Tài liệu chuyên đề khảo sát sự biến thiên và vẽ đồ thị của hàm số

Tài liệu chuyên đề khảo sát sự biến thiên và vẽ đồ thị của hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn:

Toán 12 3.9 K tài liệu

Thông tin:
181 trang 1 năm trước
Tác giả:
Student
Mai Nguyệt
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Tài liệu chuyên đề khảo sát sự biến thiên và vẽ đồ thị của hàm số

Tài liệu chuyên đề khảo sát sự biến thiên và vẽ đồ thị của hàm số được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

62 31 lượt tải Tải xuống

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu

Môn: Toán 12 3.9 K tài liệu

Thông tin:

181 trang 1 năm trước

Tác giả:

Profile Mai Nguyệt
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 197
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
A. SƠ ĐỒ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Bước 1. Tìm tập xác định của hàm số;
Bước 2. Tính đạo hàm
()y fx
′′
=
;
Bước 3. Tìm nghiệm của phương trình
() 0fx
′
=
;
Bước 4. Tính giới hạn
lim ; lim
xx
yy
→+∞ →−∞
và tìm tiệm cận đứng, ngang (nếu có);
Bước 5. Lập bảng biến thiên;
Bước 6. Kết luận tính biến thiên và cực trị (nếu có);
Bước 7. Tìm các điểm đặc biệt của đồ thị (giao với trục
Ox
,
Oy
, các điểm đối xứng, …);
Bước 8. Vẽ đồ thị.
CHƯƠNG
I
ĐỂ KHẢO SÁT HÀM SỐ
LÝ THUY
Ế
T.
I
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 198
B. CÁC DẠNG ĐỒ THỊ CỦA CÁC HÀM SỐ THƯỜNG GẶP
1. HÀM SỐ BẬC BA
( )
32
0 y ax bx cx d a
= + ++ ≠
TRƯỜNG HỢP
0a >
0a
<
Phương trình
/
0y =
có
2 nghiệm phân biệt
Phương trình
/
0y
có
nghiệm kép
Phương trình
/
0y
=
vô
nghiệm
MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Câu 1. Khảo sát và vẽ đồ thị hàm số
32
32yx x=−+
Lời giải:
Tập xác định:
D =
Sự biến thiên:
+ Chiều biến thiên:
2
36yxx
′
= −
.Xét
0
0
2
x
y
x
=
′
= ⇔
=
+ Các giới hạn tại vô cực
3
3
32
lim lim 1 ;
xx
yx
x
x
→+∞ →+∞

= − + = +∞


3
3
32
lim lim 1 .
xx
yx
x
x
→−∞ →−∞

= − + = −∞


x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 199
+ Bảng biến thiên:
Hàm số đồng biến trên các khoảng
(
)
;0−∞
và
( )
+∞
2;
;
Hàm số nghịch biến trên khoảng
( )
0;2
+ Cực trị :
Hàm số đạt cực đại tại
0;x =
(
)
02
cd
yy= =
.Hàm số đạt cực tiểu tại
2;x =
( )
22
ct
yy= = −
+ Đồ thị
Ta có
32
2
1
3 20
2 20
x
xx
xx
=
− +=⇔
− −=
⇒
đồ thị hàm số qua điểm
(
)
1; 0 .
A
Cho
02xy=⇒=
:Đồ thị hàm số cắt
Oy
tại
(
)
0;2 .B
Lưu ý: Đồ thị hàm số nhận điểm
( )
1;0
I
làm tâm đối xứng. Hoành độ điểm
I
là nghiệm của phương
trình
0y
′′
=
(Điểm uốn)
Câu 2. Khảo sát và vẽ đồ thị hàm số
32
3 31yx x x=−+ − +
Lời giải:
Tập xác định:
D =
Sự biến thiên:
+ Chiều biến thiên:
( )
2
2
3 633 1 0y xx x x
′
=− + − =− − ≤ ∀∈
.Xét
0 1.yx
′
=⇔=
Suy ra hàm số nghịch biến trên khoảng
( )
;.−∞ + ∞
+ Cực trị : Hàm số không có cực trị
+ Các giới hạn tại vô cực
3
23
33 1
lim lim 1 ;
xx
yx
x
xx
→+∞ →+∞

= − + − + = −∞


3
23
33 1
lim lim 1 .
xx
yx
x
xx
→−∞ →−∞

= − + − + = +∞


x
0
2
+∞
y
′
+
0
−
0
+
y
−∞
2
2−
+∞
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 200
+ Bảng biến thiên:
x
−∞
1
+∞
y
′
−
0
−
y
+∞
−∞
Đồ thị
Ta có
32
3 3 10 1xxx x− + − +=⇔ =
⇒
đồ thị hàm số qua
( )
1; 0 .A
Cho
01xy=⇒=
⇒
Đồ thị hàm số cắt
Oy
tại
( )
0;1B
.
Cho
21xy=⇒=−
Đồ thị hàm số qua
( )
2; 1 .C −
Lưu ý: Đồ thị hàm số nhận điểm
( )
1;0I
làm tâm đối xứng.Hoành độ điểm
I
là nghiệm của phương
trình
0y
′′
=
(Điểm uốn).
Câu 3. Khảo sát và vẽ đồ thị hàm số
3
1yx
Lời giải:
Tập xác định:
D =
Sự biến thiên:
+ Chiều biến thiên:
2
30yx x
′
= ≥ ∀∈
.Xét
0 0.yx
′
=⇔=
Suy ra hàm số luôn đồng biến trên khoảng
(
)
;.−∞ + ∞
+ Cực trị : Hàm số không có cực trị
+ Các giới hạn tại vô cực
3
lim lim ;
xx
yx
→+∞ →+∞
= = +∞
3
lim lim .
xx
yx
→−∞ →−∞
= = −∞
+ Bảng biến thiên:
x
0
y
′
+
0
y
−∞
0
+∞
Đồ thị
Ta có
3
00xx=⇔=
.Vậy đồ thị hàm số qua
( )
0;0O
⇒
−∞
+∞
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 201
Cho
11
xy=⇒=
:Đồ thị hàm số cắt
Oy
tại
1; 1B
.Cho
11xy=−⇒ =−
:Đồ thị hàm số cắt
qua
( )
1; 1 .
C −−
Lưu ý: Đồ thị hàm số nhận điểm
( )
0;0O
làm tâm đối xứng. Hoành độ điểm
O
là nghiệm của phương
trình
0y
′′
=
(Điểm uốn)
2. HÀM SỐ TRÙNG PHƯƠNG
(
)
42
0
yaxbxca=++ ≠
TRƯỜNG HỢP
0a
0a
<
Phương trình
/
0y =
có
3 nghiệm phân biệt
Phương trình
/
0
y =
có
1 nghiệm.
MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Câu 1. Khảo sát và vẽ đồ thị hàm số
=−−
42
23yx x
Lời giải:
Tập xác định:
D =
Sự biến thiên:
+ Chiều biến thiên:
x
y
O
1
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 202
(
)
32
4 44 1y x x xx
′
= −= −
.Xét
0
0
1
x
y
x
=
′
= ⇔
= ±
+ Các giới hạn tại vô cực
4
24
23
lim lim 1 .
xx
yx
xx
→+∞ →±∞

= − − = +∞


+ Bảng biến thiên
x
−∞
1
−
0
1
+∞
y
′
−
0
0
−∞
0
+
y
+∞
4
−
3−
4−
+∞
Hàm số đồng biến trên các khoảng
( )
1;0−
và
( )
+∞1;
Hàm số nghịch biến trên các khoảng
( )
;1−∞ −
và
( )
0; 1
+ Cực trị :
Hàm số đạt cực đại tại
0;x =
( )
03
cd
yy
= = −
.
Hàm số đạt cực tiểu tại
1;x = ±
( )
14
ct
yy= ±=−
Đồ thị
Ta có
42
2 30 1xx x− −=⇔=±
.Vậy đồ thị hàm số qua
( )
1;0 ,A
( )
1; 0 .B −
Cho
03xy=⇒=−
:Đồ thị hàm số cắt
Oy
tại
(
)
0; 3C
−
.Cho
25xy=±⇒ =
: Đồ thị hàm số
qua
( )
2;5 ,D −
( )
2;5 .E
Lưu ý: Đồ thị hàm số nhận
Oy
làm trục đối xứng.
Câu 2. Khảo sát và vẽ đồ thị hàm số
24
4
28
xx
y =−−
Lời giải:
Tập xác định:
D =
Sự biến thiên:
+ Chiều biến thiên:
32
1
22
xx
yx x

′
=−− =− +


.Xét
0 0.yx
′
=⇔=
+ Các giới hạn tại vô cực
4
24
11
lim lim 1 .
28
xx
yx
xx
→+∞ →±∞

= − − − = −∞


+ Bảng biến thiên:
O
1
−
1
x
y
3−
4−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 203
x
−∞
0
+∞
y
′
+
0
−
y
−∞
4
−∞
Hàm số đồng biến trên các khoảng
(
)
−∞;0
Hàm số nghịch biến trên các khoảng
(
)
+∞0;
+ Cực trị :
Hàm số đạt cực đại tại
0;
x
=
( )
03
cd
yy
= = −
.
Hàm số không có cực tiểu.
Đồ thị
Cho
20xy=±⇒ =
:Đồ thị hàm qua
( )
2; 0 ,
C −
( )
2; 0D
Lưu ý: Đồ thị hàm số nhận
Oy
làm trục đối xứng.
3. HÀM SỐ NHẤT BIẾN
( )
00,
ax b
y c ad bc
cx d
+
= ≠ −≠
+
0D ad bc=−>
0D ad bc=−<
MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Câu 1. Khảo sát và vẽ đồ thị hàm số
1
1
x
x
Lời giải:
x
y
-1
4
-2
2
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 204
Tập xác định:
{ }
\1
D =
Sự biến thiên:
+ Chiều biến thiên:
( )
2
2
1
y
x
−
′
=
−
.Ta thấy
y
′
không xác định khi
1;x =
y
′
luôn âm với mọi
1x ≠
Vậy hàm số nghịch biến trên các khoảng
( )
1;+∞
và
( )
;1 .−∞
+ Cực trị :
Hàm số không có cực trị
+ Tiệm cận
1
lim lim 1.
1
x
x
y
x
→±∞
+
= =
−
Vậy đường thẳng
1y =
là tiệm cận ngang
1
1
1
lim lim ;
1
x
x
x
y
x
+
+
→
→
+
= = +∞
−
1
1
1
lim lim .
1
x
x
x
y
x
−
−
→
→
+
= = −∞
−
Vậy đường thẳng
1
x =
là tiệm cận ngang
+ Bảng biến thiên:
x
−∞
1
+∞
′
y
– –
y
1
−∞
+∞
1
Đồ thị
Đồ thị cắt trục tung tại điểm
( )
0; 1
A
−
và cắt trục hoành tại điểm
( )
1;0B −
(Hình vẽ)
Lưu ý : Giao điểm
( )
1 ;1I
của hai tiệm cận là tâm đối xứng của đồ thị
x
y
-2
1
0
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 205
Câu 2. Khảo sát và vẽ đồ thị của hàm số
1
21
x
y
x
+
=
−
Lời giải
Tập xác định:
1
\
2
D

=


Ta có
(
)
'
2
3
0
21
y
x
−
= <
−
với mọi
1
2
x
≠
1
lim lim
2
xx
yy
→+∞ →−∞
= =
. Đồ thị hàm số có tiệm cận ngang là
1
2
y =
11
22
lim , lim
xx
yy
+−
 
→→
 
 
= +∞ = −∞
. Đồ thị hàm số có tiệm cận đứng là
1
2
x =
Bảng biến thiên của hàm số có dạng:
x
−∞
1
2
+∞
'
y
−
−
y
1
2
−∞
+ ∞
1
2
Đồ thị hàm số có dạng:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 206
C. MỘT SỐ PHÉP BIẾN ĐỔI ĐỒ THỊ
Cho hàm số
( )
y fx=
có đồ thị
( )
C
với số
0a >
ta có:
Hàm số
( )
y fx a= +
có đồ thị
( )
C
′
là tịnh tiến
(
)
C
theo phương của
Oy
lên trên
a
đơn vị.
Hàm số
( )
y fx a= −
có đồ thị
( )
C
′
là tịnh tiến
( )
C
theo phương của
Oy
xuống dưới
a
đơn
vị.
Hàm số
( )
y fx a= +
có đồ thị
( )
C
′
là tịnh tiến
(
)
C
theo phương của
Ox
qua trái
a
đơn vị.
Hàm số
(
)
y fx a= −
có đồ thị
( )
C
′
là tịnh tiến
( )
C
theo phương của
Ox
qua phải
a
đơn vị.
Hàm số
( )
y fx
= −
có đồ thị
( )
C
′
là đối xứng của
( )
C
qua trục
Ox
.
Hàm số
(
)
yfx= −
có đồ thị
C
là đối xứng của
(
)
C
qua trục
Oy
.
Từ đồ thị
( ) ( )
:C y fx=
suy ra đồ thị
( )
( )
:C y fx
′
=
.
Ta có
( )
( )
( )
khi
khi
0
0
fx x
y fx
fx x
≥
= =
−<
và
( )
y fx=
là hàm chẵn nên đồ thị
( )
C
′
nhận Oy làm trục đối xứng.
* Cách vẽ
(
)
C
′
từ
( )
C
:
+ Giữ nguyên phần đồ thị bên phải Oy của đồ thị
(
) (
)
:C y fx=
.
+ Bỏ phần đồ thị bên trái Oy của
( )
C
, lấy đối xứng phần đồ thị được giữ qua Oy.
Ví dụ: Từ đồ thị
( )
( )
3
:3C y fx x x
= = −
suy ra đồ thị
( )
3
:3Cyx x
′
= −
.
Ta có:
( )
3
3
33
30
3
330
x x khi x
yx x
x x x x khi x
−≥
=−=
−+ =− − <
Cách vẽ đồ thị
( )
C
′
:
+ Bỏ phần đồ thị của
( )
C
bên trái
,Oy
giữ nguyên
( )
C
bên phải
.Oy
+ Lấy đối xứng phần đồ thị được giữ qua
Oy
.
( )
3
:3Cyx x
′
= −
(
)
3
:3
Cyx x= −
x
y
O
-2
2
-1
1
x
y
O
-2
-1
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 207
Từ đồ thị
( ) ( )
:C y fx=
suy ra đồ thị
( ) ( )
:C y fx
′
=
.
Ta có:
( )
( ) ( )
( ) ( )
khi
khi
0
0
fx fx
y fx
fx fx
≥
= =
−<
* Cách vẽ
( )
C
′
từ
( )
C
:
+ Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C):
( )
y fx=
.
+ Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị
( ) ( )
3
:3C y fx x x= = −
suy ra đồ thị
( )
3
:3C yx x
′
= −
.
Cách vẽ đồ thị
( )
C
′
:
+ Bỏ phần đồ thị của
( )
C
dưới
,Ox
giữ nguyên
(
)
C
phía trên
.Ox
+ Lấy đối xứng phần đồ thị bị bỏ qua
Ox
.
(
)
y fx
=
ta lần lượt biến
Chú ý: Với dạng:
đổi 2 đồ thị
( )
y fx=
và
( )
y fx=
Ví dụ: Từ đồ thị
( ) ( )
3
:3C y fx x x= = −
suy ra đồ thị
3
3yx x= −
Biến đổi
( )
C
để được đồ thị
( )
3
:3Cyx x
′
= −
.
Biến đổi
( )
3
:3Cyx x
′
= −
ta được đồ thị
( )
3
:3
C yx x
′′
= −
.
Từ đồ thị
( ) ( ) ( )
:.C y ux vx=
suy ra đồ thị
( ) ( ) ( )
:.C y ux vx
′
=
.
Ta có:
( )
( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
khi
khi
.0
.
.0
ux vx f x ux
y ux vx
ux vx f x ux
= ≥
= =
−= <
* Cách vẽ
( )
C
′
từ
( )
C
:
+ Giữ nguyên phần đồ thị trên miền
( )
0ux≥
của đồ thị
( ) ( )
:C y fx=
.
+ Bỏ phần đồ thị trên miền
( )
0ux<
của
( )
C
, lấy đối xứng phần đồ thị bị bỏ qua Ox.
( )
3
:3Cyx x= −
( )
3
:3Cyx x
′
= −
x
y
O
-2
2
-1
1
x
y
2
-1
O
1
( )
3
:3C yx x
′′
= −
x
y
2
-1
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 208
Ví dụ:
a) Từ đồ thị
( ) ( )
32
: 231C y fx x x= =−+
suy ra
đồ thị
( )
( )
2
: 12 1Cyx xx
′
= − −−
Ta có:
(
)
(
)
(
)
khi
khi
2
1
12 1
1
fx x
yx x x
fx x
≥
= − −− =
−<
Đồ thị (C’):
+ Giữ nguyên (C) với
1x ≥
.
+ Bỏ (C) với
1x <
. Lấy đối xứng phần đồ thị bị
bỏ qua Ox.
Nhận xét: Trong quá trình thực hiện phép suy đồ
thị nên lấy đối xứng các điểm đặc biệt của (C):
giao điểm với Ox, Oy, CĐ, CT…
b) Từ đồ thị
( ) ( )
:
1
x
C y fx
x
= =
−
suy ra đồ
thị
(
)
:
1
x
Cy
x
′
=
−
Ta có:
(
)
( )
khi
khi
1;
1
.
1
;1
1
x
x
x
x
y
x
x
x
x
∈ +∞
−
= =
−
− ∈ −∞
−
Đồ thị (C’):
+ Bỏ phần đồ thị của
( )
C
với
1x <
, giữ
nguyên
( )
C
với
1.x >
+ Lấy đối xứng phần đồ thị bị bỏ qua
.
Ox
Nhận xét: Đối với hàm phân thức thì nên lấy
đối xứng các đường tiệm cận để thực hiện
phép suy đồ thị một cách tương đối chính
xác.
x
y
(C)
(C')
1
O
1
x
y
1
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 209
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Hàm số nào dưới đây có bảng biến thiên như sau:
A.
42
2.yx x= −
B.
3
3.yx x=−+
C.
42
2.yx x=−+
D.
3
3.yx x= −
Câu 2: (MĐ 102-2022) Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3yx x=−+
. B.
3
3yx x= −
. C.
42
2yx x=−+
. D.
42
2yx x= −
.
Câu 3: (MĐ 103-2022) Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3yx x= −
. B.
3
3yx x=−+
. C.
2
2yx x= −
. D.
2
2yx x=−+
.
+
∞
∞
2
2
+
+
+
∞
∞
0
0
1
-1
y'
x
y
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 210
Câu 4: (MĐ 104-2022) Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3yx x= −
. B.
2
2yx x= −
. C.
3
3
yx x=−+
. D.
2
2yx x=−+
.
Câu 5: (TK 2020-2021) Đồ thị của hàm số nào dưới đây có dang như đường cong trong hình bên?
A.
42
2 1.yx x=−+ −
B.
42
2 1.yx x=−−
C.
32
3 1.yx x=−−
D.
32
3 1.yx x
=−+ −
Câu 6: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A.
3
31
yx x=−+
. B.
42
241y xx=−+ +
. C.
3
31
yx x=−+ +
. D.
42
241
yx x=−+
.
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị hàm số
42
23yx x=−− +
cắt trục tung tại điểm có tung
độ bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A.
3
1
2
2
yx x=−− +
. B.
3
1
2
2
yx x=−+
. C.
42
1
2
2
yx x=−+ +
. D.
42
1
2
2
yx x=++
.
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình
bên?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 211
A.
3
31
yx x
=−+
. B.
42
41yx x=++
. C.
3
31yx x=−+ +
. D.
42
21yx x=−+ +
.
Câu 10: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
A.
31
2
+
=
+
x
y
x
. B.
2
2= +yx x
. C.
32
2= −y xx
. D.
42
2
= −yx x
.
Câu 11: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số
3
2
yx x
= −+
?
A. Điểm
( )
1;1M
. B. Điểm
( )
1; 2
P
. C. Điểm
( )
1; 3Q
. D. Điểm
( )
1; 0N
.
Câu 12: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số
= +−
3
2
yx x
?
A. Điểm
1; 1M
. B. Điểm
1; 2N
. C. Điểm
1; 3P
. D. Điểm
1; 0Q
.
Câu 13: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây?
A.
31
2
x
y
x
−
=
+
. B.
2
2yx x= −
. C.
32
2y xx= +
. D.
42
2yx x=−+
.
Câu 14: (MĐ 103 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số
3
1yx x 
?
A. Điểm
1; 0N
. B. Điểm
1; 2P
. C. Điểm
1; 3Q
. D. Điểm
1;1M
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 212
Câu 15: (MĐ 103 2020-2021 – ĐỢT 2) Hàm số nào dưới đây có đồ thị đường cong trong hình bên?
A.
3
3
yx x=−+
. B.
42
yx x
= −
. C.
21
2
x
y
x
+
=
+
. D.
2
yx x
= +
.
Câu 16: (MĐ 104 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số
3
1yx x 
?
A. Điểm
1; 3Q
. B. Điểm
1; 2M
. C. Điểm
1;1N
. D. Điểm
1; 0P
.
Câu 17: (MĐ 103 2020-2021 – ĐỢT 1) Biết hàm số
1
xa
y
x
+
=
−
(
a
là số thực cho trước và
1a ≠−
) có
đồ thị như hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
A.
' 0, 1
yx> ∀≠
. B.
' 0,yx
> ∀∈
. C.
' 0,yx
< ∀∈
. D.
' 0, 1yx< ∀≠
.
Câu 18: (MĐ 104 2020-2021 – ĐỢT 1) Biết hàm số
1
+
=
−
xa
y
x
(
a
là số thực cho trước,
1
≠−a
) có đồ
thị như trong hình bên. Mệnh đề nào dưới đây đúng?
A.
' 0,< ∀∈y xR
. B.
' 0, 1< ∀≠yx
. C.
' 0,> ∀∈y xR
. D.
' 0, 1
> ∀≠yx
.
Câu 19: (Đề Minh Họa 2020 Lần 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 213
A.
42
2yx x=−+
. B.
42
2yx x= −
. C.
32
3yx x= −
. D.
32
3yx x=−+
.
Câu 20: (Đề Tham Khảo 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A.
3
3= −yx x
. B.
3
3=−+yx x
. C.
42
2= −yx x
. D.
42
2=−+yx x
.
Câu 21: (Mã 101 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
32
31yx x=−+
. B.
32
31yx x=−+ +
. C.
42
21yx x=−+ +
. D.
42
21yx x=−+
.
Câu 22: (Mã 102 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A. . B. . C. . D. .
Câu 23: (Mã 104 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
42
2yx x=−+
3
3
yx x
=−+
42
2yx x= −
3
3yx x= −
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 214
A.
42
21
yx x
=−+
. B.
32
31yx x=−+ +
. C.
32
31yx x=−+
. D.
42
21yx x=−+ +
.
Câu 24: (Mã 101 - 2020 Lần 2)Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên
A.
42
y x 2x 2
=−−
B.
32
y x 2x 2=−+ −
C.
32
y x 3x 2=−−
D.
42
y x 2x 2=−+ −
Câu 25: (Mã 104 2017) Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó
là hàm số nào?
A.
3
32yx x=−+ +
B.
42
1yx x=−+
C.
42
1yx x=++
D.
3
32yx x=−+
Câu 26: (Mã 102 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình
bên?
A.
42
21yx x=−+ −
. B.
42
21yx x=−−
. C.
32
31yx x=−−
. D.
32
31yx x=−+ −
.
Câu 27: (Mã 103 - 2020 Lần 2) Đồ thị của hàm số dưới đây có dạng như đường cong bên?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 215
A.
3
31yx x=−+
. B.
42
21yx x=−+
. C.
42
21yx x=−+ +
. D.
3
31yx x
=−+ +
.
Câu 28: (Mã 104 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình
bên?
A.
42
2yx x= +
. B.
3
3yx x=−−
. C.
3
3
yx x= −
. D.
42
2yx x=−+
.
Câu 29: (Đề Tham Khảo 2019) Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
21
1
x
y
x
−
=
−
B.
1
1
x
y
x
+
=
−
C.
42
1yx x=++
D.
3
31yx x
=−−
Câu 30: (Mã 103 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
32
32yx x=−−
. B.
42
22yx x=−−
. C.
32
32yx x=−+ −
. D.
42
22yx x=−+ −
.
Câu 31: (Mã 101 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 216
A.
32
33yx x=−+
. B.
33
23
++−= xxy
. C.
32
24
+−= xxy
.s D.
32
24
+
+
−
=
x
x
y
.
Câu 32: (Mã 102 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
32
1y xx=−+ −
B.
42
21yx x=−+ −
C.
32
1yx x
=−−
D.
42
21yx x
=−−
Câu 33: (Mã 101 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
32
31yx x=−−
B.
32
31yx x=−+ −
C.
42
31yx x=−+ −
D.
42
31yx x=−−
Câu 34: (Mã 104 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
2yx x=−−
B.
42
2y xx=−+ −
C.
32
32yx x=−+ −
D.
32
32yx x=−−
Câu 35: (Mã 103 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 217
A.
3
31
yx x=−−
B.
42
31yx x=−−
C.
3
31yx x=−− −
D.
42
1
y xx=−+ −
Câu 36: (Đề Tham Khảo 2018) Đường cong trong hình bên là của đồ thị hàm số nào dưới đây?
A.
32
32
=−+yx x
B.
32
32=−+ +yx x
C.
42
22=−+ +yx x
D.
42
22=−+yx x
Câu 37: (Mã 110 2017) Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm
số đó là hàm số nào?
A.
32
31yx x
=−+ +
B.
32
33yx x=−+
C.
42
21yx x=−+ +
D.
42
21yx x=−+
.
Câu 38: (Đề Tham Khảo 2017) Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
A.
21
y
1
x
x
+
=
−
B.
23
1
x
y
x
+
=
+
C.
21
1
x
y
x
−
=
+
D.
22
1
x
y
x
−
=
−
x
y
O
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 218
Câu 39: (Đề Minh Họa 2017) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án
,,,
ABC D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
31yx x=−+
B.
3
31yx x=−+ +
C.
42
1yx x=−+
D.
2
1y xx=− +−
Câu 40: (Mã 104 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
42
241
yx x=−+
B.
3
2 31y xx=− ++
C.
3
2 31yx x= −+
D.
42
241
y xx
=−+ +
Câu 41: (Mã 102 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên
A.
3
31yx x=−+ +
. B.
3
31
yx x
=−+
. C.
42
21
yx x=−+
. D.
42
21yx x=−+ +
.
Câu 42: (Mã 123 2017) Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số
đó là hàm số nào?
A.
=−−
42
1yx x
B.
=−+ −
42
1y xx
C.
=−−
32
1yx x
D.
=−+ −
32
1y xx
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 219
Câu 43: (Mã 123 2017) Đường cong ở hình bên là đồ thị của hàm số
+
=
+
ax b
y
cx d
với
,,,
abcd
là các số
thực. Mệnh đề nào dưới đây đúng?
A.
′
< ∀∈0,yx
B.
′
> ∀≠
0, 1
yx
C.
′
< ∀≠0, 1yx
D.
′
> ∀∈0,yx
Câu 44: (Mã 105 2017) Đường cong ở hình bên là đồ thị của hàm số
+
=
+
ax b
y
cx d
với
,,,abcd
là các số
thực. Mệnh đề nào dưới đây đúng?
A.
′
> ∀≠y 0, 1x
B.
′
< ∀≠y 0, x 1
C.
′
< ∀≠y 0, x 2
D.
′
> ∀≠y 0, 2
Câu 45: (Đề Minh Họa 2020 Lần 1) Cho hàm số
( )
3
3;
y ax x d a d= ++ ∈
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0ad>>
. B.
0, 0ad<>
. C.
0, 0ad><
. D.
0, 0ad<<
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 220
Câu 46: (Đề Tham Khảo 2020 Lần 2) Cho hàm số
( )
1
ax
fx
bx c
+
=
+
( )
,,abc∈
có bảng biến thiên như
sau:
Trong các số
,ab
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Câu 47: (Mã 101 - 2020 Lần 1) Cho hàm số
32
y ax bx cx d= + ++
( )
,,,abcd∈
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số
a
,
b
,
c
,
d
?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 48: (Mã 102 - 2020 Lần 1) Cho hàm số
y ax bx cx d
= + ++
32
( )
,,,abcd
∈
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các hệ số
,,,abcd
?
A.
4
. B.
3
. C.
1
. D.
2
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 221
Câu 49: (Mã 103 - 2020 Lần 1) Cho hàm số
( )
32
,,,y ax bx cx d a b c d= + ++ ∈
có đồ thị là đường
cong trong hình bên.
Có bao nhiêu số dương trong các số
,,,abcd
?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 50: (Mã 104 - 2020 Lần 1) Cho hàm số
( )
32
,,,= + ++ ∈
y ax bx cx d a b c d
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số
,,,abcd
?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 51: (Mã 102 - 2020 Lần 2) Cho hàm số
(
)
( )
32
,,,
f x ax bx cx d a b c d= + ++ ∈
có bảng biến
thiên như sau
Có bao nhiêu số dương trong các số
,,, abcd
?
A.
2
. B.
4
. C.
1
. D.
3
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 222
Câu 52: (Mã 103 - 2020 Lần 2) Cho hàm số
( ) ( )
32
,,,f x ax bx cx d a b c d= + ++ ∈
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
,,, ?abcd
A.
3.
B.
4.
C.
2.
D.
1.
Câu 53: (Mã 101 – 2020 Lần 2) Cho hàm số
( ) ( )
32
,,,f x ax bx cx d a b c d= + ++ ∈
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
,,,abcd
?
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 54: (Mã 104 - 2020 Lần 2) Cho hàm số
( )
( )
32
,,,f x ax bx cx d a b c d
= + ++ ∈
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
,,,abcd
?
A.
4
. B.
2
. C.
3
. D.
1
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 1
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Hàm số nào dưới đây có bảng biến thiên như sau:
A.
42
2.yx x= −
B.
3
3.yx x=−+
C.
42
2.yx x=−+
D.
3
3.yx x= −
Lời giải
Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với
a 0.>
Do đó ta chọn đáp án D.
Câu 2: (MĐ 102-2022) Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3yx x=−+
. B.
3
3yx x= −
. C.
42
2yx x=−+
. D.
42
2yx x= −
.
Lời giải
Chọn B
Từ bảng biến thiên
( )
y fx⇒=
là hàm bậc 3 có hệ số
0a >
, nên Chọn B
Câu 3: (MĐ 103-2022) Hàm số nào dưới đây có bảng biến thiên như sau?
+
∞
∞
2
2
+
+
+
∞
∞
0
0
1
-1
y'
x
y
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 2
A.
3
3yx x= −
. B.
3
3yx x=−+
. C.
2
2yx x
= −
. D.
2
2yx x
=−+
.
Lời giải
Chọn B
Bảng biến đã cho là của hàm số
3
3
yx x
=−+
.
Câu 4: (MĐ 104-2022) Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3
yx x= −
. B.
2
2yx x
= −
. C.
3
3yx x=−+
. D.
2
2
yx x=−+
.
Lời giải
Chọn C
Câu 5: (TK 2020-2021) Đồ thị của hàm số nào dưới đây có dang như đường cong trong hình bên?
A.
42
2 1.
yx x=−+ −
B.
42
2 1.yx x=−−
C.
32
3 1.yx x=−−
D.
32
3 1.yx x=−+ −
Lời giải
Đây chính là dạng của đồ thị hàm trùng phương có hệ số cao nhất dương, có ba điểm cực trị và
cắt trục tung tại điểm có tung độ âm. Khi đó chỉ có
42
21yx x
là thỏa mãn.
Câu 6: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A.
3
31yx x
=−+
. B.
42
241y xx=−+ +
. C.
3
31yx x=−+ +
. D.
42
241yx x
=−+
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 3
Lời giải
Đường cong đề bài ra là đồ thị của hàm bậc 4 trùng phương có hệ số
0a >
, và
0
ab
<
. Do đó
đây là đồ thị của hàm số
42
241yx x=−+
.
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị hàm số
42
23yx x=−− +
cắt trục tung tại điểm có tung
độ bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Đồ thị hàm số
42
23
yx x=−− +
cắt trục tung tại điểm có tung độ bằng
3
.
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A.
3
1
2
2
yx x
=−− +
. B.
3
1
2
2
yx x=−+
. C.
42
1
2
2
yx x
=−+ +
. D.
42
1
2
2
yx x=++
.
Lời giải
Dựa trên hình dạng đường cong đã cho và các phương án, ta suy ra đường cong trên là đồ thị
của hàm số
3
1
2
2
yx x=−+
.
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình
bên?
A.
3
31yx x
=−+
. B.
42
41yx x=++
. C.
3
31yx x=−+ +
. D.
42
21yx x=−+ +
.
Lời giải
Đồ thị hàm số có 2 điểm cực trị nên đây là đồ thị hàm bậc 3, mặt khác
lim
x
y
→−∞
= +∞
nên
0a <
.
Câu 10: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 4
A.
31
2
+
=
+
x
y
x
. B.
2
2= +yx x
. C.
32
2= −y xx
. D.
42
2
= −yx x
.
Lời giải
Đường cong đã cho có 3 điểm cực trị nên loại các phương án A, B, C. Do đó chọn phương
án D.
Câu 11: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số
3
2yx x= −+
?
A. Điểm
( )
1;1M
. B. Điểm
( )
1; 2
P
. C. Điểm
( )
1; 3Q
. D. Điểm
( )
1; 0N
.
Lời giải
Thay
1x =
vào
3
2yx x= −+
ta được
3
1 12 2y = −+ =
.
Vậy điểm
( )
1; 2
P
thuộc đồ thị hàm số đã cho.
Câu 12: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số
= +−
3
2
yx x
?
A. Điểm
1; 1M
. B. Điểm
1; 2N
. C. Điểm
1; 3P
. D. Điểm
1; 0Q
.
Lời giải
Với
1x
, ta có:
3
1 12 0y 
Do đó điểm
1; 0Q
thuộc đồ thị hàm số
Câu 13: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây?
A.
31
2
x
y
x
−
=
+
. B.
2
2yx x= −
. C.
32
2y xx= +
. D.
42
2yx x=−+
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 5
Lời giải
Đường cong đã cho không phải là đồ thị của hàm phân thức, cũng không phải là đồ thị của hàm
đa thức bậc hai, bậc ba. Do đó chỉ có phương án D là đúng.
Câu 14: (MĐ 103 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số
3
1yx x 
?
A. Điểm
1; 0N
. B. Điểm
1; 2P
. C. Điểm
1; 3Q
. D. Điểm
1;1M
.
Lời giải
Thay tọa độ các điểm vào hàm số ta thấy tọa độ điểm
1;1M
thỏa mãn.
Câu 15: (MĐ 103 2020-2021 – ĐỢT 2) Hàm số nào dưới đây có đồ thị đường cong trong hình bên?
A.
3
3yx x=−+
. B.
42
yx x
= −
. C.
21
2
x
y
x
+
=
+
. D.
2
yx x= +
.
Lời giải
Từ đồ thị ta thấy có 2 cực trị và nhìn vào các phương án thì chỉ có đồ thị hàm bậc 3 có 2 cực trị
nên đáp án là A
Câu 16: (MĐ 104 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số
3
1yx x 
?
A. Điểm
1; 3
Q
. B. Điểm
1; 2M
. C. Điểm
1;1N
. D. Điểm
1; 0
P
.
Lời giải
Thay
1x
vào hàm số ta được
3
1 11 1y 
. Khi đó điểm
1;1N
thuộc đồ thị hàm số.
Câu 17: (MĐ 103 2020-2021 – ĐỢT 1) Biết hàm số
1
xa
y
x
+
=
−
(
a
là số thực cho trước và
1a ≠−
) có
đồ thị như hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
A.
' 0, 1yx> ∀≠
. B.
' 0,yx> ∀∈
. C.
' 0,yx< ∀∈
. D.
' 0, 1yx< ∀≠
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 6
Lời giải
Đồ thị hàm số
1
xa
y
x
+
=
−
nhận
1
x
=
làm tiệm cận đứng.
Nhìn đồ thị hàm số, hàm số đồng biến trên từng khoảng xác định nên
' 0, 1.
yx
> ∀≠
Câu 18: (MĐ 104 2020-2021 – ĐỢT 1) Biết hàm số
1
+
=
−
xa
y
x
(
a
là số thực cho trước,
1≠−a
) có đồ
thị như trong hình bên. Mệnh đề nào dưới đây đúng?
A.
' 0,< ∀∈y xR
. B.
' 0, 1< ∀≠yx
. C.
' 0,> ∀∈y xR
. D.
' 0, 1> ∀≠yx
.
Lời giải
Ta có TXĐ:
{ }
\1=
DR
và
2
1
' 0, 1
( 1)
−−
= ≠ ∀≠
−
a
yx
x
.
Vì đồ thị hàm số là đường cong đi xuống (tính từ trái sang phải) trên từng khoảng xác định nên
hàm số đã cho nghịch biến trên mỗi khoảng xác định. Vậy
' 0, 1yx< ∀≠
.
Câu 19: (Đề Minh Họa 2020 Lần 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
dưới đây?
A.
42
2yx x=−+
. B.
42
2yx x= −
. C.
32
3yx x= −
. D.
32
3yx x=−+
.
Lời giải
Chọn A
Từ hình dạng của đồ thị ta loại phương án C và D.
Nhận thấy
lim ( )
x
fx
→±∞
= −∞
suy ra hệ số của
4
x
âm nên chọn phương án A.
Câu 20: (Đề Tham Khảo 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 7
A.
3
3= −yx x
. B.
3
3=−+yx x
. C.
42
2= −yx x
. D.
42
2=−+yx x
.
Lời giải
Chọn A
Đường cong có dạng của đồ thị hàm số bậc
3
với hệ số
0a >
nên chỉ có hàm số
3
3yx x= −
thỏa yêu cầu bài toán.
Câu 21: (Mã 101 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
32
31yx x=−+
. B.
32
31yx x=−+ +
. C.
42
21yx x=−+ +
. D.
42
21yx x=−+
.
Lời giải
Chọn C
Từ hình có đây là hình dạng của đồ thị hàm bậc 4.
( ) ( )
lim lim 0
xx
fx fx a
→−∞ →+∞
= = −∞ ⇒ <
Câu 22: (Mã 102 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A. . B. . C. . D. .
Lời giải
Chọn A
Đường cong trong hình là đồ thị hàm trùng phương có hệ số .
Câu 23: (Mã 104 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
42
2yx x=−+
3
3yx x
=−+
42
2yx x= −
3
3yx x= −
42
y ax bx c=++
( )
0a ≠
0a <
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 8
A.
42
21
yx x
=−+
. B.
32
31yx x=−+ +
. C.
32
31yx x=−+
. D.
42
21yx x=−+ +
.
Lời giải
Chọn A
Dựa vào hình vẽ, ta thấy đồ thị hàm số có ba điểm cực trị nên loại các đáp án B và C.
Mặt khác, ta thấy
( )
42
lim 2 1
x
xx
→+∞
− + = +∞
nên chọn đáp án A.
Câu 24: (Mã 101 - 2020 Lần 2)Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên
A.
42
y x 2x 2=−−
B.
32
y x 2x 2=−+ −
C.
32
y x 3x 2
=−−
D.
42
y x 2x 2=−+ −
Lời giải
Chọn B
Qua đồ thị là hàm bậc 3 nên loại A, D.
Bên phải ngoài cùng của đồ thị đi xuống nên hệ số a < 0
⇒
loại đáp án C
Câu 25: (Mã 104 2017) Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó
là hàm số nào?
A.
3
32yx x=−+ +
B.
42
1yx x=−+
C.
42
1yx x=++
D.
3
32yx x=−+
Lời giải
Chọn D
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 9
Đồ thị hình vẽ là đồ thị hàm số bậc ba có hệ số
0a >
nên chỉ có hàm số
3
32yx x=−+
thỏa
mãn điều kiện trên.
Câu 26: (Mã 102 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình
bên?
A.
42
21yx x=−+ −
. B.
42
21yx x=−−
. C.
32
31
yx x
=−−
. D.
32
31yx x=−+ −
.
Lời giải
Chọn D
Dựa vào đồ thị có dạng đồ thị của hàm số bậc 3 có hệ số
0a <
nên đáp án D đúng.
Câu 27: (Mã 103 - 2020 Lần 2) Đồ thị của hàm số dưới đây có dạng như đường cong bên?
A.
3
31yx x=−+
. B.
42
21
yx x
=−+
. C.
42
21yx x=−+ +
. D.
3
31yx x=−+ +
.
Lời giải
Chọn A
Câu 28: (Mã 104 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình
bên?
A.
42
2yx x= +
. B.
3
3yx x=−−
. C.
3
3yx x= −
. D.
42
2yx x=−+
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 10
Lời giải
Chọn C
Đây là đồ thị của hàm số bậc ba với hệ số
0
a >
nên Chọn C
Câu 29: (Đề Tham Khảo 2019) Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
21
1
x
y
x
−
=
−
B.
1
1
x
y
x
+
=
−
C.
42
1
yx x=++
D.
3
31
yx x=−−
Lời giải
Chọn B
Vì từ đồ thị ta suy ra đồ thị của hàm phân thức có tiệm cận đứng và ngang
1; 1xy= =
Câu 30: (Mã 103 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
32
32yx x=−−
. B.
42
22yx x
=−−
. C.
32
32yx x=−+ −
. D.
42
22yx x
=−+ −
.
Lời giải
Chọn B
Quan sát đò thị ta thấy đây là đồ thị của hàm số
( )
42
0y ax bx c a=++ >
.
Câu 31: (Mã 101 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
32
33yx x=−+
. B.
33
23
++−= xxy
. C.
32
24
+−= xxy
.s D.
32
24
++−= xxy
.
Lời giải
Chọn A
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 11
Dạng hàm bậc ba nên loại C
Từ đồ thị ta có
0a >
. Do đó loại B, D.
Câu 32: (Mã 102 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
32
1y xx=−+ −
B.
42
21yx x=−+ −
C.
32
1
yx x=−−
D.
42
21yx x=−−
Lời giải
Chọn D
Dựa vào hình vẽ suy ra hàm số đã cho có
3
cực trị
→
loại C, D.
Mặt khác nhánh bên tay phải của đồ thị hàm số đi lên suy ra hệ số
0a >
→
Chọn D
Câu 33: (Mã 101 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
32
31yx x=−−
B.
32
31yx x=−+ −
C.
42
31yx x=−+ −
D.
42
31yx x=−−
Lời giải
Chọn C
+ Nhìn đồ thị khẳng định đồ thị hàm trùng phương loại A, B
+
lim
x
y
→±∞
= −∞
nên Chọn C
Câu 34: (Mã 104 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
2yx x=−−
B.
42
2y xx=−+ −
C.
32
32yx x=−+ −
D.
32
32yx x=−−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 12
Lời giải
Chọn C
Dựa trên hình dáng đồ thị, ta loại
32
32yx x=−−
và
42
2yx x=−−
Mặt khác từ đồ thị, ta thấy
lim
x
y
→+∞
= −∞
nên loại
42
2y xx=−+ −
Câu 35: (Mã 103 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3
31
yx x=−−
B.
42
31yx x=−−
C.
3
31yx x=−− −
D.
42
1y xx
=−+ −
Lời giải
Chọn A
Đồ thị hàm số là đồ thị của hàm số bậc ba nên loại A và B.
Đồ thi hàm số bậc ba có hệ số
0a >
nên D đúng.
Câu 36: (Đề Tham Khảo 2018) Đường cong trong hình bên là của đồ thị hàm số nào dưới đây?
A.
32
32=−+yx x
B.
32
32=−+ +
yx x
C.
42
22=−+ +yx x
D.
42
22=−+yx x
Lời giải
Chọn C
Đồ thị hàm số trên là đồ thị hàm trùng phương có 3 cực trị và có
0<a
Câu 37: (Mã 110 2017) Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm
số đó là hàm số nào?
x
y
O
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 13
A.
32
31
yx x=−+ +
B.
32
33yx x=−+
C.
42
21yx x=−+ +
D.
42
21yx x=−+
.
Lời giải
Chọn B
Dựa vào đồ thị ta thấy đây là hình ảnh đồ thị của hàm số bậc ba nên loại đáp án B và C; Mặt
khác dựa vào đồ thị ta có
lim
x
y
→+∞
= +∞
nên hệ số của
3
x
dương nên ta chọn đáp án
32
33yx x=−+
Câu 38: (Đề Tham Khảo 2017) Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
A.
21
y
1
x
x
+
=
−
B.
23
1
x
y
x
+
=
+
C.
21
1
x
y
x
−
=
+
D.
22
1
x
y
x
−
=
−
Lời giải
Chọn C
Dựa vào đồ thị suy ra tiệm cận đứng
1x
= −
loại C, D
Đồ thị hàm số giao với trục hoành có hoành độ dương suy ra chọn B
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 14
Câu 39: (Đề Minh Họa 2017) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án
,,,
ABC D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
31yx x=−+
B.
3
31yx x=−+ +
C.
42
1yx x=−+
D.
2
1y xx=− +−
Lời giải
Chọn A
Từ đồ thị :
lim
x
y
→+∞
= +∞
và đây là đồ thị hàm bậc ba nên ta chọn phương án
3
3 1.
yx x=−+
Câu 40: (Mã 104 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
42
241yx x=−+
B.
3
2 31y xx=− ++
C.
3
2 31yx x= −+
D.
42
241y xx=−+ +
Lời giải
Chọn D
Dạng đồ thị hình bên là đồ thị hàm số trùng phương
42
y ax bx c=++
có hệ số
0a <
.
Do đó, chỉ có đồ thị ở đáp án
B
là thỏa mãn.
Câu 41: (Mã 102 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên
A.
3
31yx x=−+ +
. B.
3
31yx x=−+
. C.
42
21yx x=−+
. D.
42
21yx x=−+ +
.
Lời giải
Chọn A
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 15
Trong bốn hàm số đã cho thì chỉ có hàm số
3
31
yx x=−+ +
(hàm số đa thức bậc ba với hệ số
0a <
) có dạng đồ thị như đường cong trong hình.
Câu 42: (Mã 123 2017) Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số
đó là hàm số nào?
A.
=−−
42
1yx x
B.
=−+ −
42
1
y xx
C.
=−−
32
1yx x
D.
=−+ −
32
1y xx
Lời giải
Chọn A
Đây là hình dáng của đồ thị hàm bậc bốn trùng phương có hệ số
> 0a
Câu 43: (Mã 123 2017) Đường cong ở hình bên là đồ thị của hàm số
+
=
+
ax b
y
cx d
với
,,,abcd
là các số
thực. Mệnh đề nào dưới đây đúng?
A.
′
< ∀∈0,yx
B.
′
> ∀≠0, 1
yx
C.
′
< ∀≠0, 1yx
D.
′
> ∀∈0,yx
Lời giải
Chọn C
Ta có :
Dựa vào hình dáng của đồ thị ta được:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 16
+ Điều kiện
≠ 1
x
+ Đây là đồ thị của hàm nghịch biến
Từ đó ta được
′
< ∀≠0, 1.yx
Câu 44: (Mã 105 2017) Đường cong ở hình bên là đồ thị của hàm số
+
=
+
ax b
y
cx d
với
,,,abcd
là các số
thực. Mệnh đề nào dưới đây đúng?
A.
′
> ∀≠y 0, 1x
B.
′
< ∀≠y 0, x 1
C.
′
< ∀≠y 0, x 2
D.
′
> ∀≠
y 0, 2
Lời giải
Chọn C
Dựa vào đồ thị ta nhận thấy tiệm cận đứng bằng 2, Hàm số nghịch biến vậy chọn B
Câu 45: (Đề Minh Họa 2020 Lần 1) Cho hàm số
(
)
3
3;y ax x d a d
= ++ ∈
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0ad>>
. B.
0, 0ad<>
. C.
0, 0ad><
. D.
0, 0ad<<
.
Lời giải
Chọn D
Ta có:
lim
x→+∞
= −∞ ⇒
đồ thị nhánh ngoài cùng của hàm số hướng đi xuống nên hệ số
0a <
.
Giao điểm của đồ thị hàm số với trục tung
:0Oy x =
là điểm nằm bên dưới trục hoành nên khi
00
x yd=⇒=<
.
Câu 46: (Đề Tham Khảo 2020 Lần 2) Cho hàm số
( )
1ax
fx
bx c
+
=
+
(
)
,,abc∈
có bảng biến thiên như
sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 17
Trong các số
,ab
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn C
Hàm số
(
)
1ax
fx
bx c
+
=
+
có đường tiệm cận đứng là đường thẳng
c
x
b
= −
và đường tiệm cận
ngang là đường thẳng
a
y
b
=
.
Từ bảng biến thiên ta có:
2
2
1
c
c
b
ab
a
b
−=
⇔==−
=
1
Mặt khác:
(
)
(
)
2
'
ac b
fx
bx c
−
=
+
.
Vì hàm số đã cho đồng biến trên các khoảng
( )
;2−∞
và
( )
2; +∞
nên
( )
( )
2
' 00
ac b
f x ac b
bx c
−
= >⇔ −>
+
2
Thay
1
vào
2
, ta được:
2
2
0 00 1
22
cc
cc c− +>⇔−+>⇔<<
.
Suy ra c là số dương và a, b là số âm.
Câu 47: (Mã 101 - 2020 Lần 1) Cho hàm số
32
y ax bx cx d= + ++
(
)
,,,abcd∈
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số
a
,
b
,
c
,
d
?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Ta có
lim
x
y
→+∞
= +∞
⇒
0a <
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 18
Gọi
1
x
,
2
x
là hoành độ hai điểm cực trị của hàm số suy ra
1
x
,
2
x
nghiệm phương trình
2
32 0y ax bx c
′
= + +=
nên theo định lý Viet:
+) Tổng hai nghiệm
12
2
0
3
b
xx
a
+=− >
⇒
0
b
a
<
⇒
0b >
.
+) Tích hai nghiệm
12
0
3
c
xx
a
= >
⇒
0c <
.
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
0d >
.
Vậy có
2
số dương trong các số
a
,
b
,
c
,
d
.
Câu 48: (Mã 102 - 2020 Lần 1) Cho hàm số
y ax bx cx d= + ++
32
( )
,,,abcd∈
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các hệ số
,,,
abcd
?
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Ta có
( )
lim
x
fx a
→+∞
= −∞ ⇒ < 0
Đồ thị hàm số có hai điểm cực trị nằm cùng phía của trục tung nên
ac c
>⇒<00
Đồ thị hàm số có điểm uốn nằm bên phải trục tung nên
ab b<⇒>00
Đồ thị hàm số cắt trục tung ở dưới trục hoành
d⇒<0
Câu 49: (Mã 103 - 2020 Lần 1) Cho hàm số
( )
32
,,,y ax bx cx d a b c d= + ++ ∈
có đồ thị là đường
cong trong hình bên.
Có bao nhiêu số dương trong các số
,,,abcd
?
A.
4
. B.
2
. C.
1
. D.
3
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 19
Lời giải
Chọn C
Ta có
2
32y ax bx c
′
= ++
. Dựa vào đồ thị ta thấy
0a <
Hàm số có 2 cực trị âm nên
2
90
0
0
2
00
0
3
0
0
3
y
b ac
b
b
S
c
a
P
c
a
′
−>
′
∆>
<

< ⇔ − < ⇒⇒

<

>

>

Đồ thị cắt trục
Oy
tại điểm
( )
0; d
nên
0d >
.
Vậy có đúng một số dương trong các số
,,,abcd
Câu 50: (Mã 104 - 2020 Lần 1) Cho hàm số
( )
32
,,,= + ++ ∈
y ax bx cx d a b c d
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số
,,,abcd
?
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
Ta có:
2
32
′
= ++y ax bx c
Dựa vào đồ thị ta thấy
0<a
Hàm số có 2 cực trị âm nên
2
90
0
0
2
00
0
3
0
0
3
′
−>
′
∆>
<
< ⇔− < ⇒

<

>
>
y
b ac
b
b
S
c
a
P
c
a
Đồ thị cắt trục
Oy
tại điểm
( )
0; d
nên
0>d
Vậy có đúng 1 số dương trong các số
,,,abcd
.
Câu 51: (Mã 102 - 2020 Lần 2) Cho hàm số
( ) (
)
32
,,, f x ax bx cx d a b c d= + ++ ∈
có bảng biến
thiên như sau
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 20
Có bao nhiêu số dương trong các số
,,, abcd
?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn D
Từ dáng điệu sự biến thiên hàm số ta có
0.a >
Khi
0x =
thì
10
yd
= = >
.
Mặt khác
( )
2
32f x ax bx c
′
= ++
. Từ bảng biến thiên ta có
( )
2
0
0
x
fx
x
= −
′
= ⇔
=
.
Từ đó suy ra
2
0; 2 3 0
3
b
c ba
a
−
= =−⇒ = >
.
Vậy có 3 số dương là
,, abd
.
Câu 52: (Mã 103 - 2020 Lần 2) Cho hàm số
(
) ( )
32
,,,f x ax bx cx d a b c d
= + ++ ∈
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
,,, ?abcd
A.
3.
B.
4.
C.
2.
D.
1.
Lời giải
Chọn C
( )
lim 0.
x
fx a
→+∞
= +∞ ⇒ >
( )
0 1 1 0.fd=−⇒ =−<
( )
2
32.f x ax bx c
′
= ++
Ta có
12
12
2
2
2
30
3
.
00
0
3
b
xx
ba
a
xx c c
a
−=−
+=−
= >
⇒⇒

= =
=
Có 2 số dương là a, b
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 21
Câu 53: (Mã 101 – 2020 Lần 2) Cho hàm số
( )
(
)
32
,,,
f x ax bx cx d a b c d= + ++ ∈
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
,,,abcd
?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn A
Từ bảng biến thiên, ta có
1
(0) 3 3
4
(4) 5 64 16 4 5 3
2
(0) 0 0
0
(4) 0 48 8 0
3
a
fd
f a b cd
b
fc
c
f a bc
d
=
= =


=− + + +=−

= −
⇔⇔

′
= =

=

′
= + +=

=
Vậy trong các số
,,,abcd
có 2 số dương.
Câu 54: (Mã 104 - 2020 Lần 2) Cho hàm số
( ) (
)
32
,,,f x ax bx cx d a b c d= + ++ ∈
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
,,,abcd
?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Ta có:
( ) ( )
32
,,,f x ax bx cx d a b c d= + ++ ∈
( )
2
32f x ax bx c
′
⇒ = ++
Đồ thị hàm số
( )
fx
có hai điểm cực trị
( ) ( )
0; 1 , 4; 5AB−−
nên ta có hệ:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 22
( )
( )
( )
( )
1
01
1
8
45
64 16 4 5
3
4
0
00
0
48 8 0
40
1
a
f
d
f
a b cd
b
c
f
c
a bc
f
d
=
= −
= −
= −
+ + +=−

= −
⇔⇔

=
′
=

=

+ +=
′
=
= −
. Trong các số
,,,abcd
có
1
số dương.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 223
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
DẠNG. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
A. Hàm số bậc ba
( )
= + ++ ≠y ax bx cx d a
32
0
TRƯỜNG HỢP
>a
0
0
a <
Phương trình
=y
/
0
có
2 nghiệm phân biệt
Phương trình
=y
/
0
có
nghiệm kép
Phương trình
/
0y =
vô
nghiệm
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 224
B. Hàm số trùng phương
( )
= ++ ≠y ax bx c a
42
0
TRƯỜNG HỢP
>a 0
0a <
Phương trình
=y
/
0
có
3 nghiệm phân biệt
Phương trình
=y
/
0
có
1 nghiệm.
C. Hàm số nhất biến
( )
0, 0
ax b
y c ad bc
cx d
+
= ≠ −≠
+
= −>D ad bc
0
= −<D ad bc
0
Câu 1: Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án
,,,ABC D
. Hỏi đó là hàm
số nào?
A.
3
21yx x=++
. B.
32
21yx x=−+
. C.
3
21yx x=−+
. D.
3
21yx x=−+ +
.
Câu 2: Hình vẽ bên dưới là đồ thị của hàm số nào
x
y
O
1
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 225
A.
1
1
−
=
+
x
y
x
. B.
21
1
+
=
+
x
y
x
. C.
23
1
−
=
+
x
y
x
. D.
25
1
+
=
+
x
y
x
.
Câu 3: Đường cong trong hình là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
−
=
+
. B.
21
22
x
y
x
−+
=
+
. C.
42
3yx x= −
. D.
32
3
yx x= −
.
Câu 4: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
3
31yxx
. B.
42
1
yx x
. C.
2
1y xx
. D.
3
31yx x
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 226
DẠNG 2. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ
Câu 5: Cho hàm số
32
= + ++y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0<>> <abcd
B.
0, 0, 0, 0<<><abcd
.
C.
0, 0, 0, 0><< >abcd
D.
0, 0, 0, 0<>< <abcd
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 227
Câu 6: Cho hàm số
42
y ax bx c
=++
có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?
A.
0, 0, 0abc><>
B.
0, 0, 0abc><<
C.
0, 0, 0abc>><
D.
0, 0, 0
abc<><
Câu 7: Cho hàm số
+
=
+
ax b
y
cx d
có đồ thị như sau.
Mệnh đề nào sau đây đúng?
A.
0; 0ac bd>>
B.
0; 0ab cd
<<
C.
0; 0bc ad><
D.
0; 0ad bd><
Câu 8: Cho hàm số
( )
32
0y ax bx cx d a= + ++ ≠
có đồ thị như hình vẽ dưới đây. Chọn khẳng định
đúng về dấu của
a
,
b
,
c
,
d
?
A.
0a
>
,
0b >
,
0d >
,
0c >
B.
0a >
,
0cb>>
,
0d <
C.
0, 0, 0, 0.abcd>>> >
D.
0
a >
,
0
b <
,
0c <
,
0d >
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 228
Câu 9: Cho hàm số
1
,0
1
a xb
yd
c xd



có đồ thị như hình trên. Khẳng định nào dưới đây là đúng?
A.
1, 0, 1.ab c
B.
1, 0, 1.ab c
C.
1, 0, 1.ab c
D.
1, 0, 1.ab c
Câu 10: Cho hàm số
42
y ax bx c=++
(
0a ≠
) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A.
0a <
,
0b >
,
0c <
. B.
0a <
,
0b
<
,
0c >
. C.
0a <
,
0b >
,
0c >
. D.
0a <
,
0
b <
,
0c <
.
Câu 11: Hàm số
32
y ax bx cx d 
có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0
c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 229
Câu 12: Cho hàm số
ax b
y
xc
+
=
+
có đồ thị như hình bên dưới, với
a
,
b
,
c
∈
. Tính giá trị của biểu thức
23Ta b c=++
?
A.
8T = −
. B.
2T =
. C.
6T =
. D.
0T =
.
Câu 13: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào
đúng?
A.
0, 0, 0
ab bc cd<><
B.
0, 0, 0
ab bc cd<<>
C.
0, 0, 0
ab bc cd>><
D.
0, 0, 0ab bc cd
>>>
Câu 14: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A.
0, 0, 0, 0abcd<<< <
B.
0, 0, 0, 0abcd<>> >
C.
0, 0, 0, 0
abcd<>< >
D.
0, 0, 0, 0abcd<>> <
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 230
Câu 15: Cho hàm số có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ?
A.
0, 0, 0abc><<
. B.
0, 0, 0abc<<<
.
C.
0, 0, 0abc<><
. D.
0, 0, 0abc><>
Câu 16: Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị như trong hình bên dưới. Biết rằng
a
là số thực dương, hỏi
trong các số
,,bcd
có tất cả bao nhiêu số dương?
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 17: Hàm số
32
y ax bx cx d 
có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
42
y ax bx c=++
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 231
Câu 18: Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
A.
0
0
ad
bc
<
>
. B.
0
0
ad
bc
<
<
. C.
0
0
ad
bc
>
<
. D.
0
0
ad
bc
>
>
.
Câu 19: Cho đường cong
( )
32
:
C y ax bx cx d= + ++
có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A.
0, 0, 0, 0abcd
><< <
. B.
0, 0, 0, 0abcd>>< >
.
C.
0, 0, 0, 0abcd<>> <
. D.
0, 0, 0, 0abcd>>< <
.
Câu 20: Hàm số
42
y ax bx c
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 232
Câu 21: Cho hàm số
42
y ax bx c

có đồ thị như hình vẽ. Tìm kết luận đúng
A.
0ab
. B.
0bc
. C.
0ab
. D.
0ac
.
Câu 22: Cho hàm số
42
( 0)y ax bx c a

có đồ thị như hình bên. Hãy chọn mệnh đề đúng.
A.
0, 0, 0abc
. B.
0, 0, 0
abc
.
C.
0, 0, 0abc

. D.
0, 0, 0
abc
.
Câu 23: Cho hàm số
32
()y f x ax bx cx d= = + ++
có đồ thị như hình vẽ ở bên. Mệnh đề nào sau đây
đúng?
A.
0a >
,
0b >
,
0c >
,
0
d >
. B.
0a >
,
0b >
,
0c <
,
0d >
.
C.
0a >
,
0b <
,
0c >
,
0d >
. D.
0a <
,
0b <
,
0c >
,
0d <
.
Câu 24: Cho hàm số bậc bốn trùng phương
42
y ax bx c

có đồ thị như hình vẽ bên. Mệnh đề nào
dưới đây là đúng?
A.
0, 0, 0abc
. B.
0, 0, 0
abc
.
C.
0, 0, 0abc
. D.
0, 0, 0abc

.
Câu 25: Cho hàm số
42
y ax bx c=++
có đồ thị như hình vẽ bên. Hỏi khẳng định nào sau đây đúng?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 233
A.
0, 0, 0abc><<
. B.
0, 0, 0abc>><
. C.
0, 0, 0abc><>
. D.
0, 0, 0abc<><
.
Câu 26: Cho hàm số
3ax
y
xc
+
=
+
có đồ thị như hình vẽ bên. Tính giá trị của
2.ac−
A.
2 3.ac−=
B.
2 3.ac−=−
C.
2 1.ac−=−
D.
2 2.ac−=−
Câu 27: Hình vẽ bên là đồ thị hàm số
ax b
y
cx d
+
=
+
.
.
Mệnh đề nào dưới đây đúng?
A.
0ad >
và
0bd >
. B.
0ad >
và
0ab <
. C.
0bd <
và
0ab >
. D.
0ad <
và
0ab <
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 234
Câu 28: Cho hàm số
1
ax b
y
x
−
=
−
có đồ thị như hình vẽ dưới đây:
Khẳng định nào sau đây đúng?
A.
0
ba<<
. B.
0
ab<<
. C.
ba>
và
0a <
. D.
0ab<<
.
Câu 29: Đồ thị trong hình bên dưới là của hàm số
ax b
y
xc
+
=
+
.
Khi đó tổng
abc++
bằng
A.
1−
. B.
1
. C.
2
. D.
0
.
Câu 30: Cho hàm số
2
()
ax
fx
bx c
−
=
−
(
)
,, , 0
abc b∈≠
có bảng biến thiên như sau:
Tổng các số
( )
2
abc++
thuộc khoảng nào sau đây
A.
( )
1; 2
. B.
( )
2;3
. C.
4
0;
9



. D.
4
;1
9



.
Câu 31: Cho hàm số
()
ax b
fx
cx d
+
=
+
(,,,abcd∈
và
0c ≠
). Biết rằng đồ thị hàm số đã cho đi qua điểm
( )
1;7−
và giao điểm hai tiệm cận là
( )
2;3−
. Giá trị biểu thức
234
7
a b cd
c
+++
bằng
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 235
A.
7
. B.
4
. C.
6
. D.
5−
.
Câu 32: Cho hàm số
1ax
y
bx c
+
=
+
(
,,abc
là các tham số) có bảng biến thiên như hình vẽ
Xét các phát biểu sau:
( ) ( ) ( ) ( )
1 : 1; 2 : 0; 3 : 0; 4 : 0c ab abc a> +< ++= >
. Số phát biểu đúng
là?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 33: Ta xác định được các số
,,abc
để đồ thị hàm số
32
y x ax bx c=+ ++
đi qua điểm
( )
1;0
và có
điểm cực trị
( )
2;0−
. Tính giá trị biểu thức
222
Tabc=++
.
A.
25.
B.
1.−
C.
7.
D.
14.
Câu 34: Cho hàm số có đồ thị như hình vẽ. Tính ?
A. . B. . C. . D. .
32
y ax bx cx d= + ++
S ab= +
2S = −
0S =
1S =
1S = −
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 236
Câu 35: Cho hàm số
32
y ax bx cx d
= + ++
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0abcd
<<> <
. B.
0, 0, 0, 0
abcd
<>< <
.
C.
0, 0, 0, 0abcd><< >
. D.
0, 0, 0, 0abcd<>> <
.
Câu 36: Cho hàm số
(
)
,,
1
ax b
y abc
cx
+
= ∈
+
có bảng biến thiên như sau:
Tập các giá trị
b
là tập nghiệm của bất phương trình nào dưới đây?
A.
3
8 0.b −≤
B.
2
4 0.b
− +>
C.
2
3 2 0.bb
− +<
D.
3
8 0.b −<
Câu 37: Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị như hình dưới đây. Tính giá trị biểu thức
23abd
T
c
−+
=
.
A.
6
=T
. B.
0=T
. C.
8= −T
. D.
2=T
.
Câu 38: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình vẽ. Trong các số
,,abc
và
d
có bao nhiêu
số dương?
A.
1
. B.
4
. C.
3
. D.
2
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 237
Câu 39: Cho hàm số
( )
6−
=
−
ax
fx
bx c
( )
,,∈ abc
có bảng biến thiên như sau:
Trong các số
,,abc
có bao nhiêu số âm?
A.
0
. B.
3
. C.
1
. D.
2
.
DẠNG 2. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
Dạng 1
Từ đồ thị
( ) ( )
=C y fx:
suy ra đồ thị
( ) ( )
′
=C y fx:
.
Ta có:
( )
( ) ( )
( ) ( )
≥
= =
−<
fx khi fx
y fx
fx khi fx
0
0
* Cách vẽ
( )
′
C
từ
( )
C
:
Giữ nguyên phần đồ thị phía trên Ox của đồ thị :
( )
=
y fx
.
Bỏ phần đồ thị phía dưới Ox của , lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị
( ) ( )
3
:3C y fx x x= = −
suy ra đồ thị
= −yx x
3
3
.
Biến đổi
( )
C
:
Bỏ phần đồ thị của
(
)
C
dưới
,
Ox
giữ nguyên
( )
C
phía trên
.Ox
Lấy đối xứng phần đồ thị bị bỏ qua
Ox
.
x
y
O
-2
2
-1
1
x
y
2
-1
O
1
( )
3
:3Cyx x= −
( )
′
= −Cyx x
3
:3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 238
Dạng 2
Từ đồ thị
( ) ( )
=C y fx:
suy ra đồ thị
(
)
( )
′
=
C y fx:
.
Ta có:
( )
( )
( )
f x khi x
y fx
f x khi x
0
0
≥
= =
−<
và
(
)
=y fx
là hàm chẵn nên đồ thị
( )
C
′
nhận Oy làm trục đối xứng.
* Cách vẽ
( )
′
C
từ
( )
C
:
Giữ nguyên phần đồ thị bên phải Oy của đồ thị
(
) (
)
=
C y fx
:
.
Bỏ phần đồ thị bên trái Oy của
( )
C
, lấy đối xứng phần đồ thị được giữ qua Oy.
Ví dụ: Từ đồ thị
( ) ( )
= = −C y fx x x
3
:3
suy ra đồ thị
( )
′
= −Cyx x
3
:3
.
Biến đổi
(
)
C
:
Bỏ phần đồ thị của
(
)
C
bên trái
Oy
,
giữ nguyên
(
)
C
bên
phải
.Oy
Lấy đối xứng phần đồ thị được giữ qua
Oy
.
Chú ý với dạng:
( )
=y fx
ta lần lượt biến đổi 2 đồ thị
(
)
=y fx
và
( )
=y fx
Ví dụ: Từ đồ thị
( ) ( )
= = −C y fx x x
3
:3
suy ra đồ thị
= −yx x
3
3
. Biến đổi
(
)
C
để được đồ thị
( )
′
= −Cyx x
3
:3
. Biến đổi
( )
′
= −Cyx x
3
:3
ta được đồ thị
( )
′′
= −C yx x
3
:3
.
x
y
O
-2
2
-1
1
x
y
O
-2
-1
1
x
y
2
-1
O
1
( )
′
= −Cyx x
3
:3
( )
= −Cyx x
3
:3
( )
′′
= −C yx x
3
:3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 239
Dạng 3
Từ đồ thị
(
)
(
)
( )
=C y ux vx
:.
suy ra đồ thị
(
)
(
)
(
)
′
=
C y ux vx
:.
.
Ta có:
(
)
(
)
( )
(
)
(
)
(
)
( )
(
) (
) (
)
ux vx fx khi ux
y ux vx
ux vx fx khi ux
.0
.
.0
= ≥
= =
−= <
* Cách vẽ
( )
′
C
từ
(
)
C
:
Giữ nguyên phần đồ thị trên miền
(
)
≥ux 0
của đồ thị
(
) (
)
=
C y fx
:
.
Bỏ phần đồ thị trên miền
( )
<ux 0
của
( )
C
, lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ
a) Từ đồ thị
( )
(
)
= =−+C y fx x x
32
: 231
suy ra
đồ thị
( )
( )
′
= − −−Cyx x x
2
: 12 1
Ví dụ
b) Từ đồ thị
( ) ( )
= =
−
x
C y fx
x
:
1
suy ra đồ thị
(
)
′
=
−
x
Cy
x
:
1
( )
( )
( )
≥
= − −− =
−<
f x khi x
yx x x
f x khi x
2
1
12 1
1
Đồ thị :
Giữ nguyên với
1x ≥
.
Bỏ với
<x 1
. Lấy đối xứng phần đồ thị bị bỏ qua
Ox.
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của : giao điểm
với Ox, Oy, CĐ, CT…
( )
( )
∈ +∞
−
= =
−
− ∈ −∞
−
x
khi x
x
x
y
x
x
khi x
x
1;
1
.
1
;1
1
Đồ thị :
Bỏ phần đồ thị của
( )
C
với
x ,1<
giữ nguyên
( )
C
với
1.x
>
Lấy đối xứng phần đồ thị bị bỏ qua
Ox.
Nhận xét: Đối với hàm phân thức thì nên lấy đối xứng
các đường tiệm cận để thực hiện phép suy đồ thị một
cách tương đối chính xác.
x
y
(C)
(C')
1
O
1
x
y
1
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 240
Câu 40: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Câu 41: Cho hàm số
( )
y fx=
có đồ thị hàm số
( )
y fx
=
như hình vẽ.
Chọn kết luận đúng trong các kết luận sau:
A.
( )
32
44fx x x x=−+ + −
B.
( )
32
44fx x x x=−−+
C.
(
)
32
44fx x x x=−− + −
D.
(
)
32
4 4.fx x x x=+−−
Câu 42: Cho hàm số
(
)
( )
2
21yx x
=−−
có đồ thị như hình vẽ
Một trong bốn hình dưới đây là đồ thị của hàm số
( )
2
21
yx x=−−
. Hỏi đó là hình nào?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 241
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.
Câu 43: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.
yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Câu 44: Cho hàm số
1
21
x
y
x
−+
=
−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
21
x
y
x
−+
=
−
B.
1
21
x
y
x
+
=
−
C.
1
21
x
y
x
−+
=
−
D.
1
21
x
y
x
−+
=
−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 242
Câu 45: Cho hàm số
32
69yx x x=−+
có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào
dưới đây?
A.
32
69=−+ −yx x x
. B.
32
69=−+
yx x x
.
C.
3
2
69=−+yx x x
. D.
32
69=++yx x x
.
Câu 46: Cho hàm số
21
x
y
x
có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong các đáp
án A, B, C, D dưới đây?
A.
21
x
y
x
. B.
21
x
y
x
C.
21
x
y
x
D.
21
x
y
x
Câu 47: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Câu 48: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 243
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Câu 49: Cho hàm số
21
x
y
x
=
+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
21
x
y
x
=
+
B.
21
x
y
x
=
+
C.
21
x
y
x
=
+
D.
21
x
y
x
=
+
Câu 50: Cho hàm số
1
2
x
y
x
−+
=
−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
−+
=
−
B.
1
.
2
x
y
x
+
=
−
C.
1
2
x
y
x
−+
=
−
D.
1
2
x
y
x
−+
=
−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 244
Câu 51: Cho hàm số
1
2
x
y
x
+
=
+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
+
=
+
B.
1
.
2
x
y
x
+
=
+
C.
1
.
2
x
y
x
+
=
+
D.
1
.
2
x
y
x
+
=
+
Câu 52: Cho hàm số
( )
(
)
2
1 23yx x x=− −−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới
đây?
A.
(
)
( )
2
1 2 3.yx x x=− −−
B.
( )
2
1 2 3.yx x x=− −−
C.
( )
2
1 23yxxx=−− − −
D.
( )
2
1 23yx x x=− −−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 137
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
DẠNG. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
A. Hàm số bậc ba
( )
= + ++ ≠y ax bx cx d a
32
0
TRƯỜNG HỢP
>a
0
0
a <
Phương trình
=y
/
0
có
2 nghiệm phân biệt
Phương trình
=y
/
0
có
nghiệm kép
Phương trình
/
0y =
vô
nghiệm
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 138
B. Hàm số trùng phương
( )
= ++ ≠y ax bx c a
42
0
TRƯỜNG HỢP
>a 0
0a <
Phương trình
=y
/
0
có
3 nghiệm phân biệt
(ab<0)
Phương trình
=y
/
0
có
1 nghiệm.
C. Hàm số nhất biến
( )
0, 0
ax b
y c ad bc
cx d
+
= ≠ −≠
+
= −>D ad bc
0
= −<D ad bc
0
Câu 1: (THPT Yên Phong 1 Bắc Ninh 2019) Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho
ở các đáp án
,,,ABC D
. Hỏi đó là hàm số nào?
A.
3
21yx x=++
. B.
32
21yx x=−+
. C.
3
21yx x=−+
. D.
3
21yx x=−+ +
.
Lời giải
x
y
O
1
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 139
Dựa vào đồ thị, ta có
lim
x
y
→+∞
= +∞
, loại phương án
D
.
Xét phương án
A
có
2
3 2 0,yx x
′
= + > ∀∈
, hàm số không có cực tri, loại phương án
A
.
Xét phương án
B
có
2
36yx x
′
= −
và
y
′
đổi dấu khi đi qua các điểm
0, 2xx= =
nên hàm số đạt
cực tri tại
0x =
và
2x =
, loại phương án
B
.
Vậy phương án đúng là
C
.
Câu 2: (Sở Cần Thơ - 2019) Hình vẽ bên dưới là đồ thị của hàm số nào
A.
1
1
−
=
+
x
y
x
. B.
21
1
+
=
+
x
y
x
. C.
23
1
−
=
+
x
y
x
. D.
25
1
+
=
+
x
y
x
.
Lời giải
Chọn B
Đồ thị hàm số cắt trục Oy tai điểm có tọa độ
( )
0;1
nên chọn phương án B.
Câu 3: (SGD Nam Định) Đường cong trong hình là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
−
=
+
. B.
21
22
x
y
x
−+
=
+
. C.
42
3yx x= −
. D.
32
3yx x= −
.
Lời giải
Chọn A
Hình vẽ trên là đồ thị của hàm số dạng
( )
0; 0
ax b
y c ad bc
cx d
+
= ≠ −≠⇒
+
Loại phương án C, D
Ta thấy: Đồ thị có đường tiệm cận đứng là
1x = −
và đường tiệm cận ngang là
1y =
Phương án B: Đồ thị có đường tiệm cận đứng là
2x =−⇒
loại B
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 140
⇒
A đúng.
Câu 4: (Sở Gia Lai 2019) Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
3
31
yxx

. B.
42
1yx x

. C.
2
1y xx
. D.
3
31yx x
.
Lời giải
Chọn D
Đồ thị đã cho có hình dạng của đồ thị hàm số bậc ba
32
y ax bx cx d

nên loại phương án B và
C
Dựa vào đồ thị, ta có
lim 0
x
ya


nên loại phương án A
DẠNG 2. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ
Câu 5: Cho hàm số
32
= + ++y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 141
A.
0, 0, 0, 0<>> <abcd
B.
0, 0, 0, 0<<><abcd
.
C.
0, 0, 0, 0><< >abcd
D.
0, 0, 0, 0<>< <abcd
.
Lời giải
Chọn A
Dựa vào đồ thị suy ra hệ số
0<a
⇒
loại phương án C
2
32 0
′
= + +=y ax bx c
có 2 nghiệm
12
,xx
trái dấu (do hai điểm cực trị của đồ thị hàm số nằm
hai phía với
Oy
)
3. 0 0⇒ <⇒>ac c
⇒
loại phương án D. Do
( ) ( )
0; 0.∩ = ⇒<C Oy D d d
Câu 6: (THPT Nguyễn Khuyến 2019) Cho hàm số
42
y ax bx c
=++
có đồ thị như hình bên. Mệnh đề
nào dưới đây là đúng?
A.
0, 0, 0abc
><>
B.
0, 0, 0abc><<
C.
0, 0, 0abc>><
D.
0, 0, 0abc<><
Lời giải
Chọn B
Ta có đồ thị có hình dạng như trên với hàm bậc bốn trùng phương có hai điểm cực tiểu và một
điểm cực đại nên
0, 0ab><
. Giá trị cực đại nhỏ hơn
0
nên
0c <
.
Câu 7: (Chuyên Trần Phú Hải Phòng 2019) Cho hàm số
+
=
+
ax b
y
cx d
có đồ thị như sau.
Mệnh đề nào sau đây đúng?
A.
0; 0ac bd>>
B.
0; 0ab cd<<
C.
0; 0bc ad><
D.
0; 0ad bd><
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 142
Lời giải
Theo đồ thị:
Tiệm cận ngang:
0= >
a
y
c
( )
1
Tiệm cận đứng:
00=− >⇒ <
dd
x
cc
( )
2
0 00=⇒=−<⇒ >
bb
yx
aa
( )
3
Câu 8: (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số
( )
32
0y ax bx cx d a= + ++ ≠
có đồ thị như
hình vẽ dưới đây. Chọn khẳng định đúng về dấu của
a
,
b
,
c
,
d
?
A.
0a >
,
0b >
,
0d >
,
0c >
B.
0
a
>
,
0cb>>
,
0d <
C.
0, 0, 0, 0.abcd>>> >
D.
0a >
,
0b <
,
0c
<
,
0d >
Lời giải
Chọn D
Dựa vào đồ thị ta có
0a >
, đồ thị cắt
Oy
tại
1
điểm có tung độ dương nên
0d >
, đồ thị có
2
cực trị trái dấu nên
12
.0 0 0
c
xx c
a
<⇒ <⇒<
. Vậy đáp án D
Câu 9: (Toán Học Tuổi Trẻ 2019) Cho hàm số
1
,0
1
a xb
yd
c xd



có đồ thị như hình trên. Khẳng
định nào dưới đây là đúng?
A.
1, 0, 1 .
ab c

B.
1, 0, 1 .ab c
C.
1, 0, 1 .ab c
D.
1, 0, 1 .
ab c

Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 143
Theo bài ra, đường tiệm cận đứng của đồ thị hàm số là
.
1
d
x
c

Đường tiệm cận ngang của đồ thị hàm số là:
1
.
1
a
y
c
Nhìn đồ thị ta thấy:
0
1
d
x
c

mà
0 10 1dc c 
.
1
0 10 1
1
a
y aa
c

.
Đồ thị cắt trục tung tại điểm có tung độ bằng
00
b
b
d

.
Câu 10: (Sở Ninh Bình 2019) Cho hàm số
42
y ax bx c=++
(
0a ≠
) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A.
0a <
,
0
b >
,
0c <
. B.
0a <
,
0b <
,
0
c
>
. C.
0a <
,
0
b >
,
0
c
>
. D.
0a <
,
0b
<
,
0c
<
.
Lời giải
Đồ thị cắt trục tung tại điểm
( )
0; c
, từ đồ thị suy ra
0
c <
Mặt khác đồ thị hàm số có ba điểm cực trị nên
0y
′
=
có ba nghiệm phân biệt, hay
( )
32
4 2 22 0y ax bx x ax b
′
= + = +=
có ba nghiệm phân biệt. Suy ra
,ab
trái dấu.
Mà
00
ab<⇒>
Câu 11: (Cụm Liên Trường Hải Phòng 2019) Hàm số
32
y ax bx cx d 
có đồ thị như hình vẽ
bên dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 144
+ Dựa vào hình dạng đồ thị ta khẳng định được
0a
.
+ Đồ thị cắt trục
Oy
tại điểm có tọa độ
0; d
. Dựa vào đồ thị suy ra
0d
.
+ Ta có:
2
32y ax bx c

. Hàm số có hai điểm cực trị
1
x
,
2
x
12
xx
trái dấu nên phương
trình
0y
có hai nghiệm phân biệt
1
x
,
2
x
trái dấu. Vì thế
3. 0ac
, nên suy ra
0
c
.
+ Mặt khác từ đồ thị ta thấy
1
2
1
1
x
x

nên
12
0xx
.
Mà
12
2
3
b
xx
a

nên suy ra
2
0
3
b
a
0
b
.
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 12: (THPT Ba Đình 2019) Cho hàm số
ax b
y
xc
+
=
+
có đồ thị như hình bên dưới, với
a
,
b
,
c ∈
.
Tính giá trị của biểu thức
23Ta b c=++
?
A.
8T = −
. B.
2T
=
. C.
6T =
. D.
0T =
.
Lời giải
Từ đồ thị hàm số, ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng
1x =
, tiệm cận ngang là đường thẳng
1y = −
.
Đồ thị hàm số đi qua các điểm
( )
2; 0
A
,
( )
0; 2B −
.
Từ biểu thức hàm số
ax b
y
xc
+
=
+
(vì đồ thị hàm số là đồ thị hàm nhất biến nên
0ac b−≠
), ta
suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng
xc= −
, tiệm cận ngang là đường thẳng
ya
=
.
Đồ thị hàm số đi qua
;0
b
A
a

−


,
0;
b
B
c



.
Đối chiếu lại, ta suy ra
1c = −
,
1a = −
,
2b =
.
Vậy
( ) ( )
2 3 1 2.2 3 1 0Ta b c=+ + =−+ + −=
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 145
Câu 13: (THPT Việt Đức Hà Nội 2019) Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình bên.
Trong các mệnh đề sau mệnh đề nào đúng?
A.
0, 0, 0ab bc cd<><
B.
0, 0, 0ab bc cd<<>
C.
0, 0, 0
ab bc cd>><
D.
0, 0, 0ab bc cd>>>
Lời giải
Chọn A
Từ dáng điệu của đồ thị ta có ngay được:
⊕
lim ; lim 0
xx
y ya
→+∞ →−∞
= +∞ = −∞ ⇒ >
.
⊕
Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên
0d >
.
Ta có:
2
'3 2y ax bx c= ++
Mặt khác dựa vào đồ thị ta thấy phương trình
'0y
=
có hai nghiệm trái dấu và tổng hai nghiệm
này luôn dương nên
0
0
2
0
3
ac
c
b
b
a
<
<
⇒

<
−>
(do
0a >
)
Do đó:
0, , 0ab bc cd< ><
.
Câu 14: (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình
dưới. Khẳng định nào sau đây đúng ?
A.
0, 0, 0, 0abcd<<< <
B.
0, 0, 0, 0abcd<>> >
C.
0, 0, 0, 0
abcd<>< >
D.
0, 0, 0, 0abcd<>> <
Lời giải
Chọn D
- Dựa vào hình dáng của đồ thị suy ra hệ số
0a <
.
- Đồ thị cắt trục
Oy
tại điểm có tung độ âm nên
0d <
.
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương
trình
2
32 0y ax bx c
′
= + +=
có 2 nghiệm
12
,xx
trái dấu kéo theo
3. 0 0ac c<⇒>
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 146
- Mặt khác
12
00
23
xx b
b
a
+
=− >⇒>
.
Câu 15: (THPT Chuyên Bắc Ninh 2019) Cho hàm số có đồ thị như hình vẽ. Mệnh đề
nào dưới đây đúng ?
A.
0, 0, 0abc><<
. B.
0, 0, 0abc<<<
.
C.
0, 0, 0abc<><
. D.
0, 0, 0abc><>
Lời giải
Chọn C
- Dựa vào hình dạng đồ thị suy ra
0a <
- Hàm số có 3 điểm cực trị nên
00ab b<⇒>
- Giao điểm với trục tung nằm dưới trục hoành nên
0c <
.
Câu 16: (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị như trong hình bên
dưới. Biết rằng
a
là số thực dương, hỏi trong các số
,,bcd
có tất cả bao nhiêu số dương?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
Nhìn vào đồ thị ta thấy
42
y ax bx c=++
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 147
• tiệm cận ngang
a
y
c
=
nằm trên trục hoành nên
0c >
(vì
0a >
)
• tiệm cận đứng
d
x
c
−
=
nằm bên trái trục tung nên
0.
d
c
−
<
Suy ra
0d
>
(vì
0c >
)
• giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên
0.
b
d
<
Suy ra
0b <
(vì
0d >
)
Vậy
0, 0
cd
>>
Câu 17: (Cụm liên trường Hải Phòng 2019) Hàm số
32
y ax bx cx d 
có đồ thị như hình vẽ bên
dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0
d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0
a
,
0b
,
0c
,
0d
. D.
0
a
,
0b
,
0c
,
0d
.
Lời giải
Chọn D
+ Dựa vào hình dạng đồ thị ta khẳng định được
0a
.
+ Đồ thị cắt trục
Oy
tại điểm có tọa độ
0; d
. Dựa vào đồ thị suy ra
0d
.
+ Ta có:
2
32y ax bx c

. Hàm số có hai điểm cực trị
1
x
,
2
x
12
xx
trái dấu nên phương
trình
0
y
có hai nghiệm phân biệt
1
x
,
2
x
trái dấu. Vì thế
3. 0ac
, nên suy ra
0c
.
+ Mặt khác từ đồ thị ta thấy
1
2
1
1
x
x

nên
12
0xx
.
Mà
12
2
3
b
xx
a

nên suy ra
2
0
3
b
a
0
b
.
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 18: (Chuyên Nguyễn Huệ 2019) Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị như hình vẽ bên. Khẳng định
nào sau đây là khẳng định đúng?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 148
A.
0
0
ad
bc
<
>
. B.
0
0
ad
bc
<
<
. C.
0
0
ad
bc
>
<
. D.
0
0
ad
bc
>
>
.
Lời giải
Chọn C
Nhận xét từ đồ thị:
+ Giao với trục hoành tại
0
o
b
x
a
=−>⇒
a
và
b
trái dấu (1).
+ Giao với trục tung tại
0
o
b
yb
d
= <⇒
và
d
trái dấu (2).
+ Tiệm cận đứng:
0
d
xd
c
=−<⇒
và
c
cùng dấu (3).
Từ (1) và (2) suy ra:
a
và
d
cùng dấu hay
0ad >
.
Từ (2) và (3) suy ra:
b
và
c
trái dấu hay
0
bc <
.
Câu 19: Cho đường cong
( )
32
:C y ax bx cx d= + ++
có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A.
0, 0, 0, 0abcd><< <
.
B.
0, 0, 0, 0abcd>>< >
.
C.
0, 0, 0, 0abcd<>> <
.
D.
0, 0, 0, 0
abcd
>>< <
.
Lời giải
Chọn D
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 149
Từ đồ thị ta có
00
x yd=⇒=<
, từ dạng đồ thị suy ra
0a >
.
Mặt khác
2
'3 2y ax bx c= ++
từ đồ thị ta có phương trình
'0y =
có hai nghiệm trái dấu suy ra
0ac <
mà
0
a >
suy ra
0c <
.
Hơn nữa phương trình
'0y =
có hai nghiệm phân biệt
12
2
1
3
b
xx
a
+=− =−
suy ra
32 0abb
= ⇒>
.
Vậy chọn đáp án D.
Câu 20: (Gia Lai 2019) Hàm số
42
y ax bx c
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0
b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0
a
,
0
b
,
0c
.
Lời giải
Chọn C
Dựa vào đồ thị:
+
lim
x
y


0a
.
+ Đồ thị hàm số có ba điểm cực trị
0
ab
0b
.
+ Giao điểm của đồ thị hàm số và trục tung có tung độ dương
0c
.
Vậy
0a
,
0b
,
0c
.
Câu 21: (THPT Thăng Long 2019) Cho hàm số
42
y ax bx c

có đồ thị như hình vẽ. Tìm kết luận
đúng
A.
0ab
. B.
0bc
. C.
0ab
. D.
0ac
.
Lời giải
Chọn B
Từ hình vẽ ta thấy:
Đồ thị hàm số có bề lõm hướng lên
0a
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0c
.
Đồ thị hàm số có 3 điểm cực trị
00ab b 
.
Vậy chỉ có
0bc
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 150
Câu 22: (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số
42
( 0)y ax bx c a
có đồ thị như hình
bên. Hãy chọn mệnh đề đúng.
A.
0, 0, 0abc
. B.
0, 0, 0abc
.
C.
0, 0, 0abc
. D.
0, 0, 0
abc
.
Lời giải
Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy :
Hệ số
0a
Đồ thị hàm số đi qua gốc tọa tọa
0
c
Hàm số có 3 điểm cực trị
.0 0
ab b 
Câu 23: (Chuyên Long An 2019) Cho hàm số
32
()y f x ax bx cx d= = + ++
có đồ thị như hình vẽ ở bên.
Mệnh đề nào sau đây đúng?
A.
0a >
,
0
b
>
,
0c
>
,
0d >
. B.
0
a >
,
0b
>
,
0
c
<
,
0d >
.
C.
0a
>
,
0b <
,
0
c >
,
0d >
. D.
0a <
,
0
b <
,
0c
>
,
0d <
.
Lời giải
Chọn C
Đồ thị hàm số đi qua các điểm
(0;1)A
,
(1; 5)B
và
(3;1)C
và đạt cực trị tại các điểm
B
và
C
.
2
() 3 2f x ax bx c
′
= ++
. Ta có
(0) 1 1 1
(1) 5 5 6
(1) 0 3 2 0 9
(3) 0 27 6 0 1
fd a
f abcd b
f a bc c
f a bc d
′
′
= = =


= +++ = =−

⇒⇒

= + += =


= + += =

.
Câu 24: (THPT Trần Phú 2019) Cho hàm số bậc bốn trùng phương
42
y ax bx c
có đồ thị như
hình vẽ bên. Mệnh đề nào dưới đây là đúng?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 151
A.
0, 0, 0abc
. B.
0, 0, 0abc
.
C.
0, 0, 0
abc
. D.
0, 0, 0abc
.
Lời giải
Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy :
Hệ số
0a
.
Hàm số có 3 điểm cực trị
.0 0ab b 
.
Đồ thị hàm số đi qua gốc tọa tọa
0c
.
Vậy
0, 0, 0abc
.
Câu 25: (THPT Cộng Hiền 2019) Cho hàm số
42
y ax bx c=++
có đồ thị như hình vẽ bên. Hỏi khẳng
định nào sau đây đúng?
A.
0, 0, 0abc><<
. B.
0, 0, 0abc>><
. C.
0, 0, 0abc><>
. D.
0, 0, 0abc<><
.
Lời giải
Chọn A
Nhìn vào đồ thị ta có:
Khi
x ∈
( )
2; +∞
hàm số đồng biến
0a⇒>
.
Hàm số có
3
điểm cực trị nên
0a.b <
mà
00ab
>⇒<
.
( )
01 0y cc=−= ⇒ <
.
Câu 26: (SGD Điện Biên - 2019) Cho hàm số
3ax
y
xc
+
=
+
có đồ thị như hình vẽ bên. Tính giá trị của
2.ac−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 152
A.
2 3.ac−=
B.
2 3.ac−=−
C.
2 1.ac−=−
D.
2 2.ac−=−
Lời giải
Chọn A
Đồ thị hàm số có TCN
1 1 1.
1
a
ya=−⇔ =−⇔ =−
Mặt khác Đồ thị hàm số có TCĐ
2x =
nên
2 0 2.cc+=⇔=−
( )
2 1 2. 2 3.ac⇒ − =−− − =
Dựa vào đồ thị ta thấy các điểm
( )
3; 0
và
3
0;
2

−


thuộc vào đồ thị hàm số đã cho nên ta được
hệ phương trình
.3 3
0
3
3 .0 3
20
a
c
a
c
+
=
+
+
−=
+
3 30
36
a
c
+=
⇔
−=
1
2
a
c
= −
⇔
= −
( )
2 1 2. 2 3.ac⇒ − =−− − =
Câu 27: Hình vẽ bên là đồ thị hàm số
ax b
y
cx d
+
=
+
.
.
Mệnh đề nào dưới đây đúng?
A.
0ad >
và
0bd >
. B.
0ad >
và
0ab <
. C.
0bd <
và
0ab >
. D.
0ad <
và
0ab <
.
Lời giải
Chọn B
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 153
Đồ thị hàm số giao với trục
Ox
tại điểm có hoành độ
b
x
a
= −
, giao với
Oy
tại điểm có tung độ
b
y
d
=
.
Dựa vào hình vẽ ta có
00
0
0
0
00
bb
ab
aa
ad
b b bd
dd

−> <

<

⇔ ⇔ ⇒>

<

<<


.
Trong các phương án chỉ có phương án B thỏa mãn.
Câu 28: Cho hàm số
1
ax b
y
x
−
=
−
có đồ thị như hình vẽ dưới đây:
Khẳng định nào sau đây đúng?
A.
0ba
<<
. B.
0
ab
<<
. C.
ba>
và
0a <
. D.
0ab
<<
.
Lời giải
Chọn A
Ta thấy đồ thị hàm số có tiệm cận ngang
1y = −
suy ra
1a = −
.
Do đồ thị hàm số đi qua điểm
( )
2; 0
nên
2 02 0 2ab b b−=⇔−−=⇔=−
.
Vậy
0
ba<<
.
Câu 29: (Chuyên Lương Văn Chánh - Phú Yên - 2020) Đồ thị trong hình bên dưới là của hàm số
ax b
y
xc
+
=
+
(với
,,abc∈
).
Khi đó tổng
abc++
bằng
A.
1−
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn D
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 154
Đồ thị hàm số
ax b
y
xc
+
=
+
có đường tiệm cận ngang
ya=
, đường tiệm cận đứng
xc= −
và cắt
Oy
tại điểm
0;
b
c



.
Từ đồ thị hàm số ta có đường tiệm cận ngang
1y = −
, đường tiệm cận đứng
1
x =
và cắt
Oy
tại
điểm
( )
0; 2−
.
Từ đó suy ra:
11 1
11 1
22
2
aa a
cc c
b bcb
c
=−=− =−


−=⇔=−⇔=−


=−=

= −
. Vậy
11 2 0
abc+ + =−−+ =
.
Câu 30: (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số
2
()
ax
fx
bx c
−
=
−
( )
,, , 0abc b∈≠
có
bảng biến thiên như sau:
Tổng các số
( )
2
abc++
thuộc khoảng nào sau đây
A.
( )
1; 2
. B.
(
)
2;3
. C.
4
0;
9



. D.
4
;1
9



.
Lời giải
Chọn C
Ta có
2
lim
x
ax a
bx c b
→∞
−−
=
−
, theo giả thiết suy ra
33
a
ab
b
−
=⇔=−
Hàm số không xác định tại
10
x bc bc=⇒−=⇔=
Hàm số đồng biến trên từng khoảng xác định nên
( )
( )
2
2
0
ac b
fx
bx c
−
′
= >
−
với mọi
x
khác 1
Suy ra
2
22
20 3 20 00
33
ac b b b b b− >⇔− − >⇔−<<⇔<−<
Lại có
3abc bbb b++=− ++=−
. Suy ra
( )
2
2
4
0;
9
abc b

++ = ∈


Vậy tổng
abc
++
thuộc khoảng
4
0;
9



.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 155
Câu 31: (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
()
ax b
fx
cx d
+
=
+
(,,,abcd∈
và
0
c
≠
).
Biết rằng đồ thị hàm số đã cho đi qua điểm
( )
1;7
−
và giao điểm hai tiệm cận là
(
)
2;3
−
. Giá trị
biểu thức
234
7
a b cd
c
+++
bằng
A.
7
. B.
4
. C.
6
. D.
5−
.
Lời giải
Chọn C
+ Ta có đồ thị hàm số
()
ax b
fx
cx d
+
=
+
có đường tiệm cận ngang là
a
y
c
, đường tiệm cận đứng
là
d
x
c
.
Theo bài ra, ta có:
3
3
2
2
a
ac
c
d dc
c





.
+ Điểm
( )
1;7
−
thuộc đồ thị hàm số
()fx
nên
3
7 7 10
2
ab cb
bc
cd c c
−+ − +
=⇔ =⇔=
−+ −+
.
Vậy
2 3 4 2.(3 ) 3.(10 ) 4 2
6
77
a b cd c c c c
cc
 

.
Câu 32: (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số
1ax
y
bx c
+
=
+
(
,,abc
là các tham số)
có bảng biến thiên như hình vẽ
Xét các phát biểu sau:
( ) ( ) ( ) ( )
1 : 1; 2 : 0; 3 : 0; 4 : 0
c ab abc a> +< ++= >
. Số phát biểu đúng
là?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng khoảng xác định, đồ thị hàm số
có tiệm cận đứng là đường thẳng
2x =
và tiệm cận ngang là đường thẳng
1y =
nên ta có hệ
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 156
2
2
01
22
1
10
2
02 0
1
0
0
2
0
c
c
b
cb cb
a
ab ab a
b
ac b b b
ac b
b
abc
−=
<<
=−=−


= ⇔ = ⇔ = ⇔−<<


−> − −>

−>

−<<

++=
Dựa vào hệ trên ta có các phát biểu
( ) ( )
1,4
là sai,
( ) ( )
2,3
đúng.
Câu 33: (Đô Lương 4 - Nghệ An - 2020) Ta xác định được các số
,,abc
để đồ thị hàm số
32
y x ax bx c=+ ++
đi qua điểm
( )
1;0
và có điểm cực trị
( )
2;0−
. Tính giá trị biểu thức
222
Tabc=++
.
A.
25.
B.
1.−
C.
7.
D.
14.
Lời giải
Chọn A
Ta có
32 2
32y x ax bx c y x ax b
′
= + + +⇒ = + +
.
Theo đề, ta có hệ phương trình
( )
( )
( )
( ) ( ) ( )
( ) ( )
32
32
2
0 1 .1 .1
10
2 0 0 2 .2 .2
20
0
3.2 2.2
a bc
y
y a
bc
y
ab
=+ ++
=
−=⇔ =− + − + −+


′
−=
= − + −+
13
42 8 0
4 12 4
abc a
a bc b
ab c
++=− =


⇔ − +=⇔ =


− +=− =−

.
Vậy
( )
2
22222
3 0 4 25.Tabc=++=++− =
Câu 34: (Lê Lai - Thanh Hóa - 2020) Cho hàm số có đồ thị như hình vẽ. Tính
?
A. . B. . C. . D. .
Lời giải
Chọn A
Vì đồ thị hàm số cắt trục tung tại điểm
2y =
nên
2d =
.
32
y ax bx cx d= + ++
S ab= +
2S = −
0S =
1S =
1S = −
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 157
2
32
y ax bx c
′
= ++
.
Hàm số đạt cực trị tại
0x =
và
2x =
nên
(
)
(
)
(
)
00
0
0
3 1
12 4 0
20
y
c
c
ba
a bc
y
′
=
=
=

⇔⇔

= −
+ +=
′
=
Từ đồ thị ta nhận thấy
(
)
( )
2 284 284 42 1 2
y abd ab ab=−⇔ + + =−⇔ + =−⇔ + =−
Thay
(
)
1
vào
( )
2
ta tìm được
1, 3
ab
= = −
.
Vậy
2S = −
.
Câu 35: (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0abcd<<> <
. B.
0, 0, 0, 0abcd<>< <
.
C.
0, 0, 0, 0abcd
><< >
. D.
0, 0, 0, 0abcd<>> <
.
Lời giải
Chọn D
Ta có:
2
32y ax bx c
′
= ++
,
62y ax b
′′
= +
Từ đồ thị ta thấy:
lim
x
y
→+∞
= −∞
. Ta suy ra
0a <
.
( )
00 0yd
<⇒<
loại C.
Đồ thị hàm số có hai điểm cực trị với hoành độ
1
x
,
2
x
trái dấu và
12
0xx+>
. Ta suy ra phương
trình
'0y =
có hai nghiệm trái dấu và
12
0xx+>
.
Ta suy ra
12
0
3
c
xx
a
= <
,
0c⇒>
loại B.
Hơn nữa,
12
0
0
3
0
b
xx
b
a
a
+=− >
⇒>
<
. Lọai A.
Câu 36: (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số
( )
,,
1
ax b
y abc
cx
+
= ∈
+
có bảng biến thiên như
sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 158
Tập các giá trị
b
là tập nghiệm của bất phương trình nào dưới đây?
A.
3
8 0.b −≤
B.
2
4 0.b− +>
C.
2
3 2 0.bb− +<
D.
3
8 0.b
−<
Lời giải
Chọn D
Đồ thị hàm số
1
ax b
y
cx
+
=
+
có đường tiệm cận đứng là đường thẳng
1
x
c
= −
và đường tiệm cận
ngang là đường thẳng
a
y
c
=
.
Nhìn vào bảng biến thiên, ta thấy
1
11c
c
− =−⇒ =
và
22
a
a
c
=⇒=
(vì
1c =
).
Ta có
(
)
2
1
a bc
y
cx
−
′
=
+
.
Vì hàm số đã cho đồng biến trên các khoảng
( )
;1−∞ −
và
( )
1;− +∞
nên
( )
33
2
0 0 2 0 2 8 80
a bc
y abc bbb b
bx c
−
′
= >⇔− >⇔−>⇔<⇔ <⇔ −<
+
.
Vậy tập các giá trị
b
là tập nghiệm của bất phương trình
3
8 0.b −<
Câu 37: (Tiên Du - Bắc Ninh - 2020) Cho hàm số
ax b
y
cx d
+
=
+
(với
,,,abcd
là số thực) có đồ thị như
hình dưới đây. Tính giá trị biểu thức
23abd
T
c
−+
=
.
A.
6=T
. B.
0=T
. C.
8= −T
. D.
2=T
.
Lời giải
Chọn C
Từ đồ thị ta có
TCĐ:
111
dd
x
cc
−
=⇒ =⇒=−
dc⇒=−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 159
TCN:
11
a
y ac
c
=−⇒ =−⇒ =−
Đồ thị cắt trục hoành tại điểm:
2222
b bb
x
a cc
−−
=⇒=⇒=⇒=
−
2bc⇒=
Vậy
23 43
8
abd ccc
T
cc
− + −− −
= = = −
Câu 38: (Thanh Chương 1 - Nghệ An - 2020) Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình vẽ.
Trong các số
,,
abc
và
d
có bao nhiêu số dương?
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn D
Từ hình dạng đồ thị hàm số ta có
0a >
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0d⇒<
Ta có:
2
'3 2y ax bx c= ++
Hàm số có hai điểm cực trị trái dấu
'0y⇒=
có hai nghiệm trái dấu
0ca⇔<
Mà
0a >
nên
0c <
Ta lại có:
'' 6 2y ax b= +
'' 0 6 2 0
3
b
y ax b x
a
=⇔ + =⇔=−
Từ đồ thị hàm số ta thấy tâm đối xứng có hoành độ âm. Do đó
0
3
b
a
−<
Mà
0
a >
nên
0b >
Vậy trong các số
,,
abc
và
d
có 2 số dương là
a
và
b
Câu 39: (Tiên Lãng - Hải Phòng - 2020) Cho hàm số
( )
6−
=
−
ax
fx
bx c
( )
,,∈ abc
có bảng biến thiên
như sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 160
Trong các số
,,abc
có bao nhiêu số âm?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là
đường thẳng
2
x = −
và tiệm cận ngang là đường thẳng
1
y
=
.
Suy ra
2
1
c
b
a
b
= −
=
0
0
bc
ab
<
⇒
>
( )
( )
1
0, 0, 0
2
0, 0, 0
bca
bca
><>
⇔
<><
Lại có hàm số nghịch biến trên mỗi khoảng xác định
( )
( )
2
6
0
ac b
fx
bx c
−+
′
= <
−
6
ac b
⇒>
.
Ta thấy
( )
1
không thể xảy ra do nếu
0b >
thì
60ac b>>
; và
(
)
2
có thể xảy ra do nếu
0, 0ca><
thì
60b ac<<
.
Vậy trong các số
,,abc
có hai số âm.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 161
DẠNG 2. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI (BIẾN ĐỔI ĐỒ THỊ)
Dạng 1
Từ đồ thị
(
)
( )
=C y fx:
suy ra đồ thị
( ) ( )
′
=C y fx:
.
Ta có:
(
)
(
)
( )
( )
(
)
≥
= =
−<
fx khi fx
y fx
fx khi fx
0
0
* Cách vẽ
( )
′
C
từ
(
)
C
:
Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C):
( )
=y fx
.
Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị
( ) ( )
3
:3C y fx x x= = −
suy ra đồ thị
= −yx x
3
3
.
Biến đổi
( )
C
:
Bỏ phần đồ thị của
( )
C
dưới
,Ox
giữ nguyên
( )
C
phía trên
.Ox
Lấy đối xứng phần đồ thị bị bỏ qua
Ox
.
Dạng 2
Từ đồ thị
( )
( )
=C y fx
:
suy ra đồ thị
( )
( )
′
=C y fx:
.
Ta có:
( )
( )
( )
f x khi x
y fx
f x khi x
0
0
≥
= =
−<
và
(
)
=
y fx
là hàm chẵn nên đồ thị
( )
C
′
nhận Oy làm trục đối xứng.
* Cách vẽ
( )
′
C
từ
( )
C
:
Giữ nguyên phần đồ thị bên phải Oy của đồ thị
( ) ( )
=C y fx:
.
Bỏ phần đồ thị bên trái Oy của
( )
C
, lấy đối xứng phần đồ thị được giữ qua Oy.
x
y
O
-2
2
-1
1
x
y
2
-1
O
1
( )
3
:3Cyx x= −
( )
′
= −Cyx x
3
:3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 162
Ví dụ: Từ đồ thị
( )
( )
= = −
C y fx x x
3
:3
suy ra đồ thị
( )
′
= −Cyx x
3
:3
.
Biến đổi
( )
C
:
Bỏ phần đồ thị của
( )
C
bên trái
Oy
,
giữ nguyên
( )
C
bên
phải
.Oy
Lấy đối xứng phần đồ thị được giữ qua
Oy
.
Chú ý với dạng:
( )
=y fx
ta lần lượt biến đổi 2 đồ thị
( )
=y fx
và
( )
=
y fx
Ví dụ: Từ đồ thị
( ) ( )
= = −C y fx x x
3
:3
suy ra đồ thị
= −yx x
3
3
. Biến đổi
(
)
C
để được đồ thị
( )
′
= −Cyx x
3
:3
. Biến đổi
( )
′
= −Cyx x
3
:3
ta được đồ thị
( )
′′
= −C yx x
3
:3
.
Dạng 3
Từ đồ thị
( ) ( ) ( )
=C y ux vx:.
suy ra đồ thị
( ) ( )
( )
′
=C y ux vx:.
.
Ta có:
( )
( )
( ) ( ) ( ) ( )
( ) ( ) ( )
( )
ux vx fx khi ux
y ux vx
ux vx fx khi ux
.0
.
.0
= ≥
= =
−= <
* Cách vẽ
( )
′
C
từ
(
)
C
:
Giữ nguyên phần đồ thị trên miền
( )
≥ux 0
của đồ thị
( ) ( )
=C y fx:
.
Bỏ phần đồ thị trên miền
( )
<ux 0
của
( )
C
, lấy đối xứng phần đồ thị bị bỏ qua Ox.
x
y
O
-2
2
-1
1
x
y
O
-2
-1
1
x
y
2
-1
O
1
( )
′
= −Cyx x
3
:3
( )
= −Cyx x
3
:3
( )
′′
= −C yx x
3
:3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 163
Ví dụ
a) Từ đồ thị
( ) ( )
= =−+C y fx x x
32
: 231
suy ra
đồ thị
( )
( )
′
= − −−Cyx x x
2
: 12 1
Ví dụ
b) Từ đồ thị
( ) ( )
= =
−
x
C y fx
x
:
1
suy ra đồ thị
( )
′
=
−
x
Cy
x
:
1
( )
( )
( )
≥
= − −− =
−<
f x khi x
yx x x
f x khi x
2
1
12 1
1
Đồ thị (C’):
Giữ nguyên (C) với
1x ≥
.
Bỏ (C) với
<
x
1
. Lấy đối xứng phần đồ thị bị bỏ
qua Ox.
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của (C): giao
điểm với Ox, Oy, CĐ, CT…
(
)
( )
∈ +∞
−
= =
−
− ∈ −∞
−
x
khi x
x
x
y
x
x
khi x
x
1;
1
.
1
;1
1
Đồ thị
(C’):
Bỏ phần đồ thị của
( )
C
với
x ,
1<
giữ nguyên
(
)
C
với
1.x
>
Lấy đối xứng phần đồ thị bị bỏ qua
Ox.
Nhận xét: Đối với hàm phân thức thì nên lấy đối xứng
các đường tiệm cận để thực hiện phép suy đồ thị một
cách tương đối chính xác.
Câu 40: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x
=− −−
D.
( )
2
1 2 2.yx x x=− −−
Hướng dẫn
Ta có:
( )
( )
32 2
3 2 1 22yx x x x x= − += − − −
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
x
y
(C)
(C')
1
O
1
x
y
1
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 164
Toàn bộ đồ thị ứng với
1x ≥
được giữ nguyên.
Phần đồ thị ứng với
1
x
<
lấy đối xứng qua trục hoành.
⇒
Chọn đáp án C.
Câu 41: (THPT Việt Đức Hà Nội 2019) Cho hàm số
( )
y fx=
có đồ thị hàm số
( )
y fx=
như hình
vẽ.
Chọn kết luận đúng trong các kết luận sau:
A.
( )
32
44
fx x x x=−+ + −
B.
( )
32
44fx x x x=−−+
C.
( )
32
44fx x x x=−− + −
D.
( )
32
4 4.fx x x x=+−−
Lời giải
Chọn A
Do đồ thị giao với trục
Oy
tại điểm có tung độ bằng
4−
và
lim
x
y
→+∞
= −∞
.
Câu 42: (Chu Văn An - Hà Nội - 2019) Cho hàm số
( )
( )
2
21yx x=−−
có đồ thị như hình vẽ
Một trong bốn hình dưới đây là đồ thị của hàm số
( )
2
21yx x=−−
. Hỏi đó là hình nào?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 165
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.
Lời giải
Chọn C
Gọi
( )
C
là đồ thị hàm số
( )
( )
2
21yx x=−−
.
Ta có
( )
( )
(
)
( )
( )
2
2
2
21 1 1
21
2 1 11
x x khi x hay x
yx x
x x khi x
− − ≤− ≥
= − −=
− − − −< <
.
Cách vẽ đồ thi như sau:
+ Giữ nguyên phần đồ
(
)
C
ứng với
(
]
[
)
; 1 1;x ∈ −∞ − ∪ +∞
ta được
(
)
1
C
.
+ Lấy đối xứng phần
( )
C
ứng với
( )
1;1x ∈−
qua trục hoành ta được
( )
2
C
.
Khi đó đồ thị hàm số
( )
2
21yx x
=−−
gồm
(
)
1
C
và
( )
2
C
.
Câu 43: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.
yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía “phải”
Oy
sau đó lấy đối xứng sang trái.
⇒
Chọn đáp án B.
Câu 44: Cho hàm số
1
21
x
y
x
−+
=
−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 166
A.
1
21
x
y
x
−+
=
−
B.
1
21
x
y
x
+
=
−
C.
1
21
x
y
x
−+
=
−
D.
1
21
x
y
x
−+
=
−
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải
Oy
được giữ nguyên
Sau đó, được lấy đối xứng sang trái.
Chọn đáp án B.
Câu 45: Cho hàm số
32
69yx x x=−+
có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào
dưới đây?
A.
32
69=−+ −yx x x
. B.
32
69=−+yx x x
.
C.
3
2
69=−+yx x x
. D.
32
69=++yx x x
.
Lời giải
Chọn C
+/ Loại đáp án A vì:
( )
32 32
69 69=−+ − =− − +yx x x x x x
+/ Loại đáp án B, vì đồ thị của hàm số
32
69yx x x=−+
giữ lại phần đồ thị phía trên trục
hoành và chỉ lấy đối xứng phần dưới trục hoành của đồ thị Hình 1.
+/ Loại đáp án D vì hệ số của
2
x
khác -6.
+/ Đồ thị ở đáp án C là đồ thị của hàm số dạng
( )
y fx=
. Chọn đáp án C
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 167
Câu 46: (Cụm liên trường Hải Phòng -2019) Cho hàm số
21
x
y
x
có đồ thị như Hình 1. Đồ thị Hình
2 là của hàm số nào trong các đáp án A, B, C, D dưới đây?
A.
21
x
y
x
. B.
21
x
y
x
C.
21
x
y
x
D.
21
x
y
x
Lời giải
Chọn A
Câu 47: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32
yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Hướng dẫn
Ta có:
( )
( )
32 2
3 2 1 22yx x x x x
= − += − − −
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị ứng với
13
13
x
x
≥+
≤−
được giữ nguyên.
Phần đồ thị ứng với
13 13x− ≤ ≤+
lấy đối xứng qua trục hoành.
⇒
Chọn đáp án D.
Câu 48: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 168
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Hướng dẫn
Ta có:
( )
( )
32 2
3 2 1 22
yx x x x x
= − += − − −
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm phía trên
Ox
được giữ nguyên.
Phần đồ thị phía dưới
Ox
được lấy đối xứng qua
Ox
.
⇒
Chọn đáp án A.
Câu 49: Cho hàm số
21
x
y
x
=
+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
21
x
y
x
=
+
B.
21
x
y
x
=
+
C.
21
x
y
x
=
+
D.
21
x
y
x
=
+
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía trên
Ox
giữ nguyên
Toàn bộ phần phía dưới
Ox
được lấy đối xứng lên trên
⇒
dạng
( )
fx
.
Chọn đáp án C.
Câu 50: Cho hàm số
1
2
x
y
x
−+
=
−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 169
A.
1
.
2
x
y
x
−+
=
−
B.
1
.
2
x
y
x
+
=
−
C.
1
2
x
y
x
−+
=
−
D.
1
2
x
y
x
−+
=
−
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng
1x =
được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng
1
x
=
lấy đối xứng qua
Ox
Chọn đáp án C.
Chú ý:
1
,1
1
2
1
2
,1
2
x
x
x
x
y
x
x
x
x
−+
≤
−+
−
= =
−+
−
−>
−
Câu 51: Cho hàm số
1
2
x
y
x
+
=
+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
+
=
+
B.
1
.
2
x
y
x
+
=
+
C.
1
.
2
x
y
x
+
=
+
D.
1
.
2
x
y
x
+
=
+
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải đường thẳng
2x = −
được giữ nguyên
Toàn bộ đồ thị phía bên trái đường thẳng
2x = −
lấy đối xứng qua
Ox
Chọn đáp án D.
Câu 52: Cho hàm số
( )
( )
2
1 23yx x x=− −−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới
đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 170
A.
(
)
(
)
2
1 2 3.
yx x x=− −−
B.
(
)
2
1 2 3.
yx x x
=− −−
C.
( )
2
1 23yxxx=−− − −
D.
( )
2
1 23yx x x=− −−
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm bên trái (ứng với
1)x ≤
đường thẳng
1x
=
được giữ nguyên
Toàn bộ đồ thị nằm bên phải (ứng với
1)x >
đường thẳng
1x =
được lấy đối xứng qua
.Ox
⇒
Chọn đáp án C.
Câu 53: Cho hàm số
1
2
x
y
x
+
=
−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
+
=
+
B.
1
.
2
x
y
x
+
=
−
C.
1
.
2
x
y
x
+
=
−+
D.
1
.
2
x
y
x
+
=
+
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng
1x = −
(ứng với
1)x ≤−
được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng
1x = −
(ứng với
1)
x ≤−
được lấy đối xứng qua trục
.Ox
Chọn đáp án B.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 1
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
DẠNG 1. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
1.1 HÀM SỐ BẬC BA
(
)
= + ++ ≠y ax bx cx d a
32
0
TRƯỜNG HỢP
>
a 0
0a
<
Phương trình
=y
/
0
có
2 nghiệm phân biệt
Phương trình
=y
/
0
có
nghiệm kép
Phương trình
/
0y =
vô
nghiệm
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 2
1.2. HÀM SỐ TRÙNG PHƯƠNG
( )
= ++ ≠y ax bx c a
42
0
TRƯỜNG HỢP
>a 0
0
a
<
Phương trình
=y
/
0
có
3 nghiệm phân biệt
(ab<0)
Phương trình
=y
/
0
có
1 nghiệm.
1.3. HÀM SỐ NHẤT BIẾN
( )
0, 0
ax b
y c ad bc
cx d
+
= ≠ −≠
+
= −>D ad bc
0
= −<D ad bc 0
Câu 1: Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án
,,,ABC D
. Hỏi đó là hàm
số nào?
A.
3
21yx x=++
. B.
32
21yx x=−+
. C.
3
21yx x=−+
. D.
3
21yx x=−+ +
.
Lời giải
Dựa vào đồ thị, ta có
lim
x
y
→+∞
= +∞
, loại phương án
D
.
x
y
O
1
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 3
Xét phương án
A
có
2
3 2 0,yx x
′
= + > ∀∈
, hàm số không có cực tri, loại phương án
A
.
Xét phương án
B
có
2
36yx x
′
= −
và
y
′
đổi dấu khi đi qua các điểm
0, 2xx= =
nên hàm
số đạt cực tri tại
0x =
và
2x =
, loại phương án
B
.
Vậy phương án đúng là
C
.
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
3
31yxx
. B.
42
1yx x
. C.
2
1y xx
. D.
3
31
yx x
.
Lời giải
Chọn D
Đồ thị đã cho có hình dạng của đồ thị hàm số bậc ba
32
y ax bx cx d 
nên loại phương
án B và C
Dựa vào đồ thị, ta có
lim 0
x
ya


nên loại phương án A
Câu 3: Đồ thị hàm số
3
32
yx x=−+
là hình nào trong 4 hình dưới đây?
A. Hình 1. B. Hình 2.
C. Hình 3. D. Hình 4.
Câu 4: Đường cong trong hình bên dướ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 4
A.
3
3yx x
= −
. B.
3
31yx x=−+ −
.
C.
3
3yx x=−+
. D.
42
1yx x=−+
.
Câu 5: Đường cong trong hình bên dướ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
31
yx x=−+
. B.
3
31yx x=−+ +
.
C.
2
1y xx=− +−
. D.
42
1yx x=−+
.
Câu 6: Đường cong trong hình bên dướ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
31yx x=−+ −
. B.
3
3yx x=−+
.
C.
42
1yx x=−+
. D.
3
3yx x= −
.
Câu 7: Đường cong trong hình bên dướ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 5
A.
3
31
yx x
=−+
. B.
32
31yx x=−+ +
. C.
32
3 31yx x x=− ++
.D.
32
31yx x=−− −
.
Câu 8: Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B,
C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
3yx x= −
.
B.
3
3yx x=−+
.
C.
42
2yx x=−+
.
D.
42
2yx x= −
.
x
2
-2
y
1
O
-1
Lời giải
Chọn A
Đặc trưng của đồ thị là hàm bậc ba nên loại C, D.
Hình dáng đồ thị thể hiện
0a >
nên chỉ có A phù hợp.
Câu 9: Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C,
D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2
1y xx
=− +−
.
B.
3
31yx x=−+ +
.
C.
42
1yx x=−+
.
D.
3
31yx x=−+
.
x
y
O
Lời giải
Chọn D
Đặc trưng của đồ thị là hàm bậc ba. Loại đáp án A và C.
Hình dáng đồ thị thể hiện
0a
>
.
Câu 10: Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B,
C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
32
32yx x=−− −
.
B.
32
32yx x=+−
.
C.
32
32yx x=−−
.
x
y
-2
-2
-1
O
2
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 6
D.
32
32yx x
=−+ −
.
Lời giải
Chọn B
Hình dáng đồ thị thể hiện
0a
>
. Loại đáp án A, D.
Thấy đồ thị cắt trục hoành tại điểm
1x = −
nên thay
1
0
x
y
= −
=
vào hai đáp án B và C, chỉ có B
thỏa mãn.
Câu 11: Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
3
1yx=−+
.
B.
3
32yx x=−+ +
.
C.
32
3 32yx x x=−+ − +
.
D.
3
2yx=−+
.
x
y
1
2
1
O
2x
Lời giải
Chọn D
Để ý thấy khi
0x =
thì
2y =
nên ta loại đáp án A.
Dựa vào đồ thị, suy ra hàm số không có cực trị nên ta loại đáp án B vì
2
'3 3yx=−+
có hai
nghiệm.
Đồ thị hàm số đi qua điểm có tọa độ
( )
1;1
, kiểm tra thấy C & D đều thỏa mãn.
Xét phương trình hoành độ giao điểm:
CASIO
32
3 3 2 0 2.xxx x− + − + = → =
Xét phương trình hoành độ giao điểm:
(
)
3
3
2 0 2 1; 2
xx
− + = → = ∈
. Do đó chỉ có D thỏa
mãn.
Câu 12: Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây.
Hàm số đó là hàm số nào?
A.
32
2 6 6 1.y xxx=− − −+
B.
32
2 6 6 1.yx x x= − ++
C.
32
2 6 6 1.yx x x= − −+
D.
32
2 6 1.y xx x= −++
Lời giải
Chọn B
Nhận xét: Nhìn vào đồ thị ta thấy
0a >
nên loại
32
2 6 6 1.y xxx=− − −+
Đồ thi hàm số đi qua điểm
( )
1;3A
. Thay vào từng đáp án ta chọn
32
2 6 6 1.yx x x= − ++
O
x
y
1
3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 7
Câu 13: Xác định đồ thị sau của hàm số nào?
A.
3
32
yx x=++
. B.
3
32yx x
=−− +
. C.
3
32yx x=−+
. D.
3
32yx x=−−
.
Lời giải
Chọn C
Đồ thị hàm số đi qua điểm có tọa độ
( )
1; 0
nên loại …và
3
32yx x=−+
đúng.
Câu 14: Cho hàm số
( )
y fx=
như hình vẽ dưới đây
Hỏi
( )
fx
là hàm số nào trong các hàm số dưới đây?
A.
( )
32
34fx x x=+−
. B.
( )
32
31fx x x
=−+
.
C.
(
)
3
31
fx x x=−+
. D.
( )
32
31fx x x=−+ +
.
Lời giải
Chọn B
Dựa vào hình dạng đồ thị hàm số có hai điểm cực trị tại
0x =
và
2x =
, cắt trục tung tại điểm
có tung độ
1y =
và có hệ số
0a >
.
Như vậy chỉ có hàm số
( )
32
31fx x x=−+
thỏa mãn.
Câu 15: Đồ thị trong hình dưới là đồ thị của một trong bốn hàm số cho trong các phương án sau đây, đó
là hàm số nào?
x
y
4
2
O
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 8
A.
32
32
yx x
=−+ +
. B.
32
32yx x=−+
. C.
3
32yx x=−+
. D.
32
32yx x=−−
.
Lời giải
Chọn B
Giả sử hàm số cần tìm có dạng
32
y ax bx cx d= + ++
với
0a ≠
.
Dựa vào đồ thị hàm số ta thấy
lim
x
y
→+∞
= +∞
nên suy ra
0
a >
. Vậy loại đáp án
32
32yx x=−+ +
.
Đồ thị hàm số cắt trục tung tại điểm có tọa độ là
(
)
0;2
nên suy ra
2
d
=
. Vậy loại
32
32yx x=−−
.
Đồ thị hàm số đạt cực đại tại điểm có tọa độ là
( )
0;2
nên phương trình
0y
′
=
phải có nghiệm
0x =
. Ta thấy chỉ có hàm số
32
32yx x=−+
có
2
0
3 60
2
x
yxx
x
=
′
= −=⇔
=
.
Vậy Chọn
32
32yx x=−+
Câu 16: Biết rằng đồ thị cho ở hình vẽ dưới đây là đồ thị của một trong
4
hàm số cho trong
4
phương
án
A
,
B
,
C
,
D
.
Đó là hàm số nào?
A.
32
2 9 11 3yx x x= +−+
. B.
32
4 33yx x x=− ++
.
C.
32
2 6 43yx x x= − ++
. D.
32
5 43yx x x=− ++
.
Lời giải
Chọn B
6
4
2
x
y
2
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 9
Dựa vào đồ thị ở hình
3
ta thấy hàm số cần tìm đi qua các điểm
( )
0;3
,
( )
1; 3
và
(
)
2;1
thay vào
bốn phương án ta thấy phương án
32
4 33yx x x=− ++
là thỏa mãn.
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A.
32
262
yx x=+−
B.
32
32yx x=+−
. C.
32
32yx x=−− −
. D.
32
32yx x=−−
.
Lời giải
Chọn B
Từ đồ thị hàm số ta có:
Đồ thị trong hình là của hàm số bậc 3, có hệ số
0a >
.
Đồ thị hàm số đạt cực trị tại các điểm
( ) ( )
2; 2 ; B 0; 2A −−
.
Vậy chọn đáp án
32
32yx x
=+−
.
Câu 18: Đường cong bên là đồ thị của một trong bốn hàm số đã cho sau đây. Hỏi đó là hàm số nào?
A.
32
31yx x=+−
. B.
42
1
yx x=+−
. C.
3
31yx x=−−
. D.
2
31yx x=−− −
.
Lời giải
Chọn A
Dựa vào đồ thị, ta có hàm số đã cho có hai điểm cực trị, trong đó điểm cực tiểu là
0x =
.
Xét hàm số
32
31yx x=+−
.
2
36yx x
′
= +
;
0; 1
0
2; 3
xy
y
xy
= = −
′
= ⇔
=−=
.
Bảng biến thiên:
Đồ thị:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 10
Câu 19: Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên dưới:
A.
3
3yx x= +
. B.
32
3yx x= −
. C.
32
3yx x= +
. D.
3
3yx x= −
.
Lời giải
Chọn B
Quan sát đồ thị ta thấy đây là đồ thị của hàm số bậc ba:
32
y ax bx cx d= + ++
có
0
a >
.
Đồ thị hàm số giao với trục hoành tại hai điểm có hoành độ
0x =
và
3
x
=
suy ra đồ thị có hàm
số là
32
3yx x= −
.
Câu 20: Đường cong hình bên là đồ thị của hàm số nào dưới đây?
A.
32
34yx x=−+ −
. B.
32
34yx x=−+
. C.
32
34
yx x=−− −
. D.
32
34yx x=+−
.
Lời giải
Chọn D
Từ đồ thị hàm số ta thấy đây là hàm bậc ba
32
y ax bx cx d= + ++
với hệ số
0a >
,
0d <
Và
0y
′
=
có hai nghiệm
{ }
2;1x ∈−
. Ta thấy có hàm số
3
34yx x=+−
thỏa mãn.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 11
Câu 21: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A.
32
31yx x=−+ +
. B.
32
31yx x=−− +
. C.
32
31yx x=++
. D.
32
31yx x=−+
.
Lời giải
Chọn D
Dựa vào đồ thị ta có hàm số là hàm bậc ba
32
y ax bx cx d= + ++
có hệ số
0a >
. Đồng thời
0
y
′
=
có nghiệm
1
0x =
và nghiệm
2
0
x
>
.
Do đó, ta có hàm số thỏa mãn là
32
31yx x=−+
.
Câu 22: Đường cong trong hình bên là đồ thị hàm số nào?
A.
3
31yx x=−+
. B.
3
31yx x=−+ −
. C.
3
31yx x
=−−
. D.
3
31yx x=−+ +
.
Lời giải
Chọn D
Từ đồ thị ta có hệ số
0
a <
nên ta loại đáp án
3
31yx x=−+
và
3
31yx x=−−
.
Khi
0x =
thì đồ thị cắt trục
Oy
tại điểm có tung độ dương nên
0d
>
nên ta loại
3
31yx x=−+ −
.
Câu 23: Đường cong trong hình bên cạnh là đồ thị của hàm số nào trong các hàm số sau?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 12
A.
32
32yx x=++
. B.
32
32yx x=−+
. C.
3
32yx x=−+
. D.
32
32yx x=−−
.
Lời giải
Chọn B
Đồ thị hàm số đi qua điểm
( )
0; 2
, do đó loại đáp án
32
32yx x=−−
.
Từ đồ thị, ta có
0
y
′
=
có hai nghiệm là
0
và
2
. Như vậy ta chọn đáp án
32
32
yx x
=−+
.
Câu 24: Đồ thị như hình bên là đồ thị của hàm số nào?
A.
33
31yx x=−+ +
B.
3
31yx x=−−
C.
3
31yx x=−+
D.
33
31yx x=−− −
Lời giải
Chọn C
Hàm số là hàm bậc 3 có hệ số
0.a
>
Loại
33
31yx x=−+ +
và
33
31
yx x=−− −
.
Đồ thị cắt
Oy
tại
( )
0;1
nên loại.
3
31yx x=−−
Câu 25: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A.
42
31yx x=−+
. B.
42
2yx x= +
. C.
42
2
yx x= −
. D.
42
2yx x=−−
.
Lời giải
Chọn C
Câu 26: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
-4 -2 2 4
-2
2
4
x
y
x
y
-1
1
-1
0
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 13
A.
42
21
yx x=−+
. B.
42
21yx x=−+
. C.
42
31
yx x=−+
. D.
42
21yx x=−− +
.
Lời giải
Chọn D
Câu 27: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
A.
42
31yx x=−+
. B.
42
21yx x=−+
.
C.
42
21yx x=−+ +
. D.
42
21yx x=−− +
.
Lời giải
Chọn C
Câu 28: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
x
y
1
0
1
x
y
-1
1
-1
0
1
x
y
1
-1
0
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 14
A.
42
31yx x
=++
. B.
42
21yx x
=−+
. C.
42
31yx x=−+
. D.
42
21yx x
=−+ +
.
Lời giải
Chọn A
Câu 29: Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
42
22yx x=−+ +
.
B.
42
22yx x=−+
.
C.
42
42
yx x=−+
.
D.
42
23
yx x=−+
.
x
y
O
2
1
1
-1
Lời giải
Chọn B
Hình dáng đồ thị thể hiện
0a >
. Loại đáp án A.
Để ý thấy khi
0x =
thì
2y
=
nên ta loại đáp án D.
Đồ thị hàm số đi qua điểm có tọa độ
( )
1;1
nên chỉ có B thỏa mãn.
Câu 30: Đường cong trong hình bên là đồ thị của một hàm số
trong bốn hàm số được liệt kê ở bốn phương án A, B, C,
D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
42
21yx x=−−
.
B.
42
2 41y xx=−+ −
.
C.
42
21yx x=−+ −
.
D.
42
21yx x=−+ +
.
x
-1
O
y
1
-1
1
Lời giải
Chọn B
Hình dáng đồ thị thể hiện
0a <
. Loại A.
Đồ thị cắt trục tung tại điểm có tung độ bằng
1−
nên thể hiện
1c = −
. Loại D.
Đồ thị hàm số đi qua điểm có tọa độ
( )
1;1
nên chỉ có B thỏa mãn.
Câu 31: Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
42
23yx x
=−− +
.
B.
42
23yx x=−− −
.
C.
42
23yx x=−+ +
.
D.
42
23yx x=++
.
x
-1
O
y
1
3
Lời giải
Chọn A
Hình dáng đồ thị thể hiện
0a <
. Loại D.
Dựa vào đồ thị thấy khi
0x =
thì
3y
=
. Loại B.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 15
Hàm số có một cực trị nên
, ab
cùng dấu.
Câu 32: Đường cong trong hình bên là đồ thị của một hàm số trong bốn
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi
hàm số đó là hàm số nào?
A.
42
2yx x
=++
.
B.
42
2
yx x=−+
.
C.
42
1yx x=−+
.
D.
42
1yx x=++
.
x
O
y
1
Lời giải
Chọn D
Dựa vào đồ thị ta thấy khi
0x =
thì
1y =
. Loại A, B.
Hàm số có một cực trị nên
,
ab
cùng dấu.
Câu 33: Biết hình dưới đây là đồ thị của một trong bốn hàm số sau, hỏi đó là đồ thị của hàm số nào?
A.
42
2yx x= −
. B.
42
21yx x=−+
. C.
42
2yx x= +
. D.
42
2yx x=−+
.
Lời giải
Chọn A
Dựa vào đồ thị ta chọn đáp án
42
2yx x= −
.
Câu 34: Đường cong trong hình sau là đồ thị của hàm số nào?
A.
42
23yx x=+−
. B.
42
23yx x=−−
. C.
42
23yx x
=−− +
. D.
42
23
yx x=−+ +
.
Lời giải
Chọn B
Theo hình vẽ, đồ thị của hàm số trùng phương
42
y ax bx c=++
với
0a >
, loại
42
23yx x=−− +
,
42
23yx x=−+ +
-3
-4
1
-1
O
y
x
O
x
y
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 16
Đồ thị hàm số có
3
cực trị nên
0ab <
, loại
42
23yx x=+−
.
Câu 35: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
42
2 1.yx x=−+ −
B.
42
1.y xx=−+ −
C.
42
3 3.yx x=−+ −
D.
42
3 2.yx x=−+ −
Lời giải
Chọn A
Đồ thị hàm số qua điểm có tọa độ
( )
0; 1
−⇒
Loại
42
3 3.yx x=−+ −
và
42
3 2.yx x=−+ −
Đồ thị hàm số qua điểm có tọa độ
( )
1; 0 ⇒
Loại
42
1.y xx=−+ −
Câu 36: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây
A.
42
1yx x=−+
. B.
42
41yx x=−+
.
C.
42
41yx x=−+ +
. D.
32
3 21
yx x x=− ++
.
Lời giải
Chọn B
Đây là đồ thị hàm số trùng phương có
3
cực trị và có
0a >
⇒
loại
42
41yx x=−+ +
, loại
32
3 21yx x x=− ++
.
Nhìn vào điểm cực tiểu
0
x
của hàm số thấy
0
1x >
⇒
loại
42
1
yx x=−+
.
Câu 37: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
O
x
y
1
1
−
1−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 17
A.
42
43yx x=++
. B.
42
43yx x
=−+ +
. C.
42
43yx x=−+
. D.
32
43yx x=−−
.
Lời giải
Chọn C
Quan sát đồ thị hàm số ta có đây là đồ thị của hàm số bậc bốn:
( )
42
0
y ax bx c a=++ ≠
và
0a >
nên
42
43yx x=−+ +
và
32
43yx x=−−
bị loại. Mặt khác đồ thị hàm số có ba điểm cực
trị nên
.0ab<
. Do đó
42
43yx x=++
bị loại.
Câu 38: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
42
2 1.yx x=−+ −
B.
42
1.y xx=−+ −
C.
42
3 3.yx x=−+ −
D.
42
3 2.yx x=−+ −
Lời giải
Chọn A
Đồ thị hàm số qua điểm có tọa độ
( )
0; 1−⇒
Loại
42
3 3.yx x=−+ −
và
42
3 2.yx x=−+ −
Đồ thị hàm số qua điểm có tọa độ
( )
1; 0 ⇒
Loại
42
1.y xx=−+ −
Câu 39: Đường cong ở hình bên là đồ thị của hàm số nào sau đây?
A.
2
31yx x=−+
. B.
42
31yx x=−+
. C.
42
31yx x=−+ +
. D.
32
31yx x=−+
.
Lời giải
Chọn B
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 18
Đồ thị hàm số có
3
cực trị nên từ đáp án suy ra hàm số là hàm bậc
4
Theo nhánh phải đồ thị có hướng đi lên nên ta có hệ số
0a >
nên ta chọn phương án
42
31yx x=−+
.
Câu 40: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A.
42
82
yx x
=−+ −
. B.
42
82yx x=−−
. C.
32
32yx x=−−
. D.
32
32yx x=−+ −
.
Lời giải
Chọn B
Từ đồ thị ta thấy đây là đồ thị của hàm số trùng phương với hệ số
0
a
>
.
Câu 41: Hình bên là đồ thị của hàm số nào dưới đây?
A.
42
23yx x=−−
. B.
42
2yx x=−+
. C.
42
23
yx x
=−+ −
. D.
42
2yx x= −
.
Lời giải
Chọn D
Đồ thị có hai nhanh hướng lên nên hệ số
4
x
phải dương; đồ thị hàm số có
3
cực trị nên hệ số của
4
x
và
2
x
phải trái dấu nên hệ số của
2
x
phải âm; đồ thị hàm số đi qua gốc tọa độ nên hệ số tự
do bằng
0
. Do đó đáp án
42
2yx x= −
là đáp án đúng.
Câu 42: Đồ thị hình bên là đồ thị hàm số nào trong các hàm số sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 19
A.
32
33yx x=+−
. B.
2
23yx x=−+ +
. C.
42
23yx x
=+−
. D.
42
23yx x=−− +
.
Lời giải
Chọn D
Đồ thị cắt
Oy
tại điểm có tung độ dương nên chọn
2
23
yx x=−+ +
hoặc
42
23yx x=−− +
.
Đồ thị cắt
Ox
tại hai điểm có hoành độ
1−
và
1
nên chọn
42
23yx x=−− +
.
Câu 43: Đường cong hình bên là đồ thị của một trong bốn hàm số sau. Đó là hàm số nào?
A.
42
21yx x=−+
. B.
3
21y x xx=− − ++
. C.
32
21yx x x= − −+
. D.
42
21
yx x=−+ +
.
Lời giải
Chọn D
Đồ thị hàm số có
3
điểm cực trị nên từ đáp án suy ra hàm số là hàm bậc
4
trùng phương.
Theo nhánh phải đồ thị có hướng đi xuống nên ta có hệ số
0a <
nên ta chọn phương án
42
21yx x=−+ +
.
Câu 44: Đường cong sau là đồ thị hàm số nào dưới đây
A.
42
23yx x=−+
. B.
42
23yx x=−−
. C.
42
23yx x=−+ −
. D.
32
33yx x=−−
.
Lời giải
Chọn B
Đồ thị hàm số có ba cực trị, bề lõm hướng lên và cắt trục tung tại điểm có tung độ bằng
3−
.
Câu 45: Đường cong hình bên là đồ thị của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 20
A.
42
44y xx=− ++
. B.
42
23yx x=−+
. C.
42
32yx x
=++
. D.
32
21yx x=−+
.
Lời giải
Chọn B
Đồ thị hàm số đã cho là hàm trùng phương có
0a >
và có
3
cực trị. Nên hàm số
42
23yx x=−+
TM
Câu 46: Đường cong trong hình vẽ bên là của hàm số nào dưới đây
A.
42
31=−−
yx x
. B.
32
31=−−yx x
. C.
32
31=−+ −yx x
. D.
42
31=−+ −yx x
.
Lời giải
Chọn D
Đồ thị hàm số đã cho là hàm trùng phương có
0a <
và có
3
cực trị. Nên hàm số
42
31=−+ −yx x
TM
Câu 47: Hàm số nào sau đây có đồ thị như hình vẽ.
A.
42
21yx x=−− +
. B.
42
21yx x=−+ +
. C.
42
22yx x
=−−
. D.
42
21yx x=−−
.
Lời giải
Chọn B
Ta thấy
lim
x
y
→+∞
= −∞
nên loại
42
22yx x=−−
,
42
21yx x=−−
.
Đồ thị hàm số có ba điểm cực trị nên loại
42
21yx x=−− +
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 21
Câu 48: Đường cong trong hình vẽ dưới đây là đồ thị hàm số nào?
A.
4
2
1
4
x
yx=−+−
. B.
42
1
42
xx
y =−−
. C.
4
2
23
4
x
yx=−+ −
. D.
4
2
21
4
x
yx=−−
.
Lời giải
Chọn D
Từ đồ thị ta có
0a >
⇒
loại đáp án
4
2
1
4
x
yx=−+−
,
4
2
23
4
x
yx=−+ −
Ta lại có
( )
25y = ⇒
loại
42
1
42
xx
y =−−
Đáp án đúng là
4
2
21
4
x
yx=−−
.
Câu 49: Đồ thị cho ở hình vẽ sau đây, là đồ thị của hàm số cho bởi một trong bốn số phương án A,B,C,D
dưới đây?
A.
42
21yx x=+−
. B.
42
21yx x=−−
. C.
42
1
31
4
y xx=− +−
. D.
42
31yx x=−−
.
Lời giải
Chọn A
Ta thấy
( )
( ) ( )
01
1 12
y
yy
= −
= −=
chọn đáp án
42
21yx x=+−
.
Câu 50: Đường cong trong hình bên là đồ thị một hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 22
A.
32
31yx x=−+
. B.
42
241yx x=−+
. C.
42
241y xx=−+ +
. D.
42
24y xx=−+
.
Lời giải
Chọn B
Đồ thị đã cho là đồ thị hàm trùng phương có hệ số
0a >
và đi qua điểm
( )
0;1
.
Vậy đó là đồ thị hàm số
42
241yx x=−+
.
Câu 51: Hàm số
2
1
x
y
x
−
=
−
có đồ thị là hình vẽ nào sau đây?
A.
B.
C.
D.
Lời giải
Chọn A
Câu 52: Hàm số
22
2
x
y
x
+
=
+
có đồ thị là hình vẽ nào sau đây?
x
y
-2
2
1
-1
0
1
x
y
-2
1
-1
0
1
x
y
-2
3
1
-1
0
1
x
y
-2
2
1
-1
0
1
O
1−
1−
1
1
x
y
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 23
A.
B.
C.
D.
Lời giải
Chọn B
Câu 53: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
32
31yx x=++
. B.
25
1
x
y
x
+
=
+
. C.
42
1yx x=−+
. D.
21
1
x
y
x
+
=
+
.
Lời giải
Chọn B
Câu 54: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
x
y
-2
1
2
-1
0
1
x
y
-2
-3
4
2
1
-1
0
1
x
y
-2
3
-3
2
1
-1
0
1
x
y
-2
2
1
-1
0
1
x
y
-2
2
-1
0
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 24
A.
21
1
x
y
x
−
=
+
. B.
21
1
x
y
x
+
=
−
. C.
21
1
x
y
x
+
=
+
. D.
12
1
x
y
x
−
=
−
.
Lời giải
Chọn A
Câu 55: Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào?
A.
1
.
21
x
y
x
+
=
+
B.
3
.
21
x
y
x
+
=
+
C.
.
21
x
y
x
=
+
D.
1
.
21
x
y
x
−
=
+
x
1
2
1
2
y
O
Lời giải
Chọn C
Các chi tiết đồ thị hàm số có TCĐ:
1
2
x = −
và TCN:
1
2
y =
đều giống nhau.
Chỉ có chi tiết đồ thị hàm số đi qua gốc tọa độ là phù hợp cho đáp án C.
Cách 2. Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên từng khoảng xác định tức
'0y >
.
Kiểm tra ta thấy chỉ có C & D thỏa mãn.
Đồ thị hàm số đi qua gốc tọa độ
( )
0; 0O
nên đáp án C thỏa mãn.
Câu 56: Đồ thị (hình bên) là đồ thị của hàm số nào?
A.
2
1
x
y
x
+
=
+
. B.
21
1
x
y
x
+
=
+
. C.
1
1
x
y
x
−
=
+
. D.
3
1
x
y
x
+
=
−
.
Lời giải
Chọn B
x
y
-2
-1
2
-1
0
1
x
y
-1
2
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 25
Dựa vào đồ thị ta có đường tiệm cận đứng
1x = −
và đường tiệm cận ngang
2y =
nên chọn
phương án
21
1
x
y
x
+
=
+
Câu 57: Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số sau. Hỏi đó là đồ thị của hàm
số nào?
A.
2
1
x
y
x
−
=
+
. B.
2
1
x
y
x
−
=
−
. C.
2
2
x
y
x
+
=
−
. D.
2
1
x
y
x
+
=
−
.
Lời giải
Chọn B
Đồ thị hàm số có TCĐ
1x =
nên loại đáp án
2
1
x
y
x
−
=
+
và
2
2
x
y
x
+
=
−
Đồ thị hàm số cắt trục
Oy
tại điểm
( )
0; 2
nên ta loại
2
1
x
y
x
−
=
−
Câu 58: Đồ thị sau là đồ thị của hàm số nào sau?
A.
23
22
x
y
x
−
=
−
. B.
1
x
y
x
=
−
. C.
1
1
x
y
x
−
=
+
. D.
1
1
x
y
x
+
=
−
.
Lời giải
Chọn D
1x =
là tiệm cận đứng của đồ thị
⇒
loại
1
1
x
y
x
−
=
+
C=
Đồ thị hàm số cắt
Oy
tại
1y
=−⇒
loại
23
22
x
y
x
−
=
−
,
1
x
y
x
=
−
Vậy đồ thị trên là đồ thị của hàm số
1
1
x
y
x
+
=
−
.
2
2
1
1
O
x
y
O
x
y
1
1
1−
1−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 26
DẠNG 1. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ
Câu 59: Cho hàm số
32
= + ++y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0<>> <abcd
B.
0, 0, 0, 0<<><abcd
.
C.
0, 0, 0, 0><< >abcd
D.
0, 0, 0, 0<>< <abcd
.
Lời giải
Chọn A
Dựa vào đồ thị suy ra hệ số
0<a
⇒
loại phương án C
2
32 0
′
= + +=y ax bx c
có 2 nghiệm
12
,xx
trái dấu (do hai điểm cực trị của đồ thị hàm số nằm
hai phía với
Oy
)
3. 0 0⇒ <⇒>ac c
⇒
loại phương án D. Do
( ) ( )
0; 0.∩ = ⇒<C Oy D d d
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 27
Câu 60: Cho hàm số
42
y ax bx c=++
có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?
A.
0, 0, 0abc><>
B.
0, 0, 0abc
><<
C.
0, 0, 0abc>><
D.
0, 0, 0abc<><
Lời giải
Chọn B
Ta có đồ thị có hình dạng như trên với hàm bậc bốn trùng phương có hai điểm cực tiểu và một
điểm cực đại nên
0, 0
ab><
. Giá trị cực đại nhỏ hơn
0
nên
0c <
.
Câu 61: Cho hàm số
+
=
+
ax b
y
cx d
có đồ thị như sau.
Mệnh đề nào sau đây đúng?
A.
0; 0ac bd>>
B.
0; 0ab cd<<
C.
0; 0bc ad><
D.
0; 0ad bd><
Lời giải
Chọn C
Theo đồ thị:
Tiệm cận ngang:
0= >
a
y
c
( )
1
Tiệm cận đứng:
00=− >⇒ <
dd
x
cc
( )
2
0 00=⇒=−<⇒ >
bb
yx
aa
( )
3
Câu 62: Cho hàm số
( )
32
0y ax bx cx d a= + ++ ≠
có đồ thị như hình vẽ dưới đây. Chọn khẳng định đúng
về dấu của
a
,
b
,
c
,
d
?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 28
A.
0a >
,
0
b >
,
0
d >
,
0c >
B.
0a >
,
0cb>>
,
0
d <
C.
0, 0, 0, 0.abcd>>> >
D.
0a >
,
0b <
,
0
c
<
,
0d
>
Lời giải
Chọn D
Dựa vào đồ thị ta có
0a >
, đồ thị cắt
Oy
tại
1
điểm có tung độ dương nên
0d >
, đồ thị có
2
cực trị trái dấu nên
12
.0 0 0
c
xx c
a
<⇒ <⇒<
. Vậy đáp án D
Câu 63: Cho hàm số
1
,0
1
a xb
yd
c xd



có đồ thị như hình trên. Khẳng định nào dưới đây là đúng?
A.
1, 0, 1.ab c
B.
1, 0, 1.ab c
C.
1, 0, 1.ab c
D.
1, 0, 1.ab c
Lời giải
Chọn D
Theo bài ra, đường tiệm cận đứng của đồ thị hàm số là
.
1
d
x
c

Đường tiệm cận ngang của đồ thị hàm số là:
1
.
1
a
y
c
Nhìn đồ thị ta thấy:
0
1
d
x
c

mà
0 10 1dc c 
.
1
0 10 1
1
a
y aa
c

.
Đồ thị cắt trục tung tại điểm có tung độ bằng
00
b
b
d

.
Câu 64: Cho hàm số
42
y ax bx c=++
(
0a ≠
) có đồ thị như hình vẽ dưới đây.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 29
Mệnh đề nào dưới đây đúng?
A.
0a <
,
0
b >
,
0
c <
. B.
0a <
,
0
b <
,
0
c >
.
C.
0a <
,
0b
>
,
0
c >
. D.
0a <
,
0
b
<
,
0c <
.
Lời giải
Chọn A
Đồ thị cắt trục tung tại điểm
( )
0; c
, từ đồ thị suy ra
0c
<
Mặt khác đồ thị hàm số có ba điểm cực trị nên
0y
′
=
có ba nghiệm phân biệt, hay
(
)
32
4 2 22 0y ax bx x ax b
′
= + = +=
có ba nghiệm phân biệt. Suy ra
,ab
trái dấu.
Mà
00
ab<⇒>
Câu 65: Hàm số
32
y ax bx cx d 
có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0
a
,
0
b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải
Chọn D
+ Dựa vào hình dạng đồ thị ta khẳng định được
0a
.
+ Đồ thị cắt trục
Oy
tại điểm có tọa độ
0; d
. Dựa vào đồ thị suy ra
0d
.
+ Ta có:
2
32y ax bx c

. Hàm số có hai điểm cực trị
1
x
,
2
x
12
xx
trái dấu nên phương
trình
0y
có hai nghiệm phân biệt
1
x
,
2
x
trái dấu. Vì thế
3. 0ac
, nên suy ra
0c
.
+ Mặt khác từ đồ thị ta thấy
1
2
1
1
x
x

nên
12
0
xx

.
Mà
12
2
3
b
xx
a

nên suy ra
2
0
3
b
a
0b
.
Vậy
0a
,
0b
,
0c
,
0d
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 30
Câu 66: Cho hàm số
ax b
y
xc
+
=
+
có đồ thị như hình bên dưới, với
a
,
b
,
c
∈
. Tính giá trị của biểu thức
23Ta b c=++
?
A.
8
T
= −
. B.
2T =
. C.
6T =
. D.
0
T
=
.
Lời giải
Chọn D
Từ đồ thị hàm số, ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng
1x =
, tiệm cận ngang là đường thẳng
1y = −
.
Đồ thị hàm số đi qua các điểm
( )
2; 0A
,
(
)
0; 2
B −
.
Từ biểu thức hàm số
ax b
y
xc
+
=
+
(vì đồ thị hàm số là đồ thị hàm nhất biến nên
0ac b−≠
), ta
suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng
xc= −
, tiệm cận ngang là đường thẳng
ya=
.
Đồ thị hàm số đi qua
;0
b
A
a

−


,
0;
b
B
c



.
Đối chiếu lại, ta suy ra
1c = −
,
1a = −
,
2b =
.
Vậy
( ) ( )
2 3 1 2.2 3 1 0Ta b c=+ + =−+ + −=
.
Câu 67: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào
đúng?
A.
0, 0, 0ab bc cd<><
B.
0, 0, 0ab bc cd<<>
C.
0, 0, 0ab bc cd>><
D.
0, 0, 0ab bc cd>>>
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 31
Lời giải
Chọn A
Từ dáng điệu của đồ thị ta có ngay được:
⊕
lim ; lim 0
xx
y ya
→+∞ →−∞
= +∞ = −∞ ⇒ >
.
⊕
Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên
0d >
.
Ta có:
2
'3 2y ax bx c= ++
Mặt khác dựa vào đồ thị ta thấy phương trình
'0y =
có hai nghiệm trái dấu và tổng hai nghiệm
này luôn dương nên
0
0
2
0
3
ac
c
b
b
a
<
<
⇒

<
−>
(do
0a >
)
Do đó:
0, , 0ab bc cd< ><
.
Câu 68: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A.
0, 0, 0, 0abcd<<< <
B.
0, 0, 0, 0abcd<>> >
C.
0, 0, 0, 0abcd<>< >
D.
0, 0, 0, 0abcd<>> <
Lời giải
Chọn D
- Dựa vào hình dáng của đồ thị suy ra hệ số
0a <
.
- Đồ thị cắt trục
Oy
tại điểm có tung độ âm nên
0d <
.
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương
trình
2
32 0y ax bx c
′
= + +=
có 2 nghiệm
12
,xx
trái dấu kéo theo
3. 0 0ac c<⇒>
.
- Mặt khác
12
00
23
xx b
b
a
+
=− >⇒>
.
Câu 69: Cho hàm số có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ?
A.
0, 0, 0abc><<
. B.
0, 0, 0abc<<<
. C.
0, 0, 0abc<><
. D.
0, 0, 0abc><>
Lời giải
Chọn C
42
y ax bx c=++
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 32
- Dựa vào hình dạng đồ thị suy ra
0
a
<
- Hàm số có 3 điểm cực trị nên
00
ab b
<⇒>
- Giao điểm với trục tung nằm dưới trục hoành nên
0c <
.
Câu 70: Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị như trong hình bên dưới. Biết rằng
a
là số thực dương, hỏi
trong các số
,,bcd
có tất cả bao nhiêu số dương?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
Nhìn vào đồ thị ta thấy
• tiệm cận ngang
a
y
c
=
nằm trên trục hoành nên
0
c >
(vì
0a >
)
• tiệm cận đứng
d
x
c
−
=
nằm bên trái trục tung nên
0.
d
c
−
<
Suy ra
0d
>
(vì
0c >
)
• giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên
0.
b
d
<
Suy ra
0b <
(vì
0d >
)
Vậy
0, 0cd>>
Câu 71: Hàm số
32
y ax bx cx d 
có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0
c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 33
Chọn D
+ Dựa vào hình dạng đồ thị ta khẳng định được
0a
.
+ Đồ thị cắt trục
Oy
tại điểm có tọa độ
0; d
. Dựa vào đồ thị suy ra
0d
.
+ Ta có:
2
32y ax bx c

. Hàm số có hai điểm cực trị
1
x
,
2
x
12
xx
trái dấu nên phương
trình
0y
có hai nghiệm phân biệt
1
x
,
2
x
trái dấu. Vì thế
3. 0ac
, nên suy ra
0c
.
+ Mặt khác từ đồ thị ta thấy
1
2
1
1
x
x

nên
12
0xx
.
Mà
12
2
3
b
xx
a

nên suy ra
2
0
3
b
a
0b
.
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 72: Cho hàm số
ax b
y
cx d
+
=
+
có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
A.
0
0
ad
bc
<
>
. B.
0
0
ad
bc
<
<
. C.
0
0
ad
bc
>
<
. D.
0
0
ad
bc
>
>
.
Lời giải
Chọn C
Nhận xét từ đồ thị:
+ Giao với trục hoành tại
0
o
b
x
a
=−>⇒
a
và
b
trái dấu (1).
+ Giao với trục tung tại
0
o
b
yb
d
= <⇒
và
d
trái dấu (2).
+ Tiệm cận đứng:
0
d
xd
c
=−<⇒
và
c
cùng dấu (3).
Từ (1) và (2) suy ra:
a
và
d
cùng dấu hay
0ad >
.
Từ (2) và (3) suy ra:
b
và
c
trái dấu hay
0bc <
.
Câu 73: Tìm đồ thị hàm số
( )
y fx=
được cho bởi một trong các phương án dưới đây, biết
( ) ( )( )
2
fx a xb x=−−
với
ab<
.
A. . B. .
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 34
C. . D. .
Lời giải
Chọn A
Có
( ) ( ) ( ) ( )( ) ( )( ) ( )( )
2
.2 2 2 2 3fx bx ax bx bxbx a x bxb a x
′
=−− +− − −=−− −+ − =−− + −
( )
0
2
3
xb
fx
ab
x
=
′
= ⇔
+
=
.
Có
22
33
ab bb
b
++
<=
.
Ta có bảng biến thiên
Từ đó chọn đáp án A
Câu 74: Cho đường cong
( )
32
:C y ax bx cx d= + ++
có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A.
0, 0, 0, 0abcd><< <
. B.
0, 0, 0, 0abcd>>< >
.
C.
0, 0, 0, 0abcd<>> <
. D.
0, 0, 0, 0abcd>>< <
.
Lời giải
Chọn D
Từ đồ thị ta có
00x yd=⇒=<
, từ dạng đồ thị suy ra
0a >
.
Mặt khác
2
'3 2y ax bx c= ++
từ đồ thị ta có phương trình
'0y =
có hai nghiệm trái dấu suy ra
0ac <
mà
0a >
suy ra
0c <
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 35
Hơn nữa phương trình
'0y
=
có hai nghiệm phân biệt
12
2
1
3
b
xx
a
+=− =−
suy ra
32 0
abb
= ⇒>
.
Vậy chọn đáp án D.
Câu 75: (Gia Lai 2019) Hàm số
42
y ax bx c
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
0
a
,
0
b
,
0
c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0
a
,
0
b
,
0
c
.
Lời giải
Chọn C
Dựa vào đồ thị:
+
lim
x
y


0a
.
+ Đồ thị hàm số có ba điểm cực trị
0ab
0b
.
+ Giao điểm của đồ thị hàm số và trục tung có tung độ dương
0c
.
Vậy
0a
,
0b
,
0c
.
Câu 76: Cho hàm số
42
y ax bx c

có đồ thị như hình vẽ. Tìm kết luận đúng
A.
0ab
. B.
0bc
. C.
0ab
. D.
0ac
.
Lời giải
Chọn B
Từ hình vẽ ta thấy:
Đồ thị hàm số có bề lõm hướng lên
0a
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0c
.
Đồ thị hàm số có 3 điểm cực trị
00ab b 
.
Vậy chỉ có
0bc
.
Câu 77: Cho hàm số
42
( 0)y ax bx c a
có đồ thị như hình bên. Hãy chọn mệnh đề đúng.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 36
A.
0, 0, 0
abc
. B.
0, 0, 0abc
.
C.
0, 0, 0abc

. D.
0, 0, 0abc
.
Lời giải
Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy :
Hệ số
0a
Đồ thị hàm số đi qua gốc tọa tọa
0c
Hàm số có 3 điểm cực trị
.0 0ab b 
Câu 78: Cho hàm số
32
()y f x ax bx cx d
= = + ++
có đồ thị như hình vẽ ở bên. Mệnh đề nào
sau đây đúng?
A.
0a >
,
0b >
,
0c
>
,
0d
>
. B.
0a >
,
0b
>
,
0
c <
,
0
d
>
.
C.
0a >
,
0b
<
,
0c >
,
0d >
. D.
0a <
,
0b <
,
0c
>
,
0
d <
.
Lời giải
Chọn C
Đồ thị hàm số đi qua các điểm
(0;1)A
,
(1; 5)B
và
(3;1)C
và đạt cực trị tại các điểm
B
và
C
.
2
() 3 2f x ax bx c
′
= ++
. Ta có
(0) 1 1 1
(1) 5 5 6
(1) 0 3 2 0 9
(3) 0 27 6 0 1
fd a
f abcd b
f a bc c
f a bc d
′
′
= = =


= +++ = =−

⇒⇒

= + += =


= + += =

.
Câu 79: Cho hàm số bậc bốn trùng phương
42
y ax bx c
có đồ thị như hình vẽ bên. Mệnh đề nào
dưới đây là đúng?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 37
A.
0, 0, 0abc
. B.
0, 0, 0abc
. C.
0, 0, 0abc
. D.
0, 0, 0abc
.
Lời giải
Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy :
Hệ số
0a
.
Hàm số có 3 điểm cực trị
.0 0ab b 
.
Đồ thị hàm số đi qua gốc tọa tọa
0
c
.
Vậy
0, 0, 0
abc
.
Câu 80: Cho hàm số
42
y ax bx c=++
có đồ thị như hình vẽ bên. Hỏi khẳng định nào sau đây đúng?
A.
0, 0, 0
abc><<
. B.
0, 0, 0abc>><
. C.
0, 0, 0abc><>
. D.
0, 0, 0abc<><
.
Lời giải
Chọn A
Nhìn vào đồ thị ta có:
Khi
x ∈
( )
2; +∞
hàm số đồng biến
0a⇒>
.
Hàm số có
3
điểm cực trị nên
0
a.b <
mà
00ab>⇒<
.
( )
01 0y cc=−= ⇒ <
.
Câu 81: Cho hàm số
3ax
y
xc
+
=
+
có đồ thị như hình vẽ bên. Tính giá trị của
2.ac−
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 38
A.
2 3.ac−=
B.
2 3.ac−=−
C.
2 1.ac−=−
D.
2 2.ac−=−
Lời giải
Chọn A
Đồ thị hàm số có TCN
1 1 1.
1
a
ya=−⇔ =−⇔ =−
Mặt khác Đồ thị hàm số có TCĐ
2x =
nên
2 0 2.cc+=⇔=−
( )
2 1 2. 2 3.ac⇒ − =−− − =
Dựa vào đồ thị ta thấy các điểm
( )
3; 0
và
3
0;
2

−


thuộc vào đồ thị hàm số đã cho nên ta được
hệ phương trình
.3 3
0
3
3 .0 3
20
a
c
a
c
+
=
+
+
−=
+
3 30
36
a
c
+=
⇔
−=
1
2
a
c
= −
⇔
= −
( )
2 1 2. 2 3.ac⇒ − =−− − =
Câu 82: Hình vẽ bên là đồ thị hàm số
ax b
y
cx d
+
=
+
.
.
Mệnh đề nào dưới đây đúng?
A.
0ad >
và
0bd >
. B.
0ad >
và
0ab <
. C.
0bd <
và
0ab >
. D.
0ad <
và
0ab <
.
Lời giải
Chọn B
Đồ thị hàm số giao với trục
Ox
tại điểm có hoành độ
b
x
a
= −
, giao với
Oy
tại điểm có tung độ
b
y
d
=
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 39
Dựa vào hình vẽ ta có
00
0
0
0
00
bb
ab
aa
ad
b b bd
dd

−> <

<

⇔ ⇔ ⇒>

<

<<


.
Trong các phương án chỉ có phương án B thỏa mãn.
Câu 83: Cho hàm số
1
ax b
y
x
−
=
−
có đồ thị như hình vẽ dưới đây:
Khẳng định nào sau đây đúng?
A.
0
ba<<
. B.
0ab<<
. C.
ba>
và
0a <
. D.
0ab<<
.
Lời giải
Chọn A
Ta thấy đồ thị hàm số có tiệm cận ngang
1y
= −
suy ra
1a = −
.
Do đồ thị hàm số đi qua điểm
( )
2; 0
nên
2 02 0 2ab b b−=⇔−−=⇔=−
.
Vậy
0ba<<
.
Câu 84: Đồ thị trong hình bên dưới là của hàm số
ax b
y
xc
+
=
+
(với
,,abc∈
).
Khi đó tổng
abc++
bằng
A.
1−
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn D
Đồ thị hàm số
ax b
y
xc
+
=
+
có đường tiệm cận ngang
ya=
, đường tiệm cận đứng
xc= −
và cắt
Oy
tại điểm
0;
b
c



.
Từ đồ thị hàm số ta có đường tiệm cận ngang
1y = −
, đường tiệm cận đứng
1x
=
và cắt
Oy
tại
điểm
( )
0; 2−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 40
Từ đó suy ra:
11 1
11 1
22
2
aa a
cc c
b bcb
c
=−=− =−


−=⇔=−⇔=−


=−=

= −
. Vậy
11 2 0
abc+ + =−−+ =
.
Câu 85: Cho hàm số
2
()
ax
fx
bx c
−
=
−
( )
,, , 0abc b∈≠
có bảng biến thiên như sau:
Tổng các số
( )
2
abc++
thuộc khoảng nào sau đây
A.
( )
1; 2
. B.
(
)
2;3
. C.
4
0;
9



. D.
4
;1
9



.
Lời giải
Chọn C
Ta có
2
lim
x
ax a
bx c b
→∞
−−
=
−
, theo giả thiết suy ra
33
a
ab
b
−
=⇔=−
Hàm số không xác định tại
10x bc b c=⇒−=⇔=
Hàm số đồng biến trên từng khoảng xác định nên
( )
( )
2
2
0
ac b
fx
bx c
−
′
= >
−
với mọi
x
khác 1
Suy ra
2
22
20 3 20 00
33
ac b b b b b− >⇔− − >⇔−<<⇔<−<
Lại có
3abc bbb b++=− ++=−
. Suy ra
(
)
2
2
4
0;
9
abc b

++ = ∈


Vậy tổng
abc++
thuộc khoảng
4
0;
9



.
Câu 86: Cho hàm số
()
ax b
fx
cx d
+
=
+
(,,,
abcd∈
và
0c ≠
). Biết rằng đồ thị hàm số đã cho đi qua điểm
( )
1;7−
và giao điểm hai tiệm cận là
( )
2;3−
. Giá trị biểu thức
234
7
a b cd
c
+++
bằng
A.
7
. B.
4
. C.
6
. D.
5−
.
Lời giải
Chọn C
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 41
+ Ta có đồ thị hàm số
()
ax b
fx
cx d
+
=
+
có đường tiệm cận ngang là
a
y
c
, đường tiệm cận đứng
là
d
x
c
.
Theo bài ra, ta có:
3
3
2
2
a
ac
c
d dc
c





.
+ Điểm
( )
1;7−
thuộc đồ thị hàm số
()fx
nên
3
7 7 10
2
ab cb
bc
cd c c
−+ − +
=⇔ =⇔=
−+ −+
.
Vậy
2 3 4 2.(3 ) 3.(10 ) 4 2
6
77
a b cd c c c c
cc
 

.
Câu 87: Cho hàm số
1ax
y
bx c
+
=
+
(
,,abc
là các tham số) có bảng biến thiên như hình vẽ
Xét các phát biểu sau:
( ) ( )
( ) (
)
1 : 1; 2 : 0; 3 : 0; 4 : 0c ab abc a> +< ++= >
. Số phát biểu đúng
là?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng khoảng xác định, đồ thị hàm số
có tiệm cận đứng là đường thẳng
2
x
=
và tiệm cận ngang là đường thẳng
1y =
nên ta có hệ
2
2
01
22
1
10
2
02 0
1
0
0
2
0
c
c
b
cb cb
a
ab ab a
b
ac b b b
ac b
b
abc
−=
<<
=−=−


= ⇔ = ⇔ = ⇔−<<


−> − −>

−>

−<<

++=
Dựa vào hệ trên ta có các phát biểu
( ) ( )
1,4
là sai,
( )
( )
2,3
đúng.
Câu 88: Ta xác định được các số
,,abc
để đồ thị hàm số
32
y x ax bx c=+ ++
đi qua điểm
( )
1;0
và có
điểm cực trị
( )
2;0−
. Tính giá trị biểu thức
222
Tabc=++
.
A.
25.
B.
1.−
C.
7.
D.
14.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 42
Lời giải
Chọn A
Ta có
32 2
32y x ax bx c y x ax b
′
= + + +⇒ = + +
.
Theo đề, ta có hệ phương trình
( )
( )
( )
( ) ( ) ( )
( ) ( )
32
32
2
0 1 .1 .1
10
2 0 0 2 .2 .2
20
03.2 2.2
a bc
y
y a
bc
y
ab
=+ ++
=
−=⇔
=− + − + −+


′
−=
= − + −+
13
42 8 0
4 12 4
abc a
a bc b
ab c
++=− =


⇔ − +=⇔ =


− +=− =−

.
Vậy
( )
2
22222
3 0 4 25.Tabc=++=++− =
Câu 89: Cho hàm số có đồ thị như hình vẽ. Tính ?
A. . B. . C. . D. .
Lời giải
Chọn A
Vì đồ thị hàm số cắt trục tung tại điểm
2y =
nên
2d =
.
2
32y ax bx c
′
= ++
.
Hàm số đạt cực trị tại
0x =
và
2x =
nên
( )
( )
( )
00
0
0
3 1
12 4 0
20
y
c
c
ba
a bc
y
′
=
=
=

⇔⇔

= −
+ +=
′
=
Từ đồ thị ta nhận thấy
( ) ( )
2 284 284 42 1 2y abd ab ab=−⇔ + + =−⇔ + =−⇔ + =−
Thay
( )
1
vào
( )
2
ta tìm được
1, 3ab= = −
.
Vậy
2S = −
.
Câu 90: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
32
y ax bx cx d= + ++
S ab= +
2S = −
0S =
1S =
1S = −
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 43
A.
0, 0, 0, 0abcd
<<> <
. B.
0, 0, 0, 0
abcd
<>< <
.
C.
0, 0, 0, 0
abcd><< >
. D.
0, 0, 0, 0abcd<>> <
.
Lời giải
Chọn D
Ta có:
2
32y ax bx c
′
= ++
,
62y ax b
′′
= +
Từ đồ thị ta thấy:
lim
x
y
→+∞
= −∞
. Ta suy ra
0a <
.
( )
00 0yd<⇒<
loại C.
Đồ thị hàm số có hai điểm cực trị với hoành độ
1
x
,
2
x
trái dấu và
12
0xx+>
. Ta suy ra phương
trình
'0y =
có hai nghiệm trái dấu và
12
0xx+>
.
Ta suy ra
12
0
3
c
xx
a
= <
,
0c
⇒>
loại B.
Hơn nữa,
12
0
0
3
0
b
xx
b
a
a
+=− >
⇒>
<
. Lọai A.
Câu 91: Cho hàm số
( )
,,
1
ax b
y abc
cx
+
= ∈
+
có bảng biến thiên như sau:
Tập các giá trị
b
là tập nghiệm của bất phương trình nào dưới đây?
A.
3
8 0.b −≤
B.
2
4 0.b− +>
C.
2
3 2 0.bb− +<
D.
3
8 0.
b −<
Lời giải
Chọn D
Đồ thị hàm số
1
ax b
y
cx
+
=
+
có đường tiệm cận đứng là đường thẳng
1
x
c
= −
và đường tiệm cận
ngang là đường thẳng
a
y
c
=
.
Nhìn vào bảng biến thiên, ta thấy
1
11c
c
− =−⇒ =
và
22
a
a
c
=⇒=
(vì
1c =
).
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 44
Ta có
( )
2
1
a bc
y
cx
−
′
=
+
.
Vì hàm số đã cho đồng biến trên các khoảng
( )
;1−∞ −
và
( )
1;− +∞
nên
( )
33
2
0 0 2 0 2 8 80
a bc
y abc bbb b
bx c
−
′
= >⇔− >⇔−>⇔<⇔ <⇔ −<
+
.
Vậy tập các giá trị
b
là tập nghiệm của bất phương trình
3
8 0.b −<
Câu 92: Cho hàm số
ax b
y
cx d
+
=
+
(với
,,,
abcd
là số thực) có đồ thị như hình dưới đây. Tính giá trị biểu
thức
23abd
T
c
−+
=
.
A.
6
=
T
. B.
0=T
. C.
8= −T
. D.
2=T
.
Lời giải
Chọn C
Từ đồ thị ta có
TCĐ:
111
dd
x
cc
−
=⇒ =⇒=−
dc⇒=−
TCN:
11
a
y ac
c
=−⇒ =−⇒ =−
Đồ thị cắt trục hoành tại điểm:
2222
b bb
x
a cc
−−
=⇒=⇒=⇒=
−
2bc⇒=
Vậy
23 43
8
abd ccc
T
cc
− + −− −
= = = −
Câu 93: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình vẽ. Trong các số
,,abc
và
d
có bao nhiêu
số dương?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 45
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn D
Từ hình dạng đồ thị hàm số ta có
0a >
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0
d⇒<
Ta có:
2
'3 2y ax bx c= ++
Hàm số có hai điểm cực trị trái dấu
'0y⇒=
có hai nghiệm trái dấu
0ca⇔<
Mà
0a >
nên
0c <
Ta lại có:
'' 6 2y ax b
= +
'' 0 6 2 0
3
b
y ax b x
a
=⇔ + =⇔=−
Từ đồ thị hàm số ta thấy tâm đối xứng có hoành độ âm. Do đó
0
3
b
a
−<
Mà
0a >
nên
0b >
Vậy trong các số
,,abc
và
d
có 2 số dương là
a
và
b
Câu 94: Cho hàm số
( )
6−
=
−
ax
fx
bx c
( )
,,∈ abc
có bảng biến thiên như sau:
Trong các số
,,abc
có bao nhiêu số âm?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là
đường thẳng
2x = −
và tiệm cận ngang là đường thẳng
1y =
.
Suy ra
2
1
c
b
a
b
= −
=
0
0
bc
ab
<
⇒
>
( )
( )
1
0, 0, 0
2
0, 0, 0
bca
bca
><>
⇔
<><
Lại có hàm số nghịch biến trên mỗi khoảng xác định
( )
( )
2
6
0
ac b
fx
bx c
−+
′
= <
−
6ac b⇒>
.
Ta thấy
( )
1
không thể xảy ra do nếu
0b >
thì
60ac b>>
; và
(
)
2
có thể xảy ra do nếu
0, 0ca><
thì
60b ac<<
.
Vậy trong các số
,,abc
có hai số âm.
DẠNG. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI (BIẾN ĐỔI ĐỒ THỊ)
Dạng 1
Từ đồ thị
( ) ( )
=C y fx:
suy ra đồ thị
( ) ( )
′
=C y fx:
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 46
Ta có:
(
)
( ) ( )
(
) (
)
≥
= =
−<
fx khi fx
y fx
fx khi fx
0
0
* Cách vẽ
(
)
′
C
từ
( )
C
:
Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C):
( )
=y fx
.
Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị
( ) ( )
3
:3C y fx x x= = −
suy ra đồ
thị
= −yx x
3
3
.
Biến đổi
( )
C
:
Bỏ phần đồ thị của
(
)
C
dưới
,Ox
giữ nguyên
( )
C
phía trên
.Ox
Lấy đối xứng phần đồ thị bị bỏ qua
Ox
.
Dạng 2
Từ đồ thị
(
) ( )
=C y fx:
suy ra đồ thị
( )
( )
′
=C y fx:
.
Ta có:
( )
( )
( )
f x khi x
y fx
f x khi x
0
0
≥
= =
−<
và
( )
=y fx
là hàm chẵn nên đồ thị
( )
C
′
nhận Oy làm trục đối xứng.
* Cách vẽ
( )
′
C
từ
( )
C
:
Giữ nguyên phần đồ thị bên phải Oy của đồ thị
( ) ( )
=C y fx:
.
Bỏ phần đồ thị bên trái Oy của
( )
C
, lấy đối xứng phần đồ thị được giữ qua Oy.
x
y
O
-2
2
-1
1
x
y
2
-1
O
1
( )
3
:3Cyx x= −
( )
′
= −Cyx x
3
:3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 47
Ví dụ: Từ đồ thị
( ) ( )
= = −C y fx x x
3
:3
suy ra đồ
thị
( )
′
= −Cyx x
3
:3
.
Biến đổi
( )
C
:
Bỏ phần đồ thị của
(
)
C
bên trái
Oy,
giữ nguyên
( )
C
bên phải
.Oy
Lấy đối xứng phần đồ thị được giữ qua
Oy
.
Chú ý với dạng:
( )
=y fx
ta lần lượt biến đổi 2 đồ thị
( )
=
y fx
và
( )
=y fx
Ví dụ: Từ đồ thị
( ) (
)
= = −C y fx x x
3
:3
suy ra đồ
thị
= −yx x
3
3
. Biến đổi
( )
C
để được đồ thị
( )
′
= −Cyx x
3
:3
. Biến đổi
( )
′
= −Cyx x
3
:3
ta
được đồ thị
(
)
′′
= −C yx x
3
:3
.
Dạng 3
Từ đồ thị
( ) ( ) ( )
=C y ux vx:.
suy ra đồ thị
(
)
( )
(
)
′
=
C y ux vx
:.
.
Ta có:
( )
(
)
( ) (
) ( )
( )
(
) ( ) ( ) (
)
ux vx fx khi ux
y ux vx
ux vx fx khi ux
.0
.
.0
= ≥
= =
−= <
* Cách vẽ
( )
′
C
từ
( )
C
:
Giữ nguyên phần đồ thị trên miền
( )
≥
ux 0
của đồ thị
( )
( )
=C y fx
:
.
Bỏ phần đồ thị trên miền
(
)
<ux 0
của
( )
C
, lấy đối xứng phần đồ thị bị bỏ qua Ox.
x
y
O
-2
2
-1
1
x
y
O
-2
-1
1
x
y
2
-1
O
1
( )
′
= −Cyx x
3
:3
( )
= −
Cyx x
3
:3
( )
′′
= −C yx x
3
:3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 48
Ví dụ
a) Từ đồ thị
(
)
( )
= =−+
C y fx x x
32
: 231
suy ra
đồ thị
( )
( )
′
= − −−Cyx x x
2
: 12 1
Ví dụ
b) Từ đồ thị
( ) ( )
= =
−
x
C y fx
x
:
1
suy ra đồ
thị
( )
′
=
−
x
Cy
x
:
1
( )
( )
( )
≥
= − −− =
−<
f x khi x
yx x x
f x khi x
2
1
12 1
1
Đồ thị (C’):
Giữ nguyên (C) với
1x ≥
.
Bỏ (C) với
<x 1
. Lấy đối xứng phần đồ thị bị bỏ qua
Ox.
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của (C): giao
điểm với Ox, Oy, CĐ, CT…
( )
( )
∈ +∞
−
= =
−
− ∈ −∞
−
x
khi x
x
x
y
x
x
khi x
x
1;
1
.
1
;1
1
Đồ thị (C’):
Bỏ phần đồ thị của
( )
C
với
x
,
1<
giữ nguyên
( )
C
với
1.x
>
Lấy đối xứng phần đồ thị bị bỏ qua
Ox
.
Nhận xét: Đối với hàm phân thức thì nên lấy đối
xứng các đường tiệm cận để thực hiện phép suy
đồ thị một cách tương đối chính xác.
Câu 95: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Lời giải
Chọn C
Ta có:
( )
( )
32 2
3 2 1 22yx x x x x= − += − − −
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
x
y
(C)
(C')
1
O
1
x
y
1
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 49
Toàn bộ đồ thị ứng với
1x ≥
được giữ nguyên.
Phần đồ thị ứng với
1
x
<
lấy đối xứng qua trục hoành.
⇒
Chọn đáp án C.
Câu 96: Hàm số
( )
(
)
2
21yx x
=−−
có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số
( )
2
21yx x=−−
?
A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Lời giải
Chọn A
( )
( )
( )
( )
( )
2
2
2
2 1, 2
21
2 1, 2
xx x
yx x
xx x
− −≥
=− −=
−− − <
Đồ thị gồm 2 phần:
+) Giữ nguyên phần đồ thị đã cho ứng với
2x
≥
.
+) Lấy đối xứng phần đồ thị đã cho ứng với
2
x <
qua trục
Ox
Hình 1 nhận vì đồ thị là hàm
( )
2
21yx x
=−−
Hình 2 loại vì đồ thị là hàm
( )
( )
211yx x x=− −+
Hình 3 loại vì đồ thị hàm số
( )
(
)
2
21yx x
=−−
Hình 4 loại vì đồ thị hàm
( )
( )
2
21yx x=−−
Câu 97: Cho hàm số
( )
y fx=
có đồ thị hàm số
(
)
y fx=
như hình vẽ.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 50
Chọn kết luận đúng trong các kết luận sau:
A.
( )
32
44fx x x x=−+ + −
B.
( )
32
44fx x x x=−−+
C.
( )
32
44fx x x x=−− + −
D.
( )
32
4 4.fx x x x=+−−
Lời giải
Chọn A
Do đồ thị giao với trục
Oy
tại điểm có tung độ bằng
4
−
và
lim
x
y
→+∞
= −∞
.
Câu 98: Biết phương trình
32
0ax bx cx d+ + +=
( 0)a ≠
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
32
y ax bx cx d= + ++
có bao nhiêu điểm cực trị?
A. 4. B. 5. C. 2. D. 3.
Lời giải
Chọn D
Ta có:
Phương trình
32
0ax bx cx d+ + +=
( 0)a ≠
có đúng hai nghiệm thực
Nên đồ thị hàm số
32
y ax bx cx d= + ++
được minh họa như hình vẽ.
Gọi m là số điểm cực trị của hàm số
( )
y fx=
và k là nghiệm bội lẻ
của phương trình
( )
0fx=
.
⇒
Số điểm cực trị của đồ thị hàm số
( )
y fx=
là
mk+
.
Vậy đồ thị hàm số
32
y ax bx cx d= + ++
có số điểm cực trị là
21+
.
Câu 99: Cho hàm số
( )
( )
2
21yx x=−−
có đồ thị như hình vẽ
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 51
Một trong bốn hình dưới đây là đồ thị của hàm số
( )
2
21
yx x
=−−
. Hỏi đó là hình nào?
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.
Lời giải
Chọn C
Gọi
( )
C
là đồ thị hàm số
( )
(
)
2
21yx x
=−−
.
Ta có
( )
( )
( )
( )
( )
2
2
2
21 1 1
21
2 1 11
x x khi x hay x
yx x
x x khi x
− − ≤− ≥
= − −=
− − − −< <
.
Cách vẽ đồ thi như sau:
+ Giữ nguyên phần đồ
( )
C
ứng với
(
]
[
)
; 1 1;
x ∈ −∞ − ∪ +∞
ta được
( )
1
C
.
+ Lấy đối xứng phần
( )
C
ứng với
( )
1;1x ∈−
qua trục hoành ta được
( )
2
C
.
Khi đó đồ thị hàm số
(
)
2
21yx x
=−−
gồm
( )
1
C
và
(
)
2
C
.
Câu 100: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Lời giải
Chọn B
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 52
Toàn bộ đồ thị phía “phải”
Oy
sau đó lấy đối xứng sang trái.
⇒
Chọn đáp án B.
Câu 101: Cho hàm số
1
21
x
y
x
−+
=
−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
21
x
y
x
−+
=
−
B.
1
21
x
y
x
+
=
−
C.
1
21
x
y
x
−+
=
−
D.
1
21
x
y
x
−+
=
−
Lời giải
Chọn B
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải
Oy
được giữ nguyên
Sau đó, được lấy đối xứng sang trái.
Chọn đáp án B.
Câu 102: Cho hàm số
32
69
yx x x=−+
có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào
dưới đây?
A.
32
69=−+ −yx x x
. B.
32
69=−+yx x x
.
C.
3
2
69=−+yx x x
. D.
32
69=++yx x x
.
Lời giải
Chọn C
+/ Loại đáp án A vì:
( )
32 32
69 69=−+ − =− − +yx x x x x x
+/ Loại đáp án B, vì đồ thị của hàm số
32
69
yx x x=−+
giữ lại phần đồ thị phía trên trục
hoành và chỉ lấy đối xứng phần dưới trục hoành của đồ thị Hình 1.
+/ Loại đáp án D vì hệ số của
2
x
khác -6.
+/ Đồ thị ở đáp án C là đồ thị của hàm số dạng
( )
y fx=
. Chọn đáp án C
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 53
Câu 103: Cho hàm số
21
x
y
x
có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong các đáp án
A, B, C, D dưới đây?
A.
21
x
y
x
. B.
21
x
y
x
C.
21
x
y
x
D.
21
x
y
x
Lời giải
Chọn A
Câu 104: Cho hàm số
32
32
yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
32
3 2.yx x=−+
B.
3
2
32yx x=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Lời giải
Chọn D
Ta có:
( )
( )
32 2
3 2 1 22yx x x x x= − += − − −
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị ứng với
13
13
x
x
≥+
≤−
được giữ nguyên.
Phần đồ thị ứng với
13 13x− ≤ ≤+
lấy đối xứng qua trục hoành.
Câu 105: Cho hàm số
32
32yx x=−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 54
A.
32
3 2.yx x
=−+
B.
3
2
32yx x
=−+
C.
( )
2
1 2 2.yx x x=− −−
D.
( )
2
1 2 2.yx x x=− −−
Lời giải
Chọn A
Ta có:
( )
( )
32 2
3 2 1 22yx x x x x= − += − − −
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm phía trên
Ox
được giữ nguyên.
Phần đồ thị phía dưới
Ox
được lấy đối xứng qua
Ox
.
Câu 106: Cho hàm số
21
x
y
x
=
+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
21
x
y
x
=
+
B.
21
x
y
x
=
+
C.
21
x
y
x
=
+
D.
21
x
y
x
=
+
Lời giải
Chọn C
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía trên
Ox
giữ nguyên
Toàn bộ phần phía dưới
Ox
được lấy đối xứng lên trên
⇒
dạng
( )
fx
.
Câu 107: Cho hàm số
1
2
x
y
x
−+
=
−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 55
A.
1
.
2
x
y
x
−+
=
−
B.
1
.
2
x
y
x
+
=
−
C.
1
2
x
y
x
−+
=
−
D.
1
2
x
y
x
−+
=
−
Lời giải
Chọn C
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng
1x
=
được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng
1
x
=
lấy đối xứng qua
Ox
Chú ý:
1
,1
1
2
1
2
,1
2
x
x
x
x
y
x
x
x
x
−+
≤
−+
−
= =
−+
−
−>
−
Câu 108: Cho hàm số
1
2
x
y
x
+
=
+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
+
=
+
B.
1
.
2
x
y
x
+
=
+
C.
1
.
2
x
y
x
+
=
+
D.
1
.
2
x
y
x
+
=
+
Lời giải
Chọn D
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải đường thẳng
2x = −
được giữ nguyên
Toàn bộ đồ thị phía bên trái đường thẳng
2x = −
lấy đối xứng qua
Ox
Câu 109: Cho hàm số
( )
( )
2
1 23yx x x=− −−
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới
đây?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 56
A.
( )
( )
2
1 2 3.yx x x
=− −−
B.
(
)
2
1 2 3.
yx x x=− −−
C.
( )
2
1 23
yxxx=−− − −
D.
( )
2
1 23yx x x=− −−
Lời giải
Chọn C
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm bên trái (ứng với
1)x ≤
đường thẳng
1x =
được giữ nguyên
Toàn bộ đồ thị nằm bên phải (ứng với
1)
x >
đường thẳng
1x =
được lấy đối xứng qua
.
Ox
Câu 110: Cho hàm số
1
2
x
y
x
+
=
−+
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
+
=
+
B.
1
.
2
x
y
x
+
=
−
C.
1
.
2
x
y
x
+
=
−+
D.
1
.
2
x
y
x
+
=
+
Lời giải
Chọn B
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng
1x = −
(ứng với
1)
x ≤−
được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng
1x = −
(ứng với
1)x ≤−
được lấy đối xứng qua trục
.
Ox
Câu 111: Cho hàm số
bx c
y
xa
−
=
−
(
0a ≠
và
a
,
b
,
c ∈
) có đồ thị như hình bên. Khẳng định nào dưới
đây đúng?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 57
A.
0a >
,
0
b <
,
0c ab−<
. B.
0a >
,
0b >
,
0c ab−<
.
C.
0
a <
,
0b >
,
0c ab−<
. D.
0
a <
,
0b <
,
0c ab
−>
.
Lời giải
Chọn B
Dựa vào hình vẽ, đồ thị hàm số có tiệm cận ngang
0yb= >
, tiệm cận đứng
0xa
= >
.
Hàm số nghịch biến trên từng khoảng của tập xác định nên
0c ab−<
, đáp án
0a >
,
0b >
,
0c ab−<
.
Câu 112: Đường cong hình bên là đồ thị hàm số
42
y ax bx c
=++
với
a
,
b
,
c
là các số thực. Mệnh đề
nào dưới đây đúng?
A.
0a <
,
0b >
,
0c <
. B.
0
a <
,
0b <
,
0c <
.
C.
0a >
,
0b <
,
0c <
. D.
0a >
,
0b <
,
0c >
.
Lời giải
Chọn C
Đồ thị hàm số có nhanh cuối cùng hướng lên nên
0a >
.
Đồ thị hàm số có
3
cực trị nên
0ab
<
mà
0a >
nên
0b <
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên
0c <
.
Câu 113: Cho hàm số
42
y ax bx c=++
có đồ thị như hình bên.
O
y
x
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 58
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0.abc><>
B.
0, 0, 0.
abc
><<
C.
0, 0, 0.abc>><
D.
0, 0, 0.abc<><
Lời giải
Chọn B
Do đồ thị cắt
Oy
tại
( )
0;Mc
nằm dưới trục
Ox
nên
0c <
.
Vì
lim
x
y
→±∞
= +∞
nên
0a >
.
Hàm số có ba điểm cực trị nên
00ab b
<⇒<
Câu 114: Giả sử hàm số
42
y ax bx c=++
có đồ thị là hình bên dưới.
Khẳng định nào sau đây là khẳng định đúng?
A.
0, 0, 1abc><=
. B.
0, 0, 1abc>>=
.
C.
0, 0, 1abc<>=
. D.
0, 0, 0abc
>>>
.
Lời giải
Chọn A
Dựa vào đồ thị ta có:
+ Đồ thị hướng lên nên
0a >
, loại đáp án
0, 0, 1abc<>=
+Với
0x =
1
yc⇒==
nên loại đáp án
0, 0, 0abc>>>
+Có 3 cực trị nên
0ab <
suy ra
0b <
.
Câu 115: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình vẽ
Mệnh đề nào sau đây đúng?
A.
0, 0, 0, 0abcd<>< >
. B.
0, 0, 0, 0
abcd>>< >
.
C.
0, 0, 0, 0abcd<<< >
. D.
0, 0, 0, 0abcd<>> >
.
O
x
y
O
x
y
1−
1
1
O
x
y
2−
2
−
1
−
1
2
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 59
Lời giải
Chọn A
Do đồ thị ở nhánh phải đi xuống nên
0a <
. Loại phương án
0, 0, 0, 0abcd>>< >
Do hai điểm cực trị dương nên
12
2
00
3
b
x x ab
a
+ =− >⇒ <
và
00ab<⇒>
. Loại
0, 0, 0, 0
abcd
<<< >
,
12
00
3
c
xx c
a
= >⇒<
. Loại phương án
0, 0, 0, 0abcd<>> >
Câu 116: Cho hàm số
1
ax b
y
x
−
=
−
có đồ thị như hình dưới.
Khẳng định nào dưới đây là đúng?
A.
0ba<<
. B.
0
ba<<
. C.
0ba<<
. D.
0 ab<<
.
Lời giải
Chọn C
Nhìn vào đồ thị ta thấy: Đồ thị hàm số có tiệm cận ngang
ya
=
và tiệm cận đứng
1x =
.Đồ thị
cắt trục hoành tại điểm có hoành độ
1
b
x
a
= >
. Ta có:
1
1
10
1
a
ba
b
a
=
−
⇔ < =−<
>
.
Câu 117: Cho hàm số bậc bốn
( )
42
0y ax bx c a=++ ≠
có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0abc><<
. B.
0, 0, 0abc>><
. C.
0, 0, 0abc><>
. D.
0, 0, 0abc<><
.
Lời giải
Chọn A
Dựa vào hình dáng của đồ thị suy ra
0a >
. Loại
0, 0, 0abc<><
Đồ thị hàm số có ba điểm cực trị nên
0ab <
. Loại
0, 0, 0abc>><
Giao điểm của đồ thị với trục tung tại điểm có tung độ âm nên
0c <
. Loại
0, 0, 0abc><>
Câu 118: Cho hàm số bậc ba
( )
32
0y ax bx cx d a= + ++ ≠
có đồ thị như hình vẽ
O
x
y
O
x
y
1−
1
2−
2
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 60
Mệnh đề nào dưới đây đúng?
A.
0; 0; 0; 0.abcd>>> <
B.
0; 0; 0; 0.abcd<>> <
C.
0; 0; 0; 0.
abcd
<<> <
D.
0; 0; 0; 0.abcd
<<< <
Lời giải
Chọn B
Từ hình dáng đồ thị cho ta biết
0.a <
Cho
( )
0 0 0.x fd=⇒=<
Ta có
( )
2
32 0y ax bx c a
′
= ++ ≠
. Từ đồ thị hàm số ta thấy hoành độ
hai điểm cực trị trái dấu, suy ra
0ac <
mà theo trên
0 0.ac<⇒>
Từ đồ thị hàm số ta thấy tổng hoành độ cửa cực đại và cực tiểu dương nên
2
0 0.
3
b
b
a
− >⇒>
(vì
0
a <
)
Câu 119: Cho hàm số
32
y ax bx cx d= + ++
có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0abcd<<><
. B.
0, 0, 0, 0abcd<>> <
.
C.
0, 0, 0, 0abcd<<< <
. D.
0, 0, 0, 0abcd<>< <
.
Lời giải
Chọn B
32 2
32y ax bx cx d y ax bx c
′
= + ++⇒= + +
.
Từ đồ thị ta có: hàm số có hai điểm cực trị
12
12
0xx
xx
<<
<
, đồ thị cắt trục tung tại điểm có tung độ
âm và
lim
x
y
→+∞
= −∞
.
O
x
y
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 61
Suy ra
12
12
0
0
0
0
2
0
0
3
0
.0
3
a
a
d
d
b
xx
b
a
cc
xx
a
<
<
<
<

⇔

+=− >
>


>
= <
.
Câu 120: Cho hàm số
ax b
y
xc
+
=
+
có đồ thị như hình bên với
,, .abc∈
Tính giá trị của biểu thức
32Ta b c=−+
?
A.
12T =
. B.
10T =
. C.
9T = −
. D.
7T
= −
.
Lời giải
Chọn C
Đồ thị hàm số có
1x =
là tiệm cận đứng nên
1c = −
.
Đồ thị hàm số có
1y = −
là tiệm cận ngang nên
1a = −
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
2−
nên
2
b
c
= −
do đó
2b =
.
Vậy
32Ta b c
=−+
( )
1 3.2 2 1 9=−− + − =−
.
Câu 121: Cho hàm số
( )
42
f x ax bx c=++
với
0a
≠
có đồ thị như hình vẽ:
Tìm mệnh đề đúng trong các mệnh đề sau?
A.
0a <
;
0b >
;
0c >
. B.
0a >
;
0b <
;
0c
>
.
C.
0a <
;
0b <
;
0c >
. D.
0a <
;
0b >
;
0c <
.
Lời giải
Chọn A
Ta có nhánh bên phải đồ thị đi xuống, suy ra
0a <
.
Mặt khác do đồ thị có ba cực trị suy ra
0ab <
mà
00ab<⇒>
.
Mà giao điểm của đồ thị với trục
Oy
tại điểm có tung độ
0yc= >
.
Vậy chọn đáp án
0a <
;
0b >
;
0c >
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 62
Câu 122: Từ đồ thị hàm số
42
y ax bx c=++
(
a
khác
0
) được cho dạng như hình vẽ, ta có
A.
0a >
,
0b <
,
0c <
. B.
0a
>
,
0b >
,
0c
<
.
C.
0a <
,
0b >
,
0c <
. D.
0a
>
,
0b <
,
0c >
.
Lời giải
Chọn A
Đồ thị có dạng quay lên nên
0a >
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ nhỏ hơn
0
nên
0c <
.
Do đồ thị hàm số có ba điểm cực trị nên
.0ab<
0b⇒<
.
Câu 123: Bảng biến thiên trong hình bên dưới của hàm số nào dưới đây?
A.
1
21
x
y
x
−
=
−
. B.
42
23yx x=−−
. C.
3
32yx x
=−+ +
. D.
3
34yx x=−+
.
Lời giải
Chọn C
Theo bảng biến thiên ta có hàm số là một hàm có hai cực trị và có
lim
x
y
→+∞
= −∞
nên chọn đáp án
3
32yx x=−+ +
.
Câu 124: Bảng biến thiên dưới đây là của hàm số nào?
A.
21
2
x
y
x
+
=
−
. B.
1
22
x
y
x
−
=
+
. C.
1
2
x
y
x
+
=
−
. D.
3
2
x
y
x
+
=
+
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 63
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số có tập xác định
{ }
\2D =
và
lim 1
x
y
→+∞
=
nên hàm số
phải là
1
2
x
y
x
+
=
−
.
Câu 125: Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ bên?
A.
3
32yx x=−+
. B.
32
31yx x=−+ −
. C.
32
32yx x=−+
. D.
32
31
yx x=+−
.
Lời giải
Chọn C
* Từ BBT ta thấy đây là BBT của hàm bậc ba
32
y ax bx cx d= + ++
.
* Nhánh đầu tiên đi lên nên
0a >
ta loại trừ đáp án
32
31yx x=−+ −
* Phương trình
0
0
2
x
y
x
=
′
= ⇔
=
ta loại trừ đáp án
3
32yx x=−+
và
32
31yx x=+−
Đáp án đúng là
32
32yx x=−+
Câu 126: Cho bảng biến thiên như hình vẽ bên. Hỏi đây là bảng biến thiên của hàm số nào trong các hàm
số sau?
A.
2
1
x
y
x
−+
=
−
. B.
2
1
x
y
x
+
=
−
. C.
2
1
x
y
x
+
=
+
. D.
3
1
x
y
x
−
=
−
.
Lời giải
Chọn C
Từ bảng biến thiên ta có đồ thị hàm số có đường tiệm cận đứng là
1x =
và đường tiệm cận
ngang là
1y =
nên ta loại các đáp án
2
1
x
y
x
−+
=
−
và
2
1
x
y
x
+
=
+
Mặt khác từ bảng biến thiên ta có hàm số nghịch biến nên lọai đáp án
3
1
x
y
x
−
=
−
Câu 127: Bảng biến thiên sau là của hàm số nào?
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 64
A.
32
31yx x=−− −
. B.
32
31yx x=−+ −
. C.
32
31yx x=+−
. D.
32
31yx x=−−
.
Lời giải
Chọn B
* Bảng biến thiên này là bảng biến thiên của hàm bậc ba.
* Nhánh đầu tiên của bảng biến thiên đi xuống nên ta loại
32
31yx x
=+−
và
32
31yx x
=−−
.
* Phương trình
0y
′
=
có hai nghiệm là
0x =
và
2x =
nên ta loại đáp án
32
31yx x=−− −
.
* Đáp án đúng là
32
31yx x=−+ −
.
Câu 128: Cho hàm số
( )
y fx=
có bảng biến thiên
Hỏi hàm số đó là hàm nào?
A.
2
21
x
y
x
−+
=
−
. B.
2
21
x
y
x
+
=
−
. C.
2
21
x
y
x
−−
=
−
. D.
2
21
x
y
x
−
=
−
.
Lời giải
Chọn D
Dựa vào bảng biến thiên suy ra đồ thị hàm số
(
)
y fx=
có tiệm cận đứng
1
2
x =
, tiệm cận ngang
1
2
y =
và hàm số đồng biến trên từng khoảng xác định. Do đó chọn
2
21
x
y
x
−
=
−
.
Câu 129: Bảng biến thiên dưới đây là của hàm số nào?
A.
21
2
x
y
x
+
=
−
. B.
1
22
x
y
x
−
=
+
. C.
1
2
x
y
x
+
=
−
. D.
3
2
x
y
x
+
=
+
.
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số có tập xác định
{ }
\2D =
và
lim 1
x
y
→+∞
=
nên hàm số
phải là
1
2
x
y
x
+
=
−
Câu 130: Cho hàm số
(
)
y fx=
có bảng biến thiên như sau:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 65
Hàm số
( )
y fx=
là hàm số nào dưới đây?
A.
23
23
x
y
x
+
=
−
. B.
33
23
x
y
x
−
=
−
C.
23
32
x
y
x
+
=
+
. D.
23
32
x
y
x
−
=
−
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy đồ thị hàm số có 1 tiệm cận đứng
2
3
x =
và 1 tiệm cận ngang là
2
3
y =
.
Câu 131: Bảng biến thiên như hình vẽ bên là của hàm số nào trong các hàm số sau?
A.
3
31yx x=+−
. B.
3
31yx x=−−
. C.
3
33
yx x=−+ +
. D.
42
22
yx x=−+
.
Lời giải
Chọn B
Đồ thị hàm số là hàm bậc ba và có hướng đi lên nên loại
3
33yx x=−+ +
.,
42
22yx x=−+
.
Hàm số có hai điểm cực trị
1x = −
và
1
x =
trái dấu
.0ac<
nên loại
3
31
yx x
=+−
.
Đáp án
3
31yx x=−−
đúng.
Câu 132: Cho hàm số
32
69yx x x=−+
có đồ thị như Hình
1
. Đồ thị Hình
2
là của hàm số nào trong bốn
đáp án A, B, C, D dưới đây?
x
y
4
3
1
O
x
y
4
3
1
O
-3
-1
Hình
1
Hình
2
A.
32
6 9.yx x x=−+ −
B.
32
6 9.
yx x x=++
C.
32
69yx x x=−+
D.
3
2
6 9.yx x x=−+
Lời giải
x
– ∞
2/3
+ ∞
y'
+
+
y
2/3
+ ∞
2/3
– ∞
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 66
Chọn D
Nhắc lại lí thuyết: Đồ thị hàm số
( )
y fx=
được suy ra từ đồ thị hàm số
( )
y fx=
bằng cách
● Giữ nguyên phần đồ thị hàm số
( )
y fx=
với
0.x ≥
● Sau đó lấy đối xứng phần đồ thị vừa giữ ở trên qua trục
Oy
.
Câu 133: Cho hàm số
32
32
yx x=+−
có đồ thị như Hình
1
. Đồ thị Hình
2
là của hàm số nào dưới đây?
x
y
2
3
1
O
-2
-1-2
x
y
2
1
O
-1
-2-3
Hình
1
Hình
2
A.
32
3 2.yx x
=+−
B.
32
3 2.yx x=+−
C.
3
2
3 2.yx x=+−
D.
32
3 2.yx x=−− +
Lời giải
Chọn B
Nhắc lại lí thuyết: Đồ thị hàm số
( )
y fx=
được suy ra từ đồ thị hàm số
( )
y fx=
bằng cách
● Giữ nguyên phần đồ thị hàm số
( )
y fx=
với
0.y ≥
● Lấy đối xứng phần đồ thị hàm số
(
)
y fx
=
với
0y
<
qua trục
.Ox
Câu 134: Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số
24
21
y xx= −+
?
A
B
C
D
x
y
1
2
-1
O
1
x
-1
y
-2
-1
O
1
x
y
-2
-1
-1
O
1
x
y
2
1
-1
O
1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 67
Lời giải
Chọn D
Ta có
24
2 1 0, y xx x= − + ≥ ∀ ∈ →
đồ thị luôn nằm phía trên trục hoành.
Câu 135: Cho hàm số
21
x
y
x
=
+
có đồ thị như Hình
1
. Đồ thị Hình
2
là của hàm số nào trong các đáp án
A, B, C, D dưới đây?
x
1
2
1
2
y
O
x
1
2
1
2
y
O
Hình
1
Hình
2
A.
.
21
x
y
x
=
+
B.
.
21
x
y
x
=
+
C.
.
21
x
y
x
=
+
D.
.
21
x
y
x
=
+
Lời giải
Chọn A
Câu 136: Cho hàm số
2
21
x
y
x
+
=
−
có đồ thị như Hình
1
. Đồ thị Hình
2
là của hàm số nào trong các đáp án
A, B, C, D dưới đây?
x
1
2
1
2
y
O
-2
-2
x
1
2
1
2
y
O
-2
-2
Hình
1
Hình
2
A.
2
.
21
x
y
x
+

= −

−

B.
2
21
x
y
x
+
=
−
C.
2
.
21
x
y
x
+
=
−
D.
2
.
21
x
y
x
+
=
−
Lời giải
Chọn B
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 68
Câu 137: Đồ thị hàm số
21
1
x
y
x
−
=
−
có
đồ thị như hình bên. Hỏi đồ
thị hàm số
21
1
x
y
x
−
=
−
có đồ
thị là hình nào trong các đáp
án sau:
x
O
y
2
1
1
2
1
A
x
O
y
2
1
1
2
1
B
x
O
y
2
1
1
2
C
x
O
y
2
1
1
2
1
D
x
O
y
2
1
1
2
1
Lời giải
Chọn C
Ta có
21 1
khi
21
12
.
21 1
1
khi
12
x
x
x
x
y
x
x
x
x
−
≥
−
−
−
= =
−
−
<
−
Do đó đồ thị hàm số
21
1
x
y
x
−
=
−
được suy từ đồ thị hàm số
21
1
x
y
x
−
=
−
bằng cách:
● Giữ nguyên phần đồ thị hàm số
21
1
x
y
x
−
=
−
phía bên phải đường thẳng
1
.
2
x =
● Phần đồ thị hàm số
21
1
x
y
x
−
=
−
phía bên trái đường thẳng
1
2
x =
thì lấy đối xứng qua trục hoành.
Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số
21
1
x
y
x
−
=
−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 69
Câu 138: Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số
1
x
y
x
=
−
?
A
x
O
y
1
1
B
x
O
y
1
1
C
x
O
y
1
1
D
x
O
y
1
1
Lời giải
Chọn B
Ta có
khi 1
1
.
1
khi 1
1
x
x
x
x
y
x
x
x
x
>
−
= =
−
−<
−
Do đó đồ thị hàm số
1
x
y
x
=
−
được suy từ đồ thị hàm số
1
x
y
x
=
−
bằng cách:
● Giữ nguyên phần đồ thị hàm số
1
x
y
x
=
−
phía bên phải đường thẳng
1.x =
● Phần đồ thị hàm số
1
x
y
x
=
−
phía bên trái đường thẳng
1x =
thì lấy đối xứng qua trục hoành.
Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số
1
x
y
x
=
−
.
Câu 139: Hàm số
32
y ax bx cx d= + ++
có đồ
thị như hình vẽ bên. Mệnh đề
nào sau đây là đúng?
A.
0, 0, 0, 0abcd>>< >
.
B.
0, 0, 0, 0abcd<<< <
.
C.
0, 0, 0, 0abcd><< >
.
D.
0, 0, 0, 0abcd>>><
.
x
y
1
2
-
1
O
Lời giải
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 70
Chọn C
Đồ thị hàm số thể hiện
0a >
; cắt trục tung tại điểm có tung độ dương nên
0d >
.
Hàm số có
CD CT
CD CT
CD CT
0
1 0, 1
.0
xx
xx
xx
+>
− < < > →
<
.
( )
*
Ta có
2
3 2 0.y ax bx c
′
= + +=
Do đó
( )
0
0
2
00 0
3
*.
00 0
3
a
a
bb
b
aa
cc
c
aa
>
>
− > → < → <
↔
< → < → <
Vậy
0, 0, 0, 0.abcd
><< >
Câu 140: Hàm số
32
y ax bx cx d= + ++
có đồ
thị như hình vẽ bên. Mệnh đề
nào sau đây là đúng?
A.
0, 0, 0, 0.abcd<>>>
B.
0, 0, 0, 0.abcd<<< >
C.
0, 0, 0, 0.abcd<<> >
D.
0, 0, 0, 0.abcd<>< >
x
y
1
-
1
O
Lời giải
Chọn A
Đồ thị hàm số thể hiện
0a <
; cắt trục tung tại điểm có tung độ dương nên
0d >
.
Hàm số có
CD CT
CD CT
CD CT
0
1, 1 0
.0
xx
xx
xx
+>
> − < < →
<
.
(
)
*
Ta có
2
3 2 0.y ax bx c
′
= + +=
Do đó
( )
0
0
2
00 0
3
*.
00 0
3
a
a
bb
b
aa
cc
c
aa
<
<
− > → < → >
↔
< → < → >
Vậy
0, 0, 0, 0.abcd<>>>
Câu 141: Hàm số
42
y ax bx c=++
có
đồ thị như hình vẽ bên. Mệnh
đề nào sau đây là đúng?
A.
0, 0, 0.abc
>><
B.
0, 0, 0.abc><<
C.
0, 0, 0.abc><>
D.
0, 0, 0.abc<><
x
y
O
Lời giải
Chọn C
Đồ thị hàm số thể hiện
0.a >
Đồ thị hàm số có ba điểm cực trị nên
0
0 0.
a
ab b
>
< → <
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
0.c >
Vậy
0, 0, 0.abc><>
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 71
Câu 142: Hàm số
42
y ax bx c=++
có
đồ thị như hình vẽ bên. Mệnh
đề nào sau đây là đúng?
A.
0, 0, 0.abc<>>
B.
0, 0, 0.
abc
<><
C.
0, 0, 0.abc<<>
D.
0, 0, 0.abc<<<
x
y
O
Lời giải
Chọn B
Đồ thị hàm số thể hiện
0.a <
Đồ thị hàm số có ba điểm cực trị nên
0 0.ab b< → >
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên
0.c <
Vậy
0, 0, 0abc<><
.
Câu 143: Hàm số
( )
42
0y ax bx c a=++ ≠
có đồ
thị như hình vẽ bên. Mệnh đề nào sau
đây là đúng?
A.
0, 0, 0.abc>≥<
B.
0, 0, 0.abc><≤
C.
0, 0, 0.abc
>≥>
D.
0, 0, 0.abc<<<
x
y
O
Lời giải
Chọn A
Dựa vào dáng điệu đồ thị suy ra
0
a
>
.
Hàm số có 1 điểm cực trị nên
0
0 0.
a
ab b
>
≥ → ≥
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên
0.
c <
Vậy
0, 0, 0.abc>≥<
Câu 144: Hàm số
ax b
y
cx d
+
=
+
với
0a >
có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây là đúng?
A.
0, 0, 0.bcd>> <
B.
0, 0, 0.
bcd>< <
C.
0, 0, 0.bcd<< <
D.
0, 0, 0.bcd<><
x
y
O
Lời giải
Chọn A
Từ đồ thị hàm số, ta thấy
● Khi
0
0 0 0.
a
b
yx b
a
>
= → = − < → >
● Khi
0
0 00
b
b
xy d
d
>
= → = < → <
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 72
Đồ thị hàm số có tiệm cận đứng
0
0 0.
d
d
xc
c
<
= − > → >
Vậy
0, 0, 0.
bcd>> <
Câu 145: Hàm số
bx c
y
xa
−
=
−
(
0;a ≠
)
, , abc∈
có đồ thị như
hình vẽ bên.Mệnh đề nào sau
đây là đúng?
A.
0, 0, 0.a b c ab> > −<
B.
0, 0, 0.a b c ab> > −>
C.
0, 0, 0.a b c ab> > −=
D.
0, 0, 0.
a b c ab
> < −<
x
y
O
Lời giải
Chọn A
Đồ thị hàm số có tiệm cận đứng
0xa= >
; tiệm cận ngang
0.yb= >
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định
của nó nên
( )
2
0, 0.
c ab
y x a c ab
xa
−
′
= < ∀ ≠ → − <
−
Vậy
0, 0, 0.a b c ab> > −<
Câu 146: Đồ thị hàm số
42
y ax bx c=++
cắt trục hoành tại bốn điểm
,,,
ABC D
phân biệt như hình vẽ
bên.
Biết rằng
AB BC CD= =
, mệnh đề nào sau đây là đúng?
A.
2
0, 0, 0,100 9a b c b ac><> =
.
B.
2
0, 0, 0, 9 100abc b ac>>> =
.
C.
2
0, 0, 0, 9 100a b c b ac><> =
.
D.
2
0, 0, 0, 100 9abc bac>>> =
.
Lời giải
Chọn A
Đồ thì hàm số quay lên nên
0a >
.
Đồ thị hàm số có ba điểm cực trị nên
0b <
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
0c >
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 73
Đồ thị hàm số cắt trục hoành tại 4 điểm
(
)
1
;0Ax−
,
( )
2
;0Bx
−
,
(
)
2
;0Cx
và
(
)
1
;0Ax
.
Mà
AB BC CD
= = ⇔
1 2 1 2 1 21
2 39xx x x xxx− + = ⇔ = ⇔=
.
Khi đó:
12 1
12 2
2 1 12
10
9
10
9
bb
xx x
aa
cb
xx x
aa
x x xx c

+=− =−



= ⇔=−


= =



2
9
. 9 100
10 10
bb
c b ac
aa
⇔ =⇔=
Câu 147: Biết rằng hàm số
42
()y f x ax bx c
= =++
có đồ thị là đường cong như hình vẽ bên.
Tính giá trị
()fabc++
.
A.
( )1fabc++ =−
.
B.
( )2fabc
++ =
.
C.
( )2fabc
++ =−
.
D.
( )1fabc++ =
.
Lời giải
Chọn A
Dựa vào đồ thị hàm số ta có: điểm cực tiểu và cực đại của đồ thị hàm số là
( )
1; 1A −
,
( )
0;1B
.
Ta có:
3
42y ax bx
′
= +
Do đó:
42
12
1 4 241
420 1
abc a
c b yx x
ab c
++=− =


= ⇔ =−⇒ = − +


+= =

Mà
(
) ( )
1 11abc fabc f++=−⇒ ++ = − =−
Câu 148: Cho hàm số
42
y ax bx c=++
có đồ thị như hình vẽ bên.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 74
Mệnh đề nào dưới đây là đúng?
A.
0, 0, 0abc><>
. B.
0, 0, 0abc<><
. C.
0, 0, 0abc>>>
. D.
0, 0, 0abc><<
.
Lời giải.
Chọn B
Dựa vào đồ thi hàm số ta có:
0, 0ab<>
(do hàm số có 3 cực trị ) và
0c <
.
Câu 149: Cho hàm số
42
y ax bx c=++
có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây là đúng?
A.
0, 0, 0abc><<
. B.
0, 0, 0abc<>>
. C.
0, 0, 0abc>>>
. D.
0, 0, 0abc><>
.
Lời giải.
Chọn D
Dựa vào đồ thi hàm số ta có:
0, 0ab><
(do hàm số có 3 cực trị ) và
0c >
.
Câu 150: Cho hàm số
42
y ax bx c
=++
có đồ thị như hình vẽ bên.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 75
Kết luận nào sau đây là đúng?
A.
0, 0, 0abc<≤>
. B.
0, 0, 0abc<<<
. C.
0, 0, 0abc>>>
. D.
0, 0, 0abc<>≥
.
Lời giải.
Chọn A
Dựa vào đồ thi hàm số ta có:
0, 0ab<≤
(do hàm số có 1 cực trị ) và
0
c
>
.
Câu 151: Cho hàm số
42
()f x ax bx c=++
có đồ thị của hàm số như hình vẽ bên. Kết luận nào sau đây là
đúng?
A.
0, 0, 0abc><>
. B.
0, 0, 0abc<<>
. C.
0, 0, 0abc<>>
. D.
0, 0, 0abc<><
.
Lời giải.
Chọn C
Dựa vào đồ thị hàm số ta có:
0, 0, 0abc<>>
Câu 152: Đồ thị hàm số
( )
y f x ax bx c= =++
42
như hình vẽ dưới đây.
Khẳng định nào sau đây là đúng?
A.
;;;abcbac>>> =
2
000 4
. B.
;;;a b c b ac><> =
2
000 4
.
C.
;;;abcbac>>> >
2
000 4
. D.
;;;abcbac>>> <
2
000 4
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 76
Lời giải.
Chọn B
Dựa vào đồ thị hàm số, ta nhận xét
0a >
và
00ab b<⇒<
(Do hàm số có 3 cực trị)
Dựa vào 4 đáp án, ta Chọn B
Câu 153: Hình vẽ bên là đồ thị của hàm số
y ax bx c=++
42
. Giá trị của biểu thức
Aabc=++
222
có thể
nhận giá trị nào trong các giá trị sau?
A.
A = 24
. B.
A = 20
. C.
A = 18
. D.
A = 6
.
Lời giải.
Chọn C
Ta có
' ;'
x
y ax bx c y ax bx y
b
x
a
=
= + +⇒ = + =⇔
= −
42 3
2
0
42 0
2
.
Dựa vào đồ thị hàm số, ta có
0; 0
ab<>
.
Gọi đồ thị hàm số đã cho là
( )
C
. Dựa vào đồ thị hàm số ta có:
( ) ( )
42
0; 1 .0 .0 1 1I Cabc c+ − ∈ ⇒ + + =−⇒ =−
.
+
( ) ( )
1
42
1; 2 .1 .1 2 2 3 3
c
A C a b c abc ab a b
=−
∈ ⇒ + +=⇔++=←→+=⇔ =−
.
+ Giá trị cực đại của hàm số bằng 3 nên ta có:
(
)
2
1
2
. . 3 16 *
22
c
bb
a b c ba
aa
=−

− + − + = ← → = −


.
Thế
3ab= −
vào
( )
*
ta được:
2
4
16 48 0
12
b
bb
b
=
− +=⇔
=
.
Với
41ba
=⇒=−
(thỏa mãn điều kiện
0a <
). Khi đó
Aabc=++=
222
18
⇒
Chọn C
Câu 154: Hàm số
( )
y f x ax bx c= =++
42
có bảng biến thiên như hình vẽ dưới đây.
Tính giá trị của biểu thức
P bc=++22 3
A.
P = −15
. B.
P = 15
. C.
P = −8
. D.
P = 8
.
Lời giải.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 77
Chọn A
Ta có
';y ax bx c y ax bx= + +⇒ = +
42 3
42
.
Gọi đồ thị hàm số đã cho là
( )
C
. Dựa vào BBT ta có:
( )
(
)
42
0; 3 .0 .0 3 3I Cabc c+ − ∈ ⇒ + + =−⇒ =−
( )
1
.
+ Hàm số đạt cực tiểu tại
1x =±⇒
( )
'1 0 4 2 0y ab=⇔+=
( )
2
.
+ Hàm số có cực đại
55
CD
y abc=−⇒ + + =−
( )
3
.
Giải hệ
( ) ( ) ( )
1,2,3
ta được:
2, 4, 3
ab c
= =−=−
. Vậy
P bc=++=−2 2 3 15
.
| 1/181

Tài liệu khác của Toán 12

Preview text:

CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ G ƠN I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ HƯ C
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ I LÝ THUYẾT.
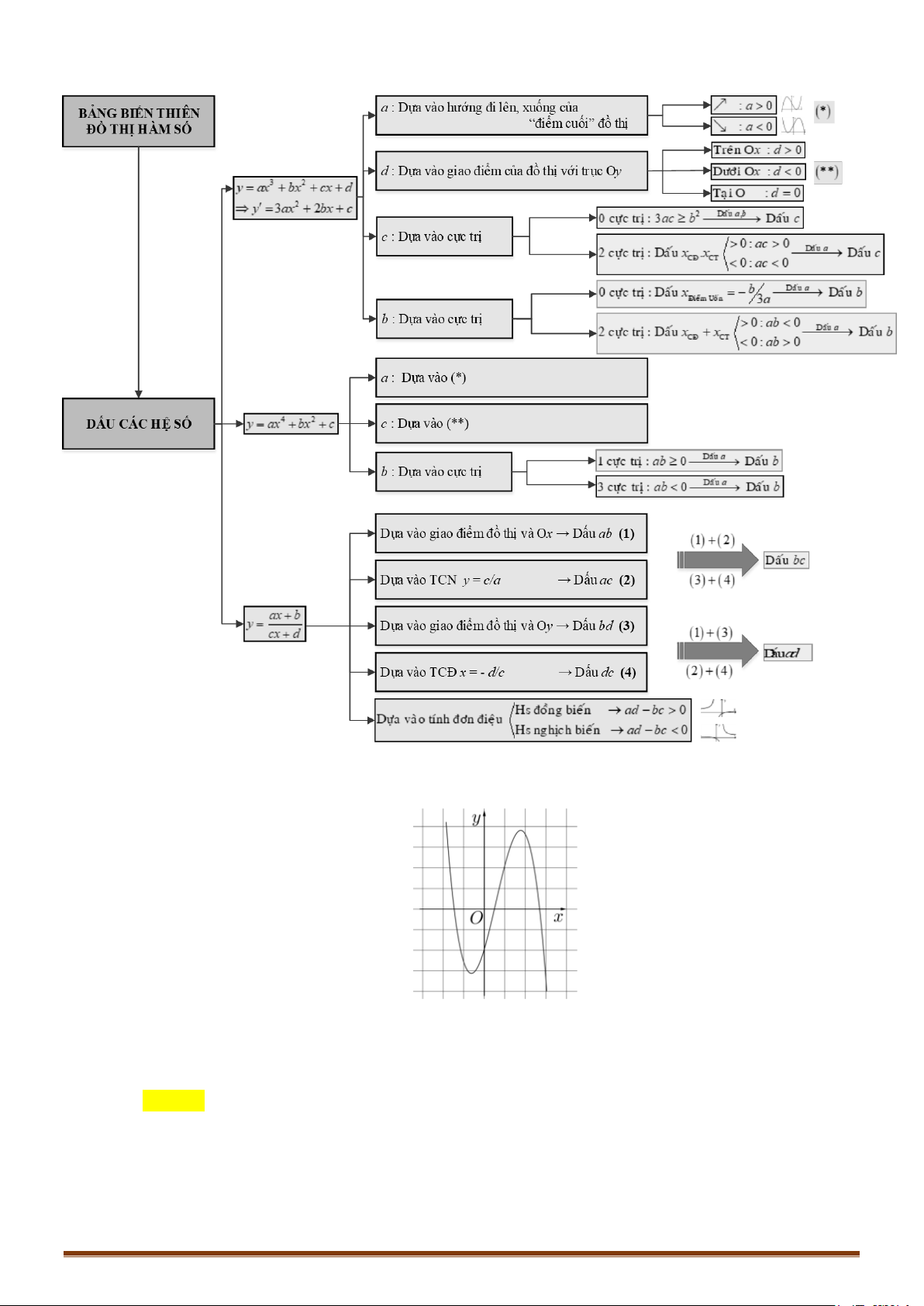
A. SƠ ĐỒ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Bước 1. Tìm tập xác định của hàm số;
Bước 2. Tính đạo hàm y′ = f (′x) ;
Bước 3. Tìm nghiệm của phương trình f (′x) = 0 ;
Bước 4. Tính giới hạn lim y; lim y và tìm tiệm cận đứng, ngang (nếu có); x→+∞ x→−∞
Bước 5. Lập bảng biến thiên;
Bước 6. Kết luận tính biến thiên và cực trị (nếu có);
Bước 7. Tìm các điểm đặc biệt của đồ thị (giao với trục Ox , Oy , các điểm đối xứng, …);
Bước 8. Vẽ đồ thị. Page 197
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
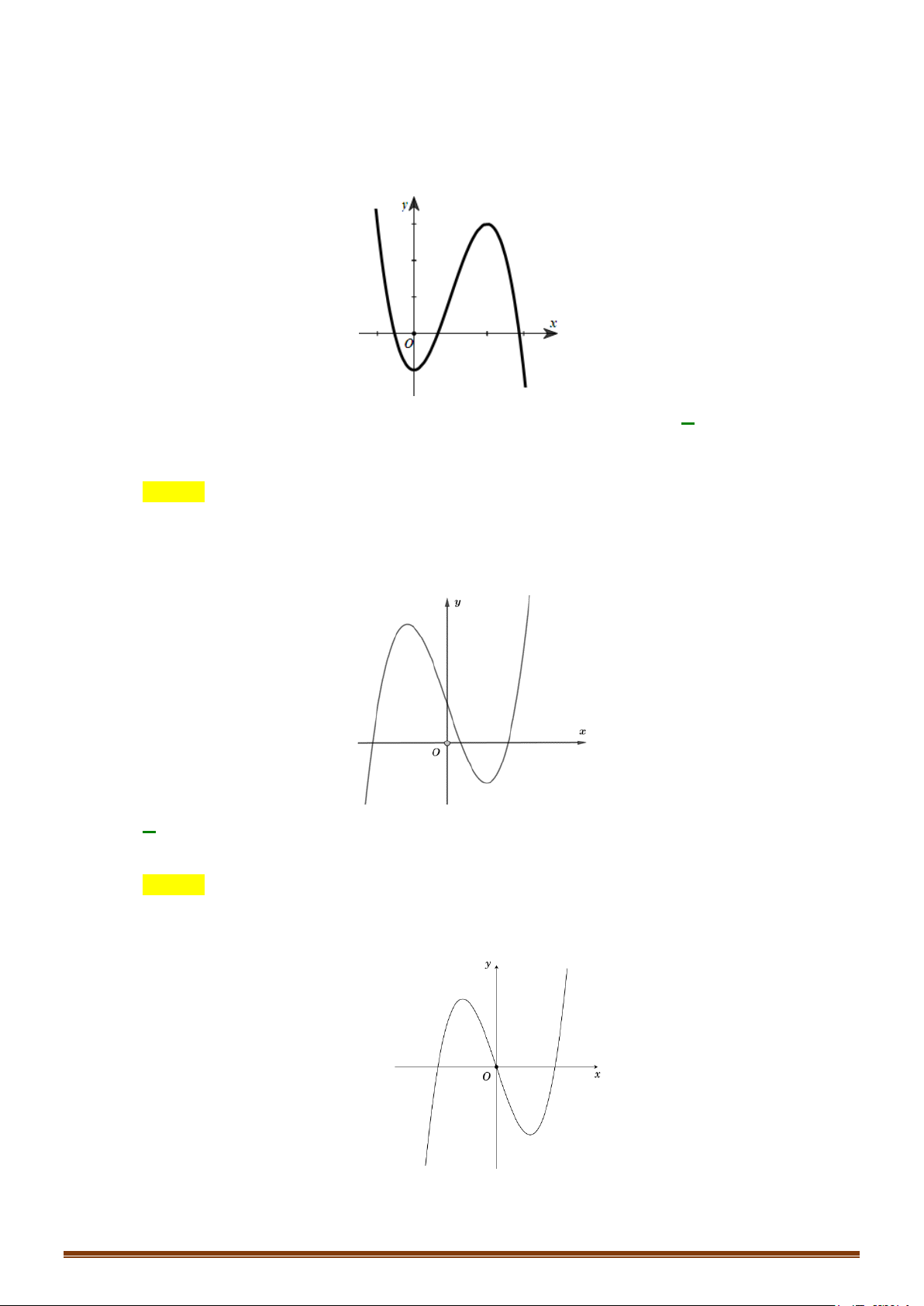
B. CÁC DẠNG ĐỒ THỊ CỦA CÁC HÀM SỐ THƯỜNG GẶP 1. HÀM SỐ BẬC BA 3 2
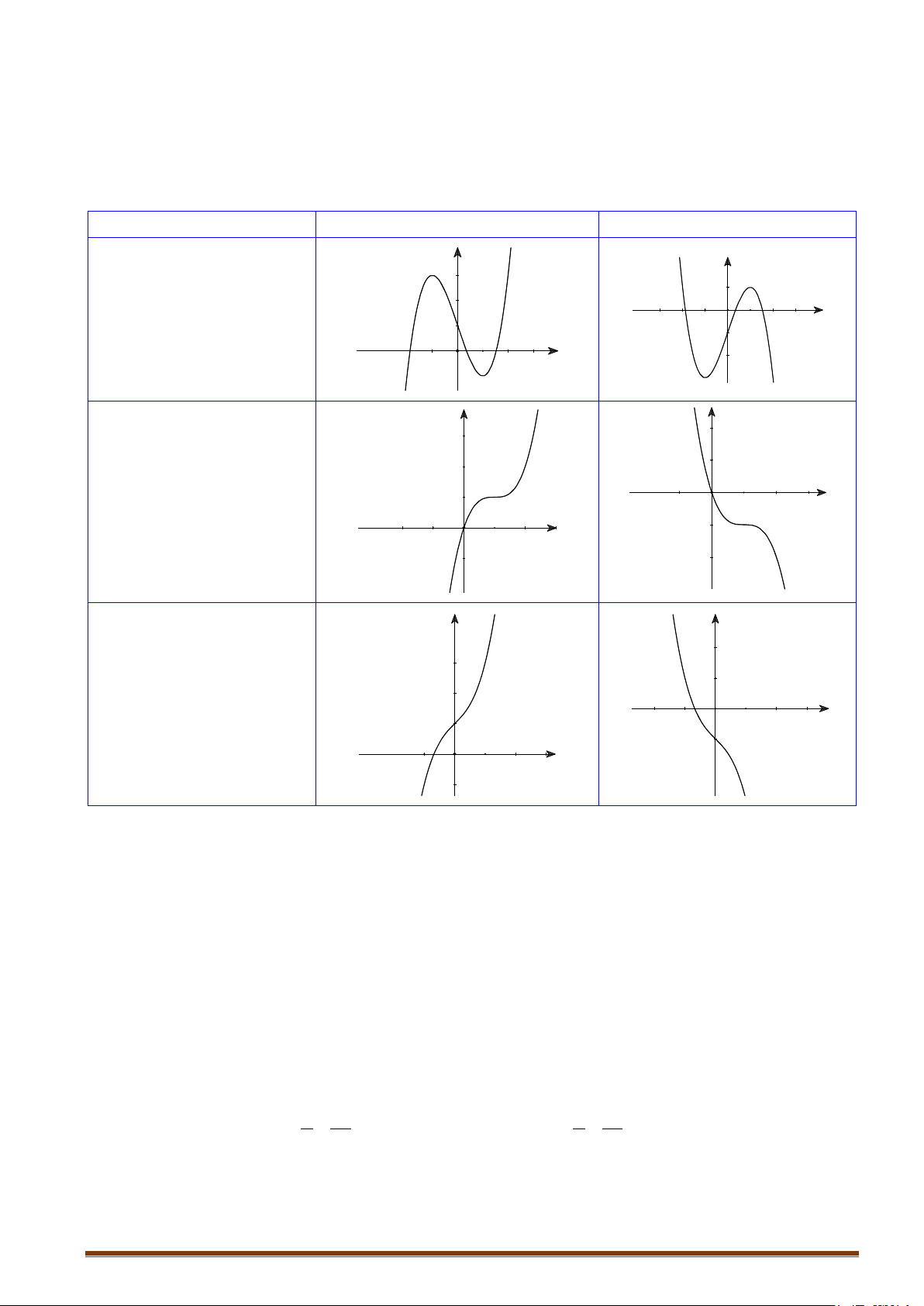
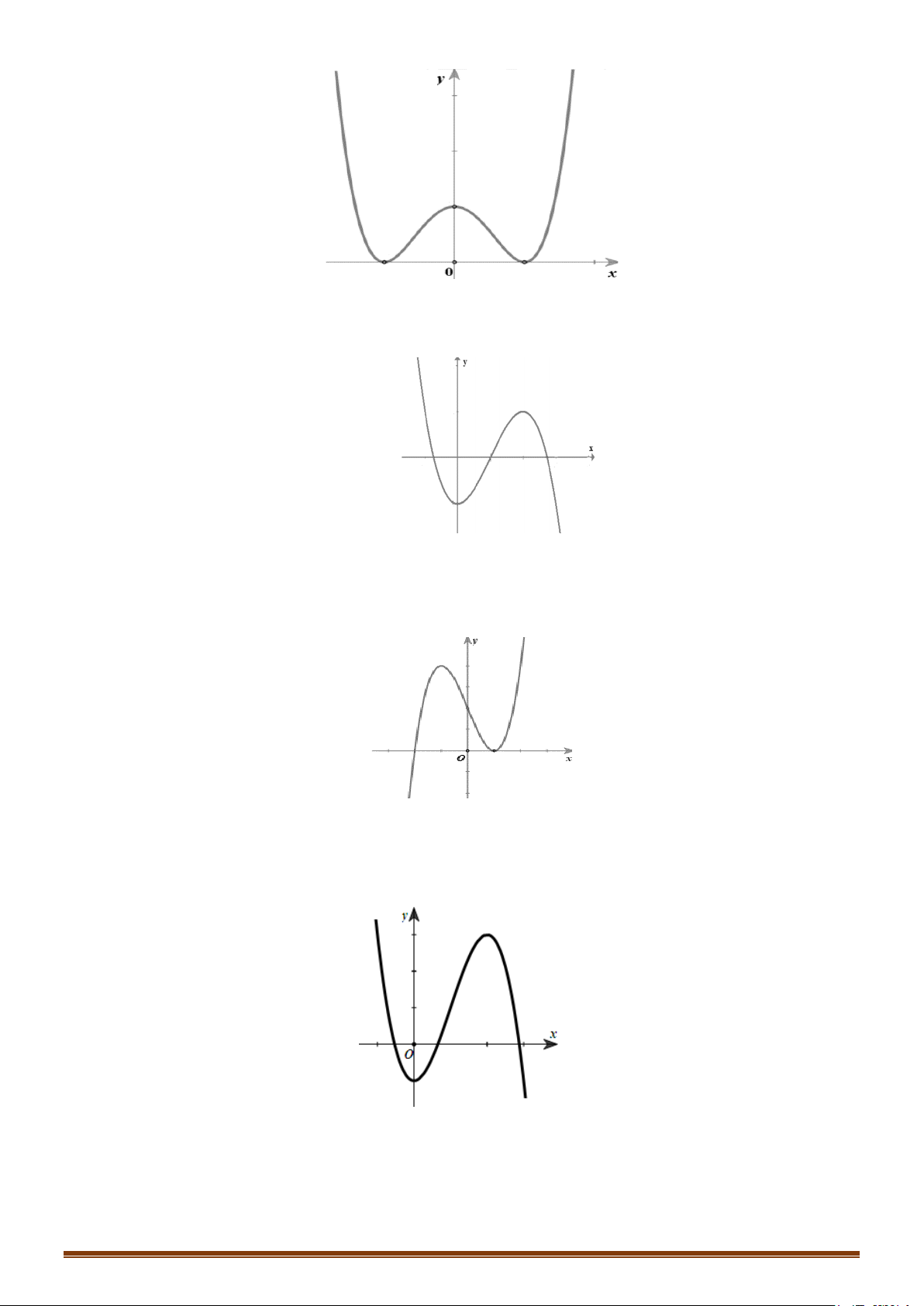
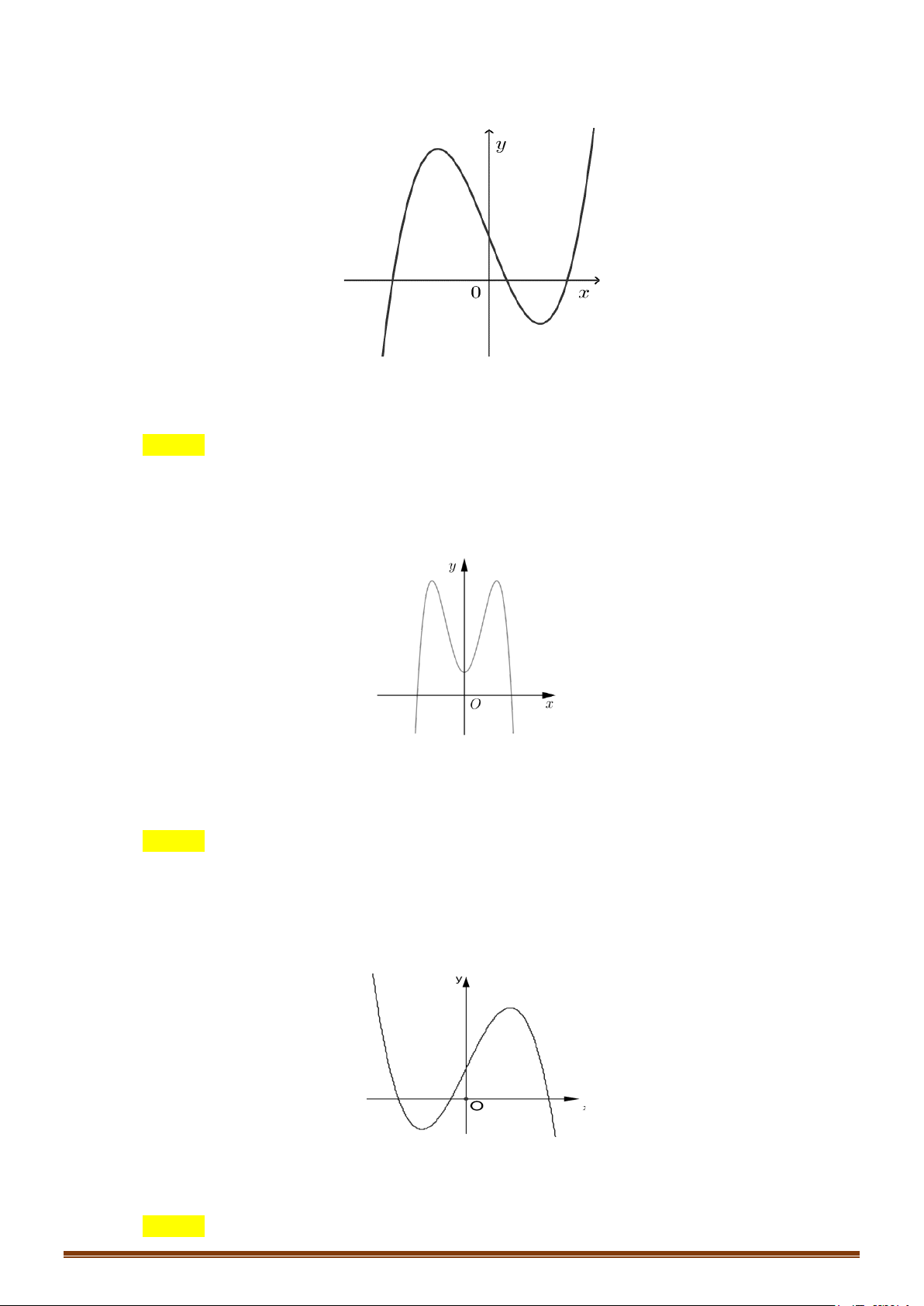
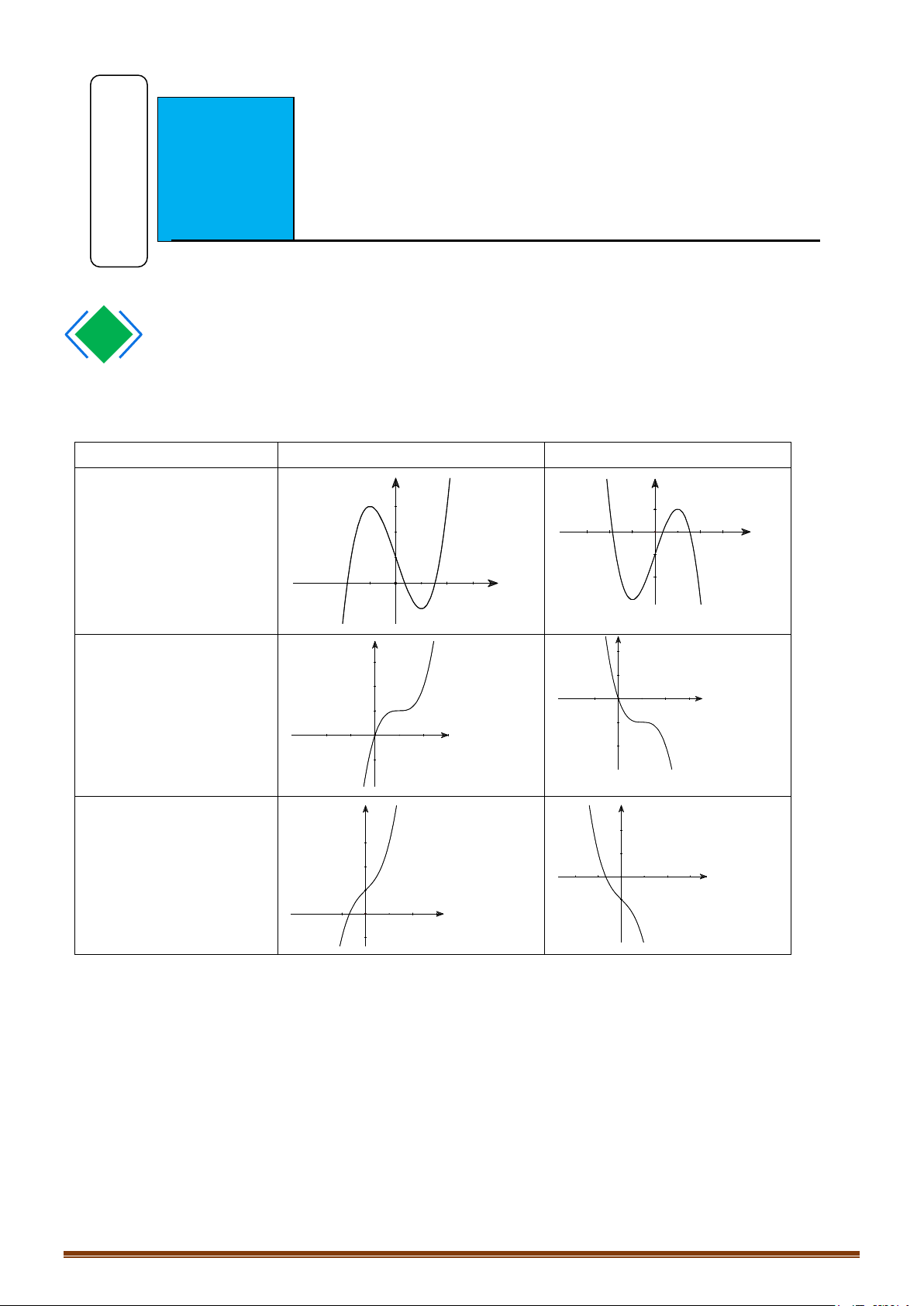
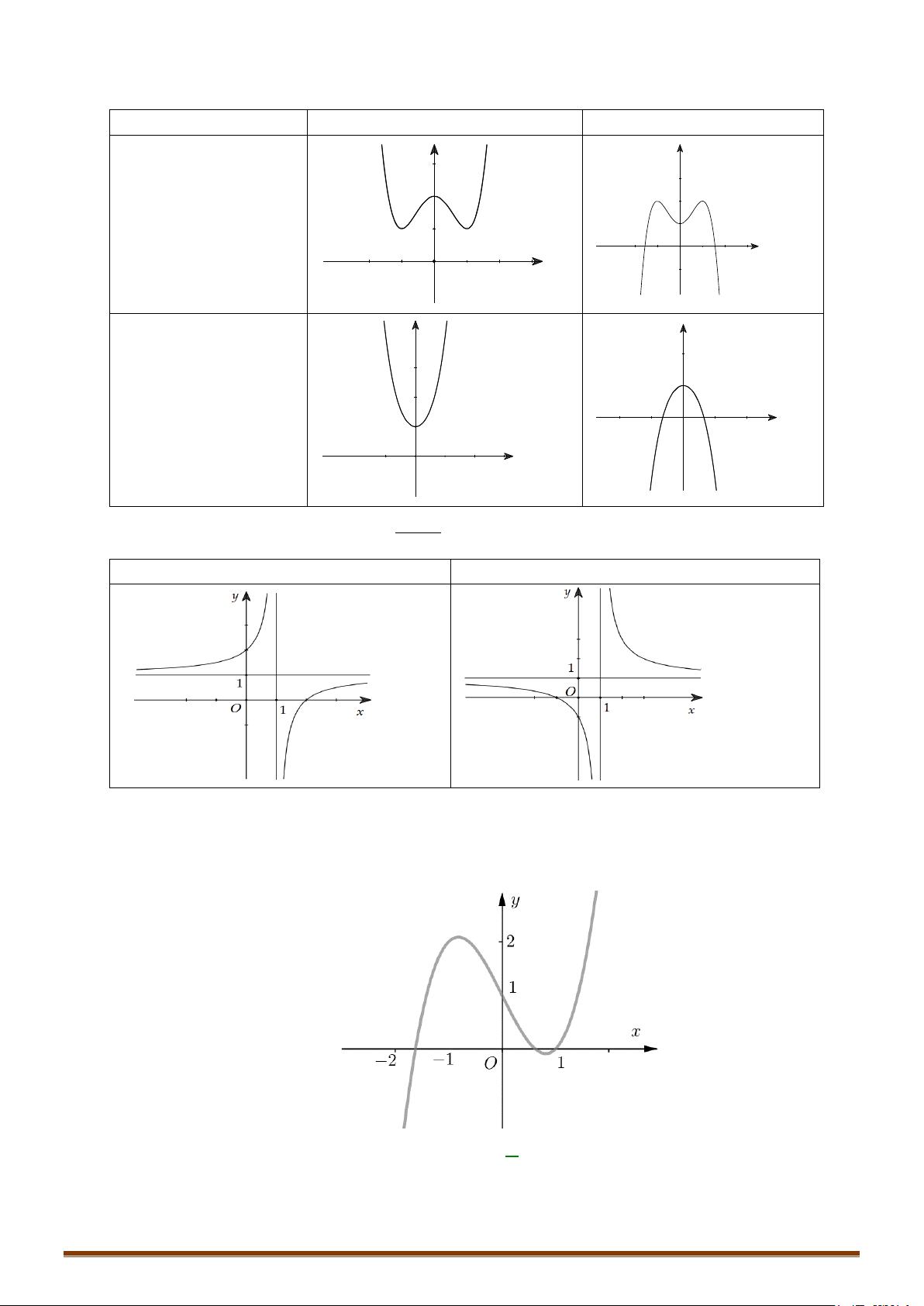
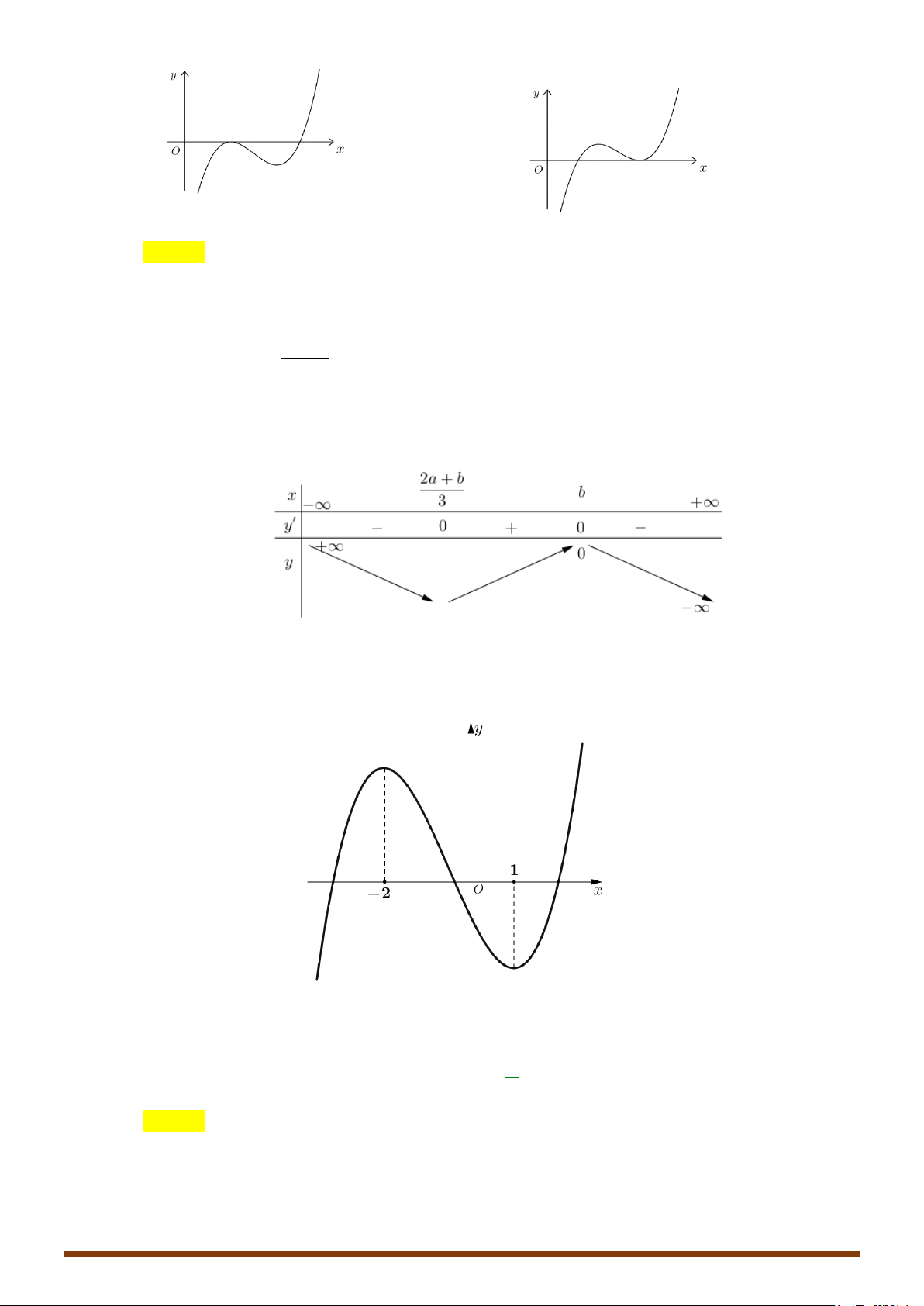
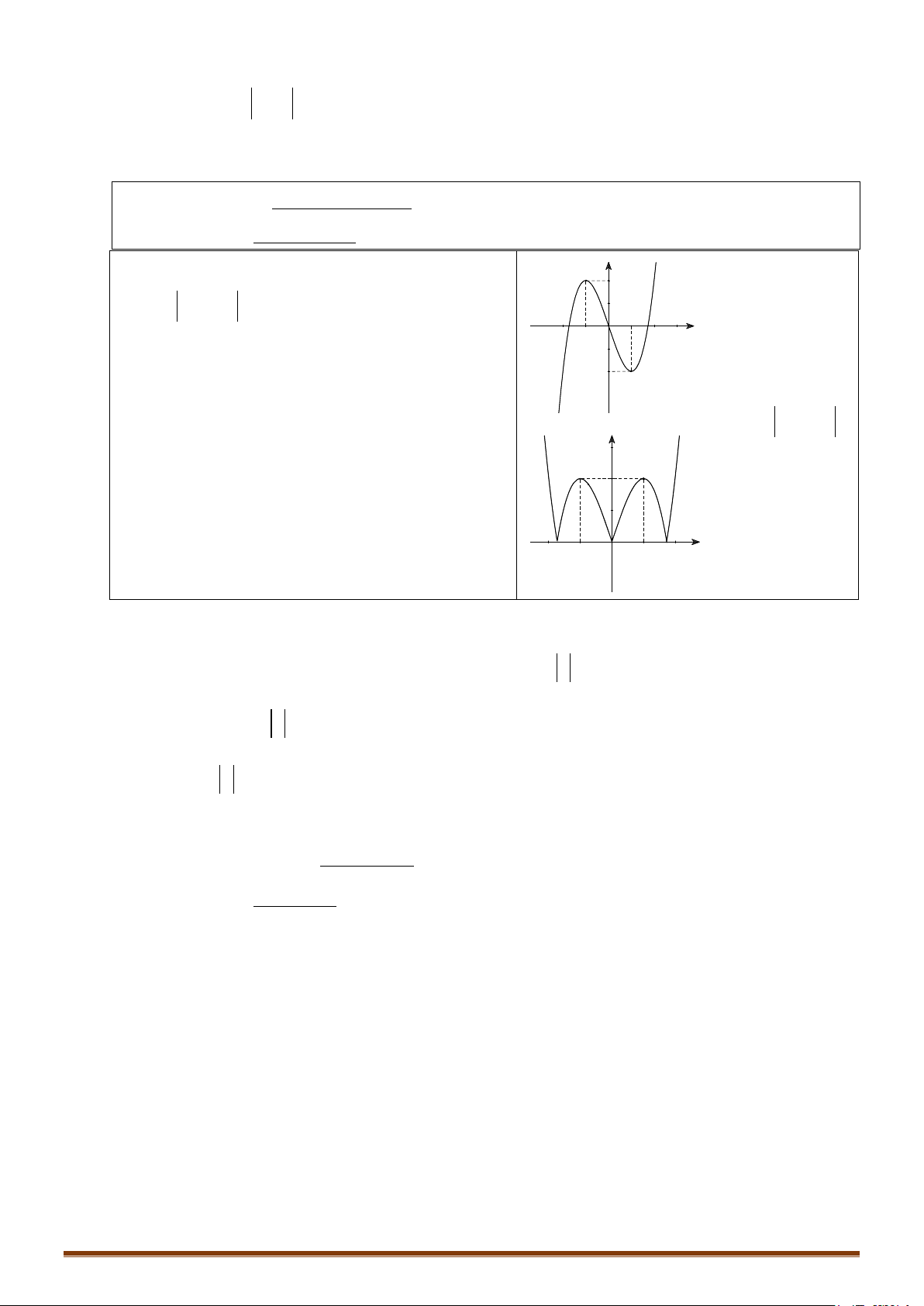
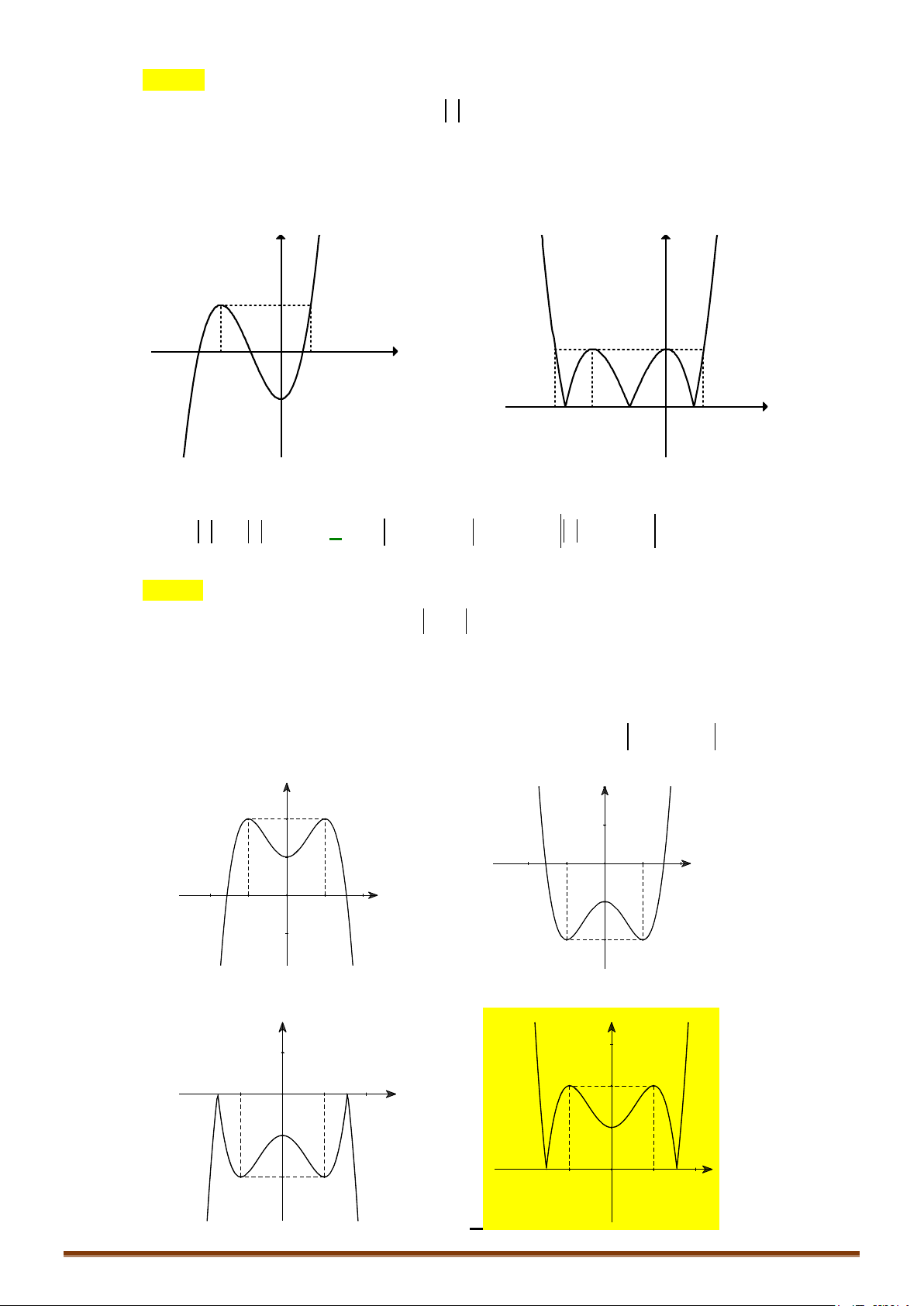
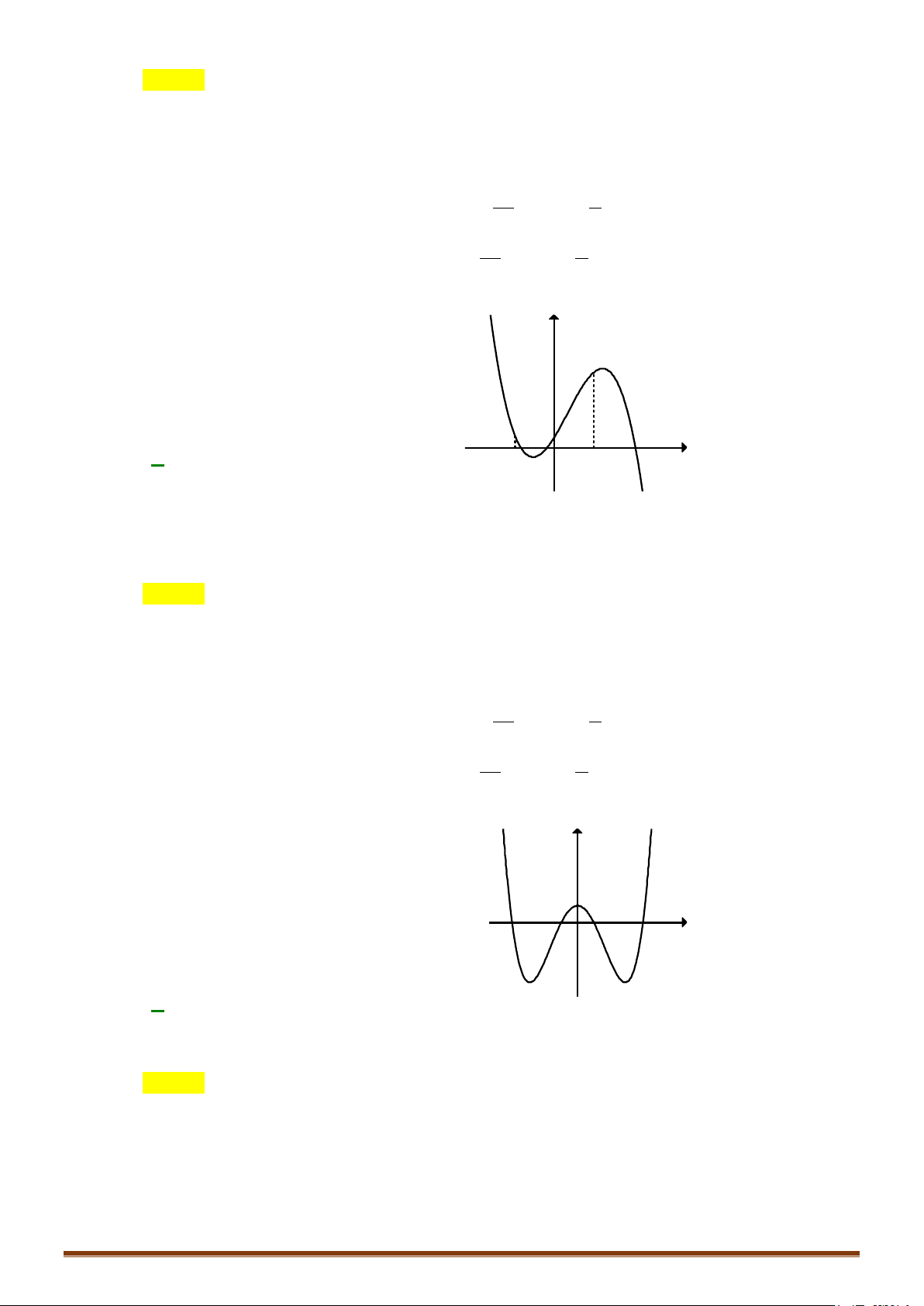
y = ax + bx + cx + d (a ≠ 0) TRƯỜNG HỢP a > 0 a < 0 y y Phương trình / y = 0 có 1 1
2 nghiệm phân biệt 1 O x 1 O x y y Phương trình / y  0 có 1 nghiệm kép 1 1 O x 1 O x y y 1 Phương trình / y = 0 vô O 1 nghiệm 1 x 1 O x
MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
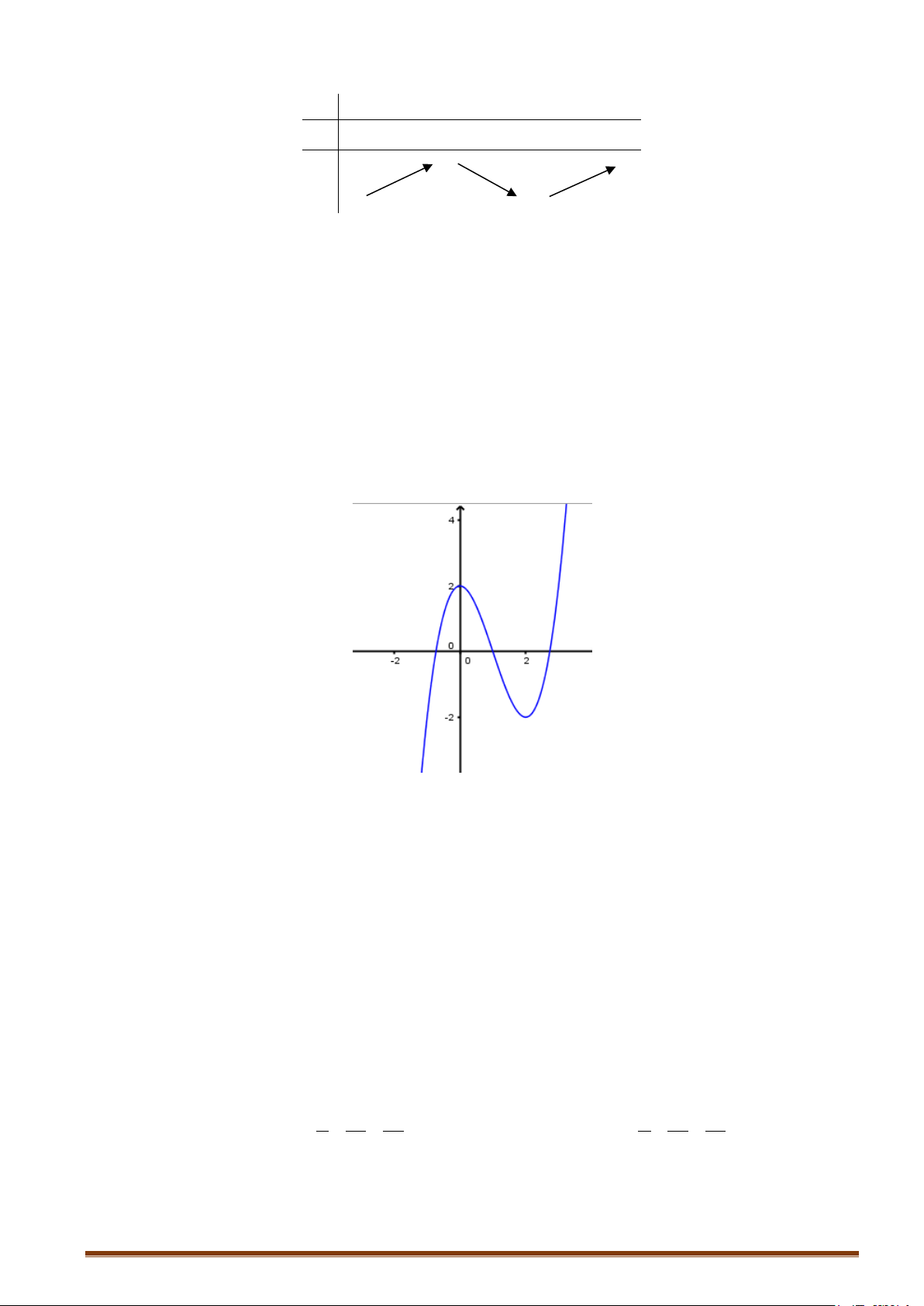
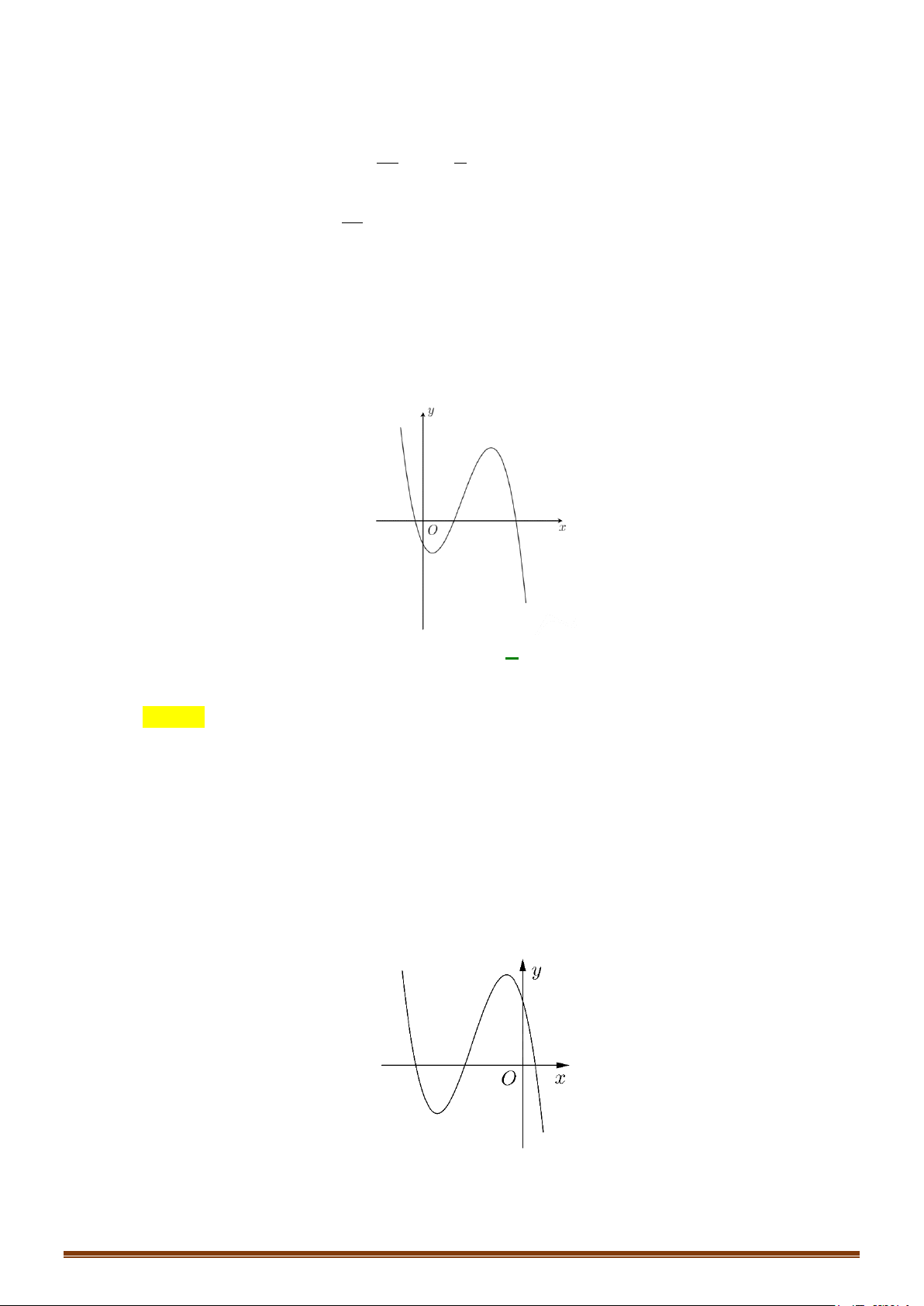
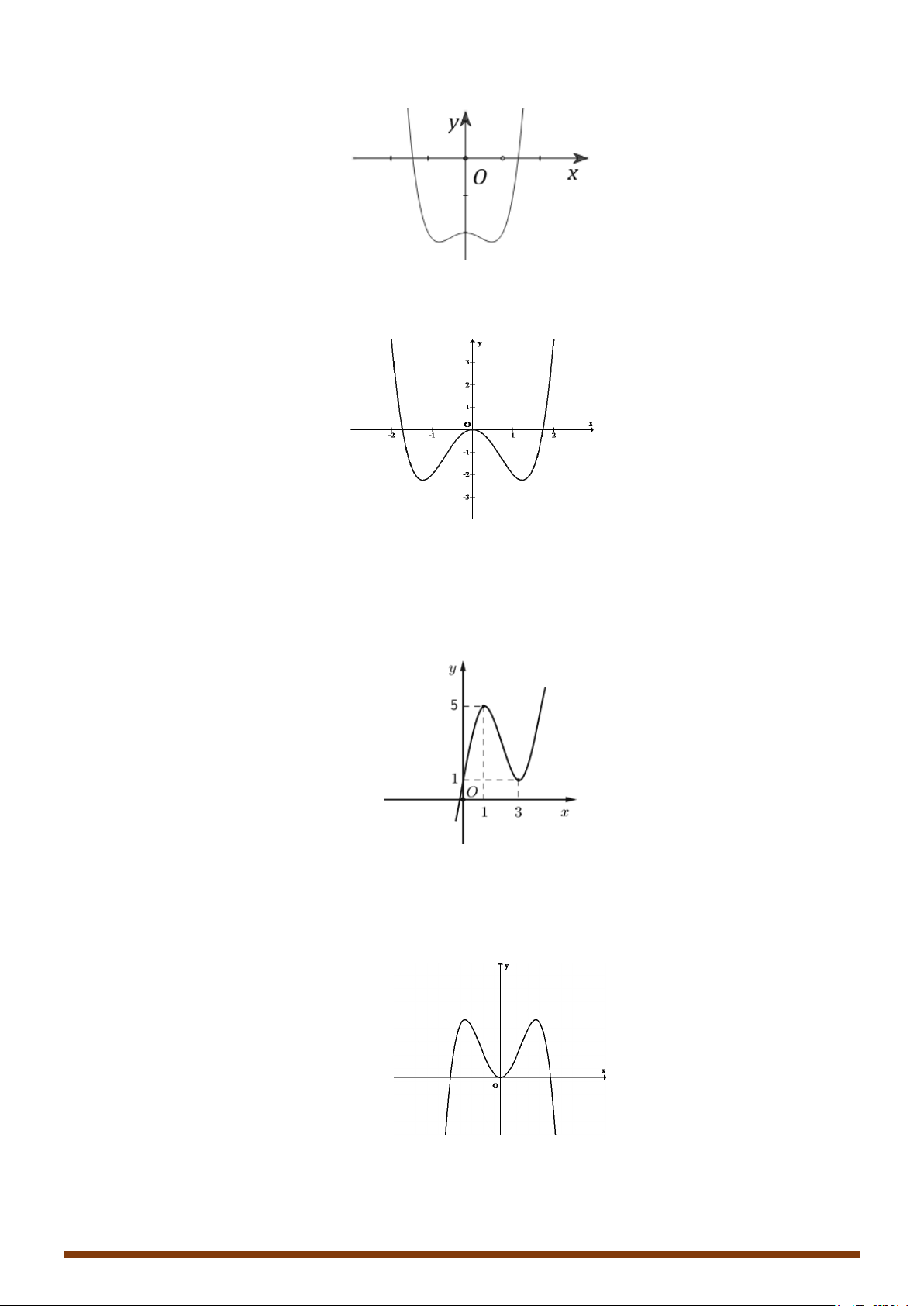
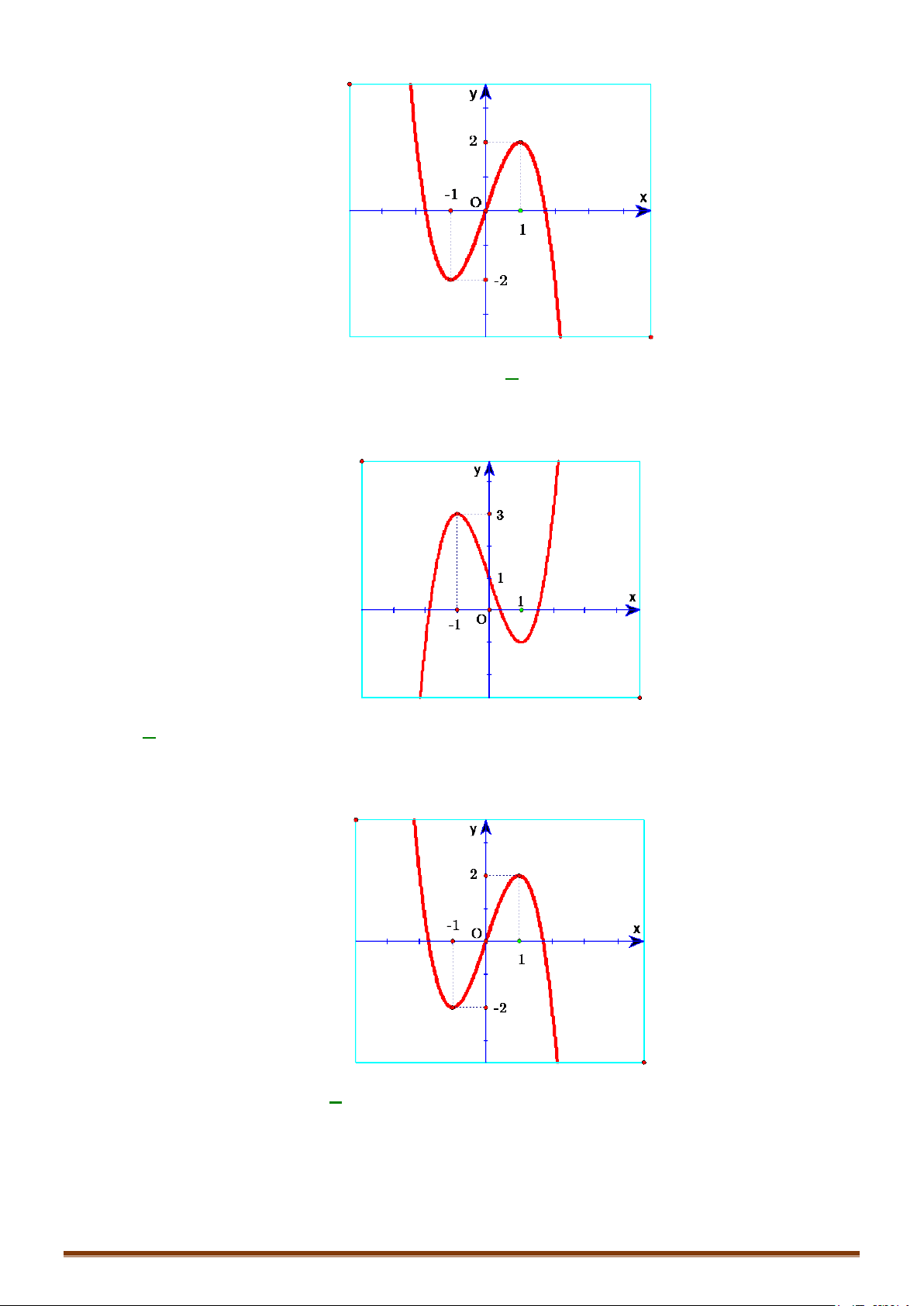
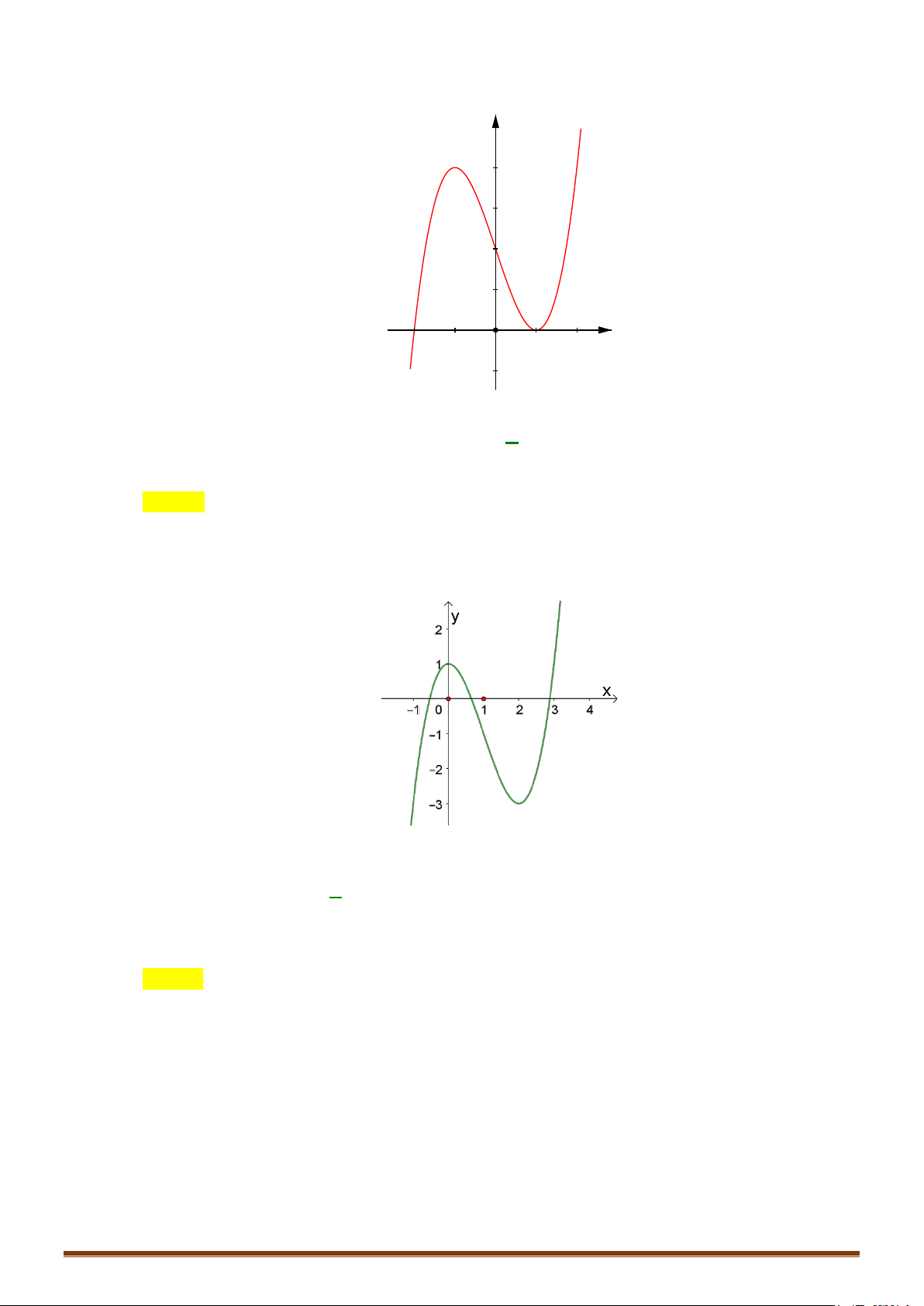
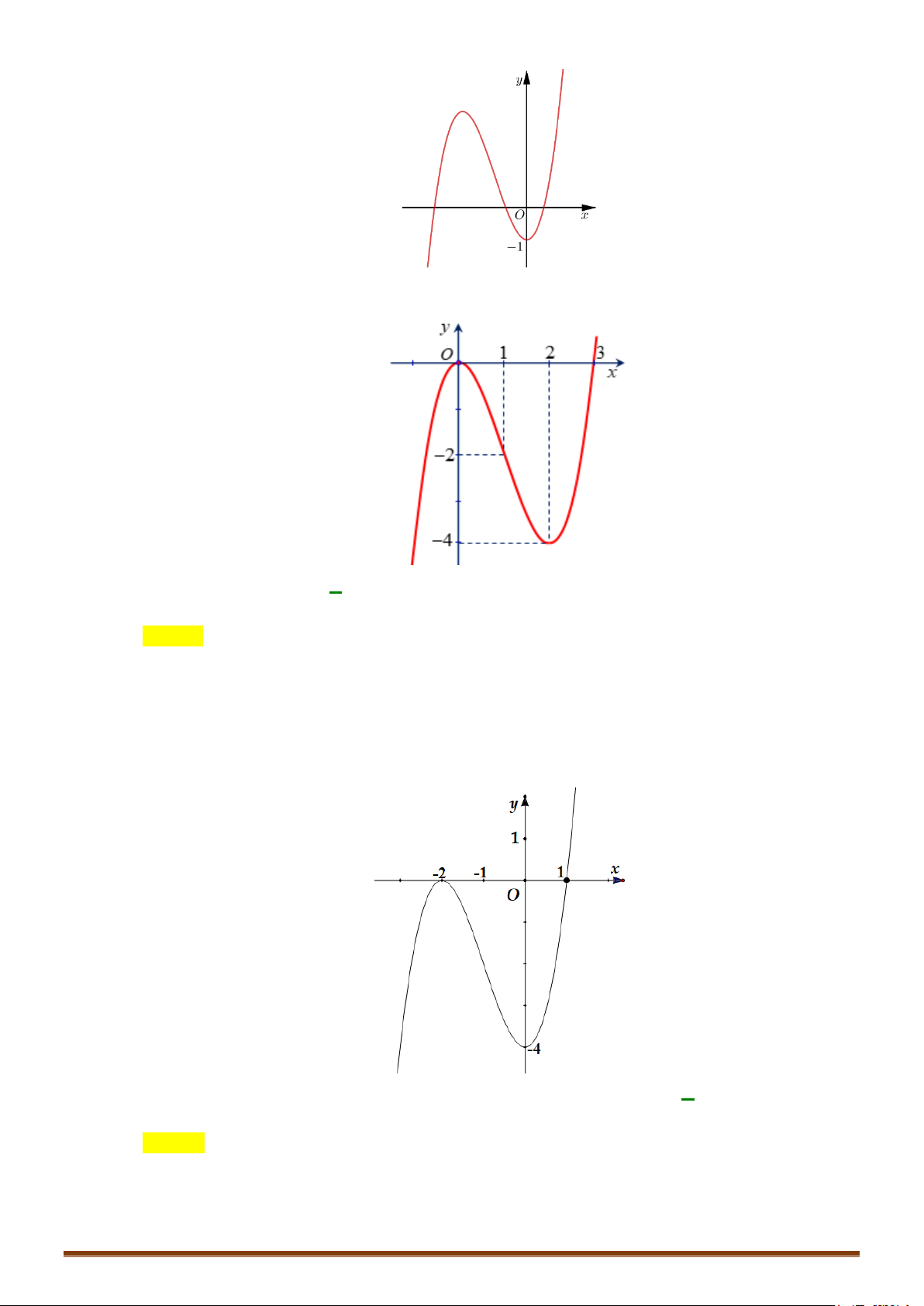
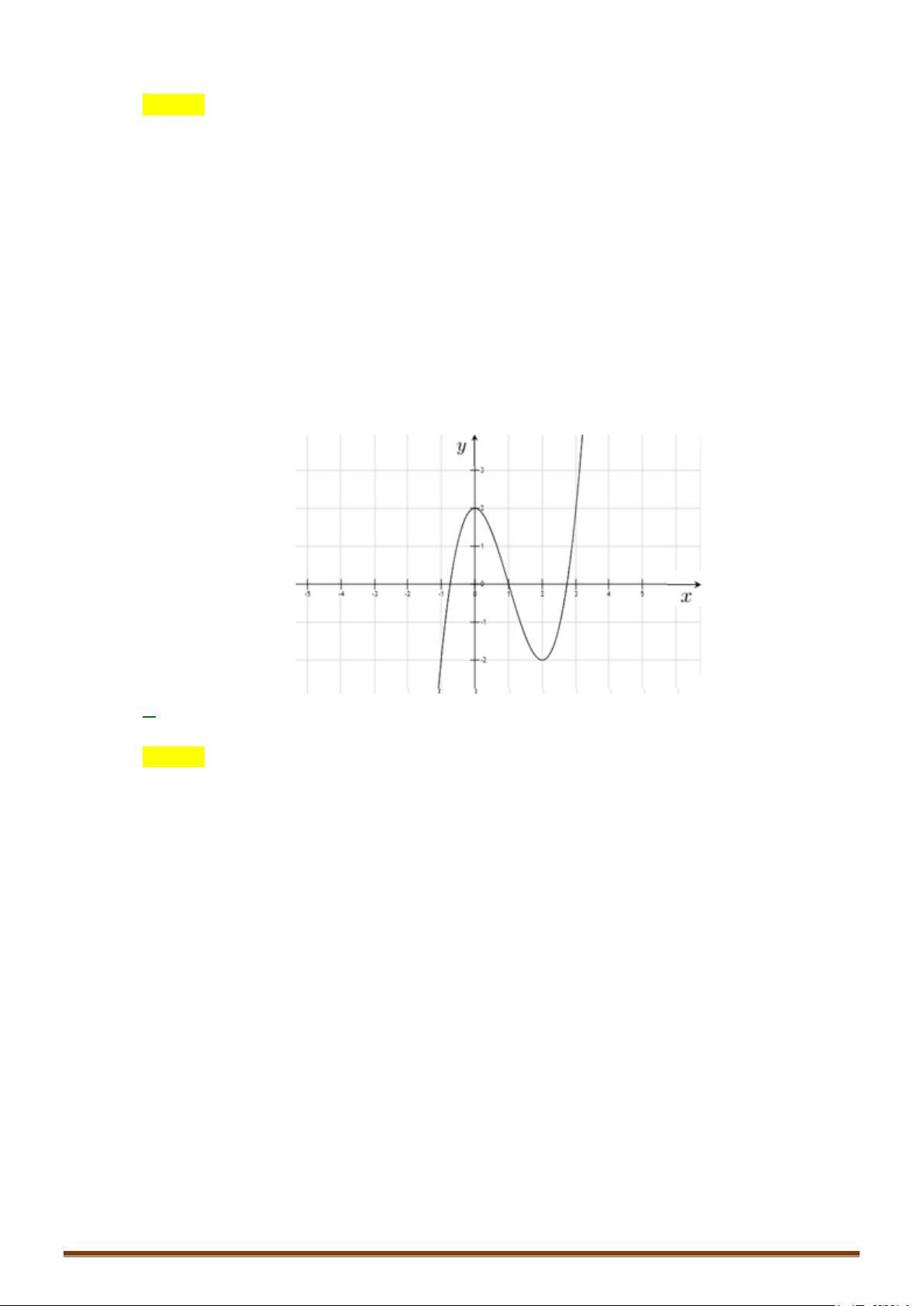
Câu 1. Khảo sát và vẽ đồ thị hàm số 3 2
y = x − 3x + 2 Lời giải:
Tập xác định: D =  Sự biến thiên: + Chiều biến thiên: x = 0 2
y′ = 3x − 6x .Xét y′ = 0 ⇔  x =  2
+ Các giới hạn tại vô cực 3  3 2 lim y lim x 1   3 2  = − + = +∞   ; 3
lim y = lim x 1− + =  . −∞ 3 x→+∞ x→+∞  x x  3 x→−∞ x→−∞  x x Page 198
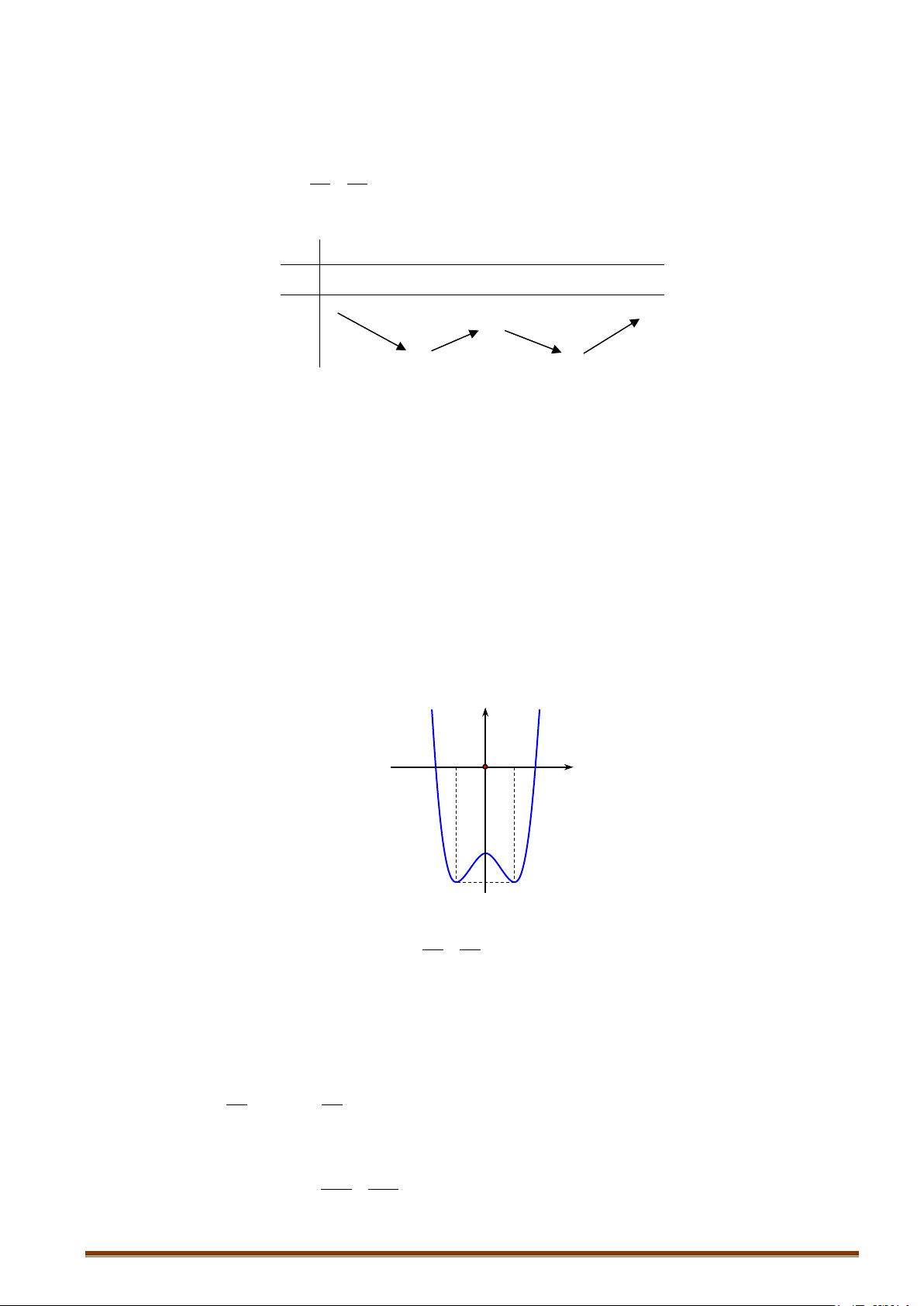
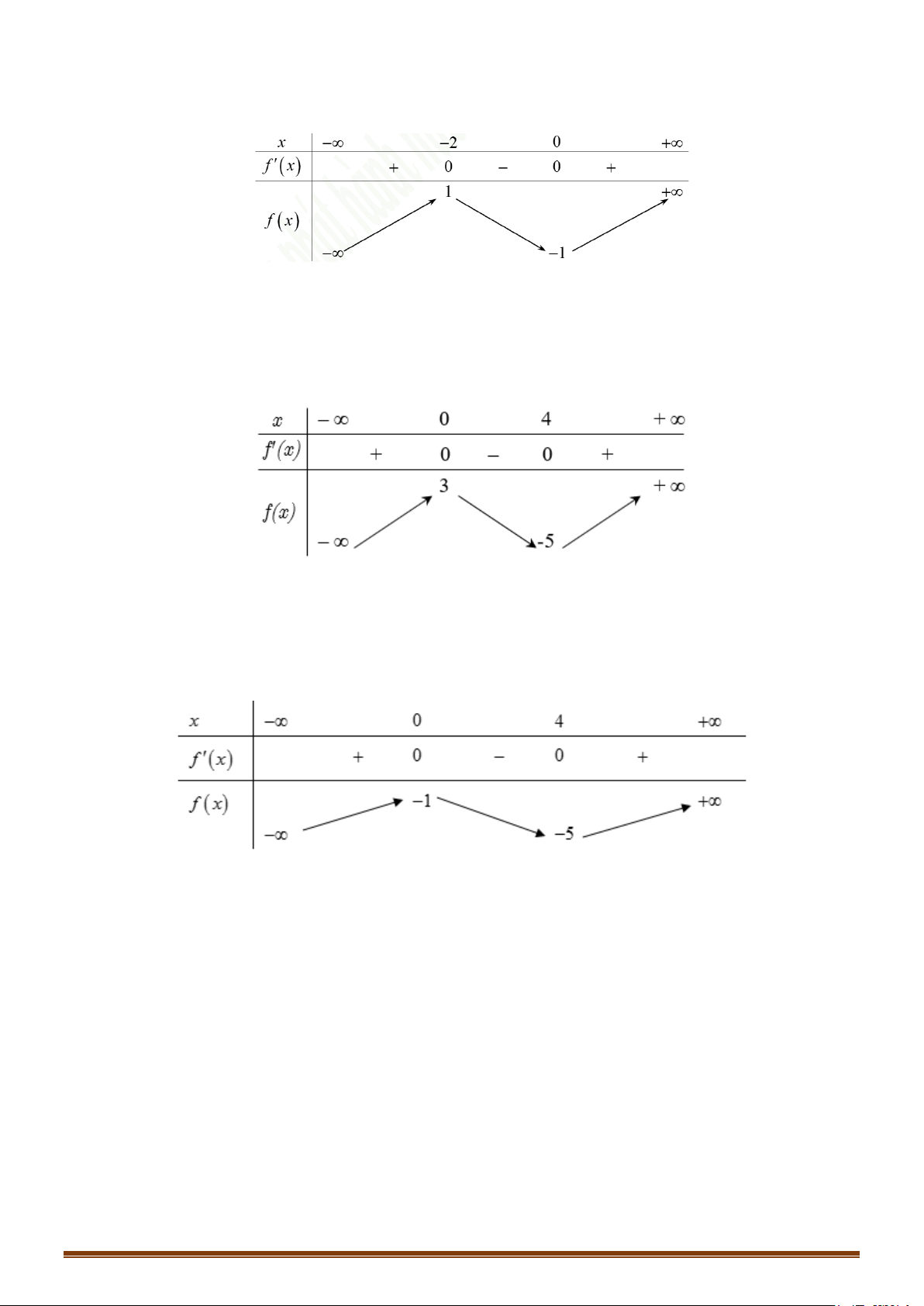
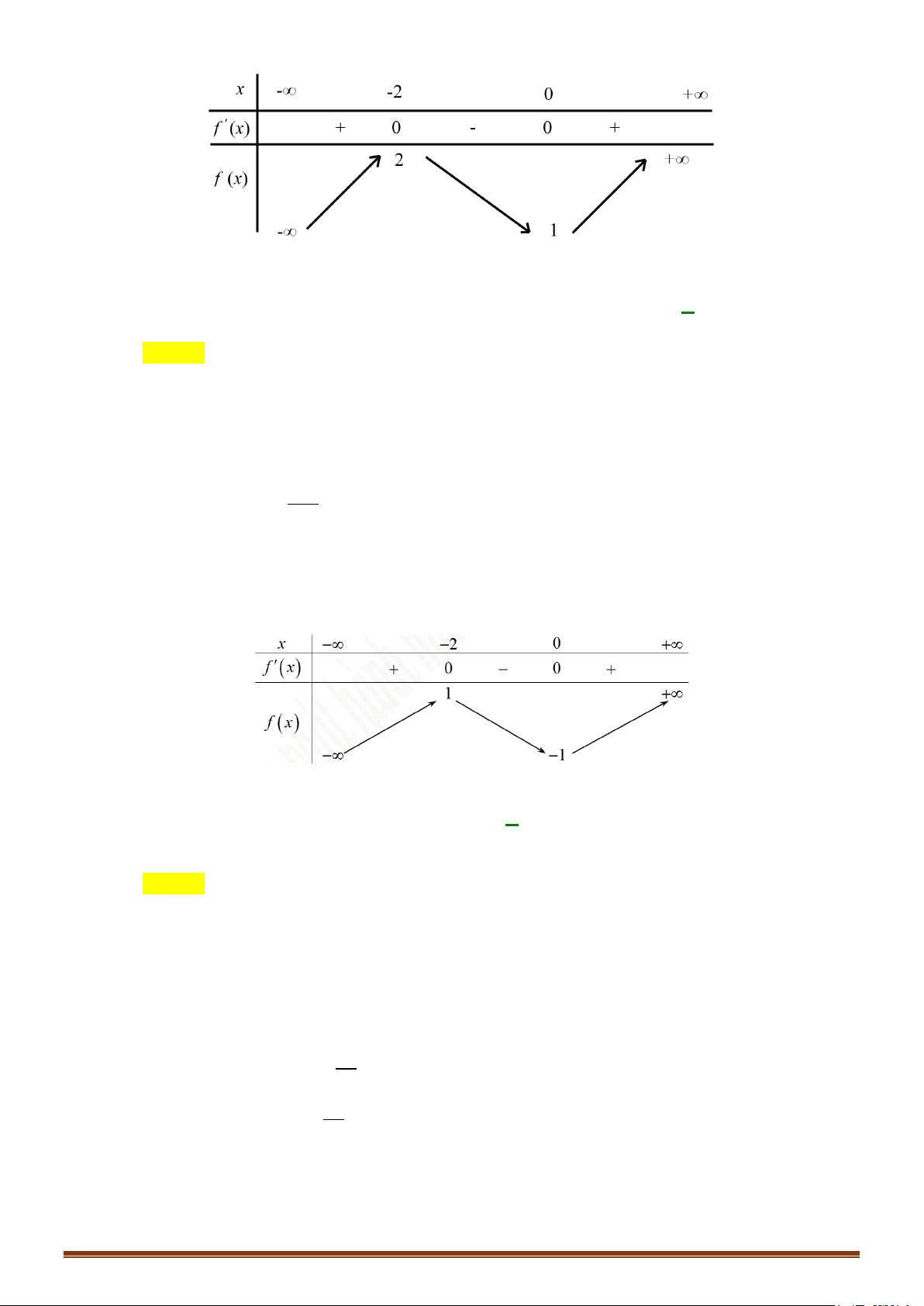
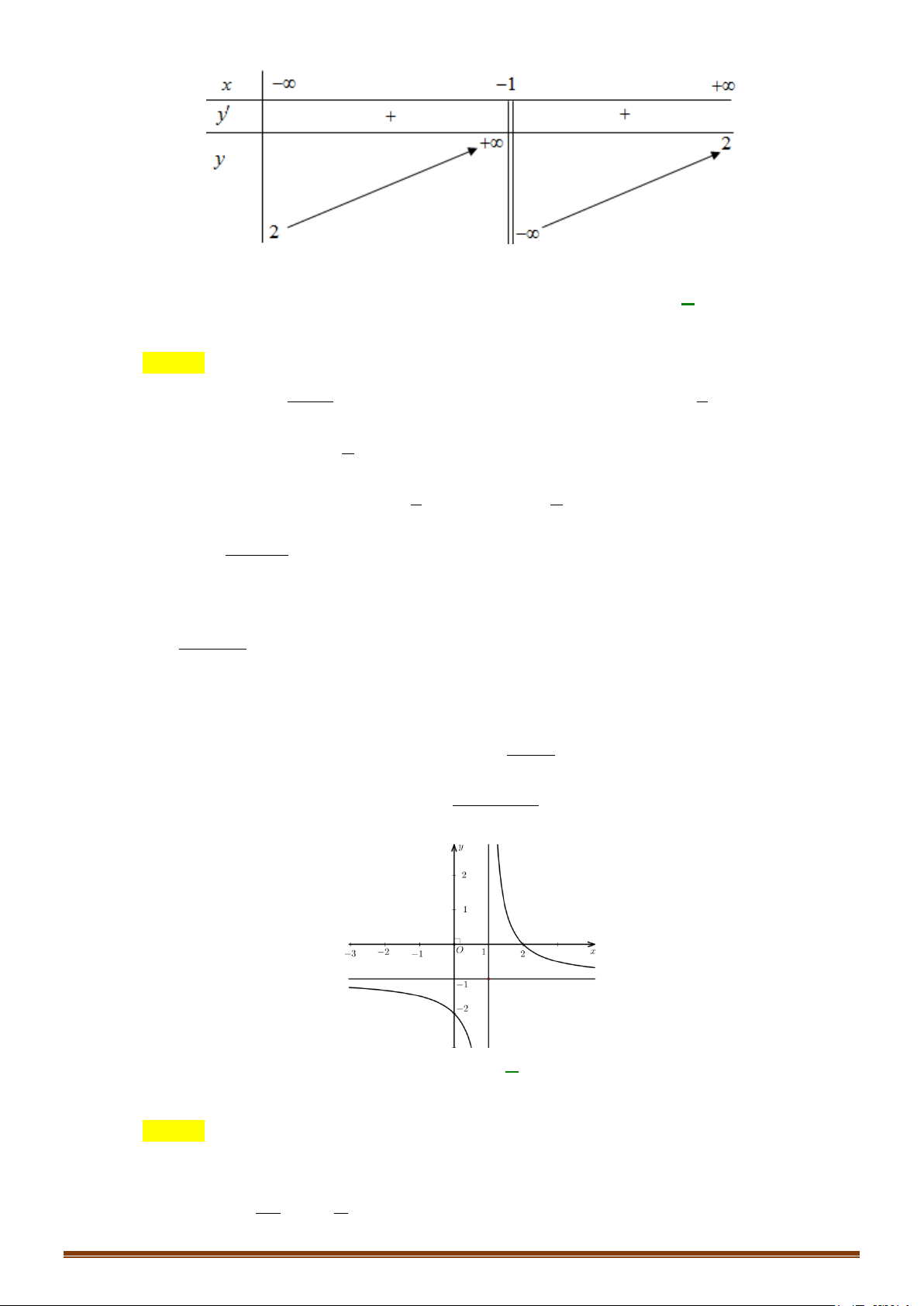
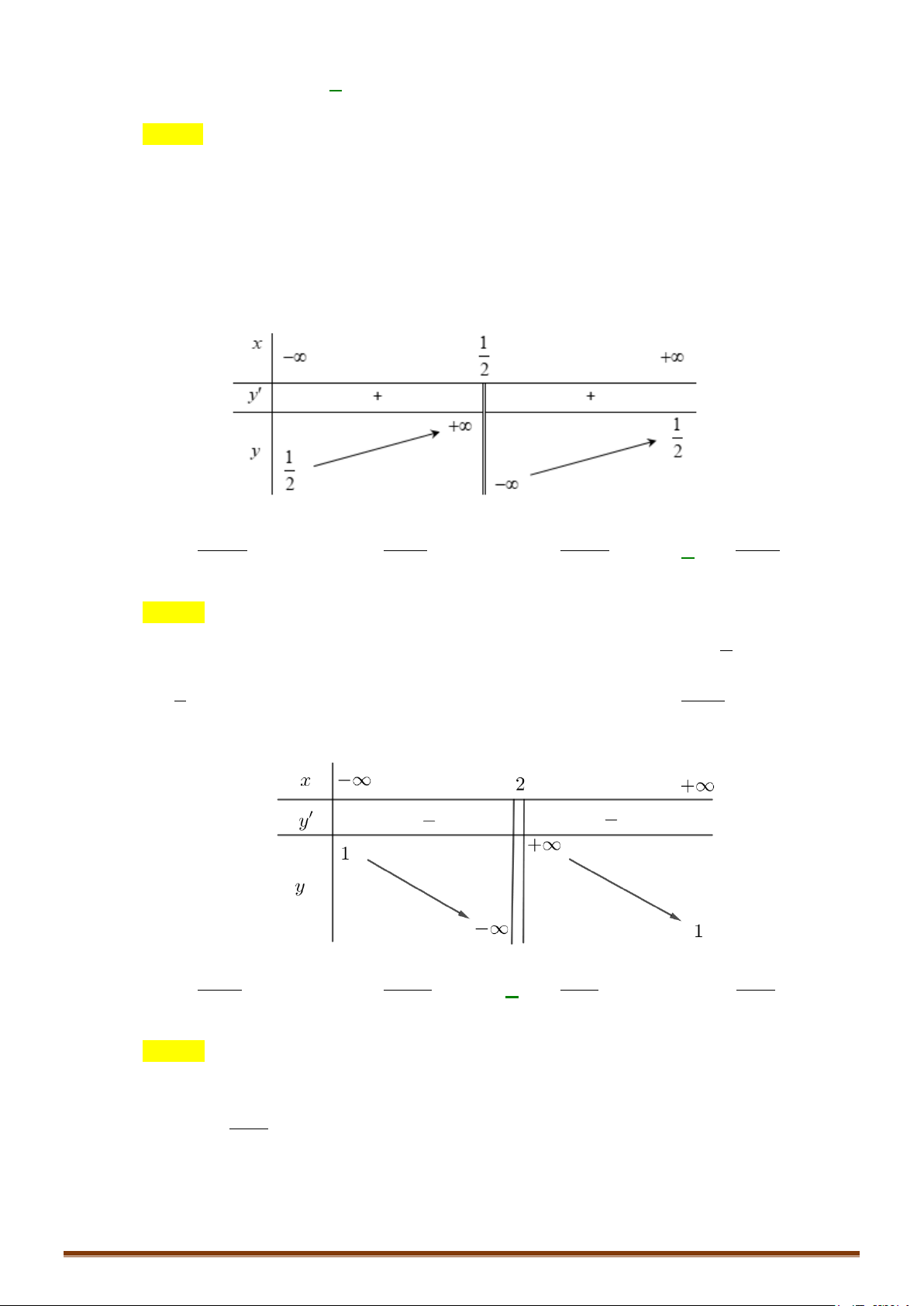
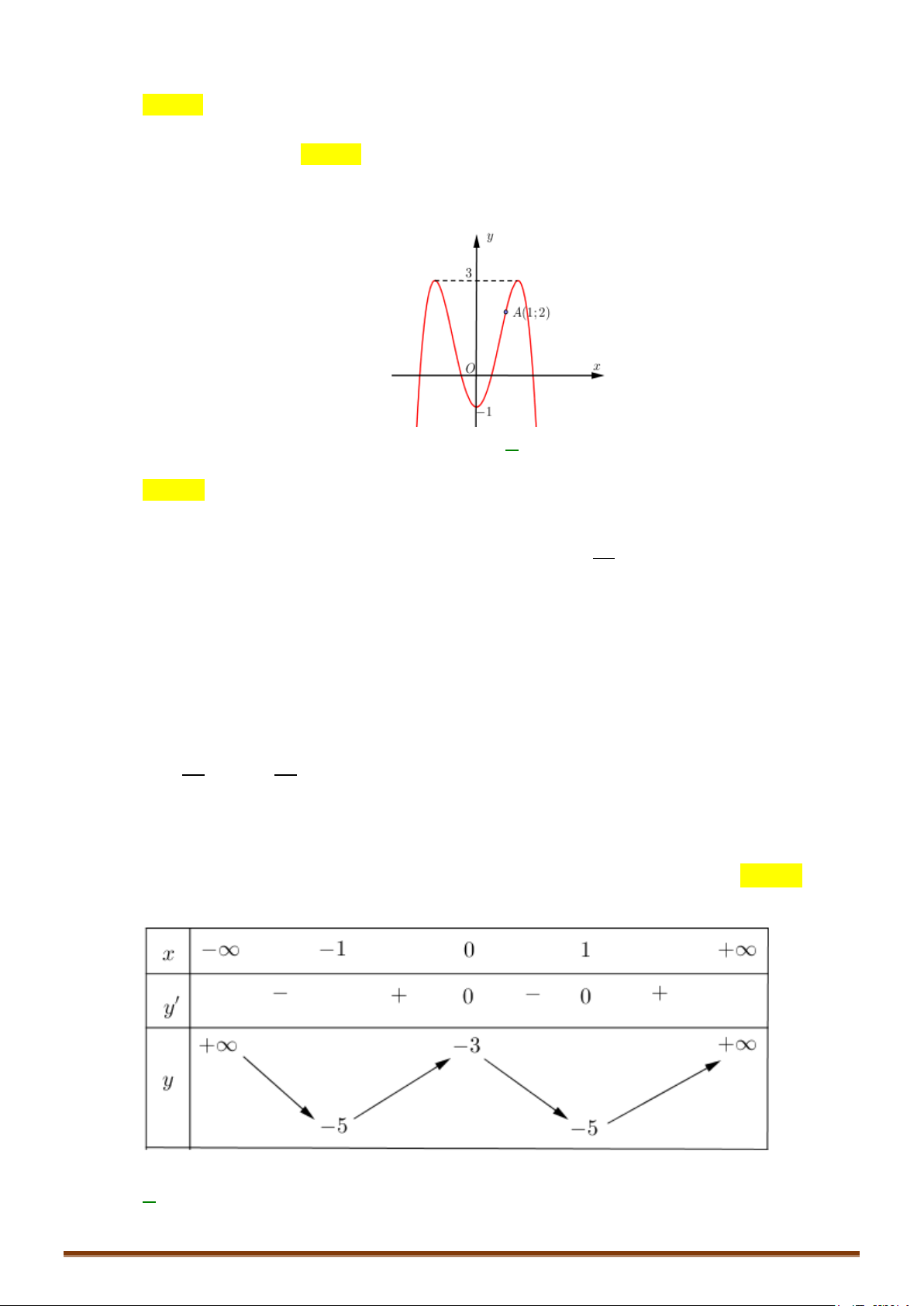
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ + Bảng biến thiên: x 0 2 +∞ y′ + 0 − 0 + 2 +∞ y −∞ 2 −
Hàm số đồng biến trên các khoảng (−∞;0) và (2;+ ∞) ;
Hàm số nghịch biến trên khoảng (0;2) + Cực trị :
Hàm số đạt cực đại tại x = 0; y = y(0) = 2 .Hàm số đạt cực tiểu tại x = 2; y = y = − ct (2) 2 cd + Đồ thị x = 1 Ta có 3 2
x − 3x + 2 = 0 ⇔ 
⇒ đồ thị hàm số qua điểm A(1;0). 2 x − 2x − 2 =  0
Cho x = 0 ⇒ y = 2 :Đồ thị hàm số cắt Oy tại B(0;2).
Lưu ý: Đồ thị hàm số nhận điểm I (1;0) làm tâm đối xứng. Hoành độ điểm I là nghiệm của phương
trình y′ = 0 (Điểm uốn)
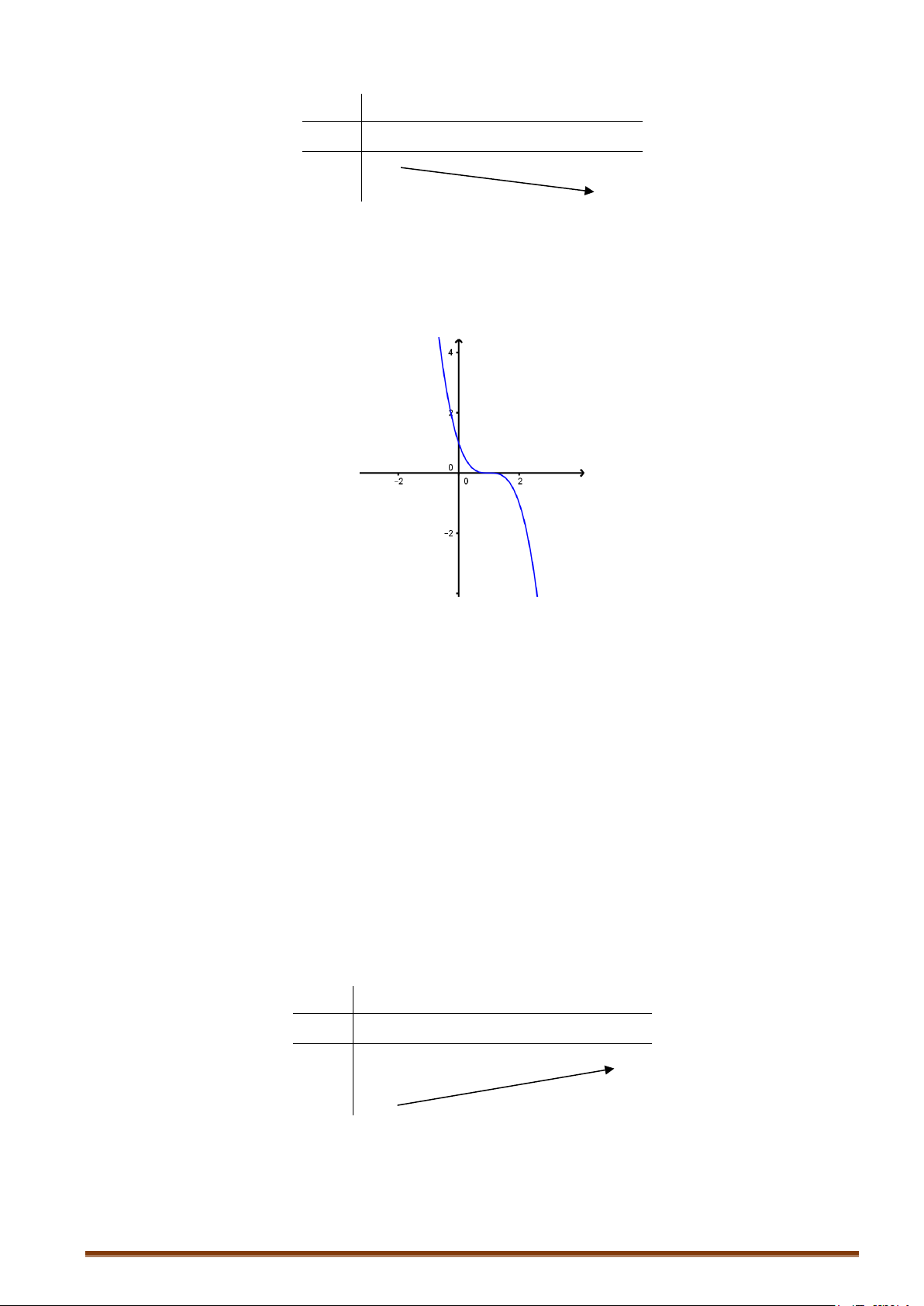
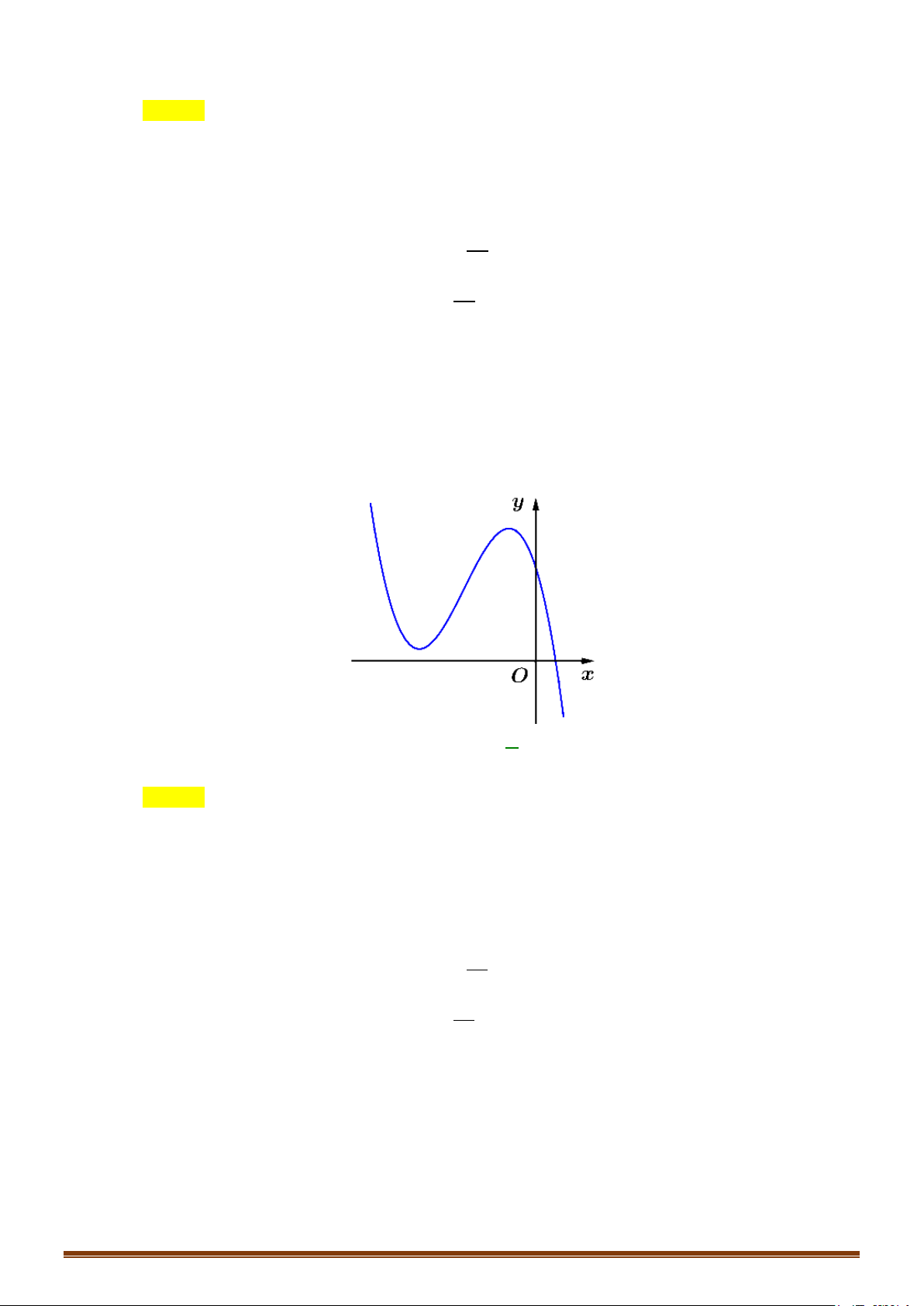
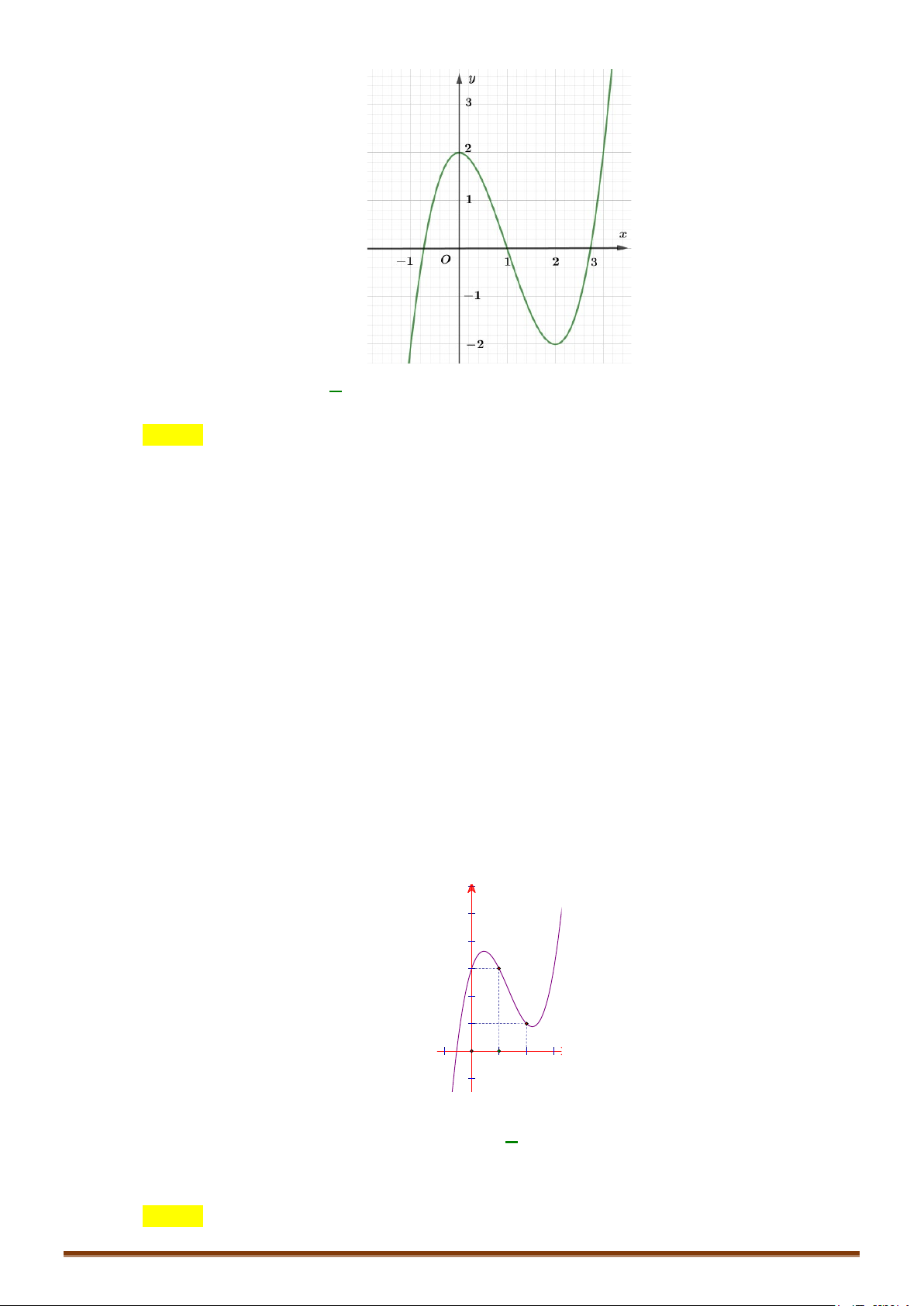
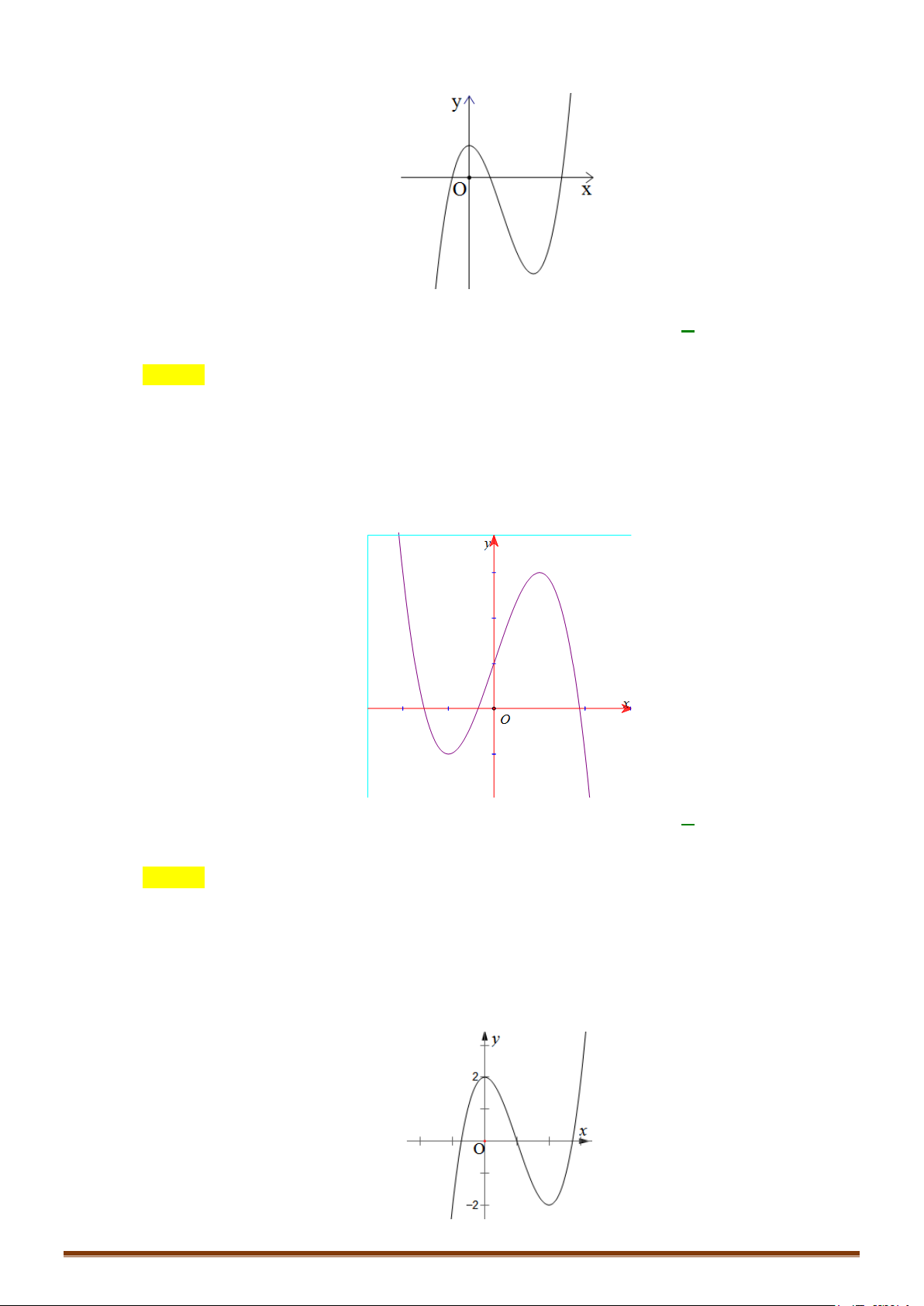
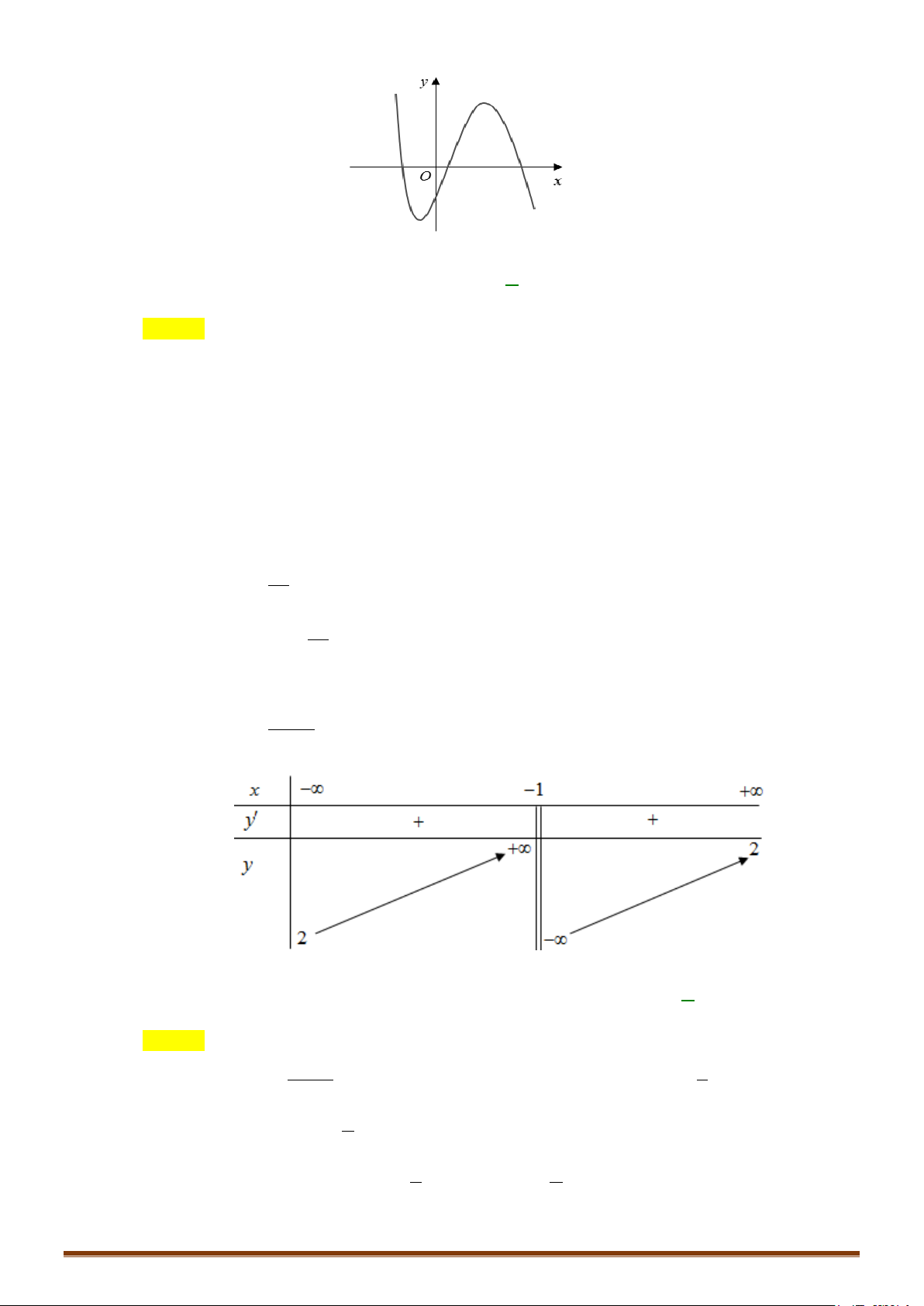
Câu 2. Khảo sát và vẽ đồ thị hàm số 3 2
y = −x + 3x − 3x + 1 Lời giải:
Tập xác định: D =  Sự biến thiên: + Chiều biến thiên:
y′ = − x + x − = − (x − )2 2 3 6 3 3 1 ≤ 0 x
∀ ∈  .Xét y′ = 0 ⇔ x = 1.
Suy ra hàm số nghịch biến trên khoảng (−∞;+ ∞).
+ Cực trị : Hàm số không có cực trị
+ Các giới hạn tại vô cực 3  3 3 1 lim y lim x 1   3 3 1  = − + − + = −∞   ; 3
lim y = lim x  1 − + − + =  . +∞ 2 3 x→+∞ x→+∞  x x x  2 3 x→−∞ x→−∞  x x x Page 199
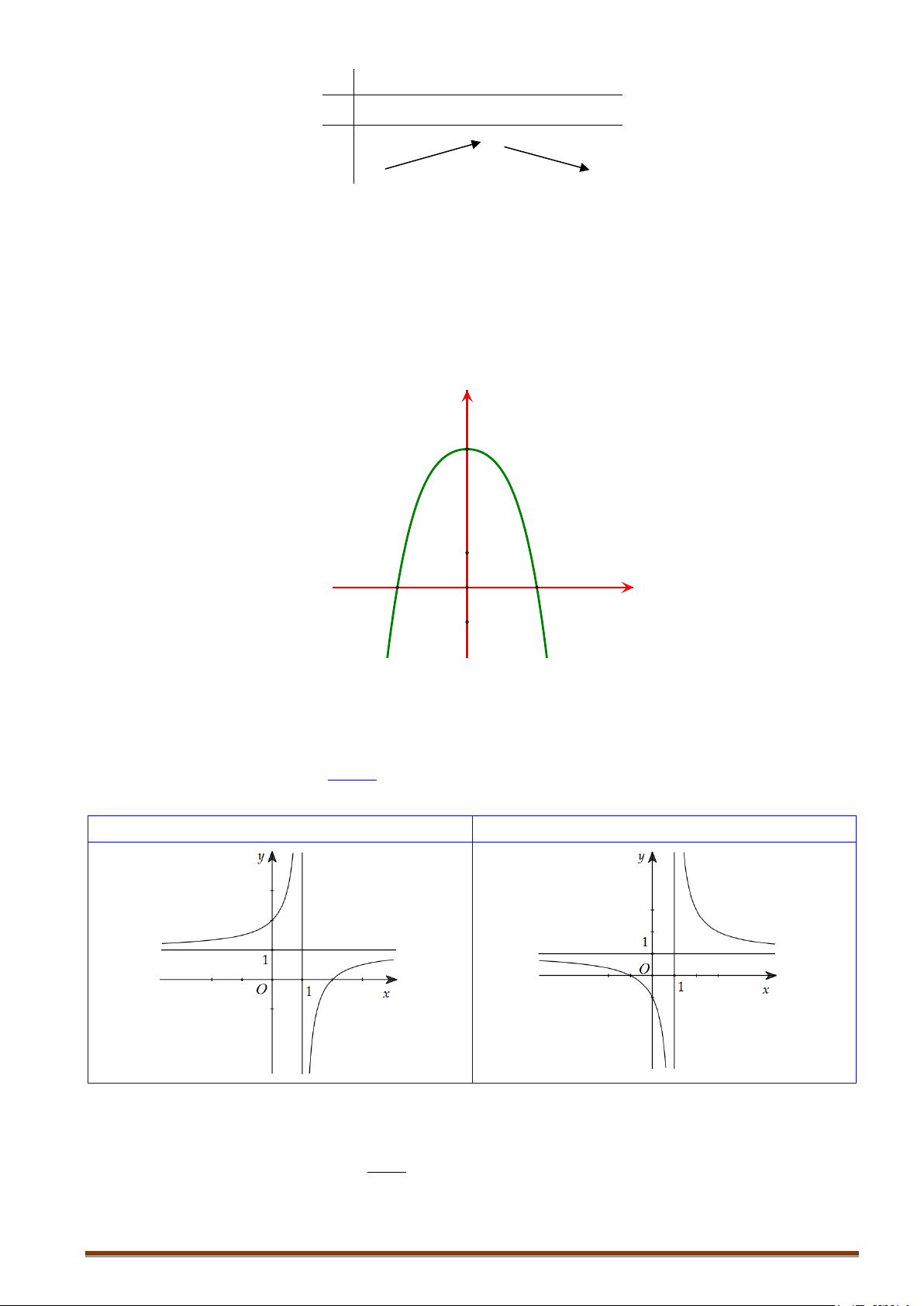
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ + Bảng biến thiên: x −∞ 1 +∞ y′ − 0 − y +∞ −∞ Đồ thị Ta có 3 2
−x + 3x − 3x + 1 = 0 ⇔ x = 1 ⇒ đồ thị hàm số qua A(1;0).
Cho x = 0 ⇒ y = 1 ⇒ Đồ thị hàm số cắt Oy tại B(0;1) .
Cho x = 2 ⇒ y = 1
− ⇒ Đồ thị hàm số qua C (2;−1).
Lưu ý: Đồ thị hàm số nhận điểm I (1;0) làm tâm đối xứng.Hoành độ điểm I là nghiệm của phương
trình y′ = 0 (Điểm uốn).
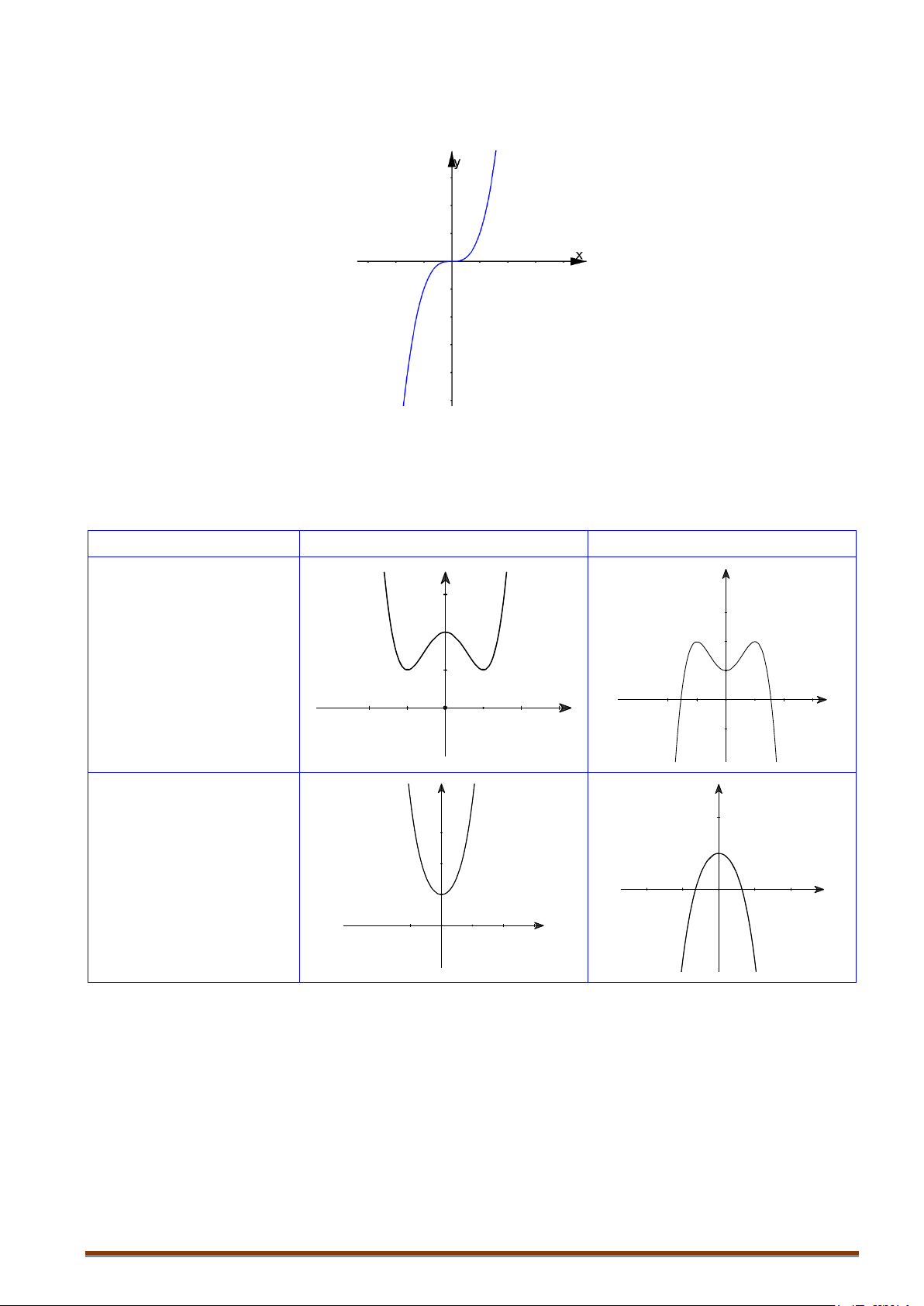
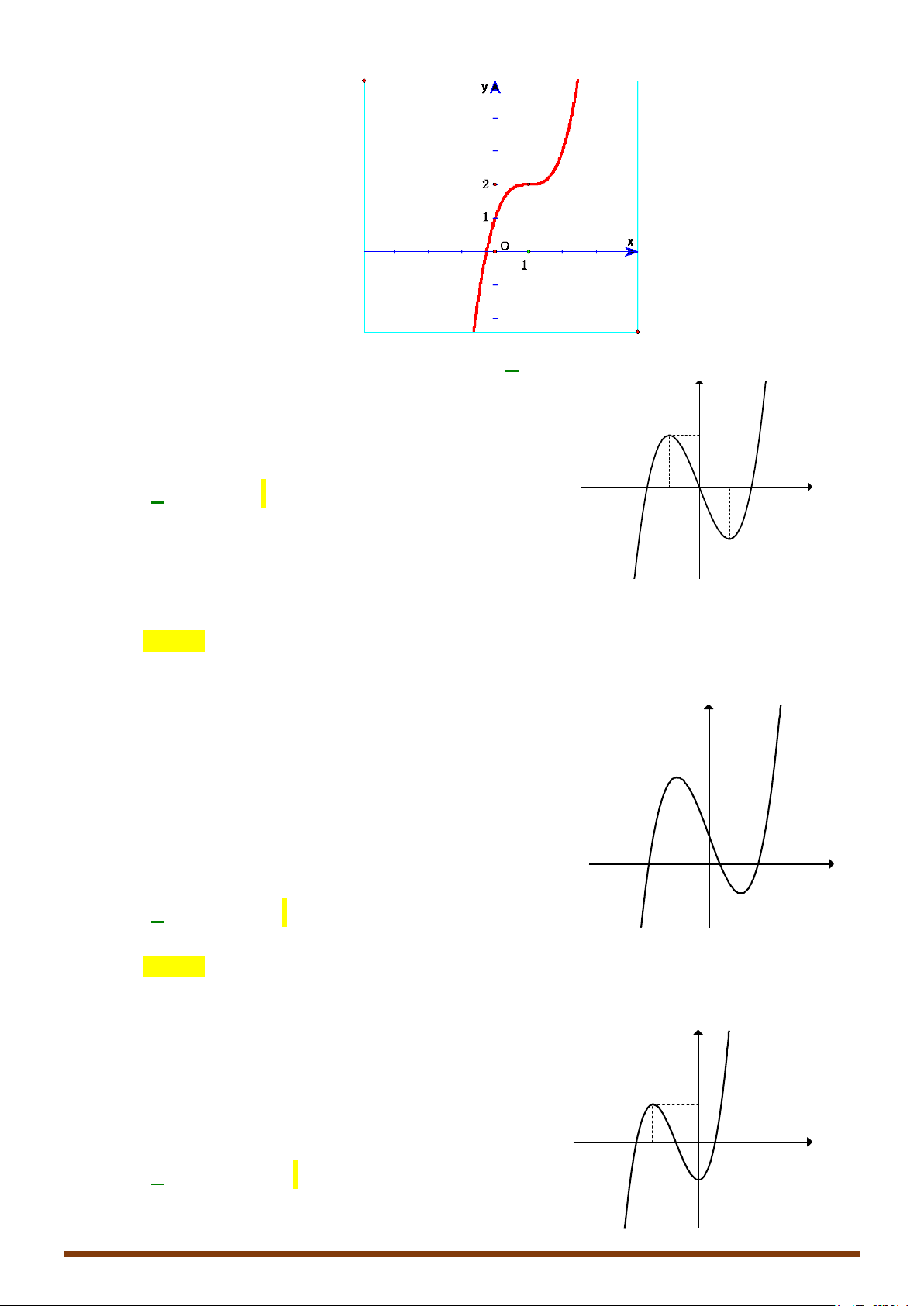
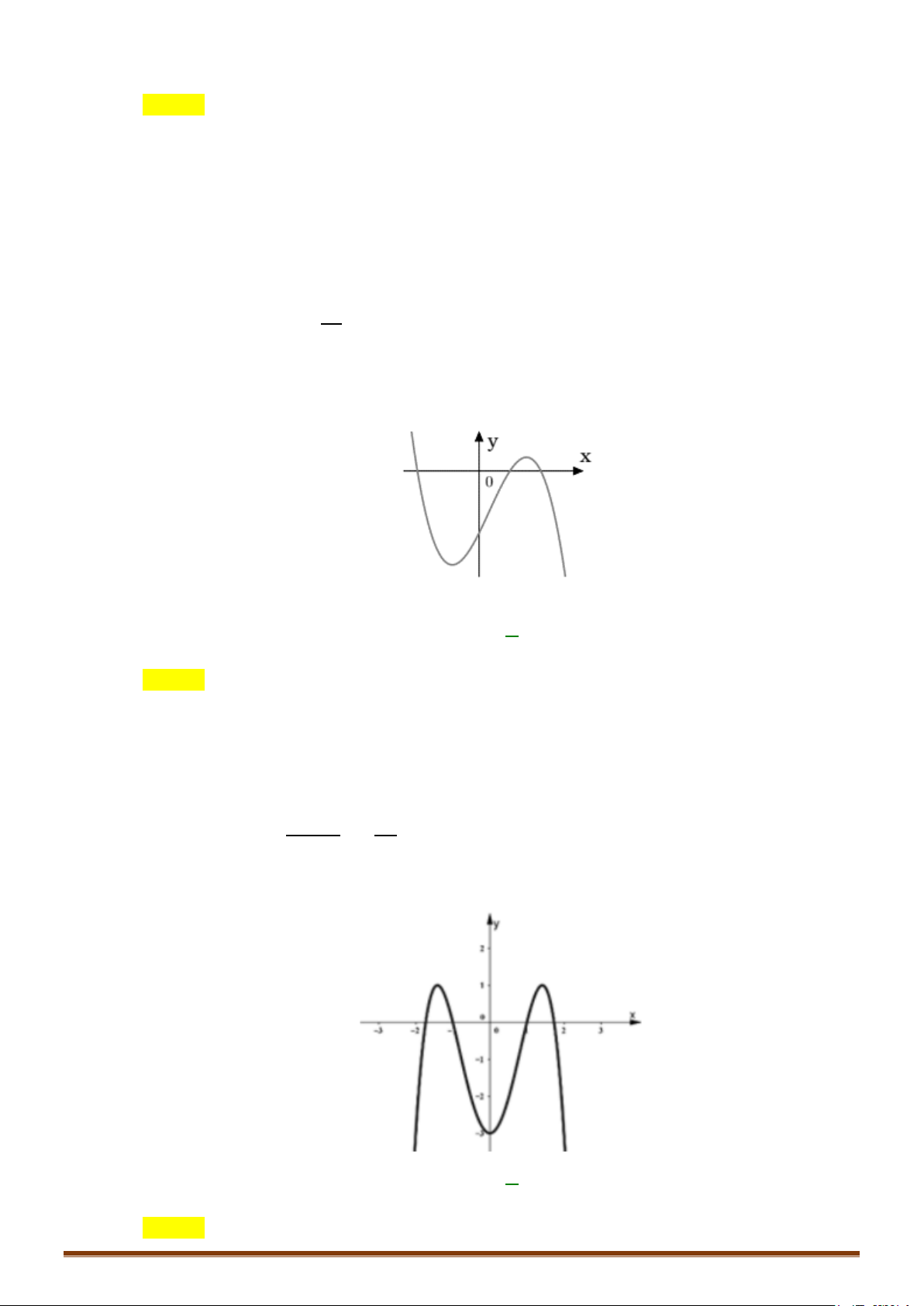
Câu 3. Khảo sát và vẽ đồ thị hàm số 3
y x 1 Lời giải:
Tập xác định: D =  Sự biến thiên: + Chiều biến thiên: 2
y′ = 3x ≥ 0 x
∀ ∈  .Xét y′ = 0 ⇔ x = 0.
Suy ra hàm số luôn đồng biến trên khoảng (−∞;+ ∞).
+ Cực trị : Hàm số không có cực trị
+ Các giới hạn tại vô cực 3
lim y = lim x = +∞; 3 lim y = lim x = . −∞ x→+∞ x→+∞ x→−∞ x→−∞ + Bảng biến thiên: x −∞ 0 +∞ y′ + 0  +∞ y 0 −∞ Đồ thị Ta có 3
x = 0 ⇔ x = 0 .Vậy đồ thị hàm số qua O(0;0) Page 200
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Cho x = 1 ⇒ y = 1 :Đồ thị hàm số cắt Oy tại B 1;  1 .Cho x = 1 − ⇒ y = 1
− :Đồ thị hàm số cắt qua C ( 1 − ; −1).
Lưu ý: Đồ thị hàm số nhận điểm O(0;0) làm tâm đối xứng. Hoành độ điểmO là nghiệm của phương
trình y′′ = 0 (Điểm uốn)
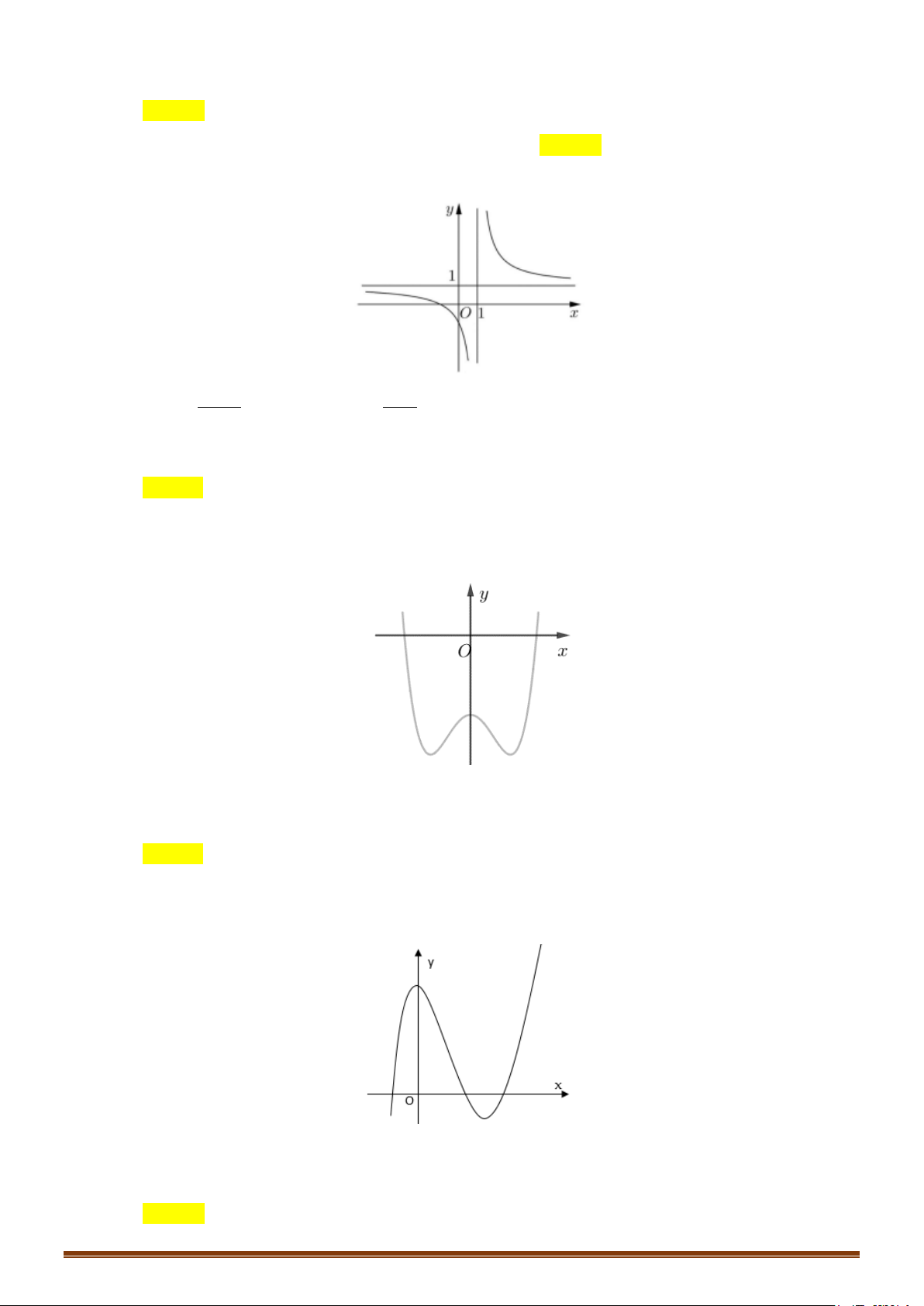
2. HÀM SỐ TRÙNG PHƯƠNG 4 2
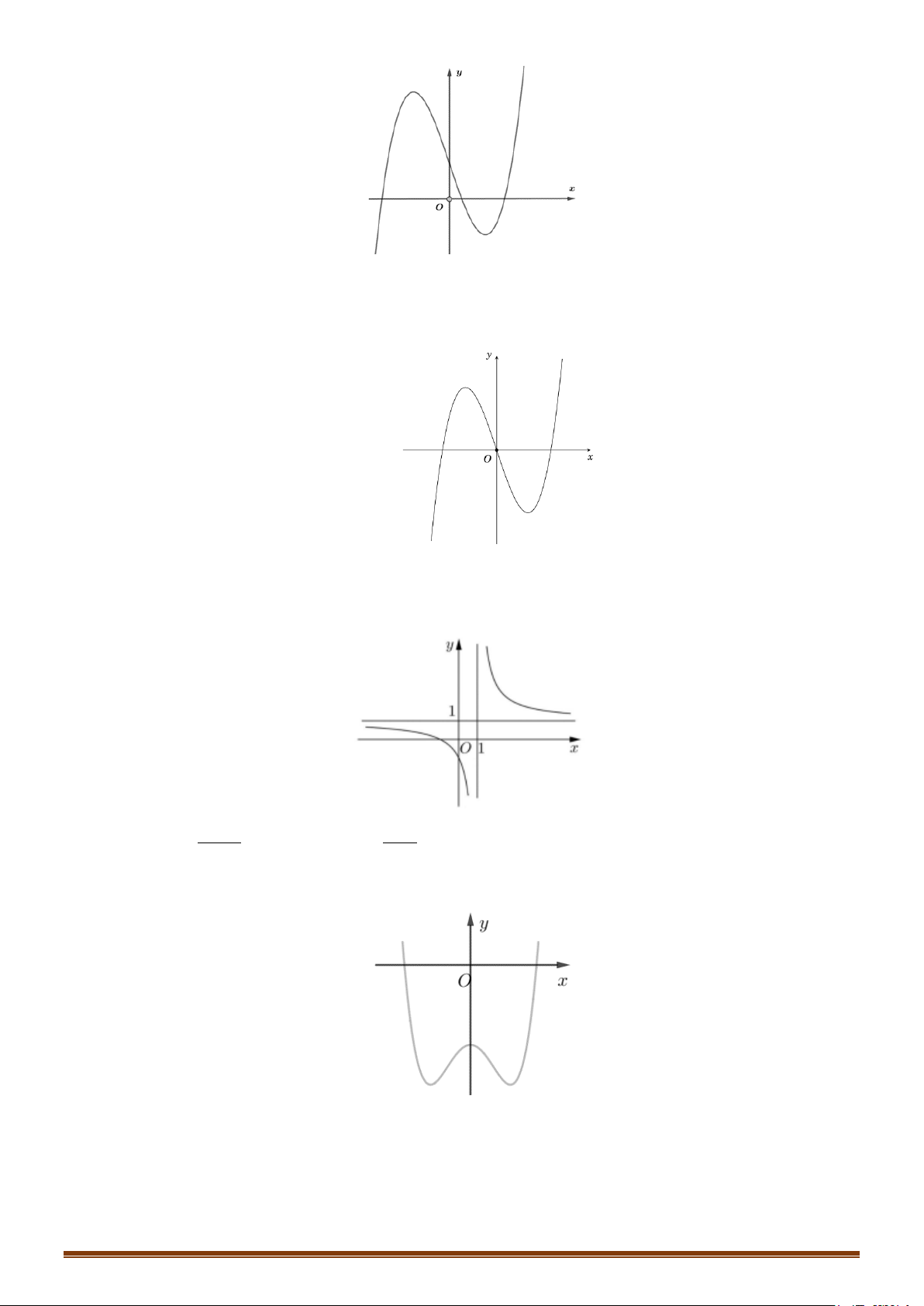
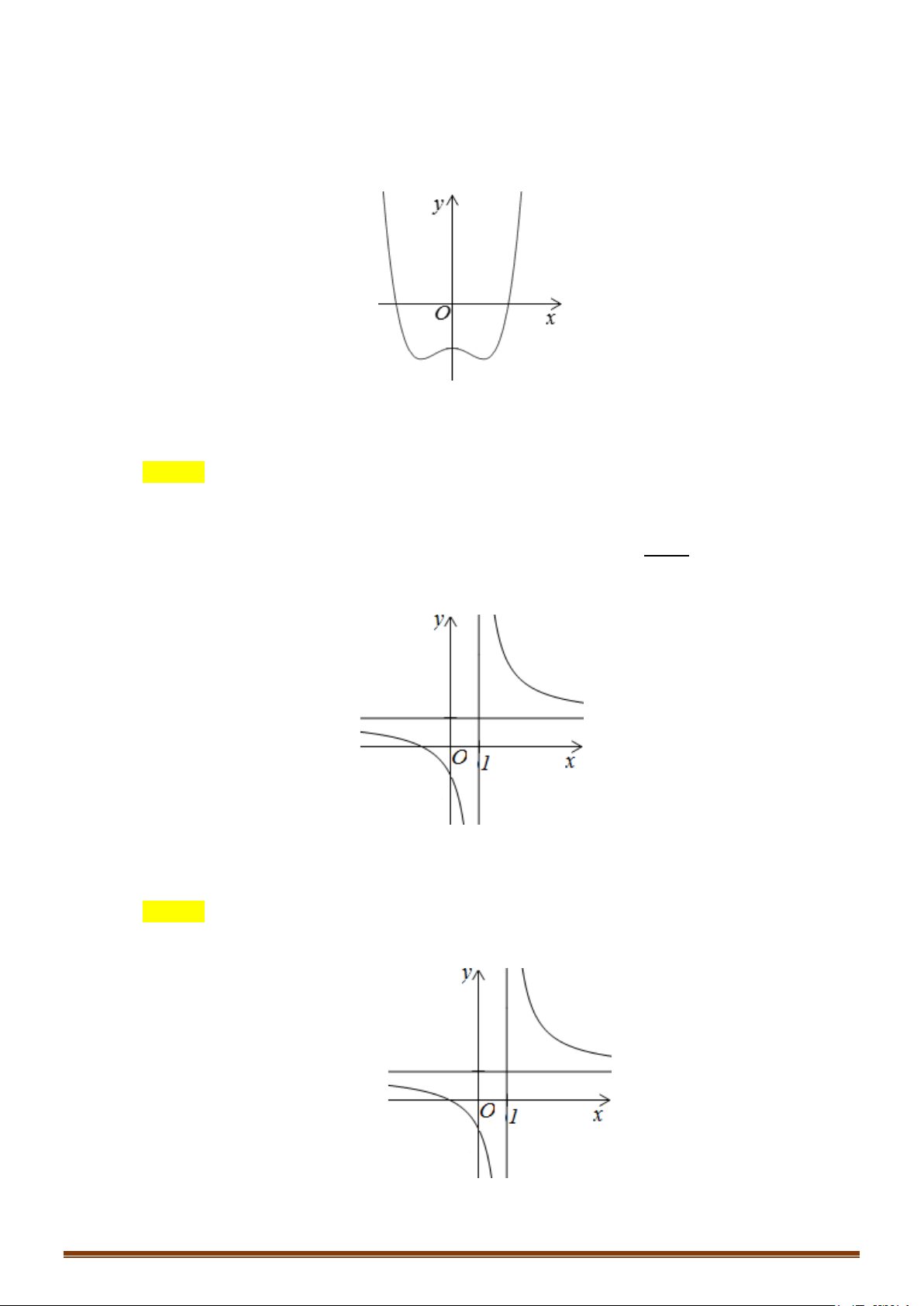
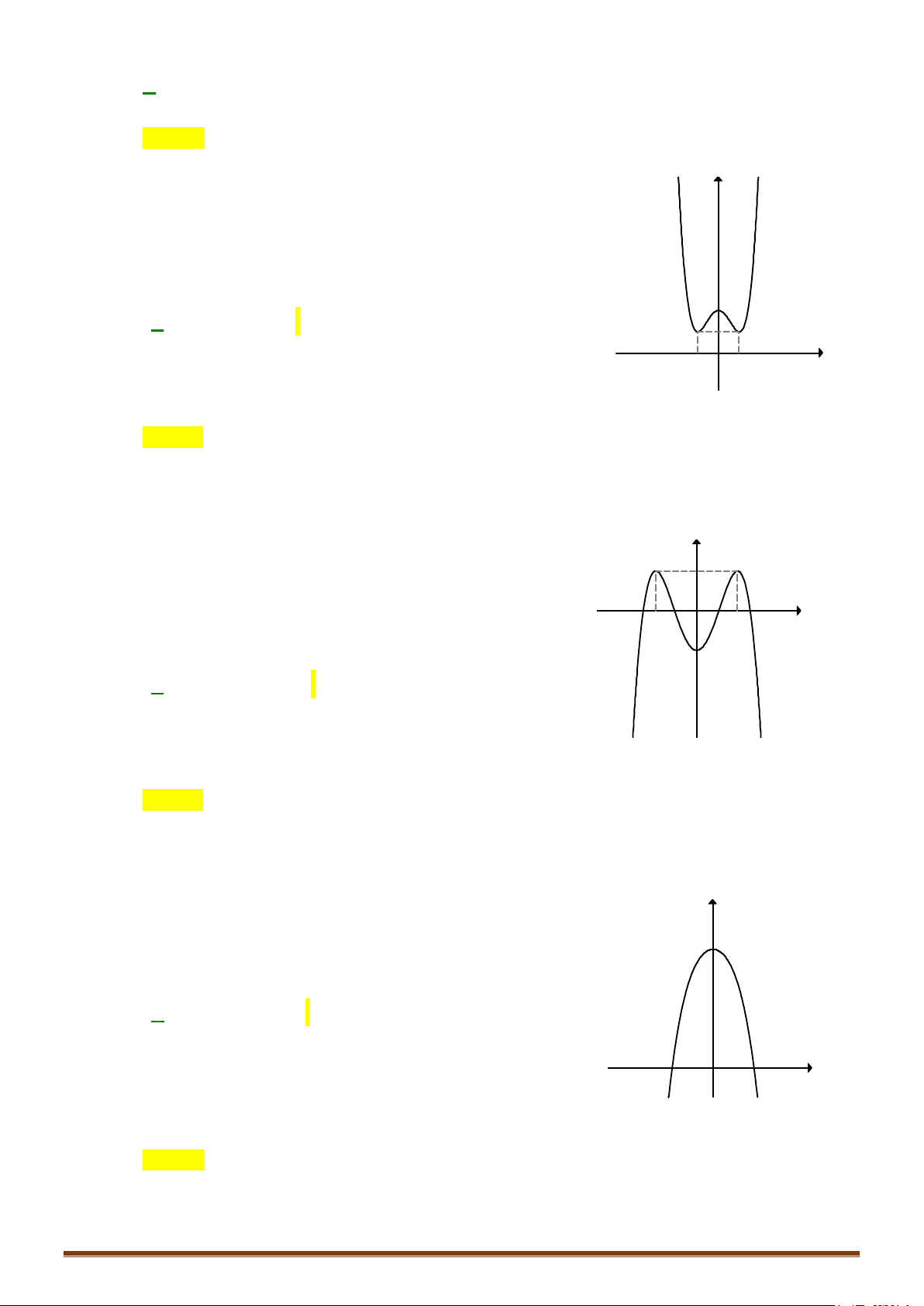
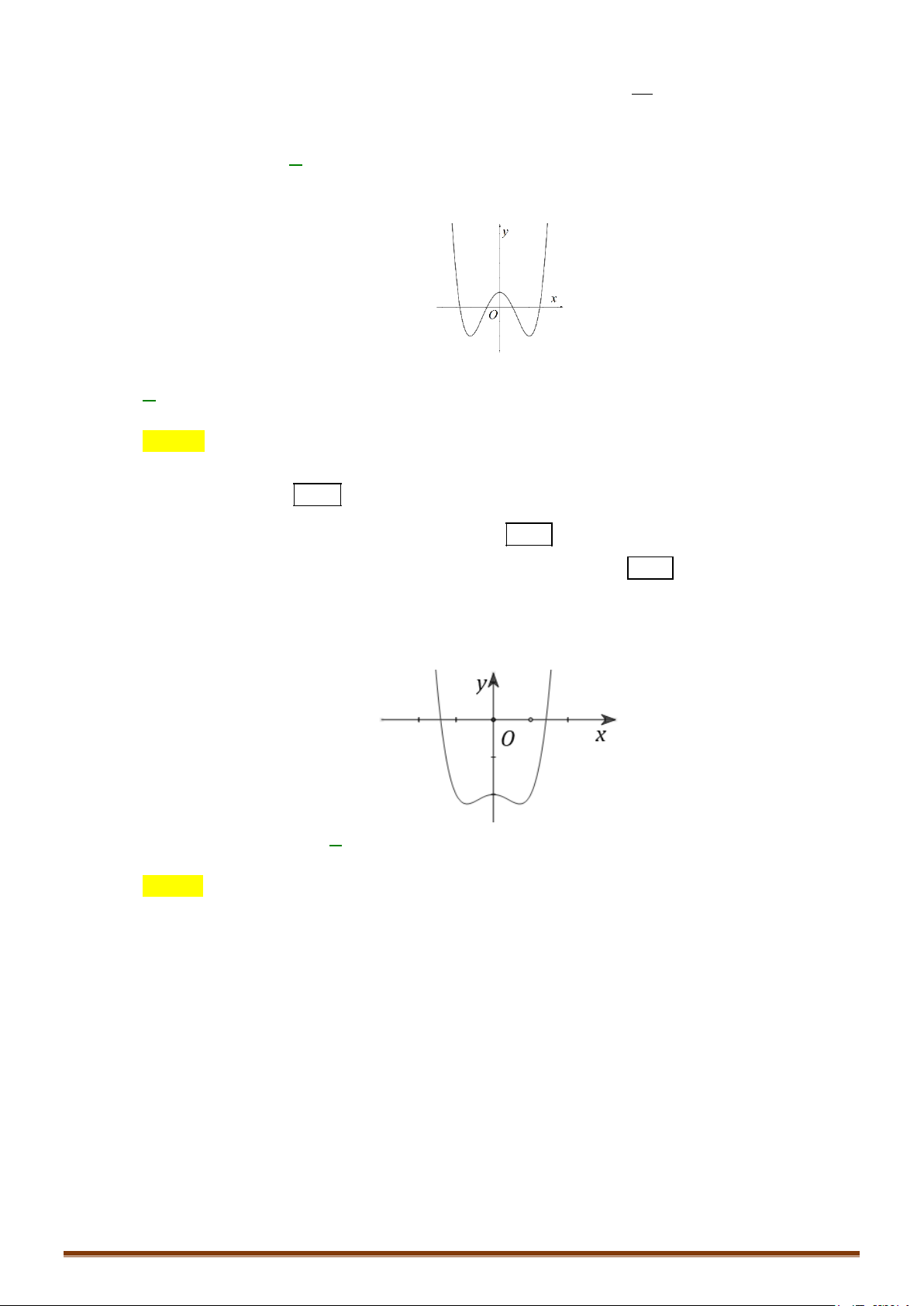
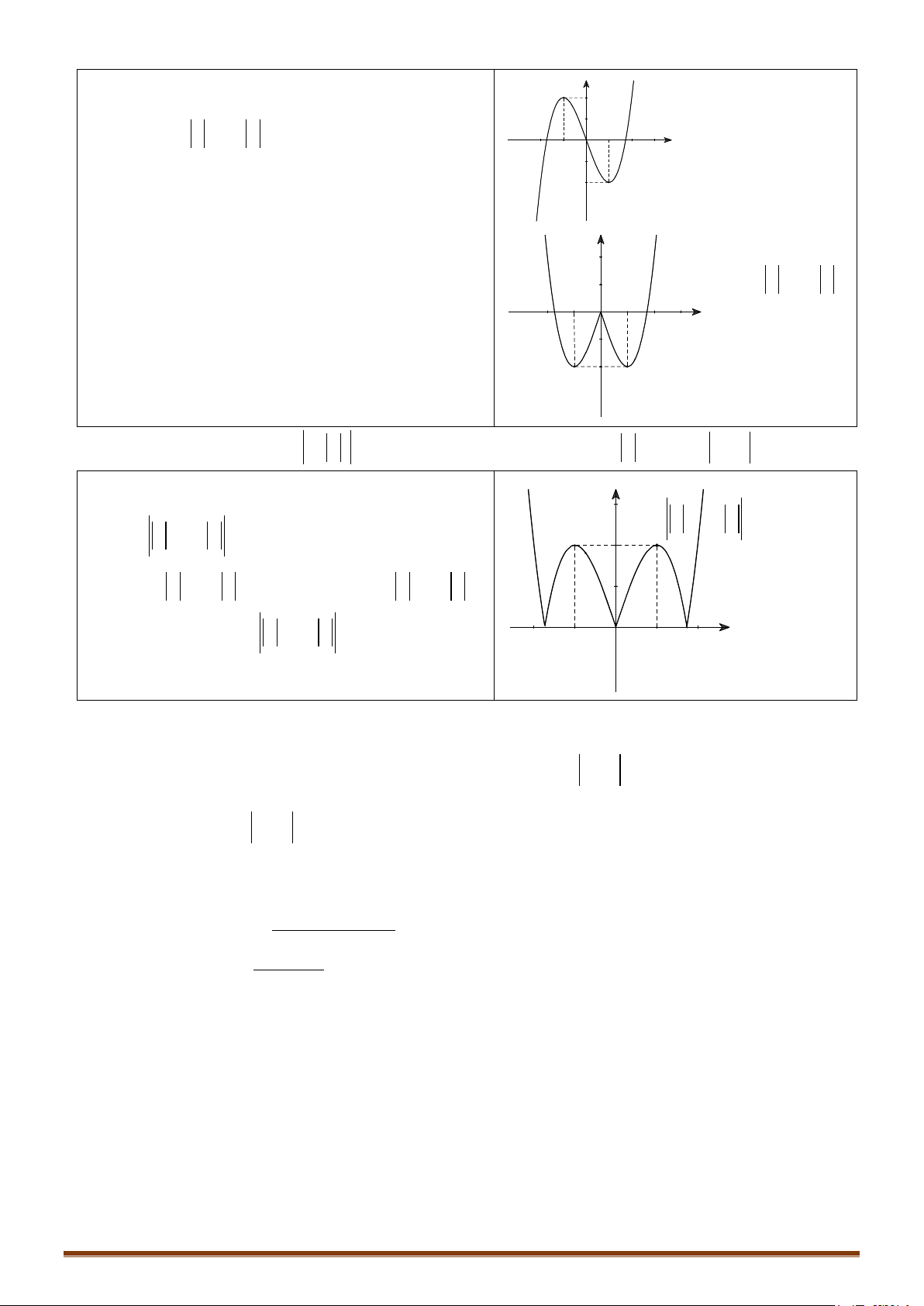
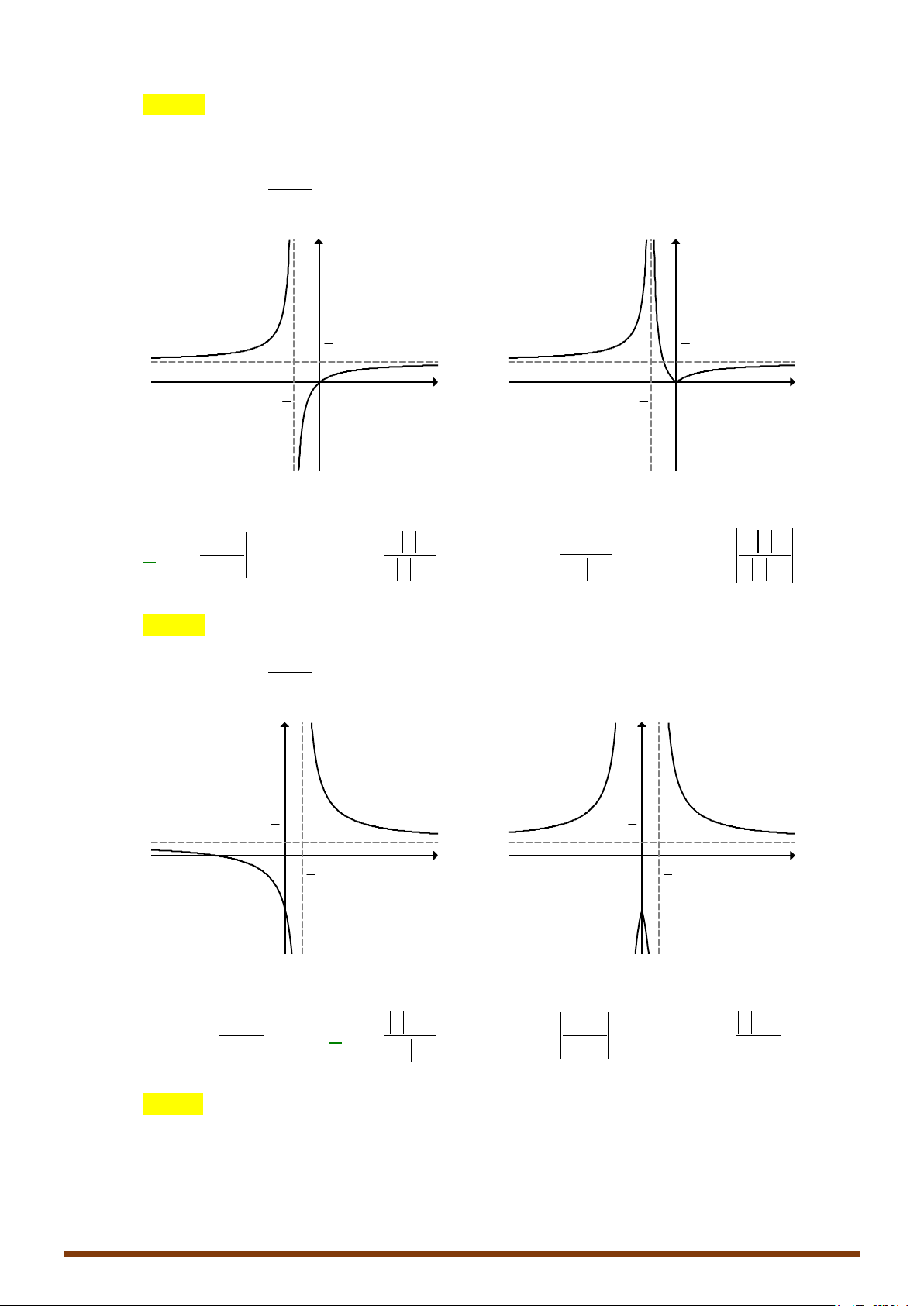
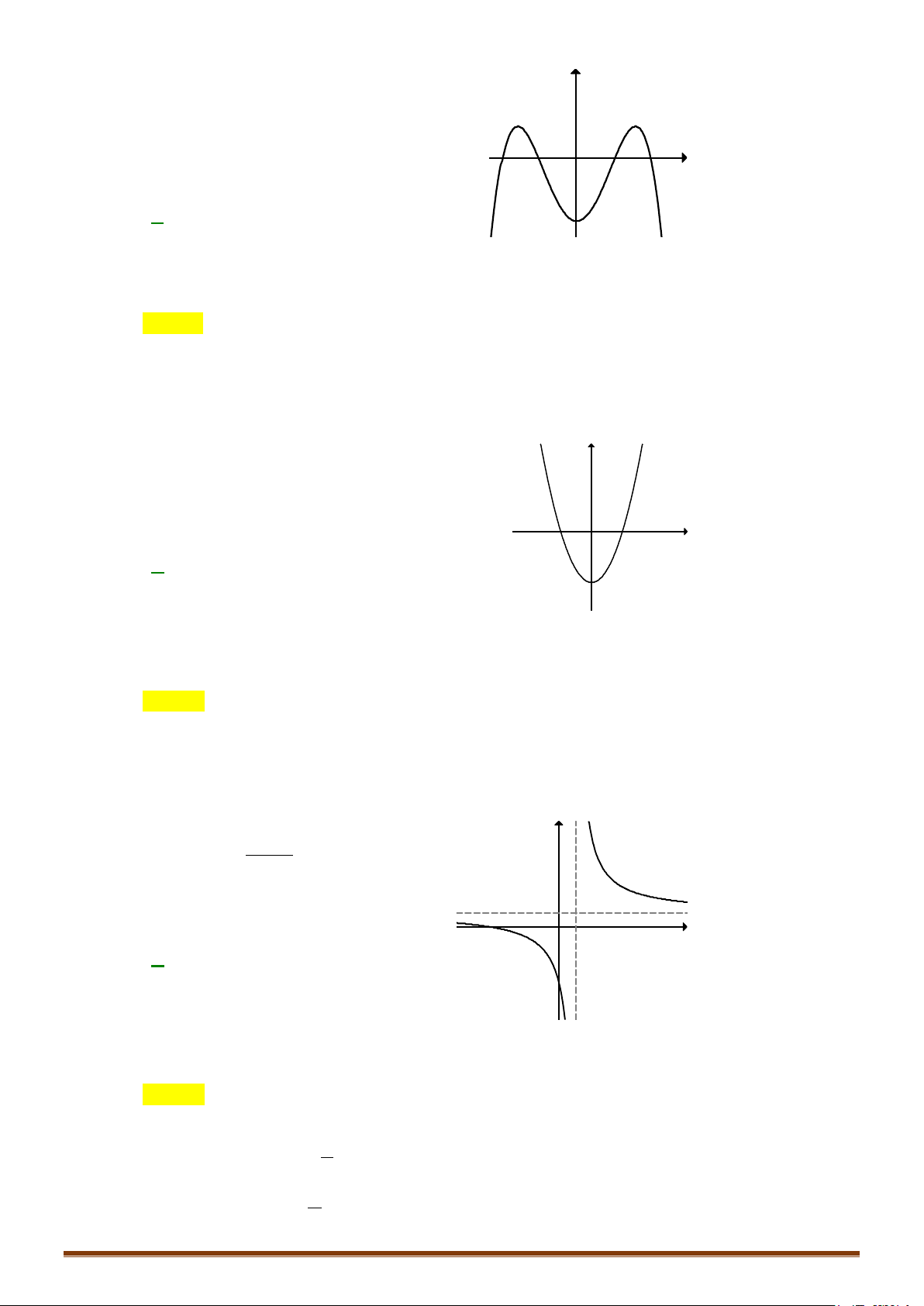
y = ax + bx + c (a ≠ 0) TRƯỜNG HỢP a  0 a < 0 y y Phương trình / y = 0 có
3 nghiệm phân biệt 1 1 1 1 O O x x y y Phương trình / y = 0 có 1 1 nghiệm. 1 1 O x 1 O x
MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
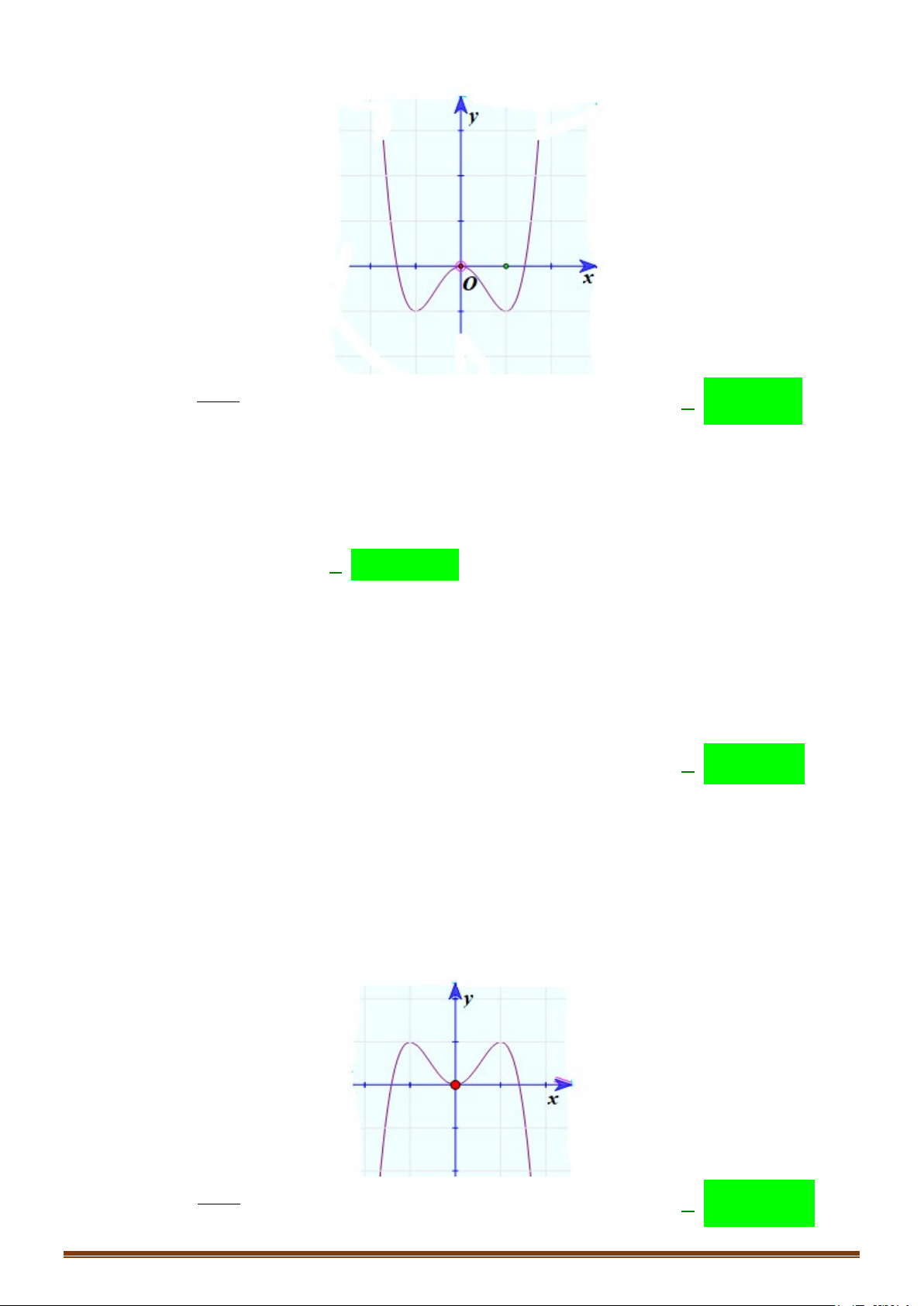
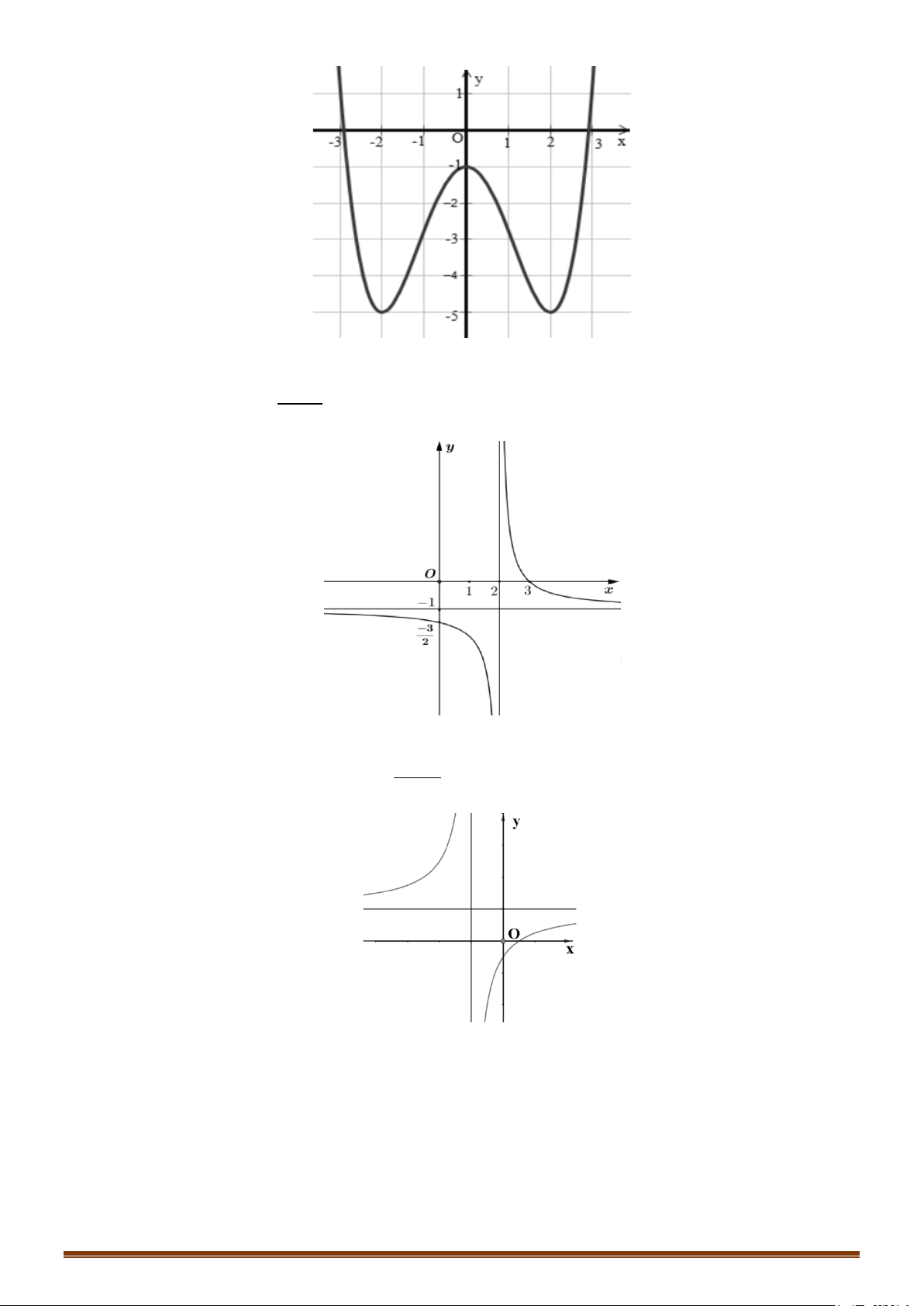
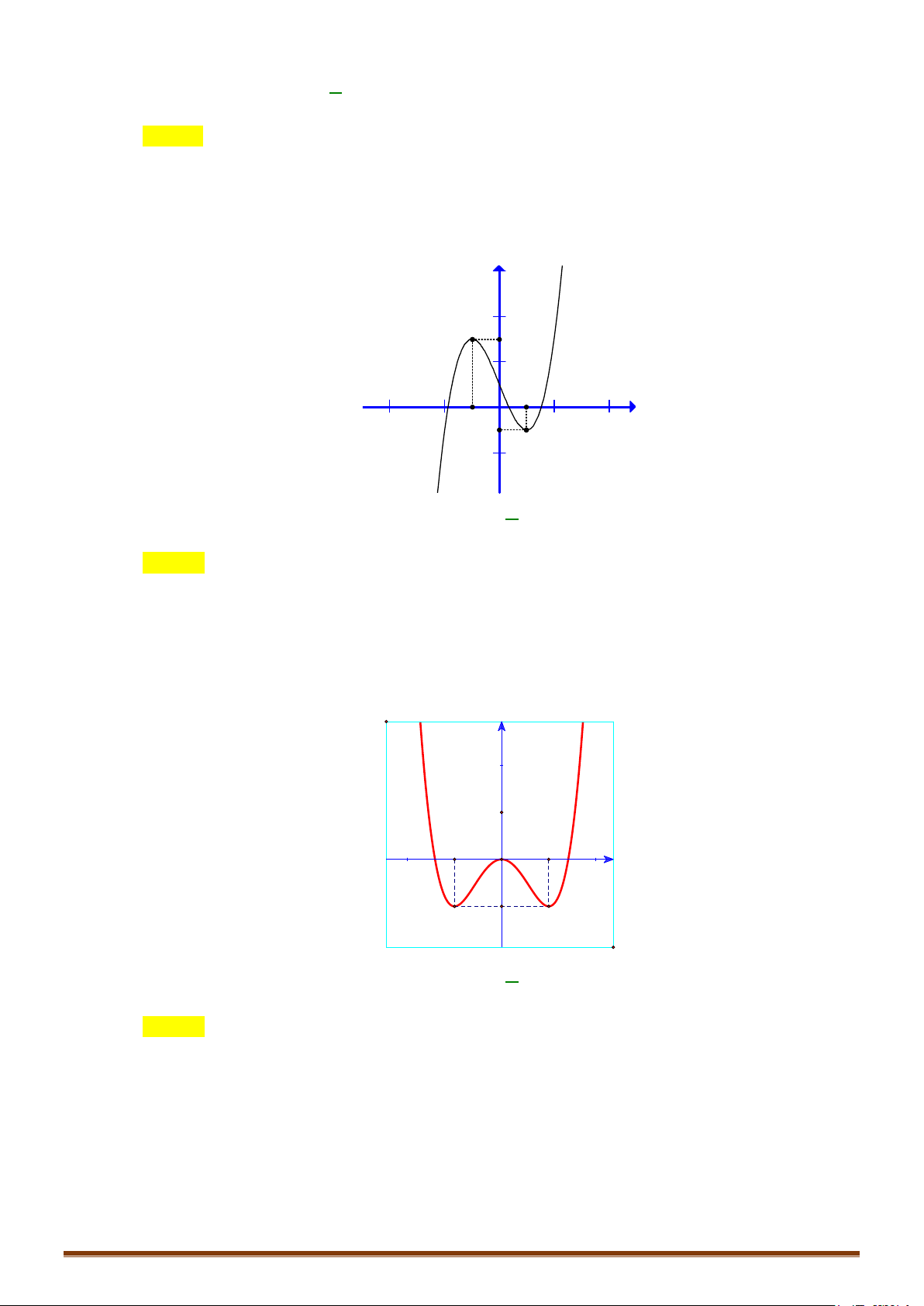
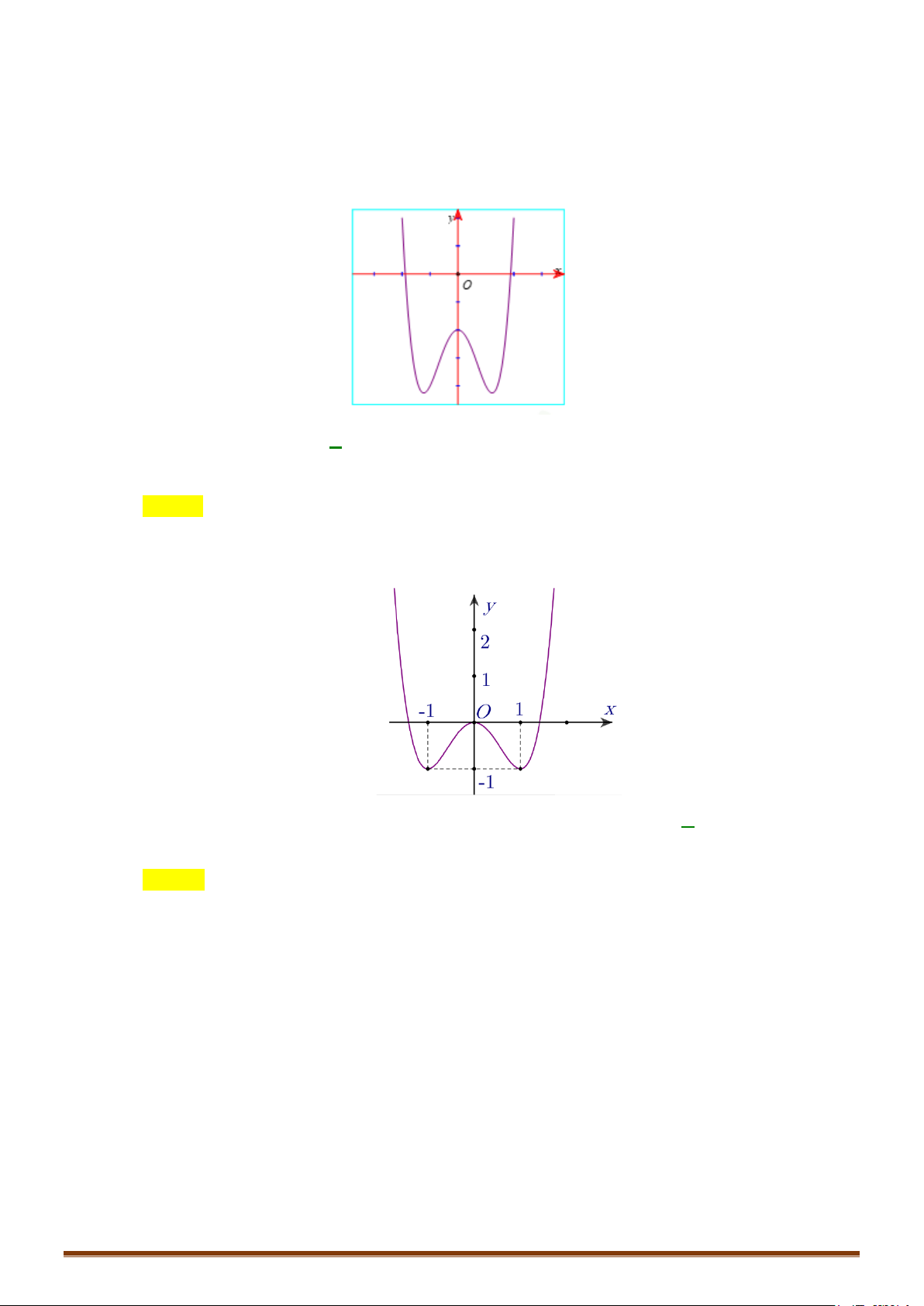
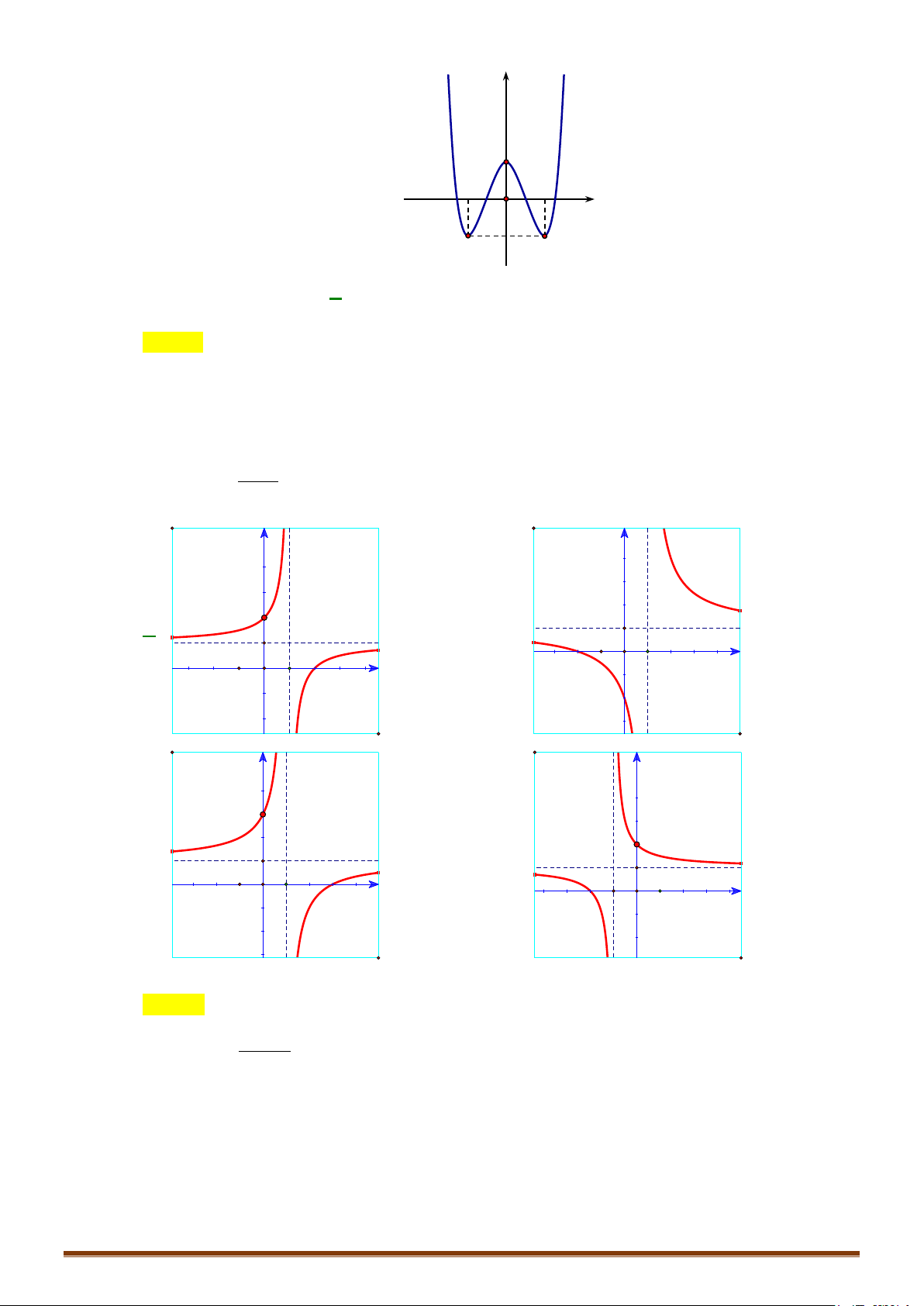
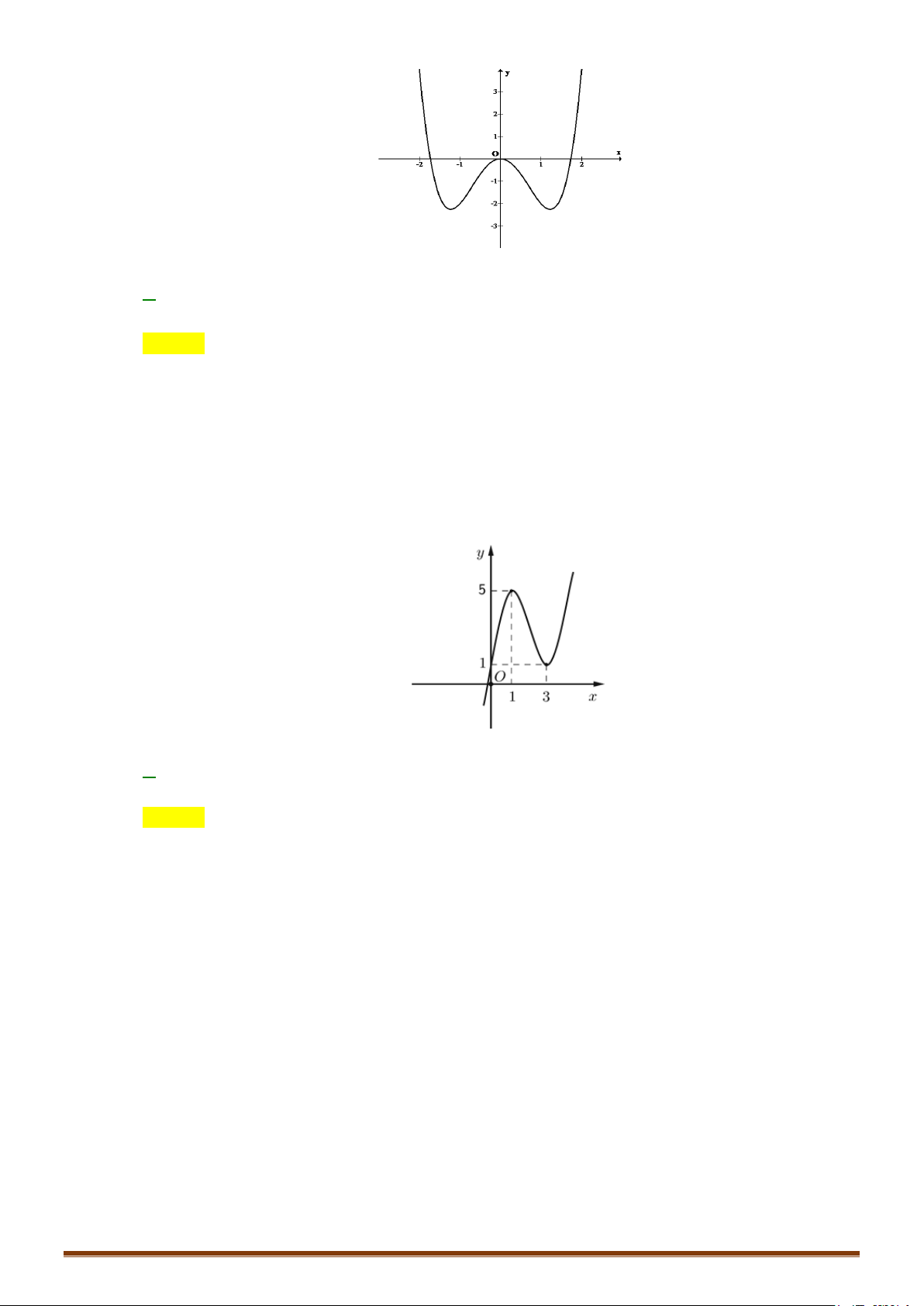
Câu 1. Khảo sát và vẽ đồ thị hàm số y = 4 x − 2 2x − 3 Lời giải:
Tập xác định: D =  Sự biến thiên: + Chiều biến thiên: Page 201
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x = 0 3
y′ = x − x = x( 2 4 4
4 x −1) .Xét y′ = 0 ⇔  x = 1 ± 
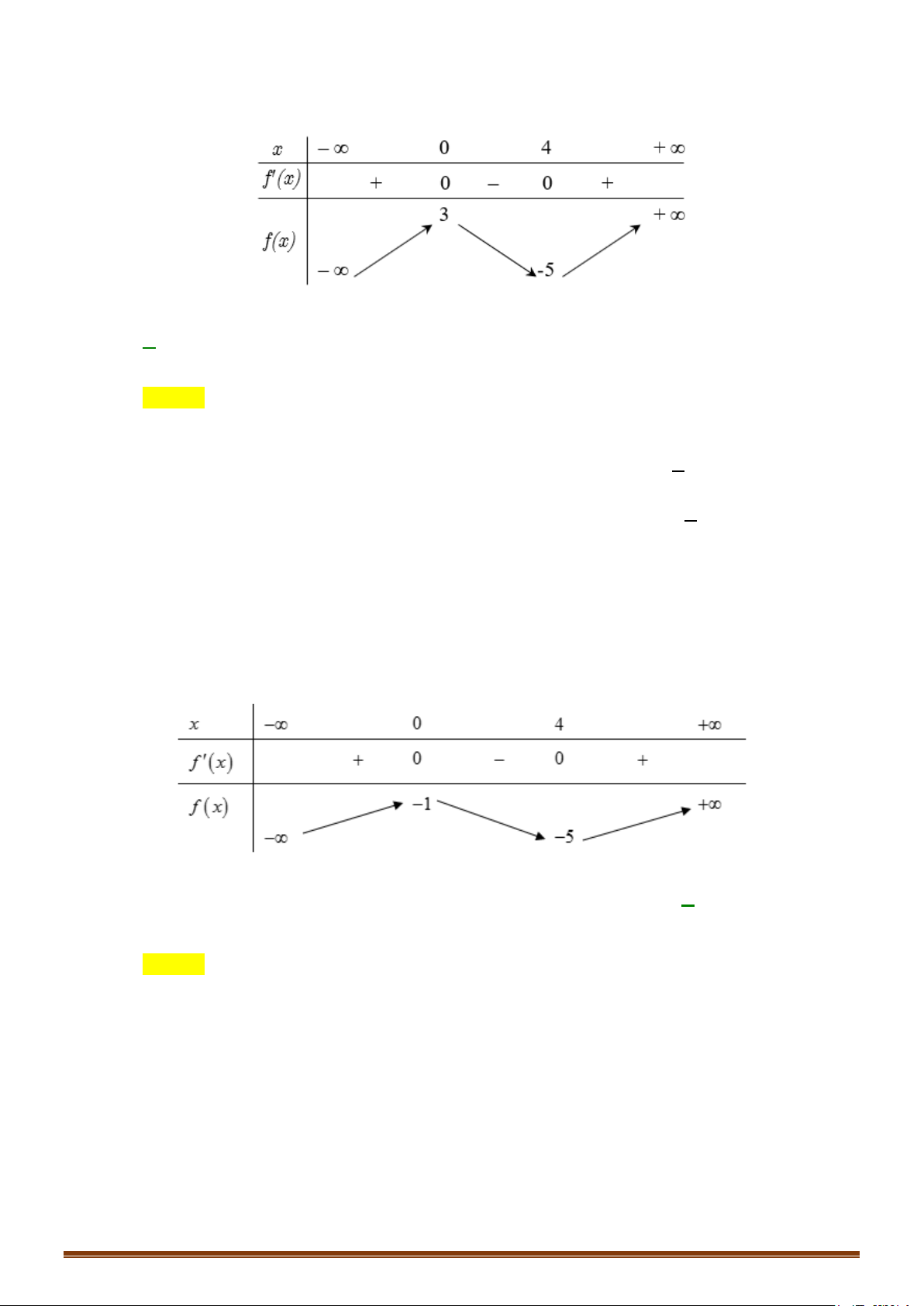
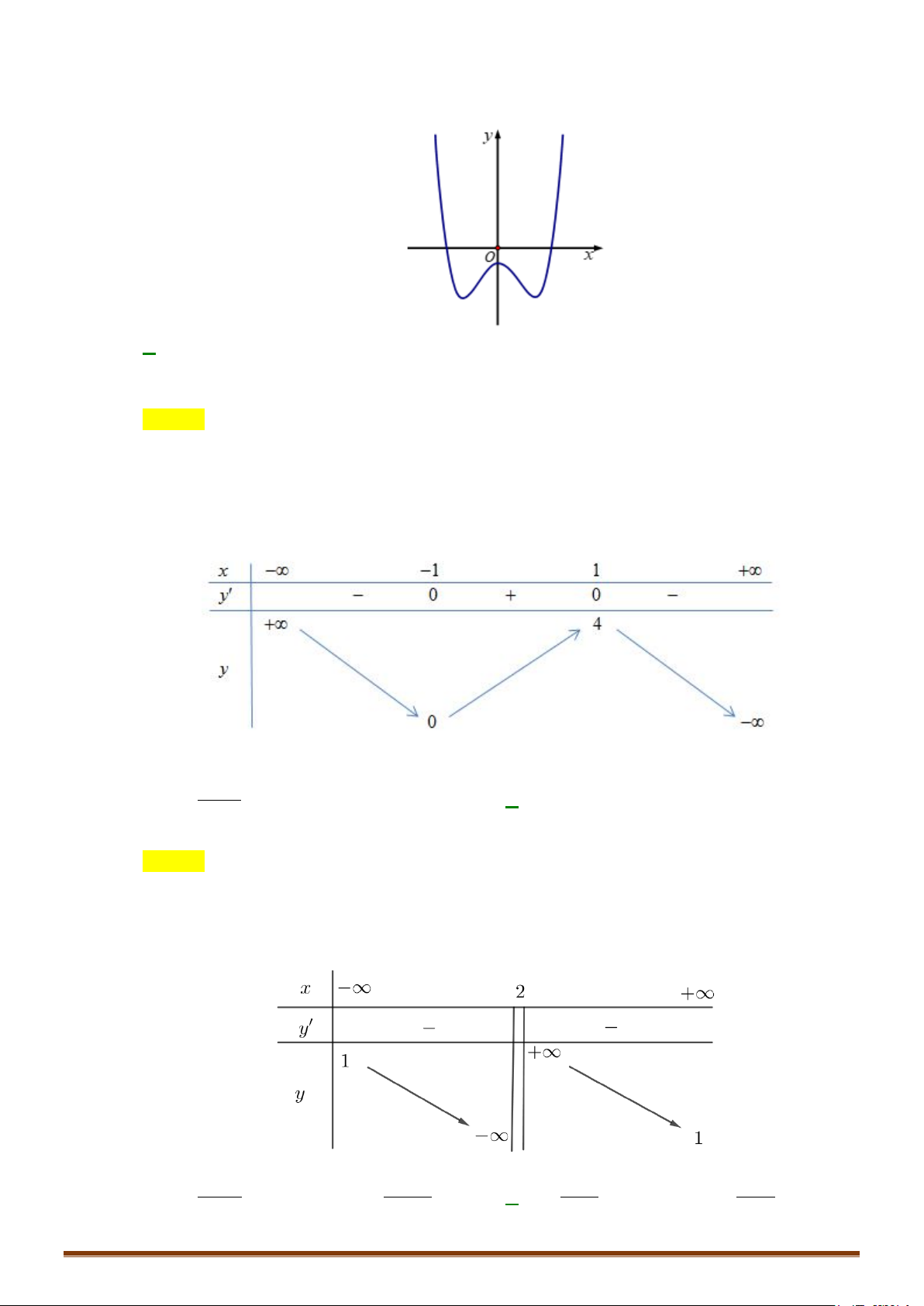
+ Các giới hạn tại vô cực 4  2 3 lim y lim x 1  = − − =  . +∞  2 4 x→+∞ x→±∞  x x  + Bảng biến thiên x −∞ 1 − 0 1 +∞ y′ − 0  0 −∞ 0 + +∞ +∞ y 3 − 4 − 4 −
Hàm số đồng biến trên các khoảng ( 1 − ; 0) và (1; + ∞)
Hàm số nghịch biến trên các khoảng (−∞ ; −1) và (0; 1) + Cực trị :
Hàm số đạt cực đại tại x = 0; y = y(0) = 3 − . cd
Hàm số đạt cực tiểu tại x = 1 ± ; y = y( 1 ± ) = 4 − ct Đồ thị Ta có 4 2
x − 2x − 3 = 0 ⇔ x = 1
± .Vậy đồ thị hàm số qua A(1;0), B( 1 − ; 0).
Cho x = 0 ⇒ y = 3
− :Đồ thị hàm số cắt Oy tại C (0;− 3) .Cho x = 2
± ⇒ y = 5 : Đồ thị hàm số qua D( 2 − ; 5), E(2 ; 5).
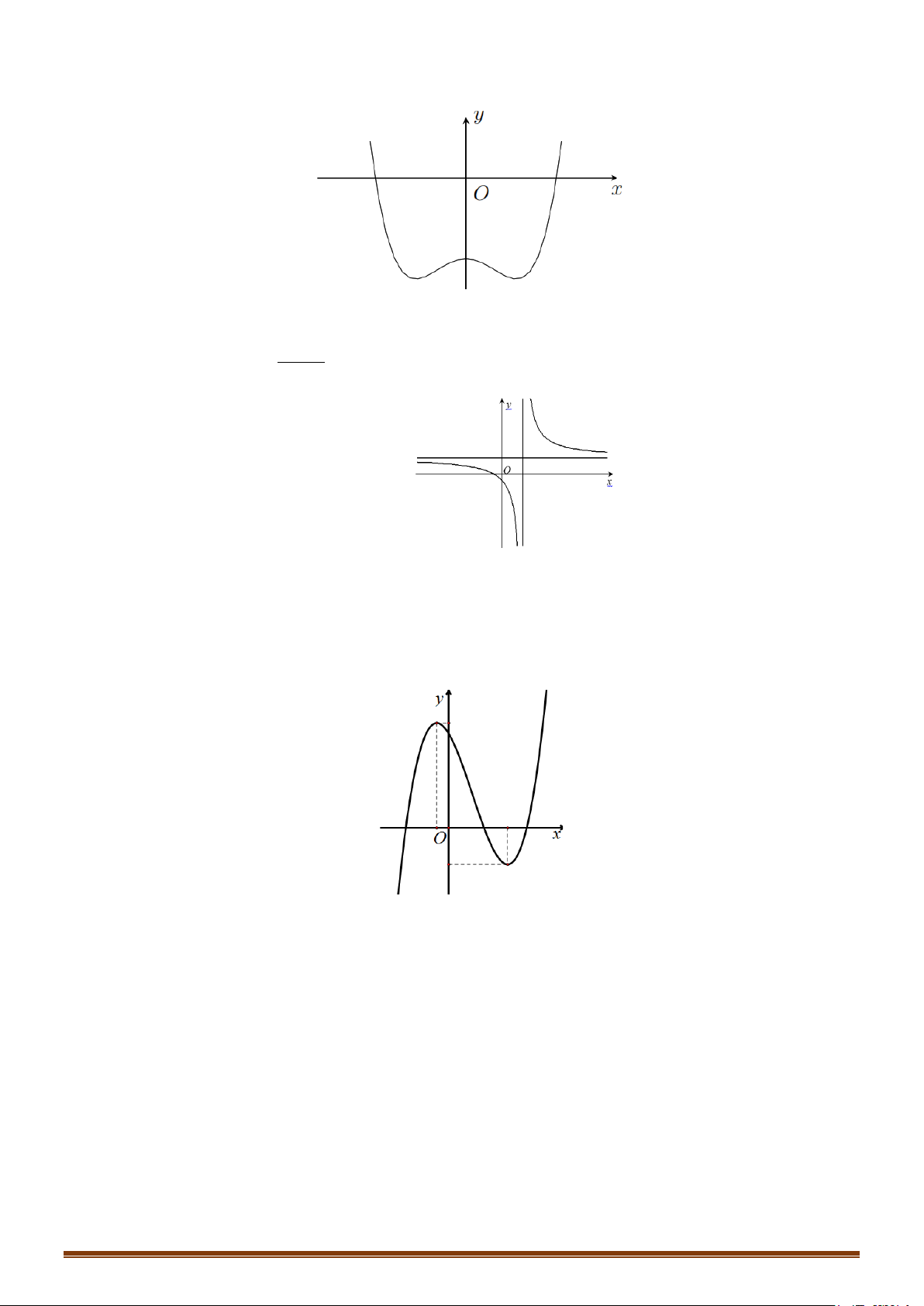
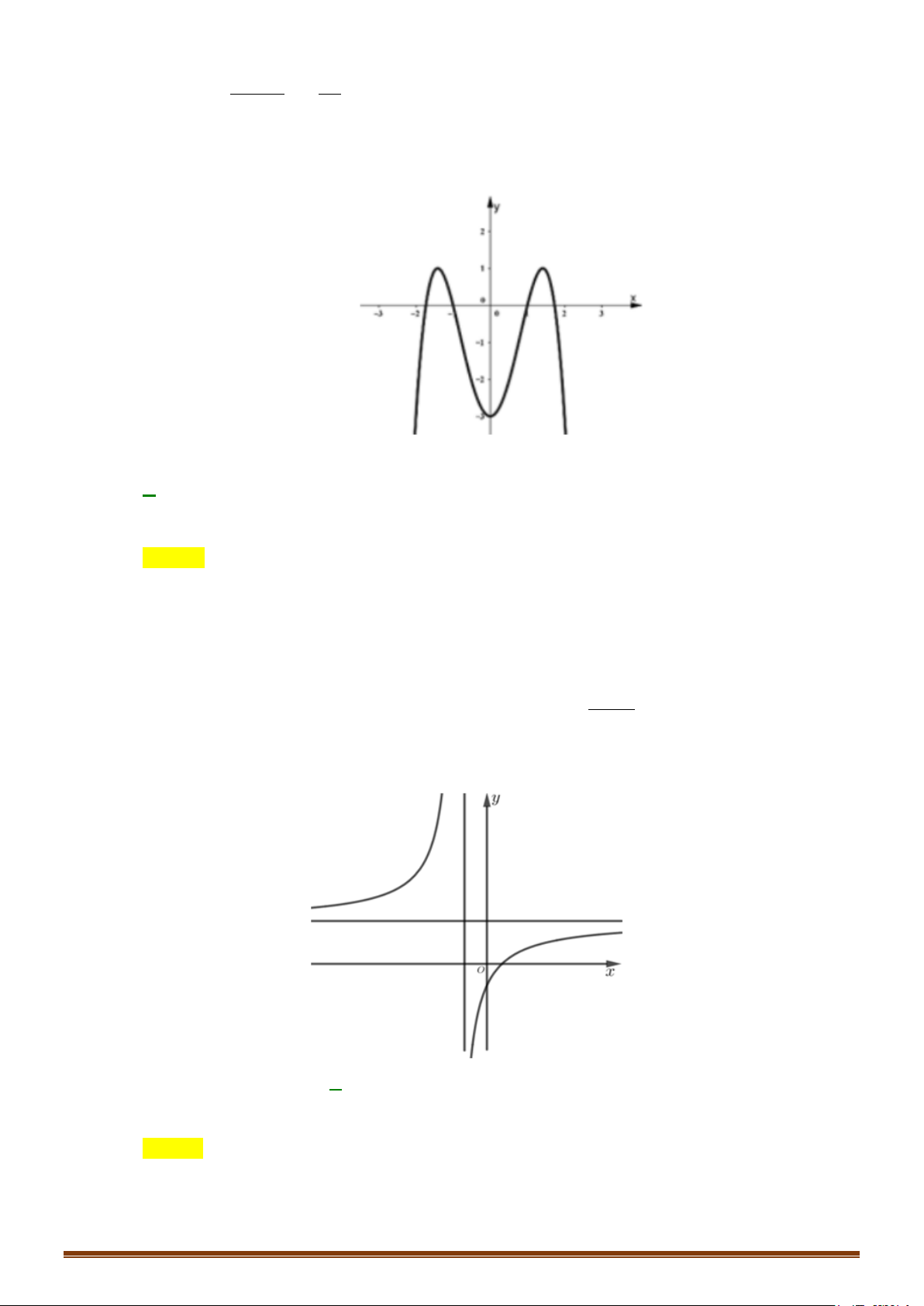
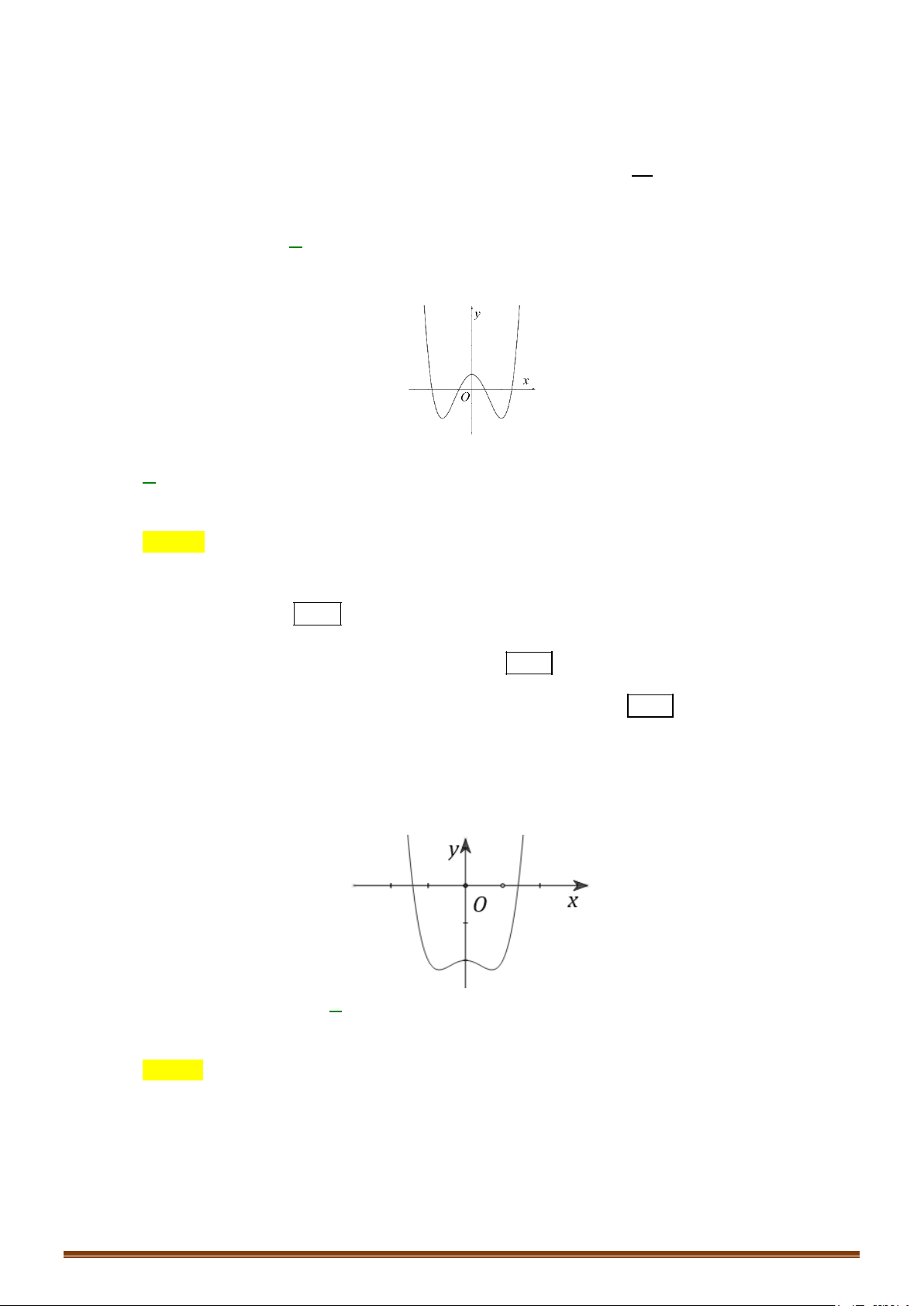
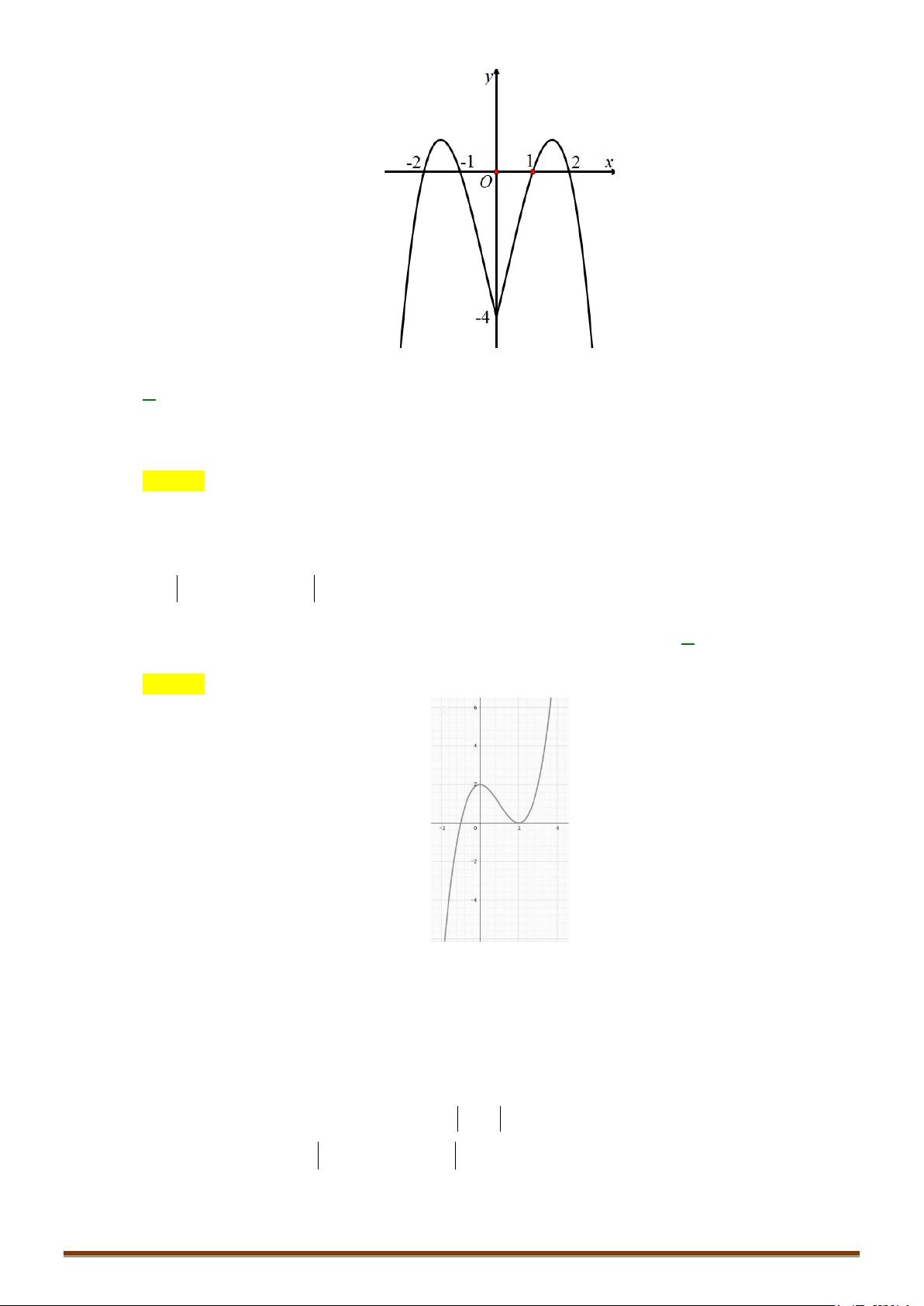
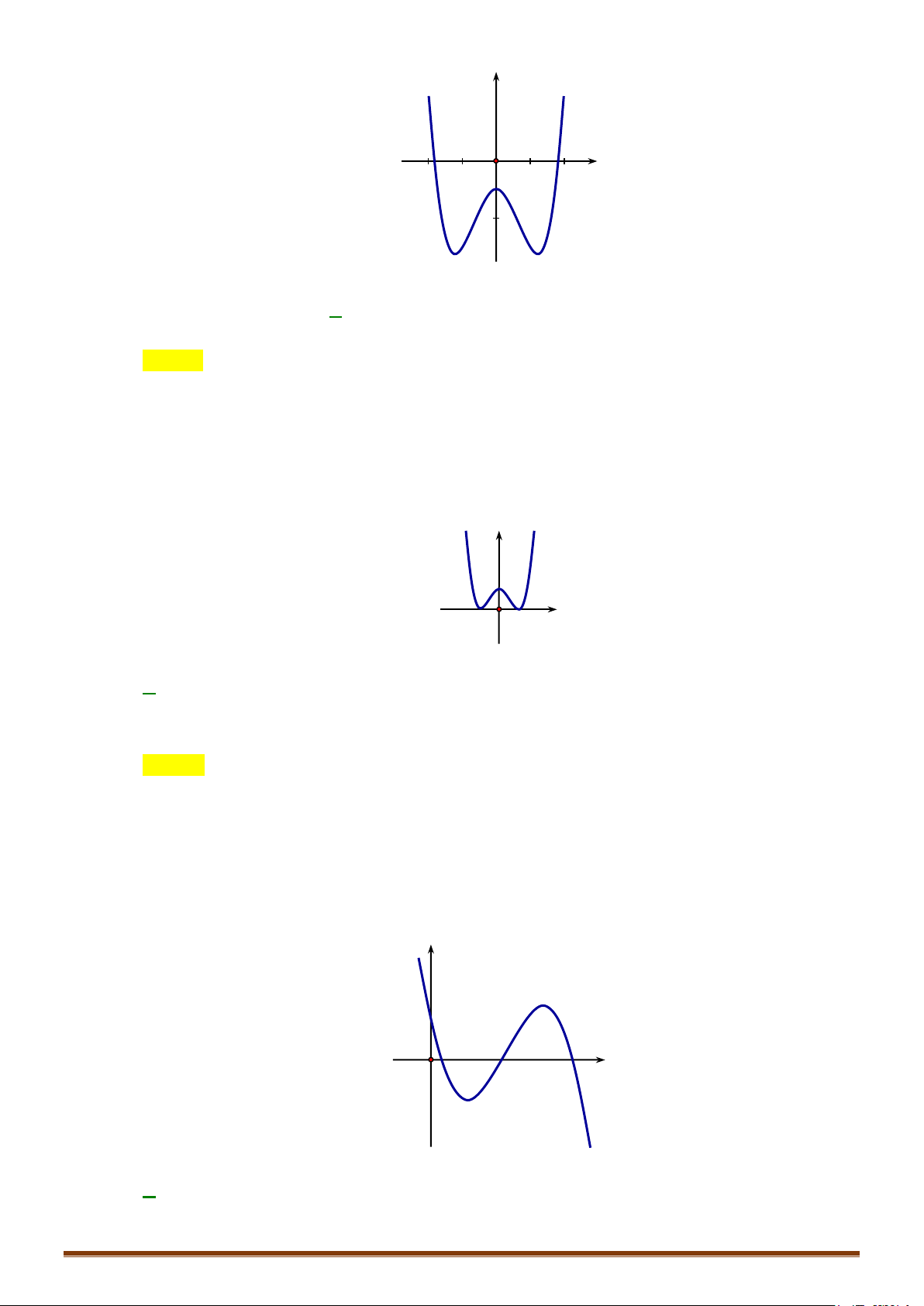
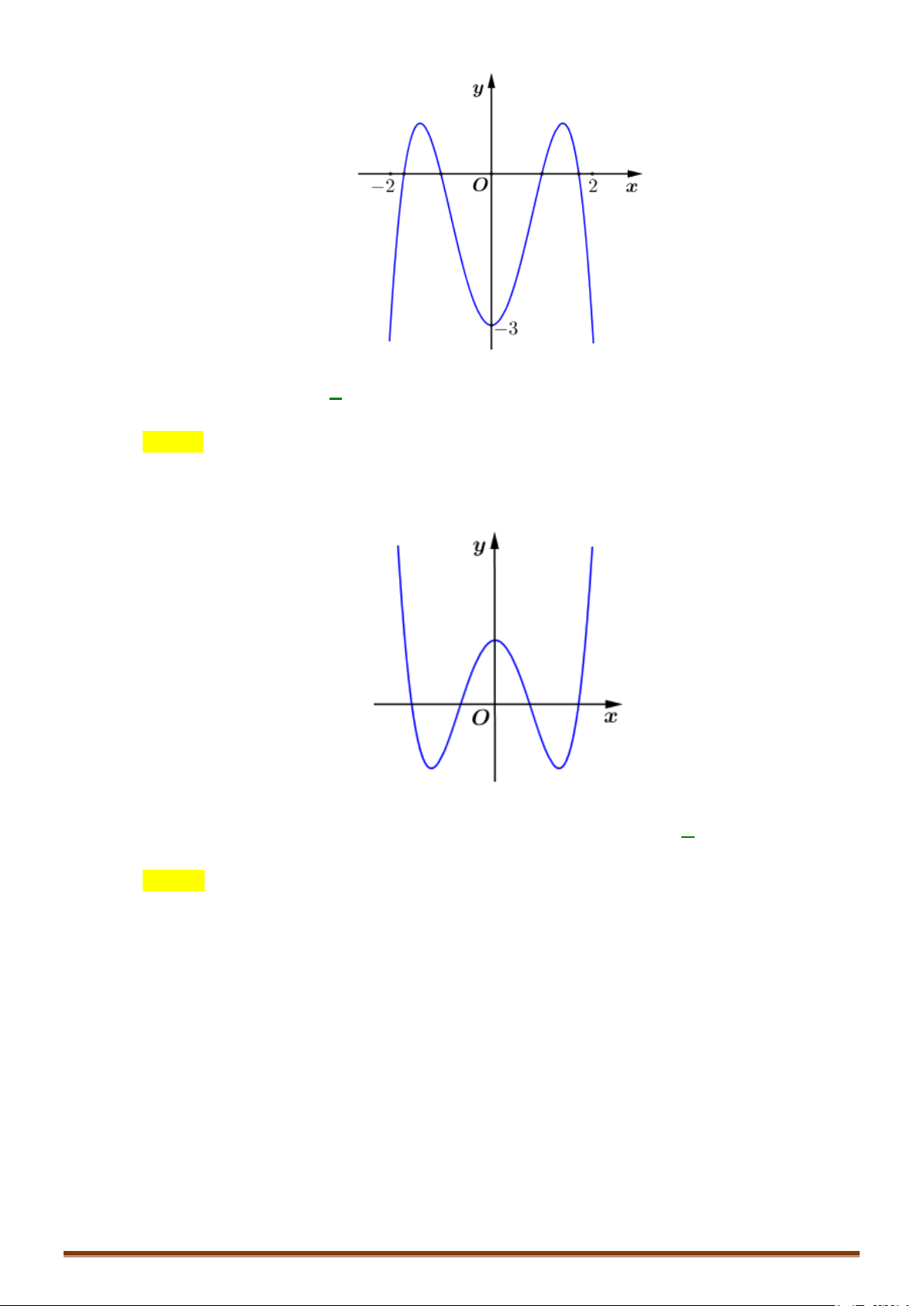
Lưu ý: Đồ thị hàm số nhận Oy làm trục đối xứng. y 1 − O 1 x 3 − 4 − 2 4
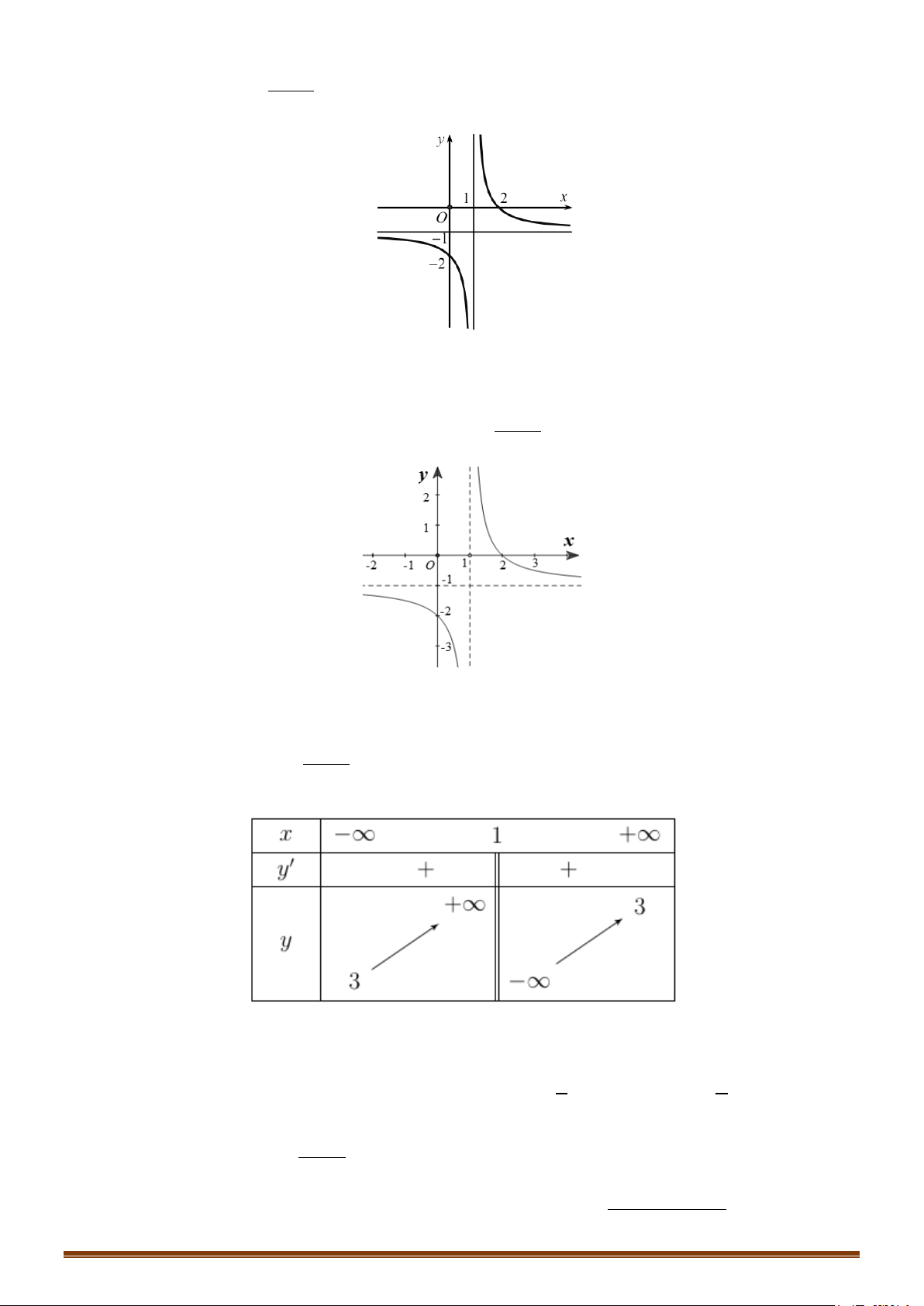
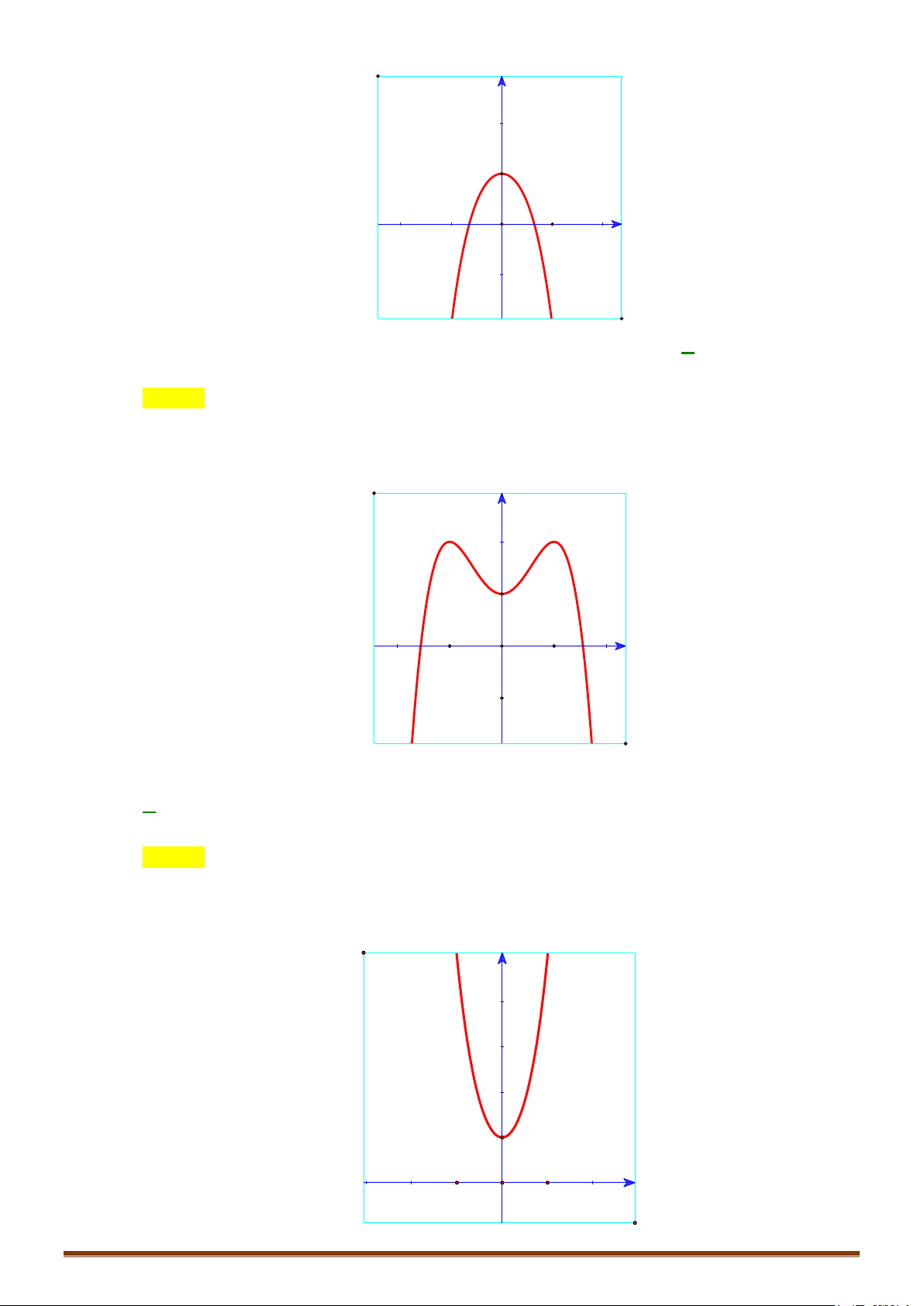
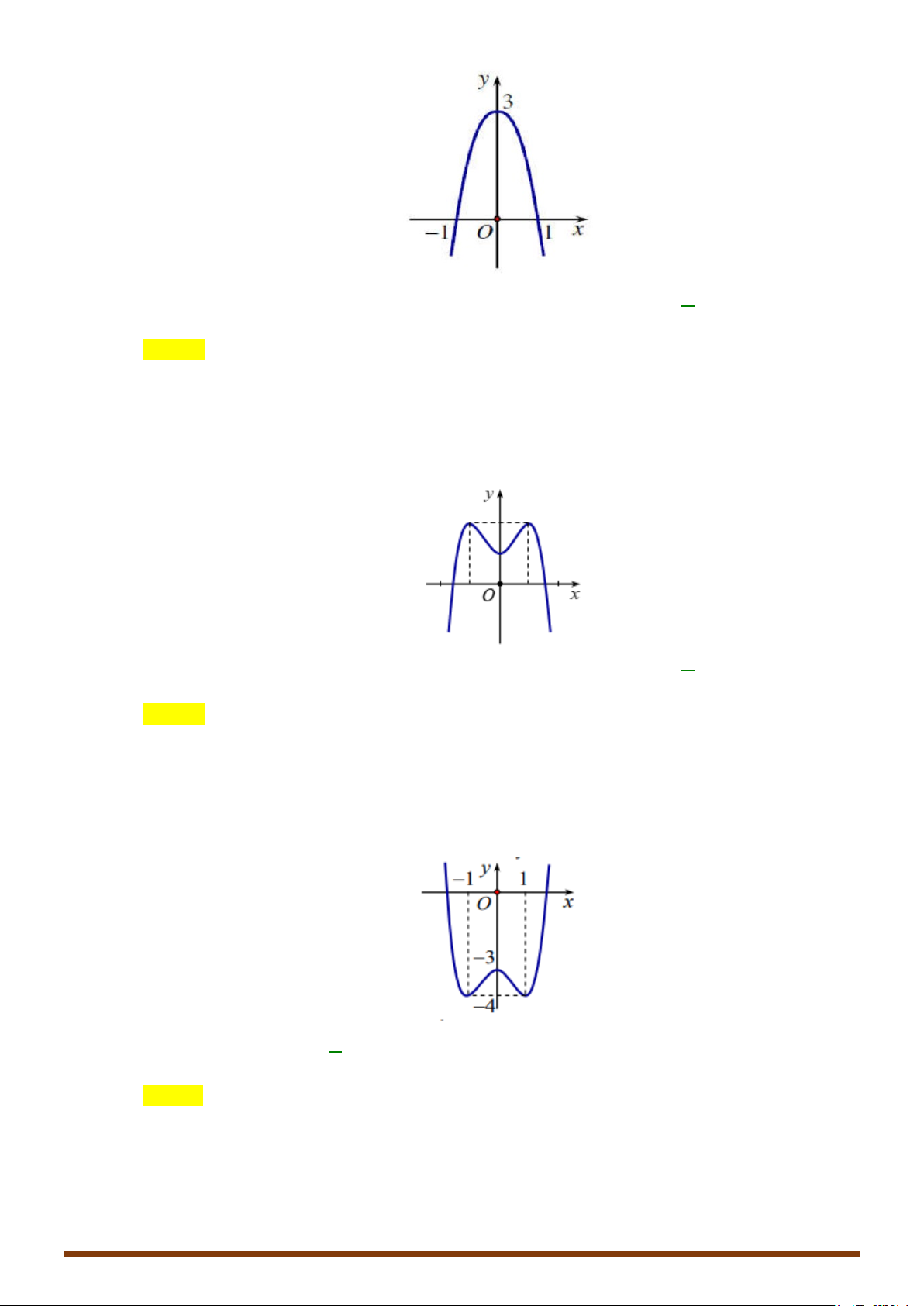
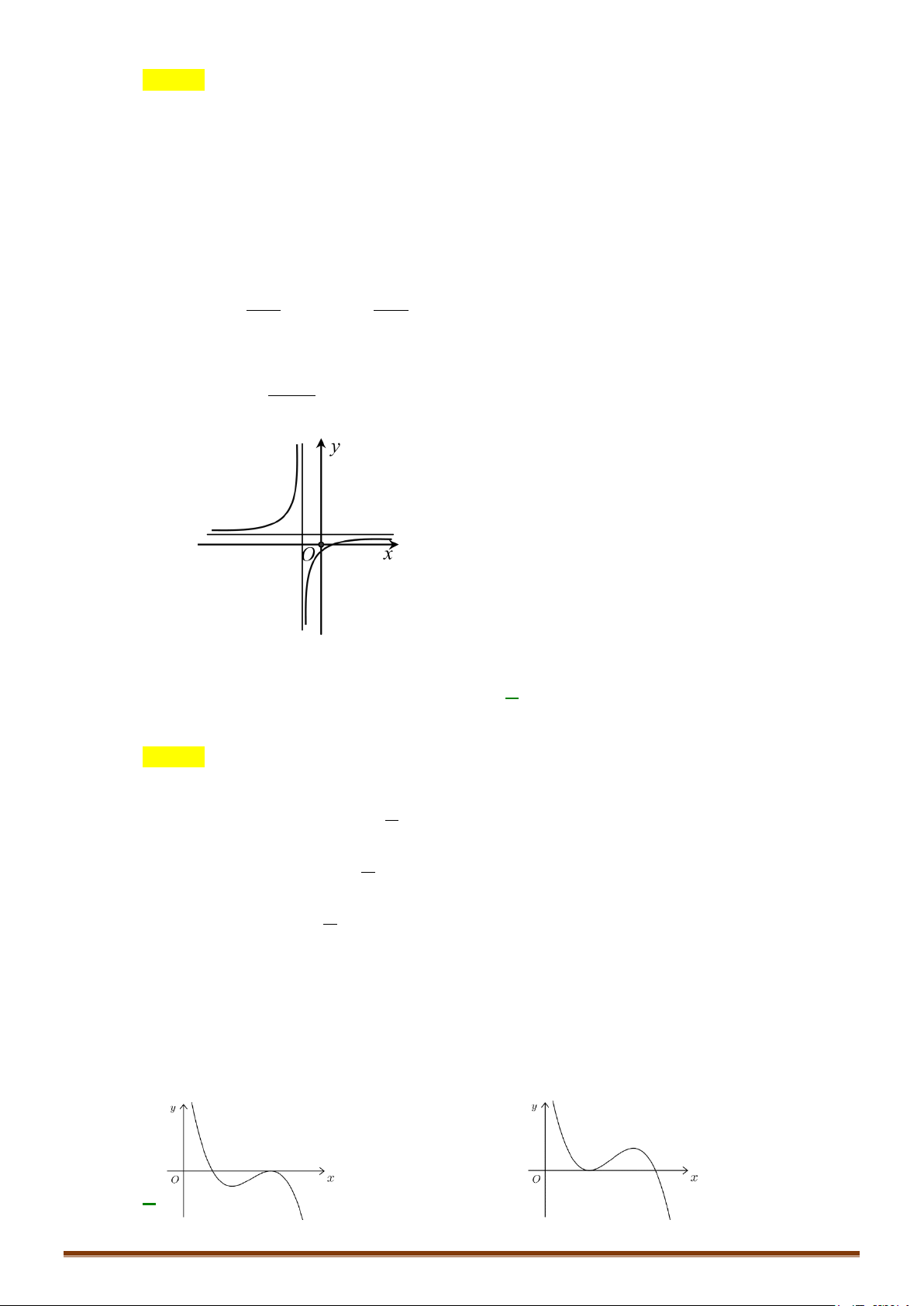
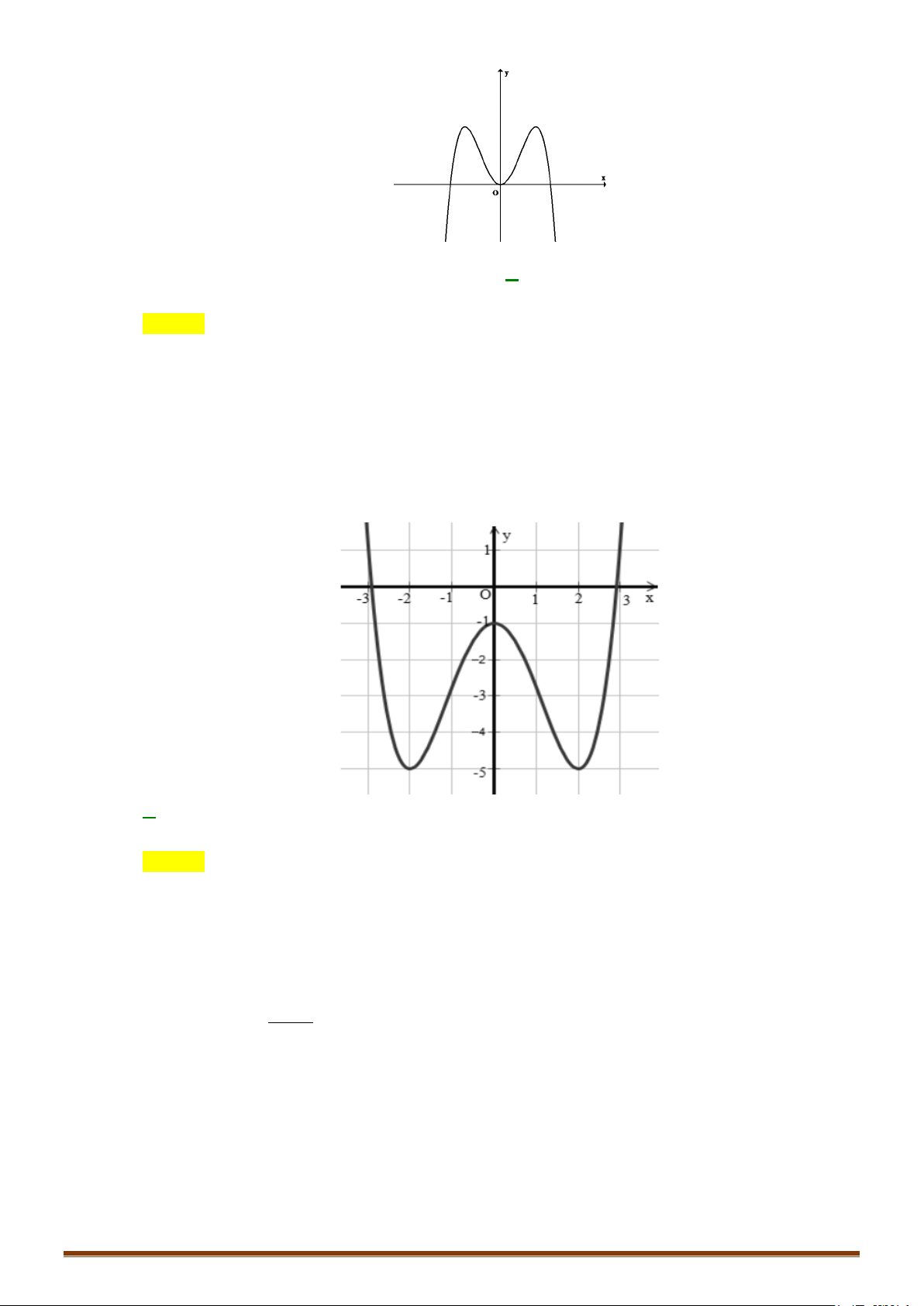
Câu 2. Khảo sát và vẽ đồ thị hàm số 4 x x y = − − 2 8 Lời giải:
Tập xác định: D =  Sự biến thiên: + Chiều biến thiên: 3 2 x   ′ = − − = − 1 x y x x +
.Xét y′ = 0 ⇔ x = 0. 2 2   
+ Các giới hạn tại vô cực 4  1 1 lim y lim x 1  = − − − =  . −∞  2 4 x→+∞ x→±∞  2x 8x  + Bảng biến thiên: Page 202
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x −∞ 0 +∞ y′ + 0 − y 4 −∞ −∞
Hàm số đồng biến trên các khoảng (−∞;0)
Hàm số nghịch biến trên các khoảng (0 ;+ ∞) + Cực trị :
Hàm số đạt cực đại tại x = 0; y = y(0) = 3 − . cd
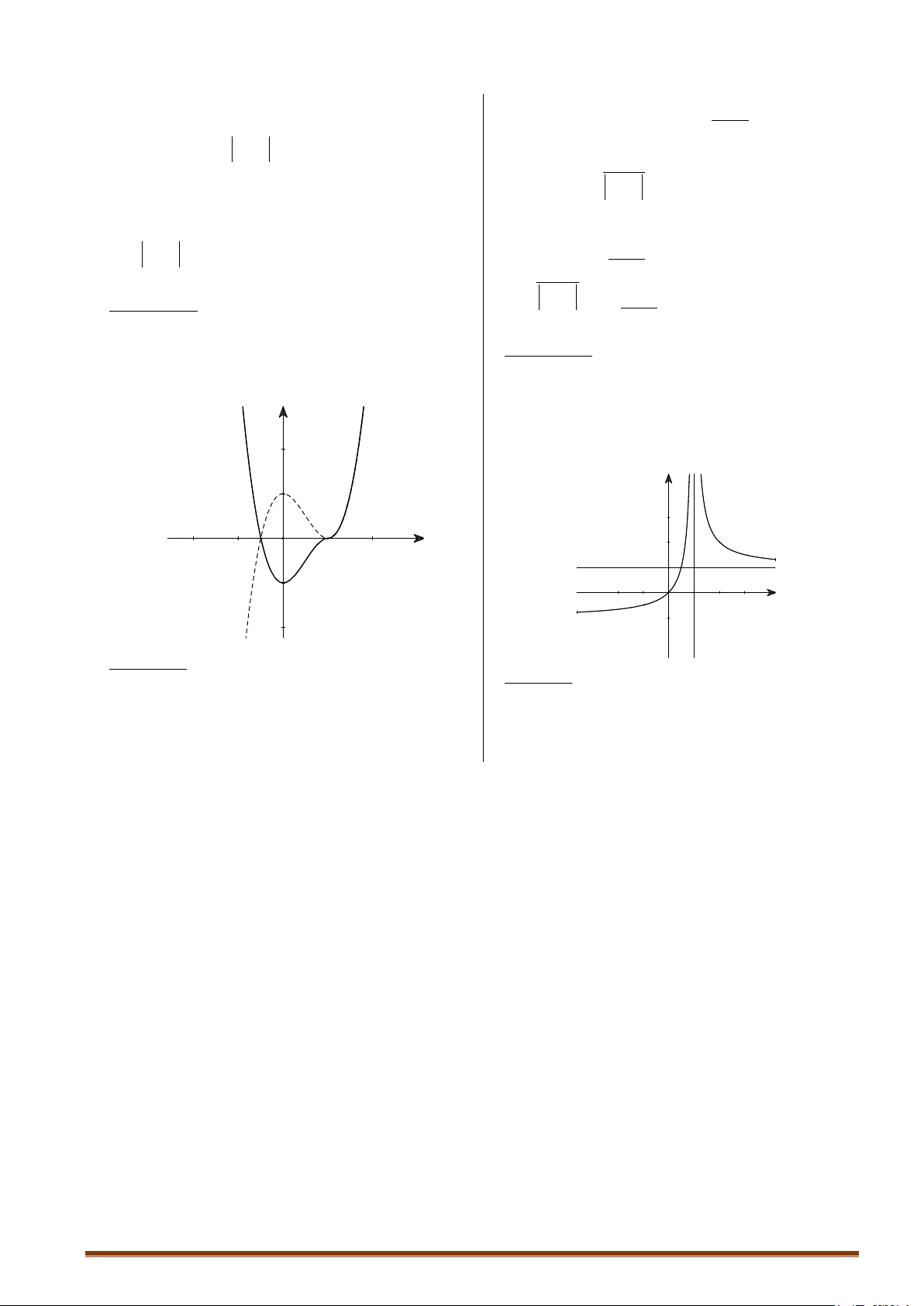
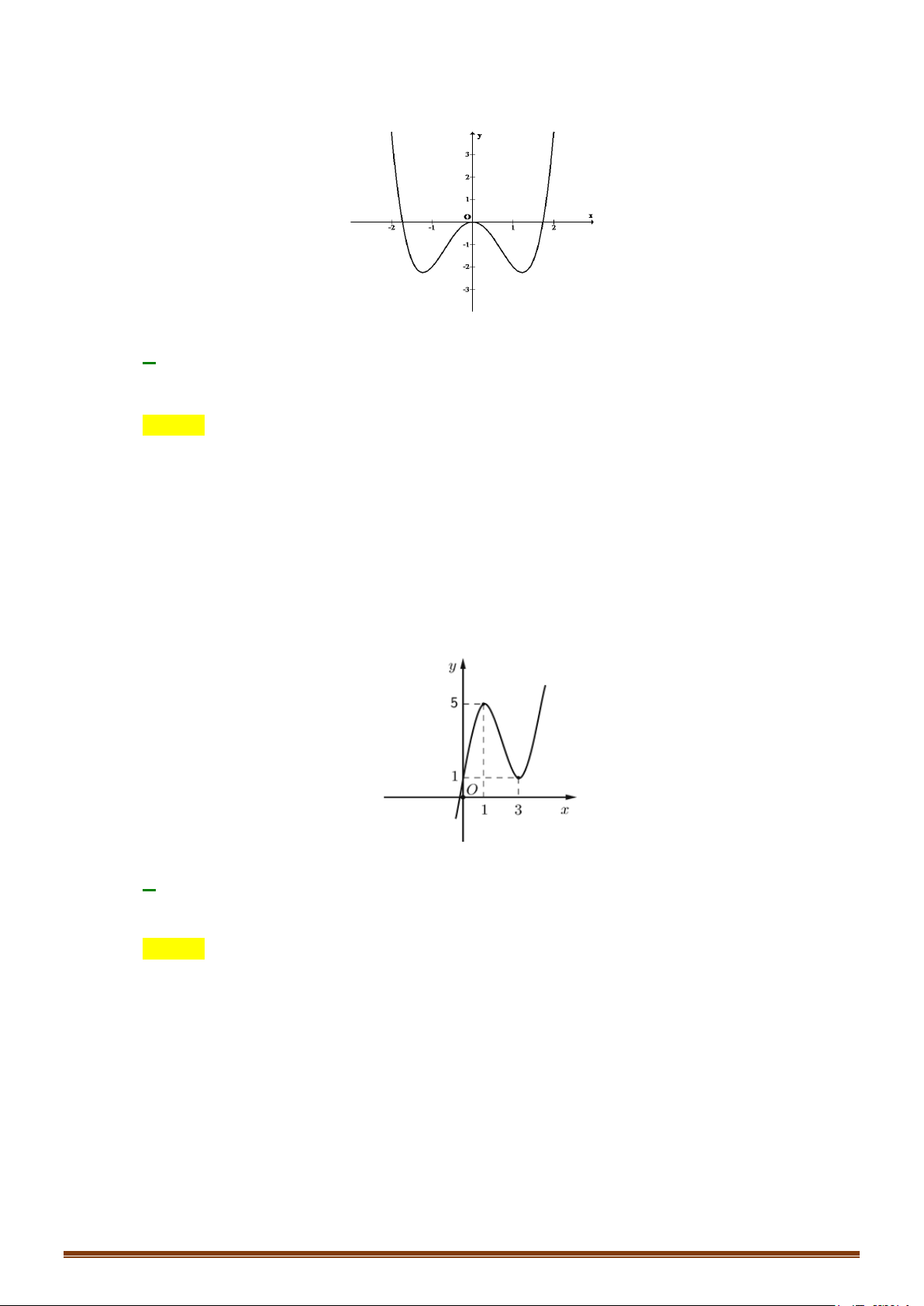
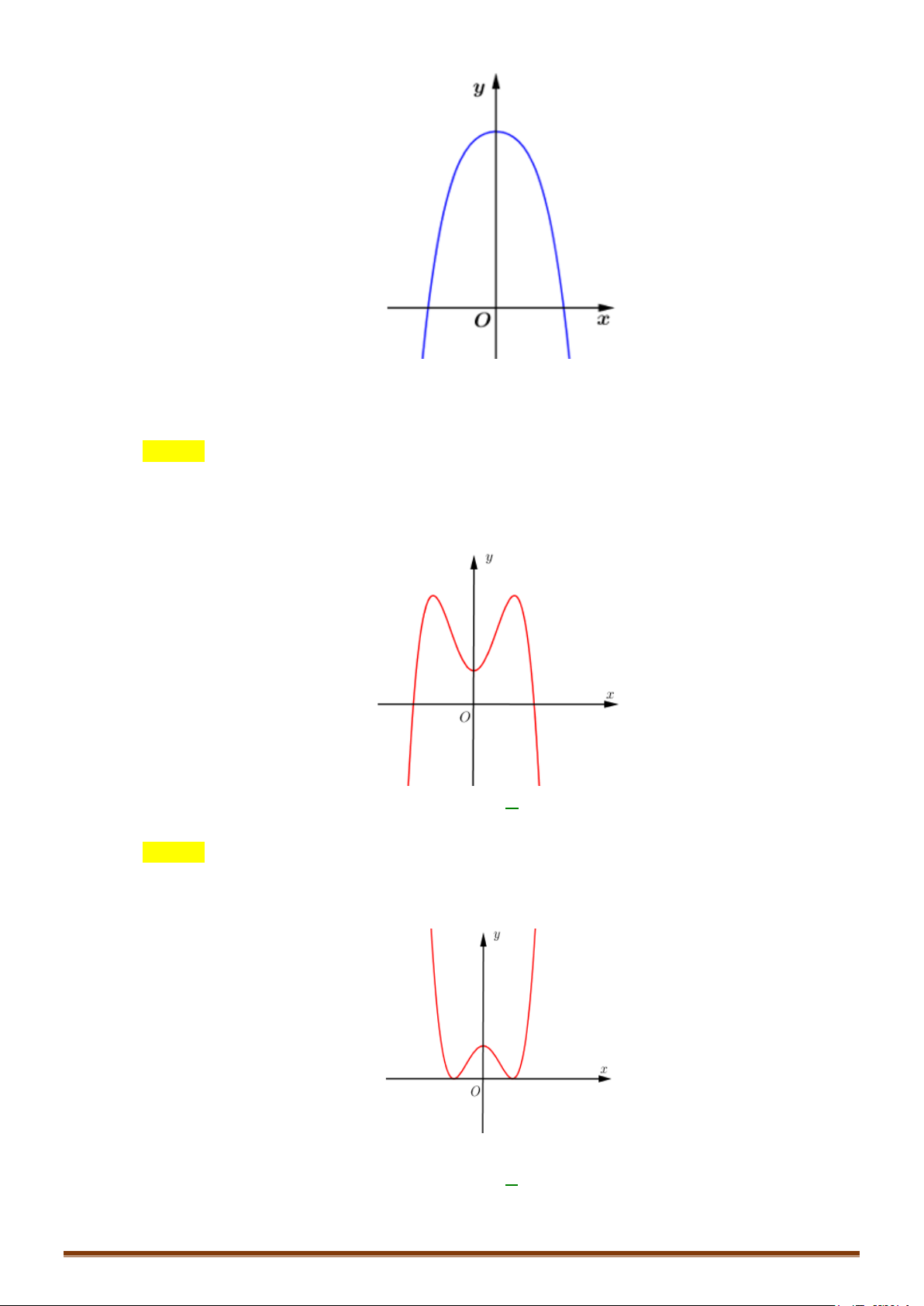
Hàm số không có cực tiểu. Đồ thị y 4 1 -2 2 x O -1 Cho x = 2
± ⇒ y = 0 :Đồ thị hàm qua C ( 2; − 0), D(2; 0)
Lưu ý: Đồ thị hàm số nhận Oy làm trục đối xứng.
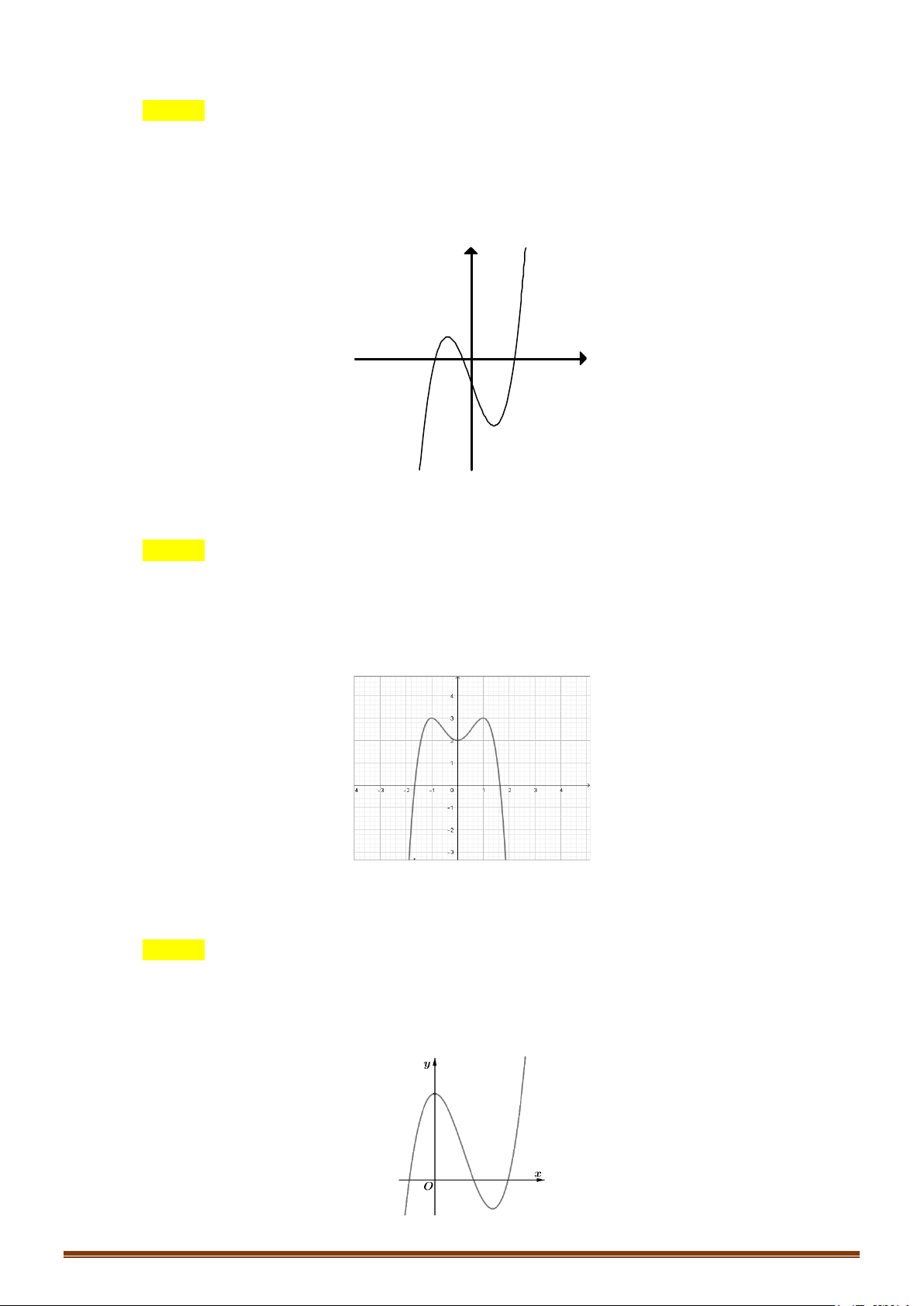
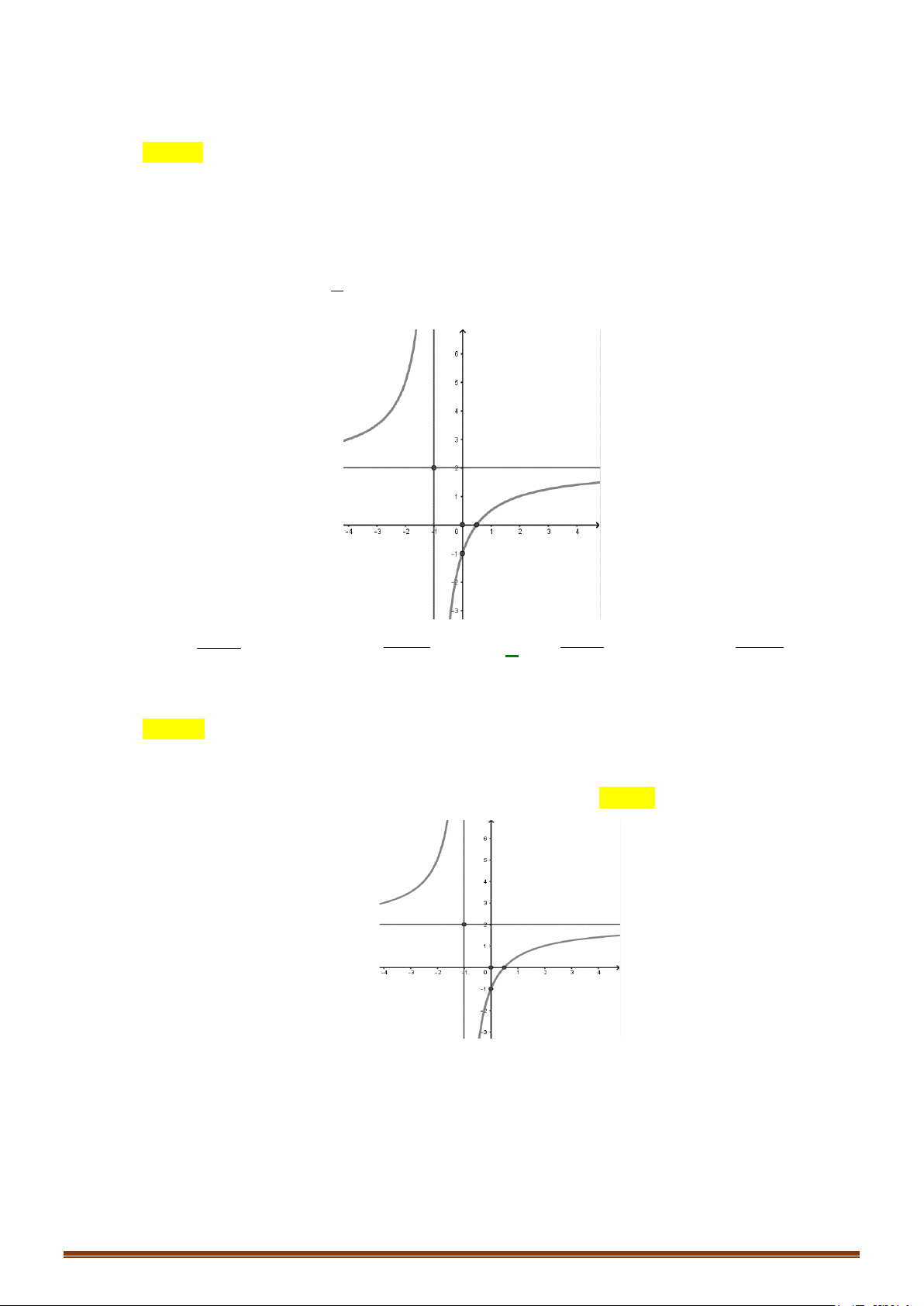
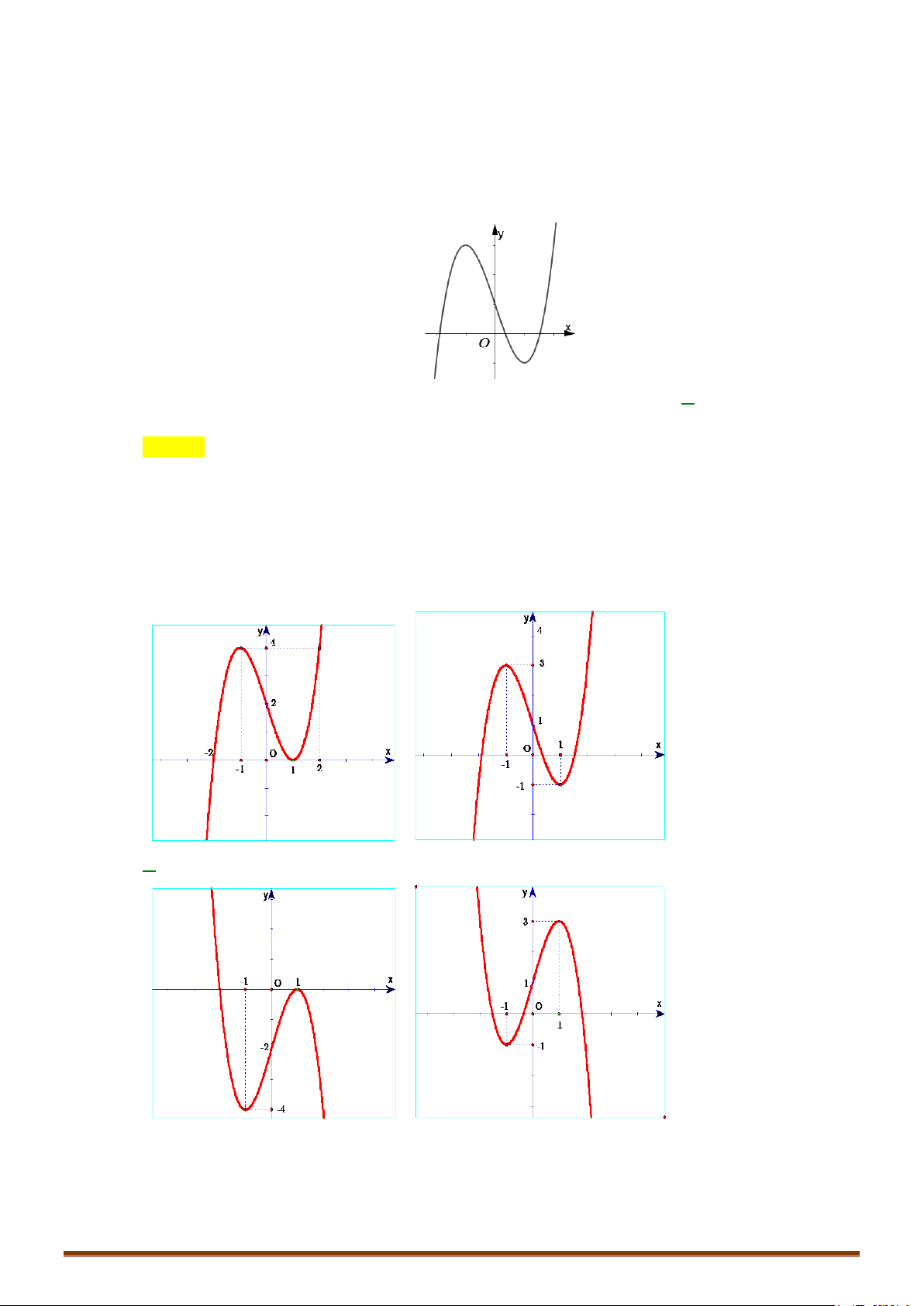
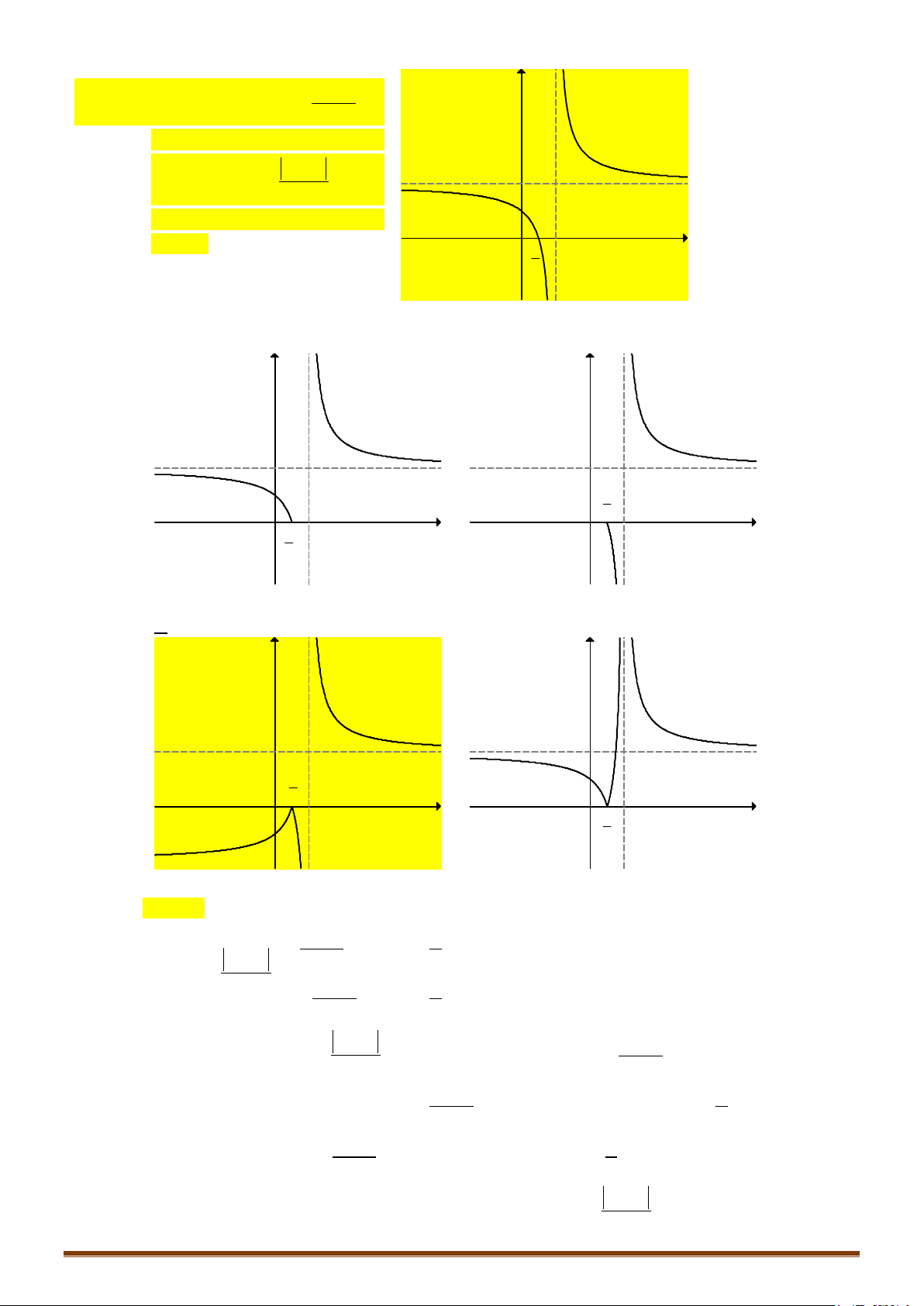
3. HÀM SỐ NHẤT BIẾN
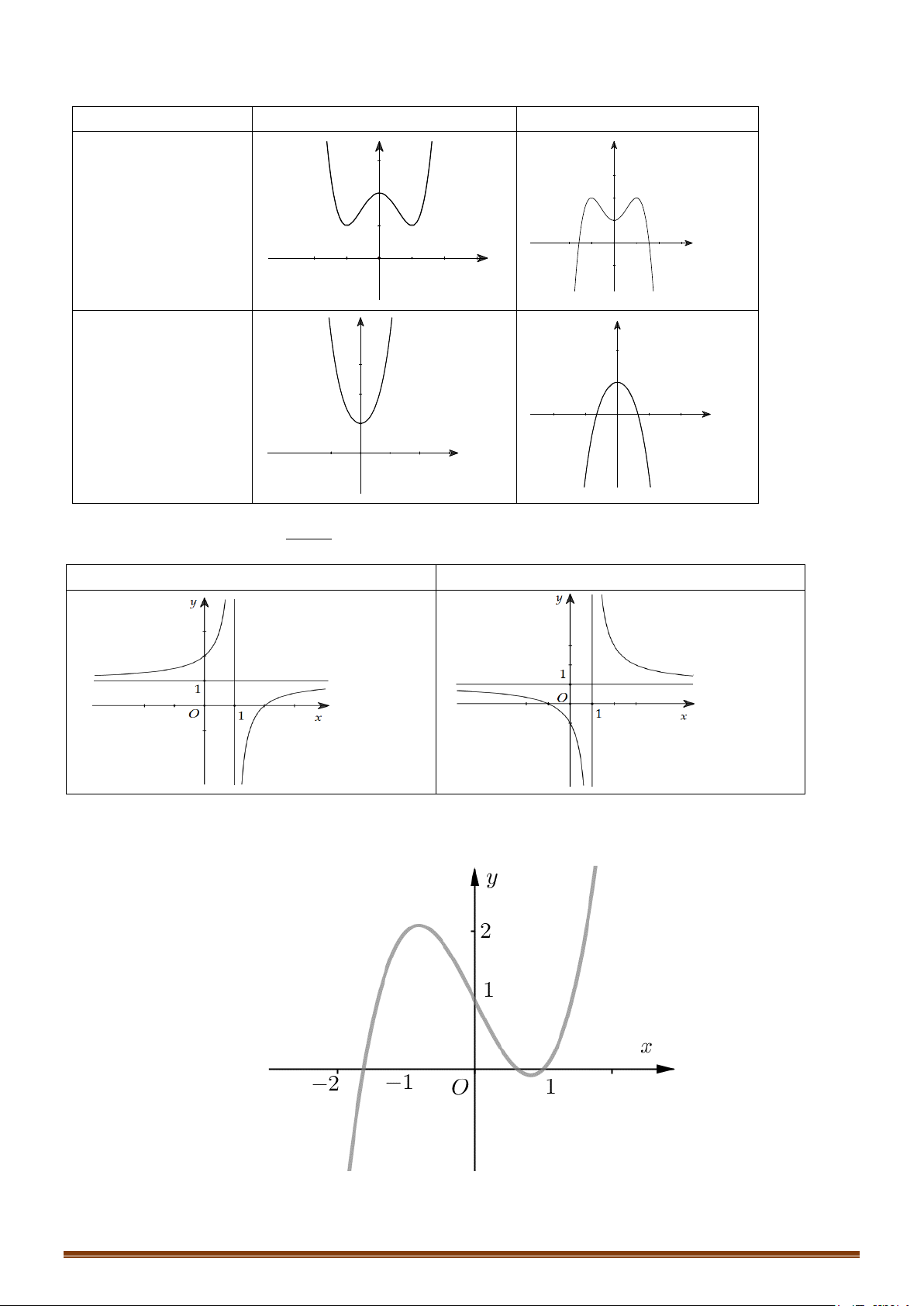
ax + b y =
(c ≠ 0, ad − bc ≠ 0)
cx + d
D = ad − bc > 0
D = ad − bc < 0
MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
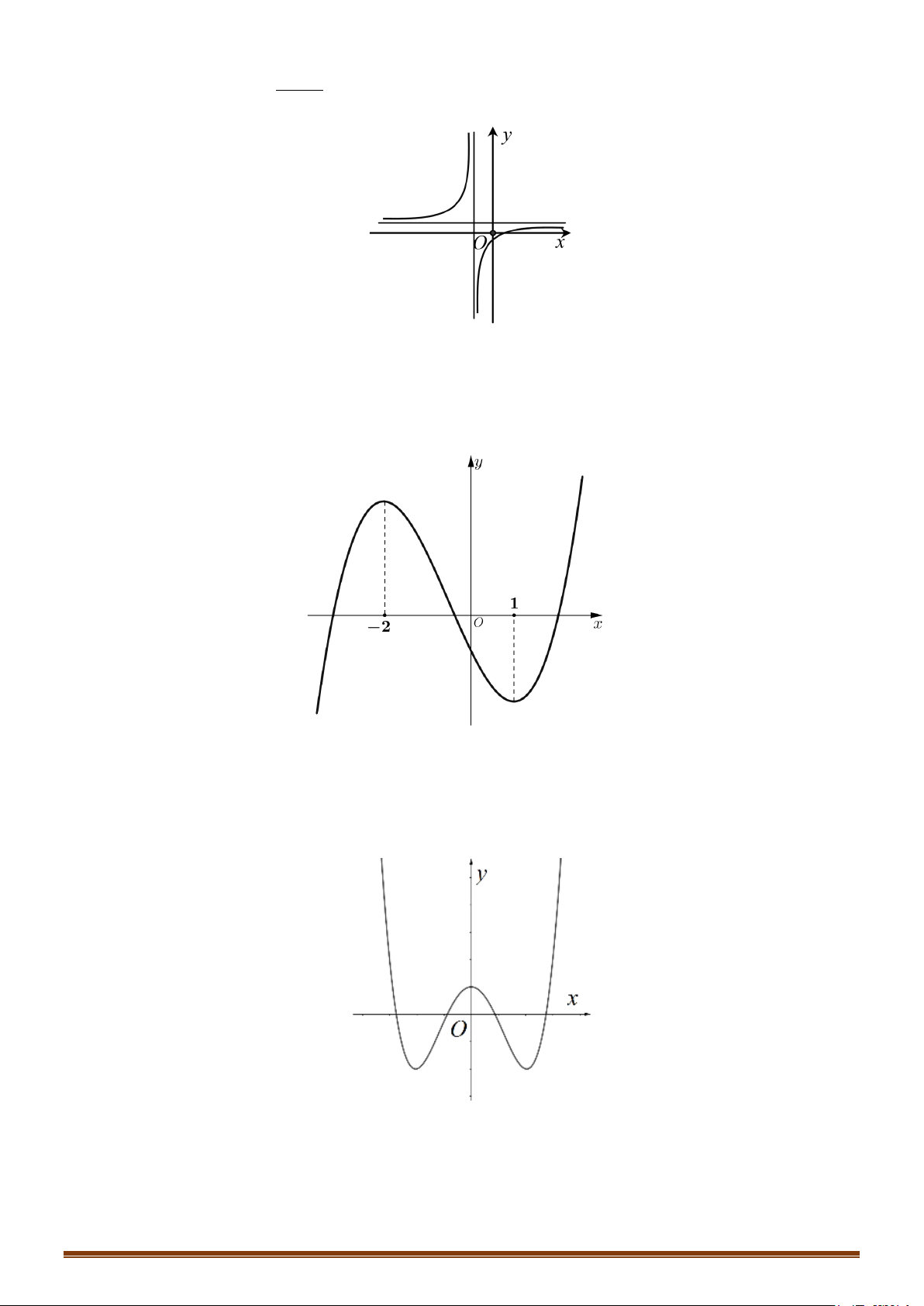
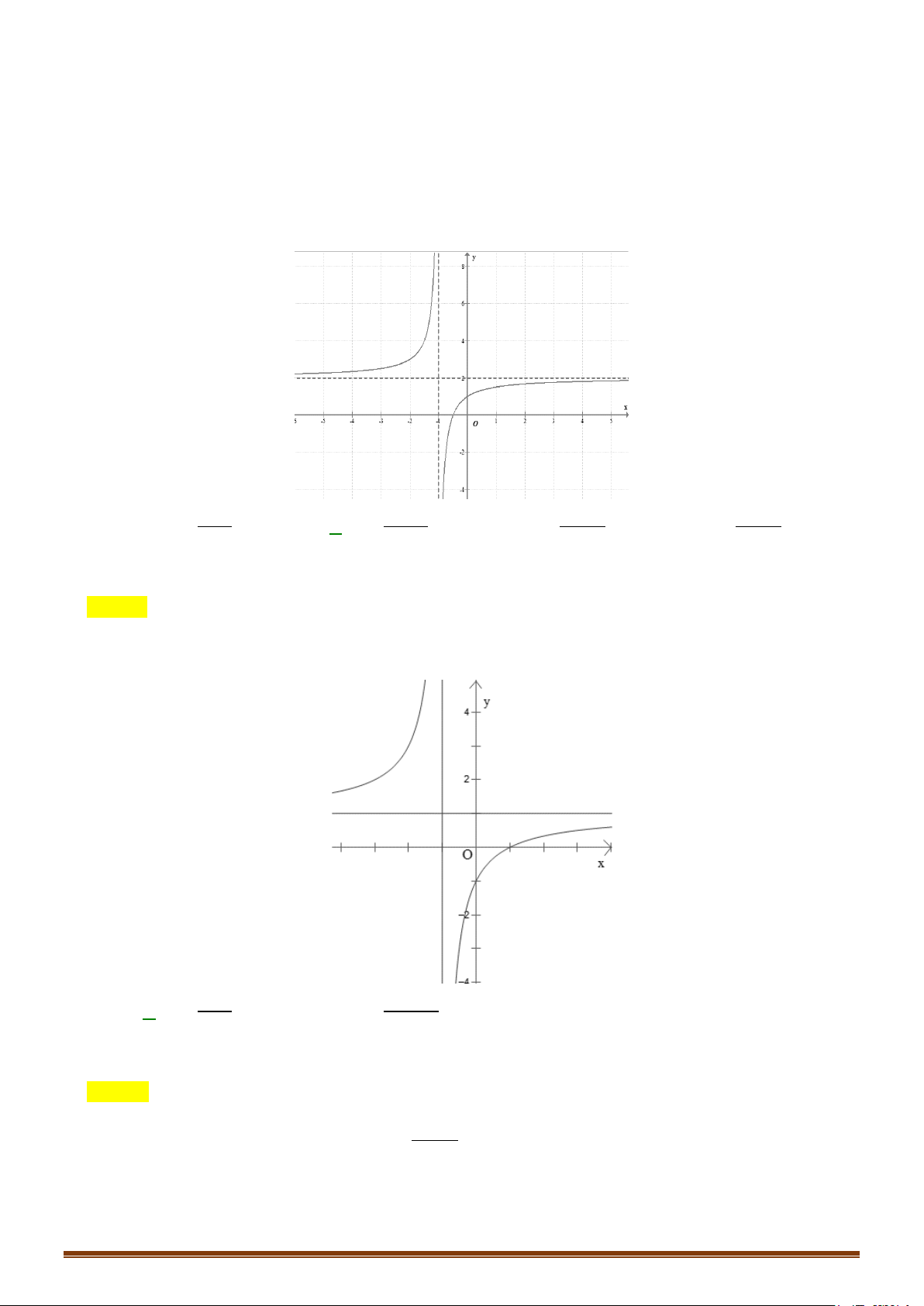
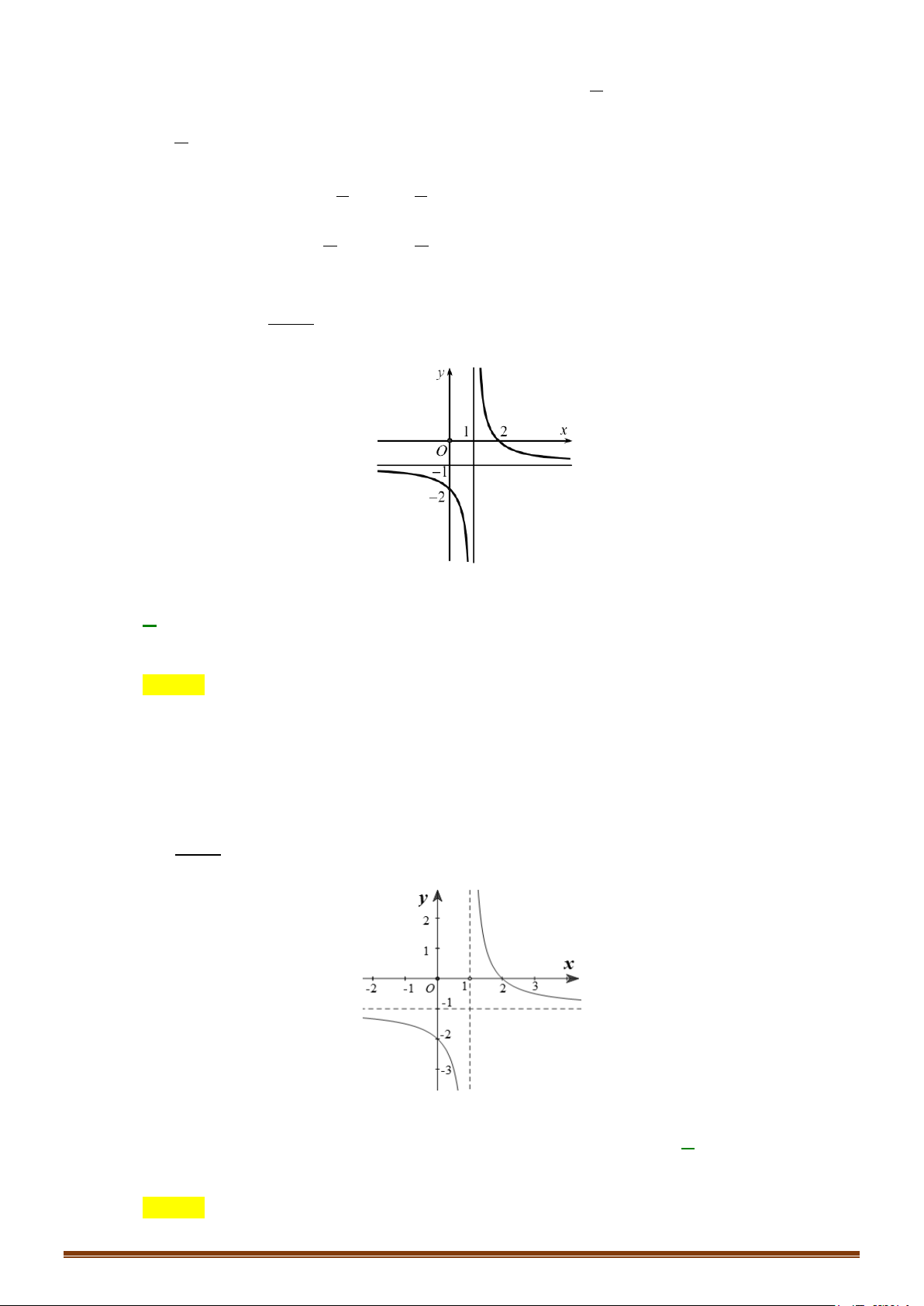
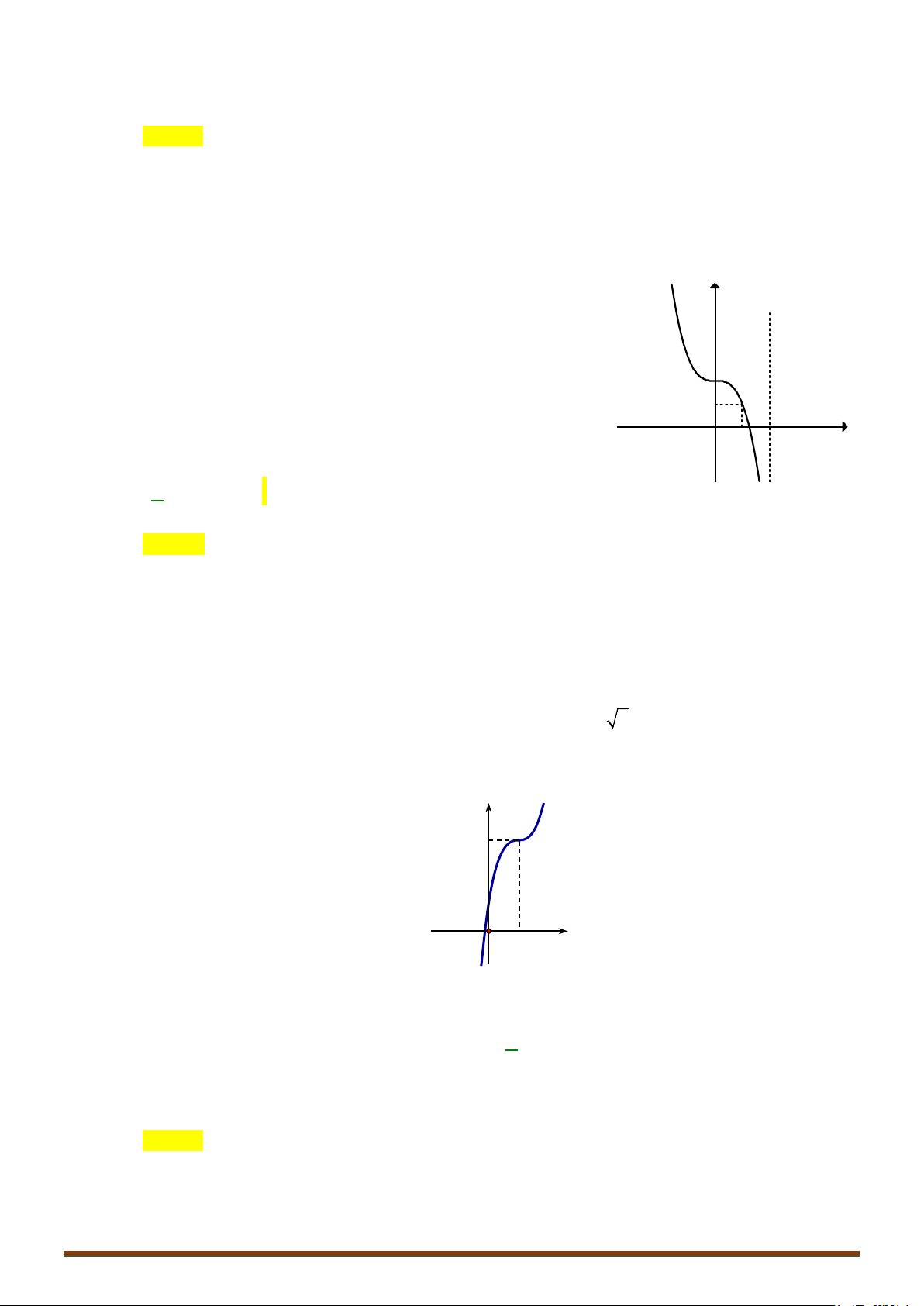
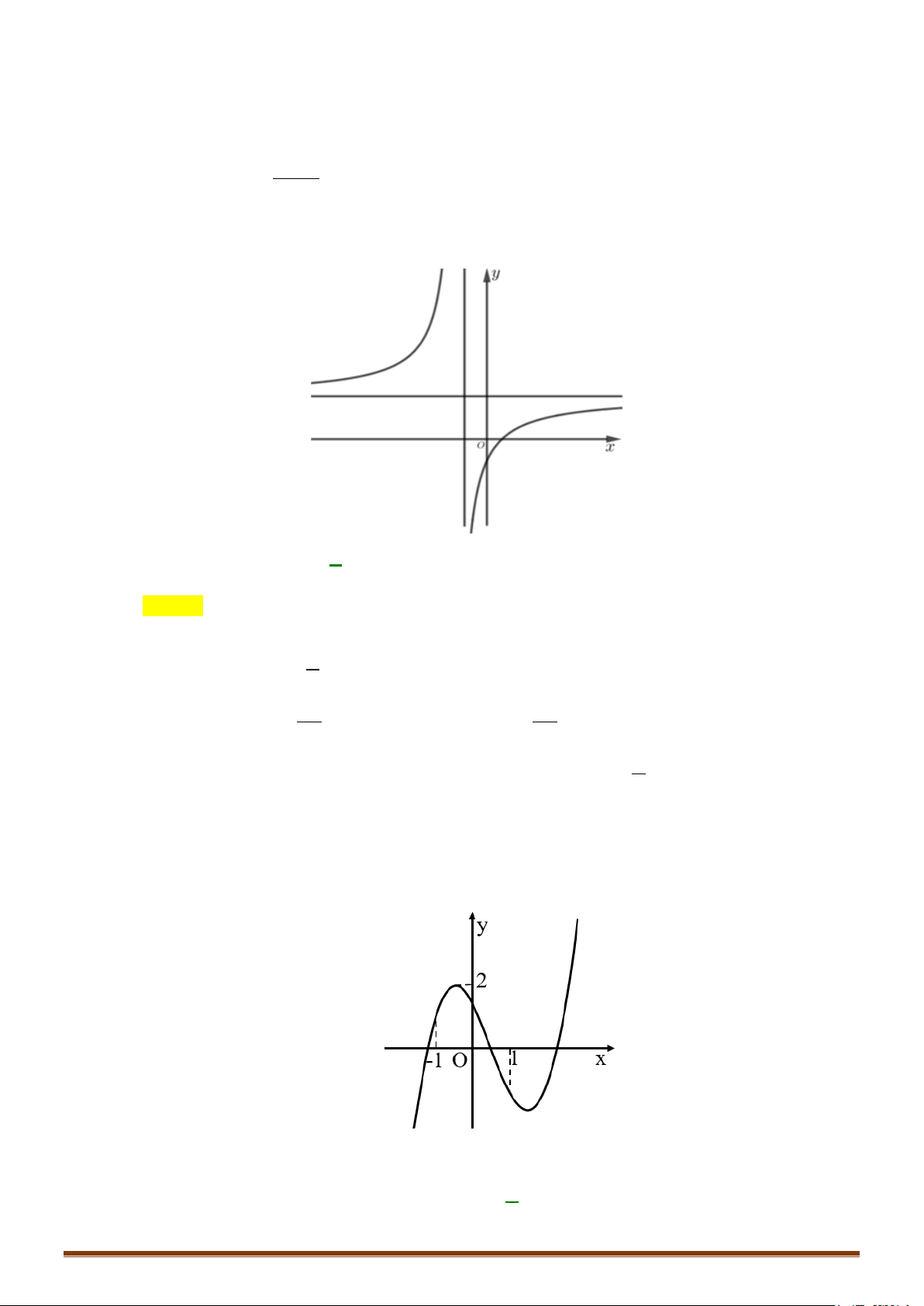
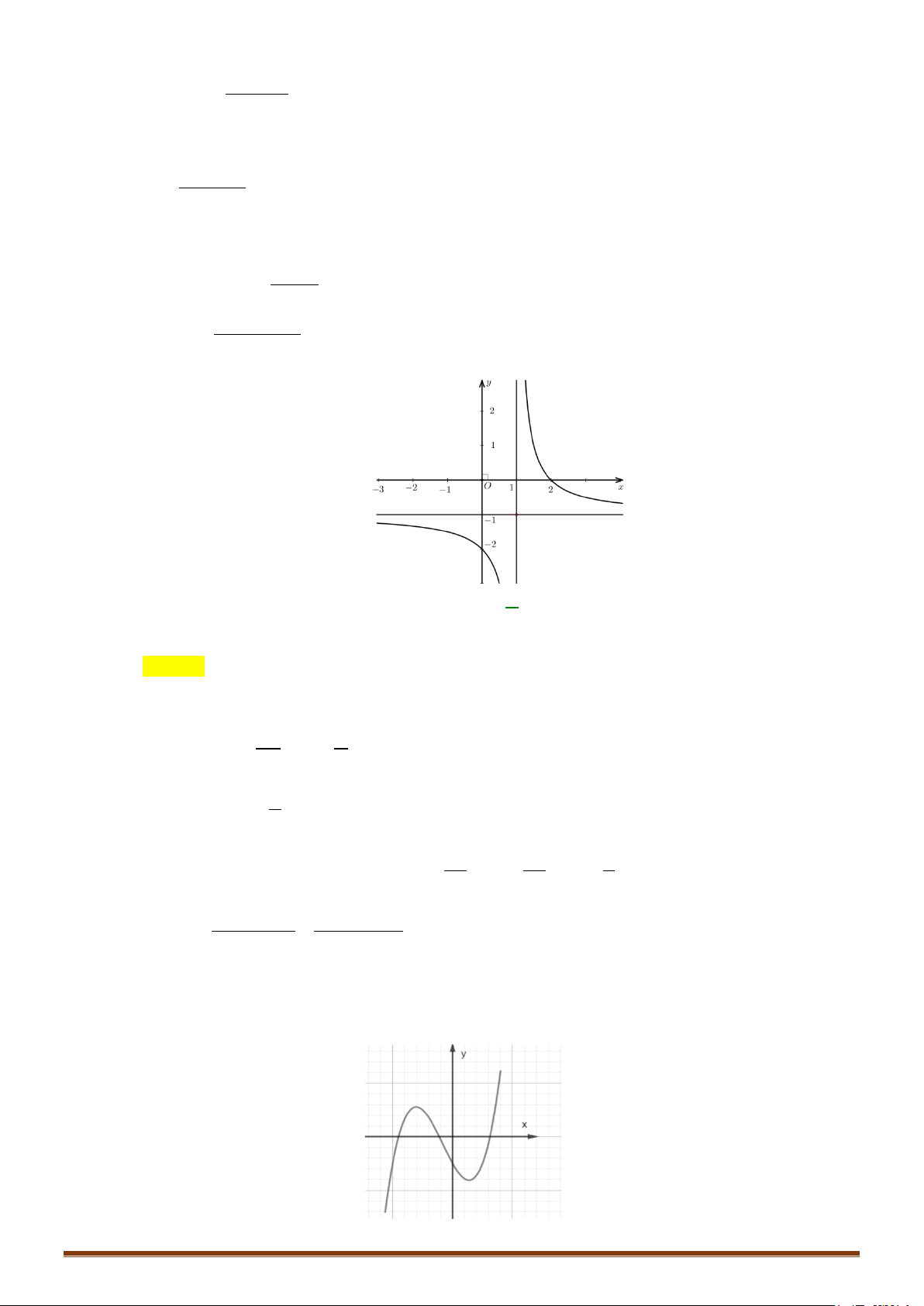
Câu 1. Khảo sát và vẽ đồ thị hàm số x 1 x1 Lời giải: Page 203
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tập xác định: D =  { \ } 1 Sự biến thiên: + Chiều biến thiên: 2 y − ′ =
.Ta thấy y′ không xác định khi x = 1; y′ luôn âm với mọi x ≠ 1 (x−1)2
Vậy hàm số nghịch biến trên các khoảng (1;+ ∞) và (−∞; 1). + Cực trị :
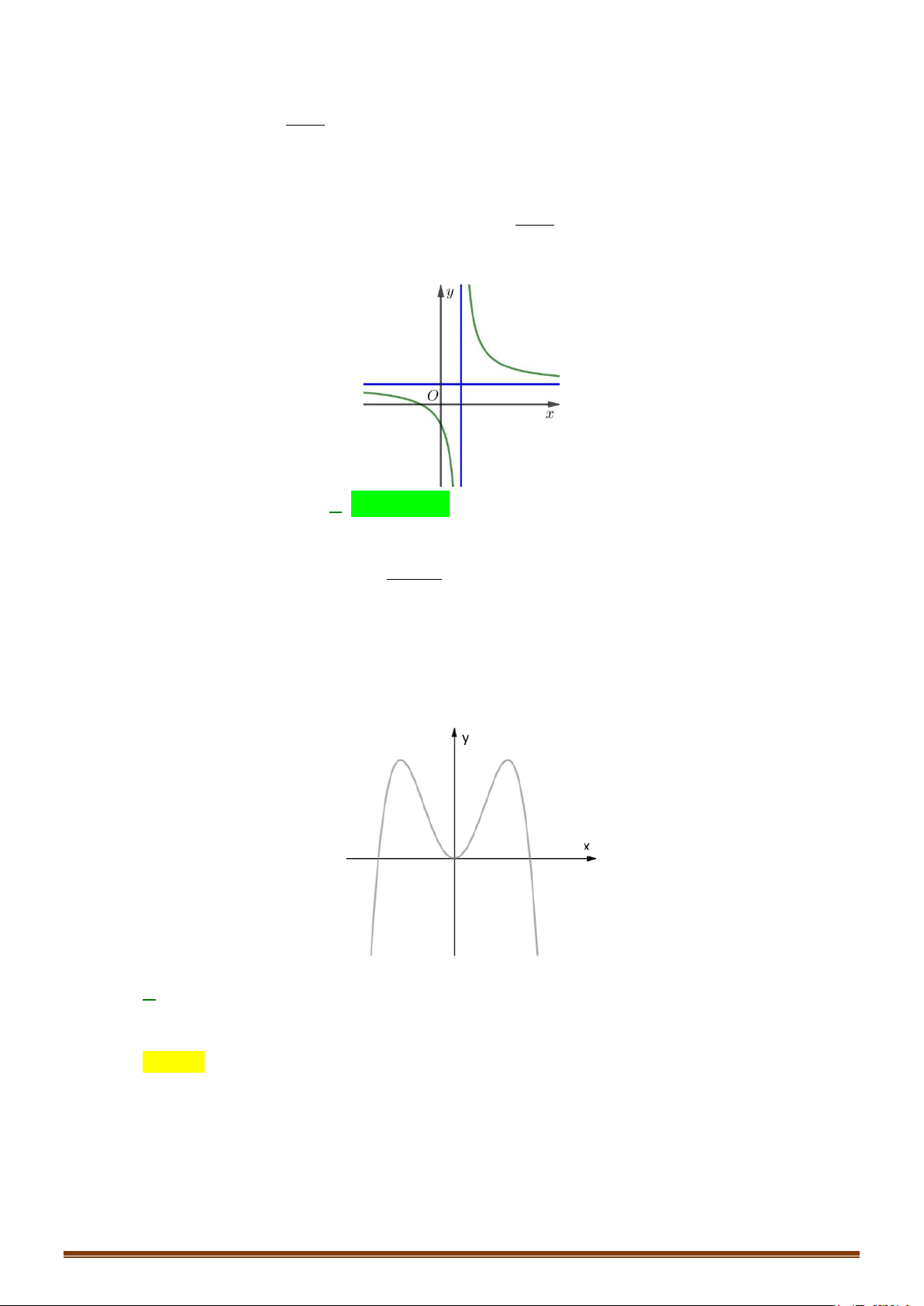
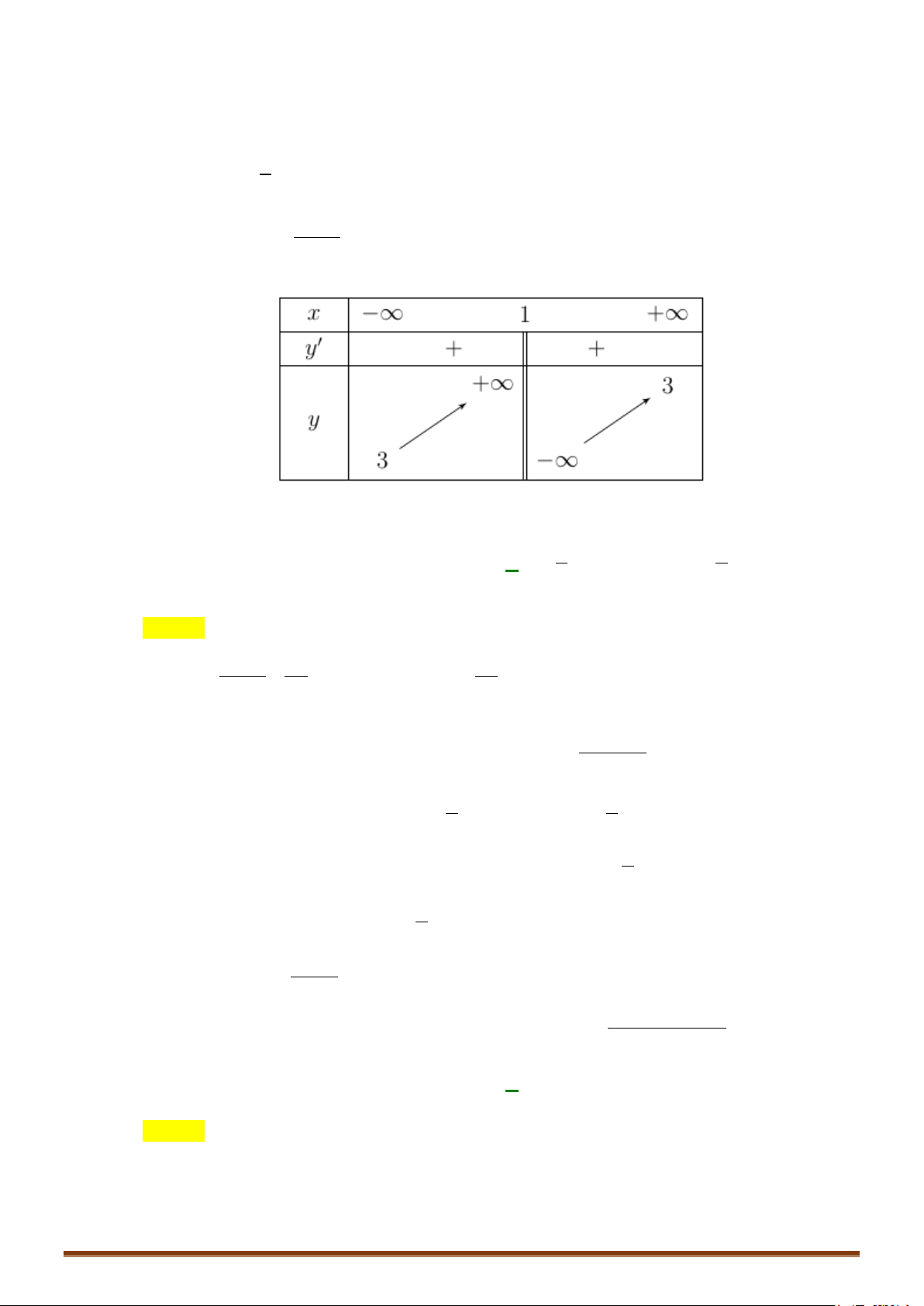
Hàm số không có cực trị + Tiệm cận x + 1 lim y = lim
= 1. Vậy đường thẳng y = 1 là tiệm cận ngang x→±∞ x −1 x + 1 lim y x + 1 = lim = +∞; lim y = lim = .
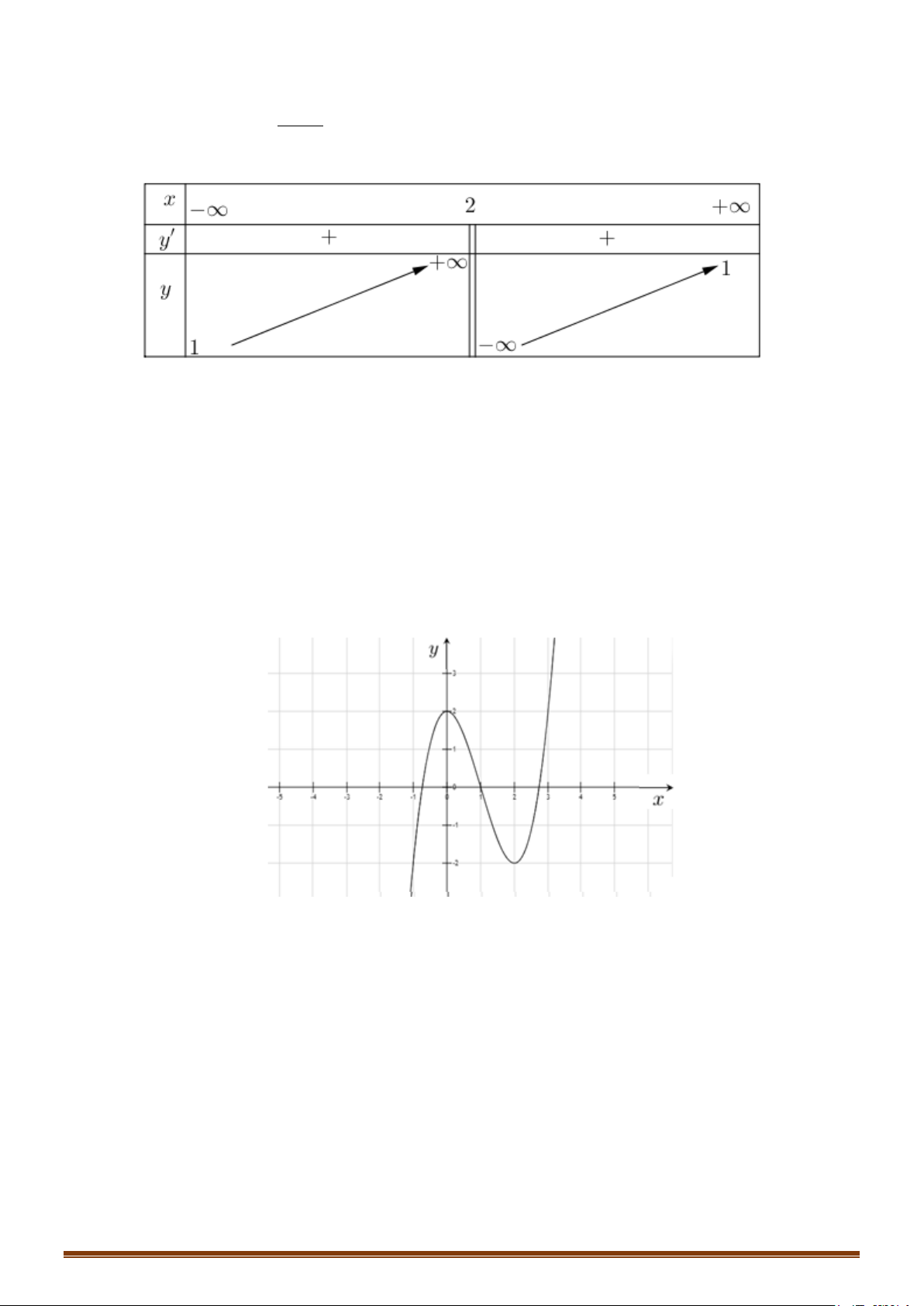
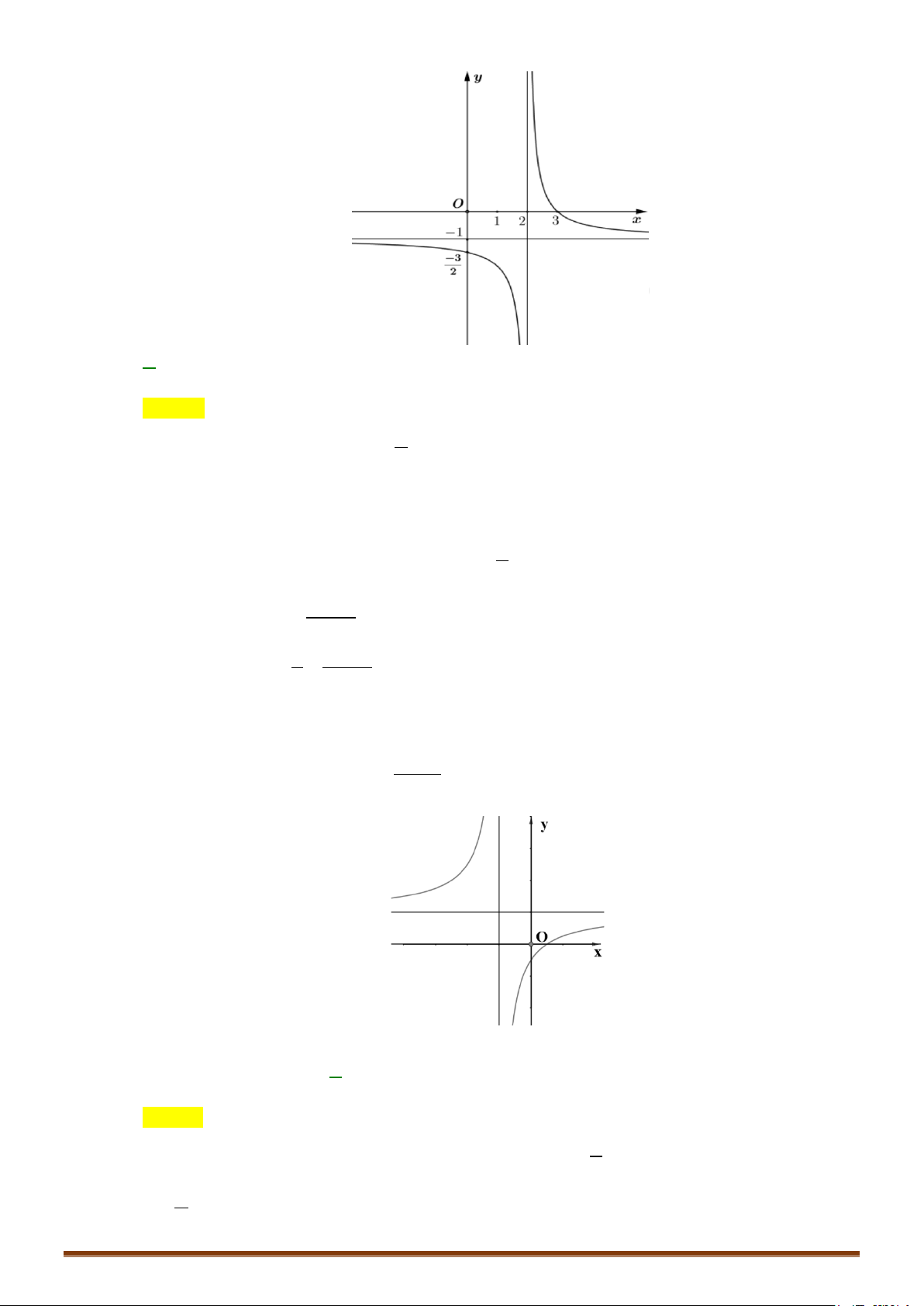
−∞ Vậy đường thẳng x = 1 là tiệm cận ngang − + x 1+ x 1 → → x −1 − x 1 x 1 → → x −1 + Bảng biến thiên: x −∞ 1 +∞ y′ – – +∞ y 1 1 −∞ Đồ thị
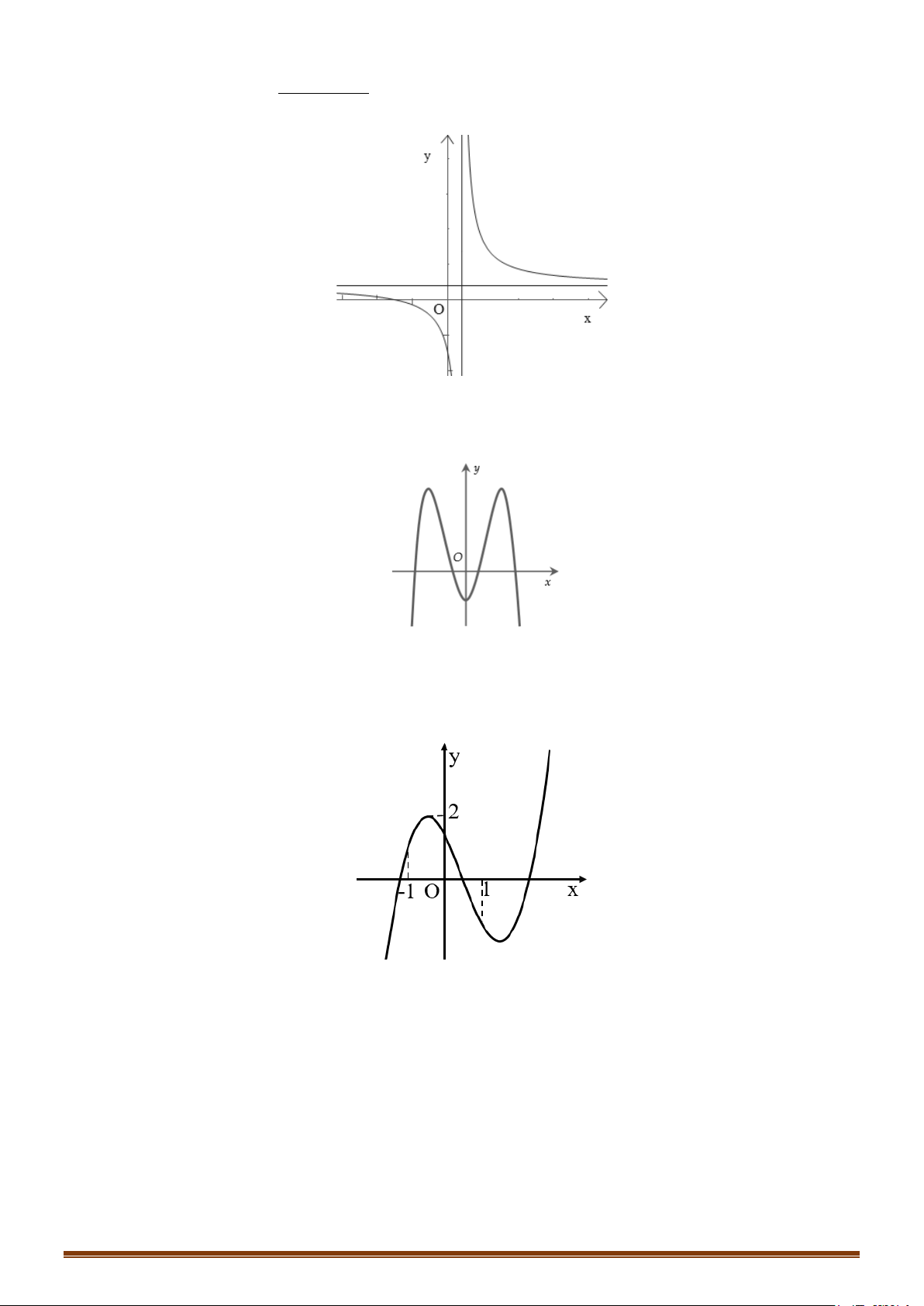
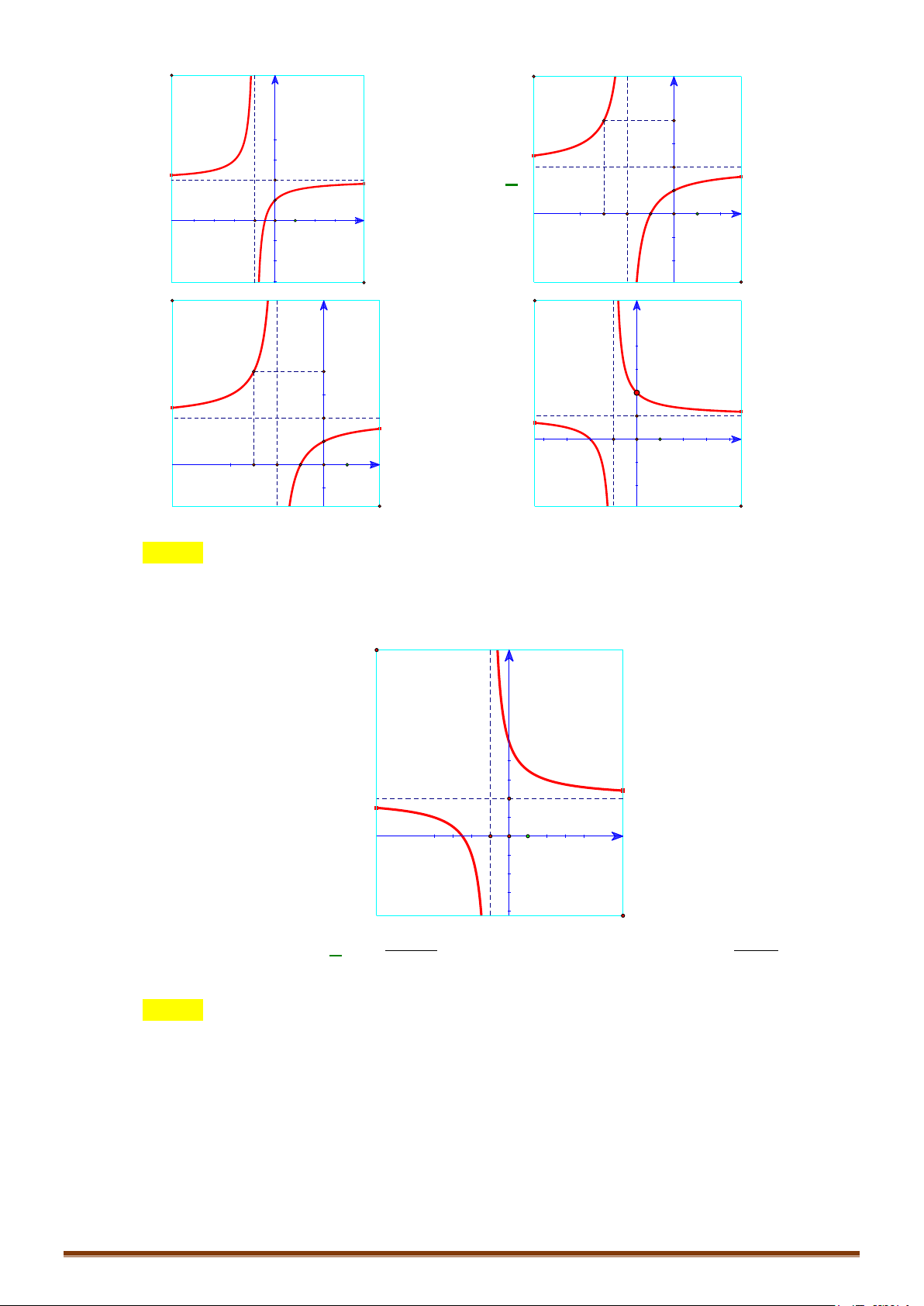
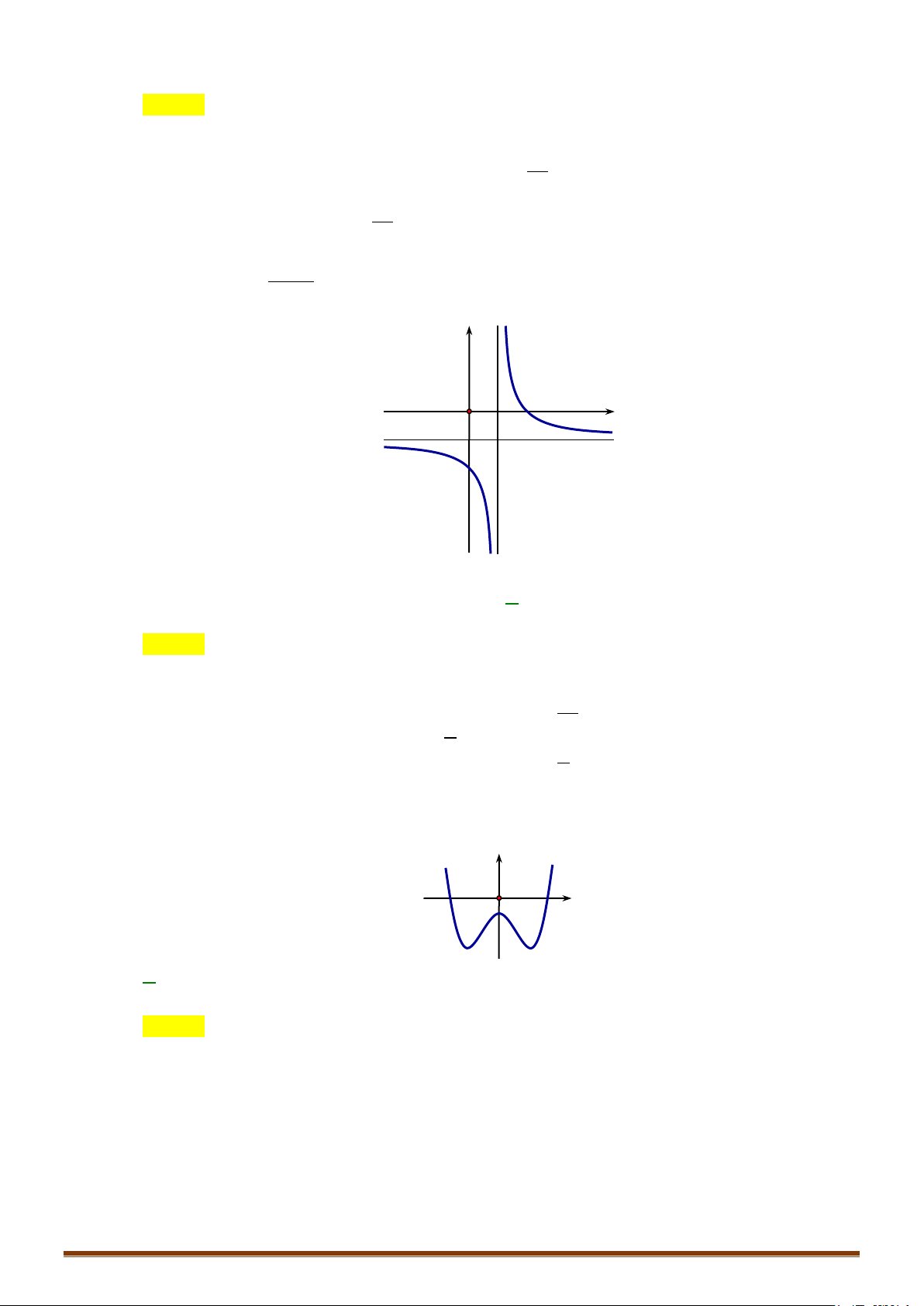
Đồ thị cắt trục tung tại điểm A(0 ;−1) và cắt trục hoành tại điểm B( 1 − ;0) (Hình vẽ) y 1 -2 0 1 x
Lưu ý : Giao điểm I (1 ;1) của hai tiệm cận là tâm đối xứng của đồ thị Page 204
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x +1
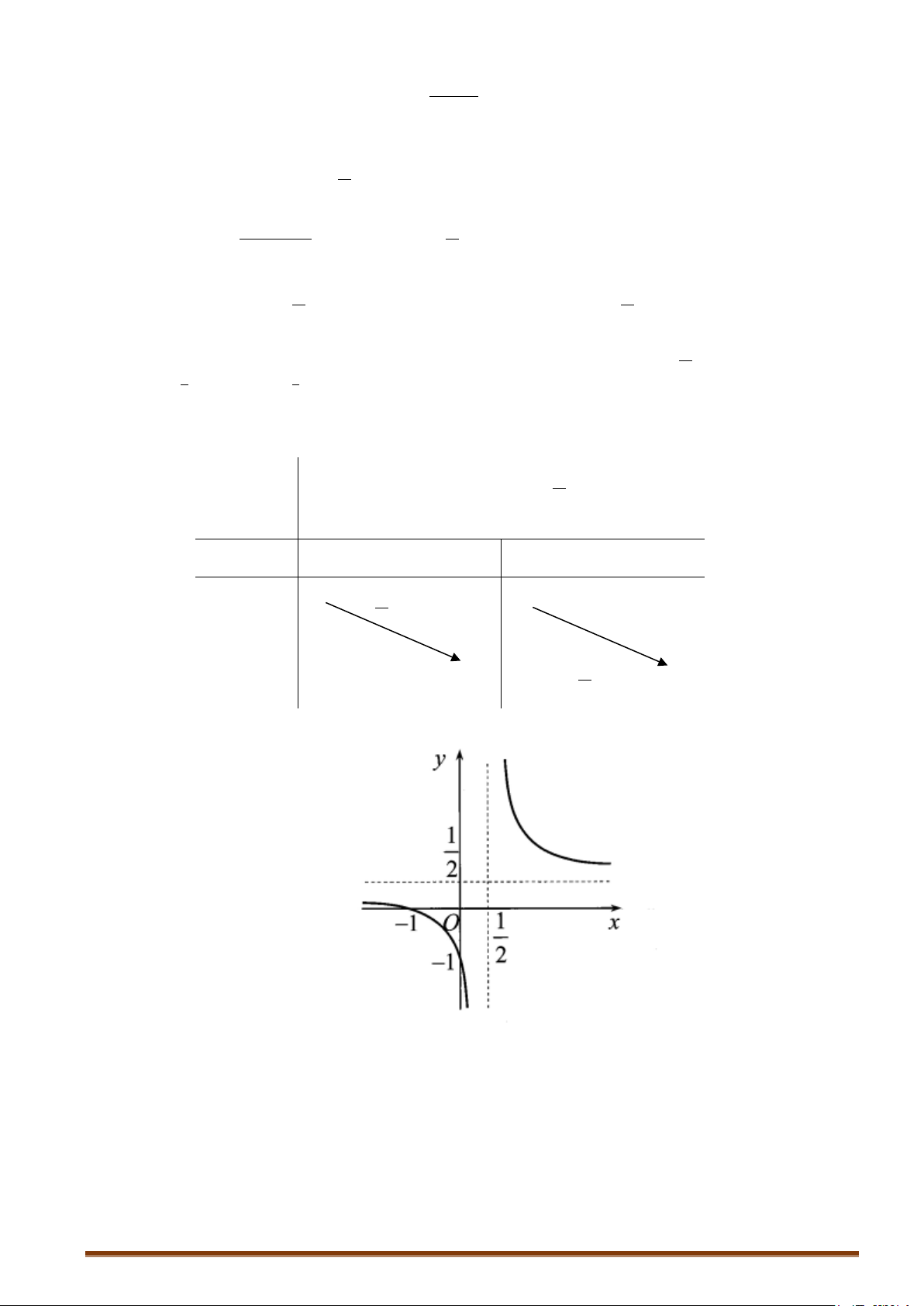
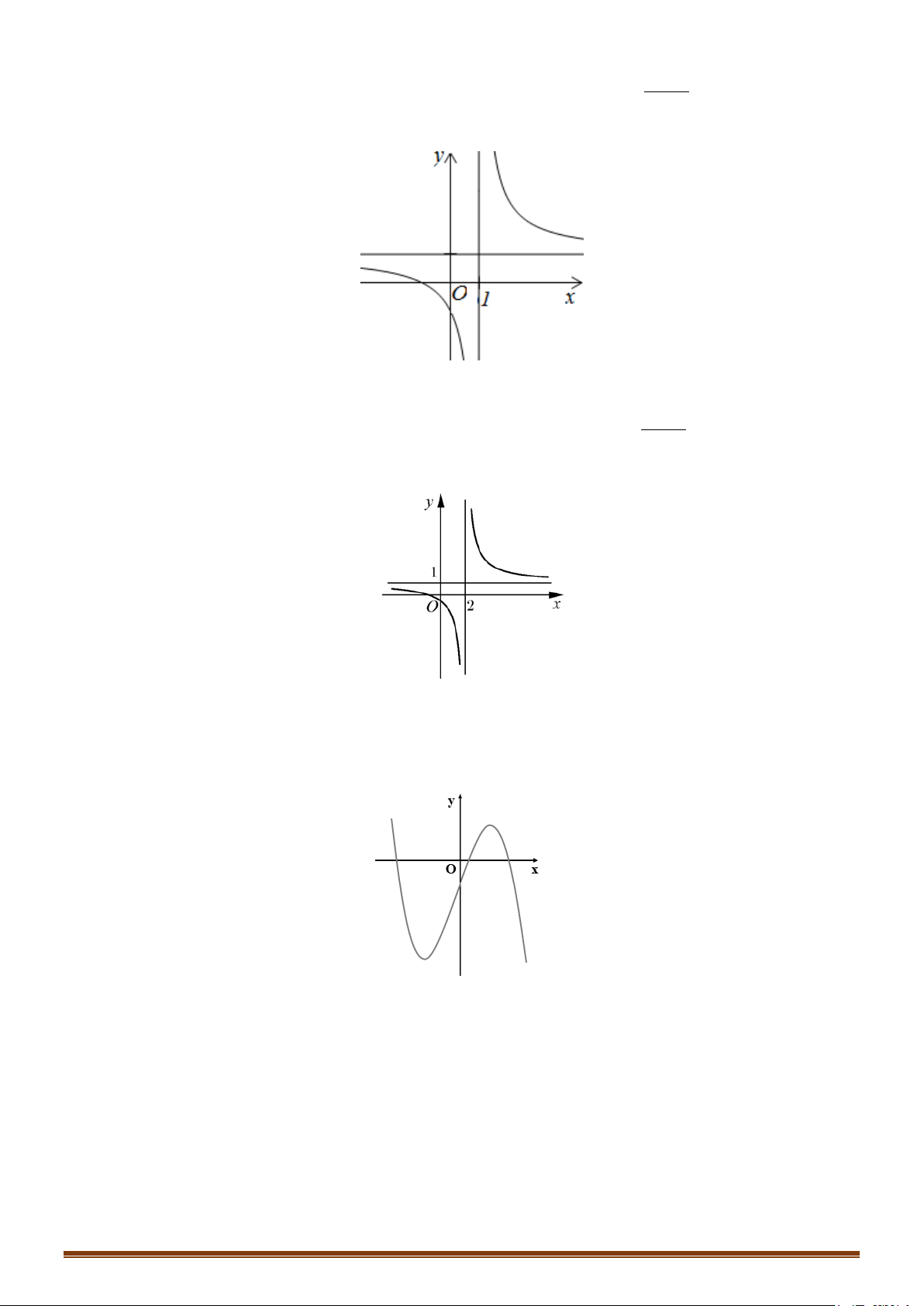
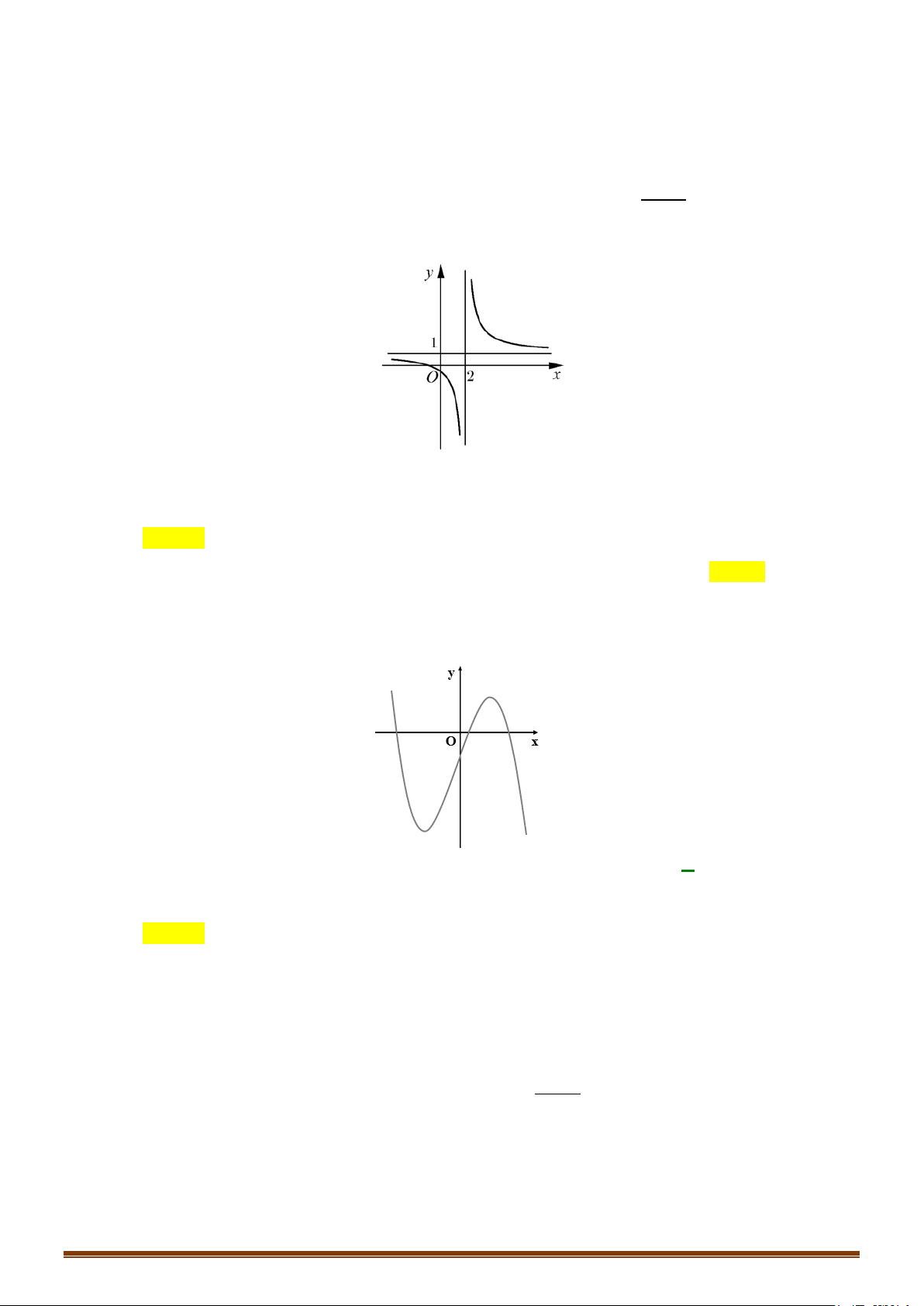
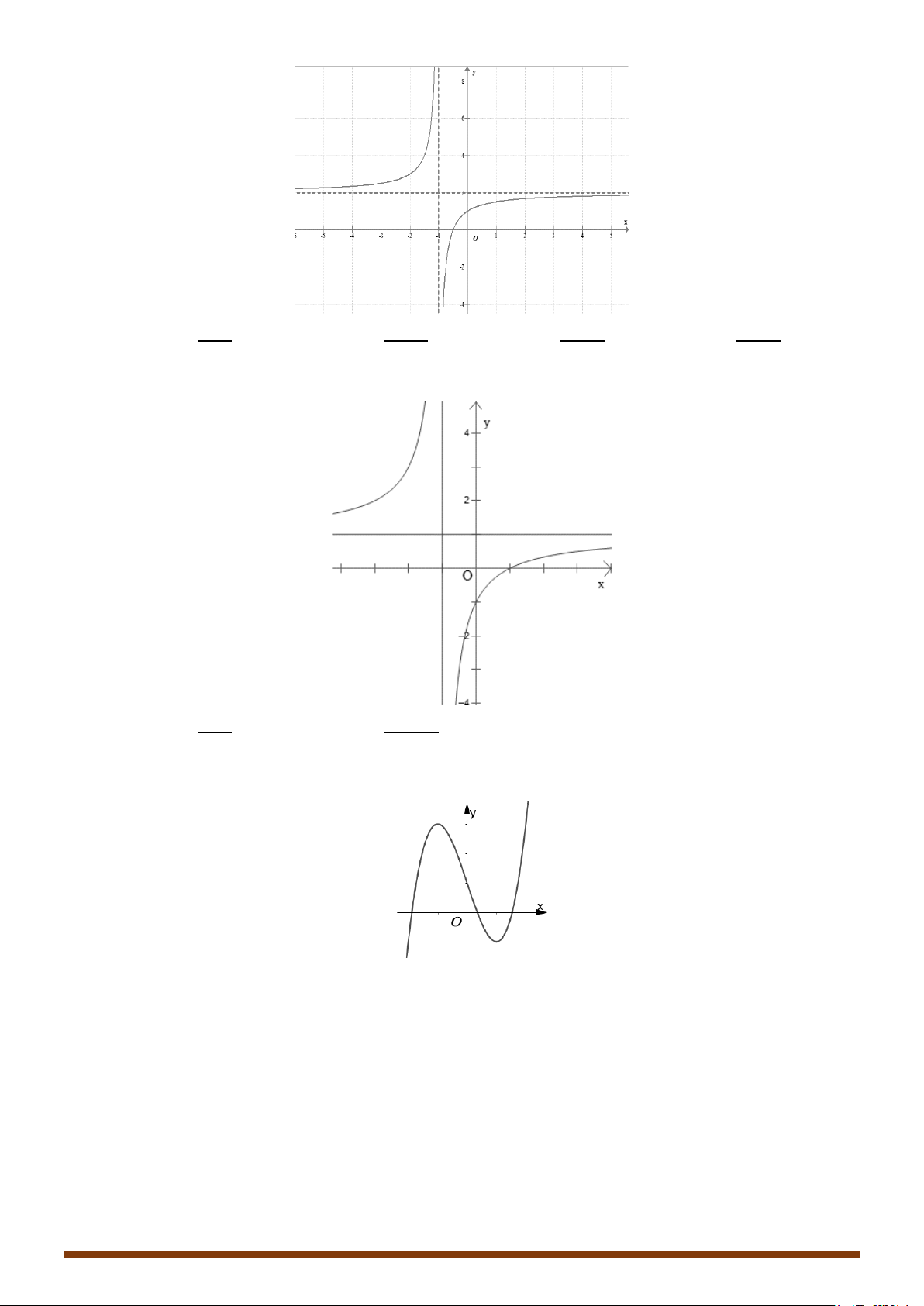
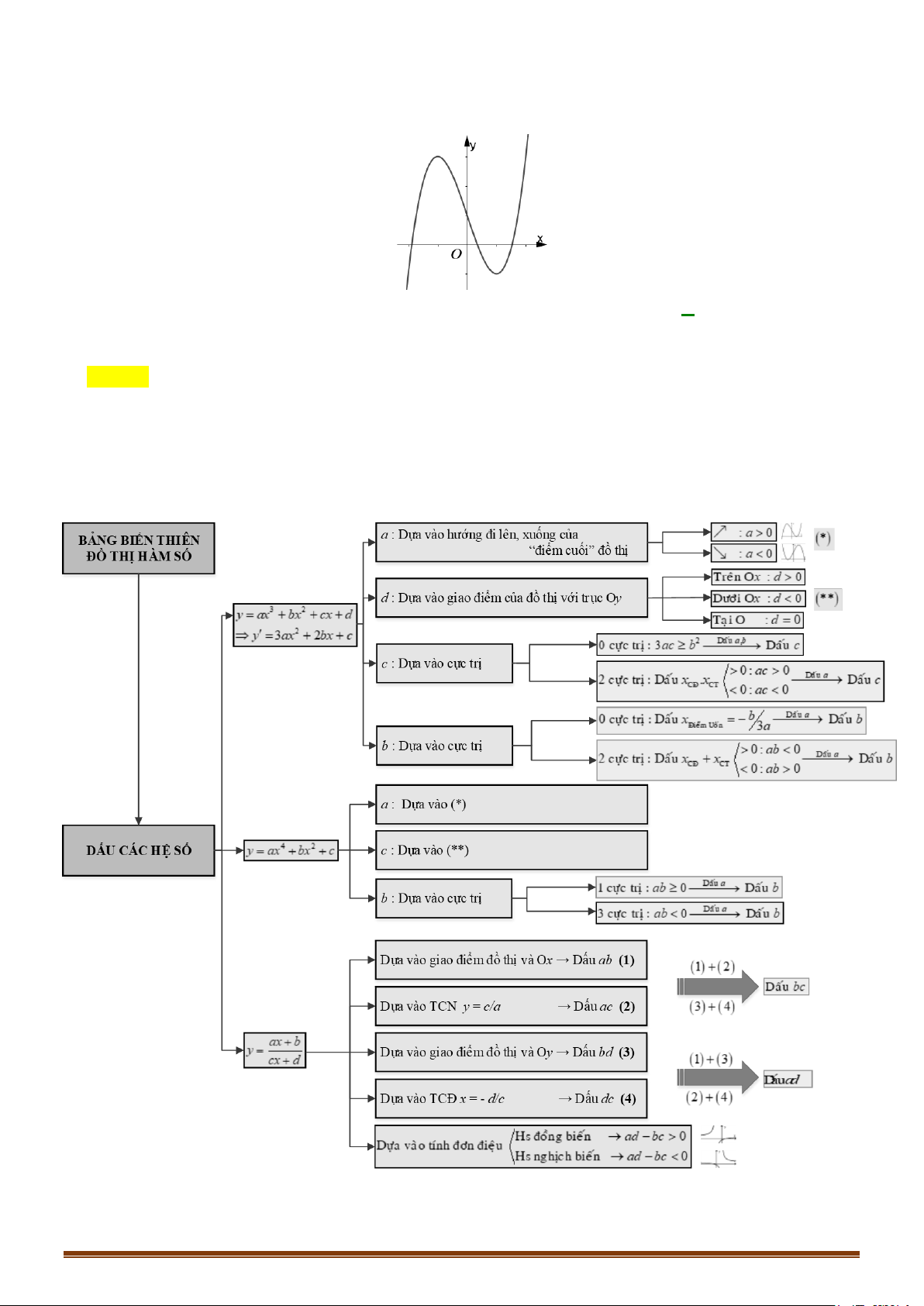
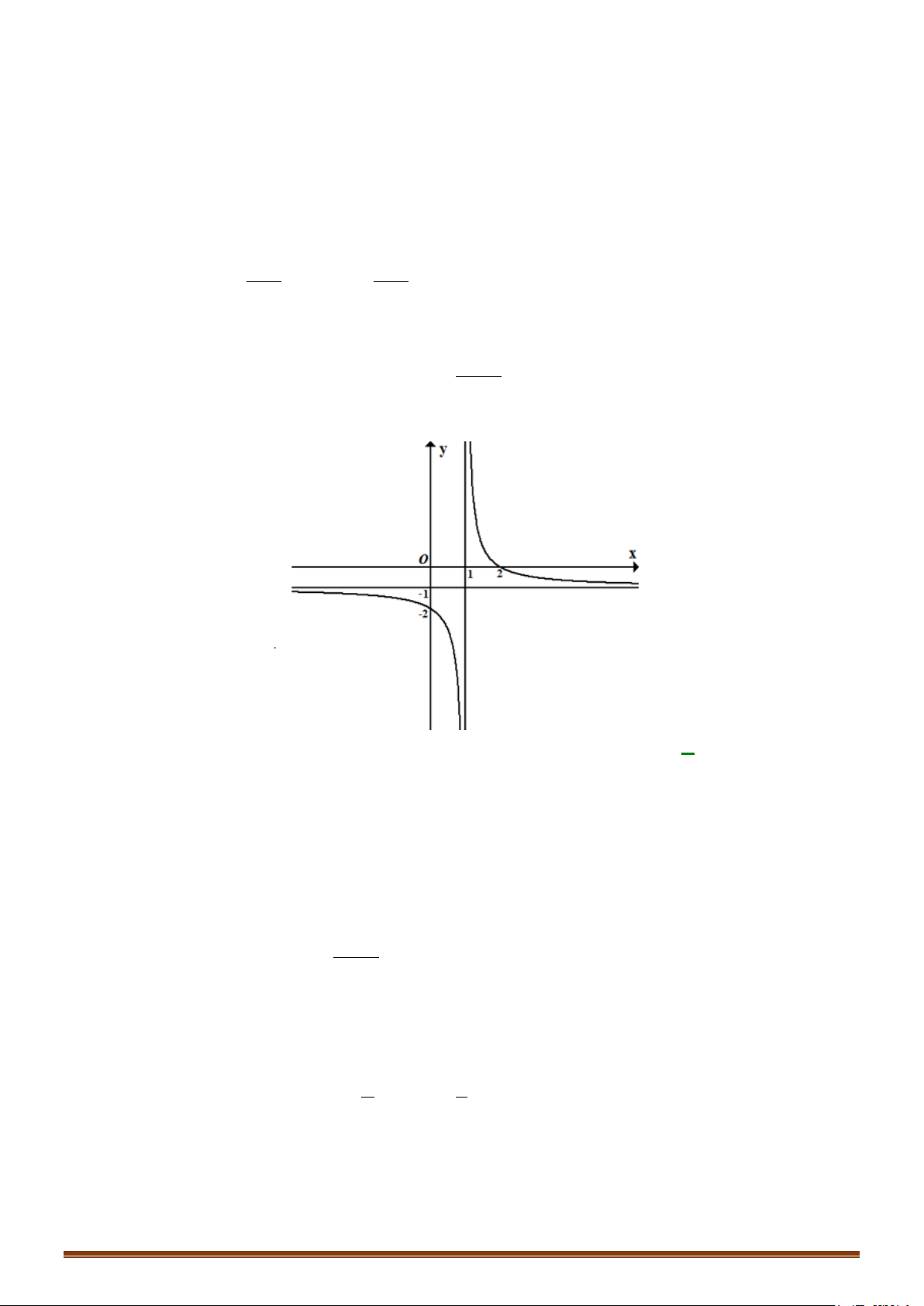
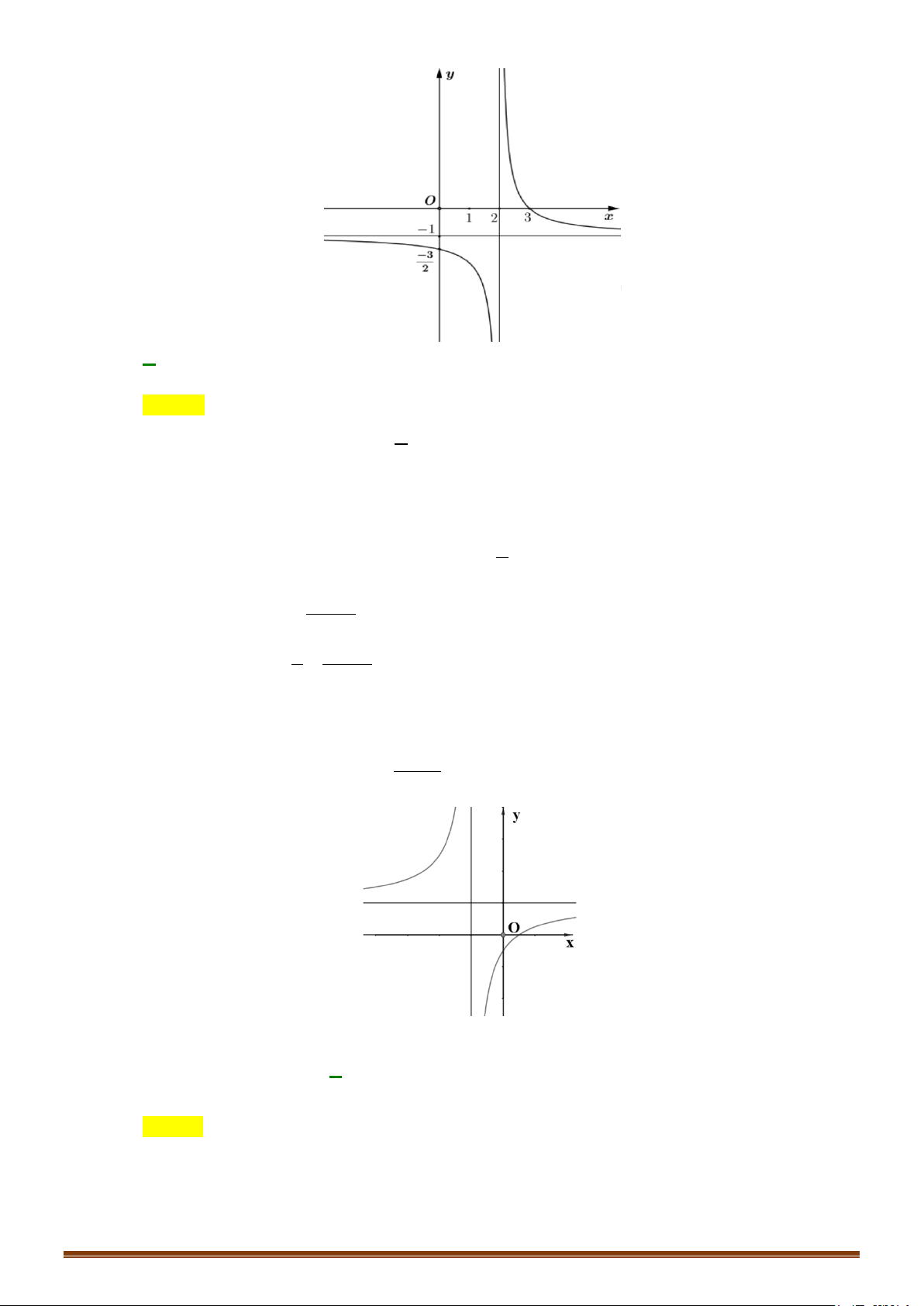
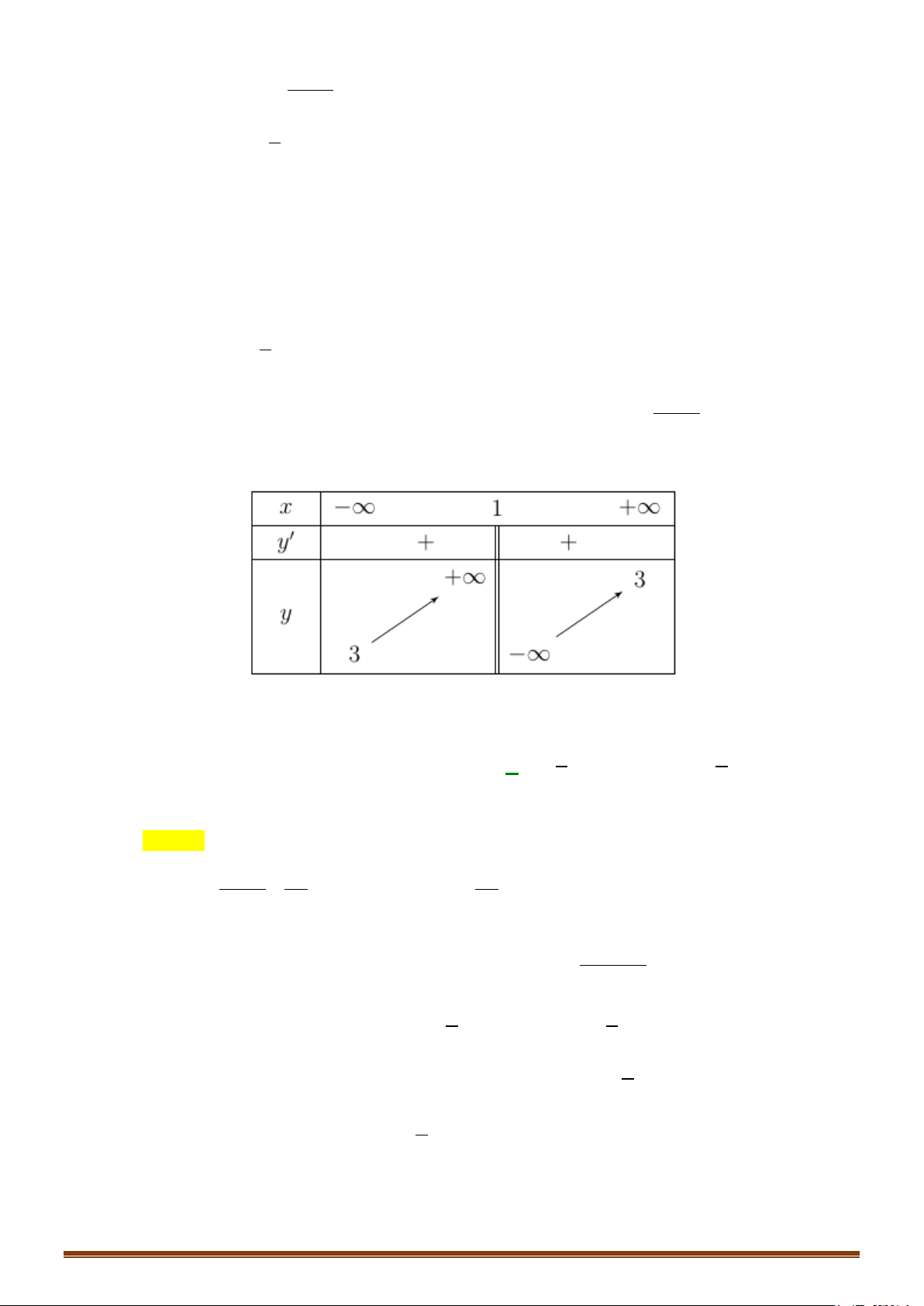
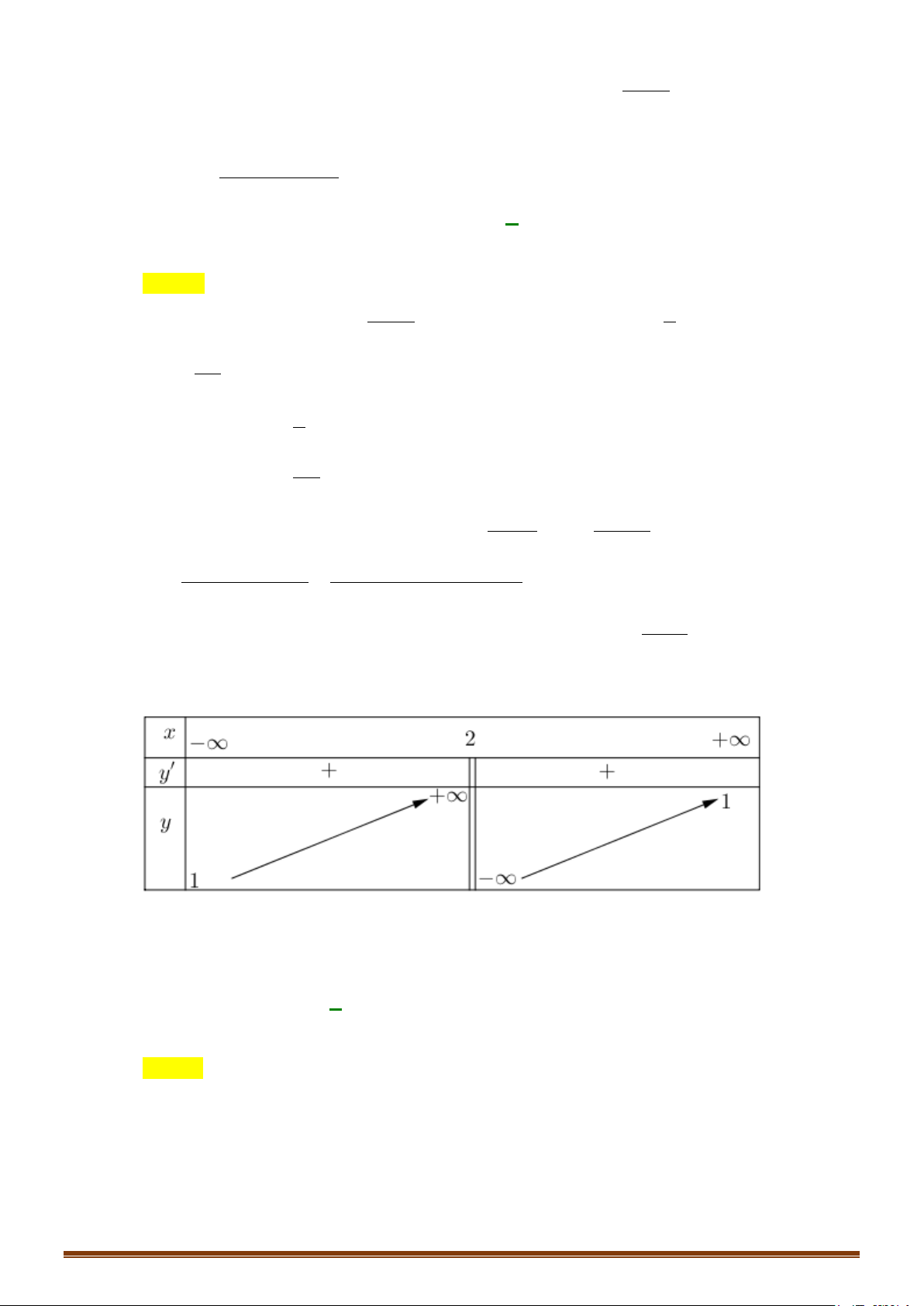
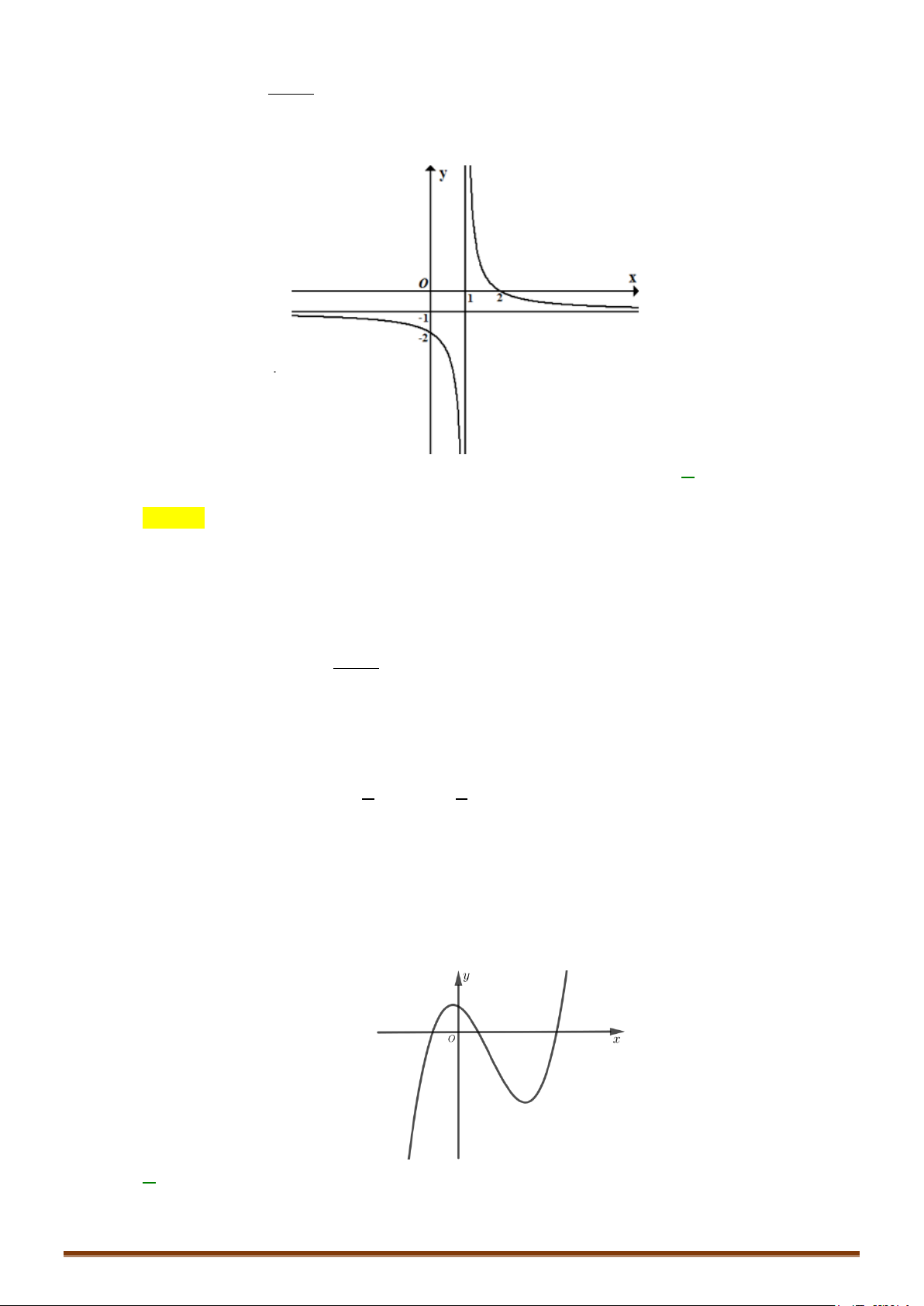
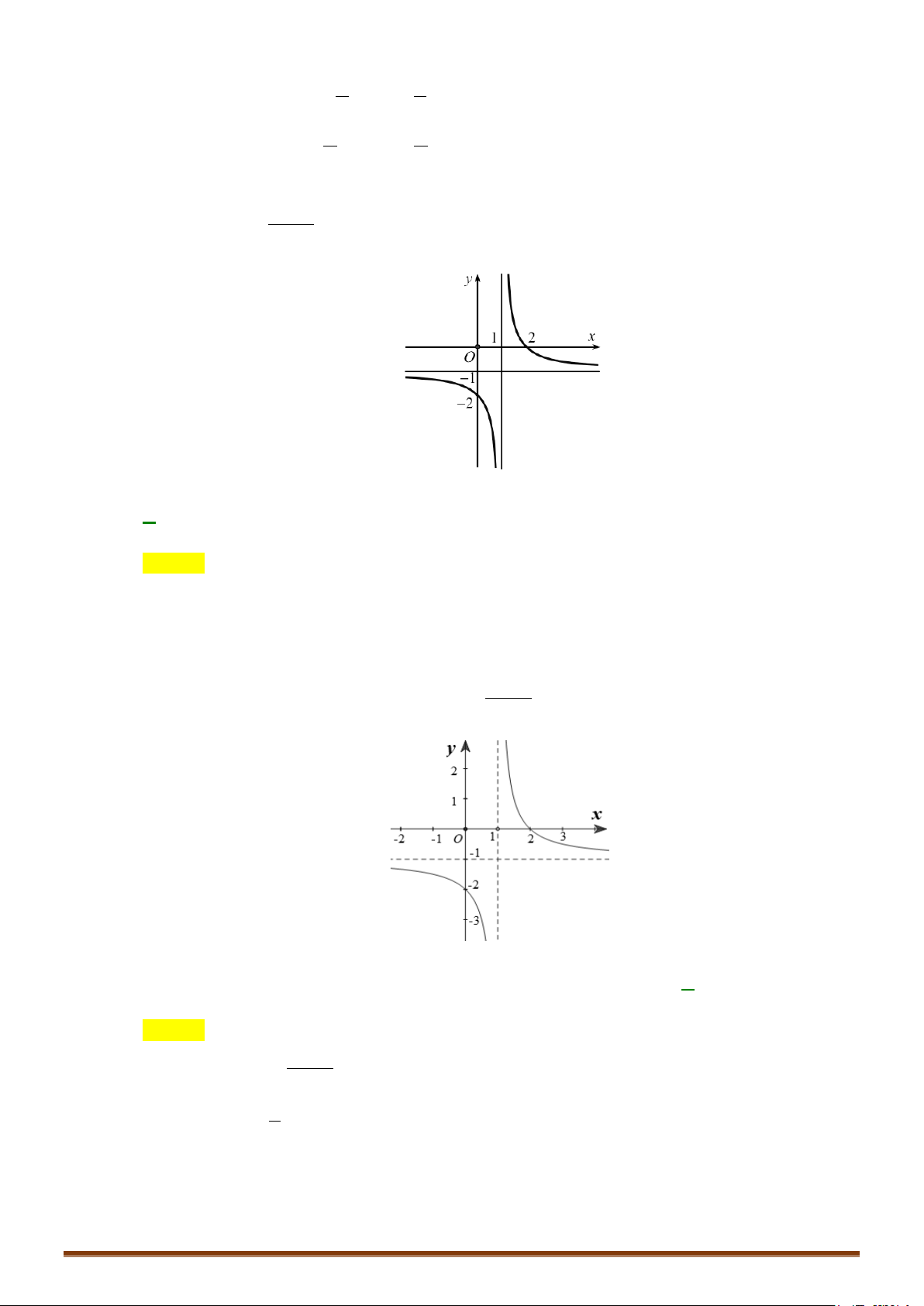
Câu 2. Khảo sát và vẽ đồ thị của hàm số y = 2x −1 Lời giải 1
Tập xác định: D  \  =  2   3 − 1 Ta có 'y = < 0 x ≠ ( với mọi 2x − )2 1 2 1 lim y = lim y = 1
. Đồ thị hàm số có tiệm cận ngang là y = x→+∞ x→−∞ 2 2
lim y = +∞, lim y = −∞ 1
. Đồ thị hàm số có tiệm cận đứng là x =  1 +   1 − 2 xx  → →  2  2    
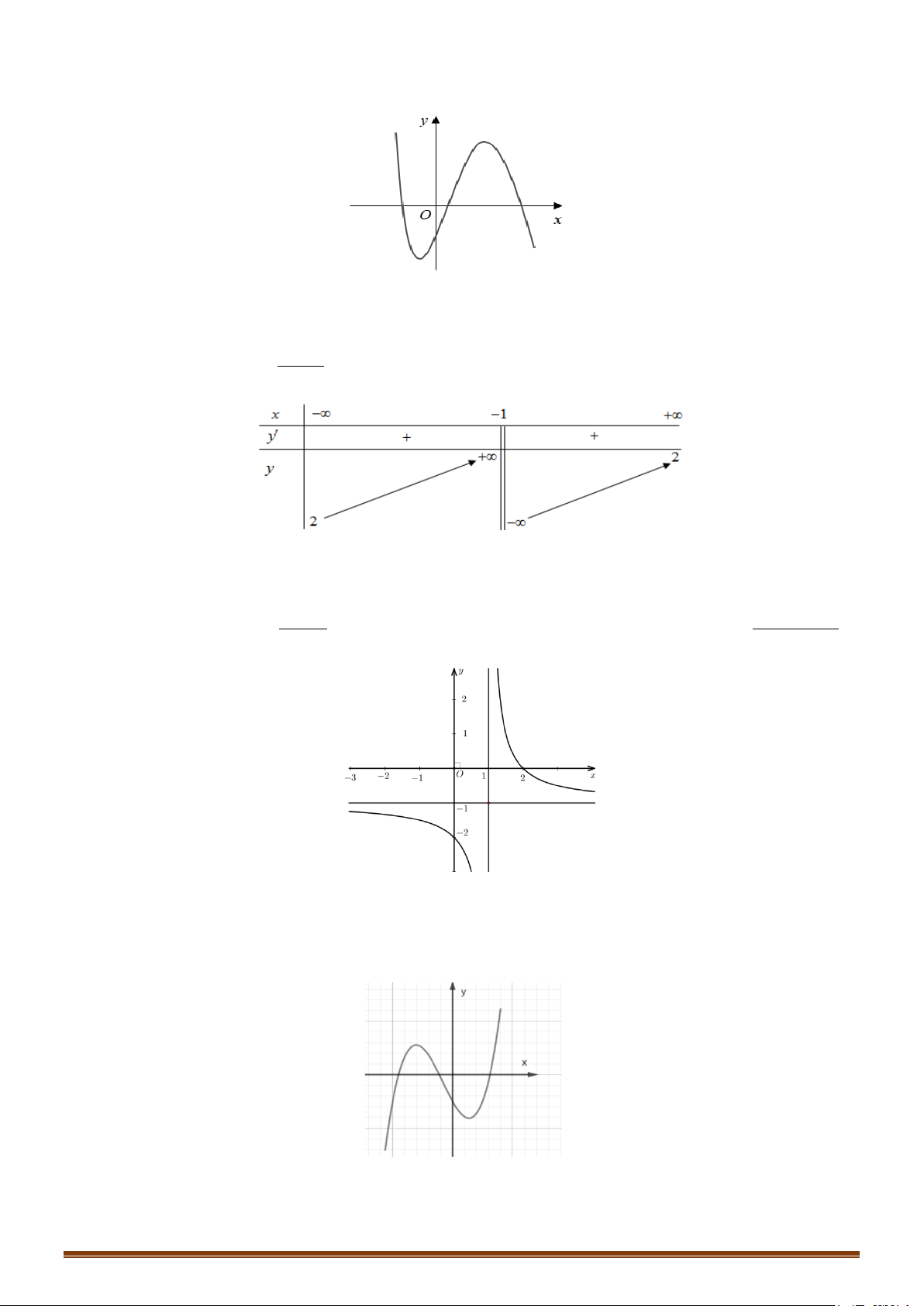
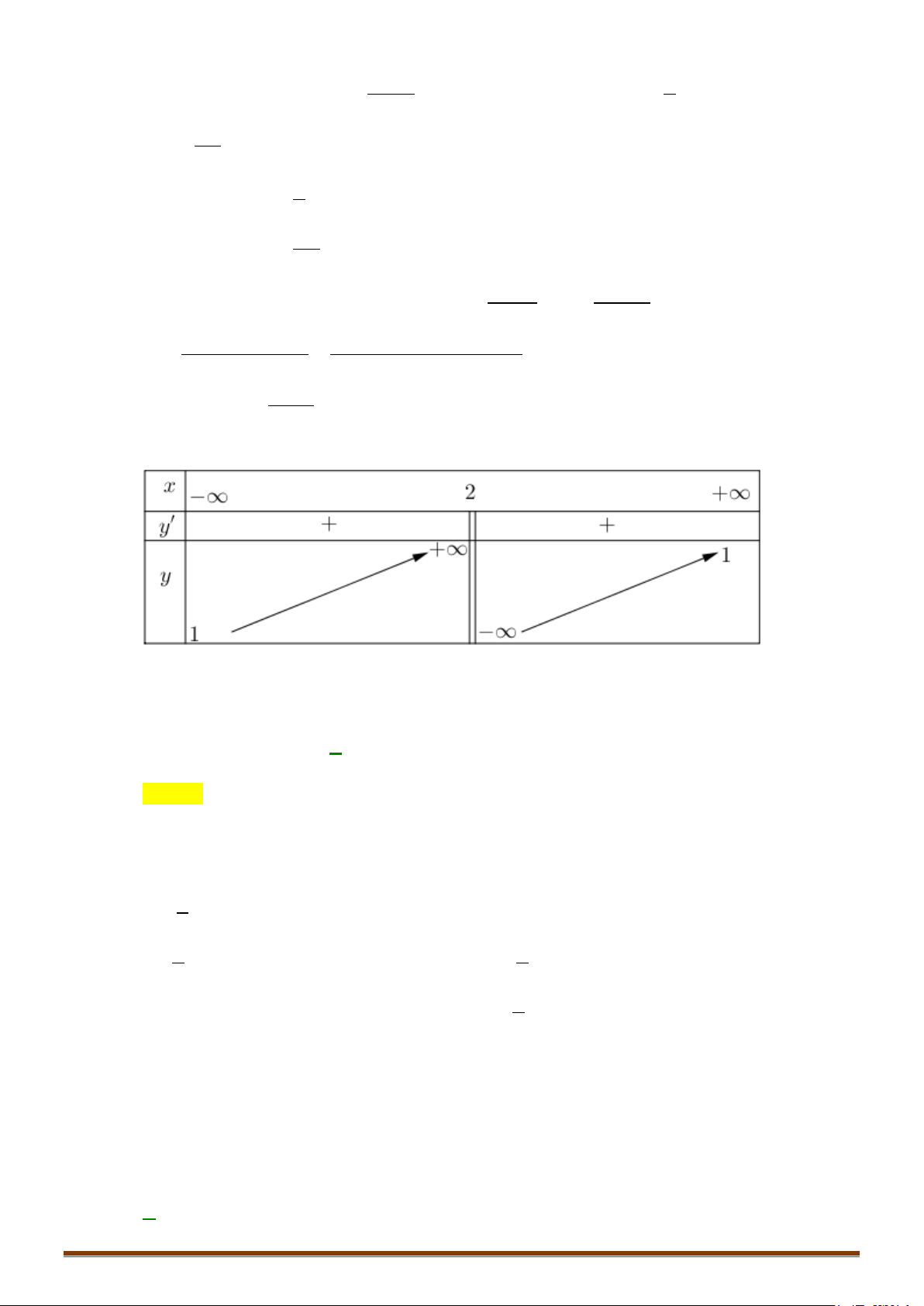
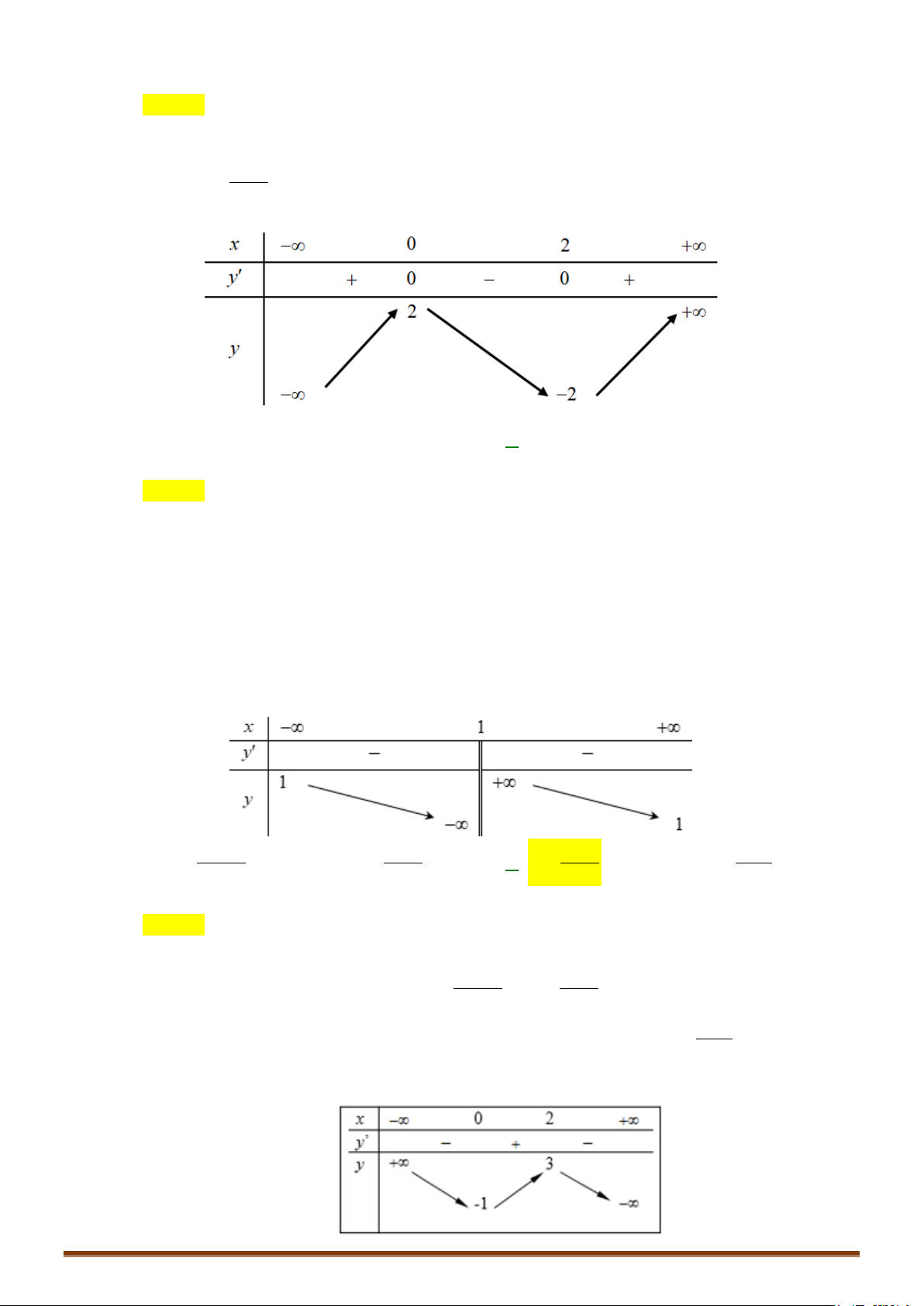
Bảng biến thiên của hàm số có dạng: x 1 −∞ 2 +∞ ' y − − y 1 + ∞ 2 −∞ 1 2
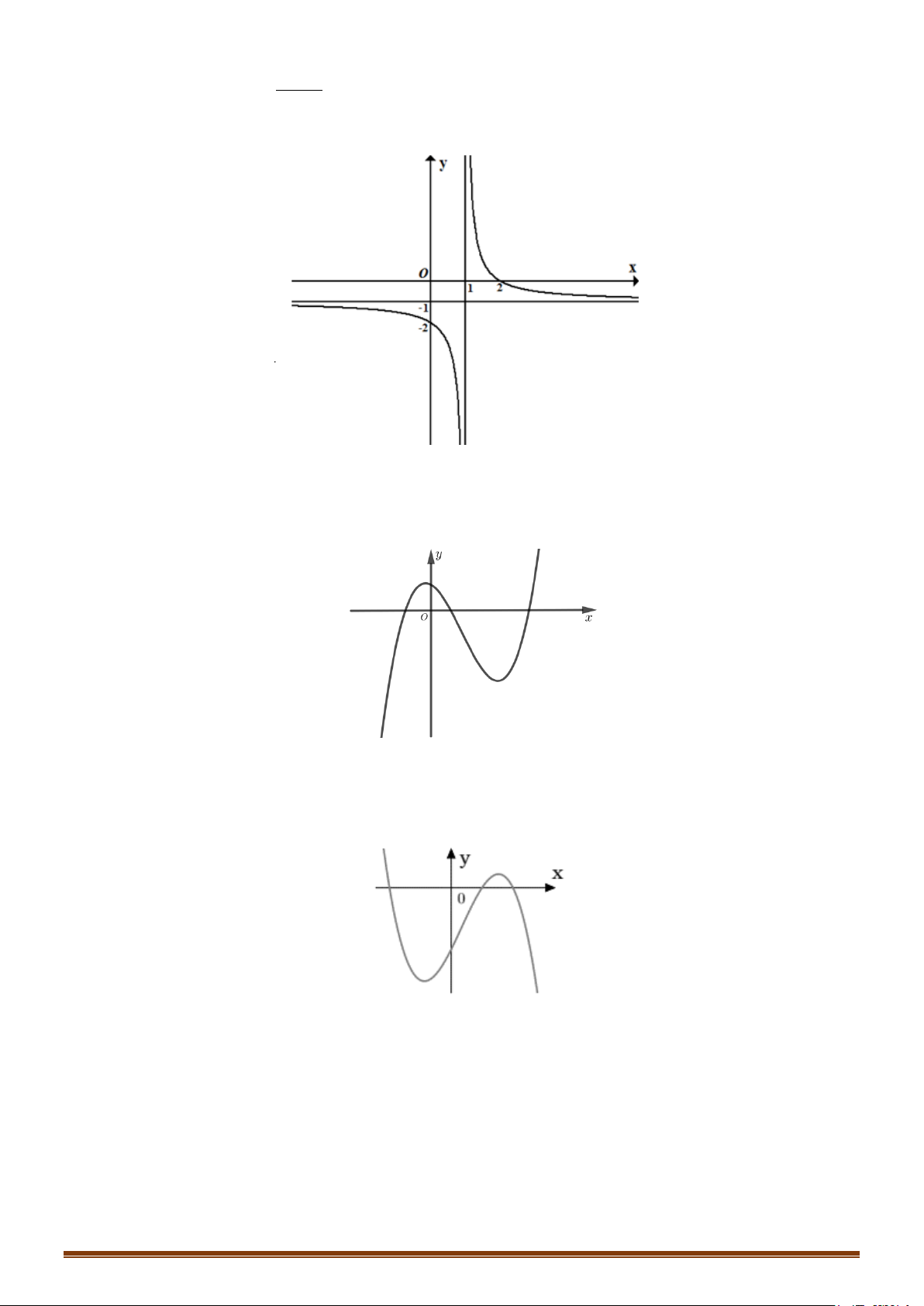
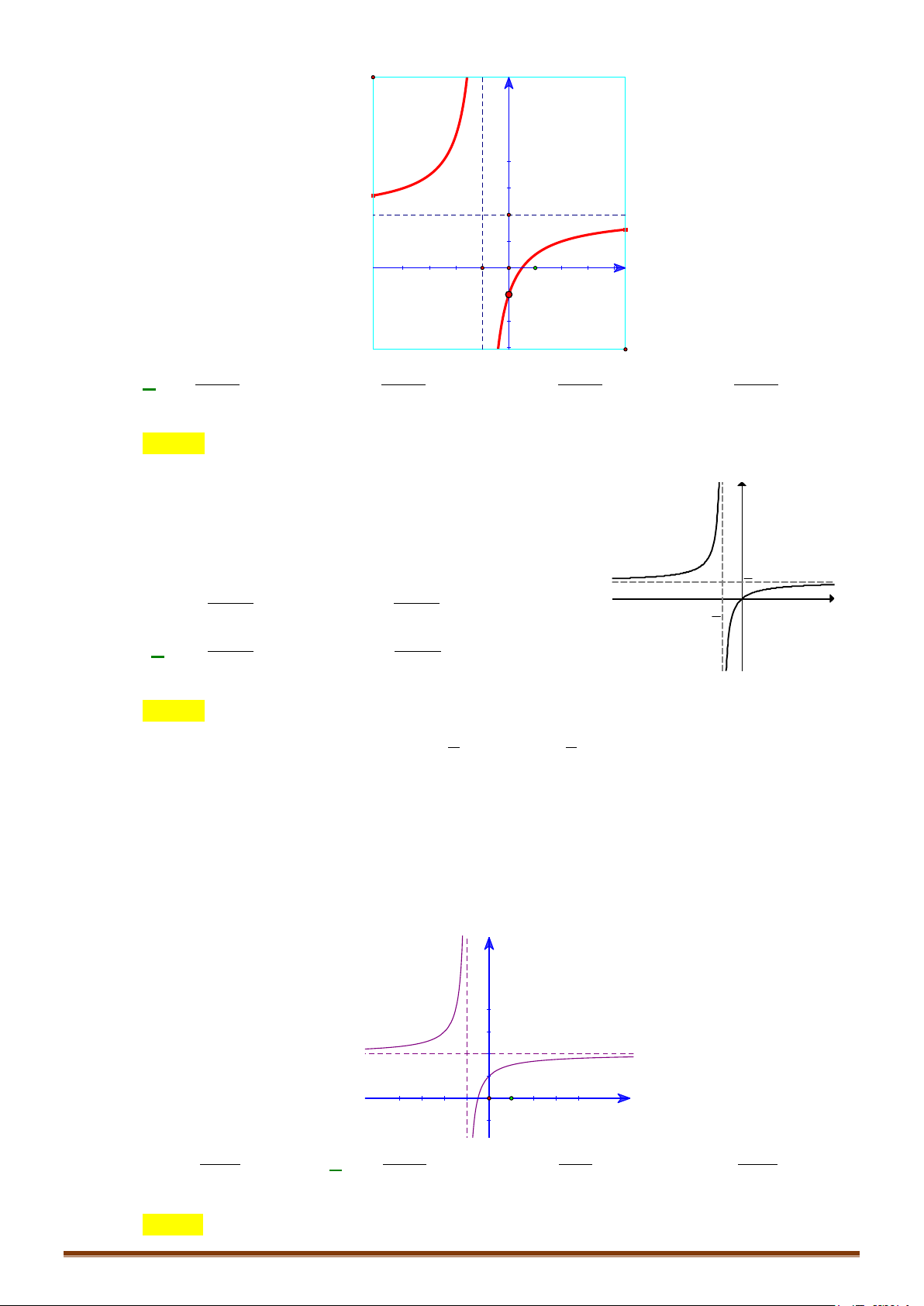
Đồ thị hàm số có dạng: Page 205
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
C. MỘT SỐ PHÉP BIẾN ĐỔI ĐỒ THỊ
Cho hàm số y = f (x) có đồ thị (C) với số a > 0 ta có:
Hàm số y = f (x) + a có đồ thị (C′) là tịnh tiến (C) theo phương của Oy lên trên a đơn vị.
Hàm số y = f (x) − a có đồ thị (C′) là tịnh tiến (C) theo phương của Oy xuống dưới a đơn vị.
Hàm số y = f (x + a) có đồ thị (C′) là tịnh tiến (C) theo phương của Ox qua trái a đơn vị.
Hàm số y = f (x − a) có đồ thị (C′) là tịnh tiến (C) theo phương của Ox qua phải a đơn vị.
Hàm số y = − f (x) có đồ thị (C′) là đối xứng của (C) qua trục Ox .
Hàm số y = f (−x) có đồ thị C  là đối xứng của (C) qua trục Oy .
Từ đồ thị (C) : y = f (x) suy ra đồ thị (C′) : y = f ( x ) .
f x khi x ≥  0
Ta có y = f ( x ) ( ) =  f
 (−x) khi x <  0
và y = f ( x ) là hàm chẵn nên đồ thị (C′) nhận Oy làm trục đối xứng.
* Cách vẽ (C′) từ (C) :
+ Giữ nguyên phần đồ thị bên phải Oy của đồ thị (C) : y = f (x).
+ Bỏ phần đồ thị bên trái Oy của (C) , lấy đối xứng phần đồ thị được giữ qua Oy. y
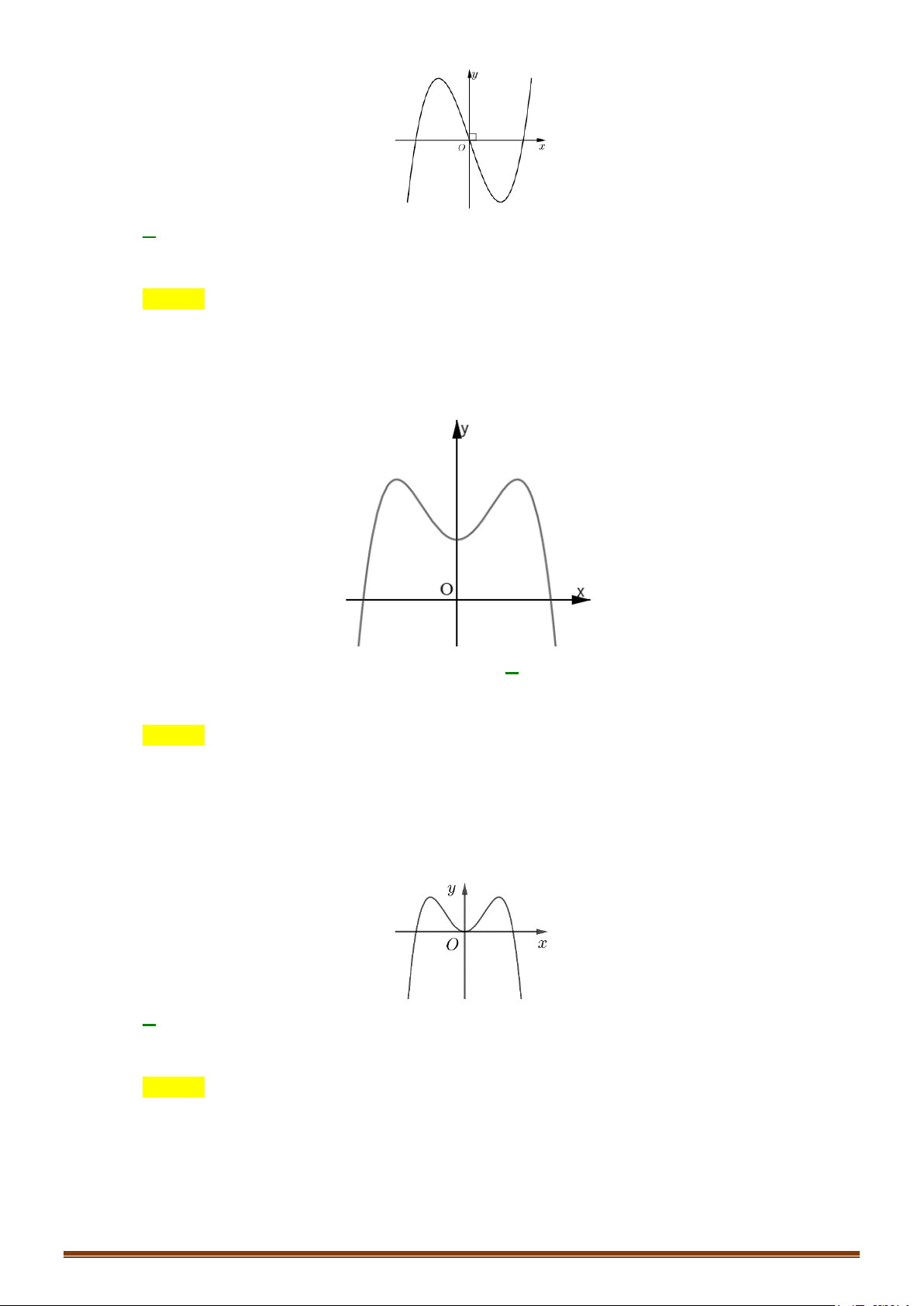
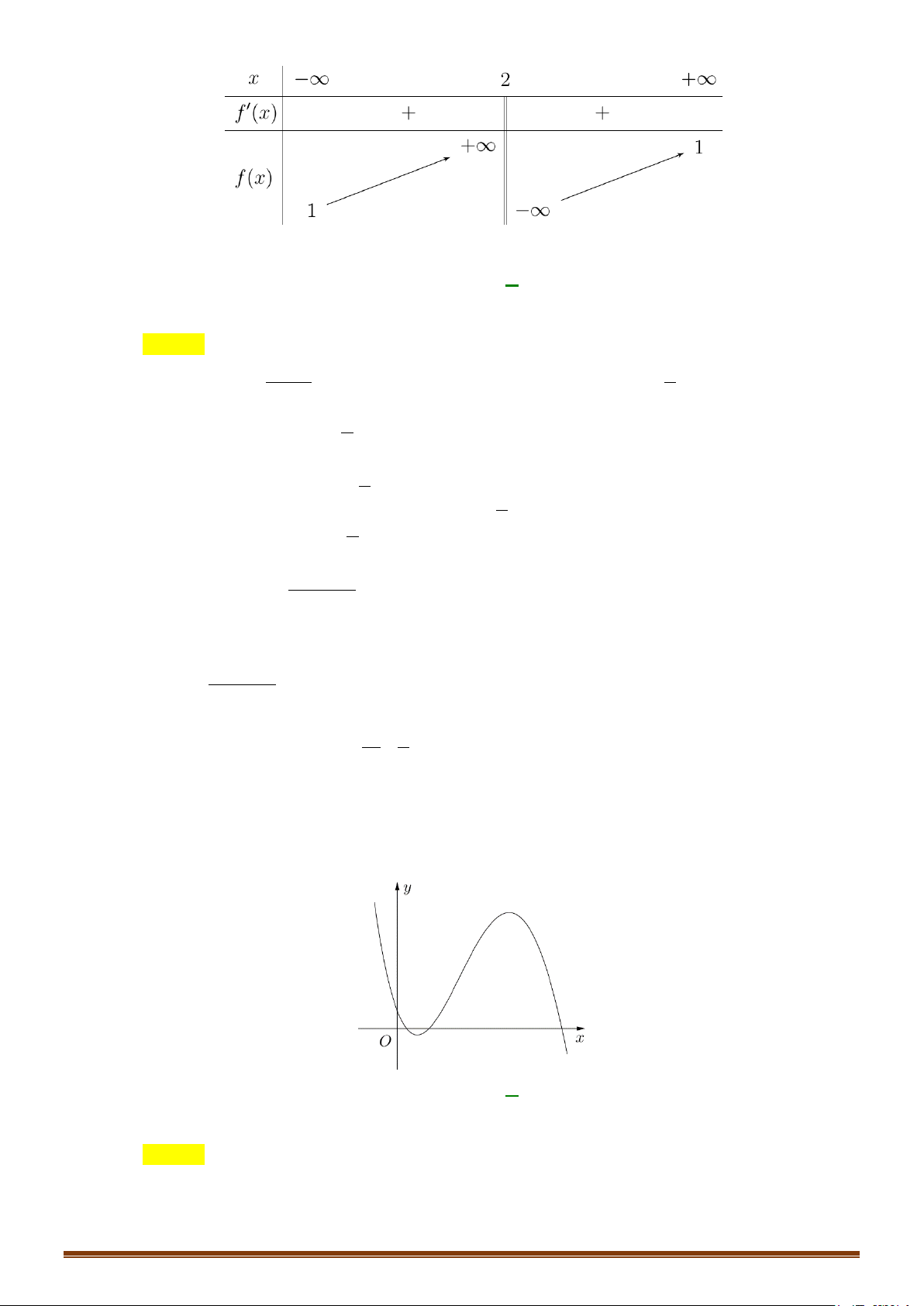
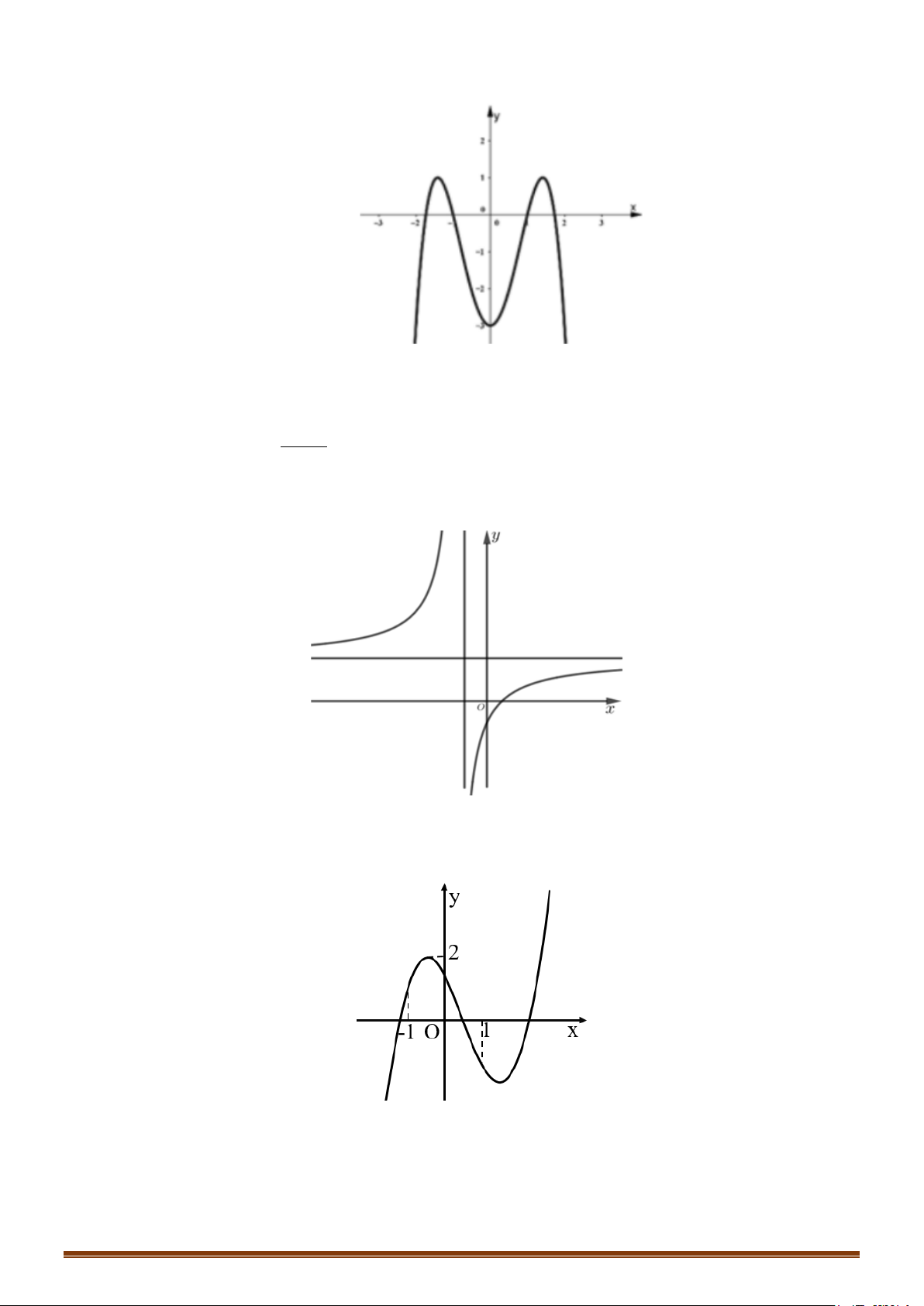
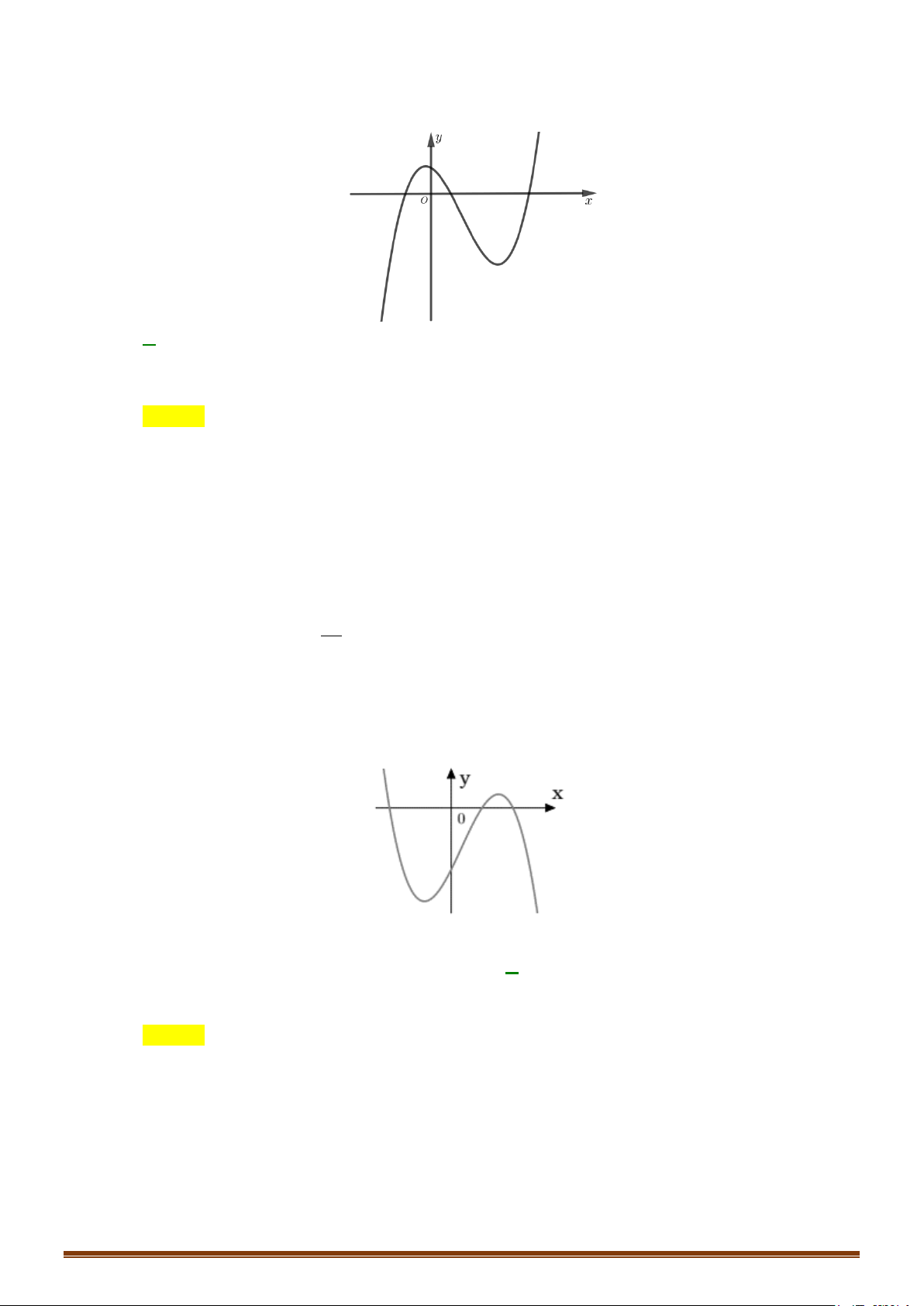
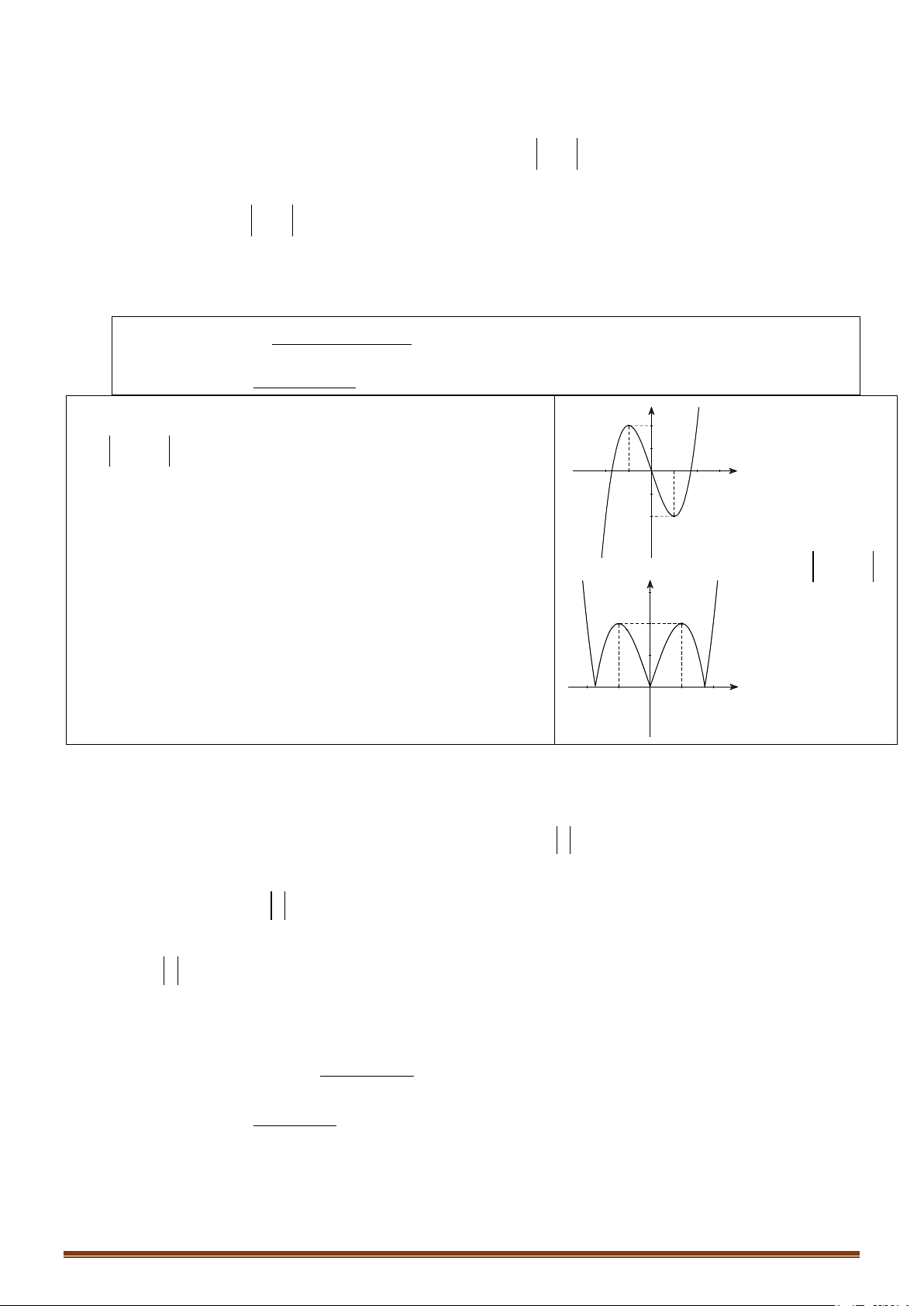
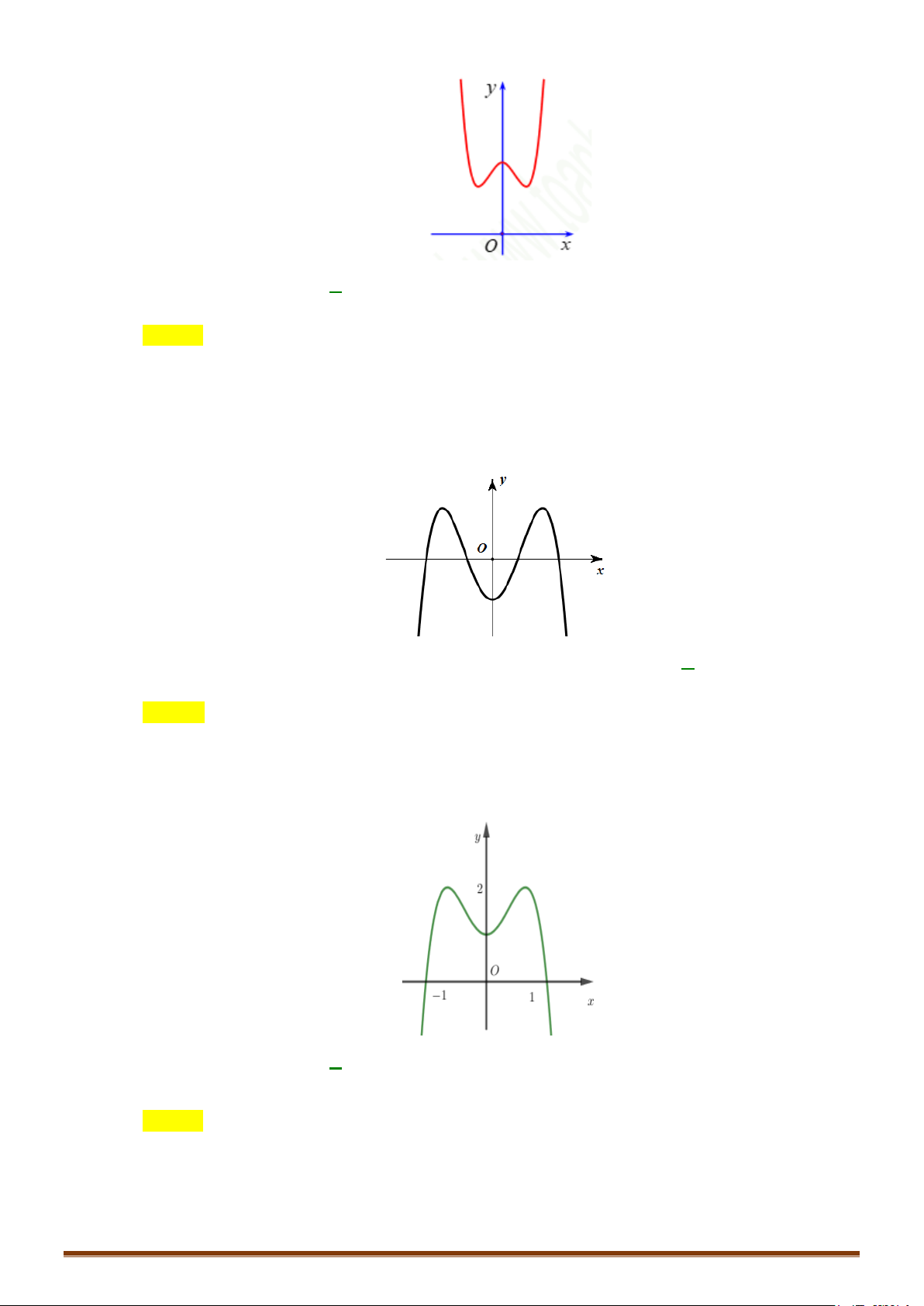
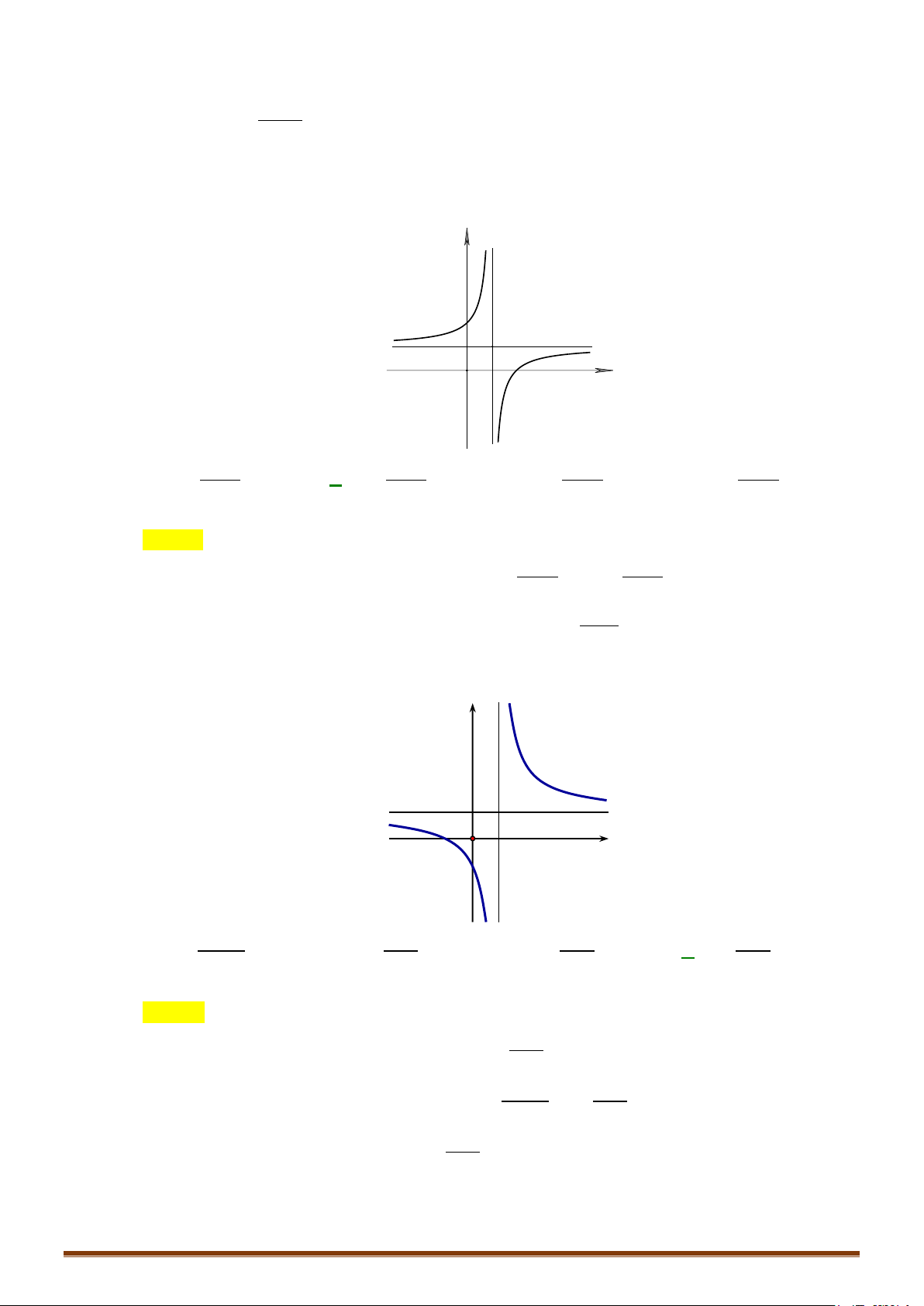
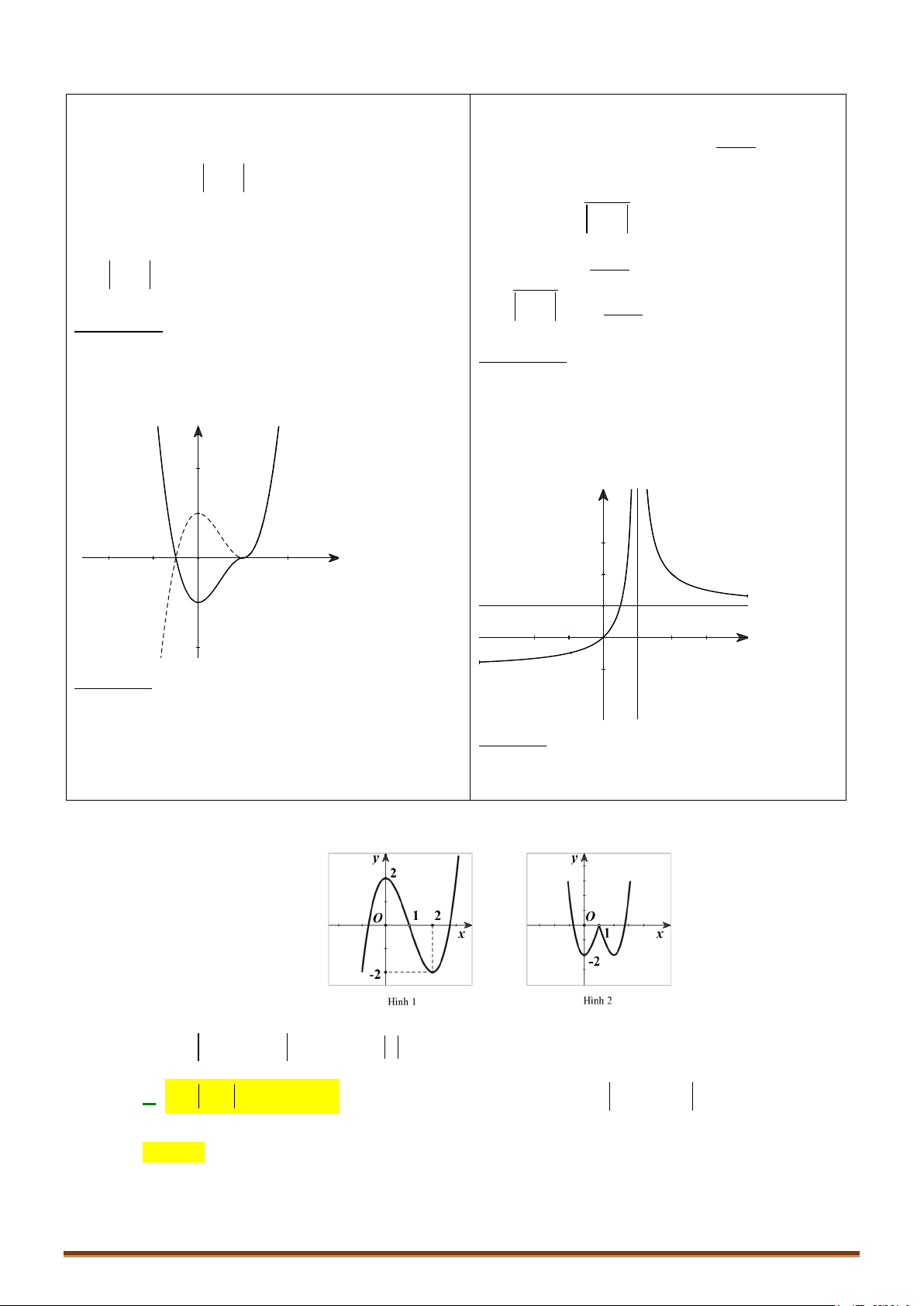
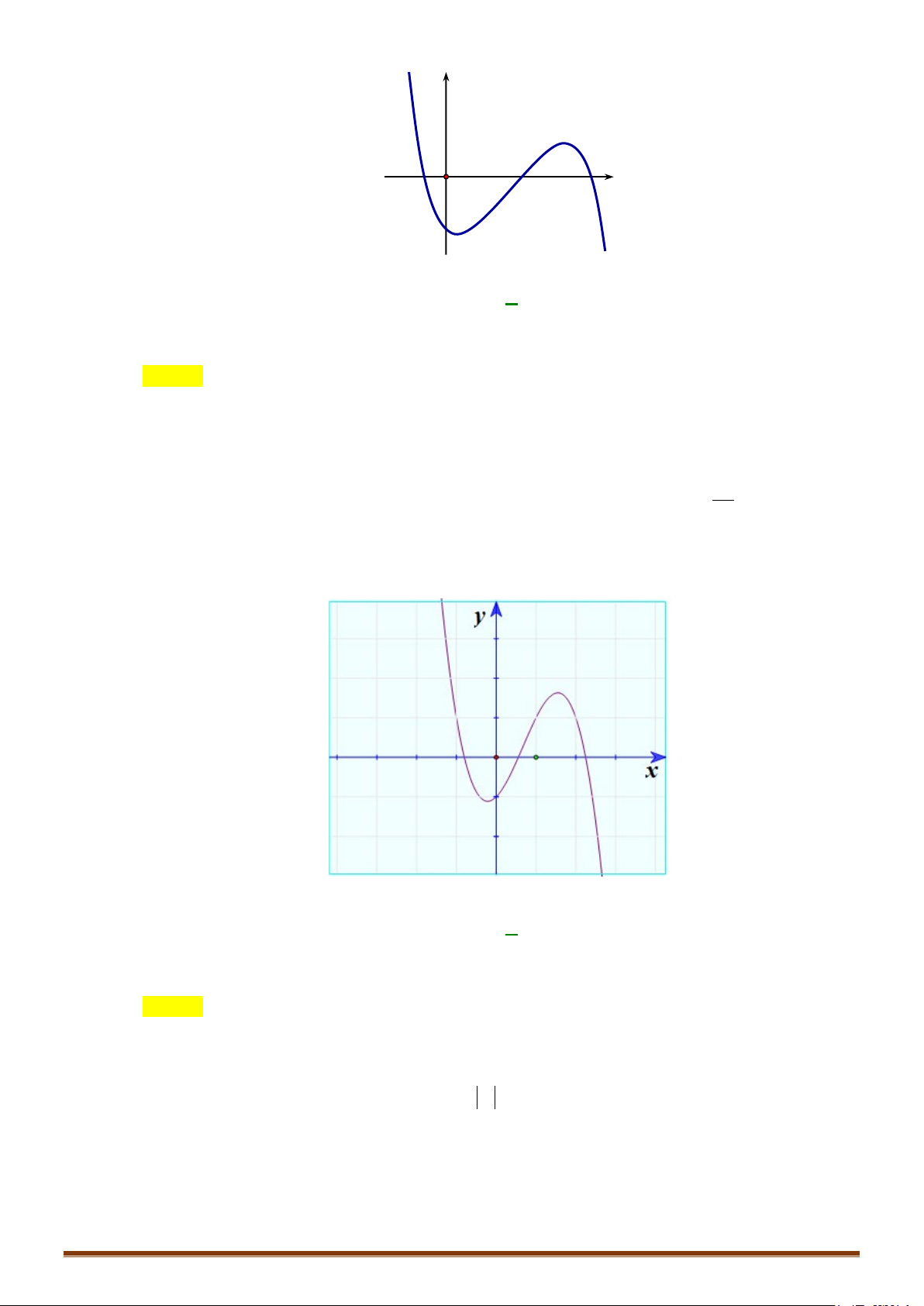
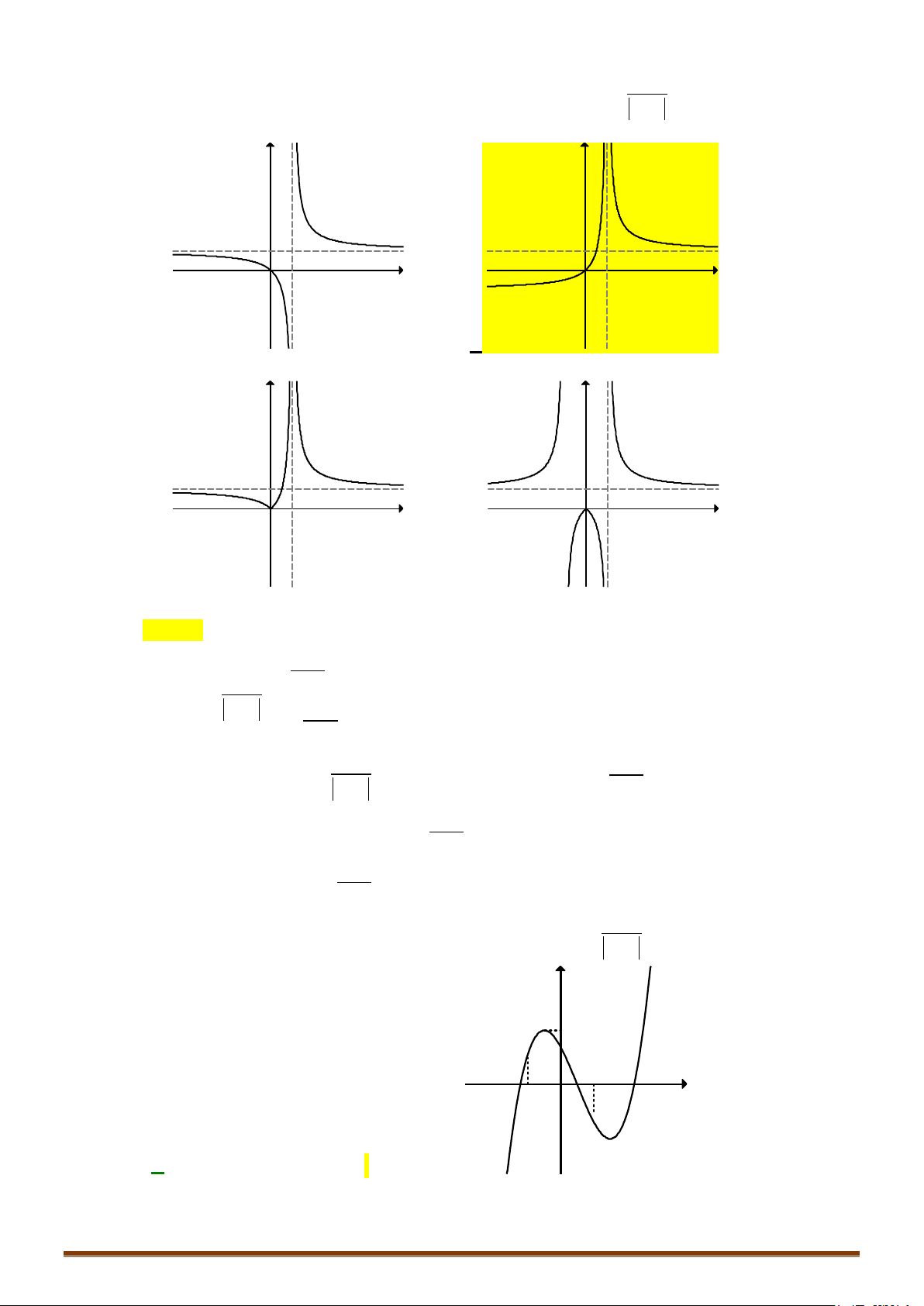
Ví dụ: Từ đồ thị (C) y = f (x) 3 :
= x − 3x suy ra đồ thị (C′) 3
: y = x − 3 x . 2 3  3
x − 3x khi x ≥  0
Ta có: y = x − 3 x = 1  -1 O 3 −x + 3x = − x  ( 3x −3x) khi x < 0 -2
Cách vẽ đồ thị (C′) : (C) 3
: y = x − 3x
+ Bỏ phần đồ thị của (C) bên trái Oy, giữ nguyên (C) bên phải . Oy y
+ Lấy đối xứng phần đồ thị được giữ qua Oy . -1 O 1 x -2 (C′) 3
: y = x − 3 x Page 206
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Từ đồ thị (C) : y = f (x) suy ra đồ thị (C′) : y = f (x) .
f x khi f x ≥  0
Ta có: y = f (x) ( ) ( ) =  − f
(x) khi f (x) <  0
* Cách vẽ (C′) từ (C) :
+ Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C): y = f (x) .
+ Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
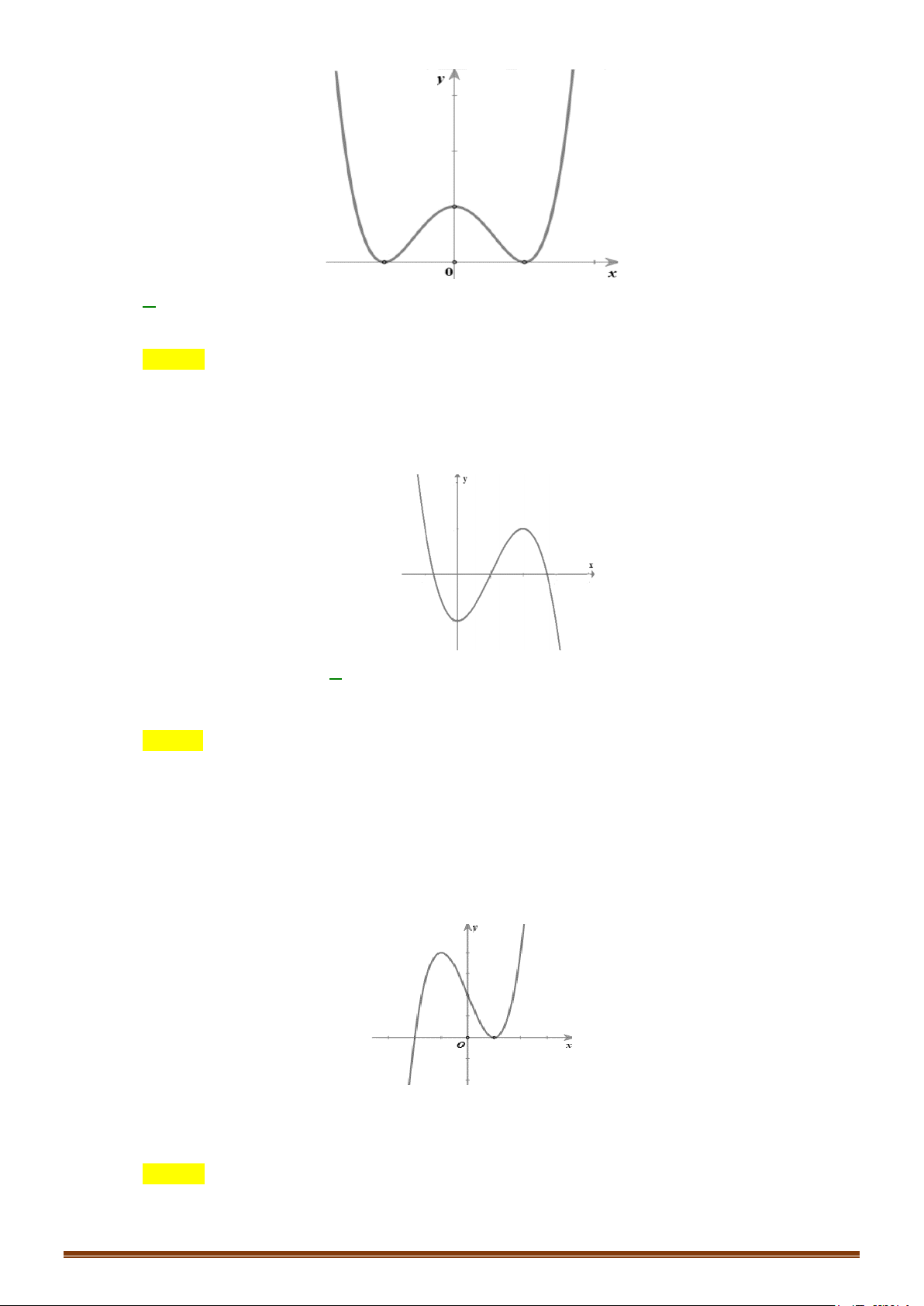
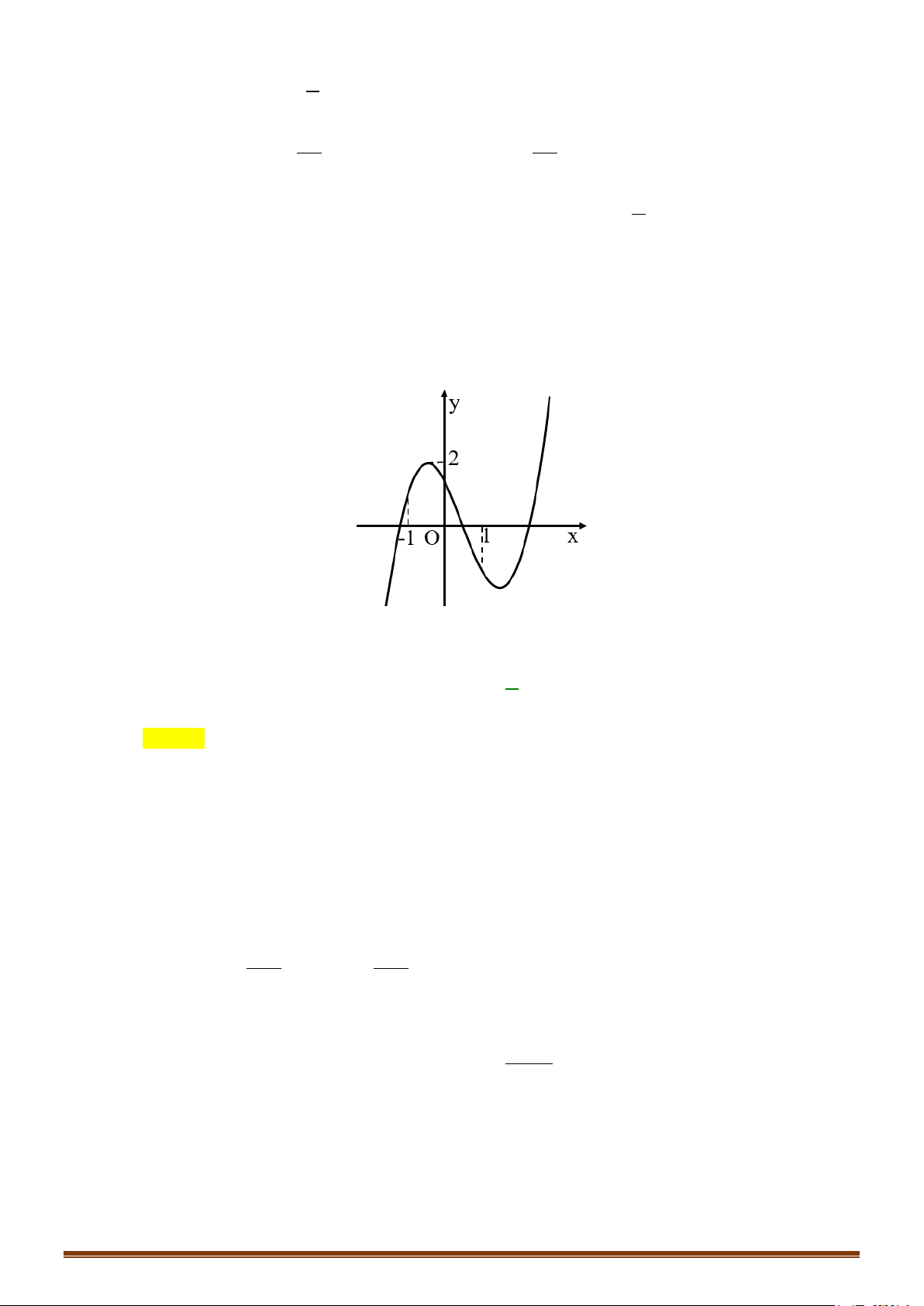
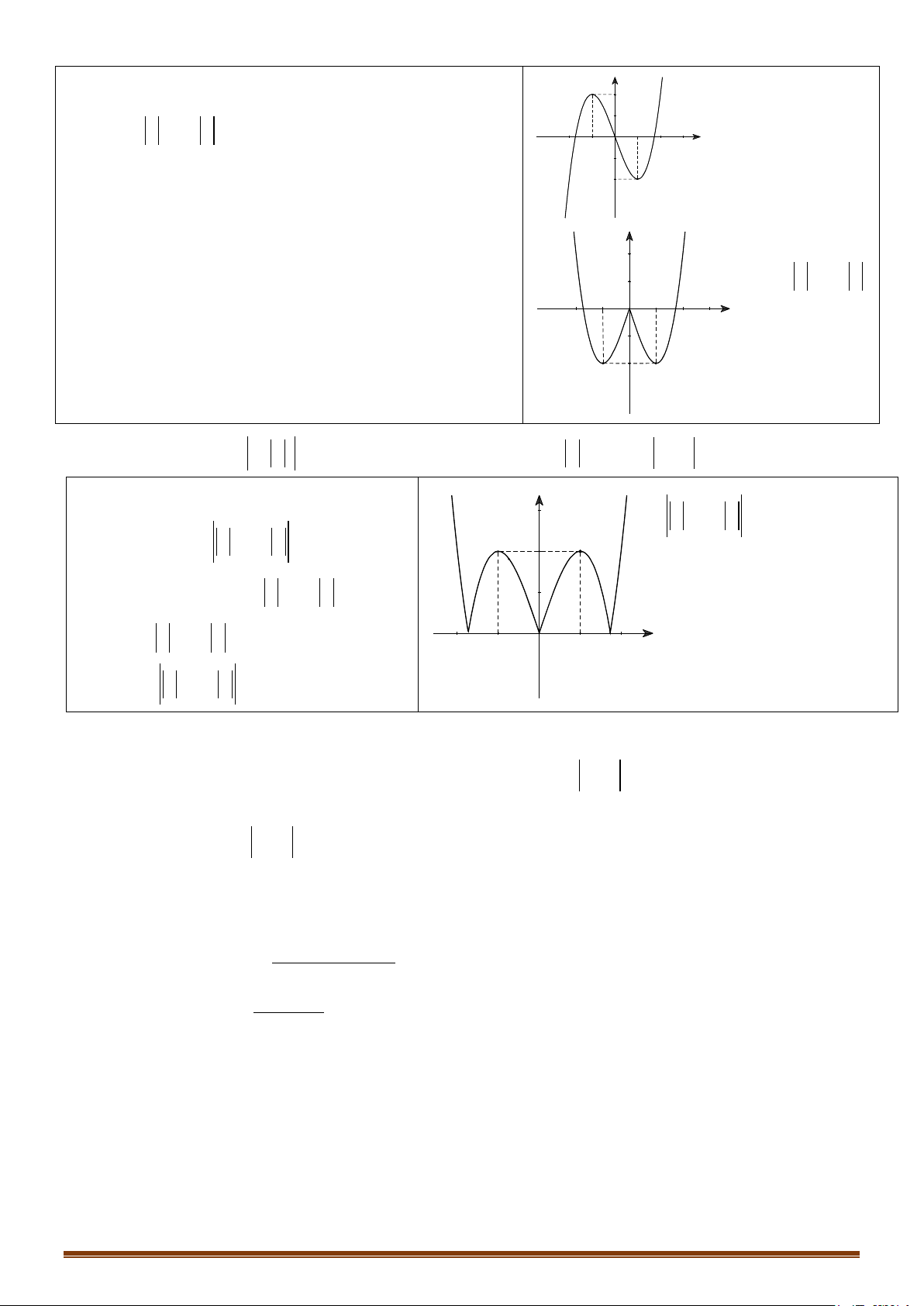
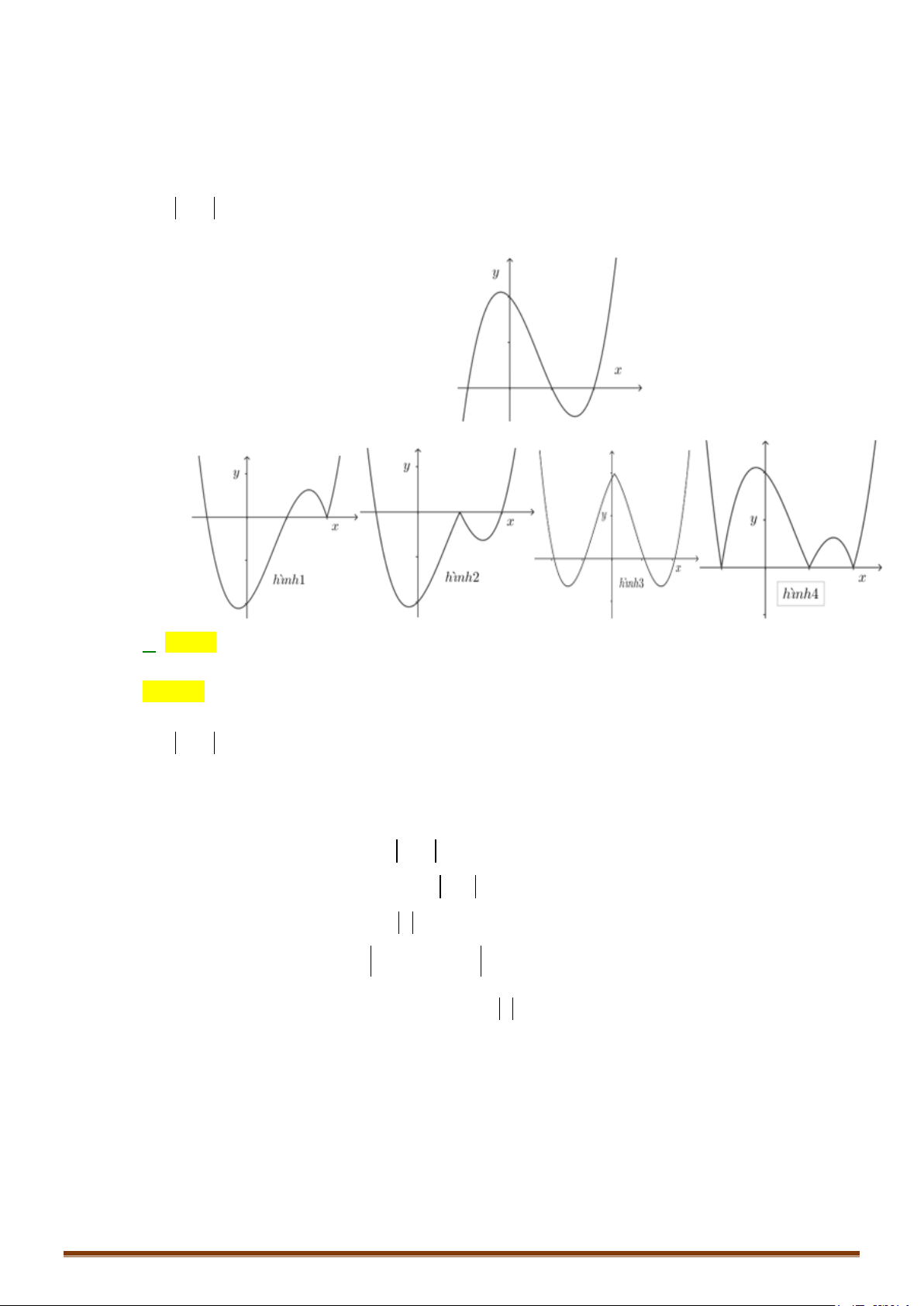
Ví dụ: Từ đồ thị (C) y = f (x) 3 :
= x − 3x suy ra đồ thị (C′) 3
: y = x − 3x .
Cách vẽ đồ thị (C′) :
+ Bỏ phần đồ thị của (C) dưới Ox, giữ nguyên (C) phía trên . Ox
+ Lấy đối xứng phần đồ thị bị bỏ qua Ox . y y 2 2 1 -1 O x (C) 3
: y = x − 3x (C′) 3
: y = x − 3x -2 -1 O 1 x
Chú ý: Với dạng:
y = f ( x ) ta lần lượt biến
đổi 2 đồ thị y = f ( x ) và y = f (x) y
Ví dụ: Từ đồ thị (C) y = f (x) 3 :
= x − 3x suy ra đồ thị 2 3
y = x − 3 x
Biến đổi (C) để được đồ thị (C′) 3
: y = x − 3 x . -1 O 1 x Biến đổi (C′) 3
: y = x − 3 x ta được đồ thị (C′′) 3
: y = x − 3 x . (C′′) 3
: y = x − 3 x
Từ đồ thị (C) : y = u(x).v(x) suy ra đồ thị (C′) : y = u(x) .v(x) . u
x .v x = f x khi u x ≥  0
Ta có: y = u(x) .v(x) ( ) ( ) ( ) ( ) =  u −
 (x).v(x) = f (x) khi u(x) <  0
* Cách vẽ (C′) từ (C) :
+ Giữ nguyên phần đồ thị trên miền u(x) ≥ 0 của đồ thị (C) : y = f (x).
+ Bỏ phần đồ thị trên miền u(x) < 0 của (C) , lấy đối xứng phần đồ thị bị bỏ qua Ox. Page 207
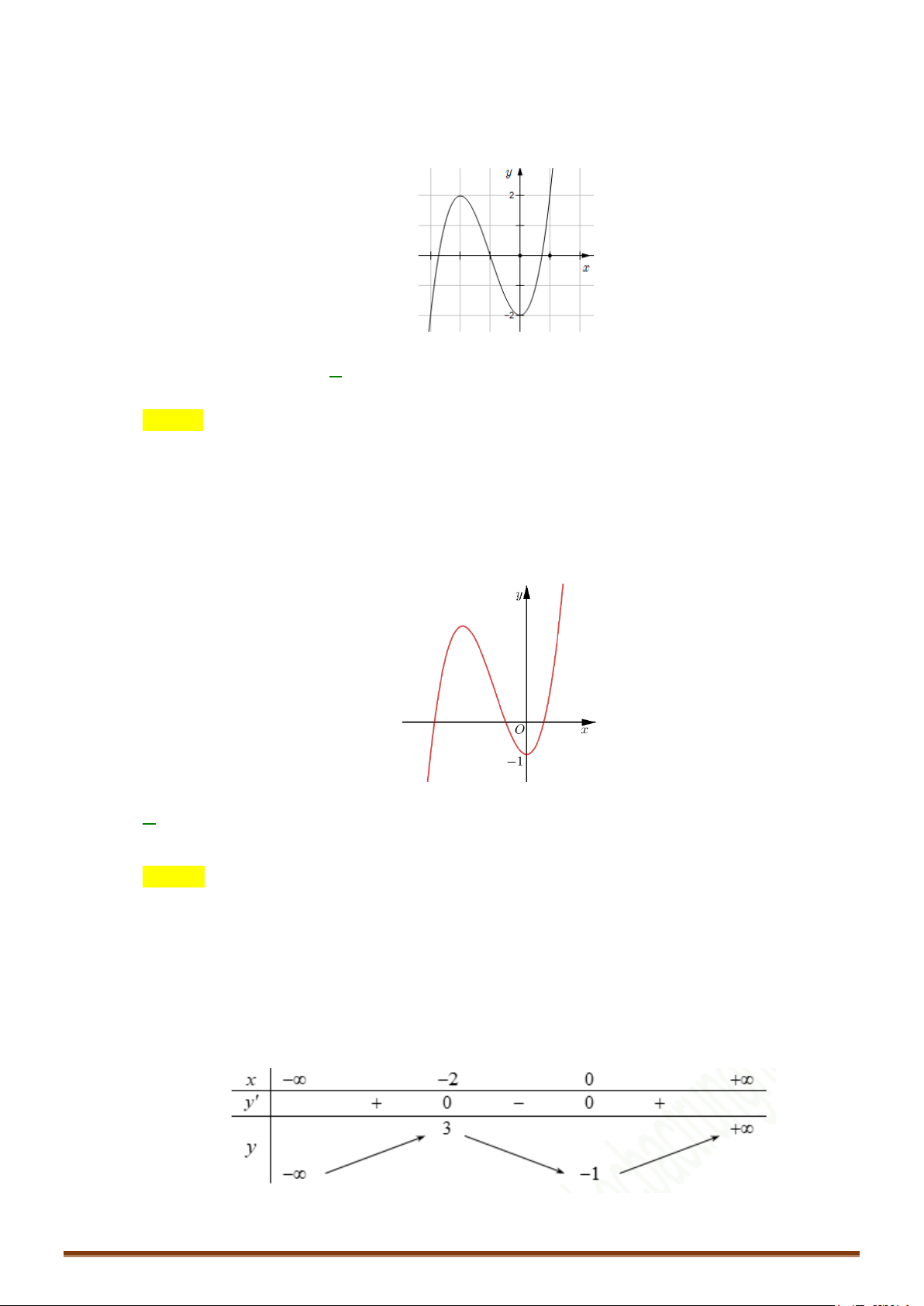
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Ví dụ:
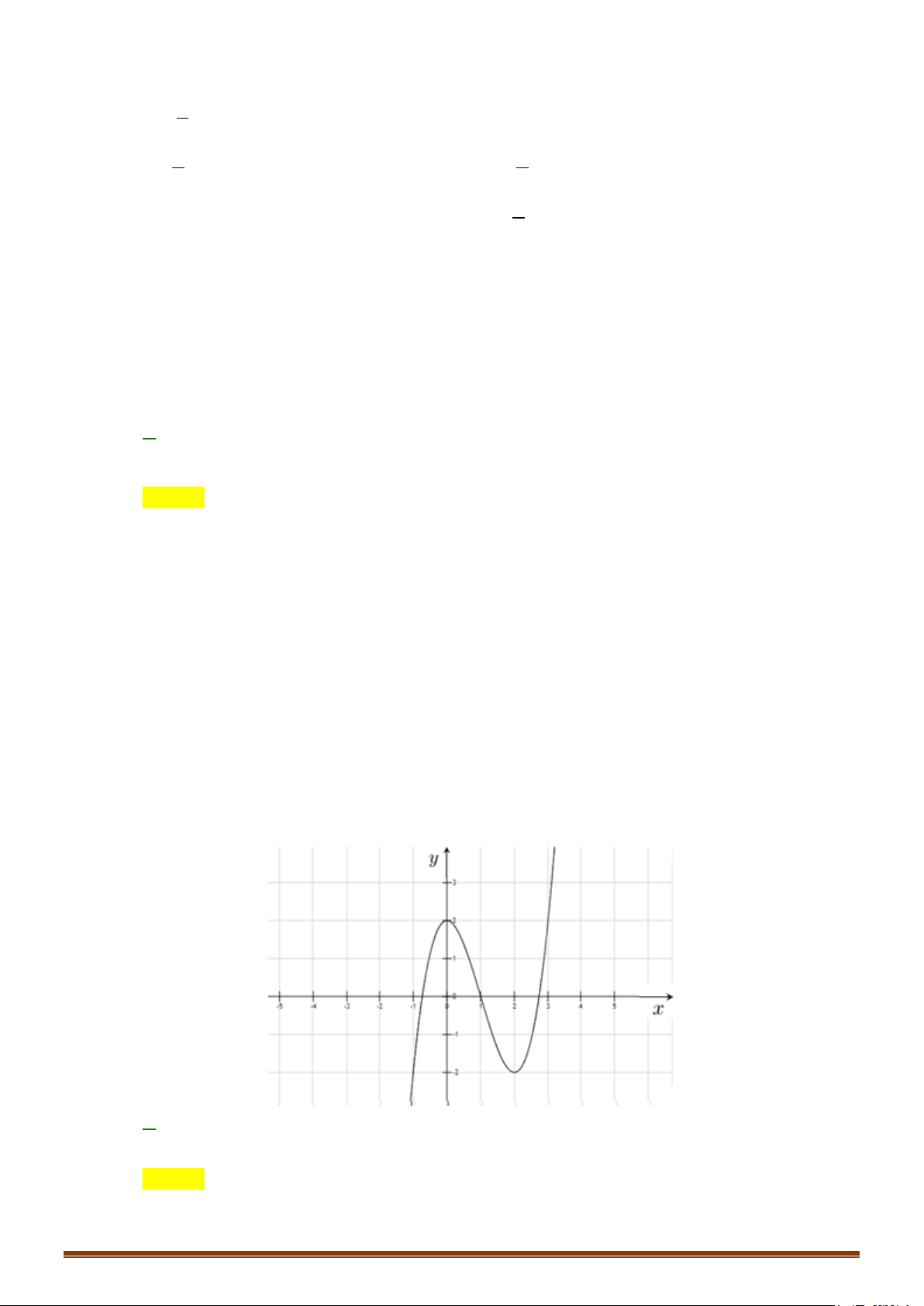
a) Từ đồ thị (C) y = f (x) 3 2 :
= 2x − 3x + 1 suy ra b) Từ đồ thị ( ): = ( ) x C y f x = suy ra đồ x −1
đồ thị (C′) y = x − ( 2 :
1 2x − x −1) x
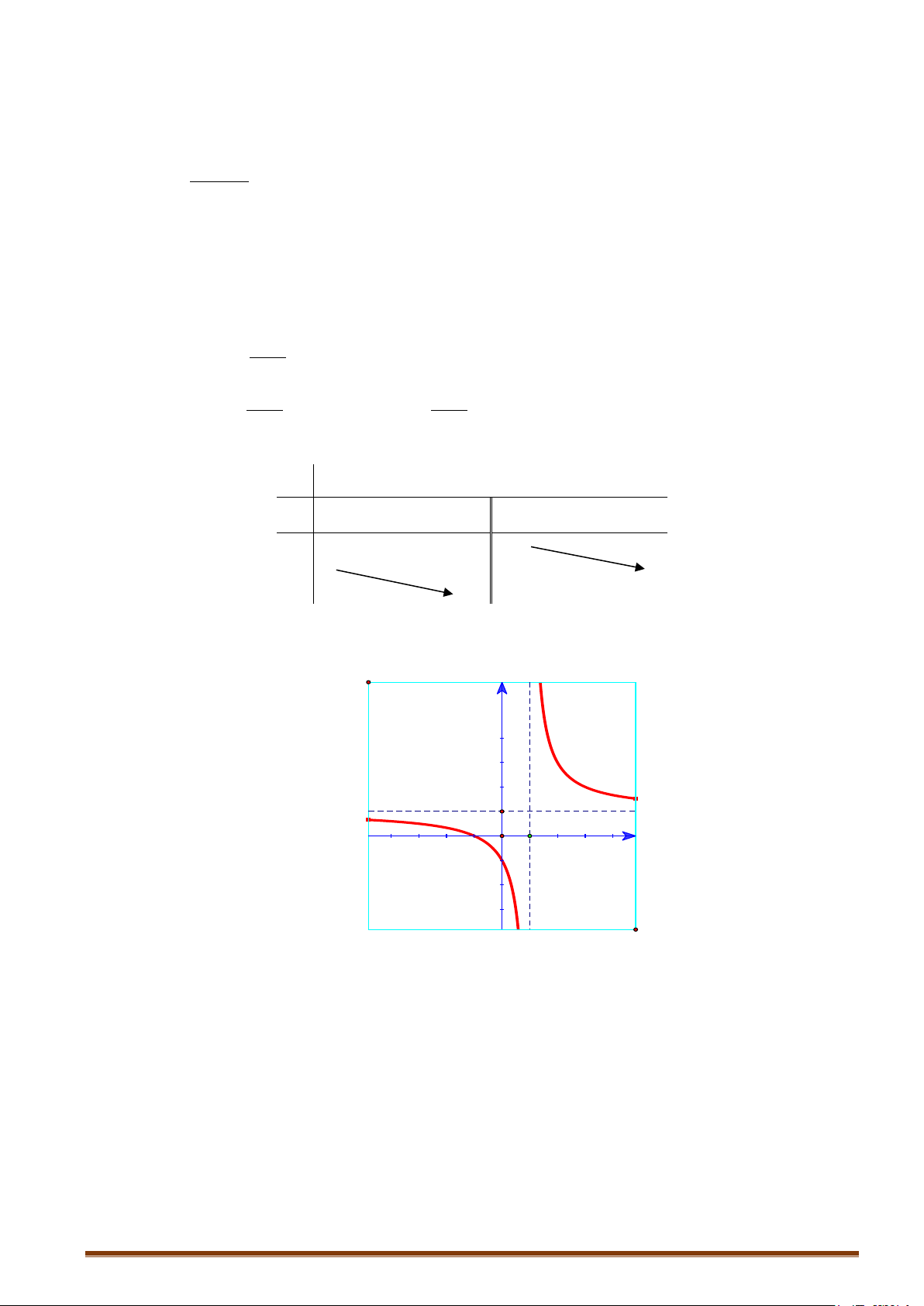
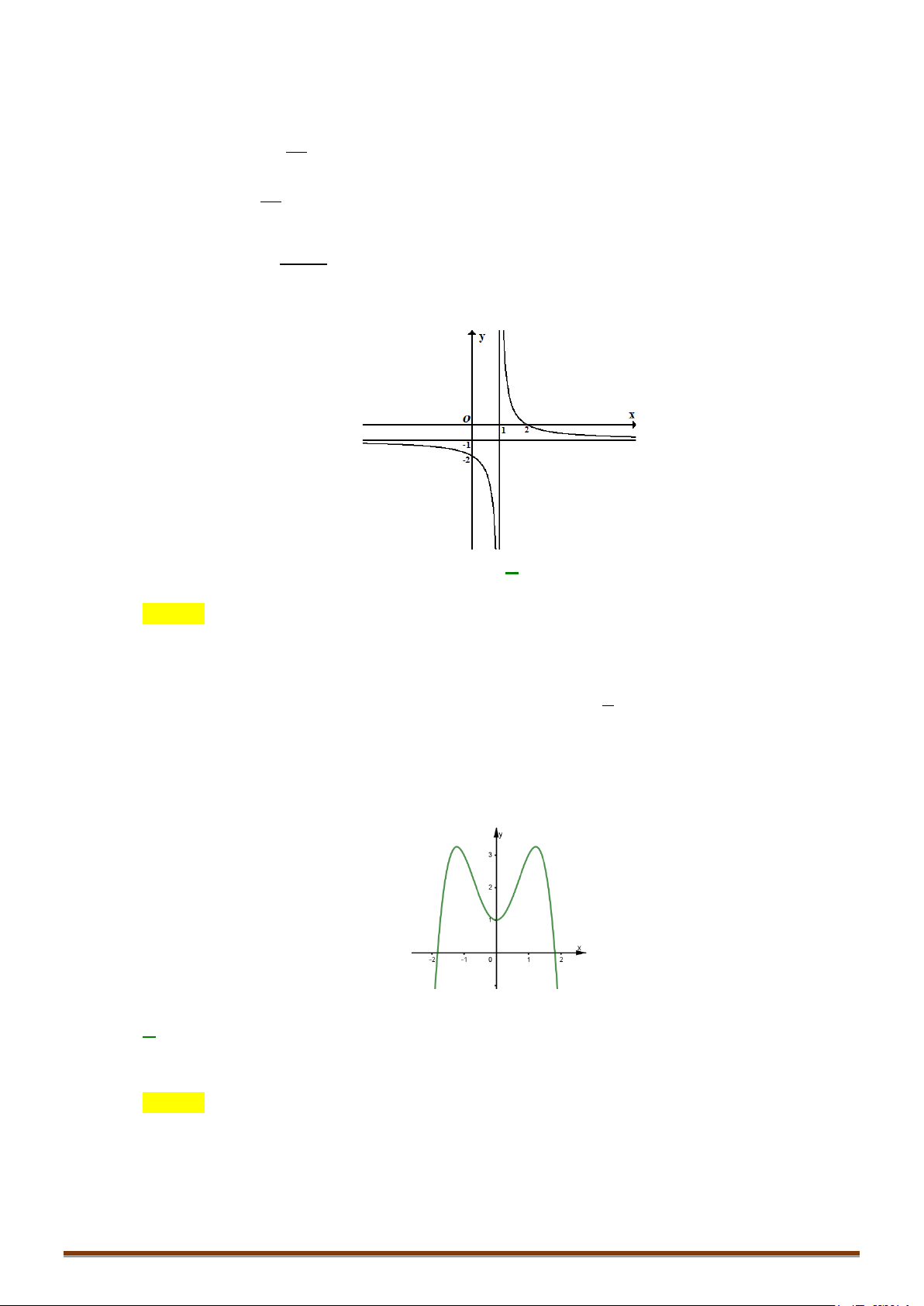
thị (C′) : y = x −1 Ta có: Ta có:  f x x ≥ y = x −1 ( 1 2 2x − x −1) ( ) khi = 
x khi x∈(1;+∞  ) − f  (x) khi x <  1 xx −1 y = =  . Đồ thị (C’): x −1 x − khi x ∈(−∞;1)
+ Giữ nguyên (C) với x ≥ 1.  x −1
+ Bỏ (C) với x < 1. Lấy đối xứng phần đồ thị bị Đồ thị (C’): bỏ qua Ox.
+ Bỏ phần đồ thị của (C) với x < 1, giữ y nguyên (C')
(C) với x > 1.
+ Lấy đối xứng phần đồ thị bị bỏ qua . Ox 1 y O 1 x 1 O 1 x (C)
Nhận xét: Trong quá trình thực hiện phép suy đồ
thị nên lấy đối xứng các điểm đặc biệt của (C):
Nhận xét: Đối với hàm phân thức thì nên lấy
giao điểm với Ox, Oy, CĐ, CT…
đối xứng các đường tiệm cận để thực hiện
phép suy đồ thị một cách tương đối chính xác. Page 208
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ G
ƠN I ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ HƯ C
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
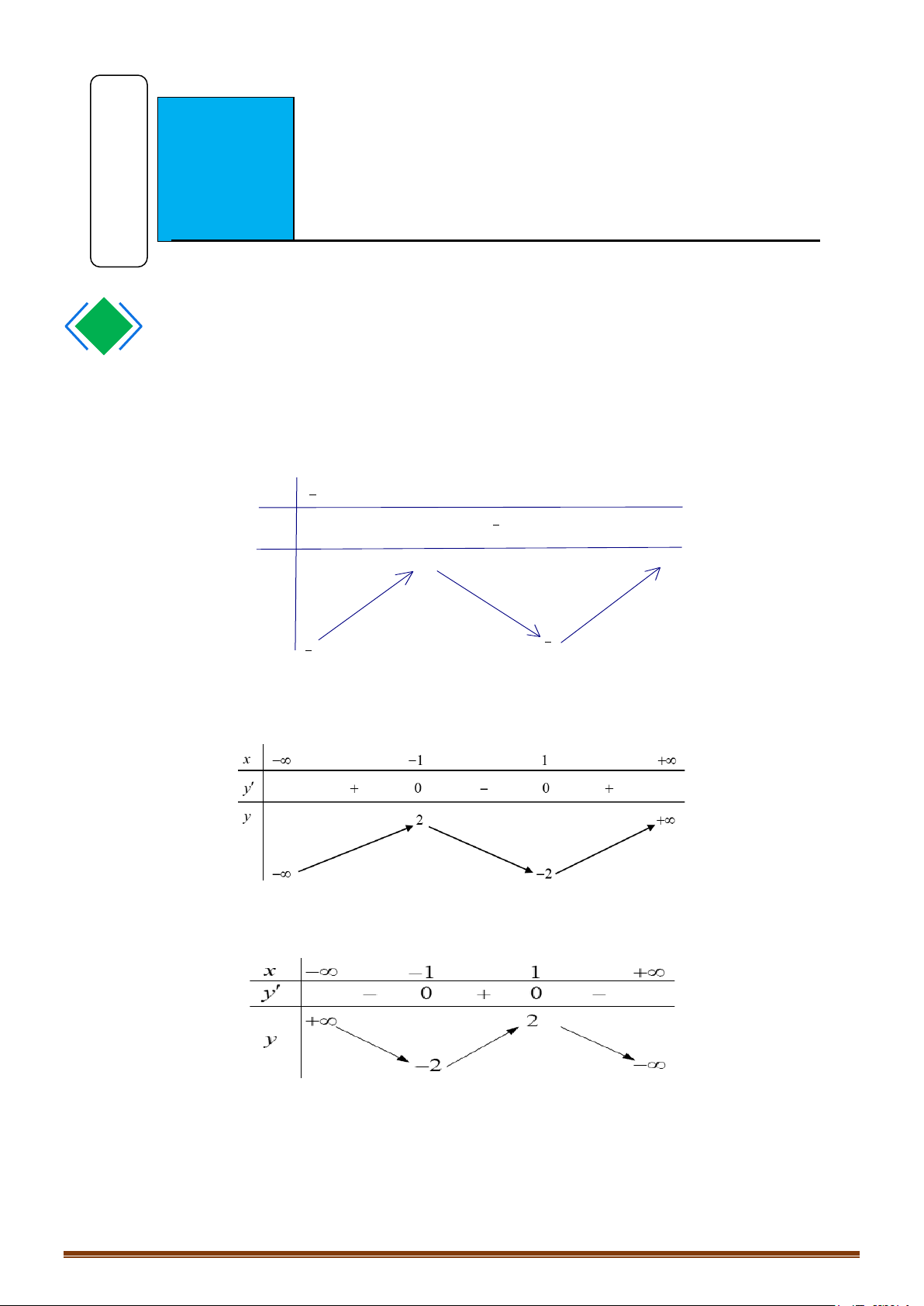
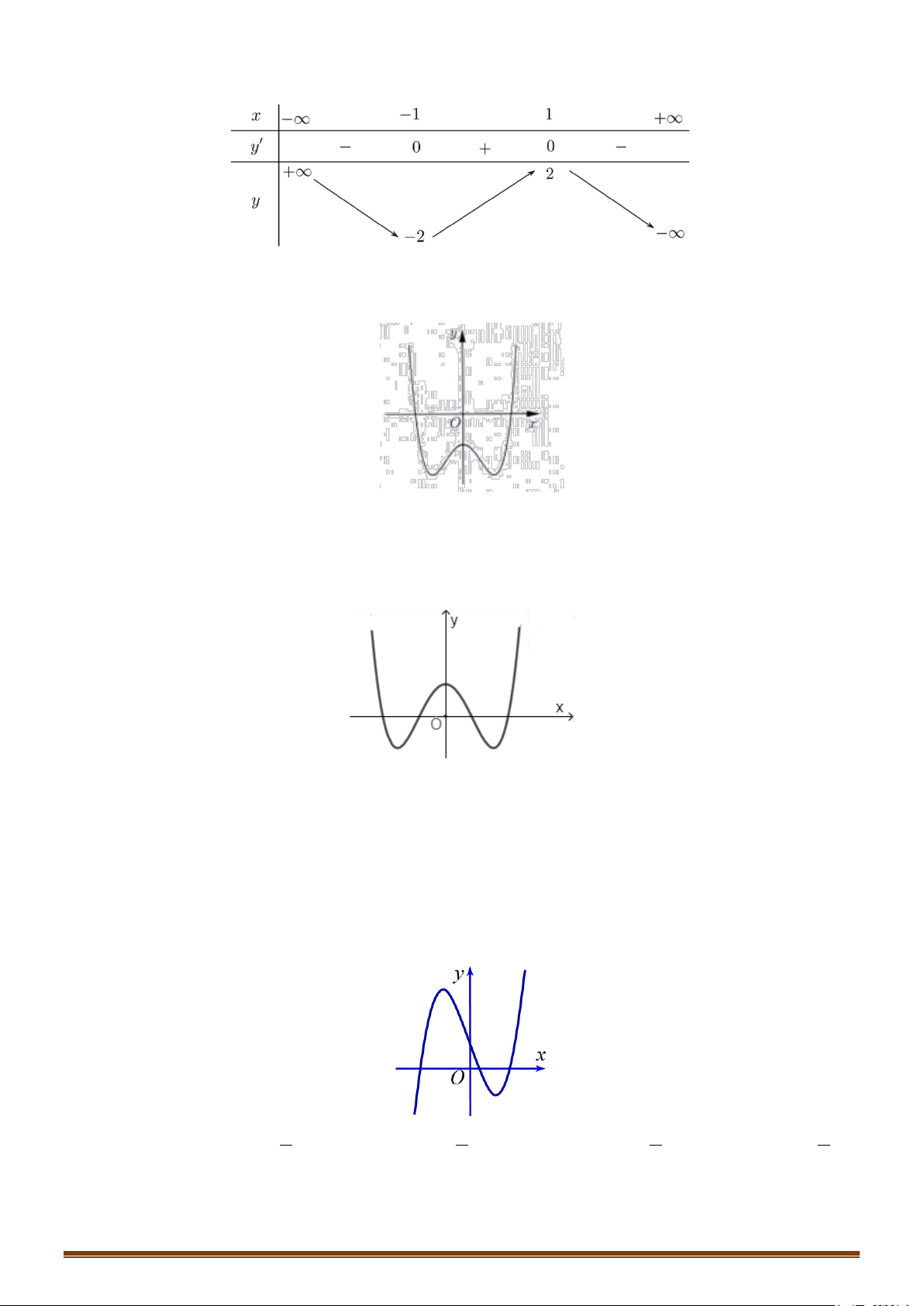
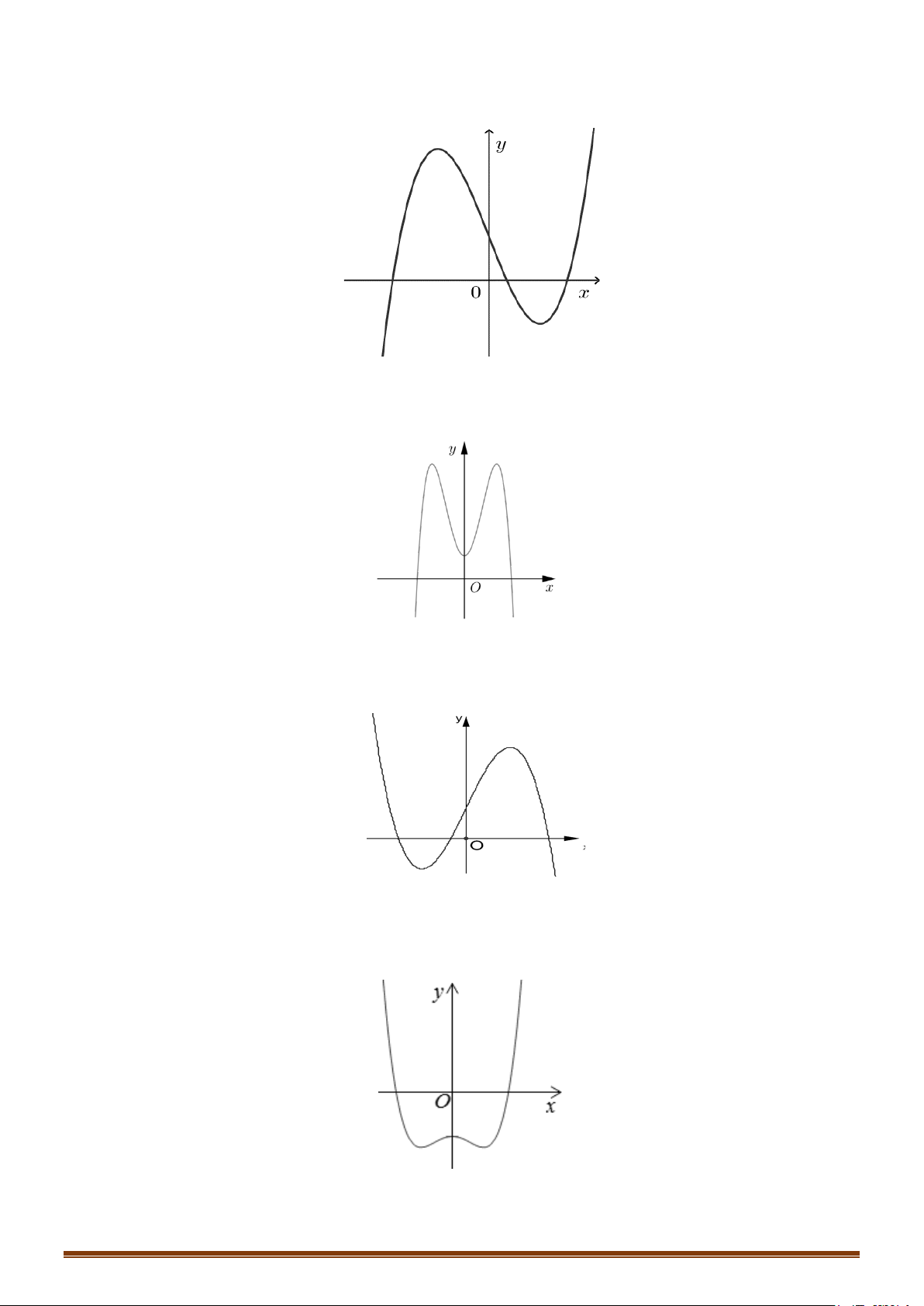
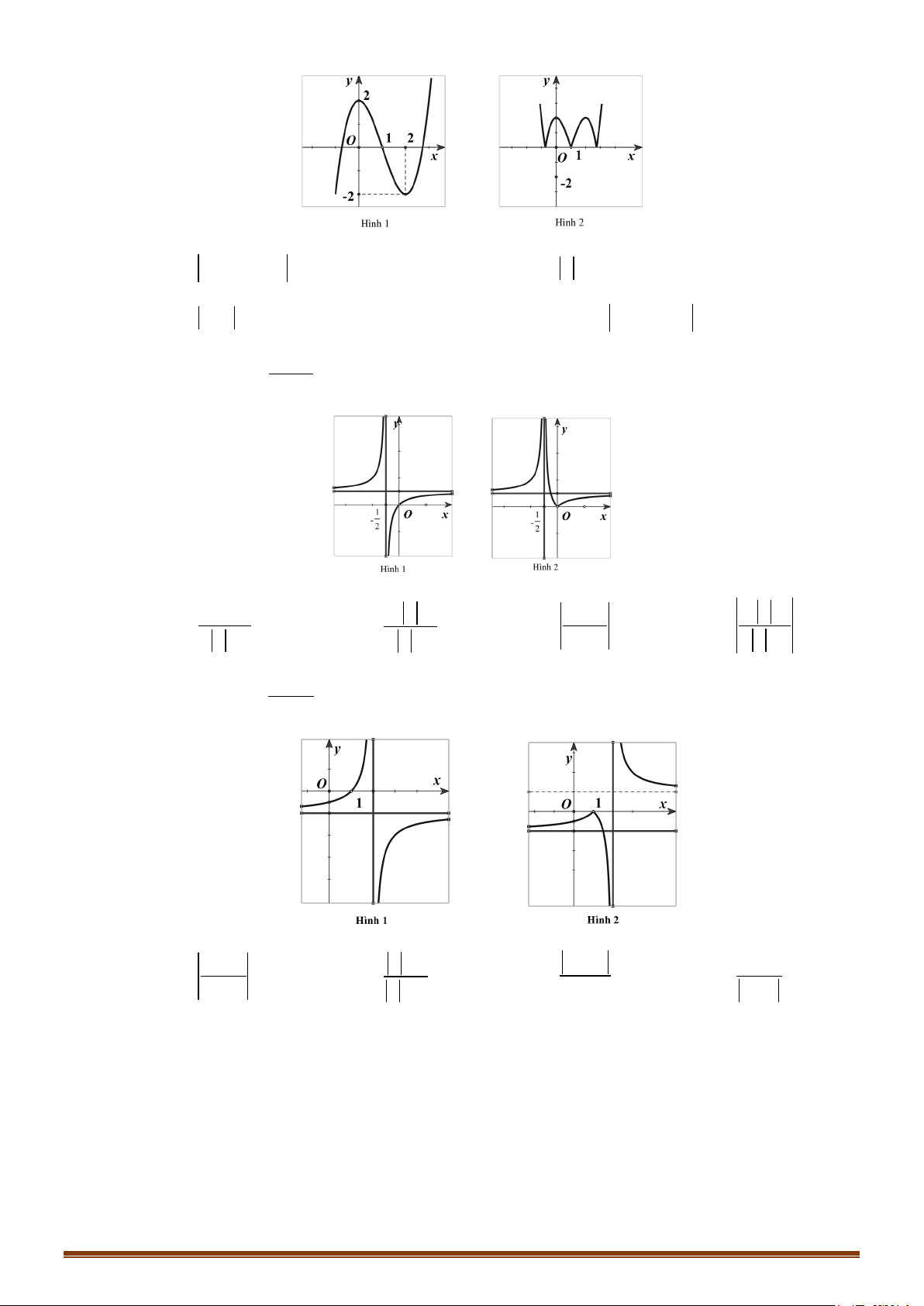
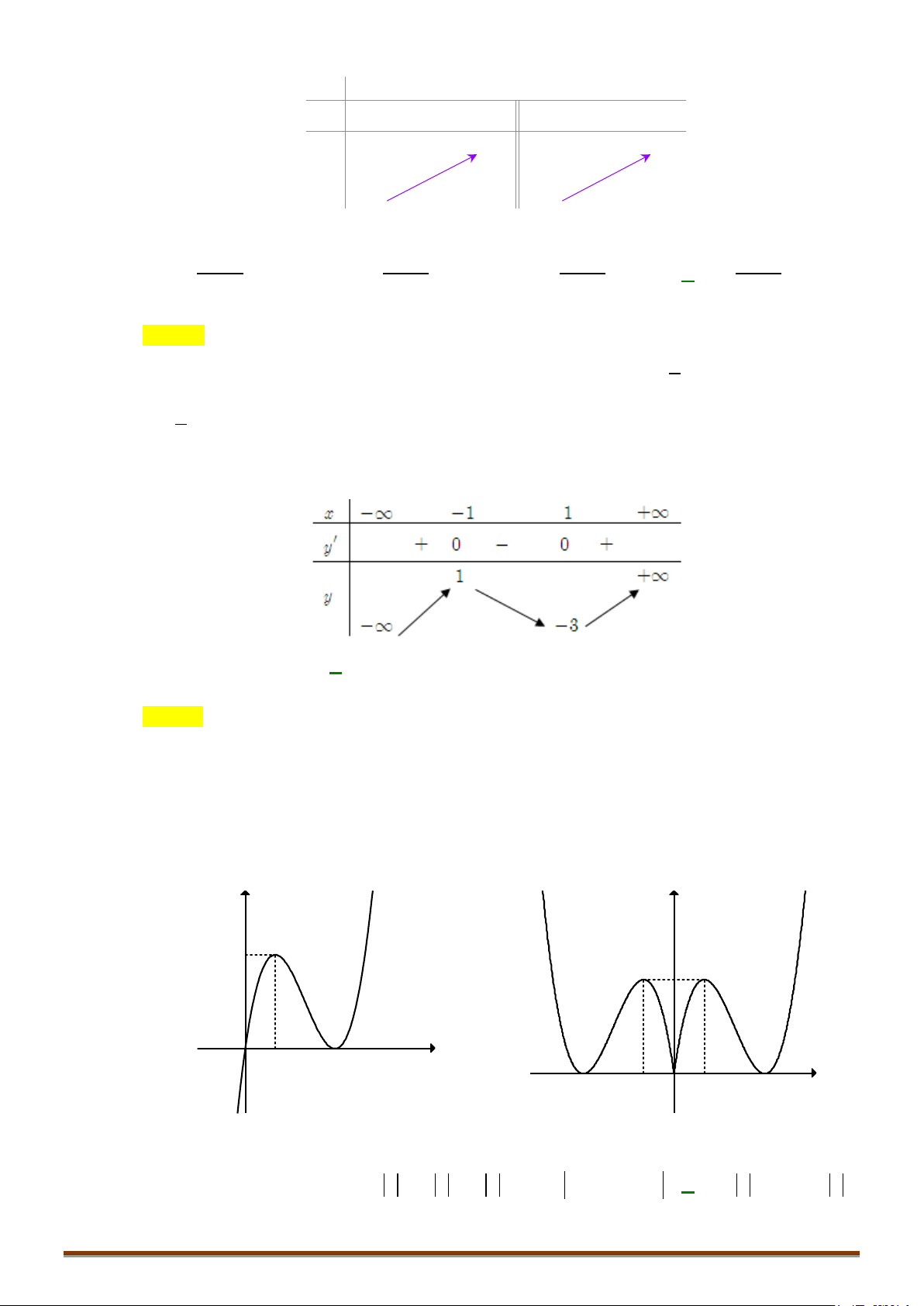
Câu 1: (MĐ 101-2022) Hàm số nào dưới đây có bảng biến thiên như sau: x ∞ -1 1 +∞ y' + 0 0 + +∞ 2 y 2 ∞ A. 4 2
y = x − 2x . B. 3
y = −x + 3 .x C. 4 2
y = −x + 2x . D. 3
y = x −3 .x
Câu 2: (MĐ 102-2022) Hàm số nào dưới đây có bảng biến thiên như sau? A. 3
y = −x + 3x . B. 3
y = x − 3x . C. 4 2
y = −x + 2x . D. 4 2
y = x − 2x .
Câu 3: (MĐ 103-2022) Hàm số nào dưới đây có bảng biến thiên như sau? A. 3
y = x − 3x . B. 3
y = −x + 3x . C. 2
y = x − 2x . D. 2
y = −x + 2x . Page 209
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 4: (MĐ 104-2022) Hàm số nào dưới đây có bảng biến thiên như sau? A. 3
y = x − 3x . B. 2
y = x − 2x . C. 3
y = −x + 3x . D. 2
y = −x + 2x .
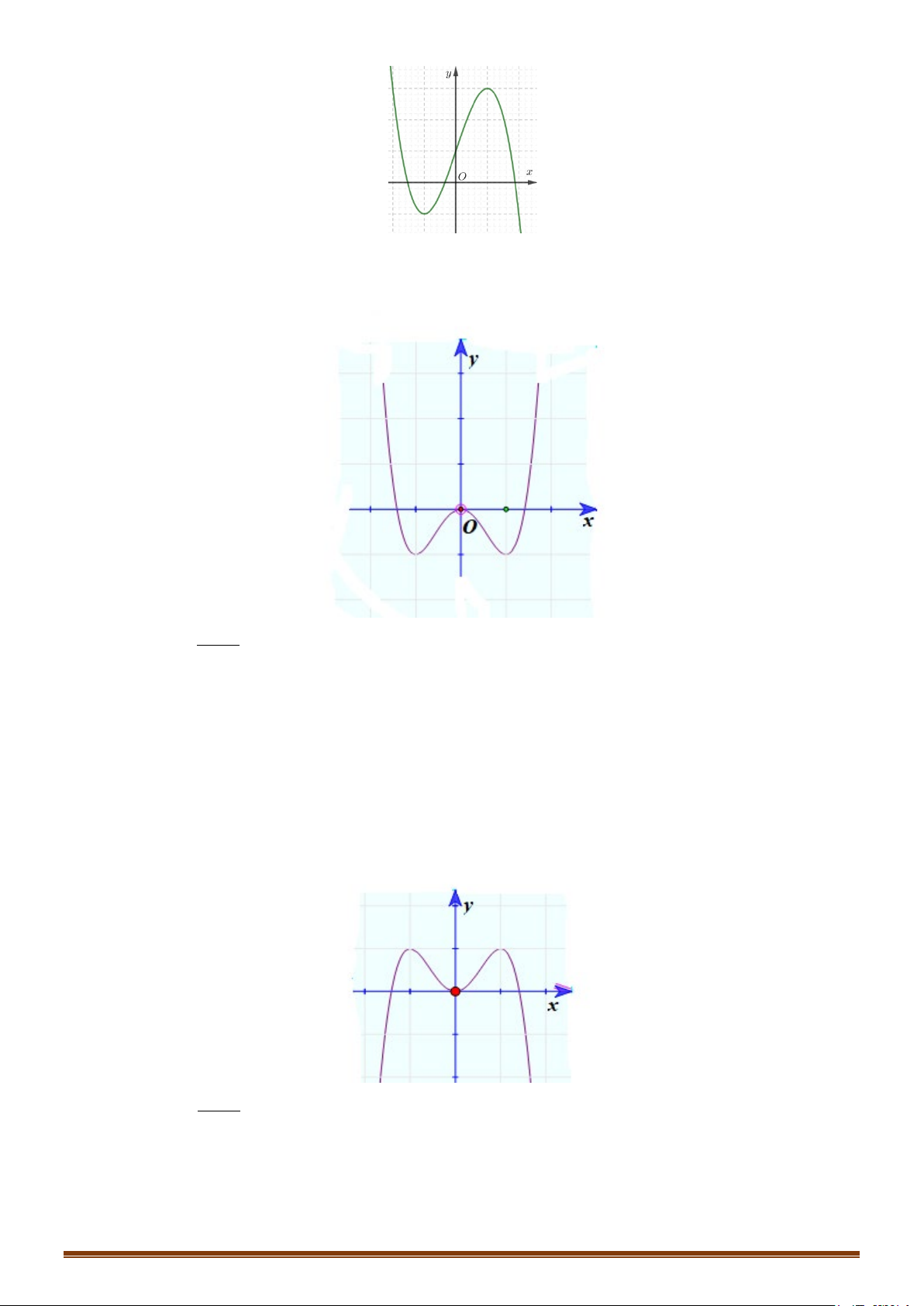
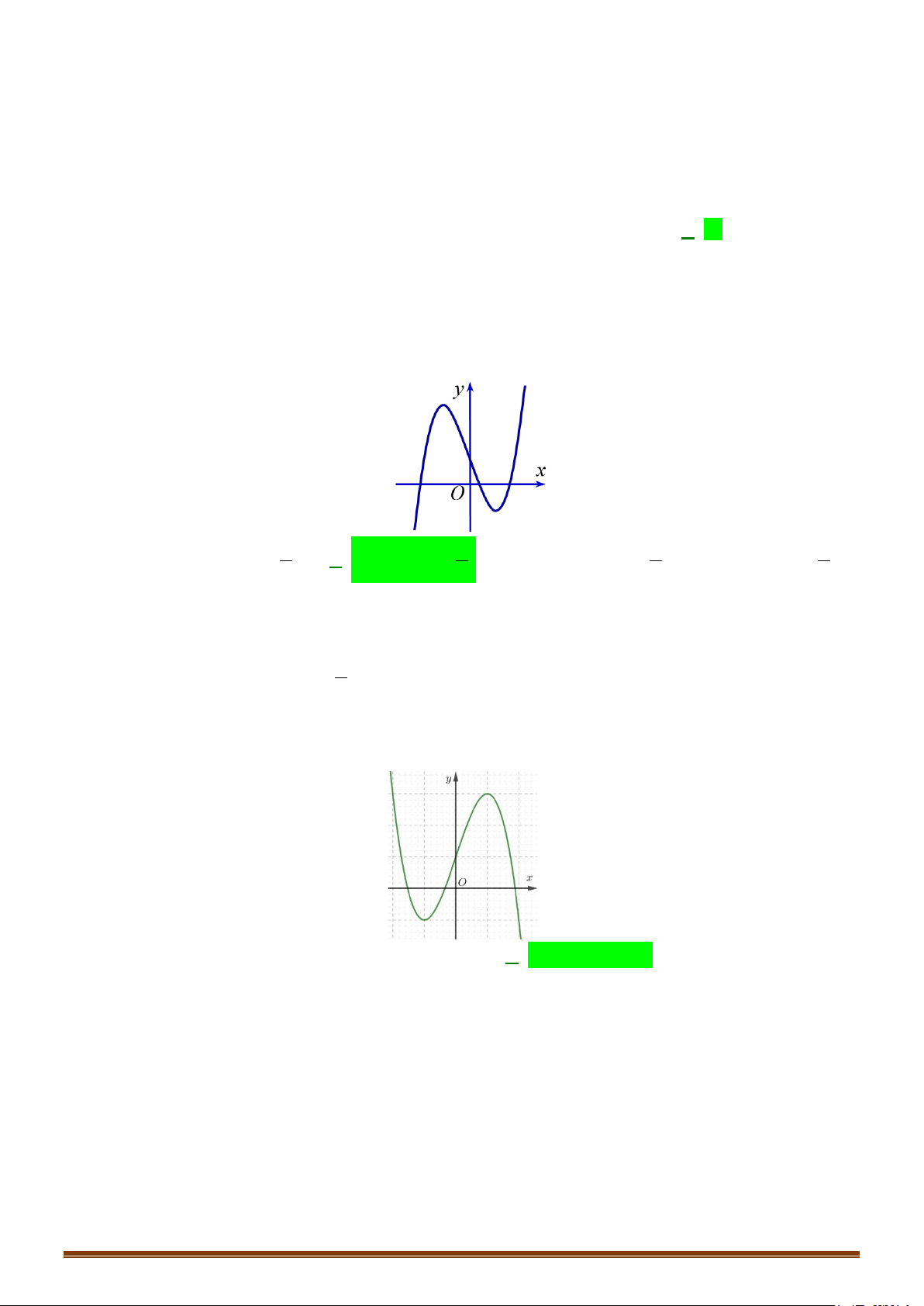
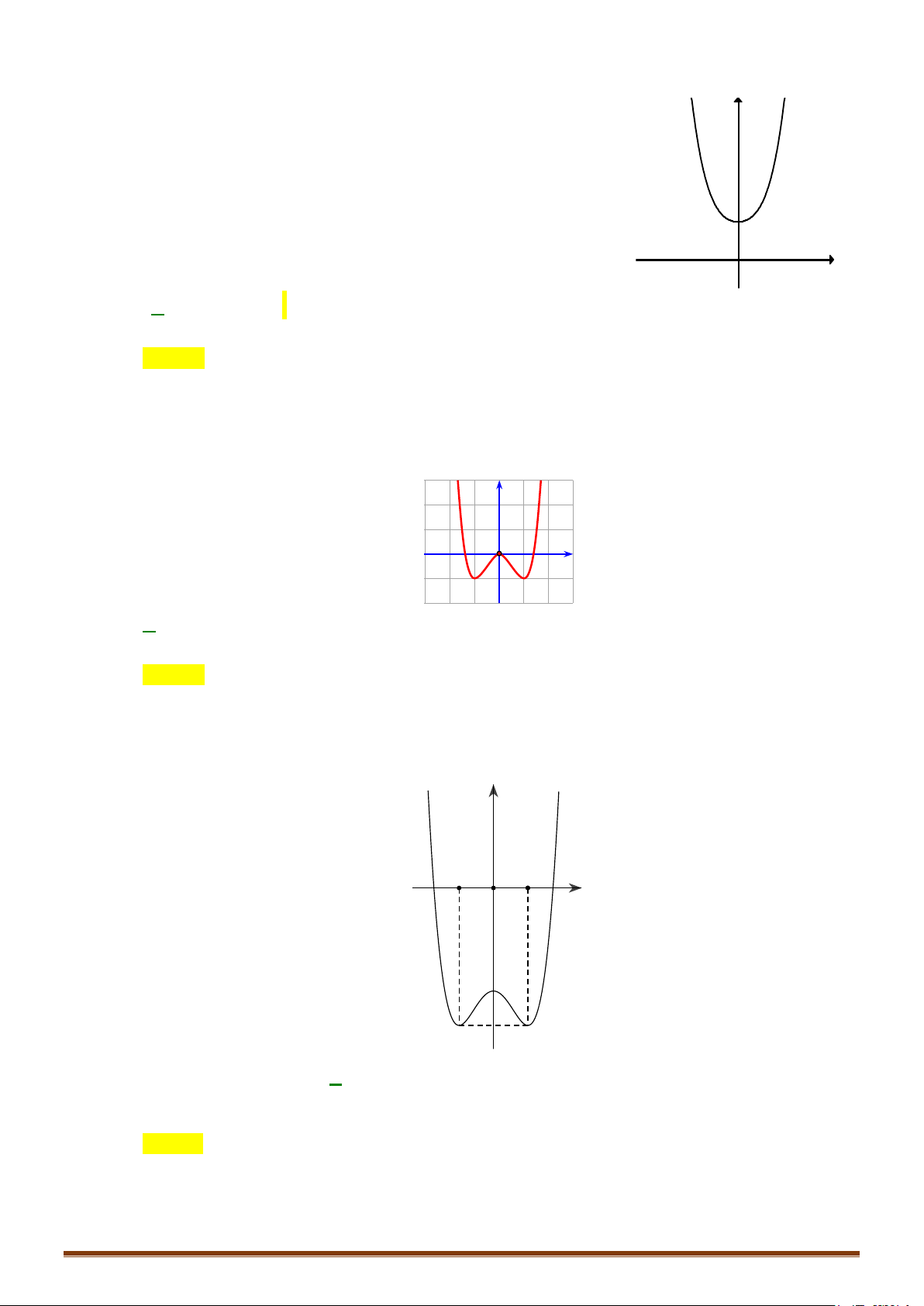
Câu 5: (TK 2020-2021) Đồ thị của hàm số nào dưới đây có dang như đường cong trong hình bên? A. 4 2
y = −x + 2x −1. B. 4 2
y = x − 2x −1. C. 3 2
y = x − 3x −1. D. 3 2
y = −x + 3x −1.
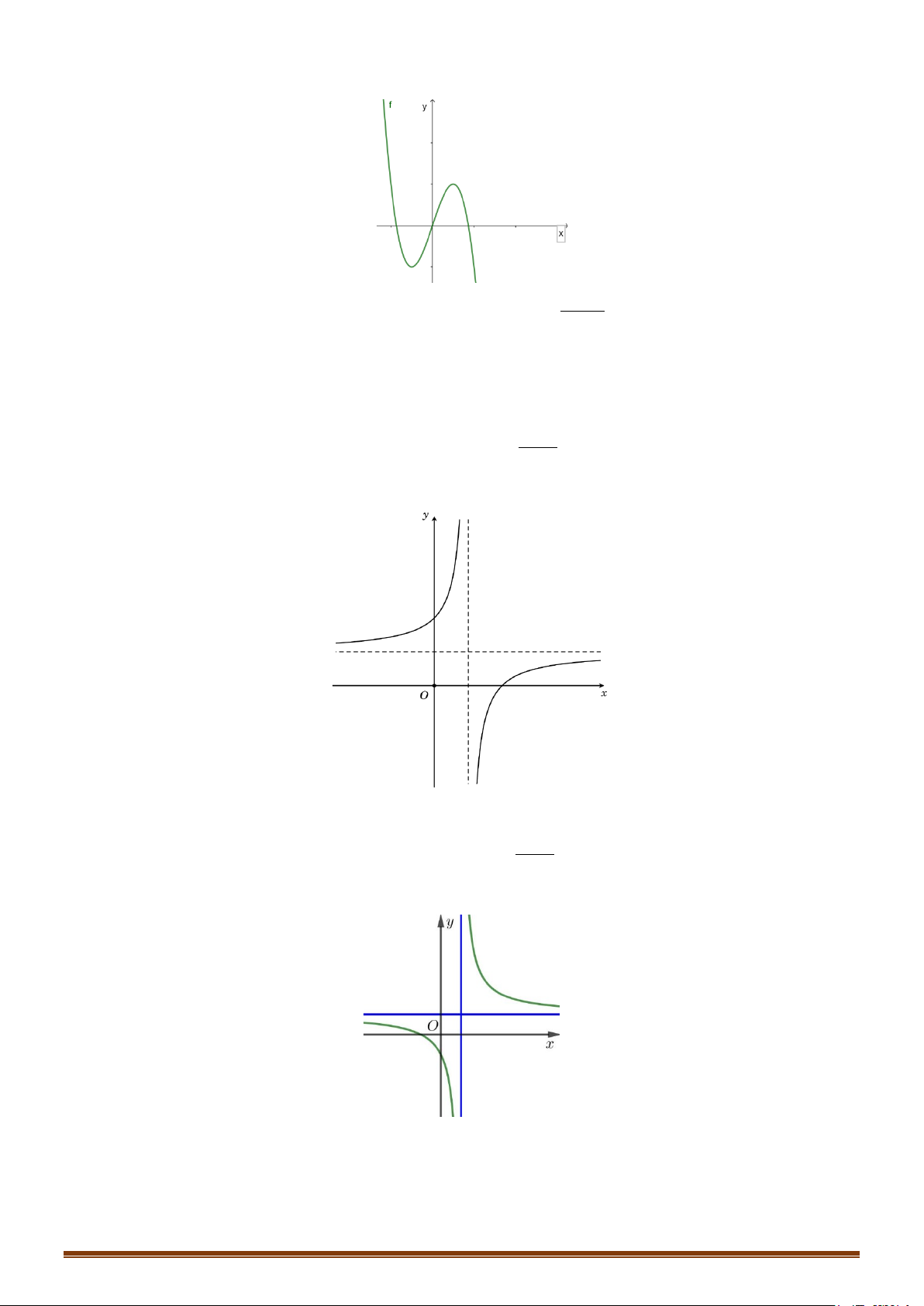
Câu 6: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x +1. B. 4 2 y = 2
− x + 4x +1. C. 3
y = −x + 3x +1. D. 4 2
y = 2x − 4x +1.
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị hàm số 4 2
y = −x − 2x + 3 cắt trục tung tại điểm có tung độ bằng A. 1. B. 0 . C. 2 . D. 3.
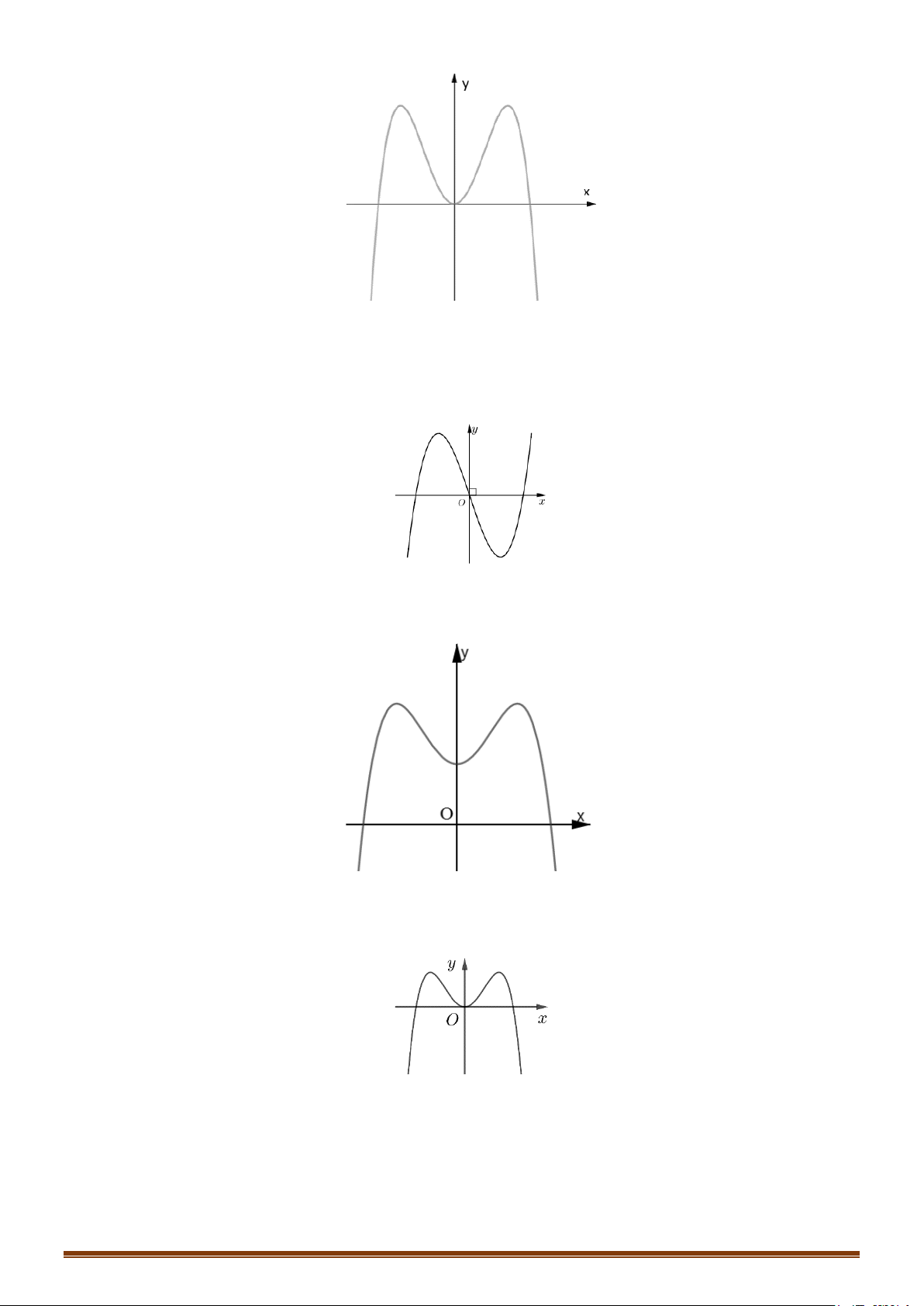
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 1
y = −x − 2x + . B. 3 1
y = x − 2x + . C. 4 2 1
y = −x + 2x + . D. 4 2 1
y = x + 2x + . 2 2 2 2
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? Page 210
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3
y = x − 3x +1. B. 4 2
y = x + 4x +1. C. 3
y = −x + 3x +1. D. 4 2
y = −x + 2x +1.
Câu 10: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình bên? A. 3x +1 y = . B. 2
y = x + 2x . C. 3 2
y = 2x − x . D. 4 2
y = x − 2x . x + 2
Câu 11: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số 3
y = x − x + 2 ?
A. Điểm M (1; ) 1 .
B. Điểm P(1;2) .
C. Điểm Q(1;3).
D. Điểm N (1;0).
Câu 12: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số y = 3
x + x − 2 ?
A. Điểm M 1; 1.
B. Điểm N 1;  2 .
C. Điểm P 1;  3 .
D. Điểm Q 1;  0 .
Câu 13: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây? A. 3x −1 y = . B. 2
y = x − 2x . C. 3 2
y = 2x + x . D. 4 2
y = −x + 2x . x + 2
Câu 14: (MĐ 103 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số 3
y x x 1?
A. Điểm N 1;0.
B. Điểm P1;2.
C. Điểm Q1;  3 .
D. Điểm M 1;  1 . Page 211
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 15: (MĐ 103 2020-2021 – ĐỢT 2) Hàm số nào dưới đây có đồ thị đường cong trong hình bên? A. 3
y = −x + 3x . B. 4 2
y = x − x . C. 2x +1 y = . D. 2
y = x + x . x + 2
Câu 16: (MĐ 104 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số 3
y x x1?
A. Điểm Q1;  3 .
B. Điểm M 1;2.
C. Điểm N 1;  1 .
D. Điểm P1;0.
Câu 17: (MĐ 103 2020-2021 – ĐỢT 1) Biết hàm số x + a y =
( a là số thực cho trước và a ≠ 1 − ) có x −1
đồ thị như hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
A. y ' > 0, x ∀ ≠ 1.
B. y ' > 0, x ∀ ∈.
C. y ' < 0, x ∀ ∈ .
D. y ' < 0, x ∀ ≠ 1.
Câu 18: (MĐ 104 2020-2021 – ĐỢT 1) Biết hàm số x + = a y
( a là số thực cho trước, a ≠ 1 − ) có đồ x −1
thị như trong hình bên. Mệnh đề nào dưới đây đúng?
A. y ' < 0,∀x∈ R .
B. y ' < 0,∀x ≠1.
C. y ' > 0,∀x∈ R .
D. y ' > 0,∀x ≠ 1.
Câu 19: (Đề Minh Họa 2020 Lần 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây? Page 212
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 4 2
y = −x + 2x . B. 4 2
y = x − 2x . C. 3 2
y = x −3x . D. 3 2
y = −x + 3x .
Câu 20: (Đề Tham Khảo 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x −3x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 4 2
y = −x + 2x .
Câu 21: (Mã 101 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 2
y = x − 3x +1. B. 3 2
y = −x + 3x +1. C. 4 2
y = −x + 2x +1. D. 4 2
y = x − 2x +1.
Câu 22: (Mã 102 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = −x + 2x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 3
y = x − 3x .
Câu 23: (Mã 104 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? Page 213
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 4 2
y = x − 2x +1. B. 3 2
y = −x + 3x +1. C. 3 2
y = x − 3x +1. D. 4 2
y = −x + 2x +1.
Câu 24: (Mã 101 - 2020 Lần 2)Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên A. 4 2 y = x − 2x − 2 B. 3 2
y = −x + 2x − 2 C. 3 2 y = x − 3x − 2 D. 4 2 y = −x + 2x − 2
Câu 25: (Mã 104 2017) Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3
y = −x + 3x + 2 B. 4 2
y = x − x +1 C. 4 2
y = x + x +1 D. 3
y = x − 3x + 2
Câu 26: (Mã 102 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = −x + 2x −1. B. 4 2
y = x − 2x −1. C. 3 2
y = x −3x −1. D. 3 2
y = −x + 3x −1.
Câu 27: (Mã 103 - 2020 Lần 2) Đồ thị của hàm số dưới đây có dạng như đường cong bên? Page 214
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3
y = x −3x +1. B. 4 2
y = x − 2x +1. C. 4 2
y = −x + 2x +1. D. 3
y = −x + 3x +1.
Câu 28: (Mã 104 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = x + 2x . B. 3
y = −x − 3x . C. 3
y = x − 3x . D. 4 2
y = −x + 2x .
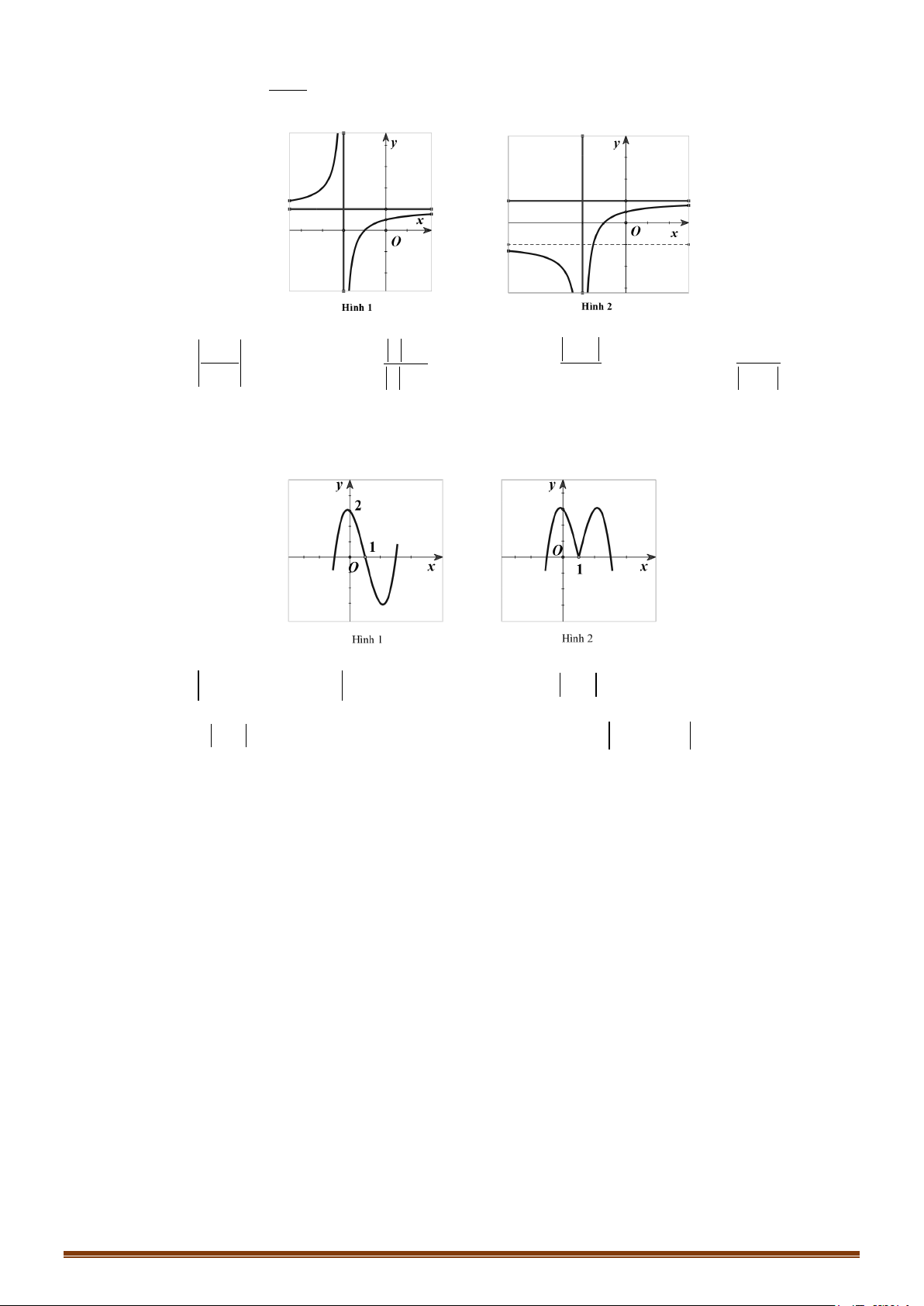
Câu 29: (Đề Tham Khảo 2019) Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 2x −1 y + = B. x 1 y = C. 4 2
y = x + x +1 D. 3
y = x − 3x −1 x −1 x −1
Câu 30: (Mã 103 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 3 2
y = x − 3x − 2 . B. 4 2
y = x − 2x − 2. C. 3 2
y = −x + 3x − 2. D. 4 2
y = −x + 2x − 2 .
Câu 31: (Mã 101 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? Page 215
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = x − 3x + 3 . B. 3 y = −x + 3 2 x + 3. C. 4 y = x − 2 2 x + 3.s D. 4 y = −x + 2 2 x + 3.
Câu 32: (Mã 102 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = −x + x −1 B. 4 2
y = −x + 2x −1 C. 3 2
y = x − x −1 D. 4 2
y = x − 2x −1
Câu 33: (Mã 101 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = x − 3x −1 B. 3 2
y = −x + 3x −1 C. 4 2
y = −x + 3x −1 D. 4 2
y = x − 3x −1
Câu 34: (Mã 104 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 4 2
y = x − x − 2 B. 4 2
y = −x + x − 2 C. 3 2
y = −x + 3x − 2 D. 3 2
y = x − 3x − 2
Câu 35: (Mã 103 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? Page 216
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y x O A. 3
y = x − 3x −1 B. 4 2
y = x − 3x −1 C. 3
y = −x − 3x −1 D. 4 2
y = −x + x −1
Câu 36: (Đề Tham Khảo 2018) Đường cong trong hình bên là của đồ thị hàm số nào dưới đây? A. 3 2
y = x −3x + 2 B. 3 2
y = −x + 3x + 2 C. 4 2
y = −x + 2x + 2 D. 4 2
y = x − 2x + 2
Câu 37: (Mã 110 2017) Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3 2
y = −x + 3x +1 B. 3 2
y = x −3x + 3 C. 4 2
y = −x + 2x +1 D. 4 2
y = x − 2x +1.
Câu 38: (Đề Tham Khảo 2017) Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 2x + 3 A. 2x +1 y = B. y = x −1 x +1 2x −1 2x − 2 C. y = D. y = x +1 x −1 Page 217
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 39: (Đề Minh Họa 2017) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án ,
A B,C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 3
y = x − 3x +1 B. 3
y = −x + 3x +1 C. 4 2
y = x − x +1 D. 2
y = −x + x −1
Câu 40: (Mã 104 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 4 2
y = 2x − 4x +1 B. 3 y = 2
− x + 3x +1 C. 3
y = 2x − 3x +1 D. 4 2 y = 2
− x + 4x +1
Câu 41: (Mã 102 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên A. 3
y = −x + 3x +1. B. 3
y = x − 3x +1. C. 4 2
y = x − 2x +1. D. 4 2
y = −x + 2x +1.
Câu 42: (Mã 123 2017) Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. y = 4 x − 2 x −1 B. y = − 4 x + 2 x −1 C. y = 3 x − 2 x −1 D. y = − 3 x + 2 x −1 Page 218
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 43: (Mã 123 2017) Đường cong ở hình bên là đồ thị của hàm số ax + b y =
với a,b,c,d là các số cx + d
thực. Mệnh đề nào dưới đây đúng?
A. y′ < 0,∀x∈ 
B. y′ > 0,∀x ≠ 1
C. y′ < 0,∀x ≠ 1
D. y′ > 0,∀x∈ 
Câu 44: (Mã 105 2017) Đường cong ở hình bên là đồ thị của hàm số ax + b y =
với a,b,c,d là các số cx + d
thực. Mệnh đề nào dưới đây đúng?
A. y′ > 0,∀x ≠ 1
B. y′ < 0,∀x ≠ 1
C. y′ < 0,∀x ≠ 2
D. y′ > 0,∀ ≠ 2
Câu 45: (Đề Minh Họa 2020 Lần 1) Cho hàm số 3
y = ax + 3x + d ( ;
a d ∈) có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A. a > 0,d > 0.
B. a < 0,d > 0 .
C. a > 0,d < 0 .
D. a < 0,d < 0 . Page 219
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 46: (Đề Tham Khảo 2020 Lần 2) Cho hàm số f (x) ax +1 =
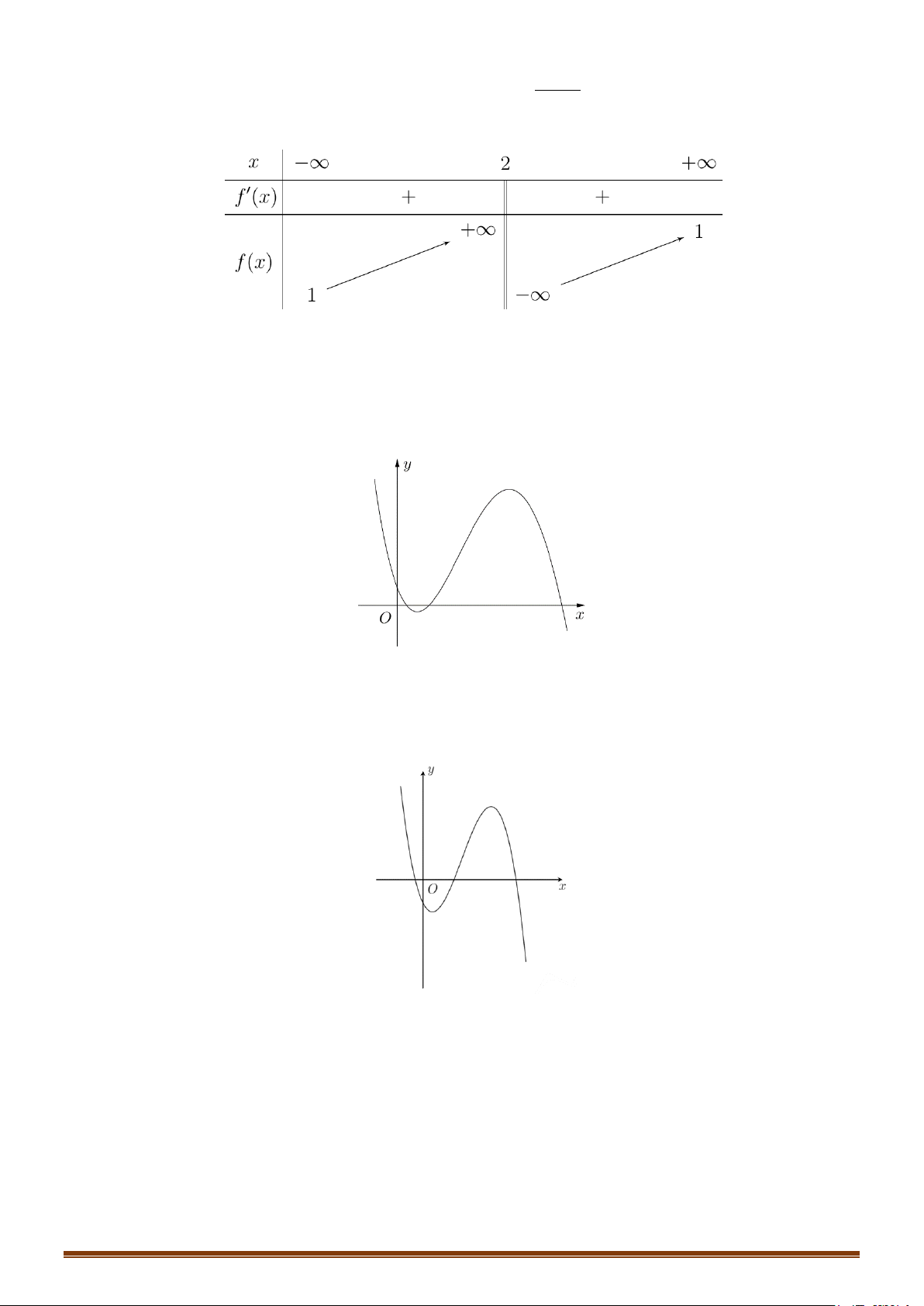
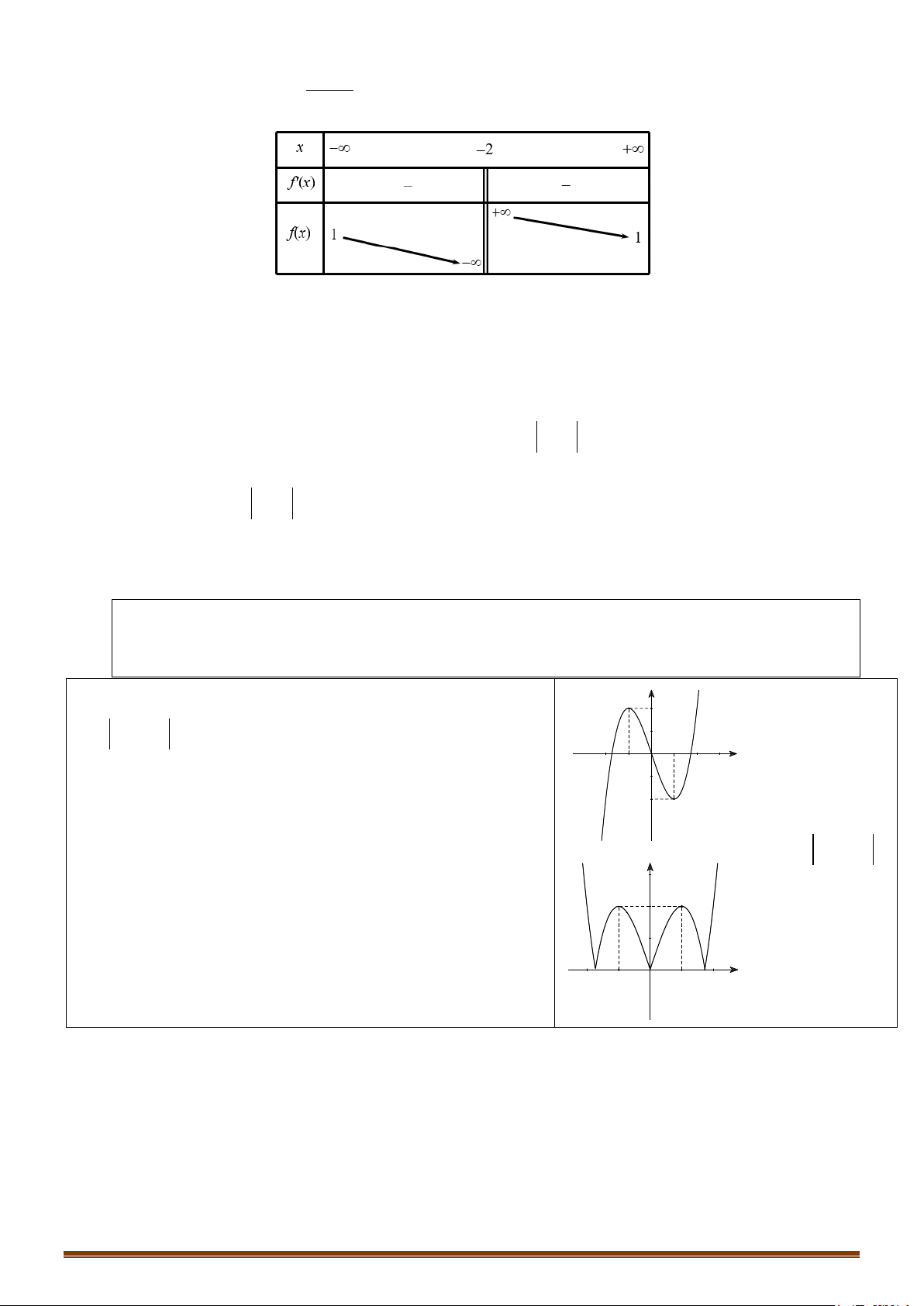
(a,b,c∈) có bảng biến thiên như bx + c sau:
Trong các số a,b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0.
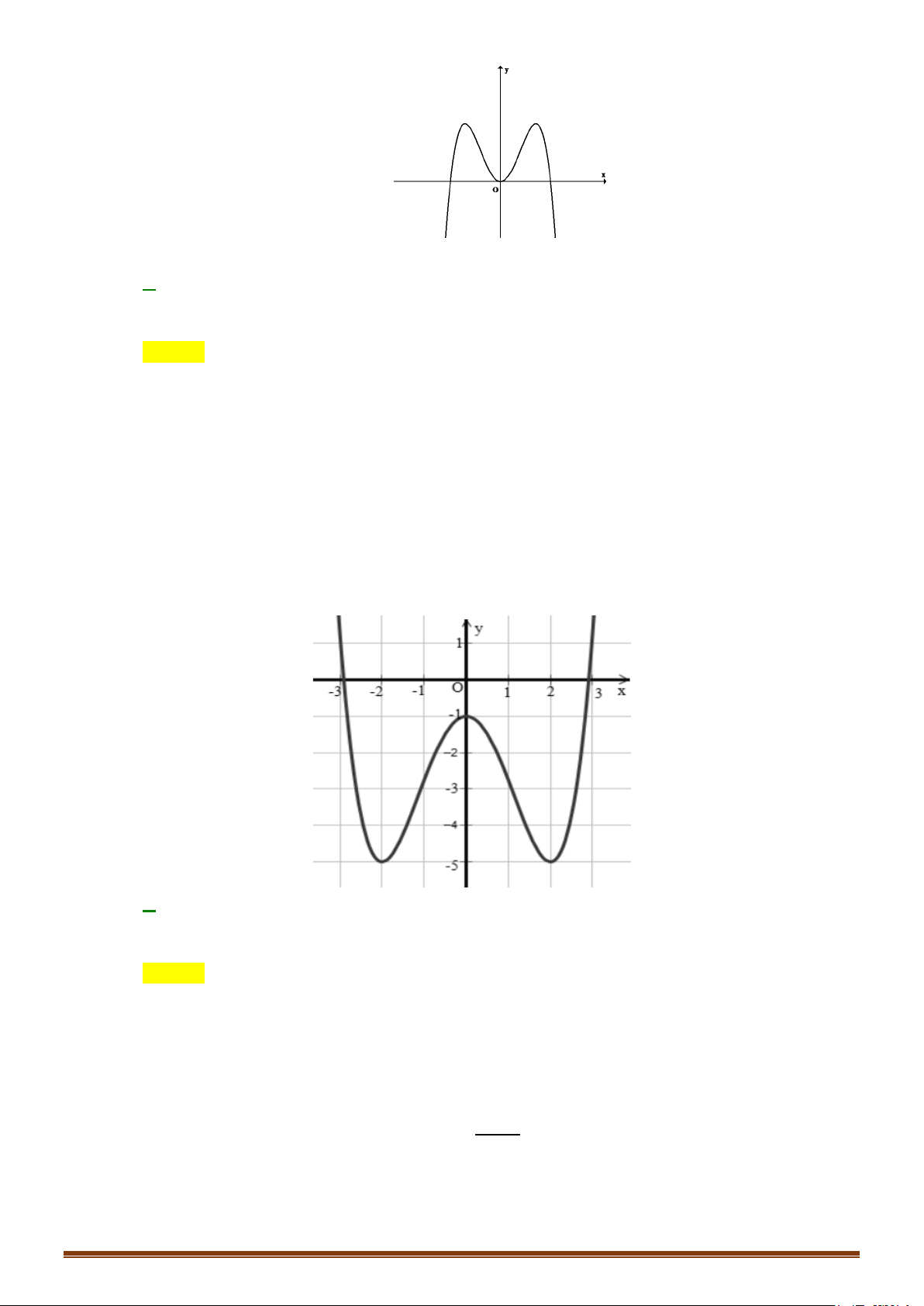
Câu 47: (Mã 101 - 2020 Lần 1) Cho hàm số 3 2
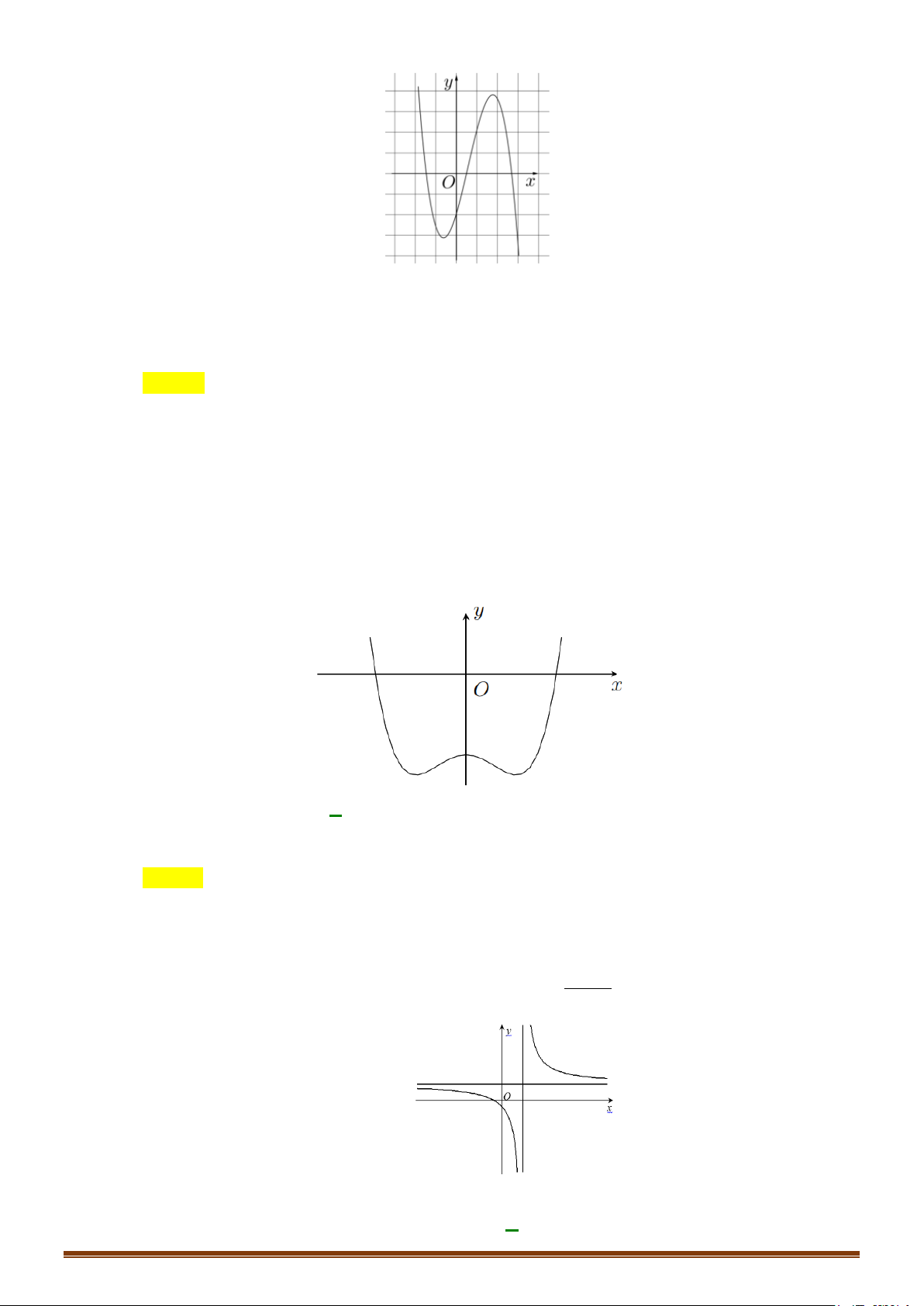
y = ax + bx + cx + d (a,b,c,d ∈) có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số a , b , c , d ? A. 4 . B. 1. C. 2 . D. 3.
Câu 48: (Mã 102 - 2020 Lần 1) Cho hàm số y = ax3 + bx2 + cx + d (a,b,c,d ∈ ) có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các hệ số a,b,c,d ? A. 4 . B. 3. C. 1. D. 2 . Page 220
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 49: (Mã 103 - 2020 Lần 1) Cho hàm số 3 2
y = ax + bx + cx + d (a,b,c,d ∈) có đồ thị là đường cong trong hình bên.
Có bao nhiêu số dương trong các số a,b,c,d ? A. 4 . B. 2 . C. 1. D. 3.
Câu 50: (Mã 104 - 2020 Lần 1) Cho hàm số 3 2
y = ax + bx + cx + d (a,b,c,d ∈) có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d ? A. 4 . B. 2 . C. 1. D. 3.
Câu 51: (Mã 102 - 2020 Lần 2) Cho hàm số f (x) 3 2
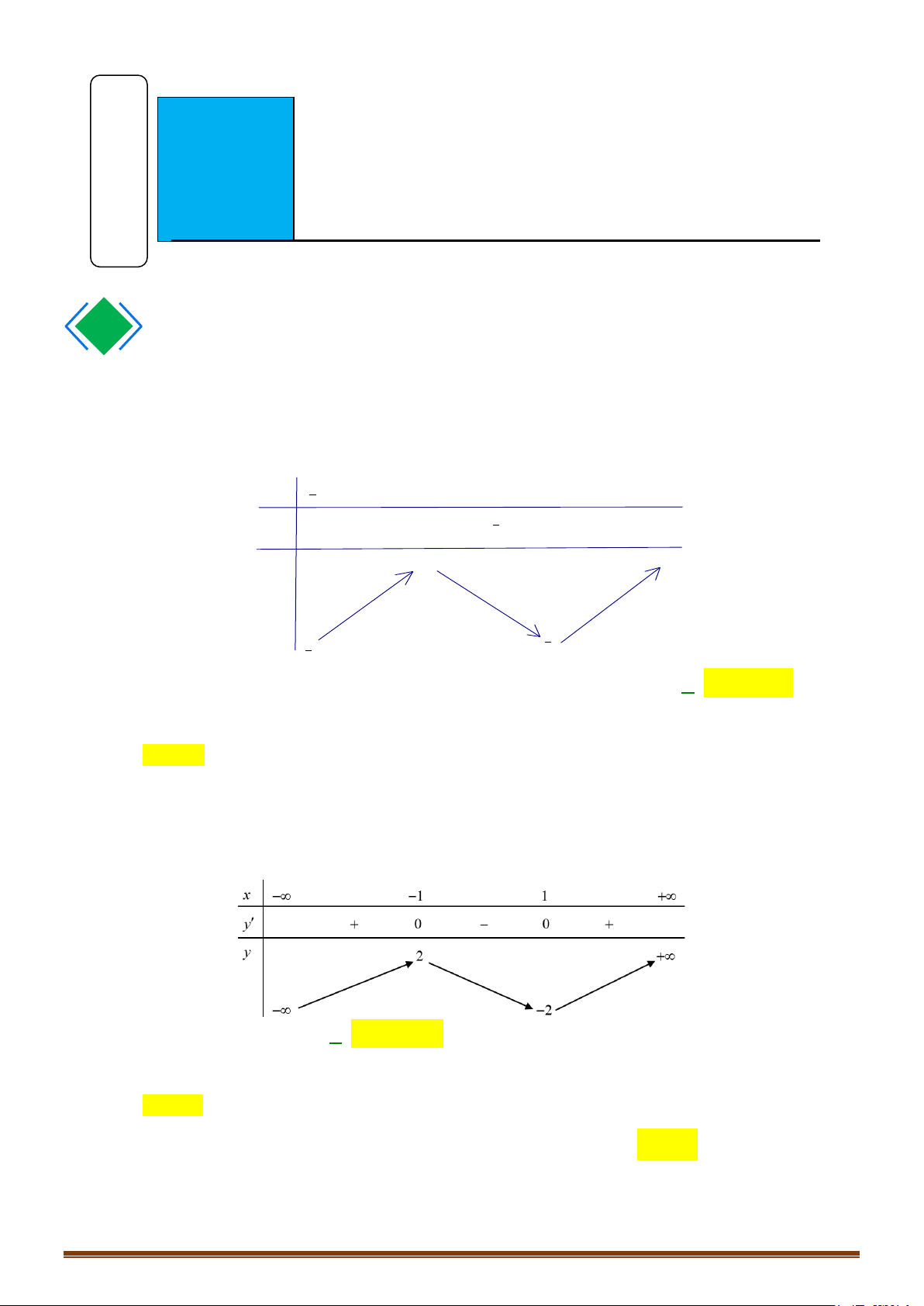
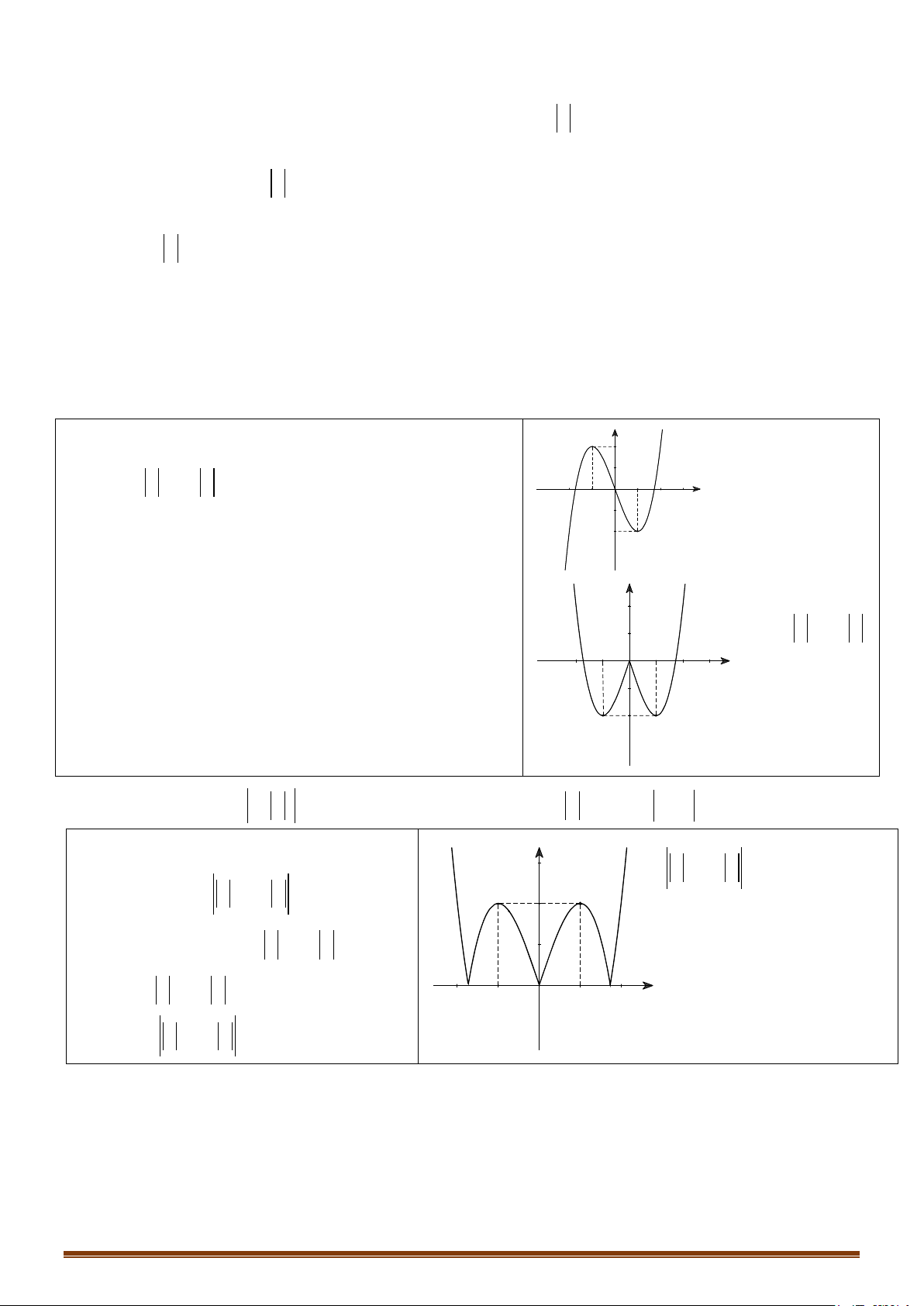
= ax + bx + cx + d (a,b,c,d ∈) có bảng biến thiên như sau
Có bao nhiêu số dương trong các số a, , b c, d ? A. 2 . B. 4 . C. 1. D. 3. Page 221
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 52: (Mã 103 - 2020 Lần 2) Cho hàm số f (x) 3 2
= ax + bx + cx + d (a, b, c, d ∈) có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a, b, c, d ? A. 3. B. 4. C. 2. D. 1.
Câu 53: (Mã 101 – 2020 Lần 2) Cho hàm số f (x) 3 2
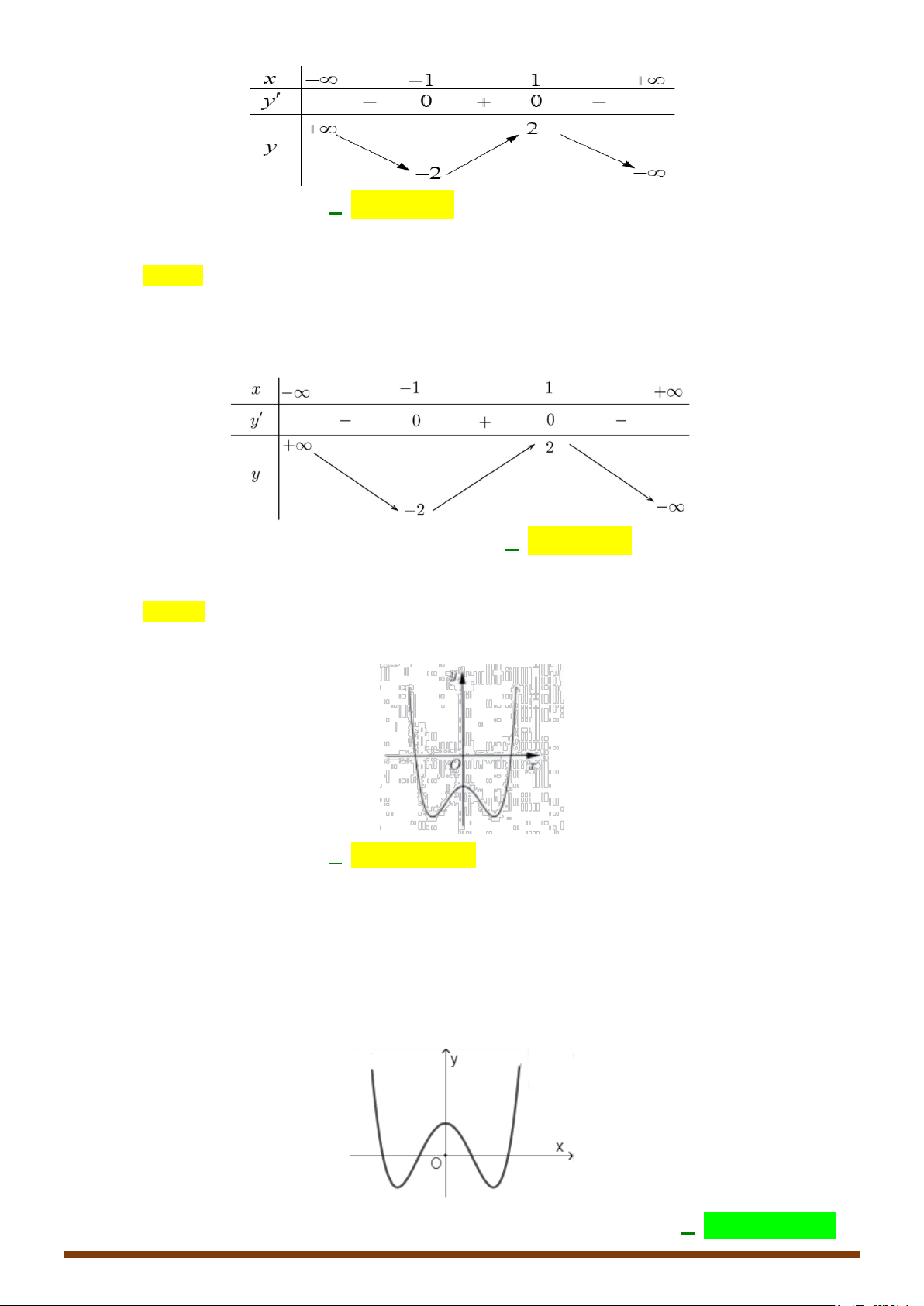
= ax + bx + cx + d (a,b,c,d ∈) có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a,b,c,d ? A. 2 . B. 4 . C. 1. D. 3.
Câu 54: (Mã 104 - 2020 Lần 2) Cho hàm số f (x) 3 2
= ax + bx + cx + d (a,b,c,d ∈) có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a,b,c,d ? A. 4 . B. 2 . C. 3. D. 1. Page 222
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ G
ƠN I ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ HƯ C
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐỀ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Hàm số nào dưới đây có bảng biến thiên như sau: x ∞ -1 1 +∞ y' + 0 0 + +∞ 2 y 2 ∞ A. 4 2
y = x − 2x . B. 3
y = −x + 3 .x C. 4 2
y = −x + 2x . D. 3
y = x −3 .x Lời giải Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với a > 0. Do đó ta chọn đáp án D.
Câu 2: (MĐ 102-2022) Hàm số nào dưới đây có bảng biến thiên như sau? A. 3
y = −x + 3x . B. 3
y = x − 3x . C. 4 2
y = −x + 2x . D. 4 2
y = x − 2x . Lời giải Chọn B
Từ bảng biến thiên ⇒ y = f (x) là hàm bậc 3 có hệ số a > 0 , nên Chọn B
Câu 3: (MĐ 103-2022) Hàm số nào dưới đây có bảng biến thiên như sau? Page 1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3
y = x − 3x . B. 3
y = −x + 3x . C. 2
y = x − 2x . D. 2
y = −x + 2x . Lời giải Chọn B
Bảng biến đã cho là của hàm số 3
y = −x + 3x .
Câu 4: (MĐ 104-2022) Hàm số nào dưới đây có bảng biến thiên như sau? A. 3
y = x − 3x . B. 2
y = x − 2x . C. 3
y = −x + 3x . D. 2
y = −x + 2x . Lời giải Chọn C
Câu 5: (TK 2020-2021) Đồ thị của hàm số nào dưới đây có dang như đường cong trong hình bên? A. 4 2
y = −x + 2x −1. B. 4 2
y = x − 2x −1. C. 3 2
y = x − 3x −1. D. 3 2
y = −x + 3x −1. Lời giải
Đây chính là dạng của đồ thị hàm trùng phương có hệ số cao nhất dương, có ba điểm cực trị và
cắt trục tung tại điểm có tung độ âm. Khi đó chỉ có 4 2
y x 2x 1 là thỏa mãn.
Câu 6: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x +1. B. 4 2 y = 2
− x + 4x +1. C. 3
y = −x + 3x +1. D. 4 2
y = 2x − 4x +1. Page 2
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải
Đường cong đề bài ra là đồ thị của hàm bậc 4 trùng phương có hệ số a > 0 , và ab < 0 . Do đó
đây là đồ thị của hàm số 4 2
y = 2x − 4x +1.
Câu 7: (MĐ 102 2020-2021 – ĐỢT 1) Đồ thị hàm số 4 2
y = −x − 2x + 3 cắt trục tung tại điểm có tung độ bằng A. 1. B. 0 . C. 2 . D. 3. Lời giải Đồ thị hàm số 4 2
y = −x − 2x + 3 cắt trục tung tại điểm có tung độ bằng 3.
Câu 8: (MĐ 103 2020-2021 – ĐỢT 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 1
y = −x − 2x + . B. 3 1
y = x − 2x + . C. 4 2 1
y = −x + 2x + . D. 4 2 1
y = x + 2x + . 2 2 2 2 Lời giải
Dựa trên hình dạng đường cong đã cho và các phương án, ta suy ra đường cong trên là đồ thị của hàm số 3 1
y = x − 2x + . 2
Câu 9: (MĐ 104 2020-2021 – ĐỢT 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x +1. B. 4 2
y = x + 4x +1. C. 3
y = −x + 3x +1. D. 4 2
y = −x + 2x +1. Lời giải
Đồ thị hàm số có 2 điểm cực trị nên đây là đồ thị hàm bậc 3, mặt khác lim y = +∞ nên a < 0 . x→−∞
Câu 10: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình bên? Page 3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3x +1 y = . B. 2
y = x + 2x . C. 3 2
y = 2x − x . D. 4 2
y = x − 2x . x + 2 Lời giải
Đường cong đã cho có 3 điểm cực trị nên loại các phương án A, B,
C. Do đó chọn phương án D.
Câu 11: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số 3
y = x − x + 2 ?
A. Điểm M (1; ) 1 .
B. Điểm P(1;2) .
C. Điểm Q(1;3).
D. Điểm N (1;0). Lời giải Thay x =1 vào 3
y = x − x + 2 ta được 3 y =1 −1+ 2 = 2 .
Vậy điểm P(1;2) thuộc đồ thị hàm số đã cho.
Câu 12: (2020-2021 – ĐỢT 1) Điểm nào dưới đây thuộc đồ thị của hàm số y = 3
x + x − 2 ?
A. Điểm M 1; 1.
B. Điểm N 1;  2 .
C. Điểm P 1;  3 .
D. Điểm Q 1;  0 . Lời giải Với x  1, ta có: 3
y  1  1  2  0
Do đó điểm Q 1; 
0 thuộc đồ thị hàm số
Câu 13: (2020-2021 – ĐỢT 1) Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây? A. 3x −1 y = . B. 2
y = x − 2x . C. 3 2
y = 2x + x . D. 4 2
y = −x + 2x . x + 2 Page 4
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải
Đường cong đã cho không phải là đồ thị của hàm phân thức, cũng không phải là đồ thị của hàm
đa thức bậc hai, bậc ba. Do đó chỉ có phương án D là đúng.
Câu 14: (MĐ 103 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số 3
y x x 1?
A. Điểm N 1;0.
B. Điểm P1;2.
C. Điểm Q1;  3 .
D. Điểm M 1;  1 . Lời giải
Thay tọa độ các điểm vào hàm số ta thấy tọa độ điểm M 1;  1 thỏa mãn.
Câu 15: (MĐ 103 2020-2021 – ĐỢT 2) Hàm số nào dưới đây có đồ thị đường cong trong hình bên? A. 3
y = −x + 3x . B. 4 2
y = x − x . C. 2x +1 y = . D. 2
y = x + x . x + 2 Lời giải
Từ đồ thị ta thấy có 2 cực trị và nhìn vào các phương án thì chỉ có đồ thị hàm bậc 3 có 2 cực trị nên đáp án là A
Câu 16: (MĐ 104 2020-2021 – ĐỢT 2) Điểm nào dưới đây thuộc đồ thị của hàm số 3
y x x1?
A. Điểm Q1;  3 .
B. Điểm M 1;2.
C. Điểm N 1;  1 .
D. Điểm P1;0. Lời giải
Thay x 1 vào hàm số ta được 3
y 1 111. Khi đó điểm N 1; 
1 thuộc đồ thị hàm số.
Câu 17: (MĐ 103 2020-2021 – ĐỢT 1) Biết hàm số x + a y =
( a là số thực cho trước và a ≠ 1 − ) có x −1
đồ thị như hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
A. y ' > 0, x ∀ ≠ 1.
B. y ' > 0, x ∀ ∈.
C. y ' < 0, x ∀ ∈ .
D. y ' < 0, x ∀ ≠ 1. Page 5
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Đồ thị hàm số x + a y =
nhận x =1 làm tiệm cận đứng. x −1
Nhìn đồ thị hàm số, hàm số đồng biến trên từng khoảng xác định nên y ' > 0, x ∀ ≠ 1.
Câu 18: (MĐ 104 2020-2021 – ĐỢT 1) Biết hàm số x + = a y
( a là số thực cho trước, a ≠ 1 − ) có đồ x −1
thị như trong hình bên. Mệnh đề nào dưới đây đúng?
A. y ' < 0,∀x∈ R .
B. y ' < 0,∀x ≠1.
C. y ' > 0,∀x∈ R .
D. y ' > 0,∀x ≠ 1. Lời giải
Ta có TXĐ: D = R \{ } 1 1 − − a và y ' = ≠ 0,∀x ≠ 1. 2 (x −1)
Vì đồ thị hàm số là đường cong đi xuống (tính từ trái sang phải) trên từng khoảng xác định nên
hàm số đã cho nghịch biến trên mỗi khoảng xác định. Vậy y ' < 0, x ∀ ≠ 1.
Câu 19: (Đề Minh Họa 2020 Lần 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới đây? A. 4 2
y = −x + 2x . B. 4 2
y = x − 2x . C. 3 2
y = x −3x . D. 3 2
y = −x + 3x . Lời giải Chọn A
Từ hình dạng của đồ thị ta loại phương án C và D.
Nhận thấy lim f (x) = −∞ suy ra hệ số của 4
x âm nên chọn phương án A. x→±∞
Câu 20: (Đề Tham Khảo 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? Page 6
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3
y = x −3x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 4 2
y = −x + 2x . Lời giải Chọn A
Đường cong có dạng của đồ thị hàm số bậc 3 với hệ số a > 0 nên chỉ có hàm số 3
y = x − 3x
thỏa yêu cầu bài toán.
Câu 21: (Mã 101 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 2
y = x − 3x +1. B. 3 2
y = −x + 3x +1. C. 4 2
y = −x + 2x +1. D. 4 2
y = x − 2x +1. Lời giải Chọn C
Từ hình có đây là hình dạng của đồ thị hàm bậc 4.
lim f (x) = lim f (x) = −∞ ⇒ a < 0 x→−∞ x→+∞
Câu 22: (Mã 102 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = −x + 2x . B. 3
y = −x + 3x . C. 4 2
y = x − 2x . D. 3
y = x − 3x . Lời giải Chọn A
Đường cong trong hình là đồ thị hàm trùng phương 4 2
y = ax + bx + c (a ≠ 0) có hệ số a < 0 .
Câu 23: (Mã 104 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? Page 7
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 4 2
y = x − 2x +1. B. 3 2
y = −x + 3x +1. C. 3 2
y = x − 3x +1. D. 4 2
y = −x + 2x +1. Lời giải Chọn A
Dựa vào hình vẽ, ta thấy đồ thị hàm số có ba điểm cực trị nên loại các đáp án B và C. Mặt khác, ta thấy ( 4 2
lim x − 2x + )1 = +∞ nên chọn đáp án A. x→+∞
Câu 24: (Mã 101 - 2020 Lần 2)Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên A. 4 2 y = x − 2x − 2 B. 3 2
y = −x + 2x − 2 C. 3 2 y = x − 3x − 2 D. 4 2 y = −x + 2x − 2 Lời giải Chọn B
Qua đồ thị là hàm bậc 3 nên loại A, D.
Bên phải ngoài cùng của đồ thị đi xuống nên hệ số a < 0 ⇒ loại đáp án C
Câu 25: (Mã 104 2017) Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. 3
y = −x + 3x + 2 B. 4 2
y = x − x +1 C. 4 2
y = x + x +1 D. 3
y = x − 3x + 2 Lời giải Chọn D Page 8
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Đồ thị hình vẽ là đồ thị hàm số bậc ba có hệ số a > 0 nên chỉ có hàm số 3
y = x − 3x + 2 thỏa mãn điều kiện trên.
Câu 26: (Mã 102 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = −x + 2x −1. B. 4 2
y = x − 2x −1. C. 3 2
y = x −3x −1. D. 3 2
y = −x + 3x −1. Lời giải Chọn D
Dựa vào đồ thị có dạng đồ thị của hàm số bậc 3 có hệ số a < 0 nên đáp án D đúng.
Câu 27: (Mã 103 - 2020 Lần 2) Đồ thị của hàm số dưới đây có dạng như đường cong bên? A. 3
y = x −3x +1. B. 4 2
y = x − 2x +1. C. 4 2
y = −x + 2x +1. D. 3
y = −x + 3x +1. Lời giải Chọn A
Câu 28: (Mã 104 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = x + 2x . B. 3
y = −x − 3x . C. 3
y = x − 3x . D. 4 2
y = −x + 2x . Page 9
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn C
Đây là đồ thị của hàm số bậc ba với hệ số a > 0 nên Chọn C
Câu 29: (Đề Tham Khảo 2019) Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 2x −1 y + = B. x 1 y = C. 4 2
y = x + x +1 D. 3
y = x − 3x −1 x −1 x −1 Lời giải Chọn B
Vì từ đồ thị ta suy ra đồ thị của hàm phân thức có tiệm cận đứng và ngang x =1; y =1
Câu 30: (Mã 103 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 3 2
y = x − 3x − 2 . B. 4 2
y = x − 2x − 2. C. 3 2
y = −x + 3x − 2. D. 4 2
y = −x + 2x − 2 . Lời giải Chọn B
Quan sát đò thị ta thấy đây là đồ thị của hàm số 4 2
y = ax + bx + c(a > 0).
Câu 31: (Mã 101 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 3 2
y = x − 3x + 3 . B. 3 y = −x + 3 2 x + 3. C. 4 y = x − 2 2 x + 3.s D. 4 y = −x + 2 2 x + 3. Lời giải Chọn A Page 10
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Dạng hàm bậc ba nên loại C
Từ đồ thị ta có a > 0. Do đó loại B, D.
Câu 32: (Mã 102 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = −x + x −1 B. 4 2
y = −x + 2x −1 C. 3 2
y = x − x −1 D. 4 2
y = x − 2x −1 Lời giải Chọn D
Dựa vào hình vẽ suy ra hàm số đã cho có 3 cực trị → loại C, D.
Mặt khác nhánh bên tay phải của đồ thị hàm số đi lên suy ra hệ số a > 0 → Chọn D
Câu 33: (Mã 101 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = x − 3x −1 B. 3 2
y = −x + 3x −1 C. 4 2
y = −x + 3x −1 D. 4 2
y = x − 3x −1 Lời giải Chọn C
+ Nhìn đồ thị khẳng định đồ thị hàm trùng phương loại A, B
+ lim y = −∞ nên Chọn C x→±∞
Câu 34: (Mã 104 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 4 2
y = x − x − 2 B. 4 2
y = −x + x − 2 C. 3 2
y = −x + 3x − 2 D. 3 2
y = x − 3x − 2 Page 11
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn C
Dựa trên hình dáng đồ thị, ta loại 3 2
y = x − 3x − 2và 4 2
y = x − x − 2 Mặt khác từ đồ thị, ta thấy
lim y = −∞ nên loại 4 2
y = −x + x − 2 x→+∞
Câu 35: (Mã 103 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y x O A. 3
y = x − 3x −1 B. 4 2
y = x − 3x −1 C. 3
y = −x − 3x −1 D. 4 2
y = −x + x −1 Lời giải Chọn A
Đồ thị hàm số là đồ thị của hàm số bậc ba nên loại A và B.
Đồ thi hàm số bậc ba có hệ số a > 0 nên D đúng.
Câu 36: (Đề Tham Khảo 2018) Đường cong trong hình bên là của đồ thị hàm số nào dưới đây? A. 3 2
y = x −3x + 2 B. 3 2
y = −x + 3x + 2 C. 4 2
y = −x + 2x + 2 D. 4 2
y = x − 2x + 2 Lời giải Chọn C
Đồ thị hàm số trên là đồ thị hàm trùng phương có 3 cực trị và có a < 0
Câu 37: (Mã 110 2017) Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? Page 12
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = −x + 3x +1 B. 3 2
y = x −3x + 3 C. 4 2
y = −x + 2x +1 D. 4 2
y = x − 2x +1. Lời giải Chọn B
Dựa vào đồ thị ta thấy đây là hình ảnh đồ thị của hàm số bậc ba nên loại đáp án B và C; Mặt
khác dựa vào đồ thị ta có lim y = +∞ nên hệ số của 3
x dương nên ta chọn đáp án x→+∞ 3 2
y = x −3x + 3
Câu 38: (Đề Tham Khảo 2017) Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào? 2x + 3 2x −1 2x − 2 A. 2x +1 y = B. y = C. y = D. y = x −1 x +1 x +1 x −1 Lời giải Chọn C
Dựa vào đồ thị suy ra tiệm cận đứng x = 1 − loại C, D
Đồ thị hàm số giao với trục hoành có hoành độ dương suy ra chọn B Page 13
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 39: (Đề Minh Họa 2017) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án ,
A B,C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 3
y = x − 3x +1 B. 3
y = −x + 3x +1 C. 4 2
y = x − x +1 D. 2
y = −x + x −1 Lời giải Chọn A
Từ đồ thị : lim y = +∞ và đây là đồ thị hàm bậc ba nên ta chọn phương án 3
y = x − 3x +1. x→+∞
Câu 40: (Mã 104 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? A. 4 2
y = 2x − 4x +1 B. 3 y = 2
− x + 3x +1 C. 3
y = 2x − 3x +1 D. 4 2 y = 2
− x + 4x +1 Lời giải Chọn D
Dạng đồ thị hình bên là đồ thị hàm số trùng phương 4 2
y = ax + bx + c có hệ số a < 0 .
Do đó, chỉ có đồ thị ở đáp án B là thỏa mãn.
Câu 41: (Mã 102 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên A. 3
y = −x + 3x +1. B. 3
y = x − 3x +1. C. 4 2
y = x − 2x +1. D. 4 2
y = −x + 2x +1. Lời giải Chọn A Page 14
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Trong bốn hàm số đã cho thì chỉ có hàm số 3
y = −x + 3x +1(hàm số đa thức bậc ba với hệ số
a < 0 ) có dạng đồ thị như đường cong trong hình.
Câu 42: (Mã 123 2017) Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A. y = 4 x − 2 x −1 B. y = − 4 x + 2 x −1 C. y = 3 x − 2 x −1 D. y = − 3 x + 2 x −1 Lời giải Chọn A
Đây là hình dáng của đồ thị hàm bậc bốn trùng phương có hệ số a > 0
Câu 43: (Mã 123 2017) Đường cong ở hình bên là đồ thị của hàm số ax + b y =
với a,b,c,d là các số cx + d
thực. Mệnh đề nào dưới đây đúng?
A. y′ < 0,∀x∈ 
B. y′ > 0,∀x ≠ 1
C. y′ < 0,∀x ≠ 1
D. y′ > 0,∀x∈  Lời giải Chọn C Ta có :
Dựa vào hình dáng của đồ thị ta được: Page 15
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
+ Điều kiện x ≠ 1
+ Đây là đồ thị của hàm nghịch biến
Từ đó ta được y′ < 0,∀x ≠ 1.
Câu 44: (Mã 105 2017) Đường cong ở hình bên là đồ thị của hàm số ax + b y =
với a,b,c,d là các số cx + d
thực. Mệnh đề nào dưới đây đúng?
A. y′ > 0,∀x ≠ 1
B. y′ < 0,∀x ≠ 1
C. y′ < 0,∀x ≠ 2
D. y′ > 0,∀ ≠ 2 Lời giải Chọn C
Dựa vào đồ thị ta nhận thấy tiệm cận đứng bằng 2, Hàm số nghịch biến vậy chọn B
Câu 45: (Đề Minh Họa 2020 Lần 1) Cho hàm số 3
y = ax + 3x + d ( ;
a d ∈) có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A. a > 0,d > 0.
B. a < 0,d > 0 .
C. a > 0,d < 0 .
D. a < 0,d < 0 . Lời giải Chọn D
Ta có: lim = −∞ ⇒ đồ thị nhánh ngoài cùng của hàm số hướng đi xuống nên hệ số a < 0 . x→+∞
Giao điểm của đồ thị hàm số với trục tung Oy : x = 0 là điểm nằm bên dưới trục hoành nên khi
x = 0 ⇒ y = d < 0.
Câu 46: (Đề Tham Khảo 2020 Lần 2) Cho hàm số f (x) ax +1 =
(a,b,c∈) có bảng biến thiên như bx + c sau: Page 16
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Trong các số a,b và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0. Lời giải Chọn C
Hàm số f (x) ax +1 =
có đường tiệm cận đứng là đường thẳng c
x = − và đường tiệm cận bx + c b ngang là đường thẳng a y = . bc − = 2 
Từ bảng biến thiên ta có:  b c
⇔ a = b = −   1 a 2  =1 b Mặt khác: '( ) ac − b f x = . (bx + c)2
Vì hàm số đã cho đồng biến trên các khoảng ( ;2 −∞ ) và (2;+∞) nên '( ) ac − b f x =
> 0 ⇔ ac − b > 0 2 (bx + c)2 2 Thay  
1 vào 2, ta được: c c 2 −
+ > 0 ⇔ −c + c > 0 ⇔ 0 < c <1. 2 2
Suy ra c là số dương và a, b là số âm.
Câu 47: (Mã 101 - 2020 Lần 1) Cho hàm số 3 2
y = ax + bx + cx + d (a,b,c,d ∈) có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số a , b , c , d ? A. 4 . B. 1. C. 2 . D. 3. Lời giải Chọn C
Ta có lim y = +∞ ⇒ a < 0 . x→+∞ Page 17
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Gọi x , x là hoành độ hai điểm cực trị của hàm số suy ra x , x nghiệm phương trình 1 2 1 2 2
y′ = 3ax + 2bx + c = 0 nên theo định lý Viet: +) Tổng hai nghiệm 2b x + x = −
> 0 ⇒ b < 0 ⇒ b > 0. 1 2 3a a +) Tích hai nghiệm c x x = > 0 ⇒ c < 0 . 1 2 3a
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d > 0 .
Vậy có 2 số dương trong các số a , b , c , d .
Câu 48: (Mã 102 - 2020 Lần 1) Cho hàm số y = ax3 + bx2 + cx + d (a,b,c,d ∈ ) có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các hệ số a,b,c,d ? A. 4 . B. 3. C. 1. D. 2 . Lời giải Chọn C
Ta có lim f (x) = −∞ ⇒ a < 0 x→+∞
Đồ thị hàm số có hai điểm cực trị nằm cùng phía của trục tung nên ac > 0 ⇒ c < 0
Đồ thị hàm số có điểm uốn nằm bên phải trục tung nên ab < 0 ⇒ b > 0
Đồ thị hàm số cắt trục tung ở dưới trục hoành ⇒ d < 0
Câu 49: (Mã 103 - 2020 Lần 1) Cho hàm số 3 2
y = ax + bx + cx + d (a, ,
b c,d ∈) có đồ thị là đường cong trong hình bên.
Có bao nhiêu số dương trong các số a,b,c,d ? A. 4 . B. 2 . C. 1. D. 3. Page 18
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn C Ta có 2
y′ = 3ax + 2bx + c . Dựa vào đồ thị ta thấy a < 0   2  b  − 9ac > 0 ∆′ > y′ 0    2b b  < 0
Hàm số có 2 cực trị âm nên S < 0 ⇔ − < 0 ⇒ ⇒ 3a    c < 0 P > 0   c > 0    3a
Đồ thị cắt trục Oy tại điểm (0;d ) nên d > 0 .
Vậy có đúng một số dương trong các số a,b,c,d
Câu 50: (Mã 104 - 2020 Lần 1) Cho hàm số 3 2
y = ax + bx + cx + d (a,b,c,d ∈) có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d ? A. 4 . B. 2 . C. 1. D. 3. Lời giải Chọn C Ta có: 2
y′ = 3ax + 2bx + c
Dựa vào đồ thị ta thấy a < 0  2
b − 9ac > 0 ∆′ > y′ 0    2bb < 0
Hàm số có 2 cực trị âm nên S < 0 ⇔ − < 0 ⇒ 3    ac < 0 P > 0   c > 0 3a
Đồ thị cắt trục Oy tại điểm (0;d ) nên d > 0
Vậy có đúng 1 số dương trong các số a, b, c, d .
Câu 51: (Mã 102 - 2020 Lần 2) Cho hàm số f (x) 3 2
= ax + bx + cx + d (a,b,c,d ∈) có bảng biến thiên như sau Page 19
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Có bao nhiêu số dương trong các số a, b, c, d ? A. 2 . B. 4 . C. 1. D. 3. Lời giải Chọn D
Từ dáng điệu sự biến thiên hàm số ta có a > 0.
Khi x = 0 thì y = d =1 > 0 . x = −
Mặt khác f ′(x) 2
= 3ax + 2bx + c . Từ bảng biến thiên ta có f ′(x) 2 = 0 ⇔  . x = 0 Từ đó suy ra 2 = 0; − b c = 2
− ⇒ b = 3a > 0 . 3a
Vậy có 3 số dương là a, b, d .
Câu 52: (Mã 103 - 2020 Lần 2) Cho hàm số f (x) 3 2
= ax + bx + cx + d (a, ,
b c, d ∈) có bảng biến thiên như sau:
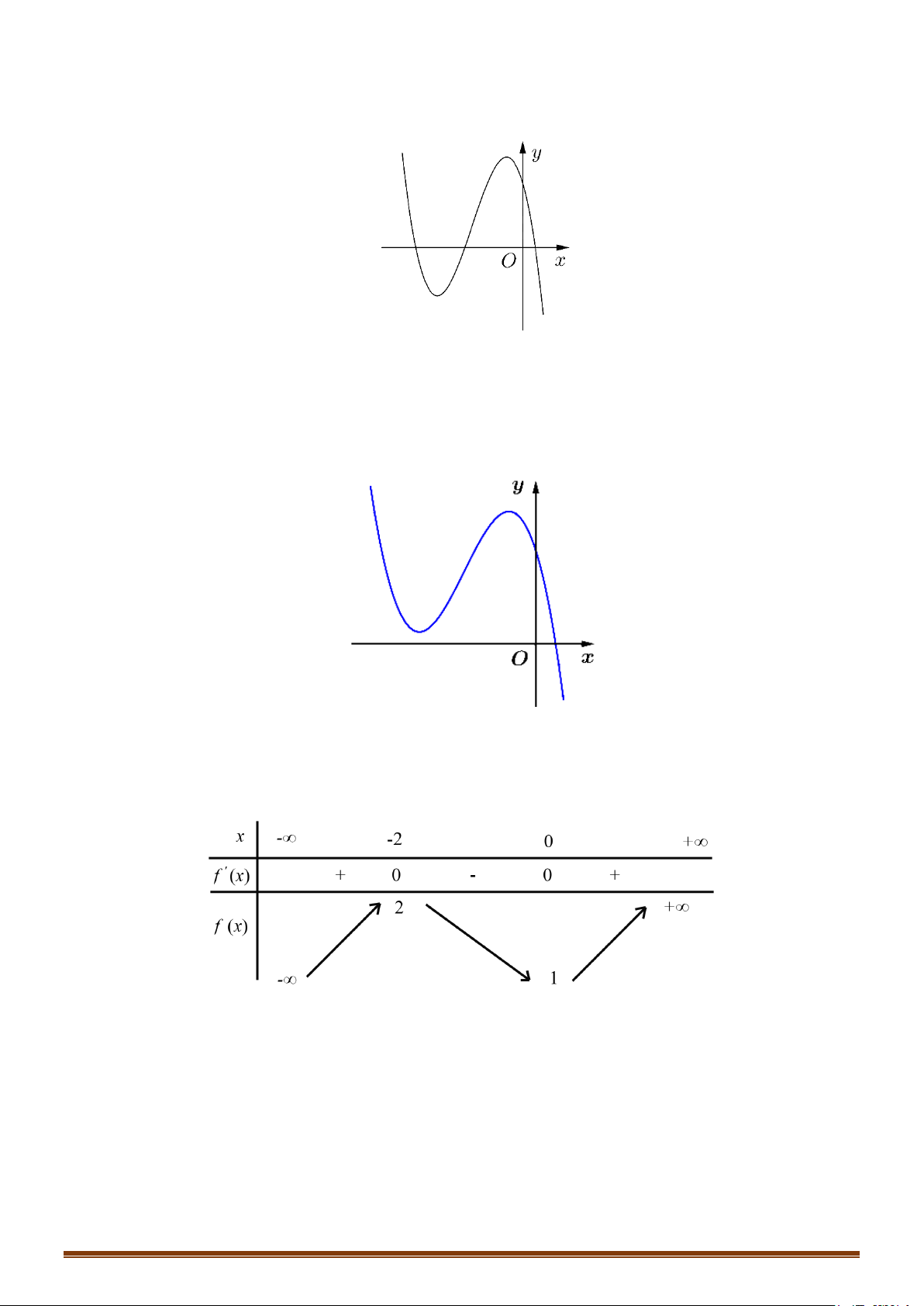
Có bao nhiêu số dương trong các số a, b, c, d ? A. 3. B. 4. C. 2. D. 1. Lời giải Chọn C
 lim f ( x) = +∞ ⇒ a > 0. x→+∞  f (0) = 1 − ⇒ d = 1 − < 0.  f ′( x) 2 = 3ax + 2bx + . c  2b − = 2 x + x = 2 − −  3a b  = 3a > 0 Ta có 1 2  ⇒  ⇒  . x x = 0 c  c = 0 1 2 = 0 3a Có 2 số dương là a, b Page 20
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 53: (Mã 101 – 2020 Lần 2) Cho hàm số f (x) 3 2
= ax + bx + cx + d (a,b,c,d ∈) có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a,b,c,d ? A. 2 . B. 4 . C. 1. D. 3. Lời giải Chọn A
Từ bảng biến thiên, ta có  1  (0) = 3  = 3 a f d =  4     f (4) = 5 −
64a +16b + 4c + d = 5 −  3  ⇔  ⇔ b = − f (0) 0 c 0  ′ = = 2     ′  =  + + = c = 0 f (4) 0 48a 8b c 0  d = 3
Vậy trong các số a, ,
b c, d có 2 số dương.
Câu 54: (Mã 104 - 2020 Lần 2) Cho hàm số f (x) 3 2
= ax + bx + cx + d (a, ,
b c,d ∈) có bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a,b,c,d ? A. 4 . B. 2 . C. 3. D. 1. Lời giải Chọn D
Ta có: f (x) 3 2
= ax + bx + cx + d (a,b,c,d ∈) ⇒ f ′(x) 2
= 3ax + 2bx + c
Đồ thị hàm số f (x) có hai điểm cực trị A(0;− ) 1 , B(4; 5 − ) nên ta có hệ: Page 21
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ  1  (0) 1  = 1 a f d = = − −  8   f (4) = 5   −
64a +16b + 4c + d = 5 −  3  ⇔  ⇔ b = − 
. Trong các số a,b,c,d có 1 số dương. f ′(0) =  0 c = 0 4    f ′  (4)  =  + + = c = 0 0 48a 8b c 0  d = 1 − Page 22
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ G
ƠN I ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ HƯ C
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
DẠNG. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
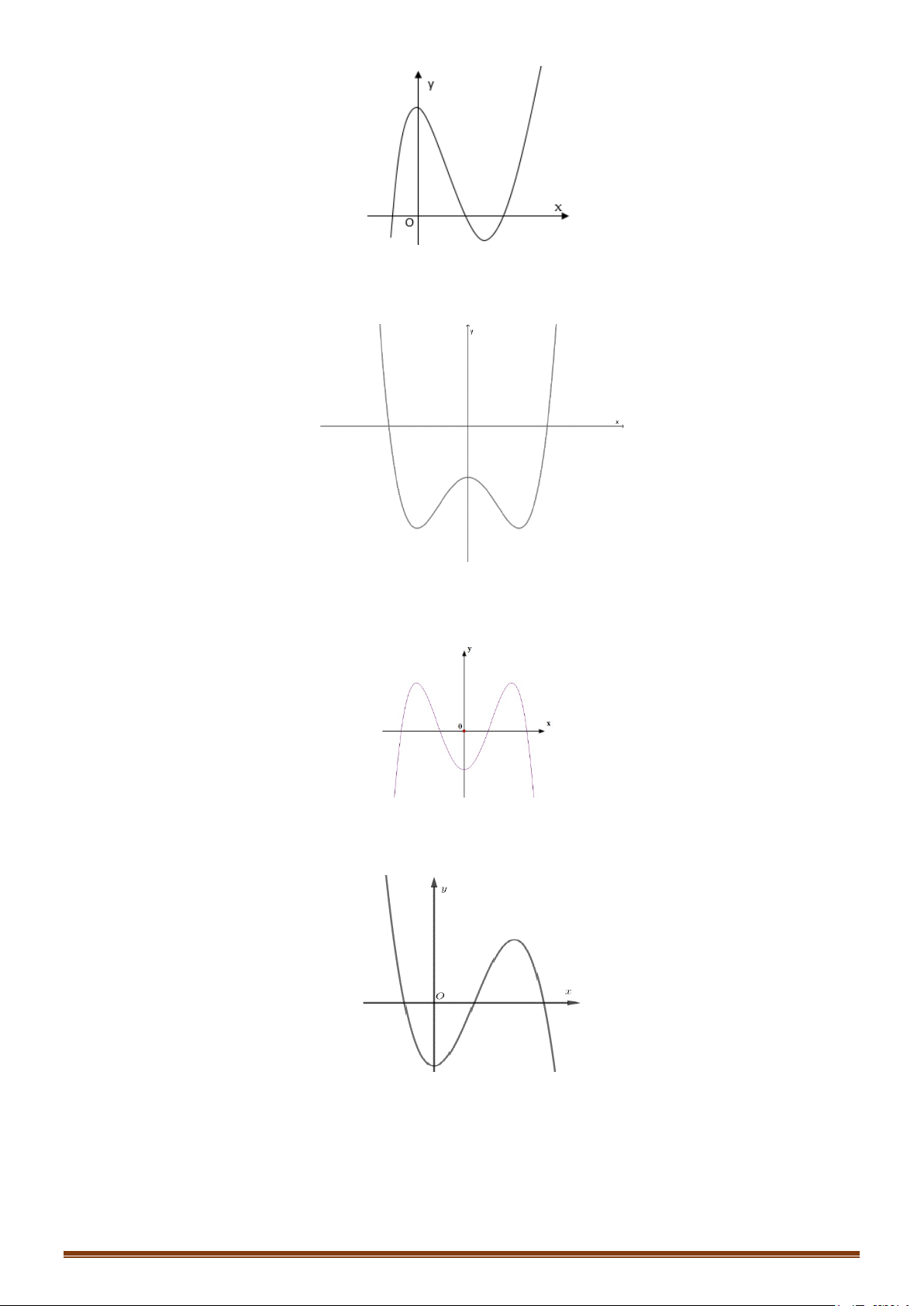
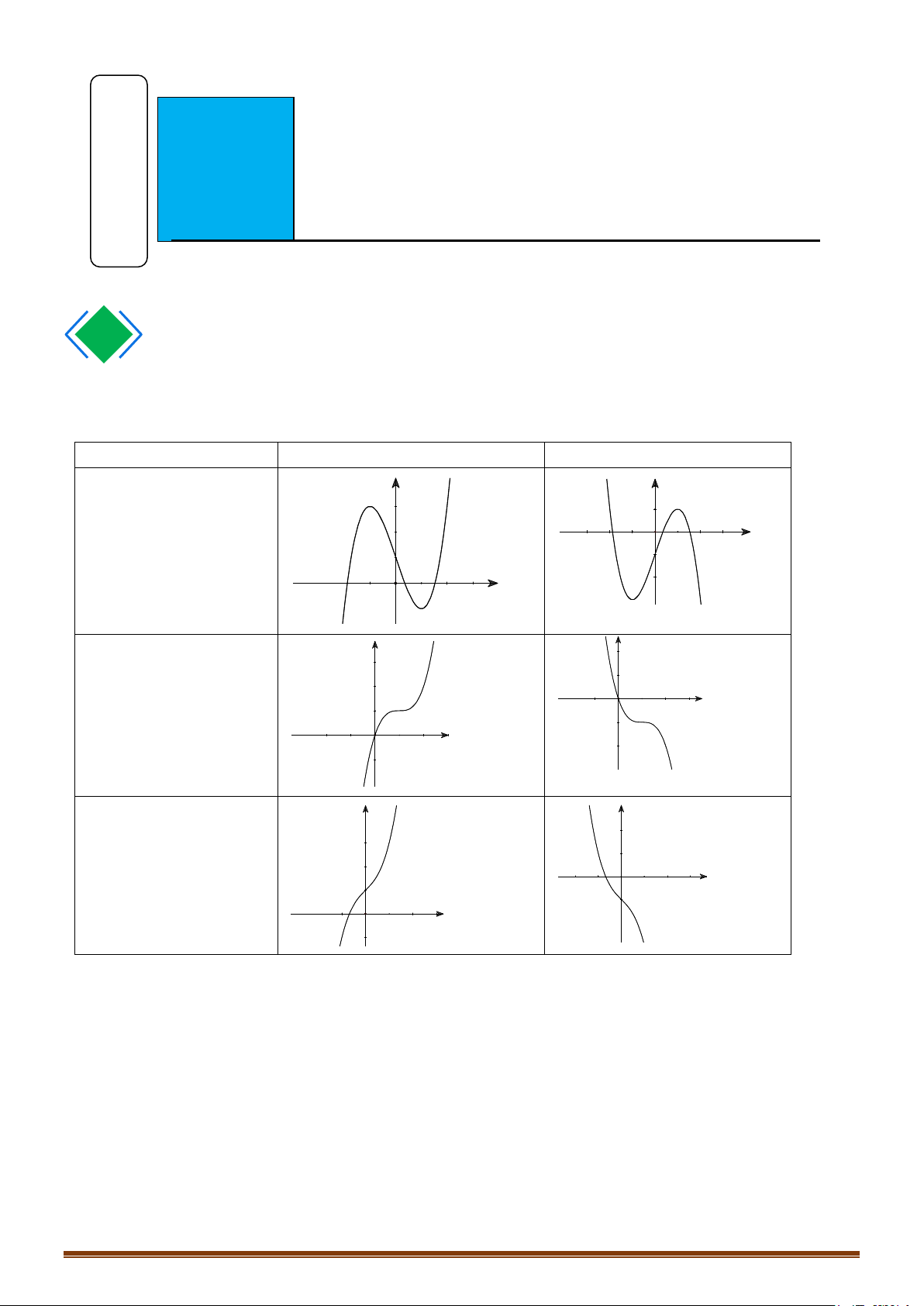
A. Hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0) TRƯỜNG HỢP a > 0 a < 0
Phương trình y/ = 0 có y y
2 nghiệm phân biệt 1 1 O x 1 1 O x Phương trình y y/ = 0 có y nghiệm kép 1 1 1 O x 1 O x Phương trình / y = 0 vô y y nghiệm 1 O 1 1 x 1 O x Page 223
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
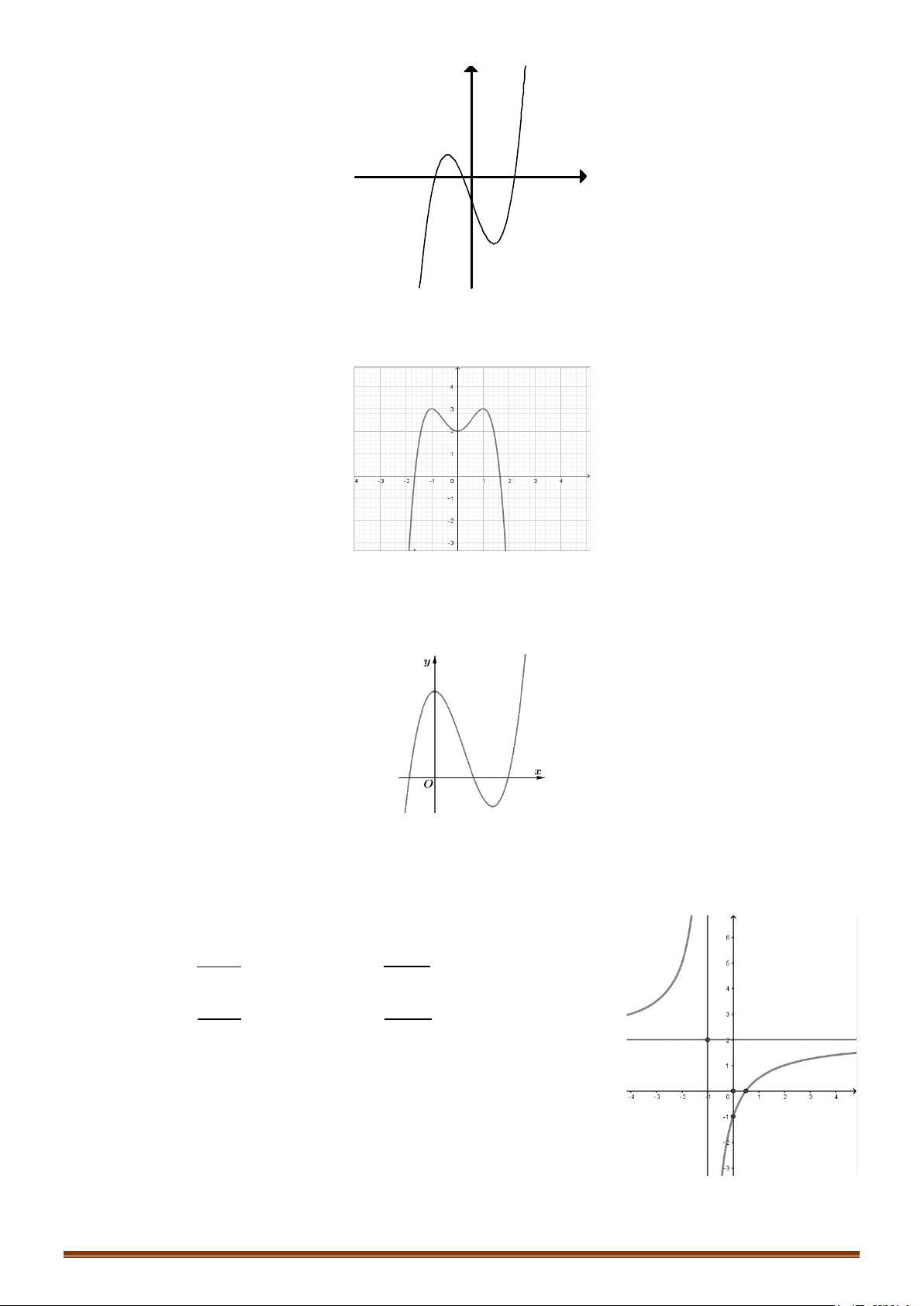
B. Hàm số trùng phương y = ax4 + bx2 + c (a ≠ 0) TRƯỜNG HỢP a > 0 a < 0
Phương trình y/ = 0 y y có
3 nghiệm phân biệt 1 1 1 1 O x O x
Phương trình y/ = 0 y y có 1 nghiệm. 1 1 1 O x 1 O x
C. Hàm số nhất biến ax + b y =
(c ≠ 0, ad − bc ≠ 0) cx + d
D = ad − bc > 0
D = ad − bc < 0
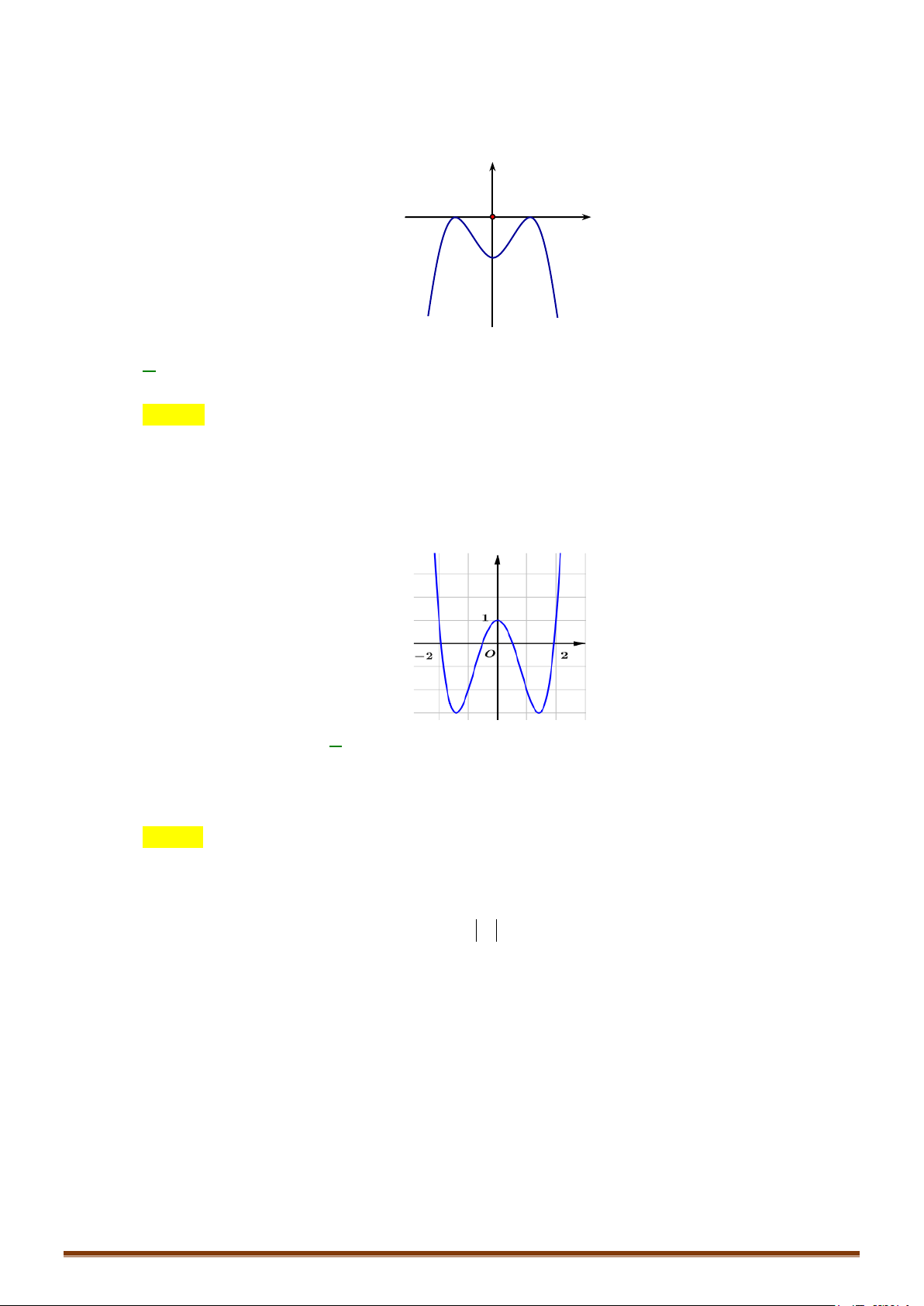
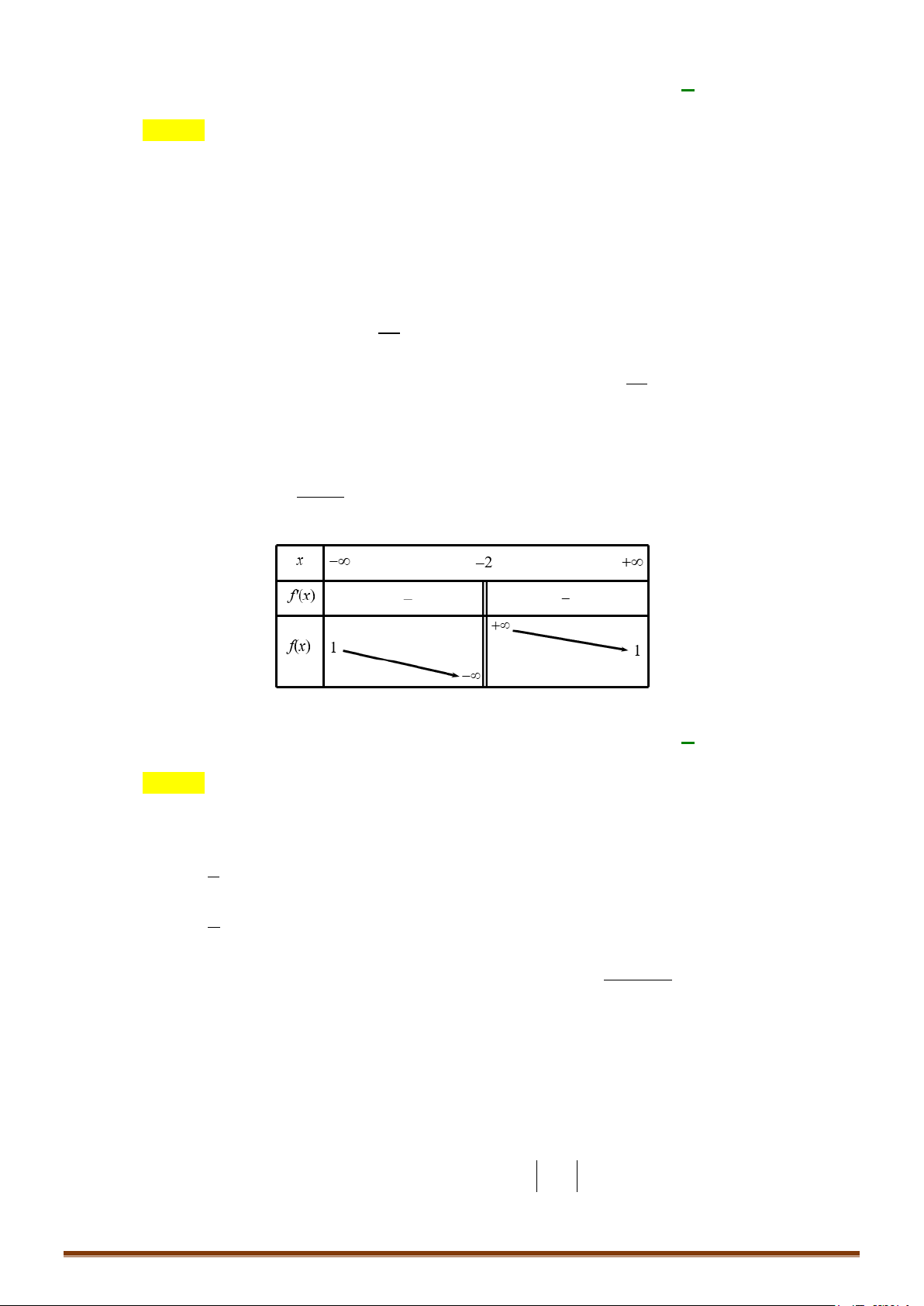
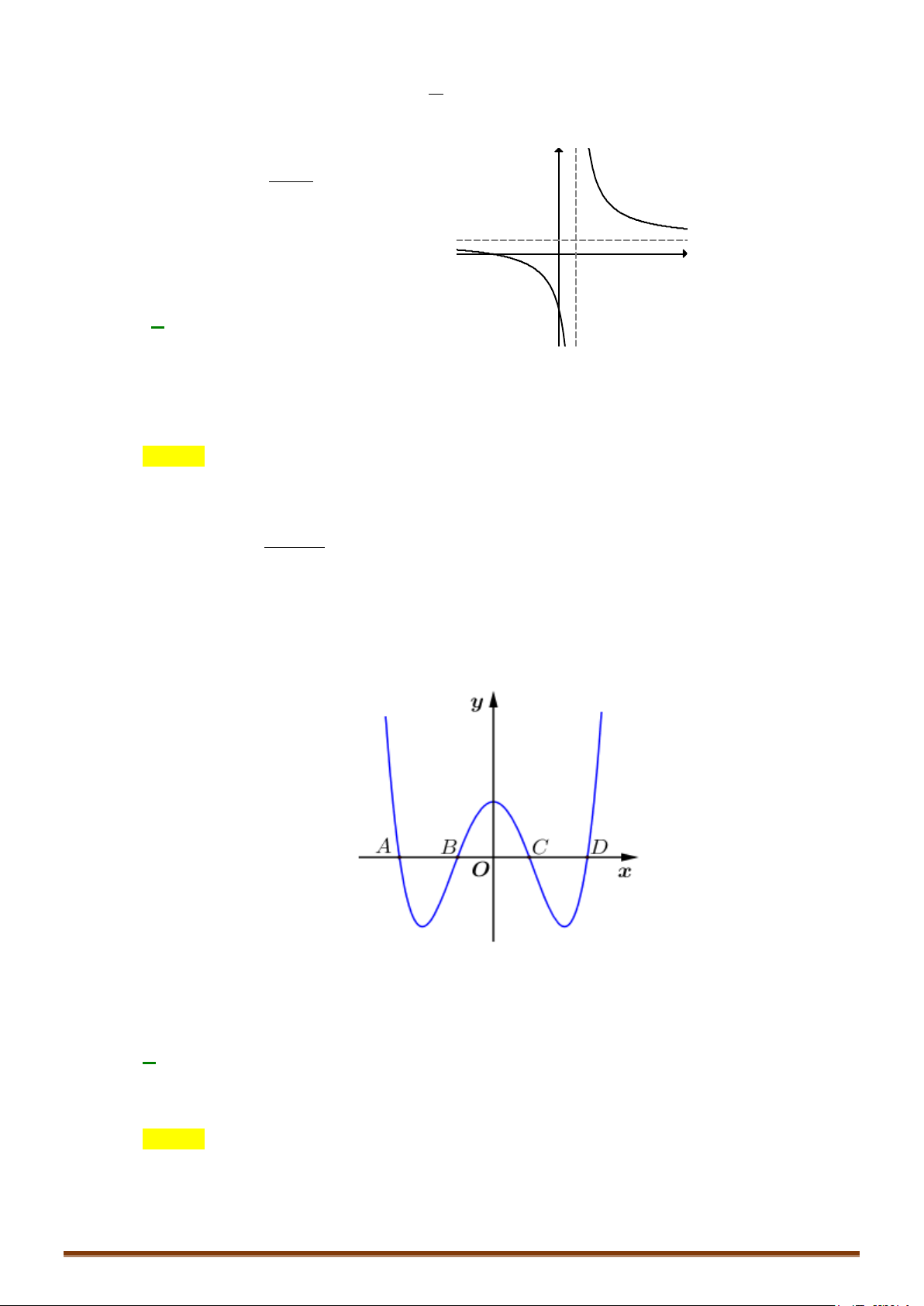
Câu 1: Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án ,
A B,C, D . Hỏi đó là hàm số nào? A. 3
y = x + 2x +1. B. 3 2
y = x − 2x +1. C. 3
y = x − 2x +1. D. 3
y = −x + 2x +1.
Câu 2: Hình vẽ bên dưới là đồ thị của hàm số nào Page 224
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. x −1 y x + x − x + = . B. 2 1 y = . C. 2 3 y = . D. 2 5 y = . x +1 x +1 x +1 x +1
Câu 3: Đường cong trong hình là đồ thị của hàm số nào dưới đây? A. x −1 y − + = . B. 2x 1 y = . C. 4 2
y = x − 3x . D. 3 2
y = x − 3x . x +1 2x + 2
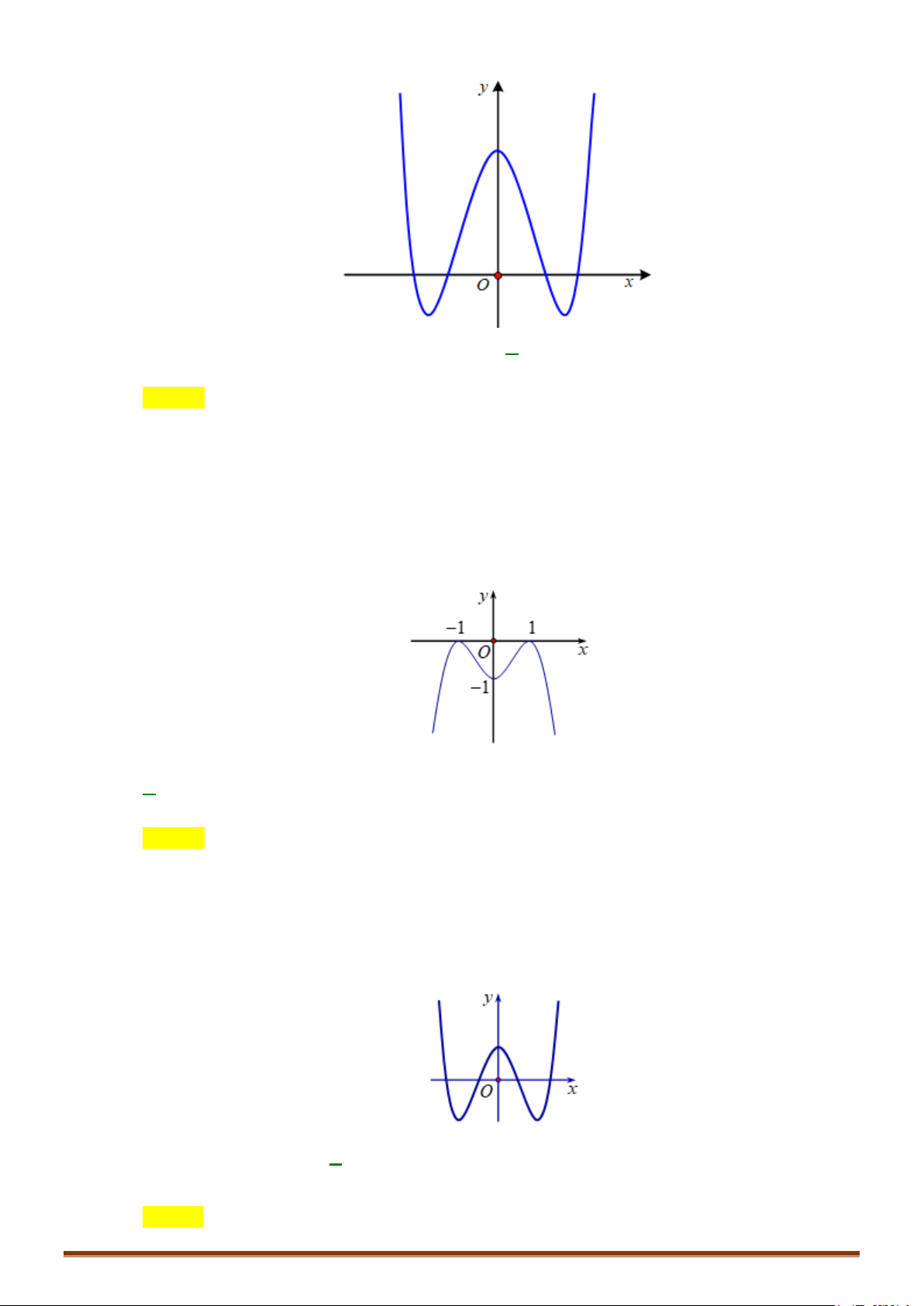
Câu 4: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây? A. 3
y  x 3x 1. B. 4 2
y x x 1. C. 2
y  x x1. D. 3
y x 3x 1. Page 225
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 2. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ Câu 5: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? A. a < 0, b > 0, 0, c > d < 0 B. a < 0, b < 0, 0, c > d < 0. C. a > 0, b < 0, c < 0, d > 0 D. a < 0, b > 0, 0, c < d < 0. Page 226
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 6: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?
A. a > 0,b < 0,c > 0
B. a > 0,b < 0,c < 0 C. a > 0,b > 0,c < 0 D. a < 0,b > 0,c < 0 Câu 7: Cho hàm số ax + = b y có đồ thị như sau. cx + d
Mệnh đề nào sau đây đúng? A. ac > 0; 0 bd > B. ab < 0; 0 cd < C. bc > 0; 0 ad < D. ad > 0; 0 bd < Câu 8: Cho hàm số 3 2
y = ax + bx + cx + d (a ≠ 0) có đồ thị như hình vẽ dưới đây. Chọn khẳng định
đúng về dấu của a , b , c , d ?
A. a > 0 ,b > 0, d > 0 , c > 0
B. a > 0 , c > 0 > b , d < 0
C. a > 0, b > 0, c > 0, d > 0.
D. a > 0 , b < 0 , c < 0 , d > 0 Page 227
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ a  1 x b
Câu 9: Cho hàm số y
, d  0 có đồ thị như hình trên. Khẳng định nào dưới đây là đúng? c  1 x d
A. a 1,b  0,c 1. B. a 1,b  0,c 1. C. a 1,b  0,c 1. D. a 1,b  0,c 1. Câu 10: Cho hàm số 4 2
y = ax + bx + c ( a ≠ 0) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A. a < 0 , b > 0, c < 0 . B. a < 0 , b < 0 , c > 0 . C. a < 0 , b > 0, c > 0 . D. a < 0 , b < 0 , c < 0 . Câu 11: Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A. a  0, b  0 , c  0, d  0 .
B. a  0 , b  0 , c  0, d  0 .
C. a  0, b  0 , c  0, d  0 .
D. a  0 , b  0 , c  0, d  0 . Page 228
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 12: Cho hàm số ax + b y =
có đồ thị như hình bên dưới, với a , b , c∈ . Tính giá trị của biểu thức x + c
T = a + 2b + 3c ? A. T = 8 − . B. T = 2. C. T = 6 . D. T = 0 . Câu 13: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào đúng?
A. ab < 0,bc > 0,cd < 0
B. ab < 0,bc < 0,cd > 0
C. ab > 0,bc > 0,cd < 0
D. ab > 0,bc > 0,cd > 0 Câu 14: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A. a < 0,b < 0,c < 0,d < 0
B. a < 0,b > 0,c > 0,d > 0
C. a < 0,b > 0,c < 0,d > 0
D. a < 0,b > 0,c > 0,d < 0 Page 229
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 15: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ?
A. a > 0,b < 0,c < 0 .
B. a < 0,b < 0,c < 0 .
C. a < 0,b > 0,c < 0 .
D. a > 0,b < 0,c > 0 Câu 16: Cho hàm số ax + b y =
có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi cx + d trong các số ,
b c,d có tất cả bao nhiêu số dương? A. 1. B. 2 . C. 0 . D. 3. Câu 17: Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A. a  0, b  0 , c  0, d  0 .
B. a  0 , b  0 , c  0, d  0 .
C. a  0, b  0 , c  0, d  0 .
D. a  0 , b  0 , c  0, d  0 . Page 230
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 18: Cho hàm số ax + b y =
có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng? cx + d ad < 0 ad < 0 ad > 0 ad > 0 A.  . B.  . C.  . D.  . bc > 0 bc < 0 bc < 0 bc > 0
Câu 19: Cho đường cong (C) 3 2
: y = ax + bx + cx + d có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A. a > 0,b < 0,c < 0,d < 0.
B. a > 0,b > 0,c < 0,d > 0 .
C. a < 0,b > 0,c > 0,d < 0.
D. a > 0,b > 0,c < 0,d < 0. Câu 20: Hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a  0, b  0 , c  0.
B. a  0, b  0 , c  0.
C. a  0, b  0 , c  0.
D. a  0, b  0 , c  0. Page 231
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 21: Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ. Tìm kết luận đúng
A. a b  0 .
B. bc  0 .
C. ab  0 .
D. ac  0. Câu 22: Cho hàm số 4 2
y ax bx c(a  0) có đồ thị như hình bên. Hãy chọn mệnh đề đúng.
A. a  0,b  0,c  0 . B. a  0,b  0,c  0 .
C. a  0,b  0,c  0 . D. a  0,b  0,c  0. Câu 23: Cho hàm số 3 2
y = f (x) = ax + bx + cx + d có đồ thị như hình vẽ ở bên. Mệnh đề nào sau đây đúng?
A. a > 0 , b > 0, c > 0 , d > 0 .
B. a > 0 , b > 0, c < 0 , d > 0 .
C. a > 0 , b < 0 , c > 0 , d > 0 .
D. a < 0 , b < 0 , c > 0 , d < 0 .
Câu 24: Cho hàm số bậc bốn trùng phương 4 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào
dưới đây là đúng?
A. a  0,b  0,c  0.
B. a  0,b  0,c  0.
C. a  0,b  0,c  0 .
D. a  0,b  0,c  0. Câu 25: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Hỏi khẳng định nào sau đây đúng? Page 232
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a > 0,b < 0,c < 0 . B. a > 0,b > 0,c < 0 . C. a > 0,b < 0,c > 0. D. a < 0,b > 0,c < 0 . Câu 26: Cho hàm số ax + 3 y =
có đồ thị như hình vẽ bên. Tính giá trị của a − 2 . c x + c
A. a − 2c = 3.
B. a − 2c = 3. −
C. a − 2c = 1. −
D. a − 2c = 2. −
Câu 27: Hình vẽ bên là đồ thị hàm số ax + b y = . cx + d .
Mệnh đề nào dưới đây đúng?
A. ad > 0 và bd > 0. B. ad > 0 và ab < 0 . C. bd < 0 và ab > 0 . D. ad < 0 và ab < 0 . Page 233
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 28: Cho hàm số ax − b y =
có đồ thị như hình vẽ dưới đây: x −1
Khẳng định nào sau đây đúng?
A. b < a < 0.
B. a < b < 0.
C. b > a và a < 0 .
D. a < 0 < b .
Câu 29: Đồ thị trong hình bên dưới là của hàm số ax + b y = . x + c
Khi đó tổng a + b + c bằng A. 1 − . B. 1. C. 2 . D. 0 .
Câu 30: Cho hàm số 2 ( ) − ax f x =
(a,b,c∈,b ≠ 0) có bảng biến thiên như sau: bx − c Tổng các số ( + + )2
a b c thuộc khoảng nào sau đây A. (1;2) . B. (2;3). C.  4 0;     . D. 4  ;1 . 9      9 
Câu 31: Cho hàm số ( ) ax + b f x =
(a,b,c,d ∈và c ≠ 0 ). Biết rằng đồ thị hàm số đã cho đi qua điểm cx + d ( 1;
− 7) và giao điểm hai tiệm cận là( 2;
− 3). Giá trị biểu thức 2a + 3b + 4c + d bằng 7c Page 234
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 7 . B. 4 . C. 6 . D. 5 − . Câu 32: Cho hàm số ax +1 y =
( a,b,c là các tham số) có bảng biến thiên như hình vẽ bx + c
Xét các phát biểu sau: ( ) 1 : c >1 (
; 2): a + b < 0 (
; 3): a + b + c = 0 (
; 4): a > 0 . Số phát biểu đúng là? A. 1. B. 2 . C. 3. D. 4 .
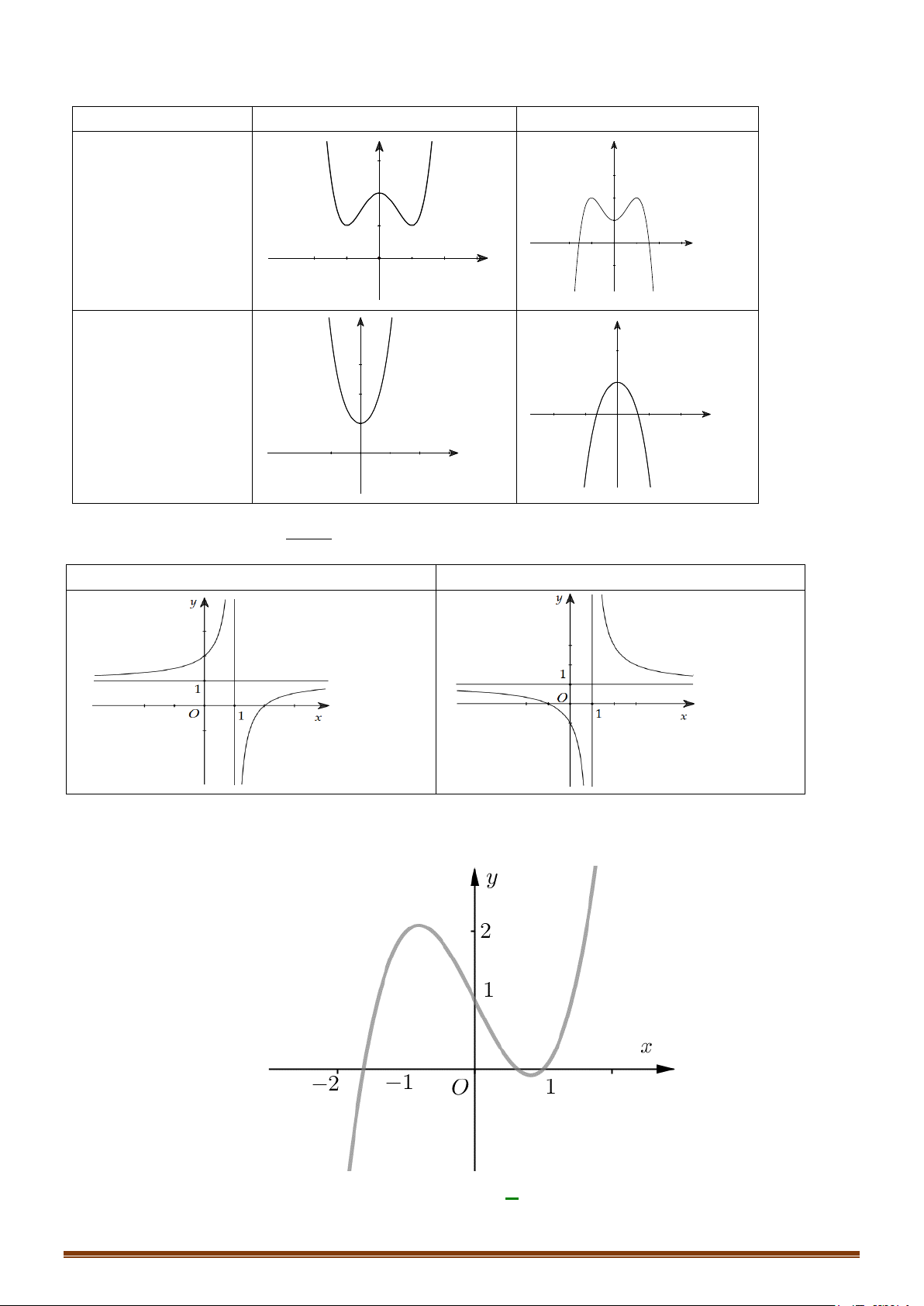
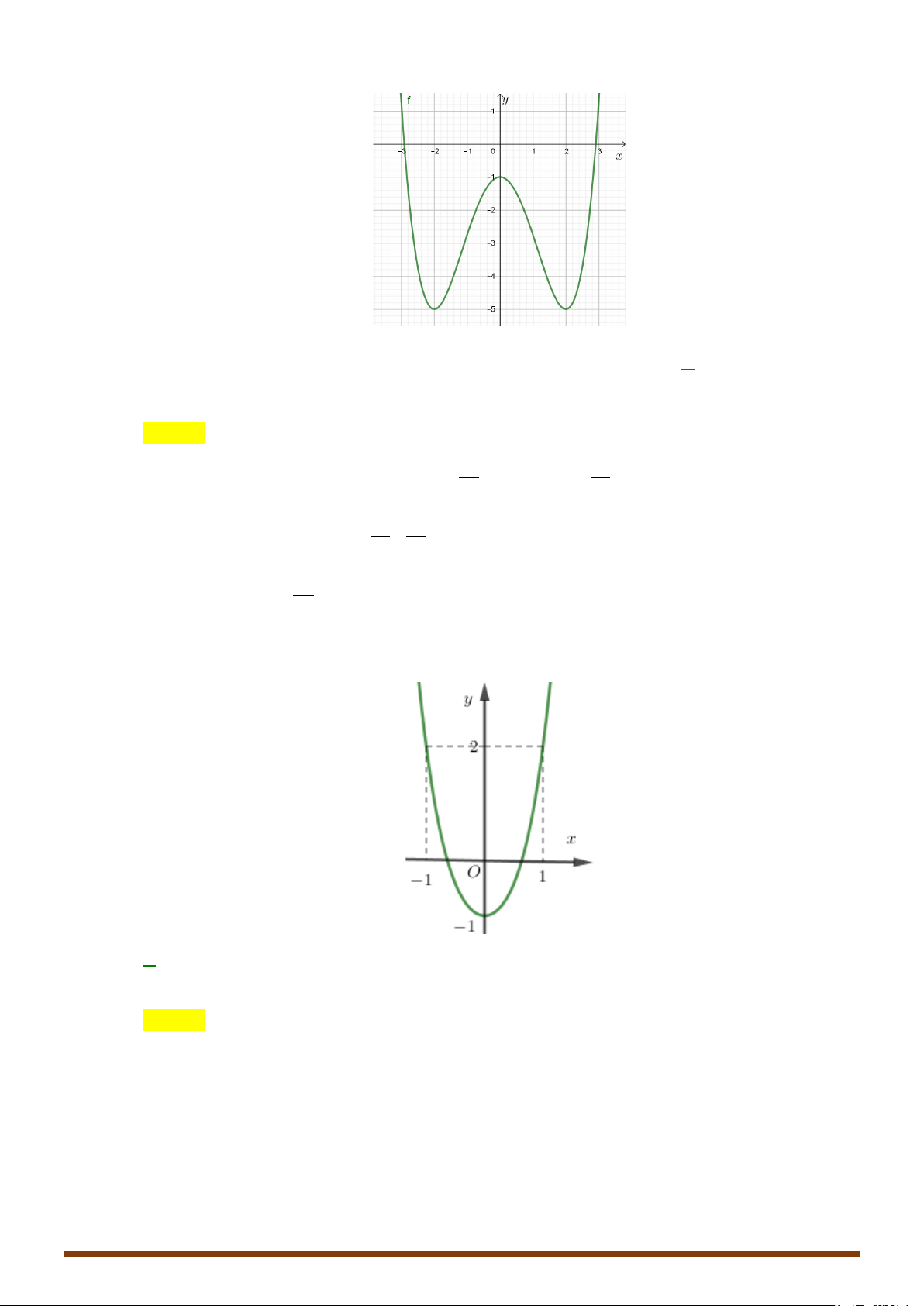
Câu 33: Ta xác định được các số a,b,c để đồ thị hàm số 3 2
y = x + ax + bx + c đi qua điểm (1;0) và có điểm cực trị ( 2;
− 0) . Tính giá trị biểu thức 2 2 2
T = a + b + c . A. 25. B. 1. − C. 7. D. 14. Câu 34: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ. Tính S = a + b ? A. S = 2 − . B. S = 0 . C. S =1. D. S = 1 − . Page 235
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 35: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A. a < 0,b < 0,c > 0,d < 0.
B. a < 0,b > 0,c < 0,d < 0 .
C. a > 0,b < 0,c < 0,d > 0.
D. a < 0,b > 0,c > 0,d < 0. Câu 36: Cho hàm số ax + b y =
(a,b,c∈) có bảng biến thiên như sau: cx +1
Tập các giá trị b là tập nghiệm của bất phương trình nào dưới đây? A. 3 b −8 ≤ 0. B. 2 b − + 4 > 0. C. 2
b − 3b + 2 < 0. D. 3 b −8 < 0. Câu 37: Cho hàm số ax + b y − + =
có đồ thị như hình dưới đây. Tính giá trị biểu thức a 2b 3d T = . cx + d c
A. T = 6 .
B. T = 0 . C. T = 8 − .
D. T = 2 . Câu 38: Cho hàm số 3 2
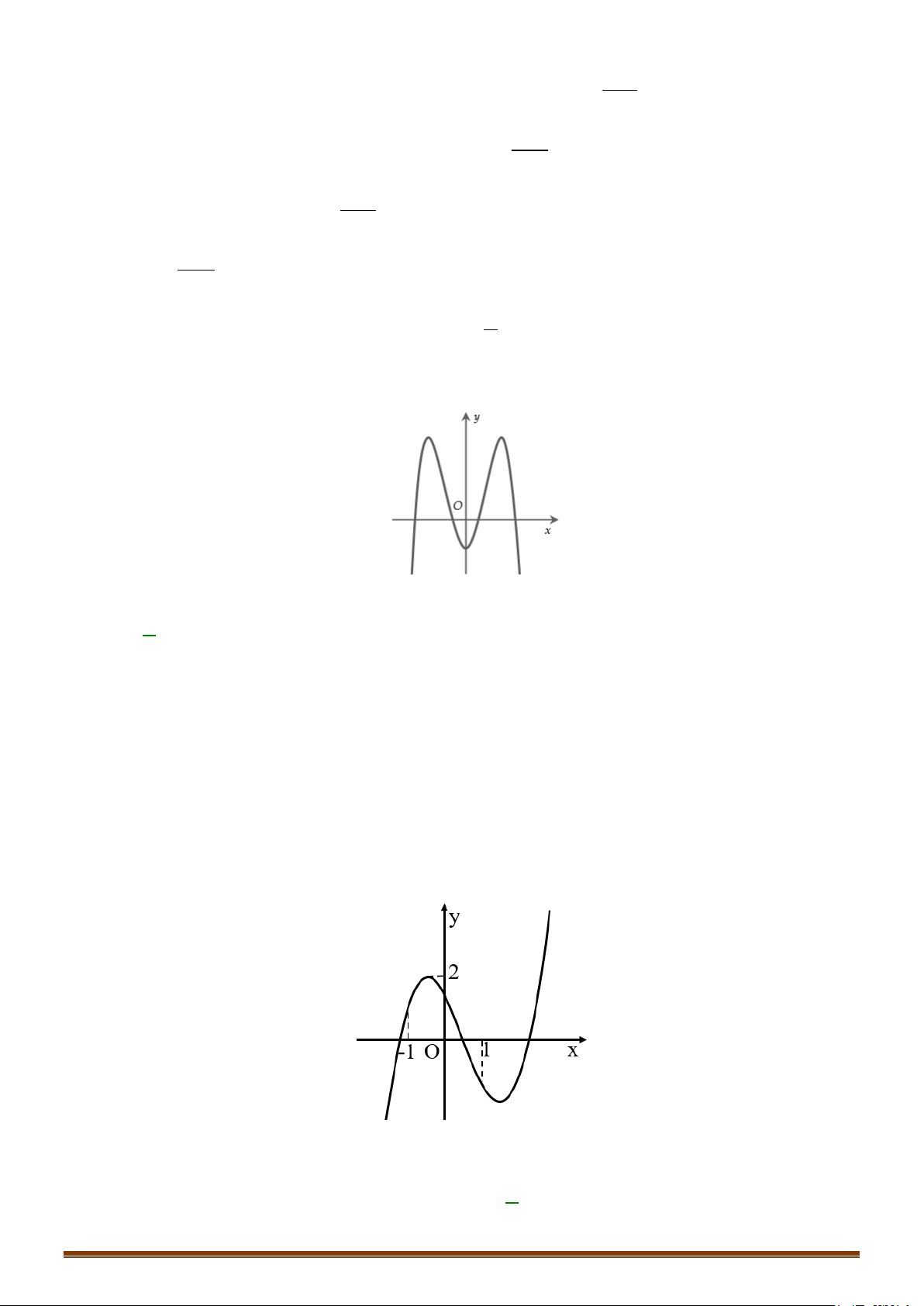
y = ax + bx + cx + d có đồ thị như hình vẽ. Trong các số a,b,c và d có bao nhiêu số dương? A. 1. B. 4 . C. 3. D. 2 . Page 236
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 39: Cho hàm số f (x) ax − 6 =
(a,b,c ∈ ) có bảng biến thiên như sau: bx − c Trong các số a, ,
b c có bao nhiêu số âm? A. 0 . B. 3. C. 1. D. 2 .
DẠNG 2. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI Dạng 1
Từ đồ thị (C ) : y = f (x ) suy ra đồ thị (C′) : y = f (x ) . f x kh i f x ≥ 0
Ta có: y = f (x ) ( ) ( ) = 
−f (x ) kh i f (x ) <  0
* Cách vẽ (C′) từ (C) :
Giữ nguyên phần đồ thị phía trên Ox của đồ thị :y = f (x ) .
Bỏ phần đồ thị phía dưới Ox của , lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị (C) y = f (x) 3 :
= x − 3x suy ra đồ thị y 2 (C) 3
: y = x − 3x
y = x 3 − x 3 . 1 Biến đổi (C) : -1 O x
 Bỏ phần đồ thị của (C ) dưới Ox, giữ nguyên (C ) phía trên -2 . Ox
(C′) y = x3 : − x 3
 Lấy đối xứng phần đồ thị bị bỏ qua Ox . y 2 -1 O 1 x Page 237
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Dạng 2
Từ đồ thị (C ) : y = f (x ) suy ra đồ thị (C′) : y = f ( x ) . f x khi x ≥ 0
Ta có: y = f ( x ) ( ) =  f  ( x − ) khi x < 0
và y = f ( x ) là hàm chẵn nên đồ thị (C′) nhận Oy làm trục đối xứng.
* Cách vẽ (C′) từ (C ) :
Giữ nguyên phần đồ thị bên phải Oy của đồ thị (C ) : y = f (x ).
Bỏ phần đồ thị bên trái Oy của (C ) , lấy đối xứng phần đồ thị được giữ qua Oy.
Ví dụ: Từ đồ thị (C ) y = f (x ) = x3 : − x 3 suy ra đồ thị y 2 ( 3 3
C ′) : y = x − 3 x .
(C ) : y = x − x3 1 -1 O x Biến đổi (C ) : -2
 Bỏ phần đồ thị của (C ) bên trái Oy, giữ nguyên (C ) bên phải . Oy y
 Lấy đối xứng phần đồ thị được giữ qua Oy . ( 3
C ′) : y = x − 3 x -1 O 1 x -2
Chú ý với dạng: y = f ( x ) ta lần lượt biến đổi 2 đồ thị y = f ( x ) và y = f (x )
Ví dụ: Từ đồ thị (C ) y = f (x ) = x3 : − x 3 y ( 3
C ′′) : y = x − 3 x suy ra đồ thị 3
y = x − 3 x . Biến đổi (C ) 2 để được đồ thị ( 3
C ′) : y = x − 3 x . Biến đổi ( 3
C ′) : y = x − 3 x ta được đồ thị -1 O 1 x ( 3
C ′′) : y = x − 3 x . Page 238
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Dạng 3
Từ đồ thị (C ) : y = u (x ) v. (x ) suy ra đồ thị (C′) : y = u (x ) v. (x ) . u
 x v. x = f x khi u x ≥ 0
Ta có: y = u (x ) v. (x ) ( ) ( ) ( ) ( ) =  u −
 (x ) v. (x ) = f (x ) khi u (x ) < 0
* Cách vẽ (C′) từ (C) :
Giữ nguyên phần đồ thị trên miền u (x ) ≥ 0 của đồ thị (C ) : y = f (x ).
Bỏ phần đồ thị trên miền u (x ) < 0 của (C ) , lấy đối xứng phần đồ thị bị bỏ qua Ox. Ví dụ Ví dụ
a) Từ đồ thị (C ) y = f (x ) = x3 − x2 : 2 3
+ 1 suy ra b) Từ đồ thị ( ) : = ( ) = x C y f x suy ra đồ thị x − 1
đồ thị (C′) y = x − ( x2 : 1 2 − x − 1) ( ′) : = x C y x − 1 f x khi x 1  x
y = x − 1 ( x2 2 − x − 1)  ( ) ≥ =  khi x ∈ x (1;+∞  )
−f (x ) khi x <  x − 1  1 y = =  .Đồ thị : x − 1  x Đồ thị : − khi x ∈ (−∞;1)  x − 1
 Giữ nguyên với x ≥ 1.
 Bỏ phần đồ thị của (C ) với < giữ nguyên (C )  Bỏ với x , 1
x < 1 . Lấy đối xứng phần đồ thị bị bỏ qua Ox. với x > 1.
 Lấy đối xứng phần đồ thị bị bỏ qua Ox. y (C') y 1 1 O 1 x O 1 x (C)
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của : giao điểm Nhận xét: Đối với hàm phân thức thì nên lấy đối xứng
với Ox, Oy, CĐ, CT…
các đường tiệm cận để thực hiện phép suy đồ thị một
cách tương đối chính xác. Page 239
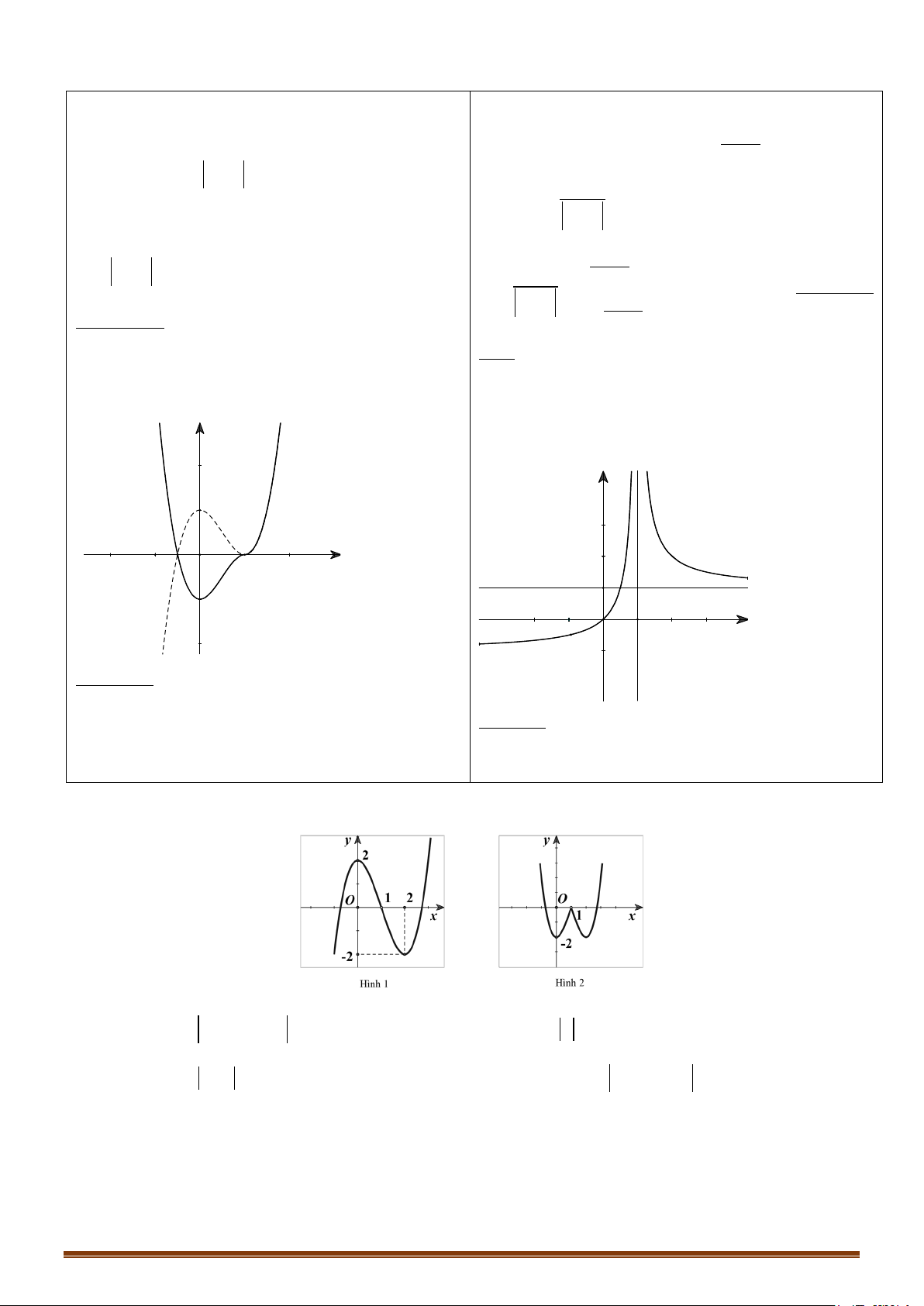
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 40: Cho hàm số 3 2
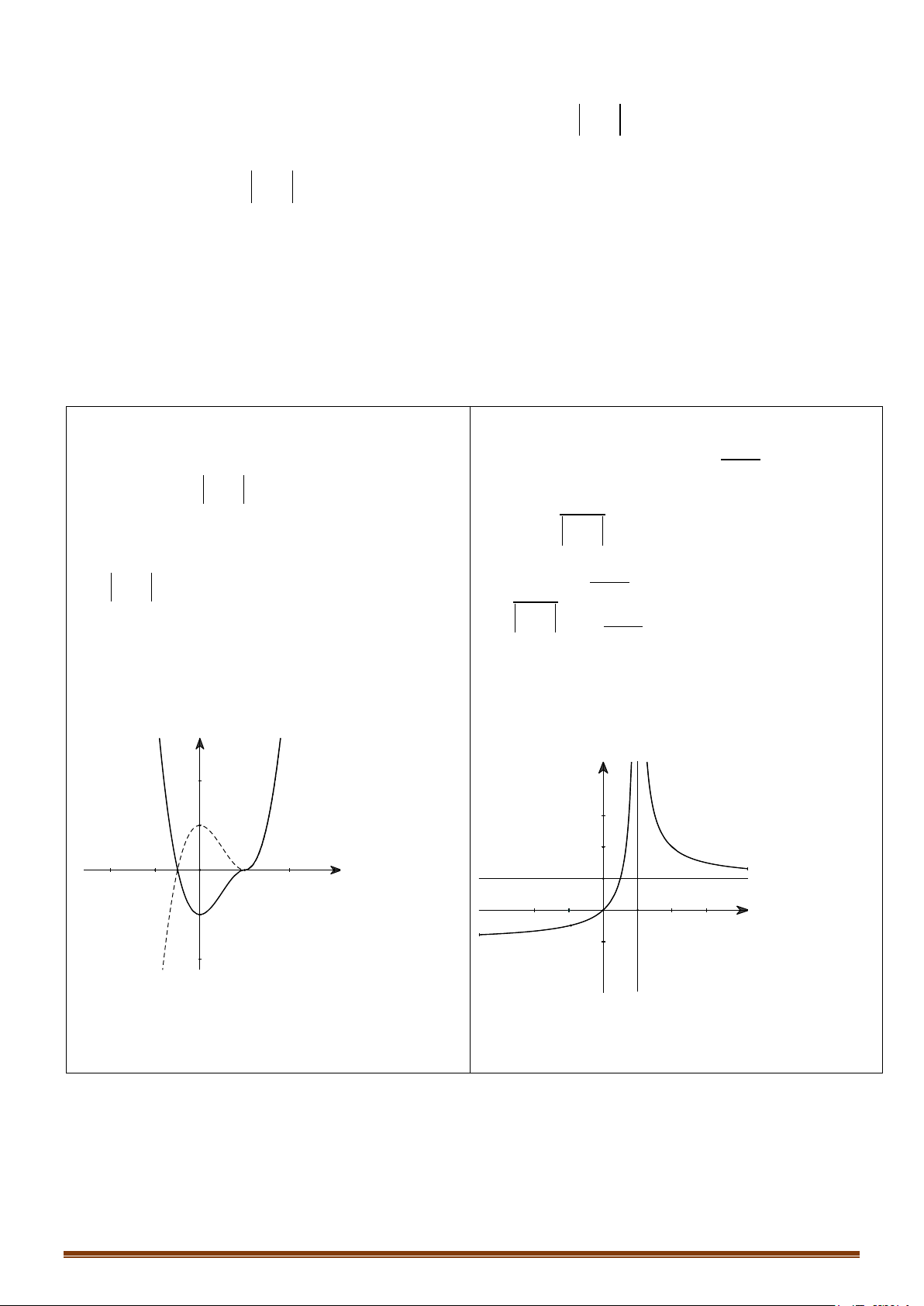
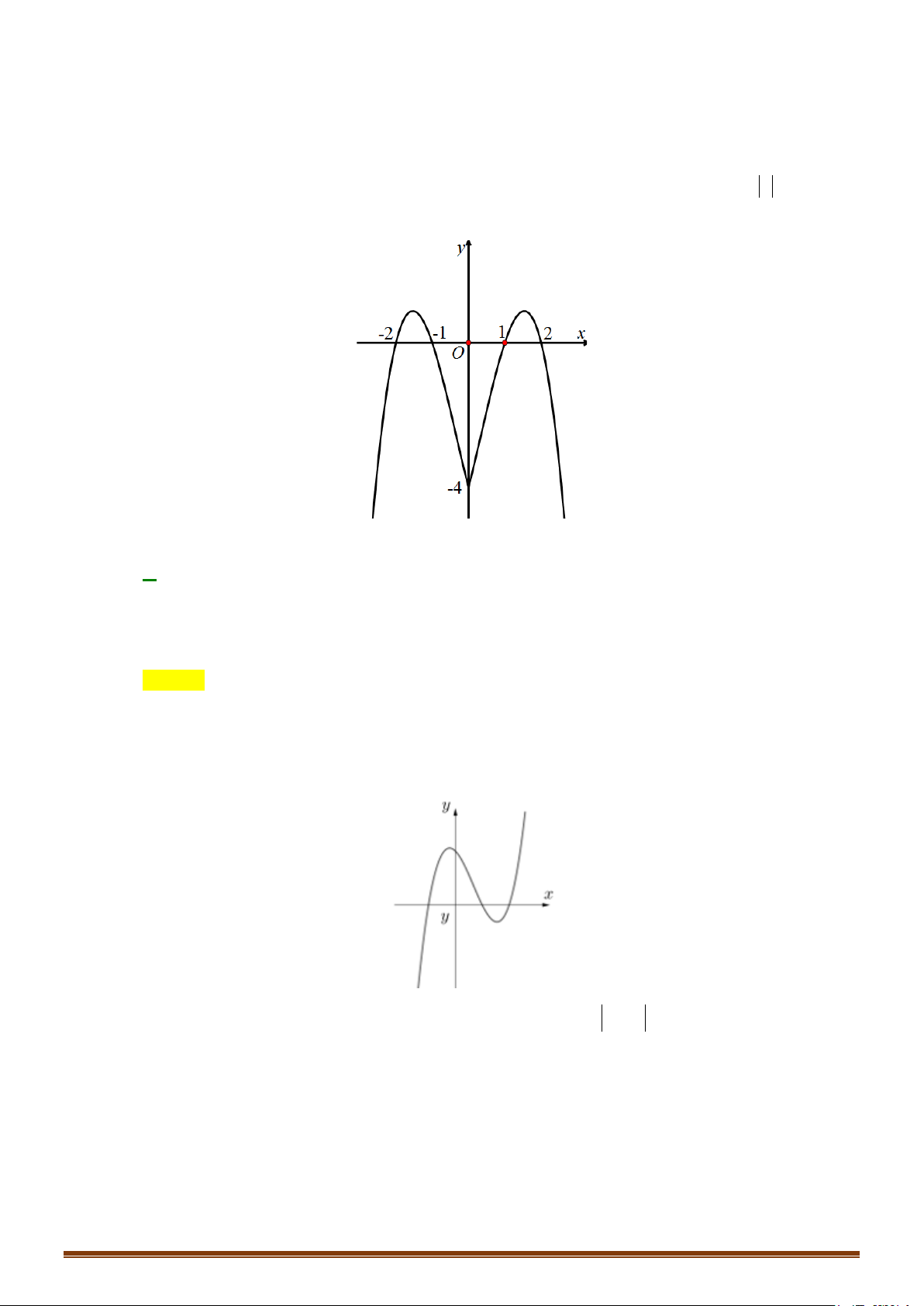
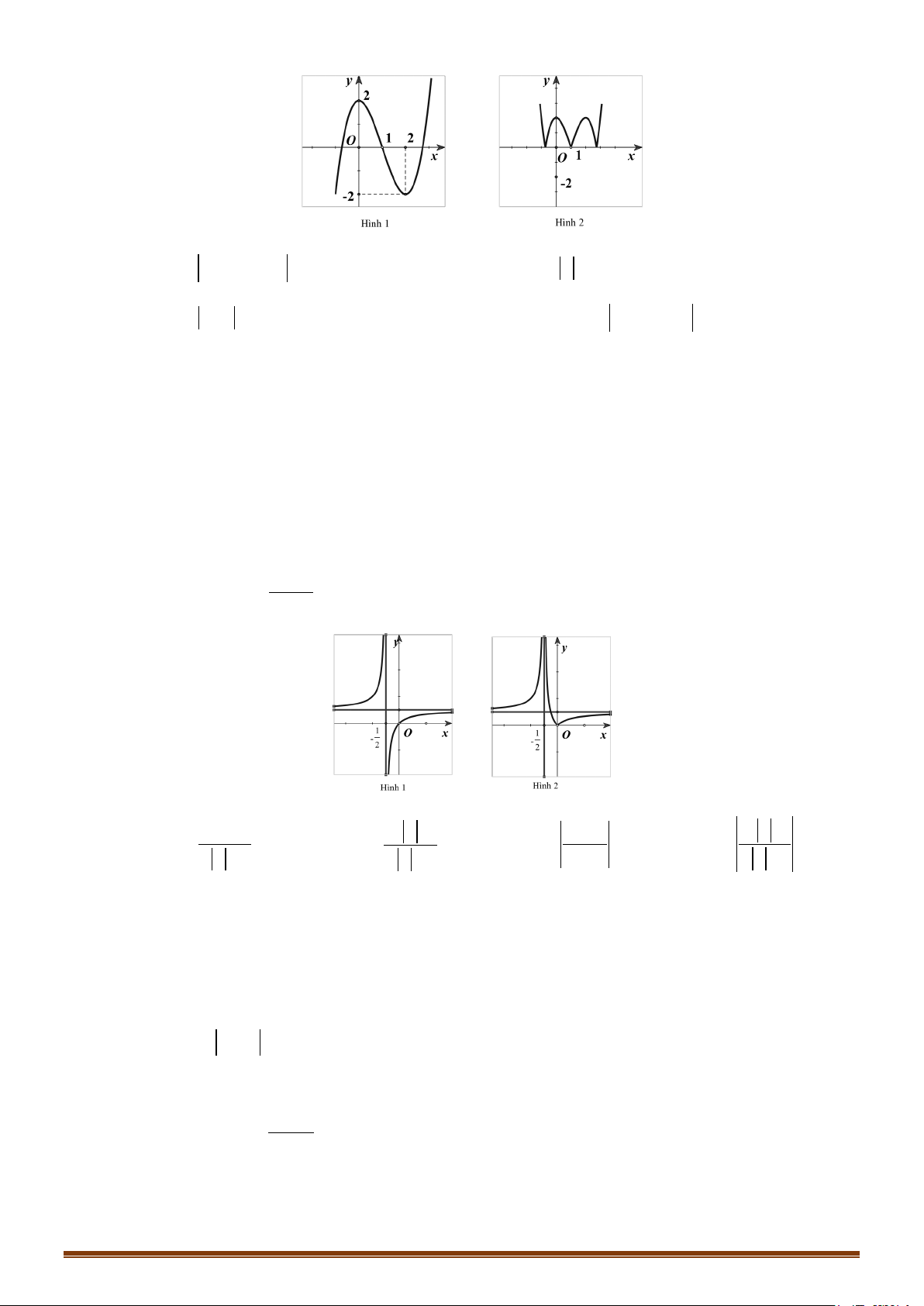
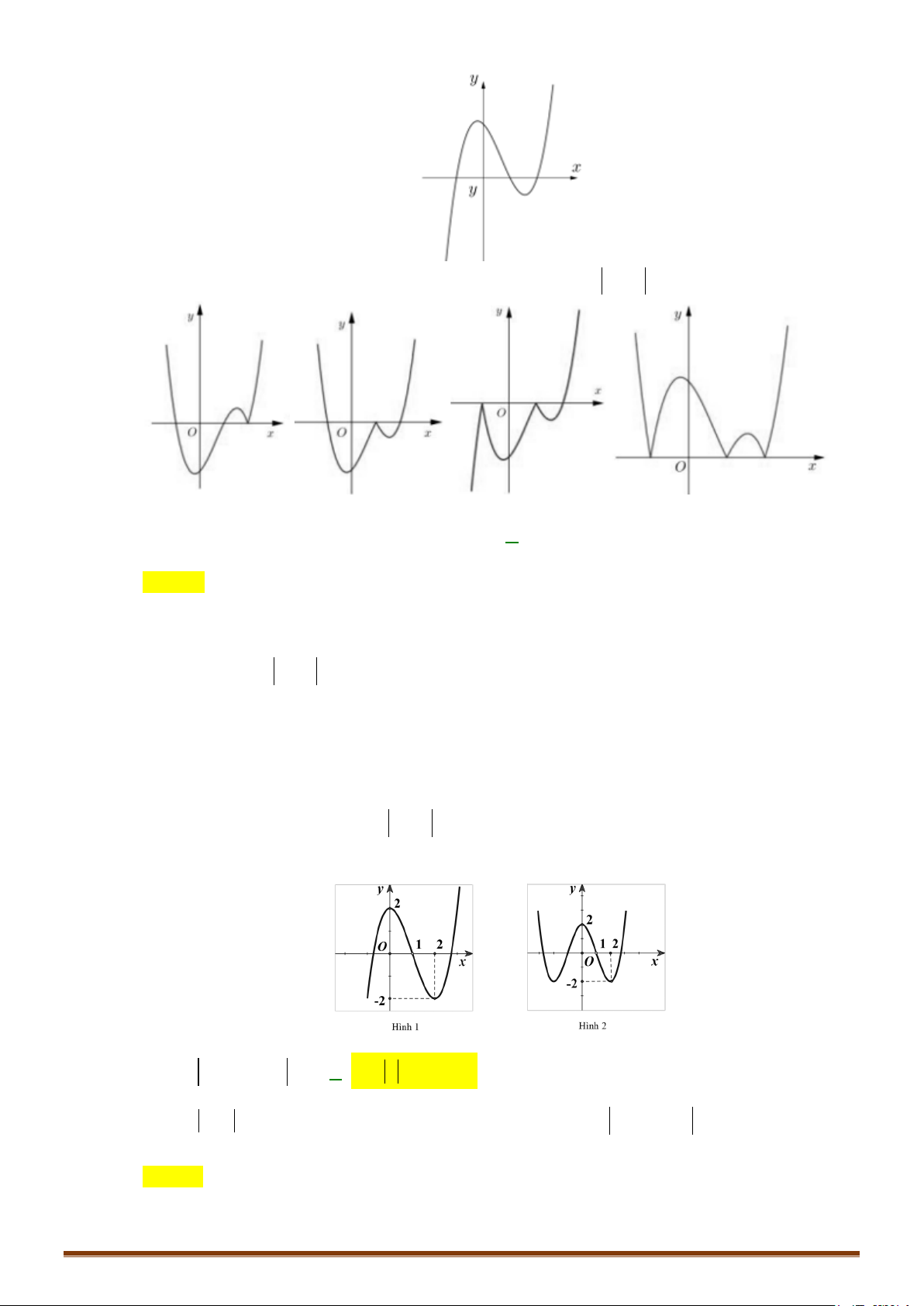
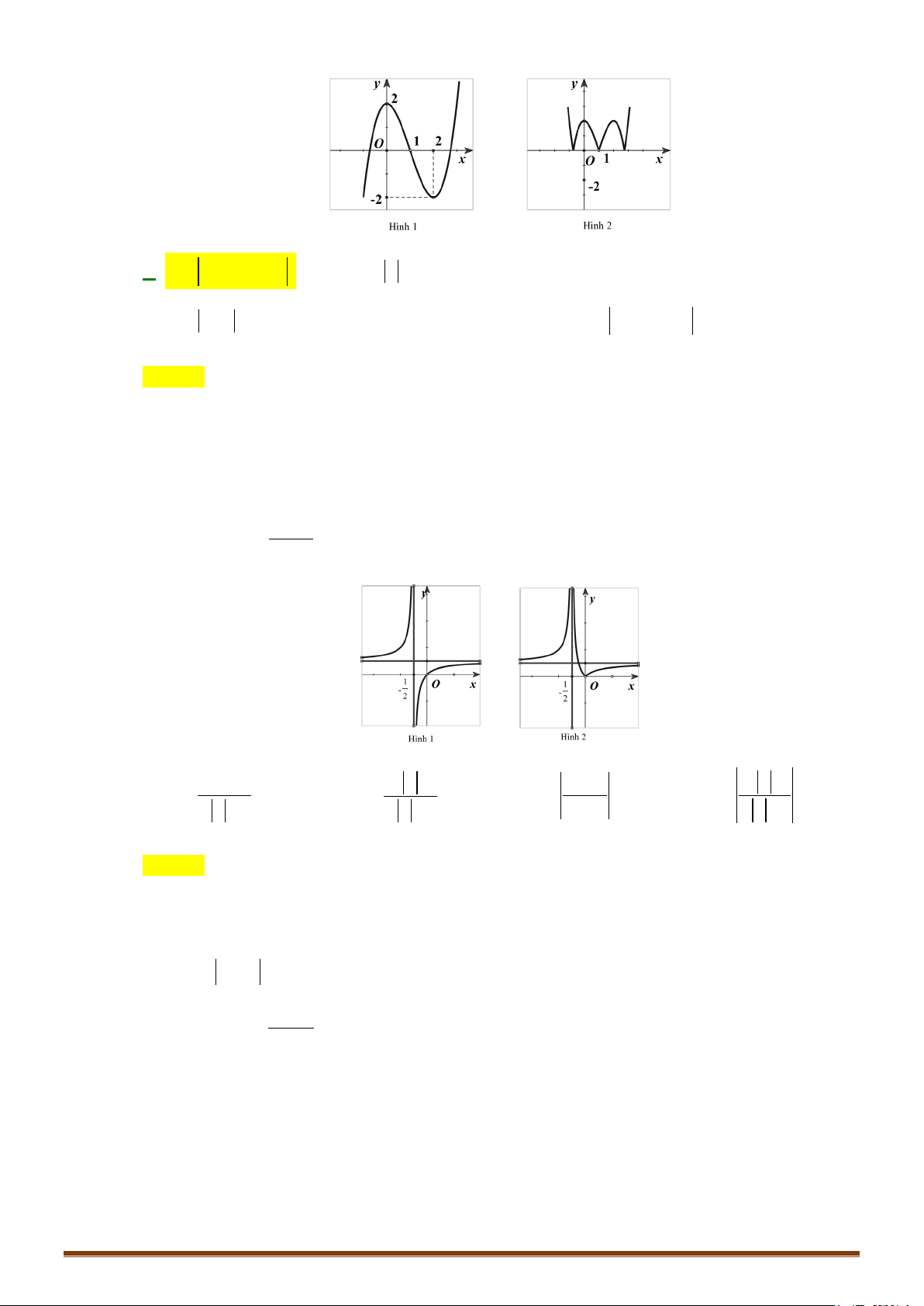
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 .
Câu 41: Cho hàm số y = f (x) có đồ thị hàm số y = f ( x ) như hình vẽ.
Chọn kết luận đúng trong các kết luận sau: A. f (x) 3 2
= −x + x + 4x − 4 B. f (x) 3 2
= x − x − 4x + 4 C. f (x) 3 2
= −x − x + 4x − 4 D. f (x) 3 2
= x + x − 4x − 4.
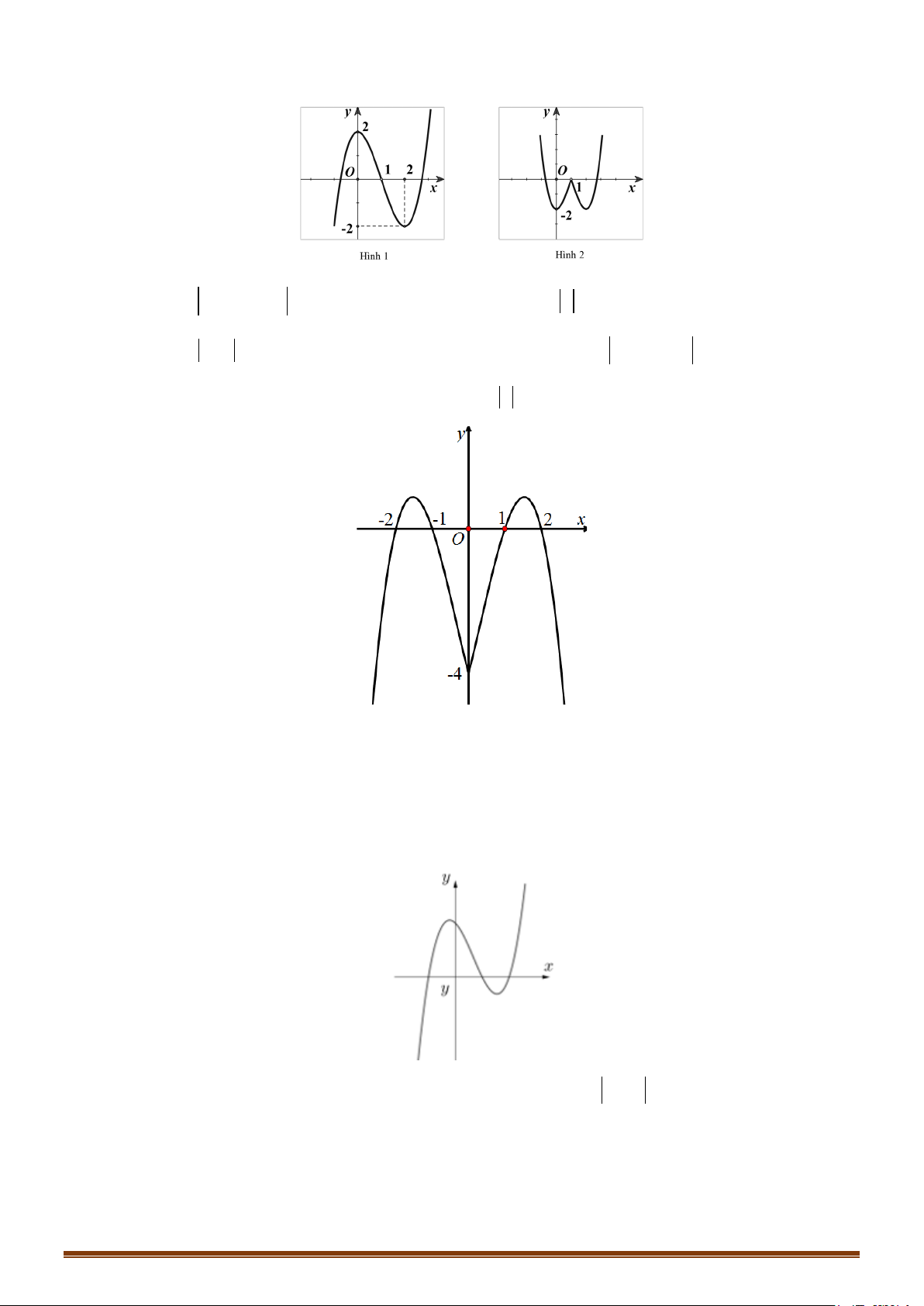
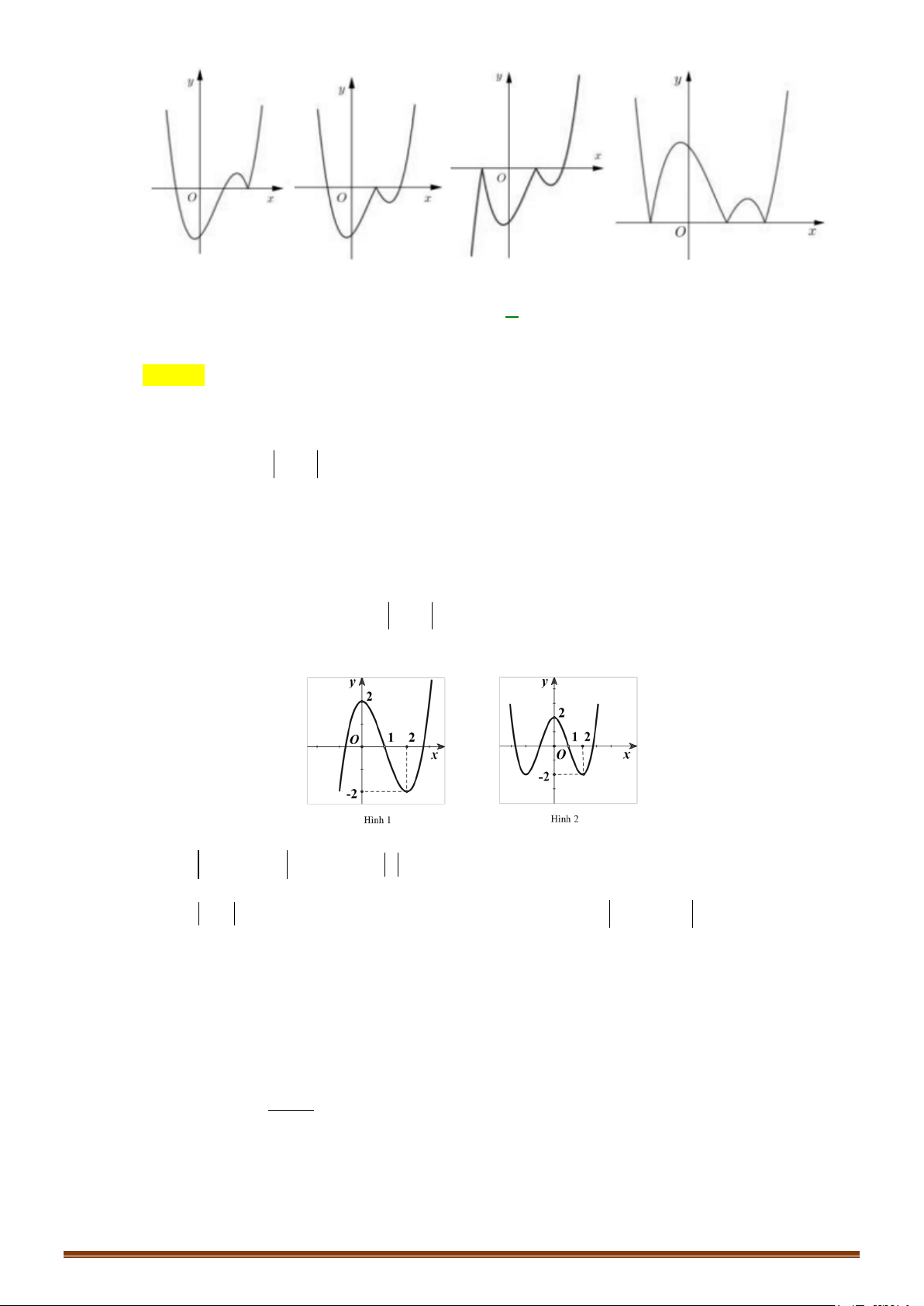
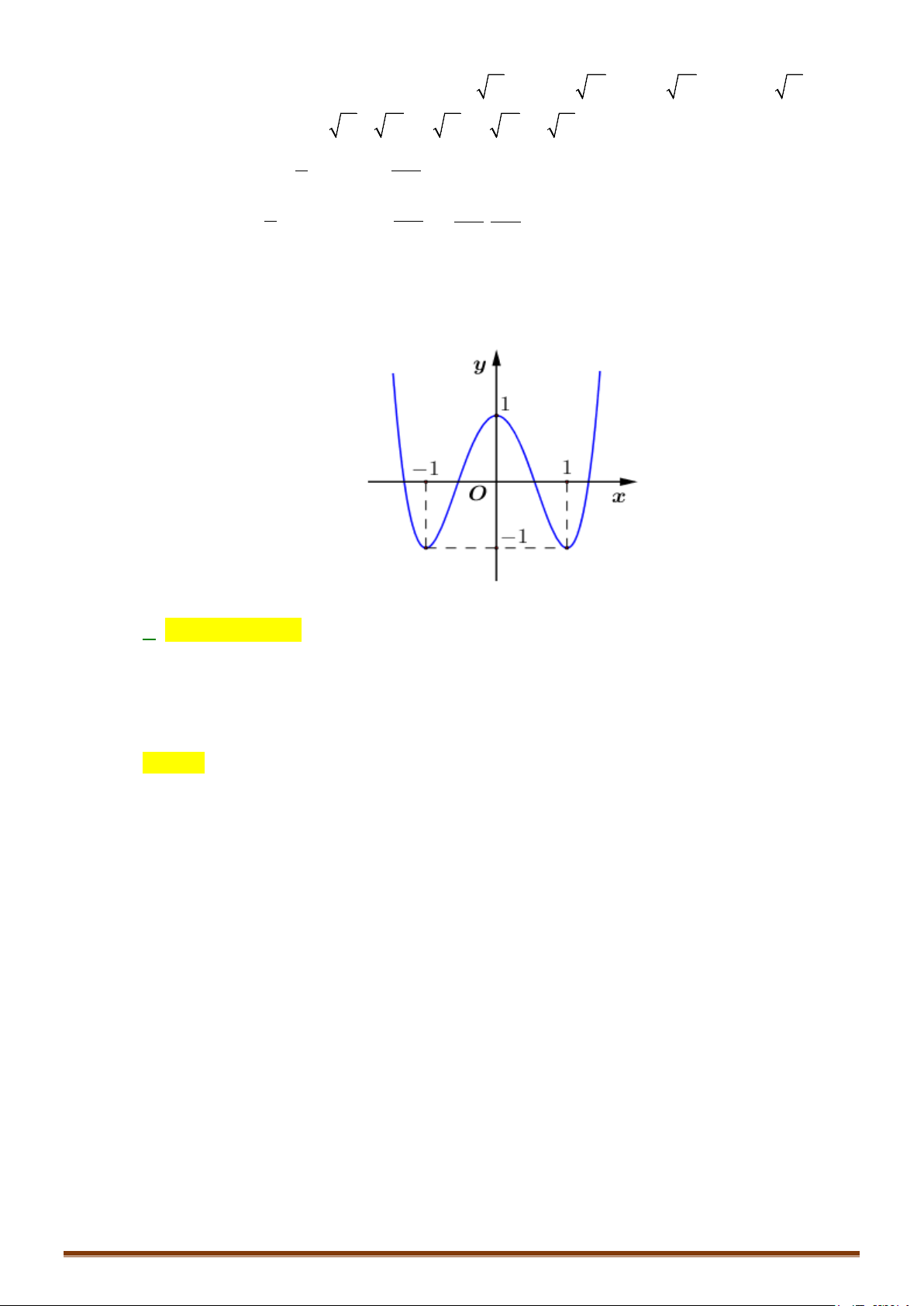
Câu 42: Cho hàm số y = (x − )( 2 2 x − )
1 có đồ thị như hình vẽ
Một trong bốn hình dưới đây là đồ thị của hàm số y = (x − ) 2
2 x −1 . Hỏi đó là hình nào? Page 240
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1. Câu 43: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
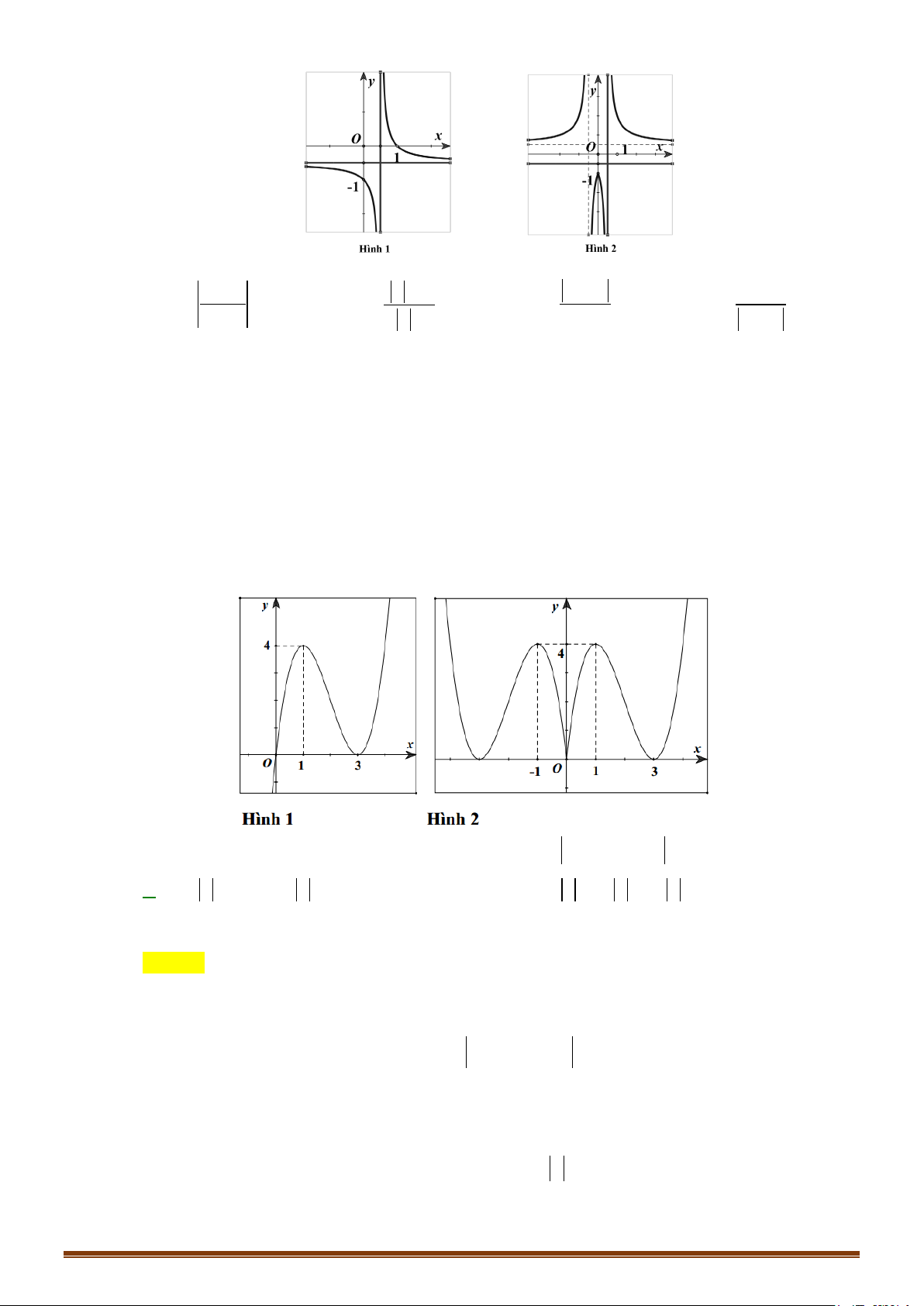
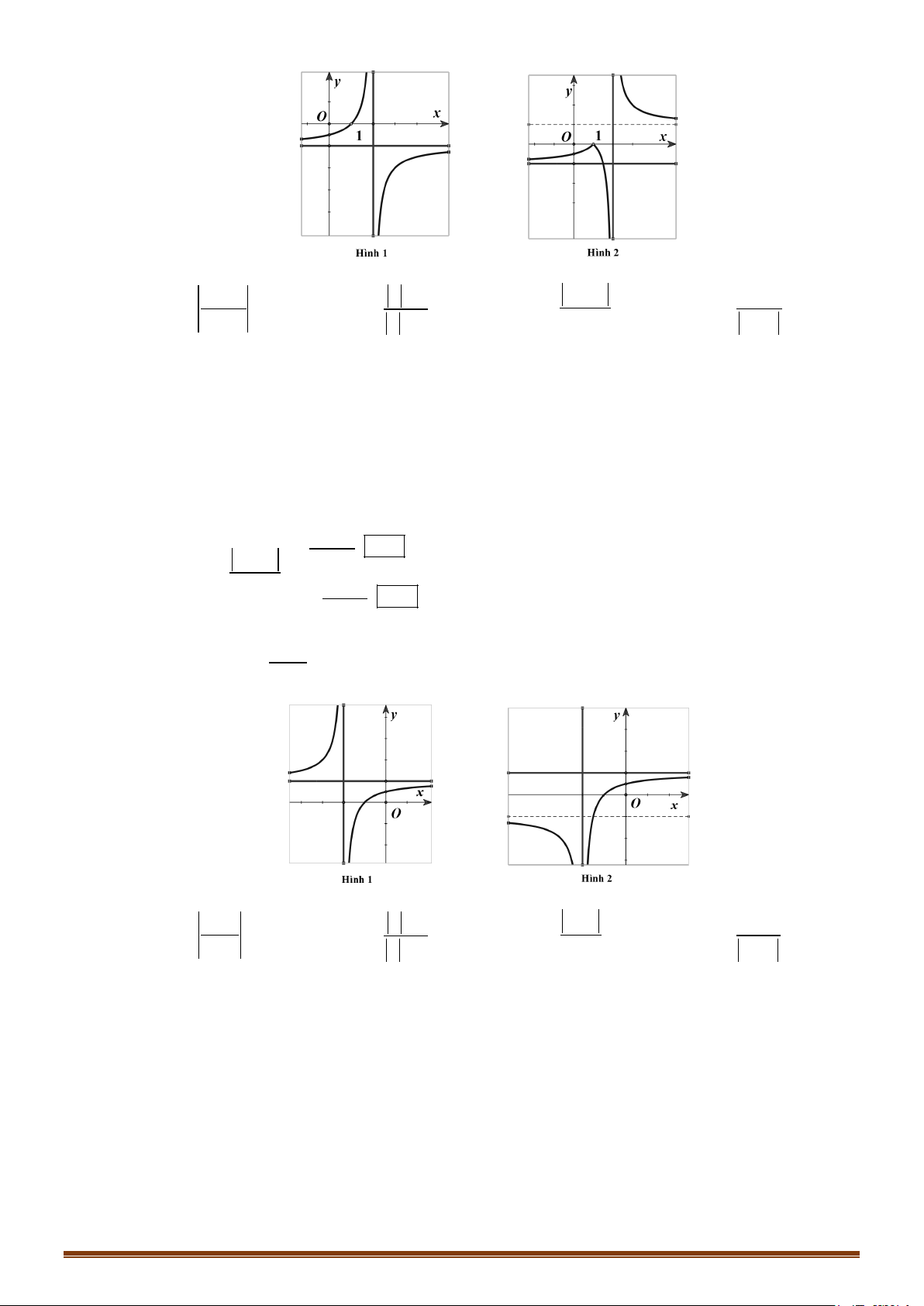
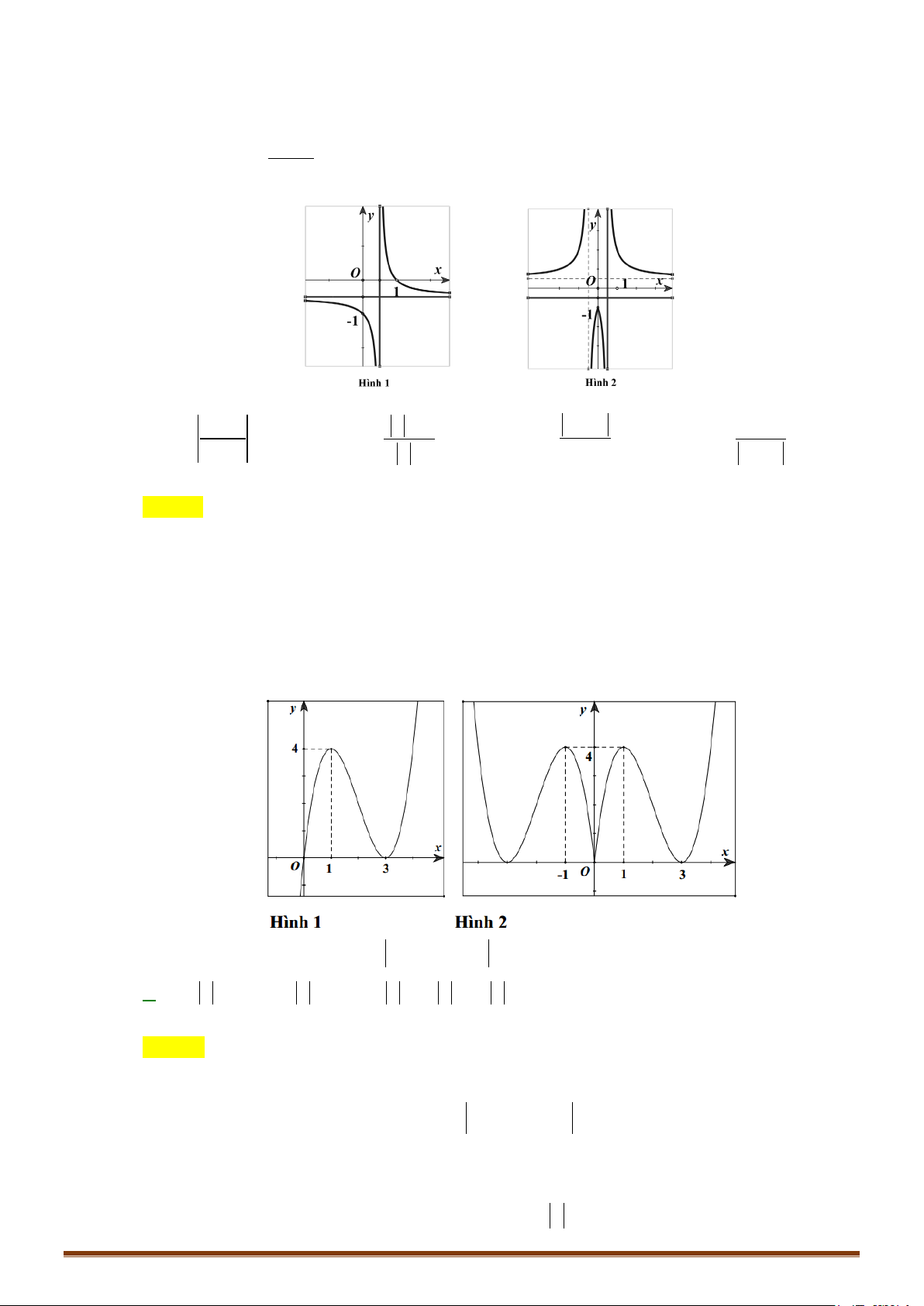
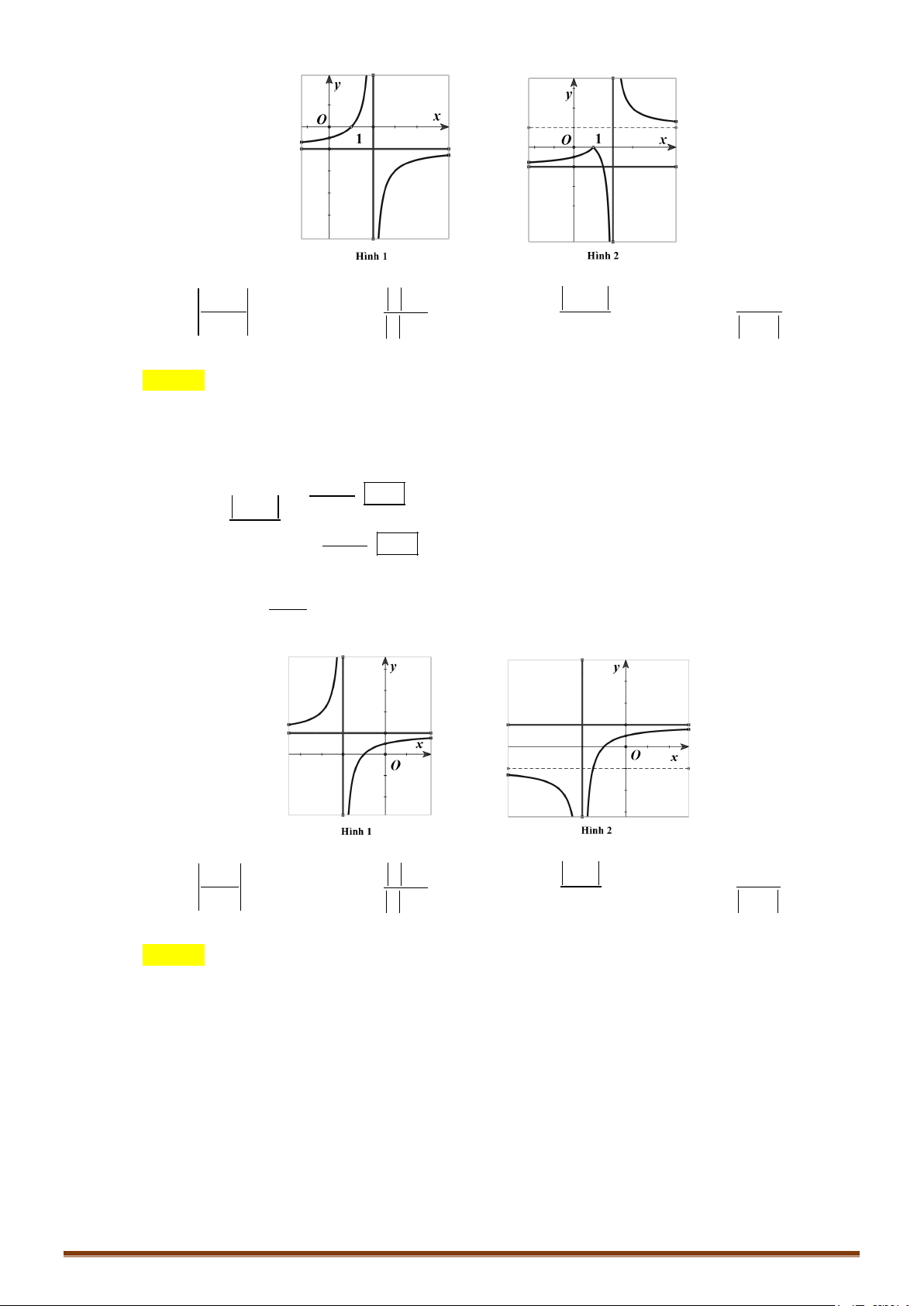
1 x − 2x − 2 . Câu 44: Cho hàm số −x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? 2x −1 − + x +1 −x +1 A. x 1 y − + = B. x y = C. y = D. 1 y = 2x −1 2 x −1 2x −1 2x −1 Page 241
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 45: Cho hàm số 3 2
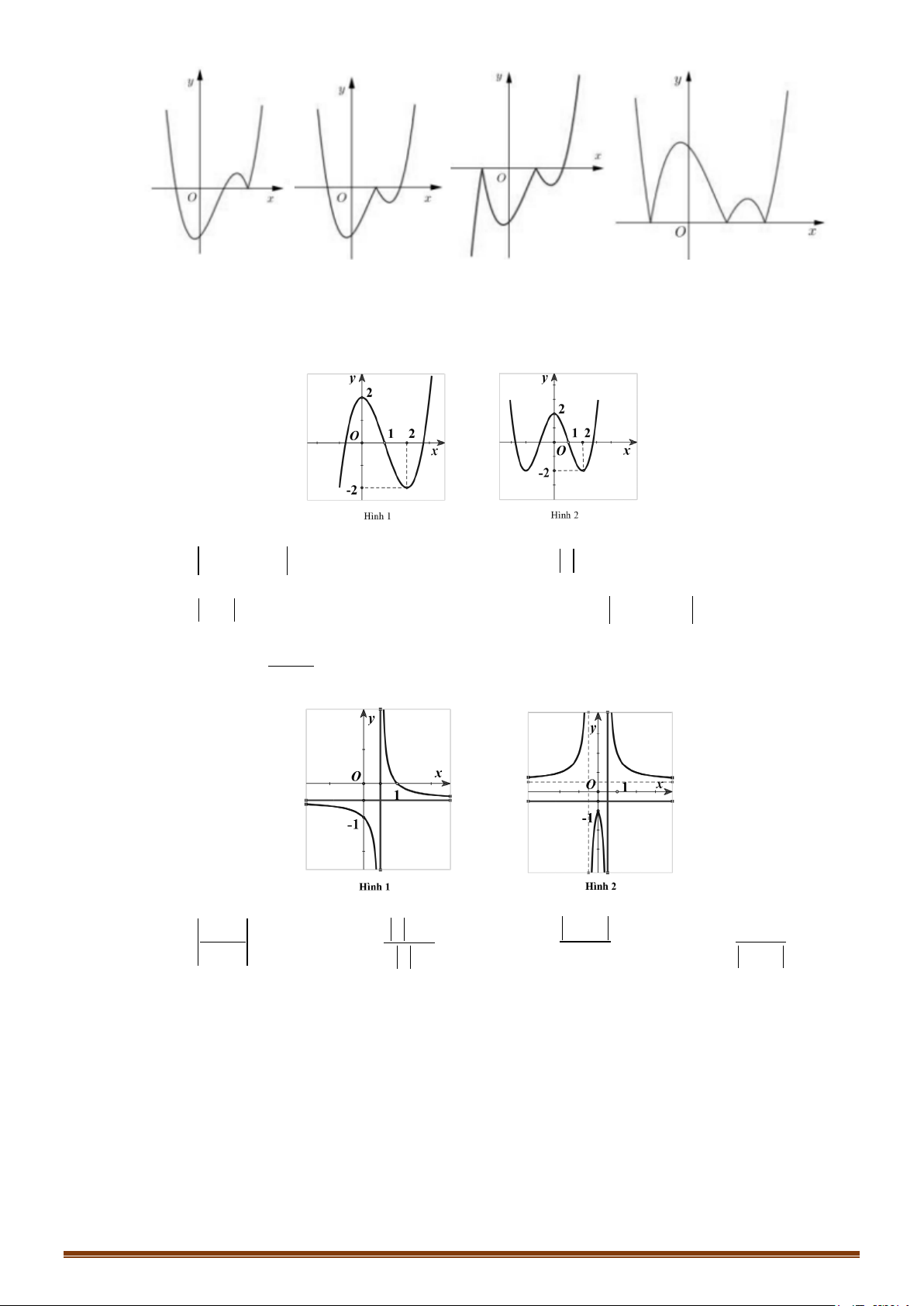
y = x − 6x + 9x có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào dưới đây? A. 3 2
y = −x + 6x − 9x . B. 3 2
y = x − 6x + 9x . C. 3 2
y = x − 6x + 9 x . D. 3 2
y = x + 6 x + 9 x . Câu 46: Cho hàm số x y
có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong các đáp 2x 1 án A, B, C, D dưới đây? x A. x y x x  . B. y C. y D. y 2x 1 2 x 1 2 x 1 2 x 1 Câu 47: Cho hàm số 3 2
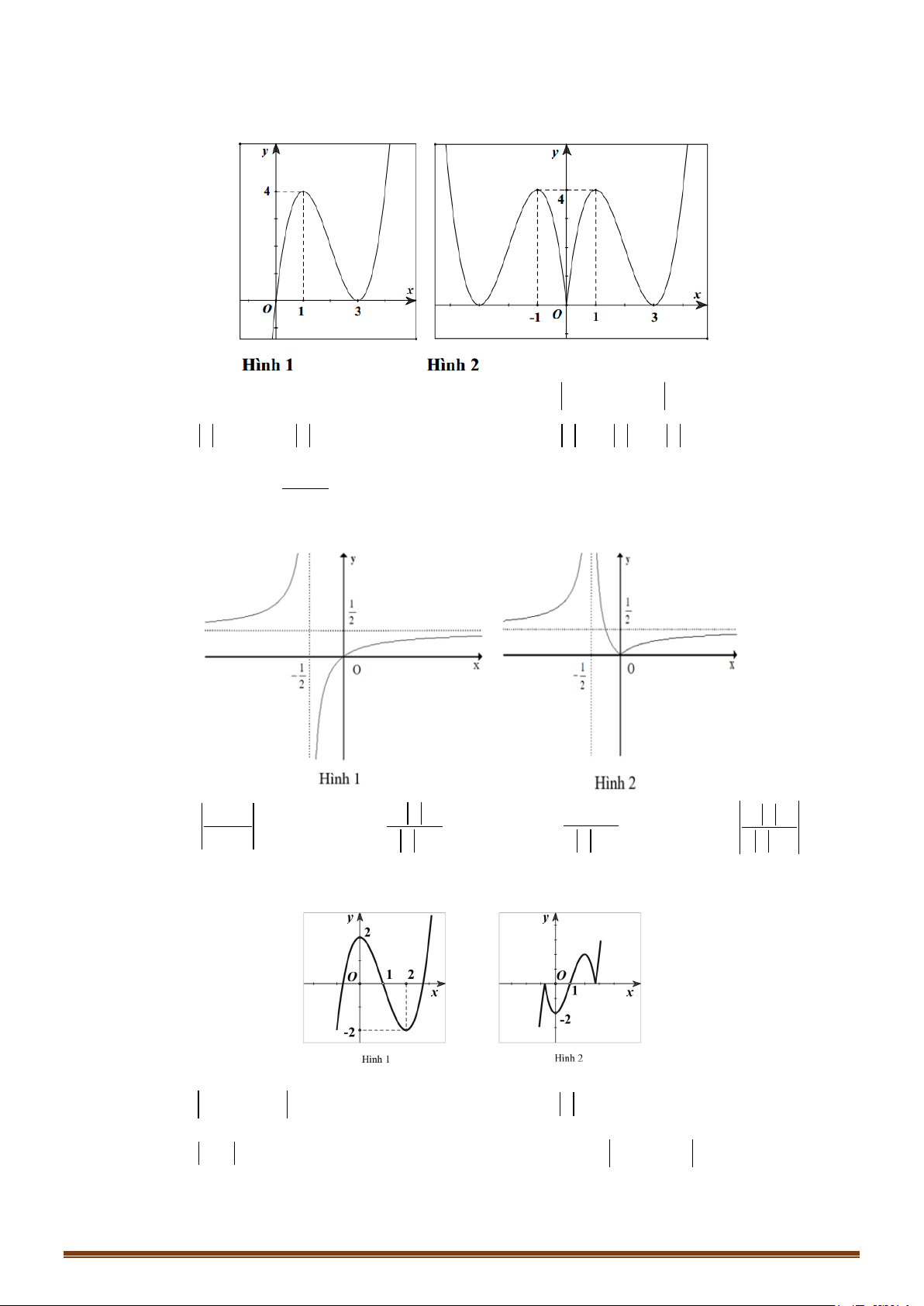
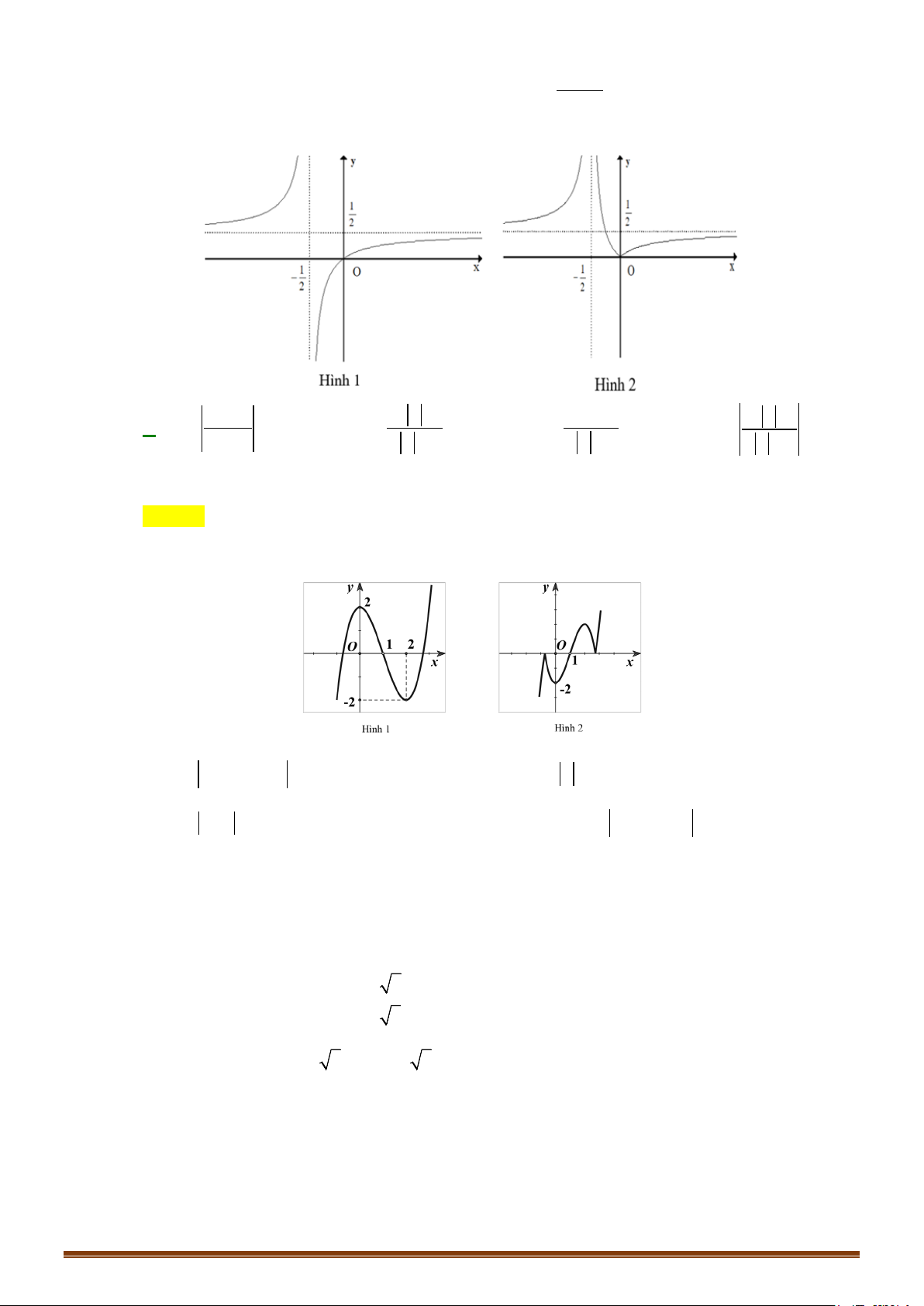
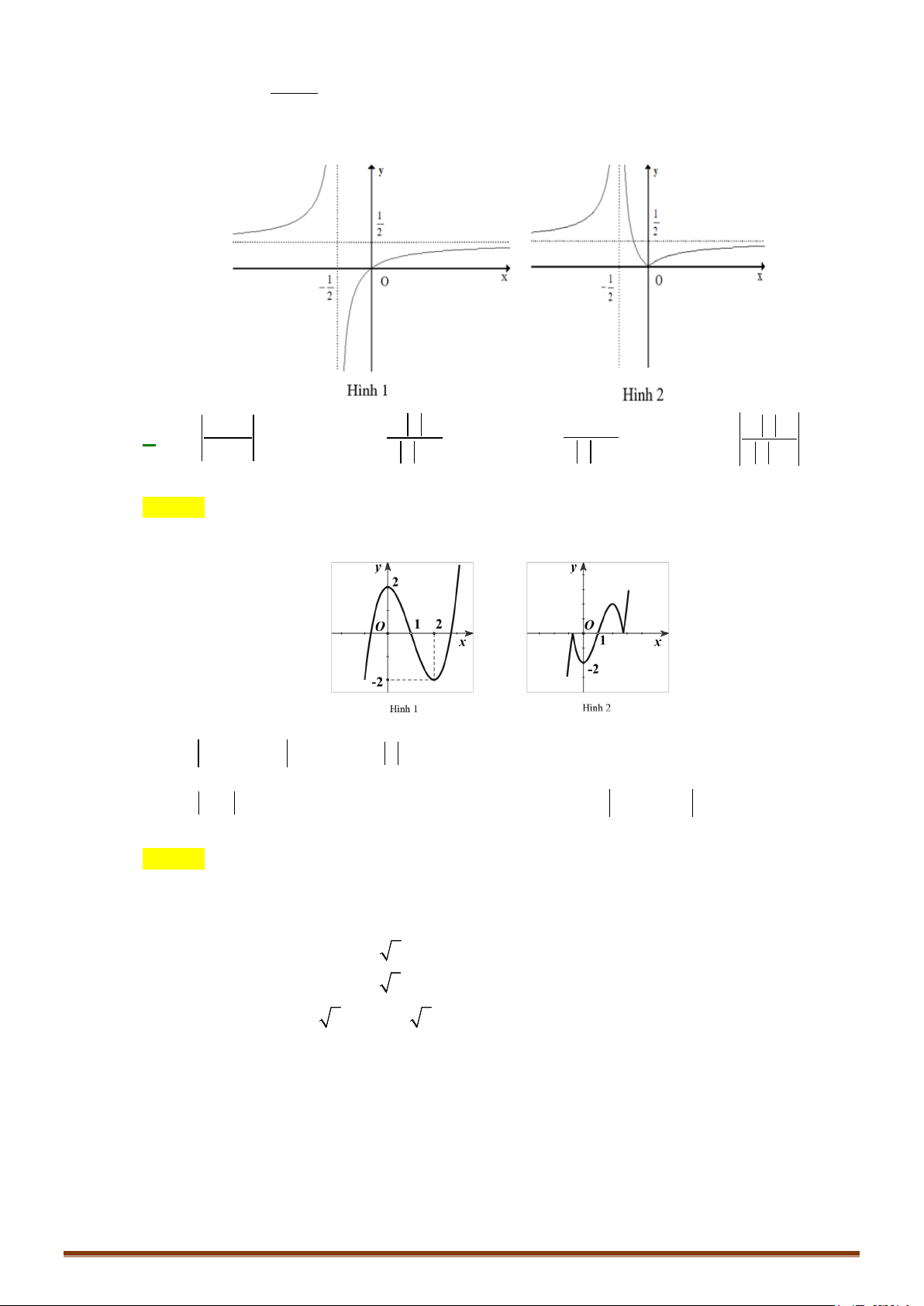
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Câu 48: Cho hàm số 3 2
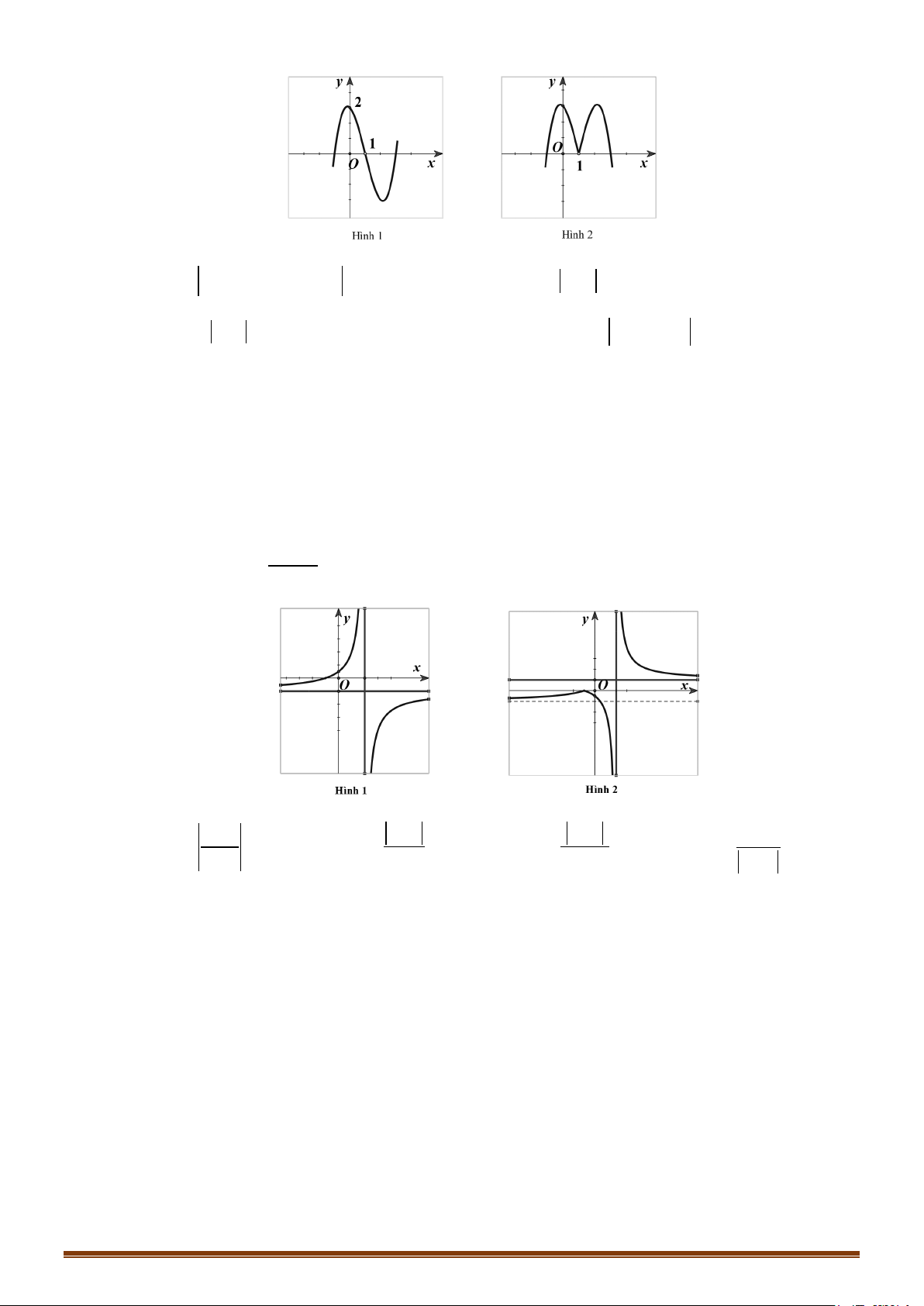
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? Page 242
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Câu 49: Cho hàm số x y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? 2x +1 x x A. x y x = B. y = C. y = D. y = 2 x +1 2 x +1 2x +1 2 x +1 Câu 50: Cho hàm số −x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? x − 2 − + x +1 −x +1 A. x 1 y − + = . B. x y = . C. y = D. 1 y = x − 2 x − 2 x − 2 x − 2 Page 243
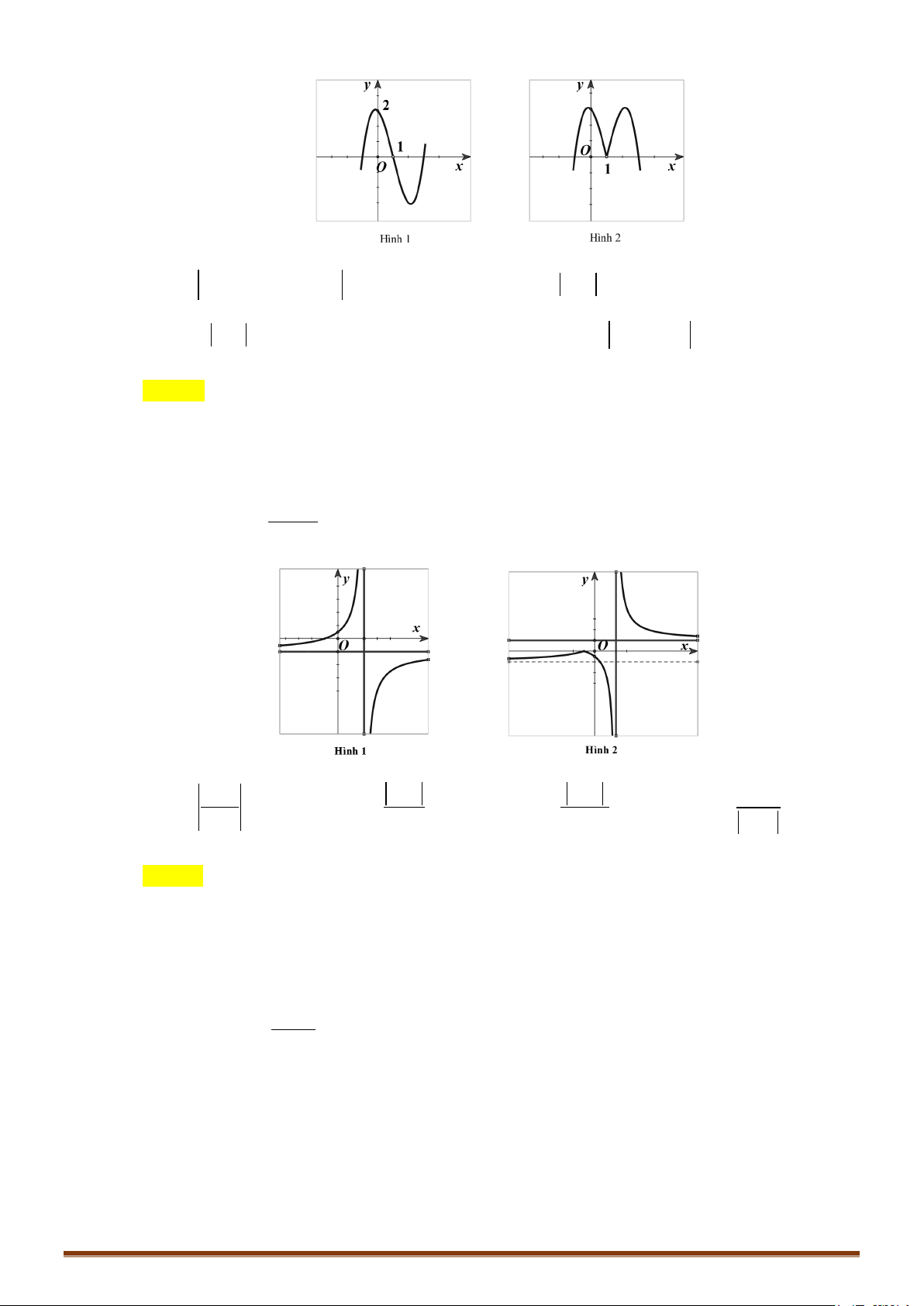
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 51: Cho hàm số x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? x + 2 + x +1 x +1 A. x 1 y + = . B. x y = . C. y = . D. 1 y = . x + 2 x + 2 x + 2 x + 2
Câu 52: Cho hàm số y = (x − )( 2
1 x − 2x − 3) có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A. y = (x − )( 2
1 x − 2x − 3) .
B. y = x − ( 2
1 x − 2x − 3).
C. y = − x − ( 2
1 x − 2x − 3)
D. y = (x − ) 2 1 x − 2x − 3 Page 244
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ G
ƠN I ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ HƯ C
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
III BÀI TẬP TRẮC NGHIỆM
DẠNG. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
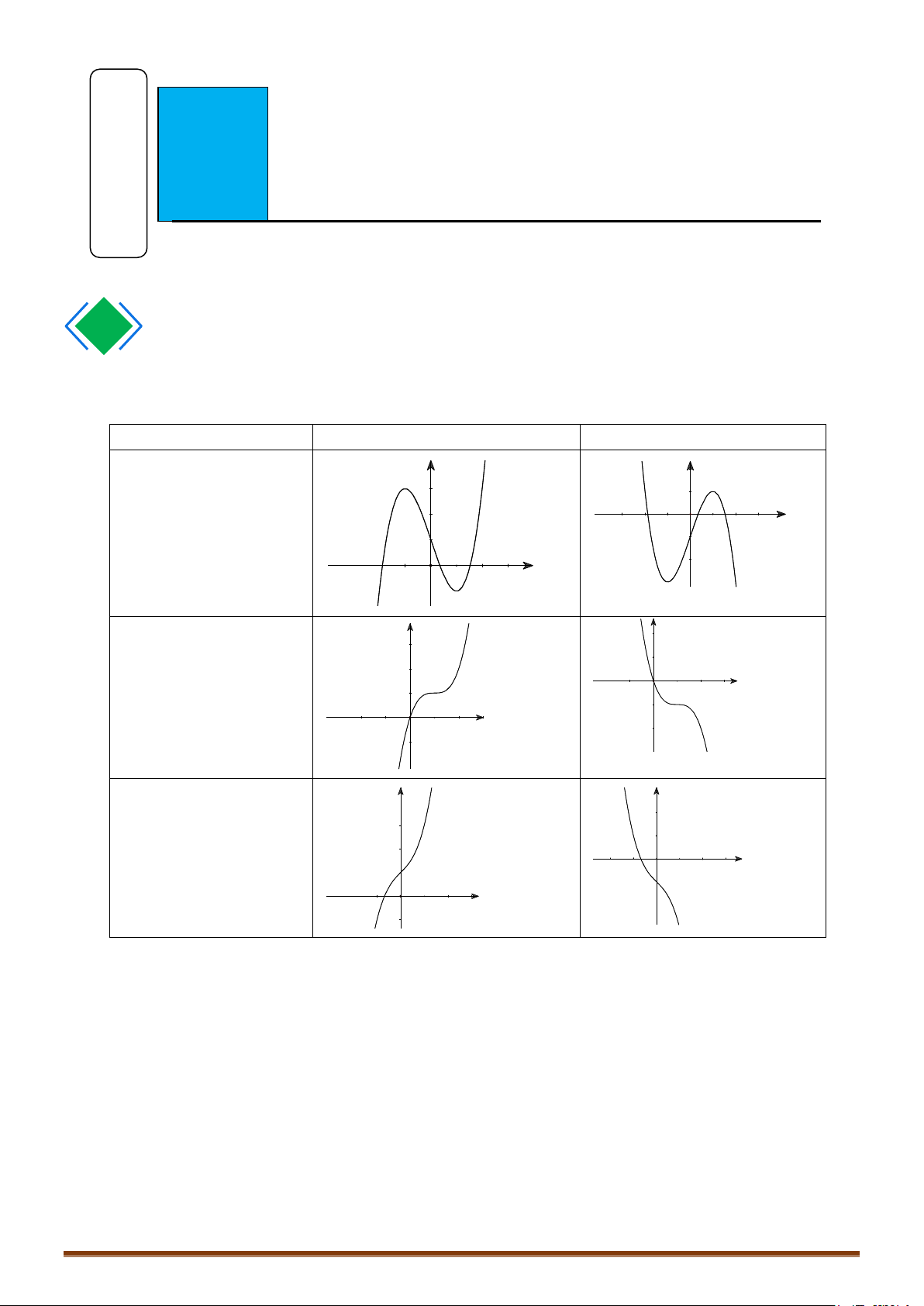
A. Hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0) TRƯỜNG HỢP a > 0 a < 0
Phương trình y/ = 0 có y y
2 nghiệm phân biệt 1 1 O x 1 1 O x Phương trình y y/ = 0 có y nghiệm kép 1 1 1 O x 1 O x Phương trình / y = 0 vô y y nghiệm 1 O 1 1 x 1 O x Page 137
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
B. Hàm số trùng phương y = ax4 + bx2 + c (a ≠ 0) TRƯỜNG HỢP a > 0 a < 0
Phương trình y/ = 0 y y có
3 nghiệm phân biệt (ab<0) 1 1 1 1 O x O x
Phương trình y/ = 0 y y có 1 nghiệm. 1 1 1 O x 1 O x
C. Hàm số nhất biến ax + b y =
(c ≠ 0, ad − bc ≠ 0) cx + d
D = ad − bc > 0
D = ad − bc < 0
Câu 1: (THPT Yên Phong 1 Bắc Ninh 2019) Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án ,
A B,C, D . Hỏi đó là hàm số nào? A. 3
y = x + 2x +1. B. 3 2
y = x − 2x +1. C. 3
y = x − 2x +1. D. 3
y = −x + 2x +1. Lời giải Page 138
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Dựa vào đồ thị, ta có lim y = +∞ , loại phương án D . x→+∞
Xét phương án A có 2
y′ = 3x + 2 > 0, x
∀ ∈  , hàm số không có cực tri, loại phương án A .
Xét phương án B có 2
y′ = 3x − 6x và y′ đổi dấu khi đi qua các điểm x = 0, x = 2 nên hàm số đạt
cực tri tại x = 0 và x = 2 , loại phương án B .
Vậy phương án đúng là C .
Câu 2: (Sở Cần Thơ - 2019) Hình vẽ bên dưới là đồ thị của hàm số nào A. x −1 y x + x − x + = . B. 2 1 y = . C. 2 3 y = . D. 2 5 y = . x +1 x +1 x +1 x +1 Lời giải Chọn B
Đồ thị hàm số cắt trục Oy tai điểm có tọa độ (0; )
1 nên chọn phương án B.
Câu 3: (SGD Nam Định) Đường cong trong hình là đồ thị của hàm số nào dưới đây? A. x −1 y − + = . B. 2x 1 y = . C. 4 2
y = x − 3x . D. 3 2
y = x − 3x . x +1 2x + 2 Lời giải Chọn A
Hình vẽ trên là đồ thị của hàm số dạng ax + b y =
(c ≠ 0;ad −bc ≠ 0) ⇒ Loại phương án C, D cx + d
Ta thấy: Đồ thị có đường tiệm cận đứng là x = 1
− và đường tiệm cận ngang là y =1
Phương án B: Đồ thị có đường tiệm cận đứng là x = 2 − ⇒ loại B Page 139
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ ⇒ A đúng.
Câu 4: (Sở Gia Lai 2019) Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây? A. 3
y  x 3x 1. B. 4 2
y x x 1. C. 2
y  x x1. D. 3
y x 3x 1. Lời giải Chọn D
Đồ thị đã cho có hình dạng của đồ thị hàm số bậc ba 3 2
y ax bx cx d nên loại phương án B và C
Dựa vào đồ thị, ta có lim y    a  0 nên loại phương án A x
DẠNG 2. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ Câu 5: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? Page 140
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. a < 0, b > 0, 0, c > d < 0 B. a < 0, b < 0, 0, c > d < 0. C. a > 0, b < 0, c < 0, d > 0 D. a < 0, b > 0, 0, c < d < 0. Lời giải Chọn A
Dựa vào đồ thị suy ra hệ số a < 0 ⇒ loại phương án C 2
y′ = 3ax + 2bx + c = 0 có 2 nghiệm x , x trái dấu (do hai điểm cực trị của đồ thị hàm số nằm 1 2
hai phía với Oy )⇒ 3 .
a c < 0 ⇒ c > 0 ⇒ loại phương án D. Do
(C)∩Oy = D(0;d) ⇒ d < 0.
Câu 6: (THPT Nguyễn Khuyến 2019) Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình bên. Mệnh đề
nào dưới đây là đúng?
A. a > 0,b < 0,c > 0
B. a > 0,b < 0,c < 0 C. a > 0,b > 0,c < 0 D. a < 0,b > 0,c < 0 Lời giải Chọn B
Ta có đồ thị có hình dạng như trên với hàm bậc bốn trùng phương có hai điểm cực tiểu và một
điểm cực đại nên a > 0,b < 0 . Giá trị cực đại nhỏ hơn 0 nên c < 0 .
Câu 7: (Chuyên Trần Phú Hải Phòng 2019) Cho hàm số ax + = b y có đồ thị như sau. cx + d
Mệnh đề nào sau đây đúng? A. ac > 0; 0 bd > B. ab < 0; 0 cd < C. bc > 0; 0 ad < D. ad > 0; 0 bd < Page 141
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Theo đồ thị: Tiệm cận ngang: a y = > 0 c ( ) 1 d d
Tiệm cận đứng: x = − > 0 ⇒ < 0 2 c c ( )
= 0 ⇒ = − b < 0 ⇒ b y x > 0 3 a a ( )
Câu 8: (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số 3 2
y = ax + bx + cx + d (a ≠ 0) có đồ thị như
hình vẽ dưới đây. Chọn khẳng định đúng về dấu của a , b , c , d ?
A. a > 0 ,b > 0, d > 0 , c > 0
B. a > 0 , c > 0 > b , d < 0
C. a > 0, b > 0, c > 0, d > 0.
D. a > 0 , b < 0 , c < 0 , d > 0 Lời giải Chọn D
Dựa vào đồ thị ta có a > 0 , đồ thị cắt Oy tại 1 điểm có tung độ dương nên d > 0 , đồ thị có 2
cực trị trái dấu nên . < 0 c x x
⇒ < 0 ⇒ c < 0 . Vậy đáp án D 1 2 aa  1 x b
Câu 9: (Toán Học Tuổi Trẻ 2019) Cho hàm số y
, d  0 có đồ thị như hình trên. Khẳng c  1 x d
định nào dưới đây là đúng?
A. a 1,b  0,c 1. B. a 1,b  0,c 1. C. a 1,b  0,c 1. D. a 1,b  0,c 1. Lời giải Page 142
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Theo bài ra, đường tiệm cận đứng của đồ thị hàm số là d x   . c1
Đường tiệm cận ngang của đồ thị hàm số là: a1 y  . c1 Nhìn đồ thị ta thấy: d x  
 0 mà d  0  c1 0  c 1. c1 a1 y
 0  a 1 0  a 1. c1
Đồ thị cắt trục tung tại điểm có tung độ bằng b  0  b  0. d
Câu 10: (Sở Ninh Bình 2019) Cho hàm số 4 2
y = ax + bx + c ( a ≠ 0) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A. a < 0 , b > 0, c < 0 . B. a < 0 , b < 0 , c > 0 . C. a < 0 , b > 0, c > 0 . D. a < 0 , b < 0 , c < 0 . Lời giải
Đồ thị cắt trục tung tại điểm (0;c), từ đồ thị suy ra c < 0
Mặt khác đồ thị hàm số có ba điểm cực trị nên y′ = 0 có ba nghiệm phân biệt, hay 3
y′ = ax + bx = x( 2 4 2
2 2ax + b) = 0 có ba nghiệm phân biệt. Suy ra a,b trái dấu.
Mà a < 0 ⇒ b > 0
Câu 11: (Cụm Liên Trường Hải Phòng 2019) Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A. a  0, b  0 , c  0, d  0 .
B. a  0 , b  0 , c  0, d  0 .
C. a  0, b  0 , c  0, d  0 .
D. a  0 , b  0 , c  0, d  0 . Lời giải Page 143
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
+ Dựa vào hình dạng đồ thị ta khẳng định được a  0 .
+ Đồ thị cắt trục Oy tại điểm có tọa độ 0;d. Dựa vào đồ thị suy ra d  0 . + Ta có: 2
y  3ax  2bx c . Hàm số có hai điểm cực trị x x 1 , 2 x x trái dấu nên phương 1 2 
trình y  0 có hai nghiệm phân biệt x x
1 , 2 trái dấu. Vì thế 3 .
a c  0 , nên suy ra c  0. x 1
+ Mặt khác từ đồ thị ta thấy  1 
nên x x  0. x 1 1 2  2 Mà 2b xbx
nên suy ra 2  0  b  0 . 1 2 3a 3a
Vậy a  0 , b  0 , c  0, d  0 .
Câu 12: (THPT Ba Đình 2019) Cho hàm số ax + b y =
có đồ thị như hình bên dưới, với a , b , c∈ . x + c
Tính giá trị của biểu thức T = a + 2b + 3c ? A. T = 8 − . B. T = 2. C. T = 6 . D. T = 0 . Lời giải
Từ đồ thị hàm số, ta suy ra
 Đồ thị hàm số có tiệm cận đứng là đường thẳng x =1, tiệm cận ngang là đường thẳng y = 1 − .
 Đồ thị hàm số đi qua các điểm A(2;0) , B(0; 2 − ) . Từ biểu thức hàm số ax + b y =
(vì đồ thị hàm số là đồ thị hàm nhất biến nên ac − b ≠ 0 ), ta x + c suy ra
 Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −c , tiệm cận ngang là đường thẳng y = a .
 Đồ thị hàm số đi qua  b A ;0 −    , 0; b B . a      c
Đối chiếu lại, ta suy ra c = 1 − , a = 1 − , b = 2 .
Vậy T = a + 2b + 3c = (− ) 1 + 2.2 + 3(− ) 1 = 0. Page 144
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 13: (THPT Việt Đức Hà Nội 2019) Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình bên.
Trong các mệnh đề sau mệnh đề nào đúng?
A. ab < 0,bc > 0,cd < 0
B. ab < 0,bc < 0,cd > 0
C. ab > 0,bc > 0,cd < 0
D. ab > 0,bc > 0,cd > 0 Lời giải Chọn A
Từ dáng điệu của đồ thị ta có ngay được: ⊕ lim y = ;
+∞ lim y = −∞ ⇒ a > 0 . x→+∞ x→−∞
⊕ Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên d > 0 . Ta có: 2
y ' = 3ax + 2bx + c
Mặt khác dựa vào đồ thị ta thấy phương trình y ' = 0 có hai nghiệm trái dấu và tổng hai nghiệm ac < 0  c < 0
này luôn dương nên  2b ⇒ (do a > 0 ) − > b    < 0  3a
Do đó: ab < 0,bc , > cd < 0 .
Câu 14: (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình
dưới. Khẳng định nào sau đây đúng ?
A. a < 0,b < 0,c < 0,d < 0
B. a < 0,b > 0,c > 0,d > 0
C. a < 0,b > 0,c < 0,d > 0
D. a < 0,b > 0,c > 0,d < 0 Lời giải Chọn D
- Dựa vào hình dáng của đồ thị suy ra hệ số a < 0 .
- Đồ thị cắt trục Oy tại điểm có tung độ âm nên d < 0 .
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương trình 2
y′ = 3ax + 2bx + c = 0 có 2 nghiệm x , x
a c < ⇒ c > 1 2 trái dấu kéo theo 3 . 0 0 . Page 145
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x + x b - Mặt khác 1 2 = − > 0 ⇒ b > 0. 2 3a
Câu 15: (THPT Chuyên Bắc Ninh 2019) Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ?
A. a > 0,b < 0,c < 0 .
B. a < 0,b < 0,c < 0 .
C. a < 0,b > 0,c < 0 .
D. a > 0,b < 0,c > 0 Lời giải Chọn C
- Dựa vào hình dạng đồ thị suy ra a < 0
- Hàm số có 3 điểm cực trị nên ab < 0 ⇒ b > 0
- Giao điểm với trục tung nằm dưới trục hoành nên c < 0 .
Câu 16: (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số ax + b y =
có đồ thị như trong hình bên cx + d
dưới. Biết rằng a là số thực dương, hỏi trong các số ,
b c,d có tất cả bao nhiêu số dương? A. 1. B. 2 . C. 0 . D. 3. Lời giải Chọn B
Nhìn vào đồ thị ta thấy Page 146
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ a
• tiệm cận ngang y = nằm trên trục hoành nên c > 0 (vì a > 0 ) c − − • tiệm cận đứng d x =
nằm bên trái trục tung nên d < 0. Suy ra d > 0 (vì c > 0 ) c c
• giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên b < 0. d
Suy ra b < 0 (vì d > 0 )
Vậy c > 0,d > 0
Câu 17: (Cụm liên trường Hải Phòng 2019) Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A. a  0, b  0 , c  0, d  0 .
B. a  0 , b  0 , c  0, d  0 .
C. a  0, b  0 , c  0, d  0 .
D. a  0 , b  0 , c  0, d  0 . Lời giải Chọn D
+ Dựa vào hình dạng đồ thị ta khẳng định được a  0 .
+ Đồ thị cắt trục Oy tại điểm có tọa độ 0;d. Dựa vào đồ thị suy ra d  0 . + Ta có: 2
y  3ax  2bx c . Hàm số có hai điểm cực trị x x 1 , 2 x x 1
2  trái dấu nên phương
trình y  0 có hai nghiệm phân biệt x x
1 , 2 trái dấu. Vì thế 3 .
a c  0 , nên suy ra c  0. x 1
+ Mặt khác từ đồ thị ta thấy  1 
nên x x  0. x 1 1 2  2 Mà 2b xbx
nên suy ra 2  0  b  0 . 1 2 3a 3a
Vậy a  0 , b  0 , c  0, d  0 .
Câu 18: (Chuyên Nguyễn Huệ 2019) Cho hàm số ax + b y =
có đồ thị như hình vẽ bên. Khẳng định cx + d
nào sau đây là khẳng định đúng? Page 147
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ ad < 0 ad < 0 ad > 0 ad > 0 A.  . B.  . C.  . D.  . bc > 0 bc < 0 bc < 0 bc > 0 Lời giải Chọn C
Nhận xét từ đồ thị:
+ Giao với trục hoành tại b x = − > ⇒ o 0
a và b trái dấu (1). a
+ Giao với trục tung tại b
y = < ⇒ b và o 0
d trái dấu (2). d + Tiệm cận đứng: d
x = − < 0 ⇒ d và c cùng dấu (3). c
Từ (1) và (2) suy ra: a và d cùng dấu hay ad > 0 .
Từ (2) và (3) suy ra: b và c trái dấu hay bc < 0 .
Câu 19: Cho đường cong (C) 3 2
: y = ax + bx + cx + d có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A. a > 0,b < 0,c < 0,d < 0.
B. a > 0,b > 0,c < 0,d > 0 .
C. a < 0,b > 0,c > 0,d < 0.
D. a > 0,b > 0,c < 0,d < 0. Lời giải Chọn D Page 148
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Từ đồ thị ta có x = 0 ⇒ y = d < 0, từ dạng đồ thị suy ra a > 0 . Mặt khác 2
y ' = 3ax + 2bx + c từ đồ thị ta có phương trình y ' = 0 có hai nghiệm trái dấu suy ra
ac < 0 mà a > 0 suy ra c < 0 .
Hơn nữa phương trình y ' = 0 có hai nghiệm phân biệt 2b x + x = − = 1 − suy ra 1 2 3a
3a = 2b ⇒ b > 0 .
Vậy chọn đáp án D.
Câu 20: (Gia Lai 2019) Hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a  0, b  0 , c  0.
B. a  0, b  0 , c  0.
C. a  0, b  0 , c  0.
D. a  0, b  0 , c  0. Lời giải Chọn C Dựa vào đồ thị:
+ lim y    a  0 . x
+ Đồ thị hàm số có ba điểm cực trị ab  0  b  0 .
+ Giao điểm của đồ thị hàm số và trục tung có tung độ dương c  0 .
Vậy a  0, b  0 , c  0.
Câu 21: (THPT Thăng Long 2019) Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ. Tìm kết luận đúng
A. a b  0 .
B. bc  0 .
C. ab  0 .
D. ac  0. Lời giải Chọn B Từ hình vẽ ta thấy:
Đồ thị hàm số có bề lõm hướng lên  a  0 .
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm  c  0 .
Đồ thị hàm số có 3 điểm cực trị  ab  0  b  0.
Vậy chỉ có bc  0 . Page 149
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 22: (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số 4 2
y ax bx c(a  0) có đồ thị như hình
bên. Hãy chọn mệnh đề đúng.
A. a  0,b  0,c  0 . B. a  0,b  0,c  0 .
C. a  0,b  0,c  0 . D. a  0,b  0,c  0. Lời giải Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy : Hệ số a  0
Đồ thị hàm số đi qua gốc tọa tọa  c  0
Hàm số có 3 điểm cực trị  .
a b  0  b  0
Câu 23: (Chuyên Long An 2019) Cho hàm số 3 2
y = f (x) = ax + bx + cx + d có đồ thị như hình vẽ ở bên.
Mệnh đề nào sau đây đúng?
A. a > 0 , b > 0, c > 0 , d > 0 .
B. a > 0 , b > 0, c < 0 , d > 0 .
C. a > 0 , b < 0 , c > 0 , d > 0 .
D. a < 0 , b < 0 , c > 0 , d < 0 . Lời giải Chọn C
Đồ thị hàm số đi qua các điểm (
A 0;1) , B(1;5) và C(3;1) và đạt cực trị tại các điểm B và C . ′ 2
f (x) = 3ax + 2bx + c . Ta có  f (0) =1 d =1 a =1   f (1) 5  a b c d 5 b  = + + + =  = 6 −  ⇒  ⇒ . f ′(1) 0 3a 2b c 0  = + + = c = 9   
 f ′(3) = 0 27a + 6b + c = 0 d =1
Câu 24: (THPT Trần Phú 2019) Cho hàm số bậc bốn trùng phương 4 2
y ax bx c có đồ thị như
hình vẽ bên. Mệnh đề nào dưới đây là đúng? Page 150
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a  0,b  0,c  0.
B. a  0,b  0,c  0.
C. a  0,b  0,c  0 .
D. a  0,b  0,c  0. Lời giải Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy : Hệ số a  0 .
Hàm số có 3 điểm cực trị  .
a b  0  b  0.
Đồ thị hàm số đi qua gốc tọa tọa  c  0 .
Vậy a  0,b  0,c  0 .
Câu 25: (THPT Cộng Hiền 2019) Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Hỏi khẳng
định nào sau đây đúng?
A. a > 0,b < 0,c < 0 . B. a > 0,b > 0,c < 0 . C. a > 0,b < 0,c > 0. D. a < 0,b > 0,c < 0 . Lời giải Chọn A
Nhìn vào đồ thị ta có:
Khi x∈ (2;+ ∞) hàm số đồng biến ⇒a > 0 .
Hàm số có 3 điểm cực trị nên a.b < 0 mà a > 0⇒b < 0 . y(0) = 1
− = c ⇒ c < 0 .
Câu 26: (SGD Điện Biên - 2019) Cho hàm số ax + 3 y =
có đồ thị như hình vẽ bên. Tính giá trị của x + c a − 2 . c Page 151
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a − 2c = 3.
B. a − 2c = 3. −
C. a − 2c = 1. −
D. a − 2c = 2. − Lời giải Chọn A
Đồ thị hàm số có TCN = 1 a y − ⇔ = 1 − ⇔ a = 1. − 1
Mặt khác Đồ thị hàm số có TCĐ x = 2 nên 2 + c = 0 ⇔ c = 2. − ⇒ a − 2c = 1 − − 2.( 2 − ) = 3.
Dựa vào đồ thị ta thấy các điểm (3;0) và  3 0;  − 
thuộc vào đồ thị hàm số đã cho nên ta được 2     .3 a + 3 0 =  3  a + 3 = 0 a = 1 − hệ phương trình  3+ c  ⇔ ⇔ 3 .0 a + 3    − =  = − − = 3c 6 c 2  2 0 + c ⇒ a − 2c = 1 − − 2.( 2 − ) = 3.
Câu 27: Hình vẽ bên là đồ thị hàm số ax + b y = . cx + d .
Mệnh đề nào dưới đây đúng?
A. ad > 0 và bd > 0. B. ad > 0 và ab < 0 . C. bd < 0 và ab > 0 . D. ad < 0 và ab < 0 . Lời giải Chọn B Page 152
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Đồ thị hàm số giao với trục Ox tại điểm có hoành độ b
x = − , giao với Oy tại điểm có tung độ a b y = . db − > 0 b < 0  a aab < 0
Dựa vào hình vẽ ta có  ⇔  ⇔  ⇒ ad > 0 . b b bd    < 0 < 0 < 0 d d
Trong các phương án chỉ có phương án B thỏa mãn. Câu 28: Cho hàm số ax − b y =
có đồ thị như hình vẽ dưới đây: x −1
Khẳng định nào sau đây đúng?
A. b < a < 0.
B. a < b < 0.
C. b > a và a < 0 .
D. a < 0 < b . Lời giải Chọn A
Ta thấy đồ thị hàm số có tiệm cận ngang y = 1 − suy ra a = 1 − .
Do đồ thị hàm số đi qua điểm (2;0) nên 2a −b = 0 ⇔ 2
− − b = 0 ⇔ b = 2 − .
Vậy b < a < 0.
Câu 29: (Chuyên Lương Văn Chánh - Phú Yên - 2020) Đồ thị trong hình bên dưới là của hàm số ax + b y =
(với a,b,c ∈ ). x + c
Khi đó tổng a + b + c bằng A. 1 − . B. 1. C. 2 . D. 0 . Lời giải Chọn D Page 153
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Đồ thị hàm số ax + b y =
có đường tiệm cận ngang y = a , đường tiệm cận đứng x = −c và cắt x + c
Oy tại điểm 0; b   . c   
Từ đồ thị hàm số ta có đường tiệm cận ngang y = 1
− , đường tiệm cận đứng x =1 và cắt Oy tại điểm (0; 2 − ) .  a = 1 − a = 1 − a = 1 − 
Từ đó suy ra:  c 1  c 1  − = ⇔ = − ⇔ c = 1
− . Vậy a + b + c = 1 − −1+ 2 = 0 . b b  2c b  = − =   2  = 2 − c
Câu 30: (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số 2 ( ) − ax f x =
(a,b,c∈,b ≠ 0) có bx − c
bảng biến thiên như sau: Tổng các số ( + + )2
a b c thuộc khoảng nào sau đây A. (1;2) . B. (2;3). C.  4 0;     . D. 4  ;1 . 9      9  Lời giải Chọn C Ta có 2 lim − ax −a − =
, theo giả thiết suy ra a = 3 ⇔ a = 3 − b
x→∞ bx − c b b
Hàm số không xác định tại x =1⇒ b − c = 0 ⇔ b = c
Hàm số đồng biến trên từng khoảng xác định nên ′( ) ac − 2b f x = > 0 với mọi ( x khác 1 bx − c)2 Suy ra 2 2 2
ac − 2b > 0 ⇔ 3
− b − 2b > 0 ⇔ − < b < 0 ⇔ 0 < b − < 3 3
Lại có a + b + c = 3
− b + b + b = b − . Suy ra (a b c)2 2 4 b 0;  + + = ∈ 9   
Vậy tổng a + b + c thuộc khoảng  4 0;   . 9    Page 154
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 31: (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số ( ) ax + b f x =
(a,b,c,d ∈và c ≠ 0 ). cx + d
Biết rằng đồ thị hàm số đã cho đi qua điểm ( 1;
− 7) và giao điểm hai tiệm cận là( 2; − 3). Giá trị
biểu thức 2a + 3b + 4c + d bằng 7c A. 7 . B. 4 . C. 6 . D. 5 − . Lời giải Chọn C
+ Ta có đồ thị hàm số ( ) ax + b f x =
có đường tiệm cận ngang là a
y  , đường tiệm cận đứng cx + d c là d x   . c a   3 c a  3c Theo bài ra, ta có:    . d   d    2   2 c   c + Điểm ( 1;
− 7) thuộc đồ thị hàm số f (x) nên −a + b 3 = 7 − c + b ⇔
= 7 ⇔ b =10c . −c + d −c + 2c
Vậy 2a 3b  4c d
2.(3c) 3.(10c)  4c  2c   6 . 7c 7c
Câu 32: (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số ax +1 y =
( a,b,c là các tham số) bx + c
có bảng biến thiên như hình vẽ
Xét các phát biểu sau: ( )
1 : c >1; (2): a + b < 0; (3): a + b + c = 0; (4): a > 0 . Số phát biểu đúng là? A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B
Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng khoảng xác định, đồ thị hàm số
có tiệm cận đứng là đường thẳng x = 2 và tiệm cận ngang là đường thẳng y =1nên ta có hệ Page 155
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ c   − = 2   b 0 < c <1   c = 2 − bc = 2 − b   a    1 
= 1 ⇔  a = b ⇔  a = b
⇔  − < a < 0 b 2    2 ac − b > 0 2 − b − b >   0 
ac − b > 0  1 − < b < 0    2 
a + b + c = 0
Dựa vào hệ trên ta có các phát biểu ( )
1 ,(4) là sai, (2),(3) đúng.
Câu 33: (Đô Lương 4 - Nghệ An - 2020) Ta xác định được các số a,b,c để đồ thị hàm số 3 2
y = x + ax + bx + c đi qua điểm (1;0) và có điểm cực trị ( 2;
− 0) . Tính giá trị biểu thức 2 2 2
T = a + b + c . A. 25. B. 1. − C. 7. D. 14. Lời giải Chọn A Ta có 3 2 2
y = x + ax + bx + c ⇒ y′ = 3x + 2ax + b . y ( ) 3 2 1 = 0 0 =1 + .1 a + .1 b + c  
Theo đề, ta có hệ phương trình y( 2) 0  − = ⇔ 0 = ( 2 − )3 + . a ( 2 − )2 + . b ( 2 − ) + c y  ( 2) 0  ′ − = 0 = 3.  ( 2 − )2 + 2 . a ( 2 − ) + b
a + b + c = 1 − a = 3  4a 2b c 8 b  ⇔ − + = ⇔  = 0 .  4a b 12  − + = − c = 4 −  
Vậy T = a + b + c = + + (− )2 2 2 2 2 2 3 0 4 = 25.
Câu 34: (Lê Lai - Thanh Hóa - 2020) Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ. Tính
S = a + b ? A. S = 2 − . B. S = 0 . C. S =1. D. S = 1 − . Lời giải Chọn A
Vì đồ thị hàm số cắt trục tung tại điểm y = 2 nên d = 2 . Page 156
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ 2
y′ = 3ax + 2bx + c .
Hàm số đạt cực trị tại x = 0 và x = 2 nên y′(0) = 0 c = 0 c = 0  ⇔  ⇔  y′  (2) = 0 12
a + 4b + c = 0 b  = 3 − a  ( )1
Từ đồ thị ta nhận thấy y(2) = 2
− ⇔ 8a + 4b + d = 2
− ⇔ 8a + 4b = 4
− ⇔ 2a + b = − 1 (2) Thay ( )
1 vào (2) ta tìm được a =1,b = 3 − . Vậy S = 2 − .
Câu 35: (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A. a < 0,b < 0,c > 0,d < 0.
B. a < 0,b > 0,c < 0,d < 0 .
C. a > 0,b < 0,c < 0,d > 0.
D. a < 0,b > 0,c > 0,d < 0. Lời giải Chọn D Ta có: 2
y′ = 3ax + 2bx + c , y′′ = 6ax + 2b Từ đồ thị ta thấy:
 lim y = −∞ . Ta suy ra a < 0 . x→+∞
y(0) < 0 ⇒ d < 0 loại C.
Đồ thị hàm số có hai điểm cực trị với hoành độ x x x + x > 0 1 , 2 trái dấu và 1 2 . Ta suy ra phương
trình y ' = 0 có hai nghiệm trái dấu và x + x > 0 1 2 . Ta suy ra c x x = < 0 , ⇒ > loại B. 1 2 c 0 3abx + x = − > 0 Hơn nữa, 1 2  3a ⇒ b > 0 . Lọai A. a < 0
Câu 36: (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số ax + b y =
(a,b,c∈) có bảng biến thiên như cx +1 sau: Page 157
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Tập các giá trị b là tập nghiệm của bất phương trình nào dưới đây? A. 3 b −8 ≤ 0. B. 2 b − + 4 > 0. C. 2
b − 3b + 2 < 0. D. 3 b −8 < 0. Lời giải Chọn D Đồ thị hàm số ax + b y =
có đường tiệm cận đứng là đường thẳng 1
x = − và đường tiệm cận cx +1 c ngang là đường thẳng a y = . c
Nhìn vào bảng biến thiên, ta thấy 1 − = 1
− ⇒ c =1 và a = 2 ⇒ a = 2 (vì c =1). c c Ta có a − bc y′ = . (cx + )2 1
Vì hàm số đã cho đồng biến trên các khoảng ( ; −∞ − ) 1 và ( 1; − +∞) nên a − bc 3 3 y′ =
> 0 ⇔ a − bc > 0 ⇔ 2 − b > 0 ⇔ b < 2 ⇔ b < 8 ⇔ b −8 < 0 . (bx + c)2
Vậy tập các giá trị b là tập nghiệm của bất phương trình 3 b −8 < 0.
Câu 37: (Tiên Du - Bắc Ninh - 2020) Cho hàm số ax + b y =
(với a,b,c,d là số thực) có đồ thị như cx + d
hình dưới đây. Tính giá trị biểu thức
a − 2b + 3d T = . c
A. T = 6 .
B. T = 0 . C. T = 8 − .
D. T = 2 . Lời giải Chọn C
Từ đồ thị ta có TCĐ: = 1 −d ⇒ = 1 d x ⇒ = 1
− ⇒ d = −c c c Page 158
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ TCN: = 1 a y − ⇒ = 1
− ⇒ a = −c c
Đồ thị cắt trục hoành tại điểm: 2 b − 2 b − = ⇒ = ⇒ = 2 b x
⇒ = 2 ⇒ b = 2c a −c c Vậy
a − 2b + 3d −c − 4c − 3c T = = = 8 − c c
Câu 38: (Thanh Chương 1 - Nghệ An - 2020) Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ.
Trong các số a,b,c và d có bao nhiêu số dương? A. 1. B. 4 . C. 3. D. 2 . Lời giải Chọn D
Từ hình dạng đồ thị hàm số ta có a > 0
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm⇒ d < 0 Ta có: 2
y ' = 3ax + 2bx + c
Hàm số có hai điểm cực trị trái dấu⇒ y ' = 0 có hai nghiệm trái dấu ⇔ ca < 0
Mà a > 0 nên c < 0
Ta lại có: y ' = 6ax + 2b ' = 0 ⇔ 6 + 2 = 0 b y ax b ⇔ x = − 3a
Từ đồ thị hàm số ta thấy tâm đối xứng có hoành độ âm. Do đó b − < 0 3a
Mà a > 0 nên b > 0
Vậy trong các số a,b,c và d có 2 số dương là a và b
Câu 39: (Tiên Lãng - Hải Phòng - 2020) Cho hàm số f (x) ax − 6 =
(a,b,c ∈ ) có bảng biến thiên bx − c như sau: Page 159
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Trong các số a, ,
b c có bao nhiêu số âm? A. 0 . B. 3. C. 1. D. 2 . Lời giải Chọn D
Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là đường thẳng x = 2
− và tiệm cận ngang là đường thẳng y =1. c = 2 −  bc  < 0
b > 0,c < 0,a > 0 ( ) 1 Suy ra b  ⇒ ⇔ a    ab > 0
b < 0,c > 0,a < 0 (2) = 1 b
Lại có hàm số nghịch biến trên mỗi khoảng xác định ′( ) −ac + 6b f x =
< 0 ⇒ ac > 6b . (bx − c)2 Ta thấy ( )
1 không thể xảy ra do nếu b > 0 thì ac > 6b > 0; và (2) có thể xảy ra do nếu
c > 0,a < 0 thì 6b < ac < 0 .
Vậy trong các số a,b,c có hai số âm. Page 160
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 2. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI (BIẾN ĐỔI ĐỒ THỊ) Dạng 1
Từ đồ thị (C ) : y = f (x ) suy ra đồ thị (C′) : y = f (x ) . f x kh i f x ≥ 0
Ta có: y = f (x ) ( ) ( ) = 
−f (x ) kh i f (x ) <  0
* Cách vẽ (C′) từ (C) :
Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C):y = f (x ) .
Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị (C) y = f (x) 3 :
= x − 3x suy ra đồ thị y 2 (C) 3
: y = x − 3x
y = x 3 − x 3 . 1 Biến đổi (C) : -1 O x
 Bỏ phần đồ thị của (C ) dưới Ox, giữ nguyên (C ) phía trên -2 . Ox
(C′) y = x3 : − x 3
 Lấy đối xứng phần đồ thị bị bỏ qua Ox . y 2 -1 O 1 x Dạng 2
Từ đồ thị (C ) : y = f (x ) suy ra đồ thị (C′) : y = f ( x ) . f x khi x ≥ 0
Ta có: y = f ( x ) ( ) =  f  ( x − ) khi x < 0
và y = f ( x ) là hàm chẵn nên đồ thị (C′) nhận Oy làm trục đối xứng.
* Cách vẽ (C′) từ (C ) :
Giữ nguyên phần đồ thị bên phải Oy của đồ thị (C ) : y = f (x ).
Bỏ phần đồ thị bên trái Oy của (C ) , lấy đối xứng phần đồ thị được giữ qua Oy. Page 161
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Ví dụ: Từ đồ thị (C ) y = f (x ) = x3 : − x 3 suy ra đồ thị y 2 ( 3 3
C ′) : y = x − 3 x .
(C ) : y = x − x3 1 -1 O x Biến đổi (C ) : -2
 Bỏ phần đồ thị của (C ) bên trái Oy, giữ nguyên (C ) bên phải Oy. y
 Lấy đối xứng phần đồ thị được giữ qua Oy . ( 3
C ′) : y = x − 3 x -1 O 1 x -2
Chú ý với dạng: y = f ( x ) ta lần lượt biến đổi 2 đồ thị y = f ( x ) và y = f (x )
Ví dụ: Từ đồ thị (C ) y = f (x ) = x3 : − x 3 y ( 3
C ′′) : y = x − 3 x suy ra đồ thị 3
y = x − 3 x . Biến đổi (C ) 2 để được đồ thị ( 3
C ′) : y = x − 3 x . Biến đổi ( 3
C ′) : y = x − 3 x ta được đồ thị -1 O 1 x ( 3
C ′′) : y = x − 3 x . Dạng 3
Từ đồ thị (C ) : y = u (x ) v. (x ) suy ra đồ thị (C′) : y = u (x ) v. (x ) . u
 x v. x = f x khi u x ≥ 0
Ta có: y = u (x ) v. (x ) ( ) ( ) ( ) ( ) =  u −
 (x ) v. (x ) = f (x ) khi u (x ) < 0
* Cách vẽ (C′) từ (C) :
Giữ nguyên phần đồ thị trên miền u (x ) ≥ 0 của đồ thị (C ) : y = f (x ).
Bỏ phần đồ thị trên miền u (x ) < 0 của (C ) , lấy đối xứng phần đồ thị bị bỏ qua Ox. Page 162
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Ví dụ Ví dụ
a) Từ đồ thị (C ) y = f (x ) = x3 − x2 : 2 3
+ 1 suy ra b) Từ đồ thị ( ) : = ( ) = x C y f x suy ra đồ thị x − 1
đồ thị (C′) y = x − ( x2 : 1 2 − x − 1) ( ′) : = x C y x − 1 f x khi x 1  x
y = x − 1 ( x2 2 − x − 1)  ( ) ≥ =  khi x ∈ x (1;+∞  )
−f (x ) khi x <  x − 1  1 y = =  .Đồ thị x − 1  x Đồ thị (C’): − khi x ∈ (−∞;1)  x − 1
 Giữ nguyên (C) với x ≥ 1. (C’):
 Bỏ (C) với x < 1. Lấy đối xứng phần đồ thị bị bỏ  Bỏ phần đồ thị của (C) với < giữ nguyên (C) qua x , 1 Ox. với x > 1. y (C')
 Lấy đối xứng phần đồ thị bị bỏ qua Ox. y 1 O 1 x 1 O (C) 1 x
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của (C): giao
điểm với Ox, Oy, CĐ, CT…
Nhận xét: Đối với hàm phân thức thì nên lấy đối xứng
các đường tiệm cận để thực hiện phép suy đồ thị một
cách tương đối chính xác. Câu 40: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Hướng dẫn Ta có: 3 2
y = x − x + = (x − )( 2 3 2
1 x − 2x − 2)
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Page 163
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Toàn bộ đồ thị ứng với x ≥1 được giữ nguyên.
Phần đồ thị ứng với x <1 lấy đối xứng qua trục hoành.
⇒ Chọn đáp án C.
Câu 41: (THPT Việt Đức Hà Nội 2019) Cho hàm số y = f (x) có đồ thị hàm số y = f ( x ) như hình vẽ.
Chọn kết luận đúng trong các kết luận sau: A. f (x) 3 2
= −x + x + 4x − 4 B. f (x) 3 2
= x − x − 4x + 4 C. f (x) 3 2
= −x − x + 4x − 4 D. f (x) 3 2
= x + x − 4x − 4. Lời giải Chọn A
Do đồ thị giao với trục Oy tại điểm có tung độ bằng 4
− và lim y = −∞ . x→+∞
Câu 42: (Chu Văn An - Hà Nội - 2019) Cho hàm số y = (x − )( 2 2 x − )
1 có đồ thị như hình vẽ
Một trong bốn hình dưới đây là đồ thị của hàm số y = (x − ) 2
2 x −1 . Hỏi đó là hình nào? Page 164
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1. Lời giải Chọn C
Gọi (C) là đồ thị hàm số y = (x − )( 2 2 x − ) 1 . (  x − 2) 
( 2x − )1 khi x ≤ 1 − hay x ≥1
Ta có y = (x − 2) 2 x −1 =  . −( x − 2) 
( 2x − )1 khi −1< x <1
Cách vẽ đồ thi như sau:
+ Giữ nguyên phần đồ (C) ứng với x∈( ; −∞ − ]
1 ∪[1;+∞) ta được (C . 1 )
+ Lấy đối xứng phần (C) ứng với x∈( 1; − )
1 qua trục hoành ta được (C . 2 )
Khi đó đồ thị hàm số y = (x − ) 2
2 x −1 gồm (C và (C . 2 ) 1 ) Câu 43: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía “phải” Oy sau đó lấy đối xứng sang trái.
⇒ Chọn đáp án B. Câu 44: Cho hàm số −x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? 2x −1 Page 165
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ − + x +1 −x +1 A. x 1 y − + = B. x y = C. y = D. 1 y = 2x −1 2 x −1 2x −1 2x −1 Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải Oy được giữ nguyên
Sau đó, được lấy đối xứng sang trái. Chọn đáp án B. Câu 45: Cho hàm số 3 2
y = x − 6x + 9x có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào dưới đây? A. 3 2
y = −x + 6x − 9x . B. 3 2
y = x − 6x + 9x . C. 3 2
y = x − 6x + 9 x . D. 3 2
y = x + 6 x + 9 x . Lời giải Chọn C
+/ Loại đáp án A vì: 3 2
y = −x + x − x = −( 3 2 6 9
x − 6x + 9x)
+/ Loại đáp án B, vì đồ thị của hàm số 3 2
y = x − 6x + 9x giữ lại phần đồ thị phía trên trục
hoành và chỉ lấy đối xứng phần dưới trục hoành của đồ thị Hình 1.
+/ Loại đáp án D vì hệ số của 2 x khác -6.
+/ Đồ thị ở đáp án C là đồ thị của hàm số dạng y = f ( x ) . Chọn đáp án C Page 166
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 46: (Cụm liên trường Hải Phòng -2019) Cho hàm số x y
có đồ thị như Hình 1. Đồ thị Hình 2x 1
2 là của hàm số nào trong các đáp án A, B, C, D dưới đây? x A. x y x x  . B. y C. y D. y 2x 1 2 x 1 2 x 1 2 x 1 Lời giải Chọn A Câu 47: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Hướng dẫn Ta có: 3 2
y = x − x + = (x − )( 2 3 2
1 x − 2x − 2)
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy x ≥1+ 3
Toàn bộ đồ thị ứng với  được giữ nguyên. x ≤1− 3
Phần đồ thị ứng với 1− 3 ≤ x ≤1+ 3 lấy đối xứng qua trục hoành.
⇒ Chọn đáp án D. Câu 48: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? Page 167
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Hướng dẫn Ta có: 3 2
y = x − x + = (x − )( 2 3 2
1 x − 2x − 2)
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm phía trên Ox được giữ nguyên.
Phần đồ thị phía dưới Ox được lấy đối xứng qua Ox .
⇒ Chọn đáp án A. Câu 49: Cho hàm số x y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? 2x +1 x x A. x y x = B. y = C. y = D. y = 2 x +1 2 x +1 2x +1 2 x +1 Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía trên Ox giữ nguyên
Toàn bộ phần phía dưới Ox được lấy đối xứng lên trên
⇒ dạng f (x) . Chọn đáp án C. Câu 50: Cho hàm số −x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? x − 2 Page 168
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ − + x +1 −x +1 A. x 1 y = . B. −x + y = . C. y = D. 1 y = x − 2 x − 2 x − 2 x − 2 Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng x =1 được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng x =1 lấy đối xứng qua Ox Chọn đáp án C.
−x +1, x ≤1 −x +1  Chú ý:  x − 2 y = = x − 2  −x+1 − , x >1  x − 2 Câu 51: Cho hàm số x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? x + 2 + x +1 x +1 A. x 1 y = . B. x + y = . C. y = . D. 1 y = . x + 2 x + 2 x + 2 x + 2 Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải đường thẳng x = 2 − được giữ nguyên
Toàn bộ đồ thị phía bên trái đường thẳng x = 2
− lấy đối xứng qua Ox Chọn đáp án D.
Câu 52: Cho hàm số y = (x − )( 2
1 x − 2x − 3) có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? Page 169
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. y = (x − )( 2
1 x − 2x − 3) .
B. y = x − ( 2
1 x − 2x − 3).
C. y = − x − ( 2
1 x − 2x − 3)
D. y = (x − ) 2 1 x − 2x − 3 Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm bên trái (ứng với x ≤1) đường thẳng x =1 được giữ nguyên
Toàn bộ đồ thị nằm bên phải (ứng với x >1) đường thẳng x =1 được lấy đối xứng qua . Ox
⇒ Chọn đáp án C. Câu 53: Cho hàm số x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? −x + 2 + x +1 x +1 A. x 1 y + = . B. y = . C. y = . D. x 1 y = . x + 2 x − 2 −x + 2 x + 2 Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng x = 1
− (ứng với x ≤ 1) − được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng x = 1
− (ứng với x ≤ 1)
− được lấy đối xứng qua trục . Ox Chọn đáp án B. Page 170
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ G ƠN I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT HÀM SỐ HƯ C
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM. III
DẠNG 1. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
1.1 HÀM SỐ BẬC BA y = ax3 + bx2 + cx + d (a ≠ 0) TRƯỜNG HỢP a > 0 a < 0
Phương trình y/ = 0 có y y
2 nghiệm phân biệt 1 1 O x 1 1 O x Phương trình y y/ = 0 có y nghiệm kép 1 1 1 O x 1 O x Phương trình / y = 0 vô y y nghiệm 1 O 1 1 x 1 O x Page 1
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
1.2. HÀM SỐ TRÙNG PHƯƠNG y = ax4 + bx2 + c (a ≠ 0) TRƯỜNG HỢP a > 0 a < 0
Phương trình y/ = 0 có y y
3 nghiệm phân biệt (ab<0) 1 1 1 1 O x O x
Phương trình y/ = 0 có y y 1 nghiệm. 1 1 1 O x 1 O x
1.3. HÀM SỐ NHẤT BIẾN ax + b y =
(c ≠ 0, ad − bc ≠ 0) cx + d
D = ad − bc > 0
D = ad − bc < 0
Câu 1: Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở các đáp án ,
A B,C, D . Hỏi đó là hàm số nào? A. 3
y = x + 2x +1. B. 3 2
y = x − 2x +1. C. 3
y = x − 2x +1. D. 3
y = −x + 2x +1. Lời giải
Dựa vào đồ thị, ta có lim y = +∞ , loại phương án D . x→+∞ Page 2
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Xét phương án A có 2
y′ = 3x + 2 > 0, x
∀ ∈  , hàm số không có cực tri, loại phương án A .
Xét phương án B có 2
y′ = 3x − 6x và y′ đổi dấu khi đi qua các điểm x = 0, x = 2 nên hàm
số đạt cực tri tại x = 0 và x = 2 , loại phương án B .
Vậy phương án đúng là C .
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây? A. 3
y  x 3x 1. B. 4 2
y x x 1. C. 2
y  x x1. D. 3
y x 3x 1. Lời giải Chọn D
Đồ thị đã cho có hình dạng của đồ thị hàm số bậc ba 3 2
y ax bx cx d nên loại phương án B và C
Dựa vào đồ thị, ta có lim y    a  0 nên loại phương án A x
Câu 3: Đồ thị hàm số 3
y = x − 3x + 2 là hình nào trong 4 hình dưới đây? A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Câu 4: Đường cong trong hình bên d ư ớ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? Page 3
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3
y = x − 3x . B. 3
y = −x + 3x −1 . C. 3
y = −x + 3x . D. 4 2
y = x − x + 1 .
Câu 5: Đường cong trong hình bên d ư ớ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 3
y = x − 3x + 1 . B. 3
y = −x + 3x + 1. C. 2
y = −x + x −1. D. 4 2
y = x − x + 1.
Câu 6: Đường cong trong hình bên d ư ớ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 3
y = −x + 3x −1 . B. 3
y = −x + 3x . C. 4 2
y = x − x + 1. D. 3
y = x − 3x .
Câu 7: Đường cong trong hình bên d ư ớ i là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? Page 4
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3
y = x − 3x + 1 . B. 3 2
y = −x + 3x + 1. C. 3 2
y = x − 3x + 3x + 1.D. 3 2
y = −x − 3x −1 .
Câu 8: Đường cong trong hình bên là đồ thị của một hàm số y
trong bốn hàm số được liệt kê ở bốn phương án A, B, 2
C, D dưới đây. Hỏi hàm số đó là hàm số nào? x 1 A. 3
y = x − 3x . -1 O B. 3
y = −x + 3x . -2 C. 4 2
y = −x + 2x . D. 4 2
y = x − 2x . Lời giải Chọn A
Đặc trưng của đồ thị là hàm bậc ba nên loại C, D.
Hình dáng đồ thị thể hiện a > 0 nên chỉ có A phù hợp.
Câu 9: Đường cong trong hình bên là đồ thị của một hàm số y
trong bốn hàm số được liệt kê ở bốn phương án A, B, C,
D dưới đây. Hỏi hàm số đó là hàm số nào? A. 2
y = −x + x −1. B. 3
y = −x + 3x +1. x C. 4 2
y = x − x +1. O D. 3
y = x − 3x +1. Lời giải Chọn D
Đặc trưng của đồ thị là hàm bậc ba. Loại đáp án A và C.
Hình dáng đồ thị thể hiện a > 0 .
Câu 10: Đường cong trong hình bên là đồ thị của một hàm số y
trong bốn hàm số được liệt kê ở bốn phương án A, B,
C, D dưới đây. Hỏi hàm số đó là hàm số nào? 2 x A. 3 2
y = −x − 3x − 2 . -2 -1 O B. 3 2
y = x + 3x − 2. -2 C. 3 2
y = x − 3x − 2 . Page 5
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ D. 3 2
y = −x + 3x − 2. Lời giải Chọn B
Hình dáng đồ thị thể hiện a > 0 . Loại đáp án A, D. x = 1 −
Thấy đồ thị cắt trục hoành tại điểm x = 1 − nên thay 
vào hai đáp án B và C, chỉ có B y = 0 thỏa mãn.
Câu 11: Đường cong trong hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? 2 A. 3 y = −x +1. 1 x B. 3
y = −x + 3x + 2. x  2 O 1 C. 3 2
y = −x + 3x − 3x + 2 . D. 3 y = −x + 2 . Lời giải Chọn D
Để ý thấy khi x = 0 thì y = 2 nên ta loại đáp án A.
Dựa vào đồ thị, suy ra hàm số không có cực trị nên ta loại đáp án B vì 2 y ' = 3 − x + 3 có hai nghiệm.
Đồ thị hàm số đi qua điểm có tọa độ (1; )
1 , kiểm tra thấy C & D đều thỏa mãn.
Xét phương trình hoành độ giao điểm: 3 2 CASIO
−x + 3x − 3x + 2 = 0 → x = 2.
Xét phương trình hoành độ giao điểm: 3 3 −x + 2 = 0 
→ x = 2 ∈(1;2). Do đó chỉ có D thỏa mãn.
Câu 12: Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. y 3 O 1 x
Hàm số đó là hàm số nào? A. 3 2 y = 2
− x − 6x − 6x +1. B. 3 2
y = 2x − 6x + 6x +1. C. 3 2
y = 2x − 6x − 6x +1. D. 3 2
y = 2x − x + 6x +1. Lời giải Chọn B
Nhận xét: Nhìn vào đồ thị ta thấy a > 0 nên loại 3 2 y = 2
− x − 6x − 6x +1.
Đồ thi hàm số đi qua điểm A(1;3) . Thay vào từng đáp án ta chọn 3 2
y = 2x − 6x + 6x +1. Page 6
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 13: Xác định đồ thị sau của hàm số nào? y 4 2 O x A. 3
y = x + 3x + 2 . B. 3
y = −x − 3x + 2. C. 3
y = x − 3x + 2. D. 3
y = x − 3x − 2 . Lời giải Chọn C
Đồ thị hàm số đi qua điểm có tọa độ (1;0) nên loại …và 3
y = x − 3x + 2 đúng.
Câu 14: Cho hàm số y = f (x) như hình vẽ dưới đây
Hỏi f (x) là hàm số nào trong các hàm số dưới đây? A. f (x) 3 2
= x + 3x − 4 . B. f (x) 3 2 = x − 3x +1. C. f (x) 3
= x − 3x +1. D. f (x) 3 2 = −x + 3x +1. Lời giải Chọn B
Dựa vào hình dạng đồ thị hàm số có hai điểm cực trị tại x = 0 và x = 2 , cắt trục tung tại điểm
có tung độ y =1 và có hệ số a > 0 .
Như vậy chỉ có hàm số f (x) 3 2
= x − 3x +1 thỏa mãn.
Câu 15: Đồ thị trong hình dưới là đồ thị của một trong bốn hàm số cho trong các phương án sau đây, đó là hàm số nào? Page 7
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = −x + 3x + 2 . B. 3 2
y = x − 3x + 2. C. 3
y = x − 3x + 2. D. 3 2
y = x − 3x − 2. Lời giải Chọn B
Giả sử hàm số cần tìm có dạng 3 2
y = ax + bx + cx + d với a ≠ 0 .
Dựa vào đồ thị hàm số ta thấy lim y = +∞ nên suy ra a > 0 . Vậy loại đáp án x→+∞ 3 2
y = −x + 3x + 2 .
Đồ thị hàm số cắt trục tung tại điểm có tọa độ là (0;2) nên suy ra d = 2 . Vậy loại 3 2
y = x − 3x − 2 .
Đồ thị hàm số đạt cực đại tại điểm có tọa độ là (0;2) nên phương trình y′ = 0 phải có nghiệm x = 0
x = 0 . Ta thấy chỉ có hàm số 3 2
y = x − 3x + 2 có 2
y′ = 3x − 6x = 0 ⇔  . x = 2 Vậy Chọn 3 2
y = x − 3x + 2
Câu 16: Biết rằng đồ thị cho ở hình vẽ dưới đây là đồ thị của một trong 4 hàm số cho trong 4 phương
án A , B , C , D . 6 y 4 2 O 1 2 x Đó là hàm số nào? A. 3 2
y = 2x + 9x −11x + 3. B. 3 2
y = x − 4x + 3x + 3 . C. 3 2
y = 2x − 6x + 4x + 3. D. 3 2
y = x − 5x + 4x + 3 . Lời giải Chọn B Page 8
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Dựa vào đồ thị ở hình3 ta thấy hàm số cần tìm đi qua các điểm (0;3), (1;3) và (2; ) 1 thay vào
bốn phương án ta thấy phương án 3 2
y = x − 4x + 3x + 3 là thỏa mãn.
Câu 17: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = 2x + 6x − 2 B. 3 2
y = x + 3x − 2. C. 3 2
y = −x − 3x − 2 . D. 3 2
y = x − 3x − 2. Lời giải Chọn B
Từ đồ thị hàm số ta có:
Đồ thị trong hình là của hàm số bậc 3, có hệ số a > 0 .
Đồ thị hàm số đạt cực trị tại các điểm A( 2; − 2);B(0; 2 − ). Vậy chọn đáp án 3 2
y = x + 3x − 2.
Câu 18: Đường cong bên là đồ thị của một trong bốn hàm số đã cho sau đây. Hỏi đó là hàm số nào? A. 3 2
y = x + 3x −1. B. 4 2
y = x + x −1. C. 3
y = x − 3x −1. D. 2
y = −x − 3x −1. Lời giải Chọn A
Dựa vào đồ thị, ta có hàm số đã cho có hai điểm cực trị, trong đó điểm cực tiểu là x = 0 . Xét hàm số 3 2
y = x + 3x −1. x = 0; y = 1 − 2
y′ = 3x + 6x ; y′ = 0 ⇔  . x = 2; − y = 3 Bảng biến thiên: Đồ thị: Page 9
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 19: Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên dưới: A. 3
y = x + 3x . B. 3 2
y = x − 3x . C. 3 2
y = x + 3x . D. 3
y = x − 3x . Lời giải Chọn B
Quan sát đồ thị ta thấy đây là đồ thị của hàm số bậc ba: 3 2
y = ax + bx + cx + d có a > 0 .
Đồ thị hàm số giao với trục hoành tại hai điểm có hoành độ x = 0 và x = 3 suy ra đồ thị có hàm số là 3 2
y = x − 3x .
Câu 20: Đường cong hình bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = −x + 3x − 4. B. 3 2
y = x − 3x + 4. C. 3 2
y = −x − 3x − 4 . D. 3 2
y = x + 3x − 4. Lời giải Chọn D
Từ đồ thị hàm số ta thấy đây là hàm bậc ba 3 2
y = ax + bx + cx + d với hệ số a > 0 , d < 0
Và y′ = 0 có hai nghiệm x∈{ 2; − } 1 . Ta thấy có hàm số 3
y = x + 3x − 4 thỏa mãn. Page 10
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 21: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? A. 3 2
y = −x + 3x +1. B. 3 2
y = −x − 3x +1. C. 3 2
y = x + 3x +1. D. 3 2
y = x − 3x +1. Lời giải Chọn D
Dựa vào đồ thị ta có hàm số là hàm bậc ba 3 2
y = ax + bx + cx + d có hệ số a > 0 . Đồng thời
y′ = 0 có nghiệm x = 0 và nghiệm x > 0 . 1 2
Do đó, ta có hàm số thỏa mãn là 3 2
y = x − 3x +1.
Câu 22: Đường cong trong hình bên là đồ thị hàm số nào? A. 3
y = x − 3x +1. B. 3
y = −x + 3x −1. C. 3
y = x − 3x −1. D. 3
y = −x + 3x +1. Lời giải Chọn D
Từ đồ thị ta có hệ số a < 0 nên ta loại đáp án 3
y = x − 3x +1 và 3
y = x − 3x −1.
Khi x = 0 thì đồ thị cắt trục Oy tại điểm có tung độ dương nên d > 0 nên ta loại 3
y = −x + 3x −1 .
Câu 23: Đường cong trong hình bên cạnh là đồ thị của hàm số nào trong các hàm số sau? Page 11
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = x + 3x + 2 . B. 3 2
y = x − 3x + 2. C. 3
y = x − 3x + 2. D. 3 2
y = x − 3x − 2. Lời giải Chọn B
Đồ thị hàm số đi qua điểm (0; 2) , do đó loại đáp án 3 2
y = x − 3x − 2 .
Từ đồ thị, ta có y′ = 0 có hai nghiệm là 0 và 2 . Như vậy ta chọn đáp án 3 2
y = x − 3x + 2.
Câu 24: Đồ thị như hình bên là đồ thị của hàm số nào? y 4 2 x -4 -2 2 4 -2 A. 3 3
y = −x + 3x +1 B. 3
y = x − 3x −1 C. 3
y = x − 3x +1 D. 3 3
y = −x − 3x −1 Lời giải Chọn C
Hàm số là hàm bậc 3 có hệ số a > 0. Loại 3 3
y = −x + 3x +1 và 3 3
y = −x − 3x −1.
Đồ thị cắt Oy tại (0; ) 1 nên loại. 3
y = x − 3x −1
Câu 25: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? y 1 -1 1 0 x -1 A. 4 2
y = x − 3x + 1. B. 4 2
y = x + 2x . C. 4 2
y = x − 2x . D. 4 2
y = −x − 2x . Lời giải Chọn C
Câu 26: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? Page 12
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y 1 1 0 x A. 4 2
y = x − 2x + 1. B. 4 2
y = x − 2x + 1. C. 4 2
y = x − 3x + 1. D. 4 2
y = −x − 2x + 1. Lời giải Chọn D
Câu 27: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? y 1 -1 1 0 x -1 A. 4 2
y = x − 3x + 1. B. 4 2
y = x − 2x + 1. C. 4 2
y = −x + 2x + 1. D. 4 2
y = −x − 2x + 1. Lời giải Chọn C
Câu 28: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ? y 1 -1 1 0 x Page 13
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 4 2
y = x + 3x + 1. B. 4 2
y = x − 2x + 1. C. 4 2
y = x − 3x + 1. D. 4 2
y = −x + 2x + 1. Lời giải Chọn A y
Câu 29: Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? A. 4 2
y = −x + 2x + 2 . 2 B. 4 2
y = x − 2x + 2 . 1 x C. 4 2
y = x − 4x + 2 . -1 O 1 D. 4 2
y = x − 2x + 3 . Lời giải Chọn B
Hình dáng đồ thị thể hiện a > 0 . Loại đáp án A.
Để ý thấy khi x = 0 thì y = 2 nên ta loại đáp án D.
Đồ thị hàm số đi qua điểm có tọa độ (1; )
1 nên chỉ có B thỏa mãn.
Câu 30: Đường cong trong hình bên là đồ thị của một hàm số y
trong bốn hàm số được liệt kê ở bốn phương án A, B, C, 1 x
D dưới đây. Hỏi hàm số đó là hàm số nào? -1 O 1 A. 4 2
y = x − 2x −1. -1 B. 4 2 y = 2
− x + 4x −1. C. 4 2
y = −x + 2x −1. D. 4 2
y = −x + 2x +1. Lời giải Chọn B
Hình dáng đồ thị thể hiện a < 0 . Loại A.
Đồ thị cắt trục tung tại điểm có tung độ bằng 1
− nên thể hiện c = 1 − . Loại D.
Đồ thị hàm số đi qua điểm có tọa độ (1; )
1 nên chỉ có B thỏa mãn.
Câu 31: Đường cong trong hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới 3
đây. Hỏi hàm số đó là hàm số nào? A. 4 2
y = −x − 2x + 3 . B. 4 2
y = −x − 2x − 3 . x -1 1 C. 4 2
y = −x + 2x + 3. O D. 4 2
y = x + 2x + 3. Lời giải Chọn A
Hình dáng đồ thị thể hiện a < 0 . Loại D.
Dựa vào đồ thị thấy khi x = 0 thì y = 3. Loại B. Page 14
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Hàm số có một cực trị nên a, b cùng dấu.
Câu 32: Đường cong trong hình bên là đồ thị của một hàm số trong bốn y
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi
hàm số đó là hàm số nào? A. 4 2
y = x + x + 2 . B. 4 2
y = x − x + 2. 1 x C. 4 2
y = x − x +1. O D. 4 2
y = x + x +1. Lời giải Chọn D
Dựa vào đồ thị ta thấy khi x = 0 thì y =1. Loại A, B.
Hàm số có một cực trị nên a, b cùng dấu.
Câu 33: Biết hình dưới đây là đồ thị của một trong bốn hàm số sau, hỏi đó là đồ thị của hàm số nào? y O x A. 4 2
y = x − 2x . B. 4 2
y = x − 2x +1. C. 4 2
y = x + 2x . D. 4 2
y = −x + 2x . Lời giải Chọn A
Dựa vào đồ thị ta chọn đáp án 4 2
y = x − 2x .
Câu 34: Đường cong trong hình sau là đồ thị của hàm số nào? y -1 1 O x -3 -4 A. 4 2
y = x + 2x − 3 . B. 4 2
y = x − 2x − 3 . C. 4 2
y = −x − 2x + 3 . D. 4 2
y = −x + 2x + 3. Lời giải Chọn B
Theo hình vẽ, đồ thị của hàm số trùng phương 4 2
y = ax + bx + c với a > 0 , loại 4 2
y = −x − 2x + 3 , 4 2
y = −x + 2x + 3 Page 15
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Đồ thị hàm số có 3 cực trị nên ab < 0 , loại 4 2
y = x + 2x − 3.
Câu 35: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 1 − 1 O x 1 − A. 4 2
y = −x + 2x −1. B. 4 2
y = −x + x −1. C. 4 2
y = −x + 3x − 3. D. 4 2
y = −x + 3x − 2. Lời giải Chọn A
Đồ thị hàm số qua điểm có tọa độ (0; ) 1 − ⇒ Loại 4 2
y = −x + 3x − 3.và 4 2
y = −x + 3x − 2.
Đồ thị hàm số qua điểm có tọa độ (1;0) ⇒ Loại 4 2
y = −x + x −1.
Câu 36: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây A. 4 2
y = x − x +1. B. 4 2
y = x − 4x +1. C. 4 2
y = −x + 4x +1. D. 3 2
y = x − 3x + 2x +1. Lời giải Chọn B
Đây là đồ thị hàm số trùng phương có 3cực trị và có a > 0 ⇒ loại 4 2
y = −x + 4x +1, loại 3 2
y = x − 3x + 2x +1.
Nhìn vào điểm cực tiểu x của hàm số thấy ⇒ loại 4 2
y = x − x +1. 0 x >1 0
Câu 37: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? Page 16
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 4 2
y = x + 4x + 3. B. 4 2
y = −x + 4x + 3. C. 4 2
y = x − 4x + 3. D. 3 2
y = x − 4x − 3. Lời giải Chọn C
Quan sát đồ thị hàm số ta có đây là đồ thị của hàm số bậc bốn: 4 2
y = ax + bx + c(a ≠ 0) và a > 0 nên 4 2
y = −x + 4x + 3 và 3 2
y = x − 4x − 3 bị loại. Mặt khác đồ thị hàm số có ba điểm cực trị nên . a b < 0 . Do đó 4 2
y = x + 4x + 3bị loại.
Câu 38: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. 4 2
y = −x + 2x −1. B. 4 2
y = −x + x −1. C. 4 2
y = −x +3x −3. D. 4 2
y = −x +3x − 2. Lời giải Chọn A
Đồ thị hàm số qua điểm có tọa độ (0; ) 1 − ⇒ Loại 4 2
y = −x +3x −3. và 4 2
y = −x +3x − 2.
Đồ thị hàm số qua điểm có tọa độ (1;0) ⇒ Loại 4 2
y = −x + x −1.
Câu 39: Đường cong ở hình bên là đồ thị của hàm số nào sau đây? A. 2
y = x −3x +1. B. 4 2
y = x −3x +1. C. 4 2
y = −x +3x +1. D. 3 2
y = x −3x +1. Lời giải Chọn B Page 17
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Đồ thị hàm số có 3 cực trị nên từ đáp án suy ra hàm số là hàm bậc 4
Theo nhánh phải đồ thị có hướng đi lên nên ta có hệ số a > 0 nên ta chọn phương án 4 2
y = x −3x +1.
Câu 40: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? A. 4 2
y = −x +8x − 2 . B. 4 2
y = x −8x − 2 . C. 3 2
y = x −3x − 2. D. 3 2
y = −x +3x − 2. Lời giải Chọn B
Từ đồ thị ta thấy đây là đồ thị của hàm số trùng phương với hệ số a > 0 .
Câu 41: Hình bên là đồ thị của hàm số nào dưới đây? A. 4 2
y = x − 2x −3. B. 4 2
y = −x + 2x . C. 4 2
y = −x + 2x −3. D. 4 2
y = x − 2x . Lời giải Chọn D
Đồ thị có hai nhanh hướng lên nên hệ số 4
x phải dương; đồ thị hàm số có 3 cực trị nên hệ số của 4 x và 2
x phải trái dấu nên hệ số của 2
x phải âm; đồ thị hàm số đi qua gốc tọa độ nên hệ số tự
do bằng 0 . Do đó đáp án 4 2
y = x −2x là đáp án đúng.
Câu 42: Đồ thị hình bên là đồ thị hàm số nào trong các hàm số sau: Page 18
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = x +3x −3. B. 2
y = −x + 2x +3. C. 4 2
y = x + 2x −3. D. 4 2
y = −x − 2x +3. Lời giải Chọn D
Đồ thị cắt Oy tại điểm có tung độ dương nên chọn 2
y = −x + 2x +3 hoặc 4 2
y = −x − 2x +3.
Đồ thị cắt Ox tại hai điểm có hoành độ 1 − và 1 nên chọn 4 2
y = −x − 2x +3.
Câu 43: Đường cong hình bên là đồ thị của một trong bốn hàm số sau. Đó là hàm số nào? A. 4 2
y = x − 2x +1. B. 3
y = −x − 2x + x +1. C. 3 2
y = x − 2x − x +1 . D. 4 2
y = −x + 2x +1. Lời giải Chọn D
Đồ thị hàm số có 3 điểm cực trị nên từ đáp án suy ra hàm số là hàm bậc 4 trùng phương.
Theo nhánh phải đồ thị có hướng đi xuống nên ta có hệ số a < 0 nên ta chọn phương án 4 2
y = −x + 2x +1.
Câu 44: Đường cong sau là đồ thị hàm số nào dưới đây A. 4 2
y = x − 2x +3. B. 4 2
y = x − 2x −3. C. 4 2
y = −x + 2x −3. D. 3 2
y = x −3x −3 . Lời giải Chọn B
Đồ thị hàm số có ba cực trị, bề lõm hướng lên và cắt trục tung tại điểm có tung độ bằng 3 − .
Câu 45: Đường cong hình bên là đồ thị của hàm số nào dưới đây? Page 19
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 4 2 y = 4
− x + x + 4. B. 4 2
y = x − 2x +3. C. 4 2
y = x +3x + 2. D. 3 2
y = x − 2x +1. Lời giải Chọn B
Đồ thị hàm số đã cho là hàm trùng phương có a > 0 và có 3 cực trị. Nên hàm số 4 2
y = x − 2x +3 TM
Câu 46: Đường cong trong hình vẽ bên là của hàm số nào dưới đây A. 4 2
y = x −3x −1. B. 3 2
y = x −3x −1. C. 3 2
y = −x +3x −1. D. 4 2
y = −x +3x −1. Lời giải Chọn D
Đồ thị hàm số đã cho là hàm trùng phương có a < 0 và có 3 cực trị. Nên hàm số 4 2
y = −x +3x −1 TM
Câu 47: Hàm số nào sau đây có đồ thị như hình vẽ. A. 4 2
y = −x − 2x +1. B. 4 2
y = −x + 2x +1. C. 4 2
y = x − 2x − 2. D. 4 2
y = x − 2x −1. Lời giải Chọn B
Ta thấy lim y = −∞ nên loại 4 2
y = x − 2x − 2, 4 2
y = x − 2x −1. x→+∞
Đồ thị hàm số có ba điểm cực trị nên loại 4 2
y = −x − 2x +1 Page 20
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 48: Đường cong trong hình vẽ dưới đây là đồ thị hàm số nào? 4 x 4 2 x x 4 x 4 x A. 2 y = − + x −1 y = − −1 2
y = − + 2x −3 2 y = − 2x −1 4 . B. 4 2 . C. 4 . D. 4 . Lời giải Chọn D 4 x 4 x
Từ đồ thị ta có a > 0 ⇒ loại đáp án 2 y = − + x −1 2
y = − + 2x −3 4 , 4 4 2 x x
Ta lại có y(2) = 5 ⇒ loại y = − −1 4 2 4 x Đáp án đúng là 2 y = − 2x −1 4 .
Câu 49: Đồ thị cho ở hình vẽ sau đây, là đồ thị của hàm số cho bởi một trong bốn số phương án A,B,C,D dưới đây? A. 4 2
y = x + 2x −1. B. 4 2
y = x − 2x −1. C. 1 4 2
y = − x + 3x −1. D. 4 2
y = x −3x −1. 4 Lời giải Chọn A y(0) = 1 − Ta thấy  chọn đáp án 4 2
y = x + 2x −1. y  ( ) 1 = y(− ) 1 = 2
Câu 50: Đường cong trong hình bên là đồ thị một hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? Page 21
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y 1 1 − 1 O x 1 − A. 3 2
y = x −3x +1. B. 4 2
y = 2x − 4x +1. C. 4 2 y = 2
− x + 4x +1. D. 4 2 y = 2 − x + 4x . Lời giải Chọn B
Đồ thị đã cho là đồ thị hàm trùng phương có hệ số a > 0 và đi qua điểm (0; ) 1 .
Vậy đó là đồ thị hàm số 4 2
y = 2x − 4x +1. Câu 51: Hàm số x − 2 y =
có đồ thị là hình vẽ nào sau đây? x − 1 y y A. 2 B. 1 1 -2 -1 0 1 x -2 -1 0 1 x y y 3 C. D. 2 1 1 -2 -1 0 1 x -2 -1 0 1 x Lời giải Chọn A Câu 52: Hàm số 2 + 2x y =
có đồ thị là hình vẽ nào sau đây? 2 + x Page 22
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y y 4 2 A. 2 B. 1 1 x -1 0 -2 -1 0 1 -3 -2 1 x y y 3 C. D. 2 2 1 1 -2 -1 0 1 x -3 -2 -1 0 1 x Lời giải Chọn B
Câu 53: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 2 x -2 -1 0 1 A. 3 2
y = x + 3x +1. B. 2x + 5 y x + = . C. 4 2
y = x − x +1. D. 2 1 y = . x + 1 x + 1 Lời giải Chọn B
Câu 54: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? Page 23
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y 2 x -2 -1 0 1 -1 A. 2x −1 y x + x + − x = . B. 2 1 y = . C. 2 1 y = . D. 1 2 y = . x + 1 x −1 x + 1 x −1 Lời giải Chọn A
Câu 55: Đường cong trong hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào? 1 A. x +1 2 y + = . B. x 3 y = . 2x +1 2x +1 1 O x  2 C. x y − = . D. x 1 y = . 2x +1 2x +1 Lời giải Chọn C
Các chi tiết đồ thị hàm số có TCĐ: 1 x = − và TCN: 1
y = đều giống nhau. 2 2
Chỉ có chi tiết đồ thị hàm số đi qua gốc tọa độ là phù hợp cho đáp án C.
Cách 2. Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên từng khoảng xác định tức y' > 0 .
Kiểm tra ta thấy chỉ có C & D thỏa mãn.
Đồ thị hàm số đi qua gốc tọa độ O(0;0) nên đáp án C thỏa mãn.
Câu 56: Đồ thị (hình bên) là đồ thị của hàm số nào? y 2 -1 1 x O A. x + 2 y + − + = . B. 2x 1 y = . C. x 1 y = . D. x 3 y = . x +1 x +1 x +1 1− x Lời giải Chọn B Page 24
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Dựa vào đồ thị ta có đường tiệm cận đứng x = 1
− và đường tiệm cận ngang y = 2 nên chọn phương án 2x +1 y = x +1
Câu 57: Đường cong trong hình vẽ bên là đồ thị của một trong bốn hàm số sau. Hỏi đó là đồ thị của hàm số nào? y 2 1 O 1 2 x A. x − 2 y − + + = . B. x 2 y = . C. x 2 y = . D. x 2 y = . x +1 x −1 x − 2 x −1 Lời giải Chọn B
Đồ thị hàm số có TCĐ x =1 nên loại đáp án x − 2 y + = và x 2 y = x +1 x − 2
Đồ thị hàm số cắt trục x −
Oy tại điểm (0;2) nên ta loại 2 y = x −1
Câu 58: Đồ thị sau là đồ thị của hàm số nào sau? y 1 1 − O 1 x 1 − A. 2x − 3 y − + = . B. x y = . C. x 1 y = . D. x 1 y = . 2x − 2 x −1 x +1 x −1 Lời giải Chọn D x −
x = 1 là tiệm cận đứng của đồ thị ⇒ loại 1 y = C= x +1 x − x
 Đồ thị hàm số cắt Oy tại y = 1 − ⇒ loại 2 3 y = , y = 2x − 2 x −1
Vậy đồ thị trên là đồ thị của hàm số x +1 y = . x −1 Page 25
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
DẠNG 1. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ Câu 59: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? A. a < 0, b > 0, 0, c > d < 0 B. a < 0, b < 0, 0, c > d < 0. C. a > 0, b < 0, c < 0, d > 0 D. a < 0, b > 0, 0, c < d < 0. Lời giải Chọn A
Dựa vào đồ thị suy ra hệ số a < 0 ⇒ loại phương án C 2
y′ = 3ax + 2bx + c = 0 có 2 nghiệm x , x trái dấu (do hai điểm cực trị của đồ thị hàm số nằm 1 2
hai phía với Oy )⇒ 3 .
a c < 0 ⇒ c > 0 ⇒ loại phương án D. Do
(C)∩Oy = D(0;d) ⇒ d < 0. Page 26
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 60: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?
A. a > 0,b < 0,c > 0
B. a > 0,b < 0,c < 0 C. a > 0,b > 0,c < 0 D. a < 0,b > 0,c < 0 Lời giải Chọn B
Ta có đồ thị có hình dạng như trên với hàm bậc bốn trùng phương có hai điểm cực tiểu và một
điểm cực đại nên a > 0,b < 0 . Giá trị cực đại nhỏ hơn 0 nên c < 0 . Câu 61: Cho hàm số ax + = b y có đồ thị như sau. cx + d
Mệnh đề nào sau đây đúng? A. ac > 0; 0 bd > B. ab < 0; 0 cd < C. bc > 0; 0 ad < D. ad > 0; 0 bd < Lời giải Chọn C Theo đồ thị: Tiệm cận ngang: a y = > 0 c ( ) 1 d d
Tiệm cận đứng: x = − > 0 ⇒ < 0 2 c c ( )
= 0 ⇒ = − b < 0 ⇒ b y x > 0 3 a a ( ) Câu 62: Cho hàm số 3 2
y = ax + bx + cx + d (a ≠ 0) có đồ thị như hình vẽ dưới đây. Chọn khẳng định đúng
về dấu của a , b , c , d ? Page 27
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a > 0 ,b > 0, d > 0 , c > 0
B. a > 0 , c > 0 > b , d < 0
C. a > 0, b > 0, c > 0, d > 0.
D. a > 0 , b < 0 , c < 0 , d > 0 Lời giải Chọn D
Dựa vào đồ thị ta có a > 0 , đồ thị cắt Oy tại 1 điểm có tung độ dương nên d > 0 , đồ thị có 2
cực trị trái dấu nên . < 0 c x x
⇒ < 0 ⇒ c < 0 . Vậy đáp án D 1 2 aa  1 x b
Câu 63: Cho hàm số y
, d  0 có đồ thị như hình trên. Khẳng định nào dưới đây là đúng? c  1 x d
A. a 1,b  0,c 1. B. a 1,b  0,c 1. C. a 1,b  0,c 1. D. a 1,b  0,c 1. Lời giải Chọn D
Theo bài ra, đường tiệm cận đứng của đồ thị hàm số là d x   . c1
Đường tiệm cận ngang của đồ thị hàm số là: a1 y  . c1 Nhìn đồ thị ta thấy: d x  
 0 mà d  0  c1 0  c 1. c1 a1 y
 0  a 1 0  a 1. c1
Đồ thị cắt trục tung tại điểm có tung độ bằng b  0  b  0. d Câu 64: Cho hàm số 4 2
y = ax + bx + c ( a ≠ 0) có đồ thị như hình vẽ dưới đây. Page 28
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Mệnh đề nào dưới đây đúng?
A. a < 0 , b > 0, c < 0 . B. a < 0 , b < 0 , c > 0 .
C. a < 0 , b > 0, c > 0 . D. a < 0 , b < 0 , c < 0 . Lời giải Chọn A
Đồ thị cắt trục tung tại điểm (0;c), từ đồ thị suy ra c < 0
Mặt khác đồ thị hàm số có ba điểm cực trị nên y′ = 0 có ba nghiệm phân biệt, hay 3
y′ = ax + bx = x( 2 4 2
2 2ax + b) = 0 có ba nghiệm phân biệt. Suy ra a,b trái dấu.
Mà a < 0 ⇒ b > 0 Câu 65: Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A. a  0, b  0 , c  0, d  0 .
B. a  0 , b  0 , c  0, d  0 .
C. a  0, b  0 , c  0, d  0 .
D. a  0 , b  0 , c  0, d  0 . Lời giải Chọn D
+ Dựa vào hình dạng đồ thị ta khẳng định được a  0 .
+ Đồ thị cắt trục Oy tại điểm có tọa độ 0;d. Dựa vào đồ thị suy ra d  0 . + Ta có: 2
y  3ax  2bx c . Hàm số có hai điểm cực trị x x 1 , 2 x x 1
2  trái dấu nên phương
trình y  0 có hai nghiệm phân biệt x x
1 , 2 trái dấu. Vì thế 3 .
a c  0 , nên suy ra c  0. x 1
+ Mặt khác từ đồ thị ta thấy  1 
nên x x  0. x 1 1 2  2 Mà 2b xbx
nên suy ra 2  0  b  0 . 1 2 3a 3a
Vậy a  0 , b  0 , c  0, d  0 . Page 29
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 66: Cho hàm số ax + b y =
có đồ thị như hình bên dưới, với a , b , c∈ . Tính giá trị của biểu thức x + c
T = a + 2b + 3c ? A. T = 8 − . B. T = 2. C. T = 6 . D. T = 0 . Lời giải Chọn D
Từ đồ thị hàm số, ta suy ra
 Đồ thị hàm số có tiệm cận đứng là đường thẳng x =1, tiệm cận ngang là đường thẳng y = 1 − .
 Đồ thị hàm số đi qua các điểm A(2;0) , B(0; 2 − ) . Từ biểu thức hàm số ax + b y =
(vì đồ thị hàm số là đồ thị hàm nhất biến nên ac − b ≠ 0 ), ta x + c suy ra
 Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −c , tiệm cận ngang là đường thẳng y = a .
 Đồ thị hàm số đi qua  b A ;0 −    , 0; b B . a      c
Đối chiếu lại, ta suy ra c = 1 − , a = 1 − , b = 2 .
Vậy T = a + 2b + 3c = (− ) 1 + 2.2 + 3(− ) 1 = 0. Câu 67: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào đúng?
A. ab < 0,bc > 0,cd < 0 B. ab < 0,bc < 0,cd > 0
C. ab > 0,bc > 0,cd < 0 D. ab > 0,bc > 0,cd > 0 Page 30
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn A
Từ dáng điệu của đồ thị ta có ngay được: ⊕ lim y = ;
+∞ lim y = −∞ ⇒ a > 0 . x→+∞ x→−∞
⊕ Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên d > 0 . Ta có: 2
y ' = 3ax + 2bx + c
Mặt khác dựa vào đồ thị ta thấy phương trình y ' = 0 có hai nghiệm trái dấu và tổng hai nghiệm ac < 0  c < 0
này luôn dương nên  2b ⇒ (do a > 0 ) − > b    < 0  3a
Do đó: ab < 0,bc , > cd < 0 . Câu 68: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A. a < 0,b < 0,c < 0,d < 0
B. a < 0,b > 0,c > 0,d > 0
C. a < 0,b > 0,c < 0,d > 0
D. a < 0,b > 0,c > 0,d < 0 Lời giải
Chọn D - Dựa vào hình dáng của đồ thị suy ra hệ số a<0.
- Đồ thị cắt trục Oy tại điểm có tung độ âm nên d < 0 .
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương trình 2
y′ = 3ax + 2bx + c = 0 có 2 nghiệm x , x
a c < ⇒ c > 1 2 trái dấu kéo theo 3 . 0 0 . x + x b - Mặt khác 1 2 = − > 0 ⇒ b > 0. 2 3a Câu 69: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ?
A. a > 0,b < 0,c < 0 .
B. a < 0,b < 0,c < 0 . C. a < 0,b > 0,c < 0 . D. a > 0,b < 0,c > 0 Lời giải Chọn C Page 31
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
- Dựa vào hình dạng đồ thị suy ra a < 0
- Hàm số có 3 điểm cực trị nên ab < 0 ⇒ b > 0
- Giao điểm với trục tung nằm dưới trục hoành nên c < 0 . Câu 70: Cho hàm số ax + b y =
có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi cx + d trong các số ,
b c,d có tất cả bao nhiêu số dương? A. 1. B. 2 . C. 0 . D. 3. Lời giải Chọn B
Nhìn vào đồ thị ta thấy a
• tiệm cận ngang y = nằm trên trục hoành nên c > 0 (vì a > 0 ) c − − • tiệm cận đứng d x =
nằm bên trái trục tung nên d < 0. Suy ra d > 0 (vì c > 0 ) c c
• giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên b < 0. d
Suy ra b < 0 (vì d > 0 )
Vậy c > 0,d > 0 Câu 71: Hàm số 3 2
y ax bx cx d có đồ thị như hình vẽ bên dưới:
Khẳng định nào là đúng?
A. a  0, b  0 , c  0, d  0 .
B. a  0 , b  0 , c  0, d  0 .
C. a  0, b  0 , c  0, d  0 .
D. a  0 , b  0 , c  0, d  0 . Lời giải Page 32
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Chọn D
+ Dựa vào hình dạng đồ thị ta khẳng định được a  0 .
+ Đồ thị cắt trục Oy tại điểm có tọa độ 0;d. Dựa vào đồ thị suy ra d  0 . + Ta có: 2
y  3ax  2bx c . Hàm số có hai điểm cực trị x x 1 , 2 x x trái dấu nên phương 1 2 
trình y  0 có hai nghiệm phân biệt x x
1 , 2 trái dấu. Vì thế 3 .
a c  0 , nên suy ra c  0. x 1
+ Mặt khác từ đồ thị ta thấy  1 
nên x x  0. x 1 1 2  2 Mà 2b xbx
nên suy ra 2  0  b  0 . 1 2 3a 3a
Vậy a  0 , b  0 , c  0, d  0 . Câu 72: Cho hàm số ax + b y =
có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng? cx + d ad < 0 ad < 0 ad > 0 ad > 0 A.  . B.  . C.  . D.  . bc > 0 bc < 0 bc < 0 bc > 0 Lời giải Chọn C Nhận xét từ đồ thị:
+ Giao với trục hoành tại b x = − > ⇒ o 0
a và b trái dấu (1). a
+ Giao với trục tung tại b
y = < ⇒ b và o 0
d trái dấu (2). d + Tiệm cận đứng: d
x = − < 0 ⇒ d và c cùng dấu (3). c
Từ (1) và (2) suy ra: a và d cùng dấu hay ad > 0 .
Từ (2) và (3) suy ra: b và c trái dấu hay bc < 0 .
Câu 73: Tìm đồ thị hàm số y = f (x) được cho bởi một trong các phương án dưới đây, biết ( ) = ( − )( − )2 f x
a x b x với a < b . A. . B. . Page 33
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ C. . D. . Lời giải Chọn A
Có f ′(x) = −(b − x)2 + (a − x).( 2
− )(b − x) = −(b − x)(b − x + 2a − 2x) = −(b − x)(b + 2a − 3x) x = b f ′(x) = 0  ⇔ 2a + bx = .  3
2a + b 2b + b Có < = b 3 3 . Ta có bảng biến thiên Từ đó chọn đáp án A
Câu 74: Cho đường cong (C) 3 2
: y = ax + bx + cx + d có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A. a > 0,b < 0,c < 0,d < 0.
B. a > 0,b > 0,c < 0,d > 0 .
C. a < 0,b > 0,c > 0,d < 0.
D. a > 0,b > 0,c < 0,d < 0. Lời giải Chọn D
Từ đồ thị ta có x = 0 ⇒ y = d < 0, từ dạng đồ thị suy ra a > 0 . Mặt khác 2
y ' = 3ax + 2bx + c từ đồ thị ta có phương trình y ' = 0 có hai nghiệm trái dấu suy ra
ac < 0 mà a > 0 suy ra c < 0 . Page 34
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Hơn nữa phương trình y ' = 0 có hai nghiệm phân biệt 2b x + x = − = 1 − suy ra 1 2 3a
3a = 2b ⇒ b > 0 .
Vậy chọn đáp án D.
Câu 75: (Gia Lai 2019) Hàm số 4 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
A. a  0, b  0 , c  0. B. a  0, b  0 , c  0.
C. a  0, b  0 , c  0. D. a  0, b  0 , c  0. Lời giải Chọn C Dựa vào đồ thị:
+ lim y    a  0 . x
+ Đồ thị hàm số có ba điểm cực trị ab  0  b  0 .
+ Giao điểm của đồ thị hàm số và trục tung có tung độ dương c  0 .
Vậy a  0, b  0 , c  0. Câu 76: Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ. Tìm kết luận đúng
A. a b  0 .
B. bc  0 .
C. ab  0 .
D. ac  0. Lời giải Chọn B Từ hình vẽ ta thấy:
Đồ thị hàm số có bề lõm hướng lên  a  0 .
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm  c  0 .
Đồ thị hàm số có 3 điểm cực trị  ab  0  b  0.
Vậy chỉ có bc  0 . Câu 77: Cho hàm số 4 2
y ax bx c(a  0) có đồ thị như hình bên. Hãy chọn mệnh đề đúng. Page 35
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a  0,b  0,c  0 . B. a  0,b  0,c  0 .
C. a  0,b  0,c  0 . D. a  0,b  0,c  0. Lời giải Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy : Hệ số a  0
Đồ thị hàm số đi qua gốc tọa tọa  c  0
Hàm số có 3 điểm cực trị  .
a b  0  b  0 Câu 78: Cho hàm số 3 2
y = f (x) = ax + bx + cx + d có đồ thị như hình vẽ ở bên. Mệnh đề nào sau đây đúng?
A. a > 0 , b > 0, c > 0 , d > 0 .
B. a > 0 , b > 0, c < 0 , d > 0 .
C. a > 0 , b < 0 , c > 0 , d > 0 .
D. a < 0 , b < 0 , c > 0 , d < 0 . Lời giải Chọn C
Đồ thị hàm số đi qua các điểm (
A 0;1) , B(1;5) và C(3;1) và đạt cực trị tại các điểm B và C . ′ 2
f (x) = 3ax + 2bx + c . Ta có  f (0) =1 d =1 a =1   f (1) 5  a b c d 5 b  = + + + =  = 6 −  ⇒  ⇒ . f ′(1) 0 3a 2b c 0  = + + = c = 9   
 f ′(3) = 0 27a + 6b + c = 0 d =1
Câu 79: Cho hàm số bậc bốn trùng phương 4 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào
dưới đây là đúng? Page 36
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a  0,b  0,c  0. B. a  0,b  0,c  0. C. a  0,b  0,c  0 . D. a  0,b  0,c  0. Lời giải Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy : Hệ số a  0 .
Hàm số có 3 điểm cực trị  .
a b  0  b  0.
Đồ thị hàm số đi qua gốc tọa tọa  c  0 .
Vậy a  0,b  0,c  0 . Câu 80: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Hỏi khẳng định nào sau đây đúng?
A. a > 0,b < 0,c < 0 . B. a > 0,b > 0,c < 0 . C. a > 0,b < 0,c > 0. D. a < 0,b > 0,c < 0 . Lời giải Chọn A
Nhìn vào đồ thị ta có:
Khi x∈ (2;+ ∞) hàm số đồng biến ⇒a > 0 .
Hàm số có 3 điểm cực trị nên a.b < 0 mà a > 0⇒b < 0 . y(0) = 1
− = c ⇒ c < 0 . Câu 81: Cho hàm số ax + 3 y =
có đồ thị như hình vẽ bên. Tính giá trị của a − 2 . c x + c Page 37
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a − 2c = 3.
B. a − 2c = 3. −
C. a − 2c = 1. −
D. a − 2c = 2. − Lời giải Chọn A
Đồ thị hàm số có TCN = 1 a y − ⇔ = 1 − ⇔ a = 1. − 1
Mặt khác Đồ thị hàm số có TCĐ x = 2 nên 2 + c = 0 ⇔ c = 2. − ⇒ a − 2c = 1 − − 2.( 2 − ) = 3.
Dựa vào đồ thị ta thấy các điểm (3;0) và  3 0;  − 
thuộc vào đồ thị hàm số đã cho nên ta được 2     .3 a + 3 0 =  3  a + 3 = 0 a = 1 − hệ phương trình  3+ c  ⇔ ⇔ 3 .0 a + 3    − =  = − − = 3c 6 c 2  2 0 + c ⇒ a − 2c = 1 − − 2.( 2 − ) = 3.
Câu 82: Hình vẽ bên là đồ thị hàm số ax + b y = . cx + d .
Mệnh đề nào dưới đây đúng?
A. ad > 0 và bd > 0. B. ad > 0 và ab < 0 . C. bd < 0 và ab > 0 . D. ad < 0 và ab < 0 . Lời giải Chọn B
Đồ thị hàm số giao với trục Ox tại điểm có hoành độ b
x = − , giao với Oy tại điểm có tung độ a b y = . d Page 38
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ b − > 0 b < 0  a aab < 0
Dựa vào hình vẽ ta có  ⇔  ⇔  ⇒ ad > 0 . b b bd    < 0 < 0 < 0 d d
Trong các phương án chỉ có phương án B thỏa mãn. Câu 83: Cho hàm số ax − b y =
có đồ thị như hình vẽ dưới đây: x −1
Khẳng định nào sau đây đúng?
A. b < a < 0.
B. a < b < 0.
C. b > a và a < 0 .
D. a < 0 < b . Lời giải Chọn A
Ta thấy đồ thị hàm số có tiệm cận ngang y = 1 − suy ra a = 1 − .
Do đồ thị hàm số đi qua điểm (2;0) nên 2a −b = 0 ⇔ 2
− − b = 0 ⇔ b = 2 − .
Vậy b < a < 0.
Câu 84: Đồ thị trong hình bên dưới là của hàm số ax + b y =
(với a,b,c ∈ ). x + c
Khi đó tổng a + b + c bằng A. 1 − . B. 1. C. 2 . D. 0 . Lời giải Chọn D Đồ thị hàm số ax + b y =
có đường tiệm cận ngang y = a , đường tiệm cận đứng x = −c và cắt x + c
Oy tại điểm 0; b   . c   
Từ đồ thị hàm số ta có đường tiệm cận ngang y = 1
− , đường tiệm cận đứng x =1 và cắt Oy tại điểm (0; 2 − ) . Page 39
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ  a = 1 − a = 1 − a = 1 − 
Từ đó suy ra:  c 1  c 1  − = ⇔ = − ⇔ c = 1
− . Vậy a + b + c = 1 − −1+ 2 = 0 . b b  2c b  = − =   2  = 2 − c
Câu 85: Cho hàm số 2 ( ) − ax f x =
(a,b,c∈,b ≠ 0) có bảng biến thiên như sau: bx − c Tổng các số ( + + )2
a b c thuộc khoảng nào sau đây A. (1;2) . B. (2;3). C.  4 0;     . D. 4  ;1 . 9      9  Lời giải Chọn C Ta có 2 lim − ax −a − =
, theo giả thiết suy ra a = 3 ⇔ a = 3 − b
x→∞ bx − c b b
Hàm số không xác định tại x =1⇒ b − c = 0 ⇔ b = c
Hàm số đồng biến trên từng khoảng xác định nên ′( ) ac − 2b f x = > 0 với mọi ( x khác 1 bx − c)2 Suy ra 2 2 2
ac − 2b > 0 ⇔ 3
− b − 2b > 0 ⇔ − < b < 0 ⇔ 0 < b − < 3 3
Lại có a + b + c = 3
− b + b + b = b − . Suy ra (a b c)2 2 4 b 0;  + + = ∈ 9   
Vậy tổng a + b + c thuộc khoảng  4 0;   . 9   
Câu 86: Cho hàm số ( ) ax + b f x =
(a,b,c,d ∈và c ≠ 0 ). Biết rằng đồ thị hàm số đã cho đi qua điểm cx + d ( 1;
− 7) và giao điểm hai tiệm cận là( 2;
− 3). Giá trị biểu thức 2a + 3b + 4c + d bằng 7c A. 7 . B. 4 . C. 6 . D. 5 − . Lời giải Chọn C Page 40
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
+ Ta có đồ thị hàm số ( ) ax + b f x =
có đường tiệm cận ngang là a
y  , đường tiệm cận đứng cx + d c là d x   . c a   3 c a  3c Theo bài ra, ta có:    . d   d    2   2 c   c + Điểm ( 1;
− 7) thuộc đồ thị hàm số f (x) nên −a + b 3 = 7 − c + b ⇔
= 7 ⇔ b =10c . −c + d −c + 2c
Vậy 2a 3b  4c d
2.(3c) 3.(10c)  4c  2c   6 . 7c 7c Câu 87: Cho hàm số ax +1 y =
( a,b,c là các tham số) có bảng biến thiên như hình vẽ bx + c
Xét các phát biểu sau: ( )
1 : c >1; (2): a + b < 0; (3): a + b + c = 0; (4): a > 0 . Số phát biểu đúng là? A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B
Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng khoảng xác định, đồ thị hàm số
có tiệm cận đứng là đường thẳng x = 2 và tiệm cận ngang là đường thẳng y =1nên ta có hệ  c   − = 2   b 0 < c <1   c = 2 − bc = 2 − b   a    1 
= 1 ⇔  a = b ⇔  a = b
⇔  − < a < 0 b 2    2 ac − b > 0 2 − b − b >   0 
ac − b > 0  1 − < b < 0    2 
a + b + c = 0
Dựa vào hệ trên ta có các phát biểu ( )
1 ,(4) là sai, (2),(3) đúng.
Câu 88: Ta xác định được các số a,b,c để đồ thị hàm số 3 2
y = x + ax + bx + c đi qua điểm (1;0) và có điểm cực trị ( 2;
− 0) . Tính giá trị biểu thức 2 2 2
T = a + b + c . A. 25. B. 1. − C. 7. D. 14. Page 41
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn A Ta có 3 2 2
y = x + ax + bx + c ⇒ y′ = 3x + 2ax + b . y ( ) 3 2 1 = 0 0 =1 + .1 a + .1 b + c  
Theo đề, ta có hệ phương trình y( 2) 0  − = ⇔ 0 = ( 2 − )3 + . a ( 2 − )2 + . b ( 2 − ) + c y  ( 2) 0  ′ − = 0 = 3.  ( 2 − )2 + 2 . a ( 2 − ) + b
a + b + c = 1 − a = 3  4a 2b c 8 b  ⇔ − + = ⇔  = 0 .  4a b 12  − + = − c = 4 −  
Vậy T = a + b + c = + + (− )2 2 2 2 2 2 3 0 4 = 25. Câu 89: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ. Tính S = a + b ? A. S = 2 − . B. S = 0 . C. S =1. D. S = 1 − . Lời giải Chọn A
Vì đồ thị hàm số cắt trục tung tại điểm y = 2 nên d = 2 . 2
y′ = 3ax + 2bx + c .
Hàm số đạt cực trị tại x = 0 và x = 2 nên y′(0) = 0 c = 0 c = 0  ⇔  ⇔  y′  (2) = 0 12
a + 4b + c = 0 b  = 3 − a  ( )1
Từ đồ thị ta nhận thấy y(2) = 2
− ⇔ 8a + 4b + d = 2
− ⇔ 8a + 4b = 4
− ⇔ 2a + b = − 1 (2) Thay ( )
1 vào (2) ta tìm được a =1,b = 3 − . Vậy S = 2 − . Câu 90: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? Page 42
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. a < 0,b < 0,c > 0,d < 0.
B. a < 0,b > 0,c < 0,d < 0 .
C. a > 0,b < 0,c < 0,d > 0.
D. a < 0,b > 0,c > 0,d < 0. Lời giải Chọn D Ta có: 2
y′ = 3ax + 2bx + c , y′′ = 6ax + 2b Từ đồ thị ta thấy:
 lim y = −∞ . Ta suy ra a < 0 . x→+∞
y(0) < 0 ⇒ d < 0 loại C.
Đồ thị hàm số có hai điểm cực trị với hoành độ x x x + x > 0 1 , 2 trái dấu và 1 2 . Ta suy ra phương
trình y ' = 0 có hai nghiệm trái dấu và x + x > 0 1 2 . Ta suy ra c x x = < 0 , ⇒ > loại B. 1 2 c 0 3abx + x = − > 0 Hơn nữa, 1 2  3a ⇒ b > 0 . Lọai A. a < 0 Câu 91: Cho hàm số ax + b y =
(a,b,c∈) có bảng biến thiên như sau: cx +1
Tập các giá trị b là tập nghiệm của bất phương trình nào dưới đây? A. 3 b −8 ≤ 0. B. 2 b − + 4 > 0. C. 2
b − 3b + 2 < 0. D. 3 b −8 < 0. Lời giải Chọn D Đồ thị hàm số ax + b y =
có đường tiệm cận đứng là đường thẳng 1
x = − và đường tiệm cận cx +1 c ngang là đường thẳng a y = . c
Nhìn vào bảng biến thiên, ta thấy 1 − = 1
− ⇒ c =1 và a = 2 ⇒ a = 2 (vì c =1). c c Page 43
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Ta có a − bc y′ = . (cx + )2 1
Vì hàm số đã cho đồng biến trên các khoảng ( ; −∞ − ) 1 và ( 1; − +∞) nên a − bc 3 3 y′ =
> 0 ⇔ a − bc > 0 ⇔ 2 − b > 0 ⇔ b < 2 ⇔ b < 8 ⇔ b −8 < 0 . (bx + c)2
Vậy tập các giá trị b là tập nghiệm của bất phương trình 3 b −8 < 0. Câu 92: Cho hàm số ax + b y =
(với a,b,c,d là số thực) có đồ thị như hình dưới đây. Tính giá trị biểu cx + d thức
a − 2b + 3d T = . c
A. T = 6 .
B. T = 0 . C. T = 8 − .
D. T = 2 . Lời giải Chọn C
Từ đồ thị ta có TCĐ: = 1 −d ⇒ = 1 d x ⇒ = 1
− ⇒ d = −c c c TCN: = 1 a y − ⇒ = 1
− ⇒ a = −c c
Đồ thị cắt trục hoành tại điểm: 2 b − 2 b − = ⇒ = ⇒ = 2 b x
⇒ = 2 ⇒ b = 2c a −c c Vậy
a − 2b + 3d −c − 4c − 3c T = = = 8 − c c Câu 93: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ. Trong các số a,b,c và d có bao nhiêu số dương? Page 44
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 1. B. 4 . C. 3. D. 2 . Lời giải Chọn D
Từ hình dạng đồ thị hàm số ta có a > 0
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm⇒ d < 0 Ta có: 2
y ' = 3ax + 2bx + c
Hàm số có hai điểm cực trị trái dấu⇒ y ' = 0 có hai nghiệm trái dấu ⇔ ca < 0
Mà a > 0 nên c < 0
Ta lại có: y ' = 6ax + 2b ' = 0 ⇔ 6 + 2 = 0 b y ax b ⇔ x = − 3a
Từ đồ thị hàm số ta thấy tâm đối xứng có hoành độ âm. Do đó b − < 0 3a
Mà a > 0 nên b > 0
Vậy trong các số a,b,c và d có 2 số dương là a và b
Câu 94: Cho hàm số f (x) ax − 6 =
(a,b,c ∈ ) có bảng biến thiên như sau: bx − c
Trong các số a,b,c có bao nhiêu số âm? A. 0 . B. 3. C. 1. D. 2 . Lời giải Chọn D
Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là đường thẳng x = 2
− và tiệm cận ngang là đường thẳng y =1. c = 2 −  bc  < 0
b > 0,c < 0,a > 0 ( ) 1 Suy ra b  ⇒ ⇔ a    ab > 0
b < 0,c > 0,a < 0 (2) = 1 b
Lại có hàm số nghịch biến trên mỗi khoảng xác định ′( ) −ac + 6b f x =
< 0 ⇒ ac > 6b . (bx − c)2 Ta thấy ( )
1 không thể xảy ra do nếu b > 0 thì ac > 6b > 0; và (2) có thể xảy ra do nếu
c > 0,a < 0 thì 6b < ac < 0 .
Vậy trong các số a,b,c có hai số âm.
DẠNG. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI (BIẾN ĐỔI ĐỒ THỊ) Dạng 1
Từ đồ thị (C ) : y = f (x ) suy ra đồ thị (C′) : y = f (x ) . Page 45
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ f x kh i f x ≥ 0
Ta có: y = f (x ) ( ) ( ) = 
−f (x ) kh i f (x ) <  0
* Cách vẽ (C′) từ (C) :
Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C):y = f (x ) .
Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị (C) y = f (x) 3 :
= x − 3x suy ra đồ y 2 (C) 3
: y = x − 3x
thị y = x3 − x 3 . 1 Biến đổi (C) : -1 O x
Bỏ phần đồ thị của (C ) dưới Ox, giữ nguyên (C ) -2 phía trên . Ox
(C′) y = x3 : − x 3
Lấy đối xứng phần đồ thị bị bỏ qua Ox . y 2 -1 O 1 x Dạng 2
Từ đồ thị (C ) : y = f (x ) suy ra đồ thị (C′) : y = f ( x ) . f x khi x ≥ 0
Ta có: y = f ( x ) ( ) =  f  ( x − ) khi x < 0
và y = f ( x ) là hàm chẵn nên đồ thị (C′) nhận Oy làm trục đối xứng.
* Cách vẽ (C′) từ (C ) :
Giữ nguyên phần đồ thị bên phải Oy của đồ thị (C ) : y = f (x ).
Bỏ phần đồ thị bên trái Oy của (C ) , lấy đối xứng phần đồ thị được giữ qua Oy. Page 46
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Ví dụ: Từ đồ thị (C ) y = f (x ) = x3 : − x 3 suy ra đồ y 2 thị ( 3 3
C ′) : y = x − 3 x .
(C ) : y = x − x3 1 -1 O x Biến đổi (C ) : -2
Bỏ phần đồ thị của (C ) bên trái Oy, giữ nguyên (C ) bên phải Oy. y
Lấy đối xứng phần đồ thị được giữ qua Oy . ( 3
C ′) : y = x − 3 x -1 O 1 x -2
Chú ý với dạng: y = f ( x ) ta lần lượt biến đổi 2 đồ thị y = f ( x ) và y = f (x )
Ví dụ: Từ đồ thị (C ) y = f (x ) = x3 : − x 3 suy ra đồ y ( 3
C ′′) : y = x − 3 x thị 3
y = x − 3 x . Biến đổi (C ) để được đồ thị 2 ( 3 3
C ′) : y = x − 3 x . Biến đổi (C ′) : y = x − 3 x ta được đồ thị ( 3
C ′′) : y = x − 3 x . -1 O 1 x Dạng 3
Từ đồ thị (C ) : y = u (x ) v. (x ) suy ra đồ thị (C′) : y = u (x ) v. (x ) . u
 x v. x = f x khi u x ≥ 0
Ta có: y = u (x ) v. (x ) ( ) ( ) ( ) ( ) =  u −
 (x ) v. (x ) = f (x ) khi u (x ) < 0
* Cách vẽ (C′) từ (C) :
Giữ nguyên phần đồ thị trên miền u (x ) ≥ 0 của đồ thị (C ) : y = f (x ).
Bỏ phần đồ thị trên miền u (x ) < 0 của (C ) , lấy đối xứng phần đồ thị bị bỏ qua Ox. Page 47
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Ví dụ Ví dụ
a) Từ đồ thị (C ) y = f (x ) = x3 − x2 : 2 3
+ 1 suy ra b) Từ đồ thị ( ) : = ( ) = x C y f x suy ra đồ x − 1
đồ thị (C′) y = x − ( x2 : 1 2 − x − 1) thị ( ′) : = x C y x − 1 f x khi x 1  x
y = x − 1 ( x2 2 − x − 1)  ( ) ≥ =  khi x ∈ x (1;+∞  )
−f (x ) khi x <  x − 1  1 y = =  . x − 1  x Đồ thị (C’): − khi x ∈ (−∞;1)  x − 1
Giữ nguyên (C) với x ≥ 1. Đồ thị (C’):
Bỏ (C) với x < 1. Lấy đối xứng phần đồ thị bị bỏ qua Bỏ phần đồ thị của (C) với x < ,1 giữ nguyên Ox. y
(C ) với x >1. (C')
Lấy đối xứng phần đồ thị bị bỏ qua Ox. y 1 O 1 x 1 O (C) 1 x
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của (C): giao điểm với Ox, Oy, CĐ, CT…
Nhận xét: Đối với hàm phân thức thì nên lấy đối
xứng các đường tiệm cận để thực hiện phép suy
đồ thị một cách tương đối chính xác. Câu 95: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Lời giải Chọn C Ta có: 3 2
y = x − x + = (x − )( 2 3 2
1 x − 2x − 2)
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Page 48
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Toàn bộ đồ thị ứng với x ≥1 được giữ nguyên.
Phần đồ thị ứng với x <1 lấy đối xứng qua trục hoành.
⇒ Chọn đáp án C.
Câu 96: Hàm số y = (x − )( 2 2 x − )
1 có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y = x − ( 2 2 x − ) 1 ? A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 Lời giải Chọn A 2  x − x − x ≥ y = x − 2 ( 2 1 , 2 2 x − ) ( )  ( ) 1 = 
Đồ thị gồm 2 phần: −( x − 2) 
( 2x − )1,x < 2
+) Giữ nguyên phần đồ thị đã cho ứng với x ≥ 2 .
+) Lấy đối xứng phần đồ thị đã cho ứng với x < 2 qua trục Ox
Hình 1 nhận vì đồ thị là hàm y = x − ( 2 2 x − ) 1
Hình 2 loại vì đồ thị là hàm y = (x − 2) x −1 (x + ) 1
Hình 3 loại vì đồ thị hàm số y = ( x − )( 2 2 x − ) 1
Hình 4 loại vì đồ thị hàm y = (x − )( 2 2 x − ) 1
Câu 97: Cho hàm số y = f (x) có đồ thị hàm số y = f ( x ) như hình vẽ. Page 49
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Chọn kết luận đúng trong các kết luận sau: A. f (x) 3 2
= −x + x + 4x − 4 B. f (x) 3 2
= x − x − 4x + 4 C. f (x) 3 2
= −x − x + 4x − 4 D. f (x) 3 2
= x + x − 4x − 4. Lời giải Chọn A
Do đồ thị giao với trục Oy tại điểm có tung độ bằng 4
− và lim y = −∞ . x→+∞
Câu 98: Biết phương trình 3 2
ax + bx + cx + d = 0 (a ≠ 0) có đúng hai nghiệm thực. Hỏi đồ thị hàm số 3 2
y = ax + bx + cx + d có bao nhiêu điểm cực trị? A. 4. B. 5. C. 2. D. 3. Lời giải Chọn D Ta có: Phương trình 3 2
ax + bx + cx + d = 0 (a ≠ 0) có đúng hai nghiệm thực Nên đồ thị hàm số 3 2
y = ax + bx + cx + d được minh họa như hình vẽ.
Gọi m là số điểm cực trị của hàm số y = f (x) và k là nghiệm bội lẻ
của phương trình f (x) = 0 .
⇒ Số điểm cực trị của đồ thị hàm số y = f (x) là m + k . Vậy đồ thị hàm số 3 2
y = ax + bx + cx + d có số điểm cực trị là 2 +1.
Câu 99: Cho hàm số y = (x − )( 2 2 x − )
1 có đồ thị như hình vẽ Page 50
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Một trong bốn hình dưới đây là đồ thị của hàm số y = (x − ) 2
2 x −1 . Hỏi đó là hình nào?
Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1. Lời giải Chọn C
Gọi (C) là đồ thị hàm số y = (x − )( 2 2 x − ) 1 . (  x − 2) 
( 2x − )1 khi x ≤ 1 − hay x ≥1
Ta có y = (x − 2) 2 x −1 =  . −( x − 2) 
( 2x − )1 khi −1< x <1
Cách vẽ đồ thi như sau:
+ Giữ nguyên phần đồ (C) ứng với x∈( ; −∞ − ]
1 ∪[1;+∞) ta được (C . 1 )
+ Lấy đối xứng phần (C) ứng với x∈( 1; − )
1 qua trục hoành ta được (C . 2 )
Khi đó đồ thị hàm số y = (x − ) 2
2 x −1 gồm (C và (C . 2 ) 1 )
Câu 100: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Lời giải Chọn B
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Page 51
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Toàn bộ đồ thị phía “phải” Oy sau đó lấy đối xứng sang trái.
⇒ Chọn đáp án B.
Câu 101: Cho hàm số −x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? 2x −1 − + x +1 −x +1 A. x 1 y = B. −x + y = C. y = D. 1 y = 2x −1 2 x −1 2x −1 2x −1 Lời giải Chọn B
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải Oy được giữ nguyên
Sau đó, được lấy đối xứng sang trái. Chọn đáp án B.
Câu 102: Cho hàm số 3 2
y = x − 6x + 9x có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào dưới đây? A. 3 2
y = −x + 6x − 9x . B. 3 2
y = x − 6x + 9x . C. 3 2
y = x − 6x + 9 x . D. 3 2
y = x + 6 x + 9 x . Lời giải Chọn C
+/ Loại đáp án A vì: 3 2
y = −x + x − x = −( 3 2 6 9
x − 6x + 9x)
+/ Loại đáp án B, vì đồ thị của hàm số 3 2
y = x − 6x + 9x giữ lại phần đồ thị phía trên trục
hoành và chỉ lấy đối xứng phần dưới trục hoành của đồ thị Hình 1.
+/ Loại đáp án D vì hệ số của 2 x khác -6.
+/ Đồ thị ở đáp án C là đồ thị của hàm số dạng y = f ( x ) . Chọn đáp án C Page 52
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 103: Cho hàm số x y
có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong các đáp án 2x 1 A, B, C, D dưới đây? x A. x y x x  . B. y C. y D. y 2x 1 2 x 1 2 x 1 2 x 1 Lời giải Chọn A
Câu 104: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Lời giải Chọn D Ta có: 3 2
y = x − x + = (x − )( 2 3 2
1 x − 2x − 2)
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy x ≥1+ 3
Toàn bộ đồ thị ứng với  được giữ nguyên. x ≤1− 3
Phần đồ thị ứng với 1− 3 ≤ x ≤1+ 3 lấy đối xứng qua trục hoành.
Câu 105: Cho hàm số 3 2
y = x − 3x + 2 có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? Page 53
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = x − 3x + 2 . B. 3 2
y = x − 3x + 2
C. y = x − ( 2
1 x − 2x − 2).
D. y = (x − ) 2
1 x − 2x − 2 . Lời giải Chọn A Ta có: 3 2
y = x − x + = (x − )( 2 3 2
1 x − 2x − 2)
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm phía trên Ox được giữ nguyên.
Phần đồ thị phía dưới Ox được lấy đối xứng qua Ox .
Câu 106: Cho hàm số x y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? 2x +1 x x A. x y x = B. y = C. y = D. y = 2 x +1 2 x +1 2x +1 2 x +1 Lời giải Chọn C
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía trên Ox giữ nguyên
Toàn bộ phần phía dưới Ox được lấy đối xứng lên trên
⇒ dạng f (x) .
Câu 107: Cho hàm số −x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? x − 2 Page 54
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ − + x +1 −x +1 A. x 1 y − + = . B. x y = . C. y = D. 1 y = x − 2 x − 2 x − 2 x − 2 Lời giải Chọn C
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng x =1 được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng x =1 lấy đối xứng qua Ox
−x +1, x ≤1 −x +1  Chú ý:  x − 2 y = = x − 2  −x+1 − , x >1  x − 2
Câu 108: Cho hàm số x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? x + 2 + x +1 x +1 A. x 1 y = . B. x + y = . C. y = . D. 1 y = . x + 2 x + 2 x + 2 x + 2 Lời giải Chọn D
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải đường thẳng x = 2 − được giữ nguyên
Toàn bộ đồ thị phía bên trái đường thẳng x = 2
− lấy đối xứng qua Ox
Câu 109: Cho hàm số y = (x − )( 2
1 x − 2x − 3) có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? Page 55
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
A. y = (x − )( 2
1 x − 2x − 3) .
B. y = x − ( 2
1 x − 2x − 3).
C. y = − x − ( 2
1 x − 2x − 3)
D. y = (x − ) 2 1 x − 2x − 3 Lời giải Chọn C
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm bên trái (ứng với x ≤1) đường thẳng x =1 được giữ nguyên
Toàn bộ đồ thị nằm bên phải (ứng với x >1) đường thẳng x =1 được lấy đối xứng qua . Ox
Câu 110: Cho hàm số x +1 y =
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây? −x + 2 + x +1 x +1 A. x 1 y = . B. y = . C. y = . D. x +1 y = . x + 2 x − 2 −x + 2 x + 2 Lời giải Chọn B
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng x = 1
− (ứng với x ≤ 1) − được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng x = 1
− (ứng với x ≤ 1)
− được lấy đối xứng qua trục . Ox
Câu 111: Cho hàm số bx − c y =
( a ≠ 0 và a , b , c∈ ) có đồ thị như hình bên. Khẳng định nào dưới x − a đây đúng? Page 56
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y O x
A. a > 0 , b < 0 , c − ab < 0.
B. a > 0 , b > 0, c − ab < 0.
C. a < 0 , b > 0, c − ab < 0.
D. a < 0 , b < 0 , c − ab > 0 . Lời giải Chọn B
Dựa vào hình vẽ, đồ thị hàm số có tiệm cận ngang y = b > 0, tiệm cận đứng x = a > 0 .
Hàm số nghịch biến trên từng khoảng của tập xác định nên c − ab < 0, đáp án a > 0 , b > 0,
c − ab < 0.
Câu 112: Đường cong hình bên là đồ thị hàm số 4 2
y = ax + bx + c với a , b , c là các số thực. Mệnh đề nào dưới đây đúng?
A. a < 0 , b > 0, c < 0 . B. a < 0 , b < 0 , c < 0 .
C. a > 0 , b < 0 , c < 0 . D. a > 0 , b < 0 , c > 0 . Lời giải Chọn C
Đồ thị hàm số có nhanh cuối cùng hướng lên nên a > 0 .
Đồ thị hàm số có 3 cực trị nên ab < 0 mà a > 0 nên b < 0 .
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên c < 0 . Câu 113: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình bên. Page 57
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y 2 − 1 − O x 1 2 2 −
Mệnh đề nào dưới đây đúng?
A. a > 0,b < 0,c > 0. B. a > 0,b < 0,c < 0. C. a > 0,b > 0,c < 0. D. a < 0,b > 0,c < 0. Lời giải Chọn B
Do đồ thị cắt Oy tại M (0;c) nằm dưới trục Ox nên c < 0 .
Vì lim y = +∞ nên a > 0 . x→±∞
Hàm số có ba điểm cực trị nên ab < 0 ⇒ b < 0
Câu 114: Giả sử hàm số 4 2
y = ax + bx + c có đồ thị là hình bên dưới. y 1 1 − O 1 x
Khẳng định nào sau đây là khẳng định đúng?
A. a > 0, b < 0, c =1. B. a > 0, b > 0, c =1.
C. a < 0, b > 0, c =1. D. a > 0, b > 0, c > 0 . Lời giải Chọn A
Dựa vào đồ thị ta có:
+ Đồ thị hướng lên nên a > 0 , loại đáp án a < 0, b > 0, c =1
+Với x = 0 ⇒ y = c =1nên loại đáp án a > 0, b > 0, c > 0
+Có 3 cực trị nên ab < 0 suy ra b < 0 .
Câu 115: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ y O x
Mệnh đề nào sau đây đúng?
A. a < 0,b > 0,c < 0,d > 0.
B. a > 0,b > 0,c < 0,d > 0 .
C. a < 0,b < 0,c < 0,d > 0.
D. a < 0,b > 0,c > 0,d > 0 . Page 58
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn A
Do đồ thị ở nhánh phải đi xuống nên a < 0 . Loại phương án a > 0,b > 0,c < 0,d > 0
Do hai điểm cực trị dương nên 2b x + x = −
> 0 ⇒ ab < 0 và a < 0 ⇒ b > 0 . Loại 1 2 3a
a < 0,b < 0,c < 0,d > 0 , c x x =
> 0 ⇒ c < 0. Loại phương án a < 0,b > 0,c > 0,d > 0 1 2 3a
Câu 116: Cho hàm số ax − b y =
có đồ thị như hình dưới. x −1 y 1 2 x O 1 − 2 −
Khẳng định nào dưới đây là đúng?
A. b < 0 < a .
B. 0 < b < a .
C. b < a < 0.
D. 0 < a < b . Lời giải Chọn C
Nhìn vào đồ thị ta thấy: Đồ thị hàm số có tiệm cận ngang y = a và tiệm cận đứng x =1.Đồ thị  a =1 
cắt trục hoành tại điểm có hoành độ b
x = >1. Ta có:  1 −  ⇔ b < a = 1 − < 0 . a b  >1 a
Câu 117: Cho hàm số bậc bốn 4 2
y = ax + bx + c(a ≠ 0) có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng? y O x
A. a > 0,b < 0,c < 0 . B. a > 0,b > 0,c < 0 . C. a > 0,b < 0,c > 0. D. a < 0,b > 0,c < 0 . Lời giải Chọn A
Dựa vào hình dáng của đồ thị suy ra a > 0 . Loại a < 0,b > 0,c < 0
Đồ thị hàm số có ba điểm cực trị nên ab < 0 . Loại a > 0,b > 0,c < 0
Giao điểm của đồ thị với trục tung tại điểm có tung độ âm nên c < 0 . Loại a > 0,b < 0,c > 0
Câu 118: Cho hàm số bậc ba 3 2
y = ax + bx + cx + d (a ≠ 0) có đồ thị như hình vẽ Page 59
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y x O
Mệnh đề nào dưới đây đúng?
A. a > 0; b > 0; c > 0; d < 0.
B. a < 0; b > 0; c > 0; d < 0.
C. a < 0; b < 0; c > 0; d < 0.
D. a < 0; b < 0; c < 0; d < 0. Lời giải Chọn B
Từ hình dáng đồ thị cho ta biết a < 0.
Cho x = 0 ⇒ f (0) = d < 0. Ta có 2
y′ = 3ax + 2bx + c (a ≠ 0) . Từ đồ thị hàm số ta thấy hoành độ
hai điểm cực trị trái dấu, suy ra ac < 0 mà theo trên a < 0 ⇒ c > 0.
Từ đồ thị hàm số ta thấy tổng hoành độ cửa cực đại và cực tiểu dương nên 2b −
> 0 ⇒ b > 0. (vì 3a a < 0 )
Câu 119: Cho hàm số 3 2
y = ax + bx + cx + d có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. a < 0,b < 0,c > 0,d < 0 .
B. a < 0,b > 0,c > 0,d < 0 .
C. a < 0,b < 0,c < 0,d < 0 .
D. a < 0,b > 0,c < 0,d < 0 . Lời giải Chọn B 3 2 2
y = ax + bx + cx + d ⇒ y′ = 3ax + 2bx + c .
x < 0 < x
Từ đồ thị ta có: hàm số có hai điểm cực trị 1 2 
, đồ thị cắt trục tung tại điểm có tung độ  x < x  1 2
âm và lim y = −∞ . x→+∞ Page 60
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ a < 0  < a < 0 d 0    d < 0 Suy ra 2bx + x = − > 0 ⇔  . 1 2  3a b > 0   c c > 0 x .x = < 0 1 2  3a
Câu 120: Cho hàm số ax + b y =
có đồ thị như hình bên với a, , b c ∈ .
 Tính giá trị của biểu thức x + c
T = a − 3b + 2c ? A. T = 12 . B. T = 10 . C. T = −9 . D. T = −7 . Lời giải Chọn C
Đồ thị hàm số có x = 1 là tiệm cận đứng nên c = −1.
Đồ thị hàm số có y = −1 là tiệm cận ngang nên a = −1.
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
− nên b = −2 do đó b = 2 . c
Vậy T = a − 3b + 2c = −1− 3.2 + 2(− ) 1 = −9 .
Câu 121: Cho hàm số ( ) 4 2
f x = ax + bx + c với a ≠ 0 có đồ thị như hình vẽ:
Tìm mệnh đề đúng trong các mệnh đề sau?
A. a < 0 ; b > 0; c > 0 . B. a > 0 ; b < 0 ; c > 0 .
C. a < 0 ; b < 0 ; c > 0 . D. a < 0 ; b > 0; c < 0 . Lời giải Chọn A
Ta có nhánh bên phải đồ thị đi xuống, suy ra a < 0 .
Mặt khác do đồ thị có ba cực trị suy ra ab < 0 mà a < 0 ⇒ b > 0 .
Mà giao điểm của đồ thị với trục Oy tại điểm có tung độ y = c > 0 .
Vậy chọn đáp án a < 0 ; b > 0; c > 0 . Page 61
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 122: Từ đồ thị hàm số 4 2
y = ax + bx + c ( a khác 0 ) được cho dạng như hình vẽ, ta có
A. a > 0 , b < 0 , c < 0 . B. a > 0 , b > 0, c < 0 .
C. a < 0 , b > 0, c < 0 . D. a > 0 , b < 0 , c > 0 . Lời giải Chọn A
Đồ thị có dạng quay lên nên a > 0 .
Đồ thị hàm số cắt trục tung tại điểm có tung độ nhỏ hơn 0 nên c < 0 .
Do đồ thị hàm số có ba điểm cực trị nên .
a b < 0 ⇒ b < 0.
Câu 123: Bảng biến thiên trong hình bên dưới của hàm số nào dưới đây? A. x −1 y = . B. 4 2
y = x − 2x − 3 . C. 3
y = −x + 3x + 2. D. 3
y = x − 3x + 4. 2x −1 Lời giải Chọn C
Theo bảng biến thiên ta có hàm số là một hàm có hai cực trị và có lim y = −∞ nên chọn đáp án x→+∞ 3
y = −x + 3x + 2.
Câu 124: Bảng biến thiên dưới đây là của hàm số nào? A. 2x +1 y − + + = . B. x 1 y = . C. x 1 y = . D. x 3 y = . x − 2 2x + 2 x − 2 2 + x Page 62
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số có tập xác định D =  \{ }
2 và lim y =1 nên hàm số x→+∞ phải là x +1 y = . x − 2
Câu 125: Hàm số nào trong bốn hàm số sau có bảng biến thiên như hình vẽ bên? A. 3
y = x − 3x + 2. B. 3 2
y = −x + 3x −1. C. 3 2
y = x − 3x + 2. D. 3 2
y = x + 3x −1. Lời giải Chọn C
* Từ BBT ta thấy đây là BBT của hàm bậc ba 3 2
y = ax + bx + cx + d .
* Nhánh đầu tiên đi lên nên a > 0 ta loại trừ đáp án 3 2
y = −x + 3x −1 x = 0
* Phương trình y′ = 0 ⇔  ta loại trừ đáp án 3
y = x − 3x + 2 và 3 2
y = x + 3x −1 x = 2 Đáp án đúng là 3 2
y = x − 3x + 2
Câu 126: Cho bảng biến thiên như hình vẽ bên. Hỏi đây là bảng biến thiên của hàm số nào trong các hàm số sau? A. −x + 2 y + + − = . B. x 2 y = . C. x 2 y = . D. x 3 y = . x −1 x −1 x +1 x −1 Lời giải Chọn C
Từ bảng biến thiên ta có đồ thị hàm số có đường tiệm cận đứng là x =1 và đường tiệm cận ngang là − + +
y =1 nên ta loại các đáp án x 2 y = và x 2 y = x −1 x +1
Mặt khác từ bảng biến thiên ta có hàm số nghịch biến nên lọai đáp án x − 3 y = x −1
Câu 127: Bảng biến thiên sau là của hàm số nào? Page 63
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ A. 3 2
y = −x − 3x −1. B. 3 2
y = −x + 3x −1 . C. 3 2
y = x + 3x −1. D. 3 2
y = x − 3x −1. Lời giải Chọn B
* Bảng biến thiên này là bảng biến thiên của hàm bậc ba.
* Nhánh đầu tiên của bảng biến thiên đi xuống nên ta loại 3 2
y = x + 3x −1 và 3 2
y = x − 3x −1.
* Phương trình y′ = 0 có hai nghiệm là x = 0 và x = 2 nên ta loại đáp án 3 2
y = −x − 3x −1. * Đáp án đúng là 3 2
y = −x + 3x −1 .
Câu 128: Cho hàm số y = f (x) có bảng biến thiên
Hỏi hàm số đó là hàm nào? A. −x + 2 y + − − − = . B. x 2 y = . C. x 2 y = . D. x 2 y = . 2x −1 2x −1 2x −1 2x −1 Lời giải Chọn D
Dựa vào bảng biến thiên suy ra đồ thị hàm số y = f (x) có tiệm cận đứng 1
x = , tiệm cận ngang 2 1 y −
= và hàm số đồng biến trên từng khoảng xác định. Do đó chọn x 2 y = . 2 2x −1
Câu 129: Bảng biến thiên dưới đây là của hàm số nào? A. 2x +1 y − + + = . B. x 1 y = . C. x 1 y = . D. x 3 y = . x − 2 2x + 2 x − 2 2 + x Lời giải Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số có tập xác định D =  \{ }
2 và lim y =1 nên hàm số x→+∞ phải là x +1 y = x − 2
Câu 130: Cho hàm số y = f ( x) có bảng biến thiên như sau: Page 64
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ x – ∞ 2/3 + ∞ y' + + + ∞ 2/3 y 2/3 – ∞
Hàm số y = f (x) là hàm số nào dưới đây? A. 2x + 3 y − + − = . B. 3x 3 y = C. 2x 3 y = . D. 2x 3 y = . 2x − 3 2x − 3 3x + 2 3x − 2 Lời giải Chọn D
Dựa vào bảng biến thiên ta thấy đồ thị hàm số có 1 tiệm cận đứng 2
x = và 1 tiệm cận ngang là 3 2 y = . 3
Câu 131: Bảng biến thiên như hình vẽ bên là của hàm số nào trong các hàm số sau? A. 3
y = x + 3x −1. B. 3
y = x − 3x −1. C. 3
y = −x + 3x + 3 . D. 4 2
y = x − 2x + 2 . Lời giải Chọn B
Đồ thị hàm số là hàm bậc ba và có hướng đi lên nên loại 3
y = −x + 3x + 3 ., 4 2
y = x − 2x + 2 .
Hàm số có hai điểm cực trị x = 1
− và x =1 trái dấu . a c < 0 nên loại 3
y = x + 3x −1. Đáp án 3
y = x − 3x −1 đúng.
Câu 132: Cho hàm số 3 2
y = x − 6x + 9x có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong bốn
đáp án A, B, C, D dưới đây? y y 4 4 x O 1 3 x -3 -1 O 1 3 Hình 1 Hình 2 A. 3 2
y = −x + 6x − 9 .x B. 3 2
y = x + 6 x + 9 x . C. 3 2
y = x − 6x + 9x D. 3 2
y = x − 6x + 9 x . Lời giải Page 65
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Chọn D
Nhắc lại lí thuyết: Đồ thị hàm số y = f ( x ) được suy ra từ đồ thị hàm số y = f (x) bằng cách
● Giữ nguyên phần đồ thị hàm số y = f (x) với x ≥ 0.
● Sau đó lấy đối xứng phần đồ thị vừa giữ ở trên qua trục Oy .
Câu 133: Cho hàm số 3 2
y = x + 3x − 2 có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào dưới đây? y y 2 x 2 -2 -1 O 1 3 x -2 -3 -2 -1 O 1 Hình 1 Hình 2 A. 3 2
y = x + 3 x − 2. B. 3 2
y = x + 3x − 2 . C. 3 2
y = x + 3x − 2 . D. 3 2
y = −x − 3x + 2. Lời giải Chọn B
Nhắc lại lí thuyết: Đồ thị hàm số y = f (x) được suy ra từ đồ thị hàm số y = f (x) bằng cách
● Giữ nguyên phần đồ thị hàm số y = f (x) với y ≥ 0.
● Lấy đối xứng phần đồ thị hàm số y = f (x) với y < 0 qua trục . Ox
Câu 134: Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số 2 4
y = 2x − x +1 ? y y 2 -1 O 1 1 x -1 -1 O 1 x -2 A B y y -1 O 1 2 x -1 1 -1 -2 O 1 x C D Page 66
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải Chọn D Ta có 2 4
y = 2x − x +1 ≥ 0, x ∀ ∈  
→ đồ thị luôn nằm phía trên trục hoành.
Câu 135: Cho hàm số x y =
có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong các đáp án 2x +1 A, B, C, D dưới đây? y y 1 1 2 2 1 O x 1 Ox  2 2 Hình 1 Hình 2 x x A. x y x = . B. y = . C. y = . D. y = . 2x +1 2 x +1 2 x +1 2 x +1 Lời giải Chọn A
Câu 136: Cho hàm số x + 2 y =
có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong các đáp án 2x −1 A, B, C, D dưới đây? y y 1 1 2 2 -2 O 1 x -2 O 1 x 2 2 -2 -2 Hình 1 Hình 2 x + 2 x + 2 A. x + 2 y  + = − x  . B. y = C. 2 y = . D. y = .  2x −1 2 x −1 2x −1 2x −1 Lời giải Chọn B Page 67
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ y
Câu 137: Đồ thị hàm số 2x −1 y = có x −1
đồ thị như hình bên. Hỏi đồ 2x −1
thị hàm số y = có đồ 2 x −1
thị là hình nào trong các đáp 1 án sau: O 1 1 x 2 A B y y 2 2 1 1 2 O 1 1 x O 1 x 2 C D y y 2 2 1 1 1 2 O 1 x O 1 1 x 2 Lời giải Chọn C 2x −1 1 khi 2 1 x x ≥ −  Ta có  x −1 2 y = =  . x −1 2x −1 1 − khi x <  x −1 2 2x −1
Do đó đồ thị hàm số y =
được suy từ đồ thị hàm số 2x −1 y = bằng cách: x −1 x −1
● Giữ nguyên phần đồ thị hàm số 2x −1 y =
phía bên phải đường thẳng 1 x = . x −1 2
● Phần đồ thị hàm số 2x −1 y =
phía bên trái đường thẳng 1
x = thì lấy đối xứng qua trục hoành. x −1 2 2x −1
Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số y = . x −1 Page 68
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 138: Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số x y = ? x −1 y y 1 1 O 1 x O 1 x A B y y 1 1 O O 1 x 1 x C D Lời giải Chọn B
x khi x >1  Ta có xx −1 y = =  . x −1 x − khi x <1  x −1 Do đó đồ thị hàm số x y =
được suy từ đồ thị hàm số x y = bằng cách: x −1 x −1
● Giữ nguyên phần đồ thị hàm số x y =
phía bên phải đường thẳng x =1. x −1
● Phần đồ thị hàm số x y =
phía bên trái đường thẳng x =1 thì lấy đối xứng qua trục hoành. x −1
Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số x y = . x −1 Câu 139: Hàm số y 3 2
y = ax + bx + cx + d có đồ 2
thị như hình vẽ bên. Mệnh đề nào sau đây là đúng? x 1 A. a > 0, b > 0, 0, c < d > 0 . -1 O B. a < 0, b < 0, c < 0, d < 0 . C. a > 0, b < 0, c < 0, d > 0 . D. a > 0, b > 0, 0, c > d < 0 . Lời giải Page 69
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Chọn C
Đồ thị hàm số thể hiện a > 0 ; cắt trục tung tại điểm có tung độ dương nên d > 0 . x + x > 0 Hàm số có CD CT 1 − < x < 0, x >1 → . (*) CD CT x .x <  0 CD CT  2b b a>0 − > 0 
→ < 0 →b < 0  Ta có 2
y′ = 3ax + 2bx + c = 0. Do đó ( )  3 * a a ↔  . c ca>0 < 0 
→ < 0 →c < 0 3a a Vậy a > 0, b < 0, c < 0, d > 0. Câu 140: Hàm số y 3 2
y = ax + bx + cx + d có đồ
thị như hình vẽ bên. Mệnh đề nào sau đây là đúng? x A. a < 0, b > 0, 0, c > d > 0. -1 O 1 B. a < 0, b < 0, c < 0, d > 0. C. a < 0, b < 0, 0, c > d > 0. D. a < 0, b > 0, 0, c < d > 0. Lời giải Chọn A
Đồ thị hàm số thể hiện a < 0 ; cắt trục tung tại điểm có tung độ dương nên d > 0 . x + x > 0 Hàm số có CD CT x >1,
−1< x < 0  → . (*) CD CT x .x <  0 CD CT  2b b a<0 − > 0 
→ < 0 →b > 0  Ta có 2
y′ = 3ax + 2bx + c = 0. Do đó ( )  3 * a a ↔  . c ca<0 < 0 
→ < 0 →c > 0 3a a Vậy a < 0, b > 0, 0, c > d > 0. Câu 141: Hàm số 4 2
y = ax + bx + c có y
đồ thị như hình vẽ bên. Mệnh
đề nào sau đây là đúng? x A. a > 0, b > 0, 0 c < . O B. a > 0, b < 0, c < 0. C. a > 0, b < 0, 0 c > . D. a < 0, b > 0, 0 c < . Lời giải Chọn C
Đồ thị hàm số thể hiện a > 0.
Đồ thị hàm số có ba điểm cực trị nên a>0
ab < 0 →b < 0.
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên c > 0. Vậy a > 0, b < 0, 0 c > . Page 70
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Câu 142: Hàm số 4 2
y = ax + bx + c có y
đồ thị như hình vẽ bên. Mệnh
đề nào sau đây là đúng? x O A. a < 0, b > 0, 0 c > . B. a < 0, b > 0, 0 c < . C. a < 0, b < 0, 0 c > . D. a < 0, b < 0, c < 0. Lời giải Chọn B
Đồ thị hàm số thể hiện a < 0.
Đồ thị hàm số có ba điểm cực trị nên ab < 0  →b > 0.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên c < 0. Vậy a < 0, b > 0, 0 c < . Câu 143: Hàm số 4 2
y = ax + bx + c ( 0 a ≠ ) có đồ y
thị như hình vẽ bên. Mệnh đề nào sau đây là đúng? x O A. a > 0, b ≥ 0, c < 0. B. a > 0, b < 0, c ≤ 0. C. a > 0, b ≥ 0, 0 c > . D. a < 0, b < 0, c < 0. Lời giải Chọn A
Dựa vào dáng điệu đồ thị suy ra a > 0 .
Hàm số có 1 điểm cực trị nên a>0
ab ≥ 0 →b ≥ 0.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên c < 0. Vậy a > 0, b ≥ 0, c < 0. y Câu 144: Hàm số ax + b y = với a > 0 cx + d
có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây là đúng? O x A. b > 0, 0, c > d < 0. B. b > 0, c < 0, d < 0. C. b < 0, c < 0, d < 0. D. b < 0, 0, c > d < 0. Lời giải Chọn A
Từ đồ thị hàm số, ta thấy ● Khi b a>0 y = 0 
→ x = − < 0 →b > 0. a ● Khi b b>0 x = 0 
→ y = < 0 →d < 0. d Page 71
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Đồ thị hàm số có tiệm cận đứng d d <0
x = − > 0 →c > 0. c Vậy b > 0, 0, c > d < 0. y Câu 145: Hàm số bx − c y = (a ≠ 0; x − a
a, b, c∈) có đồ thị như
hình vẽ bên.Mệnh đề nào sau O x đây là đúng? A. a > 0, 0, b >
c − ab < 0. B. a > 0, 0, b >
c − ab > 0. C. a > 0, 0, b >
c − ab = 0. D. a > 0, 0, b <
c − ab < 0. Lời giải Chọn A
Đồ thị hàm số có tiệm cận đứng x = a > 0 ; tiệm cận ngang y = b > 0.
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên c − ab y′ = < 0, x ∀ ≠ a 
→c − ab < 0. (x − a)2 Vậy a > 0, 0, b >
c − ab < 0.
Câu 146: Đồ thị hàm số 4 2
y = ax + bx + c cắt trục hoành tại bốn điểm ,
A B,C, D phân biệt như hình vẽ bên.
Biết rằng AB = BC = CD , mệnh đề nào sau đây là đúng? A. 2
a > 0, b < 0, c > 0,100b = 9ac . B. 2
a > 0, b > 0, c > 0, 9b =100ac . C. 2
a > 0, b < 0, c > 0, 9b =100ac . D. 2
a > 0, b > 0, c > 0,100b = 9ac . Lời giải Chọn A
Đồ thì hàm số quay lên nên a > 0 .
Đồ thị hàm số có ba điểm cực trị nên b < 0 .
Đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên c > 0 . Page 72
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Đồ thị hàm số cắt trục hoành tại 4 điểm A(− x ;0 , B(− x ;0 , C( x ;0 và A( x ;0 . 1 ) 2 ) 2 ) 1 )
Mà AB = BC = CD ⇔ − x + x = 2 x ⇔ x = 3 x ⇔ x = 9x . 1 2 1 2 1 2 1  bb x + x = − x = −  1 2  1 a 10a   Khi đó:  c  9b b 9bx x = ⇔ x = − 2 1 2 2 ⇔ .
= c ⇔ 9b =100ac a 10a   10a 10ax = 9xx x = c 2 1 1 2    
Câu 147: Biết rằng hàm số 4 2
y = f (x) = ax + bx + c có đồ thị là đường cong như hình vẽ bên.
Tính giá trị f (a + b + c) .
A. f (a + b + c) = 1 − .
B. f (a + b + c) = 2 .
C. f (a + b + c) = 2 − .
D. f (a + b + c) =1. Lời giải Chọn A
Dựa vào đồ thị hàm số ta có: điểm cực tiểu và cực đại của đồ thị hàm số là A(1;− ) 1 , B(0; ) 1 . Ta có: 3
y′ = 4ax + 2bx
a + b + c = 1 − a = 2   Do đó: 4 2 c =1 ⇔ b  = 4
− ⇒ y = 2x − 4x +1 4a 2b 0  + = c =   1
Mà a + b + c = 1
− ⇒ f (a + b + c) = f (− ) 1 = 1 −
Câu 148: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Page 73
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Mệnh đề nào dưới đây là đúng?
A. a > 0, b < 0, c > 0 . B. a < 0, b > 0, c < 0 . C. a > 0, b > 0, c > 0 . D. a > 0, b < 0, c < 0 . Lời giải. Chọn B
Dựa vào đồ thi hàm số ta có: a < 0,b > 0 (do hàm số có 3 cực trị ) và c < 0 .
Câu 149: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây là đúng?
A. a > 0, b < 0, c < 0 . B. a < 0, b > 0, c > 0 . C. a > 0, b > 0, c > 0 . D. a > 0, b < 0, c > 0 . Lời giải. Chọn D
Dựa vào đồ thi hàm số ta có: a > 0,b < 0 (do hàm số có 3 cực trị ) và c > 0 .
Câu 150: Cho hàm số 4 2
y = ax + bx + c có đồ thị như hình vẽ bên. Page 74
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Kết luận nào sau đây là đúng?
A. a < 0, b ≤ 0, c > 0 . B. a < 0, b < 0, c < 0 . C. a > 0, b > 0, c > 0 . D. a < 0, b > 0, c ≥ 0 . Lời giải. Chọn A
Dựa vào đồ thi hàm số ta có: a < 0,b ≤ 0 (do hàm số có 1 cực trị ) và c > 0 .
Câu 151: Cho hàm số 4 2
f (x) = ax + bx + c có đồ thị của hàm số như hình vẽ bên. Kết luận nào sau đây là đúng?
A. a > 0, b < 0, c > 0 . B. a < 0, b < 0, c > 0 . C. a < 0, b > 0, c > 0 . D. a < 0, b > 0, c < 0 . Lời giải. Chọn C
Dựa vào đồ thị hàm số ta có: a < 0,b > 0,c > 0
Câu 152: Đồ thị hàm số y = f (x) = ax4 + bx2 + c như hình vẽ dưới đây.
Khẳng định nào sau đây là đúng?
A. a > ;b > ;c > ;b2 0 0 0 = 4ac .
B. a > ;b < ;c > ;b2 0 0 0 = 4ac .
C. a > ;b > ;c > ;b2 0 0 0 > 4ac .
D. a > ;b > ;c > ;b2 0 0 0 < 4ac . Page 75
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Lời giải. Chọn B
Dựa vào đồ thị hàm số, ta nhận xét a > 0 và ab < 0 ⇒ b < 0 (Do hàm số có 3 cực trị)
Dựa vào 4 đáp án, ta Chọn B
Câu 153: Hình vẽ bên là đồ thị của hàm số y = ax4 + bx2 + c . Giá trị của biểu thức A = a2 + b2 + c2 có thể
nhận giá trị nào trong các giá trị sau? A. A = 24. B. A = 20. C. A = 18 .
D. A = 6. Lời giải. Chọn C x = 0
Ta có y ax4 bx2 c y ' 4ax3 2 ; bx y '  = + + ⇒ = + = 0 ⇔ . 2 bx = −  2a
Dựa vào đồ thị hàm số, ta có a < 0;b > 0 .
Gọi đồ thị hàm số đã cho là (C). Dựa vào đồ thị hàm số ta có: +I ( − )∈(C) 4 2 0; 1 ⇒ .0 a + .0 b + c = 1 − ⇒ c = 1 − . + A(1;2) (C) 4 2 c= 1 .1 a .1 b c 2 a b c 2 − ∈ ⇒ + + = ⇔ + + = ←
→a + b = 3 ⇔ a = 3− b .
+ Giá trị cực đại của hàm số bằng 3 nên ta có: 2  b   b c= 1 − 2 . a − + . b − + c = 3← →b = 16 −     a(*) .  2a   2a  b = 4
Thế a = 3− b vào (*) ta được: 2
b −16b + 48 = 0 ⇔  . b = 12
Với b = 4 ⇒ a = 1
− (thỏa mãn điều kiện a < 0 ). Khi đó A = a2 + b2 + c2 = 18 ⇒ Chọn C
Câu 154: Hàm số y = f (x) = ax4 + bx2 + c có bảng biến thiên như hình vẽ dưới đây.
Tính giá trị của biểu thức P = 2 + b 2 + 3c
A. P = −15.
B. P = 15 .
C. P = −8 .
D. P = 8 . Lời giải. Page 76
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ Chọn A
Ta có y = ax4 + bx2 + c ⇒ y ' = ax3 4 + 2 ; bx .
Gọi đồ thị hàm số đã cho là (C). Dựa vào BBT ta có: +I ( − )∈(C) 4 2 0; 3 ⇒ .0 a + .0 b + c = 3 − ⇒ c = 3 − ( ) 1 .
+ Hàm số đạt cực tiểu tại x = 1 ± ⇒ y '( )
1 = 0 ⇔ 4a + 2b = 0 (2) .
+ Hàm số có cực đại y = − ⇒ a + b + c = − (3) . CD 5 5 Giải hệ ( )
1 ,(2),(3) ta được: a = 2,b = 4, − c = 3
− . Vậy P = 2 + b 2 + 3c = −15 . Page 77
Document Outline

  • 001_01_13_GT12_BAI 5_DTHS_TỰ LUẬN_HDG_CHI TIẾT
    • A. SƠ ĐỒ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
    • B. CÁC DẠNG ĐỒ THỊ CỦA CÁC HÀM SỐ THƯỜNG GẶP
    • MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
    • MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
    • MỘT SỐ VÍ DỤ VỀ BÀI TOÁN KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
    • C. MỘT SỐ PHÉP BIẾN ĐỔI ĐỒ THỊ
  • 001_01_14_GT12_BAI 5_DTHS_TRẮC NGHIỆM BỘ_DE
  • 001_01_14_GT12_BAI 5_DTHS_TRẮC NGHIỆM BỘ_HDG
  • 001_01_15_GT12_BAI 5_DTHS_BÀI TẬP TRẮC NGHIỆM(MUC5-6)_DE
    • DẠNG. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
    • DẠNG 2. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ
    • DẠNG 2. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI
  • 001_01_15_GT12_BAI 5_DTHS_BÀI TẬP TRẮC NGHIỆM(MUC5-6)_HDG
    • DẠNG. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
    • DẠNG 2. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ
    • DẠNG 2. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI (BIẾN ĐỔI ĐỒ THỊ)
  • 001_01_15_GT12_BAI 5_DTHS_BÀI TẬP TRẮC NGHIỆM_HDG_CHI TIẾT
    • DẠNG 1. NHẬN DẠNG HÀM SỐ THƯỜNG GẶP THÔNG QUA ĐỒ THỊ
    • DẠNG 1. XÉT DẤU CỦA CÁC HỆ SỐ HÀM SỐ THÔNG QUA ĐỒ THỊ
    • DẠNG. ĐỒ THỊ HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI (BIẾN ĐỔI ĐỒ THỊ)