
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 43
BÀI 2. TÍCH PHÂN
Định nghĩa: Cho hàm số
f
liên tục trên khoảng
K
và
,ab
là hai số bất kì thuộc
K
. Nếu
F
là một nguyên hàm của
f
trên
K
thì hiệu số
( ) ( )
Fb Fa−
được gọi là tích phân của hàm số
f
từ
a
đến
b
và kí hiệu là
( )
d
b
a
fx x
∫
.
Ta gọi:
a
là cận dưới,
b
là cận trên,
f
là hàm số dưới dấu tích phân,
( )
dfx x
là biểu thức
dưới dấu tích phân,
x
biến số lấy tích phân.
Nhận xét :
a) Nếu
ab
<
thì ta gọi
( )
d
b
a
fx x
∫
là tích phân của
f
trên đoạn
[
]
;.ab
b) Hiệu số
(
) ( )
Fb Fa−
còn được kí hiệu là
( )
b
a
Fx
. Khi đó :
( ) ( )
( ) ( )
d.
b
b
a
a
f x x Fx Fb Fa= = −
∫
c) Tích phân không phụ thuộc biến số (điều này sẽ mang lại lợi ích cho ta để tính một số tích
phân đặc biệt), tức là
( ) ( ) ( ) ( ) ( )
d d d ... .
b bb
a aa
fx x ft t fu u Fb Fa= = = = −
∫ ∫∫
Tính chất: Cho
k
là hằng số
[ ]
) () 0 ) () ()
c) .() () ) () () () ()
a ba
a ab
b b b bb
a a a aa
a f x dx b f x dx f x dx
k f x dx k f x dx d f x g x dx f x dx g x dx
= = −
= += +
∫ ∫∫
∫ ∫ ∫ ∫∫
e) Tính chất chèn cận:
() () ()
b cb
a ac
f x dx f x dx f x dx= +
∫∫∫
(chèn cận
c
)
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
LÝ THUYẾT.
I

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 44
DẠNG 1: SỬ DỤNG ĐỊNH NGHĨA TÍCH PHÂN
Câu 1: Tính các tích phân sau:
1 4 ln 2
4
2
0100
1
) 3 d ) d ) 2 d ) sin d
x
a I x x bI x cI x d I xx
x
π
= = = =
∫∫∫∫
Câu 2: Gọi
( )
Fx
là nguyên hàm của hàm số
( )
x
fx e=
. Tính
( ) ( )
2 2 2.F ln F ln−
Câu 3: Gọi
( )
Fx
là nguyên hàm của hàm số
( )
1
fx
x
=
thỏa điều kiện
( )
12F =
. Tính
( )
Fe
.
Câu 4: Chứng minh
( )
(
)
2
ln 1Fx x x= ++
là một nguyên hàm của hàm số
( )
2
1
1
fx
x
=
+
. Từ đó
tính tích phân
1
2
0
1
d.
1
Ix
x
=
+
∫
Câu 5: Chứng minh
( )
1
ln
ax b
Fx
ad bc cx d
+
=
−+
là một nguyên hàm của hàm số
( )
( )
( )
1
fx
ax b cx d
=
++
. Từ đó tính tích phân
(
)( )
1
0
1
d.
21 1
Ix
xx
=
++
∫
DẠNG 2: SỬ DỤNG TÍNH CHẤT TÍCH PHÂN
Câu 6: Tính các tích phân sau:
( )
( )
12
3
0 10
1
) 4 d ) 3 d ) sin 2cos d
xx
aI x e x bI x cI x x x
x
=−=− =+
∫∫∫
π
Câu 7: Tính
( )
22
11
ln d 1 ln d .
xt
I e xx e t t= +−
∫∫
Câu 8: Tính
2
2
sin ln d sin sin d .
2 22
t uu
I t t lnu u
= +−
∫∫
π
π
π
π
DẠNG 3: SỬ DỤNG TÍNH CHẤT CHÈN CẬN ĐỂ TÍNH TÍCH PHÂN
Tích phân của hàm chứa dấu trị tuyệt đối
a) Yêu cầu: Tính tích phân
()
b
a
I f x dx=
∫
b) Phương pháp:
+ Bước 1: Xét dấu của
( )
fx
trên khoảng
( )
;ab
- Giải phương trình
( ) ( )
0;
i
f x x x ab=⇔=∈
- Lập bảng xét dấu của
( )
fx
trên khoảng
( )
;ab
+ Bước 2: Chèn cận
i
x
và đồng thời bỏ dấu
(căn cứ vào BXD) ta được các tích phân cơ bản
( ) ( ) ( )
ddd
i
i
x
bb
a ax
I fx x fx x fx x= = +
∫∫∫
Chú ý: Nếu
( )
fx
không đổi dấu trên đoạn
[ ]
;ab
thì
( ) ( )
dd
bb
aa
I fx x fx x= =
∫∫
Câu 9: Tính các tích phân:
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 45
2 32 2
22
0 04 2
) 1d ) d ) 2 3d ) 2 1 daIxx bIxxxcxx x dxx x
−−
= − = − + − −+
∫ ∫∫ ∫
Câu 10: Tính
0
1 cos 2 dI xx= −
∫
π
.
Câu 11: Tính
2
0
1 sin 2
d.
2
x
Ix
−
=
∫
π
Tích phân của hàm min, max
a) Yêu cầu: Tính tích phân
(
)
( )
{
}
min ;g d
b
a
I fx x x
=
∫
;
( ) ( )
{ }
max ;g d
b
a
I fx x x=
∫
b) Phương pháp: Tính
( ) ( )
{ }
min ;g d
b
a
I fx x x=
∫
(
( ) ( )
{ }
max ;g d
b
a
I fx x x=
∫
tương tự)
+ Bước 1: Xét dấu của
( )
()fx gx−
trên khoảng
( )
;ab
- Giải phương trình
( ) ( )
() 0 ;
i
f x g x x x ab− =⇔=∈
- Lập bảng xét dấu của
( )
()fx gx−
trên khoảng
( )
;ab
+ Bước 2: Chèn cận
i
x
và chọn hàm
( ) ( )
{ }
min ;gfx x
như sau:
- Nếu
( ) ( )
0f x gx−>
trên khoảng
K
thì
(
)
( )
{ }
( )
min ;g
f x x gx=
.
- Nếu
( ) ( )
0f x gx−<
trên khoảng
K
thì
( ) ( )
{ }
( )
min ;gfx x fx=
.
Từ đó, ta được các tích phân cơ bản.
Câu 12: Tính
{ }
2
2
0
min ; d .I xx x=
∫
Câu 13: Tính
{
}
1
1
max ;2 d .
xx
I ex
−
=
∫
Tích phân của hàm số xác định trên từng khoảng
Câu 14: Cho hàm số
( )
2
khi 0
khi 0
xx
y fx
xx
≥
= =
−≤
. Biết hàm số
f
liên tục trên
.
Tính
(
)
1
1
.I fx
−
=
∫
Câu 15: Cho hàm số
( )
( )
3
2 1 khi 1
2 1 khi 1
x
xx
y fx
x
−≥
= =
−≤
. Biết hàm số
f
liên tục trên
.
Tính
( )
3
2
d.I fx x
−
=
∫
Câu 16: Cho hàm số
( )
( )
( )
2
2 1 khi 0
1 khi 0
xx
y fx
kx x
− + ≤
= =
−≥
. Xác định
k
để
( )
1
1
d1fx x
−
=
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 46
MỘT SỐ DẠNG KHÁC
Câu 17: Cho
( ) ( )
25
12
d 3, d 4fx x fx x= =
∫∫
. Tính
( )
5
1
d.
I fx x=
∫
Câu 18: Gọi
( )
Fx
là nguyên hàm của hàm số
( )
fx
.
Biết
( )
( )
33
01
d 12, d 2fx x fx x= =
∫∫
và
( )
27F =
. Tính
( )
0.F
Câu 19: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
thỏa mãn
( )
10
0
d7fx x=
∫
;
( )
6
2
d3fx x=
∫
. Tính giá
trị của biểu thức
(
) (
)
2 10
06
d d.P fx x fx x= +
∫∫
DẠNG 4: SỬ DỤNG ĐỊNH NGHĨA TÍCH PHÂN VÀO CÁC BÀI TOÁN KHÁC
Câu 20: Cho hàm số
( )
2
sin d
x
x
g x t tt=
∫
xác định với
0
x
>
. Tìm
( )
gx
′
.
Câu 21: Cho hàm số
( )
3
2
2
2
1
d
1
x
x
t
gx t
t
−
=
+
∫
. Tìm
( )
.gx
′
Câu 22: Cho hàm số
f
và số thực
0a >
thỏa mãn điều kiện:
( )
2
d 62
x
a
ft
tx
t
+=
∫
với
0x >
.
Tìm
a
và
f
.
DẠNG 5: PHƯƠNG PHÁP ĐỔI BIẾN SỐ LOẠI 1 ĐỂ TÍNH TÍCH PHÂN
Yêu cầu : Tính tích phân
( ) ( )
12
d
b
a
I f xf x x=
∫
Phương pháp:
+ Biến đổi về dạng
( ) ( )
d.
b
a
I f ux u x x
′
=
∫
+ Đặt
(
) ( )
d d.tux tuxx
′
= ⇒=
+ Đổi cận:
( )
( )
12
;.xa tua txb tub t= ⇒= = = ⇒= =
+ Khi đó:
( )
2
1
d
t
t
I ft t=
∫
là tính phân đơn giản hơn.
Một số dấu hiệu cơ bản và cách chọn
( )
t ux=
Dấu hiệu
Cách chọn
t
Hàm số chứa mẫu số
t
là mẫu số
Hàm số chứa căn
( )
, ()f x ux
t
là căn:
()t ux=
Hàm số có dạng
[
]
()
n
fx
(xấu)
lũy thừa
t
là biểu thức (xấu) trong lũy thừa,
()t fx=
Hàm số lượng giác có góc xấu
t
là góc xấu
Hàm số mũ, mà mũ xấu
t
là mũ xấu
Hàm số
log u
mà
u
xấu
tu=

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 47
Hàm số
sin cos
()
sin cos
a xb x
fx
c xd xe
+
=
++
tan cos 0
22
xx
t
= ≠
Hàm
(
)(
)
1
()fx
xaxb
=
++
Tổng quát đặt
t xa xb= ++ +
+ Với
00xa xb+> ∧+>
, đặt
t xa xb= ++ +
+ Với
00xa xb+< ∧ +<
, đặt
(
)
(
)
t xa xb=−++−+
(cos ).sinR x xdx
(theo biến
cos x
)
Đặt
costx=
(sin ).cosR x xdx
(theo biến
sin x
)
Đặt
sintx=
2
1
(tan ).
cos
R x dx
x
(theo biến
tan x
)
Đặt
tantx=
2
1
(cot ).
sin
R x dx
x
(theo biến
cot x
)
Đặt
cottx=
Hàm có
,
xx
ea
Đặt
,
xx
t et a= =
Hàm số vừa có
ln x
vừa có
1
x
Đặt
ln
tx
=
Câu 23: Tính các tích phân sau
( )
( )
( )( )
2
2
2
2
2
cos
3
10
4
11 1
2017
2
2 2017
00 0
tan
42 2
3
2
00 0
31 1
) d ) sin 2 d ) 1 sin d
46
) d ) 4d ) 1 1 d
( 3 1)
cos
) d ) sin .cos d ) d
cos cos sin
xx
x
x
a x b x x c xe x
xx
x
x
d x e xx x f x x x
xx
e xx
g x h x xx i x
x xx x
π
π
π
ππ π
−
+
++
+
+
+ +−
++
+
∫∫ ∫
∫∫ ∫
∫∫ ∫
Câu 24: Tính các tính phân sau (Đặt giảm bậc)
( )
31
2
4
2
3
3
20
2 61
)d ) d
1
29
xx
ax b x
x
xx
−
−
−−
∫∫
Tích phân có sẵn dạng
( )
(
)
fux
Câu 25: Chứng minh rằng
( ) ( )
22
11
1
dd
x ax b
x ax b
I f ax b x f x x
a
+
+
= +=
∫∫
, với
0a ≠
.
Câu 26: Cho hàm số
( )
fx
liên tục trên
và
( )
7
3
d 2.fxx=
∫
Tính
( )
3
1
21.I f x dx= +
∫
Câu 27: Cho hàm số
( )
fx
liên tục trên
và
( )
4
1
1 2 d 2.f xx−=
∫
Tính
( )
1
7
.I f x dx
−
−
=
∫
Câu 28: Cho hàm số
( )
fx
liên tục trên
và
( )
3
1
3 1 d 3.fx x−=
∫
Tính
( )
0
6
2.I f x dx
−
= −
∫
Câu 29: Cho
( )
1
0
d2fxx=
∫
Tính
( )
4
0
cos 2 sin cos d .I f x x xx=
∫
π

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 48
Tích phân với hàm số chẵn và lẻ
+ Hàm số
( )
y fx=
là hàm số chẵn trên đoạn
[ ]
;aa−
khi và chi khi
[ ]
;
x aa∀∈−
ta có:
[ ]
;
x aa− ∈−
và
( ) ( )
f x fx−=
.
+ Hàm số
( )
y fx=
là hàm số lẻ trên đoạn
[ ]
;aa−
khi và chi khi
[ ]
;x aa∀∈−
ta có:
[
]
;x aa− ∈−
và
( ) ( )
f x fx−=−
.
+ Ta có thể thay đoạn
[ ]
;aa−
bằng một tập đối xứng thì định nghĩa hàm số chẵn, hàm số lẻ vẫn
như trên.
Câu 30: Cho
( )
fx
là hàm số chẵn, liên tục trên đoạn
[ ]
;aa−
. Chứng minh rằng:
(
)
( )
0
d 2 d.
aa
a
fx x fx x
−
=
∫∫
Câu 31: Cho
( )
fx
là hàm số chẵn, liên tục trên đoạn
[ ]
;aa−
. Chứng minh rằng:
( )
(
)
0
d
1
aa
x
a
fx
I x f x dx
b
−
= =
+
∫∫
, với
0a >
,
0b >
.
Câu 32: Tính tích phân
1
2
1
d
21
x
x
Ix
−
=
+
∫
.
Câu 33: Tính tích phân
2
2
cos
d
1
x
x
Ix
e
π
π
−
=
+
∫
Câu 34: Biết hàm số
2
y fx
= +
π
là hàm số chẵn trên
;
22
−
ππ
và
( )
sin cos
2
fx fx x x
+ += +
π
.
Tính
( )
2
0
dI fx x
π
=
∫
.
Câu 35: Cho
( )
fx
là hàm số lẻ, liên tục trên đoạn
[ ]
;aa−
. Chứng minh rằng:
( )
d 0.
a
a
fx x
−
=
∫
Câu 36: Tính tích phân
1
2
1
2
1
cos4 sin sin ln d
21
xx
I xx x
x
−
+
= +
−
∫
Câu 37: Tính tích phân
( )
2
0
sin sin dI x mx x
π
= +
∫
, với
m ∈
.
Một số kiểu đổi biến đặc biệt
Câu 38: Cho
( )
fx
là hàm số liên tục trên
[ ]
0;1
. Chứng minh rằng:
( ) ( )
22
00
sin d cos dI f xx f xx
ππ
= =
∫∫
Câu 39: Tính tích phân
( )
( )
2
2
2
0
1
tan cos d
cos sin
I xx
x
π
= −
∫
.
Câu 40: Tính
2017
2
2016 2016
0
sin .cos
d
sin cos
xx
Ix
xx
=
+
∫
π
.
Câu 41: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
1;1−
. Chứng minh rằng
( ) ( )
00
sin d sin d
2
I xf xx f xx
ππ
π
= =
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 49
Câu 42: Tính
2
0
sin
d
3 sin
xx
Ix
x
=
+
∫
π
Câu 43: Cho
( )
fx
,
( )
gx
là các hàm số liên tục trên
và
( )
27f =
;
(
)
11
f −=
;
( )
29
g =
;
(
)
13
g −=
.
Tính
( ) (
) (
)
( )
( )
(
)
2
2
1
d
f xgx f xg x
Ix
f x gx
−
′′
−
=
+
∫
Câu 44: Cho hàm số
(
)
y fx
=
thỏa mãn
( ) ( )
52
. 36fxf x x x
′
= +
. Biết
( )
02f =
. Tính
( )
2
2f
.
DẠNG 6: PHƯƠNG PHÁP ĐỔI BIẾN SỐ LOẠI 2 ĐỂ TÍNH TÍCH PHÂN
Yêu cầu: Tính tích phân
( )
d
b
a
I fx x=
∫
Phương pháp: Đặt
( )
(
)
ddx t x tt
ϕϕ
′
= ⇒=
+ Đổi cận:
12
;xa ttxb tt= ⇒= =⇒=
+ Khi đó:
( ) ( )
2
1
d
t
t
I f t tt
ϕϕ
′
=
∫
Một số cách đổi biển cần nhớ:
+
( )
2
2
: tan , ;
22
a bx c bx c a t t
ππ
+ + + = ∈−
+
( )
2
2
: sin , ;
22
a bx c bx c a t t
ππ
− + + = ∈−
+
( )
{ }
2
2
: , ; \0
sin 2 2
a
bx c a bx c t
t
ππ
+ − + = ∈−
+ Nhớ:
22 2
11 1
( ) tan
0, 0
24
2
2
11
24
b
ax t
xx t
a
aa
xx t
a
dx dt
ax bx c
b
ax
aa
−∆
+=
∆< >
= =
++
−∆
−∆
++
∫∫ ∫
Câu 45: Tính các tích phân sau:
1 11
22 2
0 00
11 1
3
22
8
00 0
12
2
2
2
0
3
11 1
)d ) d ) d
1 3 4 44
d) d ) 1 d ) 4 4 1d
1
1
g) 2 d ) d
1
aI x bI x c I x
x x xx
x
I x eI x x f I x x x
x
I x x x hI x
xx
= = =
+ + ++
= = − =− ++
+
=−=
−
∫∫∫
∫∫ ∫
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 50
DẠNG 7: PHƯƠNG PHÁP TỪNG PHẦN ĐỂ TÍNH TÍCH PHÂN
Công thức từng phần:
( ) ( ) ( ) ( ) ( ) ( )
dd
bb
b
a
aa
uxv x x uxvx vxu x x
′′
= −
∫∫
.
Viết gọn:
(
)
dd
bb
b
a
aa
u v uv v u= −
∫∫
Áp dụng: Tính tích phân
( )
d
b
a
I fx x=
∫
Phương pháp:
+ Bước 1: Biến đổi
( ) ( )
12
.d
b
a
I fxf x x=
∫
+ Bước 2: Đặt
(
)
( )
( )
( )
1
1
22
dd
dd
u fx x
u fx
dv fxx v fxx
′
=
=
⇒
= =
∫
(Chọn
dv
sao cho
v
dễ lấy nguyên hàm)
+ Bước 3: Khi đó
( )
d
b
b
a
a
I uv v u
= −
∫
● Dạng 1.
( ) ( )
sin dI P x ax b x= +
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
( )
( )
( )
( )
d .d
1
d sin d
cos
u Px x
u Px
v ax b x
v ax b
a
′
=
=
⇒
= +
=−+
.
● Dạng 2.
(
) (
)
cos d
I P x ax b x= +
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
( )
( )
( )
( )
d .d
1
d cos d
sin
u Px x
u Px
v ax b x
v ax b
a
′
=
=
⇒
= +
= +
.
● Dạng 3.
( )
d
ax b
I Pxe x
+
=
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
(
)
( )
d .d
1
dd
ax b
ax b
u Px x
u Px
ve
ve x
a
+
+
′
=
=
⇒
=
=
.
● Dạng 4.
( ) ( )
ln dI Px gx x=
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
( )
( )
ln
dd
u gx
v Px x
=
=
.
● Dạng 5.
sin
d
cos
x
x
I ex
x
=
∫
.
Với dạng này, ta đặt
sin
cos
dd
x
x
u
x
v ex
=
=
.
Câu 46: Tính các tích phân sau:
ln 2
22
1 00 0
) lnd ) d ) cosd ) sind
e
xx
aI x xx bI xe x cI x xx dI e xx
ππ
= = = =
∫ ∫∫ ∫
Câu 47: Tính các tích phân sau:
1
2
22 2
00
) d ) cos d
x
aI xe x bI x x x
π
= =
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 51
Câu 48: Tính tích phân
0
2 sin 3 d
x
I xx
π
=
∫
Câu 49: Cho hàm số
( )
y fx
=
có đạo hàm liên tục trên đoạn
[ ]
;ab
. Chứng minh rằng:
( ) ( ) ( ) ( )
d.
b
x ba
a
I f x f x e x f b e f ae
′
=+=−
∫
Câu 50: Cho hàm số
( )
y fx
=
có đạo hàm liên tục trên đoạn
[
]
1;1−
thỏa
( )
( )
23
12 6 7
fx fx x x+− = − −
Tính
( ) ( )
1
1
ln 2.
d.
2
x
f x fx
Ix
−
′
−
=
∫
Câu 51: Tính các tích phân
(
)
2
2
1
3
00
ln .ln ln
) d ) sin d ) d
e
e
x
e
xx
aI xe x bI xx cI x
x
π
= = =
∫∫ ∫
Câu 52: Tính tích phân
3
2
0
sin
cos
xx
I dx
x
π
=
∫
Câu 53: Tính tích phân
ln3
0
1
x
x
xe
I dx
e
=
+
∫
Câu 54: Chứng minh rằng:
11
22 2
00
1
1d 2 2 1d
4
Ixxx xx
= += − +
∫∫
Câu 55: Tính
( )
2
3
2
0
d
sin cos
x
Ix
xx x
=
+
∫
π
Câu 56: Cho hàm số
( )
fx
có nguyên hàm là
( )
Fx
trên đoạn
[ ]
1; 2
, biết
( )
21F =
và
(
)
2
1
d5Fx x
=
∫
.
Tính
( ) ( )
2
1
1dI x fx x= −
∫
.
Câu 57: Cho
( )
2017
2017 2017
sin
sin cos
x
fx
xx
=
+
. Tính
(
)
2
0
dI xf x x
π
′
=
∫
.
DẠNG 7. KỸ THUẬT TÍCH PHÂN TỪNG PHẦN HÀM ẨN
Câu 58: Cho hàm số
( )
fx
thỏa mãn
( )
( )
3
0
. . d8
fx
xf x e x
′
=
∫
và
( )
3 ln 3f =
. Tính
( )
3
0
d.
fx
Iex=
∫
Câu 59: Cho hàm số
( )
fx
có đạo hàm liên tục trên
0; ,
2
π
thỏa mãn
( )
2
2
0
' cos d 10f x xx
π
=
∫
và
( )
0 3.f =
Tích phân
( )
2
0
sin 2 df x xx
π
∫
bằng
Câu 60: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
2
1
1d 3
fx x−=
∫
và
( )
1 4.f =
Tích phân
( )
1
32
0
'dxf x x
∫
bằng

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 52
Câu 61: Cho hàm số
( )
fx
nhận giá trị dương, có đạo hàm liên tục trên
[
]
0; 2 .
Biết
( )
01f =
và
(
) (
)
2
24
2
xx
fxf x e
−
−=
với mọi
[ ]
0; 2 .x
∈
Tính tích phân
( )
( )
( )
32
2
0
3'
d.
x xfx
Ix
fx
−
=
∫
DẠNG 8. TÍNH TÍCH PHÂN DỰA VÀO TÍNH CHẤT
Câu 62: Cho hàm số
(
)
fx
là hàm số lẻ, liên tục trên
[ ]
4; 4 .−
Biết rằng
( )
0
2
d2f xx
−
−=
∫
và
( )
2
1
2 d 4.f xx−=
∫
Tính tích phân
( )
4
0
d.I fx x=
∫
Câu 63: Cho hàm số
( )
fx
là hàm số chẵn, liên tục trên
[ ]
1; 6 .
−
Biết rằng
( )
2
1
d8fx x
−
=
∫
và
( )
3
1
2 d 3.f xx−=
∫
Tính tích phân
(
)
6
1
d.I fx x
−
=
∫
Câu 64: Cho hàm số
(
)
fx
liên tục trên
[ ]
3; 7 ,
thỏa mãn
( ) (
)
10fx f x= −
với mọi
[
]
3; 7
x ∈
và
( )
7
3
d 4.fx x=
∫
Tính tích phân
( )
7
3
d.I xf x x=
∫
Câu 65: Cho hàm số
( )
y fx=
là hàm số chẵn và liên tục trên đoạn
[ ]
;,
ππ
−
thỏa mãn
(
)
0
d 2018.
fx x
π
=
∫
Giá trị của tích phân
(
)
d
2018 1
x
fx
Ix
π
π
−
=
+
∫
bằng
Câu 66: Biết
2018
2018 2018
0
sin
d
sin cos
a
xx
x
x xb
π
π
=
+
∫
với
,.ab
+
∈
Tính
2.P ab= +
DẠNG 9. KỸ THUẬT PHƯƠNG TRÌNH HÀM
Câu 67: Cho hàm số
( )
y fx=
liên tục trên
;
22
ππ
−
và thỏa mãn
( ) ( )
2 cos .fx f x x+ −=
Tính tích
phân
( )
2
2
d.I fx x
π
π
−
=
∫
Câu 68: Cho hàm số
( )
y fx=
liên tục trên
[ ]
2; 2−
và thỏa mãn
( ) (
)
2
1
23 .
4
fx f x
x
+ −=
+
Tính tích
phân
( )
2
2
d.I fx x
−
=
∫
Câu 69: Cho hàm số
(
)
y fx=
liên tục trên
[ ]
0;1
và thỏa mãn
(
) ( )
24
1 2.xf x f x x x+ −=−
Tính tích
phân
( )
1
0
d.I fx x=
∫
Câu 70: Cho hàm số
( )
fx
liên tục trên
1
;2
2
và thỏa mãn
( )
1
2 3.fx f x
x
+=
Tính tích phân
( )
2
1
2
d.
fx
Ix
x
=
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 53
Câu 71: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
và thỏa mãn
( ) ( )
2
2 31 1 .fx f x x+ −=−
Tính tích phân
( )
1
0
d.I fx x=
∫
DẠNG 10. KỸ THUẬT BIẾN ĐỔI
Câu 72: Cho hàm số
(
)
fx
thỏa
( )
( )
52
3 6.fxf x x x
′
= +
Biết rằng
( )
0 2,f =
tính
( )
2
2.f
Câu 73: Cho hàm số
( )
fx
thỏa mãn
( ) ( ) ( )
2
4
. 15 12
f x fxf x x x
′ ′′
+=+
với mọi
x ∈
và
( ) ( )
0 0 1.ff
′
= =
Giá trị của
( )
2
1f
bằng
Câu 74: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
1; 2
và thỏa mãn
( )
[ ]
0, 1; 2 .
fx x
> ∀∈
Biết
rằng
( )
2
1
d 10fxx
′
=
∫
và
(
)
(
)
2
1
d ln 2.
fx
x
fx
′
=
∫
Tính
( )
2.f
Câu 75: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
1;1−
, thỏa mãn
( )
0, fx x> ∀∈
và
( ) ( )
'2 0f x fx+=
. Biết rằng
( )
11f =
, giá trị của
( )
1f −
bằng
Câu 76: Cho hàm số
( )
fx
có đạo hàm liên tục trên
( )
0; +∞
, biết
( ) ( ) ( )
2
' 2 3 0,fx x f x++ =
( )
0fx>
với mọi
0x >
và
( )
1
1.
6
f
=
Tính
(
) ( )
( )
1 1 2 ... 2018 .Pff f=+ + ++
Câu 77: Cho hàm số
( )
fx
liên tục trên
0; 3 ,
thỏa mãn
( )
1,fx>−
( )
00f =
và
( ) ( )
2
1 2 1.
f x x xfx
′
+= +
Giá trị của
( )
3f
bằng
Câu 78: Cho hàm số
( )
fx
có đạo hàm và liên tục trên
[
]
1; 4 ,
đồng biến trên
[ ]
1; 4 ,
thoản mãn
(
) ( )
2
2x xf x f x
′
+=
với mọi
[ ]
1; 4 .x ∈
Biết rằng
( )
3
1,
2
f =
tính tích phân
( )
4
1
d.I fx x=
∫
Câu 79: Cho hàm số
( )
fx
liên tục, không âm trên
0;
2
π
, thỏa
( ) ( ) ( )
2
. ' cos 1
fxf x x f x= +
với mọi
0;
2
x
π
∈
và
( )
0 3.
f =
Giá trị của
2
f
π
bằng
Câu 80: Cho hàm số
( )
fx
liên tục, không âm trên
[ ]
0;3 ,
thỏa
( ) (
) ( )
2
.2 1fxf x xf x
′
= +
với mọi
[ ]
0;3x ∈
và
( )
0 0.f =
Giá trị của
(
)
3f
bằng
Câu 81: Cho hàm số
( )
fx
có đạo hàm không âm trên
[ ]
0;1 ,
thỏa mãn
( )
0fx>
với mọi
[ ]
0;1x ∈
và
( ) ( )
( )
( )
42 3
2
. ' . 11 .fx f x x fx+=+
Biết
( )
0 2,f =
hãy chọn khẳng định đúng trong các
khẳng định sau đây.
Câu 82: Cho hàm số
( )
fx
liên tục trên
{ }
,\
0; 1−
thỏa mãn
( ) ( ) ( )
2
1.xx f x f x x x
′
+ +=+
với mọi
{ }
0; 1\x ∈−
và
( )
1 2ln 2.f = −
Biết
( )
2 ln 3f ab= +
với
, ab∈
, tính
22
.Pa b= +
Câu 83: Cho hàm số
( )
fx
có đạo hàm xác định, liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
01f
′
= −
và
( ) ( )
( )
2
0
fx f x
fx
′ ′′
=
′
≠
với mọi
[ ]
0;1 .x ∈
Đặt
( ) ( )
10Pf f= −
, khẳng định nào sau đây đúng?
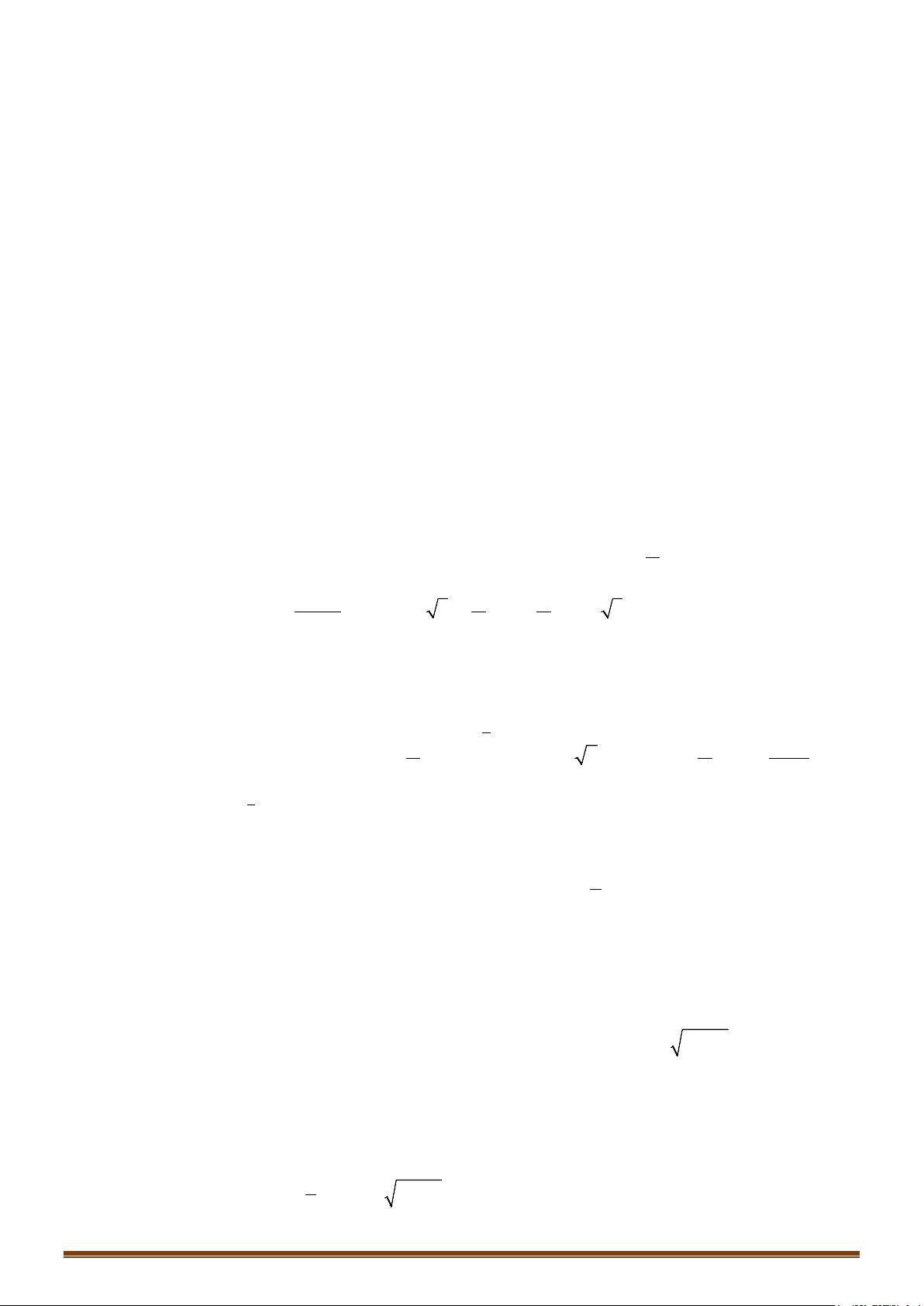
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 54
Câu 84: Cho hai hàm số
(
)
fx
và
( )
gx
có đạo hàm liên tục trên
[
]
0; 2 ,
thỏa mãn
(
)
( )
'0. '2 0
ff≠
và
(
) (
)
( )
.' 2 .
x
gx f x xx e= −
Tính tích phân
( ) ( )
2
0
. ' d.I fxg x x=
∫
Câu 85: Cho hàm số
( )
y fx
=
liên tục trên đoạn
[ ]
0;1
và thỏa mãn
( ) ( )
1
af b bf a+=
với mọi
[
]
, 0;1 .ab∈
Tính tích phân
( )
1
0
d.
I fx x
=
∫
DẠNG 11. KỸ THUẬT ĐẠO HÀM ĐÚNG
Câu 86: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[
]
0;1 ,
thoả mãn
(
)
( )
2018
3 f x xf x x
′
+=
với mọi
[ ]
0;1 .x ∈
Tính
(
)
1
0
dI fx x=
∫
.
Câu 87: Cho hàm số
( )
fx
có đạo hàm trên
,
thỏa mãn
( ) ( )
2017 2018
' 2018 2018
x
f x fx x e−=
với mọi
x ∈
và
( )
0 2018.f =
Tính giá trị
( )
1.f
Câu 88: Cho hàm số
( )
fx
có đạo hàm và liên tục trên
,
thỏa mãn
( ) ( )
2
2
x
f x xf x xe
−
′
+=
và
(
)
0 2.
f = −
Tính
( )
1.f
Câu 89: Cho hàm số
( )
fx
liên tục và có đạo hàm trên
0; ,
2
π
thỏa mãn hệ thức
( ) ( )
3
tan .
cos
x
f x xf x
x
′
+=
Biết rằng
3 3 ln 3
36
f f ab
ππ
π
−=+
trong đó
, .ab
∈
Tính
giá trị của biểu thức
.P ab= +
DẠNG 12. KỸ THUẬT ĐƯA VỀ BÌNH PHƯƠNG LOẠI 1
Câu 90: Cho hàm số
( )
fx
liên tục trên
0; ,
2
π
thỏa
( )
( )
2
2
0
2
2 2 sin d .
42
f x fx x x
π
ππ
−
− −=
∫
Tính
tích phân
( )
2
0
d.I fx x
π
=
∫
Câu 91: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
thỏa
( ) ( ) ( )
11
22
00
2
2ln d 2 ln 1 d .f x x fx x x
e
+= +
∫∫
Tích
phân
( )
1
0
d.I fx x
=
∫
Câu 92: Cho hàm số
( )
fx
có đạo liên tục trên
[ ]
0;1 ,
( )
fx
và
( )
'fx
đều nhận giá trị dương trên
[ ]
0;1
và thỏa mãn
( )
02f =
và
( ) ( ) ( ) ( )
11
2
00
' . 1d 2 ' . d.f x fx x f xfx x
+=
∫∫
Tính
( )
1
3
0
d.I fx x=
∫
Câu 93: Cho hàm số
( )
fx
có đạo hàm dương, liên tục trên đoạn
[ ]
0;1
và thỏa mãn
( )
0 1,f =
(
) ( ) ( ) ( )
11
2
00
1
3 ' . d 2 ' . d.
9
f x fx x f xfx x
+=
∫∫
Tính
( )
1
3
0
d.I fx x=
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 55
Câu 94: Cho hàm số
( )
y fx=
có đạo hàm dương, liên tục trên đoạn
[
]
0;1 ,
thỏa
( ) ( )
1 01ff−=
và
( ) ( ) ( )
( )
11
2
00
' 1d 2 ' d.fxf x x fxfxx
+=
∫∫
Giá trị của tích phân
( )
1
3
0
dfx x
∫
bằng
DẠNG 13. KỸ THUẬT ĐƯA VỀ BÌNH PHƯƠNG LOẠI 2 - KỸ THUẬT HOLDER
Câu 95: Cho hàm số
(
)
y fx
=
liên tục trên đoạn
[
]
0;1 ,
thỏa mãn
( ) ( )
11
00
d d1fx x xfx x= =
∫∫
và
( )
1
2
0
d4fx x=
∫
. Giá trị của tích phân
( )
1
3
0
dfx x
∫
bằng
Câu 96: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
0;1 ,
thỏa mãn
( )
(
)
11
00
d d1xfx x xfx x
= =
∫∫
và
( )
1
2
0
d 5.fx x=
∫
Giá trị của tích phân
( )
1
3
0
dfx x
∫
bằng
Câu 97: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
0;1 ,
thỏa mãn
( ) ( )
11
22
00
1
d d.
16
xf xx xfxx= −
∫∫
Giá trị
của tích phân
(
)
1
0
dfx x
∫
bằng
Câu 98: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[
]
1; 8
và thỏa mãn
( ) ( )
( )
2 28
2
33
1 11
2 38
d2 d d .
3 15
fx x fx x fx x
+=−
∫ ∫∫
Tích phân
( )
8
1
dfxx
∫
bằng
Câu 99: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
10f =
,
( )
1
2
0
d7fx x
′
=
∫
và
( )
1
2
0
1
d.
3
xf x x=
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Câu 100: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
11f =
,
( )
1
5
0
11
d
78
xf x x=
∫
và
( ) ( )
( )
1
0
4
d.
13
f x fx
′
=
∫
Tính
( )
2.
f
Câu 101: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
1 2, 0 0ff= =
và
( )
1
2
0
' d 4.fx x=
∫
. Tích phân
( )
1
3
0
2018 d .fx xx
+
∫
bằng
Câu 102: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
1; 2 ,
thỏa mãn
( ) ( )
2
2
1
1
1 d,
3
x fx x−=−
∫
( )
20f =
và
( )
2
2
1
' d 7.fx x=
∫
Tích phân
( )
2
1
dfx x
∫
bằng

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 56
Câu 103: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
1
2
0
9
1 1, ' d
5
f fx x= =
∫
và
( )
1
0
2
d.
5
f xx=
∫
Tích phân
(
)
1
0
dfx x
∫
bằng
Câu 104: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
0 1 0,ff+=
( ) ( )
1
0
' cos d
2
fx xx
π
π
=
∫
và
(
)
1
2
0
1
d.
2
f xx=
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Câu 105: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0; ,
π
thỏa mãn
(
)
0
' sin d 1f x xx
π
= −
∫
và
( )
2
0
2
d.f xx
π
π
=
∫
Tích phân
( )
0
dxf x x
π
∫
bằng
Câu 106: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa
( ) ( )
1
2
2
0
1 0, ' d
8
f fx x
π
= =
∫
và
( )
1
0
1
cos d .
22
x
fx x
π
=
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Câu 107: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
(
) ( )
1
0
' sin dfx xx
ππ
=
∫
và
( )
1
2
0
d 2.f xx=
∫
Tích phân
1
0
d
2
x
fx
∫
bằng
Câu 108: Cho hàm số
( )
fx
có đạo hàm liên tục trên
0; ,
2
π
thỏa
( )
2
2
0
0, d 3
2
f f xx
π
π
π
= =
∫
và
( )
0
sin d 6 .
2
x
x xf x
π
π
′
−=
∫
Tích phân
( )
2
3
0
dfx x
π
′′
∫
bằng
Câu 109: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;1 ,
thỏa mãn
( )
10f =
và
( ) ( ) ( )
11
2
2
00
1
'd 1 d .
4
x
e
f x x x ef x x
−
=+=
∫∫
Tính tích phân
( )
1
0
d.I fx x
=
∫
Câu 110: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
0 0, 1 1ff
= =
và
( )
2
1
0
'
1
d.
1
x
fx
x
ee
=
−
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Câu 111: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
0 0, 1 1ff= =
và
(
)
(
)
1
2
2
0
1
1 'd .
ln 1 2
x fx x+=
+
∫
Tích phân
( )
1
2
0
d
1
fx
x
x+
∫
bằng
Câu 112: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
1;1 ,−
thỏa mãn
( )
1 0,f −=
( )
1
2
1
' d 112fx x
−
=
∫
và
( )
1
2
1
16
d.
3
xf x x
−
=
∫
Tính tích phân
( )
1
1
d.I fx x
−
=
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 57
Câu 113: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
1 0,f =
( )
1
2
0
3
' d 2ln 2
2
fx x= −
∫
và
( )
(
)
1
2
0
3
d 2 ln 2 .
2
1
fx
x
x
= −
+
∫
Tích phân
(
)
1
0
dfx x
∫
bằng
Câu 114: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[
]
1; 2 ,
đồng biến trên
[
]
1; 2 ,
thỏa mãn
( )
10f =
,
( )
2
2
1
d2fx x
′
=
∫
và
(
) (
)
2
1
. ' d 1.fxf x x
=
∫
Tích phân
(
)
2
1
d
fx x
∫
bằng
Câu 115: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
10f =
,
( )
1
2
0
d1f xx=
∫
và
( ) ( )
1
2
2
0
3
d.
4
fx f xx
′
=
∫
Giá trị của
( )
2
2f
bằng
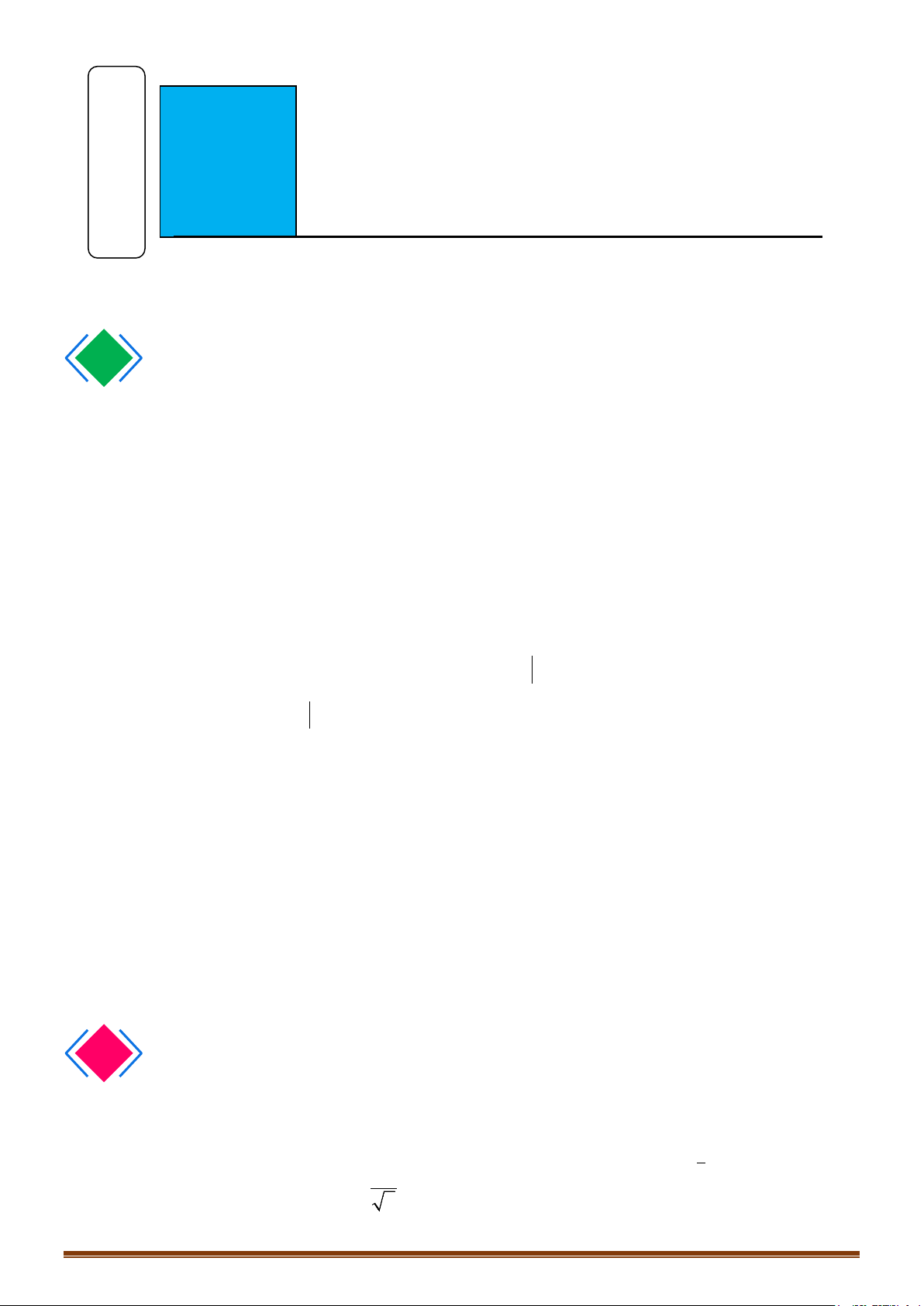
Câu 116: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
[ ]
0; 2 ,
thỏa mãn
( )
21f =
,
( )
2
2
0
8
d
15
xf x x=
∫
và
( )
2
4
0
32
'd .
5
fx x=
∫
Giá trị của tích phân
( )
2
0
dfx x
∫
bằng
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 1
BÀI 2. TÍCH PHÂN
Định nghĩa: Cho hàm số
f
liên tục trên khoảng
K
và
,ab
là hai số bất kì thuộc
K
. Nếu
F
là một nguyên hàm của
f
trên
K
thì hiệu số
( ) ( )
Fb Fa−
được gọi là tích phân của hàm số
f
từ
a
đến
b
và kí hiệu là
( )
d
b
a
fx x
∫
.
Ta gọi:
a
là cận dưới,
b
là cận trên,
f
là hàm số dưới dấu tích phân,
( )
dfx x
là biểu thức
dưới dấu tích phân,
x
biến số lấy tích phân.
Nhận xét :
a) Nếu
ab<
thì ta gọi
( )
d
b
a
fx x
∫
là tích phân của
f
trên đoạn
[ ]
;.
ab
b) Hiệu số
( ) ( )
Fb Fa−
còn được kí hiệu là
( )
b
a
Fx
. Khi đó :
(
) ( )
( )
( )
d.
b
b
a
a
f x x Fx Fb Fa
= = −
∫
c) Tích phân không phụ thuộc biến số (điều này sẽ mang lại lợi ích cho ta để tính một số tích
phân đặc biệt), tức là
( ) ( ) ( )
( ) (
)
d d d ... .
b bb
a aa
fx x ft t fu u Fb Fa= = = = −
∫ ∫∫
Tính chất: Cho
k
là hằng số
[ ]
) () 0 ) () ()
c) .() () ) () () () ()
a ba
a ab
b b b bb
a a a aa
a f x dx b f x dx f x dx
k f x dx k f x dx d f x g x dx f x dx g x dx
= = −
= += +
∫ ∫∫
∫ ∫ ∫ ∫∫
e) Tính chất chèn cận:
() () ()
b cb
a ac
f x dx f x dx f x dx= +
∫∫∫
(chèn cận
c
)
DẠNG 1: SỬ DỤNG ĐỊNH NGHĨA TÍCH PHÂN
Câu 1: Tính các tích phân sau:
1 4 ln 2
4
2
0100
1
) 3 d ) d ) 2 d ) sin d
x
a I x x bI x cI x d I xx
x
π
= = = =
∫∫∫∫
Lời giải
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
LÝ THUYẾT.
I
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
1
1
23
0
0
) 3 d 1 0 1.
aI x x x
= = =−=
∫
( )
4
4
1
1
1
) d 2 2 2 1 2.bI x x
x
= = = −=
∫
( )
1
1
10
0
0
21 1
) 2d 2 2 .
ln 2 ln 2 ln 2
x
x
cI x= = = −=
∫
4
4
0
0
11
) sin d cos 1 1 .
22
d I xx x
π
π
= =− =− −=−
∫
Câu 2: Gọi
( )
Fx
là nguyên hàm của hàm số
(
)
x
fx e
=
. Tính
(
)
( )
2 2 2.F ln F ln
−
Lời giải
Vì hàm số
( )
x
fx e=
liên tục trên đoạn
[ ]
ln 2;2ln 2
nên ta có:
(
) (
) ( )
ln 4 ln 4
ln 4
ln 2
ln 2 ln 2
ln 4 ln 2 d d 2.
xx
F F fx x ex e
−= ===
∫∫
Câu 3: Gọi
( )
Fx
là nguyên hàm của hàm số
(
)
1
fx
x
=
thỏa điều kiện
( )
12
F =
. Tính
(
)
Fe
.
Lời giải
Vì hàm số
( )
1
fx
x
=
liên tục trên đoạn
[ ]
1; e
nên ta có:
( ) ( ) ( )
1
11
1
1 d d ln 1.
ee
e
Fe F f x x x x
x
−= = = =
∫∫
Suy ra:
( ) ( )
1 1 1 2 3.Fe F=+ =+=
Câu 4: Chứng minh
( )
(
)
2
ln 1Fx x x= ++
là một nguyên hàm của hàm số
( )
2
1
1
fx
x
=
+
. Từ đó
tính tích phân
1
2
0
1
d.
1
Ix
x
=
+
∫
Lời giải
Ta có:
( )
(
)
( )
2
2
2 22
1
1
1
1
.
1 11
x
xx
x
Fx fx
xx xx x
′
+
++
+
′
= = = =
++ ++ +
Do đó:
(
)
( )
1
1
2
2
0
0
1
d ln 1 ln 1 2 .
1
I x xx
x
= = + += +
+
∫
Câu 5: Chứng minh
( )
1
ln
ax b
Fx
ad bc cx d
+
=
−+
là một nguyên hàm của hàm số
( )
( )( )
1
fx
ax b cx d
=
++
. Từ đó tính tích phân
( )( )
1
0
1
d.
21 1
Ix
xx
=
++
∫
Lời giải
Ta có:
( )
( )
( )( )
( )
1 11
ln ln .
ac
F x ax b cx d f x
ad bc ad bc ax b cx d ax b cx d
′
′
= +− + = − = =
− − ++ ++

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
Do đó:
( )( )
1
1
0
0
1 1 21 3 3
d ln ln ln1 ln
2 1 1 21 1 2 2
x
Ix
xx x
+
= = = −=
++ − +
∫
.
DẠNG 2: SỬ DỤNG TÍNH CHẤT TÍCH PHÂN
Câu 6: Tính các tích phân sau:
( )
( )
12
3
0 10
1
4 d ) 3 d ) sin 2cos d
xx
I x e x bI x cI x x x
x
π
=−= =− = +
∫ ∫∫
Lời giải
( )
( )
1
11
34
00
0
) 4 1 12.
xx
a I x e dx x e e e= − = − =−−=−
∫
( )
2
2
2
1
1
1
13 1 6
) 3 d ln 9 3 ln 2 ln 2.
ln 3 ln3 ln 3
x
x
bI x x
x
= − = − = −− = −
∫
( )
00
0
) sin 2cos d cos 2sin 2.cI x x x x x
π
ππ
= + =−+ =
∫
Câu 7: Tính
( )
22
11
ln d 1 ln d .
xt
I e xx e t t= +−
∫∫
Lời giải
(
)
22 2
2
11 1
e ln d 1 ln d d .
xx x
I xx e x x e x e e
= +− = =−
∫∫ ∫
Câu 8: Tính
2
2
sin ln d sin sin d .
2 22
t uu
I t t lnu u
= +−
∫∫
π
π
π
π
Lời giải
22
sin ln d sin ln sin d
2 22
x xx
I xx x x
ππ
ππ
= −−
∫∫
2
22
22
1 cos 1 1 1
sin sin .
2 2 2 2 42
xx
dx dx x x
ππ
ππ
ππ
ππ
π
−
= = =−=+
∫∫
DẠNG 3: SỬ DỤNG TÍNH CHẤT CHÈN CẬN ĐỂ TÍNH TÍCH PHÂN
Tích phân của hàm chứa dấu trị tuyệt đối
a) Yêu cầu: Tính tích phân
()
b
a
I f x dx=
∫
b) Phương pháp:
+ Bước 1: Xét dấu của
( )
fx
trên khoảng
( )
;ab
- Giải phương trình
(
)
( )
0;
i
f x x x ab=⇔=∈
- Lập bảng xét dấu của
( )
fx
trên khoảng
( )
;
ab
+ Bước 2: Chèn cận
i
x
và đồng thời bỏ dấu
(căn cứ vào BXD) ta được các tích phân cơ bản
( ) ( ) ( )
ddd
i
i
x
bb
a ax
I fx x fx x fx x= = +
∫∫∫
Chú ý: Nếu
(
)
fx
không đổi dấu trên đoạn
[ ]
;ab
thì
( ) ( )
dd
bb
aa
I fx x fx x= =
∫∫
Câu 9: Tính các tích phân:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
2 32 2
22
0 04 2
) 1d ) d ) 2 3d ) 2 1 daIxx bIxxxcxx x dxx x
−−
= − = − + − −+
∫ ∫∫ ∫
Lời giải
( )
( )
2 12 1 2
0 01 0 1
11
) 1d 1d 1d 1 d 1 d 1.
22
aIxxxxxx x xx x=−=−+−=−− +− =+=
∫∫∫ ∫ ∫
b) Xét trên khoảng
( )
0;3
ta có:
( )
2
0
0.
1
xl
xx
x
=
−=⇔
=
BXD:
x
0
1
3
2
xx
−
−
0
+
Suy ra:
( ) ( )
13
22
01
1 14 29
dd .
63 6
I x xx x xx=− − + − =+=
∫∫
c) Xét trên khoảng
( )
2; 2−
ta có:
2
3
2 30 .
1
x
xx
x
= −
+ −=⇔
=
BXD:
x
4−
3
−
1
2
2
23xx+−
+
0
−
0
+
Suy ra:
( ) ( ) ( )
31 2
2 22
4 31
7 32 7 46
2 3d 2 3d 2 3d .
3333
I xx x xx xxx x
−
−−
= +− − +− + +− =++=
∫∫∫
d) Xét trên khoảng
( )
2; 2−
ta có:
10 1xx
+= ⇔ =−
BXD:
x
2−
1−
2
1x +
−
0
+
Suy ra:
1 2 12
12
2 1 21
2 1d 2 1d 3 1d 1dI xxx xxx xxxxII
−−
= +++ −−= ++−=+
∫ ∫ ∫∫
Ta có:
(
) ( )
1
11
3
1
1
22
3
41
31d 31d 31d .
6
I xx xx xx
−
−−
−
= +=− ++ + =
∫∫∫
( )
22
2
11
1
1d 1 d .
2
I xxx x=−=− =
∫∫
Vậy:
41 1 22
.
62 3
I = +=
Câu 10: Tính
0
1 cos 2 dI xx= −
∫
π
.
Lời giải
2
2
0 0 00
2
1 cos 2
d cos d cos d cos d cos d 1 1 2.
2
x
I x xx x x xx xx
π
π ππ π
π
+
= = = = − =+=
∫ ∫ ∫ ∫∫
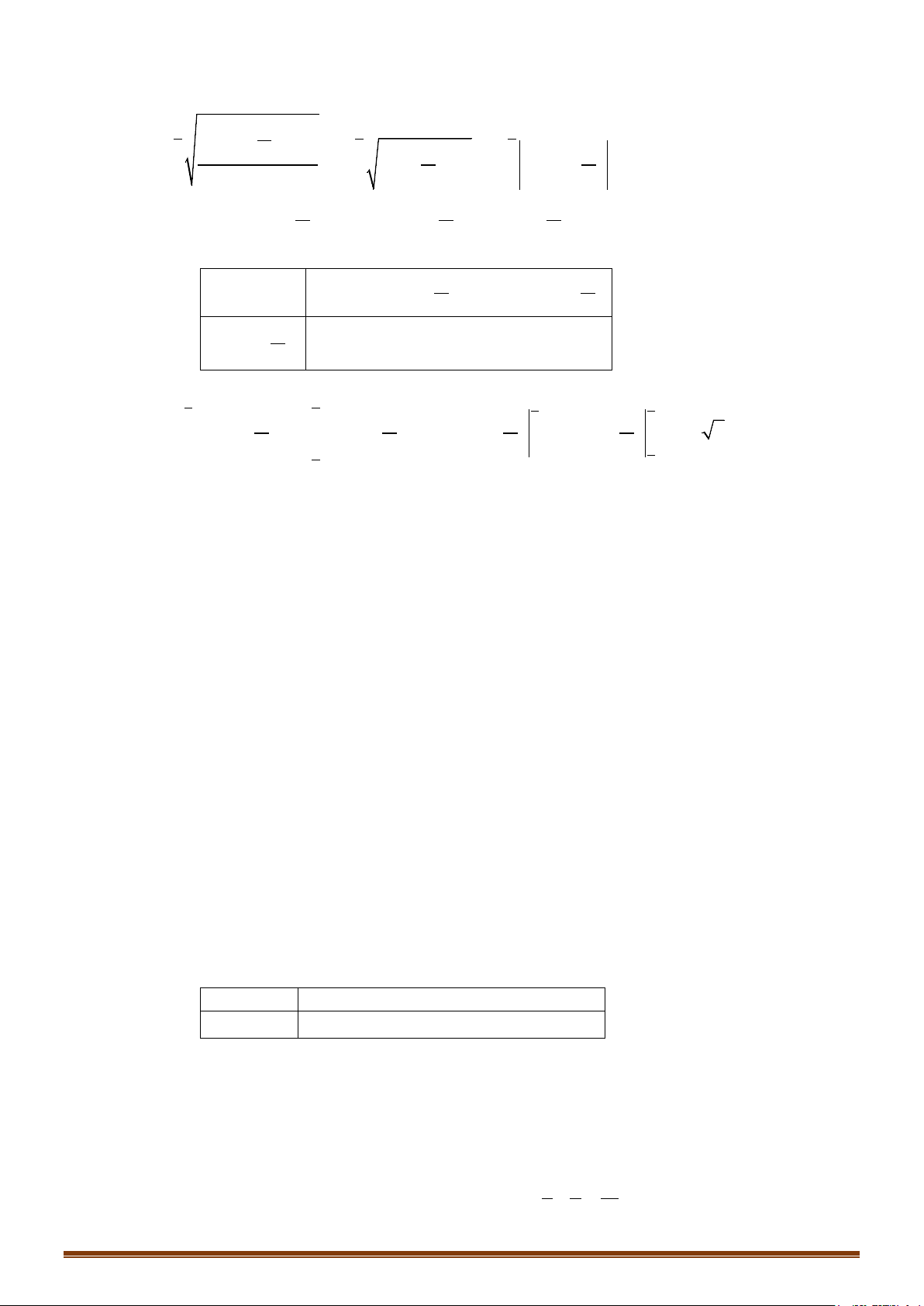
Câu 11: Tính
2
0
1 sin 2
d.
2
x
Ix
−
=
∫
π
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Lời giải
Ta có:
2 22
2
0 00
1 cos 2
2
d sin d sin d .
2 44
x
I x xx x x
π ππ
π
ππ
−−
= = −= −
∫ ∫∫
Xét trên khoảng
0;
2
π
, ta có:
sin 0
44
xx
ππ
− =⇔=
.
BXD:
x
0
4
π
2
π
sin
4
x
π
−
−
0
+
Suy ra:
42
42
0
0
4
4
sin d sin d cos cos 2 2.
4 4 44
I xx xx x x
ππ
ππ
π
π
π π ππ
=− −+ − = −− −=−
∫∫
Tích phân của hàm min, max
a) Yêu cầu: Tính tích phân
( ) ( )
{ }
min ;g d
b
a
I fx x x=
∫
;
( )
( )
{ }
max ;g d
b
a
I fx x x=
∫
b) Phương pháp: Tính
( ) ( )
{
}
min ;g d
b
a
I fx x x=
∫
(
( ) ( )
{ }
max ;g d
b
a
I fx x x=
∫
tương tự)
+ Bước 1: Xét dấu của
( )
()fx gx
−
trên khoảng
(
)
;ab
- Giải phương trình
( ) ( )
() 0 ;
i
f x g x x x ab− =⇔=∈
- Lập bảng xét dấu của
(
)
()
fx gx
−
trên khoảng
( )
;ab
+ Bước 2: Chèn cận
i
x
và chọn hàm
( ) ( )
{ }
min ;gfx x
như sau:
- Nếu
( ) ( )
0f x gx−>
trên khoảng
K
thì
( )
( )
{ }
( )
min ;gf x x gx=
.
- Nếu
( ) ( )
0f x gx−<
trên khoảng
K
thì
( ) ( )
{ }
( )
min ;gfx x fx=
.
Từ đó, ta được các tích phân cơ bản.
Câu 12: Tính
{ }
2
2
0
min ; d .I xx x=
∫
Lời giải
Xét trên khoảng
( )
0; 2
, ta có:
( )
2
0
0.
1
xl
xx
x
=
−=⇔
=
BXD:
x
0
1
2
2
xx−
+
0
−
Ta có:
2
0xx−>
với mọi
( )
0;1x ∈
nên
{ }
22
min ; .xx x=
2
0xx−<
với mọi
( )
1; 2x ∈
nên
{ }
2
min ; .xx x=
Suy ra:
{ } { }
1 2 12
2 22
0 1 01
1 3 11
min ; d min ; d d d .
32 6
I xx x xx x x x xx= + = + =+=
∫ ∫ ∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
Câu 13: Tính
{ }
1
1
max ;2 d .
xx
I ex
−
=
∫
Lời giải
Xét trên khoảng
(
)
1;1
−
, ta có:
20 0
xx
ex− =⇔=
BXD:
x
1
−
0
1
2
xx
e −
−
0
+
Ta có:
20
xx
e −<
với mọi
( )
1; 0x ∈−
nên
{ }
2
max ; 2 .
x
xx =
20
xx
e −>
với mọi
( )
0;1
x ∈
nên
{ }
2
max ; .
x
xx e=
Suy ra:
{ } {
}
0
0 1 01
1
0
1 0 10
1
21
max e ;2 d max e ;2 d 2 d e d e 1.
ln 2 2ln 2
x
xx xx x x x
I x x xx e
−−
−
= + = + = + = +−
∫ ∫ ∫∫
Tích phân của hàm số xác định trên từng khoảng
Câu 14: Cho hàm số
( )
2
khi 0
khi 0
xx
y fx
xx
≥
= =
−≤
. Biết hàm số
f
liên tục trên
.
Tính
( )
1
1
.I fx
−
=
∫
Lời giải
Ta có:
( ) ( ) ( )
1 01
1 10
d ddI fx x fx x fx x
−−
= = +
∫∫∫
01
2
10
115
dd .
236
xx x x
−
=− + =+=
∫∫
Câu 15: Cho hàm số
( )
( )
3
2 1 khi 1
2 1 khi 1
x
xx
y fx
x
−≥
= =
−≤
. Biết hàm số
f
liên tục trên
.
Tính
( )
3
2
d.I fx x
−
=
∫
Lời giải
Ta có:
( ) ( )
13
21
dd
I fx x fx x
−
= +
∫∫
( )
( )
13
3
21
7
2 1 d 2 1 d 78.
2ln 2
x
xx x
−
= −+ − = +
∫∫
Câu 16: Cho hàm số
( )
( )
( )
2
2 1 khi 0
1 khi 0
xx
y fx
kx x
− + ≤
= =
−≥
. Xác định
k
để
( )
1
1
d1fx x
−
=
∫
.
Lời giải
Ta có:
( ) ( ) ( ) (
)
( )
1 01 0 1
2
1 10 1 0
d d d 2 1d 1 d
fx x fx x fx x x x k x x
−− −
= + =−+ + −
∫∫∫∫ ∫
2
1 1 3.
3
kk⇔ =−+ ⇔ =
Một số dạng khác

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 7
Câu 17: Cho
( ) ( )
25
12
d 3, d 4fx x fx x= =
∫∫
. Tính
( )
5
1
d.I fx x=
∫
Lời giải
(
) ( ) ( )
5 25
1 12
d d d 3 4 7.I fx x fx x fx x= = + =+=
∫∫∫
Câu 18: Gọi
( )
Fx
là nguyên hàm của hàm số
( )
fx
.
Biết
( )
( )
33
01
d 12, d 2fx x fx x= =
∫∫
và
( )
27F =
. Tính
( )
0.F
Lời giải
Ta có:
(
) (
)
( ) ( ) ( )
232
003
20 d d dF F fxx fx x fx x−= = +
∫∫∫
( ) ( )
33
02
d d 12 2 10.fx x fx x= − = −=
∫∫
Suy ra:
( )
( )
0 2 10 7 10 3.FF= −=−=−
Câu 19: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
thỏa mãn
( )
10
0
d7fx x=
∫
;
( )
6
2
d3fx x
=
∫
. Tính giá
trị của biểu thức
(
) (
)
2 10
06
d d.P fx x fx x
= +
∫∫
Lời giải
( ) ( )
( )
( )
10 2 6 10
0 026
d 7 7 d d d 7 3 4.fx x fx x fx x fx x P P
=⇔= + + ⇔=+⇔ =
∫ ∫∫∫
DẠNG 4: SỬ DỤNG ĐỊNH NGHĨA TÍCH PHÂN VÀO CÁC BÀI TOÁN KHÁC
Câu 20: Cho hàm số
( )
2
sin d
x
x
g x t tt=
∫
xác định với
0x >
. Tìm
( )
gx
′
.
Lời giải
Gọi
( )
Ft
là một nguyên hàm của hàm số
(
)
sin
ft t t=
. Suy ra:
(
) ( )
.Ft ft
′
=
Ta có:
( ) ( ) ( )
( )
( )
( )
2
2
2
d *.
x
x
x
x
gx f t t Ft Fx F x= = = −
∫
Lấy đạo hàm hai vế của (*) theo biến
x
ta được:
( )
( )
( )
2
1
2.
2
g x xF x F x
x
′′ ′
= −
( )
( )
(
)
2
1
2.
2
g x xf x f x
x
′
⇔= −
( )
2
4
1
2 . sin sin
2
g x xx x x x
x
′
⇔= −
( )
22
4
1
2 sin sin .
2
gx x x x
x
′
⇔= −
Câu 21: Cho hàm số
( )
3
2
2
2
1
d
1
x
x
t
gx t
t
−
=
+
∫
. Tìm
( )
.gx
′
Lời giải
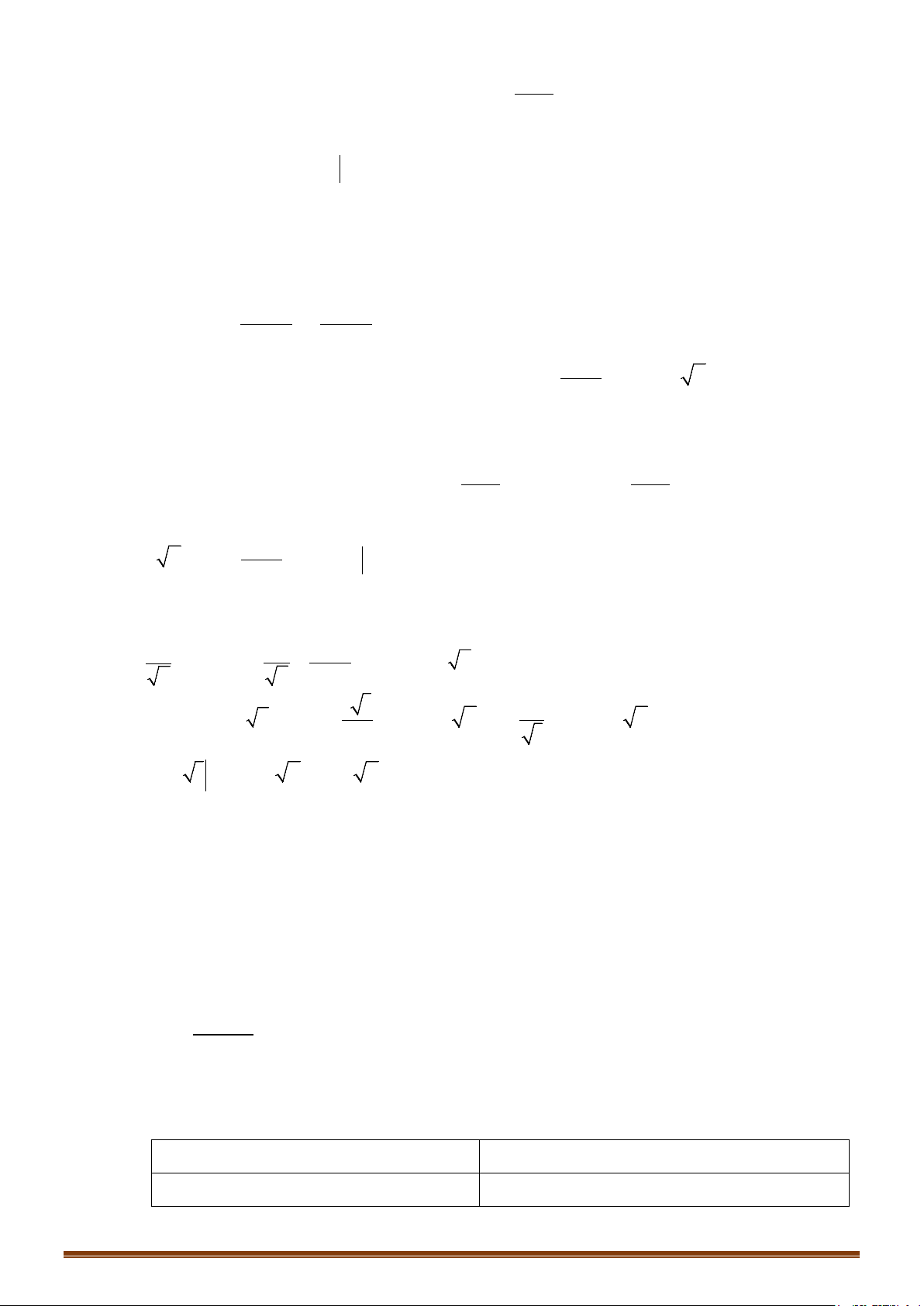
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Gọi
( )
Ft
là một nguyên hàm của hàm số
(
)
2
2
1
1
t
ft
t
−
=
+
. Suy ra:
(
)
( )
.Ft ft
′
=
Ta có:
( ) ( ) ( )
( ) ( ) ( )
3
3
2
2
d 3 2 *.
x
x
x
x
gx f t t Ft F x F x= = = −
∫
Lấy đạo hàm hai vế của (*) theo biến
x
ta được:
( ) ( ) ( )
3. 3 2 2gx F x F x
′′ ′
= −
( ) ( ) ( )
3. 3 2 2gx f x f x
′
⇔= −
( )
22
22
9141
3 2.
9141
xx
gx
xx
−−
′
⇔= −
++
Câu 22: Cho hàm số
f
và số thực
0a
>
thỏa mãn điều kiện:
( )
2
d 62
x
a
ft
tx
t
+=
∫
với
0x >
.
Tìm
a
và
f
.
Lời giải
Gọi
( )
Ft
là một nguyên hàm của hàm số
( )
2
ft
t
. Suy ra:
( )
( )
2
.
ft
Ft
t
′
=
Ta có:
(
)
(
)
(
)
(
)
(
)
2
2 6 d *.
x
x
a
a
ft
x t Ft Fx Fa
t
−= = = −
∫
Lấy đạo hàm hai vế của (*) theo biến
x
ta được:
( )
1
Fx
x
′
=
( )
( )
2
1
.
fx
fx xx
x
x
⇔= ⇔ =
Với
( )
fx xx=
, ta có:
2
1
d 62 d 62
xx
aa
tt
tx tx
t
t
+= ⇔ +=
∫∫
2 6 2 2 6 0 9.
x
a
t xa a⇔ += ⇔− +=⇔=
DẠNG 5: PHƯƠNG PHÁP ĐỔI BIẾN SỐ LOẠI 1 ĐỂ TÍNH TÍCH PHÂN
Yêu cầu : Tính tích phân
( ) ( )
12
d
b
a
I f xf x x=
∫
Phương pháp:
+ Biến đổi về dạng
( ) ( )
d.
b
a
I f ux u x x
′
=
∫
+ Đặt
( ) ( )
d d.tux tuxx
′
= ⇒=
+ Đổi cận:
( ) ( )
12
;.xa tua txb tub t= ⇒= = = ⇒= =
+ Khi đó:
( )
2
1
d
t
t
I ft t=
∫
là tính phân đơn giản hơn.
Một số dấu hiệu cơ bản và cách chọn
( )
t ux=
Dấu hiệu
Cách chọn
t
Hàm số chứa mẫu số
t
là mẫu số

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
Hàm số chứa căn
( )
, ()f x ux
t
là căn:
()t ux=
Hàm số có dạng
[ ]
()
n
fx
(xấu)
lũy thừa
t
là biểu thức (xấu) trong lũy thừa,
()t fx=
Hàm số lượng giác có góc xấu
t
là góc xấu
Hàm số mũ, mà mũ xấu
t
là mũ xấu
Hàm số
log u
mà
u
xấu
tu=
Hàm số
sin cos
()
sin cos
a xb x
fx
c xd xe
+
=
++
tan cos 0
22
xx
t
= ≠
Hàm
( )( )
1
()fx
xaxb
=
++
Tổng quát đặt
t xa xb= ++ +
+ Với
00xa xb+> ∧+>
, đặt
t xa xb= ++ +
+ Với
00xa xb
+< ∧+<
, đặt
( ) ( )
t xa xb=−+ +−+
(cos ).sinR x xdx
(theo biến
cos x
)
Đặt
costx=
(sin ).cosR x xdx
(theo biến
sin x
)
Đặt
sintx=
2
1
(tan ).
cos
R x dx
x
(theo biến
tan
x
)
Đặt
tantx=
2
1
(cot ).
sin
R x dx
x
(theo biến
cot x
)
Đặt
cottx=
Hàm có
,
xx
ea
Đặt
,
xx
t et a= =
Hàm số vừa có
ln x
vừa có
1
x
Đặt
lntx=
Câu 23: Tính các tích phân sau
( )
( )
( )( )
2
2
2
2
2
cos
3
10
4
11 1
2017
2
2 2017
00 0
tan
42 2
3
2
00 0
31 1
) d ) sin 2 d ) 1 sin d
46
) d ) 4d ) 1 1 d
( 3 1)
cos
) d ) sin .cos d ) d
cos cos sin
xx
x
x
a x b x x c xe x
xx
x
x
d x e xx x f x x x
xx
e xx
g x h x xx i x
x xx x
π
π
π
ππ π
−
+
++
+
+
+ +−
++
+
∫∫ ∫
∫∫ ∫
∫∫ ∫
Lời giải
( )
2
2
3
1
1
) .3 1daI x x
xx
= +
+
∫
Đặt
( )
32
d 3 1dtx x t x x= +⇒ = +
.
Đổi cận:
12xt
=⇒=
;
2 10xt= ⇒=
.
Suy ra:
10
10
2
2
1
d ln ln 5.I tt
t
= = =
∫
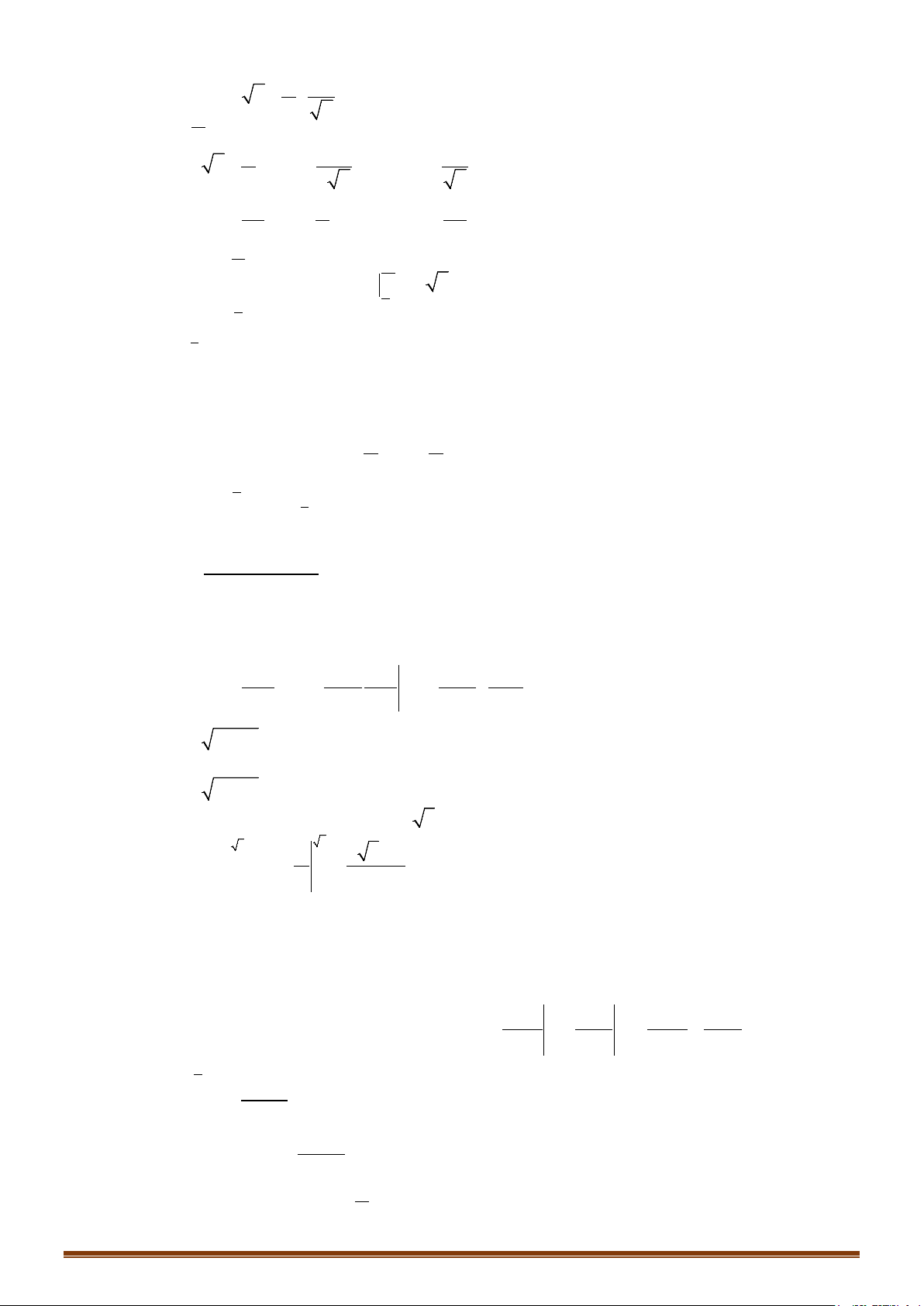
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 10
2
2
4
1
) sin d
4
bI x x
x
π
π
π
= −
∫
Đặt
11
d d 2d d
4
2
tx t x t x
xx
π
= −⇒= ⇒ =
.
Đổi cận:
2
44
xt
ππ
= ⇒=
;
2
3
4
xt
π
π
= ⇒=
.
Suy ra:
3
4
4
4
4
2sin d 2cos 2 2.
I tt t
π
π
π
π
3
= =−=
∫
(
)
2
cos
0
) 1 sin d
xx
cI e x x
π
−
= +
∫
Đặt
( )
cos d 1 sin d
tx x t xx
=− ⇒=+
.
Đổi cận:
01xt=⇒=−
;
22
xt
ππ
= ⇒=
.
Suy ra:
2
1
2
1
ed e .
t
I te
π
π
−
−
= = −
∫
(
)
1
2 2017
0
2
) 2 3d
( 3 1)
dI x x
xx
= +
++
∫
Đặt
(
)
2
3 1 d 2 3d
tx x t x x
= + +⇒ = +
.
Đổi cận:
01xt=⇒=
;
15xt=⇒=
.
Suy ra:
5
5
2017 2016 2016
1
1
2 11 1 1
d 1.
1008 1008 5
It
tt
==−=−−
∫
1
2
0
) 4. deI x xx= +
∫
Đặt
2 22
4 4d dt x t x tt xx= +⇒ = +⇒ =
.
Đổi cận:
02
xt= ⇒=
;
15xt=⇒=
.
Suy ra:
5
5
3
2
2
2
55 8
d.
33
t
I tt
−
= = =
∫
(
) ( )
1
2017
0
) 1 1dfI x x x=−+
∫
Đặt
1ddtx t x= −⇒ =
và
1xt= +
.
Đổi cận:
01xt=⇒=−
;
10xt=⇒=
.
Suy ra:
( )
( )
00
00
2019 2018
2017 2018 2017
11
11
11
2 d +2t d .
2019 1009 2019 1009
tt
Itt t t t
−−
−−
= += = + = −
∫∫
4
tan
2
0
1
) .d
cos
x
gI e x
x
π
=
∫
Đặt
2
1
tan d d
cos
t xt x
x
= ⇒=
.
Đổi cận:
00xt=⇒=
;
1
4
xt
π
= ⇒=
.
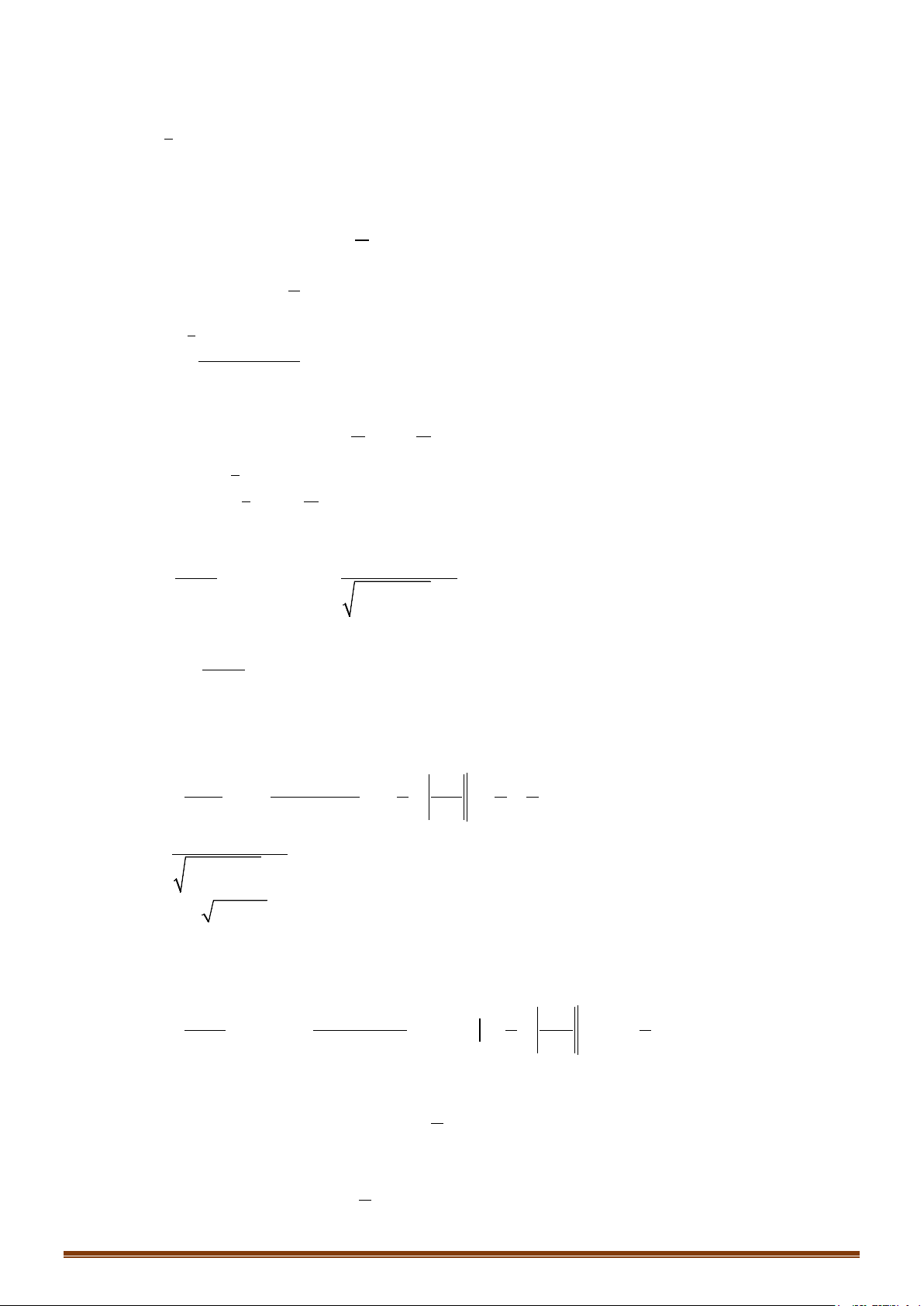
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 11
Suy ra:
1
0
d 1.
t
I et e= = −
∫
2
3
0
) sin .cos d
h x xx
π
∫
Đặt
sin d cos d
t x t xx= ⇒=
.
Đổi cận:
00xt= ⇒=
;
1
2
xt
π
= ⇒=
.
Suy ra:
1
3
0
1
td .
4
It= =
∫
2
0
cos
)d
cos sin
xx
iI x
xx x
π
=
+
∫
Đặt
cos sin d cos dt x x x t x xx= + ⇒=
.
Đổi cận:
01xt
=⇒=
;
22
xt
ππ
= ⇒=
.
Suy ra:
2
1
1
d ln .
2
It
t
π
π
= =
∫
Câu 24: Tính các tính phân sau (Đặt giảm bậc)
( )
31
2
4
2
3
3
20
2 61
)d ) d
1
29
xx
ax b x
x
xx
−
−
−−
∫∫
Lời giải
3
4
2
2
)d
1
x
aI x
x
=
−
∫
Đặt
2
d 2dt x t xx=⇒=
Đổi cận:
24xt= ⇒=
;
39xt=⇒=
.
Suy ra:
( )( )
9
99
2
44
4
1 1 1 1 14
d d ln ln .
1 1 1 2 1 23
t
It t
t tt t
−
= = = =
− −+ +
∫∫
( )
1
2
2
3
3
0
61
)d
29
x
bx
xx
−
−−
∫
Đặt
(
)
3
3 33 2 2
2 2 3 d 6 1dt xx t xx tt x x= −⇒ = −⇒ = −
Đổi cận:
00xt=⇒=
;
11xt=⇒=
Suy ra:
( )( )
1
11
2
1
2
0
00
0
3 1 13 1
d 3 1 d 3 ln 3 ln 2.
9 33 6 3 2
tt
I t tt
t tt t
−
==+ =−=+
− −+ +
∫∫
Tích phân có sẵn dạng
( )
( )
fux
Câu 25: Chứng minh rằng
( ) ( )
22
11
1
dd
x ax b
x ax b
I f ax b x f x x
a
+
+
= +=
∫∫
, với
0a ≠
.
Lời giải
Đặt
1
d d ddtaxb tax t x
a
= +⇒ = ⇒ =
.
Đổi cận:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
11
x x t ax b= ⇒= +
;
22
x x t ax b
= ⇒= +
.
Suy ra:
( ) ( )
22
11
11
dt d
ax b ax b
ax b ax b
I ft fx x
aa
++
++
= =
∫∫
(Do tích phân không phụ thuộc vào biến số).
Từ đây trở về sau, ta xem đây là một tính chất của tích phân.
Câu 26: Cho hàm số
( )
fx
liên tục trên
và
( )
7
3
d 2.fxx=
∫
Tính
( )
3
1
21.I f x dx
= +
∫
Lời giải
(
)
( )
( )
3 2.3 1 7
1 2.1 1 3
11
2 1 d d 1.
22
I f x dx fx x fx x
+
+
= += = =
∫ ∫∫
Câu 27: Cho hàm số
( )
fx
liên tục trên
và
( )
4
1
1 2 d 2.f xx−=
∫
Tính
( )
1
7
.I f x dx
−
−
=
∫
Lời giải
(
)
(
)
(
)
4 71
1 17
11
12d d d
22
f xx fx x fx x
−−
−−
−= =
−
∫ ∫∫
( )
( )
11
77
1
2 d d 4.
2
fx x fx x
−−
−−
⇔= ⇔ =
∫∫
Câu 28: Cho hàm số
(
)
fx
liên tục trên
và
( )
3
1
3 1 d 3.fx x−=
∫
Tính
( )
0
6
2.
I f x dx
−
= −
∫
Lời giải
Ta có:
( ) (
) ( )
3 88
1 22
1
3 3 1 d d d 9.
3
f x x fx x fx x= −= ⇔ =
∫ ∫∫
Ta có:
(
) ( )
( )
0 28
6 82
2 d d d 9.I f xx fxx fxx
−
= −=− = =
∫ ∫∫
Câu 29: Cho
( )
1
0
d2fxx=
∫
Tính
( )
4
0
cos 2 sin cos d .I f x x xx
π
=
∫
Lời giải
Đặt
1
cos 2 d 2sin 2 d d sin cos d
4
t x t xx t x xx= ⇒ =− ⇒− =
Đổi cận:
01xt=⇒=
;
0
4
xt
π
= ⇒=
Suy ra:
( )
1
0
1 11
d .2 .
4 42
I ft t= = =
∫
Tích phân với hàm số chẵn và lẻ
+ Hàm số
(
)
y fx=
là hàm số chẵn trên đoạn
[
]
;aa−
khi và chi khi
[ ]
;x aa∀∈−
ta có:
[ ]
;x aa− ∈−
và
( ) ( )
f x fx−=
.
+ Hàm số
( )
y fx=
là hàm số lẻ trên đoạn
[ ]
;aa−
khi và chi khi
[ ]
;x aa
∀∈−
ta có:
[ ]
;x aa− ∈−
và
( ) ( )
f x fx−=−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
+ Ta có thể thay đoạn
[ ]
;aa−
bằng một tập đối xứng thì định nghĩa hàm số chẵn, hàm số lẻ vẫn
như trên.
Câu 30: Cho
(
)
fx
là hàm số chẵn, liên tục trên đoạn
[ ]
;aa−
. Chứng minh rằng:
( ) (
)
0
d 2 d.
aa
a
fx x fx x
−
=
∫∫
Lời giải
Ta có:
( ) (
)
( )
( )
0
00
d dd
a aa
aa
I fx x fxdx fx x K fx x
−−
= = +=+
∫∫∫ ∫
Tính
( )
0
d
a
K fx x
−
=
∫
.
Đặt
ddtx t x=−⇒ =−
.
Đổi cận:
x a ta
=−⇒=
;
00xt
=⇒=
.
Suy ra:
(
) ( ) ( )
0
00
d dd
aa
a
K f xx f xx fxx=−−=−=
∫∫∫
.
Do đó:
( ) ( )
00
d 2 d.
aa
I K fx x fx x=+=
∫∫
Câu 31: Cho
( )
fx
là hàm số chẵn, liên tục trên đoạn
[ ]
;aa
−
. Chứng minh rằng:
(
)
(
)
0
d
1
aa
x
a
fx
I x f x dx
b
−
= =
+
∫∫
, với
0a >
,
0
b >
.
Lời giải
Đặt
ddtx t x=−⇒ =−
Đổi cận:
x a ta=−⇒=
;
xa t a= ⇒=−
Suy ra:
( ) ( )
( )
dt d d
11 1
tx
aa a
tt x
aa a
f t bf t b f x
I tx
bb b
−
−
−−
−
=−= =
++ +
∫∫ ∫
Do đó:
( )
( )
( ) ( ) ( )
00
2 d d 2 d d.
11
x
a a aa a
xx
aa a
fx bfx
I x x fx fx x I fx x
bb
−− −
= + = = ⇔=
++
∫ ∫ ∫∫ ∫
Câu 32: Tính tích phân
1
2
1
d
21
x
x
Ix
−
=
+
∫
.
Lời giải
Vì
( )
2
fx x=
là hàm số chẵn trên đoạn
[ ]
1;1−
nên ta có:
1
2
0
1
d
3
I xx= =
∫
.
Câu 33: Tính tích phân
2
2
cos
d
1
x
x
Ix
e
π
π
−
=
+
∫
Lời giải
Vì
( )
cosfx x=
là hàm số chẵn trên đoạn
;
22
ππ
−
nên ta có:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
2
2
0
0
cos d sin 1I xx x
π
π
= = =
∫
.
Câu 34: Biết hàm số
2
y fx
π
= +
là hàm số chẵn trên
;
22
ππ
−
và
( )
sin cos
2
fx f x x x
π
+ += +
.
Tính
(
)
2
0
dI fx x
π
=
∫
.
Lời giải
Đặt
dd
2
tx t x
π
=−⇒=
và
2
xt
π
= +
Đổi cận:
0
2
xt
π
=⇒=−
;
0
2
xt
π
= ⇒=
Suy ra:
0
2
0
2
dd
22
I ft t ft t
π
π
ππ
−
= +=+
∫∫
( Do
2
y ft
π
= +
là hàm số chẵn trên
;
22
ππ
−
)
Do đó:
( )
(
)
( )
22 2
2
0
00 0
2 dt d sin cos d cos sint 2
2
I I ft ft t t t t t
ππ π
π
π
== + + = + =−+ =
∫∫ ∫
Vậy
1I =
.
Câu 35: Cho
( )
fx
là hàm số lẻ, liên tục trên đoạn
[ ]
;aa−
. Chứng minh rằng:
(
)
d 0.
a
a
fx x
−
=
∫
Lời giải
Ta có:
( ) ( ) ( ) ( )
0
00
d dd
a aa
aa
I fx x fxdx fx x K fx x
−−
= = +=+
∫∫∫ ∫
Tính
( )
0
d
a
K fx x
−
=
∫
.
Đặt
ddtx t x=−⇒ =−
.
Đổi cận:
x a ta=−⇒=
;
00xt
=⇒=
.
Suy ra:
( ) ( ) ( )
0
00
ddd
aa
a
K f xx f xx fxx=−−=−=−
∫∫ ∫
.
Do đó:
(
) ( ) ( )
0 00
d d d0
a aa
I K fx x fx x fx x=+=−+=
∫ ∫∫
Câu 36: Tính tích phân
1
2
1
2
1
cos4 sin sin ln d
21
xx
I xx x
x
−
+
= +
−
∫
Lời giải
Xét hàm
( )
1
cos4 sin sin ln
21
xx
fx x x
x
+
= +
−
Ta thấy
( )
fx
liên tục trên đoạn
11
;
22
−
và

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
(
)
1
11
cos4 sin sin ln cos4 sin sin ln
21 21
xx xx
fxxx xx
xx
−
−+
−= + = +
+−
(
)
1
cos4 sin sin ln
21
xx
x x fx
x
+
−+ =−
−
Nên
( )
fx
là hàm số lẻ trên
11
;
22
−
Vậy
0I
=
.
Câu 37: Tính tích phân
( )
2
0
sin sin dI x mx x
π
= +
∫
, với
m
∈
.
Lời giải
Đặt
ddtx t x
π
=−⇒ =
.
Đổi cận:
0
xt
π
=⇒=−
;
2xt
ππ
= ⇒=
.
( )
( )
( ) ( ) (
)
sin sin d sin sin d 1 sin sin d
m
I t mt m t mt t m t mt t t
ππ π
ππ π
ππ π
−− −
= +++ = − + =− −
∫∫∫
Xét hàm
( ) (
)
sin sinf t mt t= −
.
Ta thấy hàm số này liên tục trên đoạn
[ ]
;
ππ
−
và
( ) ( ) ( ) ( )
sin sin sin sinf t mt t mt t f t−= − + =− − =−
Nên
(
)
ft
là hàm số lẻ trên
[ ]
;
ππ
−
Vậy
( )
1 .0 0
m
I =−=
.
Một số kiểu đổi biến đặc biệt
Câu 38: Cho
( )
fx
là hàm số liên tục trên
[ ]
0;1
. Chứng minh rằng:
( )
( )
22
00
sin d cos d
I f xx f xx
ππ
= =
∫∫
Lời giải
Đặt
dd
2
t xt x
π
= −⇒ =−
.
Đổi cận:
0
2
xt
π
=⇒=
;
0
2
xt
π
= ⇒=
.
Suy ra:
( ) ( ) ( )
0
2 22
0 00
2
sin d sin d cos d cos d .
2
I f xx f t t f tt f xx
π ππ
π
π
= =− −= =
∫ ∫ ∫∫
Câu 39: Tính tích phân
(
)
( )
2
2
2
0
1
tan cos d
cos sin
I xx
x
π
= −
∫
.
Lời giải
Ta có:
( ) ( )
22
22
00
tan cos d tan sin dxx xx
ππ
=
∫∫
và
2
2
1
tan 1
cos
α
α
−=
Do đó:
( )
( )
22
2
2
00
1
tan sin d 1d .
cos sin 2
I xx x
x
ππ
π
=−==
∫∫
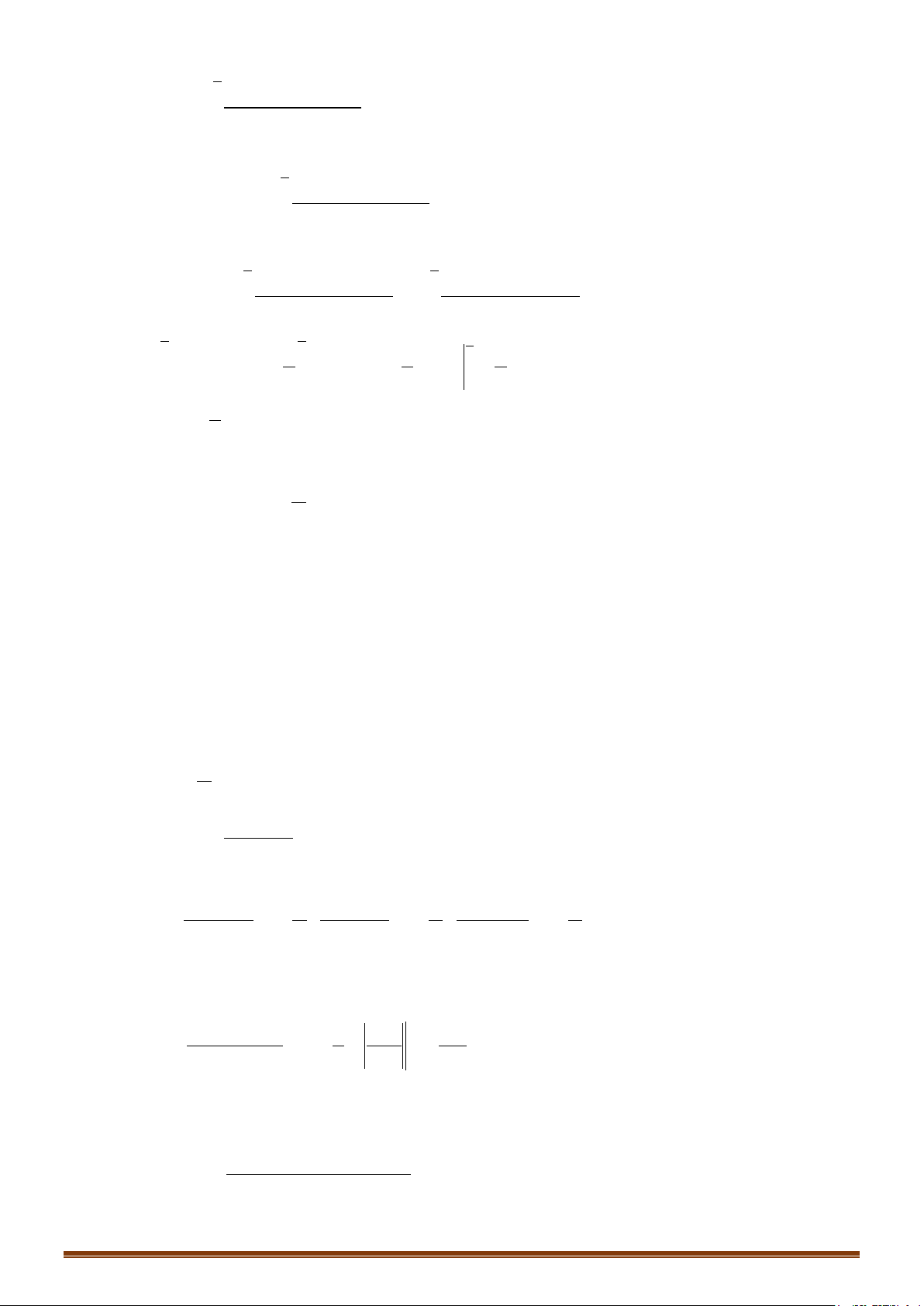
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
Câu 40: Tính
2017
2
2016 2016
0
sin .cos
d
sin cos
xx
Ix
xx
π
=
+
∫
.
Lời giải
Xét tích phân
2017
2
2016 2016
0
cos .sin
d
sin cos
xx
Jx
xx
π
=
+
∫
Ta có:
IJ=
. Suy ra:
2017 2017
22
2016 2016 2016 2016
00
sin .cos cos .sin
2 dd
sin cos sin cos
x x xx
IIJ x x
xx xx
ππ
=+= +
++
∫∫
22
2
0
00
1 11
sin .cos d sin 2 d cos 2 .
2 42
x xx xx x
ππ
π
= = =−=
∫∫
Vậy
1
.
4
I =
Câu 41: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
1;1−
. Chứng minh rằng
( )
(
)
00
sin d sin d
2
I xf xx f xx
ππ
π
= =
∫∫
Lời giải
Đặt
dd
t xt x
π
= −⇒ =−
Đổi cận:
0xt
π
=⇒=
;
0xt
π
= ⇒=
Suy ra:
( ) ( ) ( )
(
)
00
sin d sin dI xf x x t f t t
ππ
ππ
= =−−
∫∫
( ) (
) ( )
00 0
sin d . sin d sin df tt tf tt f xxI
ππ π
ππ
= −= −
∫∫ ∫
( )
0
sin d .
2
I f xx
π
π
⇔=
∫
Câu 42: Tính
2
0
sin
d
3 sin
xx
Ix
x
π
=
+
∫
Lời giải
22 2
000
sin sin sin
d d d.
3 sin 2 3 sin 2 4 cos 2
xx x x
I x x xJ
xx x
πππ
ππ π
= = = =
++−
∫∫∫
Đặt
cos d sin d
t x t xx= ⇒=−
Đổi cận:
01xt=⇒=
;
1xt
π
= ⇒=−
.
Suy ra:
( )(
)
1
1
1
1 1 2 ln 3
d ln .
2 2 42 2
t
Jt
tt t
−
−
−
= =−=
−+ +
∫
Câu 43: Cho
( )
fx
,
( )
gx
là các hàm số liên tục trên
và
( )
27f =
;
( )
11f −=
;
( )
29g =
;
( )
13g −=
.
Tính
( ) ( ) (
) ( )
( ) ( )
2
2
1
d
f xgx f xg x
Ix
f x gx
−
′′
−
=
+
∫
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
( )
( )
( )
(
) ( )
(
)
( )
(
)
(
)
2
22
22
11
.
dd
1
fx fx
gx
gx gx
I xx
f x gx
fx
gx
−−
′′
= =
+
+
∫∫
Đặt
(
)
(
)
(
)
( )
dd
fx fx
ttx
gx gx
′
= ⇒=
Đổi cận:
1
1
3
xt
=−⇒=
;
7
2
9
xt
= ⇒=
.
Suy ra:
(
)
7
7
9
9
2
1
1
3
3
1 13
d.
1 16
1
It
t
t
= =−=
+
+
∫
Chú ý: Trong lời giải trên đã sử dụng thêm giả thiết
( )
0gx≠
. Điều này không ảnh hướng đến
lời giải.
Câu 44: Cho hàm số
( )
y fx=
thỏa mãn
( ) ( )
52
. 36fxf x x x
′
= +
. Biết
( )
02f =
. Tính
(
)
2
2f
.
Lời giải
Ta có:
( )
( )
(
)
22
52
00
. d 3 6 d 48
I fxf x x x x x
′
= =+=
∫∫
Đặt
(
) (
)
ddtfx tfxx
′
= ⇒=
Đổi cận:
( )
0 02x tf=⇒= =
;
( )
22x tf= ⇒=
.
Suy ra:
( )
( )
( )
2
2
2
2
2
2
2
d2
22
f
f
f
t
I tt
= = = −
∫
( )
( )
2
2
2
48 2 2 100.
2
f
f⇔ = −⇔ =
DẠNG 6: PHƯƠNG PHÁP ĐỔI BIẾN SỐ LOẠI 2 ĐỂ TÍNH TÍCH PHÂN
Yêu cầu: Tính tích phân
( )
d
b
a
I fx x=
∫
Phương pháp: Đặt
( ) ( )
ddx t x tt
ϕϕ
′
= ⇒=
+ Đổi cận:
12
;
xa ttxb tt
= ⇒= =⇒=
+ Khi đó:
( ) ( )
2
1
d
t
t
I f t tt
ϕϕ
′
=
∫
Một số cách đổi biển cần nhớ:
+
( )
2
2
: tan , ;
22
a bx c bx c a t t
ππ
+ + + = ∈−
+
( )
2
2
: sin , ;
22
a bx c bx c a t t
ππ
− + + = ∈−
+
( )
{ }
2
2
: , ; \0
sin 2 2
a
bx c a bx c t
t
ππ
+ − + = ∈−
+ Nhớ:
22 2
11 1
( ) tan
0, 0
24
2
2
11
24
b
ax t
xx t
a
aa
xx t
a
dx dt
ax bx c
b
ax
aa
−∆
+=
∆< >
= =
++
−∆
−∆
++
∫∫ ∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
Câu 45: Tính các tích phân sau:
1 11
22 2
0 00
11 1
3
22
8
00 0
12
2
2
2
0
3
11 1
)d ) d ) d
1 3 4 44
d) d ) 1 d ) 4 4 1d
1
1
g) 2 d ) d
1
aI x bI x c I x
x x xx
x
I x eI x x f I x x x
x
I x x x hI x
xx
= = =
+ + ++
= = − =− ++
+
=−=
−
∫∫∫
∫∫ ∫
∫∫
Lời giải
1
2
0
1
)
1
a I dx
x
=
+
∫
Đặt
( )
2
tan , ; d 1 tan d
22
x tt x t t
ππ
= ∈− ⇒ = +
Đổi cận:
00xt
=⇒=
;
1
4
xt
π
=⇒=
.
Suy ra:
( )
44
2
2
00
1
. 1 tan d d
1 tan 4
I tt t
t
ππ
π
= +==
+
∫∫
.
1
2
0
1
)
3
b I dx
x
=
+
∫
Đặt
( )
2
3 tan , ; d 3 1 tan d
22
x tt x t t
ππ
= ∈− ⇒ = +
Đổi cận:
00xt= ⇒=
;
1
6
xt
π
=⇒=
.
Suy ra:
( )
66
2
2
00
11
. 3 1 tan d d
3 3tan
3 63
I tt t
t
ππ
π
= +==
+
∫∫
.
( )
1
2
0
1
)
321
c I dx
x
=
++
∫
Đặt
( ) ( )
22
3
2 1 3 tan , ; 2d 3 1 tan d d 1 tan d
22 2
x tt x tt x tt
ππ
+= ∈− ⇒ = + ⇒ = +
Đổi cận:
0
6
xt
π
=⇒=
;
1
3
xt
π
=⇒=
.
Suy ra:
( )
33
2
2
66
13 1
. 1 tan d d
3 3tan 2
23 123
I tt t
t
ππ
ππ
π
= +==
+
∫∫
.
1
3
8
0
d)
1
x
I dx
x
=
+
∫
Đặt
( ) ( )
4 3 23 2
1
tan , ; 4 d 1 tan d d 1 tan d
22 4
x tt xx t t xx t t
ππ
= ∈− ⇒ = + ⇒ = +
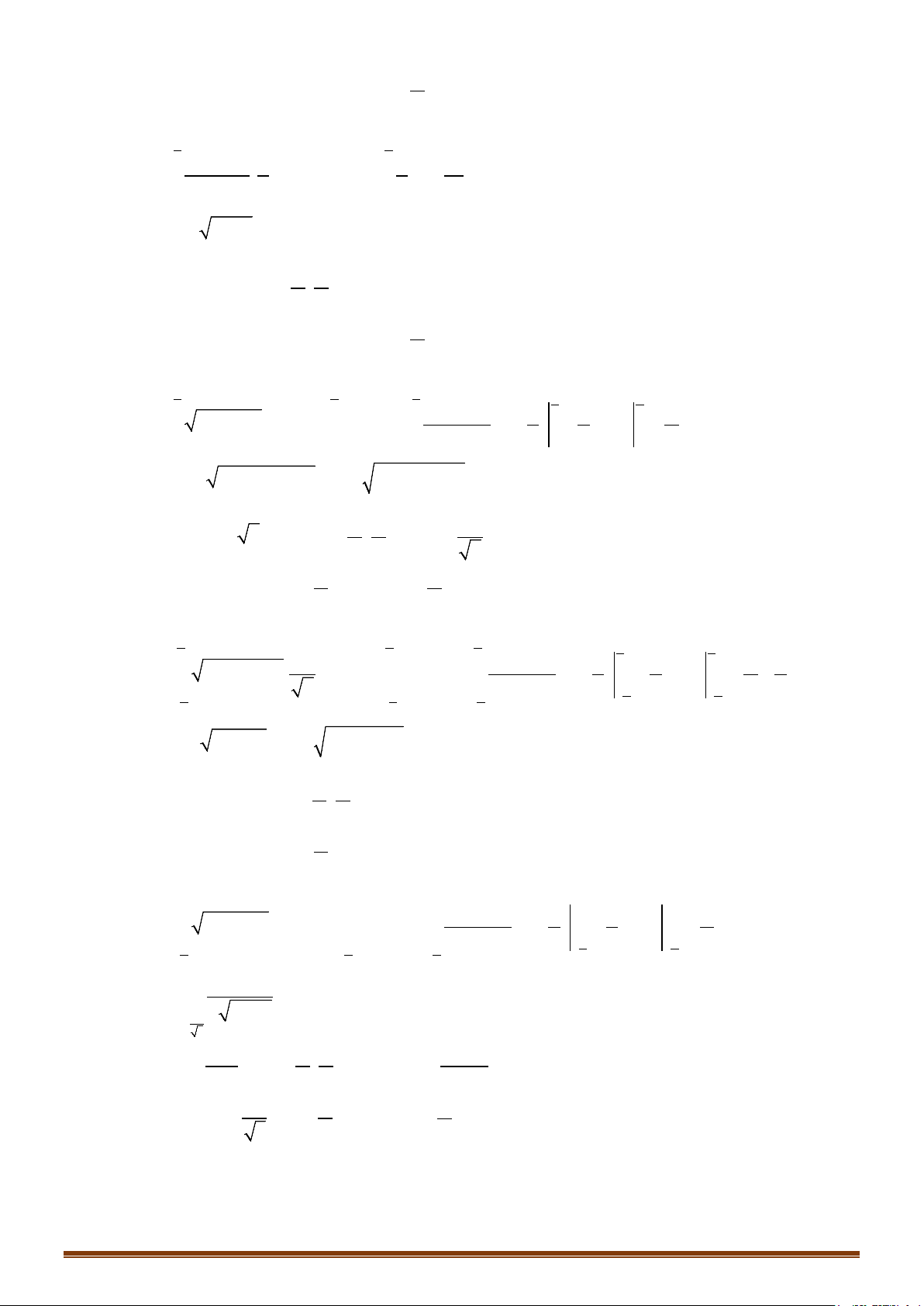
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 19
Đổi cận:
00
xt
=⇒=
;
1
4
xt
π
=⇒=
.
Suy ra:
(
)
44
2
2
00
11 1
. 1 tan d d
1 tan 4 4 16
I tt t
t
ππ
π
= +==
+
∫∫
.
1
2
0
)1e I x dx= −
∫
Đặt
sin , ; d cos d
22
x tt x tt
ππ
= ∈− ⇒ =
Đổi cận:
00
xt= ⇒=
;
1
2
xt
π
=⇒=
.
Suy ra:
2 22
22
22
00
0 00
1 cos 2 1 1
1 sin .cos d cos d d sin 2 .
2 24 4
t
I x tt tt t t t
π ππ
ππ
π
+
=− == =+=
∫ ∫∫
( )
11
2
2
00
) 4 4 1d 2 2 1 dfI x x x x x
=− ++ = − −
∫∫
Đặt
1
2 1 2 sin , ; d cos d
22
2
x tt x tt
ππ
−= ∈− ⇒ =
Đổi cận:
0
4
xt
π
=⇒=−
;
1
4
xt
π
=⇒=
.
Suy ra:
4 44
44
22
44
4 44
1 1 cos 2 1 1 1
2 2sin . cos d cos d d sin 2 .
2 2 4 42
2
t
I x tt tt t t t
π ππ
ππ
ππ
π ππ
π
−−
− −−
+
=− == =+=+
∫ ∫∫
( )
11
2
2
00
g) 2 d 1 1 dI xxx x x= − = −−
∫∫
Đặt
1 sin , ; d cos d
22
x tt x tt
ππ
−= ∈− ⇒ =
Đổi cận:
0
2
xt
π
=⇒=−
;
10xt
=⇒=
.
Suy ra:
00
0 00
22
22
2 22
1 cos 2 1 1
1 sin .cos d cos d d sin 2 .
2 24 4
t
I x tt tt t t t
ππ
π ππ
π
−−
− −−
+
=− == =+=
∫ ∫∫
2
2
2
3
1
)d
1
hI x
xx
=
−
∫
Đặt
{ }
2
1 cos
, ; \0 d d
sin 2 2 sin
t
xt x t
tt
ππ
−
= ∈− ⇒ =
Đổi cận:
2
3
3
xt
π
= ⇒=
;
2
6
xt
π
= ⇒=
.
Suy ra:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
33
2
2
66
sin cos
dd .
sin 6
1
1
sin
tt
I tt
t
t
ππ
ππ
π
= = =
−
∫∫
DẠNG 7: PHƯƠNG PHÁP TỪNG PHẦN ĐỂ TÍNH TÍCH PHÂN
Công thức từng phần:
( ) ( ) ( ) ( )
( ) ( )
dd
bb
b
a
aa
uxv x x uxvx vxu x x
′′
= −
∫∫
.
Viết gọn:
( )
dd
bb
b
a
aa
u v uv v u= −
∫∫
Áp dụng: Tính tích phân
( )
d
b
a
I fx x=
∫
Phương pháp:
+ Bước 1: Biến đổi
(
) (
)
12
.d
b
a
I fxf x x=
∫
+ Bước 2: Đặt
(
)
( )
( )
( )
1
1
22
dd
dd
u fx x
u fx
dv fxx v fxx
′
=
=
⇒
= =
∫
(Chọn
d
v
sao cho
v
dễ lấy nguyên hàm)
+ Bước 3: Khi đó
( )
d
b
b
a
a
I uv v u
= −
∫
● Dạng 1.
( ) ( )
sin dI P x ax b x= +
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
( )
( )
( )
( )
d .d
1
d sin d
cos
u Px x
u Px
v ax b x
v ax b
a
′
=
=
⇒
= +
=−+
.
● Dạng 2.
( ) ( )
cos dI P x ax b x= +
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
( )
( )
( )
( )
d .d
1
d cos d
sin
u Px x
u Px
v ax b x
v ax b
a
′
=
=
⇒
= +
= +
.
● Dạng 3.
( )
d
ax b
I Pxe x
+
=
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
( )
( )
d .d
1
dd
ax b
ax b
u Px x
u Px
ve
ve x
a
+
+
′
=
=
⇒
=
=
.
● Dạng 4.
( ) ( )
ln dI Px gx x=
∫
, trong đó
( )
Px
là đa thức.
Với dạng này, ta đặt
( )
( )
ln
dd
u gx
v Px x
=
=
.
● Dạng 5.
sin
d
cos
x
x
I ex
x
=
∫
.
Với dạng này, ta đặt
sin
cos
dd
x
x
u
x
v ex
=
=
.
Câu 46: Tính các tích phân sau:
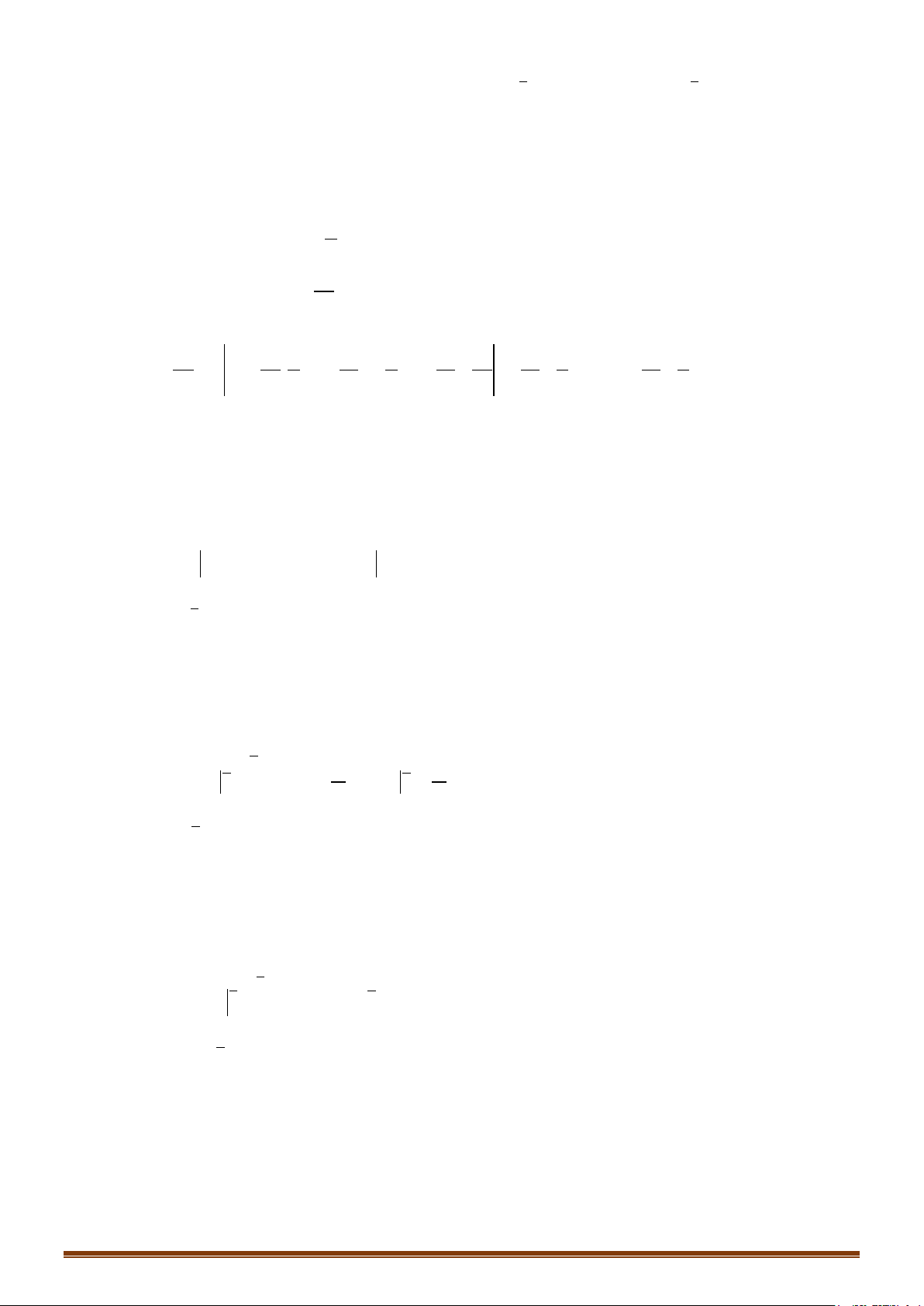
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 21
ln 2
22
1 00 0
) lnd ) d ) cosd ) sind
e
xx
aI x xx bI xe x cI x xx dI e xx
ππ
= = = =
∫ ∫∫ ∫
Lời giải
1
) ln d
e
aI x xx=
∫
Đặt
2
1
dd
ln
dd
2
ux
ux
x
v xx
x
v
=
=
⇒
=
=
Suy ra:
( )
2 2 2 22 2 2
2
11
11
1 11
ln . d d 1 .
2 2 2 2 2 4 24 44
ee
ee
x x e x ex e e
Ix x x e
x
= − = − = − = − −= +
∫∫
ln 2
0
)d
x
b I xe x=
∫
Đặt
dd
dd
xx
ux u x
vex ve
= =
⇒
= =
Suy ra:
ln 2
ln 2 ln2
00
0
d 2ln 2 2ln 2 1.
xx x
I xe e x e= − =−=−
∫
2
0
) cos dcI x xx
π
=
∫
Đặt
dd
d cos d sin
ux u x
v xx v x
= =
⇒
= =
Suy ra:
2
22
00
0
sin sin d cos 1.
22
I x x xx x
π
ππ
ππ
= − =+=−
∫
2
0
) sin d
x
dI e xx
π
=
∫
Đặt
sin d cos d
dd
xx
u x u xx
vex ve
= =
⇒
= =
Suy ra:
2
2
2
0
0
sin cos d
xx
I e x e xx e J
π
π
π
=−=−
∫
Tính
2
0
cos d
x
J e xx
π
=
∫
Đặt
cos d sin d
dd
xx
u x u xx
vex ve
= = −
⇒
= =
Suy ra:
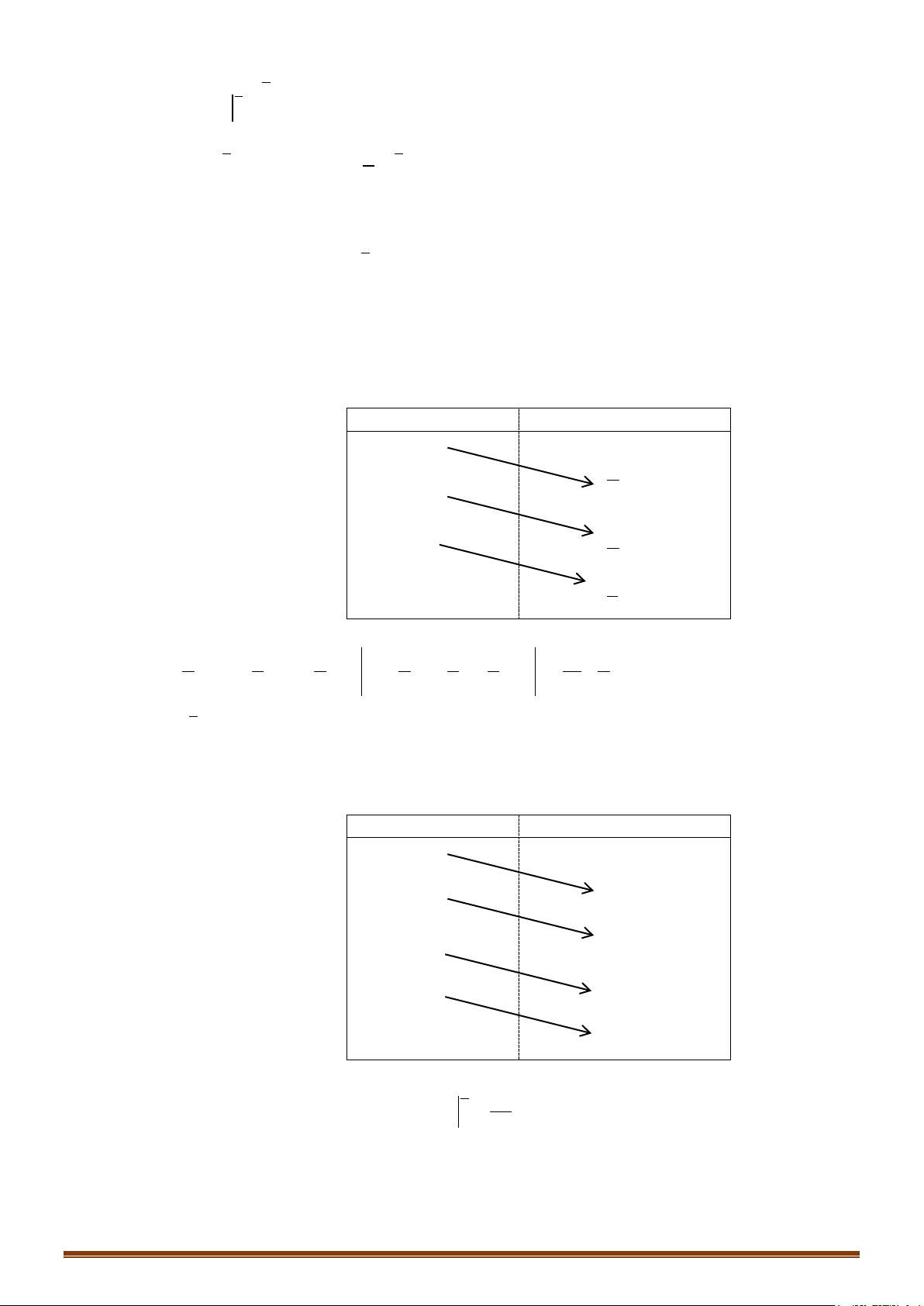
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 22
2
2
0
0
cos sin d 1
xx
J e x e xx I
π
π
= + =−+
∫
Vậy:
( )
22
1
1 1.
2
Ie I I e
ππ
= −−+ ⇔ = +
Câu 47: Tính các tích phân sau:
1
2
22 2
00
) d ) cos d
x
aI xe x bI x x x
π
= =
∫∫
Lời giải
1
22
0
)d
x
aI xe x=
∫
Cách làm nhanh
Cột
u
(cột đạo hàm)
Cột
v
(cột nguyên hàm)
2
x
2x
2
0
2x
e
2
1
2
x
e
2
1
4
x
e
2
1
8
x
e
Dựa vào bảng, ta có:
11
2
22 2 2 2 2
00
1 1 1 1 11 1
2 2 4 2 2 4 44
x xx x
e
I x e xe e x x e
= −+=−+=−
2
3
0
) cos dbI x xx
π
=
∫
Cột
u
(cột đạo hàm)
Cột
v
(cột nguyên hàm)
3
x
2
3x
6x
6
0
cos x
sin x
cos x−
sin x−
cos x
Dựa vào bảng, ta có:
( )
3
32
2
0
sin 3 cos 6 sin 6cos 3 6.
8
I x xx xxx x
π
π
π
= + − − = −+
Câu 48: Tính tích phân
0
2 sin 3 d
x
I xx
π
=
∫
Lời giải
+
−
+
+
−
+
−
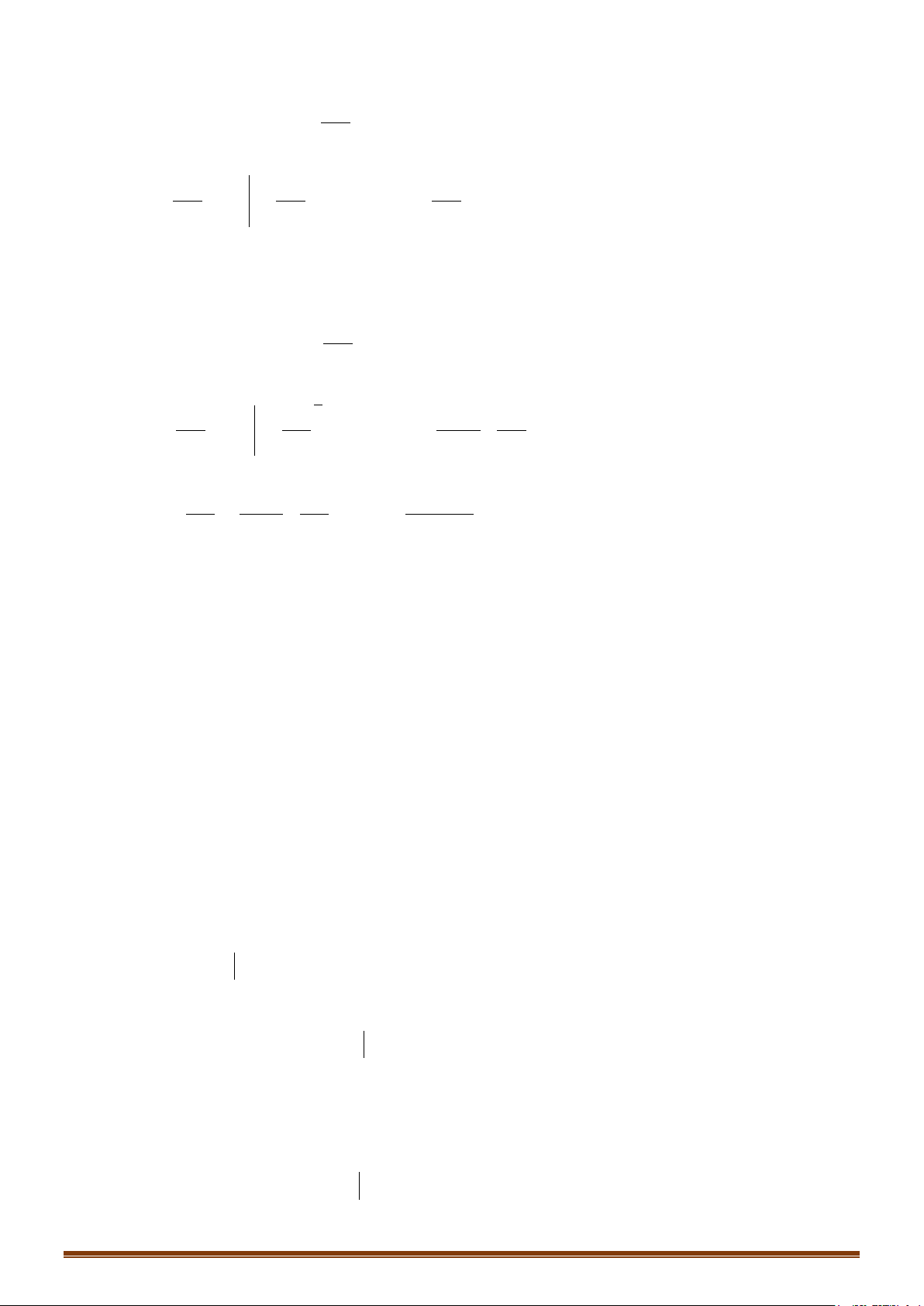
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
Đặt
d 3cos3 d
sin 3
2
d 2d
ln 2
x
x
u xx
ux
vx
v
=
=
⇒
=
=
Suy ra:
0
0
23 3
sin 3 2 cos3 d
ln 2 ln 2 ln 2
x
x
I x xx J
π
π
=−=−
∫
Tính
0
2 cos3 d
x
J xx
π
=
∫
Đặt
d 3sin 3 d
cos3
2
d 2d
ln 2
x
x
u xx
ux
vx
v
= −
=
⇒
=
=
Suy ra:
2
0
0
2 3 12 3
cos3 2 sin 3 d
ln 2 ln 2 ln 2 ln 2
x
x
J x xx I
π
π
π
+
= + =−+
∫
Do đó:
(
)
2
31 2
3 12 3
.
ln 2 ln 2 ln 2 9 ln 2
I II
π
π
+
+
=− − + ⇔=
+
Câu 49: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
;ab
. Chứng minh rằng:
( ) ( ) ( ) ( )
d.
b
x ba
a
I f x f x e x f b e f ae
′
=+=−
∫
Lời giải
Cách 1:
Ta có:
(
) (
)
( )
( )
(
)
d dd d
b bb b
x xx x
a aa a
I f x fx ex f xex fxex J fxex
′′
=+= +=+
∫ ∫∫ ∫
Tính
(
)
d
b
x
a
J f xe x
′
=
∫
Đặt
( ) ( )
dd
dd
xx
ue uex
vfxx vfx
= =
⇒
′
= =
Suy ra:
(
)
(
)
d
b
b
xx
a
a
J f xe f xe x= −
∫
Do đó:
( ) ( )
( ) ( )
d
b
b
x x ba
a
a
I J f xe x f xe f be f ae
=+==−
∫
Cách 2:
Ta có:
(
)
( )
( ) ( )
( ) ( )
x xx x
f xe f xe f xe f x f x e
′
′′
= +=+
Do đó:
( )
( )
(
) ( ) ( )
d.
b
b
x x ba
a
a
I f xe x f xe f be f ae
′
= = = −
∫
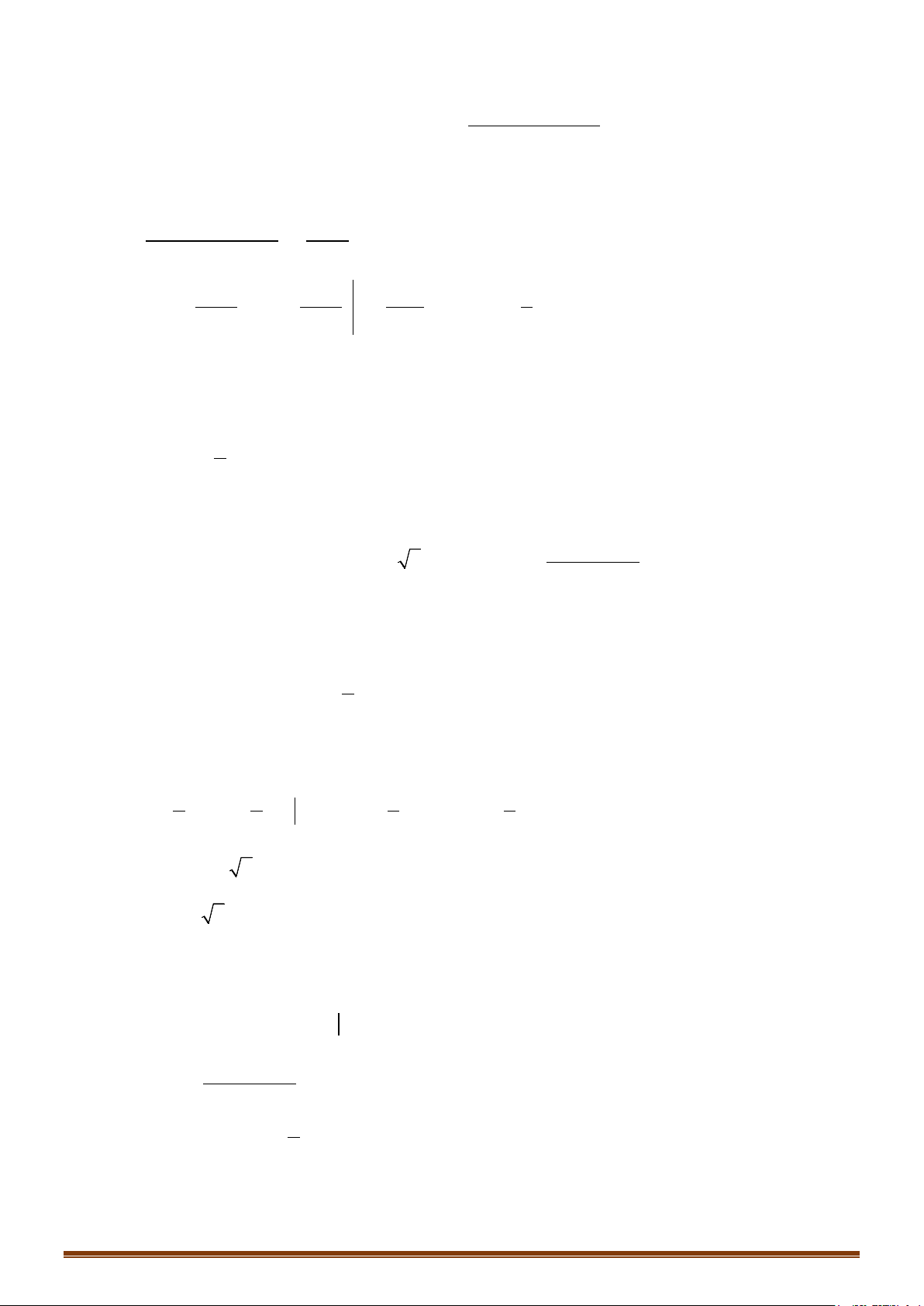
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
Câu 50: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[
]
1;1
−
thỏa
( ) ( )
23
12 6 7fx fx x x+− = − −
Tính
( ) ( )
1
1
ln 2.
d.
2
x
f x fx
Ix
−
′
−
=
∫
Lời giải
Ta có:
(
) (
)
( )
ln 2.
22
xx
f x fx fx
′
′
−
=
nên
( ) (
) (
)
(
) ( ) ( )
1
1
1
1
1
1
d 2. 1 1 4 1
2 22 2
xx
fx fx f
I x f ff
−
−
′
= = = − −= − −
∫
Ta có:
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( ) ( )
120 7 120 7
14 17
02 10 204 10
ff ff
ff
ff ff
−= −=
⇔ ⇒ − −=
− −= − −=
Vậy:
7
2
I =
.
Câu 51: Tính các tích phân
( )
2
2
1
3
00
ln .ln ln
) d ) sin d ) d
e
e
x
e
xx
aI xe x bI xx cI x
x
π
= = =
∫∫ ∫
Lời giải
22
11
32
00
)d
xx
a I x e dx x e x x
= =
∫∫
Đặt
2
1
d 2d d d
2
t x t xx t xx=⇒= ⇒ =
Đổi cận:
00xt=⇒=
;
11xt=⇒=
Suy ra:
( )
( )
11
1
0
00
11 1 1
d d 1.
22 2 2
t tt
I te t te e t e e
= = − = −− =
∫∫
2
0
) sin dbI x x
π
=
∫
Đặt
2
2d dt x t x tt x= ⇒=⇒ =
Đổi cận:
00xt=⇒=
;
2
xt
ππ
= ⇒=
Suy ra:
0
00
2 sin d 2 cos cos d 2 .I t tt t t tt
ππ
π
π
= =−+ =
∫∫
( )
5
2
ln .ln ln
)d
e
e
xx
cI x
x
=
∫
Đặt
1
ln d dt xt x
x
= ⇒=
Đổi cận:
1xe t=⇒=
;
e
xe te
= ⇒=
Suy ra:
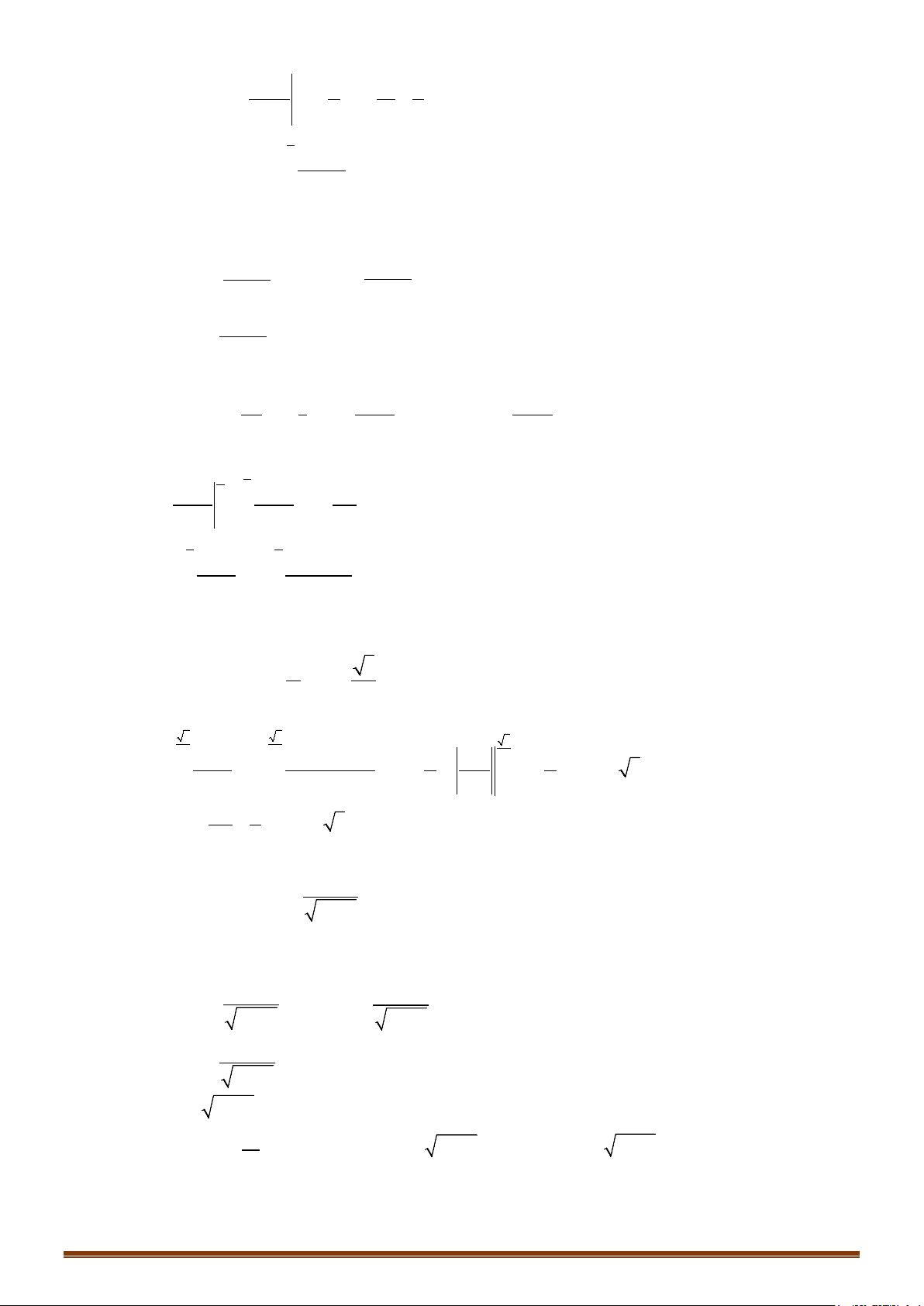
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
22
11
1
ln 1
ln d d .
2 2 44
e
ee
tt t e
I t tt t
= = −=+
∫∫
Câu 52: Tính tích phân
3
2
0
sin
cos
xx
I dx
x
π
=
∫
Lời giải
Đặt
2
2
dd
sin
sin
d
dd
cos
cos
ux
ux
x
x
vx
vx
x
x
=
=
⇒
=
=
∫
Tìm
2
sin
d
cos
x
vx
x
=
∫
Đặt
cos d sin dt x t xx= ⇒=−
Suy ra:
2
11 1
d
cos
v tC C
tt x
−
= =+= +
∫
. Chọn
1
cos
v
x
=
Do đó:
3
3
0
0
12
d.
cos cos 3
x
I xJ
xx
π
π
π
=−=−
∫
Tính
33
2
00
1 cos
dd
cos 1 sin
x
xx
xx
ππ
=
−
∫∫
Đặt
sin d cos d
t x t xx= ⇒=
và
2
1
x
et= −
Đổi cận:
00xt= ⇒=
;
3
32
xt
π
= ⇒=
Suy ra:
( )( )
( )
33
3
22
2
2
00
0
1 1 11 1
d d ln ln 7 4 3 .
1 1 1 21 2
t
Jt t
t tt t
−
= = =− =−−
− −+ +
∫∫
Vậy
( )
21
ln 7 4 3 .
32
I
π
=+−
Câu 53: Tính tích phân
ln3
0
1
x
x
xe
I dx
e
=
+
∫
Lời giải
Đặt
dd
dd
d
1
1
x
x
x
x
ux
ux
e
e
vx
vx
e
e
=
=
⇒
=
=
+
+
∫
Tìm
d
1
x
x
e
vx
e
=
+
∫
Đặt
2
1 1 2d d
xx x
t e t e tt e x= +⇒ = +⇒ =
Suy ra:
2
d 2d 2 2 1
x
t
v t t tC e C
t
= = = + = ++
∫∫
. Chọn
21
x
ve= +
Do đó:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
ln3
ln3
0
0
2 1 2 1d 4 ln 3 2 .
xx
I xe e x J= +− += −
∫
Tính
ln3
0
1d
x
J ex= +
∫
Đặt
2
1 1 2d d
xx x
t e t e tt e x= +⇒ = +⇒ =
và
2
1
x
et= −
Đổi cận:
02
xt=⇒=
;
ln 3 2xt= ⇒=
Suy ra:
( )( )
ln3 2 2
2
2
0
22
12 1
d d21 d
1 11
x
x
x
et
J ex t t
e t tt
+
= = = +
− −+
∫ ∫∫
( )
( )
2
2
2
2
1 21
2 ln 2 2 2 ln
1
3 21
t
t
t
−+
= + =−+
+
−
Vậy
( )
( )
21
4ln 3 4 2 2 2 ln .
3 21
I
+
= −−−
−
Câu 54: Chứng minh rằng:
11
22 2
00
1
1d 2 2 1d
4
Ixxx xx
= += − +
∫∫
Lời giải
( )
( )
22 3
11
22
00
1
dd
11
x x x xx
I xx
xx
++
= =
++
∫∫
Đặt
( )
3
2
2
2
d 3 1d
dd
1
1
ux x
ux x
x
vx
vx
x
= +
= +
⇒
=
= +
+
Suy ra:
( ) ( )
11
1
3 2 22 2
0
00
1 3 1 1d 2 2 3 1dIxxx x xx I xx= + +− + + = −− +
∫∫
1
2
0
1
2 2 1d .
4
I xx
⇔= − +
∫
Câu 55: Tính
( )
2
3
2
0
d
sin cos
x
Ix
xx x
π
=
+
∫
Lời giải
Ta có:
( )
2
1 cos
sin cos
sin cos
xx
xx x
xx x
′
−=
+
+
Ta có:
( )
3
2
0
cos
.d
cos
sin cos
x xx
Ix
x
xx x
π
=
+
∫
Đặt
( )
2
2
cos sin
dd
cos
cos
cos
1
dd
sin cos
sin cos
x
xx x
u
ux
x
x
xx
vx
v
xx x
xx x
+
=
=
⇒
=
= −
+
+

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 27
Suy ra:
( )
3
3
3
2
0
0
0
14 4
d tan 3.
cos sin cos cos
33 33
x
I xx
xx x x x
π
π
π
ππ
ππ
=− + =−+=−+
+
++
∫
Câu 56: Cho hàm số
( )
fx
có nguyên hàm là
(
)
Fx
trên đoạn
[ ]
1; 2
, biết
( )
21F =
và
( )
2
1
d5Fx x=
∫
.
Tính
( ) (
)
2
1
1dI x fx x= −
∫
.
Lời giải
Đặt
( ) (
)
1 dd
dd
ux u x
v f x x v Fx
=−=
⇒
= =
Suy ra:
( ) ( ) (
) (
) ( )
22
2
1
11
1 d 2 d 15 4I x Fx Fx x F Fx x=−−=−=−=−
∫∫
Câu 57: Cho
( )
2017
2017 2017
sin
sin cos
x
fx
xx
=
+
. Tính
(
)
2
0
d
I xf x x
π
′
=
∫
.
Lời giải
Ta có:
( ) ( ) ( )
( )
2 22
2
0
0 00
d d1 dI xf x x xfx fx x fx x
π ππ
π
′
= =−=−
∫ ∫∫
Đặt
( )
2017
2017 2017
cos
sin cos
x
gx
xx
=
+
. Theo phần trước, ta có:
(
)
( )
22
00
ddgxx fxx
ππ
=
∫∫
Do đó:
( )
( ) ( )
22 2
00 0
11
d d d.
2 24
fx x fx gx x x
ππ π
π
= +==
∫∫ ∫
Vậy:
1.
4
I
π
= −
DẠNG 7. KỸ THUẬT TÍCH PHÂN TỪNG PHẦN HÀM ẨN
Câu 58: Cho hàm số
( )
fx
thỏa mãn
( )
( )
3
0
. . d8
fx
xf x e x
′
=
∫
và
( )
3 ln 3f =
. Tính
( )
3
0
d.
fx
Iex=
∫
Lời giải
Đặt
( )
( )
( )
dd
.
d .d
fx
fx
ux
ux
v f xe x
ve
=
=
⇒
′
=
=
Khi đó
( )
(
) ( ) (
)
33
3
0
00
. . d . d.
fx fx fx
xfxexxe ex
′
= −
∫∫
Suy ra
(
)
( ) ( )
33
3
00
8 3. d d 9 8 1.
f fx fx
e ex ex= − → = − =
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
Câu 59: Cho hàm số
( )
fx
có đạo hàm liên tục trên
0; ,
2
π
thỏa mãn
( )
2
2
0
' cos d 10
f x xx
π
=
∫
và
( )
0 3.
f =
Tích phân
( )
2
0
sin 2 df x xx
π
∫
bằng
Lời giải
Xét
( )
2
2
0
' cos d 10f x xx
π
=
∫
, đặt
( )
( )
2
2
d sin 2 d
cos
.
d ' cos d
u xx
ux
v fx
v f x xx
= −
=
⇒
=
=
Khi đó
( )
( )
(
)
22
22
2
0
00
10 ' cos d cos sin 2 df x xx xf x f x xx
ππ
π
= = +
∫∫
( ) (
)
( ) ( )
22
00
10 0 sin 2 d sin 2 d 10 0 13.f f x xx f x xx f
ππ
⇔ = − + → = + =
∫∫
Câu 60: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
2
1
1d 3
fx x−=
∫
và
( )
1 4.f =
Tích phân
(
)
1
32
0
'd
xf x x
∫
bằng
Lời giải
Ta có
( )
( )
21
1
10
1d 3 d 3
tx
fx x ft t
= −
− = → =
∫∫
hay
( )
1
0
d 3.
fx x=
∫
Xét
( )
( ) ( )
2
1 11
32
0 00
11
' d ' d ' d.
22
tx
xfx x tftt xfxx
=
→ =
∫ ∫∫
Đặt
( ) ( )
dd
.
d 'd
ux u x
vfxx vfx
= =
⇒
= =
Khi đó
( )
( ) ( ) ( )
[ ]
2
11 1
1
32
0
00 0
1 1 11
' d ' d d 43 .
2 2 22
tx
xf x x tf t t xfx fx x
=
→ = − = − =
∫∫ ∫
Câu 61: Cho hàm số
( )
fx
nhận giá trị dương, có đạo hàm liên tục trên
[ ]
0; 2 .
Biết
( )
01f =
và
( ) ( )
2
24
2
xx
fxf x e
−
−=
với mọi
[ ]
0; 2 .x ∈
Tính tích phân
( )
( )
( )
32
2
0
3'
d.
x xfx
Ix
fx
−
=
∫
Lời giải
Từ giả thiết
( ) ( ) ( )
2
2
24
2 2 1.
x
xx
fxf x e f
=
−
− = → =
Ta có
( )
( )
( )
32
2
0
3'
d.
x xfx
Ix
fx
−
=
∫
Đặt
( )
( )
( )
( )
32
2
3
d 3 6d
.
'
dd
ln
ux x
u x xx
fx
vx
v fx
fx
= −
= −
⇒
=
=
Khi đó
( )
( )
(
)
( )
( )
( )
( )
22
2
21
32 2 2
0
00
3 ln 3 6 ln d 3 2 ln d 3 .
f
I x x fx x x fx x x x fx x J
=
=− −− =−− =−
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 29
Ta có
(
)
(
)
(
)
(
)
(
)
(
)
20
2
2
2
02
2 ln d 2 2 2 ln 2 d 2
xt
J x x fx x t t f t t
= −
= − = −− − − −
∫∫
( ) ( )
( ) ( )
( )
( )
02
2
2
20
2 2 2 ln 2 d 2 2 ln 2 d .
x xfx x xxfxx
= − − − − −= − −
∫∫
Suy ra
( )
( )
( )
( )
( )
( ) ( )
22 2
22 2
00 0
2 2 ln d 2 ln 2 d 2 ln 2 dJ x x fxx x x f xx x x fxf xx=− +− − =− −
∫∫ ∫
( )
( )( )
2
22
2 24 2 2
00
32 16
2ln d 2 2 4d .
15 15
xx
xxe x xxxxx J
−
= − = − − = → =
∫∫
Vậy
16
3.
5
IJ=−=−
DẠNG 8. TÍNH TÍCH PHÂN DỰA VÀO TÍNH CHẤT
Câu 62: Cho hàm số
( )
fx
là hàm số lẻ, liên tục trên
[ ]
4; 4 .−
Biết rằng
( )
0
2
d2f xx
−
−=
∫
và
( )
2
1
2 d 4.f xx−=
∫
Tính tích phân
( )
4
0
d.I fx x
=
∫
Lời giải
Do
( )
fx
là hàm lẻ nên
( ) ( )
.
f x fx
−=−
Xét
( )
0
2
d 2.A f xx
−
=−=
∫
Đặt
d d.tx t x= − → = −
Đổi cận:
22
.
00
xt
xt
=−→=
= →=
Khi đó
( ) ( ) ( )
022
200
d d d.A ft t ft t fx x=−= =
∫∫∫
Xét
( ) ( )
22
11
2d 2d.B f xx f xx=−=−
∫∫
Đặt
2 d 2d .ux u x= → =
Đổi cận:
12
.
24
xu
xu
=→=
=→=
Khi đó
( ) ( ) ( )
444
222
11
d d d 2 2.4 8.
22
B fu u fx x fx x B= − = − → = − = − = −
∫∫∫
Vậy
(
) ( ) ( )
4 24
0 02
d d d 2 8 6.I fx x fx x fx x
= = + =−=−
∫∫∫
Chọn B.
Câu 63: Cho hàm số
( )
fx
là hàm số chẵn, liên tục trên
[ ]
1; 6 .−
Biết rằng
( )
2
1
d8fx x
−
=
∫
và
( )
3
1
2 d 3.f xx−=
∫
Tính tích phân
( )
6
1
d.I fx x
−
=
∫
Lời giải
Vì
(
)
fx
là hàm số chẵn nên
( ) ( )
33
11
2d 2d 3.f xx f xx−= =
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 30
Xét
( )
3
1
2 d 3.K f xx= =
∫
Đặt
2 d 2d .
tx t x= → =
Đổi cận:
12
.
36
xt
xt
=→=
=→=
Khi đó
( ) ( ) ( )
66 6
22 2
11
d d d 2 6.
22
K ft t fx x fx x K
= = → = =
∫∫ ∫
Vậy
( ) (
)
( )
6 26
1 12
d d d 8 6 14.I fx x fx x fx x
−−
= = + =+=
∫∫∫
Chọn D.
Câu 64: Cho hàm số
( )
fx
liên tục trên
[
]
3; 7 ,
thỏa mãn
( ) ( )
10fx f x= −
với mọi
[ ]
3; 7x
∈
và
( )
7
3
d 4.fx x=
∫
Tính tích phân
( )
7
3
d.I xf x x=
∫
Lời giải
Đặt
( )
3 7 d d.t x tx
= + − → = −
Đổi cận
73
.
37
xt
xt
= →=
=→=
Khi đó
( ) ( ) ( ) ( ) ( ) (
)
377
733
10 10 d 10 10 d 10 10 dI tf t t tf t t xf x x=−− −= − −= − −
∫∫∫
( )
(
)
( ) ( )
( ) (
) ( )
7 77 7
10
3 33 3
10 d 10 d d 10 d .
fx f x
xfx x fx x xfx x fx x I
= −
=−= −= −
∫ ∫∫ ∫
Suy ra
( )
7
3
2 10 d 10.4 40 20.I fx x I= = = → =
∫
Chọn A.
Câu 65: Cho hàm số
( )
y fx=
là hàm số chẵn và liên tục trên đoạn
[ ]
;,
ππ
−
thỏa mãn
( )
0
d 2018.fx x
π
=
∫
Giá trị của tích phân
(
)
d
2018 1
x
fx
Ix
π
π
−
=
+
∫
bằng
Lời giải
Đặt
d d.xt x t= − → = −
Đổi cận
.
xt
xt
ππ
ππ
=−→=
= →=−
Khi đó
(
) ( ) ( )
( )
2018 2018
d d d d.
2018 1 2018 1 1 2018 1 2018
tx
tt t x
ft ft ft fx
I tt t x
ππ π π
π ππ π
−
−−
−− −
−− − −
=−= = =
+ ++ +
∫∫∫ ∫
Vì
( )
y fx=
là hàm số chẵn trên đoạn
[ ]
;
ππ
−
nên
( ) ( )
( )
2018
d.
2018 1
x
x
fx
f x fx I x
π
π
−
− = → =
+
∫
Vậy
( ) ( )
( ) ( )
0
2018
2 d d d 2 d 2.2018 2018.
2018 1 2018 1
x
xx
fx fx
I x x fx x fx x I
π π ππ
ππ π
−− −
= + = = = →=
++
∫ ∫ ∫∫
Câu 66: Biết
2018
2018 2018
0
sin
d
sin cos
a
xx
x
x xb
π
π
=
+
∫
với
,.ab
+
∈
Tính
2.P ab= +
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 31
Gọi
2018
2018 2018
0
sin
d
sin cos
xx
Ix
xx
π
=
+
∫
Đặt
d d.t x tx
π
= − → = −
Đổi cận
0
.
0
xt
xt
π
π
= →=
= →=
Khi đó
( ) ( )
( ) ( )
(
) (
)
2018 2018 2018
0
2018 2018 2018 2018 2018 2018
00
sin sin sin
d d d.
sin cos sin cos sin cos
t t tt xx
I tt x
t t tt xx
ππ
π
ππ π π
ππ
−− − −
=−==
−+ − + +
∫ ∫∫
Suy ra
( )
2018
2018 2018
2018 2018 2018 2018 2018 2018
00 0
sin
sin sin
2 ddd
sin cos sin cos sin cos
xx
xx x
I xx x
xx xx xx
ππ π
π
π
−
=+=
+++
∫∫∫
2018 2018 2018
2
2018 2018 2018 2018 2018 2018
00
2
sin sin sin
d d d.
2 sin cos 2 sin cos sin cos
x xx
I x xx
xx xx xx
π
ππ
π
ππ
→ = = +
+ ++
∫ ∫∫
Đặt
2
xu
π
= +
ta suy ra
2018 2018 2018
2
2018 2018 2018 2018 2018 2018
0
22
sin cos cos
d d d.
sin cos sin cos sin cos
xux
xux
xx uu xx
π
ππ
ππ
= =
+++
∫∫∫
Vậy
2
2
0
2
d 8.
4
24
a
Ix P
b
π
ππ
=
= = → → =
=
∫
Chọn B.
DẠNG 9. KỸ THUẬT PHƯƠNG TRÌNH HÀM
Câu 67: Cho hàm số
( )
y fx=
liên tục trên
;
22
ππ
−
và thỏa mãn
( ) ( )
2 cos .fx f x x+ −=
Tính tích
phân
(
)
2
2
d.
I fx x
π
π
−
=
∫
Lời giải
Từ giả thiết, thay
x
bằng
x
−
ta được
( ) ( )
2 cos .f x fx x−+ =
Do đó ta có hệ
( ) ( )
( ) ( )
( )
( )
( ) ( )
( )
2 cos 4 2 2cos
1
cos .
3
2 cos 2 cos
fx f x x fx f x x
fx x
f x fx x fx f x x
+ −= + −=
⇔ → =
−+ = + −=
Khi đó
( )
22
2
2
22
1 12
d cos d sin .
3 33
I f x x xx x
ππ
π
π
ππ
−
−−
= = = =
∫∫
Câu 68: Cho hàm số
( )
y fx
=
liên tục trên
[ ]
2; 2−
và thỏa mãn
( ) ( )
2
1
23 .
4
fx f x
x
+ −=
+
Tính tích
phân
( )
2
2
d.I fx x
−
=
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
Lời giải
Từ giả thiết, thay
x
bằng
x
−
ta được
( ) ( )
2
1
23 .
4
f x fx
x
−+ =
+
Do đó ta có hệ
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( )
( )
22
2
22
12
23 46
1
44
.
13
54
2 3 96
44
fx f x fx f x
xx
fx
x
f x fx fx f x
xx
+ −= + −=
++
⇔ → =
+
−+ = + −=
++
Khi đó
(
)
22
2
22
11
d d.
5 4 20
I fx x x
x
π
−−
= = =
+
∫∫
Chọn C.
Câu 69: Cho hàm số
( )
y fx=
liên tục trên
[ ]
0;1
và thỏa mãn
( ) ( )
24
1 2.
xf x f x x x+ −=−
Tính tích
phân
( )
1
0
d.
I fx x
=
∫
Lời giải
Từ giả thiết, thay
x
bằng
1 x−
ta được
(
) ( )
( ) (
) ( )
24
1 1 21 1x f x fx x x
− −+ = −−−
(
)
( ) (
)
2 2 34
2 1 1 12 6 4 .
x x f x fx x x x x⇔ −+ −+ =+− + −
( )
1
Ta có
(
) ( ) ( ) ( )
2 4 42
12 12xf x f x x x f x x x xf x+ −=−→ −=−−
. Thay vào
( )
1
ta được
(
)
(
) (
)
2 42 2 34
2 12 12 6 4x x x x xfx fx x x x x
−+ −− + =+− + −
(
)
(
)
234 6532
1 2 2221
x x x fx x x x x⇔−+− =−+−+
( )
(
)
( )( )
(
)
2 34 2 2 34
2
12 112
1.
x xxfx x x xx
fx x
⇔−+ − =− −+ −
→ = −
Vậy
( )
( )
11
1
23
0
00
12
d1d .
33
I fx x x x x x
= =−=− =
∫∫
Câu 70: Cho hàm số
( )
fx
liên tục trên
1
;2
2
và thỏa mãn
( )
1
2 3.fx f x
x
+=
Tính tích phân
( )
2
1
2
d.
fx
Ix
x
=
∫
Lời giải
Từ giả thiết, thay
x
bằng
1
x
ta được
( )
13
2.f fx
xx
+=
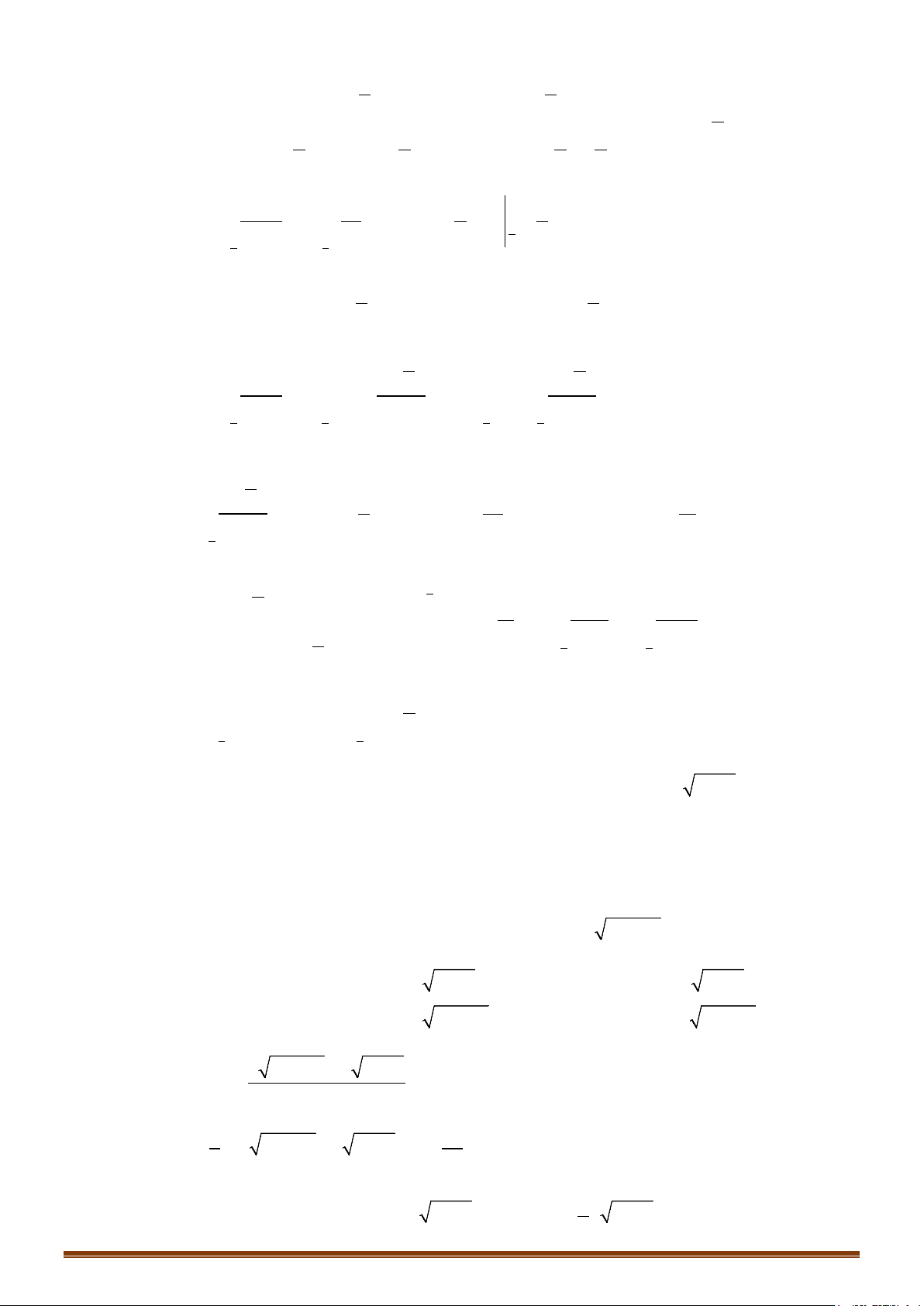
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 33
Do đó ta có hệ
(
)
(
)
(
)
(
)
( )
11
23 23
2
.
1 3 16
2 42
fx f x fx f x
xx
fx x
x
f fx fx f
x x xx
+= +=
⇔ → = −
+= + =
Khi đó
( )
22
2
1
2
11
2
22
2 23
1.
2
fx
I dx dx x
xx x
= = − =−− =
∫∫
Cách khác. Từ
( )
( )
11
2 3 32 .fx f x fx x f
xx
+ = → = −
Khi đó
(
)
2 2 22
1 1 11
2 2 22
11
d 3 2 d 3d 2 d.
ff
fx
xx
I x xx x
xx x
==−=−
∫ ∫ ∫∫
Xét
2
1
2
1
d.
f
x
Jx
x
=
∫
Đặt
1
t
x
=
, suy ra
2
22
11
d d d d d.
t x tx x t
xt
= − = − → = −
Đổi cận:
1
2
2
.
1
2
2
xt
xt
= →=
= →=
Khi đó
( )
( )
(
)
1
22
2
2
11
2
22
1
d dt d .
ft fx
J tf t t x I
ttx
= −= = =
∫ ∫∫
Vậy
22
11
22
3
3d 2 d .
2
I xI I x= − → = =
∫∫
Câu 71: Cho hàm số
(
)
fx
liên tục trên
[
]
0;1
và thỏa mãn
( ) ( )
2
2 31 1 .fx f x x+ −=−
Tính tích phân
(
)
1
0
d.I fx x=
∫
Lời giải
Từ giả thiết, thay
x
bằng
1 x−
ta được
( ) ( )
2
21 3 2 .f x fx x x−+ = −
Do đó ta có hệ
( ) ( )
( ) ( )
( ) ( )
( )
( )
22
22
2 3 1 1 4 6 1 21
21 3 2 9 61 32
fx f x x fx f x x
f x fx x x fx f x x x
+ −=− + −= −
⇔
−+ = − + −= −
( )
22
32 21
.
5
xx x
fx
−− −
→ =
Vậy
(
)
1
22
0
1
32 21 d .
5 20
I xx x x
π
= −− − =
∫
Cách khác. Từ
( ) ( )
( ) ( )
22
1
2 31 1 1 31 .
2
fx f x x fx x f x
+ − = − → = − − −

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 34
Khi đó
( ) ( )
1 11
2
0 00
1
d 1 d 3 1 d.
2
I fxx xx f xx
= = −− −
∫ ∫∫
Xét
( )
1
0
1 d.J f xx= −
∫
Đặt
1 d d.
t x tx
= − → = −
Đổi cận:
01
.
10
xt
xt
= →=
=→=
Khi đó
( ) ( ) ( )
011
100
dt dt d .J ft ft fx x I
=−= = =
∫∫∫
Vậy
11
22
00
11
1d3 1d .
2 5 20
I xx I I xx
π
= − − → = − =
∫∫
DẠNG 10. KỸ THUẬT BIẾN ĐỔI
Câu 72: Cho hàm số
( )
fx
thỏa
( ) ( )
52
3 6.
fxf x x x
′
= +
Biết rằng
( )
0 2,f =
tính
( )
2
2.f
Lời giải
Từ giả thiết ta có
(
) ( )
( )
( )
2
6
52 3
. d 3 6d 2 .
22
fx
x
fxf x x x x x x C
′
= + ⇔ =++
∫∫
Thay
0x =
vào hai vế, ta được
(
)
2
0
2.
2
f
CC=⇒=
Suy ra
( ) ( )
2 63 2 6 3
4 4 2 2 4.2 4 100.fx x x f= + + → = + + =
Câu 73: Cho hàm số
( )
fx
thỏa mãn
( ) ( ) ( )
2
4
. 15 12f x fxf x x x
′ ′′
+=+
với mọi
x ∈
và
( ) ( )
0 0 1.ff
′
= =
Giá trị của
( )
2
1f
bằng
Lời giải
Nhận thấy được
(
) ( ) (
) ( )
( )
2
. ..f x fxf x fxf x
′
′ ′′ ′
+=
Do đó giả thiết tương đương với
( ) ( )
4
. 15 12 .fxf x x x
′
′
= +
Suy ra
( ) ( )
( )
( )
( )
0 0 1.
4 52
. 15 12 d 3 6 1
ff
fxf x x x x x x C C
′
= =
′
= + = + + → =
∫
( ) ( )
52
. 361fxf x x x
′
→ = + +
( ) ( )
( )
( )
2
6
52 3
. d 3 6 1 d 2 '.
22
fx
x
fxf x x x x x x xC
′
→ = + + ⇔ = + + +
∫∫
Thay
0x =
vào hai vế ta được
( )
2
0
1
' '.
22
f
CC=⇒=
Vậy
( ) ( )
2 63 2
4 2 1 1 8.fx x x x f= + + + → =

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 35
Câu 74: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
1; 2
và thỏa mãn
( )
[ ]
0, 1; 2 .fx x> ∀∈
Biết
rằng
( )
2
1
d 10fxx
′
=
∫
và
( )
(
)
2
1
d ln 2.
fx
x
fx
′
=
∫
Tính
( )
2.f
Lời giải
Ta có
(
) ( ) ( ) ( )
2
2
1
1
d 10 10 2 1 10.
f x x fx f f
′
=⇔ =⇔ −=
∫
( )
1
Lại có
( )
( )
( )
( )
2
22
11
1
d ln 2 ln ln 2 ln ln 2
fx
x fx fx
fx
′
=⇔=⇔ =
∫
(do
( )
[ ]
0, 1; 2fx x> ∀∈
)
( ) ( )
( )
( )
(
)
(
)
22
ln 2 ln 1 ln 2 ln ln 2 2.
11
ff
ff
ff
⇔ − =⇔ =⇔=
( )
2
Từ
( )
1
và
( )
2
, suy ra
( )
2 20.f =
Câu 75: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[
]
1;1−
, thỏa mãn
( )
0, fx x> ∀∈
và
( ) ( )
'2 0f x fx+=
. Biết rằng
( )
11f =
, giá trị của
( )
1f −
bằng
Lời giải
Ta có
( ) ( ) ( ) ( )
( )
( )
'
'2 0' 2 2
fx
f x fx f x fx
fx
+ =⇔=−⇔ =−
(do
( )
0fx>
)
(
)
( )
( )
'
d 2d ln 2
fx
x x fx xC
fx
→ = − ⇔ = − +
∫∫
(do
( )
0fx>
).
Mà
( ) ( ) ( ) ( )
22 4
1 1 2 ln 2 2 1 .
x
f C fx x fx e f e
−+
= ⇒ = ⇒ = − + → = → − =
Câu 76: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
( )
0; +∞
, biết
( ) ( ) ( )
2
' 2 3 0,fx x f x++ =
( )
0fx>
với mọi
0x >
và
(
)
1
1.
6
f =
Tính
(
) ( ) ( )
1 1 2 ... 2018 .Pff f=+ + ++
Lời giải
Ta có
(
) ( )
( )
( )
( )
(
)
2
2
'
' 23 0 23
fx
fx x f x x
fx
++ =⇔ =−+
(do
( )
0fx>
)
( )
( )
(
)
( )
( )
2
22
'
11
d 2 3d 3 .
3
fx
x x x x xC fx
f x fx x xC
→ = − + ⇔ − = − − + → =
+−
∫∫
Mà
( ) ( )
22
1 1 1 1 11
12 .
6 6 1 3.1 3 2 1 2
f C fx
C xx x x
= → = ⇔ = − → = = −
+ − ++ + +
Suy ra
1 1 1 1 1 1 3029
1 ... .
2 3 3 4 2019 2020 2020
P
=+ − + − ++ − =

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
Câu 77: Cho hàm số
( )
fx
liên tục trên
0; 3 ,
thỏa mãn
( )
1,fx>−
( )
00f =
và
( )
( )
2
1 2 1.
f x x xfx
′
+= +
Giá trị của
( )
3f
bằng
Lời giải
Từ giả thiết suy ra
( )
( )
( )
( )
22
22
dd
11
11
fx fx
xx
xx
fx fx
xx
′′
= → =
++
++
∫∫
(
)
( )
( )
( )
/
2
2
2
1
2 d 2 d 2 12 1
21
21
x
fx
x x fx x C
fx
x
+
′
⇔ = ⇔ += ++
+
+
∫∫
Mà
(
) ( )
( )
2
0 0 0 3 3.
f C fx x f
= ⇒ = ⇒ = → =
Câu 78: Cho hàm số
(
)
fx
có đạo hàm và liên tục trên
[ ]
1; 4 ,
đồng biến trên
[ ]
1; 4 ,
thoản mãn
(
)
( )
2
2x xf x f x
′
+=
với mọi
[ ]
1; 4 .x ∈
Biết rằng
( )
3
1,
2
f =
tính tích phân
( )
4
1
d.I fx x=
∫
Lời giải
Nhận xét: Do
( )
fx
đồng biến trên
[ ]
1; 4
nên
( )
[ ]
' 0, 1; 4fx x≥ ∀∈
.
Từ giả thiết ta có
( ) ( ) ( )
( )
[ ]
2
12 ' .12 , 1;4x fx f x f x x fx x
′
+ = → = + ∀ ∈
( )
( )
( )
( )
( )
22
2
d d 12 .
3
21 2 21 2
fx fx
x x xx f x x x C
fx fx
′′
→ = → = ⇔ + = +
++
∫∫
Mà
( ) ( )
2
3
24
1
3 4 28 7
33
1
2 3 2 9 9 18
xx
f C fx x xx
+−
= ⇒ = → = = + +
( )
4
1
1186
d.
45
fx x → =
∫
Câu 79: Cho hàm số
(
)
fx
liên tục, không âm trên
0;
2
π
, thỏa
( ) ( ) ( )
2
. ' cos 1fxf x x f x= +
với mọi
0;
2
x
π
∈
và
( )
0 3.
f =
Giá trị của
2
f
π
bằng
Lời giải
Từ giả thiết ta có
( ) ( )
( )
2
2.
cos , 0;
2
21
fxf x
xx
fx
π
′
= ∀∈
+
( ) ( )
( )
( )
2
2
2.
d cos d 1 sin .
21
fxf x
x xx f x x C
fx
′
→ = ⇔ + = +
+
∫∫
Mà
( )
( ) ( )
2
2
0 3 2 sin 2 1 sin 4sin 3, 0;
2
f C fx x x x x
π
= ⇒ = → = + − = + + ∀ ∈

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 37
2 2.
2
f
π
→ =
Câu 80: Cho hàm số
( )
fx
liên tục, không âm trên
[
]
0;3 ,
thỏa
( ) ( )
( )
2
.2 1fxf x xf x
′
= +
với mọi
[ ]
0;3x ∈
và
( )
0 0.f
=
Giá trị của
( )
3f
bằng
Lời giải
Từ giả thiết ta có
( ) ( )
( )
[ ]
2
2.
2 , 0;3
21
fxf x
xx
fx
′
= ∀∈
+
( ) ( )
( )
( )
22
2
2.
d 2d 1 .
21
fxf x
x xx f x x C
fx
′
→ = ⇔ + = +
+
∫∫
Mà
( ) ( )
( )
[ ]
2
2 42
0 0 1 1 1 2 , 0;3f C fx x x x x= ⇒ = → = + − = + ∀ ∈
( )
3 3 11.f → =
Câu 81: Cho hàm số
( )
fx
có đạo hàm không âm trên
[ ]
0;1 ,
thỏa mãn
( )
0fx>
với mọi
[
]
0;1x ∈
và
( ) ( )
( )
( )
42 3
2
. ' . 11 .fx f x x fx+=+
Biết
( )
0 2,f =
hãy chọn khẳng định đúng trong các
khẳng định sau đây.
Lời giải
Từ giả thiết ta có
( )
( )
(
)
( ) ( )
( )
2
23
2
32
.'
1
.' . 1 1
1
1
fx f x
fx f x x fx
x
fx
+= + ⇔ =
+
+
( )
( )
( )
( )
(
)
( )
3
2
1 111
3 2 32
0 000
d1
.'
12 1
dd d
3
11
1 21
fx
fx f x
xx x
xx
fx fx
+
→ = ⇔ × =
++
++
∫ ∫∫∫
( )
(
)
( )
( )
11
3
02
2
00
2
1 ln 1 1 2,605.
3
f
fx x x f
=
⇔ × + = + + → ≈
Câu 82: Cho hàm số
( )
fx
liên tục trên
{ }
,\
0; 1−
thỏa mãn
( ) ( ) ( )
2
1.xx f x f x x x
′
+ +=+
với mọi
{ }
0; 1\x ∈−
và
( )
1 2ln 2.f = −
Biết
( )
2 ln 3f ab= +
với
, ab∈
, tính
22
.Pa b= +
Lời giải
Từ giả thiết ta có
(
)
( )
( ) { }
2
\
1
, 0; 1 .
11
1
xx
f x fx x
xx
x
′
+ = ∀∈ −
++
+
Nhận thấy
( )
( )
( ) ( )
2
1
..
11
1
xx
f x fx fx
xx
x
′
′
+=
++
+
Do đó giả thiết tương đương với
( ) { }
. , 0; 1
11
\ .
xx
fx x
xx
′
= ∀∈ −
++

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 38
Suy ra
( )
. d 1 d ln1.
11 1
xx
fx x x x x C
xx x
= = − =− ++
++ +
∫∫
Mà
(
)
( )
1 2 ln 2 1 . ln 1 1.
1
x
f C fx x x
x
= − ⇒ = − → = − + −
+
Cho
2x =
ta được
( ) ( )
3
2 33 9
2
2 . 2 ln 3 1 2 ln 3 .
3
3 22 2
2
a
ff P
b
=
= − − ⇒ = − → ⇒ =
= −
Câu 83: Cho hàm số
( )
fx
có đạo hàm xác định, liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
01f
′
= −
và
( ) ( )
( )
2
0
fx f x
fx
′ ′′
=
′
≠
với mọi
[ ]
0;1 .x ∈
Đặt
( ) ( )
10Pf f= −
, khẳng định nào sau đây đúng?
Lời giải
Nhận thấy
( ) ( ) ( )
1
0
10 dP f f fxx
′
=−=
∫
nên ta cần tìm
( )
.fx
′
Từ giả thiết ta có
(
)
( )
( )
( )
( )
( )
22
11
1 d 1d .
fx fx
x x xC f x
f x xC
fx fx
′′ ′′
′
= → = ⇔ − = + ⇔ = −
′
+
′′
∫∫
Mà
(
) (
)
1
01 1 .
1
f C fx
x
′′
= − ⇒ = → = −
+
Vậy
( )
11
00
1
d d ln 2 0,69.
1
P fxx x
x
′
= =− =− ≈−
+
∫∫
Câu 84: Cho hai hàm số
( )
fx
và
(
)
gx
có đạo hàm liên tục trên
[ ]
0; 2 ,
thỏa mãn
( ) ( )
'0. '2 0ff≠
và
(
) ( )
( )
.' 2 .
x
gx f x xx e= −
Tính tích phân
( ) ( )
2
0
. ' d.I fxg x x=
∫
Lời giải
Từ giả thiết
( ) ( )
( )
( )
'0 0
'0. '2 0 .
'2 0
f
ff
f
≠
≠ →
≠
Do đó từ
( ) ( ) ( )
.' 2
x
gx f x xx e= −
, suy ra
( )
( )
( )
( )
( )
( )
22 2
20
'2
.
00 2
00
'0
x
x
e
g
f
e
g
f
−
= =
−
= =
Tích phân từng phần ta được
( ) ( ) ( ) ( )
2
2
0
0
. .dI f x gx gx f x x
′
= −
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
( ) ( ) ( )
(
) (
) (
)
22
00
2. 2 0. 0 2 d 2 d 4.
xx
f g f g xx e x xx e x= − −−=−−=
∫∫
Câu 85: Cho hàm số
(
)
y fx
=
liên tục trên đoạn
[ ]
0;1
và thỏa mãn
( ) ( )
1af b bf a+=
với mọi
[ ]
, 0;1 .
ab∈
Tính tích phân
( )
1
0
d.I fx x=
∫
Lời giải
Đặt
sin , cosa xb x= =
với
0; .
2
x
π
∈
Từ giả thiết, suy ra
( )
( )
sin cos cos sin 1xf x xf x+=
( )
( )
22 2
00 0
sin cos d cos sin d 1d .
2
xf x x xf x x x
ππ π
π
→ + = =
∫∫∫
( )
1
Ta có
( )
( ) (
)
(
)
( ) ( )
01
2
cos
0 10
11
2
sin
0 00
sin cos d d d
.
cos sin d d d
tx
tx
xf xx ftt fxx
xf xx ftt fxx
π
π
=
=
=−=
= =
∫ ∫∫
∫ ∫∫
Do đó
( ) ( )
1
0
1 d.
4
fx x
π
⇔=
∫
DẠNG 11. KỸ THUẬT ĐẠO HÀM ĐÚNG
Câu 86: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thoả mãn
(
) (
)
2018
3
f x xf x x
′
+=
với mọi
[ ]
0;1 .x ∈
Tính
( )
1
0
d
I fx x=
∫
.
Lời giải
Từ giả thiết
( ) ( )
2018
3,f x xf x x
′
+=
nhân hai vế cho
2
x
ta được
( ) ( ) ( )
2 3 2020 3 2020
3.xf x xf x x xf x x
′
′
+ = ← → =
Suy ra
( )
2021
3 2020
d.
2021
x
xf x x x C= = +
∫
Thay
0x =
vào hai vế ta được
( )
2018
0.
2021
x
C fx= → =
Vậy
( )
1
11
2018 2019
0
00
1 11 1
d d. .
2021 2021 2019 2021 2019
fx x x x x= = =
×
∫∫
Chọn C.
Nhận xét: Ý tưởng nhân hai vế cho
2
x
là để thu được đạo hàm đúng dạng
( )
' ' '.uv u v uv= +
Câu 87: Cho hàm số
( )
fx
có đạo hàm trên
,
thỏa mãn
( ) ( )
2017 2018
' 2018 2018
x
f x fx x e−=
với mọi
x ∈
và
( )
0 2018.f =
Tính giá trị
( )
1.f

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 40
Lời giải
Nhân hai vế cho
2018x
e
−
để thu được đạo hàm đúng, ta được
(
)
( ) ( )
2018 2018 2017 2018 2017
2018 2018 2018 .
xx x
f xe f xe x f xe x
−− −
′
′
− =⇔=
Suy ra
(
)
2018 2017 2018
2018 d .
x
f xe x x x C
−
= = +
∫
Thay
0x =
vào hai vế ta được
( )
(
)
2018 2018
2018 2018 .
x
C fx x e
= → = +
Vậy
( )
2018
1 2019 .fe=
Câu 88: Cho hàm số
( )
fx
có đạo hàm và liên tục trên
,
thỏa mãn
( ) ( )
2
2
x
f x xf x xe
−
′
+=
và
( )
0 2.f = −
Tính
( )
1.f
Lời giải
Nhân hai vế cho
2
2
x
e
để thu được đạo hàm đúng, ta được
( ) ( )
( )
2 2 22 2
2 2 22 2
2 2.
x x xx x
f x e f x xe xe e f x xe
−−
′
′
+=⇔ =
Suy ra
( )
2 22
2 22
2d2 .
x xx
e f x xe x e C
−−
= =−+
∫
Thay
0x =
vào hai vế ta được
( )
2
0 2.
x
C fx e
−
= → = −
Vậy
(
)
1
2
12 .fe
e
−
=−=−
Câu 89: Cho hàm số
(
)
fx
liên tục và có đạo hàm trên
0; ,
2
π
thỏa mãn hệ thức
( ) ( )
3
tan .
cos
x
f x xf x
x
′
+=
Biết rằng
3 3 ln 3
36
f f ab
ππ
π
−=+
trong đó
, .ab∈
Tính
giá trị của biểu thức
.P ab= +
Lời giải
Từ giả thiết, ta có
(
) ( ) ( )
22
cos sin sin .
cos cos
xx
xf x xf x xf x
xx
′
′
+=⇔ =
Suy ra
( )
2
sin d tan ln cos .
cos
x
xf x x x x x C
x
= =++
∫
Với
32
. 3 ln 2 3 . 3 2ln 2 2 .
3 2 33 33
xf f C
π ππ π
π
= → = − → = − +
Với
1 31 1
. ln 3 ln 2 . 3 ln 3 2ln 2 2 .
6 2 6 63 2 6 9
x f Cf C
π ππ π
π
= → = + − + → = + − +

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 41
Suy ra
5
54
3 3 ln 3 .
9
3 69 9
1
a
f f P ab
b
ππ
π
=
− = − → → = + = −
= −
DẠNG 12. KỸ THUẬT ĐƯA VỀ BÌNH PHƯƠNG LOẠI 1
Câu 90: Cho hàm số
( )
fx
liên tục trên
0; ,
2
π
thỏa
( )
( )
2
2
0
2
2 2 sin d .
42
f x fx x x
π
ππ
−
− −=
∫
Tính
tích phân
(
)
2
0
d.I fx x
π
=
∫
Lời giải
Ta có
2
2
0
2
2sin d .
42
xx
π
ππ
−
−=−
∫
Do đó giả thiết tương đương với
( ) ( )
2
22
0
2 2 sin 2sin d 0
44
f x fx x x x
π
ππ
− −+ − =
∫
( )
( )
2
2
0
2 sin d 0 2 sin 0, 0; .
4 42
fx x x fx x x
π
π ππ
⇔−−=⇔−−=∀∈
∫
Suy ra
( )
( )
22
00
2 sin d 2 sin d 0.
44
fx x I fx x x x
ππ
ππ
= − → = = − =
∫∫
Chọn A.
Câu 91: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
thỏa
( ) ( ) ( )
11
22
00
2
2ln d 2 ln 1 d .f x x fx x x
e
+= +
∫∫
Tích
phân
( )
1
0
d.
I fx x=
∫
Lời giải
Bằng phương pháp tích phân từng phần ta tính được
( )
11
2 22
00
22
ln 1 d 2ln 2ln d .xx x
ee
+= =
∫∫
Do đó giả thiết tương đương với
(
) ( ) (
) ( )
[ ]
1
2
0
ln 1 d 0 ln 1 , 0;1 .fx x x fx x x− + = ⇔ ≡ + ∀∈
∫
Suy ra
( ) ( )
11
00
4
d ln 1 d lnfxx xx
e
= +=
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 42
Câu 92: Cho hàm số
( )
fx
có đạo liên tục trên
[ ]
0;1 ,
( )
fx
và
( )
'fx
đều nhận giá trị dương trên
[ ]
0;1
và thỏa mãn
(
)
02f =
và
( ) ( ) ( )
( )
11
2
00
' . 1d 2 ' . d.f x fx x f xfx x
+=
∫∫
Tính
( )
1
3
0
d.I fx x=
∫
Lời giải
Giả thiết tương đương với
( ) ( )
1
2
0
' . 1d 0f xfx x
−=
∫
( )
( )
[ ]
(
)
( )
( ) ( )
22
' . 1, 0;1 ' 1 ' d dfxfx x fxf x fxf xx x → = ∀ ∈ → = → =
∫∫
( )
(
)
3
02
8
.
33
f
fx
xC C
=
→ = + → =
Vậy
( ) ( )
1
3
3
0
19
38 d .
2
f x x I fx x= + → = =
∫
Câu 93: Cho hàm số
(
)
fx
có đạo hàm dương, liên tục trên đoạn
[
]
0;1
và thỏa mãn
( )
0 1,f =
( )
( ) ( )
( )
11
2
00
1
3 ' . d 2 ' . d.
9
f x fx x f xfx x
+=
∫∫
Tính
( )
1
3
0
d.
I fx x=
∫
Lời giải
Giả thiết
(
)
(
) ( )
(
)
11
2
00
1
3 '. d 2 '. d
3
f xfx x f xfx x
⇔ +=
∫∫
( )
( ) ( )
(
) ( )
( )
1 1 11
22
0 0 00
3'. d23'. d d0 3'. 1d0
f xfx x f xfx x x f xfx x
⇔ − +=⇔ − =
∫ ∫ ∫∫
( ) ( )
[ ]
( ) ( ) ( ) ( )
22
3 ' . 10, 0;1 9' . 1 9' . d dfxfx x fxf x fxf xx x → − = ∀ ∈ → = → =
∫∫
( )
( )
3
01
9. 3.
3
f
fx
xC C
=
→ = + → =
Vậy
( )
( )
1
3
3
0
17
1 d.
36
f x x fx x= + → =
∫
Câu 94: Cho hàm số
( )
y fx=
có đạo hàm dương, liên tục trên đoạn
[ ]
0;1 ,
thỏa
( ) ( )
1 01ff−=
và
( )
( ) ( ) (
)
11
2
00
' 1d 2 ' d.fxf x x fxfxx
+=
∫∫
Giá trị của tích phân
( )
1
3
0
dfx x
∫
bằng
Lời giải
Nhóm hằng đẳng thức ta có
( ) ( ) ( ) ( )
11
2
00
' 1d 2 ' dfxf x x fxfxx
+=
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 43
(
)
( )
(
)
(
)
(
)
(
)
( )
(
)
( )
( )
11
2
00
11
2
00
0 vi 1 0 1
' ' d2 ' d0
' 1 d ' 1d 0
ff
fxf x fx x fxfxx
fxfx x fx x
= −=
⇔ +− =
⇔ − + −=
∫∫
∫∫
(
)
( )
[
]
( )
( )
(
) (
)
22
' . 1, 0;1 ' 1 ' d d
fxfx x fxf x fxf xx x → = ∀ ∈ → = → =
∫∫
( )
( )
( ) ( )
3
1 01
3
5 33 27
33 .
3 54
ff
fx
xC f x x C C
−=
−
→ = + → = + → =
Vậy
( ) ( )
1
3
3
0
5 33 27 5 33
3 d.
18 18
f x x fx x
−
= + → =
∫
DẠNG 13. KỸ THUẬT ĐƯA VỀ BÌNH PHƯƠNG LOẠI 2 - KỸ THUẬT HOLDER
Câu 95: Cho hàm số
(
)
y fx=
liên tục trên đoạn
[ ]
0;1 ,
thỏa mãn
(
) ( )
11
00
d d1fx x xfx x= =
∫∫
và
( )
1
2
0
d4fx x=
∫
. Giá trị của tích phân
( )
1
3
0
dfx x
∫
bằng
Lời giải
Ở đây các hàm xuất hiện dưới dấu tích phân là
( ) ( ) ( )
2
, , fx xfx fx
nên ta sẽ liên kết với bình
phương
( )
2
.fx x
αβ
++
Với mỗi số thực
,
αβ
ta có
( ) (
) ( ) (
) ( )
1 11 1
22
2
0 00 0
d d2 d dfx x x fx x x fx x x x
αβ αβ αβ
++ = + + + +
∫ ∫∫ ∫
( )
2
2
42 .
3
α
α β αβ β
=+ ++ + +
Ta cần tìm
,
αβ
sao cho
( )
1
2
0
d0fx x x
αβ
++ =
∫
hay
( )
2
2
42 0
3
α
α β αβ β
+ ++ + +=
( )
22
3 6 3 6 12 0.
α β αβ β
⇔ + + + + +=
Để tồn tại
α
thì
( )
( )
2
2
3 6 4 3 6 12 0
β ββ
∆= + − + + ≥
( )
2
2
3 12 12 0 3 2 0 2 6.
ββ β β α
⇔− + − ≥ ⇔− − ≥ ⇔ = → =−
Vậy
( ) ( )
[ ]
( )
11
23
00
6 2 d 0 6 2, 0;1 d 10.fx x x fx x x fx x− + = → = − ∀ ∈ → =
∫∫
Chọn C.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 44
Câu 96: Cho hàm số
( )
y fx=
liên tục trên đoạn
[ ]
0;1 ,
thỏa mãn
( )
(
)
11
00
d d1
xfx x xfx x
= =
∫∫
và
( )
1
2
0
d 5.fx x=
∫
Giá trị của tích phân
( )
1
3
0
dfx x
∫
bằng
Lời giải
Ở đây các hàm xuất hiện dưới dấu tích phân là
(
) (
)
( )
2
, , fx xfx xfx
nên ta sẽ liên kết với
bình phương
( )
2
.fx x x
αβ
++
Với mỗi số thực
,
αβ
ta có
( ) ( )
( )
( )
( )
1 11 1
2
2
2
0 00 0
d d2 d dfx x x x fx x x xfx x x x x
αβ αβ αβ
++ = + + + +
∫ ∫∫ ∫
( )
22
4
52 .
352
α αβ β
αβ
=+ ++ + +
Ta cần tìm
,
αβ
sao cho
( )
1
2
0
d0fx x x x
αβ
++ =
∫
hay
(
)
22
4
5 2 0.
352
α αβ β
αβ
+ ++ + + =
Tương tự như bài trước, ta tìm được
15, 10.
αβ
=−=
Vậy
( ) ( )
[
]
( )
11
2
3
00
5
15 10 d 0 15 10 , 0;1 d .
6
fx x x x fx x x x fx x
− + = → = − ∀ ∈ → =
∫∫
Câu 97: Cho hàm số
(
)
y fx
=
liên tục trên đoạn
[
]
0;1 ,
thỏa mãn
( ) ( )
11
22
00
1
d d.
16
xf xx xfxx= −
∫∫
Giá trị
của tích phân
( )
1
0
dfx x
∫
bằng
Lời giải
Hàm bình phương không như thông thường là
( )
2
fx
hoặc
( )
2
'.fx
Ở đây các hàm xuất hiện dưới dấu tích phân là
(
) ( )
2
2
, xfx xfx
nên ta sẽ liên kết với bình
phương
( ) ( )
( ) ( )
2
2
2
??? 2??? ??? .xf x xf x xf x
+= + +
So sánh ta thấy được
??? .
2
xx
=
Do đó giả thiết được viết lại
( )
22
11
00
1
d d 0.
2 2 16
xx xx
xf x x x
− = −=
∫∫
Suy ra
( )
[ ]
( ) ( )
1
0
1
, 0;1 d .
2 24
xx x
xfx x fx fx x= ∀ ∈ → = → =
∫
Câu 98: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
1; 8
và thỏa mãn

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 45
(
) (
)
(
)
2 28
2
33
1 11
2 38
d2 d d .
3 15
fx x fx x fx x
+=−
∫ ∫∫
Tích phân
( )
8
1
dfxx
∫
bằng
Lời giải
Nhận thấy có một tích phân khác cận là
( )
8
1
d.fx x
∫
Bằng cách đổi biến
3
xt=
ta thu được tích
phân
( ) ( )
22
23 2 3
11
3 d 3 d.tf t t xf x x=
∫∫
Do đó giả thiết được viết lại
( ) ( ) ( )
2 22
2
3 3 23
1 11
38
d2 d2 d .
15
fx x fx x xfx x
+= −
∫ ∫∫
( )
*
Ở đây các hàm xuất hiện dưới dấu tích phân là
( ) ( ) ( )
2
3 32 3
, , fx fx xfx
nên ta sẽ liên kết với
bình phương
(
)
2
32
.fx x
αβ
++
Tương tự như các bài trên ta tìm được
1, 1.
αβ
=−=
Do đó
(
)
( )
( )
22
2
2
32 2
11
38
* 1d 1 d 0
15
fx x x x x
⇔ −+ =− + − =
∫∫
( )
[ ]
( )
[
]
( )
8
3
32 2
1
3
1, 1; 2 1, 1; 8 d .
2
fx x x fx x x fxx → = − ∀ ∈ → = − ∀ ∈ → =
∫
Câu 99: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
10f =
,
( )
1
2
0
d7fx x
′
=
∫
và
( )
1
2
0
1
d.
3
xf x x=
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Lời giải
Hàm dưới dấu tích phân là
( ) ( )
2
2
, f x xf x
′
không có mối liên hệ với nhau.
Dùng tích phân từng phần ta có
( ) (
) ( )
11
3
1
23
0
00
1
d ' d.
33
x
xfx x fx xf x x
= −
∫∫
Kết hợp với giả thiết
( )
10f =
, ta suy ra
( )
1
3
0
' d 1.xf x x= −
∫
Bây giờ giả thiết được đưa về
( )
( )
1
2
0
1
3
0
d7
.
'd 1
fx x
xf x x
′
=
= −
∫
∫
Hàm dưới dấu tích phân bây giờ là
( ) ( )
2
3
, 'f x xf x
′
nên ta sẽ liên kết với bình phương
( )
2
3
'.fx x
α
+
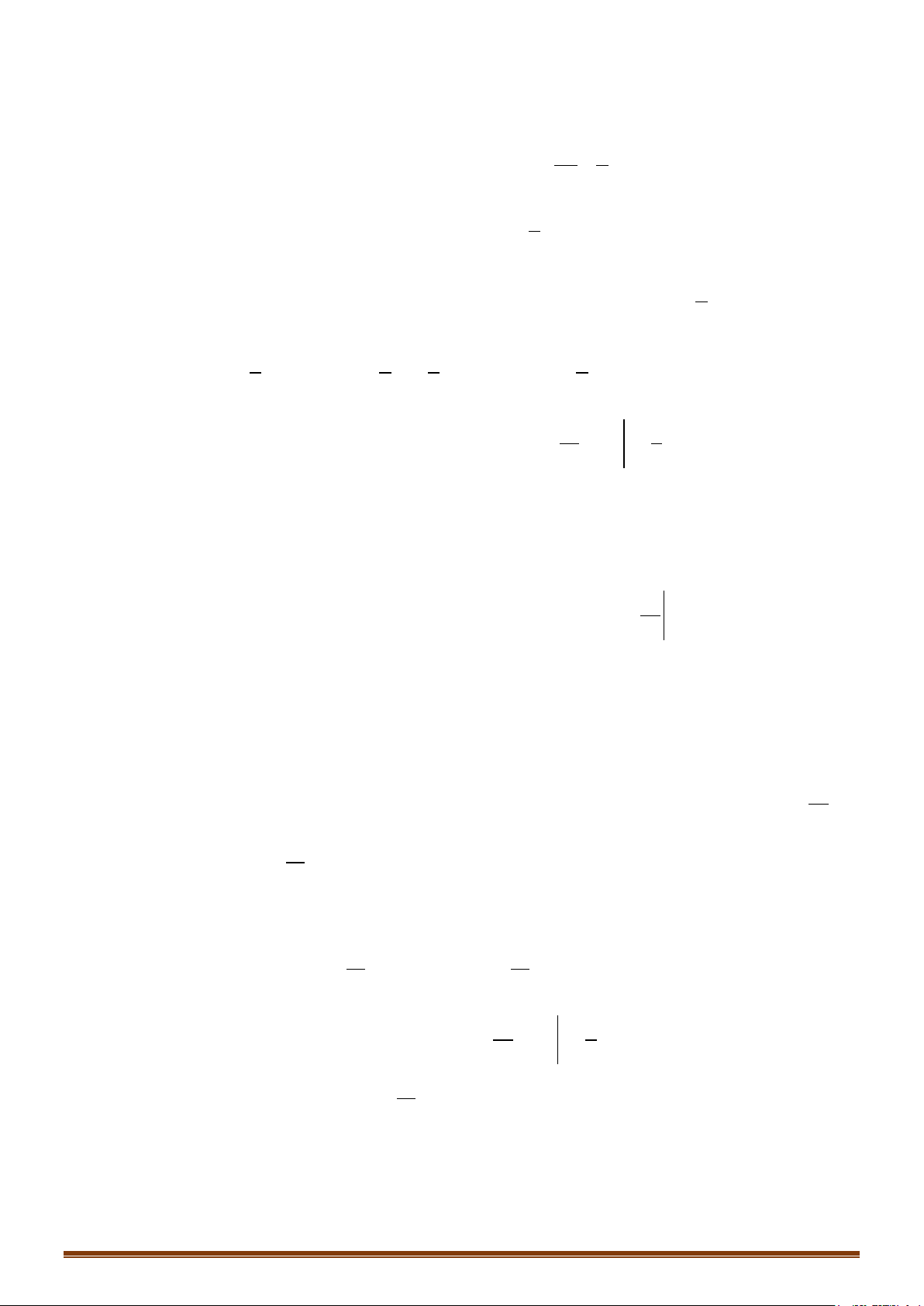
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 46
Với mỗi số thực
α
ta có
( )
(
) (
)
1 1 11
2
2
3 3 26
0 0 00
' d ' d2 'd d
fx x x fx x xfxx xx
α αα
+= + +
∫ ∫ ∫∫
( )
2
2
1
72 7.
77
α
αα
=−+= −
Ta cần tìm
α
sao cho
( )
1
2
3
0
' d0fx x x
α
+=
∫
hay
( )
2
1
7 0 7.
7
αα
− =⇔=
Vậy
(
) ( )
[ ]
( )
1
2
33 4
0
7
' 7 d 0 ' 7 , 0;1
4
fx x x fx x x fx x C
+ = → = − ∀ ∈ → = − +
∫
( )
( )
(
)
1
10
4
0
7 77 7
d.
4 44 5
f
C fx x fx x
=
→ = → = − + → =
∫
Cách 2. Dùng tích phân từng phần ta có
(
)
(
)
( )
11
3
1
23
0
00
1
d ' d.
33
x
xfx x fx xf x x= −
∫∫
Kết hợp với
giả thiết
( )
10f
=
, ta suy ra
( )
1
3
0
' d 1.xf x x
= −
∫
Theo Holder
( ) ( ) ( )
2
1 11
7
1
2
2
36
0
0 00
1 ' d d . ' d .7 1.
7
x
xfxx xx fx x
−= ≤ = =
∫ ∫∫
Vậy đẳng thức xảy ra nên ta có
( )
3
',
f x kx
=
thay vào
( )
1
3
0
'd 1xf x x= −
∫
ta được
7.k = −
Suy ra
( )
3
'7fx x
= −
(làm tiếp như trên)
Câu 100: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
11f =
,
( )
1
5
0
11
d
78
xf x x
=
∫
và
( ) ( )
( )
1
0
4
d.
13
f x fx
′
=
∫
Tính
( )
2.f
Lời giải
Viết lại
( ) ( )
( )
( )
11
2
00
44
d d.
13 13
fx fx fx x
′′
=⇔=
∫∫
Dùng tích phân từng phần ta có
( ) ( ) ( )
11
6
1
56
0
00
1
d d.
66
x
xfx x fx xf x x
′
= −
∫∫
Kết hợp với giả thiết
( )
11f =
, ta suy ra
(
)
1
6
0
2
d.
13
xf x x
′
=
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 47
Bây giờ giả thiết được đưa về
( )
( )
1
2
0
1
6
0
4
d
13
.
2
'd
13
fx x
xf x x
′
=
=
∫
∫
Hàm dưới dấu tích phân bây giờ là
(
)
( )
2
6
, '
f x xf x
′
nên ta sẽ liên kết với bình phương
(
)
2
6
'.
fx x
α
+
Tương tự như bài trên
ta tìm được
(
)
(
)
(
)
11
67
25
22 .
77
f
f x x fx x C C
α
=
′
= − → = → = + → =
Vậy
( )
(
)
7
2 5 261
2.
77 7
fx x f= + → =
Cách 2. Theo Holder
( ) ( )
2
2
1 11
2
6 12
0 00
2 14 4
d . d. .
13 13 13 169
xfxx xdx fx x
′′
=≤==
∫ ∫∫
Câu 101: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
1 2, 0 0ff= =
và
(
)
1
2
0
' d 4.fx x
=
∫
. Tích phân
(
)
1
3
0
2018 d .fx xx
+
∫
bằng
Lời giải
Từ giả thiết
( ) ( )
1 2, 0 0ff= =
suy ra
(
) ( )
1
1
0
0
' d 2.f x x fx
= =
∫
Hàm dưới dấu tích phân là
( ) ( )
2
' , 'fx fx
nên sẽ liên kết với bình phương
(
)
2
'.
fx
α
+
Ta tìm được
( ) ( )
( )
00
2 ' 2 2 0.
f
f x fx xC C
α
=
= − → = → = + → =
Vậy
( )
( )
1
3
0
2 2018 d 1011.fx x f x x x
= → + =
∫
Cách 2. Theo Holder
( )
( )
2
1 11
2
2
0 00
2 ' d d . ' d 1.4 4.fxx x fx x
=≤==
∫ ∫∫
Câu 102: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
1; 2 ,
thỏa mãn
( ) ( )
2
2
1
1
1 d,
3
x fx x−=−
∫
( )
20f =
và
( )
2
2
1
' d 7.fx x=
∫
Tích phân
(
)
2
1
d
fx x
∫
bằng
Lời giải
Chuyển thông tin
( ) ( )
2
2
1
1dx fx x−
∫
sang
( )
'fx
bằng cách tích phân từng phần, ta được
( ) ( )
2
3
1
1 ' d 1.x fxx−=
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 48
Hàm dưới dấu tích phân là
(
)
( )
( )
2
3
' , 1 '
fx x fx−
nên liên kết với
( )
( )
2
3
' 1.
fx x
α
+−
Ta tìm được
( ) ( ) ( ) ( )
( )
34
20
77
7 ' 71 1 .
44
f
f x x fx x C C
α
=
= − → = − → = − + → = −
Vậy
( )
( )
(
)
2
4
1
77 7
1 d.
44 5
fx x fx x= − − → = −
∫
Cách 2. Theo Holder
( ) ( ) ( ) ( )
2
2 22
2
36
1
1 11
1
1 1 ' d 1 d ' d .7 1.
7
x fxx x x fx x
= − ≤− ==
∫ ∫∫
Câu 103: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
(
)
( )
1
2
0
9
1 1, ' d
5
f fx x
= =
∫
và
(
)
1
0
2
d.
5
f xx
=
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Lời giải
Chuyển thông tin
( )
1
0
df xx
∫
sang
( )
'fx
bằng cách:
Đặt
(
)
1
0
1
d
5
t x tf t t
= → =
∫
hay
( )
1
0
1
d.
5
xf x x =
∫
Tích phân từng phần
( )
1
0
d,xf x x
∫
ta được
( )
1
2
0
3
'd .
5
xf x x
=
∫
Hàm dưới dấu tích phân là
( )
( )
2
2
' , '
fx xfx
nên liên kết với
( )
2
2
'.fx x
α
+
Ta tìm được
( ) ( )
( )
11
23
3 ' 3 0.
f
f x x fx x C C
α
=
= − → = → = + → =
Vậy
( ) ( )
1
3
0
1
d.
4
fx x fx x= → =
∫
Cách 2. Theo Holder
( ) ( )
2
2
1 11
2
24
0 00
3 19 9
'd d ' d . .
5 5 5 25
xfxx xx fx x
=≤==
∫ ∫∫
Câu 104: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
0 1 0,ff+=
( ) ( )
1
0
' cos d
2
fx xx
π
π
=
∫
và
( )
1
2
0
1
d.
2
f xx=
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Lời giải
Hàm dưới dấu tích phân là
( )
2
fx
và
( ) ( )
' cosfx x
π
, không thấy liên kết.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 49
Do đó ta chuyển thông tin của
( ) ( )
' cosfx x
π
về
( )
fx
bằng cách tích phân từng phần của
( ) ( )
1
0
' cos d
2
fx xx
π
π
=
∫
cùng với kết hợp
( ) ( )
0 1 0,ff+=
ta được
( )
(
)
1
0
1
sind.
2
fx x x
π
=
∫
Hàm dưới dấu tích phân bây giờ là
(
)
2
fx
và
(
) (
)
sin
fx x
π
nên ta sẽ liên kết với bình phương
( ) ( )
2
sin .
fx x
απ
+
Ta tìm được
( ) ( ) ( )
1
0
2
1 sin d .fx x fx x
απ
π
= − → = → =
∫
Cách 2. Theo Holder
( ) ( ) ( ) ( )
2
2
1 11
2
2
0 00
1 11
sin d d . sin . .
2 22
fx xx f xx x dx
ππ
=≤=
∫ ∫∫
Câu 105: Cho hàm số
(
)
fx
có đạo hàm liên tục trên
[ ]
0; ,
π
thỏa mãn
(
)
0
' sin d 1f x xx
π
= −
∫
và
( )
2
0
2
d.f xx
π
π
=
∫
Tích phân
( )
0
dxf x x
π
∫
bằng
Lời giải
Hàm dưới dấu tích phân là
(
)
2
fx
và
( )
' sinfx x
, không thấy liên kết.
Do đó ta chuyển thông tin của
( )
' sinfx x
về
( )
fx
bằng cách tích phân từng phần của
( )
0
' sin d 1,f x xx
π
= −
∫
ta được
( )
0
cos d 1.f x xx
π
=
∫
Hàm dưới dấu tích phân bây giờ là
( )
2
fx
và
( )
cosfx x
nên ta sẽ liên kết với bình phương
( )
2
cos .fx x
α
+
Ta tìm được
( )
( )
00
2 2 2 cos 4
cos d d .
xx
fx x xfx x x
ππ
α
π π ππ
= − → = → = = −
∫∫
Cách 2. Theo Holder
( ) ( ) ( )
2
2
22
0 00
2
1 cos d d cos d . 1.
2
f x xx f x x xx
π ππ
π
π
=≤==
∫ ∫∫
Câu 106: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa
( ) ( )
1
2
2
0
1 0, ' d
8
f fx x
π
= =
∫
và
( )
1
0
1
cos d .
22
x
fx x
π
=
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Lời giải
Hàm dưới dấu tích phân là
( )
2
'fx
và
( )
cos
2
x
fx
π
, không thấy liên kết.
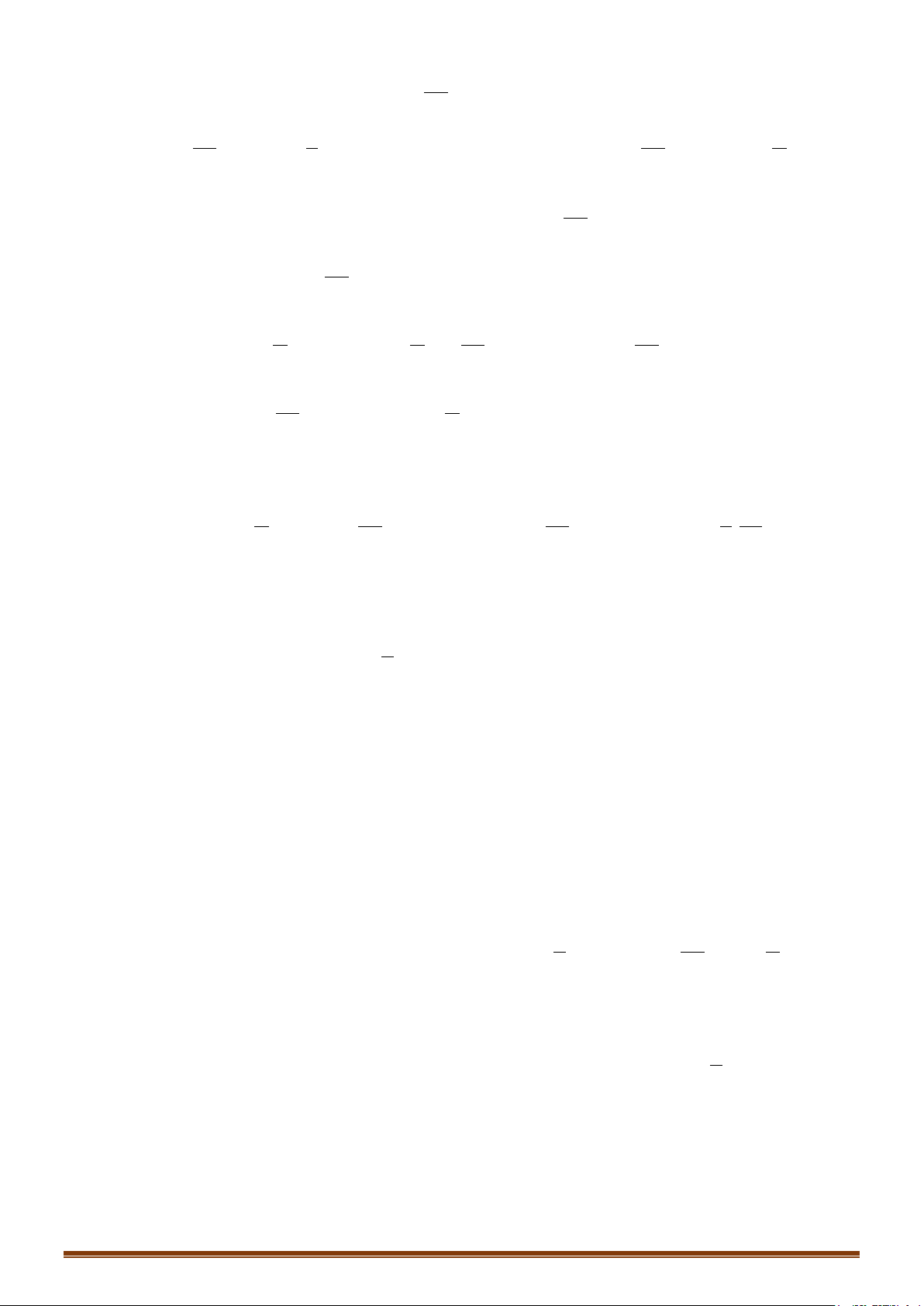
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 50
Do đó ta chuyển thông tin của
( )
cos
2
x
fx
π
về
( )
'fx
bằng cách tích phân từng phần của
(
)
1
0
1
cos d
22
x
fx x
π
=
∫
cùng với kết hợp
(
)
1 0,
f =
ta được
(
)
1
0
sin ' d .
24
x
fxx
ππ
= −
∫
Hàm dưới dấu tích phân bây giờ là
( )
2
'fx
và
( )
sin '
2
x
fx
π
nên ta sẽ liên kết với bình
phương
(
)
2
' sin .
2
x
fx
π
α
+
Ta tìm được
( )
( )
( )
10
' sin cos 0.
2 22 2
f
xx
f x fx C C
π ππ π
α
=
= → = − → = + → =
Vậy
(
) ( )
1
0
2
cos d .
2
x
fx fx x
π
π
= → =
∫
Cách 2. Theo Holder
( )
( )
2
2
1 11
2
2
2
0 00
1
sin ' d sin d . ' d . .
4 2 2 28
xx
fxx x fx x
ππ π π
−= ≤ =
∫ ∫∫
Câu 107: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) (
)
1
0
' sin dfx xx
ππ
=
∫
và
( )
1
2
0
d 2.f xx=
∫
Tích phân
1
0
d
2
x
fx
∫
bằng
Lời giải
Chuyển thông tin của
(
) ( )
' sinfx x
π
về
( )
fx
bằng cách tích phân từng phần của
( ) ( )
1
0
' sin d ,fx xx
ππ
=
∫
ta được
( ) ( )
1
0
cos d 1.fx x x
π
= −
∫
Hàm dưới dấu tích phân bây giờ là
( )
2
fx
và
(
) ( )
cos xfx
π
nên ta sẽ liên kết với bình phương
( ) ( )
2
cos .fx x
απ
+
Ta tìm được
( ) ( )
11
00
4
2 2cos d 2 cos d .
22
xx
fx x f x x
π
απ
π
= → = − → = − = −
∫∫
Cách 2. Theo Holder
( ) ( ) ( ) ( ) ( )
2
1 11
2
2
2
0 00
1
1 cos d cos d d .2.
2
fx x x x x fx x
ππ
−= ≤ =
∫ ∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 51
Câu 108: Cho hàm số
( )
fx
có đạo hàm liên tục trên
0; ,
2
π
thỏa
(
)
2
2
0
0, d 3
2
f f xx
π
π
π
= =
∫
và
( )
0
sin d 6 .
2
x
x xf x
π
π
′
−=
∫
Tích phân
( )
2
3
0
dfx x
π
′′
∫
bằng
Lời giải
Tích phân từng phần của
( )
0
sin d 6 ,
2
x
x xf x
π
π
′
−=
∫
kết hợp với
0
2
f
π
=
ta được
ta được
( )
2
2
0
3
sin d .
4
xf x x
π
π
=
∫
Hàm dưới dấu tích phân bây giờ là
( )
2
fx
và
( )
2
sin xf x
nên ta sẽ liên kết với bình phương
(
)
2
2
sin .fx x
α
+
Ta tìm được
( ) ( ) ( )
2
4 4sin ' 4sin2 '' 8cos2 .fx xfx xfx x
α
= − → = ⇒ = ⇒ =
Vậy
( )
[ ]
22
3
3
00
d 8cos2 d 0.fx x x x
ππ
′′
= =
∫∫
Cách 2. Theo Holder
( ) ( )
2
2
2 22
2 42
0 00
33
sin d sin d d .3 .
4 16
xfxx xxf xx
π ππ
ππ
π
=≤=
∫ ∫∫
Câu 109: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1 ,
thỏa mãn
( )
10f =
và
( ) ( ) ( )
11
2
2
00
1
'd 1 d .
4
x
e
f x x x ef x x
−
=+=
∫∫
Tính tích phân
(
)
1
0
d.I fx x=
∫
Lời giải
Tích phân từng phần của
( ) ( )
1
0
1 d,
x
x ef x x+
∫
kết hợp với
( )
10f =
ta được
( )
1
2
0
1
'd .
4
x
e
xe f x x
−
= −
∫
Hàm dưới dấu tích phân bây giờ là
( )
2
'fx
và
( )
'
x
xe f x
nên ta sẽ liên kết với
( )
2
.
x
f x xe
α
+
Ta tìm được
( ) ( )
( )
( )
10
1 ' d 1 0.
f
x xx
f x xe f x xe x x e C C
α
=
= → = − → = − = − + → =
∫
Vậy
( ) ( ) ( ) ( )
11
00
1 d 1 d 2.
xx
f x xe f x x xe x e= − → = − = −
∫∫
Cách 2. Theo Holder
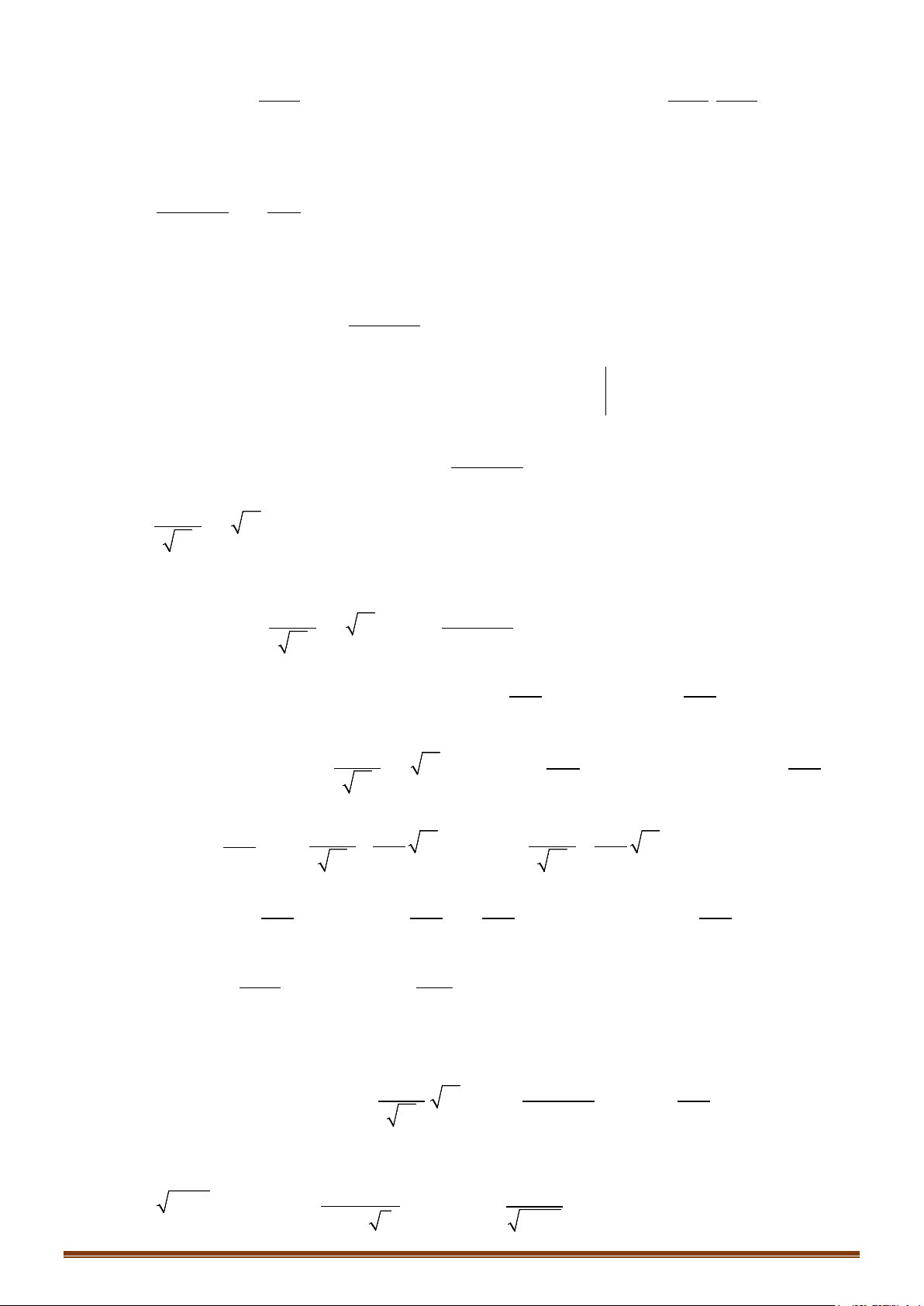
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 52
( ) ( )
2
2
1 11
2 22
2
22
0 00
1 11
' d d. ' d . .
4 44
xx
e ee
xefxx xe x fx x
− −−
−= ≤ =
∫ ∫∫
Câu 110: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
0 0, 1 1ff= =
và
( )
2
1
0
'
1
d.
1
x
fx
x
ee
=
−
∫
Tích phân
( )
1
0
dfx x
∫
bằng
Lời giải
Hàm dưới dấu tích phân là
( )
2
'
x
fx
e
nên ta cần tìm một thông tin liên quan
( )
'.fx
Từ giả thiết
(
) ( )
0 0, 1 1ff= =
ta nghĩ đến
( ) ( ) ( ) ( )
1
1
0
0
' d 1 0 1. f x x fx f f= =−=
∫
Do đó ta có hàm dưới dấu tích phân là
( )
2
'
x
fx
e
và
( )
'fx
nên sẽ liên kết với bình phương
( )
2
'
.
x
x
fx
e
e
α
+
Với mỗi số thực
α
ta có
( )
( )
( )
2
2
1 1 11
2
0 0 00
'
'
d d2 'd d
xx
x
x
fx
fx
e x x f x x ex
e
e
α αα
+= + +
∫ ∫ ∫∫
( ) (
)
2
2
11
2 1 1 1.
11
ee
ee
αα α
= + + −= − +
−−
Ta cần tìm
α
sao cho
( )
2
1
0
'
d0
x
x
fx
ex
e
α
+=
∫
hay
( )
2
11
110 .
11
e
ee
αα
− + =⇔=−
−−
Với
1
1e
α
= −
−
thì
( ) ( )
[ ]
2
1
0
''
11
d 0 , 0;1 .
11
xx
xx
fx fx
e x ex
ee
ee
− = ⇒ ≡ ∀∈
−−
∫
Suy ra
( ) ( )
( ) ( )
0 0, 1 1
1
'd .
1 11 1
x xx
ff
e ee
f x fx x C C
e ee e
= =
= → = = + → = −
− −− −
∫
Vậy
(
) ( )
1
0
12
d.
11
x
ee
fx fx x
ee
−−
= → =
−−
∫
Cách 2. Theo Holder
( )
( )
( )
( )
2
22
1 1 11
2
0 0 00
'
'
1
1 ' d . d d d . 1 1.
1
xx
x
x
fx
fx
f x x e x xe x e
ee
e
= = ≤ = −=
−
∫ ∫ ∫∫
Câu 111: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( ) ( )
0 0, 1 1ff= =
và
( )
( )
1
2
2
0
1
1 'd .
ln 1 2
x fx x+=
+
∫
Tích phân
( )
1
2
0
d
1
fx
x
x+
∫
bằng

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 53
Lời giải
Tương tự bài trước, ta có
( )
(
) (
) (
)
1
1
0
0
' d 1 0 1.f x x fx f f= =−=
∫
Do đó ta có hàm dưới dấu tích phân là
( )
2
2
1'x fx
+
và
( )
'fx
nên sẽ liên kết với bình
phương
( )
2
2
4
2
4
1' .
1
xf x
x
α
++
+
Ta tìm được
( )
( )
( )
2
1 11
'.
ln 1 2 ln 1 2
1
fx
x
α
= − → =
++
+
( )
( ) ( )
(
)
2
2
11 1
. d ln 1 .
ln 1 2 ln 1 2
1
fx x x x C
x
→ = = + + +
++
+
∫
Mà
(
) (
) ( )
(
)
( )
2
ln 1
0 0, 1 1 0 .
ln 1 2
xx
f f C fx
++
= = ⇒ = → =
+
Vậy
( )
( )
(
)
( )
(
)
(
)
2
11 1
22
22
00 0
ln 1
11
d d ln 1 d ln 1
ln 1 2 ln 1 2
11
xx
fx
x x xx xx
xx
++
= = ++ ++
++
++
∫∫ ∫
( )
(
)
( )
22
1
0
ln 1
11
. ln 1 2 .
22
ln 1 2
xx++
= = +
+
Cách 2. Theo Holder
( ) ( ) ( )
2
11 1 1
2
22 2
4
22
4
00 0 0
1d
1 ' d 1 ' . d 1 ' d.
11
x
fxx xfx x x fx x
xx
= =+ ≤+
++
∫∫ ∫ ∫
( )
( )
1
.ln 1 2 1.
ln 1 2
= +=
+
Câu 112: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
1;1 ,−
thỏa mãn
( )
1 0,f −=
( )
1
2
1
' d 112fx x
−
=
∫
và
( )
1
2
1
16
d.
3
xf x x
−
=
∫
Tính tích phân
( )
1
1
d.I fx x
−
=
∫
Lời giải
Như các bài trước, ta chuyển
( )
1
2
1
16
d
3
xf x x
−
=
∫
về thông tin của
( )
'fx
bằng cách tích phân từng
phần. Đặt
( )
( )
3
2
d 'd
.
dd
3
u fxx
u fx
x
v xx
v
=
=
⇒
=
=

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 54
Khi đó
( )
( )
(
)
(
)
( )
( )
11 1
3
1
23 3
1
11 1
1 11 1
d 'd 1 1 'd.
3 3 33 3
x
xfxx fx xfxx f f xfxx
−
−− −
= − = + −−
∫∫ ∫
Tới đây
ta bị vướng
( )
1f
vì giả thiết không cho. Do đó ta điều chỉnh lại như sau
( )
( )
3
2
d 'd
dd
3
u fxx
u fx
x
v xx
vk
=
=
⇒
=
= +
với
k
là hằng số.
Khi đó
( ) ( ) ( )
11
33
1
2
1
11
d 'd
33
xx
xfx x kfx kf x x
−
−−
=+ −+
∫∫
( )
( )
( )
( )
1
3
1
0 do 1 0
11
1 1 ' d.
33 3
f
x
kf kf kf x x
−
= −=
= + −− + − − +
∫
Ta chọn
k
sao cho
11
0.
33
kk+=⇔=−
Khi đó
( )
( )
(
)
( )
(
)
11 1
23 3
11 1
16 1
d 1 ' d 1 ' d 16.
33
xfxx x fxx x fxx
−− −
= = − − → − = −
∫∫ ∫
Hàm dưới dấu tích phân là
( )
( )
( )
2
3
' , 1 'fx x fx−
nên ta liên kết với
( )
( )
2
3
'1fx x
α
+−
.
Ta tìm được
( )
(
)
( )
( )
3 34
7
7 ' 7 1 7 1d 7
4
f x x fx x x x xC
α
= → = − − ⇒ = − − = − + +
∫
( )
(
)
10
4
35 7 35
7.
4 44
f
C fx x x
−=
→ = → = − + +
Vậy
( )
1
1
84
d.
5
I fx x
−
= =
∫
Cách 2. Theo Holder
( )
(
)
(
)
( )
( )
2
1 11
2
2
2
33
1 11
16
16 1 ' d 1 d . ' d .112 256.
7
x fxx x x fx x
− −−
−= − ≤ − = =
∫ ∫∫
Câu 113: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;1 ,
thỏa mãn
( )
1 0,f =
( )
1
2
0
3
' d 2ln 2
2
fx x= −
∫
và
( )
(
)
1
2
0
3
d 2 ln 2 .
2
1
fx
x
x
= −
+
∫
Tích phân
(
)
1
0
dfx x
∫
bằng
Lời giải
Như các bài trước, ta chuyển
( )
( )
1
2
0
3
d 2 ln 2
2
1
fx
x
x
= −
+
∫
về thông tin của
( )
'fx
bằng cách tích
phân từng phần. Đặt
( )
( )
( )
2
d 'd
.
1
1
dd
1
1
u fx
u fxx
vx
v
x
x
=
=
⇒
=
= −
+
+

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 55
Khi đó
( )
(
)
( ) ( ) ( ) (
) (
)
11 1
1
2
0
00 0
' 10 '
d d d.
1 1 21 1
1
fx fx f x f f f x
xx x
xx x
x
=− + =−+ +
++ +
+
∫∫ ∫
Tới đây ta bị vướng
( )
0
f
vì giả thiết không cho. Do đó ta điều chỉnh lại như sau
( )
( )
( )
2
d 'd
1
1
dd
1
1
u fx
u fxx
vx
vk
x
x
=
=
⇒
=
=−+
+
+
với
k
là hằng số.
Khi đó
(
)
( )
( )
( )
11
1
2
0
00
11
d 'd
11
1
fx
x kfx kf x x
xx
x
=−+ −−+ =
++
+
∫∫
(
)
(
) ( )
( )
1
10
0
1
1 0 ' d.
1
f
kf kf x x
x
=
= −−+ − − +
+
∫
Ta chọn
k
sao cho
1 0 1.
kk
−+ = ⇔ =
Khi đó
( )
( )
( )
( )
11 1
2
00 0
33
2ln 2 d ' d ' d 2ln 2.
2 1 12
1
fx
xx
x fxx fxx
xx
x
− = = − → = −
++
+
∫∫ ∫
Hàm dưới dấu tích phân là
( ) ( )
2
' , '
1
x
fx fx
x
+
nên ta liên kết với
( )
2
'.
1
x
fx
x
α
+
+
Ta tìm được
( )
( )
1 ' d ln 1
11
xx
f x fx x x x C
xx
α
= − → = ⇒ = = − + +
++
∫
( )
( ) ( )
10
ln 2 1 ln 1 ln 2 1.
f
C fx x x
=
→ = − → = − + + −
Vậy
( )
1
0
1 2 ln 2
d.
2
fx x
−
=
∫
Cách 2. Theo Holder
( ) ( )
2
22
1 11
2
0 00
3 33
2ln 2 ' d d ' d 2ln 2 2ln 2 .
2 1 1 22
xx
fxx x fx x
xx
−= ≤ =− −
++
∫ ∫∫
Câu 114: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
1; 2 ,
đồng biến trên
[ ]
1; 2 ,
thỏa mãn
( )
10f =
,
( )
2
2
1
d2fx x
′
=
∫
và
( ) ( )
2
1
. ' d 1.fxf x x=
∫
Tích phân
( )
2
1
dfx x
∫
bằng
Lời giải
Hàm dưới dấu tích phân là
( ) ( ) ( )
2
, .fx fxfx
′′
nên ta sẽ liên kết với bình phương
(
) ( )
2
.f x fx
α
′
+
Nhưng khi khai triển thì vướng
( )
2
2
1
d
fx x
∫
nên hướng này không khả thi.
Ta có
( ) ( )
( ) ( ) ( )
( )
( )
2 22 2
2
2
1
1
2 1 20
1 .' d 2 2
222
fx f f f
fxf x x f
−−
= = = = → =
∫
(do đồng
biến trên
[ ]
1; 2
nên
( ) ( )
2 10
ff>=
)

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 56
Từ
( )
10f =
và
(
)
22
f =
ta nghĩ đến
(
) (
)
(
) ( )
2
2
1
1
' d 2 1 2 0 2.
f x x fx f f= = − = −=
∫
Hàm dưới dấu tích phân bây giờ là
(
) (
)
2
,
fx fx
′′
nên ta sẽ liên kết với
(
)
2
.
fx
α
′
+
Ta tìm được
( ) ( )
( )
10
2 ' 2 2 2.
f
f x fx xC C
α
=
= − → = → = + → = −
Vậy
( ) ( )
2
1
2
22 d .
2
fx x fx x= − → =
∫
Câu 115: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[
]
0;1 ,
thỏa mãn
( )
10f =
,
( )
1
2
0
d1f xx=
∫
và
( ) ( )
1
2
2
0
3
d.
4
fx f xx
′
=
∫
Giá trị của
( )
2
2f
bằng
Lời giải
Hàm dưới dấu tích phân là
( ) ( )
2
2
fx f x
′
và
( )
2
fx
nên ta sẽ liên kết với bình phương
( ) ( ) ( )
2
.f xfx fx
α
′
+
Nhưng khi khai triển thì vướng
( )
( )
1
2
0
'df xf x x
∫
nên hướng này không
khả thi.
Tích phân từng phần
( )
1
2
0
d1
f xx
=
∫
kết hợp với
( )
1 0,f =
ta được
( ) ( )
1
0
1
'd .
2
xf x f x x = −
∫
Hàm dưới dấu tích phân bây giờ là
( ) ( )
2
2
fx f x
′
và
( ) ( )
'xf x f x
nên ta sẽ liên kết với bình
phương
( ) ( )
2
'.fxf x x
α
+
Ta tìm được
( ) ( ) ( ) ( )
( )
2
2
3 3 33
' 'd d
2 2 2 24
fx
fxf x x fxf x x xx x C
α
= → = − ⇒ = − ⇒ = − +
∫∫
( )
( )
( )
( )
10
2 22
33 3
1 2.
42 2
f
C fx x f
=
→ = → = − → = −
Câu 116: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0; 2 ,
thỏa mãn
( )
21f =
,
( )
2
2
0
8
d
15
xf x x=
∫
và
( )
2
4
0
32
'd .
5
fx x=
∫
Giá trị của tích phân
( )
2
0
dfx x
∫
bằng
Lời giải
Hàm dưới dấu tích phân
( )
4
'fx
và
( )
2
xf x
. Lời khuyên là đừng có cố liên kết với bình
phương nào, vì có tìm cũng không ra.
Tích phân từng phần
( )
2
2
0
8
d
15
xf x x=
∫
kết hợp với
( )
21f =
, ta được
( )
2
3
0
32
d.
5
xf x x
′
=
∫
Áp dụng Holder
2
lần ta được

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 57
( ) ( ) ( )
4 42 2
4
2 2 22
2
3 2 42
0 0 00
32
d . d d 'd
5
xfxx xxfxx xx x fx x
′′
= = ≤
∫ ∫ ∫∫
( )
( )
2
2 22
4
44
0 00
3
4
22
4
4
00
d d. ' d
1048576 32
d 'd .
625 5
xx xx f x x
xx f x x
≤×
=×==
∫ ∫∫
∫∫
Dấu
'' ''=
xảy ra, tức là
( ) ( )
2
''
xf x kx f x kx
=⇒=
thay vào
( )
2
4
0
32
'd
5
fx x=
∫
tìm được
1
k =
( ) (
)
( )
2
21
' d 1.
2
f
x
f x x f x xx C C
=
→ = ⇒ = = + → = −
∫
Vậy
( ) ( )
2
2
0
2
1 d.
23
x
fx fx x= − → = −
∫
Cách 2. Áp dụng bất đẳng thức AM – GM ta có
( ) (
)
4
444 3
' 4 '.
fx x x x xfx+++≥
Do vậy
(
) (
)
2 22
4
43
0 00
' d 3 d 4 d.f x x x x xf x x
′
+≥
∫ ∫∫
Mà giá trị của hai vế bằng nhau, có nghĩa là dấu
'' ''=
xảy ra nên
( )
'.fx x=
(Làm tiếp như trên).
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 58
BÀI 2. TÍCH PHÂN
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐÊ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Nếu
( )
2
0
4dfx x=
∫
thì
(
)
2
0
d
1
2
2
fx x
+
∫
bằng
A.
6
. B.
8
. C.
4
. D.
2
.
Câu 2: (MĐ 101-2022) Nếu
( )
5
1
3dfx x
−
= −
∫
thì
(
)
1
5
dfx x
−
∫
bằng
A.
5
. B.
6
. C.
4
. D.
3
.
Câu 3: (MĐ 102-2022) Nếu
( )
2
0
d4
fx x=
∫
thì
(
)
2
0
1
2d
2
fx x
+
∫
bằng
A.
2
. B.
6
. C.
4
. D.
8
.
Câu 4: (MĐ 102-2022) Nếu
(
)
5
1
d3
−
= −
∫
fx x
thì
(
)
1
5
d
−
∫
fx x
bằng
A.
3
. B.
4
. C.
6
. D.
5
.
Câu 5: (MĐ 103-2022) Nếu
(
)
3
0
d6
fx x=
∫
thì
(
)
3
0
1
2d
3
fx x
+
∫
bằng
A.
8
. B.
5
. C.
9
. D.
6
.
Câu 6: (MĐ 103-2022) Nếu
( )
2
1
d2fx x
−
=
∫
và
( )
5
2
d5fx x= −
∫
thì
( )
5
1
d
fx x
−
∫
bằng
A.
7−
. B.
3−
. C.
4
. D.
7
.
Câu 7: (MĐ 104-2022) Nếu
(
)
2
1
d2
fx x
−
=
∫
và
( )
5
2
d5fx x= −
∫
thì
( )
5
1
dfx x
−
∫
bằng
A.
7
. B.
3−
. C.
7−
. D.
4−
.
Câu 8: (MĐ 104-2022) Nếu
( )
3
0
6f x dx =
∫
thì
( )
3
0
1
2
3
f x dx
+
∫
bằng
A.
6
. B.
5
. C.
9
. D.
8
.
Câu 9: (TK 2020-2021) Nếu
( )
2
1
5f x dx =
∫
và
( )
3
2
2f x dx = −
∫
thì
( )
3
1
f x dx
∫
bằng
A.
3.
B.
7.
C.
10.−
D.
7.−
Câu 10: (TK 2020-2021) Tích phân
2
3
1
x dx
∫
bằng
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
- ỨNG DỤNG TÍCH PHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 59
A.
15
.
3
B.
17
.
4
C.
7
.
4
D.
15
.
4
Câu 11: (TK 2020-2021) Nếu
( )
3
1
2 15f x dx
+=
∫
thì
(
)
3
1
f x dx
∫
bằng
A.
3.
B.
2.
C.
3
.
4
D.
3
.
2
Câu 12: (MĐ 101 2020-2021 – ĐỢT 1) Nếu
( )
4
1
d3fxx=
∫
và
( )
4
1
d2gx x= −
∫
thì
( ) ( )
( )
4
1
df x gx x−
∫
bằng
A.
1−
. B.
5
−
. C.
5
. D.
1
.
Câu 13: (MĐ 102 2020-2021 – ĐỢT 1) Nếu
( )
4
1
d6fx x
=
∫
và
(
)
4
1
d5
gx x
= −
∫
thì
( ) ( )
4
1
df x gx x
−
∫
bằng
A.
1
−
. B.
11−
. C.
1
. D.
11
.
Câu 14: (MĐ 102 2020-2021 – ĐỢT 1) Nếu
3
0
() 3f x dx =
∫
thì
3
0
2 ()f x dx
∫
bằng
A.
3.
B.
18.
C.
2.
D.
6.
Câu 15: (MĐ 102 2020-2021 – ĐỢT 1) Nếu
(
)
2
0
3f x dx =
∫
thì
( )
2
0
21f x dx−
∫
bằng
A.
6
. B.
4
. C.
8
. D.
5
.
Câu 16: (MĐ 103 2020-2021 – ĐỢT 1) Nếu
( )
4
1
d5fx x=
∫
và
( )
4
1
d4gx x= −
∫
thì
(
) (
)
4
1
gdfx x x
−
∫
bằng
A.
1−
. B.
9−
. C.
1
. D.
9
.
Câu 17: (MĐ 103 2020-2021 – ĐỢT 1) Nếu
( )
3
0
d2fxx=
∫
thì
( )
3
0
3dfxx
∫
bằng
A.
6
. B.
2
. C.
18
. D.
3
.
Câu 18: (MĐ 104 2020-2021 – ĐỢT 1) Nếu
(
)
4
1
d4fx x=
∫
và
( )
4
1
d3gx x= −
∫
thì
(
) ( )
4
1
df x gx x
−
∫
bằng
A.
1
. B.
7−
. C.
1−
. D.
7
.
Câu 19: (MĐ 104 2020-2021 – ĐỢT 1) Nếu
( )
3
0
d3fxx=
∫
thì
( )
3
0
4dfxx
∫
bằng
A.
3
. B.
12
. C.
36
. D.
4
.
Câu 20: (2020-2021 – ĐỢT 2) Nếu
( )
1
0
d2fx x=
∫
và
( )
3
1
d5fx x=
∫
thì
( )
3
0
d
fx x
∫
bằng
A.
10
. B.
3
. C.
7
. D.
3−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 60
Câu 21: (2020-2021 – ĐỢT 2) Cho
(
)
fx
là hàm số liên tục trên đoạn
[
]
1; 2
. Biết
(
)
Fx
là nguyên hàm
của
(
)
fx
trên đoạn
[ ]
1; 2
thỏa mãn
(
)
12= −
F
và
(
)
24
=
F
. Khi đó
( )
2
1
d
∫
fx x
bằng
A.
6
. B.
2
. C.
6−
. D.
2−
.
Câu 22: (2020-2021 – ĐỢT 2) Nếu
( )
1
0
d5fx x=
∫
và
( )
3
1
d2fx x=
∫
thì
( )
3
0
dfx x
∫
bằng
A.
10
. B.
−3
. C.
3
. D.
7
.
Câu 23: (MĐ 103 2020-2021 – ĐỢT 2) Nếu
1
0
() 3f x dx =
∫
và
3
1
() 4
f x dx =
∫
thì
3
0
()
f x dx
∫
bằng
A.
1
−
. B.
1
. C.
7
. D.
12
.
Câu 24: (MĐ 103 2020-2021 – ĐỢT 2) Cho
f
là một hàm số liên tục trên đoạn
[ ]
1; 2
. Biết
F
là nguyên
hàm của hàm
f
trên đoạn
[ ]
1; 2
thỏa mãn
(
)
11F = −
và
(
)
23
F =
. Khi đó
( )
2
1
dfx x
∫
.
A.
4
. B.
2−
. C.
2
. D.
4−
.
Câu 25: (MĐ 104 2020-2021 – ĐỢT 2) Nếu
(
)
1
0
d4
fx x
=
∫
và
( )
3
1
d3fx x=
∫
thì
(
)
3
0
dfx x
∫
bằng
A.
1.−
B.
1.
C.
7.
D.
12.
Câu 26: (MĐ 104 2020-2021 – ĐỢT 2) Cho
f
là hàm số liên tục trên đoạn
[ ]
1; 2
. Biết
F
là nguyên
hàm của
f
trên đoạn
[
]
1; 2
thỏa mãn
( )
11F = −
và
( )
2 4.F =
Khi đó
( )
2
1
dfx x
∫
bằng
A.
5.−
B.
3.
C.
5.
D.
3.−
Câu 27: (MĐ 103 2020-2021 – ĐỢT 1) Nếu
2
0
( )d 6fx x=
∫
thì
( )
2
0
21f x dx−
∫
bằng
A.
12
. B.
10
. C.
11
. D.
14
.
Câu 28: (MĐ 104 2020-2021 – ĐỢT 1) Nếu
( )
2
0
4dfxx=
∫
thì
( )
2
0
21dfx x−
∫
bằng
A.
8
. B.
10
. C.
7
. D.
6
.
Câu 29: (2020-2021 – ĐỢT 2) Nếu
( )
2
0
d2fx x=
∫
thì
( )
2
0
4dx fx x
−
∫
bằng
A.
12
. B.
10
. C.
4
. D.
6
.
Câu 30: (2020-2021 – ĐỢT 2) Cho
f
là hàm số liên tục trên đoạn
[ ]
1; 2
. Biết
F
là nguyên hàm của
f
trên đoạn
[ ]
1; 2
thỏa mãn
( )
12F
= −
và
(
)
23F =
. Khi đó
(
)
2
1
dfx x
∫
bằng
A.
−5
. B.
1
. C.
−1
. D.
5
.
Câu 31: (2020-2021 – ĐỢT 2) Nếu
( )
2
0
d2fx x=
∫
thì
( )
2
0
2dx fx x
−
∫
bằng
A.
2
. B.
8
. C.
6
. D.
0
.
Câu 32: (MĐ 103 2020-2021 – ĐỢT 2) Nếu
( )
2
0
d3fxx=
∫
thì
( )
( )
2
0
2dx fx x−
∫
bằng
A.
7
. B.
2−
. C.
10
. D.
1
.
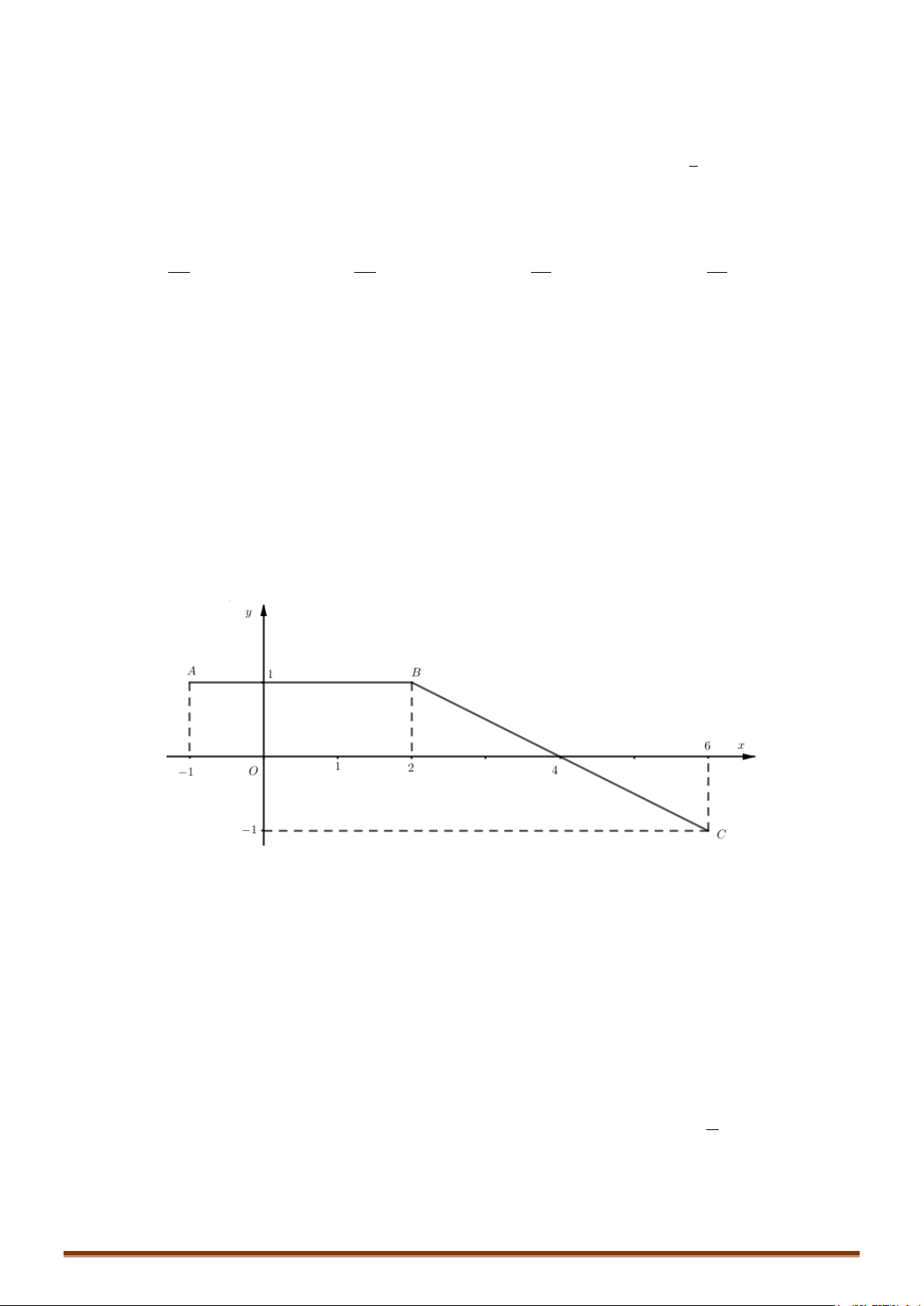
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 61
Câu 33: (MĐ 104 2020-2021 – ĐỢT 2) Nếu
( )
2
0
d3fxx=
∫
thì
( )
2
0
4dx fx x
−
∫
bằng
A.
14
. B.
5
. C.
2−
. D.
11
.
Câu 34: (TK 2020-2021) Cho hàm số
(
)
2
2
12
.
23 2
x khi x
fx
x x khi x
−≥
=
−+ <
Tích phân
( )
2
0
2sin 1 cosf x xdx
π
+
∫
bằng
A.
23
.
3
B.
23
.
6
C.
17
.
6
D.
17
.
3
Câu 35: (MĐ 102 2020-2021 – ĐỢT 1) Cho hàm số
(
)
2
21 1
32 1
x khi x
fx
x khi x
−≥
=
−<
. Giả sử
F
là nguyên
hàm của
f
trên
thỏa mãn
( )
02F =
. Giá trị
( )
( )
122FF
−+
A.
9
B.
15
C.
11
D.
6
Câu 36: (MĐ 104 2020-2021 – ĐỢT 1) Cho hàm số
( )
2
22 1
.
31 1
x khi x
fx
x khi x
+≥
=
+<
Giả sử
F
là nguyên hàm
của
f
trên
thỏa mãn
( )
0 2.F
=
Giá trị của
( ) ( )
122FF−+
bằng
A.
18
. B.
20
. C.
9
. D.
24
.
Câu 37: Cho hàm số
y fx
liên tục trên đoạn
1; 6
và có đồ thị là đường gấp khúc
ABC
trong hình
bên. Biết
F
là nguyên hàm của
f
thỏa mãn
11F
. Giá trị của
46FF
bằng
A.
10
. B.
5
. C.
6
. D.
7
.
Câu 38: (Đề Minh Họa 2020 Lần 1) Nếu
( )
2
1
d2fx x= −
∫
và
( )
3
2
d1fx x=
∫
thì
( )
3
1
dfx x
∫
bằng
A.
3
−
. B.
1−
. C.
1
. D.
3
.
Câu 39: (Đề Tham Khảo 2020 Lần 2) Nếu
( )
1
0
d4fx x=
∫
thì
( )
1
0
2dfx x
∫
bằng
A.
16
. B.
4
. C.
2
. D.
8
.
Câu 40: (Mã 101 - 2020 Lần 1) Biết
( )
3
1
d3fx x=
∫
. Giá trị của
( )
3
1
2dfx x
∫
bằng
A.
5
. B.
9
. C.
6
. D.
3
2
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 62
Câu 41: (Mã 101 - 2020 Lần 1) Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
( )
fx
trên
. Giá trị
của
( )
2
1
2dfx x+
∫
bằng
A.
5
. B.
3
. C.
13
3
. D.
7
3
.
Câu 42: (Mã 102 - 2020 Lần 1) Biết . Giá trị của bằng
A. . B. . C. . D. .
Câu 43: (Mã 102 - 2020 Lần 1) Biết là một nguyên hàm của hàm số trên . Giá trị
của bằng
A. . B. . C. . D. .
Câu 44: (Mã 103 - 2020 Lần 1) Biết
( )
2
1
2f x dx =
∫
. Giá trị của
( )
3
1
3 f x dx
∫
bằng
A.
5
. B.
6
. C.
2
3
. D.
8
.
Câu 45: (Mã 103 - 2020 Lần 1) Biết
3
()Fx x=
là một nguyên hàm của hàm số
()fx
trên
. Giá trị
của
3
1
(1 ( ) d)x xf+
∫
bằng
A. 20. B. 22. C. 26. D. 28.
Câu 46: (Mã 104 - 2020 Lần 1) Biết
( )
3
2
d 6.fx x=
∫
Giá trị của
( )
3
2
2dfx x
∫
bằng.
A.
36
. B.
3
. C.
12
. D.
8
.
Câu 47: (Mã 104 - 2020 Lần 1) Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
()fx
trên
. Giá trị
của
[ ]
3
1
1 ()f x dx+
∫
bằng
A.
10
. B.
8
. C.
26
3
. D.
32
3
.
Câu 48: (Mã 101 - 2020 Lần 2) Biết
( )
3
2
f x dx 4=
∫
và
( )
3
2
g x dx 1=
∫
. Khi đó:
( ) ( )
3
2
f x g x dx
−
∫
bằng:
A.
3−
. B.
3
. C.
4
. D.
5
.
Câu 49: (Mã 101 - 2020 Lần 2) Biết
( )
1
0
f x 2x dx=2
+
∫
. Khi đó
( )
1
0
f x dx
∫
bằng :
A.
1
. B.
4
. C.
2
. D.
0
.
Câu 50: (Mã 102 - 2020 Lần 2) Biết
( )
3
2
3f x dx =
∫
và
( )
3
2
1g x dx =
∫
. Khi đó
( ) ( )
3
2
f x g x dx+
∫
bằng
A.
4
. B.
2
. C.
2−
. D.
3
.
Câu 51: (Mã 102 - 2020 Lần 2) Biết
( )
1
0
23f x x dx+=
∫
. Khi đó
( )
1
0
dfx x
∫
bằng
( )
5
1
d4fx x=
∫
( )
5
1
3dfx x
∫
7
4
3
64
12
( )
3
Fx x=
( )
fx
( )
2
1
2 ()dfx x+
∫
23
4
7
9
15
4

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 63
A.
1
. B.
5
. C.
3
. D.
2
.
Câu 52: (Mã 103 - 2020 Lần 2) Biết
(
)
2
1
d3fx x=
∫
và
(
)
2
1
d2
gx x
=
∫
. Khi đó
( ) ( )
2
1
df x gx x
−
∫
bằng?
A.
6
. B.
1
. C.
5
. D.
1−
.
Câu 53: (Mã 103 - 2020 Lần 2) Biết
( )
1
0
2d 4
fx x x
+=
∫
. Khi đó
( )
1
0
dfx x
∫
bằng
A.
3
. B.
2
. C.
6
. D.
4
.
Câu 54: (Mã 104 - 2020 Lần 2) Biết
2
1
() 2f x dx =
∫
và
2
1
( ) 3.g x dx =
∫
Khi đó
2
1
[ () ()]f x g x dx+
∫
bằng
A.
1
. B.
5
. C.
1
−
. D.
6
.
Câu 55: (Mã 104 - 2020 Lần 2) Biết
( )
1
0
2d 5fx x x+=
∫
. Khi đó
( )
1
0
d
fx x
∫
bằng
A.
7
. B.
3
. C.
5
. D.
4
.
Câu 56: (Mã 103 - 2019) Biết
( )
2
1
d2fx x=
∫
và
(
)
2
1
d6
gx x=
∫
, khi đó
( )
( )
2
1
d
f x gx x
−
∫
bằng
A.
8
. B.
4−
. C.
4
. D.
8−
.
Câu 57: (Mã 102 - 2019) Biết tích phân
(
)
1
0
3f x dx
=
∫
và
(
)
1
0
4g x dx
= −
∫
. Khi đó
( ) ( )
1
0
f x g x dx+
∫
bằng
A.
7−
. B.
7
. C.
1−
. D.
1
.
Câu 58: (Mã 104 - 2019) Biết
1
0
( )d 2fx x=
∫
và
1
0
( )d 4gx x= −
∫
, khi đó
[
]
1
0
() ()df x gx x
+
∫
bằng
A.
6
. B.
6
−
. C.
2−
. D.
2
.
Câu 59: (Mã 101 2019) Biết
( )
1
0
d2fxx= −
∫
và
(
)
1
0
d3gx x
=
∫
, khi đó
( ) ( )
1
0
df x gx x
−
∫
bằng
A.
1−
. B.
1
. C.
5−
. D.
5
.
Câu 60: (Đề Tham Khảo 2019) Cho
( )
1
0
d2fx x=
∫
và
( )
1
0
d5gx x=
∫
, khi
( ) ( )
1
0
2d
f x gx x
−
∫
bằng
A.
8−
B.
1
C.
3−
D.
12
Câu 61: (Mã 104 2018)
2
1
23
dx
x +
∫
bằng
A.
1
ln 35
2
B.
7
ln
5
C.
17
ln
25
D.
7
2ln
5
Câu 62: (Mã 103 2018)
2
1
32
dx
x −
∫
bằng
A.
2ln 2
B.
1
ln 2
3
C.
2
ln 2
3
D.
ln 2

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 64
Câu 63: (Đề Tham Khảo 2018) Tích phân
2
0
3
dx
x
+
∫
bằng
A.
2
15
B.
16
225
C.
5
log
3
D.
5
ln
3
Câu 64: (Mã 105 2017) Cho
−=+
++
∫
1
0
11
d ln 2 ln 3
12
xa b
xx
với
,ab
là các số nguyên. Mệnh đề nào
dưới đây đúng?
A.
+=
20ab
B.
+=2ab
C.
−=20ab
D.
+=−2
ab
Câu 65: (Mã 110 2017) Cho
( )
Fx
là một nguyên hàm của hàm số
( )
ln x
fx
x
=
. Tính:
( ) ( )
1I Fe F= −
?
A.
1
2
I
=
B.
1
I
e
=
C.
1I
=
D.
Ie=
Câu 66: (Mã 102 2018)
1
31
0
d
x
ex
+
∫
bằng
A.
( )
4
1
3
ee+
B.
3
ee−
C.
( )
4
1
3
ee−
D.
4
ee−
Câu 67: (Mã 101 2018)
2
31
1
ed
−
∫
x
x
bằng
A.
( )
52
1
ee
3
+
B.
( )
52
1
ee
3
−
C.
52
1
ee
3
−
D.
52
ee−
Câu 68: (Mã 123 2017) Cho
6
0
( ) 12f x dx
=
∫
. Tính
2
0
(3 ) .I f x dx=
∫
A.
= 5I
B.
= 36I
C.
= 4I
D.
=
6I
Câu 69: (Mã 103 - 2019) Cho hàm số
( )
fx
. Biết
( )
04f =
và
( )
2
' 2 sin 1, fx x x= + ∀∈
, khi đó
( )
4
0
d
fx x
π
∫
bằng
A.
2
16 4
.
16
ππ
+−
B.
2
4
.
16
π
−
C.
2
15
.
16
ππ
+
D.
2
16 16
.
16
ππ
+−
Câu 70: (Mã 104 - 2019) Cho hàm số
(
)
fx
. Biết
( )
04f =
và
( )
2
2sin 3fx x
′
= +
,
xR∀∈
, khi đó
( )
4
0
dfx x
π
∫
bằng
A.
2
2
8
π
−
. B.
2
88
8
ππ
+−
. C.
2
82
8
ππ
+−
. D.
2
3 23
8
ππ
+−
.
Câu 71: (Mã 102 - 2019) Cho hàm số
()fx
.Biết
(0) 4f =
và
2
( ) 2 cos 3,fx x x
′
= + ∀∈
, khi đó
4
0
()f x dx
π
∫
bằng?
A.
2
88
8
ππ
++
. B.
2
82
8
ππ
++
. C.
2
68
8
ππ
++
. D.
2
2
8
π
+
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 65
Câu 72: (Đề Tham Khảo -2019) Cho
( )
1
2
0
ln 2 ln 3
2
xdx
ab c
x
=++
+
∫
với
,,abc
là các số hữu tỷ. Giá trị
của
3abc++
bằng
A.
2
B.
1
C.
2−
D.
1−
Câu 73: (Đề Minh Họa 2020 Lần 1) Cho hàm số
(
)
fx
có
( )
33f =
và
( )
11
x
fx
xx
′
=
+− +
,
0
x∀>
. Khi đó
( )
8
3
dfx x
∫
bằng
A.
7
. B.
197
6
. C.
29
2
. D.
181
6
.
Câu 74: (Mã 102 2018) Cho
21
5
ln 3 ln 5 ln 7
4
dx
abc
xx
=++
+
∫
, với
,,abc
là các số hữu tỉ. Mệnh đề nào
sau đây đúng?
A.
2ab c−=−
B.
2ab c+=−
C.
abc+=
D.
ab c−=−
Câu 75: (Mã 101 2018) Cho
55
16
d
ln 2 ln 5 ln11
9
x
abc
xx
=++
+
∫
, với
,,abc
là các số hữu tỉ. Mệnh đề nào
dưới đây đúng?
A.
3ab c+=
B.
3ab c−=−
C.
ab c−=−
D.
abc+=
Câu 76: (Đề Tham Khảo 2017) Tính tích phân
2
2
1
21I x x dx= −
∫
bằng cách đặt
2
1ux= −
, mệnh đề nào
dưới đây đúng?
A.
3
0
I udu=
∫
B.
2
1
1
2
I udu=
∫
C.
3
0
2I udu
=
∫
D.
2
1
I udu
=
∫
Câu 77: (Đề Tham Khảo 2018) Biết
2
1
( 1) 1
dx
dx a b c
x x xx
=−−
+ ++
∫
với
,,abc
là các số nguyên
dương. Tính
P abc=++
A.
18P =
B.
46P =
C.
24P
=
D.
12P =
Câu 78: (Đề Tham Khảo 2020 Lần 2) Cho hàm số
( )
fx
có
( )
00
f =
và
( )
2
cos cos 2 ,fx x x R
′
= ∀∈
.
Khi đó
( )
0
dfx x
π
∫
bằng
A.
1042
225
. B.
208
225
. C.
242
225
. D.
149
225
.
Câu 79: (Đề Minh Họa 2017) Tính tích phân
3
0
cos .sin dI x xx
π
=
∫
.
A.
1
4
I = −
B.
4
1
4
I
π
= −
C.
4
I
π
= −
D.
0I =
Câu 80: (Đề Tham Khảo 2017) Cho
1
0
d1
ln
12
x
xe
ab
e
+
= +
+
∫
, với
,a
b
là các số hữu tỉ. Tính
33
Sa b= +
.
A.
2S = −
. B.
0S =
. C.
1S =
. D.
2S =
.
Câu 81: (Đề Tham Khảo 2020 Lần 2) Xét
2
2
0
ed
x
xx
∫
, nếu đặt
2
ux=
thì
2
2
0
ed
x
xx
∫
bằng

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 66
A.
2
0
2 ed
u
u
∫
. B.
4
0
2 ed
u
u
∫
. C.
2
0
1
ed
2
u
u
∫
. D.
4
0
1
ed
2
u
u
∫
.
Câu 82: (Đề Minh Họa 2017) Tính tích phân
1
ln
e
I x xdx=
∫
:
A.
2
1
4
e
I
−
=
B.
1
2
I =
C.
2
2
2
e
I
−
=
D.
2
1
4
e
I
+
=
Câu 83: (Mã 103 2018) Cho
(
)
e
2
1
1 ln d e exxxa b c+ = ++
∫
với
a
,
b
,
c
là các số hữu tỷ. Mệnh đề nào
dưới đây đúng?
A.
abc+=
B.
ab c
+=−
C.
ab c−=
D.
ab c−=−
Câu 84: (Mã 104 2018) Cho
(
)
2
1
2 ln d
e
x x x ae be c
+ = ++
∫
với
,,
abc
là các số hữu tỉ. Mệnh đề nào sau
đây đúng?
A.
abc
+=
B.
ab c−=
C.
ab c−=−
D.
ab c+=−
Câu 85: (Đề tham khảo 2017) Cho hàm số
( )
fx
thỏa mãn
( ) ( )
1
0
1 d 10x fxx
′
+=
∫
và
( ) (
)
21 0 2ff−=
. Tính
( )
1
0
dfx x
∫
.
A.
12
I = −
B.
8
I
=
C.
1
I =
D.
8
I = −
Câu 86: (Mã 104 - 2019) Cho hàm số
(
)
fx
có đạo hàm liên tục trên
. Biết
(
)
31
=f
và
( )
1
0
3d 1=
∫
xf x x
, khi đó
( )
3
2
0
d
′
∫
xf x x
bằng
A.
25
3
. B.
3
. C.
7
. D.
9
−
.
Câu 87: (Mã 101 - 2019) Cho hàm số
( )
fx
có đạo hàm liên tục trên
.
Biết
( )
41f =
và
( )
1
0
4 1,xf x dx =
∫
khi đó
( )
4
2
0
x f x dx
′
∫
bằng
A. 8. B. 14. C.
31
2
. D.
16
−
.
Câu 88: (Mã 103 - 2019) Cho hàm số
( )
fx
có đạo hàm liên tục trên
. Biết
( )
61f =
và
( )
1
0
6d 1xf x x =
∫
, khi đó
( )
6
2
0
dxf x x
′
∫
bằng
A.
107
3
. B.
34
. C.
24
. D.
36
−
.
Câu 89: (Mã 102 - 2019) Cho hàm số
()fx
có đạo hàm liên tục trên
. Biết
(5) 1f
và
1
0
(5 ) 1xf x dx
, khi đó
5
2
0
()x f x dx
bằng
A.
15
B.
23
C.
123
5
D.
25
Câu 90: (Đề Tham Khảo 2018) Cho hàm số
(
)
y fx=
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
[ ]
1
2
0
1 0, ( ) d 7f fx x
′
= =
∫
và
1
2
0
1
( )d
3
xfx x=
∫
. Tính tích phân
1
0
( )dfx x
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 67
A.
4
B.
7
5
C.
1
D.
7
4
Câu 91: (Mã 102 2018) Cho hàm số
()fx
thỏa mãn
1
(2)
3
f
= −
và
[ ]
2
() ()f x xfx
′
=
với mọi
.x ∈
Giá trị của
(1)f
bằng
A.
2
3
−
B.
2
9
−
C.
7
6
−
D.
11
6
−
Câu 92: (Mã 104 2018) Cho hàm số
( )
fx
thỏa mãn
(
)
1
2
5
f
= −
và
(
)
( )
2
3
f x x fx
′
=
với mọi
x ∈
. Giá trị của
( )
1f
bằng
A.
4
35
−
B.
71
20
−
C.
79
20
−
D.
4
5
−
Câu 93: (Minh họa 2020 Lần 1) Cho hàm số
( )
fx
liên tục trên
thảo mãn
(
)
( )
3 2 10 6
1 2,xf x f x x x x x+ − =− + − ∀∈
. Khi đó
( )
0
1
dfxx
−
∫
?
A.
17
20
−
. B.
13
4
−
. C.
17
4
. D.
1−
.
Câu 94: (Đề Tham Khảo 2017) Cho hàm số
(
)
fx
liên tục trên
và thoả mãn
( ) (
)
2 2cos 2fx f x x+ −= +
,
x
∀∈
. Tính
( )
3
2
3
2
.I f x dx
π
π
−
=
∫
A.
6
I = −
B.
0I =
C.
2I = −
D.
6I =

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 1
BÀI 2. TÍCH PHÂN
BÀI TẬP TRẮC NGHIỆM TRÍCH TỪ ĐÊ THAM KHẢO VÀ ĐỀ CHÍNH THỨC
CỦA BỘ GIÁO DỤC TỪ NĂM 2017 ĐẾN NAY
Câu 1: (MĐ 101-2022) Nếu
( )
2
0
d4
fx x
=
∫
thì
( )
2
0
1
2d
2
fx x
+
∫
bằng
A.
6
. B.
8
. C.
4
. D.
2
.
Lời giải
Chọn A
Ta có
( )
( )
2 22
0 00
dd .
11 1
2 2 .4 4 6
22
d
2
fx x fx x x
+ = + = +=
∫ ∫∫
Câu 2: (MĐ 101-2022) Nếu
( )
5
1
3dfx x
−
= −
∫
thì
(
)
1
5
dfx x
−
∫
bằng
A.
5
. B.
6
. C.
4
. D.
3
.
Lời giải
Chọn D
Ta có
( ) ( )
15
51
3ddfx x fx x
−
−
=−=
∫∫
Câu 3: (MĐ 102-2022) Nếu
( )
2
0
d4fx x=
∫
thì
( )
2
0
1
2d
2
fx x
+
∫
bằng
A.
2
. B.
6
. C.
4
. D.
8
.
Lời giải
Chọn B
Ta có
( ) ( ) ( )
2 22
2
0
0 00
11 1
2d d 2d .42 2220 6
22 2
fx x fx x x x
+ = + = + =+ −=
∫ ∫∫
.
Câu 4: (MĐ 102-2022) Nếu
( )
5
1
d3
−
= −
∫
fx x
thì
( )
1
5
d
−
∫
fx x
bằng
A.
3
. B.
4
. C.
6
. D.
5
.
Lời giải
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
- ỨNG DỤNG TÍCH PHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
Chọn A
Theo tính chất tích phân thì
( )
(
) (
)
15
51
d d 33
−
−
=− =−− =
∫∫
fx x fx x
.
Câu 5: (MĐ 103-2022) Nếu
(
)
3
0
d6
fx x=
∫
thì
( )
3
0
1
2d
3
fx x
+
∫
bằng
A.
8
. B.
5
. C.
9
. D.
6
.
Lời giải
Chọn A
Ta có:
( )
( )
3 33
3
0
0 00
11 1
2 d d 2d .6 2 2 6 8
33 3
fx x fx x x x
+ = + = + =+=
∫ ∫∫
.
Câu 6: (MĐ 103-2022) Nếu
( )
2
1
d2fx x
−
=
∫
và
(
)
5
2
d5fx x
= −
∫
thì
( )
5
1
dfx x
−
∫
bằng
A.
7−
. B.
3
−
. C.
4
. D.
7
.
Lời giải
Chọn B
Ta có
( ) ( ) ( ) ( )
5 25
1 12
d d d2 5 3fx x fx x fx x
−−
= + = +− =−
∫∫∫
.
Câu 7: (MĐ 104-2022) Nếu
( )
2
1
d2fx x
−
=
∫
và
( )
5
2
d5fx x
= −
∫
thì
(
)
5
1
dfx x
−
∫
bằng
A.
7
. B.
3−
. C.
7−
. D.
4
−
.
Lời giải
Chọn B
Ta có
5 25
1 12
d d d 2 5 3.fx x fx x fx x
Câu 8: (MĐ 104-2022) Nếu
(
)
3
0
6f x dx =
∫
thì
( )
3
0
1
2
3
f x dx
+
∫
bằng
A.
6
. B.
5
. C.
9
. D.
8
.
Lời giải
Chọn D
Ta có:
( )
( )
3 33
0 00
11 1
2 2 .6 6 8
33 3
f x dx f x dx dx
+ = + = +=
∫ ∫∫
.
Câu 9: (TK 2020-2021) Nếu
( )
2
1
5f x dx =
∫
và
( )
3
2
2f x dx = −
∫
thì
( )
3
1
f x dx
∫
bằng
A.
3.
B.
7.
C.
10.−
D.
7.−
Lời giải
Ta có
3 23
112
( )d ( )d ( )d 5 2 3.fx x fx x fx x

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
Câu 10: (TK 2020-2021) Tích phân
2
3
1
x dx
∫
bằng
A.
15
.
3
B.
17
.
4
C.
7
.
4
D.
15
.
4
Lời giải
Ta có
2
4 44
2
3
1
1
2 1 15
d.
4 44
x
xx
Câu 11: (TK 2020-2021) Nếu
( )
3
1
2 15f x dx+=
∫
thì
( )
3
1
f x dx
∫
bằng
A.
3.
B.
2.
C.
3
.
4
D.
3
.
2
Lời giải
Ta có
3 33
1 11
3
5 2 () 1d 2 ()d 2 ()d .
2
fx x fx x fx x
Câu 12: (MĐ 101 2020-2021 – ĐỢT 1) Nếu
( )
4
1
d3fxx=
∫
và
( )
4
1
d2gx x= −
∫
thì
(
)
( )
( )
4
1
df x gx x−
∫
bằng
A.
1−
. B.
5−
. C.
5
. D.
1
.
Lời giải
Ta có
( ) ( )
( )
4
1
df x gx x−
∫
( ) ( )
44
11
dd
fxx gxx= −
∫∫
( )
3 25= −− =
.
Câu 13: (MĐ 102 2020-2021 – ĐỢT 1) Nếu
4
1
d6fx x
và
4
1
d5gx x
thì
4
1
df x gx x
bằng
A.
1−
. B.
11−
. C.
1
. D.
11
.
Lời giải
4
1
df x gx x
44
11
d d 6 5 11fxx gxx
.
Câu 14: (MĐ 102 2020-2021 – ĐỢT 1) Nếu
3
0
() 3f x dx =
∫
thì
3
0
2 ()f x dx
∫
bằng
A.
3.
B.
18.
C.
2.
D.
6.
Lời giải
Chọn D
Ta có
33
00
2 ( ) 2 ( ) 2.3 6.f x dx f x dx= = =
∫∫
Câu 15: (MĐ 102 2020-2021 – ĐỢT 1) Nếu
( )
2
0
3f x dx =
∫
thì
( )
2
0
21
f x dx−
∫
bằng
A.
6
. B.
4
. C.
8
. D.
5
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
Lời giải
(
) (
)
2 22
2
0
0 00
2 1 2 2.3 6 2 4
f x dx f x dx dx x− = − = − =−=
∫ ∫∫
Câu 16: (MĐ 103 2020-2021 – ĐỢT 1) Nếu
(
)
4
1
d5
fx x
=
∫
và
( )
4
1
d4gx x= −
∫
thì
( )
( )
4
1
gdfx x x−
∫
bằng
A.
1
−
. B.
9−
. C.
1
. D.
9
.
Lời giải
Ta có:
( ) ( )
( ) ( )
4 44
1 11
[ g ]d d d 5 4 9
fx x x fx x gx x− = − =+=
∫ ∫∫
.
Câu 17: (MĐ 103 2020-2021 – ĐỢT 1) Nếu
( )
3
0
d2fxx=
∫
thì
( )
3
0
3dfxx
∫
bằng
A.
6
. B.
2
. C.
18
. D.
3
.
Lời giải
Theo tính chất của tích phân ta có:
( ) ( )
33
00
3 3 3.2 6
f x dx f x dx= = =
∫∫
.
Câu 18: (MĐ 104 2020-2021 – ĐỢT 1) Nếu
( )
4
1
d4fx x=
∫
và
( )
4
1
d3gx x
= −
∫
thì
(
) ( )
4
1
df x gx x−
∫
bằng
A.
1
. B.
7−
. C.
1−
. D.
7
.
Lời giải
Ta có
( ) ( ) ( ) ( ) ( )
4 44
1 11
d d d4 37f x gx x f x x gx x− = − = −− =
∫ ∫∫
.
Câu 19: (MĐ 104 2020-2021 – ĐỢT 1) Nếu
( )
3
0
d3fxx=
∫
thì
( )
3
0
4dfxx
∫
bằng
A.
3
. B.
12
. C.
36
. D.
4
.
Lời giải
Ta có:
(
) ( )
33
00
4 d 4 d 4.3 12
fxx fxx= = =
∫∫
.
Câu 20: (2020-2021 – ĐỢT 2) Nếu
( )
1
0
d2fx x=
∫
và
( )
3
1
d5fx x=
∫
thì
(
)
3
0
dfx x
∫
bằng
A.
10
. B.
3
. C.
7
. D.
3−
.
Lời giải
Ta có
(
) ( ) ( )
3 13
0 01
d d d 257fx x fx x fx x= + =+=
∫∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Câu 21: (2020-2021 – ĐỢT 2) Cho
(
)
fx
là hàm số liên tục trên đoạn
[
]
1; 2
. Biết
(
)
Fx
là nguyên hàm
của
(
)
fx
trên đoạn
[ ]
1; 2
thỏa mãn
(
)
12= −F
và
(
)
24
=
F
. Khi đó
(
)
2
1
d
∫
fx x
bằng
A.
6
. B.
2
. C.
6−
. D.
2−
.
Lời giải
Ta có
( ) ( )
( ) ( )
2
2
1
1
d 2 16f x x Fx F F= = −=
∫
.
Câu 22: (2020-2021 – ĐỢT 2) Nếu
( )
1
0
d5fx x=
∫
và
(
)
3
1
d2fx x
=
∫
thì
( )
3
0
dfx x
∫
bằng
A.
10
. B.
−3
. C.
3
. D.
7
.
Lời giải
Ta có:
(
) ( ) ( )
3 13
0 01
d d d 527fx x fx x fx x= + =+=
∫∫∫
.
Câu 23: (MĐ 103 2020-2021 – ĐỢT 2) Nếu
1
0
() 3f x dx
=
∫
và
3
1
() 4f x dx
=
∫
thì
3
0
()
f x dx
∫
bằng
A.
1−
. B.
1
. C.
7
. D.
12
.
Lời giải
0
3 13
01
() () () 3 4 7.f x dx f x dx f x dx= + =+=
∫∫∫
Vậy Chọn C
Câu 24: (MĐ 103 2020-2021 – ĐỢT 2) Cho
f
là một hàm số liên tục trên đoạn
[ ]
1; 2
. Biết
F
là nguyên
hàm của hàm
f
trên
đoạn
[ ]
1; 2
thỏa mãn
( )
11F
= −
và
( )
23F =
. Khi đó
( )
2
1
dfx x
∫
.
A.
4
. B.
2−
. C.
2
. D.
4−
.
Lời giải
Ta có
( ) ( ) (
) ( ) ( )
2
1
2
d 2 13 14
1
f x x Fx F F= = − = −− =
∫
.
Câu 25: (MĐ 104 2020-2021 – ĐỢT 2) Nếu
( )
1
0
d4
fx x=
∫
và
( )
3
1
d3fx x=
∫
thì
( )
3
0
dfx x
∫
bằng
A.
1.−
B.
1.
C.
7.
D.
12.
Lời giải
Ta có
( )
( ) ( )
3 13
0 01
d d d 4 3 7.fx x fx x fx x= + =+=
∫∫∫
Câu 26: (MĐ 104 2020-2021 – ĐỢT 2) Cho
f
là hàm số liên tục trên đoạn
[ ]
1; 2
. Biết
F
là nguyên
hàm của
f
trên đoạn
[ ]
1; 2
thỏa mãn
( )
11F = −
và
( )
2 4.F =
Khi đó
( )
2
1
dfx x
∫
bằng
A.
5.−
B.
3.
C.
5.
D.
3.−

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
Lời giải
Ta có
( ) ( )
( )
( )
( )
2
2
1
1
d 2 1 4 1 5.f x x Fx F F= = − = −− =
∫
Câu 27: (MĐ 103 2020-2021 – ĐỢT 1) Nếu
2
0
( )d 6fx x=
∫
thì
(
)
2
0
21f x dx−
∫
bằng
A.
12
. B.
10
. C.
11
. D.
14
.
Lời giải
( )
( )
2 22
0 00
2 1 2 1 12 2 10
− = − = −=
∫ ∫∫
f x dx f x dx dx
.
Câu 28: (MĐ 104 2020-2021 – ĐỢT 1) Nếu
( )
2
0
4
d
fxx=
∫
thì
( )
2
0
21dfx x−
∫
bằng
A.
8
. B.
10
. C.
7
. D.
6
.
Lời giải
Ta có:
( )
( )
2 22
0 00
2 1 2 2.4 2 6d ddfx x fx x x
− = − = −=
∫ ∫∫
.
Câu 29: (2020-2021 – ĐỢT 2) Nếu
( )
2
0
d2fx x
=
∫
thì
( )
2
0
4dx fx x
−
∫
bằng
A.
12
. B.
10
. C.
4
. D.
6
.
Lời giải
Ta có
( ) ( )
2 22
0 00
4 d 4d−=−
∫ ∫∫
x fx x xx fxdx
2
2
0
2 26= −=x
.
Câu 30: (2020-2021 – ĐỢT 2) Cho
f
là hàm số liên tục trên đoạn
[ ]
1; 2
. Biết
F
là nguyên hàm của
f
trên đoạn
[ ]
1; 2
thỏa mãn
(
)
12F = −
và
( )
23F =
. Khi đó
( )
2
1
dfx x
∫
bằng
A.
−5
. B.
1
. C.
−1
. D.
5
.
Lời giải
Ta có:
( ) ( ) ( ) ( ) (
)
2
2
1
1
d 2 13 25
f x x Fx F F= = − = −− =
∫
.
Câu 31: (2020-2021 – ĐỢT 2) Nếu
( )
2
0
d2fx x=
∫
thì
( )
2
0
2dx fx x−
∫
bằng
A.
2
. B.
8
. C.
6
. D.
0
.
Lời giải
Ta có
( ) ( )
2 22
0 00
2 d 2d d 4 2 2x fx x xx fx x− = − =−=
∫ ∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 7
Câu 32: (MĐ 103 2020-2021 – ĐỢT 2) Nếu
(
)
=
∫
2
0
d3
fx x
thì
( )
( )
−
∫
2
0
2dx fx x
bằng
A.
7
. B.
2
−
. C.
10
. D.
1
.
Lời giải
Ta có:
(
)
(
)
( )
− = − = −=−=
∫ ∫∫
2 22
2
0 00
2
2 d 2d d 2 3 4 3 1
20
x
x fx x xx fxx
.
Câu 33: (MĐ 104 2020-2021 – ĐỢT 2) Nếu
( )
2
0
d3fxx=
∫
thì
( )
2
0
4dx fx x−
∫
bằng
A.
14
. B.
5
. C.
2−
. D.
11
.
Lời giải
Ta có
( ) ( )
2 22
2
2
0
0 00
4 d 4d d 2 3 8 3 5x fx x xx fxx x− = − = −=−=
∫ ∫∫
.
Câu 34: (TK 2020-2021) Cho hàm số
(
)
2
2
12
.
23 2
x khi x
fx
x x khi x
−≥
=
−+ <
Tích phân
( )
2
0
2sin 1 cosf x xdx
π
+
∫
bằng
A.
23
.
3
B.
23
.
6
C.
17
.
6
D.
17
.
3
Lời giải
Trong tích phân
I
đã cho, đặt
2sin 1
tx
thì
d 2cos dt xx
. Ta có
32 3
22
11 1
1 1 1 23
( )d ( 2 3)d ( 1)d .
22 2 6
I ft t t t t t t
Câu 35: (MĐ 102 2020-2021 – ĐỢT 1) Cho hàm số
(
)
2
21 1
32 1
x khi x
fx
x khi x
−≥
=
−<
. Giả sử
F
là nguyên
hàm của
f
trên
thỏa mãn
( )
02
F =
. Giá trị
(
)
( )
122
FF−+
A.
9
B.
15
C.
11
D.
6
Lời giải
Ta có:
( )
2
1
3
2
1
21
x x C khi x
Fx
x x C khi x
−+ ≥
=
−+ <
.
( )
2
02 2FC=⇔=
.
Hàm số liên tục tại
1x =
nên ta có:
23
11
1 1 1 22 1CC
−+ = − + ⇔ =
.
Do đó
( )
2
3
11
22 1
x x khi x
Fx
x x khi x
−+ ≥
=
−+ <
.
Vậy
( ) ( ) ( ) ( )
( )
3
2
122 1 21222219FF−+ =− − −++ −+=
.
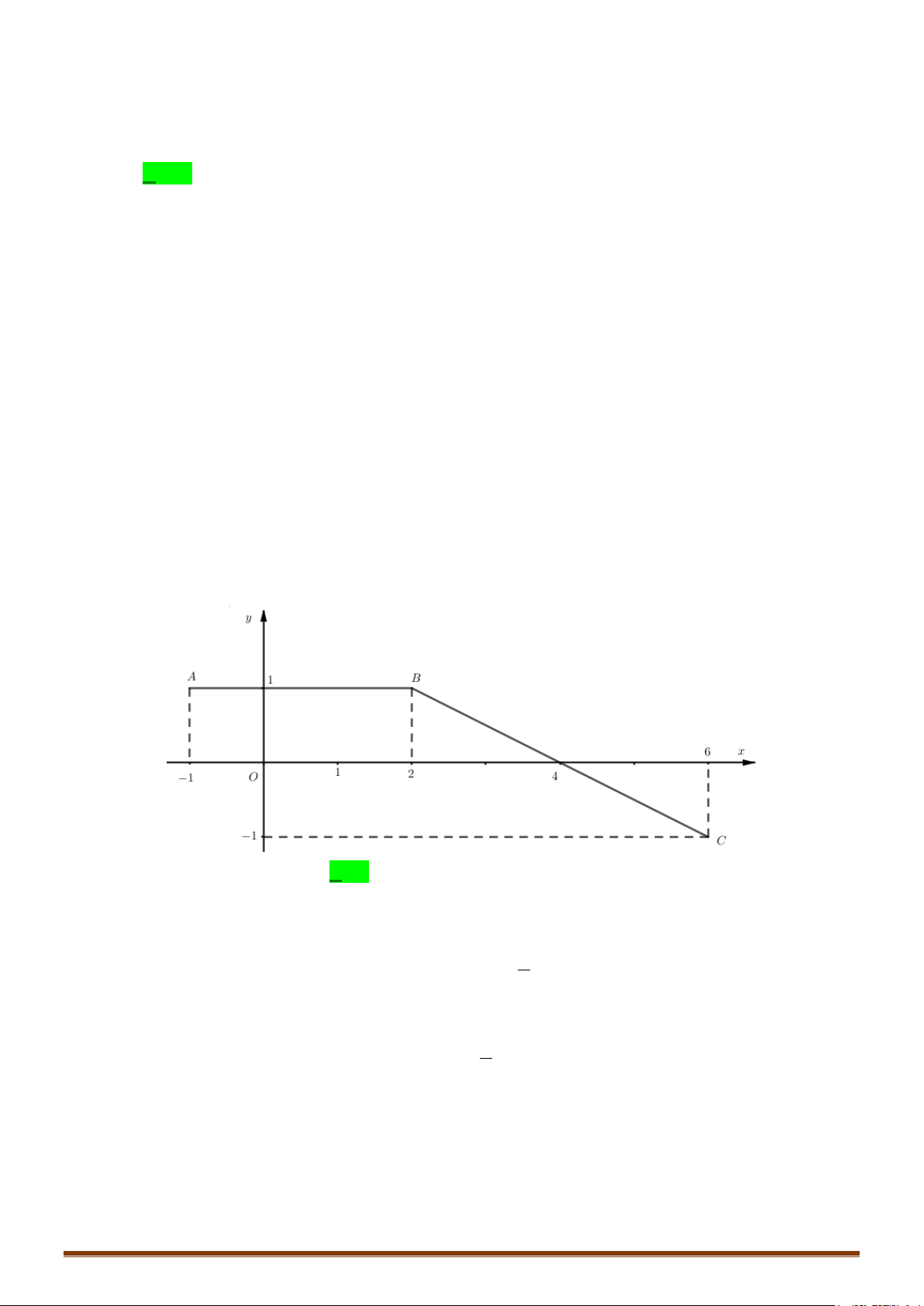
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Câu 36: (MĐ 104 2020-2021 – ĐỢT 1) Cho hàm số
( )
2
22 1
.
31 1
x khi x
fx
x khi x
+≥
=
+<
Giả sử
F
là nguyên hàm
của
f
trên
thỏa mãn
(
)
0 2.
F
=
Giá trị của
( ) ( )
122FF−+
bằng
A.
18
. B.
20
. C.
9
. D.
24
.
Lời giải
Ta có:
(
)
(
)
( )
(
) (
)
( )
11
2
00
3 1 2 1 0 12 04f x dx x dx F F F F= +==− ⇒ =+ =
∫∫
Trên khoảng
( )
;1−∞
, ta có:
( )
( )
23
1
31F x x dx x x C= + = ++
∫
Mà
(
)
( )
3
1
0 2 2 2.
F C Fx x x=⇒ =⇒ = ++
Trên nửa khoảng
[
)
1; +∞
, ta có:
( )
(
)
2
2
22 2
F x x dx x x C= + =++
∫
Mà
( ) ( )
2
2
1 4 1 2 1.F C Fx x x=⇒=⇒ =++
Do đó:
( ) ( )
1 2 2 0 2.9 18.FF−+ =+ =
Câu 37: Cho hàm số
y fx
liên tục trên đoạn
1; 6
và có đồ thị là đường gấp khúc
ABC
trong hình
bên. Biết
F
là nguyên hàm của
f
thỏa mãn
11F
. Giá trị của
46FF
bằng
A.
10
. B.
5
. C.
6
. D.
7
.
Lời giải
Từ đồ thị của hàm số ta xác định được
1 khi 1 2
1
2 khi 2 6
2
x
fx
xx
.
Do
F
là nguyên hàm của
f
nên
1
2
2
khi 1 2
1
2 khi 2 6
4
xC x
Fx
x xC x
.
Ta có
11
111 1 0F CC
.
Hàm số
y fx
liên tục trên đoạn
1; 6
Fx
liên tục trên đoạn
1; 6
Fx
liên tục tại
2x

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
1 22
22
lim lim 2 3 1.
xx
Fx Fx C C C
Suy ra
1
2
1
khi 1 2
1
2 khi
4
26
xx
F
C
x
xx x
.
Vậy
4 65FF
.
Câu 38: (Đề Minh Họa 2020 Lần 1) Nếu
( )
2
1
d2fx x= −
∫
và
( )
3
2
d1fx x=
∫
thì
( )
3
1
dfx x
∫
bằng
A.
3
−
. B.
1−
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có
( ) (
) ( )
323
112
d d d 21 1fx x fx x fx x= + =−+=−
∫∫∫
.
Câu 39: (Đề Tham Khảo 2020 Lần 2) Nếu
( )
1
0
d4fx x=
∫
thì
( )
1
0
2dfx x
∫
bằng
A.
16
. B.
4
. C.
2
. D.
8
.
Lời giải
Chọn D
Ta có:
(
) (
)
11
00
2 d 2 d 2.4 8fx x fx x
= = =
∫∫
.
Câu 40: (Mã 101 - 2020 Lần 1) Biết
(
)
3
1
d3
fx x=
∫
. Giá trị của
( )
3
1
2dfx x
∫
bằng
A.
5
. B.
9
. C.
6
. D.
3
2
.
Lời giải
Chọn C
Ta có:
( ) ( )
33
11
2 d 2 d 2.3 6fx x fx x= = =
∫∫
.
Câu 41: (Mã 101 - 2020 Lần 1) Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
( )
fx
trên
. Giá trị
của
( )
2
1
2dfx x+
∫
bằng
A.
5
. B.
3
. C.
13
3
. D.
7
3
.
Lời giải
Chọn A
Ta có:
( )
( )
2
2
1
2
2 d 2 835
1
fx x x x+ = + =−=
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 10
Câu 42: (Mã 102 - 2020 Lần 1) Biết . Giá trị của bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có .
Câu 43: (Mã 102 - 2020 Lần 1) Biết là một nguyên hàm của hàm số trên . Giá trị
của bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có
Câu 44: (Mã 103 - 2020 Lần 1) Biết
( )
2
1
2f x dx =
∫
. Giá trị của
( )
3
1
3 f x dx
∫
bằng
A.
5
. B.
6
. C.
2
3
. D.
8
.
Lời giải
Chọn B
Ta có :
( ) ( )
22
11
33f x dx f x dx=
∫∫
3.2 6= =
.
Câu 45: (Mã 103 - 2020 Lần 1) Biết
3
()Fx x=
là một nguyên hàm của hàm số
()fx
trên
. Giá trị
của
3
1
(1 ( ) d)x xf+
∫
bằng
A. 20. B. 22. C. 26. D. 28.
Lời giải
Chọn D
Ta có
[ ] [ ]
3
33
3
11
1
1 ( ) d ( ) ) 30 2 28f x x x Fx x x
+ = + = + = −=
∫
.
Câu 46: (Mã 104 - 2020 Lần 1) Biết
( )
3
2
d 6.fx x=
∫
Giá trị của
( )
3
2
2dfx x
∫
bằng.
A.
36
. B.
3
. C.
12
. D.
8
.
( )
5
1
d4fx x=
∫
( )
5
1
3dfx x
∫
7
4
3
64
12
( ) ( )
55
11
3 d 3 d 3.4 12fx x fx x= = =
∫∫
( )
3
Fx x=
( )
fx
( )
2
1
2 ()dfx x+
∫
23
4
7
9
15
4
( )
2 22
3
1 11
2 2 22
2 ()d 2d ()d 2 () 2 9
1 1 11
fx x x fx x x Fx x x+ = + =+ =+=
∫ ∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 11
Lời giải
Chọn C
Ta có :
( ) (
)
33
22
2 d 2 d 12.fx x fx x= =
∫∫
.
Câu 47: (Mã 104 - 2020 Lần 1) Biết
( )
2
Fx x=
là một nguyên hàm của hàm số
()fx
trên
. Giá trị
của
[ ]
3
1
1 ()f x dx+
∫
bằng
A.
10
. B.
8
. C.
26
3
. D.
32
3
.
Lời giải
Chọn A
Ta có
[
]
( )
( )
( )
3
3
3
2
1
1
1
1 ( ) 12 2 10.f x dx x F x x x+ = + = + = −=
∫
Câu 48: (Mã 101 - 2020 Lần 2) Biết
( )
3
2
f x dx 4
=
∫
và
( )
3
2
g x dx 1=
∫
. Khi đó:
(
) ( )
3
2
f x g x dx
−
∫
bằng:
A.
3−
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn B
Ta có
( ) ( ) ( ) ( )
3 33
2 22
413f x g x dx f x dx g x dx− = − = −=
∫ ∫∫
Câu 49: (Mã 101 - 2020 Lần 2) Biết
(
)
1
0
f x 2x dx=2
+
∫
. Khi đó
( )
1
0
f x dx
∫
bằng :
A.
1
. B.
4
. C.
2
. D.
0
.
Lời giải
Chọn A
Ta có
( ) ( )
1 11
0 00
f x 2x dx=2 f x dx+ 2xdx=2
+⇔
∫ ∫∫
( )
⇔=−
∫
1
1
2
0
0
f x dx 2 x
( )
⇔=−
∫
1
0
f x dx 2 1
( )
⇔=
∫
1
0
f x dx 1
Câu 50: (Mã 102 - 2020 Lần 2) Biết
( )
3
2
3f x dx =
∫
và
( )
3
2
1g x dx =
∫
. Khi đó
( ) (
)
3
2
f x g x dx+
∫
bằng
A.
4
. B.
2
. C.
2−
. D.
3
.
Lời giải
Chọn A

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
Ta có:
( ) (
) (
)
( )
3 33
2 22
4f x g x dx f x dx g x dx+= + =
∫ ∫∫
.
Câu 51: (Mã 102 - 2020 Lần 2) Biết
( )
1
0
23f x x dx+=
∫
. Khi đó
( )
1
0
dfx x
∫
bằng
A.
1
. B.
5
. C.
3
. D.
2
.
Lời giải
Chọn D
Ta có
( ) ( ) ( )
1 111
2
0 000
1
23232.3
0
2
x
f x x dx f x dx xdx f x dx+=⇔+=⇔+=
∫ ∫∫∫
.
Suy ra
( ) ( )
1
2
0
1
3 3 10 2d
0
fx x
x=− =−− =
∫
.
Câu 52: (Mã 103 - 2020 Lần 2) Biết
( )
2
1
d3fx x=
∫
và
(
)
2
1
d2gx x
=
∫
. Khi đó
(
) (
)
2
1
d
f x gx x
−
∫
bằng?
A.
6
. B.
1
. C.
5
. D.
1−
.
Lời giải
Chọn B
Ta có:
( ) ( ) (
) ( )
2 22
1 11
d d d 321f x gx x f x x gx x− = − =−=
∫ ∫∫
.
Câu 53: (Mã 103 - 2020 Lần 2) Biết
( )
1
0
2d 4
fx x x
+=
∫
. Khi đó
( )
1
0
dfx x
∫
bằng
A.
3
. B.
2
. C.
6
. D.
4
.
Lời giải
Chọn A
( ) ( ) ( )
1 11 1
0 00 0
2d4 d 2d4 d413fx x x fx x xx fx x+ = ⇔ + = ⇔ = −=
∫ ∫∫ ∫
Câu 54: (Mã 104 - 2020 Lần 2) Biết
2
1
() 2f x dx =
∫
và
2
1
( ) 3.g x dx =
∫
Khi đó
2
1
[ () ()]f x g x dx+
∫
bằng
A.
1
. B.
5
. C.
1−
. D.
6
.
Lời giải
Chọn D
Ta có:
2 22
1 11
[ () ()] () () 2 3 5
f x g x dx f x dx g x dx+ = + =+=
∫ ∫∫
.
Câu 55: (Mã 104 - 2020 Lần 2) Biết
( )
1
0
2d 5fx x x+=
∫
. Khi đó
( )
1
0
dfx x
∫
bằng
A.
7
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn D

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
( )
1
0
2d 5fx x x+=
∫
( )
11
00
d 2xd 5fx x x⇔ +=
∫∫
( ) (
) ( )
1 11
1
2
0
0 00
d5d15d4fx x x fx x fx x+ = ⇔ += ⇔ =
∫ ∫∫
.
Câu 56: (Mã 103 - 2019) Biết
( )
2
1
d2fx x=
∫
và
(
)
2
1
d6
gx x=
∫
, khi đó
( ) ( )
2
1
df x gx x
−
∫
bằng
A.
8
. B.
4−
. C.
4
. D.
8−
.
Lời giải
Chọn B
Ta có:
( ) ( ) ( ) ( )
2 22
1 11
d d d 26 4f x gx x f x x gx x− = − =−=−
∫ ∫∫
.
Câu 57: (Mã 102 - 2019) Biết tích phân
(
)
1
0
3f x dx
=
∫
và
(
)
1
0
4
g x dx
= −
∫
. Khi đó
( ) ( )
1
0
f x g x dx+
∫
bằng
A.
7−
. B.
7
. C.
1−
. D.
1
.
Lời giải
Chọn C
Ta có
( ) ( ) ( ) ( ) ( )
1 11
0 00
34 1f x g x dx f x dx g x dx+ = + = +− =−
∫ ∫∫
.
Câu 58: (Mã 104 - 2019) Biết
1
0
( )d 2
fx x=
∫
và
1
0
( )d 4gx x= −
∫
, khi đó
[ ]
1
0
() ()df x gx x+
∫
bằng
A.
6
. B.
6−
. C.
2−
. D.
2
.
Lời giải
Chọn C
[ ]
1 11
0 00
() ()d ()d g()d 2 (4) 2+ = + = +− =−
∫ ∫∫
fx gx x fx x x x
.
Câu 59: (Mã 101 2019) Biết
( )
1
0
d2fxx= −
∫
và
( )
1
0
d3gx x=
∫
, khi đó
( ) (
)
1
0
df x gx x
−
∫
bằng
A.
1−
. B.
1
. C.
5−
. D.
5
.
Lời giải
Chọn C
( ) ( ) ( ) ( )
1 11
0 00
d d d 23 5− = − =−− =−
∫ ∫∫
f x gx x f x x gx x
.
Câu 60: (Đề Tham Khảo 2019) Cho
(
)
1
0
d2fx x=
∫
và
( )
1
0
d5gx x=
∫
, khi
( ) ( )
1
0
2df x gx x
−
∫
bằng
A.
8−
B.
1
C.
3−
D.
12
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
Chọn A
Có
( ) ( ) ( ) ( )
1 11
0 00
2 d d2 df x gx x f x x gx x−=−
∫ ∫∫
2 2.5 8=−=−
.
Câu 61: (Mã 104 2018)
2
1
23
dx
x
+
∫
bằng
A.
1
ln 35
2
B.
7
ln
5
C.
17
ln
25
D.
7
2ln
5
Lời giải
Chọn C
Ta có
( )
2
2
1
1
1 1 17
ln 2 3 ln 7 ln 5 ln
2 32 2 25
dx
x
x
= += − =
+
∫
.
Câu 62: (Mã 103 2018)
2
1
32
dx
x −
∫
bằng
A.
2ln 2
B.
1
ln 2
3
C.
2
ln 2
3
D.
ln 2
Lời giải
Chọn C
Ta có
( )
2
2
1
1
11 2
ln 3 2 ln 4 ln1 ln 2
3 23 3 3
dx
x
x
= −= − =
−
∫
.
Câu 63: (Đề Tham Khảo 2018) Tích phân
2
0
3
dx
x +
∫
bằng
A.
2
15
B.
16
225
C.
5
log
3
D.
5
ln
3
Lời giải
Chọn D
2
2
0
0
5
ln 3 ln
33
dx
x
x
= +=
+
∫
Câu 64: (Mã 105 2017) Cho
−=+
++
∫
1
0
11
d ln 2 ln 3
12
xa b
xx
với
,ab
là các số nguyên. Mệnh đề nào
dưới đây đúng?
A.
+=20ab
B.
+=2ab
C.
−=20ab
D.
+=−2ab
Lời giải
Chọn A
[ ]
− = +− + = −
++
∫
1
1
0
0
11
d ln 1 ln 2 2 ln 2 ln 3
12
xx x
xx
; do đó
= = −2; 1ab

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
Câu 65: (Mã 110 2017) Cho
(
)
Fx
là một nguyên hàm của hàm số
( )
ln
x
fx
x
=
. Tính:
( ) ( )
1I Fe F= −
?
A.
1
2
I
=
B.
1
I
e
=
C.
1I
=
D.
Ie=
Lời giải
Chọn A
Theo định nghĩa tích phân:
( ) ( ) ( ) ( )
2
1 11
1
ln ln 1
1 d d ln . ln
22
e
e ee
xx
I F e F f x x x xd x
x
=−= = = = =
∫ ∫∫
.
Câu 66: (Mã 102 2018)
1
31
0
d
x
ex
+
∫
bằng
A.
( )
4
1
3
ee+
B.
3
ee−
C.
(
)
4
1
3
ee−
D.
4
ee−
Lời giải
Chọn C
1
31
0
d
x
ex
+
∫
( )
1
31
0
1
31
3
d
x
ex
+
= +
∫
1
31
0
1
3
x
e
+
=
( )
4
1
3
ee
= −
.
Câu 67: (Mã 101 2018)
2
31
1
ed
−
∫
x
x
bằng
A.
( )
52
1
ee
3
+
B.
( )
52
1
ee
3
−
C.
52
1
ee
3
−
D.
52
ee−
Lời giải
Chọn B
Ta có
2
2
31 31
1
1
1
ed e
3
−−
=
∫
xx
x
( )
52
1
ee
3
= −
.
Câu 68: (Mã 123 2017) Cho
6
0
( ) 12
f x dx =
∫
. Tính
2
0
(3 ) .I f x dx=
∫
A.
= 5I
B.
= 36I
C.
= 4I
D.
= 6I
Lời giải
Chọn C
Ta có:
= = = = =
∫∫ ∫
22
00 0
6
1 11
(3 ) (3 ) 3 ( ) .12 4.
3 33
I f x dx f x d x f t dt
Câu 69: (Mã 103 - 2019) Cho hàm số
( )
fx
. Biết
( )
04f =
và
(
)
2
' 2 sin 1, fx x x= + ∀∈
, khi đó
( )
4
0
dfx x
π
∫
bằng
A.
2
16 4
.
16
ππ
+−
B.
2
4
.
16
π
−
C.
2
15
.
16
ππ
+
D.
2
16 16
.
16
ππ
+−

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
Lời giải
Chọn A
Ta có
(
)
(
)
(
)
2
1
2sin 1 d 2 cos 2 d 2 sin 2 .
2
fx x x x x x xC
= +=− =− +
∫∫
Vì
( )
04 4fC=⇒=
Hay
( )
1
2 sin 2 4.
2
fx x x=−+
Suy ra
( )
44
00
1
d 2 sin 2 4 d
2
fx x x x x
ππ
=−+
∫∫
22
2
4
0
1 1 16 4
cos 2 4 .
4 16 4 16
x xx
π
π ππ
π
+−
= + + = +−=
Câu 70: (Mã 104 - 2019) Cho hàm số
( )
fx
. Biết
( )
04f =
và
( )
2
2sin 3fx x
′
= +
,
xR∀∈
, khi đó
(
)
4
0
d
fx x
π
∫
bằng
A.
2
2
8
π
−
. B.
2
88
8
ππ
+−
. C.
2
82
8
ππ
+−
. D.
2
3 23
8
ππ
+−
.
Lời giải
Chọn C
( )
( )
( ) ( )
2
1
d 2sin 3 d 1 cos 2 3 d 4 cos2 d 4 sin 2
2
fx x x x x x x x x xC
′
= +=− +=− =− +
∫∫ ∫ ∫
.
Ta có
( )
04f =
nên
1
4.0 sin 0 4 4
2
CC
− +=⇔=
.
Nên
( )
1
4 sin 2 4
2
fx x x
=−+
.
( )
44
2
00
11
d 4 sin24d 2 cos24
4
24
0
fx x x x x x x x
ππ
π
=− +=+ + =
∫∫
2
82
8
ππ
+−
.
Câu 71: (Mã 102 - 2019) Cho hàm số
()fx
.Biết
(0) 4f =
và
2
( ) 2 cos 3,fx x x
′
= + ∀∈
, khi đó
4
0
()f x dx
π
∫
bằng?
A.
2
88
8
ππ
++
. B.
2
82
8
ππ
++
. C.
2
68
8
ππ
++
. D.
2
2
8
π
+
.
Lời giải
Chọn B
Ta có
,
2
() () (2cos 3)f x f x dx x dx= = +
∫∫
1 cos 2
(2. 3)
2
x
dx
+
= +
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
(cos2 4)x dx= +
∫
=
1
sin 2 4
2
x xC++
do
(0) 4 4fC=⇒=
.
Vậy
1
() sin244
2
fx x x= ++
nên
44
00
1
() (sin244)
2
f x dx x x dx
ππ
= ++
∫∫
2
4
0
1
( cos 2 2 4 )
4
xx x
π
=− ++
2
82
8
ππ
++
=
.
Câu 72: (Đề Tham Khảo -2019) Cho
( )
1
2
0
ln 2 ln 3
2
xdx
ab c
x
=++
+
∫
với
,,abc
là các số hữu tỷ. Giá trị
của
3abc++
bằng
A.
2
B.
1
C.
2−
D.
1−
Lời giải
Chọn D
Đặt
2t x dt dx=+⇒ =
Đổi cận:
02xt=⇒=
;
13xt=⇒=
( )
1
2
0
2
xdx
x +
∫
( )
3
2
2
2t dt
t
−
=
∫
3
2
2
12
dt
tt
= −
∫
3
2
2
ln
t
t
= +
( )
2
ln 3 ln 2 1
3
= +− +
1
ln 2 ln 3
3
=−− +
Suy ra
1
; 1; 1
3
a bc=− =−=
3abc++
111=−−+
1= −
.
Câu 73: (Đề Minh Họa 2020 Lần 1) Cho hàm số
( )
fx
có
(
)
33
f =
và
( )
11
x
fx
xx
′
=
+− +
,
0x∀>
. Khi đó
( )
8
3
dfx x
∫
bằng
A.
7
. B.
197
6
. C.
29
2
. D.
181
6
.
Lời giải
Chọn B
Xét
( )
dd
11
x
fxx x
xx
′
=
+− +
∫∫
. Đặt
22
1 1 1 d 2dt x x t x t x tt= +⇒ += ⇒ = −⇒ =
.
Khi đó,
( )
( )
( )
( )
(
)
2
2
1. 1
1
d d 2d 2d 2 2 d
.1
11
tt
xt
f x x x tt tt t t
t t tt
xx
−+
−
′
= = ⋅= ⋅= +
−−
+− +
∫∫ ∫ ∫ ∫
( )
2
2 12 1t tC x x C= + + = + + ++
.
Mà
( ) ( )
3 3 31 231 3 5f CC= ⇔ + + ++ = ⇔ =−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
(
)
( )
1215 214
fx x x x x
⇒ = + + +−= + +−
.
( )
( )
( )
8
88
2
3
33
3
4 19 197
d 2 1 4 d 1 4 36
23 6 6
x
fx x x x x x x
⇒ = + +− = + + − = − =
∫∫
.
Câu 74: (Mã 102 2018) Cho
21
5
ln 3 ln 5 ln 7
4
dx
abc
xx
=++
+
∫
, với
,,abc
là các số hữu tỉ. Mệnh đề nào
sau đây đúng?
A.
2ab c−=−
B.
2ab c+=−
C.
abc+=
D.
ab c
−=−
Lời giải
Chọn B
Đặt
42t x tdt dx= +⇒ =
.
Với
53xt=⇒=
;
21 5xt= ⇒=
Ta có
21
5
4
dx
xx+
∫
5
2
3
2
4
dt
t
=
−
∫
( )
5
3
1
ln 2 ln 2
2
tt= −− +
111
ln 2 ln 5 ln 7
222
=+−
.
Câu 75: (Mã 101 2018) Cho
55
16
d
ln 2 ln 5 ln11
9
x
abc
xx
=++
+
∫
, với
,,abc
là các số hữu tỉ. Mệnh đề nào
dưới đây đúng?
A.
3ab c+=
B.
3ab c−=−
C.
ab c−=−
D.
abc+=
Lời giải
Chọn. A.
Đặt
9tx= +
2
9 2 dt dtx t x⇒ =+⇒ =
.
Đổi cận
16 5xt= ⇒=
,
55 8xt= ⇒=
.
Do đó
55
16
d
9
x
xx
=
+
∫
( )
8
2
5
2 dt
9
t
tt−
∫
8
2
5
dt
2
9t
=
−
∫
8
5
11 1
d
3 33
x
xx
= −
−+
∫
8
13
ln
5
33
x
x
−
=
+
1 511
ln ln
3 11 3 4
= −
211
ln 2 ln 5 ln11
333
= +−
.
Vậy
21 1
;;
33 3
abc= = = −
ab c⇒−=−
.
Câu 76: (Đề Tham Khảo 2017) Tính tích phân
2
2
1
21I x x dx= −
∫
bằng cách đặt
2
1ux= −
, mệnh đề nào
dưới đây đúng?
A.
3
0
I udu=
∫
B.
2
1
1
2
I udu=
∫
C.
3
0
2I udu=
∫
D.
2
1
I udu=
∫
Lời giải
Chọn A
2
2
1
21I x x dx= −
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 19
đặt
2
12u x du xdx= −⇒ =
. Đổi cận
10xu=⇒=
;
23xu=⇒=
Nên
3
0
I udu=
∫
Câu 77: (Đề Tham Khảo 2018) Biết
2
1
( 1) 1
dx
dx a b c
x x xx
=−−
+ ++
∫
với
,,abc
là các số nguyên
dương. Tính
P abc=++
A.
18P
=
B.
46P =
C.
24P =
D.
12P =
Lời giải
Chọn B
Cách 1
(
)
( )
22 2
2
11 1
1
( 1) 1
( 1) 1
( 1) 1
dx dx x x
dx dx
x x xx
xx x x
xx x x
++
= =
+ ++
+ ++
+ ++
∫∫ ∫
Đăt
11 1
12
2 1 2 ( 1)
xx
t x x dt dx dt dx
x x xx
++
= ++ ⇒ = + ⇔ =
++
Khi đó
23
23
2
12
12
22
2 3 4 2 2 32 12 2I dt
tt
+
+
+
+
−
= = =− + −= − −
∫
32 12 2 46.P abc⇒ =++= + +=
Cách 2
( )
( )
( )
( )
( )
22 2
11 1
22
1
11
2
2 2 1 22 2 23 22
11
( 1) 1
( 1) 1 ( 1) 1
1 11
(1
12 2
)
32
1
x xx x
dx dx
dx dx
x x xx
xx x x xx x x
x
x
x
dx dx
xx x x
x
++ +−
= =
+ ++
+ ++ + ++
+−
= =−=
+
− + = −− + = − −
+
∫∫ ∫
∫∫
Câu 78: (Đề Tham Khảo 2020 Lần 2) Cho hàm số
( )
fx
có
(
)
00f
=
và
(
)
2
cos cos 2 ,fx x x R
′
= ∀∈
.
Khi đó
( )
0
dfx x
π
∫
bằng
A.
1042
225
. B.
208
225
. C.
242
225
. D.
149
225
.
Lời giải
Chọn C
Ta có
( ) ( )
2
d cos cos 2 df x f x x x xx
′
= =
∫∫
( )
2
2
cos 1 2sin dx xx= −
∫
.
Đặt
sin d cos dt x t xx= ⇒=
.
( )
( )
2
2
12 dfx t t⇒=−
∫
( )
24
14 4 dt tt=−+
∫
35 3 5
44 4 4
sin sin sin
35 3 5
t t t C x x xC=− + += − + +
.
Mà
( )
00 0fC=⇒=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
Do đó
( )
35
44
sin sin sin
35
fx x x x=−+
24
44
sin 1 sin sin
35
x xx
=−+
.
( ) ( )
2
22
44
sin 1 1 cos 1 cos
35
x xx
= −− +−
.
Ta có
( )
(
) ( )
2
22
00
44
d sin 1 1 cos 1 cos d
35
fx x x x x x
ππ
= −− +−
∫∫
.
Đặt
cos d sin d
t x t xx= ⇒=−
Đổi cận
0 1; 1x tx t
π
=⇒= = ⇒=−
.
Khi đó,
( )
( ) ( )
1
2
22
01
44
d 11 1 d
35
fx x t t t
π
−
= − −+ −
∫∫
1
24
1
74 4
d
15 15 5
t tt
−
= −+
∫
1
34
1
74 4
15 45 5
ttt
−
=−+
=
242
225
.
Câu 79: (Đề Minh Họa 2017) Tính tích phân
3
0
cos .sin dI x xx
π
=
∫
.
A.
1
4
I = −
B.
4
1
4
I
π
= −
C.
4
I
π
= −
D.
0I =
Lời giải
Chọn D
Ta có:
3
0
cos .sinI x xdx
π
=
∫
. Đặt
cos sin sint x dt xdx dt xdx= ⇒ =− ⇔− =
Đổi cận: Với
01xt=⇒=
; với
1xt
π
= ⇒=−
.
Vậy
( )
1
4
11
44
33
11
1
1
1
0
4 44
t
I t dt t dt
−
−
−
−
=−= ==− =
∫∫
.
Cách khác : Bấm máy tính.
Câu 80: (Đề Tham Khảo 2017) Cho
1
0
d1
ln
12
x
xe
ab
e
+
= +
+
∫
, với
,a
b
là các số hữu tỉ. Tính
33
Sa b= +
.
A.
2S = −
. B.
0S =
. C.
1S =
. D.
2S =
.
Lời giải
Chọn B
Cách 1. Đặt
dd
xx
te tex=⇒=
. Đổi cận:
0 1; 1x t x te=⇒= =⇒=
( )
( )
( )
( )
( )
11
1
00 1 1
d d d 11
d ln ln 1 1 ln 1 ( ln 2)
1 11
1
ee
x
e
x
xx
x ex t
t tt e
e tt t t
ee
= = = − = − + = − + −−
+ ++
+
∫∫ ∫ ∫
33
1
21
1 ln 1 ln 0
1
12
a
e
Sa b
b
e
=
+
=+ =− ⇒ ⇒= + =
= −
+
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 21
Cách 2.
(
) (
)
1 1 11
1
1
0
0
0 0 00
1 d1
d1
d d ln 1 1 ln
11 1 2
xx x
x
xx x
ee e
xe
xx x e
ee e
+− +
+
= = − =− +=−
++ +
∫ ∫ ∫∫
.
Suy ra
1
a =
và
1
b = −
. Vậy
33
0Sa b
=+=
.
Câu 81: (Đề Tham Khảo 2020 Lần 2) Xét
2
2
0
ed
x
xx
∫
, nếu đặt
2
ux=
thì
2
2
0
ed
x
xx
∫
bằng
A.
2
0
2 ed
u
u
∫
. B.
4
0
2 ed
u
u
∫
. C.
2
0
1
ed
2
u
u
∫
. D.
4
0
1
ed
2
u
u
∫
.
Lời giải
Chọn D
Đặt
2
d
d 2d d
2
u
u x u xx xx=⇒= ⇔ =
.
Khi
00xu=⇒=
, khi
24xu=⇒=
.
Do đó
2
24
00
1
e d ed
2
xu
xx u=
∫∫
.
Câu 82: (Đề Minh Họa 2017) Tính tích phân
1
ln
e
I x xdx=
∫
:
A.
2
1
4
e
I
−
=
B.
1
2
I =
C.
2
2
2
e
I
−
=
D.
2
1
4
e
I
+
=
Lời giải
Chọn D
1
ln
e
I x xdx=
∫
. Đặt
2
1
ln
2
=
=
⇒
=
=
du dx
ux
x
dv xdx
x
v
2 2 2 2 2 22 2
00
00
1 1 11
ln .
2 2 22 2 4 2 44 4
ee
ee
x x e ex ee e
I x dx xdx
x
+
⇒= − = − = − = − +=
∫∫
.
Câu 83: (Mã 103 2018) Cho
( )
e
2
1
1 ln d e exxxa b c+ = ++
∫
với
a
,
b
,
c
là các số hữu tỷ. Mệnh đề nào
dưới đây đúng?
A.
abc+=
B.
ab c+=−
C.
ab c−=
D.
ab c−=−
Lời giải
Chọn C
Ta có
( )
e
1
1 ln dxxx+
∫
ee
11
1.d ln dx x xx= +
∫∫
e
1
e 1 ln dx xx= −+
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 22
Đặt
2
1
ln d d
d .d
2
uxu x
x
x
v xx v
= ⇒=
= ⇒=
Khi đó
e
1
ln d
x xx
∫
e
2
e
1
1
1
ln d
22
x
x xx= −
∫
2
e
2
1
e1
24
x= −
22
ee1
2 44
=−+
2
e1
44
= +
.
Suy ra
( )
e
1
1 ln dxxx+
∫
2
e1
e1
44
= −+ +
2
e3
e
44
= +−
nên
1
4
a =
,
1
b =
,
3
4
c
= −
.
Vậy
ab c−=
.
Câu 84: (Mã 104 2018) Cho
(
)
2
1
2 ln d
e
x x x ae be c
+ = ++
∫
với
,,abc
là các số hữu tỉ. Mệnh đề nào sau
đây đúng?
A.
abc
+=
B.
ab c
−=
C.
ab c−=−
D.
ab c+=−
Lời giải
Chọn B
Ta có
( )
1 11
2 ln d 2d ln d 2 2 2
1
e ee
e
xxx x xxx x I e I+ = + = += −+
∫ ∫∫
với
1
ln d
e
I x xx=
∫
Đặt
ln
dd
ux
v xx
=
=
2
1
dd
2
ux
x
x
v
=
⇒
=
2 22
1
ln d ln
1 11
2 22 4
e
e ee
x xx x
Ixxx⇒= − = −
∫
( )
22
2
11
1
24 4
ee
e
+
= − −=
( )
2
2
1
11 7
2 ln d 2 2 2
44 4
e
e
x xx e e e
+
⇒ + = −+ = + −
∫
1
4
2
7
4
a
b
c
=
⇒=
= −
ab c⇒−=
Câu 85: (Đề tham khảo 2017) Cho hàm số
( )
fx
thỏa mãn
( ) (
)
1
0
1 d 10x fxx
′
+=
∫
và
(
) ( )
21 0 2
ff
−=
. Tính
( )
1
0
dfx x
∫
.
A.
12I
= −
B.
8I =
C.
1I
=
D.
8I = −
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
Chọn D
Đặt
(
)
( )
1 dd
dd
ux u x
vfxx vfx
=+=
⇒
′
= =
. Khi đó
( )
(
)
( )
1
1
0
0
1dI x fx fx x
=+−
∫
Suy ra
(
) ( ) ( ) (
)
11
00
10 2 1 0 d d 10 2 8
f f fx x fx x= − − ⇒ =− +=−
∫∫
Vậy
( )
1
0
d8fx x= −
∫
.
Câu 86: (Mã 104 - 2019) Cho hàm số
(
)
fx
có đạo hàm liên tục trên
. Biết
( )
31=f
và
(
)
1
0
3d 1=
∫
xf x x
, khi đó
( )
3
2
0
d
′
∫
xf x x
bằng
A.
25
3
. B.
3
. C.
7
. D.
9−
.
Lời giải
Chọn D
Đặt
1
3 d 3d d d
3
=⇒= ⇒=txtxx t
.
Suy ra
(
) ( )
( )
1 33
0 00
1
1 3d d 9
9
= = ⇔=
∫ ∫∫
xf x x tf t t tf t dt
.
Đặt
( )
( )
2
dd
dd
2
′
=
=
⇒
=
=
u ft t
u ft
t
v tt
v
.
( )
( )
( )
( )
( )
3
33 3
22
2'
00 0
0
91
d d3 d
2 2 22
′
⇒= − =−
∫∫ ∫
tt
tft t ft f t t f tf t t
.
( ) ( )
33
22
00
91
9 d d9
22
′′
⇔=− ⇔ =−
∫∫
tf t t tf t t
.
Vậy
( )
3
2
0
d9
′
= −
∫
xf x x
.
Câu 87: (Mã 101 - 2019) Cho hàm số
( )
fx
có đạo hàm liên tục trên
.
Biết
( )
41f =
và
( )
1
0
4 1,xf x dx =
∫
khi đó
( )
4
2
0
x f x dx
′
∫
bằng
A. 8. B. 14. C.
31
2
. D.
16−
.
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
Chọn D
Xét
( )
1
0
4 1.xf x dx =
∫
Đặt:
( ) ( ) ( )
4 44
0 00
11
4 . . 1 . 16 . 16.
44
t x t f t dt t f t dt x f x dx=⇒ =⇒=⇒ =
∫ ∫∫
Xét
(
) ( )
44
22
00
I x f x dx x df x
′
= =
∫∫
Suy ra:
( )
( )
( )
4
4
22
0
0
. 2 . 4 4 2.16 16.I xfx xfxdx f= − = −=−
∫
Câu 88: (Mã 103 - 2019) Cho hàm số
(
)
fx
có đạo hàm liên tục trên
. Biết
(
)
61f
=
và
( )
1
0
6d 1xf x x =
∫
, khi đó
( )
6
2
0
dxf x x
′
∫
bằng
A.
107
3
. B.
34
. C.
24
. D.
36−
.
Lời giải
Chọn D
Theo bài ra:
( )
1
0
6d 1xf x x =
∫
.
Đặt
6 d 6dtx t x
= ⇒=
.
Đổi cận:
Do đó:
( ) ( )
( ) ( )
1 6 66
0 0 00
1d 1
6d1 . 1 .d1 .d36
6 6 36
t
xf x x tf t tf t t tf t t=⇔ =⇔ =⇔=
∫ ∫ ∫∫
.
Tính
( )
6
2
0
dI xf x x
′
=
∫
.
Đặt
( )
( )
2
d 2d
dd
u xx
ux
v fx
v fx x
=
=
⇔
=
′
=
( ) ( ) ( ) ( )
66
2
00
6
2 d 36 6 2 d 36.1 2.36 36
0
I xfx xfx x f xfx x⇒=−=−=−=−
∫∫
.
Câu 89: (Mã 102 - 2019) Cho hàm số
()
fx
có đạo hàm liên tục trên
. Biết
(5) 1f
và
1
0
(5 ) 1xf x dx
, khi đó
5
2
0
()x f x dx
bằng
A.
15
B.
23
C.
123
5
D.
25
Lời giải
Chọn D

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
+)
55 5
5
2 22 2
0
00 0
.I x f x dx x df x x f x f x dx
5
0
25. 5 0. .2f fx fx xdx
5
0
25 2 xf x dx
+) Ta có:
1
0
(5 ) 1xf x dx
Đặt
5xt
5
0
(t) 1
55
tt
fd
5
0
(t) 25tf dt
Vậy
25 2 25 25I = −× =−
.
Câu 90: (Đề Tham Khảo 2018) Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
[ ]
1
2
0
1 0, ( ) d 7
f fx x
′
= =
∫
và
1
2
0
1
( )d
3
xfx x=
∫
. Tính tích phân
1
0
( )dfx x
∫
A.
4
B.
7
5
C.
1
D.
7
4
Lời giải
Chọn B
Cách 1: Đặt
( ) ( )
u f x du f x dx
′
= ⇒=
,
3
2
3
x
dv x dx v= ⇒=
.
Ta có
( )
( ) ( )
1
11
33
3
00
0
1
1
33 3
xx
f x f x dx x f x dx
′′
=− ⇒=−
∫∫
Ta có
[ ]
( )
11 1 1
2
2
6 33
00 0 0
49 d 7, ( ) d 7, 2.7 . 14 7 ( ) d 0xx fx x xf xdx x fx x
′′ ′
= = =−⇒ + =
∫∫ ∫ ∫
( )
4
3
7
7 () 0
4
x
x fx fx C
′
⇒+ =⇒ =−+
, mà
( )
7
10
4
fC=⇒=
11
4
00
77 7
( )d d
44 5
x
fx x x
⇒ =−+ =
∫∫
.
Cách 2: Nhắc lại bất đẳng thức Holder tích phân như sau:
(
) ( ) ( ) ( )
2
22
.
b bb
a aa
f x g x dx f x dx g x dx
≤
∫ ∫∫
Dấu bằng xảy ra khi
( ) ( )
[ ]
( )
. , ;,= ∀∈ ∈f x kg x x ab k

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
Ta có
( ) ( )
2
1 11
36
2
0 00
11
.
93 9 9
xx
f x dx dx f x dx
′′
=≤=
∫ ∫∫
. Dấu bằng xảy ra khi
(
)
3
.
3
x
fx k
′
=
.
Mặt khác
( )
(
)
1
3
3
0
1
21 7
33
x
fxdx k fx x
−
′′
= ⇒= ⇒ =−
∫
suy ra
( )
4
77
44
x
fx=−+
.
Từ đó
11
4
00
77 7
( )d d
44 5
x
fx x x
=−+ =
∫∫
.
Câu 91: (Mã 102 2018) Cho hàm số
()fx
thỏa mãn
1
(2)
3
f = −
và
[ ]
2
() ()f x xfx
′
=
với mọi
.
x ∈
Giá trị của
(1)
f
bằng
A.
2
3
−
B.
2
9
−
C.
7
6
−
D.
11
6
−
Lời giải
Chọn A
Từ hệ thức đề cho:
[ ]
2
() ()f x xfx
′
=
(1), suy ra
0()fx
′
≥
với mọi
[1; 2]x ∈
. Do đó
()fx
là hàm
không giảm trên đoạn
[1; 2]
, ta có
(
(
0) 2)ffx≤<
với mọi
[1; 2]x ∈
.
Chia 2 vế hệ thức (1) cho
[ ]
[ ]
[ ]
2
2
()
() ,
()
1; 2 .
fx
fx x x
fx
∈
′
⇒=∀
Lấy tích phân 2 vế trên đoạn
[1; 2]
hệ thức vừa tìm được, ta được:
[
]
[ ]
2
2 22
22
1 11
1
() 1 3 1 3 1 1 3
d d d()
2()2(1)(2)2
() ()
fx
x xx fx
fx f f
fx fx
′
−
= ⇒ =⇒ =⇒− =
∫ ∫∫
Do
1
(2)
3
f = −
nên suy ra
2
(1) .
3
f = −
Chú ý: có thể tự kiểm tra các phép biến đổi tích phân trên đây là có nghĩa.
Câu 92: (Mã 104 2018) Cho hàm số
( )
fx
thỏa mãn
(
)
1
2
5
f = −
và
( ) ( )
2
3
f x x fx
′
=
với mọi
x ∈
. Giá trị của
( )
1f
bằng
A.
4
35
−
B.
71
20
−
C.
79
20
−
D.
4
5
−
Lời giải
Chọn D
Ta có:
( ) ( )
( )
( )
( )
( )
22
2
3 33
22
11
dd
fx fx
f x x fx x x xx
fx fx
′′
′
= ⇒=⇒ =
∫∫
( ) ( ) ( )
( )
2
1
1 15 1 1 15 4
1
4 2 14 5
f
fx f f
⇔ − = ⇔− + = ⇔ =−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 27
Câu 93: (Minh họa 2020 Lần 1) Cho hàm số
(
)
fx
liên tục trên
thảo mãn
( ) ( )
3 2 10 6
1 2,
xf x f x x x x x+ − =− + − ∀∈
. Khi đó
( )
0
1
dfxx
−
∫
?
A.
17
20
−
. B.
13
4
−
. C.
17
4
. D.
1−
.
Lời giải
Chọn B
Ta có
(
)
(
) (
)
( )
3 2 10 6 2 3 2 11 7 2
1212
xf x f x x x x x f x xf x x x x
+ −=−+−⇒ + −=−+−
.
Lấy tích phân hai vế cận từ
0
đến
1
ta được:
( ) ( ) ( )
( ) ( ) ( ) ( )
( )
( )
( ) ( )
( )
( )
11 1
2 3 2 11 7 2
00 0
11
33 2 2
00
10
01
11
00
1
0
1
0
d 1 d 2d
11 5
d 1 d1
32 8
11 5
dd
32 8
11 5
dd
32 8
55
d
68
3
d
4
x f x x xf x x x x x x
fx x f x x
ft t ft t
ft t ft t
ft t
ft t
+ − =−+−
⇔ − − −=−
⇒−=−
⇔+=−
⇔=−
⇔=−
∫∫ ∫
∫∫
∫∫
∫∫
∫
∫
.
Suy ra
( )
1
0
3
d
4
fx x= −
∫
.
Lấy tích phân hai vế cận từ
1−
đến
0
ta được:
( ) (
) (
)
( )
( )
(
) (
)
( )
( )
( )
( )
( )
( )
00 0
2 3 2 11 7 2
11 1
00
33 2 2
11
01
10
01
10
01
10
d 1 d 2d
1 1 17
d 1 d1
3 2 24
1 1 17
dd
3 2 24
1 1 17
dd
3 2 24
1 17 1
dd
3 24 2
xfxx xf xx x x xx
fx x f x x
ft t ft t
ft t ft t
ft t ft t
−− −
−−
−
−
−
+ − =−+−
⇔ − − −=−
⇒−=−
⇔−=−
⇔ =−+
∫∫ ∫
∫∫
∫∫
∫∫
∫∫
( ) ( )
( )
01
10
0
1
1 17 1 17 1 3 13
d d.
3 24 2 24 2 4 12
13
d
4
fx x fx x
fx x
−
−
−−
⇒ =+ =−=−
−
⇒=
∫∫
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
Câu 94: (Đề Tham Khảo 2017) Cho hàm số
( )
fx
liên tục trên
và thoả mãn
(
) (
)
2 2cos 2
fx f x x+ −= +
,
x∀∈
. Tính
(
)
3
2
3
2
.I f x dx
π
π
−
=
∫
A.
6I = −
B.
0I =
C.
2I = −
D.
6I =
Lời giải
Chọn D
Đặt
xt
= −
. Khi đó
( )
( ) ( ) (
) (
)
3
00 0
2
33 3
0
22 2
f x dx f t d t f t dt f x dx
π
ππ π
−
= − −=− − = −
∫∫ ∫∫
Ta có:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
3 33 3
0
2 22 2
33
00 0
22
I f xd x f xd x f xd x f xd x f xd x
π ππ π
ππ
−−
= = + =−+∫ ∫∫∫ ∫
Hay
( ) ( )
(
)
( ) ( ) ( )
3 33
2 22
0 00
2 2cos2 2(1 cos 2 )I f x f x dx xdx xdx
π ππ
= −+ = + = +
∫ ∫∫
( ) ( ) ( ) ( )
33
3
2 2 22
2
0 00
2
4cos 2 cos 2 cos 2 cosI xdx xdx xdx xdx
π π ππ
π
⇔= = = −
∫ ∫ ∫∫
Vậy
3
22
0
2
2sin | 2sin | 6.Ix x
ππ
π
=−=
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 68
BÀI 2. TÍCH PHÂN
Câu 1: Khẳng định nào trong các khẳng định sau đúng với mọi hàm
f
,
g
liên tục trên
K
và
a
,
b
là
các số bất kỳ thuộc
K
?
A.
[ ]
() 2()d ()d+2 ()d
b bb
a aa
f x gx x f x x gx x
+=
∫ ∫∫
. B.
( )d
()
d
()
( )d
b
b
a
b
a
a
fx x
fx
x
gx
gx x
=
∫
∫
∫
.
C.
[ ]
().()d ()d . ()d
b bb
a aa
f x gx x f x x gx x=
∫ ∫∫
. D.
2
2
()d= ()d
bb
aa
f x x fx x
∫∫
.
Câu 2: Cho
( )
2
2
d1
fx x
−
=
∫
,
( )
4
2
d4ft t
−
= −
∫
. Tính
( )
4
2
dfy y
∫
.
A.
5I =
. B.
3I = −
. C.
3I =
. D.
5I
= −
.
Câu 3: Cho
( )
2
0
3f x dx =
∫
và
( )
2
0
7g x dx =
∫
, khi đó
( ) ( )
2
0
3f x g x dx
+
∫
bằng
A.
16
. B.
18−
. C.
24
. D.
10
.
Câu 4: Cho
1
0
()fx
∫
dx
1
= −
;
3
0
()fx
∫
dx
5=
. Tính
3
1
()fx
∫
dx
A. 1. B. 4. C. 6. D. 5.
Câu 5: Cho
( )
2
1
d3fx x
= −
∫
và
( )
3
2
d4fx x=
∫
. Khi đó
( )
3
1
dfx x
∫
bằng
A. 12. B. 7. C. 1. D.
12−
.
Câu 6: Cho hàm số
( )
fx
liên tục, có đạo hàm trên
[ ]
( ) ( )
1; 2 , 1 8; 2 1ff− −= =−
. Tích phân
( )
2
1
'f x dx
−
∫
bằng
A.
1.
B.
7.
C.
9.−
D.
9.
Câu 7: Cho hàm số
( )
fx
liên tục trên
R
và có
24
02
( )d 9; ( )d 4.fx x fx x= =
∫∫
Tính
4
0
( )d .I fx x=
∫
A.
5I =
. B.
36I =
. C.
9
4
I =
. D.
13I =
.
Câu 8: Cho
( ) ( )
03
10
3 3.f x dx f x dx
−
= =
∫∫
Tích phân
( )
3
1
f x dx
∫
bằng
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 69
A.
6
B.
4
C.
2
D.
0
Câu 9: Cho hàm số
( )
fx
liên tục trên
và
( )
4
0
d 10fx x=
∫
,
( )
4
3
d4
fx x=
∫
. Tích phân
( )
3
0
d
fx x
∫
bằng
A.
4
. B.
7
. C.
3
. D.
6
.
Câu 10: Cho hàm số
fx
liên tục trên
thoả mãn
( )
8
1
d9fx x=
∫
,
( )
12
4
d3fx x=
∫
,
( )
8
4
d5fx x=
∫
.
Tính
( )
12
1
dI fx x=
∫
.
A.
17I
. B.
1I
. C.
11I
. D.
7I
.
Câu 11: Cho hàm số
(
)
fx
liên tục trên
[ ]
0;10
thỏa mãn
( )
10
0
7f x dx =
∫
,
( )
6
2
3
f x dx
=
∫
. Tính
( )
( )
2 10
06
P f x dx f x dx= +
∫∫
.
A.
10P =
. B.
4P =
. C.
7P =
. D.
6P = −
.
Câu 12: Cho
f
,
g
là hai hàm liên tục trên đoạn
[ ]
1; 3
thoả:
(
) ( )
3
1
3 d 10
f x gx x+=
∫
,
( )
(
)
3
1
2 d6f x gx x−=
∫
. Tính
( ) ( )
3
1
df x gx x+
∫
.
A. 7. B. 6. C. 8. D. 9.
Câu 13: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
và
( )
10
0
7
f x dx =
∫
;
( )
6
2
3f x dx =
∫
. Tính
( ) ( )
2 10
06
P f x dx f x dx= +
∫∫
.
A.
4P =
B.
10P =
C.
7P
=
D.
4P = −
Câu 14: Cho
,fg
là hai hàm số liên tục trên
[ ]
1; 3
thỏa mãn điều kiện
( ) ( )
3
1
3 dx=10f x gx+
∫
đồng thời
( ) ( )
3
1
2 dx=6f x gx−
∫
. Tính
( ) ( )
3
1
dx
f x gx+
∫
.
A.
9
. B.
6
. C.
7
. D.
8
.
Câu 15: Cho
f
,
g
là hai hàm liên tục trên
[ ]
1;3
thỏa:
( ) ( )
3
1
3 d 10f x gx x+=
∫
và
( ) ( )
3
1
2 d6f x gx x−=
∫
. Tính
( ) ( )
3
1
dI f x gx x= +
∫
.
A. 8. B. 7. C. 9. D. 6.
Câu 16: Cho
( )
2
0
d5fx x=
∫
π
. Tính
( )
2
0
2sin d 5I fx x x
=+=
∫
π
.
A.
7I =
B.
5
2
I
= +
π
C.
3I =
D.
5I = +
π
Câu 17: Cho
( )
2
1
d2
fx x
−
=
∫
và
( )
2
1
d1gx x
−
= −
∫
. Tính
( ) ( )
2
1
2 3dI x f x gx x
−
=+−
∫
.
A.
17
2
I =
B.
5
2
I =
C.
7
2
I =
D.
11
2
I =

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 70
Câu 18: Cho hai tích phân
( )
5
2
d8fx x
−
=
∫
và
( )
2
5
d3gx x
−
=
∫
. Tính
( ) ( )
5
2
4 1dI f x gx x
−
= −−
∫
A.
13.
B.
27.
C.
11
−
. D.
3
.
Câu 19: Cho
2
1
() 2f x dx
−
=
∫
và
2
1
() 1g x dx
−
= −
∫
, khi đó
[
]
2
1
2 () 3()
x f x g x dx
−
++
∫
bằng
A.
5
2
B.
7
2
C.
17
2
D.
11
2
Câu 20: Cho
(
)
2
0
d3
fx x
=
∫
,
( )
2
0
d1gx x= −
∫
thì
( ) ( )
2
0
5df x gx x x
−+
∫
bằng:
A.
12
. B.
0
. C.
8
. D.
10
Câu 21: Cho
( )
5
0
d2fx x
= −
∫
. Tích phân
( )
5
2
0
4 3dfx x x
−
∫
bằng
A.
140−
. B.
130
−
. C.
120−
. D.
133−
.
Câu 22: Cho
( )
2
1
421f x x dx
−=
∫
. Khi đó
( )
2
1
f x dx
∫
bằng:
A.
1
. B.
3−
. C.
3
. D.
1−
.
Câu 23: Cho
( )
1
0
1f x dx =
∫
tích phân
( )
( )
1
2
0
23f x x dx−
∫
bằng
A.
1
. B.
0
. C.
3
. D.
1−
.
Câu 24: Tính tích phân
( )
0
1
21I x dx
−
= +
∫
.
A.
0I =
. B.
1I =
. C.
2I =
. D.
1
2
I = −
.
Câu 25: Tích phân
( )( )
1
0
3 1 3dxx x++
∫
bằng
A.
12
. B.
9
. C.
5
. D.
6
.
Câu 26: Giá trị của
2
0
sin xdx
π
∫
bằng
A. 0. B. 1. C. -1. D.
2
π
.
Câu 27: Tính tích phân
2
0
(2 1)I x dx= +
∫
A.
5I =
. B.
6
I =
. C.
2I =
. D.
4I =
.
Câu 28: Với
,ab
là các tham số thực. Giá trị tích phân
( )
2
0
3 2 1d
b
x ax x−−
∫
bằng
A.
32
b ba b−−
. B.
32
b ba b++
. C.
32
b ba b−−
. D.
2
321b ab−−
.
Câu 29: Giả sử
4
0
2
sin 3
2
I xdx a b
π
= = +
∫
( )
,ab∈
. Khi đó giá trị của
ab−
là

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 71
A.
1
6
−
B.
1
6
−
C.
3
10
−
D.
1
5
Câu 30: Cho hàm số
( )
fx
liên tục trên
và
( )
( )
2
2
0
3 d 10+=
∫
fx x x
. Tính
( )
2
0
dfx x
∫
.
A.
2
. B.
2−
. C.
18
. D.
18−
.
Câu 31: Cho
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
( )
1; 2−
. B.
( )
;0−∞
. C.
( )
0; 4
. D.
( )
3;1−
.
Câu 32: Tính tích phân
2
1
11
e
I dx
xx
= −
∫
A.
1
I
e
=
B.
1
1I
e
= +
C.
1I =
D.
Ie=
Câu 33: Tính tích phân
3
0
d
2
x
I
x
=
+
∫
.
A.
21
100
I = −
. B.
5
ln
2
I =
. C.
5
log
2
I =
. D.
4581
5000
I
=
.
Câu 34:
2
1
d
32
x
x
−
∫
bằng
A.
2ln 2
. B.
2
ln 2
3
. C.
ln 2
. D.
1
ln 2
3
.
Câu 35: Tính tích phân
2
1
1
d
x
Ix
x
−
=
∫
.
A.
1 ln 2I = −
. B.
7
4
I =
. C.
1 ln 2I = +
. D.
2ln 2I =
.
Câu 36: Biết
3
1
2
ln ,
x
dx a b c
x
+
= +
∫
với
, , , 9.abc c∈<
Tính tổng
.S abc=++
A.
7S =
. B.
5S =
. C.
8S =
. D.
6
S =
.
Câu 37: Tích phân
1
0
1
d
1
Ix
x
=
+
∫
có giá trị bằng
A.
ln 2 1−
. B.
ln 2
−
. C.
ln 2
. D.
1 ln 2−
.
Câu 38: Tính
3
2
2
d
1
x
Kx
x
=
−
∫
.
A.
ln 2K =
. B.
18
ln
23
K =
. C.
2ln 2K =
. D.
8
ln .
3
K =
Câu 39: Biết rằng hàm số
( )
f x mx n= +
thỏa mãn
( )
1
0
d3fx x
=
∫
,
( )
2
0
d8fx x=
∫
. Khẳng định nào dưới
đây là đúng?
A.
4mn+=
. B.
4mn+=−
. C.
2mn+=
. D.
2mn+=−
.
Câu 40: Biết rằng hàm số
( )
2
f x ax bx c= ++
thỏa mãn
( )
1
0
7
d
2
fx x= −
∫
,
( )
2
0
d2fx x= −
∫
và
A.
3
4
−
. B.
4
3
−
. C.
4
3
. D.
3
4
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 72
Câu 41: Cho
( )
1
2
0
42 d= −
∫
I xmx
. Có bao nhiêu giá trị nguyên của
m
để
60+>I
?
A. 1. B. 5. C. 2. D. 3.
Câu 42: Có bao nhiêu giá trị nguyên dương của
a
để
(
)
0
2 3d 4
a
xx−≤
∫
?
A.
5
. B.
6
. C.
4
. D.
3
.
Câu 43: Có bao nhiêu số thực
b
thuộc khoảng
( )
;3
ππ
sao cho
4cos 2 1
b
xdx
π
=
∫
?
A. 8. B. 2. C. 4. D. 6.
Câu 44: Cho hàm số
()fx
có
(0) 4
f =
và
2
( ) 2 cos 1,fx x x
′
= + ∀∈
Khi đó
4
0
()f x dx
∫
π
bằng.
A.
2
16 16
16
ππ
++
. B.
2
4
16
π
+
. C.
2
14
16
ππ
+
. D.
2
16 4
16
ππ
++
.
Câu 45: Cho hàm số
(
)
fx
có
( )
00f =
và
( )
4
sin , fx x x
′
= ∀∈
. Tích phân
(
)
2
0
dfx x
∫
π
bằng
A.
2
6
18
−
π
. B.
2
3
32
−
π
. C.
2
3 16
64
−
π
. D.
2
36
112
−
π
.
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 73
TÍCH PHÂN HÀM SỐ HỮU TỶ
Tính
(
)
(
)
b
a
Px
I dx
Qx
=
∫
? với
(
)
Px
và
( )
Qx
là các đa thức không chứa căn.
Nếu bậc của tử
( )
Px
≥
bậc mẫu
(
)
Qx
PP
→
chia đa thức.
Nếu bậc của tử
( )
Px
<
bậc mẫu
( )
Qx
mà mẫu số phân tích được thành tích số
PP
→
đồng nhất thức để đưa thành tổng của các phân số.
Một số trường hợp đồng nhất thức thường gặp:
+
( )( )
11ab
ax m bx n an bm ax m bx n
= −
++ − ++
( )
1
+
( )
(
)
( ) ( )
( )( )
AB m
A B x Ab Ba
mx n A B
Ab Ba n
xaxb xa xb xaxb
+=
+−+
+
=+= ⇒
+=−
−− − − −−
.
+
( )
(
) ( )
22
1 A Bx C
xm
x m ax bx c ax bx c
+
= +
−
− ++ ++
với
2
40b ac∆= − <
.
+
( ) ( ) (
)
( )
22 2 2
1 ABCD
xa xb
xa xb xa xb
=+ ++
−−
−− − −
.
Nếu bậc tử
( )
Px
<
bậc mẫu
( )
Qx
mà mẫu không phân tích được thành tích số, ta xét một
số trường hợp thường gặp sau:
+
( )
(
)
1
22
, * .tan
n
PP
dx
I nN xa t
xa
= ∈ → =
+
∫
.
+
( )
2
2
2
x
,0
24
dx d
I
ax bx c
b
ax
aa
= ∆< =
++
∆
+ +−
∫∫
. Ta sẽ đặt
tan
24
b
xt
aa
∆
→ + = −
.
+
3
2
.
px q
I dx
ax bx c
+
=
++
∫
với
2
40b ac
∆= − <
. Ta sẽ phân tích:
( )
2
3
22
2
.
.
22
I
A
ax b dx
p b p dx
Iq
a ax bx c a ax bx c
+
= +−
++ ++
∫∫
và giải A bằng cách đặt
t =
mẫu số.
Câu 46: Biết
( )(
)
2
1
d
ln 2 ln 3 ln 5
12 1
x
abc
xx
= ++
++
∫
. Khi đó giá trị
abc++
bằng
A.
3−
. B.
2
. C.
1
. D.
0
.
Câu 47: Biết
( )
0
2
1
3 51 2
ln , ,
23
xx
I dx a b a b
x
−
+−
= =+∈
−
∫
. Khi đó giá trị của
4ab+
bằng
A.
50
B.
60
C.
59
D.
40
Câu 48: Biết
2
1
0
21
ln 2
1
x
dx n
xm
−−
= +
+
∫
, với
,mn
là các số nguyên. Tính
mn+
.
A.
1S =
. B.
S4=
. C.
S5= −
. D.
S1= −
.
Câu 49: Tích phân
( )
2
1
2
0
1
d ln
1
x
I xa b
x
−
= = −
+
∫
trong đó
a
,
b
là các số nguyên. Tính giá trị của biểu thức
ab+
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 74
A.
1
. B.
0
. C.
1−
. D.
3
.
Câu 50: Biết
5
2
3
1
d ln
12
xx b
xa
x
++
= +
+
∫
với
a
,
b
là các số nguyên. Tính
2Sa b
.
A.
2S =
. B.
2S = −
. C.
5S =
. D.
10S =
.
Câu 51: Cho
2
2
1
10
d ln
1
xa
xx
x bb
+=+
+
∫
với
,ab∈
. Tính
?Pab= +
A.
1P =
. B.
5P =
. C.
7P =
. D.
2P =
.
Câu 52: Cho
3
2
1
3
ln 2 ln 3 ln 5
32
x
dx a b c
xx
+
= ++
++
∫
, với a, b, c là các số nguyên. Giá trị của
abc
++
bằng
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 53: Cho
4
2
3
58
d ln 3 ln 2 ln 5
32
−
=++
−+
∫
x
xa b c
xx
, với
, ,
abc
là các số hữu tỉ. Giá trị của
3
2
−+a bc
bằng
A.
12
B.
6
C.
1
D.
64
Câu 54: Biết
5
2
3
1
d ln
12
xx b
xa
x
++
= +
+
∫
với
a
,
b
là các số nguyên. Tính
2
Sa b
.
A.
2S =
. B.
2S = −
. C.
5S =
. D.
10S =
.
Câu 55: Biết rằng
1
2
0
1
d
1
a
x
xx b
π
=
++
∫
( )
, , 10ab a
∈<
. Khi đó
ab+
có giá trị bằng
A.
14
. B.
15
. C.
13
. D.
12
.
Câu 56: Biết
2
2
2
0
52
d ln 3 ln 5
43
xx
x ab c
xx
++
=++
++
∫
,
( )
,,abc∈
. Giá trị của
abc
bằng
A.
8−
. B.
10
−
. C.
12−
. D.
16
.
Câu 57: Giả sử rằng
0
2
1
3 51 2
ln
23
xx
dx a b
x
−
+−
= +
−
∫
. Khi đó, giá trị của
2ab
+
là
A.
30
. B.
60
. C.
50
. D.
40
.
Câu 58: Biết
4
32
2
1
73
d ln 5
3
xx x a
xc
xx b
+++
= +
−+
∫
với
a
,
b
,
c
là các số nguyên dương và
a
b
là phân số tối
giản. Tính
23
P ab c=−−
.
A.
5−
. B.
4−
. C. 5. D. 0.
Câu 59: Cho
1
2
2
0
4 15 11
d ln 2 ln 3
2 52
xx
x ab c
xx
++
=++
++
∫
với
a
,
b
,
c
là các số hữu tỷ. Biểu thức
.T ac b= −
bằng
A.
4
. B.
6
. C.
1
2
−
. D.
1
2
.
Câu 60: Biết
1
2
0
21
d ln 2
1
x
xn
xm
−−
= +
+
∫
, với
m
,
n
là các số nguyên. Tính
S mn= +
.
A.
1S = −
. B.
5S = −
. C.
1S
=
. D.
4S =
.
Câu 61: Cho
1
2
0
1
d ln 2 ln 3
32
xa b
xx
= +
++
∫
, với
,ab
là các số hữu tỷ. Khi đó
ab+
bằng
A.
0
. B.
2
. C.
1
. D.
1−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 75
Câu 62: Cho
1
2
2
0
23
d ln 2 ln 3
32
xx
x ab c
xx
+
=++
++
∫
với
a
,
b
,
c
là các số nguyên. Tổng
abc++
bằng
A.
3
. B.
2
. C.
1
. D.
1−
.
Câu 63: Cho biết
2
2
0
1
ln 5 ln 3
43
x
dx a b
xx
, với
,ab
. Tính
22
Ta b
bằng
A.
13.
B.
10.
C.
25.
D.
5.
Câu 64: Biết
2
2
2
0
52
d ln 3 ln 5
43
xx
x ab c
xx
++
=++
++
∫
,
( )
,,abc∈
. Giá trị của
abc
bằng
A.
8−
. B.
10−
. C.
12−
. D.
16
.
Câu 65: Biết
4
32
2
1
73
d ln 5
3
xx x a
xc
xx b
+++
= +
−+
∫
với
,
a
,b
c
là các số nguyên dương và
a
b
là phân số tối giản.
Tính giá trị của
23
P ab c
=−−
.
A.
5−
. B.
3−
. C.
6
. D.
4
−
.
Câu 66: Cho
( )( )
3
2
d
ln 2 ln 3 ln 5
12
x
abc
xx
= ++
++
∫
với
,,
abc
là các số hữu tỉ. Giá trị của
23
ab c+−
bằng
A.
3
. B.
6
. C.
5
. D.
4
.
Câu 67: Cho
4
2
3
23
d ln 2 ln 3 ln 7
3
x
xa b c
xx
+
= ++
+
∫
với
, , abc∈
. Giá trị của
237abc
++
bằng
A.
9
−
. B.
6
. C.
15
. D.
3
.
Câu 68: Cho
(
)
2
2
1
.ln 2 .ln 3
1
x
dx a b c
x
=++
+
∫
, với
,,abc
là các số hữu tỷ. Giá trị
6abc++
bằng:
A.
2−
. B.
1
. C.
2
. D.
1−
.
Câu 69: Biết
3
2
2
5 12
d ln 2 ln 5 ln 6
56
x
xa b c
xx
+
=++
++
∫
. Tính
32S a bc
=++
.
A.
11−
. B.
14−
. C.
2−
. D.
3
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 76
TÍCH PHÂN ĐỔI BIẾN
Tích phân đổi biến:
( ) ( ) ( ) ( ) ( )
.' .
b
a
b
f x u xdx Fux Fub Fua
a
= = −
∫
.
Các bước tính tích phân đổi biến số
Bước 1. Biến đổi để chọn phép đặt
( ) ( )
'.t u x dt u x dx= ⇒=
Bước 2. Đổi cận:
(
)
(
)
t ub
xb
xa
t ua
=
=
⇒
=
=
Bước 3. Đưa về dạng
( )
( )
( )
.
ub
ua
I f t dt=
∫
đơn giản hơn và dễ tính toán.
Một số phương pháp đổi biến số thường gặp
Đổi biến dạng 1.
( )
( )
( ) ( )
( )
( )
( )
1
2
'
. . ..
b bb
a aa
I
I
fx gx
I dx h x dx f g x dx
gx gx
= = +
∫ ∫∫
với
Đổi biến dạng 2.
Nghĩa là nếu gặp tích phân chứa căn thức thì có khoảng
80%
sẽ đặt
t =
căn trừ một số trường
hợp ngoại lệ sau:
1/
(
)
22
1
. .I f a x x dx= −
∫
→
đặt
.sinxa t=
hoặc
.cosxa t=
.
Câu 70: Cho tích phân
( )
1
7
5
2
0
d
1
x
Ix
x
=
+
∫
, giả sử đặt
2
1tx= +
. Tìm mệnh đề đúng.
A.
( )
3
2
5
1
1
1
d
2
t
It
t
−
=
∫
. B.
( )
3
3
5
1
1
d
t
It
t
−
=
∫
. C.
( )
3
2
4
1
1
1
d
2
t
It
t
−
=
∫
. D.
( )
3
4
4
1
1
3
d
2
t
It
t
−
=
∫
.
Câu 71: Có bao nhiêu số thực
a
để
1
2
0
1=
+
∫
x
dx
ax
.
A.
2
B.
1
C.
0
D.
3
Câu 72: Cho hàm số
( )
fx
có
( )
10
f =
và
( )
( )
2018
2019.2020. 1 ,
f x xx x
′
= − ∀∈
. Khi đó
( )
1
0
dfx x
∫
bằng
A.
2
.
2021
B.
1
.
1011
C.
2
.
2021
−
D.
1
.
1011
−
Câu 73: Biết
1
2
2
0
2 33
dx ln
21
xx
ab
xx
++
= −
++
∫
với
,ab
là các số nguyên dương. Tính
22
Pa b= +
.
A.
13
. B.
5
. C.
4
. D.
10
.
Câu 74: Cho với
m
,
p
,
q ∈
và là các phân số tối giản. Giá trị
mpq
bằng
A.
10
. B.
6
. C.
22
3
. D.
8
.
Có sẵn Tách từ hàm Nhân thêm
chẵn

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 77
Câu 75: Biết rằng
( )
2
1
2
0
d
2
x bc
a
xe x e e
+
= −
∫
với
,,abc∈
. Giá trị của
abc++
bằng
A.
4
. B.
7
. C.
5
. D.
6
.
Câu 76: Biết
( )
2
1
1
ln
ln
e
x
dx ae b
x xx
+
= +
+
∫
với
,ab
là các số nguyên dương. Tính giá trị của biểu thức
22
.
T a ab b
=−+
A. 3. B. 1. C. 0. D. 8.
Câu 77: Biết
(
)
2
1
1
2
1
p
x
q
x
x e dx me n
−
+=−
∫
, trong đó
,, ,mnpq
là các số nguyên dương và
p
q
là phân số tối
giản. Tính
T mn pq= +++
.
A.
11T =
. B.
10
T =
. C.
7
T =
. D.
8T =
.
Câu 78: Cho hàm số
( )
y fx=
có đạo hàm trên
đồng thời thỏa mãn
( ) ( )
0 15ff= =
. Tính tích phân
( )
( )
1
0
d
fx
I f xe x
′
=
∫
.
A.
10I =
B.
5
I
= −
C.
0
I =
D.
5
I =
Câu 79: Giả sử tích phân
5
1
1
ln 3 ln 5
1 31
I dx a b c
x
= =++
++
∫
. Lúc đó
A.
5
3
abc++=
. B.
4
3
abc++=
. C.
7
3
abc++=
. D.
8
3
abc
++=
.
Câu 80: Biết tích phân
ln 6
0
e
d ln 2 ln 3
1 e3
x
x
x ab c=++
++
∫
, với
a
,
b
,
c
là các số nguyên. Tính
T abc=++
.
A.
1
T = −
. B.
0T =
. C.
2T =
. D.
1T
=
.
Câu 81: Tích phân
1
0
d
31
x
x +
∫
bằng
A.
4
3
. B.
3
2
. C.
1
3
. D.
2
3
.
Câu 82: Biết
1
ln
2
1 ln
e
x
dx a b
xx
= +
+
∫
với
,ab
là các số hữu tỷ. Tính
S ab= +
.
A.
1S =
. B.
1
2
S =
. C.
3
4
S =
. D.
2
3
S =
.
Câu 83: Cho tích phân
22
2
0
16 dI xx= −
∫
và
4sinxt=
. Mệnh đề nào sau đây đúng?
A.
( )
4
0
8 1 cos2 dI tt
π
= +
∫
. B.
4
2
0
16 sin dI tt
π
=
∫
. C.
( )
4
0
8 1 cos 2 dI tt
π
= −
∫
. D.
4
2
0
16 cos dI tt
π
= −
∫
.
Câu 84: Biết
5
1
1
dx ln 3 ln 5
1 31
ab c
x
=++
++
∫
(,, )abc Q∈
. Giá trị của
abc++
bằng
A.
7
3
. B.
5
3
. C.
8
3
. D.
4
3
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 78
Câu 85: Cho biết
7
3
3
2
0
d
1
=
+
∫
xm
x
n
x
với
m
n
là một phân số tối giản. Tính
7mn−
A.
0
. B.
1
. C.
2
. D.
91
.
Câu 86: Biết rằng
1
0
ln 2 ln 3 ln 5
3 53 1 7
dx
abc
xx
= ++
+ ++
∫
, với
,,abc
là các số hữu tỉ. Giá trị của
abc++
bằng
A.
10
3
−
B.
5
3
−
C.
10
3
D.
5
3
Câu 87: Biết
1
ln
2
1 ln
e
x
dx a b
xx
= +
+
∫
với
,ab
là các số hữu tỷ. Tính
S ab= +
.
A.
1S =
. B.
1
2
S
=
. C.
3
4
S =
. D.
2
3
S =
.
Câu 88: Cho
3
0
ln 2 ln 3
3
42 1
xa
dx b c
x
=++
++
∫
với
a,b,c
là các số nguyên. Giá trị
abc
++
bằng:
A.
9
B.
2
C.
1
D.
7
Câu 89: Cho
3
0
d ln 2 ln
42 1
xa
I x b cd
d
x
= =++
++
∫
, với
,,,abcd
là các số nguyên và
a
d
là phân số tối
giản. Giá trị của
abcd+++
bằng
A. 16. B. 4. C. 28. D.
2−
.
Câu 90: Tính
3
2
0
d
1
a
xx
Ix
x
+
=
+
∫
.
A.
( )
22
1 11Ia a= + +−
. B.
( )
22
1
1 11
3
Ia a
= + +−
.
C.
( )
22
1
1 11
3
Ia a
= + ++
. D.
(
)
22
1 11
Ia a= + ++
.
Câu 91: Giá trị của tích phân
1
2
0
d
1
x
x
x−
∫
bằng tích phân nào dưới đây?
A.
4
2
0
2sin dy
y
π
∫
. B.
1
2
2
0
sin
d
cos
x
x
x
∫
. C.
2
4
0
sin
dy
cosy
y
π
∫
. D.
2
2
0
2sin dy
y
π
∫
.
Câu 92: Biết
22
22
3
d ln 5 ln 2
11
xb
xc
a
xx
= −
++ −
∫
với
,,abc
là các số nguyên và phân số
a
b
là tối giản.
Tính
32P a bc=++
.
A.
11
. B.
12
. C.
14
. D.
13
.
Câu 93: Cho tích phân
1
2
0
d
4
x
I
x
=
−
∫
nếu đổi biến số
2sin , ;
22
x tt
= ∈−
ππ
thì ta được.
A.
3
0
d
π
It=
∫
. B.
6
0
d
π
It
=
∫
. C.
4
0
d
π
I tt=
∫
. D.
6
0
d
π
t
I
t
=
∫
.
Câu 94: Biết
1
3
2
0
15
1
x ab c
dx
xx
+
=
++
∫
với
, , abc
là các số nguyên và
0b ≥
. Tính
2
P ab c=+−
.
A.
3P =
. B.
7P =
. C.
7P = −
. D.
5P =
.
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 79
Câu 95: Cho
n
là số nguyên dương khác
0
, hãy tính tích phân
( )
1
2
0
1d
n
I x xx= −
∫
theo
n
.
A.
1
22
I
n
=
+
. B.
1
2
I
n
=
. C.
1
21
I
n
=
−
. D.
1
21
I
n
=
+
.
Câu 96: Giả sử
64
3
1
d2
ln
3
x
I ab
xx
= = +
+
∫
với
,ab
là số nguyên. Khi đó giá trị
ab−
là
A.
17−
. B. 5. C.
5−
. D.
17
.
Câu 97: Cho hàm số
( )
fx
có
( )
22f = −
và
( )
(
)
2
, 6; 6
6
x
fx x
x
′
= ∀∈−
−
. Khi đó
( )
3
0
.dfx x
∫
bằng
A.
3
4
π
−
. B.
36
4
π
+
. C.
2
4
π
+
. D.
36
4
π
+
−
.
Câu 98: Biết
2
2
1
d 2 35
3 91
x
x ab c
xx
=++
+−
∫
với
a
,
b
,
c
là các số hữu tỷ, tính
27P a bc=+ +−
.
A.
1
9
−
. B.
86
27
. C.
2−
. D.
67
27
.
Câu 99: Biết
( )
2
1
d
11
x
abc
xx x x
=−−
++ +
∫
với
a
,
b
,
c
là các số nguyên dương. Tính
P abc=++
.
A.
44P =
. B.
42P =
. C.
46P
=
. D.
48P =
.
Câu 100: Biết
( )
4
0
2 1d 5
ln 2 ln , ,
3
2 32 1 3
xx
a b c abc
xx
+
=++ ∈
+ ++
∫
. Tính
2T abc= ++
.
A.
4
T =
. B.
2T
=
. C.
1T =
. D.
3T =
.
Câu 101: Cho
2
2
0
cos 4
d ln ,
sin 5sin 6
x
xa b
xx c
π
= +
−+
∫
tính tổng
S abc=++
A.
1S =
. B.
4
S =
. C.
3S =
. D.
0
S =
.
Câu 102: Cho tích phân
2
0
2 cos .sin dI x xx
π
= +
∫
. Nếu đặt
2 costx= +
thì kết quả nào sau đây đúng?
A.
2
3
d
I tt=
∫
. B.
3
2
d
I tt
=
∫
. C.
2
3
2dI tt=
∫
. D.
2
0
dI tt
π
=
∫
.
Câu 103: Tính tích phân
2
4
4
0
sin
d
cos
x
Ix
x
π
=
∫
bằng cách đặt
tanux=
, mệnh đề nào dưới đây đúng?
A.
4
2
0
dI uu
π
=
∫
. B.
2
2
0
1
dIu
u
=
∫
. C.
1
2
0
dI uu= −
∫
. D.
1
2
0
dI uu=
∫
.
Câu 104: Tính tích phân
π
3
3
0
sin
d
cos
x
Ix
x
=
∫
.
A.
5
2
I =
. B.
3
2
I =
. C.
π9
3 20
I = +
. D.
9
4
I =
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 80
Câu 105: Cho tích phân
2
3
sin
d ln 5 ln 2
cos 2
x
xa b
x
π
π
= +
+
∫
với
,.ab∈
Mệnh đề nào dưới đây đúng?
A.
2 0.
ab+=
B.
2 0.ab−=
C.
2 0.ab−=
D.
2 0.ab+=
Câu 106: Có bao nhiêu số
( )
0;20
π
∈
a
sao cho
5
0
2
sin sin 2 d
7
a
x xx
=
∫
.
A. 10.
B. 9.
C. 20.
D. 19.
Câu 107: Biết
6
0
d3
1 sin
x ab
xc
π
+
=
+
∫
, với
,,
ab c
+
∈∈
và
,,abc
là các số nguyên tố cùng nhau. Giá trị
của tổng
abc++
bằng
A.
5
. B.
12
. C.
7
. D.
1−
.
Câu 108: Cho tích phân số
2
3
sin
d ln 5 ln 2
cos 2
x
xa b
x
π
π
= +
+
∫
với
,ab∈
. Mệnh đề nào dưới đây đúng?
A.
2 0.ab+=
B.
2 0.ab−=
C.
2 0.ab−=
. D.
2 0.ab+=
.
Câu 109: Cho
2
2
0
sin 4
d ln
cos 5cos 6
x
xa b
xx c
= +
−+
∫
π
, với
a
,
b
là các số hữu tỉ,
0c >
. Tính tổng
S abc=++
.
A.
3S =
. B.
0S =
. C.
1S =
. D.
4S =
.
Câu 110: Cho hàm số
()y fx=
có
(0) 1f =
và
3
( ) tan tan ,fx x x x
′
= + ∀∈
. Biết
4
0
() ;,
a
f x dx a b
b
π
π
+
= ∈
∫
, khi đó
ba−
bằng
A.
4
. B.
12
. C.
0
. D.
4−
.
Câu 111: Cho tích phân
e
1
3ln 1
d
x
Ix
x
+
=
∫
. Nếu đặt
lntx=
thì
A.
1
0
31
d
e
t
t
It
+
=
∫
. B.
e
1
31
d
t
It
t
+
=
∫
. C.
( )
e
1
3 1dI tt= +
∫
. D.
( )
1
0
3 1dI tt= +
∫
.
Câu 112: Cho
( )
2
1
ln
ln 3 ln 2
3
ln 2
e
xc
I dx a b
xx
= =++
+
∫
, với
,,abc
∈
. Khẳng định nào sau đâu đúng.
A.
222
1abc
++=
. B.
222
11
abc++=
. C.
222
9abc++=
. D.
222
3abc++=
.
Câu 113: Biết
( )
4
2
0
ln 9 d ln 5 ln 3I x x xa b c= += + +
∫
trong đó
,,abc
là các số thực. Giá trị của biểu thức
T abc=++
là:
A.
11.T =
B.
9.T =
C.
10.T =
D.
8.T =
Câu 114: Cho
( )
e
2
1
ln
d
ln 2
x
Ix
xx
=
+
∫
có kết quả dạng
ln
I ab= +
với
0a >
,
b ∈
. Khẳng định nào sau đây
đúng?
A.
21ab = −
. B.
21ab =
. C.
31
ln
23
b
a
−+ =−
. D.
31
ln
23
b
a
−+ =
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 81
Câu 115: Cho
(
)
e
2
1
2ln 1
d ln
ln 2
x ac
x
bd
xx
+
= −
+
∫
với
a
,
b
,
c
là các số nguyên dương, biết
;
ac
bd
là các phân số
tối giản. Tính giá trị
abcd+++
?
A.
18
. B.
15
. C.
16
. D.
17
.
Câu 116: Cho
(
)
( )
32
3
1
e
3 1 ln 3 1
d . .ln 1
1l
ee
n
x xx
x a bc
xx
− +−
= ++ +
+
∫
với
,,
abc
là các số nguyên và
ln e 1=
.
Tính
222
Pabc=++
.
A.
9P =
. B.
14P =
. C.
10P =
. D.
3P =
.
Câu 117: Biết
(
)
ln 2
0
d1
ln ln ln
4e 3e
xx
x
I abc
c
−
=
+
= −+
+
∫
với
a
,
b
,
c
là các số nguyên dương.
Tính
2P abc= −+
.
A.
3P = −
. B.
1P = −
. C.
4
P =
. D.
3P =
Câu 118: Cho
( )
( )
2
1
0
e
d .e ln e
e
−
+
=++
+
∫
x
x
xx
xa b c
x
với
a
,
b
,
∈c
. Tính
2P a bc=+−
.
A.
1
P =
. B.
1
P = −
. C.
0P =
. D.
2
P = −
.
Câu 119: Cho hàm số
( )
=y fx
biết
( )
1
0
2
=f
và
(
)
2
′
=
x
f x xe
với mọi
∈x
. Khi đó
( )
1
0
∫
xf x dx
bằng
A.
1
4
+e
. B.
1
4
−e
. C.
1
2
−e
. D.
1
2
+e
.
Câu 120: Biết rằng
2
1
2ln 1
d ln 2
ln 1
e
xb
xa
c
xx
với
,,abc
là các số nguyên dương và
b
c
là phân số tối
giản. Tính
S abc
=++
.
A.
3S =
. B.
7S =
. C.
10S =
. D.
5S =
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 82
TÍCH PHÂN TỪNG PHẦN
Nếu
,uv
có đạo hàm liên tục trên
(
)
;
ab
thì
.. .
bb
b
a
aa
I u dv u v v du= = −
∫∫
.
Chọn
............... ...........
........ ................
u du dx
dv dx v
= → =
= → =
Nhận dạng: tích hai hàm khác loại nhân nhau
Thứ tự ưu tiên chọn u là: "log – đa – lượng – mũ" và dv là phần còn lại.
Nghĩa là nếu có ln hay
log
a
x
thì chọn
ln
u
=
hay
1
log .ln
ln
a
ux x
a
= =
và
dv =
còn lại. Nếu
không có
ln; log
thì chọn
u =
đa thức và
dv
=
còn lại,…
CHÚ Ý:.
(
hàm mũ
)
. dx
b
a
tích phân từng phần luân hồi.
Nghĩa là sau khi đặt u, dv để tính tích phân từng phần và tiếp tục tính
udv sẽ xuất hiện lại tích
phân ban đầu. Giả sử tích phân được tính ban đầu là I và nếu lập lại, ta sẽ không giải tiếp mà xem
đây là phương trình bậc nhất ẩn là I
giải
I.
Câu 121: Biết
( )
1
2
0
ln 1 d ln 2
b
x x xa
c
+= −
∫
. Tính
13 10 84Pabc=++
.
A.
193
. B.
191
. C.
190
. D.
189
.
Câu 122: Cho hàm số
( )
fx
có
( )
01f = −
và
(
)
(
)
6 12 ,
x
fx x xe x
−
′
= + + ∀∈
. Khi đó
(
)
1
0
dfxx
∫
bằng
A.
3e
. B.
1
3e
−
. C.
1
43e
−
−
. D.
1
3e
−
−
.
Câu 123: Biết
( )
4
2
0
ln 9 d ln 5 ln 3I x x xa b c= += ++
∫
trong đó
a
,
b
,
c
là các số thực. Tính giá trị của biểu
thức
T abc=++
.
A.
9T =
. B.
11T =
. C.
8T =
. D.
10T =
.
Câu 124: Tích phân
( )
1
2
0
2e d
x
xx−
∫
bằng
A.
2
5 3e
.
4
−−
B.
2
5 3e
.
4
−
C.
2
5 3e
.
2
−
D.
2
5 3e
.
4
+
Câu 125: Biết rằng tích phân
( )
1
0
2+1ed= +.e
x
x x ab
∫
, tích
a.b
bằng
A.
15
−
. B.
1−
. C. 1. D. 20.
Câu 126: Cho tích phân
2
2
1
ln
ln 2
xb
I dx a
xc
= = +
∫
với
a
là số thực,
b
và
c
là các số dương, đồng thời
b
c
là
phân số tối giản. Tính giá trị của biểu thức
23P a bc
= ++
.
A.
6P
=
. B.
5P
=
. C.
6P = −
. D.
4P =
.
Vi phân
Nguyên hàm

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 83
Câu 127: Cho tích phân
( )
4
0
1 sin 2 d .I x xx
π
= −
∫
Tìm đẳng thức đúng?
A.
( )
4
0
1 cos2 cos2 dI x x xx
π
=−− −
∫
. B.
(
)
4
4
0
0
1
1 cos2 cos2 d
2
I x x xx
π
π
=−− −
∫
.
C.
( )
4
4
0
0
11
1 cos2 cos2 d
22
I x x xx
π
π
=−− +
∫
. D.
( )
4
4
0
0
1 cos2 cos2 dI x x xx
π
π
=−− +
∫
.
Câu 128: Biết rằng tồn tại duy nhất các bộ số nguyên
,,abc
sao cho
(
)
3
2
4 2 ln d ln 2 ln 3x xx a b c
+ =++
∫
.
Giá trị của
abc++
bằng
A.
19
. B.
19−
. C.
5
. D.
5
−
.
Câu 129: Cho
(
)
2
2
1
ln 1
ln 2 ln 3
x
dx a b
x
+
= +
∫
, với
,ab
là các số hữu tỉ. Tính
4Pa b= +
.
A.
0
P
B.
1P
C.
3P
D.
3P
Câu 130: Biết
( )
2
0
2 ln 1 dx a.lnbxx+=
∫
, với
*
,
ab∈
,
b
là số nguyên tố. Tính
67ab+
.
A.
6 7 33ab+=
. B.
6 7 25ab+=
. C.
6 7 42
ab
+=
. D.
6 7 39ab+=
.
Câu 131: Biết rằng
( )
1
ln 1 2 , 1 .
a
xdx a a=+>
∫
Khẳng định nào dưới đây là khẳng định đúng?
A.
(
)
18;21a
∈
. B.
( )
1; 4a ∈
. C.
( )
11;14a ∈
. D.
( )
6;9a ∈
.
Câu 132: Cho tích phân
1
0
( 2) x
x
x e d a be−=+
∫
, với
∈;
ab
. Tổng
+ab
bằng
A.
1
. B.
−3
. C.
5
. D.
1−
.
Câu 133: Tính tích phân
2
1
x
I xe dx=
∫
.
A.
2
=
Ie
. B.
2
= −Ie
. C.
=Ie
. D.
2
32= −Ie e
.
Câu 134: Biết rằng
3
2
ln d ln 3 ln 2x xx m n p= ++
∫
trong đó
,,mn p∈
. Tính
2mn p++
A.
5
4
. B.
9
2
. C.
0
. D.
5
4
−
.
Câu 135: Biết
( )
2
0
2 ln 1 d .lnx xxa b+=
∫
, với
*
,ab∈
,
b
là số nguyên tố. Tính
34ab+
.
A.
42
. B.
21
. C.
12
. D.
32
.
Câu 136: Biết
3
2
0
3
d ln
cos
x
Ixb
xa
π
π
= = −
∫
. Khi đó, giá trị của
2
ab+
bằng
A.
11
. B.
7
. C.
13
. D.
9
.
Câu 137: Cho
( )
2
2
1
ln 1 2
d ln 5 ln 3 ln 2
2
x
a
x bc
x
+
= ++
∫
, với
a
,
b
,
c
là các số nguyên. Giá trị của
( )
2a bc++
là:
A. 0. B. 9. C. 3. D. 5.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 84
Câu 138: Cho
( )
2
2
1
ln 1
d ln 2 ln 3
x
xa b
x
+
= +
∫
, với
a
,
b
là các số hữu tỉ. Tính
P ab=
.
A.
3
2
P =
. B.
0P =
. C.
9
2
P
−
=
. D.
3P = −
.
Câu 139: Cho tích phân
1
0
( 2) x
x
x e d a be
−=+
∫
, với
;ab
∈
. Tổng
+ab
bằng
A.
1
. B.
−3
. C.
5
. D.
1−
.
Câu 140: Biết
12
1
1
12
1
1
c
x
xd
a
x e dx e
xb
+
+− =
∫
trong đó
,,,
abcd
là các số nguyên dương và các phân số
,
ac
bd
là tối giản. Tính
bc ad−
.
A. 12. B. 1. C. 24. D. 64.
Câu 141: Cho
( )
(
)
2
2
0
ln 1
d ln 3
2
xx
ac
x
bd
x
++
= +
+
∫
. Tính
( )( )
P abcd=++
.
A.
7
. B.
7−
. C.
3
. D.
3−
.
Câu 142: Cho hàm số
( )
y fx=
có
( )
1
1
2
f
=
và
(
)
( )
2
1
x
fx
x
′
=
+
với
1x >−
. Biết
( )
2
1
d ln
b
fx x a d
c
= −
∫
với
,,,abcd
là các số nguyên dương,
3b ≤
và
b
c
tối giản. Khi đó
abcd+++
bằng
A.
8
. B.
5
. C.
6
. D.
10
.
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 1
BÀI 2. TÍCH PHÂN
Câu 1: Khẳng định nào trong các khẳng định sau đúng với mọi hàm
f
,
g
liên tục trên
K
và
a
,
b
là
các số bất kỳ thuộc
K
?
A.
[ ]
() 2()d ()d+2 ()d
b bb
a aa
f x gx x f x x gx x+=
∫ ∫∫
. B.
( )d
()
d
()
( )d
b
b
a
b
a
a
fx x
fx
x
gx
gx x
=
∫
∫
∫
.
C.
[ ]
().()d ()d . ()d
b bb
a aa
f x gx x f x x gx x=
∫ ∫∫
. D.
2
2
()d= ()d
bb
aa
f x x fx x
∫∫
.
Lời giải
Theo tính chất tích phân ta có
[
]
() ()d ()d+ ()d; ()d ()d
b b bb b
a a aa a
fx gx x fx x gx x kfx x k fx x
+= =
∫ ∫ ∫∫ ∫
, với
k ∈
.
Câu 2: Cho
( )
2
2
d1fx x
−
=
∫
,
( )
4
2
d4ft t
−
= −
∫
. Tính
( )
4
2
dfy y
∫
.
A.
5I =
. B.
3I = −
. C.
3I =
. D.
5I = −
.
Lời giải
Ta có:
( ) (
)
44
22
ddft t fx x
−−
=
∫∫
,
( ) ( )
44
22
ddfy y fx x=
∫∫
.
Khi đó:
( ) ( ) (
)
24 4
22 2
dd dfx x fx x fx x
−−
+=
∫∫∫
.
( ) ( ) ( )
442
2 22
d d d 41 5fx x fx x fx x
−−
⇒ = − =−−=−
∫∫∫
.
Vậy
( )
4
2
d5fy y= −
∫
.
Câu 3: Cho
( )
2
0
3f x dx =
∫
và
( )
2
0
7g x dx =
∫
, khi đó
( ) ( )
2
0
3f x g x dx
+
∫
bằng
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
A.
16
. B.
18−
. C.
24
. D.
10
.
Lời giải
Ta có
( ) ( ) ( ) ( )
2 22
0 00
3 3 3 3.7 24f x g x dx f x dx g x dx+ = + =+=
∫ ∫∫
.
Câu 4: Cho
1
0
()
fx
∫
dx
1
= −
;
3
0
()fx
∫
dx
5=
. Tính
3
1
()fx
∫
dx
A. 1. B. 4. C. 6. D. 5.
Lời giải
Ta có
3
0
()fx
∫
dx =
1
0
()fx
∫
dx +
3
1
()fx
∫
dx
3
1
()fx⇒
∫
dx =
3
0
()fx
∫
dx
1
0
()fx−
∫
dx = 5+ 1= 6
Vậy
3
1
()fx
∫
dx = 6
Câu 5: Cho
(
)
2
1
d3fx x= −
∫
và
( )
3
2
d4
fx x=
∫
. Khi đó
( )
3
1
dfx x
∫
bằng
A. 12. B. 7. C. 1. D.
12−
.
Lời giải
( )
3
1
dfx x
∫
( ) ( )
23
12
ddfx x fx x= +
∫∫
34=−+
1
=
.
Câu 6: Cho hàm số
( )
fx
liên tục, có đạo hàm trên
[ ]
(
) ( )
1; 2 , 1 8; 2 1ff− −= =−
. Tích phân
( )
2
1
'f x dx
−
∫
bằng
A.
1.
B.
7.
C.
9.−
D.
9.
Lời giải
Ta có
(
) ( ) ( ) (
)
2
2
1
1
f ' x dx f x f 2 f 1 1 8 9.
−
−
= = − − =−− =−
∫
Câu 7: Cho hàm số
( )
fx
liên tục trên
R
và có
24
02
( )d 9; ( )d 4.fx x fx x= =
∫∫
Tính
4
0
( )d .I fx x=
∫
A.
5
I =
. B.
36I =
. C.
9
4
I =
. D.
13I =
.
Lời giải
Ta có:
4 24
0 02
( )d ( )d ( )d 9 4 13.I fx x fx x fx x= = + =+=
∫∫∫
Câu 8: Cho
( ) ( )
03
10
3 3.f x dx f x dx
−
= =
∫∫
Tích phân
( )
3
1
f x dx
∫
bằng
A.
6
B.
4
C.
2
D.
0
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
Có
( ) ( ) ( ) ( ) ( )
0 3 3 03
1 0 1 10
3; 1; 3 1 4f x dx f x dx f x dx f x dx f x dx
− −−
= = = + =+=
∫ ∫ ∫∫∫
Câu 9: Cho hàm số
( )
fx
liên tục trên
và
( )
4
0
d 10fx x=
∫
,
( )
4
3
d4
fx x=
∫
. Tích phân
(
)
3
0
dfx x
∫
bằng
A.
4
. B.
7
. C.
3
. D.
6
.
Lời giải
Theo tính chất của tích phân, ta có:
( ) ( ) ( )
34 4
03 0
ddd
fx x fx x fx x
+=
∫∫∫
.
Suy ra:
( )
3
0
dfx x
∫
( ) ( )
44
03
ddfx x fx x= −
∫∫
10 4
= −
6=
.
Vậy
( )
3
0
d6
fx x=
∫
.
Câu 10: Cho hàm số
fx
liên tục trên
thoả mãn
( )
8
1
d9fx x
=
∫
,
( )
12
4
d3fx x=
∫
,
( )
8
4
d5fx x=
∫
.
Tính
( )
12
1
d
I fx x=
∫
.
A.
17I
. B.
1I
. C.
11I
. D.
7I
.
Lời giải
Ta có:
( ) ( ) ( )
12 8 12
1 18
dddI fx x fx x fx x= = +
∫∫∫
.
( ) ( ) ( )
8 12 8
144
d d d 935 7fx x fx x fx x= + − =+−=
∫∫∫
.
Câu 11: Cho hàm số
(
)
fx
liên tục trên
[ ]
0;10
thỏa mãn
( )
10
0
7f x dx =
∫
,
(
)
6
2
3f x dx =
∫
. Tính
( ) ( )
2 10
06
P f x dx f x dx
= +
∫∫
.
A.
10P =
. B.
4P =
. C.
7P =
. D.
6P = −
.
Lời giải
Ta có
( ) ( ) ( ) ( )
10 2 6 10
0 026
f x dx f x dx f x dx f x dx=++
∫∫∫∫
Suy ra
( ) ( ) ( ) ( )
2 10 10 6
06 02
734f x dx f x dx f x dx f x dx+ = − =−=
∫∫∫∫
.
Câu 12: Cho
f
,
g
là hai hàm liên tục trên đoạn
[ ]
1; 3
thoả:
( ) ( )
3
1
3 d 10f x gx x+=
∫
,
( )
( )
3
1
2 d6f x gx x−=
∫
. Tính
(
)
( )
3
1
df x gx x+
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
A. 7. B. 6. C. 8. D. 9.
Lời giải
( )
( )
3
1
3 d 10f x gx x+=
∫
⇔
( ) ( )
33
11
d 3 d 10f x x gx x+=
∫∫
( )
1
.
( )
(
)
3
1
2 d6f x gx x−=
∫
⇔
( ) ( )
33
11
2 d d6fxx gxx−=
∫∫
(
)
2
.
Đặt
( )
3
1
dX fxx=
∫
,
( )
3
1
dY gx x=
∫
.
Từ
( )
1
và
( )
2
ta có hệ phương trình:
3 10
26
XY
XY
+=
−=
⇔
4
2
X
Y
=
=
.
Do đó ta được:
( )
3
1
d4fxx=
∫
và
( )
3
1
d2gx x=
∫
.
Vậy
( ) ( )
3
1
d 426f x gx x+ =+=
∫
.
Câu 13: Cho hàm số
( )
fx
liên tục trên đoạn
[
]
0;10
và
( )
10
0
7
f x dx =
∫
;
( )
6
2
3f x dx =
∫
. Tính
( ) ( )
2 10
06
P f x dx f x dx= +
∫∫
.
A.
4P =
B.
10P =
C.
7
P =
D.
4P = −
Lời giải
Ta có:
( ) ( ) ( ) ( )
10 2 6 10
0 026
f x dx f x dx f x dx f x dx=++
∫∫∫∫
.
73 4PP⇒ = +⇒ =
.
Câu 14: Cho
,fg
là hai hàm số liên tục trên
[ ]
1; 3
thỏa mãn điều kiện
( ) ( )
3
1
3 dx=10f x gx+
∫
đồng thời
( ) ( )
3
1
2 dx=6f x gx−
∫
. Tính
(
) ( )
3
1
dx
f x gx+
∫
.
A.
9
. B.
6
. C.
7
. D.
8
.
Lời giải
Ta có:
( )
( )
3
1
3 dx=10f x gx+
∫
( ) ( )
33
11
dx+3 dx=10f x gx⇔
∫∫
.
( ) ( )
3
1
2 dx=6f x gx−
∫
(
) ( )
33
11
2 dx- dx=6f x gx⇔
∫∫
.
Đặt
( ) ( )
33
11
dx; v = dxu f x gx=
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Ta được hệ phương trình:
3 10
26
uv
uv
+=
−=
4
2
u
v
=
⇔
=
( )
( )
3
1
3
1
dx=4
dx=2
fx
gx
⇒
∫
∫
Vậy
( ) ( )
3
1
dx=6f x gx+
∫
.
Câu 15: Cho
f
,
g
là hai hàm liên tục trên
[ ]
1;3
thỏa:
(
) (
)
3
1
3 d 10f x gx x+=
∫
và
(
) (
)
3
1
2 d6
f x gx x
−=
∫
. Tính
( ) ( )
3
1
dI f x gx x= +
∫
.
A. 8. B. 7. C. 9. D. 6.
Lời giải
Đặt
( )
3
1
da fx x=
∫
và
( )
3
1
db gx x=
∫
.
Khi đó,
( ) ( )
3
1
3d 3f x gx x a b+=+
∫
,
( ) ( )
3
1
2 d2f x gx x a b−=−
∫
.
Theo giả thiết, ta có
3 10 4
26 2
ab a
ab b
+= =
⇔
−= =
.
Vậy
6I ab=+=
.
Câu 16: Cho
( )
2
0
d5fx x=
∫
π
. Tính
( )
2
0
2sin d 5I fx x x
=+=
∫
π
.
A.
7I =
B.
5
2
I
π
= +
C.
3I =
D.
5I
π
= +
Lời giải
Ta có
( ) ( )
222
0 00
2sin d d +2 sin dI fx x x fx x xx
π
ππ
=+=
∫ ∫∫
( )
(
)
2
2
0
0
d 2cos 5 2 0 1 7fx x x
π
π
= − =− −=
∫
.
Câu 17: Cho
( )
2
1
d2
fx x
−
=
∫
và
( )
2
1
d1gx x
−
= −
∫
. Tính
( ) ( )
2
1
2 3dI x f x gx x
−
=+−
∫
.
A.
17
2
I =
B.
5
2
I =
C.
7
2
I =
D.
11
2
I
=
Lời giải
Ta có:
( ) ( )
2
1
2 3dI x f x gx x
−
=+−
∫
=
( ) ( )
2
22
2
11
1
2 d3 d
2
x
fxx gxx
−−
−
+−
∫∫
=
( )
3
2.2 3 1
2
+ −−
=
17
2
.
Câu 18: Cho hai tích phân
( )
5
2
d8
−
=
∫
fx x
và
( )
2
5
d3
−
=
∫
gx x
. Tính
( ) ( )
5
2
4 1d
−
= −−
∫
I f x gx x

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
A.
13
. B.
27
. C.
11−
. D.
3
.
Lời giải
( ) ( )
5
2
4 1d
−
= −−
∫
I f x gx x
( )
(
)
55 5
22 2
d4dd
−− −
=−−
∫∫ ∫
f x x gx x x
( )
( )
5 55
2 22
d4 d d
− −−
=−−
∫ ∫∫
f x x gx x x
( ) ( )
5 25
2 52
d4 d d
−
−−
=+−
∫ ∫∫
f x x gx x x
5
8 4.3
2
=+−
−
x
8 4.3 7=+−
13=
.
Câu 19: Cho
2
1
() 2f x dx
−
=
∫
và
2
1
() 1g x dx
−
= −
∫
, khi đó
[ ]
2
1
2 () 3()
x f x g x dx
−
++
∫
bằng
A.
5
2
B.
7
2
C.
17
2
D.
11
2
Lời giải
Ta có
[ ]
2 22 2
1 11 1
35
2 () 3g(x) 2 () 3 () 4 3
22
x f x dx xdx f x dx g x dx
− −− −
+ + = + + = +−=
∫ ∫∫ ∫
Câu 20: Cho
(
)
2
0
d3fx x=
∫
,
( )
2
0
d1gx x= −
∫
thì
( ) ( )
2
0
5df x gx x x
−+
∫
bằng:
A.
12
. B.
0
. C.
8
. D.
10
Lời giải
( ) ( ) ( )
( )
2 2 22
0 0 00
5 d 5g d d− += − +
∫ ∫ ∫∫
fx gx x x fxdx x x xx
3 5 2 10
=++=
Câu 21: Cho
( )
5
0
d2
fx x= −
∫
. Tích phân
( )
5
2
0
4 3dfx x x
−
∫
bằng
A.
140−
. B.
130−
. C.
120−
. D.
133−
.
Lời giải
(
) (
)
5 55
5
2 23
0
0 00
4 3 d 4 d 3 d 8 8 125 133fx x x fx x xx x
− = − =−− =−− =−
∫ ∫∫
.
Câu 22: Cho
( )
2
1
421f x x dx
−=
∫
. Khi đó
( )
2
1
f x dx
∫
bằng:
A.
1
. B.
3−
. C.
3
. D.
1−
.
Lời giải
( ) ( ) ( )
( ) ( )
2
2 22 2
2
1 11 1
1
22
11
4 2 14 2 14 2. 1
2
44 1
x
f x x dx f x dx xdx f x dx
f x dx f x dx
−=⇔−=⇔−=
⇔ =⇔=
∫ ∫∫∫
∫∫
Câu 23: Cho
( )
1
0
1f x dx =
∫
tích phân
( )
( )
1
2
0
23f x x dx−
∫
bằng

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 7
A.
1
. B.
0
. C.
3
. D.
1−
.
Lời giải
Chọn. A.
( )
( )
( )
1 11
22
0 00
2 3 2 3 211f x x dx f x dx x dx− = − = −=
∫ ∫∫
.
Câu 24: Tính tích phân
(
)
0
1
21I x dx
−
= +
∫
.
A.
0I =
. B.
1
I =
. C.
2I =
. D.
1
2
I = −
.
Lời giải
( )
( )
0
0
2
1
1
2 1 00 0I x dx x x
−
−
= + = + =−=
∫
.
Câu 25: Tích phân
( )( )
1
0
3 1 3dxx x++
∫
bằng
A.
12
. B.
9
. C.
5
. D.
6
.
Lời giải
Ta có:
(
)
( )
( )
( )
11
1
2 32
0
00
3 1 3 d 3 10 3 d 5 3 9
x x x x x xx x x
+ + = ++ =++ =
∫∫
.
Vậy :
( )
( )
1
0
3 1 3d 9xx x
++ =
∫
.
Câu 26: Giá trị của
2
0
sin xdx
π
∫
bằng
A. 0. B. 1. C. -1. D.
2
π
.
Lời giải
+ Tính được
2
0
sin cos 1
2
0
xdx x
π
π
=−=
∫
.
Câu 27: Tính tích phân
2
0
(2 1)I x dx= +
∫
A.
5I =
. B.
6I =
. C.
2I =
. D.
4I =
.
Lời giải
Ta có
(
)
2
2
2
0
0
(2 1) 4 2 6I x dx x x= + = + =+=
∫
.
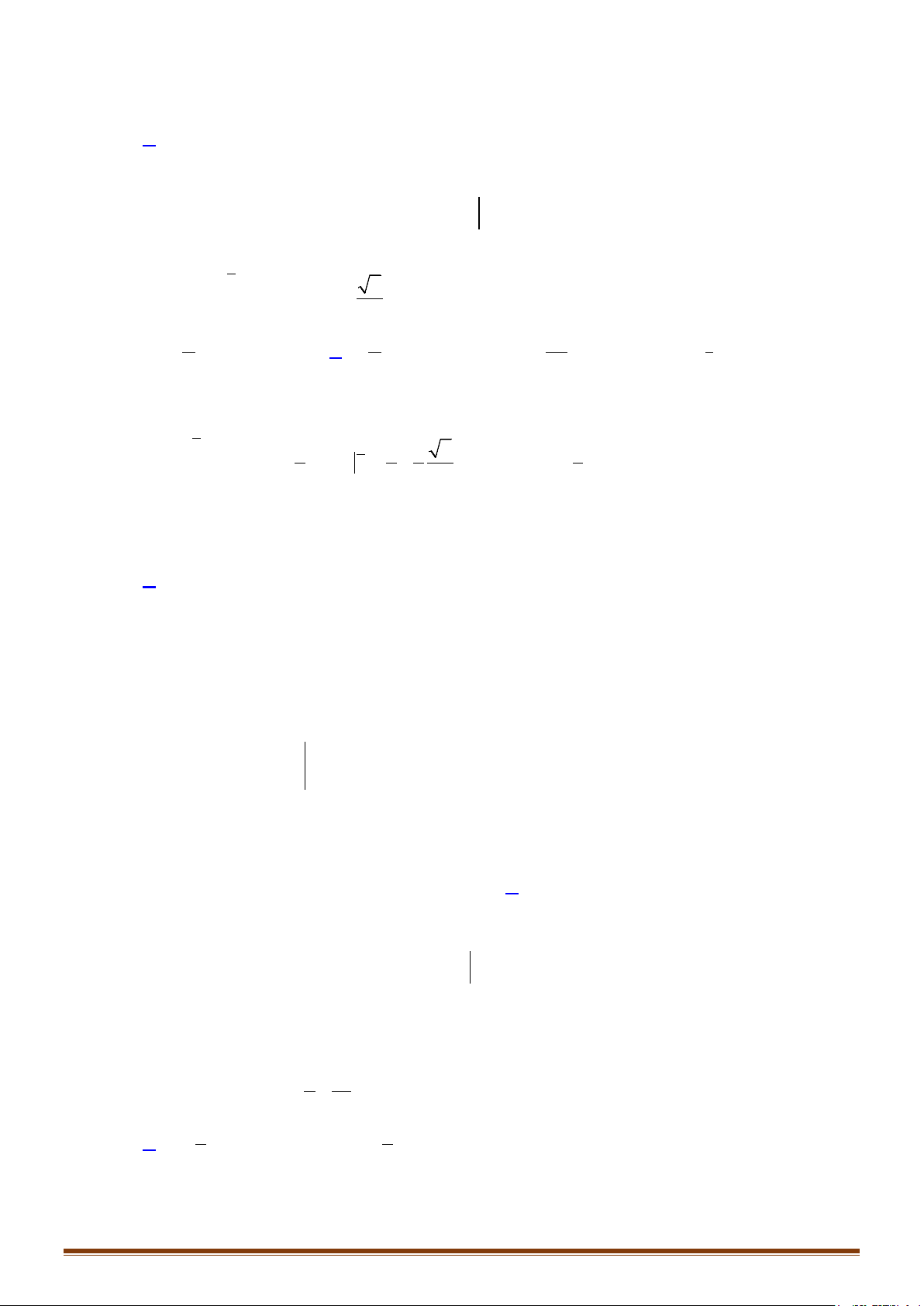
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Câu 28: Với
,ab
là các tham số thực. Giá trị tích phân
( )
2
0
3 2 1d
b
x ax x−−
∫
bằng
A.
32
b ba b−−
. B.
32
b ba b++
. C.
32
b ba b−−
. D.
2
321b ab−−
.
Lời giải
Ta có
( )
2
0
3 2 1d
b
x ax x
−−
∫
( )
32
0
b
x ax x=−−
32
b ab b=−−
.
Câu 29: Giả sử
4
0
2
sin 3
2
I xdx a b
π
= = +
∫
( )
,ab∈
. Khi đó giá trị của
ab−
là
A.
1
6
−
B.
1
6
−
C.
3
10
−
D.
1
5
Lời giải
Ta có
4
4
0
0
1 112
sin 3 cos 3
3 3 32
xdx x
π
π
=−=+
∫
. Suy ra
1
3
ab= =
0ab⇒−=
.
Câu 30: Cho hàm số
( )
fx
liên tục trên
và
(
)
( )
2
2
0
3 d 10+=
∫
fx x x
. Tính
( )
2
0
d
fx x
∫
.
A.
2
. B.
2−
. C.
18
. D.
18−
.
Lời giải
Ta có:
( )
( )
2
2
0
3 d 10+=
∫
fx x x
(
)
22
2
00
3dd10⇔ +=
∫∫
fxx xx
( )
22
2
00
1dd03⇔=−
∫∫
fxx xx
( )
2
3
0
2
0
0
d 1⇔=−
∫
fxx x
( )
2
0
10 8 2d⇔ = −=
∫
fxx
.
Câu 31: Cho
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
. Giá trị của tham số m thuộc khoảng nào sau đây?
A.
( )
1; 2−
. B.
( )
;0−∞
. C.
( )
0; 4
. D.
( )
3;1−
.
Lời giải
Ta có:
( )
2
0
3 2 1d 6
m
xx x−+ =
∫
( )
32 3 2
0
6 60 2
m
xx x mmm m⇔ − + =⇔ − + −=⇔ =
.
Vậy
( )
0; 4m∈
.
Câu 32: Tính tích phân
2
1
11
e
I dx
xx
= −
∫
A.
1
I
e
=
B.
1
1I
e
= +
C.
1I =
D.
Ie=
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
2
1
1
11 1 1
ln
e
e
I dx x
xx x e
=− = +=
∫
.
Câu 33: Tính tích phân
3
0
d
2
x
I
x
=
+
∫
.
A.
21
100
I = −
. B.
5
ln
2
I
=
. C.
5
log
2
I
=
. D.
4581
5000
I =
.
Lời giải
( )
3
3
0
0
d5
ln 2 ln 5 ln 2 ln .
22
x
Ix
x
= = +=−=
+
∫
Câu 34:
2
1
d
32
x
x −
∫
bằng
A.
2ln 2
. B.
2
ln 2
3
. C.
ln 2
. D.
1
ln 2
3
.
Lời giải
Ta có:
2
2
1
1
d1 2
ln 3 2 ln 2
3 23 3
x
x
x
= −=
−
∫
.
Câu 35: Tính tích phân
2
1
1
d
x
Ix
x
−
=
∫
.
A.
1 ln 2
I
= −
. B.
7
4
I =
. C.
1 ln 2
I = +
. D.
2ln 2I
=
.
Lời giải
Ta có
2
1
1
d
x
Ix
x
−
=
∫
2
1
1
1dx
x
= −
∫
( )
2
1
lnxx= −
( ) ( )
2 ln 2 1 ln1= − −−
1 ln 2= −
.
Câu 36: Biết
3
1
2
ln ,
x
dx a b c
x
+
= +
∫
với
, , , 9.abc c∈<
Tính tổng
.
S abc=++
A.
7S =
. B.
5S =
. C.
8S =
. D.
6S
=
.
Lời giải
Ta có
3 3 33
3
1
1 1 11
22 2
1 2 2ln 2 2ln 3.
x
dx dx dx dx x
xx x
+
=+=+=+ =+
∫ ∫ ∫∫
Do đó
2, 2, 3 7.abc S= = =⇒=
Câu 37: Tích phân
1
0
1
d
1
Ix
x
=
+
∫
có giá trị bằng
A.
ln 2 1−
. B.
ln 2−
. C.
ln 2
. D.
1 ln 2−
.
Lời giải
Chọn C
Cách 1: Ta có:
11
1
0
00
1 d( 1)
d ln 1 ln 2 ln1 ln 2
11
x
Ix x
xx
+
= = = += − =
++
∫∫
. Chọn đáp án C.
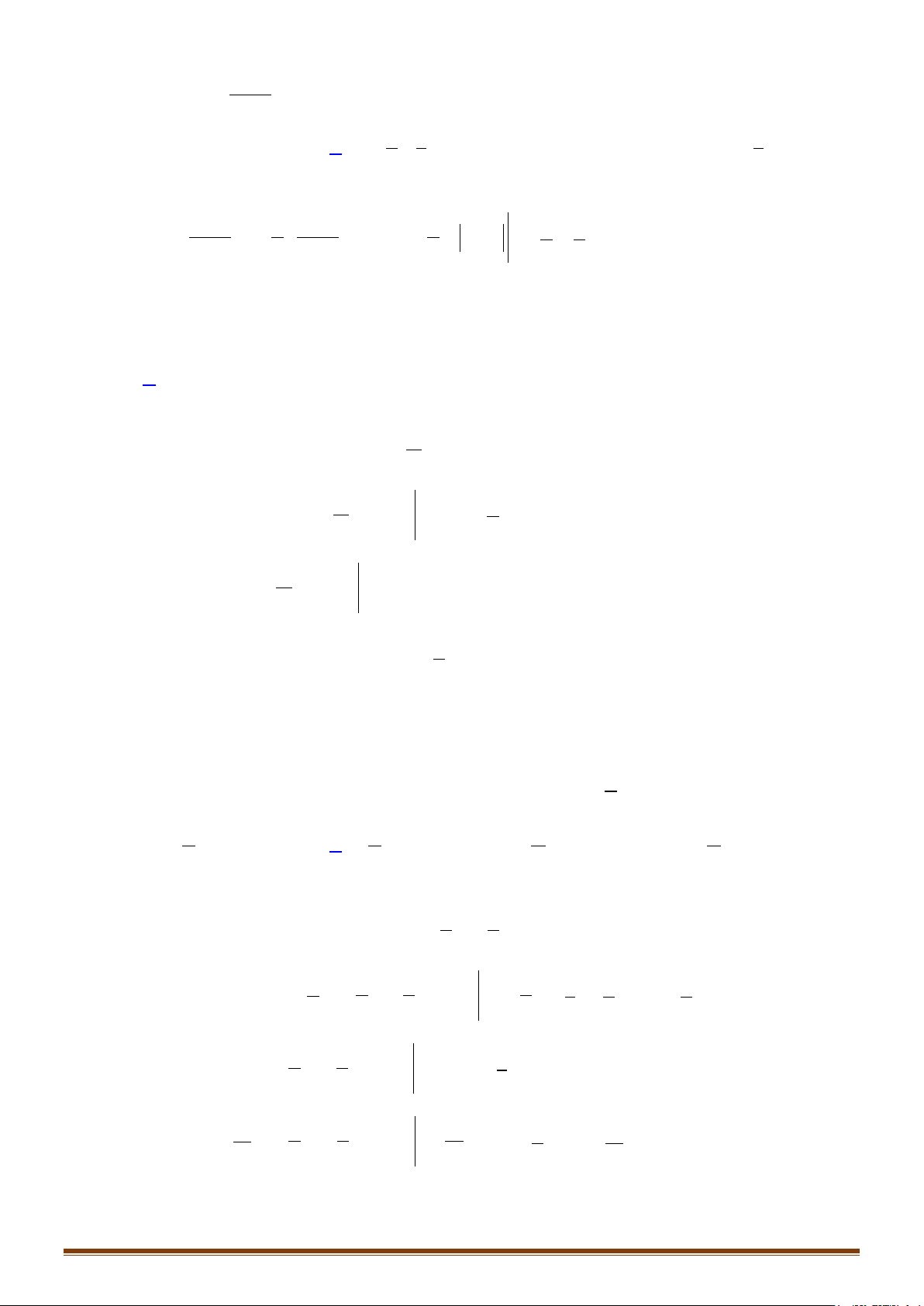
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 10
Câu 38: Tính
3
2
2
d
1
x
Kx
x
=
−
∫
.
A.
ln 2
K =
. B.
18
ln
23
K =
. C.
2ln 2K =
. D.
8
ln .
3
K =
Lời giải
3
2
2
d
1
x
Kx
x
=
−
∫
(
)
3
2
2
2
11
d1
21
x
x
= −
−
∫
2
3
1
ln 1
2
2
x= −
18
ln
23
=
Câu 39: Biết rằng hàm số
( )
f x mx n= +
thỏa mãn
( )
1
0
d3
fx x
=
∫
,
( )
2
0
d8fx x
=
∫
. Khẳng định nào dưới
đây là đúng?
A.
4
mn
+=
. B.
4mn+=−
. C.
2mn+=
. D.
2mn+=−
.
Lời giải
Ta có:
( )
( )
dd
f x x mx n x
= +
∫∫
=
2
C
2
m
x nx++
.
Lại có:
(
)
1
0
d3
fx x=
∫
2
1
3
0
2
m
x nx
⇒ +=
1
3
2
mn⇔ +=
( )
1
.
( )
2
0
d8fx x=
∫
2
2
8
0
2
m
x nx
⇒ +=
2 28
mn⇔ +=
( )
2
.
Từ
( )
1
và
( )
2
ta có hệ phương trình:
1
3
2
2 28
mn
mn
+=
+=
2
2
m
n
=
⇔
=
.
4mn⇒ +=
.
Câu 40: Biết rằng hàm số
( )
2
f x ax bx c= ++
thỏa mãn
( )
1
0
7
d
2
fx x= −
∫
,
( )
2
0
d2fx x= −
∫
và
A.
3
4
−
. B.
4
3
−
. C.
4
3
. D.
3
4
.
Lời giải
Ta có:
( )
( )
2
ddf x x ax bx c x= ++
∫∫
=
32
C
32
ab
x x cx+ ++
.
Lại có:
( )
1
0
7
d
2
fx x= −
∫
32
1
7
0
32 2
ab
x x cx
⇒ ++ =−
11 7
32 2
a bc⇔ + +=−
( )
1
.
( )
2
0
d2fx x= −
∫
32
2
2
0
32
ab
x x cx
⇒ ++ =−
8
22 2
3
abc
⇔ ++=−
( )
2
.
( )
3
0
13
d
2
fx x=
∫
32
3
13
0
32 2
ab
x x cx
⇒ ++ =
9 13
93
22
a bc⇔+ +=
( )
3
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 11
Từ
( )
1
,
(
)
2
và
( )
3
ta có hệ phương trình:
11 7
32 2
8
22 2
3
9 13
93
22
a bc
abc
a bc
+ +=−
++=−
+ +=
1
3
16
3
a
b
c
=
⇔=
= −
.
16 4
13
33
P abc
⇒ = + + =++− =−
.
Câu 41: Cho
( )
1
2
0
42 d= −
∫
I xmx
. Có bao nhiêu giá trị nguyên của
m
để
60+>
I
?
A. 1. B. 5. C. 2. D. 3.
Lời giải
Chọn D
Theo định nghĩa tích phân ta có
( ) ( )
1
1
2 22 2
0
0
42 d 2 2 2 2= − = − =−+
∫
I x m x x mx m
.
Khi đó
22
60 2 260 40 2 2+ > ⇔− + + > ⇔− + > ⇔− < <Im m m
Mà
m
là số nguyên nên
{ }
1; 0;1∈−m
. Vậy có 3 giá trị nguyên của
m
thỏa mãn yêu cầu.
Câu 42: Có bao nhiêu giá trị nguyên dương của
a
để
( )
0
2 3d 4
a
xx−≤
∫
?
A.
5
. B.
6
. C.
4
. D.
3
.
Lời giải
Chọn C
Ta có:
(
)
( )
22
0
0
2 3d 3 3
a
a
x xx x a a
−=−=−
∫
.
Khi đó:
( )
0
2 3d 4
a
xx−≤
∫
⇔
2
34
aa−≤
14a⇔− ≤ ≤
Mà
*a ∈
nên
{ }
1;2;3;4a ∈
.
Vậy có 4 giá trị của
a
thỏa đề bài.
Câu 43: Có bao nhiêu số thực
b
thuộc khoảng
( )
;3
ππ
sao cho
4cos 2 1
b
xdx
π
=
∫
?
A. 8. B. 2. C. 4. D. 6.
Lời giải
Ta có:
4cos 2 1
b
xdx
π
=
∫
2sin 2 1
b
x
π
⇔=
1
sin 2
2
b⇔=
12
5
12
bk
bk
π
π
π
π
= +
⇔
= +
.
Do đó, có 4 số thực
b
thỏa mãn yêu cầu bài toán.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
Câu 44: Cho hàm số
()fx
có
(0) 4
f =
và
2
( ) 2 cos 1,fx x x
′
= + ∀∈
Khi đó
4
0
()
f x dx
∫
π
bằng.
A.
2
16 16
16
ππ
++
. B.
2
4
16
π
+
. C.
2
14
16
ππ
+
. D.
2
16 4
16
ππ
++
.
Lời giải
Chọn D
Ta có
2
1 cos 2
( ) (2cos 1)d 2 1 d cos 2 2 d
2
sin 2
cos2 d 2d 2 .
2
x
fx x x x x x
x
xx x x C
Lại có
sin 2
(0) 4 4 ( ) 2 4.
2
x
f C fx x
4 4 4 44
0 0 0 00
2
2
sin 2 1
()d 2 4d sin2d(2) 2d 4d
24
cos2 16 4
( 4) .
44
4 16
00
π π π ππ
x
f x x x x x x xx x
ππ
x ππ
xx
.
Câu 45: Cho hàm số
( )
fx
có
( )
00f =
và
( )
4
sin , fx x x
′
= ∀∈
. Tích phân
( )
2
0
dfx x
∫
π
bằng
A.
2
6
18
−
π
. B.
2
3
32
−
π
. C.
2
3 16
64
−
π
. D.
2
36
112
−
π
.
Lời giải
Chọn C
Ta có:
( )
2
42
1 cos 2 1
sin 1 2cos 2 cos 2
24
x
x xx
−
= =−+
1 1 cos 4
1 2cos 2
42
x
x
+
=−+
( )
1
cos 4 4cos 2 3
8
xx= −+
.
Suy ra
( ) ( ) ( )
1 1 13
' d cos 4 4cos 2 3 d sin 4 sin 2
8 32 4 8
fx f x x x x x x x xC= = − + = − ++
∫∫
.
Vì
( )
00f =
nên
0C =
hay
( )
1 13
sin 4 sin 2
32 4 8
fx x x x= −+
.
Do đó
( )
2
0
dfx x
∫
π
2
2
2
0
0
1 13 1 1 3
sin 4 sin 2 d cos 4 cos 2
32 4 8 128 8 16
x x xx x x x
= − +=− + +
∫
π
π

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
22
1 1 3 1 1 3 16
128 8 64 128 8 64
−
=−−+ −−+=
ππ
.
TÍCH PHÂN HÀM SỐ HỮU TỶ
Tính
( )
( )
b
a
Px
I dx
Qx
=
∫
? với
( )
Px
và
( )
Qx
là các đa thức không chứa căn.
Nếu bậc của tử
(
)
Px
≥
bậc mẫu
(
)
Qx
PP
→
chia đa thức.
Nếu bậc của tử
(
)
Px
<
bậc mẫu
( )
Qx
mà mẫu số phân tích được thành tích số
PP
→
đồng nhất thức để đưa thành tổng của các phân số.
Một số trường hợp đồng nhất thức thường gặp:
+
( )(
)
11ab
ax m bx n an bm ax m bx n
= −
++ − ++
(
)
1
+
( )( )
( ) ( )
( )( )
AB m
A B x Ab Ba
mx n A B
Ab Ba n
xaxb xa xb xa xb
+=
+−+
+
=+= ⇒
+=−
−− − − −−
.
+
( )
( )
( )
22
1 A Bx C
xm
x m ax bx c ax bx c
+
= +
−
− ++ ++
với
2
40b ac∆= − <
.
+
(
) ( )
(
) (
)
22 2 2
1
ABCD
xa xb
xa xb xa xb
=+ ++
−−
−− − −
.
Nếu bậc tử
( )
Px
<
bậc mẫu
(
)
Qx
mà mẫu không phân tích được thành tích số, ta xét một
số trường hợp thường gặp sau:
+
( )
( )
1
22
, * .tan
n
PP
dx
I nN xa t
xa
= ∈ → =
+
∫
.
+
( )
2
2
2
x
,0
24
dx d
I
ax bx c
b
ax
aa
= ∆< =
++
∆
+ +−
∫∫
. Ta sẽ đặt
tan
24
b
xt
aa
∆
→ + = −
.
+
3
2
.
px q
I dx
ax bx c
+
=
++
∫
với
2
40b ac
∆= − <
. Ta sẽ phân tích:
( )
2
3
22
2
.
.
22
I
A
ax b dx
p b p dx
Iq
a ax bx c a ax bx c
+
= +−
++ ++
∫∫
và giải A bằng cách đặt
t
=
mẫu số.
Câu 46: Biết
( )( )
2
1
d
ln 2 ln 3 ln 5
12 1
x
abc
xx
= ++
++
∫
. Khi đó giá trị
abc++
bằng
A.
3−
. B.
2
. C.
1
. D.
0
.
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
Ta có:
( )( )
22
11
d 21
d
121 21 1
x
x
x x xx
= −
+ + ++
∫∫
22
11
11
2d d
21 1
xx
xx
= −
++
∫∫
22
1
2. ln 2 1 ln 1
11
2
xx= +− +
( )
( )
22
ln 2 1 ln 1
11
xx
= +− +
( )
ln 5 ln 3 ln 3 ln 2=−− −
ln 2 2ln 3 ln 5=−+
.
Do đó:
1, 2, 1ab c= =−=
. Vậy
( )
1 2 10abc+ + =+− + =
.
Câu 47: Biết
( )
0
2
1
3 51 2
ln , ,
23
xx
I dx a b a b
x
−
+−
= =+∈
−
∫
. Khi đó giá trị của
4ab+
bằng
A.
50
B.
60
C.
59
D.
40
Lời giải
Chọn C
Ta có
00
2
2
11
0
3 5 1 21 3
3 11 11 21.ln 2
1
2 22
xx
I dx x dx x x x
xx
−−
+−
= = ++ = + + −
−
−−
∫∫
2 19
21.ln
32
= +
. Suy ra
19
21,
2
ab= =
. Vậy
4 59ab
+=
Câu 48: Biết
2
1
0
21
ln 2
1
x
dx n
xm
−−
= +
+
∫
, với
,mn
là các số nguyên. Tính
mn+
.
A.
1
S =
. B.
S4=
. C.
S5= −
. D.
S1= −
.
Lời giải
Chọn A
1
22
1 11
1
0
0 00
0
2 ( 1) 1
( 1) ln | 1| ln 2
1 12 2
2, 1 1
x dx x
dx x dx x
xx
m n mn
− −−
= − − = − += −
++
⇒ = =−⇒ + =
∫∫∫
Câu 49: Tích phân
( )
2
1
2
0
1
d ln
1
x
I xa b
x
−
= = −
+
∫
trong đó
a
,
b
là các số nguyên. Tính giá trị của biểu thức
ab+
.
A.
1
. B.
0
. C.
1−
. D.
3
.
Lời giải
Ta có
( )
( ) (
)
2
1 1 11
1
1
22
22 2
0
0
0 0 00
1
21
d 1 d d d 1 ln 1 1 ln 2
11 1
x
x
I x xx x x x
xx x
−
= = − = − += − + =−
++ +
∫ ∫ ∫∫
1
3
2
a
ab
b
=
⇒ ⇒+=
=
.
Câu 50: Biết
5
2
3
1
d ln
12
xx b
xa
x
++
= +
+
∫
với
a
,
b
là các số nguyên. Tính
2Sa b
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
A.
2S =
. B.
2S = −
. C.
5S
=
. D.
10
S =
.
Lời giải
5
55
22
33
3
11 3
d d ln 1 8 ln
1 12 2
xx x
xx x x
xx
++
=+ =++=+
++
∫∫
8
3
a
b
=
⇒
=
22
Sa b
⇒=− =
.
Câu 51: Cho
2
2
1
10
d ln
1
xa
xx
x bb
+=+
+
∫
với
,ab∈
. Tính
?
Pab
= +
A.
1P =
. B.
5P =
. C.
7P =
. D.
2P =
.
Lời giải
Ta có
22 2
22 2
11 1
11 1
d d 1d
11 1
xx
x xx xx x
xx x
+−
+ = + = +−
++ +
∫∫ ∫
2
3
1
10 10 2 10
ln 1 ln 2 ln 3 ln ln
3 3 33
xa
xx
bb
=+−+=+−=+=+
.
Suy ra
2; 3ab= =
. Vậy
5ab+=
.
Câu 52: Cho
3
2
1
3
ln 2 ln 3 ln 5
32
x
dx a b c
xx
+
= ++
++
∫
, với a, b, c là các số nguyên. Giá trị của
abc++
bằng
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
( )( )
( )
3 3 33
2
1 1 11
3 3 21
321212
3
2ln 1 ln 2 2ln 2 ln 3 ln 5
1
xx
dx dx dx dx
xxxxxx
xx
++
= = −
++++++
= +− + = + −
∫ ∫ ∫∫
Suy ra
2, 1, 1a bc= = = −
.
Nên
211 2abc+ + = +−=
.
Câu 53: Cho
4
2
3
58
d ln 3 ln 2 ln 5
32
−
=++
−+
∫
x
xa b c
xx
, với
, , abc
là các số hữu tỉ. Giá trị của
3
2
−+a bc
bằng
A.
12
B.
6
C.
1
D.
64
Lời giải
Chọn D
Ta có:
4
2
3
58
d
32
−
=
−+
∫
x
Ix
xx
( )( )
4
3
58
d
12
−
=
−−
∫
x
x
xx
( ) ( )
( )( )
4
3
3 22 1
d
12
−+ −
=
−−
∫
xx
x
xx
4
3
32
d
12
= +
−−
∫
x
xx
( )
4
3ln 1 2ln 2 3ln3 2 ln 2 3ln 2 3ln 3 ln 2 0.ln 5
3
= −+ − = + − = − +xx
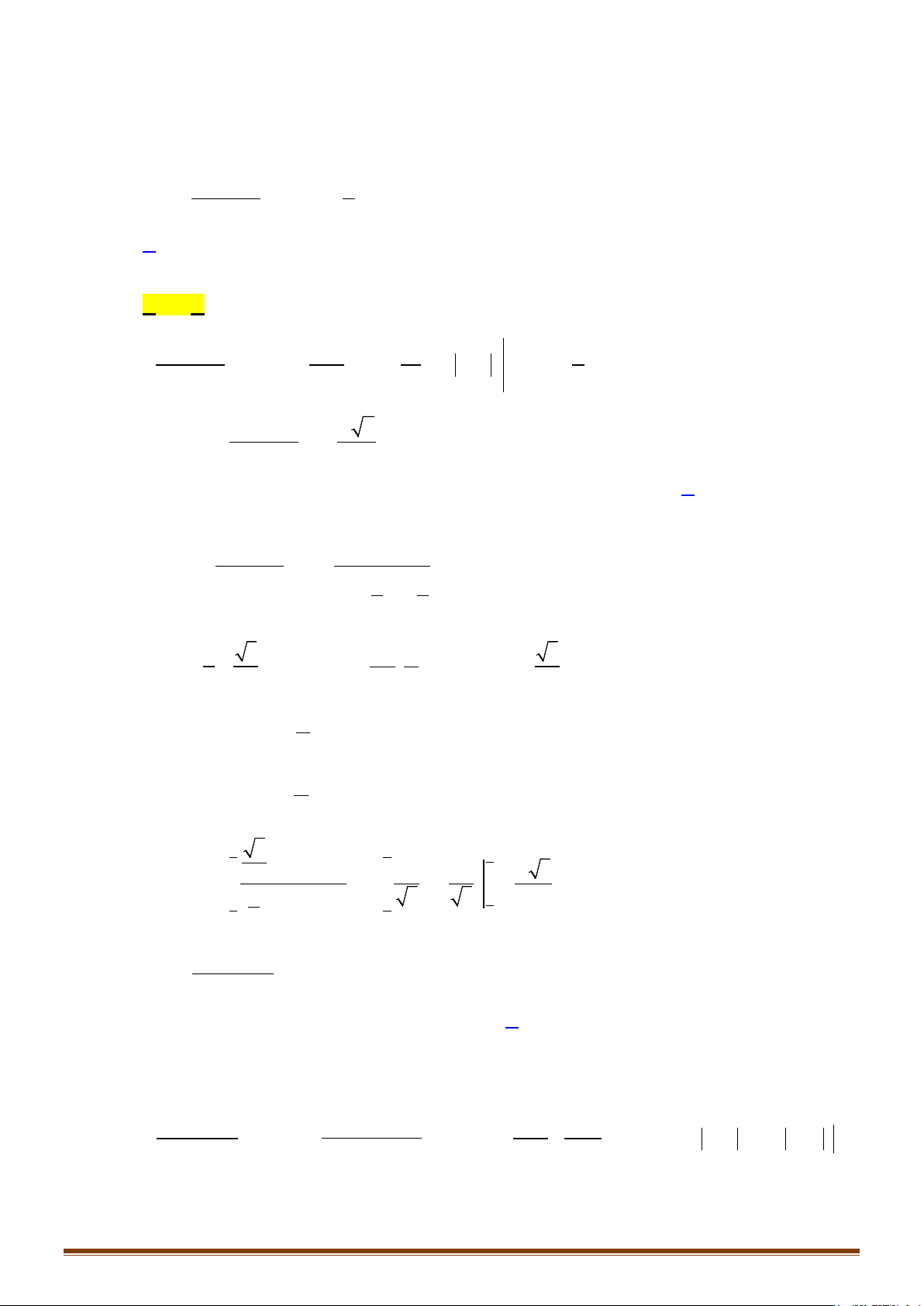
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
Suy ra
36
3
1 2 2 64
0
−+
=
=−⇒ = =
=
a bc
a
b
c
.
Câu 54: Biết
5
2
3
1
d ln
12
xx b
xa
x
++
= +
+
∫
với
a
,
b
là các số nguyên. Tính
2Sa b
.
A.
2S
=
. B.
2S = −
. C.
5
S
=
. D.
10S =
.
Lời giải
Chọn A
5
55
22
33
3
11 3
d d ln 1 8 ln
1 12 2
xx x
xx x x
xx
++
=+ =++=+
++
∫∫
8
3
a
b
=
⇒
=
22
Sa b⇒=− =
.
Câu 55: Biết rằng
1
2
0
1
d
1
a
x
xx b
π
=
++
∫
( )
, , 10ab a∈<
. Khi đó
ab+
có giá trị bằng
A.
14
. B.
15
. C.
13
. D.
12
.
Lời giải
Xét
11
2
2
00
11
dd
1
13
24
Ix x
xx
x
= =
++
++
∫∫
.
Đặt
13
tan
22
xt+=
, với
,
22
t
ππ
−
∈
. Khi đó
( )
2
3
d 1 tan dt
2
xt= +
.
Với
0x =
, ta có
6
t
π
=
.
Với
1x
=
, ta có
3
t
π
=
.
Khi đó
( )
( )
2
33
3
2
6
66
3
1 tan
22 3
2
dt dt=
3
9
33
1 tan
4
t
It
t
ππ
π
π
ππ
π
+
= = =
+
∫∫
. Từ đó suy ra
3
12
9
a
ab
b
=
⇒+=
=
.
Câu 56: Biết
2
2
2
0
52
d ln 3 ln 5
43
xx
x ab c
xx
++
=++
++
∫
,
( )
,,abc∈
. Giá trị của
abc
bằng
A.
8−
. B.
10
−
. C.
12−
. D.
16
.
Lời giải
Ta có:
2
2
2
0
52
d
43
xx
x
xx
++
++
∫
( )( )
2
0
1
1d
13
x
x
xx
−
= +
++
∫
2
0
12
1d
13
x
xx
=−+
++
∫
( )
2
0
ln 1 2 ln 3xx x= − ++ +
2 3ln 3 2ln 5=−+
.
Vậy
2, 3, 2ab c= =−=
, do đó
12abc = −
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
Câu 57: Giả sử rằng
0
2
1
3 51 2
ln
23
xx
dx a b
x
−
+−
= +
−
∫
. Khi đó, giá trị của
2ab+
là
A.
30
. B.
60
. C.
50
. D.
40
.
Lời giải
Ta có:
00
2
11
3 5 1 21
3 11
22
xx
I dx x dx
xx
−−
+−
= = ++
−−
∫∫
0
2
1
3 19
11 21.ln 2 21.ln 2 21.ln 3
22
x
I xx
−
⇒= + + − = + −
2 19
21ln
32
I⇒= +
21
19
2
a
b
=
⇒
=
2 40ab⇒+ =
.
Câu 58: Biết
4
32
2
1
73
d ln 5
3
xx x a
xc
xx b
+++
= +
−+
∫
với
a
,
b
,
c
là các số nguyên dương và
a
b
là phân số tối
giản. Tính
23
P ab c=−−
.
A.
5−
. B.
4
−
. C. 5. D. 0.
Lời giải
Ta có
4
32
2
1
73
d
3
xx x
x
xx
+++
=
−+
∫
( )
4
2
1
32 1
2d
3
x
xx
xx
−
++
−+
∫
( )
4
2
4
4
22
2
1
1
1
d3
1 27 27
2 3 3ln 3 3ln 5
2 32 2
xx
x x xx
xx
−+
= + + = + −+ = +
−+
∫
.
Mà
4
32
2
1
73
d ln 5
3
xx x a
xc
xx b
+++
= +
−+
∫
, suy ra
27a =
,
2
b =
,
3
c
=
.
Vậy
23
4P ab c
=−−=−
.
Câu 59: Cho
1
2
2
0
4 15 11
d ln 2 ln 3
2 52
xx
x ab c
xx
++
=++
++
∫
với
a
,
b
,
c
là các số hữu tỷ. Biểu thức
.
T ac b= −
bằng
A.
4
. B.
6
. C.
1
2
−
. D.
1
2
.
Lời giải
Ta có
11 1
22
22 2
00 0
4 15 11 (4 10 4) (5 7) 5 7
d d2 d
2 52 2 52 2 52
xx xx x x
x xx
xx xx xx
+ + + ++ + +
= = +
++ ++ ++
∫∫ ∫
1
0
1
13 3 5
2 d 2 ln | 2 | ln | 2 1| 2 ln 2 ln 3
0
22 1 2 2
xx x x
xx
= + + = + ++ + =− +
++
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
Vậy
2a
=
,
1b = −
,
5
2
c
=
nên
6T =
.
Câu 60: Biết
1
2
0
21
d ln 2
1
x
xn
xm
−−
= +
+
∫
, với
m
,
n
là các số nguyên. Tính
S mn= +
.
A.
1
S = −
. B.
5
S
= −
. C.
1
S =
. D.
4S =
.
Lời giải
Chọn C
Ta có:
1
2
0
2
d
1
x
x
x
−
+
∫
1
0
1
1d
1
xx
x
= −−
+
∫
1
2
0
ln 1
2
x
xx
= −− +
1
ln 2
2
−
= −
.
Suy ra
2m =
;
1n
= −
. Vậy
1S =
.
Câu 61: Cho
1
2
0
1
d ln 2 ln 3
32
xa b
xx
= +
++
∫
, với
,ab
là các số hữu tỷ. Khi đó
ab+
bằng
A.
0
. B.
2
. C.
1
. D.
1−
.
Lời giải
Chọn C
Xét
( )( )
11 1
2
00 0
1
1 1 11 1
d d d ln 2ln 2 ln 3.
0
32 1 2 1 2 2
x
xx x
xx x x x x x
+
= =−= =−
++ + + + + +
∫∫ ∫
Vậy
2, 1 1.
a b ab
= =−⇒ + =
Câu 62: Cho
1
2
2
0
23
d ln 2 ln 3
32
xx
x ab c
xx
+
=++
++
∫
với
a
,
b
,
c
là các số nguyên. Tổng
abc
++
bằng
A.
3
. B.
2
. C.
1
. D.
1−
.
Lời giải
Chọn C
Ta có:
1
2
2
0
23
d
32
xx
x
xx
+
++
∫
1
2
0
34
2d
32
x
x
xx
+
= −
++
∫
1
0
12
2d
12
x
xx
=−−
++
∫
( )
1
0
2 ln 1 2ln 2xx x= − +− +
2 ln 2 2ln 3
=+−
.
Suy ra
2a =
;
1b =
;
2c = −
.
Vậy
1abc++=
.
Câu 63: Cho biết
2
2
0
1
ln 5 ln 3
43
x
dx a b
xx
, với
,ab
. Tính
22
Ta b
bằng
A.
13.
B.
10.
C.
25.
D.
5.
Lời giải
Chọn A

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 19
Ta có:
2
11
431313
x x AB
xxxxxx
11
1, 2
13
31
xx
AB
xx
xx
22
2
00
22
1 12
ln 1 2 ln 3 ln 3 2ln 5 2ln 3
00
43 1 3
2ln 5 3ln 3 ln 5 ln 3
2, 3 13.
x
dx dx x x
xx x x
ab
ab T
Câu 64: Biết
2
2
2
0
52
d ln 3 ln 5
43
xx
x ab c
xx
++
=++
++
∫
,
( )
,,abc∈
. Giá trị của
abc
bằng
A.
8−
. B.
10−
. C.
12−
. D.
16
.
Lời giải
Chọn C
Ta có:
22 2
2
22
00 0
52 1 1 2
d1 d1 d
43 43 1 3
xx x
xx x
xx xx x x
++ − −
=+ =++
++ ++ + +
∫∫ ∫
( )
2
0
ln 1 2ln 3 2 2ln 5 3ln 3 ln 3 ln 5x x x ab c
=−++ +=+−=++
.
2
3 . . 12
2
a
b abc
c
=
⇒ =−⇒ =−
=
.
Câu 65: Biết
4
32
2
1
73
d ln 5
3
xx x a
xc
xx b
+++
= +
−+
∫
với
,a
,b
c
là các số nguyên dương và
a
b
là phân số tối giản.
Tính giá trị của
23
P ab c
=−−
.
A.
5−
. B.
3−
. C.
6
. D.
4−
.
Lời giải
Chọn D
Ta có
( )
44
32
22
11
32 1
73
d2 d
33
x
xx x
xx x
xx xx
−
+++
= ++
−+ −+
∫∫
( )
4
2
2
1
2 3ln 3
2
x
x xx
= + + −+
27
3ln 5
2
= +
.
Vậy
23
4P ab c=−−=−
.
Câu 66: Cho
( )(
)
3
2
d
ln 2 ln 3 ln 5
12
x
abc
xx
= ++
++
∫
với
,,abc
là các số hữu tỉ. Giá trị của
23
ab c+−
bằng
A.
3
. B.
6
. C.
5
. D.
4
.
Lời giải
Chọn B
Ta có
( )( )
33
22
d 11
12 1 2
x
dx
xx x x
= −
++ ++
∫∫
3
2
1
ln
2
x
x
+
=
+
43
ln ln
54
= −
4ln 2 ln 3 ln 5= −−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
Suy ra
4, 1, 1
ab c= =−=−
. Vậy
23
6
ab c
+−=
.
Câu 67: Cho
4
2
3
23
d ln 2 ln 3 ln 7
3
x
xa b c
xx
+
= ++
+
∫
với
, , abc∈
. Giá trị của
237abc
++
bằng
A.
9−
. B.
6
. C.
15
. D.
3
.
Lời giải
Chọn D
Ta có:
( )
( )
( )
( )
44 4
4
2
3
33 3
3
23 1 1
d d d ln 3 ln 28 ln18
3 .3 3
xx
x
x x x xx
x x xx x x
++
+
= =+ = +=−
++ +
∫∫ ∫
14
ln ln14 ln 9 ln 2 2ln 3 ln 7
9
= = −=− +
.
1a⇒=
,
2b = −
,
1c =
.
Vậy
2373abc++=
.
Câu 68: Cho
( )
2
2
1
.ln 2 .ln 3
1
x
dx a b c
x
=++
+
∫
, với
,,abc
là các số hữu tỷ. Giá trị
6abc++
bằng:
A.
2−
. B.
1
. C.
2
. D.
1−
.
Lời giải
Chọn D
Ta có
( )
( )
22
22
11
2
11 1 1
ln 1 ln 2 ln 3
1
1 16
11
x
dx dx x
xx
xx
= − = ++ =−− +
++
++
∫∫
.
1
, 1, 1
6
a bc⇒=− =− =
, nên
61abc++=−
.
Câu 69: Biết
3
2
2
5 12
d ln 2 ln 5 ln 6
56
x
xa b c
xx
+
=++
++
∫
. Tính
32S a bc=++
.
A.
11−
. B.
14−
. C.
2−
. D.
3
.
Lời giải
Chọn A
Ta có
( )
33
2
22
3
5 12 2 3
d d 2 ln 2 3ln 3
2
56 2 3
x
x xx x
xx x x
+
= + = ++ +
++ + +
∫∫
( ) ( )
2ln 5 3ln 6 2ln 4 3ln 5 4ln 2 ln 5 3ln 6= + − + =− −+
.
4, 1, 3abc⇒=− =− =
.
Do đó
3 2 12 2 3 11S a bc⇒ = + +=− −+=−
.
TÍCH PHÂN ĐỔI BIẾN
Tích phân đổi biến:
( ) ( ) ( ) ( ) ( )
.' .
b
a
b
f x u xdx Fux Fub Fua
a
= = −
∫
.
Có sẵn Tách từ hàm Nhân thêm

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 21
Các bước tính tích phân đổi biến số
Bước 1. Biến đổi để chọn phép đặt
( )
(
)
'.t u x dt u x dx
= ⇒=
Bước 2. Đổi cận:
( )
( )
t ub
xb
xa
t ua
=
=
⇒
=
=
Bước 3. Đưa về dạng
(
)
(
)
( )
.
ub
ua
I f t dt
=
∫
đơn giản hơn và dễ tính toán.
Một số phương pháp đổi biến số thường gặp
Đổi biến dạng 1.
( )
( )
( ) ( )
( )
( )
( )
1
2
'
. . ..
b bb
a aa
I
I
fx gx
I dx h x dx f g x dx
gx gx
= = +
∫ ∫∫
với
Đổi biến dạng 2.
Nghĩa là nếu gặp tích phân chứa căn thức thì có khoảng
80%
sẽ đặt
t =
căn trừ một số trường
hợp ngoại lệ sau:
1/
(
)
22
1
. .I f a x x dx= −
∫
→
đặt
.sinxa t=
hoặc
.cosxa t
=
.
Câu 70: Cho tích phân
( )
1
7
5
2
0
d
1
x
Ix
x
=
+
∫
, giả sử đặt
2
1tx= +
. Tìm mệnh đề đúng.
A.
( )
3
2
5
1
1
1
d
2
t
It
t
−
=
∫
. B.
( )
3
3
5
1
1
d
t
It
t
−
=
∫
. C.
( )
3
2
4
1
1
1
d
2
t
It
t
−
=
∫
. D.
(
)
3
4
4
1
1
3
d
2
t
It
t
−
=
∫
.
Lời giải
Ta có:
2
1tx= +
d 2dt xx⇒=
.
Đổi cận:
0
x =
1t⇒=
.
1x =
2t⇒=
.
( )
1
7
5
2
0
d
1
x
Ix
x
⇒=
+
∫
( )
1
6
5
2
0
.
d
1
xx
x
x
=
+
∫
( )
3
2
5
1
1
1
d
2
t
t
t
−
=
∫
.
Câu 71: Có bao nhiêu số thực
a
để
1
2
0
1=
+
∫
x
dx
ax
.
A.
2
B.
1
C.
0
D.
3
Lời giải
Chọn B
Điều kiện tích phân tồn tại là
[ ]
2
1
0, 0;1
0
<−
+ ≠ ∀∈ ⇒
>
a
ax x
a
chẵn

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 22
Đặt
2
2xdx=+⇒=t a x dt
. Khi đó
2
11
2
2
2
0
2
1
1
1 11
1
ln 1
1
22
1
1
+
=
+=
+
−
===⇔⇔
−
+
+=−
=
+
∫∫
a
a
a
a ea
x dt a
e
dx
ta
ax
a ea
a
e
So sánh điều kiện ta được
2
1
1
=
−
a
e
.
Câu 72: Cho hàm số
(
)
fx
có
( )
10f =
và
(
) ( )
2018
2019.2020. 1 ,f x xx x
′
= − ∀∈
. Khi đó
( )
1
0
dfx x
∫
bằng
A.
2
.
2021
B.
1
.
1011
C.
2
.
2021
−
D.
1
.
1011
−
Lời giải
Chọn C
Cần nhớ:
( ) ( )
df x x fx C
′
= +
∫
và
( )
( )
( )
1
1
d1
1
ax b
ax b x C
a
α
α
α
α
+
+
+ = + ≠−
+
∫
.
Ta có
( ) ( ) ( ) ( )
2018 2018
d 2019.2020. 1 d 2019.2020 1 df x f x x xx x xx x
′
= = −= −
∫∫ ∫
.
Đặt
1ddtx t x= −⇒ =
và
1xt= +
.
Suy ra
( )
(
)
(
)
2018 2019 2018
2019.2020 1 d 2019.2020 dfx t t t t t t
= += +
∫∫
2020 2019
2020 2019
2019.2020 2019 2020
2020 2019
tt
C t tC
= + += + +
.
Từ đó
( ) ( ) (
)
2020 2019
2019 1 2020 1fx x x C= −+ −+
.
Mà
( ) ( ) ( )
2020 2019
1 0 2019 1 1 2020 1 1 0 0.f CC=⇔ −+ −+=⇔=
Suy ra
( ) ( ) (
)
2020 2019
2019 1 2020 1
fx x x= −+ −
.
Vậy
( ) ( ) ( )
( )
( )
1
2021 2020
11
2020 2019
00
0
11
d 2019 1 2020 1 d 2019. 2020.
2021 2020
xx
fx x x x x
−−
= −+ − = +
∫∫
2019 2
1
2021 2021
=−− + =−
.
Câu 73: Biết
1
2
2
0
2 33
dx ln
21
xx
ab
xx
++
= −
++
∫
với
,ab
là các số nguyên dương. Tính
22
Pa b= +
.
A.
13
. B.
5
. C.
4
. D.
10
.
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
Ta có
1
2
2
0
2 33
d
21
xx
Ix
xx
++
=
++
∫
Đặt
1
1
dt dx
tx
xt
=
= +⇒
= −
suy ra
01
12
xt
xt
= ↔=
=↔=
Khi đó
( )
( )
2
2
2
1
2 1 3 13
dt
tt
I
t
− + −+
= =
∫
2
2
2
1
22
dt
tt
t
−+
=
∫
2
2
1
12
2 dt
tt
−+ =
∫
2
1
2
2 lntt
t
−−
3 ln 2= −
.
Suy ra
22
3 2 13P =+=
.
Câu 74: Cho với
m
,
p
,
q ∈
và là các phân số tối giản. Giá trị
mpq
bằng
A.
10
. B.
6
. C.
22
3
. D.
8
.
Lời giải
Chọn C
Ta có
2
31 5 2
1
11
33
x
e ee
. Suy ra
1
3
m
,
5p
và
2q
.
Vậy
1 22
52
33
mpq
.
Câu 75: Biết rằng
( )
2
1
2
0
d
2
x bc
a
xe x e e
+
= −
∫
với
,,abc∈
. Giá trị của
abc
++
bằng
A.
4
. B.
7
. C.
5
. D.
6
.
Lời giải
Ta có:
( )
( )
22 2
11
2 2 2 2 32
00
1
1 11
d d2 .
0
2 22
xx x
xe x e x e e e
++ +
= += = −
∫∫
Nên
1a =
,
3b =
,
2
c =
.
Vậy
6abc++=
.
Câu 76: Biết
( )
2
1
1
ln
ln
e
x
dx ae b
x xx
+
= +
+
∫
với
,ab
là các số nguyên dương. Tính giá trị của biểu thức
22
.T a ab b=−+
A. 3. B. 1. C. 0. D. 8.
Lời giải
Chọn B

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
(
)
( )
( )
2
1
1 11
1
1
1 ln
ln ln ln 1
ln ln ln
e ee
e
x dx x
x
dx dx x x e
xxx xx xx
+
++
= = =+=+
+++
∫ ∫∫
Vậy
1, 1ab= =
nên
22
1.T a ab b=−+=
Câu 77: Biết
( )
2
1
1
2
1
p
x
q
x
x e dx me n
−
+=−
∫
, trong đó
,, ,mnpq
là các số nguyên dương và
p
q
là phân số tối
giản. Tính
T mn pq= +++
.
A.
11T =
. B.
10
T
=
. C.
7T =
. D.
8T =
.
Lời giải
Chọn B
Ta có:
( )
( ) ( )
11
22
11
2
2
2
11
2
2
11
1 21 1 2
x x xx
x x xx
I x e dx x x e dx x e dx xe dx
− − −−
= + = ++ = + +
∫∫ ∫∫
Xét
(
)
1
22 2 2
1
11 1
11 1
2
2
1
222
2
1
1 .. .
1
xx x x
xx x x
x
I x e dx x e dx x e d xx
x
de
x
−− − −
+
=+= = =
−
∫∫ ∫ ∫
( )
22
22
11
11
1
1
2
1
1
22
2
xx x x
xx x x
xe e d x xe xe dx
−− − −
=−=−
∫∫
11
22
2
1
1
11
1
3
22
2
2 41
xx x
xx x
I xe dx xe I xe e
−− −
⇒ + = ⇒= = −
∫
Do
( )
2
1
1
2
1
p
x
q
x
x e dx me n
−
+=−
∫
, trong đó
,, ,mn pq
+
∈
và
p
q
là phân số tối giản
4
1
3
2
m
n
p
q
=
=
⇒
=
=
Khi đó,
413210T mnpq= + + + = +++ =
.
Câu 78: Cho hàm số
( )
y fx=
có đạo hàm trên
đồng thời thỏa mãn
( ) (
)
0 15
ff= =
. Tính tích phân
( )
( )
1
0
d
fx
I f xe x
′
=
∫
.
A.
10I =
B.
5I = −
C.
0I =
D.
5I =
Lời giải
Chọn C
(
)
( )
1
0
d
fx
I f xe x
′
=
∫
( )
( )
( )
( ) ( ) ( )
1
1
10
55
0
0
d0
fx fx f f
e fx e e e e e= = = − =−=
∫
.
Câu 79: Giả sử tích phân
5
1
1
ln 3 ln 5
1 31
I dx a b c
x
= =++
++
∫
. Lúc đó
A.
5
3
abc++=
. B.
4
3
abc++=
. C.
7
3
abc++=
. D.
8
3
abc++=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
Lời giải
Chọn B
Đặt
31tx= +
. Ta có
2
2
31
3
t x dx tdt
= +⇒ =
.
Đổi cận
Ta có
54
12
1 12
.
13
1 31
I dx tdt
t
x
= =
+
++
∫∫
4
2
2
31
t
dt
t
=
+
∫
4
2
21
1
31
dt
t
= −
+
∫
( )
4
2
ln 1
2
3
tt
=−+
42 2
ln 3 ln 5
33 3
=+−
.
Do đó
42 2
;;
33 3
abc= = = −
.
Vậy
4
3
abc++=
.
Câu 80: Biết tích phân
ln 6
0
e
d ln 2 ln 3
1 e3
x
x
x ab c=++
++
∫
, với
a
,
b
,
c
là các số nguyên. Tính
T abc=++
.
A.
1T = −
. B.
0T =
. C.
2T =
. D.
1T =
.
Lời giải
Đặt
2
e3 e32ded
xx x
t t tt x= +⇒ = +⇒ =
.
Đổi cận
ln 6 3
02
xt
xt
= =
⇒
= =
.
Suy ra
ln 6 3
02
e 2d
d
1
1 e3
x
x
tt
x
t
=
+
++
∫∫
( )
3
3
2
2
2
2 d 2 2ln 1
1
tt t
t
=− =−+
+
∫
( ) ( )
6 2ln 4 4 2ln 3=− −−
2
2 4ln 2 2ln 3 4
2
a
b
c
=
=− + ⇒=−
=
.
Vậy
0T =
.
Câu 81: Tích phân
1
0
d
31
x
x +
∫
bằng
A.
4
3
. B.
3
2
. C.
1
3
. D.
2
3
.
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
Đặt
31tx= +
2
31tx⇒= +
2 d 3dtt x⇒=
2
dd
3
t
tx⇒=
Đổi cận:
01
xt
=⇒=
;
12
xt=⇒=
Khi đó
11
00
d 21
.d
3
31
x
tt
t
x
=
+
∫∫
1
0
2
d
3
t=
∫
1
0
2
3
t=
2
3
=
.
Cách khác: Sử dụng công thức
d2x
ax b C
a
ax b
= ++
+
∫
thì
1
1
0
0
d2
31
3
31
x
x
x
= +
+
∫
2
3
=
.
Câu 82: Biết
1
ln
2
1 ln
e
x
dx a b
xx
= +
+
∫
với
,ab
là các số hữu tỷ. Tính
S ab= +
.
A.
1S =
. B.
1
2
S =
. C.
3
4
S =
. D.
2
3
S
=
.
Lời giải
Đặt
2
1 ln ln 1 2
dx
x t x t tdt
x
+ =⇒ = −⇒ =
Đổi cận
11
2
xt
xe t
=→=
=→=
Vậy
( )
( )
2
2
22
3
2
111
1
12
ln 4 2
2 12 2
3 33
1 ln
e
t tdt
xt
dx t dt t
t
xx
−
= = −= − =−
+
∫∫∫
Suy ra
42 2
;
33 3
a b S ab= =−⇒ =+=
Câu 83: Cho tích phân
22
2
0
16 dI xx= −
∫
và
4sinxt=
. Mệnh đề nào sau đây đúng?
A.
( )
4
0
8 1 cos2 dI tt
π
= +
∫
. B.
4
2
0
16 sin dI tt
π
=
∫
.
C.
( )
4
0
8 1 cos 2 dI tt
π
= −
∫
. D.
4
2
0
16 cos dI tt
π
= −
∫
.
Lời giải
Đặt
4sin d 4 cos dx t x tt= ⇒=
.
Đổi cận:
00xt= ⇒=
;
22
4
xt
π
= ⇒=
.
4
2
0
16 16sin .4cos dI t tt
π
= −
∫
4
0
4 cos .4cos dt tt
π
=
∫
4
0
4 cos .4cos dt tt
π
=
∫
4
0
16 cos .cos dt tt
π
=
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 27
Mà vì
0;
4
t
π
∈
thì
cos 0t >
nên khi đó
4
2
0
16 cos dI tt
π
=
∫
( )
4
0
8 1 cos2 dtt
π
= +
∫
.
Câu 84: Biết
5
1
1
dx ln 3 ln 5
1 31
ab c
x
=++
++
∫
(,, )abc Q∈
. Giá trị của
abc++
bằng
A.
7
3
. B.
5
3
. C.
8
3
. D.
4
3
.
Lời giải
Đặt
3x 1t = +
2
31tx⇒= +
2tdt 3dx
⇒=
2
dx tdt
3
⇒=
Đổi cận:
12xt=⇒=
;
54xt=⇒=
5 44
1 22
4
1 2 t 2 1 2 42 2
d dt (1 )dt (t ln t 1) ln 5 ln 3
2
31t 3 1t 3 3 3 3
1 3x 1
x = = − =−+ =− +
++
++
∫ ∫∫
.
42 2
,,
33 3
abc⇒= = =−
4
3
abc⇒++=
.
Câu 85: Cho biết
7
3
3
2
0
d
1
=
+
∫
xm
x
n
x
với
m
n
là một phân số tối giản. Tính
7mn
−
A.
0
. B.
1
. C.
2
. D.
91
.
Lời giải
Đặt
2
3
23 2 2
3d
1 1 3 d 2d d
2
tt
t x t x t t xx xx
= + ⇒=+ ⇒ = ⇒ =
.
Đổi cận:
( )
2
72 2
3 3 2 52
4
3
2
01 1
1
1 3 3 3 141
d .d. d.
2 2 2 5 2 20
1
x t t tt
x t t tt
t
x
−
= = −= − =
+
∫∫ ∫
.
7 141 7.20 1mn
⇒− = − =
.
Câu 86: Biết rằng
1
0
ln 2 ln 3 ln 5
3 53 1 7
dx
abc
xx
= ++
+ ++
∫
, với
,,abc
là các số hữu tỉ. Giá trị của
abc++
bằng
A.
10
3
−
B.
5
3
−
C.
10
3
D.
5
3
Lời giải
Chọn A
1
0
3 53 1 7
dx
A
xx
=
+ ++
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
Đặt
2
31 312 3t x t x tdt dx= +⇒ = +⇒ =
Đổi cận:
0 1; 1 2x tx t=⇒= =⇒=
( )( )
( )
22 2
2
2
1
11 1
2
2 2 23 2
3
2ln 2 3ln 3
3 23 3 2 3 3
56
tdt
t
A dt dt t t
tt t t
tt
−
= = = + = − ++ +
++ ++
++
∫∫ ∫
( ) ( )
2 2 20 4
2ln 4 3ln5 2 ln3 3ln 4 10 ln 2 2 ln 3 3ln 5 ln 2 ln 3 2 ln5
3 3 33
=−++− =− ++ =− + +
Vậy:
20 4 10
2
33 3
abc++=− + +=−
.
Câu 87: Biết
1
ln
2
1 ln
e
x
dx a b
xx
= +
+
∫
với
,ab
là các số hữu tỷ. Tính
S ab= +
.
A.
1S =
. B.
1
2
S =
. C.
3
4
S =
. D.
2
3
S =
.
Lời giải
Chọn D
Đặt
2
1 ln ln 1 2
dx
x t x t tdt
x
+ =⇒ = −⇒ =
Đổi cận
11
2
xt
xe t
=→=
=→=
Vậy
( )
( )
2
2
22
3
2
111
1
12
ln 4 2
2 12 2
3 33
1 ln
e
t tdt
xt
dx t dt t
t
xx
−
= = −= − =−
+
∫∫∫
Suy ra
42 2
;
33 3
a b S ab= =−⇒ =+=
Câu 88: Cho
3
0
ln 2 ln 3
3
42 1
xa
dx b c
x
=++
++
∫
với
a,b,c
là các số nguyên. Giá trị
abc++
bằng:
A.
9
B.
2
C.
1
D.
7
Lời giải
Chọn C

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 29
3
0
2
8 88
2 32 2
6 66
32
42 1
4 2 1 ( 4) 4( 1)
2( 4) 4
06
38
8 16 4 12 44 48 3 11 6
.( 4)
8 8 822
8
3 11 7
( 6 ln ) 12 ln 2 6ln 3
6
24 4 2 3
1
x
dx
x
t xt x
t dt dx
xt
xt
tt t t t t t
I t dt dt dt
ttt
tt
tt
abc
=
++
=+ +⇒ − = +
⇒− =
=⇒=
=⇒=
−+− − + −
= − = = −+−
= −+− =− +
⇒++=
∫
∫ ∫∫
Câu 89: Cho
3
0
d ln 2 ln
42 1
xa
I x b cd
d
x
= =++
++
∫
, với
,,,abcd
là các số nguyên và
a
d
là phân số tối
giản. Giá trị của
abcd+++
bằng
A. 16. B. 4. C. 28. D.
2−
.
Lời giải
Đặt
2
11t x xt= +⇒ = −
d 2dx tt⇒=
Đổi cận:
0 1;xt= →=
32xt
=→=
2
22
23
22
11
1
16 7
.2 d 2 3 d 3 6ln 2 12ln 2 6ln 3.
42 2 3 3
tt
I tt t t t t t t
tt
−
= = − +− = − + − + = − +
++
∫∫
Suy ra
7, 12, 6, 3ab cd
==−==
. Do đó
4.
abcd
+++ =
Câu 90: Tính
3
2
0
d
1
a
xx
Ix
x
+
=
+
∫
.
A.
( )
22
1 11Ia a= + +−
. B.
( )
22
1
1 11
3
Ia a
= + +−
.
C.
(
)
22
1
1 11
3
Ia a
= + ++
. D.
(
)
22
1 11
Ia a= + ++
.
Lời giải
Ta có
( )
2
3
2
22
00 0
1
d d 1d
11
aa a
xx
xx
I x x xx x
xx
+
+
= = = +
++
∫∫ ∫
.
Đặt
2 22
1 1d du x u x uu xx= +⇒ = +⇒ =
.
Đổi cận:
01xu=⇒=
,
2
1xa u a=⇒= +
.
Vậy
( )
2
2
1
1
3
2 22
1
1
1
d 1 11
33
a
a
u
I uu a a
+
+
= = = + +−
∫
.
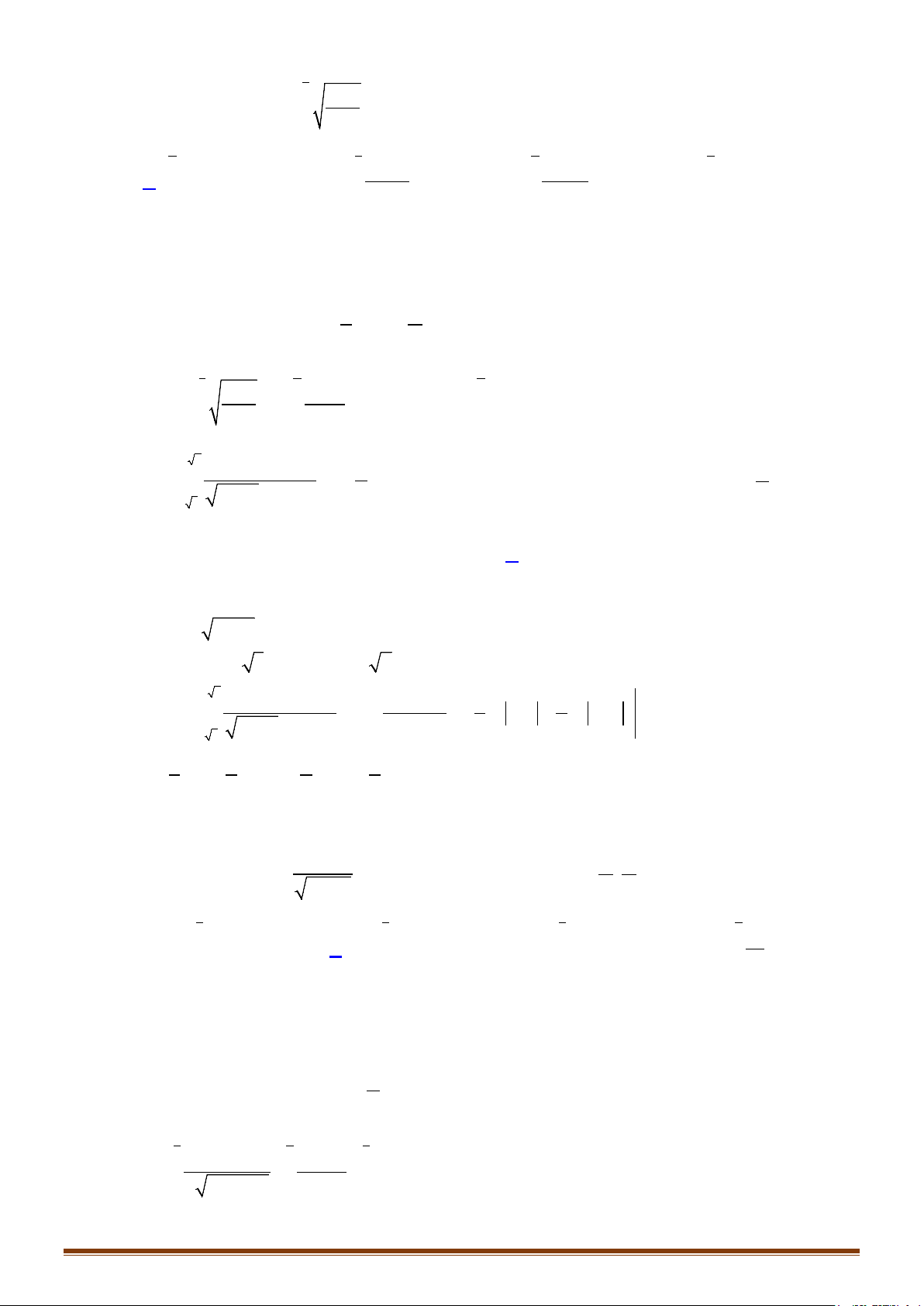
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 30
Câu 91: Giá trị của tích phân
1
2
0
d
1
x
x
x−
∫
bằng tích phân nào dưới đây?
A.
4
2
0
2sin dyy
π
∫
. B.
1
2
2
0
sin
d
cos
x
x
x
∫
. C.
2
4
0
sin
dy
cosy
y
π
∫
. D.
2
2
0
2sin dy
y
π
∫
.
Lời giải
Đặt
2
sinxy=
ta có
( )
2
d d sinxy=
d 2sin .cos dx y yy⇔=
Khi
00xy=⇒=
và
1
24
xy
π
=⇒=
.
Suy ra
1
24
00
sin
d .2sin cos dy
1 cos
xy
x yy
xy
π
=
−
∫∫
4
2
0
2sin dyy
π
=
∫
.
Câu 92: Biết
22
22
3
d ln 5 ln 2
11
xb
xc
a
xx
= −
++ −
∫
với
,,abc
là các số nguyên và phân số
a
b
là tối giản.
Tính
32
P a bc=++
.
A.
11
. B.
12
. C.
14
. D.
13
.
Lời giải
Đặt
2 22
11t x t x xdx tdt= +⇒ = +⇒ =
Đổi cận:
32,223
x tx t= ⇒= = ⇒=
.
Khi đó
3
22 3
2
22
2
2
3
12
ln 1 ln 2
23 3
11
x tdt
dx t t
tt
xx
= = −+ +
+−
++ −
∫∫
12 2 2
ln 2 ln 5 ln 4 ln 5 ln 2
33 3 3
=+− =−
.
Vậy
3, 2, 1 3 2 14a b c a bc
= = =⇒ + +=
.
Câu 93: Cho tích phân
1
2
0
d
4
x
I
x
=
−
∫
nếu đổi biến số
2sin , ;
22
x tt
= ∈−
ππ
thì ta được.
A.
3
0
d
π
It=
∫
. B.
6
0
d
π
It
=
∫
. C.
4
0
d
π
I tt=
∫
. D.
6
0
d
π
t
I
t
=
∫
.
Lời giải
2sin d 2cos dx t x tt
= ⇒=
.
Với
0 0; 1
6
x tx t
π
=⇒= =⇒=
.
6 66
2
0 00
2cos d cos d
d
cos
2 1 sin
π ππ
tt tt
It
t
t
= = =
−
∫ ∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 31
Câu 94: Biết
1
3
2
0
15
1
x ab c
dx
xx
+
=
++
∫
với
, , abc
là các số nguyên và
0
b ≥
. Tính
2
P ab c=+−
.
A.
3
P
=
. B.
7
P =
. C.
7
P = −
. D.
5
P
=
.
Lời giải.
(
)
1 1 11
3
3 2 32 4
2
0 0 00
1
11
5
1
x
I dx x x x dx x x dx x dx A
xx
= = +− = + − =−
++
∫ ∫ ∫∫
+ Tính A: Đặt
2
1 ddt x tt xx=+⇒=
( )
( )
2
22
53
2 2 42
11
1
2 22
1.
5 3 15
tt
A t t dt t t dt
+
=− =−=− =
∫∫
122
2; 2; 1
15
I abc
−+
= ⇒= = =−
2
7
P ab c=+ −=
Câu 95: Cho
n
là số nguyên dương khác
0
, hãy tính tích phân
( )
1
2
0
1d
n
I x xx
= −
∫
theo
n
.
A.
1
22
I
n
=
+
. B.
1
2
I
n
=
. C.
1
21
I
n
=
−
. D.
1
21
I
n
=
+
.
Lời giải
Với
*
n ∈
, khi đó:
Đặt
2
1 d 2dt x t xx=−⇒=−
1
dd
2
xx t⇒=−
Đổi cận:
0 1; 1 0x tx t= →= =→=
Khi đó
01
1
1
0
10
111 1
d d.
2 2 2122
n
nn
t
I tt tt
nn
+
=−== =
++
∫∫
Cách 2: Ta có
( ) (
)
22
1
d1 2d d1 d
2
x xx x xx−=− →− −=
( ) ( ) ( )
( )
1
2
11
1
2 22
0
00
1
1 11
1 d 1 d1 .
2 2122
n
nn
x
I x xx x x
nn
+
−
=− =− − −=− =
++
∫∫
Câu 96: Giả sử
64
3
1
d2
ln
3
x
I ab
xx
= = +
+
∫
với
,ab
là số nguyên. Khi đó giá trị
ab−
là
A.
17−
. B. 5. C.
5−
. D.
17
.
Lời giải
Đặt
6
tx=
6
xt⇒=
5
d 6. dx tt⇒=
.
Đổi cận:
1 1; 64 2x tx t=⇒= = ⇒=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
Suy ra
2
5
32
1
6
d
t
It
tt
=
+
∫
2
3
1
6d
1
t
t
t
=
+
∫
2
2
1
1
6 1d
1
tt t
t
= −+−
+
∫
( )
(
)
22
2
11
1
6 1d 6 d 1
1
tt t t
t
= −+ − +
+
∫∫
2
32
2
1
1
6 6ln 1
32
tt
tt
= −+ − +
( )
85
6 6 ln 3 ln 2
36
= −− −
3
11 6ln
2
= −
2
6ln 11
3
= +
.
Từ đó suy ra
6
11
a
b
=
=
5
ab⇒−=−
.
Câu 97: Cho hàm số
( )
fx
có
( )
22f = −
và
( )
(
)
2
, 6; 6
6
x
fx x
x
′
= ∀∈−
−
. Khi đó
( )
3
0
.dfx x
∫
bằng
A.
3
4
π
−
. B.
36
4
π
+
. C.
2
4
π
+
. D.
36
4
π
+
−
.
Lời giải
Chọn D
Ta có
( )
( ) ( )
2
6; 6 .d .d
6
x
x fx f x x x
x
′
∀∈− ⇒ = =
−
∫∫
( )
2
2
11
.d 6
2
6
x
x
=−−
−
∫
2
1
.2 6
2
xC=− −+
.
Mà
( )
2 2 62 2 0f CC=−⇔− − + =−⇔ =
.
Suy ra
( )
2
6fx x=−−
.
Do đó
(
)
33
2
00
.d 6 .d
I fx x x x= =−−
∫∫
.
Đặt
6 sin , ; 6 cos .d
22
x t t dx t t
ππ
= ∈− ⇒ =
.
Đổi cận
0 0; 3
4
x tx t
π
=⇒= = ⇒=
.
Suy ra
( )
4 44
22
0 00
6 6 sin . 6.cos .d 6 cos .d 3 cos 2 1 .dI t tt tt t t
π ππ
=−− =− =− +
∫ ∫∫
4
0
1
3 sin 2
2
tt
π
=−+
1 36
3 sin
2 24 4
ππ π
+
=− +=−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 33
Câu 98: Biết
2
2
1
d 2 35
3 91
x
x ab c
xx
=++
+−
∫
với
a
,
b
,
c
là các số hữu tỷ, tính
27
P a bc=+ +−
.
A.
1
9
−
. B.
86
27
. C.
2−
. D.
67
27
.
Lời giải
Ta có
2
2
1
d
3 91
x
x
xx+−
∫
(
)
2
2
1
3 9 1dxx x x
= +−
∫
(
)
2
22
1
3 9 1dx xx x=−−
∫
22
22
11
3 d 9 1d
xx x x x=−−
∫∫
2
2
32
1
1
9 1dx xx x=+−
∫
2
2
1
7 9 1d
xx x=+−
∫
.
Tính
2
2
1
9 1dxx x−
∫
.
Đặt
2
91
xt
−=
22
91
xt
⇒ −=
d
d
9
tt
xx⇒=
.
Khi
1x
=
thì
22t =
; khi
2x =
thì
35t =
.
Khi đó
2
2
1
9 1dxx x−
∫
35
35
3
22
22
d
9 27
tt t
t= =
∫
35 16
35 2
27 27
= −
.
Vậy
2
2
1
35 16
d 7 35 2
27 27
3 91
x
x
xx
=−+
+−
∫
7a⇒=
,
16
27
b =
,
35
27
c = −
.
Vậy
27P a bc=+ +−
32 35 1
77
27 27 9
=+ − −=−
.
Câu 99: Biết
( )
2
1
d
11
x
abc
xx x x
=−−
++ +
∫
với
a
,
b
,
c
là các số nguyên dương. Tính
P abc=++
.
A.
44P =
. B.
42
P =
. C.
46
P =
. D.
48P =
.
Lời giải
Đặt
( )
( )
(
)
22
11
dd
11
11
xx
I
xx x x
xx x x
= =
++ +
+ ++
∫∫
.
Đặt
( )
1
1d d
21
xx
txx t x
xx
++
= + +⇒ =
+
( )
dd
2
1
xt
t
xx
⇔=
+
.
Khi
1x =
thì
21t
= +
, khi
2x =
thì
32t = +
.
( )
( )
32
2 32
2
21
1
21
d d1
22
11
xt
I
tt
xx x x
+
+
+
+
= = = −
+ ++
∫∫
11
2
3 2 21
=−−
++
42 23 2=−−
32 12 4=−−
32a⇒=
,
12b =
,
4
c =
Vậy
48P abc=++=

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 34
Câu 100: Biết
( )
4
0
2 1d 5
ln 2 ln , ,
3
2 32 1 3
xx
a b c abc
xx
+
=++ ∈
+ ++
∫
. Tính
2T abc= ++
.
A.
4T =
. B.
2T =
. C.
1
T =
. D.
3T =
.
Lời giải
(
)
( )
( ) ( )
( )( )
44 4
00 0
2211 212d
2 1d 2 1d
2 32 1 3
211 212 211 212
x xx
xx xx
I
xx
xx xx
++ − ++
++
= = =
+ ++
++ ++ ++ ++
∫∫ ∫
( ) ( )
44
00
2d d
212 211
xx
xx
= −
++ ++
∫∫
.
Đặt
21 d du x uu x= +⇒ =
. Với
01xu=⇒=
, với
43xu=⇒=
.
Suy ra
.3 .3 .3 .3
1 11 1
2d d 4 1
2 d1 d
21 2 1
uu uu
I uu
uu u u
= − = − −−
++ + +
∫∫∫ ∫
( )
3
5
4ln 2 ln 1 2 4ln ln 2
1
3
uu u= − ++ + =− +
2a⇒=
,
1b =
,
1c =
2.1 1 4 1T
⇒ = +− =
.
Câu 101: Cho
2
2
0
cos 4
d ln ,
sin 5sin 6
x
xa b
xx c
π
= +
−+
∫
tính tổng
S abc=++
A.
1
S =
. B.
4
S =
. C.
3S =
. D.
0S =
.
Lời giải
Đặt
sin d cos dt x t xx= ⇒=
.
00xt= ⇒=
,
1
2
xt
π
= ⇒=
.
2
2
0
cos
d
sin 5sin 6
x
x
xx
π
−+
∫
1
2
0
1
dt
56tt
=
−+
∫
1
0
11
dt
32tt
= −
−−
∫
1
0
3
ln
2
t
t
−
=
−
3
ln 2 ln
2
= −
4
ln
3
=
1, b 0, 3ac⇒= = =
4
S abc⇒ =++=
.
Câu 102: Cho tích phân
2
0
2 cos .sin dI x xx
π
= +
∫
. Nếu đặt
2 costx= +
thì kết quả nào sau đây đúng?
A.
2
3
dI tt=
∫
. B.
3
2
dI tt=
∫
. C.
2
3
2dI tt=
∫
. D.
2
0
dI tt
π
=
∫
.
Lời giải
Ta có
2
0
2 cos .sin dI x xx
π
= +
∫
( )
2
0
2 cos d cosxx
π
=−+
∫
( )
2
0
2 cos d cos 2xx
π
=−+ +
∫
2
3
dtt= −
∫
3
2
dtt=
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 35
Câu 103: Tính tích phân
2
4
4
0
sin
d
cos
x
Ix
x
π
=
∫
bằng cách đặt
tanux=
, mệnh đề nào dưới đây đúng?
A.
4
2
0
dI uu
π
=
∫
. B.
2
2
0
1
dIu
u
=
∫
. C.
1
2
0
dI uu= −
∫
. D.
1
2
0
dI uu=
∫
.
Lời giải
2
4
4
0
sin
d
cos
x
Ix
x
π
= =
∫
4
2
2
0
1
tan . d
cos
xx
x
π
∫
.
Đặt
tan
ux=
2
1
dd
cos
ux
x
⇒=
.
Đổi cận:
00
xu=⇒=
,
1
4
xu
π
= ⇒=
Suy ra:
1
2
0
d
I uu=
∫
.
Câu 104: Tính tích phân
π
3
3
0
sin
d
cos
x
Ix
x
=
∫
.
A.
5
2
I
=
. B.
3
2
I =
. C.
π9
3 20
I = +
. D.
9
4
I
=
.
Lời giải
Đặt
costx=
d sin dt xx⇒=−
.
Đổi cận:
0
x =
1t
⇒=
;
π1
32
xt= ⇒=
.
Khi đó:
1
2
3
1
1
d
It
t
−
=
∫
1
3
1
2
1
dt
t
=
∫
1
2
1
2
1
2t
−
=
13
2
22
=−+=
.
Câu 105: Cho tích phân
2
3
sin
d ln 5 ln 2
cos 2
x
xa b
x
π
π
= +
+
∫
với
,.ab∈
Mệnh đề nào dưới đây đúng?
A.
2 0.ab+=
B.
2 0.ab
−=
C.
2 0.ab−=
D.
2 0.ab+=
Lời giải
Đặt
cos 2tx= +
d sin dt xx⇒=−
Đổi cận
5
32
xt
π
= ⇒=
,
2
2
xt
π
= ⇒=
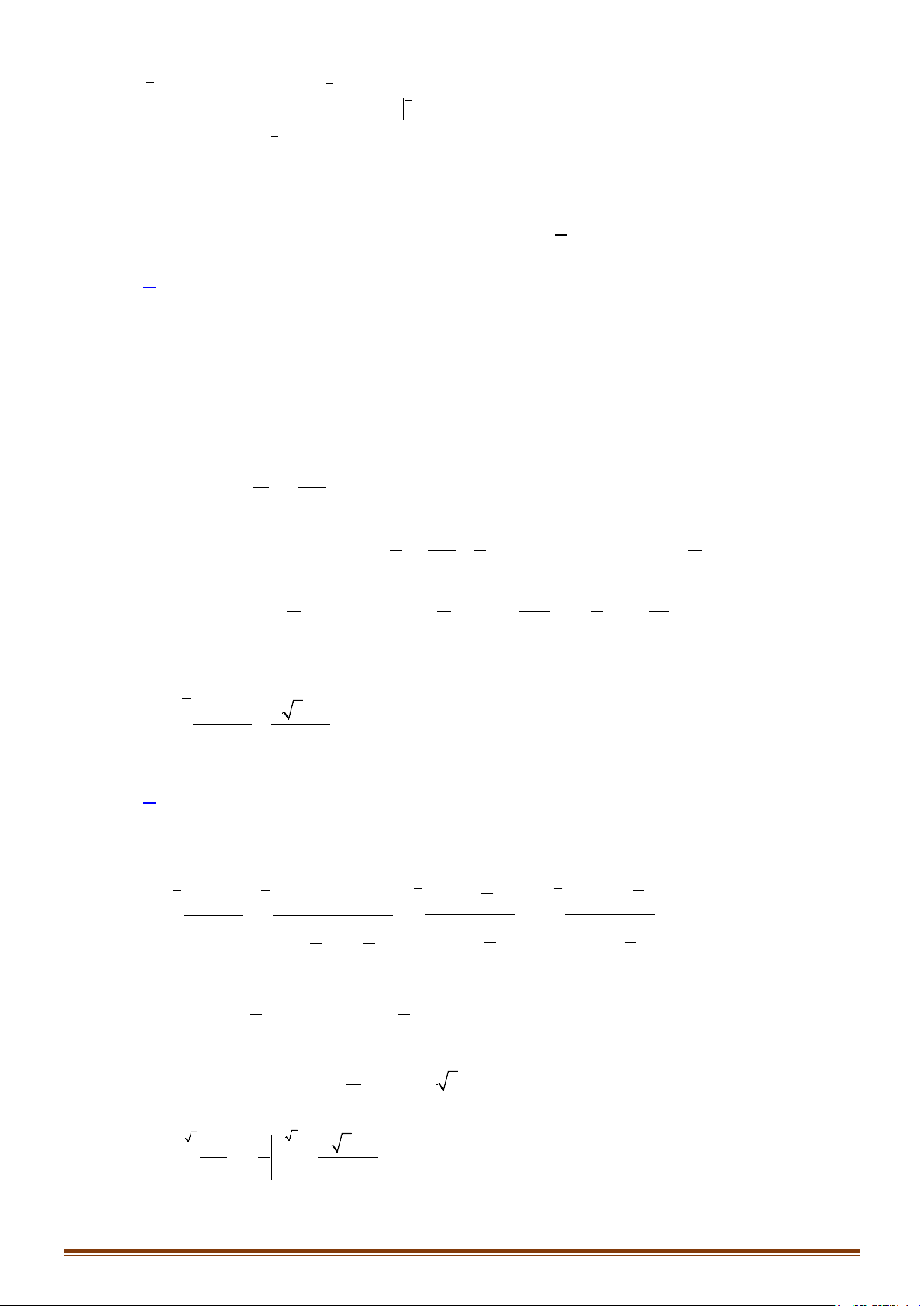
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
2
3
sin
d
cos 2
x
x
x
π
π
+
∫
2
5
2
1
d
t
t
= −
∫
5
2
2
1
dt
t
=
∫
5
2
2
ln
t
=
5
ln ln 2
2
= −
ln 5 2ln 2
= −
Vậy ta được
1; 2ab= = −
.
Câu 106: Có bao nhiêu số
( )
0;20
π
∈a
sao cho
5
0
2
sin sin 2 d
7
a
x xx
=
∫
.
A. 10.
B. 9.
C. 20.
D. 19.
Lời giải
56
00
sin sin 2 d 2 sin .cos d
aa
I x xx x xx
= =
∫∫
Đặt
sin d cos dt x t xx
= ⇒=
và
[ ]
sin ; 1;1
.
sin 0 0
abb
= ∈−
=
77
6
0
0
2
2 d 2. .
77
b
b
tb
I tt= = =
∫
Theo giả thiết:
7
5
0
22 2
sin sin 2 d 1 sin 1 2 ; .
7 77 2
a
b
x xx b a a k k
π
π
=⇒ =⇔=⇔ =⇔= + ∈
∫
( )
39 1 39
0;20 0 2 20 2 .
2 2 244
a kkk
π ππ
π ππ π
∈ ⇔ < + < ⇔− < < ⇔− < <
Mà
k ∈
nên suy ra
{ }
0;1;2;...;9 .k ∈
Câu 107: Biết
6
0
d3
1 sin
x ab
xc
π
+
=
+
∫
, với
,,
ab c
+
∈∈
và
,,abc
là các số nguyên tố cùng nhau. Giá trị
của tổng
abc
++
bằng
A.
5
. B.
12
. C.
7
. D.
1−
.
Lời giải
66
2
00
dd
1 sin
cos sin
22
xx
I
x
xx
ππ
= =
+
+
∫∫
2
2
66
22
00
1
1 tan
cos
2
2
dd
1 tan 1 tan
22
x
x
xx
xx
ππ
+
= =
++
∫∫
.
Đặt
2
1 tan 2d 1 tan d
22
xx
t tx
=+ ⇒=+
Đổi cận:
0 1; 3 3
6
x tx t
π
=⇒= = ⇒=−
.
33
33
2
1
1
2dt 2 3 3
3
I
tt
−
−
−+
= =−=
∫
.
Suy ra
1, 3, 3a bc=−= =
nên
5abc++=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 37
Câu 108: Cho tích phân số
2
3
sin
d ln 5 ln 2
cos 2
x
xa b
x
π
π
= +
+
∫
với
,ab∈
. Mệnh đề nào dưới đây đúng?
A.
2 0.ab+=
B.
2 0.ab−=
C.
2 0.ab−=
. D.
2 0.ab+=
.
Lời giải
+ Xét:
2
3
sin
d
cos 2
x
Ix
x
π
π
=
+
∫
+ Đặt
2 d sin d sin d d
u cosx u xx xx u= +⇒ =− ⇒ =−
+ Đổi cận:
5
32
2
2
xu
xu
π
π
= ⇒=
= ⇒=
2
5
2
2
1
15
d ln ln 2 ln ln 5 2ln 2 .
5
2
2
2
a
I uu
b
u
=
−
⇒= =− =− − = − ⇒
= −
∫
Câu 109: Cho
2
2
0
sin 4
d ln
cos 5cos 6
x
xa b
xx c
= +
−+
∫
π
, với
a
,
b
là các số hữu tỉ,
0c >
. Tính tổng
S abc
=++
.
A.
3S =
. B.
0S
=
. C.
1
S =
. D.
4S =
.
Lời giải
Đặt
costx=
d sin dt xx⇒=−
.
Đổi cận:
0x =
1t⇒=
;
2
x
π
=
0t⇒=
Ta có:
( )
2
2
0
sin
d
cos 5cos 6
x
x
xx
π
−+
∫
0
2
1
1
d
56
t
tt
= −
−+
∫
1
0
11
d
32
t
tt
= −
−−
∫
1
0
3
ln
2
t
t
−
=
−
3
ln 2 ln
2
= −
4
ln
3
=
4
lnab
c
= +
.
Do đó:
1
3
0
a
c
b
=
=
=
.
Vậy
S abc=++
4=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 38
Câu 110: Cho hàm số
()y fx=
có
(0) 1f =
và
3
( ) tan tan ,
fx x x x
′
= + ∀∈
. Biết
4
0
() ;,
a
f x dx a b
b
π
π
+
= ∈
∫
, khi đó
ba
−
bằng
A.
4
. B.
12
. C.
0
. D.
4−
.
Lời giải
Chọn A
Từ giả thiết
3
( ) tan tan ,fx x x x
′
= + ∀∈
ta có
3
( ) ( ) (tan tan )
f x f x dx x x dx
′
= = +
∫∫
2
tan (1 tan )x x dx= +
∫
tan . (tan )xd x=
∫
2
1
tan
2
xC
= +
,
Ta có
(0) 1f
=
suy ra
1C =
vậy
2
1
( ) tan 1
2
fx x= +
.
Tích phân
44
2
00
1
( ) (tan 2)
2
f x dx x dx
ππ
= +
∫∫
4
4
2
0
0
1 1 14
(tan 1 1) (tan ) (1 )
2 2 24 8
x dx x x
π
π
ππ
+
= ++ = + = + =
∫
.
Từ đây ta được
4
4
8
a
ba
b
=
⇒−=
=
.
Vậy
4
ba−=
.
Câu 111: Cho tích phân
e
1
3ln 1
d
x
Ix
x
+
=
∫
. Nếu đặt
lntx=
thì
A.
1
0
31
d
e
t
t
It
+
=
∫
. B.
e
1
31
d
t
It
t
+
=
∫
. C.
( )
e
1
3 1dI tt= +
∫
. D.
( )
1
0
3 1dI tt= +
∫
.
Lời giải
Đặt
lntx=
1
ddtx
x
⇒=
. Đổi cận
e1xt=⇒=
;
10xt=⇒=
.
Khi đó
(
)
e1
10
3ln 1
d 3 1d
x
I x tt
x
+
= = +
∫∫
.
Câu 112: Cho
( )
2
1
ln
ln 3 ln 2
3
ln 2
e
xc
I dx a b
xx
= =++
+
∫
, với
,,abc∈
. Khẳng định nào sau đâu đúng.
A.
222
1abc++=
. B.
222
11abc++=
. C.
222
9abc++=
. D.
222
3abc++=
.
Lời giải
Chọn D

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
Ta có
( )
2
1
ln
ln 2
e
x
I dx
xx
=
+
∫
, đặt
ln 2
dx
x t dt
x
+=⇒ =
3 33
33
22
22
2 22
2 1 1 2 22 1
2 ln ln 3 ln 2 ln 3 ln 2
32 3
t
I dt dt dt t
t tt t
−
= = − = +=−+−=−−
∫ ∫∫
Suy ra
1; 1; 1ab c= =−=−
, vậy
222
3abc++=
. Chọn D
Câu 113: Biết
( )
4
2
0
ln 9 d ln 5 ln 3
I x x xa b c
= += + +
∫
trong đó
,,abc
là các số thực. Giá trị của biểu thức
T abc=++
là:
A.
11.T =
B.
9.T =
C.
10.T =
D.
8.T =
Lời giải
Đặt
2
1
9 2d d d d
2
x t xx t xx t+=⇒ = ⇔ =
.
Khi đó
( ) ( ) ( )
25
9
25
11 1
. ln .d .ln 25ln 25 25 9ln 9 9 25ln 5 9ln 3 8
9
22 2
I tt t t t= = − = −− −= − −
∫
.
Suy ra
25988T abc=++= −−=
.
Câu 114: Cho
( )
e
2
1
ln
d
ln 2
x
Ix
xx
=
+
∫
có kết quả dạng
lnI ab
= +
với
0a >
,
b
∈
. Khẳng định nào sau đây
đúng?
A.
21ab = −
. B.
21ab =
. C.
31
ln
23
b
a
−+ =−
. D.
31
ln
23
b
a
−+ =
.
Lời giải
Đặt
ln 2xt+=
ln 2xt⇔=−
1
dd
xt
x
⇒=
.
Đổi cận: khi
1x =
thì
2
t =
; khi
ex =
thì
3t
=
.
Khi đó
3
2
2
2
d
t
It
t
−
=
∫
3
2
2
12
dt
tt
= −
∫
3
2
2
ln t
t
= +
31
ln
23
= −
3
2
1
3
a
b
=
⇒
= −
.
Vậy
21
ab = −
.
Câu 115: Cho
( )
e
2
1
2ln 1
d ln
ln 2
x ac
x
bd
xx
+
= −
+
∫
với
a
,
b
,
c
là các số nguyên dương, biết
;
ac
bd
là các phân số
tối giản. Tính giá trị
abcd+++
?
A.
18
. B.
15
. C.
16
. D.
17
.
Lời giải
Đặt
d
ln d
x
txt
x
= ⇒=
.
Đổi cận:
1 0; e 1=⇒= =⇒=x tx t
. Khi đó:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 40
( )
( )
e1
22
10
2ln 1 2 1
dd
ln 2 2
xt
I xt
xx t
++
= =
++
∫∫
( )
1
1
2
0
0
3 2 3 91
d 2ln 2 ln
2 2 42
2
tt
tt
t
−
= + = + +=−
++
+
∫
.
Vậy
9 4 1 2 16abcd
+++ = + ++ =
.
Câu 116: Cho
(
)
( )
32
3
1
e
3 1 ln 3 1
d . .ln 1
1l
ee
n
x xx
x a bc
xx
− +−
= ++ +
+
∫
với
,,abc
là các số nguyên và
ln e 1=
.
Tính
222
Pabc=++
.
A.
9P =
. B.
14P =
. C.
10
P
=
. D.
3P =
.
Lời giải
Ta có
( )
( ) ( )
( )
32
2
23
11
ee e
1
e
1
3 1 ln 3 1
3 1 ln 1 ln 1 ln
d d 3d d 1
1 ln 1 ln 1 ln
e
x xx
x xx x x
I x x xx x A
xx xx xx
− +−
+ −+ +
= = = − = −−
++ +
∫ ∫ ∫∫
Tính
(
)
1
e
1 ln
d
1 ln
x
Ax
xx
+
=
+
∫
. Đặt
( )
1 ln d 1 ln dt xx t xx=+ ⇒=+
.
Đổi cận:
e
1
1
e
1xt
xt
=⇒=
=⇒=+
. Khi đó
e1
1
e1
1
d
ln ln( 1)e
t
At
t
+
+
= = = +
∫
.
Vậy
3
1 ln( 1)eeI
= −− +
222
1
13
1
a
b Pabc
c
=
→ = − ⇒ = + + =
= −
.
Câu 117: Biết
( )
ln 2
0
d1
ln ln ln
4e 3e
xx
x
I abc
c
−
=
+
= −+
+
∫
với
a
,
b
,
c
là các số nguyên dương.
Tính
2P abc
= −+
.
A.
3P = −
. B.
1P = −
. C.
4P =
. D.
3
P =
Lời giải
Ta có
ln 2 n
0
l2
2
0
d ed
e3e e e344
x
x x xx
xx
I
−
= =
+++ +
∫∫
.
Đặt:
e d ed
xx
t tx=⇒=
. Đổi cận:
01xt=⇒=
,
ln 2 2
xt= ⇒=
.
Khi đó
( )
2
22
11
2
1
1 1 1 1 1 11
d d ln ln 3 ln 5 ln 2
32 1 3 2 34
2
t
It t
tt t t t
+
= = − = = −+
+ ++ +
+
∫∫
.
Suy ra
3a =
,
5b =
,
2c =
. Vậy
23P abc= −+=
.
Câu 118: Cho
( )
( )
2
1
0
e
d .e ln e
e
−
+
=++
+
∫
x
x
xx
xa b c
x
với
a
,
b
,
∈c
. Tính
2P a bc=+−
.
A.
1P =
. B.
1P = −
. C.
0P =
. D.
2P = −
.
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 41
Ta có:
( )
2
1
0
e
d
e
−
+
=
+
∫
x
x
xx
Ix
x
( )
1
0
1e e
d
e1
+
=
+
∫
xx
x
xx
x
x
.
Đặt
e1= +
x
tx
⇒
( )
d 1 ed= +
x
t xx
.
Đổi cận:
01xt
=⇒=
;
1 e1=⇒=+xt
.
Khi đó:
e1
1
1
d
+
−
=
∫
t
It
t
e1
1
1
1d
+
= −
∫
t
t
(
)
e1
ln
1
+
= −
tt
( )
e ln e 1=−+
.
Suy ra:
1=a
,
1= −b
,
1=c
.
Vậy:
22Pa bc
=+ −=−
.
Câu 119: Cho hàm số
( )
=y fx
biết
( )
1
0
2
=f
và
( )
2
′
=
x
f x xe
với mọi
∈
x
. Khi đó
(
)
1
0
∫
xf x dx
bằng
A.
1
4
+e
. B.
1
4
−
e
. C.
1
2
−e
. D.
1
2
+e
.
Lời giải
Chọn B
Ta có
(
) ( )
( )
22 2
2
11
.d . d .d
22
′
= = = = +
∫∫∫
xx x
f x f x x xe x e x e C
.
Mà
( )
(
)
2
11 1 1
00
22 2 2
=⇔+=⇔=⇒ =
x
f C C fx e
.
( )
( )
22 2
1
1 11
2
0
0 00
1 1 11
2 4 44
−
⇒== ==
∫ ∫∫
xx x
e
xf x dx xe dx e d x e
.
Câu 120: Biết rằng
2
1
2ln 1
d ln 2
ln 1
e
xb
xa
c
xx
với
,,abc
là các số nguyên dương và
b
c
là phân số tối
giản. Tính
S abc=++
.
A.
3S
=
. B.
7S =
. C.
10
S =
. D.
5S
=
.
Lời giải
Chọn D
Đặt
ln 1xt
. Ta có:
1
ddxt
x
=
.
Đổi cận:
11xt=⇒=
;
2xe t=⇒=
.
Ta có:
2
2
2
11
2 11
2ln 1
dd
ln 1
e
t
x
xt
t
xx
2
2
1
21
dt
tt
2
1
1
2ln t
t
1
2ln 2
2
.
Suy ra:
2a =
;
1b
=
;
2c =
. Khi đó:
5S abc=++=
.
TÍCH PHÂN TỪNG PHẦN
Nếu
,uv
có đạo hàm liên tục trên
( )
;ab
thì
.. .
bb
b
a
aa
I u dv u v v du= = −
∫∫
.
Vi phân
Nguyên hàm

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 42
Chọn
............... ...........
........ ................
u du dx
dv dx v
= → =
= → =
Nhận dạng: tích hai hàm khác loại nhân nhau
Thứ tự ưu tiên chọn u là: "log – đa – lượng – mũ" và dv là phần còn lại.
Nghĩa là nếu có ln hay
log
a
x
thì chọn
ln
u
=
hay
1
log .ln
ln
a
ux x
a
= =
và
dv
=
còn lại. Nếu
không có
ln; log
thì chọn
u =
đa thức và
dv
=
còn lại,…
CHÚ Ý:.
(
hàm mũ
)
. dx
b
a
tích phân từng phần luân hồi.
Nghĩa là sau khi đặt u, dv để tính tích phân từng phần và tiếp tục tính
udv sẽ xuất hiện lại tích
phân ban đầu. Giả sử tích phân được tính ban đầu là I và nếu lập lại, ta sẽ không giải tiếp mà xem
đây là phương trình bậc nhất ẩn là I
giải
I.
Câu 121: Biết
(
)
1
2
0
ln 1 d ln 2
b
x x xa
c
+= −
∫
. Tính
13 10 84P abc=++
.
A.
193
. B.
191
. C.
190
. D.
189
.
Lời giải
Chọn B
Đặt:
( )
2
ln 1
dd
ux
v xx
= +
=
2
2
2
dd
1
1
22
x
ux
x
x
v
=
+
⇒
= +
Khi đó:
( )
1
2
0
ln 1 dxx x+
∫
( )
1
1
2
2
0
0
1
ln 1 d
2
x
x xx
+
= +−
∫
1
ln 2
2
= −
⇒
1, 1, 2abc= = =
. Vậy
13 10 84Pabc=++
191=
.
Câu 122: Cho hàm số
( )
fx
có
( )
01f = −
và
( )
( )
6 12 ,
x
fx x xe x
−
′
= + + ∀∈
. Khi đó
( )
1
0
dfxx
∫
bằng
A.
3e
. B.
1
3e
−
. C.
1
43e
−
−
. D.
1
3e
−
−
.
Lời giải
Chọn B
Ta có:
( )
(
)
6 12 ,
x
fx x xe x
−
′
= + + ∀∈
nên
( )
fx
là một nguyên hàm của
( )
fx
′
.
( )
( ) ( )
2
d 6 12 d 6 12 d d
xx
f x x x x e x x x x xe x
−−
′
= ++ = + +
∫∫ ∫ ∫
Mà
( )
2 23
6 12 d 3 4x x x x xC+ =++
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 43
Xét
d
x
xe x
−
∫
: Đặt
dd
dd
xx
ux u x
ve x v e
−−
= =
⇒
= = −
( )
dd 1
xxxxx x
xe x xe e x xe e C x e C
−−−−− −
=−+ =−−+=−+ +
∫∫
Suy ra
( ) ( )
23
34 1 ,
x
fx x x x e C x
−
= + − + + ∀∈
.
Mà
( )
01 0fC=−⇒ =
nên
( ) ( )
23
3 4 1,
x
fx x x x e x
−
= + − + ∀∈
.
Ta có
( ) ( )
( ) ( )
( ) ( )
11 1 1
1
2 3 34
0
00 0 0
d 3 4 1 d 1d2 1d
x xx
fxx x xxexxx xex xex
− −−
= +−+ =+ −+ =−+
∫∫ ∫ ∫
Xét
(
)
1
0
1d
x
x ex
−
+
∫
: Đặt
1 dd
dd
xx
ux u x
ve x v e
−−
=+=
⇒
= = −
(
) ( )
11
11
1 11 1
00
00
1d 1 d21 21 123
x xx x
x ex x e ex e e e e e
− − − −− −− −
+ =− + + =− +− =− +− += −
∫∫
Vậy
( )
1
1
0
d3fx x e
−
=
∫
.
Câu 123: Biết
(
)
4
2
0
ln 9 d ln 5 ln 3I x x xa b c
= += + +
∫
trong đó
a
,
b
,
c
là các số thực. Tính giá trị của biểu
thức
T abc=++
.
A.
9T
=
. B.
11T =
. C.
8T =
. D.
10T =
.
Lời giải
Chọn C
Cách 1
Đặt
( )
2
ln 9
dd
= +
=
ux
v xx
, ta có
2
2
2
dd
9
9
2
=
+
+
=
x
ux
x
x
v
.
Do đó
( )
4
4
22
2
2
0
0
9 92
ln 9 . d
2 29
x xx
Ix x
x
++
= +−
+
∫
( )
4
4
2
2
0
0
9
ln 9 d
2
x
x xx
+
= +−
∫
( )
4
4
22
2
0
0
9
ln 9
22
xx
x
+
= +−
25 9
ln 25 ln 9 8
22
= −−
25ln 5 9ln 3 8
= −−
ln 5 ln 3abc=++
.
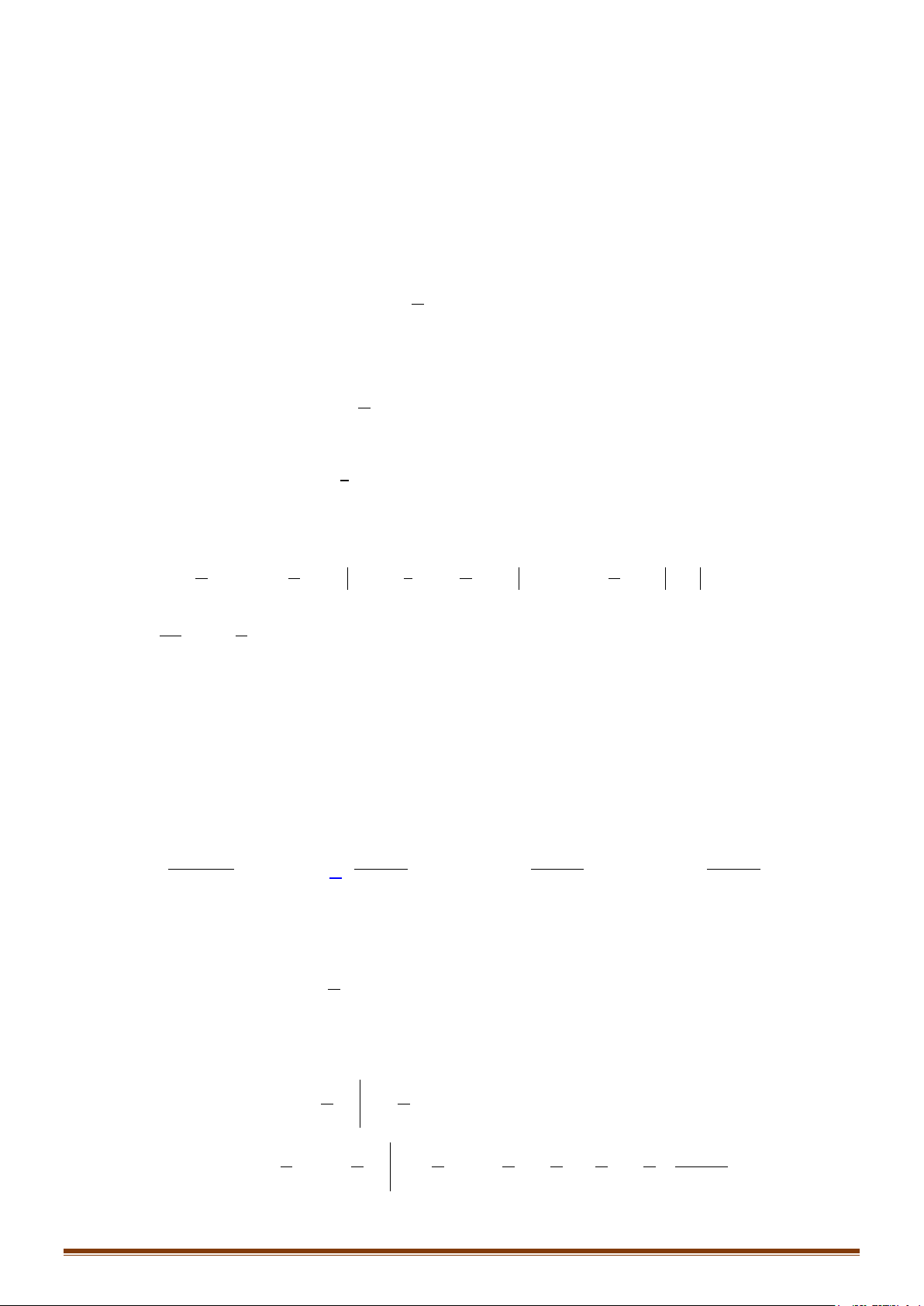
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 44
Suy ra
25
98
8
a
b abc
c
=
=−⇒ + + =
= −
.
Cách 2
Ta có
( )
4
2
0
ln 9 dI xx x= +
∫
Đặt
2
1
9 d 2d d d
2
t x t xx xx t= +⇒ = ⇒ =
Đổi cận:
09xt=⇒=
,
4 25xt= ⇒=
Suy ra
(
)
4 25
2
09
1
ln 9 d ln d
2
I x x x tt
= +=
∫∫
Đặt
ln
dd
=
=
ut
vt
, ta có
1
dd
=
=
ut
t
vt
.
25 25
25
9
99
11 1
ln d .ln . d
22
⇒= = −
∫∫
I t tt t t t t
t
25
25
9
9
1
.ln d
2
tt t
= −
∫
(
)
25 25
99
1
.ln
2
tt t= −
25 9
ln 25 ln 9 8
22
= −−
25ln 5 9ln 3 8= −−
ln 5 ln 3abc=++
.
Suy ra
25
98
8
a
b abc
c
=
=−⇒ + + =
= −
.
Câu 124: Tích phân
( )
1
2
0
2e d
x
xx−
∫
bằng
A.
2
5 3e
.
4
−−
B.
2
5 3e
.
4
−
C.
2
5 3e
.
2
−
D.
2
5 3e
.
4
+
Lời giải
Đặt
2
2
dd
2
.
1
e
d ed
2
x
x
ux
ux
v
vx
=
= −
⇒
=
=
Suy ra
( ) ( )
1
11
2 22
0
00
1
2
22 22 2
0
11
2ed 2 e ed
22
11 1113553e
e1 e e1 e e .
2 4 2 4444 4
x xx
x
x xx x−=− −
−
=−+− =−+−+=−+=
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 45
Câu 125: Biết rằng tích phân
( )
1
0
2+1ed= +.e
x
x x ab
∫
, tích
a.b
bằng
A.
15−
. B.
1−
. C. 1. D. 20.
Lời giải
Chọn C
Điều kiện:
a
,
b ∈
.
Đặt
21
d ed
x
ux
vx
= +
=
d 2d
e
x
ux
v
=
⇒
=
.
( )
1
0
2 +1 e d
x
xx⇒
∫
(
)
1
1
0
0
= 2 +1 e 2 e d
xx
xx
−
∫
( )
1
0
= 2 1e
x
x −
=1+e
= + .eab
.
=1
=1
a
b
⇒
. Vậy tích
1a.b =
.
Câu 126: Cho tích phân
2
2
1
ln
ln 2
xb
I dx a
xc
= = +
∫
với
a
là số thực,
b
và
c
là các số dương, đồng thời
b
c
là
phân số tối giản. Tính giá trị của biểu thức
23P a bc= ++
.
A.
6P =
. B.
5P
=
. C.
6P = −
. D.
4P
=
.
Lời giải
Đặt
2
2
1
2
ln
22
ln 1 ln 1 1 ln 2
11 1
22
dx
ux
du
xx
x
I dx
dx
x x xx
dv
v
x
x
=
=
− −−
⇒ ⇒= + = + =−
−
=
=
∫
1
1, 2, 2 3 4
2
b c a P a bc
−
⇒= = = ⇒ = + +=
.
Câu 127: Cho tích phân
( )
4
0
1 sin 2 d .I x xx
π
= −
∫
Tìm đẳng thức đúng?
A.
(
)
4
0
1 cos2 cos2 d
I x x xx
π
=−− −
∫
. B.
( )
4
4
0
0
1
1 cos2 cos2 d
2
I x x xx
π
π
=−− −
∫
.
C.
( )
4
4
0
0
11
1 cos2 cos2 d
22
I x x xx
π
π
=−− +
∫
. D.
( )
4
4
0
0
1 cos2 cos2 dI x x xx
π
π
=−− +
∫
.
Lời giải
Đặt
( )
1
d sin 2 d
ux
v xx
= −
=
, ta có
dd
1
cos 2
2
ux
vx
=
= −
. Do đó:
( ) ( )
44
4
0
0
11
1 sin 2 d 1 cos 2 cos 2 d
22
o
I x xx x x xx
ππ
π
=− =−− +
∫∫
.
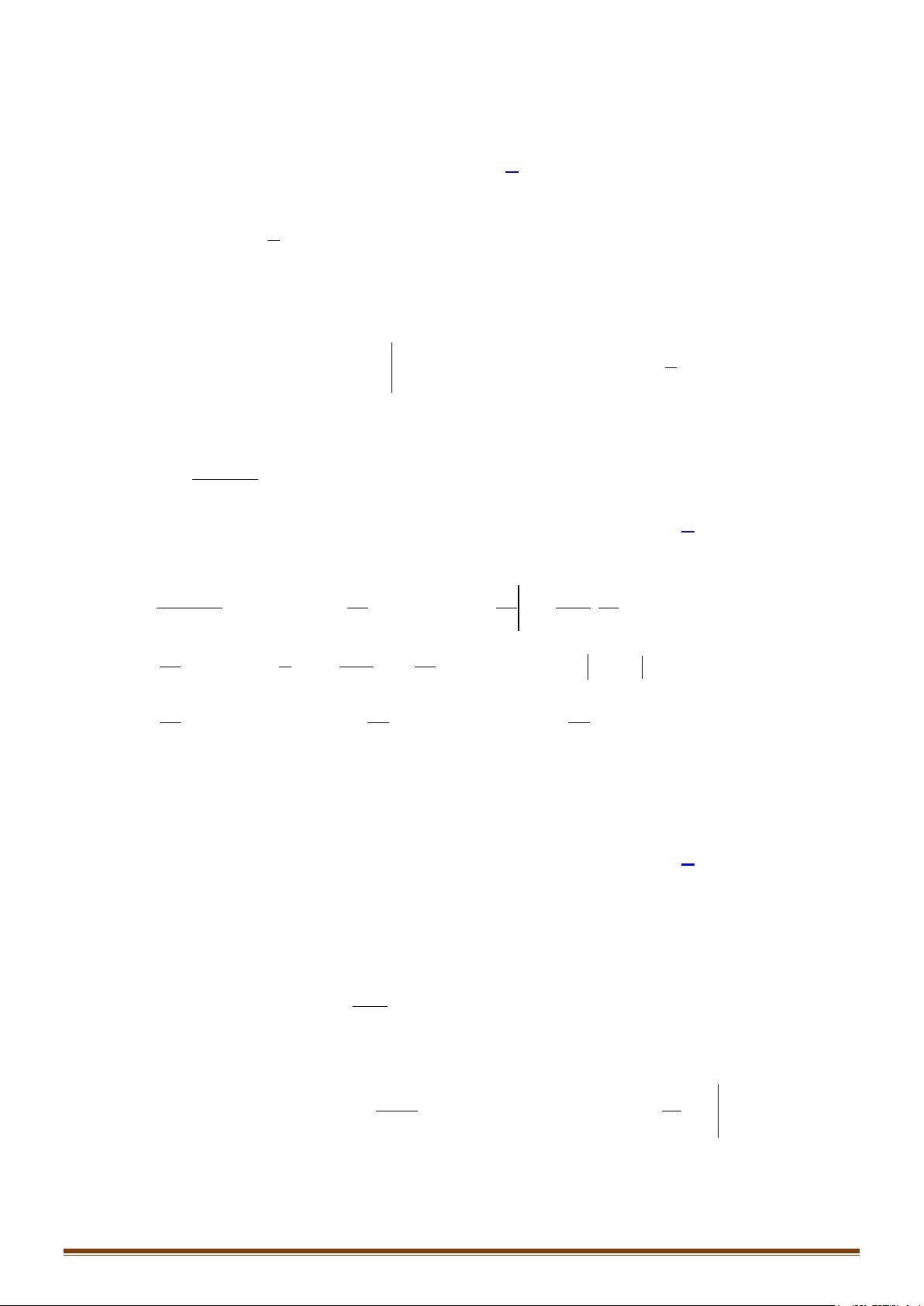
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 46
Câu 128: Biết rằng tồn tại duy nhất các bộ số nguyên
,,abc
sao cho
(
)
3
2
4 2 ln d ln 2 ln 3x xx a b c+ =++
∫
.
Giá trị của
abc
++
bằng
A.
19
. B.
19−
. C.
5
. D.
5−
.
Lời giải
Đặt
( )
2
1
ln d d
4 2d d 2 2
xu x u
x
x x v x xv
=⇒=
+ =⇒ +=
Khi đó
( )
( )
( )
33
2
22
3
7
4 2 ln d ln . 2 2 2 1 d 24ln 3 12ln 2 2. 7 12ln 2 24ln 3
2
2
x xx x x x x x+ = +−+=−−=−−+
∫∫
.
Vậy
7; 12; 24 5a b c abc=− =− = ⇒++=
.
Câu 129: Cho
( )
2
2
1
ln 1
ln 2 ln 3
x
dx a b
x
+
= +
∫
, với
,
ab
là các số hữu tỉ. Tính
4Pa b= +
.
A.
0P
B.
1P
C.
3
P
D.
3
P
Lời giải
( )
( )
22
2
11
ln 1
1
d ln 1 d
x
x xx
xx
′
+
−
= +
∫∫
( )
2
2
1
1
1 11
ln 1 . . d
1
xx
x xx
−−
=+−
+
∫
22
11
1 11
ln 3 ln 2 d d
21
xx
xx
−
= ++ −
+
∫∫
( )
2
2
1
1
1
ln 3 ln 2 ln 1 ln
2
xx
−
= +− ++
1 33
ln 3 ln 2 ln 3 2ln 2 ln 3 3ln 2 3,
2 22
ab
− −−
= + − + = + ⇒= =
.
Vậy
43ab
.
Câu 130: Biết
( )
2
0
2 ln 1 dx a.lnbxx+=
∫
, với
*
,ab∈
,
b
là số nguyên tố. Tính
67ab
+
.
A.
6 7 33ab
+=
. B.
6 7 25
ab
+=
. C.
6 7 42ab
+=
. D.
6 7 39ab
+=
.
Lời giải
Xét
( )
2
0
2 ln 1I x x dx= +
∫
.
Đặt
( )
2
1
ln 1
1
2
1
du dx
ux
x
dv xdx
vx
=
= +
⇔
+
=
= −
.
Ta có
( )
( ) ( )
2
22
22
22
0
00
0
1
1 ln 1 | 3ln 3 1 3ln3 3ln3
12
xx
I x x dx x dx x
x
−
=− +− = −− = −− =
+
∫∫
.
Vậy
3, 3 6 7 39a b ab= =⇒+=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 47
Câu 131: Biết rằng
( )
1
ln 1 2 , 1 .
a
xdx a a=+>
∫
Khẳng định nào dưới đây là khẳng định đúng?
A.
(
)
18;21a ∈
. B.
( )
1; 4a ∈
. C.
( )
11;14a ∈
. D.
( )
6;9a ∈
.
Lời giải
Đặt
lnux=
1
du dx
x
⇒=
dv dx
=
vx⇒=
Ta có
11
ln .ln ln 1 1 2
aa
xdx a a dx a a a a= − = − +=+
∫∫
3
ln 3 ln 3 .aa a a ae
⇒ = ⇔ =⇔=
Vậy
( )
18;21 .
a ∈
Câu 132: Cho tích phân
1
0
( 2) x
x
x e d a be−=+
∫
, với
∈;ab
. Tổng
+ab
bằng
A.
1
. B.
−
3
. C.
5
. D.
1−
.
Chọn A
Đặt
11
11
00
00
2x
( 2) x ( 2) x= 2 3 2e =
x
x xx x
xx
u x du d
x ed x e ed e e a be
dved ve
=−=
⇒ ⇒− =− − −+−=− +
= =
∫∫
với
; 3, 2 1
ab a b a b
∈ ⇒ = =−⇒ + =
Câu 133: Tính tích phân
2
1
x
I xe dx=
∫
.
A.
2
=Ie
. B.
2
= −Ie
. C.
=Ie
. D.
2
32
= −Ie e
.
Lời giải
Chọn A
Đặt
= =
⇒
= =
xx
u x du dx
dv e dx v e
( )
22
2 2 22 2 2
11
11
22= = − = −− = −− − =
∫∫
x xx x
I xedxxe edx eee eeeee
.
Câu 134: Biết rằng
3
2
ln d ln 3 ln 2x xx m n p= ++
∫
trong đó
,,mn p∈
. Tính
2mn p++
A.
5
4
. B.
9
2
. C.
0
. D.
5
4
−
.
Lời giải
Chọn C
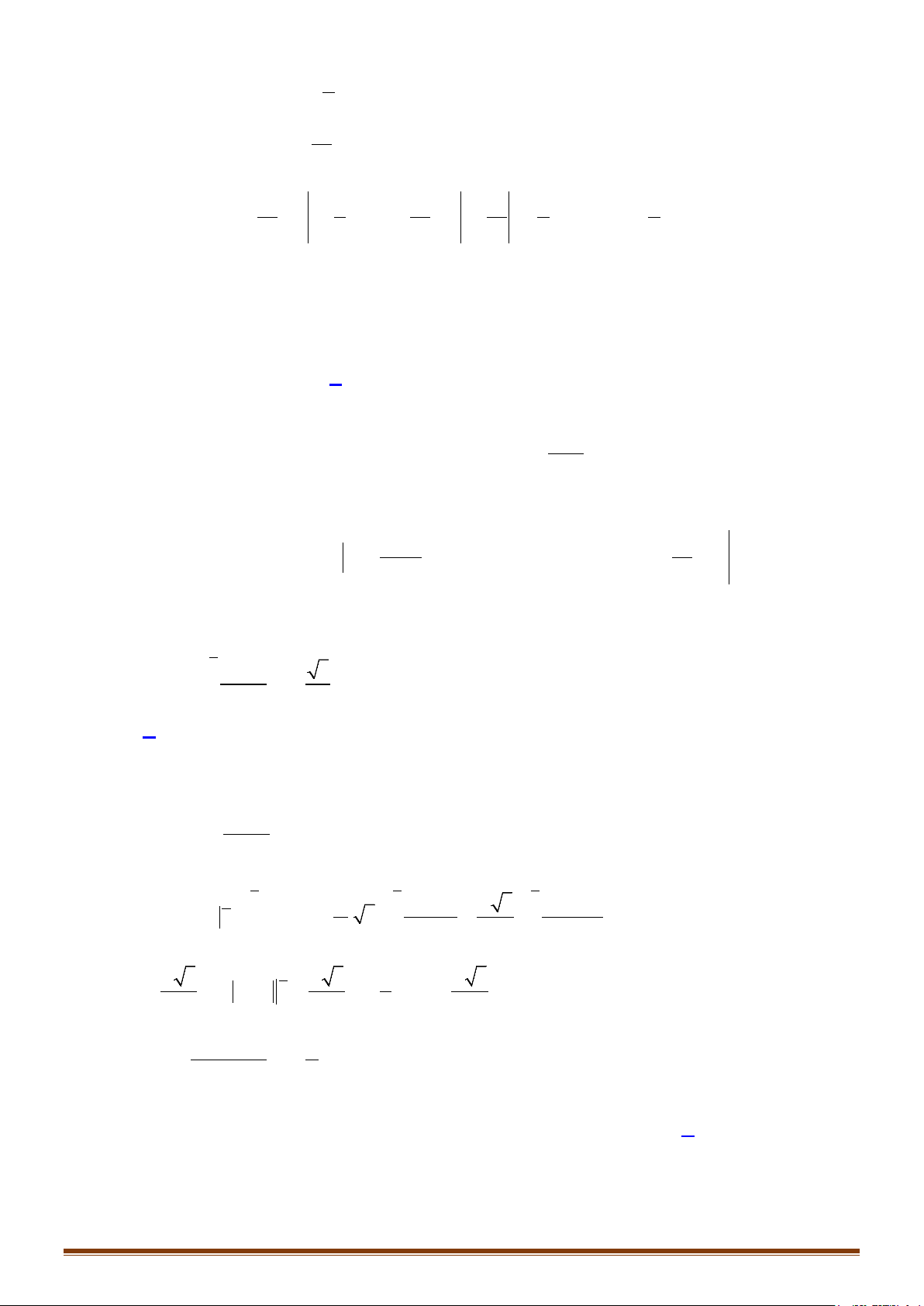
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 48
Đặt
2
1
dd
ln
dd
2
ux
ux
x
v xx
x
v
=
=
⇒
=
=
.
⇒
3
33
2
22
2
1
ln d ln d
22
x
x xx x xx= −
∫∫
33
22
22
ln
24
xx
x= −
95
ln 3 2ln 2
24
= −−
.
Suy ra
20mn p++ =
.
Câu 135: Biết
( )
2
0
2 ln 1 d .lnx xxa b+=
∫
, với
*
,ab
∈
,
b
là số nguyên tố. Tính
34ab+
.
A.
42
. B.
21
. C.
12
. D.
32
.
Lời giải
Xét
(
)
2
0
2 ln 1 dI x xx
= +
∫
. Đặt
( )
ln 1
d 2d
ux
v xx
= +
=
2
1
dd
1
1
ux
x
vx
=
⇒
+
= −
.
Ta có:
( )
( )
2
2
2
2
0
0
1
1 ln 1 d
1
x
Ix x x
x
−
=− +−
+
∫
( )
2
0
3ln 3 1 dxx= −−
∫
2
2
0
3ln 3 3ln3
2
x
x
= −−=
.
Vậy
3a =
,
3b =
3 4 21ab⇒+=
.
Câu 136: Biết
3
2
0
3
d ln
cos
x
Ixb
xa
π
π
= = −
∫
. Khi đó, giá trị của
2
ab+
bằng
A.
11
. B.
7
. C.
13
. D.
9
.
Lời giải
Đặt
2
dd
1
tan
dd
cos
ux
ux
vx
vx
x
=
=
⇒
=
=
3 33
3
0
0 00
sin d 3 d(cos )
tan tan d . 3
3 cos 3 cos
xx x
I x x xx
xx
π ππ
π
ππ
=−=−=+
∫ ∫∫
3
0
3 31 3
ln cos ln ln1 ln 2
3 32 3
x
π
π ππ
= + = + −= −
3; 2ab⇒= =
. Vậy
2
11ab+=
.
Câu 137: Cho
( )
2
2
1
ln 1 2
d ln 5 ln 3 ln 2
2
x
a
x bc
x
+
= ++
∫
, với
a
,
b
,
c
là các số nguyên. Giá trị của
( )
2a bc++
là:
A. 0. B. 9. C. 3. D. 5.
Lời giải
Áp dụng phương pháp tích phân từng phần:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 49
Đặt:
( )
( )
2
2
dd
ln 1 2
21
1
21
1
dd
chän 2
ux
ux
x
x
vx
v
x
xx
=
= +
+
⇒
−+
=
=−−=
.
( )
( )
( )
2
22
2
11
1
ln 1 2 2 1
2
d ln 1 2 d
xx
x xx
xx x
+ −+
⇒ = ⋅+ +
∫∫
2
1
5
ln 5 3ln 3 2ln
2
x
=−+ +
5
ln 5 3ln 3 2ln 2
2
−
= ++
.
5a⇒=−
,
3b =
,
2c =
.
Vậy
( )
25a bc+ +=
.
Câu 138: Cho
(
)
2
2
1
ln 1
d ln 2 ln 3
x
xa b
x
+
= +
∫
, với
a
,
b
là các số hữu tỉ. Tính
P ab=
.
A.
3
2
P
=
. B.
0P =
. C.
9
2
P
−
=
. D.
3P = −
.
Lời giải
Ta có
(
)
2
2
1
ln 1
d ln 2 ln 3
x
I xa b
x
+
= = +
∫
.
Đặt
2
1
ln(1 )
du d
1
1
1
dd
.
ux
x
x
vx
v
x
x
= +
=
+
⇒
=
= −
Khi đó
22
2
1
11
1 1 1 11
ln (1 ) d ln 3 ln 2 d
(1 ) 2 1
Ix x x
x xx x x
=− ++ =− ++ −
++
∫∫
2
1
11
ln 3 ln 2 ln 3 ln 2 2ln 2 ln 3 3ln 2 ln3.
22
3
ln
1 2
x
x
+
=− ++ =− ++ −= −
Suy ra
3
a =
,
3
2
b = −
. Vậy
9
2
P ab
−
= =
.
Câu 139: Cho tích phân
1
0
( 2) x
x
x e d a be−=+
∫
, với
;ab∈
. Tổng
+ab
bằng
A.
1
. B.
−3
. C.
5
. D.
1−
.
Lời giải
Chọn A
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 50
Đặt
=−=
⇒ ⇒ − = − − −+− =− +
= =
∫∫
11
11
00
00
2x
( 2) x ( 2) x= 2 3 2e =
x
x xx x
xx
u x du d
x ed x e ed e e a be
dved ve
với
∈ ⇒ = =−⇒ + =
; 3, 2 1ab a b a b
Câu 140: Biết
12
1
1
12
1
1
c
x
xd
a
x e dx e
xb
+
+− =
∫
trong đó
,,,abcd
là các số nguyên dương và các phân số
,
ac
bd
là tối giản. Tính
bc ad−
.
A. 12. B. 1. C. 24. D. 64.
Lời giải
Ta có:
12 12 12
1 11
22
1 11
12 12 12
11
11 1
x xx
x xx
I x e dx x e dx e dx
xx
+ ++
= −+ = − +
∫ ∫∫
.
Đặt:
1
1
2
1
1
x
x
x
x
ux
du dx
dv e dx
ve
x
+
+
=
=
→
= −
=
.
Khi đó:
12
12 12 12 12
11111
2
1
1 1 11
12
12 12 12 12
1
1.
xx xxx
xx xxx
I x e dx e dx x e e dx e dx
x
+++++
=− +=−+
∫ ∫ ∫∫
1 1 145
12 12
12 12 12
1 143
12
12 12
ee e
++
=−=
.
Vậy:
143; 12; 145; 12.a bc d= = = =
Dó đó:
12.145 143.12 24bc ad
−= − =
.
Câu 141: Cho
( )
(
)
2
2
0
ln 1
d ln 3
2
xx
ac
x
bd
x
++
= +
+
∫
. Tính
( )( )
P abcd=++
.
A.
7
. B.
7−
. C.
3
. D.
3−
.
Lời giải
Ta có
( )
( )
( )
( )
( )
2 22 2
2 22
0 00 0
ln 1 ln 1
12
dd d d
2
2 22
xx x
xx x x
x
x xx
++ +
=−+
+
+ ++
∫ ∫∫ ∫
.
( )
2
22
2
00
0
12 2 1
d d ln 2 ln 2
2 22
2
x xx
xx
x
− = ++ = −
++
+
∫∫
.
( )
( )
2
2
0
ln 1
d
2
x
Ix
x
+
=
+
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 51
Đặt
( )
( )
( )
2
1
ln 1
dd
1
1
11
dd
1
2
22
ux
ux
x
x
vx
v
x
xx
= +
=
+
⇒
−+
=
= +=
+
++
Suy ra
( )
( ) (
)
2
2
0
0
1 ln( 1)
13
d ln 3 ln 2
2 24
xx
Ix
xx
++
= −=−
++
∫
.
Do đó
( )
( )
2
2
0
ln 1
13
d ln 3
24
2
xx
x
x
++
=−+
+
∫
( )( )
1234 7
P⇒ =−+ + =
.
Câu 142: Cho hàm số
( )
y fx=
có
(
)
1
1
2
f =
và
( )
( )
2
1
x
fx
x
′
=
+
với
1x >−
. Biết
( )
2
1
d ln
b
fx x a d
c
= −
∫
với
,,,
abcd
là các số nguyên dương,
3
b
≤
và
b
c
tối giản. Khi đó
abcd+++
bằng
A.
8
. B.
5
. C.
6
. D.
10
.
Lời giải
Chọn D
Ta có
(
) ( )
(
)
22
11 1
d d ln 1
11
11
x
x xx C
xx
xx
= − = ++ +
++
++
∫∫
, với
C
là hằng số tùy ý.
Do
( )
1 11
1 ln 2 ln 2
2 22
f CC=⇒ ++=⇔ =−
.
Khi đó, ta có
(
) ( ) ( )
22 2 22
11 1 11
1d
d ln 1 ln 2 d ln 1 d ln 2 d
11
x
fx x x x x x x
xx
= ++ − = + + −
++
∫∫ ∫ ∫∫
.
Xét
(
)
2
1
ln 1 dI xx
= +
∫
. Đặt
( )
d
ln 1
d
1
dd
x
ux
u
x
vx
vx
= +
=
⇒
+
=
=
, khi đó ta có
( )
2222 2
2
1
1111 1
dd d d
.ln 1 2 ln3 ln 2 2ln 3 ln 2 d 2ln 3 ln 2 1
11 1 1
xx xx x x
Ix x x
xx x x
= +− = −− = −−+ = −−+
++ + +
∫∫∫∫ ∫
Khi đó,
( )
2 12
1 01
d3
d 2ln 3 ln 2 1 2 ln 2 d 2ln 3 ln 2 1 2ln 3 2 ln 2 ln 2 4ln 1
12
x
fx x x
x
= − −+ − = − −+ − − = −
+
∫ ∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 52
Suy ra
4
3
10
2
1
a
b
abcd
c
d
=
=
⇒+++ =
=
=
.
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 85
BÀI 2. TÍCH PHÂN
MỨC ĐỘ VẬN DỤNG – VẬN DỤNG CAO
DẠNG 1. TÍCH PHÂN HÀM ẨN
DẠNG 1.1 GIẢI BẰNG PHƯƠNG PHÁP ĐỔI BIẾN
Câu 1: Cho hàm số
(
)
fx
liên tục trên
và thỏa mãn
( )
1
5
d9
fx x
−
=
∫
. Tích phân
(
)
2
0
1 3 9dfx x
−+
∫
bằng
A.
15
. B.
27
. C.
75
. D.
21
.
Câu 2: Cho hàm số
(
)
fx
liên tục trên đoạn
[ ]
0;10
thỏa mãn
( ) (
)
10 10
02
d 7, d 1fx x fx x
= =
∫∫
. Tính
( )
1
0
2d
P f xx=
∫
.
A.
6
P =
. B.
6P = −
. C.
3
P =
. D.
12P
=
.
Câu 3: Cho
( )
5
1
d 26I fx x= =
∫
. Khi đó
( )
2
2
0
1 1dJ xfx x
= ++
∫
bằng
A.
15
. B.
13
. C.
54
. D.
52
.
Câu 4: Cho hàm số
()y fx=
liên tục trên
thỏa mãn
( )
9
1
4
fx
dx
x
=
∫
và
( )
2
0
sin cos 2.f x xdx
π
=
∫
Tích phân
3
0
()I f x dx
=
∫
bằng
A.
8I =
. B.
6I =
. C.
4I =
. D.
10I =
.
Câu 5: Cho biết
( )
5
1
d 15fxx
−
=
∫
. Tính giá trị của
( )
2
0
5 3 7dPf x x= −+
∫
.
A.
15P =
. B.
37P =
. C.
27P =
. D.
19P =
.
Câu 6: Cho
(
)
4
0
20 8d
1fx x=
∫
. Tính tích phân
( ) ( )
2
0
24d2I fx f x x= +−
∫
.
A.
0I
=
. B.
2018I =
. C.
4036I =
. D.
1009I
=
.
Câu 7: Cho
( )
y fx=
là hàm số chẵn, liên tục trên
[ ]
6;6−
. Biết rằng
( )
2
1
d8fx x
−
=
∫
;
( )
3
1
2d 3f xx−=
∫
.
Giá trị của
( )
6
1
dI fx x
−
=
∫
là
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
– ỨNG DỤNG TÍCH PHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 86
A.
5
I =
. B.
2I =
. C.
14I
=
. D.
11
I
=
.
Câu 8: Cho hàm số
( )
fx
liên tục trên
và
(
)
2
0
d 2018
fx x
π
=
∫
, tính
(
)
2
0
d.
I xf x x
π
=
∫
A.
1008I =
. B.
2019I =
. C.
2017I =
. D.
1009I
=
.
Câu 9: Cho
( )
2
1
d2fxx=
∫
. Khi đó
( )
4
1
d
fx
x
x
∫
bằng
A.
1
. B.
4
. C.
2
. D.
8
.
Câu 10: Cho
(
)
d
f x xx+=
∫
2
2
1
12
. Khi đó
( )
dI fx x=
∫
5
2
bằng
A.
2
. B.
1
. C.
4
. D.
1−
.
Câu 11: Cho
,fg
là hai hàm số liên tục trên
[
]
1; 3
thỏa mãn điều kiện
(
)
( )
3
1
3 dx=10
f x gx+
∫
đồng thời
( ) ( )
3
1
2 dx=6f x gx−
∫
. Tính
( )
3
1
4 dxfx−
∫
+2
( )
2
1
2 1 dxgx−
∫
A.
9
. B.
6
. C.
7
. D.
8
.
Câu 12: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
1
0
d2fx x=
∫
và
(
)
2
0
3 1d 6fx x+=
∫
. Tính
( )
7
0
dI fx x=
∫
.
A.
16I =
. B.
18I =
. C.
8I =
. D.
20I =
.
Câu 13: Cho
(
)
fx
liên tục trên
thỏa mãn
( )
(
)
10fx f x
= −
và
( )
7
3
d4
fx x=
∫
. Tính
( )
7
3
dI xf x x
=
∫
.
A.
80
. B.
60
. C.
40
. D.
20
.
Câu 14: Cho
(
)
1
0
d9
fx x
=
∫
. Tính
( )
6
0
sin 3 cos3 dI f x xx
π
=
∫
.
A.
5I =
. B.
9I =
. C.
3I =
. D.
2I =
.
Câu 15: Cho tích phân
( )
4
0
d 32.
= =
∫
I fx x
Tính tích phân
( )
2
0
2 d.=
∫
J f xx
A.
32J
=
B.
64J =
C.
8J =
D.
16J =
Câu 16: Biết
( )
fx
là hàm liên tục trên
và
( )
9
0
d9fx x=
∫
. Khi đó giá trị của
( )
4
1
3 3dfx x−
∫
là
A.
0
. B.
24
. C.
27
. D.
3
.
Câu 17: Cho hàm số
()fx
thỏa mãn
1
0
(2 ) 2f x dx =
∫
.Tích phân
2
0
()f x dx
∫
bằng
A. 8. B. 1. C. 2. D. 4.
Câu 18: Cho hàm
( )
fx
thỏa mãn
( )
2017
0
d1fx x=
∫
. Tính tích phân
( )
1
0
2017 dI f xx=
∫
.
A.
1
2017
I =
. B.
0I =
. C.
2017I =
. D.
1I =
.
Câu 19: Cho tích phân
( )
2
1
dfx x a=
∫
. Hãy tính tích phân
( )
1
2
0
1dI xf x x= +
∫
theo
a
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 87
A.
4Ia=
. B.
4
a
I =
. C.
2
a
I =
. D.
2
Ia
=
.
Câu 20: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
4
2
0
tan . cos d 2xf x x
π
=
∫
và
( )
2
2
ln
d2
ln
e
e
fx
x
xx
=
∫
.
Tính
(
)
2
1
4
2
d
fx
x
x
∫
.
A.
0
. B.
1
. C.
4
. D.
8
.
Câu 21: Cho hàm số
(
)
22
3; 1
5;1
x xx
y fx
xx
+≥
= =
−<
. Tính
( ) ( )
1
2
00
2 sin cos 3dd32I f x xx f x x
π
= +−
∫∫
.
A.
71
6
I =
. B.
31I =
. C.
32I =
. D.
32
3
I =
.
Câu 22: Cho
( )
2
1
d2I fx x= =
∫
. Giá trị của
( )
2
0
sin 3cos 1
d
3cos 1
xf x
x
x
π
+
+
∫
bằng
A.
2
. B.
4
3
−
. C.
4
3
. D.
2−
.
Câu 23: Biết
( )
4
1
5f x dx =
∫
và
( )
5
4
20f x dx =
∫
. Tính
( )
( )
2 ln 2
22
10
43
xx
f x dx f e e dx−−
∫∫
.
A.
15
4
I =
. B.
15I
=
. C.
5
2
I =
. D.
25I =
.
Câu 24: Cho
()fx
là hàm số liên tục trên
thỏa mãn
2
( ) (2 ) . ,
x
f x f x xe x+ − = ∀∈
. Tính tích phân
2
0
()
I f x dx=
∫
.
A.
4
1
4
e
I
−
=
. B.
21
2
e
I
−
=
. C.
4
2Ie= −
. D.
4
1Ie= −
.
Câu 25: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
(
) ( )
23f x fx=
,
x∀∈
. Biết rằng
( )
1
0
d1fx x=
∫
.
Tính tích phân
( )
2
1
dI fx x=
∫
.
A.
5I =
B.
6I =
C.
3I =
D.
2I =
Câu 26: Cho hàm số
()fx
liên tục trên
thỏa mãn
8
3
3
2
01
()
tan . (cos ) 6
fx
x f x dx dx
x
π
= =
∫∫
. Tính tích phân
2
2
1
2
()fx
dx
x
∫
A. 4 B. 6 C. 7 D. 10

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 88
Câu 27: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
2018
0
d2fx x=
∫
. Khi đó tích phân
( )
(
)
2018
e1
2
2
0
ln 1 d
1
x
fx x
x
−
+
+
∫
bằng
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 28: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
4
0
tan d 3f xx
π
=
∫
và
( )
2
1
2
0
d 1.
1
xf x
x
x
=
+
∫
Tính
( )
1
0
d.I fx x=
∫
A.
2I =
. B.
6
I
=
. C.
3I =
. D.
4I =
.
Câu 29: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
(
)
16
2
2
1
4
cot . sin d d 1
fx
xf x x x
x
π
π
= =
∫∫
. Tính tích
phân
( )
1
1
8
4
d
fx
x
x
∫
.
A.
3
I =
. B.
3
2
I =
. C.
2I =
. D.
5
2
I =
.
Câu 30: Cho hàm số
( )
fx
liên tục và là hàm số lẻ trên đoạn
[ ]
2; 2−
. Biết rằng
( )
( )
01
1
1
2
1, 2 2f x dx f x dx
−
=−−=
∫∫
.Mệnh đề nào sau đây đúng?
A.
( ) ( )
22
20
2f x dx f x dx
−
=
∫∫
. B.
(
)
1
1
2
4f x dx
= −
∫
.
C.
( )
1
0
1f x dx = −
∫
. D.
(
)
2
0
3f x dx = −
∫
.
Câu 31: Cho
( )
fx
là hàm số liên tục trên
thỏa
( )
11f =
và
( )
1
0
1
d
3
ft t=
∫
. Tính
( )
2
0
sin 2 . sin dI xf x x
π
′
=
∫
A.
4
3
I =
. B.
2
3
I =
. C.
2
3
I = −
D.
1
3
I
=
.
Câu 32: Cho hàm số
fx
liên tục trên
và
9
2
10
d4, sincosd2
fx
x f x xx
x
. Tính tích phân
3
0
dI fx x
.
A.
6I =
. B.
4I =
. C.
10I =
. D.
2I =
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 89
Câu 33: Cho
(
)
fx
liên tục trên
thỏa mãn
( ) ( )
2020fx f x= −
và
(
)
2017
3
x 4.
f xd =
∫
Khi đó
( )
2017
3
xxf x d
∫
bằng
A.
16160.
B.
4040.
C.
2020.
D.
8080.
Câu 34: Cho hàm số
()
y fx=
liên tục trên
và thỏa mãn
23
3
4 ( ) 6 (2 ) 4
5
xf x f x x+=+
. Giá trị
4
0
( )d
fx x
∫
bằng
A.
52
25
. B. 52. C.
48
25
. D. 48.
Câu 35: Cho
( )
fx
liên tục trên
và thỏa mãn
( ) ( )
1
0
2 16, 2 d 2f f xx= =
∫
. Tích phân
( )
2
0
dxf x x
′
∫
bằng
A.
30
. B.
28
. C.
36
. D.
16
.
Câu 36: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;1
và
( )
2
0
sin d 5f xx
π
=
∫
. Tính
( )
0
sin dI xf x x
π
=
∫
A.
5
2
I
π
=
. B.
10I
π
=
. C.
5I =
. D.
5I
π
=
.
Câu 37: Cho hàm số
()y fx=
liên tục trên
1
;3
3
thỏa mãn
3
1
() .
f x xf x x
x
+=−
. Giá trị tích phân
3
2
1
3
()fx
I dx
xx
=
+
∫
bằng:
A.
8
.
9
B.
16
.
9
C.
2
.
3
D.
3
.
4
DẠNG 1.2 GIẢI BẰNG PHƯƠNG PHÁP TỪNG PHẦN
Thông thường nếu bài toán xuất hiện
( ) ( )
'd
b
a
gxf x x
∫
ta sẽ đặt
( )
( )
d 'd
u gx
v fxx
=
=
Câu 38: Cho
( )
fx
là hàm số có đạo hàm liên tục trên
[
]
0;1
và
( )
1
1
18
f = −
,
( )
1
0
1
.d
36
xf x x
′
=
∫
. Giá trị
của
( )
1
0
dfx x
∫
bằng
A.
1
12
−
. B.
1
36
. C.
1
12
. D.
1
36
−
.
Câu 39: Cho hàm số
( )
fx
có
( )
2
1fe=
và
( )
2
2
21
x
x
fx e
x
−
′
=
với mọi
x
khác
0
. Khi đó
( )
ln3
1
d
xf x x
∫
bằng
A.
2
6
e−
. B.
2
6
2
e−
. C.
2
9 e−
. D.
2
9
2
e−
.
Câu 40: Cho hàm số
()y fx=
có đạo hàm liên tục trên
và thỏa mãn
2
0
(2) 16, ( ) 4f f x dx= =
∫
. Tính
1
0
(2 )I xf x dx
′
=
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 90
A.
20I =
B.
7
I
=
C.
12I =
D.
13I =
Câu 41: Cho hàm số
fx
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
1
2
0
1
21
x f x dx = −
∫
,
( )
10f =
và
(
)
1
2
0
1
'
7
f x dx
=
∫
. Giá trị của
( )
1
0
f x dx
∫
bằng
A.
5
12
. B.
1
5
−
. C.
4
5
. D.
7
10
−
.
Câu 42: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[
]
01;
thỏa mãn
( )
10f =
,
( )
1
2
0
1
3
x f x dx =
∫
Tính
( )
1
3
0
' .x f x dx
∫
A.
1−
B.
1
C.
3
D.
3−
Câu 43: Cho hàm số
(
)
y fx
=
có đạo hàm liên tục trên đoạn
[ ]
0;1
và
( ) ( )
0 10ff+=
. Biết
(
) ( ) ( )
11
2
00
1
d , cos d
22
f xx fx xx
π
π
′
= =
∫∫
. Tính
( )
1
0
dfx x
∫
.
A.
π
. B.
3
2
π
. C.
2
π
. D.
1
π
.
Câu 44: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
thỏa mãn
(
)
10
f
=
,
(
)
1
2
0
d7fx x
′
=
∫
và
( )
1
2
0
1
d
3
xf x x=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
7
5
B.
1
C.
7
4
D.
4
Câu 45: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
14
=f
,
( )
1
2
0
d 36
′
=
∫
fx x
và
(
)
1
0
1
.d
5
=
∫
xf x x
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
5
6
B.
3
2
C.
4
D.
2
3
Câu 46: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0; 2
thỏa mãn
( )
23=
f
,
( )
2
2
0
d4
′
=
∫
fx x
và
( )
2
2
0
1
d
3
=
∫
xf x x
. Tích phân
( )
2
0
d
∫
fx x
bằng
A.
2
115
B.
297
115
C.
562
115
D.
266
115
Câu 47: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
14=f
,
( )
1
2
0
d5
′
=
∫
fx x
và
( )
1
0
1
.d
2
xf x x= −
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
15
19
B.
17
4
C.
17
18
D.
15
4

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 91
Câu 48: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0; 2
thỏa mãn
( )
26
f
=
,
( )
2
2
0
d7fx x
′
=
∫
và
( )
2
0
17
.d
2
xf x x
=
∫
. Tích phân
( )
2
0
dfx x
∫
bằng
A.
8
B.
6
C.
7
D.
5
Câu 49: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;3
thỏa mãn
( )
36f =
,
( )
3
2
0
d2
′
=
∫
fx x
và
( )
3
2
0
154
.d
3
=
∫
xfx x
. Tích phân
( )
3
0
dfx x
∫
bằng
A.
53
5
B.
117
20
C.
153
5
D.
13
5
Câu 50: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
12
f =
,
( )
1
2
0
d8fx x
′
=
∫
và
( )
1
3
0
. d 10xfx x=
∫
. Tích phân
(
)
1
0
dfx x
∫
bằng
A.
2
285
−
B.
194
95
C.
116
57
D.
584
285
Câu 51: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
thỏa mãn
( )
10
f =
và
( ) (
) ( )
11
2
2
00
1
d 1e d
4
x
e
f x x x fx x
−
′
=+=
∫∫
. Tính tích phân
( )
1
0
dI fx x=
∫
.
A.
2e
I = −
. B.
e2I = −
. C.
e
2
I
=
. D.
e1
2
I
−
=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 92
Câu 52: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
0;
4
π
và
0
4
f
π
=
. Biết
( )
4
2
0
d
8
f xx
π
π
=
∫
,
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Tính tích phân
( )
8
0
2dI f xx
π
=
∫
A.
1I =
. B.
1
2
I =
. C.
2I =
. D.
1
4
I
=
.
Câu 53: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[ ]
0;1
và
( ) ( )
0 10
ff+=
. Biết
( ) ( ) ( )
11
2
00
1
d , cos d
22
f xx fx xx
π
π
′
= =
∫∫
. Tính
( )
1
0
d
fx x
∫
.
A.
π
. B.
1
π
. C.
2
π
. D.
3
2
π
.
Câu 54: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[
]
0;1
thỏa mãn
( )
11f =
,
(
)
1
2
0
d9fx x
′
=
∫
và
( )
1
3
0
1
d
2
xf x x=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng:
A.
2
3
. B.
5
2
. C.
7
4
. D.
6
5
.
Câu 55: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[ ]
1; 2
thỏa mãn
( ) ( )
2
2
1
1
1d
3
x fx x−=−
∫
,
( )
20f =
và
( )
2
2
1
d7fx x
′
=
∫
. Tính tích phân
( )
2
1
dI fx x=
∫
.
A.
7
5
I =
. B.
7
5
I = −
. C.
7
20
I = −
. D.
7
20
I =
.
Câu 56: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn:
( ) ( )
1
2
0
1 0, d 7f fx x
′
= =
∫
và
( )
1
2
0
1
.d
3
xfx x=
∫
. Tính tích phân
( )
1
0
dI fx x=
∫
.
A.
1I =
. B.
7
5
I =
. C.
4I =
. D.
7
4
I =
.
Câu 57: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
( )
1
2
0
4
1 3,
11
f f x dx
′
= =
∫
và
( )
1
4
0
7
11
x f x dx =
∫
. Giá trị của
( )
1
0
f x dx
∫
là
A.
35
11
. B.
65
21
. C.
23
7
. D.
9
4
.
Câu 58: Cho hàm số
()fx
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
01f =
;
( )
[
]
1
2
0
1
d
30
fx x
′
=
∫
và
(
) ( )
1
0
1
21 d
30
x fx x−=−
∫
. Tích phân
( )
1
0
dfx x
∫
bằng

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 93
A.
11
30
. B.
11
12
. C.
11
4
. D.
1
30
.
Câu 59: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
0;
4
π
và
0
4
f
π
=
. Biết
(
)
4
2
0
d
8
f xx
π
π
=
∫
,
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Tính tích phân
( )
8
0
2dI f xx
π
=
∫
.
A.
1
I
=
. B.
1
2
I =
. C.
2
I
=
. D.
1
4
I =
.
Câu 60: Cho hàm số
( )
fx
liên tục, có đạo hàm trên
,
( )
2 16f
=
và
( )
2
0
4f x dx =
∫
. Tích phân
4
0
2
x
xf dx
′
∫
bằng
A.
112
. B.
12
. C.
56
. D.
144
.
Câu 61: Cho hàm số
( )
fx
liên tục trên
và
(
) (
)
2
0
2 16, d 4f fx x= =
∫
. Tính
( )
1
0
. 2dI xf x x
′
=
∫
.
A.
7
. B.
12
. C.
20
. D.
13
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 94
DẠNG 1.3 BIẾN ĐỔI
Dạng 1. Bài toán tích phân liên quan đến đẳng thúrc
'
() () () () ()uxf x uxfx hx
′
+=
Phương pháp:
Dễ dàng thấy rằng
() () () () [() ()]uxf x u xfx uxfx
′′ ′
+=
Do dó
() () () () () [() ()] ()uxf x u xfx hx uxfx hx
′′ ′
+=⇔ =
Suy ra
() () ()dux f x hx x=
∫
Từ đây ta dễ dàng tính được
()fx
Dang 2. Bài toán tích phân liên quan đến biếu thúrc
() () ()f x f x hx
′
+=
Phương pháp:
Nhân hai vế vói
x
e
ta durọc
() () () () ()
x xx x x
efx efx ehx efx ehx
′
′
⋅ +⋅ =⋅ ⇔ ⋅ =⋅
Suy ra
() ()d
xx
e f x e hx x⋅=⋅
∫
Từ đây ta dễ dàng tính được
()fx
Dang 3. Bài toán tích phân liên quan đến biếu thúc
() () ()f x f x hx
′
−=
Phương pháp:
Nhân hai vế vói
x
e
−
ta durọc
() () () () ()
x xx x x
efxefxehx efx ehx
′
−′ − − − −
⋅ −⋅ =⋅ ⇔ ⋅ =⋅
Suy ra
() ()d
xx
e f x e hx x
−−
⋅=⋅
∫
Từ đây ta dễ dàng tính được
()fx
Dạng 4. Bài toán tích phân liên quan đến biếu thúrc
() () () ()
f x px f x hx
′
+⋅=
Phương pháp:
Nhân hai vế với
()p x dx
e
∫
ta được
() () () () ()
() () () () () ()
p x dx p x dx p x dx p x dx p x dx
fxe pxe fx hxe fxe hxe
′
′
∫∫ ∫ ∫ ∫
⋅ +⋅ ⋅=⋅ ⇔ ⋅ =⋅
Suy ra
() ()
() ()d
p x dx p x dx
f x e e hx x
∫∫
⋅=
∫
Từ đây ta dễ dàng tính được
()fx
Dang 5. Bài toán tích phân liên quan đến biếu thúc
() () () 0f x px f x
′
+⋅=
Phương pháp:
Chia hai vế với
()fx
ta đựơc
() ()
() 0 ()
() ()
fx fx
px px
fx fx
′′
+=⇔ =−
Suy ra
()
d ()d ln| ()| ()d
()
fx
x px x f x px x
fx
′
=−⇔ =−
∫∫ ∫
Từ đây ta dễ dàng tính được
()fx
Dạng 6. Bài toán tích phân liên quan đến biểu thức
() ()[ ()] 0
n
f x px f x
′
+⋅ =
Phương pháp:
Chia hai vế với
[ ( )]
n
fx
ta được
() ()
() 0 ()
[ ( )] [ ( )]
nn
fx fx
px px
fx fx
′′
+=⇔ =−
Suy ra
1
() [ ()]
d ( )d ( )d
[ ( )] 1
n
n
f x fx
x px x px x
fx n
′ −+
=−⇔ =−
−+
∫∫ ∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 95
Câu 62: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
thỏa mãn
( )
( )
23
6
16
31
f x xf x
x
−= −
+
. Khi đó
( )
1
0
dfx x
∫
bằng
A.
4
. B.
1−
. C.
2
. D.
6
.
Câu 63: Cho hàm số
( )
fx
xác định và liên tục trên
{ }
\0
thỏa mãn
( ) ( ) ( ) ( )
22 '
21 1x f x x f x xf x+− = −
, với mọi
{ }
\0x ∈
đồng thời thỏa
( )
12f = −
. Tính
( )
2
1
dfxx
∫
A.
ln 2
1
2
−−
. B.
1
ln 2
2
−−
. C.
3
ln 2
2
−−
. D.
ln 2 3
22
−−
.
Câu 64: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
( )
2 3 532
1 33
1 4 5 7 6,
4 42
fx x f x x x x x x x
+ − − − = − − + + ∀∈
. Tích phân
( )
2
1
dfx x
∫
bằng
A.
1
7
. B.
1
3
. C.
7
. D.
19
3
−
.
Câu 65: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
11f =
và
( )
( )
( )
( )
[ ]
2
2 642
4 6 1 . 40 44 32 4, 0;1f x x fx x x x x
′
+ − = − + − ∀∈
. Tích phân
( )
1
0
f x dx
∫
bằng?
A.
23
15
. B.
13
15
. C.
17
15
−
. D.
7
15
−
.
Câu 66: Cho hàm số có đạo hàm liên tục trên và thỏa mãn và
. Tích phân bằng
A. . B. . C. . D.
Câu 67: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
2; 4
và
( )
[ ]
0, 2; 4fx x
′
> ∀∈
. Biết
( ) ( )
[ ]
( )
3
33
7
4 , 2; 4 , 2
4
xf x f x x x f
′
= − ∀∈ =
. Giá trị của
( )
4f
bằng
A.
40 5 1
2
−
. B.
20 5 1
4
−
. C.
20 5 1
2
−
. D.
40 5 1
4
−
.
Câu 68: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;2
và thỏa
( )
10f =
,
( )
( )
( )
2
2
4 8 32 28f x fx x x
′
+ =−+
với mọi
x
thuộc
[ ]
0;2
. Giá trị của
( )
1
0
dfx x
∫
bằng
A.
5
3
−
. B.
4
3
. C.
2
3
−
. D.
14
3
−
.
Câu 69: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
và
( ) ( )
2
23
1
1
xx
fx f x
x
++
+ −=
+
,
[ ]
0;1x∀∈
. Tính
( )
1
0
dfx x
∫
A.
3
2ln 2
4
+
. B.
3 ln 2+
. C.
3
ln 2
4
+
. D.
3
2ln 2
2
+
.
()fx
(0) 3f =
2
( ) (2 ) 2 2,fx f x x x x+ − = − + ∀∈
2
0
( )dxf x x
′
∫
4
3
−
2
3
5
3
10
3
−

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 96
Câu 70: Cho hàm số
()
y fx
=
liên tục trên thỏa mãn
(
) (
)
( )
2
21
3 2 2 1e 4
xx
fx f x x
−+
+ −= − +
. Tính tích
phân
(
)
2
0
dI fx x=
∫
ta được kết quả:
A.
e4
I = +
. B.
8I =
. C.
2I
=
. D.
e2I = +
.
Câu 71: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
(
)
(
)
2 73
2 23 1
f x xf x x x x+ = + −−
với
x ∈
.
Tính tích phân
( )
1
0
dxf x x
′
∫
.
A.
1
4
. B.
5
4
. C.
3
4
. D.
1
2
−
.
Câu 72: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
43
2
22 44
1 2 , 0, 1
− −++ −
− + = ∀≠ ≠
x xx x
xf x f x x
xx
. Khi đó
( )
1
1
d
−
∫
fx x
có giá trị là
A.
0
. B.
1
. C.
1
2
. D.
3
2
.
Câu 73: Cho hàm số
()
y fx=
thỏa mãn
2
' '' 3
() (). () 2,f x fxf x x x x R
+ = − ∀∈
và
'
(0) (0) 2ff= =
.
Tính giá trị của
2
(2)Tf
=
A.
160
15
B.
268
15
C.
4
15
D.
268
30
Câu 74: Cho
fx
là hàm số liên tục trên tập xác đinh
và thỏa mãn
2
31 2fx x x
. Tính
5
1
d
I fx x
A.
37
6
. B.
527
3
. C.
61
6
. D.
464
3
.
Câu 75: Cho hàm số
( )
y fx=
liên tục, có đạo hàm trên
R
thỏa mãn điều kiện
( )
2
() () 2sin cos,f x x f x x x xx R
′
+ −= ∈
và
22
f
=
ππ
.Tính
( )
2
0
xf x dx
′′
∫
π
A.
0
. B.
2
π
. C.
1
. D.
π
.
Câu 76: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
( )
22
4. 3 1 1xf x f x x+ −=−
. Tính
( )
1
0
d
I fx x
=
∫
.
A.
4
π
. B.
16
π
. C.
20
π
. D.
6
π
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 97
Câu 77: Cho hàm số
( )
fx
liên tục trên khoảng
( )
0; .+∞
Biết
( )
33f =
và
( ) ( )
(
)
3
'21 21 , 0; .xf x f x x x+ − + = ∀ ∈ +∞
Giá trị của
( )
5
3
f x dx
∫
bằng
A.
914
3
. B.
59
3
. C.
45
4
. D.
88
.
Câu 78: Cho hàm số
(
)
fx
có đạo hàm và đồng biến trên
[ ]
1; 4
, thỏa mãn
(
) (
)
2
2
x xf x f x
′
+=
với mọi
[ ]
1; 4x ∈
. Biết
( )
3
1
2
f =
, tính
( )
4
1
I f x dx=
∫
A.
1188
45
. B.
1187
45
. C.
1186
45
. D.
9
2
.
Câu 79: Cho hàm số
()
y fx=
có đạo hàm liên tục trên
thỏa mãn
2
.(). '() () ,xf x f x f x x x= − ∀∈
và
có
(2) 1f =
. Tích phân
2
2
0
()f x dx
∫
A.
3
2
B.
4
3
C.
2
D.
4
Câu 80: Cho hàm số
( )
fx
nhận giá trị không âm và có đạo hàm liên tục trên
thỏa mãn
( ) ( ) ( )
2
21 ,f x x fx x
′
= + ∀∈
và
( )
01f = −
. Giá trị của tích phân
( )
1
0
dfxx
∫
bằng
A.
1
6
−
. B.
ln 2−
. C.
3
9
π
−
. D.
23
9
π
−
.
Câu 81: Cho số thực
0a >
. Giả sử hàm số
()fx
liên tục và luôn dương trên đoạn
[
]
0;
a
thỏa mãn
( ). ( ) 1fx fa x−=
. Tính tích phân
( )
0
1
d
1
a
Ix
fx
=
+
∫
?
A.
2
3
a
I =
. B.
2
a
I =
. C.
3
a
I =
. D.
Ia=
.
Câu 82: Cho hàm số
( )
fx
đồng biến, có đạo hàm đến cấp hai trên đoạn
[ ]
0; 2
và thỏa mãn
( ) (
) ( )
( )
22
.0fx fxf x f x
′′ ′
− +=
. Biết
( )
01f =
,
( )
6
2fe
=
. Khi đó
( )
1f
bằng
A.
2
e
. B.
3
2
e
. C.
3
e
. D.
5
2
e
.
Câu 83: Cho hàm số
( )
y fx=
là hàm số lẻ trên
và đồng thời thỏa mãn hai điều kiện
(
) ( )
11fx fx+= +
,
x∀∈
và
( )
2
1
fx
f
xx
=
,
0x∀≠
. Gọi
( )
( )
1
2
0
.d
1
fx
Ix
fx
=
+
∫
. Hãy chọn
khẳng định đúng về giá trị của
I
.
A.
( )
1; 0I ∈−
. B.
( )
1; 2I ∈
. C.
( )
0;1I ∈
. D.
( )
2; 1I ∈− −
.
Câu 84: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;
π
. Biết
( )
0 2ef =
và
( )
fx
thỏa mãn hệ thức
( ) ( )
[ ]
cos
sin . cos .e , 0;
x
f x xf x x x
π
′
+ = ∀∈
. Tính
( )
0
dI fx x
π
=
∫
.
A.
6,55I ≈
. B.
17,30I ≈
. C.
10,31I ≈
. D.
16,91I ≈
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 98
Câu 85: Cho hàm số
( )
fx
liên tục và nhận giá trị dương trên
[ ]
0;1
. Biết
( ) ( )
.1 1fxf x−=
với
[ ]
0;1x∀∈
. Tính giá trí
( )
1
0
d
1
x
I
fx
=
+
∫
A.
3
2
. B.
1
2
. C.
1
. D.
2
.
Câu 86: Cho hàm số
( )
y fx=
có đạo hàm trên khoảng
(
)
0;
+∞
thỏa mãn
( )
(
) ( )
3
.ln
.
x
fx x
xf x f x
=
′
−
và
( )
10f =
. Tính tích phân
(
)
5
1
d
I fx x=
∫
.
A.
12ln13 13−
. B.
13ln13 12
−
. C.
12ln13 13+
. D.
13ln13 12+
.
Câu 87: Cho hàm số
( )
y fx=
liên tục trên
{ }
\ 0; 1−
thỏa mãn điều kiện
( )
1 2ln 2f =
và
( ) ( ) ( )
2
1. 3 2xx f x f x x x
′
+ + =++
. Giá trị
(
)
2 ln 3
f ab
= +
, với
,ab∈
. Tính
22
ab+
.
A.
5
2
. B.
13
4
. C.
25
4
. D.
9
2
.
Câu 88: Cho hàm số
()y fx=
liên tục trên
thỏa mãn:
2
21
3 ( ) (2 ) 2( 1) 4,
xx
fx f x x e x
−+
+ − = − + ∀∈
.
Tính giá trị của tích phân
2
0
()I f x dx=
∫
.
A.
2Ie= +
. B.
24Ie= +
. C.
2I =
. D.
8
I =
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 99
DẠNG 2. TÍCH PHÂN MỘT SỐ HÀM ĐẶC BIỆT
DẠNG 2.1 TÍCH PHÂN CỦA HÀM SỐ LẺ VÀ HÀM SỐ CHẴN
Nhắc lại kiến thức về hàm số lẻ và hàm số chẵn:
Hàm số
(
)
y fx
=
có miền xác định trên tập đối xứng D và
Nếu
( )
( )
(
)
,
f x fx x D y fx
− = ∀∈ ⇒ =
: là hàm số chẵn.
Nếu
(
)
( )
,f x fx x D
− =− ∀∈
(
)
y fx
⇒=
: là hàm số lẻ.
.
Thường gặp cung góc đối nhau của
(
)
( )
cos cos , sin sin
xx x x
−= −=−
.
Nếu hàm số
( )
fx
liên tục và lẻ trên
[ ]
;aa−
thì
( )
.0
a
a
f x dx
−
=
∫
.
Nếu hàm số
(
)
fx
liên tục và chẵn trên
[
]
;aa
−
thì
( ) ( )
( )
( )
0
0
2
1
aa
a
a
x
a
f x dx f x dx
fx
dx f x dx
b
α
−
−
=
=
+
∫∫
∫∫
.
Do những kết quả này không có trong SGK nên về mặt thực hành, ta làm theo các bước sau:
Bước 1. Phân tích:
( ) ( ) ( )
0
0
. ..
aa
aa
I f x dx f x dx f x dx A B
−−
= = +=+
∫ ∫∫
.
Bước 2. Tính
(
)
0
.
a
A f x dx
−
=
∫
? bằng cách đổi biến
tx= −
và cần nhớ rằng: tích phân không phụ
thuộc vào biến, mà chỉ phụ thuộc vào giá trị của hai cận, chẳng hạn luôn có:
0
22
0
22
2014
2014
3 cos 3 cos
1 sin 1 sin
tt xx
dt dx
tx
−
−
=
++
∫∫
.
2. Tích phân của hàm số liên tục
Nếu hàm số
(
)
fx
liên tục trên
[ ]
;ab
thì
( ) (
)
bb
aa
f x dx f a b x dx= +−
∫∫
.
Nếu hàm số
( )
fx
liên tục trên
[ ]
0;1
thì
+
(
) ( )
22
00
sin cos
f x dx f x dx
ππ
=
∫∫
.
+
(
) ( )
sin sin
2
aa
aa
xf x dx f x dx
ππ
π
−−
=
∫∫
và
( ) (
)
00
. sin sin
2
x f x dx f x dx
ππ
π
=
∫∫
.
+
( ) ( )
22
cos cos
aa
aa
xf x dx f x dx
ππ
π
−−
=
∫∫
và
( ) ( )
22
00
. cos cosx f x dx f x dx
ππ
π
=
∫∫
→
Về mặt thực hành, sẽ đặt
x =
cận trên
+
cận dưới
t−
( )
x abt=+−
. Từ đó tạo tích phân
xoay vòng, rồi giải phương trình bậc nhất với ẩn I.
Nếu hàm số
( )
fx
liên tục trên
và tuần hoàn với chu kỳ T thì
( ) ( )
0
aT T
a
f x dx f x dx
+
=
∫∫
và
( ) ( )
00
nT T
f x dx n f x dx=
∫∫
.
Lưu ý: Hàm số
( )
fx
có chu kỳ T thì
( ) ( )
fxT fx+=
.
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 100
→
Về mặt thực hành, ta sẽ làm theo các bước sau:
Bước 1. Tách:
( ) ( ) ( ) ( )
0
0
aT T aT
aa T
C
AB
I f x dx f x dx f x dx f x dx
++
= =++
∫ ∫∫ ∫
( )
i
Bước 2. Tính
( )
aT
T
C f x dx
+
=
∫
?
Đặt
x t T dx dt=+⇒ =
. Đổi cận:
0
x aT t a
xT t
=+=
⇒
= =
. Khi đó:
(
) ( )
(
)
00
0
a
aa
C f t T dt f t dt f x dx A
=+=− =− =−
∫ ∫∫
( )
ii
Thế
( )
i
vào
( )
ii
ta được:
( )
0
T
I B f x dx= =
∫
.
Câu 89: Cho
( )
fx
là hàm số chẵn trên đoạn
[ ]
;aa−
và
0k >
. Giá trị tích phân
(
)
d
1e
a
kx
a
fx
x
−
+
∫
bằng
A.
(
)
0
d
a
fx x
∫
. B.
( )
d
a
a
fx x
−
∫
. C.
(
)
2d
a
a
fx x
−
∫
. D.
( )
0
2d
a
fx x
∫
.
Câu 90: Cho
(
) (
)
,
fx f x−
liên tục trên
và thỏa mãn
( ) ( )
2
1
23
4
fx f x
x
+ −=
+
. Biết
( )
2
2
I f x dx
m
π
−
= =
∫
. Khi đó giá trị của
m
là
A.
2m
=
. B.
20m =
. C.
5m =
. D.
10
m =
.
Câu 91: Cho hàm số
(
)
y fx
=
là hàm lẻ và liên tục trên
[ ]
4; 4−
biết
(
)
0
2
d2f xx
−
−=
∫
và
( )
2
1
2d 4
f xx−=
∫
. Tính
( )
4
0
dI fx x=
∫
.
A.
10I = −
. B.
6I = −
. C.
6I =
. D.
10I =
.
Câu 92: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
ln 2;ln 2−
và thỏa mãn
( ) ( )
1
1
x
fx f x
e
+ −=
+
. Biết
(
)
ln 2
ln 2
d ln 2 ln 3fx x a b
−
= +
∫
( )
;ab∈
. Tính
P ab= +
.
A.
1
2
P =
. B.
2P = −
. C.
1P = −
. D.
2P =
.
Câu 93: Cho
( )
y fx=
là hàm số chẵn và liên tục trên
.
Biết
(
) ( )
12
01
1
d d1
2
fx x fx x= =
∫∫
. Giá trị của
( )
2
2
d
31
x
fx
x
−
+
∫
bằng
A.
1
. B.
6
. C.
4
. D.
3
.
Câu 94: Hàm số
( )
fx
là hàm số chẵn liên tục trên
và
(
)
2
0
d 10
fx x=
∫
. Tính
( )
2
2
d
21
x
fx
Ix
−
=
+
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 101
A.
10I
=
. B.
10
3
I =
. C.
20I
=
. D.
5I =
.
Câu 95: Cho hàm số
(
)
y fx=
là hàm số chẵn, liên tục trên đoạn
[ ]
1;1−
và
(
)
1
1
6f x dx
−
=
∫
. Kết quả của
( )
1
1
1 2018
x
fx
dx
−
+
∫
bằng
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 96: Tích phân
2
2020
2
2
.d
1
a
x
x
x
eb
−
=
+
∫
. Tính tổng
S ab= +
.
A.
0S =
. B.
2021S =
. C.
2020S =
. D.
4042S
=
.
Câu 97: Cho hàm số
(
)
fx
liên tục trên đoạn
[ ]
ln 2;ln 2−
và thỏa mãn
( )
( )
1
e1
x
fx f x+ −=
+
. Biết
(
)
( )
ln 2
ln 2
d ln 2 ln 3, ,f x x a b ab
−
=+∈
∫
. Tính
P ab= +
.
A.
2P = −
. B.
1
2
P =
. C.
1P = −
. D.
2
P
=
.
Câu 98: Cho
( )
fx
là hàm số chẵn và
( )
1
0
2f x dx =
∫
. Giá trị của tích phân
( )
1
1
1 2019
x
fx
dx
−
+
∫
là
A.
2
.
2019
B.
2
. C.
4
. D.
0
.
DẠNG 2.2 TÍCH PHÂN CỦA HÀM CHỨA DẤU TRỊ TUYỆT ĐỐI
Tính tích phân:
( )
.
b
a
I f x dx=
∫
?
Bước 1. Xét dấu
( )
fx
trên đoạn
[
]
;
ab
. Giả sử trên đoạn
[
]
;ab
thì phương trình
( )
0
fx=
có
nghiệm
[
]
;
o
x ab∈
và có bảng xét dấu sau:
x
a
o
x
b
( )
fx
+
0
−
Bước 2. Dựa vào công thức phân đoạn và dấu của trên
[ ] [ ]
;,;
oo
ax x b
ta được:
( ) ( ) ( )
.
o
o
x
bb
a ax
I f x dx f x dx f x dx A B= = +− =+
∫ ∫∫
.
Sử dụng các phương pháp tính tích phân đã học tính
,AB
I⇒
.
Câu 99: Cho
a
là số thực dương, tính tích phân
1
d
a
I xx
−
=
∫
theo
a
.
A.
2
1
2
a
I
+
=
. B.
2
2
2
a
I
+
=
. C.
2
21
2
a
I
−+
=
. D.
2
31
2
a
I
−
=
.
Câu 100: Cho số thực
1m >
thỏa mãn
1
211
m
mx dx−=
∫
. Khẳng định nào sau đây đúng?
A.
( )
4;6m ∈
. B.
( )
2; 4m ∈
. C.
( )
3; 5m ∈
. D.
( )
1; 3m ∈
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 102
Câu 101: Cho tích phân
5
1
2
ln 2 ln 3
1
x
dx a b c
x
−
=++
+
∫
với a, b, c là các số nguyên. Tính P = abc.
A.
36
P
= −
B.
0P =
C.
18P = −
D.
18
P
=
Câu 102: Tính tích phân
1
1
22
xx
I dx
−
−
= −
∫
.
A.
1
ln 2
. B.
ln 2
. C.
2ln 2
. D.
2
ln 2
.
Câu 103: Cho hàm số
( )
fx
liên tục trên
và có
( )
1
0
d2fx x=
∫
;
( )
3
0
d6fx x=
∫
. Tính
(
)
1
1
2 1dI fx x
−
= −
∫
A.
8
I =
B.
6I =
C.
3
2
I =
D.
4I =
Câu 104: Cho hàm số
()fx
liên tục trên
và có
3
0
() 8f x dx =
∫
và
5
0
( ) 4.f x dx =
∫
Tính
1
1
(4 1) .f x dx
−
−
∫
A.
9
.
4
B.
11
.
4
C.
3.
D.
6.
Câu 105: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
1
0
2d 2f xx=
∫
và
(
)
2
0
6 d 14f xx=
∫
. Tính
( )
2
2
5 2dfx x
−
+
∫
.
A.
30
. B.
32
. C.
34
. D.
36
.
Câu 106: Cho số thực
a
và hàm số
( )
( )
2
20
0
x khi x
fx
a x x khi x
≤
=
−>
. Tính tích phân
(
)
1
1
f x dx
−
∫
bằng:
A.
1.
6
a
−
B.
2
1.
3
a
+
C.
1.
6
a
+
D.
2
1.
3
a
−
Câu 107: Cho hàm số
( )
2
e khi 0
2 3 khi 0
x
mx
fx
xx x
+≥
=
+<
liên tục trên
và
( )
1
1
d=e 3f x xa b c
−
++
∫
,
( )
,,abc Q∈
. Tổng
3ab c++
bằng
A.
15
. B.
10−
. C.
19−
. D.
17−
.
Câu 109: Cho hàm số
2
31
51
x khi x
y fx
x khi x
. Tính
1
2
00
2 sin cos 3 3 2I f x xdx f x dx
π
A.
71
6
I
. B.
31I
. C.
32I
. D.
32
3
I
.
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 1
BÀI 2. TÍCH PHÂN
MỨC ĐỘ VẬN DỤNG – VẬN DỤNG CAO
DẠNG 1. TÍCH PHÂN HÀM ẨN
DẠNG 1.1 GIẢI BẰNG PHƯƠNG PHÁP ĐỔI BIẾN
Câu 1: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
1
5
d9fx x
−
=
∫
. Tích phân
( )
2
0
1 3 9d
fx x−+
∫
bằng
A.
15
. B.
27
. C.
75
. D.
21
.
Lời giải
Chọn D
Ta có
( ) ( )
2 22
0 00
13 9d 13 d 9dfx xfxxx−+ = − +
∫ ∫∫
(
)
2
0
1 3 d 18
f xx=−+
∫
.
Xét
( )
2
0
13 df xx−
∫
, đặt
13tx= −
d
d 3d d
3
t
t xx⇒=− ⇒=−
.
Đổi cận khi
01xt=⇒=
;
25xt
= ⇒=−
. Suy ra
( )
2 51
0 15
11
1 3 d ( )d ( )d
33
f x x ft t ft t
−
−
−=− =
∫ ∫∫
.
Khi đó
( )
2 11
0 55
11
1 3 9 d ( )d 18 ( )d 18 21
33
f x x ft t fx x
−−
− + = += +=
∫ ∫∫
.
Câu 2: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;10
thỏa mãn
( ) ( )
10 10
02
d 7, d 1fx x fx x= =
∫∫
. Tính
( )
1
0
2dP f xx=
∫
.
A.
6P
=
. B.
6P = −
. C.
3P =
. D.
12
P =
.
Lời giải
Chọn C
CHƯƠNG
III
NGUYÊN HÀM – TÍCH PHÂN
- ỨNG DỤNG TÍCH PHÂN
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
Ta có:
( ) (
) ( )
2 10 10
002
d d d6fx x fx x fx x=−=
∫∫∫
.
Xét
( )
1
0
2dP f xx=
∫
. Đặt
1
2 d 2d d d
2
txt xx t= ⇒= ⇒=
.
Đổi cận:
Lúc đó:
( )
( ) ( )
1 22
0 00
11
2d d d 3
22
P f x x ft t fx x= = = =
∫ ∫∫
.
Câu 3: Cho
( )
5
1
d 26I fx x= =
∫
. Khi đó
( )
2
2
0
1 1dJ xfx x
= ++
∫
bằng
A.
15
. B.
13
. C.
54
. D.
52
.
Lời giải
Chọn A
+ Ta có:
( )
2
2
0
1 1dJ xfx x
= ++
∫
( )
22
2
00
d 1dx x xf x x=++
∫∫
.
+ Xét
2
0
dA xx
=
∫
.
2
0
dA xx=
∫
2
2
0
2
2
x
= =
.
+ Xét
( )
2
2
0
1dB xf x x= +
∫
.
Đặt
2
1tx
= +
d 2dt xx⇒=
.
Đổi cận:
( )
2
2
0
1dB xf x x= +
∫
(
)
5
1
1
d
2
ft t=
∫
( )
5
1
1
d
2
fx x
=
∫
Ta có:
1
.26 13
2
= =
.
Vậy
15J AB=+=
.
x
0
2
t
1
5

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
Câu 4: Cho hàm số
()
y fx=
liên tục trên
thỏa mãn
( )
9
1
4
fx
dx
x
=
∫
và
( )
2
0
sin cos 2.f x xdx
π
=
∫
Tích phân
3
0
()I f x dx
=
∫
bằng
A.
8I =
. B.
6I =
. C.
4I =
. D.
10I =
.
Lời giải
Chọn C
Đặt
1
t x dt dx
2x
= ⇒=
. Khi đó
1 1; 9 3x tx t=⇒= =⇒=
Suy ra
(
)
93 3
11 1
2 () 4 () 2.
fx
dx f t dt f t dt
x
= =⇒=
∫∫∫
Đặt
; cos
2
sin ;
2
txx dt dx
ππ
∈− ⇒ =
=
. Khi đó.
0 0; 1
2
x tx t
π
=⇒= = ⇒=
Suy ra
31 3
00 1
() () () 2 2 4.f x dx f x dx f x dx= + =+=
∫∫∫
Câu 5: Cho biết
(
)
5
1
d 15fxx
−
=
∫
. Tính giá trị của
( )
2
0
5 3 7dPf x x= −+
∫
.
A.
15P =
. B.
37P =
. C.
27P =
. D.
19P =
.
Lời giải
Đặt
53
tx= −
d 3dtx⇒=−
1
d= d
3
xt
⇒−
.
Đổi cận:
0
x =
thì
5
t =
;
2
x =
thì
1
t = −
.
Ta có:
( )
2
0
5 3 7dPf x x= −+
∫
( )
22
00
5 3 d + 7d
f xx x= −
∫∫
( )
1
2
0
5
d
7
3
t
ft x
−
= +
−
∫
( )
5
1
1
d 14
3
ft t
−
= +
∫
1
.15 14 19
3
= +=
.
Câu 6: Cho
( )
4
0
20 8d 1fx x=
∫
. Tính tích phân
( ) ( )
2
0
24d2I fx f x x= +−
∫
.
A.
0I =
. B.
2018I =
. C.
4036I =
. D.
1009I =
.
Lời giải
Ta có
( ) ( )
22
00
2 42ddI f xx f xxHK= +− =+
∫∫
Tính
( )
2
0
2K f x dx=
∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
Đặt
d22dtx t x= ⇒=
; đổi cận:
02;24x tx t= ⇒= = ⇒=
. Nên
(
)
4
0
1
100d 9
2
K ft t= =
∫
Tính
( )
2
0
d42H f xx= −
∫
,
Đặt
42 2t x dt dx=−⇒=−
; đổi cận:
0 4; 2 0x tx t= ⇒= = ⇒=
. Nên
( )
4
0
1
100
d 9
2
H ft t= =
∫
Suy ra
2018I KH=+=
.
Câu 7: Cho
( )
y fx=
là hàm số chẵn, liên tục trên
[ ]
6;6−
. Biết rằng
( )
2
1
d8fx x
−
=
∫
;
( )
3
1
2d 3f xx−=
∫
.
Giá trị của
(
)
6
1
dI fx x
−
=
∫
là
A.
5I =
. B.
2I =
. C.
14I =
. D.
11I =
.
Lời giải
Ta có
( )
y fx=
là hàm số chẵn, suy ra
( ) ( )
22f x fx−=
. Khi đó:
( ) ( )
33
11
2d 2d 3f xx f xx−= =
∫∫
.
Xét tích phân:
( )
3
1
1
2dI f xx=
∫
.
Đặt
1
2 d 2d d d
2
tx t x tx= ⇒= ⇔ =
. Đổi cận:
12xt=⇒=
;
36xt=⇒=
.
⇒
( ) ( ) ( )
666
1
222
11
.d d 3 d 6
22
I ft t ft t ft t= = =⇒=
∫∫∫
( )
6
2
d6
fx x⇒=
∫
.
Vậy
( ) ( ) ( )
6 26
1 12
d d d 8 6 14I fx x fx x fx x
−−
= = + =+=
∫∫∫
.
Câu 8: Cho hàm số
( )
fx
liên tục trên
và
( )
2
0
d 2018fx x
π
=
∫
, tính
( )
2
0
d.I xf x x
π
=
∫
A.
1008I =
. B.
2019I =
. C.
2017I =
. D.
1009I =
.
Lời giải
Xét
(
)
2
0
d.
I xf x x
π
=
∫
Đặt
2
1
d 2 d d d.
2
t x t xx xx t=⇒= ⇒ =
Đổi cận:
2
0 0; .x tx t
ππ
=⇒= = ⇒=

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Khi đó
( ) ( )
22
00
11
d d 1009.
22
I ft t fx x
ππ
= = =
∫∫
Câu 9: Cho
( )
2
1
d2fxx=
∫
. Khi đó
( )
4
1
d
fx
x
x
∫
bằng
A.
1
. B.
4
. C.
2
. D.
8
.
Lời giải
Đặt
xt=
1
dd
2
xt
x
⇒=
1
d 2dxt
x
⇒=
. Khi
1
x =
thì
1t =
;
4
x =
thì
2t =
.
Suy ra
( )
( )
( )
42 2
11 1
d .2d 2 d 2.2
fx
x ft t ft t
x
= = =
∫∫∫
4
=
.
Vậy
(
)
4
1
d4
fx
x
x
=
∫
.
Câu 10: Cho
( )
df x xx+=
∫
2
2
1
12
. Khi đó
( )
dI fx x=
∫
5
2
bằng
A.
2
. B.
1
. C.
4
. D.
1
−
.
Lời giải
Đặt
d
dd d .
t
x t xx t xx+=⇒ = ⇒ =
2
12
2
Đổi cận
;.x tx t=⇒= = ⇒=1 22 5
Suy ra:
( )
(
)
2
2
1
5
2
1
dd
2
21x ft tfx == +
∫∫
(
)
5
2
d4
ft t =⇒
∫
( )
dI fx x⇒= =
∫
5
2
4
.
Câu 11: Cho
,fg
là hai hàm số liên tục trên
[ ]
1; 3
thỏa mãn điều kiện
( ) ( )
3
1
3 dx=10f x gx+
∫
đồng thời
( ) (
)
3
1
2 dx=6f x gx−
∫
. Tính
( )
3
1
4 dxfx−
∫
+2
( )
2
1
2 1 dxgx−
∫
A.
9
. B.
6
. C.
7
. D.
8
.
Lời giải
Ta có:
( ) ( )
3
1
3 dx=10
f x gx+
∫
( )
( )
33
11
dx+3 dx=10
f x gx⇔
∫∫
.
( ) ( )
3
1
2 dx=6f x gx−
∫
( ) ( )
33
11
2 dx- dx=6f x gx⇔
∫∫
.
Đặt
( ) ( )
33
11
dx; v = dx
u f x gx=
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
Ta được hệ phương trình:
3 10
26
uv
uv
+=
−=
4
2
u
v
=
⇔
=
( )
( )
3
1
3
1
dx=4
dx=2
fx
gx
⇒
∫
∫
+ Tính
( )
3
1
4 dxfx−
∫
Đặt
4 dt dx; 1 3; 3 1t x x tx t=−⇒ =− =⇒= =⇒=
.
( )
(
)(
) (
)
( )
3 1 33
1 3 11
4 d dt dt dx 4f x x ft ft fx− = −= = =
∫ ∫ ∫∫
.
+ Tính
(
)
2
1
2 1 dxgx
−
∫
Đặt
2 1 dz 2dx; 1 1; 2 3zx x z x z= −⇒ = =⇒= =⇒=
.
( ) ( )
( )
2 33
1 11
11
2 1 d dz dx 1.
22
g x x gz gx−= = =
∫ ∫∫
Vậy
( )
3
1
4 dxfx−
∫
+2
( )
2
1
2 1 dx = 6gx−
∫
.
Câu 12: Cho hàm số
(
)
fx
liên tục trên
thỏa
( )
1
0
d2fx x=
∫
và
( )
2
0
3 1d 6fx x+=
∫
. Tính
( )
7
0
dI fx x=
∫
.
A.
16I
=
. B.
18I =
. C.
8I =
. D.
20I =
.
Lời giải
(
)
1
0
d2
A fx x= =
∫
,
( )
2
0
3 1d 6B fx x= +=
∫
đặt
31 3t x dt dx
= +⇒ =
.
Đổi cận :
01
27
=⇒=
= ⇒=
xt
xt
Ta có:
( ) ( ) ( )
77 7
11 1
1
dt 6 dt 18 d =18
3
B ft ft fx x= =⇒=⇒
∫∫ ∫
.
Vậy
( ) ( ) ( )
7 17
0 01
d d d 20I fx x fx x fx x==+=
∫∫∫
.
Câu 13: Cho
( )
fx
liên tục trên
thỏa mãn
( ) ( )
10fx f x= −
và
( )
7
3
d4fx x=
∫
. Tính
( )
7
3
dI xf x x=
∫
.
A.
80
. B.
60
. C.
40
. D.
20
.
Lời giải
Đặt
10tx= −
. Khi đó
ddtx= −
.
Đổi cận:
37xt=⇒=
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 7
73xt= ⇒=
.
Khi đó
( ) (
)
( ) ( )
37
73
10 10 d 10 10 d
I tf t t tf t t
=−−−=−−
∫∫
( ) ( )
7
3
10 10 dxf x x=−−
∫
( ) ( ) ( ) ( )
7 77
3 33
10 d 10 d dxfx x fx x xfx x=−= −
∫ ∫∫
( )
7
3
10 dfx x I= −
∫
.
Suy ra
(
)
7
3
2 10 d 10.4 40
I fx x
= = =
∫
. Do đó
20I =
.
Câu 14: Cho
(
)
1
0
d9
fx x
=
∫
. Tính
(
)
6
0
sin 3 cos3 d
I f x xx
π
=
∫
.
A.
5I =
. B.
9I =
. C.
3I =
. D.
2I =
.
Lời giải
Đặt
sin 3 d 3 cos 3 .dt x t xx= ⇒=
Đổi cận:
00
1
6
xt
xt
π
=⇒=
= ⇒=
( )
(
)
1
6
00
11
sin 3 cos3 d d .9 3
33
I f x xx f t t
π
= = = =
∫∫
Câu 15: Cho tích phân
(
)
4
0
d 32.
= =
∫
I fx x
Tính tích phân
( )
2
0
2 d.
=
∫
J f xx
A.
32J =
B.
64J =
C.
8J =
D.
16J =
Lời giải
Đặt
d
2 d 2d d .
2
= ⇒= ⇒ =
t
tx t x x
Đổi cận:
0 0; 2 4.=⇒= = ⇒=x tx t
( ) ( ) ( )
24 4
00 0
11 1
2 d d d 16.
22 2
= = = = =
∫∫ ∫
J f x x ft t ft t I
Câu 16: Biết
( )
fx
là hàm liên tục trên
và
( )
9
0
d9fx x=
∫
. Khi đó giá trị của
( )
4
1
3 3dfx x−
∫
là
A.
0
. B.
24
. C.
27
. D.
3
.
Lời giải
Xét
( )
4
1
3 3dI fx x= −
∫
.
Đặt
3 3 d 3dtx t x= −⇒ =
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Đổi cận:
49
10
xt
xt
= ⇒=
=⇒=
. Vậy
( )
(
)
99
00
11 1
d d .9 3
33 3
I ft t fx x
= = = =
∫∫
.
Câu 17: Cho hàm số
()fx
thỏa mãn
1
0
(2 ) 2f x dx =
∫
.Tích phân
2
0
()f x dx
∫
bằng
A. 8. B. 1. C. 2. D. 4.
Lời giải
Đặt
2
tx=
⇒
2dt dx
=
⇒
2
dt
dx
=
,
00
12
xt
xt
=⇒=
=⇒=
Ta có
12 2
00 0
() 1
2 (2 ) ( )
22
f t dt
f x dx f t dt= = =
∫∫∫
2
0
() 4f t dt⇒=
∫
Theo tính chất tích phân
22
00
(x) (t) 4f dx f dt
= =
∫∫
Vậy
2
0
() 4f x dx =
∫
Câu 18: Cho hàm
( )
fx
thỏa mãn
( )
2017
0
d1fx x=
∫
. Tính tích phân
( )
1
0
2017 dI f xx=
∫
.
A.
1
2017
I =
. B.
0I =
. C.
2017
I =
. D.
1I =
.
Lời giải
Đặt
2017 d 2017dt xt x= ⇒=
1
dd
2017
xt⇒=
Đổi cận:
0 0 ; 1 2017x t xt=⇒= =⇒=
Vậy
( ) ( )
2017 2017
00
11 1
.d d
2017 2017 2017
I ft t ft t= = =
∫∫
.
Câu 19: Cho tích phân
( )
2
1
dfx x a=
∫
. Hãy tính tích phân
(
)
1
2
0
1dI xf x x= +
∫
theo
a
.
A.
4Ia=
. B.
4
a
I =
. C.
2
a
I =
. D.
2Ia=
.
Lời giải
Đặt
2
1 d 2dt x t xx= +⇒ =
.
Đổi cận

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
( )
(
)
( )
( )
1 2 22
2
0 1 11
d1 1
1d . d d
22 2 2
ta
I xfx x ft ft t fx x= += = = =
∫ ∫ ∫∫
.
Câu 20: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
4
2
0
tan . cos d 2xf x x
π
=
∫
và
( )
2
2
ln
d2
ln
e
e
fx
x
xx
=
∫
.
Tính
( )
2
1
4
2
d
fx
x
x
∫
.
A.
0
. B.
1
. C.
4
. D.
8
.
Lời giải
*
( )
( )
2
44
2
1
2
00
cos
1
tan . cos d .sin2 d
2 cos
fx
I xf x x xx
x
ππ
= =
∫∫
.
Đặt
2
cos xt=
sin 2 d dxx t
⇒=−
.
Đổi cận
x
0
4
π
t
1
1
2
Khi đó
( )
1
2
1
1
1
d
2
ft
It
t
= −
∫
( )
1
1
2
d4
ft
t
t
⇒=
∫
.
*
( )
(
)
22
22
ee
2
2
ee
ln ln
1 2ln
d .d
ln 2 ln
fx fx
x
Ix x
xx x x
= =
∫∫
.
Đặt
2
ln xt=
2ln
dd
x
xt
x
⇒=
.
Đổi cận
x
e
2
e
t
1
4
Khi đó
(
)
4
2
1
1
d
2
ft
It
t
=
∫
( )
4
1
d4
ft
t
t
⇒=
∫
.
* Tính
( )
2
1
4
2
d
fx
Ix
x
=
∫
. Đặt
2xt=
1
d
2
x dt
⇒=
.
Đổi cận
x
1
4
2
t
1
2
4
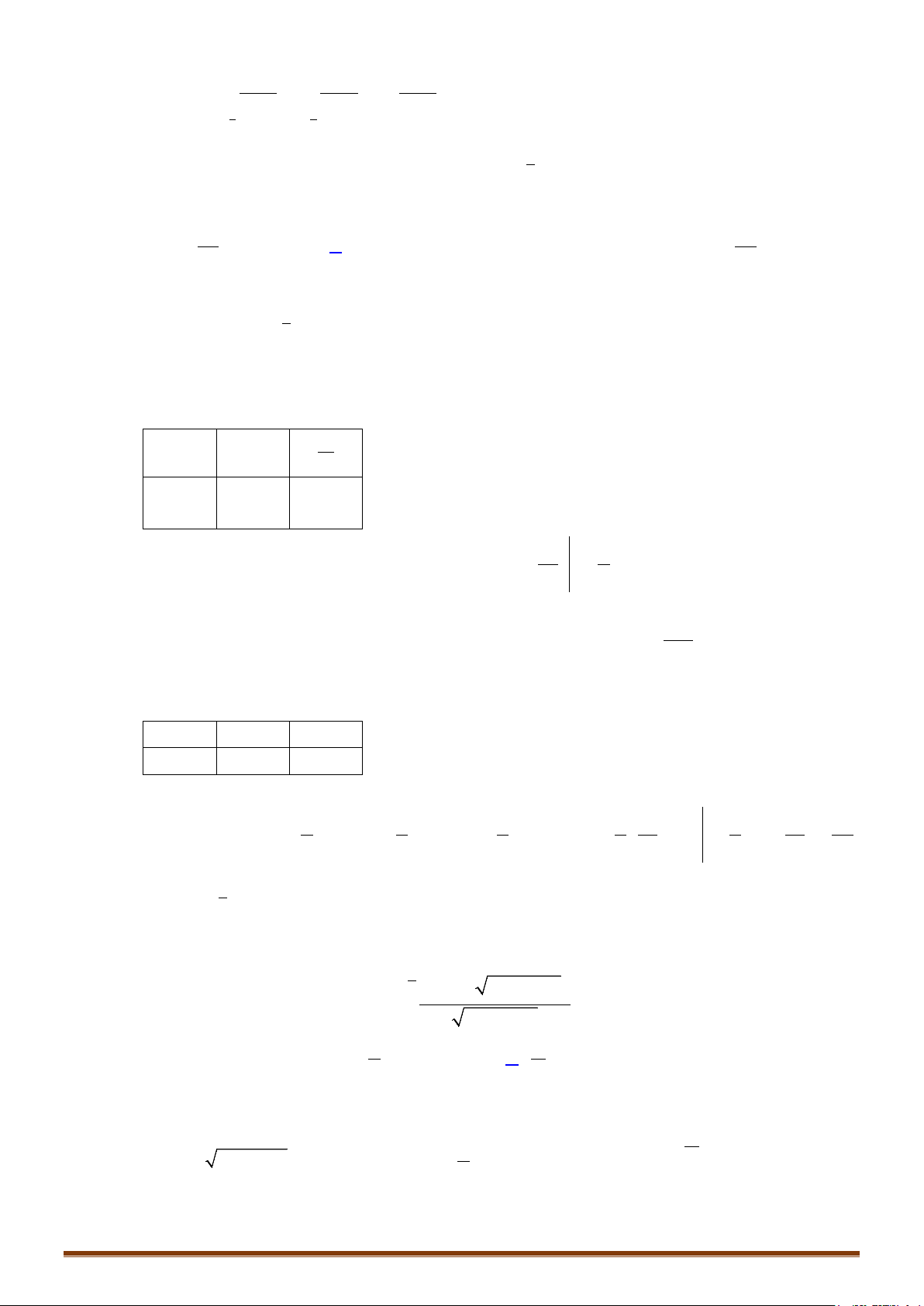
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 10
Khi đó
( )
(
)
( )
4 14
11
1
22
d d d 448
ft ft ft
I ttt
ttt
= = + =+=
∫∫∫
.
Câu 21: Cho hàm số
( )
22
3; 1
5;1
x xx
y fx
xx
+≥
= =
−<
. Tính
( ) (
)
1
2
00
2 sin cos 3dd32I f x xx f x x
π
= +−
∫∫
.
A.
71
6
I =
. B.
31I =
. C.
32I =
. D.
32
3
I =
.
Lời giải
Xét tích phân
( )
2
1
0
sin co
ds
I f x xx
π
=
∫
.Đặt
sin dcosdt x t xx= ⇒=
Đổi cận
x
0
2
π
t
0
1
Ta có
( ) ( ) ( )
1
11 1
2
1
00 0
0
dd d
9
55
22
x
I ftt fxx xx x
= = =−=− =
∫∫ ∫
Xét tích phân
( )
1
2
0
32 dI f xx= −
∫
.Đặt
32 2
d
dd
2
d
t
t xt xx
−
=−⇒=− ⇒=
Đổi cận
x
0
1
t
3
1
Ta có
( ) ( ) (
)
(
)
3
1 33 3
3
2
2
0 11 1
1
ddd d
1 1 1 1 1 10 22
3 2 3 3 18
2 2 2 23 2 3 3
x
I f xx ftt fxx x x x
= − = = = + = + = −=
∫ ∫∫ ∫
Vậy
( ) ( )
1
2
00
2 sin cos 3 3 2 9 31d 2d 2I f x xx f x x
π
= + − =+=
∫∫
.
Câu 22: Cho
( )
2
1
d2I fx x= =
∫
. Giá trị của
( )
2
0
sin 3cos 1
d
3cos 1
xf x
x
x
π
+
+
∫
bằng
A.
2
. B.
4
3
−
. C.
4
3
. D.
2−
.
Lời giải
Đặt
2
2
3cos 1 3cos 1 d sin d .
3
u x u x uu xx= + ⇒ = + ⇒− =
Đổi cận
1
.
2
02
xu
xu
π
= ⇒=
=⇒=
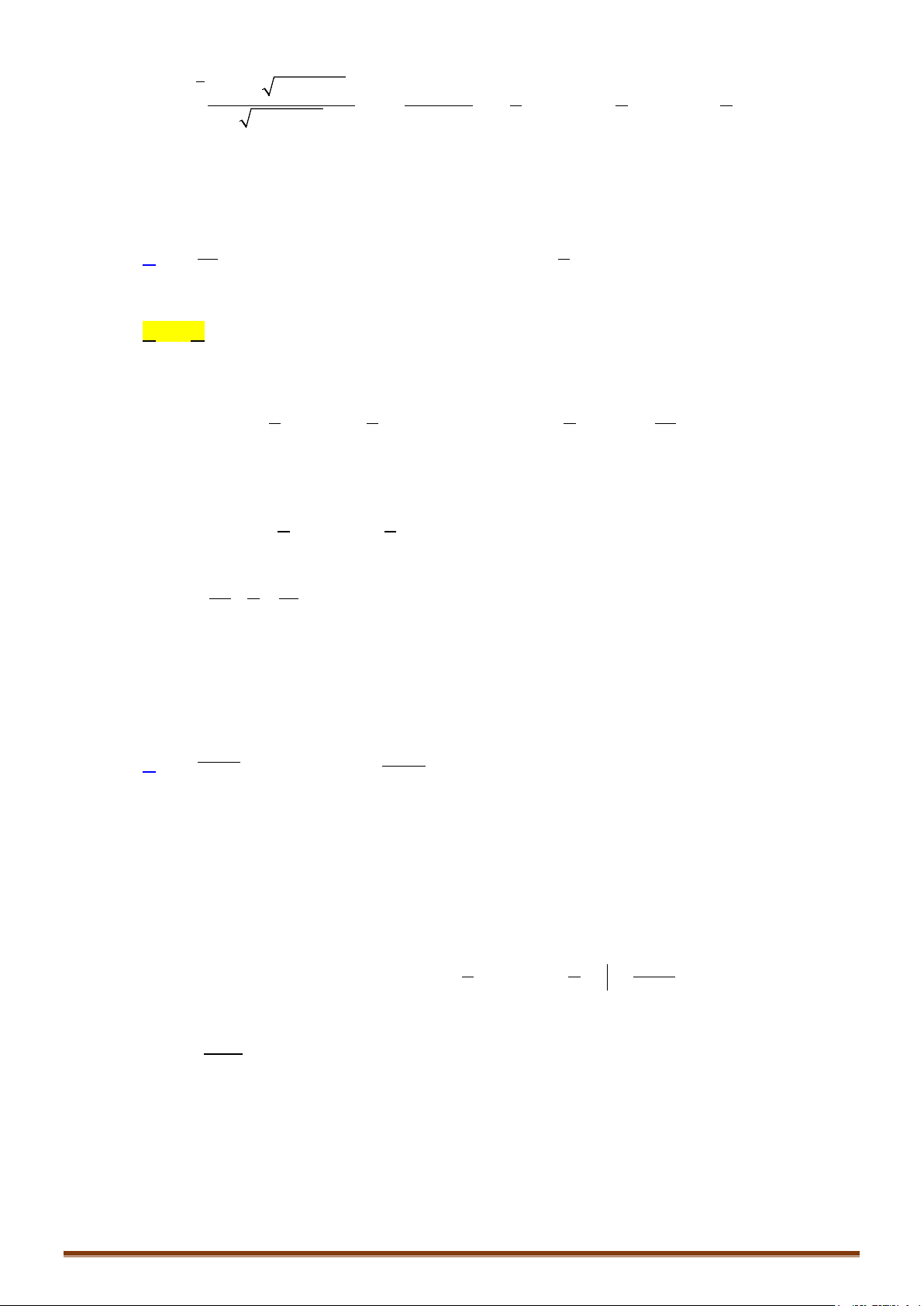
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 11
Do đó
( )
( )
( )
( )
1 22
2
0 2 11
sin 3cos 1
2
224
d ddd.
33 3 3
3cos 1
xf x
uf u
x ufuufxx
u
x
π
+
−
= = = =
+
∫ ∫ ∫∫
Câu 23: Biết
( )
4
1
5
f x dx =
∫
và
( )
5
4
20f x dx =
∫
. Tính
( )
( )
2 ln 2
22
10
43
xx
f x dx f e e dx−−
∫∫
.
A.
15
4
I =
. B.
15I
=
. C.
5
2
I =
. D.
25I =
.
Lời giải
Chọn A
Đặt
43 4t x dt dx= −⇒ =
thì
( ) (
) (
) (
)
( )
2 5 45
1 1 14
1 1 1 25
4 3 5 20
44 44
f x dx f t dt f t dt f t dt
− = = + = +=
∫ ∫ ∫∫
.
Đặt
22
2
xx
u e du e dx=⇒=
thì
( )
( )
ln 2 4
22
01
15
22
xx
f e e dx f u du
= =
∫∫
.
Vậy
25 5 15
424
I
= −=
.
Câu 24: Cho
()
fx
là hàm số liên tục trên
thỏa mãn
2
( ) (2 ) . ,
x
f x f x xe x+ − = ∀∈
. Tính tích phân
2
0
()I f x dx
=
∫
.
A.
4
1
4
e
I
−
=
. B.
21
2
e
I
−
=
. C.
4
2Ie= −
. D.
4
1Ie= −
.
Lời giải
Đặt
2x t dx dt= −⇒ =−
.
( )( ) ( )( ) ( )
0 22
2 00
2 22I f t dt f t dt f x dx⇒= − − = − = −
∫ ∫∫
.
( ) ( )
( )
22 2
2 22
4
22
0
0 00
1 11
22
2 22
xx x
e
I f x f x dx xe dx e d x e
−
⇒= + − = = = =
∫ ∫∫
.
Vậy
4
1
4
e
I
−
=
.
Câu 25: Cho hàm số
(
)
fx
liên tục trên
thỏa mãn
( ) ( )
23f x fx=
,
x∀∈
. Biết rằng
( )
1
0
d1fx x=
∫
.
Tính tích phân
(
)
2
1
dI fx x=
∫
.
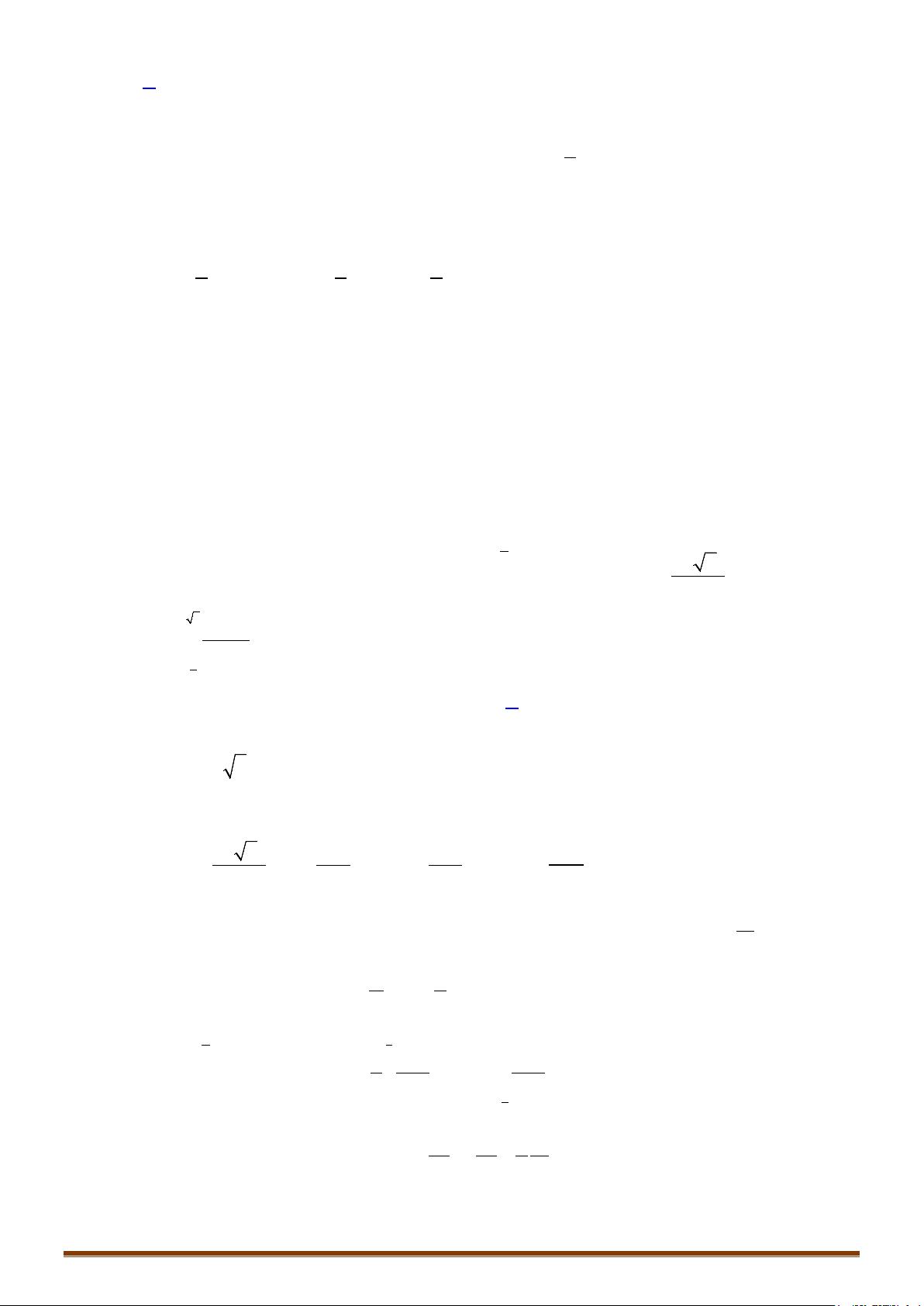
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
A.
5I =
B.
6
I
=
C.
3I =
D.
2I =
Lời giải.
Ta có:
( ) ( ) ( )
( ) ( )
11 1 1
00 0 0
1
3 3.1 3. d 3 d 2 d 2 d 2 ,
2
fxx fxx f xx f x x x= = = = = ∀∈
∫∫ ∫ ∫
.
Đặt
( )
2 d2 dxt x t=⇒=
, với
00xt=⇒=
;
12xt=⇒=
.
( ) (
)
(
)
(
)
1 22
0 00
1 11
3 2 d2 d d,
2 22
f x x ft t fx x x⇔ = = = ∀∈
∫ ∫∫
.
⇔
(
)
2
0
d 6,fx x x
= ∀∈
∫
( ) ( )
12
01
d d 6,fx x fx x x⇔ + = ∀∈
∫∫
.
( )
2
1
1 d 6,
fx x x⇔ + = ∀∈
∫
.
( )
2
1
d 5,fx x x⇔ = ∀∈
∫
.
Câu 26: Cho hàm số
()fx
liên tục trên
thỏa mãn
8
3
3
2
01
()
tan . (cos ) 6
fx
x f x dx dx
x
π
= =
∫∫
. Tính tích
phân
2
2
1
2
()fx
dx
x
∫
A. 4 B. 6 C. 7 D. 10
Lời giải
+) Đặt
32
3
3
t x t x t dt dx= ⇒=⇒ =
Đổi cận
11xt=⇒=
và
82
xt=⇒=
.
Khi đó
82 2
3
2
3
11 1
( ) (t) (t)
33 6
fx f f
dx t dt dt
xt t
= = =
∫∫ ∫
2
1
(t)
2
f
dt
t
⇒=
∫
+) Đặt
22
1
cos 2cos sin 2cos tan tan
2
t x dt x xdx dt x xdx xdx dt
t
= ⇒=− ⇒=− ⇒ =−
Đổi cận:
01xt=⇒=
và
1
34
xt
π
= ⇒=
.
Khi đó
1
1
3
4
2
1
01
4
1 (t) (t)
tan . (cos ) 6 12
2
ff
x f x dx dt dt
tt
π
=− =⇒=
∫ ∫∫
+) Đặt
22
1
22
2
dx dx dt
t x dt xdx dt x
xx t
=⇒= ⇒= ⇒ =

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
Đổi cận:
11
24
xt= ⇒=
và
22
xt= ⇒=
Khi đó
2 2 12
2
1 11
1
2 44
( ) 1 (t) 1 (t) 1 (t) 2 12
7
222 2
fx f f f
dx dt dt dt
x t tt
+
==+==
∫ ∫∫∫
Câu 27: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
2018
0
d2
fx x
=
∫
. Khi đó tích phân
(
)
(
)
2018
e1
2
2
0
ln 1 d
1
x
fx x
x
−
+
+
∫
bằng
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Đặt
( )
( )
2018
e1
2
2
0
ln 1 d
1
x
I fx x
x
−
= +
+
∫
.
Đặt
( )
2
ln 1tx= +
2
2
dd
1
x
tx
x
⇒=
+
.
Đổi cận:
0x =
0t⇒=
;
2018
e1x = −
2018t⇒=
.
Vậy
( )
2018
0
dI ft t=
∫
(
)
2018
0
d2fx x= =
∫
.
Câu 28: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
4
0
tan d 3f xx
π
=
∫
và
( )
2
1
2
0
d 1.
1
xf x
x
x
=
+
∫
Tính
( )
1
0
d.I fx x=
∫
A.
2I =
. B.
6I =
. C.
3I =
. D.
4I =
.
Lời giải
Ta có
( )
4
0
tan d 3K f xx
π
= =
∫
. Đặt
(
)
2
2
1
tan d d tan d 1 d
cos
xt t x x t x
x
=⇒= = = +
.
Vậy
( ) (
)
11
22
00
11
. d . d3
11
K ft t fx x
tx
= = =
++
∫∫
.
Lại có
( )
( ) ( ) ( ) ( )
2
1 1 11
22 2
0 0 00
11
d dd d
11 1
xf x
x fx fx x fx x fx x
xx x
=−=−
++ +
∫ ∫ ∫∫
.
Vậy suy ra
( )
1
0
d4I fx x= =
∫
.
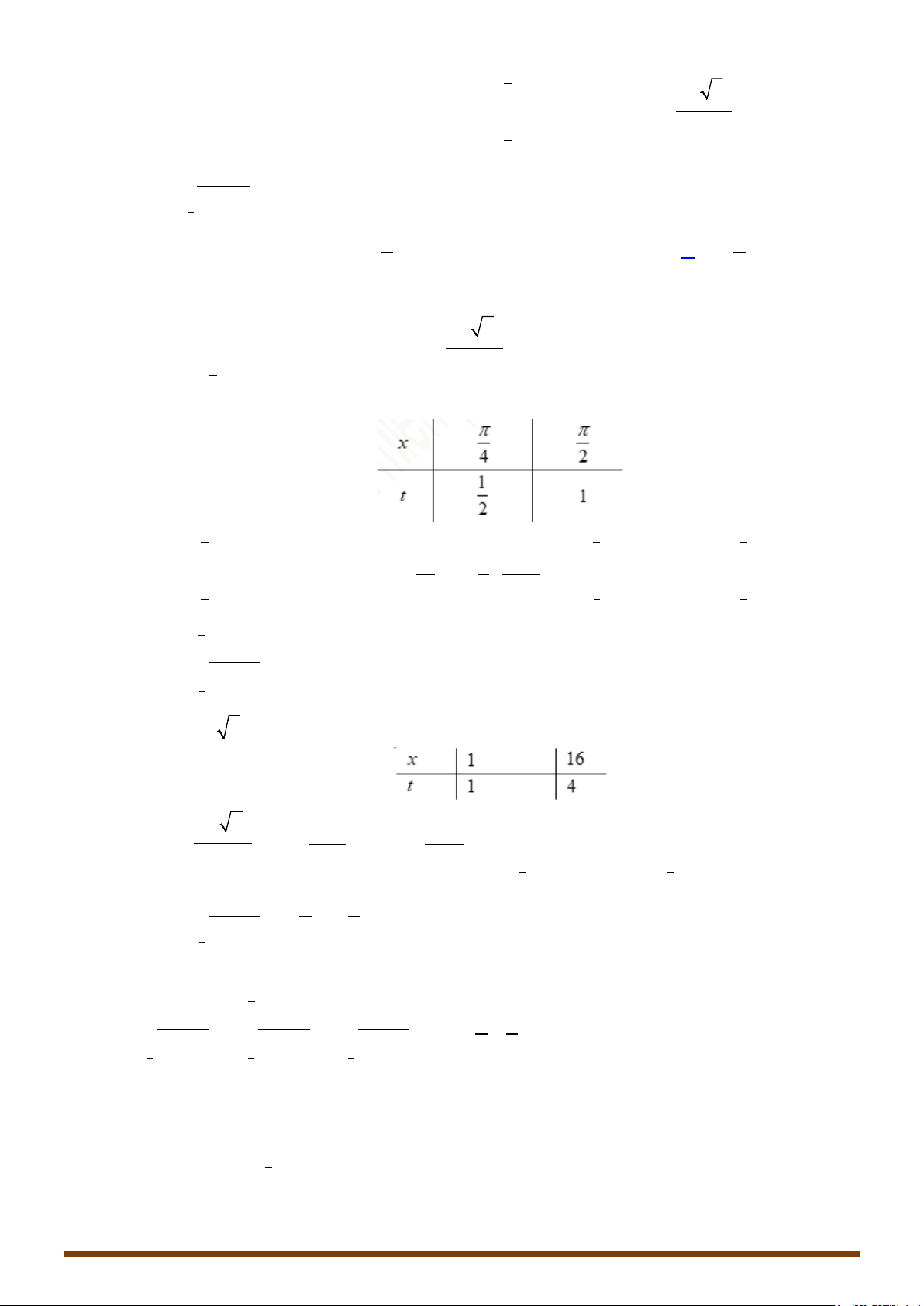
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
Câu 29: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
( )
16
2
2
1
4
cot . sin d d 1
fx
xf x x x
x
π
π
= =
∫∫
. Tính tích
phân
( )
1
1
8
4
d
fx
x
x
∫
.
A.
3I =
. B.
3
2
I =
. C.
2I =
. D.
5
2
I
=
.
Lời giải
Đặt
(
)
2
2
1
4
cot . sin d 1I xf x x
π
π
= =
∫
,
( )
16
2
1
d1
fx
Ix
x
== =
∫
.
Đặt
2
sintx=
d 2sin .cos dt x xx
⇒=
2
2sin .cot dx xx=
2 .cot d
t xx=
.
( )
2
2
1
4
cot . sin dI xf x x
π
π
=
∫
( )
1
1
2
1
.d
2
ft t
t
=
∫
( )
1
1
2
1
d
2
ft
t
t
=
∫
( )
( )
1
4
1
8
4
1
d4
24
fx
x
x
=
∫
( )
1
4
1
8
4
1
d
2
fx
x
x
=
∫
.
Suy ra
( )
1
4
1
1
8
4
d2 2
fx
xI
x
= =
∫
Đặt
tx=
2d dtt x⇒=
.
( )
16
2
1
d
fx
Ix
x
=
∫
( )
4
2
1
2d
ft
tt
t
=
∫
( )
4
1
2d
ft
t
t
=
∫
( )
( )
1
1
4
4
2 d4
4
fx
x
x
=
∫
( )
1
1
4
4
2d
fx
x
x
=
∫
.
Suy ra
(
)
1
2
1
4
4
11
d
22
fx
xI
x
= =
∫
Khi đó, ta có:
( ) ( )
( )
1
11
4
1 11
8 84
444
ddd
fx fx fx
xxx
xxx
= +
∫∫∫
15
2
22
=+=
.
Câu 30: Cho hàm số
( )
fx
liên tục và là hàm số lẻ trên đoạn
[ ]
2; 2−
. Biết rằng
( ) ( )
01
1
1
2
1, 2 2f x dx f x dx
−
=−− =
∫∫
.Mệnh đề nào sau đây đúng?

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
A.
(
)
( )
22
20
2
f x dx f x dx
−
=
∫∫
. B.
( )
1
1
2
4f x dx
= −
∫
.
C.
(
)
1
0
1
f x dx = −
∫
. D.
( )
2
0
3f x dx = −
∫
.
Lời giải
Chọn D
Đặt
tx=−⇒
(
) ( ) ( )
0 01
1 10
f x dx f t dt f t dt
−
=−−=−
∫ ∫∫
( )
1
0
1
f t dt⇒=
∫
.
Đặt
( )
(
)
(
)
11 2
11
1
22
1
22 2
2
t x f x dx f x dx f t dt
−
=⇒− =− =
∫∫ ∫
( ) ( )
22
11
1
2 4.
2
f t dt f t dt
−
⇒ =⇒=−
∫∫
Vậy
( ) ( ) ( )
2 12
0 01
1 4 3.f x dx f x dx f x dx= + =−=−
∫∫∫
Câu 31: Cho
( )
fx
là hàm số liên tục trên
thỏa
( )
11f =
và
( )
1
0
1
d
3
ft t=
∫
. Tính
( )
2
0
sin 2 . sin dI xf x x
π
′
=
∫
A.
4
3
I
=
. B.
2
3
I =
. C.
2
3
I = −
D.
1
3
I =
.
Lời giải
Chọn A
Đặt
sin , d cos dt x t xx= =
.
Đổi cận
( ) ( )
1
2
00
sin 2 . sin d 2 . dI xf x x tf t t
π
′′
= =
∫∫
.
Đặt
( ) ( )
2 d 2d
dd
ut u t
vftt vft
= =
⇒
′
= =

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
( )
(
)
(
)
(
)
1
0
1
14
2 . 2 d 2. 1 2.
0
33
I tft ft t f
= − = −=
∫
.
Câu 32: Cho hàm số
fx
liên tục trên
và
9
2
10
d4, sincosd2
fx
x f x xx
x
. Tính tích phân
3
0
dI fx x
.
A.
6I
=
. B.
4I =
. C.
10
I
=
. D.
2I =
.
Lời giải
Chọn B
Ta có:
99 3
11 1
d2 d 2 d
fx
x f x x ft t
x
.
Mà
9
1
d4
fx
x
x
nên
33
11
2 d4 d2ft t ft t
Vì tích phân không phụ thuộc vào biến số nên
33
11
d2 d2ft t fx x
.
Ta có:
1
22
00 0
sin cos d sin d sin dfxxx fx x ftt
.
Mà
2
0
sin cos d 2f x xx
nên
1
0
d2
ft t
.
Vì tích phân không phụ thuộc vào biến số nên
11
00
d2 d2ft t fx x
.
Khi đó
3 13
0 01
d d d 224I fx x fx x fx x
.
Câu 33: Cho
( )
fx
liên tục trên
thỏa mãn
( ) ( )
2020fx f x
= −
và
( )
2017
3
x 4.f xd =
∫
Khi đó
( )
2017
3
xxf x d
∫
bằng
A.
16160.
B.
4040.
C.
2020.
D.
8080.
Lời giải
Chọn B
Đặt
2020 2020u xx u= −⇒= −
. Ta có
xd du= −
.
Với
3x =
thì
2017u =
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
Với
2017x =
thì
3u
=
.
Khiđó
( )
2017
3
x
xf x d
∫
=
( ) ( )
(
) (
)
2017 2017
33
2020 2020 2020u f u du x f x dx
− −= −
∫∫
Suy ra
( ) ( )
2017 2017
33
2 x = 2020 x = 8080.xf xd f xd
∫∫
Do đó
( )
2017
3
x = 4040.xf x d
∫
Câu 34: Cho hàm số
()
y fx=
liên tục trên
và thỏa mãn
23
3
4 ( ) 6 (2 ) 4
5
xf x f x x+=+
. Giá trị
4
0
( )d
fx x
∫
bằng
A.
52
25
. B. 52. C.
48
25
. D. 48.
Lời giải
Chọn A
22
2 32 3
00
2 2 44
22
0 0 00
44 4 4
00 0 0
33
4 ( ) 6 (2 ) 4 4 ( ) 6 (2 ) d 4 d
55
52 52
2 ( )d( ) 3 (2 )d(2 ) 2 ( )d 3 ( )d
55
52 52 52
2 ( )d 3 ( )d 5 ( )d ( )d
5 5 25
xf x f x x xf x f x x x x
fx x f x x ft t fu u
fx x fx x fx x fx x
+ = +⇒ + = +
⇒ + =⇒+ =
⇒ + =⇒ =⇒=
∫∫
∫ ∫ ∫∫
∫∫ ∫ ∫
Câu 35: Cho
( )
fx
liên tục trên
và thỏa mãn
( ) ( )
1
0
2 16, 2 d 2f f xx= =
∫
. Tích phân
(
)
2
0
d
xf x x
′
∫
bằng
A.
30
. B.
28
. C.
36
. D.
16
.
Lời giải
Chọn B
Ta có:
( ) ( ) ( )
( )
11 2
00 0
1
2d 2 2d2 2 d 4
2
f xx f x x fxx=⇔ =⇔=
∫∫ ∫
.
Đặt
(
) (
)
dd
d dx
ux u x
vfx vfx
= =
⇒
′
= =
(
) ( ) ( ) (
)
22
2
0
00
d d 2 2 4 32 4 28xf x x xf x f x x f
′
⇒ = − = −= −=
∫∫
.
Câu 36: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;1
và
( )
2
0
sin d 5
f xx
π
=
∫
. Tính
( )
0
sin dI xf x x
π
=
∫
A.
5
2
I
π
=
. B.
10I
π
=
. C.
5I =
. D.
5I
π
=
.
Lời giải
Chọn D

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
Ta có
( ) ( ) ( )
2
00
2
sin d sin d sin dI xf x x xf x x xf x x
π
ππ
π
= = +
∫∫∫
,
Tính
( )
2
sin dxf x x
π
π
∫
Đặt
xt
π
= −
d dtx
= −
( ) ( ) ( ) ( ) ( ) ( )
sin d sin dt sin dtxf x x t f t t f t
ππ π
=− − −=−
Đổi cận
22
0
xt
xt
ππ
π
= ⇒=
= ⇒=
(
) ( )
( ) ( )
( ) ( )
( )
0
22 2 2
00 0 0
22
sin d sin dt sin dt sin dt sin d sin dxfxxtft ft tft fxxxfxx
ππ π π
π
ππ
ππ π
=− = −= −
∫ ∫ ∫∫ ∫ ∫
Do đó
(
)
( )
(
)
(
)
22
00 0
2
sin d sin d sin d sin d 5
Ixfxxxfxxxfxx fxx
ππ
ππ
π
ππ
==+= =
∫∫∫ ∫
Vậy Chọn D
Câu 37: Cho hàm số
()y fx=
liên tục trên
1
;3
3
thỏa mãn
3
1
() .f x xf x x
x
+=−
. Giá trị tích phân
3
2
1
3
()fx
I dx
xx
=
+
∫
bằng:
A.
8
.
9
B.
16
.
9
C.
2
.
3
D.
3
.
4
Lời giải
Chọn A
3
2
1
1 ()
() . 1
1
f
fx
x
f x xf x x x
x xxx
+ = −⇒ + =−
++
33 3
2
11 1
33 3
1
( ) 16
d d (x 1)d
19
f
fx
x
x xx
xx x
⇒ + =−=
++
∫∫ ∫
.
Xét
3
1
3
1
'd
1
f
x
Ix
x
=
+
∫
.
Đặt
22
11 d
dd d
t
t xt x
xx t
−
=⇒ =⇒=
−
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 19
1
3 33
3
22 2
1 11
3
3 33
1
() d () ( )
'd d
1
1
1
f
ft t ft fx
x
I x dt x I
x t tt xx
t
= = = = =
+ −+ +
+
∫ ∫ ∫∫
.
Suy ra
16 8
2
99
II= ⇒=
.
DẠNG 1.2 GIẢI BẰNG PHƯƠNG PHÁP TỪNG PHẦN
Thông thường nếu bài toán xuất hiện
( ) ( )
'd
b
a
gxf x x
∫
ta sẽ đặt
( )
( )
d 'd
u gx
v fxx
=
=
Câu 38: Cho
(
)
fx
là hàm số có đạo hàm liên tục trên
[ ]
0;1
và
( )
1
1
18
f = −
,
( )
1
0
1
.d
36
xf x x
′
=
∫
. Giá trị
của
( )
1
0
d
fx x
∫
bằng
A.
1
12
−
. B.
1
36
. C.
1
12
. D.
1
36
−
.
Lời giải
Chọn A
Đặt
( ) ( )
dd
d
ux u x
dvfxx vfx
= =
⇒
′
= =
, khi đó ta có
( )
( ) ( ) ( )
( )
1 11
1
0
0 00
1
. d. d 1 d
36
xf x x xfx fx x f fx x
′
=−=−=
∫ ∫∫
( ) ( )
1
0
11
d1
36 12
fx x f⇒ = −=−
∫
.
Câu 39: Cho hàm số
( )
fx
có
( )
2
1fe=
và
( )
2
2
21
x
x
fx e
x
−
′
=
với mọi
x
khác
0
. Khi đó
( )
ln3
1
dxf x x
∫
bằng
A.
2
6 e−
. B.
2
6
2
e−
. C.
2
9 e−
. D.
2
9
2
e−
.
Lời giải
Chọn D
Xét tích phân
( )
2
2
21
dd
x
x
fxx e x
x
−
′
=
∫∫
Đặt
( )
2
2
2
21
d4d
1
1
dd
x
x
u xe
u xe x
v
vx
x
x
= −
=
⇒
= −
=
, khi đó
( )
( )
2 22
2
21 1
d d 21 4 d
x xx
x
fxx ex x e ex
xx
−
′
= =− −+
∫∫ ∫
( )
22
1
21 2
xx
xe eC
x
=− − ++
.
Do
( )
2
10f eC=⇒=
. Vậy
( ) ( )
22
1
21 2
xx
fx x e e
x
=− −+
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
Khi đó, ta có
( ) ( )
(
)
ln3
ln3 ln 3 ln 3
2
22 2 2
11 1
1
1
d 12 2 d d 9
22
x
xx x
e
xf x x x e xe x e x e
=−+ = ==−
∫∫ ∫
.
Câu 40: Cho hàm số
()y fx
=
có đạo hàm liên tục trên
và thỏa mãn
2
0
(2) 16, ( ) 4f f x dx= =
∫
. Tính
1
0
(2 )I xf x dx
′
=
∫
.
A.
20I =
B.
7I =
C.
12
I =
D.
13I =
Lời giải
Ta có:
(
)
( )
( ) ( )
1
1 11
0
0 00
1 1 11
(2 ) 2 2 d (2) 2 d 2
2 2 24
I xfxdx xfx fxx f fx x
′
==−=−
∫ ∫∫
2
0
1 1 11
(2) ( ) .16 .4 7
2 4 24
I f f x dx
= − = −=
∫
.
Câu 41: Cho hàm số
fx
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
1
2
0
1
21
x f x dx = −
∫
,
( )
10f =
và
( )
1
2
0
1
'
7
f x dx
=
∫
. Giá trị của
( )
1
0
f x dx
∫
bằng
A.
5
12
. B.
1
5
−
. C.
4
5
. D.
7
10
−
.
Lời giải
Đặt
( )
( )
3
2
'
.
3
du f x dx
u fx
x
dv x dx
v
=
=
⇒
=
=
(
)
111
21
0
000
1
21
x f x dx udv uv vdu−= = = −
∫∫∫
( )
( )
33
1
1
0
0
'
33
xx
f x f x dx= −
∫
( )
1
3
0
1
'
3
x f x dx= −
∫
( )
1
3
0
1
'
7
x f x dx⇒=
∫
.
( )
(
)
( ) ( )
1 11 1
2
2
3 63
0 00 0
1 11
' 2 ' ' 2. 0
7 77
x f x dx x dx x f x dx f x dx− = − + =− +=
∫ ∫∫ ∫
( )
( )
[ ]
( )
[ ]
2
33
' 0, 0;1 ' , 0;1fx x x fx x x⇒ − = ∀∈ ⇒ = ∀∈
.
Kết hợp điều kiện
( )
10f =
ta có
( )
( )
[ ]
4
1
1 ; 0;1
4
fx x x= − ∀∈
Vậy
( )
( )
( )
11 1
44
00 0
11 1
11
44 5
f x dx x dx x dx= −= −=−
∫∫ ∫
.
Câu 42: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
01;
thỏa mãn
( )
10f =
,
( )
1
2
0
1
3
x f x dx
=
∫
Tính
( )
1
3
0
' .x f x dx
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 21
A.
1−
B.
1
C.
3
D.
3−
Lời giải
Chọn A
3
2
() '()
3
u f x du f x dx
x
dv x dx v
= ⇒=
= ⇒=
11
3 33 3
00
11
33
00
1
1
() '() (1) 0.(0) '()
0
3 33 3
11
'( ) '( ) 1
33
xx x
I f x f x dx f f f x dx
x f x dx x f x dx
α
= − = −−
−
= ⇒=−
∫∫
∫∫
Câu 43: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[
]
0;1
và
( ) ( )
0 10ff+=
. Biết
( ) ( ) ( )
11
2
00
1
d , cos d
22
f xx fx xx
π
π
′
= =
∫∫
. Tính
( )
1
0
dfx x
∫
.
A.
π
. B.
3
2
π
. C.
2
π
. D.
1
π
.
Lời giải
Xét tích phân
( ) ( )
1
0
cos d
2
I fx xx
′
= =
∫
π
π
Đặt
(
)
( )
( )
(
)
cos sin
'
u x du x dx
dv f x dx v f x
= π = −π π
⇒
= =
, ta có
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
1 11
1
0
0 00
cos sin 1 0 sin sinI fx x fx xdx f f fx xdx fx xdx=π+ππ=−−+ππ=ππ
∫ ∫∫
Mà
(
) (
)
( ) (
)
11
00
1
sin sin
2 22
I f x x dx f x x dx
ππ
=⇔π π=⇔ π=
∫∫
Mặt khác:
( ) ( ) ( )
1
11
2
00
0
1 11 1
sin 1 cos 2 sin 2
2 22 2
x dx x dx x x
π= − π =− π=
π
∫∫
( )
( ) ( ) (
)
1
22
0
1 11
2. sin sin 2. 0
2 22
f x f x x x dx
⇒ − π+ π =− +=
∫
.
Khi đó
( ) ( )
1
2
0
sin 0f x x dx−π =
∫
Vì
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
và
( ) ( )
[ ]
2
sin 0, 0;1
fx x x
− π ≥ ∀∈
nên ta suy ra
( ) ( ) ( ) ( )
sin 0 sinfx x fx x− π=⇔ = π
.
Do đó
( ) ( ) ( )
1
11
0
00
12
d sin cosf x x x dx x==−=
∫∫
ππ
ππ
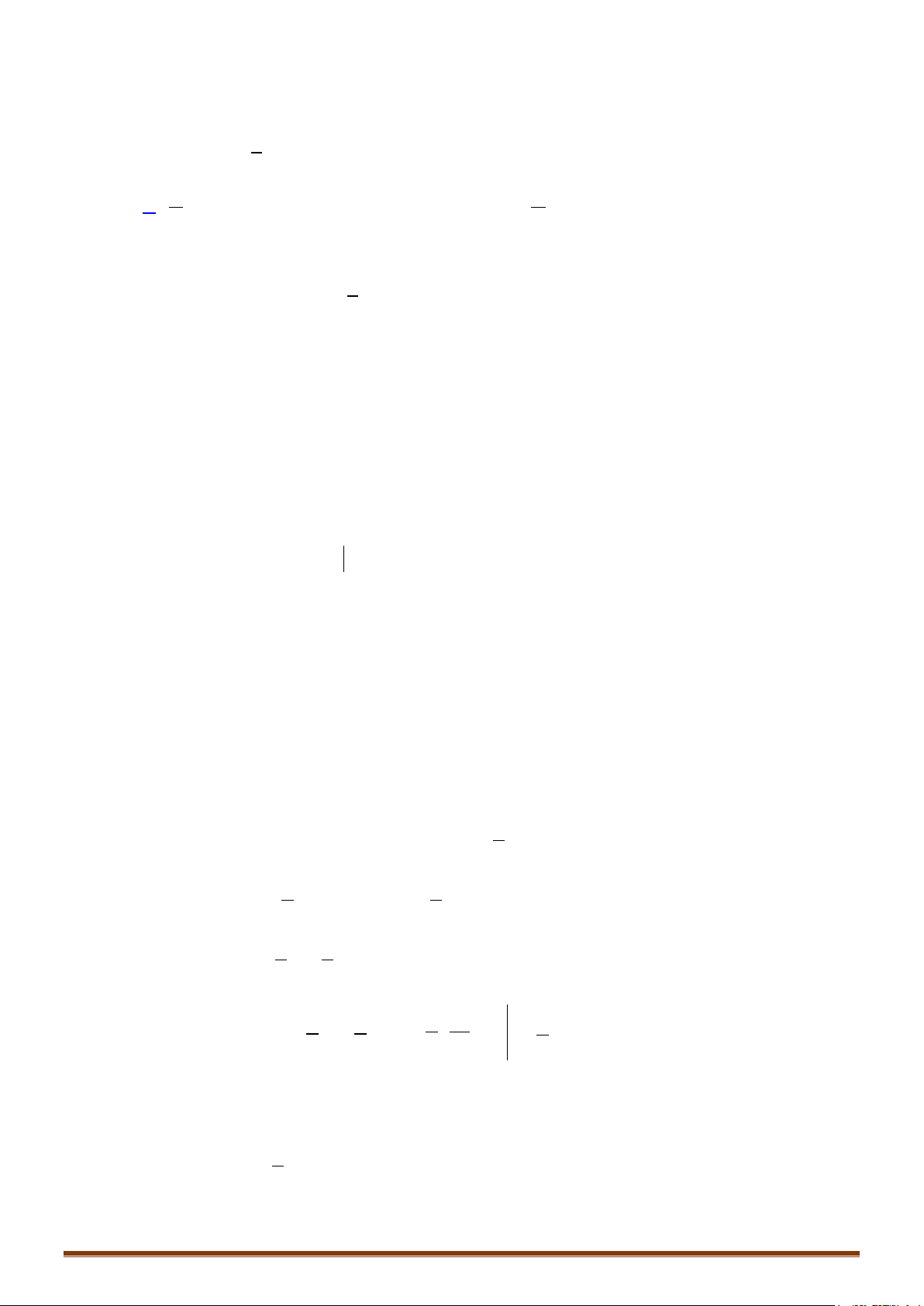
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 22
Câu 44: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
(
)
10f =
,
( )
1
2
0
d7fx x
′
=
∫
và
( )
1
2
0
1
d
3
xf x x
=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
7
5
B.
1
C.
7
4
D.
4
Lời giải
Từ giả thiết:
( )
1
2
0
1
d
3
=
∫
xf x x
(
)
1
2
0
3 d1
⇒=
∫
xf x x
.
Tính:
( )
1
2
0
3d
=
∫
I xf x x
.
Đặt:
( ) (
)
23
dd
d 3d
′
= =
⇒
= =
ufx ufxx
v xx v x
.
Ta có:
( ) ( ) ( )
11
1
233
0
00
3 d .d
′
= = −
∫∫
I xfx x xfx xf x x
(
) ( )
( )
1
3
0
1. 1 0. 0 . d
′
=−−
∫
f f xf x x
(
)
1
3
0
.d
′
= −
∫
xf x x
.
Mà:
( )
1
2
0
3 d1=
∫
xf x x
( )
1
3
0
1 .d
′
⇒=−
∫
xf x x
( )
1
3
0
. d1
′
⇔=−
∫
xf x x
( )
1
3
0
7. d 7
′
⇔=−
∫
xf x x
( ) ( )
11
2
3
00
7. d d
′′
⇔=−
∫∫
xfxx fx x
,.
( ) ( )
(
)
1
2
3
0
7. + d 0
′′
⇔=
∫
xfx fx x
( ) (
)
1
3
0
7+ d 0
′′
⇔=
∫
fx x fx x
( )
3
7+ 0
′
⇒=x fx
( )
3
7
′
⇔=−fx x
(
)
4
7
4
⇒ =−+fx x C
.
Với
( )
10=f
4
7
.1 0
4
⇒− + =C
7
4
⇒=
C
.
Khi đó:
( )
4
77
44
=−+fx x
.
Vậy:
( )
11
4
00
77
dd
44
=−+
∫∫
fx x x x
1
5
0
7
45
=−−
x
x
7
5
=
.
Câu 45: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
14=f
,
( )
1
2
0
d 36
′
=
∫
fx x
và
( )
1
0
1
.d
5
=
∫
xf x x
. Tích phân
( )
1
0
dfx x
∫
bằng
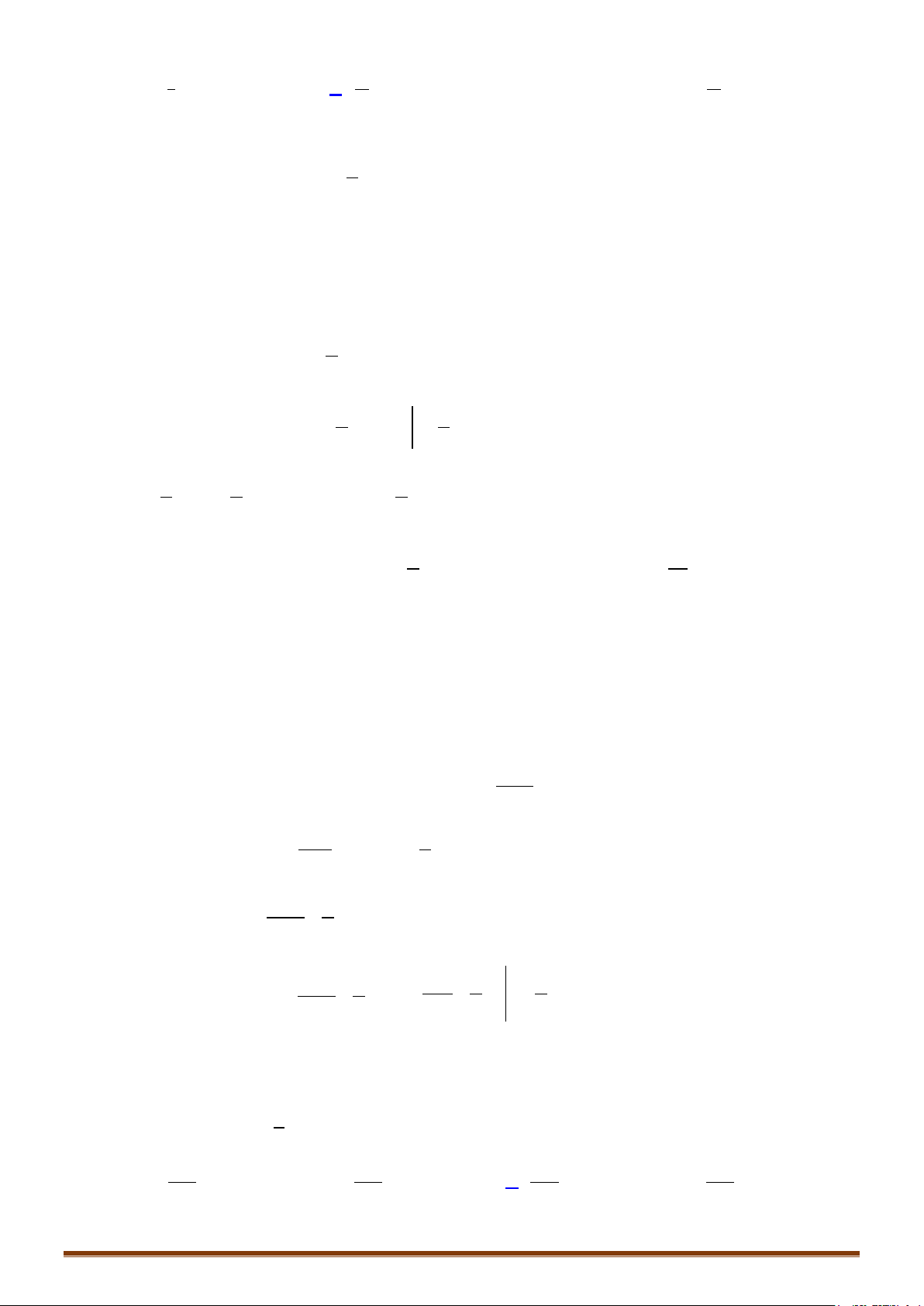
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
A.
5
6
B.
3
2
C.
4
D.
2
3
Lời giải
Từ giả thiết:
( )
1
0
1
.d
5
=
∫
xf x x
( )
1
0
5. d 1⇒=
∫
xf x x
.
Tính:
( )
1
0
5. d=
∫
I xf x x
.
Đặt:
( )
( )
2
dd
5
d 5d
2
′
=
=
⇒
=
=
u fxx
u fx
v xx
vx
.
Ta có:
( ) (
) (
)
1
11
22
0
00
55
5. d . . d
22
′
= = −
∫∫
I xfx x xfx xf x x
( )
( )
1
2
0
55
.1 . d
22
′
= −
∫
f xf x x
(
)
1
2
0
5
10 . d
2
′
= −
∫
xf x x
,
Mà:
( )
1
0
5. d 1= =
∫
I xf x x
( )
1
2
0
5
1 10 . d
2
′
⇒= −
∫
xf x x
( )
1
2
0
18
.d
5
′
⇔=
∫
xf x x
( )
1
2
0
10 . d 36
′
⇔=
∫
xf x x
( ) ( )
11
2
2
00
10 . d d
′′
⇔=
∫∫
xfxx fx x
,
( ) ( )
1
2
2
0
10 . d 0
′′
⇔ −=
∫
xfx fx x
( ) ( )
1
2
0
10 d 0
′′
⇔ −=
∫
fx x fx x
( )
2
10 0
′
⇒− =x fx
(
)
2
10
′
⇔=fx x
( )
3
10
3
⇒=+
x
fx C
Với
( )
14=f
10.1
4
3
⇒= +C
2
3
⇒=
C
.
Khi đó:
( )
3
10 2
33
= +
x
fx
.
Vậy:
( )
11
3
00
10 2
dd
33
= +
∫∫
x
fx x x
1
4
0
52 3
63 2
=+=
x
x
.
Câu 46: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0; 2
thỏa mãn
( )
23=f
,
( )
2
2
0
d4
′
=
∫
fx x
và
( )
2
2
0
1
d
3
=
∫
xf x x
. Tích phân
( )
2
0
d
∫
fx x
bằng
A.
2
115
B.
297
115
C.
562
115
D.
266
115
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
Từ giả thiết:
(
)
2
2
0
1
d
3
=
∫
xf x x
(
)
2
2
0
3 d1⇒=
∫
xf x x
.
Tính:
( )
2
2
0
3d=
∫
I xf x x
.
Đặt:
( )
(
)
23
dd
d 3d
′
= =
⇒
= =
ufx ufxx
v xx v x
.
Ta có:
(
) ( ) ( )
22
2
23 3
0
00
3 d. .d
′
= = −
∫∫
I xfx x xfx xf x x
(
)
2
3
0
24 . d
′
= −
∫
xf x x
,
Mà:
(
)
2
2
0
3 d1
= =
∫
I xf x x
( )
2
3
0
1 24 . d
′
⇒= −
∫
xf x x
(
)
2
3
0
. d 23
′
⇔=
∫
xf x x
( )
2
3
0
4
. d4
23
′
⇔=
∫
xf x x
(
) (
)
22
2
3
00
4
.d d
23
′′
⇔=
∫∫
xfxx fx x
,
( ) ( )
2
2
3
0
4
. d0
23
′′
⇔ −=
∫
xfx fx x
( ) (
)
2
3
0
4
d0
23
′′
⇔ −=
∫
fx x fx x
( )
3
4
0
23
′
⇒− =x fx
( )
3
4
23
′
⇔=fx x
(
)
4
1
23
⇒=+fx x C
Với
( )
23=f
16
3
23
⇒= +C
53
23
⇒=C
.
Khi đó:
( )
4
1 53
23 23
= +fx x
.
Vậy
( )
22
4
00
1 53
dd
23 23
= +
∫∫
fx x x x
2
5
0
1 53 562
115 23 115
= +=
xx
.
Câu 47: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
14=f
,
( )
1
2
0
d5
′
=
∫
fx x
và
( )
1
0
1
.d
2
xf x x= −
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
15
19
B.
17
4
C.
17
18
D.
15
4
Lời giải
Tính:
( )
1
0
.dI xf x x=
∫
. Đặt:
( )
( )
2
dd
1
dd
2
u fxx
u fx
v xx
vx
′
=
=
⇒
=
=
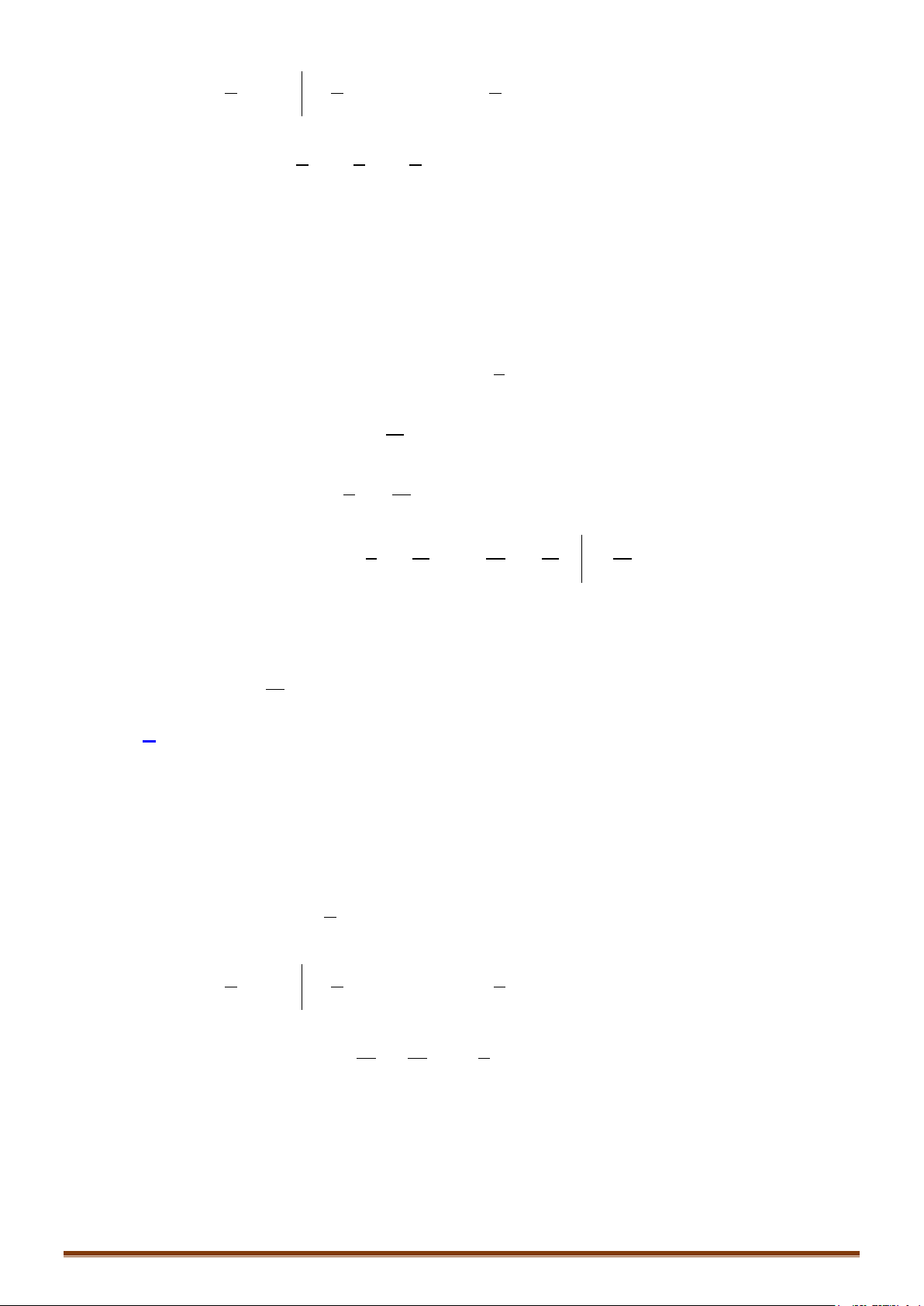
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
Ta có:
(
) ( )
1
22
0
1
11
.d
0
22
I x f x xf x x
′
= −
∫
(
)
1
2
0
1
2d
2
xf x x
′
= −
∫
,.
Mà:
( )
1
0
1
.d
2
xf x x= −
∫
( )
1
2
0
11
2d
22
′
⇒− = −
∫
xf x x
( )
1
2
0
d5
′
⇔=
∫
xf x x
,
( ) ( )
11
2
2
00
dd
′′
⇔=
∫∫
xfxx fx x
( ) ( )
(
)
1
2
2
0
d0
′′
⇔− =
∫
xfx fx x
( ) ( )
1
2
0
. d0
′′
⇔ −=
∫
fx x fx x
⇒
( )
2
0x fx
′
−=
⇔
( )
2
fx x
′
=
⇒
( )
3
1
3
fx x C= +
.
Với
( )
14=f
⇒
11
3
C =
.
Khi đó:
( )
3
1 11
33
fx x
= +
.
Vậy
( )
11
34
00
1
1 11 1 11 15
dd
0
3 3 12 3 4
=+=+ =
∫∫
fx x x x x x
.
Câu 48: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[ ]
0; 2
thỏa mãn
( )
26f =
,
( )
2
2
0
d7fx x
′
=
∫
và
( )
2
0
17
.d
2
xf x x=
∫
. Tích phân
( )
2
0
d
fx x
∫
bằng
A.
8
B.
6
C.
7
D.
5
Lời giải
Tính:
(
)
2
0
.dI xf x x
=
∫
.
Đặt:
( )
( )
2
dd
1
dd
2
u fxx
u fx
v xx
vx
′
=
=
⇒
=
=
Ta có:
( ) ( )
2
22
0
2
11
.d
0
22
I x f x xf x x
′
= −
∫
( )
2
2
0
1
12 d
2
xf x x
′
= −
∫
,.
Theo giả thiết:
( )
2
0
17
.d
2
xf x x=
∫
( )
2
2
0
17 1
12 d
22
′
⇒=−
∫
xf x x
( )
2
2
0
d7
′
⇔=
∫
xf x x
⇔
( ) ( )
22
2
2
00
ddxfxx fx x
′′
=
∫∫
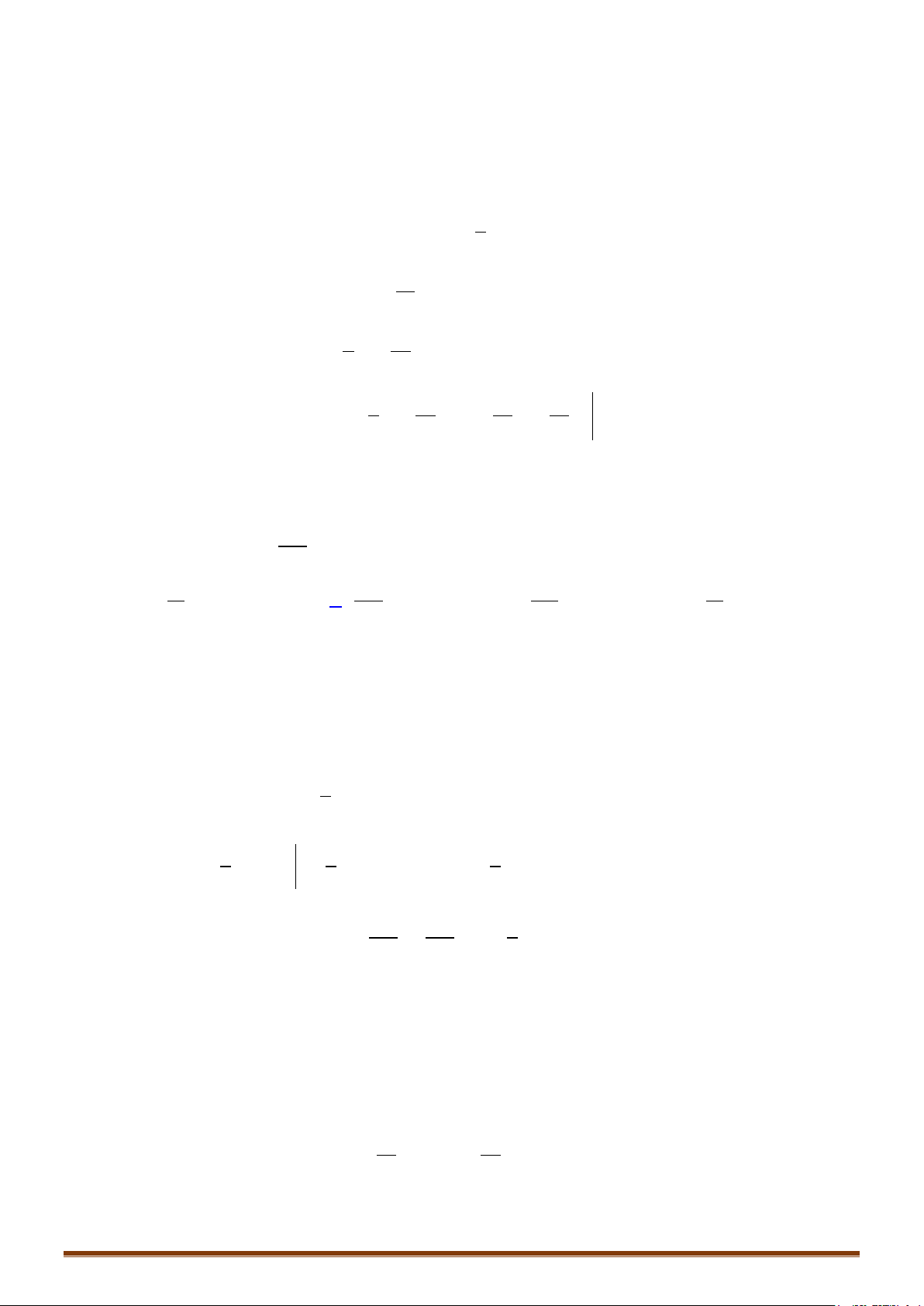
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
⇔
(
)
( )
(
)
2
2
2
0
d0xfx fx x
′′
−=
∫
⇔
( ) (
)
2
2
0
. d0fx x fx x
′′
−=
∫
⇒
( )
2
0x fx
′
−=
( )
2
′
⇔=fx x
( )
3
1
3
⇒=+fx x C
.
Với
( )
26f =
⇒
10
3
C =
.
Khi đó:
( )
3
1 10
33
fx x= +
.
Vậy
(
)
22
34
00
2
1 10 1 10
dd 8
0
3 3 12 3
=+=+ =
∫∫
fx x x x x x
.
Câu 49: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;3
thỏa mãn
( )
36f =
,
( )
3
2
0
d2
′
=
∫
fx x
và
( )
3
2
0
154
.d
3
=
∫
xfx x
. Tích phân
(
)
3
0
dfx x
∫
bằng
A.
53
5
B.
117
20
C.
153
5
D.
13
5
Lời giải
Tính
( )
3
2
0
.dI xfx x=
∫
.
Đặt
(
)
(
)
3
2
dd
1
dd
3
u fxx
u fx
vx
v xx
′
=
=
⇒
=
=
.
Ta có
( )
( )
3
33
0
3
11
.d
0
33
I x f x xf x x
′
= −
∫
( )
3
3
0
1
54 d
3
′
= −
∫
xf x x
,.
Theo giả thiết:
( )
3
2
0
154
.d
3
=
∫
xfx x
( )
3
3
0
154 1
54 d
33
′
⇒=−
∫
xf x x
( )
3
3
0
d8
′
⇔=
∫
xf x x
( ) ( )
33
2
3
00
d4 d
′′
⇔=
∫∫
xfxx fx x
( ) ( )
(
)
3
2
3
0
4 d0
′′
⇔− =
∫
xfx fx x
( ) ( )
3
3
0
4 d0
′′
⇔−=
∫
fxx fx x
.
( )
3
40
′
⇒− =x fx
( )
3
4
′
⇔=
x
fx
( )
4
16
⇒=+
x
fx C
.
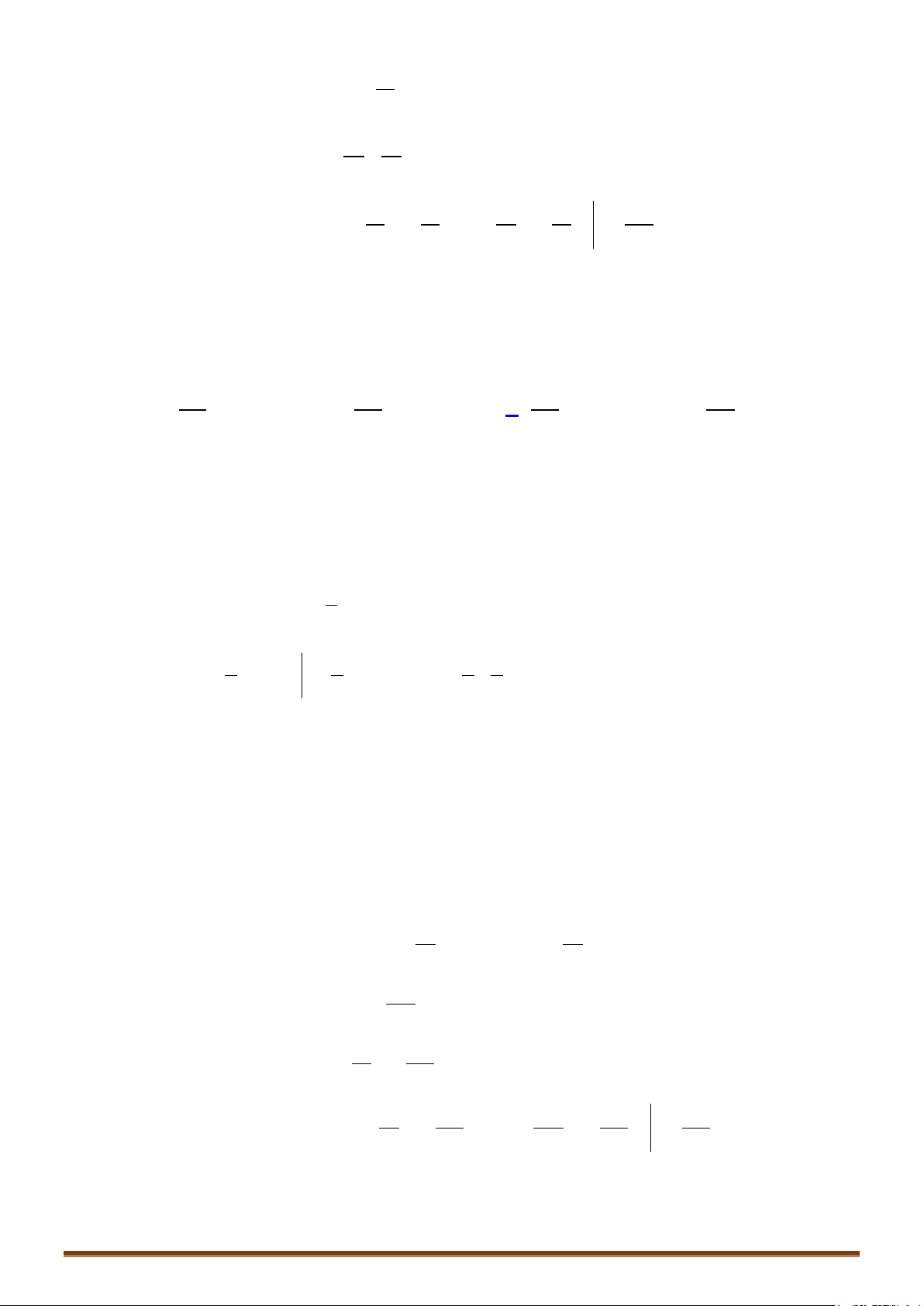
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 27
Với
( )
36f =
15
16
⇒=C
.
Khi đó:
( )
4
15
16 16
= +
x
fx
.
Vậy
(
)
33
45
00
3
1 15 1 15 117
dd
0
16 16 80 16 20
= +=+ =
∫∫
fx x x x x x
.
Câu 50: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
12f =
,
( )
1
2
0
d8fx x
′
=
∫
và
(
)
1
3
0
. d 10xfx x=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng
A.
2
285
−
B.
194
95
C.
116
57
D.
584
285
Lời giải
Tính:
( )
1
3
0
.dI xfx x=
∫
.
Đặt:
( )
( )
4
3
dd
1
dd
4
u fxx
u fx
vx
v xx
′
=
=
⇒
=
=
.
Ta có:
( ) ( )
1
44
0
1
11
.d
0
44
I x f x xf x x
′
= −
∫
( )
1
4
0
11
d
24
xf x x
′
= −
∫
,.
Theo giả thiết:
( )
1
3
0
. d 10
xfx x=
∫
⇒
( )
1
4
0
d 38xf x x
′
= −
∫
( )
1
4
0
8. d 38.8
′
⇔=−
∫
xf x x
( ) ( )
11
2
4
00
8. d 38. d
′′
⇔=−
∫∫
xfxx fx x
( ) ( )
(
)
1
2
4
0
8 38 d 0
′′
⇔+ =
∫
xfx fx x
( ) ( )
1
4
0
. 8 38 d 0
′′
⇔ +=
∫
fx x fx x
⇒
( )
4
8 38 0
′
+=x fx
⇔
( )
4
4
19
′
= −fx x
⇒
( )
5
4
95
=−+fx x C
.
Với
(
)
12f
=
⇒
194
95
=C
.
Khi đó:
( )
5
4 194
95 95
=−+fx x
.
Vậy
( )
11
56
00
1
4 194 2 194 116
dd
0
95 95 285 95 57
=−+ =− + =
∫∫
fx x x x x x
.
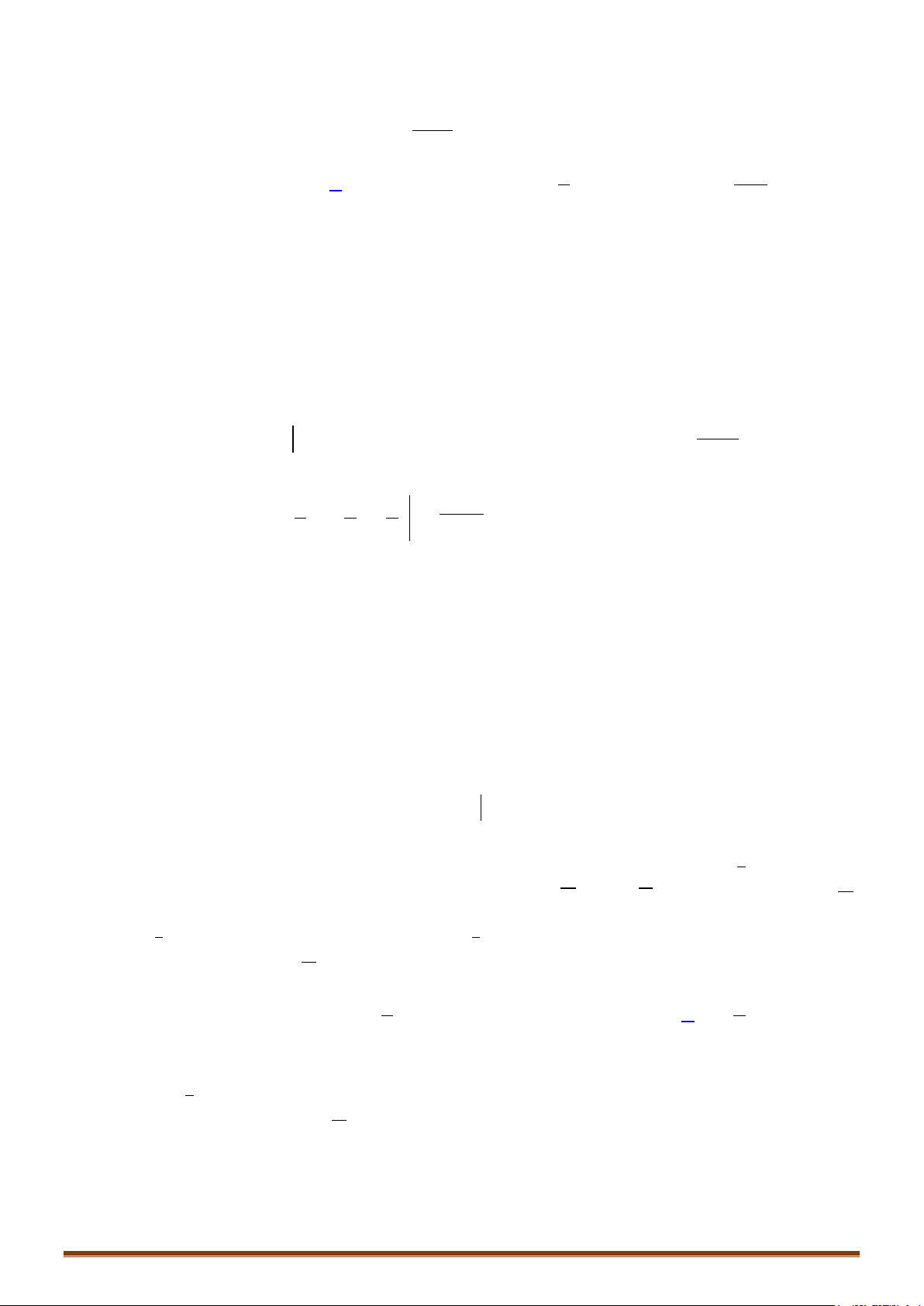
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
Câu 51: Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
10
f =
và
(
)
( ) ( )
11
2
2
00
1
d 1e d
4
x
e
f x x x fx x
−
′
=+=
∫∫
. Tính tích phân
( )
1
0
dI fx x=
∫
.
A.
2eI = −
. B.
e2I = −
. C.
e
2
I =
. D.
e1
2
I
−
=
.
Lời giải
Xét
(
)
(
)
1
0
1e d
x
A x fx x= +
∫
Đặt
( )
( )
d 1d
x
u fx
v x ex
=
= +
( )
dd
e
x
u fxx
vx
′
=
⇒
=
Suy ra
( )
( )
1
1
0
0
e ed
xx
Axfx xfxx
′
= −
∫
( )
1
0
d
x
xe f x x
′
= −
∫
( )
1
2
0
1
d
4
x
e
xe f x x
−
′
⇒=
∫
Xét
1
22
0
d
x
xe x
∫
1
22
0
1 11
2 24
x
exx
= −+
2
1
4
e −
=
Ta có :
(
) (
)
1 11
2
22
0 00
d2 d d0
xx
fx x xefxx xe x
′′
+ +=
∫ ∫∫
( )
( )
1
2
0
d0
x
f x xe x
′
⇔+=
∫
Suy ra
( )
[ ]
0, 0;1
x
f x xe x
′
+ = ∀∈
( )
x
f x xe
′
⇒=−
( ) ( )
1
x
f x xe C⇒ =−+
Do
( )
10f =
nên
( ) ( )
1
x
f x xe= −
Vậy
( ) ( ) ( )
11
1
0
00
d 1 d2 2
xx
I f x x xe x xe e= =− =−=−
∫∫
.
Câu 52: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
0;
4
π
và
0
4
f
π
=
. Biết
( )
4
2
0
d
8
f xx
π
π
=
∫
,
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Tính tích phân
( )
8
0
2dI f xx
π
=
∫
A.
1I =
. B.
1
2
I =
. C.
2I =
. D.
1
4
I =
.
Lời giải
Tính
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Đặt
( ) ( )
sin 2 2cos 2 d d
dd
x u xx u
f x x v fx v
= =
⇒
′
= =
, khi đó

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 29
( ) ( )
( )
44
4
0
00
sin 2 d sin 2 . 2 cos2 df x xx xf x f x xx
ππ
π
′
= −
∫∫
( ) ( )
4
0
sin . sin 0. 0 2 cos2 d
24
f f f x xx
π
ππ
= −−
∫
( )
4
0
2 cos2 df x xx
π
= −
∫
.
Theo đề bài ta có
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
⇒
( )
4
0
cos2 d
8
f x xx
π
π
=
∫
.
Mặt khác ta lại có
4
2
0
cos 2 d
8
xx
π
π
=
∫
.
Do
( ) ( ) ( )
44
2
22
00
cos2 d 2 .cos2 cos 2 dfx x x f x fx x x x
ππ
−=− +
∫∫
20
8 88
π ππ
=−+=
nên
( )
cos 2fx x
=
.
Ta có
8
8
0
0
11
cos 4 d sin 4
44
I xx x
π
π
= = =
∫
.
Câu 53: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
[
]
0;1
và
( ) ( )
0 10ff+=
. Biết
( ) ( ) ( )
11
2
00
1
d , cos d
22
f xx fx xx
π
π
′
= =
∫∫
. Tính
( )
1
0
dfx x
∫
.
A.
π
. B.
1
π
. C.
2
π
. D.
3
2
π
.
Lời giải
Đặt
( )
( )
( )
( )
cos d sin d
dd
u x u xx
vfxx vfx
π ππ
= = −
⇔
′
= =
. Khi đó:
( ) ( ) ( ) ( )
( ) ( )
11
1
0
00
cos d cos sin df x x x xfx fx x x
π πππ
′
= +
∫∫
( ) ( )
( )
( ) ( ) ( ) ( ) ( ) ( )
1 11
0 00
1
1 0 sin d sin d sin d
2
f f fx x x fx x x fx x x
ππππ π
=−+ + = ⇒ =
∫ ∫∫
.
Cách 1: Ta có
(
) ( ) ( ) ( ) (
)
( )
1 11 1
2
2 22
0 00 0
sin d d 2 sin d sin dfx k x x f xx kfx xxk xx
π ππ
−=− +
∫ ∫∫ ∫
2
1
01
22
k
kk= −+ =⇔ =
.
Do đó
( ) ( ) ( ) ( )
1
2
0
sin d 0 sinfx x x fx x
ππ
− =⇒=
∫
. Vậy
( ) ( )
11
00
2
d sin dfxx xx
π
π
= =
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 30
Cách 2: Sử dụng BĐT Holder.
( ) ( ) ( ) ( )
2
22
d d. d
b bb
a aa
fxgxx f xxgxx
≤
∫ ∫∫
.
Dấu “=” xảy ra
( )
( )
[ ]
,;f x kg x x a b⇔ = ∀∈
.
Áp dụng vào bài ta có
( ) ( ) ( ) ( )
2
1 11
22
0 00
11
sin d d . sin d
44
fx xx f xx xx
ππ
=≤=
∫ ∫∫
,
suy ra
(
)
( )
sinfx k x
π
=
.
Mà
( ) ( )
( ) ( ) ( )
11
2
00
11
sin d sin d 1 sin
22
fx x x k x x k fx x
ππ π
=⇔ =⇔=⇒ =
∫∫
.
Vậy
(
) ( )
11
00
2
d sin dfxx xx
π
π
= =
∫∫
.
Câu 54: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
11f =
,
( )
1
2
0
d9fx x
′
=
∫
và
( )
1
3
0
1
d
2
xf x x=
∫
. Tích phân
( )
1
0
dfx x
∫
bằng:
A.
2
3
. B.
5
2
. C.
7
4
. D.
6
5
.
Lời giải
Ta có:
( )
1
2
0
d9fx x
′
=
∫
( )
1
- Tính
( )
1
3
0
1
d.
2
xf x x=
∫
Đặt
(
)
3
d .d
u fx
vxx
=
=
( )
4
dd
4
u fxx
x
v
′
=
⇒
=
( )
1
3
0
1
d
2
xf x x⇒=
∫
( )
1
4
0
.
4
x
fx
=
( )
1
4
0
1
.d
4
xf x x
′
−
∫
( )
1
4
0
11
.d
44
xf x x
′
= −
∫
( )
1
4
0
. d1xf x x
′
⇒=−
∫
( )
1
4
0
18 . d 18xf x x
′
⇒=−
∫
( )
2
- Lại có:
1
1
9
8
0
0
1
d
99
x
xx= =
∫
1
8
0
81 d 9xx⇒=
∫
( )
3
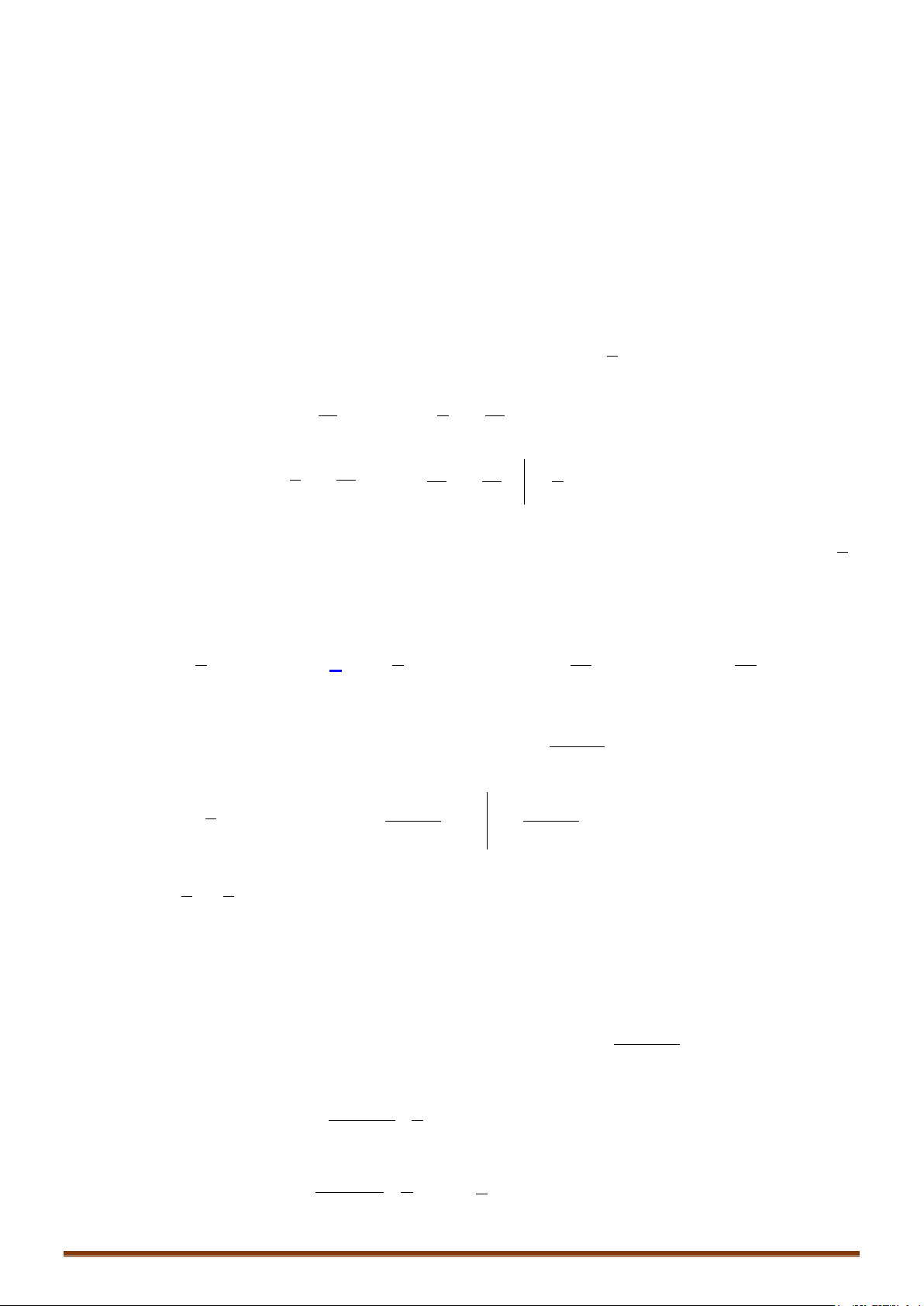
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 31
- Cộng vế với vế các đẳng thức
( )
1
,
( )
2
và
(
)
3
ta được:
(
)
( )
1
2
48
0
18 . 81 d 0
fx xfx x x
′′
+ +=
∫
(
)
1
4
0
9d0
fx x x
′
⇔ +=
∫
( )
1
4
0
. 9d0fx x x
π
′
⇔ +=
∫
Hay thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hàm số
( )
4
9y fx x
′
= +
,
trục hoành
Ox
, các đường thẳng
0x =
,
1x =
khi quay quanh
Ox
bằng
0
(
)
4
90fx x
′
⇒ +=
( )
4
9fx x
′
⇒=−
( )
(
)
.dfx f x x
′
⇒=
∫
4
9
5
xC=−+
.
Lại do
( )
11f =
14
5
C⇒=
( )
5
9 14
55
fx x⇒ =−+
( )
1
0
dfx x⇒=
∫
1
5
0
9 14
d
55
xx
−+
∫
1
6
0
3 14 5
10 5 2
xx
=−+ =
.
Câu 55: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
1; 2
thỏa mãn
( ) ( )
2
2
1
1
1d
3
x fx x−=−
∫
,
( )
20f =
và
( )
2
2
1
d7fx x
′
=
∫
. Tính tích phân
( )
2
1
d
I fx x=
∫
.
A.
7
5
I =
. B.
7
5
I = −
. C.
7
20
I = −
. D.
7
20
I =
.
Lời giải
Đặt
( ) ( )
ddufx ufxx
′
= ⇒=
,
( )
(
)
3
2
1
d 1d
3
x
vx xv
−
= − ⇒=
Ta có
( ) ( )
2
2
1
1
1d
3
x fx x−= −
∫
( )
( )
( )
( )
2
33
2
1
1
11
.d
33
xx
fx f x x
−−
′
= −
∫
( ) ( )
2
3
1
11
1d
33
x fxx
′
⇔− =− −
∫
( ) ( )
2
3
1
1 d1x fxx
′
⇔− =
∫
( ) ( )
2
3
1
2.7 1 d 14x fxx
′
⇒− − =−
∫
Tính được
( )
2
6
1
49 1 d 7xx−=
∫
( )
2
2
1
dfx x
′
⇒
∫
( ) ( )
2
3
1
2.7 1 dx fxx
′
−−
∫
( )
2
6
1
49 1 d 0xx+ −=
∫
( ) ( )
2
2
3
1
7 1 d0x fx x
′
⇒ −− =
∫
(
) ( )
3
71fx x
′
⇒=−
( )
( )
4
71
4
x
fx C
−
⇒= +
.
Do
(
)
20f
=
( )
( )
4
71
7
44
x
fx
−
⇒= −
.
Vậy
( )
2
1
dI fx x=
∫
(
)
4
2
1
71
7
d
44
x
x
−
= −
∫
7
5
= −
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
Câu 56: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn:
(
)
(
)
1
2
0
1 0, d 7
f fx x
′
= =
∫
và
( )
1
2
0
1
.d
3
xfx x=
∫
. Tính tích phân
( )
1
0
d
I fx x=
∫
.
A.
1
I
=
. B.
7
5
I
=
. C.
4I =
. D.
7
4
I =
.
Lời giải
Xét tích phân
( )
1
2
0
.dxfx x
∫
.
Đặt
( )
( )
3
2
dd
dd
3
u fxx
u fx
x
vxx
v
′
=
=
⇒
=
=
( ) (
)
( )
11
3
23
00
1
11
.d d
0
3 33
x
xfx x fx xf x x
′
= = −
∫∫
( )
1
3
0
1
d
3
xf x x
′
= −
∫
(
)
1
3
0
d1xf x x
′
⇒=−
∫
1
6
0
1
7
x dx =
∫
.
Ta có:
( ) (
)
1 11
2
36
0 00
d 14 d 49 d 0fx x xfxx xx
′′
+ +=
∫ ∫∫
(
)
( )
1
2
3
0
7 d0
fx x x
′
⇒+=
∫
Mà
(
)
( )
1
2
3
0
7 d0
fx x x
′
+≥
∫
. Dấu “=” xảy ra khi
(
) ( )
33
70 7fx x fx x
′′
+=⇒ =−
( ) ( )
3
d 7dfx f x x x x
′
⇒= =−
∫∫
4
7
4
x
C
=−+
.
( )
7
10
4
fC=⇒=
( )
4
77
44
x
fx⇒ =−+
.
(
)
1
0
d
I fx x=
∫
1
45
0
11
77 7 7
d
00
4 4 20 4
x xx
x
=−+ =− +
∫
7 77
20 4 5
=− +=
.
Câu 57: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
( )
1
2
0
4
1 3,
11
f f x dx
′
= =
∫
và
( )
1
4
0
7
11
x f x dx =
∫
. Giá trị của
( )
1
0
f x dx
∫
là
A.
35
11
. B.
65
21
. C.
23
7
. D.
9
4
.
Lời giải
Xét
( )
1
4
0
7
11
x f x dx =
∫
Đặt
( )
( )
5
4
5
du f x dx
u fx
x
dv x dx
v
′
=
=
⇒
=
=

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 33
( )
( )
( )
1
11
455
0
00
11
55
x f x dx x f x x f x dx
′
⇒=−
∫∫
( )
1
5
0
31
55
x f x dx
′
= −
∫
( )
1
5
0
37 2
5
5 11 11
x f x dx
′
⇒ = −=−
∫
.
Xét
(
)
( )
1
2
0
1
5
0
1
1
10 11
0
0
4
11
2
11
11
11 11
f x dx
x f x dx
x dx x
′
=
′
= −
= =
∫
∫
∫
( )
( )
1 11
2
5 10
0 00
4 40f x dx x f x dx x dx
′′
⇒ + +=
∫ ∫∫
( )
( )
1
2
5
0
20f x x dx
′
⇒+=
∫
( ) ( )
6
5
2
3
x
f x x fx C
−
′
⇒ =−⇒ = +
. Do
(
)
10
13
3
fC=⇒=
nên
( )
11
6
00
10 23
33 7
x
f x dx dx
−
=+=
∫∫
Câu 58: Cho hàm số
()fx
có đạo hàm liên tục trên
[ ]
0;1
thỏa mãn
( )
01f =
;
(
)
[
]
1
2
0
1
d
30
fx x
′
=
∫
và
(
) ( )
1
0
1
21 d
30
x fx x−=−
∫
. Tích phân
( )
1
0
d
fx x
∫
bằng
A.
11
30
. B.
11
12
. C.
11
4
. D.
1
30
.
Lời giải
Đặt
( )
( )
( )
2
dd
d 2 1d
u fxx
u fx
vx x
vx x
′
=
=
⇒
= −
= −
.
Suy ra
( ) ( )
( )
( )
( )
( )
11
1
22
0
00
21 d dx fx x x xfx x xf x x
′
− =− −−
∫∫
( )
( )
1
2
0
dx xf x x
′
=−−
∫
( )
( )
1
2
0
1
d
30
x xf x x
′
⇒− =
∫
Ta có:
( ) ( )
11
2
2 4 32
00
d 2dxxx x xxx− = −+
∫∫
1
543
0
523
xxx
= −+
1
30
=
.
Do đó,
( )
[ ]
( )
( )
( )
11 1
2
2
22
00 0
d2 d d0fx x x xfxx x x x
′′
− − +− =
∫∫ ∫
( )
( )
1
2
2
0
d0fx x x x
′
⇔ −− =
∫
( )
2
fx x x
′
⇒=−
( )
32
32
xx
fx C⇒ =−+
.
Vì
( )
01f =
nên
1C =
( )
32
1
32
xx
fx⇒ =−+
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 34
Vậy
(
)
11
32
00
d 1d
32
xx
fx x x
= −+
∫∫
1
43
0
12 6
xx
x
= −+
11
12
=
.
Câu 59: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên đoạn
0;
4
π
và
0
4
f
π
=
. Biết
(
)
4
2
0
d
8
f xx
π
π
=
∫
,
( )
4
0
sin 2 d
4
f x xx
π
π
′
= −
∫
. Tính tích phân
(
)
8
0
2dI f xx
π
=
∫
.
A.
1I =
. B.
1
2
I =
. C.
2I =
. D.
1
4
I =
.
Lời giải
Ta có
(
)
( )
44
00
sin 2 d sin 2 d
f x xx xf x
ππ
′
=
∫∫
( )
( )
4
4
0
0
sin 2 dsin 2fx x fx x
π
π
= −
∫
(
)
( )
( )
4
0
sin 2. 0 sin 2.0 2 cos2 d
44
f f f x xx
π
ππ
= −−
∫
( )
4
0
2 cos 2 d
4
f f x xx
π
π
= −
∫
( )
4
0
2 cos 2 df x xx
π
= −
∫
.
Do đó
( )
4
0
2 cos 2 d
4
f x xx
π
π
=
∫
.
Mặt khác:
( )
44
2
00
1
cos 2 d 1 cos 4 d
2
xx x x
ππ
= +
∫∫
4
0
11
sin 4
28
xx
π
= +
8
π
=
.
Bởi vậy:
( ) ( )
44 4
22
00 0
d 2 cos 2 d cos 2 d
848
f x x f x xx xx
ππ π
πππ
− + =−+
∫∫ ∫
(
) ( )
4
22
0
2 cos 2 cos 2 d 0f x fx x x x
π
⇔− + =
∫
( )
( )
4
2
0
cos 2 d 0 cos 2fx x x fx x
π
⇔ − =⇒=
∫
.
Nên:
( )
8
0
2dI f xx
π
=
∫
8
0
cos 4 dxx
π
=
∫
8
0
11
sin 4
44
x
π
= =
.
Câu 60: Cho hàm số
( )
fx
liên tục, có đạo hàm trên
,
( )
2 16f =
và
( )
2
0
4f x dx =
∫
. Tích phân
4
0
2
x
xf dx
′
∫
bằng
A.
112
. B.
12
. C.
56
. D.
144
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 35
Lời giải
Đặt
22
2
x
t x t dx dt=⇒= ⇒ =
.
Đổi cận:
00
42
xt
xt
=⇒=
= ⇒=
. Do đó
( ) ( )
4 22
0 00
44
2
x
xf dx tf t dt xf x dx
′ ′′
= =
∫ ∫∫
.
Đặt
( ) ( )
44u x du dx
dv f x dx v f x
= =
⇒
′
= =
.
Suy ra
( )
[ ]
( ) ( ) ( )
2 22
2
0
0 00
4 4 ( ) 4 8 2 4 8.16 4.4 112.xf x dx xf x f x dx f f x dx
′
=−=−=−=
∫ ∫∫
Câu 61: Cho hàm số
( )
fx
liên tục trên
và
( ) ( )
2
0
2 16, d 4f fx x= =
∫
. Tính
( )
1
0
. 2dI xf x x
′
=
∫
.
A.
7
. B.
12
. C.
20
. D.
13
.
Lời giải
Đặt
2tx=
d 2dtx⇒=
. Với
00xt=⇒=
; Với
12
xt=⇒=
.
Suy ra:
( )
( )
22
00
d1
d
2 24
tt
I ft tft t
′′
= =
∫∫
( )
2
0
1
d
4
xf x x
′
=
∫
.
Đặt
( ) ( )
dd
dd
ux u x
vfxx vfx
= =
⇒
′
= =
.
Ta có
( ) ( ) ( )
( )
2
0
2
11
d 22004
0
44
I xfx fx x f f
= − = −−
∫
( )
1
2.16 4 7
4
= −=
.
DẠNG 1.3 BIẾN ĐỔI
Dạng 1. Bài toán tích phân liên quan đến đẳng thúrc
'
() () () () ()uxf x uxfx hx
′
+=
Phương pháp:
Dễ dàng thấy rằng
() () () () [() ()]uxf x u xfx uxfx
′′ ′
+=
Do dó
() () () () () [() ()] ()uxf x u xfx hx uxfx hx
′′ ′
+=⇔ =
Suy ra
() () ()dux f x hx x=
∫
Từ đây ta dễ dàng tính được
()fx
Dang 2. Bài toán tích phân liên quan đến biếu thúrc
() () ()f x f x hx
′
+=
Phương pháp:
Nhân hai vế vói
x
e
ta durọc
() () () () ()
x xx x x
efx efx ehx efx ehx
′
′
⋅ +⋅ =⋅ ⇔ ⋅ =⋅

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
Suy ra
() ()d
xx
e f x e hx x⋅=⋅
∫
Từ đây ta dễ dàng tính được
()fx
Dang 3. Bài toán tích phân liên quan đến biếu thúc
() () ()
f x f x hx
′
−=
Phương pháp:
Nhân hai vế vói
x
e
−
ta durọc
() () () () ()
x xx x x
efxefxehx efx ehx
′
−′ − − − −
⋅ −⋅ =⋅ ⇔ ⋅ =⋅
Suy ra
() ()d
xx
e f x e hx x
−−
⋅=⋅
∫
Từ đây ta dễ dàng tính được
()fx
Dạng 4. Bài toán tích phân liên quan đến biếu thúrc
() () () ()
f x px f x hx
′
+⋅=
Phương pháp:
Nhân hai vế với
()
p x dx
e
∫
ta được
() () () () ()
() () () () () ()
p x dx p x dx p x dx p x dx p x dx
fxe pxe fx hxe fxe hxe
′
′
∫∫ ∫ ∫ ∫
⋅ +⋅ ⋅=⋅ ⇔ ⋅ =⋅
Suy ra
() ()
() ()d
p x dx p x dx
f x e e hx x
∫∫
⋅=
∫
Từ đây ta dễ dàng tính được
()fx
Dang 5. Bài toán tích phân liên quan đến biếu thúc
() () () 0f x px f x
′
+⋅=
Phương pháp:
Chia hai vế với
()fx
ta đựơc
() ()
() 0 ()
() ()
fx fx
px px
fx fx
′′
+=⇔ =−
Suy ra
()
d ()d ln| ()| ()d
()
fx
x px x f x px x
fx
′
=−⇔ =−
∫∫ ∫
Từ đây ta dễ dàng tính được
()fx
Dạng 6. Bài toán tích phân liên quan đến biểu thức
() ()[ ()] 0
n
f x px f x
′
+⋅ =
Phương pháp:
Chia hai vế với
[ ( )]
n
fx
ta được
() ()
() 0 ()
[ ( )] [ ( )]
nn
fx fx
px px
fx fx
′′
+=⇔ =−
Suy ra
1
() [ ()]
d ( )d ( )d
[ ( )] 1
n
n
f x fx
x px x px x
fx n
′ −+
=−⇔ =−
−+
∫∫ ∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 37
Câu 62: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
thỏa mãn
( )
( )
23
6
16
31
f x xf x
x
−= −
+
. Khi đó
( )
1
0
d
fx x
∫
bằng
A.
4
. B.
1
−
. C.
2
. D.
6
.
Lời giải
Chọn A
Ta có
( )
( )
23
6
16
31
f x xf x
x
−= −
+
( )
( )
23
6
16
31
f x xf x
x
⇔ −− =−
+
( )
( )
11 1
23
00 0
6
1d6 d d
31
f x x xf x x x
x
⇔ −− =−
+
∫∫ ∫
( )
*
.
Ta có
( ) ( ) ( ) ( ) ( )
1 1 01
1
0 0 10
1d 1d1 d d
ux
f xx f x x fuu fxx
= −
− =− − −=− =
∫ ∫ ∫∫
.
Và
( ) ( ) ( )
(
) ( )
3
1 1 11
23 3 3
0 0 00
6 d2 d 2d2d
ux
xfx x fx x fu u fx x
=
= = =
∫ ∫ ∫∫
.
Ta có
( ) ( ) ( )
( )
11 1 1 1
00 0 0 0
11
* d2d6d d6d4
31 31
fx x fx x x fx x x
xx
⇔− =− ⇔= =
++
∫∫ ∫ ∫∫
.
Vậy
( )
1
0
d4fx x=
∫
.
Câu 63: Cho hàm số
( )
fx
xác định và liên tục trên
{ }
\0
thỏa mãn
( ) ( ) ( ) ( )
22 '
21 1x f x x f x xf x+− = −
, với mọi
{
}
\0x ∈
đồng thời thỏa
(
)
12
f
= −
. Tính
( )
2
1
dfxx
∫
A.
ln 2
1
2
−−
. B.
1
ln 2
2
−−
. C.
3
ln 2
2
−−
. D.
ln 2 3
22
−−
.
Lời giải
Chọn D
Ta có
( ) ( )
( ) ( ) ( )
( )
( )
( )
2'
22 '
21 1 1x f x xf x xf x f x xf x xf x+ += + ⇔ + = +
Do đó
( )
( )
(
)
( )
(
)
( )
(
)
( )
( )
''
22
11
1
11
1
11
xf x xf x
dx dx x c
xf x
xf x xf x
++
= ⇒ = ⇒− = +
+
++
∫∫
( )
1
1xf x
xc
⇒ +=−
+
Mặt khác
( )
12f = −
nên
( ) ( )
2
1 1 11
21 0 1
1
c xfx fx
c x xx
−+=− ⇒ =⇒ +=− ⇒ =− −
+
Vậy
( )
22
2
1
2
11
11 1 1
d ln | ln 2
2
f x x dx x
xx x
=−− =− + =− −
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 38
Câu 64: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
( )
2 3 532
1 33
1 4 5 7 6,
4 42
fx x f x x x x x x x
+ − − − = − − + + ∀∈
. Tích phân
( )
2
1
dfx x
∫
bằng
A.
1
7
. B.
1
3
. C.
7
. D.
19
3
−
.
Lời giải
Mặt khác :
( )
( ) ( )
22 2
2 3 532
11 1
1 33
(*) d 1 d 4 5 7 6 d
4 42
fx x x f x x x x x x x x
⇒ + − − − = − − ++
∫∫ ∫
( )
22
33
11
4 1 33 1 331
dd
3 4 42 4 423
fxx fxx xx
⇔ + −− −−=
∫∫
( ) ( ) ( )
22 2
11 1
41 1
dd d
33 7
fx x fx x fx x⇒+ =⇔=
∫∫ ∫
.
Câu 65: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
11f =
và
( )
(
)
(
)
(
)
[ ]
2
2 642
4 6 1 . 40 44 32 4, 0;1
f x x fx x x x x
′
+ − = − + − ∀∈
. Tích phân
(
)
1
0
f x dx
∫
bằng?
A.
23
15
. B.
13
15
. C.
17
15
−
. D.
7
15
−
.
Lời giải
Chọn B
( )
( )
( )
( )
2
2 642
4 6 1 . 40 44 32 4f x x fx x x x
′
+ − =−+−
( )
( )
( )
( )
( )
( )
11 1
2
2 642
00 0
4 6 1 . 40 44 32 4 . 1f x dx x f x dx x x x dx⇒ + − = −+−
′
∫∫ ∫
Xét
( )
( )
( )
( )
11
22
00
4 6 1 . 24 4I x f x dx x f x dx=−=−
∫∫
.
Đặt
(
)
( )
( )
2
3
24 4
84
u fx
du f x dx
dv x dx
vx x
=
′
=
⇒
= −
= −
.
( )
( )
(
)
( )
( )
( )
11
1
33 3
0
00
8 4. 8 4. = 424 2. .I x xfx x xf xdx x xf xdx
′′
⇒= − − − − −
∫∫
Do đó:
( ) ( )
(
)
( )
( )
( ) ( )
11 1 1
2
2
3 3 642
00 0 0
1 2 4 2 . 4 2 56 60 36 8 .f x dx x x f x dx x x dx x x x dx
′′
⇒ − − + − = −+−
∫∫ ∫ ∫
( )
( )
( ) ( )
1
2
3 3 42
0
42 0 42 .fx x x dx fx x x fx x x c
⇒ −− =⇒ =−
′′
⇒ =−+
∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
Mà
( )
11 1fc=⇒=
⇒
( )
42
1.fx x x=−+
Do đó
( )
( )
11
42
00
13
1.
15
f x dx x x dx= −+ =
∫∫
Câu 66: Cho hàm số có đạo hàm liên tục trên và thỏa mãn và
. Tích phân bằng
A. . B. . C. . D.
Lời giải
Chọn D
Cách 1.
Áp dụng công thức tích phân từng phần, ta có: .
Từ
Thay
vào ta được .
Xét
Đặt , đổi cận:
Khi đó
Do đó ta có
Vậy
Cách 2.
Từ
Thay
vào ta được .
Xét hàm số từ giả thiết trên ta có
.
Vậy suy ra .
()fx
(0) 3f =
2
( ) (2 ) 2 2,fx f x x x x+ − = − + ∀∈
2
0
( )dxf x x
′
∫
4
3
−
2
3
5
3
10
3
−
22
2
0
00
()d () ()dxf x x xf x f x x
′
= −
∫∫
( )
2
( ) (2 ) 2 2, 1fx f x x x x+ − = − + ∀∈
0x =
( )
1
(0) (2) 2 (2) 2 (0) 2 3 1ff f f+ =⇒ =− =−=−
2
0
( )dI fx x=
∫
2x t dx dt= −⇒ =−
02
20
xt
xt
=⇒=
= ⇒=
02 2
20 0
(2 ) (2 ) (2 )I f t dt f t dt I f x dx=− − = − ⇒= −
∫∫ ∫
( )
( )
2 2 22
2
0 0 00
84
() (2 )d 2 2d 2 ()d ()d .
33
fx f x x x x x fx x fx x+ − = −+ ⇔ =⇔ =
∫ ∫ ∫∫
22
2
0
00
4 10
()d () ()d 2.(1) .
33
xf x x xf x f x x
′
= − = −−=−
∫∫
( )
2
( ) (2 ) 2 2 1
(0) 3
fx f x x x
f
+ −=−+
=
0; 1xx= =
( )
1
1
(2) 1; (1)
2
ff=−=
2
()f x ax bx c= ++
33
11
22
42 1 3
cc
abc a
a bc b
= =
++= ⇔ =
+ +=− =−
2
1
() 3 3 () 3
2
fx x x f x x
′
= − +⇒ =−
( )
22
00
10
( )d 3 d
3
xf x x x x x
′
= −=−
∫∫

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 40
Câu 67: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
[ ]
2; 4
và
( )
[ ]
0, 2; 4fx x
′
> ∀∈
. Biết
( ) ( )
[ ]
( )
3
33
7
4 , 2; 4 , 2
4
xf x f x x x f
′
= − ∀∈ =
. Giá trị của
( )
4f
bằng
A.
40 5 1
2
−
. B.
20 5 1
4
−
. C.
20 5 1
2
−
. D.
40 5 1
4
−
.
Lời giải
Chọn D
Ta có:
(
)
[
]
0, 2; 4
fx x
′
> ∀∈
nên hàm số
( )
y fx=
đồng biến trên
[ ]
2; 4
( ) ( )
2fx f⇒≥
mà
( )
7
2
4
f =
. Do đó:
( )
[ ]
0, 2; 4fx x> ∀∈
.
Từ giả thiết ta có:
( ) ( ) ( ) ( )
33
3 33
4 41xfx f x x x fx f x
′′
= −⇔ +=
(
)
(
)
(
)
(
)
3
3
.4 1
41
fx
x fx f x x
fx
′
′
⇔ += ⇔ =
+
.
Suy ra:
( )
( )
( )
( )
2
33
d4 1
1
dd
42
41 41
fx
fx
x
x xx C
fx fx
+
′
=⇔=+
++
∫ ∫∫
( )
2
2
3
3
41
82
x
fx C⇔ +=+
.
( )
73 1
22
42 2
f CC=⇔=+⇔=−
.
Vậy:
( )
( )
3
2
4
11
3
4
x
fx
−−
=
( )
40 5 1
4
4
f
−
⇒=
.
Câu 68: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;2
và thỏa
( )
10f =
,
( )
( )
(
)
2
2
4 8 32 28f x fx x x
′
+ =−+
với mọi
x
thuộc
[ ]
0;2
. Giá trị của
( )
1
0
dfx x
∫
bằng
A.
5
3
−
. B.
4
3
. C.
2
3
−
. D.
14
3
−
.
Lời giải
Chọn B
Đặt
( )
2
1
2dI fx x=
∫
.
Dùng tích phân từng phần, ta có:
( )
d 2d
u fx
vx
=
=
( )
dd
24
u fxx
vx
′
=
⇒
= −
.
( ) ( ) ( ) ( ) ( ) ( )
22
2
1
11
24 24 d 24 dIxfx xfxx xfxx
′′
=− − − =−−
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 41
Ta có
( )
( )
( )
2
2
4 8 32 28f x fx x x
′
+ =−+
(
)
(
)
( )
22
2
11
d 22 d
f x x fx x
′
⇒+
∫∫
(
)
2
2
1
8 32 28 d
xx x= −+
∫
( )
( )
( ) ( ) ( )
22 2
2
2
11 1
d224 d 24dfx x x fxx x x
′′
⇔ − − +−
∫∫ ∫
(
)
(
)
22
2
2
11
8 32 28 d 2 4 d
xx xx x
= −+ + −
∫∫
(
)
( )
2
2
1
2 4d 0fx x x
′
⇔ −− =
∫
( )
24fx x
′
⇔=−
( )
2
4fx x xC⇒ =−+
,
C ∈
.
Mà
( )
10 3fC=⇒=
(
)
2
43
fx x x⇒ =−+
( )
( )
11
2
00
4
d 4 3d
3
fx x x x x⇒ = −+ =
∫∫
.
Câu 69: Cho hàm số
( )
fx
liên tục trên
[ ]
0;1
và
( ) ( )
2
23
1
1
xx
fx f x
x
++
+ −=
+
,
[ ]
0;1x∀∈
. Tính
( )
1
0
dfx x
∫
A.
3
2ln 2
4
+
. B.
3 ln 2+
. C.
3
ln 2
4
+
. D.
3
2ln 2
2
+
.
Lời giải
Chọn C
Theo giả thiết, ta có:
( ) ( )
2
23
1
1
xx
fx f x
x
++
+ −=
+
,
[ ]
0;1x∀∈
và
( )
fx
liên tục trên
[ ]
0;1
nên
( ) ( )
11
2
00
23
1d d
1
xx
fx f x x x
x
++
+− =
+
∫∫
( ) ( )
( )
2
11 1
00 0
12
d 1d d
1
x
fxx f xx x
x
++
⇔ +−=
+
∫∫ ∫
Đặt
1 xt−=
thì
ddxt= −
, với
01xt=⇒=
, với
10xt=⇒=
Do đó:
(
) ( )
( ) (
)
1 011
0 100
1d d d d
f x x ft t ft t fx x−=− = =
∫ ∫∫∫
( ) ( ) ( )
11 1
00 0
d 1 d2 dfxx f xx fxx⇒ +−=
∫∫ ∫
.
Lại có
( )
1
2
11
2
00
0
12
23
d 1 d 2ln 1 2 ln 2
1 12 2
x
x
xx x x x
xx
++
= ++ = + + + = +
++
∫∫
Từ, và suy ra
( ) ( )
11
00
33
2 d 2ln 2 d ln 2
24
fx x fx x=+⇔ =+
∫∫
.
Câu 70: Cho hàm số
()y fx=
liên tục trên thỏa mãn
( ) ( ) ( )
2
21
3 2 2 1e 4
xx
fx f x x
−+
+ −= − +
. Tính tích
phân
( )
2
0
dI fx x=
∫
ta được kết quả:
A.
e4I = +
. B.
8I =
. C.
2I =
. D.
e2I
= +
.
Lời giải
Chọn C

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 42
Theo giả thuyết ta có
( )
( )
(
) ( )
2
22
21
00
3 2 d 2 1e 4 d *
xx
fx f x x x x
−+
+− = − +
∫∫
.
Ta tính
(
) ( ) ( ) ( )
22 2
00 0
2d 2d2 df xx f x x fxx− =− − −=
∫∫ ∫
.
Vì vậy
(
)
( )
(
)
22
00
3 2 d4 d
fx f x x fx x+− =
∫∫
.
Hơn nữa
( )
( )
22 2
22
2
21 21 2 21
0
00
2 1 d e d 21e 0
xx xx xx
xe x x x
−+ −+ −+
− = − += =
∫∫
và
2
0
4d 8
x =
∫
.
Suy ra
( ) (
)
22
00
4 d8 d2fx x fx x=⇔=
∫∫
.
Câu 71: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
( )
2 73
2 23 1f x xf x x x x+ = + −−
với
x ∈
.
Tính tích phân
( )
1
0
dxf x x
′
∫
.
A.
1
4
. B.
5
4
. C.
3
4
. D.
1
2
−
.
Lời giải
Chọn B
Áp dụng công thức tích phân từng phần, ta có:
( ) (
) ( ) ( )
11
00
1
d d*
0
xf x x xf x f x x
′
= −
∫∫
Từ
( )
( )
( )
2 73
2 2 3 11
f x xf x x x x+ = + −−
Thay
1x =
vào
( )
1
ta được
( ) ( ) ( ) ( )
1213 112ff f+ =⇒=
Mặt khác từ
( )
1
ta có
( )
( ) ( )
11 1
2 73
00 0
d 2 d 2 3 1df x x xf x x x x x x
+ = + −−
∫∫ ∫
( )
( ) ( )
( ) ( )
( )
11 1 1
22
00 0 0
1 11
d d 2d d 3
2 24
fx x fx x fx x fx x⇒ + =−⇒ =−⇒ =−
∫∫ ∫ ∫
Thay
(
) ( )
2, 3
vào
( )
*
ta được
( )
1
0
15
d1
44
xf x x
′
=+=
∫
Câu 72: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( )
43
2
22 44
1 2 , 0, 1
− −++ −
− + = ∀≠ ≠
x xx x
xf x f x x
xx
. Khi đó
( )
1
1
d
−
∫
fx x
có giá trị là
A.
0
. B.
1
. C.
1
2
. D.
3
2
.
Lời giải
Chọn A

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 43
Từ giả thiết suy ra
(
)
43
23
2 22 44
1
− −++ −
−+ =
x xx x
fx f
xx x
Ta có:
( )
22 2
43
23
11 1
222 44
1 d .d d
x xx x
f xx f x x
xx x
− −++ −
−+ =
∫∫ ∫
( ) ( )
22 2
23
11 1
22 22 44
1 d1 d 1 d
−−
⇔− − − + = − + + −
∫∫ ∫
xx
fx xf x x
x x xx
( ) (
)
11
2
2
00
2
42
dd
1
2
−
⇔− + = − + − +
∫∫
x
ft t ft t x
xx
( )
(
)
01
10
d d0
−
⇔+=
∫∫
ft t ft t
( )
1
1
d0
−
⇔=
∫
ft t
.
Vậy
( )
1
1
d0
−
=
∫
fx x
.
Cách trắc nghiệm
Ta có:
( )
43
2
22 44
1 2 , 0, 1
x xx x
xf x f x x
xx
− −++ −
− + = ∀≠ ≠
(
)
43
2
22 44
1 2 , 0, 1
x xx x
xf x f x x
x xx
− −+ −
⇔ − + = + ∀≠ ≠
( )
(
)
22
22 22
12 12 ,0,1
xx
xf x f x x x x
xx
−−
⇔ −+ = −+ ∀≠ ≠
Chọn
( ) ( )
11
11
.d .d 0fx x fx x xx
−−
=⇒==
∫∫
.
Câu 73: Cho hàm số
()y fx=
thỏa mãn
2
' '' 3
() (). () 2,f x fxf x x x x R
+ = − ∀∈
và
'
(0) (0) 2ff= =
.
Tính giá trị của
2
(2)
Tf=
A.
160
15
B.
268
15
C.
4
15
D.
268
30
Lời giải
Chọn B
Ta có:
2
' '' 3
() (). () 2,f x fxf x x x x R
+ = − ∀∈
( )
'
'3
().() 2,f x fx x x x R⇔ = − ∀∈
Lấy nguyên hàm hai vế ta có:
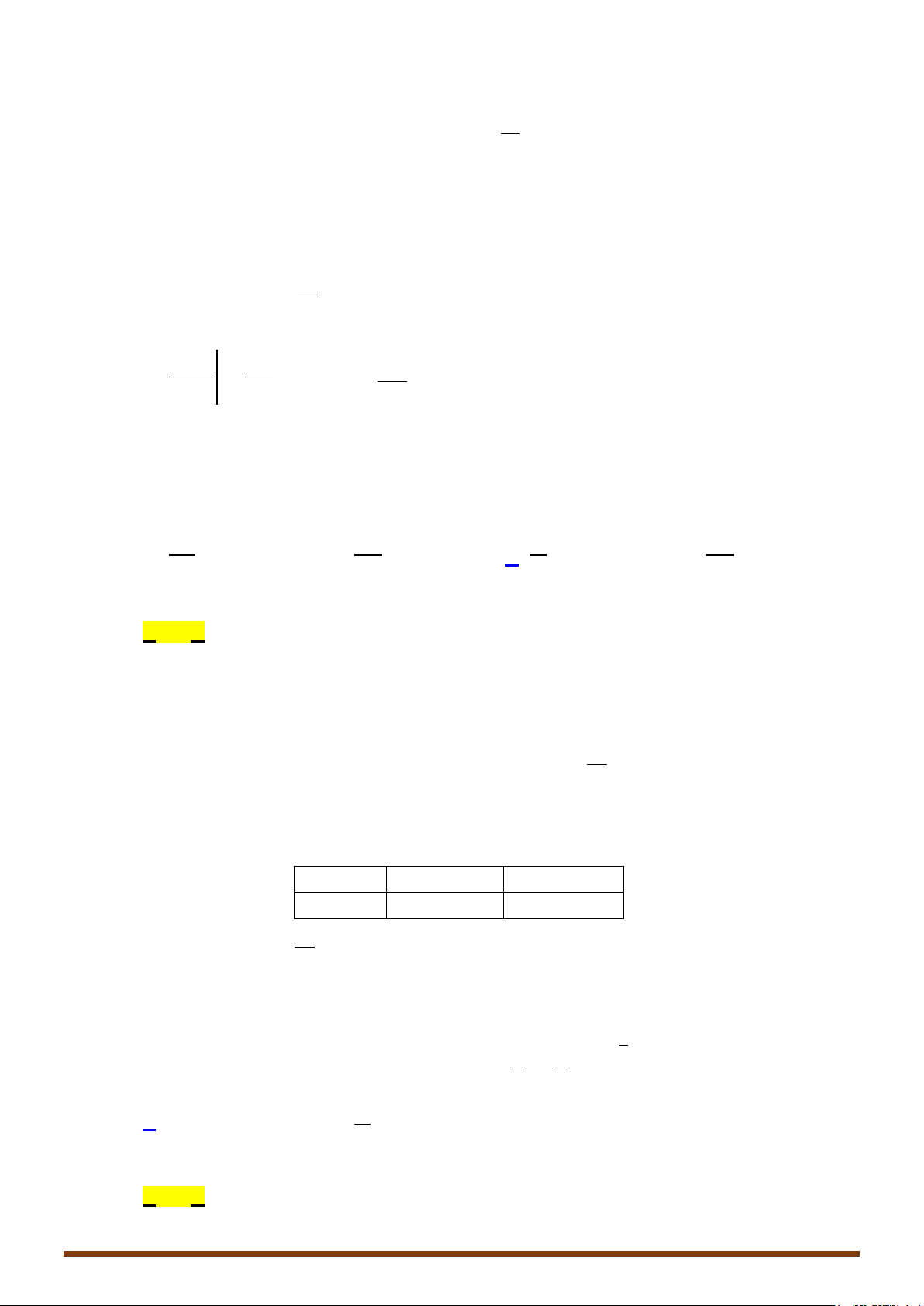
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 44
( ) ( )
'
'3
4
'2
(). () 2
(). ()
4
f x f x dx x x dx
x
f xfx x C
= −
⇔ = −+
∫∫
Theo đề ra ta có:
'
(0). (0) 4ff C= =
Suy ra:
22
4
'2
00
(). (). 4
4
x
f x f x dx x dx
= −+
∫∫
2
2
0
( ) 104
2 15
fx
⇔=
2
268
(2)
15
f⇔=
.
Câu 74: Cho
fx
là hàm số liên tục trên tập xác đinh
và thỏa mãn
2
31 2fx x x
. Tính
5
1
d
I fx x
A.
37
6
. B.
527
3
. C.
61
6
. D.
464
3
.
Lời giải
Chọn C
2
2
11
2
00
31 2
23 31 23 2
61
23 31d 23 2d
6
fx x x
x fx x x x
x fx x x x x x
Đặt
2
3 1 d 2 3dtx x t x x
x
0
1
t
1
5
Suy ra
5
1
61
d
6
ft t
.
Câu 75: Cho hàm số
( )
y fx=
liên tục, có đạo hàm trên
R
thỏa mãn điều kiện
(
)
2
() () 2sin cos,f x x f x x x xx R
′
+ −= ∈
và
22
f
=
ππ
.Tính
( )
2
0
xf x dx
′′
∫
π
A.
0
. B.
2
π
. C.
1
. D.
π
.
Lời giải
Chọn A

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 45
Từ giả thiết
( )
2
() () 2sin cos
fx xf x x x x
′
+ −=
( )
( )
( )
( )
2
2
2
() () cos 2sin
sin
sin
f x xf x x x x x
xf x x x
xf x x x C
′
⇔+ = +
′
′
⇔=
⇔=+
Mặt khác:
( )
0 sin .
22
f C fx x x
=⇒=⇒ =
ππ
Ta có:
(
)
( ) ( ) (
)
22
2
22
00
00
cos 2 sin 2xf x dx xf x f x dx x x x x f x
′′ ′ ′
= − = + −
∫∫
ππ
ππ
2
2
0
2
2
0
cos 2 sin 2 sin
cos 0
x xxxxx
xx
= + −
= =
π
π
Câu 76: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
0;1
thỏa mãn
( )
( )
22
4. 3 1 1xf x f x x+ −=−
. Tính
( )
1
0
dI fx x=
∫
.
A.
4
π
. B.
16
π
. C.
20
π
. D.
6
π
.
Lời giải
Chọn C
Lấy tích phân hai vế, ta có
( )
(
)
( )
11
22
00
4. 3 1 d 1 d *xf x f x x x x
+− =−
∫∫
.
Xét tích phân
1
2
0
1dJ xx= −
∫
. Đặt
sin d cos dx t x tt= ⇒=
. Khi đó, ta có
1
22
22 2
00 0
1 d 1 sin .cos d cos dJ x x t tt tt
ππ
=−=− =
∫∫ ∫
( )
2
2
0
0
1 1 sin 2
1 cos 2 d
2 22 4
t
tt t
π
π
π
=+=+=
∫
.
Xét tích phân
( )
1
2
0
4. dK xf x x=
∫
. Đặt
2
d 2dt x t xx=⇒=
. Khi đó, ta có
( )
( ) ( )
1 11
2
0 00
4. d 2 d 2 dK xf x x f t t f x x= = =
∫ ∫∫
.
Xét tích phân
( )
1
0
31 d
L f xx= −
∫
. Đặt
1 ddt xt x=−⇒ =−
. Khi đó, ta có
( ) ( )( ) ( ) ( )
1 0 11
0 1 00
31 d 3 d 3 d 3 dL f x x ft t ft t fx x= − = −= =
∫ ∫ ∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 46
Vậy
(
)
( )
( )
11
00
*5 d d
4 20
fx x fx x
ππ
⇔ =⇒=
∫∫
.
Câu 77: Cho hàm số
(
)
fx
liên tục trên khoảng
(
)
0; .
+∞
Biết
( )
33
f =
và
(
) ( ) ( )
3
'21 21 , 0; .xf x f x x x+ − + = ∀ ∈ +∞
Giá trị của
( )
5
3
f x dx
∫
bằng
A.
914
3
. B.
59
3
. C.
45
4
. D.
88
.
Lời giải
Chọn B
Ta có:
( ) ( )
( ) ( )
( )
( ) (
)
( )
2
3
4
22
'
2 '212 21
'21 21 2, 0; .
21 21
2 2 .1
x f x xf x
xf x f x x x
x
fx fx
xC
xx
+− +
+ − + = ⇔ = ∀ ∈ +∞
++
⇔ =⇔=+
Cho
1x =
từ
( )
1
( )
( ) ( )
2 32
22
3
3
2.1 2.1 1 2 1 2 1 2 .
11
f
C C C fx x x xx⇒ = +⇔ = +⇒=⇒ += += +
( )
( )
2
22
43
32
11
1
59
21 2 2 .
43 6
xx
f x dx x x dx
⇒ += + = + =
∫∫
( )
( )
52
31
59
2 21 .
3
f x dx f x dx⇒ = +=
∫∫
Câu 78: Cho hàm số
( )
fx
có đạo hàm và đồng biến trên
[ ]
1; 4
, thỏa mãn
( ) ( )
2
2x xf x f x
′
+=
với mọi
[ ]
1; 4x ∈
. Biết
( )
3
1
2
f =
, tính
( )
4
1
I f x dx=
∫
A.
1188
45
. B.
1187
45
. C.
1186
45
. D.
9
2
.
Lời giải
Chọn C
Do
(
)
fx
đồng biến trên
[ ]
1; 4
nên
( ) ( )
31
1
22
fx f≥ = >−
, ngoài ra
( )
[ ]
0, 1; 4
fx x
′
≥ ∀∈
. Khi
đó ta có biến đổi sau:
( ) ( )
( )
( )
2
2
21
fx
x xf x f x x
fx
′
′
+= ⇔ =
+
( )
( )
( )
33
22
21 21
33
fx x C fx x C
′
′
⇔ + = + ⇔ += +

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 47
Mà
( )
34
1
23
fC=⇒=
( )
2
3
33
24
1
28 7
33
2 9 9 18
x
fx x x
+−
⇒= =+ +
.
Vậy
(
)
4
4
42
1
1
1 16 7 1186
18 45 18 45
I f x dx x x x x
= =+ +=
∫
.
Câu 79: Cho hàm số
()y fx=
có đạo hàm liên tục trên
thỏa mãn
2
.(). '() () ,xf x f x f x x x= − ∀∈
và
có
(2) 1f =
. Tích phân
2
2
0
()f x dx
∫
A.
3
2
B.
4
3
C.
2
D.
4
Lời giải
Chọn C
Ta có:
(
)
( )
22
2 22
22 2 2
0 00
2
.(). '() () 2.(). '() 2 () 2
2.(). '() () 3 () 2 . ()'x 3 () 2
2
.() 34 234 2
0
xf x f x f x x xf x f x f x x
xfxfx fx fx x xfxd fxdx xdx
xf x I I I
= −⇔ = −
⇔ + = −⇔ = −
⇔ = −⇔= −⇔=
∫ ∫∫
Câu 80: Cho hàm số
( )
fx
nhận giá trị không âm và có đạo hàm liên tục trên
thỏa mãn
( ) ( ) (
)
2
21 ,f x x fx x
′
= + ∀∈
và
( )
01f = −
. Giá trị của tích phân
( )
1
0
dfxx
∫
bằng
A.
1
6
−
. B.
ln 2−
. C.
3
9
π
−
. D.
23
9
π
−
.
Lời giải
( ) ( ) ( )
( )
( )
( )
( )
( )
2
2
21 , 21,
1
2 1,
fx
f x x fx x x x
fx
xx
fx
′
−
′
= + ∀∈ ⇒ =− + ∀∈
′
⇒ =− + ∀∈
Vậy
( )
( )
( )
2
2
11
2 1dx x x xC fx
fx x xC
=− + =− −+ ⇒ =
− −+
∫
.
Do
( )
01 1fC=−⇒ =−
. Vậy
( )
2
1
1
fx
xx
= −
++
.
( )
11 1
2
2
00 0
11
dd d
1
13
24
I fxx x x
xx
x
==−=−
++
++
∫∫ ∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 48
Đặt
13
tan , ;
2 2 22
x tt
ππ
−
+= ∈
. Suy ra
(
)
( )
2
33
2
66
3
1 tan
23 3
2
dt dt .
3
39
1 tan
4
t
I
t
ππ
ππ
π
+
=− =−=−
+
∫∫
Câu 81: Cho số thực
0a
>
. Giả sử hàm số
()fx
liên tục và luôn dương trên đoạn
[ ]
0; a
thỏa mãn
( ). ( ) 1
fx fa x−=
. Tính tích phân
(
)
0
1
d
1
a
Ix
fx
=
+
∫
?
A.
2
3
a
I =
. B.
2
a
I =
. C.
3
a
I =
. D.
Ia=
.
Lời giải
Đặt
ddt ax t x=−⇒ =−
.
Thay vào ta được
( )
0
1
d
1
a
Ix
fx
=
+
∫
( )
0
1
dt
1
a
fa t
=
+−
∫
( )
0
1
d
1
a
x
fa x
=
+−
∫
.
Suy ra
( )
(
)
( )
(
)
(
)
(
)
0
0d
11
a
fa x fx
x
fx fa x
−−
=
+ +−
∫
, do hàm số
()fx
liên tục và luôn dương trên đoạn
[ ]
0; a
. Suy ra
( ) ( )
fa x fx−=
, trên đoạn
[
]
0;
a
.
Mà
( ). ( ) 1fx fa x−=
( )
1fx⇒=
. Vậy
0
1
d
22
a
a
Ix
= =
∫
.
Câu 82: Cho hàm số
( )
fx
đồng biến, có đạo hàm đến cấp hai trên đoạn
[ ]
0; 2
và thỏa mãn
( ) ( ) ( ) ( )
22
.0fx fxf x f x
′′ ′
− +=
. Biết
( )
01f =
,
( )
6
2fe=
. Khi đó
( )
1f
bằng
A.
2
e
. B.
3
2
e
. C.
3
e
. D.
5
2
e
.
Lời giải
Theo bài ra ta có hàm số
( )
fx
đồng biến trên
[ ]
0; 2
( ) ( )
0 10fx f⇒≥=>
do đó
( )
[ ]
0 0; 2fx x> ∀∈
.
Ta có
( )
(
)
( )
( )
( )
(
)
2
2
.
f xfx f x
fx
fx
fx
′
′′ ′
−
′
=
Theo đề bài
( ) ( ) ( ) ( )
22
.0fx fxf x f x
′′ ′
− +=
( ) ( ) ( ) ( )
22
.f xfx f x fx
′′ ′
⇒ −=
( )
( )
1
fx
fx
′
′
⇒=
( )
( )
fx
xC
fx
′
⇒=+
(
)
( )
( )
22
00
dd
fx
x xC x
fx
′
⇒=+
∫∫
( )
( )
( )
2
2
2
0
0
1
d
2
x
f x Cx
fx
⇒=+
∫
( )
2
0
ln 2 2fx C⇒=+
6
ln e ln 1 2 2 2CC⇒ − =+ ⇒=
( )
( )
2
fx
x
fx
′
⇒=+
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 49
Do đó
( )
11
2
00
ln 2
2
x
fx x
= +
( )
5
ln 1
2
f⇒=
( )
5
2
1ef⇒=
.
Câu 83: Cho hàm số
( )
y fx=
là hàm số lẻ trên
và đồng thời thỏa mãn hai điều kiện
( ) ( )
11fx fx+= +
,
x∀∈
và
( )
2
1
fx
f
xx
=
,
0x∀≠
. Gọi
(
)
(
)
1
2
0
.d
1
fx
Ix
fx
=
+
∫
. Hãy chọn
khẳng định đúng về giá trị của
I
.
A.
(
)
1; 0I ∈−
. B.
( )
1; 2I ∈
. C.
( )
0;1I ∈
. D.
( )
2; 1I ∈− −
.
Lời giải
- Đặt
( )
y fx=
. Khi đó từ giả thiết ta có :
(
)
11fx y+=+
,
( )
2
11
1
1
y
f
x
x
+
=
+
+
,
(
)
2
11
1
1
y
f
x
x
+
−=−
+
+
.
Suy ra
1
1
11
x
ff
xx
=−+
++
1
1
1
f
x
=−+
+
( )
2
1
1
1
y
x
+
=−+
+
( )
2
2
2
1
x xy
x
+−
=
+
( )
1
Và
11
1
x
ff
xx
+
= +
2
1
11
y
f
xx
=+=+
2
2
xy
x
+
=
,
1
1
1
x
ff
x
x
x
=
+
+
2
2
22
1
11
x
xy
f
x
x
xx
xx
+
+
= =
++
( )
2
2
1
xy
x
+
=
+
( )
2
.
- Từ
( )
1
và
( )
2
suy ra :
( ) ( )
22
22
2
11
x xy x y
xx
+− +
=
++
22
2
x xyx y⇒ + −= +
yx⇒=
hay
( )
fx x=
.
Do đó:
(
)
(
)
1
2
0
.d
1
fx
Ix
fx
=
+
∫
1
2
0
.d
1
x
x
x
=
+
∫
( )
2
1
2
0
d1
1
21
x
x
+
=
+
∫
( )
1
2
0
1
ln 1
2
x= +
1
ln 2 0,35
2
= ≈
.
Vậy
(
)
0;1I ∈
.
Câu 84: Cho hàm số
( )
fx
có đạo hàm liên tục trên
[ ]
0;
π
. Biết
( )
0 2ef =
và
(
)
fx
thỏa mãn hệ thức
( ) ( )
[ ]
cos
sin . cos .e , 0;
x
f x xf x x x
π
′
+ = ∀∈
. Tính
(
)
0
dI fx x
π
=
∫
.
A.
6,55I ≈
. B.
17,30I ≈
. C.
10,31I ≈
. D.
16,91I ≈
.
Lời giải
Chọn C
Giả thiết
( ) ( )
cos
sin . cos .e
x
f x xf x x
′
+=
( ) ( )
cos cos
e. e.sin. cos
xx
f x xf x x
−−
′
⇔+ =
( )
cos
e . cos
x
fx x
−
′
⇔=
( )
cos
1
e . sin
x
fx xC
−
⇒=+
.
Do
( )
0 2ef =
, thế vào ta được
1
2C =
suy ra
( ) ( )
cos
2 sin e
x
fx x= +
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 50
Dùng máy tính thì
( ) ( )
cos
00
d 2 sin .e d 10,30532891
x
I fx x x x
ππ
==+≈
∫∫
.
Câu 85: Cho hàm số
(
)
fx
liên tục và nhận giá trị dương trên
[
]
0;1
. Biết
( ) ( )
.1 1fxf x−=
với
[ ]
0;1x∀∈
. Tính giá trí
( )
1
0
d
1
x
I
fx
=
+
∫
A.
3
2
. B.
1
2
. C.
1
. D.
2
.
Lời giải
Ta có:
( ) (
)
( ) ( )
.1 1fxf x fx fx−+ =+
( )
( )
( )
1
1 11
fx
f x fx
⇒=
−+ +
Xét
( )
1
0
d
1
x
I
fx
=
+
∫
Đặt
11t xx t=−⇔=−
ddxt⇒=−
. Đổi cận:
01xt=⇒=
;
10xt=⇒=
.
Khi đó
( )
( )
(
)
( )
( )
011 1
100 0
d
ddd
11 11 11 1
fx x
ttx
I
ft ft fx fx
=−= = =
+− +− +− +
∫∫∫∫
Mặt khác
( )
( )
( )
( )
11 1 1
00 0 0
d1
d
d d1
1 1 1 ()
fx x fx
x
xx
fx fx ft
+
+= ==
++ +
∫∫∫ ∫
hay
21I =
. Vậy
1
2
I
=
.
Câu 86: Cho hàm số
( )
y fx=
có đạo hàm trên khoảng
( )
0; +∞
thỏa mãn
( )
( ) ( )
3
.ln
.
x
fx x
xf x f x
=
′
−
và
( )
10f =
. Tính tích phân
( )
5
1
dI fx x=
∫
.
A.
12ln13 13−
. B.
13ln13 12−
. C.
12ln13 13+
. D.
13ln13 12+
.
Lời giải
Chọn B
Từ giả thiết và
( )
( ) ( )
3
.ln
.
x
fx x
xf x f x
=
′
−
( )
( ) ( )
3
ln
.
fx
x
x xf x f x
⇔=
′
−
( )
( ) ( )
3
e
.
fx
x
x
xf x f x
⇔=
′
−
(
) ( )
( )
2
.
.e
fx
x
xf x f x
x
x
′
−
⇔=
( )
( )
.e
fx
x
fx
x
x
′
⇔=
Lấy nguyên hàm hai vế của suy ra
( )
2
e
2
fx
x
x
C= +
.
Do
( )
10f =
⇒
1
2
C =
, nên
( )
( )
22
11
e ln
22
fx
x
xx
fx x
++
= ⇒=
với
( )
0;x ∈ +∞
.
( )
55
2
11
1
d .ln d
2
x
I fx x x x
+
= =
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 51
Đặt
2
2
12
ln d d
21
xx
u ux
x
+
= ⇒=
+
;
ddv xx
=
, chọn
2
1
2
x
v
+
=
.
Theo công thức tích phân từng phần, ta được:
5
5
5
22 2
1
1
1
11
.ln d 13ln13
22 2
xx x
I xx
++
= −= −
∫
13ln13 12= −
.
Câu 87: Cho hàm số
( )
y fx=
liên tục trên
{ }
\ 0; 1−
thỏa mãn điều kiện
(
)
1 2ln 2f =
và
( )
(
) (
)
2
1. 3 2
xx f x f x x x
′
+ + =++
. Giá trị
( )
2 ln 3f ab= +
, với
,ab∈
. Tính
22
ab
+
.
A.
5
2
. B.
13
4
. C.
25
4
. D.
9
2
.
Lời giải
Chọn D
Do hàm số
( )
y fx=
liên tục trên
{ }
\ 0; 1−
nên
(
)
( )
( )
2
1 32xx f x f x x x
′
+ + =++
( )
( )
( )
( )
2
12
11
1
2
11
xx
f x fx
xx
x
xx
fx
xx
+
′
⇔+ =
++
+
′
+
⇔=
++
( )
( )
( )
( )
( )
( )
22
11
2
1
2
11
3
1 ln
12
21 3
2 1 1 ln
32 2
2 3 33
2 ln 2 1 ln 2 ln 3.
3 2 22
xx
f x dx dx
xx
x
fx
x
ff
ff
′
+
⇒=
++
⇔=+
+
⇔ −=+
⇔ −=+ ⇔ =+
∫∫
22
39
.
22
ab a b⇒==⇒ + =
Câu 88: Cho hàm số
()y fx=
liên tục trên
thỏa mãn:
2
21
3 ( ) (2 ) 2( 1) 4,
xx
fx f x x e x
−+
+ − = − + ∀∈
.
Tính giá trị của tích phân
2
0
()I f x dx=
∫
.
A.
2Ie= +
. B.
24Ie= +
. C.
2I =
. D.
8I =
.
Lời giải
Chọn C
Cách 1:
2
21
3 ( ) f(2 ) 2(x 1)e 4,
xx
fx x x
−+
+ − = − + ∀∈
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 52
2
22
22
21
00
00
3 ( )d (2 )d (2 2) d 4 d (1)
xx
fxx f xx x e x x
−+
⇒ + −= − +
∫∫ ∫ ∫
.
Đặt
2 022
0 200
2 (2 )d( ) ( )d ( )d ( )d (2)t x f x x ft t ft t fx x=−⇒ − =− = =
∫ ∫∫∫
.
Đặt
2
21
2 21
01
2 1 d (2 2)d (2 2) d d 0 (3)
xx u
u x x u x x x e x eu
−+
= − +⇒ = − ⇒ − = =
∫∫
.
Thay
(2)
và
(3)
vào
(1)
2
2
0
0
4 ( )d 4 dfx x x⇒=
∫∫
2
0
( )d 2I fx x⇒= =
∫
. Chọn phương án
C
.
Cách 2: Do
2
21
3 ( ) f(2 ) 2(x 1) e 4, (1)
xx
fx x x
−+
+ − = − + ∀∈
Thay
2xx= −
vào
(1)
ta có:
2
21
3 (2 ) ( ) 2(x 1)e 4, (2)
xx
f x fx x
−+
− + =− − + ∀∈
Từ
(1)
và
(2)
ta có hệ phương trình:
2
2
21
21
3 ( ) f(2 ) 2(x 1) e 4,
( ) 3 (2 ) 2(x 1) e 4,
xx
xx
fx x x
fx f x x
−+
−+
+ − = − + ∀∈
+ − =− − + ∀∈
2
2
21
21
9 ( ) 3f(2 ) 6(x 1) e 12
( ) 3 (2 ) 2(x 1) e 4
xx
xx
fx x
fx f x
−+
−+
+ −= − +
⇔
+ −=−− +
2
21
( ) 2(x 1) e 1
xx
fx
−+
⇒=− +
( )
2
22
21
00
( )d 2(x 1) e 1 d 2
xx
fx x x
−+
⇒ = − +=
∫∫
DẠNG 2. TÍCH PHÂN MỘT SỐ HÀM ĐẶC BIỆT
DẠNG 2.1 TÍCH PHÂN CỦA HÀM SỐ LẺ VÀ HÀM SỐ CHẴN
Nhắc lại kiến thức về hàm số lẻ và hàm số chẵn:
Hàm số
( )
y fx=
có miền xác định trên tập đối xứng D và
Nếu
( ) ( ) ( )
, f x fx x D y fx− = ∀∈ ⇒ =
: là hàm số chẵn.
Nếu
( )
(
)
,f x fx x D− =− ∀∈
( )
y fx⇒=
: là hàm số lẻ.
.
Thường gặp cung góc đối nhau của
( ) ( )
cos cos , sin sinxx x x
−= −=−
.
Nếu hàm số
( )
fx
liên tục và lẻ trên
[ ]
;aa−
thì
( )
.0
a
a
f x dx
−
=
∫
.
Nếu hàm số
( )
fx
liên tục và chẵn trên
[ ]
;aa−
thì
( ) ( )
( )
( )
0
0
2
1
aa
a
a
x
a
f x dx f x dx
fx
dx f x dx
b
α
−
−
=
=
+
∫∫
∫∫
.
Do những kết quả này không có trong SGK nên về mặt thực hành, ta làm theo các bước sau:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 53
Bước 1. Phân tích:
( ) ( ) ( )
0
0
. ..
aa
aa
I f x dx f x dx f x dx A B
−−
= = +=+
∫ ∫∫
.
Bước 2. Tính
( )
0
.
a
A f x dx
−
=
∫
? bằng cách đổi biến
tx= −
và cần nhớ rằng: tích phân không phụ
thuộc vào biến, mà chỉ phụ thuộc vào giá trị của hai cận, chẳng hạn luôn có:
0
22
0
22
2014
2014
3 cos 3 cos
1 sin 1 sin
tt xx
dt dx
tx
−
−
=
++
∫∫
.
2. Tích phân của hàm số liên tục
Nếu hàm số
( )
fx
liên tục trên
[ ]
;
ab
thì
( ) ( )
bb
aa
f x dx f a b x dx
= +−
∫∫
.
Nếu hàm số
( )
fx
liên tục trên
[ ]
0;1
thì
+
( ) ( )
22
00
sin cosf x dx f x dx
ππ
=
∫∫
.
+
( )
( )
sin sin
2
aa
aa
xf x dx f x dx
ππ
π
−−
=
∫∫
và
( )
( )
00
. sin sin
2
x f x dx f x dx
ππ
π
=
∫∫
.
+
( ) ( )
22
cos cos
aa
aa
xf x dx f x dx
ππ
π
−−
=
∫∫
và
( ) ( )
22
00
. cos cosx f x dx f x dx
ππ
π
=
∫∫
→
Về mặt thực hành, sẽ đặt
x =
cận trên
+
cận dưới
t−
( )
x abt=+−
. Từ đó tạo tích phân
xoay vòng, rồi giải phương trình bậc nhất với ẩn I.
Nếu hàm số
( )
fx
liên tục trên
và tuần hoàn với chu kỳ T thì
( ) ( )
0
aT T
a
f x dx f x dx
+
=
∫∫
và
( ) ( )
00
nT T
f x dx n f x dx
=
∫∫
.
Lưu ý: Hàm số
( )
fx
có chu kỳ T thì
( ) ( )
fxT fx+=
.
→
Về mặt thực hành, ta sẽ làm theo các bước sau:
Bước 1. Tách:
( ) ( ) ( ) ( )
0
0
aT T aT
aa T
C
AB
I f x dx f x dx f x dx f x dx
++
= =++
∫ ∫∫ ∫
(
)
i
Bước 2. Tính
( )
aT
T
C f x dx
+
=
∫
?
Đặt
x t T dx dt=+⇒ =
. Đổi cận:
0
x aT t a
xT t
=+=
⇒
= =
. Khi đó:

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 54
( ) ( )
( )
00
0
a
aa
C f t T dt f t dt f x dx A=+=− =− =−
∫ ∫∫
(
)
ii
Thế
( )
i
vào
( )
ii
ta được:
( )
0
T
I B f x dx= =
∫
.
Câu 89: Cho
( )
fx
là hàm số chẵn trên đoạn
[ ]
;
aa−
và
0k >
. Giá trị tích phân
( )
d
1e
a
kx
a
fx
x
−
+
∫
bằng
A.
( )
0
d
a
fx x
∫
. B.
(
)
d
a
a
fx x
−
∫
. C.
(
)
2d
a
a
fx x
−
∫
. D.
( )
0
2d
a
fx x
∫
.
Lời giải
Ta có
( ) ( )
( )
0
0
d dd
1e 1e 1e
aa
kx kx kx
aa
fx fx fx
x xx
−−
= +
+ ++
∫ ∫∫
.
Xét tích phân
( )
0
d
1e
kx
a
fx
x
−
+
∫
.
Đặt
t xxt=−⇔ =−
d d ddt x tx⇒ =− ⇔− =
Đổi cận:
x a ta=−⇒=
00xt=⇒=
Khi đó,
( ) ( )
( )
( )
00
dd
1e
1e
kx
kt
aa
fx f t
xt
−
−
−
= −
+
+
∫∫
( )
0
d
1e
a
kt
ft
t
−
=
+
∫
( ) ( )
00
e. e.
dd
1e 1e
kt kx
aa
kt kx
ft fx
xx= =
++
∫∫
Do đó,
( )
( ) (
)
00
e.
d dd
1e 1e 1e
kx
aa a
kx kx kx
a
fx fx fx
x xx
−
= +
+++
∫∫ ∫
( )
( )
( )
00
e1
dd
1e
kx
aa
kx
fx
x fx x
+
= =
+
∫∫
Câu 90: Cho
( ) ( )
,fx f x−
liên tục trên
và thỏa mãn
( ) ( )
2
1
23
4
fx f x
x
+ −=
+
. Biết
(
)
2
2
I f x dx
m
π
−
= =
∫
. Khi đó giá trị của
m
là
A.
2m =
. B.
20m =
. C.
5m =
. D.
10m =
.
Lời giải
Hàm số
( ) ( )
,fx f x−
liên tục trên
và thỏa mãn
( ) ( )
2
1
23
4
fx f x
x
+ −=
+
nên ta có:
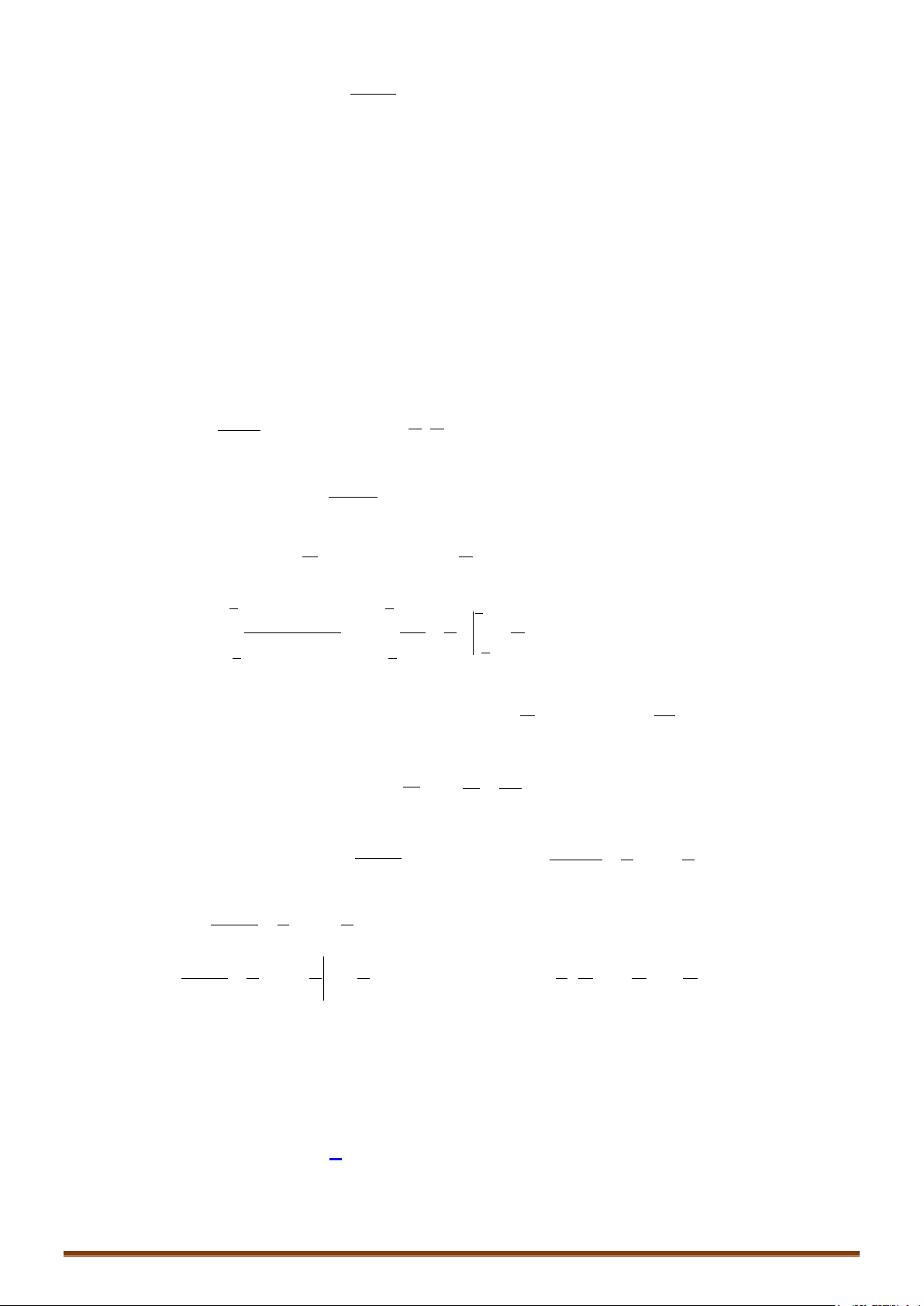
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 55
( ) ( )
( )
22
2
22
23
4
dx
f x f x dx
x
−−
+− =
+
∫∫
( )
1
Đặt
( ) ( )
( )
( ) ( )
2 22
2 22
23 2 3K f x f x dx f x dx f x dx
− −−
= +− = + −
∫ ∫∫
Đặt
( ) ( )
;x t dx dt f x f t−=⇒ =− − =
,
2 2; 2 2x tx t=−⇒= = ⇒=−
Do đó
( ) (
) (
) (
)
( )
2 2 22
2 2 22
.f x dx f t dt f t dt f x dx
−
− −−
− = −= =
∫ ∫ ∫∫
(
) ( ) (
)
( )
( )
22 22 2
22 22 2
23 235
K f x dx f x dx f x dx f x dx f x dx
−− −− −
⇒= + − = + =
∫∫ ∫∫∫
( )
2
Đặt
2
2
2
4
dx
J
x
−
=
+
∫
;
2 tan
x
α
=
,
;
22
ππ
α
∈−
,
Ta có:
( )
( )
2
2
2
2 tan 2 1 tan
cos
d
dx d d
α
α αα
α
= = = +
.
Với
2
4
x
π
α
=−⇒ =−
; Với
2
4
x
π
α
=⇒=
.
Do đó
( )
2
44
4
2
4
44
2 1 tan
1
4 tan 4 2 2 4
d
Jd
ππ
π
π
ππ
α
απ
αα
α
−
−−
+
= = = =
+
∫∫
( )
3
Từ
( )
1
,
( )
2
và
( )
3
, ta có
( ) ( )
22
22
5
4 20
K J f x dx f x dx
ππ
−−
=⇒ =⇒=
∫∫
Mà theo giả thiết,
( )
2
2
I f x dx
m
π
−
= =
∫
nên
20
20
m
m
ππ
= ⇒=
.
Chú ý: Có thể tính nhanh
2
2
2
4
dx
x
−
+
∫
bằng công thức:
22
1
arctan
dx x
C
xa a a
= +
+
∫
Từ đó:
2
1
arctan
42 2
dx x
C
x
= +
+
∫
( )
( )
2
2
2
2
2
11 1
arctan arctan1 arctan 1
4 2 2 2 24 4 4
dx x
x
πππ
−
−
⇒ = = − − = −− =
+
∫
Câu 91: Cho hàm số
( )
y fx=
là hàm lẻ và liên tục trên
[ ]
4; 4−
biết
(
)
0
2
d2
f xx
−
−=
∫
và
( )
2
1
2d 4f xx−=
∫
. Tính
( )
4
0
dI fx x=
∫
.
A.
10I = −
. B.
6I = −
. C.
6I =
. D.
10I =
.
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 56
Xét tích phân
(
)
0
2
d2
f xx
−
−=
∫
.
Đặt
xt−=
d dtx⇒=−
.
Đổi cận: khi
2x = −
thì
2t =
; khi
0x =
thì
0t =
do đó
( ) ( )
00
22
d dtf x x ft
−
−=−
∫∫
( )
2
0
dtft=
∫
( )
2
0
dt 2ft⇒=
∫
(
)
2
0
d2fx x
⇒=
∫
.
Do hàm số
( )
y fx=
là hàm số lẻ nên
( ) ( )
22f x fx−=−
.
Do đó
(
) ( )
22
11
2d 2d
f xx f xx
−=−
∫∫
( )
2
1
2d 4f xx⇒=−
∫
.
Xét
(
)
2
1
2df xx
∫
.
Đặt
2xt=
1
d dt
2
x⇒=
.
Đổi cận: khi
1x =
thì
2t =
; khi
2x =
thì
4t =
do đó
( ) ( )
24
12
1
2 d dt 4
2
f x x ft= = −
∫∫
( )
4
2
dt 8ft⇒=−
∫
( )
4
2
d8fx x⇒=−
∫
.
Do
( )
4
0
dI fx x=
∫
( ) ( )
24
02
ddfx x fx x= +
∫∫
28 6
=−=−
.
Câu 92: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
ln 2;ln 2
−
và thỏa mãn
( ) ( )
1
1
x
fx f x
e
+ −=
+
. Biết
( )
ln 2
ln 2
d ln 2 ln 3fx x a b
−
= +
∫
( )
;ab∈
. Tính
P ab= +
.
A.
1
2
P =
. B.
2P = −
. C.
1P = −
. D.
2P =
.
Lời giải
Gọi
( )
ln 2
ln 2
dI fx x
−
=
∫
.
Đặt
tx= −
⇒
d dt x= −
.
Đổi cận: Với
ln 2x = −
⇒
ln 2t =
; Với
ln 2
x =
⇒
ln 2t = −
.
Ta được
(
)
ln 2
ln 2
dI f tt
−
=−−
∫
( )
ln 2
ln 2
df tt
−
= −
∫
( )
ln 2
ln 2
df xx
−
= −
∫
.
Khi đó ta có:
2I
( ) ( )
ln 2 ln 2
ln 2 ln 2
ddfxx f xx
−−
= +−
∫∫
( ) ( )
ln 2
ln 2
dfx f x x
−
== +−
∫
ln 2
ln 2
1
d
e1
x
x
−
=
+
∫
.
Xét
ln 2
ln 2
1
d
e1
x
x
−
+
∫
. Đặt
e
x
u =
⇒
d ed
x
ux=

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 57
Đổi cận: Với
ln 2x
= −
⇒
1
2
u =
;
ln 2
x
=
2u⇒=
.
Ta được
ln 2
ln 2
1
d
e1
x
x
−
+
∫
( )
ln 2
ln 2
e
d
ee 1
x
xx
x
−
=
+
∫
( )
ln 2
ln 2
1
d
1
u
uu
−
=
+
∫
ln 2
ln 2
11
d
1
u
uu
−
= −
+
∫
( )
2
1
2
ln ln 1uu= −+
ln 2=
Vậy ta có
1
2
a =
,
1
0
2
b ab=⇒+=
.
Câu 93: Cho
(
)
y fx=
là hàm số chẵn và liên tục trên
.
Biết
( ) ( )
12
01
1
d d1
2
fx x fx x= =
∫∫
. Giá trị của
( )
2
2
d
31
x
fx
x
−
+
∫
bằng
A.
1
. B.
6
. C.
4
. D.
3
.
Lời giải
Do
( )
1
0
dfx x=
∫
( )
2
1
1
d1
2
fx x=
∫
( )
1
0
d1fx x⇒=
∫
và
(
)
2
1
d2fx x=
∫
( ) (
)
12
01
dd
fx x fx x⇒+
∫∫
(
)
2
0
d3fx x= =
∫
.
Mặt khác
( )
2
2
d
31
x
fx
x
−
=
+
∫
( )
( )
02
20
dd
31 31
xx
fx fx
xx
−
+
++
∫∫
và
(
)
y fx=
là hàm số chẵn, liên tục trên
( ) ( )
f x fx x⇒ − = ∀∈
.
Xét
( )
0
2
d
31
x
fx
Ix
−
=
+
∫
. Đặt
t x dx dt=−⇒ =−
( )
0
2
d
31
x
fx
Ix
−
⇒= =
+
∫
( )
0
2
d =
31
t
ft
t
−
−
−
+
∫
( )
2
0
d =
1
1
3
t
ft
t
−
+
∫
( )
2
0
3
d =
31
t
t
ft
t
+
∫
( )
2
0
3
d
31
x
x
fx
x
+
∫
( )
2
2
d
31
x
fx
x
−
⇒=
+
∫
( ) ( )
02
20
dd
31 31
xx
fx fx
xx
−
+=
++
∫∫
( ) ( )
22
00
3
dd
31 31
x
xx
fx fx
xx+=
++
∫∫
( )
( )
2
0
31
d
31
x
x
fx
x
+
=
+
∫
( )
2
0
d3fx x=
∫
.
Câu 94: Hàm số
( )
fx
là hàm số chẵn liên tục trên
và
( )
2
0
d 10fx x=
∫
. Tính
( )
2
2
d
21
x
fx
Ix
−
=
+
∫
.
A.
10I =
. B.
10
3
I =
. C.
20
I
=
. D.
5I =
.
Lời giải

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 58
Đặt
tx= −
ddtx⇒=−
. Đổi cận:
22xt=−⇒=
,
22xt=⇒=−
.
( )
2
2
d
21
t
ft
It
−
−
=
+
∫
(
)
2
2
2
d
21
t
t
ft t
−
=
+
∫
( )
2
2
2
d
21
x
x
fx x
−
=
+
∫
(
)
2
2
2d
21
x
fx
Ix
−
⇒=
+
∫
( )
2
2
2
d
21
x
x
fx x
−
+
+
∫
(
)
2
2
d
fx x
−
=
∫
( ) ( )
02
20
ddfx x fx x
−
= +
∫∫
( )
0
2
d 10fx x
−
= +
∫
Mặt khác do
( )
fx
là hàm số chẵn nên
(
)
( )
f x fx−=
.
Xét
(
)
0
2
dJ fx x
−
=
∫
, đặt
ddtx t x
=−⇒ =−
(
)
2
0
dJ f tt⇒= −
∫
( )
2
0
df xx
= −
∫
(
)
2
0
d 10
fx x
= =
∫
2 20I⇒=
10
I⇒=
.
Câu 95: Cho hàm số
( )
y fx=
là hàm số chẵn, liên tục trên đoạn
[ ]
1;1−
và
( )
1
1
6f x dx
−
=
∫
. Kết quả của
( )
1
1
1 2018
x
fx
dx
−
+
∫
bằng
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Xét tích phân
( )
1
1
1 2018
x
fx
dx
−
+
∫
. Đặt
xt= −
;
dx dt= −
;
11xt=−⇒ =
;
11xt=⇒=−
.
( )
1
1
1 2018
x
fx
dx
−
+
∫
=
(
)
1
1
1 2018
t
ft
dt
−
−
−
−
+
∫
=
( ) ( )
11
11
2018 .
1
1 2018
1
2018
t
t
t
ft ft
dt dt
−−
=
+
+
∫∫
=
( )
1
1
2018
1 2018
x
x
fx
dx
−
+
∫
.
Vậy
( )
1
1
1 2018
x
fx
dx
−
+
∫
+
( )
1
1
2018
1 2018
x
x
fx
dx
−
+
∫
=
( )
1
1
f x dx
−
∫
=
6
.
Do đó
( )
1
1
1 2018
x
fx
dx
−
+
∫
=
1
.6 3
2
=
.
Câu 96: Tích phân
2
2020
2
2
.d
1
a
x
x
x
eb
−
=
+
∫
. Tính tổng
S ab= +
.
A.
0S
=
. B.
2021S
=
. C.
2020S =
. D.
4042S =
.
Lời giải
Chọn D
Xét
2
2020
2
.d
1
x
x
Ix
e
−
=
+
∫
.
Đặt
ddxt x t=−⇒ =−
. Đổi cận
2 2; 2 2x tx t=−⇒= = ⇒=−
.
Ta được
( )
(
)
2020
2 22 2
2020 2020 2020
2 22 2
..
. d .d .d .d
1
1 11
1
tx
t tx
t
t
t te xe
I ttt x
e ee
e
−
−
−− −
−
= −= = =
+ ++
+
∫ ∫∫ ∫
.
Suy ra
( )
2
2021
2021
22 2
2020 2020 2021 2022
2020
22 2
2
22
.2
2 .d .d .d
1 1 2021 2021 2021
x
xx
x xe x
III x x x x
ee
−− −
−
−−
=+= + = = = =
++
∫∫ ∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 59
Do đó
2021
2
2021
I
=
. Suy ra
2021ab= =
. Vậy
4042S ab=+=
.
Câu 97: Cho hàm số
( )
fx
liên tục trên đoạn
[ ]
ln 2;ln 2−
và thỏa mãn
( ) ( )
1
e1
x
fx f x+ −=
+
. Biết
( ) ( )
ln 2
ln 2
d ln 2 ln 3, ,f x x a b ab
−
=+∈
∫
. Tính
P ab= +
.
A.
2P = −
. B.
1
2
P =
. C.
1P = −
. D.
2P =
.
Lời giải
Chọn B
Từ giả thiết suy ra
( ) ( )
ln 2 ln 2
ln 2 ln 2
1
dd
e1
x
fx f x x x
−−
+− =
+
∫∫
.
Ta có
( ) (
)
( ) ( ) ( ) ( )
ln 2 ln 2 ln 2 ln 2
ln 2 ln 2 ln 2 ln 2
d d d2 dfx f x x fx x f x x fx x
− −− −
+ − = − − −=
∫ ∫∫ ∫
.
Mặt khác
( )
( ) ( )
ln 2 ln 2 ln 2
ln 2 ln 2 ln 2
1 1 11
d de de
e1 e e1
e 1e
xx
x xx
xx
x
−− −
= = −
++
+
∫∫ ∫
( ) ( ) ( )
ln 2 ln 2
ln 2
ln 2
ln 2
ln 2
ln 2 ln 2
11 3
d e d e 1 ln e 1 ln 2 ln 2 ln 3 ln ln 2
e e1 2
xx x
xx
x
−
−
−−
= − += − + = + − + =
+
∫∫
.
Suy ra
( )
ln 2
ln 2
1
d ln 2
2
fx x
−
=
∫
11
,0
22
a b ab⇒= =⇒+=
.
Câu 98: Cho
( )
fx
là hàm số chẵn và
( )
1
0
2f x dx =
∫
. Giá trị của tích phân
( )
1
1
1 2019
x
fx
dx
−
+
∫
là
A.
2
.
2019
B.
2
. C.
4
. D.
0
.
Lời giải
Chọn B
( )
1
1
1 2019
x
fx
I dx
−
=
+
∫
Đặt
t x dt dx=− →− =
Cận
1
1
-1
-1
t
x

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 60
( )
( ) ( )
( ) ( )
( )
( )
( ) ( )
11 1
1 11
1 11
1 11
11
10
2019
1 2019
1 2019 1 2019
2019
1 2019
2019
2
1 2019 1 2019 1 2019
2 2 2.2 2.
t
t
tt
t
t
t
tt t
f t ft ft
I dt dt dt
ft
ft ft
I dt dt dt
I f t dt f t dt I
−
−
−−
− −−
−
−
=−==
+
++
+
⇒= + =
++ +
⇒ = = = ⇒=
∫∫∫
∫ ∫∫
∫∫
DẠNG 2.2 TÍCH PHÂN CỦA HÀM CHỨA DẤU TRỊ TUYỆT ĐỐI
Tính tích phân:
( )
.
b
a
I f x dx=
∫
?
Bước 1. Xét dấu
( )
fx
trên đoạn
[ ]
;
ab
. Giả sử trên đoạn
[
]
;ab
thì phương trình
( )
0
fx=
có
nghiệm
[ ]
;
o
x ab∈
và có bảng xét dấu sau:
x
a
o
x
b
(
)
fx
+
0
−
Bước 2. Dựa vào công thức phân đoạn và dấu của trên
[
] [
]
;,;
oo
ax x b
ta được:
( )
( ) ( )
.
o
o
x
bb
a ax
I f x dx f x dx f x dx A B= = +− =+
∫ ∫∫
.
Sử dụng các phương pháp tính tích phân đã học tính
,AB
I⇒
.
Câu 99: Cho
a
là số thực dương, tính tích phân
1
d
a
I xx
−
=
∫
theo
a
.
A.
2
1
2
a
I
+
=
. B.
2
2
2
a
I
+
=
. C.
2
21
2
a
I
−+
=
. D.
2
31
2
a
I
−
=
.
Lời giải
Chọn A
Vì
0a >
nên
0
22
10
11
22 2
a
aa
I x dx x dx
−
+
=− + =+=
∫∫
Câu 100: Cho số thực
1m >
thỏa mãn
1
211
m
mx dx−=
∫
. Khẳng định nào sau đây đúng?
A.
( )
4;6m ∈
. B.
( )
2; 4m ∈
. C.
( )
3; 5m ∈
. D.
( )
1; 3m ∈
.
Lời giải
Do
1
12 2 1
2
mm
m
>⇒ > ⇒ <
. Do đó với
[ ]
1, 1; 2 1 0m x m mx> ∈ ⇒ −>
.
Vậy
( )
( )
23 3
11
21 21 1 21
1
mm
m
mx dx mx dx mx x m m m m m− = − = − = −−+= − +
∫∫
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 61
Từ đó theo bài ra ta có
3
0
2 11
2
m
mm
m
=
− +=⇔
= ±
. Do
1m >
vậy
2m =
.
Câu 101: Cho tích phân
5
1
2
ln 2 ln 3
1
x
dx a b c
x
−
=++
+
∫
với a, b, c là các số nguyên. Tính P = abc.
A.
36P = −
B.
0P =
C.
18P = −
D.
18P =
Lời giải
Chọn A
Ta có
( ) ( )
( )
5 25
1 12
25
12
25
12
2 22
d dd
1 11
33
1d1d
11
3ln 1 3ln 1
2 3ln 3 1 3ln 2 5 3ln 6 2 3ln 3
2 6ln 2 3ln 3
x xx
x xx
x xx
xx
xx
xx xx
− −−
=−+
+ ++
=−− + −
++
=−−++−+
=− − +− +− − +
=−+
∫ ∫∫
∫∫
Vậy
2, 6, 3 36a b c P abc
= =− =⇒= =−
.
Câu 102: Tính tích phân
1
1
22
xx
I dx
−
−
= −
∫
.
A.
1
ln 2
. B.
ln 2
. C.
2ln 2
. D.
2
ln 2
.
Lời giải
1
1
22
xx
I dx
−
−
= −
∫
ta có
22 0
xx−
−=
0x⇒=
.
( ) ( )
1 01 0 1
1 10 1 0
22 22 22 22 22
xx xx xx xx xx
I dx dx dx dx dx
− −− − −
−− −
⇒=−=−+−=− +−
∫∫∫ ∫ ∫
01
10
22 22 1
ln 2 ln 2 ln 2
xx xx
−−
−
++
= +=
.
Câu 103: Cho hàm số
( )
fx
liên tục trên
và có
( )
1
0
d2fx x=
∫
;
( )
3
0
d6fx x=
∫
. Tính
( )
1
1
2 1dI fx x
−
= −
∫
A.
8I =
B.
6I =
C.
3
2
I =
D.
4I =
Lời giải
Chọn D

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 62
(
)
( )
( )
1
11
2
12
1
11
2
21d 12d 21dI f x x f xx f x xI I
−−
= − = − + −=+
∫ ∫∫
.
Xét
(
)
(
)
(
)
11
22
1
11
1
12 d 12 d12
2
Ifxx fx x
−−
=−=− − −
∫∫
(
) ( )
33
00
11
d d3
22
ft t fx x= = =
∫∫
.
Xét
( ) (
) (
)
11
2
11
22
1
21d 21d21
2
I fx x fx x= −= − −
∫∫
(
)
(
)
11
00
11
d d1
22
ft t fx x= = =
∫∫
Vậy
12
4II I=+=
.
Câu 104: Cho hàm số
()fx
liên tục trên
và có
3
0
() 8f x dx =
∫
và
5
0
( ) 4.f x dx =
∫
Tính
1
1
(4 1) .f x dx
−
−
∫
A.
9
.
4
B.
11
.
4
C.
3.
D.
6.
Lời giải
Ta có
1
11
4
1
11
4
(4 1) (4 1) (4 1)f x dx f x dx f x dx
−−
−= −+ −
∫∫∫
1
1
4
1
1
4
(1 4 ) (4 1)f x dx f x dx
−
=−+ −
∫∫
.IJ= +
+) Xét
1
4
1
(1 4 ) .I f x dx
−
= −
∫
Đặt
14 4 ;t x dt dx
=−⇒=−
Với
1
1 5; 0.
4
x tx t=−⇒= = ⇒=
1
0 55
4
1 5 00
11 1
(1 4 ) ()( ) () ( ) 1.
44 4
I f x dx f t dt f t dt f x dx
−
=− = −= = =
∫ ∫ ∫∫
+) Xét
1
1
4
(4 1) .J f x dx= −
∫
Đặt
4 1 4;t x dt dx= −⇒ =
Với
1
1 3; 0.
4
x tx t=⇒= = ⇒=

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 63
1 3 33
1
0 00
4
11 1
(4 1) ()( ) () ( ) 2.
44 4
J f x dx f t dt f t dt f x dx= −= = = =
∫ ∫ ∫∫
Vậy
1
1
( 4 1 ) 3.f x dx
−
−=
∫
Câu 105: Cho hàm số
( )
fx
liên tục trên
thỏa
( )
1
0
2d 2
f xx
=
∫
và
( )
2
0
6 d 14f xx=
∫
. Tính
( )
2
2
5 2dfx x
−
+
∫
.
A.
30
. B.
32
. C.
34
. D.
36
.
Lời giải
+ Xét
( )
1
0
2d 2
f xx
=
∫
.
Đặt
2 d 2dux u x=⇒=
;
00xu
=⇒=
;
12xu=⇒=
.
Nên
(
)
1
0
2 2df xx
=
∫
( )
2
0
1
d
2
fu u=
∫
( )
2
0
d4fu u⇒=
∫
.
+ Xét
(
)
2
0
6 d 14f xx
=
∫
.
Đặt
6 d 6dvx v x=⇒=
;
00xv=⇒=
;
2 12xv=⇒=
.
Nên
( )
2
0
14 6 df xx=
∫
(
)
12
0
1
d
6
fv v
=
∫
( )
12
0
d 84fv v⇒=
∫
.
+ Xét
( )
2
2
5 2d
fx x
−
+
∫
( ) ( )
02
20
5 2d 5 2dfx x fx x
−
= ++ +
∫∫
.
Tính
(
)
0
1
2
5 2dI fx x
−
= +
∫
.
Đặt
52tx= +
.
Khi
20x−< <
,
52tx=−+
d 5dtx⇒=−
;
2 12xt=−⇒=
;
02xt=⇒=
.
(
)
2
1
12
1
d
5
I ft t
−
=
∫
( ) ( )
12 2
00
1
dd
5
ft t ft t
= −
∫∫
( )
1
84 4 16
5
= −=
.
Tính
( )
2
1
0
5 2dI fx x= +
∫
.
Đặt
52tx= +
.
Khi
02x<<
,
52tx= +
d 5dtx⇒=
;
2 12xt= ⇒=
;
02xt=⇒=
.
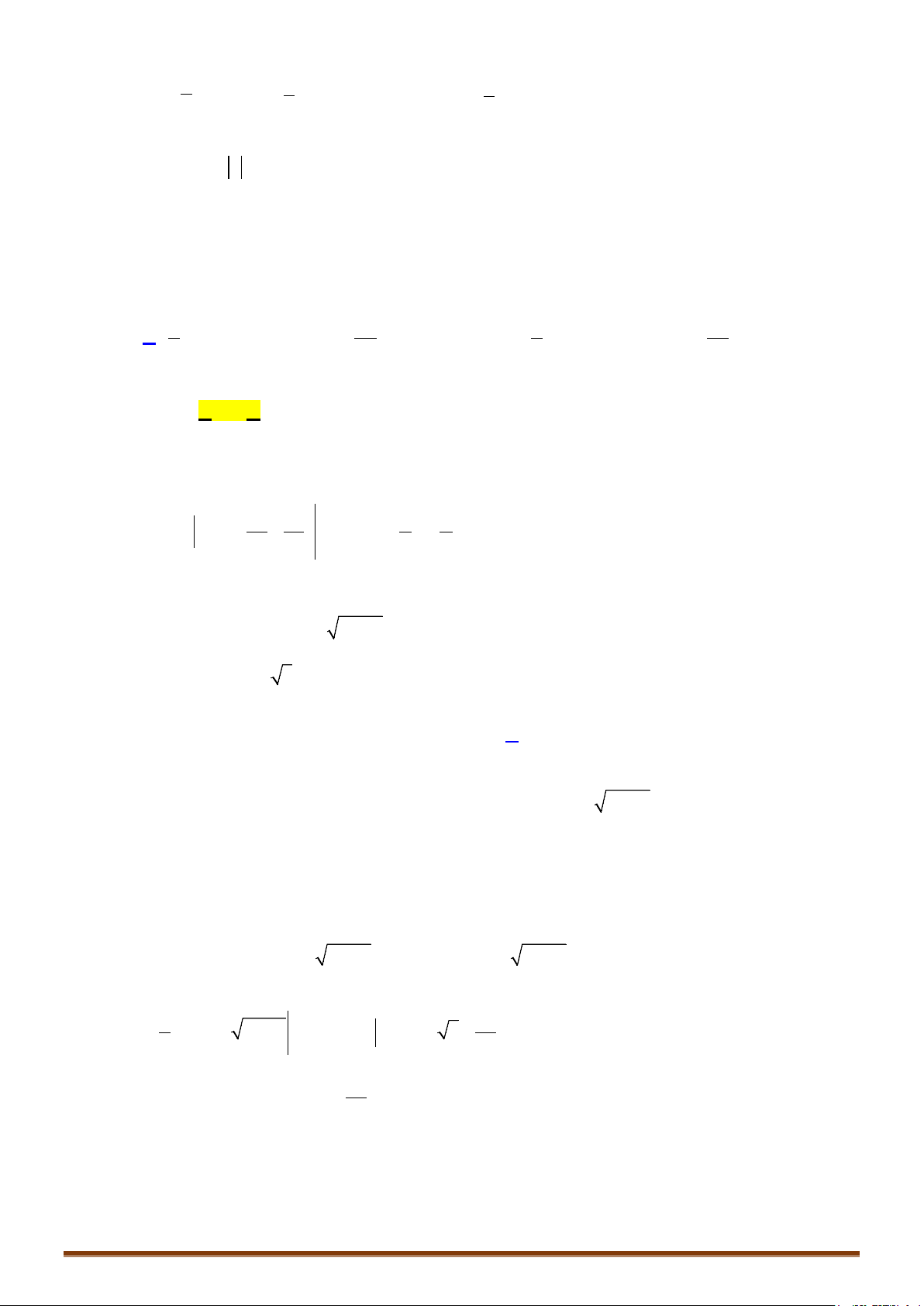
CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 64
( )
12
2
2
1
d
5
I ft t
=
∫
( ) ( )
12 2
00
1
dd
5
ft t ft t
= −
∫∫
( )
1
84 4 16
5
= −=
.
Vậy
( )
2
2
5 2 d 32fx x
−
+=
∫
.
DẠNG 2.3 TÍCH PHÂN NHIỀU HÀM
Câu 106: Cho số thực
a
và hàm số
( )
( )
2
20
0
x khi x
fx
a x x khi x
≤
=
−>
. Tính tích phân
( )
1
1
f x dx
−
∫
bằng:
A.
1.
6
a
−
B.
2
1.
3
a
+
C.
1.
6
a
+
D.
2
1.
3
a
−
Lời giải
Chọn A
Ta thấy,
(
) (
) ( )
( )
1 0 1 01
2
1 1 0 10
2f x dx f x dx f x dx xdx a x x dx
−− −
= + = +−
∫ ∫ ∫ ∫∫
( )
1
23
0
2
1
0
1
11
23 6 6
xx a
xa a
−
= + − =−+ = −
.
Câu 107: Cho hàm số
( )
2
e khi 0
2 3 khi 0
x
mx
fx
xx x
+≥
=
+<
liên tục trên
và
( )
1
1
d=e 3f x xa b c
−
++
∫
,
( )
,,abc Q
∈
. Tổng
3ab c++
bằng
A.
15
. B.
10−
. C.
19
−
. D.
17
−
.
Lời giải
Ta có
( )
( )
00
lim lim e 1
x
xx
fx m m
++
→→
= +=+
,
( )
(
)
2
00
lim lim 2 3 0
xx
fx x x
−−
→→
= +=
và
(
)
01fm= +
.
Vì hàm số đã cho liên tục trên
nên liên tục tại
0x =
.
Suy ra
( ) ( ) ( )
00
lim lim 0
xx
fx fx f
+−
→→
= =
hay
10 1mm+= ⇔ =−
.
Khi đó
(
)
( ) ( ) ( )
10 1 0 1
2 22
11 0 1 0
d = 2 3 d e 1d = 3 d 3 e 1d
xx
fxx x x x x x x x
−− −
++− + ++−
∫∫ ∫ ∫ ∫
( )
( )
0
1
22
0
1
2 22
= 3 3 e e 23
33
x
xx x
−
+ + +− =+ −
.
Suy ra
1a =
,
2b =
,
22
3
c
= −
.
Vậy tổng
3 19ab c++ =−
.
Câu 108: Tính tích phân
1
12
0
max ,
xx
e e dx

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 65
A.
1
e
−
. B.
( )
3
3
2
ee−
. C.
3
ee−
. D.
11
2
e
e
−
.
Lời giải
Ta có:
12
1
12
3
xx
ee x xx
. Suy ra:
12
12
1
0
3
max ,
1
1
3
x
xx
x
e khi x
ee
e khi x
Do đó
1
11
3
1
1
12 12 12
3
1
0
3
1
00
3
1
max ,
2
xx x x x x
I e e dx e dx e dx e e
11
3
33
11 3
22 2
e eee e e
.
Câu 109: Cho hàm số
2
31
51
x khi x
y fx
x khi x
. Tính
1
2
00
2 sin cos 3 3 2I f x xdx f x dx
π
A.
71
6
I
. B.
31I
. C.
32I
. D.
32
3
I
.
Lời giải
Chọn B
+ Xét tích phân:
2
1
0
2 sin cosI f x xdx
π
.
Đặt:
sin cost x dt xdx
.
Đổi cận: với
0x
thì
0t
, với
2
x
π
thì
1t
.
11 1
2
1
2
1
0
0 00 0
2 sin cos 2 2 2 5 10 9I f x xdx f t dt f x dx x dx x x
π
.
+ Xét tích phân:
1
2
0
3 32I f x dx
.
Đặt:
1
32 2
2
t x dt dx dx dt
Đổi cận: với
0x
thì
3t
, với
1x
thì
1t
.

CHUYÊN ĐỀ III – GIẢI TÍCH 12 – NGUYÊN HÀM – TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 66
1 11
2
0 33
1
1
23
3
3
33
3 32
22
3 19
3 22.
2 22
I f x dx f t dt f x dx
x dx x x
Vậy:
1
2
00
2 sin cos 3 3 2 9 22 31I f x xdx f x dx
π
.
Bấm Tải xuống để xem toàn bộ.




