Tài liệu Giải tích 1 | Trường đại học Bách Khoa, Đại học Đà Nẵng

Mục tiêu của môn học Giải tích II
• cách tính tích phân bội: bội 2, bội 3;
• tích phân đường: loại 1, loại 2;
• tích phân mặt: loại 1, loại 2;
• các ứng dụng hình học, cơ học của các loại tích phân này; • Chuỗi • Phương trình vi phân 1
Nhiệm vụ của sinh viên. Đi học đầy đủ
Làm tất cả các bài tập cho về nhà.
Đọc bài mới trước khi đến lớp.
Đánh giá, kiểm tra. Làm và nộp bài tập Thi giữa học kỳ Thi cuối kỳ 2 1 Tài liệu tham khảo
• [1]. Nguyễn Đình Trí, Toán cao cấp (Tập 3), NXB Giáo Dục 2002.
• [2]. Đemiđovich, Bài tập giải tích toán học, Moscow 1962.
• [3]. G.M. Fichtengon, Cơ sở giải tích toán học, Hà
Nội 1986. (Giáo trình tham khảo)
• [4] James Stewart. Calculus, second edition, 2000. 3
TRƯỜNG ĐH BÁCH KHOA ĐÀ NẴNG
-------------------------------------------------------------------------------------
Chương 1: Tích phân kép
• Giảng viên Ts. Phạm Quý Mười 4 2 Nội dung
---------------------------------------------------------------------------------------------------------------------------
1.1 – Định nghĩa, cách tính tích phân kép
1.2 – Đổi biến số. Tọa độ cực
1.3 – Ứng dụng hình học
1.4 – Ứng dụng cơ học 5
I. Định nghĩa, cách tính tích phân kép
---------------------------------------------------------------------------------------------------------------------------
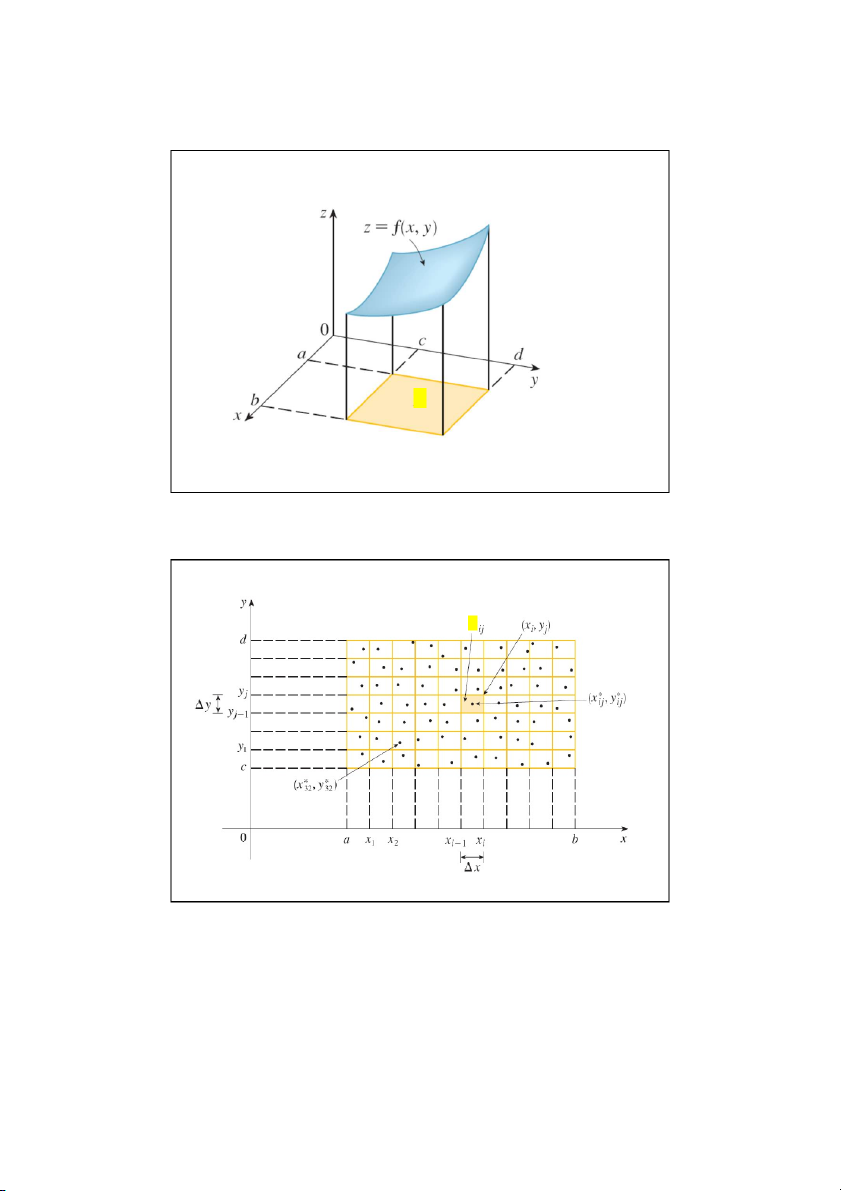
Cho vật thể (hình trụ cong) được giới hạn trên bởi mặt bậc hai z  f ( , xy )
giới hạn xung quanh bởi những đường thẳng song song oz, tựa trên biên D
giới hạn dưới bởi miền D (đóng, bị chặn). Tìm thể tích vật thể. 6 3
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- D 7
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- D 8 4
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- D 9
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- 10 5
I. Định nghĩa, cách tính tích phân kép
---------------------------------------------------------------------------------------------------------------------------
Cho vật thể được giới hạn trên bởi mặt bậc hai f ( , xy )
giới hạn dưới bởi miền D (đóng, bị chặn).
giới hạn xung quanh bởi những đường thẳng song song oz, tựa trên biên D Tìm thể tích vật thể.
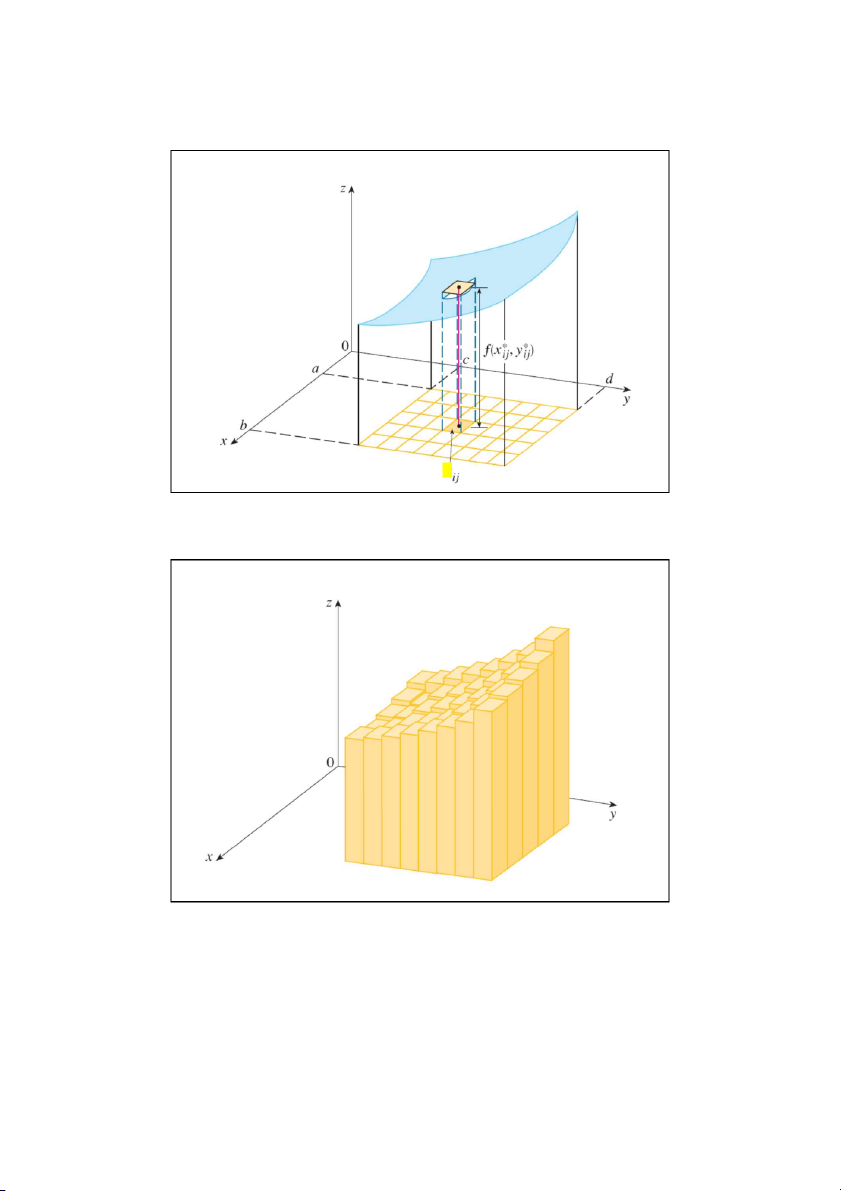
1) Chia D một cách tùy ý ra thành n miền không dẫm nhau: D1, D2, ..., D .n Có diện tích tương ứn
S gD,S D ,...,S D ;d n  maxS 1 là 2 n D i 1  ,..., i n
2) Trên mỗi miền lấy tùy ý một điểm M ( x,y ) i i i S  D i n
3) Thể tích của vật thể: V   ( fM ) i  D S V  i n i 1  4) V limV n n d 0  11
I. Định nghĩa, cách tính tích phân kép
---------------------------------------------------------------------------------------------------------------------------
Định nghĩa tích phân kép
Cho z = f(x,y) xác định trên miền đóng và bị chặn D.
Tích phân kép của f trên miền D là giới hạn (nếu có) n I  f ( , x ) ydxdy   
 lim   f (Mi)  DS  d D 0 i n  i 1  
Nếu I tồn tại (khôngphụthuộccáchchiavàcáchchọnđiểmM f i), ta nói khả tích trên D. 12 6
I. Định nghĩa, cách tính tích phân kép
---------------------------------------------------------------------------------------------------------------------------
Tính chất của tích phân kép
1) Hàm liên tục trên một miền đóng, bị chặn, có biên trơn tùng khúc thì khả tích trên miền này. 2) SD  1 dxdy D 3)  f ( , x ) ydxdy    f ( , x ) ydxdy D D 4)  f ( , x ) y  ( g , x )
y  dxdy (f ,x )ydxdy  ( g ,x )ydxdy D D D
5) Nếu D được chia làm hai miền D1 và D2 không dẫm lên nhau:  f ( , x ) ydxdy   f (x, ) ydxdy   f (x ,y)dxdy D D 1 D 2 6) (x,y ) D  ,f (x , y ) g  ( xy , ) fd  xdy gd  xdy D D 13
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- Ví dụ
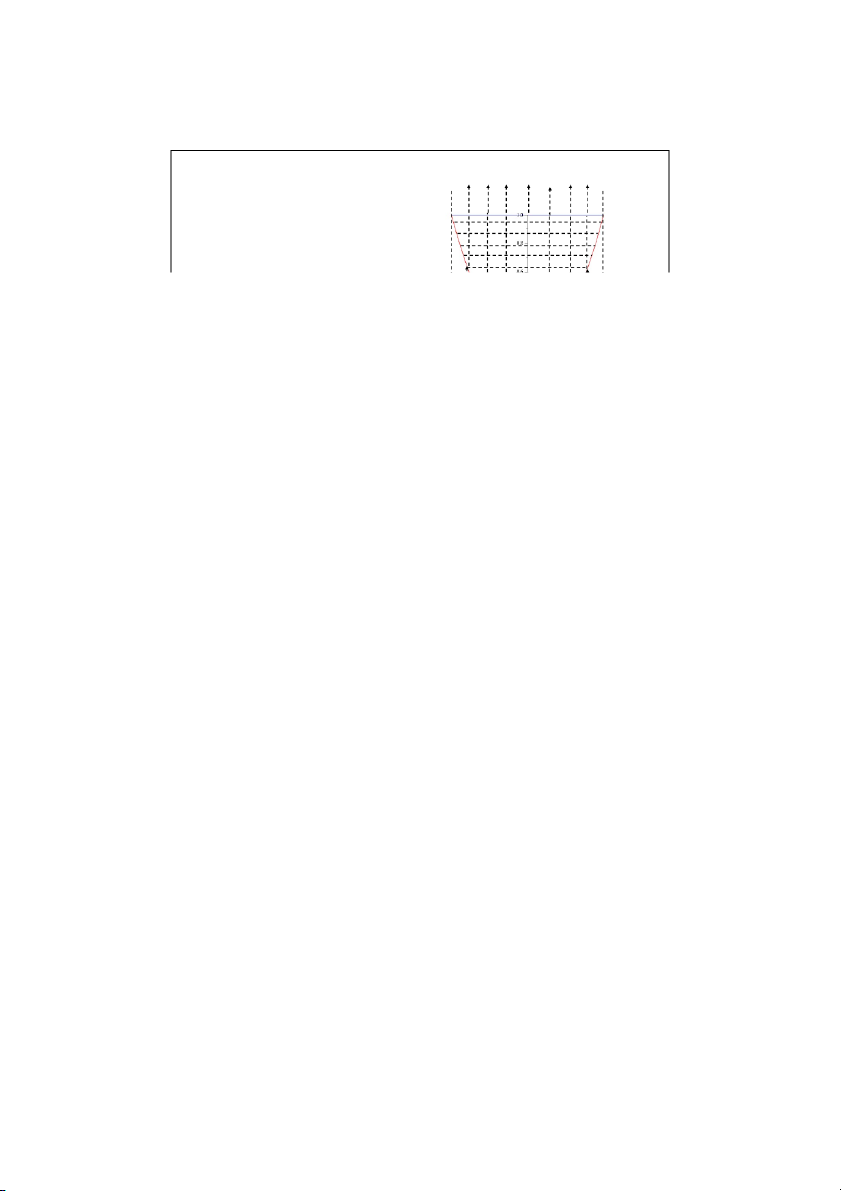
Cho vật thể được giới hạn trên bởi mặt bậc hai 2 2 f ( , xy )  16 x   2y
giới hạn dưới bởi hình vuông: R  [0,2][0,2]
giới hạn xung quanh bởi những đường thẳng song song oz, tựa trên biên R.
Ước lượng thể tích của vật thể trong các trường hợp sau:
a) Chia R thành 4 phần bằng nhau;
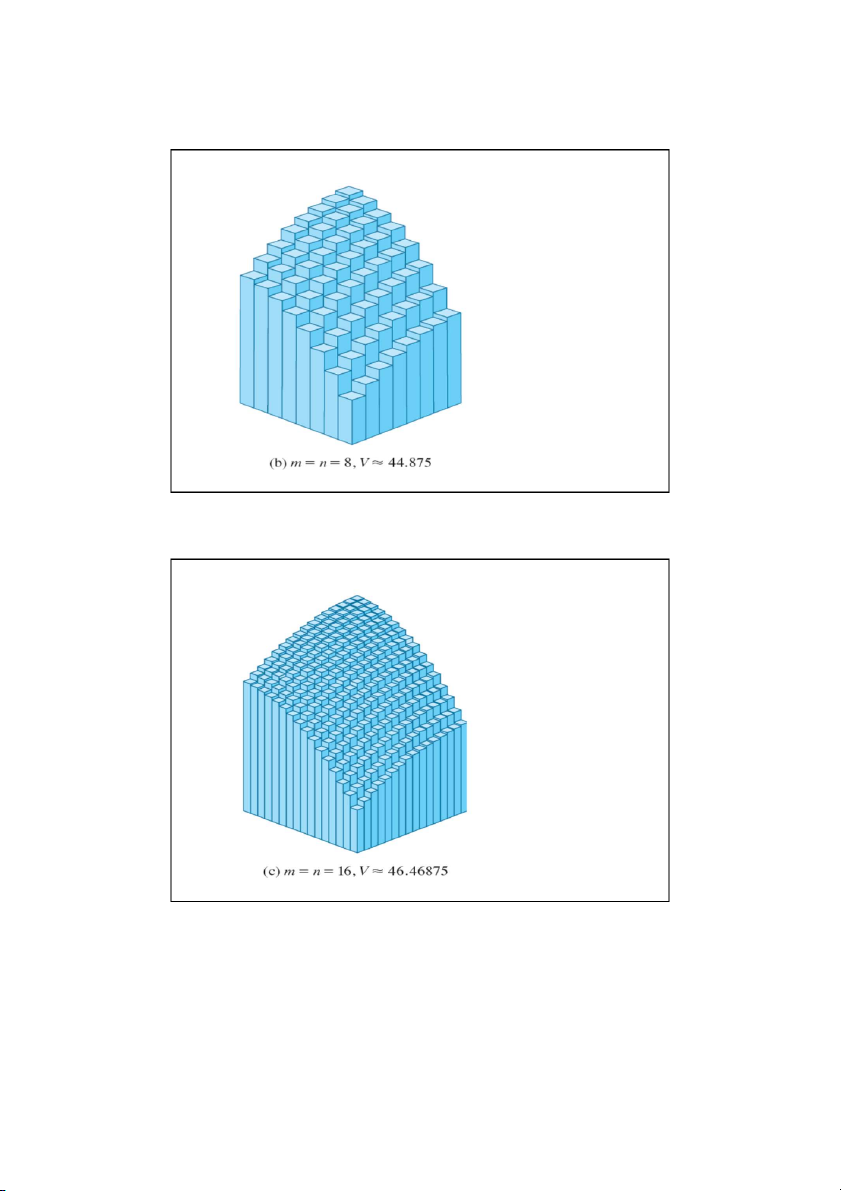
b) Chia R thành 16 phần bằng nhau;
c) Chia R thành 64 phần bằng nhau;
d) Chia R thành 256 phần bằng nhau;
e) Tính thể tích của vật thể. 14 7 4 V  n V   ( fM i)  D S i 1 i  D S 1  ,i 1  ,...,4. i V f  (1,1) f  (1,2) f  (2,1) f  (2,2)
V  13  7 10  4  34. 15
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- 16 8
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- 17
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- 18 9
I. Định nghĩa, cách tính tích phân kép
---------------------------------------------------------------------------------------------------------------------------
Cách tính (Định lý Fubini) Cho f liên tục trên miền đóng và bị chặn D. y=y2(x) y=y1(x) a b
1) Giả sử D xác định bởi: b    2 y ( x ) a x b 
I   f( ,x )ydxdy  dx  f ( , x ) ydy     1 y ( x ) y y 2(x ) D a 1 y (x ) 19
I. Định nghĩa, cách tính tích phân kép
---------------------------------------------------------------------------------------------------------------------------
Cách tính tích phân kép (Định lý Fubini) x=x1(y) d x=x2(y) c
2) Giả sử D xác định bởi: d 2 x (y ) c  y d I   f ( , x ) ydxdy  dy  f (x, y)dx  D c 1 x ( y) x1( y )  x x   2( y ) 20 10
I. Định nghĩa, cách tính tích phân kép
--------------------------------------------------------------------------------------------------------------------------- 2 0  x  2  0  y   2 2 2 2
e) Tính thể tích của vật thể.V   2 2
16  x  2 y dxdy  dx    2 2 16  x 2 y dy R 0 0 3 2 2  2 2 y  16   (16  x ) y2 d  x 2
  32 2x  dx  48 0 3    3  0 0 21 Ví dụ
Tính tích phân kép I  xy
 dxdy , trong đó D là miền phẳng giới hạn bởi D 2 y  2  x ,y x  . 2  x 1   2  x y 2 x 2 1 2 x  I    x  ydxdy   dx   x  ydy D 2 x 2 2 2x 1  y    x dx    2 2   x 2 2 2 1  (2  x ) x    x  x dx   2 2 2   22 11 Ví dụ
Tính tích phân kép I   (x  ) ydxdy
, trong đó D là tam giác OAB, với D O(0,0), ( A 1,1),B (2,0). 0  x  2  0   y   ? A
Cần chia D ra thành hai miền: D1 và D2 D
I      1 D2 D D 1 D 2  B 1 x 2 2x I  dx ( x  ) ydy  d  x  (x  y)dy 0 0 1 0
(Nếu lấy cận y trước, x sau thì không cần chia D ) 23 Ví dụ Tính tích phân kép 2 I   y  xdxdy D
D là miền phẳng giới hạn bởi 1   x 1,0 y  1. 2 I  2 2
 y xdxdy   y  xdxdy   y  x  dxdy D 1 D D 2    2
y  x  dxdy   2 x  ydxdy 1 D D 2 1 1 D1   dx   y x  2 1 x
2 dy  dx  2x  ydy 2 1  x 1  0 11 I  D D 2 2 15 24 12 Ví dụ 1 1 2 Tính tích phân kép x I   dye dx 0 y 1 2 Tích phân x  edx
không tính được ( qua các hàm sơ cấp) y
Thay đổi thứ tự lấy tích phân: 1) Xác định miền D 2) Vẽ miền D 3) Thay đổi thứ tự 25 0  y  1 D: y x 1  0  x 1 Thay đổi cận: D : 0 y x 1 x 1 2 x 1 1 1 x e1 I  2 dxe dy 2 x x 2  x  e ydx   xedx  e  0 0 0 2 2 0 0 0 26 13 Ví dụ 1 1 Tính tích phân kép 3 I dy    sin( x 1) dx 0 y 1 Tích phân 3  sin(x  1) dx
không tính được (qua các hàm sơ cấp) y  0  y  1  D :  y x 1  Thay đổi cận:  0  x 1 D:  2 0  y x 2 1 x 1 2 3 I d  x   sin( x 1) dy 3   sin( 1) x x y dx 0 0 0 0 1 2 3 cos(1) 1   x sin( x 1)dx  3 0 27 Ví dụ 2 1 y y
Thay đổi thứ tự lấy tích phân I   dy  f ( ,x ) ydx 0 0  0  y 1  D : 2 0  x y  y   Vẽ miền D: Thay đổi cận  0 x  2  D :  1   1 4 x  y   1  2 2 1 I   dx  f ( , x ) ydy 0 1 14x 2 28 14 Ví dụ 2 3 2 4 y
Thay đổi thứ tự lấy tích phân I   dy  f ( , x ) ydx 2  3 12 y   3  y  3  D D: 1  2 2  12  y x   2  4 y   Vẽ miền D: D3 Thay đổi cận Phải chia D làm 3 miền  3  x  2 3 D  2  3   x  2 3 1 D :  2 2  12  x  y  4 x x   D2 :  2 2   4x x y    12 x   2 3  x  4  D : 3  2 2
I   fdxdy  fdxdy fdxdy  4  x x y   4x x 1 D D 2 D 3 29
Phương pháp đổi biến • Xét I  f ( ,x )ydxdy  • Dùng công D
thức đổi biến x (xu ,v )  thỏa mãn:  y (yu, ) v
1. D là ảnh của miền D’ ((u,v) D’)
2. x, y là có các DHR liên tục trên D’ 3. Đinh thức Jacobi: x' y ' u u J   0, (  u,v ) D  ' Khi đó: x' y v 'v I  f ( , x ) ydxdy  f 
 x(u,v ),y (uv , )Jdudv D D ' 30 15 II. Tọa độ cực
--------------------------------------------------------------------------------------------------------------------------- y
Mối liên hệ giữa tọa độ cực và tọa độ Descartes y  M( , xy )  x r cos  r   y r sin  x x 2 2 2 Chú ý: x y R 2 2
Ví dụ. Phương trình đường tròn tâm 0, bán kính bằng 2: x y   4
Phương trình đường tròn này trong tọa độ cực là: r  2. 31 II. Tọa độ cực
---------------------------------------------------------------------------------------------------------------------------
Ví dụ. Phương trình đường tròn tâm (1,0), bán kính bằng 1: 2 2 x y   2 x
Phương trình đường tròn này trong tọa độ cực là: 2 r r  2 cos r   2cos
Ví dụ. Phương trình đường tròn tâm (0,1), bán kính bằng 1: 2 2 x y   2y
Phương trình đường tròn này trong tọa độ cực là: 2 r  2 r sin  r   2sin
Ví dụ. Phương trình đường tròn thẳng x = 2 (trong tọa độ Descartes) 2
Phương trình đường thẳng này trong tọa độ cực là: r cos  2 r   cos 32 16 II. Tọa độ cực
--------------------------------------------------------------------------------------------------------------------------- I   f ( , x ) ydxdy R Qua phép đổi biến: x  r cos y r  sin Jacobi: J=r Miền D'=[ , ] a ,b   b  f ( , x )
ydxdy   d  f (r cos ,  r sin ) r d  r R  a 33 Ví dụ
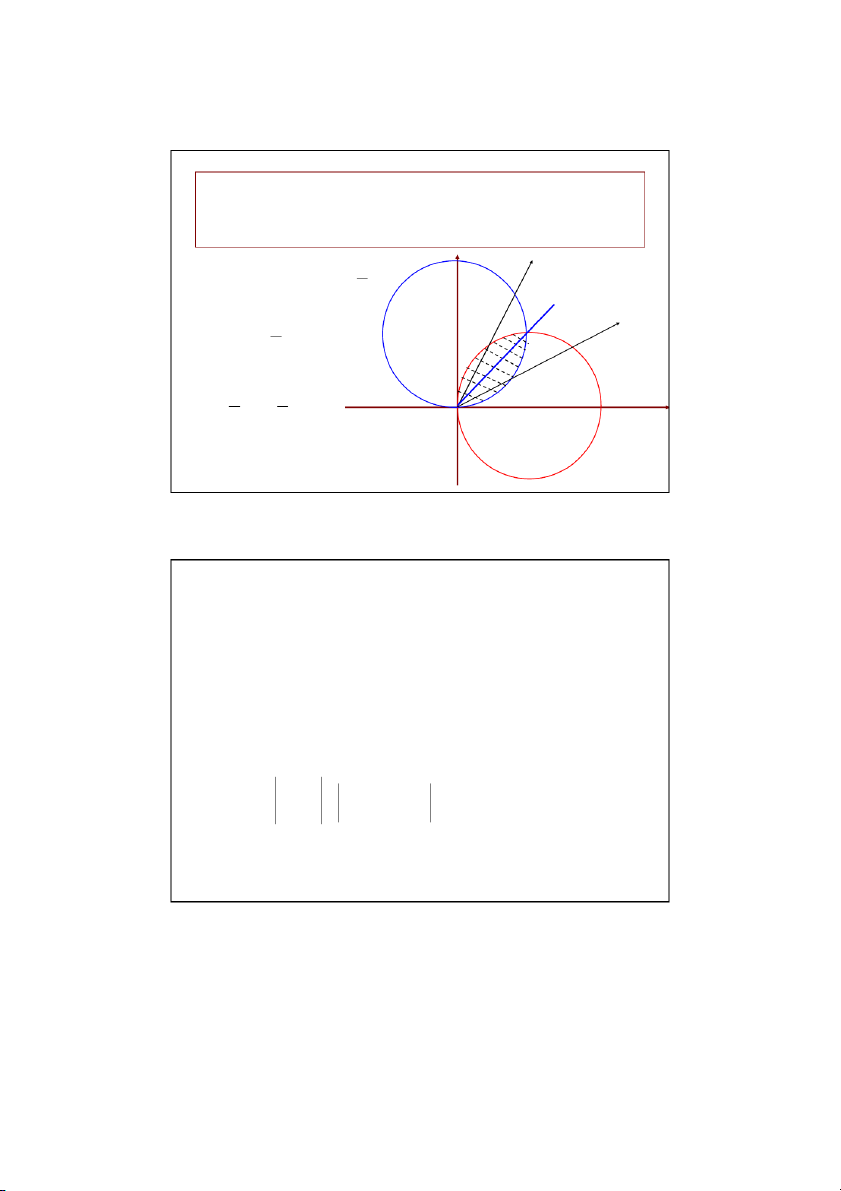
Tính tích phân kép I  ( x  )
ydxdy, trong đó D là miền phẳng giới hạn bởi D 2 2 2 2 x y  1,x y  4, y  0 y , x x r cos   y r   sin   0   D':  4  1   r  2 34 17 I   (x  y)dxdy D  / 4 2  / 4 2 I  2
 d r cosr sin  drr
  d  cos  sin  r dr 0 1 0 1 2  3 / 4    r I cos  sin  d  0 3 1  / 4 I      8 1 cos sin d        0  3 3 7 I  3 35 Ví dụ Tính 2 2
I   4 x  ydxdy , trong đó D là miền phẳng giới hạn bởi D 2 2
x  y  4, y  ,xy x 3 (y  x) x r cos   y r  sin       D ': 4 3  0  r  2  /3 2 2
I   d  4 r  drr  /4 0 2 I  4 36 18 Ví dụ Tính 2 2 I   x  ydxdy
, trong đó D là miền phẳng giới hạn bởi D 2 2 x  y  2 , xy  x  . x r cos  y r   sin           D : 2 4  0  r  2cos  / 4 2cos  I  d    r  drr  / 2 0  / 48 3 I  16 10 2  cos d    / 23 9 37 Ví dụ Tính I   (x  1) dxdy
, trong đó D là miền phẳng giới hạn bởi D 2 2 2 2 x  y  2 ; x x  y  4 ;xy   ; xy x  3 x r cos  y r   sin         D : 4 3
 2cos   r  4cos   /3 4cos  I  d 
  r( cos 1)  drr   / 4 2cos  38 19 Ví dụ Tính I  (x  ) ydxdy
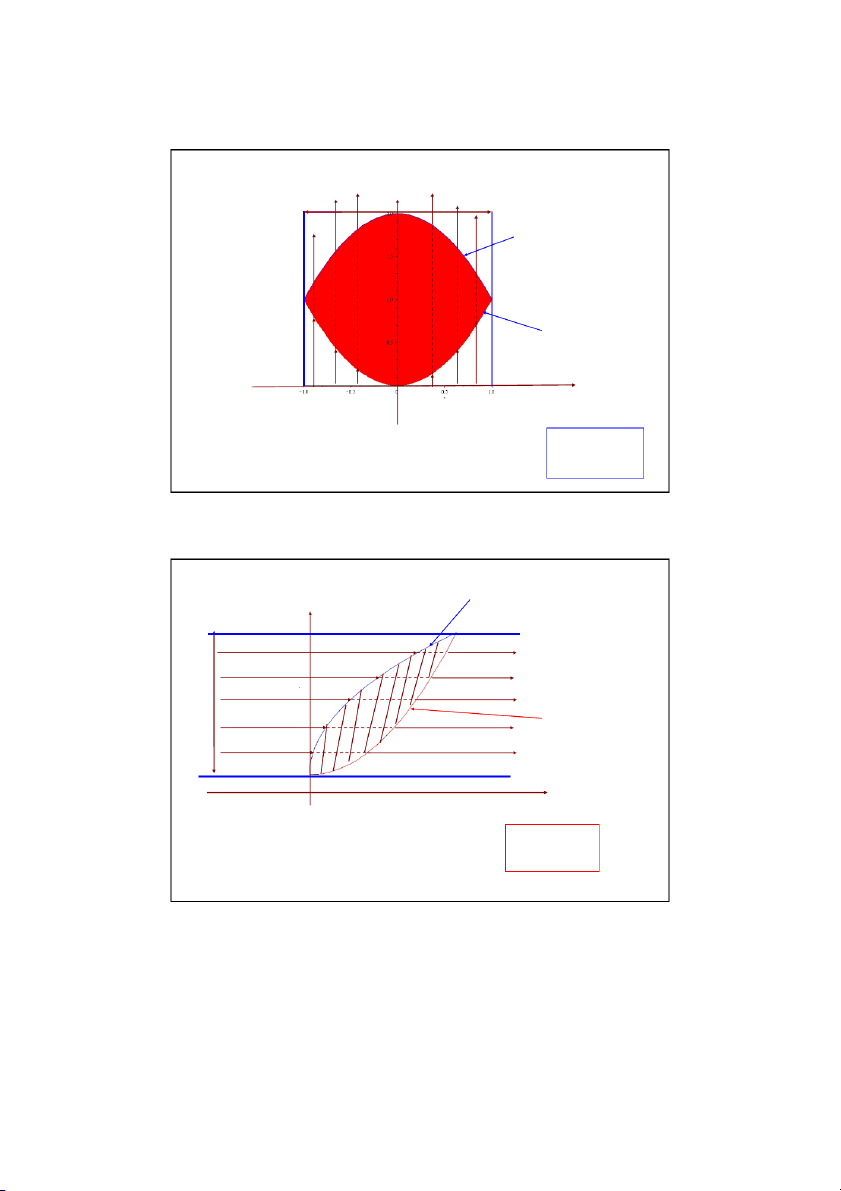
, trong đó D là miền phẳng giới hạn bởi D 2 2 2 2 x y   2 x ;x y y  2 .   x  r cos  0     D:  2 y r sin  0  r  ?   0    1 D :  4 0  r   D2  2sin D1       2 D :  4 2 0  r  2cos I     1 D D 2 39 II. Tọa độ cực
---------------------------------------------------------------------------------------------------------------------------
Toạ độ cực mở rộng:
Trường hợp 1. Miền phẳng D là hình tròn 2 2 2 (x x  )  ( y y  )  0 0 a Dùng phép đổi biến: x x  0 r cos  y y r sin  0
Khi đó định thức Jacobi: ' ' r x x cos  r.sin J    ' '  r r y y  sin r.cos Khi lấy cận của ,
r  ta coi như gốc tọa độ dời về tâm hình tròn. 40 20 II. Tọa độ cực
---------------------------------------------------------------------------------------------------------------------------
Toạ độ cực mở rộng: 2 2
Trường hợp 2. Miền phẳng D ellipse x y   1,a b  0,  0 2 2 a b  x Dùng phép đổi biến:  r cos  a  y   rsin  b
Khi đó định thức Jacobi: ' ' r x x a.cos  ar .sin  J    ' ' y y  a .b .r r  . b sin  br .cos Khi đó cận của r, : 0     2  0 r 1   41 Ví dụ Tí T n í h n I   (2x  ) ydxdy
, trong đó D là miền phẳng giới hạn bởi D 2 2 (x  1)  ( y  2)  4;x  1. x 1 r cos
Gốc tọa độ dời về đây y   2 r sin          D:  2 2  0  r  2  / 2 2
I   d 2(1r cos)  (2 r sin) rdr   / 2 0 42 21 Ví dụ Tí T n í h n I   (x 1) dxdy
, trong đó D là miền phẳng giới hạn bởi D 2 2 x y  1; y  0;x  0 9 4 x  rcos 3  y   r sin  2    0    D : 2  0 r 1  / 2 I   d 
1 r .3 cos  132 drr 0 0 43 Ví dụ Tí T n í h n I  xdxdy
, trong đó D là miền phẳng giới hạn bởi D 2 x 2  y  1; y  0; y x  3   x 0     r cos  D : 3  3   0  r  1 y r  sin  sin y/r tg    cos / x (r 3)
Vì đường y = x nên tg  3     3  / 3 1 I   d r. 3 cos  3 1 rdr 0 0 44 22
III. Ứng dụng hình học
--------------------------------------------------------------------------------------------------------------------------- Diện tích miền D: S  1 D dx  dy D
Thể tích hình trụ cong được giới hạn trên bởi f = f(x,y), giới hạn dưới bởi miền
D, giới hạn xung quanh bởi những đường thẳng song song 0z, tựa trên biên D: V   f( ,x ) ydxdy D
Thể tích hình trụ cong được giới hạn trên bởi f = f2(x,y), giới hạn dưới bởi
f = f1(x,y), giới hạn xung quanh bởi những đường thẳng song song 0z, tựa trên biên D:
V   f ( ,xy)  f ( , xy ) 2 1 dxdy D 45 Ví dụ
Tính diện tích miền phẳng giới hạn bởi 2 2 2 2 x y   2 y ;x y y  6y ; x 3 x ;  0 Diện tích miền D là:  / 2 6sin S  dx  dy D   d  rdr D  / 3 2sin  6sin  / 2 2 r  / 2 S   d  2 D   16sin   2 d  /3 2sin   / 3 4   2 3 D S  3 46 23
III. Ứng dụng hình học
---------------------------------------------------------------------------------------------------------------------------
Để tính thể tích khối 
1) Xác định mặt giới hạn bên trên: z  z ( , xy ) 2
2) Xác định mặt giới hạn bên dưới: z  1 z ( , xy )
3) Xác định hình chiếu của  xuống 0xy: D  proxy V   2z ( ,xy ) 1 z ( , xy )dxdy    D
Chú ý: 1) Có thể chiếu  xuống 0xz, hoặc 0yz. Khi đó mặt phía trên, mặt
phía dưới phải theo hướng chiếu xuống.
2) Để tìm hình chiếu của  xuống 0xy, ta khử z trong các phương trình của  47 Ví dụ
Tính thể tích vật thể giới hạn bởi 2 2 2
z  x  y ; y  x ;y 1;z  0 Mặt trên: 2 2 z x y  Mặt phía dưới: z  0 Hình chiếu: D D 48 24
III. Ứng dụng hình học
--------------------------------------------------------------------------------------------------------------------------- V   2 2 x y   0 dxdy D  1 x  1 D :  2 x y 1   1 1 V  dx  2 2 x  y dy 2 1  x 1 3 1   2 y V   x y  dx 1  3 2  x  6 1      88 2 1 4 x V   x    x     d  x   105 1   3   3     49 Ví dụ
Tính thể tích vật thể giới hạn trên bởi 2 2 ( x1)  y  ;z2x z   2 Mặt phía trên: z  2 z ( , xy )  2x  2 Mặt phía dưới: 2 2 z  z ( , xy )  (x  1)  1 y
Hình chiếu: khử z trong 2 phương trình 2 2 (x  1)  y  2 x  2 2 2  x y   1 Hình chiếu 2 2  D :x y   1 V    z  zdxdy 2 1 2 2 x y 1  50 25 Ví dụ
Tính thể tích vật thể giới hạn bởi 2 2 z  2 x  y 1; x y
 1; và các mặt tọa độ. Mặt phía trên: 2 2 z  2 x y  1  Mặt phía dưới: z  0
Hình chiếu: là tam giác màu đỏ. A 0  B 2 2 Mặt dưới V   2 x y 10dxdy tam giaùc 51 Ví dụ
Tính thể tích vật thể giới hạn bởi 2 2 z  4 y ;z y   2;x   1;x  2. z
Có thể chiếu xuống 0xy tương tự các ví dụ trước.
Chiếu vật thể xuống 0yz: Mặt phía trên: x 2 Mặt phía dưới: x 1 y x 52 26
Thể tích vật thể cần tính: z V    2 x ( ,yz ) 1 x (y,z )dydz D D 2 1 4 y V  dy  (2 (1)) dz 2 1  2 y 2 4 1  y V   3 z dy 2 y  1 2 y 1 V  3   2 2 4  y  2  y dy  1 V  8. 53
III. Ứng dụng hình học
---------------------------------------------------------------------------------------------------------------------------
Mặt S cho bởi phương trình z = z(x,y), D là hình chiếu của S xuống 0xy.
Chia miền D thành n miền con D1, D , ..., D 2
n. S được chia thành các mặt con S1, S2, ..., S .n Lấy điểm bất kỳ P ( x ,y ,0) D M x yz S  i i i  i Tương ứng điểm i ( i , i ,i ) i
T là mặt tiếp diện với S tại M T i
i là mảnh có hình chiếu Di
Với Di nhỏ ta coi diện tích của Ti là diện tích gần đúng của mảnh Si. n S  n S   S(iT ) i 1 
Gọi  là góc giữa hai mảnh D S(D ) S  ( S )  cos i và Ti : i i i i
Ta có  là góc giữa pháp tuyến tại M với mặt S và trục Oz. i i 54 27
III. Ứng dụng hình học
---------------------------------------------------------------------------------------------------------------------------
Véctơ pháp của S tại M : ' '
n  ( f ( x ,y ),f (xy , ),1) i i x i i y i i 1 cos i   f (x,y ) x i i 2 f (x ,y ) y i i 2 ' ' 1 n S  n S    f ( x,y ) x i i 2 f (xy, ) y i i 2 ' ' 1S ( D ) i i 1  n  
S  lim    xf  2 yf 2 ' ' 1  ( S iD )  n i 1   
Diện tích mặt cong có phương trình z = f(x,y), có hình chiếu xuống mặt phẳng
0xy là D được tính bởi công thức: 2 2  f   f    S   1  dxdy     D  x   y   55 Ví dụ
Tính diện tích phần mặt paraboloid 2 2 z  1 x y  nằm trong hình trụ 2 2 x y   1
Hình chiếu của S xuống 0xy: 2 2 D :x y  1 Phương trình mặt S: 2 2 z  1 x y  ' ' z  2  ; xz  2 x y  y
Diện tích phần mặt paraboloid: S    z 2  z 2 ' ' 1 dxdy x y D 2 1 2 2 S   1  4 x  4 ydxdy 2
  d 1 4r rdr 2 2 x y 1 0 0 56 28 Bài tập 57 58 29 Bài tập 59 30