Tài liệu giải tích | Trường đại học Bách Khoa, Đại học Đà Nẵng
Tài liệu giải tích | Trường đại học Bách Khoa, Đại học Đà Nẵng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Giải tích 1(GT 1) 40 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 410 tài liệu
Tác giả:
Preview text:
TÀI LIỆU GIẢI T TÀI LIỆU GI ÍCH ẢI T [PHẦN 1] [PHẦN 1] Chương 1. Vi V phân h ân àm hàm số m số ột biến Chương 2. Tích p ch hân hàm à số mộ m t biến ế Chương 3. Chuỗi số Chương 4. Hàm số nhiều ề b iến Chương 1. Vi V phân h àm số một biến Bài 1. .Giới h ạn và và liên tụ ên c Bài 2. .Đạo h ạo àm và và ứng dụng g tìm g iới hạn ạ Chương 1. Vi V phân h àm số một biến Bài 1. .Giới h ạn và và liên tụ ên c 1.1. H àm H số àm số l ượng l g ượng iác ngược ược 1.2. C ác quy y tắc tắc tính g iới hạn ạ 1.3. Đ ại lượn ư g vô cùng b
cùng é, vô cùng l ớn 1.4. H àm số l số iên tụ ên c Bài 1. Giới h ạn và liên tục 1.2.2. Các ác quy y tắc tí tắc nh g iới hạn Giả sử k và lim f(x ) , lim ( gx ) tồn tại. Khi đó: x a x a 1) lim[k.f (x )] k.lim f( ) x x a x a 2) lim[f( ) x (g ) x ] lim (f )x lim (g )x x a x a x a 3) lim[f( ) x (g ) x ] lim (f ). x lim (g )x x a x a x a lim f(x ) f(x ) 4) lim x a nếu lim ( gx ) 0 . x a g(x ) limg(x ) x a x a Bài 1. Giới h ạn và liên tục Định lý Nếu f (x )
g (x ) khi x a và lim f(x ) , lim ( gx ) x a x a tồn tại thì lim f( ) x lim (g ) x . x a x a
Định lý kẹp giữa Nếu ( x ) h ( x ) g ( x ) khi x a và lim f( ) x lim (g ) x L thì lim ( hx ) L . x a x a x a Chú ý 1 1 1 1 , , 0 , 0 Bài 1. Giới h ạn và liên tục Một số ố kết quả ả g iới hạn ạ cần nhớ h 1) sin ( ) x tan ( ) x lim lim 1 ( ) x 0 (x ) 0 ( ) x (x ) 2) lim ln x , lim lnx x x 0 x 1 3) 1 lim 1 lim 1 x x e x x 0 x n 4) lim[f(x )] n limf ( x ) , n x a x a Bài 1. Giới h ạn và liên tục Một số ố kết quả ả g iới hạn ạ cần nhớ h lim g(x ) 5) g(x ) lim [f(x )] limf ( x ) x a (lim f(x ) 0 ) x a x a x a 6) lim n f(x ) n lim f ( x ) , n x a x a
(nếu n lẻ, ta giả sử rằng lim f(x ) 0 ) x a 7) ln x x lim lim 0 nếu 1, 1 . x x x x Bài 1. Giới h ạn và liên tục 1.2.3. Mộ t số t ví v dụ cos x
VD1. Chứng tỏ rằng lim 0 . x x Giải. Ta có: 1 cosx 1, x (0; ) . x x x 1 1 cos x Vì lim lim 0 , nên lim 0 . x x x x x x Bài 1. Giới h ạn và liên tục 3x 2x 1 VD2. Tính L lim . x 2x 3 1 VD 3. Tìm giới hạn 2 4 L lim 1 tan x x . x 0 A. L ; B. L 1; C. 4 L e ; D. L e . cot x VD4. Tính sin L lim(cos 2x ) x . x 0 Chương 3. Chuỗi ỗ is ố s Bài 3. .Chuỗi số có có dấu tù ấu y ý y 3.1. C huỗi số đan a dấu 3.1.1. Đ ịnh n ghĩa 3.1.2. T i T êu chuẩn L chuẩn eibniz 3.2. C huỗi số có có dấu tù ấu y ý y 3.2.1. Đ ịnh n ghĩa 3.2.2. T i T êu chuẩn h chuẩn ội tụ tu yệt đ yệt ối Bài 3. Chuỗi s ố có dấu u tùy ý 3.1. C huỗi số đan a dấu 3.1.1. Đ ịnh n ghĩa
Cho dãy số dương (u ) , các chuỗi số có dạng n n n 1 ( 1) u , ( 1) u n n n 1 n 1
được gọi là các chuỗi số đan dấu. Bài 3. Chuỗi s ố có dấu u tùy ý
VD. Các chuỗi số sau là chuỗi số đan dấu: ( 1)n 1 1 1 1 1) 1 ... n 1 n 2 3 4 5 n 2n 2 1 3 5 9 17 1 2) 1 ( 1) ... n 1 n 1 2 4 8 16 32 Bài 3. Chuỗi s ố có dấu u tùy ý 3.1.2. T i T êu chuẩn L chuẩn eibniz
Nếu dãy (u ) giảm về 0 thì các chuỗi số đan dấu n n n 1 ( 1) u , ( 1) u n n n 1 n 1 hội t ụ tụ. Kh i Kh đ ó đó, t a t gọi c h c uỗ u i ỗ s ố s l ố à l ch c uỗi h Le i Le bni i z bni . ( 1)n
VD1. Xét sự hội tụ của chuỗi số . n 1 n 1 1 Giải. Dãy (u ) giảm và u 0 n n n n
chuỗi số đã cho hội tụ. ộ ụ Bài 3. Chuỗi s ố có dấu u tùy ý ( 1)n
VD2. Xét sự hội tụ của chuỗi số . n n 2 n ( 1) 2n n 1
VD3. Xét sự hội tụ của chuỗi số ( 1) . n 1 n 1 2 Bài 3. Chuỗi s ố có dấu u tùy ý 3.2. C huỗi số có có dấu tù ấu y ý y 3.2.1. Đ ịnh n ghĩa • u (u
) được gọi là chuỗi số có dấu tùy ý. n n n 1 •
u được gọi là hội tụ tuyệt đối nếu u hội tụ. n n n 1 n 1 •
u được gọi là bán hội tụ nếu n n 1 u hội tụ và u phân kỳ n n n 1 n 1 ( 1)n VD4. Chuỗi số là bán hội tụ. n n 1 Bài 3. Chuỗi s ố có dấu u tùy ý 33..22..2. Ti T êu i
chuẩn hội tụ tuyệt đối Nếu
u hội tụ thì chuỗi có dấu tùy ý u hội tụ. n n n 1 n 1 cos( n n )
VD5. Xét sự hội tụ của chuỗi số . 2 n 1 n n n 1 ( 1) ( 2)
VD6. Xét sự hội tụ của chuỗi số . n n 1 3 Chương 4. Lý thuyế y t chuỗi §4. CHUỖI HÀM
4.1. Khái niệm chung về chuỗi hàm 4.1.1. Các định nghĩa
• Cho dãy hàm u (x ),u (x ),..., u ( ) x ,... cùng xác định 1 2 n trên D . Tổng hình thức: u (x ) u (x ) ... u ( ) x ... u ( )x (1) 1 2 n n n 1
được gọi là chuỗi hàm số hay chuỗi hàm trên D . • Nếu tại x D , chuỗi số
u (x ) hội tụ (phân kỳ) 0 n 0 n 1
thì x0 được gọi là điểm hội tụ (phân kỳ) của chuỗi (1). Chương 4. Lý thuyế y t chuỗi
• Tập hợp các điểm hội tụ x của chuỗi (1) được gọi là 0
miền hội tụ của chuỗi (1).
• Chuỗi (1) được gọi là hội tụ tuyệt đối tại x D nếu 0 chuỗi u (x ) hội tụ. n 0 n 1 • Tổ Tổng S ( ) x u (x ) u (x) ... u ( ) x đ được g i ọ l à l n 1 2 n
tổng riêng thứ n của chuỗi (1).
Trong miền hội tụ của chuỗi (1), tổng S (x ) hội tụ về n một hàm số f ( x ) nào đó. • Hàm f(x )
lim S (x) xác định trong miền hội tụ của n n
chuỗi (1) được gọi là tổng của chuỗi (1). Chương 4. Lý thuyế y t chuỗi Ta viết là: u ( ) x ( fx ) . n n 1 Khi đó, R ( ) x ( fx ) S ( )
x được gọi là phần dư của n n
(1) và tại mỗi x thuộc miền hội tụ thì lim R (x ) 0 . n n nx
VD 1. Tìm miền hội tụ của chuỗi hàm ne . n 1 Giải • Với x 0: lim n nx x ne e 1 chuỗi hội tụ. n • Với x 0: nx ne 0 chuỗi phân kỳ.
Vậy miền hội tụ của chuỗi hàm là 0; . Chương 4. Lý thuyế y t chuỗi 2n
VD 2. Tìm miền hội tụ của chuỗi hàm x . n n 1 ! Giải • Với x 0: Chuỗi hội tụ. • Với x 0, ta có: 2( 2 n 1) 1 2n 2 x x x lim : lim 0 chuỗi hội tụ. n (n 1)! n ! n n 1
Vậy miền hội tụ của chuỗi hàm là . Chương 4. Lý thuyế y t chuỗi 4.2. Chuỗi lũy thừa 4.2.1. Định nghĩa Chuỗi hàm a ( x
x )n với a ,x là các hằng số n 0 n 0 n 0
được gọi là chuỗi lũy thừa. Nhận xét • Nếu đặt x
x x thì chuỗi lũy thừa có dạng n ax . 0 n n 0 • Miền hội tụ của n ax chứa x 0 nên khác rỗng. n n 0 n 0 Chương 4. Lý thuyế y t chuỗi 4.2.2. Bổ đề Abel Nếu chuỗi hàm n ax hội tụ tại x 0 thì chuỗi n n 0
hội tụ tuyệt đối tại mọi điểm x ; . • Hệ quả Nếu chuỗi hàm n ax phân kỳ tại x thì phân kỳ n n 0 tại mọi x thỏa x . Chương 4. Lý thuyế y t chuỗi 4.2.3. Bán kính hội tụ a) Định nghĩa • Số R 0 để n ax
hội tụ tuyệt đối trên ( R ;R ) và n n 0 phân kỳ tại x :x
R được gọi là bán kính hội tụ.
• Khoảng ( R ;R ) được gọi là khoảng hội tụ. Nhận xét • Nếu chuỗi hội tụ x thì R . • Nếu chuỗi phân kỳ x 0 thì R 0. Chương 4. Lý thuyế y t chuỗi
b) Phương pháp tìm bán kính hội tụ a Nếu tồn tại 1 lim n r hoặc lim n a r thì: n a n n n 0, r 1 R , 0 r . r , r 0 Chương 4. Lý thuyế y t chuỗi
Tìm miền hội tụ của chuỗi lũy thừa
Bước 1. Tìm bán kính hội tụ R , suy ra khoảng hội tụ của
chuỗi lũy thừa là: ( R ;R ) .
Bước 2. Xét sự hội tụ của các chuỗi số tại x R . Bước 3
• Nếu các chuỗi số phân kỳ tại x R thì kết luận:
miền hội tụ của chuỗi hàm là ( R ;R ) .
• Nếu chuỗi số phân kỳ tại x R và hội tụ tại x R
thì kết luận: miền hội tụ của chuỗi hàm là [ R ;R ) .
• Tương tự: miền hội tụ là ( ; RR ], [ R ; R ]. Chương 4. Lý thuyế y t chuỗi n
VD 4. Tìm miền hội tụ của chuỗi hàm x . n n 1 n
VD 5. Tìm miền hội tụ của chuỗi hàm (x 1) . n n 1 n.2 2 n
VD 6. Tìm miền hội tụ của chuỗi hàm 1 1 n x . n n 1 2
VD 7. Tìm miền hội tụ của chuỗi hàm 3n( x 2)n . n 0 Chương 4. Lý thuyế y t chuỗi
4.3. Sơ lược về chuỗi Fourier a) Chuỗi lượng giác a Chuỗi hàm dạng: 0 (a cos nx b sinnx ) (*) 2 n n n 1
được gọi là chuỗi lượng giác. N ế N u h c uỗi ( * ( ) h ộ h i ộ t i tụ đ ều t ê r n [ ; ] đ ế đ n h à h m số f ( x )
thì các hệ số a ,b được tính theo công thức: n n 1 a f (x)cos nxdx , n 0, 1, 2,... (2); n 1 n b f( ) x sin nxd , x n 1, 2,... (3). Chương 4. Lý thuyế y t chuỗi
b) Định nghĩa chuỗi Fourier
• Chuỗi lượng giác (*) có các hệ số được tính theo công
thức (2), (3) được gọi là chuỗi Fourier của hàm f ( x ) .
Các hệ số a ,b được gọi là hệ số Fourier của f ( x ) . n n • Mọi hàm f ( x ) khả tích trên [
; ] tương ứng với chuỗi
Fourier của nó và thông thường ta viết: a0 f(x ) (a cosnx b sinnx ) . 2 n n n 1 Chương 4. Lý thuyế y t chuỗi
Jean Baptiste Joseph Fourier (1768 – 1830)
Nhà Toán học và Vật lý học Pháp. Chương 4. Lý thuyế y t chuỗi
VD 8. Tìm chuỗi Fourier của hàm số: 1, x 0 f(x ) 1, 0 x . Giải. Do hàm f ( x ) lẻ nên: f ( x ).cosnx lẻ và f ( x ).sin x chẵn. Suy ra: • 1 a f ( ) x cos nxdx 0, n . n • 1 2 b f( ) x sin nxdx ( f ) x sin nx dx n 0 Chương 4. Lý thuyế y t chuỗi 2 2 sin nxdx (cosn 1) n 0 0, n 2k 2 [1 ( 1)n] 4 . n , n 2 k 1 (2 ( k 2 1) 1 Vậy 4 sin(2k 1)x f(x ) . k 0 2k 1 Chương 4. Lý thuyế y t chuỗi
VD 9. Tìm chuỗi Fourier của f ( x ) x trên [ ; ]. Giải. Do hàm f ( x ) chẵn nên ta có: • 1 b f( ) x sin nxdx 0, n 1,2,... n • 1 2 a x dx xdx d , 0 0 0, n 2k 2 a x cosnxdx . n 4 , n 2k 1 0 2 n Vậy 4 cos(2k 1)x f(x ) . y ( ) 2 k 0 2 (2k 1) Chương 4. Lý thuyế y t chuỗi
c) Khai triển Fourier của hàm số Định lý Dirichlet Nếu hàm số f (
x ) tuần hoàn với chu kỳ 2 , đơn điệu
từng khúc và bị chặn trên [ ; ] thì chuỗi Fourier của nó hội tụ t nó hội tụ tại ạ m ọi m đi ể đi m ể t rê t n rê [ ; ] đế n đế t n ổn t g l à l : à f (x ) f ( x ) . 2 Chương 4. Lý thuyế y t chuỗi J.P.G. Lejeune Dirichlet (1805 – 1859) Nhà Toán học Đức Chương 4. Lý thuyế y t chuỗi
VD 10. Khai triển thành chuỗi Fourier của hàm số: 0, x 0 f(x ) x , 0 x . Giải. Hàm f (
x ) thỏa mãn định lý. Ta có: 1 1 • a f ( ) x dx xdx , 0 2 0 0, n 2k 1 a x cosnxdx . n 2 , n 2k 1 0 2 n Chương 4. Lý thuyế y t chuỗi 1 , n 2k • 1 sin n b x nxdx n 1 0 , n 2k 1. n Vậy: k 1 2 cos(2k 1)x ( 1) sinkx f(x ) . 2 4 k 0 (2k 1) k 1 k
…………………………Hết………………………… Chương 4. HÀM S H Ố NHIỀU BIẾN SỐ Bài 1. .Khái n iệm cơ b ản Bài 2. .Đạo h ạo àm riêng – Vi V ip h p ân h
Bài 3. .Cực trị của hàm à hai a biến số ến Chương 4. HÀM S H Ố NHIỀU BIẾN SỐ Bài 1. .Khái n iệm cơ b ản 1.1. C ác định nghĩa 1.2. G iới h ạn của củ hàm hai a biến số ến 1.3. H àm số l số iên tụ ên c Bài 1. Khái ni n ệm cơ bản 1.1. C ác định nghĩa a) Mi a) ền phẳn ẳ g D D Bài 1. Khái ni n ệm cơ bản Miền đ ó đ n ó g n D D D D D Bài 1. Khái ni n ệm cơ bản Miền m ở D D D D \ D Bài 1. Khái ni n ệm cơ bản Miền Mi ền đ ền ơn đa l il iên ên C1 D C 2 C 2 3 D D C C C 1 2 3 Bài 1. Khái ni n ệm cơ bản Miền l iên thôn ô g • D • Bài 1. Khái ni n ệm cơ bản Miền Mi ền không l không ilên i th ên ông D Bài 1. Khái ni n ệm cơ bản b) L ) ân cận cậ của m
của ột điểm trong m ặt phẳng ε • M0 S(M0,0ε) M S (M , ) d (M ,M ) 0 0 Bài 1. Khái ni n ệm cơ bản Điểm trong Đi Đ ểm i ểm n g n o g ài oài • M1 D • M2 D • M3 Điểm biên ên
Bài 2. Đạo hàm – Vi V ip h p â h n â Sơ đ Sơ ồ đ f 2 x fx f f (x,y ) xy f f 2 y y fyx
Bài 2. Đạo hàm – Vi V ip h p â h n â • Định l ý Sch Sc warz
Nếu hàm số f (x,y ) có các đạo hàm riêng f và xy
f liên tục trong miền mở 2 D thì f f . yx xy yx
Bài 2. Đạo hàm – Vi V ip h p â h n â Hermann Ama ndus Schwarz (1843 – 19 1 2 9 1 2 ) 1
Bài 2. Đạo hàm – Vi V ip h p â h n â
VD6. Tính các đạo hàm riêng cấp 2 của hàm số 3 2 3 4 ( , ) y f x y xe x y y tại ( 1; 1) .
VD7. Tính các đạo hàm riêng cấp 2 của hàm số 2 f (x ,y ) cos(xy ) . 2
VD8. Tính các đạo hàm riêng cấp 2 của x y z e .
VD9. Tính các đạo hàm riêng cấp 2 của 2xy z . x y
VD10. Tính các đạo hàm riêng cấp 2 của hàm số z x arctan y .
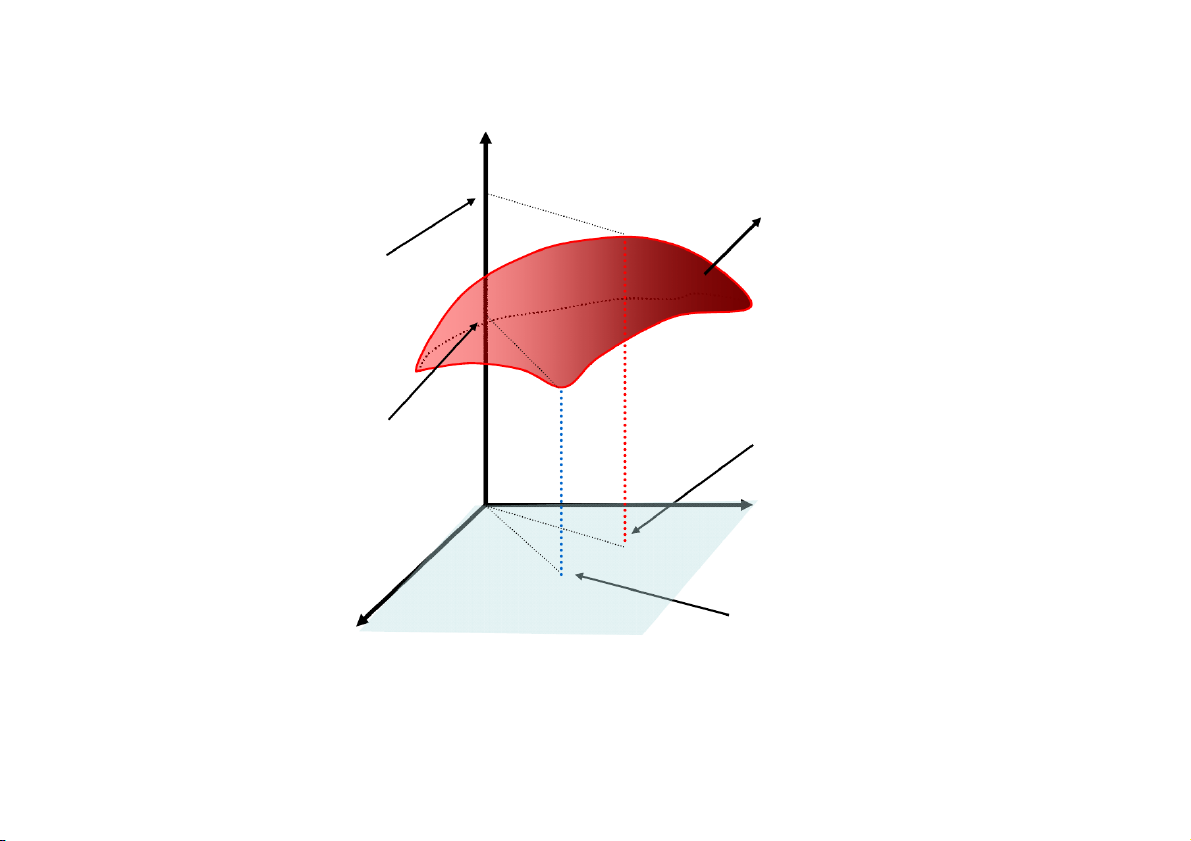
Bài 2. Đạo hàm – Vi V ip h p â h n â 2.2. 2. 2. VI VI PHÂN 2.2.1. V i V phân cấp cấ 1 Đại lượng f (x , y ) x f (x , y ) y x 0 0 y 0 0 ký hiệu df (
x y ) , được gọi là vi phân hàm số 0 0 f (x,y ) tại điểm M ( x ,y ) . 0 0
Bài 2. Đạo hàm – Vi V ip h p â h n â
Công thức vi phân của f (x,y ) tại M (x,y ) là df ( , x ) y f( ,x )ydx f( ,x )ydy x y
Bài 2. Đạo hàm – Vi V ip h p â h n â
• Vi phân của hàm nhiều hơn hai biến số
có định nghĩa tương tự, chẳng hạn df( , x ,yz) f ( ,x ,y ) z dx f ( ,x ,y )z dy (f ,x, ) yz dz x y z
Bài 2. Đạo hàm – Vi V ip h p â h n â VD11. Cho hs 3 2 2 f (x,y ) 2x y xy , tính df (1; 1) .
Giải. Ta có các đạo hàm riêng là: 2 2 f ( , x ) y 6 xy 2xy f (1; 1) 8 , x x 3 2 f ( , xy ) 4x y x f (1; 1) 5 . y y Vậy df (1 ( ; 1 1) 1 f (1 ( ; 1 1) 1 dx f (1 ( ; 1 1) 1 dy 8dx 5 dy . x y
Bài 2. Đạo hàm – Vi V ip h p â h n â
VD12. Tính vi phân của hàm số 2 (x ,y ) tan(xy ) .
Giải. Ta có các đạo hàm riêng là: 2 2xy f ( , xy ) [tan(xy )] , x x 2 2 cos (xy ) 2 2 x f (x, x ) y [ta t n a ( x ) y ] . y y 2 2 cos (xy ) 2 Vậy 2xy x df ( , xy ) dx dy . 2 2 2 2 cos (xy ) cos (xy )
Bài 2. Đạo hàm – Vi V ip h p â h n â VD13. Cho hs 2 y x 2 f ( , xy ) e cos(xy ) , tính df (1; ) .
Giải. Ta có các đạo hàm riêng là: 2 y x 2 2 f ( , xy ) 2xe [cos(xy ) y sin(xy )] x 2 y x 2 2 2 f ( , x ) y e [cos( xy) x sin( xy )] y 1 f (1; ) 2e x 1 f (1; ) e . y Vậy 1 df (1; ) (2dx dy)e .
Bài 2. Đạo hàm – Vi V ip h p â h n â 2.2.2. Vi V phân cấp ân 2 cấp
Vi phân của df (x,y ) , ký hiệu là 2
d f (x,y ) , được gọi là
vi phân cấp 2 của hàm số f (x,y ) . 2 2 2 d f( ,xy ) f ( , xy )dx 2f ( , xy )dxdy f (x,y )dy 2 2 x xy y
Bài 2. Đạo hàm – Vi V ip h p â h n â VD14. Tính 2 df (2; 1) của hàm số 2 3 2 3 5 f (x,y ) xy xy 3 x y . Giải. Ta có: 3 2 2 5 f ( ,xy ) 2xy y 9xy x 2 2 3 4 f ( ,x ) y 3 xy 2xy 15x y y 3 5 f ( , xy ) 2y 18xy f (2; 1) 34 2 x 2 x 2 2 4 f ( , xy ) 6xy +2y 45xy f (2; 1) 170 xy xy 2 3 3 f ( , xy ) 6xy +2x 60x y f (2; 1) 460. 2 y 2 y Vậy 2 2 2 df (2; 1) 34dx 340dxdy 460dy .
Bài 2. Đạo hàm – Vi V ip h p â h n â
VD15. Tính vi phân cấp 2 của hàm số 2 z sin( xy ) . Giải. Ta có: 2 2 z y cos(xy ) x 2 z 2xycos(xy ) y 4 2 z 2 y sin(xy ) 2 x 2 3 2 z 2ycos(xy ) 2xy sin(xy ) xy 2 2 2 2 z 2x cos( xy ) 4 xy sin(xy ). 2 y Vậy 2 4 2 2 dzx (y , ) y sin( xy ) dx 2 2 2 4y [cos(xy ) xy sin(xy )]dxdy 2 2 2 2
2x [cos(xy ) 2xy sin(xy )]dy .
……………….………………………………
……………….…………………… Chương 4. HÀM S H Ố NHIỀU BIẾN SỐ
Bài 3. .Cực trị của hàm à hai a biến số ến 3.1. Đ ịnh n ghĩa 3.2. C ực trị tự d o 3.3. C ực trị có c điều ề kiện
Bài 3. Cực trị của a hàm hai biến số 3.1. Đ ịnh n ghĩa • Hàm số z
f (x,y ) đạt cực trị địa phương (gọi tắt • Nếu f 0 thì
được gọi là giá trị cực
là cực trị) tại điểm fxM ( ,y )
0 (x0 ,y ) nếu với mọi điểm 0 0 0 Mtiể(xy
u ,và) SM là điểm cực tiểu của z f (x,y ) . 0 ( M )\M thì 0 0 f f (
x ,y ) fx ( y, ) có dấu không đổi. • Nếu Nếu f 0 th t ì h f ( x 0y, 0) đư đ ợ ư c ợc gọ g i ọ là là gi g á iá trị r cực cực 0 0
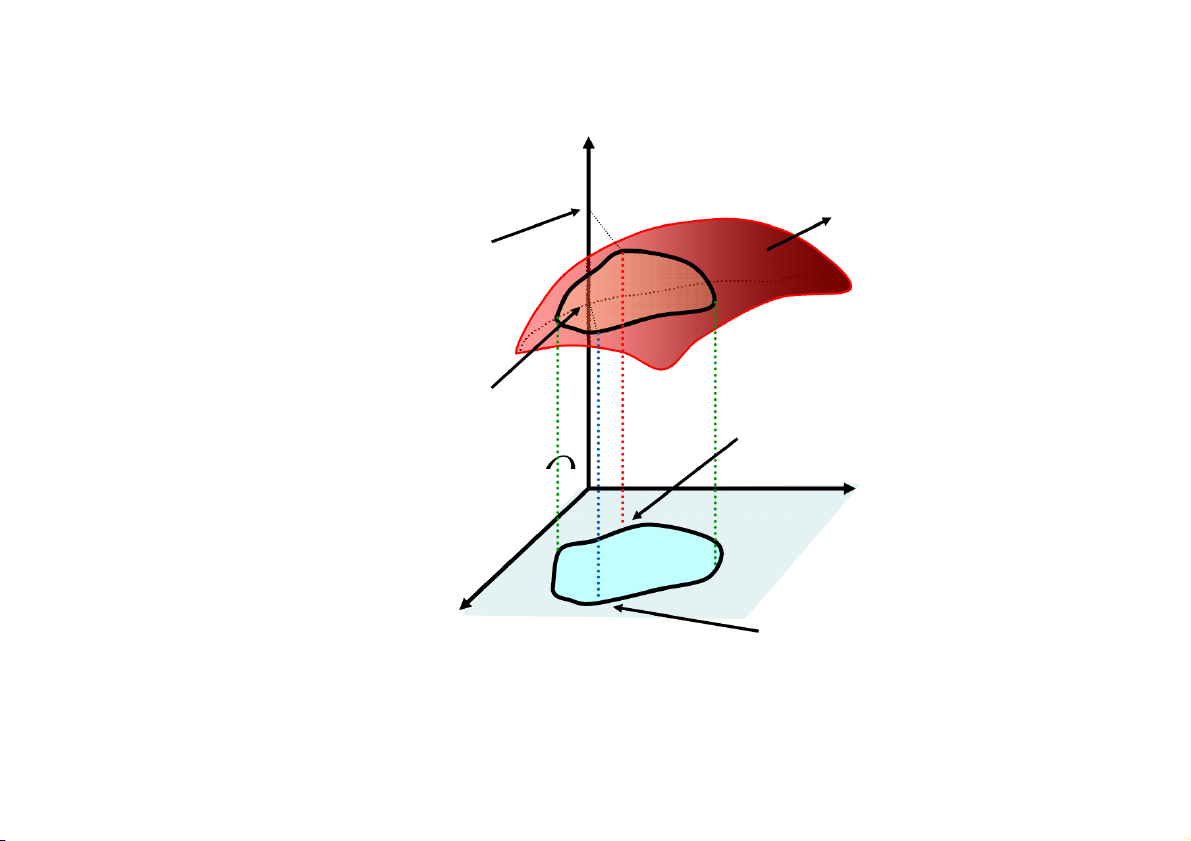
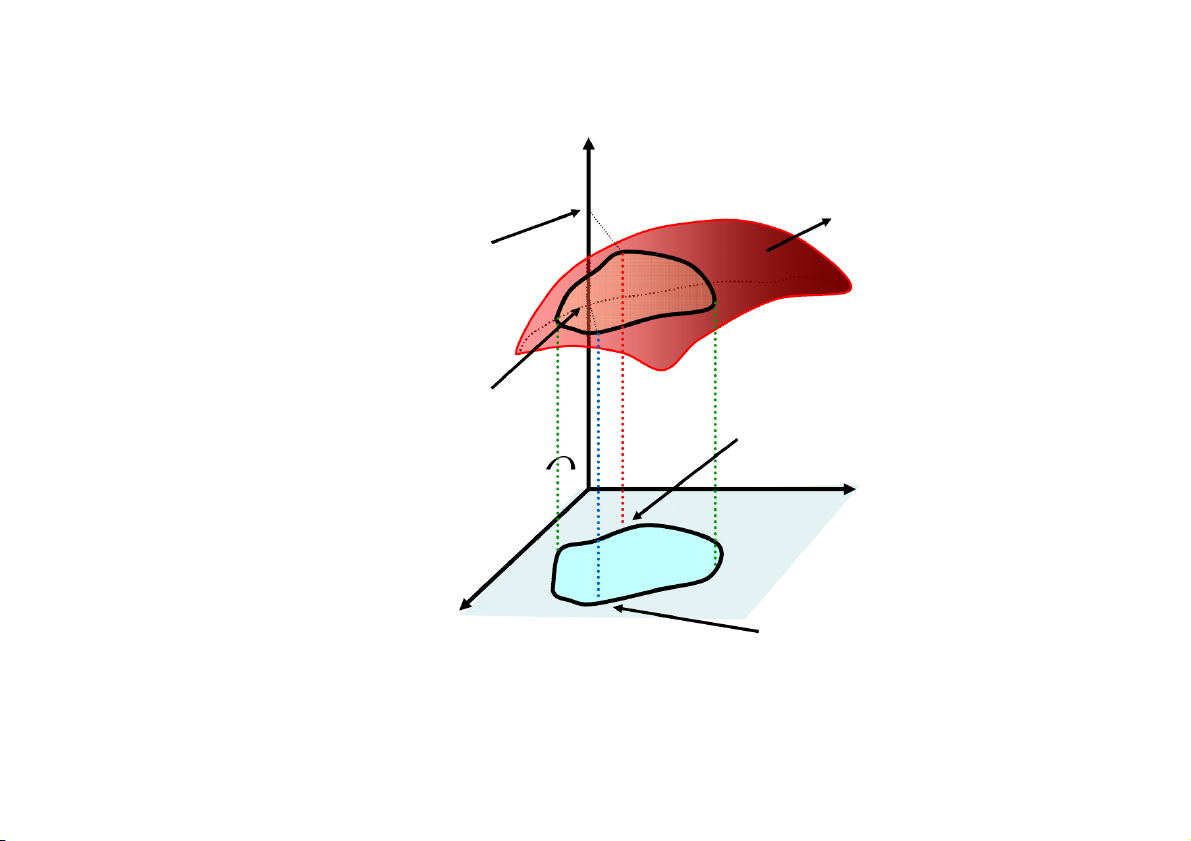
đại và M là điểm cực đại của z f (x,y ) . 0 Cực trị ực tự do z • P z f (x,y ) •2 zCÑ • S • P1 zCT Điểm cực đại O y • • M2 M x 1 Điểm cực tiểu Cực C trị ực trị có có đ i đ ều i ki ều ện ki z S z f (x,y ) • z • CÑ P2 ••P1 zCT Điểm cực đại O y •M2 ( ) x • M Điểm cực tiểu 1
Bài 3. Cực trị của a hàm hai biến số 3.2. CỰC T RỊ TỰ D O Phương
Phương pháp tìm cực trị tự do
Để tìm cực trị tự do của hàm số f (x,y ) trên 2 D ,
ta thực hiện các bước sau • B ướ B c ướ 1 . T ì T m ì đi m đ ể i m ể dừn d g ừn b ằ b n ằ g n c á c c á h c g i g ả i i ả h ệ h p h p t h r t ì r n ì h n f ( , xy ) 0 x f ( , xy ) 0. y
Bài 3. Cực trị của a hàm hai biến số
• Bước 2. Giả sử (x ,y ) là một nghiệm của hệ pt 0 0
trên và M (x ,y ) D , ta tính: 0 0 0 A f (x ,y ) 2 x 0 0 2 B f (x ,y ) AC B . xy 0 0 C f 2(x ,y ) 2 y 0 0
Bài 3. Cực trị của a hàm hai biến số
• Bước 3. Ta có các trường hợp: 0 1) nếu
thì f (x,y ) đạt cực tiểu tại M ; A 0 0 0 2) nếu
thì f (x,y ) đạt cực đại tại M ; A 0 0 0 3) nếu
0 thì f (x,y ) không đạt cực trị tại M ; 0 4) nếu
0 thì ta chưa thể kết luận.
Bài 3. Cực trị của a hàm hai biến số
VD1. Tìm điểm dừng của hàm số 3 3 2 f (x,y ) x y 3y 12x 5 .
VD2. Tìm cực trị của hs 2 2 z x y 4x 2y 8 .
VD3. Tìm cực trị của hs 3 3 f (x,y ) x y 3xy 2 .
VD4. Tìm điểm cực trị của hàm số 2 3 2 2 z 3xy y 3x 3y 2 . 1 1
VD5. Tìm cực trị của hàm số z xy . x y
VD6. Tìm cực trị của hàm số 3 2 2 2 f ( ) 2 5 4 .
Bài 3. Cực trị của a hàm hai biến số 3.3. CỰC T RỊ CÓ Đ IỀU KIỆN c ( ự cự t c rị trị vư vướ ớng n ) g
Cho hàm số f (x,y ) xác định trên lân cận của điểm M (
x y , ) thuộc đường cong ( ): (x,y ) 0 . 0 0 0
Nếu tại điểm M , hàm f (x,y ) đạt cực trị thì ta nói 0
M là điểm cực trị có điều kiện của f (x,y ) với 0 điều kiện (x,y ) 0 . Cực C trị ực trị có có đ i đ ều i ki ều ện ki z S z f (x,y ) • z • CÑ P2 ••P1 zCT Điểm cực đại O y •M2 ( ) x • M Điểm cực tiểu 1
Bài 3. Cực trị của a hàm hai biến số 3.3.1. Phươn Phư g p háp khử
• Bước 1. Từ pt (x,y )
0 , ta giải y theo x (hoặc x
theo y) và thế vào hàm số z f (x,y ) .
• Bước 2. Tìm cực trị của hàm 1 biến z f ( x ,y ( x ) ) .
Bài 3. Cực trị của a hàm hai biến số
VD7. Tìm cực trị của hàm 2 2 z x y thỏa mãn điều kiện xy 1. Giải. Ta có: 1 2 1 xy 1 y z x . 2 x x 2 x 1 y 1 z 2x 0 . 3 x 1 y 1 x 1 Lập BBT của hàm 2 z x , ta được: 2 x 2 2 z x
y đạt cực tiểu tại M ( 1; 1) , . 1 M (1; 1) 2
Bài 3. Cực trị của a hàm hai biến số 3.3.2. Phươn Phư g p háp nhân tử L tử agrange
• Bước 1. Lập hàm phụ (hàm Lagrange) ( xy, ) f ( xy , ) x(y , )
• Bước 2. Tìm điểm dừng bằng cách giải hệ pt L ( , xy ) f (x,y ) (x ,y ) 0 x x x L ( , xy ) f (x,y ) (x ,y ) 0 y y y ( , xy ) 0.
Giả sử f (x,y ) có n điểm dừng M (x ,y ) ứng với k k k k (k 1,...,n ) .
Bài 3. Cực trị của a hàm hai biến số
• Bước 3. Tính các vi phân: 2 2 2 dL (x , y ) L ( xy, ) dx 2 L ( xy ,d)xdy L ( xy ,d )y 2 2 xy x y d ( , x ) y ( ,x )ydx ( ,x )yd . y x y
• Bước 4. Tại điểm M (x ,y ) ứng với , ta giải: k k k k (M )dx (M ) dy 0 dy theo dx x k y k (hoặc ngược lại). Sau đó, thay vào 2 d ( LM ) (chú ý 2 2 dx dy 0). k
Bài 3. Cực trị của a hàm hai biến số Kết luận: 1) nếu 2
d L(M ) 0 thì f (x,y ) đạt cực tiểu tại M ; k k 2) nếu 2
d L(M ) 0 thì f (x,y ) đạt cực đại tại M . k k Chú ý 2 Trường hợp d (
LM ) 0 trong chương trình ta k không xét. Nếu từ vi phân 2 d L (
x ,y ) mà ta có thể kết luận
được cực trị thì không cần phải tính d (x,y ) .
Bài 3. Cực trị của a hàm hai biến số
VD8. Tìm điểm cực trị của hàm số f (x,y ) 2x y thỏa điều kiện 2 2 x y 5. Giải. • Hàm Lagrange: 2 2 2 2 x y 5 ( x ,y ) x y 5 2 2 L (x ,y ) 2 x y x ( y 5) .
• Tìm điểm dừng, ta có: L ( , xy ) 2 2 x 0 x L ( , xy ) 1 2 y 0 y 2 2 ( , xy ) x y 5 0
Bài 3. Cực trị của a hàm hai biến số 1 x x 2 x 2 1 1 1 y 2 2 2 1 1 y 1 y 1. 5 2 2 4
Suy ra hàm số có hai điểm dừng: 1 1 M (2; 1) với và M ( 2; 1) với . 1 1 2 2 2 2
Bài 3. Cực trị của a hàm hai biến số • Tính vi phân: 2 2 2 d L ( x ,y ) 2 (dx dy ) . • Tại điểm 1 M (2; 1) với , ta có: 1 1 2 2 2 2 d L ( M ) ( dx dy ) 0 M là điểm cực đại. 1 1
• Tại điểm M ( 2; 1) với 1 , ta có: 2 2 2 2 2 2 d L (M ) dx dy 0 M là điểm cực tiểu. 2 2
Bài 3. Cực trị của a hàm hai biến số
VD9. Tìm cực trị của hàm số 2 2 z x y thỏa điều kiện 2 2 x y 3x 4y . Giải. Ta có: 2 2 (x,y ) x y 3x 4y 2 2 2 2 L (x ,y ) x y x ( y x 3 y 4 ) . Tìm điểm dừng: L ( , xy ) 2x (2x 3) 0 (1) x L ( , xy ) 2y (2y 4) 0 (2) y 2 2 ( , xy ) x y 3x 4y 0 (3).
Bài 3. Cực trị của a hàm hai biến số 3 2 Từ (1) và (2) x ,y , thay vào (3) 2(1 ) 1 ta được 2 điểm dừng: M (0; 0) với 0 và M (3; 4) với 2. 1 1 2 2 Từ vi phân 2 2 2 L ( x ,y ) (2 2 )(dx dy ) , ta có: 2 d L ( M )
0 M (0; 0) là điểm cực tiểu. 1 1 2 d L ( M )
0 M (3; 4) là điểm cực đại. 2 2
Bài 3. Cực trị của a hàm hai biến số Chú ý
• Trong ví dụ 9, nếu ta thay 2 2 x y 3 x 4y vào 2 2 z x y thì z 3x 4y và 2 2 L ( x ,y ) 3x 4y (x y 3x 4y ) .
Giải tương tự như trên, ta có hai điểm dừng: M (0 ( ; 0) 0 ới với 1 à và M (3 ( ; 4) 4 ới với 1. 1 1 2 2
Kết quả tìm được không thay đổi nhưng nhân tử đã thay đổi. • Khi ta thay (x,y )
0 bởi một phươ ng trình tương đương thì nhân tử
sẽ thay đổi nhưng không làm h đổi kế b i
Bài 3. Cực trị của a hàm hai biến số
VD10. Tìm cực trị của hàm số f (x,y ) 10x 40y thỏa điều kiện xy 20. Giải. Biến đổi: xy 20 xy 400 (x,y ) xy 400 L ( x ,y ) 10x 40y (xy 400) . Tìm điểm dừng: L ( , xy ) 10 y 0 x M (40; 10), 1 1 1 L ( , xy ) 40 x 0 y M ( 40; 10), 1. 2 2 ( , xy ) xy 400 0
Bài 3. Cực trị của a hàm hai biến số Vi phân: 2 d L ( x ,y ) 2 dxdy và d (x,y ) ydx xdy .
• Tại M (40; 10) ứng với 1, ta có: 1 1 2 2 d (M ) 0 dx 4dy d L (M ) 8dy 0 1 1
M (40; 10) là điểm cực tiểu của f (x,y ) . 1
• Tại M ( 40; 10) ứng với 1, ta có: 2 2 2 2 d (M ) 0 dx 4dy d L (M ) 8dy 0 2 2
M ( 40; 10) là điểm cực đại của f (x,y ) . 2
Bài 3. Cực trị của a hàm hai biến số
VD11. Tìm điểm cực trị của z xy thỏa điều kiện 2 2 x y 1. 8 2 2 2 x y Giải. Biến đổi: 2 2 1 x 4y 8 0 8 2 2 2 L ( x y, ) xy (x 4y 8) 8 . Ta có: L ( , xy ) y 2 x 0 x L ( , xy ) x 8 y 0 y 2 2 ( , xy ) x 4y 8 0
Bài 3. Cực trị của a hàm hai biến số y x 2 1 1 2 . x 16 4 8y
Suy ra hàm số có 4 điểm dừng: 1
• M (2; 1) và M ( 2; 1) ứng với , 1 2 4 1
• M ( 2; 1) và M (2; 1) ứng với . 3 4 4 Vi phân: 2 2 2 dL 2dx 2dxdy 8 dy , d (x,y ) 2xdx 8ydy .
Bài 3. Cực trị của a hàm hai biến số
• Tại M (2; 1) và M ( 2; 1) , với 1 ta có: 1 2 4 2 1 2 2 d L(M ) dx 2dxdy 2dy . 1,2 2 Mặt khác: d ( M ) 0 dx 2 dy 0 1,2 2 2 d L (M ) 8dy 0 . 1,2
M (2; 1) và M ( 2; 1) là hai điểm cực đại. 1 2 • Tương tự
M ( 2; 1) và M (2; 1) là hai điểm cực tiểu. 3 4
………………………………Hết…………………………….