Tài liệu học tập HK1 Toán 12 – Huỳnh Phú Sĩ

Tài liệu học tập HK1 Toán 12 – Huỳnh Phú Sĩ được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

101 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
TÀILIỆU
HỌCTẬP
HK1
TOÁN 12
TrườngTHCS&THPTMỹThuận
VĩnhLong
KẾ HOẠCH TUẦN
L TUẦN 1
L TUẦN 2
L TUẦN 3
L TUẦN 4
L TUẦN 5
L TUẦN 6
L TUẦN 7
L TUẦN 8
L TUẦN 9
L TUẦN 10
L TUẦN 11
L TUẦN 12
L TUẦN 13
L TUẦN 14
L TUẦN 15
L TUẦN 16
L TUẦN 17
L TUẦN 18
MỤCLỤC TOÁN12
MỤC LỤC
PHẦN I GIẢI TÍCH 4
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§1. Sự đồng biến và nghịch biến của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1. Tínhđơnđiệucủahàmsố.................................................................. 5
2. Quytắcxéttínhđơnđiệucủahàmsố....................................................... 6
3. Thựchành................................................................................. 6
§2. Cực trị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1. Kháiniệmcựcđại,cựctiểu................................................................. 11
2. Điềukiệnđủđểhàmsốcócựctrị........................................................... 11
3. Quytắctìmcựctrị......................................................................... 12
4. Thựchành................................................................................. 13
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1. Địnhnghĩa................................................................................ 17
2. CáchtìmGTLN&GTNNcủahàmsốtrênmộtđoạn.......................................... 17
3. Thựchành................................................................................. 18
§4. Đường tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1. Đườngtiệmcậnngang..................................................................... 22
2. Đườngtiệmcậnđứng....................................................................... 22
3. Thựchành................................................................................. 23
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
1. Sơđồkhảosáthàmsố...................................................................... 26
2. Khảosátmộtsốhàmthườnggặp............................................................ 26
3. Sựtươnggiaocủacácđồthị................................................................ 28
4. Thựchành................................................................................. 28
Chương 2. Hàm số lũy thừa. Hàm số mũ và hàm số logarit. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
§1. Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
1. Kháiniệmlũythừa......................................................................... 34
2. Tínhchấtcủalũythừavớisốmũthực....................................................... 35
3. Thựchành................................................................................. 36
§2. Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
1. Kháiniệm................................................................................. 38
2. Đạohàmcủahàmsốlũythừa.............................................................. 38
3. Khảosáthàmsốlũythừa................................................................... 38
4. Thựchành................................................................................. 39
§3. Lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
1. Kháiniệmlôgarit.......................................................................... 41
2. Quytắctínhlôgarit......................................................................... 41
3. Lôgaritthậpphânvàlôgarittựnhiên........................................................ 42
4. Thựchành................................................................................. 42
§4. Hàm số mũ. Hàm số lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
1. Hàmsốmũ................................................................................ 45
2. Hàmsốlôgarit............................................................................. 46
3. Thựchành................................................................................. 46
§5. Phương trình mũ và phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
1. Phươngtrìnhmũ........................................................................... 50
2. Phươngtrìnhlôgarit........................................................................ 50
3. Thựchành................................................................................. 51
§6. Bất phương trình mũ và bất phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
1. Bấtphươngtrìnhmũ....................................................................... 54
2. Bấtphươngtrìnhlôgarit.................................................................... 54
3. Thựchành................................................................................. 55
PHẦN II HÌNH HỌC 58
Soạn:HuỳnhPhúSĩ 4 TrườngTHCS-THPTMỹThuận
MỤCLỤC TOÁN12
Chương 1. Khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
§1. Khái niệm về khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
1. Khốilăngtrụvàkhốichóp................................................................. 59
2. Kháiniệmvềhìnhđadiệnvàkhốiđadiện.................................................. 59
3. Haiđadiệnbằngnhau..................................................................... 60
4. Phânchiavàlắpghépcáckhốiđadiện..................................................... 61
5. Thựchành................................................................................. 61
§2. Đa diện lồi và Đa diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
1. Khốiđadiệnlồi............................................................................ 64
2. Khốiđadiệnđều........................................................................... 64
3. Thựchành................................................................................. 64
§3. Khái niệm về thể tích của khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
1. Kháiniệmvềthểtíchkhốiđadiện.......................................................... 67
2. Thểtíchkhốilăngtrụ...................................................................... 67
3. Thểtíchkhốichóp......................................................................... 67
4. Thựchành................................................................................. 68
Chương 2. Mặt nón, mặt trụ, mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
§1. Khái niệm về khối tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
1. Sựtạothànhmặttrònxoay................................................................. 71
2. Mặtnóntrònxoay.......................................................................... 71
3. Mặttrụtrònxoay........................................................................... 72
4. Thựchành................................................................................. 73
§2. Mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
1. Mặtcầuvàcáckháiniệmliênquanđếnmặtcầu............................................. 76
2. Giaocủamặtcầuvàmặtphẳng............................................................. 76
3. Giaocủamặtcầuvàđườngthẳng.Tiếptuyến................................................ 77
4. Diệntíchvàthểtích........................................................................ 77
5. Thựchành................................................................................. 78
Soạn:HuỳnhPhúSĩ 5 TrườngTHCS-THPTMỹThuận
PHẦNI
GIẢI TÍCH
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§1. Sự đồng biến và nghịch biến của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§2. Cực trị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
§4. Đường tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Chương 2. Hàm số lũy thừa. Hàm số mũ và hàm số logarit. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
§1. Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
§2. Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
§3. Lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
§4. Hàm số mũ. Hàm số lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
§5. Phương trình mũ và phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
§6. Bất phương trình mũ và bất phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Soạn:HuỳnhPhúSĩ 6 TrườngTHCS-THPTMỹThuận
Chương1.Ứngdụngđạohàmđểkhảosátvàvẽđồthịcủahàmsố TOÁN12
Chương1.
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ
ĐỒ THỊ CỦA HÀM SỐ
§1.SỰ ĐỒNG BIẾN VÀ NGHỊCH BIẾN
CỦA HÀM SỐ
Đặt vấn đề
Chohaihàmsốy =2x −6 vày =3+2x −x
2
lầnlượtcóbảngbiếnthiênnhưsau:
x
y
−∞
+∞
−∞−∞
+∞+∞
x
y
−∞
1
+∞
−∞−∞
44
−∞−∞
1)Chỉracáckhoảngđồngbiến,nghịchbiếncủamỗihàmsốtrên.
2)Giảithíchnguyênnhâncủasựbiếnthiênđó.
3)Hãychobiếtcáchtìmcácgiátrịtạihaiđầumútcủatừngmũitêntrongbảng.
1 TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1 Định nghĩa
O
x
y
1 3
Hàm số này đồng biến trên
khoảng ......, nghịch biến
trênkhoảng......,khôngđổi
trênkhoảng......
Giảsửhàmsốy =f(x) xácđịnhtrênK (khoảng,đoạnhoặcnửakhoảng).
○ f(x) đồngbiến(tăng)trênK nếuvới∀x
1
, x
2
∈ K màx
1
< x
2
thìf
(
x
1
)
... f
(
x
2
)
○ f(x)nghịchbiến(giảm)trênK nếuvới∀x
1
, x
2
∈ K màx
1
< x
2
thìf
(
x
1
)
...f
(
x
2
)
2 Tính đơn điệu và dấu của đạo hàm
Chohàmsốy =f(x) cóđạohàmtrênK.
○ Nếuf
0
(x)> 0,∀x ∈ K thìf(x) ............... trênK.
○ Nếuf
0
(x)< 0,∀x ∈ K thìf(x) ............... trênK.
○ Nếuf
0
(x)=0,∀x ∈ K thìf(x) ............... trênK.
Ví dụ 1. Xétsựbiếnthiêncủahàmsốy =3+2x −x
2
.
O
x
y
1
I
4
−1 3
Paraboly =3+2x−x
2
cóđỉnh
...... vàhướngxuốngvìa ...
Soạn:HuỳnhPhúSĩ 7 TrườngTHCS-THPTMỹThuận
§1.Sựđồngbiếnvànghịchbiếncủahàmsố TOÁN12
2 QUY TẮC XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
!
Bước1. Tìm..................
Bước2. Tìm............ f
0
(x).Tìmx đểf
0
(x)...... hoặc..................
Bước3. Lậpbảng...............
Bước4. Kếtluậnvềcáckhoảngđồngbiến,nghịchbiếncủahàmsố.
Ví dụ 2. Xétsựbiếnthiêncủacáchàmsốsau:
a)y =
x
3
3
−
x
2
2
−2x +2
b)y =
x −1
x +2
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Mệnhđềnàosauđâylàđúng?
A. Hàmsốy =f(x)đồngbiếntrênkhoảng(a;b)khivàchỉkhif
0
(x)≥ 0, ∀x ∈
(a;b).
B. Nếuf
0
(x)≥ 0, ∀x ∈ (a;b)thìhàmsốy =f(x) đồngbiếntrênkhoảng(a;b).
C. Hàmsốy =f(x)đồngbiếntrênkhoảng(a;b)khivàchỉkhif
0
(x)> 0, ∀x ∈
(a;b).
D. Nếuf
0
(x)> 0, ∀x ∈ (a;b)thìhàmsốy =f(x) đồngbiếntrênkhoảng(a;b).
Câu 2.
Chohàmsốy =f(x) cóđồthịnhưhìnhvẽ.Tìm
khoảngđồngbiếncủahàmsố.
A. (−2;1). B. (−1;2).
C. (−2;−1). D. (−1;1).
x
y
−2 −1 0 1
−3
−1
1
Câu 3. Chohàmsốy =f(x)cóđồthịnhưhìnhvẽ.Mệnhđềnàosauđâylàđúng?
x
y
−1 0 1 2
−3
−1
1
Soạn:HuỳnhPhúSĩ 8 TrườngTHCS-THPTMỹThuận
§1.Sựđồngbiếnvànghịchbiếncủahàmsố TOÁN12
A. Hàmsốđồngbiếntrênkhoảng(−3;1).
B. Hàmsốnghịchbiếntrênkhoảng(0;2).
C. Hàmsốnghịchbiếntrênkhoảng(−1;0).
D. Hàmsốđồngbiếntrênkhoảng(0;1).
Câu 4. Chohàmsốy =f(x)cóbảngbiếnthiênnhưhìnhvẽ.Hàmsốđãcho
nghịchbiếntrênkhoảngnàosauđây?
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
33
−2−2
+∞+∞
A. (0;+∞). B. (−1;1). C. (−∞;0). D. (−∞;−2).
Câu 5. Chohàmsốy =f(x) cóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
2
+∞
− −
22
−∞
+∞
22
Khẳngđịnhnàosauđâylàđúng?
A. HàmsốnghịchbiếntrênR \{2}.
B. Hàmsốđồngbiếntrên(−∞;2) và(2;+∞).
C. Hàmsốnghịchbiếntrên(−∞;2) và(2;+∞).
D. HàmsốnghịchbiếntrênR.
Câu 6. Chohàmsốy =f(x) cóbảngxétdấuđạohàmnhưsau:
x
y
0
−∞
−2
0 2
+∞
+
0
− −
0
−
Mệnhđềnàosauđâylàđúng?
A. Hàmsốnghịchbiếntrênkhoảng(−∞;−2).
B. Hàmsốđồngbiếntrênkhoảng(−∞;0).
C. Hàmsốnghịchbiếntrênkhoảng(0;2).
D. Hàmsốđồngbiếntrênkhoảng(−2;0).
Câu 7. Chohàmsốy =f(x) cóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
−4 −1
+∞
+
0
+
0
−
−∞−∞
33
−∞−∞
0
Tìmmệnhđềđúngtrongcácmệnhđềsau:
A. Hàmsốđồngbiếntrênkhoảng(−∞;3).
B. Hàmsốnghịchbiếntrênkhoảng(−2;+∞).
C. Hàmsốnghịchbiếntrênkhoảng(−∞;−2).
D. Hàmsốđồngbiếntrênkhoảng(−4;−1).
Câu 8.
Chohàmsốy =f(x).Biếtrằngf(x) cóđạohàm
f
0
(x) vớiđồthịnhưhìnhvẽ.Khẳngđịnhnàosau
đâyđúngvềhàmsốy =f(x)?
A. Hàmsốđồngbiếntrênkhoảng(−∞;−1).
B. Hàmsốđồngbiếntrênkhoảng(−1;0).
C. Hàmsốđồngbiếntrênkhoảng(1;2).
D. Hàmsốnghịchbiếntrênkhoảng(0;+∞).
x
y
−1 0 1 2
Câu 9. Hàmsốy =
x
3
3
−
x
2
2
−6x +
3
4
Soạn:HuỳnhPhúSĩ 9 TrườngTHCS-THPTMỹThuận
§1.Sựđồngbiếnvànghịchbiếncủahàmsố TOÁN12
A. Đồngbiếntrênkhoảng(−2;3).
B. Nghịchbiếntrênkhoảng(−2;3).
C. Nghịchbiếntrênkhoảng(−∞;−2).
D. Đồngbiếntrênkhoảng(−2;+∞).
Câu 10. Chohàmsốy =x
4
−8x
2
−4.Hàmsốđãchonghịchbiếntrênkhoảng
A. (−2;0) và(2;+∞). B. (−∞;−2) và(0;2).
C. (−2;0) và(0;2). D. (−∞;−2) và(2;+∞).
Câu 11. Chohàmsốy =
x +1
2−x
.Khẳngđịnhnàosauđâyđúng?
A. Hàmsốđồngbiếntrêntừngkhoảngxácđịnhcủanó.
B. HàmsốđồngbiếntrênR.
C. Hàmsốđồngbiếntrên(−∞;2)∪(2;+∞).
D. Hàmsốnghịchbiếntrêntừngkhoảngxácđịnhcủanó.
Câu 12. Chohàmsốy =x
3
−3x +1.Mệnhđềnàosauđâyđúng?
A. Hàmsốnghịchbiếntrênkhoảng(−1;3).
B. Hàmsốđồngbiếntrênkhoảng(−1;1).
C. Hàmsốđồngbiếntrênkhoảng(−∞;−1) và(1;+∞).
D. Hàmsốnghịchbiếntrênkhoảng(−2;1).
Câu 13. Chohàmsốy =
3−x
2x −1
.Mệnhđềnàosauđâylàđúng?
A. Hàmsốnghịchbiếntrên
−∞;
1
2
.
B. HàmsốđồngbiếntrênR.
C. Hàmsốđồngbiếntrên
1
2
;+∞
.
D. HàmsốnghịchbiếntrênR.
Câu 14. Hàmsốy =2x
4
+3 nghịchbiếntrênkhoảngnàodướiđây?
A. (3;+∞). B. (0;+∞). C. (−∞;−3). D. (−∞;0).
Câu 15. Hàmsốy =
√
4−x
2
nghịchbiếntrênkhoảng
A. (0;2). B. (−2;0). C. (0;+∞). D. (−2;2).
Câu 16. Hàmsốy =
√
−x
2
+3x đồngbiếntrênkhoảng
A.
−∞;
3
2
. B.
0;
3
2
. C.
3
2
;3
. D.
3
2
;+∞
.
Câu 17. HàmsốnàosauđâynghịchbiếntrênR?
A. y =x
3
−3x
2
+4. B. y =−x
4
−2x
2
−3.
C. y =x
3
+3x. D. y =−x
3
+3x
2
−3x +2.
Câu 18. HàmsốnàosauđâyđồngbiếntrênR?
A. y =
√
x
2
−3x +2. B. y =x
4
+x
2
+1.
C. y =
x −1
x +1
. D. y =x
3
+5x +13.
Câu 19. Tìmtấtcảcácgiátrịcủathamsốm đểhàmsốy =−
x
3
3
+mx
2
−(2m+
3)x +4 nghịchbiếntrênR.
A. −1≤ m ≤ 3. B. −3< m < 1. C. −1< m < 3. D. −3≤ m ≤ 1.
Câu 20. Tìmtấtcảcácgiátrịcủathamsốm đểhàmsốy =−
x
3
3
−mx
2
+(2m−
3)x −m +2 nghịchbiếntrênR.
A. m ∈ (−∞;−3)∪(1;+∞). B. m ∈ [−3;1].
C. m ∈ (−∞;1]. D. m ∈ (−3;1).
Câu 21. Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
x
3
3
−2mx
2
+4x−5
đồngbiếntrênR.
A. 0< m < 1. B. −1≤ m ≤ 1. C. 0≤ m ≤ 1. D. −1< m < 1.
Câu 22. Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
x +2−m
x +1
nghịchbiếntrêncáckhoảngxácđịnhcủanó.
A. m ≤ 1. B. m < 1. C. m < −3. D. m ≤ −3.
Câu 23. Tìmtấtcảcácgiátrịcủathamsốm đểhàmsốy =
mx +1
x +m
đồngbiến
trênkhoảng(2;+∞).
A. −2≤ m < −1 hoặcm > 1. B. m ≤ −1 hoặcm > 1.
C. −1< m < 1. D. m < −1 hoặcm ≥ 1.
Soạn:HuỳnhPhúSĩ 10 TrườngTHCS-THPTMỹThuận
§1.Sựđồngbiếnvànghịchbiếncủahàmsố TOÁN12
Câu 24. Sốgiátrịnguyêncủam đểhàmsốy =
mx −2
−2x +m
nghịchbiếntrên
khoảng
1
2
;+∞
là
A. 4. B. 5. C. 3. D. 2.
Câu 25. Hàmsốy =ax
3
+bx
2
+cx +d đồngbiếntrênR khi
A.
a =b, c > 0
b
2
−3ac ≤ 0
. B.
a =b =c =0
a > 0, b
2
−3ac < 0
.
C.
a =b =0, c > 0
a > 0, b
2
−3ac ≤ 0
. D.
a =b =0, c > 0
a > 0, b
2
−3ac ≥ 0
.
Câu 26. Chohàmsốy = f(x)cóđạohàmf
0
(x) = x(x −1)
2
(x − 2).Tìmkhoảng
nghịchbiếncủađồthịhàmsốy =f(x).
A. (−∞;0) và(1;2). B. (0;1).
C. (0;2). D. (2;+∞).
Câu 27. Chohàmsốy =f(x)cóđạohàmy
0
=x
2
(x−2).Mệnhđềnàosauđâylà
đúng?
A. HàmsốnghịchbiếntrênR.
B. Hàmsốđồngbiếntrên(0;2).
C. Hàmsốnghịchbiếntrên(−∞;0) và(2;+∞).
D. Hàmsốđồngbiếntrên(2;+∞).
Câu 28. Chohàmsốy =f(x)thỏamãnf
0
(x)=x
2
−5x+4, ∀x ∈ R.Khẳngđịnh
nàosauđâylàđúng?
A. Hàmsốđồngbiếntrênkhoảng(−∞;3).
B. Hàmsốnghịchbiếntrênkhoảng(3;+∞).
C. Hàmsốnghịchbiếntrênkhoảng(2;3).
D. Hàmsốđồngbiếntrênkhoảng(1;4).
Câu 29. Chohàmsốf(x) cóbảngxétdấucủađạohàmnhưsau:
x
y
0
−∞
1 2 3 4
+∞
−
0
+
0
+
0
−
0
+
Hàmsốy =3f(x +2)−x
3
+3x đồngbiếntrênkhoảngnàosauđây:
A. (1;+∞). B. (−∞;−1). C. (−1;0). D. (0;2).
Câu 30.
Chohàmsốy =f(x)cóđồthịhàm
sốy =f
0
(x) nhưhìnhvẽ.Hàmsốy =
f(3−2x)nghịchbiếntrênkhoảngnào
sauđây:
A. (−1;+∞). B. (0;2).
C. (−∞;−1). D. (1;3).
x
y
−2 0 2 5
L TỰ LUẬN
Câu 1 (SGK GT12). Xétsựđồngbiến,nghịchbiếncủacáchàmsố:
a)y =4+3x −x
2
b)y =
1
3
x
3
+3x
2
−7x −2
c)y =x
4
−2x
2
+3
d)y =
3x +1
1−x
Câu 2. Tìmm đểhàmsốy =
x
3
3
−
mx
2
2
+2x +2019 đồngbiếntrênR.
Soạn:HuỳnhPhúSĩ 11 TrườngTHCS-THPTMỹThuận
§1.Sựđồngbiếnvànghịchbiếncủahàmsố TOÁN12
d Vocabulary
function hàmsố
domain tậpxácđịnh
monotonic tínhđơnđiệu
increasing đồngbiến
decreasing nghịchbiến
derivative đạohàm
graph đồthị
variation chart bảngbiếnthiên
Soạn:HuỳnhPhúSĩ 12 TrườngTHCS-THPTMỹThuận
§2.Cựctrịcủahàmsố TOÁN12
§2.CỰC TRỊ CỦA HÀM SỐ
Đặt vấn đề
Chohàmsốy =f(x) cóđồthịnhưhìnhvẽdướiđây.
O
x
y
x
1
A
y
1
x
2
C
y
2
B
2
Mộtcáchtrựcquan,hãychỉranhữngđiểmlồi,điểmlõmcủađồthị.
1 KHÁI NIỆM CỰC ĐẠI, CỰC TIỂU
O
x
y
1
1
Hàmsốnàyđạtcựcđạitạix =
... vàđạtcựctiểutạix =...
Giảsửhàmsốy =f(x) xácđịnhvàliêntụctrênK vàđiểmx
0
∈ K.
○ Nếu∃h > 0saochof(x) < f
(
x
0
)
vớimọix ∈
(
x
0
−h;x
0
+h
)
vàx 6= x
0
thìta
nóif(x) đạt............ tạix
0
.
○ Nếu∃h > 0saochof(x) > f
(
x
0
)
vớimọix ∈
(
x
0
−h;x
0
+h
)
vàx 6= x
0
thìta
nóif(x) đạt............ tạix
0
.
Chú ý:
•Nếuf(x) đạtCĐtạix
0
thìtagọix
0
làđiểmCĐcủa.........,f
(
x
0
)
làgiátrịCĐcủa
.........,cònđiểmM
(
x
0
;f
(
x
0
))
làđiểmCĐcủa..........Tagọitươngtựđốivới
cựctiểu.
•CácđiểmCĐvàCTđượcgọichunglà...............,giátrịCĐvàgiátrịCTđược
gọichunglà......... củahàmsố.
•Nếuf(x) xácđịnhtrênK vàđạtcựctrịtạix
0
thìf
0
(
x
0
)
=....
O
x
y
x
1
y
1
x
2
y
2
Điểmcựcđạicủahàmsố
Giátrịcựctiểucủahàmsố
Điểmcựctiểucủahàmsố
Giátrịcựcđạicủahàmsố
ĐiểmcựcđạiA
(
x
1
;y
1
)
củađồthị
ĐiểmcựctiểuB
(
x
2
;y
2
)
củađồthị
2 ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊ
Giảsửhàmsốy =f(x) ......... trênK vàxácđịnhtrênK hoặcK \{x
0
}.
○ Nếuf
0
(
x
0
)
> 0khix < x
0
vàf
0
(
x
0
)
< 0khix > x
0
thìx
0
làmộtđiểm.........
củahàmsốf(x).
○ Nếuf
0
(
x
0
)
< 0khix < x
0
vàf
0
(
x
0
)
> 0khix > x
0
thìx
0
làmộtđiểm.........
củahàmsốf(x).
Soạn:HuỳnhPhúSĩ 13 TrườngTHCS-THPTMỹThuận
§2.Cựctrịcủahàmsố TOÁN12
Ví dụ 1. Tìmcáccựctrịcủahàmsốy =x
3
−x
2
−x +3.
3 QUY TẮC TÌM CỰC TRỊ
1 Quy tắc 1
!
Bước1. Tìm..................
Bước2. Tìm............ f
0
(x).Tìmx đểf
0
(x)...... hoặc..................
Bước3. Lậpbảng...............
Bước4. Kếtluậnvềcácđiểmcựctrị.
Ví dụ 2. Tìmcựctrịcủahàmsốy =
3x +1
x +1
.
2 Định lý
Giảsửhàmsốy =f(x) cóđạohàmcấp... trênK.
○ Nếuf
0
(
x
0
)
=0 vàf
00
(
x
0
)
> 0 thìx
0
làđiểm......... củahàmsố.
○ Nếuf
0
(
x
0
)
=0 vàf
00
(
x
0
)
< 0 thìx
0
làđiểm......... củahàmsố.
Ví dụ 3. Tìmcựctrịcủahàmsốy =
x
4
4
−2x
2
+6.
3 Quy tắc 2
!
Bước1. Tìm..................
Bước2. Tìm............ f
0
(x).Tìmx đểf
0
(x)...0.
Bước3. Tìmđạohàmcấp... rồitínhcácgiátrịf
00
(x).
Bước4. Kếtluậnvềcácđiểmcựctrị.
Soạn:HuỳnhPhúSĩ 14 TrườngTHCS-THPTMỹThuận
§2.Cựctrịcủahàmsố TOÁN12
Ví dụ 4. Chohàmsốy =
x
3
3
−(m +1)x
2
+mx −2.Tìmm đểhàmsốđạtcựcđạitại
x =−1.
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1.
Chohàmsốy = f(x)xácđịnh,liêntụctrênđoạn[−2;2]
vàcóđồthịlàđườngcongtronghìnhbên.Hàmsốđãcho
đạtcựctiểutạiđiểm
A. x =1. B. x =−2.
C. x =2. D. x =−1.
x
y
−2−1 10 2
2
4
Câu 2.
Chohàmsốy =f(x) cóđồthịnhưhìnhvẽ.Giátrịcựcđại
củahàmsốlà
A. −2. B. 0. C. −1. D. 1.
x
y
−1
−2
1
−1
Câu 3.
Chohàmsốy =f(x)liêntụctrênR vàcóđồthịnhư
hìnhvẽ.Đồthịhàmsốđãchocóbaonhiêuđiểmcực
trị?
A. 4. B. 5. C. 2. D. 3.
x
y
−1
2
1O
Câu 4. Chohàmsốy =f(x) cóbảngbiếnthiênnhưhình.
x
y
0
y
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
11
55
−∞−∞
Hàmsốđạtcựctiểutạiđiểm
A. x =1. B. x =5. C. x =2. D. x =0.
Soạn:HuỳnhPhúSĩ 15 TrườngTHCS-THPTMỹThuận
§2.Cựctrịcủahàmsố TOÁN12
Câu 5. Hàmsốy =f(x) liêntụctrênR vàcóbảngbiếnthiênnhưhìnhvẽ.
x
y
0
y
−∞
1 2
+∞
+
0
−
+
−∞−∞
33
00
+∞+∞
Mệnhđềnàosauđâylàđúng?
A. f(x) có2 điểmcựctrị. B. f(x) cóđúng1 điểmcựctrị.
C. f(x) khôngcógiátrịcựctiểu. D. f(x) khôngcógiátrịcựcđại.
Câu 6. Chohàmsốy =f(x) cóbảngbiếnthiênnhưhình.
x
y
0
y
−∞
−2
0 2
+∞
+
0
−
0
+
0
−
−∞−∞
33
11
33
−∞−∞
Giátrịcựcđạicủahàmsốbằng
A. −2. B. −1. C. 2. D. 3.
Câu 7. Chohàmsốy =f(x) xácđịnh,liêntụctrênR vàcóbảngbiếnthiênnhư
hìnhvẽ.
x
y
0
y
−∞
1 2
+∞
+
−
0
−
−∞−∞
22
−∞−∞
Khẳngđịnhnàosauđâylàđúng?
A. Hàmsốcógiátrịcựcđạibằng1. B. Hàmsốcóđúng2 cựctrị.
C. Hàmsốcógiátrịcựcđạibằng2. D. Hàmsốkhôngxácđịnhtạix =1.
Câu 8. Chohàmsốy =f(x) cóbảngbiếnthiênnhưhình.
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
+
0
−
−∞−∞
22
−1 −1
33
22
Hỏihàmsốy =f(x) cóbaonhiêuđiểmcựctrị?
A. 1. B. 3. C. 2. D. 4.
Câu 9. Chohàmsốy =f(x) cóbảngbiếnthiênnhưhình.
x
y
0
y
−∞
−1
1 3
+∞
+
−
0
+
−
−∞−∞
33
−1−1
+∞ +∞
−∞−∞
Sốđiểmcựctrịcủahàmsốy =f(x) là
A. 0. B. 2. C. 3. D. 1.
Câu 10. Tìmđiểmcựctiểucủahàmsốy =x
3
−3x
2
−9x +2.
A. x =25. B. x =3. C. x =7. D. x =−1.
Câu 11. Điểmcựctiểucủađồthịhàmsốy =x
3
−3x +5 là
A. M(1;3). B. N(−1;7). C. Q(3;1). D. P(7;−1).
Soạn:HuỳnhPhúSĩ 16 TrườngTHCS-THPTMỹThuận
§2.Cựctrịcủahàmsố TOÁN12
Câu 12. Chohàmsốy =
x
3
3
−x −11.Giátrịcựctiểucủahàmsốlà
A. 2. B. −
1
3
. C. −
5
3
. D. −1.
Câu 13. Điểmcựcđạicủahàmsốy =x
4
−8x
2
−3 là
A. S(0;−3). B. x =0. C. x =±2. D. y =0.
Câu 14. Tìmđiểmcựcđạicủađồthịhàmsốy =
x
2
+
2
x
.
A. N(−2;−2). B. x =−2. C. M(2;2). D. x =2.
Câu 15. Chohàmsốy =x +
√
12−3x
2
.Khẳngđịnhnàosauđâyđúng?
A. Hàmsốđạtcựcđạitạix =−1. B. Hàmsốđạtcựcđạitạix =1.
C. Hàmsốđạtcựctiểutạix =−1. D. Hàmsốđạtcựctiểutạix =1.
Câu 16. Chohàmsốy = −x
4
+2x
2
+3cógiátrịcựcđạivàgiátrịcựctiểulần
lượtlày
1
, y
2
.Khiđóy
1
+y
2
bằng
A. 7. B. 1. C. 3. D. −1.
Câu 17. Đồthịhàmsốy =−x
4
−x
2
+3 cóbaonhiêuđiểmcựctrị?
A. 2. B. 3. C. 1. D. 0.
Câu 18. Hàmsốy =x
3
+3 cóbaonhiêuđiểmcựctrị?
A. 3. B. 0. C. 1. D. 2.
Câu 19. Hàmsốy =
−2x +1
x −3
cóbaonhiêuđiểmcựctrị?
A. 1. B. 0. C. 3. D. 2.
Câu 20. Đồthịhàmsốnàosauđâycóbađiểmcựctrị?
A. y =2x
4
−4x
2
+3. B. y =
x
2
+2
2
.
C. y =−x
4
−3x
2
. D. y =x
3
−6x
2
+9x −5.
Câu 21. Hàmsốnàosauđâykhôngcócựctrị?
A. y =2x
3
−3x
2
. B. y =x
4
+2.
C. y =
x +1
x −2
. D. y =−x
4
+2x
2
+1.
Câu 22. Chohàmsốy =f(x)cóđạohàmf
0
(x)=x(x−1)
2
(x+1).Hỏihàmsốcó
baonhiêuđiểmcựctrị?
A. 1. B. 3. C. 2. D. 0.
Câu 23. Chohàmsốf(x)cóđạohàmf
0
(x)=(x−1)(x−2)
2
(x−3)
3
(x−4)
4
,∀x ∈ R.
Sốđiểmcựctrịcủahàmsốđãcholà
A. 3. B. 5. C. 2. D. 4.
Câu 24. Chohàmsốf(x) cóđạohàmf
0
(x)=(x +1)
x
2
−x
(x −1),∀x ∈ R.Số
điểmcựctrịcủahàmsốđãcholà
A. 1. B. 3. C. 2. D. 0.
Câu 25. Biếtrằngđồthịhàmsốy = x
3
−3x +1cóhaiđiểmcựctrịA, B.Khi
đóđườngthẳngAB cóphươngtrìnhlà
A. y =2x −1. B. y =x −2. C. y =−x +2. D. y =1−2x.
Câu 26. Tìmtấtcảgiátrịcủathamsốm đểđồthịhàmsốy =x
4
+(6m−4)x
2
+1−m
có3 điểmcựctrị.
A. m ≥
2
3
. B. m ≤
2
3
. C. m >
2
3
. D. m <
2
3
.
Câu 27. Tìmtấtcảcácgiátrịcủathamsốm đểhàmsốy =x
3
−3x
2
+mx +1
có2 điểmcựctrị.
A. m ≤ 3. B. m > 3. C. m > −3. D. m < 3.
Câu 28. Tậphợpcácgiátrịcủathamsốm đểhàmsốy =
x
3
3
−6x
2
+(m−2)x+11
có2 điểmcựctrịtráidấu.
A. (−∞;38). B. (−∞;2). C. (−∞;2]. D. (2;38).
Câu 29. Hàmsốy =x
3
−(m +2)x +m đạtcựctiểutạix =1 khi
A. m =−1. B. m =2. C. m =−2. D. m =1.
Câu 30. Vớigiátrịnàocủathamsốm thìhàmsốy =x
3
−mx
2
+(2m−3)x −3
đạtcựcđạitạix =1?
A. m ≤ 3. B. m =3. C. m < 3. D. m > 3.
Soạn:HuỳnhPhúSĩ 17 TrườngTHCS-THPTMỹThuận
§2.Cựctrịcủahàmsố TOÁN12
L TỰ LUẬN
Câu 1 (SGK GT12). Tìmcácđiểmcựctrịcủacáchàmsốsau
a)y =2x
3
+3x
2
−36x −10 b)y =x
4
−2x
2
+1
Câu 2 (SGK GT12). Xácđịnhgiátrịcủathamsốm đểhàmsốy =
x
2
+mx +1
x +m
đạtcựcđạitạix =2.
d Vocabulary
local maximum cựcđại
local minimum cựctiểu
extrema cựctrị
value giátrị
interval khoảng
closed interval đoạn
sign dấu
parameter thamsố
Soạn:HuỳnhPhúSĩ 18 TrườngTHCS-THPTMỹThuận
§3.Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố TOÁN12
§3.GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ
NHẤT CỦA HÀM SỐ
Đặt vấn đề
TheoyêucầucủavuaHùng,SơnTinhvàThủyTinhphảiđếnnôngtrạicủaBạchCốtTinhđểmangvoichínngà,gà
chíncựa,ngựachínhồngmaovàcùngxuấtphátlúc7hsángđếnchỗcủaMịNương.BiếtrằngchỗởcủaBạchCốt
Tinhlàtrongrừngrậm,cáchđườngquốclộ30 kmvàvịtrícủaMịNươngđượcmôtảnhưhình:
30 km
A
50km MịNương
g
SơnTinhđithẳngtheođườngrừngđếnchỗMịNương,cònThủyTinhđithẳngraquốclộ(điểmA),rồitheođường
quốclộđếnchỗcủaMịNương.Biếtrằngvậntốctốiđakhidichuyểntrongrừngrậmlà30 km/h,trênđườngquốclộ
là50 km/hvàđoạnquốclộtronghìnhlàđườngthẳng.
a)GiữaSơnTinhvàThủyTinh,aisẽđếnnơitrước?
b)NếucùngxuấtphátnhưSơnTinhvàThủyTinh,bạnsẽchọnđườngđithếnàođểđếntrướchọ?
1 ĐỊNH NGHĨA
O
x
y
1
A
1
−
3
2
B
−1
C
2
D
3
Quan sát đồ thị ta thấy
max
[−2;2]
f(x)=...,min
[−2;2]
f(x)=...
Chohàmsốy =f(x) xácđịnhtrêntậpD .
○ SốM đượcgọilàgiátrịlớnnhấtcủaf(x)trênD nếuf(x) ... M, ∀x ∈ D và
∃x
0
∈ D saochof
(
x
0
)
... M.KíhiệuM =max
D
f(x).
○ Sốm đượcgọilàgiátrịnhỏnhấtcủaf(x)trênD nếuf(x) ... m, ∀x ∈ D và
∃x
0
∈ D saochof
(
x
0
)
... m.Kíhiệum =min
D
f(x).
2 CÁCH TÌM GTLN & GTNN CỦA HÀM SỐ TRÊN MỘT ĐOẠN
1 Định lý
Mọihàmsố......... trênmộtđoạnđềucógiátrịlớnnhấtvàgiátrịnhỏnhất
trênđoạnđó.
2 Quy tắc
!
Bước1. Tìmcácgiátrịx ∈ (a;b) đểf
0
(x)...... hoặc............
Bước2. Tính...... củaf(x) tạia, b vàtạicácđiểmx vừatìmđượcởbước1.
Bước3. Tìmsố... nhấtvàsố... nhấttrongcácsốđãtínhđượcởbước2.
Soạn:HuỳnhPhúSĩ 19 TrườngTHCS-THPTMỹThuận
§3.Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố TOÁN12
Ví dụ 1. Tìmgiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsốy =x
3
−6x
2
+9x +2trên
đoạn[−1;2].
O
x
y
1
min
4
max
f(x) đồngbiếntrênđoạn[1;4].
Nhận xét
Nếuf
0
(x)không......... trên[a;b]thìf
(
x
)
đạtGTLNvàGTNNtạicácđầumút
của[a;b].
Ví dụ 2. Tìmgiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsốy =
2x +1
x −2
trên
[2020;2021].
Ví dụ 3. Trongtìnhhuốngđãnêuởđầubài,hãytìmrađườngđisaochothờigianđến
chỗMịNươnglàngắnnhất.
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1.
Chohàmsốy =f(x)liêntụctrênđoạn[−1;3]vàcó
đồthịnhưhìnhvẽ.GọiM vàm lầnlượtlàgiátrịlớn
nhấtvàgiátrịnhỏnhấtcủahàmsốđãchotrênđoạn
[−1;3].GiátrịcủaM −m bằng
A. 0. B. 1. C. 4. D. 5.
O
x
y
−1
1
−2
2
3
3
Câu 2. Chohàmsốy =f(x)xácđịnhtrênđoạn
h
−
√
3;
√
5
i
vàcóbảngbiếnthiên
nhưhìnhvẽ.Khẳngđịnhnàosauđâylàđúng?
x
y
0
y
−
√
3
−1
1
√
5
+
0
−
0
+
00
11
−2−2
2
√
52
√
5
Soạn:HuỳnhPhúSĩ 20 TrườngTHCS-THPTMỹThuận
§3.Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố TOÁN12
A. min
[
−
√
3;
√
5
]
f(x)=0. B. max
[
−
√
3;
√
5
]
f(x)=2.
C. max
[
−
√
3;
√
5
]
f(x)=2
√
5. D. min
[
−
√
3;
√
5
]
f(x)=2.
Câu 3. Chobảngbiếnthiêncủahàmsốy = f(x) nhưhình.Tìmgiátrịlớnnhất
M vàgiátrịnhỏnhấtm củahàmsốtrênđoạn[−2;3].
x
y
−∞
−2
0 3
+∞
−∞−∞
22
−1−1
+∞+∞
1
A.
(
M =3
m =−2
. B.
(
M =0
m =3
. C.
(
M =2
m =−1
. D.
(
M =1
m =−1
.
Câu 4. Giátrịnhỏnhấtcủahàmsốy =x
3
−3x +5 trênđoạn[2;4] là
A. 3. B. 7. C. 5. D. 0.
Câu 5. Giátrịlớnnhấtcủahàmsốy =x
3
−3x +4 trênđoạn[−2;2] là
A. 10. B. 6. C. 24. D. 4.
Câu 6. Tìmgiátrịlớnnhấtcủahàmsốf(x)=2x
3
+3x
2
− 12x +2trênđoạn
[−1;2].
A. max
[−1;2]
f(x)=10. B. max
[−1;2]
f(x)=6.
C. max
[−1;2]
f(x)=11. D. max
[−1;2]
f(x)=15.
Câu 7. Giátrịlớnnhấtcủahàmsốy =x(5−2x)
2
trênđoạn[0;3] là
A.
250
3
. B. 0. C.
250
27
. D.
125
27
.
Câu 8. Giátrịlớnnhấtcủahàmsốy =x
4
−3x
2
+2 trênđoạn[0;3] là
A. 57. B. 55. C. 56. D. 54.
Câu 9. Tìmgiátrịlớnnhấtcủahàmsốy =x
4
−2x
2
trênđoạn[0;1].
A. −1. B. 0. C. 1. D. −2.
Câu 10. Giátrịlớnnhấtcủahàmsốy =
x
2
−3x
x +1
trênđoạn[0;3] bằng
A. 3. B. 2. C. 0. D. 1.
Câu 11. Tìmgiátrịnhỏnhấtcủahàmsốy =x +1+
4
x
trênđoạn[1;3].
A. 4. B.
16
3
. C. 5. D. 6.
Câu 12. Tìm giá trị lớn nhất của hàm số y = 3 +
√
x
2
−2x +8 trên đoạn
[−2;2].
A. 7. B. 9. C. 3+2
√
2. D. 3+
√
7.
Câu 13. Tìmgiátrịlớnnhấtcủahàmsốy =
3x −1
x −3
trênđoạn[0;2].
A. −
1
3
. B. −5. C. 5. D.
1
3
.
Câu 14. Tìmgiátrịnhỏnhấtcủahàmsốy =
x +1
x −1
trênđoạn[2;3].
A. −3. B. 3. C. 2. D. 4.
Câu 15. Giátrịnhỏnhấtm củahàmsốy =x
3
−3x +5 trênđoạn[2;4] là
A. 0. B. 5. C. 7. D. 3.
Câu 16. TìmtậpgiátrịT củahàmsốy =
√
x −1+
√
9−x.
A. T =[1;9]. B. T =
h
0;2
√
2
i
. C. T =(1;9). D. T =
h
2
√
2;4
i
.
Câu 17. GọiM vàm lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố
y =x
√
1−x
2
.KhiđóM −m bằng
A. 1. B. 2. C. 4. D. 3.
Câu 18. Chohàmsốy =f(x) liêntụctrên[−3;2] vàcóbảngbiếnthiênnhưsau:
x
f(x)
−3 −1
0 1 2
22
33
00
22
11
Soạn:HuỳnhPhúSĩ 21 TrườngTHCS-THPTMỹThuận
§3.Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố TOÁN12
GọiM, m lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủaf(x) trênđoạn[−1;2].
TínhM +m.
A. 3. B. 2. C. 1. D. 4.
Câu 19. Chohàmsốy =
x +1
x −1
.GọiM, m lầnlượtlàgiátrịlớnnhất,giátrịnhỏ
nhấtcủahàmsốtrênđoạn[0;2].Khiđó4M −2m bằng
A. 10. B. 6. C. 5. D. 4.
Câu 20. Giátrịnhỏnhấtcủahàmsốy =x
2
+2x +5 trênnửakhoảng[−4;+∞)
là
A. 13. B. −17. C. 4. D. −9.
Câu 21. Tìmgiátrịnhỏnhấtm củahàmsốy =x −1+
4
x −1
trênnửakhoảng
(1;+∞).
A. m =5. B. m =4. C. m =2. D. m =3.
Câu 22. Hàmsốy =x
4
+2x
2
−3
A. khôngcógiátrịlớnnhấtvàgiátrịnhỏnhất.
B. khôngcócựctrị.
C. cógiátrịnhỏnhất.
D. cógiátrịlớnnhất.
Câu 23. Tìmgiátrịlớnnhấtcủahàmsốf(x)=−x
4
−3x
2
+2020 trênR.
A. max
R
f(x)=2020. B. max
R
f(x)=2021.
C. max
R
f(x)=2019. D. max
R
f(x)=2018.
Câu 24. Tìmtấtcảcácgiátrịthựccủathamsốm saochohàmsốy =x
4
−2(m−
1)x
2
+m −2 đồngbiếntrênkhoảng(1;3).
A. m ∈ (−∞;−5). B. m ∈ [5;2).
C. m ∈ (2;+∞). D. m ∈ (−∞;2].
Câu 25. MộtngọnhảiđăngđặttạivịtríA cáchbờbiểnBC =5 km.Trênbờbiển
cómộtcáikhoởvịtríC cáchB 7km.NgườigáchảiđăngcóthểchèođòtừA
đếnvịtríM trênbờbiểnvớivậntốc4 km/hrồiđibộđếnC vớivậntốc6 km/h.
VịtrícủađiểmM phảicáchB baonhiêukmđểngườiđóđếnC nhanhnhất?
M
A
B C
A. 0 km. B.
14+5
√
5
12
km.
C. 2
√
5 km. D. 7 km.
Câu 26. Mộttrangtrạimỗingàythuhoạchđượcmộttấnrau.Mỗingày,nếubán
rauvớigiá30000đồng/kgthìhếtsạchrau,nếugiábáncứtăngthêm1000đồng/kg
thìsốrauthừalạităngthêm20kg.Sốrauthừanàyđượcthumualàmthứcăn
chănnuôivớigiá2000đồng/kg.Hỏisốtiềnbánraunhiềunhấtmàtrangtrạicó
thểthuđượcmỗingàylàbaonhiêu?
A. 32.420.000 đồng. B. 32.400.000 đồng.
C. 34.400.000 đồng. D. 34.240.000 đồng.
Câu 27. Mộtxưởngsảnxuấtcầnlàm100chiếchộpinoxbằngnhau,hìnhdạng
làhìnhhộpchữnhậtcóđáylàhìnhvuông(khôngcónắp),vớithểtíchlà108
dm
3
/hộp.Giácủainoxlà47.000 đồng/dm
2
.Hãytínhtoánsaochotổngchiphísản
xuất100chiếchộplàítnhất,vàsốtiềntốithiểuđólàbaonhiêu(nếuchỉtínhsố
inoxvừađủđểsảnxuất100 chiếchộp,khôngcóphầndưthừa,cắtbỏ)?
A. 1.692.000.000 đồng. B. 507.666.000 đồng.
C. 1.015.200.000 đồng. D. 235.800.000 đồng.
Câu 28. MộtchấtđiểmchuyểnđộngtheophươngtrìnhS =−2t
3
+18t
2
+1,trong
đót tínhbằnggiâyvàS tínhbằngmét.Mấtbaolâukểtừlúcxuấtphátđểchất
điểmđạtvậntốclớnnhất?
A. 5 giây. B. 6 giây. C. 3 giây. D. 1 giây.
Soạn:HuỳnhPhúSĩ 22 TrườngTHCS-THPTMỹThuận
§3.Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố TOÁN12
Câu 29. Chohàmsốy =f(x) cóđồthịnhưhìnhvẽ.Tìmmax
[−2;4]
|f(x)|.
O
x
y
−2
−1
−1
−3
2
2 4
1
A. |f(0)|. B. 2. C. 3. D. 1.
Câu 30. Chox, y làhaisốkhôngâmthỏamãnx +y =2.Tìmgiátrịnhỏnhất
củabiểuthứcP =
x
3
3
+x
2
+y
2
−x +1.
A.
17
3
. B. 5. C.
115
3
. D.
7
3
.
L TỰ LUẬN
Câu 1 (SGK GT12). Tínhgiátrịlớnnhất,giátrịnhỏnhấtcủacáchàmsố
a)y =x
3
−3x
2
−9x +35 trên[−4;4]
b)y =x
4
−3x
2
+2 trên[0;3]
c)y =
2−x
1−x
trên[−3;−2]
d)y =
√
5−4x trên[−1;1]
Câu 2 (SGK GT12). Trongsốcáchìnhchữnhậtcùngcóchuvi16 cm,hãytìmhìnhchữnhậtcódiệntíchlớnnhất.
Câu 3 (SGK GT12). Trongsốcáchìnhchữnhậtcùngcódiệntích48 m
2
,hãyxácđịnhhìnhchữnhậtcóchuvinhỏnhất.
d Vocabulary
absolute maximum giátrịlớnnhất
absolute minimum giátrịnhỏnhất
continuous liêntục
exist tồntại
equation phươngtrình
root nghiệm
undefined khôngxácđịnh
square hìnhvuông
rectangle hìnhchữnhật
Soạn:HuỳnhPhúSĩ 23 TrườngTHCS-THPTMỹThuận
§4.Đườngtiệmcận TOÁN12
§4.ĐƯỜNG TIỆM CẬN
Đặt vấn đề
TrongcôngviênxãMỹThuận,ngườitaxâydựngmộtcầutrượttựavàomộtbứctườngbêtôngvàđượcmôphỏngtheo
đồthịhàmsốy =
1
x
vớimặtđấtlàtrụchoành,bứctườnglàtrụctung(nhưhìnhvẽ).
O
x
y
Đểnghiệmthucôngtrình,ngườitathảmộtquảbóngđểnódichuyểndọctheocầutrượtvềphía+∞.Hỏi:
a)Khinàothìquảbóngsẽchạmđất?
b)Phảiđặtquảbóngcáchmặtđấtbaonhiêuđểnóchạmvàomặttường?
1 ĐƯỜNG TIỆM CẬN NGANG
Chohàmsốy =f(x) xácđịnhtrênmộtkhoảngvôhạn.
Đườngthẳngy = y
0
đượcgọilàtiệmcậnngangcủađồthịhàmsốy =f
(
x
)
nếu
...... trongcácđiềukiệnsauđượcthỏamãn:
○ lim
x→+∞
f(x)=... ○ lim
x→−∞
f(x)=...
Ví dụ 1. Tìmphươngtrìnhđườngtiệmcậnngangcủađồthịhàmsốy =
2x +3
x −5
.
2 ĐƯỜNG TIỆM CẬN ĐỨNG
Đườngthẳngx = x
0
đượcgọilàtiệmcậnđứngcủađồthịhàmsốy = f
(
x
)
nếu
...... trongcácđiềukiệnsauđượcthỏamãn:
○ lim
x→x
+
0
f(x)=......
○ lim
x→x
+
0
f(x)=......
○ lim
x→x
−
0
f(x)=......
○ lim
x→x
−
0
f(x)=......
Ví dụ 2. Đồthịhàmsốy =
x
4
−12
(
x
2
−5x +6
)
√
x −1
cóbaonhiêuđườngtiệmcậnđứng?
Soạn:HuỳnhPhúSĩ 24 TrườngTHCS-THPTMỹThuận
§4.Đườngtiệmcận TOÁN12
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Đườngtiệmcậnngangcủađồthịhàmsốy =
2x −3
x +4
là
A. x =−4. B. y =2. C. x =4. D. y =−
3
4
.
Câu 2. Đườngtiệmcậnngangcủađồthịhàmsốy =
x −3
x −1
là
A. y =5. B. y =0. C. x =1. D. y =1.
Câu 3. Tìmtiệmcậnngangcủađồthịhàmsốf(x)=1+
2x +2
x −1
.
A. x =1. B. y =1. C. y =2. D. y =3.
Câu 4. Đườngthẳngnàodướiđâylàtiệmcậnngangcủađồthịhàmsốy =
1−4x
2x −1
?
A. y =2. B. y =
1
2
. C. y =4. D. y =−2.
Câu 5. Đồthịhàmsốf(x)=x
3
+2x
2
+3x +2021 cóbaonhiêuđườngtiệmcận
ngang?
A. 0. B. 1. C. 2. D. 3.
Câu 6. Đồthịcủahàmsốnàodướiđâycóđườngtiệmcậnngang?
A. y =
3x
2
−1
x +1
. B. y =x
4
−x
2
−2.
C. y =
2−x
x
. D. y =x
3
−x
2
+x −3.
Câu 7. Đườngthẳngy =2làtiệmcậnngangcủađồthịhàmsốnàodướiđây?
A. y =
2x −1
1−x
. B. y =
4x −1
2x +5
. C. y =
x +1
2x +1
. D. y =
2x −4
2x +3
.
Câu 8. Đườngtiệmcậnđứngcủađồthịhàmsốy =
3x −5
x −2
là
A. x =2. B. y =2. C. x =3. D. x =
5
3
.
Câu 9. Đườngtiệmcậnđứngcủađồthịhàmsốy =
7−2x
x −2
là
A. x =−3. B. x =2. C. x =−2. D. x =3.
Câu 10. Đồthịcủahàmsốnàosauđâynhậnđườngthẳngx = 2làmtiệmcận
đứng?
A. y =
1
x +1
. B. y =
5x
2−x
.
C. y =x −2+
1
x +1
. D. y =
1
x +2
.
Câu 11. Đồthịcủahàmsốnàodướiđâycótiệmcậnđứng?
A. y =
√
1−x
2
+1
2019
. B. y =
x
2
−1
x −1
.
C. y =
x
2
x
2
+2018
. D. y =
x
x +12
.
Câu 12. Đồthịhàmsốy =
x
2
−2x +3
2x −4
cótiệmcậnđứnglàđườngthẳng
A. y =1. B. x =1. C. x =2. D. x =−1.
Câu 13. Đồthịhàmsốy =
2x −3
x −1
cócácđườngtiệmcậnđứngvàtiệmcậnngang
lầnlượtlà
A. x =1 vày =2. B. x =2 vày =1.
C. x =1 vày =−3. D. x =−1 vày =2.
Câu 14. Đồthịhàmsốy =
x +1
x −
√
2
cócácđườngtiệmcậnđứngvàtiệmcận
nganglầnlượtlà
A. x =
√
2 vày =1. B. x =4 vày =1.
C. x =1 vày =−
1
√
2
. D. x =2 vày =1.
Câu 15. Đồthịhàmsốy =
4x +4
x
2
+2x +1
cótấtcảbaonhiêuđườngtiệmcận?
A. 2. B. 0. C. 1. D. 3.
Soạn:HuỳnhPhúSĩ 25 TrườngTHCS-THPTMỹThuận
§4.Đườngtiệmcận TOÁN12
Câu 16. Tìmsốđườngtiệmcậncủađồthịhàmsốy =
x
2
−3x +2
x
2
−4
.
A. 1. B. 2. C. 0. D. 3.
Câu 17. Chohàmsốy =
5x +5
x
2
−1
.Gọim làsốtiệmcậnđứng,n làsốtiệmcận
ngangcủađồthịhàmsốđãcho.TínhS =m+n.
A. S =2. B. S =3. C. S =1. D. S =4.
Câu 18. Đồthịhàmsốy =
x +1
√
x
2
−1
cóbaonhiêuđườngtiệmcận?
A. 3. B. 1. C. 2. D. 0.
Câu 19. Đồthịhàmsốy =
√
x +1
x
2
−1
cóbaonhiêuđườngtiệmcận?
A. 3. B. 1. C. 2. D. 0.
Câu 20. Đồthịhàmsốy =
x
2
+2x +3
√
x
4
−3x
2
+2
cóbaonhiêuđườngtiệmcận?
A. 4. B. 5. C. 3. D. 6.
Câu 21. Đồthịhàmsốnàodướiđâykhôngcóđườngtiệmcận?
A. y =
x
x
2
+1
. B. y =
1
x
.
C. y =x
4
−3x
2
+2. D. y =
2x +1
2−x
.
Câu 22. Biếtrằngđồthịhàmsốy =
ax +1
bx −2
cóđườngtiệmcậnđứnglàx =2 và
đườngtiệmcậnnganglày =3.Tínhgiátrịcủaa +b.
A. a+b =1. B. a +b =5. C. a +b =4. D. a +b =0.
Câu 23. Biếtrằngđồthịhàmsốy =
(m−2n −3)x +5
x −m −n
nhậnhaitrụctọađộlàm
haiđườngtiệmcận.TínhtổngS =m
2
+n
2
−2.
A. S =2. B. S =0. C. S =−1. D. S =1.
Câu 24. Đườngcongtronghìnhdướiđâylàđồthịcủahàmsốnào?
O
x
y
−1
−1
2
A. y =
2x −1
x +1
. B. y =
1−2x
x +1
. C. y =
2x +1
x −1
. D. y =
2x +1
x +1
.
Câu 25. Đườngcongtronghìnhsaulàđồthịcủahàmsốnào?
O
x
y
1
−1
1
A. y =−x
3
+3x +1. B. y =
x +1
x −1
.
C. y =
x −1
x +1
. D. y =x
3
−3x −1.
Soạn:HuỳnhPhúSĩ 26 TrườngTHCS-THPTMỹThuận
§4.Đườngtiệmcận TOÁN12
Câu 26. Chohàmsốy =f(x) cóbảngbiếnthiênnhưhình.
x
y
0
y
−∞
1
+∞
−
0
−
22
−∞
+∞
22
Tiệmcậnđứngcủađồthịhàmsốđãcholàđườngthẳngcóphươngtrình
A. x =2. B. y =2. C. x =1. D. y =1.
Câu 27. Chohàmsốy =f(x) cóbảngbiếnthiênnhưhình.
x
y
0
y
−∞
0 1
+∞
−
+
0
−
+∞+∞
−1 −∞
22
−2−2
Tổngsốtiệmcậnngangvàtiệmcậnđứngcủađồthịhàmsốđãcholà
A. 3. B. 4. C. 1. D. 2.
Câu 28. Tọađộgiaođiểmcủahaiđườngtiệmcậncủađồthịhàmsốy =
3x −7
x +2
là
A. (2;−3). B. (−2;3). C. (3;−2). D. (−3;2).
Câu 29. Tìmgiaođiểmcủahaiđườngtiệmcậncủađồthịhàmsốy =
x −2
x +2
.
A. M(2;1). B. N(−2;2). C. P(−2;−2). D. Q(−2;1).
Câu 30. Đồthịhàmsốnàodướiđâycótiệmcậnđứngx =1vàđiquađiểm
A(2;5)?
A. y =
2−3x
1−x
. B. y =
x +13
x +1
. C. y =
2x +1
x −1
. D. y =
x +1
x −1
.
L TỰ LUẬN
Câu 1 (SGK GT12). Tìmcáctiệmcậncủahàmsố
a)y =
2x −5
5x −2
b)y =
x
2−x
c)y =
x
2
+x +1
3−2x −5x
2
d)y =
√
x +1
√
x −1
d Vocabulary
asymptote đườngtiệmcận
horizontal asymptote tiệmcậnngang
vertical asymptote tiệmcậnđứng
distance khoảngcách
limit giớihạn
infinity vôcực
line đườngthẳng
curve đườngcong
condition điềukiện
Soạn:HuỳnhPhúSĩ 27 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
§5.KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ
THỊ CỦA HÀM SỐ
Đặt vấn đề
Theoem,khảosátmộthàmsốlàlàmnhữngviệcgì?
Tìmtậpxácđịnh
Xéttínhchẵnlẻ
Xéttínhđơnđiệu
Tìmcựctrị
Tìmđườngtiệmcận
Tìmđạohàm
1 SƠ ĐỒ KHẢO SÁT HÀM SỐ
!
Bước1. Tìm..................
Bước2. Xétsự............ củahàmsố
Bước3. Tìm............... (nếucó)
Bước4. Tìmcácđường............ (nếucó)
Bước5. Vẽ.........
Ví dụ 1. Khảosátcáchàmsốy =2x −3 vày =6−x −x
2
.
2 KHẢO SÁT MỘT SỐ HÀM THƯỜNG GẶP
1 Hàm số y =ax
3
+bx
2
+cx +d (a 6=0)
•Tậpxácđịnh:D =...
•Đạohàm:y
0
=...............
b
2
−3ac...0 và a...0
O
x
y
−1
3
1
−1
y =x
3
−3x +1
b
2
−3ac...0 và a...0
O
x
y
−1
1
y =−
x
3
3
+
x
2
2
+2x
Soạn:HuỳnhPhúSĩ 28 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
b
2
−3ac...0 và a...0
O
x
y
1
1
y =
x
3
3
−x
2
+x +
2
3
b
2
−3ac...0 và a...0
O
x
y
y =x
3
+x
2
+2x −1
b
2
−3ac...0 và a...0
O
x
y
2
y =2−x
3
b
2
−3ac...0 và a...0
O
x
y
y =1−x −x
3
2 Hàm số y =ax
4
+bx
2
+c (a 6=0)
•Tậpxácđịnh:D =...
•Đạohàm:y
0
=............... =...............
a, b...... dấu và a...0
O
x
y
−3
y =x
4
+2x
2
−3
a, b...... dấu và a...0
O
x
y
√
2
−3
−
√
2
−1
y =
x
4
2
−2x
2
−1
a, b...... dấu và a...0
O
x
y
1
y =−2x
4
−x
2
+1
a, b...... dấu và a...0
O
x
y
1
2
−1
1
y =−x
4
+2x
2
+1
3 Hàm số y =
ax +b
cx +d
(c 6=0, ad −bc 6=0)
•Tậpxácđịnh:D =...
d
c
•Đạohàm:y
0
=.........
•Tiệmcậnđứng:.........
d
c
•Tiệmcậnngang:.........
Soạn:HuỳnhPhúSĩ 29 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
y
0
...0
O
x
y
−1
−1
2
y =
2x −1
x +1
y
0
...0
O
x
y
1
−1
1
y =
x +1
x −1
3 SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ
Giảsửhàmsốy =f(x) cóđồthị
(
C
1
)
vàhàmsốy =g(x) cóđồthị
(
C
2
)
.
Đểtìmhoànhđộgiaođiểmcủa
(
C
1
)
và
(
C
2
)
,tagiảiphươngtrình............
O
x
y
−1 1 2
−1
1
2
Ví dụ 2. Tìmtọađộgiaođiểmcủađườngthẳngy =x −1 vàparaboly =x
2
−x −1
O
x
y
−4
−
8
5
1
Ví dụ 3. Chohàmsốy =f(x)cóđồthịnhưhìnhbên.Biệnluậntheothamsốm số
nghiệmcủaphươngtrìnhf(x)=m.
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1.
Đồthịtronghìnhvẽbênlàcủahàmsố
A. y =
x
4
4
−
x
2
2
−1. B. y =
x
4
4
−x
2
−1.
C. y =
x
4
4
−2x
2
−1. D. y =−
x
4
4
+x
2
−1.
O
x
y
−2
−5
2
−1
Câu 2.
Đồthịtronghìnhvẽbênlàcủahàmsố
A. y =−x
2
+x −4. B. y =x
4
−3x
2
−4.
C. y =−x
3
+2x
2
+4. D. y =−x
4
+3x
2
+4.
O
x
y
Soạn:HuỳnhPhúSĩ 30 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
Câu 3.
Đồthịtronghìnhvẽbênlàcủahàmsố
A. y =−
x
3
4
+x
2
+1. B. y =x
3
+3x
2
+1.
C. y =−x
3
+3x
2
+1. D. y =x
3
−3x
2
+1.
O
x
y
−1
−3
2
1
Câu 4.
Đườngcongnhưhìnhbênlàđồthịcủahàmsốnàodưới
đây?
A. y =x
3
−3x −2. B. y =−x
3
+3x +2.
C. y =x
3
−3x +2. D. y =−x
3
+3x −2.
O
x
y
−1
−4
−1
−2
1
Câu 5.
Đồthịtronghìnhvẽbênlàcủahàmsố
A. y =2x
3
+1. B. y =x
3
+x +1.
C. y =x
3
+1. D. y =−x
3
+2x +1.
O
x
y
−1
1
1
2
Câu 6.
Hàmsốy =f(x)cóđồthịnhưhìnhvẽlàhàm
sốnàosauđây?
A. y =
2x +1
x −1
. B. y =
2x −1
x −1
.
C. y =
2x −1
x +1
. D. y =
3x +1
2x +2
.
O
x
y
−1
2
−1
Câu 7.
Đồthịnhưhìnhbênlàcủahàmsốnào
sauđây?
A. y =
2x +1
x −1
. B. y =
x +2
x −2
.
C. y =
x +2
x +1
. D. y =
x −1
x +1
.
O
x
y
−2 2
1
−1
Câu 8. Đồthịnàosauđâykhôngthểlàđồthịhàmsốy =ax
4
+bx
2
+c với
a, b, c làcácsốthựcvàa 6=0?
O
x
y
Hình1
O
x
y
Hình2
O
x
y
Hình3
O
x
y
Hình4
Soạn:HuỳnhPhúSĩ 31 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
A. Hình1. B. Hình2. C. Hình3. D. Hình4.
Câu 9. Đồthịhàmsốy =−x
3
−3x
2
+2 làhìnhnàosauđây?
O
x
y
Hình1
O
x
y
Hình2
O
x
y
Hình3
O
x
y
Hình4
A. Hình1. B. Hình2. C. Hình3. D. Hình4.
Câu 10. Đồthịhàmsốy =
x +1
1−x
làhìnhnàosauđây?
O
x
y
Hình1
O
x
y
Hình2
O
x
y
Hình3
O
x
y
Hình4
A. Hình1. B. Hình2. C. Hình3. D. Hình4.
Câu 11.
Bảngbiếnthiêntronghìnhbênlàcủahàm
sốnàosauđây?
A. y =x
3
−5x
2
+x +6.
B. y =x
3
−6x
2
+9x −1.
C. y =−x
3
+6x
2
−9x +7.
D. y =x
4
+x
2
−3.
x
y
0
y
−∞
1 3
+∞
+
0
−
0
+
−∞−∞
33
−1−1
+∞+∞
Câu 12.
Đồthịnhưhìnhbênlàcủahàmsốnàosauđây?
A. y =x
4
−2x
2
+2.
B. y =2
x
2
−1
2
.
C. y =|x|
3
−3|x|+2.
D. y =x
2
−2|x|
2
+2.
O
x
y
2
−1 1
Câu 13.
Chohàmsốy =f(x) liêntụctrênR vàcóđồthị
nhưhìnhvẽ.Hỏiđồthịhàmsốy =|f
(
|x|
)
| có
tấtcảbaonhiêuđiểmcựctrị?
A. 9. B. 7. C. 6. D. 8.
O
x
y
−2
−1
1
2
3
−1
1
Câu 14. Chohàmsốy =(x − 2)
x
2
−5x +6
cóđồthị
(
C
)
.Mệnhđềnàosau
đâylàđúng?
A.
(
C
)
khôngcắttrụchoành. B.
(
C
)
cắttrụchoànhtại3 điểm.
C.
(
C
)
cắttrụchoànhtại1 điểm. D.
(
C
)
cắttrụchoànhtại2 điểm.
Câu 15. Sốgiaođiểmcủađồthịhàmsốy =−2x
3
−3x
2
+1vớitrụchoànhlà
A. 1. B. 0. C. 3. D. 2.
Soạn:HuỳnhPhúSĩ 32 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
Câu 16. Sốgiaođiểmcủađồthịhàmsốy =x
4
−5x
2
+4 vớitrụchoànhlà
A. 3. B. 2. C. 4. D. 1.
Câu 17. TìmtọađộgiaođiểmM củađồthịhàmsốy =
2x −1
x +2
vớitrụctung.
A. M
1
2
;0
. B. M
(
0;2
)
. C. M
0;−
1
2
. D. M
−
1
2
;0
.
Câu 18. Đồthịcủahaihàmsốy = −x
3
+3x
2
+2x −1vày = 3x
2
−2x −1có
tấtcảbaonhiêuđiểmchung?
A. 1. B. 2. C. 0. D. 3.
Câu 19. Sốgiaođiểmcủađườngcongy =x
3
− 2x
2
+2x +1vàđườngthẳng
y =1−x bằng
A. 0. B. 2. C. 1. D. 3.
Câu 20. GọiM vàN làgiaođiểmcủađồthịhaihàmsốy =x
4
− 2x
2
+2và
y =4−x
2
.TọađộtrungđiểmI củađoạnthẳngMN là
A. (1;0). B. (0;2). C. (2;0). D. (0;1).
Câu 21. GọiM vàN làgiaođiểmcủađồthịhaihàmsốy =x+1vày =
2x +4
x −1
.
TìmhoànhđộtrungđiểmI củađoạnthẳngMN.
A. x
I
=−
5
2
. B. x
I
=2. C. x
I
=
5
2
. D. x
I
=1.
Câu 22. Chohàmsốy =f(x) liêntụctrênR vàcóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Đồthịcủaf(x) cắtđườngthẳngy =2021 tạibaonhiêuđiểm?
A. 2. B. 1. C. 0. D. 4.
Câu 23. Chohàmsốy =f(x) liêntụctrênR vàcóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
−2
0
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
Tậphợpcácgiátrịthựccủathamsốm đểphươngtrìnhf(x)= m cóđúngmột
nghiệmlà
A. (−∞;−2)∪(2;+∞). B. (−∞;−2]∪[2;+∞).
C. (−2;2). D. [−2;2].
Câu 24. Chohàmsốy =f(x)xácđịnhtrênR \ {0},liêntụctrêntừngkhoảng
xácđịnhvàcóbảngbiếnthiênnhưhình.
x
y
0
y
−∞
0 1
+∞
−
+
0
−
+∞+∞
−1 −∞
22
−∞−∞
Phươngtrìnhf(x)=m vớim ∈ (−1;2) cóbaonhiêunghiệm?
A. 3. B. 1. C. 0. D. 2.
Câu 25. Chohàmsốy =f(x) liêntụctrênR vàcóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
00
−1−1
+∞+∞
Soạn:HuỳnhPhúSĩ 33 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
Tìmtấtcảcácgiátrịthựccủathamsốm đểphươngtrìnhf(x)−1 =m cóđúng
2 nghiệm.
A. −2< m < −1. B. m =−2 hoặcm ≥ −1.
C. m =−1 hoặcm > 0. D. m =−2 hoặcm > −1.
Câu 26. Tìmcácgiátrịcủathamsốm đểphươngtrìnhx
3
−12x+m−2=0 có
3 nghiệmphânbiệt.
A. m ∈ [−14;18]. B. m ∈ (−14;18).
C. m ∈ (−18;14). D.
m < −14
m > 18
.
Câu 27. Tìmm đểđườngthẳngy =x − m cắtđồthịhàmsốy =
2x +1
x +1
tại2
điểmphânbiệt.
A. m < −1. B. m > −5.
C. m < −5 hoặcm > −1. D. −5< m < −1.
Câu 28. Phươngtrìnhtiếptuyếncủađồthịhàmsốy =x
3
−3x
2
−x+3 tạiđiểm
M(1;0) là
A. y =1−x. B. y =−4x −4. C. y =−4x +4. D. y =1−4x.
Câu 29. Đườngthẳngnàosauđâylàtiếptuyếncủađồthịhàmsốy =
3x −1
x +2
tại
điểmcóhoànhđộbằng−1?
A. y =6x +1. B. y =5x +1. C. y =−4x. D. y =7x +3.
Câu 30. Trênđồthị
(
C
)
: y =
x −1
x −2
,cóbaonhiêuđiểmmàtiếptuyếntạiđóvới
(
C
)
songsongvớiđườngthẳngx +y =1?
A. 2. B. 4. C. 1. D. 0.
L TỰ LUẬN
Câu 1 (SGK GT12). Khảosátsựbiếnthiênvàvẽđồthịcủacáchàmsốsau:
a)y =2+3x −x
3
b)y =x
3
+4x
2
+4x
c)y =x
3
+x
2
+9x
d)y =−2x
3
+5
e)y =−x
4
+8x
2
−1
f)y =x
4
−2x
2
+2
g)y =
x
4
2
+x
2
−
3
2
h)y =−2x
2
−x
4
+3
i)y =
x +3
x −1
j)y =
1−2x
2x −4
k)y =
−x +2
2x +1
Câu 2. Tìmgiaođiểmcủacácđồthịhàmsốsauvớitrụchoành.
a)y =x
3
−3x
2
+5 b)y =−2x
3
+3x
2
−2 c) y =−x
4
+2x
2
+1
Câu 3 (SGK GT12). Chohàmsốy =x
3
+(m +3)x
2
+1−m (m làthamsố)cóđồthịlà
(
C
m
)
.
a)Xácđịnhm đểhàmsốcóđiểmcựcđạilàx =−1
b)Xácđịnhm đểđồthị
(
C
m
)
cắttrụchoànhtạix =−2.
Câu 4 (SGK GT12).
a)Khảosátsựbiếnthiênvàvẽđồthị
(
C
)
củahàmsốf(x)=−x
3
+3x
2
+9x +2.
b)Giảibấtphươngtrìnhf
0
(x −1)> 0
c)Viếtphươngtrìnhtiếptuyếncủađồthị
(
C
)
tạiđiểmcóhoànhđộx
0
,biếtrằngf
00
(
x
0
)
=−6.
Soạn:HuỳnhPhúSĩ 34 TrườngTHCS-THPTMỹThuận
§5.Khảosátsựbiếnthiênvàvẽđồthịcủahàmsố TOÁN12
d Vocabulary
even function hàmsốchẵn
odd function hàmsốlẻ
constant function hàmhằng
linear function hàmsốtuyếntính
quadratic function hàmsốbậc2
cubic function hàmsốbậc3
biquadratic function hàmsốtrùngphương
linear rational function hàmphântuyếntính
tangent line tiếptuyến
absolute value giátrịtuyệtđối
Soạn:HuỳnhPhúSĩ 35 TrườngTHCS-THPTMỹThuận
Chương2.Hàmsốlũythừa.Hàmsốmũvàhàmsốlogarit TOÁN12
Chương2.
HÀM SỐ LŨY THỪA. HÀM SỐ MŨ VÀ HÀM
SỐ LOGARIT
§1.LŨY THỪA
1 KHÁI NIỆM LŨY THỪA
1 Lũy thừa với số mũ nguyên
Chon ∈ N
∗
,a ∈ R.
Lũythừabậcn củaa là...... của... thừasốa.
a
n
=a·a ·a···a ·a
| {z }
n sốa
Sốa gọilà.........,sốn gọilà.........
Chú ý: Vớia 6=0 tacó
•a
0
=... •a
−n
=......
Ví dụ 1. Tính
(
1,5
)
4
,
−
2
3
3
,
√
3
−
5.
2 Phương trình x
n
=b
○ Vớin lẻ:phươngtrìnhcó............... vớimọib.
○ Vớin chẵn:
– phươngtrìnhvônghiệmnếub......
– phươngtrìnhcó1 nghiệm......... nếub......
– phươngtrìnhcó2 nghiệm......... nếub......
Ví dụ 2. Phươngtrìnhnàodướiđâycónghiệmduynhấtkhác0?
A. x
5
=0. B. x
6
=0. C. x
6
=1. D. x
5
=1.
3 Căn bậc n
Chosốb ∈ R vàsốn ∈ N
∗
(n ≥ 2).
Nếua
n
=b thìa đượcgọilà............ củab.
○ Vớin lẻ:có............... cănbậcn củab
○ Vớin chẵn:
– Nếub < 0 thì...............
– Nếub =0 thì...............
– Nếub > 0 thì...............
Soạn:HuỳnhPhúSĩ 36 TrườngTHCS-THPTMỹThuận
§1.Lũythừa TOÁN12
!
•
n
√
a·
n
√
b =......
•
n
√
a
n
√
b
=......
•
n
√
a
m
=......
•
n
√
a
n
=
(
a nếun......
|a| nếun......
Ví dụ 3. Chosốa > 0.RútgọnbiểuthứcA =
√
a
3
·
3
√
a
4
·
4
√
a
5
.
4 Lũy thừa với số mũ hữu tỉ
Chosốthựca > 0 vàsốhữutỉr =
m
n
(m ∈ Z,n ∈ N, n ≥ 2).Khiđó
a
r
=a
m
n
=......
Ví dụ 4. Chox làsốthựcdươngvàP =
3
p
x
2
√
x
5
.BiếtrằngP đượcbiểudiễndưới
dạngx
m
n
,trongđó
m
n
làphânsốtốigiảnvàm, n ∈ N
∗
.Tínhm+n.
5 Lũy thừa với số mũ vô tỉ
Chosốthựca > 0vàsốvôtỉα.Khiđó,luôncómộtdãysốhữutỉ
(
r
n
)
saocholimr
n
=α
và
a
α
=lima
r
n
=......
2 TÍNH CHẤT CỦA LŨY THỪA VỚI SỐ MŨ THỰC
Choa, b > 0 lànhữngsốthực;m, n lànhữngsốthựctùyý.
!
•a
m
·a
n
=......
•
a
m
a
n
=......
•
(
a
m
)
n
=......
•
(
ab
)
m
=......
•
a
b
m
=......
Ví dụ 5. RútgọnbiểuthứcF =
a
4
3
a
−
1
3
+a
2
3
a
1
4
a
3
4
+a
−
1
4
Soạn:HuỳnhPhúSĩ 37 TrườngTHCS-THPTMỹThuận
§1.Lũythừa TOÁN12
○ Vớia > 1:a
m
> a
n
⇔ m...n
○ Vớia < 1:a
m
> a
n
⇔ m...n
Ví dụ 6. Sosánhcáccặpsốsau:
a)
√
3−1
7
và
√
3−1
8
b)
√
2
2
!
−2020
và
√
2
2
!
−2021
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Chosốdươnga vàm, n ∈ R.Mệnhđềnàosauđâyđúng?
A. a
m
·a
n
=a
m−n
. B. a
m
·a
n
=
(
a
m
)
n
.
C. a
m
·a
n
=a
m+n
. D. a
m
·a
n
=a
m·n
.
Câu 2. Chosốthựcdươnga vàhaisốm, n ∈ R.Mệnhđềnàosauđâyđúng?
A. a
m+n
=
(
a
m
)
n
. B. a
m+n
=
a
m
a
n
.
C. a
m+n
=a
m
·a
n
. D. a
m+n
=a
m
+n.
Câu 3. Vớiα làmộtsốthựcbấtkỳ,mệnhđềnàosauđâysai?
A.
√
10
α
=10
α
2
. B.
√
10
α
=
√
10
α
.
C.
(
10
α
)
2
=100
α
. D.
(
10
α
)
2
=10
α
2
.
Câu 4. TínhgiátrịcủabiểuthứcP =
4+2
√
3
2018
·
1−
√
3
2017
1+
√
3
2019
.
A. P =−2
2017
. B. P =−1. C. P =−2
2019
. D. P =2
2018
.
Câu 5. Chobiết9
x
−12
2
=0,tínhgiátrịcủabiểuthứcP =
1
3
−x−1
−8·9
x−1
2
+19.
A. 31. B. 23. C. 22. D. 15.
Câu 6. Choa làsốthựcdương.Biểuthứca
2
·
3
√
a đượcviếtdướidạnglũythừavới
sốmũhữutỉlà
A. a
4
3
. B. a
7
3
. C. a
5
3
. D. a
2
3
.
Câu 7. Kếtquả viếtdướidạng lũythừa vớisố mũhữu tỉcủa biểuthức F =
r
a
q
a
p
a
√
a
a
11
16
vớia > 0 là
A. F =a
1
4
. B. F =a
3
8
. C. F =a
1
2
. D. F =a
3
4
.
Câu 8. Choa làmộtsốthựcdương.RútgọnbiểuthứcP =
a
√
7−3
√
7+3
a
√
11−4
·a
5−
√
11
.
A. P =
1
a
3
. B. P =a
3
. C. P =a
2
. D. P =a
2
√
7−1
.
Câu 9. RútgọnbiểuthứcA =
3
√
a
7
·a
11
3
a
4
·
7
√
a
−5
vớia > 0 tađượckếtquảA =a
m
n
trong
đóm, n ∈ N
∗
và
m
n
làphânsốtốigiản.Khẳngđịnhnàosauđâyđúng?
A. m
2
−n
2
=312. B. m
2
+n
2
=543.
C. m
2
−n
2
=−312. D. m
2
+n
2
=409.
Câu 10. Choa làmộtsốdương,biểuthứca
2
3
√
a dướidạnglũythừavớisốmũ
hữutỉlà
A. a
4
3
. B. a
5
6
. C. a
7
6
. D. a
6
7
.
Soạn:HuỳnhPhúSĩ 38 TrườngTHCS-THPTMỹThuận
§1.Lũythừa TOÁN12
Câu 11. Choa > 0.Tìmx biết
3
r
a
3
q
a
3
p
a
3
√
a =a
x
.
A. x =
4
9
. B. x =
1
81
. C. x =
40
81
. D. x =
13
27
.
Câu 12. RútgọnbiểuthứcP =
a
√
3+1
·a
2−
√
3
a
√
2−2
√
2+2
vớia > 0.
A. P =a. B. P =a
3
. C. P =a
4
. D. P =a
5
.
Câu 13. Choa, b làcácsốthựcdương.RútgọnP =
a
4
3
b+ab
4
3
3
√
a+
3
√
b
tađược
A. P =ab. B. P =a +b.
C. P =a
4
b+ab
4
. D. P =a
2
b+ab
2
.
Câu 14. RútgọnbiểuthứcP =x
1
2
·
8
√
x vớix > 0.
A. P =x
5
16
. B. P =x
5
8
. C. P =x
1
16
. D. P =x
4
.
Câu 15. Choa làsốthựcdương.Biểuthứca
2
3
·
√
a viếtdướidạnglũythừavớisố
mũhữutỉlà
A. a
1
3
. B. a
7
6
. C. a
11
6
. D. a
6
5
.
Câu 16. RútgọnbiểuthứcP =
a
√
3−1
√
3+1
a
4−
√
5
·a
√
5−2
(0< a 6=1).
A. P =2. B. P =a
2
. C. P =1. D. P =a.
Câu 17. Phátbiểunàosauđâysai?
A. e
3
> e
2
. B. (0,5)
3
>
1
2
2
.
C.
√
3
2
<
√
3
3
. D.
π
2
2
<
π
2
3
.
Câu 18. Choa, b > 0thỏamãna
1
2
> a
1
3
vàb
2
3
> b
3
4
.Khiđókhẳngđịnhnào
đúng?
A. 0< a < 1, 0< b < 1. B. 0< a < 1, b > 1.
C. a > 1, 0< b < 1. D. a > 1, b > 1.
Câu 19. Cho
√
2−1
m
<
√
2−1
n
.Khiđó
A. m =n. B. m < n. C. m > n. D. m 6=n.
Câu 20. Chobiết(x −2)
−
1
3
> (x −2)
−
1
6
,khẳngđịnhnàosauđâyđúng?
A. 2< x < 3. B. 0< x < 1. C. x > 2. D. x > 1.
L TỰ LUẬN
Câu 1 (SGK GT12). Choa, b lànhữngsốthựcdương.Viếtcácbiểuthứcsaudướidạnglũythừavớisốmũhữutỉ:
a)a
1
3
·
√
a b)b
1
2
·b
1
3
·
6
√
b c)a
4
3
:
3
√
a d)
3
√
b :b
1
6
d Vocabulary
power lũythừa
factor thừasố
base cơsố
exponent sốmũ
integer sốnguyên
rational sốhữutỉ
irrational sốvôtỉ
real sốthực
Soạn:HuỳnhPhúSĩ 39 TrườngTHCS-THPTMỹThuận
§2.Hàmsốlũythừa TOÁN12
§2.HÀM SỐ LŨY THỪA
1 KHÁI NIỆM
Chosốthựcα.
Hàmsốy =...... đượcgọilàhàmsốlũythừa.
Chú ý: Tậpxácđịnhcủahàmsốlũythừax
α
tùythuộcvàogiátrịcủa...
○ Nếuα ∈ Z
+
:tậpxácđịnhlà.........
○ Nếuα ∈ Z
−
:tậpxácđịnhlà.........
○ Nếuα /∈ Z:tậpxácđịnhlà.........
Ví dụ 1. Tìmtậpxácđịnhcủacáchàmsốsau:
a)y =(2x −1)
3
b)y =(2x −1)
−3
c)y =(2x −1)
1
3
d)y =
3
√
2x −1
2 ĐẠO HÀM CỦA HÀM SỐ LŨY THỪA
Hàmsốlũythừay =x
α
(α ∈ R)cóđạohàmvớimọix......
(
x
α
)
0
=.........
Ví dụ 2. Tìmđạohàmcủacáchàmsốsau:
a)y =x
2
3
b)y =x
π
c)y =(1−3x)
√
2
3 KHẢO SÁT HÀM SỐ LŨY THỪA
Trongtrườnghợptổngquát,takhảosáthàmsốy =x
α
trênkhoảng.........
y =x
α
,α > 0 y =x
α
,α < 0
Sựbiếnthiên
Giớihạnđặcbiệt
Tiệmcận
Đồthị
O
x
y
α > 1
α =1
α < 1
1
1
O
x
y
α < 0
1
1
Soạn:HuỳnhPhúSĩ 40 TrườngTHCS-THPTMỹThuận
§2.Hàmsốlũythừa TOÁN12
Ví dụ 3. Khảosátsựbiếnthiênvàvẽđồthịhàmsốy =x
−3
.
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Tậpxácđịnhcủahàmsốy =(x −2)
−3
là
A. R \{2}. B. [2;+∞). C. R. D. (2;+∞).
Câu 2. Tậpxácđịnhcủahàmsốy =(2−x)
−3
là
A. (−∞;2]. B. R \{2}. C. (−∞;2). D. (2;+∞).
Câu 3. Tậpxácđịnhcủahàmsốy =
x
2
−1
−4
là
A. R. B. (−1;1).
C. R \{−1;1}. D. (−∞;−1)∪(1;+∞).
Câu 4. Tậpxácđịnhcủahàmsốy =
x
2
−3x +2
π
là
A. R \{1;2}. B. (1;2).
C. (−∞;1]∪[2;+∞). D. (−∞;1)∪(2;+∞).
Câu 5. Tậpxácđịnhcủahàmsốy =
x
2
−x +1
π
là
A. R \{1}. B. R.
C. ∅. D. (−∞;−1)∪(1;+∞).
Câu 6. Tậpxácđịnhcủahàmsốy =
x
2
−5x +6
−
1
3
là
A. (−∞;2)∪(3;+∞). B. R \{2;3}.
C. (2;3). D. R.
Câu 7. Tậpxácđịnhcủahàmsốy =
3x −x
2
−
3
2
là
A. R. B. (0;3).
C. (−∞;0)∪(3;+∞). D. R \{0;3}.
Câu 8. TìmtậpxácđịnhD củahàmsốy =
5+4x −x
2
√
2019
.
A. D =R \{−1;5}. B. D =(−∞;−1)∪(5;+∞).
C. D =(1;5). D. D =(−1;5).
Câu 9. Tậpxácđịnhcủahàmsốy =
x
2
−3x −4
1
3
là
A. (−∞;−1)∪(4;+∞). B. R \{−1;4}.
C. (−1;4). D. R.
Câu 10. Tậpxácđịnhcủahàmsốy =
x
2
−4x
e
là
A. R. B. R \{0;4}.
C. (−∞;0)∪(4;+∞). D. (0;4).
Câu 11. Tìmtậpxácđịnhcủahàmsốy =(x −2)
√
3
.
A. D =R \2. B. D =(2;+∞). C. D =(−∞;2). D. D =R.
Câu 12. TìmtậpxácđịnhD củahàmsốy =(x −5)
√
3
.
A. D =[5;+∞). B. D =(5;+∞). C. D =(−∞;5). D. D =R \{5}.
Câu 13. TìmtậpxácđịnhD củahàmsốy =(x −1)
1
2
.
A. D =(0;+∞). B. D =[1;+∞). C. D =(1;+∞). D. D =R.
Câu 14. TìmtậpxácđịnhD củahàmsốy =(1−x)
√
2
.
A. D =(1;+∞). B. D =R \{1}. C. D =(−∞;1). D. D =R.
Câu 15. Tìmđạohàmcủahàmsốy =
x
2
−x +1
1
3
.
A. y
0
=
2x −1
3
q
(
x
2
−x +1
)
2
. B. y
0
=
1
3
3
q
(
x
2
−x +1
)
2
.
C. y
0
=
2x −1
3
3
√
x
2
−x +1
. D. y
0
=
2x −1
3
3
q
(
x
2
−x +1
)
2
.
Soạn:HuỳnhPhúSĩ 41 TrườngTHCS-THPTMỹThuận
§2.Hàmsốlũythừa TOÁN12
Câu 16. Chohàmsốf(x)=(2x −3)
5
6
.Tínhf
0
(2).
A.
5
6
. B.
5
3
. C. −
5
6
. D. −
5
3
.
Câu 17. Chohàmsốf(x)=
2x
2
+3x +1
3
2
.Khiđógiátrịcủaf(1) bằng
A. 8. B.
3
2
. C. 6
√
6. D. 6
2
3
.
Câu 18. Chohàmsốy =x
−
3
4
.Khẳngđịnhnàosauđâysai?
A. Đồthịhàmsốnhậntrụctunglàmtiệmcậnđứng.
B. Đồthịhàmsốnhậntrụchoànhlàmtiệmcậnngang.
C. ĐồthịhàmsốluônđiquagốctọađộO(0;0).
D. Nghịchbiếntrên(0;+∞).
Câu 19.
Chocácsốthựcα vàβ.Đồthịcáchàmsốy =x
α
vày =x
β
trênkhoảng(0;+∞)nhưhìnhvẽbên.
Mệnhđềnàodướiđâyđúng?
A. 0< β < α < 1. B. α < 0< β < 1.
C. 0< β < 1< α. D. β < 0< 1< α.
O
x
y
y =x
β
y =x
α
1
1
Câu 20.
Chobahàmsốy =x
√
3
,y =x
1
5
,y =x
−2
.Khi
đóđồthịcủabahàmsốđólầnlượtlà
A.
(
C
3
)
,
(
C
2
)
,
(
C
1
)
. B.
(
C
2
)
,
(
C
3
)
,
(
C
1
)
.
C.
(
C
2
)
,
(
C
1
)
,
(
C
3
)
. D.
(
C
1
)
,
(
C
3
)
,
(
C
2
)
.
O
x
y
(
C
2
)
(
C
1
)
(
C
3
)
1
1
L TỰ LUẬN
Câu 1 (SGK GT12). Tìmtậpxácđịnhcủacáchàmsố
a)y =(1−x)
−
1
3
b)y =
2−x
2
3
5
c)y =
x
2
−1
−2
d)y =
x
2
−x −2
√
2
Câu 2 (SGK GT12). Tìmđạohàmcủacáchàmsố
a)y =
2x
2
−x +1
1
3
b)y =
4−x −x
2
1
4
c)y =(3x +1)
π
2
d)y =(5−x)
√
3
Soạn:HuỳnhPhúSĩ 42 TrườngTHCS-THPTMỹThuận
§3.Lôgarit TOÁN12
§3.LÔGARIT
Đặt vấn đề
"Ngày6.7,nhiềukhuvựctạimiềnnambangCalifornia
củaMỹtiếptụcrungchuyểnvìtrậnđộngđấtthứhailiên
tiếptrongchưađầy48giờ.CơquanKhảosátđịachấtMỹ
(USGS)chobiếtđộngđấtmạnh7,1độRichtervớitâm
chấnởđộsâu7kmnằmgầnTP.Ridgecrest,cáchTP.Los
Angeleskhoảng200kmvềphíađôngbắc.Giớichuyêngia
chobiếtđâylàtrậnđộngđấtchính,cóbiênđộrungchấn
gấp...... lầnsovớitrậntiềnchấn6,4độRichterhôm
4.7(giờđịaphương)cũnggầnRidgecrest".
Thanh Niên ngày 7/7/2019
Hãyđiềnconsốcònthiếutrongdấu"...",biếtrằngcườngđộmộttrậnđộngđấtM độRichterđượcchobởicôngthức
M =logA−logA
0
,vớiA làbiênđộrungchấntốiđavàA
0
làbiênđộchuẩn(A
0
làhằngsố).
1 KHÁI NIỆM LÔGARIT
1 Định nghĩa
Chohaisố...... a, b vớia.......
Sốα thỏamãnđẳngthứca
α
=b đượcgọilà........................ vàkíhiệu
là.......
α =...... ⇔ a
α
=b
Sốa gọilà.........,sốn gọilà.........
Chú ý: Khôngcólôgaritcủasố...... vàsố0.
Ví dụ 1. Tínhlog
3
81 vàlog
1
2
1024.
2 Tính chất
Chohaisố...... a, b vớia.......Tacócáctínhchấtsau:
!
•log
a
1=...
•log
a
a =...
•a
log
a
b
=...
•log
a
a
b
=...
Ví dụ 2. Tính5
log
5
2021
và81
log
3
2
.
2 QUY TẮC TÍNH LÔGARIT
Chobasố...... a, b, c vớia.......Tacó
!
•log
a
(
b·c
)
=...............
•log
a
b
c
=...............
•log
a
b
α
=.........,∀α
•log
a
b =
log
c
...
log
c
...
(c 6=1)
•log
a
b =
1
......
(b 6=1)
•log
a
α
b =......log
a
b (α 6=0)
Soạn:HuỳnhPhúSĩ 43 TrườngTHCS-THPTMỹThuận
§3.Lôgarit TOÁN12
Ví dụ 3. Tính:
a)A =2log
1
2
1
3
+log
1
2
3
8
−log
1
2
2
b)C =log
5
3
√
25
Ví dụ 4. ChứngtỏrằngbiểuthứcS =log
x
x
3
·
√
x ·
5
√
x
khôngphụthuộcx.
3 LÔGARIT THẬP PHÂN VÀ LÔGARIT TỰ NHIÊN
1 Lôgarit thập phân
Lôgaritthậpphânlàlôgaritcơsố....
logb =......
Ví dụ 5. Tínhlog1000 vàlog0,01.
2 Lôgarit tự nhiên
7/2đượcxemlàngàycủasốe
Lôgarittựnhiênlàlôgaritcơsố...
lnb =......
Ví dụ 6. Dùngmáytínhcầmtaytínhln2,ln3 vàln1.
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Vớia 6=1 làsốthựcdươngtùyý,giátrịcủalog
a
3
a bằng
A. 3. B. −
1
3
. C.
1
3
. D. −3.
Câu 2. Choa 6=1 làsốthựcdươngtùyý,tínhP =log
a
2
a.
A. P =2. B. P =−
1
2
. C. P =
1
2
. D. P =−2.
Câu 3. Vớia làsốthựcdươngbấtkì,khẳngđịnhnàosauđâyđúng?
A. log
a
4
=4loga. B. log
a
4
=
1
4
loga.
C. log(4a)=4loga. D. log(4a)=
1
4
loga.
Câu 4. Choa, b > 0 vớia, b 6= 1 vàx, y làhaisốthựcdương.Trongcácmệnh
đềsauđây,mệnhđềnàosai?
A. log
a
(xy)=log
a
x +log
a
y. B. log
b
a·log
a
x =log
b
x.
C. log
a
1
x
=
1
log
a
x
. D. log
a
x
y
=log
a
x −log
a
y.
Câu 5. Chosốthực0< a 6=1vàhaisốthựcdươngx, y.Khẳngđịnhnàosau
đâylàđúng?
A. log
a
x
y
=log
a
x −log
a
y. B. log
a
x
y
=
log
a
x
log
a
y
.
C. log
a
x
y
=log
a
x +log
a
y. D. log
a
x
y
=log
a
(x −y).
Soạn:HuỳnhPhúSĩ 44 TrườngTHCS-THPTMỹThuận
§3.Lôgarit TOÁN12
Câu 6. Choa, b > 0.Khẳngđịnhnàosauđâyđúng?
A. log
ab
2
=loga+2logb. B. log(ab)=loga ·logb.
C. log
ab
2
=2loga+2logb. D. log(ab)=loga−logb.
Câu 7. Vớia làsốthựcdươngbấtkìvàa 6=1,mệnhđềnàodướiđâyđúng?
A. log
a
5
e=
1
5lna
. B. loga
5
=
1
5
lna.
C. loga
5
=
5
lna
. D. log
a
5
e=5log
a
e.
Câu 8. Vớimọisốthựcdươnga, b, x, y saochoa, b 6= 1,mệnhđềnàosauđây
không đúng?
A. log
a
1
x
=
1
log
a
x
. B. log
a
(xy)=log
a
x +log
a
y.
C. log
b
a·log
a
x =log
b
x. D. log
a
x
y
=log
a
x −log
a
y.
Câu 9. Choa, b làcácsốthựcdương,trongđóa 6=1.Đẳngthứcnàosauđây
đúng?
A. log
a
a
3
√
b
=3−2log
a
b. B. log
a
a
3
√
b
=3+2log
a
b.
C. log
a
a
3
√
b
=3−
1
2
log
a
b. D. log
a
a
3
√
b
=3+
1
2
log
a
b.
Câu 10. Vớisốthựcdươnga tùyý,tacóln(6a)−ln(2a) bằng
A. ln(4a). B. ln
12a
2
. C. 4lna. D. ln3.
Câu 11. Vớia, b làhaisốthựckhác0 tùyý.Khiđóln
a
2
b
4
bằng
A. 2lna +4lnb. B. 4lna+2lnb.
C. 2ln|a|+4ln|b|. D. 4
(
ln|a|+ln|b|
)
.
Câu 12. Choa > 0 vàa 6=1.Tìmmệnhđềđúngtrongcácmệnhđềsau:
A. log
a
x
n
=nlog
a
x (x > 0). B. log
a
x
y
=
log
a
x
log
a
y
(x, y > 0).
C. log
a
x cónghĩavớimọix. D. log
a
1=a, log
a
a =1.
Câu 13. Cho0< a 6=1vàmộtsốthựcdươngx.Đẳngthứcnàodướiđâysai?
A. a
log
a
x
=a. B. log
a
x =
lnx
lna
.
C. a
log
a
x
=x. D. log
√
a
x
3
=6log
a
x.
Câu 14. Vớia, b làhaisốdươngtùyý.Khiđóln
a
b
bằng
A.
lna
lnb
. B. lna+lnb. C. lna−lnb. D. lna·lnb.
Câu 15. Choa làsốthựcdươngkhác1,mệnhđềnàodướiđâysai?
A. loga·log
a
10=1. B. loga =
1
log10
.
C. lna =ln10·loga. D. loga =
1
log
a
10
.
Câu 16. Chox, y làcácsốthựcdương.Mệnhđềnàosauđâysai?
A. logx +logy =log(xy). B. log(x +y)=logx +logy.
C. log
√
xy =
1
2
(
logx +logy
)
. D. log
x
y
=logx −logy.
Câu 17. Choa làsốthựcdươngkhác4.TínhI =log
a
4
a
3
64
.
A. I =−
1
3
. B. I =−3. C. I =3. D. I =
1
3
.
Câu 18. Choa, b làcácsốdương(a 6=1).Khiđólog
√
a
a
√
b
bằng
A. 2+2log
a
b. B.
1
2
+log
a
b. C.
1
2
+
1
2
log
a
b. D. 2+log
a
b.
Câu 19. Choa, b làhaisốthựcdươngtùyý,khiđóln
e
2
a
7
b
5
bằng
A. 2+5lna +7lnb. B. 7lna +5lnb.
C. 2+7lna +5lnb. D. 5lna +7lnb.
Câu 20. Cho0< a 6=1.TínhgiátrịcủabiểuthứcQ =a
6log
a
4
5
.
A. Q =
√
5. B. Q =a
5
. C. Q =5
√
5. D. Q =a
3
2
.
Câu 21. RútgọnbiểuthứcA =log
a
a
3
·
√
a·
5
√
a
tađượckếtquảlà
A.
3
10
. B.
1
10
. C.
35
10
. D.
37
10
.
Soạn:HuỳnhPhúSĩ 45 TrườngTHCS-THPTMỹThuận
§3.Lôgarit TOÁN12
Câu 22. Chohaisốthực0< a, b 6=1.TínhgiátrịcủabiểuthứcP =log
a
2
a
10
b
2
+
log
√
a
a
√
b
+log
3
√
b
b
−2
.
A. P =
√
3. B. P =1. C. P =
√
2. D. P =2.
Câu 23. Vớicácsốthựcdươnga, b thỏamãna
2
+b
2
=6ab,biểuthứclog
2
(a+b)
bằng
A.
1
2
(
3+log
2
a+log
2
b
)
. B.
1
2
(
1+log
2
a+log
2
b
)
.
C. 1+
1
2
(
log
2
a+log
2
b
)
. D. 2+
1
2
(
log
2
a+log
2
b
)
.
Câu 24. Vớia, b, c làcácsốthựcdươngkhác1tùyývàx =log
a
c,y =log
b
c,
tínhgiátrịcủalog
c
(ab).
A. log
c
(ab)=
1
xy
. B. log
c
(ab)=x +y.
C. log
c
(ab)=
xy
x +y
. D. log
c
(ab)=
1
x
+
1
y
.
Câu 25. Cholog
a
b =−2vàlog
a
c =5trongđóa, b, c làcácsốthựcdương
(a 6=1).TínhS =log
a
ab
2
c
3
.
A. S =−17. B. S =−18. C. S =18. D. S =−19.
Câu 26. Cho0 < a 6=1,b > 0,c > 0saocholog
a
b =3vàlog
a
c = −2.Tính
log
a
a
3
b
2
√
c
.
A. 6. B. −18. C. −9. D. 8.
Câu 27. Nếulog
3
5=a thìlog
45
75 bằng
A.
2+a
1+2a
. B.
1+a
2+a
. C.
1+2a
2+a
. D.
1+2a
1+a
.
Câu 28. Nếulog
5
3=a thìlog
81
75 bằng
A.
1
2a
+
1
4
. B.
a
2
+
1
4
. C.
a+1
4
. D.
a+1
4a
.
Câu 29. Chocácsốthựca, b thỏamãn0< a < 1< b.Tìmkhẳngđịnhđúng.
A. log
a
b < 0. B. lna > lnb.
C. (0,5)
a
< (0,5)
b
. D. 2
a
> 2
b
.
Câu 30. Choa, b làhaisốthựcthỏamãn0< a < b < 1.Mệnhđềnàodướiđây
đúng?
A. log
a
b < 1< log
b
a. B. log
b
a < 1< log
a
b.
C. log
a
b < log
b
a < 1. D. 1< log
a
b < log
b
a.
L TỰ LUẬN
Câu 1 (SGK GT12). Rútgọnbiểuthức
a)log
3
6·log
8
9·62 b)log
a
b
2
+log
a
2
b
4
Câu 2 (SGK GT12).
a)Choa =log
30
3,b =log
30
5.Hãytínhlog
30
1350 theoa, b.
b)Choc =log
15
3.Hãytínhlog
25
15 theoc.
d Vocabulary
logarithm lôgarit
positive number sốdương
negative number sốâm
expression biểuthức
property tínhchất
prove chứngminh
rule quytắc
common logarithm lôgaritthậpphân
nutural logarithm lôgarittựnhiên
Soạn:HuỳnhPhúSĩ 46 TrườngTHCS-THPTMỹThuận
§4.Hàmsốmũ.Hàmsốlôgarit TOÁN12
§4.HÀM SỐ MŨ. HÀM SỐ LÔGARIT
Đặt vấn đề
ThạchSanhtrúnggiảiBamộttờvésốtrịgiá10.000.000
đồng.Nhưnganhchưabiếtnêndùngsốtiềnđóvàoviệc
gì.BạnthâncủaThạchSanhlàLýThôngđãđềnghịvay
sốtiềnnàyvớilãisuất6%/thángvàsẽtrảcảvốnlẫnlãisau
đúngmộtnăm.LýThôngmangsốtiềnđóđếnSacombank
gửitiếtkiệmtheohìnhthứclãikép,vớilãisuất6%/tháng,
kỳhạngửilà12 tháng.
Saumộtnăm,LýThôngđếnngânhàngnhậnsốtiềncả
vốnlẫnlãi,vàtrảchoThạchSanhsốtiềnnhưđãhứa.
a)Hỏisaucuộcgiaodịch,LýThônglãihaylỗ?
b)Hãynêusựkhácnhaugiữahaihìnhthứcgửitiềncủa
ThạchSanhvàLýThông.
1 HÀM SỐ MŨ
1
Định nghĩa
Chosốthực...... a 6=....
Hàmsốy =...... đượcgọilàhàm số mũ cơsố....
Ví dụ 1. Hàmsốnàosauđâykhông phải hàmsốmũ?
A. y =
√
3
x
. B. y =x
√
3
. C. y =5
x
3
. D. y =e
−x
.
2 Đạo hàm của hàm số mũ
Chosố...... a 6=... vàhàmhợpu =u(x).Tacó:
!
•
(
a
x
)
0
=.........
•
(
e
x
)
0
=.........
•
(
a
u
)
0
=.........
•
(
e
u
)
0
=.........
Ví dụ 2. Tìmđạohàmcủacáchàmsốsau:
a)y =7
x
b)y =e
x
3
−3x+1
3 Khảo sát hàm số mũ y =a
x
y =a
x
,a > 1 y =a
x
,a < 1
Sựbiếnthiên
Tiệmcận
Đồthị
O
x
y
a > 1
1
1
a
O
x
y
a < 1
1
1
a
Ví dụ 3. Sosánhcáccặpsốsau:
a)
√
3
−5
và
√
3
−3
b)0,3
1
5
và0,3
1
3
Soạn:HuỳnhPhúSĩ 47 TrườngTHCS-THPTMỹThuận
§4.Hàmsốmũ.Hàmsốlôgarit TOÁN12
2 HÀM SỐ LÔGARIT
1 Định nghĩa
Chosốthực...... a 6=....
Hàmsốy =...... đượcgọilàhàm số lôgarit cơsố....
Ví dụ 4. Hàmsốnàosauđâykhông phải hàmsốlôgarit?
A. y =log
5
x. B. y =log(5x). C. y =ln(5x). D. y =lne.
2 Đạo hàm của hàm số lôgarit
Chosố...... a 6=... vàhàmhợpu =u(x).Tacó:
!
•
(
log
a
x
)
0
=.........
1
xlna
•
(
lnx
)
0
=.........
1
xlna
•
(
log
a
u
)
0
=.........
1
xlna
•
(
lnu
)
0
=.........
1
xlna
Ví dụ 5. Tìmđạohàmcủacáchàmsốsau:
a)y =log
2
x b)y =ln(x
2
−3x +2)
3 Khảo sát hàm số lôgarit y =log
a
x
y =log
a
x,a > 1 y =log
a
x,a < 1
Tậpxácđịnh
Sựbiếnthiên
Tiệmcận
Đồthị
O
x
y
a > 1
1
a
1
O
x
y
a < 1
1
a
1
Ví dụ 6. Sosánhcáccặpsốsau:
a)log
0,5
√
3 vàlog
0,5
√
2 b)ln2020 vàln2021
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. TìmtậpxácđịnhD củahàmsốy =ln
x
2
−2x +1
.
A. D =R. B. D =(1;+∞). C. D =∅. D. D =R \{1}.
Câu 2. Tậpxácđịnhcủahàmsốy =log
x
2
−1
là
A. (−∞;−1)∪(1;+∞). B. (−∞;1).
C. (1;+∞). D. (−1;1).
Câu 3. TìmtậpxácđịnhD củahàmsốy =log
2
3−2x −x
2
.
A. D =(1;3). B. D =(−1;3).
C. D =(−3;1). D. D =(−∞;−3)∪(1;+∞).
Câu 4. Tậpxácđịnhcủahàmsốy =log(x −2)
2
là
A. R. B. R \{2}. C. (2;+∞). D. [2;+∞).
Soạn:HuỳnhPhúSĩ 48 TrườngTHCS-THPTMỹThuận
§4.Hàmsốmũ.Hàmsốlôgarit TOÁN12
Câu 5. Tìmtậpxácđịnhcủahàmsốy =
1
1−lnx
.
A. (0;+∞). B. (e;+∞). C. R \{e}. D. (0;+∞).
Câu 6. TìmtậpxácđịnhD củahàmsốy =
1
√
2−x
+ln(x −1).
A. D =(−∞;2)\{1}. B. D =(1;2).
C. D =[1;2). D. D =(1;2].
Câu 7. TìmtậpxácđịnhD củahàmsốy =
1
√
2−x
+ln|x −1|.
A. D =(−∞;2)\{1}. B. D =(1;2).
C. D =[1;2). D. D =(1;2].
Câu 8. TìmtậpxácđịnhD củahàmsốy =
√
3x −1
log(3x)
.
A. D =(0;+∞)\
1
3
. B. D =
1
3
;+∞
.
C. D =(0;+∞). D. D =
1
3
;+∞
.
Câu 9. Tìmđạohàmcủahàmsốy =2020
x
.
A. y
0
=2020
x−1
x. B. y
0
=2020
x
·log2020.
C. y
0
=2020
x
·ln2020. D. y
0
=
2020
x
ln2020
.
Câu 10. Hàmsốf(x)=log
3
(sinx) cóđạohàmlà
A. f
0
(x)=
tanx
ln3
. B. f
0
(x)=cotx ·ln3.
C. f
0
(x)=
1
sinx ·ln3
. D. f
0
(x)=
cotx
ln3
.
Câu 11. Tìmđạohàmcủahàmsốy =ln
x
2
+2
.
A. y
0
=
2x
x
2
+2
. B. y
0
=
x
x
2
+1
. C. y
0
=
2x +2
x
2
+2
. D. y
0
=
1
x
2
+2
.
Câu 12. Đạohàmcủahàmsốy =x ·e
x+1
là
A. y
0
=(1+x)e
x+1
. B. y
0
=(1−x)e
x+1
.
C. y
0
=e
x+1
. D. y
0
=x ·e
x
.
Câu 13. Tìmđạohàmcủahàmsốy =
x +1
lnx
.
A. y
0
=
lnx −x −1
xln
2
x
. B. y
0
=
xlnx −x −1
xln
2
x
.
C. y
0
=
lnx −x −1
ln
2
x
. D. y
0
=
lnx −x −1
xlnx
.
Câu 14. Tìmđạohàmcủahàmsốy =2
x
lnx −
1
e
x
.
A. y
0
=2
x
1
x
+ln2·lnx
+
1
e
x
. B. y
0
=2
x
ln2+
1
x
+e
−x
.
C. y
0
=
2
x
x
ln2+
1
e
x
. D. y
0
=2
x
ln2+
1
x
−e
−x
.
Câu 15. Chohàmsốf(x)=e
2x+1
.Khiđóf
0
(1) bằng
A. e
3
. B. e
2
. C. 2e
3
. D. 2e.
Câu 16. Đạohàmcủahàmsốy = log
3
(x +1)− 2ln(x − 1)+2x tạiđiểmx = 2
bằng
A.
1
3
. B.
1
3ln3
+2. C.
1
3ln3
−1. D.
1
3ln3
.
Câu 17. Chohàmsốy =e
−2x
.Mệnhđềnàosauđâyđúng?
A. y
00
+y
0
−y =0. B. y
00
+y
0
+y =0.
C. y
00
+y
0
+2y =0. D. y
00
+y
0
−2y =0.
Câu 18. Chohàmsốy =log
2019
x cóđồthị(C ).Mệnhđềnàosauđâysai?
A. (C ) cóđúngmộttiệmcận. B. (C ) khôngcótiệmcậnngang.
C. (C ) đồngbiếntrêntậpxácđịnh. D. (C ) khôngcótiệmcậnđứng.
Câu 19. Chohàmsốy =log
2
x.Khẳngđịnhnàosauđâysai?
A. Đồthịhàmsốnhậntrụctunglàmtiệmcậnđứng.
B. ĐồthịhàmsốcắttrụchoànhtạiđiểmA(1;0).
C. Đồthịhàmsốluônnằmphíatrêntrụchoành.
D. Hàmsốđồngbiếntrênkhoảng(0;+∞).
Soạn:HuỳnhPhúSĩ 49 TrườngTHCS-THPTMỹThuận
§4.Hàmsốmũ.Hàmsốlôgarit TOÁN12
Câu 20. Hàmsốnàosauđâynghịchbiếntrêntậpxácđịnhcủanó?
A. y =log
π
4
x. B. y =log
π
x. C. y =
√
5
2
!
x
. D. y =2
x
.
Câu 21. HàmsốnàosauđâyđồngbiếntrênR?
A. y =log
2
x. B. y =
x −1
x +1
.
C. y =3
x
. D. y =x
4
+2x
2
+4.
Câu 22. Trongcáchàmsốdướiđây,hàmsốnàonghịchbiếntrênR?
A. y =
π
3
x
. B. y =log
π
4
2x
2
+1
.
C. y =
2
e
x
. D. y =log
2
3
x.
Câu 23. Tìmcáckhoảngđồngbiếncủahàmsốy =2
x
2
−6x+5
.
A. (−∞;3). B. R.
C. (3;+∞). D. (−∞;1) và(5;+∞).
Câu 24. Sốđiểmcựctrịcủahàmsốy =e
x
+x +1 là
A. 0. B. 3. C. 2. D. 1.
Câu 25.
Choa, b, c dươngvàkhác1.Đồthịhàmsố
y = log
a
x,y =log
b
x vày = log
c
x đượccho
tronghìnhvẽ.
Khẳngđịnhnàodướiđâylàđúng?
A. a > c > b. B. b > c > a.
C. c > b > a. D. a > b > c.
O
x
y
y =log
a
x
y =log
b
x
y =log
c
x
1 2
Câu 26.
Chobasốthựcdươnga, b, c khác1.Đồthị
hàmsốy =a
x
,y =b
x
vày =c
x
đượccho
tronghìnhvẽ.
Mệnhđềnàodướiđâylàđúng?
A. a < b < c. B. a < c < b.
C. b < c < a. D. c < a < b.
O
x
y
a
x
b
x
c
x
1 2
Câu 27.
Chocáchàmsốy =log
a
x,y =b
x
,y =c
x
cóđồthị
nhưhìnhvẽ.Mệnhđềnàodướiđâylàđúng?
A. b > c > a. B. a > b > c.
C. b > a > c. D. c > b > a.
O
x
y
log
a
x
b
x
c
x
1 2
Câu 28. Mộtngườigửitiếtkiệmsốtiền80.000.000đồngvớilãisuất6,9%/năm.
Biếtrằngtiềnlãihàngnămđượcnhậpvàotiềngốc,hỏisauđúng5 nămngườiđó
rútđượccảgốclẫnlãivớisốtiềngầnvớiconsốnàonhấtsauđây?
A. 116.570.000 đồng. B. 107.667.000 đồng.
C. 105.370.000 đồng. D. 111.680.000 đồng.
Câu 29. Mộtkhurừngcótrữlượnggỗ4· 10
5
métkhối.Biếttốcđộsinhtrưởng
củacáccâytrongrừngđólà4% mỗinăm.Hỏisau10 nămkhurừngđócósốmét
khốigỗgầnnhấtvớisốnàosauđây?
A. 5,9·10
5
. B. 5,92·10
5
. C. 5,93·10
5
. D. 5,94·10
5
.
Câu 30. ViệtNamlàquốcgianằmởphíaĐôngbánđảoĐôngDươngthuộckhu
vựcĐôngNamÁ.Vớidânsốướctính93,7 triệudânvàođầunăm2018,ViệtNam
Soạn:HuỳnhPhúSĩ 50 TrườngTHCS-THPTMỹThuận
§4.Hàmsốmũ.Hàmsốlôgarit TOÁN12
làquốcgiađôngdânthứ15trênthếgiớivàlàquốcgiađôngdânthứ8ởchâuÁ,tỉ
lệtăngdânsốhàngnăm1,2%.Giảsửrằngtỉlệtăngdânsốtừnăm2018đếnnăm
2030khôngthayđổithìdânsốnướctađầunăm2030khoảngbaonhiêu?
A. 118,12 triệudân. B. 106,12 triệudân.
C. 128,12 triệudân. D. 108,12 triệudân.
L TỰ LUẬN
Câu 1 (SGK GT12). Tìmđạohàmcủacáchàmsố:
a)y =2xe
x
+3sin2x
b)y =5x
2
−2
x
cosx
c)y =
x +1
3
x
d)y =3x
2
−lnx +4sinx
e)y =log
x
2
+x +1
f)y =
log
3
x
x
Câu 2 (SGK GT12). Tìmtậpxácđịnhcủacáchàmsố:
a)y =log
2
(5−2x) b)y =log
3
x
2
−2x
c)y =log
1
5
x
2
−4x +5
d)y =log
0,4
3x +2
1−x
d Vocabulary
exponential function hàmsốmũ
compound-interest lãikép
composite function hàmhợp
logarithmic function hàmsốlôgarit
Soạn:HuỳnhPhúSĩ 51 TrườngTHCS-THPTMỹThuận
§5.Phươngtrìnhmũvàphươngtrìnhlôgarit TOÁN12
§5.PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG
TRÌNH LÔGARIT
Đặt vấn đề
Nobitamuốndùngtiềncủamìnhđểmuachiếcxemáy
LATTEcủahãngYAMAHAtrịgiá37.490.000đồng.Cậu
quyết định gửi tiết kiệm 200.000 đồng tiền mừng tuổi
hồiTếtvàoAgribankvớilãisuất6%/tháng.Hỏisaubao
lâu thì số tiền vốn và lãi của Nobita đủ để mua xe?
1 PHƯƠNG TRÌNH MŨ
1 Phương trình mũ cơ bản
Phươngtrìnhmũcơbảncódạng......... (a > ...,a 6=...).
b > 0
b ≤ 0
Ví dụ 1. Tìmm đểphươngtrình2020
x+1
=m cónghiệm.
2 Cách giải một số phương trình mũ đơn giản
Ví dụ 2. Giảicácphươngtrìnhsau:
a)2
x−1
=32
b)9
x
−4·3
x
−45=0
c)2
x
3
+2x
2
−3x
·3
x−1
=1
d)9
x
−6
x
=2
2x+1
2 PHƯƠNG TRÌNH LÔGARIT
1 Định nghĩa
Phươngtrìnhlôgaritlàphươngtrìnhcóchứaẩntrongbiểuthứcdướidấu......
2 Phương trình lôgarit cơ bản
Phươngtrìnhlôgaritcơbảncódạng............ (a > ...,a 6=...).
log
a
x =b ⇔ x =......
Soạn:HuỳnhPhúSĩ 52 TrườngTHCS-THPTMỹThuận
§5.Phươngtrìnhmũvàphươngtrìnhlôgarit TOÁN12
Ví dụ 3. Tìmsốnghiệmcủaphươngtrìnhlog
3
x =2021.
3 Cách giải một số phương trình lôgarit đơn giản
Ví dụ 4. Giảicácphươngtrìnhsau:
a)log
2
x +log
2
(x −1)=1 b)log
2
3
x −2log3x −7=0
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Phươngtrình5
2x+1
=125 cónghiệmlà
A. x =
53
2
. B. x =
3
2
. C. x =3. D. x =1.
Câu 2. Phươngtrình3
x
=2 cónghiệmlà
A. x =log
2
3. B. x =2
3
. C. x =log
3
2. D. x =
2
3
.
Câu 3. Tìmtậpnghiệmcủaphươngtrình4
x+1
+4
x−1
=272.
A. {3;2}. B. {2}. C. {3}. D. {3;5}.
Câu 4. Giảiphươngtrình2
x
2
−5x+7
=8.
A. x =1, x =−4. B. x =
5±
√
29
2
.
C. x =1, x =4. D. x =
5±
√
5
2
.
Câu 5. Nghiệmcủaphươngtrình9
√
x−1
=e
ln81
là
A. x =4. B. x =5. C. x =6. D. x =17.
Câu 6. TìmtậpnghiệmS củaphươngtrình4
x+
1
2
−5·2
x
+2=0.
A. S ={−1;1}. B. S ={−1}. C. S ={1}. D. S =(−1;1).
Câu 7. Nghiệmcủaphươngtrình9
x
−4·3
x
−45=0 là
A. x =9. B. x =−5, x =9.
C. x =2, x =log
3
5. D. x =2.
Câu 8. Tìmsốnghiệmthựccủaphươngtrình4
x
−2
x+2
+3=0.
A. 3. B. 2. C. 1. D. 0.
Câu 9. Phươngtrình3
1−x
=2+
1
9
x
cóbaonhiêunghiệmâm?
A. 0. B. 1. C. 2. D. 3.
Câu 10. Tìmsốnghiệmcủaphươngtrình2
x
3
+2x
2
−3x
·3
x−1
=1.
A. 2. B. 1. C. 0. D. 3.
Câu 11. Tìmsốnghiệmcủaphươngtrình4
x−1
+2
x+3
−4=0.
A. 1. B. 0. C. 3. D. 2.
Câu 12. Chophươngtrình2
1+2x
+15·2
x
−8=0(1).Khẳngđịnhnàosauđâylà
đúng?
A. (1)cóhainghiệmdương. B. (1)cóhainghiệmtráidấu.
C. (1)cóhainghiệmâm. D. (1)cómộtnghiệm.
Câu 13. Tínhtổngcácnghiệmcủaphươngtrình3
x+1
+3
1−x
=10.
A. 1. B. 3. C. −1. D. 0.
Câu 14. Tínhtổngcácnghiệmcủaphươngtrìnhlog
6
(
3·4
x
+2·9
x
)
=x+1.
A. 2. B. 1. C. 0. D. 3.
Câu 15. Tíchcácnghiệmcủaphươngtrình3
x
2
−3x+1
=81 bằng
A. 3. B. 4. C. −3. D. 5.
Soạn:HuỳnhPhúSĩ 53 TrườngTHCS-THPTMỹThuận
§5.Phươngtrìnhmũvàphươngtrìnhlôgarit TOÁN12
Câu 16. Giảiphươngtrìnhlog
3
(x −1)=2.
A. x =10. B. x =11. C. x =8. D. x =7.
Câu 17. Giátrịnàosauđâylàmộtnghiệmcủaphươngtrìnhlog
3
2x
2
+1
=
2?
A. x =2. B. x =4. C. x =3. D. x =1.
Câu 18. Tìmtậpnghiệmcủaphươngtrình
1
2
log
2
(x +2)
2
−1=0.
A. {−1;0}. B. {−4}. C. {0;−4}. D. {0}.
Câu 19. Tậpnghiệmcủaphươngtrìnhlog
2
x +log
2
(x −1)=1 là
A. {−1}. B. {2}. C. {2;−1}. D. {−2;1}.
Câu 20. Tìmnghiệmcủaphươngtrìnhlog
5
(x−1)+log
5
(x+3)=log
5
(4x−3).
A. x =2. B. x =0, x =2. C. x =0. D. x =
5
2
.
Câu 21. Tìmsốnghiệmcủaphươngtrìnhlog
2
(x −3)+log
2
(x −1)=3.
A. 2. B. 3. C. 1. D. 0.
Câu 22. Tìmsốnghiệmcủaphươngtrìnhlog
3
x
2
+4x
+log
1
3
(2x+3)=0.
A. 2. B. 3. C. 0. D. 1.
Câu 23. Chophươngtrìnhlog
4
(x +1)
2
+2 = log
√
2
√
4−x +log
8
(4+x)
3
.Tổng
cácnghiệmcủaphươngtrìnhđãcholà
A. 4+2
√
6. B. −4. C. 4−2
√
6. D. 2−2
√
3.
Câu 24. Tínhtổngcácnghiệmcủaphươngtrìnhlog
2
2
x−log
2
9·log
3
x =3.
A. 2. B. −2. C.
17
2
. D. 8.
Câu 25. Biếtrằngphươngtrìnhlog
2
2
(2x)− 5log
2
x = 0cóhainghiệmphânbiệt
x
1
, x
2
.Tínhx
1
·x
2
.
A. x
1
·x
2
=8. B. x
1
·x
2
=5. C. x
1
·x
2
=3. D. x
1
·x
2
=1.
Câu 26. Tínhtíchcácnghiệmcủaphươngtrìnhlog
2
3
x −2log
3
x −7=0.
A. 2. B. −7. C. 1. D. 9.
Câu 27. Chophươngtrìnhlog
2
2
(4x)−log
√
2
(2x)=5.Nghiệmnhỏnhấtcủaphương
trìnhthuộckhoảng
A. (1;3). B. (5;9). C. (3;5). D. (0;1).
Câu 28. Tậphợpcácgiátrịthựccủathamsốm đểphươngtrìnhlog
2
x = m có
nghiệmlà
A. (0;+∞). B. [0;+∞). C. (−∞;0). D. R.
Câu 29. Mộtngười gửi số tiền 50triệu đồngvào một ngân hàng vớilãi suất
8,4%/năm.Cứmỗinăm,sốtiềnlãisẽđượcnhậpvàovốnbanđầuđểtínhlãicho
nămtiếptheo.Ngườiđósẽlĩnhđượcsốtiềncảvốnlẫnlãilà80 triệusaun năm.
Hỏinếutrongkhoảngthờigiannàyngườiđókhôngrúttiềnvàlãisuấtkhôngthay
đổithìn gầnnhấtvớisốnàosauđây?
A. 4. B. 5. C. 6. D. 7.
Câu 30. ÔngBìnhgửisốtiền58triệuđồngvàomộtngânhàngtheohìnhthức
lãiképvàổnđịnhtrong9 thángthìlãnhđược61.758.000 đồng.Hỏilãisuấtngân
hàngmỗithánglàbaonhiêu,biếtrằnglãisuấtkhôngthayđổitrongsuốtthờigian
gửi?
A. 0,8%. B. 0,6%. C. 0,7%. D. 0,5%.
L TỰ LUẬN
Câu 1 (SGK GT12). Giảicácphươngtrìnhsau:
a)(0,3)
3x−2
=1
b)
1
5
x
=25
c)2
x
2
−3x+2
=4
d)(0,5)
x+7
·(0,5)
1−2x
=2
e)3
2x−1
+3
2x
=108
f)2
x+1
+2
x−1
+2
x
=28
g)64
x
−8
x
−56=0
h)3·4
x
−2·6
x
=9
x
Câu 2 (SGK GT12). Giảicácphươngtrìnhsau:
a)log
3
(5x +3)=log
3
(7x +5)
b)log(x −1)−log(2x −11)=log2
c)log
2
(x −5)+log
2
(x +2)=3
d)log
x
2
−6x +7
=log(x −3)
e)
1
2
log
x
2
+x −5
=log5x +log
1
5x
f)
1
2
log
x
2
−4x −1
=log8x −log4x
g)log
√
2
x +4log
4
x +log
8
x =13
Soạn:HuỳnhPhúSĩ 54 TrườngTHCS-THPTMỹThuận
§5.Phươngtrìnhmũvàphươngtrìnhlôgarit TOÁN12
d Vocabulary
exponential equation phươngtrìnhmũ
logarithmizing lôgarithóa
substitutive variable ẩnphụ
logarithmic equation phươngtrìnhlôgarit
exponentializing mũhóa
solve the equation giảiphươngtrình
Soạn:HuỳnhPhúSĩ 55 TrườngTHCS-THPTMỹThuận
§6.Bấtphươngtrìnhmũvàbấtphươngtrìnhlôgarit TOÁN12
§6.BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT
PHƯƠNG TRÌNH LÔGARIT
1 BẤT PHƯƠNG TRÌNH MŨ
1 Bất phương trình mũ cơ bản
Bấtphươngtrình mũcơbản có dạng......... hoặc......... hoặc......... hoặc
......... (a > ...,a 6=...).
a
x
> b a > 1 0< a < 1
b > 0
b ≤ 0
2 Bất phương trình mũ đơn giản
Ví dụ 1. Giảicácbấtphươngtrìnhsau:
a)5
x
2
−x
> 25 b)2
x
+2
−x
−3< 0 c) 4
x
−2·6
x
< 9
x
2 BẤT PHƯƠNG TRÌNH LÔGARIT
1 Bất phương trình lôgarit cơ bản
Bấtphươngtrìnhlôgaritcơbảncódạng............hoặc............hoặc............
hoặc............ (a > ...,a 6=...).
log
a
x > b a > 1 0< a < 1
Nghiệm
2 Bất phương trình lôgarit đơn giản
Ví dụ 2. Giảicácbấtphươngtrìnhsau:
a)log
1
2
(2x +3)> log
1
2
(3x +1) b)log
3
(x −3)+log
3
(x −2)≤ 1
Soạn:HuỳnhPhúSĩ 56 TrườngTHCS-THPTMỹThuận
§6.Bấtphươngtrìnhmũvàbấtphươngtrìnhlôgarit TOÁN12
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. TìmtậpnghiệmS củabấtphươngtrình
1
2
x
> 8.
A. S =(−3;+∞). B. S =(−∞;3).
C. S =(−∞;−3). D. S =(3;+∞).
Câu 2. Tìmtậpnghiệmcủabấtphươngtrình
1
3
x
2
+2x
>
1
27
.
A. S =(−3;1). B. S =(1;3).
C. S =(−1;3). D. S =(−∞;−3)∪(1;+∞).
Câu 3. Tìmtậpnghiệmcủabấtphươngtrình2
3x
<
1
2
−2x−6
.
A. (−∞;6). B. (0;6). C. (0;64). D. (6;+∞).
Câu 4. Tìmtậpnghiệmcủabấtphươngtrình
e
π
x
> 1.
A. R. B. (−∞;0). C. (0;+∞). D. [0;+∞).
Câu 5. Tìmtậpnghiệmcủabấtphươngtrình
1
3
x
> 9.
A. (−∞;−2). B. (−∞;2). C. (−2;+∞). D. (2;+∞).
Câu 6. Tìmtậpnghiệmcủabấtphươngtrình2
x
+2
x+1
≤ 3
x
+3
x−1
.
A. (2;+∞). B. (−∞;2). C. (−∞;2]. D. [2;+∞).
Câu 7. Tậpnghiệmcủabấtphươngtrình3
x+2
≥
1
9
là
A. [−4;+∞). B. (−∞;0). C. [0;+∞). D. (−∞;4).
Câu 8. TìmtậpnghiệmS củabấtphươngtrình
1
2
−x
2
+3x
<
1
4
.
A. S =[1;2]. B. S =(−∞;1). C. S =(1;2). D. S =(2;+∞).
Câu 9. Tìmtậpnghiệmcủabấtphươngtrình5
1−2x
>
1
125
.
A. S =(0;2). B. S =(−∞;2).
C. S =(−∞;−3). D. S =(2;+∞).
Câu 10. Tìmtậpnghiệmcủabấtphươngtrình4
x+1
≤ 8
x−2
.
A. [8;+∞). B. ∅. C. (0;8). D. (−∞;8].
Câu 11. Tìmtậpnghiệmcủabấtphươngtrình
tan
π
7
x
2
−x−9
≤
tan
π
7
x−1
.
A. S =(−∞;−2]∪[4;+∞). B. S =
h
−2
√
2;2
√
2
i
.
C. S =
−∞;−2
√
2
i
∪
h
2
√
2;+∞
. D. S =[−2;4].
Câu 12. TìmtậpnghiệmS củabấtphươngtrình
2
5
1−3x
≥
25
4
.
A. S =(−∞;1]. B. S =
1
3
;+∞
.
C. S =
−∞;
1
3
. D. S =[1;+∞).
Câu 13. Giảibấtphươngtrình
10+3
√
11
x
+
10−3
√
11
x
≤ 20.
A. 0≤ x ≤ 1. B. −1≤ x < 1. C. −1< x ≤ 1. D. −1≤ x ≤ 1.
Câu 14. Giảibấtphươngtrình64·9
x
−84·12
x
+27·16
x
< 0.
A.
9
16
< x <
3
4
. B.
x < 1
x > 2
. C. 1< x < 2. D. Vônghiệm.
Câu 15. Tìmsốnghiệmnguyêncủabấtphươngtrình2
x+2
+8·2
−x
−33< 0.
A. 4. B. 6. C. 7. D. Vôsố.
Câu 16. TìmtậpnghiệmcủaS củabấtphươngtrìnhlog
1
5
(x+1)< log
1
5
(2x−1).
A. S =(2;+∞). B. S =(−1;2). C. S =(−∞;2). D. S =
1
2
;2
.
Câu 17. Tìmtậpnghiệmcủabấtphươngtrìnhlog
2
(x −1)< 3.
A. (1;9). B. (−∞;9). C. (−∞;10). D. (1;10).
Soạn:HuỳnhPhúSĩ 57 TrườngTHCS-THPTMỹThuận
§6.Bấtphươngtrìnhmũvàbấtphươngtrìnhlôgarit TOÁN12
Câu 18. Tìmtậpnghiệmcủabấtphươngtrìnhlog
0,5
(x −1)> 1.
A.
−∞;
3
2
. B.
1;
3
2
. C.
3
2
;+∞
. D.
1;
3
2
.
Câu 19. Tìmtậpnghiệmcủabấtphươngtrìnhln(3x)< ln(2x +6).
A. [0;6). B. (0;6). C. (6;+∞). D. (−∞;6).
Câu 20. TìmtậpnghiệmS củabấtphươngtrìnhlog
1
2
(x −3)≥ log
1
2
4.
A. S =(−∞;7]. B. S =[7;+∞). C. S =(3;7]. D. S =[3;7].
Câu 21. Tìmtậpnghiệmcủabấtphươngtrìnhlog
4
(x +7)> log
2
(x +1).
A. (−1;2). B. (2;4). C. (−3;2). D. (5;+∞).
Câu 22. Tìmtậpnghiệmcủabấtphươngtrìnhlog
1
2
x
2
−5x +7
> 0.
A. (−∞;2). B. (−∞;2)∪(3;+∞).
C. (2;3). D. (3;+∞).
Câu 23. Tìmtậpnghiệmcủabấtphươngtrìnhlog
1
3
(x−1)+log
3
(11−2x)≥ 0.
A. S =(1;4]. B. S =(−∞;4]. C. S =
4;
11
2
. D. S =(1;4).
Câu 24. Giảibấtphươngtrìnhlog
x
(
log
3
(
9
x
−72
))
≤ 1.
A. S =(−∞;2]. B. S =
log
3
√
73;2
i
.
C. S =
log
3
√
72;2
i
. D. S =
h
log
3
√
73;2
i
.
Câu 25. Sốnghiệmnguyêncủabấtphươngtrìnhlog
0,8
(15x +2)> log
0,8
(13x +8)
là
A. Vôsố. B. 4. C. 2. D. 3.
Câu 26. Cóbaonhiêusốnguyêntrênđoạn[0;10] nghiệmđúngbấtphươngtrình
log
2
(3x −4)> log
2
(x −1)?
A. 9. B. 10. C. 8. D. 11.
Câu 27. Cóbaonhiêusốnguyênx thỏamãnbấtphươngtrìnhlog
1
2
log
2
2−x
2

>
0?
A. Vôsố. B. 1. C. 0. D. 2.
Câu 28. Tậpnghiệmcủabấtphươngtrìnhlog
2
2
x − 3log
2
x +2< 0làkhoảng
(a;b).Tínha
2
+b
2
.
A. 16. B. 5. C. 20. D. 10.
Câu 29. TìmtậpxácđịnhD củahàmsốy =
p
log(x +1)−1.
A. D =(10;+∞). B. D =[9;+∞).
C. D =(−∞;9]. D. D =R \{1}.
Câu 30. Mộtngườigửitiếtkiệmvớilãisuất5%/nămvàlãihàngnămđượcnhập
vàovốn.Sauítnhấtbaonhiêunămthìngườiđónhậnđượcsốtiềnlớnhơn150%
sốtiềngửibanđầu?
A. 8 năm. B. 10 năm. C. 9 năm. D. 11 năm.
L TỰ LUẬN
Câu 1 (SGK GT12). Giảicácbấtphươngtrìnhsau:
a)2
−x
2
+3x
< 4 b)3
x+2
+3
x−1
≤ 28 c)4
x
−3·2
x
+2> 0
Câu 2 (SGK GT12). Giảicácbấtphươngtrìnhsau:
a)log
8
(4−2x)≥ 2 b)log
1
5
(3x −5)> log
1
5
(x +1) c) log
2
3
x −5log
3
x +6≤ 0
Soạn:HuỳnhPhúSĩ 58 TrườngTHCS-THPTMỹThuận
§6.Bấtphươngtrìnhmũvàbấtphươngtrìnhlôgarit TOÁN12
Soạn:HuỳnhPhúSĩ 59 TrườngTHCS-THPTMỹThuận
PHẦNII
HÌNH HỌC
Chương 1. Khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
§1. Khái niệm về khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
§2. Đa diện lồi và Đa diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
§3. Khái niệm về thể tích của khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
Chương 2. Mặt nón, mặt trụ, mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
§1. Khái niệm về khối tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
§2. Mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
Soạn:HuỳnhPhúSĩ 60 TrườngTHCS-THPTMỹThuận
Chương1.Khốiđadiện TOÁN12
Chương1.
KHỐI ĐA DIỆN
§1.KHÁI NIỆM VỀ KHỐI ĐA DIỆN
Đặt vấn đề
MặtngoàicủaKimtựthápAiCậpcóhìnhdánglàmộthình......,đượctạothànhbởi...... đagiác.
Nếumỗiđỉnhvàcạnhcủacácđagiácđóđềuđượcgọilàđỉnhvàcạnhcủahìnhchópthìhìnhchópđãchocóbao
nhiêuđỉnh,baonhiêucạnh?
1 KHỐI LĂNG TRỤ VÀ KHỐI CHÓP
•Khốilăngtrụlàphần............ đượcgiớihạnbởimột...... lăngtrụ,kểcả
...... lăngtrụấy.
•Khốichóplàphần............ đượcgiớihạnbởimột...... chóp,kểcả......
chópấy.
S
B
C
D
A
KhốichópS.ABCD có... đỉnh,... cạnh,
... mặt.
A B
C
A
0
C
0
B
0
KhốilăngtrụABC.A
0
B
0
C
0
có... đỉnh,...
cạnh,... mặt.
2 KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN
1 Khái niệm về hình đa diện
Hình đa diện là hình được tạo bởi một số hữu hạn các ......... thỏa mãn hai
tính chất sau:
•Hai đa giác phân biệt chỉ có thể hoặc không có ...... chung, hoặc chỉ có một
...... chung, hoặc chỉ có một ...... chung.
•Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng ...... đa giác.
Soạn:HuỳnhPhúSĩ 61 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốiđadiện TOÁN12
Ví dụ 1. Hìnhnàosauđâylàhìnhđadiện?
Hình1 Hình2 Hình3 Hình4
2 Khái niệm về khối đa diện
Khối đa diện là phần ............ được giới hạn b ởi một ...... đa diện, kể cả
...... đa diện đó.
•Nhữngđiểmkhôngthuộckhốiđadiệnđượcgọilàđiểm ......,những
điểmthuộc...... đadiệnnhưngkhôngthuộc...... đadiệngiớihạn
khốiđadiệnấyđượcgọilàđiểm trong.
•Tậphợpcácđiểm...... đượcgọilàmiền trong củakhốiđadiện,tậphợp
cácđiểmngoàiđượcgọilà............ củakhốiđadiện.
•Chỉcómiền...... làchứahoàntoànmộtđườngthẳngnàođấy.
Ví dụ 2. Hìnhvẽnàosauđâylàkhốiđadiện?
3 HAI ĐA DIỆN BẰNG NHAU
1 Phép dời hình trong không gian
Trongkhông gian, quy tắc đặttương ứng mỗi điểm M với điểm M
0
xácđịnh ............
được gọi là một phép biến hình trong không gian.
Phépbiếnhìnhtrongkhônggianđượcgọilàphép dời hình nếunóbảotoàn............
giữa hai điểm tùy ý.
~v
M M
0
P
M
I
M
0
M
M
0
∆
•Phép tịnh tiến theo vectơ
−Ï
v làphépbiếnhìnhbiếnmỗiđiểmM thànhđiểmM
0
saocho.........
•Phép đối xứng qua mặt phẳng (P)làphépbiếnhìnhbiếnmỗiđiểmN ∈ (P)
thành.........,biếnmỗiđiểmM /∈ (P)thànhđiểmM
0
saocho(P)làmặtphẳng
............ củađoạnthẳngMM
0
.
•Phép đối xứng tâm O làphépbiếnhìnhbiếnđiểmO thành.........,biếnmỗi
điểmM 6=O thànhđiểmM
0
saochoO là............ củađoạnthẳngMM
0
.
Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là
............... của (H).
•Phép đối xứng qua đường thẳng ∆ (hayphépđốixứngqua...... ∆)làphépbiến
hìnhbiếnmọiđiểmN ∈ ∆ thành.........,biếnmỗiđiểmM /∈ ∆ thànhđiểmM
0
saocho∆làđường............ củađoạnthẳngMM
0
.Nếu phép đối xứng trục ∆
biến hình (H) thành chính nó thì ∆ được gọi là ............... của (H).
Soạn:HuỳnhPhúSĩ 62 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốiđadiện TOÁN12
2 Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có một phép ............ biến hình này
thành hình kia.Hai đa diện được gọi là bằng nhau nếu có một phép ............
biến đa diện này thành đa diện kia.
−Ï
v
O
(H)
(H1)
(H2)
Cácđadiện(H),(H1) và(H2) bằngnhauvì.........
4 PHÂN CHIA VÀ LẮP GHÉP CÁC KHỐI ĐA DIỆN
Nếukhốiđadiện(H) làhợpcủahaikhốiđadiện(H1),(H2) saocho(H1) và(H2)
......... điểmchungnàothìtanóikhốiđadiện(H)cóthểchiađượcthànhhai
khốiđadiện(H1) và(H2).Ngượclại,tacóthể......... haikhốiđadiện(H1) và
(H2) vớinhauđểđượckhốiđadiện(H).
Mộtkhốiđadiệnbấtkìluôncóthểphânchiađượcthànhcáckhối.........
Ví dụ 3. Hãychiamộtkhốilậpphươngthành5 khốitứdiện.
5 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Mỗicạnhcủamộtkhốiđadiệnlàcạnhchungcủabaonhiêumặtcủakhối
đadiện?
A. Bốnmặt. B. Haimặt. C. Bamặt. D. Nămmặt.
Câu 2. Hãychọntừ/cụmtừthíchhợpđểđiềnvàochỗtrốngtrongphátbiểu:"Số
cạnhcủamộthìnhđadiệnluôn...... sốmặtcủahìnhđadiệnấy".
A. bằng. B. nhỏhơnhoặcbằng.
C. nhỏhơn. D. lớnhơn.
Câu 3. Mỗiđỉnhcủamộthìnhlậpphươnglàđỉnhchungcủađúngbaonhiêu
mặt?
A. 3. B. 4. C. 2. D. 5.
Câu 4. Mỗiđỉnhcủahìnhđadiệnlàđỉnhchungcủaítnhấtbaonhiêucạnh?
A. 5. B. 4. C. 3. D. 2.
Câu 5. Trongcácmệnhđềsau,mệnhđềnàolàđúng?
A. Sốcạnhcủamộthìnhđadiệnluônlớnhơn7.
B. Sốcạnhcủamộthìnhđadiệnluônlớnhơnhoặcbằng8.
C. Sốcạnhcủamộthìnhđadiệnluônlớnhơn6.
D. Sốcạnhcủamộthìnhđadiệnluônlớnhơnhoặcbằng6.
Soạn:HuỳnhPhúSĩ 63 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốiđadiện TOÁN12
Câu 6. Sốcạnhcủamộtkhốichóptamgiáclà
A. 6. B. 4. C. 7. D. 5.
Câu 7. Tổngsốđỉnh,cạnh,mặtcủahìnhlậpphươnglà
A. 26. B. 14. C. 24. D. 28.
Câu 8. Hìnhlăngtrụngũgiáccóbaonhiêumặt?
A. 9. B. 5. C. 7. D. 2.
Câu 9.
Hìnhđadiệnởhìnhbêncóbaonhiêumặt?
A. 8. B. 12. C. 10. D. 11.
Câu 10.
Đadiệntronghìnhbêncóbaonhiêumặt?
A. 11. B. 14. C. 12. D. 13.
Câu 11.
Hìnhđadiệnbêncóbaonhiêucạnh?
A. 15. B. 12. C. 20. D. 16.
Câu 12.
Sốđỉnhcủahìnhđadiệnbênlà
A. 8. B. 9. C. 10. D. 11.
Câu 13. Trongcáchìnhdướiđây,hìnhnàolàhìnhđadiện?
Hình1
Hình2 Hình3 Hình4
A. Hình4. B. Hình2. C. Hình1. D. Hình3.
Câu 14. Trongcáchìnhdướiđây,hìnhnàokhông phải hìnhđadiện?
Hình1 Hình2
Hình3
Hình4
A. Hình1. B. Hình2. C. Hình3. D. Hình4.
Câu 15. Trongcáchìnhdướiđây,hìnhnàokhông phải hìnhđadiện?
Soạn:HuỳnhPhúSĩ 64 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốiđadiện TOÁN12
Hình1 Hình2 Hình3 Hình4
A. Hình1. B. Hình2. C. Hình3. D. Hình4.
Câu 16. Hìnhlăngtrụcóthểcósốcạnhlàsốnàosauđây?
A. 3000. B. 3001. C. 3005. D. 3007.
Câu 17. Cho khối chóp có đáy là đa giác n cạnh. Mệnhh đềnào sauđây là
đúng?
A. Sốmặtcủakhốichóplà2n.
B. Sốđỉnhcủakhốichópbằng2n +1.
C. Sốcạnhcủakhốichópbằngn +1.
D. Sốmặtcủakhốichópbằngsốđỉnhcủanó.
Câu 18. CóthểchiakhốichópS.ABCD thànhhaikhốitứdiệnlà
A. SBCD vàSACD. B. SACD vàSABD.
C. SABC vàSABD. D. SABC vàSACD.
Câu 19. ChokhốilậpphươngABCD.A
0
B
0
C
0
D
0
.Mặtphẳng
(
BDD
0
B
0
)
chiakhốilập
phươngthành
A. Haikhốilăngtrụtamgiác. B. Haikhốitứdiện.
C. Haikhốilăngtrụtứgiác. D. Haikhốichóptứgiác.
Câu 20. CắtkhốilăngtrụABC.A
0
B
0
C
0
bởimặtphẳng
(
A
0
BC
)
tađược
A. Mộtkhốichóptamgiácvàmộtkhốichópngũgiác.
B. Haikhốichóptứgiác.
C. Mộtkhốichóptamgiácvàmộtkhốichóptứgiác.
D. Haikhốichóptamgiác.
L TỰ LUẬN
Câu 1 (SGK GT12). Chiamộtkhốilậpphươngthànhsáukhốitứdiệnbằngnhau.
d Vocabulary
solid polyhedra khốiđadiện
solid prisms khốilăngtrụ
solid pyramids khốichóp
solid cube khốilậpphương
tetrahedron tứdiện
vertice đỉnh
edge cạnh
face mặt
polygon đagiác
space khônggian
translation phéptịnhtiến
reflection phépđốixứng
Soạn:HuỳnhPhúSĩ 65 TrườngTHCS-THPTMỹThuận
§2.ĐadiệnlồivàĐadiệnđều TOÁN12
§2.ĐA DIỆN LỒI VÀ ĐA DIỆN ĐỀU
1 KHỐI ĐA DIỆN LỒI
Miềntrongcủakhốiđadiệnluôn
nằmvề......phíađốivớimỗimặt
phẳngchứamộtmặtcủanó
Khối đa diện (H)được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm
......... của (H) luôn ...... (H).
Khi đó đa diện xác định (H) được gọi là ................
Ví dụ 1. Trongcáchìnhdướiđâyhìnhnàokhôngphảiđadiệnlồi?
Hình1 Hình2
Hình3
Hình4
2 KHỐI ĐA DIỆN ĐỀU
Định nghĩa
Khối đa diện đều là khối đa diện ...... có các tính chất sau đây:
•Mỗi mặt của nó là một ..................... p cạnh
•Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khốiđadiệnđềunhưvậyđượcgọilàkhốiđadiệnđềuloại.......
Ví dụ 2. Khốitứdiệnđềulàkhốiđadiệnđềuloại......,khốilậpphươnglàkhốiđa
diệnđềuloại.......
Các mặt của khối đa diện đều là những đa giác ............... nhau.
Định lý
Chỉcó...... loạikhốiđadiệnđềulàloại...... (tứdiệnđều),...... (lậpphương),
...... (bátdiệnđều),...... (thậpnhịdiệnđều)và...... (nhịthậpdiệnđều).
Tứdiệnđều
•...... đỉnh
•...... cạnh
•...... mặt
Lậpphương
•...... đỉnh
•...... cạnh
•...... mặt
Bátdiệnđều
•...... đỉnh
•...... cạnh
•...... mặt
Thậpnhịdiệnđều
•...... đỉnh
•...... cạnh
•...... mặt
Nhịthậpdiệnđều
•...... đỉnh
•...... cạnh
•...... mặt
3 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Chohìnhlăngtrụtamgiácđều.Trongcácmệnhđềsau,mệnhđềnào
sai?
A. Haiđáylàcáctamgiácđềubằngnhau.
B. Cácmặtbênlàhìnhvuông.
Soạn:HuỳnhPhúSĩ 66 TrườngTHCS-THPTMỹThuận
§2.ĐadiệnlồivàĐadiệnđều TOÁN12
C. Cáccạnhbênvuônggócvớimặtđáy.
D. Cáccạnhbênbằngnhau.
Câu 2. Trongcácmệnhđềsau,mệnhđềnàosai?
A. Khốitứdiệnlàkhốiđadiệnlồi.
B. Khốihộplàkhốiđadiệnlồi.
C. Lắpghéphaikhốihộpbấtkìthìđượcmộtkhốiđadiệnlồi.
D. Khốilăngtrụtamgiáclàkhốiđadiệnlồi.
Câu 3. Trongcáchìnhdướiđâyhìnhnàokhôngphảiđadiệnlồi?
Hình1 Hình2
Hình3
Hình4
A. Hình1. B. Hình2. C. Hình3. D. Hình4.
Câu 4. Chocáckhốihìnhsau:
Hình1
Hình2
Hình3
Hình4
Mỗihìnhtrêngồmmộtsốhữuhạnđagiácphẳng(kểcảcácđiểmtrongcủanó),
sốđadiệnlồilà
A. 3. B. 2. C. 4. D. 1.
Câu 5. Chomộtkhốiđadiệnlồicó10 đỉnh,7 mặt.Hỏikhốiđadiệnnàycómấy
cạnh?
A. 20. B. 18. C. 15. D. 12.
Câu 6. Sốđỉnhcủahìnhbátdiệnđềulà
A. 10. B. 7. C. 8. D. 6.
Câu 7. Sốđỉnhcủahình12 mặtđềulà
A. Bamươi. B. Mườisáu. C. Mườihai. D. Haimươi.
Câu 8. Khối20 mặtđềucótấtcảbaonhiêucạnh?
A. 30. B. 20. C. 12. D. 60.
Câu 9. Hìnhbátdiệnđềucótấtcảbaonhiêucạnh?
A. 8. B. 9. C. 12. D. 20.
Câu 10. Hìnhbátdiệnđềucóbaonhiêumặt?
A. 9. B. 8. C. 6. D. 4.
Câu 11. Trongcáckhốiđadiệnđều,đadiệnnàocócácmặtlàcáchìnhngũgiác
đều?
A. Bátdiệnđều. B. Hìnhlậpphương.
C. Mườihaimặtđều. D. Haimươimặtđều.
Câu 12. Phátbiểunàosauđâylàđúng?
A. Hìnhmườihaimặtđềucó20 đỉnh,30 cạnh,12 mặt.
B. Hìnhmườihaimặtđềucó30 đỉnh,12 cạnh,12 mặt.
C. Hìnhmườihaimặtđềucó30 đỉnh,20 cạnh,12 mặt.
D. Hìnhmườihaimặtđềucó30 đỉnh,12 cạnh,30 mặt.
Câu 13. Trongcáchìnhđadiệnđềusau,hìnhnàocósốđỉnhnhỏhơnsốmặt?
A. Hìnhtứdiệnđều. B. Hình20 mặtđều.
C. Hìnhlậpphương. D. Hình12 mặtđều.
Câu 14. Khốilậpphươnglàkhốiđadiệnđềuloại
A. {5;3}. B. {3;4}. C. {4;3}. D. {3;5}.
Câu 15. Khốimườihaimặtđềulàkhốiđadiệnđềuloại?
A. {4;3}. B. {3;5}. C. {3;4}. D. {5;3}.
Soạn:HuỳnhPhúSĩ 67 TrườngTHCS-THPTMỹThuận
§2.ĐadiệnlồivàĐadiệnđều TOÁN12
Câu 16. Tínhtổngsốđỉnhvàsốmặtcủakhốiđadiệnđềuloại{5;3}.
A. 50. B. 20. C. 32. D. 42.
Câu 17. Hìnhchóptứgiácđềucóbaonhiêumặtphẳngđốixứng?
A. 1. B. 4. C. 3. D. 2.
Câu 18. Mộthìnhlăngtrụtamgiácđềucóbaonhiêumặtphẳngđốixứng?
A. 2. B. 3. C. 4. D. 6.
Câu 19. Hìnhđadiệnnàodướiđâykhông cótâmđốixứng?
Khốitứdiệnđều
Khốilậpphương
Lăngtrụlụcgiácđều
Khốibátdiệnđều
A. Tứdiệnđều. B. Bátdiệnđều.
C. Lăngtrụlụcgiácđều. D. Hìnhlậpphương.
Câu 20. Hìnhđadiệnnàosauđâykhôngcótâmđốixứng?
A. Tứdiệnđều. B. Bátdiệnđều.
C. Lăngtrụlụcgiácđều. D. Hìnhlậpphương.
L TỰ LUẬN
Câu 1 (SGK GT12). Chohìnhlậpphương(H).Gọi
(
H
0
)
làhìnhbátdiệnđềucócácđỉnhlàtâmcácmặtcủa(H).Tínhtỉsố
diệntíchtoànphầncủa(H) và
(
H
0
)
.
d Vocabulary
convex polyhedra đadiệnlồi
non-convex polyhedra đadiệnkhônglồi
regular polyhedra đadiệuđều
regular polygon đagiácđều
regular tetrahedron tứdiệnđều
regular octahedron bátdiệnđều
regular dodecahedron thậpnhịdiệnđều
regular icosahedron nhịthậpdiệnđều
Soạn:HuỳnhPhúSĩ 68 TrườngTHCS-THPTMỹThuận
§3.Kháiniệmvềthểtíchcủakhốiđadiện TOÁN12
§3.KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI
ĐA DIỆN
Đặt vấn đề
DãTràngdựđịnhxâydựngmộtkimtựthápcao100m,
cạnhđáy50mbằngnhữngviêngạchhìnhhộpchữnhật
cóđộdàicáccạnhlầnlượtlà5cm,10cm,20cm.
Nếu bỏ qua phần xi măng thì Dã Tràng cần
chuẩn bị tối thiểu bao nhiêu viên gạch như trên?
1 KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN
Thể tích của một khối hộp chữ nhật bằng ......... ba kích thước của nó.
Ví dụ 1. Tínhthểtíchcủamộtviêngạchcóđộdàicáccạnhlầnlượtlà5cm,10cm,20cm.
Thể tích khối lập phương cạnh a là ......
2 THỂ TÍCH KHỐI LĂNG TRỤ
Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là
V =.........
Ví dụ 2. Chokhốilăngtrụđứngtamgiácđềucótấtcảcáccạnhbằng5cm.Tínhthểtích
khốilăngtrụđãcho.
3 THỂ TÍCH KHỐI CHÓP
Thể tích khối chóp có diện tích đáy B và chiều cao h là
V =.........
Ví dụ 3. KimtựthápKê-ốpởAiCậpđượcxâydựngvàokhoảng2500nămtrướcCông
nguyên.Kimtựthápnàylàmộtkhốichóptứgiácđềucóchiềucao147m,cạnhđáydài
230m.Hãytínhthểtíchcủanó.
Soạn:HuỳnhPhúSĩ 69 TrườngTHCS-THPTMỹThuận
§3.Kháiniệmvềthểtíchcủakhốiđadiện TOÁN12
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. ThểtíchV củakhốilăngtrụcóchiềucaoh vàdiệntíchđáyB là
A. V =Bh. B. V =
1
2
Bh. C. V =
1
6
Bh. D. V =
1
3
Bh.
Câu 2. ThểtíchV củakhốichópcódiệntíchđáyB vàchiềucaoh là
A. V =
1
3
Bh. B. V =3Bh. C. V =
1
2
Bh. D. V =Bh.
Câu 3. ChokhốilăngtrụcóthểtíchbằngV.BiếtdiệntíchđáycủalăngtrụlàB,
tínhchiềucaoh củakhốilăngtrụđãcho.
A. h =
V
3B
. B. h =
2V
B
. C. h =
3V
B
. D. h =
V
B
.
Câu 4. Thểtíchcủakhốilậpphươngcạnh2a bằng
A. 8a
3
. B. 2a
3
. C. a
3
. D. 6a
3
.
Câu 5. Thểtíchcủakhốichópcóchiềucaoh =a vàdiệntíchđáyS =3a
2
là
A. V =
1
3
a
3
. B. V =a
3
. C. V =3a
3
. D. V =
1
6
a
3
.
Câu 6. ChokhốichópcódiệntíchđáyB = a
2
√
2 vàchiềucaoh = 2a.Thểtích
V củakhốichóplà
A. V =
2a
3
√
2
3
. B. V =
2a
3
√
2
9
. C. V =2a
3
√
2. D. V =
a
3
√
2
3
.
Câu 7. ChohìnhchóptứgiácS.ABCD có đáy ABCD làhìnhvuôngcạnha,
SA ⊥ (ABCD) vàSA =a
√
6.ThểtíchcủakhốichópS.ABCD bằng
A. a
3
√
6. B. a
3
√
6
3
. C. a
3
√
6
6
. D. a
3
√
6
2
.
Câu 8. ChokhốichópS.ABC cóđáyABC làtamgiácđều,SA vuônggócvớimặt
phẳng(ABC)vàSA =a.BiếtrằngthểtíchcủakhốichópS.ABC bằng
√
3a
3
.Tính
độdàicạnhđáycủakhốichópS.ABC.
A. 2a
√
3. B. 3a
√
3. C. 2a. D. 2a
√
2.
Câu 9. ChokhốichópS.ABC cóđáylàtamgiácđềucạnh2a vàthểtíchbằnga
3
.
Tínhchiềucaoh củahìnhchópđãcho.
A. h =
√
3a
6
. B. h =
√
3a
2
. C. h =
√
3a
3
. D. h =
√
3a.
Câu 10. ChokhốichópS.ABC cóđáyABC làtamgiácđều,SA vuônggócvớimặt
phẳng(ABC)vàSA =a.BiếtrằngthểtíchcủakhốichópS.ABC bằng
√
3a
3
.Tính
độdàicạnhđáycủakhốichópS.ABC.
A. 2a
√
3. B. 3a
√
3. C. 2a. D. 2a
√
2.
Câu 11. Chokhốilăngtrụcódiệntíchđáylà30a
2
vàthểtíchlà150a
3
.Tínhtheo
a khoảngcáchgiữahaimặtphẳngđáycủakhốilăngtrụđãcho.
A. h =5. B. h =5a. C. h =
a
5
. D. h =15a.
Câu 12. Nếubakíchthướccủamộtkhốihộpchữnhậttănglên3 lầnthìthểtích
củanótănglênbaonhiêulần?
A. 3 lần. B. 9 lần. C. 18 lần. D. 27 lần.
Câu 13. Mộtviêngạchdạngkhốihộpchữnhậtcóbakíchthướclà3cm,10cm,
20cm.Tínhthểtíchviêngạchđó.
A. 300cm. B. 200cm. C. 600cm. D. 1200cm.
Câu 14. Tínhthểtíchkhốirubiclậpphươngcócạnhbằng8cm(Bỏcáckhehở
củakhốirubic,xemthểtíchcủakhehởkhôngđángkể).
A. 24cm
3
. B. 8cm
3
. C. 512cm
3
. D.
512
3
cm
3
.
Câu 15. ChohìnhchóptứgiácđềuS.ABCD cócạnhđáybằnga,cạnhbênhợp
vớimặtđáymộtgóc60
◦
.Tínhtheoa thểtíchV củakhốichópS.ABCD.
A. V =
a
3
√
6
6
. B. V =
a
3
√
6
2
. C. V =
a
3
√
6
3
. D. V =
a
3
3
.
Câu 16. CholăngtrụABC.A
0
B
0
C
0
cóđáyABC làtamgiácđềucạnhbằng2a.Hình
chiếuvuônggóccủaA
0
lênmặtphẳng(ABC)trùngvớitrungđiểmH củacạnh
BC vàA
0
H =a
√
3.Tínhtheoa thểtíchV củakhốilăngtrụABC.A
0
B
0
C
0
.
A. V =3a
3
. B. V =a
3
. C. V =
3a
3
4
. D. V =
3a
3
2
.
Soạn:HuỳnhPhúSĩ 70 TrườngTHCS-THPTMỹThuận
§3.Kháiniệmvềthểtíchcủakhốiđadiện TOÁN12
Câu 17. Chokhốichóptứgiácđềucótấtcảcáccạnhbằng2a.Thểtíchcủakhối
chópđãchobằng
A.
4
√
2a
3
3
. B.
8a
3
3
. C.
8
√
2a
3
3
. D.
2
√
2a
3
3
.
Câu 18. ChohìnhchópđềuS.ABCD cóchiềucaobằnga
√
2 vàđộdàicạnhbên
bằnga
√
6.TínhthểtíchkhốichópS.ABCD.
A.
8a
3
√
2
3
. B.
10a
3
√
2
3
. C.
8a
3
√
3
3
. D.
10a
3
√
3
3
.
Câu 19. Chokhốilăngtrụtamgiácđềucótấtcảcáccạnhbằngnhauvàthểtích
củakhốilăngtrụbằng2
√
3.Tínhcạnhcủakhốilăngtrụ.
A. 6. B. 4. C. 3. D. 2.
Câu 20.
ChohìnhchóptamgiácS.ABC cóđáyABC là
tamgiácđềucạnh2a vàSA vuônggócvớimặt
phẳng(ABC)(thamkhảohìnhvẽ).Biếtthểtích
củakhốichópS.ABC là
a
3
√
3
2
vàgócgiữahai
mặtphẳng(SBC) và(ABC) làgócnhọnα.Chọn
phátbiểuđúng.
A. α =60
◦
. B. α =45
◦
.
C. α =30
◦
. D. tanα =
√
3
2
.
S
B
A C
Câu 21. ChotứdiệnMNPQ.GọiI, J, K lầnlượtlàtrungđiểmcủacáccạnh
MN, MP, MQ.Tỉsố
V
MIJK
V
MNPQ
bằng
A.
1
3
. B.
1
4
. C.
1
8
. D.
1
6
.
Câu 22. ChohìnhchópS.ABC,gọiM,N lầnlượtlàtrungđiểmcủacạnhSA,SB.
Tínhtỉsố
V
S.ABC
V
S.MNC
.
A. 4. B.
1
2
. C. 2. D.
1
4
.
Câu 23. ChotứdiệnABCD.C ácđiểmM,N,P lầnlượtthuộccáccạnhAB,AC,
AD saochoMA = MB,NA = 2NC,PA = 3PD.BiếtthểtíchkhốitứdiệnAMNP
bằngV thìkhốitứdiệnABCD tínhtheoV cógiátrịlà
A. 4V. B. 6V. C. 12V. D. 8V.
Câu 24. ChokhốichópS.ABCD cóđáylàhìnhbìnhhànhvàcóthểtích48.Trên
cáccạnhSA, SB, SC, SD lầnlượtlấycácđiểmA
0
, B
0
, C
0
vàD
0
saocho
SA
0
SA
=
SC
0
SC
=
1
3
và
SB
0
SB
=
SD
0
SD
=
3
4
.TínhthểtíchV củakhốiđadiệnS.A
0
B
0
C
0
D
0
.
A. V =4. B. V =9. C. V =
3
2
. D. V =6.
Câu 25. ChokhốilăngtrụABC.A
0
B
0
C
0
cóthểtíchbằngV.Thểtíchcủakhốiđa
diệnABCC
0
B
0
bằng
A.
3V
4
. B.
2V
3
. C.
V
2
. D.
V
4
.
Câu 26. Mộtbểcáhìnhhộpchữnhậtcóthểtích0,36m
3
.Biếtkíchthướccủađáy
bểlầnlượtbằng0,5mvà1,2m.Chiềucaocủabểcábằng
A. 0,65m. B. 0,6m. C. 0,7m. D. 0,5m.
Câu 27. Tínhthểtíchcủakhốigỗcóhìnhdạngdướiđây
6cm
7cm
14cm
15cm
4cm
A. 328cm
3
. B. 456cm
3
. C. 584cm
3
. D. 712cm
3
.
Soạn:HuỳnhPhúSĩ 71 TrườngTHCS-THPTMỹThuận
§3.Kháiniệmvềthểtíchcủakhốiđadiện TOÁN12
Câu 28. Mộttấmbìahìnhvuôngcócạnh44cm,ngườitacắtbỏđiởmỗigóctấm
bìamộthìnhvuôngcạnh12cmrồigấplạithànhmộtcáihộpchữnhậtkhôngcó
nắp.Tínhthểtíchcáihộpnày.
A. 4800cm
3
. B. 9600cm
3
. C. 2400cm
3
. D. 2400
√
3cm
3
.
Câu 29. Mộtngườibángạomuốnđóngmộtthùngtônđựnggạocóthểtíchkhông
đổibằng8m
3
,thùngtônhìnhhộpchữnhậtcóđáylàhìnhvuông,khôngnắp.
Trênthịtrường,giátônlàmđáythùnglà100.000đồng/m
2
,giátônlàmthànhxung
quanhthùnglà50.000đồng/m
2
.Hỏingườibángạođócầnđóngthùngđựnggạo
vớicạnhđáybằngbaonhiêuđểchiphímuanguyênliệulànhỏnhất?
A. 3m. B. 1,5m. C. 2m. D. 1m.
Câu 30.
Cáckíchthướccủamộtbểbơiđược
chotrênhìnhvẽ(mặtnướccódạng
hìnhchữnhật).Hãytínhxembểbơi
chứađượcbaonhiêumétkhốinước
khinóđầyắpnước?
A. 1000m
3
. B. 640m
3
.
C. 570m
3
. D. 500m
3
.
10m
25m
2m
4m
7m
L TỰ LUẬN
Câu 1 (SGK GT12). Tínhthểtíchkhốitứdiệnđềucạnha.
Câu 2 (SGK GT12). ChohìnhchópS.ABC.TrêncácđoạnthẳngSA, SB, SC lầnlượtlấybađiểmA
0
, B
0
, C
0
khácvớiS.
Chứngminhrằng
V
S.A
0
B
0
C
0
V
S.ABC
=
SA
0
SA
·
SB
0
SB
·
SC
0
SC
Câu 3 (SGK GT12). ChohìnhlậpphươngABCD.A
0
B
0
C
0
D
0
cạnha.GọiM làtrungđiểmcủaA
0
B
0
,N làtrungđiểmcủaBC.
a)TínhthểtíchkhốitứdiệnADMN
b)Mặtphẳng(DMN)chiakhốilậpphươngđãchothànhhaikhốiđadiện.Gọi(H)làkhốiđadiệnchứađỉnhA,(H
0
)là
khốiđadiệncònlại.
Tínhtỉsố
V
(H)
V
(H
0
)
.
d Vocabulary
volume thểtích
area diệntích
base mặtđáy
height chiềucao
ratio tỉsố
rectangular hìnhhộpchữnhật
Soạn:HuỳnhPhúSĩ 72 TrườngTHCS-THPTMỹThuận
Chương2.Mặtnón,mặttrụ,mặtcầu TOÁN12
Chương2.
MẶT NÓN, MẶT TRỤ, MẶT CẦU
§1.KHÁI NIỆM VỀ KHỐI TRÒN XOAY
Đặt vấn đề
Xungquanhchúng tacónhiều vậtthểmàmặtngoàicủanó
cóhìnhdạnglà những mặttrònxoay như bìnhhoa,nónlá,
cáibát(chén)ăncơm,cáicốcuốngnước,mộtsốchitiếtmáy...
Nhờ có bàn xoay với sựkhéo léo của đôibàn tay, người thợ
gốmcóthểtạonênnhữngvậtdụng códạngtrònxoaybằng
đấtsét.Dựavàosựquaytròncủatrụcmáyđiện,ngườithợcơ
khícóthểtạonênnhữngchitiếtmáybằngkimloạicódạng
trònxoay.Vậycácmặttrònxoayđượchìnhthànhnhưthếnào?
1 SỰ TẠO THÀNH MẶT TRÒN XOAY
Trongkhônggianchomặtphẳng(P)chứađườngthẳng∆vàmộtđườngC .Khi
...... mặtphẳng(P) quanh∆ mộtgóc...... thìmỗiđiểmM trênđườngC vạch
ramộtđường...... cótâmO ∈ ∆vànằmtrênmặtphẳngvuônggócvới∆.Như
vậykhiquaymặtphẳng(P)quanhđườngthẳng∆ thìđườngC sẽtạonênmộthình
đượcgọilà..................
•ĐườngC đượcgọilà............
•Đườngthẳng∆đượcgọilà......
NếuC làđườngthẳngcắt∆ thìtađượcmộtmặt...... trònxoay,nếuC làđườngthẳng
songsongvới∆ thìtađượcmộtmặt...... trònxoay.
2 MẶT NÓN TRÒN XOAY
1 Định nghĩa
Trongmặtphẳng(P)chohaiđườngthẳngd và∆...... nhautạiđiểmO vàtạo
thànhgócβ với... < β < ... Khiquaymặtphẳng(P)xungquanh∆thìđường
thẳngd sinhramộtmặt......... đượcgọilàmặt...... trònxoayđỉnhO,gọitắt
là............
Đườngthẳng...... gọilàtrục,đườngthẳng...... gọilàđườngsinh.
2 Hình nón tròn xoay và khối nón tròn xoay
ChotamgiácOIM vuôngtạiI.Khiquay4OIM quanh
cạnhOI thìđường......... OIM tạothànhmột......
đượcgọilàhìnhnóntrònxoay,gọitắtlà............
•HìnhtròntâmI,bánkínhIM gọilà.........
•ĐiểmO gọilà...... củahìnhnón
•Đoạn OI gọi là ........., đoạn OM là độ dài
............
Khối nón tròn xoay làphần............ đượcgiớihạnbởimột...... nóntrònxoay,kể
cả...... nónđó.
Soạn:HuỳnhPhúSĩ 73 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốitrònxoay TOÁN12
Ví dụ 1. ChotamgiácđềuABC cạnh3cm,gọiH làtrungđiểmcủacạnhBC.Nếuxoay
4ABC quanhđườngcaoAH thìtathuđượcmộthìnhnóncóchiềucaoh = ......cm,
độdàiđườngsinh` =......cmvàdiệntíchđáyS
đ
=.........
3 Diện tích và thể tích
Chohìnhnóncóchiềucaoh,độdàiđườngsinh` vàbánkínhđáyr.Khiđó:
Diệntíchxungquanh Diệntíchtoànphần Thểtích
Ví dụ 2. Chohìnhnóncóchiềucaoh = 4cmvàbánkínhđáyr =3cm.Hãytínhdiện
tíchxungquanh,diệntíchtoànphầncủahìnhnónvàthểtíchcủakhốinóntạobởihình
nónđãcho.
3 MẶT TRỤ TRÒN XOAY
1 Định nghĩa
Trongmặtphẳng(P)chohaiđườngthẳng` và∆............ vớinhau,cáchnhau
mộtkhoảngr.Khiquaymặtphẳng(P)xungquanh∆thìđườngthẳng` sinhra
mộtmặt......... đượcgọilàmặt...... trònxoay,gọitắtlà............
Đườngthẳng...... gọilàtrục,đườngthẳng...... gọilàđườngsinh,r là.........
củamặttrụđó.
2 Hình trụ tròn xoay và khối trụ tròn xoay
ChohìnhchữnhậtABCD.KhiquayABCD quanhcạnhAB thì
đường......... ADCB tạothànhmột...... đượcgọilàhìnhtrụ
trònxoay,gọitắtlà............
•HìnhtròntâmA,bánkínhAD gọilà.........
•ĐoạnAB gọilà.........,đoạnCD làđộdài............
Khối trụ tròn xoay làphần............ đượcgiớihạnbởimột
...... trụtrònxoay,kểcả...... trụđó.
Ví dụ 3. ChohìnhvuôngABCD cạnh3cm,gọiM, N lầnlượtlà
trungđiểmcủacáccạnhAB, CD.NếuxoayABCD quanhđường
thẳngMN thìtathuđượcmộthình...... cóchiềucaoh =...cm,
độdàiđườngsinh` =...cmvàdiệntíchđáyS
đ
=..........
3 Diện tích và thể tích
Chohìnhtrụcóchiềucaoh vàbánkínhđáyr.Khiđó:
Diệntíchxungquanh Diệntíchtoànphần Thểtích
Ví dụ 4. HộpsữađặcÔngThọcóchiềucao8cmvàđườngkínhđáy7,5cm.Hãytính
diệntíchphầnnhãndánbaoquanhthânhộpsữavàdungtíchsữatốiđatronghộp.
Soạn:HuỳnhPhúSĩ 74 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốitrònxoay TOÁN12
4 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. Gọil, h, R lầnlượtlàđộdàiđườngsinh,chiềucaovàbánkínhđáycủa
mộtkhốinón.ThểtíchV củakhốinónđólà
A. V =
1
3
πR
2
h. B. V =πR
2
h. C. V =
1
3
πR
2
l. D. V =πR
2
l.
Câu 2. ThểtíchcủakhốitrụcóbánkínhđáyR vàchiềucaoh là
A. V =2πR
2
h. B. V =
4
3
πR
2
h. C. V =πR
2
h. D. V =
1
3
πR
2
h.
Câu 3. Chohìnhtrụcóbánkínhđáybằng2a,mộtmặtphẳngđiquatrụccủa
hìnhtrụvàcắthìnhtrụtheothiếtdiệnlàhìnhvuông.TínhthểtíchV củakhối
trụđãcho.
A. V =18πa
3
. B. V =4πa
3
. C. V =8πa
3
. D. V =16πa
3
.
Câu 4. Chohìnhtrụcóbánkínhđáyr =3vàdiệntíchxungquanhS =6π.Tính
thểtíchV củakhốitrụ.
A. V =3π. B. V =9π. C. V =18π. D. V =6π.
Câu 5. Mộthìnhtrụcóhaiđáylàhaihìnhtrònnộitiếphaimặtcủamộthìnhlập
phươngcạnha.Tínhthểtíchcủakhốitrụđãcho.
A. V =
πa
3
12
. B. V =
πa
3
6
. C. V =
πa
3
2
. D. V =
πa
3
4
.
Câu 6. Cắtmộtkhốitrụbởimộtmặtphẳngquatrụctađượcthiếtdiệnlàhình
chữnhậtABCD cóAB vàCD thuộchaiđáycủahìnhtrụ,biếtAB =4a,AC =5a.
Tínhthểtíchcủakhốitrụ.
A. V =4πa
3
. B. V =16πa
3
. C. V =12πa
3
. D. V =8πa
3
.
Câu 7. ChohìnhchữnhậtABCD cóAB =a,BC =b.GọiM, N lầnlượtlàtrung
điểmcủaAB vàCD.TínhthểtíchkhốitrụthuđượckhiquayhìnhchữnhậtABCD
quanhtrụcMN.
A. V =
πa
2
b
4
. B. V =πa
2
b. C. V =
πa
2
b
12
. D. V =
πa
2
b
3
.
Câu 8. Chohìnhtrụcóbánkínhđườngtrònđáybằng4,diệntíchxungquanh
bằng48π.Tínhthểtíchcủakhốitrụđãcho.
A. V =24π. B. V =32π. C. V =96π. D. V =72π.
Câu 9. Mộthìnhtrụcóđườngkínhđáy12cm,chiềucao10cm.Thểtíchkhốitrụ
nàylà
A. 1440π cm
3
. B. 360π cm
3
. C. 480π cm
3
. D. 1440 cm
3
.
Câu 10. Mộtkhốinóncóđộdàiđườngsinhl = 13cmvàbánkínhđáyr =5cm.
Tínhthểtíchkhốinónđãcho.
A. V =100πcm
3
. B. V =300πcm
3
.
C. V =20πcm
3
. D. V =
325π
3
cm
3
.
Câu 11. Chohìnhnón(N) cóchiềucaoh,bánkínhđáyR vàđộdàiđườngsinh
l.CôngthứctínhdiệntíchxungquanhS của(N) là
A. S =
1
3
πRl. B. S =πRl. C. S =4πR
2
. D. S =2πRl.
Câu 12. Chomộthìnhtrụcóthiếtdiệnquatrụclàmộthìnhchữnhậtcódiện
tíchbằng18.Tínhdiệntíchxungquanhcủahìnhtrụđãcho.
A. S
xq
=9. B. S
xq
=18. C. S
xq
=9π. D. S
xq
=18π.
Câu 13. Chohìnhtrụcóthiếtdiệnquatrụclàmộthìnhvuông.GọiS
1
,S
2
lần
lượtlàdiệntíchxungquanhvàdiệntíchtoànphầncủahìnhtrụ.Tínhgiátrịcủa
S
1
S
2
.
A.
1
2
. B.
2
3
. C.
3
4
. D.
4
5
.
Câu 14. Cắtmộthìnhtrụbởimộtmặtphẳngquatrụccủanó,tađượcthiếtdiện
làmộthìnhvuôngcócạnhbằng3a.Tínhdiệntíchtoànphầncủahìnhtrụđã
cho.
A. S
tp
=
9πa
2
2
. B. S
tp
=
13πa
2
6
. C. S
tp
=9πa
2
. D. S
tp
=
27πa
2
2
.
Câu 15. DiệntíchxungquanhcủahìnhtrụcóbánkínhđáyR =3 vàđườngsinh
l =6 bằng
A. 54π. B. 18π. C. 108π. D. 36π.
Soạn:HuỳnhPhúSĩ 75 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốitrònxoay TOÁN12
Câu 16. Chohìnhtrụcóbánkínhđáybằnga,chiềucaobằng3a.Diệntíchxung
quanhcủahìnhtrụbằng
A. 6πa
2
. B. 3πa
2
. C. 9πa
2
. D. 4πa
2
.
Câu 17. Chohìnhnóncóbánkínhđáybằng4a vàchiềucaobằng3a.Diệntích
xungquanhcủahìnhnónbằng
A. 18πa
2
. B. 20πa
2
. C. 12πa
2
. D. 15πa
2
.
Câu 18. Tínhchiềucaoh củakhốinóncóbánkínhđáybằng3 vàthểtíchbằng
36π.
A. h =18. B. h =12. C. h =6. D. h =16.
Câu 19.
ChotamgiácABC vuôngtạiA cóAB =a,
AC = 2a.Tínhđộdàiđườngsinhl củahình
nónnhậnđượckhiquaytamgiácABC quanh
trụcAB.
A. l =a
√
2. B. l =2a.
C. l =a
√
3. D. l =a
√
5.
A
C
B
2a
a
?
Câu 20.
ChotamgiácOAB vuôngtạiO cóAB =a vàgóc
b
A =30
◦
.
Tínhdiệntíchxungquanhcủahìnhnóncóđượckhiquay
tamgiácOAB quanhtrụcAO.
A.
πa
2
4
. B. 2πa
2
. C. πa
2
. D.
πa
2
2
.
O
B
A
a
30
◦
Câu 21. Chohìnhnóncódiệntíchxungquanhbằng3πa
2
vàbánkínhđáybằng
2a.Độdàiđườngsinhcủahìnhnónđãchobằng
A. 2a
√
2. B. 3a. C. 2a. D.
3a
2
.
Câu 22. Mộthìnhnóncóthiếtdiệnquatrụclàmộttamgiácvuôngcâncócạnh
gócvuôngbằnga.Tínhdiệntíchxungquanhcủahìnhnónđãcho.
A. S
xq
=
πa
2
2
. B. S
xq
=
πa
2
√
2
2
.
C. S
xq
=
3πa
2
2
. D. S
xq
=πa
2
.
Câu 23. Tìmbánkínhđáycủahìnhnóncódiệntíchxungquanhlà3πa
2
vàđộ
dàiđườngsinhlà3a.
A. 3a. B. a. C. 2a. D. 4a.
Câu 24. Chohìnhnóncódiệntíchxungquanhbằng3πa
2
vàbánkínhđáybằng
a.Tínhtangcủagócgiữamộtđườngsinhvàmặtđáycủahìnhnón.
A. 8. B. 2
√
2. C.
2
√
2
3
. D.
1
3
.
Câu 25. Chohìnhnóncóthiếtdiệnquatrụclàmộttamgiácđềucạnhbằnga.
Tínhdiệntíchmặtxungquanhcủahìnhnónđãcho.
A.
1
2
πa
2
. B. πa
2
. C.
2
3
πa
2
. D.
1
3
πa
2
.
Câu 26. Chohìnhnóncóbánkínhđáyr =
√
2 vàđộdàiđườngsinhl =3.Tính
diệntíchxungquanhcủahìnhnónđãcho.
A. S
xq
=2π. B. S
xq
=3π
√
2. C. S
xq
=6π. D. S
xq
=6π
√
2.
Câu 27. Chohìnhnóncóbánkínhđáybằnga,chiềucao2a.Độdàiđườngsinh
củahìnhnónbằng
A. a
√
3. B. 2a
√
3. C. a
√
5. D. 4a.
Câu 28. Chohìnhnóncóbánkínhđáybằnga vàđộdàiđườngsinhbằng2a.
Diệntíchxungquanhcủahìnhnónđóbằng
A. 4πa
2
. B. 2a
2
. C. 2πa
2
. D. 3πa
2
.
Câu 29. Chohìnhnóncóbánkínhđáybằnga vàđộdàiđườngsinhbằng3a.
Diệntíchxungquanhcủahìnhnónđóbằng
A. 3πa
2
. B. 2πa
2
. C. πa
2
. D.
3
2
πa
2
.
Soạn:HuỳnhPhúSĩ 76 TrườngTHCS-THPTMỹThuận
§1.Kháiniệmvềkhốitrònxoay TOÁN12
Câu 30. BìnhĐịnhcócâucadao:
"Cưới nàng đôi nón Gò Găng
Xấp lãnh An Thái một khăn trầu nguồn."
Nóiđếncâucadaonàylànóiđếnmộtlàngnghềtruyềnthốngcóhàngtrămnăm
tuổicủathịxãAnNhơn,tỉnhBìnhĐịnh-làngnghềlàmnónláGòGăng.Nhân
kỷniệm10nămđượccôngnhậnthịxã,thịxãAnNhơnlênkếhoạchlàmcácmô
hìnhbiểutượnglàngnghềtruyềnthốngtrênđịabàn,trongđócómôhìnhchiếc
nónláGòGăng.Chiếcnóncóbánkínhđáy1métvàchiềucao1,5mét,khung
thépdùnglàmđườngtrònđáyvà10đườngnốitừđỉnhcủanónđếnđườngtròn
đáycógiáthành40.000đồng/mét,làcủacâylánónLicualaFatouaBeccdùngđể
làmmặtnóncógiáthành20.000đồng/métvuông.Hỏinếubỏquadiệntíchcác
mépnốithìkinhphíđểlàmchiếcnónbiểutượngnàylàbaonhiêu?
A. 1.085.000 đồng. B. 1.086.000 đồng.
C. 834.000 đồng. D. 833.000 đồng.
L TỰ LUẬN
Câu 1 (SGK GT12). Chohìnhnóntrònxoaycóđườngcaoh =20cm,bánkínhđáyr =25cm.
a)Tínhdiệntíchxungquanhcủahìnhnónđãcho
b)Tínhthểtíchcủakhốinónđượctạothànhbởihìnhnónđó.
c)Mộtthiếtdiệnđiquađỉnhcủahìnhnóncókhoảngcáchtừtâmcủađáyđếnmặtphẳngchứathiếtdiệnlà12cm.Tính
diệntíchthiếtdiệnđó.
Câu 2 (SGK GT12). Mộthìnhtrụcóbánkínhđáyr =5cmvàcókhoảngcáchgiữahaiđáybằng7cm.
a)Tínhdiệntíchxungquanhcủahìnhtrụvàthểtíchcủakhốitrụtạonên
b)Cắtkhốitrụbởimộtmặtphẳngsongsongvớitrụcvàcáchtrục3cm.Hãytínhdiệntíchcủathiếtdiệnđượctạonên.
d Vocabulary
circular trònxoay
conical surface mặtnón
cylinder surface mặttrụ
generator line đườngsinh
axis trục
radius bánkính
curved surface area diệntíchxungquanh
surface area diệntíchtoànphần
cross-section thiếtdiện
Soạn:HuỳnhPhúSĩ 77 TrườngTHCS-THPTMỹThuận
§2.Mặtcầu TOÁN12
§2.MẶT CẦU
Đặt vấn đề
HìnhdạngcủaTráiĐấtrấtgầnvớihìnhphỏngcầulàhìnhcầu
bịnéndọctheohướngtừđịacựctớichỗphìnhraởxíchđạo.
Phầnphìnhranàylàkếtquảcủaquátrìnhtựquayvàkhiếncho
độdàiđườngkínhtạiđườngxíchđạodàihơn43kmsovớiđộ
dàiđườngkínhtínhtừcựctớicực.Độdàiđườngkínhtrungbình
củahìnhphỏngcầuthamchiếuvàokhoảng12.745km.
(TheoWikipedia)
Nếu xem Trái Đất là một hình cầu với đường kính như
trên thì diện tích bề mặt của Trái Đất là bao nhiêu km
2
?
1 MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN ĐẾN MẶT CẦU
1 Mặt cầu
Tập hợp những điểm M trong ............ cách điểm O cố định một khoảng
............ bằng r > 0 được gọi là mặt cầu tâm O bán kính r.
Kíhiệu:.........
•NếuhaiđiểmC, D ∈ S
(
S;r
)
thìđoạnthẳngCD gọilà.............
•Dâycungđiquatâmđượcgọilà............ củamặtcầu.
2 Điểm nằm trong và nằm ngoài mặt cầu. Khối cầu
ChomặtcầuS
(
O;r
)
vàđiểmM bấtkì.
!
•NếuOM =r thìM nằm...... mặtcầuS
(
O;r
)
•NếuOM < r thìM nằm...... mặtcầuS
(
O;r
)
•NếuOM > r thìM nằm...... mặtcầuS
(
O;r
)
TậphợpcácđiểmA saochoOA ≤ r đượcgọilà...... cầuhay...... cầutâmO bán
kínhr.
3 Đường kinh tuyến và vĩ tuyến của mặt cầu
¹ Giao......... củamặtcầuvớicácnửamặtphẳngcóbờlàtrụccủamặtcầuđược
gọilàkinh tuyến củamặtcầu.
¹ Giaotuyếncủamặtcầuvớicácmặtphẳng............ vớitrục(nếucó)đượcgọi
là............ củamặtcầu.
¹ Haigiao...... củamặtcầuvớitrụcđượcgọilàcực củamặtcầu.
2 GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG
ChomặtcầuS
(
O;r
)
vàmặtphẳng(P).GọiH làhìnhchiếuvuônggóccủaO lên(P),khi
đóOH =d
(
O,(P)
)
.
○ NếuOH > r thì(P) và(S) ......... điểmchung.
○ NếuOH =r thì(P) ......... với(S) tại....
Khiđó,(P) gọilà............,H gọilà............
○ NếuOH < r thì(P)cắt(S)theogiaotuyếnlà............ tâm...,bánkính
r
0
=......... (Pitago).
Soạn:HuỳnhPhúSĩ 78 TrườngTHCS-THPTMỹThuận
§2.Mặtcầu TOÁN12
OH ... r
OH ... r
OH ... r
3 GIAO CỦA MẶT CẦU VÀ ĐƯỜNG THẲNG. TIẾP TUYẾN
ChomặtcầuS
(
O;r
)
vàđườngthẳng∆.GọiH làhìnhchiếuvuônggóccủaO lên∆,khi
đóOH =d
(
O,∆
)
.
○ NếuOH > r thì∆và(S) ......... điểmchung.
○ NếuOH =r thì∆......... với(S) tại....
Khiđó,∆ gọilà............,H gọilà............
○ NếuOH < r thì∆cắt(S) tại... điểm.
OH ... r
OH ... r
OH ... r
Nhận xét.
•QuamộtđiểmM nằmtrênmặtcầu,có...... tiếptuyếnvớimặtcầu.Cáctiếptuyến
nàytạothànhmột............ củamặtcầu.
•QuamộtđiểmM nằmngoàimặtcầu,có...... tiếptuyếnvớimặtcầu.Cáctiếp
tuyếnnàytạothànhmột......... đỉnhA.
•NếuOM > r thìM nằm...... mặtcầuS
(
O;r
)
4 DIỆN TÍCH VÀ THỂ TÍCH
Chomặtcầubánkínhr.Khiđó:
Diệntích Thểtích
Ví dụ 1. Cómộtconquạđangkhátnước.Nótìmthấymộtcáihộphìnhtrụtròncóbán
kínhđáy5cmvàcao20cm.Tronghộpướcchừngcókhoảng1lítnước.Nóbayrabờ
sôngvàtìmthấymấyviênbicủacácbạnnhỏlớpsáubỏlại,nódùngmỏgắptừngviên
vàbỏvàotronghộp.Biếtrằngmỗiviênbicóđườngkính1cm,hỏiconquạcầnbỏvào
tốithiểubaonhiêuviênbiđểnướcdânglênđếnmiệnghộp?
Soạn:HuỳnhPhúSĩ 79 TrườngTHCS-THPTMỹThuận
§2.Mặtcầu TOÁN12
5 THỰC HÀNH
Í TRẮC NGHIỆM
Câu 1. ChohìnhcầucódiệntíchS vàbánkínhR.Mệnhđềnàosauđâylà
đúng?
A. S =
4
3
πR
3
. B. S =2πR
2
. C. S =πR
2
. D. S =4πR
2
.
Câu 2. Chomặtcầucầucódiệntíchbằng
8πa
2
3
.TínhbánkínhR củamặtcầu
đó.
A. R =
a
√
6
3
. B. R =
a
√
6
2
. C. R =
a
√
2
3
. D. R =
a
√
6
6
.
Câu 3. ChomặtcầucóbánkínhR =3.Thểtíchmặtcầuđóbằng
A. 9π. B.
81
4
π. C. 36π. D.
4π
3
.
Câu 4. Chomặtcầucóthểtích
16π
3
.Tínhđườngkínhmặtcầuđãcho.
A. 1. B. 2. C. 4. D. 4π.
Câu 5. ChomặtcầucóbánkínhR =3.Diệntíchhìnhtrònquatâmbằng
A. 3π. B. 6π. C. 4π. D. 9π.
Câu 6. Mộtkhốicầucóđườngkínhbằng10cm.Ngườitadùngmộtmặtphẳng
cáchtâmkhốicầu3cmđểcắtkhốicầuthànhhaiphần.Diệntíchcủamặtcắt
bằng
A. 16cm. B. 16πcm
2
. C. 16cm
2
. D. 16πcm
3
.
Câu 7. Trongcáclăngtrụsau,lăngtrụnàonộitiếpđượctrongmộtmặtcầu?
A. Lăngtrụcóđáylàhìnhchữnhật.
B. Lăngtrụcóđáylàhìnhvuông.
C. Lăngtrụđứngcóđáylàhìnhthoi.
D. Lăngtrụđứngcóđáylàhìnhthangcân.
Câu 8. Trongcácmệnhđềsauđây,mệnhđềnàosai?
A. Bấtkìmộthìnhtứdiệnnàocũngcómộtmặtcầungoạitiếp.
B. Bấtkìmộthìnhchópđềunàocũngcómộtmặtcầungoạitiếp.
C. Bấtkìmộthìnhhộpnàocũngcómộtmặtcầungoạitiếp.
D. Bấtkìmộthìnhhộpchữnhậtnàocũngcómộtmặtcầungoạitiếp.
Câu 9. Mộthìnhhộpchữnhậtnộitiếpmặtcầuvàcóbakíchthướclàa, b, c.Khi
đóbánkínhr củamặtcầubằng
A.
1
2
√
a
2
+b
2
+c
2
. B.
√
a
2
+b
2
+c
2
.
C.
p
2
(
a
2
+b
2
+c
2
)
. D.
√
a
2
+b
2
+c
2
3
.
Câu 10. ChohìnhchópS.ABC cóđáylàtamgiácABC vuôngtạiA,cóSA vuông
gócvớimặtphẳng(ABC) vàcóSA =a,AB =b,AC =c.Mặtcầuđiquacácđỉnh
A, B, C, S cóbánkínhr bằng
A.
2(a+b +c)
3
. B. 2
√
a
2
+b
2
+c
2
.
C.
1
2
√
a
2
+b
2
+c
2
. D.
√
a
2
+b
2
+c
2
.
L TỰ LUẬN
Câu 1 (SGK GT12). ChohìnhchóptứgiácđềuS.ABCD cótấtcảcáccạnhđềubằnga.Hãyxácđịnhtâmvàbánkínhmặt
cầungoạitiếphìnhchópđó.
Câu 2 (SGK GT12). ChohìnhchópS.ABC cóbốnđỉnhnằmtrênmộtmặtcầu,SA =a,SB =b,SC =c vàbacạnh
SA, SB, SC đôimộtvuônggóc.Tínhdiệntíchmặtcầuvàthểtíchkhốicầuđượctạonênbởimặtcầuđó.
Soạn:HuỳnhPhúSĩ 80 TrườngTHCS-THPTMỹThuận
§2.Mặtcầu TOÁN12
d Vocabulary
sphere mặtcầu
chord dâycung
diameter đườngkính
meridian of longitude kinhtuyến
inscribe nộitiếp
circumscribe ngoạitiếp
tangent plane tiếpdiện
parallel of of latitude vĩtuyến
Soạn:HuỳnhPhúSĩ 81 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
PHỤ LỤC
1 HÀM SỐ
1 Tập xác định của hàm số
Tậpxácđịnhcủahàmsốy =f
(
x
)
làtậphợpcácsốthựcx saochobiểuthứcf
(
x
)
XÁC
ĐỊNH(cónghĩa).
•
√
A xácđịnhkhiA ≥ 0.
•
A
B
xácđịnhkhiB 6= 0.
2 Hàm số chẵn, hàm số lẻ
Chohàmsốy =f
(
x
)
cótậpxácđịnhD.
f
(
x
)
chẵn⇔
(
∀x ∈ D Ñ −x ∈ D
f
(
−x
)
=f
(
x
)
O
x
y
Đồ thị hàm chẵn nhận trục tung làm
TRỤC ĐỐI XỨNG
f
(
x
)
lẻ⇔
(
∀x ∈ D Ñ −x ∈ D
f
(
−x
)
=−f
(
x
)
O
x
y
Đồ thị hàm lẻ nhận gốc tọa độ làm TÂM
ĐỐI XỨNG
3 Một vài hàm số thông dụng
O
x
y
c
y =c
d
x =d
Hàm hằng
Hàmhằnglàhàmsốcódạngy =c (c làhằngsố).Hàmhằngcóđồthịlàđườngthẳng
songsongvớitrụchoành,cắttrụctungtạiđiểmcógiátrịlàc.
Tươngtự,đườngthẳngx =d songsongvớitrụctung,cắttrụchoànhtạiđiểmcógiátrị
bằngd.
Hàm số bậc nhất một ẩn (Hàm số tuyến tính)
Dạng:y =ax +b (a 6=0 gọilàhệ số góc).
•Đồthị:đườngthẳng.
•Sựbiếnthiên:
(
a > 0 ĐồngbiếntrênR
a < 0 NghịchbiếntrênR.
O
x
y
y =2x +3
y =2x
Haiđườngthẳngy =2x+3và
y =2x cóhệsốgócbằngnhau
nênsongsong.
!
Chohaiđườngthẳng∆
1
: y =a
1
x +b
1
và∆
2
: y =a
2
x +b
2
,khiđó:
◦ ∆
1
∥ ∆
2
⇔ a
1
=a
2
. ◦ ∆
1
⊥∆
2
⇔ a
1
·a
2
=−1.
Hàm số bậc hai một ẩn
Hàmsốy =ax
2
+bx +c
(
a 6=0
)
cótậpxácđịnhR,đồthịlàmộtparabol:
•Đỉnh:I
−
b
2a
;−
∆
4a
.
•Trụcđốixứng:x =−
b
2a
.
•Bềlõmhướnglênnếua > 0,hướngxuốngnếua < 0.
•Bảngbiếnthiên:
Soạn:HuỳnhPhúSĩ 82 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
a > 0
x
y
−∞
−
b
2a
+∞
+∞+∞
−
∆
4a
−
∆
4a
+∞+∞
a < 0
x
y
−∞
−
b
2a
+∞
−∞−∞
−
∆
4a
−
∆
4a
−∞−∞
4 Xét dấu biểu thức
Nhị thức bậc nhất f
(
x
)
=ax +b
(
a 6=0
)
x
f
(
x
)
−∞
−
b
a
+∞
Tráidấuvớia
0
Cùngdấuvớia
Tam thức bậc hai f
(
x
)
=ax
2
+bx +c
(
a 6=0
)
•∆< 0
x
f
(
x
)
−∞
+∞
Cùngdấuvớia
•∆=0
x
f
(
x
)
−∞
−
b
2a
+∞
Cùngdấuvớia
0
Cùngdấuvớia
•∆> 0
x
f
(
x
)
−∞
x
1
x
2
+∞
CÙNG
0
TRÁI
0
CÙNG
!
Hệ quả
•ax
2
+bx +c ≥ 0, ∀x ∈ R ⇔
(
a > 0
∆≤ 0
•ax
2
+bx +c > 0, ∀x ∈ R ⇔
(
a > 0
∆< 0
•ax
2
+bx +c ≤ 0, ∀x ∈ R ⇔
(
a < 0
∆≤ 0
•ax
2
+bx +c < 0, ∀x ∈ R ⇔
(
a < 0
∆< 0
5 Giới hạn của hàm số
Giới hạn một bên
• lim
xÏx
+
0
f
(
x
)
Giớihạnbênphải
(
x > x
0
)
.
• lim
xÏx
−
0
f
(
x
)
Giớihạnbêntrái
(
x < x
0
)
.
• lim
xÏx
0
f
(
x
)
=L ⇔
lim
xÏx
+
0
f
(
x
)
=L
lim
xÏx
−
0
f
(
x
)
=L
O
x
y
2
Hàm số y =
x +1
x −2
liên tục
trên khoảng (−∞;2) và
(2;+∞).
Hàm số liên tục
•Hàmsốf
(
x
)
liêntụctạix
0
⇔ lim
xÏx
0
f
(
x
)
=f
(
x
0
)
.
•HàmđathứcliêntụctrênR.
•Hàmsốlượnggiác,hàmphânthức...liêntụcTRÊNTỪNGKHOẢNGcủatập xác định.
6 Đạo hàm của hàm số
♥ Quy tắc tính đạo hàm
•
(
u±v
)
0
=u
0
±v
0
•
(
u·v
)
0
=u
0
·v +u ·v
0
•
u
v
0
=
u
0
·v −u ·v
0
v
2
•y
0
x
=y
0
u
·u
0
x
(hàmhợp)
Soạn:HuỳnhPhúSĩ 83 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
♥ Đạo hàm của một số hàm thường gặp
•
hằngsố
0
=0
•
(
x
n
)
0
=n·x
n−1
◦
(
x
)
0
=1
◦
1
x
0
=−
1
x
2
◦
√
x
0
=
1
2
√
x
•
(
sinx
)
0
=cosx
•
(
cosx
)
0
=−sinx
•
(
tanx
)
0
=
1
cos
2
x
=1+tan
2
x
•
(
cotx
)
0
=−
1
sin
2
x
=−
1+cot
2
x
♥ Đạo hàm cấp n: y
(n)
=
y
(n−1)
0
♥ Vi phân: dy =y
0
·dx
Ứng dụng của đạo hàm
•Trong Vật Lý: Nếumộtchấtđiểmchuyểnđộngtheophươngtrìnhs
(
t
)
thì
◦ Vậntốctứcthờitạithờiđiểmtlàv
(
t
)
=s
0
(
t
)
.
◦ Giatốctứcthờitạithờiđiểmtlàa
(
t
)
=v
0
(
t
)
.
•Trong Hình Học: Phươngtrìnhtiếptuyếncủađồthịhàmsốy =f
(
x
)
tạiđiểmM
(
x
0
;y
0
)
là
y =f
0
(
x
0
)
·
(
x −x
0
)
+y
0
◦ y
0
=f
(
x
0
)
.
◦ f
0
(
x
0
)
làhệsốgóccủatiếptuyến.
2 PHƯƠNG TRÌNH
1 Phương trình bậc hai ax
2
+bx +c =0
(
a 6=0
)
•∆< 0:Phươngtrìnhvônghiệm.
•∆=0:Phươngtrìnhcónghiệmképx =−
b
2a
.
•∆> 0:Phươngtrìnhcó2nghiệmphânbiệt
x =
−b+
√
∆
2a
x =
−b−
√
∆
2a
Trường hợp đặc biệt
•a +b+c =0Ñ
x =1
x =
c
a
. •a −b+c =0Ñ
x =−1
x =−
c
a
.
Định lý Vi-ét
•Nếuphươngtrìnhax
2
+bx +c =0
(
a 6=0
)
cóhainghiệmx
1
, x
2
thì
x
1
+x
2
=S =−
b
a
x
1
·x
2
=P =
c
a
•Nếuhaisốu, v cótổngu +v =S vàtíchu·v =P thìu, v làhainghiệmcủaphươngtrình
x
2
−Sx +P =0.
2 Phương trình bậc 4 trùng phương ax
4
+bx
2
+c =0
•Đặtt =x
2
(
t ≥ 0
)
.
•Giảiphươngtrìnhat
2
+bt +c =0.
•Chọnnghiệmt ≥ 0.
•Kếtluậnnghiệmx.
Soạn:HuỳnhPhúSĩ 84 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
3 Phương trình tích
A
(
x
)
·B
(
x
)
···Z
(
x
)
=0⇔
A
(
x
)
=0
B
(
x
)
=0
...
Z
(
x
)
=0
4 Phương trình chứa ẩn trong dấu giá trị tuyệt đối
•|f
(
x
)
| =g
(
x
)
⇔
g
(
x
)
≥ 0
"
f
(
x
)
=g
(
x
)
f
(
x
)
=−g
(
x
)
•|f
(
x
)
| =|g
(
x
)
| ⇔
"
f
(
x
)
=g
(
x
)
f
(
x
)
=−g
(
x
)
5 Phương trình vô tỉ
•
p
f
(
x
)
=g
(
x
)
⇔
(
g
(
x
)
≥ 0
f
(
x
)
=[g
(
x
)
]
2
•
p
f
(
x
)
=
p
g
(
x
)
⇔
"
f
(
x
)
≥ 0
g
(
x
)
≥ 0
f
(
x
)
=g
(
x
)
3 LŨY THỪA VÀ CĂN THỨC
1 Lũy thừa
a
n
=a·a···a
| {z }
n sốa
(
n ∈ N
∗
)
•a gọilàcơsố,n gọilàsốmũ.
•0
n
=0,1
n
=1.
•Lũythừabậc2gọilàbìnhphương,lũythừabậc3gọilàlậpphương.
Tính chất
•Vớia, b 6=0 vàm, n ∈ Z,tacó
◦ a
0
=1,a
1
=a.
◦ a
−n
=
1
a
(
n ∈ N
∗
)
.
◦ a
m+n
=a
m
·a
n
.
◦ a
m−n
=
a
m
a
n
.
◦ a
m.n
=
(
a
m
)
n
.
◦ a
m
n
=
n
√
a
m
(
a > 0, n ∈ N
∗
)
.
◦
(
a·b
)
n
=a
n
·b
n
.
◦
a
b
n
=
a
n
b
n
.
•Với
(
a > 1
m > n
thìa
m
> a
n
Với
(
0< a < 1
m > n
thìa
m
< a
n
•Với
(
a > b > 0
n > 0
thìa
n
> b
n
Với
(
a > b > 0
n < 0
thìa
n
< b
n
2 Căn bậc n
Chosốtựnhiênn ≥ 2,sốb đượcgọilàcănbậcn củasốa nếub
n
=a,kíhiệu:b =
n
√
a.
•Nếun lẻthìcóduynhấtmộtcănbậcn củaa.
•Nếun chẵnvàa ≥ 0 thìcó2cănbậcn củaa là
n
√
a và−
n
√
a.
Soạn:HuỳnhPhúSĩ 85 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
4 CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC
1 Điểm và đường trong tam giác
B C
A
M N
Ù Đường trung bình
•Đườngtrungbìnhcủatamgiáclàđoạnthẳngnốihaitrungđiểmcủahaicạnh,nó
luônsongsongvàbằngmộtnửađộdàicủacạnhcònlại.
•Mỗitamgiáccó3đườngtrungbình.
B C
A
G
K
NM
Ù Đường trung tuyến và trọng tâm
•Đườngtrungtuyếnlàmộtđoạnthẳngnốitừđỉnhđếntrungđiểmcủacạnhđối
diện.
•Mỗitamgiáccó3đườngtrungtuyến,chúngđồngquytạimộtđiểm,gọilàTRỌNG
TÂM.Khoảngcáchtừtrọngtâmđếnmỗiđỉnhbằng2/3 độdàitrungtuyếnứngvớiđỉnhđó.
B C
A
H
K
N
M
Ù Đường cao và trực tâm
•Đườngcaocủamộttamgiáclàđoạnthẳnghạtừmộtđỉnhxuốngcạnhđốidiện
(còngọilàcạnhđáyứngvớiđỉnhđó)vàvuônggócvớicạnhđó.
•Mỗitamgiáccó3đườngcao,chúngđồngquytạimộtđiểm,gọilàTRỰCTÂM.
B C
A
M
O
K
N
Ù Đường trung trực và tâm đường tròn ngoại tiếp
•Mỗiđoạnthẳngđềucóduynhấtmộtđườngtrungtrực,dođómỗitamgiáccũng
có3đườngtrungtrực.
•Bađườngtrungtrựcđồngquytạimộtđiểm,chínhlàTÂMĐƯỜNGTRÒNNGOẠITIẾP
củatamgiác,nócáchđều3đỉnhcủatamgiác.
B C
A
I
Ù Đường phân giác và tâm đường tròn nội tiếp
•Đườngphângiáclàđoạnthẳngnốitừđỉnhđếncạnhđốidiệnvàchiagócởđỉnh
làm2phầncósốđogócbằngnhau.
•Mỗitamgiáccó3đườngphângiác,chúngđồngquytạimộtđiểm,chínhlàTÂM
ĐƯỜNGTRÒNNỘITIẾPtamgiác.
2 Định lý sin & định lý cosin
B
a
C
b
A
c
m
a
Ù Định lý cosin
•a
2
=b
2
+c
2
−2bc ·cosA
•b
2
=a
2
+c
2
−2ac ·cosB
•c
2
=a
2
+b
2
−2ab ·cosC
Ù Định lý sin
a
sinA
=
b
sinB
=
c
sinC
=2R
•Số đo góc
cosA =
b
2
+c
2
−a
2
2bc
cosB =
a
2
+c
2
−b
2
2ac
cosC =
a
2
+b
2
−c
2
2ab
•Độ dài trung tuyến
m
2
a
=
2
b
2
+c
2
−a
2
4
m
2
b
=
2
a
2
+c
2
−b
2
4
m
2
c
=
2
a
2
+b
2
−c
2
4
Ù Chu vi & diện tích
•Chuvi=a +b+c.
•Nửachuvip =
a+b +c
2
.
Diện tích
•S =
1
2
a·h
a
=
1
2
b·h
b
=
1
2
c·h
c
.
•S =
1
2
ab ·sinC =
1
2
bc ·sinA =
1
2
ca ·sinB.
•S =
a·b ·c
4R
.
•S =p ·r (r làbánkínhđườngtrònnộitiếp).
•S =
p
p
(
p−a
)
(
p−b
)
(
p−c
)
(CôngthứcHeron).
Soạn:HuỳnhPhúSĩ 86 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Ù Tam giác bằng nhau & tam giác đồng dạng
d Tam giác bằng nhau
Haitamgiácđượcgọilàbằngnhaunếuchúngcócác
cạnhtươngứngbằngnhauvàcácgóctươngứngbằng
nhau.
•Bacặpcạnhtươngứngbằngnhau(cạnh–cạnh–
cạnh).
•Haicặpcạnhtươngứngvàmộtcặpgócxengiữa
bằngnhau(cạnh–góc–cạnh).
•Haicặpgóctươngứngvàmộtcặpcạnhbấtkìbằng
nhau(góc–cạnh–góc).
d Tam giác đồng dạng
Haitamgiácđượcgọilàđồngdạngvớinhaunếuchúng
cócáccạnhtươngứngtỉlệvớinhau(theocùngmộttỉ
số)vàcácgóctươngứngbằngnhau.
•Bacặpcạnhtươngứngtỉlệvớinhau,tỉsốđóđược
gọilàtỉsốđồngdạng.
•Haicặpgóctươngứngbằngnhau.
•Haicặpcạnhtươngứngtỉlệvớinhauvàmộtcắp
gócxengiữabằngnhau.
3 Phân loại tam giác
B C
A
M
Ù Tam giác cân
Tamgiáccânlàtamgiáccó2cạnhbấtkỳđộdàibằngnhau,haicạnhnàyđượcgọilà
haicạnhbên,cạnhcònlạiđượcgọilàcạnhđáy.
•Haicạnhbênchungnhauđỉnhnàothìtamgiácsẽcântạiđỉnhđóvàhaigócởđáy
bằngnhau.
•Đườngtrungtuyếnxuấtpháttừđỉnhcũnglàđườngcaovàlàđườngphângiác.
B C
A
M
Ù Tam giác đều
Tamgiácđềulàtamgiáccó3cạnhbằngnhauhoặctươngđươngbagócbằngnhau,và
bằng60
◦
.Tamgiácđềucó
•Đườngtrungtuyếncũnglàđườngcao,cóđộdàibằngcạnh·
√
3
2
.
•Tâmcủađườngtrònnộitiếp,tâmcủađườngtrònngoạitiếp,trọngtâmvàtrựctâm
trùngnhau.
•BánkínhđườngtrònngoạitiếpR =cạnh·
√
3
3
.
•DiệntíchS =
(
cạnh
)
2
·
√
3
4
.
B
C
A
M
H
α
Ù Tam giác vuông
Tamgiácvuônglàtamgiáccómộtvuông.Nếu4ABC vuôngtạiA thì
•CạnhBCgọilàcạnhhuyền,haicạnhcònlạigọilàcạnhgócvuông,và
AB
2
+AC
2
=BC
2
(ĐịnhlýPitago)
•TrungtuyếnAM =
BC
2
.
•NếuAHlàđườngcaothìAH ·BC =AB·AC.
sinα =
Đối
Huyền
cosα =
Kề
Huyền
tanα =
Đối
Kề
cotα =
Kề
Đối
B
C
A
M
α
Ù Tam giác vuông cân
Tamgiácvuôngcânlàtamgiácvuôngcóhaicạnhgócvuôngbằngnhau.
Nếu4ABCvuôngcântạiA thì
•Góc
b
B =
b
C =45
◦
.
•CạnhBC =cạnh·
√
2.
•DiệntíchS =
1
2
·
(
cạnh
)
2
.
Soạn:HuỳnhPhúSĩ 87 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
5 HÌNH CHÓP & HÌNH LĂNG TRỤ
1 Hình chóp
S
B
C
D
A
␣ Hình chóp
Hìnhchóplàmộtđadiệncómộtmặtlàđagiácphẳng(gọilàđáy),còncácmặtcònlại
làcáctamgiácgiáccóchungmộtđỉnhkhôngnằmtrongmặtđáy(gọilàđỉnh).
•Hìnhchópcóđáylàmộtn-giáccũngđượcgọilàhìnhchópn-giác,riênghìnhchóp
tamgiáccònđượcgọilàtứdiện.
•Đoạnthẳngkẻtừđỉnhvàhìnhchiếuvuônggóccủađỉnhxuốngmặtđáyđượcgọi
làđườngcaocủahìnhchóp.
•Tổngdiệntíchcủatấtcảcácmặtcủahìnhchópgọilàdiệntíchtoànphần,còntổng
diệntíchcácmặtbêngọilàdiệntíchxungquanhcủahìnhchóp.
␣ Hình chóp đều
Hìnhchópđềulàhìnhchópcóđáylàmộtđagiácđềuvàđoạnthẳngnốiđỉnhvớitâm
củađáylàđườngcaocủahìnhchóp.
•Cácmặtbêncủahìnhchópđềulànhữngtamgiáccânbằngnhau.
•Hìnhchóptamgiácđềucóđáylàtamgiácđềuvàchânđườngcaotrùngvớitrọng
tâmcủađáy.
•Hìnhchóptứgiácđềucóđáylàmộthìnhvuôngvàchânđườngcaotrùngvớitâm
củahìnhvuông.
•Tứ diện đều làhìnhchóptamgiácđềucócácmặtbênlàtamgiácđều.
S
B
CD
A
I
Hình chóp tứ giác đều
S
B
C
A
I
Hình chóp tam giác đều
S
B
C
A
I
Tứ diện đều
2 Hình lăng trụ
A B
C
A
0
C
0
B
0
␣ Hình lăng trụ
Hìnhlăngtrụlàmộtđadiện,cóhaimặtlànhữngn-giácbằngnhau(gọilàđáy),nmặt
cònlạilàcáchìnhbìnhhành(gọilàmặtbên).Hìnhlăngtrụcóhaimặtđáysongsong
vàcáccạnhbênsongsong.
•Tổngdiệntíchtấtcảcácmặtcủahìnhlăngtrụgọilàdiệntíchtoànphần,còntổng
diệntíchcácmặtbêngọilàdiệntíchxungquanh.
•Chiềucaocủahìnhlăngtrụlàkhoảngcáchgiữahaiđáy.
A B
C
A
0
C
0
B
0
␣ Hình lăng trụ đứng
Hìnhlăngtrụđứnglàhìnhlăngtrụcócáccạnhbênvuônggócvớiđáy.Tronghìnhlăng
trụđứng
•Cácmặtbênlàcáchìnhchữnhật.
•Mỗicạnhbênđềulàđườngcao.
•Hình lăng trụ đều làhìnhlăngtrụđứngcóđáylàđagiácđều.
␣ Hình hộp
Hìnhhộplàhìnhlăngtrụcóđáylàhìnhbìnhhành.Hìnhhộpcó6mặtlàhìnhbình
hành.
•Hình hộp đứng làhìnhhộpcócáccạnhbênvuônggócvớiđáy,nóicáchkhác,
hìnhhộpđứnglàhìnhlăngtrụđứngcóđáylàhìnhbìnhhành.
•Hình hộp chữ nhật làhìnhlăngtrụđứngcó6mặtlàhìnhchữnhật.
•Hình lập phương làhìnhlăngtrụđứngcó6mặtlàhìnhvuông.
Soạn:HuỳnhPhúSĩ 88 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
A B
CD
A
0
D
0
C
0
B
0
Hình hộp
A B
CD
A
0
D
0
C
0
B
0
Phầnnàyẩn
Hình hộp chữ nhật
A B
CD
A
0
D
0
C
0
B
0
Hình lập phương
6 VỊ TRÍ TƯƠNG ĐỐI, GÓC VÀ KHOẢNG CÁCH
1 Góc
ç Đường thẳng và mặt phẳng
Trongkhônggian,chođườngthẳng∆ vàmặtphẳng
(
α
)
.
•Nếu∆⊥
(
α
)
thì
(
∆,
(
α
))
=90
◦
.
•Nếu∆khôngvuônggócvới
(
α
)
thì
(
∆,
(
α
))
=
(
∆,d
)
vớid làhìnhchiếuvuônggóc
của∆ trên
(
α
)
.
ç Mặt phẳng và mặt phẳng
Trongkhônggian,chohaimặtphẳng
(
α
)
và
(
β
)
.
•Nếu
(
α
)
∥
(
β
)
thì
((
α
)
,
(
β
))
=0
◦
.
•Nếu
(
α
)
∩
(
β
)
=∆ thì
((
α
)
,
(
β
))
=
(
a,b
)
vớia ⊂
(
α
)
,b ⊂
(
β
)
vàa∩∆∩b =M.
∆
S
H
I
d
α
(
∆,
(
α
))
=
(
∆,d
)
∆
a
b
α
β
((
α
)
,
(
β
))
=
(
a,b
)
2 Khoảng cách
S
H
α
ç Từ điểm đến mặt phẳng
ChođiểmS vàmặtphẳng
(
α
)
.GọiH làhìnhchiếuvuônggóccủaS trên
(
α
)
.Khiđó
SH⊥
(
α
)
vàd
(
S,
(
α
))
=SH
ç Hai mặt phẳng song song
Khoảngcáchgiữahaimặtphẳngsongsonglàkhoảngcáchtừmộtđiểmbấtkìcủamặt
phẳngnàyđếnmặtphẳngkia.
3 Vị trí tương đối
ç Đường thẳng và đường thẳng
Trongkhônggian,chohaiđườngthẳng∆
1
và∆
2
.Cáctrườnghợpsaucóthểxảyra:
•∆
1
∩∆
2
=M
∆
1
cắt∆
2
tạigiaođiểmM
•∆
1
∥ ∆
2
•∆
1
≡ ∆
2
•∆
1
và∆
2
chéonhau(khôngđồngphẳng).
ç Đường thẳng và mặt phẳng
Trongkhônggian,chođườngthẳng∆ vàmặtphẳng
(
α
)
.Cáctrườnghợpsaucóthểxảy
ra:
Soạn:HuỳnhPhúSĩ 89 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
•∆∥
(
α
)
•∆∩
(
α
)
=M
∆ cắt
(
α
)
tạigiaođiểmM
•∆⊂
(
α
)
∆ nằmtrên
(
α
)
ç Mặt phẳng và mặt phẳng
Trongkhônggian,chohaimặtphẳng
(
α
)
và
(
β
)
.Cáctrườnghợpsaucóthểxảyra:
•
(
α
)
∥
(
β
)
•
(
α
)
∩
(
β
)
=∆
(
α
)
cắt
(
β
)
theogiaotuyến∆
•
(
α
)
≡
(
β
)
Các định lý và hệ quả
•Nếubamặtphẳngphânbiệtđôimộtcắtnhautheo
bagiaotuyếnthìbagiaotuyếnấyđồngquyhoặcđôi
mộtsongsong.
Ï Haimặtphẳngphânbiệtlầnlượtchứahaiđường
thẳngsongsongthìgiaotuyếncủahaimặtấy(nếu
có)sẽsongsongvớihaiđườngthẳngđó,hoặctrùng
vớimộttronghaiđườngthẳngđó.
•Nếuđườngthẳng∆khôngnằmtrênmặtphẳng
(
α
)
và∆songsongvớimộtđườngthẳngd ⊂
(
α
)
thì
∆∥
(
α
)
.
•Nếu
(
α
)
và
(
β
)
cắtnhautheogiaotuyến∆và
(
α
)
chứa
đườngthẳnga∥
(
β
)
thìa∥ ∆.
Ï Nếuhaimặtphẳngphânbiệtcùngsongsongvới
mộtđườngthẳngthìgiaotuyếncủachúng(nếucó)
cũngsongsongvớiđườngthẳngđó.
•Nếumặtphẳng
(
α
)
chứahaiđườngthẳnga, b và
a, b cùngsongsongvớimặtphẳng
(
β
)
thì
(
α
)
∥
(
β
)
.
•Nếuđườngthẳng∆ vuônggócvớimặtphẳng
(
α
)
thì
cũngvuônggócvớimọiđườngthẳngd ⊂
(
α
)
.
•Nếuđườngthẳng∆vuônggócvớihaiđườngthẳng
cắtnhautrênmặtphẳng
(
α
)
thì∆⊥
(
α
)
.
•Nếu mặt phẳng
(
α
)
chứa đường thẳng a⊥
(
β
)
thì
(
α
)
⊥
(
β
)
.
Ï Nếuhaimặtphẳngvuônggócvớinhauthìbất
cứđườngthẳngnàonằmtrongmặtphẳngthứnhất
vàvuônggócvớigiaotuyếnthìvuônggócvớimặt
phẳngthứhai.
•Nếuhaimặtphẳngcắtnhauvàcùngvuônggócvới
mộtmặtphẳngthứbathìgiaotuyếncủachúngcũng
vuônggócvớimặtphẳngthứbađó.
Soạn:HuỳnhPhúSĩ 90 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
VĨNHLONG
(Đề có 05 trang)
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019-2020
MÔN: TOÁN 12 THPT
Thời gian làm bài 90 phút (bao gồm trắc nghiệm và tự luận)
Họ và tên học sinh: ........................................................................................ Mã đề 101
I. PHẦN TRẮC NGHIỆM (40 câu, 8.0 điểm)
Câu 3. Chohàmsốy =f(x) cóbảngbiếnthiênnhưsau:
x
f
0
(x)
f(x)
−∞
1 3
+∞
−
0
+
0
−
−∞
1
−3
+∞
Hàmsốy =f(x) nghịchbiếntrênkhoảngnàodướiđây?
A. (−3;1). B. (0;+∞). C. (−∞;−2). D. (−2;0).
Câu 4. HàmsốnàosauđâyđồngbiếntrênR?
A. y =
x −1
x +3
. B. y =−x
3
−x −2. C. y =x
4
+2x
2
+3. D. y =x
3
+x
2
+2x +1.
Câu 5.
Hìnhbênlàđồthịhàmsốy =f
0
(x).Hỏihàmsốy =f(x)đồngbiếntrênkhoảngnàodưới
đây?
A. (0;1) và(2;+∞). B. (1;2). C. (2;+∞). D. (0;1).
O
x
y
1 2
Câu 6. Giảtrịcựctiểuy
CT
củahàmsốy =x
3
−3x
2
+2 là
A. y
CT
=0. B. y
CT
=−2. C. y
CT
=1. D. y
CT
=4.
Câu 7. Sốđiểmcựctrịcủahàmsốy =
1
3
x
3
−2x
2
+4 là
A. 0. B. 1. C. 2. D. 3.
Câu 8. Chohàmsốf(x)=x
3
+ax
2
+bx +c cóđồthị
(
C
)
.Mệnhđềnàosauđâysai?
A. Đồthị
(
C
)
luôncótâmđốixứng. B. Hàmsốf(x) luôncócựctrị.
C. Đồthị
(
C
)
luôncắttrụchoành. D. lim
x→+∞
f(x)=+∞.
Câu 9. Chohàmsốy =f(x) cóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞
0
3
0
+∞
Giátrịlớnnhấtcủahàmsốy =f(x) trênđoạn[−1;1] bằng
A. 1. B. 3. C. −1. D. 0.
Câu 10. Tìmgiátrịnhỏnhấtm củahàmsốy =x
4
−x
2
+13 trênđoạn[−2;3].
A. m =13. B. m =
51
4
. C. m =
49
4
. D. m =
205
16
.
Câu 11. Giátrịnhỏnhấtcủahàmsốy =
2sinx +3
sinx +1
trên
h
0;
π
2
i
là
A. 5. B. 2. C. 3. D.
5
2
.
Câu 12. Chohàmsốf(x)=
x
4
−4x
3
+4x
2
+a
.GọiM, m lầnlượtlàgiátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsốđã
chotrênđoạn[0;2].Cóbaonhiêusốnguyêna thuộcđoạn[−3;2] saochoM ≤ 2m?
A. 7. B. 5. C. 6. D. 4.
Soạn:HuỳnhPhúSĩ 91 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 13. Chohàmsốy =
x
x −1
+2 cóđồthị
(
C
)
Mệnhđềnàodướiđâyđúng?
A. Đồthị
(
C
)
cótiệmcậnngangy =1. B. Đồthị
(
C
)
cótiệmcậnngangy =3.
C. Đồthị
(
C
)
khôngcótiệmcận. D. Đồthị
(
C
)
cótiệmcậnđứngx =2.
Câu 14.
Chohàmsốy =
x +b
cx −1
cóđồthịnhưhìnhbên.Mệnhđềnàodướiđâylàđúng?
A. b < 0, c < 0. B. b < 0, c > 0. C. b > 0, c > 0. D. b > 0, c < 0.
O
x
y
Câu 15.
Đườngcongtronghìnhvẽbênlàđồthịcủahàmsốnàosauđây?
A. y =−x
3
+3x +2. B. y =x
3
−2x +2.
C. y =x
3
−3x +2. D. y =x
3
+3x +2.
O
x
y
−1
4
1
2
Câu 16.
Đườngcongtronghìnhvẽbênlàđồthịhàmsốnàodướiđây?
A. y =
x +2
−2x +4
. B. y =
−x +1
x −2
. C. y =
2x −3
x +2
. D. y =
−x +3
2x −4
.
O x
y
−
1
2
2
Câu 17.
Chohàmsốy =ax
4
+bx
2
+c cóđồthịnhưhìnhvẽbên.Mệnhđềnàodướiđâyđúng?
A. a > 0, b < 0, c < 0. B. a < 0, b < 0, c < 0.
C. a < 0, b > 0, c < 0. D. a > 0, b < 0, c > 0.
O
x
y
Câu 18.
Chohàmsố y = f(x)xácđịnh trênR \ {−1}, liêntục
trênmỗikhoảngxácđịnhvàcóbảngbiếnthiênnhưhình
bên.Tìmtậphợptấtcảcácgiátrịthựccủathamsốm sao
chophươngtrìnhf(x) = m cóđúngbanghiệmthựcphân
biệt.
A. (−4;2). B. [−4;2). C. (−4;2]. D. (−∞;2].
x
y
0
y
−∞
−1
3
+∞
+
−
0
+
−∞
2
+∞
−4
+∞
Câu 19. Cóbaonhiêugiátrịcủam đểđồthịcủahàmsốy =
x
1−x
cắtđườngthẳngy = x − m tạihaiđiểmphânbiệt
A, B saochogócgiữahaiđườngthẳngOA vàOB bằng60
◦
(O làgốctọađộ)?
A. 2. B. 1. C. 3. D. 0.
Câu 20. Choa làsốthựcdương.Biểuthứca
2
·
√
3a đượcviếtdướidạnglũythừavớisốmũhữutỉlà
A. a
4
3
. B. a
7
3
. C. a
5
3
. D. a
2
3
.
Câu 21. ChoP =
5−2
√
6
2018
5+2
√
6
2019
.Tacó
A. P ∈ (3;7). B. P ∈ (7;9). C. P ∈ (9;10). D. P ∈ (10;11).
Soạn:HuỳnhPhúSĩ 92 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 22. Chocácsốthựca, b thỏa
√
2019−
√
2018
a
>
√
2019−
√
2018
b
.Kếtluậnnàosauđâyđúng?
A. a > b. B. a < b. C. a =b. D. a ≥ b.
Câu 23. Hàmsốf(x)=
x
2
+2x
e
−x
cóđạohàm
A. f
0
(x)=
x
2
+4x +2
e
−x
. B. f
0
(x)=
(
2x +2
)
e
−x
.
C. f
0
(x)=
(
−2x =2
)
e
−x
. D. f
0
(x)=
−x
2
+2
e
−x
.
Câu 24. Tìmmệnhđềđúngtrongcácmệnhđềsau:
A. Đồthịhàmsốy =a
x
vày =
1
a
x
với0< a 6=1 đốixứngvớinhauquatrụcOy.
B. Đồthịhàmsốy =a
x
với0< a 6=1 luônđiquađiểm(a;1).
C. Hàmsốy =a
x
vớia > 1 nghịchbiếntrên(−∞;+∞).
D. Hàmsốy =a
x
với0< a < 1 đồngbiếntrên(−∞;+∞).
Câu 25. Chocácsốthựcdươnga, b vớia 6=1.Khẳngđịnhnàosauđâylàkhẳngđịnhđúng?
A. log
a
2
(ab)=2+log
a
b. B. log
a
2
(ab)=
1
2
log
a
b.
C. log
a
2
(ab)=
1
2
+
1
2
log
a
b. D. log
a
2
(ab)=
1
4
log
a
b.
Câu 26. Vớilog3=a thìlog9000 đượcbiểudiễntheoa bằng
A. a
2
. B. 3+2a. C. a
2
+3. D. 3a
2
.
Câu 27. Cholog
2
5=a vàlog
3
5=b.Khiđó,log
6
5 tínhtheoa vàb là
A. a
2
+b
2
. B.
ab
a+b
. C.
1
a+b
. D. a+b.
Câu 28.
Đườngcongtronghìnhbênlàđồthịcủamộthàmsốtrongbốnhàmsốđượcliệtkêởbốn
phươngánA, B, C, D dướiđây.Hỏihàmsốđólàhàmsốnào?
A. y =log
2
x. B. y =log
√
2
x. C. y =log
2
2x. D. y =log
1
2
x.
O
x
y
1
2
−1
1
Câu 29. ÔngAdựđịnhgửivàongânhàngmộtsốtiềnvớilãisuất7,5%mộtnăm,đểsau5năm,sốtiềnlãiđủmuamột
chiếcxemáytrịgiá85 triệuđồng.Biếtrằng,cứsaumỗinămsốtiềnlãisẽđượcnhậpvàovốnbanđầu.HỏisốtiềnôngA
cầngửichongânhànggầnnhấtvớisốtiềnnàodướiđây?
A. 60 triệuđồng. B. 189 triệuđồng. C. 196 triệuđồng. D. 210 triệuđồng.
Câu 30. Tìmtấtcảcácgiátrịthựccủathamsốm đểhàmsốy =log
2
x
2
−2x +m
cótậpxácđịnhlàR.
A. m ≥ 1. B. m ≤ 1. C. m > 1. D. m < −1.
Câu 31. TậpnghiệmS củaphươngtrình2
x+1
=8 là
A. S ={4}. B. S ={1}. C. S ={3}. D. S ={2}.
Câu 32. Cóbaonhiêusốthựcx thỏamãn9
log
3
x
=4?
A. 4. B. 0. C. 2. D. 1.
Câu 33. Nghiệmthựccủaphươngtrình9
x
−4·3
x
−45=0 là
A. x =9. B. x =−5 hoặcx =9. C. x =2 hoặcx =log
3
5. D. x =2.
Câu 34. Gọix
1
, x
2
làhainghiệmcủaphươngtrình5
x−1
=2
x
2
−1
.TínhP =
(
x
1
+1
)
(
x
2
+1
)
.
A. 0. B. 2log
2
5+2. C. 2log
2
5−1. D. log
2
25.
Câu 35. Hìnhlăngtrụtamgiáccóbaonhiêumặt?
A. 6. B. 3. C. 9. D. 5.
Câu 36. Mộthìnhchóp100 cạnhcóbaonhiêumặt?
A. 53. B. 51. C. 50. D. 52.
Câu 37. Trongcáchìnhđadiệnđềusau,hìnhnàocósốđỉnhnhỏhơnsốmặt?
A. Hìnhtứdiệnđều. B. Hình20 mặtđều. C. Hìnhlậpphương. D. Hình12 mặtđều.
Câu 38. SốmặtphẳngđốixứngcủahìnhchóptứgiácđềuS.ABCD là
A. 2. B. 4. C. 7. D. 6.
Câu 39. CholăngtrụABC.A
0
B
0
C
0
cóthểtíchV.TínhthểtíchV
1
củakhốiđadiệnBCA
0
B
0
C
0
theoV.
A. V
1
=
2
3
V. B. V
1
=
1
3
V. C. V
1
=
1
2
V. D. V
1
=
1
4
V.
Soạn:HuỳnhPhúSĩ 93 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 40. Hìnhhộpchữnhậtkhôngnắpcóthểtích3200cm
3
,tỉsốgiữachiềucaovàchiềurộngbằng2.Khitổngdiệntích
cácmặtcủahìnhhộpnhỏnhất,tínhdiệntíchmặtđáycủahìnhhộp.
A. 1200cm
2
. B. 120cm
2
. C. 160cm
2
. D. 1600cm
2
.
Câu 41. Thiếtdiệnquatrụccủamộthìnhnóntrònxoaylàtamgiácđềucódiệntíchbằnga
2
√
3.TínhthểtíchV củakhối
nónđãcho.
A. V =
πa
3
√
3
3
. B. V =
πa
3
√
3
2
. C. V =
πa
3
√
3
6
. D. V =
πa
3
√
6
6
.
Câu 42.
Trênbàncómộtcốcnướchìnhtrụchứađầynước,cóchiềucaobằng3lầnđườngkínhcủađáy;
mộtviênbivàmộtkhốinónđềubằngthủytinh.Biếtviênbilàmộtkhốicầucóđườngkínhbằng
đườngkínhcủacốcnước.Ngườitatừtừthảvàocốcnướcviênbivàkhốinónsaochođỉnhkhối
nónnằmtrênmặtcầu(nhưhìnhvẽ)thìthấynướctrongcốctrànrangoài.Tínhtỉsốthểtíchcủa
lượngnướccònlạitrongcốcvàlượngnướcbanđầu(bỏquabềdàycủalớpvỏthủytinh).
A.
1
2
. B.
2
3
. C.
4
9
. D.
5
9
.
II. PHẦN TỰ LUẬN (2.0 điểm)
Câu 43 (0.75 điểm). Tìmcácđiểmcựctrịhàmsốf(x)=x
3
−3x +1.
Câu 44 (0.5 điểm). Giảiphươngtrìnhlog
2
x +log
2
(x −6)=log
2
7.
Câu 45 (0.75 điểm). ChohìnhchópS.ABCD cóđáylàhìnhvuôngcạnha,hìnhchiếucủaS trên(ABCD) trùngvớitrung
điểmcủacạnhAB,cạnhbênSD =
3a
2
.TínhthểtíchV củakhốichópS.ABCD theoa.
Soạn:HuỳnhPhúSĩ 94 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀTHICHÍNHTHỨC
(Đề có 05 trang)
KÌ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2020
Bài thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên thí sinh: ..........................................................................................
Số báo danh: ...................................................................................................... Mã đề 101
Câu 46.
Đồthịhàmsốnàodướiđâycódạngnhưđườngcongtronghìnhbên?
A. y =x
3
−3x
2
+1. B. y =−x
3
+3x
2
+1.
C. y =−x
4
+2x
2
+1. D. y =x
4
−2x
2
+1.
O
x
y
Câu 47. Nghiệmcủaphươngtrình3
x−1
=9 là
A. x =−2. B. x =3. C. x =2. D. x =−3.
Câu 48. Chohàmf
(
x
)
cóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
0 3
+∞
+
0
−
0
+
−∞−∞
22
−5−5
+∞+∞
Giátrịcựctiểucủahàmsốđãchobằng
A. 3. B. −5. C. 0. D. 2.
Câu 49. Chohàmsốf
(
x
)
cóbảngbiếnthiênnhưsau:
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
44
−1−1
+∞+∞
Hàmsốđãchođồngbiếntrênkhoảngnàodướiđây?
A.
(
−∞;−1
)
. B.
(
0;1
)
. C.
(
−1;1
)
. D.
(
−1;0
)
.
Câu 50. Chokhốihộpchữnhậtcóbakíchthước3; 4; 5.Thểtíchcủakhốihộpđãchobằng
A. 10. B. 20. C. 12. D. 60.
Câu 51. Sốphứcliênhợpcủasốphứcz =−3+5i là
A. z =−3−5i. B. z =3+5i. C. z =−3+5i. D. z =3−5i.
Câu 52. Chohìnhtrụcóbánkínhđáyr =8vàđộdàiđườngsinh` =3.Diệntíchxungquanhcủahìnhtrụđãcho
bằng
A. 24π. B. 192π. C. 48π. D. 64π.
Câu 53. Chokhốicầucóbánkínhr =4.Thểtíchcủakhốicầuđãchobằng
A.
256π
3
. B. 64π. C.
64π
3
. D. 256π.
Câu 54. Vớia, b làcácsốthựcdươngtùyývàa 6=1,log
a
5
b bằng
A. 5log
a
b. B.
1
5
+log
a
b. C. 5+log
a
b. D.
1
5
log
a
b.
Câu 55. TrongkhônggianOxyz,chomặtcầu
(
S
)
: x
2
+y
2
+
(
z+2
)
2
=9.Bánkínhcủa
(
S
)
bằng
A. 6. B. 18. C. 9. D. 3.
Câu 56. Tiệmcậnngangcủađồthịhàmsốy =
4x +1
x −1
là
A. y =
1
4
. B. y =4. C. y =1. D. y =−1.
Câu 57. Chokhốinóncóbánkínhđáyr =5 vàchiềucaoh =2.Thểtíchkhốinónđãchobằng:
A.
10π
3
. B. 10π. C.
50π
3
. D. 50π.
Soạn:HuỳnhPhúSĩ 95 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 58. Nghiệmcủaphươngtrìnhlog
3
(
x −1
)
=2 là
A. x =8. B. x =9. C. x =7. D. x =10.
Câu 59.
Z
x
2
dx bằng
A. 2x +C. B.
1
3
x
3
+C. C. x
3
+C. D. 3x
3
+C.
Câu 60. Cóbaonhiêucáchxếp6 họcsinhthànhmộthàngdọc?
A. 36. B. 720. C. 6. D. 1.
Câu 61.
Chohàmsốbậcbay =f
(
x
)
cóđồthịlàđườngcongtronghìnhbên.Sốnghiệmthựccủa
phươngtrìnhf
(
x
)
=−1 là
A. 3. B. 1. C. 0. D. 2.
O
x
y
−1
1
2
−2
Câu 62. TrongkhônggianOxyz,hìnhchiếuvuônggóccủađiểmA
(
3;2;1
)
trêntrụcOx cótọađộlà
A.
(
0;2;1
)
. B.
(
3;0;0
)
. C.
(
0;0;1
)
. D.
(
0;2;0
)
.
Câu 63. ChokhốichópcódiệntíchđáyB =6 vàchiềucaoh =2.Thểtíchcủakhốichópđãchobằng
A. 6. B. 3. C. 4. D. 12.
Câu 64. TrongkhônggianOxyz,chođườngthẳngd·
x −3
2
=
y −4
−5
=
z+1
3
.Vectơnàodướiđâylàmộtvectơchỉphương
củad?
A.
−Ï
u
2
=
(
2;4;−1
)
. B.
−Ï
u
1
=
(
2;−5;3
)
. C.
−Ï
u
3
=
(
2;5;3
)
. D.
−Ï
u
4
=
(
3;4;1
)
.
Câu 65. TrongkhônggianOxyz,chobađiểmA
(
3;0;0
)
,B
(
0;1;0
)
vàC
(
0;0;−2
)
.Mặtphẳng
(
ABC
)
cóphươngtrìnhlà:
A.
x
3
+
y
−1
+
z
2
=1. B.
x
3
+
y
1
+
z
−2
=1. C.
x
3
+
y
1
+
z
2
=1. D.
x
−3
+
y
1
+
z
2
=1.
Câu 66. Chocấpsốnhân
(
u
n
)
vớiu
1
=3 vàcôngbộiq =2.Giátrịcủau
2
bằng
A. 8. B. 9. C. 6. D.
3
2
.
Câu 67. Chohaisốphứcz
1
=3−2i vàz
2
=2+i.Sốphứcz
1
+z
2
bằng
A. 5+i. B. −5+i. C. 5−i. D. −5−i.
Câu 68. Biết
3
Z
1
f
(
x
)
dx =3.Giátrịcủa
3
Z
1
2f
(
x
)
dx bằng
A. 5. B. 9. C. 6. D.
3
2
.
Câu 69. Trênmặtphẳngtọađộ,biếtM
(
−3;1
)
làđiểmbiểudiễnsốphứcz.Phầnthựccủaz bằng
A. 1. B. −3. C. −1. D. 3.
Câu 70. Tậpxácđịnhcủahàmsốy =log
5
x là
A. [0;+∞
)
. B.
(
−∞;0
)
. C.
(
0;+∞
)
. D.
(
−∞;+∞
)
.
Câu 71. Sốgiaođiểmcủađồthịhàmsốy =x
3
+3x
2
vàđồthịhàmsốy =3x
2
+3x là
A. 3. B. 1. C. 2. D. 0.
Câu 72.
ChohìnhchópS.ABC cóđáyABC làtamgiácvuôngtạiB,AB = a,BC = 2a,SA
vuônggócvớimặtphẳngđáyvàSA =
√
15a (thamkhảohìnhbên).Gócgiữađường
thẳngSC vàmặtphẳngđáybằng
A. 45
◦
. B. 30
◦
. C. 60
◦
. D. 90
◦
.
A
B
C
S
Soạn:HuỳnhPhúSĩ 96 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
Câu 73. BiếtF
(
x
)
=x
2
làmộtnguyênhàmcủahàmsốf
(
x
)
trênR.Giátrịcủa
2
Z
1
[2+f
(
x
)
]dx bằng
A. 5. B. 3. C.
13
3
. D.
7
3
.
Câu 74. Diệntíchhìnhphẳnggiớihạnbởihaiđườngy =x
2
−4 vày =2x −4 bằng
A. 36. B.
4
3
. C.
4π
3
. D. 36π.
Câu 75. TrongkhônggianOxyz,chođiểmM
(
2;−2;3
)
vàđườngthẳngd:
x −1
3
=
y +2
2
=
z−3
−1
.MặtphẳngđiquaM
vàvuônggócvớid cóphươngtrìnhlà
A. 3x +2y −z +1=0. B. 2x −2y +3z −17=0. C. 3x +2y −z −1=0. D. 2x −2y +3z +17=0.
Câu 76. Gọiz
0
lànghiệmphứccóphầnảodươngcủaphươngtrìnhz
2
+6z +13 =0.Trênmặtphẳngtọađộ,điểmbiểu
diễnsốphức1−z
0
là
A. N
(
−2;2
)
. B. M
(
4;2
)
. C. P
(
4;−2
)
. D. Q
(
2;−2
)
.
Câu 77. TrongkhônggianOxyz,chobađiểmA
(
1;0;1
)
,B
(
1;1;0
)
vàC
(
3;4;−1
)
.ĐườngthẳngđiquaA vàsongsongvới
BC cóphươngtrìnhlà
A.
x −1
4
=
y
5
=
z−1
−1
. B.
x +1
2
=
y
3
=
z+1
−1
. C.
x −1
2
=
y
3
=
z−1
−1
. D.
x +1
4
=
y
5
=
z+1
−1
.
Câu 78. Chohàmsốf
(
x
)
liêntụctrênR vàcóbảngxétdấucủaf
0
(
x
)
nhưsau:
x
f
0
(x)
−∞
−1
0 1 2
+∞
+
0
−
0
+
−
0
−
Sốđiểmcựcđạicủahàmsốđãcholà
A. 4. B. 1. C. 2. D. 3.
Câu 79. Tậpnghiệmcủabấtphươngtrình3
x
2
−13
< 27 là
A.
(
4;+∞
)
. B.
(
−4;4
)
. C.
(
−∞;4
)
. D.
(
0;4
)
.
Câu 80. Chohìnhnóncóbánkínhđáybằng2vàgócởđỉnhbằng60
◦
.Diệntíchxungquanhcủahìnhnónđãchobằng
A. 8π. B.
16
√
3π
3
. C.
8
√
3π
3
. D. 16π.
Câu 81. Giátrịnhỏnhấtcủahàmsốf
(
x
)
=x
3
−24x trênđoạn[2;19] bằng
A. 32
√
2. B. −40. C. −32
√
2. D. −45.
Câu 82. Chohaisốphứcz =1+2i vàw =3+i.Môđuncủasốphứcz·w bằng
A. 5
√
2. B.
√
26. C. 26. D. 50.
Câu 83. Choa vàb làhaisốthựcdươngthỏamãn4
log
2
(
a
2
b
)
=3a
3
.Giátrịcủaab
2
bằng
A. 3. B. 6. C. 12. D. 2.
Câu 84. Chohàmsốf
(
x
)
=
x
√
x
2
+2
.Họtấtcảcácnguyênhàmcủahàmsốg
(
x
)
=
(
x +1
)
·f
0
(
x
)
là
A.
x
2
+2x −2
2
√
x
2
+2
+C. B.
x −2
√
x
2
+2
+C. C.
x
2
+x +2
√
x
2
+2
+C. D.
x +2
2
√
x
2
+2
+C.
Câu 85. Tậphợptấtcảcácgiátrịthựccủathamsốm đểhàmsốy =
x +4
x +m
đồngbiếntrênkhoảng
(
−∞;−7
)
là
A. [4;7
)
. B.
(
4;7]. C.
(
4;7
)
. D.
(
4;+∞
)
.
Câu 86. Trongnăm2019,diệntíchrừngtrồngmớicủatỉnhAlà600ha.GiảsửdiệntíchrừngtrồngmớicủatỉnhAmỗi
nămtiếptheođềutăng6% sovớidiệntíchrừngtrồngmớicủanămliềntrước.Kểtừsaunăm2019,nămnàodướiđâylà
nămđầutiêntỉnhAcódiệntíchrừngtrồngmớitrongnămđóđạttrên1000 ha?
A. Năm2028. B. Năm2047. C. Năm2027. D. Năm2046.
Câu 87. ChohìnhchópS.ABC cóđáylàtamgiácđềucạnh4a,SA vuônggócvớimặtphẳngđáy,gócgiữamặtphẳng
(
SBC
)
vàmặtphẳngđáybằng60
◦
.DiệntíchcủamặtcầungoạitiếphìnhchópS.ABC bằng
A.
172πa
2
3
. B.
76πa
2
3
. C. 84πa
2
. D.
172πa
2
9
.
Câu 88.
Soạn:HuỳnhPhúSĩ 97 TrườngTHCS-THPTMỹThuận
Phụlục TOÁN12
ChohìnhlăngtrụđứngABC.A
0
B
0
C
0
cótấtcảcáccạnhbằnga.GọiM làtrungđiểmcủa
CC
0
(thamkhảohìnhbên).KhoảngcáchtừM đếnmặtphẳng
(
A
0
BC
)
bằng
A.
√
21a
14
. B.
√
2a
2
. C.
√
21a
7
. D.
√
2a
4
.
A
B
C
A
0
B
0
C
0
M
Câu 89. Chohàmsốbậcbốnf
(
x
)
cóbảngbiếnthiênnhưsau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
33
−2−2
+∞+∞
Sốđiểmcựctrịcủahàmsốg
(
x
)
=x
4
[f
(
x +1
)
]
2
là
A. 11. B. 9. C. 7. D. 5.
Câu 90.
Chohàmsốy =ax
3
+bx
2
+cx +d (a, b, c, d ∈ R)cóđồthịlàđườngcongtrong
hìnhbên.Cóbaonhiêusốdươngtrongcácsốa,b,c,d?
A. 4. B. 1. C. 2. D. 3.
O
x
y
Câu 91. GọiS làtậphợptấtcảcácsốtựnhiêncó4chữsốđôimộtkhácnhauvàcácchữsốthuộctập{1, 2, 3, 4, 5, 6, 7, 8, 9}.
ChọnngẫunhiênmộtsốthuộcS,xácsuấtđểsốđókhôngcóhaichữsốliêntiếpnàocùngchẵnbằng
A.
25
42
. B.
5
21
. C.
65
126
. D.
55
126
.
Câu 92. ChohìnhchópđềuS.ABCD cócạnhđáybằnga,cạnhbênbằng2a vàO làtâmcủađáy.GọiM,N,P,Q lầnlượt
làcácđiểmđốixứngvớiO quatrọngtâmcủacáctamgiácSAB,SBC,SCD,SDA vàS
0
làđiểmđốixứngvớiS quaO.Thể
tíchcủakhốichópS
0
.MNPQ bằng
A.
20
√
14a
3
81
. B.
40
√
14a
3
81
. C.
10
√
14a
3
81
. D.
2
√
14a
3
9
.
Câu 93. Xétcácsốthựckhôngâmx vày thỏamãn2x+y4
x+y−1
≥ 3.GiátrịnhỏnhấtcủabiểuthứcP =x
2
+y
2
+4x+6y
bằng
A.
33
4
. B.
65
8
. C.
49
8
. D.
57
8
.
Câu 94. Cóbaonhiêusốnguyênx saochoứngvớimỗix cókhôngquá728sốnguyêny thỏamãnlog
4
x
2
+y
≥
log
3
(x +y)?
A. 59. B. 58. C. 116. D. 115.
Câu 95.
Chohàmsốbậcbay =f(x)cóđồthịlàđườngcongtronghình
bên.Sốnghiệmthựcphânbiệtcủaphươngtrìnhf
x
3
f(x)
+
1=0 là
A. 8. B. 5. C. 6. D. 4.
O
x
y
Soạn:HuỳnhPhúSĩ 98 TrườngTHCS-THPTMỹThuận
CHỈ MỤC
B
Bấtphươngtrình
bấtphươngtrìnhlôgarit........................56
bấtphươngtrìnhmũ...........................56
C
Cănbậcn..........................................36
G
Góc
Gócgiữahaimặtphẳng........................89
Gócgiữađườngthẳngvàmặtphẳng.............89
H
Hàmsố.............................................7
Cựctrịcủahàmsố.............................13
Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố..19
Giớihạncủahàmsố...........................83
Hàmhằng.....................................82
Hàmphântuyếntính...........................29
Hàmsốbậcba.................................28
Hàmsốbậcbốntrùngphương..................29
Hàmsốbậchai................................82
Hàmsốbậcnhất...............................82
Hàmsốchẵn,hàmsốlẻ........................82
Hàmsốliêntục................................83
Hàmsốlôgarit.................................48
Hàmsốlũythừa...............................40
Hàmsốmũ....................................47
Quytắctìmcựctrịcủahàmsố..................14
Quytắcxéttínhđơnđiệucủahàmsố............8
Sựđồngbiếnvànghịchbiếncủahàmsố.........7
TìmthamsốđểhàmsốđơnđiệutrênR ........10
Tìmthamsốđểhàmsốđơnđiệutrênmộtkhoảng10
Tươnggiaocủacácđồthị.......................30
Tậpxácđịnhcủahàmsố.......................82
Xétdấunhịthứcbậcnhất.......................83
Xétdấutamthứcbậchai.......................83
Xéttínhđơnđiệucủahàmsốdựavàobảngbiến
thiên.......................................9
Xéttínhđơnđiệucủahàmsốdựavàođồthị......8
Xéttínhđơnđiệucủahàmsốdựavàođồthịcủa
đạohàm...................................9
Xéttínhđơnđiệucủahàmẩn...................11
Điềukiệnđủđểhàmsốcócựctrị..............13
Đườngtiệmcận................................24
Đườngtiệmcậnngang.........................24
Đườngtiệmcậnđứng..........................24
Đạohàm......................................83
K
Khoảngcách
Khoảngcáchgiữahaimặtphẳngsongsong.....89
Khoảngcáchtừđiểmđếnmặtphẳng............89
Khốiđadiện
Haiđadiệnbằngnhau.........................62
Hìnhchóp.....................................88
Hìnhchópđều.................................88
Hìnhhộp......................................88
Hìnhhộpchữnhật.............................88
Hìnhlăngtrụ..................................88
Hìnhlăngtrụđứng.............................88
Hìnhlậpphương...............................88
Hìnhđadiện...................................61
Hìnhđadiệnlồi...............................66
Hìnhđadiệnđều...............................66
Khốiđadiện...................................62
L
Lôgarit.............................................43
Lôgaritthậpphân..............................44
Lôgarittựnhiên................................44
Lũythừa........................................36,85
M
Mặtcầu
Giaocủamặtcầuvàmặtphẳng.................78
Giaocủamặtcầuvàđườngthẳng...............79
Kinhtuyến....................................78
Mặtcầu........................................78
Vĩtuyến.......................................78
Mặttrònxoay
Mặtnón.......................................73
Mặttrụ........................................74
P
Phươngtrình.......................................84
Phươngtrìnhbậc4trùngphương...............84
Phươngtrìnhbậchai...........................84
Phươngtrìnhchứaẩntrongdấugiátrịtuyệtđối.85
Phươngtrìnhlôgarit............................52
Phươngtrìnhmũ...............................52
Phươngtrìnhtích..............................85
Phươngtrìnhvôtỉ.............................85
ĐịnhlýVi-ét...................................84
T
Tamgiác...........................................86
Chuvitamgiác................................86
CôngthứcHeron..............................86
Diệntíchtamgiác..............................86
Tamgiácbằngnhau............................87
Tamgiáccân..................................87
Tamgiácvuông................................87
Tamgiácvuôngcân............................87
Tamgiácđều..................................87
Tamgiácđồngdạng............................87
Trọngtâmcủatamgiác........................86
Trựctâmcủatamgiác..........................86
99
Phụlục TOÁN12
Đườngcaocủatamgiác........................86
Đườngtrungbìnhcủatamgiác.................86
Đườngtrungtuyếncủatamgiác.................86
Đườngtrònngoạitiếptamgiác.................86
Đườngtrònnộitiếptamgiác....................86
Địnhlýcosin..................................86
Địnhlýsin....................................86
Thểtích
Thểtíchkhốichóp.............................69
Thểtíchkhốihộpchữnhật.....................69
Thểtíchkhốilăngtrụ..........................69
V
Vịtrítươngđối
Vịtrítươngđốigiữahaimặtphẳng.............90
Vịtrítươngđốigiữahaiđườngthẳng............89
Vịtrítươngđốigiữađườngthẳngvàmặtphẳng..89
Soạn:HuỳnhPhúSĩ 100 TrườngTHCS-THPTMỹThuận
| 1/101
| | Tải xuống

Có thể bạn quan tâm:

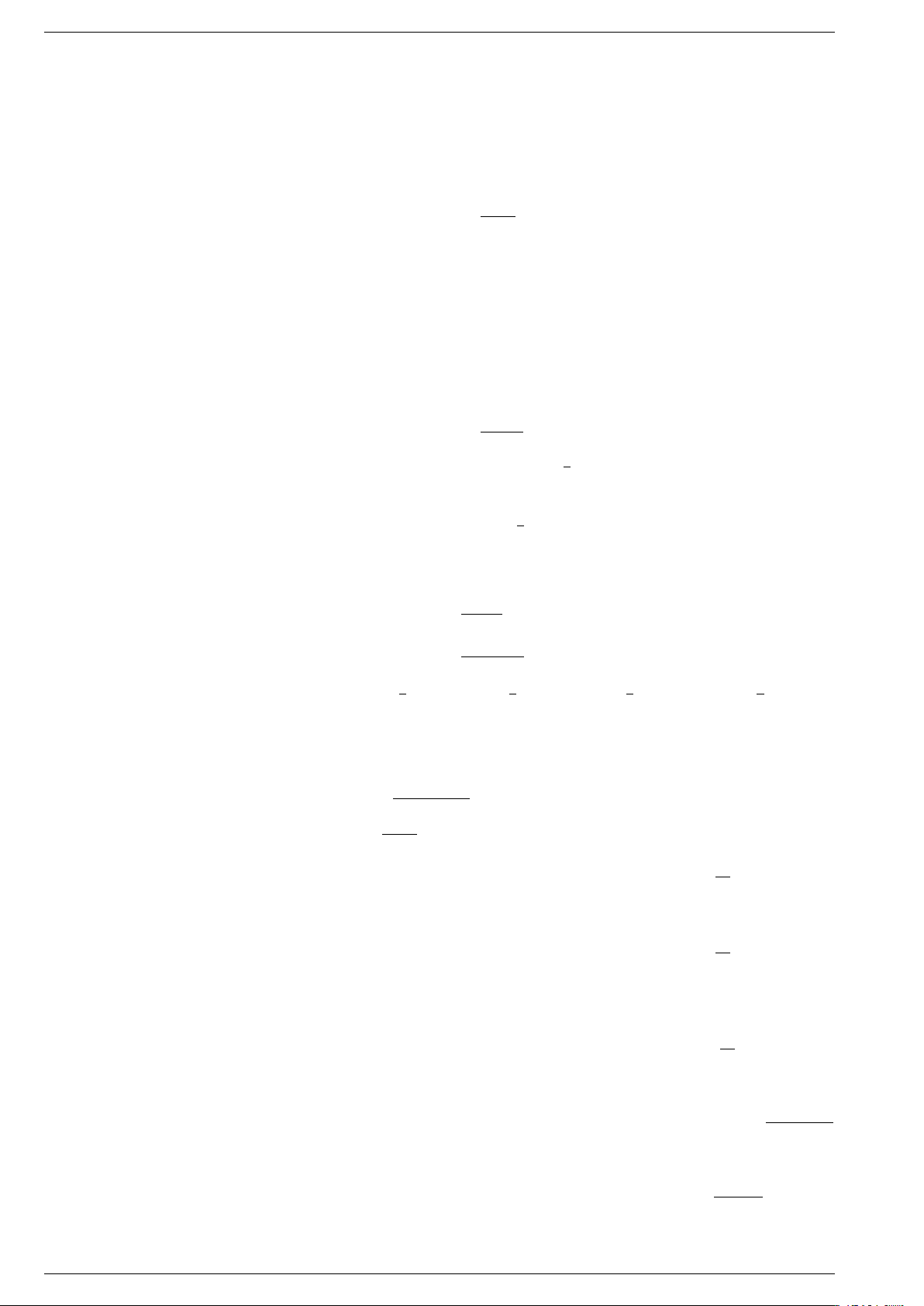
Preview text:

TÀI LIỆU HỌC TẬP HK1 TOÁN 12
Trường THCS&THPT Mỹ Thuận Vĩnh Long KẾ HOẠCH TUẦN L TUẦN 4 L TUẦN 1 L TUẦN 2 L TUẦN 5 L TUẦN 3 L TUẦN 6 L TUẦN 7 L TUẦN 10 L TUẦN 11 L TUẦN 8 L TUẦN 9 L TUẦN 12 L TUẦN 13 L TUẦN 16 L TUẦN 14 L TUẦN 17 L TUẦN 15 L TUẦN 18 MỤC LỤC TOÁN 12 MỤC LỤC PHẦN I GIẢI TÍCH 4
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§1. Sự đồng biến và nghịch biến của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 1.
Tính đơn điệu của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2.
Quy tắc xét tính đơn điệu của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
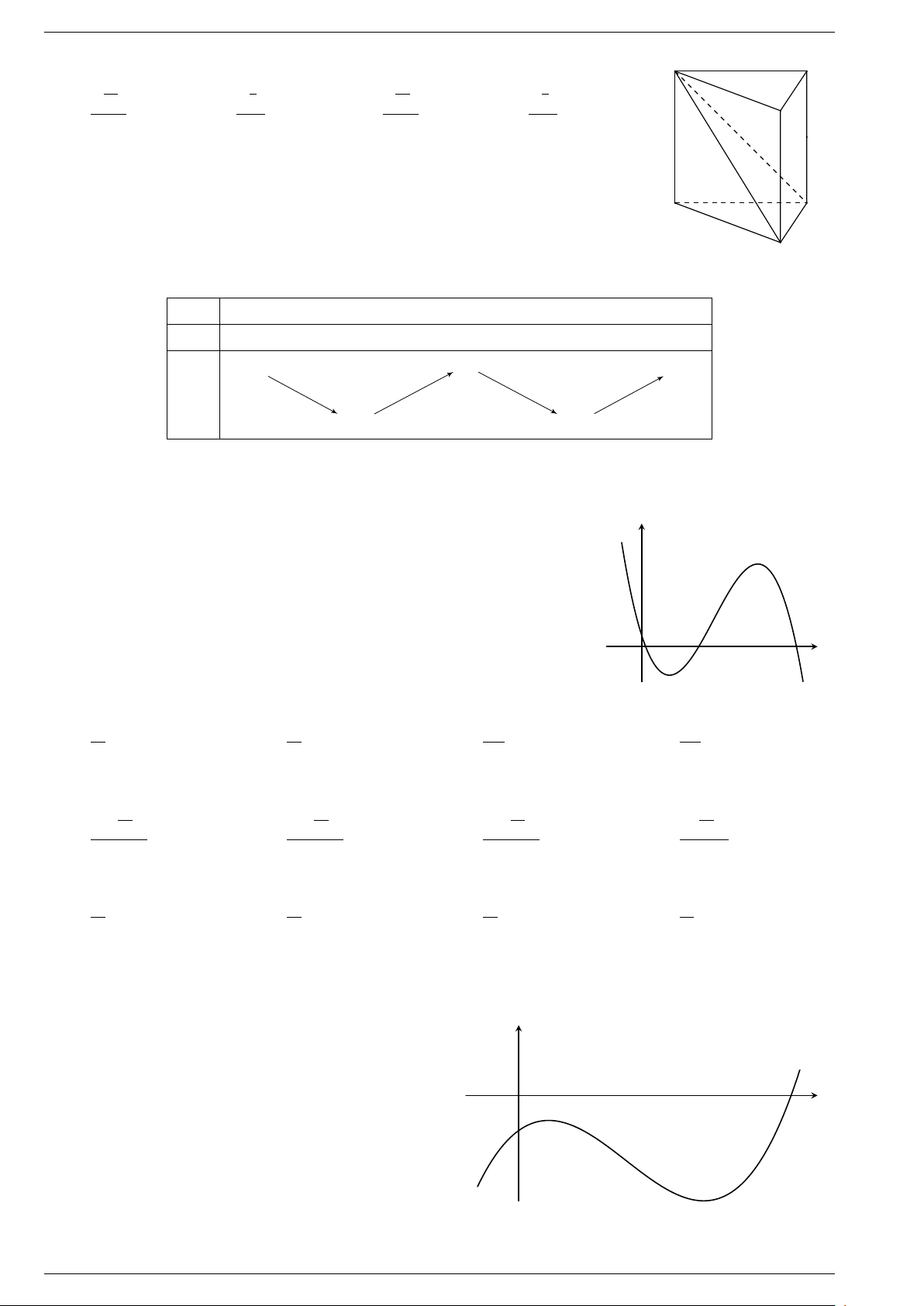
§2. Cực trị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 1.
Khái niệm cực đại, cực tiểu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2.
Điều kiện đủ để hàm số có cực trị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 3.
Quy tắc tìm cực trị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 1.
Định nghĩa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 2.
Cách tìm GTLN & GTNN của hàm số trên một đoạn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
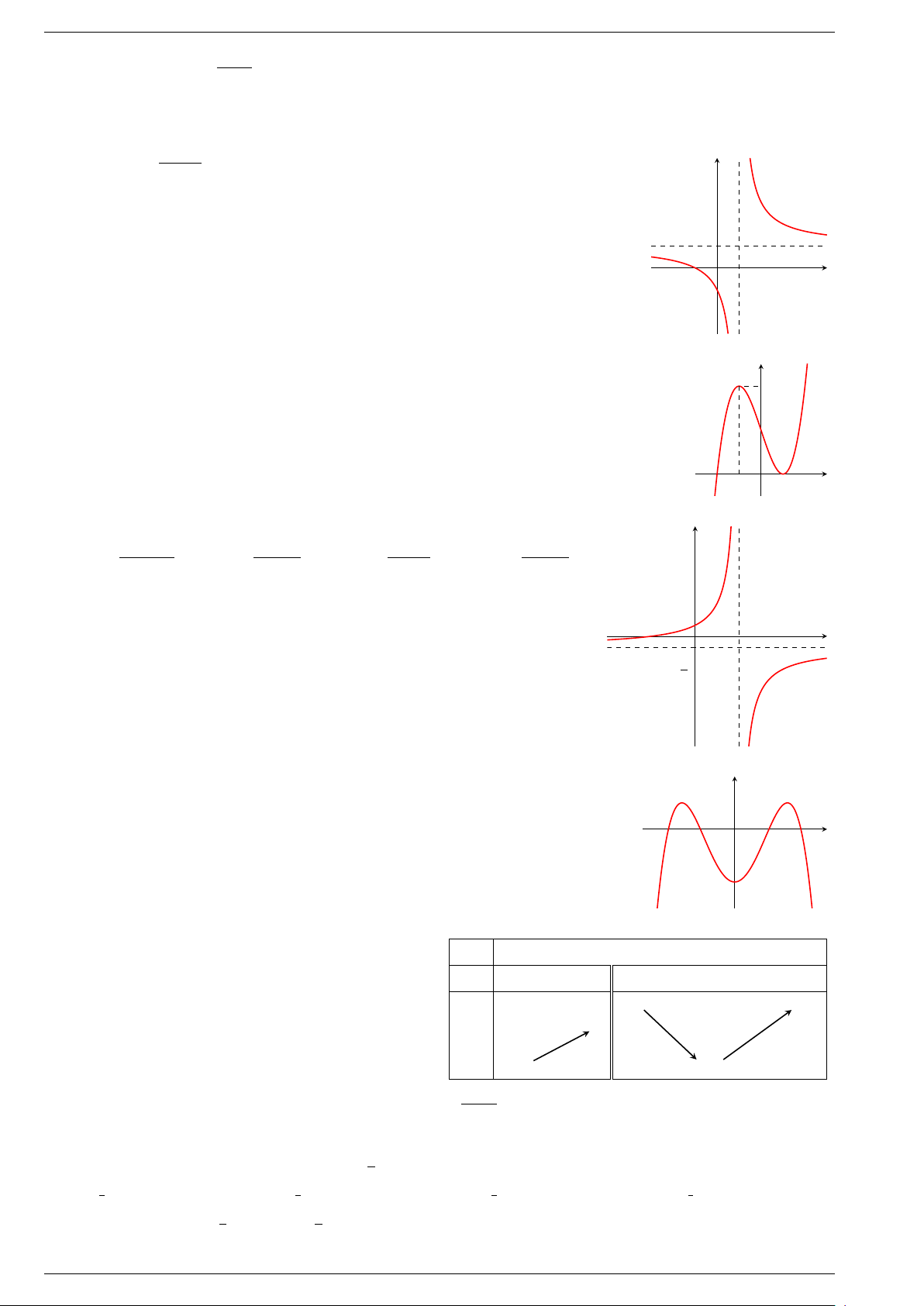
§4. Đường tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 1.
Đường tiệm cận ngang . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 2.
Đường tiệm cận đứng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 1.
Sơ đồ khảo sát hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 2.
Khảo sát một số hàm thường gặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 3.
Sự tương giao của các đồ thị . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Chương 2. Hàm số lũy thừa. Hàm số mũ và hàm số logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
§1. Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 1.
Khái niệm lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 2.
Tính chất của lũy thừa với số mũ thực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
§2. Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 1.
Khái niệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 2.
Đạo hàm của hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 3.
Khảo sát hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
§3. Lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 1.
Khái niệm lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 2.
Quy tắc tính lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 3.
Lôgarit thập phân và lôgarit tự nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
§4. Hàm số mũ. Hàm số lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 1.
Hàm số mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 2.
Hàm số lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
§5. Phương trình mũ và phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 1.
Phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 2.
Phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
§6. Bất phương trình mũ và bất phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 1.
Bất phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 2.
Bất phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 PHẦN II HÌNH HỌC 58 Soạn: Huỳnh Phú Sĩ 4
Trường THCS-THPT Mỹ Thuận MỤC LỤC TOÁN 12
Chương 1. Khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
§1. Khái niệm về khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 1.
Khối lăng trụ và khối chóp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 2.
Khái niệm về hình đa diện và khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 3.
Hai đa diện bằng nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60 4.
Phân chia và lắp ghép các khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 5.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
§2. Đa diện lồi và Đa diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 1.
Khối đa diện lồi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 2.
Khối đa diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 3.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
§3. Khái niệm về thể tích của khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 1.
Khái niệm về thể tích khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 2.
Thể tích khối lăng trụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 3.
Thể tích khối chóp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
Chương 2. Mặt nón, mặt trụ, mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
§1. Khái niệm về khối tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 1.
Sự tạo thành mặt tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 2.
Mặt nón tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 3.
Mặt trụ tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72 4.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
§2. Mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 1.
Mặt cầu và các khái niệm liên quan đến mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 2.
Giao của mặt cầu và mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 3.
Giao của mặt cầu và đường thẳng. Tiếp tuyến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 4.
Diện tích và thể tích . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 5.
Thực hành . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 Soạn: Huỳnh Phú Sĩ 5
Trường THCS-THPT Mỹ Thuận PHẦN I GIẢI TÍCH
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§1. Sự đồng biến và nghịch biến của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§2. Cực trị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
§4. Đường tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Chương 2. Hàm số lũy thừa. Hàm số mũ và hàm số logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
§1. Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
§2. Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
§3. Lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
§4. Hàm số mũ. Hàm số lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
§5. Phương trình mũ và phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
§6. Bất phương trình mũ và bất phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 Soạn: Huỳnh Phú Sĩ 6
Trường THCS-THPT Mỹ Thuận
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số TOÁN 12 Chương 1.
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
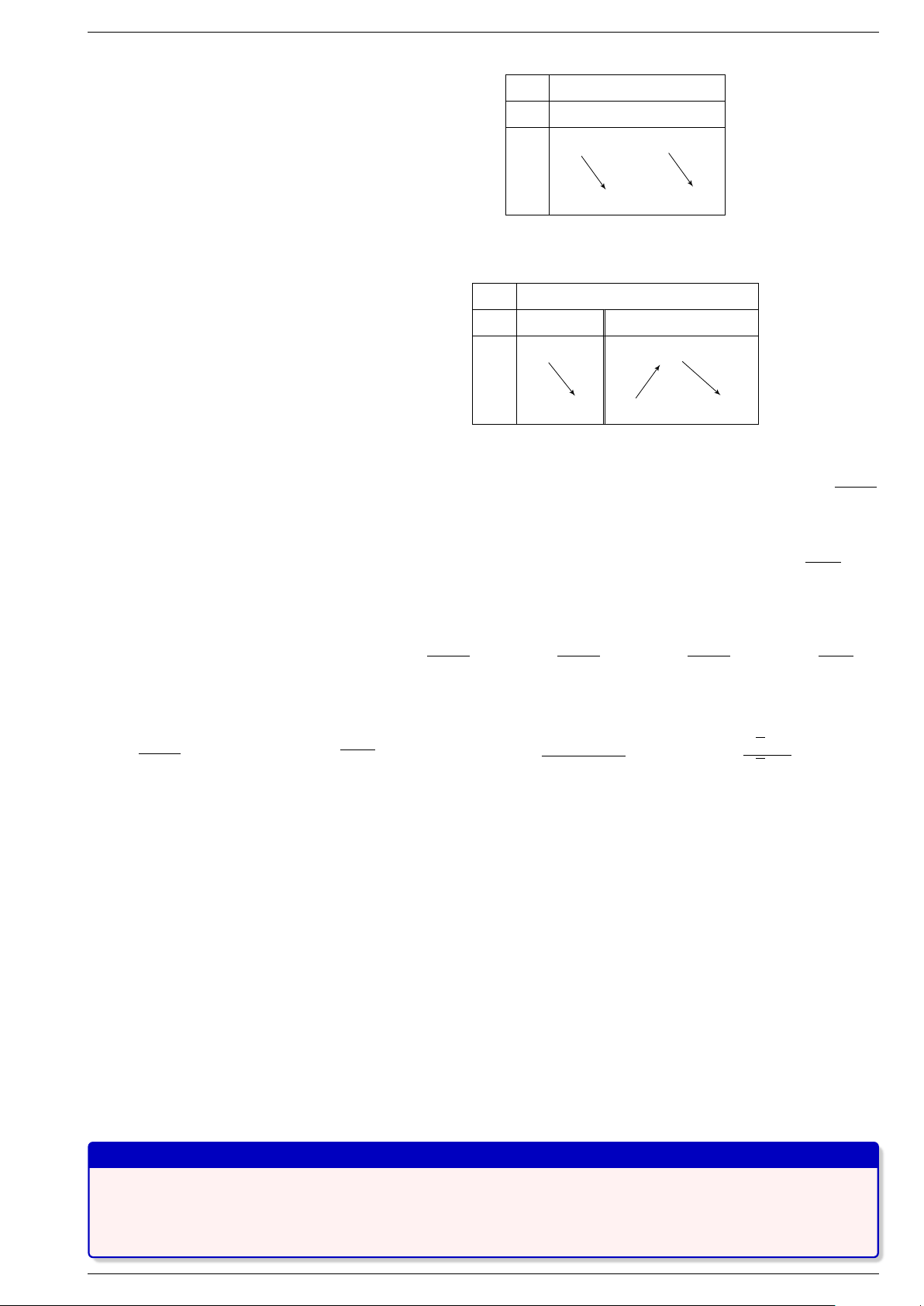
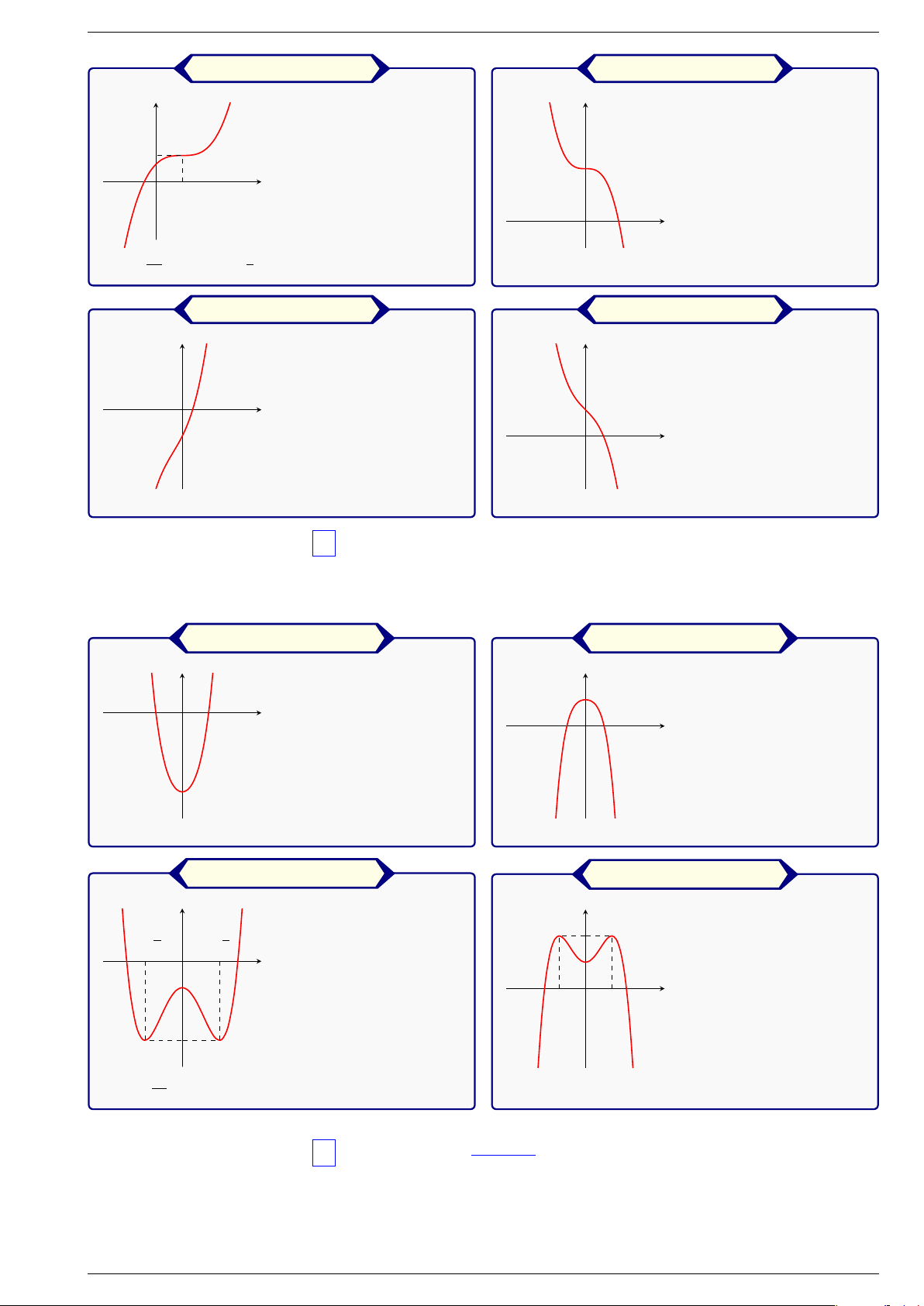
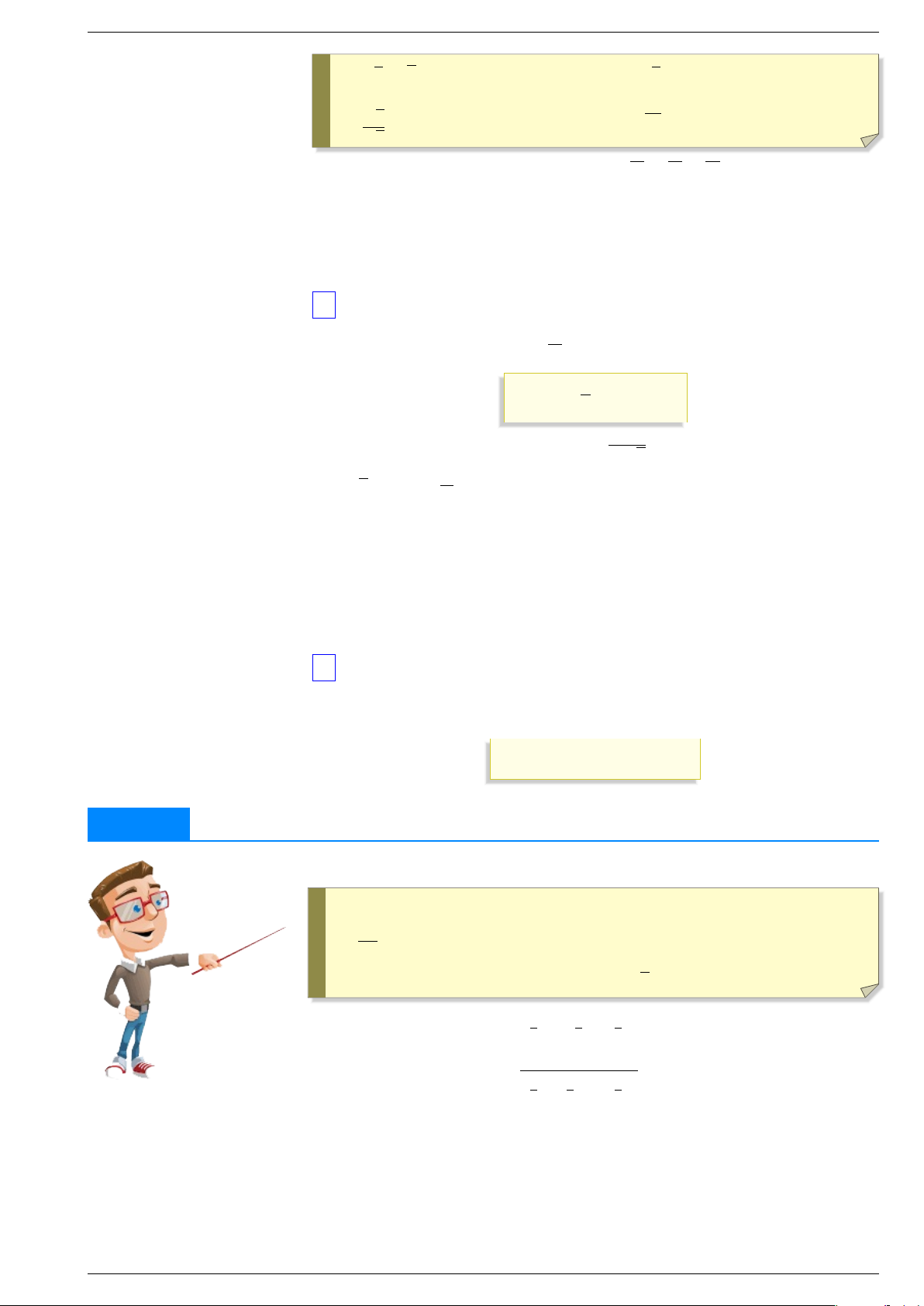
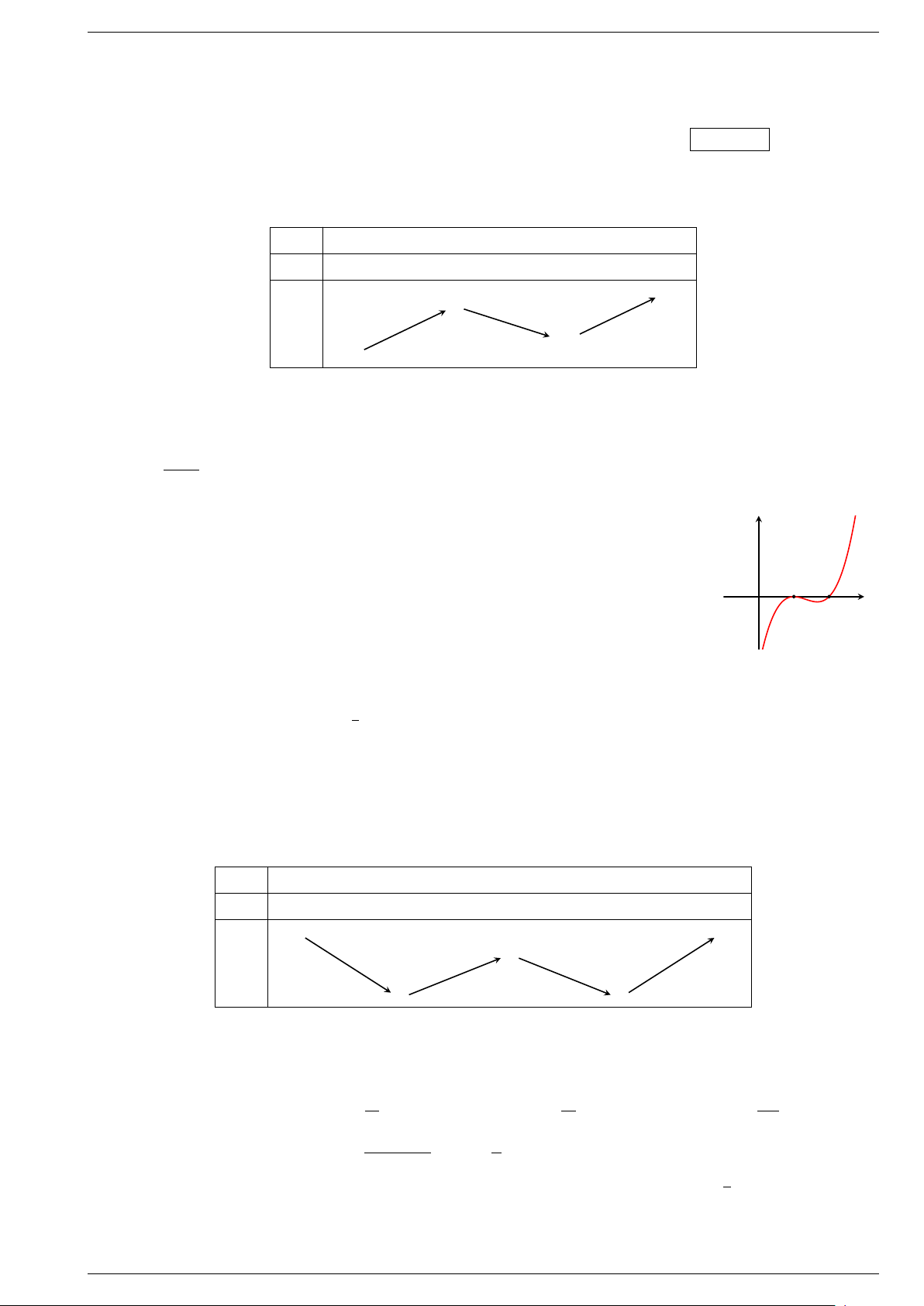
§1.SỰ ĐỒNG BIẾN VÀ NGHỊCH BIẾN CỦA HÀM SỐ Đặt vấn đề y x − y x − x2 Cho hai hàm số = 2 6 và = 3 + 2
lần lượt có bảng biến thiên như sau: x −∞ ∞ x −∞ ∞ + 1 + ∞ + 4 y y −∞ −∞ −∞ 1)
Chỉ ra các khoảng đồng biến, nghịch biến của mỗi hàm số trên. 2)
Giải thích nguyên nhân của sự biến thiên đó. 3)
Hãy cho biết cách tìm các giá trị tại hai đầu mút của từng mũi tên trong bảng. 1
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ y 1 Định nghĩa y f x K Giả sử hàm số = ( ) xác định trên
(khoảng, đoạn hoặc nửa khoảng). ○ f x K ∀x , x ∈ K x < x f x . . . f x ( ) đồng biến (tăng) trên nếu với 1 2 mà 1 2 thì ( 1 ) ( 2 ) ○ f x K ∀x , x ∈ K x < x f x . . . f x (
) nghịch biến (giảm) trên nếu với 1 2 mà 1 2 thì ( 1 ) ( 2 ) O x 1 3
2 Tính đơn điệu và dấu của đạo hàm Hàm số này đồng biến trên y f x K . . . . . . Cho hàm số = ( ) có đạo hàm trên . khoảng , nghịch biến . . . . . . trên khoảng , không đổi ○ f 0 x > ∀x ∈ K
f x . . . . . . . . . . . . . . . K . . . . . . Nếu ( ) 0, thì ( ) trên . trên khoảng ○ f 0 x < ∀x ∈ K
f x . . . . . . . . . . . . . . . K Nếu ( ) 0, thì ( ) trên . ○ f 0 x ∀x ∈ K
f x . . . . . . . . . . . . . . . K Nếu ( ) = 0, thì ( ) trên . y I Ví dụ 1. y x − x2
Xét sự biến thiên của hàm số = 3 + 2 . 4 − O x 1 1 3 y x −x2 Parabol = 3 + 2 có đỉnh . . . . . . a . . . và hướng xuống vì Soạn: Huỳnh Phú Sĩ 7
Trường THCS-THPT Mỹ Thuận
§1. Sự đồng biến và nghịch biến của hàm số TOÁN 12 2
QUY TẮC XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
. . . . . . . . . . . . . . . . . . Bước 1. Tìm !
. . . . . . . . . . . . f 0 x x f 0 x . . . . . .
. . . . . . . . . . . . . . . . . . Bước 2. Tìm ( ). Tìm để ( ) hoặc
. . . . . . . . . . . . . . . Bước 3. Lập bảng Bước 4.
Kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Ví dụ 2. Xét sự biến thiên của các hàm số sau: x x − 3 x2 y − − x y 1 a) = 2 + 2 b) = x 3 2 + 2 3 THỰC HÀNH Í TRẮC NGHIỆM
Câu 1. Mệnh đề nào sau đây là đúng? A y f x a b f 0 x ≥ , ∀x ∈ . Hàm số = (
) đồng biến trên khoảng ( ; ) khi và chỉ khi ( ) 0 a b ( ; ). B
f 0 x ≥ , ∀x ∈ a b y f x a b . Nếu ( ) 0 ( ; ) thì hàm số = (
) đồng biến trên khoảng ( ; ). C y f x a b f 0 x > , ∀x ∈ . Hàm số = (
) đồng biến trên khoảng ( ; ) khi và chỉ khi ( ) 0 a b ( ; ). D
f 0 x > , ∀x ∈ a b y f x a b . Nếu ( ) 0 ( ; ) thì hàm số = (
) đồng biến trên khoảng ( ; ). Câu 2. y f x Cho hàm số = (
) có đồ thị như hình vẽ. Tìm y 1
khoảng đồng biến của hàm số. A − B − . ( 2; 1). . ( 1; 2). C − − D − x − − . ( 2; 1). . ( 1; 1). 2 1 0 1 −1 −3 Câu 3. y f x Cho hàm số = (
) có đồ thị như hình vẽ. Mệnh đề nào sau đây là đúng? y 1 x −1 0 1 2 −1 −3 Soạn: Huỳnh Phú Sĩ 8
Trường THCS-THPT Mỹ Thuận
§1. Sự đồng biến và nghịch biến của hàm số TOÁN 12 A − .
Hàm số đồng biến trên khoảng ( 3; 1).
B. Hàm số nghịch biến trên khoảng (0; 2). C − .
Hàm số nghịch biến trên khoảng ( 1; 0).
D. Hàm số đồng biến trên khoảng (0; 1). Câu 4. y f x Cho hàm số = (
) có bảng biến thiên như hình vẽ. Hàm số đã cho
nghịch biến trên khoảng nào sau đây? x −∞ − ∞ 1 0 1 + y0 − − 0 + 0 0 + ∞ ∞ + 3 + y − − 2 2 A ∞ B − C −∞ D −∞ − . (0; + ). . ( 1; 1). . ( ; 0). . ( ; 2). Câu 5. y f x Cho hàm số = (
) có bảng biến thiên như sau: x −∞ ∞ 2 + y0 − − ∞ + 2 y −∞ 2
Khẳng định nào sau đây là đúng? A R \ { } .
Hàm số nghịch biến trên 2 . B −∞ ∞ .
Hàm số đồng biến trên ( ; 2) và (2; + ). C −∞ ∞ .
Hàm số nghịch biến trên ( ; 2) và (2; + ). D R .
Hàm số nghịch biến trên . Câu 6. y f x Cho hàm số = (
) có bảng xét dấu đạo hàm như sau: x −∞ − ∞ 2 0 2 + y0 − − − + 0 0
Mệnh đề nào sau đây là đúng? A −∞ − .
Hàm số nghịch biến trên khoảng ( ; 2). B −∞ .
Hàm số đồng biến trên khoảng ( ; 0).
C. Hàm số nghịch biến trên khoảng (0; 2). D − .
Hàm số đồng biến trên khoảng ( 2; 0). Câu 7. y f x Cho hàm số = (
) có bảng biến thiên như sau: x −∞ − − ∞ 4 1 + y0 − + 0 + 0 3 y 0 −∞ −∞
Tìm mệnh đề đúng trong các mệnh đề sau: A −∞ .
Hàm số đồng biến trên khoảng ( ; 3). B − ∞ .
Hàm số nghịch biến trên khoảng ( 2; + ). C −∞ − .
Hàm số nghịch biến trên khoảng ( ; 2). D − − .
Hàm số đồng biến trên khoảng ( 4; 1). Câu 8. y f x f x Cho hàm số = ( ). Biết rằng ( ) có đạo hàm y f 0 x (
) với đồ thị như hình vẽ. Khẳng định nào sau y f x đây đúng về hàm số = ( )? A −∞ − .
Hàm số đồng biến trên khoảng ( ; 1). B − x .
Hàm số đồng biến trên khoảng ( 1; 0). − C 1 0 1 2 .
Hàm số đồng biến trên khoảng (1; 2). D ∞ .
Hàm số nghịch biến trên khoảng (0; + ). Câu 9. x3 x2 y − − x 3 Hàm số = 6 + 3 2 4 Soạn: Huỳnh Phú Sĩ 9
Trường THCS-THPT Mỹ Thuận
§1. Sự đồng biến và nghịch biến của hàm số TOÁN 12 A − .
Đồng biến trên khoảng ( 2; 3). B − .
Nghịch biến trên khoảng ( 2; 3). C −∞ − .
Nghịch biến trên khoảng ( ; 2). D − ∞ .
Đồng biến trên khoảng ( 2; + ). Câu 10. y
x4− x2− Cho hàm số = 8
4. Hàm số đã cho nghịch biến trên khoảng A − ∞ B −∞ − . ( 2; 0) và (2; + ). . ( ; 2) và (0; 2). C − D −∞ − ∞ . ( 2; 0) và (0; 2). . ( ; 2) và (2; + ). Câu 11. x y + 1 Cho hàm số =
− x . Khẳng định nào sau đây đúng? 2
A. Hàm số đồng biến trên từng khoảng xác định của nó. B R . Hàm số đồng biến trên . C −∞ ∪ ∞ .
Hàm số đồng biến trên ( ; 2) (2; + ).
D. Hàm số nghịch biến trên từng khoảng xác định của nó. Câu 12. y x3 − x Cho hàm số = 3
+ 1. Mệnh đề nào sau đây đúng? A − .
Hàm số nghịch biến trên khoảng ( 1; 3). B − .
Hàm số đồng biến trên khoảng ( 1; 1). C −∞ − ∞ .
Hàm số đồng biến trên khoảng ( ; 1) và (1; + ). D − .
Hàm số nghịch biến trên khoảng ( 2; 1). Câu 13. − x y 3 Cho hàm số =
x − . Mệnh đề nào sau đây là đúng? 2 1 A −∞ 1 .
Hàm số nghịch biến trên ; . 2 B R . Hàm số đồng biến trên . C 1 ∞ . Hàm số đồng biến trên ; + . 2 D R .
Hàm số nghịch biến trên . Câu 14. y x4 Hàm số = 2
+ 3 nghịch biến trên khoảng nào dưới đây? A ∞ B ∞ C −∞ − D −∞ . (3; + ). . (0; + ). . ( ; 3). . ( ; 0). √ Câu 15. y − x2 Hàm số = 4 nghịch biến trên khoảng A B − C ∞ D − . (0; 2). . ( 2; 0). . (0; + ). . ( 2; 2). √ Câu 16. y −x2 x Hàm số = + 3 đồng biến trên khoảng A −∞ 3 B 3 C 3 D 3 ∞ . ; . . 0; . . ; 3 . . ; + . 2 2 2 2 Câu 17. R
Hàm số nào sau đây nghịch biến trên ? A y x3 − x2 B y
−x4 − x2 − . = 3 + 4. . = 2 3. C y x3 x D y −x3 x2 − x . = + 3 . . = + 3 3 + 2. Câu 18. √ R
Hàm số nào sau đây đồng biến trên ? A y x2 − x B y x4 x2 . = 3 + 2. . = + + 1. C x − y 1 D y x3 x . = x . . = + 5 + 13. + 1 Câu 19. x3 m y − mx2 − m
Tìm tất cả các giá trị của tham số để hàm số = + (2 + 3 x R 3) + 4 nghịch biến trên . A − ≤ m ≤ B − < m < C − < m < D − ≤ m ≤ . 1 3. . 3 1. . 1 3. . 3 1. Câu 20. x3 m y − − mx2 m −
Tìm tất cả các giá trị của tham số để hàm số = + (2 3 x − m R 3) + 2 nghịch biến trên . A m ∈ −∞ − ∪ ∞ B m ∈ − . ( ; 3) (1; + ). . [ 3; 1]. C m ∈ −∞ D m ∈ − . ( ; 1]. . ( 3; 1). Câu 21. x3 m y − mx2 x−
Tìm tất cả các giá trị thực của tham số để hàm số = 2 +4 5 3 R đồng biến trên . A < m < B − ≤ m ≤ C ≤ m ≤ D − < m < . 0 1. . 1 1. . 0 1. . 1 1. Câu 22. x − m m y + 2
Tìm tất cả các giá trị thực của tham số để hàm số = x + 1
nghịch biến trên các khoảng xác định của nó. A m ≤ B m < C m < − D m ≤ − . 1. . 1. . 3. . 3. Câu 23. mx m y + 1
Tìm tất cả các giá trị của tham số để hàm số = x m đồng biến + ∞ trên khoảng (2; + ). A − ≤ m < − m > B m ≤ − m > . 2 1 hoặc 1. . 1 hoặc 1. C − < m < D m < − m ≥ . 1 1. . 1 hoặc 1. Soạn: Huỳnh Phú Sĩ 10
Trường THCS-THPT Mỹ Thuận
§1. Sự đồng biến và nghịch biến của hàm số TOÁN 12 Câu 24. mx − m y 2 Số giá trị nguyên của để hàm số = − x m nghịch biến trên 2 + 1 ∞ khoảng ; + là 2 A B C D . 4. . 5. . 3. . 2. Câu 25. y ax3 bx2 cx d R Hàm số = + + + đồng biến trên khi   a b, c > a b c A = 0 B = = = 0 .  . .  . b2 − ac ≤
a > , b2 − ac < 3 0 0 3 0   a b , c > a b , c > C = = 0 0 D = = 0 0 .  . .  .
a > , b2 − ac ≤
a > , b2 − ac ≥ 0 3 0 0 3 0 Câu 26. y f x f 0 x x x − 2 x − Cho hàm số = ( ) có đạo hàm ( ) = ( 1) ( 2). Tìm khoảng y f x
nghịch biến của đồ thị hàm số = ( ). A −∞ B . ( ; 0) và (1; 2). . (0; 1). C D ∞ . (0; 2). . (2; + ). Câu 27. y f x y0 x2 x − Cho hàm số = ( ) có đạo hàm = (
2). Mệnh đề nào sau đây là đúng? A R .
Hàm số nghịch biến trên .
B. Hàm số đồng biến trên (0; 2). C −∞ ∞ .
Hàm số nghịch biến trên ( ; 0) và (2; + ). D ∞ .
Hàm số đồng biến trên (2; + ). Câu 28. y f x f 0 x x2 − x , ∀x ∈ R Cho hàm số = ( ) thỏa mãn ( ) = 5 + 4 . Khẳng định nào sau đây là đúng? A −∞ .
Hàm số đồng biến trên khoảng ( ; 3). B ∞ .
Hàm số nghịch biến trên khoảng (3; + ).
C. Hàm số nghịch biến trên khoảng (2; 3).
D. Hàm số đồng biến trên khoảng (1; 4). Câu 29. f x Cho hàm số (
) có bảng xét dấu của đạo hàm như sau: x −∞ ∞ 1 2 3 4 + y0 − − 0 + 0 + 0 0 + y f x − x3 x Hàm số = 3 ( + 2) + 3
đồng biến trên khoảng nào sau đây: A ∞ B −∞ − C − D . (1; + ). . ( ; 1). . ( 1; 0). . (0; 2). Câu 30. y f x Cho hàm số = ( ) có đồ thị hàm y y f 0 x y số = ( ) như hình vẽ. Hàm số = f − x (3 2
) nghịch biến trên khoảng nào sau đây: A − ∞ B . ( 1; + ). . (0; 2). C −∞ − D . ( ; 1). . (1; 3). x −2 0 2 5 L TỰ LUẬN
Câu 1 (SGK GT12). Xét sự đồng biến, nghịch biến của các hàm số: y x − x2 y x4 − x2 a) = 4 + 3 c) = 2 + 3 x y 1 x 3 + 1 3 x2 − x − y b) = + 3 7 2 d) = − x 3 1 Câu 2. x3 mx2 m y − x R Tìm để hàm số = + 2 + 2019 đồng biến trên . 3 2 Soạn: Huỳnh Phú Sĩ 11
Trường THCS-THPT Mỹ Thuận
§1. Sự đồng biến và nghịch biến của hàm số TOÁN 12 d Vocabulary function monotonic decreasing graph hàm số tính đơn điệu nghịch biến đồ thị domain increasing derivative variation chart tập xác định đồng biến đạo hàm bảng biến thiên Soạn: Huỳnh Phú Sĩ 12
Trường THCS-THPT Mỹ Thuận
§2. Cực trị của hàm số TOÁN 12
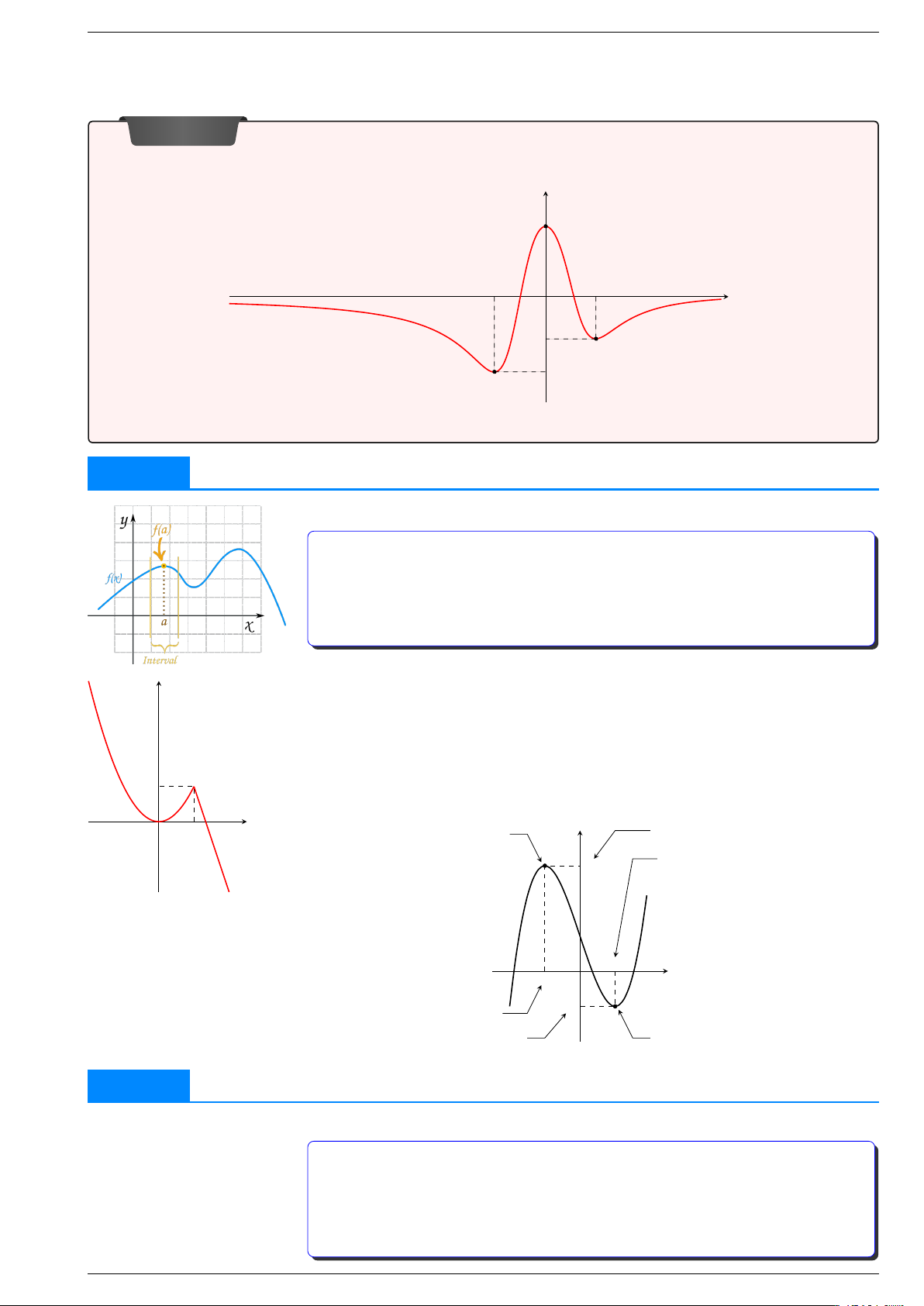
§2.CỰC TRỊ CỦA HÀM SỐ Đặt vấn đề y f x Cho hàm số = (
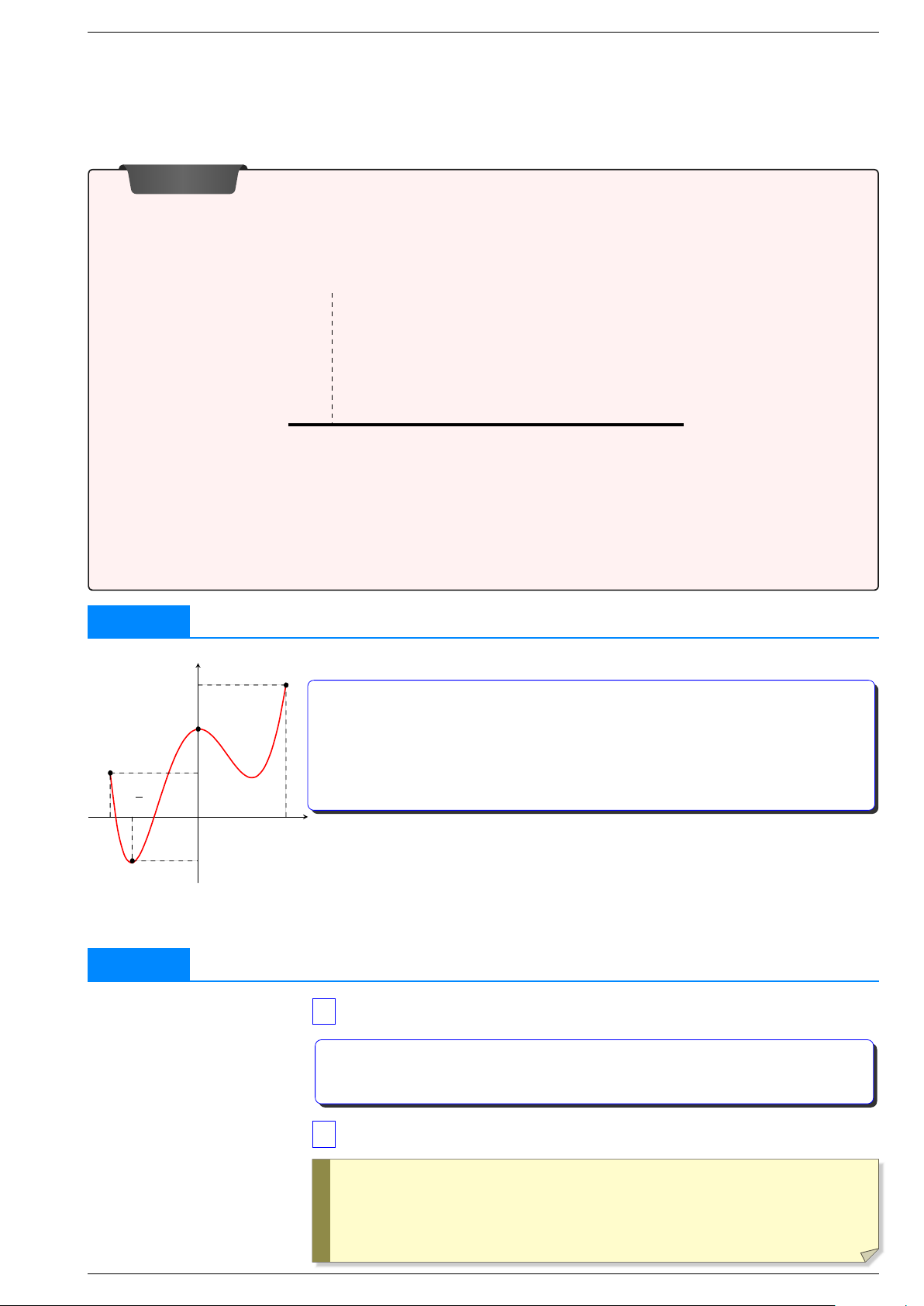
) có đồ thị như hình vẽ dưới đây. y B 2 x x x 1 2 O y2 C y A 1
Một cách trực quan, hãy chỉ ra những điểm lồi, điểm lõm của đồ thị. 1
KHÁI NIỆM CỰC ĐẠI, CỰC TIỂU y f x K x ∈ K Giả sử hàm số = (
) xác định và liên tục trên và điểm 0 . ○ ∃h > f x < f x x ∈ x − h x h x 6 x Nếu 0 sao cho ( ) ( 0 ) với mọi ( 0 ; 0 + ) và = 0 thì ta f x . . . . . . . . . . . . x nói ( ) đạt tại 0 . ○ ∃h > f x > f x x ∈ x − h x h x 6 x Nếu 0 sao cho ( ) ( 0 ) với mọi ( 0 ; 0 + ) và = 0 thì ta f x . . . . . . . . . . . . x nói ( ) đạt tại 0 . Chú ý: y f x x x . . . . . . . . . f x • Nếu ( ) đạt CĐ tại 0 thì ta gọi 0 là điểm CĐ của , ( 0 ) là giá trị CĐ của . . . . . . . . . M x f x . . . . . . . . . , còn điểm ( 0 ; ( 0 )) là điểm CĐ của
. Ta gọi tương tự đối với cực tiểu.
. . . . . . . . . . . . . . . •
Các điểm CĐ và CT được gọi chung là
, giá trị CĐ và giá trị CT được . . . . . . . . . gọi chung là của hàm số. 1 f x K x f 0 x . . . • Nếu ( ) xác định trên và đạt cực trị tại 0 thì ( 0 ) = . O x y A x y 1
Giá trị cực đại của hàm số Điểm cực đại ( 1 ; 1 ) của đồ thị y
Điểm cực tiểu của hàm số 1 x
Hàm số này đạt cực đại tại = . . . x . . . và đạt cực tiểu tại = x2 x1 O x y2
Điểm cực đại của hàm số B x y
Giá trị cực tiểu của hàm số Điểm cực tiểu ( 2 ; 2 ) của đồ thị 2
ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊ y f x . . . . . . . . . K K K \ {x } Giả sử hàm số = ( ) trên và xác định trên hoặc 0 . ○ f 0 x > x < x f 0 x < x > x x . . . . . . . . . Nếu ( 0 ) 0 khi 0 và ( 0 ) 0 khi 0 thì 0 là một điểm f x của hàm số ( ). ○ f 0 x < x < x f 0 x > x > x x . . . . . . . . . Nếu ( 0 ) 0 khi 0 và ( 0 ) 0 khi 0 thì 0 là một điểm f x của hàm số ( ). Soạn: Huỳnh Phú Sĩ 13
Trường THCS-THPT Mỹ Thuận
§2. Cực trị của hàm số TOÁN 12 Ví dụ 1. y
x3 − x2 − x
Tìm các cực trị của hàm số = + 3. 3 QUY TẮC TÌM CỰC TRỊ 1 Quy tắc 1
. . . . . . . . . . . . . . . . . . Bước 1. Tìm !
. . . . . . . . . . . . f 0 x x f 0 x . . . . . .
. . . . . . . . . . . . . . . . . . Bước 2. Tìm ( ). Tìm để ( ) hoặc
. . . . . . . . . . . . . . . Bước 3. Lập bảng Bước 4.
Kết luận về các điểm cực trị. Ví dụ 2. x y 3 + 1
Tìm cực trị của hàm số = x . + 1 2 Định lý y f x . . . K Giả sử hàm số = ( ) có đạo hàm cấp trên . ○ f 0 x f 00 x > x . . . . . . . . . Nếu ( 0 ) = 0 và ( 0 ) 0 thì 0 là điểm của hàm số. ○ f 0 x f 00 x < x . . . . . . . . . Nếu ( 0 ) = 0 và ( 0 ) 0 thì 0 là điểm của hàm số. Ví dụ 3. x4 y − x2
Tìm cực trị của hàm số = 2 + 6. 4 3 Quy tắc 2
. . . . . . . . . . . . . . . . . . Bước 1. Tìm !
. . . . . . . . . . . . f 0 x x f 0 x . . . Bước 2. Tìm ( ). Tìm để ( ) 0. . . . f 00 x Bước 3. Tìm đạo hàm cấp rồi tính các giá trị ( ). Bước 4.
Kết luận về các điểm cực trị. Soạn: Huỳnh Phú Sĩ 14
Trường THCS-THPT Mỹ Thuận
§2. Cực trị của hàm số TOÁN 12 Ví dụ 4. x3 y − m x2 mx − m Cho hàm số = ( + 1) + 2. Tìm
để hàm số đạt cực đại tại 3 x − = 1. 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. y f x − Cho hàm số = (
) xác định, liên tục trên đoạn [ 2; 2] y
và có đồ thị là đường cong trong hình bên. Hàm số đã cho 4
đạt cực tiểu tại điểm A x B x − . = 1. . = 2. C x D x − 2 . = 2. . = 1. x − − 2 10 1 2 Câu 2. y f x Cho hàm số = (
) có đồ thị như hình vẽ. Giá trị cực đại y của hàm số là A − B C − D . 2. . 0. . 1. . 1. −1 1 x −1 −2 Câu 3. y f x R Cho hàm số = ( ) liên tục trên và có đồ thị như y
hình vẽ. Đồ thị hàm số đã cho có bao nhiêu điểm cực 2 trị?A B C D . 4. . 5. . 2. . 3. x − O 1 1 Câu 4. y f x Cho hàm số = (
) có bảng biến thiên như hình. x −∞ ∞ 0 2 + y0 − − 0 + 0 ∞ + 5 y −∞ 1
Hàm số đạt cực tiểu tại điểm A x B x C x D x . = 1. . = 5. . = 2. . = 0. Soạn: Huỳnh Phú Sĩ 15
Trường THCS-THPT Mỹ Thuận
§2. Cực trị của hàm số TOÁN 12 Câu 5. y f x R Hàm số = ( ) liên tục trên
và có bảng biến thiên như hình vẽ. x −∞ ∞ 1 2 + y0 − + 0 + ∞ 3 + y −∞ 0
Mệnh đề nào sau đây là đúng? A f x B f x . ( ) có 2 điểm cực trị. . (
) có đúng 1 điểm cực trị. C f x D f x . (
) không có giá trị cực tiểu. . (
) không có giá trị cực đại. Câu 6. y f x Cho hàm số = (
) có bảng biến thiên như hình. x −∞ − ∞ 2 0 2 + y0 − − + 0 0 + 0 3 3 y −∞ −∞ 1
Giá trị cực đại của hàm số bằng A − B − C D . 2. . 1. . 2. . 3. Câu 7. y f x R Cho hàm số = (
) xác định, liên tục trên
và có bảng biến thiên như hình vẽ. x −∞ ∞ 1 2 + y0 − − + 0 2 y −∞ −∞
Khẳng định nào sau đây là đúng? A B .
Hàm số có giá trị cực đại bằng 1. .
Hàm số có đúng 2 cực trị. C D x .
Hàm số có giá trị cực đại bằng 2. .
Hàm số không xác định tại = 1. Câu 8. y f x Cho hàm số = (
) có bảng biến thiên như hình. x −∞ − ∞ 1 0 1 + y0 − − + 0 + 0 2 3 y −∞ − − 1 1 2 y f x Hỏi hàm số = (
) có bao nhiêu điểm cực trị? A B C D . 1. . 3. . 2. . 4. Câu 9. y f x Cho hàm số = (
) có bảng biến thiên như hình. x −∞ − ∞ 1 1 3 + y0 − − + 0 + ∞ ∞ + + 3 y −∞ − −∞ 1 y f x
Số điểm cực trị của hàm số = ( ) là A B C D . 0. . 2. . 3. . 1. Câu 10. y
x3 − x2 − x
Tìm điểm cực tiểu của hàm số = 3 9 + 2. A x B x C x D x − . = 25. . = 3. . = 7. . = 1. Câu 11. y x3 − x
Điểm cực tiểu của đồ thị hàm số = 3 + 5 là A M B N − C Q D P − . (1; 3). . ( 1; 7). . (3; 1). . (7; 1). Soạn: Huỳnh Phú Sĩ 16
Trường THCS-THPT Mỹ Thuận
§2. Cực trị của hàm số TOÁN 12 Câu 12. x3 y − x − Cho hàm số =
11. Giá trị cực tiểu của hàm số là 3 A B −1 C −5 D − . 2. . . . . . 1. 3 3 Câu 13. y
x4 − x2 −
Điểm cực đại của hàm số = 8 3 là A S − B x C x ± D y . (0; 3). . = 0. . = 2. . = 0. Câu 14. x y 2
Tìm điểm cực đại của đồ thị hàm số = + x . 2 A N − − B x − C M D x . ( 2; 2). . = 2. . (2; 2). . = 2. √ Câu 15. y x − x2 Cho hàm số = + 12 3
. Khẳng định nào sau đây đúng? A x − B x .
Hàm số đạt cực đại tại = 1. .
Hàm số đạt cực đại tại = 1. C x − D x .
Hàm số đạt cực tiểu tại = 1. .
Hàm số đạt cực tiểu tại = 1. Câu 16. y −x4 x2 Cho hàm số = + 2
+ 3 có giá trị cực đại và giá trị cực tiểu lần y , y y y lượt là 1 2 . Khi đó 1 + 2 bằng A B C D − . 7. . 1. . 3. . 1. Câu 17. y −x4 − x2 Đồ thị hàm số =
+ 3 có bao nhiêu điểm cực trị? A B C D . 2. . 3. . 1. . 0. Câu 18. y x3 Hàm số =
+ 3 có bao nhiêu điểm cực trị? A B C D . 3. . 0. . 1. . 2. Câu 19. − x y 2 + 1 Hàm số = x −
có bao nhiêu điểm cực trị? 3 A B C D . 1. . 0. . 3. . 2.
Câu 20. Đồ thị hàm số nào sau đây có ba điểm cực trị? A y x 2 4 − x2 B y x2 . = 2 4 + 3. . = + 2 . C y −x4 − x2 D y x3 − x2 x − . = 3 . . = 6 + 9 5.
Câu 21. Hàm số nào sau đây không có cực trị? A y x3 − x2 B y x4 . = 2 3 . . = + 2. C x y + 1 D y −x4 x2 . = x − . . = + 2 + 1. 2 Câu 22. y f x f 0 x x x − 2 x Cho hàm số = ( ) có đạo hàm ( ) = ( 1) ( + 1). Hỏi hàm số có
bao nhiêu điểm cực trị? A B C D . 1. . 3. . 2. . 0. Câu 23. f x f 0 x x −
x − 2 x − 3 x − 4 ∀x ∈ R Cho hàm số ( ) có đạo hàm ( ) = ( 1)( 2) ( 3) ( 4) , .
Số điểm cực trị của hàm số đã cho là A B C D . 3. . 5. . 2. . 4. Câu 24. f x f 0 x x
x2 − x x − ∀x ∈ R Cho hàm số ( ) có đạo hàm ( ) = ( + 1) ( 1), . Số
điểm cực trị của hàm số đã cho là A B C D . 1. . 3. . 2. . 0. Câu 25. y x3 − x A, B
Biết rằng đồ thị hàm số = 3
+ 1 có hai điểm cực trị . Khi AB đó đường thẳng có phương trình là A y x − B y x − C y −x D y − x . = 2 1. . = 2. . = + 2. . = 1 2 . Câu 26. m y x4 m− x2 −m
Tìm tất cả giá trị của tham số để đồ thị hàm số = +(6 4) +1 có 3 điểm cực trị. A m ≥ 2 B m ≤ 2 C m > 2 D m < 2 . . . . . . . . 3 3 3 3 Câu 27. m y x3 − x2 mx
Tìm tất cả các giá trị của tham số để hàm số = 3 + + 1 có 2 điểm cực trị. A m ≤ B m > C m > − D m < . 3. . 3. . 3. . 3. Câu 28. x3 m y − x2 m − x
Tập hợp các giá trị của tham số để hàm số = 6 + ( 2) + 11 3
có 2 điểm cực trị trái dấu. A −∞ B −∞ C −∞ D . ( ; 38). . ( ; 2). . ( ; 2]. . (2; 38). Câu 29. y x3 − m x m x Hàm số = ( + 2) + đạt cực tiểu tại = 1 khi A m − B m C m − D m . = 1. . = 2. . = 2. . = 1. Câu 30. m y x3 − mx2 m − x −
Với giá trị nào của tham số thì hàm số = + (2 3) 3 x đạt cực đại tại = 1? A m ≤ B m C m < D m > . 3. . = 3. . 3. . 3. Soạn: Huỳnh Phú Sĩ 17
Trường THCS-THPT Mỹ Thuận
§2. Cực trị của hàm số TOÁN 12 L TỰ LUẬN
Câu 1 (SGK GT12). Tìm các điểm cực trị của các hàm số sau y x3 x2 − x − y x4 − x2 a) = 2 + 3 36 10 b) = 2 + 1 Câu 2 (SGK GT12). x2 mx m y + + 1 x
Xác định giá trị của tham số để hàm số = x m đạt cực đại tại = 2. + d Vocabulary local maximum extrema interval sign cực đại cực trị khoảng dấu local minimum value closed interval parameter cực tiểu giá trị đoạn tham số Soạn: Huỳnh Phú Sĩ 18
Trường THCS-THPT Mỹ Thuận
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số TOÁN 12
§3.GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ Đặt vấn đề
Theo yêu cầu của vua Hùng, Sơn Tinh và Thủy Tinh phải đến nông trại của Bạch Cốt Tinh để mang voi chín ngà, gà
chín cựa, ngựa chín hồng mao và cùng xuất phát lúc 7h sáng đến chỗ của Mị Nương. Biết rằng chỗ ở của Bạch Cốt
Tinh là trong rừng rậm, cách đường quốc lộ 30 km và vị trí của Mị Nương được mô tả như hình: 30 km g A 50km Mị Nương
Sơn Tinh đi thẳng theo đường rừng đến chỗ Mị Nương, còn Thủy Tinh đi thẳng ra quốc lộ (điểm A), rồi theo đường
quốc lộ đến chỗ của Mị Nương. Biết rằng vận tốc tối đa khi di chuyển trong rừng rậm là 30 km/h, trên đường quốc lộ
là 50 km/h và đoạn quốc lộ trong hình là đường thẳng. a)
Giữa Sơn Tinh và Thủy Tinh, ai sẽ đến nơi trước? b)
Nếu cùng xuất phát như Sơn Tinh và Thủy Tinh, bạn sẽ chọn đường đi thế nào để đến trước họ? 1 ĐỊNH NGHĨA y y f x D D Cho hàm số = ( ) xác định trên tập . 3 ○ M f x D f x . . . M, ∀x ∈ D Số
được gọi là giá trị lớn nhất của ( ) trên nếu ( ) và C ∃x ∈ D f x . . . M M f x 0 sao cho ( 0 ) . Kí hiệu = max D ( ). A ○ m f x D f x . . . m, ∀x ∈ D Số
được gọi là giá trị nhỏ nhất của ( ) trên nếu ( ) và 1 ∃x ∈ D f x . . . m m f x 0 sao cho ( 0 ) . Kí hiệu = min ( ). − 3 D 2 O x 1 2 − B 1 Quan sát đồ thị ta thấy f x . . . f x . . . max − ( ) = , min − ( ) = [ 2;2] [ 2;2] 2
CÁCH TÌM GTLN & GTNN CỦA HÀM SỐ TRÊN MỘT ĐOẠN 1 Định lý . . . . . . . . . Mọi hàm số
trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó. 2 Quy tắc x ∈ a b f 0 x . . . . . . . . . . . . . . . . . .
! Bước 1. Tìm các giá trị ( ; ) để ( ) hoặc . . . . . . f x a, b x Bước 2. Tính của ( ) tại và tại các điểm
vừa tìm được ở bước 1. . . . . . . Bước 3. Tìm số nhất và số
nhất trong các số đã tính được ở bước 2. Soạn: Huỳnh Phú Sĩ 19
Trường THCS-THPT Mỹ Thuận
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số TOÁN 12 Ví dụ 1. y x3 − x2 x
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số = 6 + 9 + 2 trên − đoạn [ 1; 2]. Nhận xét y f 0 x . . . . . . . . . a b f x Nếu ( ) không trên [ ; ] thì (
) đạt GTLN và GTNN tại các đầu mút a b max của [ ; ]. Ví dụ 2. x y 2 + 1 Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số = x − trên 2 [2020; 2021]. min O x 1 4 f x (
) đồng biến trên đoạn [1; 4].
Ví dụ 3. Trong tình huống đã nêu ở đầu bài, hãy tìm ra đường đi sao cho thời gian đến
chỗ Mị Nương là ngắn nhất. 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. y f x − y Cho hàm số = ( ) liên tục trên đoạn [ 1; 3] và có M m
đồ thị như hình vẽ. Gọi và
lần lượt là giá trị lớn 3
nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn − M − m [ 1; 3]. Giá trị của bằng A B C D . 0. . 1. . 4. . 5. 1 2 − O x 1 3 −2 √ √ Câu 2. h i y f x − Cho hàm số = ( ) xác định trên đoạn 3; 5 và có bảng biến thiên
như hình vẽ. Khẳng định nào sau đây là đúng? √ √ x − − 3 1 1 5 y0 − + 0 0 + √ 1 2 5 y − 0 2 Soạn: Huỳnh Phú Sĩ 20
Trường THCS-THPT Mỹ Thuận
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số TOÁN 12 A f x B f x . min √ √ ( ) = 0. . max √ √ ( ) = 2. − − [ 3; 5] [ 3; 5] √ C f x D f x . max √ √ ( ) = 2 5. . min √ √ ( ) = 2. − − [ 3; 5] [ 3; 5] Câu 3. y f x
Cho bảng biến thiên của hàm số = (
) như hình. Tìm giá trị lớn nhất M m − và giá trị nhỏ nhất
của hàm số trên đoạn [ 2; 3]. x −∞ − ∞ 2 0 3 + ∞ 2 + y 1 −∞ −1 ( ( ( ( A M M M M = 3 B = 0 C = 2 D = 1 . m − . . m . . m − . . m − . = 2 = 3 = 1 = 1 Câu 4. y x3 − x
Giá trị nhỏ nhất của hàm số = 3 + 5 trên đoạn [2; 4] là A B C D . 3. . 7. . 5. . 0. Câu 5. y x3 − x −
Giá trị lớn nhất của hàm số = 3 + 4 trên đoạn [ 2; 2] là A B C D . 10. . 6. . 24. . 4. Câu 6. f x x3 x2 − x
Tìm giá trị lớn nhất của hàm số ( ) = 2 + 3 12 + 2 trên đoạn − [ 1; 2]. A f x B f x . max − ( ) = 10. . max − ( ) = 6. [ 1;2] [ 1;2] C f x D f x . max − ( ) = 11. . max − ( ) = 15. [ 1;2] [ 1;2] Câu 7. y x − x 2
Giá trị lớn nhất của hàm số = (5 2 ) trên đoạn [0; 3] là A 250 B C 250 D 125 . . . 0. . . . . 3 27 27 Câu 8. y x4 − x2
Giá trị lớn nhất của hàm số = 3 + 2 trên đoạn [0; 3] là A B C D . 57. . 55. . 56. . 54. Câu 9. y x4 − x2
Tìm giá trị lớn nhất của hàm số = 2 trên đoạn [0; 1]. A − B C D − . 1. . 0. . 1. . 2. Câu 10. x2 − x y 3
Giá trị lớn nhất của hàm số = x trên đoạn [0; 3] bằng + 1 A B C D . 3. . 2. . 0. . 1. Câu 11. y x 4
Tìm giá trị nhỏ nhất của hàm số =
+ 1 + x trên đoạn [1; 3]. A B 16 C D . 4. . . . 5. . 6. 3 √ Câu 12. y x2 − x Tìm giá trị lớn nhất của hàm số = 3 + 2 + 8 trên đoạn − [ 2; 2]. √ √ A B C D . 7. . 9. . 3 + 2 2. . 3 + 7. Câu 13. x − y 3 1
Tìm giá trị lớn nhất của hàm số = x − trên đoạn [0; 2]. 3 A −1 B − C D 1 . . . 5. . 5. . . 3 3 Câu 14. x y + 1
Tìm giá trị nhỏ nhất của hàm số = x − trên đoạn [2; 3]. 1 A − B C D . 3. . 3. . 2. . 4. Câu 15. m y x3 − x Giá trị nhỏ nhất của hàm số = 3 + 5 trên đoạn [2; 4] là A B C D . 0. . 5. . 7. . 3. √ √ Câu 16. T y x − − x Tìm tập giá trị của hàm số = 1 + 9 . √ √ A h i h i T B T C T D T . = [1; 9]. . = 0; 2 2 . . = (1; 9). . = 2 2; 4 . Câu 17. M m √ Gọi và
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y x − x2 M − m = 1 . Khi đó bằng A B C D . 1. . 2. . 4. . 3. Câu 18. y f x − Cho hàm số = ( ) liên tục trên [
3; 2] và có bảng biến thiên như sau: x − − 3 1 0 1 2 3 2 f x ( ) 2 0 1 Soạn: Huỳnh Phú Sĩ 21
Trường THCS-THPT Mỹ Thuận
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số TOÁN 12 M, m f x − Gọi
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của ( ) trên đoạn [ 1; 2]. M m Tính + . A B C D . 3. . 2. . 1. . 4. Câu 19. x y + 1 M, m Cho hàm số = x − . Gọi
lần lượt là giá trị lớn nhất, giá trị nhỏ 1 M − m
nhất của hàm số trên đoạn [0; 2]. Khi đó 4 2 bằng A B C D . 10. . 6. . 5. . 4. Câu 20. y x2 x − ∞
Giá trị nhỏ nhất của hàm số = + 2 + 5 trên nửa khoảng [ 4; + ) là A B − C D − . 13. . 17. . 4. . 9. Câu 21. m y x − 4 Tìm giá trị nhỏ nhất của hàm số = 1 + x − trên nửa khoảng 1 ∞ (1; + ). A m B m C m D m . = 5. . = 4. . = 2. . = 3. Câu 22. y x4 x2 − Hàm số = + 2 3
A. không có giá trị lớn nhất và giá trị nhỏ nhất. B. không có cực trị.
C. có giá trị nhỏ nhất.
D. có giá trị lớn nhất. Câu 23. f x −x4 − x2 R
Tìm giá trị lớn nhất của hàm số ( ) = 3 + 2020 trên . A f x B f x . max ( ) = 2020. . max ( ) = 2021. R R C f x D f x . max ( ) = 2019. . max ( ) = 2018. R R Câu 24. m y x4 − m −
Tìm tất cả các giá trị thực của tham số sao cho hàm số = 2( x2 m − 1) +
2 đồng biến trên khoảng (1; 3). A m ∈ −∞ − B m ∈ . ( ; 5). . [5; 2). C m ∈ ∞ D m ∈ −∞ . (2; + ). . ( ; 2]. Câu 25. A BC
Một ngọn hải đăng đặt tại vị trí cách bờ biển = 5 km. Trên bờ biển C B A
có một cái kho ở vị trí cách
7 km. Người gác hải đăng có thể chèo đò từ M C đến vị trí
trên bờ biển với vận tốc 4 km/h rồi đi bộ đến với vận tốc 6 km/h. M B C Vị trí của điểm phải cách
bao nhiêu km để người đó đến nhanh nhất? A B M C √ A B 14 + 5 5 . 0 km. . km. √ 12 C D . 2 5 km. . 7 km.
Câu 26. Một trang trại mỗi ngày thu hoạch được một tấn rau. Mỗi ngày, nếu bán
rau với giá 30000 đồng/kg thì hết sạch rau, nếu giá bán cứ tăng thêm 1000 đồng/kg
thì số rau thừa lại tăng thêm 20 kg. Số rau thừa này được thu mua làm thức ăn
chăn nuôi với giá 2000 đồng/kg. Hỏi số tiền bán rau nhiều nhất mà trang trại có
thể thu được mỗi ngày là bao nhiêu? A . . B . . . 32 420 000 đồng. . 32 400 000 đồng. C . . D . . . 34 400 000 đồng. . 34 240 000 đồng.
Câu 27. Một xưởng sản xuất cần làm 100 chiếc hộp inox bằng nhau, hình dạng
là hình hộp chữ nhật có đáy là hình vuông (không có nắp), với thể tích là 108 3 . 2
dm /hộp. Giá của inox là 47 000 đồng/dm . Hãy tính toán sao cho tổng chi phí sản
xuất 100 chiếc hộp là ít nhất, và số tiền tối thiểu đó là bao nhiêu (nếu chỉ tính số
inox vừa đủ để sản xuất 100 chiếc hộp, không có phần dư thừa, cắt bỏ)? A . . . B . . . 1 692 000 000 đồng. . 507 666 000 đồng. C . . . D . . . 1 015 200 000 đồng. . 235 800 000 đồng. Câu 28. S − t3 t2
Một chất điểm chuyển động theo phương trình = 2 + 18 + 1, trong t S đó tính bằng giây và
tính bằng mét. Mất bao lâu kể từ lúc xuất phát để chất
điểm đạt vận tốc lớn nhất? A B C D . 5 giây. . 6 giây. . 3 giây. . 1 giây. Soạn: Huỳnh Phú Sĩ 22
Trường THCS-THPT Mỹ Thuận
§3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số TOÁN 12 Câu 29. y f x |f x | Cho hàm số = (
) có đồ thị như hình vẽ. Tìm max − ( ) . [ 2;4] y 2 1 − − 2 1 O x 2 4 −1 −3 A |f | B C D . (0) . . 2. . 3. . 1. Câu 30. x, y x y Cho
là hai số không âm thỏa mãn +
= 2. Tìm giá trị nhỏ nhất x3 P x2 y2 − x của biểu thức = + + + 1. 3 A 17 B C 115 D 7 . . . 5. . . . . 3 3 3 L TỰ LUẬN
Câu 1 (SGK GT12). Tính giá trị lớn nhất, giá trị nhỏ nhất của các hàm số y x − x 3 − x2 − x − 2 a) = 3 9 + 35 trên [ 4; 4] y − − c) = − x trên [ 3; 2] 1 √ y x4 − x2 y − x − b) = 3 + 2 trên [0; 3] d) = 5 4 trên [ 1; 1]
Câu 2 (SGK GT12). Trong số các hình chữ nhật cùng có chu vi 16 cm, hãy tìm hình chữ nhật có diện tích lớn nhất. Câu 3 (SGK GT12). 2
Trong số các hình chữ nhật cùng có diện tích 48 m , hãy xác định hình chữ nhật có chu vi nhỏ nhất. d Vocabulary absolute maximum exist undefined giá trị lớn nhất tồn tại không xác định absolute minimum equation square giá trị nhỏ nhất phương trình hình vuông continuous root rectangle liên tục nghiệm hình chữ nhật Soạn: Huỳnh Phú Sĩ 23
Trường THCS-THPT Mỹ Thuận §4. Đường tiệm cận TOÁN 12 §4.ĐƯỜNG TIỆM CẬN Đặt vấn đề
Trong công viên xã Mỹ Thuận, người ta xây dựng một cầu trượt tựa vào một bức tường bê tông và được mô phỏng theo y 1 đồ thị hàm số
= x với mặt đất là trục hoành, bức tường là trục tung (như hình vẽ). y O x ∞
Để nghiệm thu công trình, người ta thả một quả bóng để nó di chuyển dọc theo cầu trượt về phía + . Hỏi: a)
Khi nào thì quả bóng sẽ chạm đất? b)
Phải đặt quả bóng cách mặt đất bao nhiêu để nó chạm vào mặt tường? 1 ĐƯỜNG TIỆM CẬN NGANG y f x Cho hàm số = (
) xác định trên một khoảng vô hạn. y y y f x Đường thẳng = 0
được gọi là tiệm cận ngang của đồ thị hàm số = ( ) nếu
. . . . . . trong các điều kiện sau được thỏa mãn: ○ f x . . . ○ f x . . . lim x→ ∞ ( ) = lim x→−∞ ( ) = + Ví dụ 1. x y 2 + 3
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số = x − . 5 2 ĐƯỜNG TIỆM CẬN ĐỨNG x x y f x Đường thẳng = 0
được gọi là tiệm cận đứng của đồ thị hàm số = ( ) nếu
. . . . . . trong các điều kiện sau được thỏa mãn: ○ f x . . . . . . ○ f x . . . . . . lim ( ) = lim ( ) = x→x+ x→x− 0 0 ○ f x . . . . . . ○ f x . . . . . . lim ( ) = lim ( ) = x→x+ x→x− 0 0 Ví dụ 2. x4 − y 12 √ Đồ thị hàm số = x
có bao nhiêu đường tiệm cận đứng? 2 − x x − ( 5 + 6) 1 Soạn: Huỳnh Phú Sĩ 24
Trường THCS-THPT Mỹ Thuận §4. Đường tiệm cận TOÁN 12 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. x − y 2 3
Đường tiệm cận ngang của đồ thị hàm số = x là + 4 A x − B y C x D y − 3 . = 4. . = 2. . = 4. . = . 4 Câu 2. x − y 3
Đường tiệm cận ngang của đồ thị hàm số = x − là 1 A y B y C x D y . = 5. . = 0. . = 1. . = 1. Câu 3. x f x 2 + 2
Tìm tiệm cận ngang của đồ thị hàm số ( ) = 1 + x − . 1 A x B y C y D y . = 1. . = 1. . = 2. . = 3. Câu 4. y Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số = − x 1 4 x − ? 2 1 A y B y 1 C y D y − . = 2. . = . . = 4. . = 2. 2 Câu 5. f x x3 x2 x Đồ thị hàm số ( ) = + 2 + 3
+ 2021 có bao nhiêu đường tiệm cận ngang? A B C D . 0. . 1. . 2. . 3.
Câu 6. Đồ thị của hàm số nào dưới đây có đường tiệm cận ngang? A x2 − y 3 1 B y
x4 − x2 − . = x . . = 2. + 1 C − x y 2 D y x3 − x2 x − . = x . . = + 3. Câu 7. y Đường thẳng
= 2 là tiệm cận ngang của đồ thị hàm số nào dưới đây? A x − x − x x − y 2 1 B y 4 1 C y + 1 D y 2 4 . = − x . . = x . . = x . . = x . 1 2 + 5 2 + 1 2 + 3 Câu 8. x − y 3 5
Đường tiệm cận đứng của đồ thị hàm số = x − là 2 A x B y C x D x 5 . = 2. . = 2. . = 3. . = . 3 Câu 9. − x y 7 2
Đường tiệm cận đứng của đồ thị hàm số = x − là 2 A x − B x C x − D x . = 3. . = 2. . = 2. . = 3. Câu 10. x
Đồ thị của hàm số nào sau đây nhận đường thẳng = 2 làm tiệm cận đứng? A x y 1 B y 5 . = x . . = − x . + 1 2 C y x − 1 D y 1 . = 2 + x . . = x . + 1 + 2 Câu 11. Đồ thị √
của hàm số nào dưới đây có tiệm cận đứng? A − x2 x2 − y 1 + 1 B y 1 . = . . = x − . 2019 1 C x2 x y D y . = x . . = . 2 x + 2018 + 12 Câu 12. x2 − x y 2 + 3 Đồ thị hàm số = x −
có tiệm cận đứng là đường thẳng 2 4 A y B x C x D x − . = 1. . = 1. . = 2. . = 1. Câu 13. x − y 2 3 Đồ thị hàm số = x −
có các đường tiệm cận đứng và tiệm cận ngang 1 lần lượt là A x y B x y . = 1 và = 2. . = 2 và = 1. C x y − D x − y . = 1 và = 3. . = 1 và = 2. Câu 14. x y + 1 √ Đồ thị hàm số = x −
có các đường tiệm cận đứng và tiệm cận 2 ngang lần lượt √ là A x y B x y . = 2 và = 1. . = 4 và = 1. C x y − 1 √ D x y . = 1 và = . . = 2 và = 1. 2 Câu 15. x y 4 + 4 Đồ thị hàm số = x
có tất cả bao nhiêu đường tiệm cận? 2 x + 2 + 1 A B C D . 2. . 0. . 1. . 3. Soạn: Huỳnh Phú Sĩ 25
Trường THCS-THPT Mỹ Thuận §4. Đường tiệm cận TOÁN 12 Câu 16. x2 − x y 3 + 2
Tìm số đường tiệm cận của đồ thị hàm số = x . 2 − 4 A B C D . 1. . 2. . 0. . 3. Câu 17. x y 5 + 5 m n Cho hàm số = x . Gọi là số tiệm cận đứng, là số tiệm cận 2 − 1 S m n
ngang của đồ thị hàm số đã cho. Tính = + . A S B S C S D S . = 2. . = 3. . = 1. . = 4. Câu 18. x y + 1 √ Đồ thị hàm số = x
có bao nhiêu đường tiệm cận? 2 − 1 A B C D . 3. . 1. . 2. . 0. √ Câu 19. x y + 1 Đồ thị hàm số = x
có bao nhiêu đường tiệm cận? 2 − 1 A B C D . 3. . 1. . 2. . 0. Câu 20. x2 x y + 2 + 3 √ Đồ thị hàm số = x
có bao nhiêu đường tiệm cận? 4 − x2 3 + 2 A B C D . 4. . 5. . 3. . 6.
Câu 21. Đồ thị hàm số nào dưới đây không có đường tiệm cận? A x y B y 1 . = x . . = 2 x . + 1 C x y x 2 + 1 4 − x2 D y . = 3 + 2. . = − x . 2 Câu 22. ax y + 1 x
Biết rằng đồ thị hàm số = bx −
có đường tiệm cận đứng là = 2 và 2 y a b
đường tiệm cận ngang là = 3. Tính giá trị của + . A a b B a b C a b D a b . + = 1. . + = 5. . + = 4. . + = 0. Câu 23. m − n − x y ( 2 3) + 5
Biết rằng đồ thị hàm số = x − m − n
nhận hai trục tọa độ làm S m2 n2 −
hai đường tiệm cận. Tính tổng = + 2. A S B S C S − D S . = 2. . = 0. . = 1. . = 1.
Câu 24. Đường cong trong hình dưới đây là đồ thị của hàm số nào? y 2 − O x 1 −1 A x − − x x x y 2 1 B y 1 2 C y 2 + 1 D y 2 + 1 . = x . . = x . . = x − . . = x . + 1 + 1 1 + 1
Câu 25. Đường cong trong hình sau là đồ thị của hàm số nào? y 1 O x 1 −1 A x y −x + 1 3 x B y . = + 3 + 1. . = x − . 1 C x − y 1 D y x3 − x − . = x . . = 3 1. + 1 Soạn: Huỳnh Phú Sĩ 26
Trường THCS-THPT Mỹ Thuận §4. Đường tiệm cận TOÁN 12 Câu 26. y f x Cho hàm số = (
) có bảng biến thiên như hình. x −∞ ∞ 1 + y0 − − 0 ∞ + 2 y −∞ 2
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình A x B y C x D y . = 2. . = 2. . = 1. . = 1. Câu 27. y f x Cho hàm số = (
) có bảng biến thiên như hình. x −∞ ∞ 0 1 + y0 − − + 0 ∞ + 2 y − −∞ − 1 2
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A B C D . 3. . 4. . 1. . 2. Câu 28. x − y 3 7
Tọa độ giao điểm của hai đường tiệm cận của đồ thị hàm số = x + 2 là A − B − C − D − . (2; 3). . ( 2; 3). . (3; 2). . ( 3; 2). Câu 29. x − y 2
Tìm giao điểm của hai đường tiệm cận của đồ thị hàm số = x . + 2 A M B N − C P − − D Q − . (2; 1). . ( 2; 2). . ( 2; 2). . ( 2; 1). Câu 30. x
Đồ thị hàm số nào dưới đây có tiệm cận đứng = 1 và đi qua điểm A(2; 5)? A − x x x x y 2 3 B y + 13 C y 2 + 1 D y + 1 . = − x . . = x . . = x − . . = x − . 1 + 1 1 1 L TỰ LUẬN
Câu 1 (SGK GT12). Tìm các tiệm cận của hàm số √ x − x x2 x x y 2 5 y + + 1 + 1 b) = y y √ a) = x − − x c) = d) = 2 − x − x x − 5 2 2 3 2 5 1 d Vocabulary asymptote distance line đường tiệm cận khoảng cách đường thẳng horizontal asymptote limit curve tiệm cận ngang giới hạn đường cong vertical asymptote infinity condition tiệm cận đứng vô cực điều kiện Soạn: Huỳnh Phú Sĩ 27
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12
§5.KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ Đặt vấn đề
Theo em, khảo sát một hàm số là làm những việc gì? ○␣ ○␣ ○␣ Tìm tập xác định Xét tính đơn điệu Tìm đường tiệm cận ○␣ ○␣ ○␣ Xét tính chẵn lẻ Tìm cực trị Tìm đạo hàm 1
SƠ ĐỒ KHẢO SÁT HÀM SỐ
. . . . . . . . . . . . . . . . . . Bước 1. Tìm . . . . . . . . . . . . ! Bước 2. Xét sự của hàm số
. . . . . . . . . . . . . . . Bước 3. Tìm (nếu có) . . . . . . . . . . . . Bước 4. Tìm các đường (nếu có) . . . . . . . . . Bước 5. Vẽ Ví dụ 1. y x − y − x − x2 Khảo sát các hàm số = 2 3 và = 6 . 2
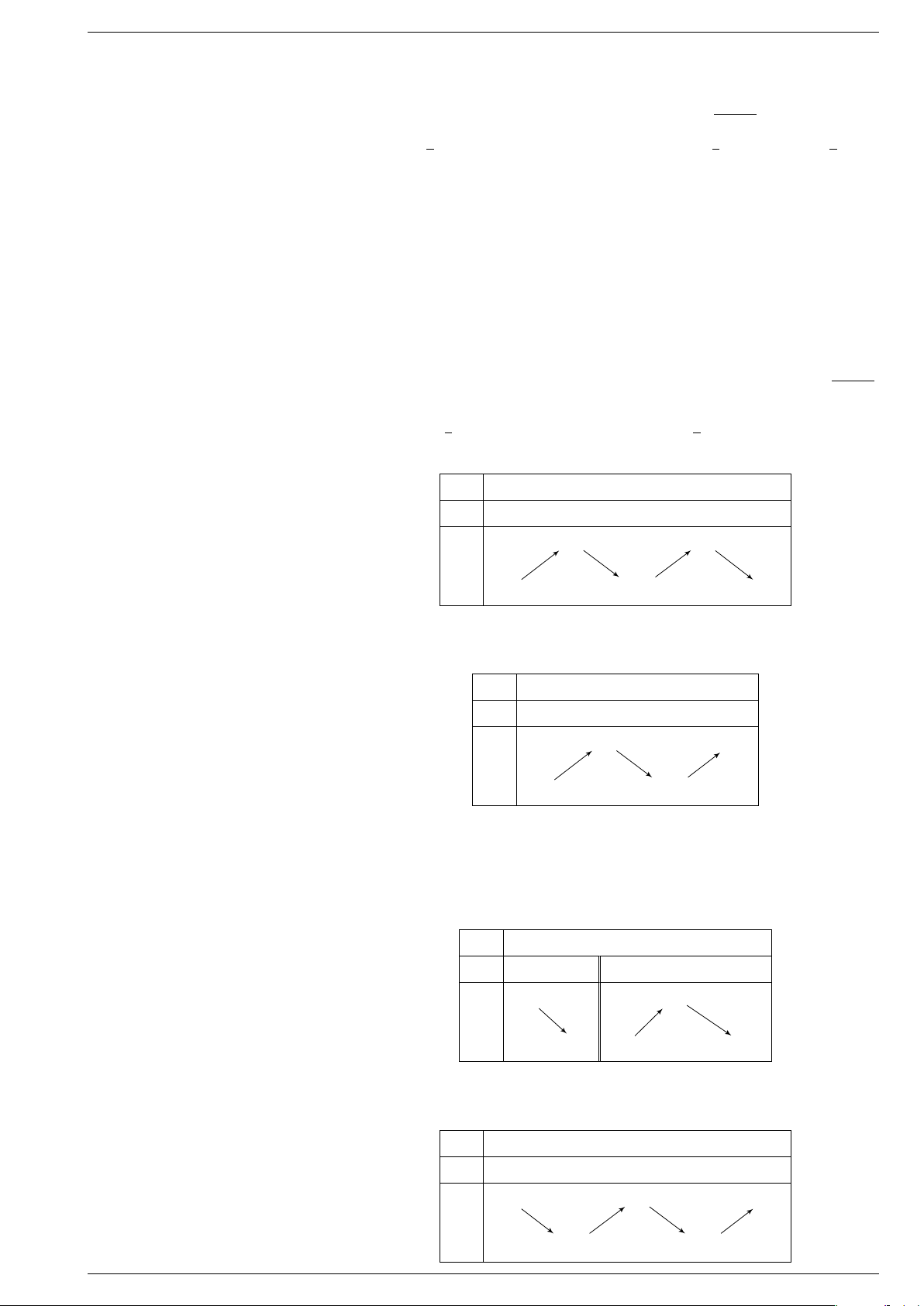
KHẢO SÁT MỘT SỐ HÀM THƯỜNG GẶP 1 Hàm số y ax3 bx2 cx d a 6 0 = + + + ( = ) D . . . • Tập xác định: = y0
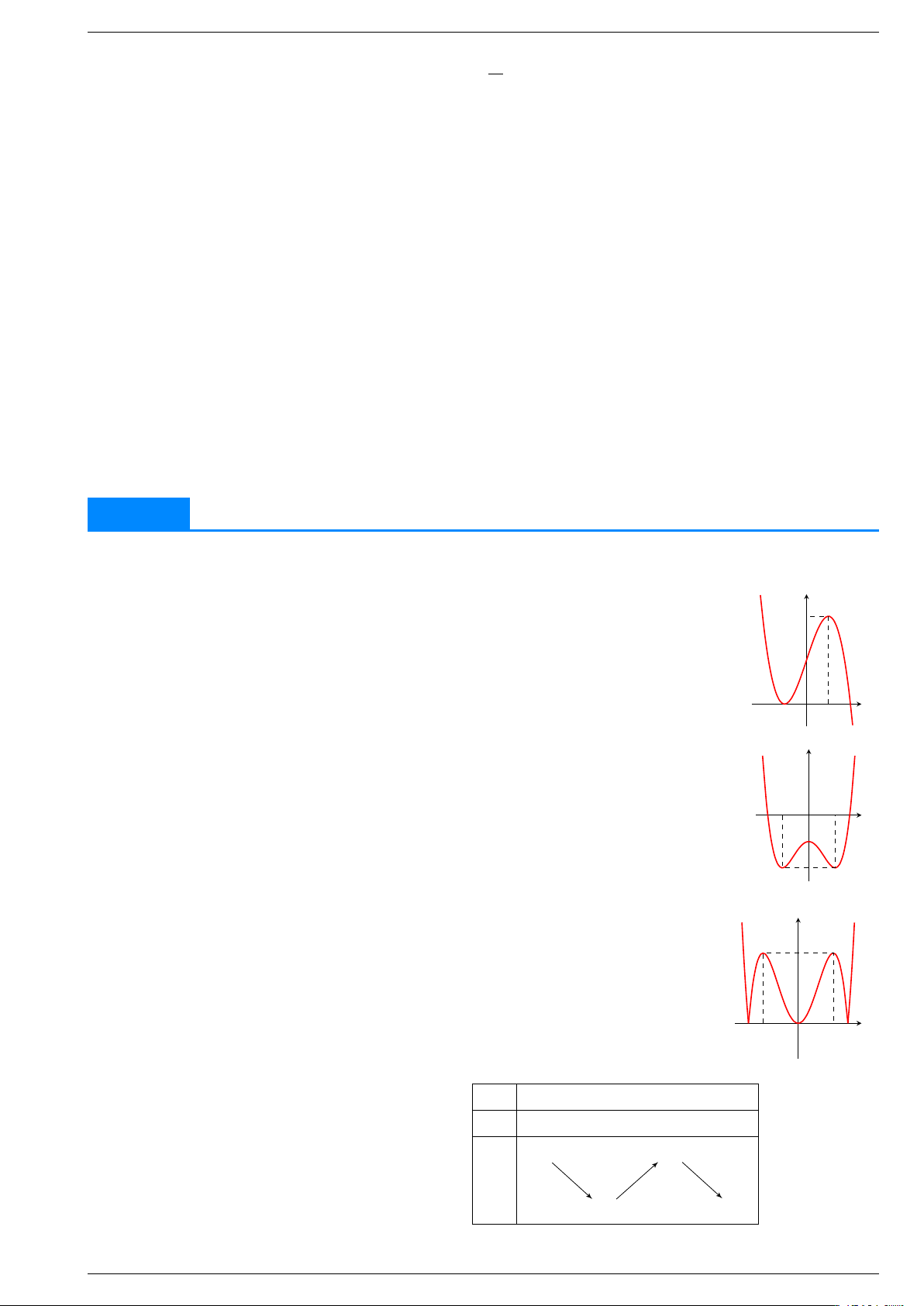
. . . . . . . . . . . . . . . • Đạo hàm: = b2 − ac . . . và a . . . b2 − ac . . . và a . . . 3 0 0 3 0 0 y y 3 O − 1 1 x − O x 1 1 −1 y x x3 x2 3 − x = 3 + 1 y − x = + + 2 3 2 Soạn: Huỳnh Phú Sĩ 28
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12 b2 − ac . . . và a . . . b2 − ac . . . và a . . . 3 0 0 3 0 0 y y 1 O x 2 1 O x x3 y − x 2 2 x y − x3 = + + = 2 3 3 b2 − ac . . . và a . . . b2 − ac . . . và a . . . 3 0 0 3 0 0 y y O x O x y x3 x2 x − y − x − x3 = + + 2 1 = 1 2 Hàm số y ax4 bx2 c a 6 0 = + + ( = ) D . . . • Tập xác định: = y0
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . • Đạo hàm: = =
a, b . . . . . . dấu và a . . .
a, b . . . . . . dấu và a . . . 0 0 y y O 1 x O x −3 y x4 x2 − y − x4 − x2 = + 2 3 = 2 + 1
a, b . . . . . . dấu và a . . .
a, b . . . . . . dấu và a . . . 0 0 y y √ √ 2 − O 2 2 x − O 1 1 x −1 1 −3 x4 y − x y −x4 x2 2 − = + 2 + 1 = 2 1 2 ax b 3 Hàm số y + c 6
0, ad − bc 6 0 = cx d ( = = ) + D d d . . . . . . . . . . . . • Tập xác định: = c • Tiệm cận đứng: c y0 . . . . . . . . . . . . . . . . . . • Đạo hàm: = • Tiệm cận ngang: Soạn: Huỳnh Phú Sĩ 29
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12 y0 . . . y0 . . . 0 0 y y 2 1 O x 1 − − O x 1 1 −1 x − x y 2 1 y + 1 = x = x − + 1 1 3
SỰ TƯƠNG GIAO CỦA CÁC ĐỒ THỊ y f x C y g x C Giả sử hàm số = ( ) có đồ thị ( 1 ) và hàm số = ( ) có đồ thị ( 2 ). y C C . . . . . . . . . . . .
Để tìm hoành độ giao điểm của ( 1 ) và ( 2 ), ta giải phương trình 2 Ví dụ 2. y x − y x2 − x −
Tìm tọa độ giao điểm của đường thẳng = 1 và parabol = 1 1 − O x 1 1 2 −1 y Ví dụ 3. y f x m Cho hàm số = (
) có đồ thị như hình bên. Biện luận theo tham số số f x m nghiệm của phương trình ( ) = . 1 O x − 8 5 −4 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. y
Đồ thị trong hình vẽ bên là của hàm số A x4 x2 x4 y − − B y − x − O 2 − 2 2 . = 1. . = 1. − x 4 2 4 1 C x4 x4 y − x2 − D y − x2 − . = 2 1. . = + 1. 4 4 −5 Câu 2. y
Đồ thị trong hình vẽ bên là của hàm số A y −x2 x − B y
x4 − x2 − . = + 4. . = 3 4. C y −x3 x2 D y −x4 x2 . = + 2 + 4. . = + 3 + 4. 4 − O 2 2 x Soạn: Huỳnh Phú Sĩ 30
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12 Câu 3. y
Đồ thị trong hình vẽ bên là của hàm số 1 A x3 y − x2 B y x3 x2 . = + + 1. . = + 3 + 1. −1 2 4 C y −x3 x2 D y x3 − x2 O x . = + 3 + 1. . = 3 + 1. −3 Câu 4. y
Đường cong như hình bên là đồ thị của hàm số nào dưới đây? A − y x 1 3 − x − B y −x3 x . = 3 2. . = + 3 + 2. C y x − O x 3 − x D y −x3 x − 1 1 . = 3 + 2. . = + 3 2. −2 −4 Câu 5. y
Đồ thị trong hình vẽ bên là của hàm số A y x3 B y x3 x . = 2 + 1. . = + + 1. C y x3 D y −x3 x . = + 1. . = + 2 + 1. 2 1 −1 O x 1 Câu 6. y f x Hàm số = (
) có đồ thị như hình vẽ là hàm y số nào sau đây? A x x − y 2 + 1 B y 2 1 . = x − . . = x − . 1 1 C x − x y 2 1 D y 3 + 1 . = x . . = x . 2 + 1 2 + 2 − O 1 x −1 Câu 7.
Đồ thị như hình bên là của hàm số nào y sau đây? A x x y 2 + 1 B y + 2 . = x − . . = x − . 1 2 C x x − y + 2 D y 1 . = x . . = x . + 1 + 1 1 − O x 2 2 −1 Câu 8. y ax4 bx2 c
Đồ thị nào sau đây không thể là đồ thị hàm số = + + với a, b, c a 6 là các số thực và = 0? y y y y O x O x O x O x Hình 1 Hình 2 Hình 3 Hình 4 Soạn: Huỳnh Phú Sĩ 31
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12 A B C D . Hình 1. . Hình 2. . Hình 3. . Hình 4. Câu 9. y −x3 − x2 Đồ thị hàm số = 3 + 2 là hình nào sau đây? y y y y O x O x O O x x Hình 1 Hình 2 Hình 3 Hình 4 A B C D . Hình 1. . Hình 2. . Hình 3. . Hình 4. Câu 10. x y + 1 Đồ thị hàm số =
− x là hình nào sau đây? 1 y y y y O O x x O O x x Hình 1 Hình 2 Hình 3 Hình 4 A B C D . Hình 1. . Hình 2. . Hình 3. . Hình 4. Câu 11.
Bảng biến thiên trong hình bên là của hàm x −∞ ∞ 1 3 + số nào sau đây? A y0 − y x + 0 0 + 3 − x2 x . = 5 + + 6. B y x ∞ 3 − x2 x − 3 + . = 6 + 9 1. C y y −x3 x2 − x . = + 6 9 + 7. D y x −∞ − 4 x2 − 1 . = + 3. Câu 12. y
Đồ thị như hình bên là của hàm số nào sau đây? A y x4 − x2 . = 2 + 2. B y x 2 2 − . = 2 1 . C y |x|3 − |x| . = 3 + 2. D 2 y x2 − |x|2 . = 2 + 2. O x −1 1 Câu 13. y f x R y Cho hàm số = ( ) liên tục trên và có đồ thị y |f |x| | 3
như hình vẽ. Hỏi đồ thị hàm số = ( ) có
tất cả bao nhiêu điểm cực trị? A B C D . 9. . 7. . 6. . 8. 1 −2 1 − O x 1 2 −1 Câu 14. y x − x 2 − x C Cho hàm số = ( 2) 5 + 6 có đồ thị ( ). Mệnh đề nào sau đây là đúng? A C B C . ( ) không cắt trục hoành. . (
) cắt trục hoành tại 3 điểm. C C D C . (
) cắt trục hoành tại 1 điểm. . (
) cắt trục hoành tại 2 điểm. Câu 15. y − x3 − x2
Số giao điểm của đồ thị hàm số = 2 3 + 1 với trục hoành là A B C D . 1. . 0. . 3. . 2. Soạn: Huỳnh Phú Sĩ 32
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12 Câu 16. y x4 − x2
Số giao điểm của đồ thị hàm số = 5 + 4 với trục hoành là A B C D . 3. . 2. . 4. . 1. Câu 17. x − M y 2 1 Tìm tọa độ giao điểm của đồ thị hàm số = x với trục tung. + 2 A M 1 B M C M − 1 D M −1 . ; 0 . . (0; 2). . 0; . . ; 0 . 2 2 2 Câu 18. y −x3 x2 x − y x2 − x −
Đồ thị của hai hàm số = + 3 + 2 1 và = 3 2 1 có
tất cả bao nhiêu điểm chung? A B C D . 1. . 2. . 0. . 3. Câu 19. y x3 − x2 x
Số giao điểm của đường cong = 2 + 2 + 1 và đường thẳng y − x = 1 bằng A B C D . 0. . 2. . 1. . 3. Câu 20. M N y x4 − x2 Gọi và
là giao điểm của đồ thị hai hàm số = 2 + 2 và y − x2 I MN = 4 . Tọa độ trung điểm của đoạn thẳng là A B C D . (1; 0). . (0; 2). . (2; 0). . (0; 1). Câu 21. x M N y x y 2 + 4 Gọi và
là giao điểm của đồ thị hai hàm số = + 1 và = x − . 1 I MN
Tìm hoành độ trung điểm của đoạn thẳng . A x − 5 B x C x 5 D x . I = . . I = 2. . I = . . I = 1. 2 2 Câu 22. y f x R Cho hàm số = ( ) liên tục trên
và có bảng biến thiên như sau: x −∞ − ∞ 1 0 1 + y0 − − + 0 0 + 0 3 3 y −∞ − −∞ 1 f x y Đồ thị của ( ) cắt đường thẳng
= 2021 tại bao nhiêu điểm? A B C D . 2. . 1. . 0. . 4. Câu 23. y f x R Cho hàm số = ( ) liên tục trên
và có bảng biến thiên như sau: x −∞ − ∞ 2 0 + y0 − + 0 0 + ∞ 2 + y −∞ −2 m f x m
Tập hợp các giá trị thực của tham số để phương trình ( ) = có đúng một nghiệm là A −∞ − ∪ ∞ B −∞ − ∪ ∞ . ( ; 2) (2; + ). . ( ; 2] [2; + ). C − D − . ( 2; 2). . [ 2; 2]. Câu 24. y f x R \ { } Cho hàm số = ( ) xác định trên 0
, liên tục trên từng khoảng
xác định và có bảng biến thiên như hình. x −∞ ∞ 0 1 + y0 − − + 0 ∞ + 2 y − −∞ −∞ 1 f x m m ∈ − Phương trình ( ) = với ( 1; 2) có bao nhiêu nghiệm? A B C D . 3. . 1. . 0. . 2. Câu 25. y f x R Cho hàm số = ( ) liên tục trên
và có bảng biến thiên như sau: x −∞ − ∞ 1 0 1 + y0 − − 0 + 0 0 + ∞ ∞ + 0 + y − − 1 1 Soạn: Huỳnh Phú Sĩ 33
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12 m f x − m
Tìm tất cả các giá trị thực của tham số để phương trình ( ) 1 = có đúng 2 nghiệm. A − < m < − B m − m ≥ − . 2 1. . = 2 hoặc 1. C m − m > D m − m > − . = 1 hoặc 0. . = 2 hoặc 1. Câu 26. m x3 − x m −
Tìm các giá trị của tham số để phương trình 12 + 2 = 0 có 3 nghiệm phân biệt. A m ∈ − B m ∈ − . [ 14; 18]. . ( 14; 18).  m < − C m ∈ − D 14 . ( 18; 14). .  . m > 18 Câu 27. x m y x − m y 2 + 1 Tìm để đường thẳng = cắt đồ thị hàm số = x tại 2 + 1 điểm phân biệt. A m < − B m > − . 1. . 5. C m < − m > − D − < m < − . 5 hoặc 1. . 5 1. Câu 28. y
x3 − x2 − x
Phương trình tiếp tuyến của đồ thị hàm số = 3 + 3 tại điểm M(1; 0) là A y − x B y − x − C y − x D y − x . = 1 . . = 4 4. . = 4 + 4. . = 1 4 . Câu 29. x − y 3 1
Đường thẳng nào sau đây là tiếp tuyến của đồ thị hàm số = x tại + 2 −
điểm có hoành độ bằng 1? A y x B y x C y − x D y x . = 6 + 1. . = 5 + 1. . = 4 . . = 7 + 3. Câu 30. C x − y 1 Trên đồ thị ( ) :
= x − , có bao nhiêu điểm mà tiếp tuyến tại đó với 2 C x y (
) song song với đường thẳng + = 1? A B C D . 2. . 4. . 1. . 0. L TỰ LUẬN
Câu 1 (SGK GT12). Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: y x − x x 3 y −x4 x2 − + 3 a) = 2 + 3 e) = + 8 1 y i) = x − 1 y x y x4 − x2 3 x2 x f) = 2 + 2 b) = + 4 + 4 − x 1 2 x y 4 j) = y x x − 3 x2 x y x2 − 3 2 4 c) = + + 9 g) = + 2 2 −x y − x y + 2 3 y − x2 − x4 d) = 2 + 5 h) = 2 + 3 k) = x 2 + 1
Câu 2. Tìm giao điểm của các đồ thị hàm số sau với trục hoành. y x3 − x2 y − x3 x2 − y −x4 x2 a) = 3 + 5 b) = 2 + 3 2 c) = + 2 + 1 Câu 3 (SGK GT12). y x3 m x2 − m m C Cho hàm số = + ( + 3) + 1 (
là tham số) có đồ thị là m ( ). m x − a) Xác định
để hàm số có điểm cực đại là = 1 m C x − b) Xác định để đồ thị m ( ) cắt trục hoành tại = 2. Câu 4 (SGK GT12). C f x −x3 x2 x a)
Khảo sát sự biến thiên và vẽ đồ thị ( ) của hàm số ( ) = + 3 + 9 + 2. f 0 x − > b) Giải bất phương trình ( 1) 0 C x f 00 x − c)
Viết phương trình tiếp tuyến của đồ thị (
) tại điểm có hoành độ 0 , biết rằng ( 0 ) = 6. Soạn: Huỳnh Phú Sĩ 34
Trường THCS-THPT Mỹ Thuận
§5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số TOÁN 12 d Vocabulary even function cubic function hàm số chẵn hàm số bậc 3 odd function biquadratic function hàm số lẻ hàm số trùng phương constant function linear rational function hàm hằng hàm phân tuyến tính linear function tangent line hàm số tuyến tính tiếp tuyến quadratic function absolute value hàm số bậc 2 giá trị tuyệt đối Soạn: Huỳnh Phú Sĩ 35
Trường THCS-THPT Mỹ Thuận
Chương 2. Hàm số lũy thừa.
Hàm số mũ và hàm số logarit TOÁN 12 Chương 2.
HÀM SỐ LŨY THỪA. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT §1.LŨY THỪA 1 KHÁI NIỆM LŨY THỪA
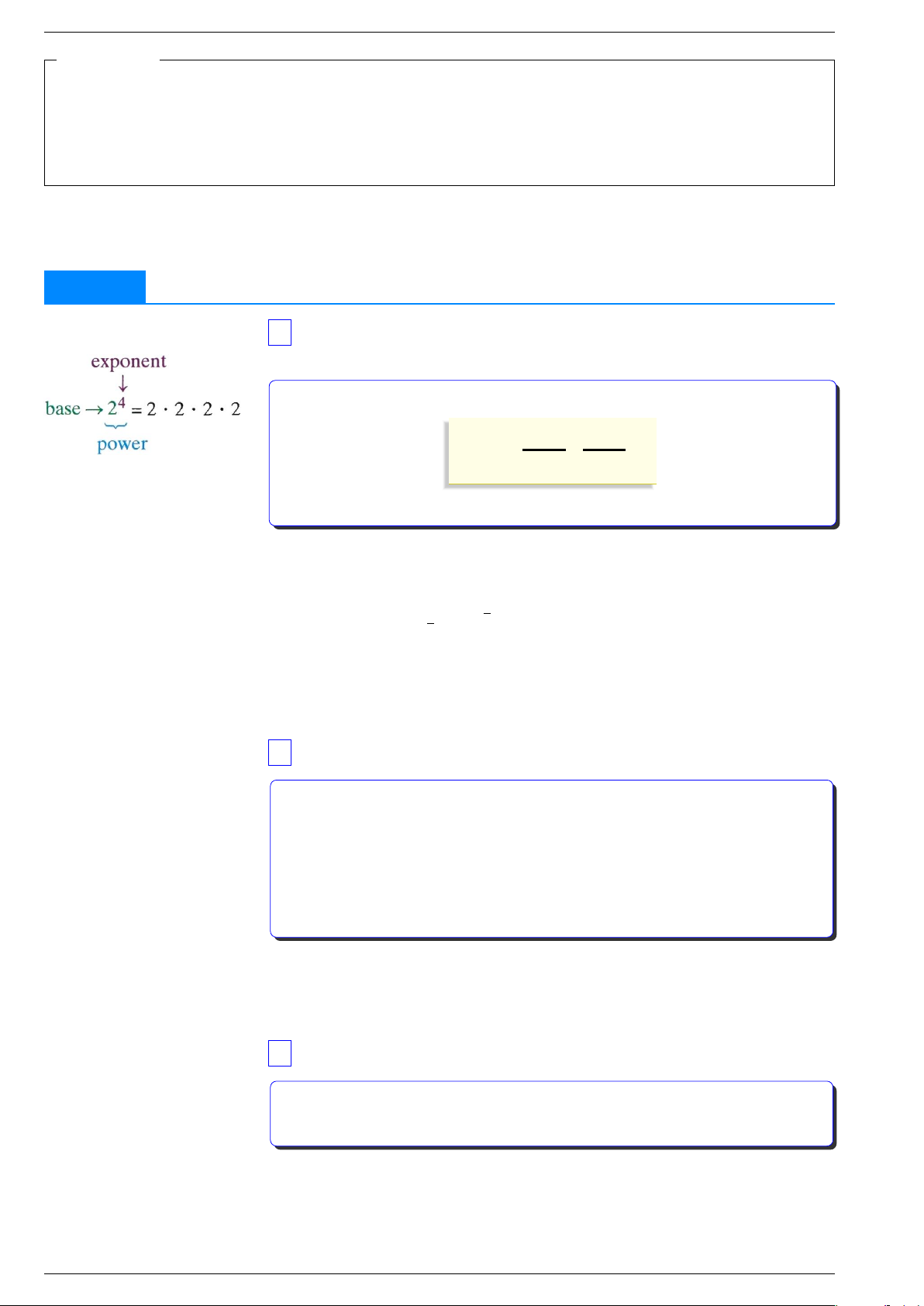
1 Lũy thừa với số mũ nguyên n ∈ ∗ N a ∈ R Cho , . n a . . . . . . . . . a Lũy thừa bậc của là của thừa số . an
a · a · a · · · a · a = | {z } n số a a . . . . . . . . . n . . . . . . . . . Số gọi là , số gọi là Chú ý: a 6 Với = 0 ta có a0 . . . a−n . . . . . . • = • = 3 Ví dụ 1. √ − , 4 − 2 Tính (1 5) , , 3 5. 3 2 Phương trình xn b = ○ n
. . . . . . . . . . . . . . . b Với lẻ: phương trình có với mọi . ○ n Với chẵn: – b . . . . . .
phương trình vô nghiệm nếu – . . . . . . . . . b . . . . . . phương trình có 1 nghiệm nếu – . . . . . . . . . b . . . . . . phương trình có 2 nghiệm nếu
Ví dụ 2. Phương trình nào dưới đây có nghiệm duy nhất khác 0? A x5 B x6 C x6 D x5 . = 0. . = 0. . = 1. . = 1. 3 Căn bậc n b ∈ ∗ R n ∈ N n ≥ Cho số và số ( 2). an b a . . . . . . . . . . . . b Nếu = thì được gọi là của . ○ n
. . . . . . . . . . . . . . . n b Với lẻ: có căn bậc của ○ n Với chẵn: – b <
. . . . . . . . . . . . . . . Nếu 0 thì – b
. . . . . . . . . . . . . . . Nếu = 0 thì – b >
. . . . . . . . . . . . . . . Nếu 0 thì Soạn: Huỳnh Phú Sĩ 36
Trường THCS-THPT Mỹ Thuận §1. Lũy thừa TOÁN 12 √ √ √ n a · n b . . . . . . n am . . . . . . ! • = • = √ ( n √ a a n . . . . . . n nếu √ . . . . . . an • = • n b = |a| n . . . . . . nếu √ √ √ Ví dụ 3. a > A
a3 · 3 a4 · 4 a5 Cho số 0. Rút gọn biểu thức = .
4 Lũy thừa với số mũ hữu tỉ m a > r
m ∈ Z n ∈ N, n ≥ Cho số thực 0 và số hữu tỉ = n ( , 2). Khi đó m ar a n . . . . . . = = √ Ví dụ 4. p 5 x P 3 x2 x P Cho là số thực dương và = . Biết rằng được biểu diễn dưới m m x n m, n ∈ ∗ N m n dạng , trong đó
n là phân số tối giản và . Tính + .
5 Lũy thừa với số mũ vô tỉ a > α r r α Cho số thực 0 và số vô tỉ
. Khi đó, luôn có một dãy số hữu tỉ n n ( ) sao cho lim = và aα arn . . . . . . = lim = 2
TÍNH CHẤT CỦA LŨY THỪA VỚI SỐ MŨ THỰC a, b > m, n Cho 0 là những số thực;
là những số thực tùy ý. am · an . . . . . . ab m . . . . . . • = • ( ) = ! am ...... • an = a m am n . . . . . . . . . . . . • • = ( ) = b   4 − 1 2 a a a 3  3 + 3  Ví dụ 5. F Rút gọn biểu thức =   1 3 − 1 a a a 4  4 + 4  Soạn: Huỳnh Phú Sĩ 37
Trường THCS-THPT Mỹ Thuận §1. Lũy thừa TOÁN 12 ○ a >
am > an ⇔ m . . . n Với 1: ○ a <
am > an ⇔ m . . . n Với 1:
Ví dụ 6. So sánh các cặp số sau: √ √ √ √ !− !− 7 8 2020 2021 − − a) 3 1 và 3 1 2 2 b) và 2 2 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. a m, n ∈ R Cho số dương và
. Mệnh đề nào sau đây đúng? A am · an am−n B am · an am n . = . . = ( ) . C am · an am n + D am · an am·n . = . . = . Câu 2. a m, n ∈ R Cho số thực dương và hai số
. Mệnh đề nào sau đây đúng? A am am n n n + am B am+ . = ( ) . . = an . C am n n + am · an D am+ am n . = . . = + . Câu 3. α sai Với
là một số thực bất kỳ, mệnh đề nào sau đây ? √ α √ A √ α α B α . 10 = 10 2 . . 10 = 10 . C α α α α2 2 D 2 . (10 ) = 100 . . (10 ) = 10 . √ √ 2018 2017 · − Câu 4. 4 + 2 3 1 3 P
Tính giá trị của biểu thức = √ . 2019 1 + 3 A P − 2017 B P − C P − 2019 D P 2018 . = 2 . . = 1. . = 2 . . = 2 . x− Câu 5. x 1 − 1 2 P − · Cho biết 9 12
= 0, tính giá trị của biểu thức = −x− 8 9 2 +19. 1 3 A B C D . 31. . 23. . 22. . 15. √ Câu 6. a a2 · 3 a Cho
là số thực dương. Biểu thức
được viết dưới dạng lũy thừa với số mũ hữu tỉ là A 4 7 5 2 a B a C a D a . 3 . . 3 . . 3 . . 3 . Câu 7. F Kết quả viết dưới dạng lũy thừa với số mũ hữu tỉ của biểu thức = r q √ p a a a a a > với 0 là 11 a 16 A 1 3 1 3 F a B F a C F a D F a . = 4 . . = 8 . . = 2 . . = 4 . √ √ 7+3 a − 7 3 Câu 8. a P √ √ Cho
là một số thực dương. Rút gọn biểu thức = a − − . 11 4 · a5 11 √ A P 1 B P a − 3 C P a2 D P a2 7 1 . = a . . = . . = . . = . 3 √ 11 3 m Câu 9. a7 · a A 3 √ a > A a n Rút gọn biểu thức = a với 0 ta được kết quả = trong 4 · 7 a−5 m m, n ∈ ∗ N đó và
n là phân số tối giản. Khẳng định nào sau đây đúng? A m2 − n2 B m2 n2 . = 312. . + = 543. C m2 − n2 − D m2 n2 . = 312. . + = 409. √ Câu 10. 2 a a a Cho
là một số dương, biểu thức 3
dưới dạng lũy thừa với số mũ hữu tỉ là A 4 5 7 6 a B a C a D a . 3 . . 6 . . 6 . . 7 . Soạn: Huỳnh Phú Sĩ 38
Trường THCS-THPT Mỹ Thuận §1. Lũy thừa TOÁN 12 r q √ Câu 11. p a > x 3
a 3 a 3 a 3 a ax Cho 0. Tìm biết = . A x 4 B x 1 C x 40 D x 13 . = . . = . . = . . = . 9 81 81 27 √ √ − Câu 12. a 3+1 · a2 3 P √ a > Rút gọn biểu thức = với 0. √ 2+2 a − 2 2 A P a B P a3 C P a4 D P a5 . = . . = . . = . . = . 4 4 Câu 13. a b ab a, b P 3 + 3 √ √ Cho
là các số thực dương. Rút gọn = 3 3 a b ta được + A P ab B P a b . = . . = + . C P a4b ab4 D P a2b ab2 . = + . . = + . √ Câu 14. 1 P x · 8 x x > Rút gọn biểu thức = 2 với 0. A 5 5 1 P x B P x C P x D P x4 . = 16 . . = 8 . . = 16 . . = . √ Câu 15. 2 a a · a Cho
là số thực dương. Biểu thức 3
viết dưới dạng lũy thừa với số mũ hữu tỉ là A 1 7 11 6 a B a C a D a . 3 . . 6 . . 6 . . 5 . √ √ 3+1 a − 3 1 Câu 16. P √ √ < a 6 Rút gọn biểu thức = a − − (0 = 1). 4 5 · a 5 2 A P B P a2 C P D P a . = 2. . = . . = 1. . = . Câu 17. sai Phát biểu nào sau đây ? 2 A 1 3 > 2 B , 3 > . e e . . (0 5) . 2 C √ √ π π 2 3 2 3 < D < . 3 3 . . . 2 2 Câu 18. 1 1 2 3 a, b > a > a b > b Cho 0 thỏa mãn 2 3 và 3
4 . Khi đó khẳng định nào đúng? A < a < , < b < B < a < , b > . 0 1 0 1. . 0 1 1. C a > , < b < D a > , b > . 1 0 1. . 1 1. Câu 19. √ m √ n − < − Cho 2 1 2 1 . Khi đó A m n B m < n C m > n D m 6 n . = . . . . . . = . Câu 20. x −
− 1 > x − − 1 Cho biết ( 2) 3 ( 2)
6 , khẳng định nào sau đây đúng? A < x < B < x < C x > D x > . 2 3. . 0 1. . 2. . 1. L TỰ LUẬN Câu 1 (SGK GT12). a, b Cho
là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ: √ √ √ √ 1 1 1 4 1 a · a b · b · 6 b a 3 3 a b b a) 3 b) 2 3 c) 3 : d) : 6 d Vocabulary power base integer irrational lũy thừa cơ số số nguyên số vô tỉ factor exponent rational real thừa số số mũ số hữu tỉ số thực Soạn: Huỳnh Phú Sĩ 39
Trường THCS-THPT Mỹ Thuận §2. Hàm số lũy thừa TOÁN 12 §2.HÀM SỐ LŨY THỪA 1 KHÁI NIỆM α Cho số thực . y . . . . . . Hàm số =
được gọi là hàm số lũy thừa. Chú ý: xα . . .
Tập xác định của hàm số lũy thừa
tùy thuộc vào giá trị của ○ α ∈ Z+ . . . . . . . . . Nếu : tập xác định là ○ α ∈ − Z . . . . . . . . . Nếu : tập xác định là ○ α / ∈ Z . . . . . . . . . Nếu : tập xác định là
Ví dụ 1. Tìm tập xác định của các hàm số sau: √ y x − − 3 y x − 3 1 y 3 x − a) = (2 1) b) = (2 1) y x − d) = 2 1 c) = (2 1) 3 2
ĐẠO HÀM CỦA HÀM SỐ LŨY THỪA y xα α ∈ R x . . . . . . Hàm số lũy thừa = ( ) có đạo hàm với mọi xα 0 . . . . . . . . . ( ) =
Ví dụ 2. Tìm đạo hàm của các hàm số sau: √ 2 y x y xπ y − x 2 b) = c) = (1 3 ) a) = 3 3
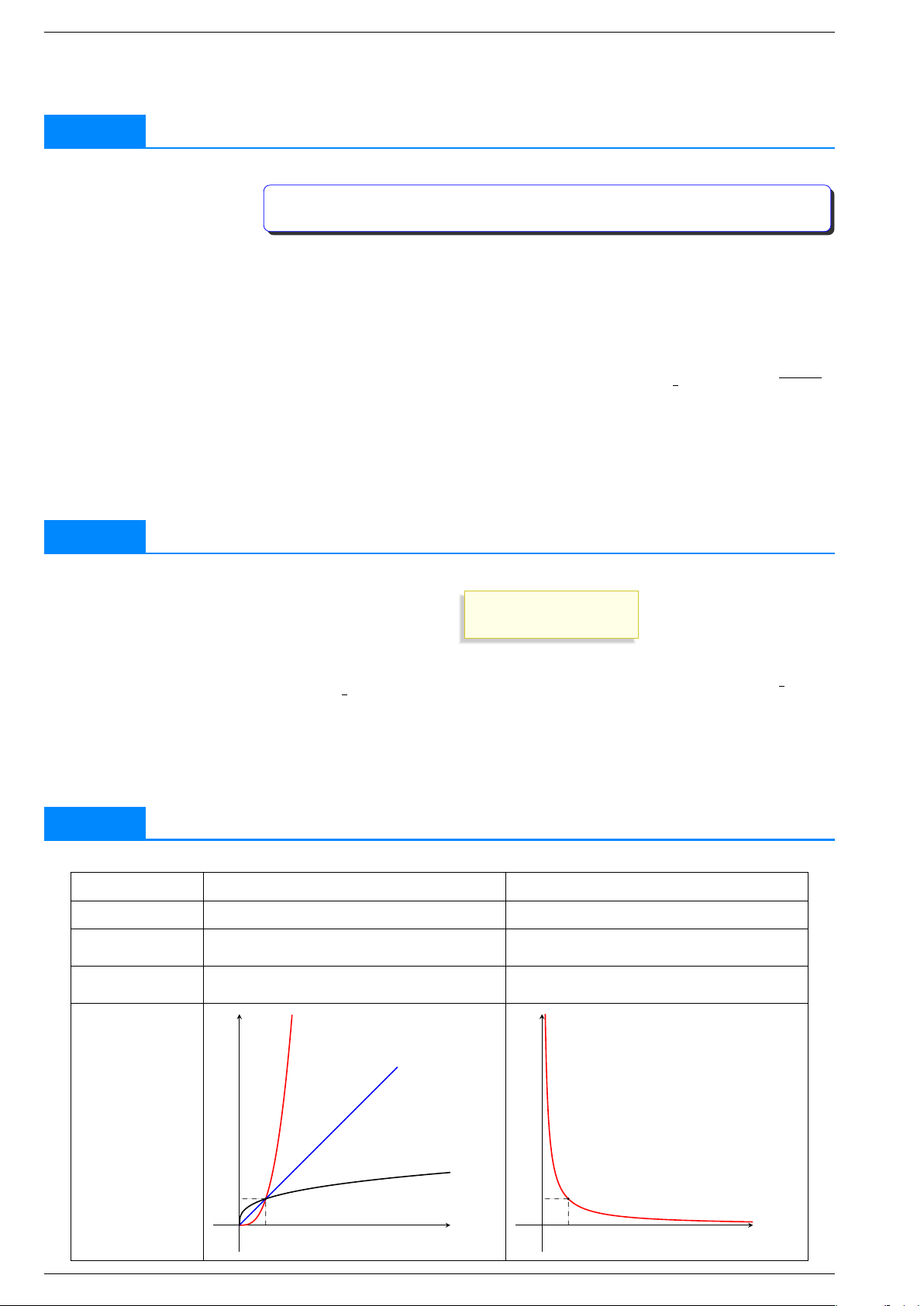
KHẢO SÁT HÀM SỐ LŨY THỪA y xα . . . . . . . . .
Trong trường hợp tổng quát, ta khảo sát hàm số = trên khoảng y xα α > y xα α < = , 0 = , 0 Sự biến thiên Giới hạn đặc biệt Tiệm cận y y α > 1 α = 1 α < 1 1 1 α < 0 O x O x 1 1 Đồ thị Soạn: Huỳnh Phú Sĩ 40
Trường THCS-THPT Mỹ Thuận §2. Hàm số lũy thừa TOÁN 12 Ví dụ 3. y x−3
Khảo sát sự biến thiên và vẽ đồ thị hàm số = . 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. y x − −3
Tập xác định của hàm số = ( 2) là A R \ { } B ∞ C R D ∞ . 2 . . [2; + ). . . . (2; + ). Câu 2. y − x −3
Tập xác định của hàm số = (2 ) là A −∞ B R \ { } C −∞ D ∞ . ( ; 2]. . 2 . . ( ; 2). . (2; + ). Câu 3. y x −4 2 −
Tập xác định của hàm số = 1 là A R B − . . . ( 1; 1). C R \ {− } D −∞ − ∪ ∞ . 1; 1 . . ( ; 1) (1; + ). Câu 4. y x π 2 − x
Tập xác định của hàm số = 3 + 2 là A R \ { } B . 1; 2 . . (1; 2). C −∞ ∪ ∞ D −∞ ∪ ∞ . ( ; 1] [2; + ). . ( ; 1) (2; + ). Câu 5. y x π 2 − x
Tập xác định của hàm số = + 1 là A R \ { } B R . 1 . . . C ∅ D −∞ − ∪ ∞ . . . ( ; 1) (1; + ). Câu 6. y x − 1 2 − x 3
Tập xác định của hàm số = 5 + 6 là A −∞ ∪ ∞ B R \ { } . ( ; 2) (3; + ). . 2; 3 . C D R . (2; 3). . . Câu 7. y x − x − 3 2 2
Tập xác định của hàm số = 3 là A R B . . . (0; 3). C −∞ ∪ ∞ D R \ { } . ( ; 0) (3; + ). . 0; 3 . √ Câu 8. D y x − x 2019 2 Tìm tập xác định của hàm số = 5 + 4 . A D R \ {− } B D −∞ − ∪ ∞ . = 1; 5 . . = ( ; 1) (5; + ). C D D D − . = (1; 5). . = ( 1; 5). Câu 9. 1 y x 2 − x − 3
Tập xác định của hàm số = 3 4 là A −∞ − ∪ ∞ B R \ {− } . ( ; 1) (4; + ). . 1; 4 . C − D R . ( 1; 4). . . Câu 10. y x2 − xe
Tập xác định của hàm số = 4 là A R B R \ { } . . . 0; 4 . C −∞ ∪ ∞ D . ( ; 0) (4; + ). . (0; 4). √ Câu 11. y x − 3
Tìm tập xác định của hàm số = ( 2) . A D R \ B D ∞ C D −∞ D D R . = 2. . = (2; + ). . = ( ; 2). . = . √ Câu 12. D y x − 3 Tìm tập xác định của hàm số = ( 5) . A D ∞ B D ∞ C D −∞ D D R \ { } . = [5; + ). . = (5; + ). . = ( ; 5). . = 5 . Câu 13. D 1 y x − Tìm tập xác định của hàm số = ( 1) 2 . A D ∞ B D ∞ C D ∞ D D R . = (0; + ). . = [1; + ). . = (1; + ). . = . √ Câu 14. D y − x 2 Tìm tập xác định của hàm số = (1 ) . A D ∞ B D R \ { } C D −∞ D D R . = (1; + ). . = 1 . . = ( ; 1). . = . Câu 15. 1 y x 2 − x 3
Tìm đạo hàm của hàm số = + 1 . A x − y0 2 1 B y0 1 . = q . . = q . 3 x 2 3 2 2 − x x2 − x ( + 1) 3 ( + 1) C x − x − y0 2 1 √ D y0 2 1 . = . . = q . 3 x2 − x 3 + 1 3 x 2 2 − x 3 ( + 1) Soạn: Huỳnh Phú Sĩ 41
Trường THCS-THPT Mỹ Thuận §2. Hàm số lũy thừa TOÁN 12 Câu 16. 5 f x x − f 0 Cho hàm số ( ) = (2 3) 6 . Tính (2). A 5 B 5 C −5 D −5 . . . . . . . . 6 3 6 3 Câu 17. 3 f x x 2 x 2 f Cho hàm số ( ) = 2 + 3 + 1 . Khi đó giá trị của (1) bằng √ A B 2 3 C D . 8. . . . 6 6. . 6 3 . 2 Câu 18. y x− 3 sai Cho hàm số =
4 . Khẳng định nào sau đây ?
A. Đồ thị hàm số nhận trục tung làm tiệm cận đứng.
B. Đồ thị hàm số nhận trục hoành làm tiệm cận ngang. C O .
Đồ thị hàm số luôn đi qua gốc tọa độ (0; 0). D ∞ . Nghịch biến trên (0; + ). Câu 19. α β y xα Cho các số thực và . Đồ thị các hàm số = y y xα y xβ ∞ = và = trên khoảng (0; + ) như hình vẽ bên.
Mệnh đề nào dưới đây đúng? A < β < α < B α < < β < y xβ . 0 1. . 0 1. = C < β < < α D β < < < α . 0 1 . . 0 1 . 1 x O 1 Câu 20. √ 1 y x 3 y x y x−2 y Cho ba hàm số = , = 5 , = . Khi C
đó đồ thị của ba hàm số đó lần lượt là A C ( 2 ) , C , C B C , C , C . ( 3 ) ( 2 ) ( 1 ). . ( 2 ) ( 3 ) ( 1 ). C C , C , C D C , C , C . ( 2 ) ( 1 ) ( 3 ). . ( 1 ) ( 3 ) ( 2 ). C ( 3 ) 1 C ( 1 ) O x 1 L TỰ LUẬN
Câu 1 (SGK GT12). Tìm tập xác định của các hàm số √ − 3 2 y − x − 1 y − x y x2 − y x 2 2 − x − 2 = 1 a) = (1 ) 3 5 c) d) = 2 b) = 2
Câu 2 (SGK GT12). Tìm đạo hàm của các hàm số π √ 1 1 y x y x y − x 3 2 − x 2 d) = (5 ) 3 y − x − x2 4 c) = (3 + 1) a) = 2 + 1 b) = 4 Soạn: Huỳnh Phú Sĩ 42
Trường THCS-THPT Mỹ Thuận §3. Lôgarit TOÁN 12 §3.LÔGARIT Đặt vấn đề "Ngày 6.7, nhiều khu vực tại miền nam bang California
của Mỹ tiếp tục rung chuyển vì trận động đất thứ hai liên
tiếp trong chưa đầy 48 giờ. Cơ quan Khảo sát địa chất Mỹ , (USGS) cho biết động đất mạnh 7 1 độ Richter với tâm
chấn ở độ sâu 7 km nằm gần TP.Ridgecrest, cách TP.Los
Angeles khoảng 200 km về phía đông bắc. Giới chuyên gia
cho biết đây là trận động đất chính, có biên độ rung chấn . . . . . . , gấp
lần so với trận tiền chấn 6 4 độ Richter hôm
4.7 (giờ địa phương) cũng gần Ridgecrest".
Thanh Niên ngày 7/7/2019 . . . M
Hãy điền con số còn thiếu trong dấu "
", biết rằng cường độ một trận động đất
độ Richter được cho bởi công thức M A − A A A A = log log 0 , với
là biên độ rung chấn tối đa và 0 là biên độ chuẩn ( 0 là hằng số). 1 KHÁI NIỆM LÔGARIT 1 Định nghĩa . . . . . . a, b a . . . . . . Cho hai số với . α aα b
. . . . . . . . . . . . . . . . . . . . . . . . Số thỏa mãn đẳng thức = được gọi là và kí hiệu . . . . . . là . α . . . . . . ⇔ aα b = = a . . . . . . . . . n . . . . . . . . . Số gọi là , số gọi là Chú ý: . . . . . . Không có lôgarit của số và số 0.
Ví dụ 1. Tính log 81 và log 1024. 3 1 2 2 Tính chất . . . . . . a, b a . . . . . . Cho hai số với
. Ta có các tính chất sau: ! . . . aloga b . . . • loga 1 = • = . . . . . . • loga a = • loga ab = Ví dụ 2. log 2021 log 2 5 3 Tính 5 và 81 . 2 QUY TẮC TÍNH LÔGARIT . . . . . . a, b, c a . . . . . . Cho ba số với . Ta có b · c
. . . . . . . . . . . . . . . logc . . . • loga ( ) = c 6 • loga b = = 1) logc . . . ( ! b
. . . . . . . . . . . . . . . • loga c = 1 b 6 •
loga b = . . . . . . ( = 1) . . . . . . . . . ∀α . . . . . . α 6 • loga bα = , • logaα b = loga b ( = 0) Soạn: Huỳnh Phú Sĩ 43
Trường THCS-THPT Mỹ Thuận §3. Lôgarit TOÁN 12 Ví dụ 3. Tính: √ 3 A 1 3 − C b) = log 25 a) = 2 log 5 1 + log 1 log 1 2 2 3 2 8 2 √ √ Ví dụ 4. S x · 5 x x
Chứng tỏ rằng biểu thức = logx x3 · không phụ thuộc . 3
LÔGARIT THẬP PHÂN VÀ LÔGARIT TỰ NHIÊN 1 Lôgarit thập phân . . .
Lôgarit thập phân là lôgarit cơ số . b . . . . . . log = Ví dụ 5. , Tính log 1000 và log 0 01. 2 Lôgarit tự nhiên . . .
Lôgarit tự nhiên là lôgarit cơ số b . . . . . . ln =
Ví dụ 6. Dùng máy tính cầm tay tính ln 2, ln 3 và ln 1.
7/2 được xem là ngày của số e 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. a 6 a Với
= 1 là số thực dương tùy ý, giá trị của loga3 bằng A B −1 C 1 D − . 3. . . . . . 3. 3 3 Câu 2. a 6 P a Cho
= 1 là số thực dương tùy ý, tính = loga2 . A P B P − 1 C P 1 D P − . = 2. . = . . = . . = 2. 2 2 Câu 3. a Với
là số thực dương bất kì, khẳng định nào sau đây đúng? A a 1 4 a B a4 a . log = 4 log . . log = log . 4 C a a D a 1 a . log(4 ) = 4 log . . log(4 ) = log . 4 Câu 4. a, b > a, b 6 x, y Cho 0 với = 1 và
là hai số thực dương. Trong các mệnh sai
đề sau đây, mệnh đề nào ? A xy B . loga (
) = loga x + loga y . .
logb a · loga x = logb x . C x 1 1 D . loga x = .
loga y = loga x − loga y. loga x . Câu 5. < a 6 x, y Cho số thực 0
= 1 và hai số thực dương . Khẳng định nào sau đây là đúng? A x B x loga x .
loga y = loga x − loga y. .
loga y = loga y . C x D x x − y .
loga y = loga x + loga y. . loga y = loga( ). Soạn: Huỳnh Phú Sĩ 44
Trường THCS-THPT Mỹ Thuận §3. Lôgarit TOÁN 12 Câu 6. a, b > Cho
0. Khẳng định nào sau đây đúng? A ab 2 a b B ab a · b . log = log + 2 log . . log( ) = log log . C ab 2 a b D ab a − b . log = 2 log + 2 log . . log( ) = log log . Câu 7. a a 6 Với
là số thực dương bất kì và
= 1, mệnh đề nào dưới đây đúng? A 1 B a 1 5 a . loga5 e = a . . log = ln . 5 ln 5 C a 5 5 D . log = a . .
loga5 e = 5 loga e. ln Câu 8. a, b, x, y a, b 6
Với mọi số thực dương sao cho
= 1, mệnh đề nào sau đây không đúng? A 1 1 B xy . loga x = . loga (
) = loga x + loga y . loga x . C D x .
logb a · loga x = logb x . .
loga y = loga x − loga y. Câu 9. a, b a 6 Cho
là các số thực dương, trong đó
= 1. Đẳng thức nào sau đây đúng? A a3 a3 √ − B √ . loga b = 3 2 loga b. . loga b = 3 + 2 loga b. C a3 a3 √ − 1 D √ 1 . loga b = 3 loga b. . loga b = 3 + loga b. 2 2 Câu 10. a a − a Với số thực dương tùy ý, ta có ln(6 ) ln(2 ) bằng A a B a 2 C a D . ln(4 ). . ln 12 . . 4 ln . . ln 3. Câu 11. a, b a 2 b4 Với
là hai số thực khác 0 tùy ý. Khi đó ln bằng A a b B a b . 2 ln + 4 ln . . 4 ln + 2 ln . C |a| |b| D |a| |b| . 2 ln + 4 ln . . 4 (ln + ln ). Câu 12. a > a 6 Cho 0 và
= 1. Tìm mệnh đề đúng trong các mệnh đề sau: A x n x > B loga x x, y > . loga x n = loga x ( 0). . loga y = 0). loga y ( C x D a, .
loga x có nghĩa với mọi . . loga 1 = loga a = 1. Câu 13. < a 6 x sai Cho 0
= 1 và một số thực dương
. Đẳng thức nào dưới đây ? A x a ln loga x a B . = . . loga x = a . ln C a √ loga x x D . = . . log a x3 = 6 loga x. Câu 14. a a, b Với
là hai số dương tùy ý. Khi đó ln b bằng A a ln B a b C a − b D a · b . b . . ln + ln . . ln ln . . ln ln . ln Câu 15. a sai Cho
là số thực dương khác 1, mệnh đề nào dưới đây ? A a · B a 1 . log loga 10 = 1. . log = . log 10 C a · a D a 1 . ln = ln 10 log . . log = . loga 10 Câu 16. x, y sai Cho
là các số thực dương. Mệnh đề nào sau đây ? A x y xy B x y x y . log + log = log( ). . log( + ) = log + log . C √ x xy 1 x y D x − y . log = (log + log ). . log y = log log . 2 Câu 17. a3 a I a Cho
là số thực dương khác 4. Tính = log . 4 64 A I − 1 B I − C I D I 1 . = . . = 3. . = 3. . = . 3 3 √ Câu 18. a, b a 6 √ a b Cho là các số dương ( = 1). Khi đó log a bằng A B 1 C 1 1 D . 2 + 2 loga b. . + loga b. . + loga b. . 2 + loga b. 2 2 2 Câu 19. a, b 2 a7b5 Cho
là hai số thực dương tùy ý, khi đó ln e bằng A a b B a b . 2 + 5 ln + 7 ln . . 7 ln + 5 ln . C a b D a b . 2 + 7 ln + 5 ln . . 5 ln + 7 ln . Câu 20. < a 6 Q a6 loga4 5 Cho 0
= 1. Tính giá trị của biểu thức = . √ √ A 3 Q B Q a5 C Q D Q a . = 5. . = . . = 5 5. . = 2 . √ √ Câu 21. A a · 5 a Rút gọn biểu thức = loga a3 · ta được kết quả là A 3 B 1 C 35 D 37 . . . . . . . . 10 10 10 10 Soạn: Huỳnh Phú Sĩ 45
Trường THCS-THPT Mỹ Thuận §3. Lôgarit TOÁN 12 Câu 22. < a, b 6 P a 10 b2 Cho hai số thực 0
= 1. Tính giá trị của biểu thức = loga2 + a √ √ √ b− 2 log a b + log 3 b . √ √ A P B P C P D P . = 3. . = 1. . = 2. . = 2. Câu 23. a, b a2 b2 ab a b Với các số thực dương thỏa mãn + = 6 , biểu thức log ( + ) 2 bằng A 1 a b B 1 a b . (3 + log + log ). . + log ). 2 2 (1 + log2 2 2 2 C 1 a b D 1 a b . 1 + (log + log ). . 2 + + log ). 2 2 (log2 2 2 2 Câu 24. a, b, c x y Với
là các số thực dương khác 1 tùy ý và = loga c, = logb c, ab
tính giá trị của logc ( ). A ab 1 B ab x y . logc ( ) = xy . . logc ( ) = + . C xy ab D ab 1 1 . logc ( ) = x y . . logc ( ) = x + y . + Câu 25. − a, b, c Cho loga b = 2 và loga c = 5 trong đó là các số thực dương ab2 a 6 S ( = 1). Tính = loga c . 3 A S − B S − C S D S − . = 17. . = 18. . = 18. . = 19. Câu 26. < a 6 b > c > − Cho 0 = 1, 0,
0 sao cho loga b = 3 và loga c = 2. Tính √c loga a3b2 . A B − C − D . 6. . 18. . 9. . 8. Câu 27. a Nếu log 5 = thì log 75 bằng 3 45 A a a a a 2 + B 1 + C 1 + 2 D 1 + 2 . a . . a . . a . . a . 1 + 2 2 + 2 + 1 + Câu 28. a Nếu log 3 = thì log 75 bằng 5 81 A a a a 1 1 B 1 C + 1 D + 1 . a + . . + . . . . a . 2 4 2 4 4 4 Câu 29. a, b < a < < b Cho các số thực thỏa mãn 0 1 . Tìm khẳng định đúng. A B a > b . loga b < 0. . ln ln . C , a < , b D a > b . (0 5) (0 5) . . 2 2 . Câu 30. a, b < a < b < Cho
là hai số thực thỏa mãn 0
1. Mệnh đề nào dưới đây đúng? A < B < . loga b < 1 logb a. . logb a < 1 loga b. C D < .
loga b < logb a < 1. . 1
loga b < logb a. L TỰ LUẬN
Câu 1 (SGK GT12). Rút gọn biểu thức · · b4 a) log 6 log 9 62 b) loga b2 + loga2 3 8 Câu 2 (SGK GT12). a b a, b a) Cho = log 3, = log 5. Hãy tính log 1350 theo . 30 30 30 c c b) Cho = log 3. Hãy tính log 15 theo . 15 25 d Vocabulary logarithm expression rule lôgarit biểu thức quy tắc positive number property common logarithm số dương tính chất lôgarit thập phân negative number prove nutural logarithm số âm chứng minh lôgarit tự nhiên Soạn: Huỳnh Phú Sĩ 46
Trường THCS-THPT Mỹ Thuận §4. Hàm số mũ. Hàm số lôgarit TOÁN 12
§4.HÀM SỐ MŨ. HÀM SỐ LÔGARIT Đặt vấn đề . .
Thạch Sanh trúng giải Ba một tờ vé số trị giá 10 000 000
đồng. Nhưng anh chưa biết nên dùng số tiền đó vào việc
gì. Bạn thân của Thạch Sanh là Lý Thông đã đề nghị vay
số tiền này với lãi suất 6%/tháng và sẽ trả cả vốn lẫn lãi sau
đúng một năm. Lý Thông mang số tiền đó đến Sacombank
gửi tiết kiệm theo hình thức lãi kép, với lãi suất 6%/tháng,
kỳ hạn gửi là 12 tháng.
Sau một năm, Lý Thông đến ngân hàng nhận số tiền cả
vốn lẫn lãi, và trả cho Thạch Sanh số tiền như đã hứa. a)
Hỏi sau cuộc giao dịch, Lý Thông lãi hay lỗ? b)
Hãy nêu sự khác nhau giữa hai hình thức gửi tiền của Thạch Sanh và Lý Thông. 1 HÀM SỐ MŨ 1 Định nghĩa . . . . . . a 6 . . . Cho số thực = . y . . . . . . hàm số mũ . . . Hàm số = được gọi là cơ số . Ví dụ 1. không phải Hàm số nào sau đây hàm số mũ? √ x A √ x y B y x −x 3 C y D y . = 3 . . = . . = 5 3 . . = e .
2 Đạo hàm của hàm số mũ . . . . . . a 6 . . . u u x Cho số = và hàm hợp = ( ). Ta có: ! ax 0 ......... au 0 . . . . . . . . . • ( ) = • ( ) = x 0 . . . . . . . . . u 0 . . . . . . . . . • (e ) = • (e ) =
Ví dụ 2. Tìm đạo hàm của các hàm số sau: y x y x3− x 3 +1 a) = 7 b) = e
3 Khảo sát hàm số mũ y ax = y ax a > y ax a < = , 1 = , 1 Sự biến thiên Tiệm cận y a > 1 y a 1 1 a a < 1 O x O x 1 1 Đồ thị
Ví dụ 3. So sánh các cặp số sau: √ − √ − 5 3 1 1 , , a) 3 và 3 b) 0 3 5 và 0 3 3 Soạn: Huỳnh Phú Sĩ 47
Trường THCS-THPT Mỹ Thuận §4. Hàm số mũ. Hàm số lôgarit TOÁN 12 2 HÀM SỐ LÔGARIT 1 Định nghĩa . . . . . . a 6 . . . Cho số thực = . y . . . . . . hàm số lôgarit . . . Hàm số = được gọi là cơ số . Ví dụ 4. không phải Hàm số nào sau đây hàm số lôgarit? A y x B y x C y x D y . = log . . = log(5 ). . = ln(5 ). . = ln e. 5
2 Đạo hàm của hàm số lôgarit . . . . . . a 6 . . . u u x Cho số = và hàm hợp = ( ). Ta có: 0 . . . . . . . . . 1 0 . . . . . . . . . 1 ! • (logax) = x a • (loga u) = x a ln ln x 0 . . . . . . . . . 1 u 0 . . . . . . . . . 1 • (ln ) = x a • (ln ) = x a ln ln
Ví dụ 5. Tìm đạo hàm của các hàm số sau: y x y x2 − x a) = log b) = ln( 3 + 2) 2
3 Khảo sát hàm số lôgarit y = loga x y a > y a < = loga x , 1 = loga x , 1 Tập xác định Sự biến thiên Tiệm cận y y a > 1 1 O a x 1 1 O a x 1 a < 1 Đồ thị
Ví dụ 6. So sánh các cặp số sau: √ √ a) log , 3 và log , 2 b) ln 2020 và ln 2021 0 5 0 5 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. D y x 2 − x Tìm tập xác định của hàm số = ln 2 + 1 . A D R B D ∞ C D ∅ D D R \ { } . = . . = (1; + ). . = . . = 1 . Câu 2. y x 2 −
Tập xác định của hàm số = log 1 là A −∞ − ∪ ∞ B −∞ . ( ; 1) (1; + ). . ( ; 1). C ∞ D − . (1; + ). . ( 1; 1). Câu 3. D y − x − x 2 Tìm tập xác định của hàm số = log 3 2 . 2 A D B D − . = (1; 3). . = ( 1; 3). C D − D D −∞ − ∪ ∞ . = ( 3; 1). . = ( ; 3) (1; + ). Câu 4. y x − 2
Tập xác định của hàm số = log( 2) là A R B R \ { } C ∞ D ∞ . . . 2 . . (2; + ). . [2; + ). Soạn: Huỳnh Phú Sĩ 48
Trường THCS-THPT Mỹ Thuận §4. Hàm số mũ. Hàm số lôgarit TOÁN 12 Câu 5. y 1
Tìm tập xác định của hàm số = − x . 1 ln A ∞ B ∞ C R \ { } D ∞ . (0; + ). . (e; + ). . e . . (0; + ). Câu 6. D y 1 √ x − Tìm tập xác định của hàm số = − x + ln( 1). 2 A D −∞ \ { } B D . = ( ; 2) 1 . . = (1; 2). C D D D . = [1; 2). . = (1; 2]. Câu 7. D y 1 √ |x − | Tìm tập xác định của hàm số = − x + ln 1 . 2 A D −∞ \ { } B D . = ( ; 2) 1 . . = (1; 2). C D D D . = [1; 2). . = (1; 2]. √ Câu 8. D x − y 3 1 Tìm tập xác định của hàm số = x . log(3 ) A D ∞ \ 1 B D 1 ∞ . = (0; + ) . . = ; + . 3 3 C D ∞ D D 1 ∞ . = (0; + ). . = ; + . 3 Câu 9. y x
Tìm đạo hàm của hàm số = 2020 . A y0 x− x 1 x B y0 · . = 2020 . . = 2020 log 2020. x C y0 x · D y0 2020 . = 2020 ln 2020. . = . ln 2020 Câu 10. f x x Hàm số ( ) = log (sin ) có đạo hàm là 3 A x f 0 x tan B f0 x x · . ( ) = . . ( ) = cot ln 3. ln 3 C x f 0 x 1 D f0 x cot . ( ) = x · . . ( ) = . sin ln 3 ln 3 Câu 11. y x 2
Tìm đạo hàm của hàm số = ln + 2 . A x x x y0 2 B y0 C y0 2 + 2 D y0 1 . = x . . = . . = . . = . 2 x2 x2 x2 + 2 + 1 + 2 + 2 Câu 12. y x · x+1 Đạo hàm của hàm số = e là A y0 x x x +1 B y0 − x +1 . = (1 + )e . . = (1 )e . C y0 x x +1 D y0 x · . = e . . = e . Câu 13. x y + 1
Tìm đạo hàm của hàm số = x . ln A x − x − x x − x − y0 ln 1 B y0 ln 1 . = x . = 2 x . x 2 x . ln ln C x − x − x − x − y0 ln 1 D y0 ln 1 . = . = 2 x . x x . ln ln Câu 14. y x x − 1
Tìm đạo hàm của hàm số = 2 ln x . e A y0 x 1 · x 1 B y0 x 1 −x . = 2 x + ln 2 ln + x . . = 2 ln 2 + x + e . e x C y0 2 1 D y0 x 1 − −x . = x ln 2 + x . . = 2 ln 2 + x e . e Câu 15. f x x 2 +1 f 0 Cho hàm số ( ) = e . Khi đó (1) bằng A 3 B 2 C 3 D . e . . e . . 2e . . 2e. Câu 16. y x − x − x x Đạo hàm của hàm số = log ( + 1) 2 ln( 1) + 2 tại điểm = 2 3 bằng A 1 B 1 C 1 − D 1 . . . + 2. . 1. . . 3 3 ln 3 3 ln 3 3 ln 3 Câu 17. y − x 2 Cho hàm số = e
. Mệnh đề nào sau đây đúng? A y00 y0 − y B y00 y0 y . + = 0. . + + = 0. C y00 y0 y D y00 y0 − y . + + 2 = 0. . + 2 = 0. Câu 18. y x C sai Cho hàm số = log có đồ thị ( ). Mệnh đề nào sau đây ? 2019 A C B C . (
) có đúng một tiệm cận. . (
) không có tiệm cận ngang. C C D C . (
) đồng biến trên tập xác định. . (
) không có tiệm cận đứng. Câu 19. y x sai Cho hàm số = log
. Khẳng định nào sau đây ? 2
A. Đồ thị hàm số nhận trục tung làm tiệm cận đứng. B A .
Đồ thị hàm số cắt trục hoành tại điểm (1; 0).
C. Đồ thị hàm số luôn nằm phía trên trục hoành. D ∞ .
Hàm số đồng biến trên khoảng (0; + ). Soạn: Huỳnh Phú Sĩ 49
Trường THCS-THPT Mỹ Thuận §4. Hàm số mũ. Hàm số lôgarit TOÁN 12
Câu 20. Hàm số nào sau đây nghịch biến trên tập xác định của nó? √ !x A y π x B y C y 5 D y x . = log . . = logπ x . . = . . = 2 . 4 2 Câu 21. R
Hàm số nào sau đây đồng biến trên ? A x − y x B y 1 . = log . . = . 2 x + 1 C y x D y x4 x2 . = 3 . . = + 2 + 4. Câu 22. R
Trong các hàm số dưới đây, hàm số nào nghịch biến trên ? A π x y B y π x2 . = . . = log 2 + 1 . 3 4 x C y 2 D y x . = . . = log 2 . e 3 Câu 23. y x2− x 6 +5
Tìm các khoảng đồng biến của hàm số = 2 . A −∞ B R . ( ; 3). . . C ∞ D −∞ ∞ . (3; + ). . ( ; 1) và (5; + ). Câu 24. y x x
Số điểm cực trị của hàm số = e + + 1 là A B C D . 0. . 3. . 2. . 1. Câu 25. a, b, c Cho
dương và khác 1. Đồ thị hàm số y y y y = loga x , = logb x và = logc x được cho y = loga x trong hình vẽ.
Khẳng định nào dưới đây là đúng? A a > c > b B b > c > a . . . . C c > b > a D a > b > c . . . . x O 1 2 y = logb x y = logc x Câu 26. a, b, c Cho ba số thực dương khác 1. Đồ thị y bx cx y ax y bx y cx hàm số = , = và = được cho trong hình vẽ.
Mệnh đề nào dưới đây là đúng? A a < b < c B a < c < b . . . . C b < c < a D c < a < b . . . . ax x O 1 2 Câu 27. y y bx y cx Cho các hàm số = loga x , = , = có đồ thị y bx cx
như hình vẽ. Mệnh đề nào dưới đây là đúng? A b > c > a B a > b > c . . . . C b > a > c D c > b > a . . . . x O 1 2 loga x Câu 28. . . ,
Một người gửi tiết kiệm số tiền 80 000 000 đồng với lãi suất 6 9%/năm.
Biết rằng tiền lãi hàng năm được nhập vào tiền gốc, hỏi sau đúng 5 năm người đó
rút được cả gốc lẫn lãi với số tiền gần với con số nào nhất sau đây? A . . B . . . 116 570 000 đồng. . 107 667 000 đồng. C . . D . . . 105 370 000 đồng. . 111 680 000 đồng. Câu 29. · 5
Một khu rừng có trữ lượng gỗ 4 10
mét khối. Biết tốc độ sinh trưởng
của các cây trong rừng đó là 4% mỗi năm. Hỏi sau 10 năm khu rừng đó có số mét
khối gỗ gần nhất với số nào sau đây? A , · 5 B , · 5 C , · 5 D , · 5 . 5 9 10 . . 5 92 10 . . 5 93 10 . . 5 94 10 .
Câu 30. Việt Nam là quốc gia nằm ở phía Đông bán đảo Đông Dương thuộc khu ,
vực Đông Nam Á. Với dân số ước tính 93
7 triệu dân vào đầu năm 2018, Việt Nam Soạn: Huỳnh Phú Sĩ 50
Trường THCS-THPT Mỹ Thuận §4. Hàm số mũ. Hàm số lôgarit TOÁN 12
là quốc gia đông dân thứ 15 trên thế giới và là quốc gia đông dân thứ 8 ở châu Á, tỉ ,
lệ tăng dân số hàng năm 1
2%. Giả sử rằng tỉ lệ tăng dân số từ năm 2018 đến năm
2030 không thay đổi thì dân số nước ta đầu năm 2030 khoảng bao nhiêu? A , B , . 118 12 triệu dân. . 106 12 triệu dân. C , D , . 128 12 triệu dân. . 108 12 triệu dân. L TỰ LUẬN
Câu 1 (SGK GT12). Tìm đạo hàm của các hàm số: y x x x x + 1 y x2 x a) = 2 e + 3 sin 2 y e) = log + + 1 c) = x 3 x y x x y log3 2 − x y x2 − x x b) = 5 2 cos d) = 3 ln + 4 sin f) = x
Câu 2 (SGK GT12). Tìm tập xác định của các hàm số: y − x y x x 2 − x y x2 − x 3 + 2 a) = log (5 2 ) b) = log 2 c) = log 4 + 5 y 2 3 1 d) = log , 0 4 − x 5 1 d Vocabulary exponential function composite function hàm số mũ hàm hợp compound-interest logarithmic function lãi kép hàm số lôgarit Soạn: Huỳnh Phú Sĩ 51
Trường THCS-THPT Mỹ Thuận
§5. Phương trình mũ và phương trình lôgarit TOÁN 12
§5.PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT Đặt vấn đề Nobita muốn dùng tiền của mình để mua chiếc xe máy . . LATTE của hãng YAMAHA trị giá 37 490 000 đồng. Cậu . quyết định gửi tiết kiệm 200 000 đồng tiền mừng tuổi hồi Tết vào Agribank với lãi suất 6%/tháng. Hỏi sau bao lâu thì số tiền vốn và lãi của Nobita đủ để mua xe? 1 PHƯƠNG TRÌNH MŨ
1 Phương trình mũ cơ bản
. . . . . . . . . a > . . . a 6 . . .
Phương trình mũ cơ bản có dạng ( , = ). b > 0 b ≤ 0 Ví dụ 1. m x+1 m Tìm để phương trình 2020 = có nghiệm.
2 Cách giải một số phương trình mũ đơn giản
Ví dụ 2. Giải các phương trình sau: x− x3 x2− x x− 1 +2 3 · 1 a) 2 = 32 c) 2 3 = 1 x − · x − x − x x 2 +1 b) 9 4 3 45 = 0 d) 9 6 = 2 2 PHƯƠNG TRÌNH LÔGARIT 1 Định nghĩa . . . . . .
Phương trình lôgarit là phương trình có chứa ẩn trong biểu thức dưới dấu
2 Phương trình lôgarit cơ bản
. . . . . . . . . . . . a > . . . a 6 . . .
Phương trình lôgarit cơ bản có dạng ( , = ). x b ⇔ x . . . . . . loga = = Soạn: Huỳnh Phú Sĩ 52
Trường THCS-THPT Mỹ Thuận
§5. Phương trình mũ và phương trình lôgarit TOÁN 12 Ví dụ 3. x
Tìm số nghiệm của phương trình log = 2021. 3
3 Cách giải một số phương trình lôgarit đơn giản
Ví dụ 4. Giải các phương trình sau: x x − 2 x − x − a) log + log ( 1) = 1 b) log 2 log 3 7 = 0 2 2 3 3 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. x 2 +1 Phương trình 5 = 125 có nghiệm là A x 53 B x 3 C x D x . = . . = . . = 3. . = 1. 2 2 Câu 2. x Phương trình 3 = 2 có nghiệm là A x B x 2 3 C x D x . = log 3. . = 2 . . = log 2. . = . 2 3 3 Câu 3. x x− +1 1
Tìm tập nghiệm của phương trình 4 + 4 = 272. A { } B { } C { } D { } . 3; 2 . . 2 . . 3 . . 3; 5 . Câu 4. x2− x 5 +7 Giải phương trình 2 = 8. √ A ± x , x − B x 5 29 . = 1 = 4. . = . √ 2 C ± x , x D x 5 5 . = 1 = 4. . = . 2 √ Câu 5. x−1 eln 81
Nghiệm của phương trình 9 = là A x B x C x D x . = 4. . = 5. . = 6. . = 17. Câu 6. 1 S x x + − · Tìm tập nghiệm của phương trình 4 2 5 2 + 2 = 0. A S {− } B S {− } C S { } D S − . = 1; 1 . . = 1 . . = 1 . . = ( 1; 1). Câu 7. x − · x −
Nghiệm của phương trình 9 4 3 45 = 0 là A x B x − , x . = 9. . = 5 = 9. C x , x D x . = 2 = log 5. . = 2. 3 Câu 8. x − x+2
Tìm số nghiệm thực của phương trình 4 2 + 3 = 0. A B C D . 3. . 2. . 1. . 0. x Câu 9. −x 1 1 Phương trình 3 = 2 + có bao nhiêu nghiệm âm? 9 A B C D . 0. . 1. . 2. . 3. Câu 10. x3 x2− x x− +2 3 · 1
Tìm số nghiệm của phương trình 2 3 = 1. A B C D . 2. . 1. . 0. . 3. Câu 11. x− x 1 +3 −
Tìm số nghiệm của phương trình 4 + 2 4 = 0. A B C D . 1. . 0. . 3. . 2. Câu 12. x x 1+2 · − Cho phương trình 2 + 15 2
8 = 0 (1). Khẳng định nào sau đây là đúng? A B . (1) có hai nghiệm dương. .
(1) có hai nghiệm trái dấu. C D . (1) có hai nghiệm âm. . (1) có một nghiệm. Câu 13. x −x +1 1
Tính tổng các nghiệm của phương trình 3 + 3 = 10. A B C − D . 1. . 3. . 1. . 0. Câu 14. · x · x x
Tính tổng các nghiệm của phương trình log 4 + 2 9 ) = + 1. 6 (3 A B C D . 2. . 1. . 0. . 3. Câu 15. x2− x 3 +1
Tích các nghiệm của phương trình 3 = 81 bằng A B C − D . 3. . 4. . 3. . 5. Soạn: Huỳnh Phú Sĩ 53
Trường THCS-THPT Mỹ Thuận
§5. Phương trình mũ và phương trình lôgarit TOÁN 12 Câu 16. x − Giải phương trình log ( 1) = 2. 3 A x B x C x D x . = 10. . = 11. . = 8. . = 7. Câu 17. x 2
Giá trị nào sau đây là một nghiệm của phương trình log 2 + 1 = 3 2? A x B x C x D x . = 2. . = 4. . = 3. . = 1. Câu 18. 1 x 2 −
Tìm tập nghiệm của phương trình log ( + 2) 1 = 0. 2 2 A {− } B {− } C { − } D { } . 1; 0 . . 4 . . 0; 4 . . 0 . Câu 19. x x −
Tập nghiệm của phương trình log + log ( 1) = 1 là 2 2 A {− } B { } C { − } D {− } . 1 . . 2 . . 2; 1 . . 2; 1 . Câu 20. x − x x −
Tìm nghiệm của phương trình log ( 1) + log ( + 3) = log (4 3). 5 5 5 A x B x , x C x D x 5 . = 2. . = 0 = 2. . = 0. . = . 2 Câu 21. x − x −
Tìm số nghiệm của phương trình log ( 3) + log ( 1) = 3. 2 2 A B C D . 2. . 3. . 1. . 0. Câu 22. x2 x x
Tìm số nghiệm của phương trình log + 4 + log (2 + 3) = 0. 3 1 3 A B C D . 2. . 3. . 0. . 1. √ Câu 23. x √ 2 − x x 3 Cho phương trình log ( + 1) + 2 = log 4 + log (4 + ) . Tổng 4 2 8 các nghiệm của √ phương trình đã cho là √ √ A B − C − D − . 4 + 2 6. . 4. . 4 2 6. . 2 2 3. Câu 24. 2 x − · x
Tính tổng các nghiệm của phương trình log log 9 log = 3. 2 2 3 A B − C 17 D . 2. . 2. . . . 8. 2 Câu 25. 2 x − x
Biết rằng phương trình log (2 ) 5 log
= 0 có hai nghiệm phân biệt 2 2 x , x x · x 1 2 . Tính 1 2 . A x · x B x · x C x · x D x · x . 1 2 = 8. . 1 2 = 5. . 1 2 = 3. . 1 2 = 1. Câu 26. 2 x − x −
Tính tích các nghiệm của phương trình log 2 log 7 = 0. 3 3 A B − C D . 2. . 7. . 1. . 9. Câu 27. √ 2 x − x Cho phương trình log (4 ) log (2
) = 5. Nghiệm nhỏ nhất của phương 2 2 trình thuộc khoảng A B C D . (1; 3). . (5; 9). . (3; 5). . (0; 1). Câu 28. m x m
Tập hợp các giá trị thực của tham số để phương trình log = có 2 nghiệm là A ∞ B ∞ C −∞ D R . (0; + ). . [0; + ). . ( ; 0). . .
Câu 29. Một người gửi số tiền 50 triệu đồng vào một ngân hàng với lãi suất , 8
4%/năm. Cứ mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu để tính lãi cho n
năm tiếp theo. Người đó sẽ lĩnh được số tiền cả vốn lẫn lãi là 80 triệu sau năm.
Hỏi nếu trong khoảng thời gian này người đó không rút tiền và lãi suất không thay n đổi thì
gần nhất với số nào sau đây? A B C D . 4. . 5. . 6. . 7.
Câu 30. Ông Bình gửi số tiền 58 triệu đồng vào một ngân hàng theo hình thức . .
lãi kép và ổn định trong 9 tháng thì lãnh được 61 758 000 đồng. Hỏi lãi suất ngân
hàng mỗi tháng là bao nhiêu, biết rằng lãi suất không thay đổi trong suốt thời gian gửi? A , B , C , D , . 0 8%. . 0 6%. . 0 7%. . 0 5%. L TỰ LUẬN
Câu 1 (SGK GT12). Giải các phương trình sau: , x− x2− x x− x x x 3 2 3 +2 2 1 2 − − a) (0 3) = 1 c) 2 = 4 e) 3 + 3 = 108 g) 64 8 56 = 0 x 1 x − x x x− x x x x b) = 25 , +7 · , 1 2 +1 1 · − · d) (0 5) (0 5) = 2 f) 2 + 2 + 2 = 28 h) 3 4 2 6 = 9 5
Câu 2 (SGK GT12). Giải các phương trình sau: x x 1 1 a) log (5 + 3) = log (7 + 5) x2 x − x 3 3 e) log + 5 = log 5 + log x x − − x − 2 5 b) log( 1) log(2 11) = log 2 1 x − x x2 − x − x − x f) log 4 1 = log 8 log 4 c) log ( 5) + log ( + 2) = 3 2 2 2 x √ 2 − x x − x x x d) log 6 + 7 = log( 3) g) log + 4 log + log = 13 2 4 8 Soạn: Huỳnh Phú Sĩ 54
Trường THCS-THPT Mỹ Thuận
§5. Phương trình mũ và phương trình lôgarit TOÁN 12 d Vocabulary exponential equation logarithmic equation phương trình mũ phương trình lôgarit logarithmizing exponentializing lôgarit hóa mũ hóa substitutive variable solve the equation ẩn phụ giải phương trình Soạn: Huỳnh Phú Sĩ 55
Trường THCS-THPT Mỹ Thuận
§6. Bất phương trình mũ và bất phương trình lôgarit TOÁN 12
§6.BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT PHƯƠNG TRÌNH LÔGARIT 1 BẤT PHƯƠNG TRÌNH MŨ
1 Bất phương trình mũ cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . Bất phương trình mũ cơ bản có dạng hoặc hoặc hoặc
. . . . . . . . . a > . . . a 6 . . . ( , = ). ax > b a > < a < 1 0 1 b > 0 b ≤ 0
2 Bất phương trình mũ đơn giản
Ví dụ 1. Giải các bất phương trình sau: x2−x > x −x − < x − · x < x a) 5 25 b) 2 + 2 3 0 c) 4 2 6 9 2 BẤT PHƯƠNG TRÌNH LÔGARIT
1 Bất phương trình lôgarit cơ bản . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bất phương trình lôgarit cơ bản có dạng hoặc hoặc
. . . . . . . . . . . . a > . . . a 6 . . . hoặc ( , = ). < a < loga x > b a > 1 0 1 Nghiệm
2 Bất phương trình lôgarit đơn giản
Ví dụ 2. Giải các bất phương trình sau: x > x x − x − ≤ a) log 1 (2 + 3) log 1 (3 + 1) b) log ( 3) + log ( 2) 1 3 3 2 2 Soạn: Huỳnh Phú Sĩ 56
Trường THCS-THPT Mỹ Thuận
§6. Bất phương trình mũ và bất phương trình lôgarit TOÁN 12 3 THỰC HÀNH Í TRẮC NGHIỆM x Câu 1. S 1 > Tìm tập nghiệm của bất phương trình 8. 2 A S − ∞ B S −∞ . = ( 3; + ). . = ( ; 3). C S −∞ − D S ∞ . = ( ; 3). . = (3; + ). x2 x +2 Câu 2. 1 > 1
Tìm tập nghiệm của bất phương trình . 3 27 A S − B S . = ( 3; 1). . = (1; 3). C S − D S −∞ − ∪ ∞ . = ( 1; 3). . = ( ; 3) (1; + ). − x− 2 6 Câu 3. x 1 3 <
Tìm tập nghiệm của bất phương trình 2 . 2 A −∞ B C D ∞ . ( ; 6). . (0; 6). . (0; 64). . (6; + ). Câu 4. e x >
Tìm tập nghiệm của bất phương trình π 1. A R B −∞ C ∞ D ∞ . . . ( ; 0). . (0; + ). . [0; + ). x Câu 5. 1 >
Tìm tập nghiệm của bất phương trình 9. 3 A −∞ − B −∞ C − ∞ D ∞ . ( ; 2). . ( ; 2). . ( 2; + ). . (2; + ). Câu 6. x x x x− +1 ≤ 1
Tìm tập nghiệm của bất phương trình 2 + 2 3 + 3 . A ∞ B −∞ C −∞ D ∞ . (2; + ). . ( ; 2). . ( ; 2]. . [2; + ). Câu 7. x+2 ≥ 1
Tập nghiệm của bất phương trình 3 là 9 A − ∞ B −∞ C ∞ D −∞ . [ 4; + ). . ( ; 0). . [0; + ). . ( ; 4). −x2 x +3 Câu 8. S 1 < 1 Tìm tập nghiệm của bất phương trình . 2 4 A S B S −∞ C S D S ∞ . = [1; 2]. . = ( ; 1). . = (1; 2). . = (2; + ). Câu 9. − x 1 2 > 1
Tìm tập nghiệm của bất phương trình 5 . 125 A S B S −∞ . = (0; 2). . = ( ; 2). C S −∞ − D S ∞ . = ( ; 3). . = (2; + ). Câu 10. x x− +1 ≤ 2
Tìm tập nghiệm của bất phương trình 4 8 . A ∞ B ∅ C D −∞ . [8; + ). . . . (0; 8). . ( ; 8]. Câu 11.
π x2−x− π x− 9 1 ≤
Tìm tập nghiệm của bất phương trình tan tan . 7 7 √ √ A h i S −∞ − ∪ ∞ B S − . = ( ; 2] [4; + ). . = 2 2; 2 2 . √ √ C i h S −∞ − ∪ ∞ D S − . = ; 2 2 2 2; + . . = [ 2; 4]. − x 1 3 Câu 12. S 2 ≥ 25 Tìm tập nghiệm của bất phương trình . 5 4 A S −∞ B S 1 ∞ . = ( ; 1]. . = ; + . 3 C S −∞ 1 D S ∞ . = ; . . = [1; + ). 3 √ √ Câu 13. x x − ≤ Giải bất phương trình 10 + 3 11 + 10 3 11 20. A ≤ x ≤ B − ≤ x < C − < x ≤ D − ≤ x ≤ . 0 1. . 1 1. . 1 1. . 1 1. Câu 14. · x − · x · x <
Giải bất phương trình 64 9 84 12 + 27 16 0.  x < A 9 < x < 3 B 1 C < x < D . . .  . . 1 2. . Vô nghiệm. 16 4 x > 2 Câu 15. x −x +2 · − <
Tìm số nghiệm nguyên của bất phương trình 2 + 8 2 33 0. A B C D . 4. . 6. . 7. . Vô số. Câu 16. S x < x− Tìm tập nghiệm của
của bất phương trình log 1 ( +1) log 1 (2 1). 5 5 A S ∞ B S − C S −∞ D S 1 . = (2; + ). . = ( 1; 2). . = ( ; 2). . = ; 2 . 2 Câu 17. x − <
Tìm tập nghiệm của bất phương trình log ( 1) 3. 2 A B −∞ C −∞ D . (1; 9). . ( ; 9). . ( ; 10). . (1; 10). Soạn: Huỳnh Phú Sĩ 57
Trường THCS-THPT Mỹ Thuận
§6. Bất phương trình mũ và bất phương trình lôgarit TOÁN 12 Câu 18. x − >
Tìm tập nghiệm của bất phương trình log , ( 1) 1. 0 5 A −∞ 3 B 3 C 3 ∞ D 3 . ; . . 1; . . ; + . . 1; . 2 2 2 2 Câu 19. x < x
Tìm tập nghiệm của bất phương trình ln(3 ) ln(2 + 6). A B C ∞ D −∞ . [0; 6). . (0; 6). . (6; + ). . ( ; 6). Câu 20. S x − ≥ Tìm tập nghiệm
của bất phương trình log 1 ( 3) log 1 4. 2 2 A S −∞ B S ∞ C S D S . = ( ; 7]. . = [7; + ). . = (3; 7]. . = [3; 7]. Câu 21. x > x
Tìm tập nghiệm của bất phương trình log ( + 7) log ( + 1). 4 2 A − B C − D ∞ . ( 1; 2). . (2; 4). . ( 3; 2). . (5; + ). Câu 22. x 2 − x >
Tìm tập nghiệm của bất phương trình log 1 5 + 7 0. 2 A −∞ B −∞ ∪ ∞ . ( ; 2). . ( ; 2) (3; + ). C D ∞ . (2; 3). . (3; + ). Câu 23. x − − x ≥
Tìm tập nghiệm của bất phương trình log 1 ( 1) + log (11 2 ) 0. 3 3 A S B S −∞ C S 11 D S . = (1; 4]. . = ( ; 4]. . = 4; . . = (1; 4). 2 Câu 24. x − ≤
Giải bất phương trình logx (log 72)) 1. 3 (9 √ A i S −∞ B S . = ( ; 2]. . = log 73; 2 . 3 √ √ C i h i S D S . = log 72; 2 . . = log 73; 2 . 3 3 Câu 25. x > x
Số nghiệm nguyên của bất phương trình log , (15 + 2) log , (13 + 8) 0 8 0 8 là A B C D . Vô số. . 4. . 2. . 3.
Câu 26. Có bao nhiêu số nguyên trên đoạn [0; 10] nghiệm đúng bất phương trình x − > x − log (3 4) log ( 1)? 2 2 A B C D . 9. . 10. . 8. . 11. Câu 27. x − x 2 > Có bao nhiêu số nguyên
thỏa mãn bất phương trình log 1 log 2 2 2 0? A B C D . Vô số. . 1. . 0. . 2. Câu 28. 2 x − x <
Tập nghiệm của bất phương trình log 3 log + 2 0 là khoảng 2 2 a b a2 b2 ( ; ). Tính + . A B C D . 16. . 5. . 20. . 10. Câu 29. D y p x − Tìm tập xác định của hàm số = log( + 1) 1. A D ∞ B D ∞ . = (10; + ). . = [9; + ). C D −∞ D D R \ { } . = ( ; 9]. . = 1 .
Câu 30. Một người gửi tiết kiệm với lãi suất 5%/năm và lãi hàng năm được nhập
vào vốn. Sau ít nhất bao nhiêu năm thì người đó nhận được số tiền lớn hơn 150% số tiền gửi ban đầu? A B C D . 8 năm. . 10 năm. . 9 năm. . 11 năm. L TỰ LUẬN
Câu 1 (SGK GT12). Giải các bất phương trình sau: −x2 x x x− x x +3 < +2 1 ≤ − · > a) 2 4 b) 3 + 3 28 c) 4 3 2 + 2 0
Câu 2 (SGK GT12). Giải các bất phương trình sau: − x ≥ x − > x 2 x − x ≤ a) log (4 2 ) 2 b) log (3 5) log ( + 1) c) log 5 log + 6 0 8 1 1 3 3 5 5 Soạn: Huỳnh Phú Sĩ 58
Trường THCS-THPT Mỹ Thuận
§6. Bất phương trình mũ và bất phương trình lôgarit TOÁN 12 Soạn: Huỳnh Phú Sĩ 59
Trường THCS-THPT Mỹ Thuận PHẦN II HÌNH HỌC
Chương 1. Khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
§1. Khái niệm về khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
§2. Đa diện lồi và Đa diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
§3. Khái niệm về thể tích của khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
Chương 2. Mặt nón, mặt trụ, mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
§1. Khái niệm về khối tròn xoay . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
§2. Mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 Soạn: Huỳnh Phú Sĩ 60
Trường THCS-THPT Mỹ Thuận Chương 1. Khối đa diện TOÁN 12 Chương 1. KHỐI ĐA DIỆN
§1.KHÁI NIỆM VỀ KHỐI ĐA DIỆN Đặt vấn đề . . . . . . . . . . . .
Mặt ngoài của Kim tự tháp Ai Cập có hình dáng là một hình , được tạo thành bởi đa giác.
Nếu mỗi đỉnh và cạnh của các đa giác đó đều được gọi là đỉnh và cạnh của hình chóp thì hình chóp đã cho có bao
nhiêu đỉnh, bao nhiêu cạnh? 1
KHỐI LĂNG TRỤ VÀ KHỐI CHÓP . . . . . . . . . . . . . . . . . . • Khối lăng trụ là phần
được giới hạn bởi một lăng trụ, kể cả
. . . . . . lăng trụ ấy. . . . . . . . . . . . . . . . . . . . . . . . . • Khối chóp là phần
được giới hạn bởi một chóp, kể cả chóp ấy. S A B C B A A0 B0 C C0 D ABC.A0B0C0 . . . . . . S.ABCD . . . . . . Khối lăng trụ có đỉnh, Khối chóp có đỉnh, cạnh, . . . . . . cạnh, mặt. mặt. 2
KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN
1 Khái niệm về hình đa diện
Hình đa diện là hình được tạo bởi một số hữu hạn các . . . . . . . . . thỏa mãn hai tính chất sau:
Hai đa giác phân biệt chỉ có thể hoặc không có . . . . . . chung, hoặc chỉ có một •
. . . . . . chung, hoặc chỉ có một . . . . . . chung.
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng . . . . . . đa giác. • Soạn: Huỳnh Phú Sĩ 61
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối đa diện TOÁN 12
Ví dụ 1. Hình nào sau đây là hình đa diện? Hình 1 Hình 2 Hình 3 Hình 4
2 Khái niệm về khối đa diện
Khối đa diện là phần . . . . . . . . . . . . được giới hạn bởi một . . . . . . đa diện, kể cả
. . . . . . đa diện đó. điểm . . . . . . •
Những điểm không thuộc khối đa diện được gọi là , những . . . . . . . . . . . . điểm thuộc
đa diện nhưng không thuộc đa diện giới hạn điểm trong
khối đa diện ấy được gọi là . . . . . . . miền trong • Tập hợp các điểm được gọi là
của khối đa diện, tập hợp . . . . . . . . . . . .
các điểm ngoài được gọi là của khối đa diện. . . . . . . • Chỉ có miền
là chứa hoàn toàn một đường thẳng nào đấy.
Ví dụ 2. Hình vẽ nào sau đây là khối đa diện? 3 HAI ĐA DIỆN BẰNG NHAU
1 Phép dời hình trong không gian
Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M0 xác định . . . . . . . . . . . .
được gọi là một phép biến hình trong không gian. ~ v
Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn . . . . . . . . . . . .
giữa hai điểm tùy ý. M M0
Phép tịnh tiến theo vectơ − Ï v M M0 •
là phép biến hình biến mỗi điểm thành điểm M . . . . . . . . . sao cho
Phép đối xứng qua mặt phẳng P N ∈ P • ( ) là phép biến hình biến mỗi điểm ( ) I . . . . . . . . . M / ∈ P M0 P thành , biến mỗi điểm ( ) thành điểm sao cho ( ) là mặt phẳng P . . . . . . . . . . . . MM0 của đoạn thẳng . M0 Phép đối xứng tâm O O . . . . . . . . . •
là phép biến hình biến điểm thành , biến mỗi M 6 O M0 O . . . . . . . . . . . . MM0 điểm = thành điểm sao cho là của đoạn thẳng . ∆
Nếu phép đối xứng tâm O biến hình H thành chính nó thì O được gọi là M0 ( )
. . . . . . . . . . . . . . . của H ( ).
Phép đối xứng qua đường thẳng ∆ . . . . . . M • (hay phép đối xứng qua ∆) là phép biến N ∈ . . . . . . . . . M / ∈ M0 hình biến mọi điểm ∆ thành , biến mỗi điểm ∆ thành điểm . . . . . . . . . . . .
MM0 Nếu phép đối xứng trục sao cho ∆ là đường của đoạn thẳng . ∆
biến hình H thành chính nó thì
được gọi là . . . . . . . . . . . . . . . của H ( ) ∆ ( ). Soạn: Huỳnh Phú Sĩ 62
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối đa diện TOÁN 12 2 Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có một phép . . . . . . . . . . . . biến hình này
thành hình kia Hai đa diện được gọi là bằng nhau nếu có một phép . . . . . . . . . . . . .
biến đa diện này thành đa diện kia. − Ï v O H ( 1) H ( ) H ( 2) H H H . . . . . . . . . Các đa diện ( ), ( 1) và ( 2) bằng nhau vì 4
PHÂN CHIA VÀ LẮP GHÉP CÁC KHỐI ĐA DIỆN H H H H H Nếu khối đa diện (
) là hợp của hai khối đa diện ( 1), ( 2) sao cho ( 1) và ( 2) . . . . . . . . . H
điểm chung nào thì ta nói khối đa diện (
) có thể chia được thành hai H H . . . . . . . . . H khối đa diện ( 1) và (
2). Ngược lại, ta có thể hai khối đa diện ( 1) và H H (
2) với nhau để được khối đa diện ( ). . . . . . . . . .
Một khối đa diện bất kì luôn có thể phân chia được thành các khối
Ví dụ 3. Hãy chia một khối lập phương thành 5 khối tứ diện. 5 THỰC HÀNH Í TRẮC NGHIỆM
Câu 1. Mỗi cạnh của một khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện? A B C D . Bốn mặt. . Hai mặt. . Ba mặt. . Năm mặt.
Câu 2. Hãy chọn từ/cụm từ thích hợp để điền vào chỗ trống trong phát biểu: "Số . . . . . .
cạnh của một hình đa diện luôn
số mặt của hình đa diện ấy". A B . bằng. . nhỏ hơn hoặc bằng. C D . nhỏ hơn. . lớn hơn.
Câu 3. Mỗi đỉnh của một hình lập phương là đỉnh chung của đúng bao nhiêu mặt? A B C D . 3. . 4. . 2. . 5.
Câu 4. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu cạnh? A B C D . 5. . 4. . 3. . 2.
Câu 5. Trong các mệnh đề sau, mệnh đề nào là đúng?
A. Số cạnh của một hình đa diện luôn lớn hơn 7.
B. Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 8.
C. Số cạnh của một hình đa diện luôn lớn hơn 6.
D. Số cạnh của một hình đa diện luôn lớn hơn hoặc bằng 6. Soạn: Huỳnh Phú Sĩ 63
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối đa diện TOÁN 12
Câu 6. Số cạnh của một khối chóp tam giác là A B C D . 6. . 4. . 7. . 5.
Câu 7. Tổng số đỉnh, cạnh, mặt của hình lập phương là A B C D . 26. . 14. . 24. . 28.
Câu 8. Hình lăng trụ ngũ giác có bao nhiêu mặt? A B C D . 9. . 5. . 7. . 2. Câu 9.
Hình đa diện ở hình bên có bao nhiêu mặt? A B C D . 8. . 12. . 10. . 11. Câu 10.
Đa diện trong hình bên có bao nhiêu mặt? A B C D . 11. . 14. . 12. . 13. Câu 11.
Hình đa diện bên có bao nhiêu cạnh? A B C D . 15. . 12. . 20. . 16. Câu 12.
Số đỉnh của hình đa diện bên là A B C D . 8. . 9. . 10. . 11.
Câu 13. Trong các hình dưới đây, hình nào là hình đa diện? Hình 1 Hình 2 Hình 3 Hình 4 A B C D . Hình 4. . Hình 2. . Hình 1. . Hình 3. Câu 14. không phải
Trong các hình dưới đây, hình nào hình đa diện? Hình 1 Hình 2 Hình 3 Hình 4 A B C D . Hình 1. . Hình 2. . Hình 3. . Hình 4. Câu 15. không phải
Trong các hình dưới đây, hình nào hình đa diện? Soạn: Huỳnh Phú Sĩ 64
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối đa diện TOÁN 12 Hình 1 Hình 2 Hình 3 Hình 4 A B C D . Hình 1. . Hình 2. . Hình 3. . Hình 4.
Câu 16. Hình lăng trụ có thể có số cạnh là số nào sau đây? A B C D . 3000. . 3001. . 3005. . 3007. Câu 17. n Cho khối chóp có đáy là đa giác cạnh. Mệnhh đề nào sau đây là đúng? A n .
Số mặt của khối chóp là 2 . B n .
Số đỉnh của khối chóp bằng 2 + 1. C n .
Số cạnh của khối chóp bằng + 1.
D. Số mặt của khối chóp bằng số đỉnh của nó. Câu 18. S.ABCD Có thể chia khối chóp
thành hai khối tứ diện là A SBCD SACD B SACD SABD . và . . và . C SABC SABD D SABC SACD . và . . và . Câu 19. ABCD.A0B0C0D0 BDD0B0 Cho khối lập phương . Mặt phẳng ( ) chia khối lập phương thành A B .
Hai khối lăng trụ tam giác. . Hai khối tứ diện. C D .
Hai khối lăng trụ tứ giác. . Hai khối chóp tứ giác. Câu 20. ABC.A0B0C0 A0BC Cắt khối lăng trụ bởi mặt phẳng ( ) ta được
A. Một khối chóp tam giác và một khối chóp ngũ giác.
B. Hai khối chóp tứ giác.
C. Một khối chóp tam giác và một khối chóp tứ giác. D. Hai khối chóp tam giác. L TỰ LUẬN
Câu 1 (SGK GT12). Chia một khối lập phương thành sáu khối tứ diện bằng nhau. d Vocabulary solid polyhedra tetrahedron polygon khối đa diện tứ diện đa giác solid prisms vertice space khối lăng trụ đỉnh không gian solid pyramids edge translation khối chóp cạnh phép tịnh tiến solid cube face reflection khối lập phương mặt phép đối xứng Soạn: Huỳnh Phú Sĩ 65
Trường THCS-THPT Mỹ Thuận
§2. Đa diện lồi và Đa diện đều TOÁN 12
§2.ĐA DIỆN LỒI VÀ ĐA DIỆN ĐỀU 1 KHỐI ĐA DIỆN LỒI
Khối đa diện H được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm ( )
. . . . . . . . . của H luôn . . . . . . H ( ) ( ).
Khi đó đa diện xác định H được gọi là . . . . . . . . . . . . . . .. ( )
Miền trong của khối đa diện luôn Ví dụ 1. . . . . . .
Trong các hình dưới đây hình nào không phải đa diện lồi? nằm về phía đối với mỗi mặt
phẳng chứa một mặt của nó Hình 1 Hình 2 Hình 3 Hình 4 2 KHỐI ĐA DIỆN ĐỀU Định nghĩa
Khối đa diện đều là khối đa diện . . . . . . có các tính chất sau đây:
Mỗi mặt của nó là một . . . . . . . . . . . . . . . . . . . . . p cạnh •
Mỗi đỉnh của nó là đỉnh chung của đúng q mặt. • . . . . . .
Khối đa diện đều như vậy được gọi là khối đa diện đều loại . Ví dụ 2. . . . . . .
Khối tứ diện đều là khối đa diện đều loại
, khối lập phương là khối đa . . . . . . diện đều loại .
Các mặt của khối đa diện đều là những đa giác . . . . . . . . . . . . . . . nhau. Định lý . . . . . . . . . . . . . . . . . . Chỉ có
loại khối đa diện đều là loại (tứ diện đều), (lập phương), . . . . . . . . . . . . . . . . . . (bát diện đều),
(thập nhị diện đều) và (nhị thập diện đều). Tứ diện đều Lập phương Bát diện đều Thập nhị diện đều Nhị thập diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . • đỉnh • đỉnh • đỉnh • đỉnh • đỉnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . • cạnh • cạnh • cạnh • cạnh • cạnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . • mặt • mặt • mặt • mặt • mặt 3 THỰC HÀNH Í TRẮC NGHIỆM
Câu 1. Cho hình lăng trụ tam giác đều. Trong các mệnh đề sau, mệnh đề nào
sai?A. Hai đáy là các tam giác đều bằng nhau.
B. Các mặt bên là hình vuông. Soạn: Huỳnh Phú Sĩ 66
Trường THCS-THPT Mỹ Thuận
§2. Đa diện lồi và Đa diện đều TOÁN 12
C. Các cạnh bên vuông góc với mặt đáy.
D. Các cạnh bên bằng nhau. Câu 2. sai
Trong các mệnh đề sau, mệnh đề nào ?
A. Khối tứ diện là khối đa diện lồi.
B. Khối hộp là khối đa diện lồi.
C. Lắp ghép hai khối hộp bất kì thì được một khối đa diện lồi.
D. Khối lăng trụ tam giác là khối đa diện lồi.
Câu 3. Trong các hình dưới đây hình nào không phải đa diện lồi? Hình 1 Hình 2 Hình 3 Hình 4 A B C D . Hình 1. . Hình 2. . Hình 3. . Hình 4.
Câu 4. Cho các khối hình sau: Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là A B C D . 3. . 2. . 4. . 1.
Câu 5. Cho một khối đa diện lồi có 10 đỉnh, 7 mặt. Hỏi khối đa diện này có mấy cạnh? A B C D . 20. . 18. . 15. . 12.
Câu 6. Số đỉnh của hình bát diện đều là A B C D . 10. . 7. . 8. . 6.
Câu 7. Số đỉnh của hình 12 mặt đều là A B C D . Ba mươi. . Mười sáu. . Mười hai. . Hai mươi.
Câu 8. Khối 20 mặt đều có tất cả bao nhiêu cạnh? A B C D . 30. . 20. . 12. . 60.
Câu 9. Hình bát diện đều có tất cả bao nhiêu cạnh? A B C D . 8. . 9. . 12. . 20.
Câu 10. Hình bát diện đều có bao nhiêu mặt? A B C D . 9. . 8. . 6. . 4.
Câu 11. Trong các khối đa diện đều, đa diện nào có các mặt là các hình ngũ giác đều? A B . Bát diện đều. . Hình lập phương. C D . Mười hai mặt đều. . Hai mươi mặt đều.
Câu 12. Phát biểu nào sau đây là đúng?
A. Hình mười hai mặt đều có 20 đỉnh, 30 cạnh, 12 mặt.
B. Hình mười hai mặt đều có 30 đỉnh, 12 cạnh, 12 mặt.
C. Hình mười hai mặt đều có 30 đỉnh, 20 cạnh, 12 mặt.
D. Hình mười hai mặt đều có 30 đỉnh, 12 cạnh, 30 mặt.
Câu 13. Trong các hình đa diện đều sau, hình nào có số đỉnh nhỏ hơn số mặt? A B . Hình tứ diện đều. . Hình 20 mặt đều. C D . Hình lập phương. . Hình 12 mặt đều.
Câu 14. Khối lập phương là khối đa diện đều loại A { } B { } C { } D { } . 5; 3 . . 3; 4 . . 4; 3 . . 3; 5 .
Câu 15. Khối mười hai mặt đều là khối đa diện đều loại? A { } B { } C { } D { } . 4; 3 . . 3; 5 . . 3; 4 . . 5; 3 . Soạn: Huỳnh Phú Sĩ 67
Trường THCS-THPT Mỹ Thuận
§2. Đa diện lồi và Đa diện đều TOÁN 12 Câu 16. { }
Tính tổng số đỉnh và số mặt của khối đa diện đều loại 5; 3 . A B C D . 50. . 20. . 32. . 42.
Câu 17. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? A B C D . 1. . 4. . 3. . 2.
Câu 18. Một hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? A B C D . 2. . 3. . 4. . 6. Câu 19. không
Hình đa diện nào dưới đây có tâm đối xứng? Khối tứ diện đều Khối lập phương Lăng trụ lục giác đều Khối bát diện đều A B . Tứ diện đều. . Bát diện đều. C D .
Lăng trụ lục giác đều. . Hình lập phương.
Câu 20. Hình đa diện nào sau đây không có tâm đối xứng? A B . Tứ diện đều. . Bát diện đều. C D .
Lăng trụ lục giác đều. . Hình lập phương. L TỰ LUẬN Câu 1 (SGK GT12). H H0 H Cho hình lập phương ( ). Gọi (
) là hình bát diện đều có các đỉnh là tâm các mặt của ( ). Tính tỉ số H H0
diện tích toàn phần của ( ) và ( ). d Vocabulary convex polyhedra regular tetrahedron đa diện lồi tứ diện đều non-convex polyhedra regular octahedron đa diện không lồi bát diện đều regular polyhedra regular dodecahedron đa diệu đều thập nhị diện đều regular polygon regular icosahedron đa giác đều nhị thập diện đều Soạn: Huỳnh Phú Sĩ 68
Trường THCS-THPT Mỹ Thuận
§3. Khái niệm về thể tích của khối đa diện TOÁN 12
§3.KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN Đặt vấn đề
Dã Tràng dự định xây dựng một kim tự tháp cao 100m,
cạnh đáy 50m bằng những viên gạch hình hộp chữ nhật
có độ dài các cạnh lần lượt là 5cm, 10cm, 20cm. Nếu bỏ qua phần xi măng thì Dã Tràng cần chuẩn bị tối thiểu bao nhiêu viên gạch như trên? 1
KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN
Thể tích của một khối hộp chữ nhật bằng . . . . . . . . . ba kích thước của nó.
Ví dụ 1. Tính thể tích của một viên gạch có độ dài các cạnh lần lượt là 5cm, 10cm, 20cm.
Thể tích khối lập phương cạnh a là . . . . . . 2 THỂ TÍCH KHỐI LĂNG TRỤ
Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là V . . . . . . . . . =
Ví dụ 2. Cho khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng 5cm. Tính thể tích khối lăng trụ đã cho. 3 THỂ TÍCH KHỐI CHÓP
Thể tích khối chóp có diện tích đáy B và chiều cao h là V . . . . . . . . . =
Ví dụ 3. Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công
nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147m, cạnh đáy dài
230m. Hãy tính thể tích của nó. Soạn: Huỳnh Phú Sĩ 69
Trường THCS-THPT Mỹ Thuận
§3. Khái niệm về thể tích của khối đa diện TOÁN 12 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. V h B Thể tích
của khối lăng trụ có chiều cao và diện tích đáy là A V Bh B V 1 Bh C V 1 Bh D V 1 Bh . = . . = . . = . . = . 2 6 3 Câu 2. V B h Thể tích
của khối chóp có diện tích đáy và chiều cao là A V 1 Bh B V Bh C V 1 Bh D V Bh . = . . = 3 . . = . . = . 3 2 Câu 3. V B
Cho khối lăng trụ có thể tích bằng
. Biết diện tích đáy của lăng trụ là , h tính chiều cao
của khối lăng trụ đã cho. A V V V V h B h 2 C h 3 D h . = B . . = B . . = B . . = B . 3 Câu 4. a
Thể tích của khối lập phương cạnh 2 bằng A a3 B a3 C a3 D a3 . 8 . . 2 . . . . 6 . Câu 5. h a S a2
Thể tích của khối chóp có chiều cao = và diện tích đáy = 3 là A V 1 a 1 3 B V a3 C V a3 D V a3 . = . . = . . = 3 . . = . 3 6 √ Câu 6. B a2 h a
Cho khối chóp có diện tích đáy = 2 và chiều cao = 2 . Thể tích
V của khối chóp là √ √ √ √ A a3 a3 a3 V 2 2 B V 2 2 C V a 2 3 D V . = . . = . . = 2 2. . = . 3 9 3 Câu 7. S.ABCD ABCD a Cho hình chóp tứ √ giác có đáy là hình vuông cạnh , SA ⊥ ABCD SA a S.ABCD ( ) và =
6. Thể tích của khối chóp bằng √ √ √ √ A a 6 6 6 3 B a3 C a3 D a3 . 6. . . . . . . 3 6 2 Câu 8. S.ABC ABC SA Cho khối chóp có đáy là tam giác đều, vuông góc √ với mặt ABC SA a S.ABC a3 phẳng ( ) và =
. Biết rằng thể tích của khối chóp bằng 3 . Tính S.ABC độ dài cạnh
√ đáy của khối chóp√ . √ A a B a C a D a . 2 3. . 3 3. . 2 . . 2 2. Câu 9. S.ABC a a3 Cho khối chóp
có đáy là tam giác đều cạnh 2 và thể tích bằng . h Tính chiều cao của hình chóp đã cho. √ √ √ √ A a a a h 3 B h 3 C h 3 D h a . = . . = . . = . . = 3 . 6 2 3 Câu 10. S.ABC ABC SA Cho khối chóp có đáy là tam giác đều, vuông góc √ với mặt ABC SA a S.ABC a3 phẳng ( ) và =
. Biết rằng thể tích của khối chóp bằng 3 . Tính S.ABC độ dài cạnh
√ đáy của khối chóp√ . √ A a B a C a D a . 2 3. . 3 3. . 2 . . 2 2. Câu 11. a2 a3
Cho khối lăng trụ có diện tích đáy là 30 và thể tích là 150 . Tính theo
a khoảng cách giữa hai mặt phẳng đáy của khối lăng trụ đã cho. A a h B h a C h D h a . = 5. . = 5 . . = . . = 15 . 5
Câu 12. Nếu ba kích thước của một khối hộp chữ nhật tăng lên 3 lần thì thể tích
của nó tăng lên bao nhiêu lần? A B C D . 3 lần. . 9 lần. . 18 lần. . 27 lần.
Câu 13. Một viên gạch dạng khối hộp chữ nhật có ba kích thước là 3cm, 10cm,
20cm. Tính thể tích viên gạch đó. A B C D . 300cm. . 200cm. . 600cm. . 1200cm.
Câu 14. Tính thể tích khối rubic lập phương có cạnh bằng 8cm (Bỏ các khe hở
của khối rubic, xem thể tích của khe hở không đáng kể). A 512 3 B 3 C 3 D 3 . 24 cm . . 8 cm . . 512 cm . . cm . 3 Câu 15. S.ABCD a
Cho hình chóp tứ giác đều có cạnh đáy bằng , cạnh bên hợp ◦ a V S.ABCD
với mặt đáy một góc 60 . Tính theo thể tích của khối chóp . √ √ √ A a3 a3 a3 a3 V 6 B V 6 C V 6 D V . = . . = . . = . . = . 6 2 3 3 Câu 16. ABC.A0B0C0 ABC a Cho lăng trụ có đáy
là tam giác đều cạnh bằng 2 . Hình A0 ABC H chiếu vuông góc √của lên mặt phẳng ( ) trùng với trung điểm của cạnh BC A0H a a V ABC.A0B0C0 và = 3. Tính theo thể tích của khối lăng trụ . A a3 a3 V a 3 3 3 B V a3 C V D V . = 3 . . = . . = . . = . 4 2 Soạn: Huỳnh Phú Sĩ 70
Trường THCS-THPT Mỹ Thuận
§3. Khái niệm về thể tích của khối đa diện TOÁN 12 Câu 17. a
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2 . Thể tích của khối chóp đã cho √ bằng √ √ A a3 a3 a3 a3 4 2 B 8 C 8 2 D 2 2 . . . . . . . . 3 3 3 3 √ Câu 18. S.ABCD a
√Cho hình chóp đều có chiều cao bằng 2 và độ dài cạnh bên a S.ABCD bằng 6. Tính √ thể tích khối chóp √ . √ √ A a3 a3 a3 a3 8 2 B 10 2 C 8 3 D 10 3 . . . . . . . . 3 3 3 3
Câu 19. Cho khối lăng trụ
√ tam giác đều có tất cả các cạnh bằng nhau và thể tích
của khối lăng trụ bằng 2
3. Tính cạnh của khối lăng trụ. A B C D . 6. . 4. . 3. . 2. Câu 20. S.ABC ABC Cho hình chóp tam giác có đáy là S a SA tam giác đều cạnh 2 và vuông góc với mặt ABC phẳng (
) (tham khảo hình vẽ). Biết thể tích √ a3 S.ABC 3 của khối chóp là và góc giữa hai 2 SBC ABC α mặt phẳng ( ) và ( ) là góc nhọn . Chọn phát biểu đúng. A α ◦ B α ◦ A C √ . = 60 . . = 45 . C α ◦ D α 3 . = 30 . . tan = . 2 B Câu 21. MNPQ I, J, K Cho tứ diện . Gọi lần lượt là trung điểm của các cạnh V MN, MP, MQ MIJK . Tỉ số V bằng MNPQ A 1 B 1 C 1 D 1 . . . . . . . . 3 4 8 6 Câu 22. S.ABC M N SA SB Cho hình chóp , gọi ,
lần lượt là trung điểm của cạnh , . VS.ABC Tính tỉ số . VS.M NC A B 1 C D 1 . 4. . . . 2. . . 2 4 Câu 23. ABCD M N P AB AC Cho tứ diện . Các điểm , ,
lần lượt thuộc các cạnh , , AD MA MB NA NC PA PD AMNP sao cho = , = 2 , = 3
. Biết thể tích khối tứ diện V ABCD V bằng thì khối tứ diện tính theo có giá trị là A V B V C V D V . 4 . . 6 . . 12 . . 8 . Câu 24. S.ABCD Cho khối chóp
có đáy là hình bình hành và có thể tích 48. Trên SA0 SA, SB, SC, SD A0, B0, C0 D0 các cạnh
lần lượt lấy các điểm và sao cho SA = SC0 SB0 SD0 1 3 V S.A0B0C0D0 SC = và SB = SD = . Tính thể tích của khối đa diện . 3 4 A V B V C V 3 D V . = 4. . = 9. . = . . = 6. 2 Câu 25. ABC.A0B0C0 V Cho khối lăng trụ có thể tích bằng . Thể tích của khối đa ABCC0B0 diện bằng A V V V V 3 B 2 C D . . . . . . . . 4 3 2 4 Câu 26. , 3
Một bể cá hình hộp chữ nhật có thể tích 0 36m . Biết kích thước của đáy , ,
bể lần lượt bằng 0 5m và 1 2m. Chiều cao của bể cá bằng A , B , C , D , . 0 65m. . 0 6m. . 0 7m. . 0 5m.
Câu 27. Tính thể tích của khối gỗ có hình dạng dưới đây 14cm 4cm 15cm 7cm 6cm A 3 B 3 C 3 D 3 . 328cm . . 456cm . . 584cm . . 712cm . Soạn: Huỳnh Phú Sĩ 71
Trường THCS-THPT Mỹ Thuận
§3. Khái niệm về thể tích của khối đa diện TOÁN 12
Câu 28. Một tấm bìa hình vuông có cạnh 44cm, người ta cắt bỏ đi ở mỗi góc tấm
bìa một hình vuông cạnh 12cm rồi gấp lại thành một cái hộp chữ nhật không có
nắp. Tính thể tích cái hộp này. √ A 3 B 3 C 3 D 3 . 4800cm . . 9600cm . . 2400cm . . 2400 3cm .
Câu 29. Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không 3
đổi bằng 8m , thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. . 2
Trên thị trường, giá tôn làm đáy thùng là 100 000 đồng/m , giá tôn làm thành xung . 2
quanh thùng là 50 000 đồng/m . Hỏi người bán gạo đó cần đóng thùng đựng gạo
với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất? A B , C D . 3m. . 1 5m. . 2m. . 1m. Câu 30.
Các kích thước của một bể bơi được 25m
cho trên hình vẽ (mặt nước có dạng 2 m m
hình chữ nhật). Hãy tính xem bể bơi 10
chứa được bao nhiêu mét khối nước khi nó đầy ắp nước? A 3 B 3 . 1000m . . 640m . m C 4 3 D 3 . 570m . . 500m . 7m L TỰ LUẬN Câu 1 (SGK GT12). a
Tính thể tích khối tứ diện đều cạnh . Câu 2 (SGK GT12). S.ABC SA, SB, SC A0, B0, C0 S Cho hình chóp . Trên các đoạn thẳng lần lượt lấy ba điểm khác với . Chứng minh rằng VS.A0B0C0 SA0 SB0 SC0 · · V = S.ABC SA SB SC Câu 3 (SGK GT12). ABCD.A0B0C0D0 a M A0B0 N BC Cho hình lập phương cạnh . Gọi là trung điểm của , là trung điểm của . ADMN a)
Tính thể tích khối tứ diện DMN H A H0 b) Mặt phẳng (
) chia khối lập phương đã cho thành hai khối đa diện. Gọi (
) là khối đa diện chứa đỉnh , ( ) là khối đa diện còn lại. V H ( ) Tính tỉ số V . H0 ( ) d Vocabulary volume base ratio thể tích mặt đáy tỉ số area height rectangular diện tích chiều cao hình hộp chữ nhật Soạn: Huỳnh Phú Sĩ 72
Trường THCS-THPT Mỹ Thuận
Chương 2. Mặt nón, mặt trụ, mặt cầu TOÁN 12 Chương 2.
MẶT NÓN, MẶT TRỤ, MẶT CẦU
§1.KHÁI NIỆM VỀ KHỐI TRÒN XOAY Đặt vấn đề Xung quanh chúng ta có nhiều vật thể mà mặt ngoài của nó có hình dạng là những mặt tròn xoay như bình hoa, nón lá,
cái bát (chén) ăn cơm, cái cốc uống nước, một số chi tiết máy... Nhờ có bàn xoay với sự khéo léo của đôi bàn tay, người thợ gốm có thể tạo nên những vật dụng có dạng tròn xoay bằng đất sét. Dựa vào sự quay tròn của trục máy điện, người thợ cơ
khí có thể tạo nên những chi tiết máy bằng kim loại có dạng
tròn xoay. Vậy các mặt tròn xoay được hình thành như thế nào? 1
SỰ TẠO THÀNH MẶT TRÒN XOAY P C
Trong không gian cho mặt phẳng (
) chứa đường thẳng ∆ và một đường . Khi . . . . . . P . . . . . . M C mặt phẳng ( ) quanh ∆ một góc thì mỗi điểm trên đường vạch . . . . . . O ∈ ra một đường có tâm
∆ và nằm trên mặt phẳng vuông góc với ∆. Như P C vậy khi quay mặt phẳng (
) quanh đường thẳng ∆ thì đường sẽ tạo nên một hình
. . . . . . . . . . . . . . . . . . được gọi là C . . . . . . . . . . . . • Đường được gọi là . . . . . . •
Đường thẳng ∆ được gọi là C . . . . . . C Nếu
là đường thẳng cắt ∆ thì ta được một mặt tròn xoay, nếu là đường thẳng . . . . . .
song song với ∆ thì ta được một mặt tròn xoay. 2 MẶT NÓN TRÒN XOAY 1 Định nghĩa P d . . . . . . O Trong mặt phẳng ( ) cho hai đường thẳng và ∆ nhau tại điểm và tạo β
. . . < β < . . . P thành góc với Khi quay mặt phẳng (
) xung quanh ∆ thì đường d . . . . . . . . . . . . . . . O thẳng sinh ra một mặt được gọi là mặt tròn xoay đỉnh , gọi tắt . . . . . . . . . . . . là . . . . . . . . . . . . Đường thẳng
gọi là trục, đường thẳng gọi là đường sinh.
2 Hình nón tròn xoay và khối nón tròn xoay OIM I 4OIM Cho tam giác vuông tại . Khi quay quanh OI . . . . . . . . . OIM . . . . . . cạnh thì đường tạo thành một . . . . . . . . . . . .
được gọi là hình nón tròn xoay, gọi tắt là I IM . . . . . . . . . • Hình tròn tâm , bán kính gọi là O . . . . . . • Điểm gọi là của hình nón OI . . . . . . . . . OM • Đoạn gọi là , đoạn là độ dài . . . . . . . . . . . . Khối nón tròn xoay . . . . . . . . . . . . . . . . . . là phần
được giới hạn bởi một nón tròn xoay, kể . . . . . . cả nón đó. Soạn: Huỳnh Phú Sĩ 73
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối tròn xoay TOÁN 12 Ví dụ 1. ABC H BC Cho tam giác đều cạnh 3cm, gọi là trung điểm của cạnh . Nếu xoay 4ABC AH h . . . . . . quanh đường cao
thì ta thu được một hình nón có chiều cao = cm, ` . . . . . . S . . . . . . . . . độ dài đường sinh = cm và diện tích đáy đ =
3 Diện tích và thể tích h ` r Cho hình nón có chiều cao , độ dài đường sinh và bán kính đáy . Khi đó: Diện tích xung quanh Diện tích toàn phần Thể tích Ví dụ 2. h r Cho hình nón có chiều cao = 4cm và bán kính đáy = 3cm. Hãy tính diện
tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón tạo bởi hình nón đã cho. 3 MẶT TRỤ TRÒN XOAY 1 Định nghĩa P ` . . . . . . . . . . . . Trong mặt phẳng ( ) cho hai đường thẳng và ∆ với nhau, cách nhau r P ` một khoảng . Khi quay mặt phẳng (
) xung quanh ∆ thì đường thẳng sinh ra . . . . . . . . . . . . . . . . . . . . . . . . . . . một mặt được gọi là mặt tròn xoay, gọi tắt là . . . . . . . . . . . . r . . . . . . . . . Đường thẳng
gọi là trục, đường thẳng gọi là đường sinh, là của mặt trụ đó.
2 Hình trụ tròn xoay và khối trụ tròn xoay ABCD ABCD AB Cho hình chữ nhật . Khi quay quanh cạnh thì . . . . . . . . . ADCB . . . . . . đường tạo thành một được gọi là hình trụ . . . . . . . . . . . . tròn xoay, gọi tắt là A AD . . . . . . . . . • Hình tròn tâm , bán kính gọi là AB . . . . . . . . . CD . . . . . . . . . . . . • Đoạn gọi là , đoạn là độ dài Khối trụ tròn xoay . . . . . . . . . . . . là phần được giới hạn bởi một . . . . . . . . . . . . trụ tròn xoay, kể cả trụ đó. Ví dụ 3. ABCD M, N Cho hình vuông cạnh 3cm, gọi lần lượt là AB, CD ABCD
trung điểm của các cạnh . Nếu xoay quanh đường MN . . . . . . h . . . thẳng
thì ta thu được một hình có chiều cao = cm, ` . . . S . . . . . . . . . độ dài đường sinh = cm và diện tích đáy đ = .
3 Diện tích và thể tích h r
Cho hình trụ có chiều cao và bán kính đáy . Khi đó: Diện tích xung quanh Diện tích toàn phần Thể tích Ví dụ 4. ,
Hộp sữa đặc Ông Thọ có chiều cao 8cm và đường kính đáy 7 5cm. Hãy tính
diện tích phần nhãn dán bao quanh thân hộp sữa và dung tích sữa tối đa trong hộp. Soạn: Huỳnh Phú Sĩ 74
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối tròn xoay TOÁN 12 4 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. l, h, R Gọi
lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của V một khối nón. Thể tích của khối nón đó là A V 1 πR 1 2 h B V πR2h C V πR2l D V πR2l . = . . = . . = . . = . 3 3 Câu 2. R h
Thể tích của khối trụ có bán kính đáy và chiều cao là A V πR 4 1 2 h B V πR2h C V πR2h D V πR2h . = 2 . . = . . = . . = . 3 3 Câu 3. a
Cho hình trụ có bán kính đáy bằng 2
, một mặt phẳng đi qua trục của V
hình trụ và cắt hình trụ theo thiết diện là hình vuông. Tính thể tích của khối trụ đã cho. A V πa3 B V πa3 C V πa3 D V πa3 . = 18 . . = 4 . . = 8 . . = 16 . Câu 4. r S π
Cho hình trụ có bán kính đáy
= 3 và diện tích xung quanh = 6 . Tính V thể tích của khối trụ. A V π B V π C V π D V π . = 3 . . = 9 . . = 18 . . = 6 .
Câu 5. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập a phương cạnh
. Tính thể tích của khối trụ đã cho. A πa3 πa3 πa3 πa3 V B V C V D V . = . . = . . = . . = . 12 6 2 4
Câu 6. Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình ABCD AB CD AB a AC a chữ nhật có và
thuộc hai đáy của hình trụ, biết = 4 , = 5 .
Tính thể tích của khối trụ. A V πa3 B V πa3 C V πa3 D V πa3 . = 4 . . = 16 . . = 12 . . = 8 . Câu 7. ABCD AB a BC b M, N Cho hình chữ nhật có = , = . Gọi lần lượt là trung AB CD ABCD điểm của và
. Tính thể tích khối trụ thu được khi quay hình chữ nhật MN quanh trục . A πa2b πa2b πa2b V B V πa2b C V D V . = . . = . . = . . = . 4 12 3
Câu 8. Cho hình trụ có bán kính đường tròn đáy bằng 4, diện tích xung quanh π bằng 48
. Tính thể tích của khối trụ đã cho. A V π B V π C V π D V π . = 24 . . = 32 . . = 96 . . = 72 .
Câu 9. Một hình trụ có đường kính đáy 12cm, chiều cao 10cm. Thể tích khối trụ này là A π 3 B π 3 C π 3 D 3 . 1440 cm . . 360 cm . . 480 cm . . 1440 cm . Câu 10. l r
Một khối nón có độ dài đường sinh = 13cm và bán kính đáy = 5cm.
Tính thể tích khối nón đã cho. A V π 3 B V π 3 . = 100 cm . . = 300 cm . C π V π 325 3 D V 3 . = 20 cm . . = cm . 3 Câu 11. N h R Cho hình nón ( ) có chiều cao , bán kính đáy và độ dài đường sinh l S N
. Công thức tính diện tích xung quanh của ( ) là A S 1 πRl B S πRl C S πR2 D S πRl . = . . = . . = 4 . . = 2 . 3
Câu 12. Cho một hình trụ có thiết diện qua trục là một hình chữ nhật có diện
tích bằng 18. Tính diện tích xung quanh của hình trụ đã cho. A S B S C S π D S π . xq = 9. . xq = 18. . xq = 9 . . xq = 18 . Câu 13. S S
Cho hình trụ có thiết diện qua trục là một hình vuông. Gọi 1 , 2 lần
lượt là diện tích xung quanh và diện tích toàn phần của hình trụ. Tính giá trị của S1 S . 2 A 1 B 2 C 3 D 4 . . . . . . . . 2 3 4 5
Câu 14. Cắt một hình trụ bởi một mặt phẳng qua trục của nó, ta được thiết diện a
là một hình vuông có cạnh bằng 3
. Tính diện tích toàn phần của hình trụ đã cho. A πa2 πa2 πa2 S 9 B S 13 C S πa 27 2 D S . tp = . . tp = . . tp = 9 . . tp = . 2 6 2 Câu 15. R
Diện tích xung quanh của hình trụ có bán kính đáy = 3 và đường sinh l = 6 bằng A π B π C π D π . 54 . . 18 . . 108 . . 36 . Soạn: Huỳnh Phú Sĩ 75
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối tròn xoay TOÁN 12 Câu 16. a a
Cho hình trụ có bán kính đáy bằng , chiều cao bằng 3 . Diện tích xung quanh của hình trụ bằng A πa2 B πa2 C πa2 D πa2 . 6 . . 3 . . 9 . . 4 . Câu 17. a a
Cho hình nón có bán kính đáy bằng 4 và chiều cao bằng 3 . Diện tích
xung quanh của hình nón bằng A πa2 B πa2 C πa2 D πa2 . 18 . . 20 . . 12 . . 15 . Câu 18. h Tính chiều cao
của khối nón có bán kính đáy bằng 3 và thể tích bằng π 36 . A h B h C h D h . = 18. . = 12. . = 6. . = 16. Câu 19. ABC A AB a Cho tam giác vuông tại có = , AC a l = 2
. Tính độ dài đường sinh của hình B ABC
nón nhận được khi quay tam giác quanh AB trục . √ a ? A l a B l a . = √2. . = 2 . √ C l a D l a . = 3. . = 5. A a 2 C Câu 20. OAB O AB a ◦ b A Cho tam giác vuông tại có = và góc = 30 .
Tính diện tích xung quanh của hình nón có được khi quay A OAB AO tam giác quanh trục . ◦ A πa2 B πa2 πa 30 2 C πa2 D . . . 2 . . . . . a 4 2 O B Câu 21. πa2
Cho hình nón có diện tích xung quanh bằng 3 và bán kính đáy bằng a 2
. Độ dài đường sinh của hình nón đã cho bằng √ A a a B a C a D 3 . 2 2. . 3 . . 2 . . . 2
Câu 22. Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh a góc vuông bằng
. Tính diện tích xung quanh của hình nón √ đã cho. A πa2 πa2 S B S 2 . xq = . . xq = . 2 2 C πa2 S 3 D S πa2 . xq = . . xq = . 2 Câu 23. πa2
Tìm bán kính đáy của hình nón có diện tích xung quanh là 3 và độ a dài đường sinh là 3 . A a B a C a D a . 3 . . . . 2 . . 4 . Câu 24. πa2
Cho hình nón có diện tích xung quanh bằng 3 và bán kính đáy bằng
a. Tính tang của góc giữa một đường sinh và mặt đáy √ của hình nón. √ A B C 2 2 D 1 . 8. . 2 2. . . . . 3 3 Câu 25. a
Cho hình nón có thiết diện qua trục là một tam giác đều cạnh bằng .
Tính diện tích mặt xung quanh của hình nón đã cho. A 1πa 2 1 2 B πa2 C πa2 D πa2 . . . . . . . . 2 3 3 √ Câu 26. r l
Cho hình nón có bán kính đáy =
2 và độ dài đường sinh = 3. Tính
diện tích xung quanh của hình nón đã √ cho. √ A S π B S π C S π D S π . xq = 2 . . xq = 3 2. . xq = 6 . . xq = 6 2. Câu 27. a a
Cho hình nón có bán kính đáy bằng , chiều cao 2 . Độ dài đường sinh của hình nón √ bằng √ √ A a B a C a D a . 3. . 2 3. . 5. . 4 . Câu 28. a a
Cho hình nón có bán kính đáy bằng
và độ dài đường sinh bằng 2 .
Diện tích xung quanh của hình nón đó bằng A πa2 B a2 C πa2 D πa2 . 4 . . 2 . . 2 . . 3 . Câu 29. a a
Cho hình nón có bán kính đáy bằng
và độ dài đường sinh bằng 3 .
Diện tích xung quanh của hình nón đó bằng A πa 3 2 B πa2 C πa2 D πa2 . 3 . . 2 . . . . . 2 Soạn: Huỳnh Phú Sĩ 76
Trường THCS-THPT Mỹ Thuận
§1. Khái niệm về khối tròn xoay TOÁN 12
Câu 30. Bình Định có câu ca dao:
"Cưới nàng đôi nón Gò Găng
Xấp lãnh An Thái một khăn trầu nguồn."
Nói đến câu ca dao này là nói đến một làng nghề truyền thống có hàng trăm năm
tuổi của thị xã An Nhơn, tỉnh Bình Định - làng nghề làm nón lá Gò Găng. Nhân
kỷ niệm 10 năm được công nhận thị xã, thị xã An Nhơn lên kế hoạch làm các mô
hình biểu tượng làng nghề truyền thống trên địa bàn, trong đó có mô hình chiếc ,
nón lá Gò Găng. Chiếc nón có bán kính đáy 1 mét và chiều cao 1 5 mét, khung
thép dùng làm đường tròn đáy và 10 đường nối từ đỉnh của nón đến đường tròn .
đáy có giá thành 40 000 đồng/mét, là của cây lá nón Licuala Fatoua Becc dùng để .
làm mặt nón có giá thành 20 000 đồng/mét vuông. Hỏi nếu bỏ qua diện tích các
mép nối thì kinh phí để làm chiếc nón biểu tượng này là bao nhiêu? A . . B . . . 1 085 000 đồng. . 1 086 000 đồng. C . D . . 834 000 đồng. . 833 000 đồng. L TỰ LUẬN Câu 1 (SGK GT12). h r
Cho hình nón tròn xoay có đường cao = 20cm, bán kính đáy = 25cm. a)
Tính diện tích xung quanh của hình nón đã cho b)
Tính thể tích của khối nón được tạo thành bởi hình nón đó. c)
Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12cm. Tính
diện tích thiết diện đó. Câu 2 (SGK GT12). r
Một hình trụ có bán kính đáy
= 5cm và có khoảng cách giữa hai đáy bằng 7cm. a)
Tính diện tích xung quanh của hình trụ và thể tích của khối trụ tạo nên b)
Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3cm. Hãy tính diện tích của thiết diện được tạo nên. d Vocabulary circular generator line curved surface area tròn xoay đường sinh diện tích xung quanh conical surface axis surface area mặt nón trục diện tích toàn phần cylinder surface radius cross-section mặt trụ bán kính thiết diện Soạn: Huỳnh Phú Sĩ 77
Trường THCS-THPT Mỹ Thuận §2. Mặt cầu TOÁN 12 §2.MẶT CẦU Đặt vấn đề
Hình dạng của Trái Đất rất gần với hình phỏng cầu là hình cầu
bị nén dọc theo hướng từ địa cực tới chỗ phình ra ở xích đạo.
Phần phình ra này là kết quả của quá trình tự quay và khiến cho
độ dài đường kính tại đường xích đạo dài hơn 43 km so với độ
dài đường kính tính từ cực tới cực. Độ dài đường kính trung bình
của hình phỏng cầu tham chiếu vào khoảng 12.745 km. (Theo Wikipedia) Nếu xem Trái Đất là một hình cầu với đường kính như 2 trên thì diện tích bề mặt của Trái Đất là bao nhiêu km ? 1
MẶT CẦU VÀ CÁC KHÁI NIỆM LIÊN QUAN ĐẾN MẶT CẦU 1 Mặt cầu
Tập hợp những điểm M trong . . . . . . . . . . . . cách điểm O cố định một khoảng
. . . . . . . . . . . . bằng r >
được gọi là mặt cầu tâm O bán kính r. 0 . . . . . . . . . Kí hiệu: C, D ∈ S S r CD . . . . . . . . . . . . • Nếu hai điểm ( ; ) thì đoạn thẳng gọi là . . . . . . . . . . . . . •
Dây cung đi qua tâm được gọi là của mặt cầu.
2 Điểm nằm trong và nằm ngoài mặt cầu. Khối cầu S O r M Cho mặt cầu ( ; ) và điểm bất kì. OM r M . . . . . . S O r • Nếu = thì nằm mặt cầu ( ; ) ! OM < r M . . . . . . S O r • Nếu thì nằm mặt cầu ( ; ) OM > r M . . . . . . S O r • Nếu thì nằm mặt cầu ( ; ) A OA ≤ r . . . . . . . . . . . . O Tập hợp các điểm sao cho được gọi là cầu hay cầu tâm bán r kính .
3 Đường kinh tuyến và vĩ tuyến của mặt cầu ¹ . . . . . . . . . Giao
của mặt cầu với các nửa mặt phẳng có bờ là trục của mặt cầu được kinh tuyến gọi là của mặt cầu. ¹ . . . . . . . . . . . .
Giao tuyến của mặt cầu với các mặt phẳng
với trục (nếu có) được gọi . . . . . . . . . . . . là của mặt cầu. ¹ . . . . . . cực Hai giao
của mặt cầu với trục được gọi là của mặt cầu. 2
GIAO CỦA MẶT CẦU VÀ MẶT PHẲNG S O r P H O P Cho mặt cầu ( ; ) và mặt phẳng ( ). Gọi
là hình chiếu vuông góc của lên ( ), khi OH O, P đó = d ( ( )). ○ OH > r P S . . . . . . . . . Nếu thì ( ) và ( ) điểm chung. ○ OH r P . . . . . . . . . S . . . Nếu = thì ( ) với ( ) tại . P
. . . . . . . . . . . . H . . . . . . . . . . . . Khi đó, ( ) gọi là , gọi là ○ OH < r P S . . . . . . . . . . . . . . . Nếu thì ( ) cắt ( ) theo giao tuyến là tâm , bán kính r0 . . . . . . . . . = (Pitago). Soạn: Huỳnh Phú Sĩ 78
Trường THCS-THPT Mỹ Thuận §2. Mặt cầu TOÁN 12 OH . . . r OH . . . r OH . . . r 3
GIAO CỦA MẶT CẦU VÀ ĐƯỜNG THẲNG. TIẾP TUYẾN S O r H O Cho mặt cầu ( ;
) và đường thẳng ∆. Gọi
là hình chiếu vuông góc của lên ∆, khi OH O, đó = d ( ∆). ○ OH > r S . . . . . . . . . Nếu thì ∆ và ( ) điểm chung. ○ OH r . . . . . . . . . S . . . Nếu = thì ∆ với ( ) tại .
. . . . . . . . . . . . H . . . . . . . . . . . . Khi đó, ∆ gọi là , gọi là ○ OH < r S . . . Nếu thì ∆ cắt ( ) tại điểm. OH . . . r OH . . . r OH . . . r Nhận xét. M . . . . . . • Qua một điểm nằm trên mặt cầu, có
tiếp tuyến với mặt cầu. Các tiếp tuyến . . . . . . . . . . . . này tạo thành một của mặt cầu. M . . . . . . • Qua một điểm nằm ngoài mặt cầu, có
tiếp tuyến với mặt cầu. Các tiếp . . . . . . . . . A
tuyến này tạo thành một đỉnh . OM > r M . . . . . . S O r • Nếu thì nằm mặt cầu ( ; ) 4 DIỆN TÍCH VÀ THỂ TÍCH r Cho mặt cầu bán kính . Khi đó: Diện tích Thể tích
Ví dụ 1. Có một con quạ đang khát nước. Nó tìm thấy một cái hộp hình trụ tròn có bán
kính đáy 5cm và cao 20cm. Trong hộp ước chừng có khoảng 1 lít nước. Nó bay ra bờ
sông và tìm thấy mấy viên bi của các bạn nhỏ lớp sáu bỏ lại, nó dùng mỏ gắp từng viên
và bỏ vào trong hộp. Biết rằng mỗi viên bi có đường kính 1cm, hỏi con quạ cần bỏ vào
tối thiểu bao nhiêu viên bi để nước dâng lên đến miệng hộp? Soạn: Huỳnh Phú Sĩ 79
Trường THCS-THPT Mỹ Thuận §2. Mặt cầu TOÁN 12 5 THỰC HÀNH Í TRẮC NGHIỆM Câu 1. S R Cho hình cầu có diện tích và bán kính . Mệnh đề nào sau đây là đúng? A S 4 πR3 B S πR2 C S πR2 D S πR2 . = . . = 2 . . = . . = 4 . 3 Câu 2. πa2 8 R
Cho mặt cầu cầu có diện tích bằng . Tính bán kính của mặt cầu 3 đó. √ √ √ √ A a a a a R 6 B R 6 C R 2 D R 6 . = . . = . . = . . = . 3 2 3 6 Câu 3. R Cho mặt cầu có bán kính
= 3. Thể tích mặt cầu đó bằng A π π B 81π C π D 4 . 9 . . . . 36 . . . 4 3 Câu 4. π 16
Cho mặt cầu có thể tích
. Tính đường kính mặt cầu đã cho. 3 A B C D π . 1. . 2. . 4. . 4 . Câu 5. R Cho mặt cầu có bán kính
= 3. Diện tích hình tròn qua tâm bằng A π B π C π D π . 3 . . 6 . . 4 . . 9 .
Câu 6. Một khối cầu có đường kính bằng 10cm. Người ta dùng một mặt phẳng cách tâm khối cầu 3cm để cắt khối cầu thành hai phần. Diện tích của mặt cắt bằng A B π 2 C 2 D π 3 . 16cm. . 16 cm . . 16cm . . 16 cm .
Câu 7. Trong các lăng trụ sau, lăng trụ nào nội tiếp được trong một mặt cầu?
A. Lăng trụ có đáy là hình chữ nhật.
B. Lăng trụ có đáy là hình vuông.
C. Lăng trụ đứng có đáy là hình thoi.
D. Lăng trụ đứng có đáy là hình thang cân. Câu 8. sai
Trong các mệnh đề sau đây, mệnh đề nào ?
A. Bất kì một hình tứ diện nào cũng có một mặt cầu ngoại tiếp.
B. Bất kì một hình chóp đều nào cũng có một mặt cầu ngoại tiếp.
C. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp.
D. Bất kì một hình hộp chữ nhật nào cũng có một mặt cầu ngoại tiếp. Câu 9. a, b, c
Một hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là . Khi r đó bán kính của mặt cầu bằng √ √
A 1 a2 b2 c2 B a2 b2 c2 . + + . . + + . √ 2 C a b c p 2 2 2 a + + 2 b2 c2 D . 2 ( + + ). . . 3 Câu 10. S.ABC ABC A SA Cho hình chóp có đáy là tam giác vuông tại , có vuông ABC SA a AB b AC c góc với mặt phẳng ( ) và có = , = , =
. Mặt cầu đi qua các đỉnh A, B, C, S r có bán kính bằng √ A a b c 2( + + ) B a2 b2 c2 . . . 2 + + . 3 √ √
C 1 a2 b2 c2 D a2 b2 c2 . + + . . + + . 2 L TỰ LUẬN Câu 1 (SGK GT12). S.ABCD a
Cho hình chóp tứ giác đều
có tất cả các cạnh đều bằng
. Hãy xác định tâm và bán kính mặt
cầu ngoại tiếp hình chóp đó. Câu 2 (SGK GT12). S.ABC SA a SB b SC c Cho hình chóp
có bốn đỉnh nằm trên một mặt cầu, = , = , = và ba cạnh
SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó. Soạn: Huỳnh Phú Sĩ 80
Trường THCS-THPT Mỹ Thuận §2. Mặt cầu TOÁN 12 d Vocabulary sphere inscribe mặt cầu nội tiếp chord circumscribe dây cung ngoại tiếp diameter tangent plane đường kính tiếp diện meridian of longitude parallel of of latitude kinh tuyến vĩ tuyến Soạn: Huỳnh Phú Sĩ 81
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 PHỤ LỤC 1 HÀM SỐ
1 Tập xác định của hàm số y f x x f x
Tập xác định của hàm số = (
) là tập hợp các số thực sao cho biểu thức ( ) XÁC ĐỊNH (có nghĩa). √A A ≥ • xác định khi 0. A B 6 • B xác định khi = 0.
2 Hàm số chẵn, hàm số lẻ y f x D Cho hàm số = ( ) có tập xác định . ( (
∀x ∈ D Ñ −x ∈ D
∀x ∈ D Ñ −x ∈ D f x ⇔ f x ⇔ ( ) chẵn f −x f x ( ) lẻ f −x −f x ( ) = ( ) ( ) = ( ) y y O x O x
Đồ thị hàm chẵn nhận trục tung làm
Đồ thị hàm lẻ nhận gốc tọa độ làm TÂM TRỤC ĐỐI XỨNG ĐỐI XỨNG
3 Một vài hàm số thông dụng x d y = Hàm hằng y c y c c c =
Hàm hằng là hàm số có dạng = (
là hằng số). Hàm hằng có đồ thị là đường thẳng c
song song với trục hoành, cắt trục tung tại điểm có giá trị là . x d
Tương tự, đường thẳng =
song song với trục tung, cắt trục hoành tại điểm có giá trị d x d bằng . O
Hàm số bậc nhất một ẩn (Hàm số tuyến tính) y ax b a 6 hệ số góc Dạng: = + ( = 0 gọi là ). y x y = 2 + 3 •
Đồ thị: đường thẳng. (a > R 0 Đồng biến trên y x • Sự biến thiên: = 2 a < R. 0 Nghịch biến trên ! y a x b y a x b
Cho hai đường thẳng ∆1 : = 1 + 1 và ∆2 : = 2 + 2 , khi đó: ◦ ∥ ⇔ a a ◦ ⊥ ⇔ a · a − ∆ ∆ ∆ ∆ 1. x 1 2 1 = 2 . 1 2 1 2 = O
Hàm số bậc hai một ẩn y ax2 bx c a 6 R Hàm số = + + ( = 0) có tập xác định
, đồ thị là một parabol: b y x I − − ∆ Hai đường thẳng = 2 + 3 và • Đỉnh: a ; a . y x 2 4 = 2 có hệ số góc bằng nhau b nên song song. x − • Trục đối xứng: = a . 2 a > a < • Bề lõm hướng lên nếu 0, hướng xuống nếu 0. • Bảng biến thiên: Soạn: Huỳnh Phú Sĩ 82
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 a > a < 0 0 b b x −∞ − ∞ x −∞ − ∞ a + a + 2 2 ∞ ∞ + + − ∆ − a y y 4 − ∆ − a −∞ −∞ 4
4 Xét dấu biểu thức
Nhị thức bậc nhất f x ax b a 6 ( ) = + ( = 0) b x −∞ − ∞ a + f x ( ) Trái dấu với a 0 Cùng dấu với a
Tam thức bậc hai f x ax2 bx c a 6 ( ) = + + ( = 0) < • ∆ 0 x −∞ ∞ + f x ( ) Cùng dấu với a • ∆ = 0 b x −∞ − ∞ a + 2 f x ( ) Cùng dấu với a 0 Cùng dấu với a > • ∆ 0 x −∞ x x ∞ 1 2 + f x ( ) CÙNG 0 TRÁI 0 CÙNG Hệ quả ( ( ! a > a < ax 0 0 2 bx
c ≥ , ∀x ∈ R ⇔ ax2 bx
c ≤ , ∀x ∈ R ⇔ • + + 0 ≤ • + + 0 ≤ ∆ 0 ∆ 0 ( ( a > a < ax 0 0 2 bx
c > , ∀x ∈ R ⇔ ax2 bx
c < , ∀x ∈ R ⇔ • + + 0 < • + + 0 < ∆ 0 ∆ 0
5 Giới hạn của hàm số  Giới hạn một bên f x x > x • lim ) Giới hạn bên phải xÏx ( ( 0 ). + 0 f x x < x • lim ) Giới hạn bên trái xÏx− ( ( 0 ). 0  f x L y  lim ( ) =  xÏx+ f x L ⇔ 0 • lim xÏx ( ) = f x L 0   lim ) = xÏx− ( 0  Hàm số liên tục f x x ⇔ f x f x • Hàm số ( ) liên tục tại 0 lim xÏx ( ) = ( 0 ). 0 O R x •
Hàm đa thức liên tục trên . 2 tập xác định •
Hàm số lượng giác, hàm phân thức. . . liên tục TRÊN TỪNG KHOẢNG của .
6 Đạo hàm của hàm số
♥ Quy tắc tính đạo hàm x y + 1 Hàm số = x − liên tục 0 u 0 u0 · v − u · v0 2 u ± v u0 ± v0 −∞ • ( ) = • = trên khoảng ( ; 2) và v v2 ∞ (2; + ). u · v 0 u0 · v u · v0 y0 y0 · u0 • ( ) = + • x = u x (hàm hợp) Soạn: Huỳnh Phú Sĩ 83
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12
♥ Đạo hàm của một số hàm thường gặp 0 x 0 x • hằng số = 0 • (sin ) = cos xn 0 n · xn−1 0 • ( ) = x − x • (cos ) = sin ◦ x 0 ( ) = 1 0 x 0 1 2 x ◦ 1 − 1 • (tan ) = 2 x = 1 + tan x = x cos 2 √ ◦ x0 1 √ x 0 − 1 − 2 x = x • (cot ) = 1 + cot 2 2 x = sin
♥ Đạo hàm cấp n: y n n− 0 ( ) y( 1) = ♥ Vi phân: dy y0 · dx = Ứng dụng của đạo hàm Trong Vật Lý: s t •
Nếu một chất điểm chuyển động theo phương trình ( ) thì ◦ v t s0 t
Vận tốc tức thời tại thời điểm t là ( ) = ( ). ◦ a t v0 t
Gia tốc tức thời tại thời điểm t là ( ) = ( ). Trong Hình Học: y f x M x y •
Phương trình tiếp tuyến của đồ thị hàm số = ( ) tại điểm ( 0 ; 0 ) là y f 0 x · x − x y = ( 0 ) ( 0 ) + 0 ◦ y f x 0 = ( 0 ). ◦ f 0 x ( 0 )
là hệ số góc của tiếp tuyến. 2 PHƯƠNG TRÌNH
1 Phương trình bậc hai ax2 bx c a 6 + + = 0 ( = 0) < • ∆
0: Phương trình vô nghiệm. b x − •
∆ = 0: Phương trình có nghiệm kép = a . 2 √−b x + ∆ = >a  2 √ • ∆
0: Phương trình có 2 nghiệm phân biệt  −b − x ∆ = a 2 Trường hợp đặc biệt xx − = 1 = 1 a b c Ñ c a − b c Ñ c • + + = 0   x . • + = 0 x − . = a = a Định lý Vi-ét ax2 bx c a 6 x , x • Nếu phương trình + + = 0 ( = 0) có hai nghiệm 1 2 thì  bx x S − 1 + 2 = = a cx · x P 1 2 = = a u, v u v S u · v P u, v • Nếu hai số có tổng + = và tích = thì
là hai nghiệm của phương trình x2 − Sx P . + = 0
2 Phương trình bậc 4 trùng phương ax4 bx2 c + + = 0 t x2 t ≥ • Đặt = ( 0). at2 bt c • Giải phương trình + + = 0. t ≥ • Chọn nghiệm 0. x • Kết luận nghiệm . Soạn: Huỳnh Phú Sĩ 84
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 3 Phương trình tích A x ( ) = 0 B x A x · B x · · · Z x ⇔  ( ) = 0 ( ) ( ) ( ) = 0  . . .Z x ( ) = 0
4 Phương trình chứa ẩn trong dấu giá trị tuyệt đối g x ≥ "f x g x ( ) 0  ( ) = ( )  |f x | |g x | ⇔ " |f x | g x ⇔ f x g x • ( ) = ( ) f x −g x • ( ) = ( ) ( ) = ( ) ( ) = ( )   f x −g x ( ) = ( )
5 Phương trình vô tỉ (g x ≥  " f x ≥ pf x g x ⇔ ( ) 0  ( ) 0  • ( ) = ( ) p p f x g x 2 f x g x ⇔ g x ≥ ( ) = [ ( )] • ( ) = ( ) ( ) 0  f x g x ( ) = ( ) 3 LŨY THỪA VÀ CĂN THỨC 1 Lũy thừa an a · a · · · a n ∈ ∗ N = ( ) | {z } n số a a n • gọi là cơ số, gọi là số mũ. n n • 0 = 0, 1 = 1. •
Lũy thừa bậc 2 gọi là bình phương, lũy thừa bậc 3 gọi là lập phương. Tính chất a, b 6 m, n ∈ Z • Với = 0 và , ta có ◦ a n 0 a1 a ◦ am.n am = 1, = . = ( ) . √ m ◦ a n n am ◦ a−n 1 n ∈ ∗ N = = a ( ). a > , n ∈ ∗ N ( 0 ). ◦ am n n + am · an ◦ a · b an · bn = . ( ) = . am a n an ◦ am−n ◦ = an . b = bn . ( ( a > a > b > 1 am > an 0 an > bn • Với m > n thì • Với n > thì 0 ( ( < a < a > b > 0 1 am < an 0 an < bn Với m > n thì Với n < thì 0 2 Căn bậc n √ n ≥ b n a bn a b n a Cho số tự nhiên 2, số được gọi là căn bậc của số nếu = , kí hiệu: = . n n a • Nếu
lẻ thì có duy nhất một căn bậc của . √ √ n a ≥ n a n a − n a • Nếu chẵn và 0 thì có 2 căn bậc của là và . Soạn: Huỳnh Phú Sĩ 85
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 4
CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC
1 Điểm và đường trong tam giác A Ù Đường trung bình M N •
Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm của hai cạnh, nó
luôn song song và bằng một nửa độ dài của cạnh còn lại. B C A •
Mỗi tam giác có 3 đường trung bình.
Ù Đường trung tuyến và trọng tâm M N •
Đường trung tuyến là một đoạn thẳng nối từ đỉnh đến trung điểm của cạnh đối G diện. B C K •
Mỗi tam giác có 3 đường trung tuyến, chúng đồng quy tại một điểm, gọi là TRỌNG A /
TÂM. Khoảng cách từ trọng tâm đến mỗi đỉnh bằng 2 3 độ dài trung tuyến ứng với đỉnh đó. N
Ù Đường cao và trực tâm M H •
Đường cao của một tam giác là đoạn thẳng hạ từ một đỉnh xuống cạnh đối diện
(còn gọi là cạnh đáy ứng với đỉnh đó) và vuông góc với cạnh đó. B C K •
Mỗi tam giác có 3 đường cao, chúng đồng quy tại một điểm, gọi là TRỰC TÂM. A
Ù Đường trung trực và tâm đường tròn ngoại tiếp •
Mỗi đoạn thẳng đều có duy nhất một đường trung trực, do đó mỗi tam giác cũng M N có 3 đường trung trực. B O C •
Ba đường trung trực đồng quy tại một điểm, chính là TÂM ĐƯỜNG TRÒN NGOẠI TIẾP K
của tam giác, nó cách đều 3 đỉnh của tam giác.
Ù Đường phân giác và tâm đường tròn nội tiếp A •
Đường phân giác là đoạn thẳng nối từ đỉnh đến cạnh đối diện và chia góc ở đỉnh
làm 2 phần có số đo góc bằng nhau. •
Mỗi tam giác có 3 đường phân giác, chúng đồng quy tại một điểm, chính là TÂM I
ĐƯỜNG TRÒN NỘI TIẾP tam giác. B C
2 Định lý sin & định lý cosin A Ù Định lý cosin Ù Định lý sin a a b c 2 b2 c2 − bc · A • = + 2 cos R c m A = B = C = 2 a b b sin sin sin 2 a2 c2 − ac · B • = + 2 cos c2 a2 b2 − ab · C • = + 2 cos B a C Số đo góc Độ dài trung tuyến • • b 2 c2 − a2 b2 c2 − a2 A + m 2 + 2 cos = bc a = 2 a 4 2 c2 − b2 a2 c2 − b2 B + m 2 + 2 cos = ac b = 2 a 4 2 b2 − c2 a2 b2 − c2 C + m 2 + 2 cos = ab c = 2 4 Ù Chu vi & diện tích a b c a b c + + • Chu vi = + + . p • Nửa chu vi = . 2 Diện tích S 1 a · h 1 b · h 1 c · h • = a = b = c . 2 2 2 S 1 ab · C 1 bc · A 1 ca · B • = sin = sin = sin . 2 2 2 a · b · c S • = R . 4 S p · r r • = (
là bán kính đường tròn nội tiếp). S
pp p − a p − b p − c • = ( ) ( ) ( ) (Công thức Heron). Soạn: Huỳnh Phú Sĩ 86
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12
Ù Tam giác bằng nhau & tam giác đồng dạng d Tam giác bằng nhau d Tam giác đồng dạng
Hai tam giác được gọi là bằng nhau nếu chúng có các
Hai tam giác được gọi là đồng dạng với nhau nếu chúng
cạnh tương ứng bằng nhau và các góc tương ứng bằng
có các cạnh tương ứng tỉ lệ với nhau (theo cùng một tỉ nhau.
số) và các góc tương ứng bằng nhau. •
Ba cặp cạnh tương ứng bằng nhau (cạnh – cạnh – •
Ba cặp cạnh tương ứng tỉ lệ với nhau, tỉ số đó được cạnh).
gọi là tỉ số đồng dạng. •
Hai cặp cạnh tương ứng và một cặp góc xen giữa •
Hai cặp góc tương ứng bằng nhau.
bằng nhau (cạnh – góc – cạnh). •
Hai cặp cạnh tương ứng tỉ lệ với nhau và một cắp •
Hai cặp góc tương ứng và một cặp cạnh bất kì bằng góc xen giữa bằng nhau.
nhau (góc – cạnh – góc).
3 Phân loại tam giác A Ù Tam giác cân
Tam giác cân là tam giác có 2 cạnh bất kỳ độ dài bằng nhau, hai cạnh này được gọi là
hai cạnh bên, cạnh còn lại được gọi là cạnh đáy. •
Hai cạnh bên chung nhau đỉnh nào thì tam giác sẽ cân tại đỉnh đó và hai góc ở đáy bằng nhau. •
Đường trung tuyến xuất phát từ đỉnh cũng là đường cao và là đường phân giác. B C Ù Tam giác đều M
Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc tương đương ba góc bằng nhau, và A ◦
bằng 60 . Tam giác đều có √ · 3 •
Đường trung tuyến cũng là đường cao, có độ dài bằng cạnh . 2 •
Tâm của đường tròn nội tiếp, tâm của đường tròn ngoại tiếp, trọng tâm và trực tâm trùng nhau. √ B C 3 M R · •
Bán kính đường tròn ngoại tiếp = cạnh . 3 √ S 3 2 · • Diện tích = (cạnh) . 4 Ù Tam giác vuông 4ABC A
Tam giác vuông là tam giác có một vuông. Nếu vuông tại thì C •
Cạnh BC gọi là cạnh huyền, hai cạnh còn lại gọi là cạnh góc vuông, và AB2 AC2 BC2 + = (Định lý Pitago) BC M AM • Trung tuyến = . 2 H AH · BC AB · AC •
Nếu AH là đường cao thì = . α Đối α Đối α sin = tan = Huyền Kề A B α Kề α Kề cos = cot = Huyền Đối C Ù Tam giác vuông cân
Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau. 4 A Nếu ABC vuông cân tại thì M ◦ b B b C 1 • Góc = = 45 . √ S · 2 • Diện tích = (cạnh) . BC · 2 • Cạnh = cạnh 2. α A B Soạn: Huỳnh Phú Sĩ 87
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 5
HÌNH CHÓP & HÌNH LĂNG TRỤ 1 Hình chóp S ␣ Hình chóp
Hình chóp là một đa diện có một mặt là đa giác phẳng (gọi là đáy), còn các mặt còn lại
là các tam giác giác có chung một đỉnh không nằm trong mặt đáy (gọi là đỉnh). •
Hình chóp có đáy là một n-giác cũng được gọi là hình chóp n-giác, riêng hình chóp
tam giác còn được gọi là tứ diện. •
Đoạn thẳng kẻ từ đỉnh và hình chiếu vuông góc của đỉnh xuống mặt đáy được gọi B
là đường cao của hình chóp. A •
Tổng diện tích của tất cả các mặt của hình chóp gọi là diện tích toàn phần, còn tổng
diện tích các mặt bên gọi là diện tích xung quanh của hình chóp. ␣ Hình chóp đều C
Hình chóp đều là hình chóp có đáy là một đa giác đều và đoạn thẳng nối đỉnh với tâm D
của đáy là đường cao của hình chóp. •
Các mặt bên của hình chóp đều là những tam giác cân bằng nhau. •
Hình chóp tam giác đều có đáy là tam giác đều và chân đường cao trùng với trọng tâm của đáy. •
Hình chóp tứ giác đều có đáy là một hình vuông và chân đường cao trùng với tâm của hình vuông. Tứ diện đều •
là hình chóp tam giác đều có các mặt bên là tam giác đều. S S S A B B B A A I I I D C C C
Hình chóp tứ giác đều
Hình chóp tam giác đều Tứ diện đều 2 Hình lăng trụ A B ␣ Hình lăng trụ C
Hình lăng trụ là một đa diện, có hai mặt là những n-giác bằng nhau (gọi là đáy), n mặt
còn lại là các hình bình hành (gọi là mặt bên). Hình lăng trụ có hai mặt đáy song song
và các cạnh bên song song. •
Tổng diện tích tất cả các mặt của hình lăng trụ gọi là diện tích toàn phần, còn tổng
diện tích các mặt bên gọi là diện tích xung quanh. A0 B0 •
Chiều cao của hình lăng trụ là khoảng cách giữa hai đáy. C0 A B ␣ Hình lăng trụ đứng C
Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với đáy. Trong hình lăng trụ đứng •
Các mặt bên là các hình chữ nhật. •
Mỗi cạnh bên đều là đường cao. A0 B0
Hình lăng trụ đều •
là hình lăng trụ đứng có đáy là đa giác đều. C0 ␣ Hình hộp
Hình hộp là hình lăng trụ có đáy là hình bình hành. Hình hộp có 6 mặt là hình bình hành. Hình hộp đứng •
là hình hộp có các cạnh bên vuông góc với đáy, nói cách khác,
hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.
Hình hộp chữ nhật •
là hình lăng trụ đứng có 6 mặt là hình chữ nhật. Hình lập phương •
là hình lăng trụ đứng có 6 mặt là hình vuông. Soạn: Huỳnh Phú Sĩ 88
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 A B A B Phần này ẩn D C A B D C D C A0 B0 A0 B0 A0 B0 D0 C0 D0 C0 D0 C0 Hình hộp
Hình hộp chữ nhật Hình lập phương 6
VỊ TRÍ TƯƠNG ĐỐI, GÓC VÀ KHOẢNG CÁCH 1 Góc
ç Đường thẳng và mặt phẳng α
Trong không gian, cho đường thẳng ∆ và mặt phẳng ( ). ⊥ α , α ◦ • Nếu ∆ ( ) thì (∆ ( )) = 90 . α , α , d d •
Nếu ∆ không vuông góc với ( ) thì (∆ ( )) = (∆ ) với là hình chiếu vuông góc α của ∆ trên ( ).
ç Mặt phẳng và mặt phẳng α β
Trong không gian, cho hai mặt phẳng ( ) và ( ). α ◦ ∥ β α , β • Nếu ( ) ( ) thì (( ) ( )) = 0 . α ∩ β α , β a, b • Nếu ( ) ( ) = ∆ thì (( ) ( )) = ( ) a ⊂ α b ⊂ β a ∩ ∩ b M với ( ), ( ) và ∆ = . β ∆ S α , β a, b (( ) ( )) = ( ) b d α H I α a , α , d (∆ ( )) = (∆ ) ∆ S 2 Khoảng cách
ç Từ điểm đến mặt phẳng S α H S α Cho điểm và mặt phẳng ( ). Gọi
là hình chiếu vuông góc của trên ( ). Khi đó SH⊥ α d S, α SH α ( ) và ( ( )) = H ç Hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt
phẳng này đến mặt phẳng kia.
3 Vị trí tương đối
ç Đường thẳng và đường thẳng
Trong không gian, cho hai đường thẳng ∆1 và ∆2 . Các trường hợp sau có thể xảy ra: ∩ M • ∆1 ∆2 =
∆1 cắt ∆2 tại giao điểm M ∥ • ∆1 ∆2 ≡ • ∆1 ∆2 •
∆1 và ∆2 chéo nhau (không đồng phẳng).
ç Đường thẳng và mặt phẳng α
Trong không gian, cho đường thẳng ∆ và mặt phẳng (
). Các trường hợp sau có thể xảy ra: Soạn: Huỳnh Phú Sĩ 89
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 ∥ α • ∆ ( ) ∩ α M α • ∆ ( ) = ∆ cắt ( ) tại giao điểm M ⊂ α α • ∆ ( ) ∆ nằm trên ( )
ç Mặt phẳng và mặt phẳng α β
Trong không gian, cho hai mặt phẳng ( ) và (
). Các trường hợp sau có thể xảy ra: α ∥ β • ( ) ( ) α ∩ β α β • ( ) ( ) = ∆ ( ) cắt ( ) theo giao tuyến ∆ α ≡ β • ( ) ( )
Các định lý và hệ quả a, b β α ∥ β •
Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo
cùng song song với mặt phẳng ( ) thì ( ) ( ).
ba giao tuyến thì ba giao tuyến ấy đồng quy hoặc đôi α một song song. •
Nếu đường thẳng ∆ vuông góc với mặt phẳng ( ) thì Ï d ⊂ α
Hai mặt phẳng phân biệt lần lượt chứa hai đường
cũng vuông góc với mọi đường thẳng ( ).
thẳng song song thì giao tuyến của hai mặt ấy (nếu
có) sẽ song song với hai đường thẳng đó, hoặc trùng •
Nếu đường thẳng ∆ vuông góc với hai đường thẳng α ⊥ α
với một trong hai đường thẳng đó.
cắt nhau trên mặt phẳng ( ) thì ∆ ( ). α •
Nếu đường thẳng ∆ không nằm trên mặt phẳng α a⊥ β ( ) • Nếu mặt phẳng ( ) chứa đường thẳng ( ) thì d ⊂ α và ∆ song song với một đường thẳng α ⊥ β ( ) thì ( ) ( ). ∥ α ∆ Ï ( ).
Nếu hai mặt phẳng vuông góc với nhau thì bất α β α
cứ đường thẳng nào nằm trong mặt phẳng thứ nhất • Nếu ( ) và (
) cắt nhau theo giao tuyến ∆ và ( ) chứa a ∥ β a ∥
và vuông góc với giao tuyến thì vuông góc với mặt đường thẳng ( ) thì ∆. Ï phẳng thứ hai.
Nếu hai mặt phẳng phân biệt cùng song song với
một đường thẳng thì giao tuyến của chúng (nếu có) •
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với
cũng song song với đường thẳng đó.
một mặt phẳng thứ ba thì giao tuyến của chúng cũng α a, b • Nếu mặt phẳng ( ) chứa hai đường thẳng và
vuông góc với mặt phẳng thứ ba đó. Soạn: Huỳnh Phú Sĩ 90
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019-2020 MÔN: TOÁN 12 THPT VĨNH LONG Đề có 05 trang
Thời gian làm bài 90 phút (bao gồm trắc nghiệm và tự luận) ( ) Họ và tên học sinh: Mã đề 101
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
I. PHẦN TRẮC NGHIỆM (40 câu, 8.0 điểm) Câu 3. y f x Cho hàm số = (
) có bảng biến thiên như sau: x −∞ ∞ 1 3 + f 0 x − − ( ) 0 + 0 ∞ + 1 f x ( ) −3 −∞ y f x Hàm số = (
) nghịch biến trên khoảng nào dưới đây? A − B ∞ C −∞ − D − . ( 3; 1). . (0; + ). . ( ; 2). . ( 2; 0). Câu 4. R
Hàm số nào sau đây đồng biến trên ? A x − y 1 B y −x3 − x − C y x4 x2 D y x3 x2 x . = x . . = 2. . = + 2 + 3. . = + + 2 + 1. + 3 Câu 5. y f 0 x y f x
Hình bên là đồ thị hàm số = ( ). Hỏi hàm số = (
) đồng biến trên khoảng nào dưới y đây? A ∞ B C ∞ D . (0; 1) và (2; + ). . (1; 2). . (2; + ). . (0; 1). 1 2 O x Câu 6. y y x3 − x2 Giả trị cực tiểu CT của hàm số = 3 + 2 là A y B y − C y D y . CT = 0. . CT = 2. . CT = 1. . CT = 4. Câu 7. y 1 x3 − x2
Số điểm cực trị của hàm số = 2 + 4 là 3 A B C D . 0. . 1. . 2. . 3. Câu 8. f x x3 ax2 bx c C sai Cho hàm số ( ) = + + + có đồ thị ( ). Mệnh đề nào sau đây ? A C B f x . Đồ thị (
) luôn có tâm đối xứng. . Hàm số ( ) luôn có cực trị. C C D f x ∞ . Đồ thị ( ) luôn cắt trục hoành. . lim x→ ∞ ( ) = + . + Câu 9. y f x Cho hàm số = (
) có bảng biến thiên như sau: x −∞ − ∞ 1 0 1 + y0 − − 0 + 0 0 + ∞ ∞ + + y 3 0 0 y f x −
Giá trị lớn nhất của hàm số = ( ) trên đoạn [ 1; 1] bằng A B C − D . 1. . 3. . 1. . 0. Câu 10. m y x4 − x2 − Tìm giá trị nhỏ nhất của hàm số = + 13 trên đoạn [ 2; 3]. A m B m 51 C m 49 D m 205 . = 13. . = . . = . . = . 4 4 16 Câu 11. x h π i y 2 sin + 3
Giá trị nhỏ nhất của hàm số = x trên 0; là sin + 1 2 A B C D 5 . 5. . 2. . 3. . . 2 Câu 12. f x x 4 − x3 x2 a M, m Cho hàm số ( ) = 4 + 4 + . Gọi
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã a − M ≤ m
cho trên đoạn [0; 2]. Có bao nhiêu số nguyên thuộc đoạn [ 3; 2] sao cho 2 ? A B C D . 7. . 5. . 6. . 4. Soạn: Huỳnh Phú Sĩ 91
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 Câu 13. x y C Cho hàm số = x − + 2 có đồ thị (
) Mệnh đề nào dưới đây đúng? 1 A C y B C y . Đồ thị ( ) có tiệm cận ngang = 1. . Đồ thị ( ) có tiệm cận ngang = 3. C C D C x . Đồ thị ( ) không có tiệm cận. . Đồ thị ( ) có tiệm cận đứng = 2. Câu 14. x b y + Cho hàm số = cx −
có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng? y 1 A b < , c < B b < , c > C b > , c > D b > , c < . 0 0. . 0 0. . 0 0. . 0 0. O x Câu 15.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây? y A y −x3 x B y x3 − x . = + 3 + 2. . = 2 + 2. 4 C y x3 − x D y x3 x . = 3 + 2. . = + 3 + 2. 2 − O x 1 1 Câu 16.
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây? y A x −x x − −x y + 2 B y + 1 C y 2 3 D y + 3 . = − x . . = x − . . = x . . = x − . 2 + 4 2 + 2 2 4 O x 2 − 1 2 Câu 17. y ax4 bx2 c Cho hàm số = + +
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? y
A a > , b < , c <
B a < , b < , c < . 0 0 0. . 0 0 0.
C a < , b > , c <
D a > , b < , c > O . 0 0 0. . 0 0 0. x Câu 18. y f x R \ {− } Cho hàm số = ( ) xác định trên 1 , liên tục x −∞ − ∞ 1 3 +
trên mỗi khoảng xác định và có bảng biến thiên như hình m y0 −
bên. Tìm tập hợp tất cả các giá trị thực của tham số sao + 0 + f x m ∞ ∞ cho phương trình ( ) =
có đúng ba nghiệm thực phân + + biệt. A − B − C − D −∞ y 2 . ( 4; 2). . [ 4; 2). . ( 4; 2]. . ( ; 2]. −∞ −4 Câu 19. x m y y x − m
Có bao nhiêu giá trị của
để đồ thị của hàm số =
− x cắt đường thẳng = tại hai điểm phân biệt 1 A, B OA OB ◦ O
sao cho góc giữa hai đường thẳng và bằng 60 ( là gốc tọa độ)? A B C D . 2. . 1. . 3. . 0. √ Câu 20. a a2 · a Cho
là số thực dương. Biểu thức 3
được viết dưới dạng lũy thừa với số mũ hữu tỉ là A 4 7 5 2 a B a C a D a . 3 . . 3 . . 3 . . 3 . √ √ Câu 21. 2018 2019 P − Cho = 5 2 6 5 + 2 6 . Ta có A P ∈ B P ∈ C P ∈ D P ∈ . (3; 7). . (7; 9). . (9; 10). . (10; 11). Soạn: Huỳnh Phú Sĩ 92
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 √ √ Câu 22. √ a √ b a, b − > − Cho các số thực thỏa 2019 2018 2019 2018
. Kết luận nào sau đây đúng? A a > b B a < b C a b D a ≥ b . . . . . = . . . Câu 23. f x x −x 2 x Hàm số ( ) = + 2 e có đạo hàm A f0 x x −x −x 2 x B f0 x x . ( ) = + 4 + 2 e . . ( ) = (2 + 2) e . C f0 x − x −x D f0 x −x −x 2 . ( ) = ( 2 = 2) e . . ( ) = + 2 e .
Câu 24. Tìm mệnh đề đúng trong các mệnh đề sau: x A y ax y 1 < a 6 Oy . Đồ thị hàm số = và = a với 0
= 1 đối xứng với nhau qua trục . B y ax < a 6 a . Đồ thị hàm số = với 0 = 1 luôn đi qua điểm ( ; 1). C y ax a > −∞ ∞ . Hàm số = với 1 nghịch biến trên ( ; + ). D y ax < a < −∞ ∞ . Hàm số = với 0 1 đồng biến trên ( ; + ). Câu 25. a, b a 6 Cho các số thực dương với
= 1. Khẳng định nào sau đây là khẳng định đúng? A ab B ab 1 . loga2 ( ) = 2 + loga b. . loga2 ( ) = loga b. 2 C ab 1 1 D ab 1 . loga2 ( ) = + loga b. . loga2 ( ) = loga b. 2 2 4 Câu 26. a a Với log 3 =
thì log 9000 được biểu diễn theo bằng A a2 B a C a2 D a2 . . . 3 + 2 . . + 3. . 3 . Câu 27. a b a b Cho log 5 = và log 5 = . Khi đó, log 5 tính theo và là 2 3 6 A ab a 1 2 b2 B C D a b . + . . a b . . a b . . + . + + Câu 28.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn y A, B, C, D phương án
dưới đây. Hỏi hàm số đó là hàm số nào? A y x B y √ x C y x D y x . = log . . = log . . = log 2 . . = log . 1 2 1 2 2 2 2 O x 1 −1 Câu 29. ,
Ông A dự định gửi vào ngân hàng một số tiền với lãi suất 7
5% một năm, để sau 5 năm, số tiền lãi đủ mua một
chiếc xe máy trị giá 85 triệu đồng. Biết rằng, cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Hỏi số tiền ông A
cần gửi cho ngân hàng gần nhất với số tiền nào dưới đây? A B C D . 60 triệu đồng. . 189 triệu đồng. . 196 triệu đồng. . 210 triệu đồng. Câu 30. m y x2 − x m R
Tìm tất cả các giá trị thực của tham số để hàm số = log 2 + có tập xác định là . 2 A m ≥ B m ≤ C m > D m < − . 1. . 1. . 1. . 1. Câu 31. S x+1 Tập nghiệm của phương trình 2 = 8 là A S { } B S { } C S { } D S { } . = 4 . . = 1 . . = 3 . . = 2 . Câu 32. x x log3 Có bao nhiêu số thực thỏa mãn 9 = 4? A B C D . 4. . 0. . 2. . 1. Câu 33. x − · x −
Nghiệm thực của phương trình 9 4 3 45 = 0 là A x B x − x C x x D x . = 9. . = 5 hoặc = 9. . = 2 hoặc = log 5. . = 2. 3 Câu 34. x , x x− x2− 1 1 P x x Gọi 1 2
là hai nghiệm của phương trình 5 = 2 . Tính = ( 1 + 1) ( 2 + 1). A B C − D . 0. . 2 log 5 + 2. . 2 log 5 1. . log 25. 2 2 2
Câu 35. Hình lăng trụ tam giác có bao nhiêu mặt? A B C D . 6. . 3. . 9. . 5.
Câu 36. Một hình chóp 100 cạnh có bao nhiêu mặt? A B C D . 53. . 51. . 50. . 52.
Câu 37. Trong các hình đa diện đều sau, hình nào có số đỉnh nhỏ hơn số mặt? A B C D . Hình tứ diện đều. . Hình 20 mặt đều. . Hình lập phương. . Hình 12 mặt đều. Câu 38. S.ABCD
Số mặt phẳng đối xứng của hình chóp tứ giác đều là A B C D . 2. . 4. . 7. . 6. Câu 39. ABC.A0B0C0 V V BCA0B0C0 V Cho lăng trụ có thể tích . Tính thể tích 1 của khối đa diện theo . A V 2 V B V 1 V C V 1 V D V 1 V . 1 = . . 1 = . . 1 = . . 1 = . 3 3 2 4 Soạn: Huỳnh Phú Sĩ 93
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 Câu 40. 3
Hình hộp chữ nhật không nắp có thể tích 3200cm , tỉ số giữa chiều cao và chiều rộng bằng 2. Khi tổng diện tích
các mặt của hình hộp nhỏ nhất, tính diện tích mặt đáy của hình hộp. A 2 B 2 C 2 D 2 . 1200cm . . 120cm . . 160cm . . 1600cm . √ Câu 41. a2 V
Thiết diện qua trục của một hình nón tròn xoay là tam giác đều có diện tích bằng 3. Tính thể tích của khối √ √ √ √ nón đã cho. A πa3 πa3 πa3 πa3 V 3 B V 3 C V 3 D V 6 . = . . = . . = . . = . 3 2 6 6 Câu 42.
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy;
một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng
đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối
nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của
lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh). A 1 B 2 C 4 D 5 . . . . . . . . 2 3 9 9
II. PHẦN TỰ LUẬN (2.0 điểm) Câu 43 (0.75 điểm). f x x3 − x
Tìm các điểm cực trị hàm số ( ) = 3 + 1. Câu 44 (0.5 điểm). x x − Giải phương trình log + log ( 6) = log 7. 2 2 2 Câu 45 (0.75 điểm). S.ABCD a S ABCD Cho hình chóp
có đáy là hình vuông cạnh , hình chiếu của trên ( ) trùng với trung a AB SD 3 V S.ABCD a điểm của cạnh , cạnh bên = . Tính thể tích của khối chóp theo . 2 Soạn: Huỳnh Phú Sĩ 94
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12
BỘ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2020 Bài thi: TOÁN ĐỀ THI CHÍNH THỨC Đề có 05 trang
Thời gian làm bài: 90 phút, không kể thời gian phát đề ( )
Họ và tên thí sinh: .......................................................................................... Số báo danh: Mã đề 101
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 46.
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? y A y x3 − x2 B y −x3 x2 . = 3 + 1. . = + 3 + 1. C y −x4 x2 D y x4 − x2 . = + 2 + 1. . = 2 + 1. O x Câu 47. x−1
Nghiệm của phương trình 3 = 9 là A x − B x C x D x − . = 2. . = 3. . = 2. . = 3. Câu 48. f x Cho hàm (
) có bảng biến thiên như sau: x −∞ ∞ 0 3 + y0 − + 0 0 + ∞ 2 + y −∞ −5
Giá trị cực tiểu của hàm số đã cho bằng A B − C D . 3. . 5. . 0. . 2. Câu 49. f x Cho hàm số (
) có bảng biến thiên như sau: x −∞ − ∞ 1 0 1 + y0 − − 0 + 0 0 + ∞ ∞ + 4 + y − − 1 1
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A −∞ − B C − D − . ( ; 1). . (0; 1). . ( 1; 1). . ( 1; 0).
Câu 50. Cho khối hộp chữ nhật có ba kích thước 3; 4; 5. Thể tích của khối hộp đã cho bằng A B C D . 10. . 20. . 12. . 60. Câu 51. z − i
Số phức liên hợp của số phức = 3 + 5 là A z − − i B z i C z − i D z − i . = 3 5 . . = 3 + 5 . . = 3 + 5 . . = 3 5 . Câu 52. r `
Cho hình trụ có bán kính đáy
= 8 và độ dài đường sinh
= 3. Diện tích xung quanh của hình trụ đã cho bằng A π B π C π D π . 24 . . 192 . . 48 . . 64 . Câu 53. r
Cho khối cầu có bán kính
= 4. Thể tích của khối cầu đã cho bằng A π π 256 B π C 64 D π . . . 64 . . . . 256 . 3 3 Câu 54. a, b a 6 b Với
là các số thực dương tùy ý và = 1, loga5 bằng A B 1 C D 1 . 5 loga b. . + loga b. . 5 + loga b. . loga b. 5 5 Câu 55. Oxyz S x2 y2 z 2 S Trong không gian , cho mặt cầu ( ) : + + ( + 2) = 9. Bán kính của ( ) bằng A B C D . 6. . 18. . 9. . 3. Câu 56. x y 4 + 1
Tiệm cận ngang của đồ thị hàm số = x − là 1 A y 1 B y C y D y − . = . . = 4. . = 1. . = 1. 4 Câu 57. r h
Cho khối nón có bán kính đáy = 5 và chiều cao
= 2. Thể tích khối nón đã cho bằng: A π π 10 B π C 50 D π . . . 10 . . . . 50 . 3 3 Soạn: Huỳnh Phú Sĩ 95
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 Câu 58. x −
Nghiệm của phương trình log 1) = 2 là 3 ( A x B x C x D x . = 8. . = 9. . = 7. . = 10. Z Câu 59. x2 x d bằng A x C B 1x3 C C x3 C D x3 C . 2 + . . + . . + . . 3 + . 3
Câu 60. Có bao nhiêu cách xếp 6 học sinh thành một hàng dọc? A B C D . 36. . 720. . 6. . 1. Câu 61. y f x Cho hàm số bậc ba = (
) có đồ thị là đường cong trong hình bên. Số nghiệm thực của y f x − 2 phương trình ( ) = 1 là A B C D . 3. . 1. . 0. . 2. 1 − O x 1 −2 Câu 62. Oxyz A Ox Trong không gian
, hình chiếu vuông góc của điểm (3; 2; 1) trên trục có tọa độ là A B C D . (0; 2; 1). . (3; 0; 0). . (0; 0; 1). . (0; 2; 0). Câu 63. B h
Cho khối chóp có diện tích đáy = 6 và chiều cao
= 2. Thể tích của khối chóp đã cho bằng A B C D . 6. . 3. . 4. . 12. Câu 64. x − y − z Oxyz d · 3 4 + 1 Trong không gian , cho đường thẳng = − =
. Vectơ nào dưới đây là một vectơ chỉ phương 2 5 3 d của ? A − Ï − Ï − Ï − Ï u − B u − C u D u . 2 = (2; 4; 1) . . 1 = (2; 5; 3). . 3 = (2; 5; 3). . 4 = (3; 4; 1). Câu 65. Oxyz A B C − ABC Trong không gian , cho ba điểm (3; 0; 0), (0; 1; 0) và (0; 0; 2). Mặt phẳng ( ) có phương trình là: A x y z B x y z C x y z D x y z . + − + = 1. . + + − = 1. . + + = 1. . − + + = 1. 3 1 2 3 1 2 3 1 2 3 1 2 Câu 66. u u q u Cho cấp số nhân n ( ) với 1 = 3 và công bội = 2. Giá trị của 2 bằng A B C D 3 . 8. . 9. . 6. . . 2 Câu 67. z − i z i z z Cho hai số phức 1 = 3 2 và 2 = 2 + . Số phức 1 + 2 bằng A i B − i C − i D − − i . 5 + . . 5 + . . 5 . . 5 . 3 3 Z Z Câu 68. f x x f x x Biết ( ) d = 3. Giá trị của 2 ( ) d bằng 1 1 A B C D 3 . 5. . 9. . 6. . . 2 Câu 69. M − z z
Trên mặt phẳng tọa độ, biết (
3; 1) là điểm biểu diễn số phức . Phần thực của bằng A B − C − D . 1. . 3. . 1. . 3. Câu 70. y x
Tập xác định của hàm số = log là 5 A ∞ B −∞ C ∞ D −∞ ∞ . [0; + ). . ( ; 0). . (0; + ). . ( ; + ). Câu 71. y x3 x2 y x2 x
Số giao điểm của đồ thị hàm số = + 3 và đồ thị hàm số = 3 + 3 là A B C D . 3. . 1. . 2. . 0. Câu 72. S.ABC ABC B AB a BC a SA Cho hình chóp có đáy là tam √ giác vuông tại , = , = 2 , S SA a
vuông góc với mặt phẳng đáy và = 15
(tham khảo hình bên). Góc giữa đường SC thẳng và mặt phẳng đáy bằng A ◦ B ◦ C ◦ D ◦ . 45 . . 30 . . 60 . . 90 . A C B Soạn: Huỳnh Phú Sĩ 96
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 2 Z Câu 73. F x x2 f x R f x x Biết ( ) =
là một nguyên hàm của hàm số ( ) trên . Giá trị của [2 + ( )] d bằng 1 A B C 13 D 7 . 5. . 3. . . . . 3 3 Câu 74. y x2 − y x −
Diện tích hình phẳng giới hạn bởi hai đường = 4 và = 2 4 bằng A B π 4 C 4 D π . 36. . . . . . 36 . 3 3 Câu 75. x − y z − Oxyz M − d 1 + 2 3 M Trong không gian , cho điểm (2; 2; 3) và đường thẳng : = = − . Mặt phẳng đi qua 3 2 1 d và vuông góc với có phương trình là A x y − z B x − y z − C x y − z − D x − y z . 3 + 2 + 1 = 0. . 2 2 + 3 17 = 0. . 3 + 2 1 = 0. . 2 2 + 3 + 17 = 0. Câu 76. z z2 z Gọi 0
là nghiệm phức có phần ảo dương của phương trình + 6
+ 13 = 0. Trên mặt phẳng tọa độ, điểm biểu − z diễn số phức 1 0 là A N − B M C P − D Q − . ( 2; 2). . (4; 2). . (4; 2). . (2; 2). Câu 77. Oxyz A B C − A Trong không gian , cho ba điểm (1; 0; 1), (1; 1; 0) và (3; 4; 1). Đường thẳng đi qua và song song với
BC có phương trình là A x − y z − x y z x − y z − x y z 1 1 B + 1 + 1 C 1 1 D + 1 + 1 . = = − . . = = − . . = = − . . = = − . 4 5 1 2 3 1 2 3 1 4 5 1 Câu 78. f x R f 0 x Cho hàm số ( ) liên tục trên
và có bảng xét dấu của ( ) như sau: x −∞ − ∞ 1 0 1 2 + f 0 x − − − ( ) + 0 0 + 0
Số điểm cực đại của hàm số đã cho là A B C D . 4. . 1. . 2. . 3. Câu 79.
x2−13 <
Tập nghiệm của bất phương trình 3 27 là A ∞ B − C −∞ D . (4; + ). . ( 4; 4). . ( ; 4). . (0; 4). Câu 80. ◦
Cho hình nón có bán kính đáy bằng 2 và góc ở đỉnh bằng 60 . Diện tích xung quanh của hình nón đã cho bằng √ √ A π π π B 16 3 C 8 3 D π . 8 . . . . . . 16 . 3 3 Câu 81. f x x3 − x
Giá trị nhỏ nhất của hàm số ( ) = 24 trên đoạn [2; 19] bằng √ √ A B − C − D − . 32 2. . 40. . 32 2. . 45. Câu 82. z i w i z · w Cho hai số phức = 1 + 2 và = 3 + . Môđun của số phức bằng √ √ A B C D . 5 2. . 26. . 26. . 50. Câu 83. a b a2b log2 ( ) a3 ab2 Cho và
là hai số thực dương thỏa mãn 4 = 3 . Giá trị của bằng A B C D . 3. . 6. . 12. . 2. Câu 84. x f x √ g x x · f 0 x Cho hàm số ( ) = x
. Họ tất cả các nguyên hàm của hàm số ( ) = ( + 1) ( ) là 2 + 2 A x2 x − x − x2 x x + 2 2 √ C B 2 √ C C + + 2 √ C D + 2 √ C . x + . . + . . + . . + . 2 x2 x2 x2 2 + 2 + 2 + 2 2 + 2 Câu 85. x m y + 4 −∞ −
Tập hợp tất cả các giá trị thực của tham số để hàm số = x
m đồng biến trên khoảng ( ; 7) là + A B C D ∞ . [4; 7). . (4; 7]. . (4; 7). . (4; + ).
Câu 86. Trong năm 2019, diện tích rừng trồng mới của tỉnh A là 600 ha. Giả sử diện tích rừng trồng mới của tỉnh A mỗi
năm tiếp theo đều tăng 6% so với diện tích rừng trồng mới của năm liền trước. Kể từ sau năm 2019, năm nào dưới đây là
năm đầu tiên tỉnh A có diện tích rừng trồng mới trong năm đó đạt trên 1000 ha? A B C D . Năm 2028. . Năm 2047. . Năm 2027. . Năm 2046. Câu 87. S.ABC a SA SBC Cho hình chóp
có đáy là tam giác đều cạnh 4 ,
vuông góc với mặt phẳng đáy, góc giữa mặt phẳng ( ) ◦ S.ABC
và mặt phẳng đáy bằng 60 . Diện tích của mặt cầu ngoại tiếp hình chóp bằng A πa2 πa2 πa2 172 B 76 C πa 172 2 D . . . . . 84 . . . 3 3 9 Câu 88. Soạn: Huỳnh Phú Sĩ 97
Trường THCS-THPT Mỹ Thuận Phụ lục TOÁN 12 ABC.A0B0C0 a M Cho hình lăng trụ đứng
có tất cả các cạnh bằng . Gọi là trung điểm của A0 C0 CC0 M A0BC
(tham khảo hình bên). Khoảng cách từ đến mặt phẳng √ √ √ ( ) bằng√ A a a a a 21 B 2 C 21 D 2 . . . . . . . . B0 14 2 7 4 M A C B Câu 89. f x Cho hàm số bậc bốn (
) có bảng biến thiên như sau: x −∞ − ∞ 1 0 1 + f 0 x − − ( ) 0 + 0 0 + ∞ ∞ + 3 + f x ( ) − − 2 2 g x x4 f x 2
Số điểm cực trị của hàm số ( ) = [ ( + 1)] là A B C D . 11. . 9. . 7. . 5. Câu 90. y ax3 bx2 cx d a, b, c, d ∈ R Cho hàm số = + + + (
) có đồ thị là đường cong trong y a b c d
hình bên. Có bao nhiêu số dương trong các số , , , ? A B C D . 4. . 1. . 2. . 3. O x Câu 91. S { , , , , , , , , } Gọi
là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập 1 2 3 4 5 6 7 8 9 . S
Chọn ngẫu nhiên một số thuộc
, xác suất để số đó không có hai chữ số liên tiếp nào cùng chẵn bằng A 25 B 5 C 65 D 55 . . . . . . . . 42 21 126 126 Câu 92. S.ABCD a a O M N P Q Cho hình chóp đều có cạnh đáy bằng , cạnh bên bằng 2 và là tâm của đáy. Gọi , , , lần lượt O SAB SBC SCD SDA S0 S O
là các điểm đối xứng với
qua trọng tâm của các tam giác , , , và
là điểm đối xứng với qua . Thể S0.MNPQ tích của khối √ chóp bằng √ √ √ A a3 a3 a3 a3 20 14 B 40 14 C 10 14 D 2 14 . . . . . . . . 81 81 81 9 Câu 93. x y x y x y− + 1 ≥ P x2 y2 x y
Xét các số thực không âm và thỏa mãn 2 + 4
3. Giá trị nhỏ nhất của biểu thức = + + 4 + 6 bằng A 33 B 65 C 49 D 57 . . . . . . . . 4 8 8 8 Câu 94. x x y x2 y ≥ Có bao nhiêu số nguyên sao cho ứng với mỗi
có không quá 728 số nguyên thỏa mãn log + 4 x y log ( + )? 3 A B C D . 59. . 58. . 116. . 115. Câu 95. y f x Cho hàm số bậc ba = (
) có đồ thị là đường cong trong hình y f x 3 f x
bên. Số nghiệm thực phân biệt của phương trình ( ) + 1 = 0 là A B C D . 8. . 5. . 6. . 4. O x Soạn: Huỳnh Phú Sĩ 98
Trường THCS-THPT Mỹ Thuận CHỈ MỤC B Khối đa diện
Hai đa diện bằng nhau . . . . . . . . . . . . . . . . . . . . . . . . . 62 Bất phương trình
Hình chóp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
bất phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . 56
Hình chóp đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
bất phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
Hình hộp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
Hình hộp chữ nhật . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88 C
Hình lăng trụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
Hình lăng trụ đứng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
Hình lập phương . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
Căn bậc n . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Hình đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 G
Hình đa diện lồi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Hình đa diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62 Góc
Góc giữa hai mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . 89 L
Góc giữa đường thẳng và mặt phẳng . . . . . . . . . . . . . 89 H
Lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
Lôgarit thập phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
Lôgarit tự nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
Hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36, 85
Cực trị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số . . 19 M
Giới hạn của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
Hàm hằng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 Mặt cầu
Hàm phân tuyến tính . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Giao của mặt cầu và mặt phẳng . . . . . . . . . . . . . . . . . 78
Hàm số bậc ba . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
Giao của mặt cầu và đường thẳng . . . . . . . . . . . . . . . 79
Hàm số bậc bốn trùng phương . . . . . . . . . . . . . . . . . . 29
Kinh tuyến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Hàm số bậc hai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
Mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Hàm số bậc nhất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
Vĩ tuyến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Hàm số chẵn, hàm số lẻ . . . . . . . . . . . . . . . . . . . . . . . . 82 Mặt tròn xoay
Hàm số liên tục . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
Mặt nón . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Hàm số lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
Mặt trụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Hàm số mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 P
Quy tắc tìm cực trị của hàm số . . . . . . . . . . . . . . . . . . 14
Quy tắc xét tính đơn điệu của hàm số . . . . . . . . . . . . 8
Sự đồng biến và nghịch biến của hàm số . . . . . . . . . 7
Phương trình . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 R
Tìm tham số để hàm số đơn điệu trên . . . . . . . . 10
Phương trình bậc 4 trùng phương . . . . . . . . . . . . . . . 84
Tìm tham số để hàm số đơn điệu trên một khoảng10
Phương trình bậc hai . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
Tương giao của các đồ thị . . . . . . . . . . . . . . . . . . . . . . . 30
Phương trình chứa ẩn trong dấu giá trị tuyệt đối . 85
Tập xác định của hàm số . . . . . . . . . . . . . . . . . . . . . . . 82
Phương trình lôgarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
Xét dấu nhị thức bậc nhất . . . . . . . . . . . . . . . . . . . . . . . 83
Phương trình mũ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
Xét dấu tam thức bậc hai . . . . . . . . . . . . . . . . . . . . . . . 83
Phương trình tích . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
Xét tính đơn điệu của hàm số dựa vào bảng biến
Phương trình vô tỉ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
thiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Định lý Vi-ét . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
Xét tính đơn điệu của hàm số dựa vào đồ thị . . . . . . 8 T
Xét tính đơn điệu của hàm số dựa vào đồ thị của
đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Xét tính đơn điệu của hàm ẩn . . . . . . . . . . . . . . . . . . . 11
Tam giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Điều kiện đủ để hàm số có cực trị . . . . . . . . . . . . . . 13
Chu vi tam giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Đường tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Công thức Heron . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Đường tiệm cận ngang . . . . . . . . . . . . . . . . . . . . . . . . . 24
Diện tích tam giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Đường tiệm cận đứng . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Tam giác bằng nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Đạo hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
Tam giác cân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Tam giác vuông . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 K
Tam giác vuông cân . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Tam giác đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87 Khoảng cách
Tam giác đồng dạng . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Khoảng cách giữa hai mặt phẳng song song . . . . . 89
Trọng tâm của tam giác . . . . . . . . . . . . . . . . . . . . . . . . 86
Khoảng cách từ điểm đến mặt phẳng . . . . . . . . . . . . 89
Trực tâm của tam giác . . . . . . . . . . . . . . . . . . . . . . . . . . 86 99 Phụ lục TOÁN 12
Đường cao của tam giác . . . . . . . . . . . . . . . . . . . . . . . . 86
Thể tích khối hộp chữ nhật . . . . . . . . . . . . . . . . . . . . . 69
Đường trung bình của tam giác . . . . . . . . . . . . . . . . . 86
Thể tích khối lăng trụ . . . . . . . . . . . . . . . . . . . . . . . . . . 69
Đường trung tuyến của tam giác . . . . . . . . . . . . . . . . . 86 V
Đường tròn ngoại tiếp tam giác . . . . . . . . . . . . . . . . . 86
Đường tròn nội tiếp tam giác . . . . . . . . . . . . . . . . . . . . 86
Định lý cosin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 Vị trí tương đối
Định lý sin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
Vị trí tương đối giữa hai mặt phẳng . . . . . . . . . . . . . 90 Thể tích
Vị trí tương đối giữa hai đường thẳng . . . . . . . . . . . . 89
Thể tích khối chóp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
Vị trí tương đối giữa đường thẳng và mặt phẳng . . 89 Soạn: Huỳnh Phú Sĩ 100
Trường THCS-THPT Mỹ Thuận