

Preview text:
NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
THỂ TÍCH TRONG PHÂN CHIA KHỐI ĐA DIỆN
Trong các bài toán thể tích khối đa diện diện , một số bài toán vận dụng hoặc vận dụng cao thường
đề cập đến việc phân chia đa diện , tính thể tích khối đa diện mới theo thể tích khối đa diện đã cho NH . Ó
Thầy cô cần tạo tình huống cho học trò có tư duy về việc so sánh thể tích các khối chóp , khối lăng M
trụ từ những tư duy đơn giản như so sánh đường cao , so sánh diện tích đáy để đi đến quyết định T
chuyển những khối đa diện khó tính thể tích thành những khối dễ hơn , dễ so sánh với khối ban OÁ
đầu. Cũng cần tạo cho học sinh quen với các bài toán tính thể tích các khối không cơ bản như chóp N
hoặc lăng trụ bằng cách phân chia thể tích với yêu cầu học sinh quan sát tốt để phân chia khối đa V
diện thành những khối dễ tính hơn với giả thiết được cho , từ đó hình thành các kĩ năng tổng hợp và D
có phản xạ tốt trong những bài phân chia đa diện . –
Trong phần thể tích khối đa diện việc ra đề và ôn tập cho học sinh thường được chú trọng đến các VD
bài toán về phân chia khối đa diện thành các phần khác nhau. Việc phân chia và tính toán khối đa C
diện thường dựa vào tỷ số thể tích, dựa vào việc dựng thiết diện, dựa vào việc lấy thêm điểm thỏa
mãn các hệ thức tỷ số hoặc vecto…
A. CÁC CÔNG THỨC TỈ SỐ THỂ TÍCH ÁP DỤNG
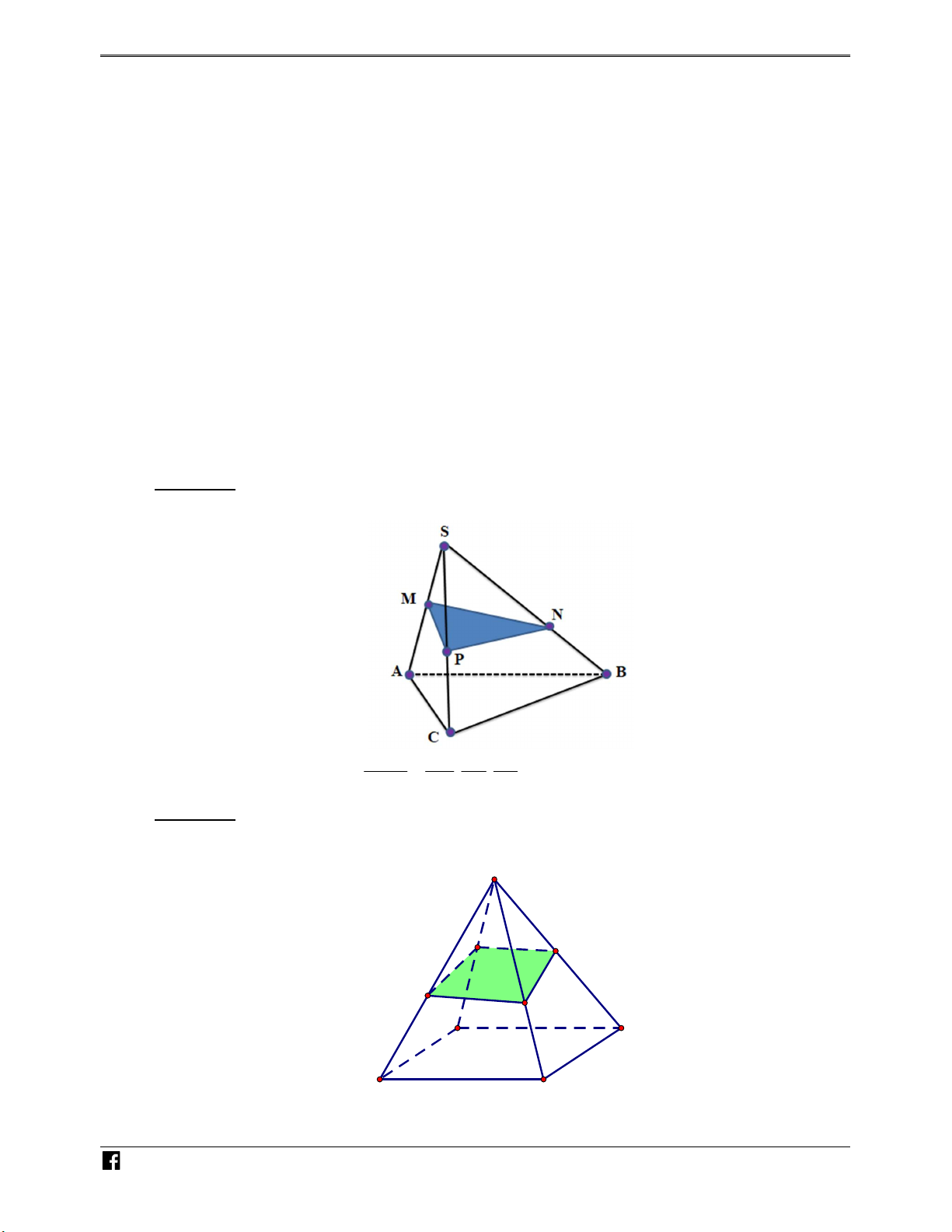
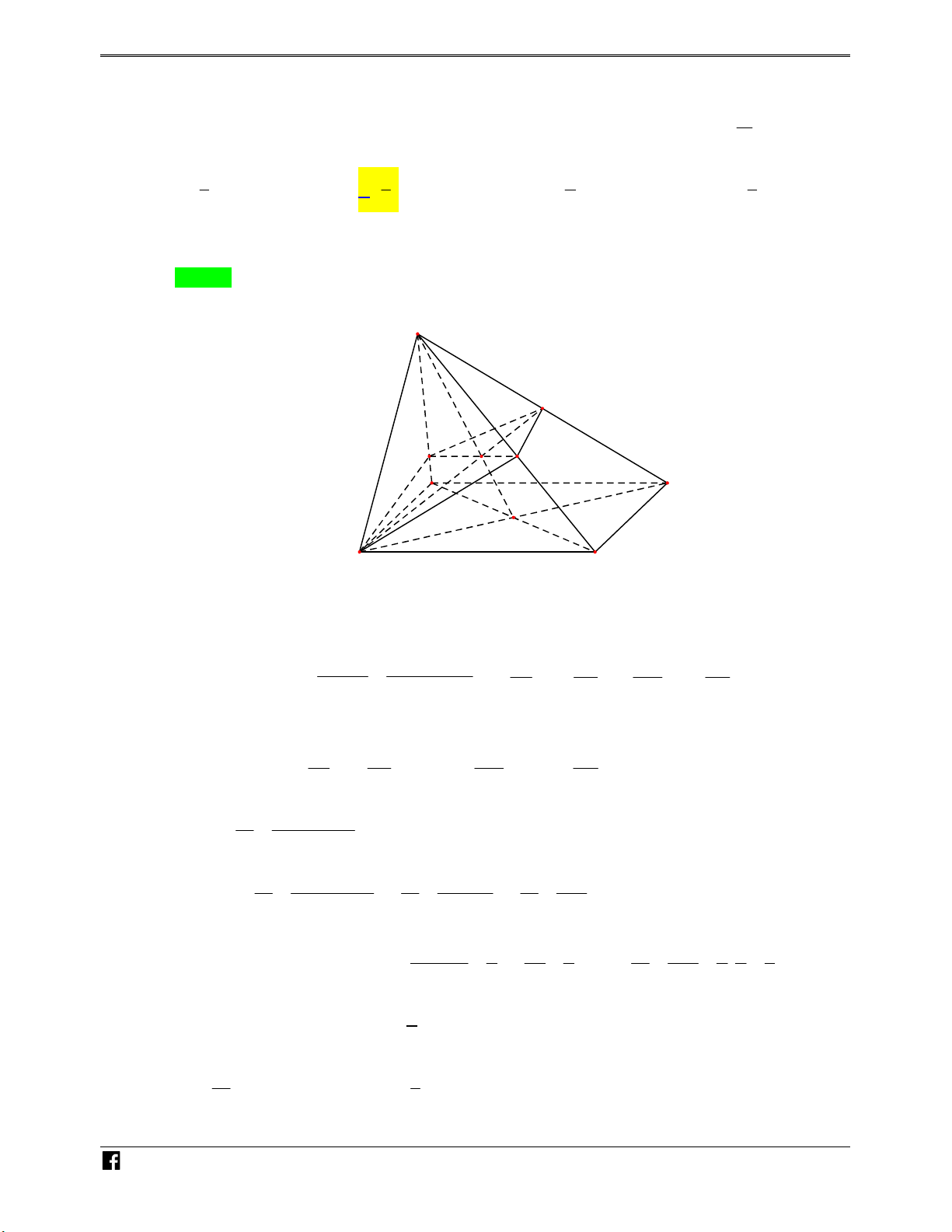
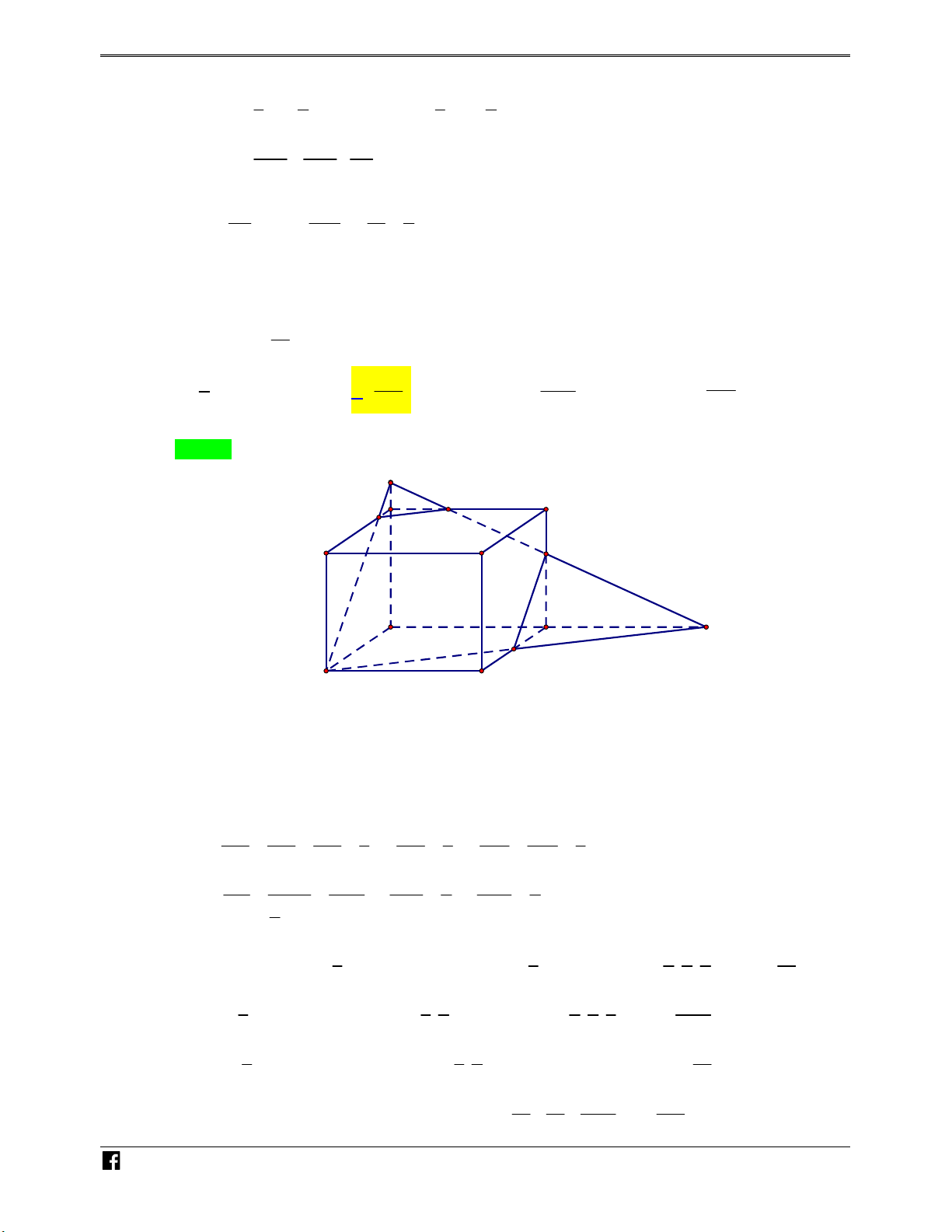
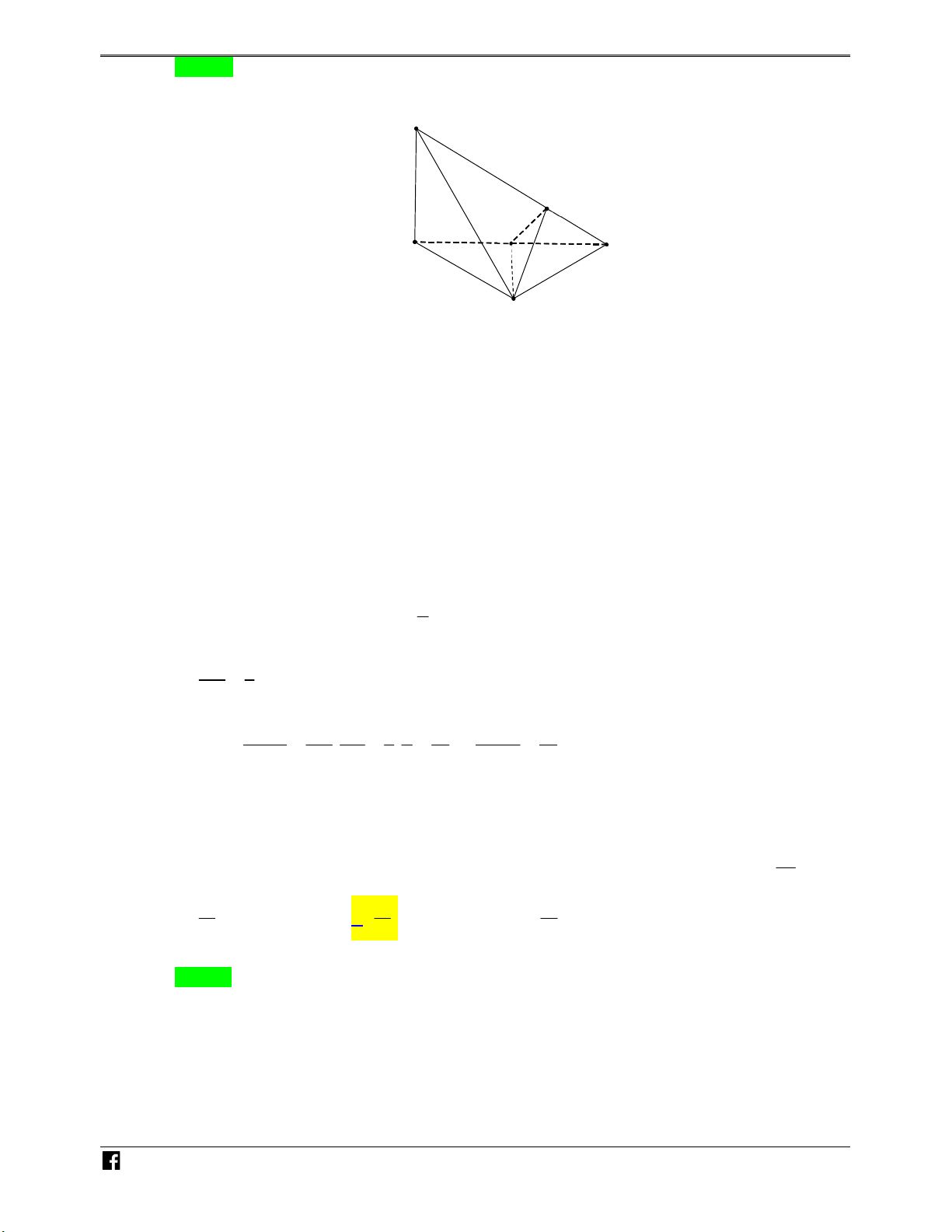
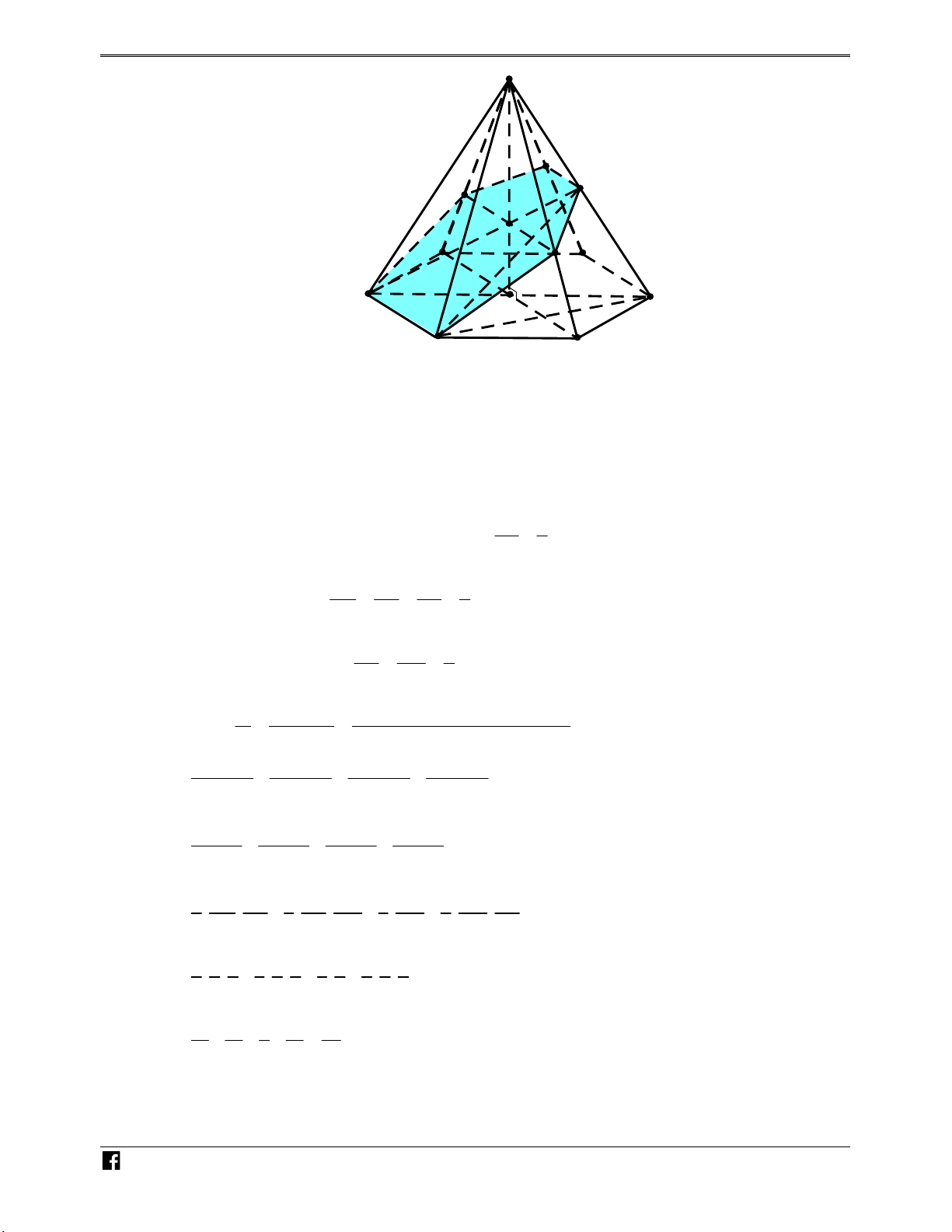
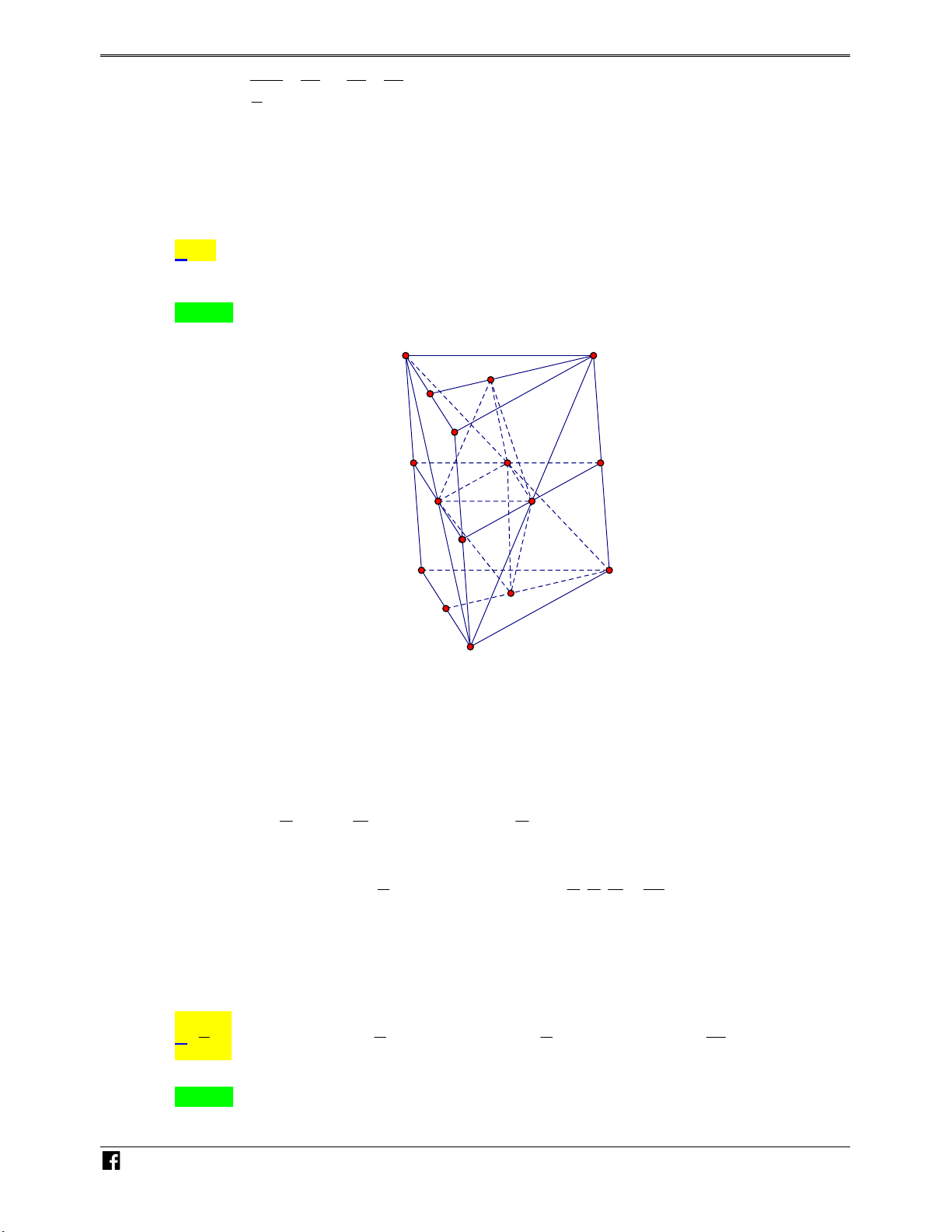
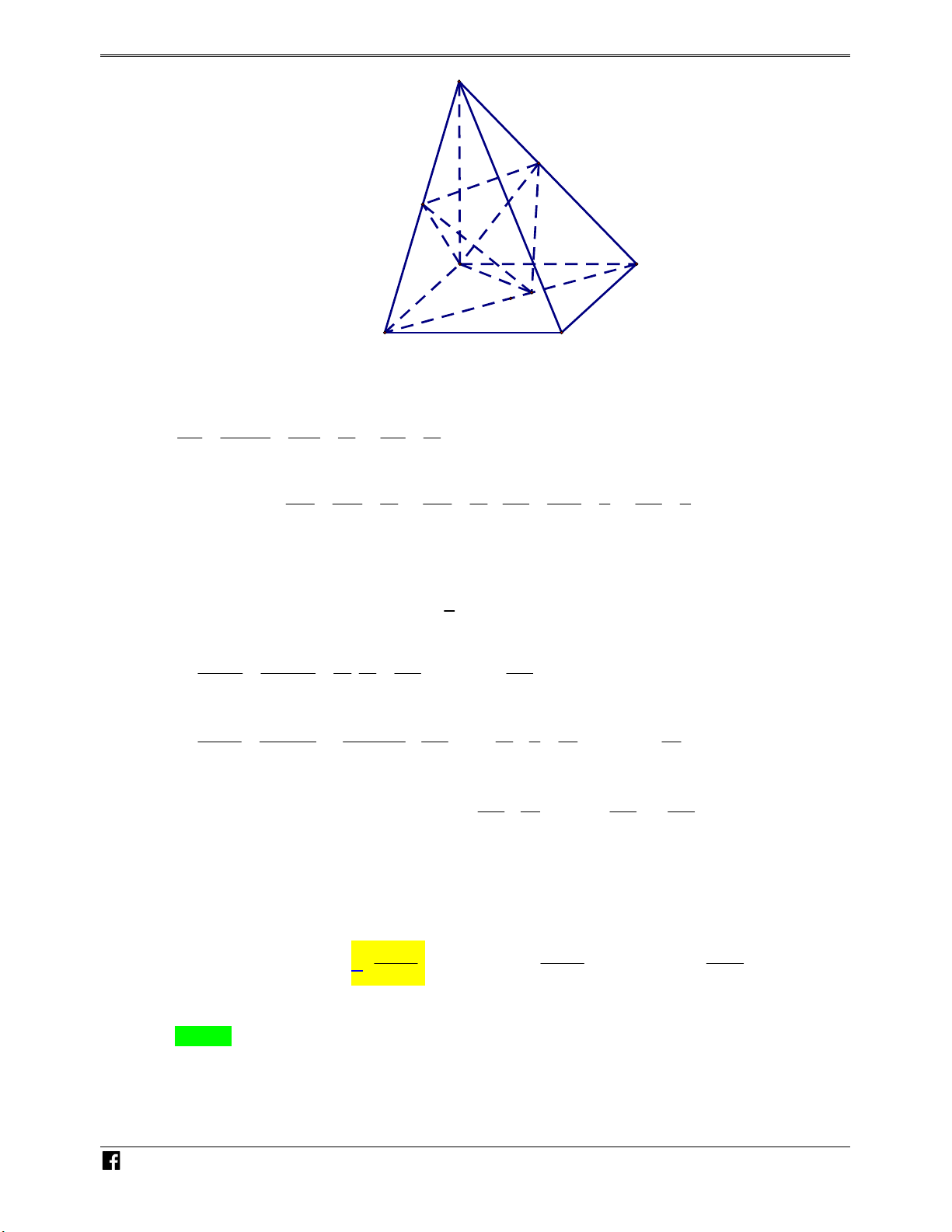
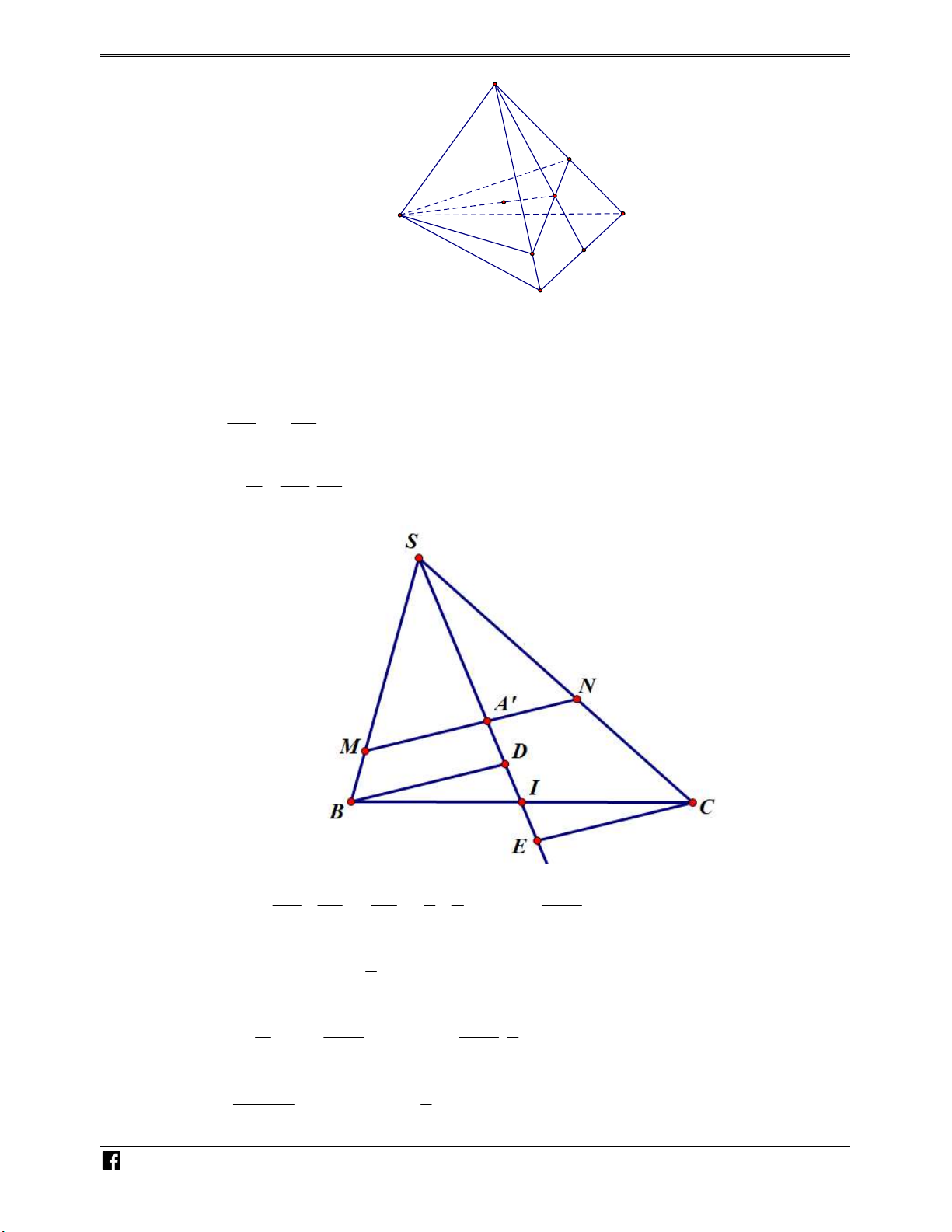
Bài toán 1. Cho hình chóp S.ABC . Một mặt phẳng P cắt các cạnh S , A SB, SC lần lượt tại
M , N , P như hình vẽ bên. N H Ó M TOÁN V SM SN SP S MNP V
Khi đó ta có các kết quả sau: . . . D V SA SB SC S.ABC –
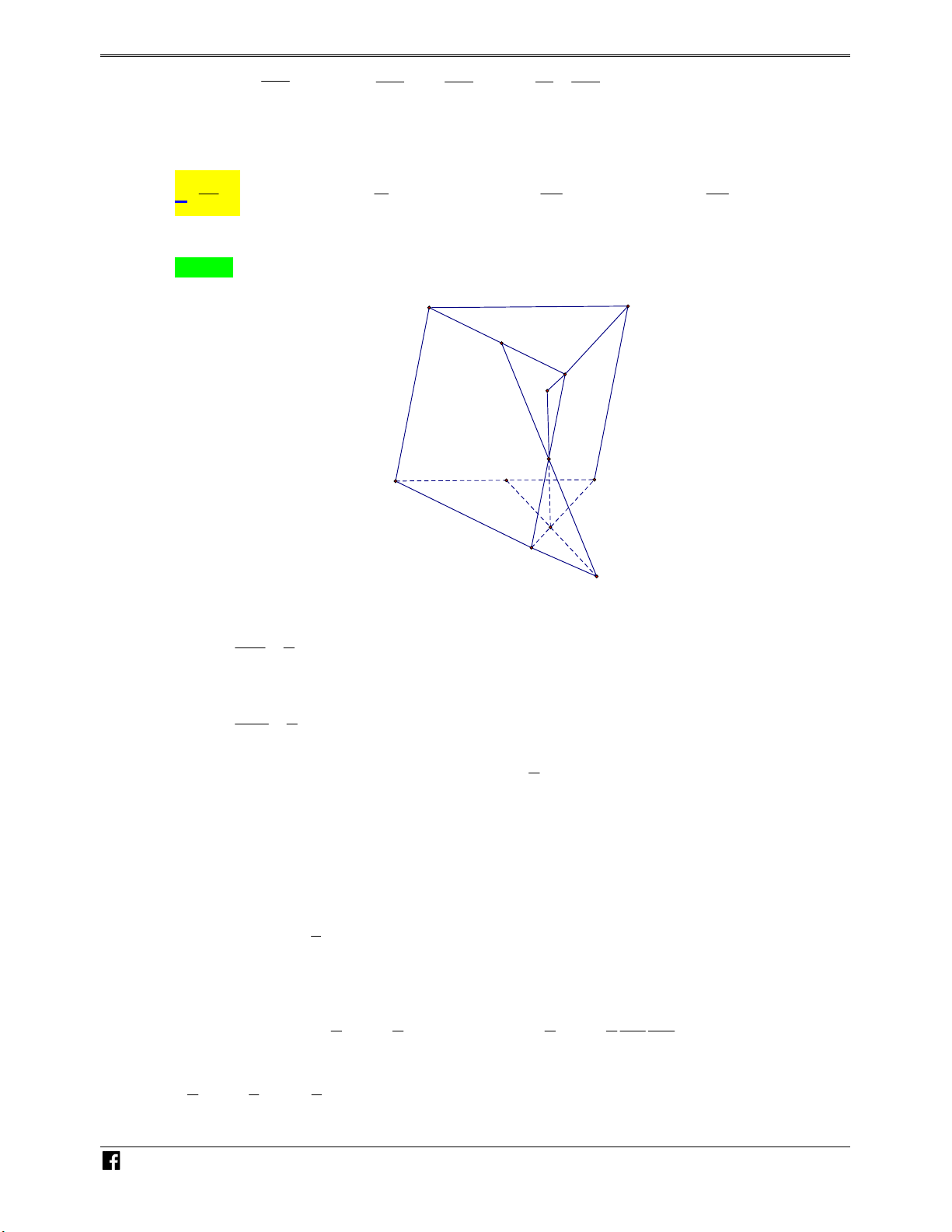
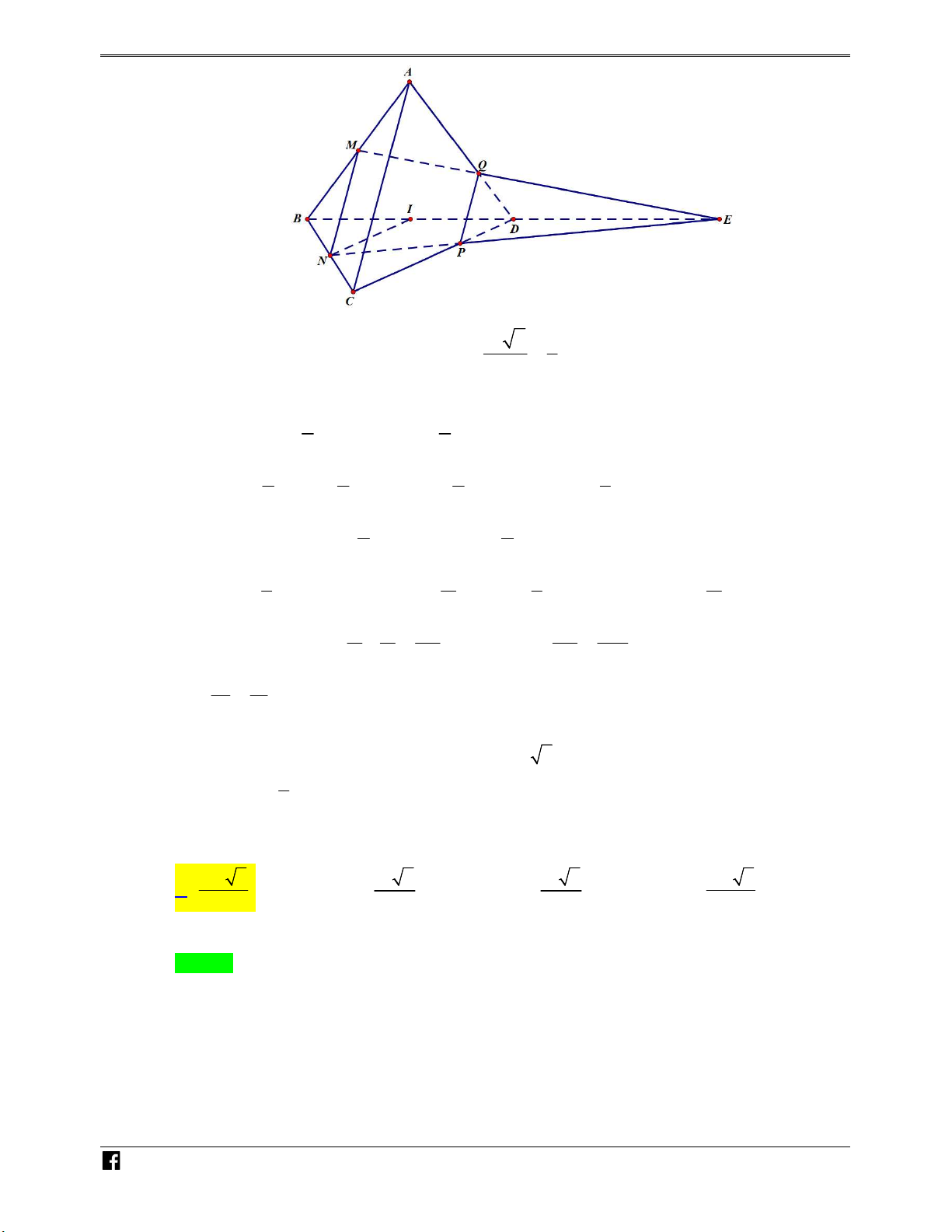
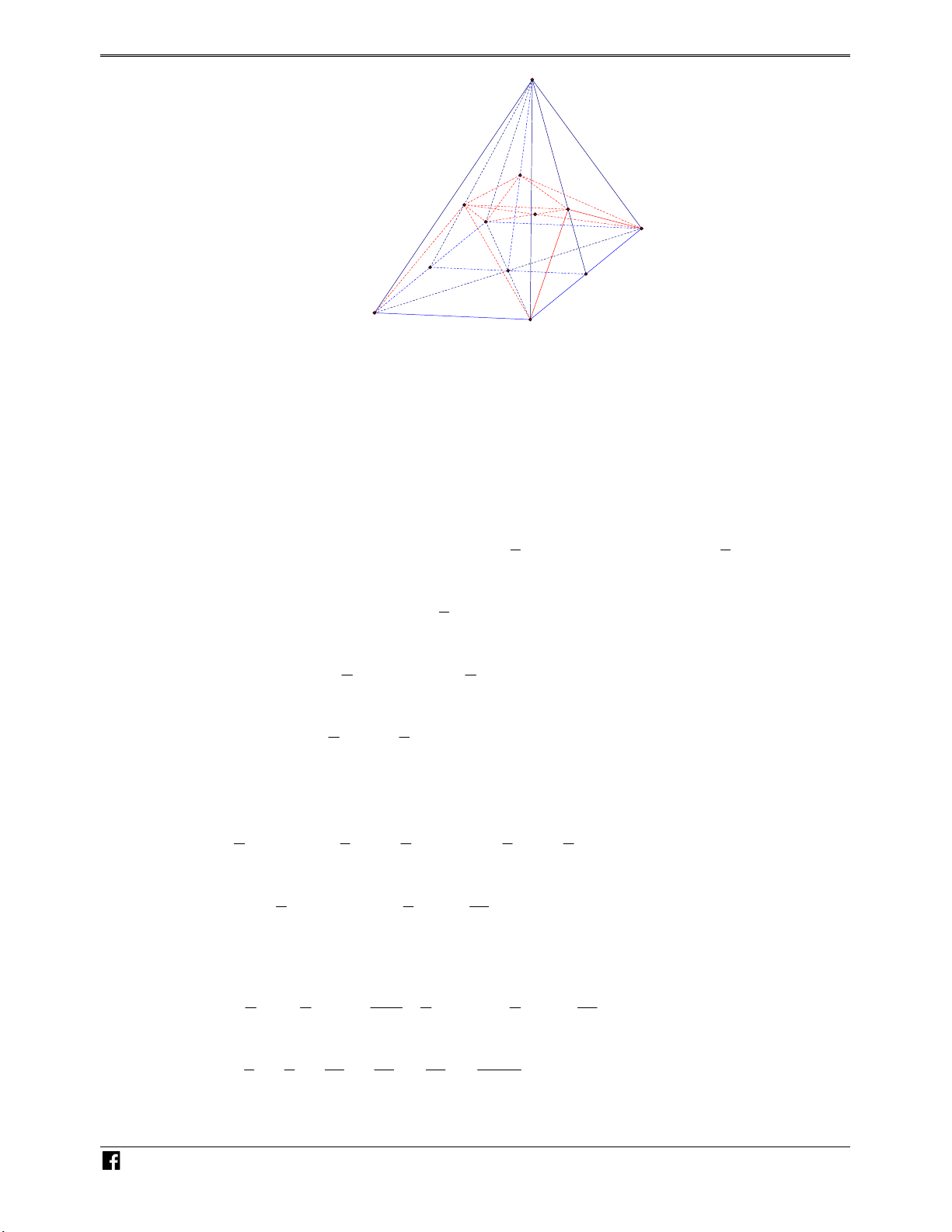
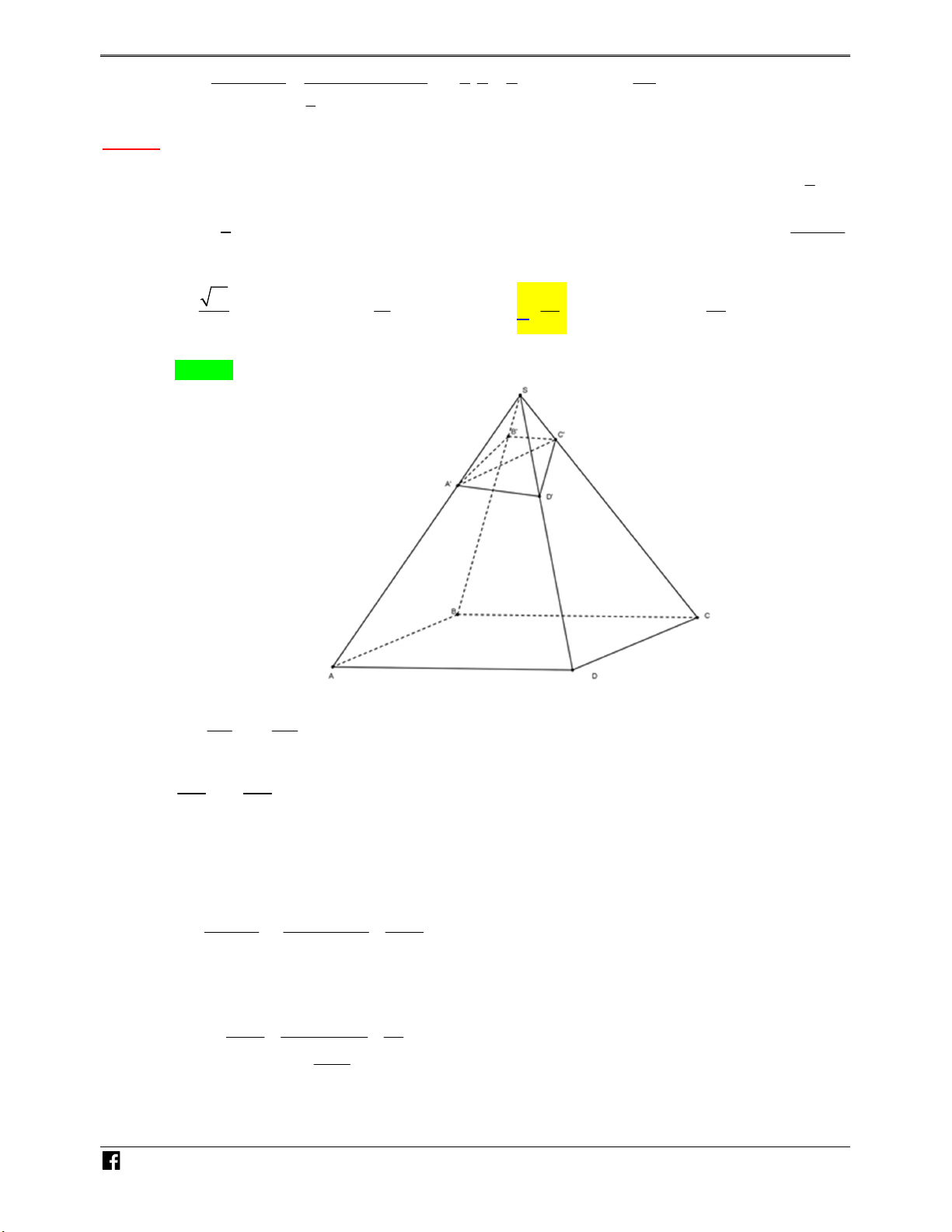
Bài toán 2. Cho hình chóp S.ABCD có đáy là hình bình hành, một mặt phẳng P cắt các cạnh V S ,
A SB, SC, SD lần lượt tại M , N , P, Q như hình vẽ bên. D C S M Q N P D A B C
https:/www.facebook.com/groups/toanvd. Trang 1 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 SA SB SC SD Đặt x, y, z,
t . Khi đó ta có các kết quả sau: SM SN SP SQ + x z y t V x y z t + S.MNPQ N V 4xyzt S.ABCD H Ó
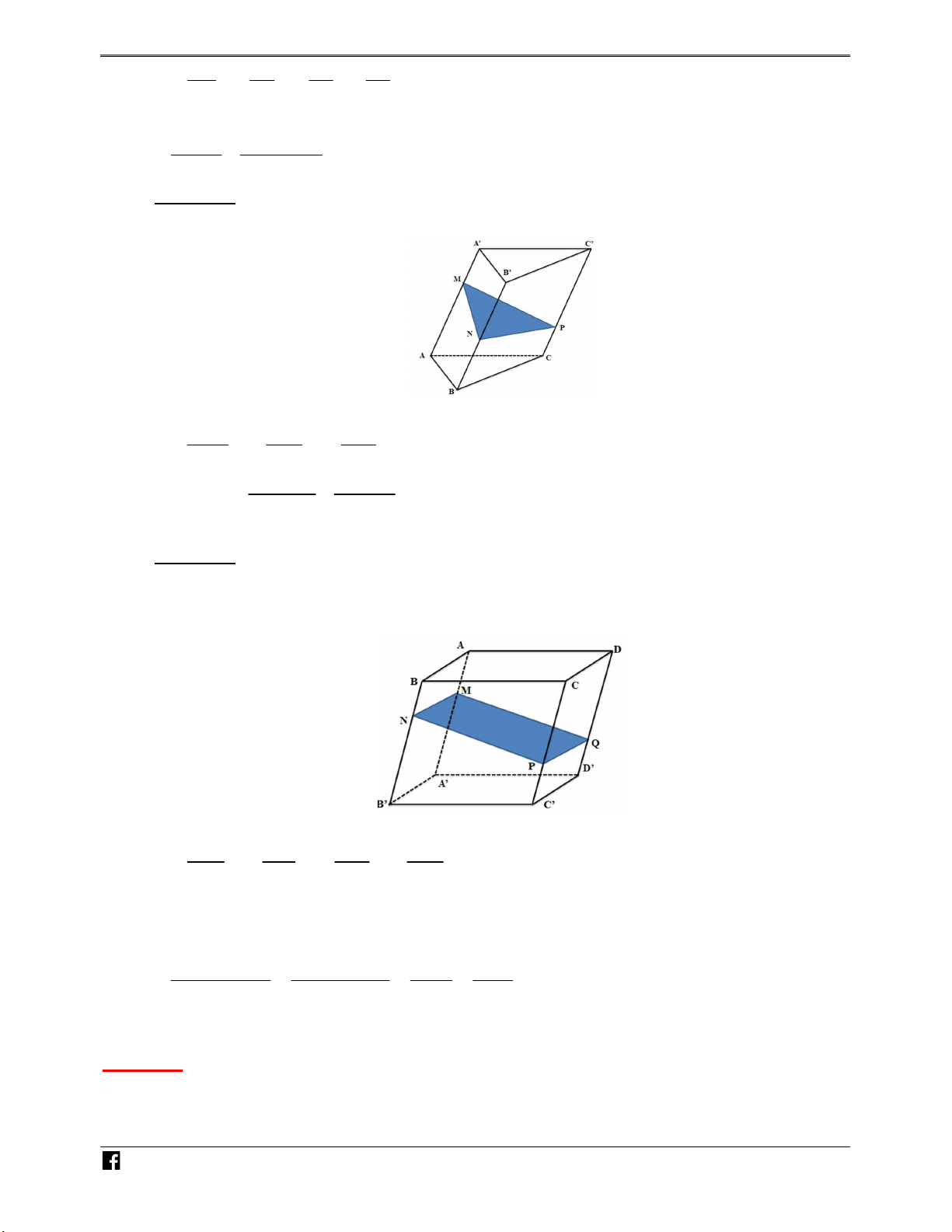
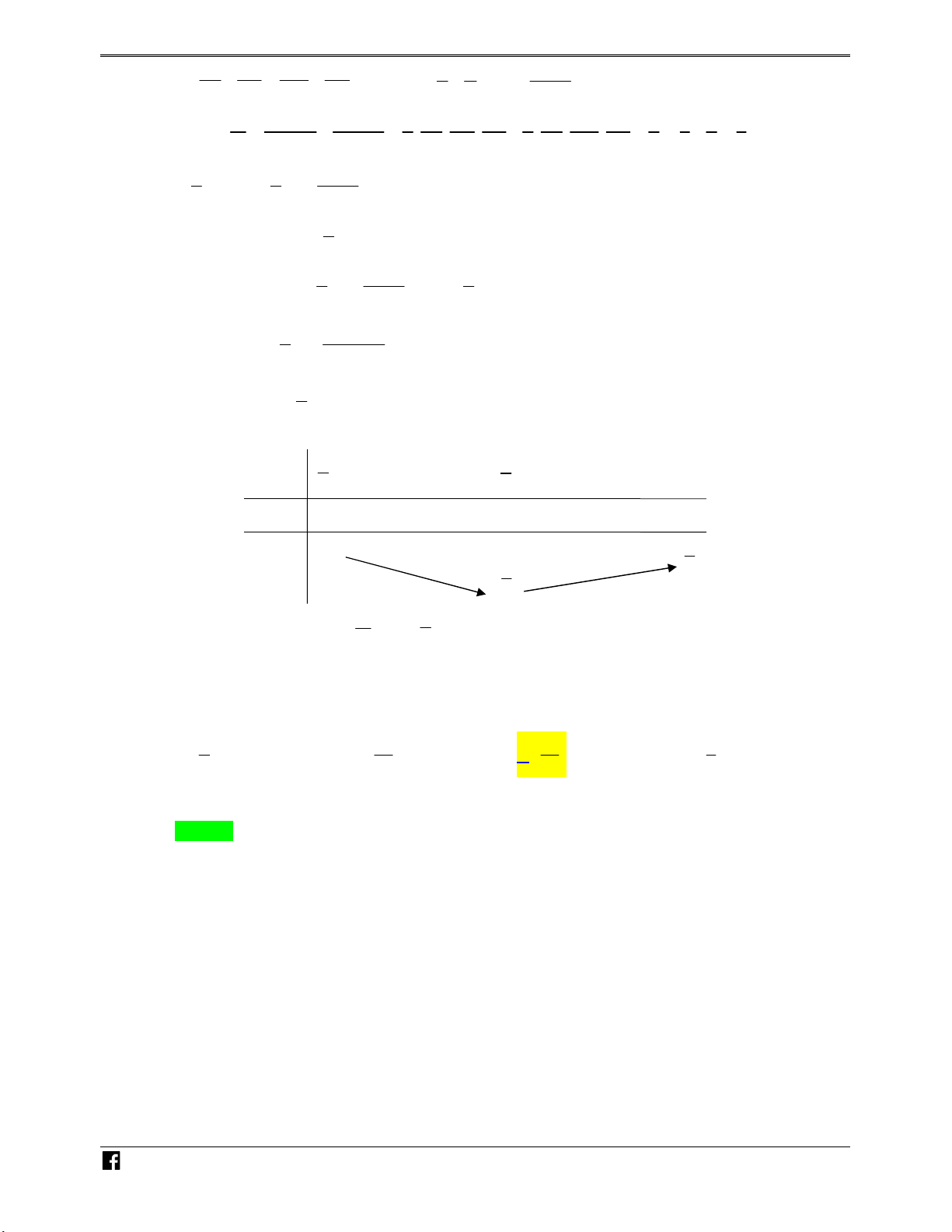
Bài toán 3. Cho hình lăng trụ ABC.A' B 'C '. Một mặt phẳng P cắt các cạnh bên M
AA', BB ', CC ' lần lượt tại M , N , P như hình vẽ bên. TOÁN VD – VD C A M B N C P Đặt x, y, z AA BB CC V x y z Khi đó ta có MNP.A'B'C' V 3 ABC.A'B'C '
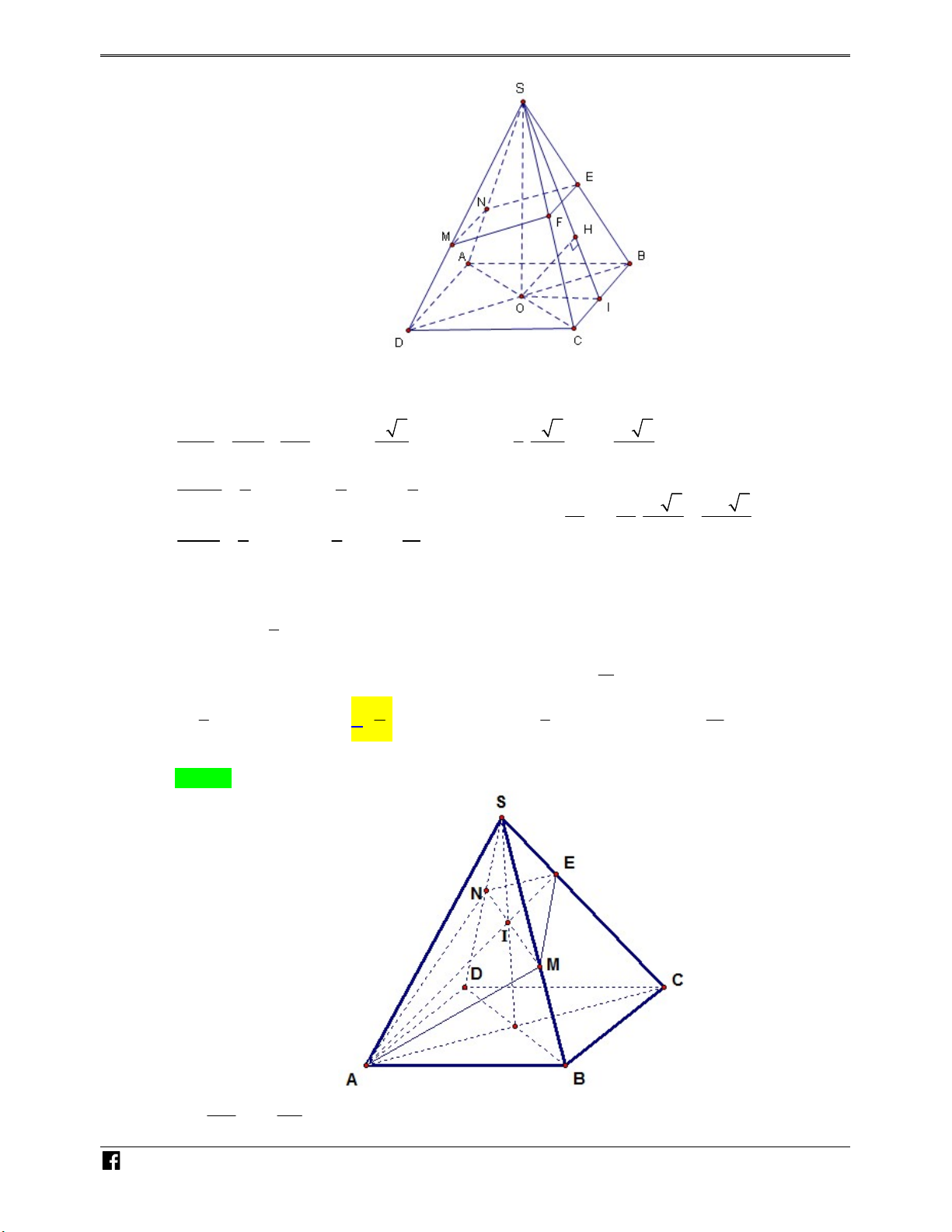
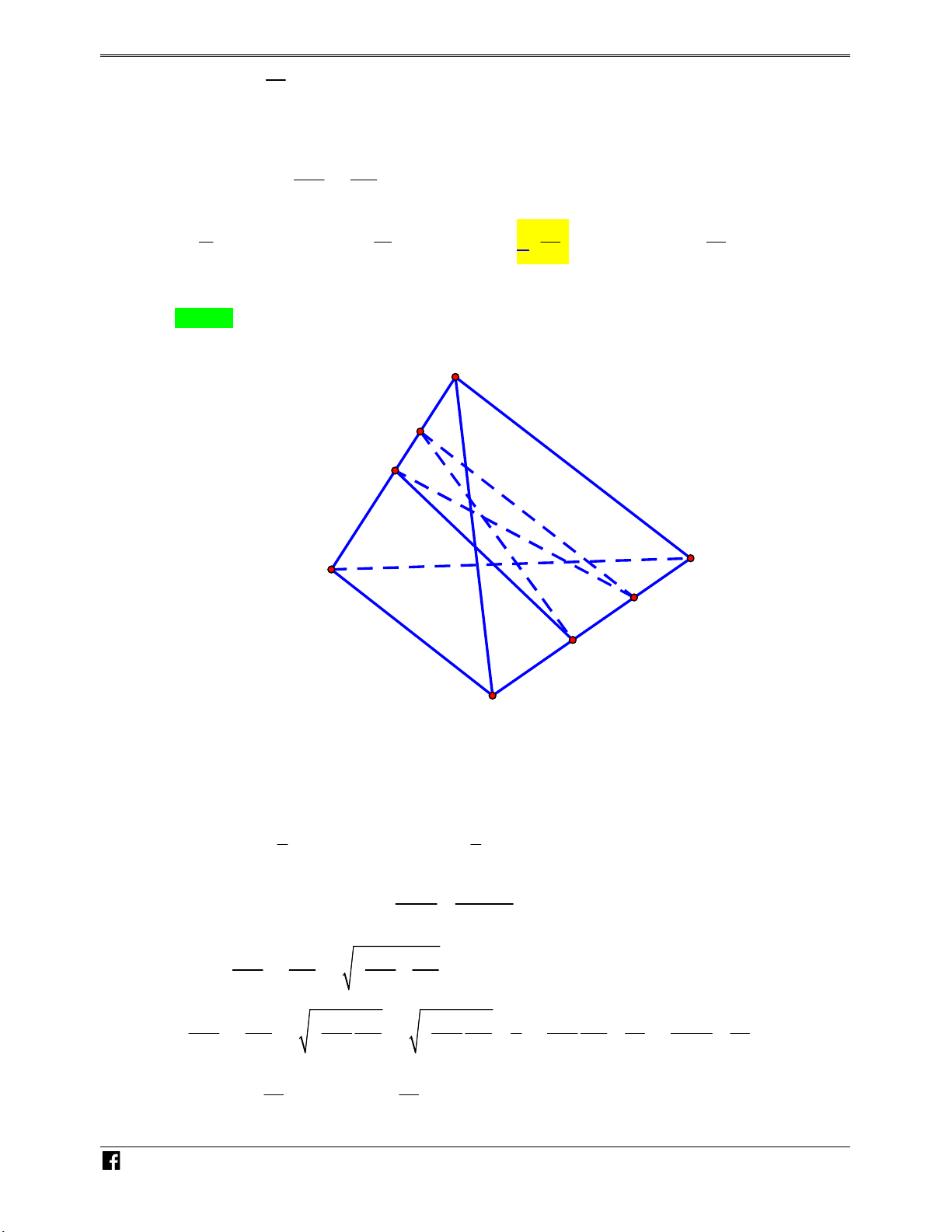
Bài toán 4. Cho hình lăng trụ ABC .
D A' B 'C 'D' . Một mặt phẳng P cắt các cạnh bên
AA ', BB ', CC ', DD' lần lượt tại M , N , P,Q như hình vẽ bên. N H Ó M TOÁN VD – VD AM BN CP DQ C Đặt x, y, z, t . AA BB CC DD Khi đó ta có + x z y t. V x y z t x z y t + ABCDMNQP V 4 2 2 ABCD.A' B 'C 'D '
B. CÁC DẠNG BÀI VÀ VÍ DỤ MINH HỌA
Bài toán 1. CHIA HÌNH CHÓP, HÌNH LĂNG TRỤ THÀNH 2 PHẦN BỞI MỘT MẶT PHẲNG
CHO TRƯỚC. TÍNH THỂ TÍCH MỘT TRONG HAI PHẦN HAY TỈ SỐ THỂ TÍCH
https:/www.facebook.com/groups/toanvd. Trang 2 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
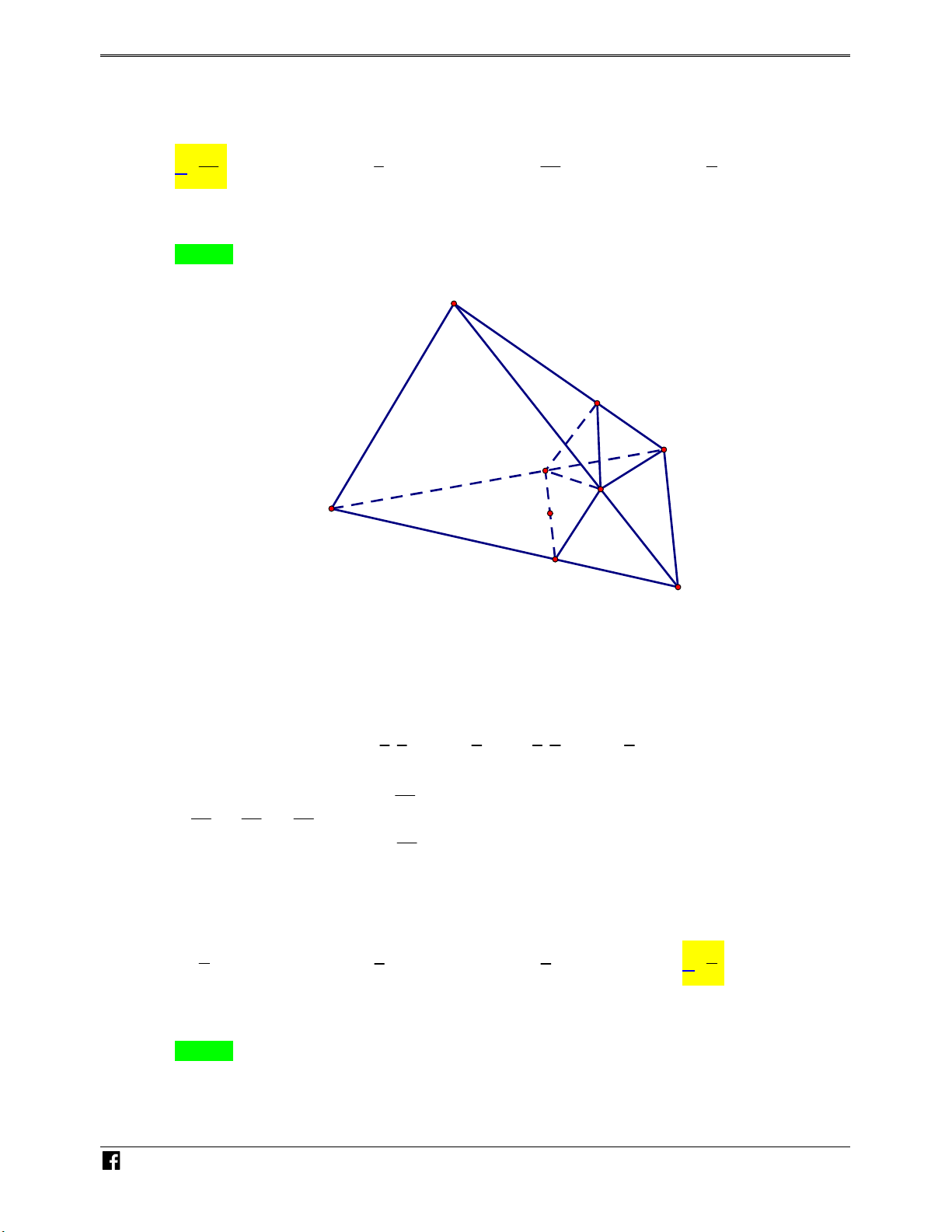
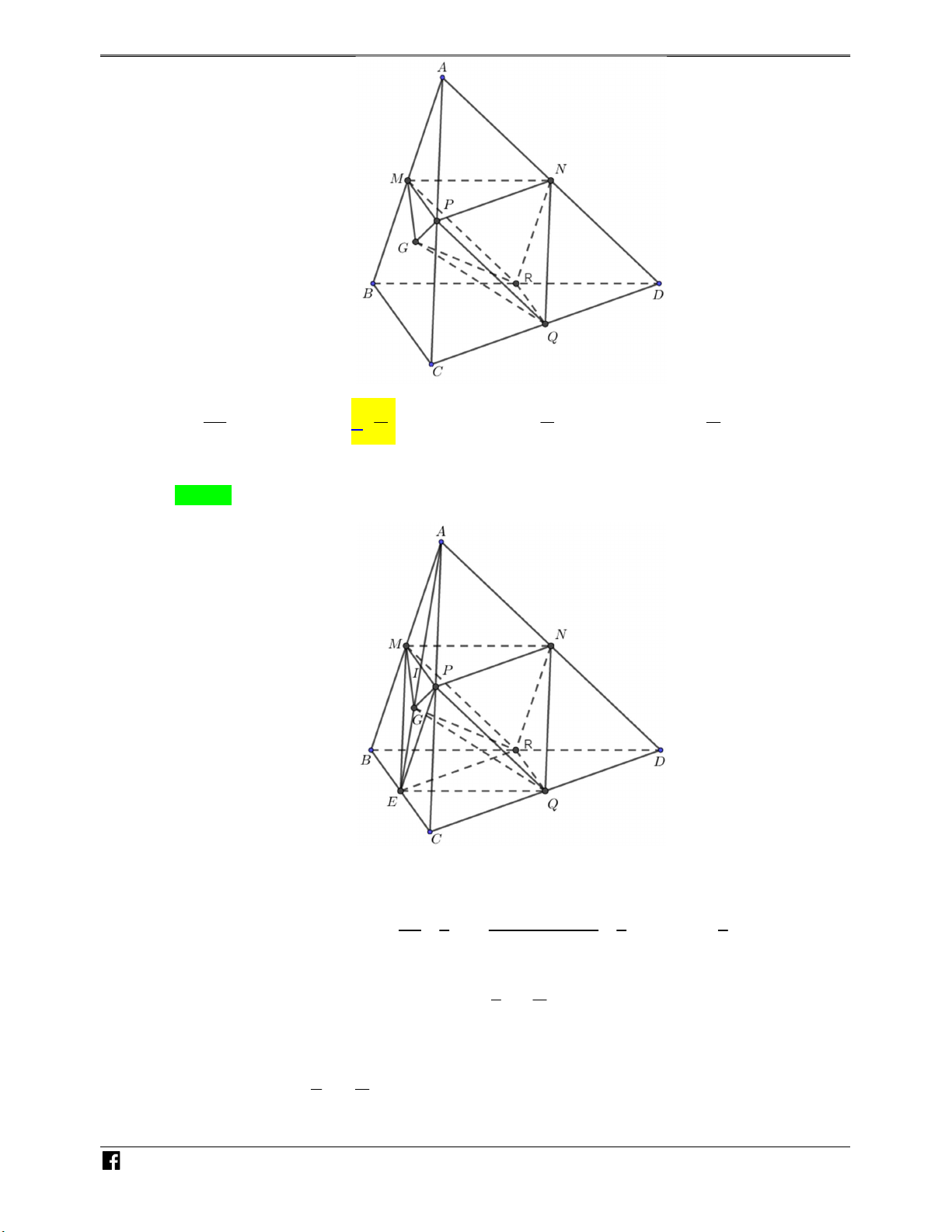
Ví dụ minh họa 1: Cho hình chóp S.ABC và G là trọng tâm tam giác ABC. Với hai số thực
x, y thay đổi và tập hợp các điểm M thỏa mãn GM xSB y AC là mặt phẳng (P) . Tính tỉ
số thể tích hai phần của khối chóp S.ABC được phân chia bởi mpP . 7 1 8 2 N A. . B. . C. . D. . H 20 3 27 5 Ó M Lời giải TO Chọn A Á N S VD – VD H C C F K G A E B
Với hai số thực x, y thay đổi và tập hợp các điểm M thỏa mãn GM xSB y AC là mặt N H
phẳng (P) đi qua G và song song song với SA ; BC . Nên thiết diện khi cắt hình chóp S.ABC ÓM
bởi P là hình bình hành EFHK như hình vẽ. T
Gọi V ,V ,V lần lượt là thể tích của khối chóp S.ABC , khối đa diện SAEFHK và BCEFHK O 1 2 Á 1 1 5 1 2 1 N Ta có V V V . d . S . d . S 2 H .BCEF K .HCF S,ABC ABC B,SAC 3 3 9 3 3 9 SAC VD 20 V V 1 – 5 2 7 V V V 27 . Chọn A. V 27 27 27 7 V V D 2 27 C
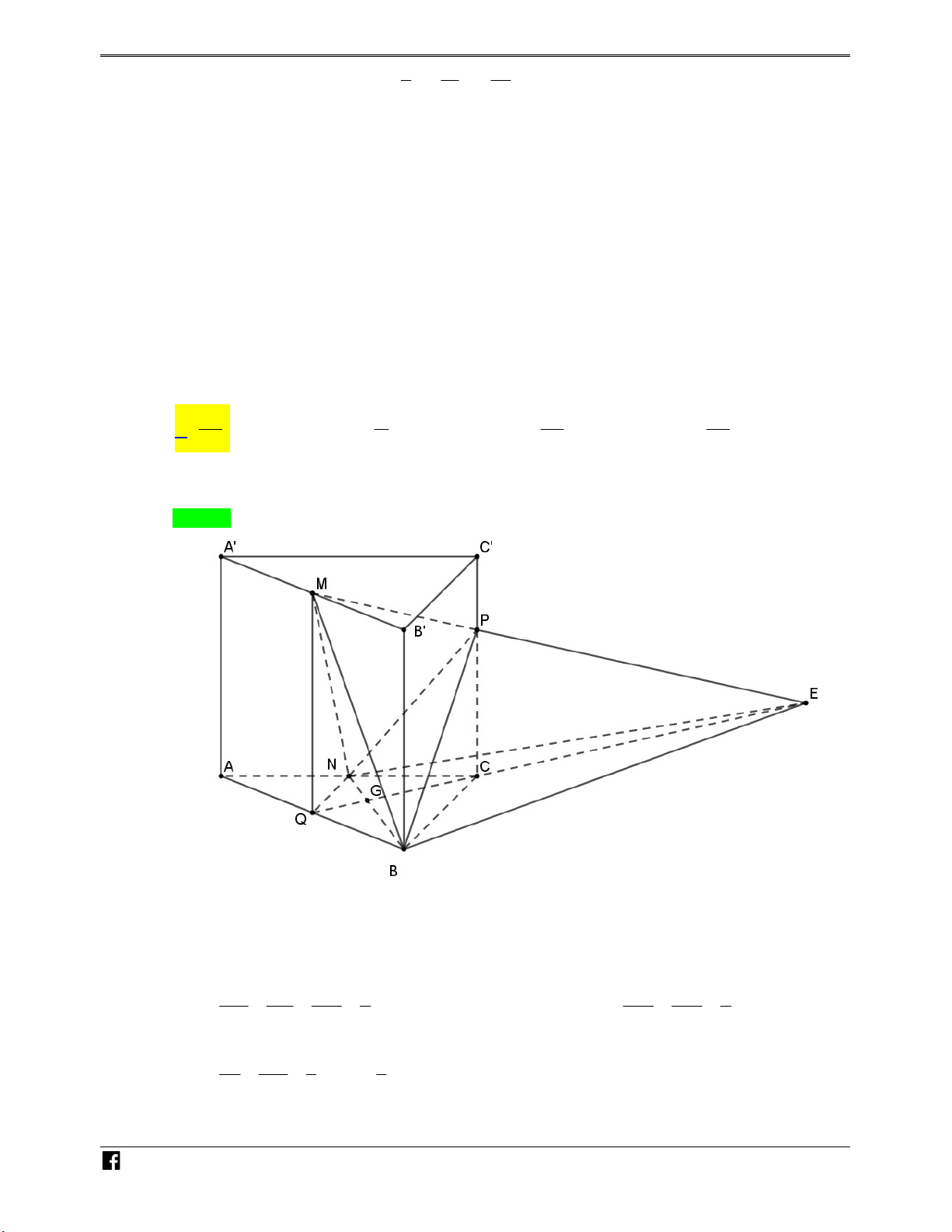
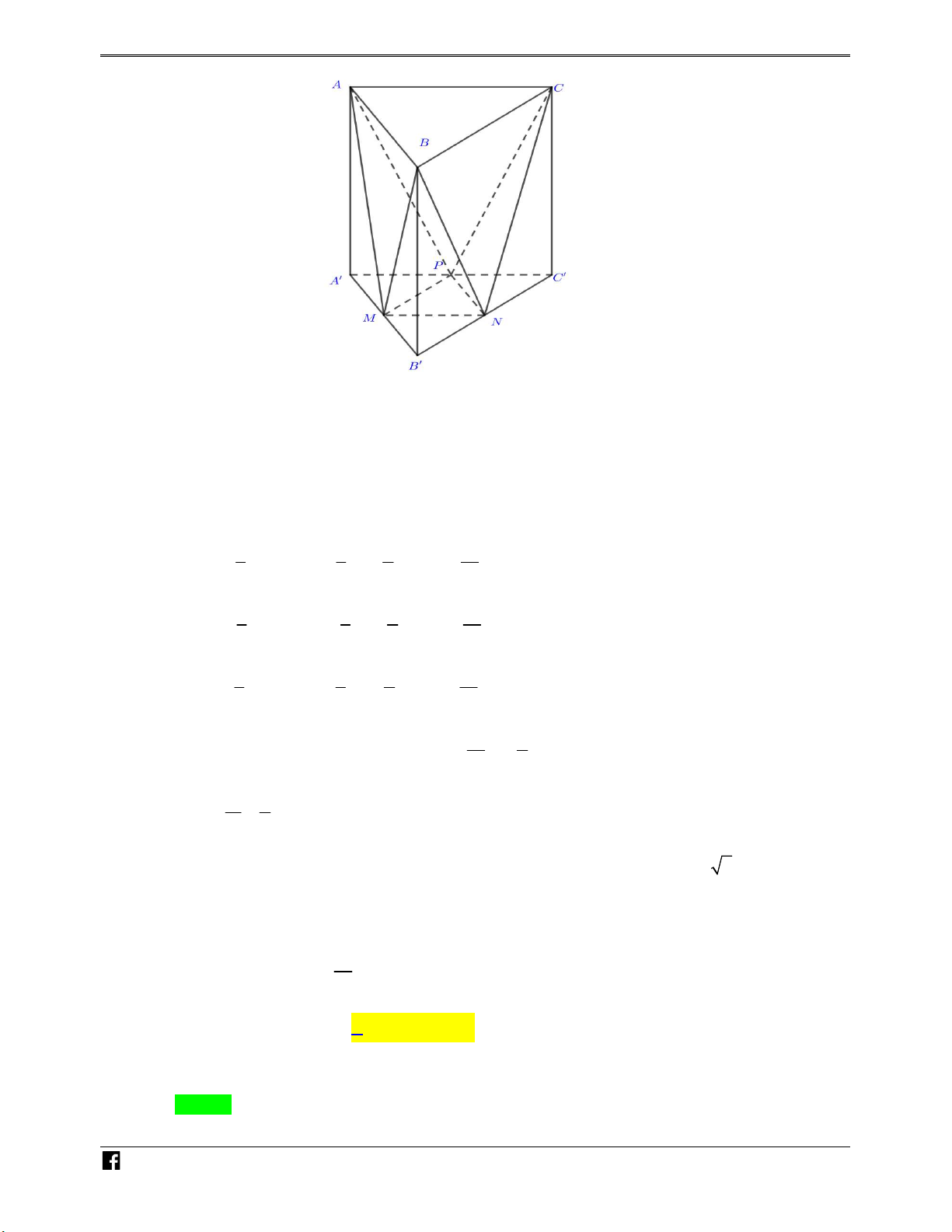
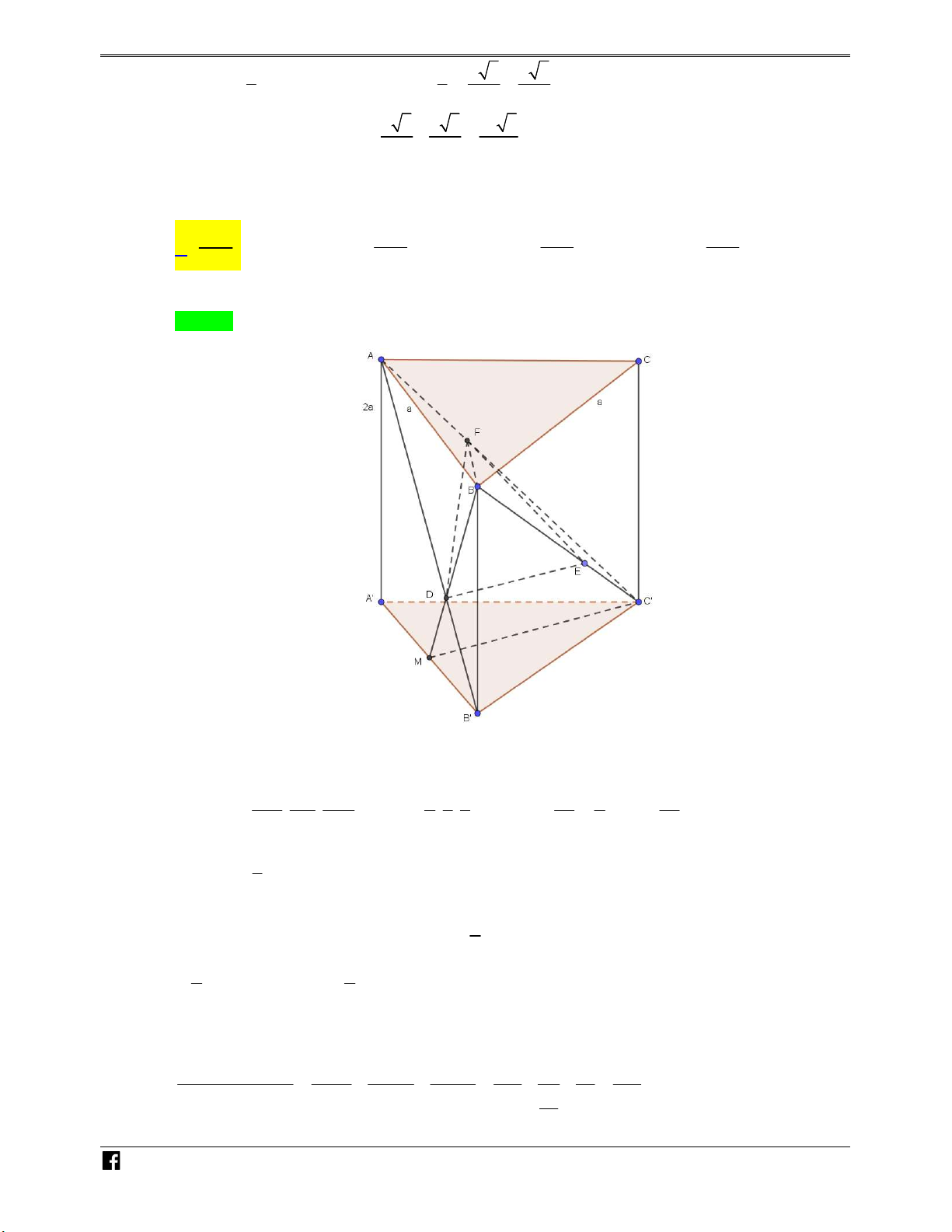
Ví dụ minh họa 2: Cho khối lăng trụ ABC.A B C
. Gọi E là trọng tâm tam giác A B C và F
là trung điểm BC . Tính tỉ số thể tích giữa khối B .EAF và khối lăng trụ ABC.A B C . 1 1 1 1 A. . B. . C. . D. . 4 8 5 6 Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 3 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 B A F C N H Ó M TOÁ B' N A' V E M D – C' V D C 1
Ta có M là trung điểm của B C khi đó S S
và d B , AAMF d B , AEF . EAF 2 AA M F 1 2 Vì V V V V V V B .AA MF ABF .A B M B .ABF ABF .A B M ABF . 3 A B M . 3 ABF AB M 1 1 2 1 1 1 Suy ra V V . .V . .V .V . B EAF B . 2 AA M F . 2 3 ABF A B M . 3 2 ABC A B C . 6 ABC A B C
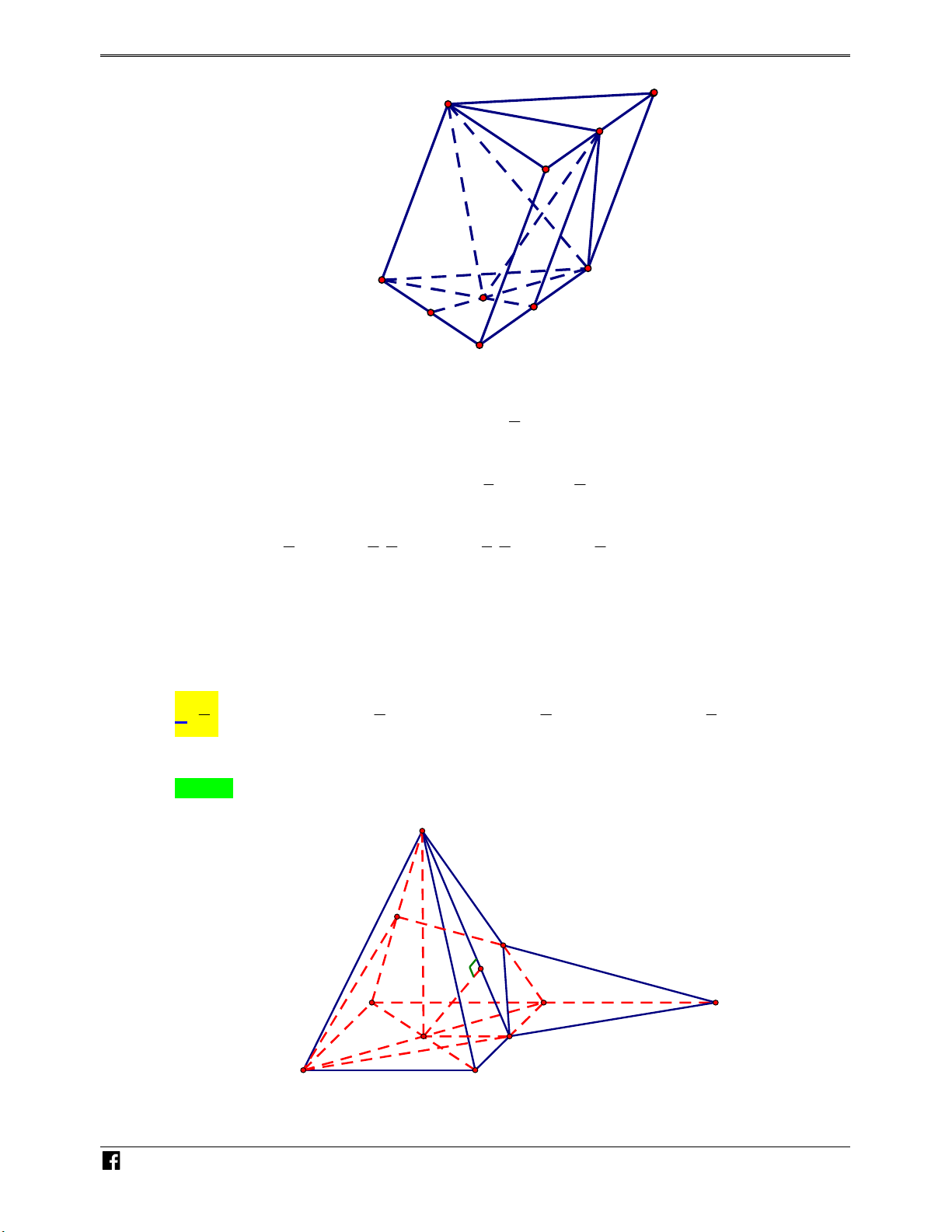
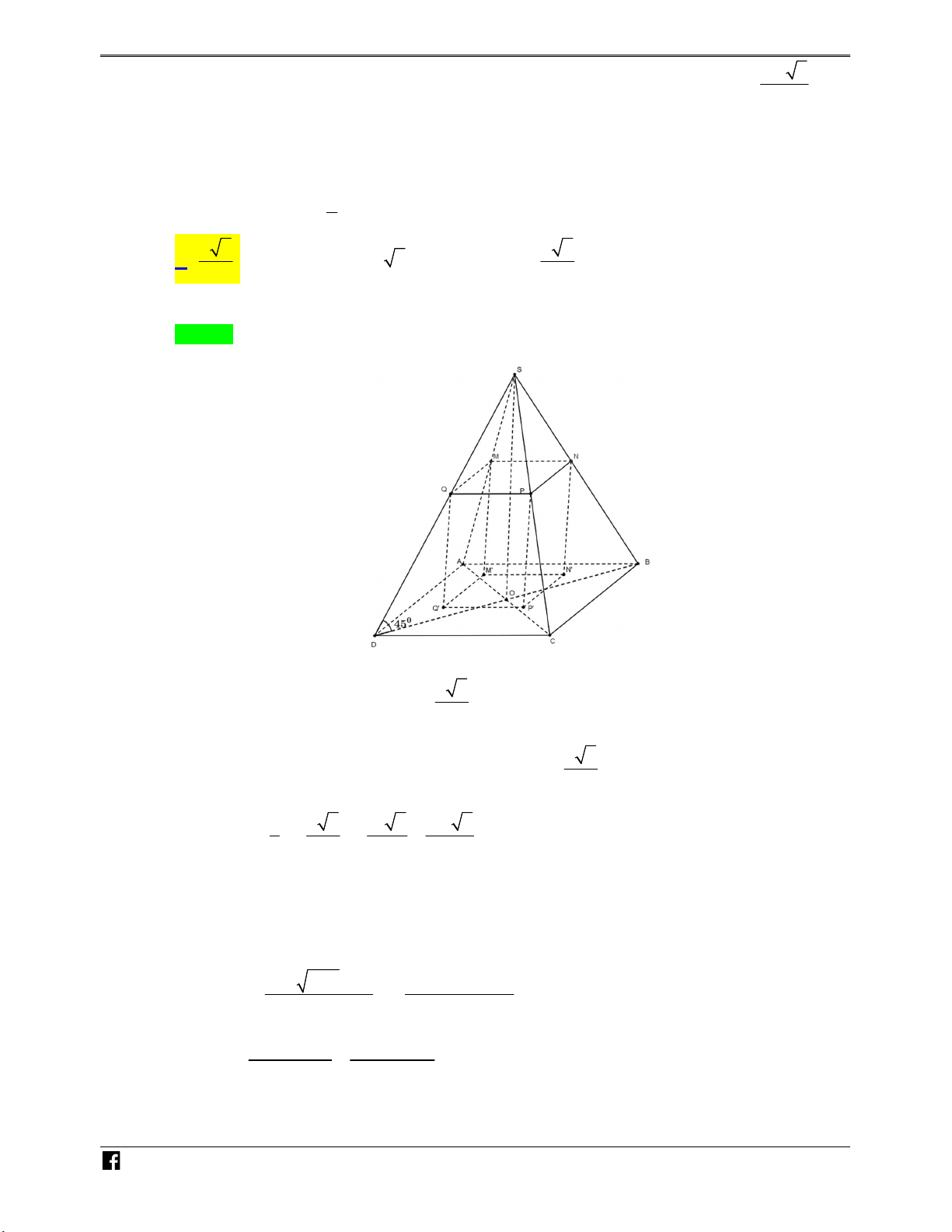
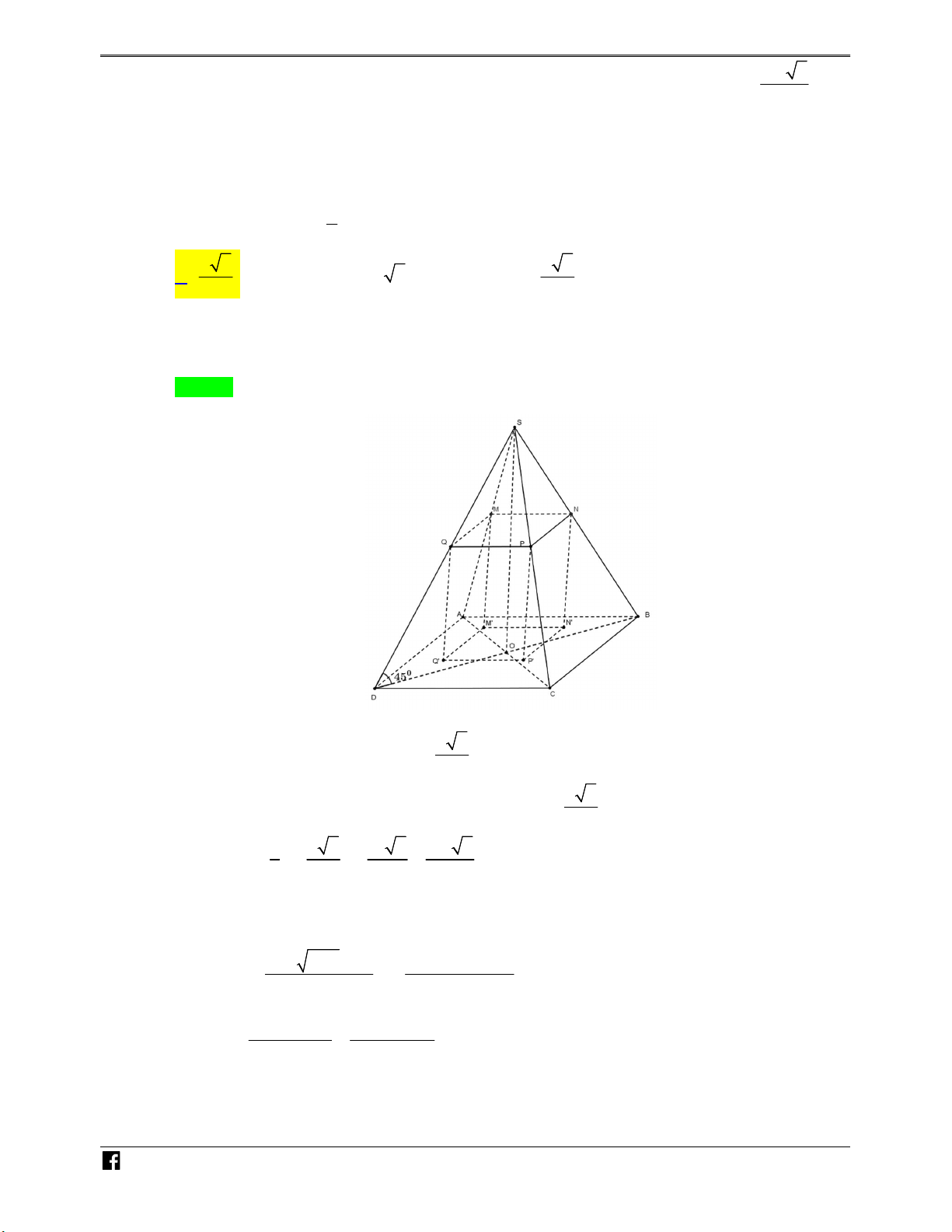
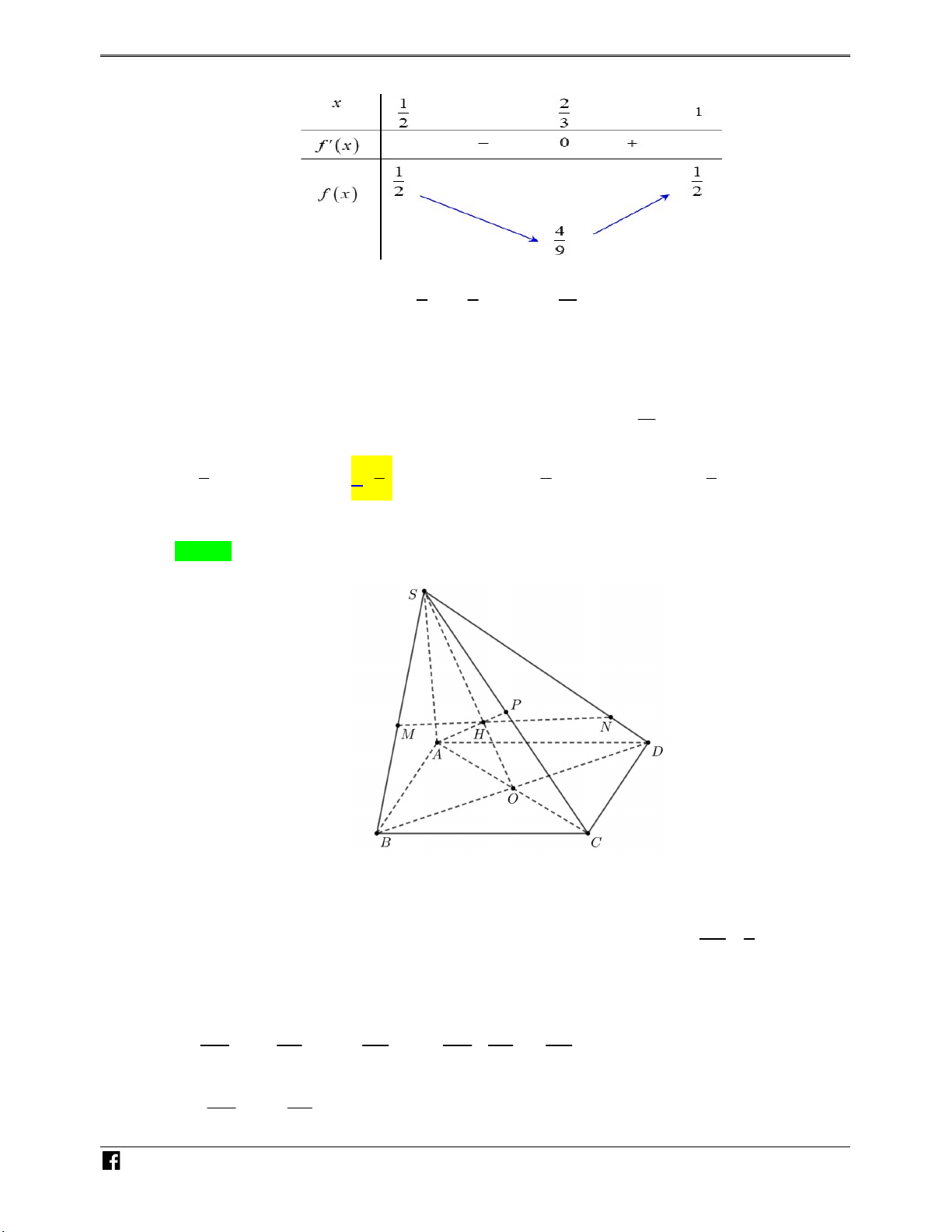
Ví dụ minh họa 3: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với N
đáy một góc 60 . Gọi M là điểm đối xứng của C qua D , N là trung điểm SC. Mặt phẳng H
BMN chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên ÓM phần bé) bằng T 7 1 7 6 O A. . B. . C. . D. . Á 5 7 3 5 N Lời giải VD Chọn A – S VDC N E H C D M O F B A
Giả sử các điểm như hình vẽ.
https:/www.facebook.com/groups/toanvd. Trang 4 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
E SD MN E là trọng tâm tam giác SCM , DF // BC F là trung điểm BM . a a Ta có: SD ABCD 6 , SDO 60 SO , 2 2 7 SF SO OF 2 2 N a a H d O SAD 2 6 1 7 , OH h ; S SF.AD Ó 2 7 SAD 2 4 M V ME MF MD 1 MEFD T O V MN MB MC 6 MNBC Á N a V V d M SAD S h S V BFDCNE MNBC 3 5 5 1 1 5 1 5 6 , 4 6 6 3 2 SBC 18 2 SAD 72 D – 3 3 1 a 6 7a 6 V S . O S V V V V S.ABCD ABCD SABFEN S. 3 6 ABCD BFDCNE 36 D C V 7 Suy ra: SABFEN V 5 BFDCNE
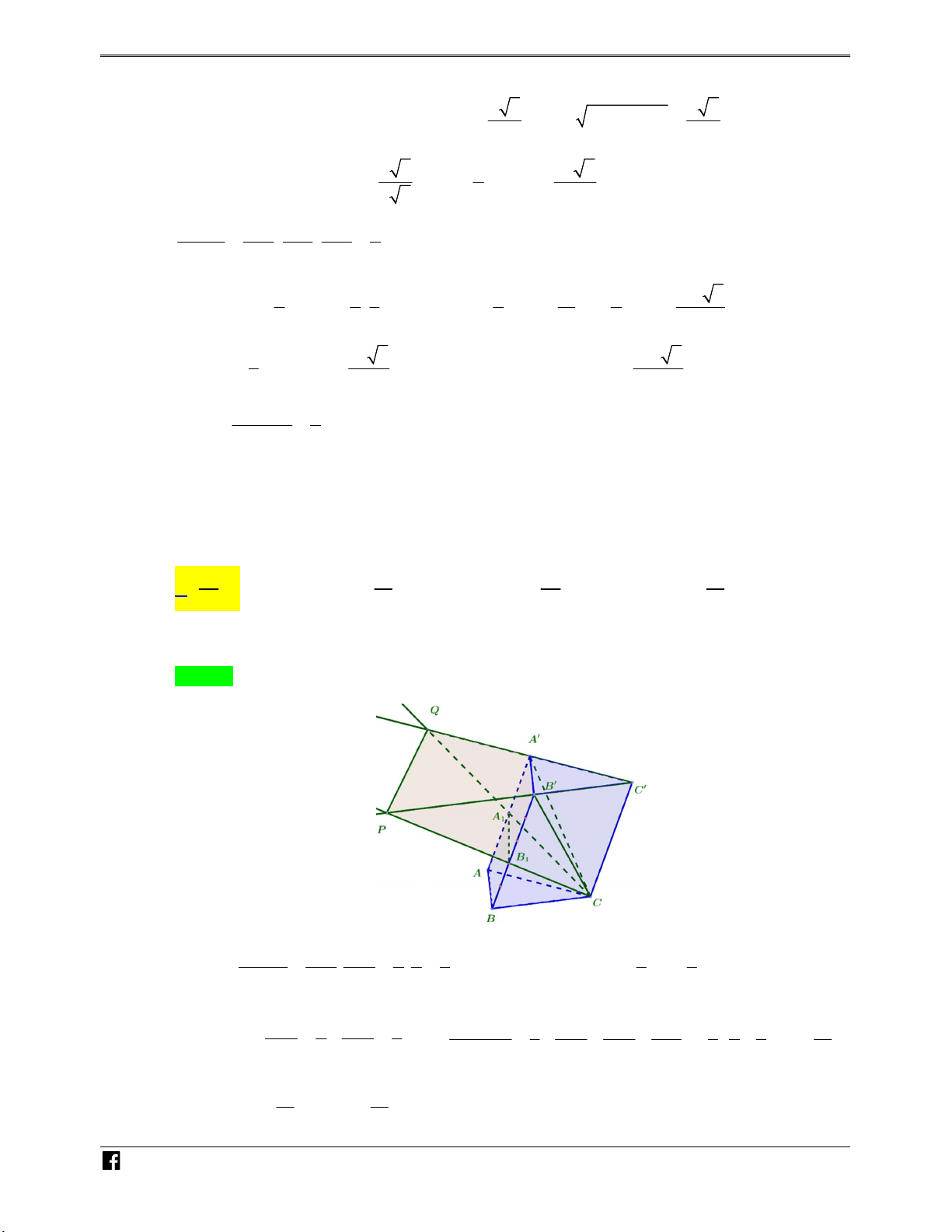
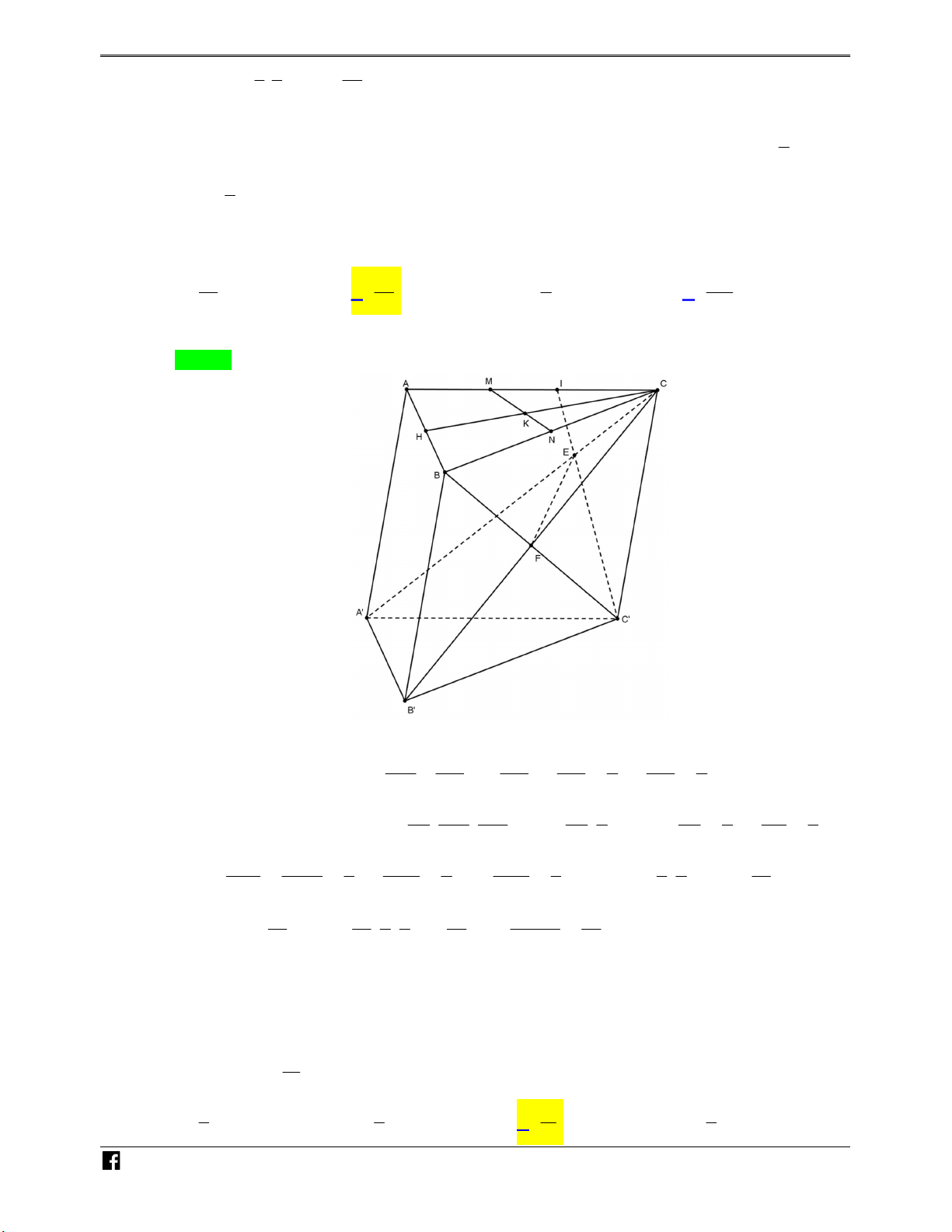
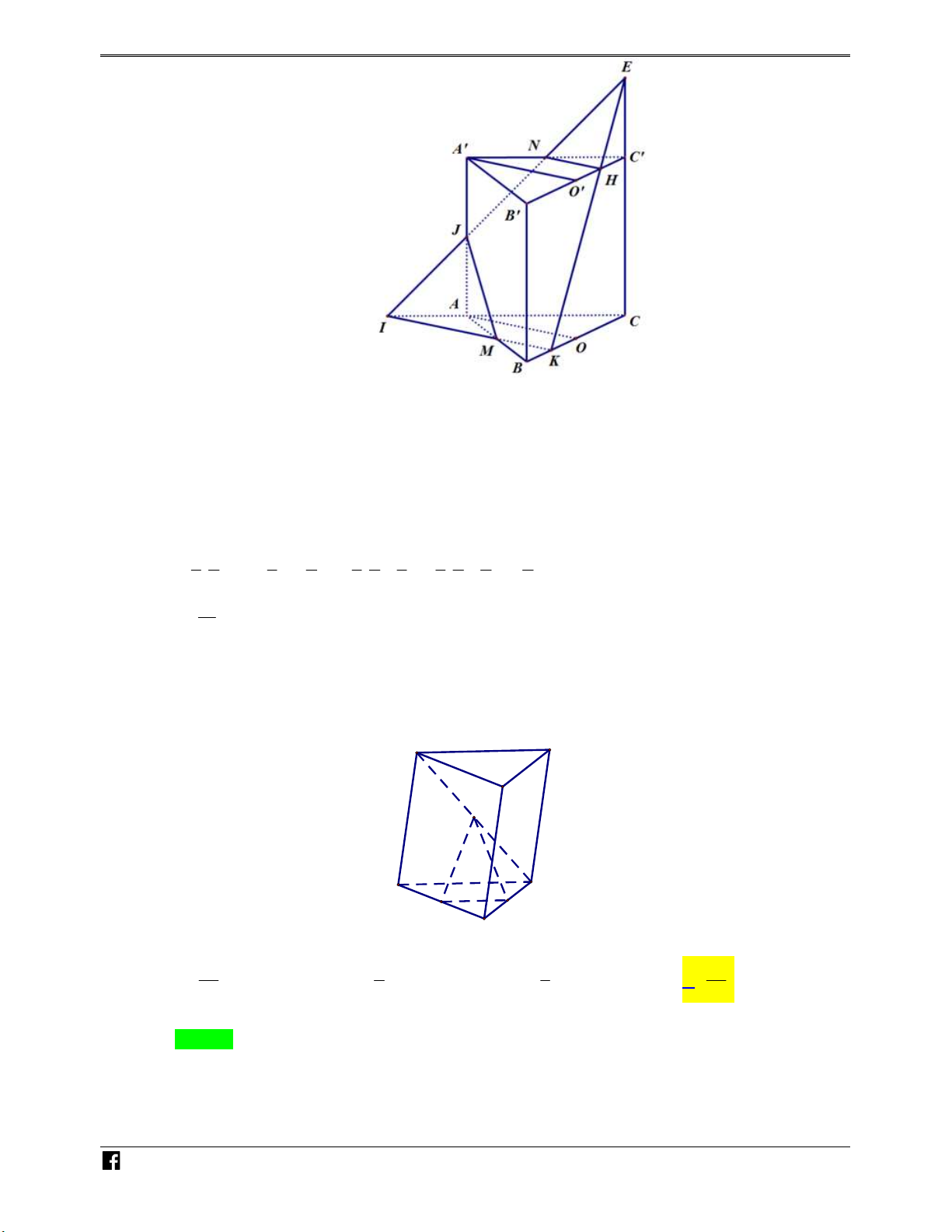
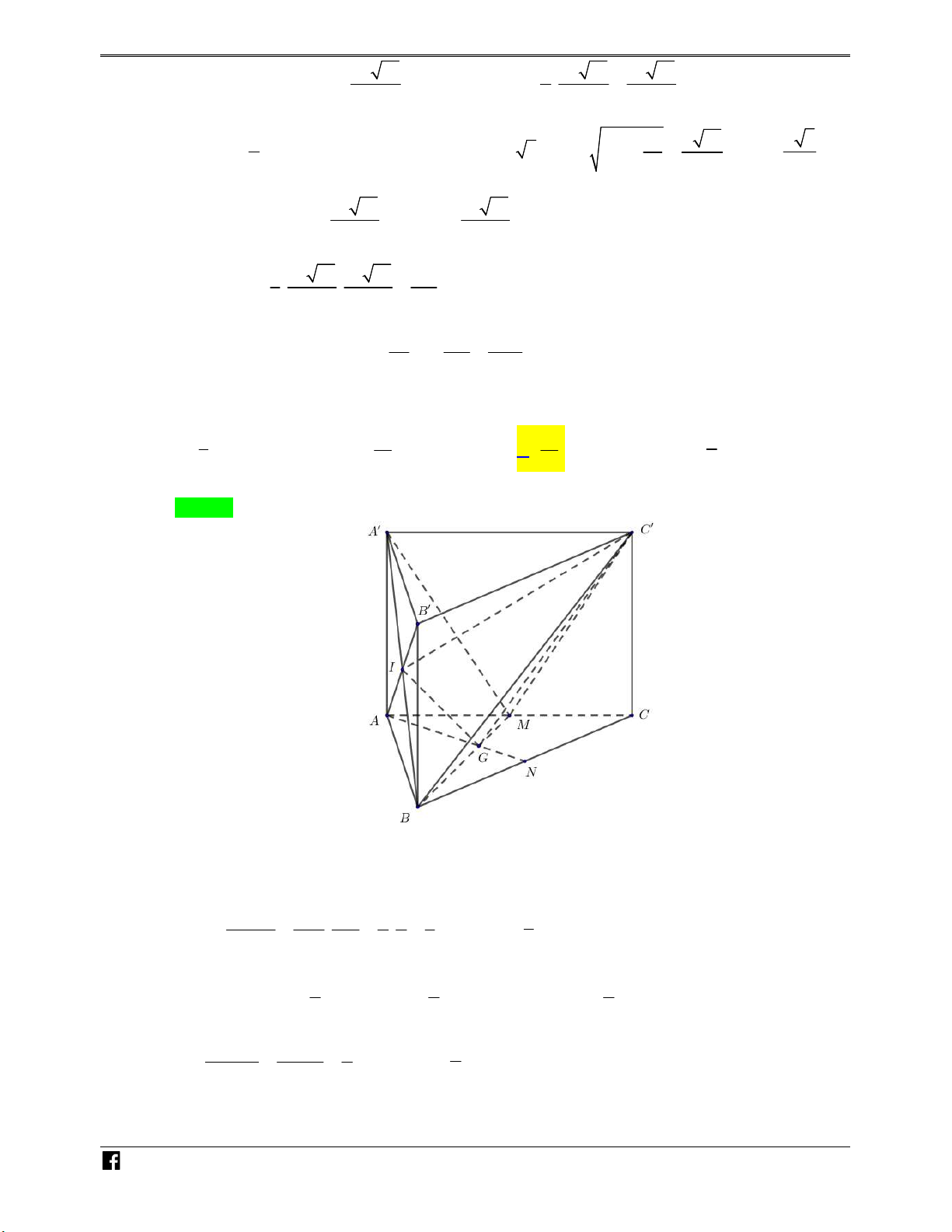
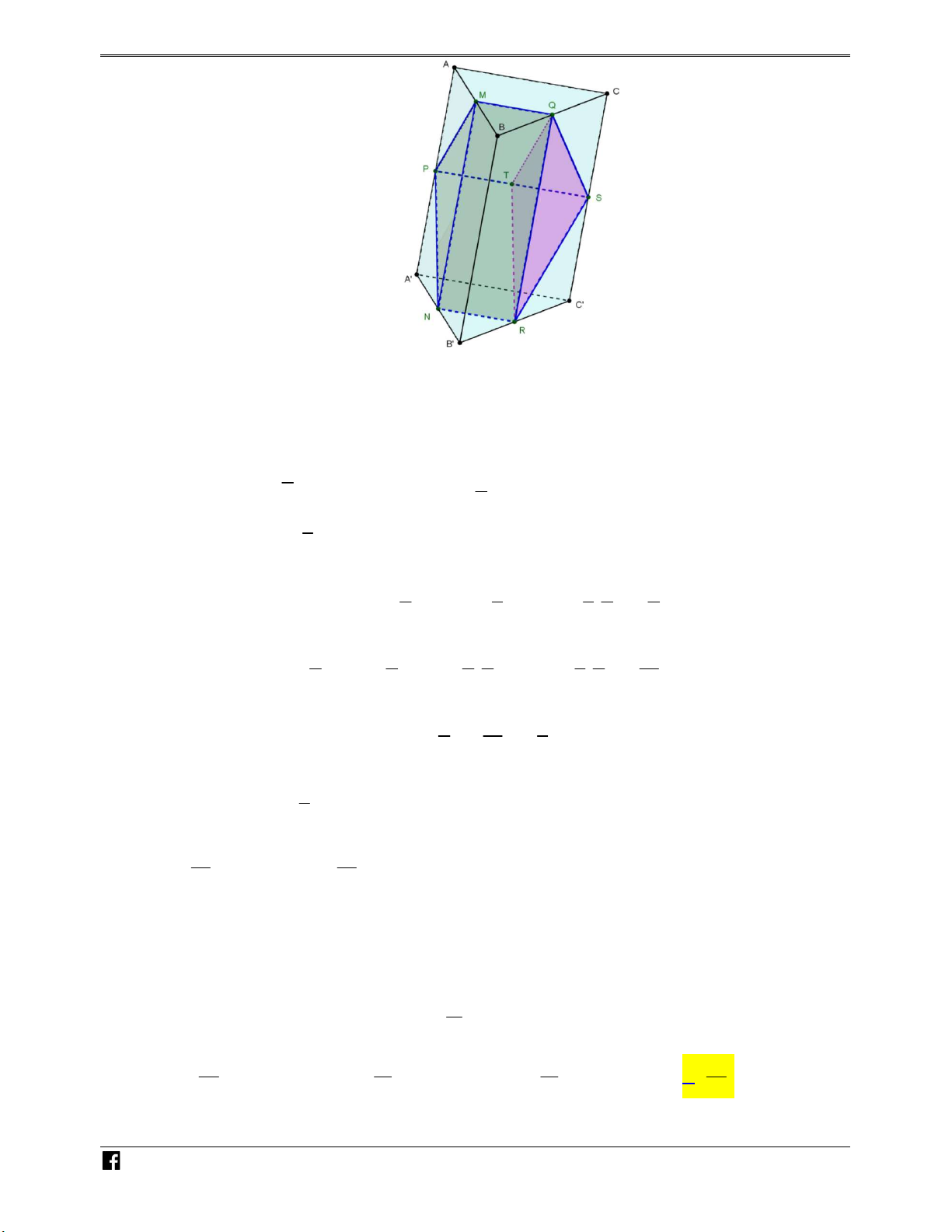
Ví dụ minh họa 4: Cho lăng trụ ABC.A B C
có thể tích bằng V . Gọi A , B lần lượt là hai 1 1
điểm nằm trên hai cạnh AA và BB sao cho A là trung điểm của AA và 5.B B 3.BB . Tia 1 1 CA cắt tia C A
tại Q và tia CB cắt tia C B
tại P . Thể tích khối đa diện lồi A A QB B P 1 1 1 1 bằng: 29 7 37 10 A. V . B. V . C. V . D. V . 30 10 90 9 N H Lời giải Ó M Chọn A TOÁN VD – VDC V C A C B 1 2 1 1 5 Ta có: C .AB C . . V 5.V 5. V V . V C .QPC C .A B C C Q C P 2 5 5 3 3 C .QPC V A A 1 B B 3 AB C A B C 1 A A B B CC 1 1 3 7 Mặt khác: 1 , 1 1 1 1 1 . 1 AA 2 BB 5 V 3 AA BB CC 3 2 5 10 A B C ABC 7 7 V V V . A B C 1 A 1 B C 10 A BC ABC 10
https:/www.facebook.com/groups/toanvd. Trang 5 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 V 5 7 29 V V V V V . A 1 A QB 1 B P C .QPC A B C 1 A 1 B C 3 10 30
Bài toán 2 : TÍNH THỂ TÍCH KHỐI ĐA DIỆN ĐƯỢC PHÁT TRỂN TỪ CÁC KHỐI CHO
TRƯỚC BẰNG CÁCH LẤY THÊM CÁC ĐIỂM . N H
Phương pháp : với các khối có đáy như chóp , lăng trụ ta chuyển đáy của các khối này về mặt đáy Ó
của các khối ban đầu , sau đó so sánh đường cao của khối này với đường cao của khối M ban đầu. T
Với các khối không phải là chóp hoặc lăng trụ ta có thể dùng phân chia đa diện để tạo ra OÁ
các khối chóp hoặc lăng trụ , N
Cũng có thể căn cứ vào khối đã cho cộng trừ đi các khối không thuộc , hoặc cộng thêm V
khối thuộc khối đa diện yêu cầu tính thể tích . D
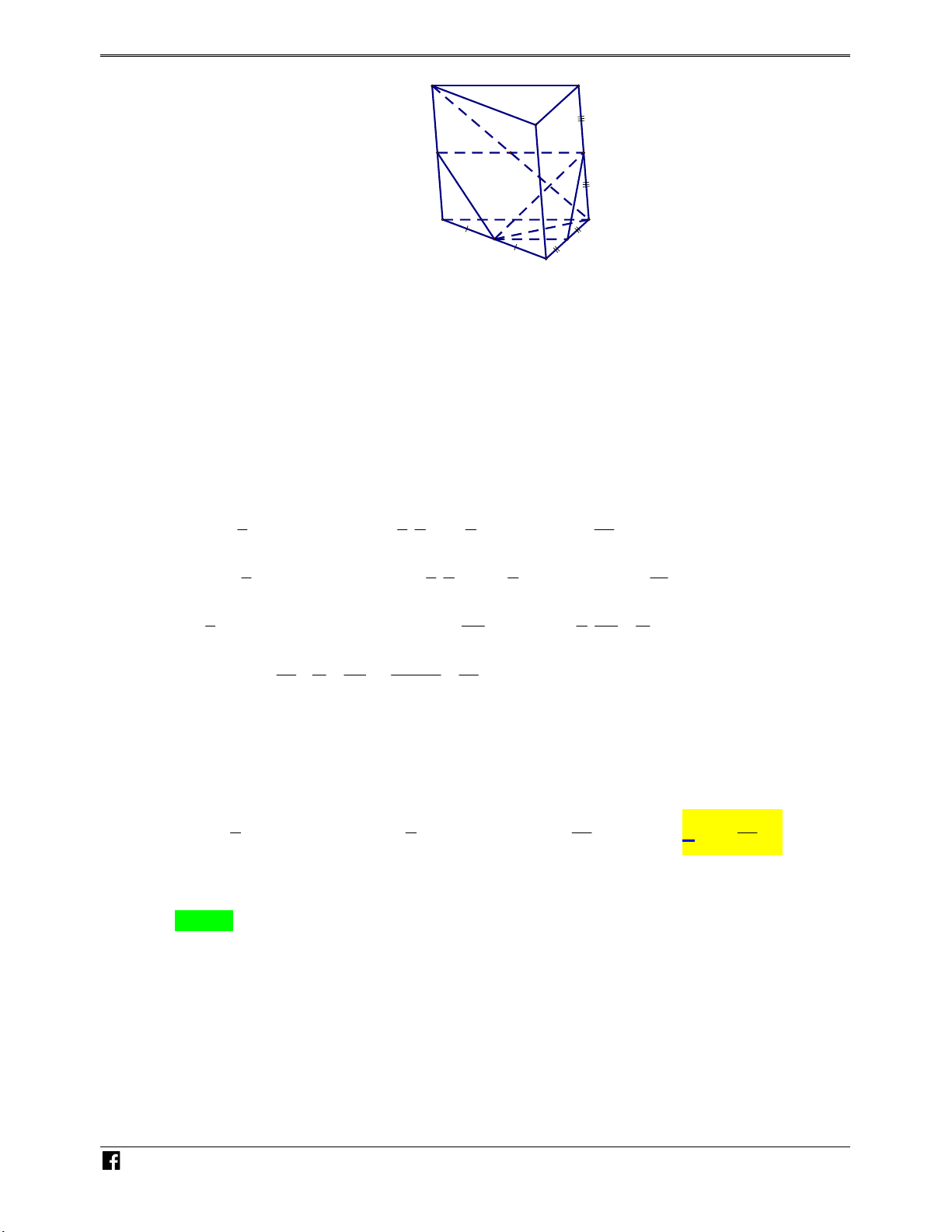
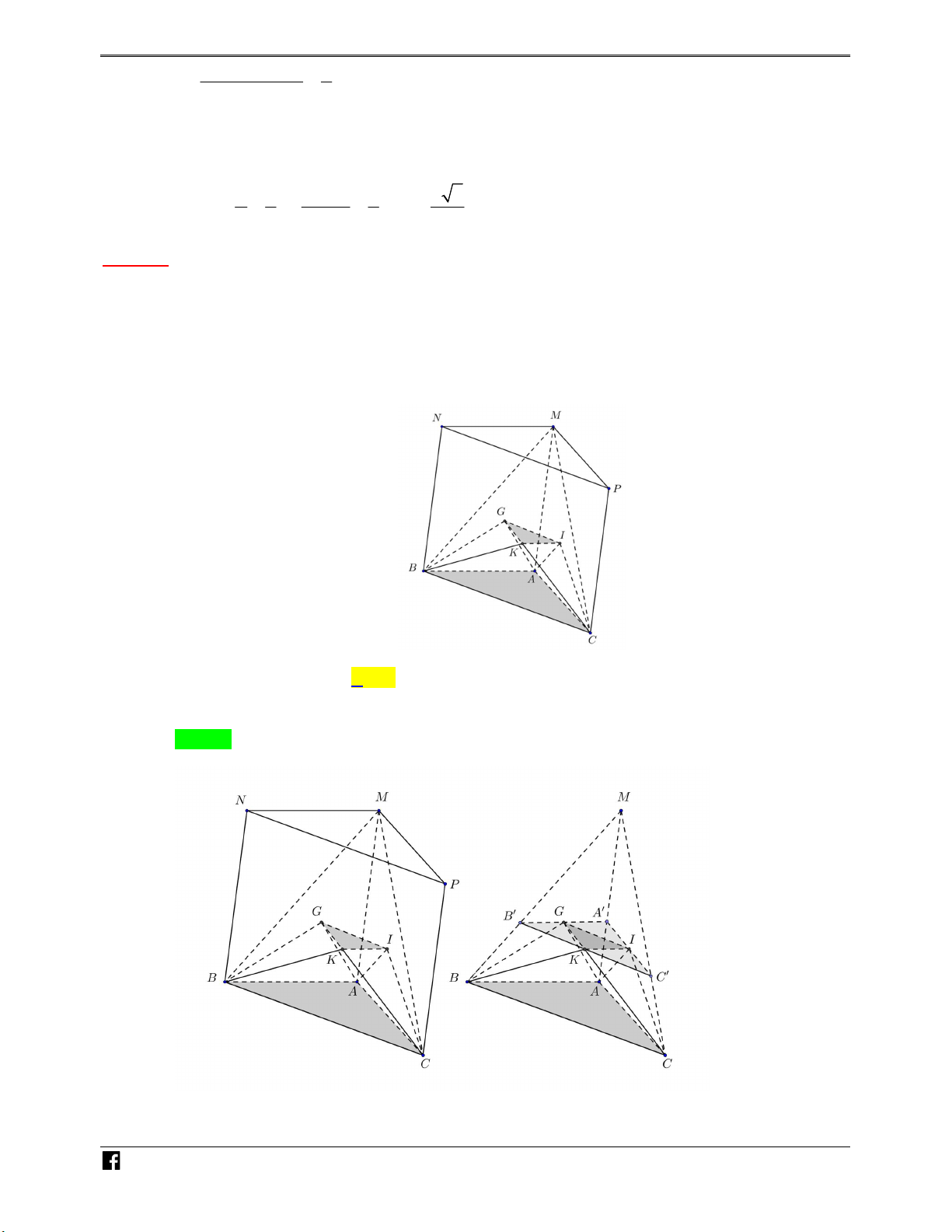
Ví dụ minh họa 1: Cho hình lăng trụ ABC.A' B 'C ' có thể tích bằng V. Gọi M, N lần lượt là –
trung điểm của A' B ', AC và P là điểm thuộc cạnh CC ' sao cho CP 2C ' P . Tính thể tích VD
khối tứ diện BMNP theo V. C 2V V 5V 4V A. . B. . C. . D. . 9 3 24 9 Lời giải Chọn A N H Ó M TOÁN VD – VDC
Gọi B là diện tích tam giác ABC , h là độ dại đường cao của hình lăng trụ, suy ra V . B h . Gọi
Q là trung điểm AB , G là trọng tâm tam giác ABC . Gọi V là thể tích khối chóp BMNP , V 1 2
là thể tích khối chóp MBNE với E QC MP . PE CE PC 2 PC PC 2 Ta có
do PC // MQ và PC 2PC nên . ME QF MQ 3 MQ CC 3 V MP 1 1 Ta có 1 V V . 1 2 V ME 3 3 2
https:/www.facebook.com/groups/toanvd. Trang 6 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 2 8
Do GC QC,CE 2QC GE GC CE QC . 3 3 1 Ta lại có V S
.h . Ta tính diện tích tam giác BNE theo diện tích tam giác ABC ta có 2 3 BNE N H 8 8 Ó S S S S S S . BNE BGE NGE NQC BQC 3 3 QBNC M T S 8 AQN AQ AN 1 3 O Mà . S S do đó S S 2B . QBCN ABC BNE QBNC Á S AB AC 4 4 3 ABC N V 1 1 2V 1 2V D Nên V S .h .2 . B h V V . 2 BNE 1 2 3 3 3 3 9 – V
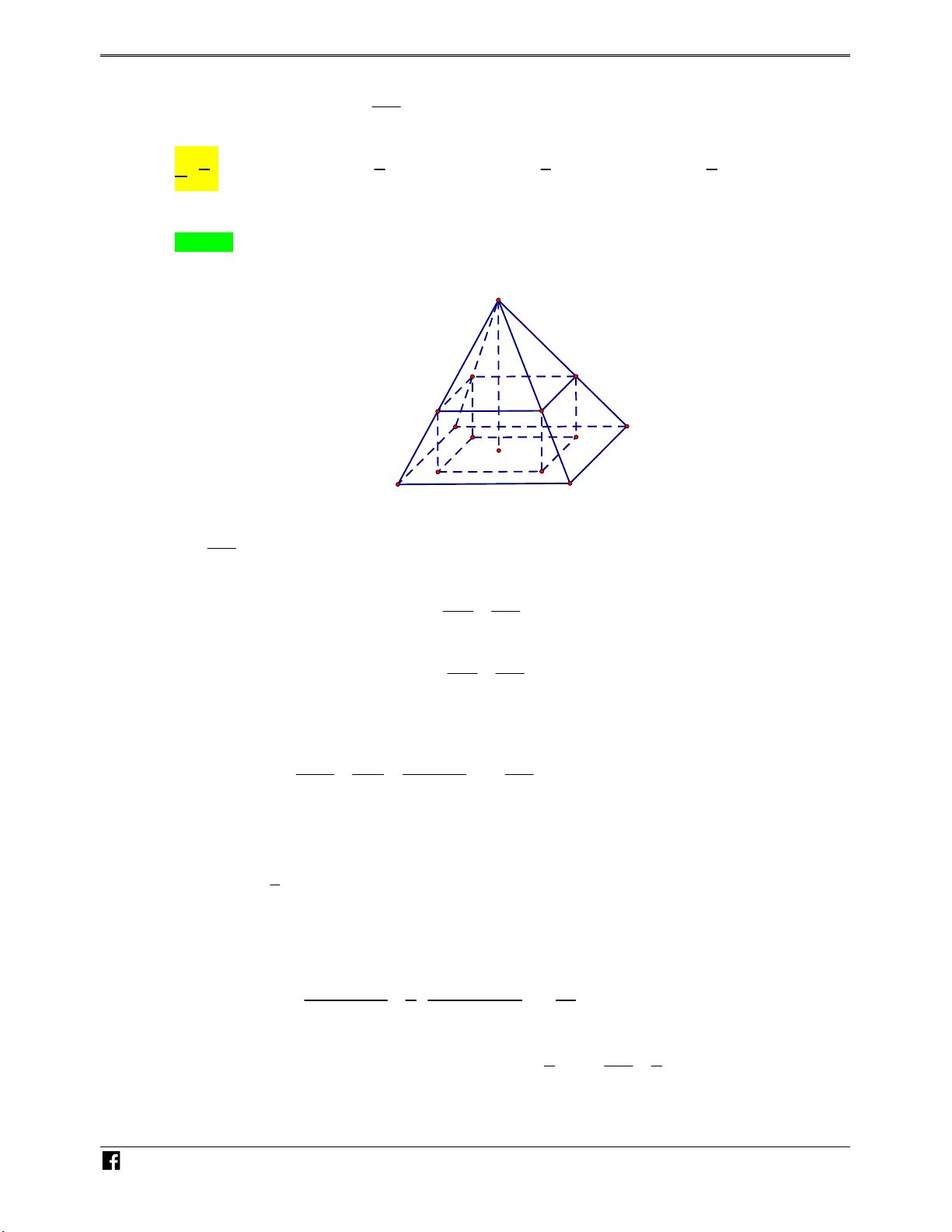
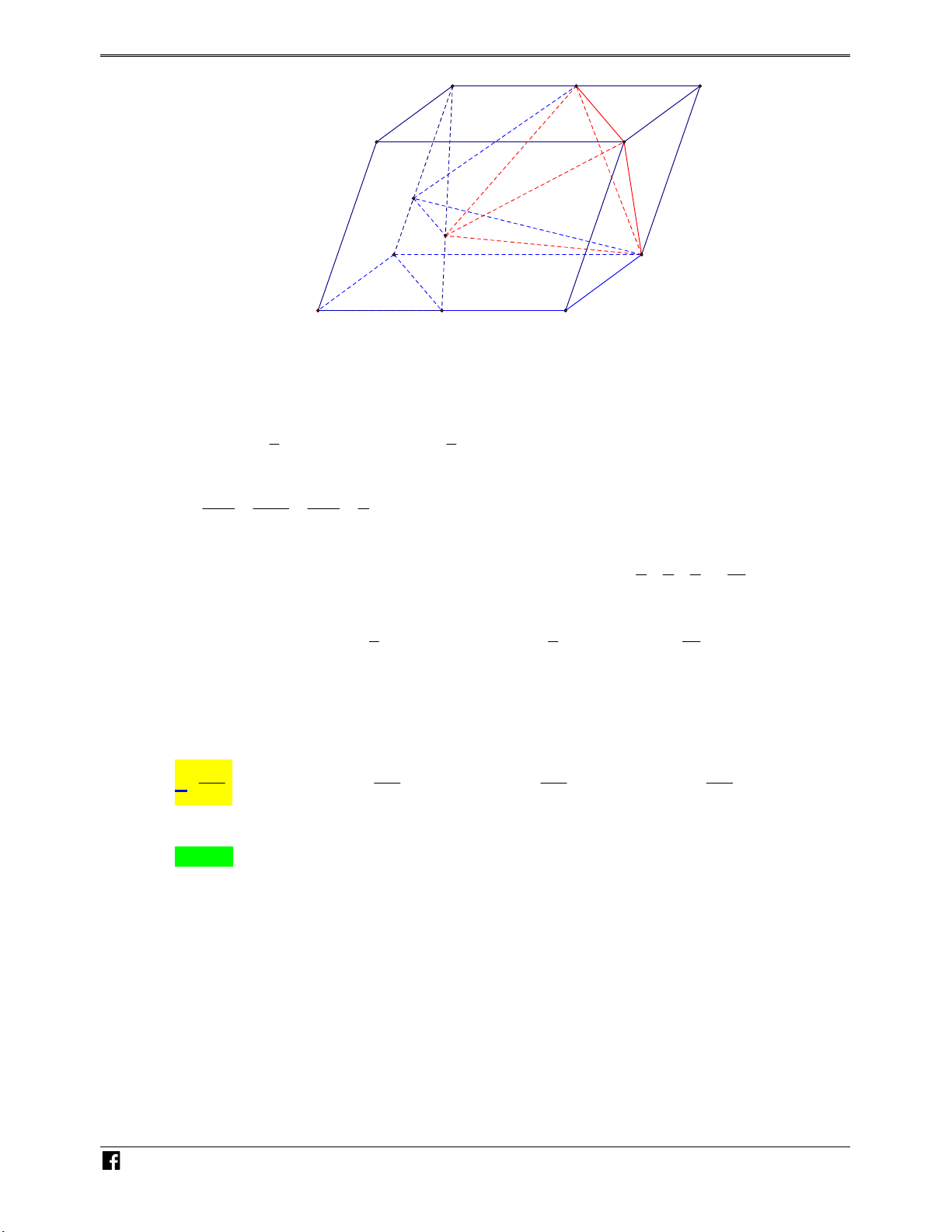
Ví dụ minh họa 3: Cho hình hộp ABC . D A' B 'C ' D ' M N P Q E F D
có thể tích bằng V . Gọi , , , , , C
lần lượt là tâm các hình bình hành ABC ,
D A' B 'C ' D ', ABB ' A', BCC ' B ',CDD 'C ', DAA' D '. Thể
tích khối đa diện có các đỉnh M , , P , Q E, F, N bằng V V V V A. . B. . C. . D. . 4 2 6 3 Lời giải Chọn C N H Ó M TOÁN VD – VDC
Gọi h là chiều cao của hình hộp ABC . D A' B 'C ' D ' V . h S . ABCD
Thấy hình đa diện MPQEFN là một bát diện nên 1 1 1 V 2.V 2. . . . h S . . h S . MPQEFN N .PQEF 3 2 PQEF 3 PQEF 1 1
Lại có: PQEF là hình bình hành và có PQ EF AC; QE PF BD nên 2 2 1 1 1 1 1 V S S . Do đó: V . h S . . h .S . . h S . PQEF 2 ABCD MPQEFN 3 PQEF 3 2 ABCD 6 ABCD 6
https:/www.facebook.com/groups/toanvd. Trang 7 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
Ví dụ minh họa 4: Cho hình hộp ABC .
D A' B 'C ' D ' có chiều cao bằng 8 và diện tích đáy bằng
9. Gọi M , N, P và Q lần lượt là tâm của các mặt bên ABB ' A', BCC ' B ',CDD 'C ' và DAA ' D '.
Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B,C, D, M , N, P và Q bằng N A. 27. B. 30. C. 18. D. 36 H Lời giải Ó M Chọn B TOÁN VD – VDC
Mặt MNPQcắt các cạnh AA', BB',CC', DD'tại A , B ,C , D . Thể tích khối đa diện cần tìm là N 1 1 1 1 H V , thì: Ó M V V V V V V 1 A 1 B 1 C 1 D .A ' B 'C ' D ' A '.QM 1 A B '.MN 1 B C '.PN 1 C D '.QP 1 D TO 8.9 V 4 . Á 2 24 N V 30 VD
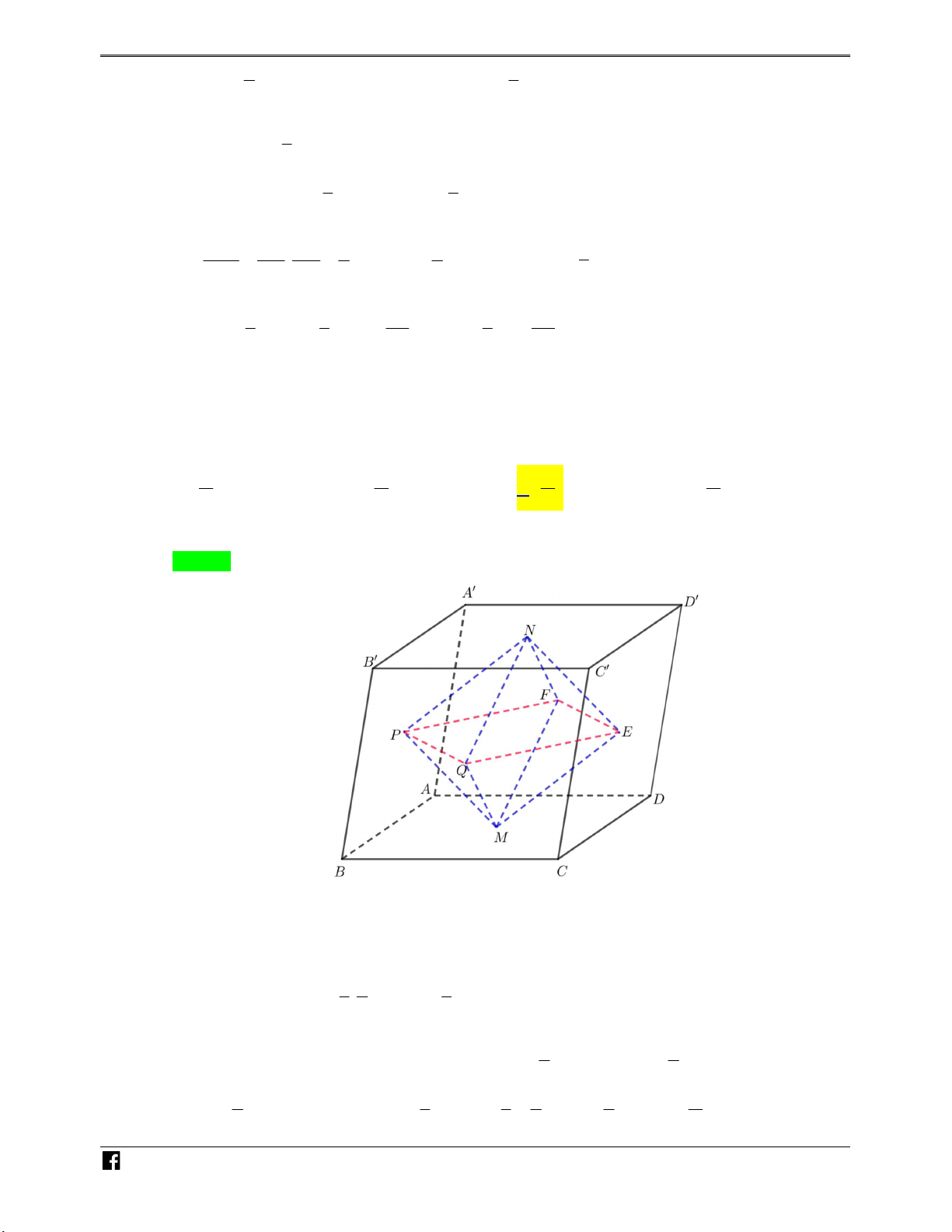
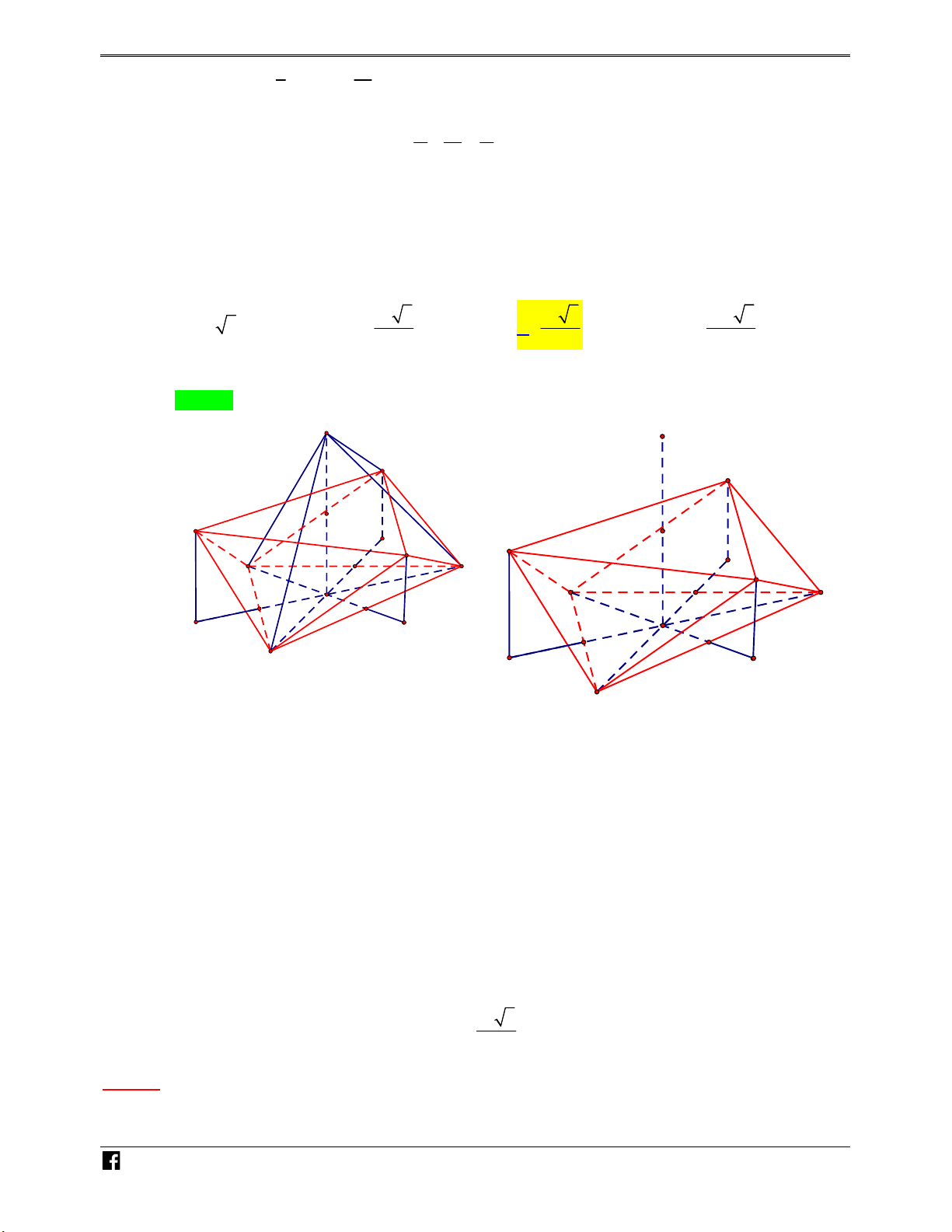
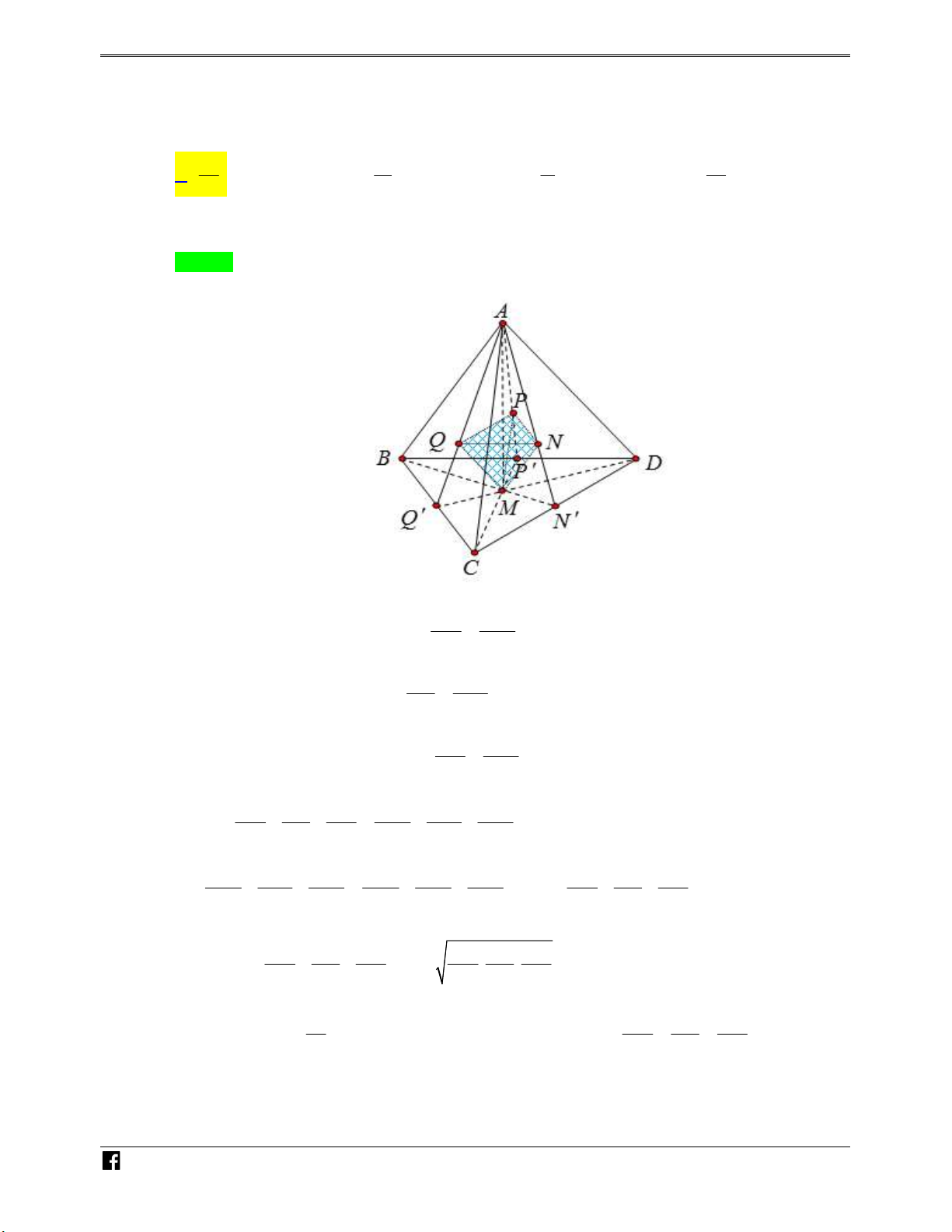
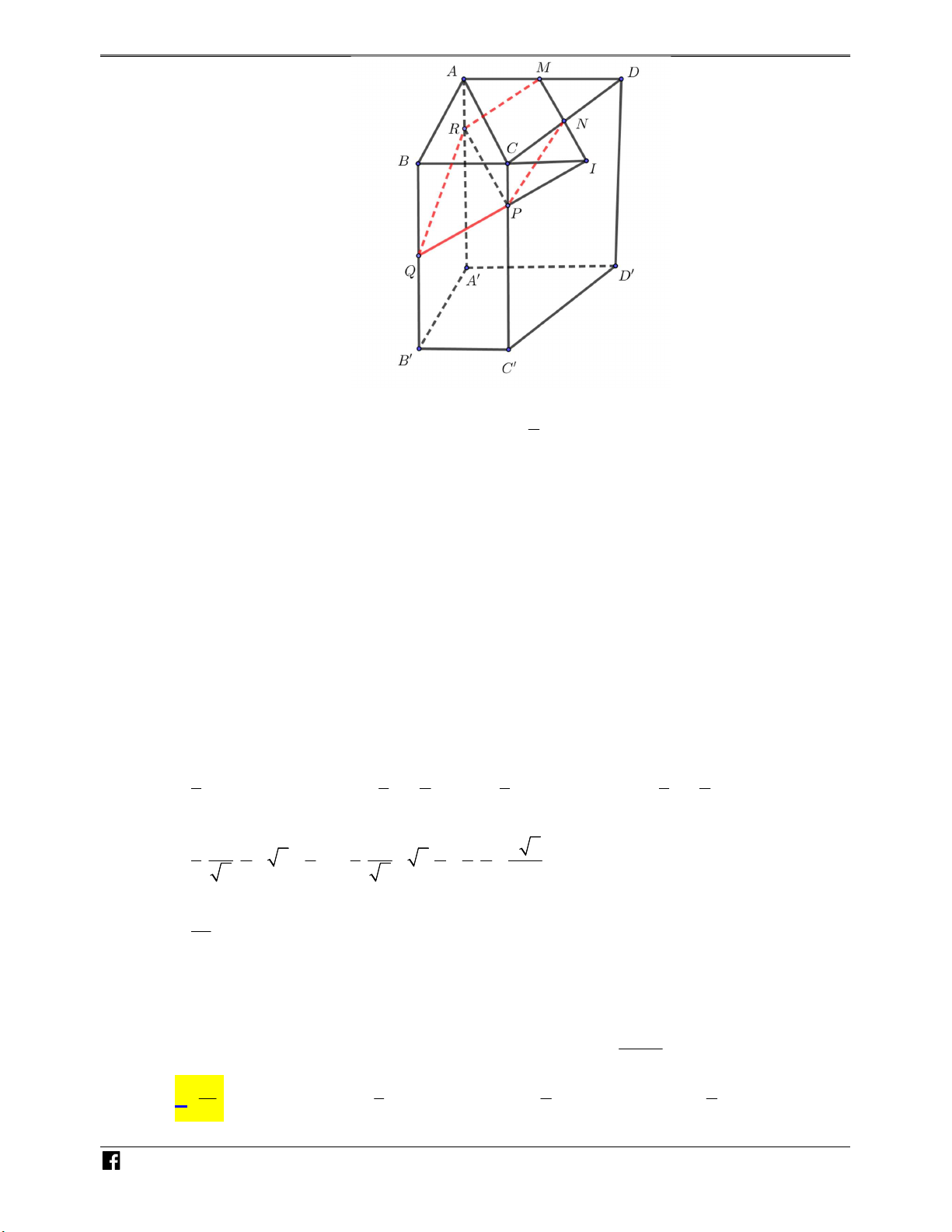
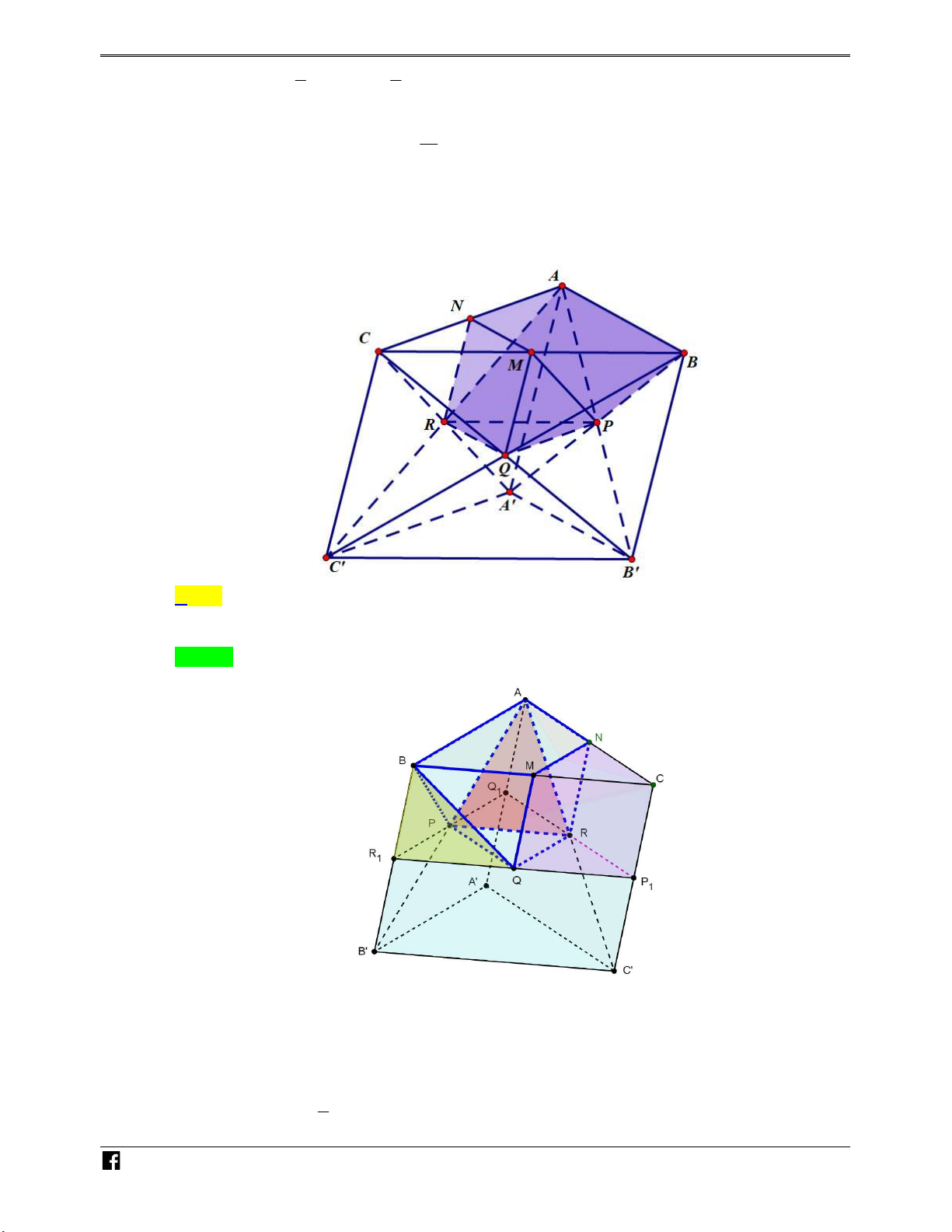
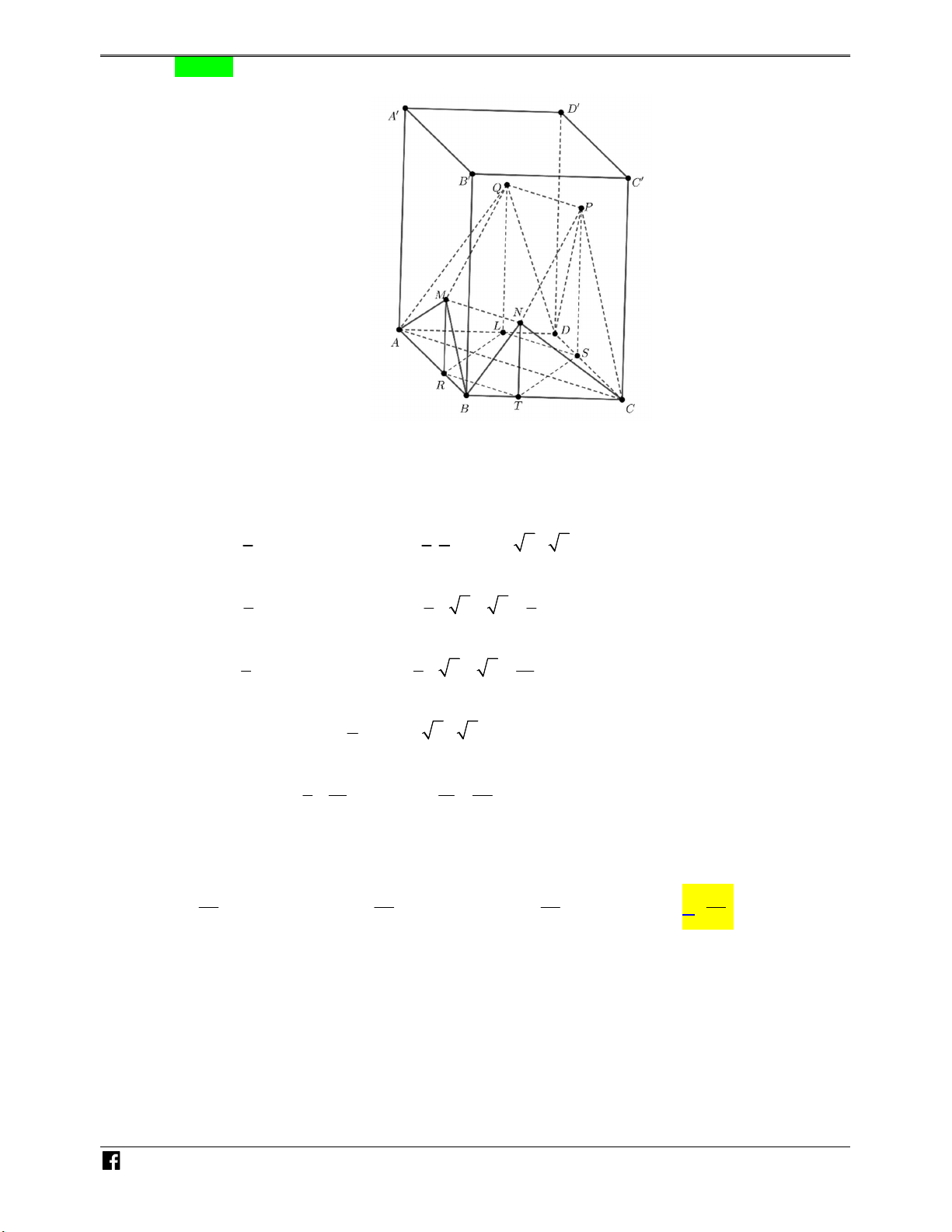
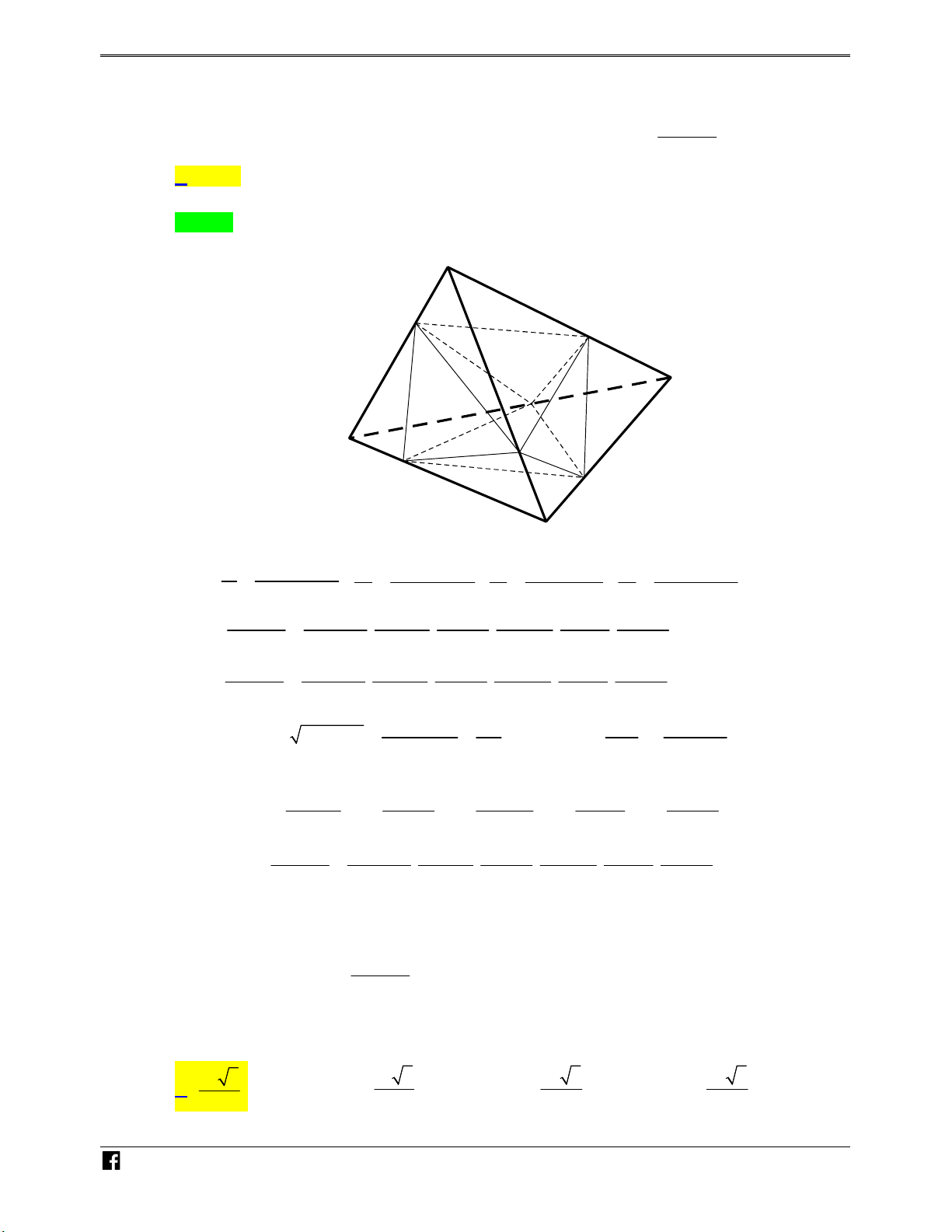
Ví dụ minh họa 5: Cho tứ diện ABCD có thể tích là V . Gọi M , N, P,Q, R lần lượt là trung – V
điểm các cạnh AB, AD, AC, DC, BD và G là trọng tâm tam giác ABC (như hình vẽ ). Tính thể DC
tích khối đa diện lồi MNPQRG theo V .
https:/www.facebook.com/groups/toanvd. Trang 8 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 N H Ó M TOÁN VD – V D C 2V V V V A. . B. . C. . D. . 5 3 2 6 Lời giải Chọn B N H Ó M TOÁN VD – V D C
Gọi E là trung điểm BC . GI 1 d G,MPQR 1 1
Gọi I là giao AE với MP thì nên V V . EI 3 d E,MPQR G.MPQR E. 3 3 MPQR 1 V Gọi V V thì V V 4.V V 4. V . 1 EMPQRN 1 AMNP 8 2
Mặt khác do MNQE là hình bình hành nên EN cắt MQ tại trung điểm nên 1 V V V V . N .MPQR E.MPQR 1 2 4
https:/www.facebook.com/groups/toanvd. Trang 9 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 1 V Mà V V . G.MPQR E. 3 MPQR 12 V V V Vậy V V V . MNPQRG N .MPQR G.MPQR 4 12 3 N H Ó
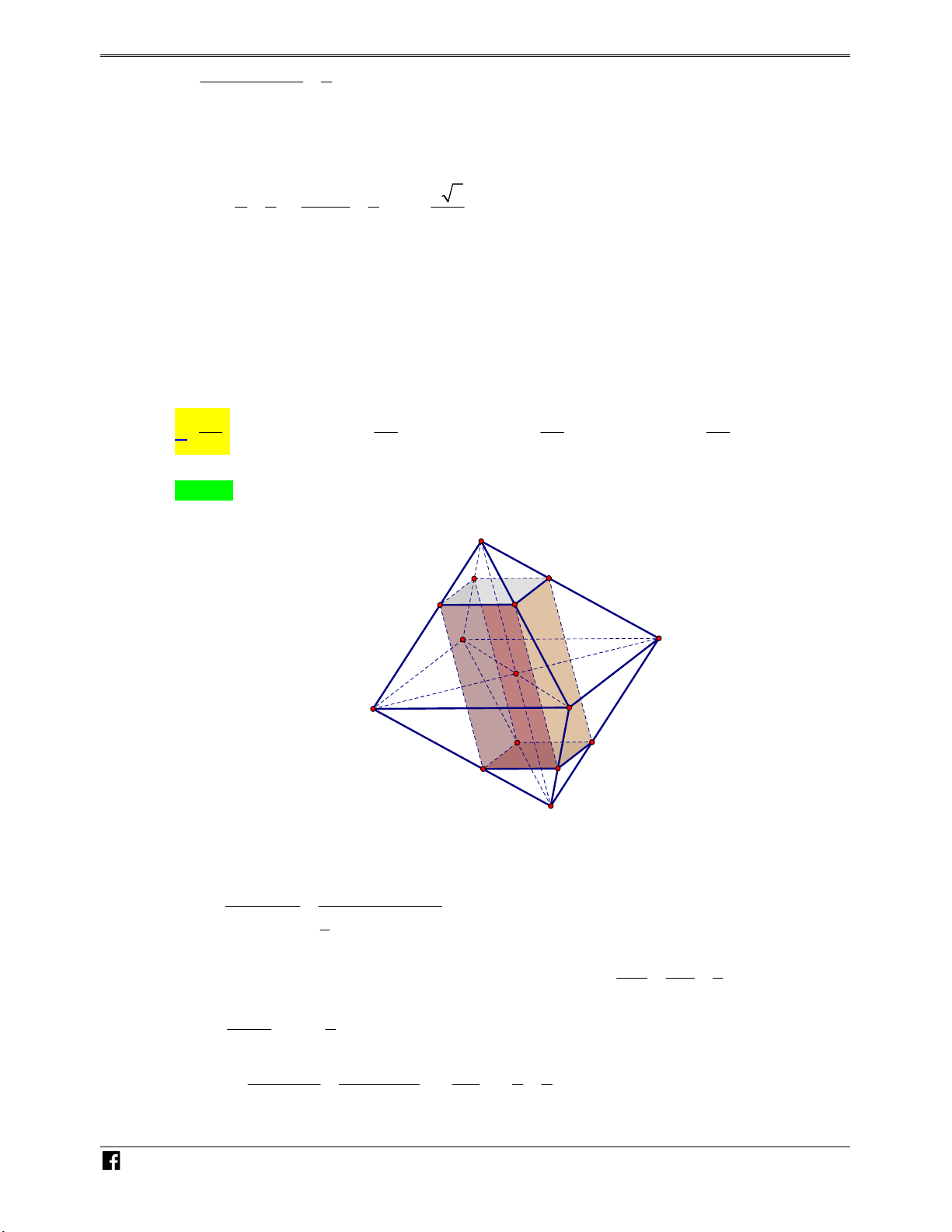
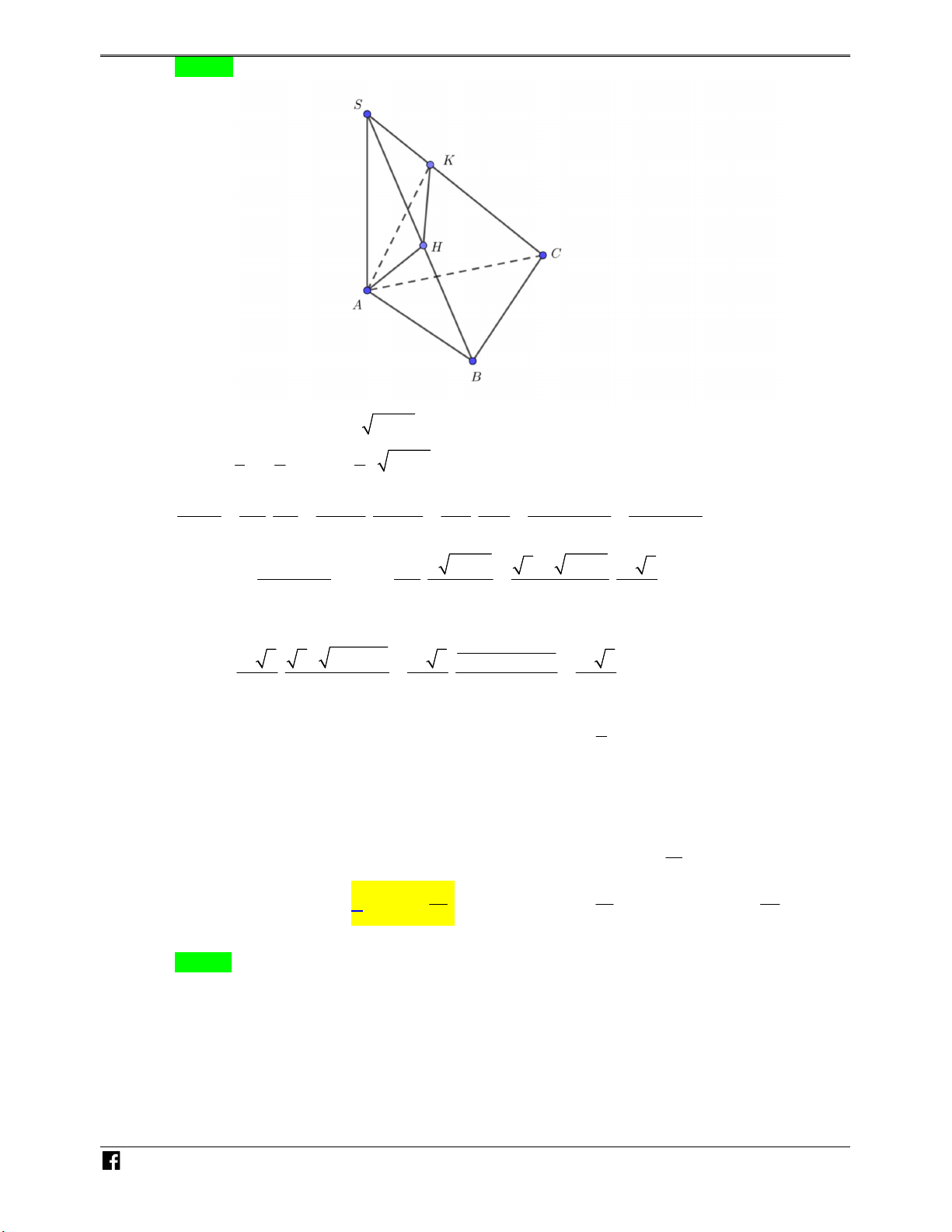
Ví dụ minh họa 6:Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , đường cao M
SH 2a . Gọi I , J , K lần lượt là tâm mặt cầu ngoại tiếp hình chóp S.HAB , S.HBC , S.HCA . TOÁ
Tính thể tích khối bát diện ABCIJK N V 3 a 3 3 a 3 3 4a 3 D A. 3 a 3 . B. . C. . D. 2 3 3 – Lời giải VD Chọn C C S S K K O I O F J I F A C J H A C M N E G H H M Ó B E G M T B OÁN V
Gọi G , E , F lần lượt là tâm đường tròn ngoại tiếp tam giác HAB , HBC , HAC . Suy ra D –
G, E, F đối xứng với H qua AB, BC ,CA . Suy ra tam giác GEF đều cạnh a . VD
Gọi O là trung điểm SH , theo bài ra I , J , K lần lượt là tâm mặt cầu ngoại tiếp hình chóp C
S.HAB , S.HBC , S.HCA nên ta có GI EJ FK HO suy ra IJK ABC
Mặt khác có ABJK , ACJI là hình bình hành nên IC AJ tại trung điểm của AJ
Suy ra d I, ABJK d C, ABJK 3 a 3 Vậy V 2V 4V 2V ABCIJK C.ABJK C.ABJ SABC 3
Dạng 3. MAX- MIN THỂ TÍCH CÁC KHỐI KHI PHÂN CHIA
Ví dụ minh họa 1: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng
thay đổi nhưng luôn song song với đáy và cắt các cạnh bên SA , SB , SC , SD lần lượt tại M ,
https:/www.facebook.com/groups/toanvd. Trang 10 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
N , P , Q . Gọi M , N, P, Q lần lượt là hình chiếu vuông góc của M , N , P , Q lên mặt SM
phẳng ABCD . Tính tỉ số
để thể tích khối đa diện MNP . Q M N P Q
đạt giá trị lớn nhất. SA 2 1 1 3 N A. . B. . C. . D. . H 3 2 3 4 Ó Lời giải M T Chọn A O Á N S VD – M Q VD N P C A D M' Q' H N' P' B C SM Đặt k với k 0; 1 . SA MN SM
Xét tam giác SAB có MN // AB nên k MN k.AB N AB SA H Ó MQ SM M
Xét tam giác SAD có MQ // AD nên k MQ k.AD AD SA TO
Kẻ đường cao SH của hình chóp. Xét tam giác SAH có: Á N MM AM SA SM SM V MM // SH nên 1
1 k MM 1 k .SH . D SH SA SA SA – 2 Ta có V A . B A . D SH.k .1 k . MN.M . Q MM V MNPQ.M N P Q D C 1 Mà V SH.A . B AD 2 V 3.V .k . 1 k . MNPQ.M N P Q S.ABCD S .ABCD 3
Thể tích khối chóp không đổi nên V
đạt giá trị lớn nhất khi 2
k .1 k lớn nhất. MNPQ.M N P Q 2 1 k .k.k 1 2 2k k k 4 Ta có k .k 3 2 1 . 2 2 3 27 SM 2
Đẳng thức xảy ra khi và chỉ khi: 21 k 2 k k . Vậy . 3 SA 3
https:/www.facebook.com/groups/toanvd. Trang 11 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
Ví dụ minh họa 2: Cho tứ diện ABCD . Hai điểm M , N lần lượt di động trên hai đoạn thẳng BC BD BC và BD sao cho 2 3
10 . Gọi V , V lần lượt là thể tích của các khối tứ diện BM BN 1 2 V
ABMN và ABCD . Tìm giá trị nhỏ nhất của 1 . N V2 H Ó 13 11 1 2 M A. . B. . C. . D. . 16 12 6 3 TO Lời giải Á N Chọn A VD – VDC AB AD Đặt x ; y , x, y 1. AM AN N H 1 Ó AM .AN.sin DAB M V S 1 AM AN 1 Ta có S.AMN AMN 2 . . . V S AB AD DAB AB AD yx S ABCD ABCD . .sin 2 2 T . O Á AB AD 3 N Theo bài ra 2 3
8 2x 3y 8 x 4 y . AM AN 2 VD V 1 S AMN – Suy ra . ; 1 y 2 (do x 1). V 3 S.ABCD V 2y 4 y D 2 C V V 1 Ta có 1 S. 1 AMN 1 ; 1 y 2 . V V y 8 3y S. ABCD 2 3y 8 3y
Áp dụng BĐT Côsi ta có 3y(8 3y) 16 2 V 3 13 V 13 4 Suy ra 1 1 1 max
. Dấu bằng xảy ra khi y , x 2 . V 16 16 V 16 3
https:/www.facebook.com/groups/toanvd. Trang 12 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
Ví dụ minh họa 3: Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V .
Điểm P là trung điểm của SC . Một mặt phẳng qua AP cắt hai cạnh SB và SD lần lượt tại V
M và N . Gọi V là thể tích của khối chóp S.AMPN . Tìm giá trị nhỏ nhất của 1 ? 1 V N H 3 1 2 1 A. . B. . C. . D. . Ó 8 3 3 8 M T Lời giải O Á Chọn B N VD S – VD P C I M N C B O A D N
Do đi qua A , P , M , N nên bốn điểm này đồng phẳng. H Ó V a b c d SA SC SD SB M
Áp dụng công thức S.AMNP với a , c , d , b thỏa mãn V 4. . a . b . c d SA SP SM SN S.ABCD TO a c b d . Á N SA SC SD SB V Theo đề bài ta có: 1, 2 và đặt d 0 , b 0 . SA SP SM SN D – V 1 2 b d Khi đó:
với 1 2 b d b d 3. V V 4.1.2. . b d D C V 1 2 b d V 1 2 3 V 3 Vậy ta có: . V 4.1.2. . b d V 4.2. . b d V 4bd b d2 9 1 4 V 3 3 4 1
Theo bất đẳng thức cơ bản: bd suy ra . . 4 4 bd 9 V 4bd 4 9 3 3
Dấu “=” xảy ra b d b d . 2 V 1 Vậy
có giá trị nhỏ nhất bằng . V 3
https:/www.facebook.com/groups/toanvd. Trang 13 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
Ví dụ minh họa 4: Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác
BCD . Các đường thẳng qua M và song song với AB , AC , AD lần lượt cắt các mặt phẳng
ACD, ABD, ABC tại N , P , Q. Giá trị lớn nhất của khối MNPQ là: N V V V V A. . B. . C. . D. . H 27 16 8 54 Ó M Lời giải TO Chọn A Á N VD – VDC N MN N M
+ Tam giác ABN có MN // AB . H AB N B Ó M MP P M
+ Tam giác ACP có MP // AC . T AC P C O Á N MQ Q M
+ Tam giác ADQ có QM // AD . V AD Q D D – MN MP MQ N M P M Q M Khi đó: V AB AC AD N B P C Q D D C N M P M Q M S S S MN MP MQ Mà MCD MBD MBC 1 nên 1 N B P C Q D S S S AB AC AD BCD BCD BCD 3 3 MN MP MQ MN MP MQ Lại có 3 3 1 3 . . (Cauchy) AB AC AD AB AC AD 1 MN MP MQ MN.M . P MQ A . B AC.AD MN.M . P MQ lớn nhất khi 27 AB AC AD
https:/www.facebook.com/groups/toanvd. Trang 14 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 MN MP MQ 1
M là trọng tâm tam giác BCD
NPQ // BCD , AB AC AD 3 2 SNPQ 2 1 1 1 , Mà S d M , NPQ d , A BCD S nên S S và S N P Q BCD NPQ BCD 3 4 9 2 N P Q N H 1 Ó
Vậy giá trị lớn nhất của khối tứ diện MNPQ là V S .d M NPQ MNPQ NPQ , M 3 TO 1 1 1 V 1 V . S . d A BCD , với V S .d A BCD V ABCD BCD , MNPQ BCD , Á 3 9 3 27 3 N V
Ví dụ minh họa 5: Cho hình lập phương ABCD.A ' B 'C ' D ' cạnh 1. Điểm M , N lần lượt nằm D C M D N –
trên đoạn thẳng AC và CD sao cho x . Khi tứ diện CC N M có thể tích lớn C A 2D C VD
nhất thì giá trị của x bằng C 1 1 1 1 A . B. . C. . D. . 2 3 4 6 Lời giải Chọn C A B N H Ó M TOÁ D C N A' V B' D – N M VDC D' C' 1 Ta có. CD ' 2 D N
2x 2 CN 2 2x 2 2(1 2x) , đk : 0 x 2 Ta có AC ' 3 C M x 3
https:/www.facebook.com/groups/toanvd. Trang 15 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 1 V 1 .C M .CN.d(C M ,CN ).sin(C M
,CN) . 6.x(1 2x).d(C , A CD ').sin(C , A CD ') CC ' NM 6 6 Do d (C , A CD ').sin(C ,
A CD ') không đổi nên tứ diện CC N
M có lớn nhất khi g(x) x(1 2x) lớn nhất. N H 2 Ó 1 1 (2x 1 2x) 1 M
Ta có g(x) .2x(1 2x) 2 2 4 8 TO 1 Á
Dấu bằng xảy ra 2x 1 2x x . N 4 VD
C. BÀI TẬP THEO CÁC DẠNG –
Dạng 1. CHIA HÌNH CHÓP, HÌNH LĂNG TRỤ THÀNH 2 PHẦN BỞI MỘT MẶT PHẲNG V
CHO TRƯỚC. TÍNH THỂ TÍCH MỘT TRONG HAI PHẦN HAY TỈ SỐ THỂ TÍCH D C
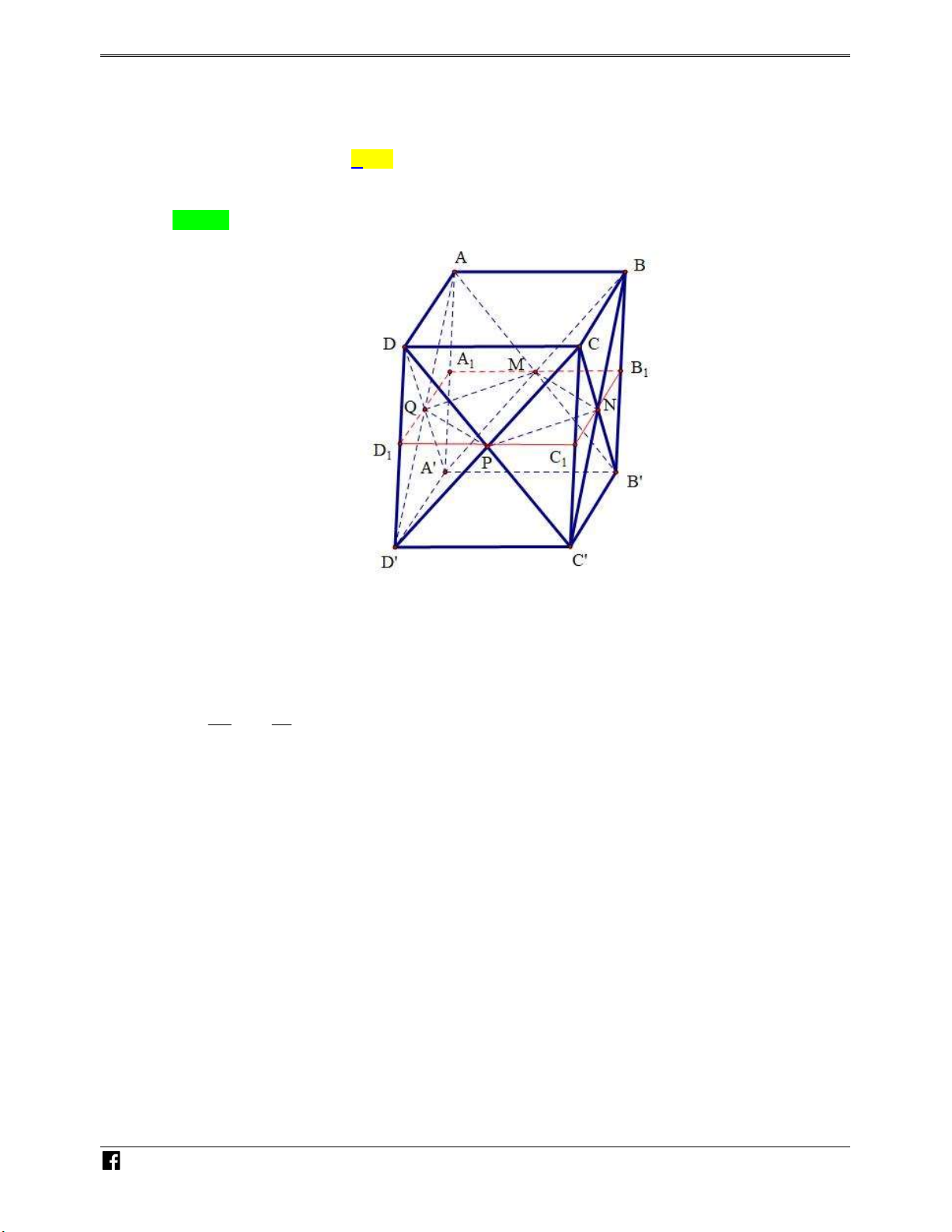
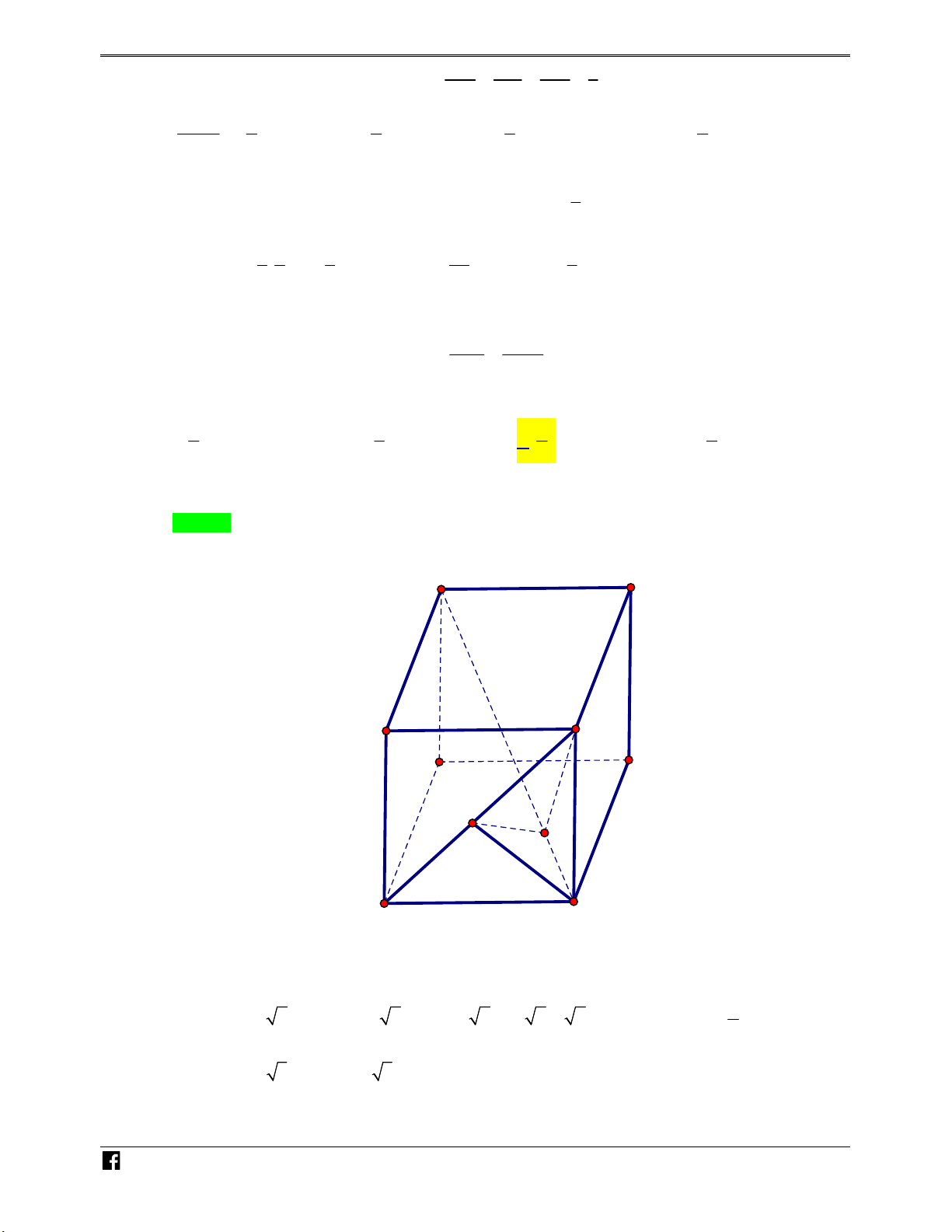
Câu 1: Cho hình lập phương ABC .
D A B C D , gọi M và N lần lượt là tâm của các hình vuông ABCD và CDD C
. Mặt phẳng A M
N chia khối lập phương trình hai phần có thể tích là V và V 1 2 V V V . Tính tỷ số 1 . 1 2 V2 1 1 2 A. . B. . C. . D. 2 . 3 2 3 Lời giải Chọn B N H Ó M TOÁN VD – VDC
Gọi I AM CC ; F IN CD ; G IN C D ; E FM AB .
Vậy thiết diện của hình hộp cắt bởi mặt phẳng AMN là hình bình hành A E FG . AE MA Ta có:
1 AE FD CF FD CD. CF MC
Tương tự: FD GD CD .
https:/www.facebook.com/groups/toanvd. Trang 16 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 V V V AEFDA GD A .AEFD A .FDD G 1 1 AA AE DF 1 1 . .AD A D
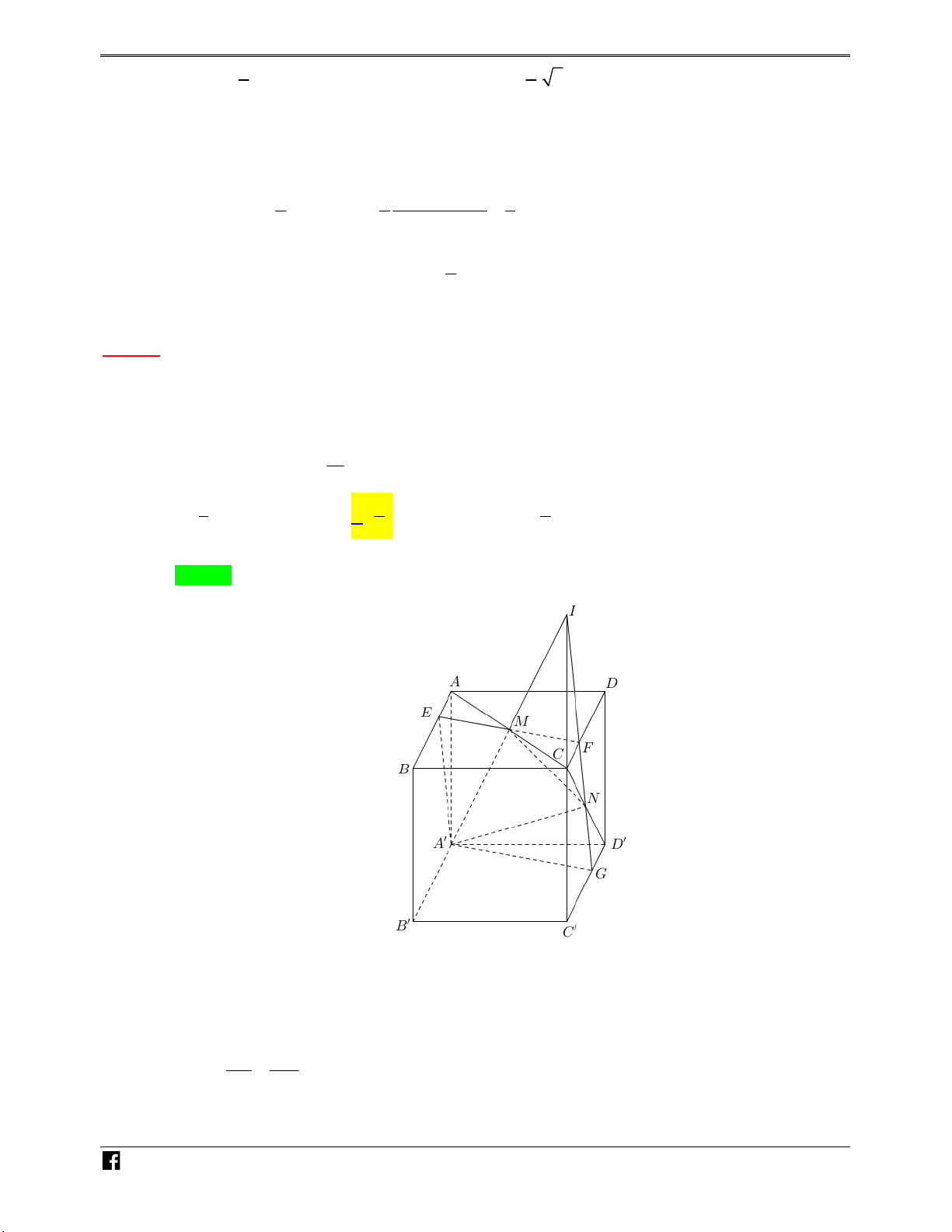
. FD GD.DD 3 2 3 2 3 3 CD CD Vhh N 6 6 3 H Ó M V 2V V 1 hh V hh V 1 . 1 2 T 3 3 V 2 2 O Á Câu 2: Cho khối hộp ABC .
D A' B 'C ' D ' . M là trung điểm C ' D '. N là điểm trên cạnh AD sao cho N
DN 3AN . Mặt phẳng B 'MN chia khối hộp thành hai phần có thể tích là V ,V thỏa mãn 1 2 VD V V V .Tỉ số 1 bằng 1 2 – V2 V 1 149 448 299 D A. . B. . C. . D. . C 4 299 1344 448 Lời giải Chọn B K A N D Q B C P A' I N D' H Ó M M B' C' T
GọiV là thể tích khối hộp. Gọi: I BM A' D ' ; P RN DD'; K RN AA'; O Á Q B ' K AB . N Ta có V V V V . AQNA'B 'MD ' P K .A' B 'I I .D 'PM K . ANQ VD
Do M là trung điểm của C ' D 'suy ra D ' là trung điểm của A' I . Mặt khác PM //B ' K nên P là – trung điểm của IK . V AK KN AN 1 KN 1 KA KQ 1 D Ta có DP NP ND 3 KI 8 KA' KB ' 8 C DP DP 7DP DP 3 D ' P 4 3 . KA 1 DD ' DD ' 7 DD ' 7 AA' 7 1 1 1 1 4 1 Khi đó ta có:V d I; CDD'C ' .S d I; CDD 'C ' . . . S V . I .D'PM D'PM CDD'C ' 3 3 2 2 7 21 1 1 1 1 1 1 1 V d K; ABCD .S . d A'; ABCD . . . S V . K .ANQ AQN 3 3 7 2 4 8 ABCD 1344 1 1 8 8 V d K; A'B 'C 'D ' .S . d ; A A' B 'C ' D ' .S V . K.A'B'I A'B'I A'B'C'D' 3 3 7 21 8 1 1 149 Suy ra V V V V = V V AQNA'B 'MD ' P K .A' B 'I I .D 'PM K . ANQ 21 21 1344 448
https:/www.facebook.com/groups/toanvd. Trang 17 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 149 149 299 V 149 Khi đó V V ,V 1 V V . Vậy 1 . 1 448 2 448 448 V 299 2
Câu 3: Cho lăng trụ ABC.A B C
có thể tích V . Gọi M, N, P lần lượt là trung điểm của AB, BB và N A C
. Tính theo V thể tích của khối tứ diện CMNP . H 5 V 5V 7V Ó A. V . B. . C. . D. . 24 4 27 24 M Lời giải TOÁ Chọn A N A C VD – M V B D K C N A' C' P E B' Q
Gọi Q là giao điểm của MN và AB . N H B Q 1 Khi đó:
và N là trung điểm của MQ . Ó AB 2 M
Gọi E là giao điểm của B C và PQ. TO B E 1 Khi đó:
và E là trung điểm của PQ. Á B C 4 N 1 V
Gọi K là giao điểm của BC và NE . Khi đó BK BC . D 4 –
Ta có: EN là đường trung bình của M PQ V NE//MP D C
NE// CMP hay NK // CMP
d N;(CMP) d K;(CMP) 1 V V S .d P ABC CMNP CMPK CMK ;( ) 3
Trong đó: d P;(ABC) h là chiều cao của lăng trụ. 1 1 BK 1 1 AB BC S S S S BM. .sin ABC S sin ABC CMK MBC BMK 2 ABC 2 2 ABC 2 2 4 1 1 5 = S S S . 2 ABC 8 ABC 8 ABC
https:/www.facebook.com/groups/toanvd. Trang 18 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 1 5 5 V . S h V . CMNP 3 8 ABC 24 2
Câu 4: Cho khối lăng trụ ABC.A'B 'C ' . Trên AC, BC lần lượt lấy M, N sao cho CM CB N 3 H 1 Ó
CN CB . Gọi K là giao điểm của MN và đường trung tuyến hạ từ đỉnh C của tam giác M 2
ABC , I là giao điểm của BK và AC , E là giao điểm của C 'I và CA' , F là giao điểm của TO
BC ' và BC . Tính tỉ số thể tích của khối đa diện C.EFBI và khối lăng trụ ABC.A'B 'C ' . Á N 1 3 1 26 A. . B. . C. . D. . V 21 35 7 105 D Lời giải – Chọn B VDC N H Ó M TO Á
Gọi thể tích khối lăng trụ là V N CA CB CH CH 7 CK 4 V
Gọi H là trung điểm AB 2. D CM CN CK CK 4 CH 7 – CI HK BA CI 3 CI 2 CI 2
Áp dụng định lí Menelaus ta có: . . 1 . .2 1 V IA CK BH IA 4 IA 3 CA 5 D C IE IC 2 C 'E 5 C 'F 1 1 5 5 Ta có: , mà V . V V EC ' A'C ' 5 C 'I 7 C '.CEF C 'CIB C ' C 'B 2 2 7 14 CIB 9 9 1 2 3 VC.EFBI 3 V V . . V V C .EFBI C ' 14 CIB 14 3 5 35 V 35
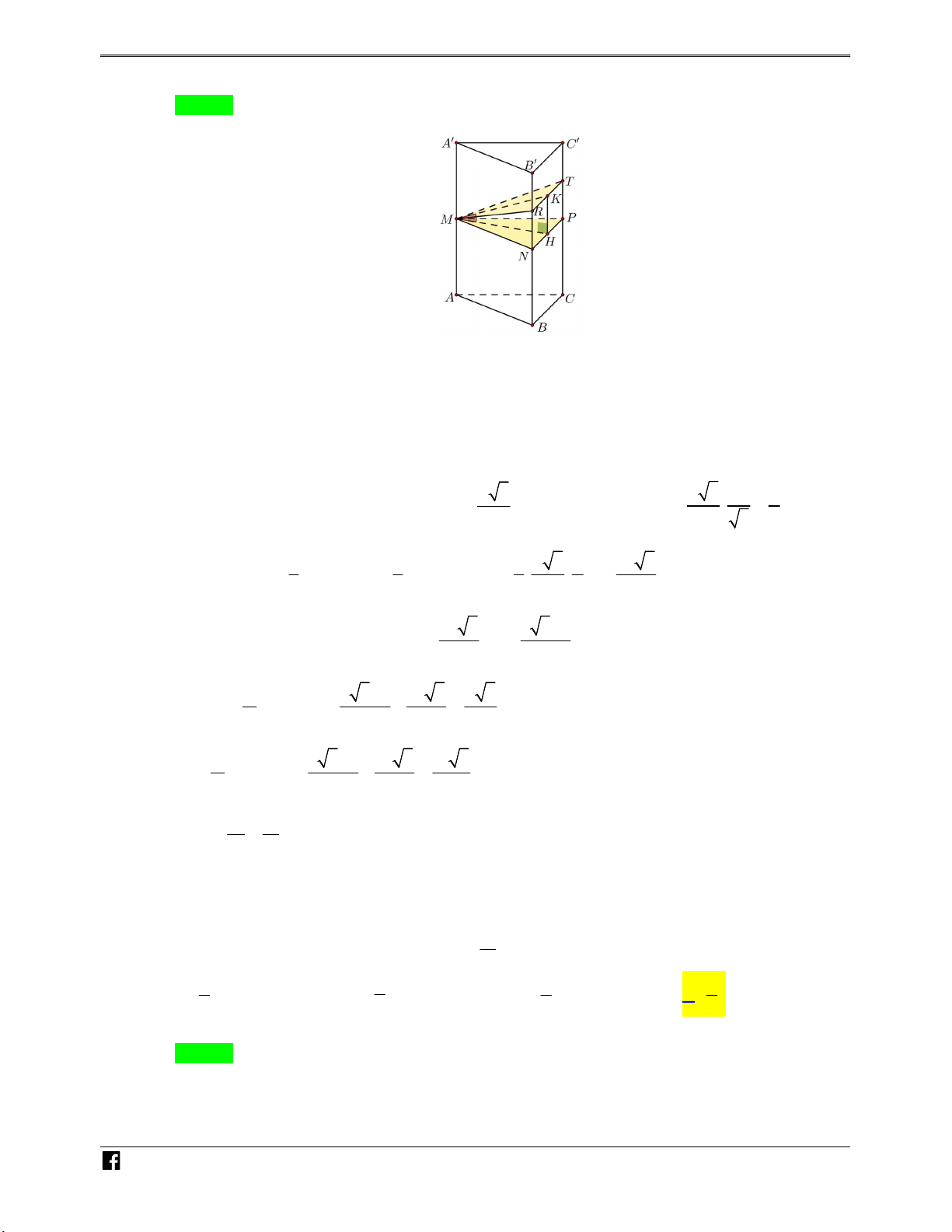
Câu 5: Cho lăng trụ đều ABC.A B C
có cạnh đáy bằng a cạnh bên 3a . Gọi M là trung điểm của AA
. Mặt phẳng đi qua M và song song với BC đồng thời tạo với mặt phẳng đáy ABC một
góc 30 . Mặt phẳng chia khối chóp làm 2 phần có thể tích lần lượt là V và V biết V V 1 2 1 2 V
. Tỉ số thể tích 1 bằng V2 4 7 7 7 A. . B. . C. . D. . 5 8 11 9
https:/www.facebook.com/groups/toanvd. Trang 19 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 Lời giải Chọn C N H Ó M TOÁN VD –
Gọi N; P lần lượt là trung điểm của BB và CC suy ra MNP // ABC . VDC
Mặt phẳng cắt các cạnh BB và CC lần lượt tại R và T . Gọi H;K lần lượt là trung điểm
của NP và RT . Mặt phẳng tạo với ABC một góc 30 suy ra KMH 30 . a 3 a 3 1 a
Tam giác MNP đều cạnh a suy ra MH và HK MH.tan 30 . . 2 2 3 2 3 1 1 1 a 3 a a 3 Ta có V .MH.S .MH.HK.NP . . .a . M .NPTR 3 NPTR 3 3 2 2 12 N 2 3 a 3 3 3.a H
Thể tích lặng trụ ABC.A B C là V .3a . Ó 4 4 M 3 3 V 3 3.a a 3 7 3 T Vậy 3 V V a O 1 M . 2 NPTR 8 12 24 Á N 3 3 V 3 3.a a 3 11 3 3 V V V a . 2 M .NPTR D 2 8 12 24 – V 7 V Suy ra 1 . D V 11 2 C
Câu 6: Cho lăng trụ đều ABC.A B C
. Gọi M, N và P lần lượt là trung điểm của A B ; B C và C A .
Thể tích của khối đa diện lồi có các đỉnh là các điểm ,
A B,C, M , N, P là V và thể tích của khối 1 V lăng trụ đều ABC.A B C
là V . Tính tỷ số 1 ? V 4 1 2 3 A. . B. . C. . D. . 5 4 3 4 Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 20 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 N H Ó M TOÁN VD – V DC
Thể tích khối lăng trụ ABC.A B C là V AA .S . A B C
Gọi thể tích của khối đa diện lồi có các đỉnh là các điểm , A , B C, M , N, P là V . 1 Ta có V V V V V . 1 AA MP BB MN CC N P 1 1 1 1 V . AA .S .AA . S V AA MP A MP A'B'C ' 3 3 4 12 1 1 1 1 N V BB .S .BB . S . V BB MN B 'MN A B C H 3 3 4 12 Ó M 1 1 1 1 V . CC .S .CC . S V CC NP C NP A B C T 3 3 4 12 O Á 3 3 N Vậy V V V . V V V V V 1 AA MP BB MN CC NP 12 4 VD V 3 – Do đó 1 V 4 VDC
Câu 7: Cho hình lăng trụ đứng ABC.AB C
, đáy là tam giác đều cạnh a , AA a 2 . Gọi M, N lần
lượt là trung điểm các cạnh A ; B A C
. Gọi là mặt phẳng qua MN vuông góc với BB C C
.Giả sử chia lăng trụ ABC.AB C
thành 2 phần có thể tích V ;V với V là thể tích khối đa 1 2 1 V diện chứa A . Đặt 1 k
, mệnh đề nào dưới đây đúng V2 A. k 0,6; 0,9 . B. k 0,9; 1, 2 . C. k 1,2; 1,5 . D. k 1,5; 1,8 . Lời giải Chọn B
https:/www.facebook.com/groups/toanvd. Trang 21 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 N H Ó M TOÁN VD – V D C Gọi ;
O O lần lượt là trung điểm của BC; B C , ta có A ; O AO BCC B
/ /A ; O AO.
Gọi K, H lần lượt là trung điểm B ; O O C
. Gọi MK AC I;IN AA J .
Ta có IN; KH;CC đồng quy tại E . Gọi h AA ; S S ; V V . ABC ABCA B C V V V V 1 IKEC ENHC AIJM 1 3 1 1 1 1 1 1 1 1 1 . . h (S S S) . . h S . . h S V . 3 2 8 4 3 2 8 3 2 4 2 V1 1. N V2 H Ó
Câu 8: Cho khối lăng trụ ABC.A' B 'C '. Gọi M , N, P lần lượt là trung điểm các cạnh AB, BC, A C . Mặt M
phẳng MNP cắt các cạnh AA ,CC tại các điểm I, J. Tỷ số thể tích của khối đa diện AIMCJN TO
và khối lăng trụ ABC.A' B 'C ' là Á N A' C' VD B' – P VDC A C N M B 7 1 1 5 A. . B. . C. . D. . 24 4 3 24 Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 22 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 A' C' B' I P J N H Ó M A C TO M N Á B N V
Xét mặt phẳng MNP và ACC A
có AC//MN , điểm P chung. Suy ra giao tuyến của MNP D và ACC A
là đường thẳng d qua P song song với AC – V Trong mặt phẳng ACC A
đường thẳng d cắt AA ,CC tại các điểm I, J. Dó đó I, J là giao DC
điểm của MNP với AA ,CC .
Mặt khác P là trung điểm của AC suy ra I, J là trung điểm của AA ,CC .
Gọi V là thể tích khối lăng trụ ABC.A' B 'C ' Ta có V V V AIMCJN J .MNC M .ACJI 1 1 1 1 V V S .d J , ABC . S . d C , ABC J .MNC MNC ABC 3 3 4 2 24 1 1 1 1 1 V S .d M , ACC A . .S . d B, ACC A .S .d B, ACC A M .ACJI ACJI ACC A ACC A 3 3 2 2 12 1 2V 1 2V V N Mà S .d B ACC A V V . ACC A , B.ACCA M .ACJI H 3 3 4 3 6 Ó V V 5V V 5 AIMCJN M Vậy V . AIMCJN 24 6 24 V 24 TO
Câu 9: Cho hình lăng trụ đứng ABC . D A B C D
có AA 2a , đáy ABCD là hình thang vuông tại A Á N và B có AB BC ,
a AD 2a . Gọi M ,Q lần lượt là trung điểm của các cạnh A , D BB. Mặt V
phẳng P chứa MQ và vuông góc với CDD C
chia khối lăng trụ ABC . D A B C D thành D
hai khối đa diện, trong đó V là thể tích khối đa diện chứa đỉnh A . Tính V ? 1 1 – 5 7 11 13 V A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 1 1 1 1 D 9 9 24 24 C Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 23 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 N H Ó M TOÁN VD – V D C 1
Tứ giác ABCM là hình vuông CM AB a AD A CD vuông tại C . 2 AC CD Ta có AC CDD C
mà P CDD C AC// P AC CC
P ABCD MN,N CD sao cho MN //AC .
Gọi MN BC I, IQ CC P . N H
AC // P P ACC A
PR,R AA sao cho PR//AC . Ó M
Thiết diện của hình lăng trụ ABC . D A B C D
cắt bởi P là ngũ giác MNPQR . TOÁ V V V V V 1 Q.ACPR Q.ABC M .ACPR P.MCN N V 1 1 1 1 1 1 D
d B, ACPR.AC.CP Q . B A .
B BC d M , AC.AC.CP C . P MN.CN 3 3 2 3 3 2 – V 2 D 1 a a 1 3 1 a a 1 a a 2 . . .a 2 a . .a 2. . . C 3 2 2 6 3 2 2 6 2 2 13 3 a . 24
Câu 10: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , 0
(SB,(ABC)) 60 , SA (ABC) . Mặt
phẳng () qua B và vuông góc với SC phân chia khối chóp S.ABC thành hai khối đa diện. V
Gọi V là thể tích của khối đa diện mà chứa đỉnh S . Tính tỉ số 1 . 1 VS.ABC 15 5 3 2 A. . B. . C. . D. . 16 8 4 3 Lời giải
https:/www.facebook.com/groups/toanvd. Trang 24 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 Chọn A S N H Ó D M E T C O A Á N V B D – V
Gọi E là trung điểm AC , kẻ ED SC(D SC) . D C BE AC Ta có
BE (SAC) BE SC BE SA SC ED Vậy
SC (BED) suy ra () (BED) . SC BE Ta có SB ABC 0 SBA 0 ( ,( )) 60 SCA 60 (vì S AB S AC) a SC 4a , 0 CD EC.cos60 . N 2 H Ó CD 1 M . CS 8 TOÁ V CD CE 1 1 1 V 15 C BED SABED N Ta lại có . . . . V CS CA 8 2 16 V 16 S.ABC S.ABC VD
Câu 11: Cho tứ diện đều ABCD cạnh a . Gọi M , N lần lượt là trung điểm của các cạnh A , B BC và E –
là điểm đối xứng với B qua D . Mặt phẳng MNE chia khối tứ diện thành hai phần, trong đó VD V C
khối đa diện chứa đỉnh A có thể tích là V , khối đa diện còn lại có thể tích V . Tỉ số 1 là: 1 2 V2 7 11 13 A. . B. . C. . D. 2 . 11 7 5 Lời giải Chọn B
https:/www.facebook.com/groups/toanvd. Trang 25 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 N H Ó M TOÁN V D 3 a 2 1 –
Ta có: Thể tích khối tứ diện ABCD là V Sh với S S h d , A BCD , . BCD 12 3 VD
Gọi P EN CD , Q EM AD , I là trung điểm đoạn thẳng BD . C 4 9 Dễ thấy, S S S S . PDE 9 N EI NEI 4 PDE 1 1 3 1 Mà S S S S S . Do đó S S . B NI 4 BCD 4 N EI 4 PDE 3 h h
Lại có, d M ,BCD , d Q,BCD 2 3 1 V 1 V V S d M BCD , V S d Q BCD . QPDE PDE , MBNE B NE , 3 2 3 9 N V V 7V 7V 11V H Từ đó suy ra V V , V V . QPDMNB 2 1 Ó 2 9 18 18 18 M V 11 Vậy 1 . TO V 7 2 Á N
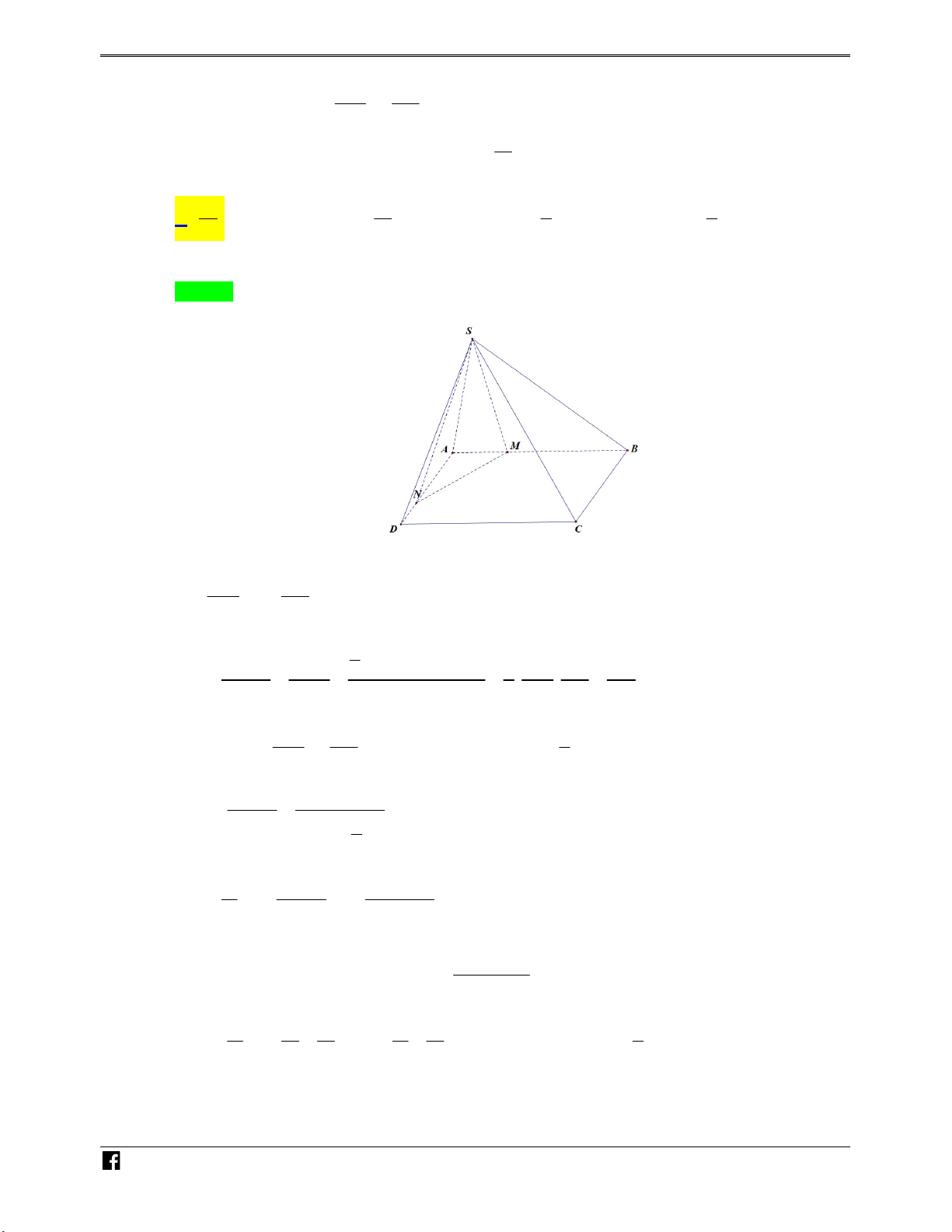
Câu 12: Cho khối chóp đều S.ABCD có cạnh đáy bằng a 2 , biết khoảng cách từ tâm O của đáy đến V a D
mặt bên bằng . Gọi E, F lần lượt là trung điểm của các cạnh SB, SC ; M là điểm trên cạnh 2 –
SD sao cho MS 2MD . Mặt phẳng MEF cắt SA tại N. Tính theo a thể tích khối chóp VD S.EFMN. C 3 3 3 3 7a 2 a 2 a 2 7a 2 A. . B. . C. . D. . 108 9 36 36 Lời giải Chọn A
https:/www.facebook.com/groups/toanvd. Trang 26 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 N H Ó M TOÁN VD – V
Gọi I là trung điểm BC . Dựng OH SI,H SI OH SBC D C 1 1 1 a 2 3 1 a 2 a 2 OS . 2 V V . .2a . 2 2 2 OH OS OI 2 S. ABCD 3 2 3 V 2 2 1 S .MNF V V V S .MNF S. V 9 9 DAC 9 3 3 S .DAC 7 7 a 2 7a 2 ; Suy ra V V . V 1 1 1 S.MNEF 36 36 3 108 S .NEF V V V S .NEF S . V 6 6 ABC 12 S .ABC
Câu 13: Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V . Điểm E thuộc cạnh SC 1 N
sao cho SE SC , một mặt phẳng qua AE cắt các cạnh SD và SB lần lượt tại M và N . Gọi H 3 Ó V M
V là thể tích khối chóp S.AMEN . Tìm giá trị nhỏ nhất của 1 ? 1 V T 1 1 1 1 O A. . B. . C. . D. . Á 9 6 3 12 N Lời giải V Chọn B D – VDC SM SN Đặt x , y , 0 x , y 1. SB SD
https:/www.facebook.com/groups/toanvd. Trang 27 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 SA SC SB SD 1 1 x Vì nên 1 3 y . SA SE SM SN x y 4x 1 V V V 1 SA SN SE 1 SA SM SE 1 1 1 1 Khi đó 1 S .ANE S .AME . . . . . . .y. . . x . V 2V 2V 2 SA SD SC 2 SA SB SC 2 3 2 3 S .ADC S.ABC N 1 1 x H x y x . Ó 6 6 4x 1 M 1
Vì x 0 , y 0 nên x 1. T 4 O Á x 1 N Xét hàm số f x 1 x trên ;1 . 6 4x 1 4 VD 1 1
Ta có f x 1 . – 6 4x 2 1 VD f x 1 0 x . C 2 Bảng biến thiên x 1 1 1 4 2 f x – 0 2 f x 1 9 6 V 1 N
Vậy giá trị nhỏ nhất của 1 bằng . H V 6 Ó M
Câu 14: Cho khối tứ diện ABCD có thể tích bằng 1. Trên cạnh AB lấy điểm M sao cho BM 2AM ,
N, P lần lượt là trung điểm của BC ,CD . Biết MNP cắt T
AD tại Q . Khối đa diện MAQNCP O có thể tích bằng Á N 7 5 7 5 A. . B. . C. . D. . V 9 16 18 8 D Lời giải – V Chọn C D C
https:/www.facebook.com/groups/toanvd. Trang 28 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 A Q M N H Ó M TOÁ B D N VD N P – V C D C NP MNP Ta thấy BD ABD
MNP ABD MQ / /BD Q AD . M MNP ABD
Chia khối đa diện MAQNCP thành các khối chóp tam giác : . A NCP, . A MNP, . A MPQ . S 1 1 Ta có : NCP V .V .1 . . A NCP ABCD S 4 4 BCD N H AM 1 1 S 1 1 1 Ó V .V .V . BNP .V . . . A MNP . A BNP . A BNP ABCD M AB 3 3 S 3 4 12 BCD TO AM AQ 1 1 S 1 BPD Á V . .V . . V . . A MPQ . A BPD ABCD N AB AD 3 3 S 18 BCD VD 1 1 1 7 Vậy V . MAQNCP – 4 12 18 18 VD
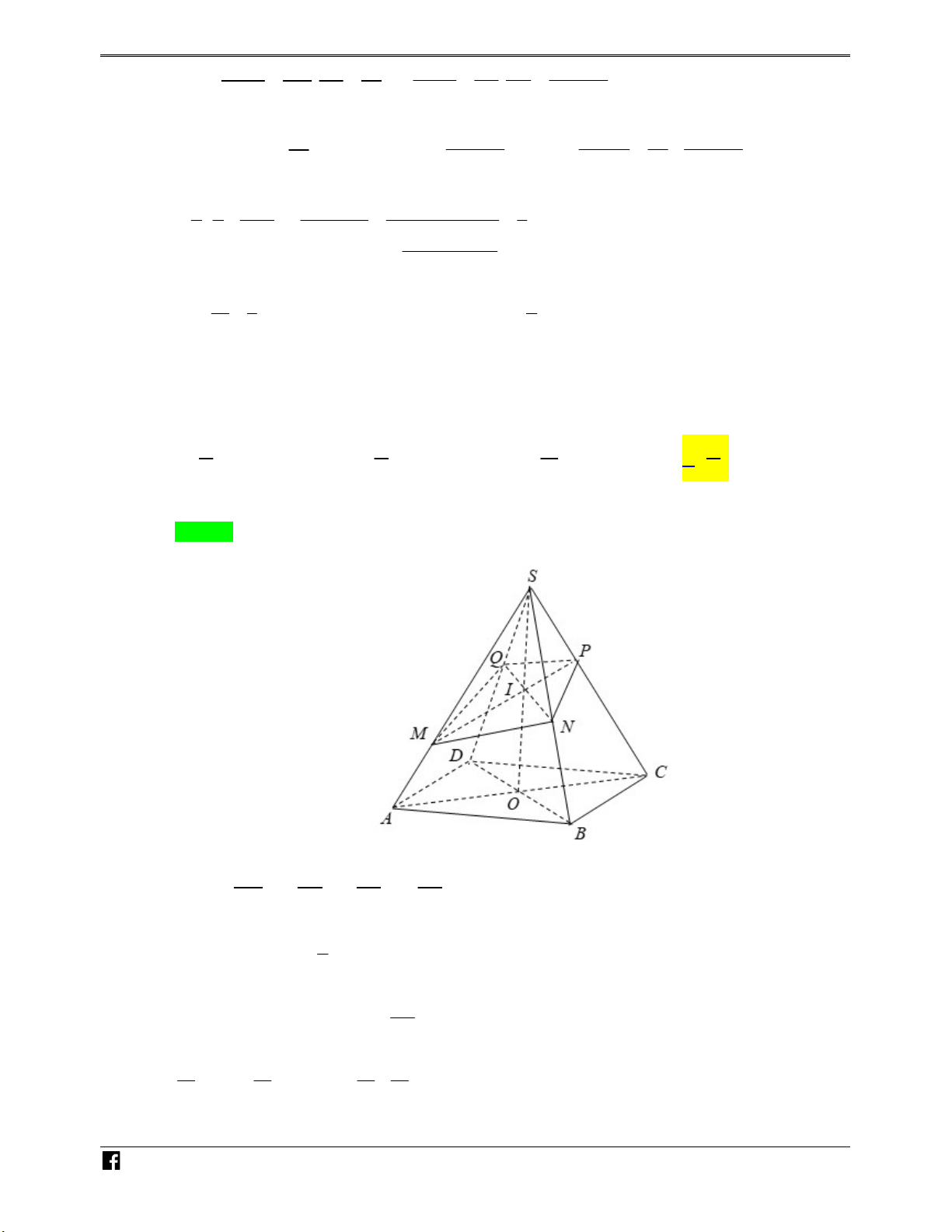
Câu 15: Cho hình chóp S.ABCDEF có đáy ABCDEF là hình lục giác đều tâm O . Gọi M là trung điểm C
của cạnh SD . Mặt phẳng AMF cắt các cạnh S ,
B SC, SE lần lượt tại H, K, N . Gọi V ,V lần 1 V
lượt là thể tích của các khối chóp S.AHKMNF và S.ABCDEF . Tính tỉ số 1 V V V V V A. 1 1 . B. 1 1 . C. 1 13 . D. 1 14 . V 3 V 9 V 36 V 27 Lời giải Chọn C
https:/www.facebook.com/groups/toanvd. Trang 29 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 S N K H H M Ó M J T B C O Á N N D V A O D – F E VD Gọi J AM SO . C
Vì AF / /CD nên AMF SCD MK với MK / /CD
Vì AF / /BE nên AMF SBE HN với HN / /BE SJ 2
Ta có J là trọng tâm của tam giác SAD nên SO 3 SH SN SJ 2 Mà HN / /BE suy ra SB SE SO 3 N H SK SM 1 Ó Lại có MK / /CD suy ra M SC SD 2 TO V V V V V V Khi đó: 1 S .AHKMNF S .AHK S .AKM S .AMF S.FMN Á V V V N S .ABCDEF S .ABCDEF V V V V V S .AHK S .AKM S .AMF S .FMN D V V V V S .ABCDEF S .ABCDEF S .ABCDEF S .ABCDEF – V V V V V S .AHK S .AKM S.AMF S .FMN (vì V 6V 3V 3V 6V ) D 6V 3V 3V 6V S.ABCDEF S.ABC S .ACD S .ADF S .FDE C S .ABC S .ACD S .ADF S .FDE 1 SH SK 1 SK SM 1 SM 1 SM SN . . . . . . . 6 SB SC 3 SC SD 3 SD 6 SD SE 1 2 1 1 1 1 1 1 1 1 2 . . . . . . . 6 3 2 3 2 2 3 2 6 2 3 1 1 1 1 13 . 18 12 6 18 36
https:/www.facebook.com/groups/toanvd. Trang 30 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 3 8a 2
Câu 16: Cho hình chóp đều S.ABCD có các cạnh bên tạo với đáy góc 45o và thể tích bằng . Mặt 6
phẳng thay đổi song song với mặt phẳng ABCD lần lượt cắt các cạnh S , A SB, SC, SD
tại M , N, P, Q . Qua M , N, P, Q kẻ các đường thẳng song song với nhau, lần lượt cắt mặt đáy N
ABCD tại M , N , P , Q . Biết tỉ số thể tích giữa khối hộp MNP . Q M N P Q
và khối chóp cụt HÓ 3 M MNP .
Q ABCD bằng . Tính chiều cao của hình chóp cụt MNP . Q ABCD ? 7 T a 2 a 2 O A. . B. a 2. C. . D. . a Á 2 4 N Lời giải VD Chọn A – VDC N H Ó M x 2 T Đặt AB x thì 2 S x và DO . ABCD O 2 Á N x 2 V Ta có , 45o SD ABCD SDO , do đó: SO DO . D 2 – 3 3 1 x 2 x 2 8a 2 2 V Mà V .x . x 2a . S .ABCD D 3 2 6 6 C
Đặt MN y và h là chiều cao của hình chóp cụt MNP . Q ABCD . Suy ra 2 V y h và MNPQ.M N P Q S S S S 2 2 x xy y h 1 1 2 2 V .h MNPQ.ABCD 3 3 2 VMNPQ M N P Q 3y Theo bài: . 2 2 V x xy y MNPQ.ABCD
https:/www.facebook.com/groups/toanvd. Trang 31 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 2 3y 3 2 2 4a 2ay y 7 2 2 6y 2ay 4a 0 y a N H Ó y 1 SO h 1 a 2 Khi đó: h M x 2 SO 2 2 TO
Dạng 2. CHIA HÌNH CHÓP, HÌNH LĂNG TRỤ THÀNH CÁC KHỐI ĐA DIỆN KHÁC NHAU Á
BỞI VIỆC LẤY THÊM CÁC ĐIỂM THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC. TÍNH N
THỂ TÍCH MỘT TRONG HAI KHỐI ĐÓ VD
Câu 1: Cho hình lăng trụ ABC.MNP có chiều cao h 3 và diện tích đáy S 27 . Gọi G, I , K lần lượt –
là trọng tâm các tam giác ABM , ACM , BCM . Tính thể tích khối đa diện tạo bởi các điểm VD G, I , K , , A B,C . C N H Ó M A. 15 . B. 16. C. 18 . D. 21. T Lời giải O Á Chọn B N VD – VDC
https:/www.facebook.com/groups/toanvd. Trang 32 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
Ta xét khối tứ diện M .ABC , vẽ mặt phẳng A' B 'C ' // ABC và đi qua các điểm G, I, K như hình vẽ. 3 2 19 Nhận xét: V .V V V . N M .A' B 'C ' MABC A' B 'C '.ABC M . 3 27 ABC H Ó 3 M 1 1 1 1 1 2 1 V V . .V . . V B.B'GK M .B 'GK M .A'B 'C ' M.ABC T 2 2 4 2 4 3 27 M.ABC O Á 16 16 1 N Vậy V V 3V V . V 16 . GKI .ABC A'B 'C '.ABC B.B'GK M .ABC ABC.MNP 27 27 3 VD
Câu 2: Cho hình lăng trụ đều ABC.A B C
có độ dài tất cả các cạnh bằng 2 . Gọi M là trung điểm AB – V
và N là điểm thỏa mãn AC 3AN . Thể tích của khối đa diện lồi có các đỉnh là các điểm D ,
A M , N , A , B và C bằng C 10 3 2 3 10 3 2 3 A. . B. . C. . D. . 3 9 9 3 Lời giải Chọn C N H Ó M TOÁN VD – V D C
Gọi V là thể tích của của khối đa diện lồi có các đỉnh là các điểm ,
A M , N, A , B và C . Khi đó ta có: V V V . M .AA C N M .AB C 1 1 2 8 Ta có S AA AN A C . AA C N .2. 2 2 2 3 3
Gọi H là trung điểm của AC thì BH ACC A
và BH 3 (do ABC là tam giác đều cạnh 1 1 3
bằng 2 ), suy ra d M , ACC A
d B, ACC A BH . 2 2 2 1 1 3 8 4 3 Suy ra V . d M , ACC A .S . . M .AA C N 3 AA C N 3 2 3 9
https:/www.facebook.com/groups/toanvd. Trang 33 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 1 1 4 3 2 3 V d M , A B C .S .2. M .A B C 3 A B C 3 4 3 4 3 2 3 10 3 Vậy V V V . M .AA C N M .AB C 9 3 9 N H
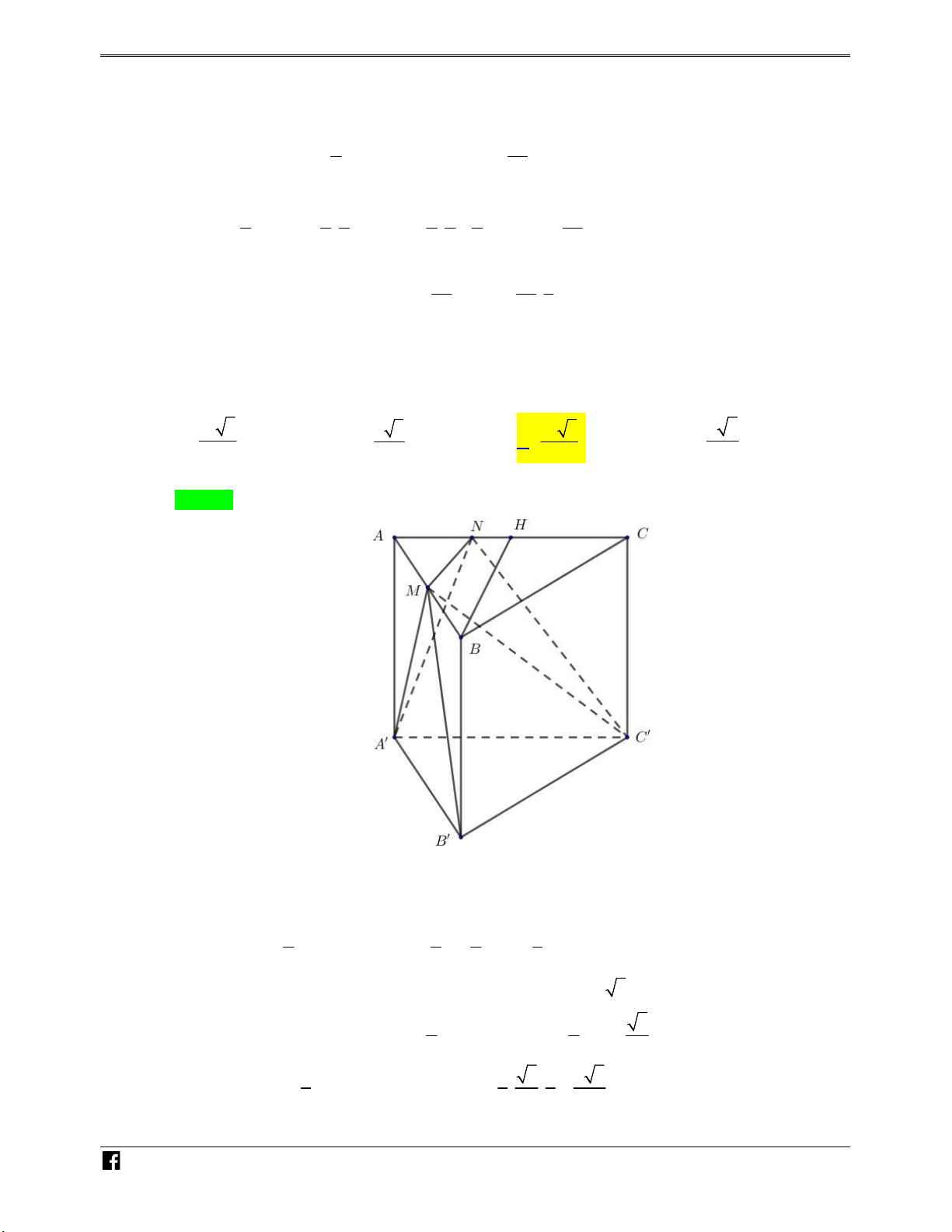
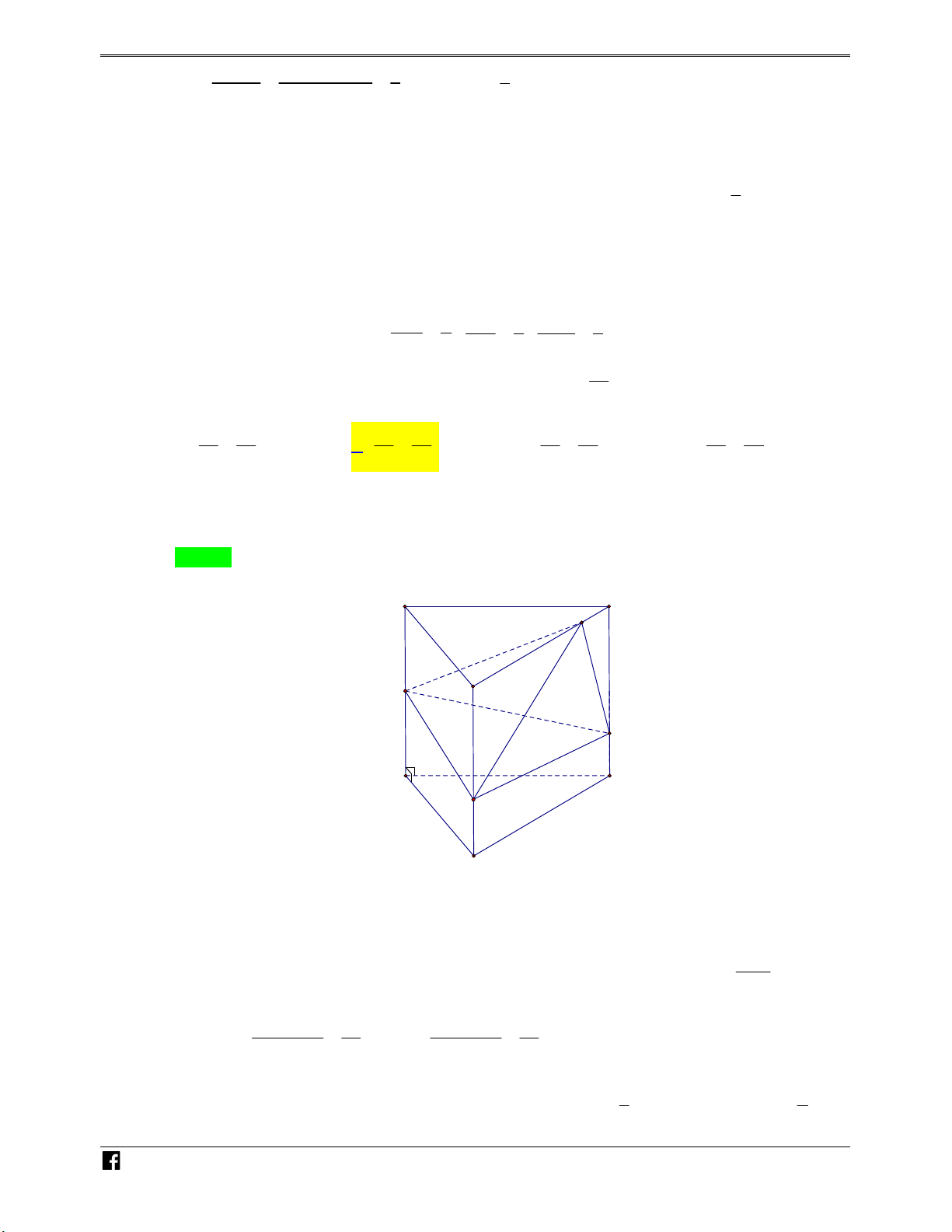
Câu 3: Cho hình lăng trụ đứng ABC.A ' B 'C ' có AA a AB BC a 0 ' 2 ,
, ABC 90 . Gọi D, E, F lần Ó
lượt là trọng tâm của các tam giác BA ' B ',CC ' B ', A ' AC . Tính thể tích khối đa diện AEBDF M 3 3 3 3 14a 16a 14a 16a T A. . B. . C. . D. . O 81 81 49 27 Á N Lời giải VD Chọn A – VDC N H Ó M TO Á N +)Ta có V V V AEBDF A.BDF E.BDF VD AD AB AF 2 1 1 2 1 2 3 – +)V . . .V . . A . B S . . a .2 . a a a A.BDF A.B 'BC ' BB 'C ' AB ' AB AC ' 3 3 3 27 2 27 VDC 1 +)V d F; BDE .S E.BDF 3 B DE 2
+)Ta có d F;BDE d F;BMC ' d ; A BMC ' 3 2 d B BMC 4 .2. ';
' d B ';BMC ' . 3 3
+) Mặt khác tứ diện B ' BMC ' có 3 góc đỉnh B ' vuông nên: 1 1 1 1 1 1 1 21 . 2 d B ';BMC ' 2 2 2 2 2 2 2 B ' B B ' M B 'C ' 4a a a 4a 4
https:/www.facebook.com/groups/toanvd. Trang 34 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 a a a
Suy ra d B BMC 2 21 '; '
d F BDE 4 2 21 8 21 ; . . 21 3 21 63 4 2 a a 17 a 5 +) S S , tam giác BMC ' có: 2 BC ' a 5, BM 4a , MC ' . BDE BMC ' N 9 4 2 2 H Ó 2 2 M a 21 a 21 Từ đó suy ra S S . BMC ' BDE 4 9 TOÁ 2 3 1 8a 21 a 21 8a N Nên V . . . E.BDF 3 63 9 81 VD 3 3 2 8a 14a 3 – Vậy V V V a AEBDF A.BDF E.BDF 27 81 81 VD
Câu 4: Cho khối lăng trụ tam giác ABC.AB C
có diện tích đáy bằng 6 và chiều cao bằng 8. Gọi I là C
tâm của hình bình hành ABB A
và G là trọng tâm tam giác ABC . Thể tích tứ diện BIGC bằng 8 16 16 8 A. . B. . C. . D. . 3 9 3 9 Lời giải Chọn C N H Ó M TOÁN VD – VD Ta có V 48 . ABC.A B C C
Gọi M là trung điểm của AC . V 1 BG BI 2 1 1 Ta có: B.GIC . . V V 1 . B.GIC B.MA C V 3 BM BA 3 2 3 B.MA C 1 1 1 Mặt khác S . d A C d A C S S MA C . . M , A C A,A C 2 2 AA C 2 ACC A V 1 S 1 Mà B.MA C MA C V V 2 . B.MA C B.ACC A V 2 S 2 B.ACC A ACC A
https:/www.facebook.com/groups/toanvd. Trang 35 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 2 2 Lại có V .V .48 32 3 . B.ACC A ABC.A B C 3 3 16 Từ
1 , 2 và 3 suy ra V . B.GIC 3 N H Ó
Câu 5: Cho lăng trụ tam giác ABC.A ' B 'C ' có diện tích đáy bằng 12 và chiều cao bằng 6 . Gọi M , N M
lần lượt là trung điểm của CB,CA và P,Q, R lần lượt là tâm các hình bình hành T
ABB ' A', BCC ' B ',CAA'C '. Thể tích của khối đa diện PQRABMN bằng O Á N VD – VDC A. 21. B. 42. C. 14. D. 18. N Lời giải H Ó Chọn A M TOÁN VD – VDC
Gọi P,Q , R lần lượt là các giao điểm của CC ', AA', BB ' và mặt phẳng PQR . 1 1 1
Đặt V V ABC.A' B'C ' và V V PQRABMN , ta có V 72 . 1 1 Lại có: V V 36 và V V V V V * . ABCPQ R 1 AQ RP BR PQ CMNPQR ABC 1 P 1 Q 1 R 2 1 1 1 1 1 1
https:/www.facebook.com/groups/toanvd. Trang 36 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 V AQ PR AQ .A . R AP 1 1 Vì 1 1 mà V V 24 nên V 3. V AA'.AC ' AB ' 8 AA'C 'B' 3 A 1 Q PR AA'C ' B' Tương tự có V 3 . B 1 R PQ N H 1 Ó
Do CMNPQR là hình lăng trụ tam giác nên V S .d P , ABC V 9 . CMN 1 PQR CMN 1 1 8 M T
Thay vào * 36 V 3 3 9 V 21. O 1 1 Á N
Câu 6: Cho lăng trụ đứng tam giác ABC.A ' B 'C '. Gọi M , N , P,Q là các điểm lần lượt thuộc các cạnh V AM 1 D BN 1 C 'Q 1
AA', BB ',CC ', B 'C ' thỏa mãn , , . Gọi 1 V , 2
V lần lượt là thể tích khối – AA' 2 BB ' 3 B 'C ' 5 V V
tứ diện MNPQ và khối lăng trụ ABC.A ' B 'C '. Tính tỷ số 1 . D 2 V C V 11 V 11 V 19 V 22 A. 1 . B. 1 . C. 1 . D. 1 . 2 V 30 2 V 45 2 V 45 2 V 45 Lời giải . Chọn B C' A' Q' N H Ó M B' b M TOÁ P N V A D C – N a VDC B Đặt BC a,CC ' , b a,b 0 . 11ab
Diện tích tam giác NPQ ' là: SNPQ' SBCC'B' SNB'Q' SPC'Q' SBCPN 30 M V NPQ 11 V 11 Suy ra: . ' . Tức là: 1 . VA'.BCC'B' 30 V '. ' ' 30 A BCC B 1 2
Mặt khác: VA'.BCC'B' VA'.ABC VABC.A'B'C' VA'.BCC'B' 2 V 2 V VA'.BCC'B' 2 V 3 3
https:/www.facebook.com/groups/toanvd. Trang 37 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 V 11 V 11 Do đó: 1 1 . 2 30 2 V 45 2 V 3
Câu 7: Cho khối lăng trụ ' ' ' ABC.A B C , gọi M , N , P N
là tâm của ba mặt bên H ' ' ' ' ' ' ABA B , ACA C , BCB C và '
G,G là trọng tâm của hai đáy ' ' '
ABC, A B C biết thể tích khối ÓM
lăng trụ bằng 24. Tính thể tích khối đa diện lồi có các đỉnh là G G MNP . 1 2 TO A. 2 . B. 6. C. 4 . D. 3. Á Lời giải N V Chọn A D – A B G VDC E C K M H P N A' T B' F G' N H Ó C' M TO
Gọi h, S là chiều cao và diện tích đáy của khối lăng trụ ' ' ' ABC. A B C Á N
Qua M , N , P kẻ các đường thẳng song song với ' ' ' ' ' ' A B , B C , AC VD – 1 S h Ta có S S , d G,MNP MNP HTK V 4 4 2 D C 1 2 h S 1 Mà V 2V 2. d G, MNP .S . . .V 2 ' G MNP ' ' ' . MNP GG MNP ABC. 3 3 2 4 12 A B C
Câu 8: Cho hình lăng trụ ABC.A' B 'C ' . Gọi M , N , P , Q , R , S lần lượt là trung điểm của các cạnh
AB , A'B', AA' , BC , B 'C ', CC ' . Biết thể tích khối lăng trụ ABC.A' B 'C ' bằng V . Tính
thể tích khối đa diện MNPQRS . 1 1 2 3 A. V . B. V . C. V . D. V . 3 4 9 10 Lời giải Chọn A
https:/www.facebook.com/groups/toanvd. Trang 38 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 N H Ó M TOÁN VD – V
Gọi T là trung điểm của PS thì MN .
P QRT là hình lăng trụ. Lúc đó: D C V V V 1 MNPQRS MNP.QRT T .QRS 1 S .S 2 MNP ABB ' A' V V Vì: 4 nên C. ABB ' A' 3 2 1 V V V 3.V C.A' B 'C ' 3 MNP.QRT Q.MNP 3 3 3 2 1 2 V 3.V V V . V V 3 MNP.QRT Q.MNP Q.ABB ' A ' C.ABB ' A' 4 8 8 3 4 N H Ó 1 1 1 1 1 2 1 M Lúc đó: V V V . V . V V 4 T .QRS P.QRS . A QRS A.BCC ' B ' 2 2 2 4 8 3 12 TO 1 1 1 Á
1 , 3 và 4 suy ra: V V V V . MNPQRS N 4 12 3 VD 1 Vậy V V . – MNPQRS 3 VD 5 5 C V . ABCD A B C D 36 36
Câu 9: Cho hình lăng trụ tứ giác ABC .
D A' B 'C ' D ' có hai đáy ABCD và A' B 'C ' D ' là các hình bình
hành. Gọi M , N, P,Q lần lượt là các điểm thoả mãn 2MB MA' ; 3BN BC ' ; 3CP 2CD '
và 3AQ 2AD ' . Biết rằng V ,V lần lượt là thể tích khối lăng trụ đã cho và khối đa diện lồi có 1 V các đỉnh ,
A B, C, D, M , N , P, Q . Tỉ số 1 bằng V 16 7 5 11 A. . B. . C. . D. . 27 12 12 27 Lời giải
https:/www.facebook.com/groups/toanvd. Trang 39 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 Chọn D N H Ó M TOÁN VD – VDC Đặc biệt hóa ABC .
D A' B 'C ' D ' thành hình lập phương có cạnh bằng 6 V 216 . Ta có V V V V V V 1 A.MRLQ C.TSPN B.RMNT D.LSPQ BLQM .TSPN 1 1 1 V S .d ; A MRLQ . 2 4 .4 2.2 2 16 A.MRLQ MRLQ 3 3 2 1 1 8 V S .d B; RMNT .2 2.2. 2 ; B.RMNT RMNT N 3 3 3 H Ó 1 1 16 M V S .d ; D LSPQ .2 2.4. 2 ; D.LSPQ LSPQ 3 3 3 TO 1 Á V S .RT 4 2 .4 2.2 2 48 . RLQM .TSPN RLQM N 2 VD 8 16 V 11 Suy ra 1 V 16.2 48 88 . 1 – 3 3 V 27 VD Câu 10: Cho hình hộp ABC . D
A BCD có thể tích bằng 1. Gọi G là trọng tâm tam giác A BC và I là C trung điểm của A
D . Thể tích khối tứ diện GDCI bằng: 7 5 7 5 A. . B. . C. . D. . 24 24 36 36
https:/www.facebook.com/groups/toanvd. Trang 40 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 A' I' D' C' B' N H Ó K M G T A O D Á N V B D M C –
Qua G kẻ đường thẳng song song với AM, cắt AA’ tại K. Khi đó: GK // AM // I’C’ GK // VD (DI’C’). C 1
V d G ICD 1 ,(
) .S d K,(ICD).S GI C D I C D I C D K V IC 3 3 D A K A G GK 2 Và A A A M AM 3 1 1 1 5 Ta có: SI ' KD SAD A D S A I K SID S D KAD SAD A D 1 SAD A D 6 4 6 12 N 1 1 5 H
Suy ra V V d , D (ICD).S ' GI C D KI C D I KD d , D (AD D A ) . SAD A D Ó 3 3 12 M
Câu 11: Cho hình chóp S.ABCD có ABCD là hình chữ nhật. AB 1, AD 2 . SA vuông góc với đáy và TO
SA 3. Gọi M , N , P lần lượt là chân đường cao hạ từ A lên các cạnh SB, SD, DB . Thể tích ÁN
khối đa diện ABMNP bằng V 17 113 81 147 D A. . B. . C. . D. . 130 130 130 130 – Lời giải VD Chọn A C Ta có 2 2 2 2 2 2 2 2 2
SD SA AD 13, SB SA AB 10, BD AB AD 5
https:/www.facebook.com/groups/toanvd. Trang 41 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 S M N H Ó N M TO A B Á N P V O D D C – V Ta có D C 2 SN SN.SD SA 9 SN 9 , 2 2 SD SD SD 13 SD 13 2 SM SA 9 SM 9 2 DP DA 4 DP 4 Tương tự ta có , . 2 SB SB 10 SB 10 2 DB DB 5 DB 5
Ta có thể tích khối đa diện V V V V . ABMNP S .ABD S .AMN D.ANP 1
+) Ta có thể tích khối tứ diện V AS.A . B AD 1. S .ABD N 6 H Ó V SM .SN 9 9 81 81 S AMN M +) . . V V . S .AMN S . V S . B SD 10 13 130 130 ABD S .ABD TOÁ V DN.DP SD SN DP 9 4 16 16 +) D.ANP . 1 . V V N D.ANP S. V DS.DB SD DB 13 5 65 65 ABD D.ASB VD 81 16 17 17 – Vậy V V V V 1 V .1 . ABMNP S.ABD S.AMN D.ANP S.ABD 130 65 130 130 VDC
Câu 12: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi M , N lần lượt là trọng tâm các
tam giác SAB và SCD ; I là trung điểm của SO . Biết thể tích khối chóp S.ABCD bằng 2020 ,
tính thể tích khối đa diện IMNABCD . 18685 17675 4040 A. 1010 . B. . C. . D. . 18 18 3 Lời giải Chọn B
https:/www.facebook.com/groups/toanvd. Trang 42 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 S N I H Ó M N M A K D TO E Á O F N V B D C –
Gọi E, F lần lượt là trung điểm của AB,CD MN //EF MN //AD//BC . VDC
Gọi V là thể tích của khối chóp S.ABCD và V là thể tích khối đa diện IMNABCD . Ta có: V V V . MNABCD I .ADNM V V V MNABCD M .ABCD MNCD 1 1
Vì M là trọng tâm SAB d M ; ABCD d S; ABCD V V . M . 3 ABCD 3 1
Vì N là trọng tâm SCD S S NCD SCD N 3 H Ó 2 2 M
Lại có d M ;SCD d E;SCD d ; A SCD 3 3 TO 2 1 Á Từ đó suy ra V V V MNCD A.SCD N 9 9 VD V V V I .ADNM AMNI BAIN – V 4 1 1 1 1 S S ; S S S ; S S S D SMN 9 SEF SMI 3 SEO 6 SEF SNI 3 SFO 6 SEF C 1 1 1 Suy ra S S V V V IMN 9 SEF AMNI 9 ASEF 36
Gọi K là giao điểm của AN và MD 2 2 KM 2 3 1 Vì MN EF AD V V V 3 3 KD 3 DANI 2 MANI 24 1 1 1 1 37 18685 Vậy V V V V V V 3 9 36 24 72 18
https:/www.facebook.com/groups/toanvd. Trang 43 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 3 8a 2
Câu 13: Cho hình chóp đều S.ABCD có các cạnh bên tạo với đáy góc 45o và thể tích bằng . Mặt 6
phẳng thay đổi song song với mặt phẳng ABCD lần lượt cắt các cạnh S , A SB, SC, SD
tại M , N, P, Q . Qua M , N, P, Q kẻ các đường thẳng song song với nhau, lần lượt cắt mặt đáy NH
ABCD tại M , N , P , Q . Biết tỉ số thể tích giữa khối hộp MNP . Q M N P Q
và khối chóp cụt ÓM 3 MNP .
Q ABCD bằng . Tính chiều cao của hình chóp cụt MNP . Q ABCD ? T 7 O a 2 a 2 Á A. . B. a 2. C. . D. . a N 2 4 V D – Lời giải VD Chọn A C N H Ó M T O Á N x 2 Đặt AB x thì 2 S x và DO . ABCD V 2 D x 2 – Ta có , 45o SD ABCD SDO , do đó: SO DO . 2 V 3 3 D 1 x 2 x 2 8a 2 Mà 2 V .x . x 2a . C S .ABCD 3 2 6 6
Đặt MN y và h là chiều cao của hình chóp cụt MNP . Q ABCD . Suy ra 2 V y h và MNPQ.M N P Q S S S S 2 2 x xy y h 1 1 2 2 V .h . MNPQ.ABCD 3 3 2 VMNPQ M N P Q 3y Theo bài: . 2 2 V x xy y MNPQ.ABCD
https:/www.facebook.com/groups/toanvd. Trang 44 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 2 3y 3 2 2 4a 2ay y 7 2 2 6y 2ay 4a 0 y a N H Ó y 1 SO h 1 a 2 Khi đó: h . M x 2 SO 2 2 TO
Câu 14: Cho hình chóp S.ABCD đáy là hình bình hành tâm O có thể tích bằng V .Lấy điểm S ' đối xứng Á
với S qua O . Trên các cạnh SA, S' A lần lượt lấy các điểm M, E sao cho N V
AM 2MS, AE 2ES'. Mặt phẳng đi qua M và song song với (ABC ) D cắt các cạnh D
SB, SC, SD lần lượt tại N, P, Q . Mặt phẳng đi qua E và song song với (ABC ) D cắt các –
cạnh S' B, S'C, S' D lần lượt tại F, G, H . Thể tích của khối đa diện có các đỉnh VD M , N, P, Q, E, F, G, H là C 4V 2V 4V 4V A. . B. . C. . D. . 9 9 3 27 Lời giải Chọn A S P Q M N N D C H Ó M B TO A Á H N G V E F D – S' V
Ta có khối đa diện có các đỉnh M, N, P, Q, E, F, G, H là khối lăng trụ có đáy là MNPQ D C và EFGH V S .d Do đó MNPQ.EFGH MNPQ (M ,( EFGH )) V 1 S.ABCD S .d ABCD (S ,( ABCD)) 3 MN SM 1
Ta thấy MNPQ và ABCD đồng dạng với nhau theo tỷ số k AB SA 3 SMNPQ 2 1 Suy ra k S 9 ABCD d 2d (M ,(EFGH )) (M ,( ABCD )) MA 2 4 Mặt khác 2. 2. d d SA (S ,( ABCD )) S,( ABCD) 3 3
https:/www.facebook.com/groups/toanvd. Trang 45 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 V S .d MNPQ.EFGH MNPQ (M ,(EFGH )) 1 4 4 4V Vậy 3. . V V 1 9 3 9 MNPQ.EFGH 9 S. ABCD S .d 3 ABCD (S,(ABCD))
Dạng 3. MAX- MIN THỂ TÍCH CÁC KHỐI KHI PHÂN CHIA N 1 H
Câu 1: Cho hình chóp tứ giác SABCD đáy là hình bình hành,các điểm A ,C thỏa mãn SA = SA , Ó 3 M 1 V
SC SC . Mặt phẳng P chứa A ,C cắt các cạnh SB, SD lần lượt tại B , D . Đặt k= SA B C D T 5 V O SABCD Á
, giá trị nhỏ nhất của k là bao nhiêu? N 15 4 1 1 V A. . B. . C. . D. . D 6 15 60 30 – Lời giải V Chọn C D C N H Ó M TO SA SB Á Đặt = a = b N SA SB VD SC SD = c = d , b d 1 – SC SD V Ta có a c 8 D C
Áp dụng công thức tính nhanh tỉ lệ thể tích ta có: V a b c d 16 K = SAB C D = =
,với a c b d 8 V 4abcd 60bd ABCD
Áp dụng bất đẳng thức Cauchy cho 2 số dương b,d 16 16 1 Ta có: ≥ = 60bd 2 b d 60 60. 2
https:/www.facebook.com/groups/toanvd. Trang 46 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 1 Vậy k min =
.Dấu = xảy ra b d 4 . 60
Câu 2: Cho tứ diện ABCD có thể tích bằng V . Trên AB lấy hai điểm M , N , trên CD lấy hai điểm N MN PQ H P,Q thỏa mãn 2 3
1. Thể tích khối MNPQ đạt giá trị lớn nhất bằng Ó CD AB M V V V V T A. . B. . C. . D. . O 8 16 24 32 Á N Lời giải V Chọn C D – A VDC M N D B Q N H Ó P M TO C Á N
Gọi d , lần lượt là khoảng cách và góc giữa AB và CD . 1 VD
Gọi d , lần lượt là khoảng cách và góc giữa MN và PQ . 2 – V 1 1 Ta có V A . B C . D d .sin , V MN.P . Q d .sin D ABCD 1 6 MNPQ 2 6 C V MN PQ Do d d và sin MNPQ . sin 1 2 V A . B CD ABCD MN PQ MN PQ Ta có 2 3 2 2 .3 CD AB CD AB MN PQ MN PQ MN PQ MN PQ V 2 3 1 1 2 6 6 MNPQ 1 CD AB CD AB CD AB 2 CD AB 24 V 24 ABCD V V VậyV MaxV . MNPQ 24 MNPQ 24
https:/www.facebook.com/groups/toanvd. Trang 47 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020
Câu 3: Trên các cạnh AB, BC,CD, D ,
A AC và BD của tứ diện ABCD lần lượt lấy các điểm
M , N , P,Q, S và R . Gọi V ,V ,V ,V và V lần lượt là thể tích của các khối tứ diện 1 2 3 4 4 V
AMSQ, BMNR, CNPR, DPQR và ABCD . Giá trị nhỏ nhất của tỉ số là VV V V 1 2 3 4 N H A. 4096 . B. 256 . C. 64 . D. 1024. Ó Lời giải M Chọn A TO A Á N V M D Q – VD R D C B S N P C V AM.AS.AQ V BM .BN.BR V CN.C . P CS V D . Q D . R DP Ta có 1 ; 2 ; 3 ; 4 . V A . B A . C AD V B . A BC.BD V C . B C . D CA V D . A D . B DC VV V V N AM .BM BN.CN C . P DP D . Q AQ AS.CS B . R DR Suy ra 1 2 3 4 . . . . . . H 4 2 2 2 2 2 2 V AB BC CD DA AC BD Ó 4 2 2 2 2 2 2 M V AB BC CD DA AC BD Do đó . . . . . . VV V V AM.BM BN.CN C . P DP D . Q AQ AS.CS B . R DR T 1 2 3 4 O 2 2 AM BM AB AB AB Á Mặt khác, ta có AM .BM AM .BM 4 . N 2 2 4 AM .BM V
Dấu “=” xảy ra khi và chỉ khi AM BM . D 2 2 2 2 2 BC CD DA AC BD – Tương tự ta có 4 ; 4 ; 4 ; 4 ; 4 BN.CN C . P DP DQ.AQ AS.CS BR.DR VD 4 2 2 2 2 2 2 V AB BC CD DA AC BD 6 C Từ đó suy ra . . . . . 4 . VV V V AM.BM BN.CN C . P DP D . Q AQ AS.CS B . R DR 1 2 3 4
Dấu “=” xảy ra khi và chỉ khi M , N , P,Q, S và R lần lượt là trung điểm của AB, BC,CD, D , A AC và BD . 4 V
Vậy giá trị nhỏ nhất của là 6 4 4096 . VV V V 1 2 3 4
Câu 4: Cho hình chóp S.ABC có SA 4, SA ABC . Tam giác ABC vuông tại B và AC 2 . H, K
lần lượt là hình chiếu vuông góc của A lên S ,
B SC . Tìm GTLN của thể tích chóp S.AHK . 32 5 16 5 24 5 40 5 A. . B. . C. . D. . 75 75 75 75 Lời giải
https:/www.facebook.com/groups/toanvd. Trang 48 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 Chọn A N H Ó M TOÁN VD – VD C Gọi cạnh 2
AB x BC 4 x . Điều kiện 0 x 2 . 1 1 2 2 V .S . A BC.BA x 4 x . S.ABC 3 2 3 2 2 V SH SK SH.SB SK.SC SA SA 256 64 S.AHK . . . 2 2 2 2 V SB SC SB SC SB SC x x S ABC 2 16 20 5 2 16 . 2 2 64 128 x 4 x 5 . x 2 4 x 64 5 V .V . . S.AHK 5 2 16 x S.ABC 2 2 15 16 x 16 x 75 N 2 2 H 5x 16 4x Ó 2 64 5 5 . x 16 4x 64 5 32 5 2 M V . . . S.AHK 2 2 75 16 x 75 16 x 75 TO 4 Á
Dấu đẳng thức xảy ra khi 2 2 2
5x 16 4x 9x 16 x 0;2 . N 3 VD
Câu 5: Cho tứ diện S.ABC và G là trọng tâm của tứ diện. Một mp quay quanh AG , cắt các cạnh –
SB, SC lần lượt tại M và N ( M , N không trùng S ). Gọi V là thể tích tứ diện S.ABC , V là 1 VD V
thể tích tứ diện SAMN và gọi m, n lần lượt là GTLN và GTNN của 1 . Hãy tính m n . C V 17 18 19 A. m n 1. B. m n . C. m n . D. m n . 18 19 20 Lời giải Chọn B
https:/www.facebook.com/groups/toanvd. Trang 49 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 S N N H G A' Ó M A C TO M I Á N B V D –
+) Gọi A là trọng tâm SBC , I là trung điểm BC Ta có A,G , A thẳng hàng và S , A , I V thẳng hàng. D C SM SN +) Đặt x , y với 0 x, y 1. SB SC V SM SN +) Ta có: 1 . xy . V SB SC N H Ó M TOÁN VD – VD C SB SC SI 1 1 x +) Mặt khác: 2 3 y . SM SN SA x y 3x 1 1
+) Vì 0 y 1 nên ta có : x 1. 2 2 V x 2 x 1 +) Khi đó: 1 xy . Xét f (x) , x 1. V 3x 1 3x 1 2 2 3x 2x 2 f '(x) , f '(x) 0 x . 3x 2 1 3
https:/www.facebook.com/groups/toanvd. Trang 50 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 +) Bảng biến thiên: N H Ó M TO Á N 1 4 17
+) Từ bảng biến thiên suy ra: m , n m n . V 2 9 18 D –
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích là V . Gọi P là trung V
điểm của SC. Mặt phẳng chứa AP và cắt hai cạnh SD, SB lần lượt tại M và N. Gọi V DC V
là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của tỉ số . V 3 1 2 1 A. . B. . C. . D. . 8 3 3 8 Lời giải Chọn B N H Ó M TOÁN VD – VD C
Gọi O là tâm hình bình hành ABCD và H SO A . P SO 3
Khi đó ta cũng có MN SO H. Tam giác SAC có H là trọng tâm nên . SH 2
Trong tam giác SBD có SB SD 2SO
SB SD SO SB SD SO .SM .SN 2. .SH 2. 3. SM SN SH SM SN SH SB SD Đặt x
3 x với x 1;2. SM SN
https:/www.facebook.com/groups/toanvd. Trang 51 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 V SM SP 1 V SP SN 1 Ta có S.AMP . và S.APN . . V SB SC 2x V SC SD 2 3 x S.ACD S .ABC 1 1 V 1 1 Khi đó V V và S.AMPN V V S .AMP S .ABCD S.APN S.ABCD N 4x 43 x V 4x 4 3 x S.ABCD H Ó 1 1 1 3 3 1 M .
4 x 3 x 4x3 x x 3 x 3 T 2 O 4. 4 Á N V 1 3 V Vậy
. Dấu bằng xảy ra x 3 x x . Khi đó MN / /B . D D V 3 2 –
Câu 7: Cho hình chóp S.ABCD có thể tích là V , ABCD là hình bình hành có tâm . O Gọi I là trung VD
điểm của SO,P là mặt phẳng qua I sao cho P cắt cạnh S , A S ,
B SC, SD lần lượt tại các điểm C M , N, , P .
Q Tìm giá trị nhỏ nhất của thể tích của khối chóp S.MNP . Q V V V V A. . B. . C. . D. . 4 2 12 8 Lời giải Chọn D N H Ó M TOÁN VD – V D C SA SB SC SD Đặt a ,b ,c , d SM SN SP SQ 1 V V V V;V V ,V V SABD SBCD 0 SMNQ 1 SNPQ 2 2 SO
Ta có kết quả a c b d 2 4 SI V V V V 0 0 . a . b d; . c b.d 0 0 .
b d a c 4b4 b 16 với 0 b 3 V V V V 1 2 1 2
https:/www.facebook.com/groups/toanvd. Trang 52 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 V V V V V 2V 2V Mặc khác: 0 0 0 0 2 . V V V V V V V V V 1 2 1 2 1 2 1 2 S .MNPQ 2V V V Do đó: 16 V
. Vậy giá trị nhỏ nhất của khối chóp S.MNPQ là . N S.MNPQ V 8 8 S.MNPQ H Ó M
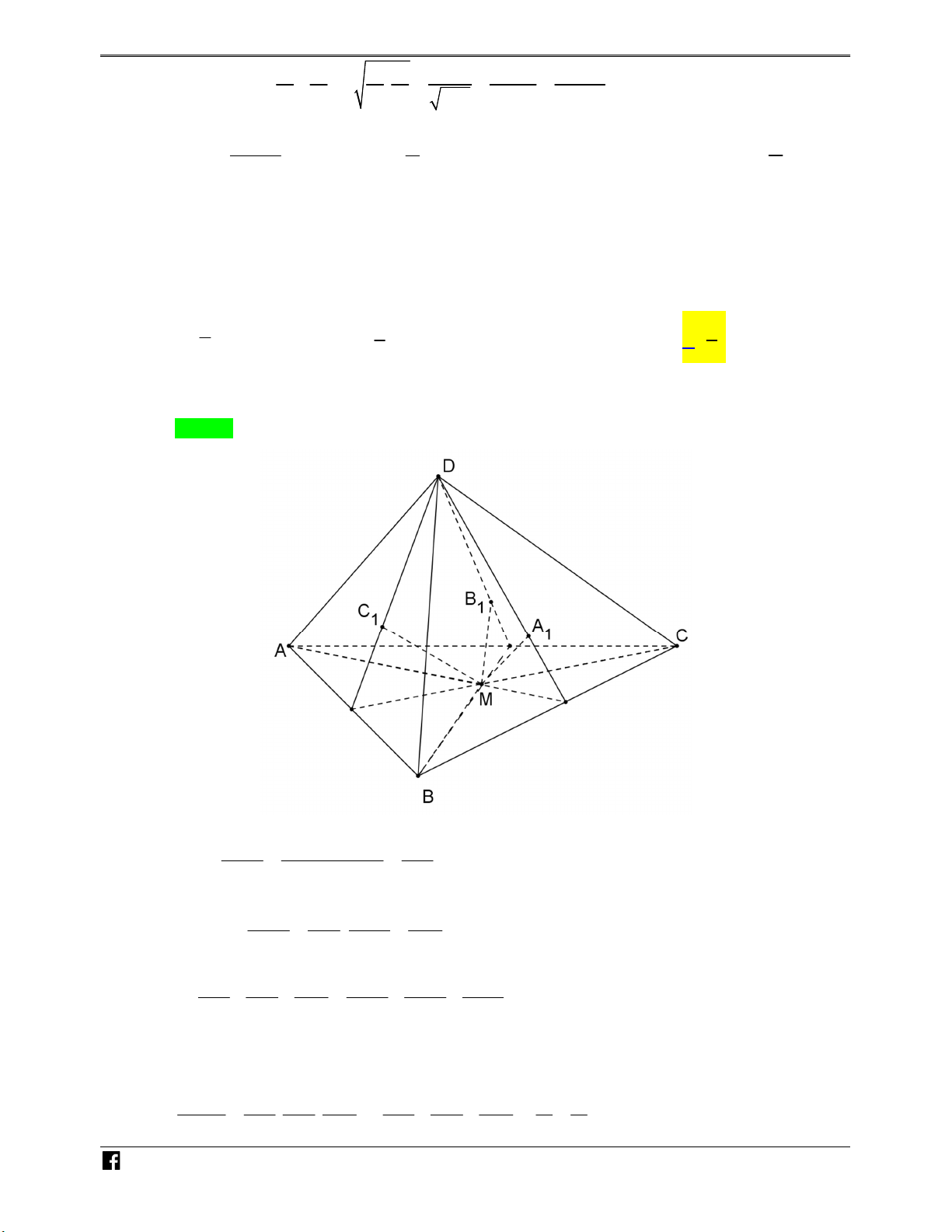
Câu 8: Cho tứ diện ABCD có D ,
A DB, DC đôi một vuông góc với nhau và có thể tích bằng 36 , M là T
điểm thay đổi trong tam giác ABC . Các đường thẳng qua M song song với D , A DB, DC theo O
thứ tự cắt các mặt phẳng BCD , CAD , ABD lần lượt tại A , B ,C . Tìm thể tích lớn nhất của Á 1 1 1 N
khối nhất của khối tứ diện MA B C khi M thay đổi. 1 1 1 VD 1 2 4 A. . B. . C. 1. D. . – 3 3 3 VD Lời giải C Chọn D N H Ó M TOÁN VD – VD V d M BCD MA MBCD , Ta có C V d A BCD AD ABCD , 1 V MB V MC Tương tự MADC 1 MABD 1 , V AD V AD ABCD ABCD MA MB MC V V V 1 1 1 MBCD MADC MABD 1 AD AD AD V V V ABCD ABCD ABCD Do D ,
A DB, DC đôi một vuông suy ra MA , MB , MC đôi một vuông. Như vậy: 1 1 1 3 VMA BC MA MB MC MA MB MC 1 1 1 1 1 1 1 1 1 1 1 . . . 3 3 V AD AD AD AD AD AD 3 3 ABCD
https:/www.facebook.com/groups/toanvd. Trang 53 NHÓM TOÁN VD–VDC NĂM HỌC 2019 – 2020 VMA B C 1 V 36 4 1 1 1 ABCD V 3 M 1 A 1 B 1 C 3 3 V 3 3 3 3 ABCD
Dấu " " xảy ra khi M là trọng tâm tam giác ABC . N H 4
Vậy thể tích lớn nhất của khối nhất của khối tứ diện MA B C bằng khi M là trọng tâm tam Ó 1 1 1 3 M giác ABC . TO Á N VD – VD C N H Ó M TOÁN VD – VDC
https:/www.facebook.com/groups/toanvd. Trang 54




