22 trang 48 lượt tải

Thiết kế sàn sườn toàn khối có bản loại dầm | Báo cáo bài tập lớn số 1 môn Kết cấu bê tông Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

95

1.3. Xác định nội lực. Để tìm nội lực lớn nhất trong dầm chính, cần xét nhiều trường hợp đặt hoạt tải khác nhau. Do dầm chính là dầm 3 nhịp, đối xứng nên moment lớn nhất tại gối C cũng chính là moment tại gối B. 1.3.1. Xác định biểu đồ bao momen cho từng trường hợp tải: Tung độ của biểu đồ momen tại tiết diện bất kì của từng trường hợp tải trọng được xác định theo công thức: Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

Môn: kết cấu bê tông & bê tông cốt thép 3 tài liệu

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh 3.1 K tài liệu

Tác giả:

Profile

Lê Kim Dung

6 tháng trước
Danh sách Quiz
/22
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT THÀNH PHỐ HỒ CHÍ MINH
KHOA XÂY DỰNG

BÁO CÁO BÀI TẬP LỚN SỐ 1
KẾT CẤU CÔNG TRÌNH BTCT
THIẾT KẾ SÀN SƯỜN TOÀN KHỐI CÓ BẢN LOẠI DẦM
GVHD : NGÔ VIỆT DŨNG
NHÓM : 12
THÀNH VIÊN:
1. Phan Hoàng Phúc-22149145
2. Phạm Thái Toàn-22149185
TP. Hồ Chí Minh, tháng 10 năm 2024
SƠ ĐỒ I, B15 , L1= 2,4 (m) , L2 = 6,3 (m) , PTC = 9 ( Kn/m2) ,
CB240T – Rs = 210 MPA , ES = 2*10^5 (N/m2) , Hs = 12cm , Rs
= 260 MPA ( CB300V)
Bài làm
1.1. Sơ đồ tính
- Kích thước dầm phụ:
b
dp
=250(mm ;h mm)
dp
=500 ( )
- Kích thước dầm chính:
b
dc
=350 (mm mm); h
dc
=700( )
- Kích thước cột :
b
c
=300(mm ;h mm)
c
=300( )
Hình 1.1. Sơ đồ tính dầm chính
+ Đối với nhịp biên:
L
ob
= 3L -
1
b
c
2
= 3 x 2400 -
300
2
= 7050 (mm)
+ Đối với nhịp giữa:
L
o
= 3L = 3 x 2400 = 7200 (mm)
1
Chênh lệch giữa nhịp biên và nhịp giữa không quá 10 % nên
xem là dầm đều nhịp
1.2. Xác định tải trọng
Hình 1.2. phần diện tích tính trọng lượng bản thân
do dầm chính
1.2.1. Tĩnh tải :
+ Tĩnh tải của sàn:
g
S
tt
=∑ n
i
x γi x δ
i
¿
g
S
tt
= 0.02×18×1.1 + 0.02×20×1.2 + 0.12×25×1.1 +
0.015×20×1.2
= 4.536 (kN/m )
2
+ Tĩnh tải từ sàn truyền vào:
L
1
=4.536×2.4 = 10.886 (kN/m)
+Trọng lượng bản thân dầm phụ:
g
0
=b (h )n
dp dp
- h
s g
γ
bt
= 0.25×(0.5 – 0.12) ×1.1×25 = 2.6125
(kN/m)
+ Tổng tĩnh tải dầm phụ:
g
dp
=
g
1
+
g
0
= 10.886 + 2.6125 = 13.4989 (kN/m)
- Trọng lượng bản thân dầm phụ truyền xuống dầm chính:
G =
1
g
dp
L
2
= 13.4989×6.3 = 85.043(kN)
- Trọng lượng bản thân dầm chính
G (h (h
o
= 1.1 b
dc dc
- h ) γ - 1.1b
s bt
L
1 dp dp
- h ) γ
s bt
b
dc
G
0
=1.1 × 0.35×
(
0.7 0.12−
)
× 25× 2.5−1.1 ×0.25 ×
(
0.5 0.12−
)
×25 × 0.35
=
13.0418 (kN)
G
0
=¿
13.0418 (kN)
- Tổng tĩnh tải tính toán
G=
G
1
+
G
0
= 85.043 +13.0418 =98.0848(kN)
1.2.2. Hoạt tải :
- Hoạt tải tính toán sàn: Ps = n
×
p
tc
= 1.2
×
9= 10.8 (Kn/m )
2
Trong đó: n là hệ số tin cậy của hoạt tải lấy theo TCVN
2737-1995
P
tc
là tải trọng tình toán lấy theo đề bài
- Hoạt tải tác dụng lên dầm phụ:
P
dp
= Ps × L1 = 10.8x2.4 =
25.92 (Kn/m)
- Hoạt tải của dầm chính (từ sàn và dầm phụ truyền vào)
P= p
dp
× L
2
=25.92× 6.3 163.296= (kN )
1.3. Xác định nội lực
Để tìm nội lực lớn nhất trong dầm chính, cần xét nhiều trường
hợp đặt hoạt tải khác nhau. Do dầm chính là dầm 3 nhịp, đối
xứng nên moment lớn nhất tại gối C cũng chính là moment tại
gối B
a) M (G):
b) M (P1):
c) M (P2):
d) M (P3):
e) M (P4):
f) M (P5):
g) M (P6):
Hình 1.3. Các trường hợp dặt tải cho dầm chính
1.3.1. Xác định biểu đồ bao momen cho từng trường hợp
tải:
Tung độ của biểu đồ momen tại tiết diện bất kì của từng trường
hợp tải trọng được xác định theo công thức:
M
G
¿
α
.GL =
α
× 98.0848 × 7.2 = 706.21
α
(kN.m)
M
Pi
¿
α
.PL =
α
× 163.296×7.2 = 1175.7312
α
(kN.m)
Sơ Đồ D
Nhịp dầm AB
M
max
=
P xL
3
=
163.296 7.2×
3
Xét tam giác đồng
dạng tại tiết diện 1:
X
391.91
=
L/3
L
x=
391.91
3
M
1
=
M
max
- X =
163.296 7.2×
3
-
391.91
3
=261.2737(Kn.m)
Xét tam giác đồng dạng tại tiết diện 2:
X
391.91
=
2 L/3
L
=> x=
2× 391.91
3
M
2
=
M
max
– X =
163.296 7.2×
3
-
2× 391.91
3
= 130.637 (Kn.m)
Nhịp dầm BC
M
max
=
P xL
3
=
163.296 7.2×
3
Xét tam giác đồng
dạng tại tiết diện 3:
X
391.91 104.64−
=
2 L/3
L
x=
2×(391.91−104.64 )
3
M
3
=
M
max
–X–
104.64
=
163.296 7.2×
3
-
2×(391.91−104.64 )
3
-
104.64
= 95.757 (Kn.m)
Xét tam giác đồng dạng tại tiết diện 4:
X
391.91 104.64−
=
L/3
L
=> x=
(391.91−104.64 )
3
M
4
=
M
max
–X–
107,234
=
163.296 7.2×
3
-
(391.91−104.64 )
3
-
104.64
= 191.513 (Kn.m)
Nhịp dầm CD
Xét tam giác đồng dạng tại tiết diện 5:
X
104.64
=
2 L/3
L
=> x=
2× 104.64
3
M
5
=
2× 104.64
3
= 69.76(Kn.m)
Xét tam giác đồng dạng tại tiết diện 6:
X
104.64
=
L/3
L
=> x=
104.64
3
=
M
6
=
104.64
3
= 34.88 (Kn.m)
Sơ Đồ E
Nhịp dầm AB
Xét tam giác đồng dạng tại tiết diện 1:
X
51.732
=
L/3
L
=> x=
51.732
3
M
1
=
51.732
3
= 17.244 (Kn.m)
Xét tam giác đồng dạng tại tiết diện 2:
X
51.732
=
2 L/3
L
=> x=
51.732
3
=> x=
2× 51.732
3
M
2
=
2× 51.732
3
= 34.488(Kn.m)
Nhịp dầm BC
Xét tam giác đồng dạng tại tiết diện 3:
X+51.732
51.732+209. 28
=
L/3
L
M
3
=
(51. 732+209.28 )
3
- 51.732 = 35.272(Kn.m)
M
3
= -35.272 (Kn.m)
Xét tam giác đồng dạng tại tiết diện 4:
X+51.732
51.732+209. 28
=
2 L/3
L
M
4
=
2×(51. 732+209.28)
3
– 51.732 = 122.276 (Kn.m)
Nhịp dầm CD
M
max
=
P xL
3
=
163.296 7.2×
3
Xét tam giác đồng dạng tại tiết diện 5:
X
214.468
=
2 L/3
L
=> x=
2× 209.28
3
M
5
=
M
max
– X =
163.296 7.2×
3
-
2× 209.28
3
= 252.39 (Kn.m)
Xét tam giác đồng dạng tại tiết diện 6:
X
209.28
=
L/3
L
=> x=
209.28
3
M
6
=
M
max
– X
163.296 7.2×
3
-
209.28
3
= 322.15 (Kn.m)
Bảng 1 Bảng tính tung độ biểu đồ moment cho
từng trường hợp tải trọng
Đoạn
sơ đồ
1 2 Gối B 3 4
Gối
C
5 6
A
α
0.24
4
0.15
6
-
0.26
7
0.06
7
0.06
7
-
0.2
67
0.15
6
0.24
4
M
G
172.
941
110.
569
-
189.
24
47.4
879
47.4
879
-
189.
24
110.
569
172.
941
B
α
0.28
9
0.24
4
-
0.13
3
-
0.13
3
-
0.13
3
-
0.1
33
0.24
4
0.28
9
MP
1
339.
786
286.
878
-
156.
37
-
156.
37
-
156.
37
-
156.
37
286.
878
339.
786
C
α
-
0.04
4
-
0.08
9
-
0.13
3
0.2 0.2
-
0.1
33
-
0.08
9
-
0.04
4
MP
2
-
51.7
32
-
104.
64
-
156.
37
235.
146
235.
146
-
156.
37
-
104.
64
-
51.7
32
D
α
- -
-
0.31
1
- -
-
0.0
89
- -
MP
3
o o
-
365.
65
o o
-
104.
64
o o
E
α - -
0.04
4
- -
-
0.1
78
- -
MP o o 51.7 o o - o o
4 322
209.
28
Hình 1.4. Biểu đồ moment cho các trường hợp tổ hợp
tải trọng
Tiết diện 1 2
Gối
B
3 4
Gối
C
5 6
M1=M(G)
+M(P1)
512
.73
397.
447
-
345
.62
-
108.8
843
-
108.
88
-
345
.62
397.
447
512.
727
M2=M(G)
+M(P2)
121
.21
5.92
885
-
345
.62
282.6
3418
282.
634
-
345
.62
5.92
885
121.
209
M3=M(G)
+M(P3)
434
.21
241.
206
-
554
.89
143 239
-
398
.52
40.8
09
138.
061
M4=M(G)
+M(P4)
190
.19
145.
057
-
137
.51
12.21
5
-
74.7
89
-
398
.52
362.
959
495.
091
M5=M(G)
+M(P5)
138
.06
40.8
09
-
262
.47
239
143.
244
-
518
.35
241.
206
434.
214
M6=M(G)
+M(P6)
495
.09
362.
96
-
365
.05
-
74.78
9
12.2
15
-
109
.18
145.
017
155.
717
Mmax
512
.73
397.
447
-
554
.89
282.6
3418
282.
634
-
109
.18
397.
447
512.
727
Mmin
121
.21
5.92
885
-
137
.51
-
108.8
843
-
108.
88
-
518
.35
5.92
885
121.
209
Bảng 1 . Bảng tính tung độ biểu đồ bao moment
Hình 1.5. Biểu đồ bao moment
-TÍNH CỐT THÉP
-Tiết diện ở nhịp với giá trị moment dương, bản cánh chịu
lực nén, tiết diện tính toán là tiết chữ T
Xác định S
f
S
f
≤
{
1
2
(
l
1
-
b
dp
),
1
6
(l
¿
¿ 2−b
dc
)¿
,6
h
s
}
S
f
≤
{1075, 1008.3 ,720}
→
Chọn
S
f
=720 (mm)
Chiều rộng bản cánh
b
f
=
b
dc
+ 2
S
f
=¿
350 +2
×
720=1790 (mm)
- Với moment dương ta có kích thước tiết diện chữ T:
b
f
'
=1790(mm);
h
f
'
=120(mm);b=350(mm);
b
dc
=350(mm);h
dc
=750(mm);
h
0
=750-50=700(mm)
M
f
'
=
γ
b
× R
b
×b
f
'
×
(
h
0
-
h
f
'
2
)=1
×
8.5
×
10
3
×
1.79
×
0.12
×
(0.7-
0.5
2
)=1168.512(kN.m)> M
-Trục trung hòa qua cánh, tính cốt thép theo tiết diện
hình chữ nhật
b
f
'
x
h
dc
❑
=(1790x700)mm
-Tiết diện tại gối
Tương ứng với moment âm, cốt thép tính toán với tiết diện HCN
nhỏ bxh với b=350(mm); h=750(mm)
Giả thiết: a gối= 70mm; h0=h-a gối=750-70=680(mm)
Do tính theo sơ đồ đàn hồi nén điều kiện hạn chế
α
m
<
α
R
=0.583
α
m
=
M
Rb . b
dc
.h 0
2
=> ξ=1-
√
1−2 α
m
=
A
st
=
ξx R
b
x b
f
'
x h
0
R
s
µ
max
=
ξ
r
x R
b
x γ
b
R
s
Kết quả cốt thép được tính như sau
-Moment mép gối
X +241.206
241.206
+554.89
=
2400 150−
2400
=>x=M =505.134(kN.m)
T
mg
X+143
143
+554.89
=
2400 150−
2400
=>x=M =511.271(kN.m)
P
mg
Tiết diện M(kN.m)
α
m
ξ
Ast(m
m
2
)
Chọn cốt thép
µ
Chọn
As(mm
2)
Nhịp
biên
512.73 0.351 0.454
4502.1
6
4d25+4
d30
4790.9
28
1.837
Gối 2 511.271 0.35 0.452 4482.3
4d25+4
d30
4790.9
28
1.829
Nhịp
giữa
282.634 0.193 0.216 2142 4d28
2463,0
08
0.874
Tiết
diện
Cắt Cốt
Thép
As(mm
2
)
Att(m
m)
Hott(m
m)
ξ
α
m
[M](K
DENT
A
Nhịp
biên
4d25+4d30
4790.9
28 65 685 0.493 0.371
540.8
25
5.479
cắt 2d30
còn
4d25+2d30
3377.2
12 65 685 0.348 0.287
419.0
27
Cắt 2d30
còn 4d25
1963.4
95 37.5 712.5 0.194 0.175 255.1
cắt 2d25
còn 2d25
981.74
7 37.5 712.5 0.0972 0.092
134.1
13
Gối 2
4d25+4d30
4790.9
28 65 685 0.493 0.371
540.8
25
5.78
Cắt 2d30
còn
4d25+2d30
3377.2
12 65 685 0.348 0.287
419.0
27
Cắt 2d30
còn 4d25
1963.4
95 37.5 712.5 0.194 0.175 255.1
Cắt 2d25
còn 2d25
981.74
7 37.5 712.5 0.0972 0.092
134.1
13
Nhịp
giữa
4d28
2463.0
08 42 708 0.245 0.214
311.9
58
10.37
5Cắt 2d28
còn 2d28 1231.5 42 708 0.1227 0.115
167.6
4
Xác định vị trí cắt lý thuyết : e=3.4
Cắt 2d30:
255.1
512.73
=
x
2400
=>x=1194.078(mm)
Cắt 2d25:
134 .113
512.73
=
x
2400
=>x=627.759(mm)
Nhịp gối 2
Gối 2 bên trái
Cắt 2d25:
255.1
511.271
=
x
2400
=>x=1197.486(mm)
Cắt 2d25:
134 .113
511. 271
=
x
2400
=>x=629.551(mm)
Cắt 2d25:
167.0896 10.87+
362.285
+10.87
=
x
2500
=>x=1191.9438(mm)
-Gối 2 bên phải
Cắt 2d28:
166.793 490.83+
166.793
+576.853
=
x
2500
=>x=2210.8066(mm)
Cắt 2d28:
166.793 376.599+
166.793
+576.853
=
x
2500
=>x=826.7905(mm)

Tài liệu khác của Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Preview text:

BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT THÀNH PHỐ HỒ CHÍ MINH KHOA XÂY DỰNG 
BÁO CÁO BÀI TẬP LỚN SỐ 1
KẾT CẤU CÔNG TRÌNH BTCT
THIẾT KẾ SÀN SƯỜN TOÀN KHỐI CÓ BẢN LOẠI DẦM
GVHD : NGÔ VIỆT DŨNG NHÓM : 12 THÀNH VIÊN:
1. Phan Hoàng Phúc-22149145
2. Phạm Thái Toàn-22149185
TP. Hồ Chí Minh, tháng 10 năm 2024
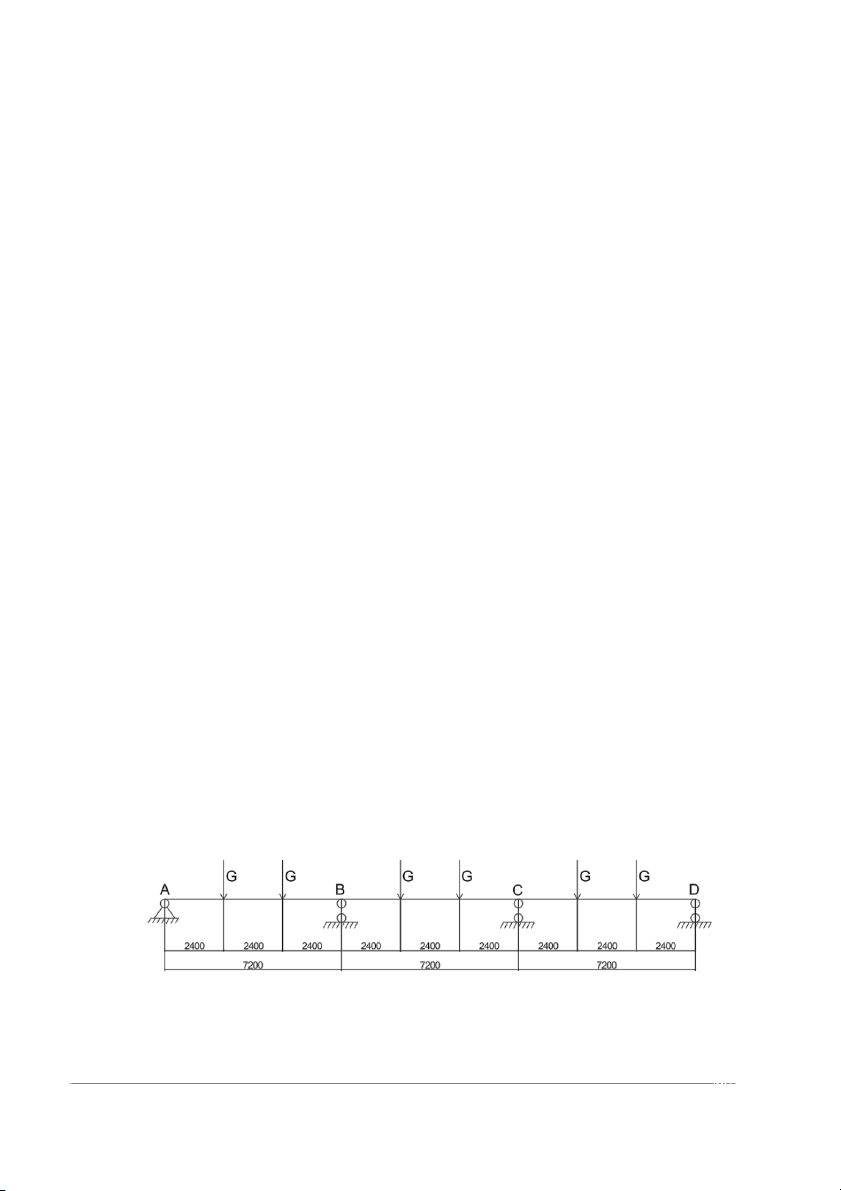
SƠ ĐỒ I, B15 , L1= 2,4 (m) , L2 = 6,3 (m) , PTC = 9 ( Kn/m2) ,
CB240T – Rs = 210 MPA , ES = 2*10^5 (N/m2) , Hs = 12cm , Rs = 260 MPA ( CB300V) Bài làm 1.1. Sơ đồ tính
- Kích thước dầm phụ: b =250(mm);h =500( ) dp mm dp
- Kích thước dầm chính: b =350(mm); h =700( ) dc mm dc
- Kích thước cột : b =300(mm);h =300( ) c mm c
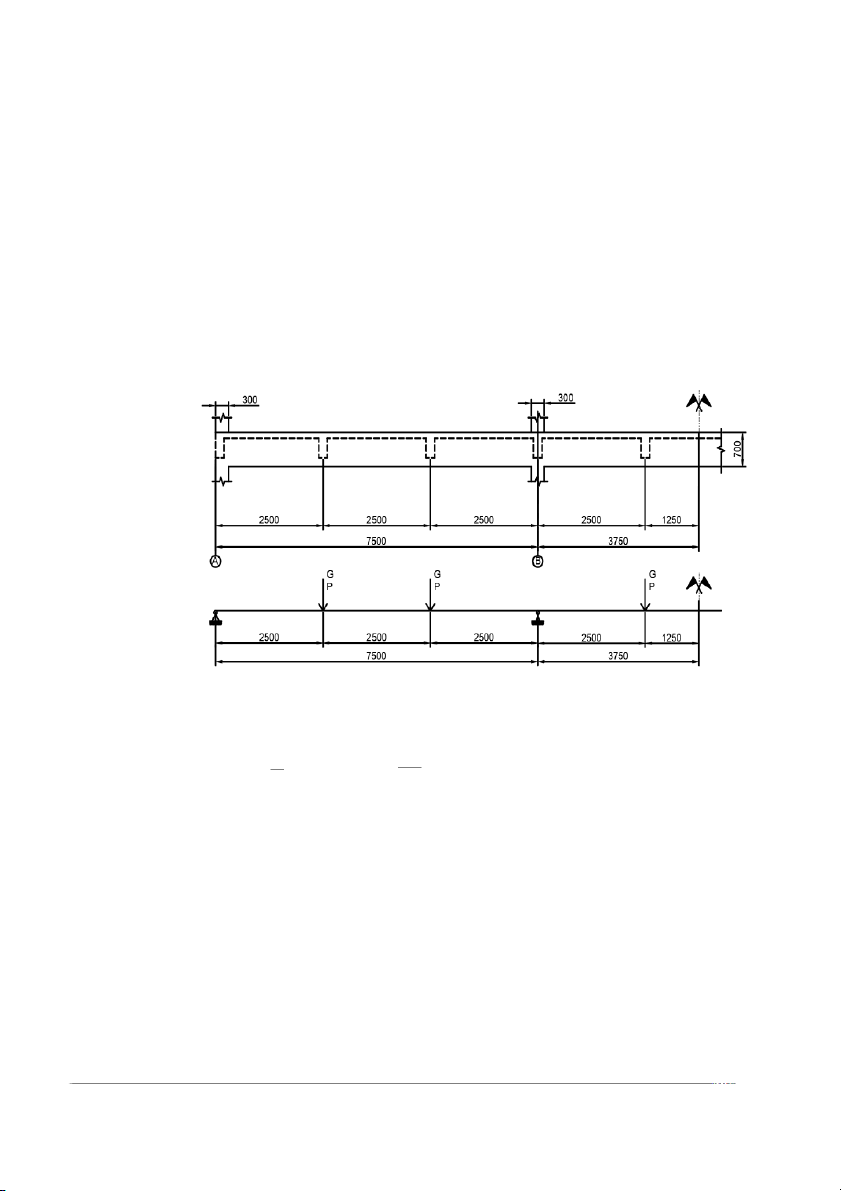
Hình 1.1. Sơ đồ tính dầm chính
+ Đối với nhịp biên: L bc ob = 3L1 - = 3 x 2400 -300 = 7050 (mm) 2 2 + Đối với nhịp giữa:
Lo = 3L1 = 3 x 2400 = 7200 (mm)
Chênh lệch giữa nhịp biên và nhịp giữa không quá 10 % nên xem là dầm đều nhịp
1.2. Xác định tải trọng
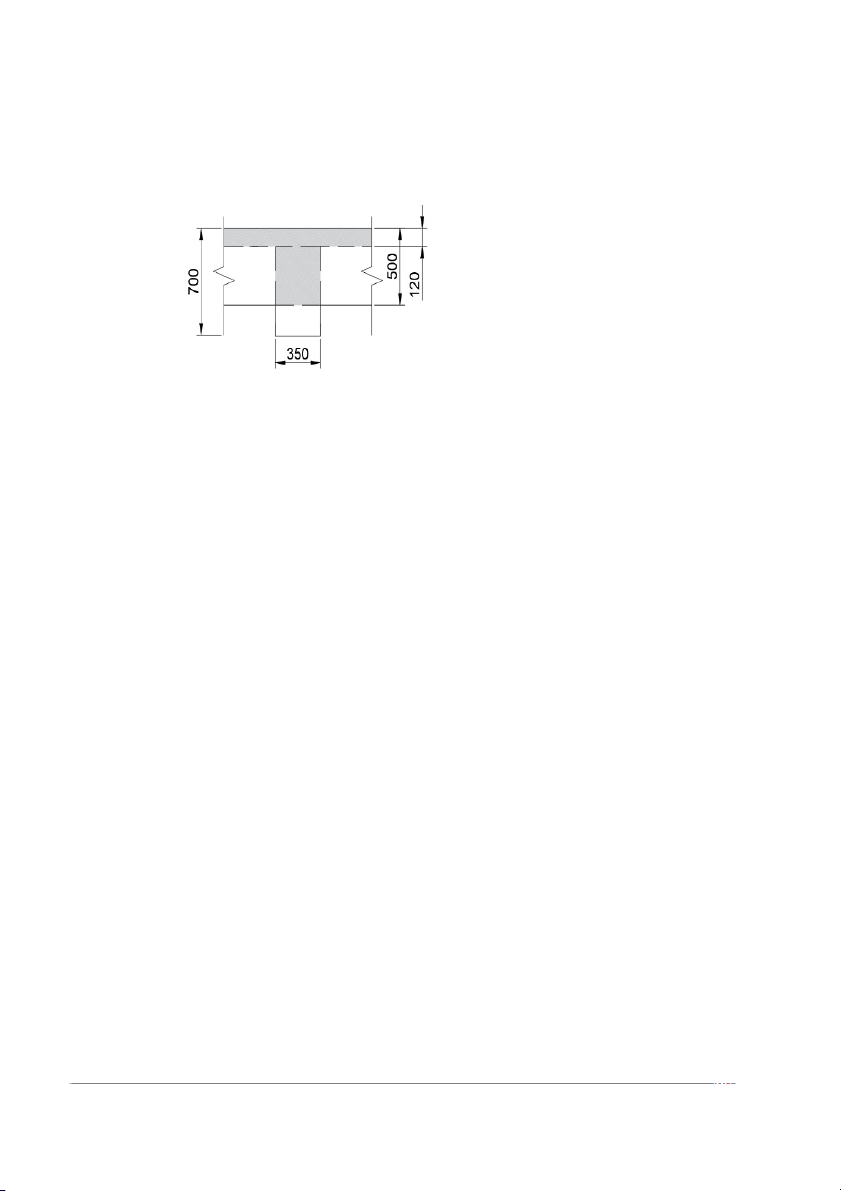
Hình 1.2. phần diện tích tính trọng lượng bản thân do dầm chính 1.2.1. Tĩnh tải : + Tĩnh tải của sàn: gtt = ¿ S ∑ n x γi x δ i i
g tt= 0.02×18×1.1 + 0.02×20×1.2 + 0.12×25×1.1 + S 0.015×20×1.2 = 4.536 (kN/m2)
+ Tĩnh tải từ sàn truyền vào: g =g L 1 s 1 =4.536×2.4 = 10.886 (kN/m)
+Trọng lượng bản thân dầm phụ: g =bdp(hdp - hs)n
= 0.25×(0.5 – 0.12) ×1.1×25 = 2.6125 0 gγbt (kN/m)
+ Tổng tĩnh tải dầm phụ:
g =g +g = 10.886 + 2.6125 = 13.4989 (kN/m) dp 1 0
- Trọng lượng bản thân dầm phụ truyền xuống dầm chính:
G1=g L = 13.4989×6.3 = 85.043(kN) dp 2
- Trọng lượng bản thân dầm chính
Go = 1.1 bdc (hdc - hs) γbt L1 - 1.1bdp (hdp - hs) γbt bdc
G =1.1 × 0.35× (0.7−0.12 )× 25× 2.5−1.1 ×0.25 × (0.5−0.12) ×25 × 0.35= 0 13.0418 (kN) G =¿ 13.0418 (kN) 0
- Tổng tĩnh tải tính toán
G=G +G = 85.043 +13.0418 =98.0848(kN) 1 0 1.2.2. Hoạt tải :
- Hoạt tải tính toán sàn: Ps = n×p 2
tc = 1.2× 9= 10.8 (Kn/m )
Trong đó: n là hệ số tin cậy của hoạt tải lấy theo TCVN 2737-1995
Ptc là tải trọng tình toán lấy theo đề bài
- Hoạt tải tác dụng lên dầm phụ: P = Ps × L1 = 10.8x2.4 = dp 25.92 (Kn/m)
- Hoạt tải của dầm chính (từ sàn và dầm phụ truyền vào)
P= p × L = 25.92× 6.3=163.296( kN ) dp 2
1.3. Xác định nội lực
Để tìm nội lực lớn nhất trong dầm chính, cần xét nhiều trường
hợp đặt hoạt tải khác nhau. Do dầm chính là dầm 3 nhịp, đối
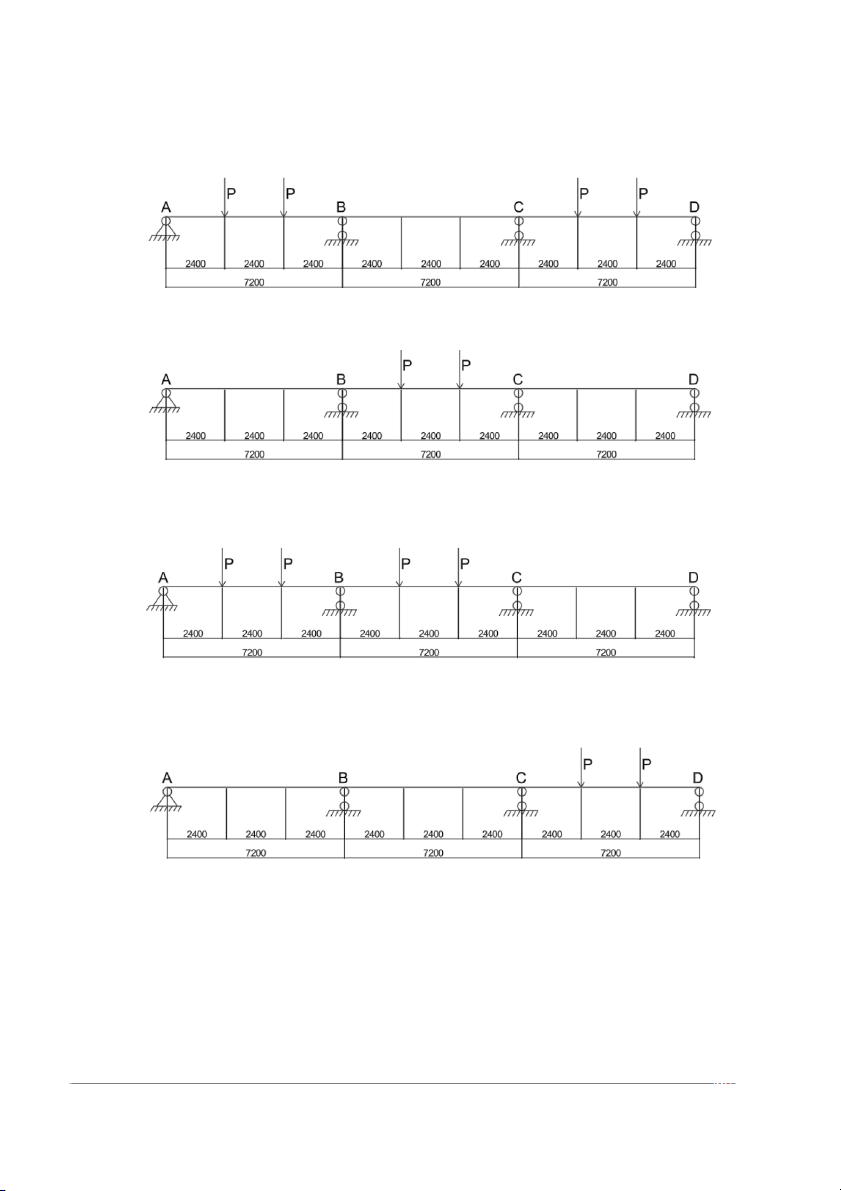
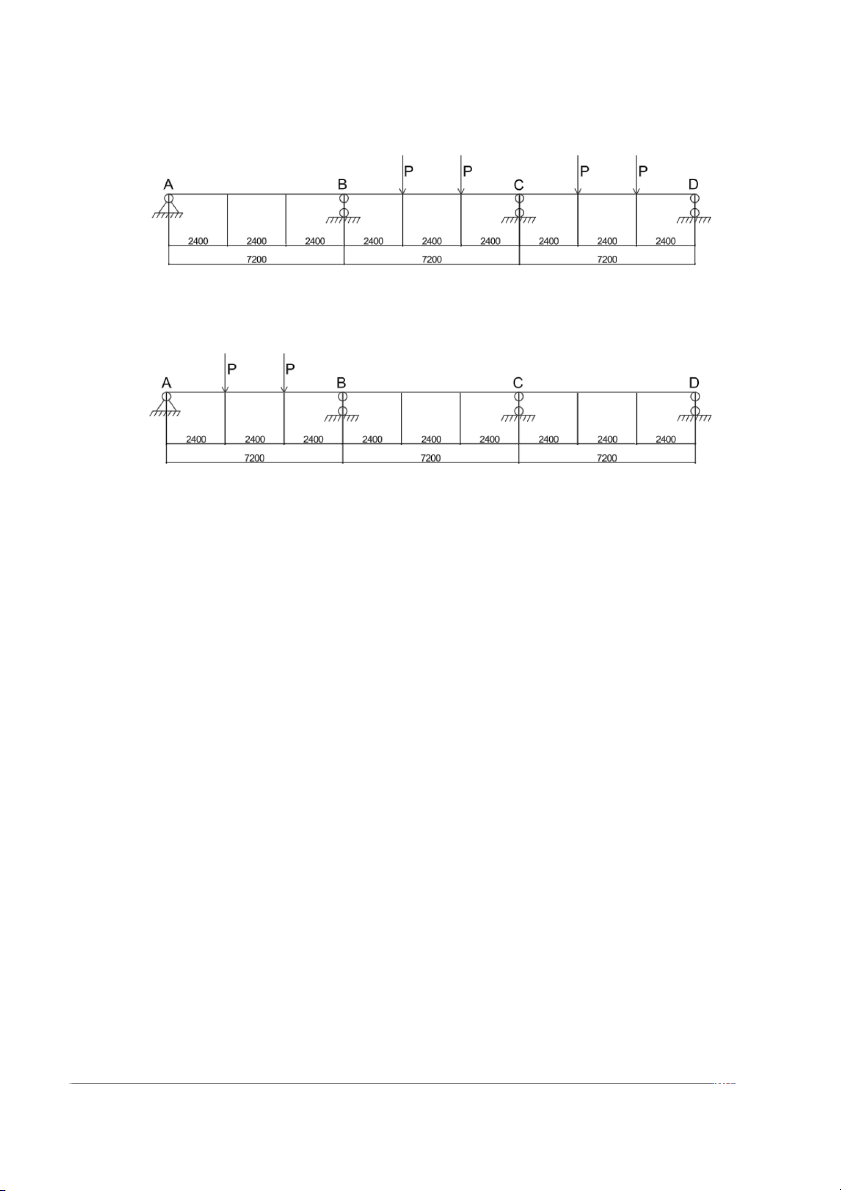
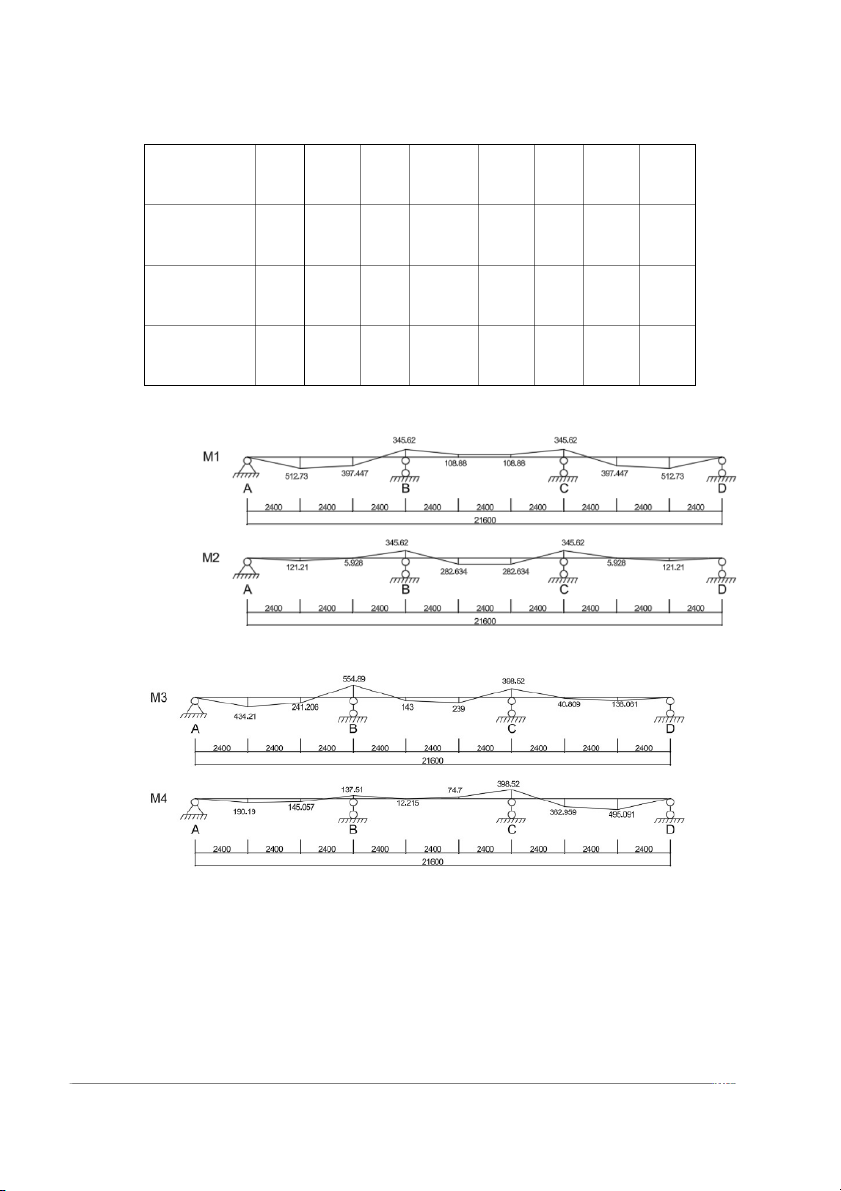
xứng nên moment lớn nhất tại gối C cũng chính là moment tại gối B a) M (G): b) M (P1): c) M (P2): d) M (P3): e) M (P4): f) M (P5): g) M (P6):
Hình 1.3. Các trường hợp dặt tải cho dầm chính
1.3.1. Xác định biểu đồ bao momen cho từng trường hợp tải:
Tung độ của biểu đồ momen tại tiết diện bất kì của từng trường
hợp tải trọng được xác định theo công thức:
MG ¿ α.GL = α × 98.0848 × 7.2 = 706.21 α (kN.m)
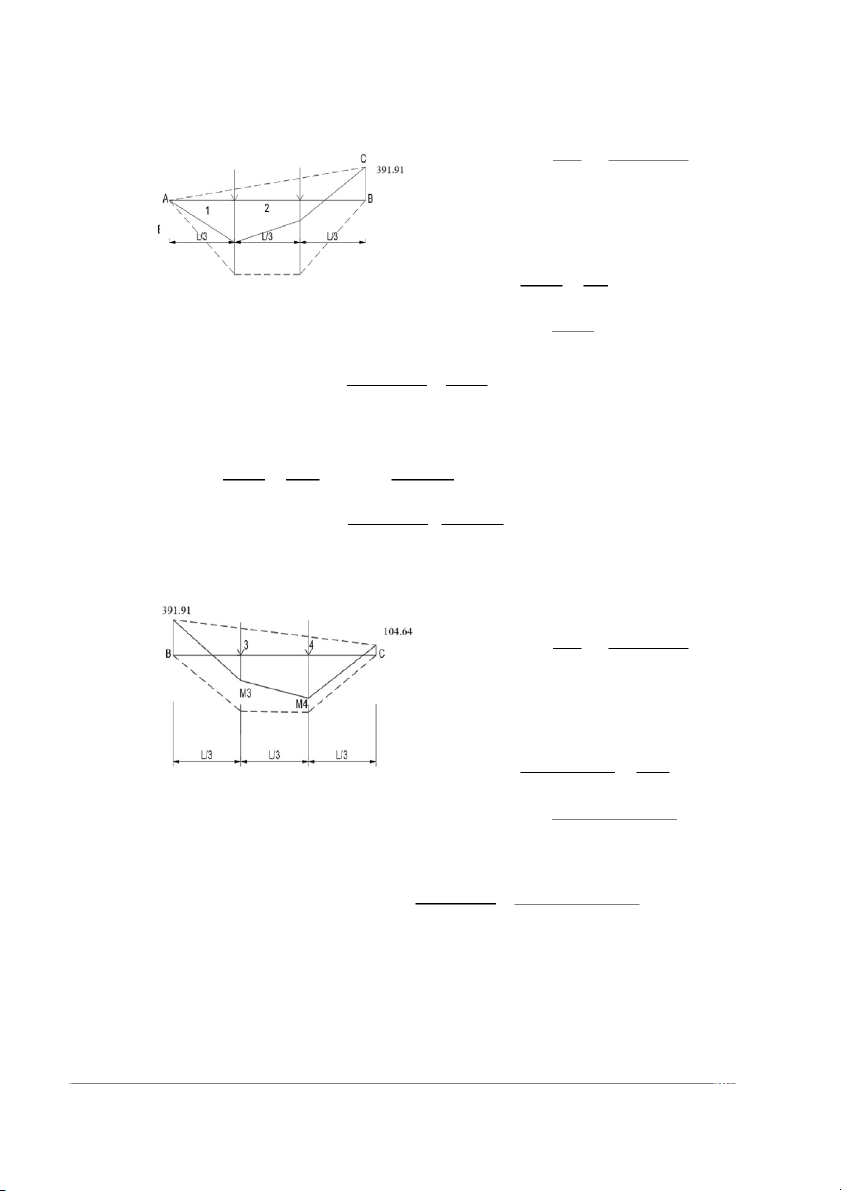
MPi ¿ α .PL = α × 163.296×7.2 = 1175.7312 α (kN.m) Sơ Đồ D × M = P xL = 163.296 7.2 max 3 3 Xét tam giác đồng dạng tại tiết diện 1:  X = L/3 391.91 L Nhịp dầm AB  x= 391.91 3 × M = M
- X = 163.296 7.2 - 391.91 =261.2737(Kn.m) 1 max 3 3
Xét tam giác đồng dạng tại tiết diện 2: X
= 2L/3 => x= 2×391.91 391.91 L 3 × M = M
– X = 163.296 7.2- 2×391.91= 130.637 (Kn.m) 2 max 3 3 × M = P xL = 163.296 7.2 max 3 3 Xét tam giác đồng dạng tại tiết diện 3: X = 2L/3 391.91−104.64 L Nhịp dầm BC
 x= 2×(391.91−104.64 ) 3 × M = M
–X–104.64 = 163.296 7.2 - 2×(391.91−104.64)- 104.64 3 max 3 3 = 95.757 (Kn.m)
Xét tam giác đồng dạng tại tiết diện 4:  X
= L/3 => x= (391.91−104.64) 391.91−104.64 L 3 × M = M –X– - (391.91−104.64)- 4 max 107,234 = 163.296 7.2 104.64 3 3 = 191.513 (Kn.m) Nhịp dầm CD
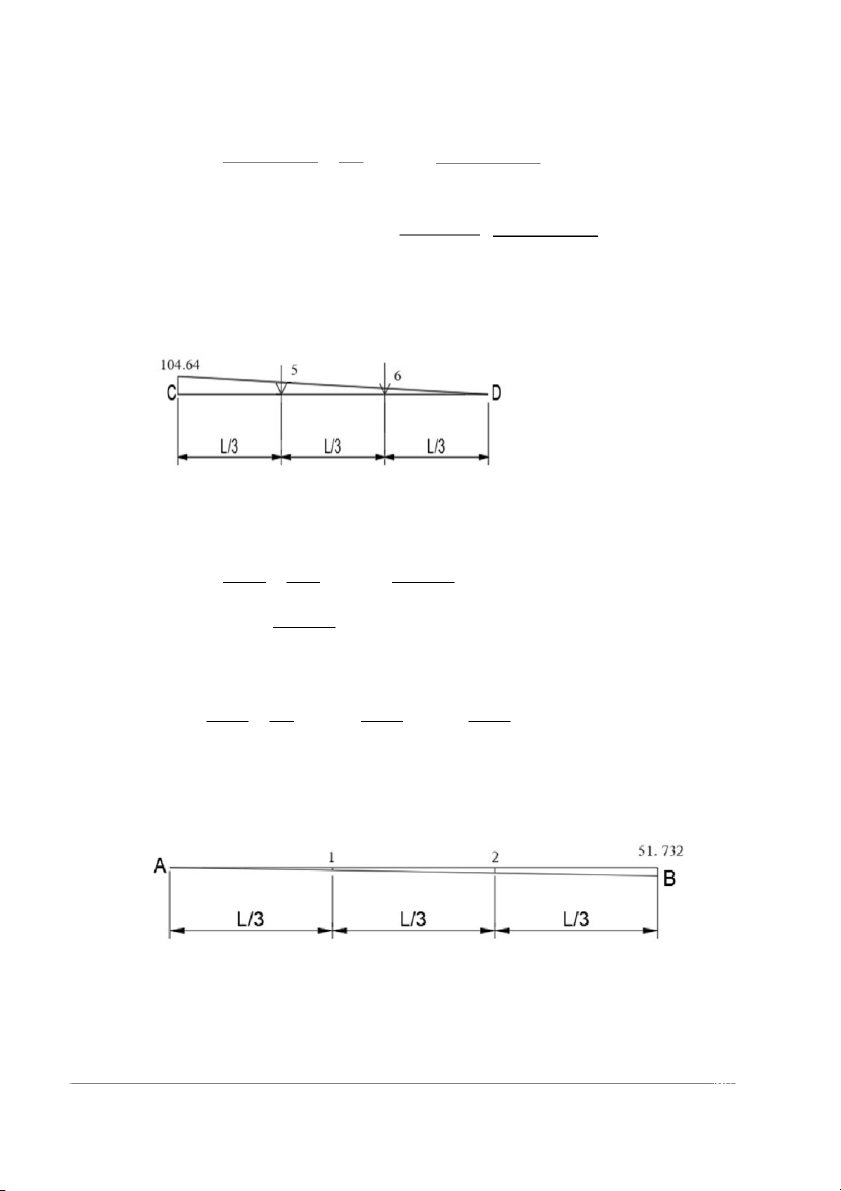
Xét tam giác đồng dạng tại tiết diện 5: X
= 2L/3 => x= 2×104.64 104.64 L 3
M = 2× 104.64 = 69.76(Kn.m) 5 3
Xét tam giác đồng dạng tại tiết diện 6: X
= L/3 => x= 104.64=M = 104.64 = 34.88 (Kn.m) 104.64 L 3 6 3 Sơ Đồ E Nhịp dầm AB
Xét tam giác đồng dạng tại tiết diện 1: X = L/3 => x= 51.732 51.732 L 3
M = 51.732 = 17.244 (Kn.m) 1 3
Xét tam giác đồng dạng tại tiết diện 2: X
= 2L/3 => x= 51.732 => x= 2×51.732 51.732 L 3 3
M = 2× 51.732= 34.488(Kn.m) 2 3 Nhịp dầm BC
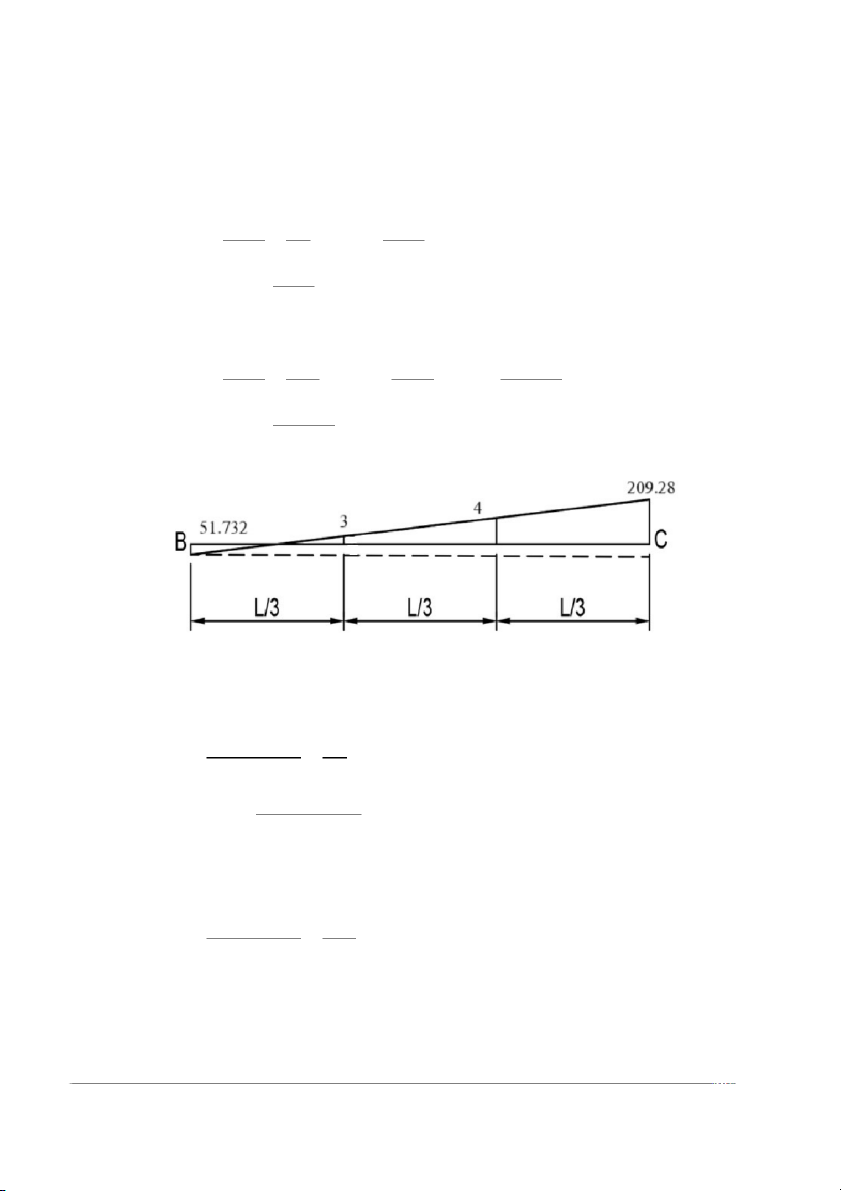
Xét tam giác đồng dạng tại tiết diện 3: X+ 51.732 = L/3 51.732+209. 28 L
M = (51. 732+ 209.28) - 51.732 = 35.272(Kn.m) 3 3  M = -35.272 (Kn.m) 3
Xét tam giác đồng dạng tại tiết diện 4: X+ 51.732 = 2L/3 51.732+209. 28 L
M = 2×(51. 732+ 209.28) – 51.732 = 122.276 (Kn.m) 4 3 Nhịp dầm CD × M = P xL = 163.296 7.2 max 3 3
Xét tam giác đồng dạng tại tiết diện 5: X
= 2L/3 => x= 2×209.28 214.468 L 3 × M = M
– X = 163.296 7.2 - 2×209.28= 252.39 (Kn.m) 5 max 3 3
Xét tam giác đồng dạng tại tiết diện 6: X = L/3 => x= 209.28 209.28 L 3 × M = M
– X 163.296 7.2 - 209.28= 322.15 (Kn.m) 6 max 3 3
Bảng 1 Bảng tính tung độ biểu đồ moment cho
từng trường hợp tải trọng Đoạn sơ đồ 1 2 Gối B 3 4 Gối C 5 6 - - α 0.24 0.15 0.06 0.06 0.15 0.24 4 6 0.26 7 7 0.2 6 4 A 7 67 - - M 172. 110. 47.4 47.4 110. 172. G 941 569 189. 189. 24 879 879 24 569 941 - - - - α 0.28 0.24 0.24 0.28 9 4 0.13 0.13 0.13 0.1 4 9 B 3 3 3 33 MP 339. 286. - - - - 286. 339. 1 786 878 156. 156. 156. 156. 37 37 37 37 878 786 - - - - - - α 0.04 0.08 0.13 0.2 0.2 0.1 0.08 0.04 C 4 9 3 33 9 4 - - - - - - MP 235. 235. 2 51.7 104. 156. 156. 104. 51.7 32 64 37 146 146 37 64 32 - - α - - 0.31 - - 0.0 - - 1 89 D MP - - o o 3 o o 365. 104. o o 65 64 E - α - - 0.04 4 - - 0.1 - - 78 MP o o 51.7 o o - o o 4 322 209. 28
Hình 1.4. Biểu đồ moment cho các trường hợp tổ hợp tải trọng Tiết diện 1 2 Gối B 3 4 Gối C 5 6 - - - - M1=M(G) 512 397. 397. 512. +M(P1) .73 447 345 108.8 108. 345 .62 843 88 .62 447 727 M2=M(G) 121 5.92 - 282.6 282. - 5.92 121. +M(P2) .21 885 345 345 .62 3418 634 .62 885 209 M3=M(G) 434 241. - - 40.8 138. +M(P3) .21 143 239 206 554 398 .89 09 .52 061 M4=M(G) 190 145. - 12.21 - - 362. 495. +M(P4) .19 057 137 74.7 398 .51 5 89 .52 959 091 M5=M(G) 138 40.8 - - 241. 434. +M(P5) .06 262 239 143. 518 09 .47 244 206 .35 214 - - - M6=M(G) 495 362. 12.2 145. 155. +M(P6) .09 96 365 74.78 109 .05 9 15 .18 017 717 - - Mmax 512 397. 282.6 282. 397. 512. .73 447 554 109 .89 3418 634 .18 447 727 - - - - Mmin 121 5.92 5.92 121. .21 885 137 108.8 108. 518 .51 843 88 .35 885 209
Bảng 1 . Bảng tính tung độ biểu đồ bao moment
Hình 1.5. Biểu đồ bao moment -TÍNH CỐT THÉP
-Tiết diện ở nhịp với giá trị moment dương, bản cánh chịu
lực nén, tiết diện tính toán là tiết chữ T Xác định Sf S
(l -b ), 1 (l )¿,6 h } f ≤ {1 ¿¿ 2−b 2 1 dp 6 dc s
Sf ≤{1075, 1008.3 ,720}
→Chọn S =720 (mm) f Chiều rộng bản cánh b + 2 S =¿350 +2 f=b dc f ×720=1790 (mm)
- Với moment dương ta có kích thước tiết diện chữ T:
b '=1790(mm);h' =120(mm);b=350(mm); f f
bdc=350(mm);hdc=750(mm); h =750-50=700(mm) 0 '
M' = γ × R ×b'
- hf )=1×8.5×103×1.79×0.12× (0.7- 0.5 f b b f ×(h0 2 2 )=1168.512(kN.m)> M
-Trục trung hòa qua cánh, tính cốt thép theo tiết diện hình chữ nhật ❑
b' xh =(1790x700)mm f dc -Tiết diện tại gối
Tương ứng với moment âm, cốt thép tính toán với tiết diện HCN
nhỏ bxh với b=350(mm); h=750(mm)
Giả thiết: a gối= 70mm; h0=h-a gối=750-70=680(mm)
Do tính theo sơ đồ đàn hồi nén điều kiện hạn chế α <α =0.583 m R α = M => ξ=1-√1−2α = m Rb . b .h 02 m dc x b' x h A = ξx Rb f 0 st Rs x R x γ µ = ξr b b max Rs
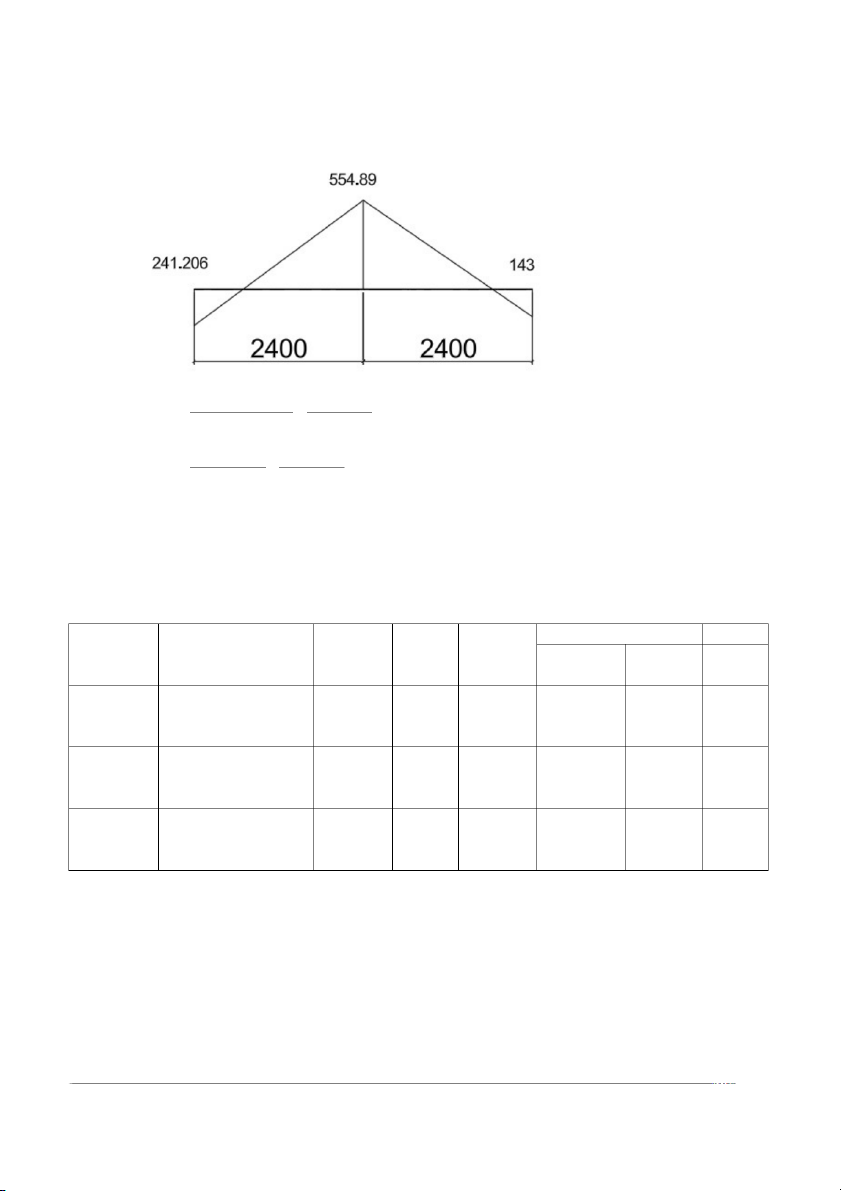
 Kết quả cốt thép được tính như sau -Moment mép gối X +241.206 −
= 2400 150 =>x=MTmg=505.134(kN.m) 241.206+ 554.89 2400 X+ 143 −
= 2400 150 =>x=MPmg=511.271(kN.m) 143+554.89 2400 Chọn cốt thép µ Tiết diện M(kN.m) Ast(m α As(mm m ξ m2) Chọn 2) Nhịp 4d25+4 4790.9 biên 512.73 0.351 0.454 4502.1 6 d30 28 1.837 Gối 2 511.271 0.35 0.452 4482.3 4d25+4 4790.9 d30 28 1.829 Nhịp giữa 282.634 0.193 0.216 2142 4d28 2463,0 08 0.874 Tiết Cắt Cốt As(mm Att(m Hott(m DENT diện Thép 2) m) m) ξ α [M](K A m 4790.9 540.8 4d25+4d30 28 65 685 0.493 0.371 25 cắt 2d30 còn 3377.2 419.0 Nhịp 4d25+2d30 12 65 685 0.348 0.287 27 biên 5.479 Cắt 2d30 1963.4 còn 4d25 95 37.5 712.5 0.194 0.175 255.1 cắt 2d25 981.74 134.1 còn 2d25 7 37.5 712.5 0.0972 0.092 13 4790.9 540.8 4d25+4d30 28 65 685 0.493 0.371 25 Cắt 2d30 còn 3377.2 419.0 Gối 2 4d25+2d30 12 65 685 0.348 0.287 27 5.78 Cắt 2d30 1963.4 còn 4d25 95 37.5 712.5 0.194 0.175 255.1 Cắt 2d25 981.74 134.1 còn 2d25 7 37.5 712.5 0.0972 0.092 13 2463.0 311.9 Nhịp 4d28 08 42 708 0.245 0.214 58 10.37 giữa Cắt 2d28 167.6 5 còn 2d28 1231.5 42 708 0.1227 0.115 4
Xác định vị trí cắt lý thuyết : e=3.4
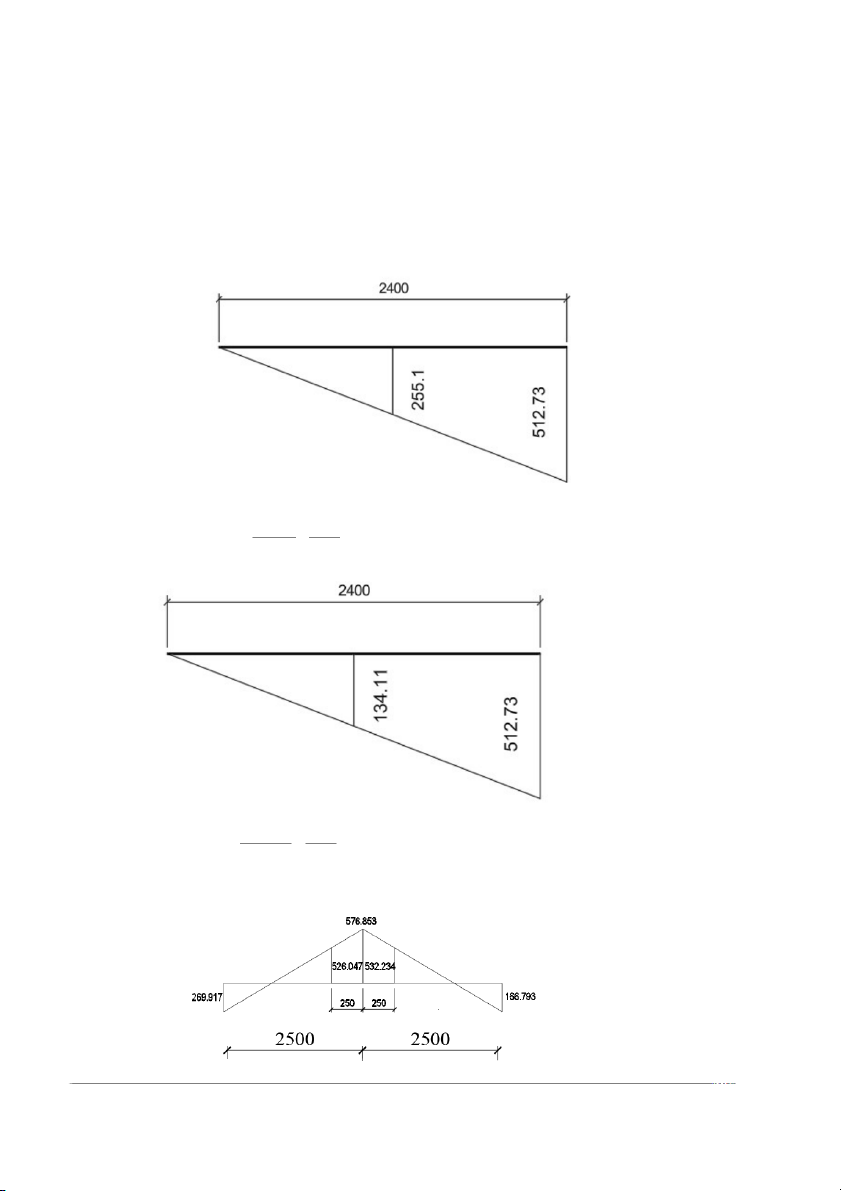
Cắt 2d30: 255.1 = x =>x=1194.078(mm) 512.73 2400
Cắt 2d25: 134.113= x =>x=627.759(mm) 512.73 2400 Nhịp gối 2 Gối 2 bên trái
Cắt 2d25: 255.1 = x =>x=1197.486(mm) 511.271 2400
Cắt 2d25: 134.113= x =>x=629.551(mm) 511. 271 2400
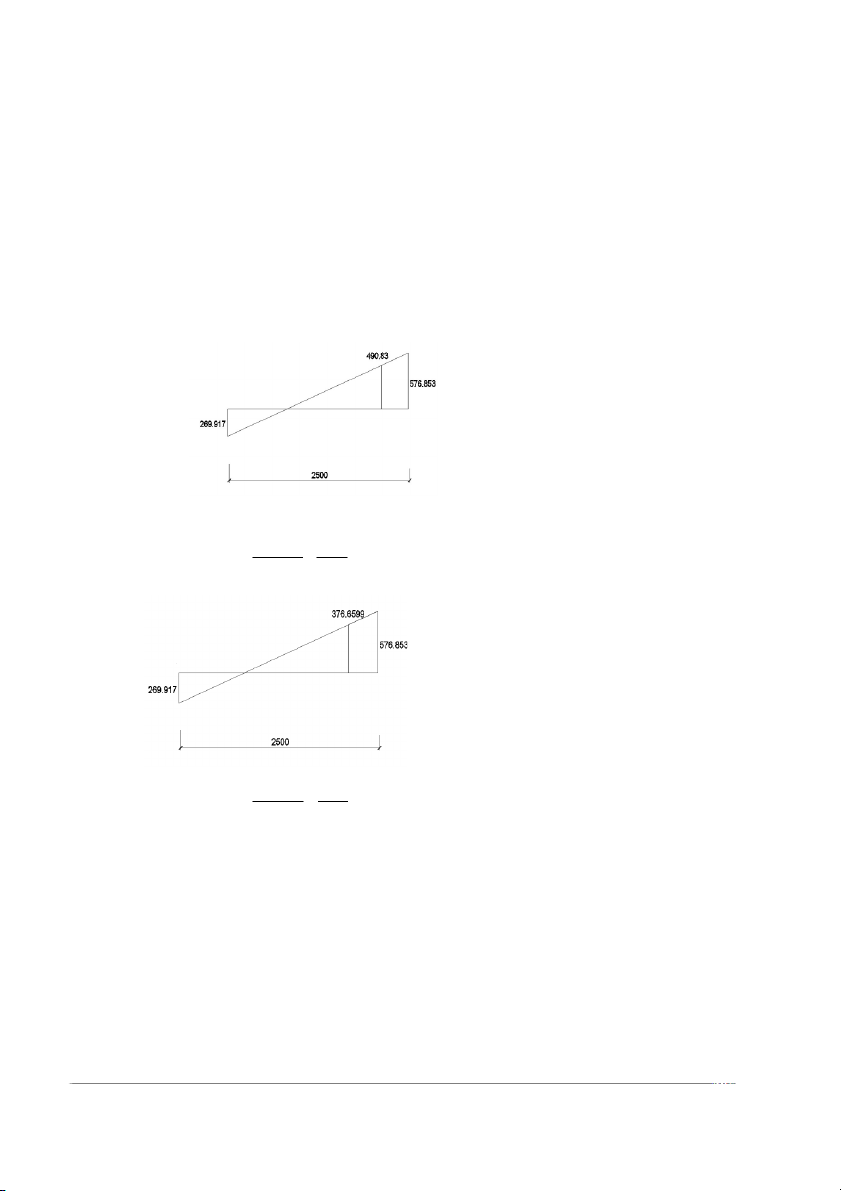
Cắt 2d25: 167.0896+10.87= x =>x=1191.9438(mm) 362.285+10.87 2500 -Gối 2 bên phải
Cắt 2d28: 166.793+490.83 = x =>x=2210.8066(mm) 166.793+ 576.853 2500
Cắt 2d28: 166.793+376.599= x =>x=826.7905(mm) 166.793+ 576.853 2500

Tài liệu liên quan: