Tích phân suy rộng loại 1- Giải tích 1| Trường đại học Bách Khoa, Đại học Đà Nẵng

Tích phân suy rộng loại 1- Giải tích 1| Trường đại học Bách Khoa, Đại học Đà Nẵng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 1(GT 1)

Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng

Thông tin:

120 trang 2 tháng trước

Tác giả:

Profile Kim Oanh
I. Tích phân suy rộng loại một
Bài toán
Tìm diện tích S miền vô hạn giới hạn bởi đường cong:
, trục hoành, đường thẳng x = a.
( ) 0y f x
b
( )
a
s f x dx

lim ( )
b
b
a
f x dx

CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tích suy phân rộng loại một
Tích phân
( )
a
f x dx

lim ( )
b
b
a
f x dx

tích trên , khả đoạn với mọi
,a b
b a
được gọi là tích phân suy rộng loại một.
Các tích phân sau cũng là tích suy phân rộng loại một
( )
a
f x dx

lim ( )
a
b
b
f x dx

( )f x dx


( ) ( )
a
a
f x dx f x dx


CuuDuongThanCong.com https://fb.com/tailieudientucntt
Hai vấn đề đối tích với phân suy rộng
1) Tính tích suy phân rộng (thường rất phức tạp)
2) Khảo sát sự hội tụ.
( ) lim ( )
b
b
a a
f x dx f x dx


Nếu giới tồn tại hạn và hữu hạn thì tích phân gọi là hội tụ.
Ngược lại, nếu giới hạn không tồn tại hoặc bằng vô
cùng, thì tích phân gọi là phân kỳ.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tính tích suy phân rộng (công thức – Newton Leibnitz)
( ) lim ( )
b
b
a a
f x dx f x dx


Giả sử F(x) nguyên là hàm của f(x) trên
,a 
lim ( ) ( )
b
F b F a

Tích phân tồn tại khi khi và chỉ tồn tại
lim ( ) : ( )
b
F b F

( ) ( ) ( ) ( )
a
a
f x dx F x F F a



CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính diện tích miền giới bởi phẳng hạn
2
1
y
x
, trục hoành và đường thẳng x = 1.
2
1
dx
S
x

2
1
lim
b
b
dx
x

1
1
lim
b
b
x

1
lim 1 1
x
b

Diện của miền tích S
bằng 1, hữu hạn.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
S là miền có diện tích
vô hạn, bằng
Ví dụ Tính diện tích miền phẳng giới bởi hạn
1
y
x
, trục hoành và đường thẳng x = 1.
1
dx
S
x

1
lim
b
b
dx
x

1
lim ln | |
b
b
x

lim ln
b
b


CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính diện tích miền giới bởi phẳng hạn
2
1
1
y
x
, . trục hoành
2
1
dx
S
x


0
2 lim arctan
b
b
x

2
0
2
1
dx
x

Diện của miền tích S
bằng .
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính tích phân
2
1
x
I e dx

2
1
x
I e dx

2
1
2
x
e

2
2 2
e e

2
1
2e
Ví dụ Tính tích phân
2
ln
e
dx
I
x x

2
ln
e
dx
I
x x

2
(ln )
ln
e
d x
x

1
ln
e
x

1 1
ln( ) lne

1.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính tích phân
2
4
5 6
dx
I
x x

2
1 1
( 2)( 3)
5 6
x x
x x
1 1
3 2x x
4
1 1
3 2
I dx
x x

4
3
ln
2
x
I
x

3 4 3
lim ln ln
2 4 2
x
x
x

1
ln1 ln
2
ln 2
4 4
ln | 3| ln | 2 |x x
 
( ) ( )  
Dạng vô định.?
Không được phép dùng :
lim ( ) lim lim
x x x
f g f g
  
khi chưa đảm bảo hạn hai giới vế phải chắc chắn tồn . tại
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính
5 10
1
1
dx
I
x x x

Đổi biến :
Đổi cận :
6
1
10 5
1 1
1
dx
I
x
x x

5
1
t
x
6
1
dt dx
x
1 1x t
0x t
0
2
1
1
dt
I
t t
1
2
0
1/ 2 3/ 4
dt
t
1
2
0
ln 1/ 2 1/ 2 3/ 4t t
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính
2
0
cos
x
I e xdx

Đặt
2 2
2
x x
u e du e dx
cos sindv xdx v x
2 2
0
0
sin 2 sin
x x
I e x e xdx


2
0
2 sin
x
I e xdx

Ta có nên
2
lim sin 0
x
x
e x

2 2
2
x x
u e du e dx
sin cosdv xdx v x
2 2
0
0
2 cos 4 cos
x x
I e x e xdx


2 4I
2
5
I
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính
3/ 2
2
0
arctan
1
x
I dx
x

arctant x
Đổi biến :
3/ 2
2
0
arctan
1
x
I dx
x

2
2
1
tan 1
cos
x t x
t
Đổi cận :
2
1
dx
dt
x
0 0x t
2
x t

2
2
0
arctan
1
1
x dx
x
x

/ 2
0
cost tdt
1
2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
0
1
a
dx
x

Kết quả (được sử dụng để sát khảo sự hội tụ)
Trường hợp 1:
1
1
1 1
1
a
x

1
1 1
1 a
hữu hạn, khác 0.
0
1
a
dx
x

Trường hợp 2:
1
1
1
a
x

Tích phân phân . kỳ
tích . phân hội tụ
Trường hợp 3:
1
0
1
a
dx
x

ln | |
a
x

Tích phân phân . kỳ
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Kết quả (được sử dụng để sát khảo sự hội tụ)
0
1
1
1
hoäi tuï, neáu
phaân kyø, neáu
a
dx
x

2
1
ln
I dx
x x

1,Neáu thì hoäi tuI
1,Neáu thì phaân kyI
1, 1,Neáu thì hoäi tuI
1, 1,Neáu thì PKI
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tích phân hàm không âm
và tích trên khả
( ) 0, ( ) 0x a f x g x
,a 
( ) ( )f x g x
ở cận lân của
.
Khi : đó
1) Nếu hội thìtụ, hội tụ.
( )
a
g x dx

( )
a
f x dx

2) Nếu phân thìkỳ, phân . kỳ
( )
a
f x dx

( )
a
g x dx

Tiêu chuẩn so sánh 1.
Để khsát sự hội tụ của , thường đem so sánh
( )
a
I f x dx

với đã biết . kết quả
a
dx
x

CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
2 2
1
2 sin 3
dx
I
x x

Ta có
2 2 2
1 1
( ) ( )
2 sin 3 2
f x g x
x x x
Vì
hội tụ
2
1
2
dx
x

, theo nên hội tụ tchuẩn so sánh 1.
I
Chú ý (trong tiêu chuẩn 1):
2) Chỉ cần tồn tại
, ( ) ( )a x f x g x
3) Cận dưới của tích phân là số dương ( )
a
dx
x

0.a
1) f(x) và g(x) là hai hàm không âm.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
2 2
1
sin 3
dx
I
x x

Ta có
22 2
1 2
( ) ( )
sin 3
f x g x
x xx
Vì
hội tụ
2
1
dx
x

, theo nên hội tụ tchuẩn so sánh 1.
I
Ví dụ Khảo sát sự hội tụ
3
1
ln
5
xdx
I
x

Ta có
3
ln 1 1
( ) ( )
5 5 2
x
f x g x
x x x
Vì
phân kỳ
1
2
dx
x

, theo ssánh 1.nên phân kỳ tchuẩn
I
5x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tích phân hàm không âm
và tích trên khả
( ) 0, ( ) 0x a f x g x
,a 
( )
lim
( )
x
f x
K
g x

Khi : đó
nếu hội tụ, thì . hội tụ
( )
a
g x dx

( )
a
f x dx

và cùng HT cùng hoặc PK.
( )
a
f x dx

( )
a
g x dx

Tiêu chuẩn so sánh 2.
1) :0 K
2) :0 höõu haïn, K
nếu hội tụ, thì . hội tụ
( )
a
f x dx

( )
a
g x dx

3) : K
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Để sát khảo sự hội tụ của
( )
a
f x dx

Cách sử dụng tiêu chuẩn so sánh 2.
1) tra f(x) không (trong lân kiểm có là hàm âm
cận của )
2) Tìm g(x) cách: hàm bằng tìm hàm tương
đương của f(x) khi x tiến ra dương vô cùng.
3) Tính , kết luận.
( )
lim
( )
x
f x
K
g x

Hai f(x) hàm và g(x) không âm: nếu , thì
( )
x
f x

( ) ( ) vaø
a a
f x dx g x dx
 
cùng tính . chất
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Hội tụ tuyệt đối
Nếu hội thì . tụ, hội tụ
( )
a
f x dx

( )
a
f x dx

Định lý
Nếu hội thì tụ, gọi hội là tụ tuyệt đối
( )
a
f x dx

( )
a
f x dx

Định nghĩa
Nếu f(x) hàm có tùy dấu ý, để sát khảo sự hội tụ của
( )
a
f x dx

( )
a
f x dx

ksát sự HT của
tích phân hàm
không âm
để dụng sử
được hai tiêu
chuẩn so sánh
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
1
5 ln
dx
I
x x

Ta có
1 1
( )
5 ln 5
x
f x
x x x
Chọn
1/ 2
1
( )g x
x
Khi : đó
( ) 1
lim
( )
5
x
f x
g x

hữu hạn, khác 0.
Tích cùng phân và hội tụ hay phân kỳ.
1
( )f x dx

1
( )g x dx

Vì phân ( kỳ ), nên phân tích I . phân kỳ
1
( )g x dx

1
1
2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
3
1
3
2 sin3
xdx
I
x x

Ta có
3 2
3 3 3
( )
2 sin3 2 2
x
x x
f x
x x x x
Chọn
2
1
( )g x
x
( ) 1
lim
( )
5
x
f x
g x

hữu hạn, khác 0.
Tích phân và cùng hội tụ hay phân kỳ.
1
( )f x dx

1
( )g x dx

Vì hội tụ ( tích ), nên phân I hội . tụ
1
( )g x dx

2 1
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
2
1
arctan
2 2ln
xdx
I
x x

Ta có
2
arctan
( )
2 2ln
x
x
f x
x x
Chọn
2
1
( )g x
x
( )
lim
( ) 4
x
f x
g x

hữu hạn, khác 0.
Tích phân và cùng hội tụ hay phân kỳ.
1
( )f x dx

1
( )g x dx

Vì hội tụ ( tích ), nên phân I hội . tụ
1
( )g x dx

2 1
2 2
2 2 4x x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
0
(3 1) 1
dx
I
x x

Ta có
1 1
( )
3
(3 1) 1
x
f x
x
x x
Chọn
3/ 2
1
( )g x
x
Khi : đó
( ) 1
lim
( ) 3
x
f x
g x

hữu hạn, khác 0.
Tích cùng phân và hội tụ hay phân kỳ.
0
( )f x dx

0
( )g x dx

Vì hội tụ ( ), tích nên phân I hội . tụ
0
( )J g x dx

3
1
2
Sai! J vì phân (xem tích suy kỳ phần phân rộng hai)loại
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
0
(3 1) 1
dx
I
x x

Ta có
1 1
( )
3
(3 1) 1
x
f x
x
x x
Chọn
3/ 2
1
( )g x
x
Khi : đó
( ) 1
lim
( ) 3
x
f x
g x

hữu hạn, khác 0.
Tích phân và cùng hội tụ hay phân kỳ.
1
( )f x dx

1
( )g x dx

Vì HT ( ), I HT, suy I nên
1
ra HT.
( )g x dx

3
1
2
Cách giải đúng!
1
1 2
0 1
(3 1) 1 (3 1) 1
dx dx
I I I
x x x x

I
1
là tích phân xác định nên hội tụ. Xét tích phân I
2
1
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
2
1
x
I e dx

2
1 ( ) ( )
x x
x f x e e g x
1
1
1
x x
e dx e
e


HT
1
( )g x dx

Tích phân đã hội cho tụ theo tiêu chuẩn so sánh 1.
Ví dụ Khảo sát sự hội tụ
2
1/
1
1
cos
x
I e dx
x

2
1/
1
( ) cos
x
f x e
x
2 2
1 1 3
2 2x x x
HTI
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
1
x
e
I dx
x

Ta : có
1
x
x e x
1 1
x
e x
2
1 1
( ) ( )
x
f x g x
xe x
Tích phân đã cho hội tụ.
Ví dụ Khảo sát sự hội tụ
3 2
3
1
1
3 1
x x
I dx
x x

3 2 3/ 2
3 3/ 2
1 1
( )
3 1
x
x x x
f x
x x x x

Tích phân hội tụ.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
0
arctan
2
x
x
I dx
e

arctan
( ) ( )
2 2
x
x
x
f x g x
e e

Tính HT, tích nên phân đã cho HT.
0
0
1
x x
e dx e


Ví dụ Khảo sát sự hội tụ
3
3/
1
2arctan
1
x
x
I dx
e

3
3/
2arctan
1
x
x
e
3
3/
1
2 / 2 arctan
1
x
x
e
3
2
2/ 2
3/ 3
x
x
x x

HT
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Chứng minh tích phân hội tụ và tính
2
3
1
dx
I
x x

2
1 1
( )
1
x
f x
x
x x
nên phân tích I . hội tụ
2 1
2
1t x
2 2
1t x
2 2tdt xdx
2 2
3
1
xdx
I
x x

2
2
1
tdt
t t

2
1
ln
1
t
t

1
ln1 ln ln3
3
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví
dụ
Chứng minh tích
phân hội tính tụ và
4 2
80
1
dx
I
x x

3/ 2
4 2
1 1 1
( )
1
x
f x
x x
x x
nên I hội . tụ
3
1
2
2
4
1t x
4 2
1t x
3
4 2t dt xdx
42 2
80
1
xdx
I
x x

3
4
9
2
1
t dt
t t

2 2
9 9
1 1
dt dt
t t
 
9
9
1
ln arctan
1
t
t
t


8
ln arctan9
10 2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví
dụ
Chứng minh tích phân phân kỳ và tính giới hạn
1
x
e
I dx
x

1
lim
t
x
x
x
e
dt
t
e

1
1 ( ) ( )
x
e
x f x g x
x x
1
( )g x dx

FK I nên phân kỳ.
Giới hạn có dạng vô định , dùng qui Lôpital tắc
'
1
'
lim
t
x
x
x
e
dt
t
e

lim
x
x
x
e
x e

1
lim
x
x

0
1
lim
t
x
x
x
e
dt
t
e

CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
2
1
sin
ln 2
xdx
I
x x

Hội tụ.
2
sin
( )
ln 2
x
f x
x x
1
( )
x
x
x

Sai! vì f(x) có dấu tùy không ý, sử dụng so sánh được.
Xét tích phân hàm không âm
2
1
sin
ln 2
x
J dx
x x

Hội tụ.
2
sin
( )
ln 2
x
f x
x x
1
( )
x
x
x

Tích phân đã hội cho tụ tuyệt . đối
2
1
ln 2x x
2
1
ln 2x x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
1
sin xdx
I
x

Tích phân từng phần:
2
1
1 1
sin cos cosx x x
I dx dx
x x
x

 
2
1 1
u du dx
x x
sin cosdv xdx v x
cos1
1
J
Xét tích phân
2
1
cos x
J dx
x

2 2
cos 1x
x x
hội tụ
hội suy tụ, ra hội tụ.
I
J
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
1
sin xdx
I
x

Xét tích phân hàm không âm
1
sin x
J dx
x

2
sin sin 1 cos2
2
x x x
x x x
1 1 1
1 cos2 cos2
2 2 2
x dx x
dx dx
x x x
  
1 2
I I
1
1
2
dx
I
x

phân kỳ
2
1
cos2
2
xdx
I
x

hội tụ (tương
tự ví dụ trước)
Tích phân đã hội cho tụ, không nhưng hội tụ tuyệt đối
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Chú ý:
1) tích Với phân chỉ có một suy điểm rộng
( )
a
f x dx

khi tách ra có dạng vô định
( ) ( )
a a
G x H x
 
vẫn chưa kết t/phân luận ban phân đầu . kỳ
2) tích Với phân hai có điểm rộng suy
( )f x dx


khi tách ra thành tích phân
( ) ( )
a
a
f x dx f x dx


chỉ cần một trong tphân thì tphân . hai PK, ban đầu PK
CuuDuongThanCong.com https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai
Định nghĩa
Điểm x
0
được gọi là điểm kỳ dị của đường cong y = f(x),
nếu
0
lim ( )
x x
f x
Tích phân suy rộng
loại hai của f(x)
trên [a,b] đoạn
( ) : lim ( )
b t
t b
a a
f x dx f x dx
Giả sử trên đoạn [a,b] hàm y = f(x) có một điểm kỳ dị duy
nhất x = b. là
0
CuuDuongThanCong.com https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai
Tích phân suy rộng
loại hai của f(x) trên
đoạn [a,b]
( ) : lim ( )
b b
t a
a t
f x dx f x dx
Giả sử trên đoạn [a,b] hàm y = f(x) có một điểm kỳ dị duy
nhất x = a. là
0
CuuDuongThanCong.com https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai
Tích phân suy rộng loại
hai f(x) trên [a,b] của đoạn
( ) ( ) ( )
b c b
a a c
f x dx f x dx f x dx
Giả sử trên đoạn [a,b] hàm y = f(x) có một điểm kỳ dị duy
nhất là
,c a b
lim ( ) lim ( )
t b
t c t c
a t
f x dx f x dx
Tích phân trái khi khivế là hội tụ và chỉ cả hai tích phân ở
vế phải hội tụ.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai
Các khái niệm hội tụ, phân kỳ giống như trong tích phân
suy rộng loại một.
Khái niệm hội tụ tuyệt đối cũng tương tự trong tích phân
suy rộng loại Hội một: tụ tuyệt đối hội thì tụ.
Tương tự tích phân suy : tiêu rộng loại một có hai chuẩn
so sánh cho tích không . phân hàm âm
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tích phân tồn tại khi và chỉ khi tồn tại
lim ( ) : ( )
t b
F t F b
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
Tính tích suy (công phân rộng thức Newton – Leibnitz)
( ) lim ( )
b t
t b
a a
f x dx f x dx
Giả sử F(x) nguyên là hàm của f(x) trên
,a b
lim ( ) ( )
t b
F t F a
Cho x = b
0
là điểm kỳ dị nhất duy f(x) trên [a,b] của
Tương tự cho trường hợp điểm x = a
0
là kỳ dị.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính tích phân
4
2
2
dx
I
x
4
2
2
dx
I
x
4
1/ 2
2
( 2)
lim
2
t
t
d x
x
4
2
lim 2 2
t
t
x
2
2 2 lim 2 2
t
t
Theo định nghĩa
2 2
Theo công Newton thức – Leibnitz (gọn hơn)
4
2
2
dx
I
x
4
2
2 2x
2 4 2 2 2
2 2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tích phân
3
0
1
dx
I
x
3
0
1
dx
I
x
3
0
ln | 1|x
Sai! vì có điểm kỳ dị x = 1 trong [0,3]. đoạn
ln 2 ln1 ln 2
1 3
0 1
1 1
dx dx
I
x x
1
1
1
0
lim
1
t
dx
I
x
1
lim ln | 1|
t
t
1 2
I I
Xét tích phân

Vậy tích phân phân . kỳ
1
I
Suy tích cho ra phân đã phân kỳ
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Tính tích phân
1
0
(2 ) 1
dx
I
x x
Đặt
1 x t
2
1 x t
2dx tdt
Đổi cận :
0 1x t
1 0x t
1
0
(2 ) 1
dx
I
x x
0
2
1
2
1
tdt
t t
1
2
0
2
1
dt
t
1
0
2arctanI t
2 arctan1 arctan0
2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tích phân hàm không âm
và tích trên khả
( ) 0, ( ) 0x a f x g x
,a b
( ) ( )f x g x
ở cận lân của trái của
.b
Khi : đó
1) Nếu hội thìtụ, hội tụ.
( )
b
a
g x dx
( )
b
a
f x dx
2) Nếu phân thìkỳ, phân . kỳ
( )
b
a
f x dx
( )
b
a
g x dx
Tiêu chuẩn so sánh 1.
Trường hợp x = b
0
là điểm kỳ dị nhất duy .
Tương tự cho trường hợp điểm x = a
0
là kỳ dị duy nhất.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Tích phân hàm không âm
và tích trên khả
( ) 0, ( ) 0x a f x g x
,a b
( )
lim
( )
x b
f x
K
g x
Khi : đó
nếu hội tụ, thì . hội tụ
( )
b
a
g x dx
( )
b
a
f x dx
và cùng HT cùng hoặc PK.
( )
b
a
f x dx
( )
b
a
g x dx
Tiêu chuẩn so sánh 2. (x
0
= b là điểm kỳ dị duy nhất)
1) :0 K
2) :0 höõu haïn, K
nếu hội tụ, thì . hội tụ
( )
b
a
f x dx
( )
b
a
g x dx
3) : K 
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Kết quả (được sử dụng để sát khảo sự hội tụ)
1
1
1
phaân kyø, neáu
hoäi tuï, neáu
b
a
dx
x a
1
1
1
phaân kyø, neáu
hoäi tuï, neáu
b
a
dx
b x
Chú ý: Kết luận ngược lại so tích với phân loại một!
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
2
2
1
1
dx
I
x
Ta có
1
1/ 2
1 1
( )
( 1)( 1)
2 1
x
f x
x x
x
Chọn
1/ 2
1
( )
1
g x
x
( ) 1
lim
( )
2
x
f x
g x

hữu hạn,
khác 0.
Tích phân và cùng hội tụ hay phân kỳ.
2
1
( )f x dx
2
1
( )g x dx
Vì hội tụ ( tích ), nên phân I hội . tụ
2
1
( )g x dx
1
1
2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
5
3
1
0
ln 1
1
x
x dx
I
e
5
3
3/ 5
0
2/ 5
ln 1
1
( )
1 ( 0)
x
x
x
x
f x
x
e x
hội tụ vì
1
1
2
Ví dụ Khảo sát sự hội tụ
3
3
2
0
2
9
x dx
I
x
3
2
( )
3 (3 )
x
f x
x x
hội tụ vì
1
1
2
3
1/ 2
18
( 3)
x
x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
1
3
0
5
tan
x x
I dx
x x
3 1/ 2
0
5/ 2
5 3
tan
/3 ( 0)
x
x x x
x x
x x
phân kỳ vì
5
1
2
Ví dụ Khảo sát sự hội tụ
4
0
2
dx
I
x
1
( )
2
f x
x
phân kỳ vì
1
4
1
4
( 4)
x
x
3
3
tan ( )
3
x
x x x x x
3
3
( )
3
x
x
2
4
x
x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Ví dụ Khảo sát sự hội tụ
2
2
0
sin xdx
I
x

Ta có
2
2 2
sin 1
( )
x
g x
x x
Vì HT , I HT, suy nên
1
ra I HT.
1
( )g x dx

1
2 2
1 2
2 2
0 1
sin sinxdx xdx
I I I
x x

I
1
không tích suy là phân rộng
mà tích là phân xác định nên HT
2
2
0
sin
lim 1
x
x
x
CuuDuongThanCong.com https://fb.com/tailieudientucntt
I. Tính các tích phân sau
3
1
1)
( 1)( 2)
dx
x x

2
1
2)
( 1)( 2)( 3)
dx
x x x

2
3
(5 3)
3)
( 2)(3 2 1)
x
dx
x x x

2
3
2
( 1)
4)
( 1)
x
dx
x x

2
3
2
5)
1 ( 1)
dx
x x

1 ln 2
2
ln 2
3
1 2
ln 5 ln 2
4 3
11 1
ln 2 ln3
5 5
3 17
ln 2
16 128
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2
0
1
6)
2
dx
x x

2
1
3
7)
( 1)
x
dx
x x x

2
6
0
8)
1
x
dx
x

2
0
9)
4 4 5
dx
x x

0
10)
x x
dx
e e

arctan 2
4
2 7
arctan 7
7
3 3
ln 3
2 18
6
4
CuuDuongThanCong.com https://fb.com/tailieudientucntt
0
1
11)
x x
dx
e e

2
1
1
12)
(ln 1)
dx
x x

2
0
1
13)
cosh ( )
dx
x

2
0
14)
x
xe dx

6
1
15)
( 3)
dx
x x

1
4
2 2ln 2
2
1
ln 2
9
CuuDuongThanCong.com https://fb.com/tailieudientucntt
4
0
16)
1
x
dx
e

0
2
17)
4 1
x
x
dx

0
18)
1
x
dx
e

2 2
2
19)
1
dx
x x

1
20)
sinh
dx
x

1
1
ln
1
e
e
4ln 2
ln 2
4
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3
1
21)
x
e dx

2
22)
ln
e
dx
x x

0
23)
2
x
xdx

1
24)
(1 )
dx
x x

3
2
25)
1
xdx
x

2
2
1
3e
1
2
1
ln 2
ln 7 1 5
arctan
6 2
3 3
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2
20
26)
1
dx
x x

2
0
27) cos3
x
e xdx

2 3
28)
( 1)
dx
x x


2 2
0
29)
(4 1) 1
dx
x x

2
2
2
1
12
30)
1
x
dx
x

3
9
2
3
3
13
4
3 3
13
4
CuuDuongThanCong.com https://fb.com/tailieudientucntt
2
1
31)
2 3
dx
x

3/ 2
2
32)
( 3)
dx
x

3
2
0
33)
x
x e dx

3
1
ln
34)
xdx
x

5
1
1
35)
1
dx
x

1
4
1
10
2 5
5
1
3
1
64
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3
3
1
5
3
0
2
36)
x x dx
x
1
2
1
37)
(4 ) 1
dx
x x
4
2
2 2
2
38)
(1 ) 4
x dx
x x
2
1
39)
1
dx
x x
2
2
1
40)
1
dx
x x
2
625
187
15
5
5
3
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3/
1
1
1) ln 1 , 0
x
e
dx

0
arctan3
2)
(2 )
x
dx
x

1
I. Tìm tất cả các giá trị để chuỗi hội tụ
không tồn tại
2
1
1
3)
2
dx
x x

1
4)
x
x
dx
e x

1
1
5)
2
dx
x x

1
CuuDuongThanCong.com https://fb.com/tailieudientucntt
1
0
ln 1
6)
1
x
x
dx
e
4 2 5
0
7)
ln(1 )
dx
x x x

3
7 5
1
( 1)
8)
1
x
dx
x x

3
1
9)
sin
dx
x x x

1
0
1
10)
cosh cos
x
e x
dx
x x
3
2
3 1
5 5
5
6
2
1
2
CuuDuongThanCong.com https://fb.com/tailieudientucntt
| 1/120
| | Tải xuống

Có thể bạn quan tâm:

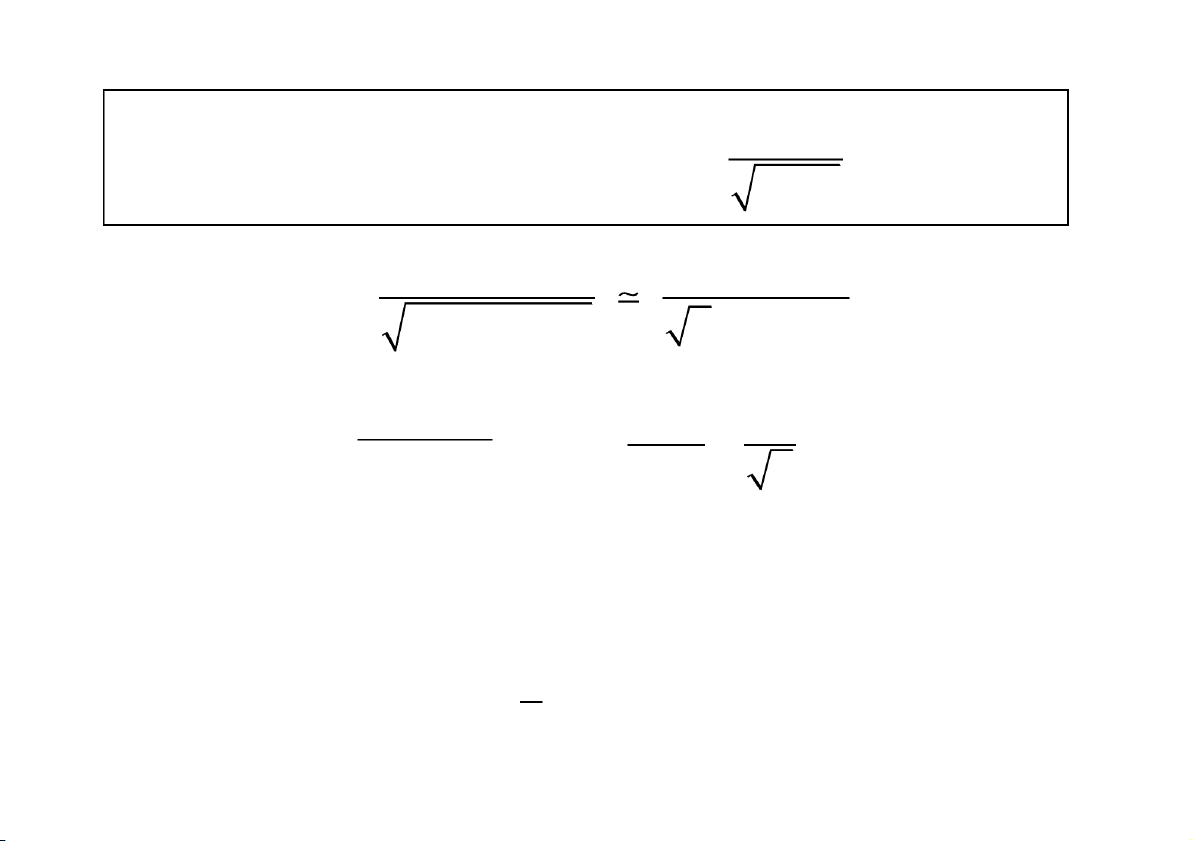
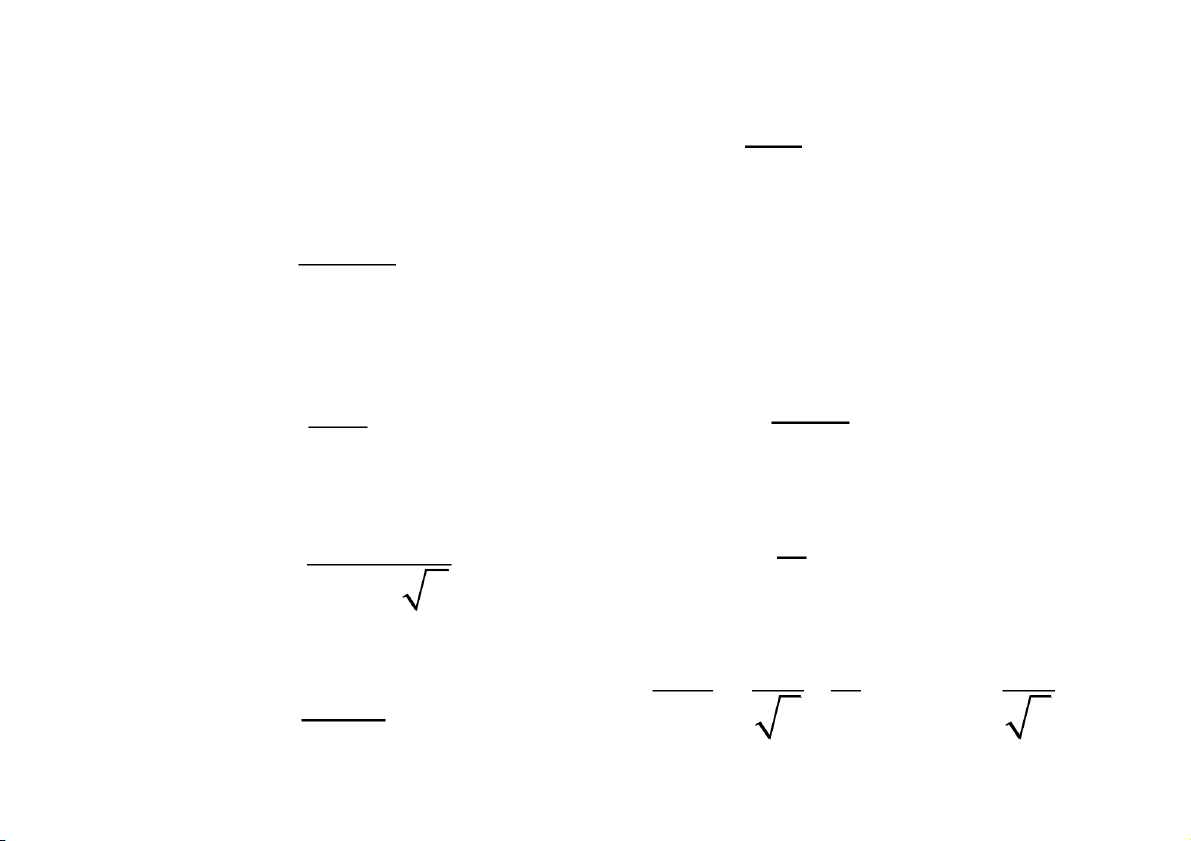
Preview text:

I. Tích phân suy rộng loại một Bài toán
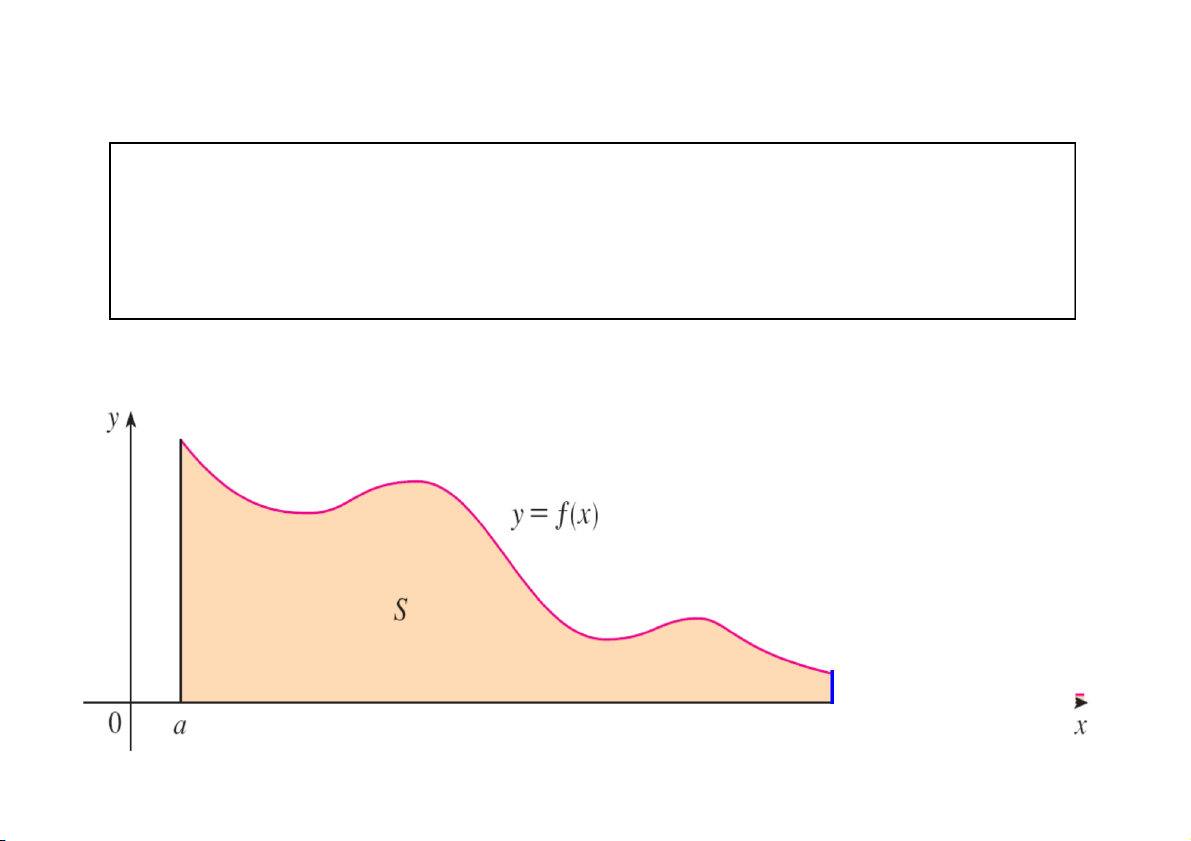
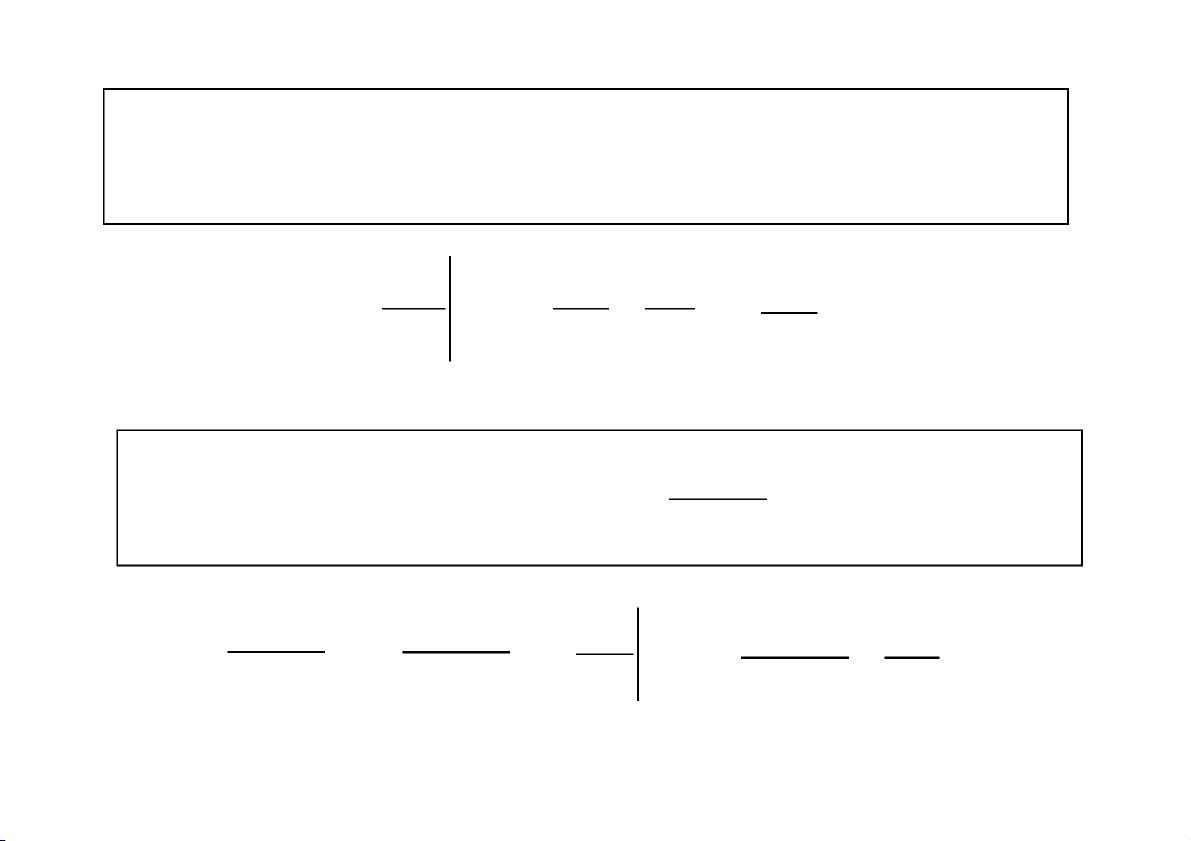
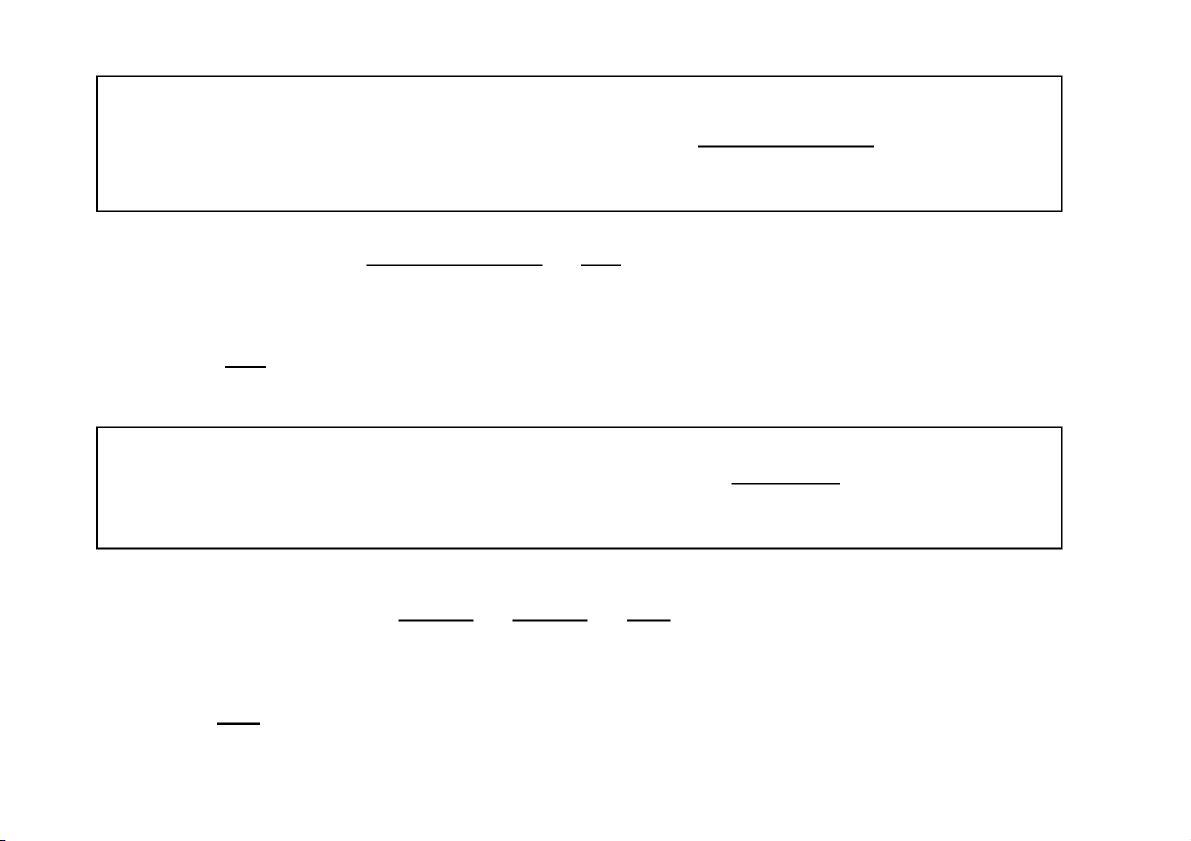
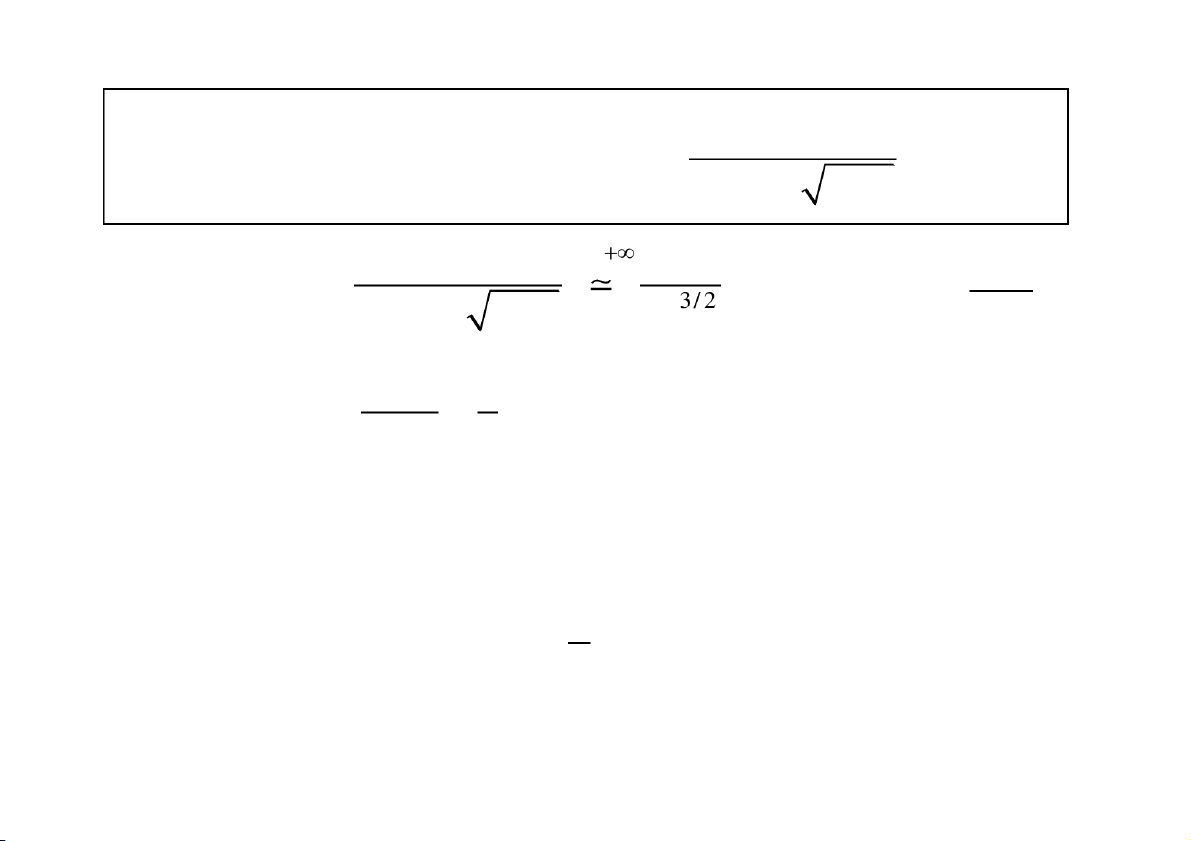
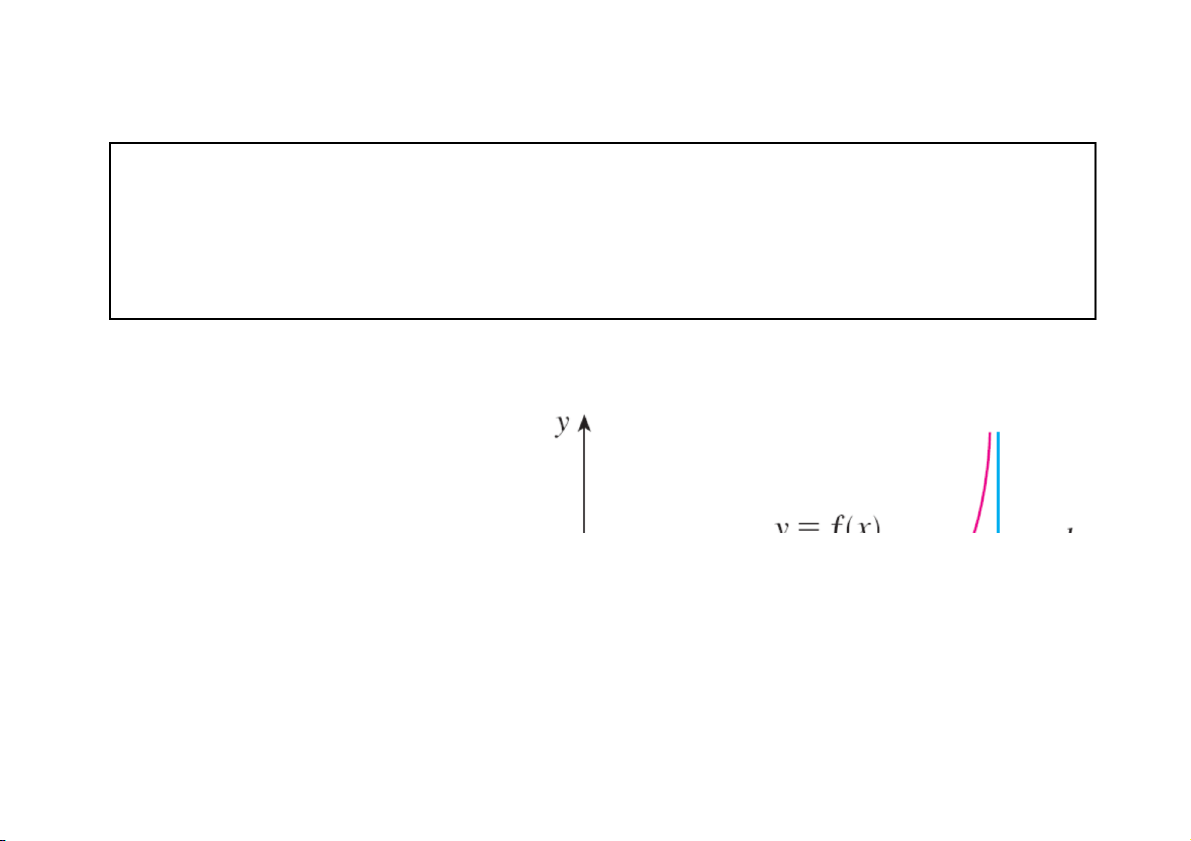
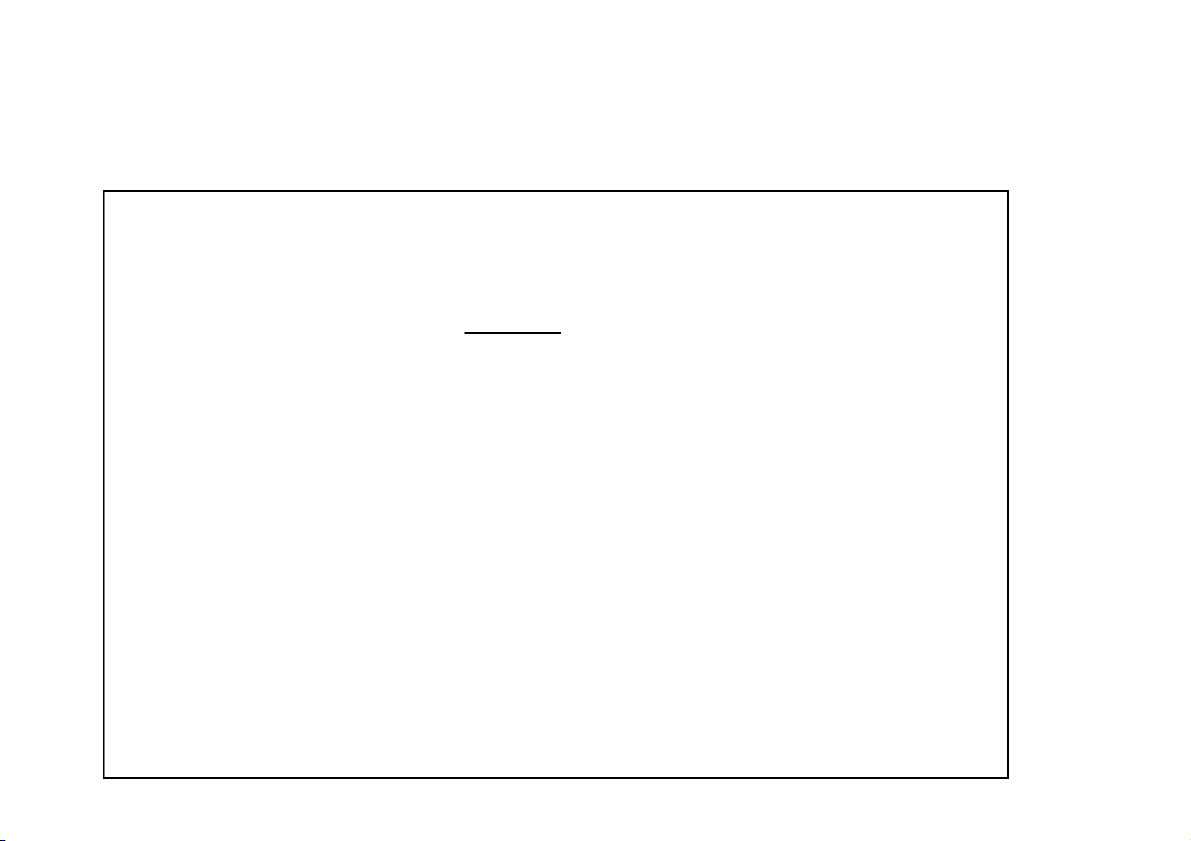
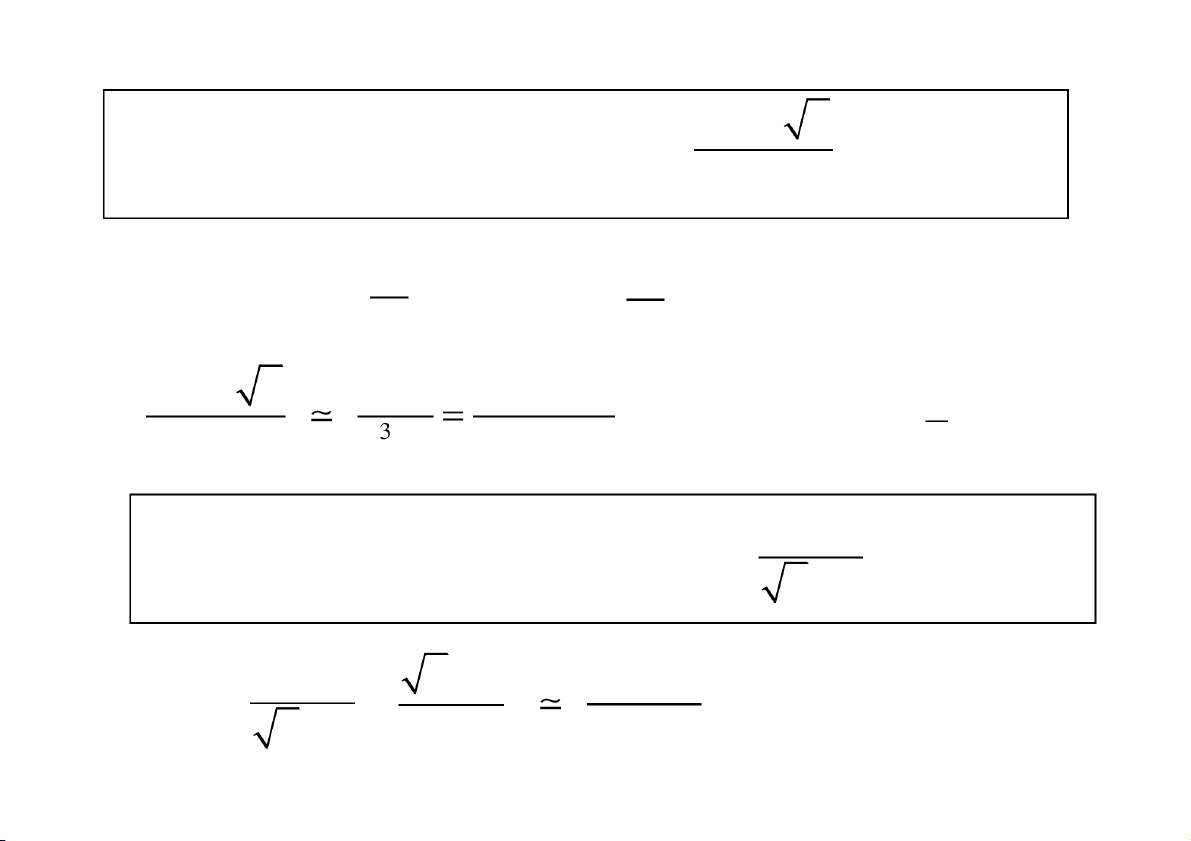
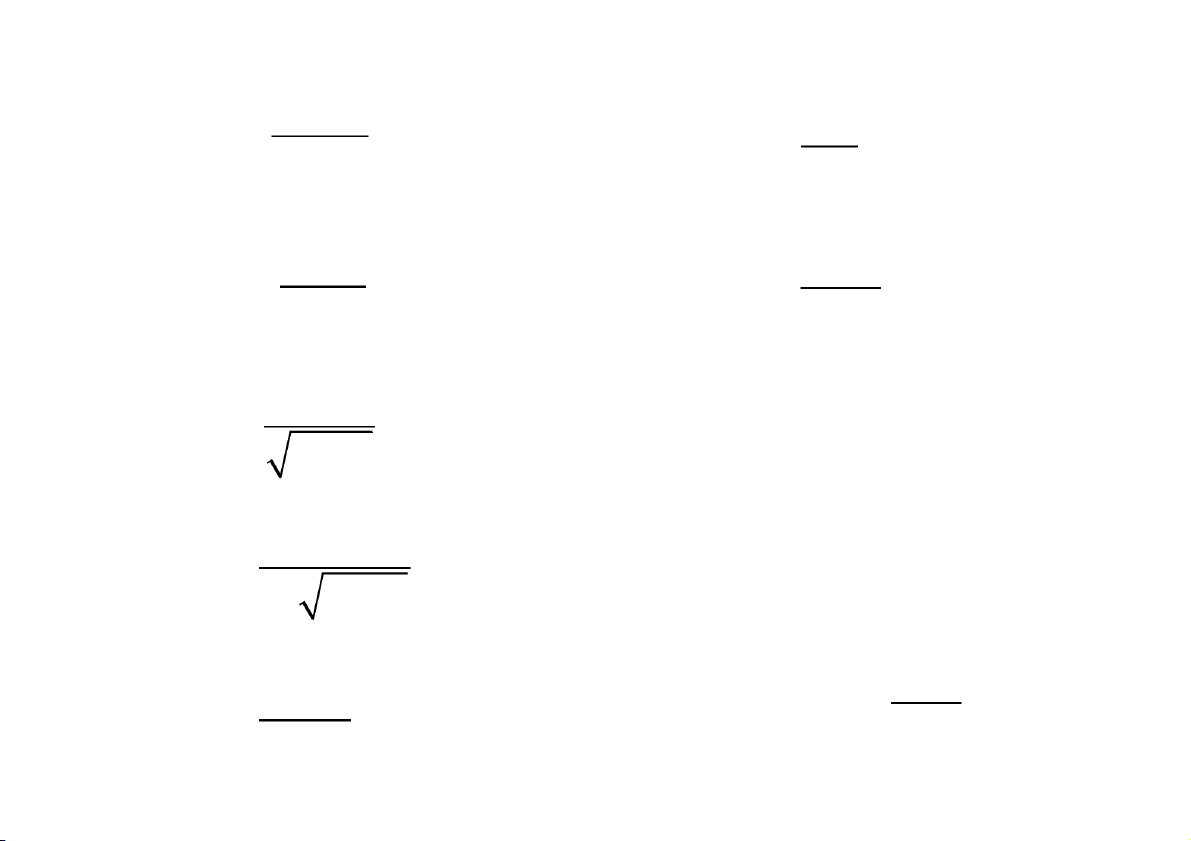
Tìm diện tích S miền vô hạn giới hạ n bởi đường cong: y f ( x )  ,
0 trục hoành, đường thẳng x = a.  b
s   f (x)dx  lim  f (x)dx b a a b   CuuDuongThanCong.com
https://fb.com/tailieudientucntt Tích phâ n suy rộng loại một
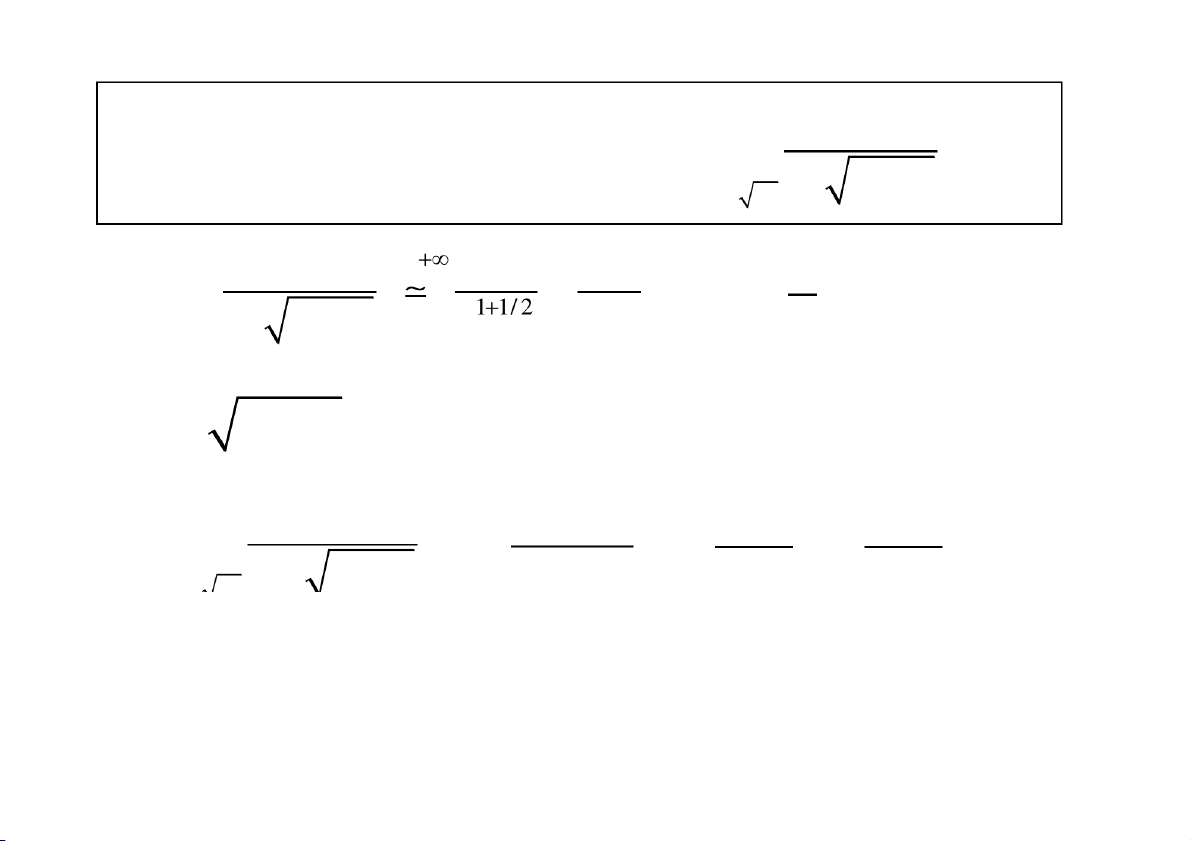
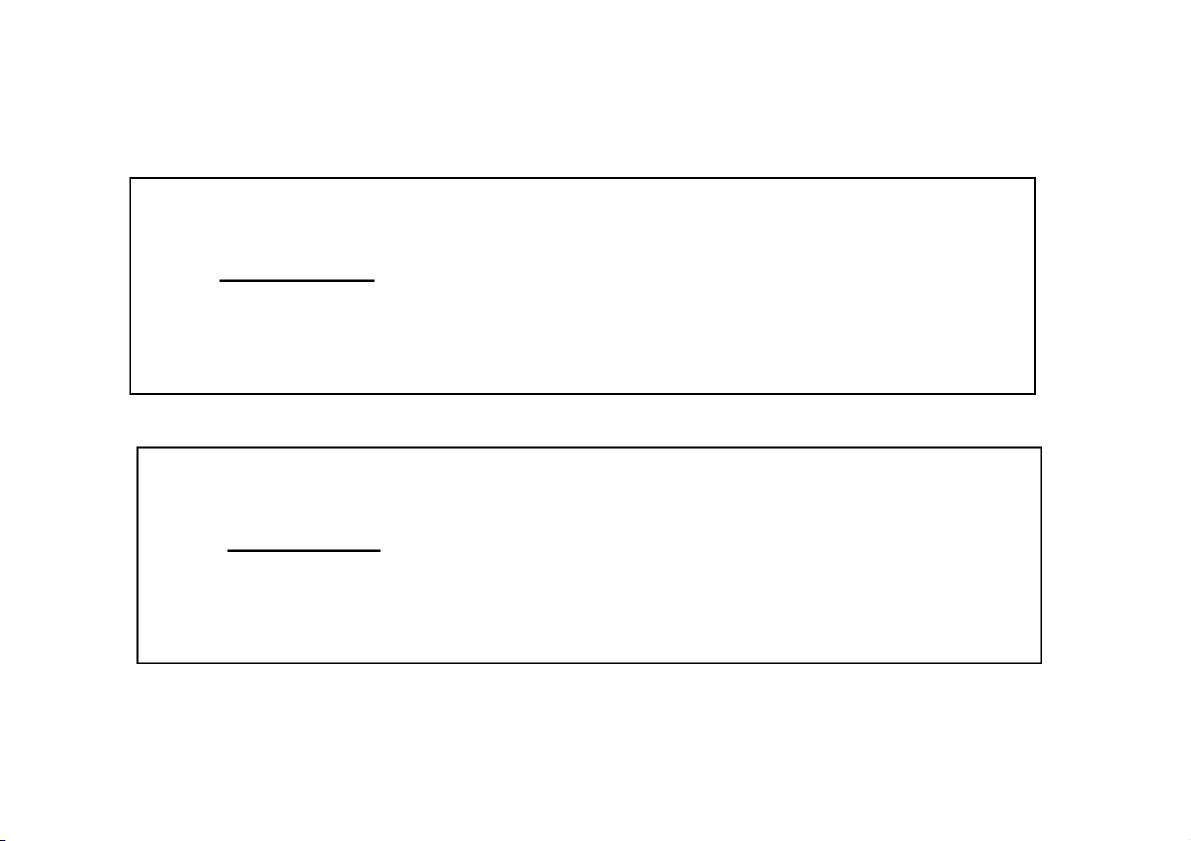
y f (x) khả tích trên đoạ n
a , b , với mọi b a  b Tích phâ
n  f (x)dx  lim  f (x)dx b a a
được gọi là tích phân suy rộng loại một.
Các tích phân sau cũng là tích phâ n suy rộng loại mộ t a a
f (x)dx  lim  f (x)dx  b b  a 
f (x)dx   f (x)dx   f (x)dx   a CuuDuongThanCong.com
https://fb.com/tailieudientucntt  b
f (x)dx  lim  f (x)dx b a a
Nếu giới hạn tồn tại và hữu hạn thì tích phâ n gọ i là hội tụ.
Ngược lại, nếu giới hạn không tồn tại hoặc bằng vô
cùng, thì tích phân gọi l à phân kỳ.
Hai vấn đề đối với tích phân suy rộng 1) Tính tích phâ
n suy rộng (thường rất phức tạp)
2) Khảo sát sự hội tụ. CuuDuongThanCong.com
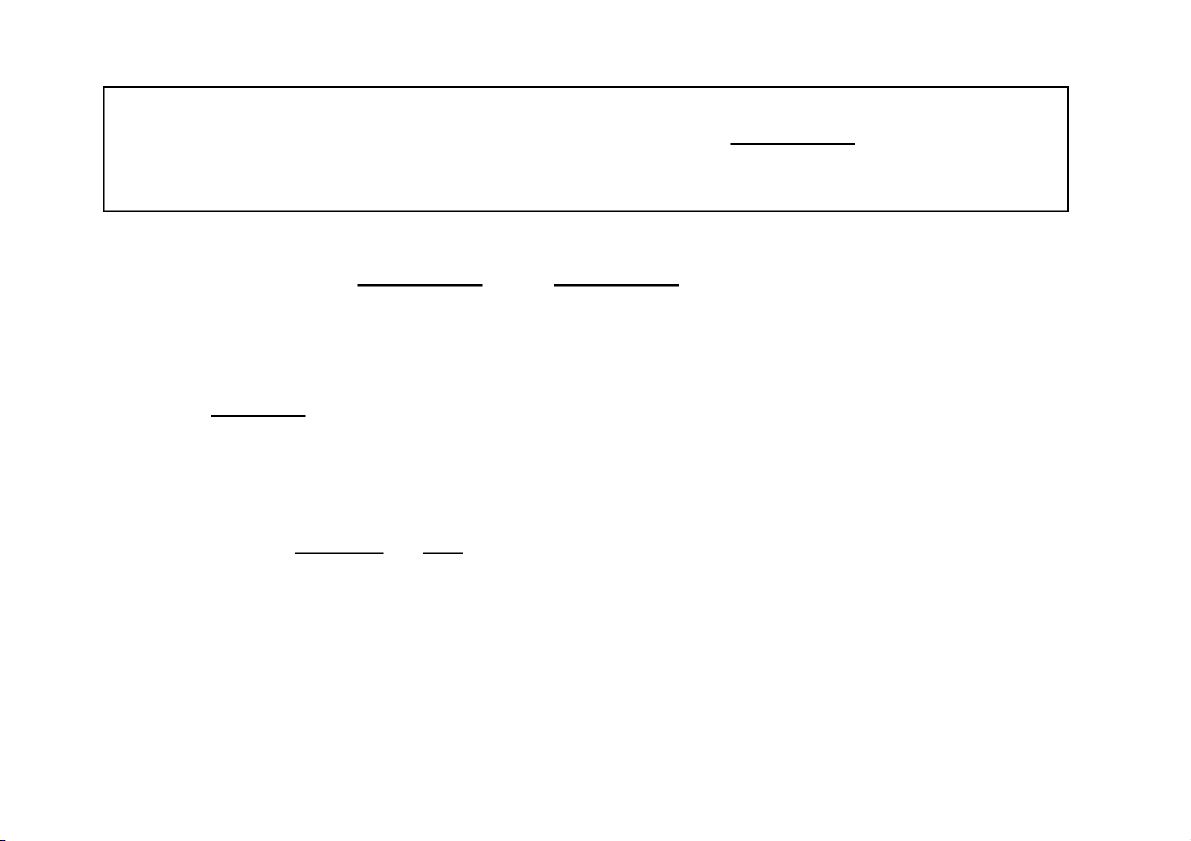
https://fb.com/tailieudientucntt Tính tích phâ
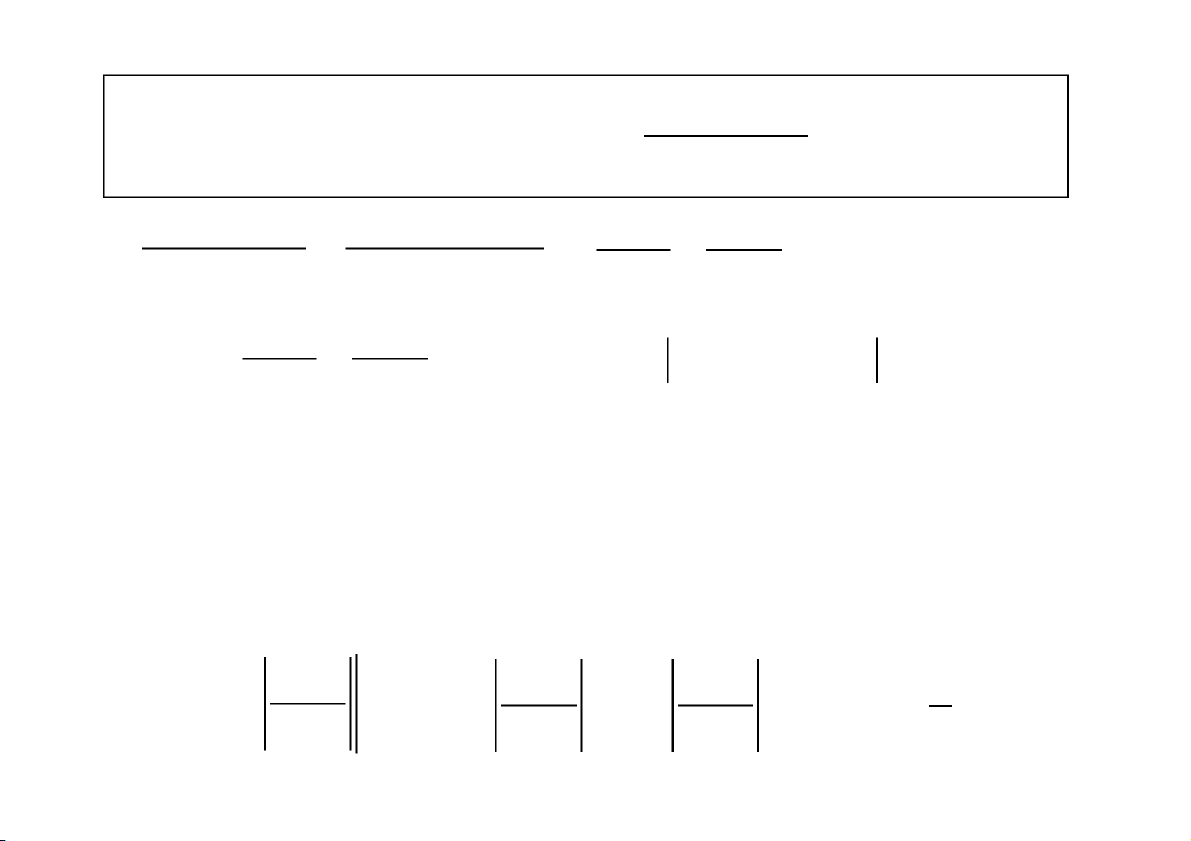
n suy rộng (công thức Newton – Leibnitz) Giả sử F(x) l à nguyên hà
m của f(x) trên a,   b
f (x)dx  lim  f (x)dx  lim F(b)  F(a) b b a a Tích phâ
n tồn tại khi và chỉ khi tồn tại lim F(b) : F() b  
f (x)dx F (x)
F()  F(a) a a CuuDuongThanCong.com
https://fb.com/tailieudientucntt Ví dụ
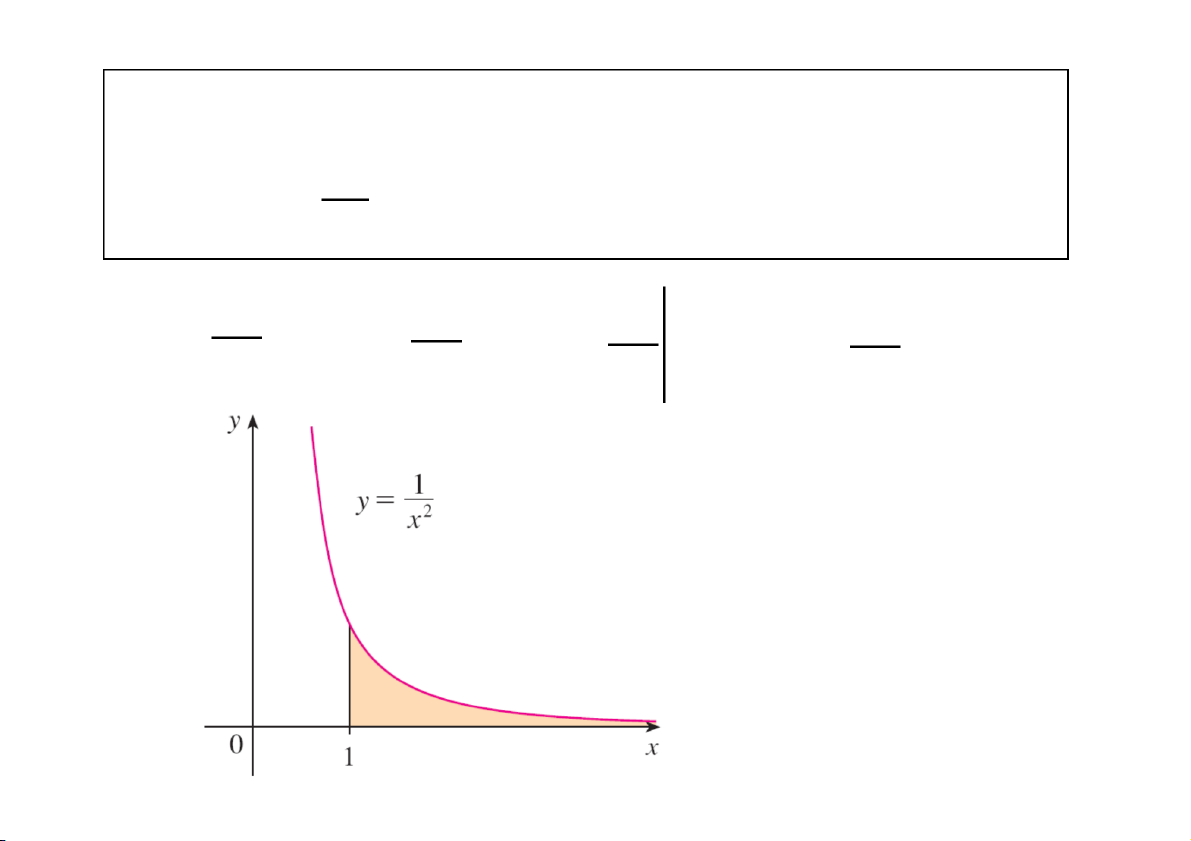
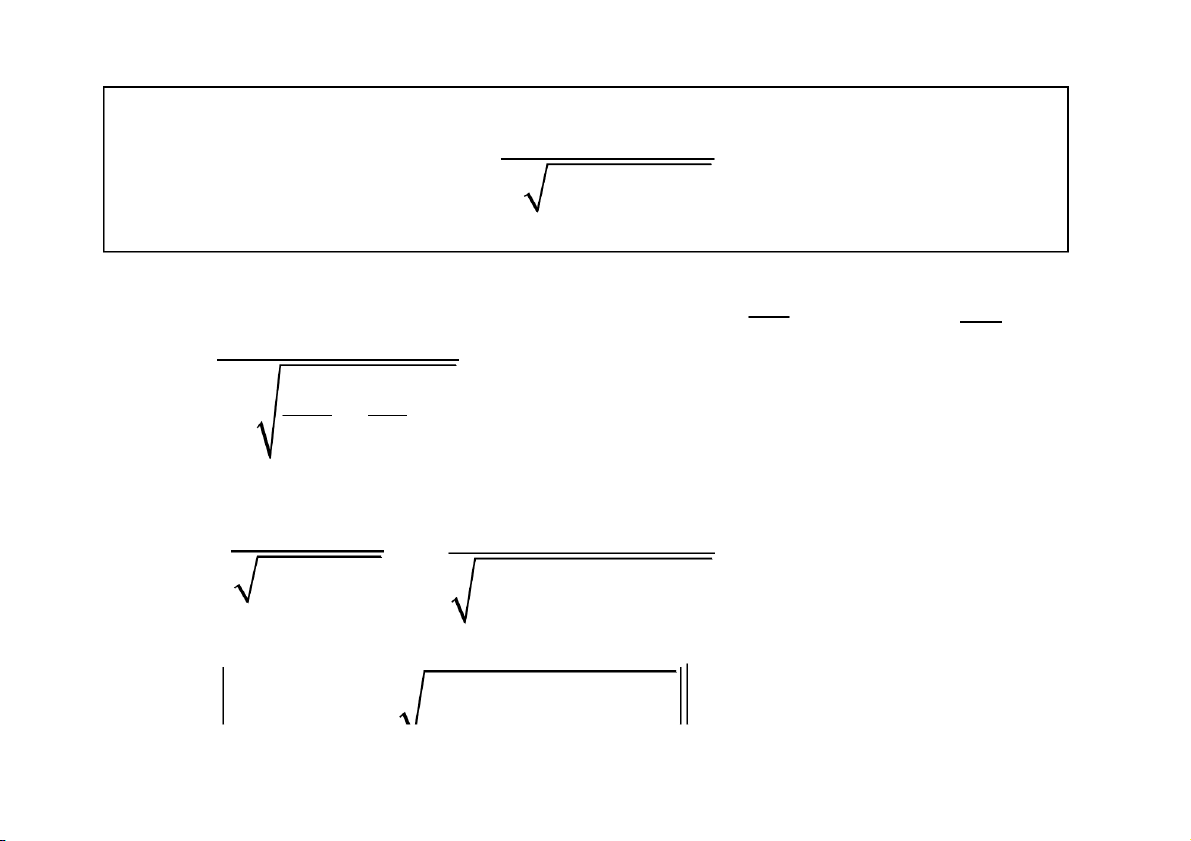
Tính diện tích miền phẳng giới hạn bởi 1 y  , trục hoàn
h và đường thẳng x = 1. 2 x  dx b b dx  1    1   S    lim   lim  lim 1 1 2   2    1 x b   1 x b x xb  1   Diện tích của miền S bằng 1, hữu hạn. CuuDuongThanCong.com
https://fb.com/tailieudientucntt Ví dụ
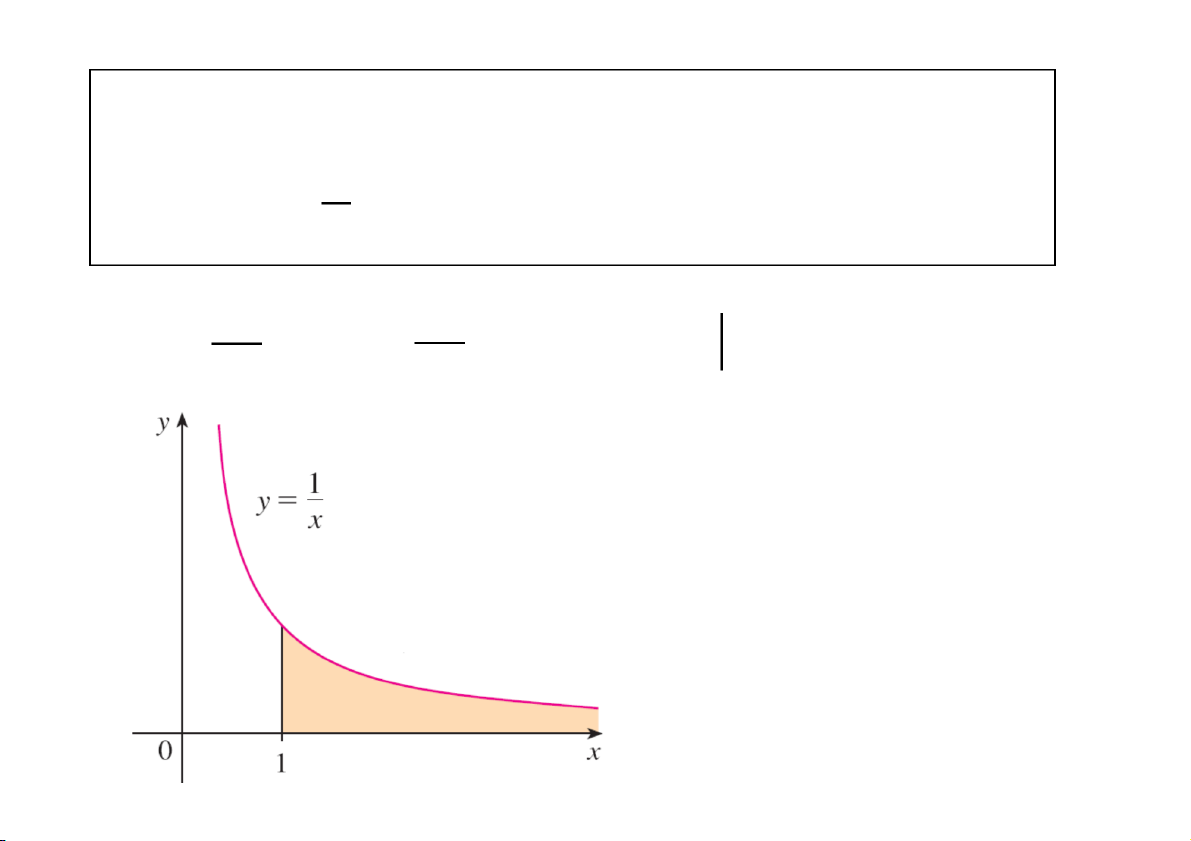
Tính diện tích miền phẳng giới hạn bởi 1 y  , trục hoàn
h và đường thẳng x = 1. x  dx b dx S    lim   lim x
 limlnb   b  ln | | b1  b b 1 x 1 x S là miền có diện tích
vô hạn, bằng  CuuDuongThanCong.com
https://fb.com/tailieudientucntt Ví dụ
Tính diện tích miền phẳng giới hạn bởi 1 y  , trục hoàn . h 2 x  1  dx  dx S    2   2  lim x   2 b  arctan b 0  2  x  1 0 x 1 Diện tích của miền S bằng  . CuuDuongThanCong.com
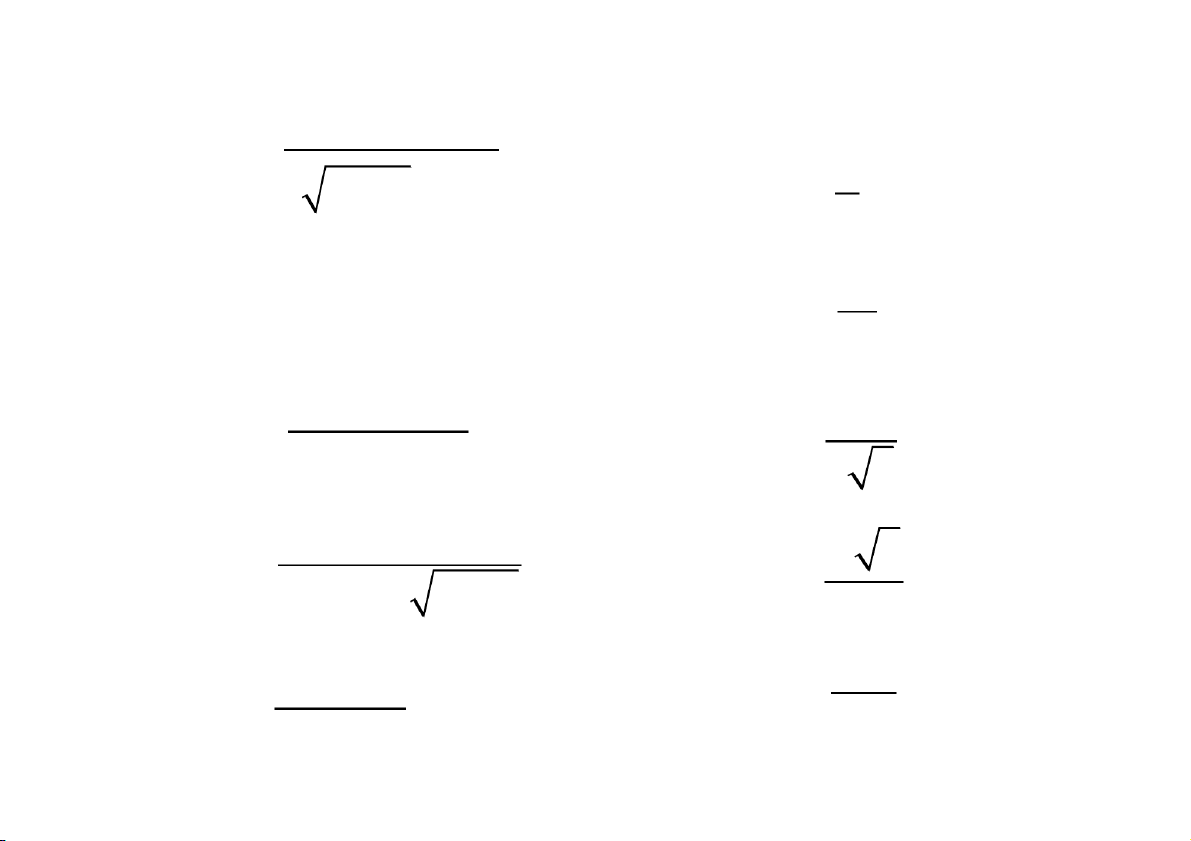
https://fb.com/tailieudientucntt   Ví dụ Tính tích phâ n 2 x I e dx 1   2  x e  2   2  e e x 1 I e dx          2 2 2 2 1   2 e 1  dx Ví dụ Tính tích phâ n I   2 x ln x e   dx  d(ln x)   I     1   1 1     2   1. x ln x 2 ln x ln x   e e ln( ) ln e e  CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx Ví dụ
Tính tích phân I   2 x  5x  6 4 1 1  1 1   2 x  5 x  6
(x  2)(x  3) x  3 x  2   1 1    I   dx     ln | x  3|  ln | x  2 |
x  3 x  2  4 4 4
 ()  () Dạng vô định.?
Không được phép dùng: lim ( f g )  lim f  lim g x x x
khi chưa đảm bảo hai giới hạn vế phải chắc chắn tồn tại.  x  3  x  3  4  3 1 I  ln  lim ln  ln    ln1 ln  ln 2 x  2 x  x  2  4  2 2 4 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx Ví dụ Tính I   5 10
1 x 1  x x 1 1  Đổi biến: t     dx dt dx 6 I   5 x x 1 1 1 6 x  1 x 1 t 1 10 5 x x Đổi cận:
x    t  0 0 dt 1 dt I     2 2 1 t t  1 0 t 1/2  3/4 1
 ln t 1/ 2  t 1/ 22  3/ 4 0 CuuDuongThanCong.com
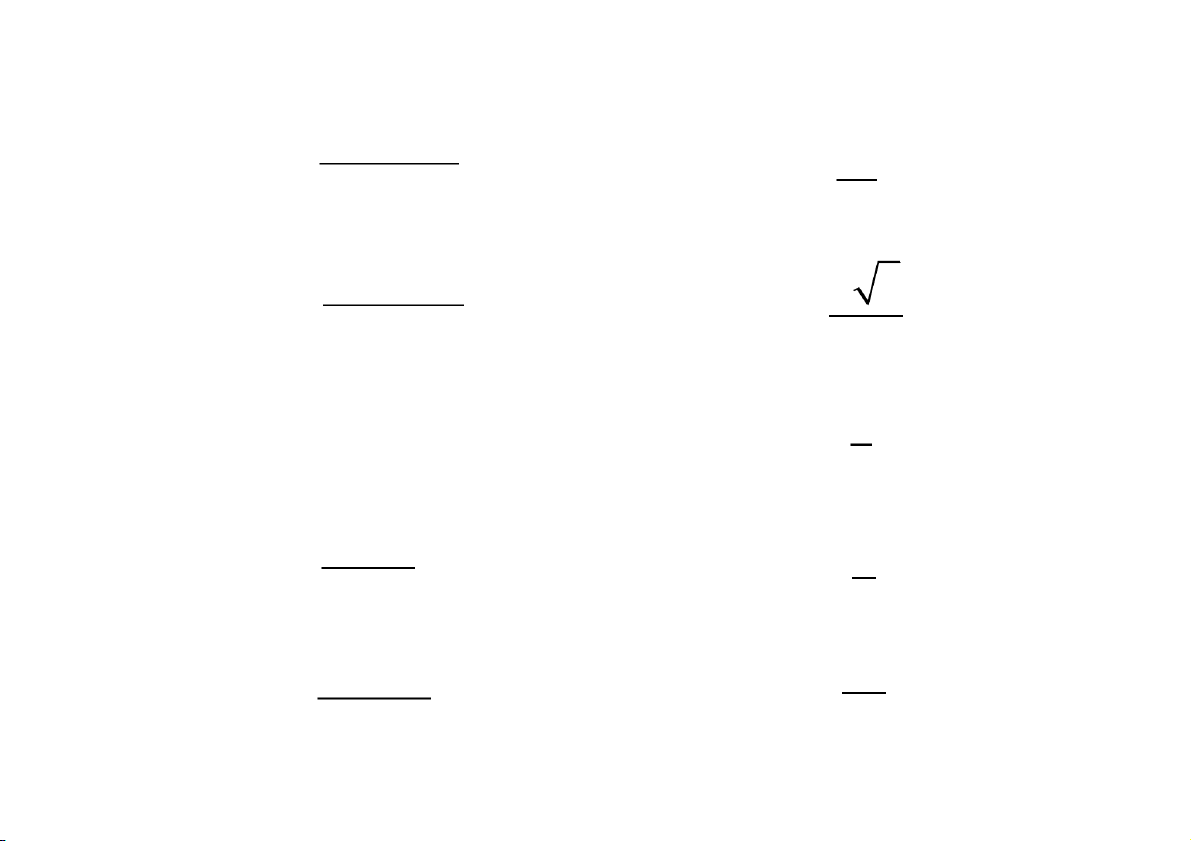
https://fb.com/tailieudientucntt  Ví dụ Tính 2x I e cos xdx 0 Đặt 2  x 2    2  x u e due dx
dv  cos xdx v  sin x   2x 2  sin  2 x I e x e sin xdx  0 0  2x 2 Ta có l i m  e s i n x   0nê n  2 x I e sin xdx x 0 2  x 2    2  x u e du
e dx dv  sin xdx v  cos x    2   2x cos  2  4 x I e x e cos xdx   2  2 4I I  0 0 5 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  arctan x Ví dụ Tính I    dx 1  x 3/2 2 0 dx
Đổi biến: t  arctan x dt  2 1 x
Đổi cận: x  0  t  0 x    t  2 2 1
x  tant  1 x  2 cos t   arctan  x arctan x dx / 2  I       dxt costdt   1 2 1  2 x 3/2 2 1 x 1  x 2 0 0 0 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
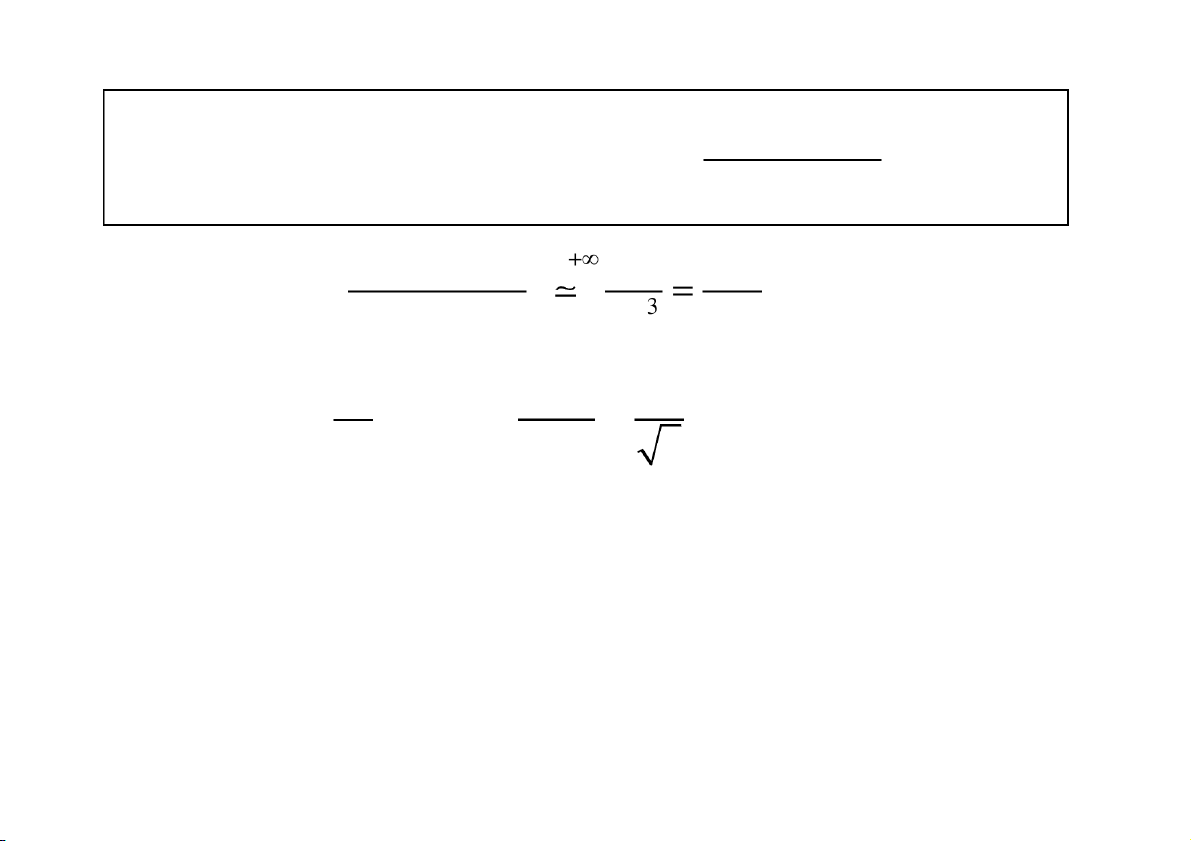
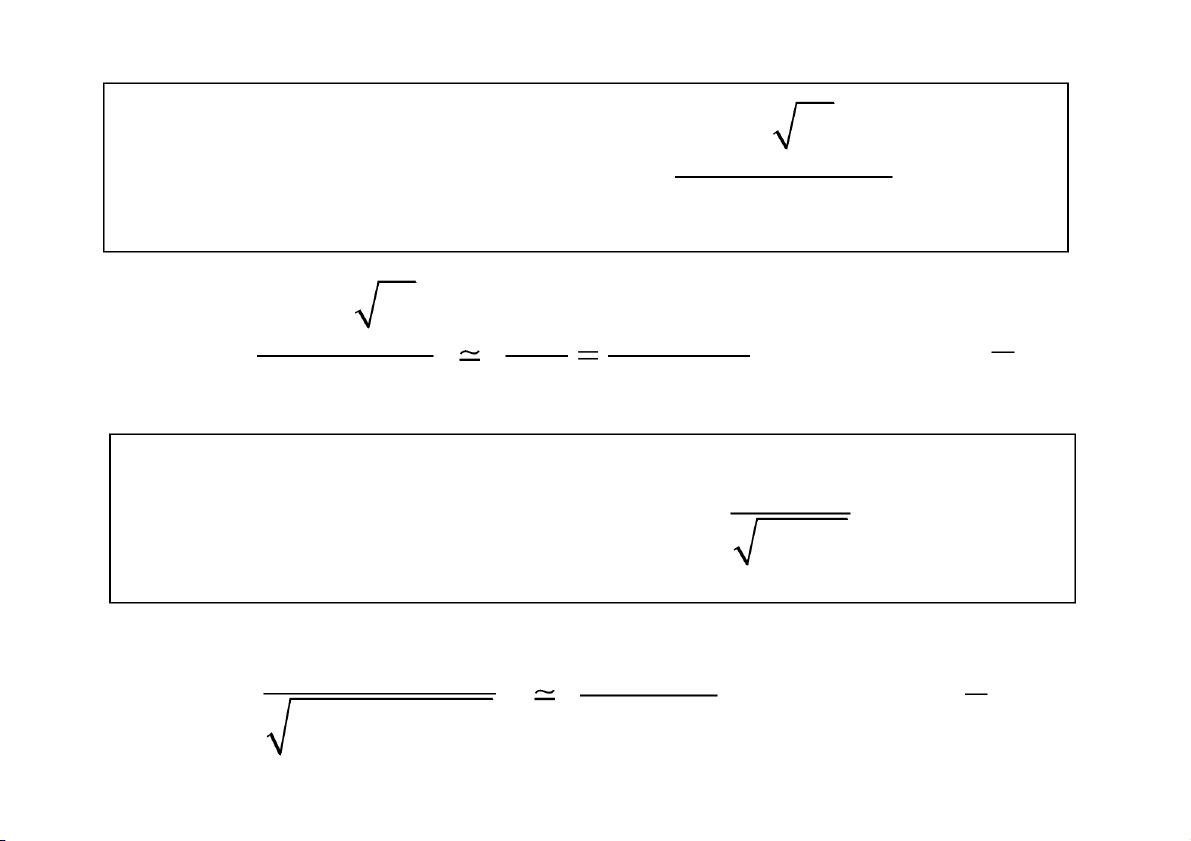
Kết quả (được sử dụng để khảo sát sự hội tụ) Trường hợp 1:  1   1 1 1  1 1 dx     hữu hạn, khác 0. 1   1 a0 x 1 x  1 a   a tích phâ n hộ i t . ụ Trường hợp 2:   1   1 1 x   dx    Tích phâ n phân kỳ.  a0 x 1 a Trường hợp 3:   1  1  
dx  ln | x |   Tích phâ n phân kỳ. a a0 x CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Kết quả (được sử dụng để khảo sát sự hội tụ)  1  hoäi tuï, neáu  1  dx      a 0 x phaân kyø, neáu 1 Neáu  1, thì h I oäi tu  1
Neáu   1, thì pIhaân ky I   dx   2 x ln x
Neáu  1, 1, thì h I oäi tu
Neáu  1, 1, thì I PK CuuDuongThanCong.com
https://fb.com/tailieudientucntt Tích phân hàm không âm Tiêu chuẩn so sánh 1.   x a f ( x )  0 , g ( x ) 
0 và khả tích trên a, 
f (x)  g(x) ở lân cận của  .  Khi đ : ó   1) Nếu g ( x ) d
x hội tụ, thì f x d x hội tụ.  ( )  a a   2) Nếu f ( x ) d x phân kỳ, thì g x d x phân kỳ.  ( )  a a 
Để khsát sự hội tụ của If ( x ) d
x, thường đem so sánh   a với dx đ ã biết kết qu . ả  x a CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Chú ý (trong tiêu chuẩn 1):
1) f(x) và g(x) là hai hàm không âm. 2) Chỉ cần tồn tại   a   x
, f (x)  g(x)  dx
3) Cận dưới của tích phâ n l à số dương ( a  )  0. xa  dx Ví dụ
Khảo sát sự hội tụ I   2 2 2x  sin 3x 1 1 1 Ta có f (x)    g(x) 2 2 2 2x  sin 3x 2x  dx Vì hội tụ  , nên I hội t
ụ theo tchuẩn so sánh 1. 2 2x 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx Ví dụ
Khảo sát sự hội tụ I   2 2 x  sin 3x 1 1 2 Ta có f (x)    g(x) 2 2 2 x  sin 3x x  dx Vì hội tụ  , nên I hội t
ụ theo tchuẩn so sánh 1. 2 x 1  3 ln xdx Ví dụ
Khảo sát sự hội tụ I   x 5 1 3 ln x 1 1 Ta có f (x)     g(x) x   5 x  5 x  5 2x  dx Vì phân kỳ  , nên I phâ
n kỳ theo tchuẩn ssánh 1. 2x 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Tích phân hàm không âm Tiêu chuẩn so sánh 2.   x
a f ( x )  0 , g ( x ) 
0 và khả tích trên a,  f (x) K  lim Khi đ : ó
x g (x)   1) K  0 : nếu g ( x ) d x hộ
i tụ, thì f x d x hộ i t . ụ  ( )  a a 2) h K öõu haïn, 0  :   f ( x ) d x và g x d x cùng HT hoặ c cùng PK.  ( )  a a  
3) K   : nếu f ( x ) d x hộ i tụ, thì g x d x hộ i t . ụ  ( )  a a CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Cách sử dụng tiêu chuẩn so sánh 2. 
Để khảo sát sự hội tụ của f ( x ) d x a
1) kiểm tra f(x) có là hà m không â m (trong lân cận của   ) 2) Tìm hà m g(x) bằn g cách: tìm hàm tương
đương của f(x) khi x tiến ra dương vô cùng. f (x) 3) Tính K  l i m , kết luận.
x  g (x) x  Hai hà
m f(x) và g(x) không âm: nếu f ( x ) , thì  
f (x)dx vaø g(x)dx   cùng tính chất. a a CuuDuongThanCong.com
https://fb.com/tailieudientucntt Hội tụ tuyệt đối Định lý   Nếu f ( x ) d
x hội tụ, thì f x d x hộ i t . ụ  ( )  a a Định nghĩa   Nếu f ( x ) d x hội tụ, thì f x d x gọi l à hội tụ tuyệt đố i  ( )  a a Nếu hà m f(x) có dấ
u tùy ý, để khảo sát sự hội tụ của   ksát sự HT của để sử dụng f (x)dx f (x) dx  tích phân hàm  được hai tiêu a a không âm chuẩn so sánh CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx Ví dụ
Khảo sát sự hội tụ I   5x lnx 1 1 x 1 1 Ta có f (x)  Chọn g(x)  5x  ln x 5x 1/ 2 x f ( ) x 1 Khi đ : ó lim  hữu hạn, khác 0.
x g (x ) 5   Tích phâ n f ( x ) d x và g ( x )
d x cùng hội tụ hay phân kỳ.   1 1  Vì g ( x ) d x phân kỳ (  
 ), nên tích phân I phâ n kỳ.  1 1 2 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  3xdx Ví dụ
Khảo sát sự hội tụ I   3 2x  sin 3x 1 3 x x  3x 3 Ta có f (x)  3 2 2x  sin 3x 2x 2x 1 f x Chọn g(x)  ( ) 1  lim  hữu hạn, khác 0. 2 x
x g (x) 5   Tích phâ n f ( x ) d x và g ( x )
d x cùng hội tụ hay phân kỳ.   1 1  Vì g ( x ) d x hội tụ (    ), nê n tích phân I hội t . ụ  2 1 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  arctan xdx Ví dụ
Khảo sát sự hội tụ I   2 2x  2ln x 1 arctan x x    Ta có f (x)   2 2x  2ln x 2 2 2  2x 4x 1 f x  Chọn g(x)  ( )  lim  hữu hạn, khác 0. 2 x
x g(x) 4   Tích phâ n f ( x ) d x và g ( x )
d x cùng hội tụ hay phân kỳ.   1 1  Vì g ( x ) d x hội tụ (    ), nê n tích phân I hội t . ụ  2 1 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx Ví dụ
Khảo sát sự hội tụ I   (3x 1) x 1 0 1 x 1 1 Ta có f (x)  Chọn g(x)  (3x 1) x 1 3x 3/ 2 x f ( ) x 1 Khi đ : ó lim  hữu hạn, khác 0.
x  g (x ) 3   Tích phâ n f ( x ) d x và g ( x )
d x cùng hội tụ hay phân kỳ.   0 0  Vì J g ( x ) d x hội tụ (    ), nê n tích phân I hội t . ụ  3 1 2 0
Sai! vì J phân kỳ (xem phầ n tích phâ
n suy rộng loại hai) CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx Ví dụ
Khảo sát sự hội tụ I   (3x 1) x 1 0 1  dx dx Cách giả i đúng! I    I I   1 2 (3x 1) x 1 (3x 1) x 1 0 1 I phân
1 là tích phân xác định nên hội tụ. Xét tích I2 1 x 1 1 Ta có f (x)  Chọn g(x)  (3x 1) x 1 3x 3/ 2 x f (x) 1 Khi đ : ó lim  hữu hạn, khác 0.
x  g (x) 3   Tích phâ n f ( x ) d x và g ( x )
d x cùng hội tụ hay phân kỳ.    1 1 Vì  3 g ( x ) d x HT (    ) 1 , nê n I HT, suy ra I HT. 1 2 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  2 Ví dụ
Khảo sát sự hội tụ x I e dx 1    2 1 ( ) xx x f x e
e g(x)    xx 1 e dx  e  
g(x)dx HT  1 e 1 1 Tích phâ
n đã cho hội tụ theo tiêu chuẩn so sánh 1.  2   x 1 Ví dụ
Khảo sát sự hội tụ 1/ I e  cos dx     x  1 2 1/ 1 1 3 x 1
f (x)  e  cos   I HT x 2 2 x 2x 2x CuuDuongThanCong.com
https://fb.com/tailieudientucntt  x e Ví dụ
Khảo sát sự hội tụ I dxx 1 Ta có:    1 x x e  1 1 x   x e x 1 1  f ( ) x    g( ) x Tích phâ n đã cho hội tụ. x 2 xe x  3 2 x x 1 Ví dụ
Khảo sát sự hội tụ I dx  3 x  3x 1 1 3 2 3/ 2 1 x x x    x 1 f (x)  Tích phâ n hội tụ. 3 3/ 2 x  3x 1 x x CuuDuongThanCong.com
https://fb.com/tailieudientucntt  arctan x Ví dụ
Khảo sát sự hội tụ I dx  2 xe 0 arctan x x   f ( ) x g( ) x 2 xe 2e   xx Tính e d x   e   1 HT, nê n tích phân đã cho HT. 0 0  3   2arctan x Ví dụ
Khảo sát sự hội tụ I dx  3/ x e 1 1  1      3   2 / 2 arctan 2arctan   x 3  3
x x 2 / x 2   3/ HT x e 1 3/ x 2 e 1 3/ x 3x CuuDuongThanCong.com
https://fb.com/tailieudientucntt Ví dụ
Chứng minh tích phân hội tụ và tính  dx I   2 3 x 1  x 1 x 1 f (x) 
  2 1 nên tích phân I hội t . ụ 2 1 x x x 2 t  1 x 2 2
t x 1  2tdt  2xdx   xdx  tdt t 1 1 I      ln  ln1 ln  ln3 2 2  t  2  2 t 1 3 x 1 x t 1 3 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  Ví dụ Chứng minh tích dx I   phân hội t ụ và tính 4 2 80 x x 1 1 x 1 1 3 f (x)     1 tụ 3/ 2 nên I hội . 4 2  1 x x x x 2 4 2 t  1 x 4 2  t x 1 3
 4t dt  2xdx  xdx  3 2t dt   dt dt I         2 4 2   t  4  2 2 t 1 t 1 9 t 1 80 x 1 x 9 9  t 1     8  ln  arctant  ln   arctan9   9 t 1 10  2  9 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Ví dụ Chứng minh tích phân phân kỳ và tính giới hạn t x e  x edt I dx  1 t x lim 1 x x e x   x    e 1 1 f (x)    g(x) g
 (x)dx FK nê n I phân kỳ. x x 1 
Giới hạn có dạng vô định , dùn g qui tắc Lôpital  ' t t x xeedtdt   1 tx 1 t  lim  e 1 lim  lim  x lim  0 x x exe ' x
x x e x x CuuDuongThanCong.com
https://fb.com/tailieudientucntt  sin xdx Ví dụ
Khảo sát sự hội tụ I   2 x  ln 2x 1 sin x x 1 1 f (x)   x 2 2 ( ) Hội tụ. x  ln 2x x  ln 2x x
Sai! vì f(x) có dấu tùy ý, không sử dụng so sánh được.  sin x
Xét tích phân hàm không âm J dx  2x ln2x 1 sin x x 1 1 f (x)   2 (x) 2 Hội tụ. x  ln 2x x  ln 2x x Tích phâ
n đã cho hội tụ tuyệt đố . i CuuDuongThanCong.com
https://fb.com/tailieudientucntt  sin xdx Ví dụ
Khảo sát sự hội tụ I   x 1 1 1 Tích phâ
n từng phần: u   du   dx 2 x x
dv  sin xdx v  cos x   sin  x cos x cos x cos1 I dx    dx     J 2 x x x 1 1 1 1  cos x cos x 1 Xét tích phân J dx   hội tụ 2 2 2 x x x 1
J hội tụ, suy ra I hội tụ. CuuDuongThanCong.com
https://fb.com/tailieudientucntt  sin xdx Ví dụ
Khảo sát sự hội tụ I   x 1  sin x
Xét tích phân hàm không âm J dxx 1 2 sin x sin x 1 cos 2x   x x 2x  1 cos2x  dx   cos 2x dx   dx     I I 2x 2x 2x 1 2 1 1 1  dx  cos2xdx I I  1  phân kỳ  hội tụ (tương 2x 2 2x
tự ví dụ trước) 1 1 Tích phâ
n đã cho hội tụ, nhưng không hộ i t ụ tuyệt đối CuuDuongThanCong.com
https://fb.com/tailieudientucntt Chú ý: 1) Vớ
i tích phân chỉ có một điểm suy rộng    f ( ) x dx  khi tách ra có dạn
g vô định G(x)  H (x) a a
a    vẫn chưa kết luận t/phân ban đầu phân kỳ. 2) Vớ
i tích phân có hai điểm suy rộng  a  f (x)dx
khi tách ra thành tích phâ n
f (x)dx f (x)dx     a
chỉ cần một trong ha itphân PK , thì tphân ba n đầ u P . K CuuDuongThanCong.com
https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai Định nghĩa
Điểm x được gọi là điểm kỳ dị của đường cong y = f(x), 0
nếu lim f (x)   x 0 x
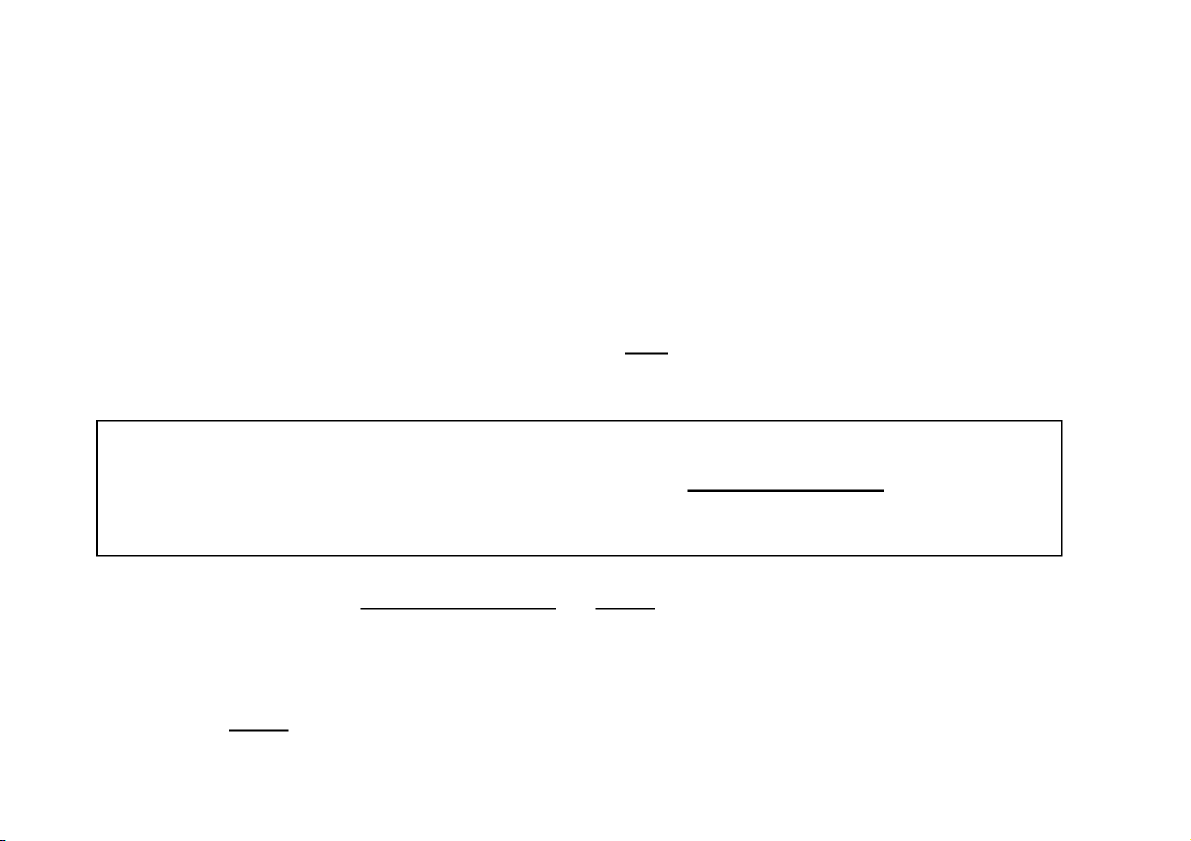
Giả sử trên đoạn [a,b] hàm y = f(x) có một điểm kỳ dị duy nhất l à x = b. 0 b t
f (x)dx : lim  f (x)dx tba a Tích phân suy rộng loại hai của f(x) trên đoạ n [a,b] CuuDuongThanCong.com
https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai
Giả sử trên đoạn [a,b] hàm y = f(x) có một điểm kỳ dị duy nhất l à x = a. 0 Tích phân suy rộng loại hai của f(x) trên đoạn [a,b] b b
f (x)dx : lim  f (x)dxt aa t CuuDuongThanCong.com
https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai
Giả sử trên đoạn [a,b] hàm y = f(x) có một điểm kỳ dị duy nhất là
c a,b Tích phân suy rộng loại hai của f(x) trên đoạ n [a,b] b c b
f (x)dx   f (x)dx   f (x)dx a a c t b  lim  f ( )
x dx  lim  f ( ) x dx   tc tc a t
Tích phân vế trái là hội t
ụ khi và chỉ khi cả hai tích phâ n ở vế phải hội tụ. CuuDuongThanCong.com
https://fb.com/tailieudientucntt
I. Tích phân suy rộng loại hai
Các khái niệm hội tụ, phâ
n kỳ giống như trong tích phâ n suy rộng loại một.
Tương tự tích phân suy rộng loại mộ : t có ha itiêu chuẩn so sánh cho tích phâ n hà m không â . m Khái niệm hộ i t
ụ tuyệt đối cũng tương tự trong tích phâ n
suy rộng loại một: Hội t
ụ tuyệt đối thì hội tụ. CuuDuongThanCong.com
https://fb.com/tailieudientucntt Tính tích phâ
n suy rộng (công thức Newton – Leibnitz) Cho x = b l
à điểm kỳ dị duy nhất của f(x) trên [a,b] 0 Giả sử F(x) l à nguyên hà
m của f(x) trên a,bb t
f (x)dx  lim  f (x)dx  limF(t)  F(a)  t b  tb a a Tích phâ
n tồn tại khi và chỉ khi tồn tại lim F (t) : F(b ) tbb b f (x)dx F (x) F (b   )  F (a) a a
Tương tự cho trường hợp x = a l à điểm kỳ dị. 0 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 4 dx Ví dụ Tính tích phâ
n I   x 2 2 Theo định nghĩa 4 dx 4 d(x  2) I    lim  x  2 t  
t x  21/ 2 2 2 4
 lim 2 x  2  2 2  lim 2 t  2  2 2   t2 t t 2
Theo công thức Newton – Leibnitz (gọn hơn) 4 dx I   4
 2 x  2  2 4  2  2 2  2 2 x  2 2 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 3 dx Ví dụ Tích phâ n I   x 1 0 3 dx I   3
 ln | x 1|  ln 2  ln1 ln 2 x 1 0 0
Sai! vì có điểm kỳ dị x = 1 trong đoạ n [0,3]. 1 3 dx dx I      I I 1 2 x 1 x 1 0 1 1 dx
Xét tích phân I  lim
 limln |t 1|   1  t 1   0 x  1 t1 Vậy tích phân I p hân kỳ. 1 Suy ra tích phâ n đ ã cho phâ n kỳ CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1 dx Ví dụ
Tính tích phân I   (2 x) 1 x 0
Đặt 1 x t 2
1 x t dx  2  tdt
Đổi cận: x  0  t 1 x 1 t  0 1 dx 0 2tdt 1 2dt I       (2  x) 1   2 2 1 1 t  1 t 0 x t 0 1  I  2arctan t
 2arctan1 arctan0  0 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Tích phân hàm không âm Tiêu chuẩn so sánh 1. Trường hợp x = b l
à điểm kỳ dị duy nhất. 0   x a f ( x )  0 , g ( x ) 
0 và khả tích trên a,b
f (x)  g(x) ở lân cận của trái của . b Khi đ : ó b b 1) Nếu g ( x ) d
x hội tụ, thì f x d x hội tụ.  ( )  a a b b 2) Nếu f ( x ) d x phân kỳ, thì g x d x phân kỳ.  ( )  a a
Tương tự cho trường hợp x = a l à điểm kỳ dị du y nhất. 0 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Tích phân hàm không âm
Tiêu chuẩn so sánh 2. (x = b là điểm kỳ dị duy nhất) 0   x
a f ( x )  0 , g ( x ) 
0 và khả tích trên a,bf (x) K  lim đó  Khi : x bg(x) b b 1) K  0 : nếu g ( x ) d x hộ i tụ, thì f x d x hộ i t . ụ  ( )  a a 2) h K öõu haïn, 0  : b b f ( x ) d x và g x d x cùng HT hoặ c cùng PK.  ( )  a a b b
3) K   : nếu f ( x ) d x hộ i tụ, thì g x d x hộ i t . ụ  ( )  a a CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Kết quả (được sử dụng để khảo sát sự hội tụ) b 1 phaân kyø, neáu  1  dx       a x a  hoäi tuï, neáu 1 b 1 phaân kyø, neáu  1  dx       a b x  hoäi tuï, neáu 1
Chú ý: Kết luận ngược lại so với tích phân loại một! CuuDuongThanCong.com
https://fb.com/tailieudientucntt 2 dx Ví dụ
Khảo sát sự hội tụ I   2 1 x 1 x 1 1   1
Ta có f (x)  (x 1)(x 1) 2 x  1/2 1 1 f ( ) x 1 Chọn g( ) x    hữu hạn,  lim x  1/2 1
x g(x) 2 khác 0. 2 2 Tích phâ n f ( x ) d x và g ( x ) d
x cùng hội tụ hay phân kỳ.   1 1 2 Vì g ( x ) d x hội tụ (    ), nê n tích phân I hội t . ụ  1 1 2 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt ln 5 3 1 1 x dx Ví dụ
Khảo sát sự hội tụ I   x e 1 0 ln 5 3 1 x    3/ 5 x 0 x 1 1 f (x) 
hội tụ vì   1 x 2 / 5 e 1 x (x  0) 2 3 3 2x dx Ví dụ
Khảo sát sự hội tụ I   2 0 9  x 3 2  x x 3  18 1 f (x)  hội     tụ vì 1 3  1/ 2 x(3  x) (x 3) 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1 3 5x x Ví dụ
Khảo sát sự hội tụ I dx  tanxx 0 3 x 3 3 x
tan x x x
 (x )  x 3  ( x ) 3 3 3   1/ 2 x 0 5x x x 3 kỳ 5 vì    5/ 2 1 tan x x x / 3 (x  phân 0) 2 4 dx Ví dụ
Khảo sát sự hội tụ
I   x  2 0 1  x4 x  2 4 f (x)  
phân kỳ vì   1 x  2 1 x  4 ( x  4) CuuDuongThanCong.com
https://fb.com/tailieudientucntt  2 sin xdx Ví dụ
Khảo sát sự hội tụ I   2 x 0 1 2  2 sin xdx sin xdx I    I I   2 2 1 2 x x 0 1 2 sin x I là phân rộng  1 không tích suy lim 1 2 x 0  x mà l
à tích phân xác định nê n HT 2 Ta có sin x 1   g(x) 2 2 x x  Vì g ( x ) d x HT , nê n I HT, suy ra I HT.  1 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt I. Tính các tích phân sau  1 1)  2 dx ln 2
3 (x  1)(x  2) 3  1 2)  1 2 dx  ln 5  ln 2
2 ( x 1)( x  2)( x  3) 4 3  (5x  3) 11 1 3)  dx  2 ln 2 ln 3 3 ( x  2)(3x  2x 1) 5 5 2  ( x 1) 4)  dx 1 ln 2 3 2 x(x  1)  3 17 dx   5)  ln 2  16 128 x  2 3 2 1 (x 1) CuuDuongThanCong.com
https://fb.com/tailieudientucntt  1 6)  dx 2 7 2 arctan 7 0 x x  2 7  x  3 3  3 7)  dx ln 3  2 1 x( xx 1) 2 18 2  x  8)  dx 6 0 x  1 6  dx arctan 2 9)  2
0 4x  4x  5 4   dx 10)  4 xx 0 e e CuuDuongThanCong.com
https://fb.com/tailieudientucntt  1 11)  dx 2  2ln 2 x x 0 e e  1  12)  dx 2 1 x(ln x  1) 2  1 13)  dx 1 2 0 cosh ( ) x  1 2 14)  xxe dx 4 0  dx ln 2 15)  6 9 1 x( x  3) CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx 16)  ln 2 4 x 0 e 1 4  2x  17)  dx x 0 4  1 4ln 2  dx 18)   x 0 e 1  dx 19)  1 2 2 2 x x 1    e 1 dx 20)  ln    e 1  1 sinh x CuuDuongThanCong.com
https://fb.com/tailieudientucntt  3 1 21) xe dx 2 1 3e  dx 22)  1 2 e x ln x  xdx 1 23)  2 0 2x ln 2  dx  24)  2 1 (1 x) x ln 7 1   5   xdx   arctan   25)  6 3  2 3 3  2 x  1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx 26)  2
0  x 1 x2 2 3  2 27)  x  3 e cos3xdx 0 13  dx  28)  4 2 3
 (x x  1) 3 3  dx 29)   3 2 2
0 (4x 1) x 1 9 2  13 x 12 30)   4 x   dx 2 2 1 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt  dx 31)  1 2x  32 1 10  dx 32)  2 5 3/ 2 2 ( x  3) 5  3 2 33)  x  1 x e dx 0 3  ln xdx 34)  1 3 1 x 4  1 1 35)  dxx 5 1 1 64 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1  3 3
2  x x dx 36)  625 5 3 0 x 187 1 dx 37)   2
1 (4  x) 1 x 15 4 2 x dx 38)   5 2 2
2 (1 x ) 4  x   5 2 dx 39)   1 x x 1 2 2  dx 40)  2 3 1 x x  1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt I. Tìm tấ t cả các giá trị  để chuỗi hộ it ụ  3/ xe 1 1)  ln 1 d  , x   0 không tồn tại 1     arctan3x 2)  dx  1  0 (2  x)  1   3)  dx 2  1 x  2x  x 4)   dx x  1 e x  1   1 5)  dx  1 x  2 x CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1 ln 1 x  3 6)  dx    2 0 x e 1  dx   7)  3 1     4 2 
x  ln(1  x )  5 0 x 5 5 3 (x 1)   5 8)  dx   7 5 6 1 x x 1  dx 9)      2 3 1
x  sin xx 1  x e  1 x 1   10)  dx 2
0 cosh x  cos x CuuDuongThanCong.com
https://fb.com/tailieudientucntt