







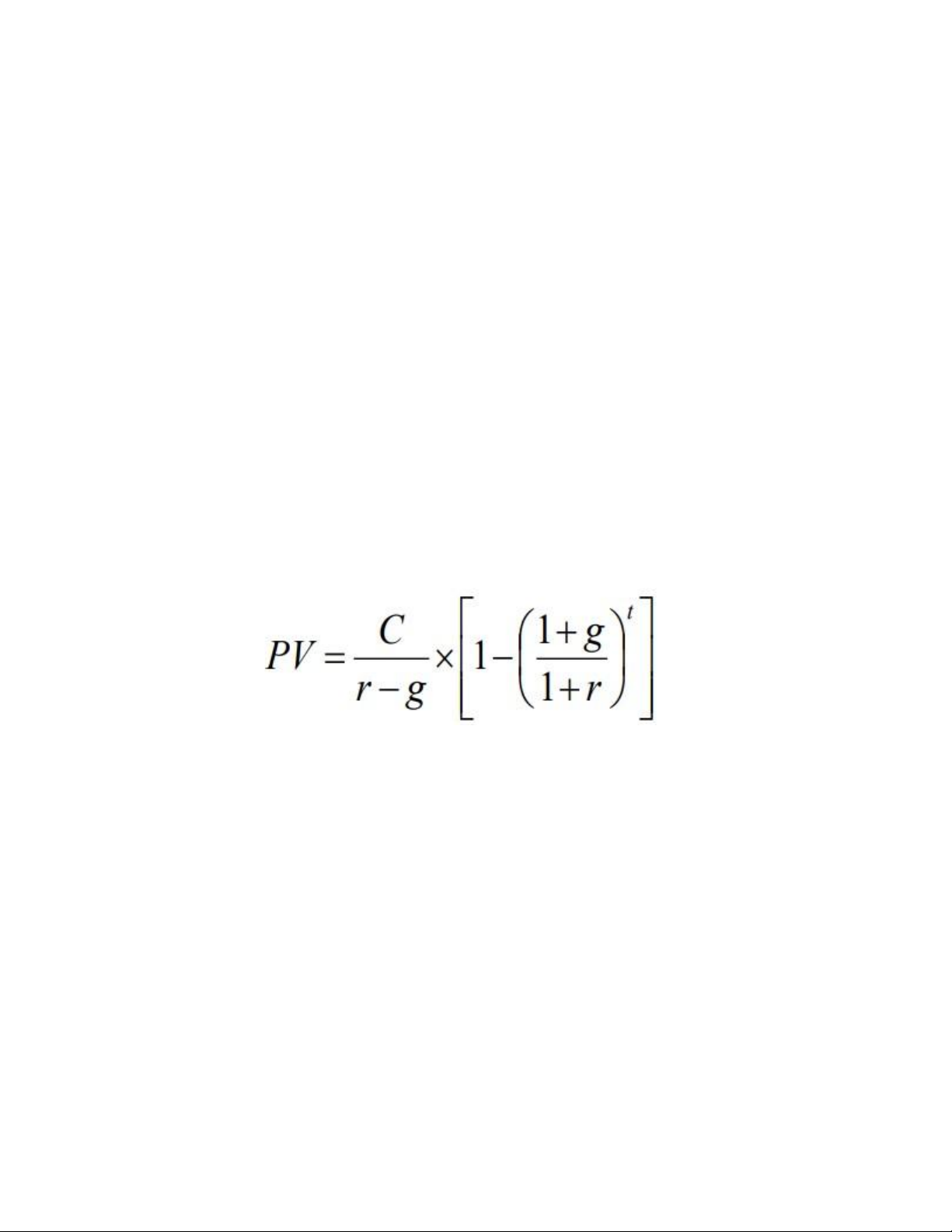




Preview text:
lOMoAR cPSD| 58562220 TIME VALUE OF MONEY
“Time Value of Money” states: “A dollar in hand today is worth more
than a dollar promised at some time in the future.”
Simple interest rate: Interest paid (earned) on only the original amount (principal). FV= PV(1+r*t)
Compound interest rate: Interest that is earned on both the principal and
any interest that has been earned previously. FV = PV(1+r)^t
FV: Future value received after t periods
PV: present value t: number of periods r: interest rate of each period
Special notes: Interest rate = Discount rate = Cost of capital =
Opportunity cost of capital = Required Return
Ex1. Suppose you great great grandparents deposited $10 at 5.5% interest
200 years ago. How much would you have today? 447,189
2. Suppose you have $500 to invest and you believe that you can earn 8%
per year over the next 15 years. a)
How much would you have at the end of 15 years using compoundinterest? b)
How much would you have at the end of 15 years using simple
interest?I. Basic concepts:
1. Present Value (PV): Value today of a future cash flow
2. Future Value (FV): Amount to which an investment will grow after earning interest lOMoAR cPSD| 58562220
Ex: You lent $10,000 to John in 1997 and he returned $13,000 to you in 2000,
which amount should be called PV and FV?
-> Although both $10,000 and $13,000 are cash flows that occurred in the
past, $10,000 is still called PV, and $13,000 is called FV. This is because
$10,000 is the cash flow at the beginning, and $13,000 is the cash flow at
the end of the time period being considered.
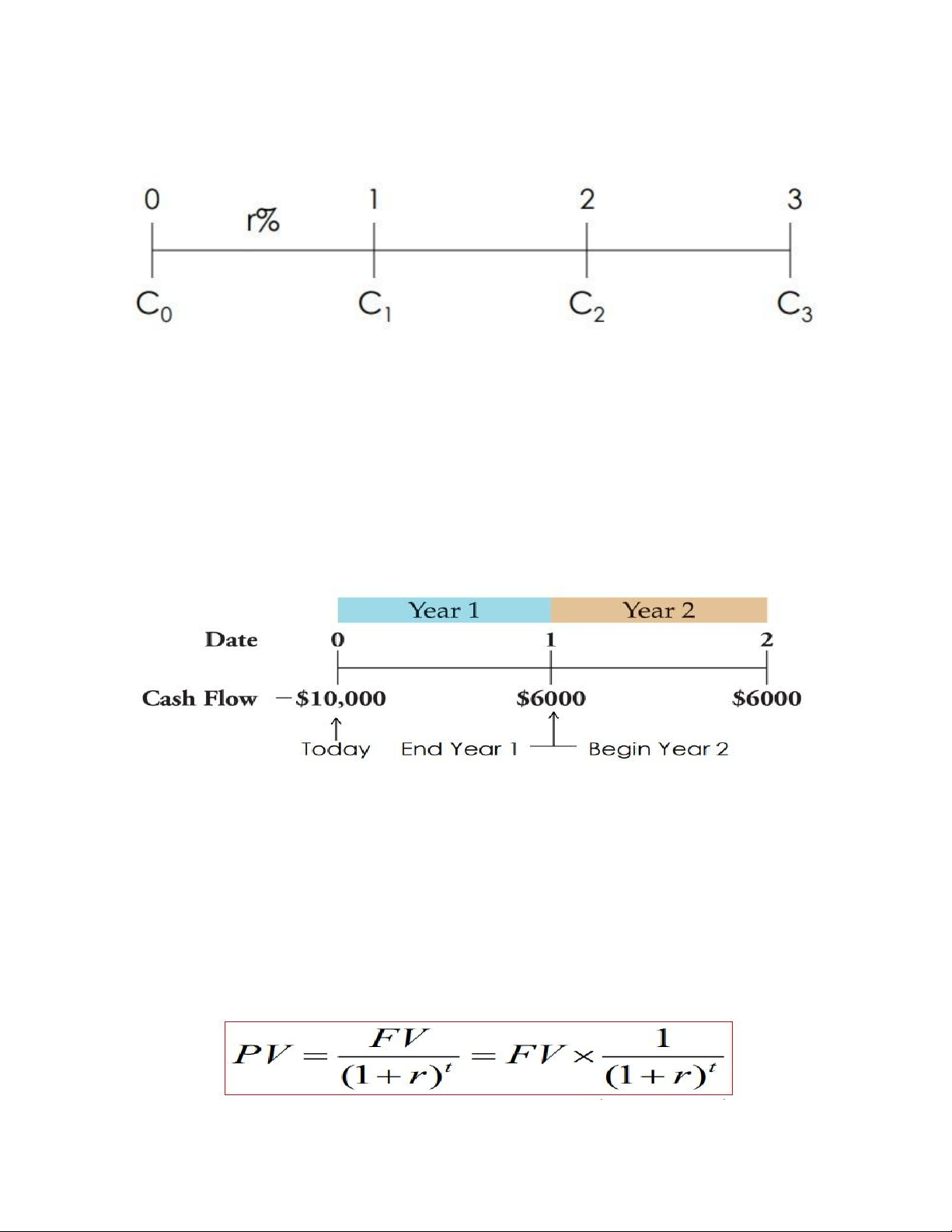
FUTURE VALUE – GENERAL FORMULA Where: PV = present value r = period interest rate (decimal) t = number of periods lOMoAR cPSD| 58562220 II. Timeline Cash flows: 2 types
- Cash inflows (i.e. money we receive) – represented by positive numbers.
- Cash outflows (i.e. money we pay) – represented by negative numbers
Ex1: Assume that you are lending $10,000 today and that the loan will be
repaid in two annual $6,000 payments. III. PV and Discouting
- “How much do I have to invest today to have some amount in the future?”
- Discounting: finding the present value of some future amount Discounting formula lOMoAR cPSD| 58562220
Ex1: Suppose you need $10,000 in one year for the down payment on a new
car. If you can earn 7% annually, how much do you need to invest today?
Ex2: Ms. Hoa wants to begin saving for her daughter’s college education
and she estimates that she will need $150,000 in 17 years. If Ms. Hoa feels
confident that by depositing money in the bank, she can earn 8% per year,
how much does she need to invest today?
Ex3: Your parents set up a trust fund for you 10 years ago that is now worth
$19,671.51. If the fund earned 7% per year, how much did your parents invest?
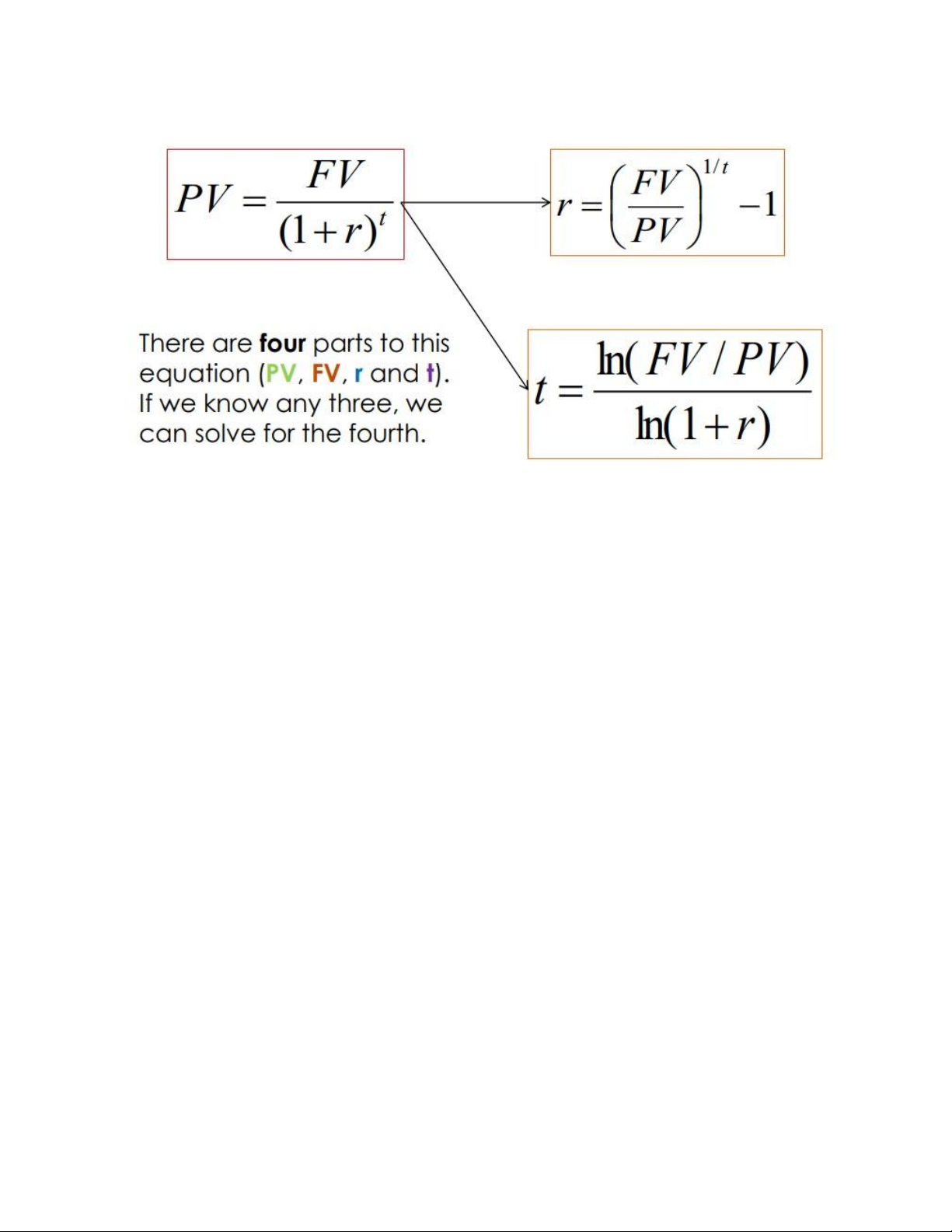
PV - Important relationship
- For a given interest rate – the longer the time period, the lower the present value
- For a given time period – the higher the interest rate, the smaller the present value lOMoAR cPSD| 58562220
IV. FV and PV of uneven CF
Uneven CF: là dòng tiền gồm những khoản gt ko giống nhau xảy ra trong
1 số thời kỳ nhất định lOMoAR cPSD| 58562220 lOMoAR cPSD| 58562220
Ex: You are planning to save money. You deposit $7000 and $8000 in Y1
and Y2, respectively. How much money is in your account at the end of Y2?
Assume you can earn interest at 10% p.a REVISION EXERCISES
1. Joe just inherited the family business, and having no desire to
run the family business, he has decided to sell it to an
entrepreneur. In exchange for the family business, Joe has been
offered an immediate payment of $100,000. Joe will also receive
payments of $50,000 in one year, $50,000 in two years, and
$75,000 in three years. The current market rate of interest for Joe
is 6%. In terms of present value, how much will Joe receive for
selling the family business?
2. You invest a single amount of $10,000 for 5 years at 10%. At the
end of 5 years you take the proceeds and invest them for 12 years
at 15%. How much will you have after 17 years? I. Perpetuity
1. Perpetual CF: Infinite series of equal payments starting one period from now. lOMoAR cPSD| 58562220
Note: Dấu hiệu nhận biết
- The first cash flow does not occur immediately; it arrives at the end of thefirst period (C0 = 0).
- All the cash flows in a perpetuity are the same (constant).
Ex: 1. An investment offers a perpetual cash flow of $500 every year. The
return you require on such investment is 8%. What is the value of this investment?
2. You decide to endow a scholarship of $100,000 per year in perpetuity
for IU. How much do you need to donate if IU can earn a return of 10% p.a on the endowment?
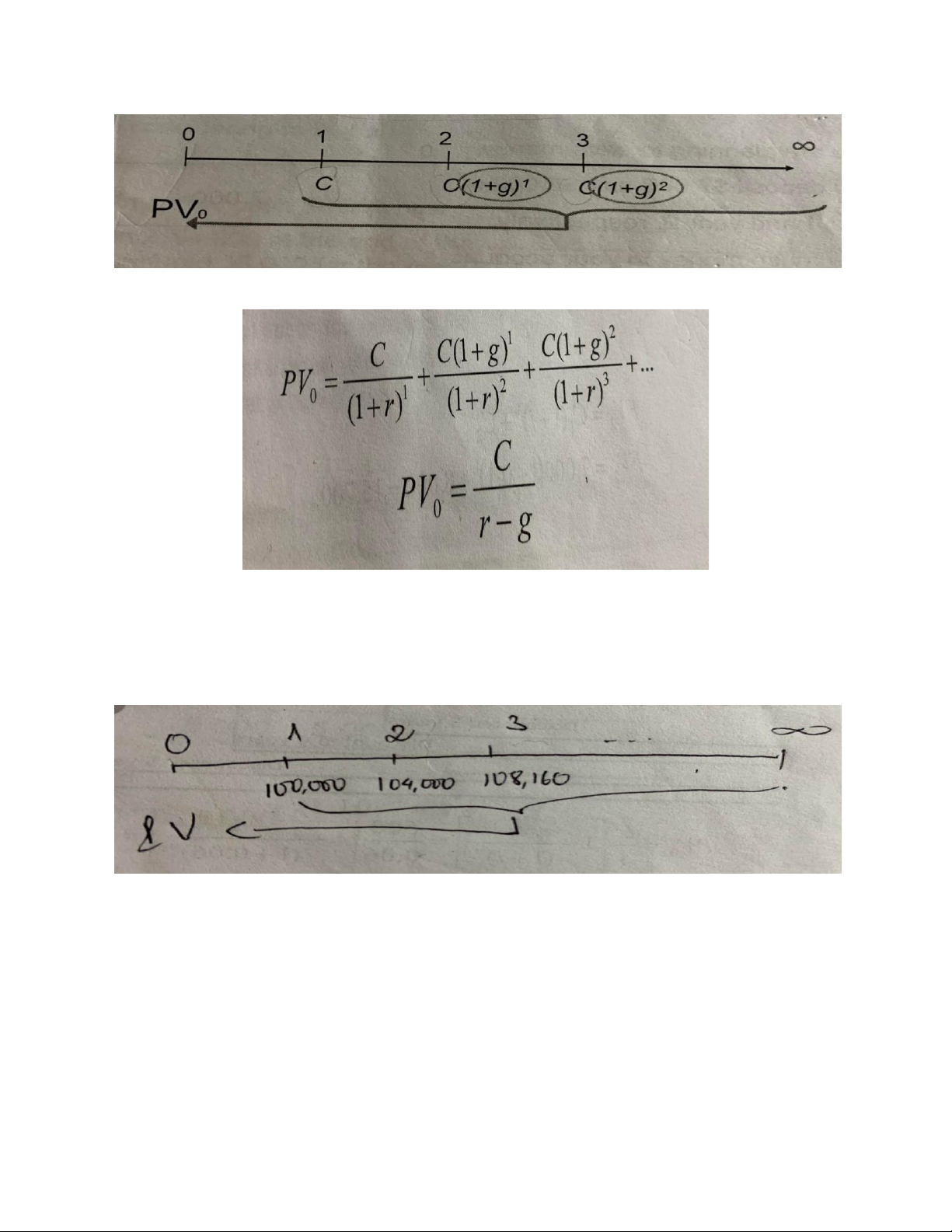
2. Constant growth perpetual CF: series of equal growing payments
occur at the end of each period forever lOMoAR cPSD| 58562220
Ex: After careful consideration, you decide that the scholarship you endow
at IU should keep pace with inflation, which is expected to be 4% per year.
How does this change the donate amount
II. Annuity (mỗi năm đều gửi 1 khoảng tiền giống nhau, có xác định thời hạn)
- Ordinary Annuity: The first payment occurs at the end of the period
- Annuity Due: The first payment occurs at the beginning of the period (starts immediately) lOMoAR cPSD| 58562220
1. Ordinary Annuity: (CF xảy ra vào cuối mỗi period)
Present value of an ordinary annuity of C dollars per period for t periods when the interest is r
Ex: 1. You will receive $12,000 a year for the next ten years from a trust fund
your grandmother is establishing. What is this gift worth today at a 9% discount rate?
2. Your company recently borrowed $50,000 to buy some office
equipment. The financing terms call for eight equal quarterly
payments. The interest rate is 10%. What is the amount of each quarterly payment?
3. You ran a little short on your spring break vacation, so you put $1000
on your credit card. You can only afford to make the minimum lOMoAR cPSD| 58562220
payment of $20 per month. The interest rate on the credit card is
1.5% per month. How long will you need to pay off the $1,000? Future value
Ex: 1. Suppose you begin saving for your retirement by depositing $2,000
per year to a retirement account paying 7.5%. How much will you have if you retire in 40 years?
2. Ellen is 35 years old, and she has decided it is time to plan seriously for
her retirement. At the end of each year until she is 65, she will save $10,000
in a retirement account. If the account earns 10% per year, how much will Ellen have saved at age 65?
2. Annuity due: payment occurs at the beginning of each period lOMoAR cPSD| 58562220
Ex: 1. You are saving for a new house, and you put $10,000 per year in an
account paying 8%. The first payment is made today. How much will you have at the end of 3 years?
2. You are buying some land from your parents today. You agreed to pay
them $5,000 a year for six years. The first payment is due today. What is the
actual selling price of the land if your parents are only charging you 3% interest?
Growing Annuities: A series of payments that grow at a constant rate for a specified number of years.
Example: A defined-benefit retirement plan offers to pay $20,000 per year
for 40 years and increase the annual payment by 3% each year. What is the
present value at retirement if the discount rate is 10%? Ex: mixed O.A and A.D
There are two options. Which one is better?
1. HN Ltd is selling TVs on the following terms:
- No payments until 13rd month after purchase lOMoAR cPSD| 58562220
- After 13 months, make 12 monthly payments of $75 each, opportunity cost 6% p.a 2. Pay cash $750 II. Interest rate:
Real interest rate: Rates of return that have been adjusted for inflation
Nominal interest rate: Rates of return that have been adjusted for inflation lOMoAR cPSD| 58562220
Ex: If the interest rate on the one year government bond is 5.9% and the
inflation rate is 3.3%, what is the real interest rate?
ANNUAL PERCENTAGE RATE (APR): lãi suất hằng năm,
What is the APR if the monthly rate is 0.5% 0.5 12 = 6%
What is the APR if the semiannual rate is 0.5% 0.5 2 = 1%
What is the monthly rate if the APR is 12% with monthly compounding? 12/ 12 = 1%
-> Note: Interest rate và time period phải match với nhau. Nếu period là
annual thì interest rate cũng phải là annual rate, period là month thì interest rate là monthly rate
EFFECTIVE ANNUAL RATE (EAR): dùng để so sánh lãi suất giữa các ngân hàng
Ex: You are looking at two savings accounts. One pays 5.25%, with daily
compounding. The other pays 5.3% with semiannual compounding. Which account should you use? lOMoAR cPSD| 58562220
Ex: The following interest rates are being offered by three competing banks:
4% compounded monthly; 4.1% compounded quarterly; 4.15%
compounded annually. Which one is the most attractive? III. Loans
Pure discount loan: Người vay nhận tiền ngay hôm nay và hoàn trả
một lần duy nhất vào một thời điểm nào đó trong tương lai.
Interest-only loan: Người vay trả lãi mỗi kỳ và trả lại toàn bộ tiền gốc
(khoản vay ban đầu số tiền) tại một số thời điểm trong tương lai lOMoAR cPSD| 58562220
Amortized loan: Người cho vay yêu cầu người đi vay hoàn trả các
phần của số tiền cho vay theo thời gian.
- > Amortizing: The process of providing a loan to be paid off by making regular principal reductions
Formula: (bản chất của amortized loan là ordinary annuity) Ex: Monthly Mortgage Payments
Assuming a 30-year loan with monthly compounding, and a rate of 6% . The
loan is needed for a $300,000 home and the down payment is $50,000. Ex retirement savings:
Susan, 35 years old, who would like to retire at age 65 (30 years from today).
Her goal is to have enough in her retirement account to provide an income
of $75,000 a year, starting a year after retirement or year 31, for 25 years
thereafter. She had a late start on saving for retirement, with a current
balance of $10,000. To help her meet this goal, estimate how much she will
need to save every year starting from now. Assume an average annual 8%
return in the retirement account. lOMoAR cPSD| 58562220
Refinance: đổi “chủ nợ”, từ tổ chức cho vay (lender) này sang một tổ chức
cho vay (lender) khác, với lãi suất có thể tốt hơn.
Ex: A 2-year, $8,000 loan quoted at an 8.5%, compounded monthly interest
rate is refinanced 10 months later. The borrower asks for a new 2-year loan
where the principal is the current remaining balance of the original loan in
order to reduce the monthly payment. Refinancing this loan requires a 0.5%
fee of the remaining balance. What are the monthly payments of both the
first loan and the refinanced one?




