Tính thể tích khối chóp biết góc giữa hai mặt phẳng Toán 12

Tài liệu gồm 38 trang, hướng dẫn giải bài toán tính thể tích khối chóp biết góc giữa hai mặt phẳng, đây là các bài toán được phát triển dựa trên câu 49 trong đề minh họa THPT Quốc gia môn Toán năm 2020 của Bộ Giáo dục và Đào tạo.Mời bạn đọc đón xem.

17 9 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 758

BÀI TẬP MẪU

(ĐỀ MINH HỌA BDG 2019-2020) Cho khối chóp

.S ABC

có đáy

ABC

là tam giác vuông cân tại

AB a



90SBA SCA 

, góc giữa hai mặt phẳng

 

SAB và

 

SAC bằng

. Thể tích của khối đã cho

bằng

a . B.

. C.

. D.

CÁCH 1: Xác định góc giữa hai mặt phẳng.

Phân tích hướng dẫn giải

1. Dạng toán: Tính thể tích khối chóp , biết góc giữa hai mặt phẳng..

Phương pháp:

Tìm đường cao của hình và khai thác được giả thiết góc của đề bài

2. Hướng giải:

B1: Tìm đường cao của hình : học sinh phải tìm đường cao bằng cách suy ra từ các quan hệ vuông góc

giữa đường với đường để chứng mình được đường vuông góc với mặt, hay phục dựng hình ẩn để xác

định đường cao.

B2:



Để khai thác được giả thiết góc ta thường làm :

+ Xác định được góc. Trong quá trình xác định góc phải tránh bẫy khi đưa về góc giữa hai đường

thẳng cắt nhau nó là góc không tù.

+ Cần chọn ẩn (Là chiều cao hay cạnh đáy nếu giả thiết chưa có) sau đó sử dụng giả thiết góc để tìm

ẩn.



Có thể sử dụng nhiều phương pháp khác ngoài hai cách truyền thống để tính góc giữa hai mặt bên.

Phương pháp khoảng cách : giả sử



là góc giữa hai mặt bên

 



và

 



( ,( ))

sin

( , )

d M

d M d





 ở đây

     

,d M

  

  

Phương pháp diện tích hai mặt bên : giả sử



là góc giữa hai mặt bên

 

ABC

và

 

ABD

2 3.

sin sin

3 2

ABC ABD ABCD

ABCD

ABC ABD

S S V AB

AB S S

 

 

   



 

Công thức đa giác chiếu : cos







Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn D

TÍNH THỂ TÍCH KHỐI CHÓP BIẾT GÓC GIỮA HAI MẶT PHẲNG

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 759

Hai tam giác vuông SAB và SAC bằng nhau chung cạnh huyền SA .

Kẻ BI vuông góc với SA suy ra CI cũng vuông góc với SA và IB IC .

 

,SA IC SA IB SA IBC    tại

 

. . .

1 1 1 1

3 3 3 3

S ABC A IBC S IBC IBC IBC IBC IBC

V V V S AI S SI S AI SI S SA

   

      

   

 

   



0 0

, , , 60 60SAB SAC IB IC IB IC BIC    

hoặc



120BIC  .

Ta có IC IB AB a   mà 2BC a nên tam giác IBC không thể đều suy ra



120BIC  .

Trong tam giác IBC đặt

 

0IB IC x x  

có:

 

2 2 2

2 2

1 6 6

cos120

2 . 2 3 3

x a

IB IC BC a a

x IB IC

IB IC



 

        

Trong tam giác ABI vuông tại I có:

2 2 2

6 3

3 3

a a

AI AB IB a

 

    

 

 

Trong tam giác SAB vuông tại B đường cao BI có:

2 2

. 3

AB a

AB IA SA SA a

    

Vậy



1 1 1 1 6

. . sin a 3 sin120

3 3 2 6 3 6

S ABC IBC

a a

V S SA IB IC SA BIC



 

   

 

 

CÁCH 2: Xác định đường cao của hình chóp.

Phân tích hướng dẫn giải

1.Dạng toán: Đây là dạng toán tính thể tích khối chóp có lồng ghép góc giữa hai mặt phẳng.

Phương pháp

Sử dụng công thức tính thể tích khối chóp

V S h

2. Hướng giải:

B1: Gọi

là chân đường cao kẻ từ S . Khi đó tứ giác ABHC là hình vuông.

a 2

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 760

B2: Xác định góc giữa hai mặt phẳng

 

SAB

và

 

SAC

rồi từ đó tính độ dài đường cao SH .

B3: Áp dụng công thức tính thể tích khối chóp.

Từ đó, ta có thể giải bài toán cụ thể như sau:

Lời giải

Chọn D

Gọi

là hình chiếu của S trên phẳng

   

ABC SH ABC 

Ta có

 

SH AB

AB SDH AB BH

SB AB





   







. Chứng minh tương tự

AC HC

Lại có AB AC .

ABHC là hình vuông.

Gọi

là hình chiếu vuông góc của

lên SA. Khi đó CK SA ( SBA SCA   ).

Suy ra góc giữa hai mặt phẳng

 

SAB

và

 

SAC

bằng góc giữa hai đường

và CK .

Đặt

SB x

, khi đó:

2 2 2 2 2 2

2 2

2 2 2 2 2 2

. .SC CA a x a x

BK CK

SC CA a x a x

   

  

và



2 2 2

0 2 2 2

cos cos 60 2.

2 . 2

BK CK BC

BKC BK BC BK

BK CK

 

     

2 2

2 2 2 2 2

2 2

2 2 2 2 2 2 2

2 2

( )

2. 3. .

3. 2

a x

x a l

BK BC BK BK BC

a x

BK BC BK BK BC a x

x a

a x









  

  





   



 

   







 











Với

2x a S H a  

1 1 1

. . . . .

3 3 2 6

S ABC ABC

V S SH AB AC HS



  

Bài tập tương tự:

Câu 49.1: Cho hình chóp .S ABC có đáy ABC là tam giác cân tại A , với 5AB  , 2BC  . Các cạnh

bên đều bằng

9 2

và cùng tạo với mặt đáy góc 60. Thể tích V của khối chóp .S ABC bằng.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 761

3 3

V 

. B.

3 3

V 

. C.

V 

. D.

V 

Lời giải

Chọn C

Kẻ

   

,SH ABC H ABC 

Ta có

2 2 2

HA SA SH

HB SB SH

HC SC SC



 



 





 



Mà SA SB SC  HA HB HC   . Suy ra H là tâm đường tròn ngoại tiếp tam giác ABC .

Đặt

5AB AC x  

2 2

4 4 2

ABC

AB BC CA x x

HA HA HA

 

    (1).

Từ ( )SH ABC



;( ))SA ABC SAH 



60SAH  .

3 3 3 9 2 9 6

sin 60

2 2 2 4 8

1 1 1 9 2 9 2

cos60

2 2 2 4 8

SH SA

HA SA



       









       





Gọi

I AH BC 

mà

AB AC

IB IC    .

2 2 2

1AI AB BI x     .

ABC

S BC AI  

2 2

2 1 1

x x     .

Thay vào (1) ta được

2 2

9 9

x x

x   

 

4 2

8 81 1

x x







   









NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 762

Kết hợp với 5x  ta được 3x  .

Suy ra 2 2

ABC



 .

Vậy

1 1 9 6 3 3

. . .2 2

3 3 8 2

ABC

V SH S  

Câu 49.2: Cho hình chóp

.S ABCD

có đáy

ABCD

là hình chữ nhật. E là điểm trên cạnh AD sao cho

BE vuông góc với AC tại H và AB AE , cạnh SH vuông góc với mặt phẳng đáy, góc



45BSH  

. Biết

AH  ,

5BE a

. Thể tích khối chóp .S ABCD bằng

3 5

. B.

32 5

. C.

. D.

8 5

Lời giải

Chọn B

Đặt AB x ,

ABE

vuông tại

2 2 2

AB AE BE   .

2 2 2 2 2 2

( 5) 5AE BE AB a x a x       .

Xét

ABE

vuông tại

, đường cao

có

2 2 2

1 1 1

AE AB AH

 

2 2 2 2

1 1 5

5 4a x x a

  



4 2 2 4

5 4 0x a x a   

x a













Loại x a và

2AE a AB a  

Suy ra 2AB a



2 2

4 4

5 5

tan

a BH a

BH AB AH SH

BSH

      

Xét ABC vuông tại B , đường cao

2 2 2

1 1 1

AB BC BH

  

2 2

AB BH

BC a

AB BH

  



1 1 4 32 5

. . .2 .4

3 3 15

S ABCD ABCD

a a

V SH S a a   .

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 763

Câu 49.3: Cho tứ diện ABCD có

2AC AD a 

, BC BD a  , khoảng cách từ điểm B đến mặt phẳng

 

ACD bằng

và thể tích tứ diện ABCD bằng

. Góc giữa hai mặt phẳng

 

ACD

và

 

BCD bằng

A. 90. B. 45. C. 30. D. 60.

Lời giải

Chọn B

Gọi M là trung điểm của CD .

Xét ACD cân tại

và BCD cân tại

nên

   



 



,ACD BCD AMB 

Kẻ BH vuông góc với AM tại

H BH AM 

Mà

 

CD ABM

 

CD BH BH ACD   

Suy ra

ABCD ACD

V BH S



 với

 

BH d B ACD  .

3 5

ACD

V a



   .

Đặt 2CD x .

Suy ra

2 2 2 2

2AM AC MC a x   

2 2

1 5

. 2

2 3

ACD

S AM CD x a x



    

2 2

2 6

3 3

a a a

x CD BM BC CM       

Xét tam giác BHM vuông tại H có



sin sin

BMH AMB

  



   







45 , 45AMB ACD BCD     

Câu 49.4: Cho hình lăng trụ đứng .ABCD A B C D

   

, đáy ABCD là hình thoi, góc



60BAD  . Gọi M là

điểm thuộc miền trong của hình thoi ABCD , biết A M



tạo với mặt phẳng

 

ABC một góc 60

và 4A M



 . Độ dài cạnh AB bằng bao nhiêu nếu thể tích khối lăng trụ bằng 12 ?

2AB 

. B. 2 3AB  . C.

4AB 

. D. 4 3AB  .

Lời giải

Chọn A

 

AM CD

CD ABM

BM CD





 







NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 764

Đặt



, 60

ABCD

BD x

AB x BAD S

AC x







     









Ta có

 

AA ABCD AM



 

là hình chiếu của

A M



trên mặt phẳng

 

ABC

 



 



 



, , 60A M ABCD A M AM A MA

  

     .

Xét

A AM





vuông tại

, có



sin 2 3

A MA AA

A M



 

  



Ta lại có

12 . 12

ABCD A B C D ABCD

V AA S

   



  

2 3

ABCD

S  

2 2x AB    .

Vậy

2AB 

Câu 49.5: Cho hình lăng trụ tam giác đều .ABC A B C

  

cạnh đáy bằng 1, khoảng cách từ tâm của tam giác

ABC đến mặt phẳng

 

A BC



bằng

. Thể tích của khối lăng trụ bằng

. B.

. C.

3 2

. D.

3 2

Lời giải

Chọn C

Gọi I là tâm tam giác ABC , M là trung điểm của AB .

 

1 1 1

, 3.

3 6 2

d I A BC

d A A BC



     



Xét tứ diện .A ABC



có

 

A A ABC





. Kẻ

AH A M





(1).

Ta có

 

AM BC

BC AA M BC AH

A M BC







   









(2).

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 765

Từ (1), (2) ta có

   

 

AH A BC AH d A A BC

 

    .

Xét

A AM





vuông:

2 2 2

2 2

1 1 1 . 6

AM AH

A A

AH AM A A

AM AH



    





Vậy

6 3 3 2

. .

4 4 16

ABC A B C ABC

V AA S

  





   .

Câu 49.6: Cho hình chóp .S ABC có đáy ABC là tam giác vuông cân tại B với 5BA BC a  ;



90SAB SCB  . Biết góc giữa hai mặt phẳng

 

SBC

và

 

SBA

bằng



với

cos





. Thể

tích của khối chóp

.S ABC

bằng

. B.

125 7

. C.

125 7

. D.

Lời giải

Chọn C

Ta có hai tam giác vuông SAB và SBC bằng nhau và chung cạnh huyền SB .

Kẻ AI SB CI SB   và góc giữa hai mặt phẳng

( )SBA

và

( )SBC

là góc giữa hai đường

thẳng AI và

( ; )CI AI CI



 



  

90 180 90 180 cos

CBA AIC AIC AIC



   

         

Có

5 2 ,AC a AIC  cân tại I, nên có :



2 2 2 2

2 2

2 2 9

cos 16 4

2 2

AI AC AI AC

AIC AI a AI a

AI AI

 

       

16 25

3 3

AI a

BI a SI a SB

       .

Cách 1 :

Dựng ( )SD ABC tại

. Ta có:

BA SA

BA AD

BA SD





 







. Tương tự BC CD

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 766

Nên tứ giác ABCD là vuông cạnh 5a

5 2BD a 

2 2

5 7

SD SB BD a   

Vậy

2 3

1 1 1 5 7 1 125 7

. . . .25

3 2 3 3 2 18

SABC

V SD BA a  

Cách 2 :

. . .

1 1 1

. . .

3 3 3

S ABC S ACI B ACI ACI ACI ACI

V V V SI S BI S SB S    

A IC

cân tại I, nên

2 2

1 1 5 7 5 7

sin .16 .

2 2 16 2

ACI

S AI a  

Vậy

2 3

1 25 5 7 125 7

. .

3 3 2 18

S ABC

a a a

V  

Câu 49.7: Cho hình chóp .S ABC có 2 4BC BA a  ,



90ABC BAS  

. Biết góc giữa hai mặt phẳng

 

SBC

và

 

SBA bằng 60



và SC SB . Thể tích của khối chóp .S ABC bằng

. B.

. C.

. D.

Lời giải

Chọn B

Tam giác SBC cân cạnh đáy 4BC a . Gọi E là trung điểm BC thì ta có SEB vuông tại

, 2E BE a BA  . Đưa về bài toán gốc với chóp .S ABE .

Hai tam giác vuông SAB , SEB bằng nhau vì chung cạnh huyền SB ,

AB EB BC a   .

Kẻ AI SB EI SB   và góc giữa hai mặt phẳng

 

SBA

và

 

SBC

góc giữa hai mặt phẳng

 

SBA

và

 

SBE

là góc giữa hai đường thẳng AI và

 

; 60EI AI EI  



90 180 90CBA AIE   

  

 

120 cos

AIE AIE    



Có

2 2AE a

, AIE cân tại I, nên có :



2 2 2 2

2 2

2 2 1

cos

2 2 2

AI AE AI AE

AIC

AI AI

 

  

8 2 2

AI AI a   

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 767

2 4 6

3 3 3

a AI a a

BI SI SB

      

Cách 1 :

Dựng

 

SD ABC

tại D . Ta có:

BA SA

BA SD











BA AD  . Tương tự BE ED

Nên tứ giác ABED là hình vuông cạnh 2a .

2 2

2 2 2BD a SD SB BD a      .

Thể tích.

1 1 1 8

2 4

3 2 3 3

S ABC

V SD BC BA a a      

Cách 2 :

SABC AEI

V SB S 

2 2

1 1 8 3 2 3

sin

2 2 3 2 3

AEI

a a

S AI



    

Vậy

2 3

1 6 4 3 8

3 3 3

S ABC

a a a

V    

Câu 49.8: Cho hình chóp .S ABC có đáy ABC là tam giác đều cạnh a ,



90SAB SCB  góc giữa hai

mặt phẳng ( )SAB và ( )SCB bằng

60 . Thể tích của khối chóp .S ABC bằng

. B.

. C.

. D.

Lời giải

Chọn B

Gọi M là trung điểm của SB , và G là trọng tâm tam giác đều ABC .

Theo giả thiết



90SAB SCB MS MB MA MC M



      

thuộc trục đường tròn ngoại

tiếp

( )ABC MG ABC  

Gọi D là điểm đối xứng với G qua cạnh AC thì ( )SD ABC  .

Từ giả thiết suy ra hai tam giác vuông bằng nhau

SAB

và

SCB

Do đó từ A kẻ

,AI SB I SB 

thì

CI SB

Nên góc giữa hai mặt phẳng ( )SAB và ( )SCB bằng góc ( , ) 60AI CI



 .

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 768



2 2

2 1

60 120

2 2

AI AC a

ABC AIC AI

 



       

2 3

3 2

a a

BI SB   

Ta có

2 2

4 3 2 3 4

3 2 2 3

3 6

a a a

BD a a SD SB BD        

Thể tích

1 1 1 3 2

3 3 4 24

S ABC ABC

V SD S a      .

Câu 49.9: Cho tứ diện

ABCD

có

 



90 ; ; 5; 135DAB CBD AB a AC a ABC

 

     . Biết góc giữa hai

mặt phẳng ( ),( )ABD BCD bằng 30



. Thể tích của tứ diện ABCD bằng

2 3

. B.

. C.

3 2

. D.

Lời giải

Chọn D

Dựng

( )DH ABC

Ta có

BA DA

BA AH

BA DH





 







. Tương tự

BC DB

BC BH

BC DH





 







Tam giác AHB có



, 45AB a ABH HAB



    vuông cân tại A AH AB a   , 2HB a

Áp dụng định lý cosin, ta có 2BC a .

Vậy



1 1 2

sin 2

2 2 2 2

ABC

S BA BC CBA a a



        

Dựng ( )

HE DA

HE DAB

HF DB





 







và

( )HF DBC

Suy ra



(( ),( )) ( , )DBA DBC HE HF EHF  và tam giác HEF vuông tại E .

a 5

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 769

Đặt DH x , khi đó

2 2 2 2

ax xa

HE HF

a x a x

 

 

Suy ra:



2 2

3 2

cos

2 2

HE x a

EHF x a

x a



    



Vậy

3 6

ABCD ABC

V DH S



    .

Câu 49.10: Cho hình chóp .S ABC có 2 , , 3AB a AC a BC a   ,



90SBA SCA 



và hai mặt

phẳng

 

SAB và

 

SAC tạo với nhau một góc



sao cho

cos





. Thể tích của khối chóp

.S ABC bằng

. B.

. C.

. D.

Lời giải

Chọn D

Từ giả thiết :

2 , , 3AB a AC a BC a  

2 2 2 2 2 2

3 2BC a a a AB AC     

ABC vuông tại

Dựng

 

SD ABC . Dễ chứng minh được ABDC là hình chữa nhật .

, 2DB AC a DC AB a   

. Gọi

SD h

Áp dụng công thức tính nhanh :

. cos

DB DC

SB SC



Chọn 1a  :

2 2

1 2 1

1 2h h



 

4 2 2

3 4 0 1 1h h h h       

1h SD  

1 1 2

. . .

3 2 6

SABC

V SD AB AC 

Vì chọn 1a  , theo đề bài ta chọn được

V 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 770

Câu 49.11: Cho hình chóp .S ABC có AB a , 3AC a , 2SB a và



90ABC BAS BCS   . Biết

sin của góc giữa đường thẳng SB và mặt phẳng

 

SAC

bằng

. Thể tích của khối chóp

.S ABC bằng

2 3

. B.

. C.

. D.

Lời giải

Chọn C

- Dựng

 

SD ABC

tại D . Ta có:

BA SA

BA SD











BA AD  .

Và:

BC SD

BC CD

BC SC





 







ABCD là hình chữ nhật

2DA BC a  

, DC AB a  .

- Sử dụng công thức

 

sin , SAC

d B SAC



 

 

;d B SAC

 

;d D SAC



 

1 11

;

d D SAC

 

 

1 .

- Lại có:

 

2 2 2

1 1 1 1

;

DS DA DC

d D SAC

  

2 2 2 2

1 1 1

SB BD DA DC

  



2 2 2

1 3

3 2SB a a

 



 

- Từ

 

và

 

suy ra:

2 2 2

1 3

3 2SB a a

 



2 2

SB a

















SB a

















Theo giả thiết 2SB a

6 3SB a SD a    .

Vậy

1 1 6

. .

3 2 6

SABC

V SD BA BC 

Câu 49.12: Cho hình chóp .S ABC có

4, 6, 12SA SB SC  

và



60 , 90ASB BSC    và



120CSA  

. Thể tích của khối chóp

.S ABC

bằng

A. 36 3 . B.

36 2

. C. 24 3 . D.

24 2

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 771

Trên tia ,SA SB lần lượt lấy cá điểm ,M N sao cho 12SM SN  . Khi đó ta có:

Tam giác SMN đều 12MN  .

Tam giác SNC vuông tại S nên 2 12 2CN SC  .

Tam giác SMC cân tại S có



2 2

2 . .cos 12 3MC SC SM SC SM CSM    .

Từ đó suy ra

2 2 2

MC MN CN 



tam giác CMN vuông tại N .

Gọi H là hình chiếu vuông góc của S trên mặt phẳng

 

CMN .

Vì 12SC SM SN   nên H là tâm đường tròn ngoại tiếp tam giác CMN

H là trung điểm của MC

2 2

6SH SC CH    .

. 72 2

CMN

S MN NC 

. . 144 2

S CMN CMN

V SH S  

Mặt khác, ta có

. .

S ABC

S MNC

SA SB SC

V SM SN SC

 

. .

24 2

S ABC S MNC

V V  

Câu 49.13: Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại

,AB a



90SAB SCB  

, góc

giữa

và

 

SBC bằng 60. Thể tích của khối chóp đã cho bằng

4 3

Lời giải

Chọn A

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 772

Dựng hình vuông ABCD tâm O . Gọi

là trung điểm SB .



90SAB SCB  nên hình chóp .S ABC nội tiếp mặt cầu tâm

đường kính SB .

là tâm đường tròn ngoại tiếp tam giác

ABC

 OI là trục của đường tròn ngoại tiếp tam giác ABC .

Suy ra

 

OI ABC

 

SD ABC 

Mà

 



, , , 60AB SBC DC SBC CD CS DCS



   



.tan 60 3SD CD a 

Từ đây ta suy ra:

2 3

1 1 3

. . . 3.

3 3 2 6

ABC

a a

V SD S a  



Câu 49.14: Cho hình chóp .S ABC có đáy là tam giác cân tại A , AB a ,



,120BAC  



90SBA SCA  

. Gọi



là góc giữa SB và

 

SAC thỏa mãn

sin





, khoảng cách từ S

đến mặt đáy nhỏ hơn 2a . Thể tích của khối chóp .S ABC bằng

. B.

. C.

. D.

Lời giải

Chọn C

+ Gọi D là hình chiếu vuông góc của S lên đáy

 

ABC

, đặt

 

0 2SD x x a  

Ta có

 

AC SC

AC SDC AC DC

AC SD





   







. Tương tự ta cũng có

AB DB

+ Tam giác ABC cân tại A và



120CAB  

3BC a  và



60DBC DCB  

DBC  đều cạnh

3a .

+ Tam giác

SDC

vuông tại

2 2

3SB a x  

+ Kẻ DK SC tại

 

K DK SAC 

 

2 2

. 3

;

x a

d D SAC DK

a x

  



+ Gọi

I BD AC 

, xét

DIC

vuông tại

và



60BDC  

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 773



2 3

DI a

cosBDC

   B là trung điểm của DI

 

; ;

d B SAC d D SAC 

Theo giả thiết

 

;

; sin

d B SAC

SB SAC

 

  

 

2 2

3 3

2 3

a x

 



2 2

3 4 0x a ax   

4 3 0

x x

a a

 

   

 

 

x a













. So sánh với điều kiện suy ra

x a

Vậy

1 3

. .

3 12

S ABC ABC

V S SD



 

Câu 49.15: Cho hình chóp .S ABC có đáy là tam giác đều cạnh 2a ,



90SAB SCB  . Gọi

là trung

điểm của SA . Biết khoảng cách từ

đến

 

MBC

bằng

. Thể tích của khối chóp đã cho

bằng

8 39

. B.

10 3

. C.

4 13

. D.

2 3a .

Lời giải

Chọn A

Trong mp

 

ABC

xác định điểm D sao cho tứ giác ABCD vuông tại A và C

Khi đó ta có:

AB AD

AB SD

AB SA





 







;

CB CD

CB SD

CB SC





 







Vậy

 

SD ABCD

S ABC ABC

V SD S



 

Có tam giác ABC là tam giác đều cạnh 2a

ABC

S a



 

Ta đi tìm

Gọi

là trung điểm AC

vì tam giác

ABC

đều,

ABCD

nội tiếp đường tròn đường kính BD 

I BD AC BD  

Gọi G là trọng tâm tam giác ABC và N là trung điểm BC

Vì tam giác ABC đều AN BC  // AN CD , tương tự // CG BD

Dễ thấy AGCD là hình thoi

2 2 3 2 3

3 3 2 3

CD AG AN a    

 

Xét hình chóp .S ANCD có đáy ANCD là hình thang vuông tại C, N.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 774

Khoảng cách từ

đến mặt phẳng

 

MNC

bằng

vì

   

MNC MBC

Trong mp

 

ABCD gọi

 

E CN AD 

Trong mp

 

SAD

kẻ tia / /At SD gọi

 

P EM At 

Gọi K là hình chiếu của G trên mặt phẳng

 

CMB

Khi đó ta có

 

/ /AP SD AP CN

APN CN

AN CN

 



 







Trong mp

 

APN kẻ AH PN ta có

 

AH d A MCN 

Mà tam giác ABC là tam giác đều cạnh 2a

3AN a 

Từ

2 2 2

1 1 1

AH AP AN

 

2 2 2 2

1 21 1 1

36 3 4AP a a a

   

2AP a 

Dễ thấy APM SFM   2SF AP a  

 

Xét tam giác EAN có / /CD AN nên

ED CD

EA AN

 

(theo

 

)

Xét tam giác EAP có / /FD PA nên

FD ED

PA EA



2 4

3 3

FD a

   

 

Từ

 

và

 

ta có

SD SF FD  

Vậy

1 1 10 10 3

. . . 3

3 3 3 9

S ABC ABC

a a

V SD S a



  

Câu 49.16: Cho hình chóp .S ABC có đáy là tam giác ABC đều cạnh

, tam giác SBA vuông tại

tam giác SAC vuông tại C . Biết góc giữa hai mặt phẳng

 

SAB

và

 

ABC

bằng 60 . Tính

thể tích khối chóp .S ABC theo

. B.

. C.

. D.

Lời giải.

Chọn B

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 775

Gọi

là hình chiếu của

lên mặt phẳng





ABC

, suy ra





SD ABC



Ta có

SD AB



và

SB AB







, suy ra





AB SBD BA BD

  

Tương tự có

AC DC



hay tam giác

ACD

vuông ở

Dễ thấy

SBA SCA

  

(cạnh huyền và cạnh góc vuông), suy ra

SB SC



Từ đó ta chứng minh được

SBD SCD

  

nên cũng có

DB DC



Vậy

là đường trung trực của

, nên cũng là đường phân giác của góc



BAC

Ta có



DAC

 

, suy ra

DC 

. Ngoài ra góc giữa hai mặt phẳng





SAB

và





ABC

là



SBD

 

, suy ra

 

tan tan . 3

SD a

SBD SD BD SBD a

    

Vậy

2 3

1 1 3 3

. . . .

3 3 4 12

S ABC ABC

a a

V S SD a



  

Câu 49.17: Cho hình chóp

S A B C

có tam giác

ABC

vuông cân tại

A B a



. Gọi

là trung

điểm của

. Hình chiếu vuông góc của

lên mặt phẳng





ABC

là điểm

thỏa mãn

B I IH



 

. Góc giữa hai mặt phẳng





SAB

và





SBC

là

. Thể tích của khối chóp

S A B C

là

V 

. B.

V 

. C.

V 

. D.

V 

Lời giải.

Chọn A

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 776

Dễ thấy hai tam giác

SAB

và

SAC

bằng nhau ( cạnh chung

), gọi K là chân đường cao

hạ từ

trong tam giác SAB suy ra

   

 



,SAB SBC AKC

Trường hợp 1:



60AKC  

kết hợp I là trung điểm

suy ra



30IKC 

Ta có

2 2

AC a

IB IC  

4 2 2

3 3

BH BI 

Từ giả thiết tam giác ABC vuông cân tại

ta được AC BI IC IK  .

Trong tam giác

ICK

vuông tại I có



tan

tan30 2

IC IC a

IKC IK

   



Như vậy

IK IB

( vô lý).

Trường hợp 2:



120AKC  

tương tự phần trên ta có



tan

tan60 6

IC IC a

IKC IK

   



 

SB AKC SB IK  

nên tam giác

BIK

vuông tại

và

2 2

BK IB IK  

Như vậy tam giác

BKI

đồng dạng với tam giác

BHS

suy ra:

. 2

IK BH a

 

Vậy thể tích của khối chóp .S ABC là:

2 3

1 2

3 2 3 9

S ABC

a a a

V  

Câu 49.18: Cho tứ diện ABCD có



9 0A B C B C D C D A   

,B C C D a 

2A D a

. Góc giữa

hai mặt phẳng

 

ABC

và

 

ACD

bằng

A. 60 . B. 30 . C. 45 . D. 90 .

Lời giải.

Chọn A

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 777

Gọi E là hình chiếu của A lên mặt phẳng

 

BCD

Kết hợp đề bài

BC AB

BC BE

BC AE





 







;

CD AD

CD ED

CD AE





 







và

BC CD a 

Suy ra tứ giác

BCDE

là hình vuông cạnh

Khi đó

2 2

AE AD ED a  

Gọi ,H K lần lượt là hình chiếu của E lên

   

,ABC ACD

thì

   

,EH ABC EK ACD 

nên góc tạo bởi hai mặt phẳng

 

ABC

và

 

ACD

là góc

 

,EH EK

Nhận xét 2 tam giác AEB và AED là vuông cân tại E nên

EH EK 

;

2 2

BD a

HK  

suy ra tam giác EHK đều.

Vậy số đo góc tạo bởi hai mặt phẳng

 

ABC

và

 

ACD

là

60

Câu 49.19: Cho tứ diện

ABCD

có

 

90DAB CBD  º

;



; 5; 135AB a AC a ABC   

. Biết góc

giữa hai mặt phẳng

   

,ABD BCD bằng

30

. Thể tích của tứ diện

ABCD

bằng

2 3

. B.

. C.

3 2

. D.

Lời giải.

Chọn D

a 2

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 778

Dựng

 

DH ABC

Ta có

BA DA

BA AH

BA DH





 







. Tương tự

BC DB

BC BH

BC DH





 







Tam giác AHB có

AB a



45ABH 

HAB 

vuông cân tại A

AH AB a  

Áp dụng định lý cosin, ta có

2BC a

Vậy



1 1 2

. . .sin . . 2.

2 2 2 2

ABC

S BA BC CBA a a



  

Dựng

HE DA

HF DB











 

HE DAB 

và

 

HF DBC

Suy ra

   

 



 



, ,DBA DBC HE HF EHF 

và tam giác HEF vuông tại E .

Đặt

DH x

, khi đó

2 2

a x





2 2

a x





Suy ra



2 2

3 2

cos

2 2

HE x a

EHF x a

x a



    



Vậy

. .

3 6

ABCD ABC

V DH S



  .

Câu 49.20: Cho hình chóp

.S ABC

có đáy là tam giác vuông cân tại B ,

3AB BC a 



90SAB SCB  

và khoảng cách từ điểm A đến

 

SBC

bằng

. Diện tích của mặt cầu

ngoại tiếp hình chóp

.S ABC

bằng

2 a



. B.

8 a



. C.

16 a



. D.

12 a



Lời giải.

Chọn D

a 5

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 779

Gọi

là hình chiếu của S lên

 

ABC .

Ta có:

BC SC

HC BC

SH BC





 







Tương tự AH AB .

Và

ABC

vuông cân tại B nên

ABCH

là hình vuông. Gọi

O AC BH 

là tâm hình

vuông.

Dựng một đường thẳng

qua

vuông góc với

 

ABCH , dựng mặt phẳng trung trực của

qua trung điểm

cắt

tại

I I

là tâm mặt cầu ngoại tiếp.

Ta hoàn toàn có

//IJ SA IJ AB I  

là trung điểm

, hay

I d SC 

Bán kính mặt cầu ngoại tiếp:

2 2

;

2 2

S ABC

r AI IJ JA IJ



    

   

 

// , ,AH SBC d A SBC d H SBC HK  

( K là hình chiếu của H lên

và

   

BC SHC HK SBC  

2HK a 

. Tam giác

SHC

vuông tại

6SH a 

Tam giác

SHA

vuông tại H 3SA a  .

2 2

3 4 12

2 2

S ABC mc

SA a

JA r AI a S r a

 

       

Câu 49.21: Tứ diện ABCD có 3BC  , 4CD  ,



90ABC BCD ADC   



 

, 60AD BC  

. Cosin

của góc giữa hai mặt phẳng

 

ABC và

 

ACD bằng

. B.

4 43

. C.

. D.

2 43

Lời giải.

Chọn D

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 780

Gọi

là chân đường cao của tứ diện ABCD .

Ta có:

BC AB

BC HB

BC AH





 







 

1 .

Lại có:

CD AD

CD HD

CD AH





 







 

2 .

Mà



90BCD   .

Từ đây ta suy ra HBCD là hình chữ nhật.

Mặt khác:



 



 



, , 60AD BC AD HD ADH   . Suy ra: tan 60 3 3AH HD   .

Chọn hệ trục .Oxyz H DBA như hình vẽ.

Ta có:

 

0;0;0H

 

0;0;3 3A ,

 

0;4;0B

 

3; 4;0C

 

3;0;0D

 

3; 3; 3 3AD   



 

3;4; 3 3AC  



 

0;4; 3 3AB  



Gọi





lần lượt là một véc tơ pháp tuyến của

 

ABC và

 

ABD .

Suy ra:

 

, 0; 9 3; 12n AB AC

 

   

 

  

;

 

, 21 3;0;21n AD AC

 

 

 

  

Vậy

   

 

1 2

cos ,

n n

ABC ADC

n n



 

 

2 2

0.21 3 9 3.0 12.21

2 43

0 9 3 12 . 21 3 0 21

 

 

     

Câu 49.22: Cho tứ diện

ABCD

có



90ABC ADC   và

1BC 

, 3CD  , 2BD  ,

3AB 

Khoảng cách từ B đến

 

ACD bằng

. B.

. C.

. D.

Lời giải.

Chọn B

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 781

1BC 

3CD 

, 2BD 

2 2 2

BC DC BD   BCD 

vuông tại

Dựng hình chữ nhật

BCDE

//BC ED mà

DC BC DC DE  

, lại có

DC AD

 

DC ADE 

DC AE 

 

1 .

Chứng minh tương tự

 

BC ABE

BC AE 

 

2 .

Từ

 

1 và

 

2 suy ra

 

AE BCDE .

Kẻ EH AD tại H . Do

 

DC ADE nên

DC EH

 

EH ACD  .

//BE CD

 

, ,d B ACD d E ACD EH  

2 2

AE AB BE 

 

3 3 6   .

2 2 2

1 1 1

EH EA ED

 

1 7

6 6

  

6 42

EH  

Vậy

 

d B ACD EH 

Câu 49.23: Cho hình chóp .S ABC có SA vuông góc với mặt đáy, SA BC và



120BAC  

. Hình

chiếu vuông góc của A lên các cạnh SB và SC lần lượt là M và N . Góc giữa hai mặt phẳng

 

ABC

và

 

AMN

bằng

A. 45. B. 60. C. 15. D. 30.

Lời giải.

Chọn A

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 782

Gọi

là tâm đường tròn ngoại tiếp tam giác

ABC

có đường kính là AD .

Khi đó tam giác ABD vuông tại B AB BD  .

Ta có

 

BD AM

AB BD

BD SAB

SA BD





   







Ta có

 

BD AM

AM SBD AM SD

SB AM





   







Tương tự, ta chứng minh được

AN SD

Do đó

 

SD AMN

suy ra

   

 



 



, ,ABC AMN SA SD ASD  .

Xét tam giác

SAD

vuông tại A có



tan

ASD

 .

Với

2 2

sin120 3

ABC

AD R SA



  



Do đó

 

tan 30

ASD ASD   

   

 



, 30ABC AMN  .

Câu 49.24: Cho hình chóp

.S ABC

có đáy là tam giác cân tại A ,

AB a



120 ,BAC  



90SBA SCA   . Gọi



là góc giữa

và

 

SAC

thỏa mãn

sin





, khoảng cách từ

đến mặt đáy nhỏ hơn

. Thể tích của khối chóp

.S ABC

bằng

. B.

. C.

. D.

Lời giải.

Chọn C

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 783

Gọi D là hình chiếu vuông góc của

lên đáy

 

ABC , đặt

 

0 2SD x x a   .

Ta có

 

AC SC

AC SDC AC DC

AC SD





   







. Tương tự ta cũng có

AB DB

Tam giác

ABC

cân tại

và



120CAB   3BC a  và



60DBC DCB DBC     đều

cạnh

Tam giác

SDC

vuông tại

2 2

3SC a x SB   

Kẻ

DK SC

tại

 

K DK SAC 

 

2 2

. 3

x a

d D SAC DK

a x

  



Gọi

I BD AC 

, xét

DIC

vuông tại

và



60BDC  



2 3

DI a

cosBDC

  

B

là trung điểm của DI

 

, ,

d B SAC d D SAC  .

Theo giả thiết



 

,( sin

d B SAC

SB SAC

 

  

 

2 2

3 3

2 3

a x

 



2 2

3 4 0x a ax   

4 3 0

x x

a a

 

   

 

 

x a













. So sánh với điều kiện suy ra x a .

Vậy

1 3

. .

3 12

S ABC ABC

V S SD



 

Câu 49.25: Cho hình chóp

.S ABC

có 3SA AB  ; 6SB  ;

2 2AC BC 

; 5SC  . Khoảng

cách từ

đến

 

SBC

bằng

. B.

. C.

. D.

Lời giải.

Chọn D

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 784

Dựng điểm

sao cho

ABCD

là hình chữ nhật.

Áp dụng định lý Pitago ta có các tam giác ; ;SAB ABC SBC lần lượt vuông góc tại , ,A B C .

Ta có

AB AD

BA SA











 

1AB SD 

BC CD

BC SC











 

2BC SD 

Từ

   

1 ; 2

 

SD ABCD SD BC   

Vậy

   

SBC SDC

theo giao tuyến

. Kẻ

vuông góc với

tại

thì

 

DH SBC

Có

 

//AD SBC

 

2 2

. 2. 3 30

, ,

DS DC

d A SBC d D SBC DH

DS DC

     



Câu 49.26: Cho hình chóp

.S ABC

, đáy là tam giác đều

ABC

có cạnh bằng a . Biết rằng các mặt bên

của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng

. Tính thể tích nhỏ

nhất của khối chóp

.S ABC

. B.

. C.

. D.

Lời giải

Chọn C

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 785

Gọi H là hình chiếu của

trên mặt phẳng đáy

 

ABC

; , ,M N K lần lượt là hình chiếu của

trên , ,AB BC CA .

Vì diện tích các mặt bên của hình chóp bằng nhau nên ta có

1 1 1

. . .

2 2 2

SM AB SN BC SK CA 

và vì tam giác

ABC

đều nên ta có

SM SN SK 



HM HN HK 

TH1: nếu

nằm trong tam giác

ABC



là tâm đường tròn nội tiếp tam giác đều

ABC

Khi đó ta có

2 3

3 3

AH AN  và

3SA SB SC a  



2 2 2

3 2 6

9 3

a a

SH SA AH a    



2 3

1 1 3 2 6 2

. . .

3 3 4 3 6

S ABC ABC

a a a

V S SH  

TH2: Nếu

nằm ngoài tam giác

ABC

. Không mất tính tổng quát giả sử

nằm khác phía

với

so với đường thẳng

Tương tự như trên ta vẫn có

HM HN HK 

. Vì tam giác

ABC

đều nên

là tâm đường

tròn bàng tiếp góc

và

AM AB BN  



60 2 2

BN a

HB a

cos

  



3 3

: 30 : 3

2 2

AH AM cos a   

. Vì thế cạnh

không thể bằng 3a  3SB SC a 



2 2 2 2

3 2SH SB BH a a a    



2 3

1 1 3 6

. . . 2

3 3 4 12

S ABC ABC

a a

V S SH a  

Vậy

3 3 3

min

2 6 6

min ,

6 12 12

a a a

 

 

 

 

 

 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 786

Câu 49.27: Cho hình chóp .S ABCD có đáy ABCD là hình bình hành thỏa mãn , 3AB a AC a  ,

2aBC 

. Biết tam giác

SBC

cân tại

, tam giác

SCD

vuông tại

và khoảng cách từ D đến

mặt phẳng ( )SBC bằng

. Thể tích của khối chóp đã cho bằng

3 5

. B.

3 5

. C.

3 3

. D.

Lời giải

Chọn A

Nhận thấy tam giác ABC vuông tại A ( do

2 2 2

AB AC BC 

Gọi

là điểm đối xứng của

qua

ta có tứ giác DEAC là hình chữ nhật, và tam giác EBC

là tam giác đều cạnh 2a .

( ) ( ,( )) ( ,( )) ( ,( ))

AD SBC d D SBC d A SBC d E SBC  

Hay

2a 3

( ,( )) 2.d( ,( ))

d E SBC D SBC 

Gọi I là trung điểm của đoạn BC , ta có:

, ( )BC EI BC SI BC SEI   

Trong ( )mp SEI kẻ

vuông góc với SI tại

. Khi đó:

2 3

( ,( ))

d E SBC EH 

Ta có

D ( )C SAC

( Do

D , DC SC C AC 

) Suy ra

( )AB SAC

Xét tam giác ESB có SA vừa là trung tuyến vừa là đường cao nên tam giác ESB cân tại S .

Xét hình chóp

.S EBC

có đáy là tam giác đều

EBC

, các cạnh bên

SE SB SC 

Nên gọi

F EI CA 

ta có ( )SF EBC .

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 787

Tam giác

EHI

vuông tại

nên

2 3

sin

  



Tam giác

SIF

vuông tại F nên

1 sin 1 2a

.tan . 3.

3 3

2 15

1 sin

1 ( )

SF FI I EI a

   





. D D

1 1 1 2 2a

. . . . . 3

3 3 3

15 3 5

S ABC ABC

V SF S SF AB CA a a    .

Câu 49.28: Cho hình chóp .S ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB và tam giác

SCD cân tại S . Biết hai mặt bên

 

SAB

và

 

SCD

có tổng diện tích bằng

và chúng

vuông góc với nhau. Thể tích khối chóp .S ABCD bằng

. B.

. C.

. D.

Lời giải.

Chọn D

Gọi

lần lượt là trung điểm

và CD . Khi đó //EF AD EF AB 

Do tam giác

SAB

và tam giác

SCD

cân tại

nên SE AB và SF CD

Lúc đó có

     

SE AB

AB SEF ABCD SEF

EF AB





   







Do đó, chân đường cao hạ từ S xuống đáy là

phải nằm trên giao tuyến

của

 

ABCD

và

 

SEF .

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 788

Mặt khác, giao tuyến của hai mặt phẳng

 

SAB và

 

SCD là đường thẳng d qua

và song

song

nên SE d và SF d , tức là



ESF là góc giữa hai mặt phẳng

 

SAB

và

 

SCD

hay nói cách khác ta có SE SF

Xét tam giác

SEF

vuông tại

có

 

2 2 2 2

2 2 2

. .

2 .

SE SF SE SF

SE SF

SE SF SE SF

 



 

 

Ta có

. . 2

SEF

SE SF SH EF S



 

Từ giả thiết

2 2

. . 3

SAB SCD

S S a SE AB SF CD a

 

     hay 3SE SF a 

Thay vào

 

1 ta có

 

2 2 2 2

. .

3 2 .

2 .

SH EF SH a

SH SH a

a SH a

SE SF SH EF

   



 

Vậy thể tích hình chóp

.S ABCD

là

1 1

. . .

3 3 3

ABCD

V SH S a a   .

Câu 49.29: Cho hình chóp

.S ABC

có



, 120AB BC a ABC  



90SAB SCB  và khoảng cách từ

đến mặt phẳng

 

SAC

bằng

2 21

. Tính thể tích khối

.S ABC

V 

. B.

V 

. C.

V 

. D.

V 

Lời giải

Chọn B

Hạ

 

SE ABC

tại E có

 



AB SE

AB SAE AB AE BAE

AB SA





     







Chứng minh tương tự có



90BCE  .

Hai tam giác vuông

BCE

và

BAE

bằng nhau suy ra



60CBE ABE  .

Gọi D là trung điểm của BE suy ra tứ giác

ABCD

là hình thoi và

BD DE a 

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 789

Gọi I là tâm hình thoi

ABCD

có

 

1 1 2 21 2 21

, , , 3.

3 3 21 7

a a

BI EI d B SAC d E SAC d E SAC     

     

CA BD

CA SEI SAC SEI

CA SE





   







Hạ

EK SI

tại

ta có

 

EK SAC

tại

suy ra

 

2 21

d E SAC EK EK  

Tam giác

SBE

vuông tại

đường cao

có

2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 7 4 5 6 5

12 9 36 5

EK EI SE SE EK EI a a a

         

Vậy

0 2

1 1 1 1 3 6 5 15

. . .sin120 . . .

3 3 2 6 2 5 10

SABC ABC

a a

V S SE BA BC SE a



 

   

 

 

Câu 49.30: Cho khối chóp

.S ABC

có đáy là tam giác cân tại

AB a



120BAC   ,



90SBA SCA  

. Gọi



là góc giữa hai mặt phẳng

 

SAB và

 

SAC . Khi

cos





thì thể

tích khối chóp đã cho bằng

3a . B.

a . C.

. D.

Lời giải

Chọn D

Kẻ

   

,SH ABC H ABC 

suy ra

SH AB

và

SH AC

Khi đó ta có

 

SH AB

AB SBH AB BH

SB AB





   







Chứng minh tương tự ta có

AC CH

suy ra tứ giác

ABHC

nội tiếp đường tròn đường kính

AH . Do đó góc

BHC

bằng

60

Dễ thấy

AHB AHC HB HC    

nên

HBC

đều.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 790

ABC



cân tại

có



, 120

AB a BAC

  

suy ra

2 2

BC a

 .

Do đó

2 2 2 2

HB HC BC a

   .

Dễ thấy

SHB SHC SB SC

    

nên

SAB SAC

  

Trong mặt phẳng





SAB

kẻ





BK SA K SA

  .

Trong mặt phẳng





SAC

kẻ





1 1

CK SA K SA

  .

Xét hai tam giác vuông

KAB



và

K AC



có

AB AC





BAK CAK



(vì

SAB SAC

  

) suy

1 1

KAB K AC AK AK

    

mà

và

nằm giữa

và

nên

K K



Từ đó ta có

CK SA



và

BK CK



Do đó



cos cos

BKC





2 2 2

2 . 4

BK CK BC

BK CK

 

 

 

2 2

2 3

BK BC



  .

Đặt





, 0 .

SH x x 

Xét

SHB



có

2 2 2 2 2

SB SH HB a x

   

Xét

SAB



vuông tại

có

2 2 2

1 1 1

BK BA BS

 

2 2 2 2

1 1 1

BK a a x

  







2 2 2

2 2

a a x

a x



 



Thay vào





ta có





 

2 2 2

2 2

2 2 2

2 2

2 3

a a x

a x

a a x

a x











x a

  .

Vậy thể tích khối chóp

S ABC

là



1 1 1 1

. . . . .sin . 3. . sin120

3 2 3 2 4

SH AB AC BAC a a  

Vậy chọn đáp án D.

Câu 49.31: Cho khối chóp

S ABC

có đáy

ABC

là tam giác vuông cân tại

AB a



, tam giác

SAB

vuông tại

, tam giác

SBC

cân tại

và khoảng cách giữa hai đường thẳng

và

bằng

. Thể tích của khối chóp đã cho bằng

. B.

. C.

. D.

Lời giải

Tác giả: Lê Văn Quý ; Fb:Lê V

ăn Quý

Chọn D

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 791

Gọi M trung điểm của



SM BC

(1)

Lấy điểm

( )H ABC

sao cho

ABMH

là hình chữ nhật

Cùng với giả thiết ta có:

AB SA

AB SH

AB AH





 







(2)

Lại có

BC SM

BC SH

BC MH





 







(2)

Từ (1) và (2) suy ra

 

SH ABC

Gọi

K AC BH 

và

là điểm trên đoạn

sao cho

HI HS



// ( ) ( , ) ( ,( )) ( ,( )) 2 ( ,( ))

SB IAC d SB AC d SB IAC d S IAC d H IAC    



( ,( ))

d H IAC 

Ta có

 

2 2 2 2 2 2 2 2

1 1 1 1 1 9 4 4 1

( ,( ))

HI a

HA HO HI HI a a a a

d H IAC

         



3SH a

Vậy

1 1 1

. 3

3 3 2 2

S ABC ABC

V SH S a a



   .

Câu 49.32: Cho tứ diện đều ABCD có cạnh bằng

. Gọi

,M N

lần lượt là trung điểm của các cạnh

,AB BC và

là điểm đối xứng với

qua

. Mặt phẳng

 

MNE

chia khối tứ diện ABCD thành

hai khối đa diện. Trong đó, khối tứ diện ABCD có thể tích là V , khối đa diện chứa đỉnh

có thể tích

'.V

Tính tỉ số



. B.

. C.

. D.

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 792

Lời giải

Chọn B

Gọi

 P EN CD

và

 Q EM AD

Suy ra

, P Q

lần lượt là trọng tâm của BCE và

ABE

Gọi

là diện tích tam giác

BCD

, suy ra .

 

 

CDE BNE

S S S

Ta có

. .

3 3

 

 

PDE CDE

S S

Gọi

là chiều cao của tứ diện

ABCD

, suy ra

   

, ; , .

2 3

    

   

h h

d M BCD d Q BCD

Khi đó

 

1 .

. , ;

3 6



  

 

M BNE BNE

S h

V S d M BCD

 

1 .

. , .

3 27



  

 

Q PDE PDE

S h

V S d Q BCD

Suy ra

. . .

. . 7 . 7 . 7

. .

6 27 54 18 3 18

PQD NMB M BNE Q PDE ABCD

S h S h S h S h

V V V V      

7 11 ' 11

' .

18 18 18

V V V V

      .

Vậy





Câu 49.33: Cho hình chóp

SABC

có đáy

ABC

là tam giác đều cạnh 2a ,



90SAB SCB  

và góc

giữa hai mặt phẳng

 

SAB

và

 

SBC

bằng

60 . Tính thể tích khối chóp

?SABC

a . B.

a . C.

a . D.

a .

Lời giải

Chọn D

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 793

Ta có SAB SBC   (c.g.c), trong tam giác SAB kẻ đường cao AE SB khi đó CE SB . Khi

đó góc giữa hai mặt phẳng

 

SAB

và

 

SBC

là góc giữa hai đường thẳng AE và CE . Dễ dàng

nhận thấy góc



120AEC  

(vì nếu



60AEC  

thì 2AE AC AB a  

điều này vô lí vì tam

giác AEB

vuông tại E ).

Trong tam giác AEC cân tại E kẻ đường cao EK ta có:

2 3

cos30

AE a 

Trong tam giác vuông ABE có:

2 2

2 6

BE AB AE a  

Trong tam giác SAB có:

 

0 3

1 1 1 2 2

. . . . . . .sin120

3 3 2 9

B EAC EAC

V BE S BE AE EC a



  

3 3

. .

6 2 2 2

. . . .

9 3

2 6

B EAC

B SAC B EAC

B SAC

BE BA BC BE BS

V V a a

V BS BA BC BS BE

     

Câu 49.34: Cho tứ diện đều có cạnh bằng , và lần lượt là hai điểm di động trên hai

cạnh ( và

không trùng với ) sao cho mặt phẳng luôn vuông góc

với mặt phẳng . Gọi lần lượt là thể tích lớn nhất và nhỏ nhất của tứ diện

. Tính tích .

A. . B. . C. . D. .

Lời giải

Chọn C

ABCD

AB AC





DMN





ABC

1 2

V V

ADMN

1 2

V V

1 2

V V 

1 2

V V 

1 2

324

V V 

1 2

V V



NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 794

Kẻ

(vì ). Suy ra là trọng tâm của tam giác

đều .

Như vậy và là hai điểm di động nhưng luôn đi qua trọng tâm của tam giác .

Đặt , ( , )

+ .

+ (*)

+ (**)

Do đó (***)

Mặt khác từ (*) và (**) suy ra , ( , ).

Đặt . Điều kiện: .

Khi đó là nghiệm của phương trình , .

Ta tìm để có nghiệm phân biệt thuộc hoặc có nghiệm kép thuộc

DH MN







DH ABC

 









DMN ABC



ABC

 

AM x AN y

0 1

 

0 1

 

2 2 2

1 2

3 3

DH DA AH

    

DH 



1 3

. .sin

2 4

AMN

S AM AN MAN xy



 

AMN AMH ANH

S S S

  

 

 

. .sin 30

AH x y

  

 

x y

 

ADMN AMN

V DH S





1 3 2 2

3 4 12

xy xy

 

 

 

 

x y xy

 

0 1

 

0 1

 

xy t x y t

   

0 3 2

9 4 0

t t

 





 





 

























4 2

9 3

  

x y





3 0 1

X tX t  

4 2

9 3

 

4 2

;

9 3

 



 

 









0;1





0;1

NHÓM WORD – BIÊN SOẠN TÀI LIỆU ĐỀ THI THỬ THPTQG – 2019-2020

Trang 795

Ta có không phải là nghiệm của nên .

Đặt , . Ta có: .

Bảng biến thiên của

Dựa vào BBT, có nghiệm phân biệt thuộc hoặc có nghiệm kép thuộc

(thỏa điều kiện) hay .

Kết hợp (***) ta có , .







 

3 1

 



 

3 1

g X









0;1

X 

 

3 2

3 1

X X

g X





 





















g X









0;1





0;1

4 1

9 2

  

4 1

9 2

 

2 2

27 24

ADMN

V 

V 

V 

1 2

324

V V 

Bấm Tải xuống để xem toàn bộ.

| 1/38

| | Tải xuống

Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
TÍNH THỂ TÍCH KHỐI CHÓP BIẾT GÓC GIỮA HAI MẶT PHẲNG BÀI TẬP MẪU
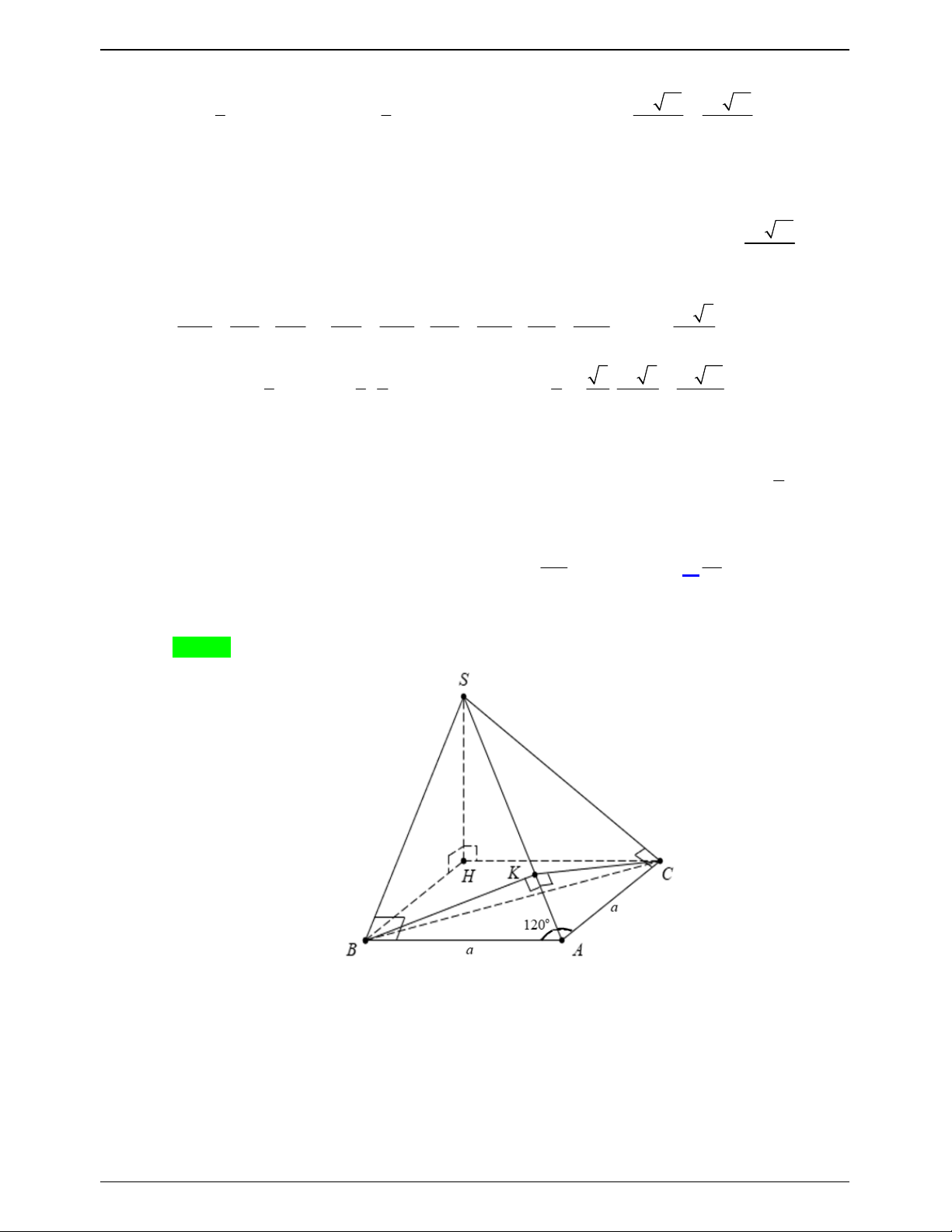
(ĐỀ MINH HỌA BDG 2019-2020) Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB  a ,   0
SBA  SCA  90 , góc giữa hai mặt phẳng  SAB và  SAC  bằng 0
60 . Thể tích của khối đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6
CÁCH 1: Xác định góc giữa hai mặt phẳng.
Phân tích hướng dẫn giải
1. Dạng toán: Tính thể tích khối chóp , biết góc giữa hai mặt phẳng.. Phương pháp:
Tìm đường cao của hình và khai thác được giả thiết góc của đề bài 2. Hướng giải:
B1: Tìm đường cao của hình : học sinh phải tìm đường cao bằng cách suy ra từ các quan hệ vuông góc
giữa đường với đường để chứng mình được đường vuông góc với mặt, hay phục dựng hình ẩn để xác định đường cao.
B2:  Để khai thác được giả thiết góc ta thường làm :
+ Xác định được góc. Trong quá trình xác định góc phải tránh bẫy khi đưa về góc giữa hai đường
thẳng cắt nhau nó là góc không tù.
+ Cần chọn ẩn (Là chiều cao hay cạnh đáy nếu giả thiết chưa có) sau đó sử dụng giả thiết góc để tìm ẩn.
 Có thể sử dụng nhiều phương pháp khác ngoài hai cách truyền thống để tính góc giữa hai mặt bên.
Phương pháp khoảng cách : giả sử  là góc giữa hai mặt bên  và 
d (M , ( )) sin  
ở đây d      , M  
d (M , d )
Phương pháp diện tích hai mặt bên : giả sử  là góc giữa hai mặt bên  ABC  và  ABD 2S  S 3.V  AB  ABC  ABD V   sin   sin ABCD   ABCD 3AB 2S  S  ABC  ABD S
Công thức đa giác chiếu : cos  S
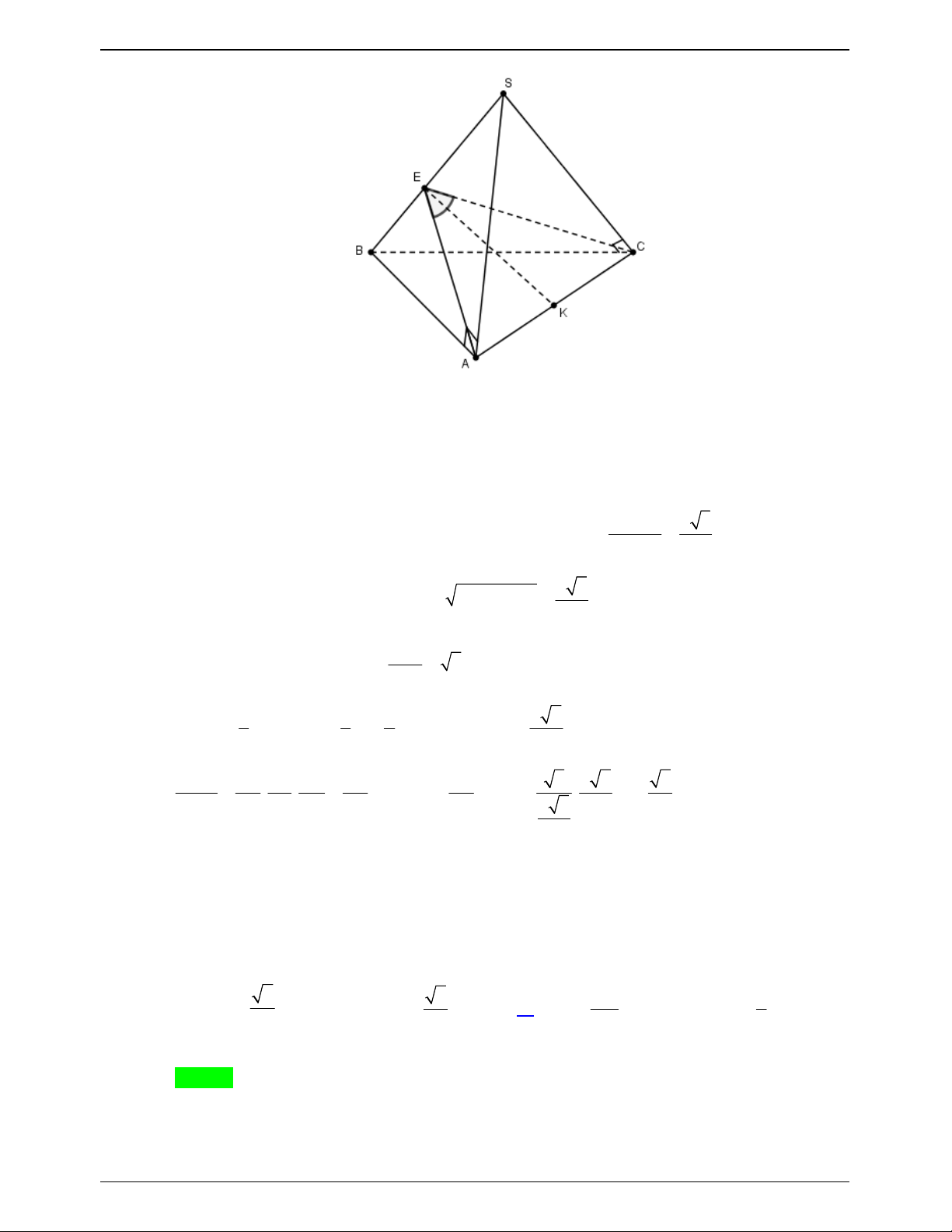
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn D Trang 758
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
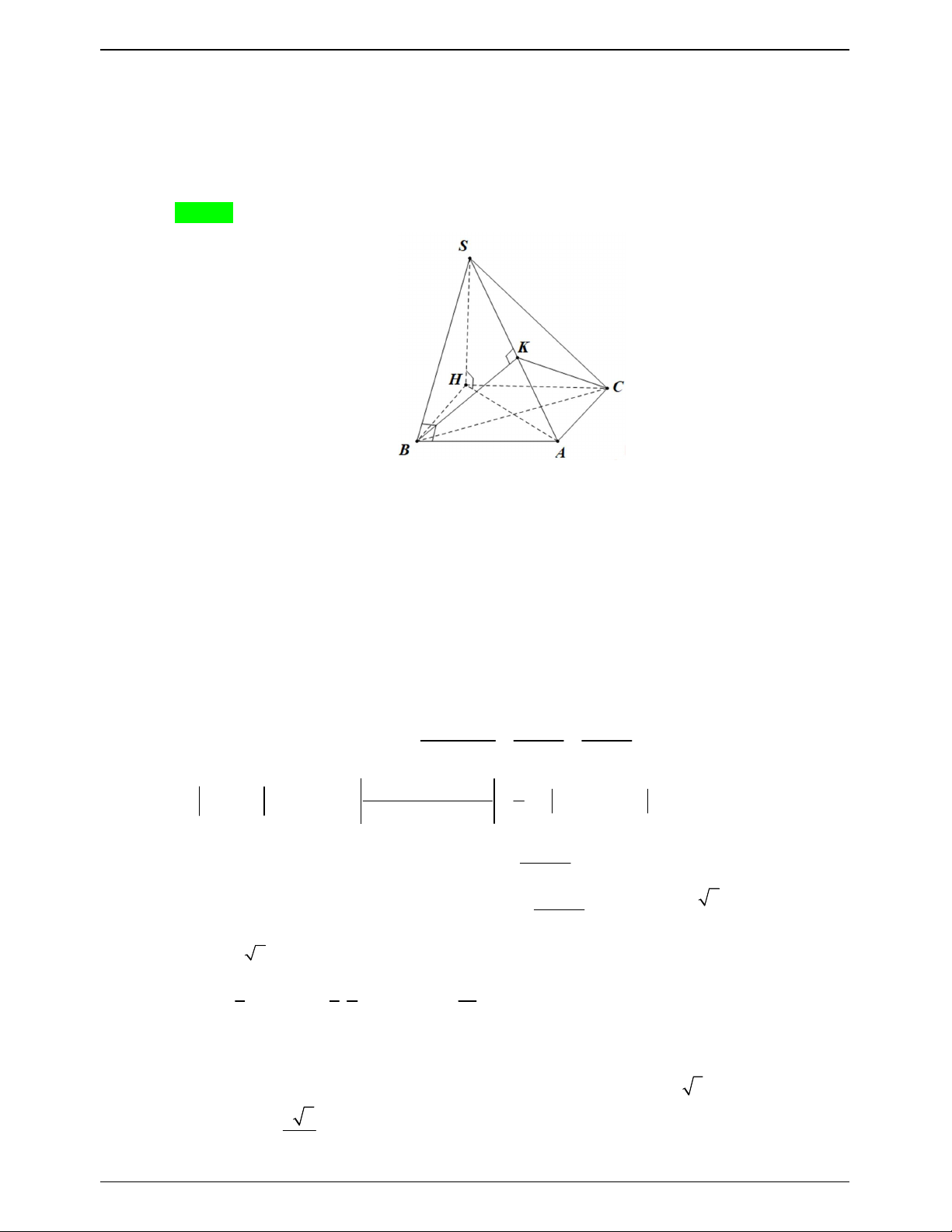
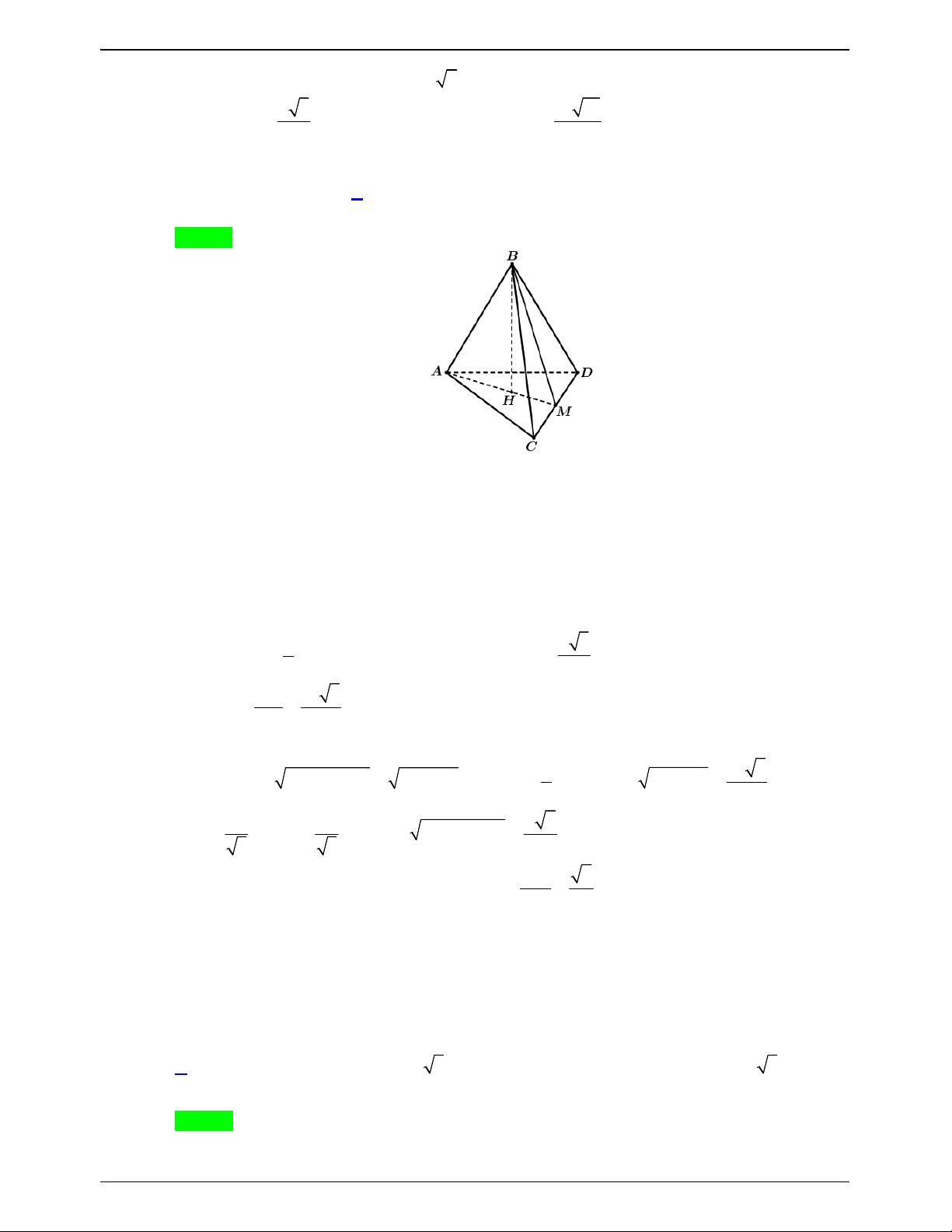
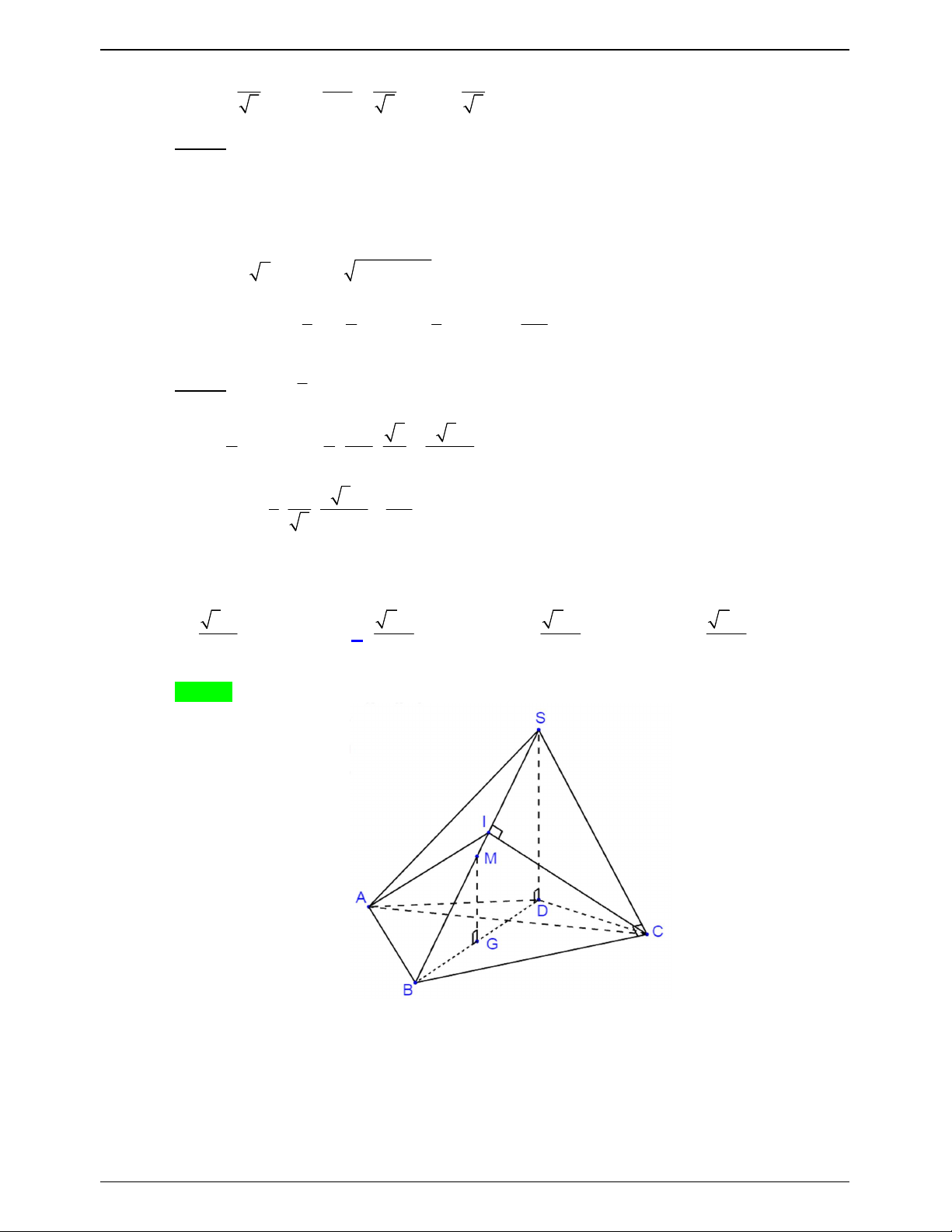
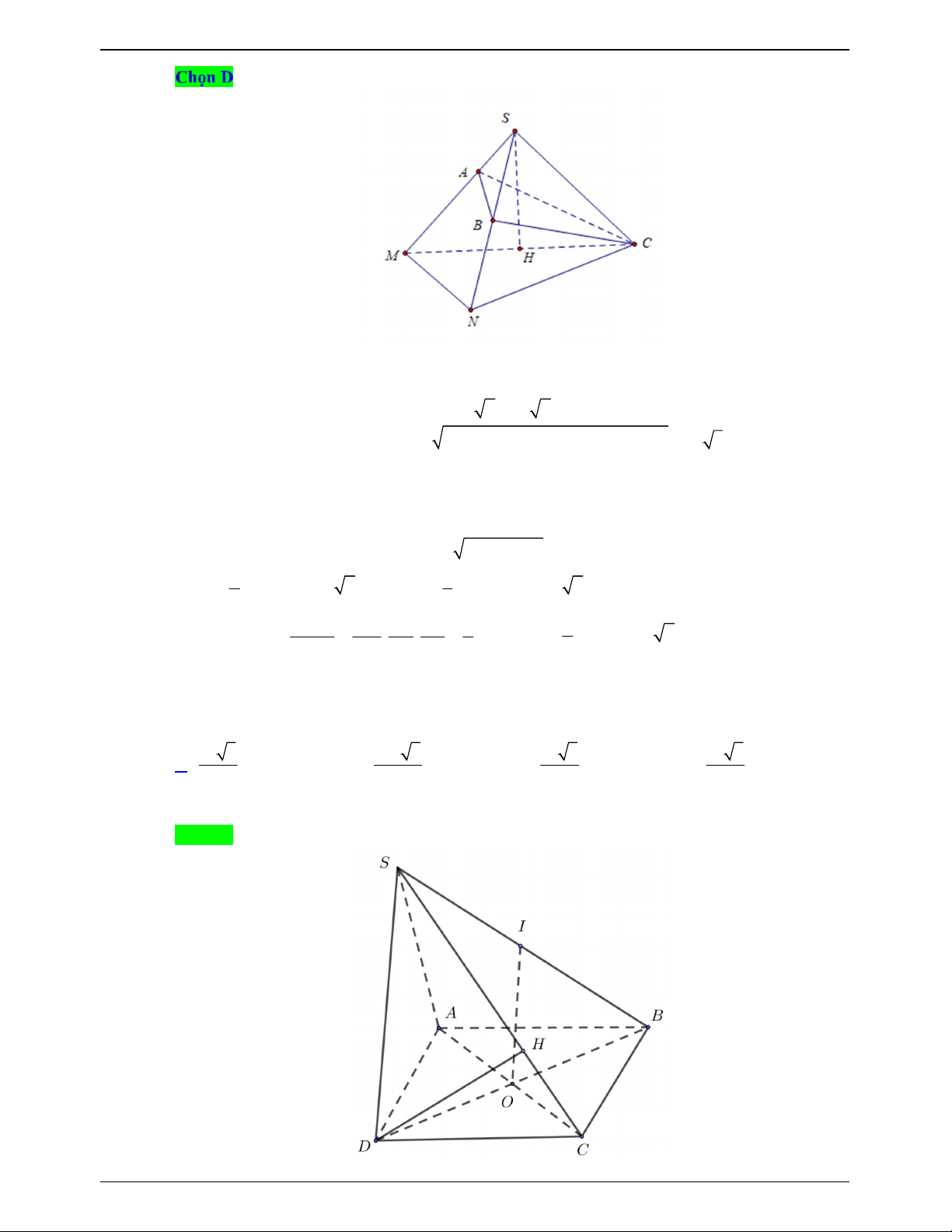
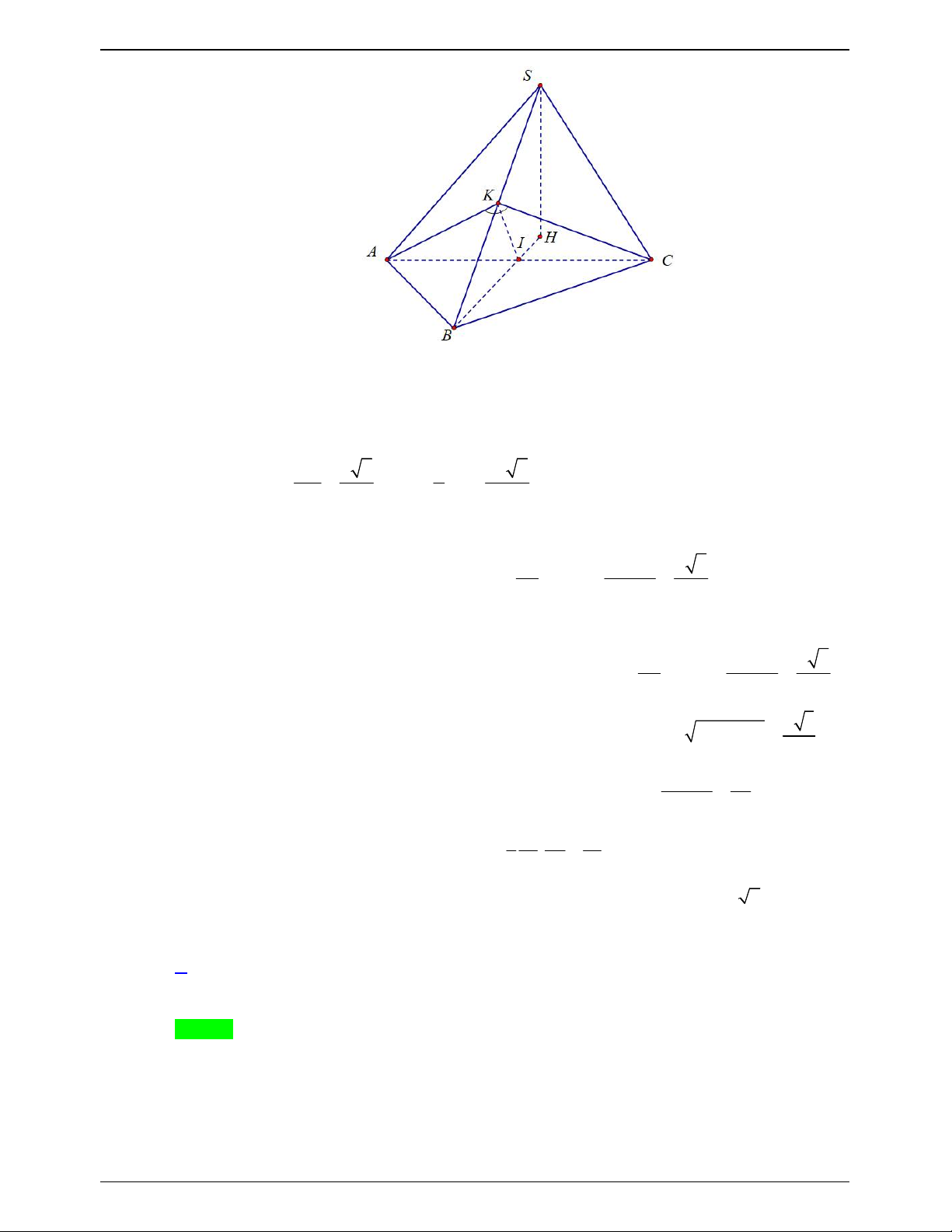
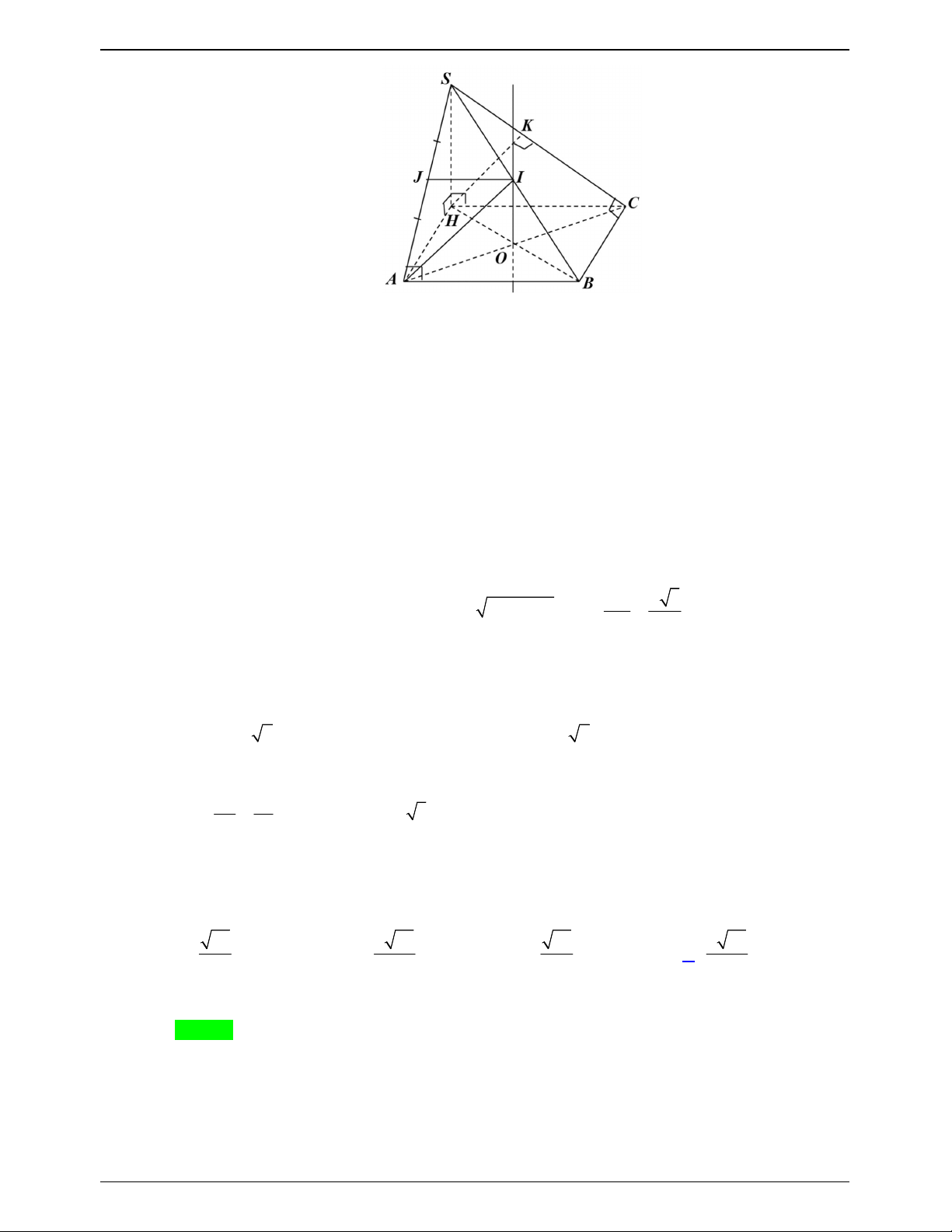
ĐỀ THI THỬ THPTQG – 2019-2020 S I A C a a 2 B
Hai tam giác vuông SAB và SAC bằng nhau chung cạnh huyền SA .
Kẻ BI vuông góc với SA suy ra CI cũng vuông góc với SA và IB  IC .
SA  IC, SA  IB  SA   IBC  tại I . 1 1 1 1 V  V V  S AI  S SI  S AI  SI  S SA . S. ABC . A IBC S.IBC IBC I  BC I  BC   3 3 3 3 IBC
SAB SAC  IB IC  IB IC 0  0 , , ,
 60  BIC  60 hoặc  0 BIC  120 .
Ta có IC  IB  AB  a mà BC  a 2 nên tam giác IBC không thể đều suy ra  0 BIC  120 .
Trong tam giác IBC đặt IB  IC  x  x  0 có: 2x IB IC BC    a 2 1 2 2 2 2 2 a 6 a 6 0 cos120      x 
 IB  IC  . 2 2I . B IC 2 2x 3 3 2  a 6  a 3
Trong tam giác ABI vuông tại I có: 2 2 2 AI  AB  IB  a     .  3  3   2 2 AB a
Trong tam giác SAB vuông tại 2
B đường cao BI có: AB  I . A SA  SA    a 3 . IA a 3 3 2 3 1 1 1 1  a 6  a Vậy  0 V  S SA  I .
B IC.SAsin BIC    a 3 sin120  . S. ABC 3 I  BC 3 2 6  3  6  
CÁCH 2: Xác định đường cao của hình chóp.
Phân tích hướng dẫn giải
1.Dạng toán: Đây là dạng toán tính thể tích khối chóp có lồng ghép góc giữa hai mặt phẳng. Phương pháp 1
Sử dụng công thức tính thể tích khối chóp V  S .h . 3 2. Hướng giải:
B1: Gọi H là chân đường cao kẻ từ S . Khi đó tứ giác ABHC là hình vuông. Trang 759
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
B2: Xác định góc giữa hai mặt phẳng  SAB và SAC rồi từ đó tính độ dài đường cao SH .
B3: Áp dụng công thức tính thể tích khối chóp.
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn D
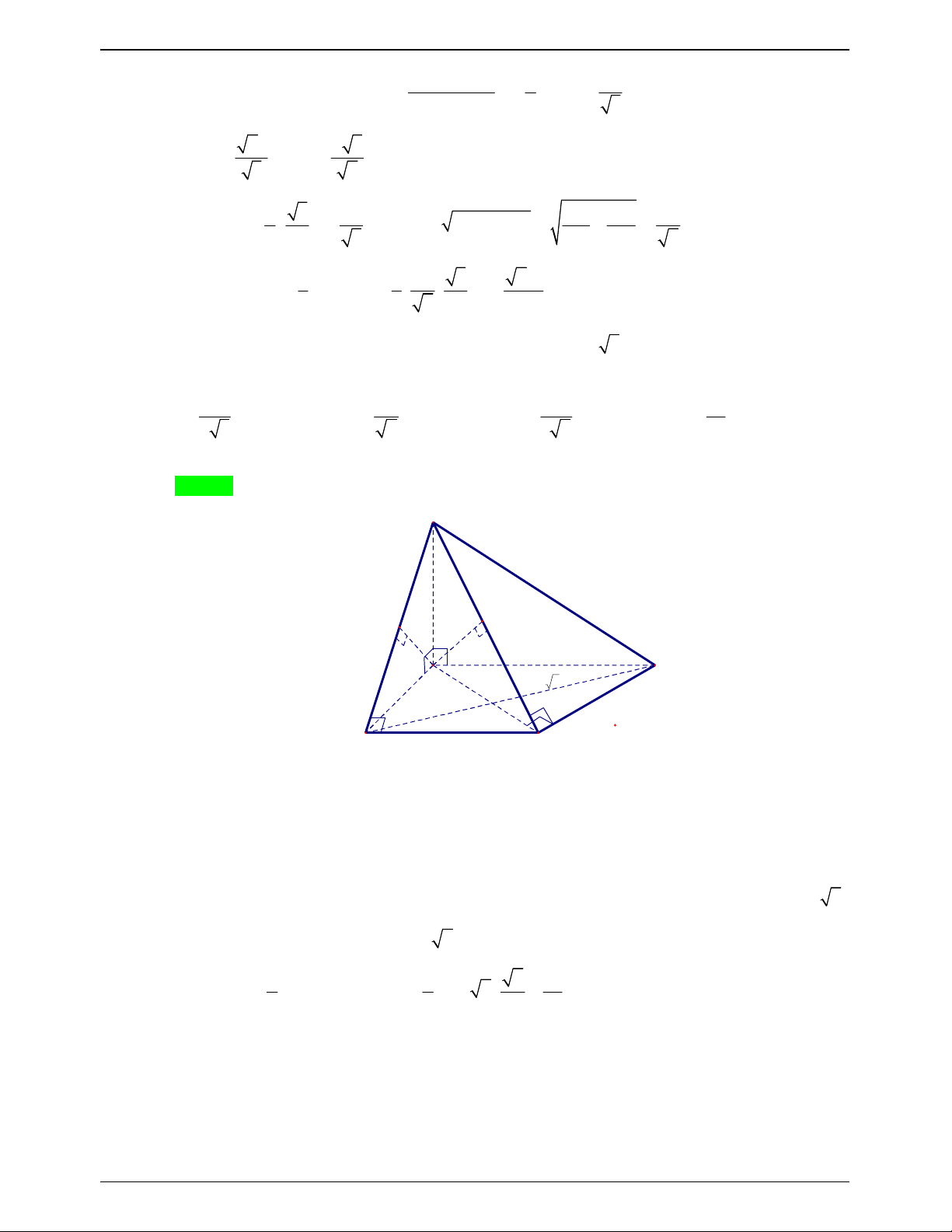
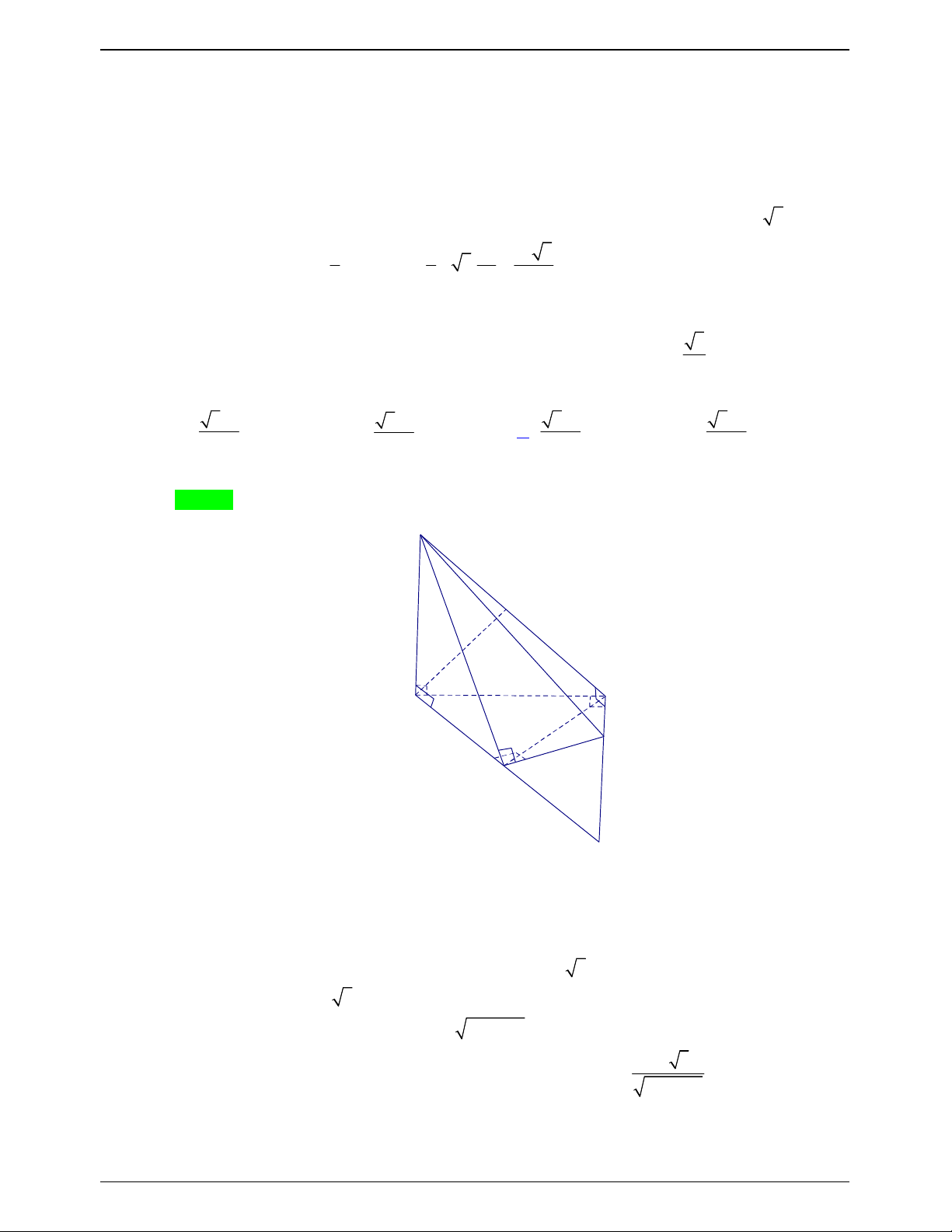
Gọi H là hình chiếu của S trên phẳng  ABC  SH   ABC . SH  AB Ta có
  AB   SDH   AB  BH . Chứng minh tương tự AC  HC . SB  AB 
Lại có AB  AC .
 ABHC là hình vuông.
Gọi K là hình chiếu vuông góc của B lên SA. Khi đó CK  SA ( S  BA  S  CA ).
Suy ra góc giữa hai mặt phẳng SAB và  SAC bằng góc giữa hai đường BK và CK . 2 2 2 2 2 2 SC .CA a x a .x 2 2
Đặt SB  x , khi đó: BK  CK    2 2 2 2 2 2 SC CA a  x a  x
BK  CK  BC 1 và  2 2 2 0 2 2 2 cos BKC  cos 60    2.BK  BC  BK 2BK .CK 2 2 2  a .x 2 2 2 2 2 2  2a 2 2  2 2
2.BK  BC  BK BK  BC
 x  a (l) a  x         2 2 2 2 2 2 2
2.BK  BC  BK 3.BK  BC  a .x   2  x  a 2 3. 2a    2 2  a  x
Với x  a 2  SH  a 3 1 1 1 a V  S .SH  . .A . B A . C HS  S.ABC . 3 A  BC 3 2 6
Bài tập tương tự:
Câu 49.1: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , với AB  5 , BC  2 . Các cạnh 9 2 bên đều bằng
và cùng tạo với mặt đáy góc 60 . Thể tích V của khối chóp S.ABC bằng. 4 Trang 760
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 3 3 3 3 3 3 A. V  . B. V  . C. V  . D. V  . 3 4 2 4 Lời giải Chọn C
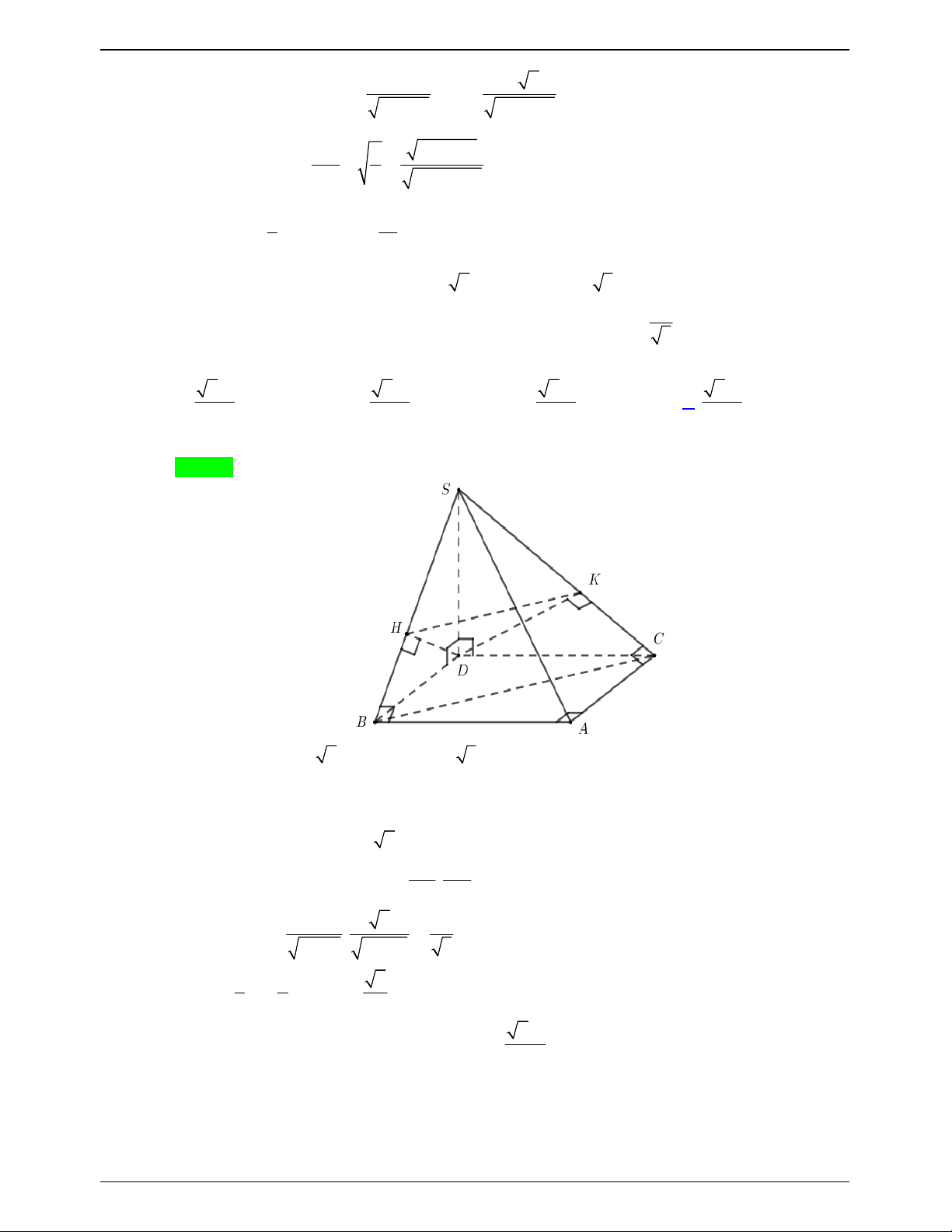
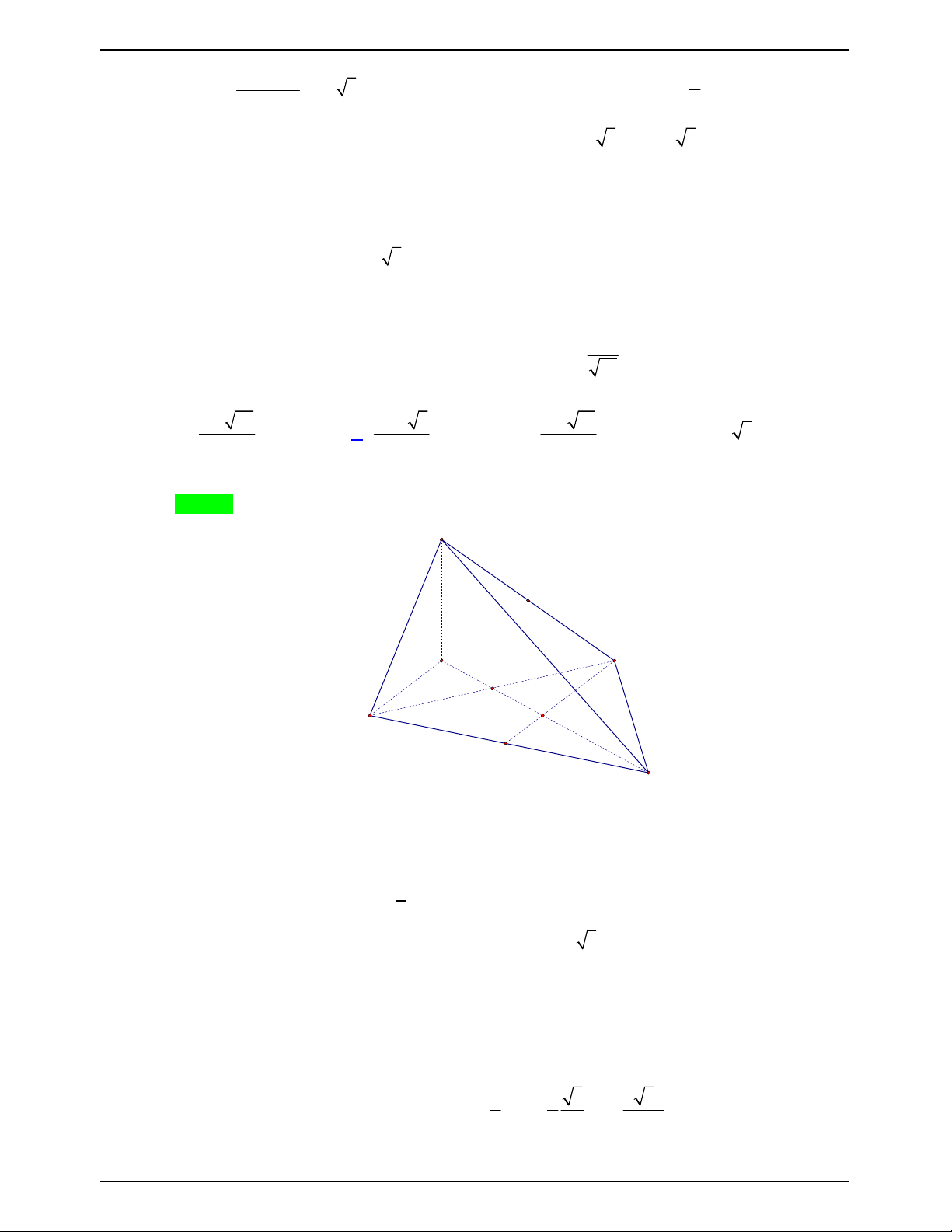
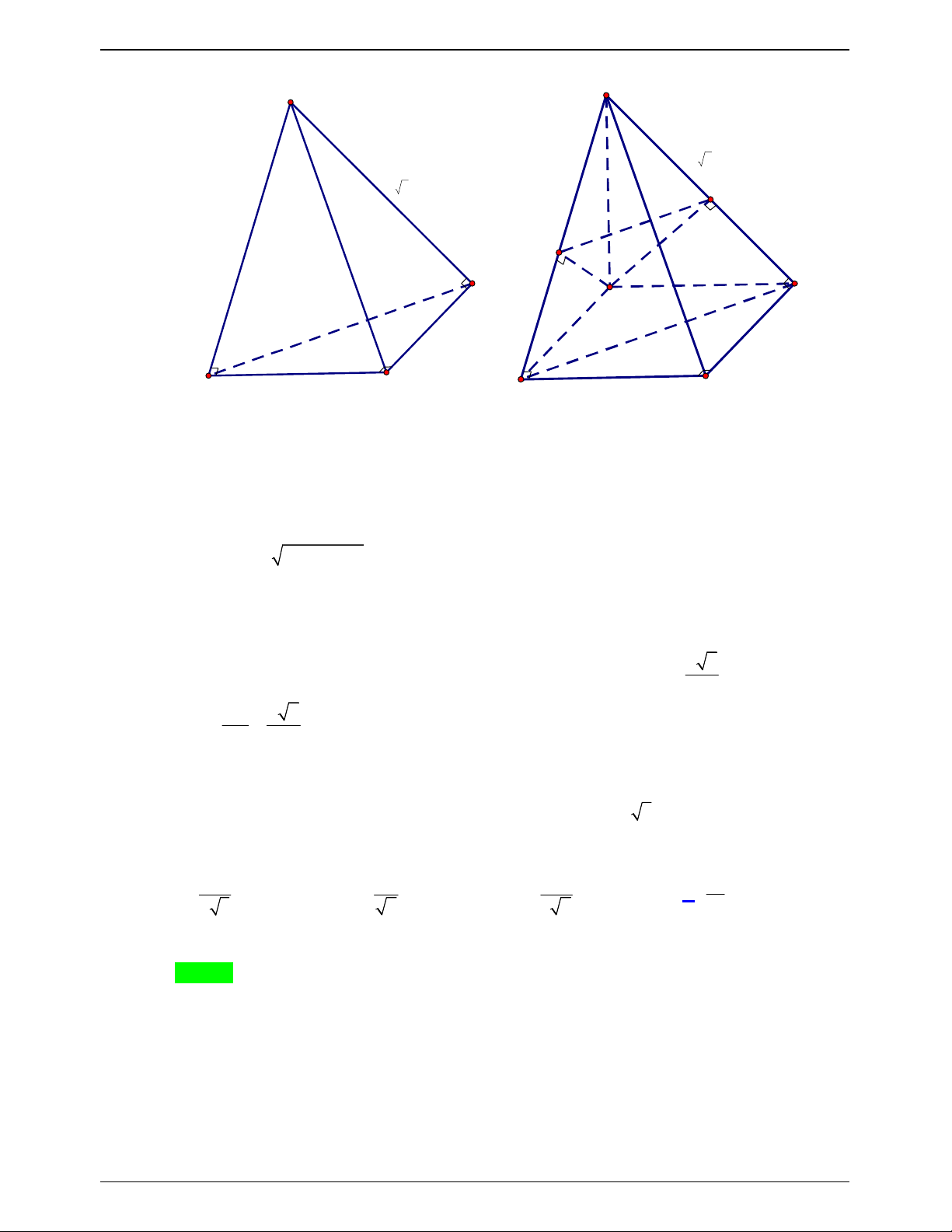
Kẻ SH   ABC , H  ABC  . 2 2 2
HA  SA  SH  Ta có 2 2 2
HB  SB  SH .  2 2 2
HC  SC  SC 
Mà SA  SB  SC  HA  HB  HC . Suy ra H là tâm đường tròn ngoại tiếp tam giác ABC .
Đặt AB  AC  x  5 . 2 2
AB  BC CA 2x x  S    (1). ABC 4HA 4HA 2HA   Từ 
SH  ( ABC)  S ;
A (ABC))  SAH  SAH  60 .  SH 3 3 3 9 2 9 6 sin 60    SH  SA      SA 2 2 2 4 8   .  HA 1 1 1 9 2 9 2 cos 60    HA  SA      SA 2 2 2 4 8 BC
Gọi I  AH  BC mà AB  AC  IB  IC   1. 2 2 2 2  AI  AB  BI  x 1 . 1 1  S  BC  AI 2 2   2 x 1  x 1 . ABC 2 2 2 2 2 x  9 x 2x 2 Thay vào (1) ta được 2 x 1   4 8x 81 2 x  1      9 . 9 9 2 x   8 Trang 761
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Kết hợp với x  5 ta được x  3 . Suy ra S  2 2 . ABC 1 1 9 6 3 3 Vậy V  SH .S  . .2 2  . 3 ABC 3 8 2
Câu 49.2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. E là điểm trên cạnh AD sao cho
BE vuông góc với AC tại H và AB  AE , cạnh SH vuông góc với mặt phẳng đáy, góc  2a
BSH  45 . Biết AH 
, BE  a 5 . Thể tích khối chóp S.ABCD bằng 5 3 16a 3 32a 5 3 32a 3 8a 5 A. . B. . C. . D. . 3 5 15 5 5 Lời giải Chọn B
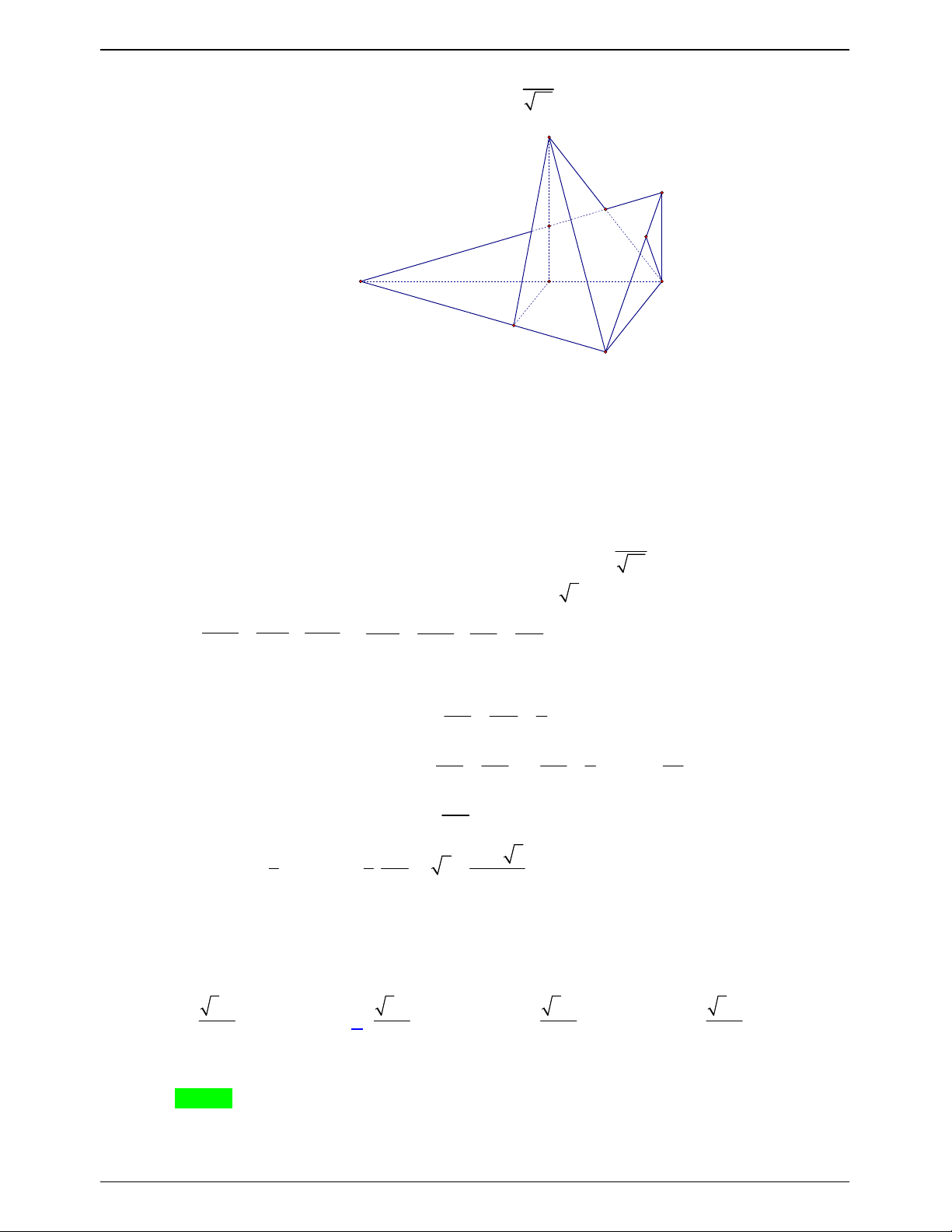
Đặt AB  x , ABE vuông tại A 2 2 2
 AB  AE  BE . 2 2 2 2 2 2  AE 
BE  AB  (a 5)  x  5a  x . Xét A
 BE vuông tại A , đường cao AH có 1 1 1 1 1 5      2 2 2 AE AB AH 2 2 2 2 5a  x x 4a x  a 4 2 2 4
 x  5a x  4a  0   . x  2a 
Loại x  a và AE  2a  AB  a . 4a BH 4a Suy ra AB  2a 2 2  BH  AB  AH   SH    . 5 tan BSH 5 1 1 1 A . B BH Xét A
 BC vuông tại B , đường cao BH     BC   4a . 2 2 2 AB BC BH 2 2 AB  BH 3 1 1 4a 32a 5 V  SH.S  . .2 . a 4a  . S .ABCD 3 ABCD 3 5 15 Trang 762
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
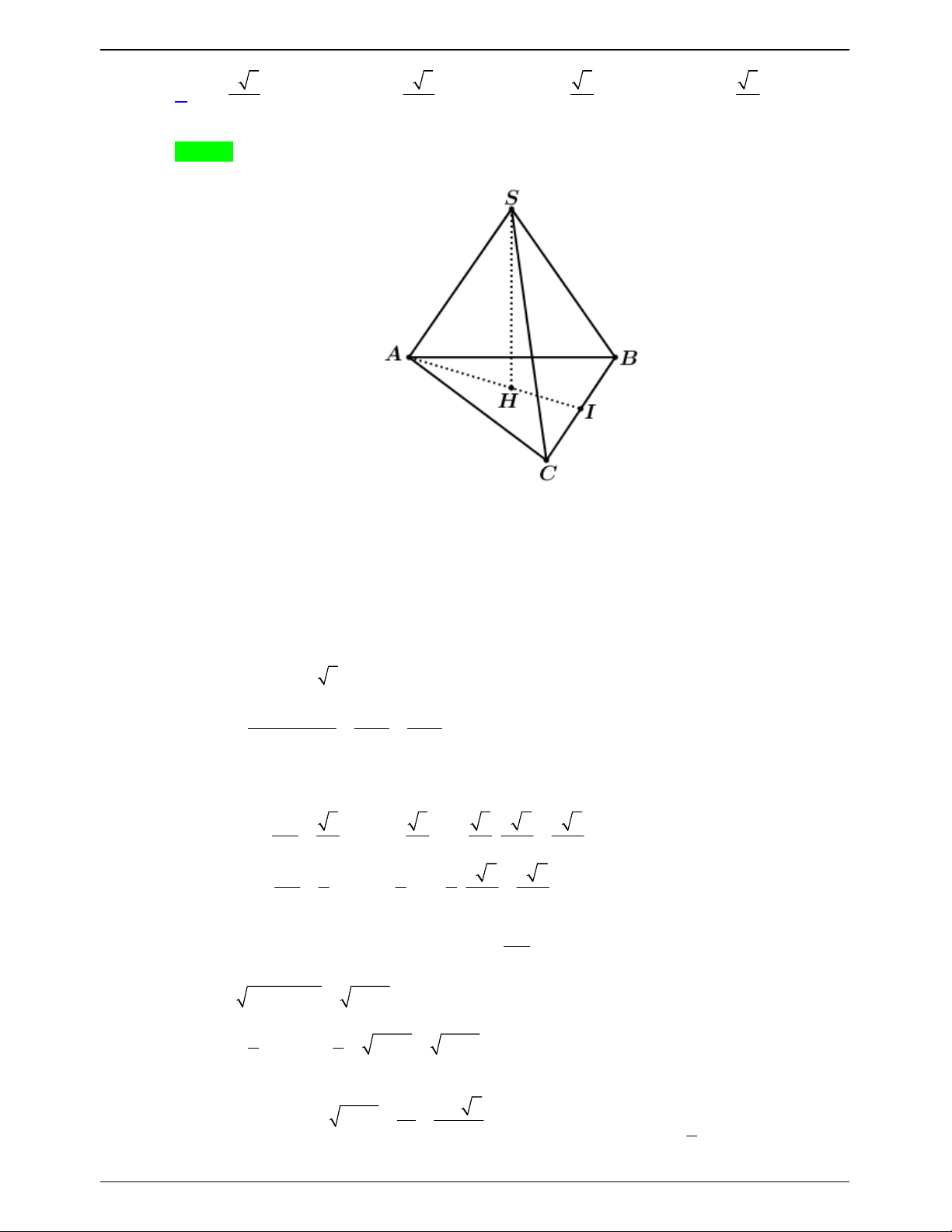
Câu 49.3: Cho tứ diện ABCD có AC  AD  a 2 , BC  BD  a , khoảng cách từ điểm B đến mặt phẳng a 3 3 a 15
 ACD bằng
và thể tích tứ diện ABCD bằng
. Góc giữa hai mặt phẳng  ACD 3 27
và  BCD bằng A. 90 . B. 45 . C. 30 . D. 60 . Lời giải Chọn B
Gọi M là trung điểm của CD .  AM  CD Xét A
 CD cân tại A và B
 CD cân tại B nên 
 CD   ABM  BM  CD 
  ACD BCD     ,  AMB .
Kẻ BH vuông góc với AM tại H  BH  AM .
Mà CD   ABM   CD  BH  BH   ACD . 1 a Suy ra V  BH.S
với BH  d  B  ACD 3 ,  . ABCD 2 ACD 3 2 3V a 5  S   . A  CD BH 3
Đặt CD  2x . 2 1 a 5 Suy ra 2 2 2 2 AM 
AC  MC  2a  x 2 2  S 
AM.CD  x 2a  x  A  CD 2 3 a 2a a 6 2 2  x   CD   BM  BC  CM  . 3 3 3  BH 2 
Xét tam giác BHM vuông tại H có sin BMH    sin AMB BM 2 
 AMB  45   ACD,  BCD     45 .
Câu 49.4: Cho hình lăng trụ đứng ABC . D A B  C  D
  , đáy ABCD là hình thoi, góc 
BAD  60 . Gọi M là
điểm thuộc miền trong của hình thoi ABCD , biết AM tạo với mặt phẳng  ABC một góc 60 và A M 
 4 . Độ dài cạnh AB bằng bao nhiêu nếu thể tích khối lăng trụ bằng 12 ?
A. AB  2 . B. AB  2 3 . C. AB  4 . D. AB  4 3 . Lời giải Chọn A Trang 763
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020  2 BD  x  x 3
Đặt AB  x, BAD  60    S  . ABCD  AC  x 3 2 
Ta có AA   ABCD  AM là hình chiếu của AM trên mặt phẳng  ABC .  A M   ABCD       A M  AM   , ,
 AMA  60 . AA
Xét AAM vuông tại A , có  sin AMA   AA  2 3 . AM 2 x 3 Ta lại có V
 12  AA .S  12  S  2 3 
 x  2  AB  2 .
ABCD. AB C  D   ABCD ABCD 2 Vậy AB  2 .
Câu 49.5: Cho hình lăng trụ tam giác đều AB . C AB C
  cạnh đáy bằng 1, khoảng cách từ tâm của tam giác 1
ABC đến mặt phẳng  A B
 C  bằng . Thể tích của khối lăng trụ bằng 6 3 12 3 2 3 2 A. . B. . C. . D. . 16 16 16 8 Lời giải Chọn C
Gọi I là tâm tam giác ABC , M là trung điểm của AB .
d  I,  ABC IM 1     d  1 1 ,
A  ABC  3.  . d  , A  A B  C  AM 3 6 2
Xét tứ diện A .ABC có AA   ABC  . Kẻ AH  AM (1).  AM  BC Ta có 
 BC   AA M 
  BC  AH (2).
AM  BC  Trang 764
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Từ (1), (2) ta có AH   ABC   AH  d  A  ABC  1 ,  . 2 1 1 1 AM .AH 6
Xét AAM vuông:    AA   . 2 2 2 2 2 AH AM AA 4 AM  AH 6 3 3 2 Vậy V  AA .S  .  .
ABC. AB C   ABC 4 4 16
Câu 49.6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với BA  BC  5a ;   9 0
SAB  SCB  90 . Biết góc giữa hai mặt phẳng  SBC  và SBA bằng với cos  . Thể 16
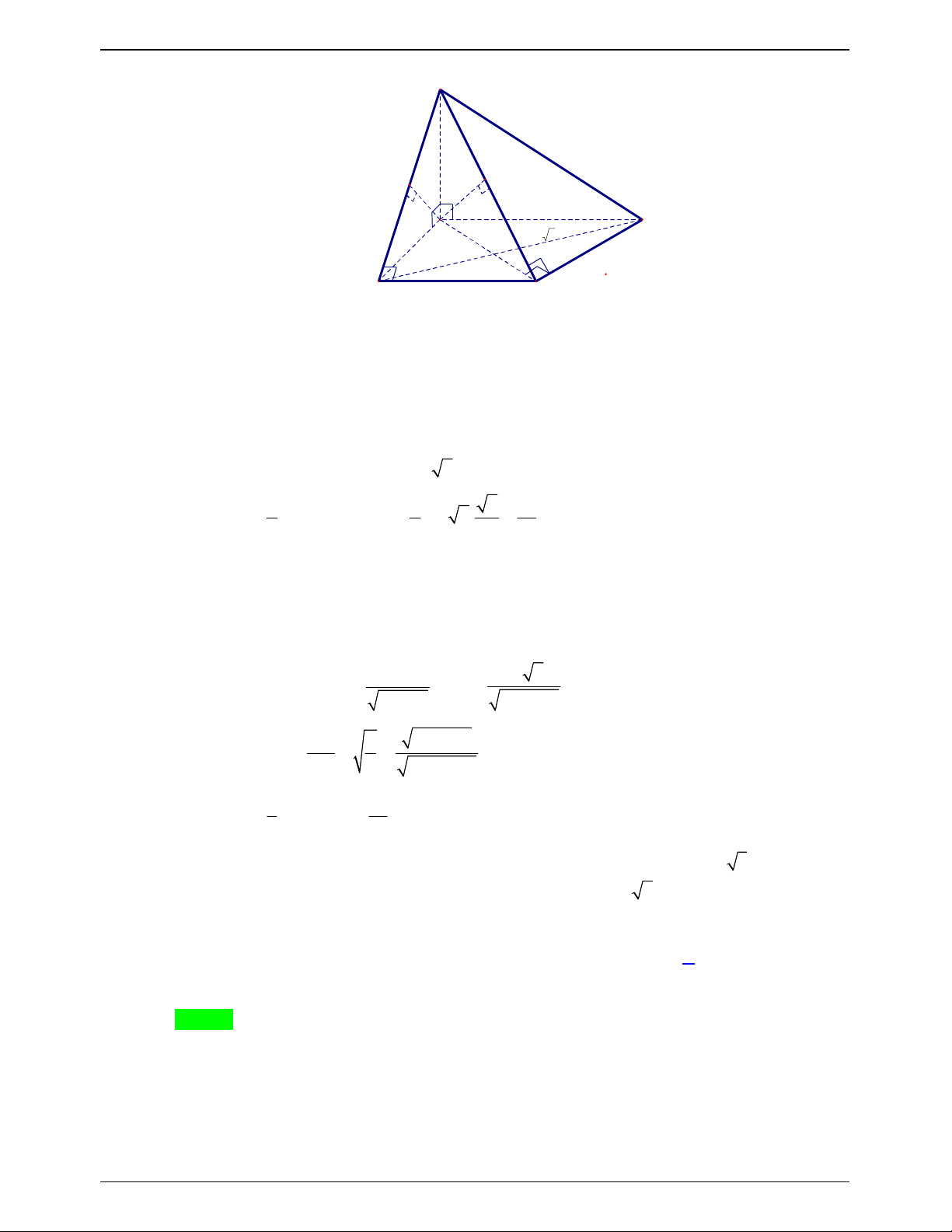
tích của khối chóp S.ABC bằng 3 50a 3 125 7a 3 125 7a 3 50a A. . B. . C. . D. . 3 9 18 9 Lời giải Chọn C
Ta có hai tam giác vuông SAB và SBC bằng nhau và chung cạnh huyền SB .
Kẻ AI  SB  CI  SB và góc giữa hai mặt phẳng (SBA) và (SBC) là góc giữa hai đường
thẳng AI và CI  ( AI ;CI )   .         9
Do CBA  90  180  AIC  90  AIC  180    cos AIC   16
Có AC  5 2a, AIC cân tại I, nên có : 2 2 2AI  AC  2 2 2 AI  AC 9 2 2  cos AIC   
 AI  16a  AI  4a 2 2 2 AI 2 AI 16 2 AI 16 25a
 BI  3a  SI   a  SB  . IB 3 3 Cách 1 : BA  SA
Dựng SD  ( ABC ) tại D . Ta có: 
 BA  AD . Tương tự BC  CD BA  SD  Trang 765
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 5 7
Nên tứ giác ABCD là vuông cạnh 5a  BD  5 2a 2 2
 SD  SB  BD  a 3 3 1 1 1 5 7 1 125 7a Vậy 2 3 V  SD. BA  . . .25 a  . SABC 3 2 3 3 2 18 1 1 1
Cách 2 : V V V  SI.S  BI.S  S . B S S .ABC S .ACI B.ACI 3 ACI 3 ACI 3 ACI 2 1 1 5 7 5 7a
 A IC cân tại I, nên 2 2 S
 AI sin   .16a .  . ACI 2 2 16 2 2 3 1 25a 5 7a 125 7a Vậy V  . .  . S .ABC 3 3 2 18
Câu 49.7: Cho hình chóp S.ABC có BC  2BA  4a ,  
ABC  BAS  90 . Biết góc giữa hai mặt phẳng
SBC  và SBA bằng 60 và SC  SB . Thể tích của khối chóp S.ABC bằng 3 32a 3 8a 3 16a 3 16a A. . B. . C. . D. . 3 3 3 9 Lời giải Chọn B
Tam giác SBC cân cạnh đáy BC  4a . Gọi E là trung điểm BC thì ta có S  EB vuông tại
E, BE  2a  BA . Đưa về bài toán gốc với chóp S.ABE . 1
Hai tam giác vuông SAB , SEB bằng nhau vì chung cạnh huyền SB , AB  EB  BC  2a . 2
Kẻ AI  SB  EI  SB và góc giữa hai mặt phẳng  SB 
A và SBC  góc giữa hai mặt phẳng
SBA và SBE là góc giữa hai đường thẳng AI và EI   AI; EI   60 .    1 Do    
CBA  90  180  AIE  90  AIE  120  cos AIE   2
Có AE  2 2a ,  AIE cân tại I, nên có : 2 2 2 AI  AE 2  2 2 2 AI  AE 1  8a 2 2 cos AIC    2  AI   AI  a . 2 2 2 AI 2 AI 2 3 3 Trang 766
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 2 2a AI 4a 6a  BI   SI    SB  . 3 IB 3 3 Cách 1 : BA  SA
Dựng SD   ABC  tại D . Ta có: 
 BA  AD . Tương tự BE  ED BA  SD 
Nên tứ giác ABED là hình vuông cạnh 2a . 2 2
 BD  2 2a  SD  SB  BD  2a . 3 1 1 1 8a Thể tích. 2 V  SD  BC  BA 
 2a  4a  S .ABC 3 2 3 3 1
Cách 2 : V  SB  2S SABC 3 AEI 2 2 1 1 8a 3 2 3a 2 S  AI sin      AEI 2 2 3 2 3 2 3 1 6a 4 3a 8a Vậy V     S .ABC 3 3 3 3
Câu 49.8: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a ,   0
SAB  SCB  90 góc giữa hai
mặt phẳng (SAB) và (SCB) bằng 0
60 . Thể tích của khối chóp S.ABC bằng 3 3a 3 2a 3 2a 3 2a A. . B. . C. . D. . 24 24 8 12 Lời giải Chọn B
Gọi M là trung điểm của SB , và G là trọng tâm tam giác đều ABC . Theo giả thiết   SAB SCB 90  
 MS  MB  MA  MC  M thuộc trục đường tròn ngoại
tiếp ABC  MG  ( ABC) .
Gọi D là điểm đối xứng với G qua cạnh AC thì  SD  ( ABC) .
Từ giả thiết suy ra hai tam giác vuông bằng nhau SAB và SCB .
Do đó từ A kẻ AI  SB, I  SB thì CI  SB
Nên góc giữa hai mặt phẳng (SAB) và (SCB) bằng góc ( AI , CI ) 60  . Trang 767
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020    2 AI AC 1 a Do   2 2
ABC  60  AIC  120     AI  2 2 AI 2 3 2a a 3  BI   SB  3 2 2 2 4 3 2 3a 4a a Ta có 2 2 BD   a  a  SD  SB  BD    3 2 3 2 3 6 3 1 1 1 3 2a Thể tích 3 V  SD  S    a  . S. ABC 3 ABC 3 6 4 24    
Câu 49.9: Cho tứ diện ABCD có DAB CBD 90 ; AB ; a AC a 5; ABC 135     
. Biết góc giữa hai
mặt phẳng ( ABD), (BCD) bằng 30 . Thể tích của tứ diện ABCD bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 2 3 2 3 2 6 Lời giải Chọn D D E F C H a 5 A a B
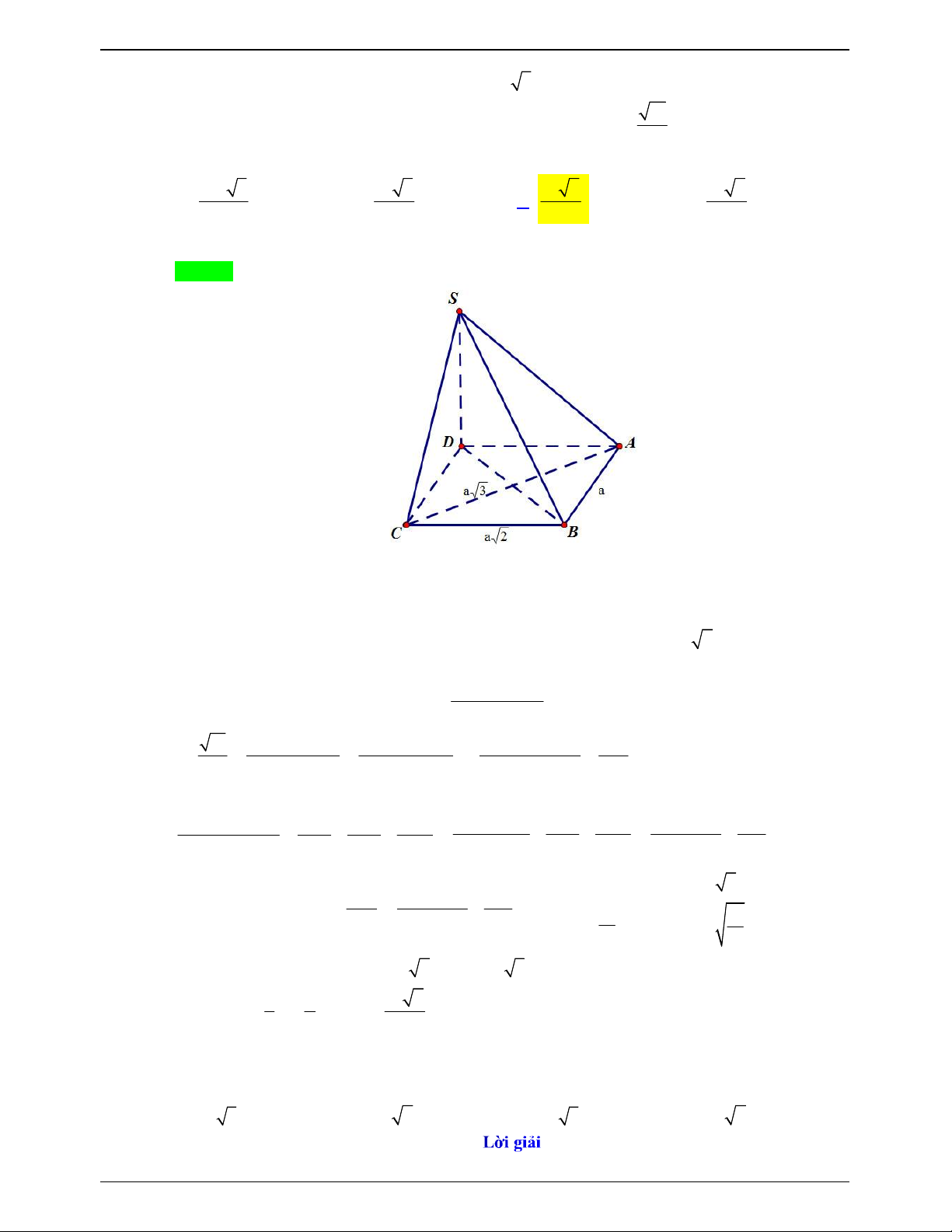
Dựng DH  ( ABC) . BA  DA BC  DB Ta có 
 BA  AH . Tương tự   BC  BH . BA  DH  BC  DH  
Tam giác AHB có AB a, ABH 45    H
 AB vuông cân tại A  AH  AB  a , HB  a 2
Áp dụng định lý cosin, ta có BC  a 2 .  2 1 1 2 a Vậy S 
 BA BC  sin CBA 
 a  a 2   . ABC 2 2 2 2 HE  DA Dựng 
 HE  (DAB) và HF  (DBC ) . HF  DB    Suy ra ((DB )
A ,(DBC))  (HE, HF)  EHF và tam giác HEF vuông tại E . Trang 768
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 ax xa 2
Đặt DH  x , khi đó HE  , HF  . 2 2 2 2 a  x 2a  x HE 3 x  2a Suy ra:  2 2 cos EHF     x  a . 2 2 HF 4 2x  2a 3 1 a Vậy V   DH  S  . ABCD 3 ABC 6 Câu 49.10:
Cho hình chóp S.ABC có AB 
2a, AC  a, BC  3a ,  
SBA  SCA  90 và hai mặt 1
phẳng SAB và SAC tạo với nhau một góc  sao cho cos 
. Thể tích của khối chóp 3 S.ABC bằng 3 2a 3 2a 3 2a 3 2a A. . B. . C. . D. . 12 2 3 6 Lời giải Chọn D
Từ giả thiết : AB  2a, AC  a, BC  3a 2 2 2 2 2 2
 BC  3a  2a  a  AB  AC
ABC vuông tại A
Dựng SD   ABC  . Dễ chứng minh được ABDC là hình chữa nhật .
DB  AC  a, DC  AB 
2a . Gọi SD  h . DB DC
Áp dụng công thức tính nhanh : .  cos . SB SC 1 2 1 Chọn a  1 : .  4 2 2
 h 3h 4  0  h 1 h 1  h  SD  1 2 2 h 1 h  2 3 1 1 2 V
 .SD. AB.AC  SABC 3 2 6 3 2a
Vì chọn a  1, theo đề bài ta chọn được V  . 6 Trang 769
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020    Câu 49.11:
Cho hình chóp S.ABC có AB  a , AC  a 3 , SB  2a và ABC  BAS  BCS  90 . Biết 11
sin của góc giữa đường thẳng SB và mặt phẳng SAC  bằng
. Thể tích của khối chóp 11 S.ABC bằng 3 2a 3 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 9 9 6 3 Lời giải Chọn C BA  SA
- Dựng SD   ABC  tại D . Ta có:   BA  AD . BA  SD  BC  SD Và: 
 BC  CD  ABCD là hình chữ nhật  DA  BC  a 2 , DC  AB  a . BC  SC 
d  B,SAC 
- Sử dụng công thức sin SB,SAC   . SB 11 d  ; B  SAC 
d  D;SAC  1 11        1 . 11 SB SB 2
d D;SAC  2 SB - Lại có: 1 1 1 1 1 1 1 1 3         2 . 2
d  D;SAC  2 2 2 DS DA DC 2 2 2 2 SB  BD DA DC 2 2 2 SB  3a 2a 2 2 SB  6a SB  a 6 11 1 3 
- Từ 1 và 2 suy ra:      2 11 SB 2 2 2 SB  3a 2a 2 2   11 SB  a SB  a  3   3
Theo giả thiết SB  2a  SB  a 6  SD  a 3 . 3 1 1 a 6 Vậy V  SD. B . A BC  . SABC 3 2 6   Câu 49.12:
Cho hình chóp S.ABC có SA  4, SB  6, SC  12 và ASB  60 ,
 BSC  90 và  CSA  120
. Thể tích của khối chóp S.ABC bằng A. 36 3 . B. 36 2 . C. 24 3 . D. 24 2 . Trang 770
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 Trên tia S ,
A SB lần lượt lấy cá điểm M , N sao cho SM  SN  12 . Khi đó ta có:
Tam giác SMN đều  MN  12 .
Tam giác SNC vuông tại S nên CN  SC 2  12 2 .
Tam giác SMC cân tại S có 2 2  MC 
SC  SM  2SC.SM .cos CSM  12 3 . Từ đó suy ra 2 2 2
MC  MN  CN  tam giác CMN vuông tại N .
Gọi H là hình chiếu vuông góc của S trên mặt phẳng CMN  .
Vì SC  SM  SN  12 nên H là tâm đường tròn ngoại tiếp tam giác CMN
 H là trung điểm của MC 2 2
 SH  SC  CH  6 . 1 1 S 
MN.NC  72 2  V  .SH.S  144 2 . CMN 2 S.CMN 3 CMN V SA SB SC 1 1
Mặt khác, ta có S.ABC  . .   V  V  24 2 . S. ABC S .MNC V SM SN SC 6 6 S .MNC Câu 49.13:
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  a,  
SAB  SCB  90 , góc
giữa AB và SBC  bằng 60 . Thể tích của khối chóp đã cho bằng 3 a 3 3 4a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 9 9 3 Lời giải Chọn A Trang 771
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Dựng hình vuông ABCD tâm O . Gọi I là trung điểm SB . Do   0
SAB  SCB  90 nên hình chóp S.ABC nội tiếp mặt cầu tâm I đường kính SB .
Do O là tâm đường tròn ngoại tiếp tam giác ABC
 OI là trục của đường tròn ngoại tiếp tam giác ABC .
Suy ra OI   ABC   SD   ABC 
Mà  AB SBC DC SBC CD CS   , , , DCS 60      0 SD  C .
D tan 60  a 3 . 2 3 1 1 a a 3
Từ đây ta suy ra: V  .SD.S  .a 3.  .  3 ABC 3 2 6 Câu 49.14: Cho hình chóp .
S ABC có đáy là tam giác cân tại A , AB  a ,  BAC 120 ,    3
SBA  SCA  90 . Gọi  là góc giữa SB và SAC  thỏa mãn sin  , khoảng cách từ S 8
đến mặt đáy nhỏ hơn 2a . Thể tích của khối chóp S.ABC bằng 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 4 6 12 24 Lời giải Chọn C S K C D A B I
+ Gọi D là hình chiếu vuông góc của S lên đáy  ABC  , đặt SD  x 0  x  2a  .  AC  SC Ta có 
 AC   SDC   AC  DC . Tương tự ta cũng có AB  DB . AC  SD 
+ Tam giác ABC cân tại A và 
CAB  120  BC  a 3 và  
DBC  DCB  60  D
 BC đều cạnh a 3 .
+ Tam giác SDC vuông tại D 2 2
 SB  3a  x . x a 3
+ Kẻ DK  SC tại K  DK  SAC   d  D;SAC   DK  . 2 2 3a  x
+ Gọi I  BD  AC , xét D
 IC vuông tại C và  BDC  60 Trang 772
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 DC 1  DI 
  2a 3  B là trung điểm của DI  d  ;
B SAC   d  ;
D SAC  . cosBDC 2
d  B;SAC  3 xa 3
Theo giả thiết   SB;SAC   sin    SB 8 2 2 2 3a  x  2  x  x x  a 2 2
 x  3a  4ax  0   4  3  0    
. So sánh với điều kiện suy ra x  a .  a  a x  3a  3 1 a 3 Vậy V  .S .SD  . S .ABC 3 ABC 12 Câu 49.15:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a ,  
SAB  SCB  90 . Gọi M là trung 6a
điểm của SA . Biết khoảng cách từ A đến  MBC  bằng
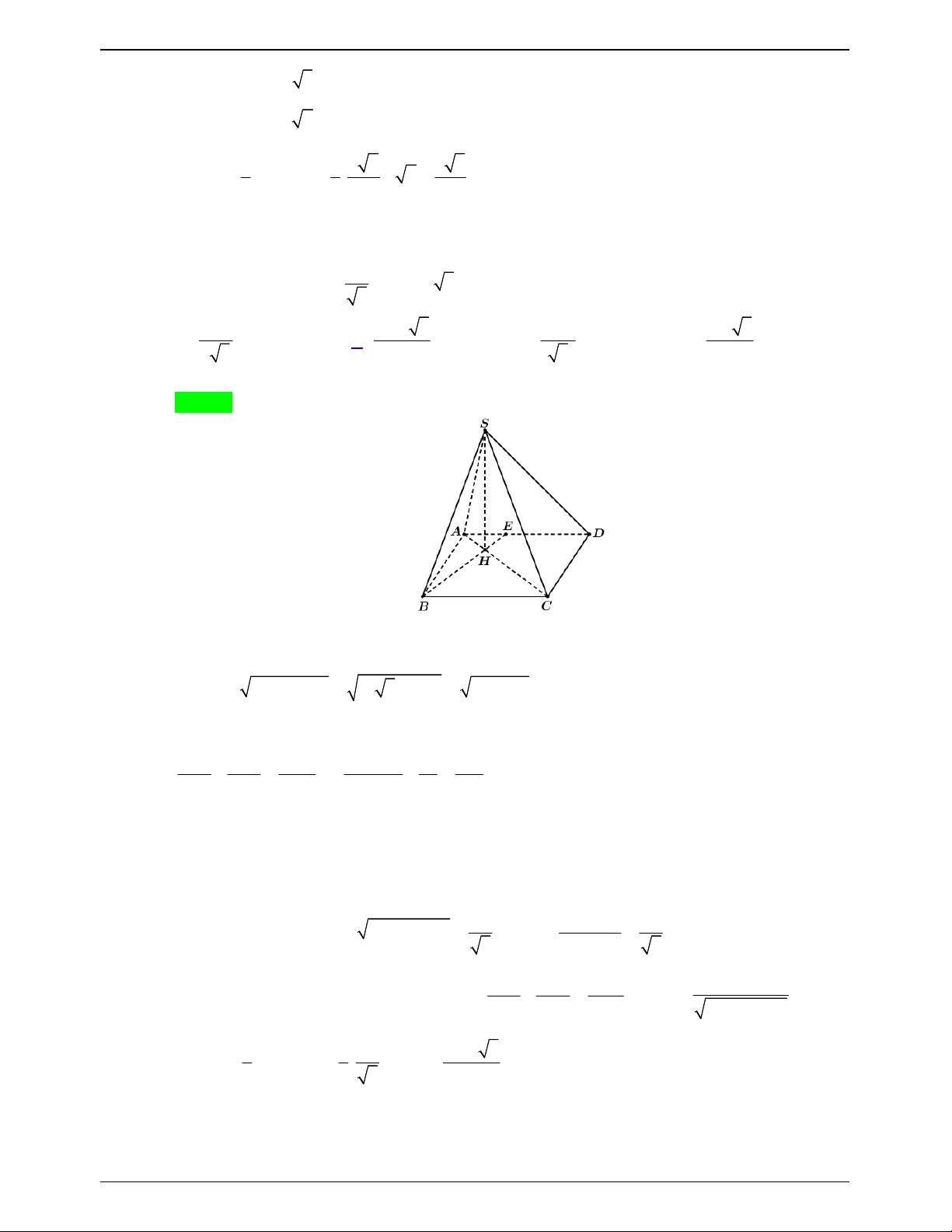
. Thể tích của khối chóp đã cho 21 bằng 3 8a 39 3 10a 3 3 4a 13 A. . B. . C. . D. 3 2a 3 . 3 9 3 Lời giải Chọn A S M D A I C G N B
Trong mp  ABC  xác định điểm D sao cho tứ giác ABCD vuông tại A và C AB  AD C  B  CD Khi đó ta có:  AB  SD  ;  CB  SD  AB  SA  CB  SC  1
Vậy SD   ABCD  V  SD.S S. ABC 3 A  BC
Có tam giác ABC là tam giác đều cạnh 2a 2  S  a 3 ABC Ta đi tìm SD
Gọi I là trung điểm AC
vì tam giác ABC đều, ABCD nội tiếp đường tròn đường kính BD  I  BD  AC  BD
Gọi G là trọng tâm tam giác ABC và N là trung điểm BC
Vì tam giác ABC đều  AN  BC  AN // CD , tương tự CG // BD 2 2 3 2 3a
Dễ thấy AGCD là hình thoi  CD  AG  AN  2a  1 3 3 2 3
Xét hình chóp S.ANCD có đáy ANCD là hình thang vuông tại C, N. Trang 773
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 6a
Khoảng cách từ A đến mặt phẳng MNC  bằng
vì  MNC    MBC  . 21 S P M F H E A D C N
Trong mp  ABCD gọi  
E  CN  AD
Trong mp SAD kẻ tia At / /SD gọi  
P  EM  At
Gọi K là hình chiếu của G trên mặt phẳng CMB
AP / /SD  AP  CN Khi đó ta có 
  APN   CN AN  CN  a
Trong mp  APN  kẻ AH  PN ta có AH  d  A MCN  6 ,  21
Mà tam giác ABC là tam giác đều cạnh 2a  AN  a 3 1 1 1 1 21 1 1 Từ        AP  2a 2 2 2 AH AP AN 2 2 2 2 AP 36a 3a 4a Dễ thấy A  PM  S
 FM  SF  AP  2a 2 ED CD 2
Xét tam giác EAN có CD / / AN nên   (theo 1 ) EA AN 3 FD ED FD 2 4a
Xét tam giác EAP có FD / / PA nên     FD  3 PA EA PA 3 3 10a
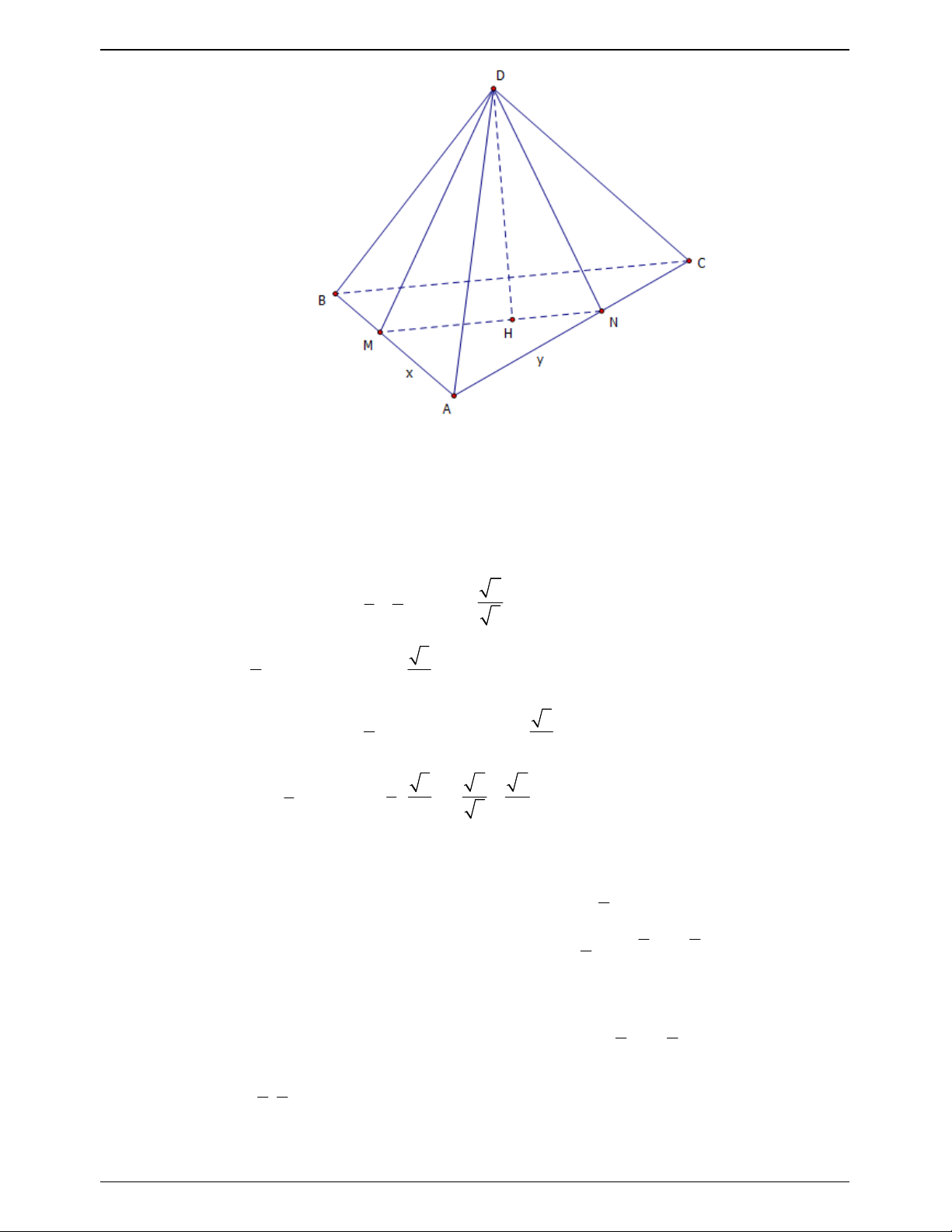
Từ 2 và 3 ta có SD  SF  FD  3 3 1 1 10a 10a 3 Vậy 2 V  SD.S  . .a 3  . S.ABC 3 ABC 3 3 9 Câu 49.16:
Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B ,
tam giác SAC vuông tại C . Biết góc giữa hai mặt phẳng  SAB và  ABC bằng 60 . Tính
thể tích khối chóp S.ABC theo a. 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 8 12 6 4 Lời giải. Chọn B Trang 774
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 S D C B A
Gọi D là hình chiếu của S lên mặt phẳng  ABC , suy ra SD   ABC .
Ta có SD  AB và SB  AB  gt , suy ra AB   SBD  BA  BD .
Tương tự có AC  DC hay tam giác ACD vuông ở C . Dễ thấy S  BA  S
 CA (cạnh huyền và cạnh góc vuông), suy ra SB  SC .
Từ đó ta chứng minh được SBD  SCD nên cũng có DB  DC . 
Vậy DA là đường trung trực của BC , nên cũng là đường phân giác của góc BAC .  a
Ta có DAC  30, suy ra DC 
. Ngoài ra góc giữa hai mặt phẳng SAB và  ABC là 3  SD a SBD  60   , suy ra tan SBD 
 SD  BD tan SBD  . 3  a . BD 3 2 3 1 1 a 3 a 3 Vậy V  .S .SD  . .a  . S.ABC 3 A  BC 3 4 12 Câu 49.17:
Cho hình chóp S . A B C có tam giác ABC vuông cân tại B , A B  a . Gọi I là trung
điểm của AC . Hình chiếu vuông góc của S lên mặt phẳng  ABC là điểm H thỏa mãn  
B I  3 IH . Góc giữa hai mặt phẳng  SAB và  SBC là 6 0 o . Thể tích của khối chóp
S . A B C là 3 a 3 a 3 a 3 a A. V  . B. V  . C. V  . D. V  . 9 6 18 3 Lời giải. Chọn A Trang 775
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Dễ thấy hai tam giác SAB và SAC bằng nhau ( cạnh chung SB ), gọi K là chân đường cao
hạ từ A trong tam giác SAB suy ra SAB SBC  ,  AKC .  
Trường hợp 1: AKC  60 kết hợp I là trung điểm AC suy ra IKC 30. AC a 2 4 2a 2
Ta có IB  IC   , BH  BI  . 2 2 3 3
Từ giả thiết tam giác ABC vuông cân tại B ta được AC  BI  IC  IK .  IC IC a 6
Trong tam giác ICK vuông tại I có tan IKC   IK   . IK tan 30 2
Như vậy IK  IB ( vô lý).   IC IC a 6
Trường hợp 2: AKC 120 tương tự phần trên ta có tan IKC   IK   . IK tan 60 6 a 3
Do SB   AKC  SB  IK nên tam giác BIK vuông tại K và 2 2
BK  IB  IK  . 3 IK .BH 2a
Như vậy tam giác BKI đồng dạng với tam giác BHS suy ra: SH   . BK 3 2 3 1 a 2a a
Vậy thể tích của khối chóp S.ABC là: V  .  S.ABC . 3 2 3 9 Câu 49.18:
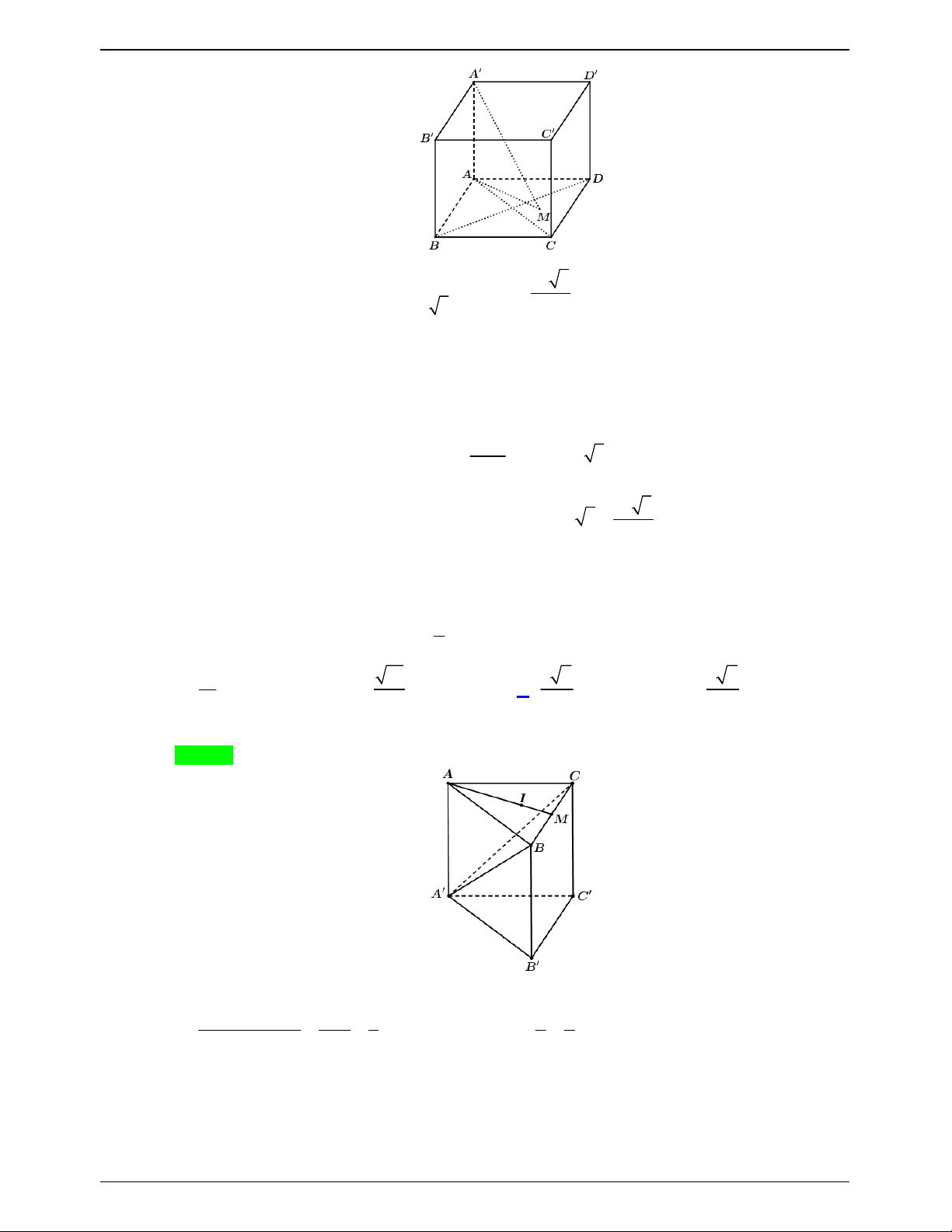
Cho tứ diện ABCD có   
A B C  B C D  C D A  9 0  , B C  C D  a , A D  a 2 . Góc giữa
hai mặt phẳng  ABC và  AC  D bằng A. 60 . B. 30 . C. 45 . D. 90 . Lời giải. Chọn A Trang 776
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 A A a 2 a 2 K H D D E a a a C B B a C
Gọi E là hình chiếu của A lên mặt phẳng  BCD  . BC  AB  CD  AD Kết hợp đề bài
  BC  BE ;
  CD  ED và BC  CD  a . BC  AE  CD  AE 
Suy ra tứ giác BCDE là hình vuông cạnh a . Khi đó 2 2 AE 
AD  ED  a
Gọi H , K lần lượt là hình chiếu của E lên  ABC , ACD thì EH   ABC , EK   ACD 
nên góc tạo bởi hai mặt phẳng  ABC  và  ACD  là góc  EH , EK  a 2
Nhận xét 2 tam giác AEB và AED là vuông cân tại E nên EH  EK  ; 2 BD a 2 HK  
suy ra tam giác EHK đều. 2 2
Vậy số đo góc tạo bởi hai mặt phẳng  ABC  và  ACD  là 60 . Câu 49.19:
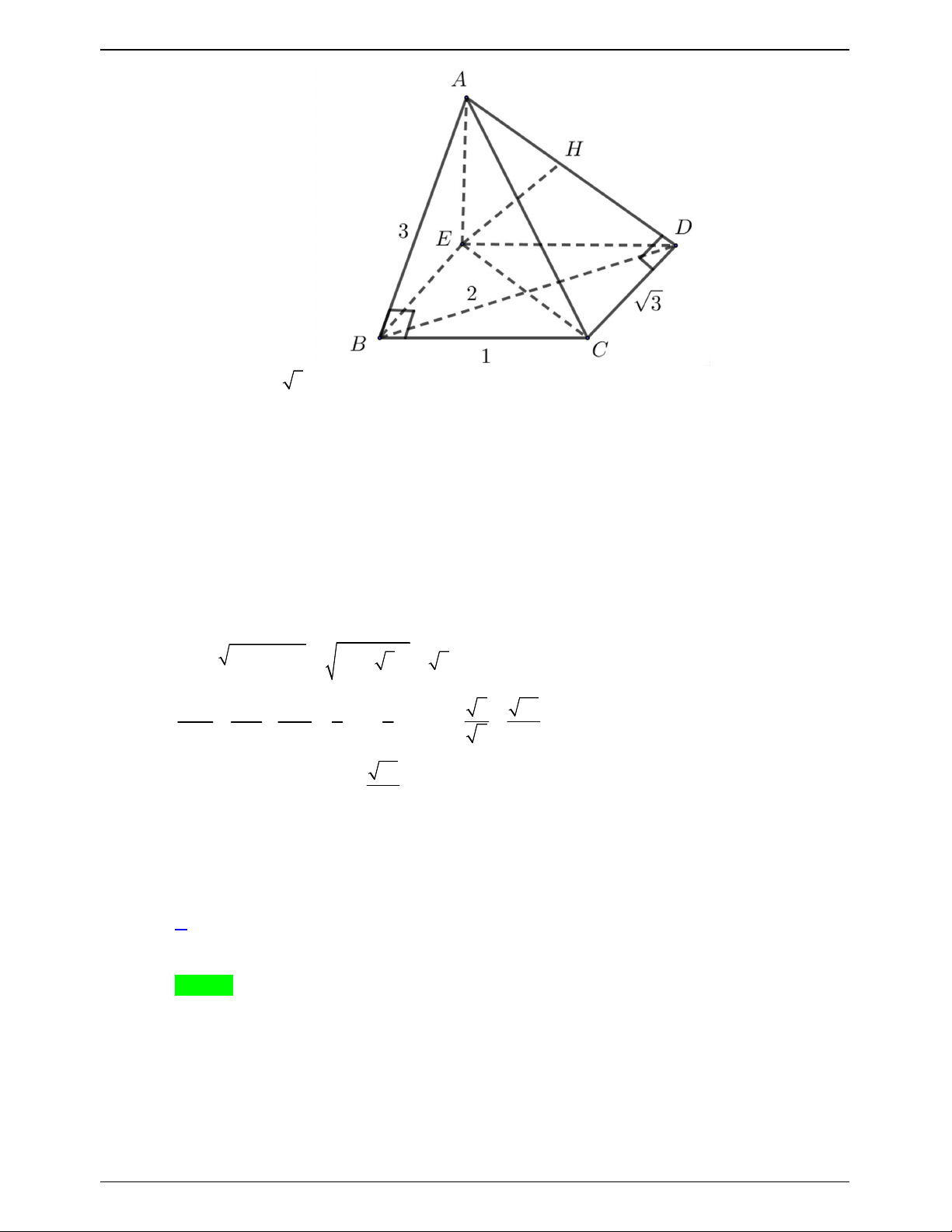
Cho tứ diện ABCD có  
DAB  CBD  90º ; 
AB  a; AC  a 5; ABC  135 . Biết góc
giữa hai mặt phẳng  ABD ,  BCD  bằng 30 . Thể tích của tứ diện ABCD bằng 3 3 a 3 a 3 a a A. . B. . C. . D. . 2 3 2 3 2 6 Lời giải. Chọn D Trang 777
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 D E F C H a 5 A a B
Dựng DH   ABC  . BA  DA BC  DB Ta có 
 BA  AH . Tương tự   BC  BH . BA  DH  BC  DH 
Tam giác AHB có AB  a ,  o
ABH  45  HAB vuông cân tại A  AH  AB  a .
Áp dụng định lý cosin, ta có BC  a 2 . a Vậy  2 1 1 2 S  .B . A BC.sin CBA  . . a a 2.  . ABC 2 2 2 2 HE  DA Dựng 
 HE   DAB và HF   DBC  . HF  DB 
Suy ra  DBA  DBC    HE HF   , ,
 EHF và tam giác HEF vuông tại E . ax xa 2
Đặt DH  x , khi đó HE  , HF  . 2 2 a  x 2 2 2a  x HE 3 x  2a Suy ra  2 2 cos EHF     x  a . 2 2 HF 4 2x  2a 3 1 a Vậy V  .DH .S  . ABCD 3 ABC 6 Câu 49.20:
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  BC  a 3 ,  
SAB  SCB  90 và khoảng cách từ điểm A đến SBC  bằng a 2 . Diện tích của mặt cầu
ngoại tiếp hình chóp S.ABC bằng A. 2 2 a . B. 2 8 a . C. 2 16 a . D. 2 12 a . Lời giải. Chọn D Trang 778
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Gọi H là hình chiếu của S lên  ABC  . BC  SC Ta có:  HC  BC  . SH  BC 
Tương tự AH  AB .
Và ABC vuông cân tại B nên ABCH là hình vuông. Gọi O  AC  BH , O là tâm hình vuông.
Dựng một đường thẳng d qua O vuông góc với  ABCH  , dựng mặt phẳng trung trực của SA
qua trung điểm J cắt d tại I  I là tâm mặt cầu ngoại tiếp.
Ta hoàn toàn có IJ  SA  IJ // AB  I là trung điểm SB , hay I  d  SC .  a 3
Bán kính mặt cầu ngoại tiếp: 2 2 r  AI 
IJ  JA ; IJ   S . ABC 2 2
Do AH //  SBC  d  ,
A SBC   d  H ,SBC   HK .
( K là hình chiếu của H lên SC và BC   SHC  HK  SBC  ).
 HK  a 2 . Tam giác SHC vuông tại H  SH  a 6 .
Tam giác SHA vuông tại H  SA  3a . SA 3a 2 2 JA    r
 AI  a 3  S
 4 r  12 a . . 2 2 S ABC mc Câu 49.21:
Tứ diện ABCD có BC  3, CD  4 ,   
ABC  BCD  ADC  90 , 
AD,BC  60. Cosin
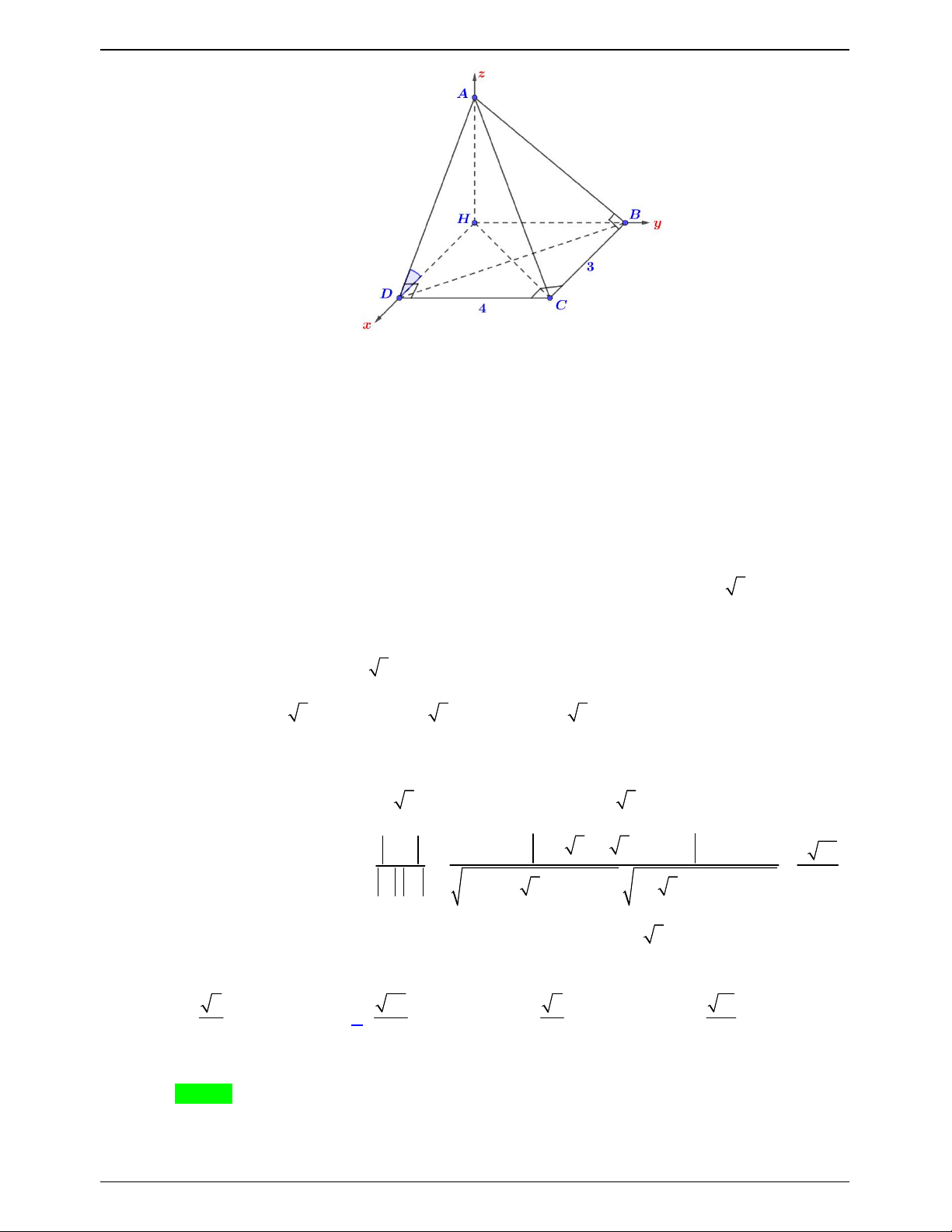
của góc giữa hai mặt phẳng  ABC và  ACD bằng 43 4 43 43 2 43 A. . B. . C. . D. . 86 43 43 43 Lời giải. Chọn D Trang 779
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Gọi H là chân đường cao của tứ diện ABCD . BC  AB Ta có: 
 BC  HB   1 . BC  AH  C  D  AD Lại có: 
 CD  HD 2 . CD  AH  Mà  BCD  90 .
Từ đây ta suy ra HBCD là hình chữ nhật. Mặt khác:  AD BC    AD HD  , ,
 ADH  60 . Suy ra: AH  HD tan 60  3 3 .
Chọn hệ trục Oxyz  H .DBA như hình vẽ.
Ta có: H 0;0;0 , A0;0;3 3, B0;4;0 , C 3;4;0 , D3;0;0 .   
AD  3; 3; 3 3 , AC  3;4;  3 3 , AB  0;4; 3 3 .  
Gọi n , n lần lượt là một véc tơ pháp tuyến của  ABC và  ABD . 1 2      
Suy ra: n   AB, AC   0;  9 3; 12 ; n   AD, AC   21 3;0; 21 . 2     1       n .n 0.21 3  9 3.0 12.21 2 43
Vậy cos  ABC , ADC  1 2      . n . n 2 2 2 2 2 2 43 1 2 0   9  3   1
 2 . 21 3  0  2  1 Câu 49.22:
Cho tứ diện ABCD có  
ABC  ADC  90 và BC  1 , CD  3 , BD  2 , AB  3 .
Khoảng cách từ B đến  ACD bằng 6 42 7 14 A. . B. . C. . D. . 7 7 7 7 Lời giải. Chọn B Trang 780
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
BC  1 , CD  3 , BD  2 2 2 2
 BC  DC  BD  BCD vuông tại C .
Dựng hình chữ nhật BCDE  BC // ED mà DC  BC  DC  DE , lại có DC  AD .
 DC   ADE  DC  AE   1 .
Chứng minh tương tự BC   ABE  BC  AE 2 . Từ  
1 và 2 suy ra AE   BCDE .
Kẻ EH  AD tại H . Do DC   ADE nên DC  EH  EH   ACD .
BE // CD  d  ,
B  ACD  d  E, ACD  EH . 2 2 AE  AB  BE    2 2 3 3  6 . 1 1 1 1 7 6 42     1   EH   . 2 2 2 EH EA ED 6 6 7 7
Vậy d  B  ACD 42 ,  EH  . 7 Câu 49.23: Cho hình chóp .
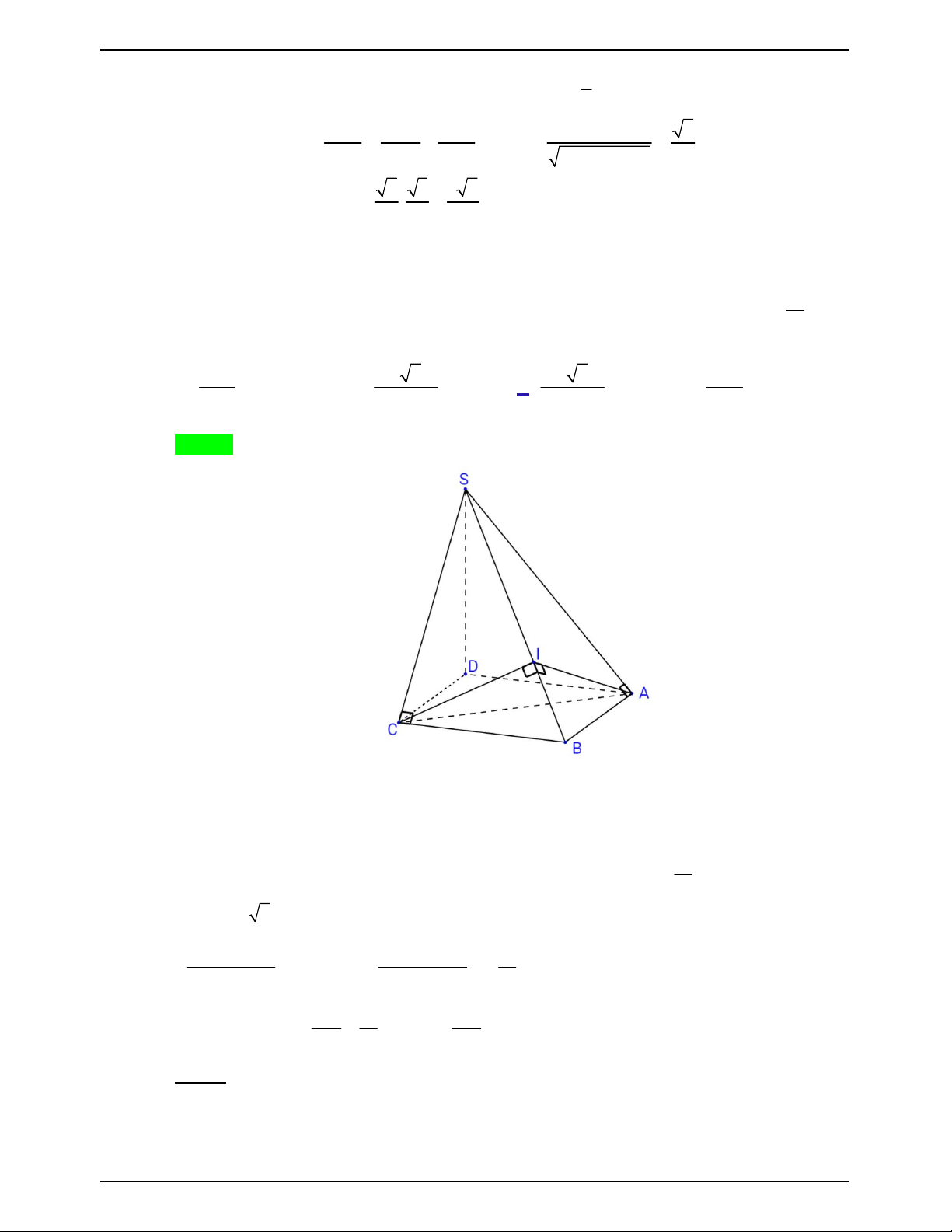
S ABC có SA vuông góc với mặt đáy, SA  BC và  BAC  120 . Hình
chiếu vuông góc của A lên các cạnh SB và SC lần lượt là M và N . Góc giữa hai mặt phẳng
 ABC và AMN  bằng A. 45. B. 60 . C. 15 . D. 30 . Lời giải. Chọn A Trang 781
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC có đường kính là AD .
Khi đó tam giác ABD vuông tại B  AB  BD .  AB  BD Ta có 
 BD  SAB  BD  AM . SA  BD  BD  AM Ta có 
 AM  SBD  AM  SD . SB  AM 
Tương tự, ta chứng minh được AN  SD .
Do đó SD   AMN  suy ra  ABC   AMN    SA SD   , ,  ASD . AD
Xét tam giác SAD vuông tại A có  tan ASD  . SA BC 3 Với AD  2R  2  SA . ABC sin120 3  3  Do đó tan ASD 
 ASD  30   ABC   AMN   ,  30 . 3  Câu 49.24:
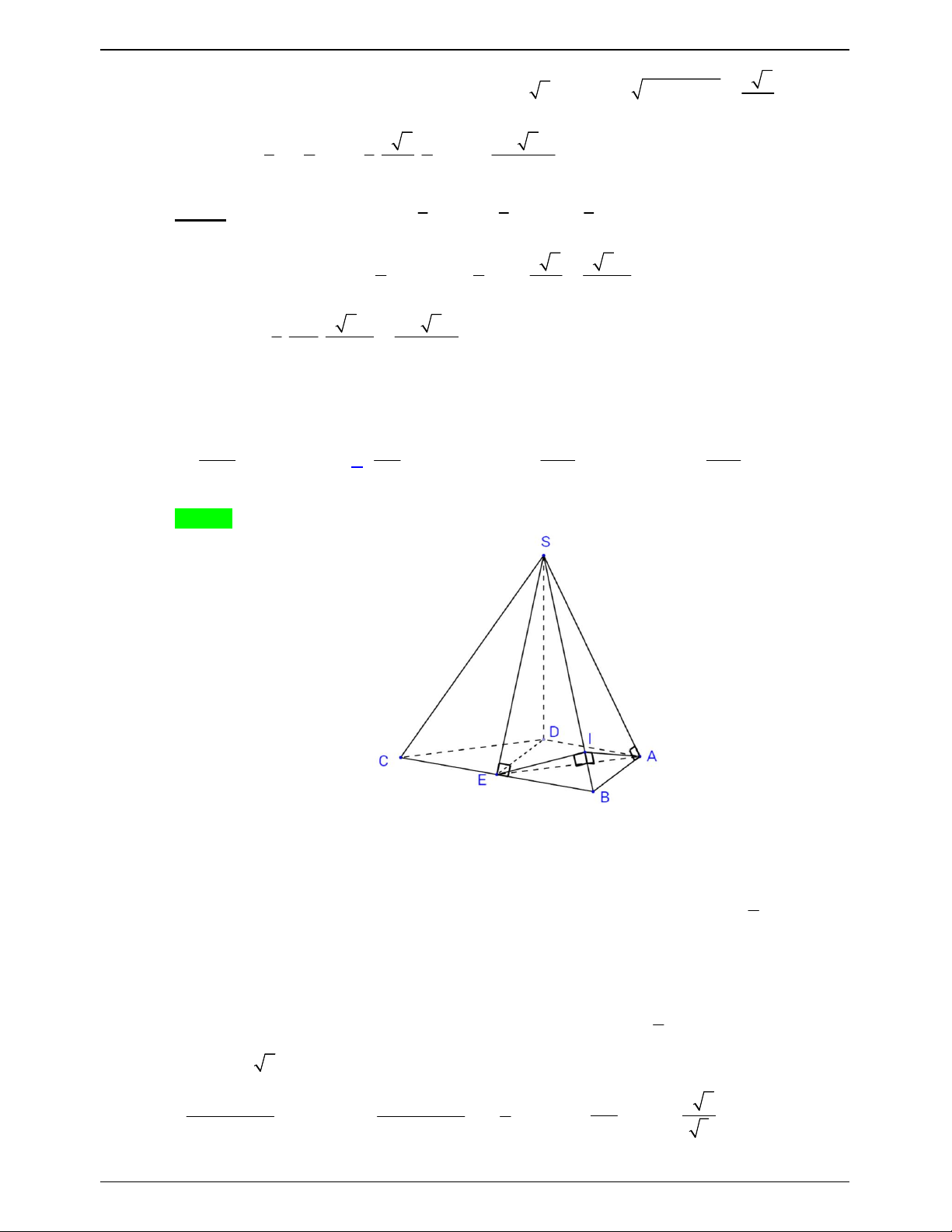
Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB  a , BAC  120 ,    3
SBA  SCA  90 . Gọi  là góc giữa SB và  SAC  thỏa mãn sin  , khoảng cách từ S 8
đến mặt đáy nhỏ hơn 2a . Thể tích của khối chóp S.ABC bằng 3 3 3 3 3a 3a 3a 3a A. . B. . C. . D. . 4 6 12 24 Lời giải. Chọn C Trang 782
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 S K C D A B I
Gọi D là hình chiếu vuông góc của S lên đáy  ABC , đặt SD  x 0  x  2a  .  AC  SC Ta có  AC  
SDC  AC  DC . Tương tự ta cũng có AB  DB . AC  SD 
Tam giác ABC cân tại A và 
CAB  120  BC  a 3 và  
DBC  DCB  60  D  BC đều cạnh a 3 .
Tam giác SDC vuông tại D 2 2
 SC  3a  x  SB . x a 3
Kẻ DK  SC tại K  DK  SAC   d  D,SAC   DK  . 2 2 3a  x
Gọi I  BD  AC , xét DIC vuông tại C và  BDC  60 DC 1  DI 
  2a 3  B là trung điểm của DI  d  B, SAC   d  D,SAC  . cosBDC 2 
d  B, SAC  3 xa 3
Theo giả thiết   SB,(SAC     sin    SB 8 2  2 2 3a  x  2  x  x x  a 2 2
 x  3a  4ax  0   4  3  0    
. So sánh với điều kiện suy ra x  a .  a  a x  3a  3 1 a 3 Vậy V  .S .SD  . S .ABC 3 ABC 12 Câu 49.25:
Cho hình chóp S.ABC có SA  AB  3 ; SB  6 ; AC  2BC  2 ; SC  5 . Khoảng
cách từ A đến  SBC  bằng 30 5 13 30 A. . B. . C. . D. . 6 2 6 5 Lời giải. Chọn D Trang 783
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Dựng điểm D sao cho ABCD là hình chữ nhật.
Áp dụng định lý Pitago ta có các tam giác SAB; ABC; SBC lần lượt vuông góc tại , A B, C .  AB  AD Ta có 
 AB  SD   1 . BA  SA  BC  CD 
 BC  SD 2 . BC  SC  Từ  
1 ;2  SD   ABCD  SD  BC .
Vậy SBC   SDC  theo giao tuyến SC . Kẻ DH vuông góc với SC tại H thì DH  SBC  . DS.DC 2. 3 30
Có AD //  SBC   d  ,
A SBC   d  D, SBC   DH    . 2 2 DS  DC 5 5 Câu 49.26:
Cho hình chóp S.ABC , đáy là tam giác đều ABC có cạnh bằng a . Biết rằng các mặt bên
của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng a 3 . Tính thể tích nhỏ
nhất của khối chóp S.ABC . 3 a 2 3 a 2 3 a 6 3 a 6 A. . B. . C. . D. . 6 2 12 4 Lời giải 4 Chọn C Trang 784
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Gọi H là hình chiếu của S trên mặt phẳng đáy  ABC  ; M , N, K lần lượt là hình chiếu của S trên A , B BC,CA . 1 1 1
Vì diện tích các mặt bên của hình chóp bằng nhau nên ta có SM .AB  SN.BC  SK.CA 2 2 2
và vì tam giác ABC đều nên ta có SM  SN  SK  HM  HN  HK .
TH1: nếu H nằm trong tam giác ABC  H là tâm đường tròn nội tiếp tam giác đều ABC . 2 a 3 Khi đó ta có AH  AN 
và SA  SB  SC  a 3 3 3 2 3a 2a 6  2 2 2 SH 
SA  AH  3a   9 3 2 3 1 1 a 3 2a 6 a 2  V  S .SH  . .  . S. ABC 3 ABC 3 4 3 6
TH2: Nếu H nằm ngoài tam giác ABC . Không mất tính tổng quát giả sử H nằm khác phía
với A so với đường thẳng BC
Tương tự như trên ta vẫn có HM  HN  HK . Vì tam giác ABC đều nên H là tâm đường 3a BN a 1
tròn bàng tiếp góc A và AM  AB  BN   HB   :  a , 2 cos60 2 2 3a 3
AH  AM : cos30  :
 a 3 . Vì thế cạnh SA không thể bằng a 3  SB  SC  a 3 2 2 2 3 1 1 a 3 a 6  2 2 2 2 SH  SB  BH 
3a  a  a 2  V  S .SH  . .a 2  . S. ABC 3 ABC 3 4 12 3 3 3  a 2 a 6    a 6 Vậy V  min  ,   . min 6 12 12     Trang 785
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 Câu 49.27:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành thỏa mãn AB  a, AC  a 3 ,
BC  2a . Biết tam giác SBC cân tại S , tam giác SCD vuông tại C và khoảng cách từ D đến a 3
mặt phẳng (SBC ) bằng
. Thể tích của khối chóp đã cho bằng 3 3 2a 3 a 3 a 3 a A. . B. . C. . D. . 3 5 3 5 3 3 5 Lời giải Chọn A
Nhận thấy tam giác ABC vuông tại A ( do 2 2 2
AB  AC  BC ).
Gọi E là điểm đối xứng của B qua A ta có tứ giác A D
C E là hình chữ nhật, và tam giác EBC
là tam giác đều cạnh 2a . 1
AD  (SBC)  d (D, (SBC))  d ( , A (SBC)) 
d (E,(SBC)) 2 2a 3
Hay d (E, (SBC))  2.d(D, (SBC))  3
Gọi I là trung điểm của đoạn BC , ta có: BC  EI , BC  SI  BC  (SEI ) . 2a 3
Trong mp(SEI ) kẻ EH vuông góc với SI tại H . Khi đó: d (E, (SBC))  EH  . 3
Ta có CD  (SAC ) ( Do CD  SC, CD  AC ) Suy ra AB  (SAC ) . Xét tam giác S E
B có SA vừa là trung tuyến vừa là đường cao nên tam giác S E
B cân tại S .
Xét hình chóp S.EBC có đáy là tam giác đều EBC , các cạnh bên SE  SB  SC .
Nên gọi F  EI  CA ta có SF  (EBC) . Trang 786
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 2a 3 HE 2
Tam giác EHI vuông tại H nên  3 sin I    . EI a 3 3 2 1 sin I 1 2a  Tam giác 3
SIF vuông tại F nên SF  FI. tan I  EI.  a 3.  . 2 3  3 2  I 2 15 1 sin 1 ( ) 3 3 1 1 1 2a 2a V  SF.S  SF.A . B CA  . . a a 3  . S . AB D C AB D 3 C 3 3 15 3 5 Câu 49.28:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB và tam giác 3
SCD cân tại S . Biết hai mặt bên SAB và SCD có tổng diện tích bằng 2 a và chúng 2
vuông góc với nhau. Thể tích khối chóp S.ABCD bằng 2 a 2 a 2 a 2 a A. . B. . C. . D. . 4 12 6 3 Lời giải. Chọn D
Gọi E , F lần lượt là trung điểm AB và CD . Khi đó EF // AD  EF  AB
Do tam giác SAB và tam giác SCD cân tại S nên SE  AB và SF  CD SE  AB Lúc đó có 
 AB  SEF  ABCD  SEF EF  AB 
Do đó, chân đường cao hạ từ S xuống đáy là H phải nằm trên giao tuyến EF của  ABCD và SEF . Trang 787
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Mặt khác, giao tuyến của hai mặt phẳng SAB và SCD là đường thẳng d qua S và song 
song AB nên SE  d và SF  d , tức là ESF là góc giữa hai mặt phẳng SAB và SCD ,
hay nói cách khác ta có SE  SF 2 2 2 2 SE .SF SE .SF
Xét tam giác SEF vuông tại S có 2 SH     1 2 2 SE  SF
SE  SF2  2SE.SF
Ta có SE.SF  SH.EF  2SSEF 3 Từ giả thiết 2 2 S  S 
a  SE.AB  SF.CD  3a hay SE  SF  3a SAB S  CD 2 2 2 2 2 SH .EF SH .a Thay vào   1 ta có 2 SH    SH  a
SE  SF 2 2  2SH.EF
3a  2SH.a 2 1 1 a
Vậy thể tích hình chóp S.ABCD là 2 V  SH.S  . . a a  . 3 ABCD 3 3   Câu 49.29:
Cho hình chóp S.ABC có  0
AB  BC  a, ABC  120 , 0
SAB  SCB  90 và khoảng cách từ 2a 21
B đến mặt phẳng  SAC  bằng
. Tính thể tích khối S.ABC . 21 3 a 5 3 a 15 3 a 15 3 a 5 A. V  . B. V  . C. V  . D. V  . 10 10 5 2 Lời giải Chọn B S S K E D A I a a E B C B D I
Hạ SE   ABC  tại E có AB  SE 
  AB   SAE   0
 AB  AE  BAE  90 . AB  SA   Chứng minh tương tự có 0 BCE  90 .  
Hai tam giác vuông BCE và BAE bằng nhau suy ra 0
CBE  ABE  60 .
Gọi D là trung điểm của BE suy ra tứ giác ABCD là hình thoi và BD  DE  a . Trang 788
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Gọi I là tâm hình thoi ABCD có 1 BI  EI  d  1 2a 21 2a 21
B, SAC   d  E, SAC   d E,SAC   3.  . 3 3 21 7 CA  BD
  CA   SEI    SAC    SEI  . CA  SE  a
Hạ EK  SI tại K ta có EK  SAC  tại K suy ra d E SAC  2 21 ,
 EK  EK  . 7
Tam giác SBE vuông tại E đường cao EK có 1 1 1 1 1 1 7 4 5 6a 5          SE  . 2 2 2 2 2 2 2 2 2 EK EI SE SE EK EI 12a 9a 36a 5 3 1 1  1  1 3 6a 5 a 15 Vậy 0 2 V  S .SE  B . A BC.sin120 .SE  a . .  . SABC   3 ABC 3  2  6 2 5 10 Câu 49.30:
Cho khối chóp S.ABC có đáy là tam giác cân tại A , AB  a ,  BAC  120 ,   3
SBA  SCA  90 . Gọi  là góc giữa hai mặt phẳng SAB và SAC  . Khi cos  thì thể 4
tích khối chóp đã cho bằng 3 3a 3 a A. 3 3a . B. 3 a . C. . D. . 4 4 Lời giải Chọn D
Kẻ SH   ABC , H   ABC  suy ra SH  AB và SH  AC . SH  AB Khi đó ta có 
 AB  SBH   AB  BH . SB  AB 
Chứng minh tương tự ta có AC  CH suy ra tứ giác ABHC nội tiếp đường tròn đường kính
AH . Do đó góc BHC bằng 60 .
Dễ thấy AHB  AHC  HB  HC nên HBC đều. Trang 789
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 
ABC cân tại A có AB  ,
a BAC  120 suy ra 2 2 BC  3a . Do đó 2 2 2 2
HB  HC  BC  3a .
Dễ thấy SHB  SHC  SB  SC nên SAB  SAC .
Trong mặt phẳng SAB kẻ BK  ,
SA K  SA .
Trong mặt phẳng SAC  kẻ CK  S , A K  SA . 1  1   
Xét hai tam giác vuông K  AB và K 
AC có AB  AC , BAK  CAK (vì SAB  SAC ) suy 1 1 ra K  AB  K 
AC  AK  AK mà K và K nằm giữa S và A nên K  K . 1 1 1 1
Từ đó ta có CK  SA và BK  CK .  2 2 2
BK  CK  BC 3 2 2 2BK  BC 3
Do đó cos  cos BKC       1 . 2BK.CK 4 2 2BK 4 Đặt SH  ,
x  x  0. Xét SHB có 2 2 2 2 2
SB  SH  HB  3a  x . 1 1 1 1 1 1
Xét SAB vuông tại B có      2 2 2 BK BA BS 2 2 2 2 BK a 3a  x 2 a  2 2 3a  x 2   BK  . 2 2 4a  x 2 2a  2 2 3a  x  2  3a 2 2 3 4a  x Thay vào   1 ta có   x  a 3 . 2 2a  2 2 3a  x  4 2 2 4a  x 1 1  3 1 1 a
Vậy thể tích khối chóp S.ABC là 2 .SH. .A . B A .
C sin BAC  .a 3. . a sin120  . 3 2 3 2 4
Vậy chọn đáp án D. Câu 49.31:
Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB  a , tam giác SAB
vuông tại A , tam giác SBC cân tại S và khoảng cách giữa hai đường thẳng SB và AC bằng
2a . Thể tích của khối chóp đã cho bằng 3 3 a 3 3a 3 a 3 a A. . B. . C. . D. . 6 2 2 3 Lời giải
Tác giả: Lê Văn Quý ; Fb:Lê Văn Quý Chọn D Trang 790
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 S I C O H M K A B
Gọi M trung điểm của BC  SM  BC (1)
Lấy điểm H  ( ABC) sao cho ABMH là hình chữ nhật  AB  SA
Cùng với giả thiết ta có:  AB  SH  (2) AB  AH  BC  SM Lại có 
 BC  SH (2) BC  MH 
Từ (1) và (2) suy ra SH   ABC . 1
Gọi K  AC  BH và I là điểm trên đoạn SH sao cho HI  HS . 3 2a
 SB // (IAC)  d (S ,
B AC)  d(S ,
B (IAC))  d (S, (IAC))  2d (H , (IAC))  . 3 a
 d (H ,(IAC))  . 3 1 1 1 1 1 9 4 4 1 Ta có          HI  a .
d(H,(IAC))2 2 2 2 2 2 2 2 2 HA HO HI HI a a a a  SH  3a . 3 1 1 1 a Vậy 2 V  SH.S  3a a  . S. ABC 3 ABC 3 2 2 Câu 49.32:
Cho tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm của các cạnh
AB, BC và E là điểm đối xứng với B qua D . Mặt phẳng MNE  chia khối tứ diện ABCD thành
hai khối đa diện. Trong đó, khối tứ diện ABCD có thể tích là V , khối đa diện chứa đỉnh A có thể tích V  V '. Tính tỉ số . V 7 11 13 1 A. . B. . C. . D. . 18 18 18 18 Trang 791
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 Lời giải Chọn B
Gọi P  EN  CD và Q  EM  AD .
Suy ra P, Q lần lượt là trọng tâm của BCE và ABE .
Gọi S là diện tích tam giác BCD , suy ra S  S  S. CDE BNE 1 S Ta có S  .S  . PDE 3 CDE 3 A M Q D E B P N C
Gọi h là chiều cao của tứ diện ABCD , suy ra h h
d M , BCD  ; d  ,
Q  BCD  .   2   3 1 S.h 1 S.h Khi đó V  S
.d M , BCD   ; V  S .d  , Q BCD   . Q.PDE PDE   M .BNE BNE   3   6 3   27 S.h S.h 7S.h 7 S.h 7 Suy ra V  V V     .  .V PQD.NMB M .BNE Q.PDE 6 27 54 18 3 18 ABCD 7 11 V ' 11
 V '  V  .V  V   . 18 18 V 18 V  11 Vậy  . V 18 Câu 49.33:
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a,  
SAB  SCB  90 và góc
giữa hai mặt phẳng SAB  và SBC  bằng 0
60 . Tính thể tích khối chóp SABC ? 2 2 2 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 2 4 6 3 Lời giải Chọn D Trang 792
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 Ta có S  AB  S
 BC (c.g.c), trong tam giác SAB kẻ đường cao AE  SB khi đó CE  SB . Khi
đó góc giữa hai mặt phẳng  SAB và SBC  là góc giữa hai đường thẳng AE và CE . Dễ dàng nhận thấy góc 
AEC  120 (vì nếu 
AEC  60 thì AE  AC  AB  2a điều này vô lí vì tam
giác AEB vuông tại E ). AK 2 3
Trong tam giác AEC cân tại E kẻ đường cao EK ta có: AE   a 0 cos 30 3
Trong tam giác vuông ABE có: 2 2 2 6 BE  AB  AE  a 3 2 AB
Trong tam giác SAB có: BS   6 BE 1 1 1 0 2 2 3 V  .BE.S
 .BE. .AE.EC.sin120  a B.EAC 3 E  AC 3 2 9 V BE BA BC BE BS 6 2 2 2 B.EAC 3 3  . .   V  .V  . a  a B.SAC B.EAC V BS BA BC BS BE B SAC 2 6 9 3 . 3 Câu 49.34:
Cho tứ diện đều ABCD có cạnh bằng 1 , M và N lần lượt là hai điểm di động trên hai
cạnh AB, AC ( M và N không trùng với A ) sao cho mặt phẳng DMN  luôn vuông góc
với mặt phẳng  ABC  . Gọi V , V lần lượt là thể tích lớn nhất và nhỏ nhất của tứ diện 1 2
ADMN . Tính tích V .V . 1 2 2 2 1 8
A. V .V  .
B. V .V  .
C. V .V  .
D. V .V  . 1 2 27 1 2 24 1 2 324 1 2 9 Lời giải Chọn C Trang 793
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020
Kẻ DH  MN  DH   ABC  (vì DMN    ABC  ). Suy ra H là trọng tâm của tam giác đều ABC .
Như vậy M và N là hai điểm di động nhưng MN luôn đi qua trọng tâm của tam giác ABC .
Đặt AM  x, AN  y , ( 0  x 1, 0  y  1 ) 1 2 2 + 2 2 2
DH  DA  AH  1   DH  . 3 3 3 1 3 +  S 
AM .AN.sin MAN  xy (*) AMN 2 4 1 3 + S  S  S 
AH . x  y.sin 30   x  y (**) A  MN A  MH ANH 2 12 1 1  3  2 2 Do đó V  DH .S   xy   xy (***) ADMN 3 A  MN 3  4  3 12  
Mặt khác từ (*) và (**) suy ra x  y  3xy , ( 0  x 1, 0  y  1 ).  2 0  t   3 0   3t  2  4 2
Đặt xy  t  x  y  3t . Điều kiện:   4   t  .  2 9t  4t  0  t   9 3 9 t  0  4 2 Khi đó ,
x y là nghiệm của phương trình 2
X  3tX  t  0   1 ,  t  . 9 3  4 2  Ta tìm t  ; để  
1 có 2 nghiệm phân biệt thuộc 0 
;1 hoặc có nghiệm kép thuộc  0  ;1 9 3    Trang 794
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
ĐỀ THI THỬ THPTQG – 2019-2020 1 2 X Ta có X 
không phải là nghiệm của   1 nên   1  t  . 3 3X 1  X  0 2 X 2 3X  2 X
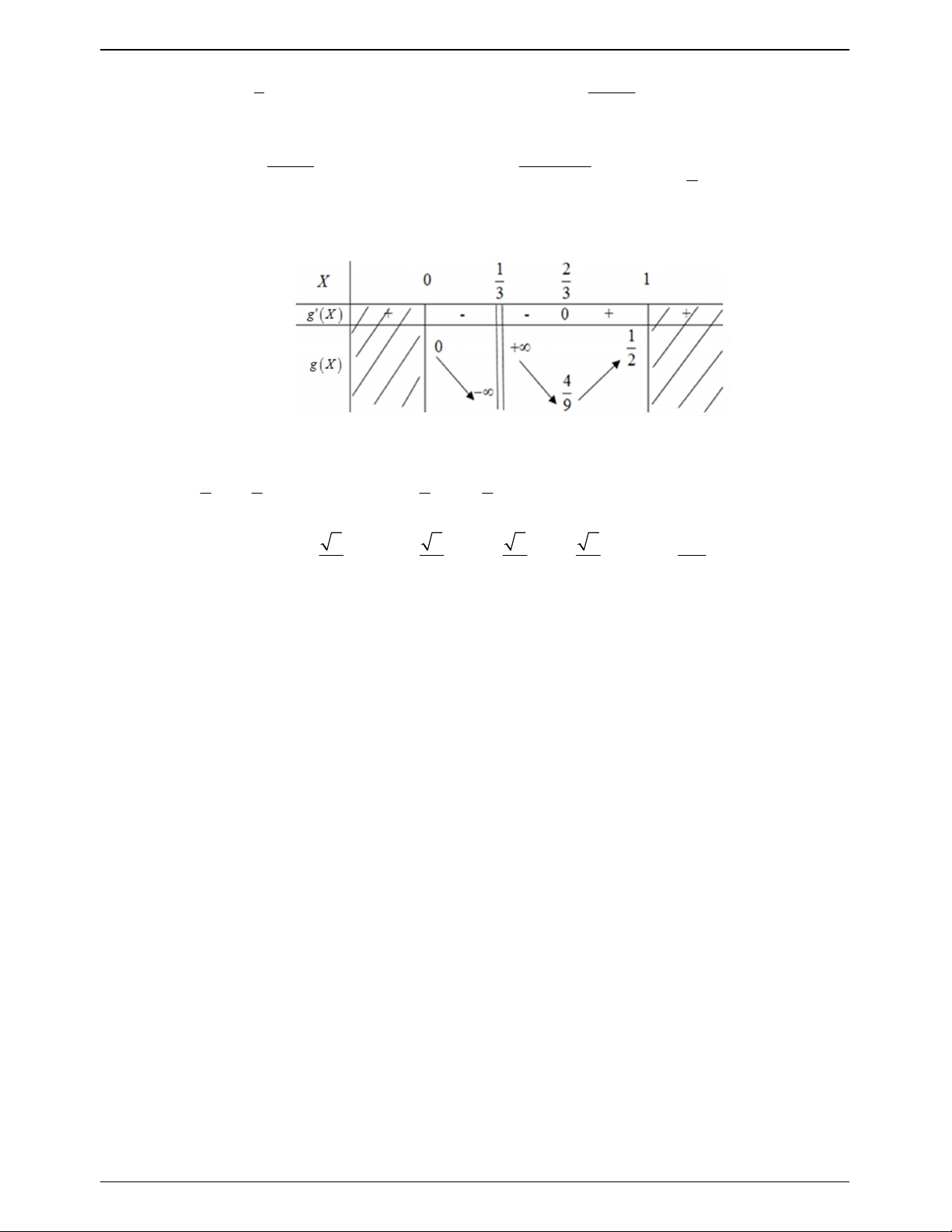
Đặt g  X   , X  0 
;1 . Ta có: g X    0   2 . 3X 1 3X  2 1  X   3
Bảng biến thiên của g  X  Dựa vào BBT,  
1 có 2 nghiệm phân biệt thuộc 0 
;1 hoặc có nghiệm kép thuộc 0  ;1 4 1 4 1   t  (thỏa điều kiện) hay  xy  . 9 2 9 2 2 2 2 2 1 Kết hợp (***) ta có  V   V  , V   V .V  . 27 ADMN 24 1 24 2 27 1 2 324 Trang 795

Tính thể tích khối chóp biết góc giữa hai mặt phẳng Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên Đề Thể Tích Khối Đa Diện Có Yếu Tố Góc Ôn Thi Tốt Nghiệp THPT Có Đáp Án Và Lời Giải

10 Đề Trắc Nghiệm Ôn Tập Chương Khối Đa Diện Hình 12 Có Đáp Án

TOP 600 bài tập chọn lọc khối tròn xoay – Lê Minh Tâm Toán 12

Phương pháp giải các bài toán HH không gian trong đề thi Quốc gia Toán 12

Các bài tập khối đa diện trong đề thi Đại học Toán 12