
Phan Nhật Linh Fanpage: Tài liệu Luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
LÝ THUYẾT
CHỦ ĐỀ 01: CƠ BẢN VỀ TÍNH ĐƠN ĐIỆU HÀM SỐ
❖ Điều kiện để hàm số đơn điệu trên khoảng
K
.
• Định nghĩa 1.
Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và
( )
=y f x
là một hàm số xác định
trên K, ta nói:
Hàm số
( )
=y f x
được gọi là đồng biến (tăng) trên K nếu
( ) ( )
1 2 1 2 1 2
,, x x K x x f x f x
Hàm số
( )
=y f x
được gọi là nghịch biến (giảm) trên K nếu
( ) ( )
1 2 1 2 1 2
,, x x K x x f x f x
Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.
❖ Nhận xét.
• Nhận xét 1.
▪ Nếu hàm số
( )
fx
và
( )
gx
cùng đồng biến (nghịch biến) trên D thì hàm số
( ) ( )
+f x g x
cũng
đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu
( ) ( )
−f x g x
.
• Nhận xét 2.
▪ Nếu hàm số
( )
fx
và
( )
gx
là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì
hàm số
( ) ( )
.f x g x
cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi
các hàm số
( ) ( )
,f x g x
không là các hàm số dương trên D.
• Nhận xét 3.
▪ Cho hàm số
( )
=u u x
, xác định với
( )
;x a b
và
( ) ( )
;u x c d
. Hàm số
( )
f u x
cũng xác
định với
( )
;x a b
. Ta có nhận xét sau:
▪ Giả sử hàm số
( )
=u u x
đồng biến với
( )
;x a b
. Khi đó, hàm số
( )
f u x
đồng biến với
( ) ( )
;x a b f u
đồng biến với
( )
;u c d
.
▪ Giả sử hàm số
( )
=u u x
nghịch biến với
( )
;x a b
. Khi đó, hàm số
( )
f u x
nghịch biến với
( ) ( )
;x a b f u
nghịch biến với
( )
;u c d
.
❖ Định lí 1.
• Giả sử hàm số
f
có đạo hàm trên khoảng K. Khi đó:
Nếu hàm số đồng biến trên khoảng K thì
( )
' 0, f x x K
.
Nếu hàm số nghịch biến trên khoảng K thì
( )
' 0, f x x K
.
❖ Định lí 2.
• Giả sử hàm số
f
có đạo hàm trên khoảng K. Khi đó:
Nếu
( )
' 0, f x x K
thì hàm số
f
đồng biến trên K.
Nếu
( )
' 0, f x x K
thì hàm số
f
nghịch biến trên K.
Nếu
( )
' 0,= f x x K
thì hàm số
f
không đổi trên K.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu Luyện thi THPT 03 mức độ: Nhận biết – Thông hiểu và Vận dụng | 2
❖ Định lý về điều kiện đủ để hàm số đơn điệu:
• Giả sử hàm số
f
có đạo hàm trên khoảng
K
. Khi đó:
Nếu
( )
0fx
,
xK
và
( )
0fx
=
chỉ tại hữu hạn điểm thuộc
K
thì hàm số
f
đồng biến
trên
K
.
Nếu
( )
0fx
,
xK
và
( )
0fx
=
chỉ tại hữu hạn điểm thuộc
K
thì hàm số
f
nghịch biến
trên
K
Bài toán 1. Tìm tham số
m
để hàm số
( )
;y f x m=
đơn điệu trên khoảng
( )
;
.
• Bước 1: Ghi điều kiện để
( )
;y f x m=
đơn điệu trên
( )
;
. Chẳng hạn:
▪ Đề yêu cầu
( )
;y f x m=
đồng biến trên
( )
;
( )
;0y f x m
=
.
▪ Đề yêu cầu
( )
;y f x m=
nghịch biến trên
( )
;
( )
;0y f x m
=
.
• Bước 2: Độc lập
m
ra khỏi biến số và đặt vế còn lại là
( )
gx
, có hai trường hợp thường gặp :
▪
( )
m g x
,
( )
;x
( )
( )
;
maxm g x
.
▪
( )
m g x
,
( )
;x
( )
( )
;
minm g x
.
• Bước 3: Khảo sát tính đơn điệu của hàm số
( )
gx
trên
D
(hoặc sử dụng Cauchy) để tìm giá trị
lớn nhất và giá trị nhỏ nhất. Từ đó suy ra
m
.
Bài toán 2. Tìm tham số
m
để hàm số
ax b
y
cx d
+
=
+
đơn điệu trên khoảng
( )
;
.
• Tìm tập xác định, chẳng hạn
d
x
c
−
. Tính đạo hàm
y
.
• Hàm số đồng biến
0y
(hàm số nghịch biến
0y
). Giải ra tìm được
m
( )
1
.
• Vì
d
x
c
−
và có
( )
;x
nên
( )
;
d
c
−
. Giải ra tìm được
m
( )
2
.
• Lấy giao của
( )
1
và
( )
2
được các giá trị
m
cần tìm.
➢ Cần nhớ: “Nếu hàm số
( )
ft
đơn điệu một chiều trên miền
D
(luôn đồng biến hoặc luôn nghịch
biến) thì phương trình
( )
0ft=
có tối đa một nghiệm và
u
,
vD
thì
( ) ( )
f u f v u v= =
.

Phan Nhật Linh Fanpage: Tài liệu Luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
VÍ DỤ MINH HỌA.
CÂU 1.
A.
1
2
x
y
x
+
=
−
B.
2
2y x x=+
C.
32
y x x x= − +
D.
42
32y x x= − +
Lời giải.
CÂU 2.
A.
B.
C.
D.
Lời giải.
CÂU 3.
42
2y x x=−
A.
( )
;2− −
B.
( )
;2− −
C.
( )
1;1−
D.
( )
1;1−
Lời giải.
2
21yx=+
( )
1;1−
( )
0;+
( )
;0−
( )
0;+

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu Luyện thi THPT 03 mức độ: Nhận biết – Thông hiểu và Vận dụng | 4
CÂU 4.
2
1
x
y
x
−
=
+
A.
( )
;1− −
B.
( )
;1− −
C.
( )
;− +
D.
( )
1;− +
Lời giải.
CÂU 5.
( )
;− +
A.
3
3 3 2y x x= + −
B.
3
2 5 1y x x= − +
C.
42
3y x x=+
D.
2
1
x
y
x
−
=
+
Lời giải.
CÂU 6.
32
21= − + +y x x x
A.
1
;1
3
B.
1
;
3
−
C.
1
;1
3
D.
( )
1; +
Lời giải.

Phan Nhật Linh Fanpage: Tài liệu Luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
CÂU 7.
4
21yx=+
A.
1
;
2
− −
B.
( )
0;+
C.
1
;
2
− +
D.
( )
;0 .−
Lời giải.
CÂU 8.
( )
fx
( )
fx
( )
52y f x=−
A.
( )
;3− −
B.
( )
4;5
C.
( )
3;4
D.
( )
1;3
Lời giải.
CÂU 9.
m
( )
32
34y x x m x= − + −
( )
2;+
A.
(
;1−
B.
(
;4−
C.
( )
;1−
D.
( )
;4−
Lời giải.
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu Luyện thi THPT 03 mức độ: Nhận biết – Thông hiểu và Vận dụng | 6
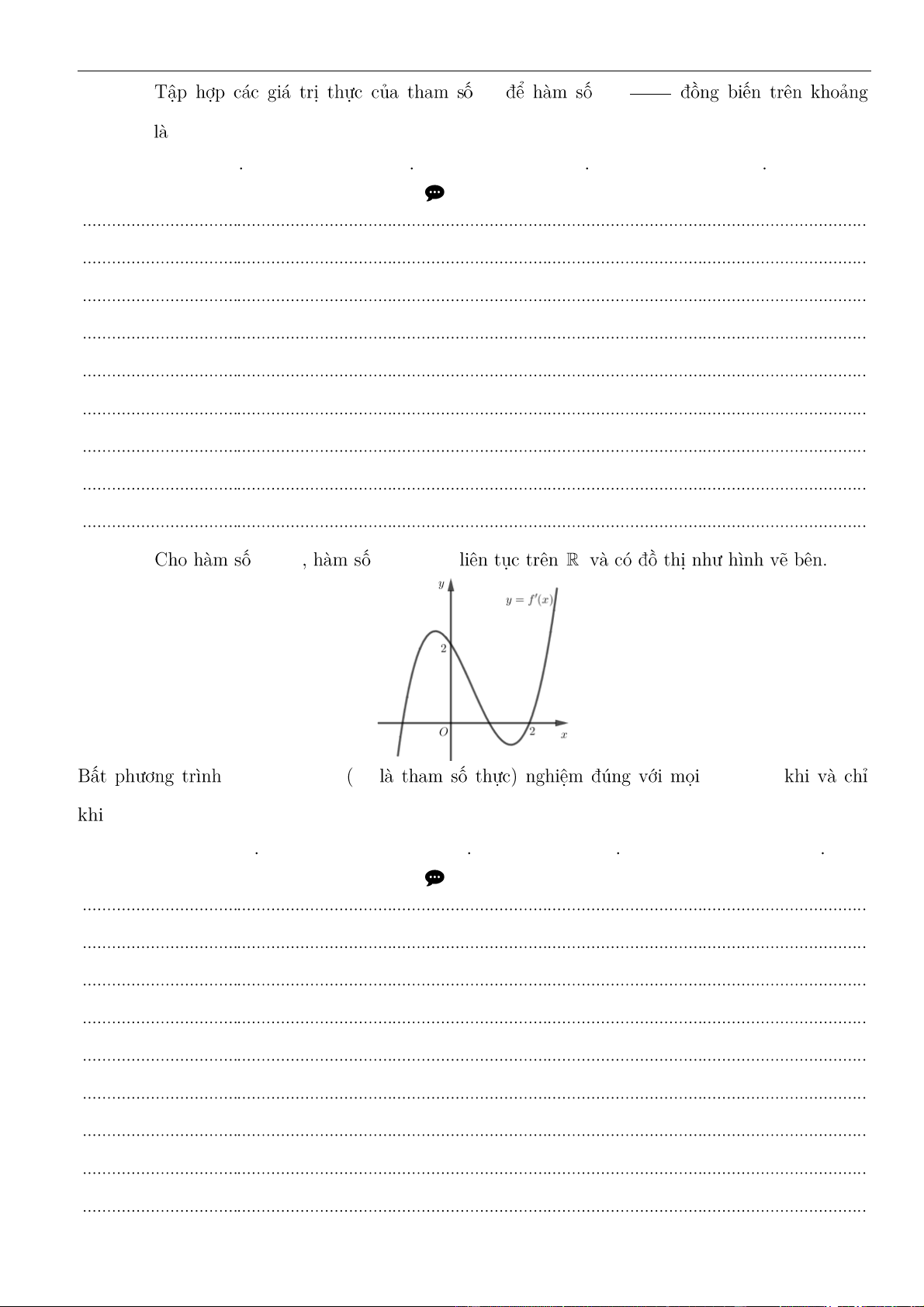
CÂU 10.
m
5x
y
xm
+
=
+
( )
;8− −
A.
( )
5;+
B.
(
5;8
C.
)
5;8
D.
( )
5;8
Lời giải.
CÂU 11.
( )
fx
( )
y f x
=
( )
2f x x m+
m
( )
0;2x
A.
( )
0mf
B.
( )
24mf−
C.
( )
0mf
D.
( )
24mf−
Lời giải.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1. Hàm số
( )
fx
có đạo hàm
( )
0,f x x
, khi đó hàm số đã cho
A. đồng biến trên .
B. nghịch biến trên .
C. là hàm số hằng trên .
D. đồng biến trên khoảng
( )
;0−
và nghịch biến trên khoảng
( )
0;+
.
Câu 2. Hàm số
( )
2
1
x
fx
x
−
=
−
đồng biến trên khoảng nào dưới đây?
A.
( )
1;2−
. B.
( )
2; 1−−
. C.
( )
;2−
. D.
( )
1;− +
.
Câu 3. Hàm số nào sau đây nghịch biến trên
A.
1
3
x
y
x
+
=
−
. B.
3
3y x x= − −
. C.
3
y x x=+
. D.
42
y x x= − −
.
Câu 4. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
21
3
x
y
x
−
=
+
. B.
42
2y x x=−
. C.
3
2 2020y x x= + −
. D.
2
21y x x= + −
.
Câu 5. Cho hàm số
21
1
x
y
x
+
=
−
mệnh đề đúng là
A. Hàm số nghịch biến trên khoảng
( )
;1−
và
( )
1; +
.
B. Hàm số nghịch biến trên tập
( ) ( )
;1 1;− +
.
C. Hàm số nghịch biến trên các khoảng
( )
;1− −
và
( )
1;− +
.
D. Hàm số nghịch biến trên tập
\1−
.
Câu 6. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
3
y x x=+
. B.
3
y x x=−
. C.
2
1yx=+
. D.
2
1yx=−
.
Câu 7. Hàm số nào dưới đây đồng biến trên
( )
;− +
?
A.
3
3y x x=−
. B.
1
2
x
y
x
−
=
−
. C.
1
3
x
x
+
+
. D.
3
3y x x=+
.
Câu 8. Hàm số nào sau đây đồng biến trên ?
Tính đơn điệu của hàm số cho bởi công thức
DẠNG 1
Phương pháp:
•
Bưc 1. Tm tập xác định
D
ca hàm số. Tính đạo hàm
( )
y f x
=
•
Bưc 2. Tm các điểm tại đó
( )
0fx
=
hoặc
( )
fx
không xác định
•
Bưc 3. Sp xếp các điểm
i
x
theo th t tăng dn và lập bảng xét dấu
•
Bưc 4. Nêu kết luận về các khoảng đồng biến và nghịch biến da vào bảng xét dấu

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
42
2y x x=+
. B.
1
1
x
y
x
−
=
+
. C.
3
31y x x= − − +
. D.
3
2 3 1y x x= + +
.
Câu 9. Hàm số nào sau đây nghịch biến trên khoảng
;
?
A.
21yx= − +
. B.
yx=
. C.
2yx= − +
. D.
5yx=−
.
Câu 10. Cho hàm số
21
3
x
y
x
−
=
+
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên mỗi khoảng
( ) ( )
;3 , 3;− +
.
B. Hàm số đồng biến trên mỗi khoảng
11
; , ;
22
− +
.
C. Hàm số đồng biến trên mỗi khoảng
( ) ( )
; 3 , 3;− − − +
.
D. Hàm số đồng biến trên .
Câu 11. Cho hàm số
3
1
x
y
x
−
=
+
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên
( )
;1− −
. B. Hàm số đồng biến trên
( )
;1− −
.
C. Hàm số nghịch biến trên
( )
;− +
. D. Hàm số nghịch biến trên
( )
1;− +
.
Câu 12. Cho hàm số
32
11
61
32
y x x x= − + + −
. Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
( )
3; +
.
B. Hàm số nghịch biến trên khoảng
( )
;0−
.
C. Hàm số đồng biến trên khoảng
( )
2;3−
.
D. Hàm số nghịch biến trên khoảng
( )
2;3−
.
Câu 13. Hàm số nào sau đây nghịch biến trên từng khoảng xác đinh?
A.
21
3
x
y
x
+
=
−
. B.
1
1
x
y
x
−
=
+
. C.
5
1
x
y
x
+
=
−−
. D.
2
21
x
y
x
−
=
−
.
Câu 14. Tm các khoảng đồng biến ca hàm số
1
1
x
y
x
−
=
+
.
A. Không tồn tại. B.
( ) ( )
; 1 1;− − − +
.
C.
( ) ( )
; 1 ; 1;− − − +
. D.
( )
;− +
.
Câu 15. Hàm số nào sau đây nghịch biến trên
;
?
A.
21yx= − +
. B.
yx=
. C.
2yx= − +
. D.
5yx=−
.
Câu 16. Cho hàm số
21
3
x
y
x
−
=
+
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên mỗi khoảng
( ) ( )
;3 , 3;− +
.
B. Hàm số đồng biến trên mỗi khoảng
11
; , ;
22
− +
.
C. Hàm số đồng biến trên mỗi khoảng
( ) ( )
; 3 , 3;− − − +
.
D. Hàm số đồng biến trên .

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 17. Hàm số
2
1
x
y
x
+
=
−
nghịch biến trên các khoảng.
A.
( )
1; .− +
B.
\1
. C.
( )
;1−
và
( )
1; .+
D.
( )
1; .+
Câu 18. Hàm số nào trong các hàm số dưới đây đồng biến trên ?
A.
42
1.y x x= + −
B.
32
3 11.y x x x= − + +
C.
tan .yx=
D.
2
.
4
x
y
x
+
=
+
Câu 19. Hàm số nào dưới đây nghịch biến trên ?
A.
1
2
x
y
x
+
=
−
. B.
2
2y x x=−
. C.
32
y x x x= − + −
. D.
42
257y x x= − −
.
Câu 20. Cho hàm số
1
1
x
y
x
+
=
−+
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên các khoảng
( )
;1−
và
( )
1; +
.
B.
Hàm số đồng biến trên các khoảng
( )
;1−
và
( )
1; +
.
C.
Hàm số nghịch biến trên khoảng
( ) ( )
;1 1;− +
.
D.
Hàm số đồng biến trên khoảng
( ) ( )
;1 1;− +
.
Câu 21. Hàm số
2
2y x x=−
nghịch biến trên khoảng:
A.
( )
0;1
. B.
( )
1; +
. C.
( )
0;2
. D.
( )
1;2
.
Câu 22. Cho hàm số
42
21y x x= − +
. Tm khẳng định đúng?
A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên
( )
;0−
.
C. Hàm số nghịch biến trên
( )
0;1
. D. Hàm số đồng biến trên
( )
2;0−
.
Câu 23. Hàm số
42
23y x x= + −
đồng biến trên khoảng nào dưới đây?
A.
( )
1;0−
và
( )
1; +
. B.
( )
0;+
. C.
( )
;1− −
và
( )
0;1
. D.
( )
;0−
.
Câu 24. Hàm số nào sau đây luôn đồng biến trên từng khoảng xác định ca nó?
A.
3 10
57
x
y
x
+
=
+
. B.
1
53
x
y
x
−+
=
−
. C.
8
3
x
y
x
−−
=
+
. D.
35
1
x
y
x
+
=
+
.
Câu 25. Cho hàm số
( )
21
3
x
fx
x
+
=
−
. Chọn mệnh đề sai trong các mệnh đề sau đây:
A. Hàm số nghịch biến trên khoảng
( )
;3−
.
B. Hàm số nghịch biến trên
\3
.
C. Hàm số nghịch biến trên các khoảng
( )
;3−
và
( )
3;+
.
D. Hàm số nghịch biến trên khoảng
( )
3;+
.
Câu 26. Hàm số
42
81y x x= − + −
nghịch biến trên khoảng nào dưới đây?
A.
( )
1; +
. B.
( )
;2− −
. C.
( )
0;1
. D.
( )
2;0−
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 27. Hàm số
43
42y x x= − + −
đồng biến trên khoảng nào sau đây?
A.
( )
3;+
. B.
( )
4; +
. C.
( )
;4−
. D.
( )
;3−
.
Câu 28. Hàm số
42
2y x x= − +
nghịch biến trên khoảng nào sau đây?
A.
( )
0;2
. B.
( )
;0−
. C.
( )
1;1−
. D.
( )
1; +
.
Câu 29. Cho hàm số
( )
y f x=
có đạo hàm trên là
( ) ( )
2
1f x x x
=−
. Hàm số
( )
y f x=
đồng biến
trên khoảng nào sau đây?
A.
( )
;− +
. B.
( )
1; +
. C.
( )
;1−
. D.
( )
0;1
.
Câu 30. Hàm số
4
9yx=−
A. đồng biến trên khoảng
( )
0;+
. B. nghịch biến trên khoảng
( )
;3−
.
C. đồng biến trên khoảng
( )
;0−
. D. nghịch biến trên khoảng
( )
3;+
.
Câu 31. Cho hàm số
2
2
1
xx
y
x
−
=
−
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên các khoảng
( )
;1−
và
( )
1; +
.
C. Hàm số nghịch biến trên .
D. Hàm số nghịch biến trên các khoảng
( )
;1−
và
( )
1; +
.
Câu 32. Hàm số nào dưới đây đồng biến trên ?
A.
1
2
x
y
x
+
=
−
. B.
2
2y x x=+
. C.
32
y x x x= − +
. D.
42
32y x x= − +
.
Câu 33. Hàm số nào sau đây đồng biến trên
A.
5
4
x
y
=
. B.
4
3
x
y
x
+
=
+
. C.
42
21y x x= − +
. D.
tanyx=
.
Câu 34. Hàm số
32
3 9 1y x x x= − − + +
đồng biến trên khoảng nào sau đây?
A.
( )
1;3−
. B.
( )
3;1−
. C.
( )
1; +
. D.
( )
;3− −
.
Câu 35. Hàm số
( )
y f x=
có đạo hàm
( )
2
1yx
=−
. Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên
( )
;1−
và nghịch biến trên
( )
1; +
.
B. Hàm số nghịch biến trên .
C. Hàm số nghịch biến trên
( )
;1−
và đồng biến trên
( )
1; +
.
D. Hàm số đồng biến trên .
Câu 36. Hàm số nào sau đây nghịch biến trên ?
A.
1
3
x
y
x
+
=
+
. B.
3
3y x x= − −
. C.
3
y x x=+
. D.
1
2
x
y
x
−
=
−
.
Câu 37. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
1
3
x
y
x
+
=
+
. B.
2
1yx=+
. C.
42
51y x x= + −
. D.
3
y x x=+
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Câu 38. Mệnh đề nào dưới đây về hàm số
( )
2
2
41yx= − +
là đúng?
A. Nghịch biến trên
( )
2;2−
. B. Đồng biến trên .
C. Đồng biến trên
( )
;2− −
và
( )
2;+
. D. Đồng biến trên
( )
2;0−
và
( )
2;+
.
Câu 39. Hàm số nào sau đây đồng biến trên ?
A.
32
45y x x x= − +
. B.
42
2 6 7y x x= − +
. C.
2
1
x
y
x
−
=
−
. D.
2
y x x= − +
.
Câu 40. Hàm số
42
1
42
xx
y = − +
đồng biến trên khoảng nào sau đây?
A.
( )
0; +
. B.
( )
;1− −
. C.
( )
1; +
. D.
( )
0;1
.
Câu 41. Trong các hàm số sau, hàm số nào đồng biến trên khoảng
( )
1; +
?
A.
3
1y x x= − + −
. B.
3
1
x
y
x
−
=
+
. C.
42
3y x x= − +
. D.
2
23
x
y
x
−
=
−
.
Câu 42. Cho hàm số
2
2.y x x=−
Hàm số nghịch biến trên khoảng nào dưới đây?
A.
( 1;1)−
. B.
(0;2)
. C.
(0;1)
. D.
(1;2)
.
Câu 43. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
( )
32
3 3 4f x x x x= − + −
. B.
( )
42
24f x x x= − −
.
C.
( )
2
41f x x x= − +
. D.
( )
21
1
x
fx
x
−
=
+
.
Câu 44. Cho hàm số
1
2
x
y
x
−
=
+
. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên
\2−
.
C. Hàm số đồng biến trên
\2−
.
D. Hàm số đồng biến trên các khoảng
( )
;2− −
và
( )
2;− +
.
Câu 45. Hàm số nào dưới đây đồng biến trên ?
A.
3
3y x x=+
. B.
42
32y x x= − +
.
C.
1
2
x
y
x
+
=
+
. D.
2
2y x x=−
.
Câu 46. Hàm số nào dưới đây nghịch biến trên ?
A.
3
31y x x= − − +
. B.
3
31y x x= − + +
. C.
3
31y x x= + +
. D.
3
3 10y x x= − +
.
Câu 47. Hàm số nào dưới đây nghịch biến trên ?
A.
3
31y x x= − − +
. B.
3
31y x x= − + +
. C.
3
31y x x= + +
. D.
3
3 10y x x= − +
.
Câu 48. Gọi
S
là tập hợp tất cả các giá trị nguyên ca tham số
m
để hàm số
( )
( )
3 2 2
3 4 2020f x x x m m x= − + − +
đồng biến trên
( )
0;4
. Tính tổng
T
tất cả các phn tử
ca tập
S
.
A.
2T =
. B.
6T =
. C.
8T =
. D.
3T =
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 49. Giá trị ca
m
để hàm số
cot 2
cot
x
y
xm
−
=
−
nghịch biến trên
;
42
là
A.
0
12
m
m
. B.
0m
. C.
12m
. D.
2m
.
Câu 50. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
( )
42
24f x x x= − −
. B.
( )
21
1
x
fx
x
−
=
+
.
C.
( )
32
3 3 4f x x x x= − + −
. D.
( )
2
41f x x x= − +
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Hàm số
( )
fx
có đạo hàm
( )
0,f x x
, khi đó hàm số đã cho
A. đồng biến trên .
B. nghịch biến trên .
C. là hàm số hằng trên .
D. đồng biến trên khoảng
( )
;0−
và nghịch biến trên khoảng
( )
0;+
.
Lời giải
Chọn A
V hàm số
( )
fx
có đạo hàm
( )
0,f x x
nên hàm số đồng biến trên .
Câu 2. Hàm số
( )
2
1
x
fx
x
−
=
−
đồng biến trên khoảng nào dưới đây?
A.
( )
1;2−
. B.
( )
2; 1−−
. C.
( )
;2−
. D.
( )
1;− +
.
Lời giải
Chọn B
Tập xác định
\1D =
.
Ta có
( )
2
1
0, \ 1
1
yx
x
=
−
.
Suy ra hàm số đồng biến trên
( )
;1−
và
( )
1; +
.
Câu 3. Hàm số nào sau đây nghịch biến trên
A.
1
3
x
y
x
+
=
−
. B.
3
3y x x= − −
. C.
3
y x x=+
. D.
42
y x x= − −
.
Lời giải
Chọn B
Ta thấy hàm số
3
3y x x= − −
có tập xác định và đạo hàm
2
3 3 0,y x x
= − −
nên nó
nghịch biến trên .
Câu 4. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
21
3
x
y
x
−
=
+
. B.
42
2y x x=−
. C.
3
2 2020y x x= + −
. D.
2
21y x x= + −
.
Lời giải
Chọn C
Ha số
3
2 2020y x x= + −
có
2
3 2 0y x x
= +
, suy ra hàm số
3
2 2020y x x= + −
đồng
biến trên .
Câu 5. Cho hàm số
21
1
x
y
x
+
=
−
mệnh đề đúng là
A. Hàm số nghịch biến trên khoảng
( )
;1−
và
( )
1; +
.
B. Hàm số nghịch biến trên tập
( ) ( )
;1 1;− +
.
C. Hàm số nghịch biến trên các khoảng
( )
;1− −
và
( )
1;− +
.
D. Hàm số nghịch biến trên tập
\1−
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Lời giải
Chọn A
Câu 6. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
3
y x x=+
. B.
3
y x x=−
. C.
2
1yx=+
. D.
2
1yx=−
.
Lời giải
Chọn A
32
' 3 1 0,y x x y x x= + = +
Nên hàm số
3
y x x=+
đồng biến trên .
Câu 7. Hàm số nào dưới đây đồng biến trên
( )
;− +
?
A.
3
3y x x=−
. B.
1
2
x
y
x
−
=
−
. C.
1
3
x
x
+
+
. D.
3
3y x x=+
.
Lời giải
Chọn D
Ta có
( )
32
3 3 3 0, ;y x x y x x
= + = + − +
.
Nên hàm số đồng biến trên .
Câu 8. Hàm số nào sau đây đồng biến trên ?
A.
42
2y x x=+
. B.
1
1
x
y
x
−
=
+
. C.
3
31y x x= − − +
. D.
3
2 3 1y x x= + +
.
Lời giải
Chọn D
Hàm số
3
2 3 1y x x= + +
có
2
6 3 0,y x x
= +
.
Vậy hàm số
3
2 3 1y x x= + +
đồng biến trên ?
Câu 9. Hàm số nào sau đây nghịch biến trên khoảng
;
?
A.
21yx= − +
. B.
yx=
. C.
2yx= − +
. D.
5yx=−
.
Lời giải
Chọn A
Xét hàm số
21yx= − +
có
20a
nên hàm số nghịc biến trên
;
.
Câu 10. Cho hàm số
21
3
x
y
x
−
=
+
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên mỗi khoảng
( ) ( )
;3 , 3;− +
.
B. Hàm số đồng biến trên mỗi khoảng
11
; , ;
22
− +
.
C. Hàm số đồng biến trên mỗi khoảng
( ) ( )
; 3 , 3;− − − +
.
D. Hàm số đồng biến trên .
Lời giải
Chọn C
Tập xác định:
\3−
Ta có:
( )
2
7
0, 3
3
yx
x
= −
+
Hàm số đồng biến trên mỗi khoảng
( ) ( )
; 3 , 3;− − − +
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Câu 11. Cho hàm số
3
1
x
y
x
−
=
+
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên
( )
;1− −
. B. Hàm số đồng biến trên
( )
;1− −
.
C. Hàm số nghịch biến trên
( )
;− +
. D. Hàm số nghịch biến trên
( )
1;− +
.
Lời giải
Chọn B
Ta có:
( )
2
4
01
1
yx
x
= −
+
Hàm số đồng biến trên từng khoảng
( )
;1− −
và
( )
1;− +
.
Câu 12. Cho hàm số
32
11
61
32
y x x x= − + + −
. Khẳng định nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
( )
3; +
.
B. Hàm số nghịch biến trên khoảng
( )
;0−
.
C. Hàm số đồng biến trên khoảng
( )
2;3−
.
D. Hàm số nghịch biến trên khoảng
( )
2;3−
.
Lời giải
Chọn C
Tập xác định
D =
.
Ta có
2
2
60
3
x
y x x
x
=−
= − + + =
=
.
Bảng xét dấu:
Suy ra, hàm số đồng biến trên khoảng
( )
2;3−
.
Câu 13. Hàm số nào sau đây nghịch biến trên từng khoảng xác đinh?
A.
21
3
x
y
x
+
=
−
. B.
1
1
x
y
x
−
=
+
. C.
5
1
x
y
x
+
=
−−
. D.
2
21
x
y
x
−
=
−
.
Lời giải
Chọn A
Xét hàm số
21
3
x
y
x
+
=
−
Ta có
( )
2
7
0
3
y
x
−
=
−
nên hàm số
21
3
x
y
x
+
=
−
nghịch biến trên từng khoảng xác định ca nó.
Câu 14. Tm các khoảng đồng biến ca hàm số
1
1
x
y
x
−
=
+
.
A. Không tồn tại. B.
( ) ( )
; 1 1;− − − +
.
C.
( ) ( )
; 1 ; 1;− − − +
. D.
( )
;− +
.
Lời giải

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Chọn C
TXĐ
\1D =−
.
( )
2
2
0
1
y x D
x
−
=
+
.
Do đó hàm số luôn nghịch biến trên từng khoảng xác định.
Câu 15. Hàm số nào sau đây nghịch biến trên
;
?
A.
21yx= − +
. B.
yx=
. C.
2yx= − +
. D.
5yx=−
.
Lời giải
Chọn A
Hàm số bậc nhất
0y ax b a
nghịch biến trên khoảng
;
0a
.
Do đó ta chọn đáp án A.
Câu 16. Cho hàm số
21
3
x
y
x
−
=
+
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên mỗi khoảng
( ) ( )
;3 , 3;− +
.
B. Hàm số đồng biến trên mỗi khoảng
11
; , ;
22
− +
.
C. Hàm số đồng biến trên mỗi khoảng
( ) ( )
; 3 , 3;− − − +
.
D. Hàm số đồng biến trên .
Lời giải
Chọn C
TXĐ:
\3D =−
.
Ta có
( )
2
7
0,
3
y x D
x
=
+
.
Vậy hàm số đồng biến trên mỗi khoảng
( )
;3− −
và
( )
3;− +
.
Câu 17. Hàm số
2
1
x
y
x
+
=
−
nghịch biến trên các khoảng.
A.
( )
1; .− +
B.
\1
. C.
( )
;1−
và
( )
1; .+
D.
( )
1; .+
Lời giải
Chọn C
Tập xác định:
\1D =
.
Ta có
( )
2
3
0,
1
y x D
x
−
=
−
.
Vậy hàm số nghịch biến trên các khoảng
( )
;1−
và
( )
1; .+
Câu 18. Hàm số nào trong các hàm số dưới đây đồng biến trên ?
A.
42
1.y x x= + −
B.
32
3 11.y x x x= − + +
C.
tan .yx=
D.
2
.
4
x
y
x
+
=
+
Lời giải

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Chọn B
Xét hàm số
32
3 11y x x x= − + +
có
2
2
18
3 2 3 3 0,
3
3
y x x x x
= − + = − +
nên hàm số
đồng biến trên .
Câu 19. Hàm số nào dưới đây nghịch biến trên ?
A.
1
2
x
y
x
+
=
−
. B.
2
2y x x=−
. C.
32
y x x x= − + −
. D.
42
257y x x= − −
.
Lời giải
Chọn C
Xét hàm số
32
y x x x= − + −
.
Tập xác định
D =
.
Ta có
2
2
12
' 3 2 1 3 0,
33
y x x x x
= − + − = − − −
.
Nên hàm số
32
y x x x= − + −
nghịch biến trên .
Câu 20: Cho hàm số
1
1
x
y
x
+
=
−+
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số nghịch biến trên các khoảng
( )
;1−
và
( )
1; +
.
B. Hàm số đồng biến trên các khoảng
( )
;1−
và
( )
1; +
.
C. Hàm số nghịch biến trên khoảng
( ) ( )
;1 1;− +
.
D. Hàm số đồng biến trên khoảng
( ) ( )
;1 1;− +
.
Lời giải
Chọn B
Tập xác định:
\1D =
.
Ta có
( )
2
2
0,
1
y x D
x
=
−+
nên hàm số đồng biến trên các khoảng
( )
;1−
và
( )
1; +
Câu 20. Hàm số
2
2y x x=−
nghịch biến trên khoảng:
A.
( )
0;1
. B.
( )
1; +
. C.
( )
0;2
. D.
( )
1;2
.
Lời giải
Chọn D
Tập xác định:
0;2
.
2
1
'
2
x
y
xx
−
=
−
.
' 0 1yx= =
( ) ( )
' 0 1;2 , ' 0 0;1y x y x
.
Vậy hàm số nghịch biến trên khoảng
( )
1;2
.
Câu 21. Cho hàm số
42
21y x x= − +
. Tm khẳng định đúng?
A. Hàm số đồng biến trên . B. Hàm số nghịch biến trên
( )
;0−
.
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
C. Hàm số nghịch biến trên
( )
0;1
. D. Hàm số đồng biến trên
( )
2;0−
.
Lời giải
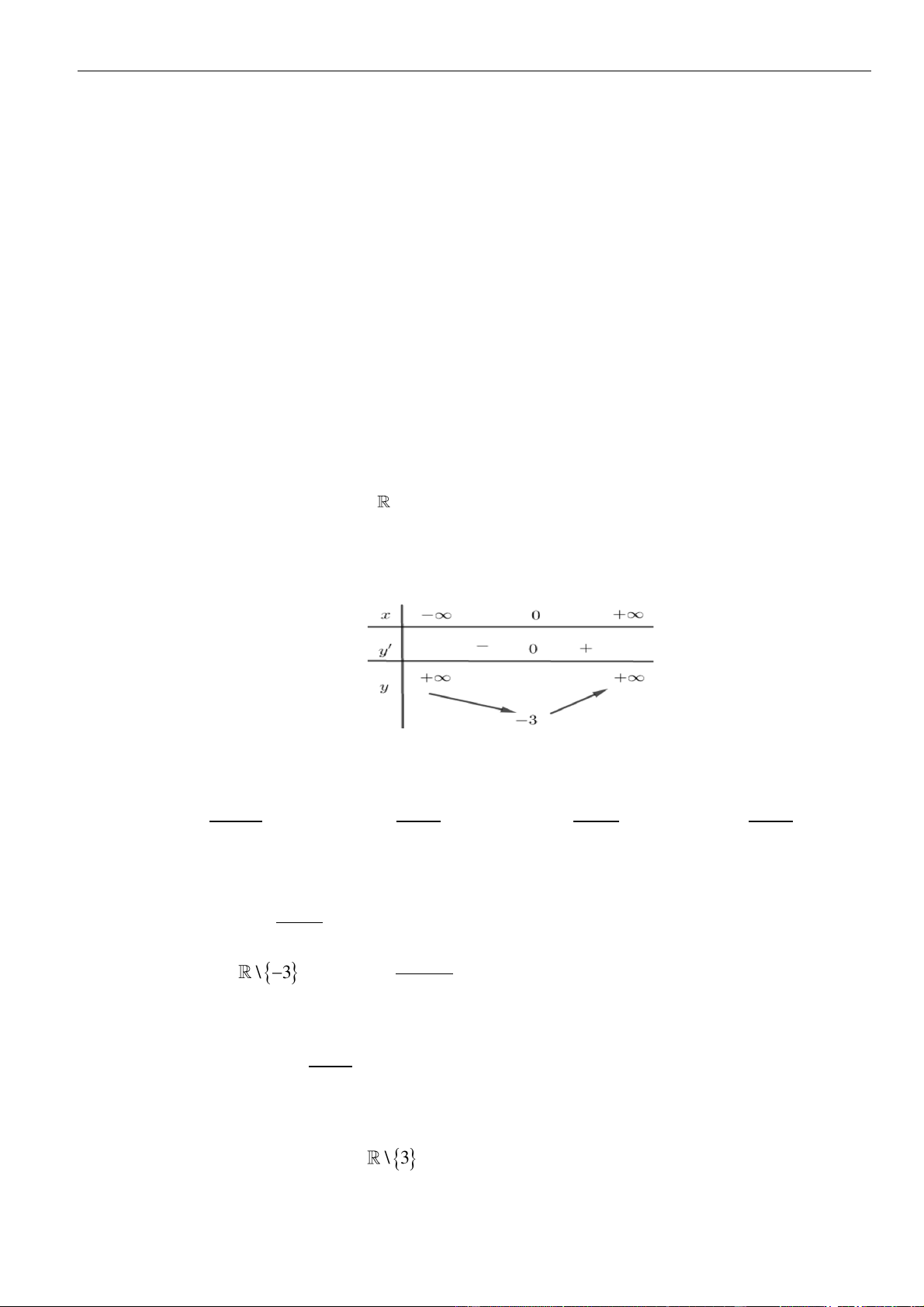
Chọn C
Ta có :
( )
32
1
' 4 4 4 1 0 0
1
x
y x x x x x
x
=−
= − = − = =
=
Bảng xét dấu ca
'y
Da vào bẳng xét dấu ta có đáp án đúng là C
là các nghiệm đơn và
4
xx=
là nghiệm kép, ta có bảng dấu ca
( )
'fx
như sau:
+) Da vào dấu ca
( )
'fx
ta có đồ thị hàm số có 3 cc trị.
Câu 22. Hàm số
42
23y x x= + −
đồng biến trên khoảng nào dưới đây?
A.
( )
1;0−
và
( )
1; +
. B.
( )
0;+
. C.
( )
;1− −
và
( )
0;1
. D.
( )
;0−
.
Lời giải
Chọn B
Hàm số xác định với mọi
x
.
Ta có:
( )
32
4 4 4 1 ,y x x x x x
= + = +
.
00yx
= =
.
Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng
( )
0;+
.
Câu 23. Hàm số nào sau đây luôn đồng biến trên từng khoảng xác định ca nó?
A.
3 10
57
x
y
x
+
=
+
. B.
1
53
x
y
x
−+
=
−
. C.
8
3
x
y
x
−−
=
+
. D.
35
1
x
y
x
+
=
+
.
Lời giải
Chọn C
Xét hàm số
8
3
x
y
x
−−
=
+
TXĐ:
\3D =−
. Ta có
2
5
' 0, 3
( 3)
yx
x
= −
+
.
Vậy hàm số đồng biến trên các khoảng
( ; 3)− −
và
( 3; )− +
.
Câu 24. Cho hàm số
( )
21
3
x
fx
x
+
=
−
. Chọn mệnh đề sai trong các mệnh đề sau đây:
A. Hàm số nghịch biến trên khoảng
( )
;3−
.
B. Hàm số nghịch biến trên
\3
.
C. Hàm số nghịch biến trên các khoảng
( )
;3−
và
( )
3;+
.
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
D. Hàm số nghịch biến trên khoảng
( )
3;+
.
Lời giải
Chọn B
Vì
( )
( )
2
7
0
3
fx
x
−
=
−
nên đồ thị hàm số luôn nghịch biến trên các khoảng
( )
;3−
và
( )
3;+
.
Câu 25. Hàm số
42
81y x x= − + −
nghịch biến trên khoảng nào dưới đây?
A.
( )
1; +
. B.
( )
;2− −
. C.
( )
0;1
. D.
( )
2;0−
.
Lời giải
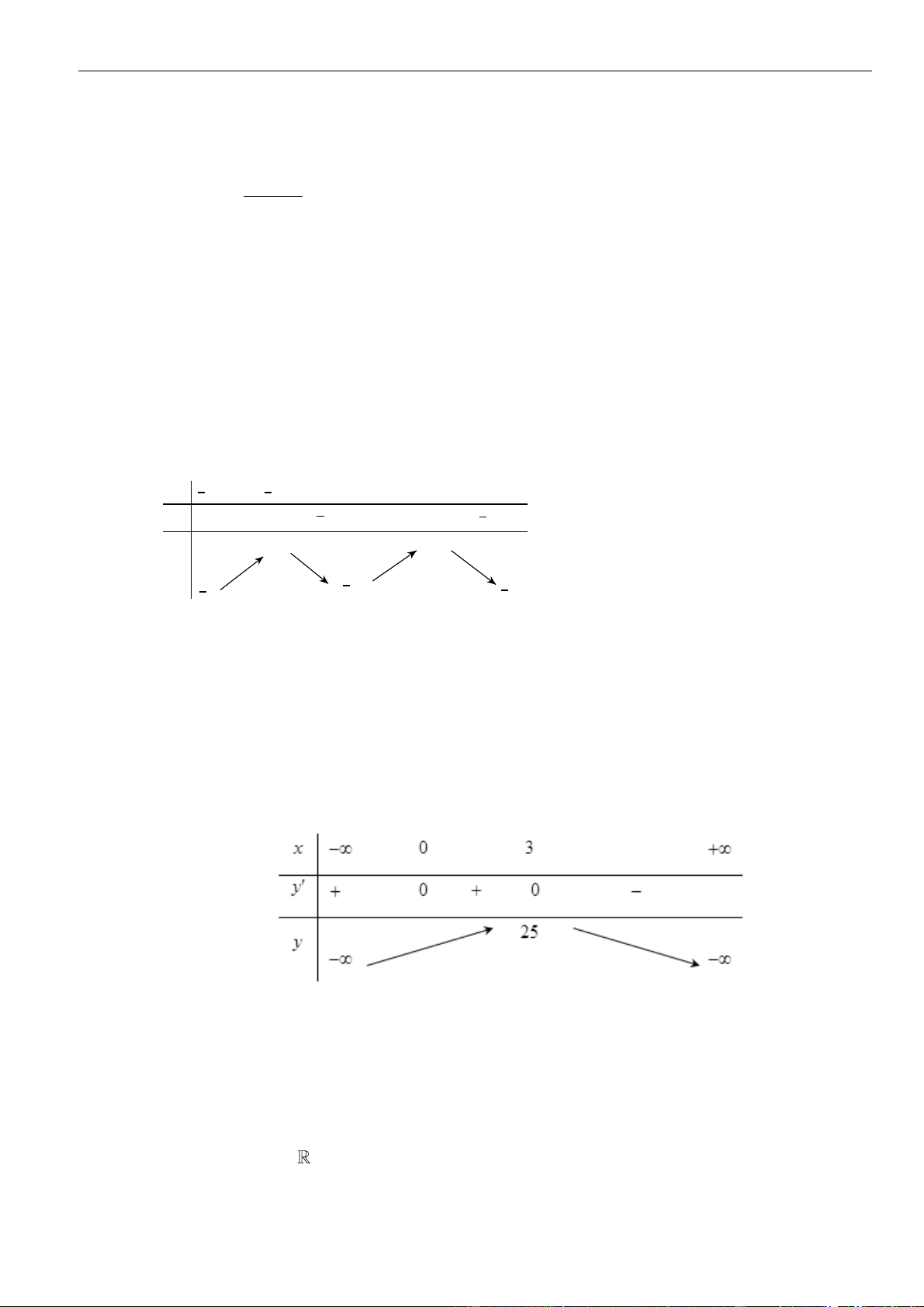
Chọn D
Ta có
( )
32
4 16 4 4y x x x x
= − + = − +
;
0
0
2
x
y
x
=
=
=
.
Bảng biến thiên :
Da vào bảng biến thiên ta có Hàm số nghịch biến trên khoảng
( )
2;0−
và
( )
2;+
.
Câu 26. Hàm số
43
42y x x= − + −
đồng biến trên khoảng nào sau đây?
A.
( )
3;+
. B.
( )
4; +
. C.
( )
;4−
. D.
( )
;3−
.
Lời giải
Chọn C
Xét
( )
3 2 2
4 12 4 3y x x x x
= − + = − −
Xét BBT:
Vậy hàm số đồng biến trên
( )
;3−
.
Câu 27. Hàm số
42
2y x x= − +
nghịch biến trên khoảng nào sau đây?
A.
( )
0;2
. B.
( )
;0−
. C.
( )
1;1−
. D.
( )
1; +
.
Lời giải
Chọn D
Tập xác định:
D =
.
∞
∞
1
+
+
15
15
0
2
2
0
0
+
∞∞
y
y'
x
0
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
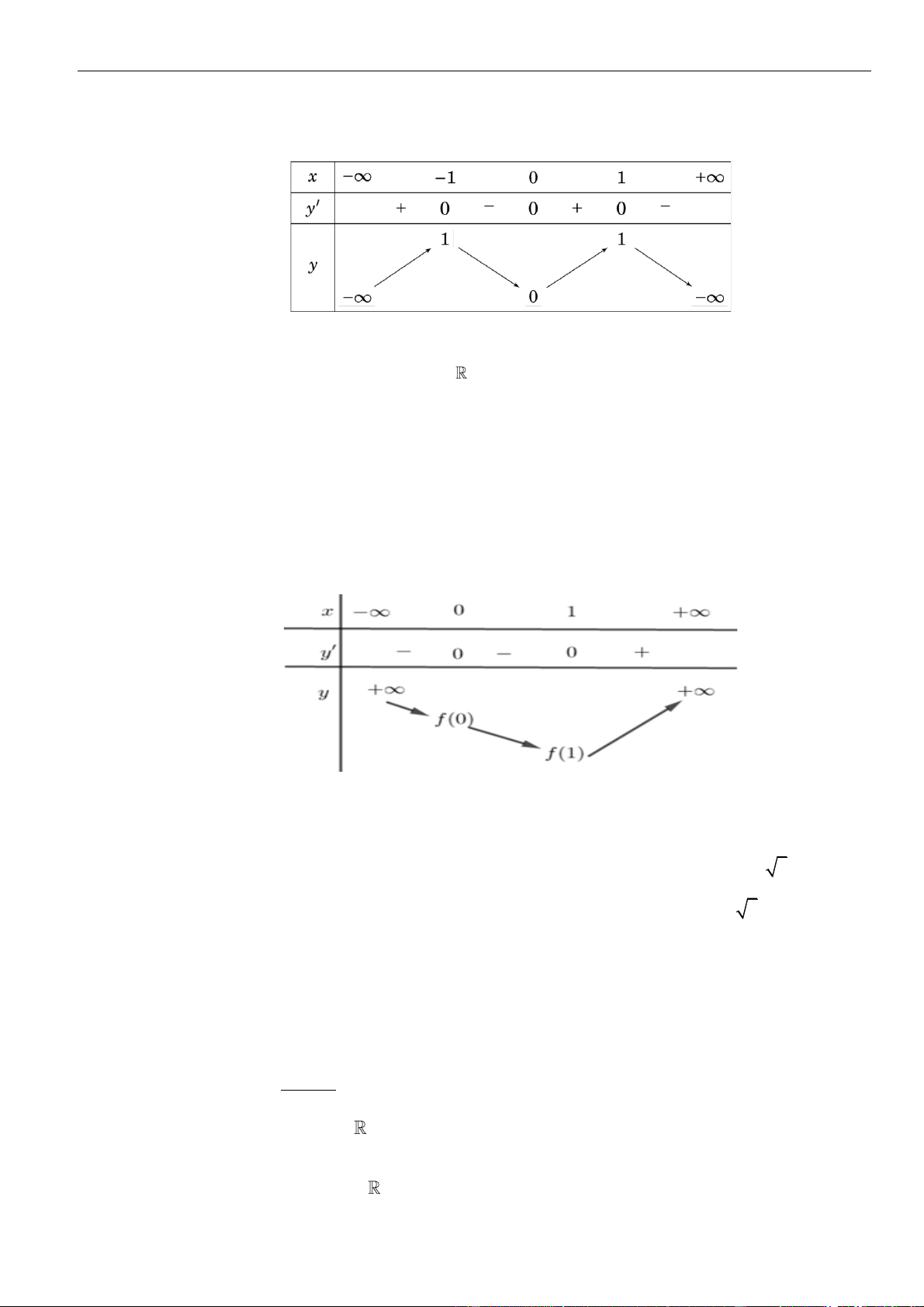
Ta có
3
0
4 4 , 0 1
1
x
y x x y x
x
=
= − + = =
=−
. Bảng biến thiên
Từ bảng biến thiên, suy ra hàm số nghịch biến trên khoảng
( )
1; +
.
Câu 28. Cho hàm số
( )
y f x=
có đạo hàm trên là
( ) ( )
2
1f x x x
=−
. Hàm số
( )
y f x=
đồng biến
trên khoảng nào sau đây?
A.
( )
;− +
. B.
( )
1; +
. C.
( )
;1−
. D.
( )
0;1
.
Lời giải
Chọn B
( )
0
0
1
x
fx
x
=
=
=
.
Bảng biến thiên:
Da vào bảng biến thiên suy ra hàm số
( )
y f x=
đồng biến trên khoảng
( )
1; +
Câu 29. Hàm số
4
9yx=−
A. đồng biến trên khoảng
( )
0;+
. B. nghịch biến trên khoảng
( )
;3−
.
C. đồng biến trên khoảng
( )
;0−
. D. nghịch biến trên khoảng
( )
3;+
.
Lời giải
Chọn A
Ta có:
3
' 4 .yx=
Từ đó:
' 0 0.yx= =
Ta thấy
' 0, 0yx
. Do đó, hàm số đồng biến trên khoảng
( )
0;+
.
Câu 30. Cho hàm số
2
2
1
xx
y
x
−
=
−
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên các khoảng
( )
;1−
và
( )
1; +
.
C. Hàm số nghịch biến trên .
D. Hàm số nghịch biến trên các khoảng
( )
;1−
và
( )
1; +
.
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn D
Ta có:
TXĐ:
( ) ( )
;1 1;D = − +
Và
( )
2
1
1 0, .
1
y x D
x
= − −
−
Do đó, hàm số nghịch biến trên các khoảng xác định.
Câu 31. Hàm số nào dưới đây đồng biến trên ?
A.
1
2
x
y
x
+
=
−
. B.
2
2y x x=+
. C.
32
y x x x= − +
. D.
42
32y x x= − +
.
Lời giải
Chọn C
2
3 2 2
12
' 3 2 1 3 0
33
y x x x y x x x x
= − + = − + = − +
Vậy hàm số đồng biến trên .
Câu 32. Hàm số nào sau đây đồng biến trên
A.
5
4
x
y
=
. B.
4
3
x
y
x
+
=
+
. C.
42
21y x x= − +
. D.
tanyx=
.
Lời giải
Chọn A
Ta có hàm số
5
4
x
y
=
có cơ số
5
1
4
a =
nên đồng biến trên
(Ngoài ra: các hàm số hàm số
4
3
x
y
x
+
=
+
,
42
21y x x= − +
,
tanyx=
không thể đồng biến hoặc
nghịch biến trên ).
Câu 33. Hàm số
32
3 9 1y x x x= − − + +
đồng biến trên khoảng nào sau đây?
A.
( )
1;3−
. B.
( )
3;1−
. C.
( )
1; +
. D.
( )
;3− −
.
Lời giải
Chọn B
Ta có
2
3 6 9y x x
= − − +
.
2
1
0 3 6 9 0
3
x
y x x
x
=
= − − + =
=−
.
Bảng biến thiên
Da vào bảng biến thiên suy ra hàm số đồng biến trên khoảng
( )
3;1−
.
Câu 34. Hàm số
( )
y f x=
có đạo hàm
( )
2
1yx
=−
. Mệnh đề nào sau đây đúng?
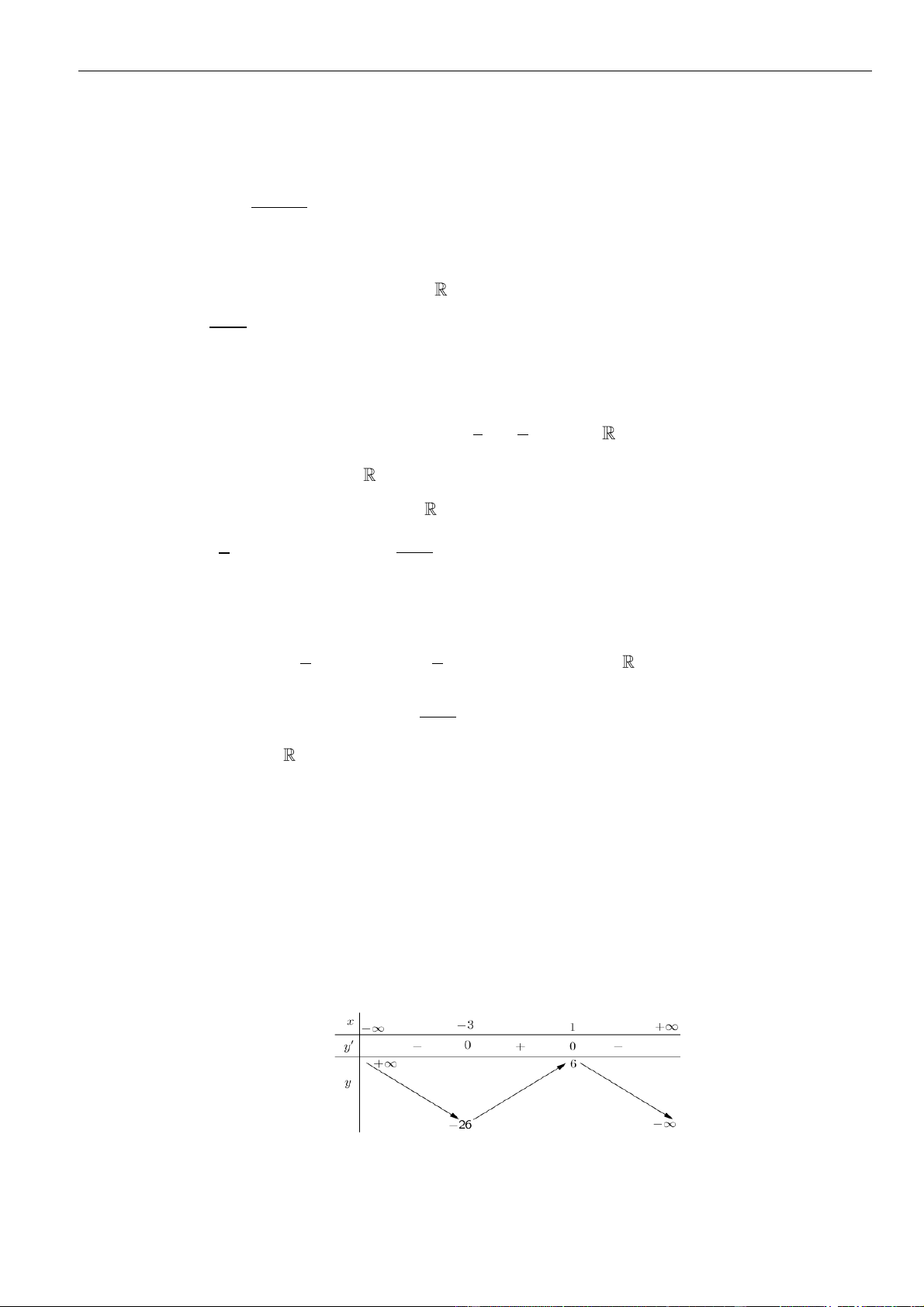
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
A. Hàm số đồng biến trên
( )
;1−
và nghịch biến trên
( )
1; +
.
B. Hàm số nghịch biến trên .
C. Hàm số nghịch biến trên
( )
;1−
và đồng biến trên
( )
1; +
.
D. Hàm số đồng biến trên .
Lời giải
Chọn D
Ta có
( )
2
1 0,y x x
= −
.
Vậy hàm số đã cho đồng biến trên .
Câu 35. Hàm số nào sau đây nghịch biến trên ?
A.
1
3
x
y
x
+
=
+
. B.
3
3y x x= − −
. C.
3
y x x=+
. D.
1
2
x
y
x
−
=
−
.
Lời giải
Chọn B
Hàm số
1
3
x
y
x
+
=
+
có TXĐ:
\3D =−
nên hàm số không nghịch biến trên .
Hàm số
3
3y x x= − −
có TXĐ:
D =
và
2
3 3 0yx
= − −
,
x
nên hàm số nghịch biến
trên .
Hàm số
3
y x x=+
có TXĐ:
D =
và
2
3 1 0yx
= +
,
x
nên hàm số không nghịch biến
trên .
Hàm số
1
2
x
y
x
−
=
−
có TXĐ:
\2D =
nên hàm số không nghịch biến trên .
Câu 36. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
1
3
x
y
x
+
=
+
. B.
2
1yx=+
. C.
42
51y x x= + −
. D.
3
y x x=+
.
Lời giải
Chọn D
+) Hàm số
2
1
,1
3
x
y y x
x
+
= = +
+
và
42
51y x x= + −
không đơn điệu trên
.
+) Hàm số
3
y x x=+
có
2
3 1 0,y x x
= +
nên đồng biến trên
.
Câu 37. Mệnh đề nào dưới đây về hàm số
( )
2
2
41yx= − +
là đúng?
A. Nghịch biến trên
( )
2;2−
. B. Đồng biến trên .
C. Đồng biến trên
( )
;2− −
và
( )
2;+
. D. Đồng biến trên
( )
2;0−
và
( )
2;+
.
Lời giải
Chọn D
42
8 17y x x= − +
3
4 16y x x
=−
0 0; 2y x x
= = =
.
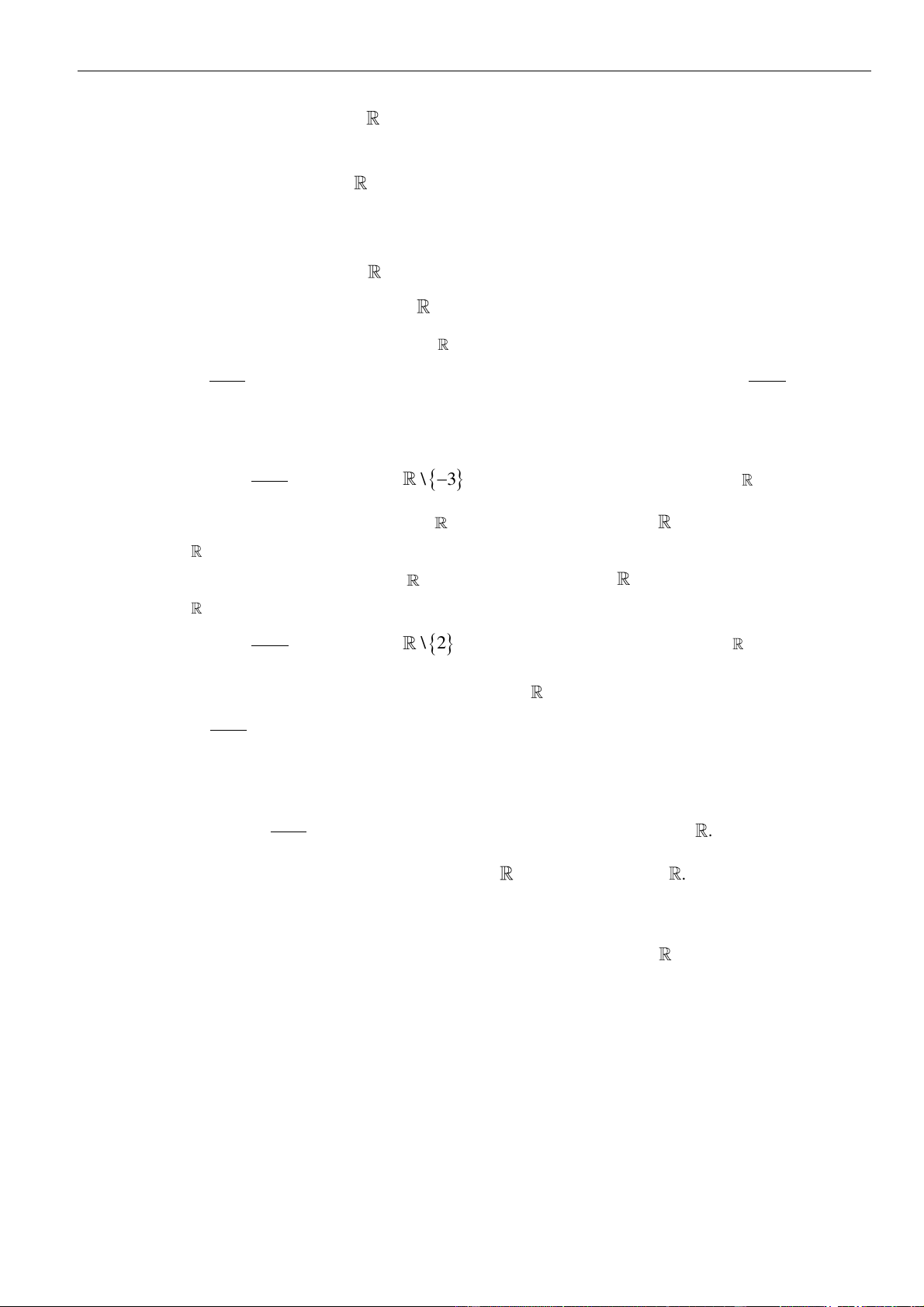
Bảng xét dấu
y
:
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Từ bảng xét dấu
y
ta thấy đáp án đúng là
D
.
Câu 38. Hàm số nào sau đây đồng biến trên ?
A.
32
45y x x x= − +
. B.
42
2 6 7y x x= − +
. C.
2
1
x
y
x
−
=
−
. D.
2
y x x= − +
.
Lời giải
Chọn A
Xét hàm số
32
45y x x x= − +
, có tập xác định
D =
Ta có
2
12 2 5 0,y x x x
= − +
. Do đó hàm số luôn đồng biến trên .
Câu 39. Hàm số
42
1
42
xx
y = − +
đồng biến trên khoảng nào sau đây?
A.
( )
0; +
. B.
( )
;1− −
. C.
( )
1; +
. D.
( )
0;1
.
Lời giải
Chọn C
TXĐ:
D =
3
'
0
' 0 1
1
y x x
x
yx
x
=−
=
= =
=−
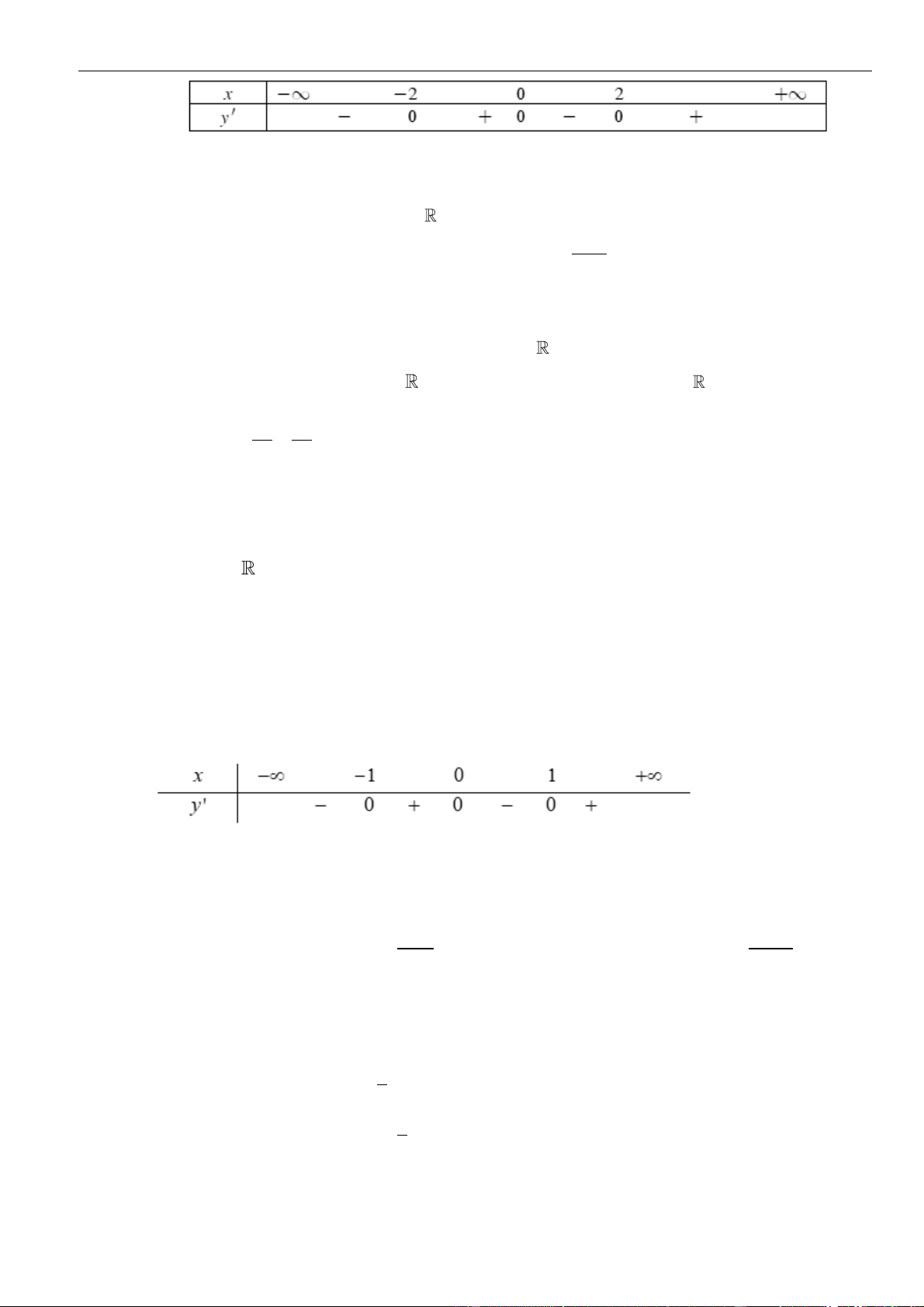
Ta có bảng xét dấu:
Từ bảng xét dấu, suy ra hàm số đồng biến trên
( )
1; 0−
và
( )
1; +
. Chọn C
Câu 40. Trong các hàm số sau, hàm số nào đồng biến trên khoảng
( )
1; +
?
A.
3
1y x x= − + −
. B.
3
1
x
y
x
−
=
+
. C.
42
3y x x= − +
. D.
2
23
x
y
x
−
=
−
.
Lời giải
Chọn C
A sai vì
23
nhưng
( ) ( )
2 7 3 25ff= − = −
.
B sai vì
23
nhưng
( ) ( )
1
2 3 0
3
ff= =
.
D sai vì
1,1 2
nhưng
( ) ( )
9
1,1 2 0
8
ff= =
.
C đúng v
( )
32
4 2 2 2 1 0, 1y x x x x x
= − = −
nên hàm số
42
3y x x= − +
đồng biến trên
khoảng
( )
1; +
.
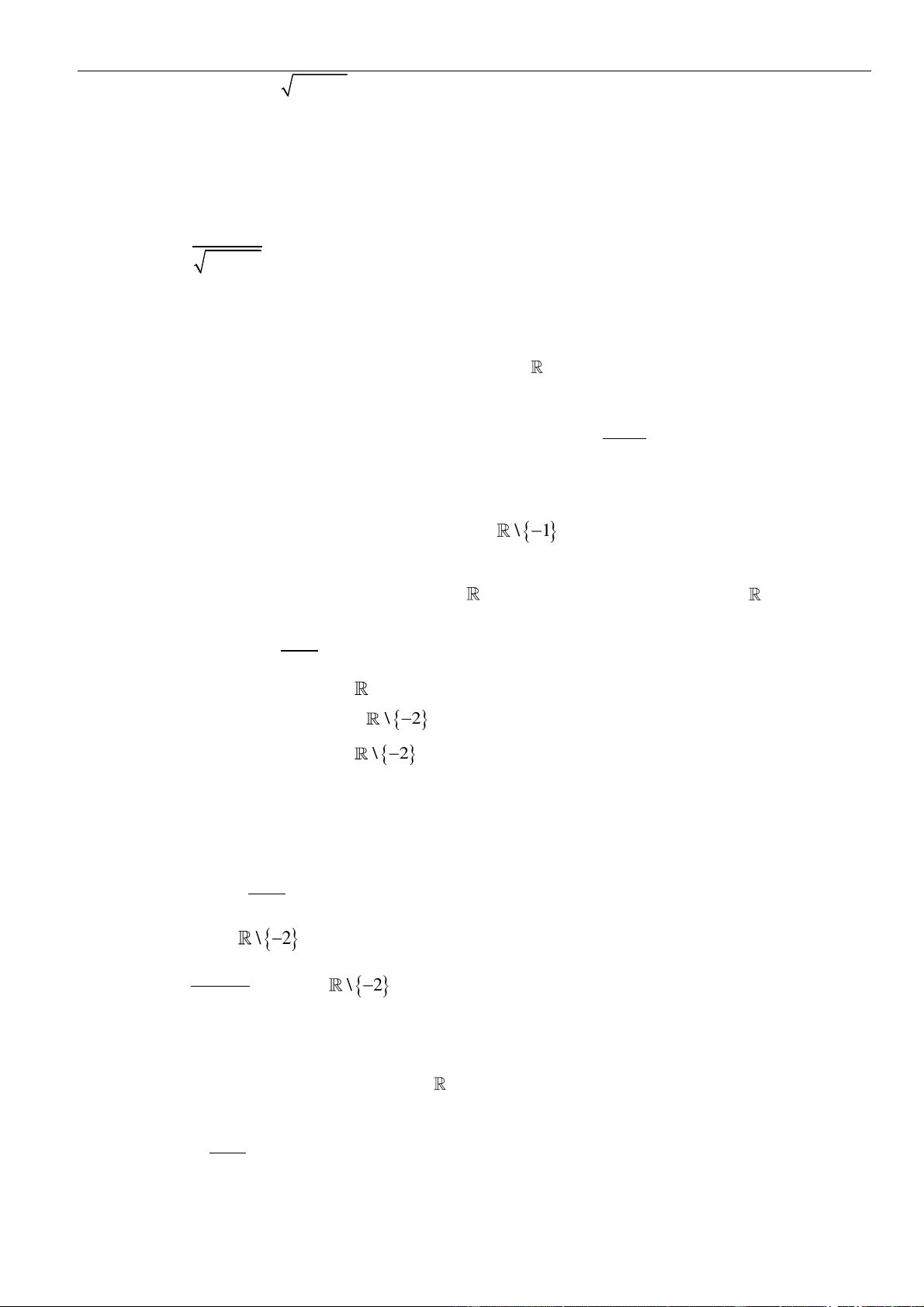
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Câu 41. Cho hàm số
2
2.y x x=−
Hàm số nghịch biến trên khoảng nào dưới đây?
A.
( 1;1)−
. B.
(0;2)
. C.
(0;1)
. D.
(1;2)
.
Lời giải
Chọn D
TXĐ:
0;2D =
2
1
'
2
x
y
xx
−
=
−
' 0 1yx= =
Nhận thấy
( )
' 0, 1;2yx
nên hs nghịch biến trên khoảng
(1;2)
Câu 42. Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
( )
32
3 3 4f x x x x= − + −
. B.
( )
42
24f x x x= − −
.
C.
( )
2
41f x x x= − +
. D.
( )
21
1
x
fx
x
−
=
+
.
Lời giải
Chọn A
Loại đáp án D v hàm số có tập xác định
\1D =−
.
Loại đáp án B v hàm trùng phương và hàm bậc hai luôn có cc trị.
Chọn A vì
( )
2
3 6 3 0f x x x x
= − +
. Do đó hàm số nào đồng biến trên .
Câu 43. Cho hàm số
1
2
x
y
x
−
=
+
. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên
\2−
.
C. Hàm số đồng biến trên
\2−
.
D. Hàm số đồng biến trên các khoảng
( )
;2− −
và
( )
2;− +
.
Lời giải
Chọn D
Hàm số
1
2
x
y
x
−
=
+
.
TXĐ:
\2D =−
.
( )
2
3
0, \ 2
2
yx
x
= −
+
.
Suy rs hàm số đồng biến trên các khoảng
( )
;2− −
và
( )
2;− +
.
Câu 44. Hàm số nào dưới đây đồng biến trên ?
A.
3
3y x x=+
. B.
42
32y x x= − +
.
C.
1
2
x
y
x
+
=
+
. D.
2
2y x x=−
.
Lời giải
Chọn A

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Xét hàm số
3
3y x x=+
TXĐ:
D =
.
2
3 3 0yx
= +
,
x
nên hàm số
3
3y x x=+
đồng biến trên .
Câu 45. Hàm số nào dưới đây nghịch biến trên ?
A.
3
31y x x= − − +
. B.
3
31y x x= − + +
. C.
3
31y x x= + +
. D.
3
3 10y x x= − +
.
Lời giải
Chọn A
Xét phương án A, ta có:
TXĐ:
D =
.
2
3 3 0,y x x
= − −
.
Do đó hàm số
3
31y x x= − − +
nghịch biến trên .
Câu 46. Hàm số nào dưới đây nghịch biến trên ?
A.
3
31y x x= − − +
. B.
3
31y x x= − + +
. C.
3
31y x x= + +
. D.
3
3 10y x x= − +
.
Lời giải
Chọn A
- Xét hàm số
3
31y x x= − − +
:
( )
22
3 3 3 1 0,y x x x
= − − = − +
nên hàm số nghịch biến
trên .
- Xét hàm số
3
31y x x= − + +
:
2
33yx
= − +
,
(
)
' 0 ; 1 1;yx − − +
nên hàm số không
nghịch biến trên .
- Xét hàm số
3
31y x x= + +
:
2
3 3 0,y x x
= +
nên hàm số không nghịch biến trên .
- Xét hàm số
3
3 10y x x= − +
:
2
33yx
=−
,
0 1;1yx
−
nên hàm số không nghịch biến
trên .
Câu 47. Gọi
S
là tập hợp tất cả các giá trị nguyên ca tham số
m
để hàm số
( )
( )
3 2 2
3 4 2020f x x x m m x= − + − +
đồng biến trên
( )
0;4
. Tính tổng
T
tất cả các phn tử ca tập
S
.
A.
2T =
. B.
6T =
. C.
8T =
. D.
3T =
.
Lời giải
Chọn B
Hàm số đã cho đồng biến
( )
22
0 3 6 4 0f x x x m m
− + −
( )
( )
( )
2 2 2
0;4
4 3 6 4 minm m x x f x m m f x − − = −
Xét hàm số
( )
2
36f x x x=−
trên khoảng
( )
0;4
Ta có
( ) ( )
6 6; 0 1f x x f x x
= − = =
Bảng biến thiên

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Da vào bảng biến thiên, ta có
( )
( )
0;4
min 3fx=−
Do đó
( )
( )
2 2 2
0;4
4 min 4 3 4 3 0 1;3m m f x m m m m m− − − − +
Mà
m
nên
1;2;3m
Vậy
6.T =
Câu 48. Giá trị ca
m
để hàm số
cot 2
cot
x
y
xm
−
=
−
nghịch biến trên
;
42
là
A.
0
12
m
m
. B.
0m
. C.
12m
. D.
2m
.
Lời giải
Chọn A
Đặt
cottx=
2
1
0
sin
t
x
= −
,
;
42
x
cot cot
24
t
hay
01t
.
Bài toán trở thành: tm
m
để hàm số
2t
y
tm
−
=
−
đồng biến trên
( )
0;1
.
+) TXĐ:
\Dm=
.
+) Ta có
( )
2
2 m
y
tm
−
=
−
.
+) Hàm số
2t
y
tm
−
=
−
đồng biến trên
( )
0;1
0y
,
( )
0;1t
( )
2
20
1
0;1
0
m
m
m
m
m
−
12
0
m
m
.
Câu 50: Trong các hàm số sau, hàm số nào đồng biến trên ?
A.
( )
42
24f x x x= − −
. B.
( )
21
1
x
fx
x
−
=
+
.
C.
( )
32
3 3 4f x x x x= − + −
. D.
( )
2
41f x x x= − +
.
Lời giải
Chọn C
Xét hàm số
( )
32
3 3 4f x x x x= − + −
Ta có
( )
2
3 6 3f x x x
= − +
( )
2
3 1 0x= −
với
x
( )
32
3 3 4f x x x x= − + −
đồng biến trên .
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
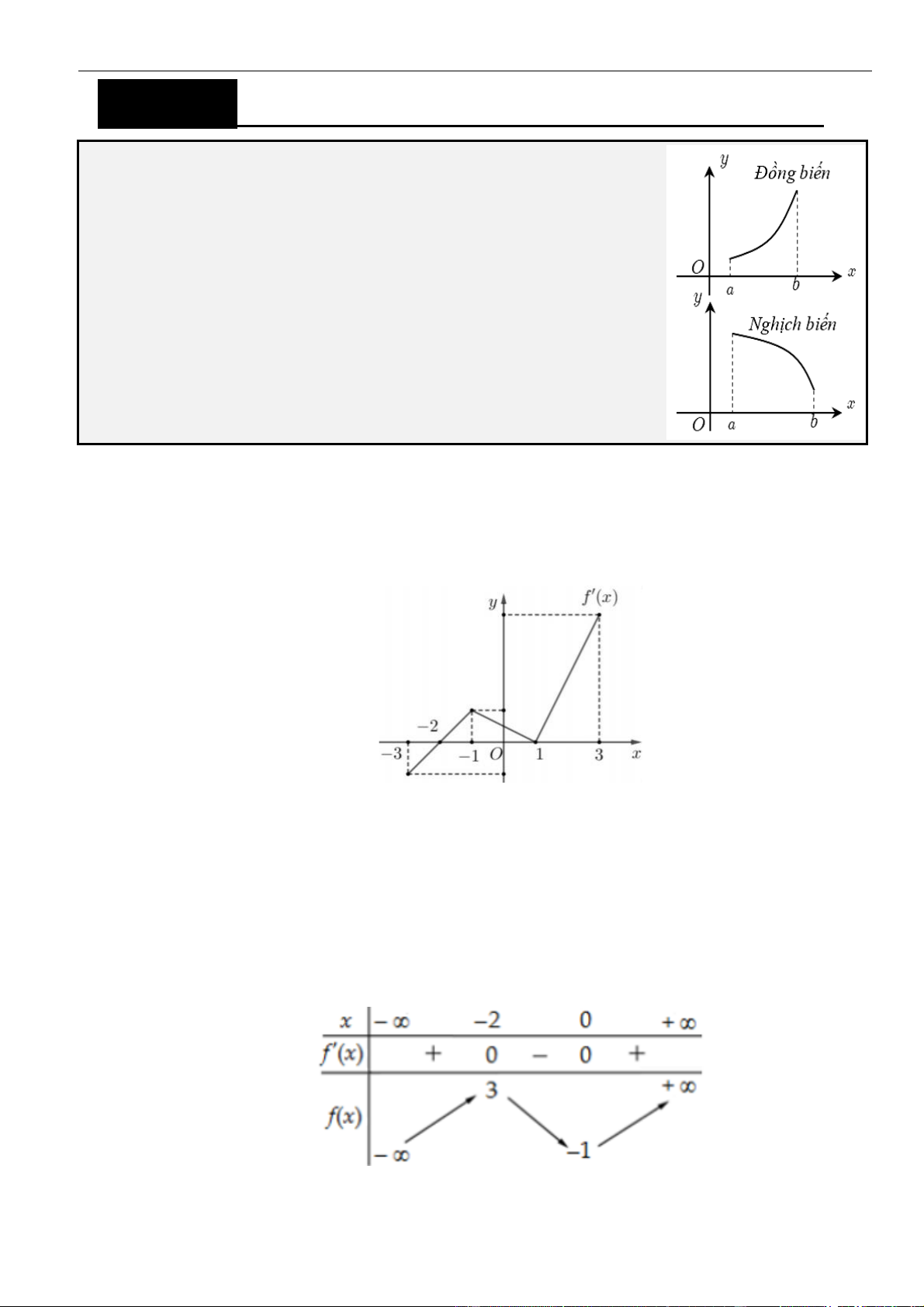
Câu 1: Cho hàm số
( )
fx
xác định và liên tục trên đoạn
−
3; 3
và có đạo hàm
( )
fx
trên khoảng
( )
−3; 3
. Đồ thị của hàm số
( )
=y f x
như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên các khoảng
( )
−−3; 1
và
( )
1; 3
.
B. Hàm số nghịch biến trên các khoảng
( )
−1;1
.
C. Hàm số đồng biến trên các khoảng
( )
−2; 3
.
D. Hàm số nghịch biến trên các khoảng
( )
−−3; 1
và
( )
1; 3
.
Câu 2: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
1;− +
. B.
( )
0;+
. C.
( )
;0−
D.
( )
2;0−
.
Xét tính đơn điệu cho bởi đồ thị, bảng biến thiên
DẠNG 2
Phương pháp:
▪ Định lí (thừa nhận): Giả sử hàm số
()y f x=
có đạo hàm trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số đồng biến trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số nghịch biến trên khoảng
.K
Nếu
( ) 0, f x x K
=
thì hàm số không đổi trên khoảng
.K
▪ Hình dáng đồ thị
Nếu hàm số đồng biến trên
K
thì từ trái sang phải đồ thị đi lên.
Nếu hàm số nghịch biến trên
K
thì từ trái sang phải đồ thị đi xuống.
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
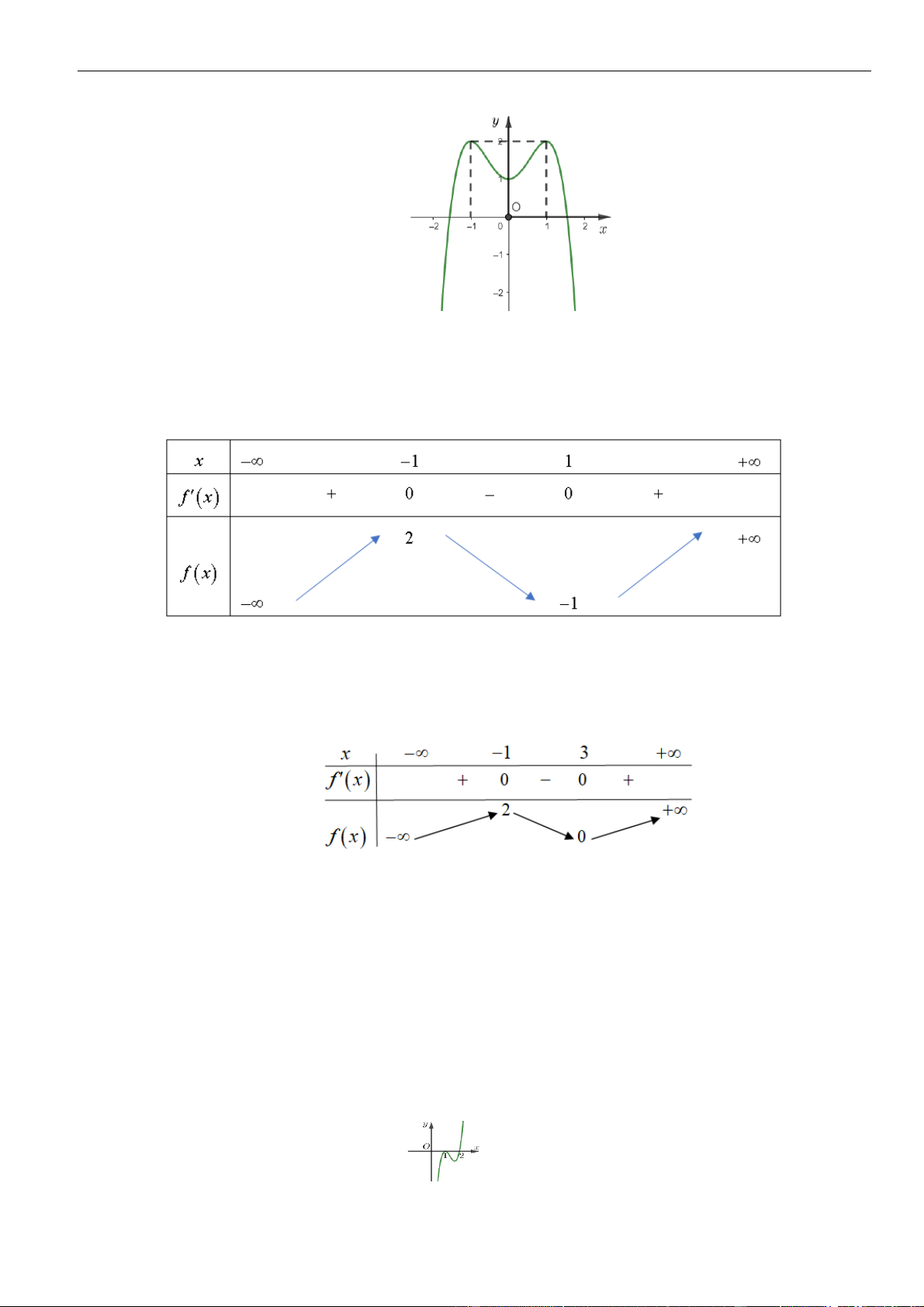
Câu 3: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
1;1−
. B.
( )
0;1
. C.
( )
1; +
. D.
( )
1;0−
.
Câu 4: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào, trong các khoảng dưới đây?
A.
( )
1; +
. B.
( )
;1− −
. C.
( )
1;2−
. D.
( )
1;1−
.
Câu 5: Cho hàm số
( )
fx
có bảng biến thiên như hình bên.
Hàm số đã cho nghịch biến trên khoảng nào trongcác khoảng dưới đây?
A.
( )
;3−
. B.
( )
1;5−
. C.
( )
1;− +
. D.
( )
1;3−
.
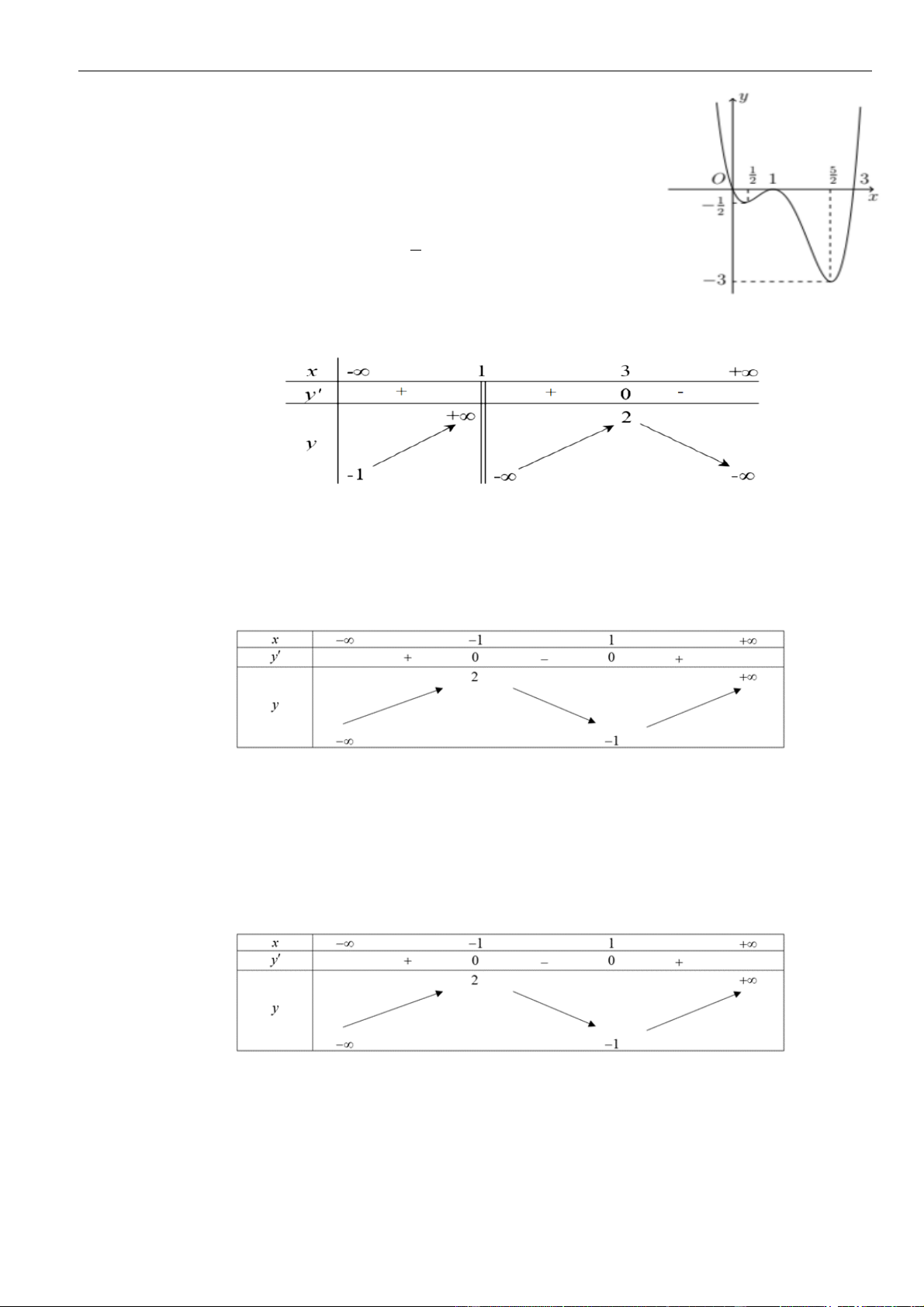
Câu 6: Hình bên là đồ thị hàm số
( )
'y f x=
. Hỏi hàm số
( )
y f x=
đồng biến trên khoảng nào dưới
đây?
A.
( )
2; +
. B.
( )
0; 1
và
( )
1; +
. C.
( )
0; 1
. D.
( )
1; 2
.
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
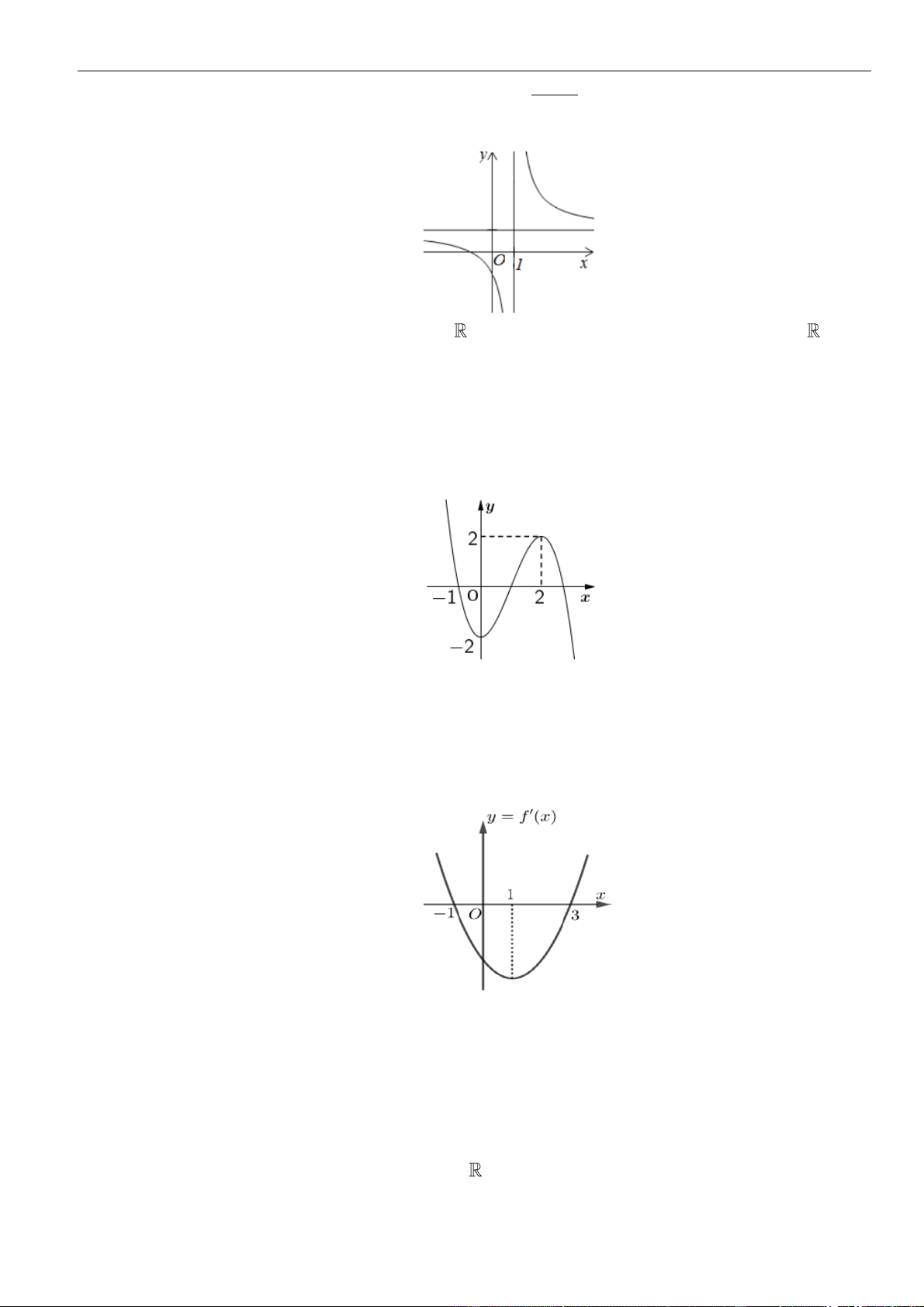
Câu 7: Cho hàm số
( )
y f x=
có đạo hàm
( )
fx
trên khoảng
( )
;− +
.
Đồ thị của hàm số
( )
y f x
=
như hình vẽ. Hàm số
( )
y f x=
nghịch biến trên khoảng nào trong các khoảng sau
A.
( )
0;3
. B.
( )
;0−
.
C.
( )
3;+
. D.
5
;
2
−
.
Câu 8: Cho hàm số
( )
y f x=
có bảng biên thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
0;2 .
B.
( )
4;10 .
C.
( )
2;5 .
D.
( )
;5 .−
Câu 9: Cho hàm số
( )
y f x=
xác định và liên tục trên khoảng
( )
;− +
, có bảng biến thiên như hình
sau:
Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
;1−
. B. Hàm số đồng biến trên khoảng
( )
1;− +
.
C. Hàm số nghịch biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
;2− −
.
Câu 10: Cho hàm số
( )
y f x=
xác định và liên tục trên khoảng
( )
;− +
, có bảng biến thiên như hình
sau:
Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
;1−
. B. Hàm số đồng biến trên khoảng
( )
1;− +
.
C. Hàm số nghịch biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
;2− −
.
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
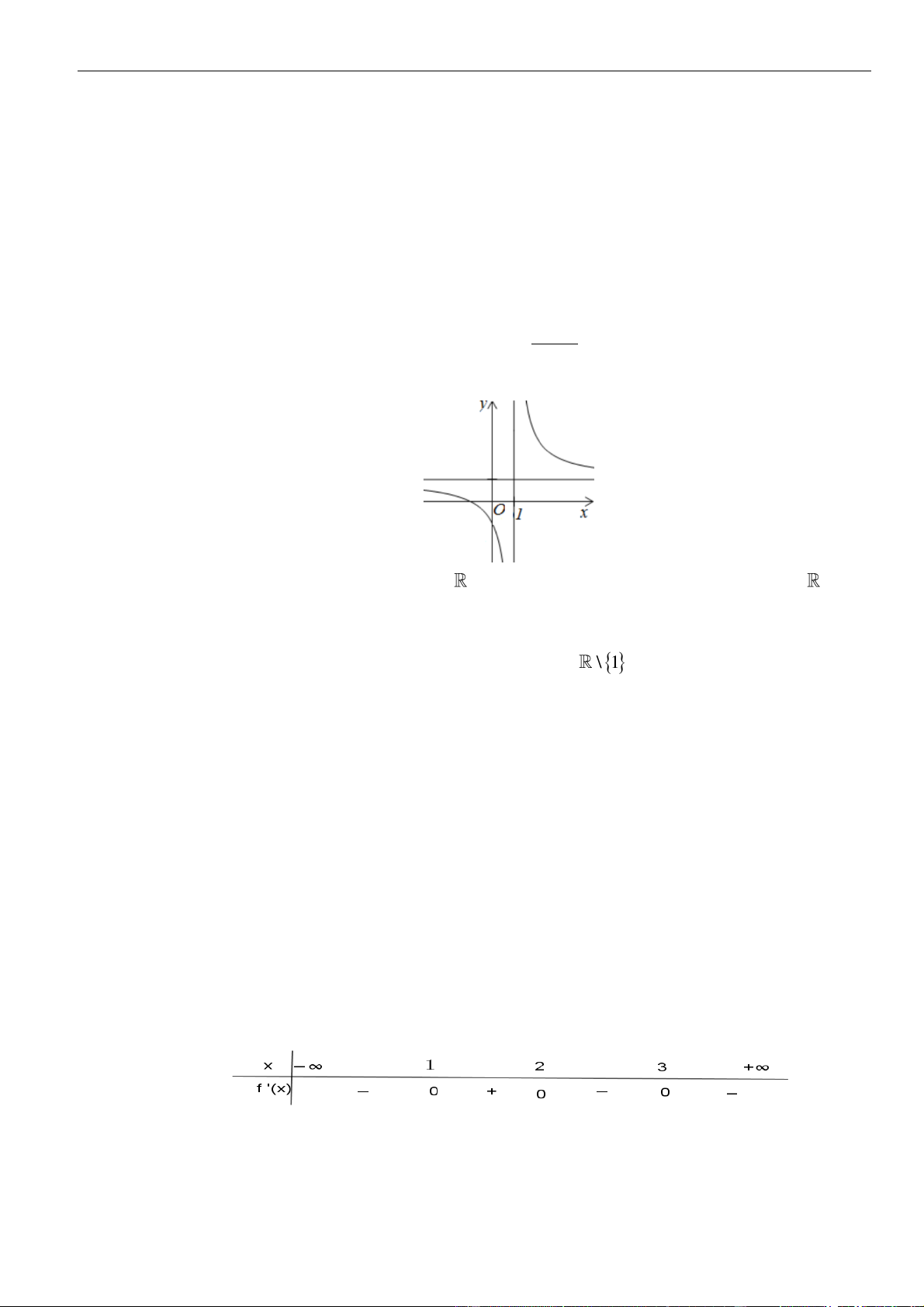
Câu 11: Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
+
=
+
với
, , ,a b c d
là các số thực. Mệnh đề
nào sau đây đúng?
A.
' 0, 1yx
. B.
' 0,yx
.C.
' 0, 1yx
. D.
' 0,yx
.
Câu 12: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )( )
32
1 2 3f x x x x
= − − −
. Hàm số đồng biến trên khoảng
nào dưới đây?
A.
( )
1;1−
và
( )
3; +
. B.
( )
;1−
và
( )
2;+
. C.
( )
1;2
. D.
( )
3; +
Câu 13: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ
Hàm số
( )
y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;2
. C.
( )
2;2−
. D.
( )
2;+
.
Câu 14: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
là parabol như hình vẽ bên. Khẳng định nào sau đây là
đúng
A. Hàm số đồng biến trên
( )
1; +
.
B. Hàm số đồng biến trên
( )
;1− −
và
( )
3; +
.
C. Hàm số nghịch biến trên
( )
;1−
.
D. Hàm số đồng biến trên
( )
1;3−
.
Câu 15: Cho hàm số
()fx
xác định, liên tục trên và có đồ thị của hàm số
()fx
là đường cong như
hình vẽ bên dưới. Hỏi khẳng định nào đúng?
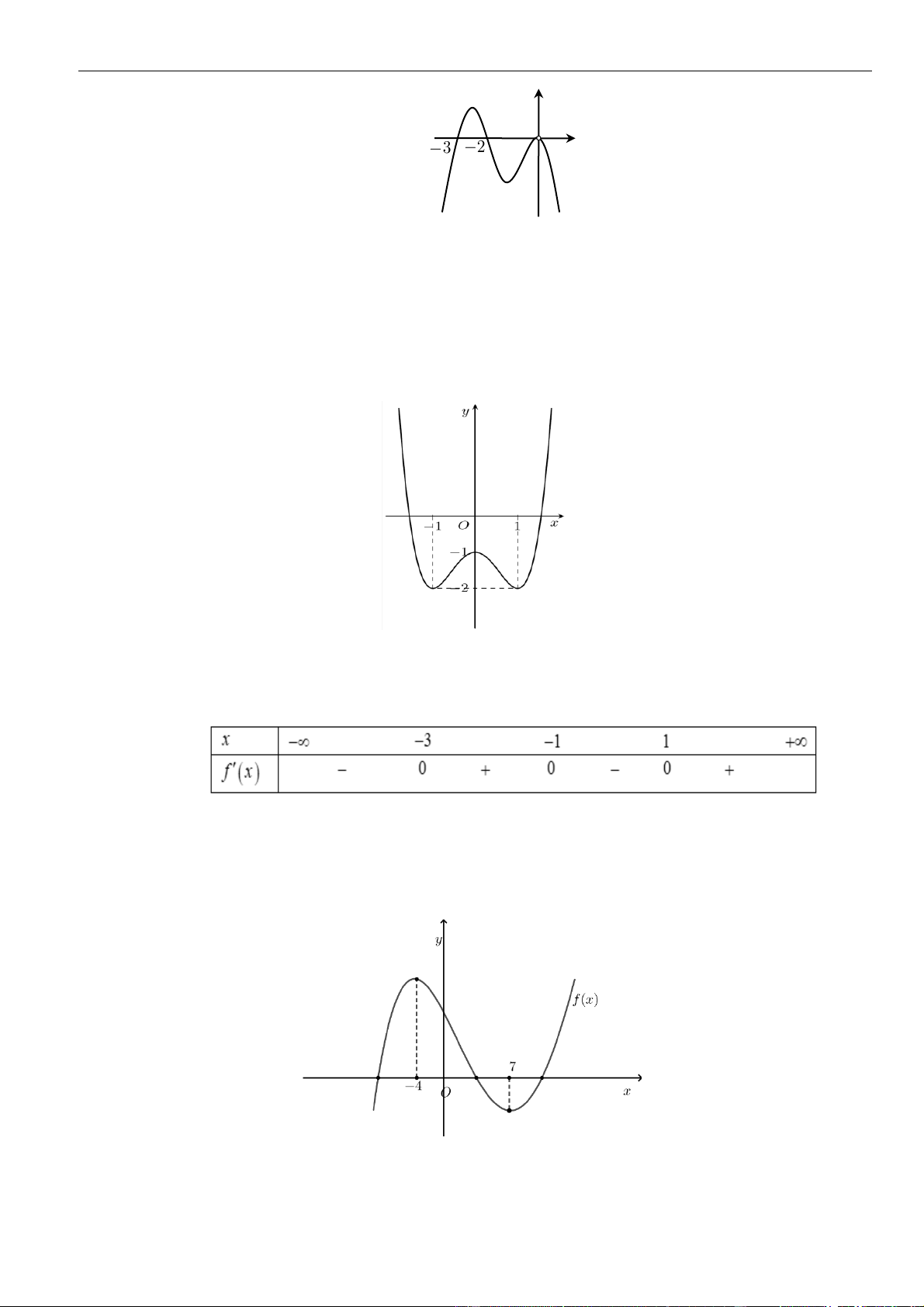
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A. Hàm số
()y f x=
đồng biến trên khoảng
( 2;0).−
B. Hàm số
()y f x=
nghịch biến trên khoảng
(0; ).+
C. Hàm số
()y f x=
đồng biến trên khoảng
( ; 3).− −
D. Hàm số
()y f x=
nghịch biến trên khoảng
( 3; 2).−−
Câu 16: Cho hàm số
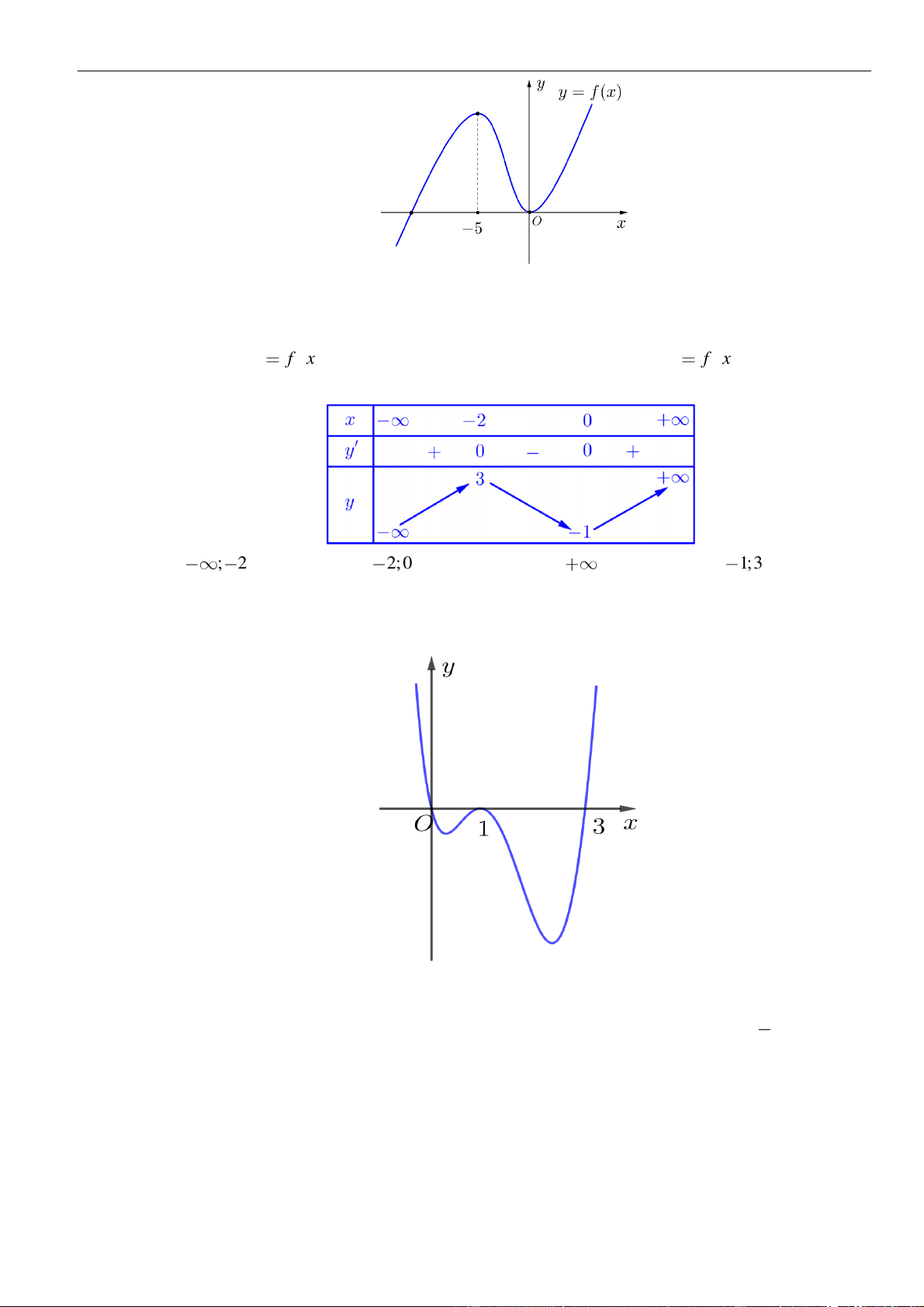
()y f x=
có đồ thị là đường cong hình bên. Hàm số đã cho nghịch biến trên khoảng
nào dưới đây
A.
(1; )+
. B.
(0;1)
. C.
( 1;0)−
. D.
( ;0)−
.
Câu 17: Cho hàm số
()fx
có bảng xét dấu
( )
fx
như hình bên
Hàn số
(2 1)fx+
nghịch biến trên khoảng nào dưới đây
A.
( )
1;2−
. B.
( )
2;0−
. C.
( )
1;0−
. D.
( )
0;+
.
Câu 18: Cho đồ thị hàm số
( )
y f x=
như hình vẽ. Hàm số
( ) ( )
2 2021g x f x=+
đồng biến trên
A.
( )
;3− −
. B.
( )
4;7−
. C.
( )
4;+
. D.
( )
8;+
.
Câu 19: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới.
O
x
y
2
3
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Hỏi hàm số
( ) ( )
32g x f x= − +
đồng biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
;6− −
. C.
( )
5;0−
. D.
( )
0;+
.
Câu 20: Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên. Hàm số
y f x
nghịch biến trên
khoảng nào dưới đây?
A.
;2
. B.
2;0
. C.
0;
. D.
1;3
Câu 21: Cho hàm số
( )
y f x=
có đạo hàm
( )
fx
trên khoảng
( )
;− +
. Đồ thị hàm số
( )
y f x
=
như
hình vẽ.
Hàm số
( )
y f x=
nghịch biến trên khoảng nào trong các khoảng sau?
A.
( )
;0−
. B.
( )
0;3
. C.
( )
3; +
. D.
5
;
2
−
.
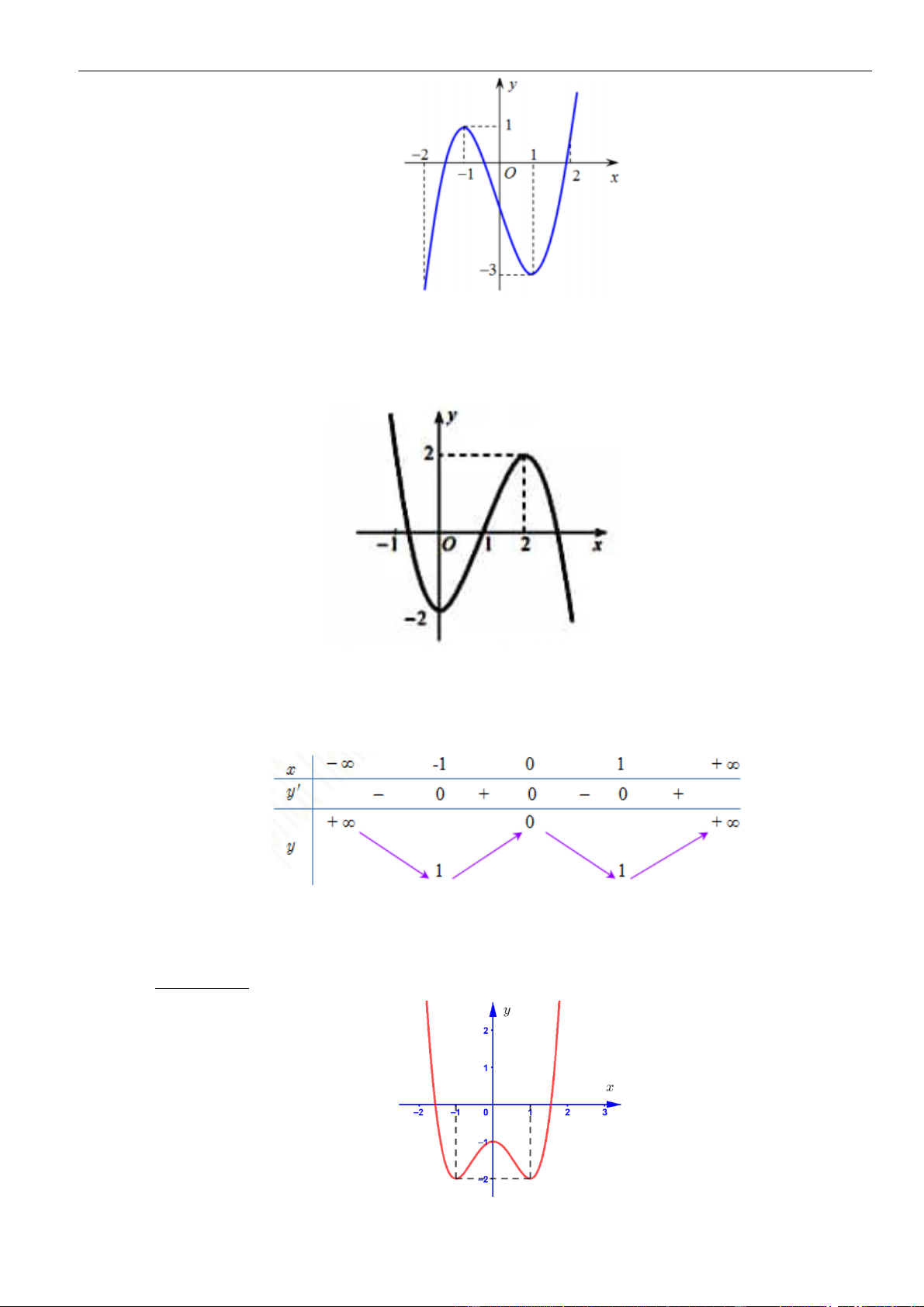
Câu 22: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ sau:
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
y f x=
đồng biến trên khoảng nào dưới đây?
A.
( )
1;1−
.
B.
( )
2;1−
.
C.
( )
2; 1−−
.
D.
( )
1;2−
.
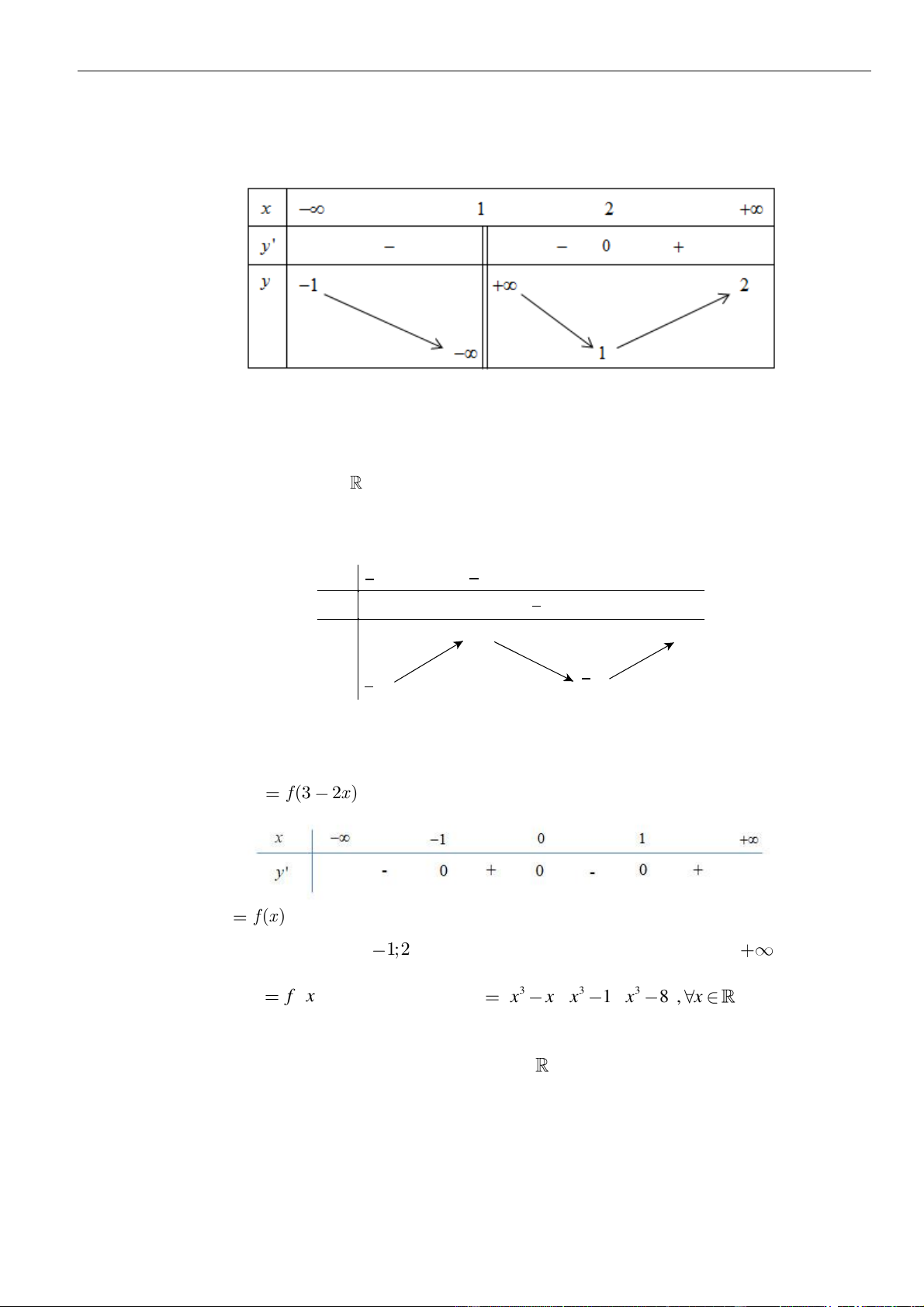
Câu 23: Cho đồ thị hàm số
()y f x=
có đồ thị như hình vẽ.
Hàm số
()y f x=
đồng biến trên khoảng nào dưới đây?
A.
(2; )+
. B.
( ;0)−
. C.
(0;2)
. D.
( 2;2)−
.
Câu 24: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số
( )
y f x=
nghịch biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
1; +
. C.
( )
0;1
. D.
( )
1;0−
.
Câu 25: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
A.
( )
1;1−
. B.
( )
0;1
. C.
( )
1;0−
. D.
( )
;1− −
.
Câu 26: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ. Có bao nhiêu khẳng định sai trong các
khẳng định dưới đây
I. Đồ thị hàm số có ba đường tiệm cận
II. Hàm số có cực tiểu tại
2x =
.
III. Hàm số nghịch biến trên mỗi khoảng
( ) ( )
; 1 ; 1;− − +
.
IV. Hàm số xác định trên .
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 27: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Hàm số
( )
2021y f x=−
đồng biến trên trên khoảng nào sau đây?
A.
( )
1; .− +
B.
( )
1;0 .−
C.
( )
; 2 .− −
D.
( )
0;2 .
Câu 28: Cho hàm số
(3 2 )y f x
có bảng xét dấu đạo hàm như sau:
Hàm số
()y f x
nghịch biến trên các khoảng nào dưới đây?
A.
3;5
. B.
1;2
. C.
1;3
. D.
5;
.
Câu 29: Cho hàm số
y f x
có đạo hàm là
' 3 3 3
1 8 ,f x x x x x x
. Tìm các khoảng
đồng biến của hàm số đã cho?
Câu 30: Cho hàm số
( )
y f x=
có đạo hàm và liên tục trên . Hàm số
( )
1y f x
=−
có đồ thị như hình
vẽ sau:
1
2
0
f'
(
x
)
f
(
x
)
∞
∞
+
0
+
∞
3
x
+
∞
0
+
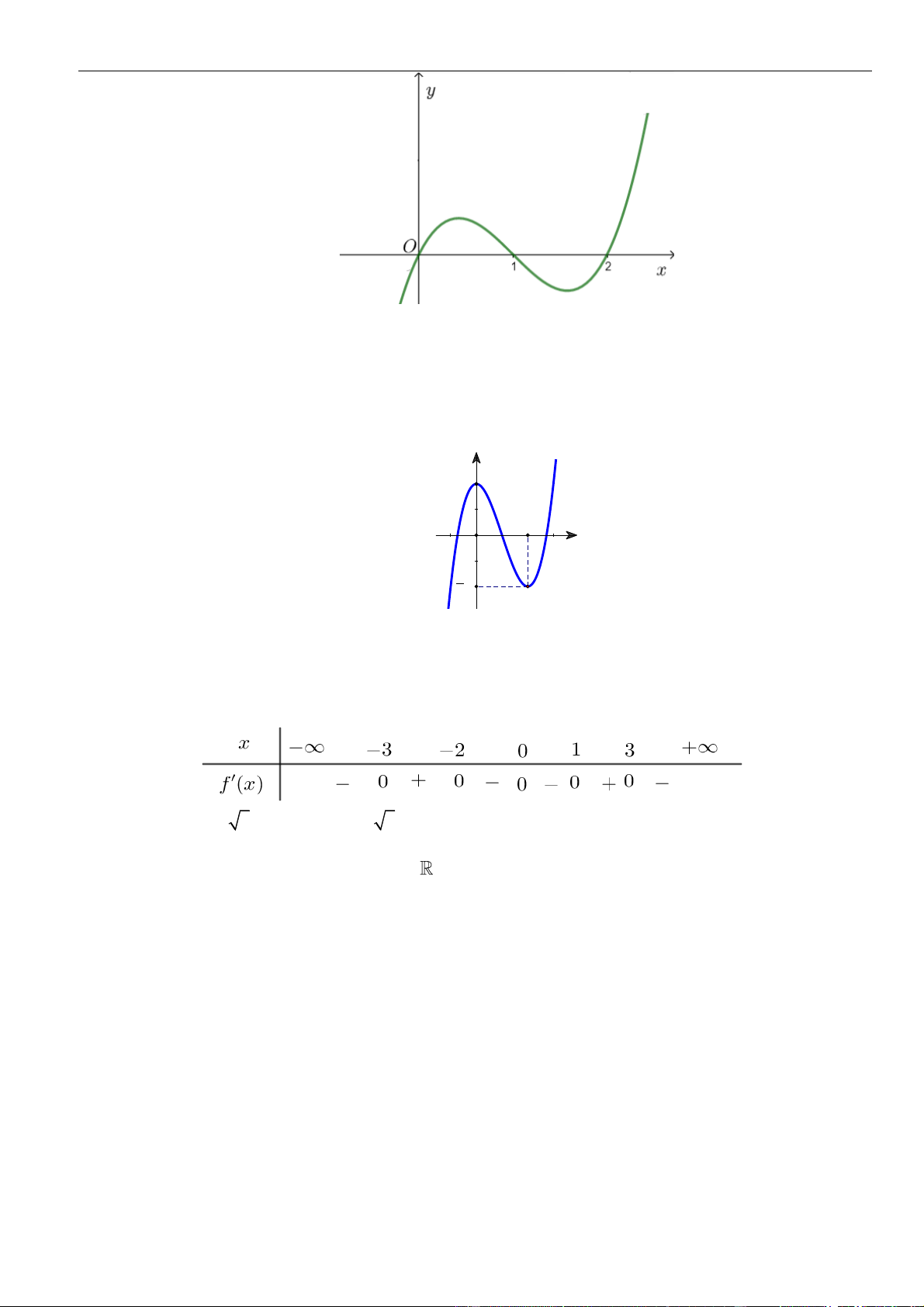
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
y f x=
nghịch biến trên khoảng nào sau đây?
A.
( )
2; 1 .−−
B.
( )
0;1 .
C.
( )
1;0 .−
D.
( )
3; 2 .−−
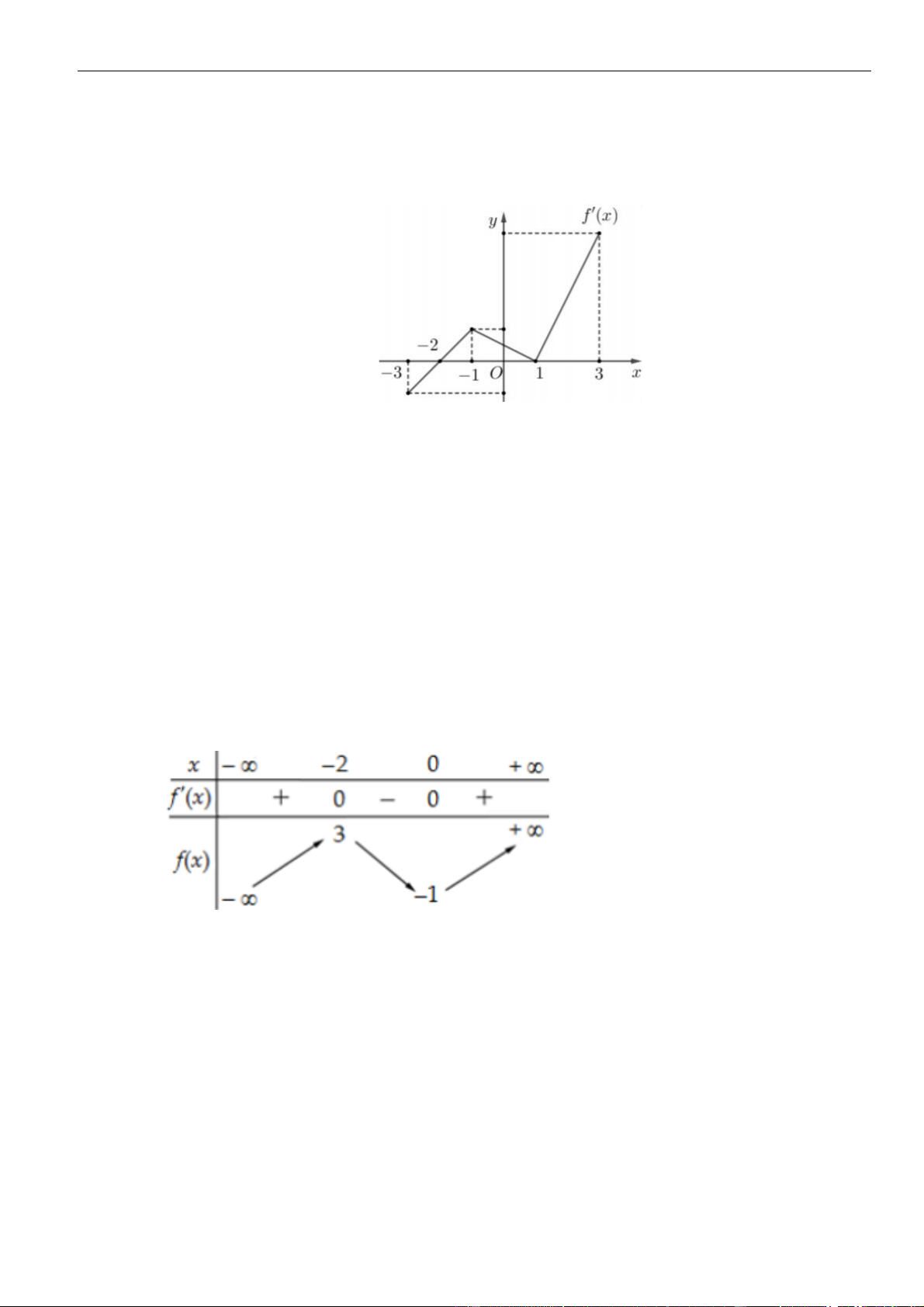
Câu 31: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên. Hàm số
( )
32y f x= − −
nghịch biến trên
khoảng
A.
( )
2;4
. B.
( )
0;3
. C.
( )
;1−
. D.
( )
3; +
.
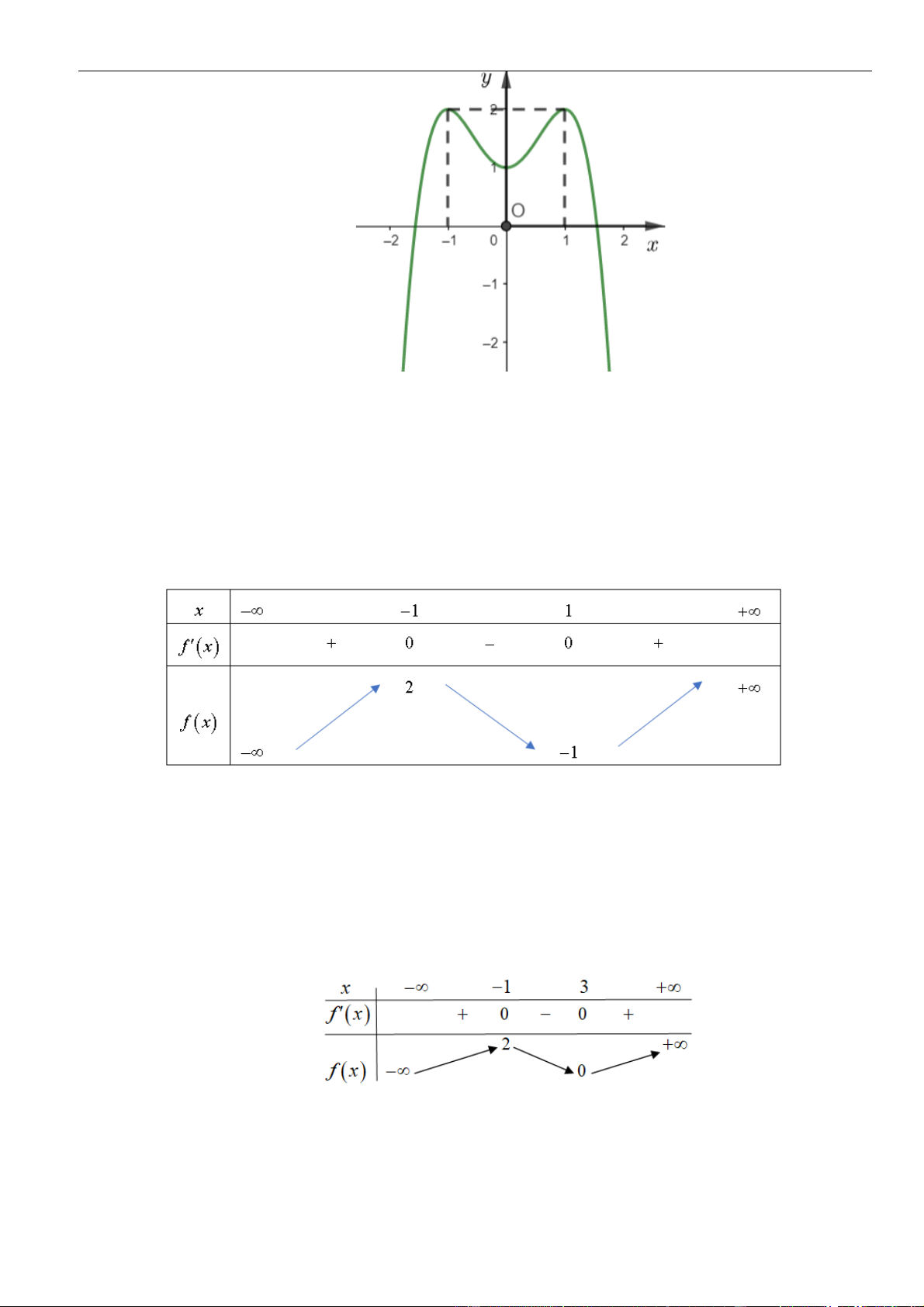
Câu 32: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên. Hàm số
( )
2
1y f x=−
nghịch biến
trên khoảng
A.
( )
2; 3−−
. B.
( )
3;2
. C.
( )
2;+
. D.
( )
1;1−
.
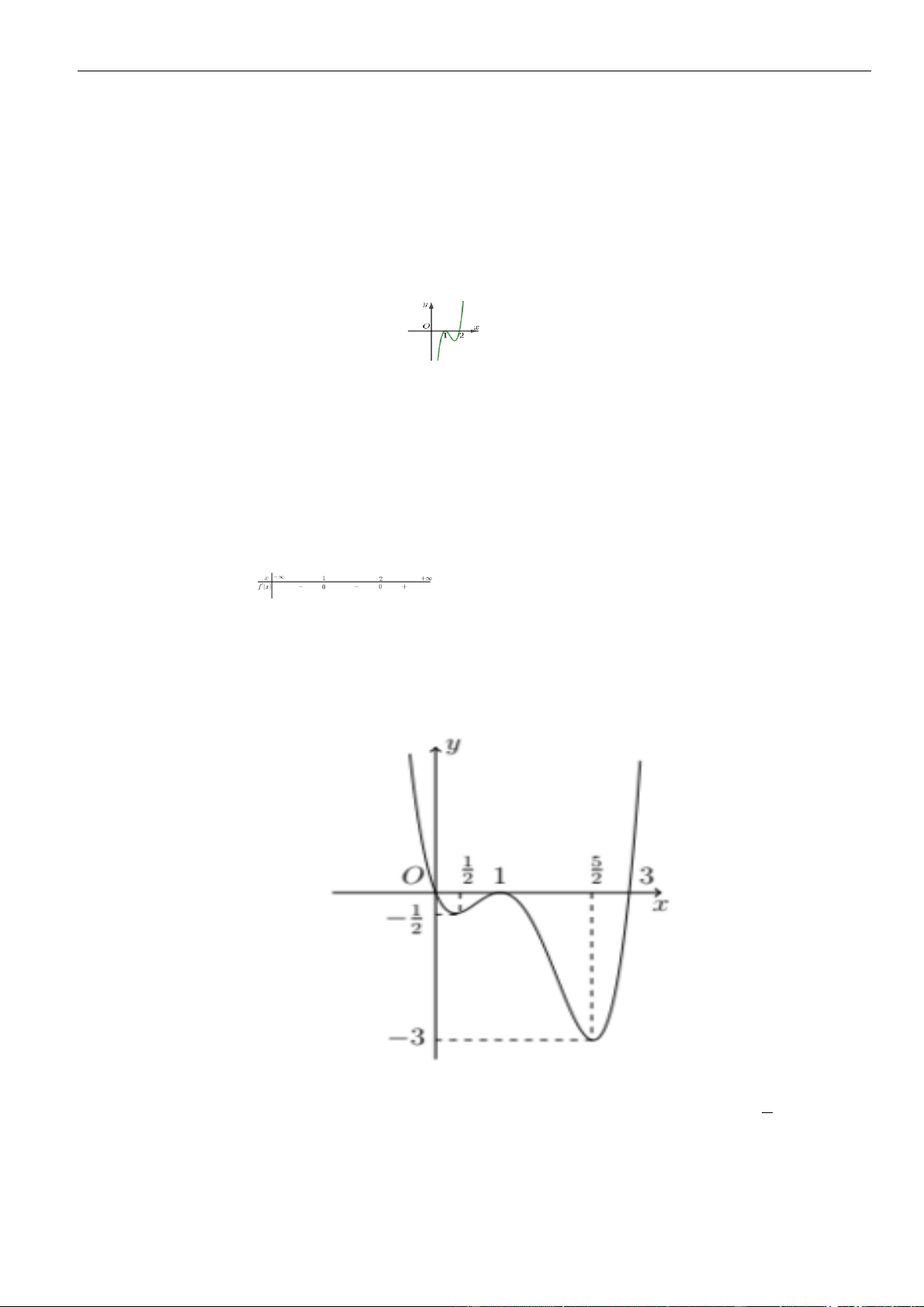
Câu 33: Cho hàm số
( )
fx
có đạo hàm trên là
( ) ( )( )
' 1 3f x x x= − +
. Có bao nhiêu giá trị nguyên của
tham số
m
thuộc đoạn
10;2021−
để hàm số
( )
2
3y f x x m= + −
đồng biến trên khoảng
( )
0;2
?
A.
2016
. B.
2019
. C.
2018
. D.
2017
.
x
y
2
2
2
O
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
fx
xác định và liên tục trên đoạn
−
3; 3
và có đạo hàm
( )
fx
trên khoảng
( )
−3; 3
. Đồ thị của hàm số
( )
=y f x
như hình vẽ sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên các khoảng
( )
−−3; 1
và
( )
1; 3
.
B. Hàm số nghịch biến trên các khoảng
( )
−1;1
.
C. Hàm số đồng biến trên các khoảng
( )
−2; 3
.
D. Hàm số nghịch biến trên các khoảng
( )
−−3; 1
và
( )
1; 3
.
Lời giải
Chọn C
Dựa vào đồ thị ta thấy
( ) ( )
−0, 2; 3f x x
và dấu
""=
chỉ xảy ra tại
1x =
nên hàm số đồng
biến trên khoảng
( )
−2; 3
.
Câu 2: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
1;− +
. B.
( )
0;+
. C.
( )
;0−
D.
( )
2;0−
.
Lời giải
Chọn B
Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng
( )
;2− −
và
( )
0;+
.
Do đó chọn đáp án B.
Câu 3: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
1;1−
. B.
( )
0;1
. C.
( )
1; +
. D.
( )
1;0−
.
Lời giải
Chọn B
Dựa vào đồ thị dễ dàng thấy hàm số đồng biến trên
( )
0;1
.
Câu 4: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào, trong các khoảng dưới đây?
A.
( )
1; +
. B.
( )
;1− −
. C.
( )
1;2−
. D.
( )
1;1−
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng
( )
1;1−
.
Câu 5: Cho hàm số
( )
fx
có bảng biến thiên như hình bên.
Hàm số đã cho nghịch biến trên khoảng nào trongcác khoảng dưới đây?
A.
( )
;3−
. B.
( )
1;5−
. C.
( )
1;− +
. D.
( )
1;3−
.
Lời giải
Chọn D
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Do
( ) ( )
0 1;3f x x
−
nên hàm số
( )
fx
nghịch biến trên khoảng
( )
1;3−
.
Câu 6: Hình bên là đồ thị hàm số
( )
'y f x=
. Hỏi hàm số
( )
y f x=
đồng biến trên khoảng nào dưới
đây?
A.
( )
2; +
. B.
( )
0; 1
và
( )
1; +
. C.
( )
0; 1
. D.
( )
1; 2
.
Lời giải
Chọn C
Từ đồ thị
( )
'y f x=
ta có bảng xét dấu
( )
'y f x=
như sau:
Vậy hàm số đồng biến trên khoảng
( )
2; +
.
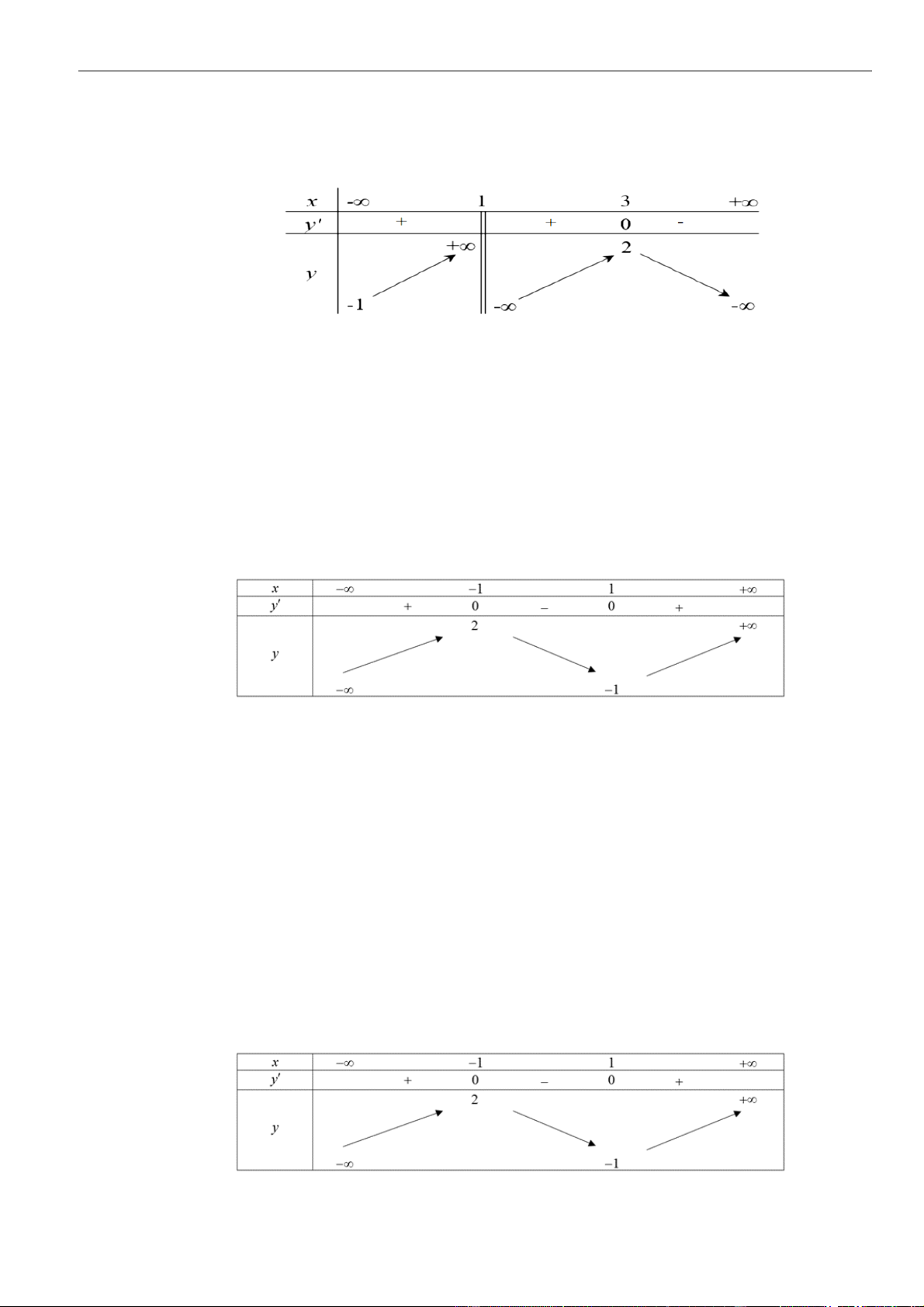
Câu 7: Cho hàm số
( )
y f x=
có đạo hàm
( )
fx
trên khoảng
( )
;− +
. Đồ thị của hàm số
( )
y f x
=
như hình vẽ. Hàm số
( )
y f x=
nghịch biến trên khoảng nào trong các khoảng sau
A.
( )
0;3
. B.
( )
;0−
. C.
( )
3;+
. D.
5
;
2
−
.
Lời giải
Chọn A
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Từ đồ thị ta thấy trên khoảng, đồ thị hàm số
( )
y f x
=
nằm phía dưới trục hoành nên
( ) ( )
0, 0;3
f x x
. Từ đó hàm số
( )
y f x=
nghịch biến trên khoảng
( )
0;3
.
Câu 8: Cho hàm số
( )
y f x=
có bảng biên thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
0;2 .
B.
( )
4;10 .
C.
( )
2;5 .
D.
( )
;5 .−
Lời giải
Chọn B
Từ BBT ta thấy hàm số nghịch biến trên
( )
3; +
Suy ra hàm số nghịch biến trên
( )
4;10 .
Câu 9: Cho hàm số
( )
y f x=
xác định và liên tục trên khoảng
( )
;− +
, có bảng biến thiên như hình
sau:
Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
;1−
. B. Hàm số đồng biến trên khoảng
( )
1;− +
.
C. Hàm số nghịch biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
;2− −
.
Lời giải
Chọn D
Dựa vài bảng biến thiên ta có:
Hàm số nghịch biến trên khoảng:
( )
1;1−
.
Hàm số đồng biến trên khoảng:
( ) ( )
; 1 1;− − +
.
Vậy đáp án D đúng.
Câu 10: Cho hàm số
( )
y f x=
xác định và liên tục trên khoảng
( )
;− +
, có bảng biến thiên như hình
sau:
Mệnh đề nào sau đây đúng?
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
A. Hàm số nghịch biến trên khoảng
( )
;1−
. B. Hàm số đồng biến trên khoảng
( )
1;− +
.
C. Hàm số nghịch biến trên khoảng
( )
1; +
. D. Hàm số đồng biến trên khoảng
( )
;2− −
.
Lời giải
Chọn D
Dựa vài bảng biến thiên ta có:
Hàm số nghịch biến trên khoảng:
( )
1;1−
.
Hàm số đồng biến trên khoảng:
( ) ( )
; 1 1;− − +
.
Vậy đáp án D đúng.
Câu 11: Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
+
=
+
với
, , ,a b c d
là các số thực. Mệnh đề
nào sau đây đúng?
A.
' 0, 1yx
. B.
' 0,yx
.C.
' 0, 1yx
. D.
' 0,yx
.
Lời giải
Chọn B
Dựa vào đồ thị ta thấy hàm số có tập xác định là
\1D =
, hàm số luôn nghịch biến trên
khoảng
( ) ( )
;1 , 1;− +
nên
' 0, 1yx
.
Câu 12: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )( )
32
1 2 3f x x x x
= − − −
. Hàm số đồng biến trên khoảng
nào dưới đây?
A.
( )
1;1−
và
( )
3; +
. B.
( )
;1−
và
( )
2;+
. C.
( )
1;2
. D.
( )
3; +
Lời giải
Chọn C
Ta có:
( ) ( ) ( )( ) ( ) ( ) ( )( )
3 2 3 2
1 2 3 0 1 2 3 0f x x x x f x x x x
= − − − = − − − =
.
1
2
3(ke p)
x
x
x
=
=
=
.
Bảng xét dấu
( )
fx
.
Từ bảng xét dấu của
( )
fx
, suy ra hàm số đồng biến trên khoảng
( )
1;2
.
Câu 13: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ
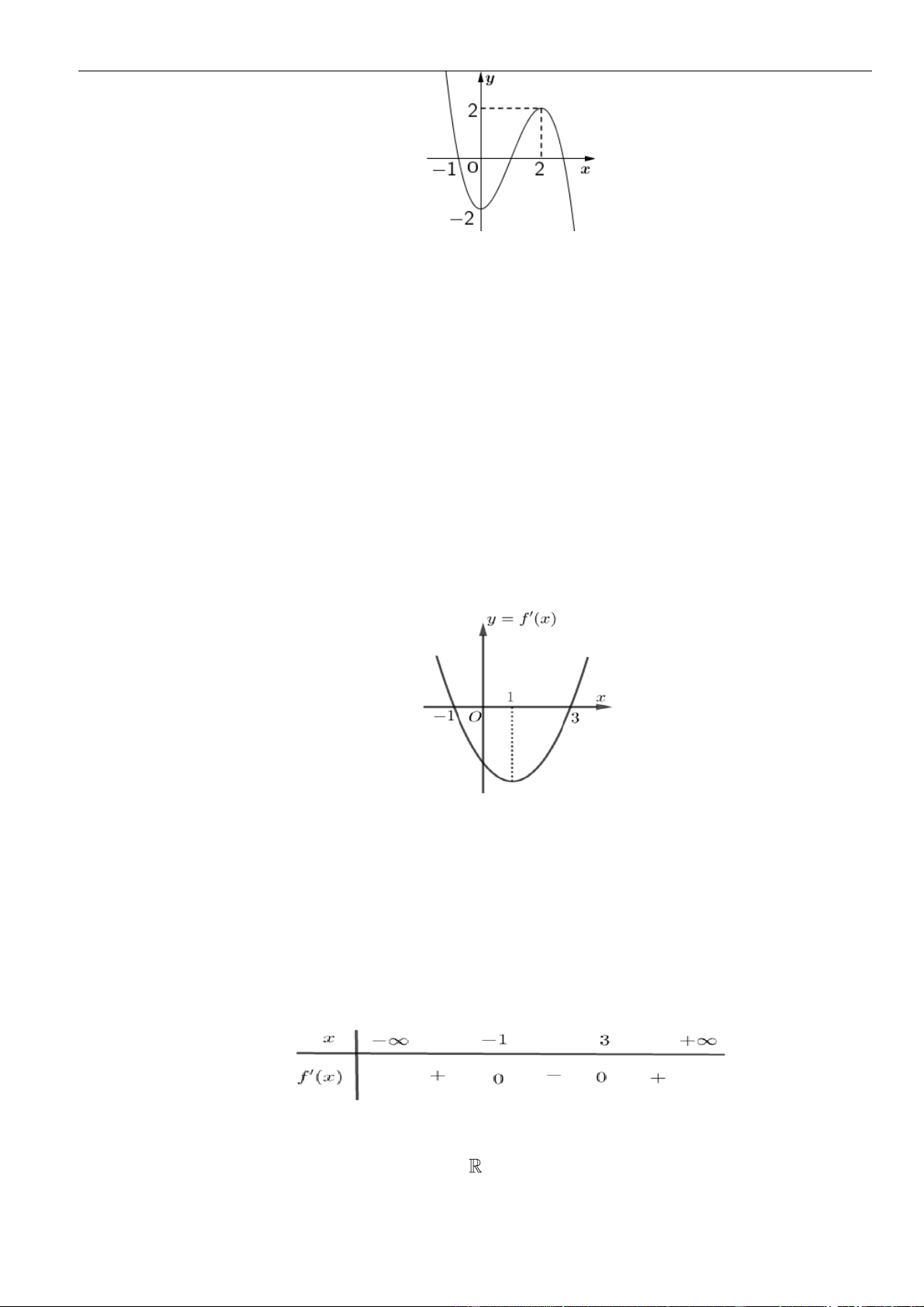
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;2
. C.
( )
2;2−
. D.
( )
2;+
.
Lời giải
Chọn A
Từ đồ thị, hàm số
( )
y f x=
đồng biến trên
( ) ( )
0;2 0 0 2f x x
.
Xét hàm số
( )
y f x=−
.
Có
( )
y f x = − −
.
( ) ( )
0 0 0 0 2 2 0y f x f x x x − − − − −
.
Suy ra hàm số
( )
y f x=−
nghịch biến trên khoảng
( )
2;0−
.
Câu 14: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
là parabol như hình vẽ bên. Khẳng định nào sau đây là
đúng
A. Hàm số đồng biến trên
( )
1; +
.
B. Hàm số đồng biến trên
( )
;1− −
và
( )
3; +
.
C. Hàm số nghịch biến trên
( )
;1−
.
D. Hàm số đồng biến trên
( )
1;3−
.
Lời giải
Chọn B
Từ đồ thị ta có bảng biến thiên :
Vậy hàm số đồng biến trên
( )
;1− −
và
( )
3; +
.
Câu 15: Cho hàm số
()fx
xác định, liên tục trên và có đồ thị của hàm số
()fx
là đường cong như
hình vẽ bên dưới. Hỏi khẳng định nào đúng?
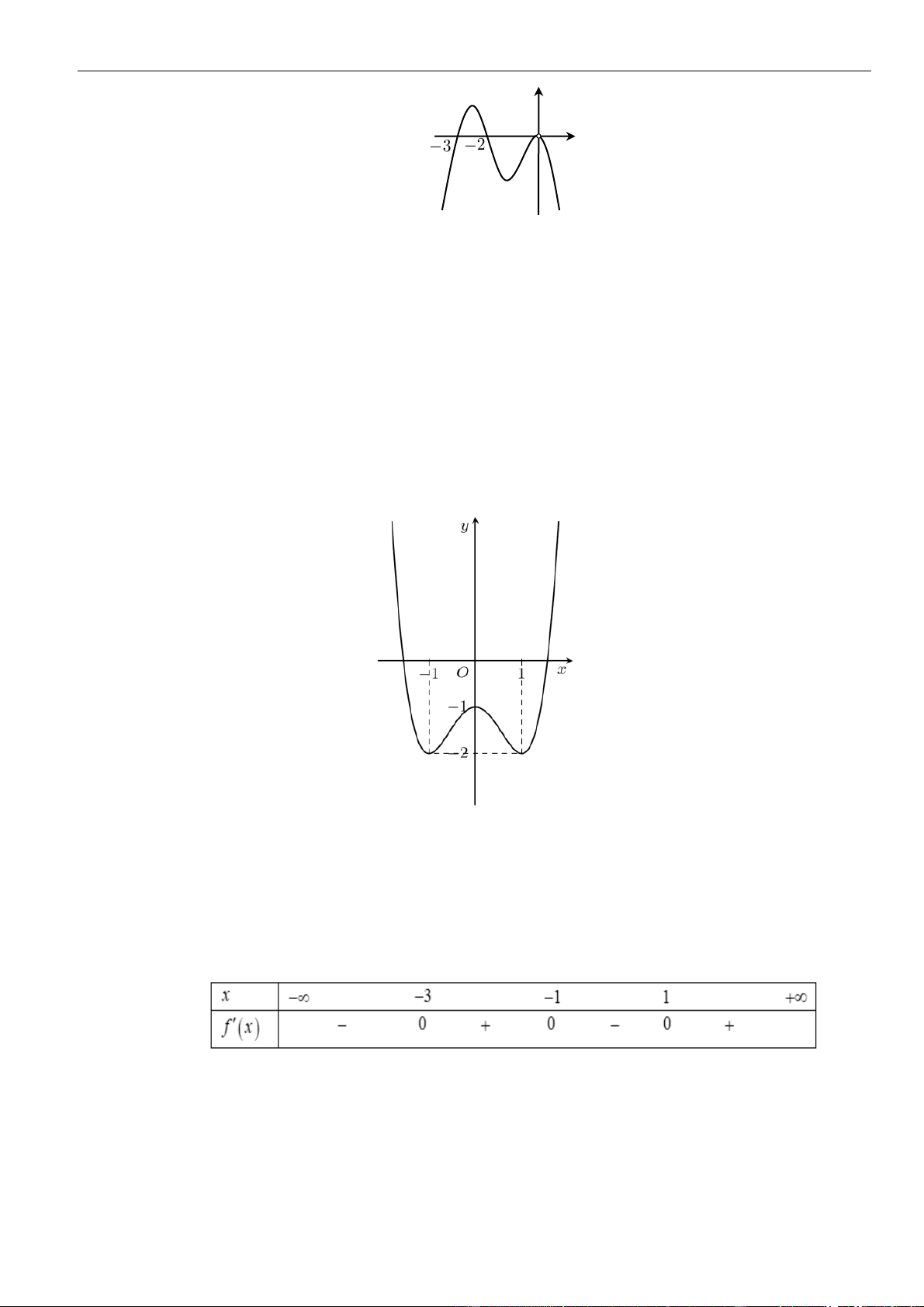
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
A. Hàm số
()y f x=
đồng biến trên khoảng
( 2;0).−
B. Hàm số
()y f x=
nghịch biến trên khoảng
(0; ).+
C. Hàm số
()y f x=
đồng biến trên khoảng
( ; 3).− −
D. Hàm số
()y f x=
nghịch biến trên khoảng
( 3; 2).−−
Lời giải
Chọn B
Từ đồ thị của hàm số
( )
fx
, ta có:
( ) ( ) ( )
0, ; 3 2;f x x
− − − +
. Vậy hàm số
()y f x=
nghịch biến trên khoảng
(0; ).+
Câu 16: Cho hàm số
()y f x=
có đồ thị là đường cong hình bên. Hàm số đã cho nghịch biến trên khoảng
nào dưới đây
A.
(1; )+
. B.
(0;1)
. C.
( 1;0)−
. D.
( ;0)−
.
Lời giải
Chọn B
Trên khoảng
(0;1)
đồ thị hàm số đi xuống nên hàm số đã cho nghịch biến trên
(0;1)
.
Câu 17: Cho hàm số
()fx
có bảng xét dấu
( )
fx
như hình bên
Hàn số
(2 1)fx+
nghịch biến trên khoảng nào dưới đây
A.
( )
1;2−
. B.
( )
2;0−
. C.
( )
1;0−
. D.
( )
0;+
.
Lời giải
Chọn C
Ta có:
( ) ( )
2 1 3 2
2 1 2. 2 1 0
1 2 1 1 1 0
xx
f x f x
xx
+ − −
+ = +
− + −
.
O
x
y
2
3
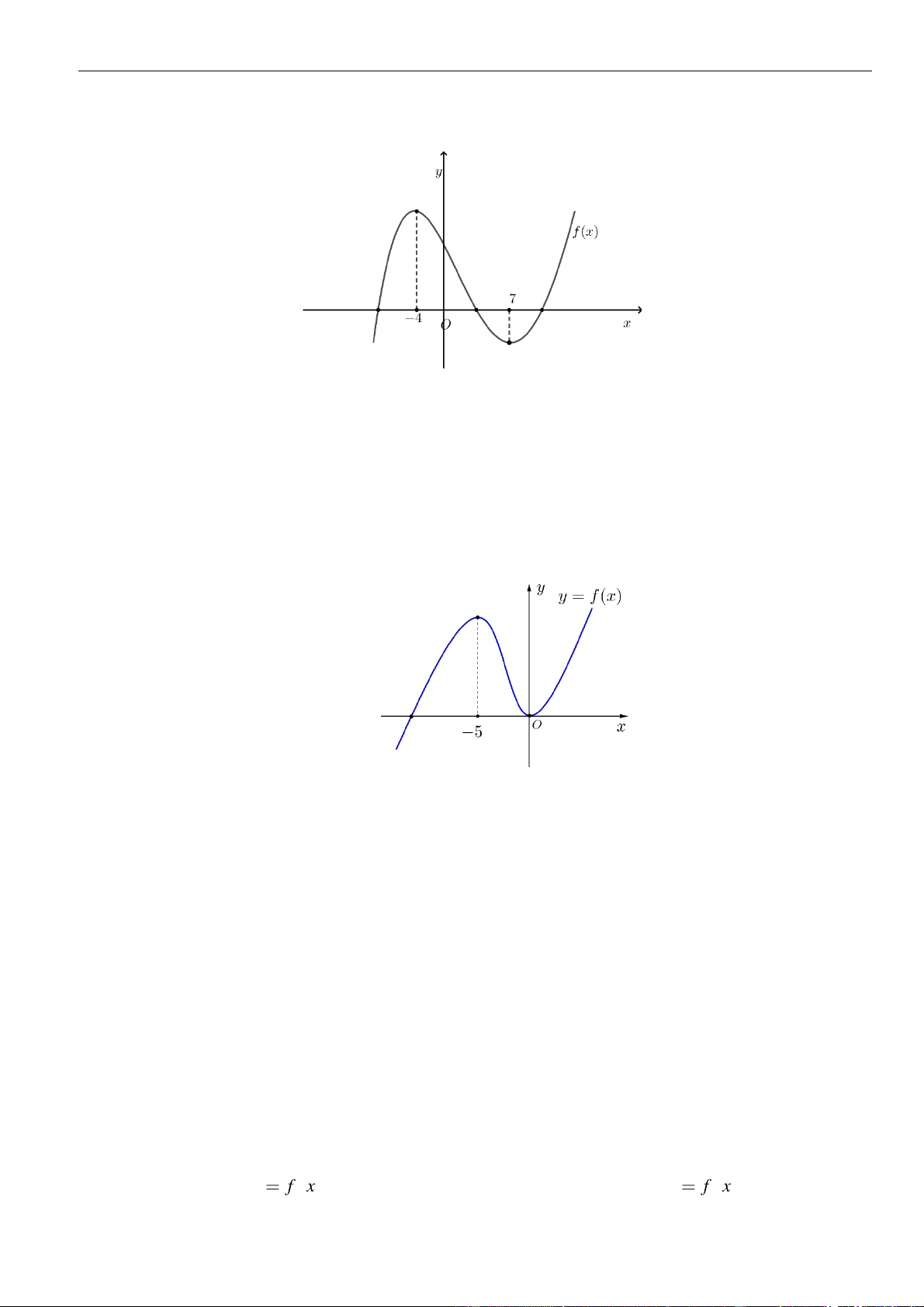
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Vậy khoảng nghịch biến của hàm số
(2 1)fx+
là khoảng
( )
1;0−
Câu 18: Cho đồ thị hàm số
( )
y f x=
như hình vẽ. Hàm số
( ) ( )
2 2021g x f x=+
đồng biến trên
A.
( )
;3− −
. B.
( )
4;7−
. C.
( )
4;+
. D.
( )
8;+
.
Lời giải
Chọn D
Ta có
( ) ( ) ( ) ( ) ( )
2 0 0 ; 4 7;g x f x f x x
= − − +
Nên suy ra hàm số cũng đồng biến trên
( )
8;+
.
Câu 19: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới.
Hỏi hàm số
( ) ( )
32g x f x= − +
đồng biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
;6− −
. C.
( )
5;0−
. D.
( )
0;+
.
Lời giải
Chọn C
GV phản biện: Đỗ Hoàng Tú – Minh Hiệp.
Từ đồ thị hàm số
( )
y f x=
ta có
( )
5
0
0
x
fx
x
−
và
( )
0 5 0f x x
−
.
Ta có
( ) ( )
3g x f x
=−
.
Ta có
+
( ) ( ) ( )
0 3 0 0g x f x f x
−
50x −
.
+
( ) ( ) ( )
0 3 0 0g x f x f x
−
5
0
x
x
−
.
Vậy hàm số
( ) ( )
32g x f x= − +
đồng biến trên
( )
5;0−
.
Câu 20: Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên. Hàm số
y f x
nghịch biến trên
khoảng nào dưới đây?
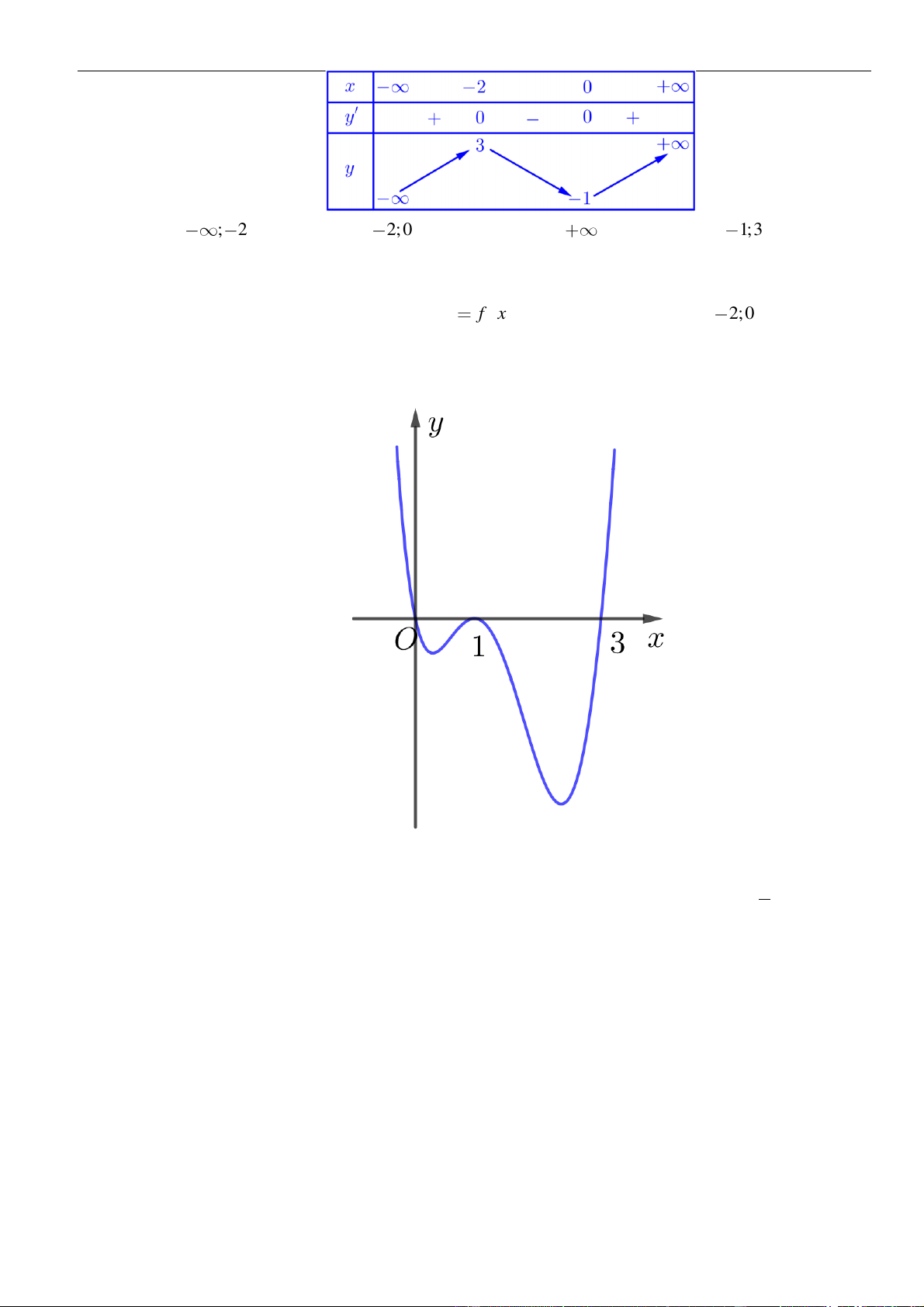
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
A.
;2
. B.
2;0
. C.
0;
. D.
1;3
Lời giải
Chọn B
Dựa vào bảng biến thiên ta có hàm số
y f x
nghịch biến trên khoảng
2;0
.
Câu 21: Cho hàm số
( )
y f x=
có đạo hàm
( )
fx
trên khoảng
( )
;− +
. Đồ thị hàm số
( )
y f x
=
như
hình vẽ.
Hàm số
( )
y f x=
nghịch biến trên khoảng nào trong các khoảng sau?
A.
( )
;0−
. B.
( )
0;3
. C.
( )
3; +
. D.
5
;
2
−
.
Lời giải
Chọn B
Từ đồ thị hàm số
( )
y f x
=
suy ra
( )
0
01
3
x
f x x
x
=
= =
=
và
( )
0 0 3f x x
.
Vậy hàm số
( )
y f x=
nghịch biến trên khoảng
( )
0;3
.
Câu 22: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ sau:
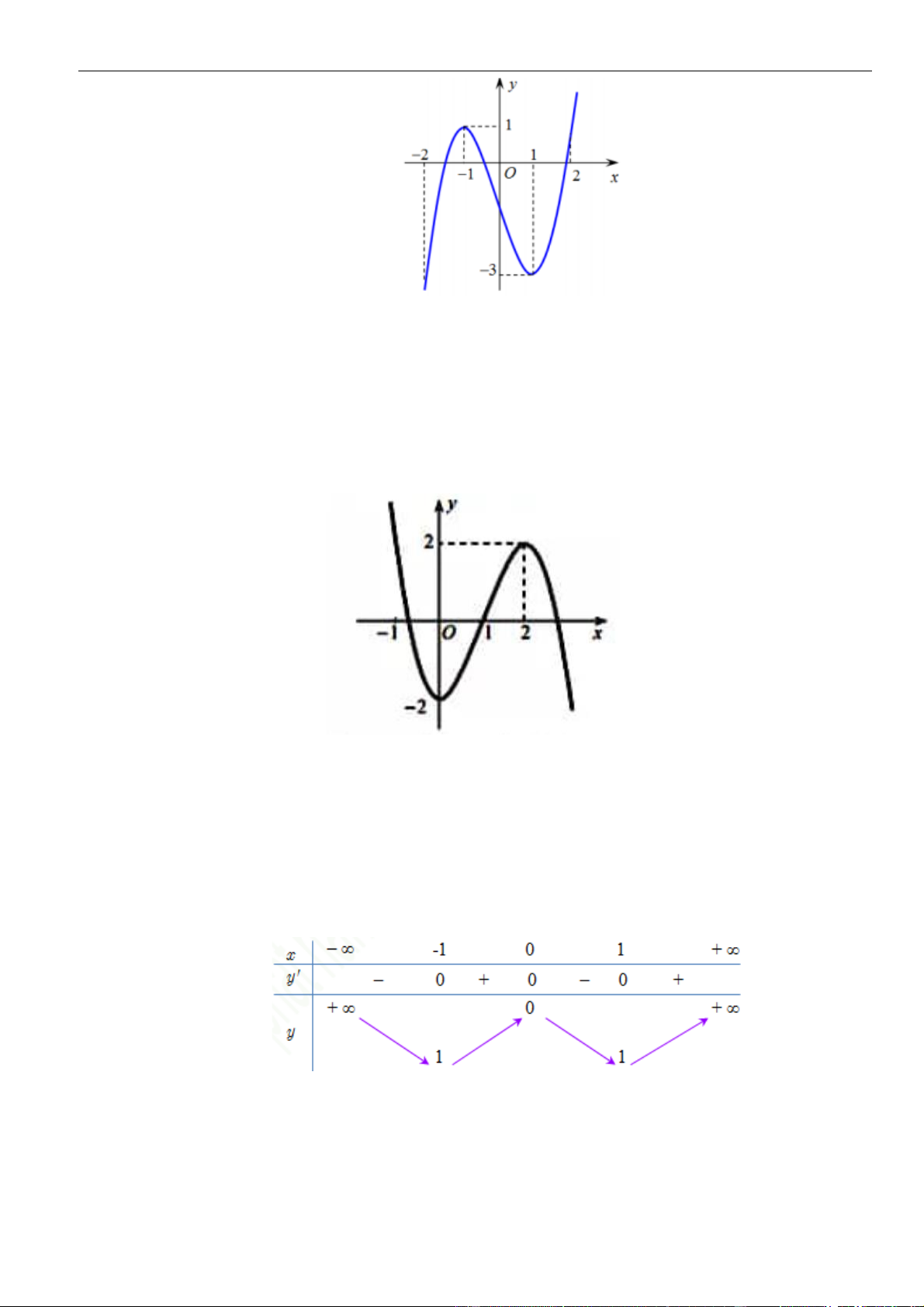
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
y f x=
đồng biến trên khoảng nào dưới đây?
A.
( )
1;1−
.
B.
( )
2;1−
.
C.
( )
2; 1−−
.
D.
( )
1;2−
.
Lời giải
Chọn
C
Từ đồ thị của hàm số
( )
y f x=
ta xác định được hàm số đồng biến trên khoảng
( )
2; 1−−
.
Câu 23: Cho đồ thị hàm số
()y f x=
có đồ thị như hình vẽ.
Hàm số
()y f x=
đồng biến trên khoảng nào dưới đây?
A.
(2; )+
. B.
( ;0)−
. C.
(0;2)
. D.
( 2;2)−
.
Lời giải
Chọn C
Dựa vào đồ thị hàm số
()y f x=
suy ra hàm số
()y f x=
đồng biến trên khoảng
(0;2)
Câu 24: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số
( )
y f x=
nghịch biến trên khoảng nào dưới đây?
A.
( )
;0−
. B.
( )
1; +
. C.
( )
0;1
. D.
( )
1;0−
.
Lời giải
Chọn C
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên
( )
0;1
.
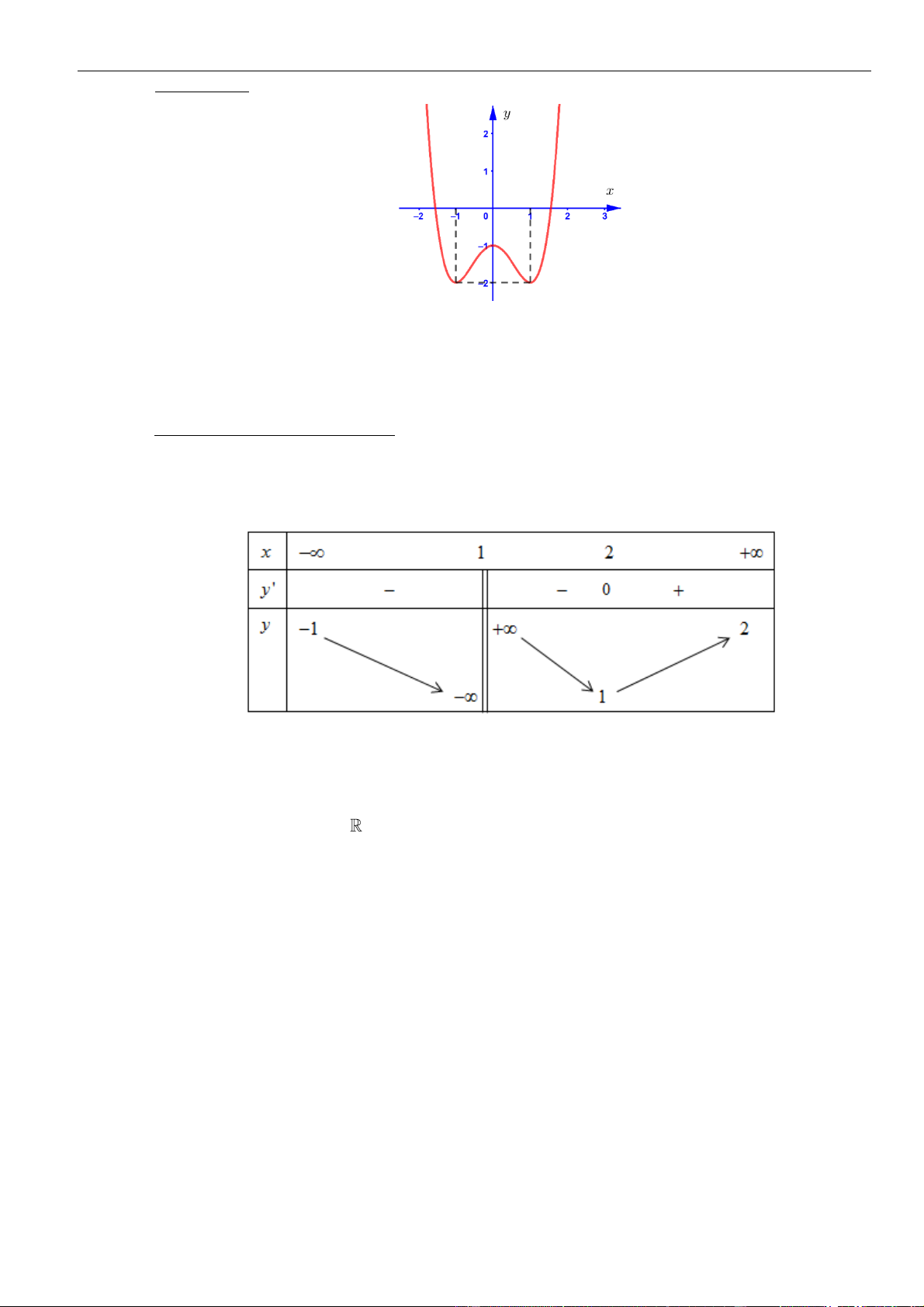
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Câu 25: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
1;1−
. B.
( )
0;1
. C.
( )
1;0−
. D.
( )
;1− −
.
Lời giải
Chọn C
Dựa vào hình vẽ ta thấy hàm số đồng biến trên khoảng
( )
1;0−
.
Câu 26: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ. Có bao nhiêu khẳng định sai trong các
khẳng định dưới đây
I. Đồ thị hàm số có ba đường tiệm cận
II. Hàm số có cực tiểu tại
2x =
.
III. Hàm số nghịch biến trên mỗi khoảng
( ) ( )
; 1 ; 1;− − +
.
IV. Hàm số xác định trên .
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn A
Do
( ) ( )
lim 1; lim 2
xx
f x f x
→− →+
= − =
nên đồ thị hàm số có hai đường tiệm cận ngang;
( )
1
lim
x
fx
→
=
nên đồ thị hàm số có một tiệm cận đứng. Do đó, đồ thị hàm số có ba đường tiệm
cận. (I) đúng
Hàm số có cực tiểu tại
2x =
đúng nên (II) đúng.
Hàm số nghịch biến trên
( ) ( )
; 1 ; 1;2− −
nên (III) sai.
Hàm số không xác định tại
1x =
nên (IV) sai.
Câu 27: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
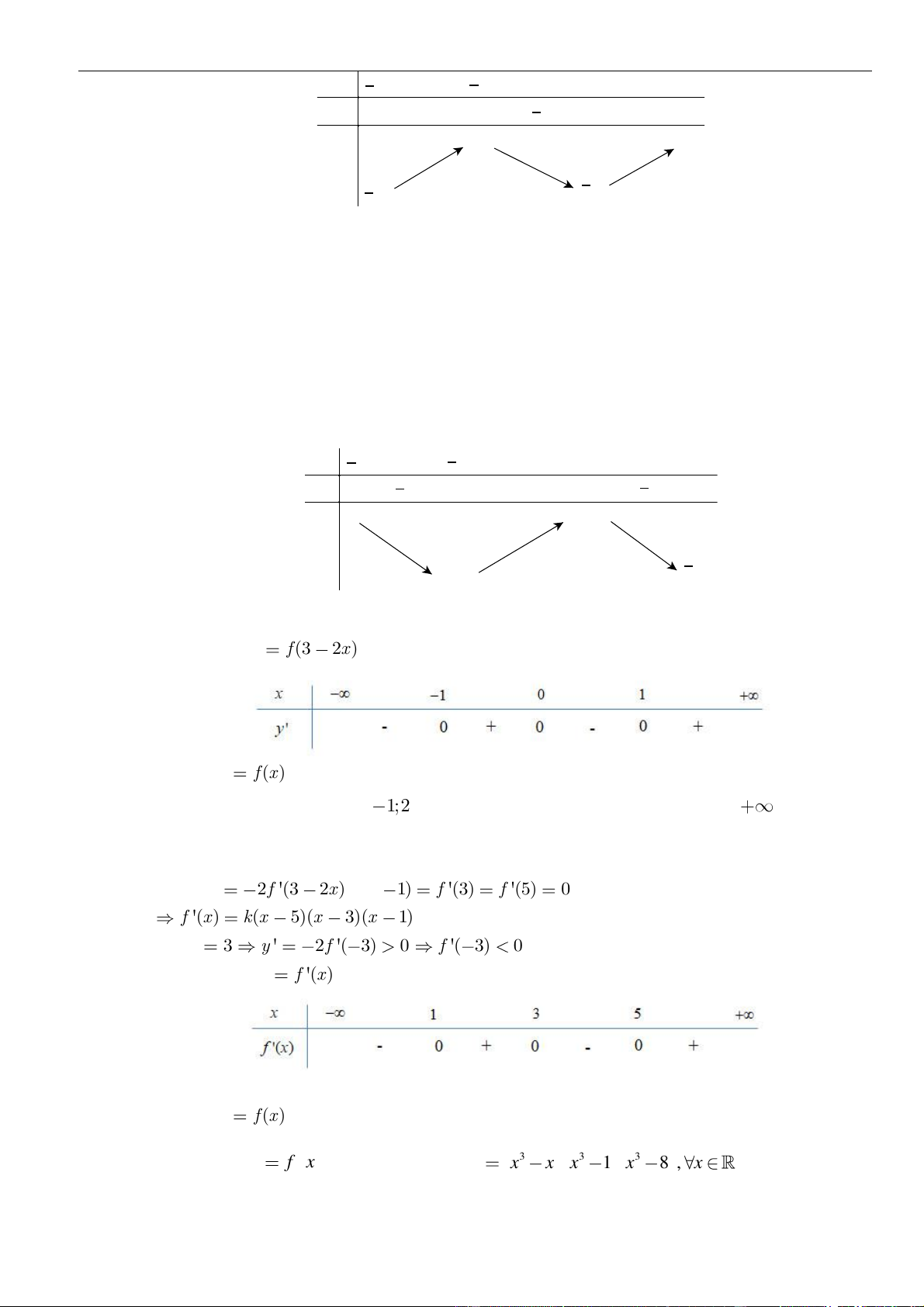
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
2021y f x=−
đồng biến trên trên khoảng nào sau đây?
A.
( )
1; .− +
B.
( )
1;0 .−
C.
( )
; 2 .− −
D.
( )
0;2 .
Lời giải
Tác giả: Nguyễn Chí Trung
Chọn B
Hàm số
( )
2021y f x=−
có
( )
y f x
=−
;
( ) ( )
2
0 0 0
0
x
y f x f x
x
=−
= − = =
=
.
Từ bảng biến thiên của hàm số
( )
y f x=
ta có bảng biến thiên của hàm số
( )
2021y f x=−
:
Dựa vào bảng biến thiên, ta có hàm số
( )
2021y f x=−
đồng biến trong khoảng
( )
2;0 .−
Câu 28: Cho hàm số
(3 2 )y f x
có bảng xét dấu đạo hàm như sau:
Hàm số
()y f x
nghịch biến trên các khoảng nào dưới đây?
A.
3;5
. B.
1;2
. C.
1;3
. D.
5;
.
Lời giải
Chọn A
Ta có
' 2 '(3 2 )y f x
;
'( 1) '(3) '(5) 0f f f
'( ) ( 5)( 3)( 1)f x k x x x
Xét
3 ' 2 '( 3) 0 '( 3) 0x y f f
Bảng xét dấu
'( )y f x
là
Căn cứ bảng xét dấu ta thấy
Hàm số
()y f x
nghịch biến trên khoảng
3;5
.
Câu 29: Cho hàm số
y f x
có đạo hàm là
' 3 3 3
1 8 ,f x x x x x x
. Tìm các khoảng
đồng biến của hàm số đã cho?
Lời giải
1
2
0
f'
(
x
)
f
(
x
)
∞
∞
+
0
+
∞
3
x
+
∞
0
+
2018
x
∞
+
0
2022
0
2
+
∞∞
y
y'
+
∞
0
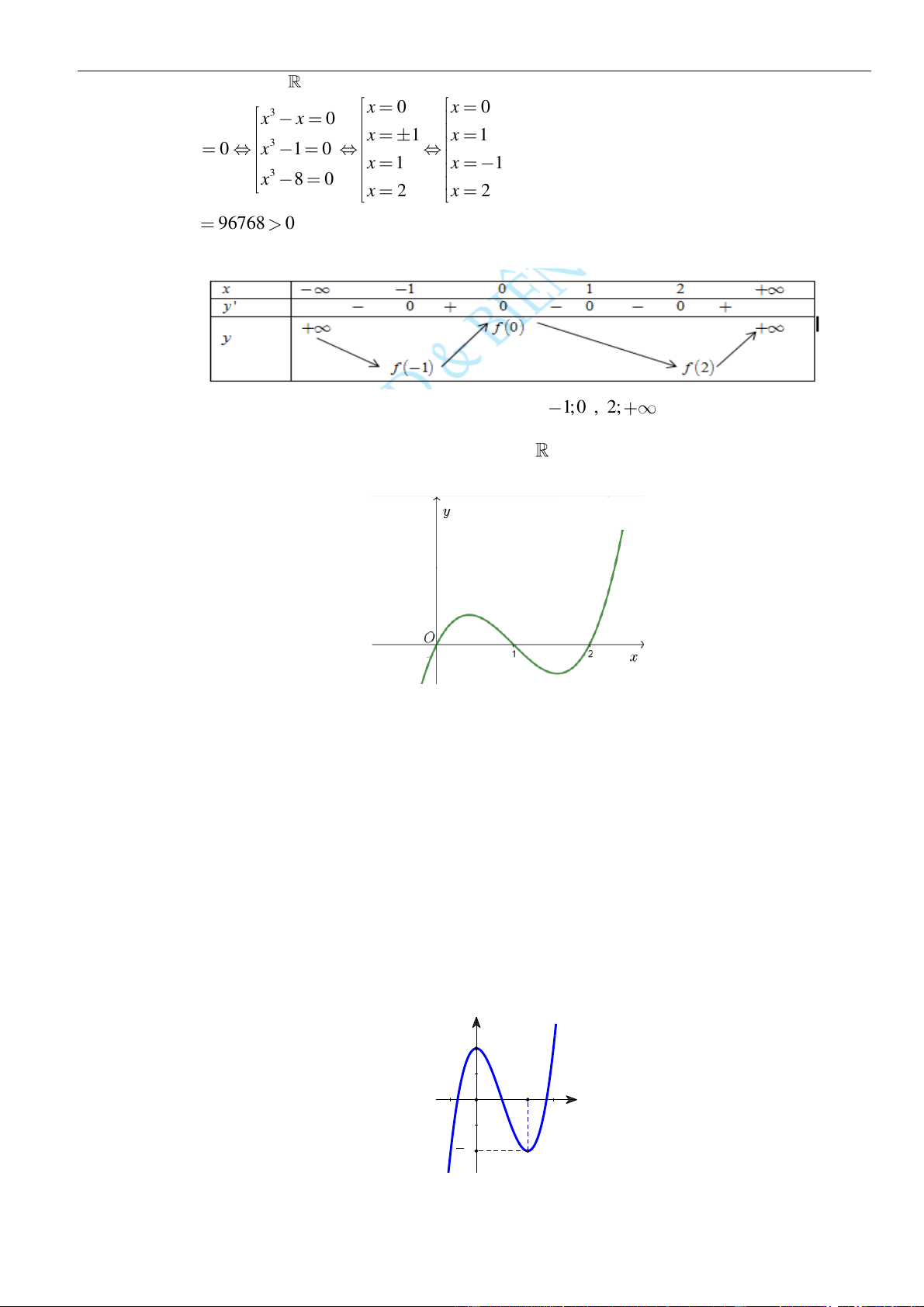
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Tập xác định
D =
3
'3
3
00
0
11
0 1 0
11
80
22
xx
xx
xx
f x x
xx
x
xx
'
3 96768 0f
Ta có bảng biến thiên
Từ BBT suy ra hàm số đồng biến trên các khoảng :
1;0 , 2;
.
Câu 30: Cho hàm số
( )
y f x=
có đạo hàm và liên tục trên . Hàm số
( )
1y f x
=−
có đồ thị như hình
vẽ sau:
Hàm số
( )
y f x=
nghịch biến trên khoảng nào sau đây?
A.
( )
2; 1 .−−
B.
( )
0;1 .
C.
( )
1;0 .−
D.
( )
3; 2 .−−
Lời giải
Chọn C
Hàm số
( )
y f x=
nghịch biến
( )
0fx
( )
10ft
−
với
1xt=−
0 1 0 1
1 2 1 1 2 1 0
t x x
t x x
−
− −
.
Vậy hàm số
( )
y f x=
nghịch biến trên
( )
1;0 .−
Câu 31: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên. Hàm số
( )
32y f x= − −
nghịch biến trên
khoảng
A.
( )
2;4
. B.
( )
0;3
. C.
( )
;1−
. D.
( )
3; +
.
Lời giải
x
y
2
2
2
O
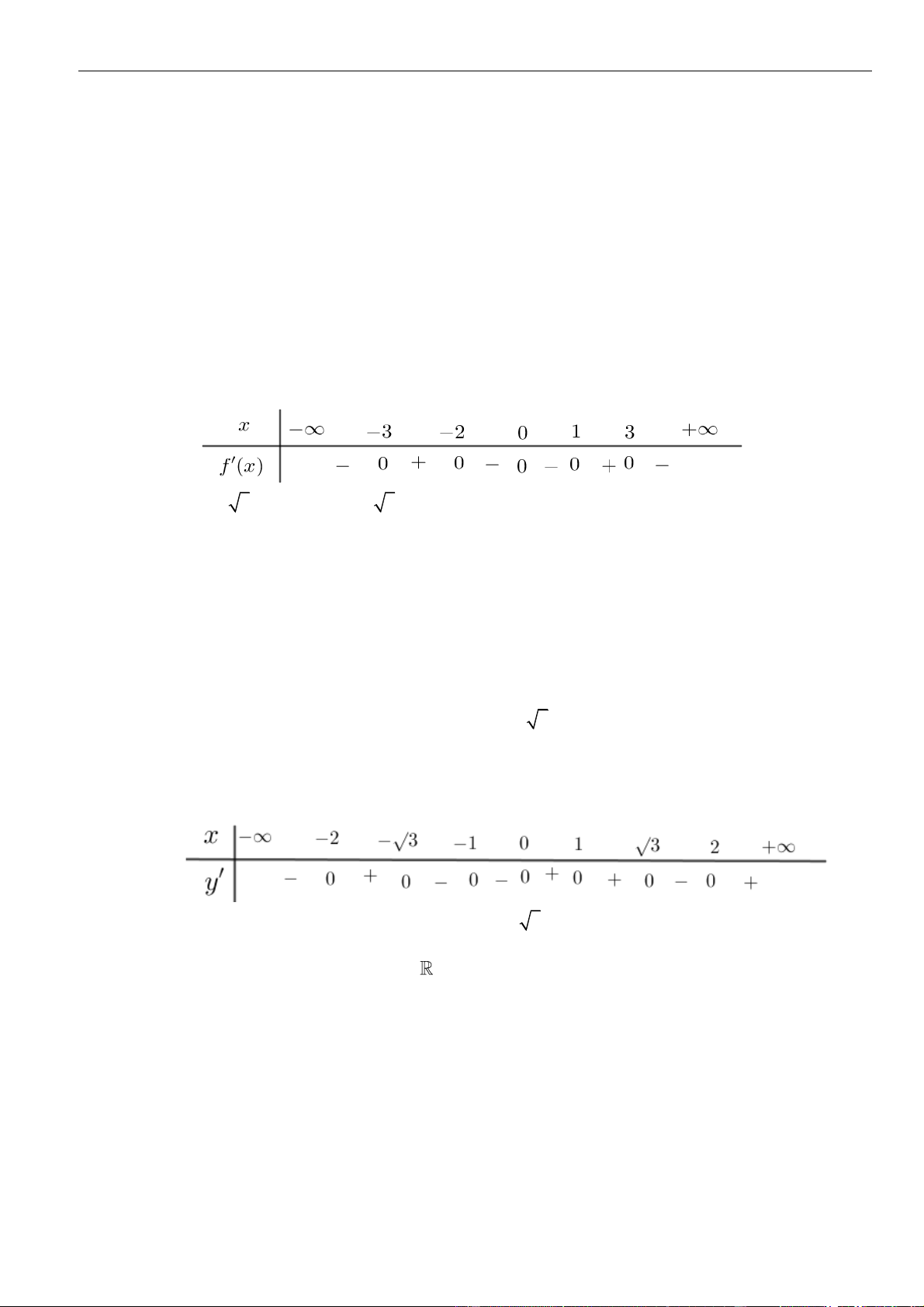
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Chọn C
Theo đồ thị hàm số ta có hàm số
( )
y f x=
đồng biến trên khoảng
( )
;0−
và
( )
2;+
( ) ( ) ( )
0, ;0 2;f x x
− +
Mặt khác:
( ) ( )
3 2 3 2y f x y f x
= − − = − −
Vậy hàm số
( )
32y f x= − −
nghịch biến
( ) ( )
0 3 2 0 2 0y f x f x
− − −
(
)
2 0 2
;2 4:
2 2 4
xx
x
xx
−
− +
−
Vậy hàm số
( )
32y f x= − −
nghịch biến trên
( )
;1−
.
Câu 32: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên. Hàm số
( )
2
1y f x=−
nghịch biến
trên khoảng
A.
( )
2; 3−−
. B.
( )
3;2
. C.
( )
2;+
. D.
( )
1;1−
.
Lời giải
Chọn B
( )
2
2 . 1y x f x
= − −
.
( )
2
2
2
2
2
2
0
13
0
0
2
12
0
10
10
3
1
11
13
x
x
x
x
x
x
y
fx
x
x
x
x
x
=
− = −
=
=
=
− = −
=
−=
− =
=
=
−=
−=
.
Bảng biến thiên
Hàm số
( )
2
1y f x=−
nghịch biến trên khoảng
( )
3;2
.
Câu 33: Cho hàm số
( )
fx
có đạo hàm trên là
( ) ( )( )
' 1 3f x x x= − +
. Có bao nhiêu giá trị nguyên của
tham số
m
thuộc đoạn
10;2021−
để hàm số
( )
2
3y f x x m= + −
đồng biến trên khoảng
( )
0;2
?
A.
2016
. B.
2019
. C.
2018
. D.
2017
.
Lời giải
Ta có
( )
( )
( )
( )( )
2 2 2
' 2 3 ' 3 2 3 3 1 3 3y x f x x m x x x m x x m= + + − = + + − − + − +
Vì
( )
2 3 0, 0;2xx+
nên yêu cầu bài toán tương đương với

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
( )
( )
( )
( )
( ) ( ) ( )
( ) ( ) ( )
2
2
2
2
2
2
3 1 0, 0;2
3 3 0, 0;2
3 1 , 0;2 1
3 3 , 0;2 . 2
3 1 0, 0;2
3 3 0, 0;2
x x m x
x x m x
m x x g x x
m x x h x x
x x m x
x x m x
+ − −
+ − +
+ − =
+ + =
+ − −
+ − +
Ta có
( ) ( ) ( )
2 3 0, 0;2g x x x g x
= +
đồng biến trên
( )
0;2
Từ
( ) ( )
1 0 1.mg = −
Lại có
( ) ( ) ( )
2 3 0, 0;2h x x x h x
= +
đồng biến trên
( )
0;2 .
Từ
( ) ( )
2 2 14.mh =
Vì
m
và
10;2021m−
nên suy ra
10; 9; 8;...; 1;14;15;16;...;2021 .m − − − −
Có tất cả
2018
giá trị của
m
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
( )
32
1
x
x
x
f
+
=
−
. Hàm số nghịch biến trên khoảng nào?
A.
( )
;− +
. B.
( )
;1−
. C.
( )
1; +
. D.
( )
;1−
và
( )
1; +
.
Câu 2: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( ) ( )
23
' 1 1 2f x x x x= + − −
. Hàm số
( )
y f x=
đồng biến
trên khoảng nào dưới đây?
Xét tính đơn điệu của hàm tổng và hàm hợp
DẠNG 3
Phương pháp:
❖ Dạng 1. Tìm khoảng đơn điệu của hàm số
( ) ( )
g x f u x=
khi biết đồ thị hàm số
( )
fx
Cách 1:
▪ Bước 1: Tính đạo hàm của hàm số
( )
gx
,
( ) ( ) ( )
.g x u x f u x
=
.
▪ Bước 2: Sử dụng đồ thị của
( )
fx
, lập bảng xét dấu của
( )
gx
.
▪ Bước 3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.
Cách 2:
▪ Bước 1: Tính đạo hàm của hàm số
( )
gx
,
( ) ( ) ( )
.g x u x f u x
=
.
▪ Bước 2: Hàm số
( )
gx
đồng biến
( )
0gx
; (Hàm số
( )
gx
nghịch biến
( )
0gx
) (*)
▪ Bước 3: Giải bất phương trình
( )
*
(dựa vào đồ thị hàm số
( )
y f x
=
) từ đó kết luận khoảng đồng
biến, nghịch biến của hàm số.
❖ Dạng 2. Tìm khoảng đơn điệu của hàm số
( ) ( )
g x f u x=
khi biết đồ thị, bảng biến thiên của
hàm số
( )
fx
Cách 1:
▪ Bước 1: Tính đạo hàm của hàm số
( )
gx
,
( ) ( ) ( ) ( )
.g x u x f u x v x
=+
.
▪ Bước 2: Sử dụng đồ thị của
( )
fx
, lập bảng xét dấu của
( )
gx
.
▪ Bước 3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.
Cách 2:
▪ Bước 1: Tính đạo hàm của hàm số
( )
gx
,
( ) ( ) ( ) ( )
.g x u x f u x v x
=+
.
▪ Bước 2: Hàm số
( )
gx
đồng biến
( )
0gx
; (Hàm số
( )
gx
nghịch biến
( )
0gx
) (*)
▪ Bước 3: Giải bất phương trình
( )
*
(dựa vào đồ thị hàm số
( )
y f x
=
) từ đó kết luận khoảng đồng
biến, nghịch biến của hàm số.
Cách 3: CÁCH LÀM TRẮC NGHIỆM
▪ Bước 1: Tính đạo hàm của hàm số
( )
gx
,
( ) ( ) ( ) ( )
.g x u x f u x v x
=+
.
▪ Bước 2: Hàm số
( )
gx
đồng biến trên
K
( )
0,g x x K
; (Hàm số
( )
gx
nghịch biến trên
K
( )
0,g x x K
) (*)
▪ Bước 3: Lần lượt chọn thay giá trị từ các phương án vào
( )
gx
để loại các phương án sai.
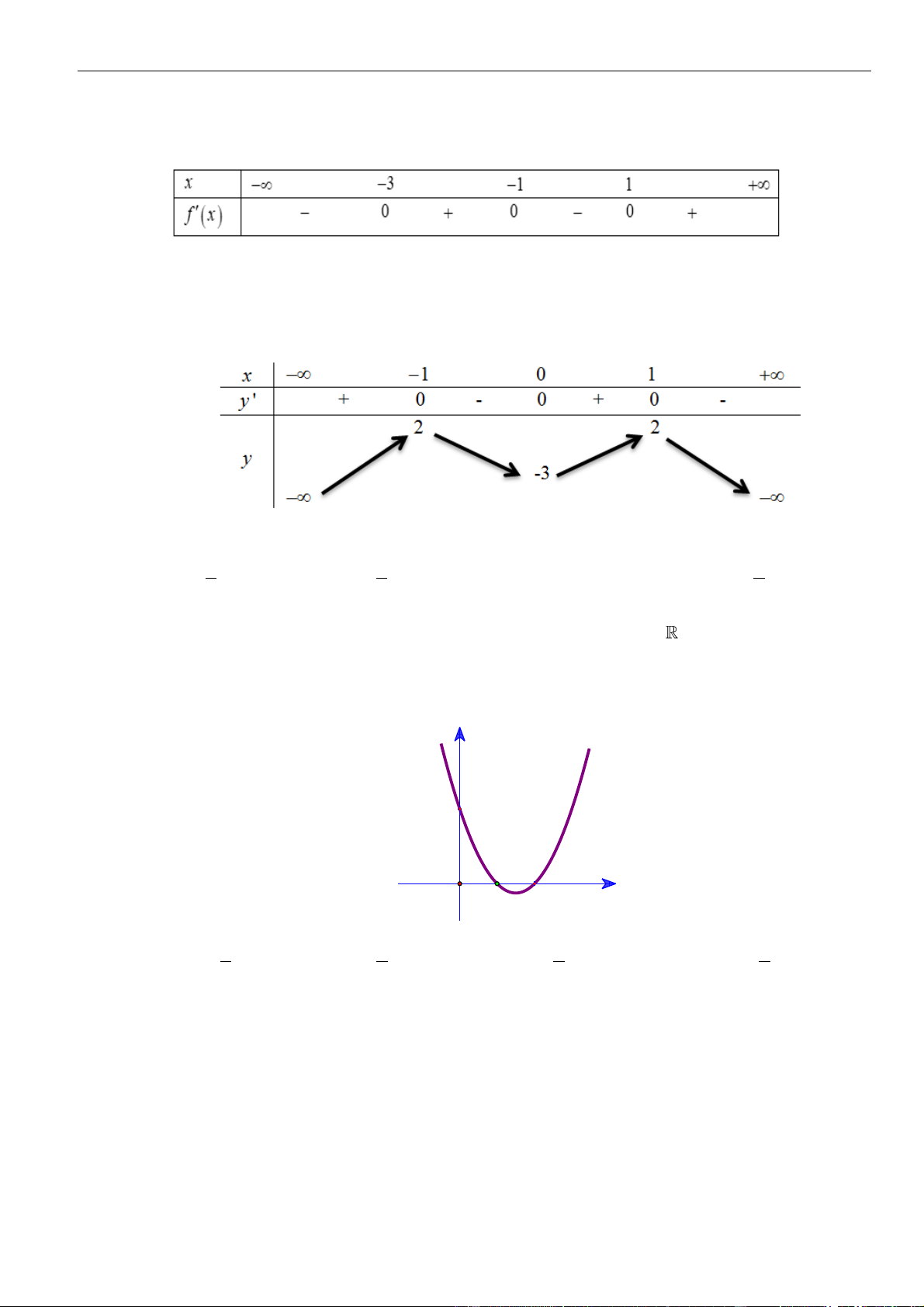
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
( )
1;1−
. B.
( )
2;+
. C.
( )
;1−
. D.
( )
1;2
.
Câu 3: Cho hàm số
()fx
có bảng xét dấu
( )
fx
như hình bên
Hàn số
(2 1)fx+
nghịch biến trên khoảng nào dưới đây
A.
( )
1;2−
. B.
( )
2;0−
. C.
( )
1;0−
. D.
( )
0;+
.
Câu 4: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau
Hàm số
( )
1 2 1y f x= − +
đồng biến trên khoảng
A.
3
0;
2
. B.
1
;1
2
. C.
( )
1; +
. D.
1
1;
2
−
.
Câu 5: Cho hàm số
( )
y f x=
có đạo hàm
( )
fx
xác định và liên tục trên . Hình vẽ bên dưới là đồ
thị của hàm số
( )
y f x
=
. Hàm số
( )
( )
2
g x f x x=−
nghịch biến trên khoảng nào trong các
khoảng dưới đây ?
A.
3
;
2
−
. B.
3
;
2
+
. C.
1
;
2
+
. D.
1
;
2
−
.
Câu 6: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( )( )
2
1 2 3f x x x x
= − + −
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên các khoảng
( )
2;1−
và
( )
3; +
.
B. Hàm số đồng biến trên các khoảng
( )
2;1−
và
( )
3; +
.
C. Hàm số đồng biến trên khoảng
( )
2;3−
.
D. Hàm số nghịch biến trên khoảng
( )
2;3−
.
Câu 7: Cho hàm số có đạo hàm
( ) ( ) ( ) ( )
23
2 2 3f x x x x
= + − −
. Hàm số
( )
y f x=
đồng biến trên
khoảng nào dưới đây?
x
y
f'
(x)
2
2
1
O
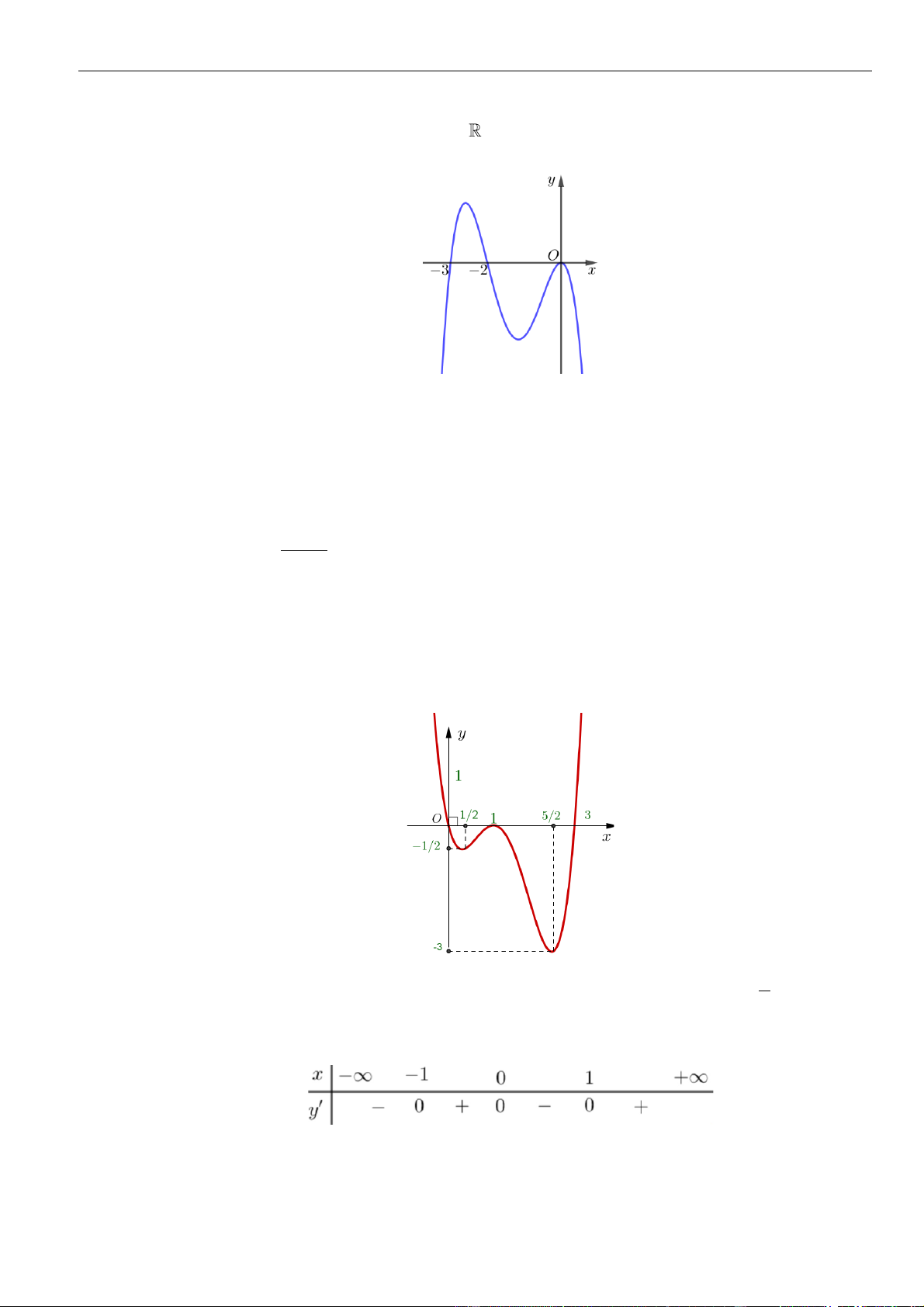
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
( )
2;3
. B.
( )
2;2−
C.
( )
3; +
D.
( )
;2− −
Câu 8: Cho hàm số
( )
fx
xác định, liên tục trên và có đồ thị của hàm số
( )
fx
là đường cong như
hình vẽ bên dưới. Hỏi khẳng định nào đúng ?
A. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
2;0−
.
B. Hàm số
( )
=y f x
nghịch biến trên khoảng
( )
3; 2−−
.
C. Hàm số
( )
=y f x
nghịch biến trên khoảng
( )
0;+
.
D. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
;3− −
.
Câu 9: Cho hàm số
22
1
x
y
x
+
=
−
. Trong các khẳng định sau, khẳng định nào đúng:
A. Hàm số nghịch biến trên khoảng
( )
0;+
. B. Hàm số đồng biến trên khoảng
( )
;2−
.
C. Hàm số nghịch biến trên khoảng
( )
2;+
. D. Hàm số đồng biến trên khoảng
( )
0;+
.
Câu 10: Cho hàm số
()y f x=
có đạo hàm
()fx
trên khoảng
( ; )− +
. Đồ thị hàm số
()y f x
=
như
hình vẽ. Hàm số
()y f x=
nghịch biến trên khoảng nào trong các khoảng sau?
A.
( ;0)−
. B.
( )
0;3
. C.
(3; )+
. D.
5
;
2
−
.
Câu 11: Hàm số
( )
32y f x=−
có bảng xét dấu của đạo hàm như sau:
Hàm số
( )
y f x=
nghịch biến trên khoảng nào dưới đây?
A.
( )
3;5
. B.
( )
1;2−
. C.
( )
1;3
. D.
( )
5;+
.
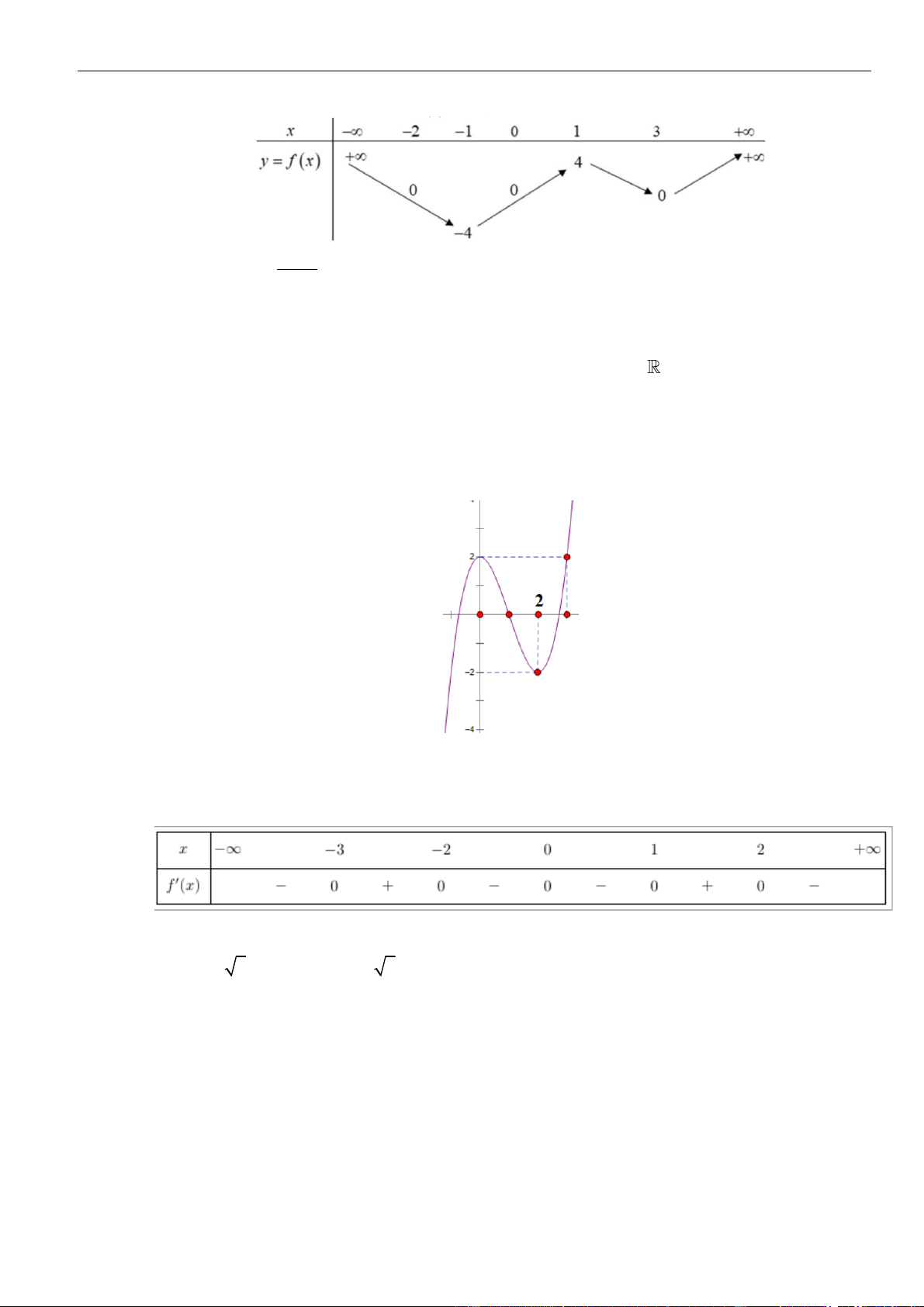
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 12: Cho hàm số
( )
=y f x
có bảng biến thiên như sau:
Hàm số
( )
( )
=
1
gx
fx
đồng biến trên khoảng nào sau đây?
A.
( )
−2 ; 0
. B.
( )
+3;
. C.
( )
1; 2
. D.
( )
− −;1
Câu 13: Cho hàm số
( )
y f x=
có đạo hàm
( )
( )
22
' 1 ,y f x x x x= = −
. Hàm số
( )
y f x=−
đồng
biến trên khoảng nào
A.
( )
2;+
. B.
( )
0;2
. C.
( )
1;1−
. D.
( )
;1− −
.
Câu 14: Cho hàm số
( )
fx
có đồ thị như hình vẽ bên. Hàm số
( )
32y f x= − −
nghịch biến trên khoảng
A.
( )
2;4
. B.
( )
;1−
. C.
( )
0;3
. D.
( )
3; +
.
Câu 15: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên dưới.
Hàm số
( )
2
1y f x=−
nghịch biến trên khoảng
A.
( )
2; 3−−
. B.
( )
3;2
. C.
( )
2;+
. D.
( )
1;1−
.
Câu 16: Cho hàm số đa thức bậc bốn
()fx
. Đồ thị hàm số
( )
32y f x
=−
được cho như hình sau:
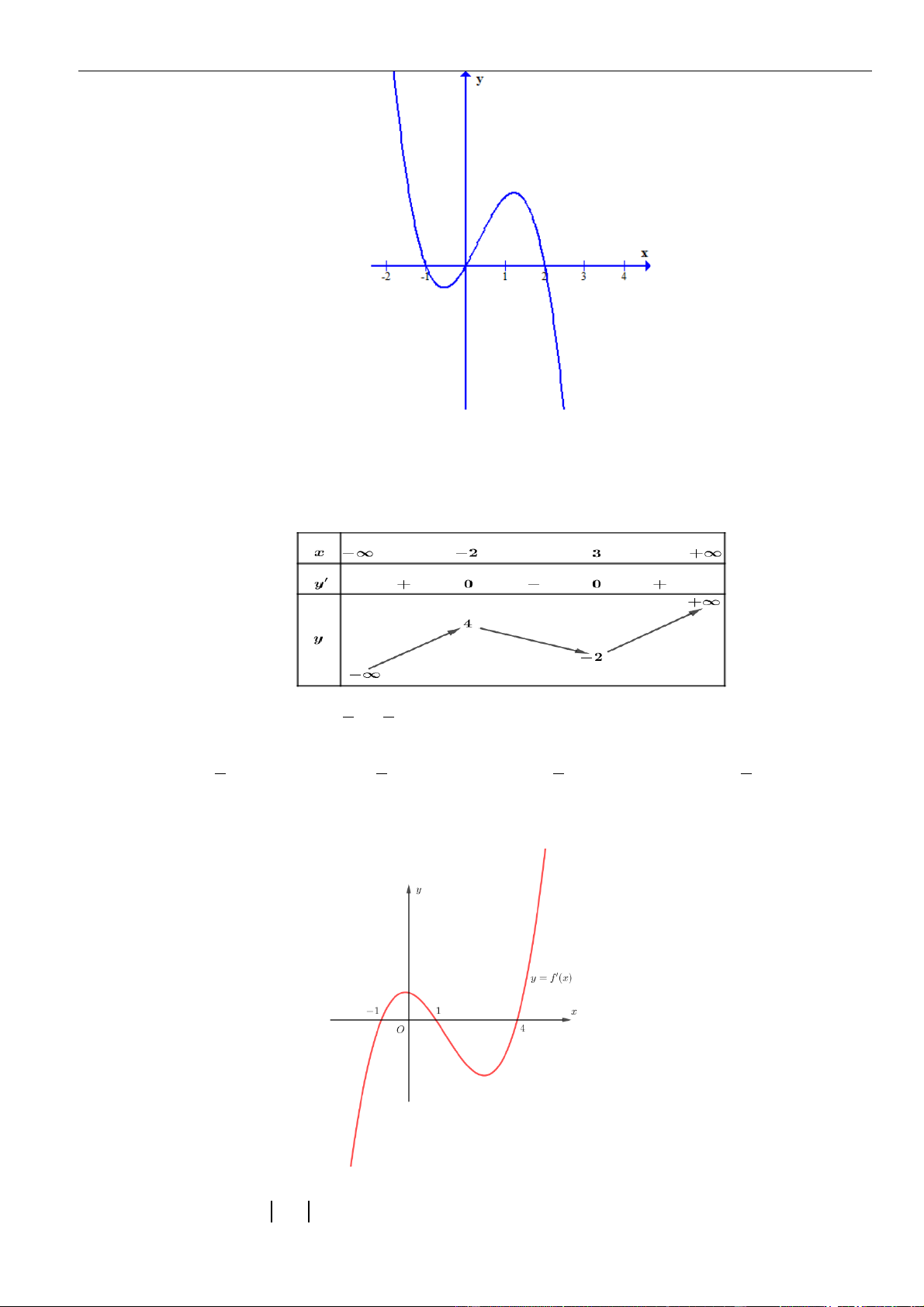
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Hàm số
()y f x=
nghịch biến trên khoảng
A.
( )
;1− −
. B.
( )
5;+
. C.
( )
1;1−
. D.
( )
1;5
.
Câu 17: Cho hàm số
( )
y f x=
có bảng biên thiên như hình vẽ
Hàm số
( )
2
53
2
22
g x f x x
= − −
nghịch biến trên khoảng nào trong các khoảng sau?
A.
1
1;
4
−
. B.
1
;1
4
. C.
9
;
4
+
. D.
5
1;
4
.
Câu 18: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
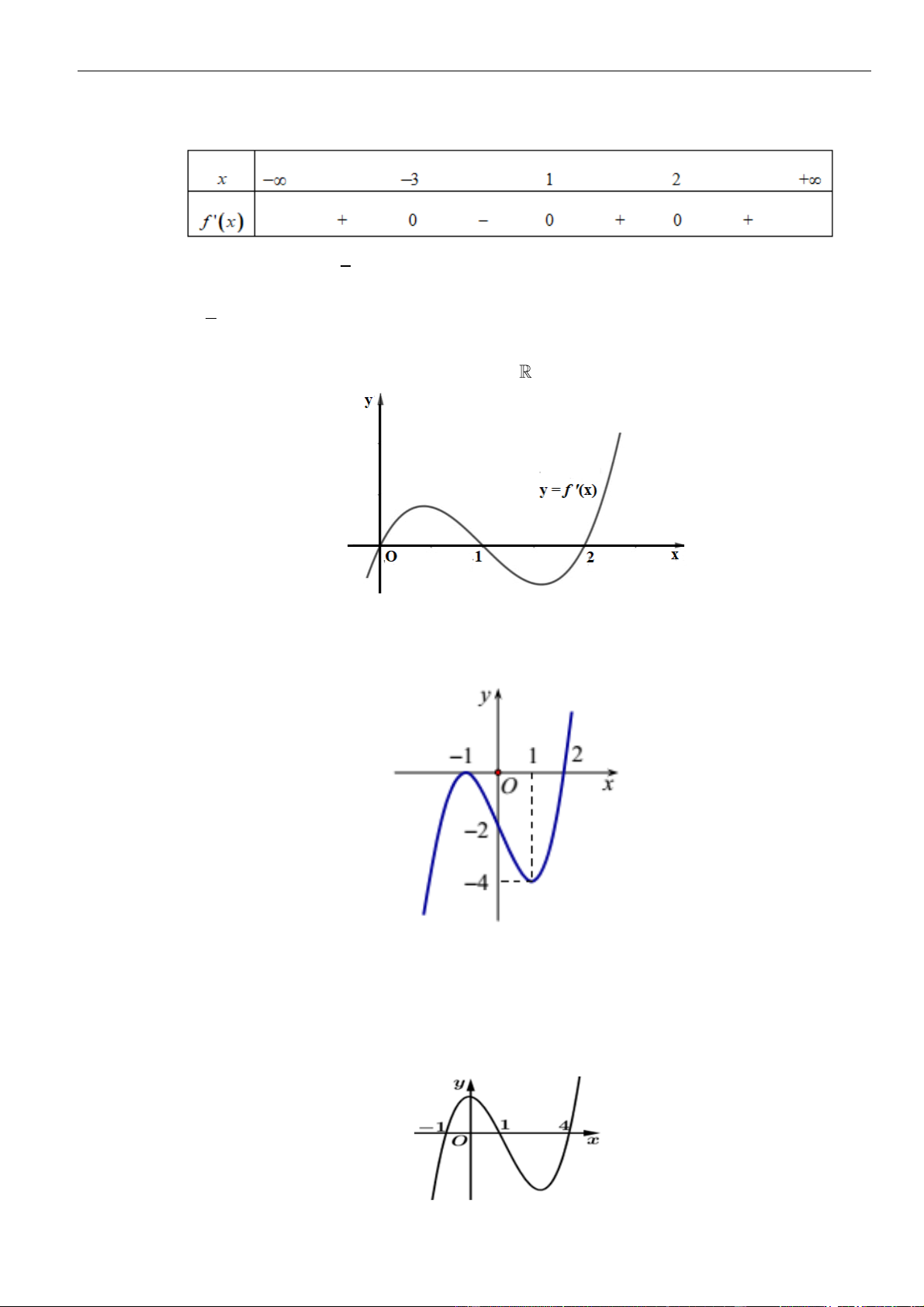
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
A.
( )
2;3
. B.
( )
4;7
. C.
( )
;1− −
. D.
( )
1;2−
.
Câu 19: Cho hàm số
( )
fx
có bảng xét dấu của
( )
'fx
như sau:
Hàm số
( )
32
1
2 3 5 1
3
x x x x
y f e e e e= − − + − +
đồng biến trên khoảng nào dưới đây?
A.
3
0;
2
. B.
( )
1;3
. C.
( )
3;0−
. D.
( )
4; 3−−
.
Câu 20: Cho hàm số
( )
y f x=
liên tục, có đạo hàm trên . Đồ thị hàm số
( )
'y f x=
như hình vẽ sau:
Hàm số
( )
3y f x=−
nghịch biến trên khoảng
( )
2;b
. Giá trị lớn nhất của
b
bằng bao nhiêu?
Câu 21: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị như hình vẽ
Gọi
S
là tập hợp tất cả các giá trị nguyên dương của tham số
m
sao cho hàm số
( )
y f x m=−
đồng biến trên khoảng
( )
2020;+
. Số phần tử của tập
S
là
A.
2020
. B.
2019
. C.
2018
. D. vô số.
Câu 22: Cho hàm số
( )
=y f x
. Hàm số
( )
=y f x
có đồ thị như hình bên dưới.
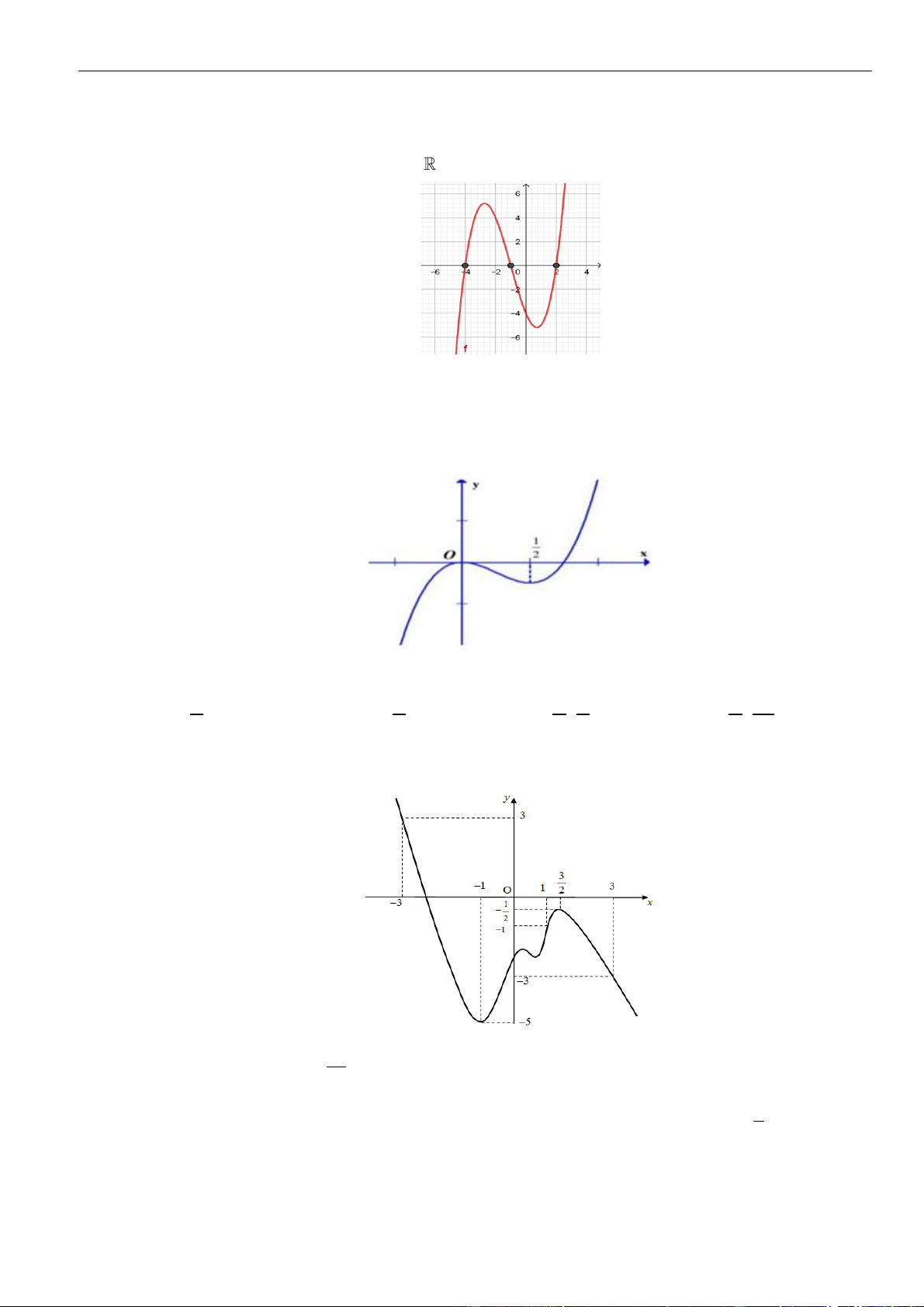
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
3 2 2020= − +y f x
nghịch biến trên khoảng nào?
A.
( )
1;1−
. B.
( )
2;+
. C.
( )
1;2
. D.
( )
;1−
.
Câu 23: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị
( )
y f x
=
như hình vẽ sau
Hàm số
( )
2
5y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;2
. B.
( )
0;1
. C.
( )
1;0−
. D.
( )
1;1−
.
Câu 24: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ
Hàm số
( )
sinfx
nghịch biến trên các khoảng nào sau đây
A.
;
2
. B.
0;
3
. C.
;
62
. D.
5
;
66
.
Câu 25: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
như hình vẽ
Hàm số
( )
2
1
2
x
y f x x= − + −
nghịch biến trên khoảng nào?
A.
( )
1;3
. B.
( )
−3;1
. C.
( )
−2;0
. D.
−
3
1;
2
Câu 26: Cho hàm số
( )
=y f x
có đạo hàm
( ) ( )( )
2
2
94f x x x x
= − −
. Khi đó hàm số
( )
2
y f x=
nghịch
biến trên khoảng nào
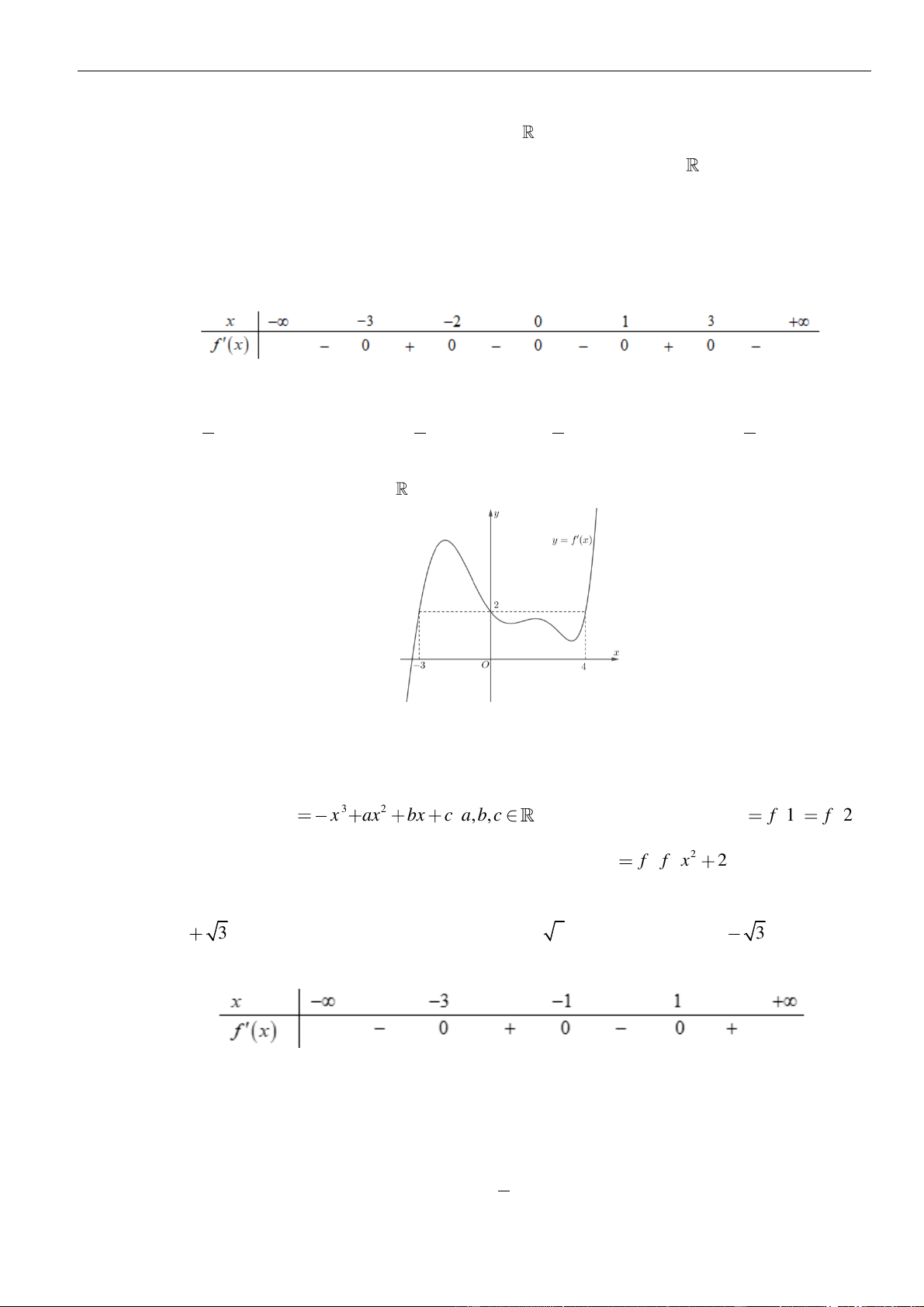
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
A.
( )
−3;0
. B.
( )
+3;
.
C.
( )
− −;3
. D.
( )
−2;2
Câu 27: Cho hàm số
()y f x=
xác định trên và có đạo hàm
()fx
thỏa mãn
( )( )
( ) 1 2 ( ) 2018f x x x g x
= − + +
trong đó
( ) 0,g x x
. Hàm số
( )
1 2018 2019y f x x= − + +
đồng biến trên khoảng nào?
A.
( )
1; +
. B.
( )
0;3
. C.
( )
3; +
. D.
( )
;3−
.
Câu 28: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên dưới
Hàm số
( )
12y f x=−
đồng biến trên khoảng
A.
1
;1
2
−
. B.
1
2;
2
−−
. C.
3
;3
2
. D.
3
0;
2
.
Câu 29: Cho hàm số
( )
fx
liên tục trên . Hàm số
( )
y f x
=
có đồ thị như hình bên dưới.
Hỏi hàm số
( )
( )
22
3 2 6g x f x x x x= − − +
nghịch biến trên khoảng nào dưới đây
A.
( )
;0−
. B.
( )
0;4
. C.
( )
1;0−
. D.
( )
0;1
.
Câu 30: Cho hàm số
32
1
,,
6
f x x ax bx c a b c
thỏa mãn điều kiện
0 1 2f f f
.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của
c
để hàm số
2
2g x f f x
nghịch biến trên
khoảng
0;1
là
A.
13
. B.
1
. C.
3
. D.
13
.
Câu 31: Cho hàm số
()fx
, bảng xét dấu của
()fx
như sau
Hàm số
( )
12y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;3
. B.
( )
3; +
. C.
( )
2;0−
. D.
( )
0;1
.
Câu 32: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên
( )
1;3−
. Bảng biến thiên của hàm số
( )
y f x
=
được cho như hình vẽ sau. Hàm số
1
2
x
y f x
= − +
nghịch biến trên khoảng nào sau đây?
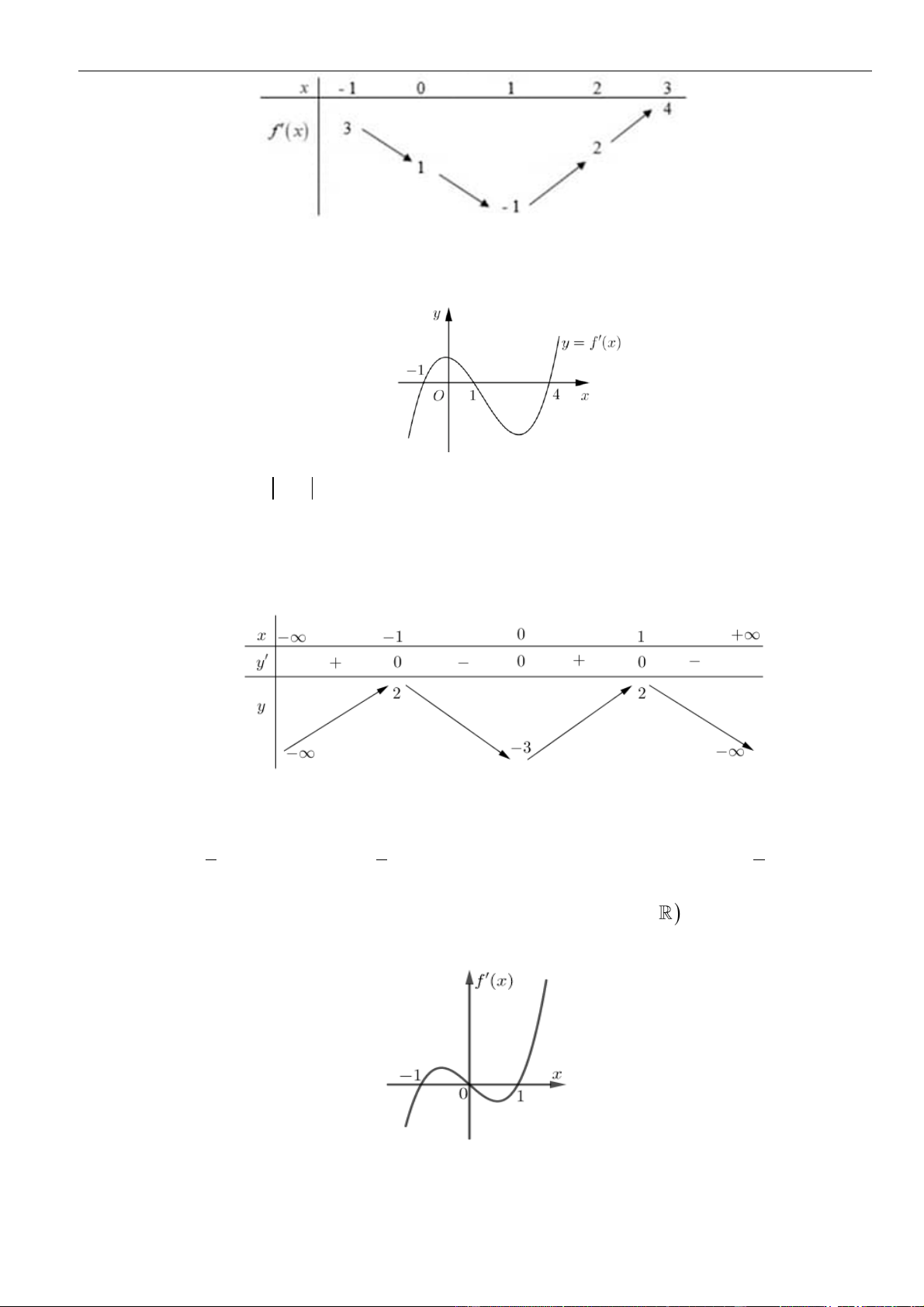
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
A.
( )
4; 2−−
. B.
( )
2;0−
. C.
( )
0;2
. D.
( )
2;4
.
Câu 33: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
4;7
. B.
( )
;1− −
. C.
( )
2;3
. D.
( )
1;2−
.
Câu 34: Cho hàm số
( )
y f x=
có bảng biến thiên như hình bên
Hàm số
( )
1 2x 1yf= − +
đồng biến trên khoảng
A.
3
0;
2
. B.
1
;1
2
. C.
( )
1; +
. D.
1
1;
2
−
.
Câu 35: Cho hàm số
( )
y f x=
, hàm số
( ) ( )
32
,,f x x ax bx c a b c
= + + +
có đồ thị như hình vẽ.
Hàm số
( ) ( )
( )
g x f f x
=
có mấy khoảng đồng biến?
A.
3
. B.
2
. C.
1
. D.
4
.
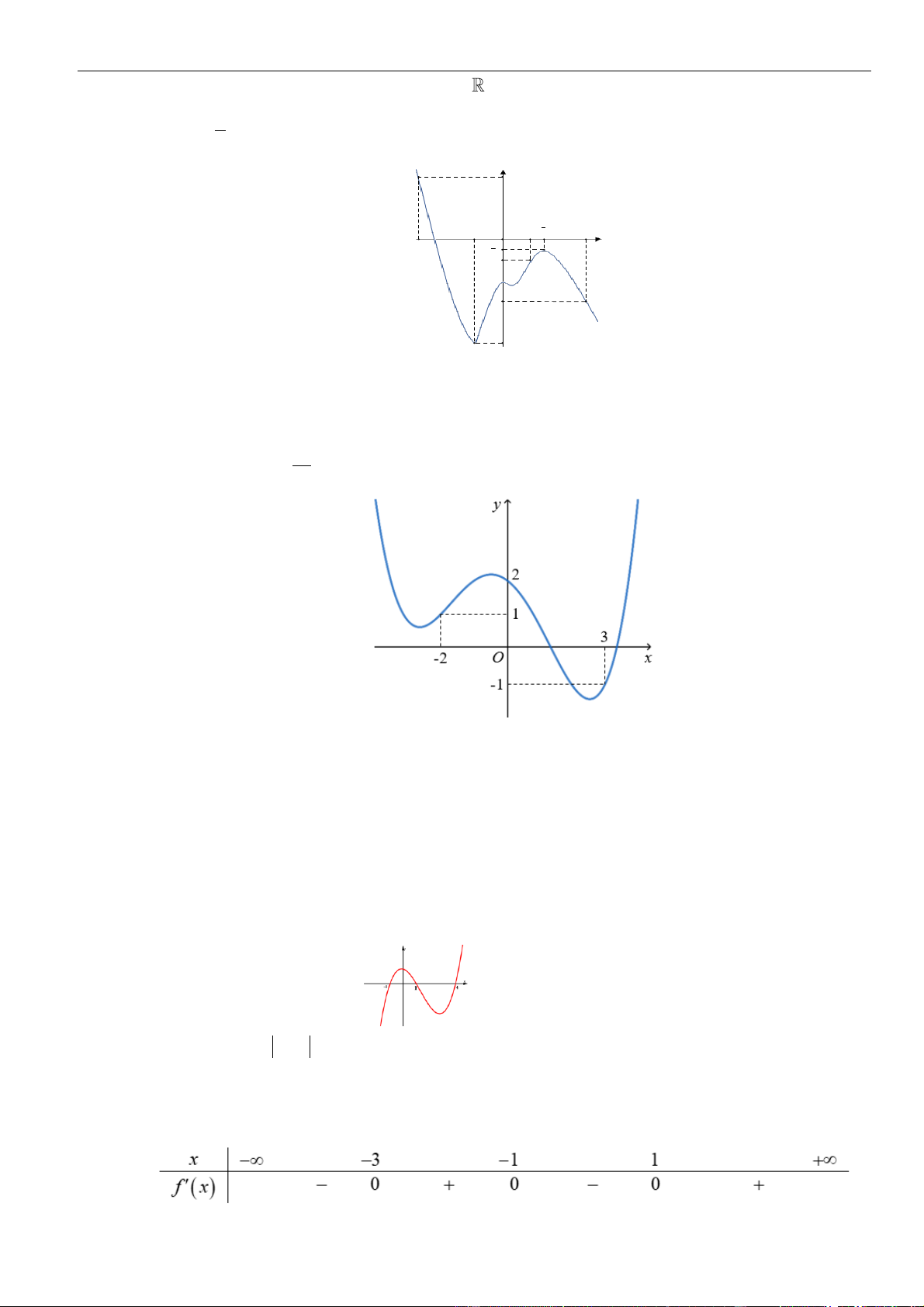
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Câu 36: Cho hàm số
( )
fx
có đạo hàm trên
và
( )
fx
có đồ thị như hình bên. Hàm số
( ) ( )
2
1
2 1 2020
2
g x f x x x= − + − +
nghịch biến trên khoảng nào dưới đây?
A.
( )
1; +
. B.
( )
;1− −
. C.
( )
1;1−
. D.
( )
1;2
.
Câu 37: Cho hàm số
( )
fx
. Hàm số
( )
y f x
=
có đồ thị như hình bên. Hàm số
( ) ( )
3
13
3
x
g x f x x= + + −
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;2−
. B.
( )
2;0−
. C.
( )
0;4
. D.
( )
1;5
.
Câu 38: Cho hàm số
( )
y f x=
mà đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
2;3
. B.
( )
4;7
. C.
( )
;1− −
. D.
( )
1;2−
.
Câu 39: Cho hàm số
( )
y f x=
có bảng xét dấu của hàm
( )
fx
như sau:
y = f '(x)
3
-
3
2
3
-
1
2
-1
-3
-5
-3
-1
1
y
x
O
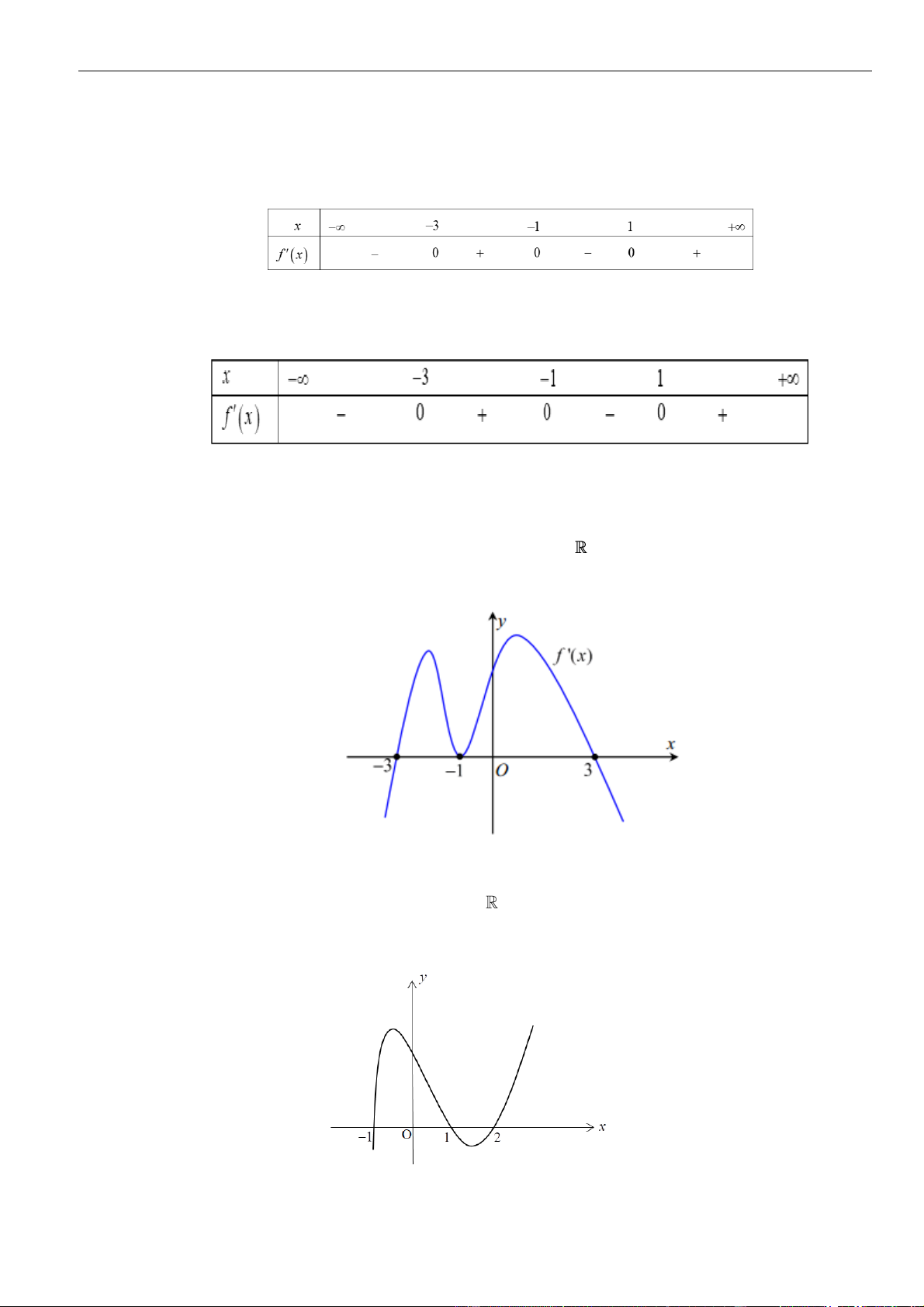
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
32y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;4
B.
( )
4;+
C.
( )
1;2
D.
( )
2;1−
Câu 40: Cho hàm số
( )
fx
, bảng xét dấu
( )
fx
như hình bên. Hàm số
( )
21fx+
đồng biến trên khoảng
nào dưới đây?
A.
( )
1;0−
. B.
( )
0;+
. C.
( )
1;2−
. D.
( )
2;0−
.
Câu 41: Cho hàm số
( )
y f x=
có bảng xét dấu
( )
fx
như hình dưới đây
Hàm số
( )
1fx+
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;1−
. B.
( )
0;1
. C.
( )
2;0−
. D.
( )
1;3
.
Câu 42: Cho hàm số
( )
fx
có đạo hàm liên tục và xác định trên và có đồ thị hàm số
( )
fx
như hình
vẽ bên dưới. Hàm số
( )
( )
2
2g x f x x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
2;3
. B.
( )
;1−
. C.
( )
0;2
. D.
( )
2;4
.
Câu 43: Cho hàm số
( )
fx
liên tục và xác định trên có đồ thị đạo hàm
( )
fx
được cho như hình vẽ.
Hàm số
( )
2
1y f x= − −
đồng biến trong khoảng nào sau đây?
A.
( )
1;5−
. B.
( )
2;6
. C.
( )
2; 1−−
. D.
( )
1;3−
.
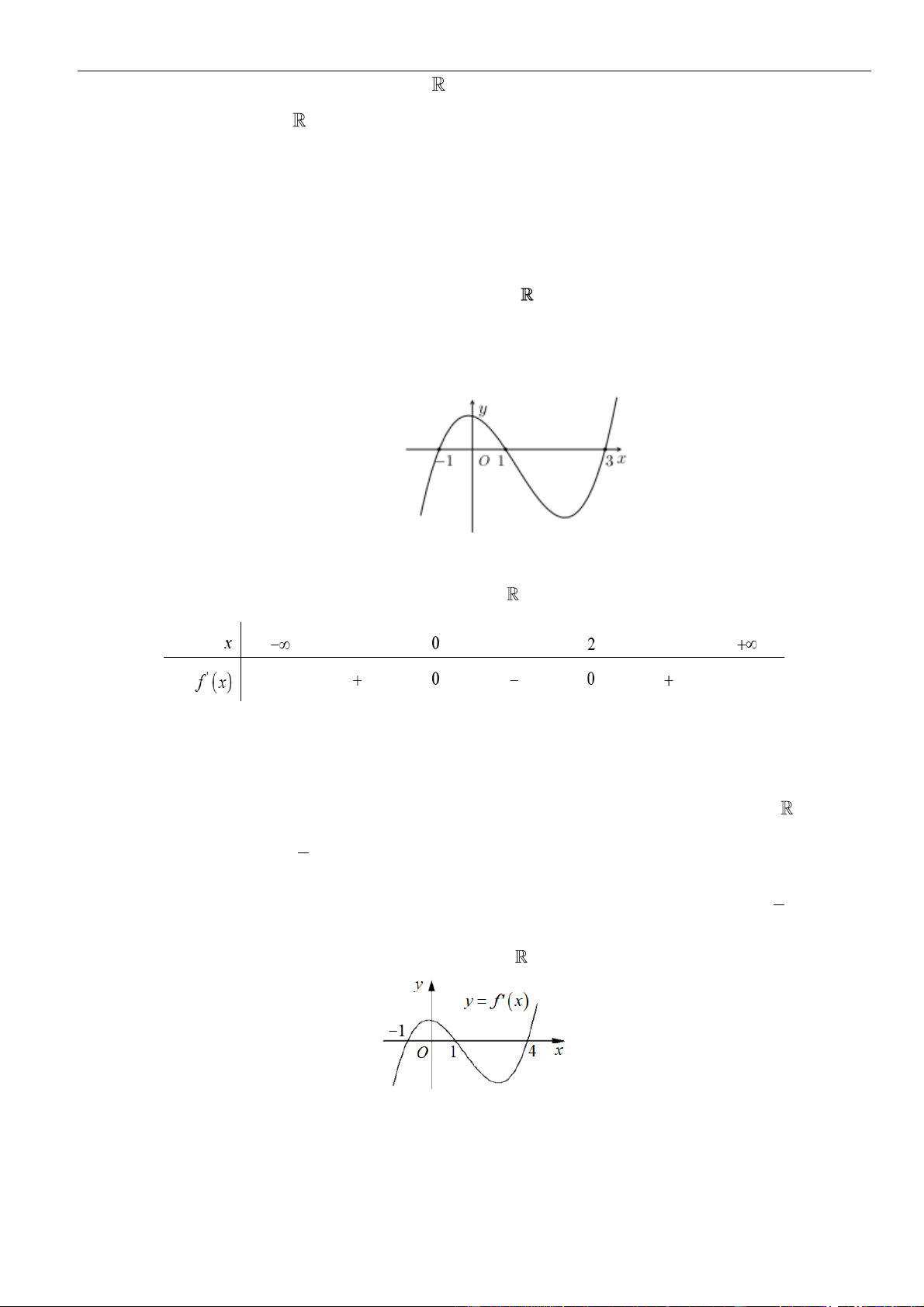
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Câu 44: Cho hàm số
( )
y f x=
xác định trên và có đạo hàm
( ) ( )( ) ( )
2 3 2021f x x x g x
= − + +
trong
đó
( )
0,g x x
. Hàm số
( )
1 2021 2022y f x x= − + +
đồng biến trên khoảng nào?
A.
( )
;1− −
. B.
( )
1;4−
. C.
( )
3;2−
. D.
( )
4;+
.
Câu 45: Cho hàm số
()y f x=
xác định trên
R
và có đạo hàm
'( ) (2 )( 3). ( ) 2021f x x x g x= − + +
trong
đó
( ) 0, .g x x R
Hàm số
(1 ) 2021 2022y f x x= − + +
đồng biến trên khoảng nào?
A.
( ; 1)− −
. B.
( 1;4)−
. C.
( 3;2)−
. D.
(4; )+
.
Câu 46: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên . Biết hàm số
( )
y f x
=
có đồ thị như hình
vẽ. Gọi
S
là tập hợp các giá trị nguyên
2021;2021m−
để hàm số
( ) ( )
g x f x m=+
nghịch
biến trên khoảng
( )
1;2
. Hỏi
S
có bao nhiêu phần tử?
A.
2020.
B.
2021.
C.
2022.
D.
2019.
Câu 47: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên , dấu của đạo hàm được cho bởi bảng:
Hàm số
( )
22y f x=−
nghịch biến trong khoảng nào?
A.
( )
;1−
. B.
( )
1;2
. C.
( )
1;1−
. D.
( )
2;+
.
Câu 48: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( ) ( )
22
' 3 10 3 2f x x x x= − − −
với mọi
x
. Hàm số
( ) ( )
( )
3
2
1
31
6
g x f x x= − + −
đồng biến trên khoảng nào trong các khoảng sau
A.
( )
1; +
. B.
( )
0;1
. C.
( )
;0−
. D.
1
;
2
− −
.
Câu 49: Cho hàm số
( )
y f x=
xác định và liên tục trên . Hàm số
( )
y f x=
có đồ thị như hình dưới.
Hàm số
( ) ( )
2y g x f x= = −
đồng biến trên khoảng nào dưới đây?
A.
( )
;2− −
. B.
( )
3; +
. C.
( )
1;3
. D.
( )
2;+
.
Câu 50: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị (như hình bên). Hàm số
( )
2y f x=−
đồng
biến trên khoảng
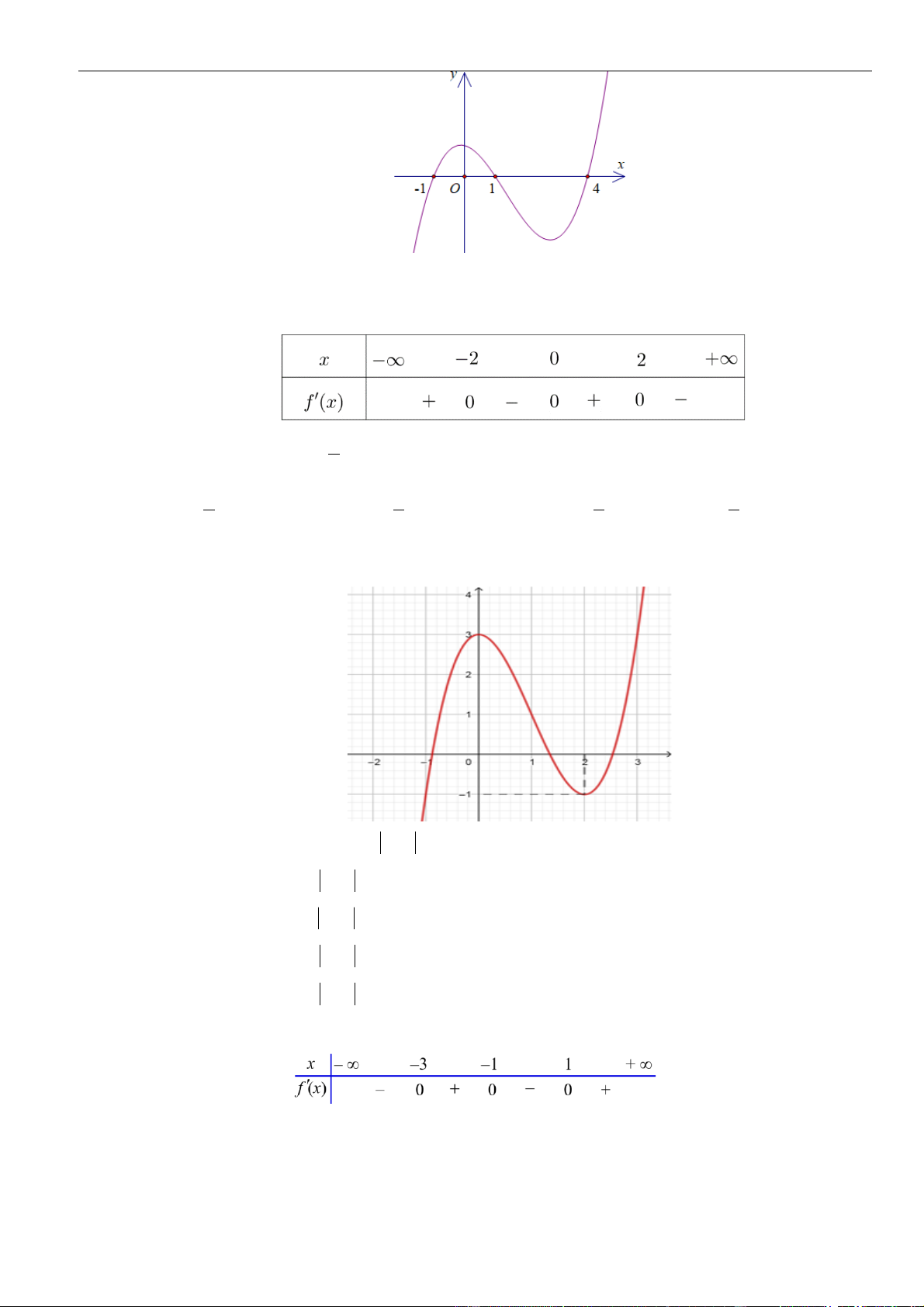
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
A.
( )
3;5
. B.
( )
4;1−
. C.
( )
;2−
. D.
( )
2;+
.
Câu 51: Cho hàm số
( )
y f x=
có bảng xét dấu đạo hàm như bảng sau.
Hỏi hàm số
1
y f x
x
=+
nghịch biến trên khoảng nào?
A.
1
;0
2
−
. B.
1
0;
2
. C.
1
2;
2
−−
. D.
1
;2
2
.
Câu 52: Cho hàm số đa thức
( )
y f x=
có đồ thị như hình vẽ bên dưới.
Xét hàm số
( )
( )
1h x f x=−
. Chọn khẳng định đúng:
A. Hàm số
( )
( )
1h x f x=−
đồng biến trên khoảng
( )
;1− −
.
B. Hàm số
( )
( )
1h x f x=−
đồng biến trên khoảng
( )
1;1−
và
( )
3; +
.
C. Hàm số
( )
( )
1h x f x=−
nghịch biến trên khoảng
( )
3; +
.
D. Hàm số
( )
( )
1h x f x=−
nghịch biến trên khoảng
( )
1;3
.
Câu 53: Cho hàm số
()fx
, bảng xét dấu của
()fx
như sau:
Hàm số
(1 2 )y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;3
. B.
( )
3; +
. C.
( )
2;0−
. D.
( )
0;1
.
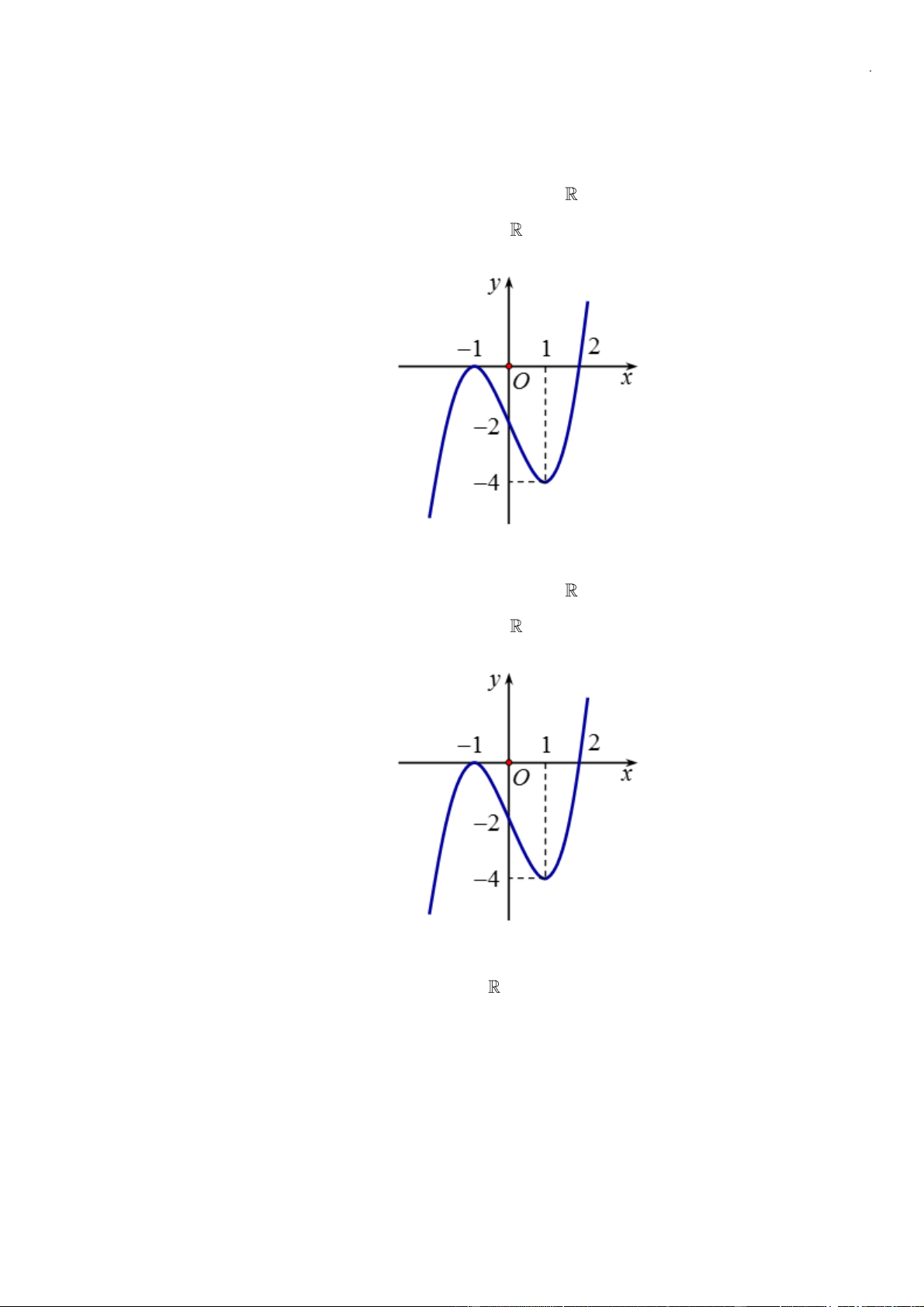
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Câu 54: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )
2
2
' 2 6f x x x x= + −
. Có bao nhiêu giá trị nguyên của
tham số
m
để hàm số
( )
( )
2
4g x f x x m= − +
đồng biến trên
( )
0;2
?
A.
5
. B.
6
. C.
3
. D.
4
.
Câu 55: Cho hàm số
( )
y f x=
là hàm bậc 4, có đạo hàm trên . Đường cong trong hình vẽ bên là đồ
thị hàm số
( )
y f x
=
, (
( )
y f x
=
liên tục trên ). Xét hàm số
( )
( )
2
2g x f x=−
. Hàm số g(x)
đồng biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;1
. C.
( )
;2− −
. D.
( )
1;1−
.
Câu 56: Cho hàm số
( )
y f x=
là hàm bậc 4, có đạo hàm trên . Đường cong trong hình vẽ bên là đồ
thị hàm số
( )
y f x
=
, (
( )
y f x
=
liên tục trên ). Xét hàm số
( )
( )
2
2g x f x=−
. Hàm số g(x)
đồng biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;1
. C.
( )
;2− −
. D.
( )
1;1−
.
Câu 57: Cho hàm số
( )
fx
có đạo hàm liên tục trên và có đồ thị của hàm số
( )
y f x
=
như hình vẽ
bên dưới.
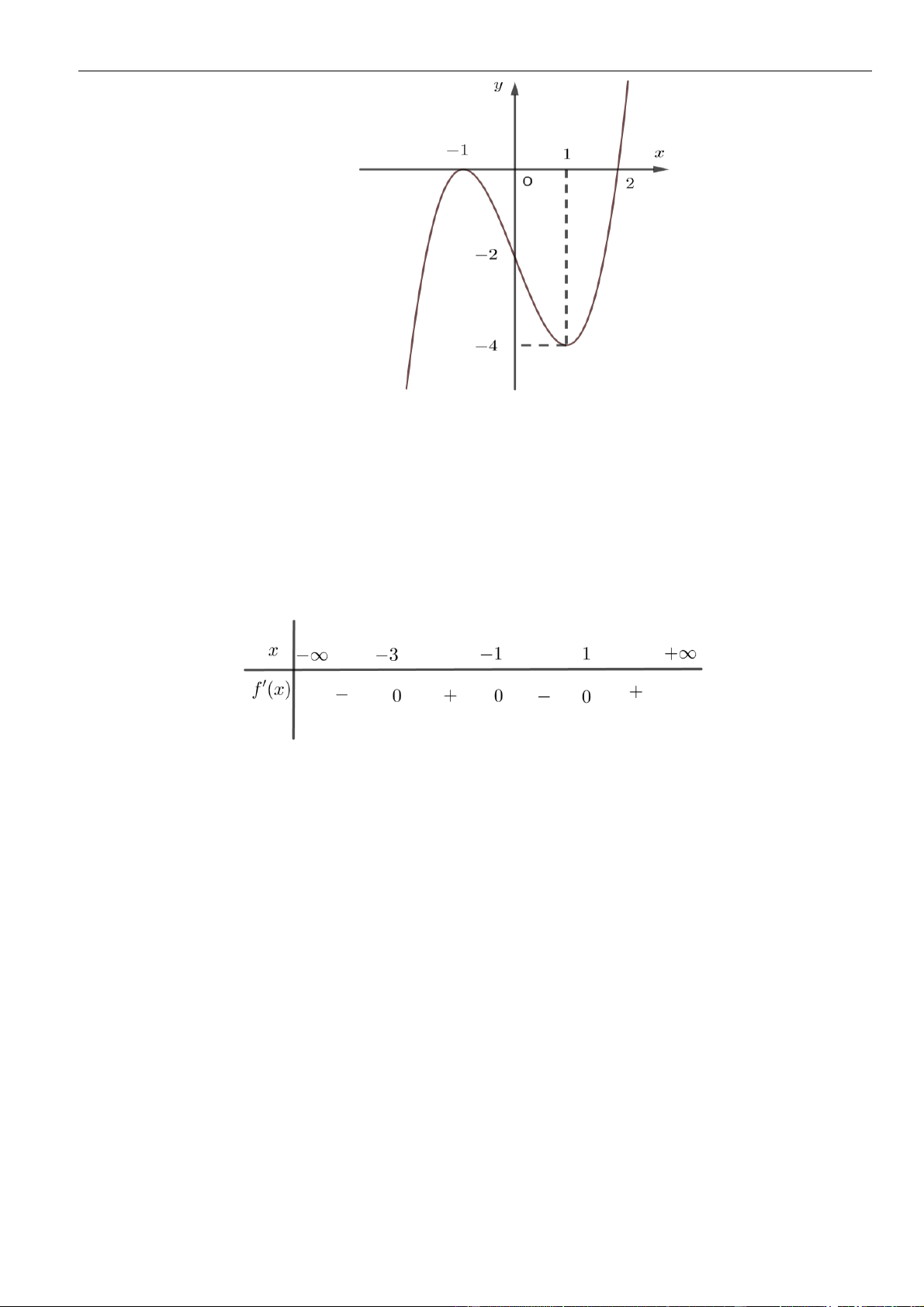
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Xét hàm
( )
( )
2
2g x f x=−
. Mệnh đề nào dưới đây sai?
A. Hàm số
( )
gx
nghịch biến trên
( )
;2− −
.
B. Hàm số
( )
gx
nghịch biến trên
( )
0;2
.
C. Hàm số
( )
gx
nghịch biến trên
( )
1;0−
.
D. Hàm số
( )
gx
đồng biến trên
( )
2;+
.
Câu 58: Cho hàm số
()y f x=
có bảng xét dấu
'( )fx
như sau:
Hàm số
(5 2 )y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
3;4
. B.
( )
1;3
. C.
( )
;3− −
. D.
( )
4;5
.
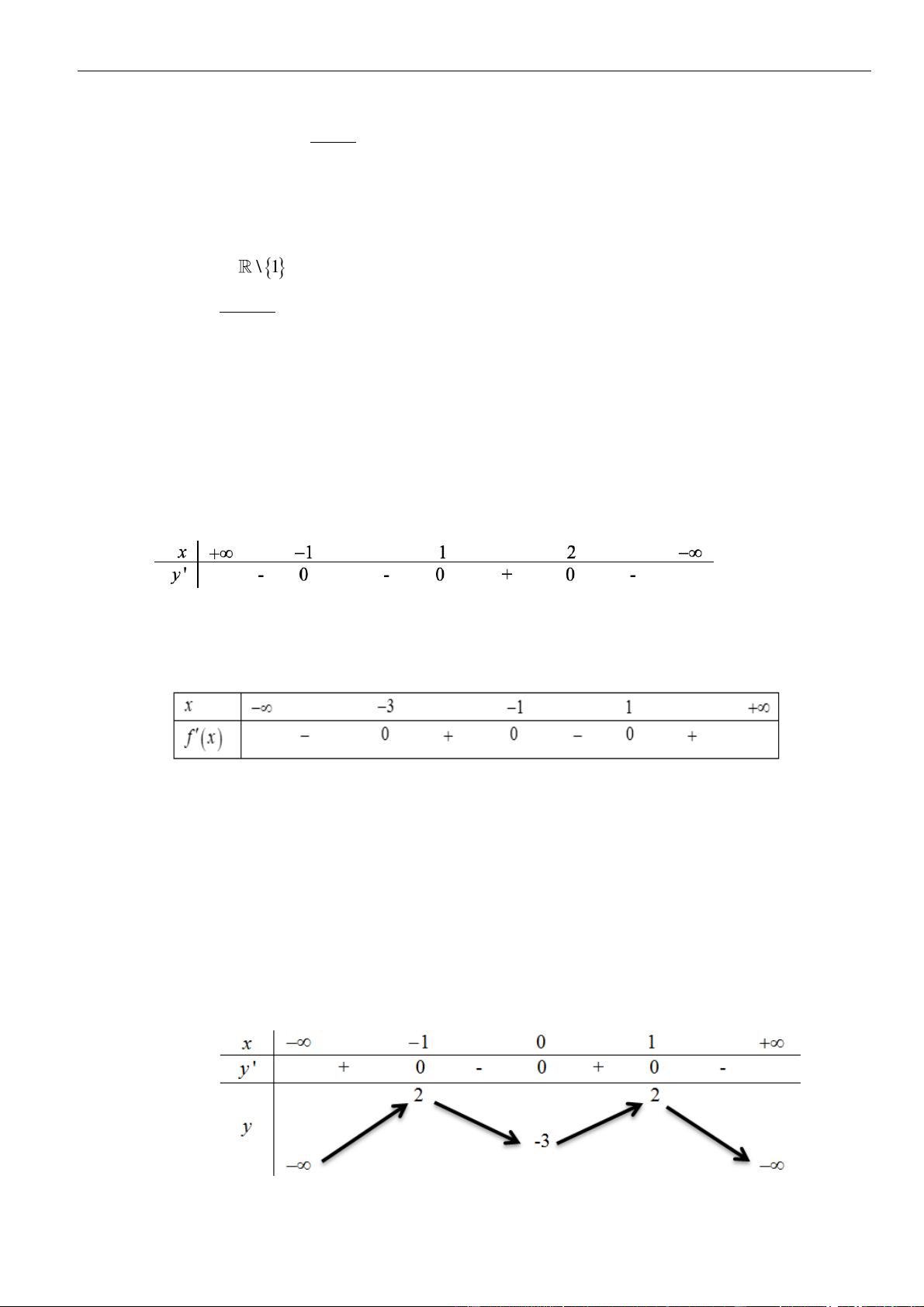
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
32
1
x
x
x
f
+
=
−
. Hàm số nghịch biến trên khoảng nào?
A.
( )
;− +
. B.
( )
;1−
. C.
( )
1; +
. D.
( )
;1−
và
( )
1; +
.
Lời giải
Chọn D
TXD:
\1D =
.
( )
( )
2
5
0,
1
f x x D
x
−
=
−
hàm số nghịch biến trên
( )
;1−
và
( )
1; +
.
Câu 2: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( ) ( )
23
' 1 1 2f x x x x= + − −
. Hàm số
( )
y f x=
đồng biến
trên khoảng nào dưới đây?
A.
( )
1;1−
. B.
( )
2;+
. C.
( )
;1−
. D.
( )
1;2
.
Lời giải
Chọn D
Bảng xét dấu của
'y
Từ bảng trên, hàm số
( )
y f x=
đồng biến trên
( )
1;2
.
Câu 3: Cho hàm số
()fx
có bảng xét dấu
( )
fx
như hình bên
Hàn số
(2 1)fx+
nghịch biến trên khoảng nào dưới đây
A.
( )
1;2−
. B.
( )
2;0−
. C.
( )
1;0−
. D.
( )
0;+
.
Lời giải
Chọn C
Ta có:
( ) ( )
2 1 3 2
2 1 2. 2 1 0
1 2 1 1 1 0
xx
f x f x
xx
+ − −
+ = +
− + −
.
Vậy khoảng nghịch biến của hàm số
(2 1)fx+
là khoảng
( )
1;0−
Câu 4: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau
Hàm số
( )
1 2 1y f x= − +
đồng biến trên khoảng
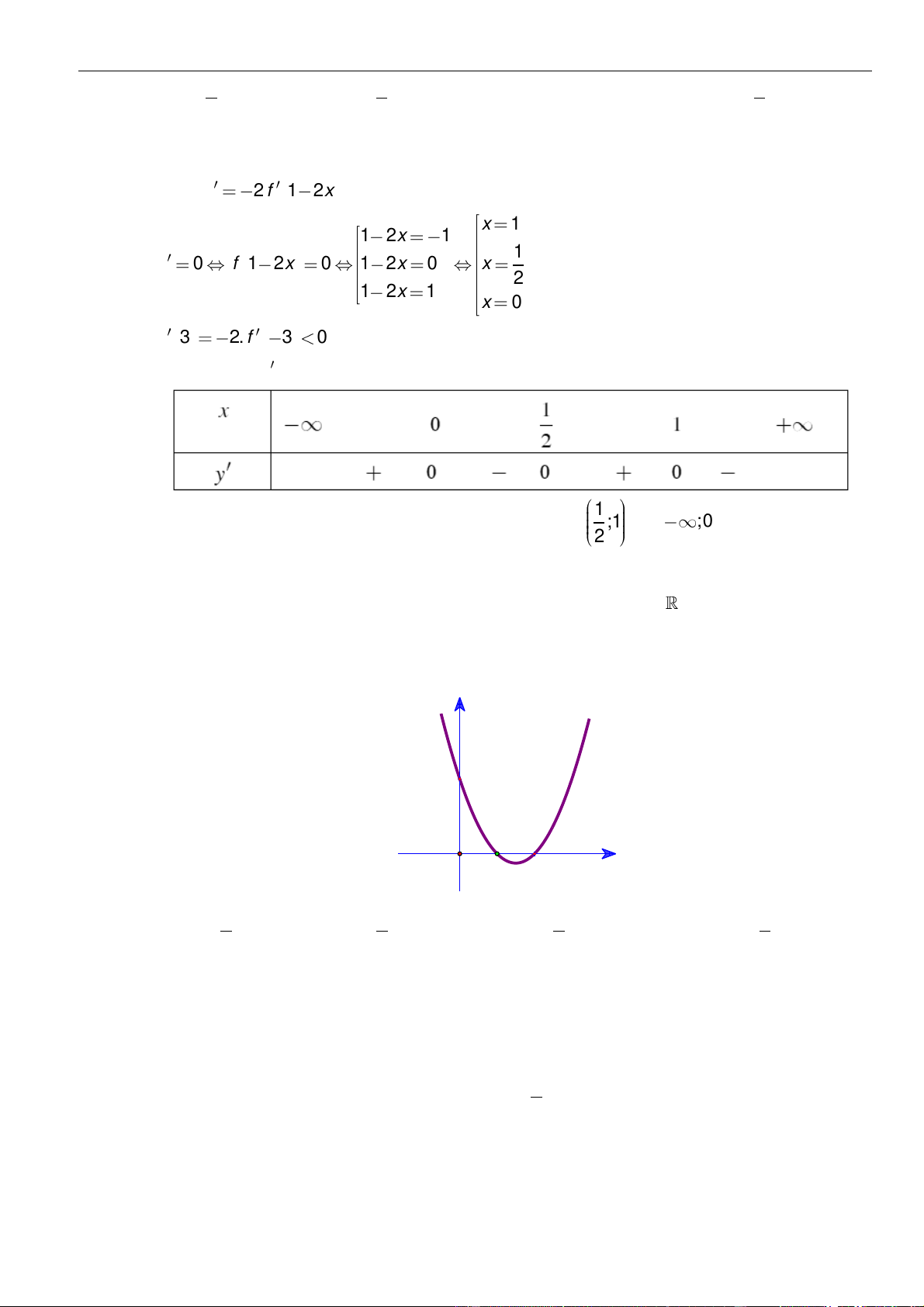
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
A.
3
0;
2
. B.
1
;1
2
. C.
( )
1; +
. D.
1
1;
2
−
.
Lời giải
Chọn B
Ta có
2 1 2y f x
1
1 2 1
1
0 1 2 0 1 2 0
2
1 2 1
0
x
x
y f x x x
x
x
3 2. 3 0yf
.
Bảng xét dấu
y
:
Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng
1
;1
2
và
;0
.
Chọn đáp án B.
Câu 5: Cho hàm số
( )
y f x=
có đạo hàm
( )
fx
xác định và liên tục trên . Hình vẽ bên dưới là đồ
thị của hàm số
( )
y f x
=
. Hàm số
( )
( )
2
g x f x x=−
nghịch biến trên khoảng nào trong các
khoảng dưới đây ?
A.
3
;
2
−
. B.
3
;
2
+
. C.
1
;
2
+
. D.
1
;
2
−
.
Lời giải
Chọn C
Có
( )
( )
( )
2
. 1 2g x f x x x
= − −
.
( )
( )
2
2
2
1
0
1
02
2
1 2 0
1 2 0
xx
f x x
g x x x x
x
x
−=
−=
= − = =
−=
−=
.
Với
0x =
có
( )
( )
( )
2
0 0 0 . 1 2.0 2 0gf
= − − =
, ta có bảng xét dấu của
( )
gx
như sau :
x
y
f'
(x)
2
2
1
O
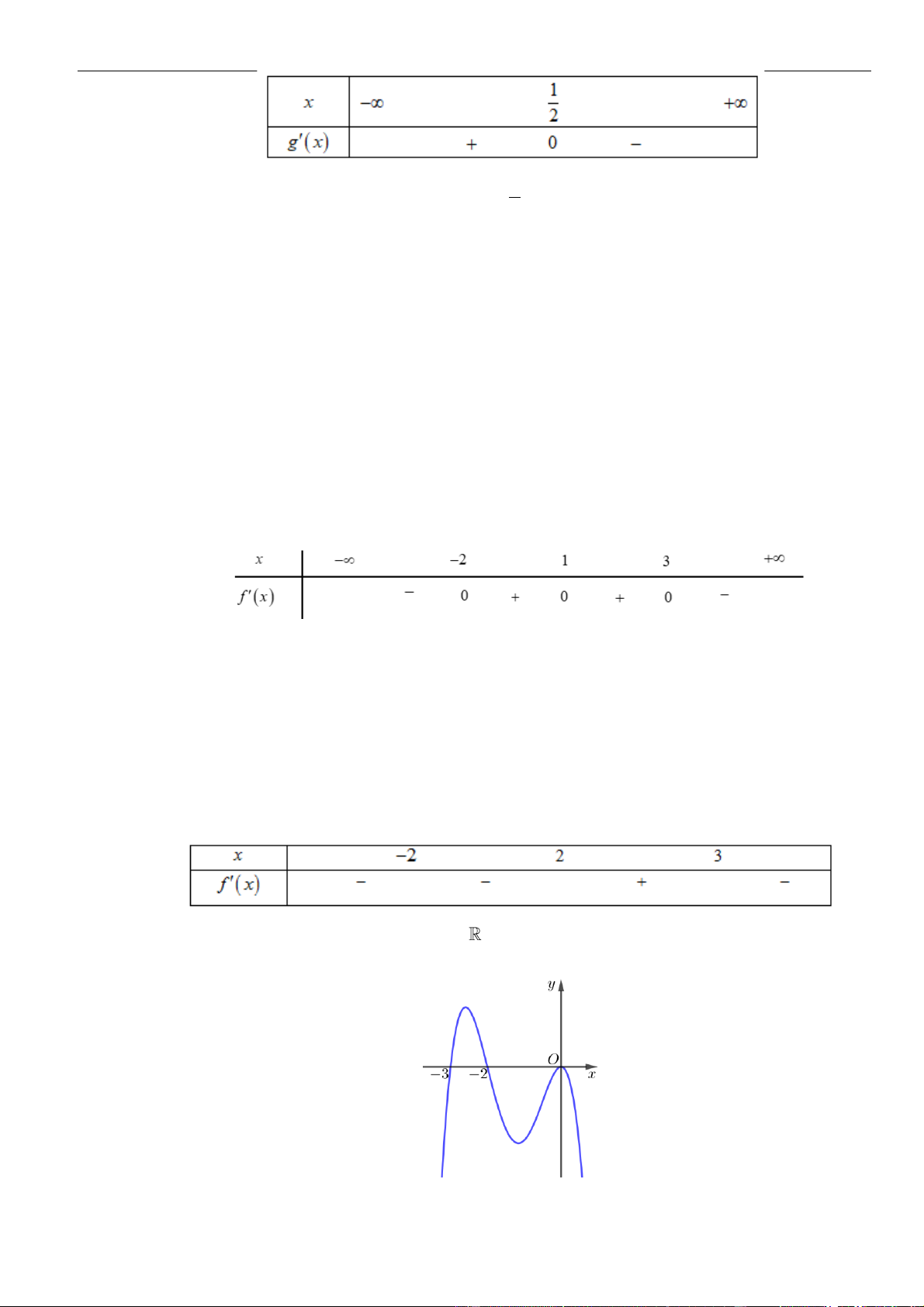
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Suy ra hàm số
( )
gx
nghịch biến trên khoảng
1
;
2
+
.
Câu 6: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( )( )
2
1 2 3f x x x x
= − + −
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên các khoảng
( )
2;1−
và
( )
3; +
.
B. Hàm số đồng biến trên các khoảng
( )
2;1−
và
( )
3; +
.
C. Hàm số đồng biến trên khoảng
( )
2;3−
.
D. Hàm số nghịch biến trên khoảng
( )
2;3−
.
Lời giải
Chọn C
Xét
( )
1
02
3
x
f x x
x
=
= = −
=
. Ta có bảng xét dấu của
( )
fx
như sau:
Dựa vào bảng xét dấu, ta thấy hàm số nghịch biến trên các khoảng
( )
;2− −
và
( )
3; +
, hàm
số đồng biến trên khoảng
( )
2;3−
Câu 7: Cho hàm số có đạo hàm
( ) ( ) ( ) ( )
23
2 2 3f x x x x
= + − −
. Hàm số
( )
y f x=
đồng biến trên
khoảng nào dưới đây?
A.
( )
2;3
. B.
( )
2;2−
C.
( )
3; +
D.
( )
;2− −
Lời giải
Chọn A
Câu 8: Cho hàm số
( )
fx
xác định, liên tục trên và có đồ thị của hàm số
( )
fx
là đường cong như
hình vẽ bên dưới. Hỏi khẳng định nào đúng ?
A. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
2;0−
.
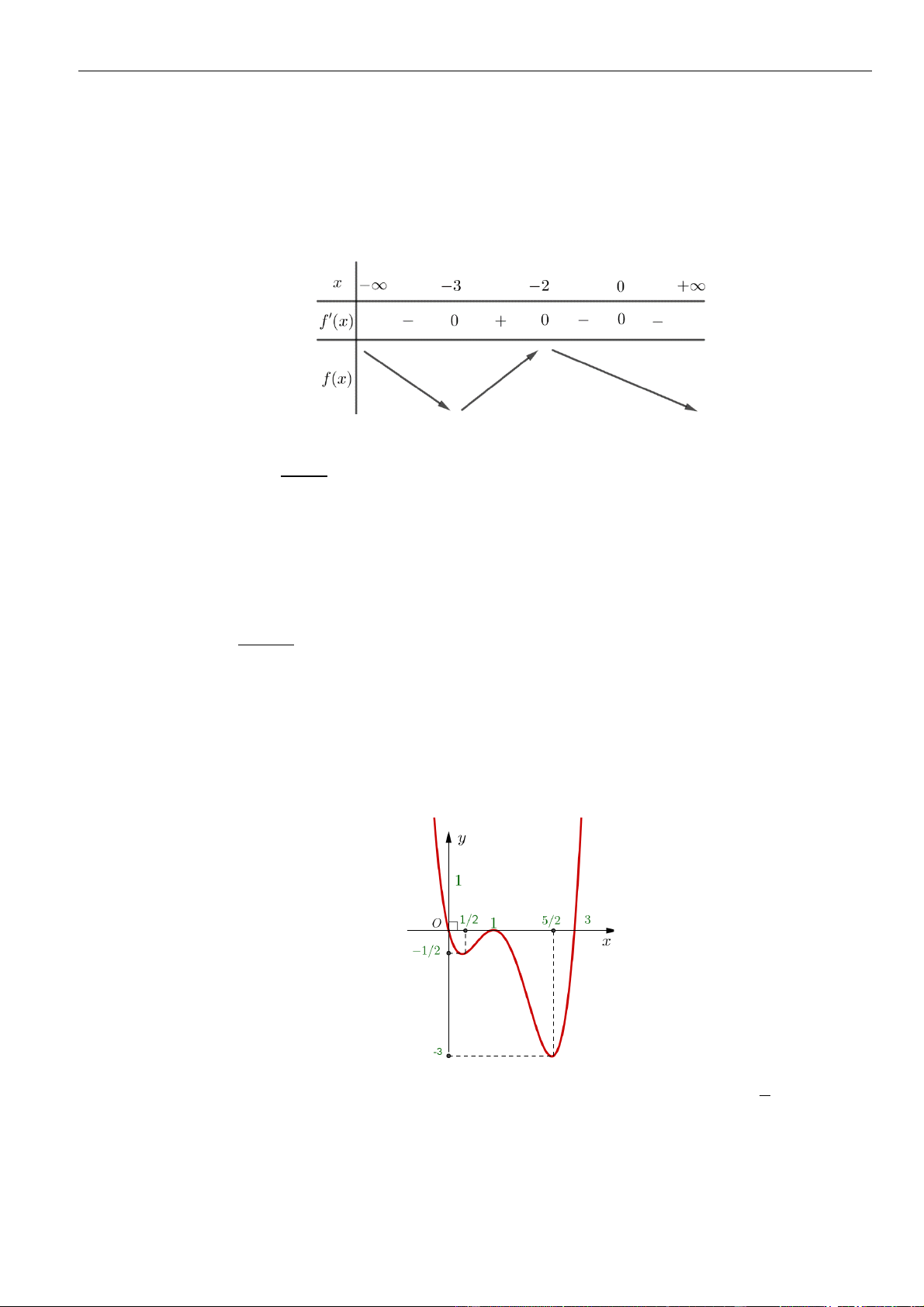
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
B. Hàm số
( )
=y f x
nghịch biến trên khoảng
( )
3; 2−−
.
C. Hàm số
( )
=y f x
nghịch biến trên khoảng
( )
0;+
.
D. Hàm số
( )
=y f x
đồng biến trên khoảng
( )
;3− −
.
Lời giải
Chọn C
Từ đồ thị hàm số
( )
fx
ta có bảng biến thiên:
Từ bảng biến thiên suy ra chỉ có khẳng định C đúng.
Câu 9: Cho hàm số
22
1
x
y
x
+
=
−
. Trong các khẳng định sau, khẳng định nào đúng:
A. Hàm số nghịch biến trên khoảng
( )
0;+
. B. Hàm số đồng biến trên khoảng
( )
;2−
.
C. Hàm số nghịch biến trên khoảng
( )
2;+
. D. Hàm số đồng biến trên khoảng
( )
0;+
.
Lời giải
Chọn C
Ta có
( )
2
4
' 0, 1
1
yx
x
−
=
−
hàm số nghịch biến trên khoảng
( )
;1−
và
( )
1; +
Mà
( ) ( )
2; 1;+ +
nên hàm số cũng nghịch biến trên khoảng
( )
2;+
Câu 10: Cho hàm số
()y f x=
có đạo hàm
()fx
trên khoảng
( ; )− +
. Đồ thị hàm số
()y f x
=
như
hình vẽ. Hàm số
()y f x=
nghịch biến trên khoảng nào trong các khoảng sau?
A.
( ;0)−
. B.
( )
0;3
. C.
(3; )+
. D.
5
;
2
−
.
Lời giải
Chọn B
Hàm số
( )
y f x=
nghịch biến khi
( ) ( )
0 0;3f x x
.
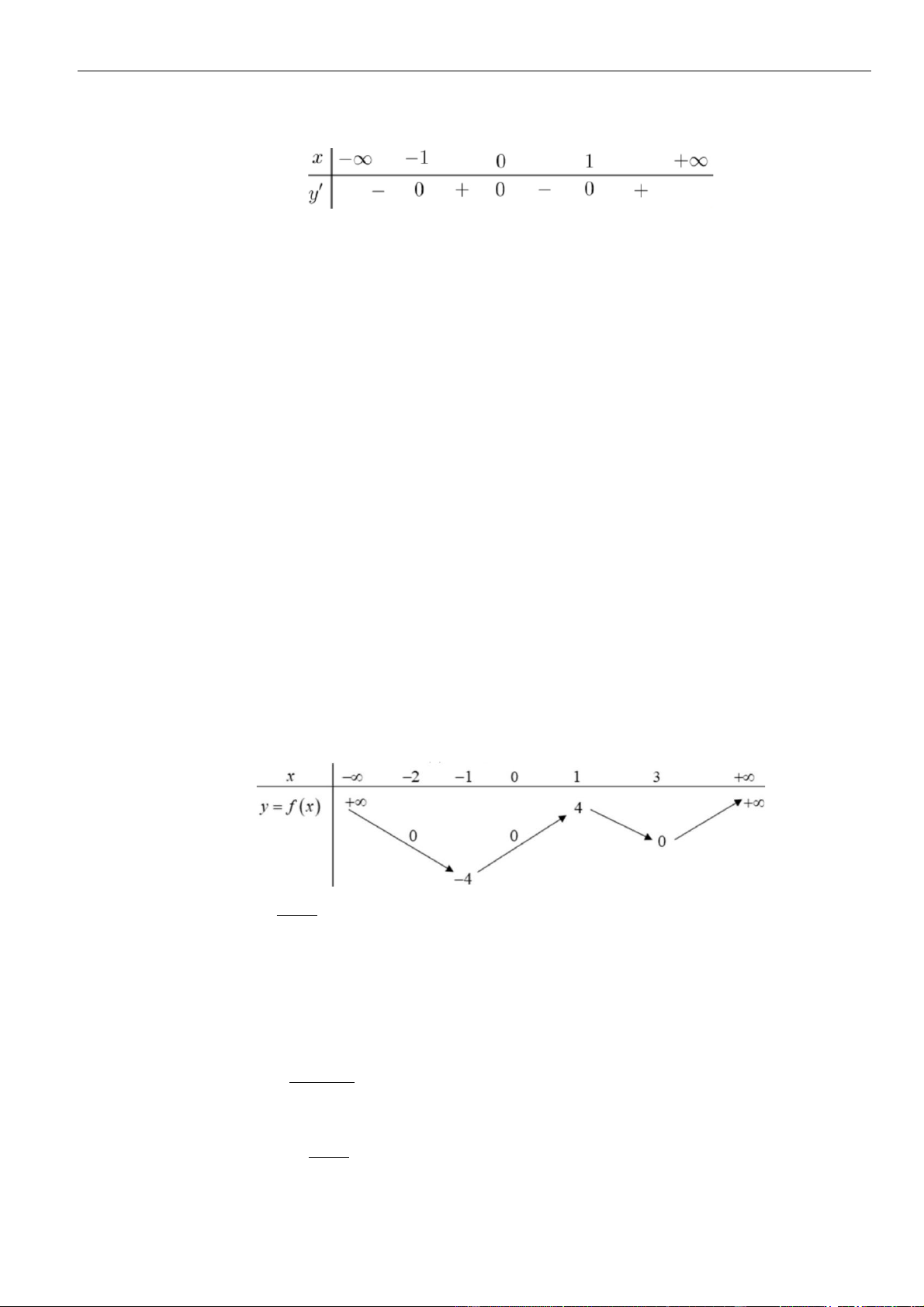
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
(Đồ thị
( )
y f x
=
nằm phía dưới trục hoành,
( )
0fx
=
khi
1x =
)
Câu 11: Hàm số
( )
32y f x=−
có bảng xét dấu của đạo hàm như sau:
Hàm số
( )
y f x=
nghịch biến trên khoảng nào dưới đây?
A.
( )
3;5
. B.
( )
1;2−
. C.
( )
1;3
. D.
( )
5;+
.
Lời giải
Chọn A
Xét hàm số
( )
32y f x=−
Ta có
( )
2. 3 2y f x
= − −
Từ bảng xét dấu, ta có
1 3 2 5
0 0 3 2 3
1 3 2 1
xx
y x x
xx
= − − =
= = − =
= − =
( ) ( )
1 0 3 3 2 5
0 2. 3 2 0 3 2 0
1 3 2 1
xx
y f x f x
xx
− −
− − −
−
Đặt
( )
35
3 2 0
1
t
t x f t
t
= −
Xét hàm số
( )
y f x=
có
( )
y f x
=
Hàm số nghịch biến khi
( )
35
00
1
x
y f x
x
.
Câu 12: Cho hàm số
( )
=y f x
có bảng biến thiên như sau:
Hàm số
( )
( )
=
1
gx
fx
đồng biến trên khoảng nào sau đây?
A.
( )
−2 ; 0
. B.
( )
+3;
. C.
( )
1; 2
. D.
( )
− −;1
Lời giải
Chọn C
Ta có :
( )
( )
( )
( )
( )
( )
− −
= − − −
−
2
12
0
0 1 3 2 1
0
13
2;0 ;3
xx
fx
fx
g x x x
fx
fx
x
x
.
Vậy hàm số
( )
( )
=
1
gx
fx
đồng biến trên các khoảng
( )
− −;2
,
( )
−−2 ; 1
và
( )
1; 3
.
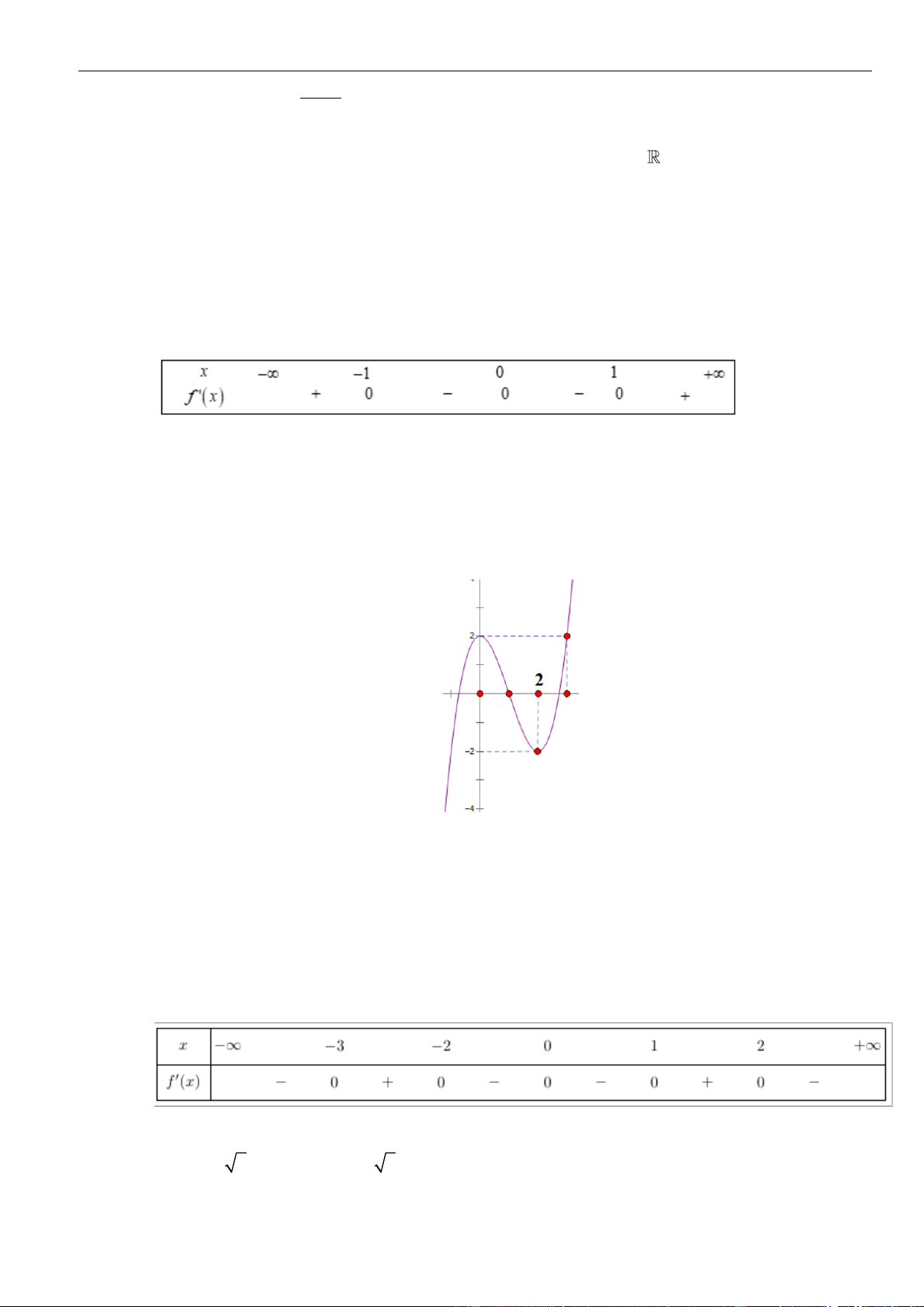
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
hàm số
( )
( )
=
1
gx
fx
đồng biến trên khoảng
( )
1; 2
.
Câu 13: Cho hàm số
( )
y f x=
có đạo hàm
( )
( )
22
' 1 ,y f x x x x= = −
. Hàm số
( )
y f x=−
đồng
biến trên khoảng nào
A.
( )
2;+
. B.
( )
0;2
. C.
( )
1;1−
. D.
( )
;1− −
.
Lời giải
Chọn C
Ta có:
( )
0
'0
1
x
fx
x
=
=
=
( )
' '( )y f x y f x= − = − −
Hàm số
( )
y f x=−
đồng biến khi và chỉ khi
( )
'( ) 0 ' 0f x f x− − −
1 1 1 1xx − − −
Câu 14: Cho hàm số
( )
fx
có đồ thị như hình vẽ bên. Hàm số
( )
32y f x= − −
nghịch biến trên khoảng
A.
( )
2;4
. B.
( )
;1−
. C.
( )
0;3
. D.
( )
3; +
.
Lời giải
Chọn B
Ta có:
( ) ( )
22
' 3 2 0 2 0
20
x
y f x f x
x
−
= − − −
−
4
2
x
x
Câu 15: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên dưới.
Hàm số
( )
2
1y f x=−
nghịch biến trên khoảng
A.
( )
2; 3−−
. B.
( )
3;2
. C.
( )
2;+
. D.
( )
1;1−
.
Lời giải
Chọn B
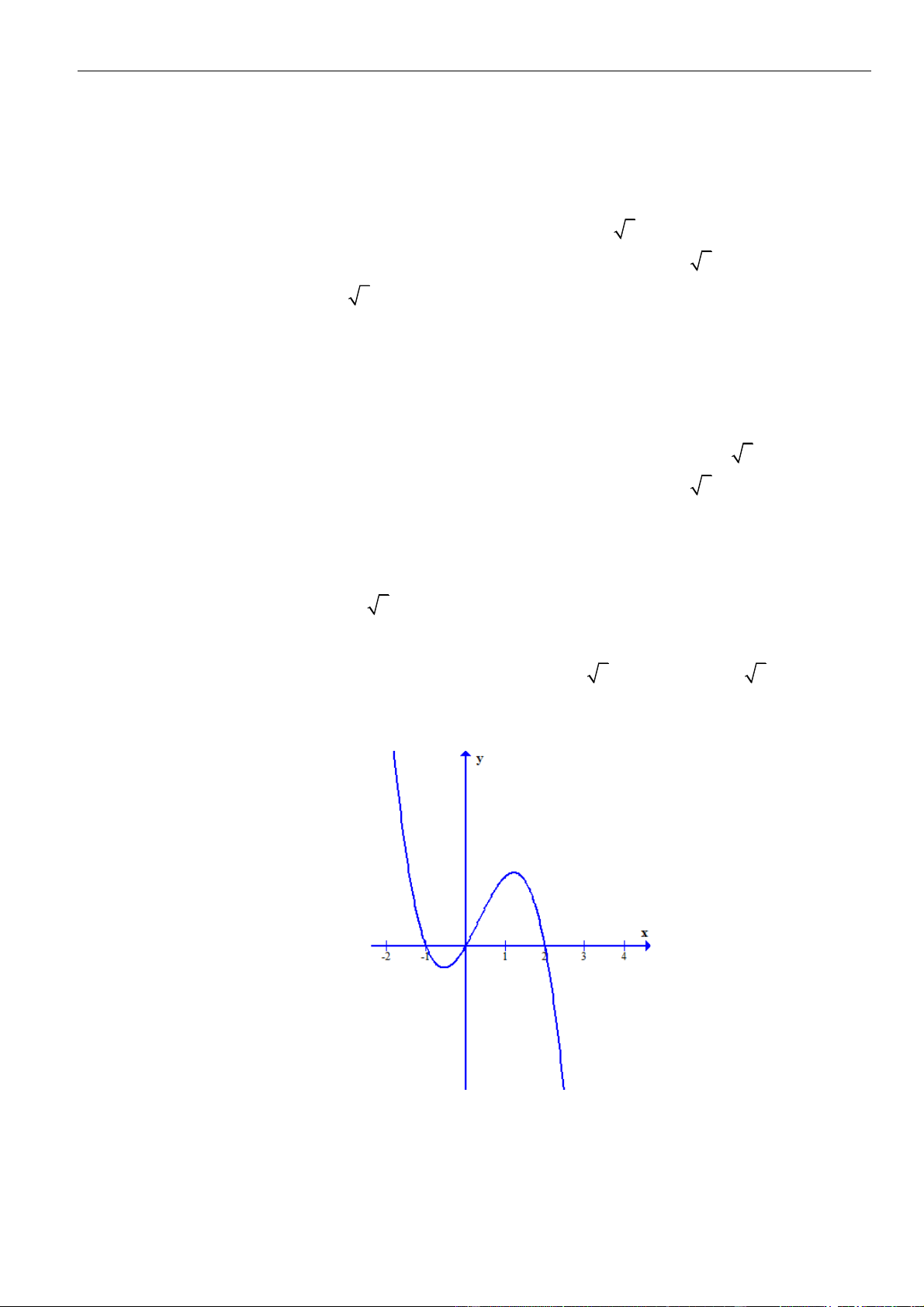
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Ta có
( )
2
21y xf x
= − −
.
Xét
( ) ( )
22
2 1 0 1 0xf x xf x
− − −
.
TH1:
( )
( )
2
0
1 0 1
x
fx
−
.
Từ giả thiết ta có
( )
22
22
3 1 2 3 4 3 2
1
1 1 2 1 0
23
x x x
xx
x
− − −
− −
− −
.
Kết hợp với
0x
suy ra
32x
.
TH2:
( )
( )
2
0
1 0 2
x
fx
−
.
Từ giả thiết ta có
( )
22
22
22
22
2
2
1 3 4
2 1 0 1 3 1 3
2
0 1 1 0 1
31
01
1 2 1
10
x
x
xx
xxx
xx
x
x
xx
x
−
− −
− −
−
− −
− −
−
.
Kết hợp với
0x
suy ra
2
31
10
x
x
x
−
− −
−
.
Từ đó suy ra
( )
2
1y f x=−
nghịch biến trên
( )
;2− −
,
( )
3; 1−−
,
( )
1;0−
và
( )
3;2
.
Câu 16: Cho hàm số đa thức bậc bốn
()fx
. Đồ thị hàm số
( )
32y f x
=−
được cho như hình sau:
Hàm số
()y f x=
nghịch biến trên khoảng
A.
( )
;1− −
. B.
( )
5;+
. C.
( )
1;1−
. D.
( )
1;5
.
Lời giải
Chọn A
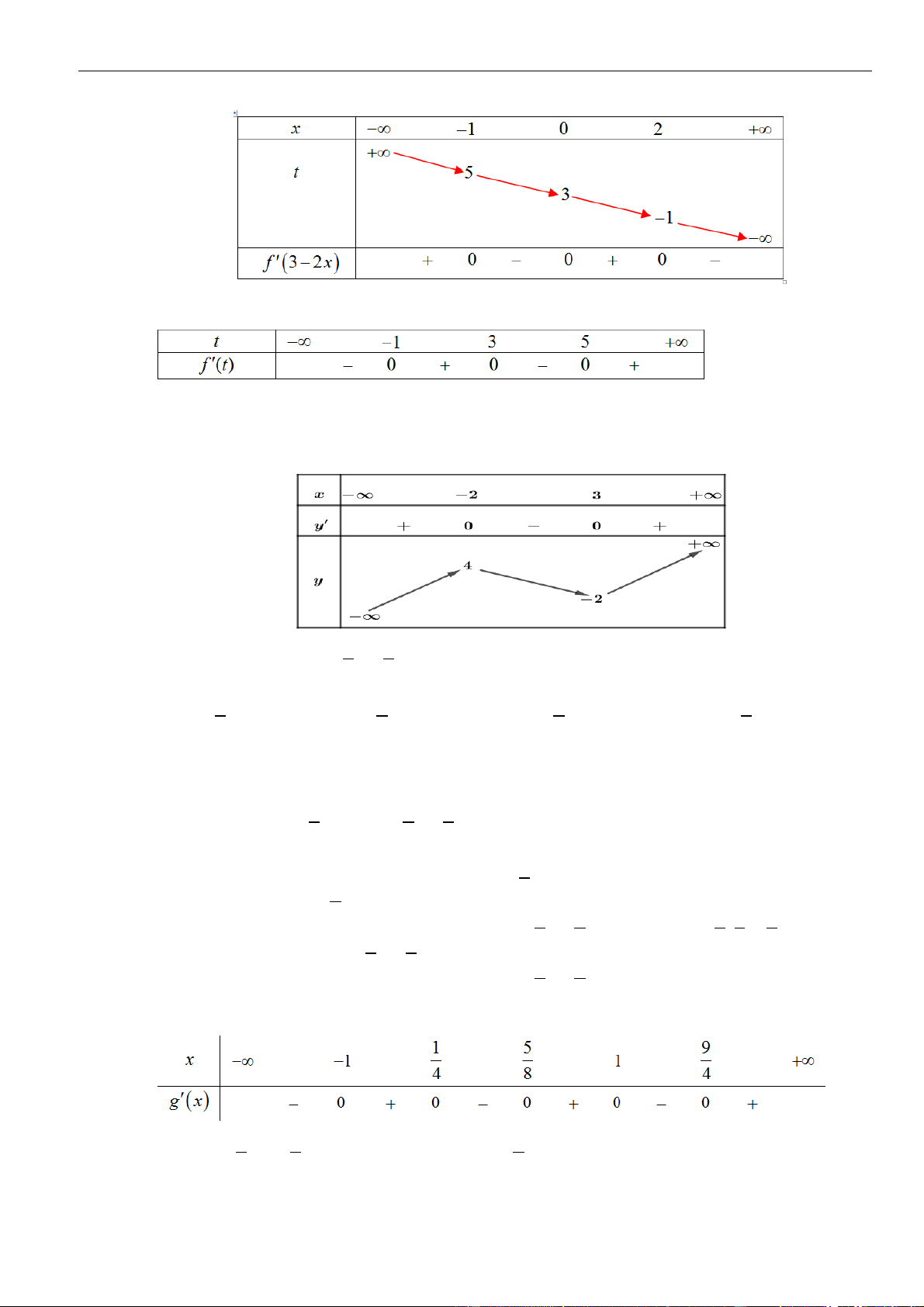
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Đặt
32tx=−
. Ta có bảng xét dấu của
( )
32fx
−
được mô tả lại như sau:
Từ đó suy ra bảng xét dấu của
()ft
:
Vậy hàm số
()y f x=
nghịch biến trên các khoảng
( )
;1− −
và
( )
3;5
.
Câu 17: Cho hàm số
( )
y f x=
có bảng biên thiên như hình vẽ
Hàm số
( )
2
53
2
22
g x f x x
= − −
nghịch biến trên khoảng nào trong các khoảng sau?
A.
1
1;
4
−
. B.
1
;1
4
. C.
9
;
4
+
. D.
5
1;
4
.
Lời giải
Chọn D
Ta có
( )
2
5 5 3
42
2 2 2
g x x f x x
= − − −
.
Xét
( )
2
2
2
5
5
8
40
2
5 3 1 5 9
0 2 2 1; ; ;1;
53
2 2 4 8 4
20
53
22
23
22
x
x
g x x x x
f x x
xx
=
−=
= − − = − −
− − =
− − =
.
Bảng biến thiên:
(
( ) ( )
5 3 1
0 0 0, 1;
2 2 4
g f g x x
= − − −
)
Đối chiếu các đáp án ta Chọn D
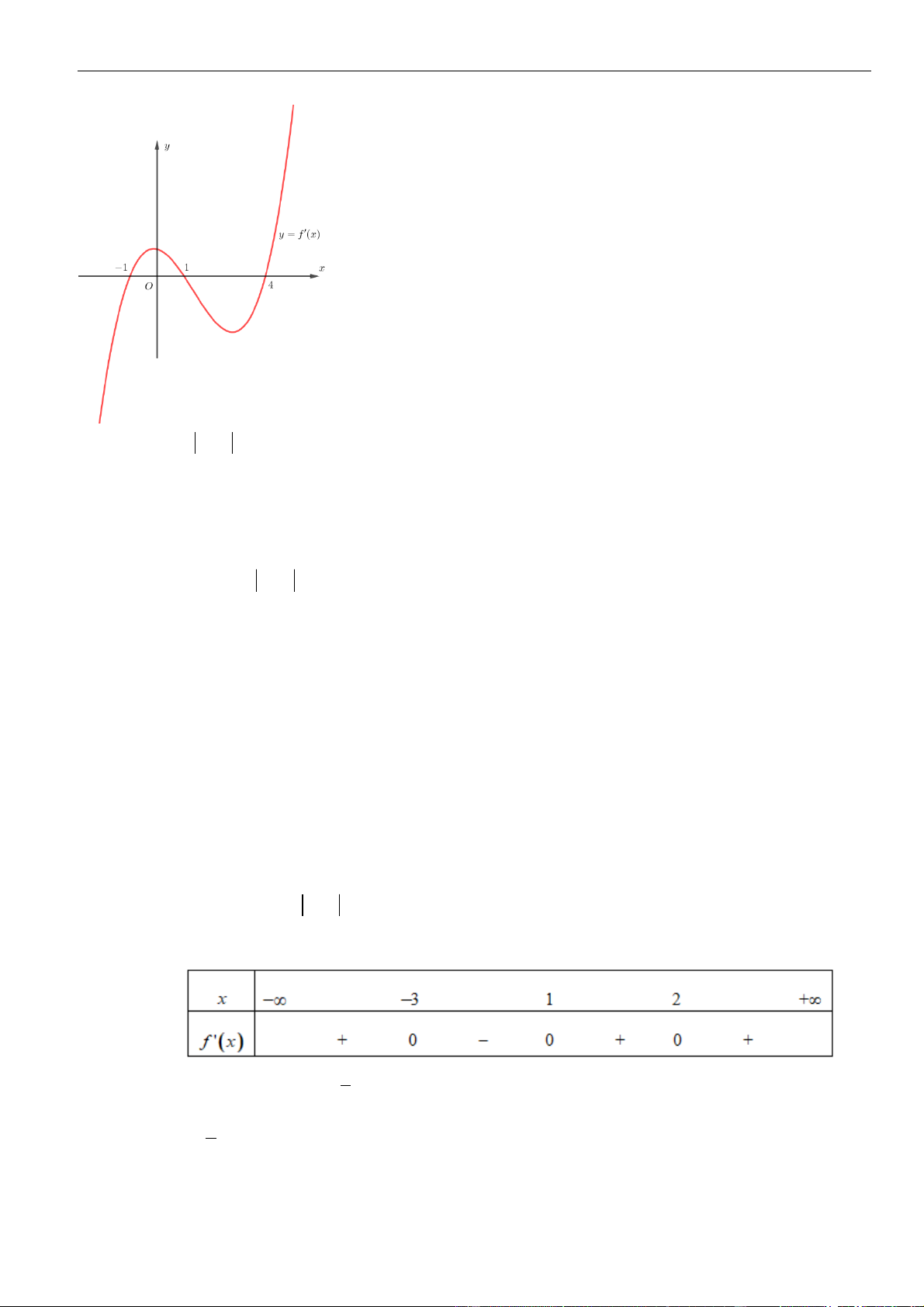
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Câu 18: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
2;3
. B.
( )
4;7
. C.
( )
;1− −
. D.
( )
1;2−
.
Lời giải
Chọn D
Ta có
( )
( )
( )
33
3
33
f x khi x
y f x
f x khi x
−
= − =
−
.
Suy ra
( )
( )
33
33
f x khi x
y
f x khi x
− −
=
−
.
Với
3x
ta có
( ) ( )
3 1 4
3 0 3 0
1 3 4 1 2
xx
y f x f x
xx
− −
= − − −
− −
.
Kết hợp với điều kiện
3x
ta có
12x−
.
Với
3x
ta có
( )
3 4 7
30
1 3 1 2 4
xx
y f x
xx
−
= −
− −
.
Kết hợp với điều kiện
3x
ta có
7
34
x
x
.
Vậy hàm số
( )
3y f x=−
đồng biến trên mỗi khoảng
( ) ( ) ( )
1;2 ; 3;4 ; 7;− +
.
Câu 19: Cho hàm số
( )
fx
có bảng xét dấu của
( )
'fx
như sau:
Hàm số
( )
32
1
2 3 5 1
3
x x x x
y f e e e e= − − + − +
đồng biến trên khoảng nào dưới đây?
A.
3
0;
2
. B.
( )
1;3
. C.
( )
3;0−
. D.
( )
4; 3−−
.
Lời giải
Chọn C
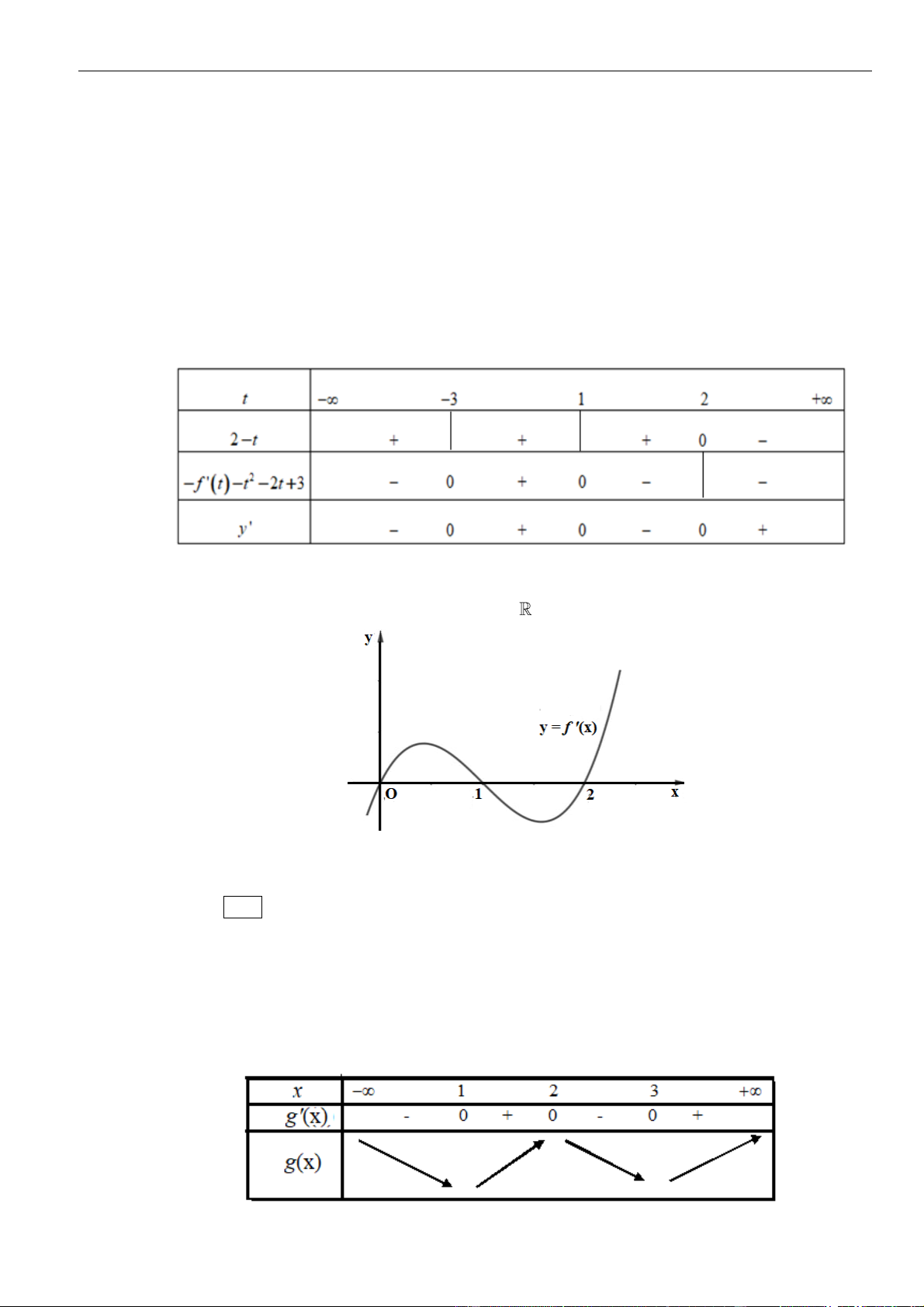
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
Ta có
( ) ( )
3 2 2
' . ' 2 6 5 ' 2 6 5
x x x x x x x x x
y e f e e e e e f e e e
= − − − + − = − − − + −
.
Đặt
2
x
te=−
, ta được:
( ) ( ) ( ) ( ) ( ) ( )
2
2
' 2 ' 2 6 2 5 2 ' 2 3y t f t t t t f t t t
= − − − − + − − = − − − − +
.
( ) ( )
( )
2
2
2
' 0 2 ' 2 3 0
' 2 3
t
y t f t t t
f t t t
=
= − − − − + =
= − − +
Hàm số
( )
2
23g x x x= − − +
là parabol có trục đối xứng
1x =−
và cắt trục hoành tại 2 điểm
có hoành độ
1
3
x
x
=
=−
. Suy ra
( )
2
1
' 2 3
3
t
f t t t
t
=
= − − +
=−
.
Bảng xét dấu:
Dựa vào bảng xét dấu
( )
' 0, 3;0yx −
.
Câu 20: Cho hàm số
( )
y f x=
liên tục, có đạo hàm trên . Đồ thị hàm số
( )
'y f x=
như hình vẽ sau:
Hàm số
( )
3y f x=−
nghịch biến trên khoảng
( )
2;b
. Giá trị lớn nhất của
b
bằng bao nhiêu?
Lời giải
Đáp án: 31aa
Đặt
( ) ( ) ( ) ( )
3 ' ' 3g x f x g x f x= − = − −
Ta có:
( ) ( )
3 0 3
0 3 0 3 1 2
3 2 1
xx
g x f x x x
xx
− = =
= − = − = =
− = =
Bảng biến thiên
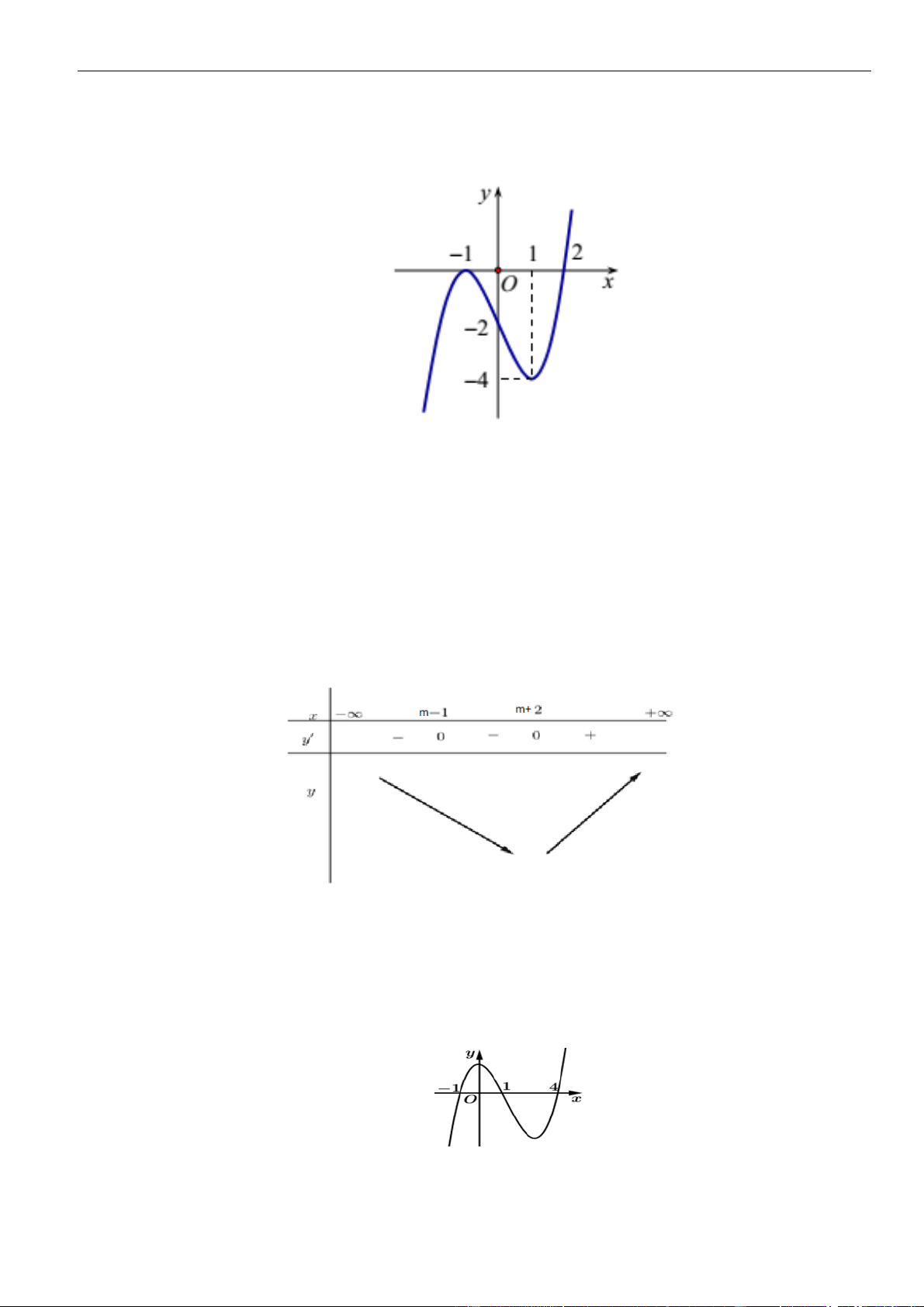
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
Dựa vào bảng biến thiên ta có hàm số
( ) ( )
3y g x f x= = −
nghịch biến trên khoảng
( )
2;3
, suy
ra
3b
. Vậy giá trị lớn nhất của
b
là
3
Câu 21: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị như hình vẽ
Gọi
S
là tập hợp tất cả các giá trị nguyên dương của tham số
m
sao cho hàm số
( )
y f x m=−
đồng biến trên khoảng
( )
2020;+
. Số phần tử của tập
S
là
A.
2020
. B.
2019
. C.
2018
. D. vô số.
Lời giải
Chọn C
Xét hàm số
( ) ( )
y f x m y f x m
= − = −
, đồ thị hàm số
( )
y f x m
=−
chính là đồ thị hàm
số
( )
y f x
=
tịnh tiến dọc theo trục hoành sang phải
m
đơn vị nên hàm số
( )
y f x m=−
có
BBT như sau:
Dựa vào BBT ta thấy hàm số đồng biến trên khoảng
( )
2;m + +
. Để hàm số đồng biến trên
khoảng
( )
2020;+
thì
2 2020 2018mm+
Do
m
nguyên dương nên có
2018
giá trị thỏa mãn.
Câu 22: Cho hàm số
( )
=y f x
. Hàm số
( )
=y f x
có đồ thị như hình bên dưới.
Hàm số
( )
3 2 2020= − +y f x
nghịch biến trên khoảng nào?
A.
( )
1;1−
. B.
( )
2;+
. C.
( )
1;2
. D.
( )
;1−
.
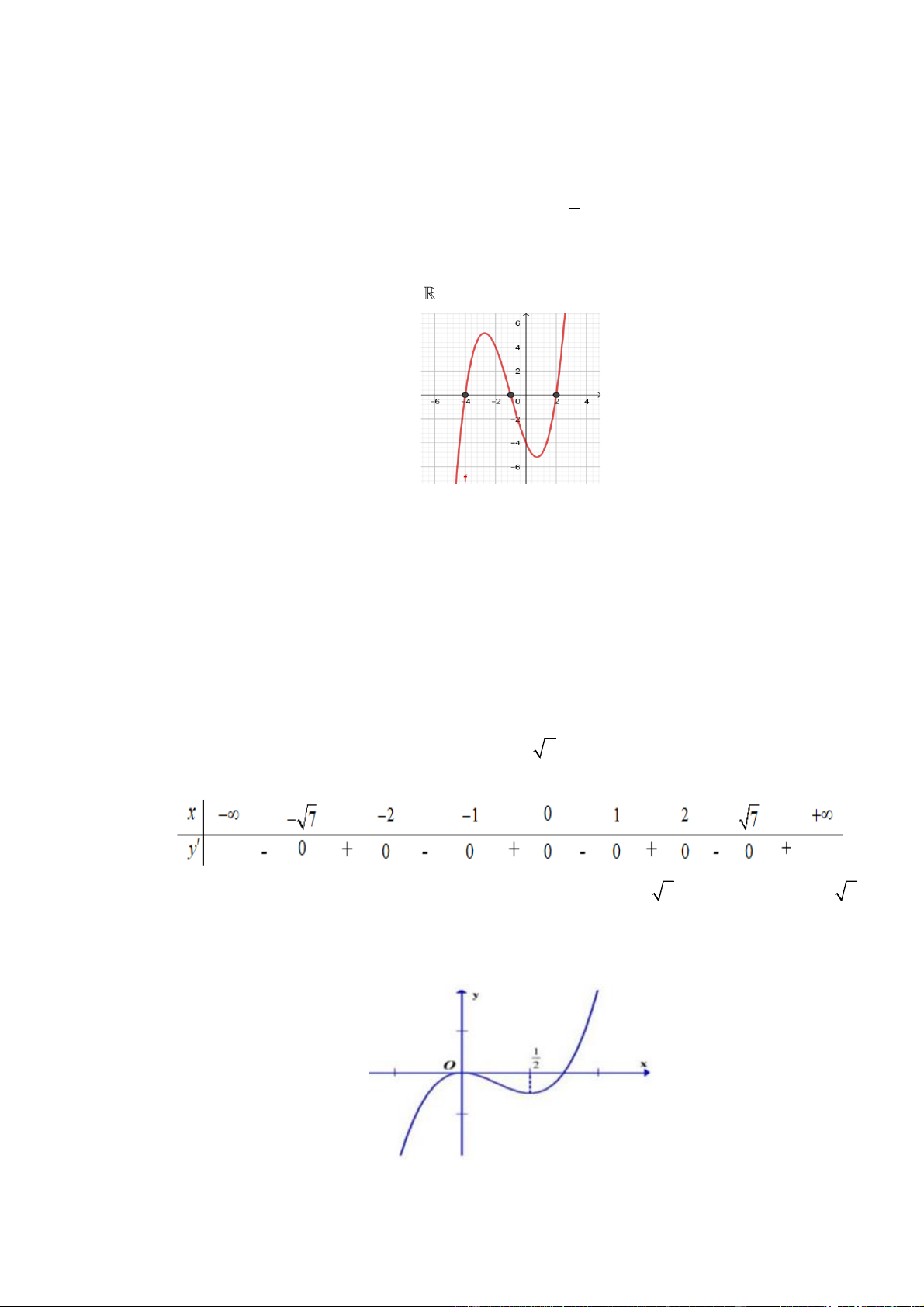
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
27 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn C
( )
2 3 2y f x
= − −
.
( )
12
1 3 2 1
0 3 2 0
1
3 2 4
2
x
x
y f x
x
x
− −
−
−
−
.
Vậy hàm số
( )
3 2 2020y f x= − +
nghịch biến trên khoảng
( )
1;2
.
Câu 23: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị
( )
y f x
=
như hình vẽ sau
Hàm số
( )
2
5y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;2
. B.
( )
0;1
. C.
( )
1;0−
. D.
( )
1;1−
.
Lời giải
Chọn B
Ta có:
( )
2
' 2 ' 5y xf x=−
.
( )
2
2
2
2
0
0
0
1
54
0
2
50
51
52
7
x
x
x
x
x
y
x
fx
x
x
x
=
=
=
=
− = −
=
=
−=
− = −
−=
=
.
Bảng xét dấu đạo hàm
Ta thấy hàm số
( )
2
5y f x=−
nghịch biến trên các khoảng
( )
;7− −
,
( )
2;1−
,
( )
0;1
,
( )
2; 7
, do đó chọn phương án. B.
Câu 24: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ
Hàm số
( )
sinfx
nghịch biến trên các khoảng nào sau đây
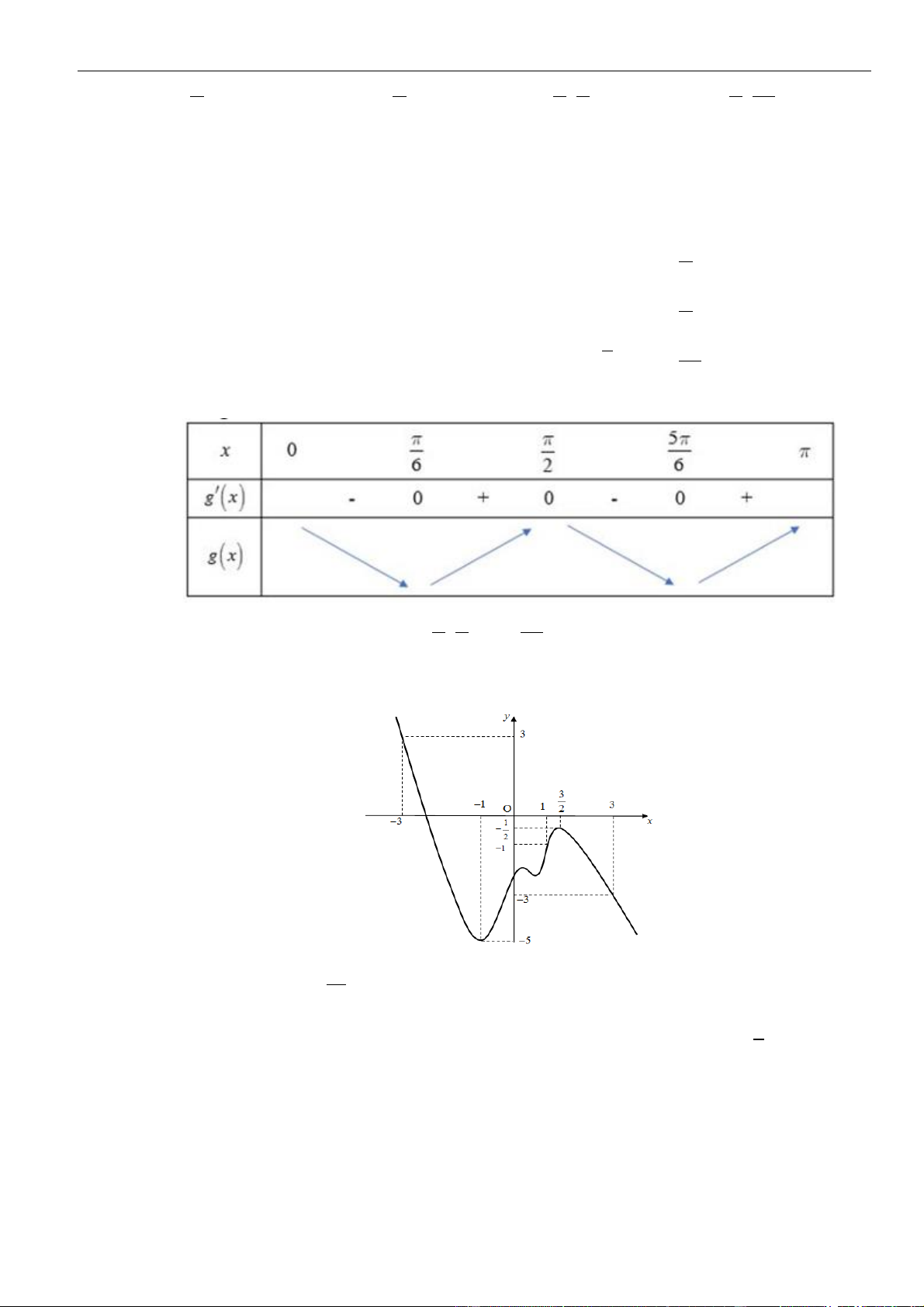
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 28
A.
;
2
. B.
0;
3
. C.
;
62
. D.
5
;
66
.
Lời giải
Chọn C
Dựa vào đồ thị hàm số
()y f x=
ta có:
Đặt
( ) (sin ) ( ) cos . (sin ).g x f x g x x f x
= =
Ta xét trên khoảng
(0; )
2
cos 0
cos 0
( ) 0 cos . (sin ) 0 sin 0
(sin ) 0
6
1
5
sin
2
6
x
x
x
g x x f x x x
fx
x
x
=
=
=
= = = =
=
=
=
Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng
;
62
và
5
;
6
.
Câu 25: Cho hàm số
( )
y f x=
có đồ thị
( )
fx
như hình vẽ
Hàm số
( )
2
1
2
x
y f x x= − + −
nghịch biến trên khoảng nào?
A.
( )
1;3
. B.
( )
−3;1
. C.
( )
−2;0
. D.
−
3
1;
2
Lời giải
Chọn C
Ta có
( )
= − − + − 1 1 0y f x x
.
Đặt
1tx=−
ta được:
( ) ( )
0f t t f t t
− − −
.
Dựa vào tương giao đồ thị hai hàm số
( )
y f t
=
và
yt=−
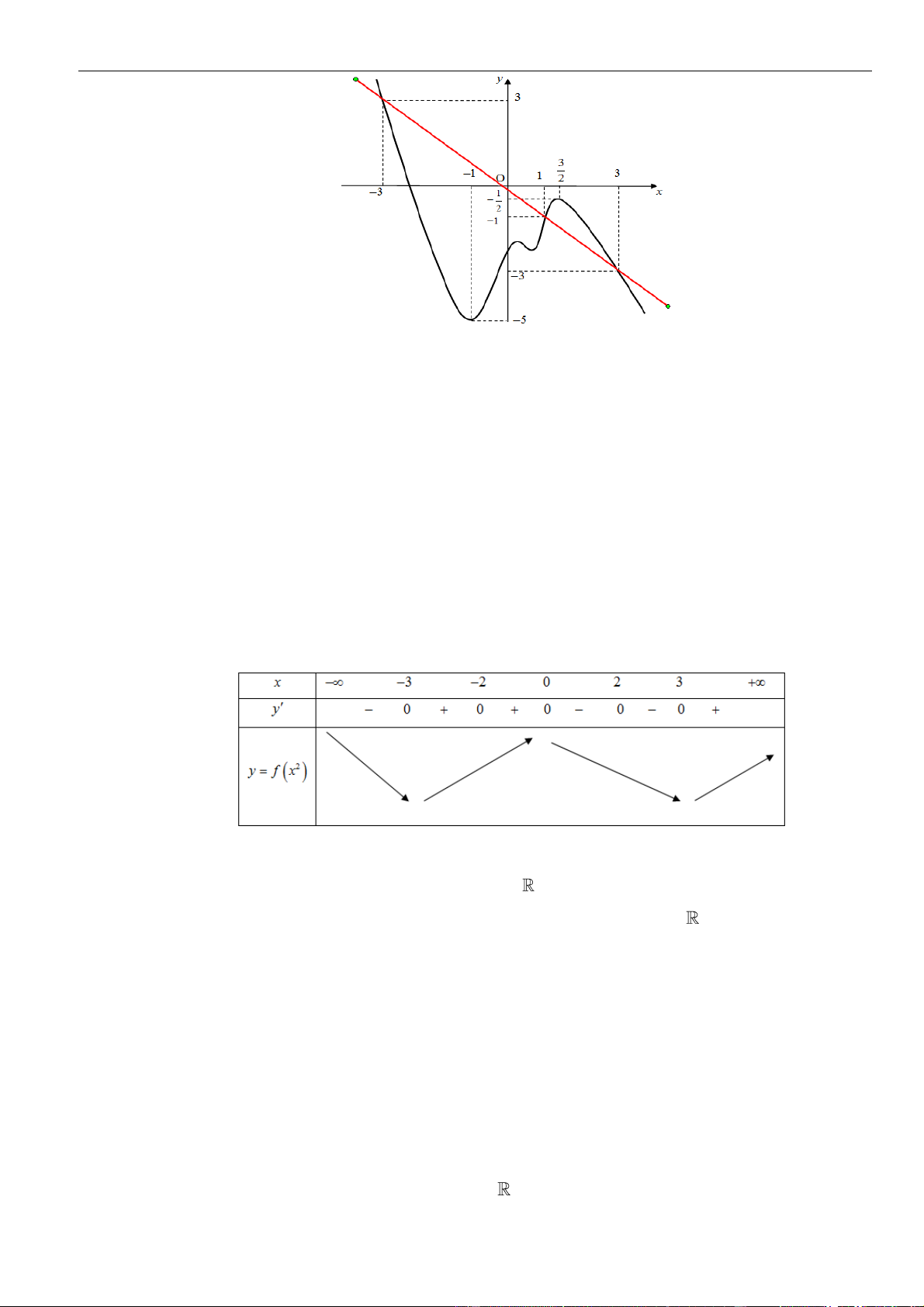
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
29 | Facebook tác giả: Phan Nhật Linh
Ta được:
3 1 3 4
1 3 1 1 3 2 0
t x x
t x x
− − −
− −
.
Câu 26: Cho hàm số
( )
=y f x
có đạo hàm
( ) ( )( )
2
2
94f x x x x
= − −
. Khi đó hàm số
( )
2
y f x=
nghịch
biến trên khoảng nào
A.
( )
−3;0
. B.
( )
+3;
.
C.
( )
− −;3
. D.
( )
−2;2
Lời giải
Chọn C
Ta có
( )
( )
( )
22
' 2 . 0y f x x f x
= = =
( )( )
2
4 2 2
0
0
3
9 4 0
2
x
x
x
x x x
x
=
=
=
− − =
=
Bảng biến thiên
Dựa vào BBT ta có hàm số nghịch biến trên
( )
;3− −
và
( )
0;3
.
Câu 27: Cho hàm số
()y f x=
xác định trên và có đạo hàm
()fx
thỏa mãn
( )( )
( ) 1 2 ( ) 2018f x x x g x
= − + +
trong đó
( ) 0,g x x
. Hàm số
( )
1 2018 2019y f x x= − + +
đồng biến trên khoảng nào?
A.
( )
1; +
. B.
( )
0;3
. C.
( )
3; +
. D.
( )
;3−
.
Lời giải
Chọn C
Ta có:
( )( ) ( ) ( )
( ) 1 2 ( ) 2018 (1 ) 3 1 2018f x x x g x f x x x g x
= − + + − = − − +
( )
1 2018 2019y f x x= − + +
( ) ( ) ( ) ( ) ( )
' 1 3 1 2018 2018 3 1y f x x x g x x x g x
= − − = − − − − + = − − −
Suy ra
0
'0
3
x
y
x
=
=
=
. Vì
( )
1 0,g x x−
nên ta có bảng xét dấu của
y
như sau:
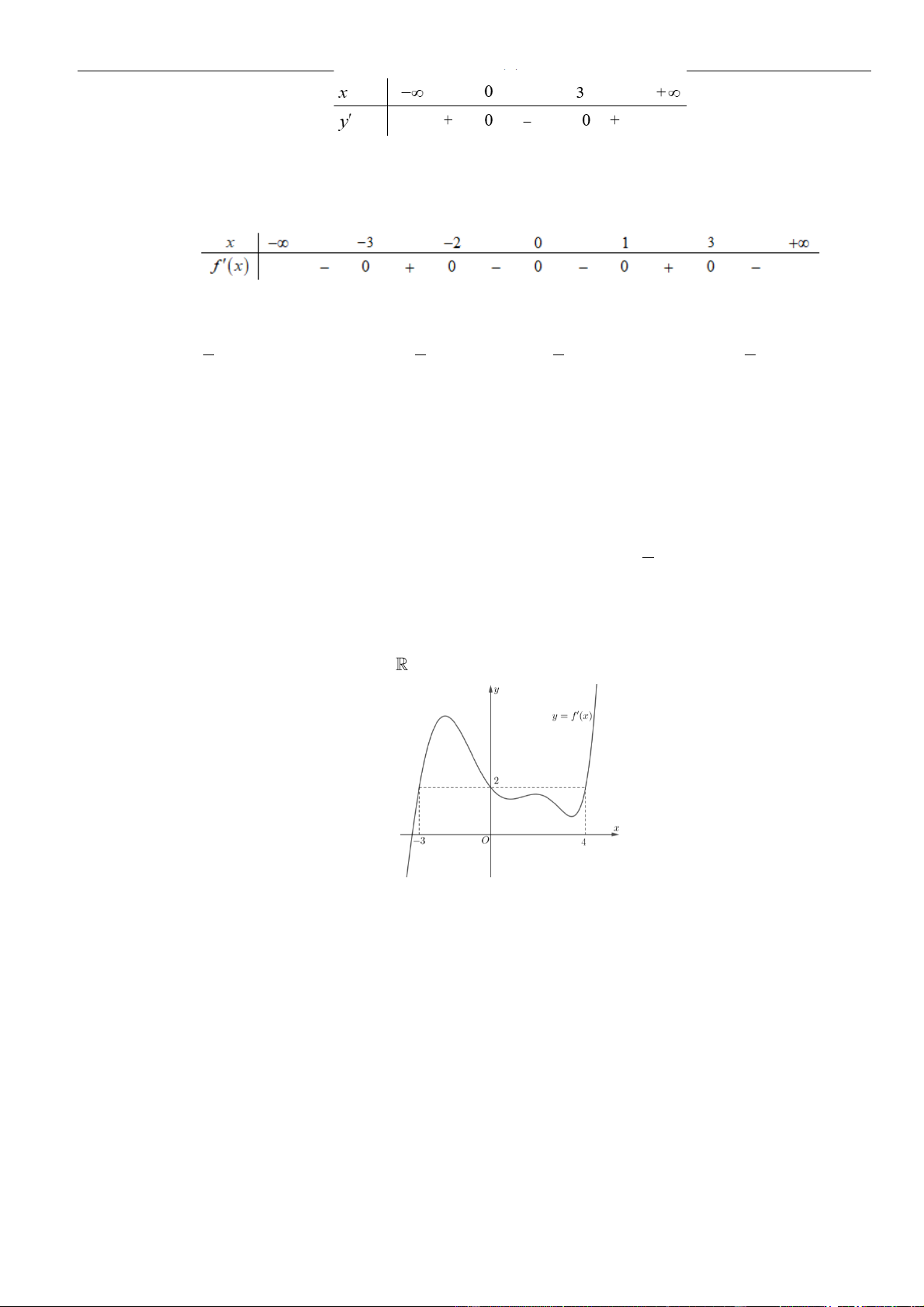
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 30
Vậy hàm số
( )
1 2018 2019y f x x= − + +
đồng biến trên mỗi khoảng
( )
;0−
và
( )
3; +
.
Câu 28: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm như hình bên dưới
Hàm số
( )
12y f x=−
đồng biến trên khoảng
A.
1
;1
2
−
. B.
1
2;
2
−−
. C.
3
;3
2
. D.
3
0;
2
.
Lời giải
Chọn D
Đặt
( ) ( )
12g x f x=−
có
( ) ( )
2 1 2g x f x
= − −
.
( )
gx
đồng biến khi và chỉ khi
( ) ( )
2
1 2 3
3
2 1 2 0 1 2 0 2 1 2 1 0
2
3 1 2
1
x
x
f x f x x x
x
x
− −
− − − − −
−
−
.
So sánh với các phương án ta thấy phương án D thỏa mãn yêu cầu đề bài.
Câu 29: Cho hàm số
( )
fx
liên tục trên . Hàm số
( )
y f x
=
có đồ thị như hình bên dưới.
Hỏi hàm số
( )
( )
22
3 2 6g x f x x x x= − − +
nghịch biến trên khoảng nào dưới đây
A.
( )
;0−
. B.
( )
0;4
. C.
( )
1;0−
. D.
( )
0;1
.
Lời giải
Chọn C
Đặt
2
3x x t−=
xét hàm số
( ) ( )
2g t f t t=−
.
Ta có:
( ) ( )
2g t f t
=−
.
Hàm số
( )
y g t=
nghịch biến khi
( ) ( )
2
2
3 3 3
20
04
0 3 4
t x x
g t f t
t
xx
− − −
= −
−
2
2
33
1;0 3;4
0 3 4
xx
x
xx
− −
−
−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
31 | Facebook tác giả: Phan Nhật Linh
Ta chọn đáp án. C.
Câu 30: Cho hàm số
32
1
,,
6
f x x ax bx c a b c
thỏa mãn điều kiện
0 1 2f f f
.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của
c
để hàm số
2
2g x f f x
nghịch biến trên
khoảng
0;1
là
A.
13
. B.
1
. C.
3
. D.
13
.
Lời giải
Chọn B
0
1
1
6
4
2 4 2
3
fc
f a b c
f a b c
Vì
0 1 2f f f
nên
11
1
66
2
1
44
4 2 4 2
3
33
c a b c a b
a
b
c a b c a b
Lúc đó :
32
1 1 1
6 2 3
f x x x x c
.
2
11
23
f x x x
.
3 3 3 3
0
33
f x x
.
Hàm số
2
2g x f f x
nghịch biến trên khoảng
0;1
0, 0;1g x x
22
2 . 2 . 2 0, 0;1x f f x f x x
1
Vì với
0;1x
:
20x
và
2
2 2 3x
nên
2
20fx
nên
1
2
2 0, 0;1f f x x
Với
0;1x
:
2
2 2 3f f x f
nên
2
3 3 3 3
2 0, 0;1 2 3
33
3 3 3 3
31
3 3 3
33
33
3 3 3 3
2
33
f f x x f f
fc
c
fc
Tổng giá trị lớn nhất và giá trị nhỏ nhất của
c
thỏa mãn yêu cầu đề bài là
3 3 3
1
33
.
Câu 31: Cho hàm số
()fx
, bảng xét dấu của
()fx
như sau
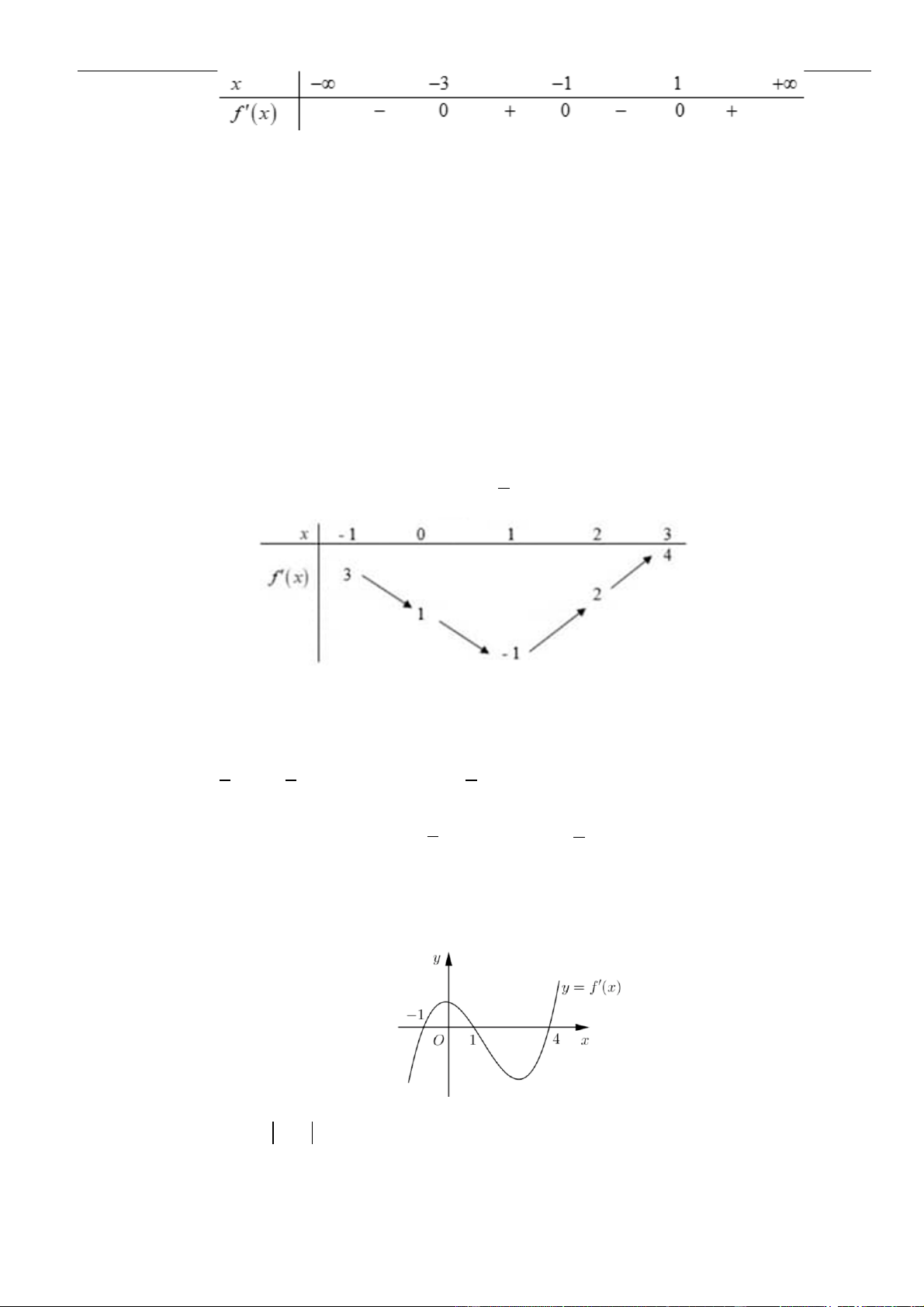
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 32
Hàm số
( )
12y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;3
. B.
( )
3; +
. C.
( )
2;0−
. D.
( )
0;1
.
Lời giải
Chọn C
Xét hàm số
( ) ( )
1 2 2 1 2y f x y f x
= − = − −
.
Hàm số nghịch biến
( )
2 1 2 0y f x
= − −
( )
1 2 0fx
−
3 1 2 1
1 2 1
x
x
− − −
−
12
0
x
x
.
Vậy, hàm số
( )
12y f x=−
nghịch biến trên khoảng
( )
1;2
và
( ) ( )
;0 2;0− −
.
Câu 32: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên
( )
1;3−
. Bảng biến thiên của hàm số
( )
y f x
=
được cho như hình vẽ sau. Hàm số
1
2
x
y f x
= − +
nghịch biến trên khoảng nào sau đây?
A.
( )
4; 2−−
. B.
( )
2;0−
. C.
( )
0;2
. D.
( )
2;4
.
Lời giải
Chọn A
1
11
22
x
yf
= − − +
;
0 1 2
2
x
yf
−
.
Ta thấy với mọi
( )
4; 2x − −
thì
( )
1 2;3
2
x
−
12
2
x
f
−
. Do đó hàm số nghịch biến trên
khoảng
( )
4; 2−−
.
Câu 33: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
4;7
. B.
( )
;1− −
. C.
( )
2;3
. D.
( )
1;2−
.
Lời giải
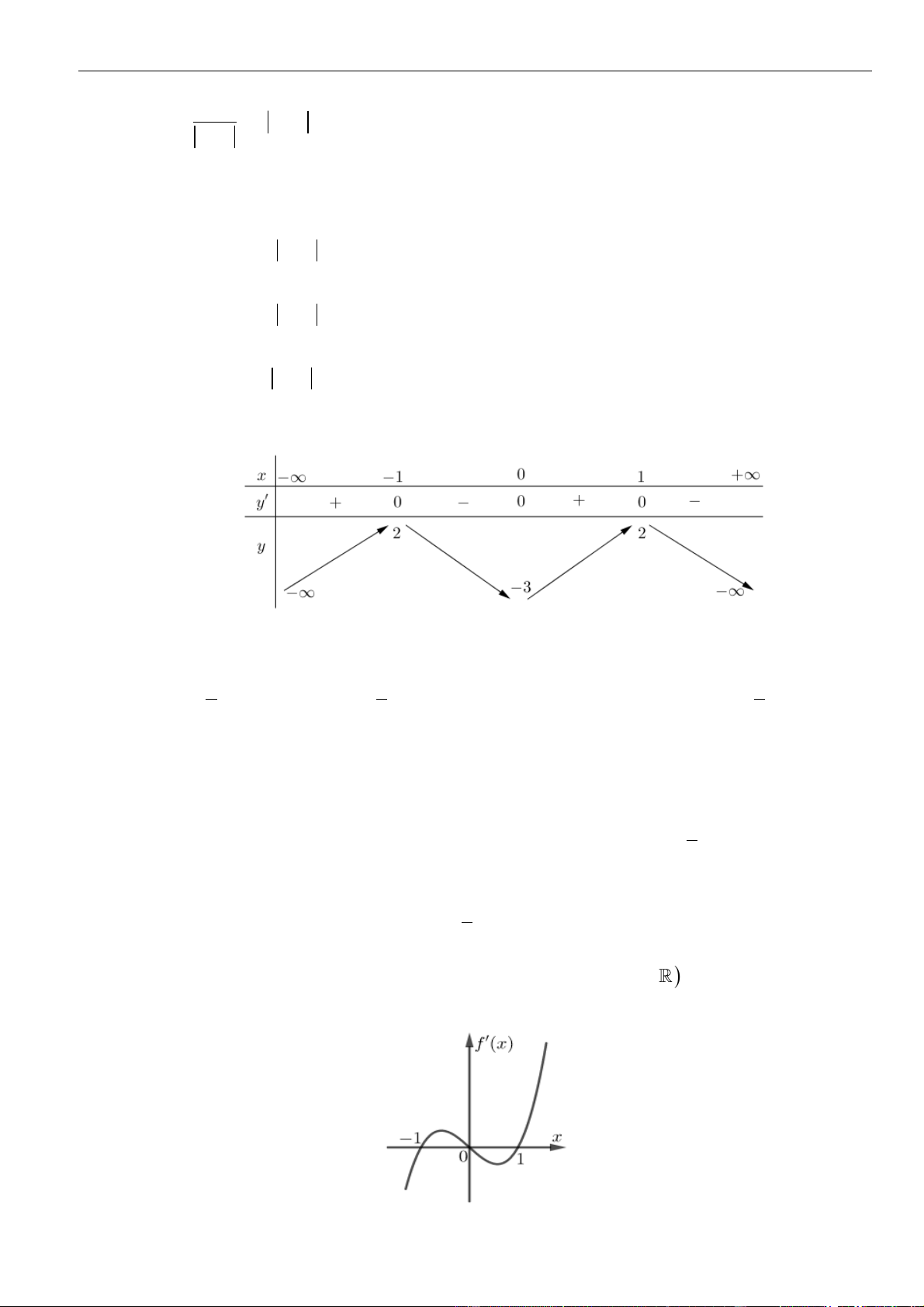
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
33 | Facebook tác giả: Phan Nhật Linh
Chọn D
( )
3
3
3
x
y f x
x
−
=−
−
. Ta có:
y
không xác định tại điểm
3x =
.
Hàm số đồng biến khi
( )
( )
33
30
1 3 1 2 4
30
3 4 1
34
0
12
3 0 3 3
1 3 4 1 2
30
3 1 4
xx
x
xx
fx
xx
x
y
x
x x x
xx
fx
xx
−
− −
−
−
−
−
− −
−
− −
.
Hàm số
( )
3y f x=−
đồng biến trên khoảng
( )
1;2−
và
( )
3;4
.
Câu 34: Cho hàm số
( )
y f x=
có bảng biến thiên như hình bên
Hàm số
( )
1 2x 1yf= − +
đồng biến trên khoảng
A.
3
0;
2
. B.
1
;1
2
. C.
( )
1; +
. D.
1
1;
2
−
.
Lời giải
Chọn B
Ta có:
( )
2 1 2xyf
= − −
.
Hàm số đồng biến khi
0y
( )
1 2x 0f
−
1 1 2x 0
1 1 2x
− −
−
1
1
2
0
x
x
.
Vậy hàm số đồng biến trên các khoảng
1
;1
2
và
( )
;0−
.
Câu 35: Cho hàm số
( )
y f x=
, hàm số
( ) ( )
32
,,f x x ax bx c a b c
= + + +
có đồ thị như hình vẽ.
Hàm số
( ) ( )
( )
g x f f x
=
có mấy khoảng đồng biến?
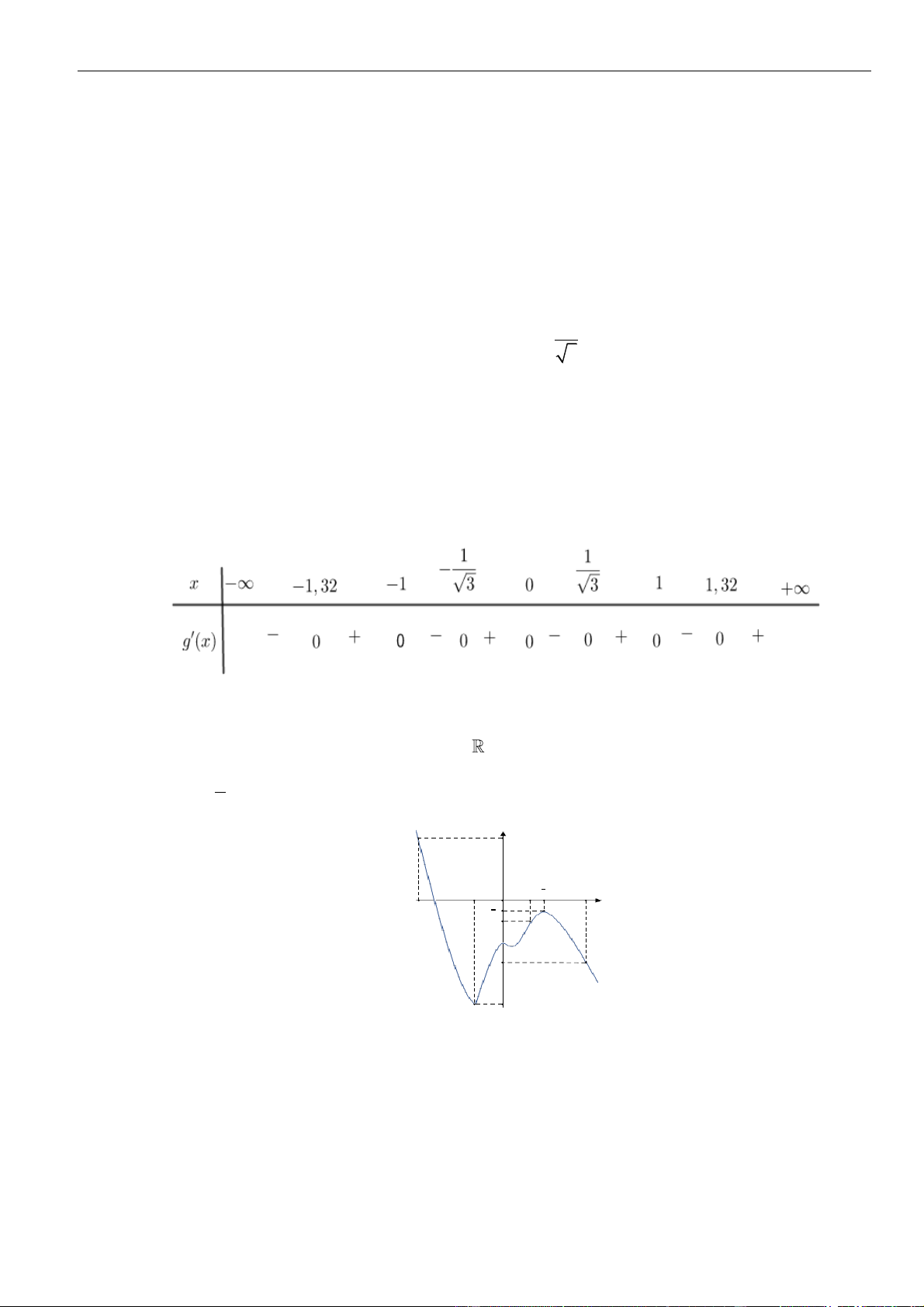
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 34
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn D
Ta có:
( )
( )
( )
10
10
0 0 0 1
10
10
f
a b c a
f c b
a b c c
f
−=
− + = =
= = = −
+ + = − =
=
.
Do đó:
( )
3
f x x x
=−
và
( )
2
31f x x
=−
.
Ta có:
( ) ( ) ( )
( )
.g x f x f f x
=
;
( )
( )
( )
( )
( )
2
3
3
3
1
3
0
3 1 0
1,32
1
10
0
0
0
0
1
10
1
1
1,32
x
fx
x
x
fx
xx
x
gx
fx
xx
x
x
fx
x
x
=
=
−=
=−
=
− − =
=
=
=
−=
=
− + =
=−
=−
=
.
Bảng xét dấu của
( )
gx
:
Vậy hàm số
( ) ( )
( )
g x f f x
=
có khoảng
4
đồng biến.
Câu 36: Cho hàm số
( )
fx
có đạo hàm trên
và
( )
fx
có đồ thị như hình bên. Hàm số
( ) ( )
2
1
2 1 2020
2
g x f x x x= − + − +
nghịch biến trên khoảng nào dưới đây?
A.
( )
1; +
. B.
( )
;1− −
. C.
( )
1;1−
. D.
( )
1;2
.
Lời giải
Chọn C
y = f '(x)
3
-
3
2
3
-
1
2
-1
-3
-5
-3
-1
1
y
x
O
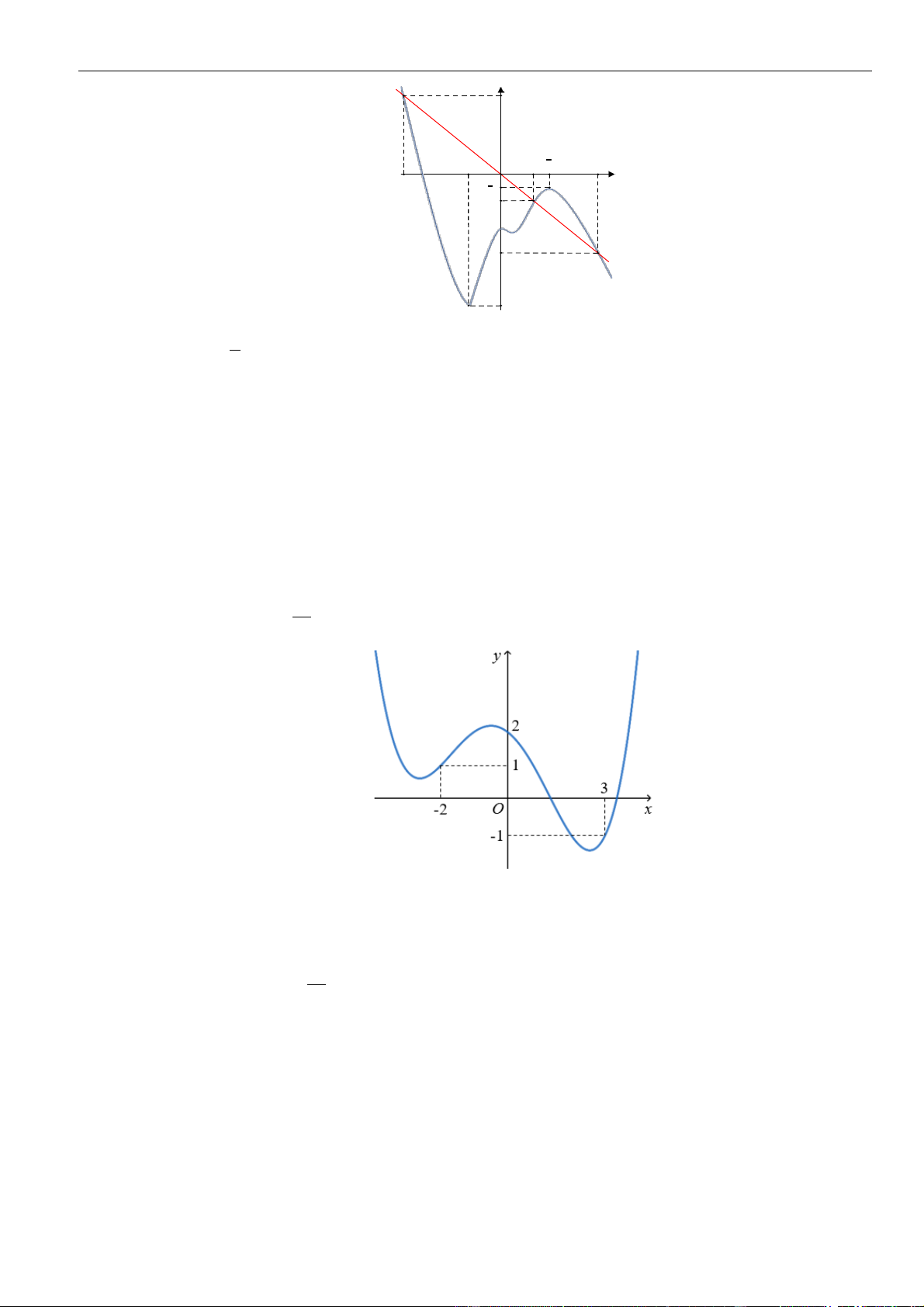
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
35 | Facebook tác giả: Phan Nhật Linh
( ) ( )
2
1
2 1 2020
2
g x f x x x= − + − +
.
( ) ( ) ( ) ( )
2 1 2 1 0 2 1 2 1g x f x x f x x
= − + − = − − −
Đặt
21xt−=
ta có
( )
'f t t= −
.
Đường thẳng
yt=−
đi qua các điểm
( )
3;3−
và
( )
1;1−
nằm trên đồ thị
( )
'ft
do đó
( )
'f t t−
trên
( )
3;1−
hay ta có:
3 2 1 1 1 1xx− − −
.
Câu 37: Cho hàm số
( )
fx
. Hàm số
( )
y f x
=
có đồ thị như hình bên. Hàm số
( ) ( )
3
13
3
x
g x f x x= + + −
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;2−
. B.
( )
2;0−
. C.
( )
0;4
. D.
( )
1;5
.
Lời giải
Chọn A
( ) ( )
3
13
3
x
g x f x x= + + −
;
( ) ( )
2
13g x f x x
= + + −
Đặt:
1xt+=
;
( )
;t − +
( ) ( ) ( )
2
13g t f t t
= + −
−
( ) ( )
( )
2
22g t f t t t
= − +
−+
Vẽ đồ thị
2
22y t t= − + +
trên cùng hệ trục tọa độ với đồ thị
( )
y f t=
như hình vẽ:
y= - t
y = f '(t)
3
-
3
2
3
-
1
2
-1
-3
-5
-3
-1
1
y
t
O
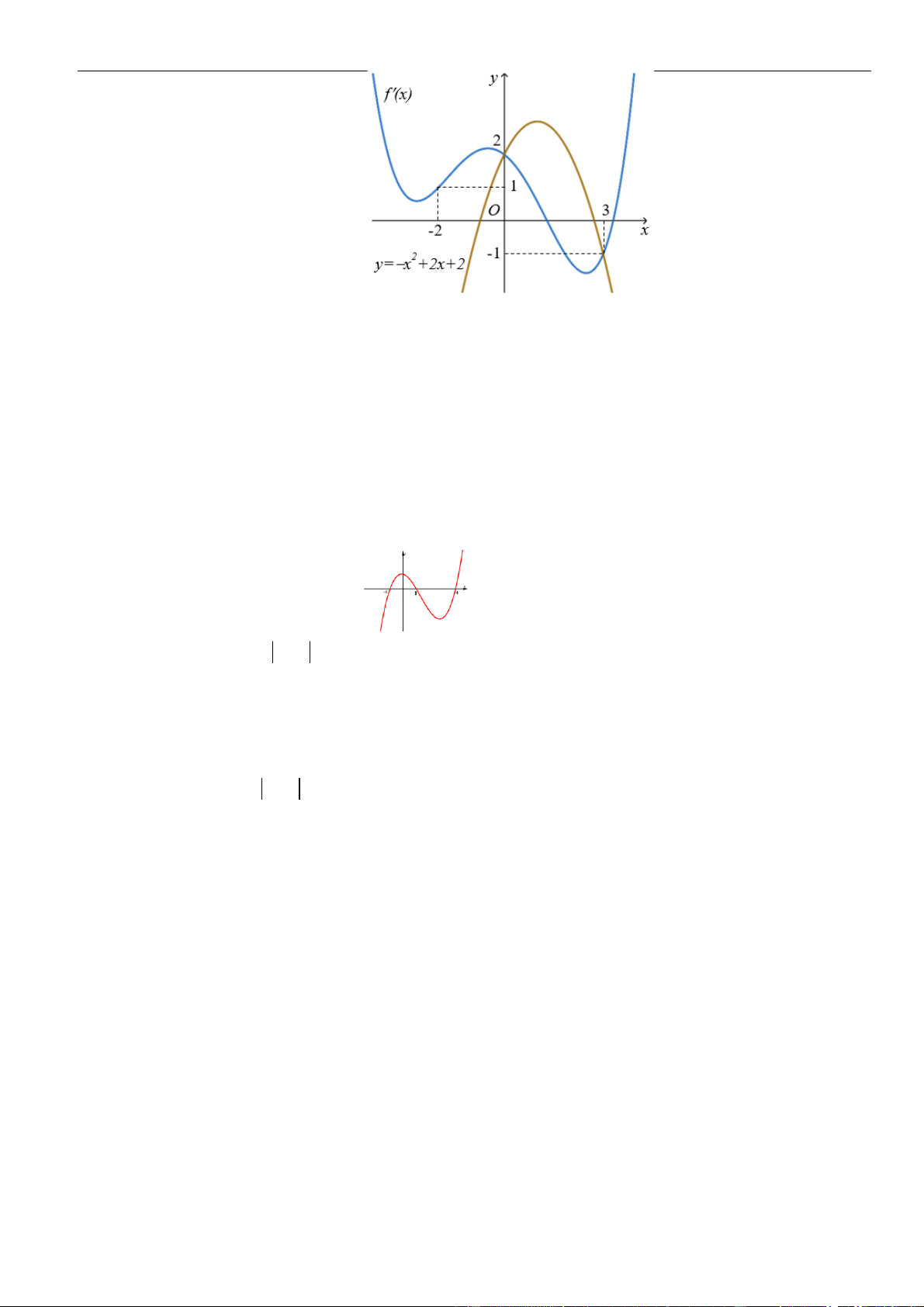
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 36
Ycbt:
( )
0gt
( )
2
22f t t t − +
+
03t
0 1 3x +
12x −
.
Câu 38: Cho hàm số
( )
y f x=
mà đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Hàm số
( )
3y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
2;3
. B.
( )
4;7
. C.
( )
;1− −
. D.
( )
1;2−
.
Lời giải
Chọn D
Ta có:
( )
( )
( )
( )
( )
3 khi 3 3 khi 3
3
3 khi 3 3 khi 3
f x x f x x
y f x y
f x x f x x
− − −
= − = =
− −
( )
( )
30
0
30
fx
y
fx
− − =
=
−=
.
Xét
3x
, phương trình
( )
( )
4
31
3 0 3 1 2
3 4 1
xl
x
f x x x
xx
=
− = −
− − = − = =
− = = −
Xét
3x
, phương trình
( )
( )
2
31
3 0 3 1 4
3 4 7
xl
x
f x x x
xx
=
− = −
− = − = =
− = =
Bảng xét dấu của
y
.
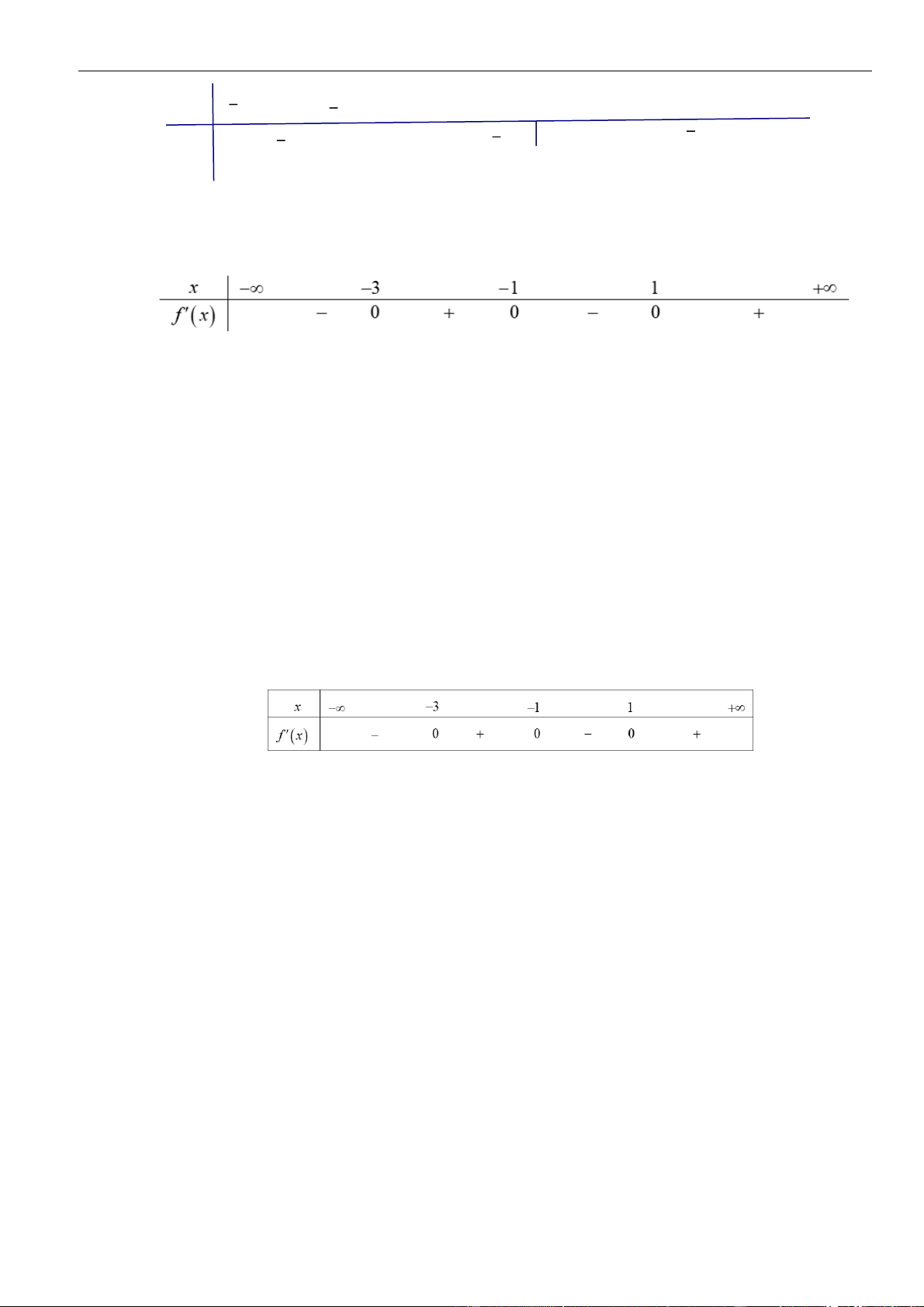
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
37 | Facebook tác giả: Phan Nhật Linh
Từ bảng xét dấu suy ra hàm số đã cho đồng biến trên khoảng
( )
1;2−
.
Câu 39: Cho hàm số
( )
y f x=
có bảng xét dấu của hàm
( )
fx
như sau:
Hàm số
( )
32y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;4
B.
( )
4;+
C.
( )
1;2
D.
( )
2;1−
Lời giải
Chọn D
Ta có
( )
2 3 2 .y f x
= − −
( )
3 3 2 1 2 3
0 3 2 0
3 2 1 1
xx
y f x
xx
− − −
−
−
Hàm số
( )
32y f x=−
nghịch biến trên các khoảng
( )
;1−
và
( )
2;3
.
Do dó hàm số nghịch biến trên khoảng
( )
2;1−
.
Câu 40: Cho hàm số
( )
fx
, bảng xét dấu
( )
fx
như hình bên. Hàm số
( )
21fx+
đồng biến trên khoảng
nào dưới đây?
A.
( )
1;0−
. B.
( )
0;+
. C.
( )
1;2−
. D.
( )
2;0−
.
Lời giải
Chọn B
Ta có
( )
( )
( ) ( ) ( )
2 1 2 1 . 2 1 2. 2 1f x f x x f x
+ = + + = +
Để hàm số
( )
21fx+
đồng biến thì
( )
2 1 0fx
+
Dựa vào bảng biến thiên ta được
3 2 1 1
2 1 1
4 2 2
20
21
0
x
x
x
x
x
x
− + −
+
− −
− −
Hàm số
(2 1)fx+
đồng biến trên
( )
2; 1−−
và
( )
0;+
Vậy ta chọn đáp án B
Câu 41: Cho hàm số
( )
y f x=
có bảng xét dấu
( )
fx
như hình dưới đây
+
+
+
0
0
0
0
3
7
4
2
1
+
∞
∞
y'
x
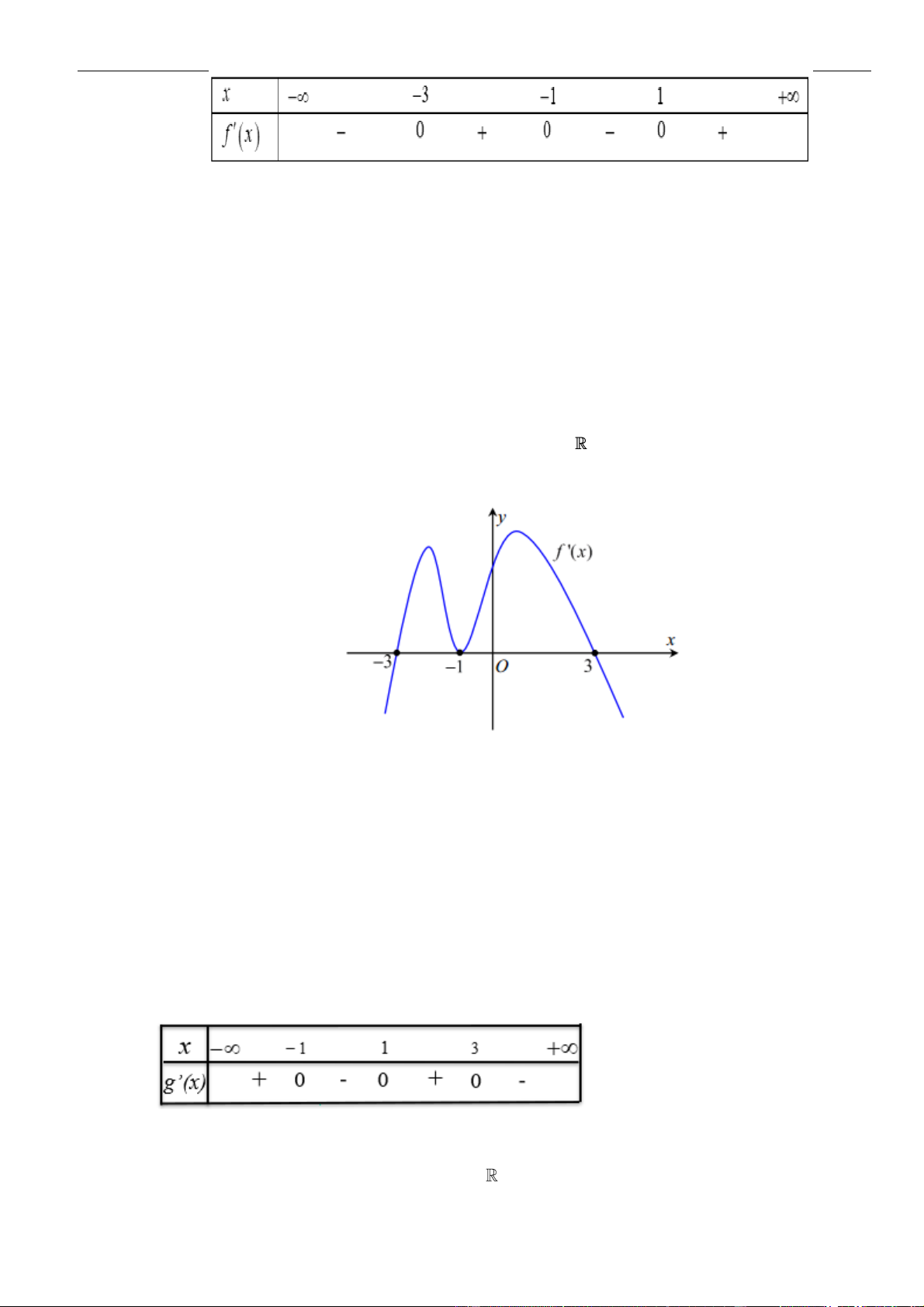
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 38
Hàm số
( )
1fx+
nghịch biến trên khoảng nào dưới đây?
A.
( )
2;1−
. B.
( )
0;1
. C.
( )
2;0−
. D.
( )
1;3
.
Lời giải
Chọn C
Đặt
( ) ( )
1g x f x=+
Ta có
( ) ( )
1 3 4
10
1 1 1 2 0
xx
g x f x
xx
+ − −
= +
− + −
.
Khi đó hàm số
( ) ( )
1g x f x=+
nghịch biến trên
( )
;4− −
và
( )
2;0−
.
Câu 42: Cho hàm số
( )
fx
có đạo hàm liên tục và xác định trên và có đồ thị hàm số
( )
fx
như hình
vẽ bên dưới. Hàm số
( )
( )
2
2g x f x x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
2;3
. B.
( )
;1−
. C.
( )
0;2
. D.
( )
2;4
.
Lời giải
Chọn A
Ta có:
( )
( )
2
2g x f x x=−
;
( )
( )
( )
2
2g x f x x
=−
( )
( )
2
2 2 . 2x f x x
= − −
.
( )
0gx
=
( )
( )
2
2 2 . 2 0x f x x
− − =
( )
2
2 2 0
20
x
f x x
−=
−=
2
2
2
1
2 3( )
21
23
x
x x vn
xx
xx
=
− = −
− = −
− =
1
1
3
x
x
x
=
= −
=
.
Ta có bảng xét dấu:
Dựa vào bảng xét dấu, suy ra hàm số
( )
( )
2
2g x f x x=−
đồng biến trên khoảng
( )
2;3
.
Câu 43: Cho hàm số
( )
fx
liên tục và xác định trên có đồ thị đạo hàm
( )
fx
được cho như hình vẽ.
Hàm số
( )
2
1y f x= − −
đồng biến trong khoảng nào sau đây?
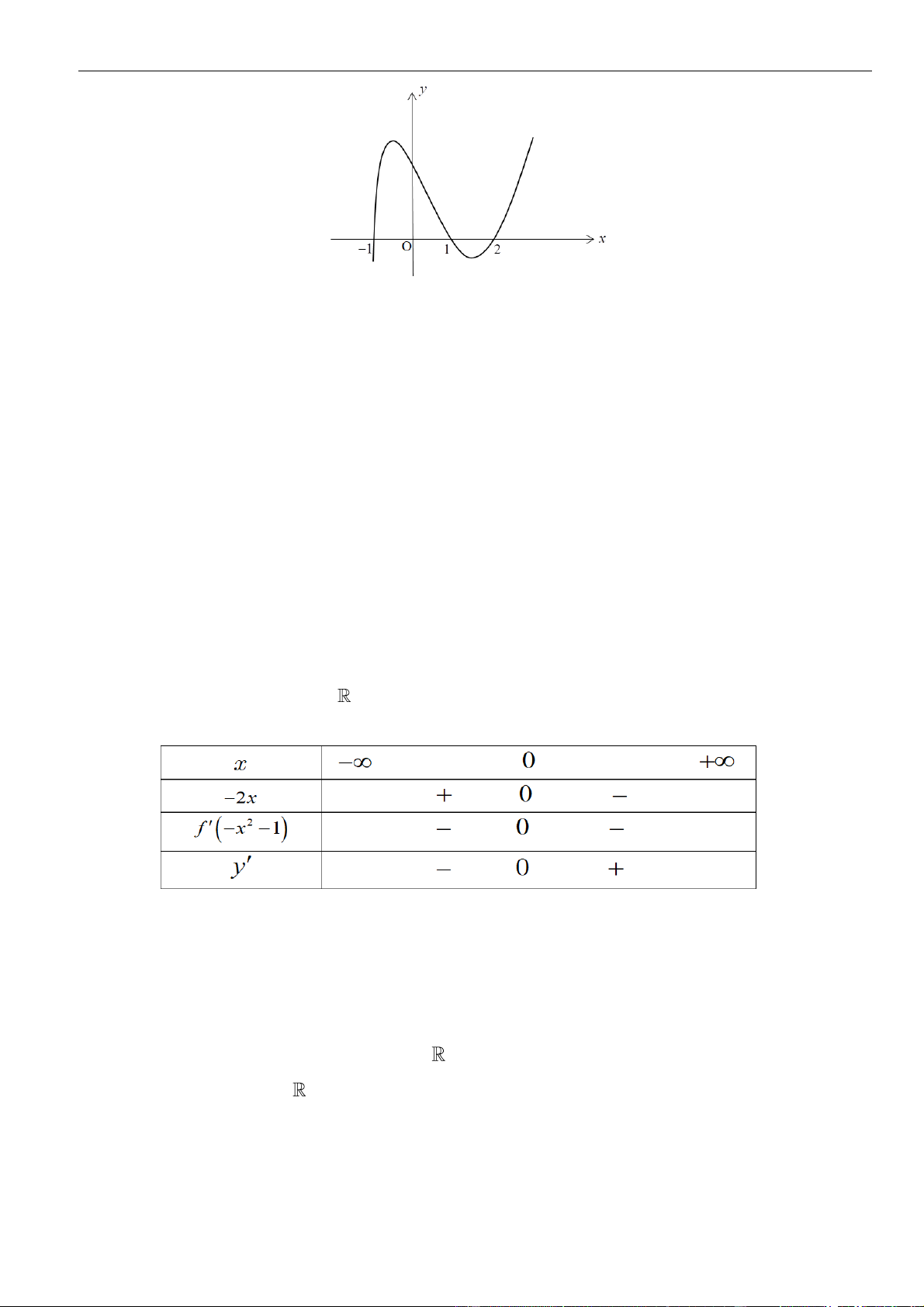
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
39 | Facebook tác giả: Phan Nhật Linh
A.
( )
1;5−
. B.
( )
2;6
. C.
( )
2; 1−−
. D.
( )
1;3−
.
Lời giải
Chọn B
Từ đồ thị của hàm số
( )
y f x=
ta thấy
( )
0fx
=
2
1
x
x
=
=
.
Với
( )
2
1y f x= − −
ta có
( )
2
2 . 1y x f x
= − − −
.
Suy ra
0y
=
( )
2
2
2
0
20
12
10
11
x
x
x
fx
x
=
−=
− − =
− − =
− − =
0x=
.
Từ đồ thị của hàm số
( )
y f x=
ta thấy
( )
11
0
2
x
fx
x
−
.
suy ra
( )
2
2
2
1 1 1
10
12
x
fx
x
− − −
− −
− −
không tồn tại
x
để
( )
2
10fx
− −
.
( )
2
1 0,f x x
− −
.
Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta có
( )
0 0;yx
+
.
Suy ra hàm số
( )
2
1y f x= − −
đồng biến trên khoảng
( )
0;+
.
Vậy hàm số đồng biến trên khoảng
( )
2;6
.
Chú ý: Dùng ghép trục thì đơn giản hơn.
Câu 44: Cho hàm số
( )
y f x=
xác định trên và có đạo hàm
( ) ( )( ) ( )
2 3 2021f x x x g x
= − + +
trong
đó
( )
0,g x x
. Hàm số
( )
1 2021 2022y f x x= − + +
đồng biến trên khoảng nào?
A.
( )
;1− −
. B.
( )
1;4−
. C.
( )
3;2−
. D.
( )
4;+
.
Lời giải
Chọn B
Ta có:
( )
1 2021y f x
= − − +
;
( )( ) ( )
1 4 . 1 2021 2021y x x g x
= − + − − + +
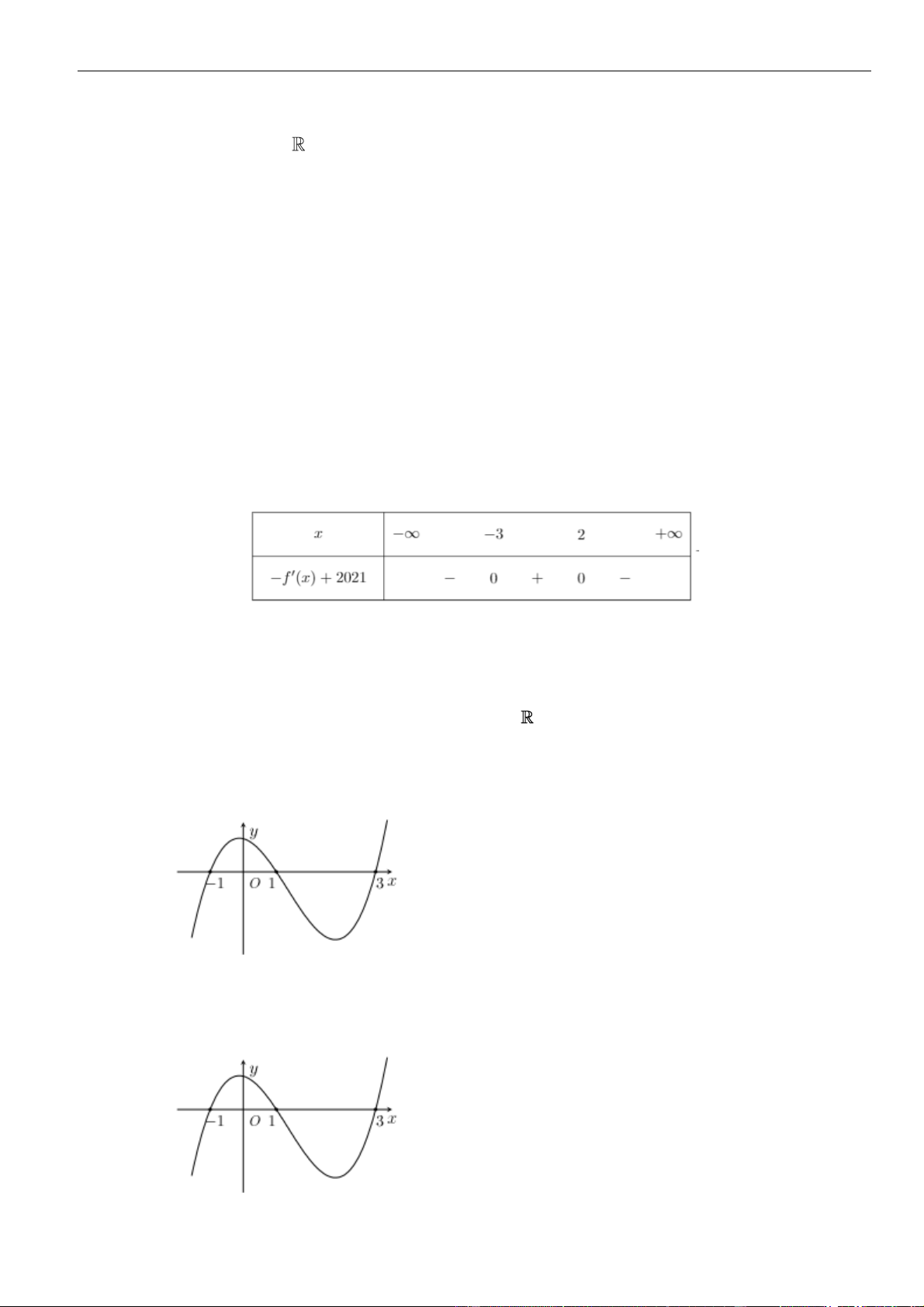
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 40
( )( ) ( )
1 4 . 1y x x g x
= + − −
. Suy ra
1
0
4
x
y
x
=−
=
=
.
Vì
( )
0,g x x
nên
( )
0, 1;4yx
−
. Suy ra hàm số đồng biến trên
( )
1;4−
.
Câu 45: Cho hàm số
()y f x=
xác định trên
R
và có đạo hàm
'( ) (2 )( 3). ( ) 2021f x x x g x= − + +
trong
đó
( ) 0, .g x x R
Hàm số
(1 ) 2021 2022y f x x= − + +
đồng biến trên khoảng nào?
A.
( ; 1)− −
. B.
( 1;4)−
. C.
( 3;2)−
. D.
(4; )+
.
Lời giải
Chọn B
Ta có:
(1 ) 2021 2022 ' '(1 ) 2021y f x x y f x= − + + = − − +
Theo giả thuyết của đề, ta có:
'( ) (2 )( 3). ( ) 2021 '( ) (2 )( 3). ( ) 2021
'( ) 2021 (2 )( 3). ( )
3
'( ) 2021 0 (2 )( 3). ( ) 0
2
f x x x g x f x x x g x
f x x x g x
x
f x x x g x
x
= − + + − = − − + −
− + = − − +
=−
− + = − + =
=
Ta có bảng xét dấu như sau:
Dựa vào bảng xét dấu, ta suy ra
'( ) 2021 0, ( 3;2)f x x− + −
' '(1 ) 2021 0 3 1 2 1 4.y f x x x = − − + − − −
Vậy hàm số
(1 ) 2021 2022y f x x= − + +
đồng biến trên khoảng
( 1;4)−
.
Câu 46: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên . Biết hàm số
( )
y f x
=
có đồ thị như hình
vẽ. Gọi
S
là tập hợp các giá trị nguyên
2021;2021m−
để hàm số
( ) ( )
g x f x m=+
nghịch
biến trên khoảng
( )
1;2
. Hỏi
S
có bao nhiêu phần tử?
A.
2020.
B.
2021.
C.
2022.
D.
2019.
Lời giải
Chọn B
( ) ( ) ( ) ( )
''g x f x m g x f x m= + = +

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
41 | Facebook tác giả: Phan Nhật Linh
Để hàm số
( ) ( )
g x f x m=+
nghịch biến thì
( ) ( )
' ' 0.g x f x m= +
(Bằng 0 tại hữu hạn điểm)
Nhìn vào đồ thị hàm
( )
y f x
=
ta có
( )
1
0
13
x
fx
x
−
.
Vậy
( )
11
0
1 3 1 3
x m x m
f x m
x m m x m
+ − − −
+
+ − −
Do đó để hàm số
( ) ( )
g x f x m=+
nghịch biến trên khoảng
( )
1;2
thì
1 2 3
1 1 2 3 0 1
mm
m m m
− − −
− −
Mà
2021;2021 ,mm −
nên
2021; 2020...., 3 0;1m − − −
Suy ra có 2021 giá trị m thỏa ycbt.
Câu 47: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên , dấu của đạo hàm được cho bởi bảng:
Hàm số
( )
22y f x=−
nghịch biến trong khoảng nào?
A.
( )
;1−
. B.
( )
1;2
. C.
( )
1;1−
. D.
( )
2;+
.
Lời giải
Chọn B
Từ bảng xét dấu của đạo hàm ta có:
( )
' 0 0 2f x x
.
( )
0
'0
2
x
fx
x
.
( )
' 2 ' 2 2y f x=−
.
( )
' 0 ' 2 2 0 0 2 2 2 1 2y f x x x − −
.
Câu 48: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( ) ( )
22
' 3 10 3 2f x x x x= − − −
với mọi
x
. Hàm số
( ) ( )
( )
3
2
1
31
6
g x f x x= − + −
đồng biến trên khoảng nào trong các khoảng sau
A.
( )
1; +
. B.
( )
0;1
. C.
( )
;0−
. D.
1
;
2
− −
.
Lời giải
Chọn D
( ) ( )
( )
2
2
3
' ' 3 2 1
6
g x f x x x= − − + −
( )
( )
2
2
' 3 1f x x x= − − + −
( ) ( ) ( )
( )
2
2
2
2
3 3 10 3 3 3 2 1x x x x x= − − − − − − − + −
( ) ( ) ( ) ( )
2 2 2 2
. 1 3 1 1 1x x x x x x= − + − + − +
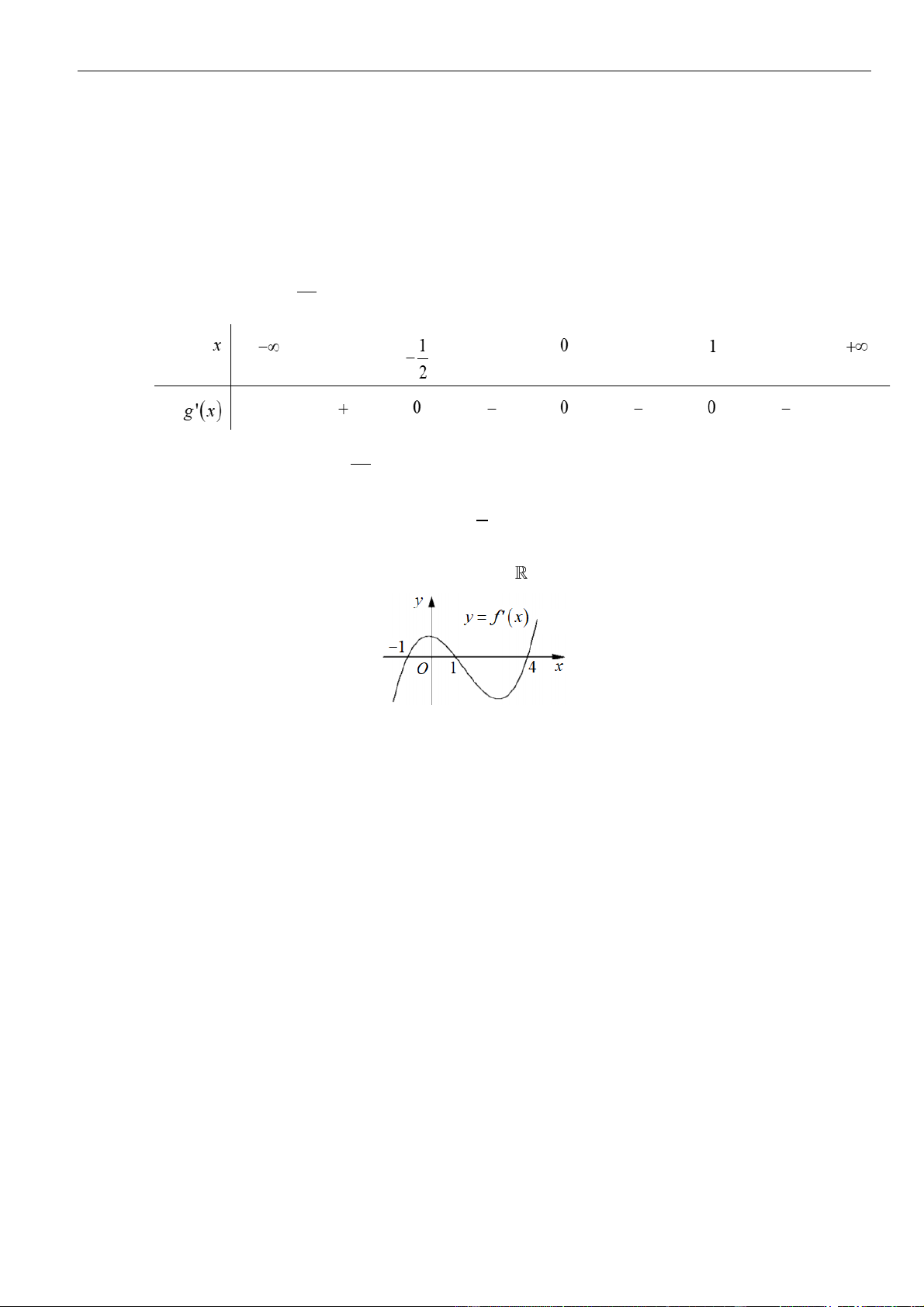
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 42
( )
( )
2
3 2 2
= 1 2 9 6 1x x x x x x x
− + + − + +
( )
( )
2
32
1 8 4x x x= − − −
=
( ) ( )
2
2
4 1 2 1x x x− − +
( )
0
' 0 1
1
2
x
g x x
x
=
= =
−
=
( )
1
' 0 ;
2
g x x
−
−
.
Vậy hàm số đồng biến trên khoảng
1
;
2
− −
.
Câu 49: Cho hàm số
( )
y f x=
xác định và liên tục trên . Hàm số
( )
y f x=
có đồ thị như hình dưới.
Hàm số
( ) ( )
2y g x f x= = −
đồng biến trên khoảng nào dưới đây?
A.
( )
;2− −
. B.
( )
3; +
. C.
( )
1;3
. D.
( )
2;+
.
Lời giải
Chọn B
Xét hàm số
( ) ( )
2y g x f x= = −
có đạo hàm:
( ) ( )
2y g x f x = = − −
.
Hàm số đồng biến khi
( ) ( ) ( )
2 0 2 0y g x f x f x = = − − −
(1)
Dựa vào đồ thị hàm số
( )
y f x=
, bất phương trình
( )
1
tương đương với
2 1 3
1 2 4 2 1
xx
xx
− −
− −
.
Vậy hàm số
( )
y g x=
đồng biến trên trên từng khoảng
( )
3; +
và
( )
2;1−
. Chọn
B
.
Câu 50: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị (như hình bên). Hàm số
( )
2y f x=−
đồng
biến trên khoảng

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
43 | Facebook tác giả: Phan Nhật Linh
A.
( )
3;5
. B.
( )
4;1−
. C.
( )
;2−
. D.
( )
2;+
.
Lời giải
Chọn A
Xét hàm số
( ) ( )
2y g x f x= = −
ta có
( ) ( )
2g x f x
= − −
, suy ra
( )
0gx
( )
20fx
−
Từ đồ thị hàm số ta có
21
1 2 4
x
x
− −
−
3
21
x
x
−
.
Suy ra hàm số đồng biến trên khoảng
( )
3;5
.
Câu 51: Cho hàm số
( )
y f x=
có bảng xét dấu đạo hàm như bảng sau.
Hỏi hàm số
1
y f x
x
=+
nghịch biến trên khoảng nào?
A.
1
;0
2
−
. B.
1
0;
2
. C.
1
2;
2
−−
. D.
1
;2
2
.
Lời giải
Chọn A
Đặt
( ) ( ) ( )
22f x a x x x
= + −
(với
0a
)
1 1 1 1
22f x a x x x
x x x x
+ = + + + + −
( )
( )
( )
22
2
3
1 1 1
1
a x x x
fx
xx
+ + −
+ =
.
Ta có
( )
( )
( )
( )
22
22
2
25
1 1 1 1
1 1 1
a x x x x
x
y f x y f x
x x x x
− + + −
−
= + = + =
.
1
0
1
x
y
x
=
=
=−
.
Ta có bảng xét dấu đạo hàm
Dựa vào bảng xét dấu suy ra hàm số nghịch biến trên khoảng
( )
1
1;0 ;0
2
− −
.
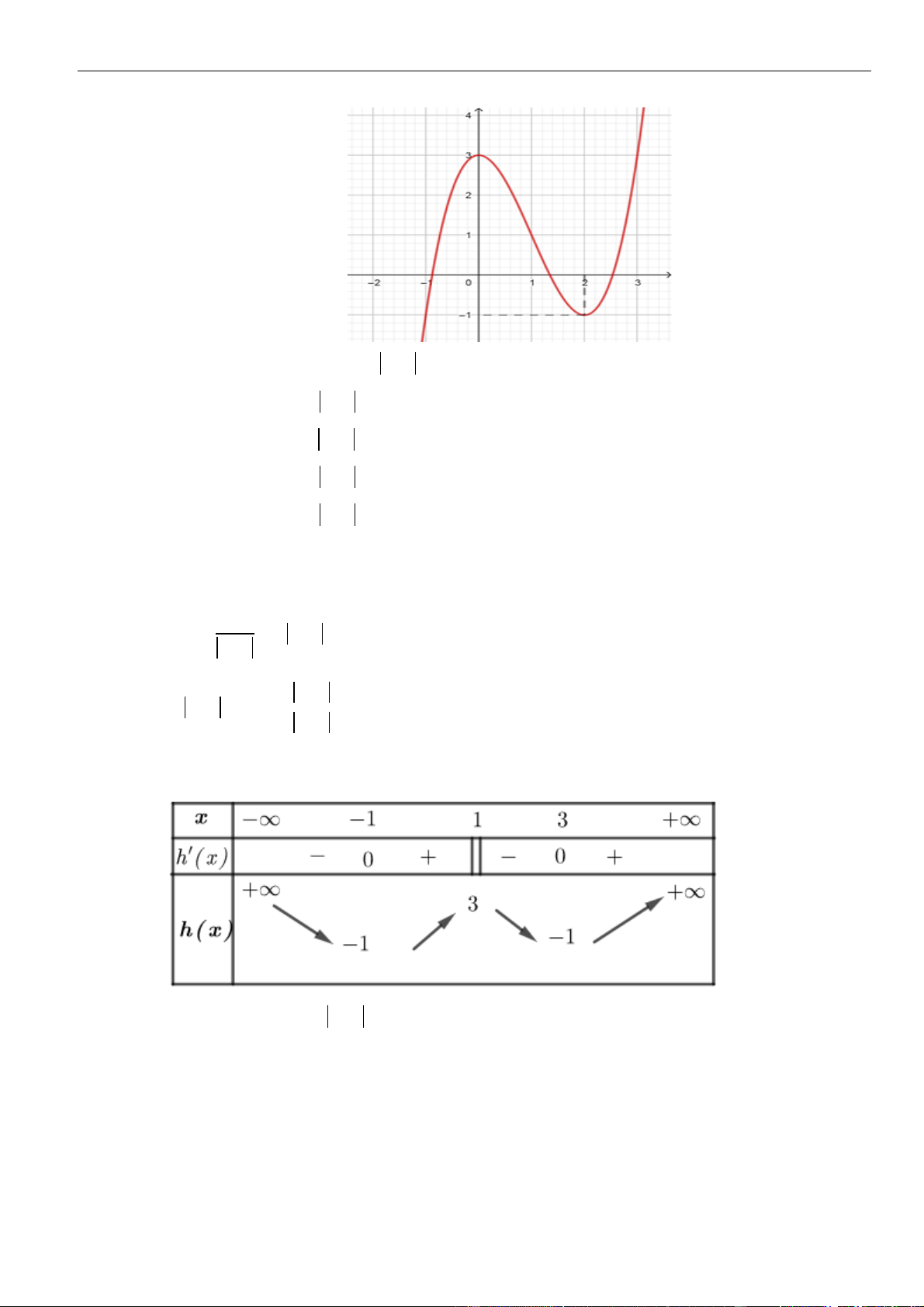
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 44
Câu 52: Cho hàm số đa thức
( )
y f x=
có đồ thị như hình vẽ bên dưới.
Xét hàm số
( )
( )
1h x f x=−
. Chọn khẳng định đúng:
A. Hàm số
( )
( )
1h x f x=−
đồng biến trên khoảng
( )
;1− −
.
B. Hàm số
( )
( )
1h x f x=−
đồng biến trên khoảng
( )
1;1−
và
( )
3; +
.
C. Hàm số
( )
( )
1h x f x=−
nghịch biến trên khoảng
( )
3; +
.
D. Hàm số
( )
( )
1h x f x=−
nghịch biến trên khoảng
( )
1;3
.
Lời giải
Chọn B
Cách 1.
( )
( )
1
.1
1
x
h x f x
x
−
=−
−
( )
1
10
1 0 3
12
1
x
x
f x x
x
x
=
− =
− = =
−=
=−
Bảng biến thiên của hàm số
( )
y h x=
Vậy hàm số
( )
( )
1h x f x=−
đồng biến trên khoảng
( )
1;1−
và
( )
3; +
Cách 2. Ghép trục
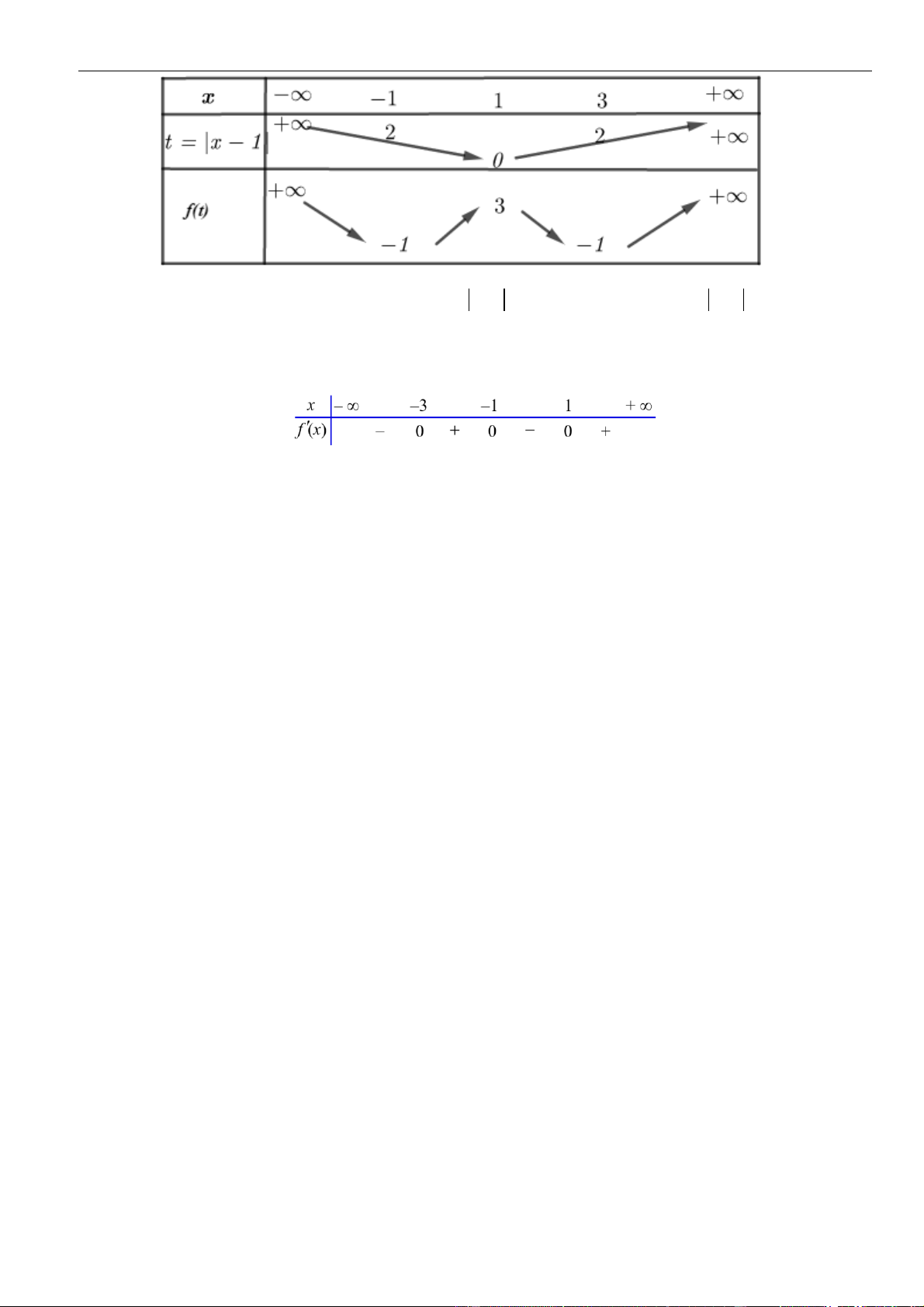
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
45 | Facebook tác giả: Phan Nhật Linh
Từ bảng biến thiên của hàm số
( )
( )
1h x f x=−
suy ra hàm số
( )
( )
1h x f x=−
đồng biến trên
khoảng
( )
1;1−
và
( )
3; +
.
Câu 53: Cho hàm số
()fx
, bảng xét dấu của
()fx
như sau:
Hàm số
(1 2 )y f x=−
nghịch biến trên khoảng nào dưới đây?
A.
( )
1;3
. B.
( )
3; +
. C.
( )
2;0−
. D.
( )
0;1
.
Lời giải
Chọn C
Ta có
2 (1 2 )y f x
= − −
.
Hàm số
(1 2 )y f x=−
nghịch biến khi và chỉ khi
2 (1 2 ) 0 (1 2 ) 0y f x f x
= − − −
.
Từ bảng xét dấu đã cho, ta có
3 1 2 1 1 2
(1 2 ) 0
1 2 1 0
xx
fx
xx
− − −
−
−
.
Do đó, hàm số
(1 2 )y f x=−
nghịch biến trên các khoảng
( )
;0−
và
( )
1;2
.
Vậy, hàm số
(1 2 )y f x=−
nghịch biến trên khoảng
( )
2;0−
.
Câu 54: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )
2
2
' 2 6f x x x x= + −
. Có bao nhiêu giá trị nguyên của
tham số
m
để hàm số
( )
( )
2
4g x f x x m= − +
đồng biến trên
( )
0;2
?
A.
5
. B.
6
. C.
3
. D.
4
.
Lời giải
Chọn C
Ta có:
( )
' 0 0;6f x x
Ta có:
( ) ( )
( )
2
' 2 4 . ' 4g x x f x x m= − − +
. Khi
( )
0;2x
thì
2 4 0x −
.
Vậy:
( ) ( )
( )
( )
2
' 0 , 0;2 ' 4 0, 0;2g x x f x x m x − +
( )
2
0 4 6, 0;2x x m x − +
( )
2
4 6 , 0;2m x x m x − − −
.
Xét
( ) ( )
2
4 , 0;2h x x x x= −
Bảng biến thiên:
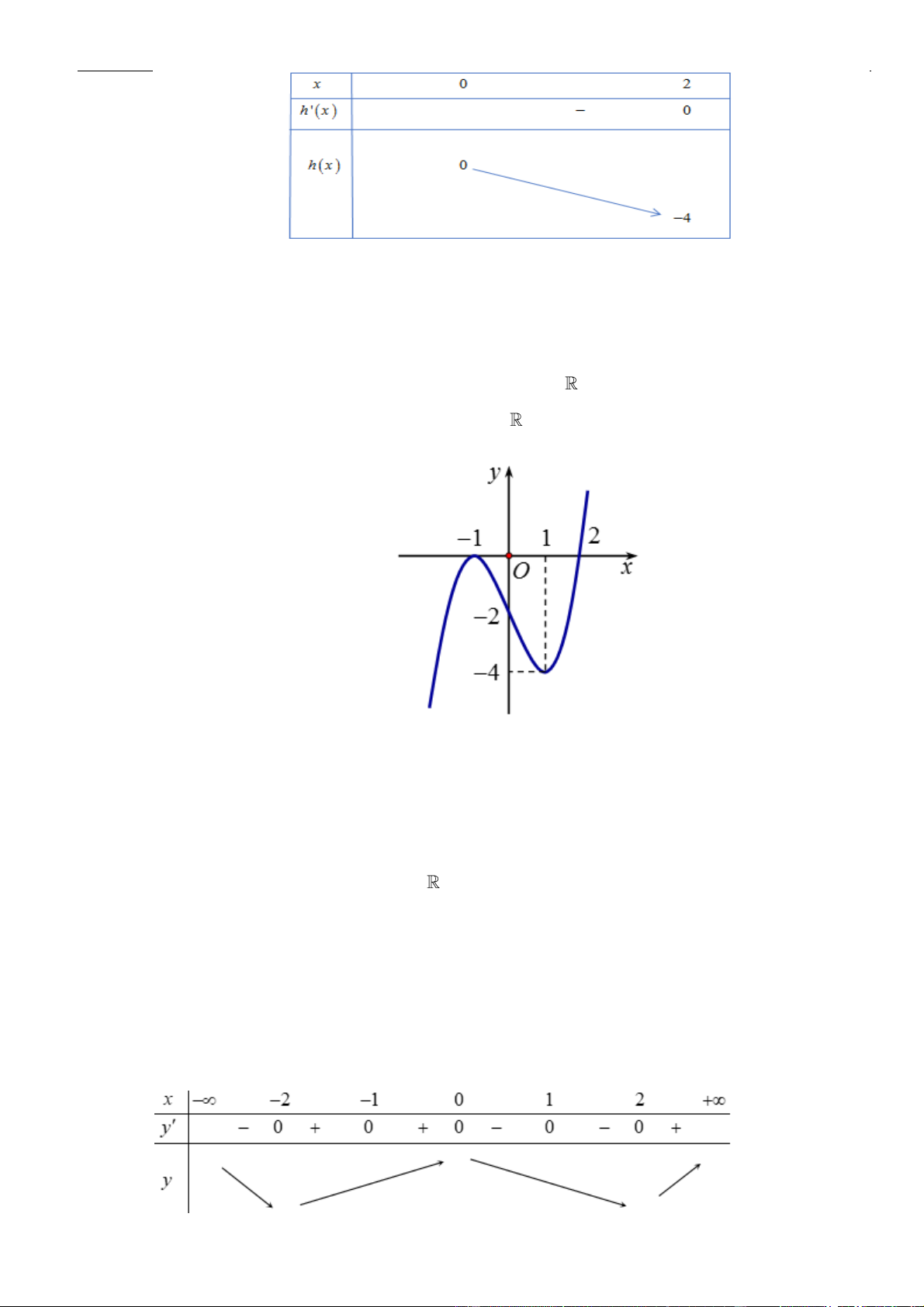
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 46
Từ bảng biến thiên ta có kết quả:
4
46
60
m
m
m
− −
−
. Vì
4,5,6m Z m =
.
Có 3 giá trị nguyên của
m
thỏa mãn bài toán. Chọn C
Câu 55: Cho hàm số
( )
y f x=
là hàm bậc 4, có đạo hàm trên . Đường cong trong hình vẽ bên là đồ
thị hàm số
( )
y f x
=
, (
( )
y f x
=
liên tục trên ). Xét hàm số
( )
( )
2
2g x f x=−
. Hàm số g(x)
đồng biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;1
. C.
( )
;2− −
. D.
( )
1;1−
.
Lời giải
Chọn A
Từ đồ thị thấy
( )
1
0
2
x
fx
x
=−
=
=
và
( )
02f x x
.
Xét
( )
( )
2
2g x f x=−
có TXĐ
D =
.
( ) ( )
2g x xf t
=
với
2
2tx=−
.
( )
2
2
0
0
0 2 1 1
2
22
x
x
g x t x x
x
tx
=
=
= = − = − =
=
= − =
.
Có
( )
2
0 2 2 2 2f t t x x x
= − −
.
Bảng biến thiên:
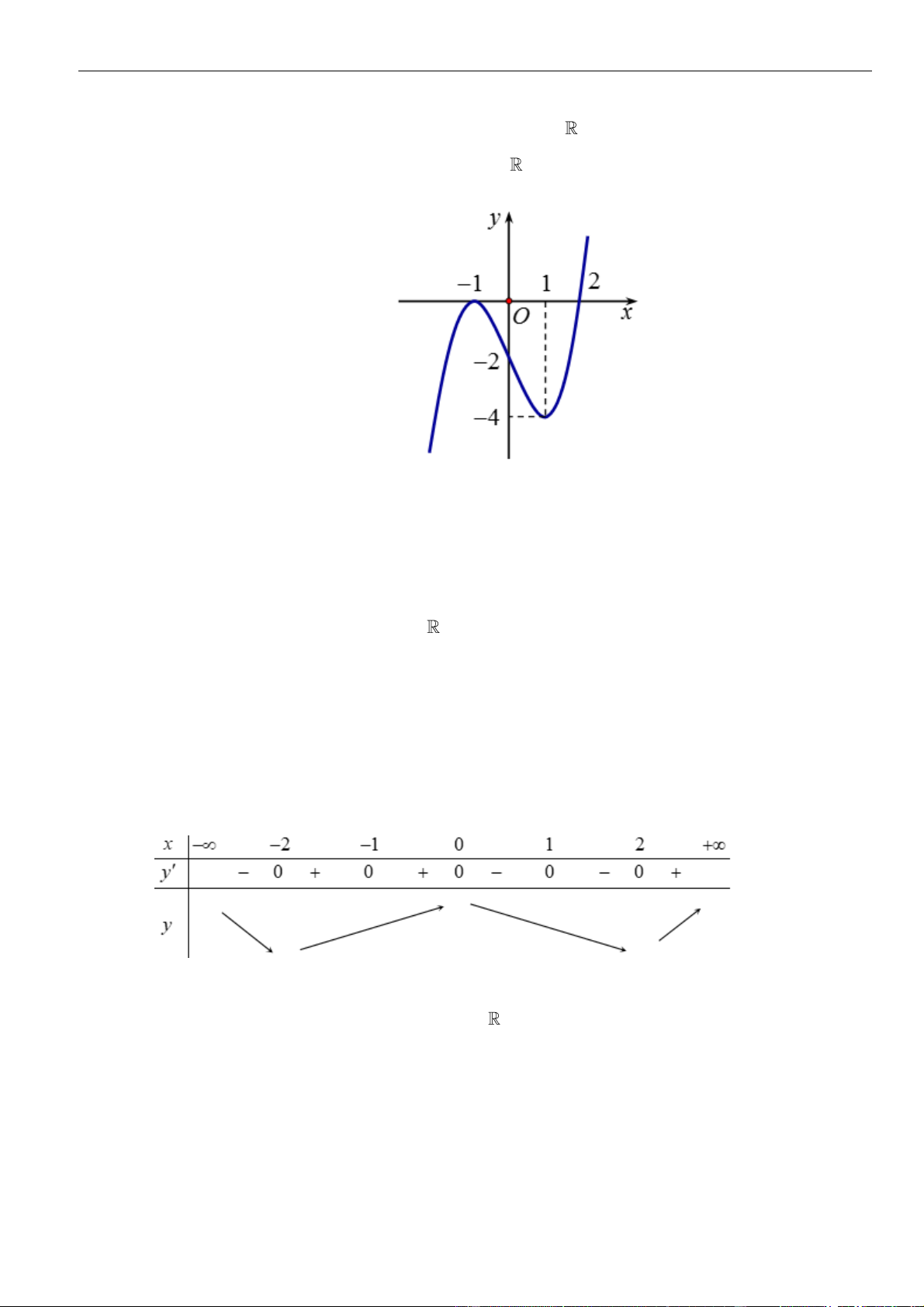
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
47 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
gx
đồng biến trên
( )
2;0−
.
Câu 56: Cho hàm số
( )
y f x=
là hàm bậc 4, có đạo hàm trên . Đường cong trong hình vẽ bên là đồ
thị hàm số
( )
y f x
=
, (
( )
y f x
=
liên tục trên ). Xét hàm số
( )
( )
2
2g x f x=−
. Hàm số g(x)
đồng biến trên khoảng nào dưới đây?
A.
( )
2;0−
. B.
( )
0;1
. C.
( )
;2− −
. D.
( )
1;1−
.
Lời giải
Chọn A
Từ đồ thị thấy
( )
1
0
2
x
fx
x
=−
=
=
và
( )
02f x x
.
Xét
( )
( )
2
2g x f x=−
có TXĐ
D =
.
( ) ( )
2g x xf t
=
với
2
2tx=−
.
( )
2
2
0
0
0 2 1 1
2
22
x
x
g x t x x
x
tx
=
=
= = − = − =
=
= − =
.
Có
( )
2
0 2 2 2 2f t t x x x
= − −
.
Bảng biến thiên:
Hàm số
( )
gx
đồng biến trên
( )
2;0−
.
Câu 57: Cho hàm số
( )
fx
có đạo hàm liên tục trên và có đồ thị của hàm số
( )
y f x
=
như hình vẽ
bên dưới.
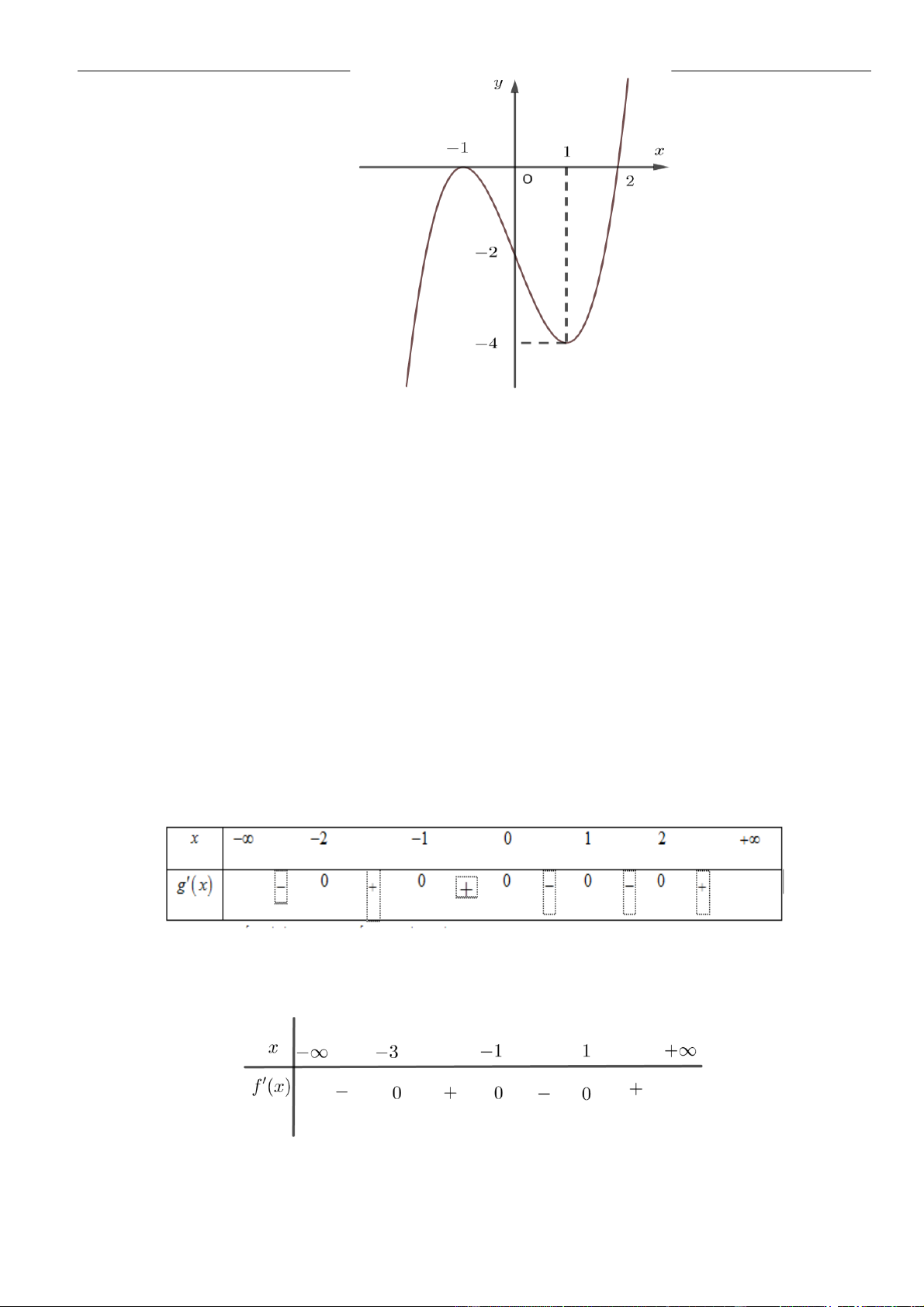
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 48
Xét hàm
( )
( )
2
2g x f x=−
. Mệnh đề nào dưới đây sai?
A. Hàm số
( )
gx
nghịch biến trên
( )
;2− −
.
B. Hàm số
( )
gx
nghịch biến trên
( )
0;2
.
C. Hàm số
( )
gx
nghịch biến trên
( )
1;0−
.
D. Hàm số
( )
gx
đồng biến trên
( )
2;+
.
Lời giải
Chọn C
Ta có
( )
( )
2
2 . 2g x x f x
=−
( )
( )
2
2
2
0
0
0
0 2 1 1
20
2
22
x
x
x
g x x x
fx
x
x
=
=
=
= − = − =
−=
=
−=
Dựa vào đồ thị ta thấy
( )
2 2 2
2
2 0 2 2 4 0
2
x
f x x x
x
−
− − −
Vậy hàm số
( )
gx
nghịch biến trên
( )
1;0−
là sai.
Câu 58: Cho hàm số
()y f x=
có bảng xét dấu
'( )fx
như sau:
Hàm số
(5 2 )y f x=−
đồng biến trên khoảng nào dưới đây?
A.
( )
3;4
. B.
( )
1;3
. C.
( )
;3− −
. D.
( )
4;5
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
49 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn D
' 2 (5 2 )y f x
= − −
.
5 2 3 4
' 2 (5 2 ) 0 (5 2 ) 0
1 5 2 1 2 3
xx
y f x f x
xx
− −
= − − −
− −
Vậy hàm số
(5 2 )y f x=−
đồng biến trên
( )
4;5

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
8
2
mx
y
xm
−
=
−
. Tìm tất cả các giá trị thực của tham số
m
để hàm số đồng biến trên
từng khoảng xác định:
A.
4m −
. B.
8m
. C.
44m−
. D.
4m
.
Câu 2: Tìm tất cả các giá trị của tham số
m
để hàm số
32
1
21
3
y x x mx= − − + −
nghịch biến trên
A.
4m −
. B.
4m −
. C.
4m −
. D.
4m −
.
Câu 3: Có bao nhiêu giá trị nguyên của
m
để hàm số
76mx m
y
xm
+−
=
+
nghịch biến trên từng khoảng
xác định?
A.
6.
B.
5.
C.
4.
D.
3.
Câu 4: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
32
1
2 3 2
3
y x mx m x m= − − − − +
luôn đồng biến trên ?
A.
5
. B.
1
. C.
2
. D.
3
.
Câu 5: Tập hợp tất cả các giá trị của tham số
m
để hàm số
( )
3 2 2
21y x x m x m= + + + −
đồng biến trên
khoảng
( )
;− +
là
A.
(
;3−
. B.
( )
;3−
. C.
1
;
3
+
. D.
1
;
3
+
.
Câu 6: Tìm tất cả giá trị của tham số
m
để hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
Tìm m để hàm số đơn điệu trên khoảng xác định
DẠNG 4
Phương pháp:
Xt hm s bc ba
32
( ) .y f x ax bx cx d= = + + +
▪ Bước 1: Tập xác định:
.D =
▪ Bước 2: Tnh đo hàm
2
( ) 3 2 .y f x ax bx c
= = + +
o Để
()fx
đồng biến trên
()
2
()
30
( ) 0, ?
4 12 0
fx
fx
aa
y f x x m
b ac
=
=
= −
o Đ
()fx
nghịch biến trên
()
2
()
30
( ) 0, ?
4 12 0
fx
fx
aa
y f x x m
b ac
=
=
= −
Lưu ý: Dấu của tam thc bậc hai
2
( ) .f x ax bx c= + +
•
Để
0
( ) 0,
0
a
f x x
•
0
( ) 0,
0
a
f x x

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
4m −
. B.
4m
. C.
4m
. D.
4m
.
Câu 7: Có bao nhiêu số nguyên
m
thỏa mãn điu kiện hàm số
3 2 2
2 9 12 2y x mx m x m= + + + −
đồng
biến trên khoảng
( )
;− +
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 8: Số giá trị nguyên của tham số
m
để hàm số
32
1
2 4 5
3
y x mx x= − + −
đồng biến trên là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 9: Cho hàm số
32
1
31
3
y x mx mx= − + +
. Tìm điu kiện của
m
để hàm số đồng biến trên .
A.
( ;0) (3; )m − +
. B.
( ;0] [3; )m − +
.
C.
[0;3]m
. D.
( 3;0)m−
.
Câu 10: Tổng tất cả các giá trị nguyên của
m
để hàm số
( )
32
1
1
3
y x m x x m= − − + −
đồng biến trên tập
xác định bằng:
A.
3
. B.
2
. C.
4
. D.
1
Câu 11: Cho hàm số
( )
32
1
2 1 1
3
y x mx m x= + + − −
(
m
là tham số). Có bao nhiêu giá trị nguyên của tham
số
m
để hàm số đồng biến trên ?
A.
3
. B.
0
. C.
1
. D. Vô số.
Câu 12: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
1y x x mx= + + +
đồng biến trên
( )
;− +
.
A.
4
3
m
. B.
4
3
m
. C.
1
3
m
. D.
1
3
m
.
Câu 13: Tìm tất cả các giá trị thực của tham số
m
để hàm số
1
xm
y
x
−
=
+
đồng biến trên từng khoảngxác
định?
A.
1m −
. B.
1m
. C.
1m
. D.
1m −
.
Câu 14: Cho hàm số
( )
32
1
( ) 3 2 5
3
f x x mx m x= − + + + −
. Tập hợp các giá trị của tham số
m
để hàm số
nghịch biến trên là
;ab
. Khi đó
2ab−
bằng
A.
6
. B.
3−
. C.
5
. D.
1−
.
Câu 15: Tìm tất cả giá trị của tham số
m
để hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
A.
4m −
. B.
4m
. C.
4m
. D.
4m
.
Câu 16: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
16−
=
−
mx
y
xm
đồng biến trên khoảng
( )
5;2−
?.
A.
7
. B.
2
. C.
1
. D.
6
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 17: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đon
[ 20;2]−
để hàm số
32
31y x x mx= +−−
đồng biến trên ?
A.
2
. B.
23
. C.
20
. D.
3
.
Câu 18: Cho hàm số
( ) ( )
32
3 1 3 2 1 2020y x m x m x= − − + + − +
. Có bao nhiêu giá trị nguyên của
m
để
hàm số nghịch biến trên khoảng
( )
;− +
?
A.
4
.
B.
6
.
C.
2
.
D.
5
.
Câu 19: Tìm tất cả các giá trị của tham số
m
để hàm số
32
21y x x mx= + − +
đồng biến trên .
A.
4
3
m −
. B.
4
3
m −
. C.
4
3
m −
. D.
4
3
m
.
Câu 20: Tổng tất cả các giá trị nguyên của tham số
m
để hàm số
43mx m
y
xm
+−
=
+
nghịch biến trên từng
khoảng xác định là
A.
3
. B.
6
. C.
1
. D.
2
.
Câu 21: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
32
1
2 3 2
3
y x mx m x m= − − − − +
luôn
đồng biến trên ?
A.
1
. B.
2
. C.
3
. D.
5
.
Câu 22: Tìm tất cả giá trị của
m
sao cho hàm số
2
xm
y
x
+
=
+
đồng biến trên các khoảng xác định?
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Câu 23: Hàm số
2
4
xm
y
x
−
=
−
đồng biến trên các khoảng
( )
;4−
và
( )
4;+
khi
A.
2 2.m−
B.
2
.
2
m
m
−
C.
2
.
2
m
m
−
D.
2 2.m−
Câu 24: Tồn ti bao nhiêu số nguyên
m
để hàm số
2x
y
xm
−
=
−
đồng biến trên khoảng
( )
;1− −
.
A.
3
. B.
4
. C.
2
. D. Vô số.
Câu 25: Số giá trị nguyên của
m
để hàm số
3
3
mx
y
xm
−+
=
−
nghịch biến trên từng khoảng xác định là.
A.
2
. B.
5
. C.
3
. D.
7
.
Câu 26: Cho hàm số
( )
4x
fx
xm
−
=
+
. Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số đồng biến
trên từng khoảng xác định.
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 27: Cho hàm số
( )
32
11y mx mx m x= + − + +
. Tìm tất cả các giá trị của m để hàm số nghịch biến
trên R.
A.
3
0
4
m
−
. B.
3
0
4
m
−
. C.
0m
. D.
3
4
m
−
.
Câu 28: Có bao nhiêu giá tị nguyên của tham số
m
để hàm số

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
( )
32
1
( 2) 3
3
f x x mx m x= − + + −
đồng biến trên ?
A. Vô số. B.
3
. C.
2
. D.
4
.
Câu 29: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
1y x x mx= + + +
đồng biến trên
( )
;− +
.
A.
1
3
m
. B.
1
3
m
. C.
4
3
m
. D.
4
3
m
.
Câu 30: Số giá trị nguyên của tham số
m
để hàm số
( )
( )
2 3 2
11y m x m x x= − + − −
nghịch biến trên
là
A. 2. B. 3. C. 1. D. 0.
Câu 31: Cho hàm số , là tham số thực. Có bao nhiêu giá trị nguyên của tham số để hàm
số nghịch biến trên từng khoảng xác định.
A. . B. . C. . D. .
Câu 32: Số giá trị nguyên của
m
để hàm số
( ) ( )
32
7 7 2 1y m x m x mx= − + − − −
nghịch biến trên
bằng
A.
7
. B.
9.
C.
4
. D.
6
.
Câu 33: Tìm tất cả các giá trị của tham số
m
để hàm số
32
1
21
3
y x x mx= + − −
đồng biến trên ?
A.
4m −
. B.
4m −
. C.
4m −
. D.
4m −
.
Câu 34: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
1
mx
y
xm
−
=
−+
đồng biến trên mỗi khoảng
xác định?
A. 4. B. 6. C. Vô số. D. 2.
Câu 36: Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
32
31f x x mx= − −
đồng biến trên
A.
0m =
. B.
0m
. C.
0m
. D.
0m
.
Câu 37: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
32
35y x m x= − −
đồng biến
trên
A.
1
. B.
3
. C.
2
. D.
5
.
Câu 38: Tất cả các giá trị thực của tham số
m
để hàm số
( )
32
2021 2022f x x mx= + +
đồng biến trên
là
A.
0m
. B.
0m =
. C.
0m
. D.
0m
.
Câu 39: Hỏi có tất cả bao nhiêu giá trị m nguyên để hàm số
32
( ) 3 6(2 ) 1f x x mx m x= − + − +
đồng biến
trên ?
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 40: Hỏi có tất cả bao nhiêu số nguyên
m
để hàm số
( )
32
35y x m x= − −
đồng biến trên .
A. 1. B. 3. C. 2. D. 5.
2
2
mx
y
xm
+
=
+
m
m
1
3
2
5

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Câu 41: Hãy tìm tất cả các giá trị thực của m để hàm số
32
3 2 1y x mx m= − + −
đồng biến trên .
A.
0m
. B.
0m =
. C.
0m
. D.
0m
.
Câu 42: Tìm tất cả các giá trị của tham số
m
để hàm số
3sin cos 5y x x mx= + − +
nghịch biến trên tập
xác định.
A.
2.m
B.
2.m
C.
2.m −
D.
2 2.m−
Câu 43: Tìm tất cả các giá trị của tham số
m
để hàm số
3sin cos 5y x x mx= + − +
nghịch biến trên tập
xác định.
A.
2m
. B.
2m
. C.
2m −
. D.
22m−
.
Câu 44: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
3
9y x m x= − + −
nghịch biến
trên
.
A.
9
. B.
10
. C.
7
. D.
8
.
Câu 45: Tìm tất cả các giá trị thực của tham số
m
để hàm số
osy mx c x=+
đồng biến trên .
A.
1m
. B.
1m
. C.
1m −
. D.
1m −
.
Câu 46: Tìm giá trị nhỏ nhất của tham số
m
sao cho hàm số
3
2
3
x
y mx mx m= + − −
luôn đồng biến trên
.
A.
0m =
. B.
1m =−
. C.
6m =−
. D.
5m =−
.
Câu 47: Tìm tất cả các giá trị của tham số
m
để hàm số
2
1
xm
y
x
+−
=
+
nghịch biến trên mỗi khoảng xác
định của nó?
A.
1m
. B.
3m −
. C.
1m
. D.
3m −
.
Câu 48: Cho hàm số
( )
32
1
( ) 3 2 5.
3
f x x mx m x= − + + + −
Tập hợp các giá trị của tham số
m
để hàm số
nghịch biến trên là
;.ab
Khi đó
2ab−
bằng:
A.
5
. B.
1−
. C.
6
. D.
3−
.
Câu 49: Tất cả các giá trị thực của
m
để hàm số
32
61y x x mx= − + +
đồng biến trên
( )
0;+
là:
A.
12m
. B.
0m
. C.
12m
. D.
0m
.
Câu 50: Có tất cả bao nhiêu giá trị nguyên của tham số thực
m
sao cho hàm số
( ) ( )
32
1
2 5 2021
3
f x mx mx m x= − + − +
nghịch biến trên ?
A. 1. B. 0. C. 3. D. 2.
Câu 51: Tìm tất cả giá trị thực của tham số
m
để hàm số
( ) ( )
32
1 2 3
3
m
y x m x m x m= − + + − −
nghịch
biến trên ?
A.
1
4
m −
. B.
0m
. C.
0m
. D.
1
0
4
m−
.
Câu 52: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
6 3 1y x mx x= − + − +
nghịch biến trên
A.
11
;;
22
m
− − +
. B.
11
;
22
m
−
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
C.
11
;
22
m
−
. D.
11
;;
22
m
− − +
.
Câu 53: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
4
xm
y
x
+
=
+
đồng biến trên từng khoảng
xác định của nó?
A.
5
. B.
1
. C.
2
. D.
3
.
Câu 54: Có bao nhiêu giá trị nguyên của tham số
m
sao cho hàm số
( )
32
1
9 23
3
f x x mx x= − + − +
nghịch biến trên
A.
6
. B.
8
. C.
7
. D.
5
.
Câu 55: Tập tất cả giá trị của tham số
m
để hàm số
32
3 3 1y x mx x
đồng biến trên là
A.
; 1 1;m
. B.
1;1
.
C.
; 1 1;
. D.
1;1
.
Câu 57: Điu kiện cần và đủ để hàm số
32
y x ax bx c= + + +
(
,,abc
là các hằng số thực) đồng biến trên
khoảng
( )
;− +
là
A.
2
30ab−
. B.
2
30ab−
. C.
2
30ab−
. D.
2
30ab−
.
Câu 58: Tìm các giá trị của
m
để hàm số
32
3y x mx x= + +
đồng biến trên .
A.
3;3m−
. B.
( )
3;3m−
.
C.
(
)
; 3 3;m − − +
D.
( ) ( )
; 3 3;m − − +
Câu 59: Tìm các giá trị của
m
để hàm số
32
3y x mx x= + +
đồng biến trên .
A.
3;3m−
. B.
( )
3;3m−
.
C.
(
)
; 3 3;m − − +
D.
( ) ( )
; 3 3;m − − +
Câu 60: Cho hàm số
( )
32
3 2 3 1y x mx m x m= − + + + −
. Tổng các giá trị nguyên của tham số
m
để hàm
số đồng biến trên là
A.
2−
. B.
1−
. C.
1
. D.
2
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
8
2
mx
y
xm
−
=
−
. Tìm tất cả các giá trị thực của tham số
m
để hàm số đồng biến trên
từng khoảng xác định:
A.
4m −
. B.
8m
. C.
44m−
. D.
4m
.
Lời giải
Chọn C
( )
2
2
16
'
2
m
y
xm
−+
=
−
và điu kiện xác định
2
m
x
Để hàm số đồng biến trên khoảng xác định thì
2
' 0 16 0 4 4y m m − + −
.
Câu 2: Tìm tất cả các giá trị của tham số
m
để hàm số
32
1
21
3
y x x mx= − − + −
nghịch biến trên
A.
4m −
. B.
4m −
. C.
4m −
. D.
4m −
.
Lời giải
Chọn C
Ta có
2
'4y x x m= − − +
Hàm số nghịch biến trên
2
40x x m − − +
với mọi x
10
16 4 0 4
0
mm
−
+ −
Câu 3: Có bao nhiêu giá trị nguyên của
m
để hàm số
76mx m
y
xm
+−
=
+
nghịch biến trên từng khoảng
xác định?
A.
6.
B.
5.
C.
4.
D.
3.
Lời giải
Chọn C
Ta có
( )
2
2
76
,
mm
y x m
xm
−+
= −
+
Để hàm số nghịch biến trên từng khoảng xác định thì
0,y x m
−
2
7 6 0 1 6m m m − +
Mà
2;3;4;5mm
có
4
giá trị nguyên của
m
thỏa mãn
Câu 4: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
32
1
2 3 2
3
y x mx m x m= − − − − +
luôn đồng biến trên ?
A.
5
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
2
2 2 3y x mx m
= − − +
.
Kh đó
22
0, 2 2 3 0, 2 3 0 3 1y x x mx m x m m m
− − + = + − −
.
Do
m
nguyên dương nên
1m =
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Câu 5: Tập hợp tất cả các giá trị của tham số
m
để hàm số
( )
3 2 2
21y x x m x m= + + + −
đồng biến trên
khoảng
( )
;− +
là
A.
(
;3−
. B.
( )
;3−
. C.
1
;
3
+
. D.
1
;
3
+
.
Lời giải
Chọn C
Hàm số đồng biến trên khi và chỉ khi
2
' 3 4 1 0,= + + + y x x m x
( )
2
30
1
' 2 3. 1 0
3
=
= − +
a
m
m
.
Câu 6: Tìm tất cả giá trị của tham số
m
để hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
A.
4m −
. B.
4m
. C.
4m
. D.
4m
.
Lời giải
Chọn A
Ta có: Hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
2
4 0;y x x m x R
= + −
.
Dễ thấy:
2
10
4 0; 4
40
x x m x R m
m
+ − −
= +
Vậy: Hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
4m −
.
Câu 7: Có bao nhiêu số nguyên
m
thỏa mãn điu kiện hàm số
3 2 2
2 9 12 2y x mx m x m= + + + −
đồng
biến trên khoảng
( )
;− +
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn A
Ta có:
22
' 6 18 12y x mx m= + +
Hàm số đồng biến trên khoảng
( )
; ' 0yx− +
2 2 2
3 2 0, 0 0 0x mx m x m m + + =
.
Vậy có 1 số nguyên
m
thỏa mãn điu kiện hàm số
3 2 2
2 9 12 2y x mx m x m= + + + −
đồng biến
trên khoảng
( )
;− +
.
Câu 8: Số giá trị nguyên của tham số
m
để hàm số
32
1
2 4 5
3
y x mx x= − + −
đồng biến trên là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A
Ta có
2
44y x mx
= − +
.
Hàm số
32
1
2 4 5
3
y x mx x= − + −
đồng biến trên

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
2
10
0, 1 1
4 4 0
a
y x m
m
=
−
= −
.
Vì
m
nên
1;0;1m−
.
Vậy số giá trị nguyên của
m
để hàm số đã cho đồng biến trên
là
3
.
Câu 9: Cho hàm số
32
1
31
3
y x mx mx= − + +
. Tìm điu kiện của
m
để hàm số đồng biến trên .
A.
( ;0) (3; )m − +
. B.
( ;0] [3; )m − +
.
C.
[0;3]m
. D.
( 3;0)m−
.
Lời giải
Chọn C
TXĐ:
D =
.
2
23y x mx m
= − +
.
Hàm số đồng biến trên
2
0
0, 3 0 0; 3
0
a
y x m m m
−
.
Câu 10: Tổng tất cả các giá trị nguyên của
m
để hàm số
( )
32
1
1
3
y x m x x m= − − + −
đồng biến trên tập
xác định bằng:
A.
3
. B.
2
. C.
4
. D.
1
Lời giải
Chọn A
Tập xác định :
D =
.
( )
2
2 1 1y x m x
= − − +
.
Để hàm số đồng biến trên tập xác định thì
2
0, 2 0 0 2y x m m m
= −
.
Vì
m
nên
0;1;2m
.
Vậy
0 1 2 3S = + + =
.
Câu 11: Cho hàm số
( )
32
1
2 1 1
3
y x mx m x= + + − −
(
m
là tham số). Có bao nhiêu giá trị nguyên của tham
số
m
để hàm số đồng biến trên ?
A.
3
. B.
0
. C.
1
. D. Vô số.
Lời giải
Chọn C
Ta có
2
2 2 1y x mx m
= + + −
.
Hàm số đồng biến trên khi
0,yx
2
2 1 0 1m m m − + =
.
Câu 12: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
1y x x mx= + + +
đồng biến trên
( )
;− +
.
A.
4
3
m
. B.
4
3
m
. C.
1
3
m
. D.
1
3
m
.
Lời giải
Chọn D
Tập xác định
D =
.
Đo hàm
2
32y x x m
= + +
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Hàm hàm số
32
1y x x mx= + + +
đồng biến trên
( )
;− +
khi và chỉ khi
0,yx
hay
1
0 1 3 0
3
mm
−
.
Câu 13: Tìm tất cả các giá trị thực của tham số
m
để hàm số
1
xm
y
x
−
=
+
đồng biến trên từng khoảngxác
định?
A.
1m −
. B.
1m
. C.
1m
. D.
1m −
.
Lời giải
Chọn D
Tập xác định
\1D =−
.
Ta có
( )
2
1
1
m
y
x
+
=
+
xác định với mọi
1x −
.
Hàm số đã cho đồng biến trên từng khoảng xác định
0 1 0 1y m m
+ −
.
Vậy
1m −
.
Câu 14: Cho hàm số
( )
32
1
( ) 3 2 5
3
f x x mx m x= − + + + −
. Tập hợp các giá trị của tham số
m
để hàm số
nghịch biến trên là
;ab
. Khi đó
2ab−
bằng
A.
6
. B.
3−
. C.
5
. D.
1−
.
Lời giải
Chọn B
Hàm số xác định với mọi
x
.
Ta có:
( )
2
2 3 2f x x mx m
= − + + +
.
Hàm số nghịch biến trên khi
( )
0,f x x
.
0
2
3 2 0 2 1m m m + + − −
Vậy
2, 1 2 3a b a b= − = − − = −
.
Câu 15: Tìm tất cả giá trị của tham số
m
để hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
A.
4m −
. B.
4m
. C.
4m
. D.
4m
.
Lời giải
Chọn A
Ta có: Hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
2
4 0;y x x m x R
= + −
.
Dễ thấy:
2
10
4 0; 4
40
x x m x R m
m
+ − −
= +
Vậy: Hàm số
3
2
2 2020
3
x
y x mx= + − +
đồng biến trên
4m −
.
Câu 16: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
16−
=
−
mx
y
xm
đồng biến trên khoảng
( )
5;2−
?.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
A.
7
. B.
2
. C.
1
. D.
6
.
Lời giải
Chọn B
Tnh được
( )
2
2
16−+
=
−
m
y
xm
với
xm
.
Để hàm số đã cho đồng biến trên khoảng
( )
5;2−
ta có:
( )
( )
( )
0 5;2
44
5;2
5;2
−
−
−
−
yx
m
m
m
Do
m
là giá trị nguyên nên:
2;3m
.
Câu 17: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đon
[ 20;2]−
để hàm số
32
31y x x mx= +−−
đồng biến trên ?
A.
2
. B.
23
. C.
20
. D.
3
.
Lời giải
Chọn A
23
31y x x mx= − + −
đồng biến trên
2
' 3 2 3 0y x x m x = − +
1
0 1 9 0
9
mm
−
mà
m
nguyên thuộc
[ 20;2]−
1;2m
có hai giá trị
m
.
Câu 18: Cho hàm số
( ) ( )
32
3 1 3 2 1 2020y x m x m x= − − + + − +
. Có bao nhiêu giá trị nguyên của
m
để
hàm số nghịch biến trên khoảng
( )
;− +
?
A.
4
.
B.
6
.
C.
2
.
D.
5
.
Lời giải
Chọn D
TXĐ:
D =
( ) ( )
2
' 3 6 1 3 2 1y x m x m= − − + + −
.
Hàm số nghịch biến trên
( )
;− +
khi
( )
' 0, ;yx − +
( ) ( )
2
2
30
9 36 0 4 0
' 9 1 9 2 1 0
a
m m m
mm
= −
+ −
= + + −
4;0m −
có 5 giá trị nguyên của m thỏa mãn.
Câu 19: Tìm tất cả các giá trị của tham số
m
để hàm số
32
21y x x mx= + − +
đồng biến trên .
A.
4
3
m −
. B.
4
3
m −
. C.
4
3
m −
. D.
4
3
m
.
Lời giải
Chọn A
Ta có
3 2 2
2 1 3 4y x x mx y x x m
= + − + = + −
.
Hàm số
32
21y x x mx= + − +
đồng biến trên khi và chỉ khi
'
0,yx

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
2
3 4 0,x x m x + −
( )
22
4
3 4 , 3 4
3
x x m x m Min x x m + + −
.
Câu 20: Tổng tất cả các giá trị nguyên của tham số
m
để hàm số
43mx m
y
xm
+−
=
+
nghịch biến trên từng
khoảng xác định là
A.
3
. B.
6
. C.
1
. D.
2
.
Lời giải
Chọn D
Tập xác định:
\Dm=−
. Ta có:
( )
2
2
43mm
y
xm
−+
=
+
.
Hàm số nghịch biến trên từng khoảng xác định khi
2
0 4 3 0 1 3y m m m
− +
.
Vì
m
nên
2m
. Vậy tổng các giá trị nguyên của tham số
m
bằng 2.
Câu 21: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
32
1
2 3 2
3
y x mx m x m= − − − − +
luôn
đồng biến trên ?
A.
1
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn D
Ta có
2
2 2 3y x mx m
= − − +
Để thỏa yêu cầu bài toán thì
0,yx
2
0 2 3 0 3 1.
y
m m m
+ − −
Do
m
là số nguyên nên
3; 2; 1;0;1m − − −
. Vậy có
5
giá trị
m
thỏa bài toán.
Câu 22: Tìm tất cả giá trị của
m
sao cho hàm số
2
xm
y
x
+
=
+
đồng biến trên các khoảng xác định?
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Lời giải
Chọn B
Hàm số
2
xm
y
x
+
=
+
đồng biến trên các khoảng xác định
( )
2
2
0, 2 2 0 2
2
m
y x m m
x
−
= − −
+
.
Câu 23: Hàm số
2
4
xm
y
x
−
=
−
đồng biến trên các khoảng
( )
;4−
và
( )
4;+
khi
A.
2 2.m−
B.
2
.
2
m
m
−
C.
2
.
2
m
m
−
D.
2 2.m−
Lời giải
Chọn A
TXĐ:
\4D =
.
Ta có
( )
2
2
4
'
4
m
y
x
−+
=
−
.
Để hàm số đồng biến trên từng khoảng xác định thì
2
' 0 4 0 2 2y m m − + −
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Câu 24: Tồn ti bao nhiêu số nguyên
m
để hàm số
2x
y
xm
−
=
−
đồng biến trên khoảng
( )
;1− −
.
A.
3
. B.
4
. C.
2
. D. Vô số.
Lời giải
Chọn A
( )
2
2
'
m
y
xm
−
=
−
Để hàm số đồng biến trên khoảng
( )
;1− −
thì
( )
20
' 0 2
12
;1
1
m
ym
m
m
x m m
−
−
− −
−
Mà
1;0;1m Z m = −
.
Câu 25: Số giá trị nguyên của
m
để hàm số
3
3
mx
y
xm
−+
=
−
nghịch biến trên từng khoảng xác định là.
A.
2
. B.
5
. C.
3
. D.
7
.
Lời giải
ĐKXĐ:
3
m
x
.
Xét 2 khoảng
;
3
m
x
−
và
;
3
m
x
+
. Để hàm số nghịch biến
( )
2
2
2
9
' 0 9 0 3 3.
3
m
y m m
xm
−
= − −
−
Câu 26: Cho hàm số
( )
4x
fx
xm
−
=
+
. Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số đồng biến
trên từng khoảng xác định.
A.
4
. B.
5
. C.
3
. D.
6
.
Lời giải
Chọn C
TXĐ:
\Dm=−
. Ta có:
( )
2
4m
y
xm
+
=
+
Hàm số đồng biến trên từng khoảng xác định
0,y x D
4 0 4mm + −
.
Vì
m
nguyên âm nên
3; 2; 1m − − −
Vậy có
3
giá trị thỏa mãn.
Câu 27: Cho hàm số
( )
32
11y mx mx m x= + − + +
. Tìm tất cả các giá trị của m để hàm số nghịch biến
trên R.
A.
3
0
4
m
−
. B.
3
0
4
m
−
. C.
0m
. D.
3
4
m
−
.
Lời giải
Chọn B
Yêu cầu cần đt:
Biết tnh đo hàm.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Xác định được điu kiện để hàm số nghịch biến trên R.
Tìm m để bất phương trình bậc hai đúng với mọi x.
Ta có:
( )
32
2
11
' 3 2 1
y mx mx m x
y mx mx m
= + − + +
= + − −
TH 1:
0 ' 1 0my= = −
. Hàm số nghịch biến trên R
( )
1
TH 2:
0m
. Hàm số nghịch biến trên
R
khi:
( ) ( )
2
2
0
0
0
0
3
0
3
0
4
0
16 12 0
2 4.3 . 1 0
4
m
m
m
a
m
m
mm
m m m
−
−
+
− − −
( )
2
Từ
( )
1
và
( )
2
3
0
4
m
−
Câu 28: Có bao nhiêu giá tị nguyên của tham số
m
để hàm số
( )
32
1
( 2) 3
3
f x x mx m x= − + + −
đồng biến trên ?
A. Vô số. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn D
Để hàm số đồng biến trên thì:
( )
0fx
,
x
2
2 2 0x mx m − + +
,
x
2
20mm = − −
12m −
Vậy có 4 giá trị nguyên của tham số
m
thỏa đ bài.
Câu 29: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
1y x x mx= + + +
đồng biến trên
( )
;− +
.
A.
1
3
m
. B.
1
3
m
. C.
4
3
m
. D.
4
3
m
.
Lời giải
Chọn B
Xét hàm số
32
1y x x mx= + + +
.
Tập xác định:
D =
.
Ta có
2
32y x x m
= + +
.
Để hàm số đồng biến trên thì
2
30
1
0,
3
1 3 0
y x m
m
= −
.
Câu 30: Số giá trị nguyên của tham số
m
để hàm số
( )
( )
2 3 2
11y m x m x x= − + − −
nghịch biến trên
là
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn A

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Yêu cầu đ bài tương đương với
( )
( )
22
3 1 2 1 1 0,y m x m x x
= − + − −
.
+) Khi
2
1 0 1mm− = =
.
Với
1m =
thì
1 0,yx
= −
do đó giá trị
1m =
thỏa mãn.
Với
1m =−
thì
1
4 1 0
4
y x x
= − − −
, do đó giá trị
1m =−
không thỏa mãn.
+) Khi
2
1 0 1mm−
, YCBT tương đương với
( )
( )
2
2
2
11
10
1
1
1
2
1
1 3 1 0
2
m
m
m
m
mm
−
−
−
−
− + −
.
Vậy
1
1
2
m−
nên có 2 giá trị nguyên của tham số
m
là
0; 1mm==
thoả mãn.
Câu 31: Cho hàm số , là tham số thực. Có bao nhiêu giá trị nguyên của tham số để hàm
số nghịch biến trên từng khoảng xác định.
A. . B. . C. . D. .
Lời giải
Chọn B
TXĐ:
\
2
m
D
−
=
,
2
2
4
'
(2 )
m
y
xm
−
=
+
.
Để hàm số nghịch biến trên từng khoảng xác định của nó thì
2
4 0 2 2mm− −
.
Do đó có giá trị nguyên của tham số thỏa mãn.
Câu 32: Số giá trị nguyên của
m
để hàm số
( ) ( )
32
7 7 2 1y m x m x mx= − + − − −
nghịch biến trên
bằng
A.
7
. B.
9.
C.
4
. D.
6
.
Lời giải
Chọn A
Tập xác định:
D =
.
Ta có
( ) ( )
2
3 7 2 7 2y m x m x m
= − + − −
.
TH1:
7 14 0,m y x
= = −
Hàm số nghịch biến trên
7m=
.
TH2:
7m
Hàm số nghịch biến trên
2
7
70
0,
0
7 56 49 0
m
m
yx
mm
−
− +
7
17
17
m
m
m
.
Vậy hàm số nghịch biến trên khi
17m
.
Do
m
nên có 7 giá trị nguyên của
m
.
Câu 33: Tìm tất cả các giá trị của tham số
m
để hàm số
32
1
21
3
y x x mx= + − −
đồng biến trên ?
A.
4m −
. B.
4m −
. C.
4m −
. D.
4m −
.
Lời giải
Chọn A
2
2
mx
y
xm
+
=
+
m
m
1
3
2
5
3
m

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Ta có:
2
4y x x m
= + −
.
Hàm số đồng biến trên
0,yx
2
10
4 0, 4 0 4
0
x x m x m m
+ − + −
.
Câu 34: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
1
mx
y
xm
−
=
−+
đồng biến trên mỗi khoảng
xác định?
A. 4. B. 6. C. Vô số. D. 2.
Lời giải
Chọn D
TXĐ:
\1Dm=−
.
Ta có:
( )
( ) ( )
2
22
12
22
'
1
11
mm
mx m m
yy
xm
x m x m
−+
− − + +
= = =
−+
− + − +
.
Để hàm số đồng biến trên mỗi khoảng xác định thì
'0y x D
Hay
2
2 0 1 2m m m− + + −
.
Các giá trị nguyên của tham số
m
thỏa mãn đ bài là: 0; 1.
Vậy có 2 giá trị nguyên của tham số
m
thỏa mãn đ bài.
Câu 36: Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
32
31f x x mx= − −
đồng biến trên
A.
0m =
. B.
0m
. C.
0m
. D.
0m
.
Lời giải
Chọn A
Tập xác định
D =
.
2
36y x mx
=−
.
Hàm số đồng biến trên
0,yx
2
3 6 0,x mx x −
( )
2
30m −
0m=
.
Câu 37: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
32
35y x m x= − −
đồng biến
trên
A.
1
. B.
3
. C.
2
. D.
5
.
Lời giải
Chọn D
+ Tập xác định:
D =
.
+ Ta có:
( )
22
' 3 3 5y x m= − −
; hàm số đồng biến trên
'0y
,
x
( )
2
36 5 0m = −
55m−
.
Do
m
nguyên nên có 5 giá trị
m
thỏa mãn là:
2; 1;0;1;2−−
.
Câu 38: Tất cả các giá trị thực của tham số
m
để hàm số
( )
32
2021 2022f x x mx= + +
đồng biến trên
là
A.
0m
. B.
0m =
. C.
0m
. D.
0m
.
Lời giải
Chọn B

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Ta có
( )
2
3 4042f x x mx
=+
;
( )
0fx
=
0
4042
3
x
m
x
=
=−
.
Hàm số đồng biến trên
( )
0,f x x
0.m =
Cách 2: Ta có
( )
2
3 4042f x x mx
=+
.
( )
( )
2
2
3 4042 0,
4042 4.3.0 0 0
f x x mx x
mm
= +
= − =
Câu 39: Hỏi có tất cả bao nhiêu giá trị m nguyên để hàm số
32
( ) 3 6(2 ) 1f x x mx m x= − + − +
đồng biến
trên ?
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn A
TXĐ:
DR=
;
'2
( ) 3 6 6(2 )f x x mx m= − + −
.
Hàm số đã cho đồng biến trên
R
khi và chỉ khi:
'
( ) 0,f x x R
'
0
2
9 18 36 0mm + −
1 5 1 5m − − − +
.
Vì
mZ
nên
3; 2; 1;0;1m − − −
.
Vậy có 5 giá trị nguyên của m thỏa mãn.
Câu 40: Hỏi có tất cả bao nhiêu số nguyên
m
để hàm số
( )
32
35y x m x= − −
đồng biến trên .
A. 1. B. 3. C. 2. D. 5.
Lời giải
Chọn D
Ta có
( ) ( )
3 2 ' 2 2
3 5 3 3 5y x m x y x m= − − = − −
.
Hàm số đồng biến trên khi và chỉ khi
'2
0, 5 0 5 5y x m m − −
.
Vì
m
nguyên suy ra
2; 1;0;1;2m − −
.
Vậy có 5 giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 41: Hãy tìm tất cả các giá trị thực của m để hàm số
32
3 2 1y x mx m= − + −
đồng biến trên .
A.
0m
. B.
0m =
. C.
0m
. D.
0m
.
Lời giải
Chọn B
Ta có
2
36y x mx
=−
.
Hàm số đồng biến trên
2
0 0 9 0 0y x m m
=
Chọn đáp án B.
Câu 42: Tìm tất cả các giá trị của tham số
m
để hàm số
3sin cos 5y x x mx= + − +
nghịch biến trên
tập xác định.
A.
2.m
B.
2.m
C.
2.m −
D.
2 2.m−
Lời giải
Chọn A
Tập xác định
.D =

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
3cos siny x x m
= − −
Hàm số
3sin cos 5y x x mx= + − +
nghịch biến trên
3cos sin 0, y x x m x
= − −
31
cos sin , sin ,
2 2 2 3 2
mm
x x x x x
− −
(1)
Vì
1 sin 1,
3
xx
− −
nên
(1) 1 2
2
m
m
.
Câu 43: Tìm tất cả các giá trị của tham số
m
để hàm số
3sin cos 5y x x mx= + − +
nghịch biến trên
tập xác định.
A.
2m
. B.
2m
. C.
2m −
. D.
22m−
.
Lời giải
Chọn A
Tập xác định:
D =
Ta có
3cos sin ,y x x m x
= − −
Hàm số nghịch biến trên tập xác định
0,yx
(dấu bằng xảy ra tại hữu hạn điểm)
0, 3cos sin 0, y x x x m x
− −
31
2 cos sin ,
22
m x x x
−
2cos , 2
6
m x x m
+
.
Câu 44: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
3
9y x m x= − + −
nghịch biến
trên
.
A.
9
. B.
10
. C.
7
. D.
8
.
Lời giải
Chọn A
Ta có
2
3 9.y x m
= − + −
Để hàm số nghịch biến trên
0,yx
( )
2
3 9 0, 0 3 9 0 9.x m x m m
− + − −
Vì
m
+
nên
1;2; ;9 .m
Câu 45: Tìm tất cả các giá trị thực của tham số
m
để hàm số
osy mx c x=+
đồng biến trên .
A.
1m
. B.
1m
. C.
1m −
. D.
1m −
.
Lời giải
Chọn B
Xét hàm số
osy mx c x=+
liên tục và xác định trên .
Hàm số đồng biến trên khi và chỉ khi

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
' sin 0 sin maxsin 1y m x x m x x m x= − =
.
Câu 46: Tìm giá trị nhỏ nhất của tham số
m
sao cho hàm số
3
2
3
x
y mx mx m= + − −
luôn đồng biến trên
.
A.
0m =
. B.
1m =−
. C.
6m =−
. D.
5m =−
.
Lời giải
Chọn B
Ta có:
2
2y x mx m
= + −
Hàm số đồng biến trên
22
0 2 0 0y x x mx m x m m
+ − +
1;0m−
Vậy giá trị nhỏ nhất của tham số
m
bằng
1−
.
Câu 47: Tìm tất cả các giá trị của tham số
m
để hàm số
2
1
xm
y
x
+−
=
+
nghịch biến trên mỗi khoảng xác
định của nó?
A.
1m
. B.
3m −
. C.
1m
. D.
3m −
.
Lời giải
Chọn C
TXĐ:
D =
1−
.
Ta có
( )
2
1
1
m
y
x
−
=
+
. Để thỏa mãn yêu cầu bài toán thì
1 0 1mm−
Câu 48: Cho hàm số
( )
32
1
( ) 3 2 5.
3
f x x mx m x= − + + + −
Tập hợp các giá trị của tham số
m
để hàm số
nghịch biến trên là
;.ab
Khi đó
2ab−
bằng:
A.
5
. B.
1−
. C.
6
. D.
3−
.
Lời giải
Chọn D
Ta có:
2
( ) 2 3 2.f x x mx m
= − + + +
Hàm số nghịch biến trên
2
( ) 0, 3 2 0 2 1.f x x m m m
= + + − −
Suy ra:
( ) ( )
2, 1 2 2 2 1 3.a b a b= − = − − = − − − = −
.
Câu 49: Tất cả các giá trị thực của
m
để hàm số
32
61y x x mx= − + +
đồng biến trên
( )
0;+
là:
A.
12m
. B.
0m
. C.
12m
. D.
0m
.
Lời giải
Chọn C
Có
2
3 12y x x m
= − +
,
' 36 3m = −
.
Hàm số đồng biến trên
( )
0;+
( )
0 0;yx
+
( )
2
3 12 , 0;m x x x − + +
Bảng biến thiên của
2
( ) 3 12g x x x= − +
trên khoảng
( )
0;+
:

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Từ bảng biến thiên ta có
( )
( )
2
0;
3 12 12Max x x
+
− + =
.
Hàm số đồng biến trên
( )
0;+
( )
( )
2
0;
3 12m Max x x
+
− +
12m
.
Câu 50: Có tất cả bao nhiêu giá trị nguyên của tham số thực
m
sao cho hàm số
( ) ( )
32
1
2 5 2021
3
f x mx mx m x= − + − +
nghịch biến trên ?
A. 1. B. 0. C. 3. D. 2.
Lời giải
Chọn D
Ta có:
( )
2
45f x mx mx m
= − + −
Ycbt
( )
0fx
,
x
TH1:
0m =
Khi đó:
( )
50fx
= −
,
x
Suy ra: nhận
0m =
.
TH2:
0m
Khi đó:
( )
0fx
,
x
( )
2
0
0
0
5
0
5
0
4 5 0
3
0
3
m
m
a
m
m m m
m
−
− −
−
Vậy
5
0
3
m−
thoả ycbt.
Do
m
nên
1;0m−
.
Câu 51: Tìm tất cả giá trị thực của tham số
m
để hàm số
( ) ( )
32
1 2 3
3
m
y x m x m x m= − + + − −
nghịch
biến trên ?
A.
1
4
m −
. B.
0m
. C.
0m
. D.
1
0
4
m−
.
Lời giải
Chọn A
TXĐ
2
, 2 1 2D y mx m x m
TH1:
0;m =
2 2 0 1y x x
= − − −
hàm số không nghịch biến trên , nên loi
0;m =
TH2:
0;m
( ) ( )
2
0
0
1
0,
4 1 0
4
1 2 0
m
m
y x m
m
m m m
−
+
+ − −
Câu 52: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
6 3 1y x mx x= − + − +
nghịch biến trên
A.
11
;;
22
m
− − +
. B.
11
;
22
m
−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
C.
11
;
22
m
−
. D.
11
;;
22
m
− − +
.
Lời giải
Chọn B
Ta có:
32
6 3 1y x mx x= − + − +
.
2
3 12 3y x mx
= − + −
Hàm số
32
6 3 1y x mx x= − + − +
nghịch biến trên
0,yx
(
0y
=
ti hữu hn điểm)
( )
2
2
6 9 0
1
4
11
22
11
;.
22
m
m
m
m
= −
−
−
Câu 53: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
4
xm
y
x
+
=
+
đồng biến trên từng khoảng
xác định của nó?
A.
5
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
Tập xác định:
\4D =−
.
( )
22
2
4
4
4
x m m
yy
x
x
+−
= =
+
+
.
Hàm số
2
4
xm
y
x
+
=
+
đồng biến trên từng khoảng xác định của nó khi và chỉ khi
2
0, 4 4 0 2 2y x m m
− − −
.
Do
m
nên
1;0;1m−
.
Câu 54: Có bao nhiêu giá trị nguyên của tham số
m
sao cho hàm số
( )
32
1
9 23
3
f x x mx x= − + − +
nghịch biến trên
A.
6
. B.
8
. C.
7
. D.
5
.
Lời giải
Chọn C
Để hàm số nghịch biến trên thì
( )
0f x x
2
2 9 0x mx− + −
x
2
4 36 0
33
10
m
m
= −
−
−
. Vậy có các giá trị nguyên của
m
là:
3; 2; 1;0;1;2;3− − −
Câu 55: Tập tất cả giá trị của tham số
m
để hàm số
32
3 3 1y x mx x
đồng biến trên là

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
A.
; 1 1;m
. B.
1;1
.
C.
; 1 1;
. D.
1;1
.
Lời giải
Chọn B
Ta có:
3 2 2
3 3 1 3 6 3y x mx x y x mx
.
Hàm số
32
3 3 1y x mx x
đồng biến trên khi
2
3 6 3 0,y f x x mx x
( )
2
30
9 9 0 1 1 1;1 .
0
fx
m m m
− − −
Câu 57: Điu kiện cần và đủ để hàm số
32
y x ax bx c= + + +
(
,,abc
là các hằng số thực) đồng biến trên
khoảng
( )
;− +
là
A.
2
30ab−
. B.
2
30ab−
. C.
2
30ab−
. D.
2
30ab−
.
Lời giải
Chọn A
Ta có:
2
' 3 2y x ax b= + +
Hàm số đồng biến trên
( )
;− +
' 0,yx
2
3 2 0,x ax b x + +
2
' 3 0ab = −
.
Câu 58: Tìm các giá trị của
m
để hàm số
32
3y x mx x= + +
đồng biến trên .
A.
3;3m−
. B.
( )
3;3m−
.
C.
(
)
; 3 3;m − − +
D.
( ) ( )
; 3 3;m − − +
Lời giải
Chọn A
Hàm số
32
3y x mx x= + +
đồng biến trên thì
0,yx
.
Suy ra
22
3 2 3 0, 9 0 3 3.
y
y x mx x m m
= + + = − −
Câu 59: Tìm các giá trị của
m
để hàm số
32
3y x mx x= + +
đồng biến trên .
A.
3;3m−
. B.
( )
3;3m−
.
C.
(
)
; 3 3;m − − +
D.
( ) ( )
; 3 3;m − − +
Lời giải
Chọn A
Hàm số
32
3y x mx x= + +
đồng biến trên thì
0,yx
.
Suy ra
22
3 2 3 0, 9 0 3 3.
y
y x mx x m m
= + + = − −
Câu 60: Cho hàm số
( )
32
3 2 3 1y x mx m x m= − + + + −
. Tổng các giá trị nguyên của tham số
m
để hàm
số đồng biến trên là
A.
2−
. B.
1−
. C.
1
. D.
2
.
Lời giải
Chọn C
Ta có
2
' 3 6 2y x mx m= − + +
.
Hàm số đã cho đồng biến trên khi
' 0,y x R
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
2
3 6 2 0,x mx m x R − + +
.
( )
( )
2
30
0
'0
9 3 2 0
Ðúng
a
mm
− +
.
2
9 3 6 0mm − −
.
2
1
3
m
−
.
Vì
mZ
nên
0;1m
.
Vậy tổng các giá trị nguyên của tham số
m
bằng
1
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Tập hợp các giá trị thực của tham số
m
để hàm số
5x
y
xm
+
=
+
đồng biến trên khoảng
( )
;8− −
là
A.
( )
5;+
. B.
(
5;8
. C.
)
5;8
. D.
( )
5;8
.
Câu 2: Tìm tất cả các giá trị nguyên của tham số
m
để hàm số
24x
y
xm
+
=
−
đồng biến trên
( )
;4− −
A. 1. B. 3. C. 4. D. 2.
Câu 3: Cho hàm số
( )
( )
23
22
2
3
m m x
y m m x mx
−
= + − + +
. Có bao nhiêu giá trị nguyên của
m
để hàm
số đồng biến trên ?
A.
3
. B.
5
. C.
1
. D.
2
.
Câu 4: Cho hàm số
32
y x mx m= + +
. Điều kiện cần và đủ của
m
để hàm số nghịch biến trên
( )
0;2
là
A.
3m −
. B.
0m
. C.
0m
. D.
3m −
.
Câu 5: Gọi
S
là tập hợp các số nguyên
2020;2020m−
để hàm số
2
5
21
mx
y
mx
+
=
+
nghịch biến trên
khoảng
( )
3; +
. Khi đó số phần tử của
S
bằng
A. 2020. B. 9. C. 45. D. 2021.
Câu 6: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
32
34y x x m x= − + −
đồng biến trên
khoảng
( )
2;+
là
A.
(
;1−
. B.
(
;4−
. C.
( )
;1−
. D.
( )
;4−
.
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
xm
+
=
+
nghịch biến trên khoảng
( )
15;+
?
A.
3
. B.
4
. C.
5
. D. Vô số.
Câu 8: Hàm số
32
6
32
x mx
yx= + + +
đồng biến trên nửa khoảng
)
1; +
khi
A.
2m −
. B.
2m
. C.
2m
. D.
2m −
.
Tìm m để hàm số đơn điệu trên khoảng cho trước
DẠNG 5
Phương pháp:
•
Bưc 1. Tìm tập xác định
D
của hàm số.
•
Bưc 2. Tnh đo hàm
( ).y f x
=
Tìm các điểm
, ( 1,2,3,..., )
i
x i n=
mà ti đó đo hàm bằng 0 hoc
không xác định.
•
Bưc 3. Sp xếp các điểm
i
x
theo th tự tăng dần và lập bảng biến thiên.
•
Bưc 4. Nêu kết luận về các khoảng đồng biến và nghịch biến dưa vào bảng biến thiên.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 9: Tập hợp tất cả các giá trị của tham số thực của tham số
m
để hàm số
( )
32
6 4 9 4y x x m x= − − + − +
nghịch biến trên khoảng
( )
;3− −
là
A.
(
;0−
. B.
)
0;+
. C.
3
;
4
− −
. D.
3
;
4
− +
.
Câu 10: Cho hàm số
( )
18
2
mx
fx
xm
−
=
−
. Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
đồng biến trên khoảng
( )
2;+
. Tổng các phần tử của
S
bằng
A.
2−
. B.
3−
. C.
2
. D.
5−
.
Câu 11: Cho hàm số
32
y x mx m= + +
. Điều kiện cần và đủ của
m
để hàm số nghịch biến trên
( )
0;2
là
A.
3m −
. B.
0m
. C.
0m
. D.
3m −
.
Câu 12: Tìm tất cả các giá trị của
m
để hàm số
( ) ( )
32
1 3 1 3 2y m x m x x= − − − + +
đồng biến biến trên
?
A.
12m
. B.
12m
. C.
12m
. D.
12m
Câu 13: Số giá trị nguyên của tham số thực
m
để hàm số
2
2
mx
y
xm
−
=
−+
nghịch biến trên khoảng
1
;
2
+
là
A.
4
. B.
3
. C.
5
. D.
2
.
Câu 14: Có bao nhiêu giá trị nguyên của tham số m thuộc đon
10;10−
để hàm số
32
3 3 2020y x x mx= − + +
nghịch biến trên khoảng
( )
1;2
?
A.
10
. B.
20
. C.
11
. D.
21
.
Câu 15: Có bao nhiêu giá trị nguyên của tham số m thuộc đon
10;10−
để hàm số
32
3 3 2020y x x mx= − + +
nghịch biến trên khoảng
( )
1;2
?
A.
10
. B.
20
. C.
11
. D.
21
.
Câu 16: Hàm số
32
( ) 3 (2 1) 1f x x x m x= − + + − −
nghịch biến trên khoàng
(0; )+
khi và chỉ khi
A.
3m −
. B.
1m −
. C.
1m
. D.
3m
Câu 17: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
1
2
x
y
xm
−
=
+−
nghịch biến trên khoảng
( )
6;+
là:
A.
( )
4;1−
. B.
( )
1;4
. C.
)
4;1−
. D.
(
4;1−
.
Câu 18: Tìm tất cả các giá trị của tham số
m
để hàm số
32
1
21
3
y x x mx= − − + −
nghịch biến trên
A.
4m −
. B.
4m −
. C.
4m −
. D.
4m −
.
Câu 19: Số giá trị nguyên của tham số
m
để hàm số
32
1
2 4 5
3
y x mx x= − + −
đồng biến trên là
A.
3
. B.
0
. C.
2
. D.
1
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 20: Cho hàm số
18
2
mx
y
xm
−
=
−
. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
đồng biến trên khoảng
(2; )+
. Tổng các phần tử của
S
bằng
A.
3−
. B.
5−
. C.
2
. D.
2−
.
Câu 21: Gọi
T
là tập hợp tất cả các giá trị nguyên dương của tham số
m
để hàm số
42
21y x mx
đồng biến trên khoảng
( )
3; +
. Tổng giá trị các phần tử của
T
là
A.
45
. B.
55
. C.
9
. D.
36
.
Câu 22: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
32
4 9 5y x mx m x= − − + + +
nghịch
biến trên ?
A.
4
. B.
6
. C.
7
. D.
5
.
Câu 23: Tìm
m
để hàm số
21x
y
xm
−
=
+
đồng biến trên khoảng
( )
;5− −
.
Câu 24: Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
( )
42
2 1 2020y x m x m= − − + +
đồng
biến trên khoảng
( )
3; 1−−
.
A.
10m
. B.
10m
. C.
10m
. D.
10m
.
Câu 25: Có tất cả bao nhiêu số nguyên
m
để hàm số
3x
y
xm
+
=
−
nghịch biến trên khoảng
( )
1; +
?
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 26: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
3 2 2
3 3 2y x mx m x= − + −
đồng
biến trên khoảng
( )
12;+
?
A.
11
. B.
10
. C.
13
. D.
0
.
Câu 27: Hàm số
2x
y
xm
−
=
−
nghịch biến trên khoảng
( )
;3−
khi
A.
2m
. B.
2m
. C.
3m
. D.
3m −
.
Câu 28: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
4
mx
y
xm
+
=
+
nghịch biến trên khoảng
( )
0;4
?
A.
6
. B.
7
C.
5
. D.
11
Câu 29: Cho hàm số
18
2
mx
y
xm
−
=
−
. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số đồng
biến trên khoảng
( )
2;+
. Tổng các phần tử của S bằng
A.
2−
.
B.
5−
.
C.
2
.
D.
3−
.
Câu 30: Cho hàm số
( ) ( )
32
3 1 3 2 1 2020y x m x m x= − − + + − +
. Có bao nhiêu giá trị nguyên
m
để hàm
số nghịch biến trên
( ; )− +
?
A.
4
B.
6
C.
2
D.
5

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 31: Cho hàm số
( )
32
1
32
3
y x mx m x= − + −
với
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá
trị của
m
để hàm số nghịch biến trên một khoảng có độ dài đúng bằng
25
. Tnh tổng các phần
tử của
.S
A.
6−
. B.
2−
. C.
2
. D.
6
.
Câu 32: Cho hàm số
23mx m
y
xm
++
=
+
với
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị nguyên
của
m
để hàm số nghịch biến trên khoảng
( )
2;+
. Tìm số phần tử của
S
.
A.
4
. B.
2
. C.
5
. D.
3
.
Câu 33: Gọi
S
là tập hợp các giá trị thực của tham số
m
để hàm số
32
11
2 3 4
32
y x mx mx m= − + − +
nghịch biến trên một đon có độ dài bằng
3
. Tnh tổng tất cả các phần tử của
S
.
A.
17
. B.
8
. C.
13
. D.
9
.
Câu 34: Cho hàm số
23mx m
y
xm
−−
=
−
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá trị nguyên của
m
để hàm số đồng biến trên khoảng
( )
2;+
. Tìm số phần tử của
S
.
A.
1
. B.
5
. C.
4
. D.
3
.
Câu 35: Cho hàm số
( )
y f x=
liên tục trên và có đo hàm
( ) ( )
( )
22
26f x x x x x m
= − − +
với mọi
x
. Có bao nhiêu số nguyên
m
thuộc đon
2019;2019−
để hàm số
( ) ( )
1g x f x=−
nghịch biến trên khoảng
( )
;1− −
?
A.
2010
. B.
2012
. C.
2011
. D.
2009
.
Câu 36: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
32
1
14
3
y x m x mx= − − −
đồng biến trên
đon
1;4
?
A.
1
2
2
m
. B.
m
. C.
2m
. D.
1
2
m
.
Câu 37: ] Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
1
2 1 2
3
y x mx m x m= − + − − +
nghịch biến
trên khoảng
( )
3;0−
.
A.
1m −
. B.
2m =−
. C.
1m −
. D.
1
2
m −
.
Câu 38: Tổng các giá trị nguyên âm của
m
để hàm số
3
5
1
5
y x mx
x
= + −
đồng biến trên khoảng
(0; )+
là
A.
10−
. B.
3−
. C.
6−
. D.
7−
.
Câu 39: Số các giá trị nguyên của tham số
m
thuộc đon
20;20−
để hàm số
16mx
y
xm
−
=
−
nghịch biến
trên khoảng
( )
;8−
là
A.
14.
B.
11.
C.
13.
D.
12.
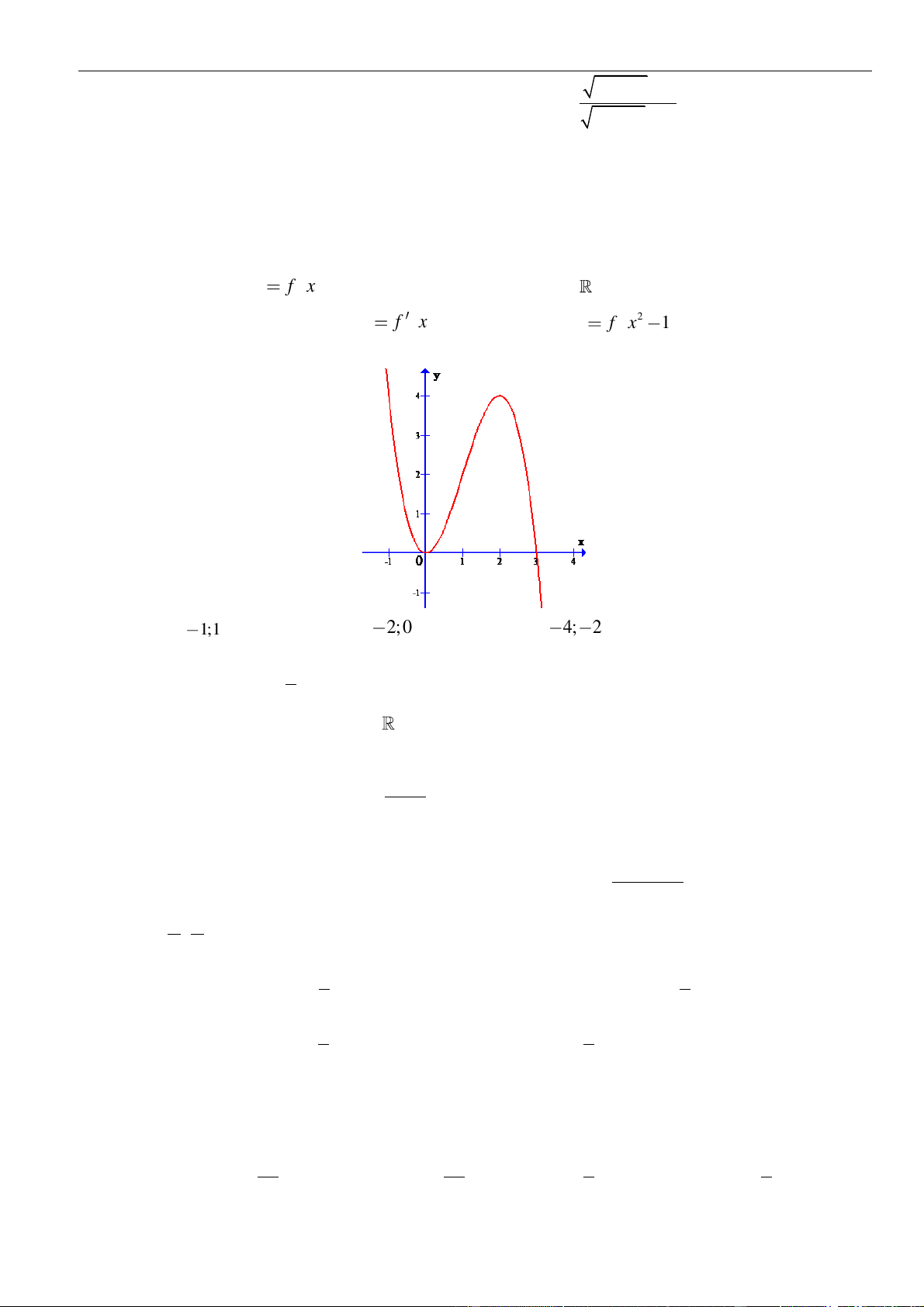
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Câu 40: Tập hợp tất cả các giá trị của tham số
m
để hàm số
2
2
84
8
xx
y
x x m
−−
=
−+
nghịch biến trên
( )
1;0−
là
A.
( )
;4−
. B.
(
)
4; 3 0;− − +
. C.
( ) ( )
4; 3 0;− − +
. D.
( )
4;− +
.
Câu 41: Cho hàm số
( )
32
2 3 1 6 1y x m x mx= − + + +
nghịch biến trên khoảng
( )
1;3
khi và chỉ khi
A.
1m
. B.
13m
. C.
3m
. D.
3m
.
Câu 42: Cho hàm số
y f x
có đo hàm liên tục liên tục trên . Biết đường cong trong hình vẽ bên
dưới là đồ thị của hàm số
y f x
. Khi đó, hàm số
2
1y f x
nghịch biến trên khoảng
nào sau đây?
A.
1;1
. B.
2;0
. C.
4; 2
. D.
0;2
.
Câu 43: Cho hàm số
( )
32
1
4 3 2017
3
y x mx m x= − + − +
. Tìm giá trị lớn nhất của tham số thực
m
để
hàm số đã cho đồng biến trên
A.
4m =
. B.
3m =
. C.
1m =
. D.
2m =
.
Câu 44: Kết quả của
m
để hàm số
2
xm
y
x
+
=
+
nghịch biến trên từng khoảng xác định là:
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Câu 45: Tìm tất cả các giá trị của tham số thực
m
để hàm số
2cot 1
cot
x
y
xm
+
=
+
đồng biến trên khoảng
;
42
.
A.
( )
1
; 1 0;
2
m
− −
. B.
(
1
; 1 0;
2
m
− −
.
C.
(
1
; 1 0;
2
m
− −
. D.
1
;
2
m
+
.
Câu 46: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
.
A.
5
;
2
m
−
−
. B.
5
;
2
m
−
−
. C.
5
;
2
m
+
. D.
5
;
2
m
+
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 47: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
.
A.
5
;
2
m
−
−
. B.
5
;
2
m
−
−
. C.
5
;
2
m
+
. D.
5
;
2
m
+
.
Câu 48: Cho hàm số
( )
fx
có đo hàm trên là
( ) ( )( )
' 1 3f x x x= − +
. Có bao nhiêu giá trị nguyên của
tham số
m
thuộc đon
10;2021−
để hàm số
( )
2
3xy f x m= + −
đồng biến trên khoảng
( )
0;2
?
A.
2016.
B.
2019.
C.
2018.
D.
2017.
Câu 49: Tìm tất cả các giá trị của tham số
m
để hàm số
4mx
y
xm
+
=
+
nghịch biến trên khoảng
( )
;1 .−
A.
( )
2;2 .m−
B.
( )
2; 1 .m − −
C.
(
2;2 .m−
D.
(
2; 1 .m − −
Câu 50: Cho hàm số
11
.
1
x
fx
xm
Có bao nhiêu giá trị nguyên của tham số
m
thuộc
10;10
để đã cho đồng biến trên khoảng
3;0
?
A. 8. B. 9. C. 10. D. 11.
---------------------------HẾT---------------------------

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Tập hợp các giá trị thực của tham số
m
để hàm số
5x
y
xm
+
=
+
đồng biến trên khoảng
( )
;8− −
là
A.
( )
5;+
. B.
(
5;8
. C.
)
5;8
. D.
( )
5;8
.
Lời giải
Chọn B
Tập xác định của hàm số là
\Dm=−
.
Hàm số
5x
y
xm
+
=
+
đồng biến trên khoảng
( )
;8− −
( )
0, ; 8yx
xm
− −
−
( )
( )
( )
2
5
0, ; 8
;8
m
x
xm
m
−
− −
+
− − −
55
58
88
mm
m
mm
− −
.
Vậy
(
5;8m
thỏa mãn yêu cầu bài toán.
Câu 2: Tìm tất cả các giá trị nguyên của tham số
m
để hàm số
24x
y
xm
+
=
−
đồng biến trên
( )
;4− −
A. 1. B. 3. C. 4. D. 2.
Lời giải
Chọn D
Ta có
( )
2
24
'
m
y
xm
−−
=
−
Hàm số đã cho đồng biến trên khoảng
( )
)
44
; 4 4; 2
2 4 0 2
mm
x
mm
− −
− − − −
− − −
Do
m
nên
4; 3m − −
.
Câu 3: Cho hàm số
( )
( )
23
22
2
3
m m x
y m m x mx
−
= + − + +
. Có bao nhiêu giá trị nguyên của
m
để hàm
số đồng biến trên ?
A.
3
. B.
5
. C.
1
. D.
2
.
Lời giải
Chọn D
Xét
2
02
0
12
my
mm
m y x
= =
− =
= = +
, chọn
1m =
.
Xét
2
0mm−
.
Hàm số đồng biến trên khi
( ) ( )
2
2 2 2
3a 0 0b c m m m m m− − − −
( )( )
( )( )
2 2 2
0
2 0 1 2 0
12
m
m m m m m m m
m
=
− − − −
.
Như vậy
12m
dẫn đến 2 giá trị nguyên
m
cần tìm.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Câu 4: Cho hàm số
32
y x mx m= + +
. Điều kiện cần và đủ của
m
để hàm số nghịch biến trên
( )
0;2
là
A.
3m −
. B.
0m
. C.
0m
. D.
3m −
.
Lời giải
Chọn A
Tập xác định:
.D =
2
32y x mx
=+
.
Đề hàm số nghịch biến trên
( )
0;2
thì
( )
0, 0;2yx
( )
2
3 2 0, 0;2x mx x +
( )
2
2 3 , 0;2mx x x −
( )
3
, 0;2
2
m x x −
( )
0;2
3
min 3
2
x
mx
− = −
.
Vậy giá trị
m
cần tìm là
3m −
.
Câu 5: Gọi
S
là tập hợp các số nguyên
2020;2020m−
để hàm số
2
5
21
mx
y
mx
+
=
+
nghịch biến trên
khoảng
( )
3; +
. Khi đó số phần tử của
S
bằng
A. 2020. B. 9. C. 45. D. 2021.
Lời giải
Chọn B
Xét
05= =my
là hàm hằng nên hàm số không nghịch biến. Vậy
0m =
không thỏa mãn.
Xét
0m
.
Tập xác định:
11
;;
22
D
mm
−−
= − +
.
Để hàm số nghịch biến trên khoảng
( )
3; +
khi và chỉ khi
( )
2
2
2
0 10
10
0
10 0
1
21
0 10
61
6
0
1
2
3
0
2
m
mm
y
mm
mx
m
m
m
m
m
m
−
=
−
−
+
+
−
.
Mà
m
và
2020;2020m−
nên
1;2;3;4;5;6;7;8;9m
.
Vậy có 9 giá trị của
S
.
Câu 6: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
32
34y x x m x= − + −
đồng biến trên
khoảng
( )
2;+
là
A.
(
;1−
. B.
(
;4−
. C.
( )
;1−
. D.
( )
;4−
.
Lời giải
Chọn B
Tập xác định:
D =
.
Ta có:
2
3 6 4y x x m
= − + −
.
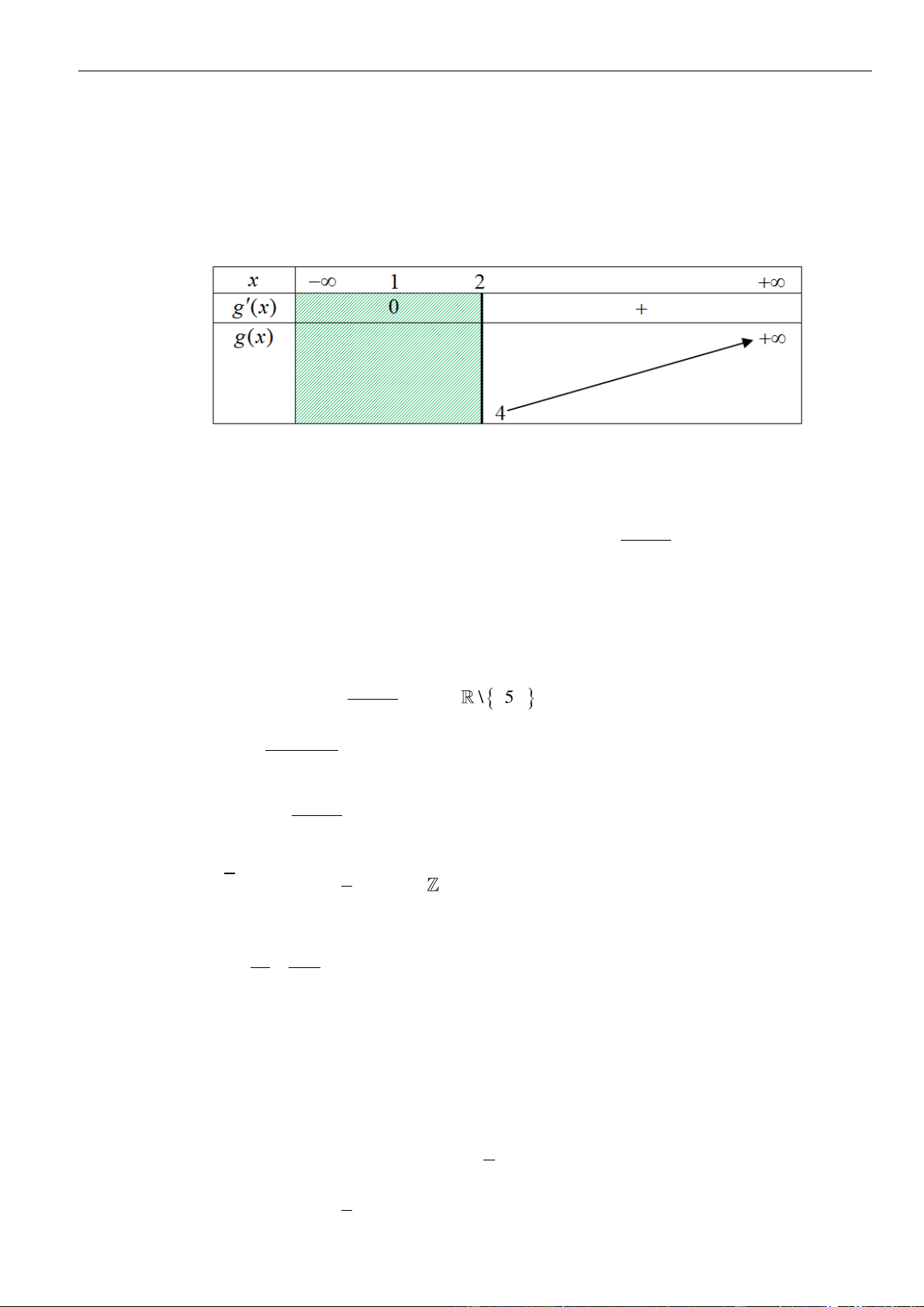
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Hàm số đồng biến trên khoảng
( )
2;+
( )
0, 2;yx
+
( )
2
3 6 4, 2;m x x x − + +
.
Xét hàm số
( )
2
3 6 4g x x x= − +
trên khoảng
( )
2;+
.
Ta có:
( )
66g x x
=−
;
( )
01g x x
= =
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có:
( )
( ), 2;m g x x +
4m
.
Vậy
4m
thoả yêu cầu bài toán.
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
xm
+
=
+
nghịch biến trên khoảng
( )
15;+
?
A.
3
. B.
4
. C.
5
. D. Vô số.
Lời giải
Chọn C
Tập xác định hàm số
6
5
x
y
xm
+
=
+
là
\5Dm=−
.
Đo hàm
( )
2
56
'
5
m
y
xm
−
=
+
.
Hàm số
6
5
x
y
xm
+
=
+
nghịch biến trên khoảng
( )
15;+
5 6 0
5 15
m
m
−
−
6
6
3
5
5
3
m
m
m
−
−
. Do
m
nên có 5 giá trị
m
.
Câu 8: Hàm số
32
6
32
x mx
yx= + + +
đồng biến trên nửa khoảng
)
1; +
khi
A.
2m −
. B.
2m
. C.
2m
. D.
2m −
.
Lời giải
Chọn A
Có
2
1y x mx
= + +
.
Để hàm số đồng biến trên nửa khoảng
)
1; +
)
' 0, 1;yx +
)
2
1 0, 1;x mx x + + +
)
1
, 1;m x x
x
− − +
Xét hàm số
( )
1
g x x
x
= − −
trên nửa khoảng
)
1; +
.
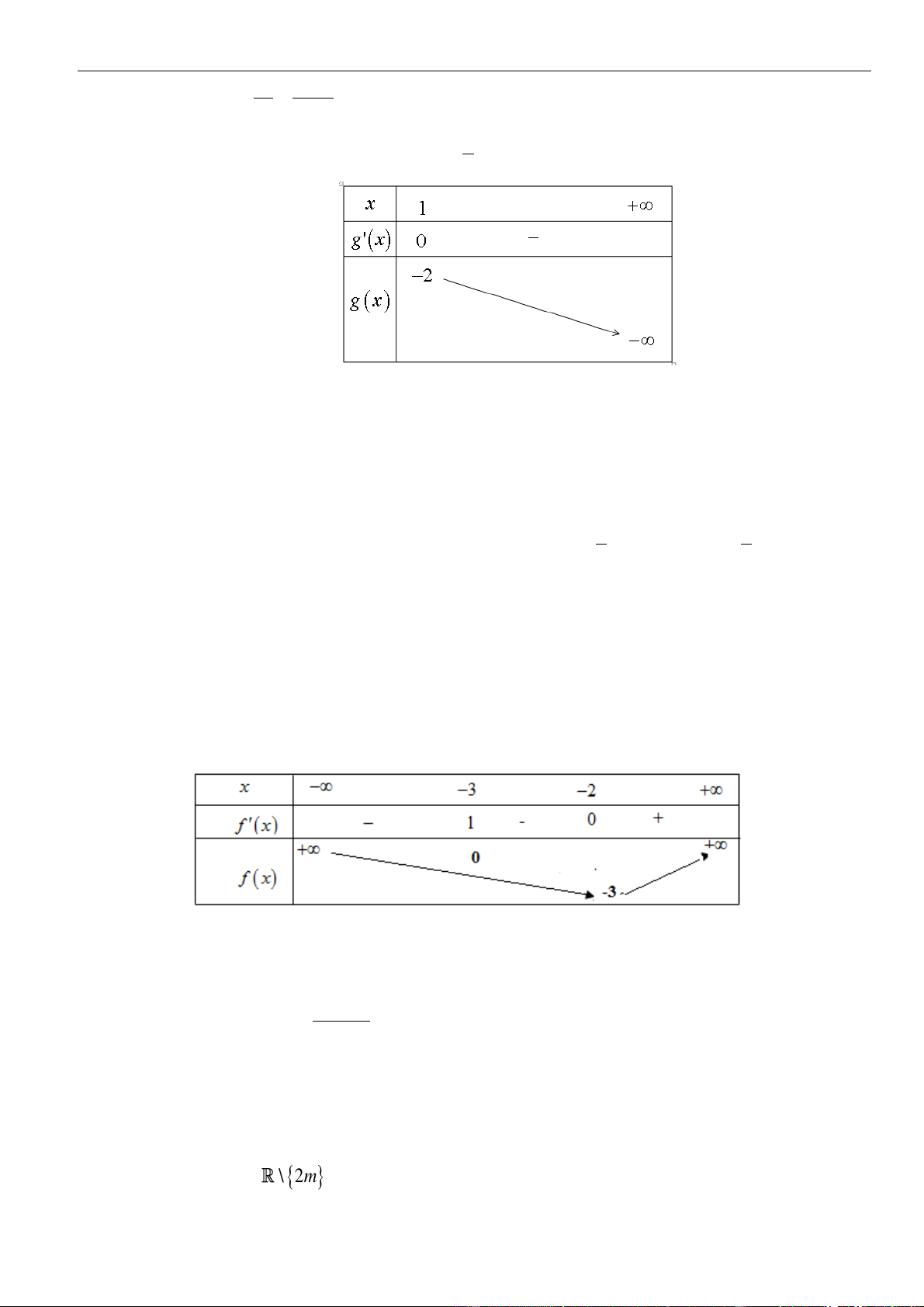
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
( )
2
22
11
1
x
gx
xx
−
= − + =
;
( )
1
0
1
x
gx
x
=
=
=−
.
Bảng biến thiên của hàm số
( )
1
g x x
x
= − −
trên nửa khoảng
)
1; +
.
Từ bảng biến thiên suy ra:
)
( ) ( )
1;
max 1 2g x g
+
= = −
.
Vậy
( )
)
, 1;m g x x +
khi và chỉ khi
2m −
.
Câu 9: Tập hợp tất cả các giá trị của tham số thực của tham số
m
để hàm số
( )
32
6 4 9 4y x x m x= − − + − +
nghịch biến trên khoảng
( )
;3− −
là
A.
(
;0−
. B.
)
0;+
. C.
3
;
4
− −
. D.
3
;
4
− +
.
Lời giải
Chọn A
Ta có
2
3 12 4 9y x x m
= − − + −
.
Hàm số nghịch biến trên khoảng
( )
;3− −
khi
( )
0 ; 3yx
− −
( )
2
3 12 4 9 0 ; 3x x m x − − + − − −
2
4 3 12 9m x x + +
( )
;3x − −
. Đt
( )
2
3 12 9f x x x= + +
có
( )
6 12f x x
=+
Ta có bảng biến thiên của
( )
fx
:
Dựa vào bảng biến thiên ta thấy
2
4 3 12 2m x x + +
( )
;3x − −
40m
0m
.
Vậy
0m
hàm số nghịch biến trên khoảng
( )
;3− −
.
Câu 10: Cho hàm số
( )
18
2
mx
fx
xm
−
=
−
. Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
đồng biến trên khoảng
( )
2;+
. Tổng các phần tử của
S
bằng
A.
2−
. B.
3−
. C.
2
. D.
5−
.
Lời giải
Chọn A
Tập xác định
\2m
.
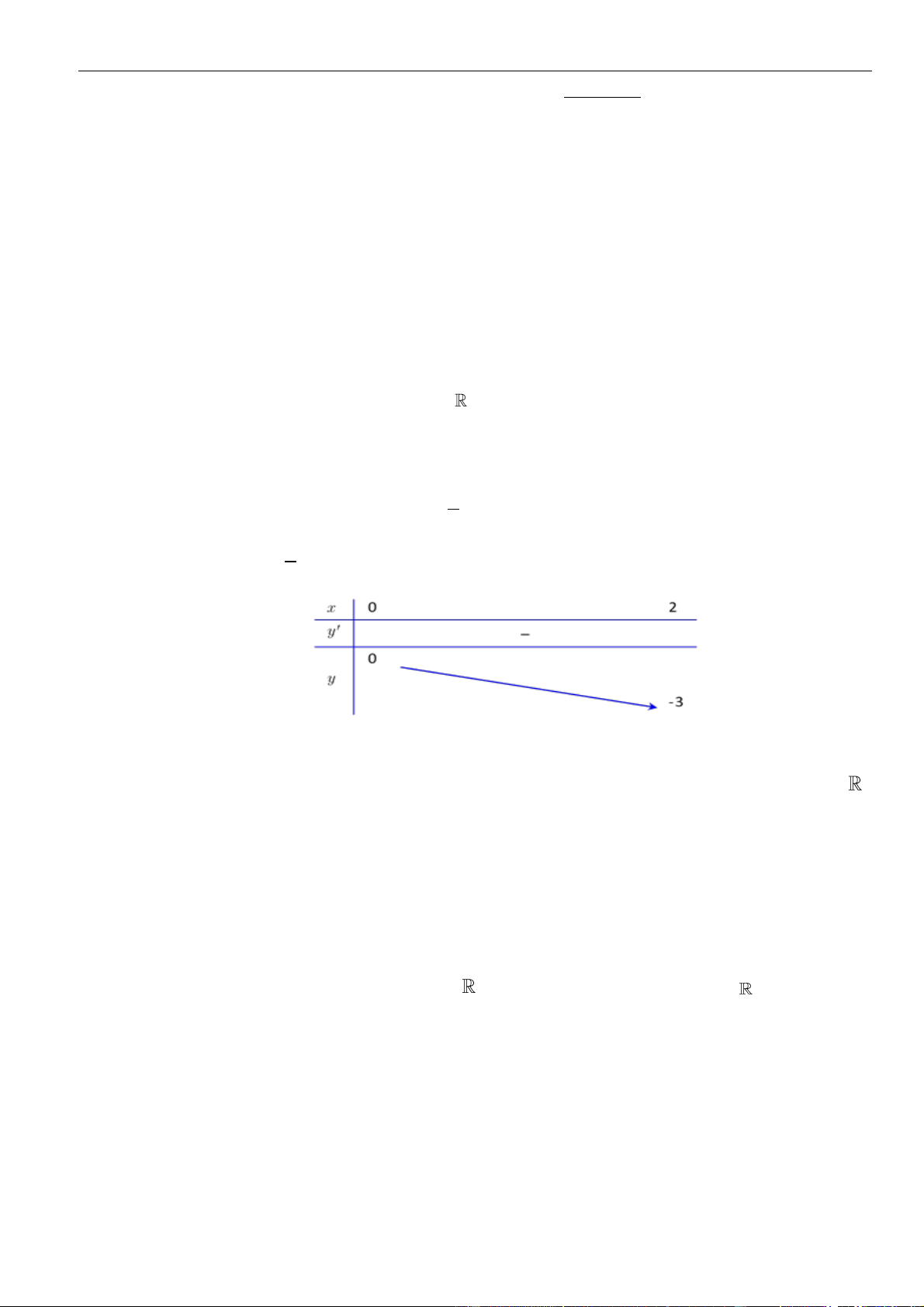
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Để hàm số đồng biến trên khoảng
( )
2;+
( )
( )
( )
2
2
2 18
' 0, 2;
2
m
f x x
xm
−+
= +
−
( )
( )
(
2
2 18 0
3;3
3;1
2 2;
1
m
m
m
xm
m
− +
−
−
= +
.
Suy ra
2; 1;0;1S = − −
.
Vậy tổng các phần tử của
S
bằng
2−
.
Câu 11: Cho hàm số
32
y x mx m= + +
. Điều kiện cần và đủ của
m
để hàm số nghịch biến trên
( )
0;2
là
A.
3m −
. B.
0m
. C.
0m
. D.
3m −
.
Lời giải
Chọn A
Hàm số
32
y x mx m= + +
xác định trên .
Ta có:
2
32y x mx
=+
Hàm số nghịch biến trên
( )
0;2
( )
2' 0, 0;yx
( )
2
23 2 0 0, ;x mx x +
( )
2
3
, 0
2
;m x x −
Xét hàm số
3
2
yx=−
trên khoảng
( )
0;2
, ta có bảng biến thiên như sau:
Vậy để hàm số nghịch biến trên
( )
0;2
thì
3m −
.
Câu 12: Tìm tất cả các giá trị của
m
để hàm số
( ) ( )
32
1 3 1 3 2y m x m x x= − − − + +
đồng biến biến trên
?
A.
12m
. B.
12m
. C.
12m
. D.
12m
Lời giải
Chọn C
Ta có
( ) ( )
2
3 1 6 1 3y m x m x
= − − − +
.
Hàm số đã cho đồng biến trên
khi và chỉ khi
0,yx
10
10
0
m
m
−=
−
( ) ( )
2
1
1
9 1 9 1 0
m
m
mm
=
− − −
1
1
12
m
m
m
=
12m
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Câu 13: Số giá trị nguyên của tham số thực
m
để hàm số
2
2
mx
y
xm
−
=
−+
nghịch biến trên khoảng
1
;
2
+
là
A.
4
. B.
3
. C.
5
. D.
2
.
Lời giải
Chọn B
Hàm số
2
2
mx
y
xm
−
=
−+
có tập xác định là
;;
22
mm
D
= − +
Ta có:
( )
2
2
4
,
2
2
mm
yx
xm
−
=
−+
.
Hàm số nghịch biến trên khoảng
1
;
2
+
2
40
22
21
1
1
22
m
m
m
m
m
−
−
−
mà
m
nên
1;0;1m−
.
Câu 14: Có bao nhiêu giá trị nguyên của tham số m thuộc đon
10;10−
để hàm số
32
3 3 2020y x x mx= − + +
nghịch biến trên khoảng
( )
1;2
?
A.
10
. B.
20
. C.
11
. D.
21
.
Lời giải
Chọn C
T a có
2
3 6 3 0y x x m
= − +
( )
1;2x
2
2m x x − +
( )
1;2x
Xét
( )
2
2f x x x= − +
( )
/ 1;2
Có
( )
2 2 0f x x
= − + =
1x=
Bảng biến thiên
Vậy
0m
,mà
10;10m−
,
mz
nên
10; 9; 8; 7; 6; 5; 4; 3; 2; 1;0m = − − − − − − − − − −
Có
11
giá trị của m thỏa mãn.
Câu 15: Có bao nhiêu giá trị nguyên của tham số m thuộc đon
10;10−
để hàm số
32
3 3 2020y x x mx= − + +
nghịch biến trên khoảng
( )
1;2
?
A.
10
. B.
20
. C.
11
. D.
21
.
Lời giải
Chọn C
T a có
2
3 6 3 0y x x m
= − +
( )
1;2x
2
2m x x − +
( )
1;2x
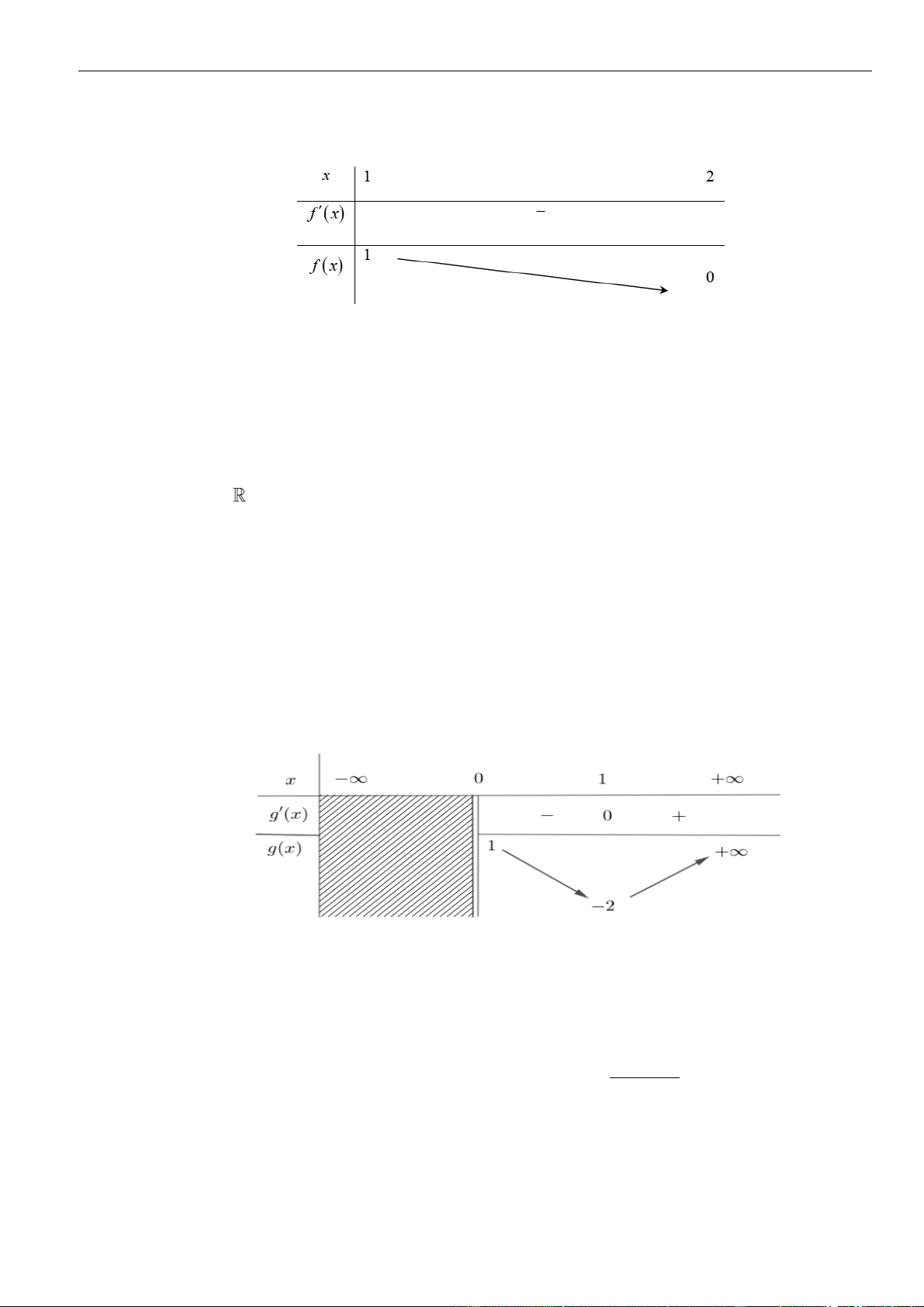
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Xét
( )
2
2f x x x= − +
( )
/ 1;2
Có
( )
2 2 0f x x
= − + =
1x=
Bảng biến thiên
Vậy
0m
,mà
10;10m−
,
mz
nên
10; 9; 8; 7; 6; 5; 4; 3; 2; 1;0m = − − − − − − − − − −
Có
11
giá trị của m thỏa mãn.
Câu 16: Hàm số
32
( ) 3 (2 1) 1f x x x m x= − + + − −
nghịch biến trên khoàng
(0; )+
khi và chỉ khi
A.
3m −
. B.
1m −
. C.
1m
. D.
3m
Lời giải
Chọn B
TXĐ:
D =
.
Đt
( ) ( )
32
3 2 1 1y f x x x m x= = − + + − −
2
3 6 2 1y x x m
= − + + −
.
Hàm số nghịch biến trên khoảng
( )
0;+
( )
0, 0;yx
+
( )
2
2 3 6 1, 0;m x x x − + +
( )
1
.
Xét hàm số
( )
2
3 6 1g x x x= − +
trên khoảng
( )
0;+
.
( )
66g x x
=−
;
( )
01g x x
= =
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có
( )
( )
0;
min 2gx
+
=−
.
Do đó
( )
1
( )
( )
1;
2 minm g x
− +
2 2 1mm − −
.
Vậy
1m −
thoả yêu cầu bài toán.
Câu 17: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
1
2
x
y
xm
−
=
+−
nghịch biến trên khoảng
( )
6;+
là:
A.
( )
4;1−
. B.
( )
1;4
. C.
)
4;1−
. D.
(
4;1−
.
Lời giải
Chọn C

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Ta có: TXĐ
\2Dm=−
( )
2
11
'
2
2
xm
yy
xm
xm
−−
= =
+−
+−
( )
y f x=
nghịch biến trên khoảng
( )
6;+
( )
' 0, 6;yx +
1 0 1
2 6 4
mm
mm
−
− −
Câu 18: Tìm tất cả các giá trị của tham số
m
để hàm số
32
1
21
3
y x x mx= − − + −
nghịch biến trên
A.
4m −
. B.
4m −
. C.
4m −
. D.
4m −
.
Lời giải
Chọn C
Ta có
2
'4y x x m= − − +
Hàm số nghịch biến trên
2
40x x m − − +
với mọi x
10
16 4 0 4
0
mm
−
+ −
Câu 19: Số giá trị nguyên của tham số
m
để hàm số
32
1
2 4 5
3
y x mx x= − + −
đồng biến trên là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A
Yêu cầu đề bài
2
2
10
' 4 4 0, 1 1
' 4 4 0
a
y x mx x m
m
=
= − + −
= −
.
Vậy có 3 giá trị nguyên của
m
thỏa mãn là
1;0;1−
.
Câu 20: Cho hàm số
18
2
mx
y
xm
−
=
−
. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
đồng biến trên khoảng
(2; )+
. Tổng các phần tử của
S
bằng
A.
3−
. B.
5−
. C.
2
. D.
2−
.
Lời giải
Chọn D
Điều kiện xác định
2xm
. Ta có
2
2
18 2 18
2 ( 2 )
mx m
yy
x m x m
− − +
= =
−−
.
Hàm số đồng biến trên
(2; )+
khi và chỉ khi
22
33
2 18 0 9
3 1 2; 1;0;1 .
1
2 (2; ) 2 2
m
mm
mm
m
mm
−
− +
− − −
+
Khi đó tổng các giá trị nguyên của tham số
m
bằng
2−
.
Câu 21: Gọi
T
là tập hợp tất cả các giá trị nguyên dương của tham số
m
để hàm số
42
21y x mx
đồng biến trên khoảng
( )
3; +
. Tổng giá trị các phần tử của
T
là
A.
45
. B.
55
. C.
9
. D.
36
.
Lời giải
Chọn A

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Yêu cầu đề bài
( )
3
' 4 4 0, 3;y x mx x= − +
( )
( ) ( )
22
4 0, 3; , 3;x x m x m x x − +
Do đó, ta có
9m
1;2;3;...;8;9T =
.
Tổng giá trị các phần tử của
T
là
45
.
Câu 22: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
32
4 9 5y x mx m x= − − + + +
nghịch
biến trên ?
A.
4
. B.
6
. C.
7
. D.
5
.
Lời giải
Chọn C
Ta có
2
3 2 4 9y x mx m
= − − + +
Hàm số
( )
32
4 9 5y x mx m x= − − + + +
nghịch biến trên
( )
2
2
10
0
12 27 0 9; 3
0
3 4 9 0
a
m m m
mm
−
+ + − −
+ +
.
Câu 23: Tìm
m
để hàm số
21x
y
xm
−
=
+
đồng biến trên khoảng
( )
;5− −
.
Lời giải
Điều kiện :
xm−
.
Ta có
( )
2
21m
y
xm
+
=
+
.
Hàm số
21x
y
xm
−
=
+
đồng biến trên khoảng
( )
( )
( )
2
21
; 5 0 ; 5
m
yx
xm
+
− − = − −
+
và
xm−
( )
11
2 1 0
1
5
22
;5
2
55
m
mm
m
m
mm
+
− −
−
− − −
− −
.
Câu 24: Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
( )
42
2 1 2020y x m x m= − − + +
đồng
biến trên khoảng
( )
3; 1−−
.
A.
10m
. B.
10m
. C.
10m
. D.
10m
.
Lời giải
Chọn D
Ta có
( ) ( )
4 2 3
2 1 2020 4 4 1y x m x m y x m x
= − − + + = − −
.
Hàm số đồng biến trên khoảng
( )
3; 1−−
( )
0, 3; 1yx
− −
( ) ( ) ( )
32
4 4 1 0, 3; 1 1, 3; 1x m x x x m x − − − − − − −
2
3; 1
1 Max 1 9 10m x m m
−−
− −
.
Câu 25: Có tất cả bao nhiêu số nguyên
m
để hàm số
3x
y
xm
+
=
−
nghịch biến trên khoảng
( )
1; +
?
A.
3
. B.
4
. C.
2
. D.
5
.
Lời giải
Chọn B

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
TXĐ
\Dm=
.
Hàm số đã cho nghịch biến trên khoảng
( )
1; +
( )
0, 1;yx
+
30
31
1
m
m
m
− −
−
.
Vậy có 4 giá trị nguyên của
m
thỏa mãn yêu cầu.
Câu 26: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( )
3 2 2
3 3 2y x mx m x= − + −
đồng
biến trên khoảng
( )
12;+
?
A.
11
. B.
10
. C.
13
. D.
0
.
Lời giải
Chọn B
Ta có:
( )
22
3 6 3 2y x mx m
= − + −
.
( )
( )
( )
22
22
2
0 3 6 3 2 0
2 2 0
2
2
2
2
2
y x mx m
x mx m
xm
xm
xm
xm
xm
− + −
− + −
−
−
− −
+
− +
Yêu cầu bài toán ta có
2 12 12 2mm+ −
. Vì
1;2;3;4;5;6;7;8;9;10mm
+
Câu 27: Hàm số
2x
y
xm
−
=
−
nghịch biến trên khoảng
( )
;3−
khi
A.
2m
. B.
2m
. C.
3m
. D.
3m −
.
Lời giải
Chọn C
Tập xác định:
\Dm=
.
Ta có:
( )
2
2m
y
xm
−+
=
−
.
Hàm số
2x
y
xm
−
=
−
nghịch biến trên khoảng
( )
;3−
khi:
( )
;3
3
3
2
20
m
m
m
m
m
−
− +
Câu 28: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
4
mx
y
xm
+
=
+
nghịch biến trên khoảng
( )
0;4
?
A.
6
. B.
7
C.
5
. D.
11
Lời giải
Chọn A
Tập xác định:
\
4
m
D
=−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Ta có:
( )
2
2
36
4
m
y
xm
−
=
+
.
Hàm số nghịch biến trên
( )
0;4
khi và chỉ khi
( )
2
36 0
0;4
4
m
m
−
−
66
06
0
16
m
m
m
m
−
−
.
Vậy có 6 giá trị nguyên của
m
là
0;1;2;3;4;5
.
Câu 29: Cho hàm số
18
2
mx
y
xm
−
=
−
. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số đồng
biến trên khoảng
( )
2;+
. Tổng các phần tử của S bằng
A.
2−
.
B.
5−
.
C.
2
.
D.
3−
.
Lời giải
Chọn A
Điều kiện:
2xm
.
Ta có:
( )
2
2
2 18
2
m
y
xm
−+
=
−
.
Để hàm số đồng biến trên khoảng
( )
2;+
thì:
( )
2
0
33
2 18 0
31
2 2;
1
22
y
m
m
m
m
m
m
−
− +
−
+
.
Vậy
2; 1;0;1S = − −
. Tổng các phần tử của
S
:
2−
.
Câu 30: Cho hàm số
( ) ( )
32
3 1 3 2 1 2020y x m x m x= − − + + − +
. Có bao nhiêu giá trị nguyên
m
để hàm
số nghịch biến trên
( ; )− +
?
A.
4
B.
6
C.
2
D.
5
Lời giải
Chọn D
2
' 3 6( 1) 3(2 1)y x m x m= − − + + −
.
Để hàm số nghịch biến trên
2
2
' 0 ' 0
9( 2 1) 18 9 0
9 36 0
40
y
m m m
mm
m
+ + + −
+
−
Vậy có 5 giá trị nguyên
m
.
Câu 31: Cho hàm số
( )
32
1
32
3
y x mx m x= − + −
với
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá
trị của
m
để hàm số nghịch biến trên một khoảng có độ dài đúng bằng
25
. Tnh tổng các phần
tử của
.S
A.
6−
. B.
2−
. C.
2
. D.
6
.
Lời giải
Chọn B
Ta có:
22
' 2 3 2 ' 2 3.y x mx m m m= − + − = + −

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Nhận xét: nếu
'0
hàm số luôn đồng biến trên nên trường hợp này không thỏa mãn.
YCBT
( )
2
2
12
1 2 1 2
'0
2 3 0
25
4 20
mm
xx
x x x x
+ −
−=
+ − =
(theo Viet ta có:
12
12
2
32
x x m
x x m
+=
=−
).
( ) ( )
( )
( ) ( )
2
; 3 1;
; 3 1;
4
4;2 .
4
2
4 4 3 2 20
2
m
m
m
S
m
m
mm
m
− − +
− − +
=−
= −
=−
=
− − =
=
Vậy tổng các phần tử của tập
S
là
2.−
Câu 32: Cho hàm số
23mx m
y
xm
++
=
+
với
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị nguyên
của
m
để hàm số nghịch biến trên khoảng
( )
2;+
. Tìm số phần tử của
S
.
A.
4
. B.
2
. C.
5
. D.
3
.
Lời giải
Chọn D
Ta có:
*
( )
( ) ( )
2
2
22
23
2 3 2 3
'
mm
mx m m m
yy
xm
x m x m
−+
+ + − −
= = =
+
++
* YCBT
( )
' 0, 2;yx +
2
13
2 3 0
2
2
m
mm
m
m
−
− −
−
−
13m −
Mà
m
nên
0,1,2m
Suy ra:
0,1,2S =
Kết luận: Số phần tử của
S
là
3
.
Câu 33: Gọi
S
là tập hợp các giá trị thực của tham số
m
để hàm số
32
11
2 3 4
32
y x mx mx m= − + − +
nghịch biến trên một đon có độ dài bằng
3
. Tnh tổng tất cả các phần tử của
S
.
A.
17
. B.
8
. C.
13
. D.
9
.
Lời giải
Chọn B
32
11
2 3 4
32
y x mx mx m= − + − +
2
2y x mx m
= − +
,
2
0 2 0y x mx m
= − + =
(*)
Gọi
12
,xx
là hai nghiệm của (*), khi đó ta có bảng biến thiên:

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Hàm số
y
nghịch biến trên một khoảng có độ dài đúng bằng
3
khi và chỉ khi phương trình (*)
có hai nghiệm phân biệt
12
,xx
thoả mãn
12
3xx−=
.
(*) có hai nghiệm phân biệt
2
0
80
8
m
mm
m
= −
(**)
( ) ( )
22
2
1 2 1 2 1 2 1 2
9
3 9 4 9 8 9 0
1
m
x x x x x x x x m m
m
=
− = − = + − = − − =
=−
(thoả (**) )
Suy ra
9; 1S =−
.
Vậy: tổng tất cả các phần tử của
S
là
8
.
Câu 34: Cho hàm số
23mx m
y
xm
−−
=
−
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá trị nguyên của
m
để hàm số đồng biến trên khoảng
( )
2;+
. Tìm số phần tử của
S
.
A.
1
. B.
5
. C.
4
. D.
3
.
Lời giải
Chọn D.
Điều kiện xác định:
xm
Ta có
( )
2
2
23mm
y
xm
− + +
=
−
.
Hàm số đã cho đồng biến trên khoảng
( )
2;+
khi và chỉ khi
( )
( )
2
2
2
23
02
13
2 3 0
12
2
2
2;
mm
yx
m
mm
xm
m
m
m
m
− + +
=
−
− + +
−
−
+
.
Suy ra
0;1;2S =
.
Vậy số phần tử của
S
là
3
.
Câu 35: Cho hàm số
( )
y f x=
liên tục trên và có đo hàm
( ) ( )
( )
22
26f x x x x x m
= − − +
với mọi
x
. Có bao nhiêu số nguyên
m
thuộc đon
2019;2019−
để hàm số
( ) ( )
1g x f x=−
nghịch biến trên khoảng
( )
;1− −
?
A.
2010
. B.
2012
. C.
2011
. D.
2009
.
Lời giải
Chọn C.
Ta có:
( ) ( )
1g x f x=−
( ) ( )
1g x f x
= − −
.
Mà:
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
2 2 2
2
1 1 1 2 1 6 1 1 1 4 5f x x x x x m x x x x m
− = − − − − − − + = − − + + + −
.
Khi đó:
( ) ( ) ( )
( )
2
2
1 1 4 5g x x x x x m
= − + + + −
.
Để hàm số
( ) ( )
1g x f x=−
nghịch biến trên khoảng
( )
;1− −
thì
( ) ( )
0, ; 1g x x
− −
.
Suy ra:
( ) ( )
( )
( )
2
2
1 1 4 5 0, ; 1x x x x m x− + + + − − −
( )
2
4 5 0, ; 1x x m x + + − − −
( )
2
4 5, ; 1m x x x − + − − −
.
Xét hàm số
( )
2
45h x x x= + −
trên khoảng
( )
;1− −
.
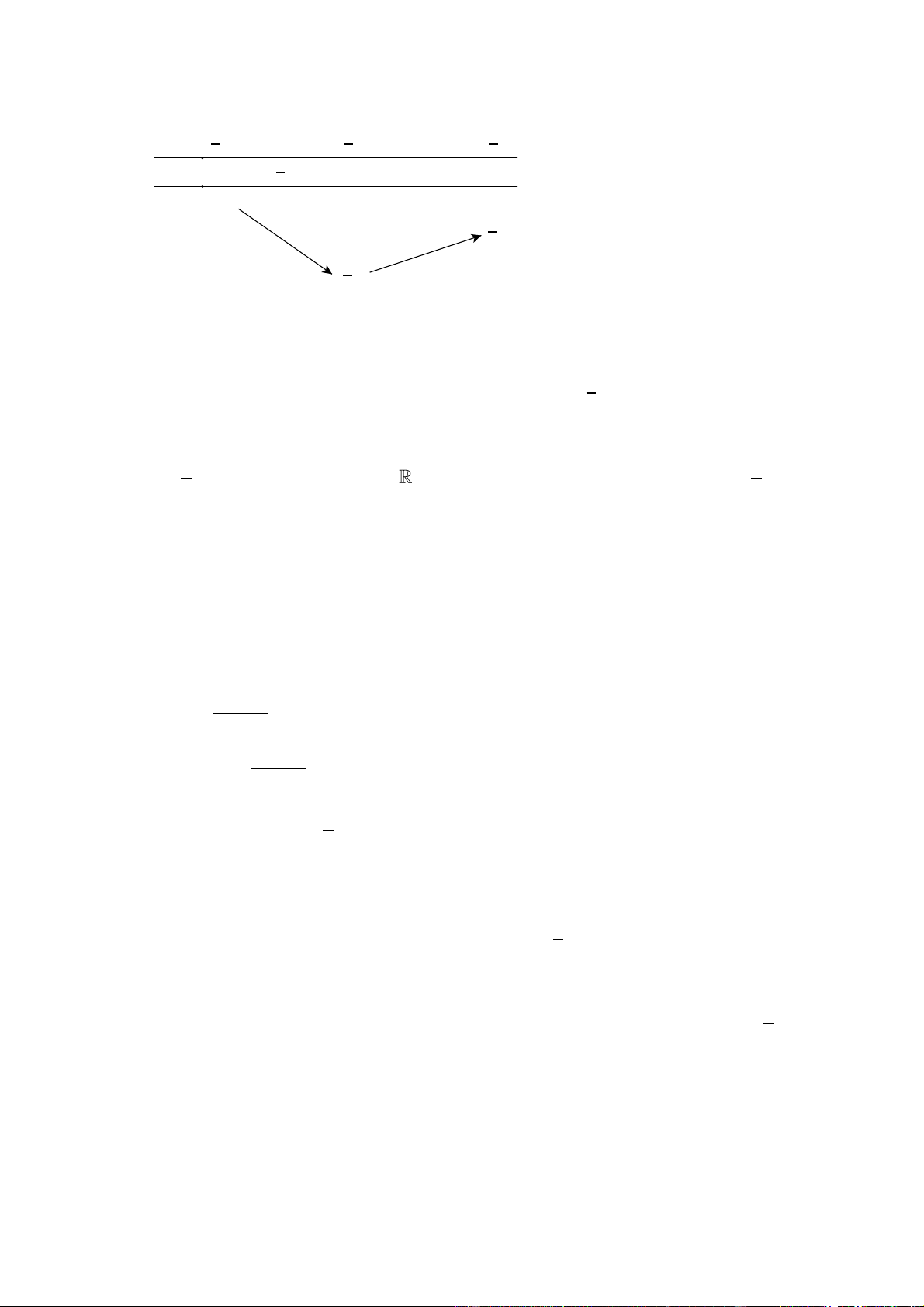
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Ta có:
( )
24h x x
=+
;
( ) ( )
0 2 ; 1h x x
= = − − −
.
Bảng biến thiên:
Từ bảng biến thiên suy ra:
99mm− −
. Mà
m
nguyên và
2019;2019m−
do đó:
9;10;...;2019m
. Vậy có 2011 giá trị thỏa mãn.
Câu 36: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
32
1
14
3
y x m x mx= − − −
đồng biến trên
đon
1;4
?
A.
1
2
2
m
. B.
m
. C.
2m
. D.
1
2
m
.
Lời giải
Chọn D
Ycbt:
( )
2
2 1 4 0y x m x m
= − − −
với
1;4x
(*)
Để hàm số đồng biến trên trên đon
1;4
( )
2
2
' 0 1;4
2 1 4 0
2
42
yx
x m x m
xx
m
x
− − −
+
+
Đt:
( )
2
2
42
xx
gx
x
+
=
+
( )
( )
2
8
' 0 1;4
42
x
g x x
x
=
+
( ) ( )
1;4
1
min 1
2
1
2
x
g x g
m
= =
Câu 37: ] Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
1
2 1 2
3
y x mx m x m= − + − − +
nghịch biến
trên khoảng
( )
3;0−
.
A.
1m −
. B.
2m =−
. C.
1m −
. D.
1
2
m −
.
Lời giải
Chọn
C
Đo hàm của hàm số:
2
2 2 1y x mx m
= − + −
.
1
0
21
x
y
xm
=
=
=−
.
Hàm số đã cho nghịch biến trên khoảng
( )
3;0−
khi
( )
3;0−
nằm trong khoảng hai nghiệm.
8
h'
(
x
)
h
(
x
)
+
∞
∞
1
2
0
+
x
9

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
1 3 0 2 1
2 1 3 0 1
m
m
− −
− −
2 1 3 1mm − − −
.
Câu 38: Tổng các giá trị nguyên âm của
m
để hàm số
3
5
1
5
y x mx
x
= + −
đồng biến trên khoảng
(0; )+
là
A.
10−
. B.
3−
. C.
6−
. D.
7−
.
Lời giải
Chọn A
Hàm số đồng biến trên khoảng
(0; )+
2
6
1
' 3 0y x m
x
= + +
với
( ) ( )
0; *x +
.
Theo bất đẳng thc Cauchy ta có
2 2 2 2 2 2 2
4
6 6 6
1 1 1
' 3 4 . . . 4y x m x x x m x x x m m
x x x
= + + = + + + + + = +
,
( )
0;x +
.
( )
* 4 0 4mm + −
Vì
m
nguyên âm nên
4; 3; 2; 1m − − − −
.
Vậy tổng các giá trị của
m
là
10−
.
Câu 39: Số các giá trị nguyên của tham số
m
thuộc đon
20;20−
để hàm số
16mx
y
xm
−
=
−
nghịch biến
trên khoảng
( )
;8−
là
A.
14.
B.
11.
C.
13.
D.
12.
Lời giải
Chọn C
Ta có
( )
2
2
16
.
m
y
xm
−+
=
−
Hàm số nghịch biến trên khoảng
( )
;8−
khi
( )
2
16 0
0, 8 4 4
8.
8
;8
m
y x m m
m
x m m
m
− +
−
−
Vì
m
và
20;20m−
nên
8;9;10;...;20 .m
Vậy có 13 giá trị
m
thỏa mãn.
Câu 40: Tập hợp tất cả các giá trị của tham số
m
để hàm số
2
2
84
8
xx
y
x x m
−−
=
−+
nghịch biến trên
( )
1;0−
là
A.
( )
;4−
. B.
(
)
4; 3 0;− − +
. C.
( ) ( )
4; 3 0;− − +
. D.
( )
4;− +
.
Lời giải
Chọn B
Đt
2
8t x x=−
.
Điều kiện xác định:
2
0
80
8
x
xx
x
−
.
Xét hàm:
2
8t x x=−
với
( )
1;0x−
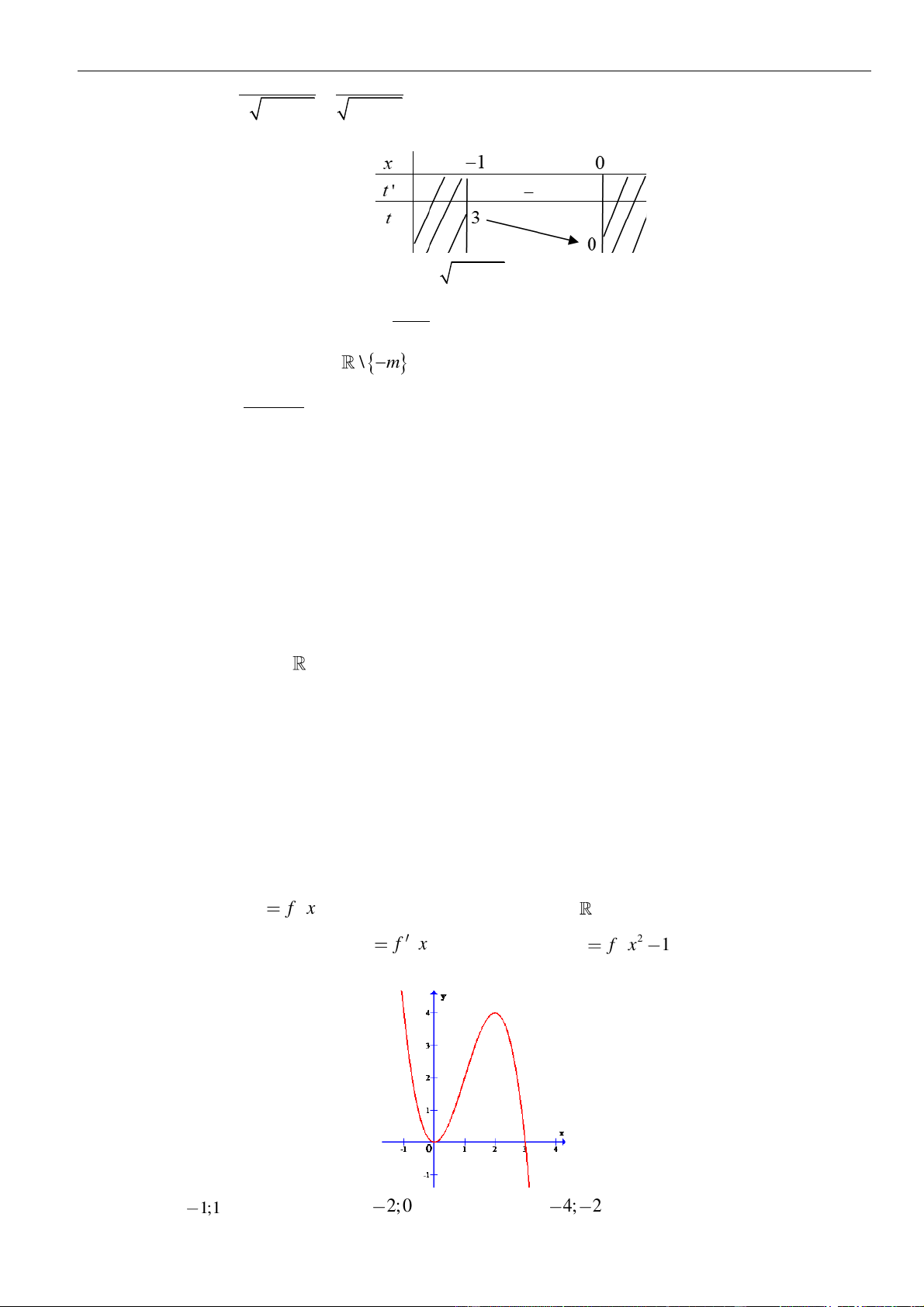
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Ta có:
( )
22
2 8 4
' 0 1;0
2 8 8
xx
tx
x x x x
−−
= = −
−−
Bảng biến thiên:
Từ bảng biến thiên ta thấy hàm số
2
8t x x=−
nghịch biến trên khoảng
( )
1;0−
và
( )
0;3t
.
Khi đó yêu cầu bài toán
4t
y
tm
−
=
+
đồng biến
( )
0;3
Điều kiện xác định:
\Dm=−
Ta có:
( )
2
4
',
m
y x D
tm
+
=
+
Để hàm số đồng biến trên
( )
0;3
thì
( )
'0
0;3
y
m
−
4 0 4
00
33
mm
mm
mm
+ −
−
− −
43
0
m
m
− −
.
Câu 41: Cho hàm số
( )
32
2 3 1 6 1y x m x mx= − + + +
nghịch biến trên khoảng
( )
1;3
khi và chỉ khi
A.
1m
. B.
13m
. C.
3m
. D.
3m
.
Lời giải
Chọn D
Tập xác định
D =
.
( ) ( )
3 2 2
2 3 1 6 1 ' 6 6 1 6y x m x mx y x m x m= − + + + = − + +
.
Hàm số nghịch biến trên khoảng
( )
1;3
.
( )
0, 1;3yx
.
( ) ( )
2
6 6 1 6 0, 1;3x m x m x − + +
.
( ) ( )
2
1 0, 1;3x m x m x − + +
( )
, 1;3m x x
.
Vậy
( )
3, 1;3mx
.
Câu 42: Cho hàm số
y f x
có đo hàm liên tục liên tục trên . Biết đường cong trong hình vẽ bên
dưới là đồ thị của hàm số
y f x
. Khi đó, hàm số
2
1y f x
nghịch biến trên khoảng
nào sau đây?
A.
1;1
. B.
2;0
. C.
4; 2
. D.
0;2
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn B
Ta có:
2
2 . 1 0y x f x
2
2
0
10
0
10
x
fx
x
fx
2
2
0
13
0
13
x
x
x
x
0
22
0
2
2
x
x
x
x
x
20
2
x
x
Câu 43: Cho hàm số
( )
32
1
4 3 2017
3
y x mx m x= − + − +
. Tìm giá trị lớn nhất của tham số thực
m
để
hàm số đã cho đồng biến trên
A.
4m =
. B.
3m =
. C.
1m =
. D.
2m =
.
Lời giải
Chọn B
TXĐ:
D =
.
Ta có:
( )
2
2 4 3y x mx m
= − + −
.
Hàm số đồng biến trên khi chỉ khi
0,yx
0
0
a
2
4 3 0 1 3m m m − +
.
Giá trị
m
lớn nhất là 3.
Câu 44: Kết quả của
m
để hàm số
2
xm
y
x
+
=
+
nghịch biến trên từng khoảng xác định là:
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Lời giải
Chọn A
Xét hàm số
2
xm
y
x
+
=
+
. TXĐ:
\2D =−
.
Ta có
( )
2
2
'
2
m
y
x
−
=
+
.
Hàm số nghịch biến trên từng khoảng xác định
' 0, 2 0 2 − y x D m m
.
Câu 45: Tìm tất cả các giá trị của tham số thực
m
để hàm số
2cot 1
cot
x
y
xm
+
=
+
đồng biến trên khoảng
;
42
.
A.
( )
1
; 1 0;
2
m
− −
. B.
(
1
; 1 0;
2
m
− −
.
C.
(
1
; 1 0;
2
m
− −
. D.
1
;
2
m
+
.
Lời giải

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Chọn B
Điều kiện:
cot xm−
.
Ta có
( ) ( )
( ) ( )
22
22
2
21
cot 2cot 1
12
sin sin
cot sin cot
x m x
m
xx
y
x m x x m
− + + +
−
==
++
.
Hàm số đồng biến trên khoảng
;
42
( )
1 2 0
1
0
1
1
0;1
0
0
2
m
m
y
m
m
m
m
−
−
−
−
(
1
; 1 0;
2
m
− −
.
Câu 46: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
.
A.
5
;
2
m
−
−
. B.
5
;
2
m
−
−
. C.
5
;
2
m
+
. D.
5
;
2
m
+
.
Lời giải
Chọn B
Ta có:
( )
2
3 12 2y x m x
= − + +
.
Hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
khi và chỉ khi:
( ) ( )
2
3 12 2 0, 2 ; 1y x m x x
= − + + − −
( )
2
4 8 0, 2 ; 1x mx x x − + + − −
( )
2
4 8 , 2 ; 1mx x x x − − −
( )
2, 2; 1
4
x
mx − − −
25
2
42
m
−−
− =
.
Câu 47: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
.
A.
5
;
2
m
−
−
. B.
5
;
2
m
−
−
. C.
5
;
2
m
+
. D.
5
;
2
m
+
.
Lời giải
Chọn B
Ta có:
( )
2
3 12 2y x m x
= − + +
.
Hàm số
( )
32
6 2 1y x m x m= − + + − +
đồng biến trên
( )
2 ; 1−−
khi và chỉ khi:
( ) ( )
2
3 12 2 0, 2 ; 1y x m x x
= − + + − −
( )
2
4 8 0, 2 ; 1x mx x x − + + − −
( )
2
4 8 , 2 ; 1mx x x x − − −
( )
2, 2; 1
4
x
mx − − −
25
2
42
m
−−
− =
.
Câu 48: Cho hàm số
( )
fx
có đo hàm trên là
( ) ( )( )
' 1 3f x x x= − +
. Có bao nhiêu giá trị nguyên của
tham số
m
thuộc đon
10;2021−
để hàm số
( )
2
3xy f x m= + −
đồng biến trên khoảng
( )
0;2
?
A.
2016.
B.
2019.
C.
2018.
D.
2017.
Lời giải
Chọn B

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
Ta có
( ) ( )( ) ( )
3
' 1 3 0 * .
1
x
f t x x
x
−
= − +
Xét hàm số
( )
2
( ) 3xy g x f x m= = + −
Có
( ) ( )
( )
2
' 2 3 ' 3g x x f x x m= + + −
Vì
( )
2 3 0, 0;2xx+
nên
( )
gx
đồng biến trên
( ) ( ) ( )
0;2 ' 0, 0;2g x x
( )
( )
2
' 3 0, 0;2f x x m x + −
( )
( )
( )
( )
22
22
3 3, 0;2 3 3, 0;2
3 1, 0;2 3 1, 0;2
x x m x x x m x
x x m x x x m x
+ − − + −
+ − + +
(**)
Có
( )
2
3h x x x=+
luôn đồng biến trên
( )
0;2
nên từ (**)
3 10 13
1 0 1
mm
mm
−
+ −
Vì
10;2021m
m
−
Có 2019 giá trị của tham số m.
Vậy có 2019 giá trị của tham số m cần tìm.
Câu 49: Tìm tất cả các giá trị của tham số
m
để hàm số
4mx
y
xm
+
=
+
nghịch biến trên khoảng
( )
;1 .−
A.
( )
2;2 .m−
B.
( )
2; 1 .m − −
C.
(
2;2 .m−
D.
(
2; 1 .m − −
Lời giải
Chọn D
* Tập xác định:
\ m=−D
.
*
( )
2
2
4m
y
xm
−
=
+
.
* ycbt
( )
( )
2
;1
1
0, ;1 2 1
22
40
m
m
y x m
m
m
− −
−
− − −
−
−
.
Câu 50: Cho hàm số
11
.
1
x
fx
xm
Có bao nhiêu giá trị nguyên của tham số
m
thuộc
10;10
để đã cho đồng biến trên khoảng
3;0
?
A. 8. B. 9. C. 10. D. 11.
Lời giải
Đt
1tx
với
3;0 1;2 .xt
Hàm số đã cho trở thành
2
11tm
f t f t
tm
tm
.
Ta có
1
0, 3;0
21
tx
x
nên
1tx
nghịch biến trên
3;0 .
Yêu cầu của bải toán tương đương với tìm
m
để hàm số
ft
nghịch biến trên
1;2
0, 1;2f t t
10
1 0 1 0
, 1;2 , 1;2
1;2
0
m
mm
tt
m
t m m t

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
10
11
2
2
1
m
m
m
m
m
. Vì
, 10;10mm
nên
10; 9;...;0 .m

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
( )
y f x=
luôn nghịch biến . Tập nghiệm của bất phương trình
( )
1
1ff
x
A.
( )
;1−
. B.
( ) ( )
;0 1;− +
. C.
( )
0;1
D.
( ) ( )
;0 0;1−
.
Câu 2: Giá trị của tham số m để bất phương trình
( 2 ) 1 4x m x m− − − −
có nghiệm là:
A.
3m
. B.
2m
. C.
0m
. D.
2m
.
Câu 3: Cho hàm số
( )
y f x=
liên tục trên và có đạo hàm
2
1,y x x
= − −
. Khẳng định nào sau
đây đúng?
A.
( ) ( )
0 2020ff
. B.
( ) ( )
22ff−=
.
C.
( ) ( )
2020 2020ff−
. D.
( ) ( )
10ff
.
Câu 4: Cho hàm số
( )
y f x=
có
( )
0,f x x
. Có bao nhiêu giá trị nguyên của
x
để
( )
( )
2
22f x f x
?
A.
23
. B.
20
. C.
21
. D.
22
.
Câu 5: Tìm
m
để bất phương trình
4
1
xm
x
+
−
có nghiệm trên khoảng
( )
;1−
A.
3m
. B.
3m −
. C.
5m
. D.
1m −
.
Câu 6: Cho hàm số
( )
fx
có đạo hàm trên và thỏa mãn
( ) ( )
1f x f x
+
với mọi số thực
x
. Bất
phương trình
( )
1
x
f x me+
nghiệm đúng với mọi
( )
0;x +
khi và chỉ khi
A.
( )
1m f e−
. B.
( )
1m f e−
. C.
( )
01mf−
. D.
( )
01mf−
.
Câu 7: Tổng các nghiệm thực của phương trình
( ) ( )
3
62
2020 5 6 2020 6 5x x x x+ = − − −
là:
A.
2021
. B.
6−
. C.
2020
D.
5
.
Câu 8: Cho hàm số
( )
fx
, hàm số
( )
fx
liên tục trên và có đồ thị như hình vẽ. Bất phương trình
( )
f x x m+
(
m
là một số thực) nghiệm đúng với mọi
( )
1;0x−
khi và chỉ khi:
Ứng dụng tính đơn điệu vào phương trình, BPT
DẠNG 6
Phương pháp:
▪ Bài toán 1: Giải phương trình
( ) ( )
=h x g x
Biến đổi và vận dụng kết quả: Nếu hàm số
( )
ft
luôn đồng biến hoặc nghịch biến trên D thì phương trình
( )
0=ft
có tối đa một nghiệm và với mọi
, u v D
thì
( ) ( )
= =f u f v u v
.
▪ Bài toán 2: Giải bất phương trình
( ) ( )
h x g x
Biến đổi bất phương trình về dạng
( ) ( )
f u f v
và sử dụng kết quả:
Hàm số
( )
ft
đồng biến trên D thì
, u v D
ta có
( ) ( )
f u f v u v
.
Hàm số
( )
ft
nghịch biến trên D thì
, u v D
ta có
( ) ( )
f u f v u v
.
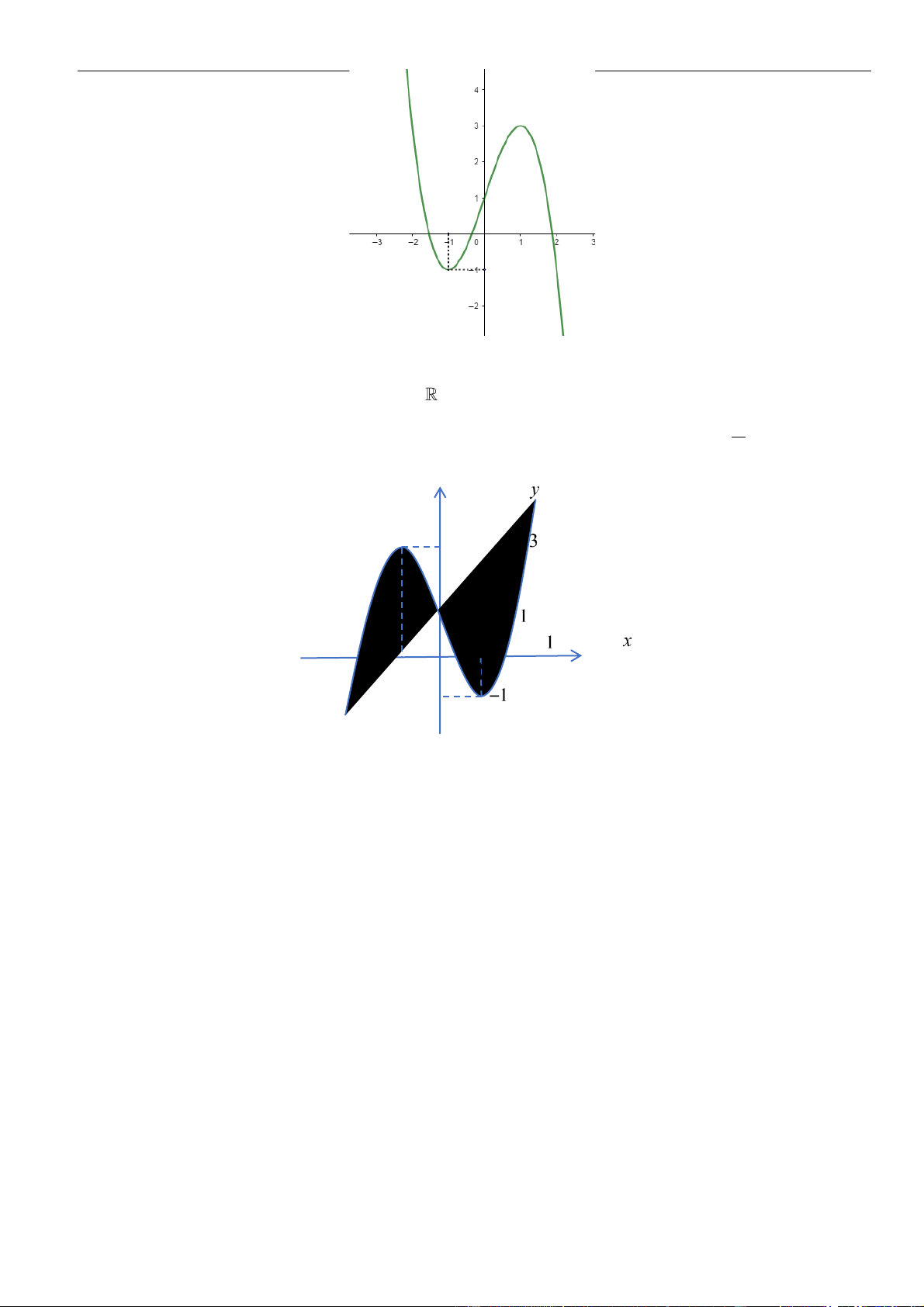
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
( )
0mf
. B.
( )
11mf − +
. C.
( )
11mf − +
. D.
( )
0mf
.
Câu 9: Cho hàm số
()y f x=
liên tục trên và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của
tham số
m
để phương trình
(cos ) 2 1f x m= − +
có nghiệm thuộc khoảng
0;
2
là
A.
( )
0;1
. B.
( )
1;1−
. C.
(
0;1
. D.
(
1;1−
.
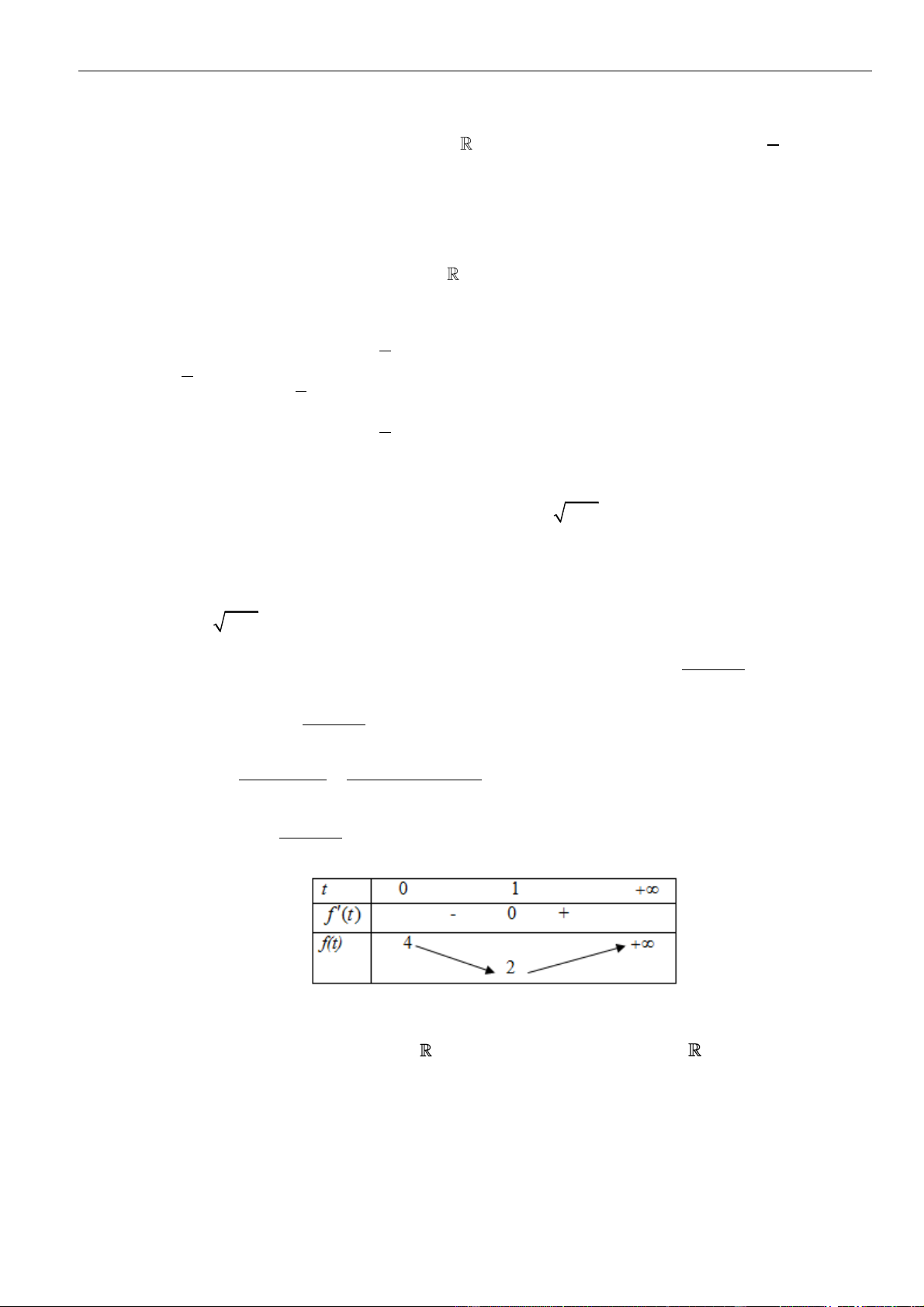
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
y f x=
luôn nghịch biến . Tập nghiệm của bất phương trình
( )
1
1ff
x
A.
( )
;1−
. B.
( ) ( )
;0 1;− +
. C.
( )
0;1
D.
( ) ( )
;0 0;1−
.
Lời giải
Chọn B
Vì hàm số
( )
y f x=
luôn nghịch biến nên ta có
( ) ( ) ( )
0
1
1
0
0
1
1 ;0 1;
1
1
1
0
1
1
x
x
x
x
f f x
x
x
x
x
x
− +
.
Vậy tập nghiệm của bất phương trình là
( ) ( )
;0 1;x − +
.
Câu 2: Giá trị của tham số m để bất phương trình
( 2 ) 1 4x m x m− − − −
có nghiệm là:
A.
3m
. B.
2m
. C.
0m
. D.
2m
.
Lời giải
Chọn B
Đặt
1; 0t x t= −
.
Khi đó bất phương trình ban đầu trở thành:
3
2
4
( 1) 4
1
tt
t m t m m
t
−+
− − −
+
.
Xét hàm số:
)
3
4
( ) , 0;
1
tt
f t t
t
−+
= +
+
.
Có
3 2 2
22
2 3 5 ( 1)(2 5 5)
()
( 1) ( 1)
t t t t t
ft
tt
+ − − + +
==
++
;
( ) 0 1f t t
= =
.
BBT của
)
3
4
( ) , 0;
1
tt
f t t
t
−+
= +
+
:
Từ BBT suy ra để bất phương trình có nghiệm thì
2m
.
Câu 3: Cho hàm số
( )
y f x=
liên tục trên và có đạo hàm
2
1,y x x
= − −
. Khẳng định nào sau
đây đúng?
A.
( ) ( )
0 2020ff
. B.
( ) ( )
22ff−=
.
C.
( ) ( )
2020 2020ff−
. D.
( ) ( )
10ff
.
Lời giải
Chọn A
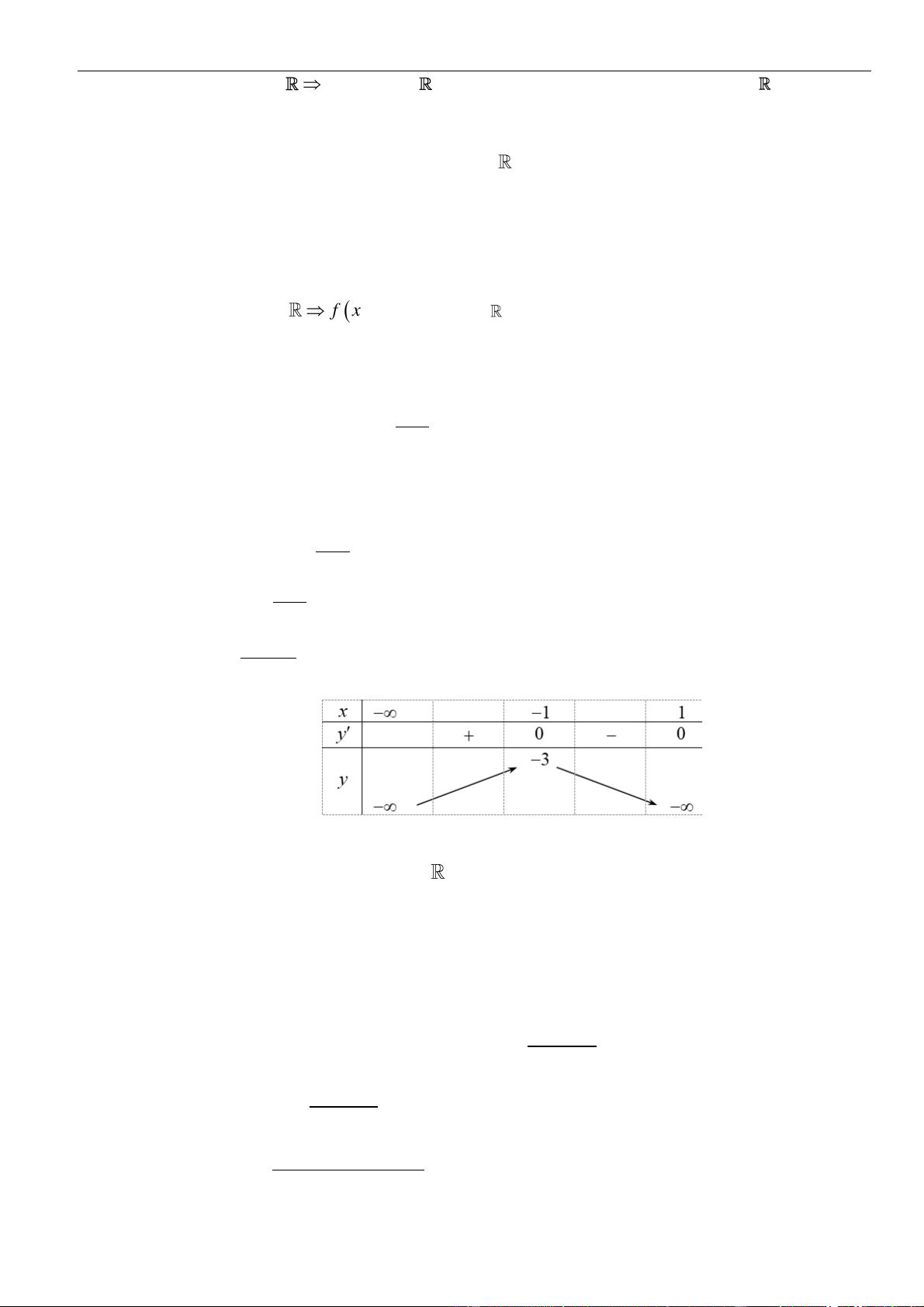
Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
2
1,y x x
= − −
0,fx
, do đó hàm số
( )
y f x=
nghịch biến trên
Do
( ) ( )
0 2020 0 2020ff
.
Câu 4: Cho hàm số
( )
y f x=
có
( )
0,f x x
. Có bao nhiêu giá trị nguyên của
x
để
( )
( )
2
22f x f x
?
A.
23
. B.
20
. C.
21
. D.
22
.
Lời giải
Chọn C
( ) ( )
0,f x x f x
đồng biến trên .
Suy ra
( )
( )
22
22 22 0 22f x f x x x x
.
Vậy có 21 giá trị nguyên của
x
.
Câu 5: Tìm
m
để bất phương trình
4
1
xm
x
+
−
có nghiệm trên khoảng
( )
;1−
A.
3m
. B.
3m −
. C.
5m
. D.
1m −
.
Lời giải
Chọn B
Bất phương trình
4
1
xm
x
+
−
có nghiệm trên khoảng
( )
;1−
(
( )
;1
m max g x
−
Với
( )
4
1
g x x
x
=+
−
( )
( )
2
4
1
1
gx
x
=−
−
;
( )
( )
( )
3 ;1
0
1 ;1
x
gx
x
= −
=
= − −
Vậy
3m −
.
Câu 6: Cho hàm số
( )
fx
có đạo hàm trên và thỏa mãn
( ) ( )
1f x f x
+
với mọi số thực
x
. Bất
phương trình
( )
1
x
f x me+
nghiệm đúng với mọi
( )
0;x +
khi và chỉ khi
A.
( )
1m f e−
. B.
( )
1m f e−
. C.
( )
01mf−
. D.
( )
01mf−
.
Lời giải
Chọn C
Ta có
( ) ( )
( )
1
11
xx
x
fx
f x me f x me m
e
−
+ −
Xét hàm
( )
( )
1
x
fx
gx
e
−
=
trên
( )
0;+
Có
( )
( ) ( )
( )
1
0, 0;
x
f x f x
g x x
e
− −
= +
Bảng biến thiên
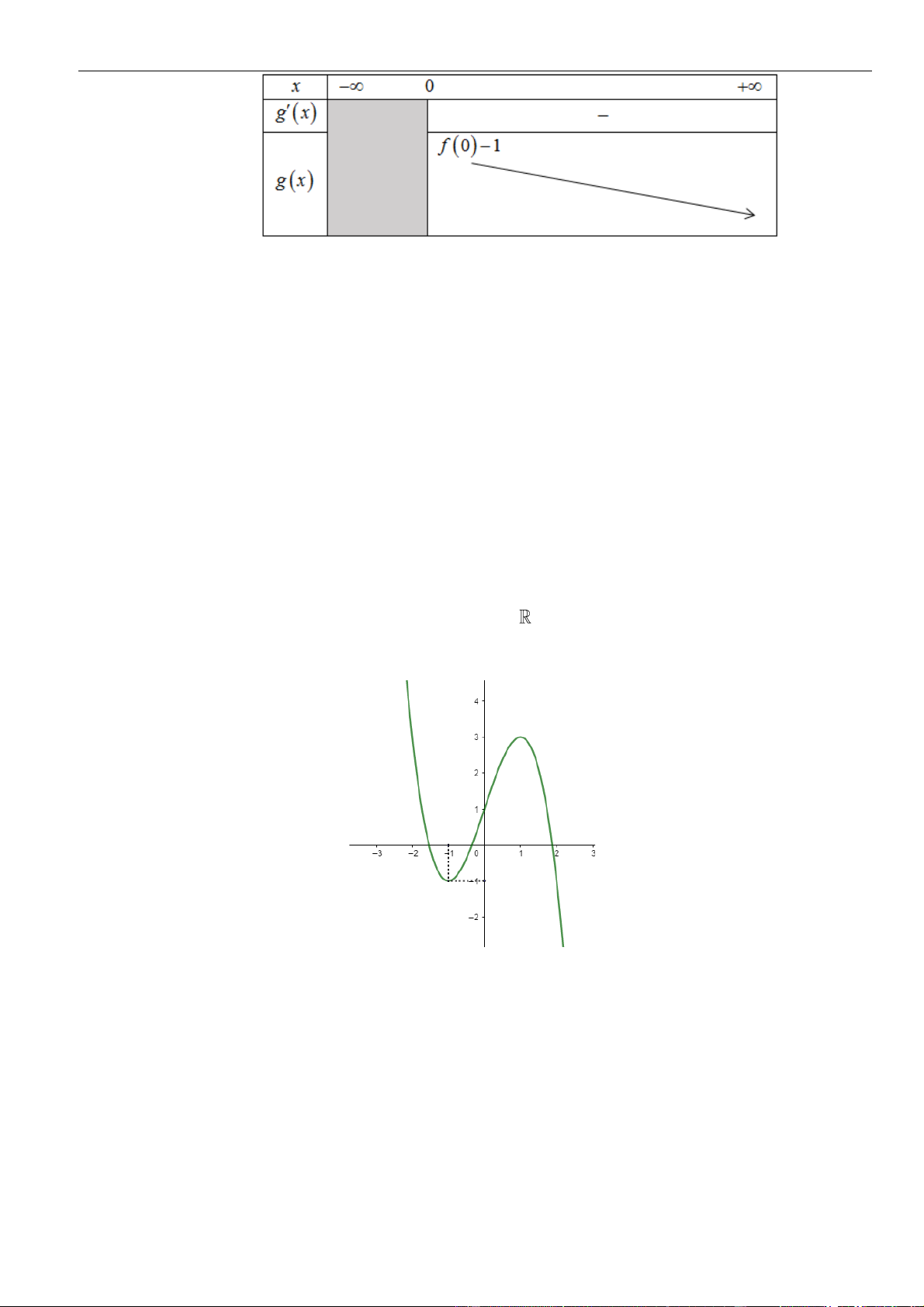
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Vậy bất phương trình
( )
1
x
f x me+
nghiệm đúng với mọi
( )
0;x +
khi và chỉ khi
( )
01mf−
Câu 7: Tổng các nghiệm thực của phương trình
( ) ( )
3
62
2020 5 6 2020 6 5x x x x+ = − − −
là:
A.
2021
. B.
6−
. C.
2020
D.
5
.
Lời giải
Chọn D
Xét hàm số
( )
3
2020f t t t=+
( )
2
' 3 2020 0,f t t t R = +
nên hàm số
( )
y f t=
đồng biến
trên khoảng
R
. Phương trình
( ) ( )
3
62
2020 5 6 2020 5 6x x x x+ = − + −
có dạng:
( )
( )
22
2
5 6 5 6
3
x
f x f x x x
x
=
= − = −
=
.
Vậy tổng các nghiệm là
5
.
Câu 8: Cho hàm số
( )
fx
, hàm số
( )
fx
liên tục trên và có đồ thị như hình vẽ. Bất phương trình
( )
f x x m+
(
m
là một số thực) nghiệm đúng với mọi
( )
1;0x−
khi và chỉ khi:
A.
( )
0mf
. B.
( )
11mf − +
. C.
( )
11mf − +
. D.
( )
0mf
.
Lời giải
Chọn B
Ta có:
( ) ( )
f x x m f x x m + −
.
Xét
( ) ( )
g x f x x=−
, ta có:
( ) ( )
1g x f x
=−
. Với mọi
( )
1;0x−
thì
( )
11fx
−
.
Từ đó
( ) ( )
10g x f x
= −
nên hàm số nghịch biến trên
( )
1;0−
.
Suy ra
( ) ( ) ( )
11g x f x x f= − − +
. Yêu cầu bài toán tương đương với
( )
11mf − +
.

Chủ đề 01: Cơ bản về tính đơn điệu của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 9: Cho hàm số
()y f x=
liên tục trên và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của
tham số
m
để phương trình
(cos ) 2 1f x m= − +
có nghiệm thuộc khoảng
0;
2
là
A.
( )
0;1
. B.
( )
1;1−
. C.
(
0;1
. D.
(
1;1−
.
Lời giải
Chọn A
Đặt
( )
cos , 0;1x t t=
.
Phương trình đã cho có nghiệm thuộc khoảng
0;
2
phương trình
( ) 2 1f t m= − +
có nghiệm
thuộc khoảng
(0;1)
. Dựa vào đồ thị trên suy ra
1 2 1 1 1 0mm− − +
.
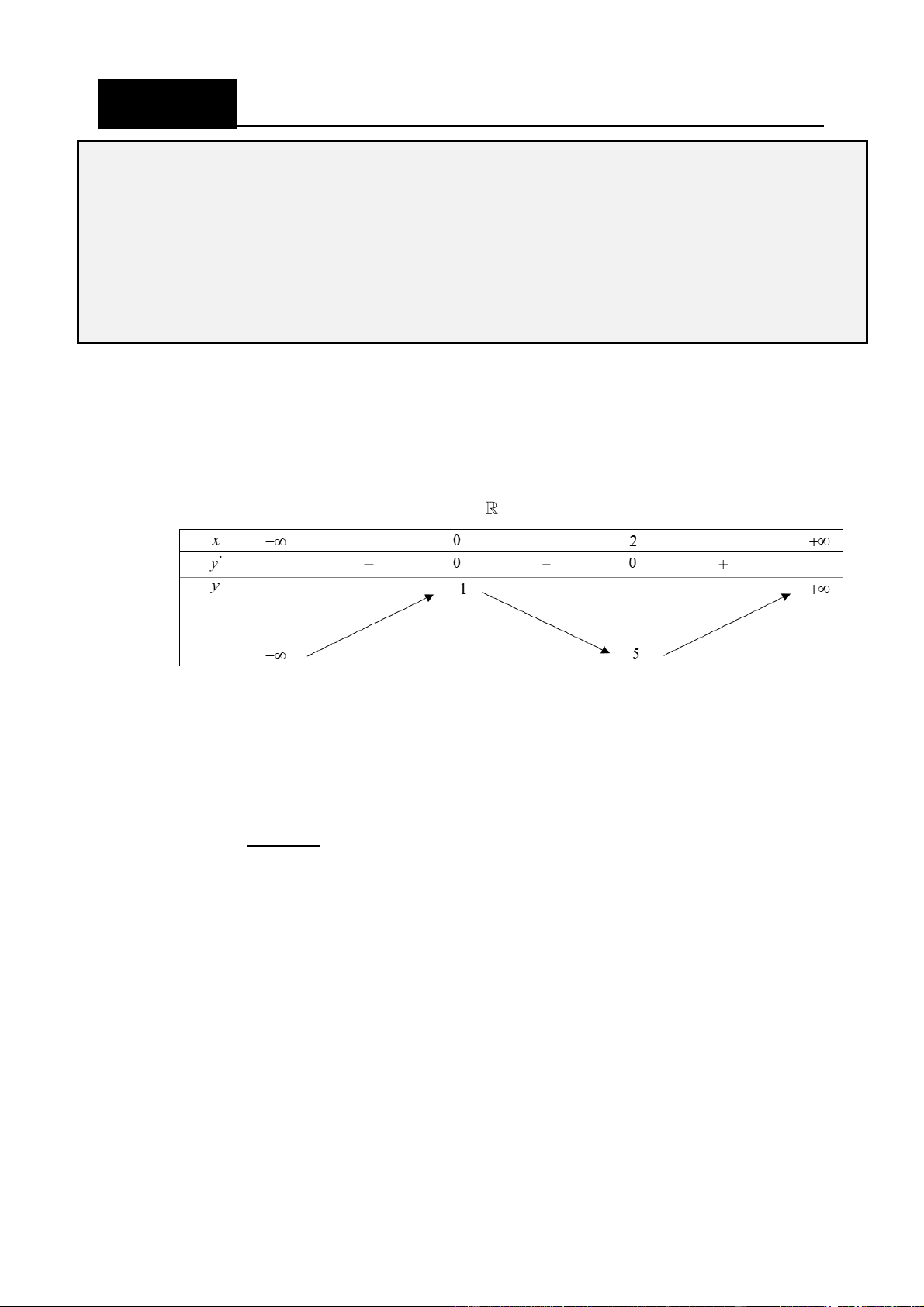
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
42
23y x x= − +
. Khẳng định nào sau đây đúng?
A. Hàm số có ba điểm cực trị. B. Hàm số chỉ có đúng hai điểm cực trị.
C. Hàm số không có cực trị. D. Hàm số chỉ có một điểm cực trị.
Câu 2: Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như hình dưới đây
Khẳng định nào dưới đây là đúng?
A. Điểm cực tiểu của hàm số là
2x =
. B. Điểm cực đại của hàm số là
1x =−
.
C. Điểm cực tiểu của hàm số là
5x =−
D. Điểm cực tiểu của hàm số là
0x =
.
Câu 3: Hàm số
3
12 3y x x= − +
đạt cực đại tại điểm
A.
19x =
. B.
2x =−
. C.
2x =
. D.
13x =−
.
Câu 4: Hàm số
2 2021
2
x
y
x
+
=
−
có bao nhiêu điểm cực trị?
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 5: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
23
1 2 2 3f x x x x
= + − +
. Tìm số điểm cực trị của hàm số
( )
fx
.
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 6: Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu?
A.
42
3y x x= − + +
. B.
42
3y x x= + +
. C.
42
3y x x= − +
. D.
42
3y x x= − − +
.
Câu 7: Điểm cực đại của đồ thị hàm số
3
35y x x= − +
là điểm
A.
( )
1;7N −
. B.
( )
7; 1P −
. C.
( )
3;1Q
. D.
( )
1;3M
.
Câu 8: Cho hàm số
42
23y x x= − +
, giá trị cực tiểu của hàm số đã cho bằng
A.
2
B.
3
. C.
1−
. D.
1
.
Tìm cực trị của hàm số cho bởi công thức
DẠNG 1
Phương pháp:
•
Bưc 1. Tìm tp xác định
D
của hàm số.
•
Bưc 2. Tnh đạo hàm
( ).y f x
=
Tìm các điểm
, ( 1,2,3,..., )
i
x i n=
mà tại đó đạo hàm bằng 0 hoc
không xác định.
•
Bưc 3. Sp xếp các điểm
i
x
theo th tự tăng dn và lp bảng biến thiên.
•
Bưc 4. Từ bảng biến thiên, suy ra các cực trị
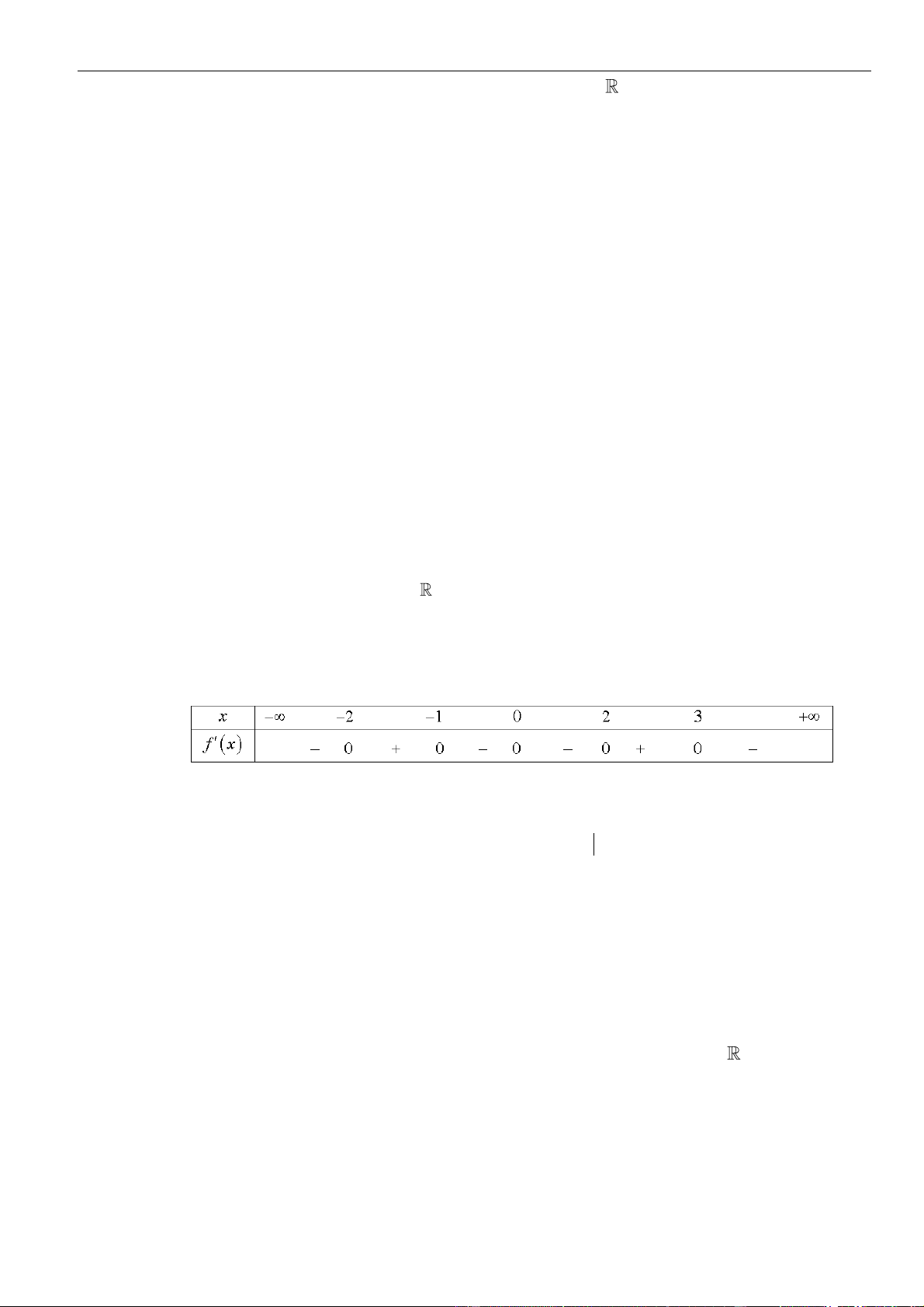
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 9: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3 1 3f x x x
= − +
trên . Tìm số điểm cực trị của hàm số
( )
y f x=
.
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 10: Hệ thc liên hệ giữa giá trị cực đại
CÐ
y
và giá trị cực tiểu
CT
y
của hàm số
3
3y x x=−
là:
A.
23
CT CÐ
yy=
. B.
0
CT CÐ
yy+=
. C.
2
CT CÐ
yy=
. D.
CT CÐ
yy=
.
Câu 11: Cho hàm số
43
3.y x x= − +
Khẳng định nào sau đây là đúng?
A. Hàm số có 3 điểm cực trị. B. Hàm số chỉ có đúng 2 cực trị.
C. Hàm số không có cực trị D. Hàm số chỉ có đúng 1 điểm cực trị.
Câu 12: Cho hàm số
32
2 4 2y x x x= − − +
. Số điểm cực trị của hàm số là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 13: Cho hàm số
32
2 4 2y x x x= − − +
. Số điểm cực trị của hàm số là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 14: Cho hàm số
( )
y f x=
là hàm đa thc. Có đạo hàm
( ) ( )( ) ( )
23
1 2 1f x x x x
= − − +
. Số điểm cực
trị của hàm số là:
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 15: Cho hàm số
( )
y f x=
xác định trên và có đạo hàm
( ) ( ) ( )
32
1 2 .f x x x x
= − +
Tìm số điểm cực
trị của hàm số đã cho?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 16: Cho hàm số
( )
fx
có bảng xét dấu của
( )
fx
như sau:
Số điểm cực trị của hàm số là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 17: Cho hàm số
42
6y x x= − +
. Số điểm cực trị của hàm số là:
A. 1. B. 0. C. 3. D. 4.
Câu 18: Cho hàm số
( )
fx
có
( ) ( )( )
2
12f x x x x
= − +
. Số điểm cực tiểu của hàm số đã cho là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 19: Hàm số
42
85y x x= − + +
có bao nhiêu điểm cực trị?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 20: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
2020 2021 2022
1 2 3 ,f x x x x x
= − − −
. Số điểm cực trị
của hàm số đã cho là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 21: Cho hàm số
()fx
có đạo hàm là
2 3 2 2
'( ) ( 2) ( 1) ( 4)( 1)f x x x x x= + − − −
, với mọi
xR
. Số điểm
cực đại của hàm số đã cho
A.
1
. B.
4
. C.
3
. D.
2
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 22: Cho hàm số
fx
có đạo hàm
2
'2f x x x x x
. Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 23: Cho hàm số
( )
fx
có đạo hàm
( )
( )
( )
2
'2f x x x x x= − −
.Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 24: Hàm số
( )( )( )
1 2 3y x x x= + − −
có số điểm cực trị là:
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 25: Trong các hàm số sau đây có bao nhiêu hàm số có đúng một điểm cực trị?
( )
( )
2
3
2 2 2
2
1) 1 2) 2 1 3) 2 1 4) .
1
x
y x y x y x x y
x
= + = − = − =
+
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 26: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( )
1 2 xf x x x x
= − −
. Tìm số điểm cực đại của hàm
số đã cho.
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 27: Điểm cực tiểu của đồ thị hàm số
3
34y x x
thuộc đường thẳng nào dưới đây?
A.
7yx
. B.
1yx
. C.
7yx
. D.
1yx
.
Câu 28: Biết rằng đồ thị hàm số
32
35y x x= − + +
có 2 điểm cực trị là
A
và
B
. Tnh độ dài đoạn thẳng A
B.
A.
10 2AB =
. B.
25AB =
. C.
32AB =
. D.
23AB =
.
Câu 29: Hàm số nào sau đây có nhiều điểm cực trị nhất?
A.
31yx= − +
. B.
42
31y x x= + +
. C.
32
31y x x= − +
. D.
21
3
x
y
x
+
=
−
.
Câu 30: Hàm số
3
1yx= − +
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 31: Hàm số
3
2
yx=
có tất cả bao nhiêu điểm cực trị?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 32: Gọi
, , A B C
là ba điểm cực trị của đồ thị hàm số
42
1
1.
2
y x x= − −
Diện tch
ABC
bằng
A.
1
2
B.
1.
C.
2.
D.
3
.
2
Câu 33: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
12f x x x x
= + −
,
x
. Số điểm cực tiểu của hàm số đã
cho là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 34: Hàm số nào dưới đây không có điểm cực trị?
A.
2
1y x x= + −
. B.
2
31y x x= + −
. C.
42
21y x x= + −
. D.
3
63y x x= + +
Câu 35: Trong các hàm số sau, hàm số nào có 3 điểm cực trị?
A.
1
2
x
y
x
+
=
+
. B.
42
23y x x= − −
. C.
42
23y x x= + −
. D.
32
3 3 1y x x x= − − +

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 36: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )
3
1 2 ,
= − + f x x x x x
. Số điểm cực trị của hàm số đã
cho là
A.
2
. B.
3
. C.
5
. D.
1
.
Câu 37: Cho hàm số
( )
fx
có đạo hàm liên tục và xác định trên . Hàm số
()fx
có biểu thc đạo hàm
( ) ( )
( )
2
11f x x x
=−−
. Hỏi hàm số có tất cả bao nhiêu cực trị?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 38: Hỏi hàm số
42
31y x x= − −
có tất cả bao nhiêu điểm cực trị?
A.
1
. B.
3
. C. 2. D. 4.
Câu 39: Hàm số
32
3 9 1y x x x= − − + −
có giá trị cực đại và giá trị cực tiểu ln lượt là M, m. Khi đó kết quả
nào sau đây đúng
A.
4Mm−=
. B.
35Mm−=
. C.
2Mm+ = −
. D.
70Mm+=
.
Câu 40: Hàm số nào sau đây có cực trị?
A.
1yx=−
. B.
2
23y x x= − +
. C.
3
89y x x= + +
. D.
21
31
x
y
x
−
=
+
.
Câu 41: Hàm số nào sau đây có cực trị?
A.
1yx
. B.
2
23y x x
. C.
3
89y x x
. D.
21
31
x
y
x
.
Câu 42: Đồ thị hàm số
32
y ax bx cx d= + + +
có hai điểm cực trị
( ) ( )
1; 7 , 2; 8AB−−
. Tính
( )
1y −
?
A.
( )
1 35y − = −
. B.
( )
1 11y −=
. C.
( )
1 11y − = −
. D.
( )
17y −=
.
Câu 43: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
32
1
3 5 1
3
y x x x
A. Có hệ số góc bằng -1.
B. song song với trục hoành.
C. song song với đường thẳng
1.x
D. Có hệ số góc dương.
Câu 44: Cho hàm số
32
2 5 4 2021y x x x= − + −
. Gọi
1
x
,
2
x
ln lượt là hoành độ hai điểm cực đại và cực tiểu
của hàm số. Kết lun nào sau đây đúng?
A.
12
1
3
xx−=
. B.
21
2
3
xx−=
. C.
21
1
2
3
xx−=
. D.
12
1
2
3
xx−=
.
Câu 45: Hàm số
42
31y x x= − −
có bao nhiêu điểm cực trị?
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 46: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
2
' 2 ,f x x x x= −
. Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 47: Cho hàm số
( )
y f x=
có
( ) ( ) ( )
2020
2021
1 1 ,f x x x x x
= − +
. Hàm số đã cho có bao nhiêu điểm
cực trị?
A. 3. B. 0. C. 2. D. 1.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Câu 48: Cho hàm số
( )
=y f x
có đạo hàm
( ) ( )( )
2
' 1 4= + −f x x x x
với mọi
.x
Hàm số có mấy điểm
cực trị?
A.
4.
B.
3.
C.
1.
D.
2.
Câu 49: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
2
3
( ) 2 1 ,f x x x x x
= − −
. Số điểm cực tiểu của hàm số
đã cho là
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 50: Số điểm cực trị của hàm số
3 2 5
( ) ( 2) ( 3) ( 2)f x x x x= + − −
là
A.
2
. B.
3
. C.
1
. D.
6
.
Câu 51: Cho hàm số
( )
y f x=
liên tục trên và có
( ) ( )( )
5
2
12f x x x x
= − +
. Số điểm cực trị của hàm
số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 52: Cho hàm số
( )
y f x=
xác định và liên tục trên và có đạo hàm
( ) ( ) ( ) ( )
2 3 4
' 1 2 3f x x x x x= − − −
. Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 53: Hàm số nào sau đây không có cực trị
A.
2
45y x x= + +
. B.
42
4 2.y x x= + +
.
C.
32
2 3 1y x x x= − + +
. D.
32
3 2 3.y x x x= + − +
Câu 54: Cho hàm số nào
( )
y f x=
có
( ) ( ) ( )( )
3
2
1 3 5f x x x x x
= − − −
. Số điểm cực trị của đồ thị hàm số
là
A.
4
. B.
2
. C.
1
.
D.
3
.
Câu 55: Cho hàm số
( )
y f x=
thỏa mãn
( ) ( )
2
1;f x x x x
= −
. Mệnh đề nào sau đây là mệnh đề
đúng?
A.
( )
fx
đạt cực tiểu tại
1x =
. B.
( )
fx
không có cực trị.
C.
( )
fx
đạt cực tiểu tại
0x =
. D.
( )
fx
có hai điểm cực trị.
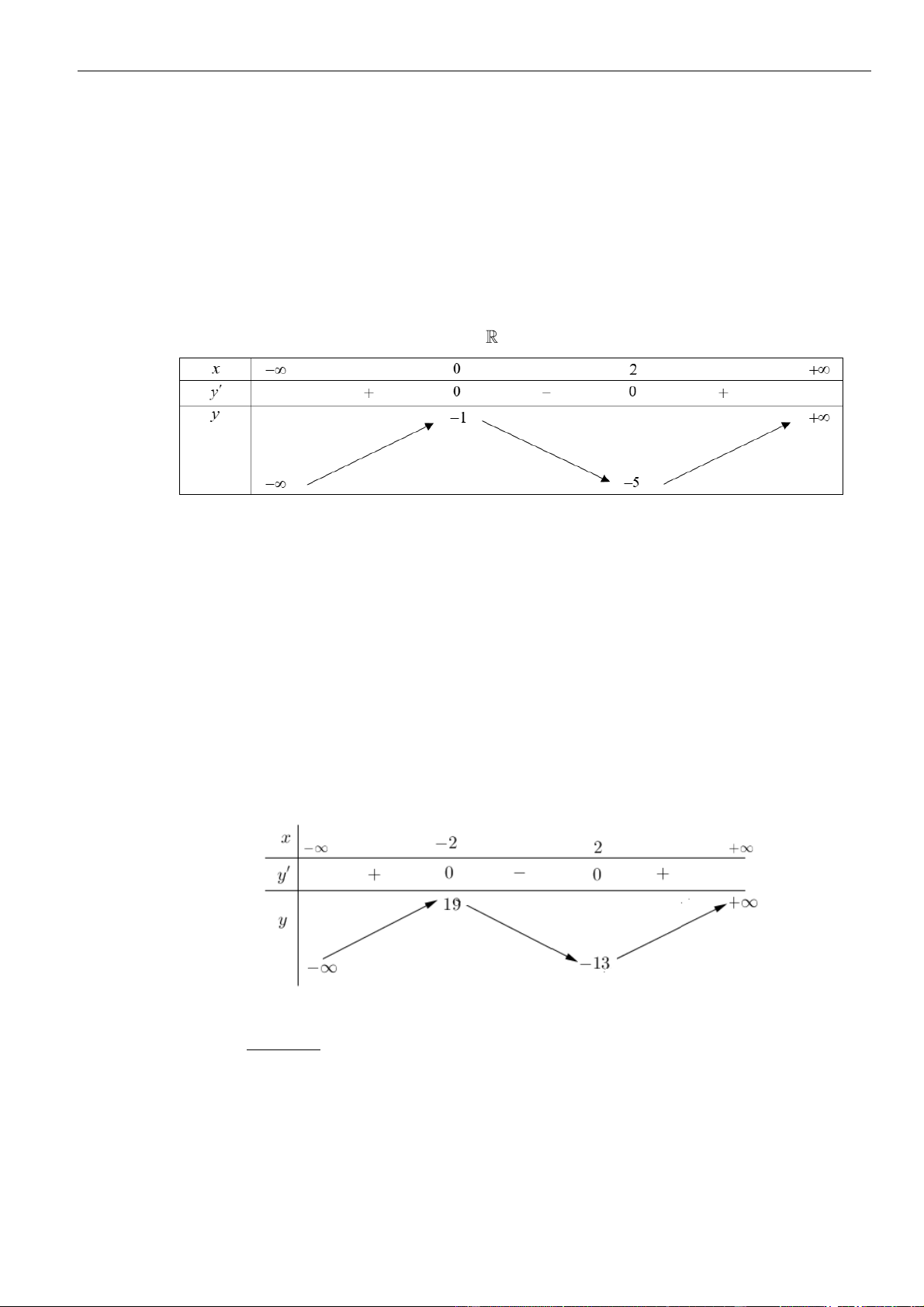
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
42
23y x x= − +
. Khẳng định nào sau đây đúng?
A. Hàm số có ba điểm cực trị. B. Hàm số chỉ có đúng hai điểm cực trị.
C. Hàm số không có cực trị. D. Hàm số chỉ có một điểm cực trị.
Lời giải
Chọn A
Ta thấy hàm số đã cho là hàm trùng phương
( )
42
0y ax bx c a= + +
với
0ab
nên
đây là trường hợp hàm số có ba điểm cực trị.
Câu 2: Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như hình dưới đây
Khẳng định nào dưới đây là đúng?
A. Điểm cực tiểu của hàm số là
2x =
. B. Điểm cực đại của hàm số là
1x =−
.
C. Điểm cực tiểu của hàm số là
5x =−
D. Điểm cực tiểu của hàm số là
0x =
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại
2x =
.
Câu 3: Hàm số
3
12 3y x x= − +
đạt cực đại tại điểm
A.
19x =
. B.
2x =−
. C.
2x =
. D.
13x =−
.
Lời giải
Chọn B
Ta có
2
3 12yx
=−
,
02yx
= =
.
Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đạt cực đại tại
2x =−
.
Câu 4: Hàm số
2 2021
2
x
y
x
+
=
−
có bao nhiêu điểm cực trị?
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn B
Tp xác định:
( ) ( )
;2 2;D = − +
.
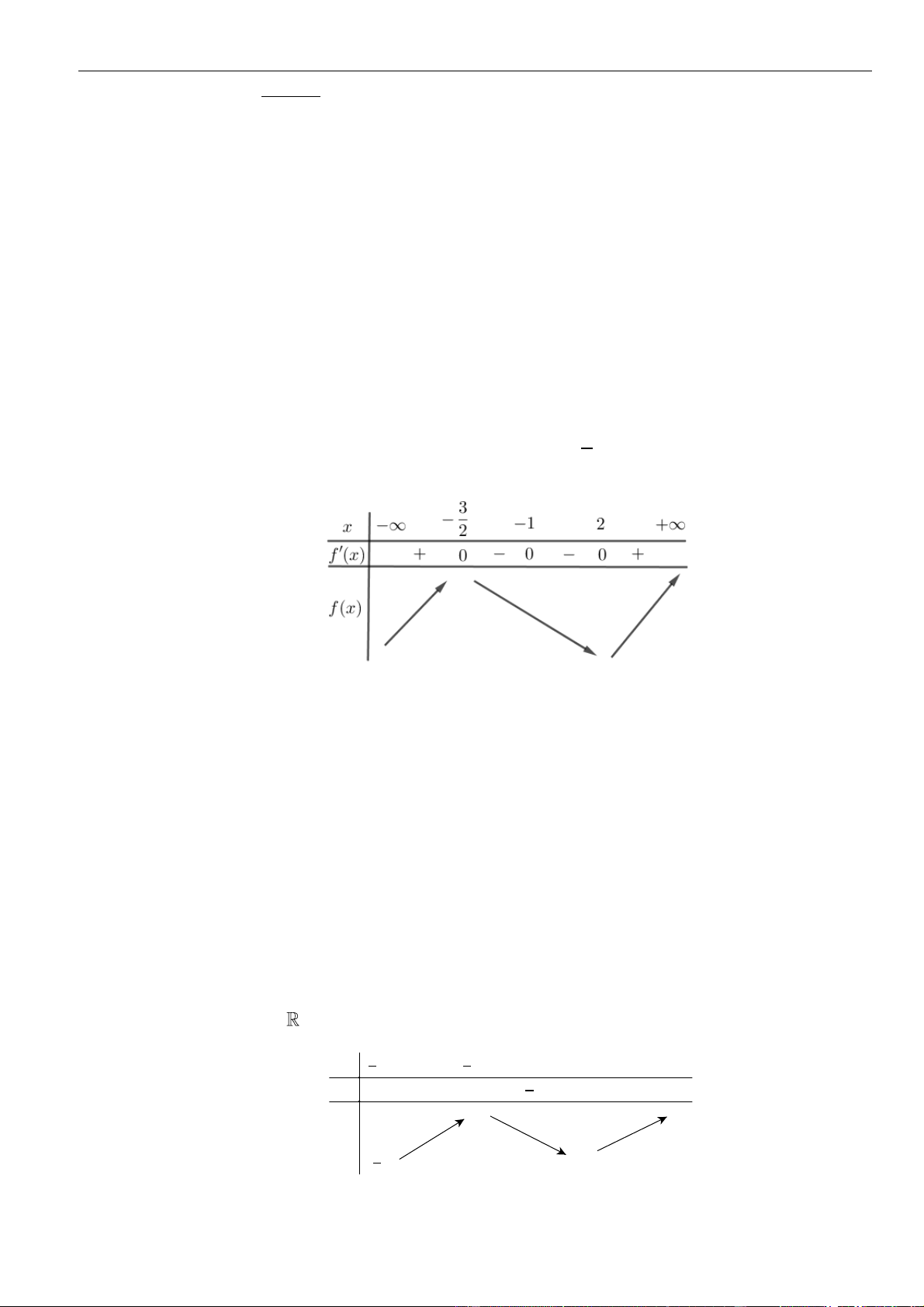
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Ta có:
( )
2
2025
0, 2
2
yx
x
= −
−
, suy ra hàm số nghịch biến trên mỗi khoảng
( )
;2−
và
( )
2;+
.
Do đó hàm số không có điểm cực trị.
Câu 5: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
23
1 2 2 3f x x x x
= + − +
. Tìm số điểm cực trị của hàm số
( )
fx
.
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
Ta có
( ) ( ) ( ) ( )
23
1
0 1 2 2 3 0 2
3
2
x
f x x x x x
x
=−
= + − + = =
=−
.
Bảng biến thiên
Vy hàm số
( )
fx
có hai điểm cực trị.
Câu 6: Trong các hàm số sau, hàm số nào có hai điểm cực đại và một điểm cực tiểu?
A.
42
3y x x= − + +
. B.
42
3y x x= + +
. C.
42
3y x x= − +
. D.
42
3y x x= − − +
.
Lời giải
Chọn A
Dựa vào dấu của hệ số
0 ; 0ab
nên hàm số
42
3y x x= − + +
có 3 điểm cực trị trong đó có 2
điểm cực đại và 1 điểm cực tiểu.
Câu 7: Điểm cực đại của đồ thị hàm số
3
35y x x= − +
là điểm
A.
( )
1;7N −
. B.
( )
7; 1P −
. C.
( )
3;1Q
. D.
( )
1;3M
.
Lời giải
Chọn A.
Ta có: TXĐ:
D =
,
2
33yx
=−
,
1
0
1
x
y
x
=
=
=−
.
Dựa vào bảng biến thiên ta có điểm cực đại của đồ thị hàm số là
( )
1;7N −
.
1
x
y'
y
+
0
3
1
+
∞∞
∞
7
+
∞
0
+
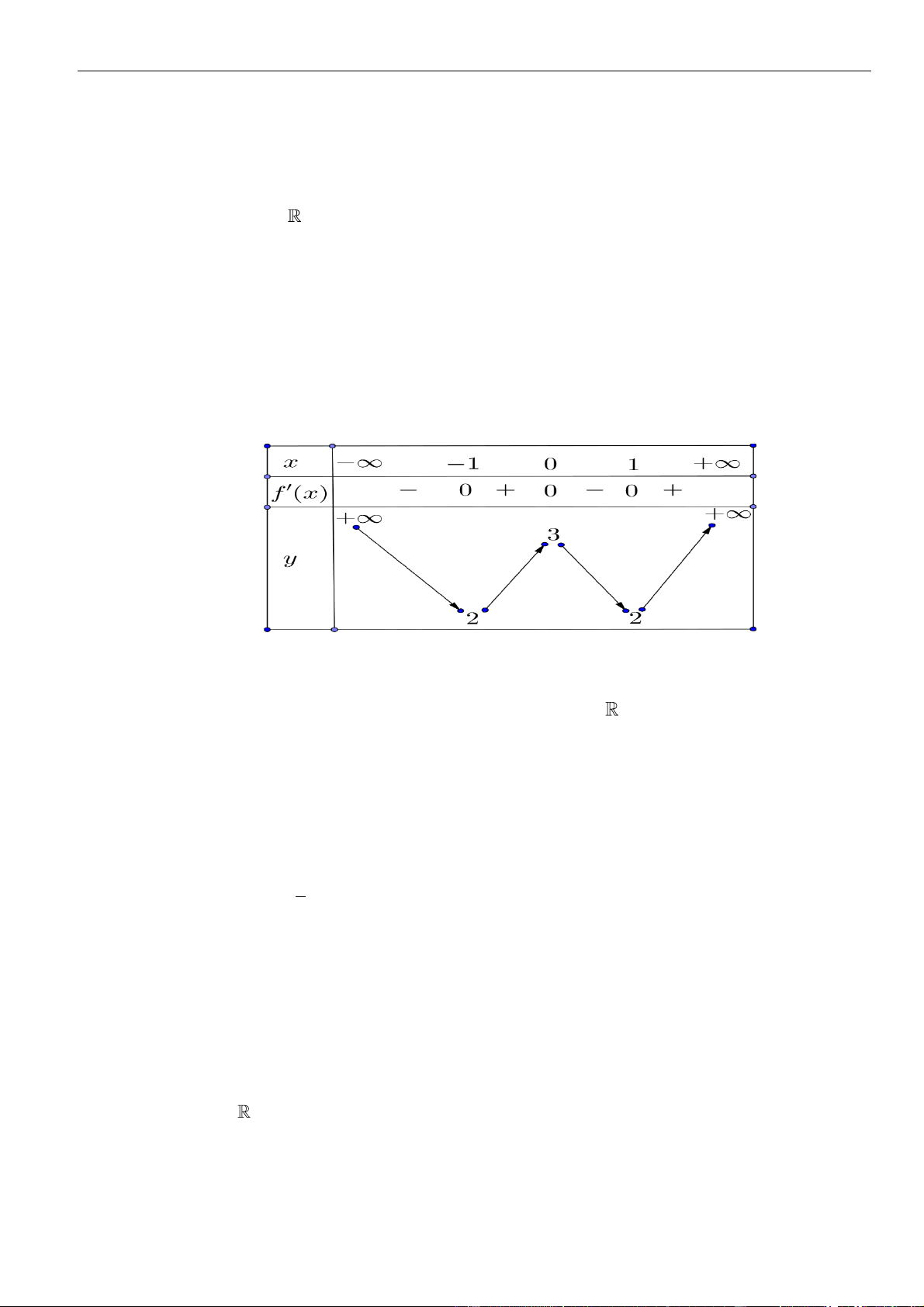
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Câu 8: Cho hàm số
42
23y x x= − +
, giá trị cực tiểu của hàm số đã cho bằng
A.
2
B.
3
. C.
1−
. D.
1
.
Lời giải
Chọn A
Xét hàm số
42
23y x x= − +
có:
Tp xác định
D =
;
( )
42
lim lim 2 3
xx
y x x
→ →
= − + = +
.
3
44y x x
=−
;
0
01
1
x
yx
x
=
= = −
=
.
Bảng biến thiên của hàm số
42
23y x x= − +
Từ bảng biến thin ta thấy
( )
12
CT
yy= =
.
Câu 9: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3 1 3f x x x
= − +
trên . Tìm số điểm cực trị của hàm số
( )
y f x=
.
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
( )
3
0.
1
3
x
fx
x
=−
=
=
( )
fx
có hai nghiệm đơn nên hàm số
( )
y f x=
có hai điểm cực trị.
Câu 10: Hệ thc liên hệ giữa giá trị cực đại
CÐ
y
và giá trị cực tiểu
CT
y
của hàm số
3
3y x x=−
là:
A.
23
CT CÐ
yy=
. B.
0
CT CÐ
yy+=
. C.
2
CT CÐ
yy=
. D.
CT CÐ
yy=
.
Lời giải
Chọn B
TXĐ:
D =
. Ta có
22
3 3 0 3 3 0y x y x
= − = − =
1
1
x
x
=
=−
Lại có
( )
6 1 6 0y x y
= =
nên
1x =
là điểm cực tiểu của hàm số
( )
1 6 0y
− = −
nên
1x =−
là điểm cực đại của hàm số

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Do đó
( ) ( )
1 2; 1 2
CÐ CT
y y y y= − = = = −
. Suy ra
0
CÐ CT
yy+=
.
Câu 11: Cho hàm số
43
3.y x x= − +
Khẳng định nào sau đây là đúng?
A. Hàm số có 3 điểm cực trị. B. Hàm số chỉ có đúng 2 cực trị.
C. Hàm số không có cực trị D. Hàm số chỉ có đúng 1 điểm cực trị.
Lời giải
Chọn D
Ta có:
32
0
4 3 0
3
4
x
y x x
x
=
= − =
=
Bảng biến thiên:
Vy hàm số đã cho có đúng 1 cực trị.
Câu 12: Cho hàm số
32
2 4 2y x x x= − − +
. Số điểm cực trị của hàm số là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Ta có
2
6 2 4 0y x x
= − − =
1
2
3
x
x
=
−
=
.
Vy hàm số có
2
điểm cực trị.
Câu 13: Cho hàm số
32
2 4 2y x x x= − − +
. Số điểm cực trị của hàm số là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Ta có
2
6 2 4 0y x x
= − − =
1
2
3
x
x
=
−
=
.
Vy hàm số có
2
điểm cực trị.
Câu 14: Cho hàm số
( )
y f x=
là hàm đa thc. Có đạo hàm
( ) ( )( ) ( )
23
1 2 1f x x x x
= − − +
. Số điểm cực
trị của hàm số là:
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có:
( ) ( )( ) ( )
23
1
1 2 1 0 2
1
x
f x x x x x
x
=
= − − + = =
=−
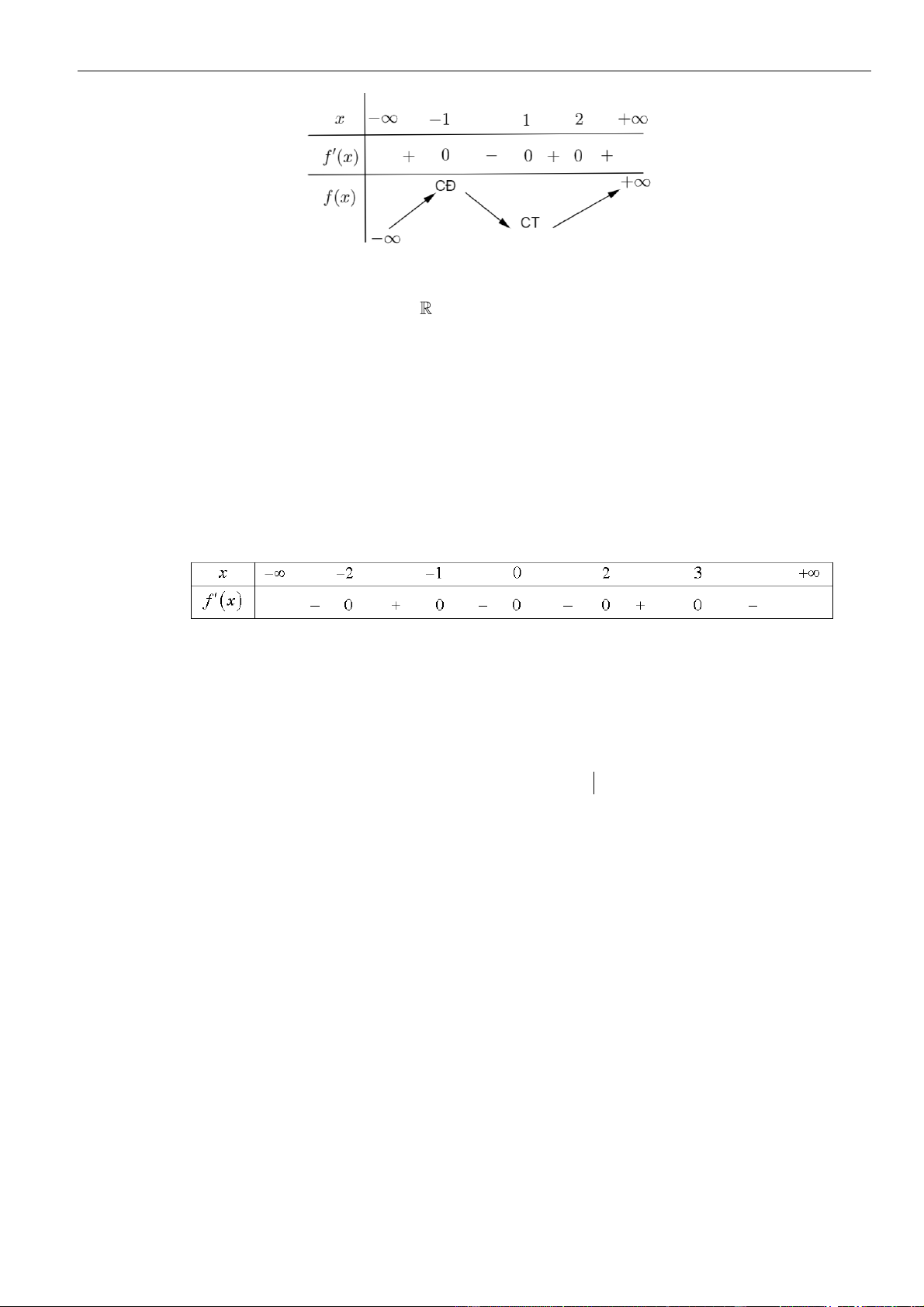
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Bảng biến thiên:
Từ bảng biến thiên ta có số điểm cực trị của hàm số là 2.
Câu 15: Cho hàm số
( )
y f x=
xác định trên và có đạo hàm
( ) ( ) ( )
32
1 2 .f x x x x
= − +
Tìm số điểm cực
trị của hàm số đã cho?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn A
Vì
( ) ( ) ( )
32
12f x x x x
= − +
nên
( )
0fx
=
có các nghiệm
0, 1, 2x x x= = = −
và
( )
fx
chỉ đổi
dấu khi
x
qua các nghiệm
0, 1xx==
.
Vy hàm số có 2 điểm cực trị.
Câu 16: Cho hàm số
( )
fx
có bảng xét dấu của
( )
fx
như sau:
Số điểm cực trị của hàm số là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn A
Dựa vào bảng xét dấu đã cho, ta thấy
( )
fx
đổi dấu 4 ln nên hàm số
( )
fx
có 4 điểm cực trị.
Câu 17: Cho hàm số
42
6y x x= − +
. Số điểm cực trị của hàm số là:
A. 1. B. 0. C. 3. D. 4.
Lời giải
Chọn C
Hàm số
42
6y x x= − +
.
Vì
. 1 0ab= −
nên hàm số đã cho có 3 cực trị.
Câu 18: Cho hàm số
( )
fx
có
( ) ( )( )
2
12f x x x x
= − +
. Số điểm cực tiểu của hàm số đã cho là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Xét phương trình
( )
0fx
=
0
1
2
x
x
x
=
=
=−
Ta có bảng xét dấu sau:
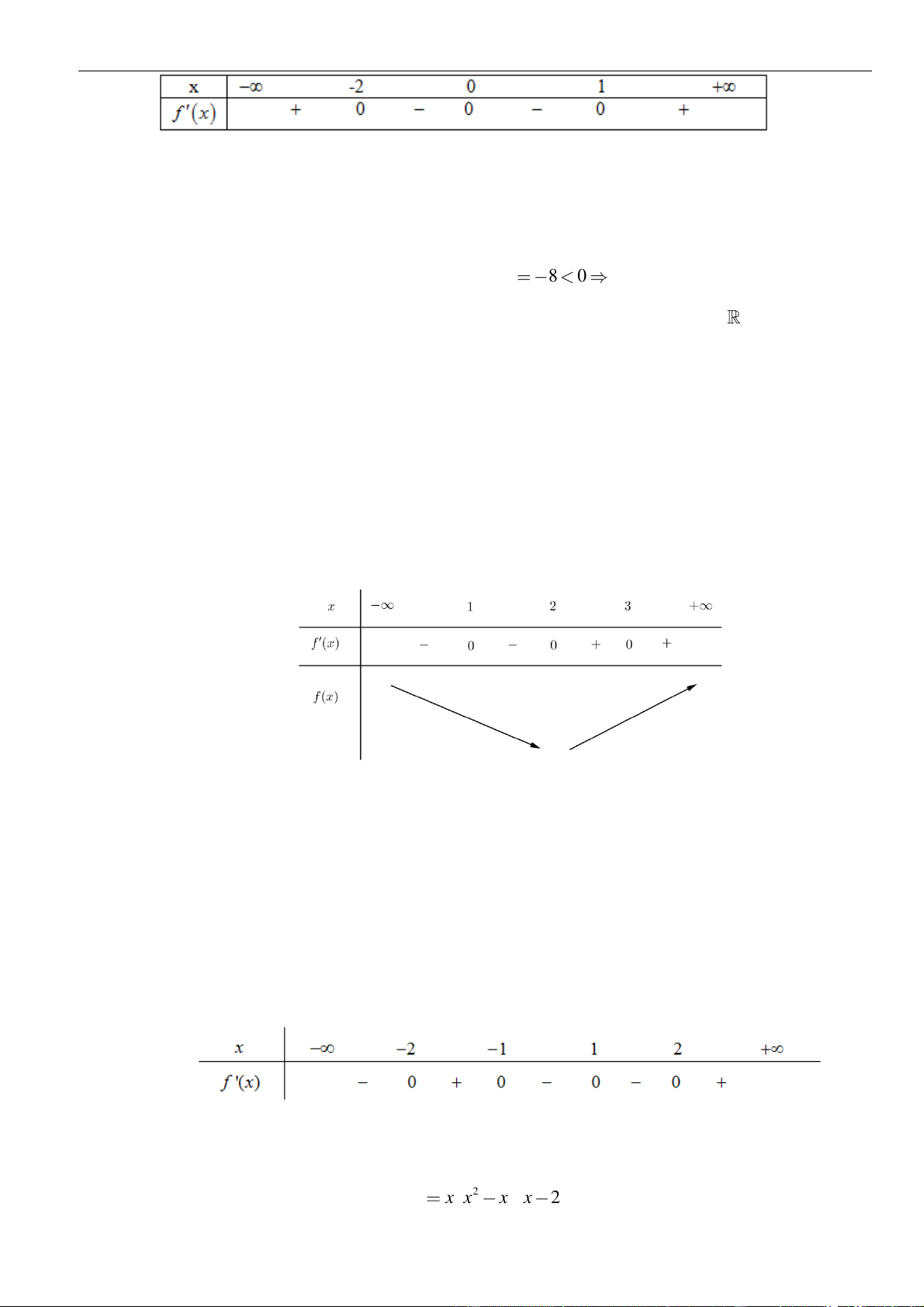
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Dựa vào bảng xét dấu suy ra hàm số có
1
điểm cực tiểu.
Câu 19: Hàm số
42
85y x x= − + +
có bao nhiêu điểm cực trị?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Hàm số đã cho là hàm trùng phương thỏa mãn
. 8 0ab
hàm số có ba điểm cực trị.
Câu 20: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
2020 2021 2022
1 2 3 ,f x x x x x
= − − −
. Số điểm cực trị
của hàm số đã cho là
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn D
Cách 1:
Ta có
( )
1
02
3
x
f x x
x
=
= =
=
.
Bảng xét dấu
( )
fx
Từ bảng xét dấu suy ra hàm số đã cho có 1 điểm cực trị.
Cách 2: (Trc nghiệm)
Nhn thấy
( )
0fx
=
có 1 nghiệm đơn và 2 nghiệm kép nên hàm số đã cho có 1 điểm cực trị.
Câu 21: Cho hàm số
()fx
có đạo hàm là
2 3 2 2
'( ) ( 2) ( 1) ( 4)( 1)f x x x x x= + − − −
, với mọi
xR
. Số điểm
cực đại của hàm số đã cho
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn A
Ta có bảng xét dấu của
2 3 2 2
'( ) ( 2) ( 1) ( 4)( 1)f x x x x x= + − − −
như sau
Quan sát bảng xét dấu ta có
'( )fx
đổi dấu từ dương sang âm tại
1x =−
. Vy hàm số có điểm cực
đại tại
1x =−
Câu 22: Cho hàm số
fx
có đạo hàm
2
'2f x x x x x
. Số điểm cực trị của hàm số đã cho là

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn A
Ta có
0
' 0 1
2
x
f x x
x
.
Vì
1x
,
2x
là nghiệm bội lẻ và
0x
là nghiệm bội chẵn nên hàm số có
2
điểm cực trị.
Câu 23: Cho hàm số
( )
fx
có đạo hàm
( )
( )
( )
2
'2f x x x x x= − −
.Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn A
Ta có
( )
( )
( ) ( )( )
22
' 2 1 2f x x x x x x x x= − − = − −
.
( )
fx
đổi dấu 2 ln.Vy hàm số
( )
fx
có 2 điểm cực trị.
Câu 24: Hàm số
( )( )( )
1 2 3y x x x= + − −
có số điểm cực trị là:
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn A
Cách 1.
TXĐ:
Ta có
( )( ) ( )( ) ( )( )
2
4 13
2 3 1 3 1 2 3 8 1 0
3
y x x x x x x x x y x
= − − + + − − + − = − + − = =
.
Suy ra bảng xét dấu của hàm số đạo hàm
Vy hàm số có hai điểm cực trị.
Cách 2.
0y =
có
3
nghiệm đơn
0y
=
có hai nghiệm đơn và là hai điểm cực trị
Câu 25: Trong các hàm số sau đây có bao nhiêu hàm số có đúng một điểm cực trị?
( )
( )
2
3
2 2 2
2
1) 1 2) 2 1 3) 2 1 4) .
1
x
y x y x y x x y
x
= + = − = − =
+
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
2
1) 1 2 0 0y x y x y x
= + = = =
và
y
đổi dấu khi
x
qua nghiệm đó nên hàm số có 1 điểm
cực trị.
( ) ( )
2
22
0
2) 2 1 2 2 1 .4 0
1
2
x
y x y x x y
x
=
= − = − =
=
và
y
đổi dấu khi
x
qua các
nghiệm đó nên hàm số có 3 điểm cực trị.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
( )
( )
33
22
33
2 2 1
10 2
3) 2 1 2
33
x
x
y x x y x
xx
−
−
= − = + =
1
0;
5
y x y
= =
không xác định khi
0x =
và
y
đổi dấu khi
x
qua
1
0;
5
nên hàm số có 2 điểm cực trị.
( )
2
2
2
2
1
4) 0 1
1
1
xx
y y y x
x
x
−
= = = =
+
+
và
y
đổi dấu khi
x
qua các nghiệm đó nên
hàm số có 2 điểm cực trị.
Vy chỉ có 1 hàm số có đúng một điểm cực trị.
Câu 26: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( )
1 2 xf x x x x
= − −
. Tìm số điểm cực đại của hàm
số đã cho.
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C
Ta có:
( ) ( )( )
0
0 1 2 0 1
2
x
f x x x x x
x
=
= − − = =
=
.
Bảng xét dấu:
Từ bảng xét dấu hàm số có 1 cực đại.
Câu 27: Điểm cực tiểu của đồ thị hàm số
3
34y x x
thuộc đường thẳng nào dưới đây?
A.
7yx
. B.
1yx
. C.
7yx
. D.
1yx
.
Lời giải
Chọn B
Ta có
2
33yx
. Do đó
2
0 3 3 0yx
1
1
x
x
.
Vì
1x
là điểm cực tiểu của hàm số nên điểm
(1;2)A
là điểm cực tiểu của đồ thị hàm số.
Điểm
(1;2)A
thuộc đường thẳng
1yx
.
Câu 28: Biết rằng đồ thị hàm số
32
35y x x= − + +
có 2 điểm cực trị là
A
và
B
. Tnh độ dài đoạn thẳng A
B.
A.
10 2AB =
. B.
25AB =
. C.
32AB =
. D.
23AB =
.
Lời giải
Chọn B
2
05
3 6 0
29
xy
y x x
xy
= =
= − + =
= =
Nhn thấy pt
0y
=
có hai nghiệm phân biệt nên đồ thị hàm số có hai điểm cưc trị là
(0;5)A
và
(2;9)B
.
22
2 4 2 5AB = + =
.
Câu 29: Hàm số nào sau đây có nhiều điểm cực trị nhất?

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
A.
31yx= − +
. B.
42
31y x x= + +
. C.
32
31y x x= − +
. D.
21
3
x
y
x
+
=
−
.
Lời giải
Chọn C
Hàm số
31yx= − +
và
21
3
x
y
x
+
=
−
không có điểm cực trị (đạo hàm không đổi dấu )
Hàm số
42
31y x x= + +
có
3
4 6 0 0y x x x
= + = =
. Đạo hàm đổi dấu qua 1 điểm
0x =
nên
hàm số
42
31y x x= + +
chỉ có một điểm cực trị.
Hàm số
32
31y x x= − +
có
2
3 6 0 0 2y x x x x
= − = = =
. Đạo hàm đổi dấu qua 2 điểm
0, 2xx==
nên hàm số
32
31y x x= − +
có hai điểm cực trị.
Suy ra đáp án C.
Câu 30: Hàm số
3
1yx= − +
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn D
Tp xác định:
D =
.
2
3 0,y x x
= −
Hàm số luôn nghịch biến trên .
Vy hàm số đã cho không có cực trị.
Câu 31: Hàm số
3
2
yx=
có tất cả bao nhiêu điểm cực trị?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
+) Tp xác định:
D =
.
+) Tnh đạo hàm.
( )
3
2
3
2
' , 0
3
y x y x
x
= =
+) Xét dấu
'y
ta có:
'0y
với
( )
0;x +
và
'0y
với
( )
;0x −
.
Vy hàm số có 1 cực trị
Câu 32: Gọi
, , A B C
là ba điểm cực trị của đồ thị hàm số
42
1
1.
2
y x x= − −
Diện tch
ABC
bằng
A.
1
2
B.
1.
C.
2.
D.
3
.
2
Lời giải
Chọn A
Ta có:
3
22y x x
=−
.
3
0
00
1
x
y x x
x
=
= − =
=
.
Ba điểm cực trị của đồ thị hàm số là
( )
0; 1A −
,
3
1;
2
B
−
,
3
1;
2
C
−−
.
Tam giác
ABC
có điểm
A
thuộc trục tung, hai điểm
,BC
đối xng nhau qua trục tung nên tam
giác
ABC
cân tại
A
. Trung điểm
3
0;
2
H
−
của
BC
thuộc trục tung và là chân đường cao hạ từ
A
của tam giác, suy ra:

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
1 1 1 3 1
. . 1 .2
2 2 2 2 2
ABC A H B C
S AH BC y y x x
= = − − = − + =
.
Câu 33: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
12f x x x x
= + −
,
x
. Số điểm cực tiểu của hàm số đã
cho là
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn A
Ta có:
( ) ( )( )
3
0
1 2 0 1
2
x
f x x x x x
x
=
= + − = = −
=
.
Bảng xét dấu
( )
fx
Căn c vào bảng xét dấu thì số điểm cực tiểu của hàm số là 2
Câu 34: Hàm số nào dưới đây không có điểm cực trị?
A.
2
1y x x= + −
. B.
2
31y x x= + −
. C.
42
21y x x= + −
. D.
3
63y x x= + +
Lời giải
Chọn D
Các hàm số
2
1y x x= + −
,
2
31y x x= + −
,
42
21y x x= + −
đều có 1 điểm cực trị.
Xét hàm số
3
63y x x= + +
, ta có
2
3 6 0y x x
= +
nên hàm số không có cực trị.
Câu 35: Trong các hàm số sau, hàm số nào có 3 điểm cực trị?
A.
1
2
x
y
x
+
=
+
. B.
42
23y x x= − −
.
C.
42
23y x x= + −
. D.
32
3 3 1y x x x= − − +
.
Lời giải
Chọn B
Xét hàm số
42
2x 3yx= − −
có
XD:TD=
3
0
' 4x 4x; ' 0
1
x
yy
x
=
= − =
=
và
y
liên tiếp đổi dấu khi đi qua các điểm
0; 1xx= =
. Vy hàm số này có 3 điểm cực trị.
Câu 36: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )
3
1 2 ,
= − + f x x x x x
. Số điểm cực trị của hàm số đã
cho là
A.
2
. B.
3
. C.
5
. D.
1
.
Lời giải
Chọn B
Phương trình
( )
0
=fx
có
3
nghiệm đơn
2, 0, 1= − = =x x x
và
( )
fx
đổi dấu khi đi qua
3
nghiệm đó. Do đó, hàm số đã cho có
3
cực trị.
+
+
-
-
0
0
0
y
+
∞
2
0
-1
-
∞
x

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Câu 37: Cho hàm số
( )
fx
có đạo hàm liên tục và xác định trên . Hàm số
()fx
có biểu thc đạo hàm
( ) ( )
( )
2
11f x x x
=−−
. Hỏi hàm số có tất cả bao nhiêu cực trị?
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn A
( )
2
1
10
0
1
10
1
x
x
fx
x
x
x
=
−=
=
=
−=
=−
1
1
x
x
=
=−
Trong đó:
1x =
là nghiệm kép,
1x =−
là nghiệm đơn.
KL: Hàm số có 1 cực trị.
Câu 38: Hỏi hàm số
42
31y x x= − −
có tất cả bao nhiêu điểm cực trị?
A.
1
. B.
3
. C. 2. D. 4.
Lời giải
Chọn B
Ta có đây là hàm bc bốn trùng phương mà
1.( 3) 0ab = −
nên hàm số có ba điểm cực trị.
Câu 39: Hàm số
32
3 9 1y x x x= − − + −
có giá trị cực đại và giá trị cực tiểu ln lượt là M, m. Khi đó kết quả
nào sau đây đúng
A.
4Mm−=
. B.
35Mm−=
. C.
2Mm+ = −
. D.
70Mm+=
.
Lời giải
Chọn D
Ta có
2
3 6 9 6 6y x x y x
= − − + = − −
.
2
1
0 2 3 0
3
x
y x x
x
=
= + − =
=−
.
( )
1 12 1, 4 .
CD CD
y x y M
= − = = =
( )
3 12 3, 28 .
CT CT
y x y m
− = = − = − =
Vy
7 7.4 28 0Mm+ = − =
.
Câu 40: Hàm số nào sau đây có cực trị?
A.
1yx=−
. B.
2
23y x x= − +
. C.
3
89y x x= + +
. D.
21
31
x
y
x
−
=
+
.
Lời giải
Chọn B
Hàm số
1yx=−
có
( )
1
0, 1; ,
21
yx
x
= +
−
suy ra hàm số không có cực trị.
Hàm số
2
23y x x= − +
có
2 2; 0 1y x y x
= − = =
và
y
đổi dẫu khi đi qua
1x =
, suy ra hàm
số có cực trị tại điểm
1x =
.
Hàm số
3
89y x x= + +
có
2
3 8 0 ,y x x
= +
suy ra hàm số không có cực trị.
Hàm số
21
31
x
y
x
−
=
+
có
( )
2
5 1 1
0, ; ; ,
33
31
yx
x
= − − − +
+
suy ra hàm số không có
cực trị.
Câu 41: Hàm số nào sau đây có cực trị?

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
A.
1yx
. B.
2
23y x x
. C.
3
89y x x
. D.
21
31
x
y
x
.
Lời giải
Chọn B.
Xét đáp án A ta có
1
'0
21
y
x
1x
(không có cực trị).
Xét đáp án B ta có
' 2 2 0 1y x x
(
'y
đổi dấu qua
1x
).
Xét đáp án C ta có
2
' 3 8 0yx
x
(không có cực trị).
Xét đáp án D ta có
2
5
'0
31
y
x
1
3
x
(không có cực trị).
Câu 42: Đồ thị hàm số
32
y ax bx cx d= + + +
có hai điểm cực trị
( ) ( )
1; 7 , 2; 8AB−−
. Tính
( )
1y −
?
A.
( )
1 35y − = −
. B.
( )
1 11y −=
. C.
( )
1 11y − = −
. D.
( )
17y −=
.
Lời giải
Chọn A
Gọi đồ thị hàm số
32
y ax bx cx d= + + +
là
( )
C
.
Ta có:
2
32y ax bx c
= + +
. Vì
( ) ( )
1; 7 , 2; 8AB−−
là hai điểm cực trị của đồ thị hàm số
32
y ax bx cx d= + + +
nên ta có:
( )
( )
( )
( )
32
2
32
2
7 .1 .1 .1
2
0
0 3 .1 2 .1 c 9
12
8 .2 .2 .2
12
0 3 .2 2 .2 c
0
A
B
AC
a b c d
a
yx
a b b
c
BC
a b c d
d
ab
yx
− = + + +
=
=
= + + = −
=
− = + + +
=−
= + +
=
Vy
32
2 9 12 12y x x x= − + −
, do dó
( )
1 35y − = −
.
Câu 43: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số
32
1
3 5 1
3
y x x x
A. Có hệ số góc bằng -1.
B. song song với trục hoành.
C. song song với đường thẳng
1.x
D. Có hệ số góc dương.
Lời giải
Chọn B
2
65y x x
1
0
5
x
y
x
26yx
1 4 0y
hàm số đạt cực đại tại
1x
5 4 0y
hàm số đạt cực tiểu tại
5x
;
28
3
ct
y

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
50y
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số:
28
3
y
.
Tiếp tuyến song song với trục hoành.
Câu 44: Cho hàm số
32
2 5 4 2021y x x x= − + −
. Gọi
1
x
,
2
x
ln lượt là hoành độ hai điểm cực đại và cực tiểu
của hàm số. Kết lun nào sau đây đúng?
A.
12
1
3
xx−=
. B.
21
2
3
xx−=
. C.
21
1
2
3
xx−=
. D.
12
1
2
3
xx−=
.
Lời giải
Chọn D
Tp xác định
D =
.
Đạo hàm
2
6 10 4y x x
= − +
,
1
0
2
3
x
y
x
=
=
=
.
12 10yx
=−
.
( )
1 1 0y
=
nên
2
1x =
là điểm cực tiểu của hàm số.
2
20
3
y
= −
nên
1
2
3
x =
là điểm cực đại của hàm số.
Suy ra
12
1
2
3
xx−=
.
Câu 45: Hàm số
42
31y x x= − −
có bao nhiêu điểm cực trị?
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn C
Ta có
3
46y x x
=−
.
3
0
0 4 6 0
6
2
x
y x x
x
=
= − =
=
Vy hàm số đã cho có
3
điểm cực trị.
Câu 46: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
2
' 2 ,f x x x x= −
. Số điểm cực trị của hàm số đã cho là
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn D
Ta có
( )
( )
2
0
0
'0
2
20
x
x
fx
x
x
=
=
=
=
−=
.
Vì
2x =
là nghiệm kép và
0x =
là nghiệm đơn nên
( )
'fx
chỉ đổi dấu khi đi qua điểm
0x =
. Suy
ra hàm số đã cho có đúng 1 điểm cực trị.
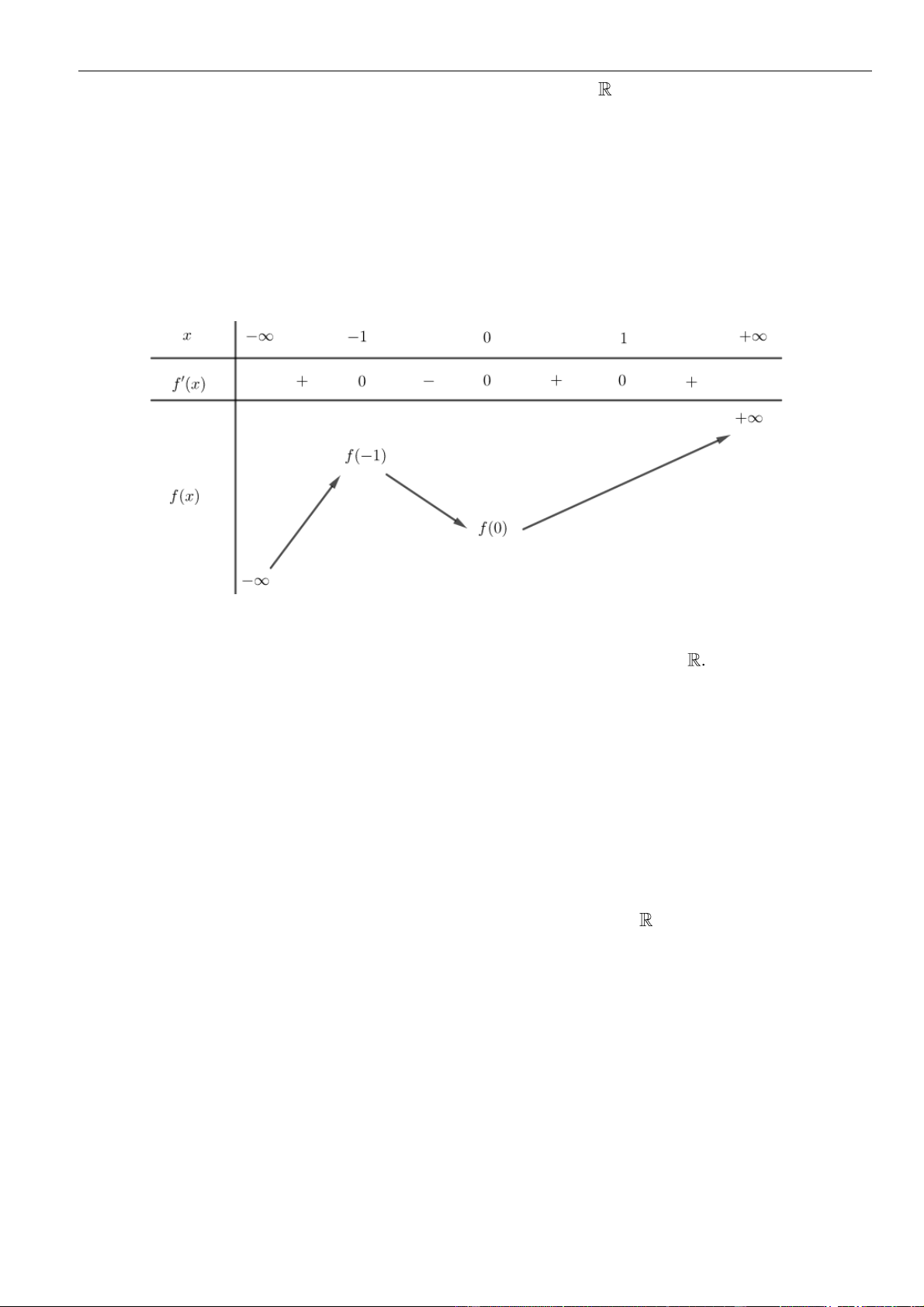
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Câu 47: Cho hàm số
( )
y f x=
có
( ) ( ) ( )
2020
2021
1 1 ,f x x x x x
= − +
. Hàm số đã cho có bao nhiêu điểm
cực trị?
A. 3. B. 0. C. 2. D. 1.
Lời giải
Chọn C
Cho
( ) ( ) ( )
2020
2021
0 1 1 0f x x x x
= − + =
0
1
1
x
x
x
=
=
=−
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có hàm số
( )
y f x=
có hai điểm cực trị.
Câu 48: Cho hàm số
( )
=y f x
có đạo hàm
( ) ( )( )
2
' 1 4= + −f x x x x
với mọi
.x
Hàm số có mấy điểm
cực trị?
A.
4.
B.
3.
C.
1.
D.
2.
Lời giải
Chọn D
Ta có:
( )
0
' 0 1
4
=
= = −
=
x
f x x
x
, trong đó
4=x
là nghiệm bội chẵn. Vy hàm số có
2
điểm cực trị
là
0=x
và
1=−x
.
Câu 49: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
2
3
( ) 2 1 ,f x x x x x
= − −
. Số điểm cực tiểu của hàm số
đã cho là
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn D
Ta có
2
( ) 0 1
0
x
f x x
x
=
= =
=
Bảng biến thiên

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Dựa vào bảng biến thiên, suy ra hàm số có một điểm cực tiểu.
Câu 50: Số điểm cực trị của hàm số
3 2 5
( ) ( 2) ( 3) ( 2)f x x x x= + − −
là
A.
2
. B.
3
. C.
1
. D.
6
.
Lời giải
Chọn B
Ta có
2 2 5 3 5 3 2 4
'( ) 3( 2) ( 3) ( 2) 2( 2) ( 3)( 2) 5( 2) ( 3) ( 2)f x x x x x x x x x x= + − − + + − − + + − −
24
'( ) [( 2) ( 3)( 2) ].[3( 3)( 2) 2( 2)( 2) 5( 2)( 3)]f x x x x x x x x x x = + − − − − + + − + + −
2 4 2 2 2
'( ) [( 2) ( 3)( 2) ].[3( 5 6) 2( 4) 5( 6)]f x x x x x x x x x = + − − − + + − + − −
2 4 2 2 2
'( ) [( 2) ( 3)( 2) ].(3 15 18 2 8 5 5 30)f x x x x x x x x x = + − − − + + − + − −
2 4 2
'( ) [( 2) ( 3)( 2) ].(10 20 20)f x x x x x x = + − − − −
.
Khi đó
2 4 2
'( ) 0 [( 2) ( 3)( 2) ].(10 20 20) 0 (*)f x x x x x x= + − − − − =
Phương trình
(*)
có
3
nghiệm bội lẻ là
3; 1 3xx= =
.
Vy hàm số ban đu có
3
điểm cực trị.
Câu 51: Cho hàm số
( )
y f x=
liên tục trên và có
( ) ( )( )
5
2
12f x x x x
= − +
. Số điểm cực trị của hàm
số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn C
Ta có
( )
0
01
2
x
f x x
x
=
= =
=−
.
Nhn xét
0x =
là nghiệm kép,
1x =
là nghiệm đơn và
2x =−
là nghiệm bội lẻ. Vy hàm số đã cho
có
2
điểm cực trị.
Câu 52: Cho hàm số
( )
y f x=
xác định và liên tục trên và có đạo hàm
( ) ( ) ( ) ( )
2 3 4
' 1 2 3f x x x x x= − − −
. Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn C
Ta có
( )
0
1
'0
2
3
x
x
fx
x
x
=
=
=
=
=
trong đó
1; 3xx==
là nghiệm bội chẵn.
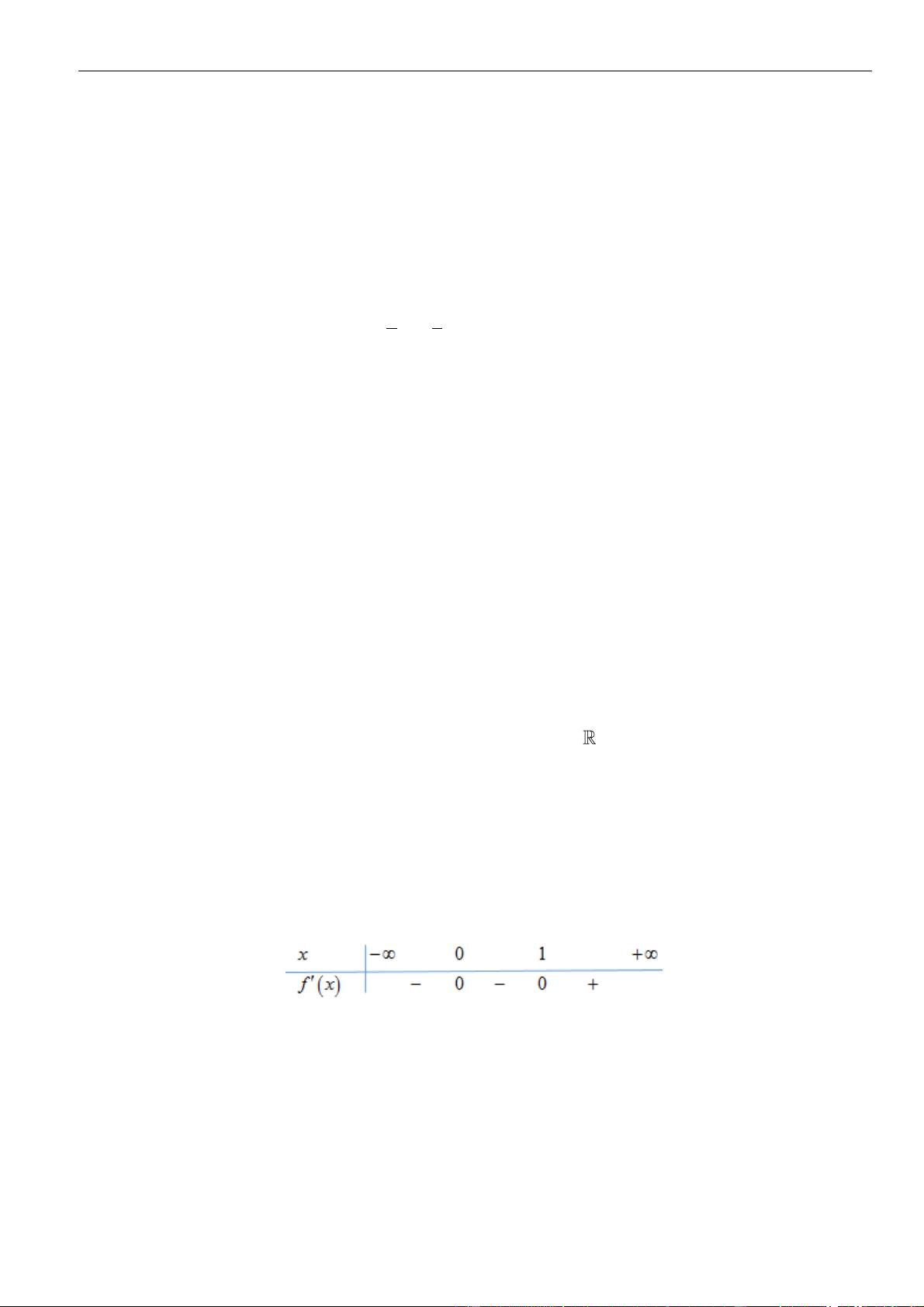
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Vy hàm số có 2 điểm cực trị.
Câu 53: Hàm số nào sau đây không có cực trị
A.
2
45y x x= + +
. B.
42
4 2.y x x= + +
.
C.
32
2 3 1y x x x= − + +
. D.
32
3 2 3.y x x x= + − +
Lời giải
Chọn C
Xét hàm số
32
2 3 1y x x x= − + +
Ta có
2
2
25
' 3 4 3 3 0,
33
y x x x x R
= − + = − +
Hàm số đã cho không có cực trị.
Câu 54: Cho hàm số nào
( )
y f x=
có
( ) ( ) ( )( )
3
2
1 3 5f x x x x x
= − − −
. Số điểm cực trị của đồ thị hàm số
là
A.
4
. B.
2
. C.
1
.
D.
3
.
Lời giải
Chọn D
( ) ( ) ( )( )
3
2
0
1
0 1 3 5 0
3
5
x
x
f x x x x x
x
x
=
=
= − − − =
=
=
.
Do
2
0x
tại
0x =
hàm số
( )
fx
không đổi dấu, tại
1; 3; 5x x x= = =
hàm số
( )
fx
đổi dấu nên
số điểm cực trị của đồ thị hàm số là 3.
Câu 55: Cho hàm số
( )
y f x=
thỏa mãn
( ) ( )
2
1;f x x x x
= −
. Mệnh đề nào sau đây là mệnh đề
đúng?
A.
( )
fx
đạt cực tiểu tại
1x =
. B.
( )
fx
không có cực trị.
C.
( )
fx
đạt cực tiểu tại
0x =
. D.
( )
fx
có hai điểm cực trị.
Lời giải
Chọn A
Từ biểu thc của
( )
fx
ta có bảng xét dấu như sau
Dễ thấy hàm số đạt cực tiểu tại
1x =
nên A đúng, C sai.
Hàm số có đúng
1
điểm cực trị nên B sai, D sai.
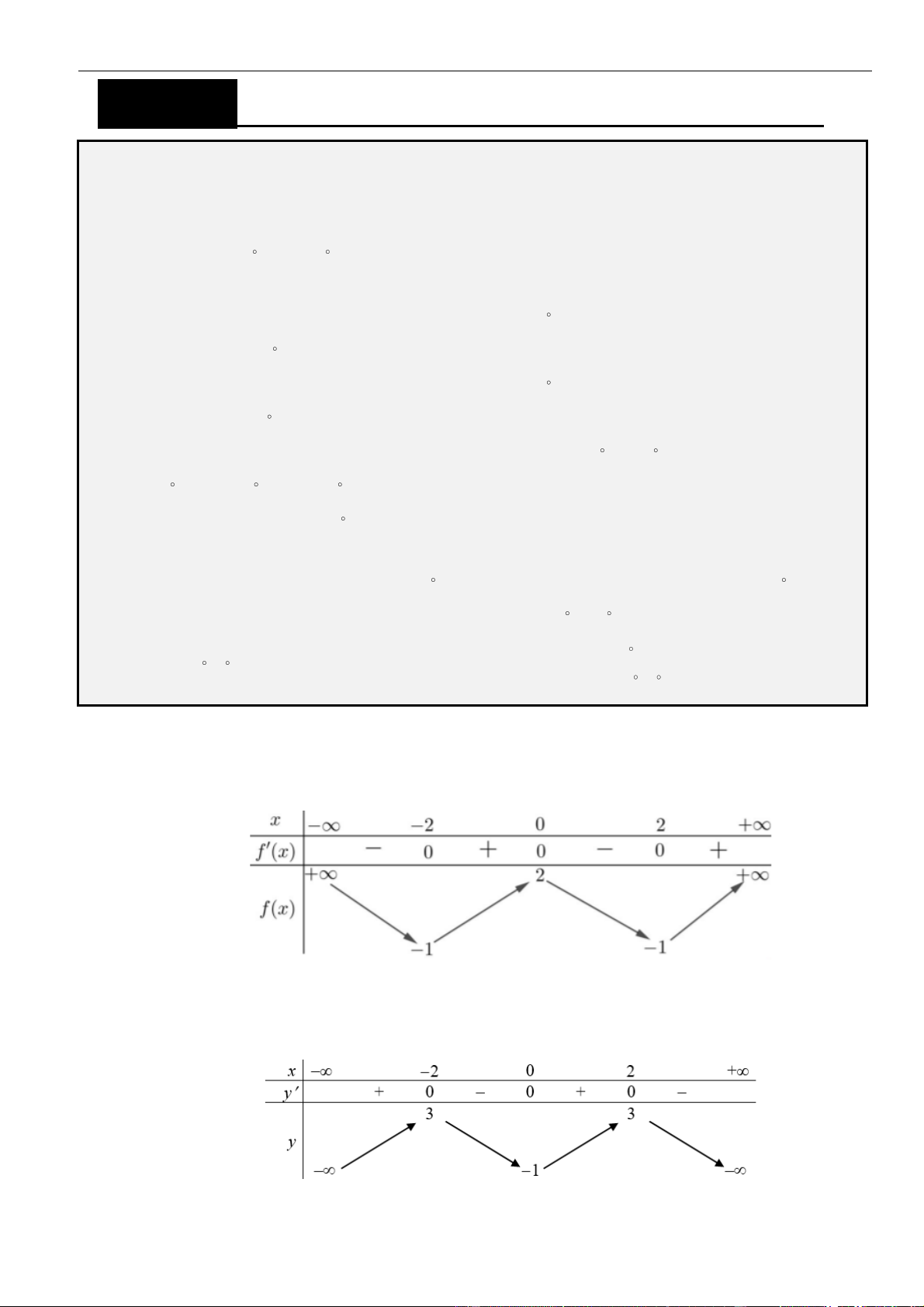
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
A.
= 0x
. B.
= 2x
. C.
=−1x
. D.
=−2x
Câu 2: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau:
Giá trị cực đại của hàm số đã cho bằng
A.
1−
. B.
2
. C.
3
. D.
2−
.
Tìm cực trị cho bởi đồ thị hoặc bảng biến thiên
DẠNG 2
Phương pháp:
❖ Định lí cực trị
• Điều kiện cần (định lí 1): Nếu hàm số
()y f x=
có đạo hàm trên khoảng
( ; )ab
và đạt cực đại
(hoặc cực tiểu) tại
x
thì
( ) 0.fx
=
• Điều kiện đủ (định lí 2):
Nếu
()fx
đi du t âm sang dương khi
x
đi qua điểm
x
(theo chiu tăng) thì hàm số
()y f x=
đạt cực tiu tại điểm
.x
Nếu
()fx
đi du t dương sang âm khi
x
đi qua điểm
x
(theo chiu tăng) thì hàm số
()y f x=
đạt cực đi tại điểm
.x
• Định lí 3: Giả s
()y f x=
có đạo hàm cp
2
trong khoảng
( ; ),x h x h−+
với
0.h
Khi đó:
Nếu
( ) 0, ( ) 0y x y x
=
thì
x
là điểm cực tiểu.
Nếu
( ) 0, ( ) 0
oo
y x y x
=
thì
x
là điểm cực đại.
❖ Lưu ý:
• Điểm cực đại (cực tiểu) của hàm số là
,x
giá trị cực đi (cực tiu) của hàm số là
()fx
(hay
y
CĐ
hoặc
CT
).y
Điểm cực đại của đồ thị hàm số là
( ; ( )).M x f x
• Nếu
( ; )M x y
là điểm cực trị của đồ thị hàm số
( ) 0
()
( ; ) ( )
yx
y f x
M x y y f x
=
=
=
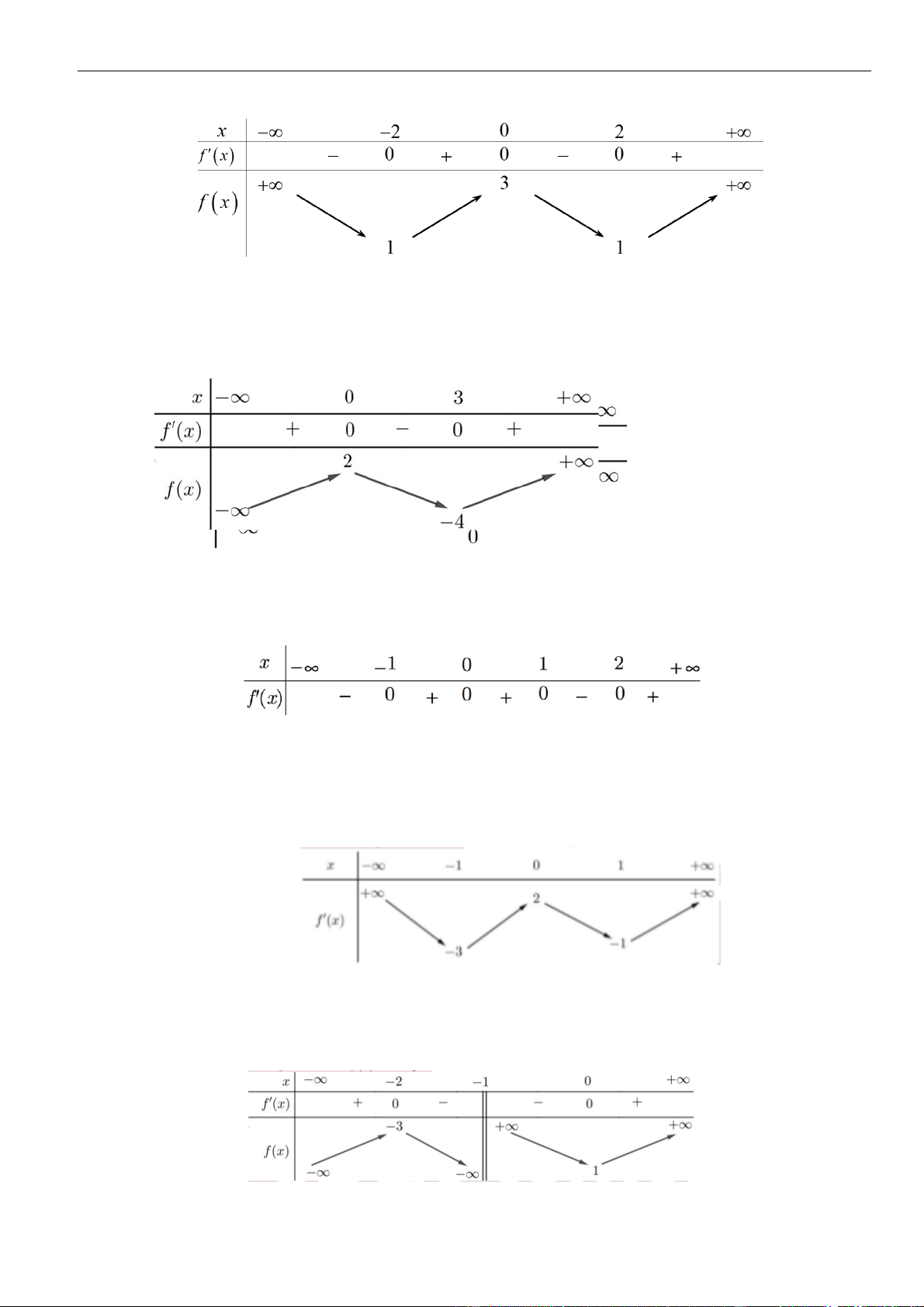
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 3: Cho hàm số
( )
fx
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 4: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
3
. C.
0
. D.
4−
Câu 5: Cho hàm số
( )
fx
có bảng xét du đạo hàm như hình vẽ bên.
Mệnh đ nào dưới đây đúng?
A. Hàm số đạt cực đại tại
0x =
. B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực đại tại
1x =
. D. Hàm số đạt cực đại tại
2x =
.
Câu 6: Cho hàm số
( )
fx
có bảng biến thiên của hàm số
( )
'fx
như hình vẽ.
Số điểm cực trị của hàm số đã cho là
A.
3.
B.
2.
C.
1.
D.
4.
Câu 7: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng:
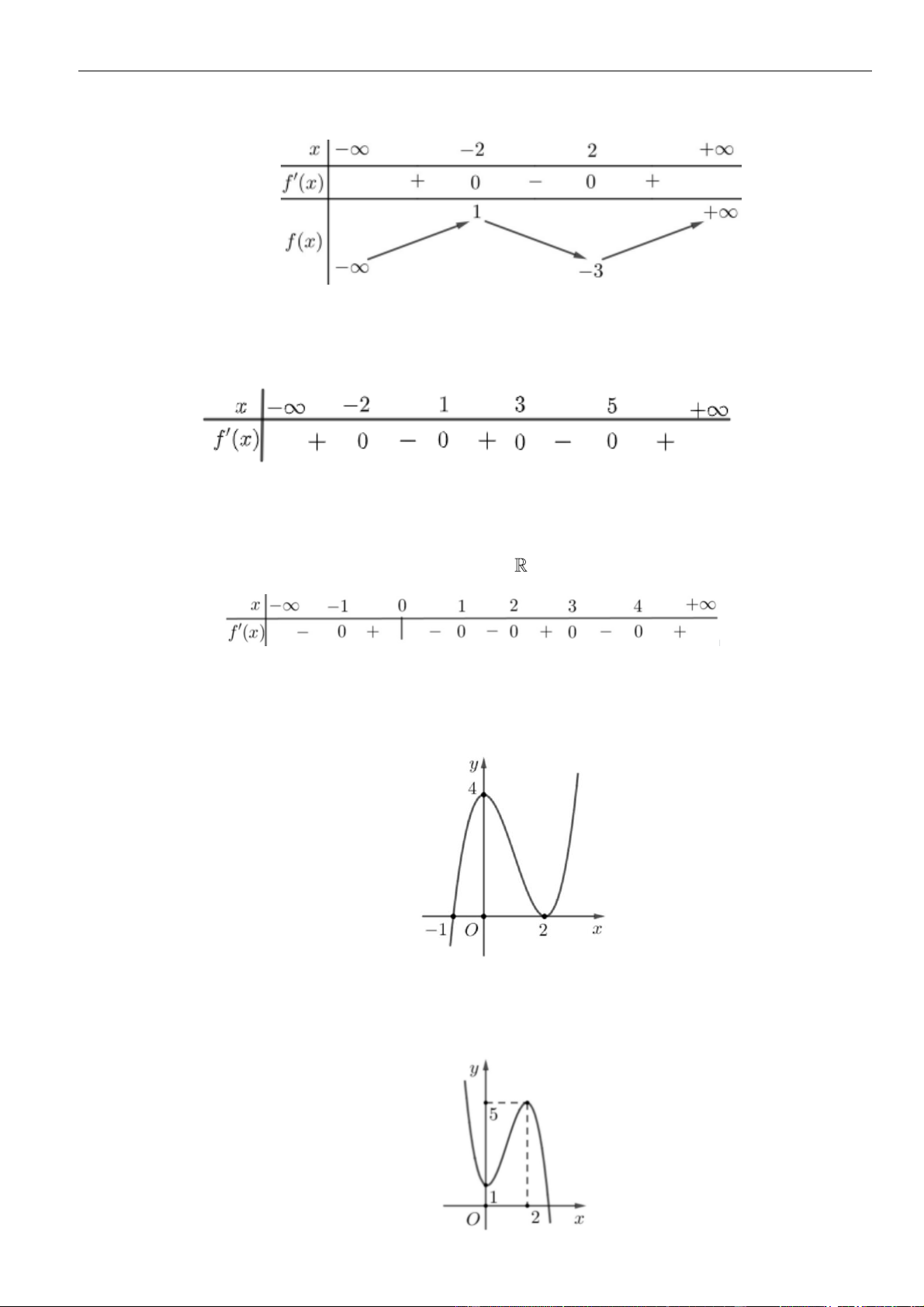
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
2−
. B.
1
. C.
0
. D.
3−
.
Câu 8: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là
A.
3x =−
. B.
1x =
. C.
2x =
. D.
2x =−
.
Câu 9: Cho hàm số
( )
fx
có bảng xét du của đạo hàm
( )
'fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
4
. B.
1
. C.
2
. D.
3
Câu 10: Cho hàm số
( )
y f x=
xác định và liên tục trên có bảng xét du như sau:
Số điểm cực trị của hàm số đã cho là:
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 11: Cho hàm số
( )
fx
có đồ thị như hình vẽ:
Điểm cực tiểu của hàm số đã cho là
A.
1x =−
. B.
0x =
. C.
2x =
. D.
4x =
.
Câu 12: Cho hàm số
( )
fx
có đồ thị như hình vẽ sau:
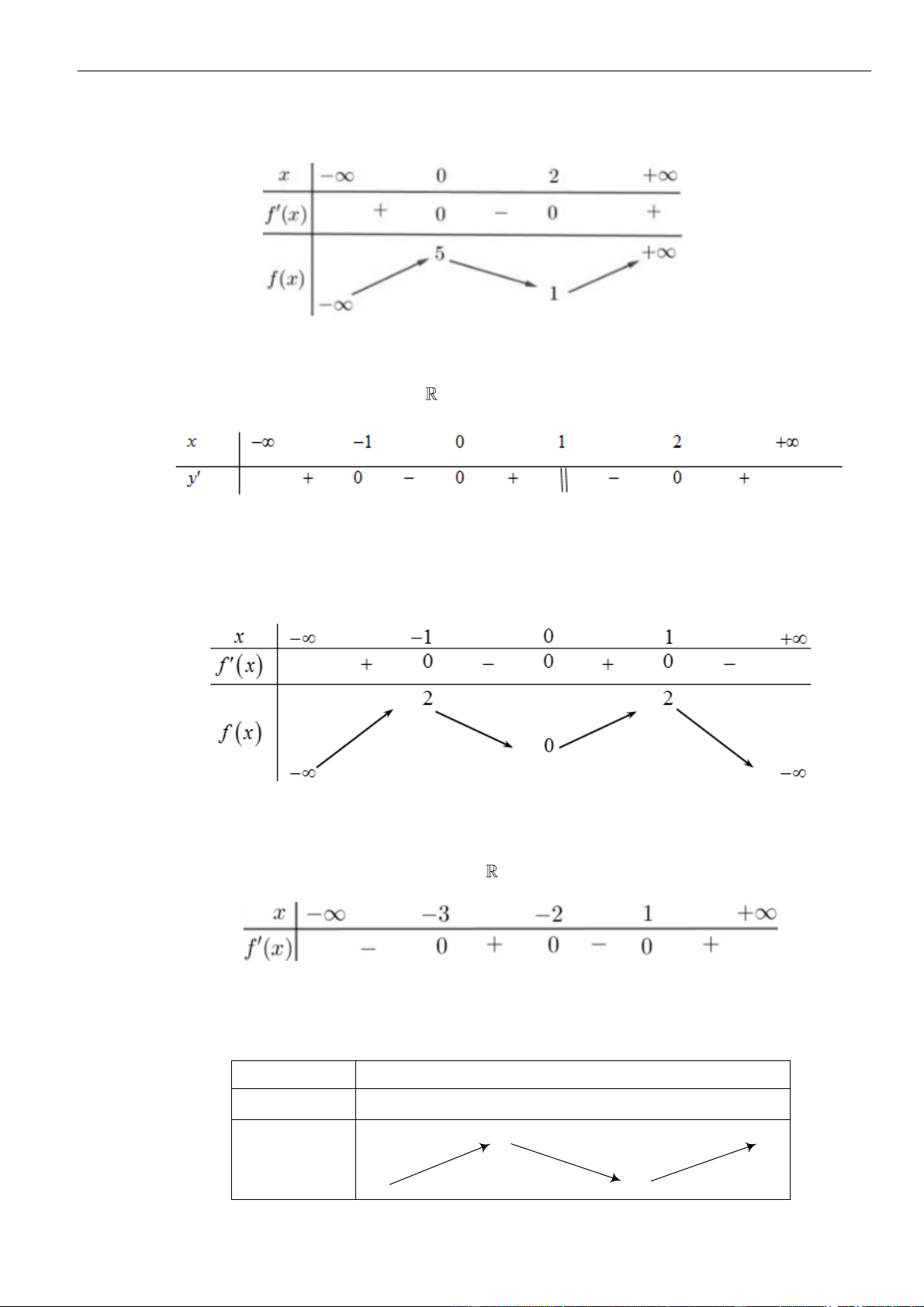
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Hàm số đạt cực tiểu tại điểm nào dưới đây?
A.
1x =
. B.
0x =
. C.
5x =
. D.
2x =
.
Câu 13: Cho hàm
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
A.
1x =
. B.
2x =
. C.
0x =
. D.
5x =
.
Câu 14: Cho hàm số
( )
fx
và xác định trên và có bảng xét du của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 15: Cho hàm số
( )
fx
có bảng biến thiên như sau
Điểm cực đại của đồ thị hàm số đã cho là
A.
1x =−
. B.
( )
1;2−
. C.
( )
0;0
. D.
0x =
.
Câu 16: Cho hàm số
( )
fx
có đạo hàm liên tục trên và có bảng xét du của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 17: Cho hàm số
( )
fx
có bảng biến thiên như sau
x
−
+
+
−
y
y
−
0
0
+
+
3−
1−
0
4−
Giá trị cực tiểu của hàm số đã cho bằng
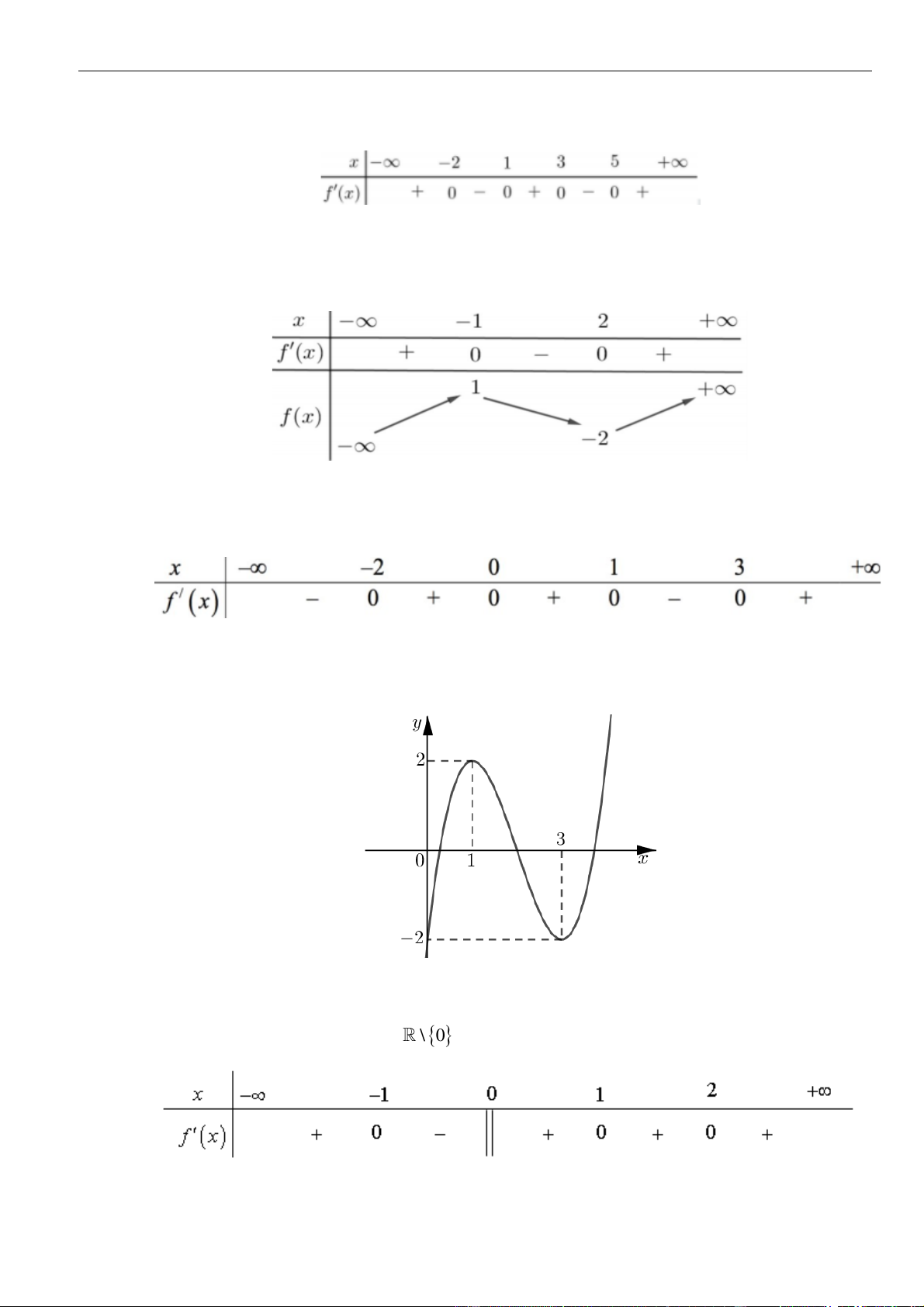
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
1−
. B.
0
. C.
4−
. D.
3−
.
Câu 18: Cho hàm số
( )
fx
có bảng xét du của đạo hàm
( )
fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 19: Cho hàm số bậc ba
( )
fx
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
2−
. C.
1
. D.
1−
.
Câu 20: Cho hàm số
( )
fx
có bảng xét du của đạo hàm như sau:
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
A.
0x =
. B.
1x =
. C.
3x =
. D.
2x =−
.
Câu 21: Cho hàm số bậc ba
( )
fx
có đồ thị như hình vẽ bên
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
3
. C.
1
. D.
2−
.
Câu 22: Cho hàm số
( )
fx
xác định trên
\0
và có bảng xét du đạo hàm
( )
fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
2
. B.
4
. C.
1
. D.
3
.
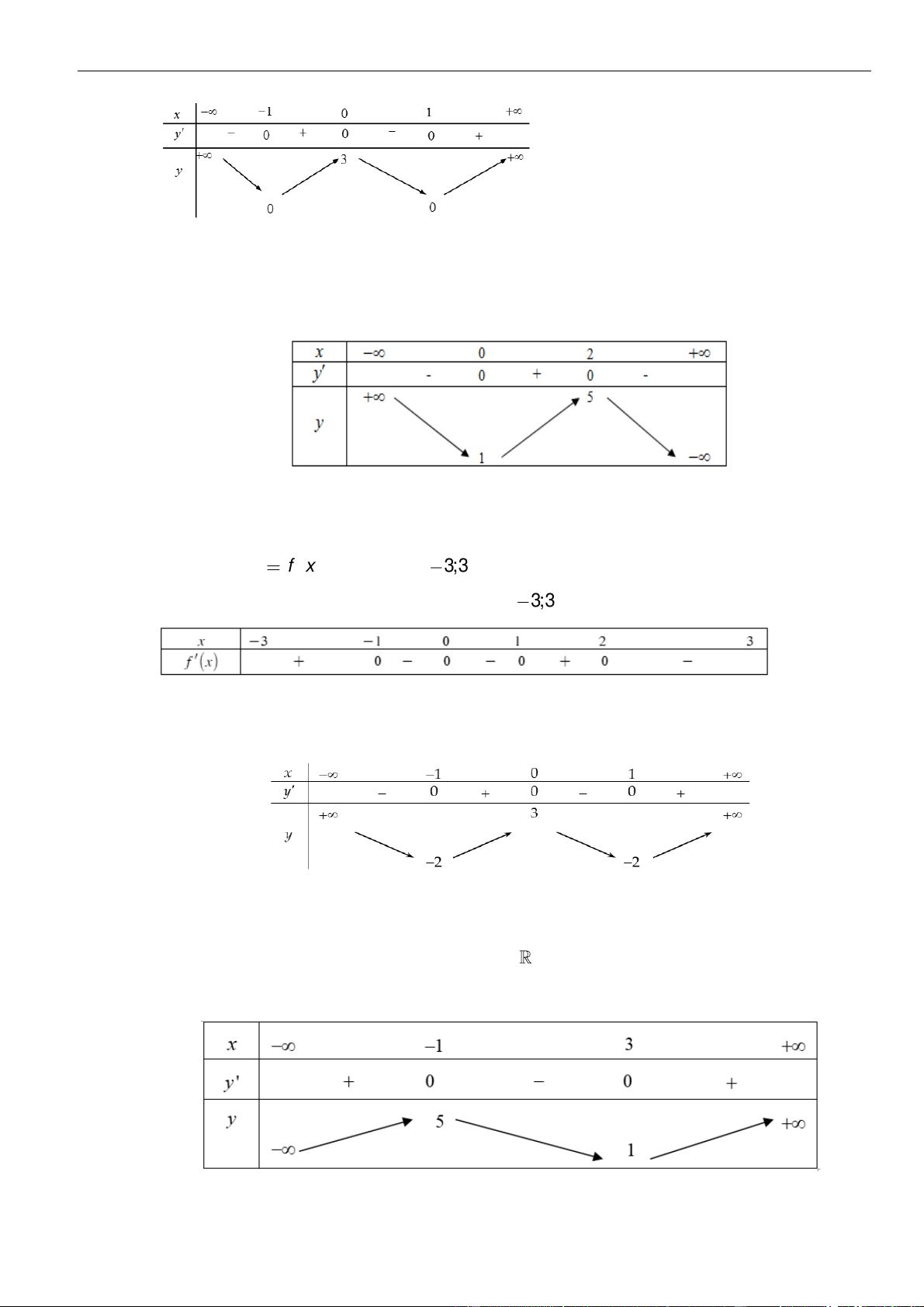
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 23: Cho hàm số
()y f x=
có bảng biến thiên như sau
Khẳng định nào sau đây đúng?
A. Điểm cực tiểu của hàm số là 0. B. Điểm cực tiểu của đồ thị hàm số là 1.
C. Điểm cực tiểu của hàm số là – 1. D. Điểm cực đại của hàm số là 3.
Câu 24: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số đạt cực tiểu tại điểm
A.
1x =
. B.
5x =
. C.
0x =
. D.
2x =
.
Câu 25: Cho hàm số
y f x
liên tục trên
3;3
và có bảng xét dy đạo hàm như hình bên. Hàm số
đã cho có bao nhiêu điểm cực trị thuộc khoảng
3;3
.
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 26: Hàm số
( )
y f x=
có bảng biến thiên như hình vẽ bên dưới
Số điểm cực trị của đồ thị hàm số là
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 27: Cho hàm số
( )
y f x=
xác định và liên tục trên , có bảng biến thiên như hình vẽ. Khi đó giá
trị cực tiểu của hàm số
( )
y f x=
bằng
A.
1−
. B.
3
. C.
1
. D.
5
.
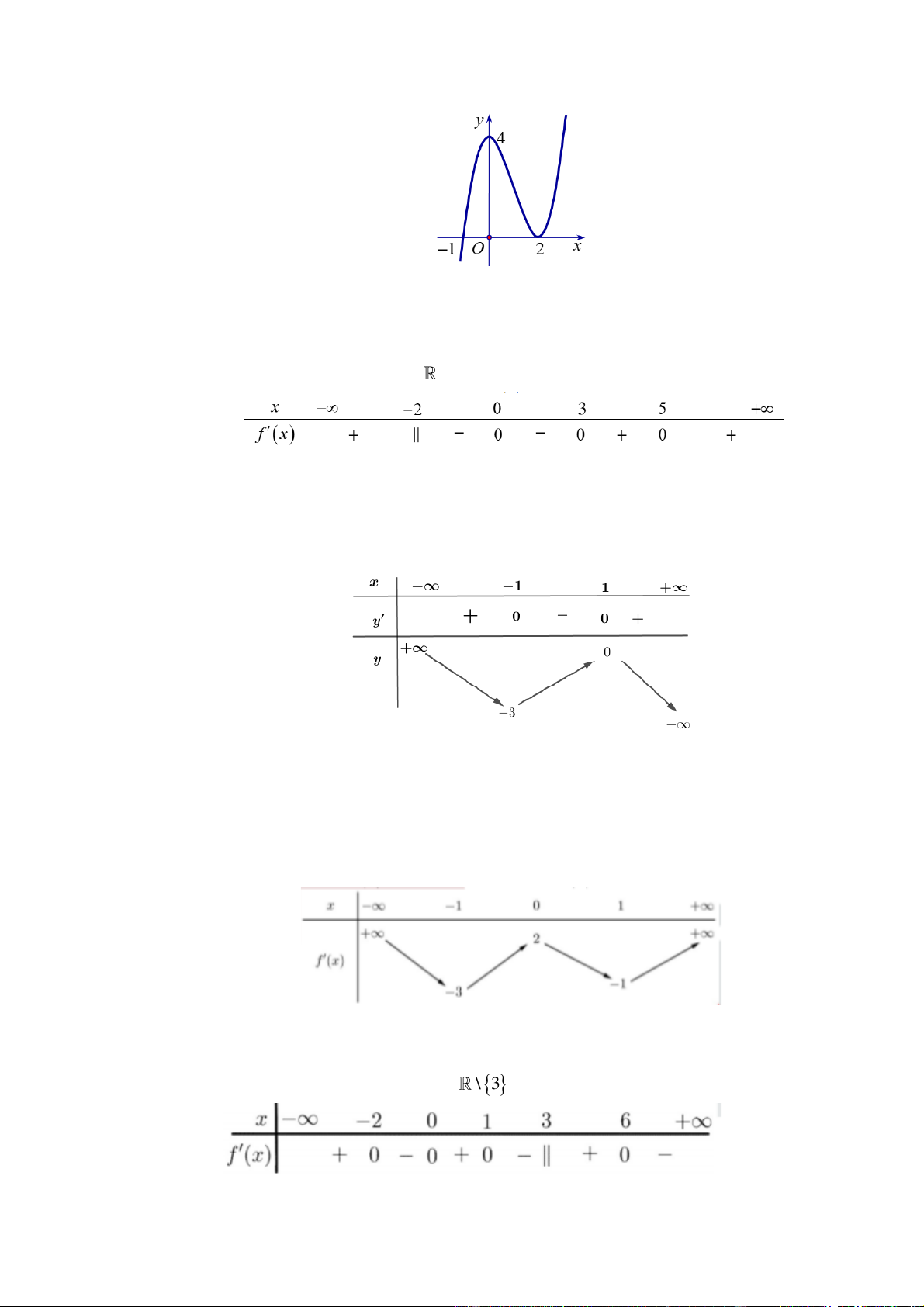
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Câu 28: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới.
Mệnh đ nào sau đây đúng?
A. Hàm số đạt cực đại tại
2x =
. B. Hàm số đạt cực tiểu tại
2x =
.
C. Hàm số đạt cực đại tại
4x =
. D. Hàm số đạt cực tiểu tại
0x =
.
Câu 29: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét du của
( )
fx
như sau:
Số điểm cực đại của hàm số
( )
y f x=
là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 30: Cho hàm số
( )
y f x=
có bảng biến thiên như sau.
Tìm giá trị cực đại
CD
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
1
CD
y =
và
0
CT
y =
. B.
CD
y =−
và
1
CT
y =−
.
C.
1
CD
y =−
và
1
CT
y =
. D.
0
CD
y =
và
3
CT
y =−
.
Câu 31: Cho hàm số
fx
có bảng biến thiên của hàm số
'fx
như hình vẽ.
Số điểm cực trị của hàm số đã cho là
A.
3.
B.
2.
C.
1.
D.
4.
Câu 32: Cho hàm số
( )
fx
xác định trên khoảng
\3
và có bảng xét du của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
4
. C.
2
. D.
5
.
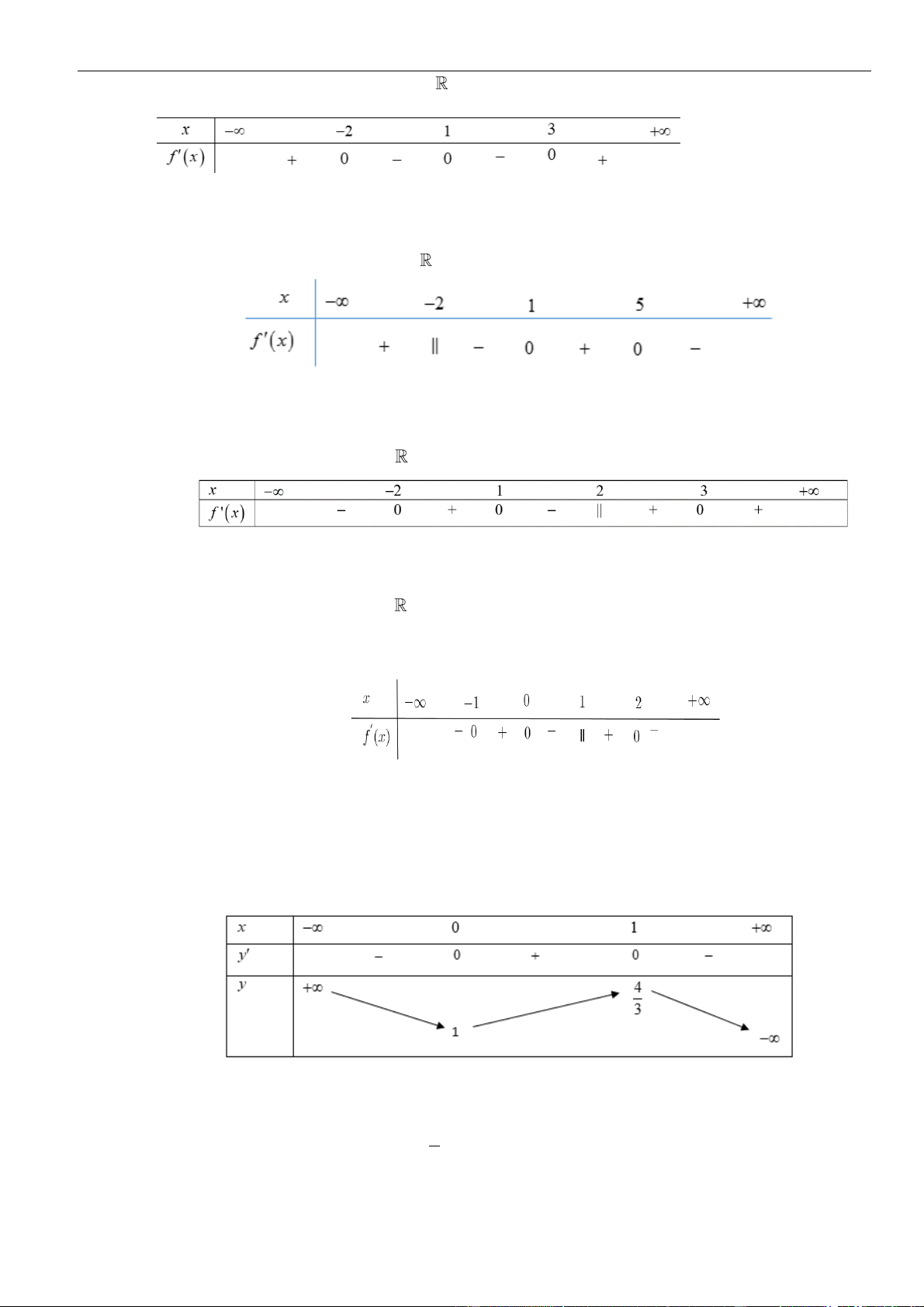
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Câu 33: ) Cho hàm số
( )
y f x=
liên tục trên có bảng xét du
( )
fx
như hình vẽ
Số điểm cực trị của hàm số
( )
y f x=
là
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 34: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét du của
( )
fx
như sau:
Số điểm cực đại của hàm số
( )
y f x=
là
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 35: Cho hàm số
( )
fx
liên tục trên và có bảng xét du của
( )
'fx
như sau:
Số điểm cực tiểu của hàm số đã cho là
A. 3. B. 2. C. 4. D. 1.
Câu 36: Cho hàm số
( )
fx
liên tục trên và có bảng xét du
( )
fx
như sau
Số điểm cực trị của
( )
fx
A.
3
. B.
4
C.
1
. D.
1
.
Câu 37: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Mệnh đ nào sau đây đúng?
A. Điểm cực đại của hàm số là
4
1; .
3
B
B. Điểm cực tiểu của đồ thị hàm số là
( )
0;1 .B
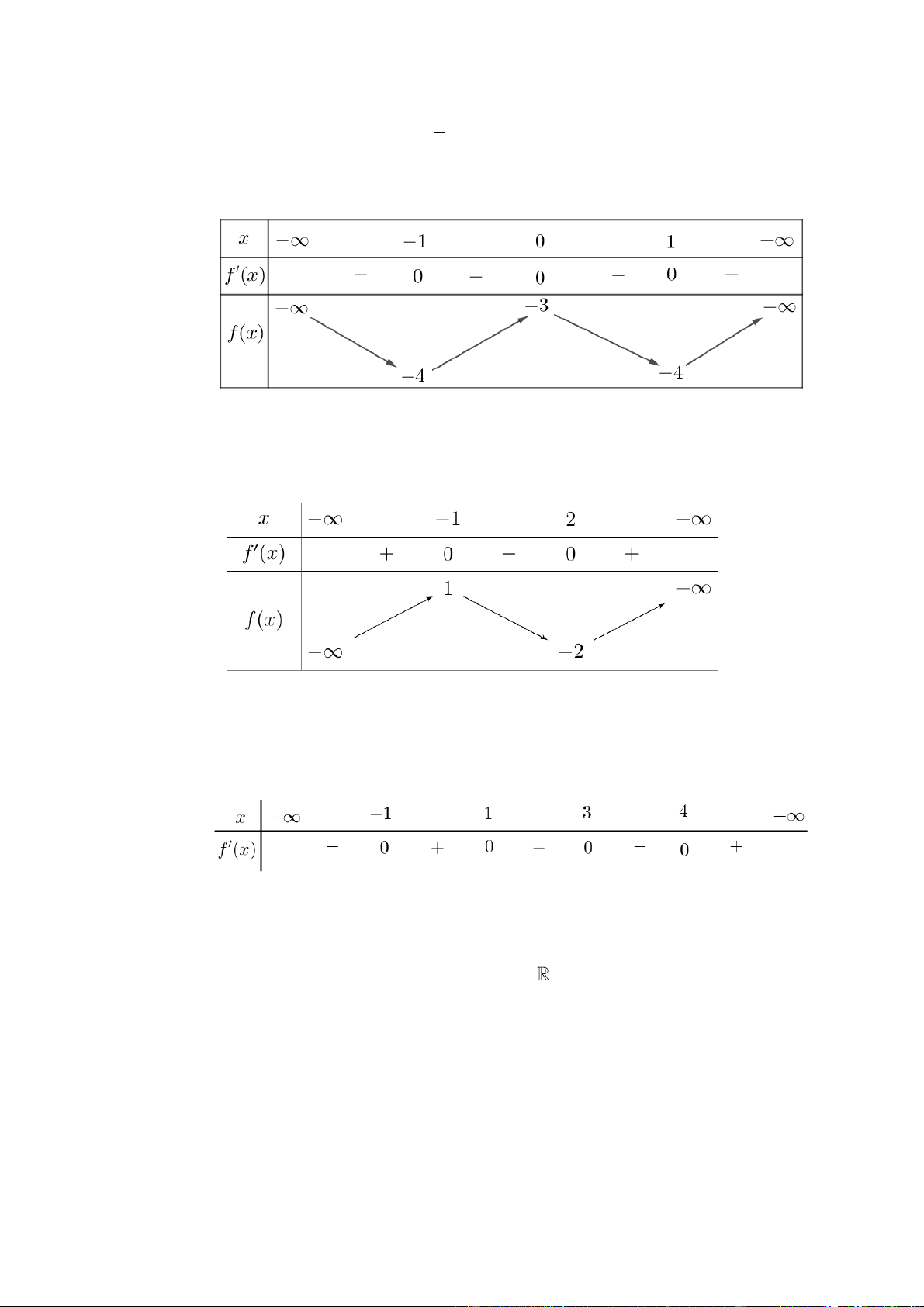
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
C. Điểm cực đại của đồ thị hàm số là
( )
0;1 .B
D. Điểm cực tiểu của hàm số là
4
1; .
3
B
Câu 38: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A.
1
. B.
0
. C.
3−
. D.
4−
.
Câu 39: Cho hàm số
()y f x=
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
2−
. C.
1
. D.
1−
.
Câu 40: Cho hàm số
( )
fx
có bảng xét du của đạo hàm
( )
fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực tiểu?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 41: Cho hàm số
( )
y f x=
liên tục và có đạo hàm trên , biết
( )
y f x
=
có đồ thị như hình bên.
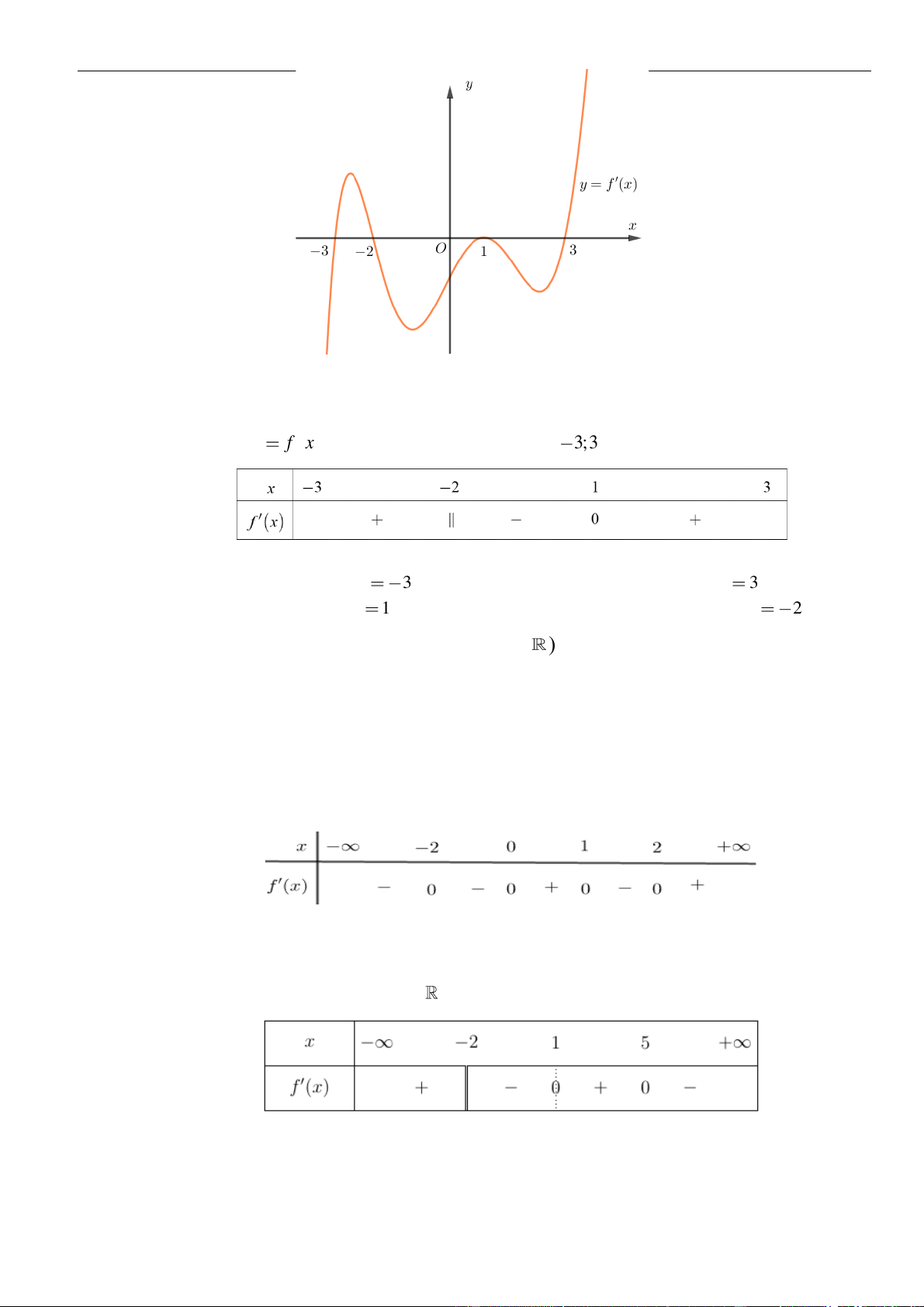
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Điểm cực đại của hàm số
( )
y f x=
đã cho là
A.
3x =
. B.
1x =
. C.
3x =−
. D.
2x =−
.
Câu 42: Cho hàm số
y f x
xác định và liên tục trên đoạn
3;3
có bảng xét du đạo hàm như sau:
Mệnh đ nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
3x
. B. Hàm số đạt cực tiểu tại
3x
.
C. Hàm số đạt cực đại tại
1x
. D. Hàm số đạt cực tiểu đại tại
2x
.
Câu 43: Cho hàm số
( )
32
, , ,y ax bx cx d a b c d= + + +
có đồ thị hàm số như hình vẽ. Mệnh đ
nào sau đây sai?
A. Giá trị cực đại của hàm số là
1−
.
B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực tiểu tại
1x =
.
D. Giá trị cực tiểu của hàm số là
0
.
Câu 44: Cho hàm số
( )
y f x=
có bảng xét du
( )
fx
như sau
Số điểm cực tiểu của hàm số
( )
y f x=
là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 45: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét du
( )
fx
như sau
Số điểm cực đại của hàm số
( )
fx
là
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 46: Cho hàm số
()fx
có bảng biến thiên như sau:
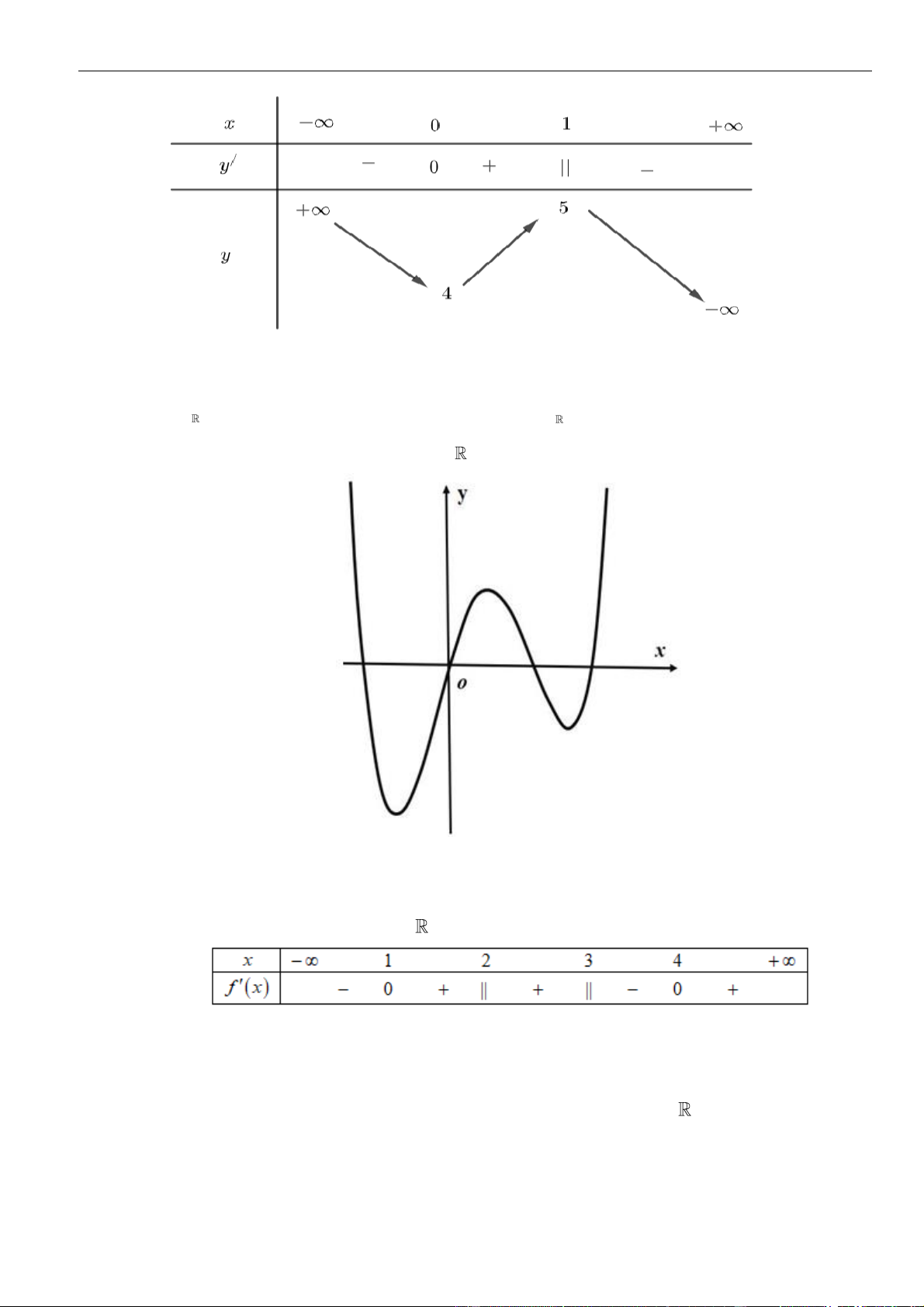
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Mệnh đ nào sau đây đúng
A.
min 4y =
. B.
=
§
15
C
y
C.
max 5y =
. D.
4
CT
y =
.
Câu 47: Cho hàm số
( )
y f x=
có đạo hàm trên và hàm số
( )
y f x
=
có đồ thị như hình bên
Tìm số điểm cực trị của hàm số
( )
y f x=
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 48: Cho hàm số
()y f x=
liên tục trên và có bảng xét du
()fx
như sau
Kết luận nào sau đây đúng?
A. Hàm số có 2 điểm cực đại. B. Hàm số có 4 điểm cực trị.
C. Hàm số có 2 điểm cực trị. D. Hàm số có 2 điểm cực tiu.
Câu 49: Cho hàm đa thức bậc năm
( )
y f x=
và đồ thị hàm số
( )
y f x
=
trên như hình vẽ. Mệnh đ
nào đúng?
A. Hàm số
( )
y f x=
có 2 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số
( )
y f x=
có 2 điểm cực đại và 2 điểm cực tiểu.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
C. Hàm số
( )
y f x=
có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số
( )
y f x=
có 1 điểm cực đại và 1 điểm cực tiểu.
Câu 50: Cho hàm số
( )
fx
liên tục trên và có bảng xét du của
( )
fx
như sau:
Số điểm cực đại của hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
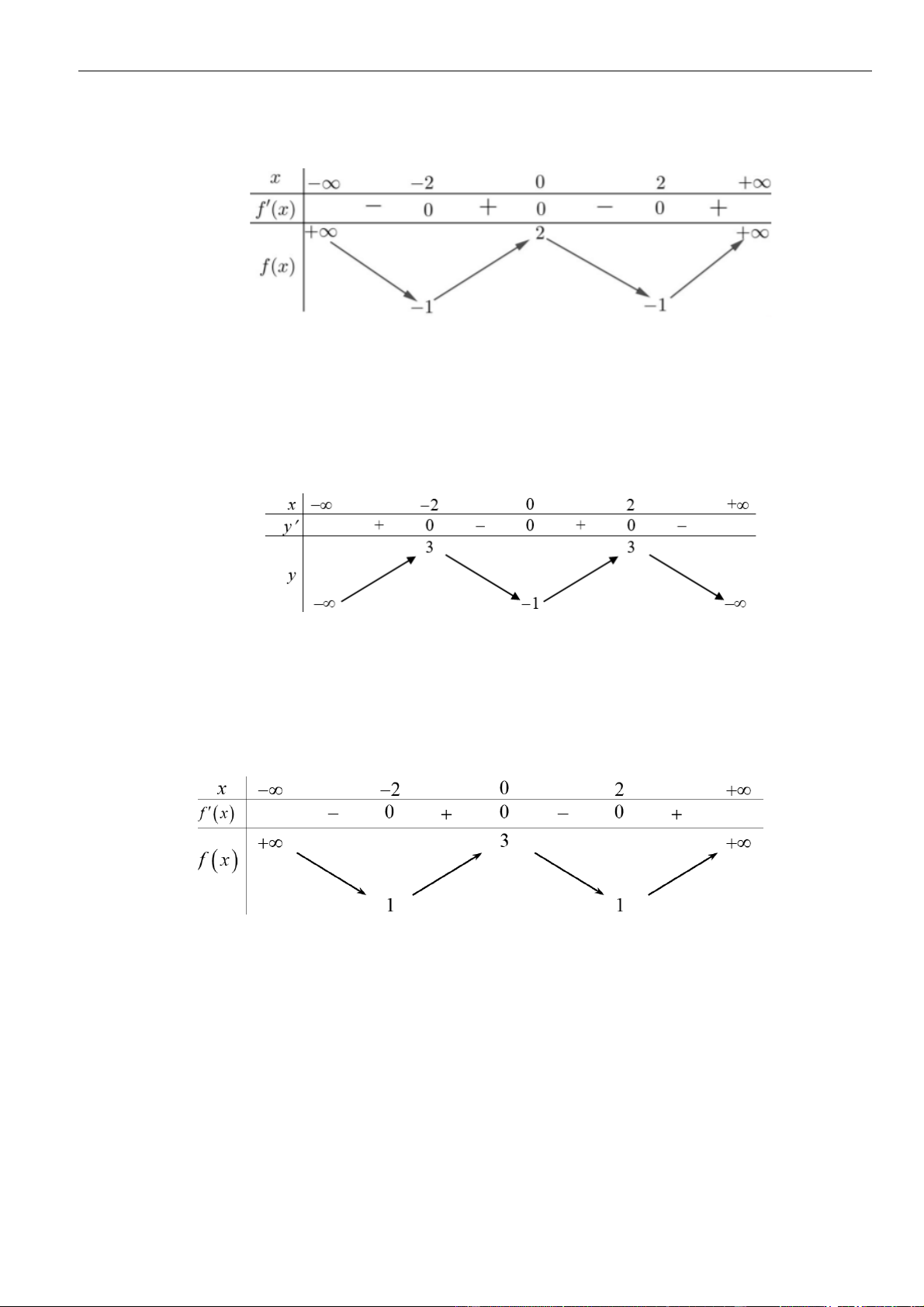
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
A.
= 0x
. B.
= 2x
. C.
=−1x
. D.
=−2x
Lời giải
Chọn A
T bảng biến thiên ta thy hàm số đạt cực đại tại
= 0x
.
Câu 2: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ sau:
Giá trị cực đại của hàm số đã cho bằng
A.
1−
. B.
2
. C.
3
. D.
2−
.
Lời giải
Chọn C
Câu 3: Cho hàm số
( )
fx
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B.
Câu 4: Cho hàm số
( )
fx
có bảng biến thiên như sau:
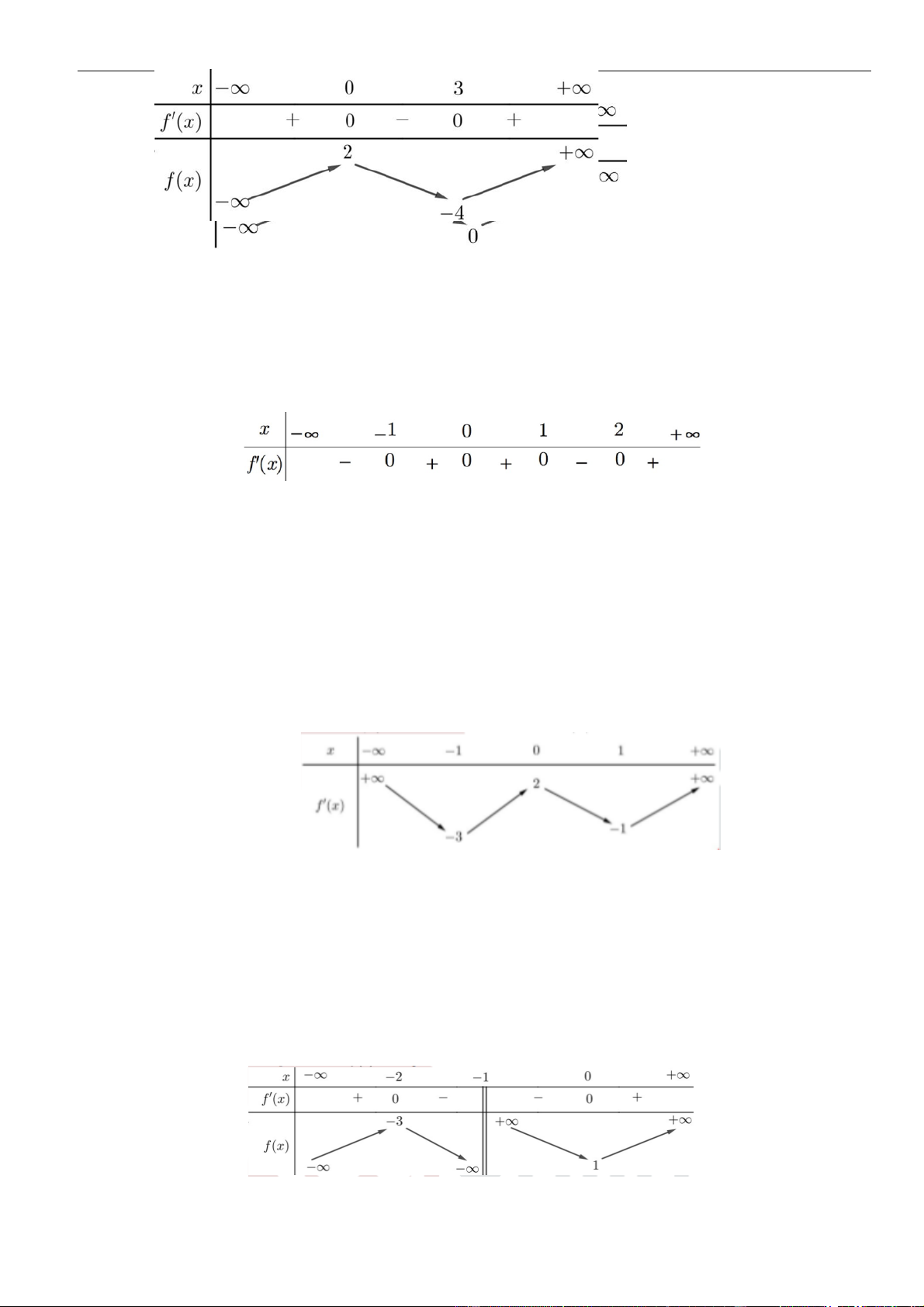
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
3
. C.
0
. D.
4−
Lời giải
Chọn D
T bảng biến thiên của hàm số ta thy hàm số đạt cực tiểu tại
3x =
, giá trị cực tiểu bằng
4−
.
Câu 5: Cho hàm số
( )
fx
có bảng xét du đạo hàm như hình vẽ bên.
Mệnh đ nào dưới đây đúng?
A. Hàm số đạt cực đại tại
0x =
. B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực đại tại
1x =
. D. Hàm số đạt cực đại tại
2x =
.
Lời giải
Chọn C
Hàm số
( )
fx
có
( )
'fx
đi du t
+
sang
−
khi
( )
'fx
đi qua điểm
1x =
.
Vậy hàm số
( )
fx
cực đại tại
1x =
.
Câu 6: Cho hàm số
( )
fx
có bảng biến thiên của hàm số
( )
'fx
như hình vẽ.
Số điểm cực trị của hàm số đã cho là
A.
3.
B.
2.
C.
1.
D.
4.
Lời giải
Chọn D
T bảng biến thiên của hàm số
( )
'fx
, ta thy rằng phương trình
( )
'0fx=
có 4 nghiệm bội lẻ.
Do đó, hàm số đã cho có 4 điểm cực trị.
Câu 7: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng:
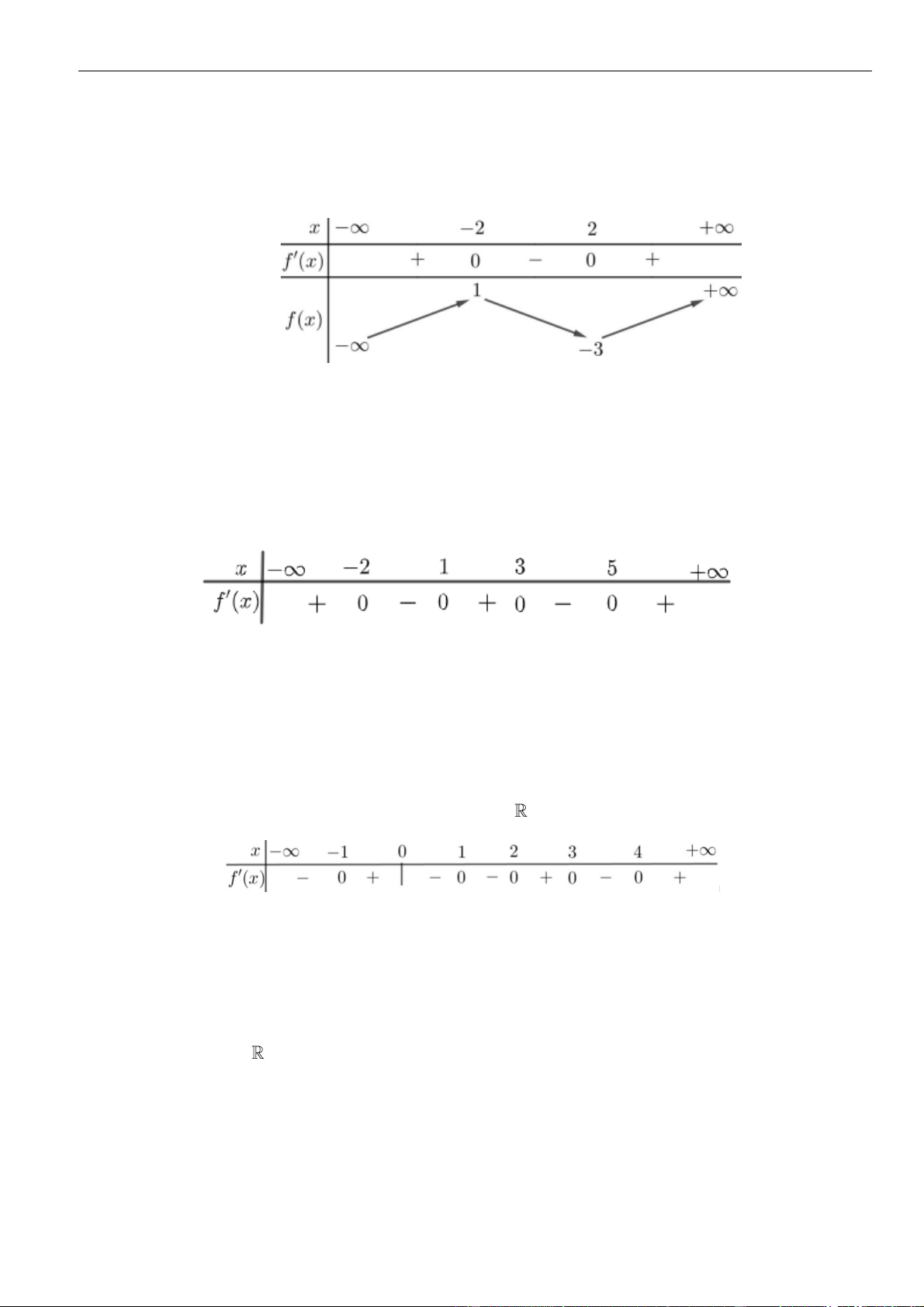
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
A.
2−
. B.
1
. C.
0
. D.
3−
.
Lời giải
Chọn B
Dựa vào BBT, hàm số đạt cực tiểu tại
0x =
, giá trị cực tiểu là
1y =
.
Câu 8: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là
A.
3x =−
. B.
1x =
. C.
2x =
. D.
2x =−
.
Lời giải
Chọn D
Hàm số đã cho đạt cực đại tại
2x =−
.
Câu 9: Cho hàm số
( )
fx
có bảng xét du của đạo hàm
( )
'fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
4
. B.
1
. C.
2
. D.
3
Lời giải
Chọn A
Dựa vào bảng xét du, ta có : Hàm số có 4 điểm cực trị
Câu 10: Cho hàm số
( )
y f x=
xác định và liên tục trên có bảng xét du như sau:
Số điểm cực trị của hàm số đã cho là:
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn B
Dựa vào bảng xét du của
( )
fx
, ta thy
( )
fx
đi du
4
lần và hàm số
( )
y f x=
xác định và
liên tục trên
( )
fx
có
4
điểm cực trị.
Câu 11: Cho hàm số
( )
fx
có đồ thị như hình vẽ:
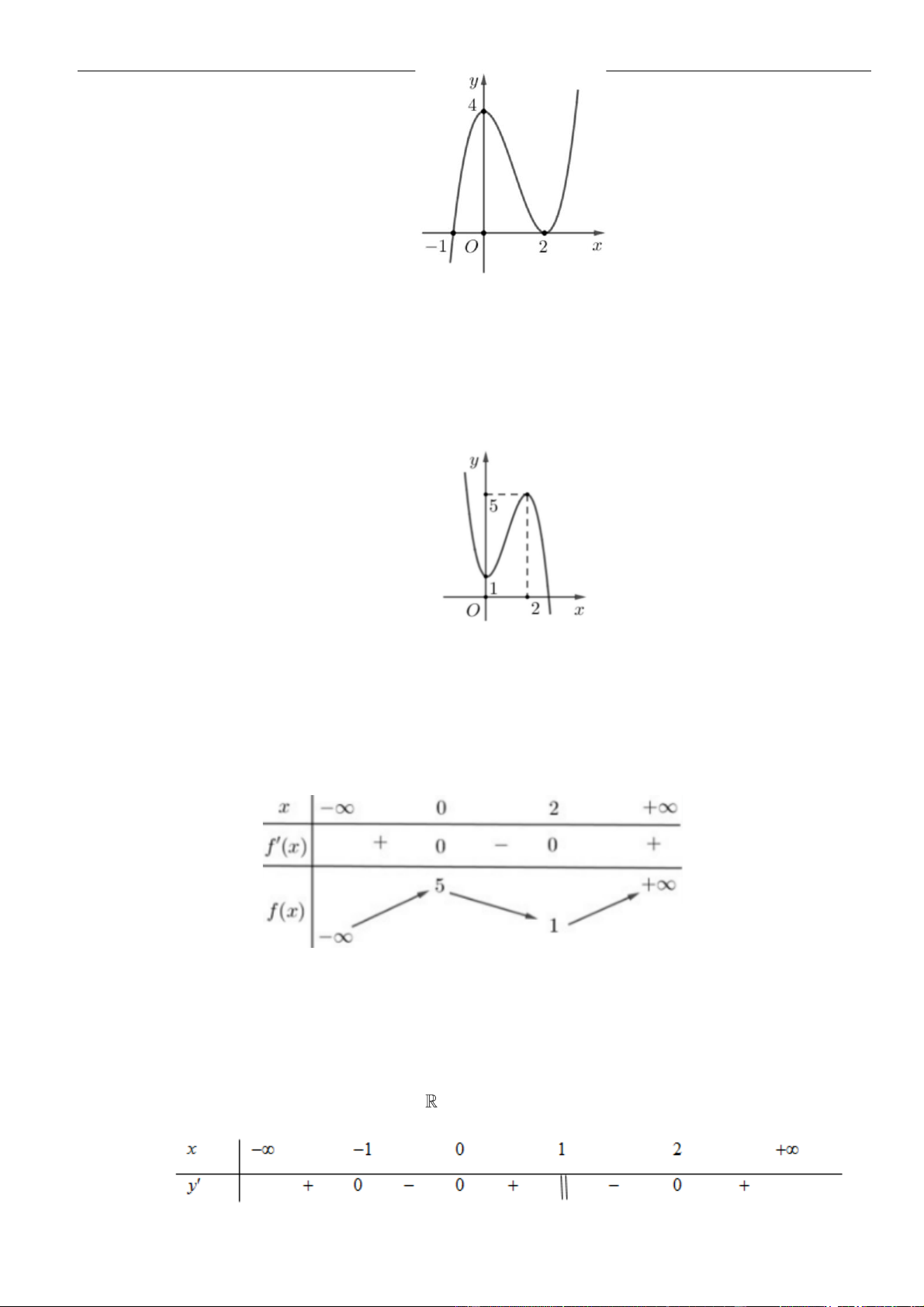
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Điểm cực tiểu của hàm số đã cho là
A.
1x =−
. B.
0x =
. C.
2x =
. D.
4x =
.
Lời giải
Chọn C
Nhìn đồ thị ta thy hàm số có điểm cực tiểu
2x =
.
Câu 12: Cho hàm số
( )
fx
có đồ thị như hình vẽ sau:
Hàm số đạt cực tiểu tại điểm nào dưới đây?
A.
1x =
. B.
0x =
. C.
5x =
. D.
2x =
.
Lời giải
Chọn B
Dựa vào đồ thị ta thy hàm số đạt cực tiểu tại
0x =
.
Câu 13: Cho hàm
( )
fx
có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
A.
1x =
. B.
2x =
. C.
0x =
. D.
5x =
.
Lời giải
Chọn C
Hàm số đã cho đạt cực đại tại
0.x =
Câu 14: Cho hàm số
( )
fx
và xác định trên và có bảng xét du của đạo hàm như sau:
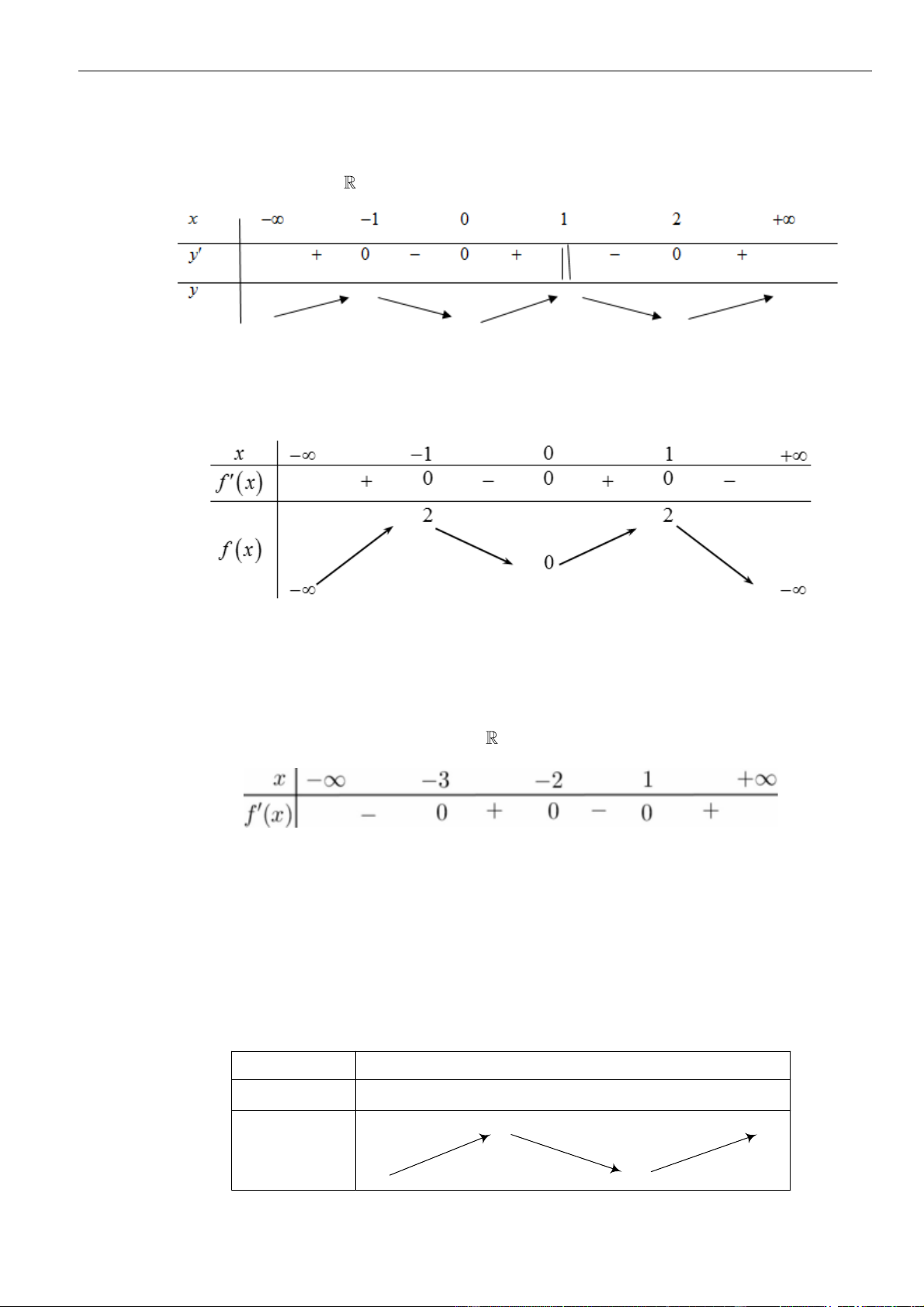
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn B
Do hàm số xác định trên nên ta có bảng biến thiên:
T đó ta có hàm số có
4
điểm cực trị.
Câu 15: Cho hàm số
( )
fx
có bảng biến thiên như sau
Điểm cực đại của đồ thị hàm số đã cho là
A.
1x =−
. B.
( )
1;2−
. C.
( )
0;0
. D.
0x =
.
Lời giải
Chọn B
Câu 16: Cho hàm số
( )
fx
có đạo hàm liên tục trên và có bảng xét du của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn A
Dựa vào bảng xét du ta có
( )
fx
đi du qua các điểm
3x =−
,
2x =−
và
1x =
nên hàm số
( )
fx
có
3
điểm cực trị.
Câu 17: Cho hàm số
( )
fx
có bảng biến thiên như sau
x
−
+
+
−
y
y
−
0
0
+
+
3−
1−
0
4−
Giá trị cực tiểu của hàm số đã cho bằng
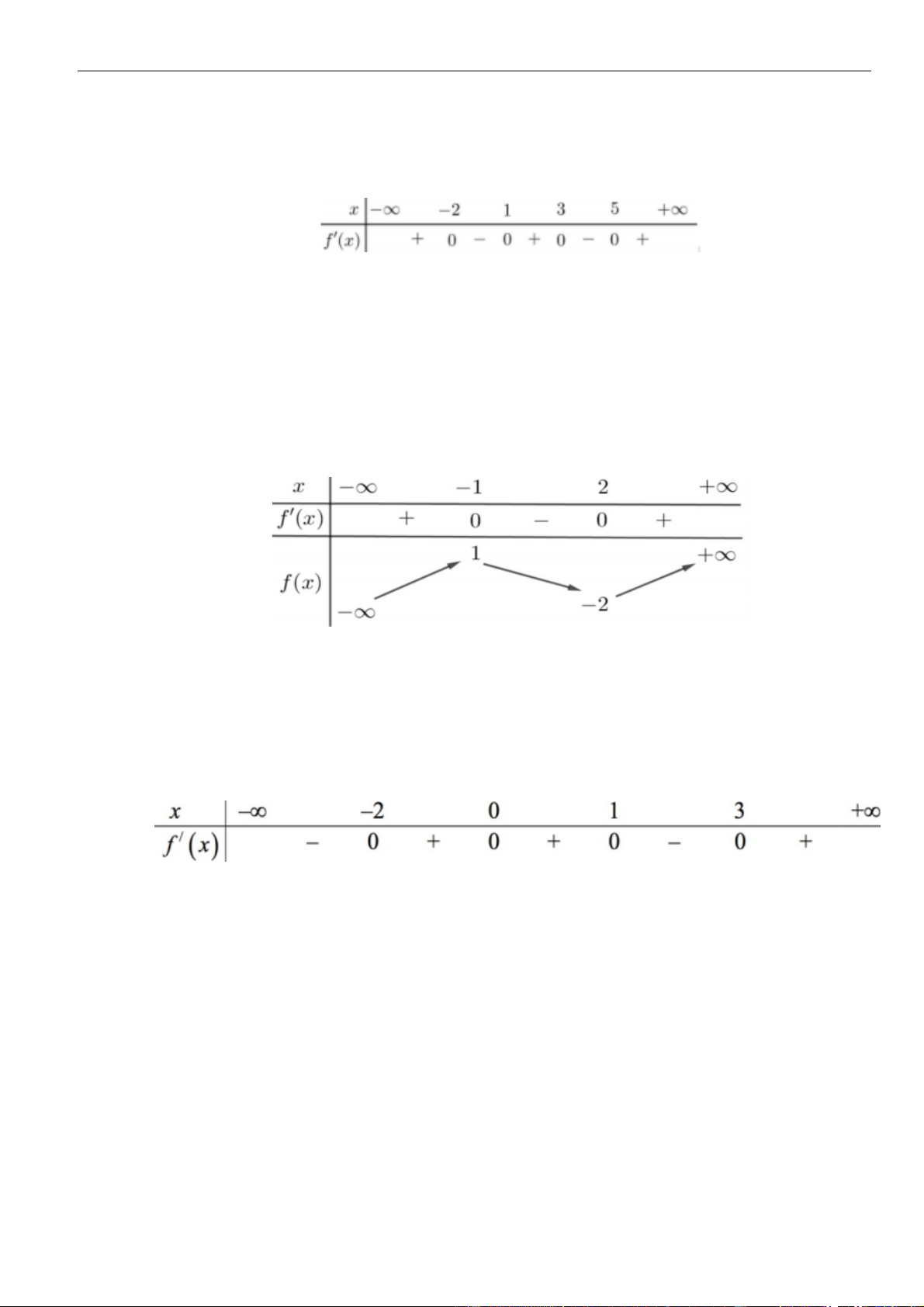
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
A.
1−
. B.
0
. C.
4−
. D.
3−
.
Lời giải
Chọn C
Câu 18: Cho hàm số
( )
fx
có bảng xét du của đạo hàm
( )
fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A
Hàm số
( )
fx
có đạo hàm
( )
fx
đi du khi đi qua các điểm
2; 1; 3; 5x x x x= − = = =
.
Vậy hàm số
( )
fx
có 4 điểm cực trị.
Câu 19: Cho hàm số bậc ba
( )
fx
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
2−
. C.
1
. D.
1−
.
Lời giải
Chọn C
T bảng biến thiên ta thy: Giá trị cực đại của hàm số đã cho
1y =
.
Câu 20: Cho hàm số
( )
fx
có bảng xét du của đạo hàm như sau:
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
A.
0x =
. B.
1x =
. C.
3x =
. D.
2x =−
.
Lời giải
Chọn B
Dựa vào bảng xét du ta thy hàm số đi du t
""+
sang
""−
khi qua
1x =
Hàm số đạt cực
đại tại điểm
1x =
.
Câu 21: Cho hàm số bậc ba
( )
fx
có đồ thị như hình vẽ bên
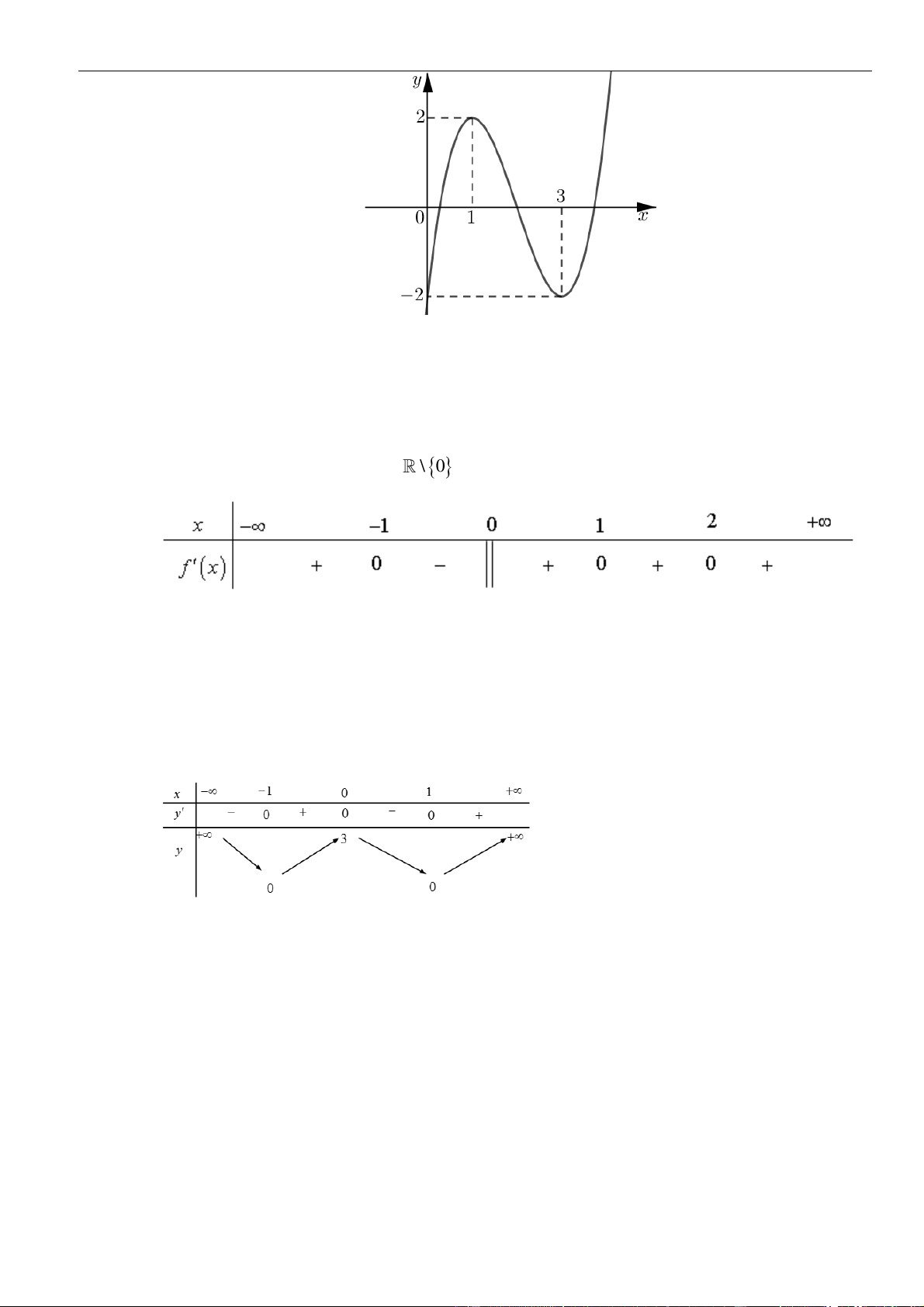
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
3
. C.
1
. D.
2−
.
Lời giải
Chọn D
Dựa vào đồ thị ta có giá trị cực tiểu của hàm số bằng
2−
.
Câu 22: Cho hàm số
( )
fx
xác định trên
\0
và có bảng xét du đạo hàm
( )
fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực trị?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn C
Dựa vào bảng xét du đạo hàm ta thy hàm số
( )
fx
có
1
điểm cực trị.
Câu 23: Cho hàm số
()y f x=
có bảng biến thiên như sau
Khẳng định nào sau đây đúng?
A. Điểm cực tiểu của hàm số là 0. B. Điểm cực tiểu của đồ thị hàm số là 1.
C. Điểm cực tiểu của hàm số là – 1. D. Điểm cực đại của hàm số là 3.
Lời giải
Chọn C
Điểm cực tiểu của hàm số là
1; 1xx= − =
.
Điểm cực tiểu của đồ thị hàm số là
( ) ( )
1;0 ; 1;0−
.
Điểm cực đại của hàm số là
0x =
.
Câu 24: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
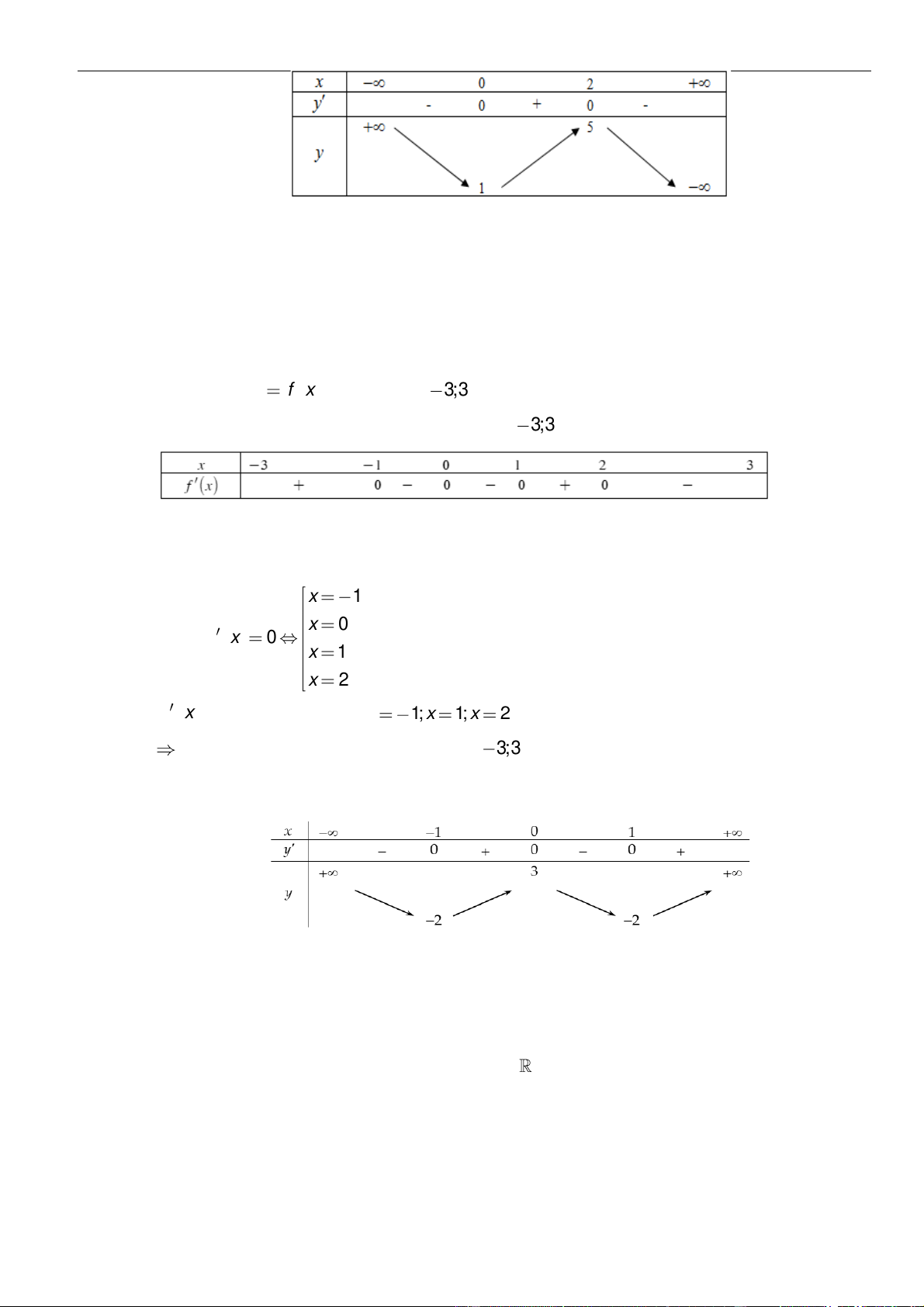
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Hàm số đạt cực tiểu tại điểm
A.
1x =
. B.
5x =
. C.
0x =
. D.
2x =
.
Lời giải
Chọn C
T BBT, hàm số đạt cực tiểu tại điểm
0x =
.
Câu 25: Cho hàm số
y f x
liên tục trên
3;3
và có bảng xét dy đạo hàm như hình bên. Hàm số
đã cho có bao nhiêu điểm cực trị thuộc khoảng
3;3
.
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
Ta có
1
0
0
1
2
x
x
fx
x
x
fx
đi du tại các điểm
1; 1; 2x x x
hàm số có 3 điểm cực trị trpng khoảng
3;3
.
Câu 26: Hàm số
( )
y f x=
có bảng biến thiên như hình vẽ bên dưới
Số điểm cực trị của đồ thị hàm số là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn A
Câu 27: Cho hàm số
( )
y f x=
xác định và liên tục trên , có bảng biến thiên như hình vẽ. Khi đó giá
trị cực tiểu của hàm số
( )
y f x=
bằng
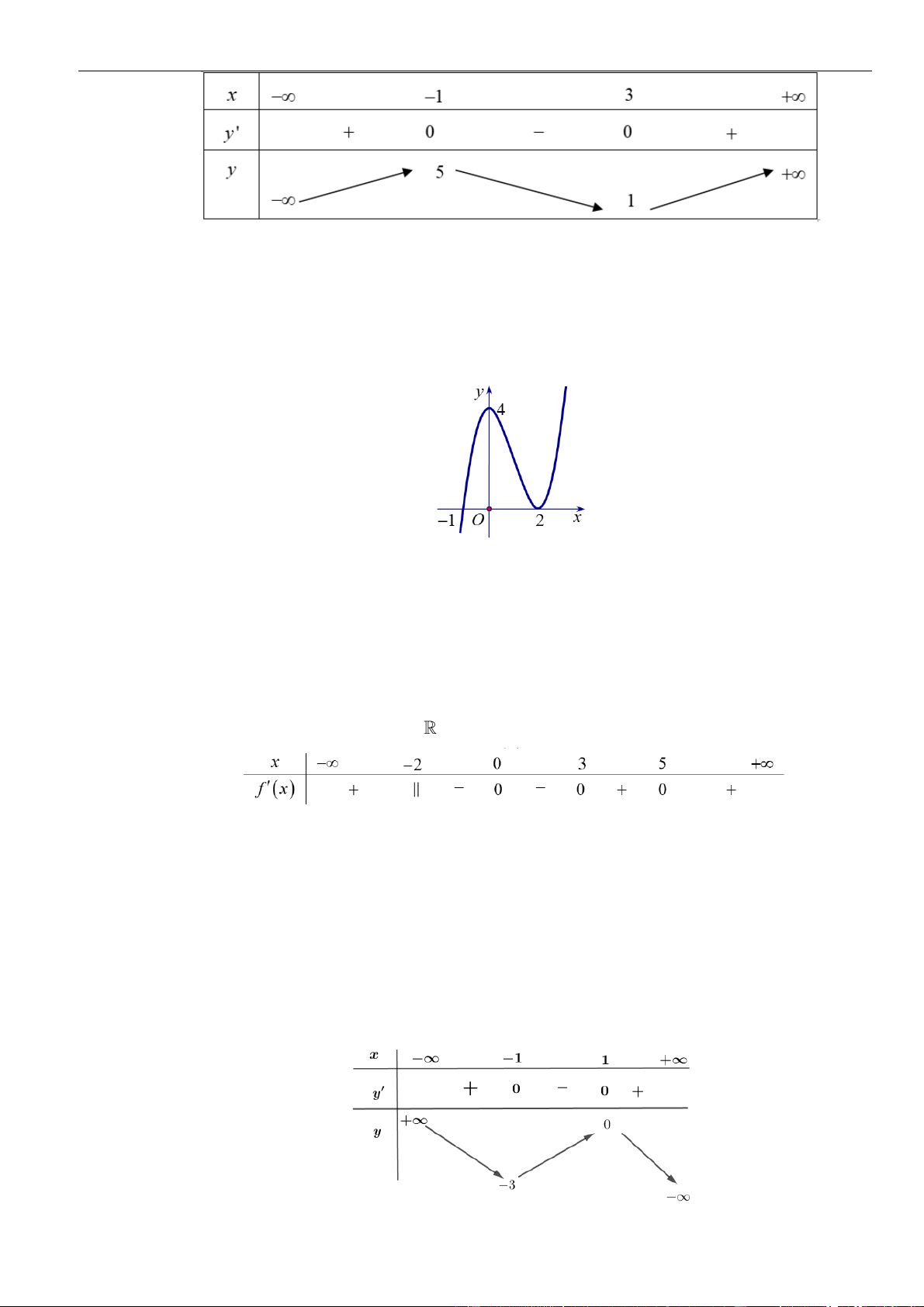
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
A.
1−
. B.
3
. C.
1
. D.
5
.
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta thy giá trị cực tiểu của hàm số
( )
y f x=
là
1
.
Câu 28: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới.
Mệnh đ nào sau đây đúng?
A. Hàm số đạt cực đại tại
2x =
. B. Hàm số đạt cực tiểu tại
2x =
.
C. Hàm số đạt cực đại tại
4x =
. D. Hàm số đạt cực tiểu tại
0x =
.
Lời giải
Chọn B
Dựa vào đồ thị ta thy, hàm số
( )
y f x=
đạt cực đại tại
0x =
và đạt cực tiểu tại
2x =
.
Câu 29: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét du của
( )
fx
như sau:
Số điểm cực đại của hàm số
( )
y f x=
là
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
Dựa vào bảng biến thiên ta thy, hàm số
( )
y f x=
đạt cực đại tại
2x =−
nên hàm số đã cho có
1
điểm cực đại.
Câu 30: Cho hàm số
( )
y f x=
có bảng biến thiên như sau.
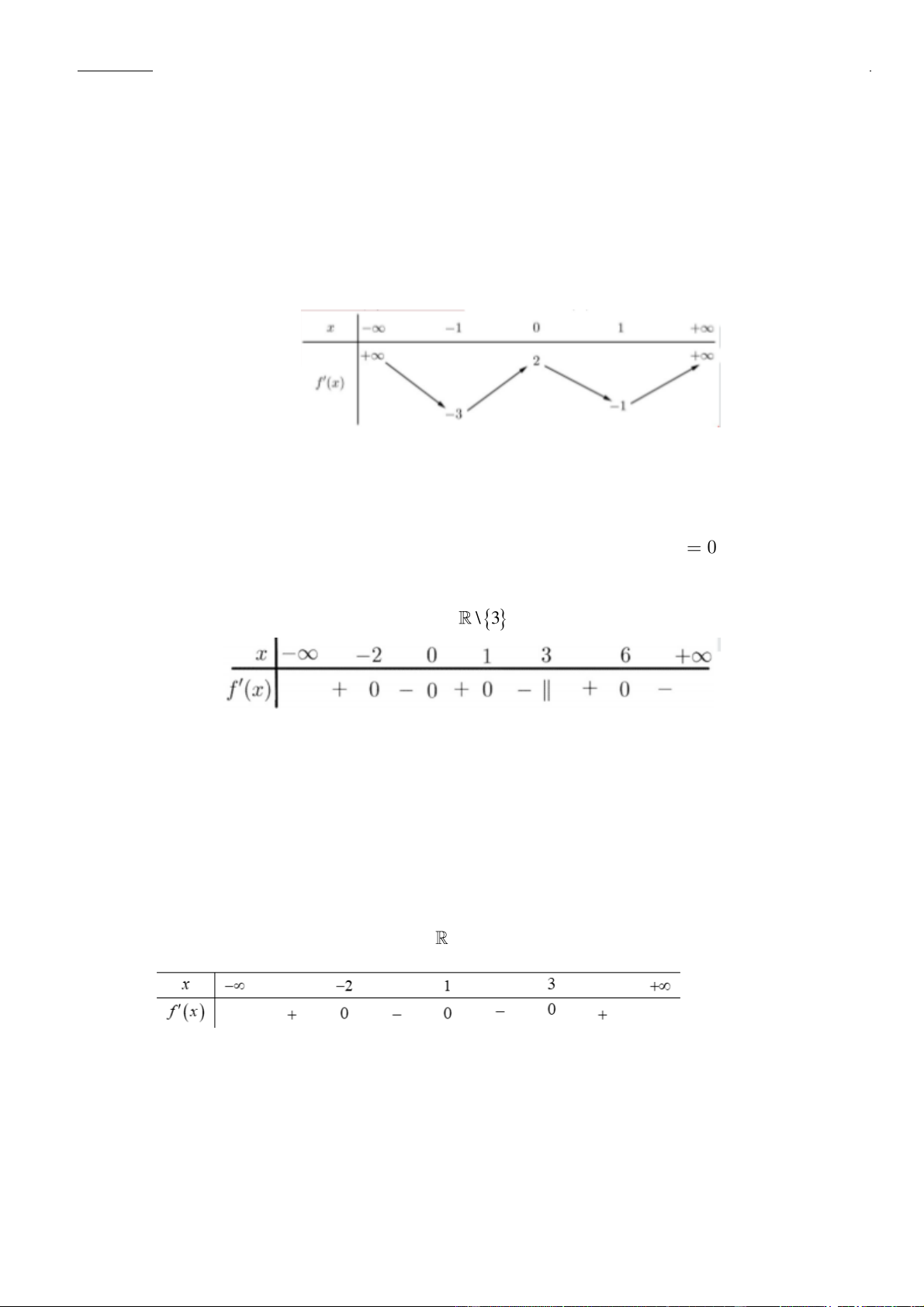
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Tìm giá trị cực đại
CD
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
1
CD
y =
và
0
CT
y =
. B.
CD
y =−
và
1
CT
y =−
.
C.
1
CD
y =−
và
1
CT
y =
. D.
0
CD
y =
và
3
CT
y =−
.
Lời giải
Chọn D
T bảng biến thiên suy ra
0
CD
y =
và
3
CT
y =−
.
Câu 31: Cho hàm số
fx
có bảng biến thiên của hàm số
'fx
như hình vẽ.
Số điểm cực trị của hàm số đã cho là
A.
3.
B.
2.
C.
1.
D.
4.
Lời giải
Chọn D
T bảng biến thiên của hàm số
'fx
, ta thy rằng phương trình
'0fx
có 4 nghiệm bội lẻ.
Do đó, hàm số đã cho có 4 điểm cực trị.
Câu 32: Cho hàm số
( )
fx
xác định trên khoảng
\3
và có bảng xét du của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
4
. C.
2
. D.
5
.
Lời giải
Chọn B
Ta có hàm số
( )
fx
không xác định tại
3x =
nên không thể đạt cực trị tại đó.
Hàm số
( )
fx
đi du tại 4 điểm
2x =−
,
0x =
,
1x =
và
6x =
.
Vậy hàm số có 4 cực trị.
Câu 33: ) Cho hàm số
( )
y f x=
liên tục trên có bảng xét du
( )
fx
như hình vẽ
Số điểm cực trị của hàm số
( )
y f x=
là
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn D
Ta có
( )
2
01
3
x
f x x
x
=−
= =
=
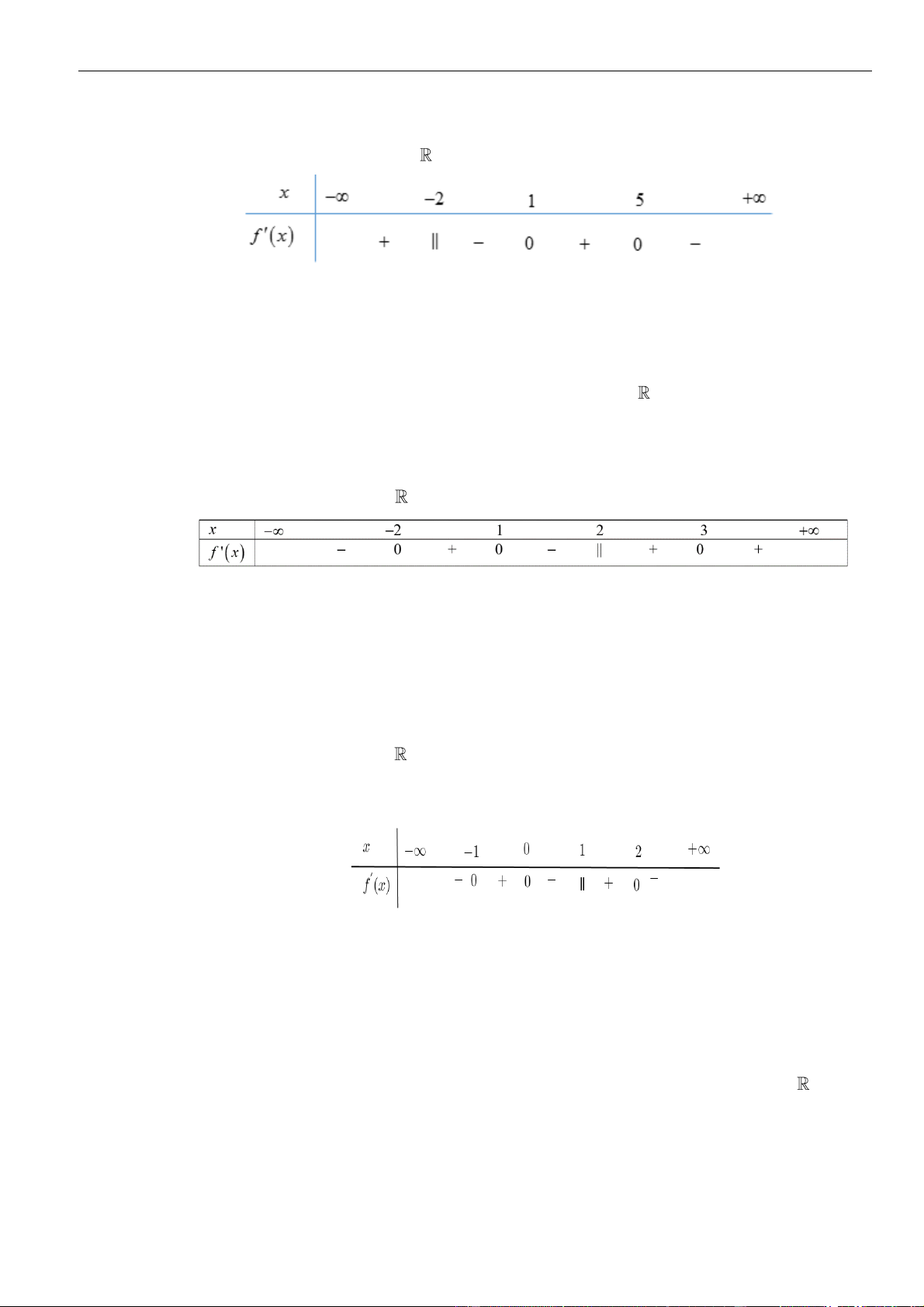
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
T bảng xét du ta thy
( )
fx
đi du khi qua nghiệm
2x =−
và nghiệm
3x =
; không đi du
khi
x
qua nghiệm
0x =
nên hàm số có hai điểm cực trị.
Câu 34: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét du của
( )
fx
như sau:
Số điểm cực đại của hàm số
( )
y f x=
là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
( )
2f
−
không xác định nhưng vì hàm số
( )
y f x=
liên tục trên nên tồn tại
( )
2f −
.
Theo bảng xét du ta thy
( )
fx
đi du t
""+
sang
""−
khi qua
2x =−
và
5x =
nên hàm số
có hai điểm cực đại.
Câu 35: Cho hàm số
( )
fx
liên tục trên và có bảng xét du của
( )
'fx
như sau:
Số điểm cực tiểu của hàm số đã cho là
A. 3. B. 2. C. 4. D. 1.
Lời giải
Chọn B
Đạo hàm
( )
'fx
đi du t âm sang dương hai lần qua các điểm
2x =−
và
2x =
nên hàm số đã
cho có hai điểm cực tiểu.
Câu 36: Cho hàm số
( )
fx
liên tục trên và có bảng xét du
( )
fx
như sau
Số điểm cực trị của
( )
fx
A.
3
. B.
4
C.
1
. D.
1
.
Lời giải
Chọn B
Hàm số
( )
fx
có 4 điểm cực trị vì
( )
fx
đi du 4 lần và hàm số
( )
fx
liên tục trên .
Câu 37: Cho hàm số
( )
fx
có bảng biến thiên như sau:
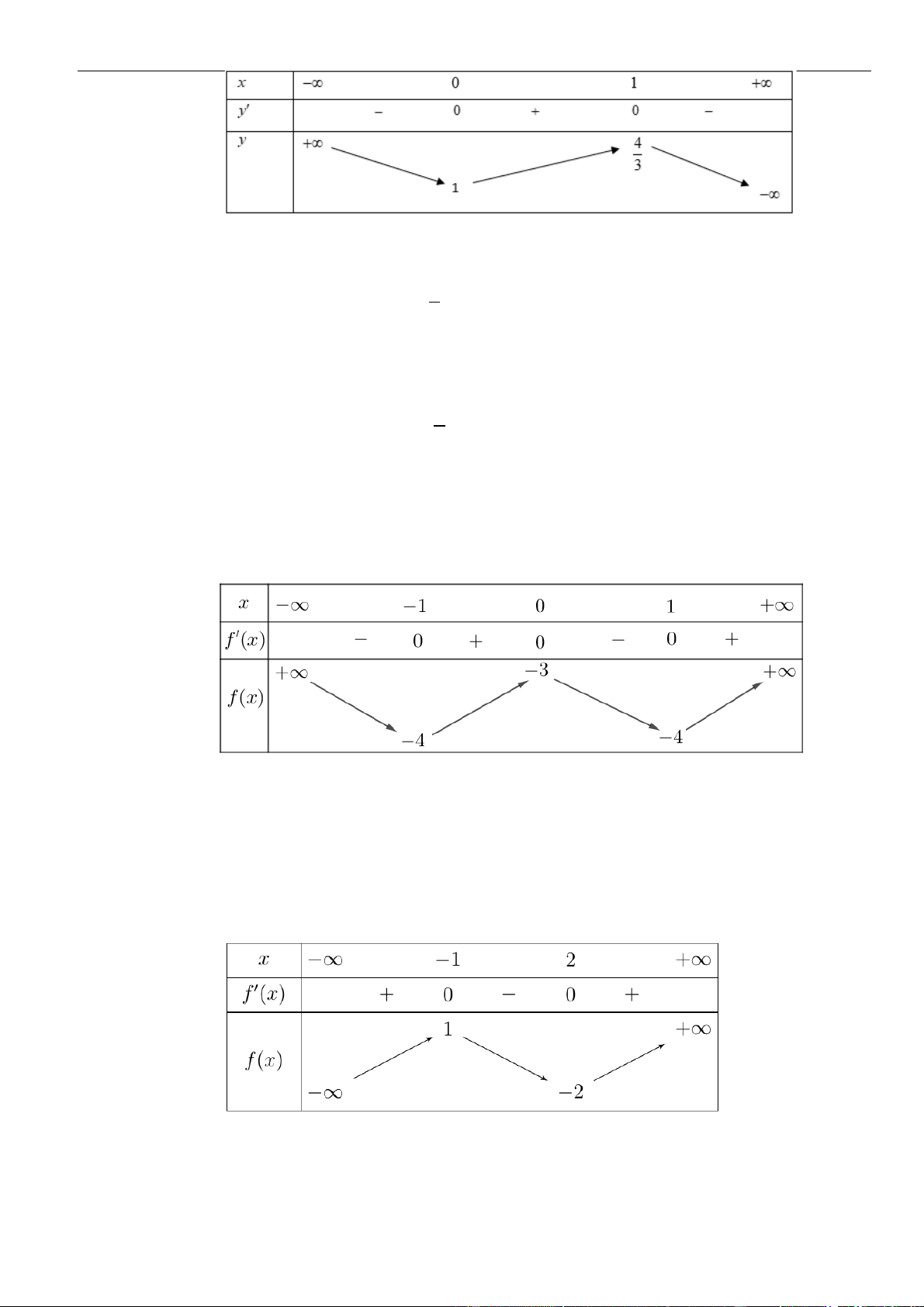
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Mệnh đ nào sau đây đúng?
A. Điểm cực đại của hàm số là
4
1; .
3
B
B. Điểm cực tiểu của đồ thị hàm số là
( )
0;1 .B
C. Điểm cực đại của đồ thị hàm số là
( )
0;1 .B
D. Điểm cực tiểu của hàm số là
4
1; .
3
B
Lời giải
Chọn B
Câu 38: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A.
1
. B.
0
. C.
3−
. D.
4−
.
Lời giải
Chọn D
Dựa vào bảng biến thiên, suy ra hàm số đạt cực tiểu tại
1−
và
1
, giá trị cực tiểu bằng
4−
.
Câu 39: Cho hàm số
()y f x=
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
2−
. C.
1
. D.
1−
.
Lời giải
Chọn C
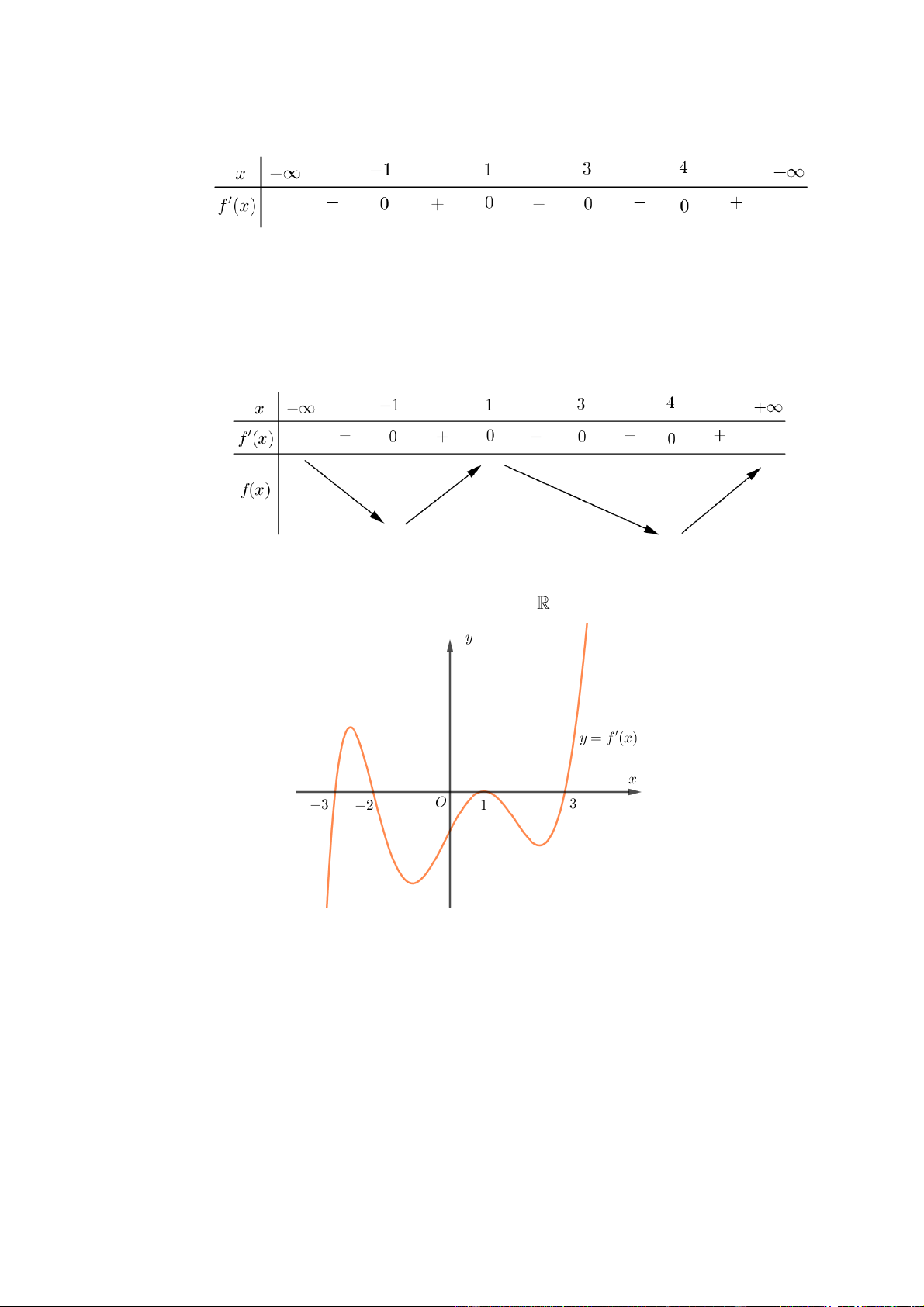
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
T bảng biến thiên ta thy giá trị cực đại của hàm số đã cho bằng 1.
Câu 40: Cho hàm số
( )
fx
có bảng xét du của đạo hàm
( )
fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực tiểu?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn A
Bảng biến thiên của hàm số
( )
fx
là:
Vậy hàm số
( )
fx
có
2
điểm cực tiểu.
Câu 41: Cho hàm số
( )
y f x=
liên tục và có đạo hàm trên , biết
( )
y f x
=
có đồ thị như hình bên.
Điểm cực đại của hàm số
( )
y f x=
đã cho là
A.
3x =
. B.
1x =
. C.
3x =−
. D.
2x =−
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số
( )
y f x
=
ta có
( )
3
2
0
1
3
x
x
fx
x
x
=−
=−
=
=
=
.
Khi đó ta có bảng xét du của
( )
fx
như sau:
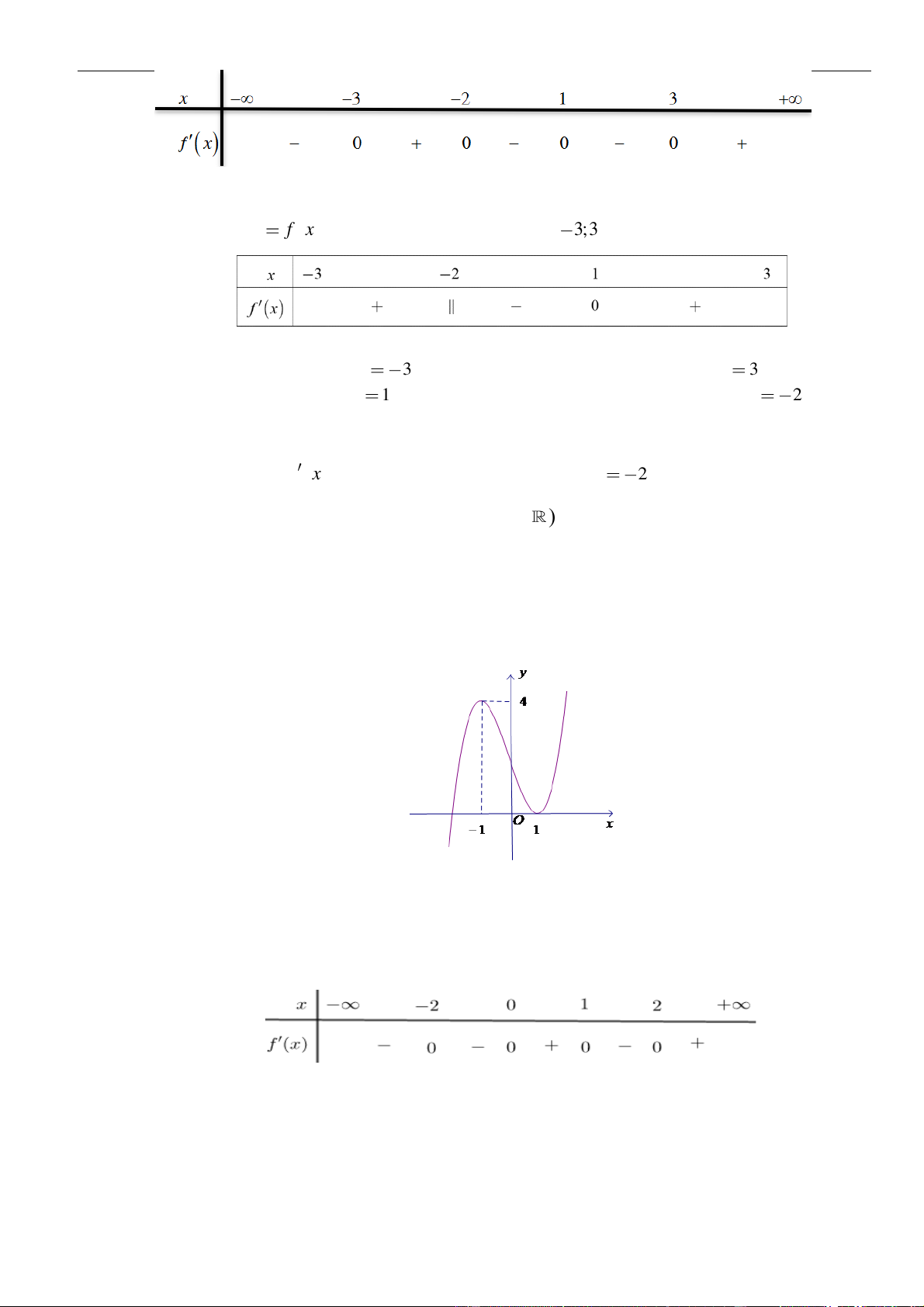
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
Dựa vào bảng xét du suy ra điểm cực đại của hàm số
( )
y f x=
là
2x =−
.
Câu 42: Cho hàm số
y f x
xác định và liên tục trên đoạn
3;3
có bảng xét du đạo hàm như sau:
Mệnh đ nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
3x
. B. Hàm số đạt cực tiểu tại
3x
.
C. Hàm số đạt cực đại tại
1x
. D. Hàm số đạt cực tiểu đại tại
2x
.
Lời giải
Chọn D
T bảng xét du
fx
ta thy hàm số đạt cực tiểu đại tại
2x
.
Câu 43: Cho hàm số
( )
32
, , ,y ax bx cx d a b c d= + + +
có đồ thị hàm số như hình vẽ. Mệnh đ
nào sau đây sai?
A. Giá trị cực đại của hàm số là
1−
.
B. Hàm số đạt cực đại tại
1x =−
.
C. Hàm số đạt cực tiểu tại
1x =
.
D. Giá trị cực tiểu của hàm số là
0
.
Lời giải
Chọn A
Giá trị cực đại cùa hàm số là 4, nên đáp án A sai.
Câu 44: Cho hàm số
( )
y f x=
có bảng xét du
( )
fx
như sau
Số điểm cực tiểu của hàm số
( )
y f x=
là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D
Hàm số đạt cực tiểu tại
0x =
và
2x =
. Vậy số điểm cực tiểu của hàm số
( )
y f x=
là
2
.
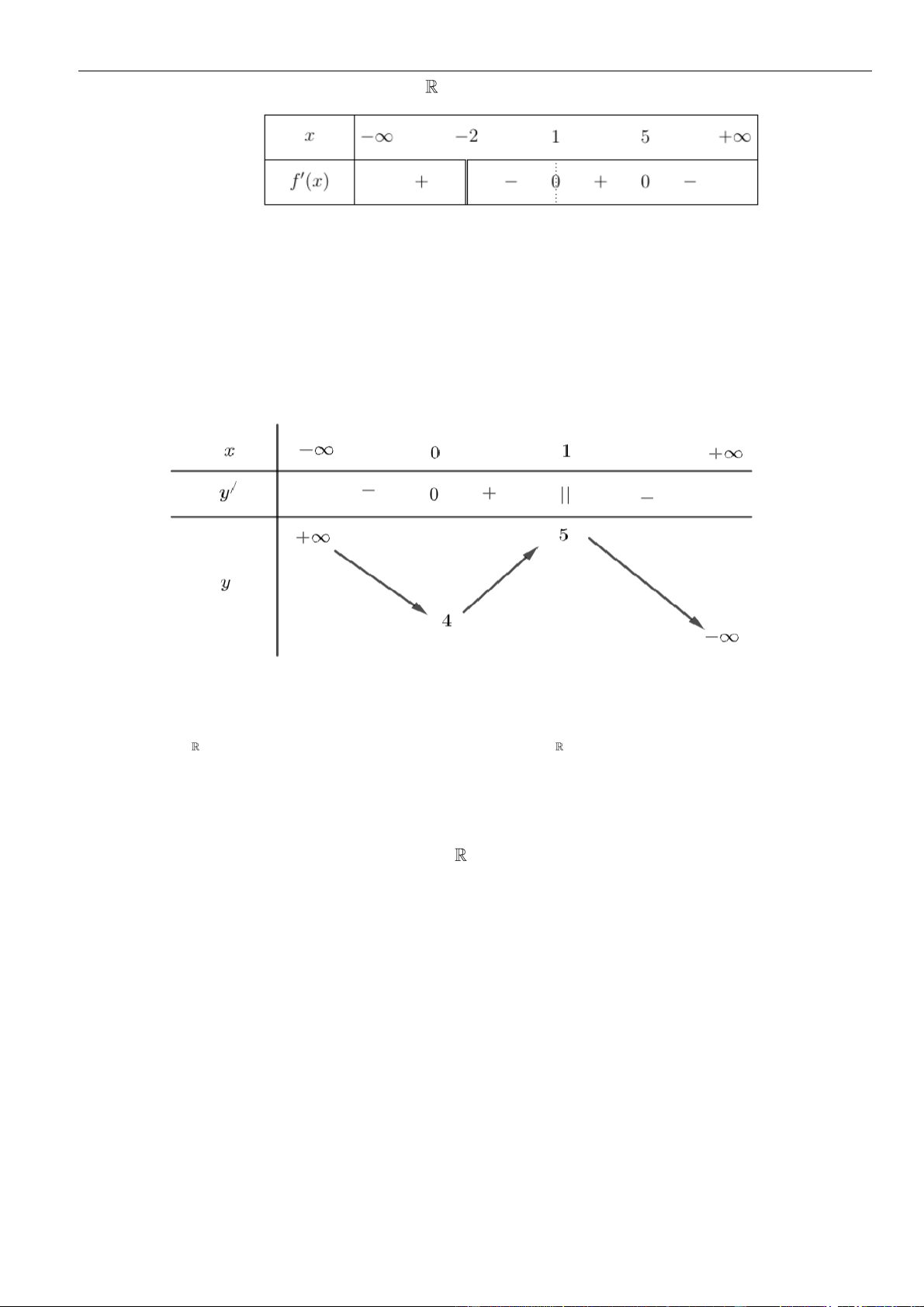
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
27 | Facebook tác giả: Phan Nhật Linh
Câu 45: Cho hàm số
( )
y f x=
liên tục trên và có bảng xét du
( )
fx
như sau
Số điểm cực đại của hàm số
( )
fx
là
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
Do đạo hàm
( )
fx
đi du t dương sang âm
2
lần nên hàm số
( )
fx
có
2
điểm cực đại.
Câu 46: Cho hàm số
()fx
có bảng biến thiên như sau:
Mệnh đ nào sau đây đúng
A.
min 4y =
. B.
=
§
15
C
y
C.
max 5y =
. D.
4
CT
y =
.
. Lời giải
Chọn D
Dựa vào bảng biến thiên dễ dàng chọn đáp án D.
Câu 47: Cho hàm số
( )
y f x=
có đạo hàm trên và hàm số
( )
y f x
=
có đồ thị như hình bên
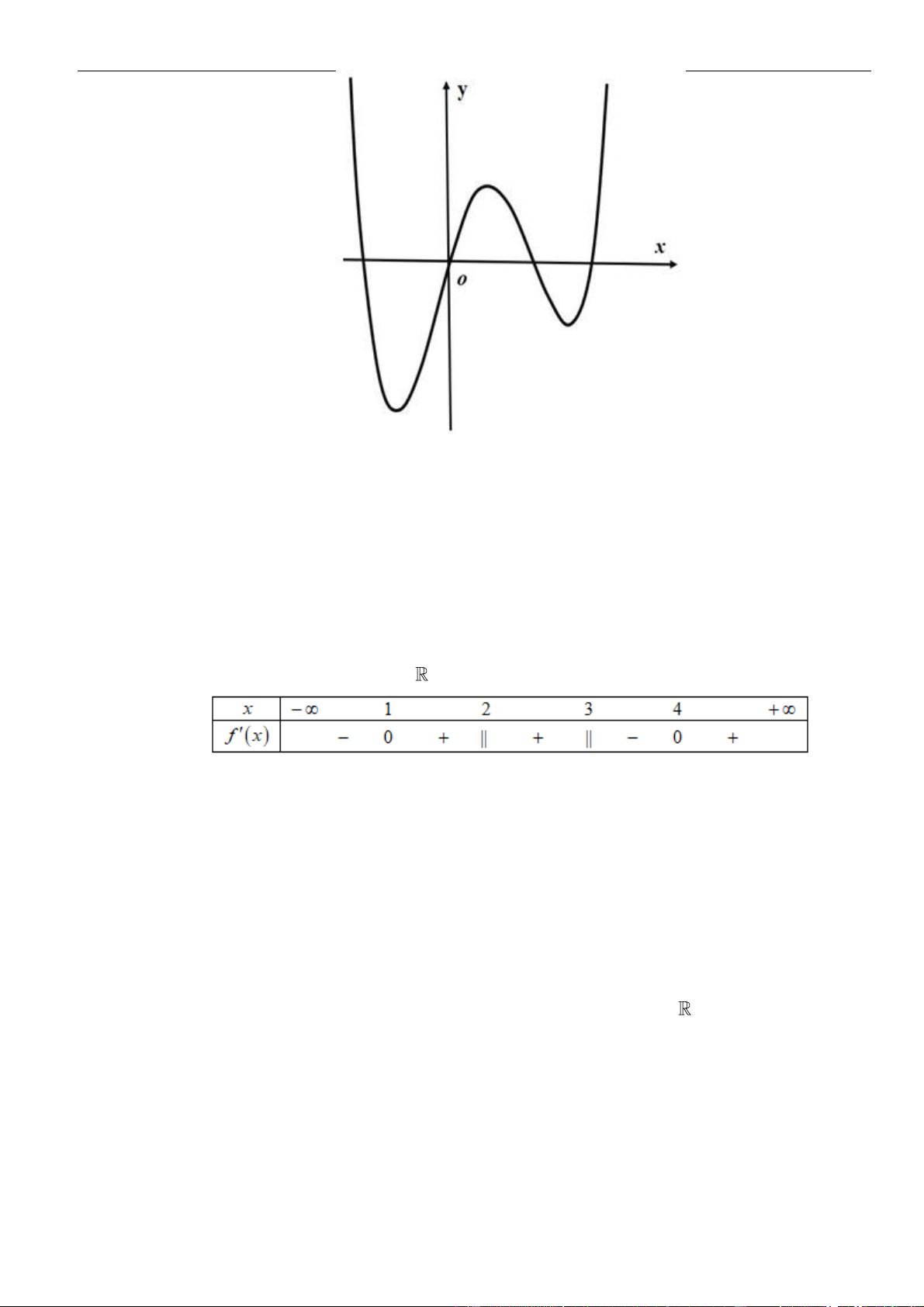
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 28
Tìm số điểm cực trị của hàm số
( )
y f x=
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn B
T đồ thị hàm số
( )
y f x
=
ta có đồ thị hàm số
( )
y f x
=
cắt trục hoành tại
4
điểm phân biệt.
Do đó, phương trình
( )
0fx
=
có
4
nghiệm phân biệt. Qua các nghiệm này
( )
fx
đu đi du
nên số cực trị của hàm số
( )
y f x=
là
4
cực trị.
Câu 48: Cho hàm số
()y f x=
liên tục trên và có bảng xét du
()fx
như sau
Kết luận nào sau đây đúng?
A. Hàm số có 2 điểm cực đại. B. Hàm số có 4 điểm cực trị.
C. Hàm số có 2 điểm cực trị. D. Hàm số có 2 điểm cực tiu.
Lời giải
Chọn D
Dựa vào bảng xét du đạo hàm ta thy: hàm số đạt cực trị tại
1; 3; 4x x x= = =
.
Tại
1; 4xx==
ta thy
( )
fx
đi du t âm sang dương nên hàm số đạt cực tiểu tại
1; 4xx==
Tại
3x =
ta thy
( )
fx
đi du t dương sang âm nên hàm số đạt cực đại tại
3x =
Câu 49: Cho hàm đa thức bậc năm
( )
y f x=
và đồ thị hàm số
( )
y f x
=
trên như hình vẽ. Mệnh đ
nào đúng?
A. Hàm số
( )
y f x=
có 2 điểm cực đại và 1 điểm cực tiểu.
B. Hàm số
( )
y f x=
có 2 điểm cực đại và 2 điểm cực tiểu.
C. Hàm số
( )
y f x=
có 1 điểm cực đại và 2 điểm cực tiểu.
D. Hàm số
( )
y f x=
có 1 điểm cực đại và 1 điểm cực tiểu.
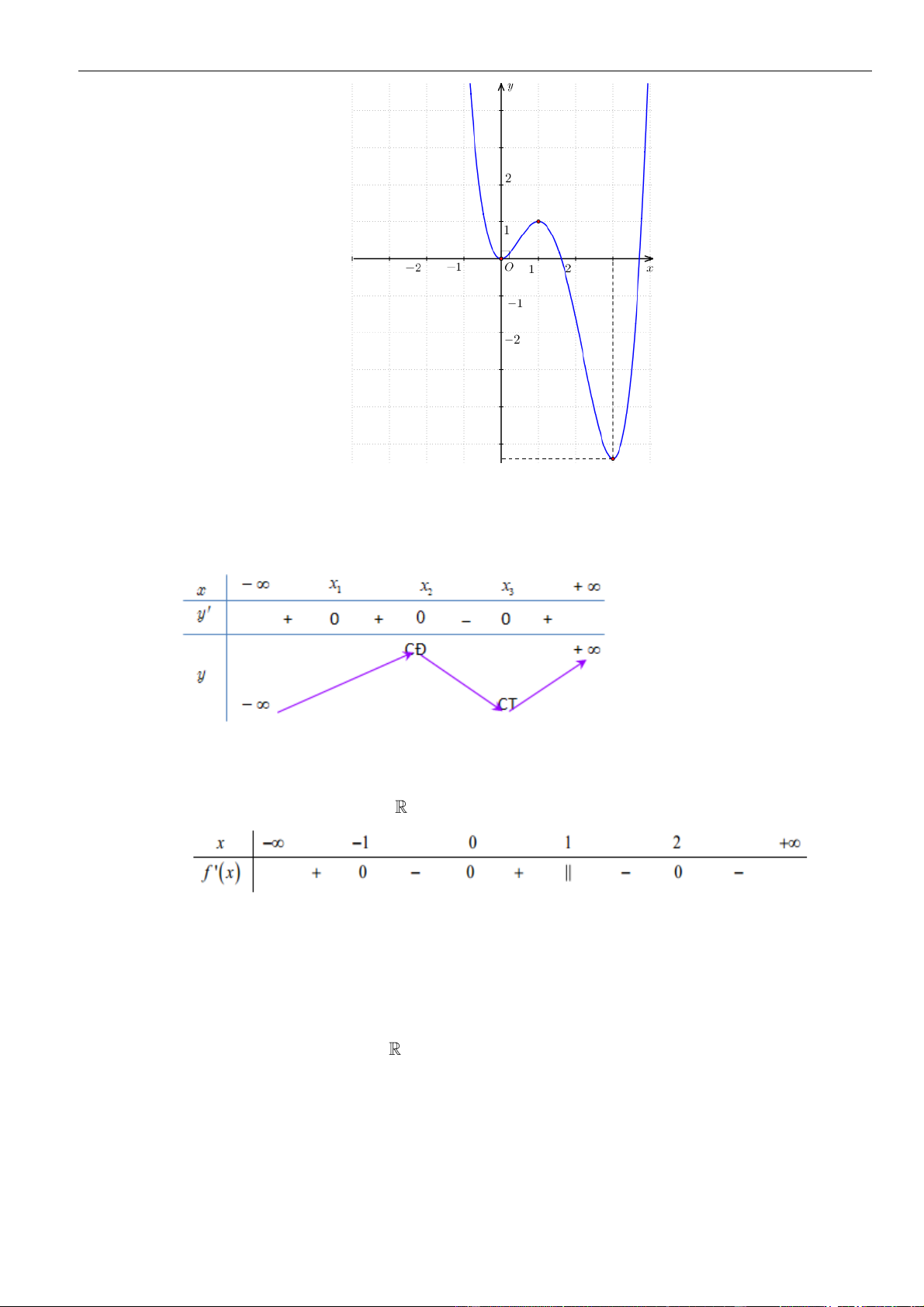
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
29 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn D
T đồ thị hàm
( )
y f x
=
ta có bảng biến thiên của hàm số
( )
y f x=
T bảng biến thiên ta thy hàm số
( )
y f x=
có 1 điểm cực đại và 1 điểm cực tiểu.
Câu 50: Cho hàm số
( )
fx
liên tục trên và có bảng xét du của
( )
fx
như sau:
Số điểm cực đại của hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
T bảng xét du ta thy:
( )
fx
đi du t dương sang âm khi qua
1x =−
và
1x =
.
Mà hàm số
( )
fx
liên tục trên .
Vậy hàm số đã cho có hai điểm cực đại là
1x =−
và
1x =
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 30
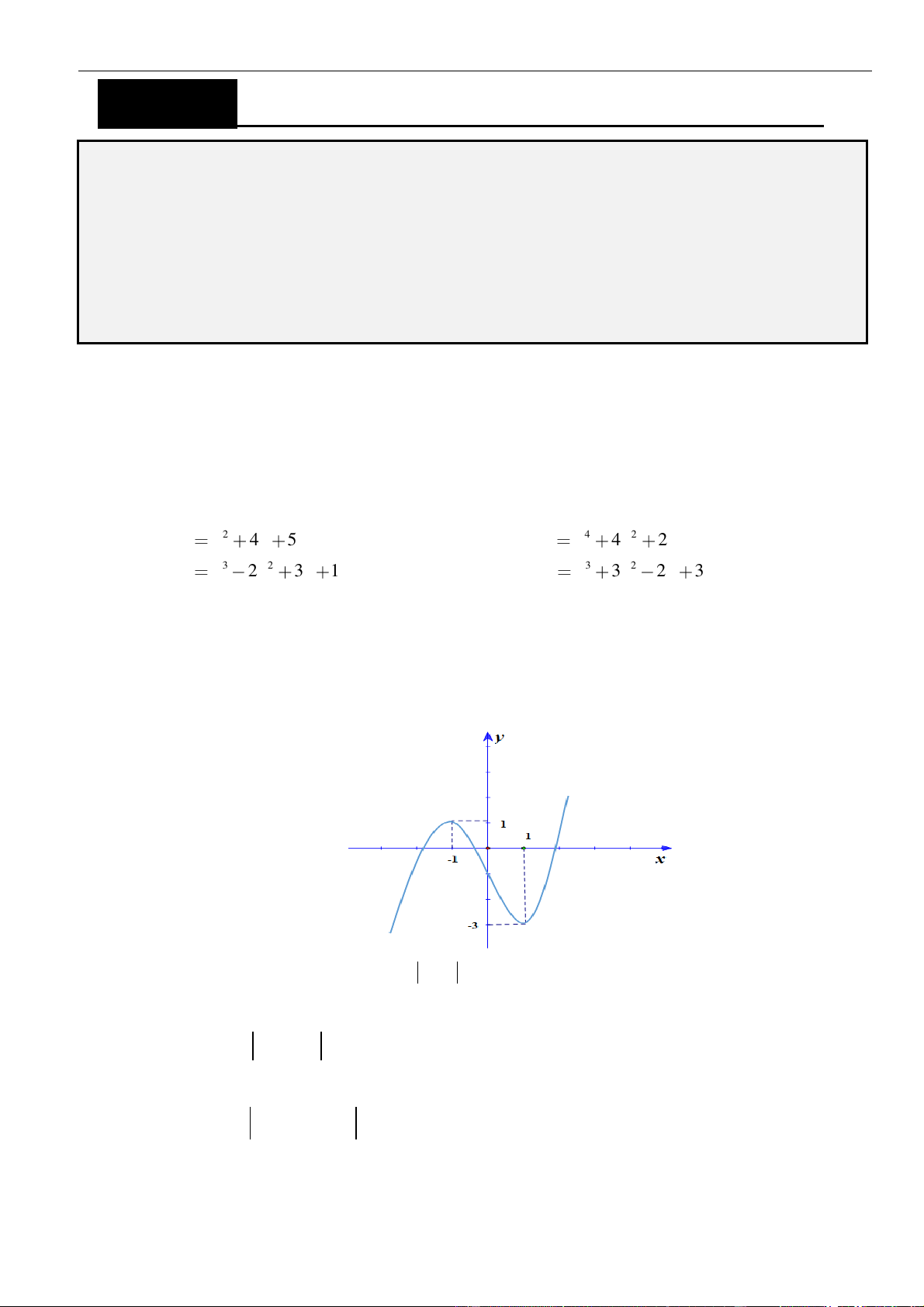
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
()fx
có đạo hàm
2
'( ) ( 1)( 2) ,= − + f x x x x R
. Số điểm cực trị của hàm số đã
cho là:
A. 3 B. 1 C. 5 D. 2
Câu 2: Hàm số nào dưới đây không có cực trị
A.
2
45y x x
. B.
42
42y x x
.
C.
32
2 3 1y x x x
. D.
32
3 2 3y x x x
.
Câu 3: Cho hàm số
( )
fx
có đạo hàm là
( ) ( ) ( )
23
23f x x x x
= − −
. Số điểm cực trị của hàm số
( )
fx
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 4: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ:
Số điểm cực trị của hàm số
( )
2.y f x=+
A.
2.
B.
1.
C.
3.
D.
5.
Câu 5: Hàm số
32
3y x x=+
đạt cực tiểu tại
A.
0x =
. B.
4x =
. C.
0x =
và
3xa= −
. D.
3x =−
và
0x =
.
Câu 6: Hàm số
( ) ( )
3
11y x x= − +
có bao nhiêu điểm cực trị?
A.
2
. B.
4
. C.
3
. D.
1
.
Tìm cực trị hàm số cho bởi nhiều công thức
DẠNG 3
Phương pháp:
•
Bưc 1. Tìm tp xc định
D
của hàm số.
•
Bưc 2.Tnh đạo hàm
( ).y f x
=
Gii phương trình
( ) 0fx
=
và k hiu
, ( 1,2,3,..., )
i
x i n=
là cc
nghim của nó.
•
Bưc 3. Tnh
()fx
và
( ).
i
fx
•
Bưc 4. Dựa vào du của
()
i
yx
suy ra tnh cht cực trị của điểm
:
i
x
+ Nu thì hàm số đạt cực đại tại điểm
+ Nu thì hàm số đạt cực tiểu tại điểm
Bưc 1. Tìm tp xc định của hàm số.
Bưc 2. Tnh đạo hàm Tìm cc điểm mà tại đó đạo hàm bng 0 hoc
không xc định.
Bưc 3. Sp xp cc điểm theo th tự tăng dn và lp bng bin thiên.
Bưc 4. Nêu kt lun v cc khong đồng bin và nghịch bin dưa vào bng bin thiên.
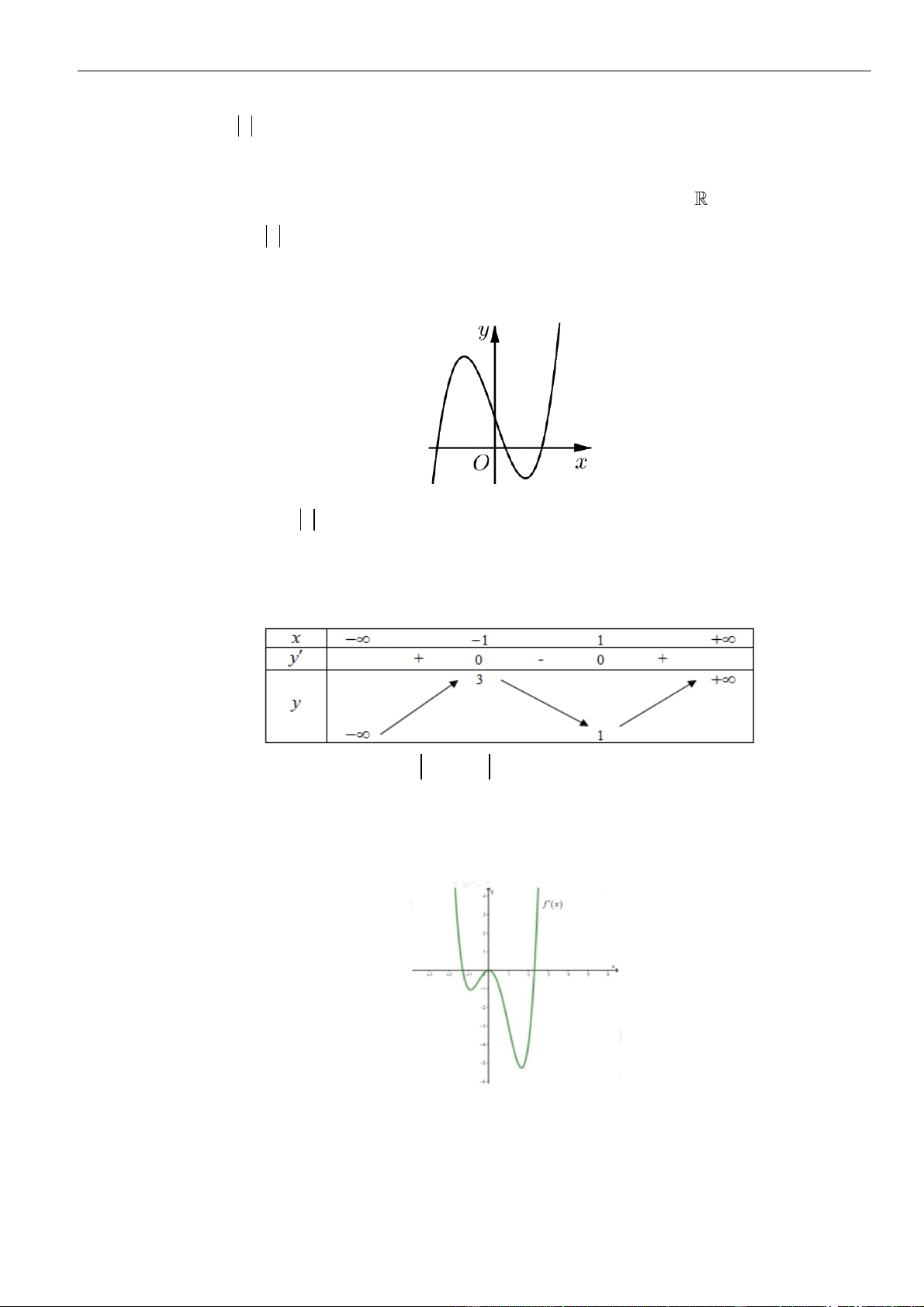
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 7: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
( )
( )
2020
2019 3
2
2 2 3f x x x x x
= − − − +
. Số điểm cực trị của
hàm số
( )
fx
là:
A.
5
. B.
1
. C.
2
. D.
3
.
Câu 8: Cho hàm số
()y f x=
có đạo hàm
( )
( )
( )
3
2
' ( 1) 1 3 , f x x x x x= + − −
. Số điểm cực trị của
hàm số
()y f x=
là:
A. 2. B. 5. C. 3. D. 1.
Câu 9: Cho hàm số
( )
.y f x=
Đồ thị của hàm số
( )
y f x
=
như hình bên.
Hàm số
( )
( )
2021g x f x=+
có bao nhiêu điểm cực trị?
A.
5
. B.
7
. C.
3
. D.
2
.
Câu 10: Cho hàm số
( )
y f x=
có bng bin thiên như hình vẽ
Số điểm cực trị của hàm số
( ) ( )
2g x f x=−
là
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 11: Cho hàm số
( )
y f x=
xc định và liên tục trên có đạo hàm
( )
y f x
=
có đồ thị như hình vẽ. Số
điểm cực tiểu của hàm số là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 12: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị như hình bên.
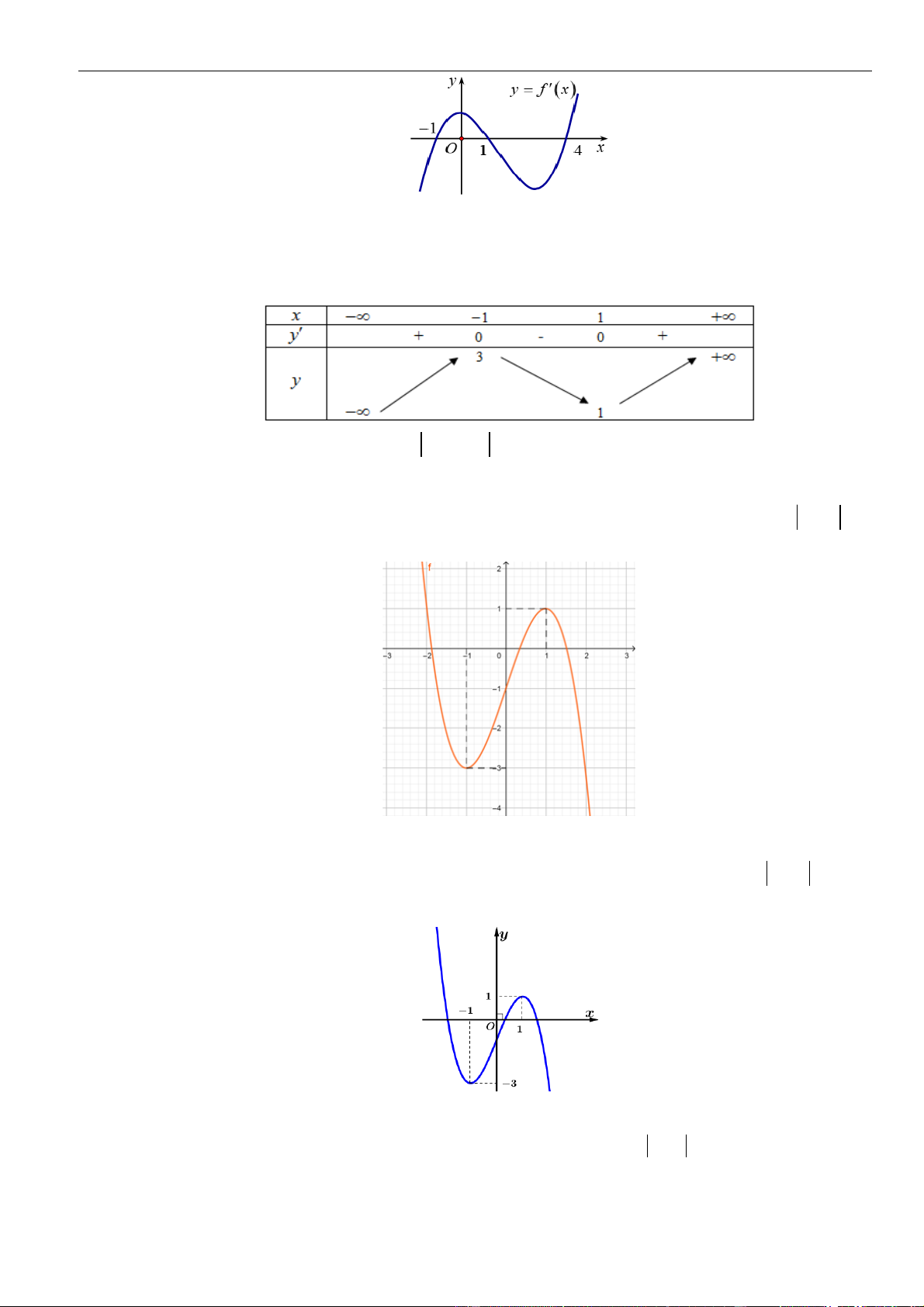
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Hàm số
( )
=y f x
có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 13: Cho hàm số
( )
y f x=
có bng bin thiên như hình vẽ
Số điểm cực trị của hàm số
( ) ( )
2g x f x=−
là
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 14: Đồ thị của hàm số
( ) ( )
32
0y f x ax bx cx d a= = + + +
như hình vẽ bên. Hàm số
( )
y f x=
có
bao nhiêu điểm cực trị?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 15: Đồ thị hàm số
( ) ( )
32
0y f x ax bx cx d a= = + + +
như hình vẽ bên. Hàm số
( )
y f x=
có bao
nhiêu điểm cực trị?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 16: Cho hàm số bc ba
()y f x=
có đồ thị như hình vẽ. Hàm số
()y f x=
có bao nhiêu điểm cực
trị?
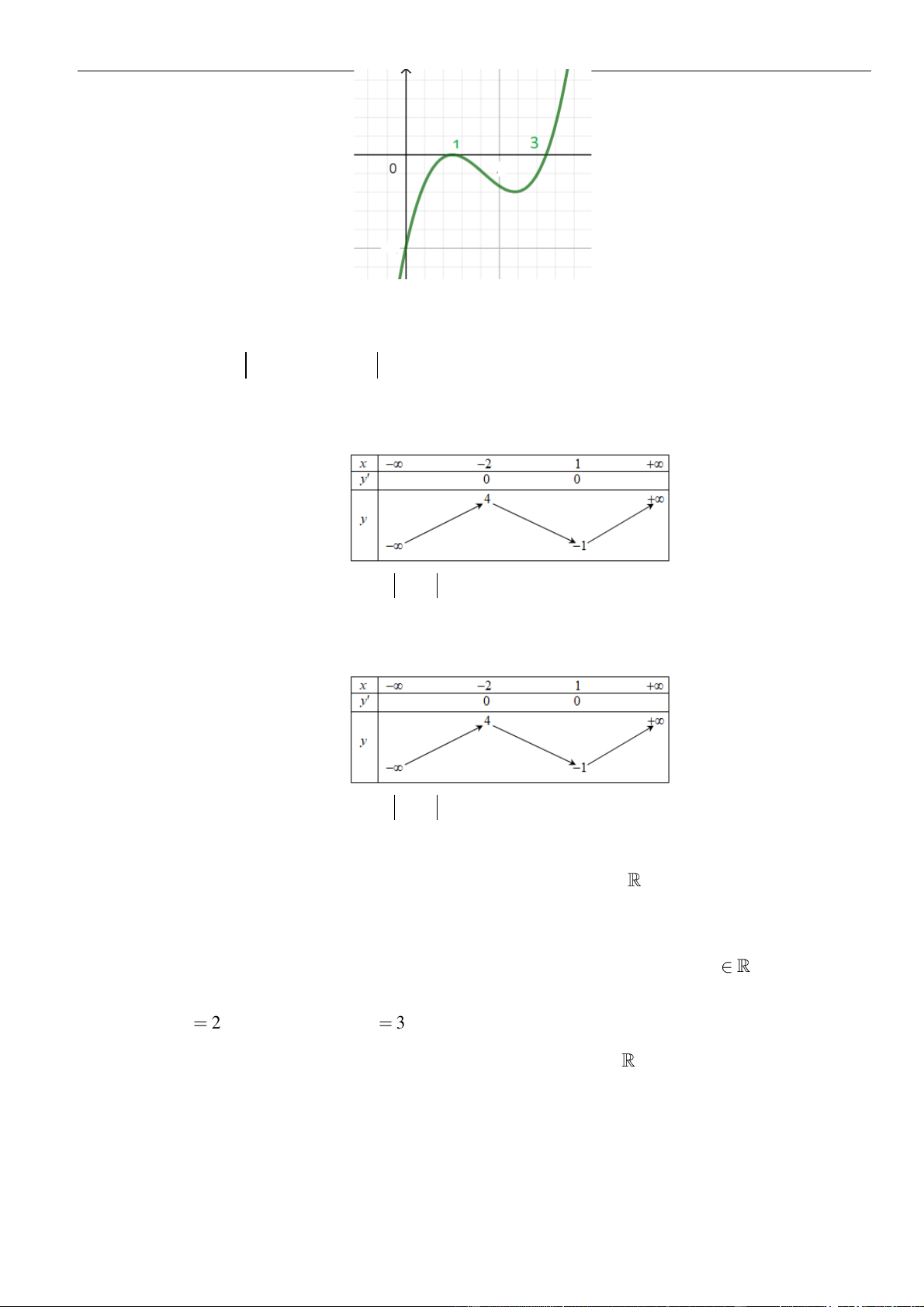
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
A.
3
. B.
5
. C.
2
. D.
1
.
Câu 17: Cho hàm số
32
y ax bx cx d= + + +
có đồ thị ct trục hoành tại ba điểm phân bit. Số cực trị của
hàm số
32
y ax bx cx d= + + +
là
A. 3. B. 5. C. 4. D. 1.
Câu 18: Cho hàm số
( )
y f x=
có bng bin thiên như hình sau:
Số điểm cực trị của hàm số
( )
y f x=
là
A.
4
. B.
3
. C.
2
D.
5
Câu 19: Cho hàm số
( )
y f x=
có bng bin thiên như hình sau:
Số điểm cực trị của hàm số
( )
y f x=
là
A.
4
. B.
3
. C.
2
D.
5
Câu 20: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
1 4 ,f x x x x x
= + −
. Số điểm cực đại của hàm số
đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 21: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
2 3 4
' 1 3 2f x x x x x= − − −
với mọi
x
. Điểm cực tiểu
của hàm số đã cho là
A.
2x
. B.
3x
. C.
0x =
. D.
1x =
.
Câu 22: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
1 2 ,f x x x x x
= − −
. Số điểm cực trị của hàm số đã
cho là
A.
1
. B.
3
. C.
5
. D.
2
.
Câu 23: Hàm số
( )
y f x=
có đạo hàm
( ) ( )( ) ( )
1 2 ... 2019f x x x x
= − − −
,
xR
. Hàm số
( )
y f x=
có tt c bao nhiêu điểm cực tiểu?
A.
1008
B.
1010
C.
1009
D.
1011

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Câu 24: Hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
2
12f x x x x
= + −
,
x
. Hỏi
( )
fx
có bao nhiêu điểm
cực đại?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 25: Cho hàm số
( )
fx
có đạo hàm là
( ) ( )( )
2
12f x x x x x
= − +
. Số điểm cực trị của hàm số
là?
A.
5
. B.
2
. C.
1
. D.
3
.
Câu 26: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( ) ( ) ( )
2 3 4
1 2 3 4 , x .f x x x x x
= − − − −
Số điểm cực trị
của hàm số đã cho là
A.
3
B.
5
C.
2
D.
4
Câu 27: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
2
1 2 ,f x x x x x
= − −
. Số điểm cực trị của hàm số đã
cho là
A.
5
. B.
2
. C.
1
. D.
3
.
Câu 28: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )( )
24
2 3 9f x x x x
= − − −
. Số điểm cực trị của hàm số
( )
y f x=
là
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 29: Nu hàm số
fx
có đạo hàm là
4
22
' 2 2 1f x x x x x x
thì tổng cc điểm cực trị
của hàm số
fx
bng
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 30: Cho hàm số
( )
y f x=
có đạo hàm trên và
( ) ( )( ) ( )
2
1 2 3f x x x x
= − − +
. Số điểm cực trị của
hàm số đã cho là:
A.
3
B.
1
C.
0
D.
2
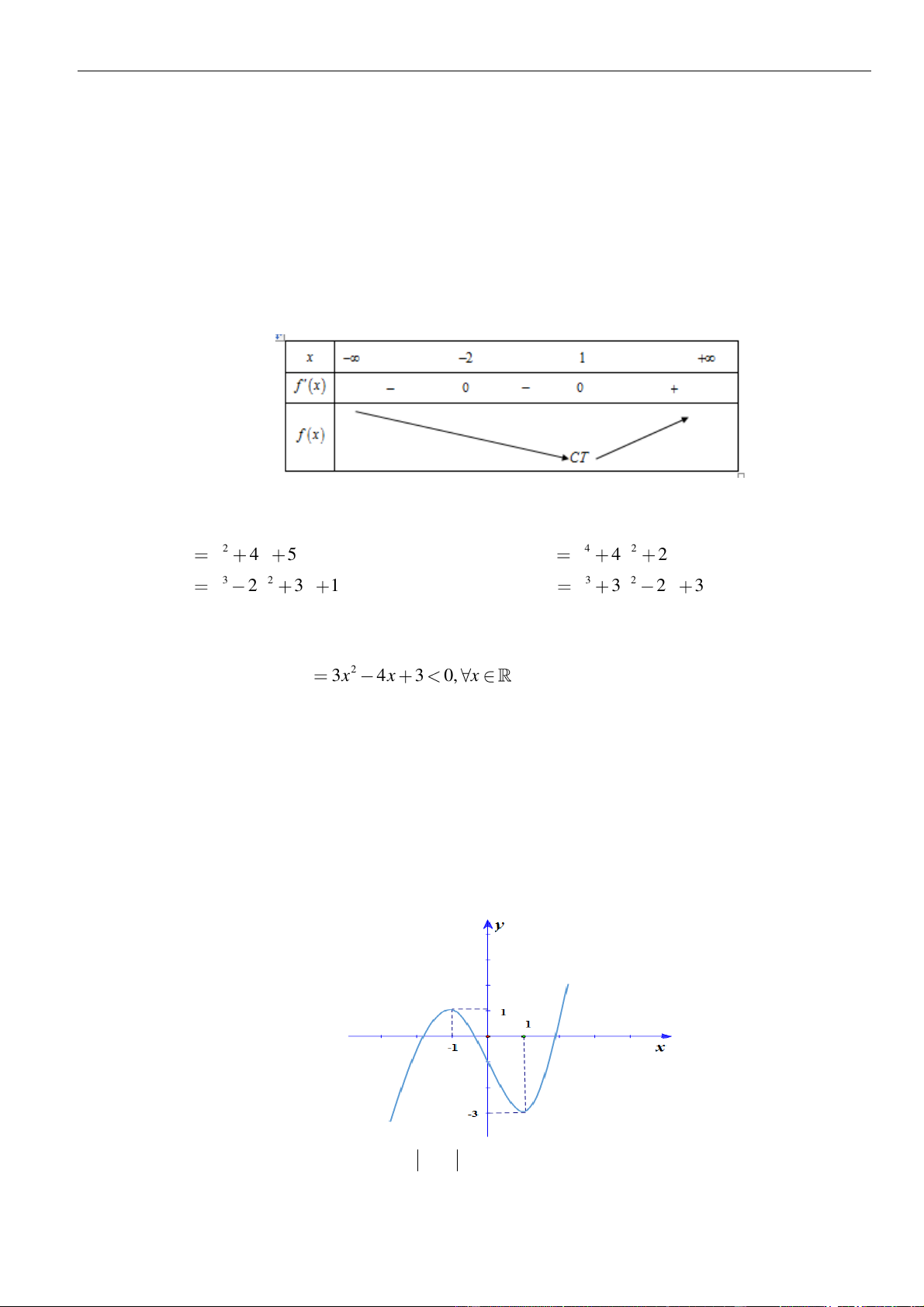
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
()fx
có đạo hàm
2
'( ) ( 1)( 2) ,= − + f x x x x R
. Số điểm cực trị của hàm số đã cho
là:
A. 3 B. 1 C. 5 D. 2
Lời giải
Chọn B
Ta có:
1
'( ) 0
2
x
fx
x
=
=
=−
Bng bin thiên:
Từ đó suy ra hàm số đã cho có 1 điểm cực trị.
Câu 2: Hàm số nào dưới đây không có cực trị
A.
2
45y x x
. B.
42
42y x x
.
C.
32
2 3 1y x x x
. D.
32
3 2 3y x x x
.
Lời giải
Chọn C
Xét phương n C:
2
' 3 4 3 0,y x x x
nên hàm số không có cực trị.
Câu 3: Cho hàm số
( )
fx
có đạo hàm là
( ) ( ) ( )
23
23f x x x x
= − −
. Số điểm cực trị của hàm số
( )
fx
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Ta có
( )
0fx
=
có hai nghim bc lẻ là
0x =
và
3x =
nên hàm số có hai điểm cực trị.
Câu 4: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ:
Số điểm cực trị của hàm số
( )
2.y f x=+
A.
2.
B.
1.
C.
3.
D.
5.
Lời giải
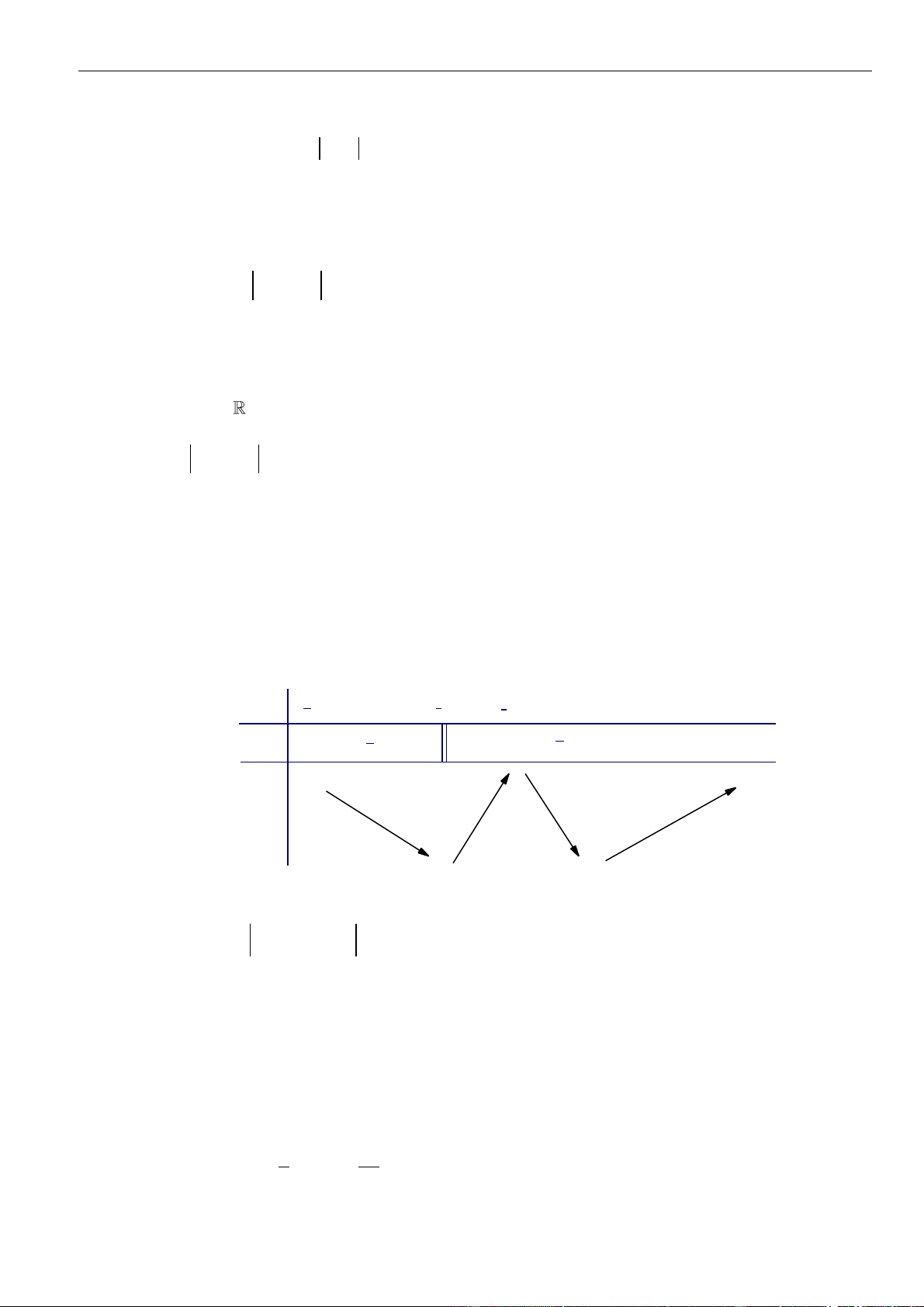
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Chọn B
Tịnh tin hàm số
( )
y f x=
sang tri hai đơn vị ta được hàm số
( )
2y f x=+
Đồ thị hàm số
( )
2.y f x=+
có được gồm 2 phn.
Phn 1: Là phn đồ thị
( )
2y f x=+
nm pha bên phi
Oy
.
Phn 2: Là phn đồ thị đối xng qua
Oy
.
Khi đó đồ thị hàm số sẽ có
1
điểm cực trị.
Câu 5: Hàm số
32
3y x x=+
đạt cực tiểu tại
A.
0x =
. B.
4x =
. C.
0x =
và
3xa= −
. D.
3x =−
và
0x =
.
Lời giải
Chọn D
TXĐ
D =
.
32
32
32
3 khi 3
3
3 khi 3
x x x
y x x
x x x
+ −
= + =
− − −
.
2
2
3 6 khi 3
3 6 khi 3
x x x
y
x x x
+ −
=
− − −
.
0
0
2
x
y
x
=
=
=−
.
Bng bin thiên.
Vy hàm số đạt cực tiểu tại
3x =−
và
0x =
.
Câu 6: Hàm số
( ) ( )
3
11y x x= − +
có bao nhiêu điểm cực trị?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
Xét hàm số
( ) ( )
3
11y x x= − +
Ta có đạo hàm
( ) ( ) ( ) ( ) ( )
2 3 2
' 3 1 1 1 1 4 2y x x x x x= − + + − = − +
10
'0
1 27
2 16
xy
y
xy
= =
=
= − = −
Bng bin thiên
∞
+
∞
+
+
0
2
x
y'
y
3
0
+
+
0
∞
∞
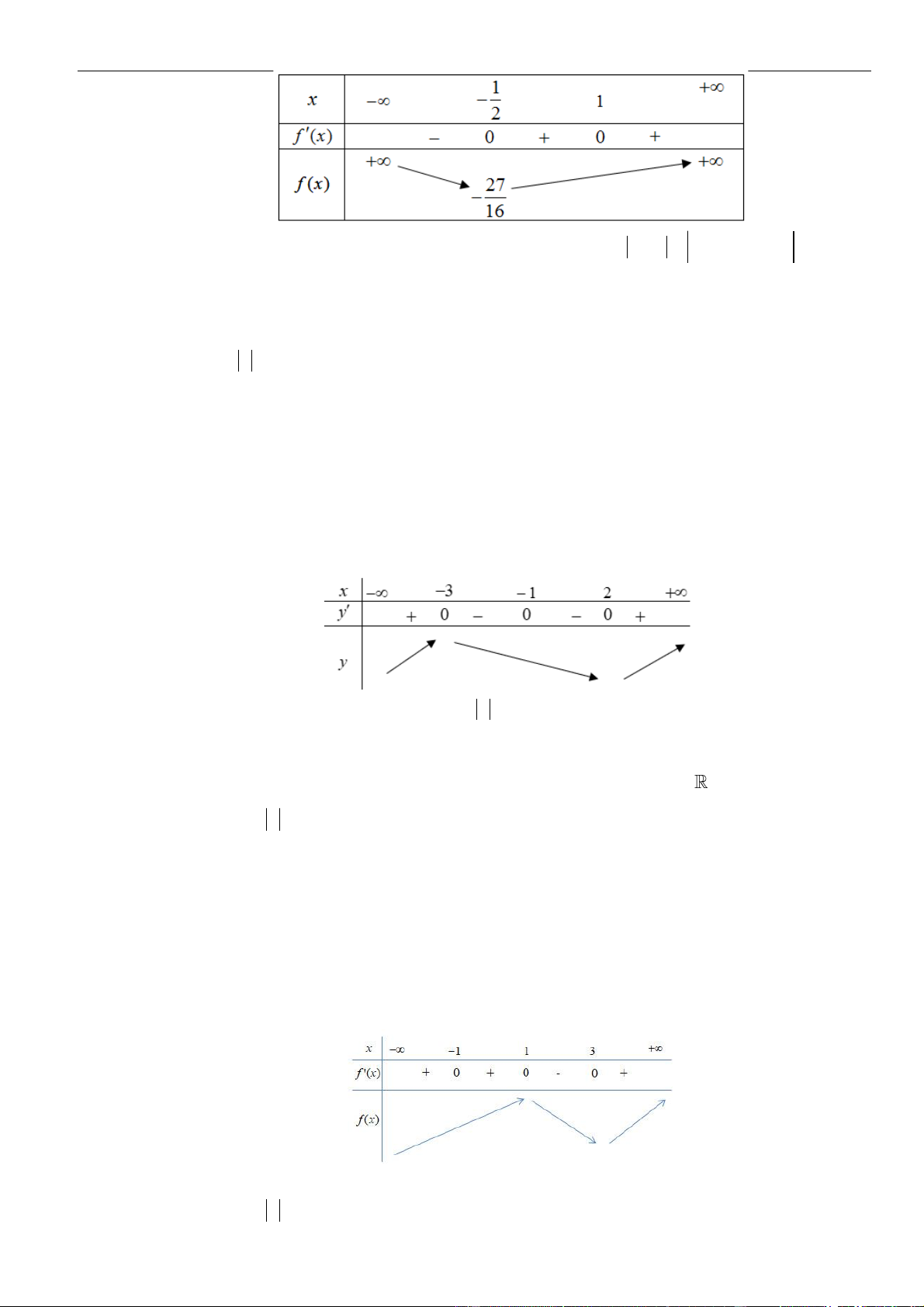
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Dựa vào bng bin thiên hàm số
()y f x=
Suy ra hàm số
( ) ( )
3
( ) 1 1y f x x x= = − +
có 3 cực
trị.
Câu 7: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
( )
( )
2020
2019 3
2
2 2 3f x x x x x
= − − − +
. Số điểm cực trị của
hàm số
( )
fx
là:
A.
5
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
Ta có:
( ) ( )
( )
( )
2020
2019 3
2
2
0 2 2 3 0 1
3
x
f x x x x x x
x
=
= − − − + = = −
=−
.
Bng bin thiên
Từ bng bin thiên: đồ thị của hàm số
( )
fx
được giữ lại phn
0x
rồi ly đối xng qua
Oy
. Khi đó hàm số có
3
cực trị.
Câu 8: Cho hàm số
()y f x=
có đạo hàm
( )
( )
( )
3
2
' ( 1) 1 3 , f x x x x x= + − −
. Số điểm cực trị của
hàm số
()y f x=
là:
A. 2. B. 5. C. 3. D. 1.
Lời giải
Chọn A
Ta có
( )
( )
( )
3
2
1
' 0 ( 1) 1 3 0 1
3
x
f x x x x x
x
=−
= + − − = =
=
Căn c BBT ta thy số điểm cực trị dương của hàm số
()y f x=
là 2 nên số điểm cực trị của
hàm số
()y f x=
là 5. Chọn đp n B.
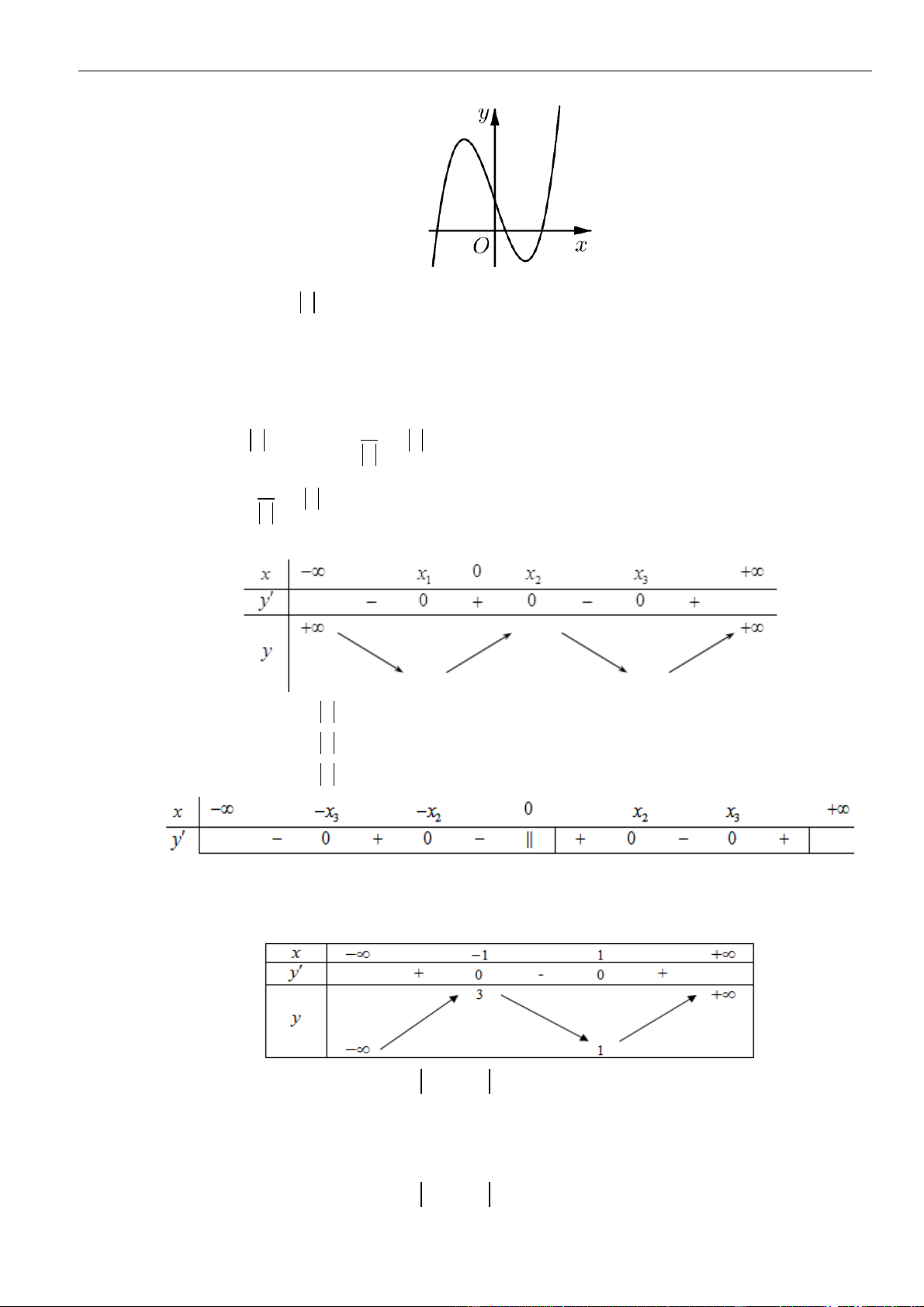
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Câu 9: Cho hàm số
( )
.y f x=
Đồ thị của hàm số
( )
y f x
=
như hình bên.
Hàm số
( )
( )
2021g x f x=+
có bao nhiêu điểm cực trị?
A.
5
. B.
7
. C.
3
. D.
2
.
Lời giải
Chọn A
( )
( )
( )
( )
2021
x
g x f x f x
x
= + =
.
( )
( )
00
x
g x f x
x
= =
. Ta có:
( )
gx
không xc định tại điểm
0x =
.
BBT
Dựa vào BBT ta có:
1
2
2
3
3
xx
xx
xx
xx
xx
=
=
=
=
=
Vy hàm số có
5
điểm cực trị.
Câu 10: Cho hàm số
( )
y f x=
có bng bin thiên như hình vẽ
Số điểm cực trị của hàm số
( ) ( )
2g x f x=−
là
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn D
Số điểm cực trị của hàm số
( ) ( )
2g x f x=−
bng
mn+
.
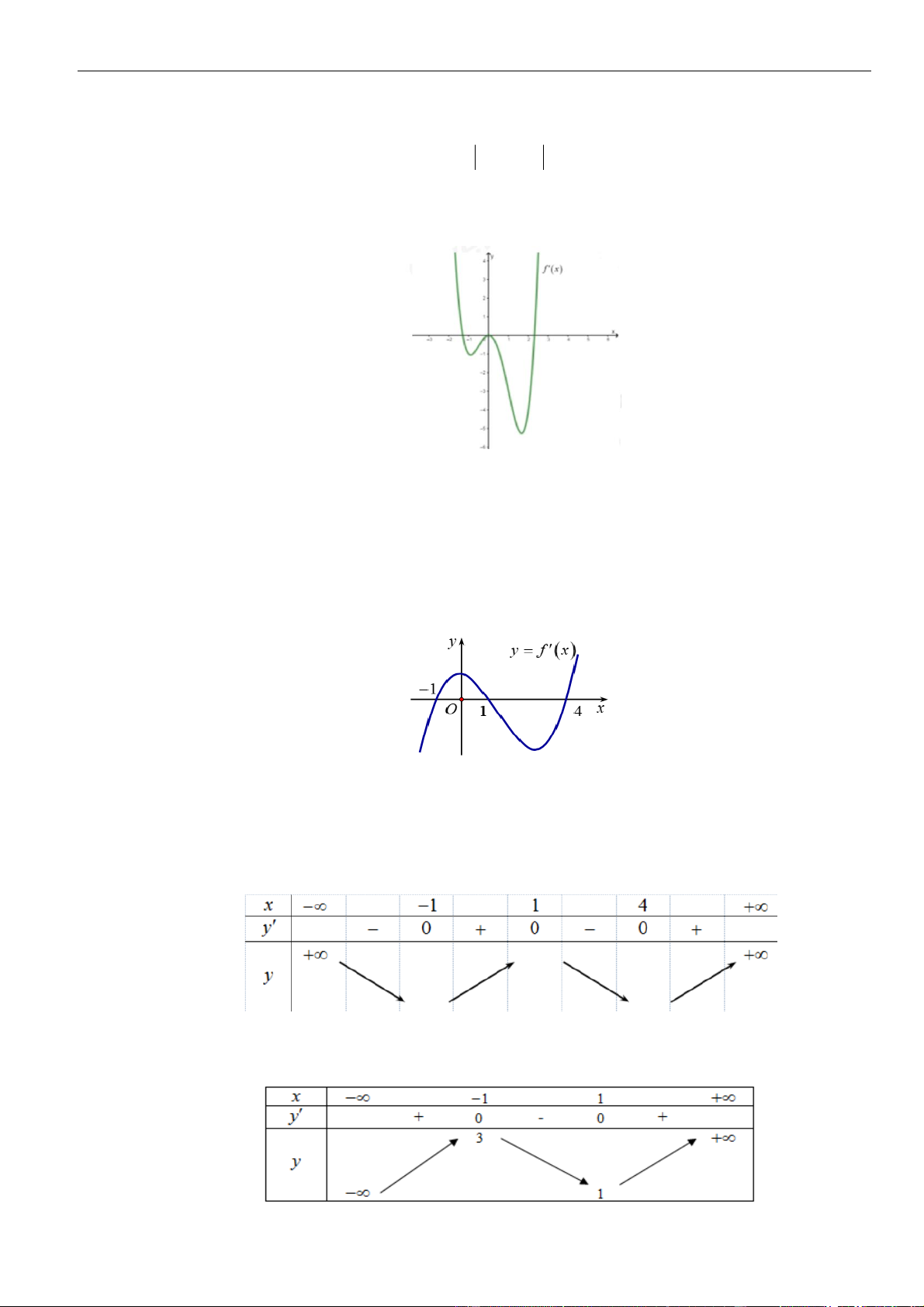
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
+
m
là số điểm cực trị của hàm số
( )
22y f x m= − =
.
+
n
là số nghim bội lẻ của phương trình
( )
23f x n= =
.
Suy ra, số điểm cực trị của hàm số
( ) ( )
2g x f x=−
bng
5
.
Câu 11: Cho hàm số
( )
y f x=
xc định và liên tục trên có đạo hàm
( )
y f x
=
có đồ thị như hình vẽ. Số
điểm cực tiểu của hàm số là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Hàm số đạt cực tiểu tại điểm có
( )
fx
đổi du từ âm sang dương. Dựa vào đồ thị thì đồ thị hàm
số có 1 điểm cực tiểu.
Câu 12: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị như hình bên.
Hàm số
( )
=y f x
có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn B
Dựa vào đồ thị ta có BBT:
Suy ra hàm số có ba điểm cực trị.
Câu 13: Cho hàm số
( )
y f x=
có bng bin thiên như hình vẽ
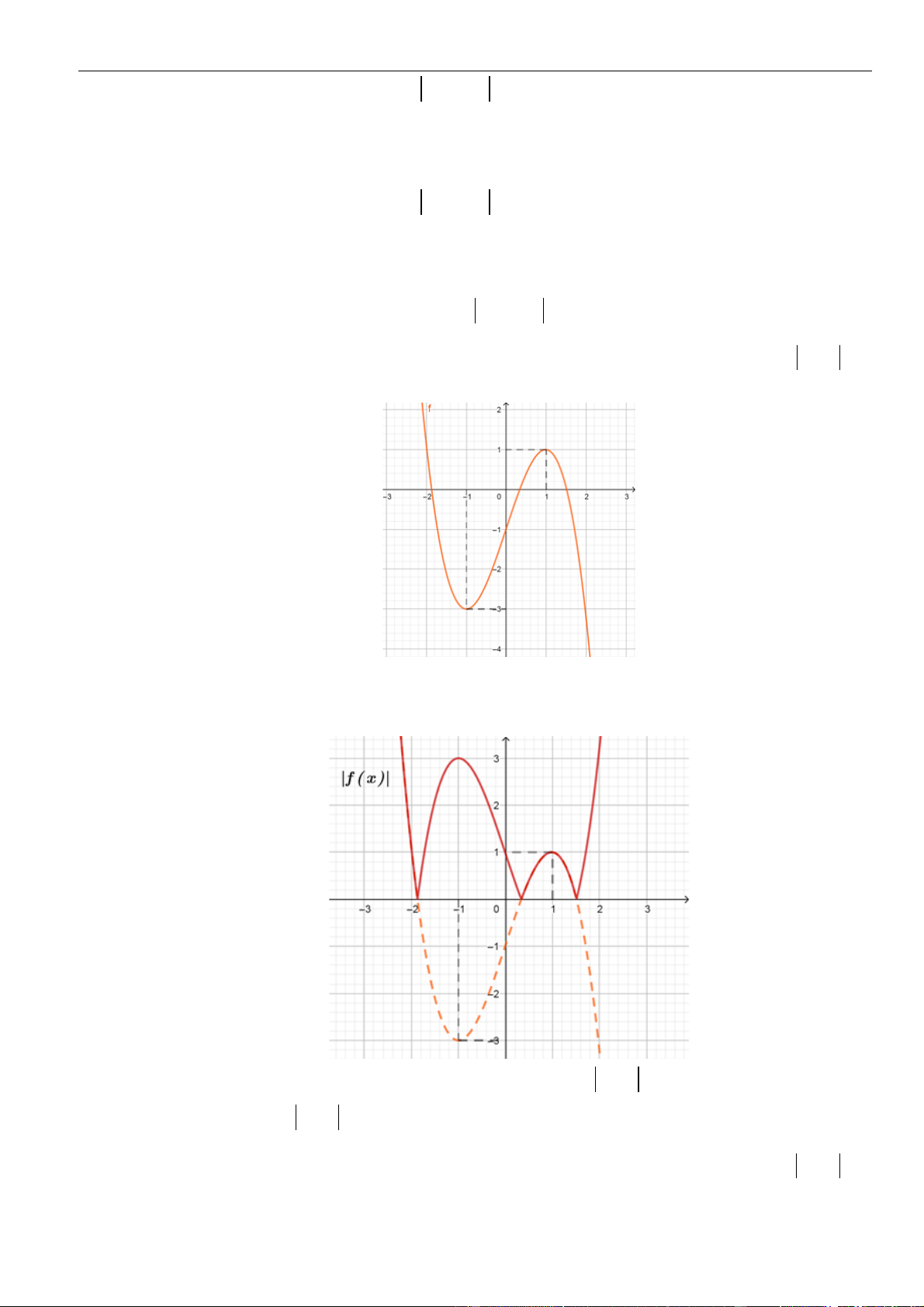
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Số điểm cực trị của hàm số
( ) ( )
2g x f x=−
là
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn D
Số điểm cực trị của hàm số
( ) ( )
2g x f x=−
bng
mn+
.
+
m
là số điểm cực trị của hàm số
( )
22y f x m= − =
.
+
n
là số nghim bội lẻ của phương trình
( )
23f x n= =
.
Suy ra, số điểm cực trị của hàm số
( ) ( )
2g x f x=−
bng
5
.
Câu 14: Đồ thị của hàm số
( ) ( )
32
0y f x ax bx cx d a= = + + +
như hình vẽ bên. Hàm số
( )
y f x=
có
bao nhiêu điểm cực trị?
A.
4
. B.
5
. C.
3
. D.
2
.
Lời giải
Chọn B
Từ đồ thị hàm số
( )
y f x=
suy ra được đồ thị hàm số
( )
y f x=
như hình vẽ.
Do đó hàm số
( )
y f x=
có 5 điểm cực trị.
Câu 15: Đồ thị hàm số
( ) ( )
32
0y f x ax bx cx d a= = + + +
như hình vẽ bên. Hàm số
( )
y f x=
có
bao nhiêu điểm cực trị?
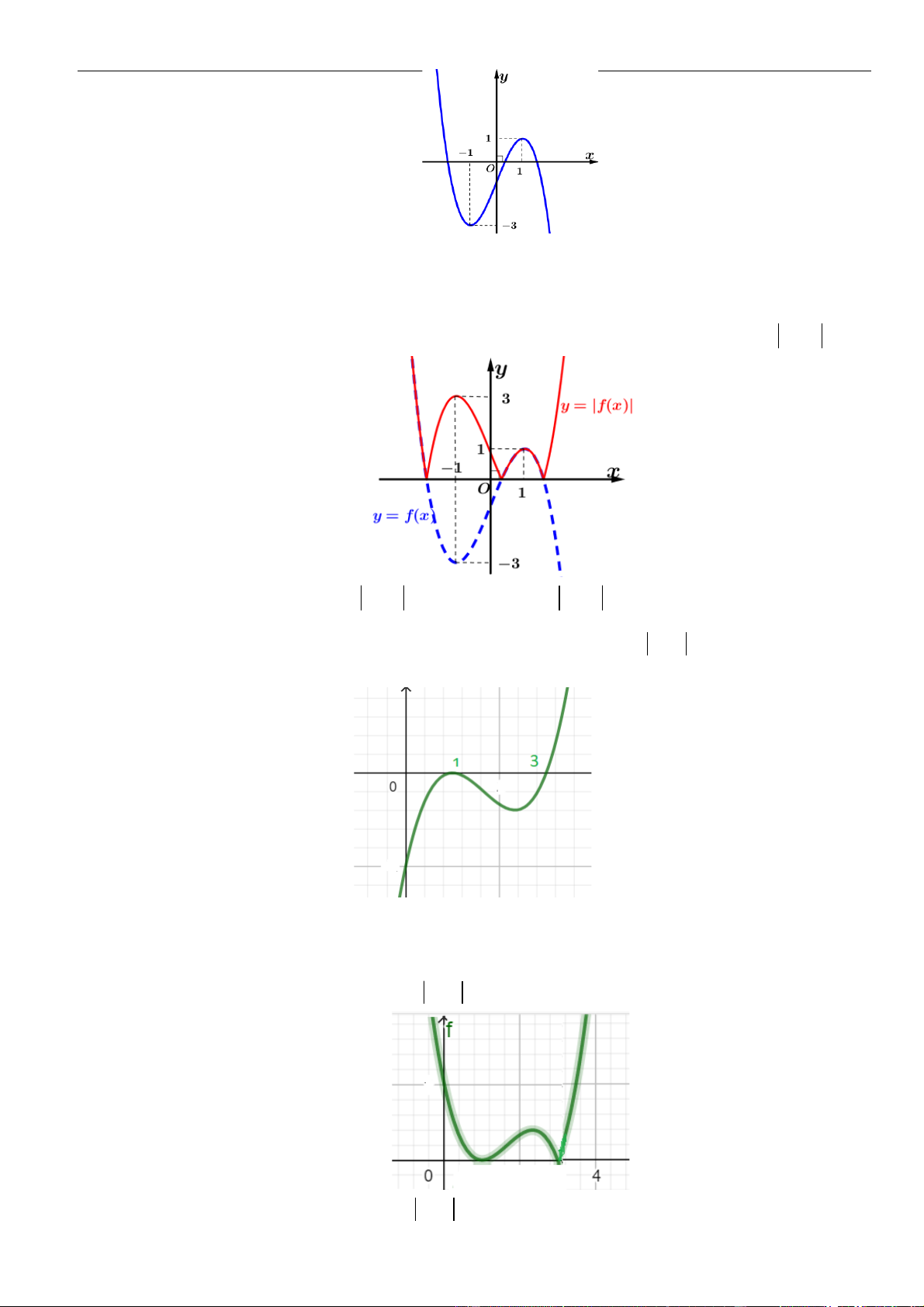
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
A.
4
. B.
5
. C.
3
. D.
2
.
Lời giải
Chọn B
Từ đồ thị hàm số
( ) ( )
32
0y f x ax bx cx d a= = + + +
ta suy ra đồ thị hàm số
( )
y f x=
.
Dựa vào đồ thị hàm số
( )
y f x=
ta thy hàm số
( )
y f x=
có điểm
5
cực trị.
Câu 16: Cho hàm số bc ba
()y f x=
có đồ thị như hình vẽ. Hàm số
()y f x=
có bao nhiêu điểm cực
trị?
A.
3
. B.
5
. C.
2
. D.
1
.
Lời giải
Chọn A
Từ gi thit ta có đồ thị hàm số
()y f x=
như sau
Dựa vào đồ thị ta thy hàm số
()y f x=
có 3 cực trị.
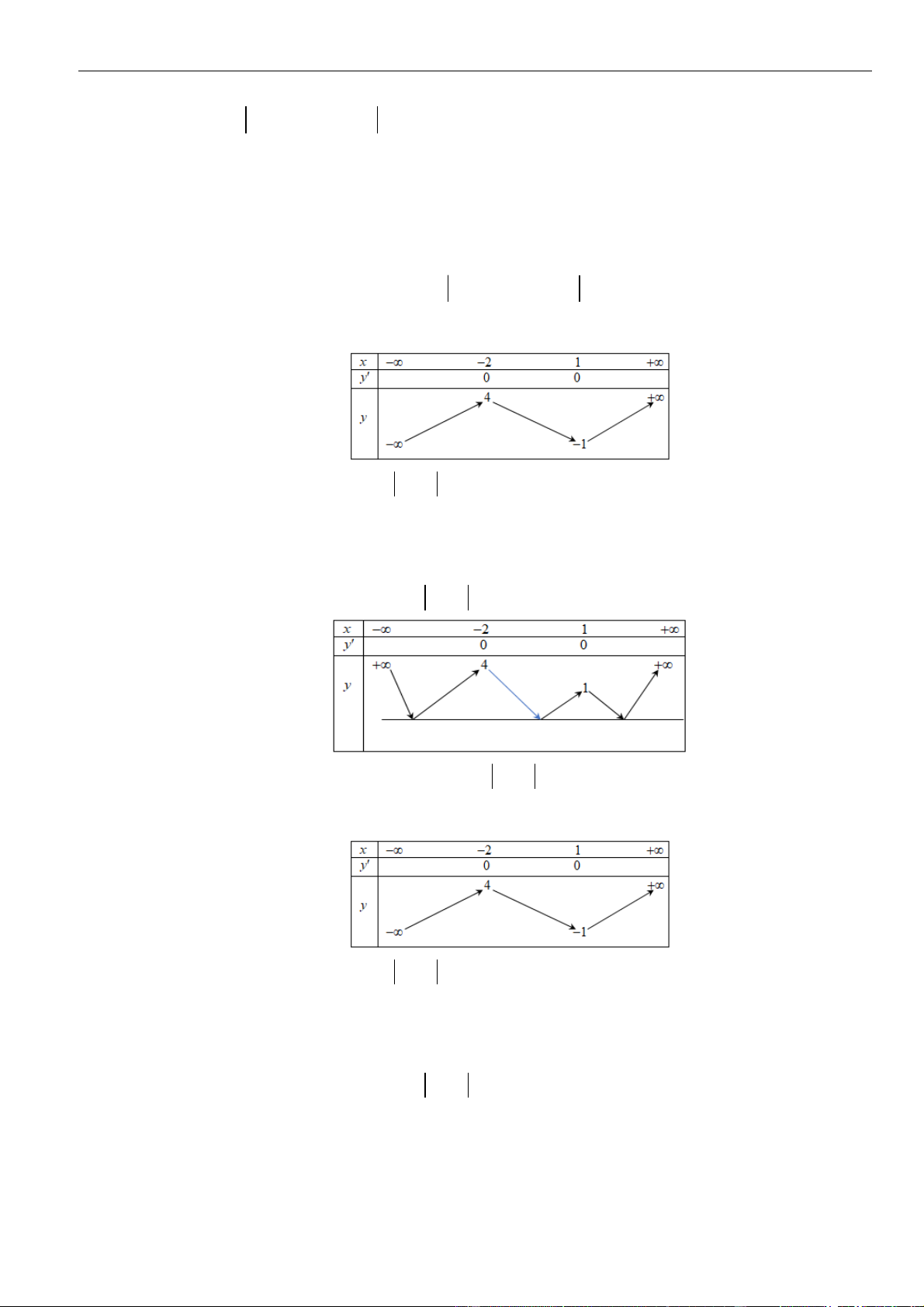
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Câu 17: Cho hàm số
32
y ax bx cx d= + + +
có đồ thị ct trục hoành tại ba điểm phân bit. Số cực trị của
hàm số
32
y ax bx cx d= + + +
là
A. 3. B. 5. C. 4. D. 1.
Lời giải
Chọn B
Vì hàm số
32
y ax bx cx d= + + +
có đồ thị ct trục hoành tại ba điểm phân bit nên hàm số này
là hàm số bc ba và có 2 điểm cực trị.
Khi đó số điểm cực trị của hàm số
32
y ax bx cx d= + + +
bng
2 3 5+=
Câu 18: Cho hàm số
( )
y f x=
có bng bin thiên như hình sau:
Số điểm cực trị của hàm số
( )
y f x=
là
A.
4
. B.
3
. C.
2
D.
5
Lời giải
Chọn D
Khi đó, bng bin thiên hàm số
( )
y f x=
sẽ có dạng
Dựa vào bng bin thiên, ta thy hàm số
( )
y f x=
có 5 điểm cực trị.
Câu 19: Cho hàm số
( )
y f x=
có bng bin thiên như hình sau:
Số điểm cực trị của hàm số
( )
y f x=
là
A.
4
. B.
3
. C.
2
D.
5
Lời giải
Chọn D
Khi đó, bng bin thiên hàm số
( )
y f x=
sẽ có dạng
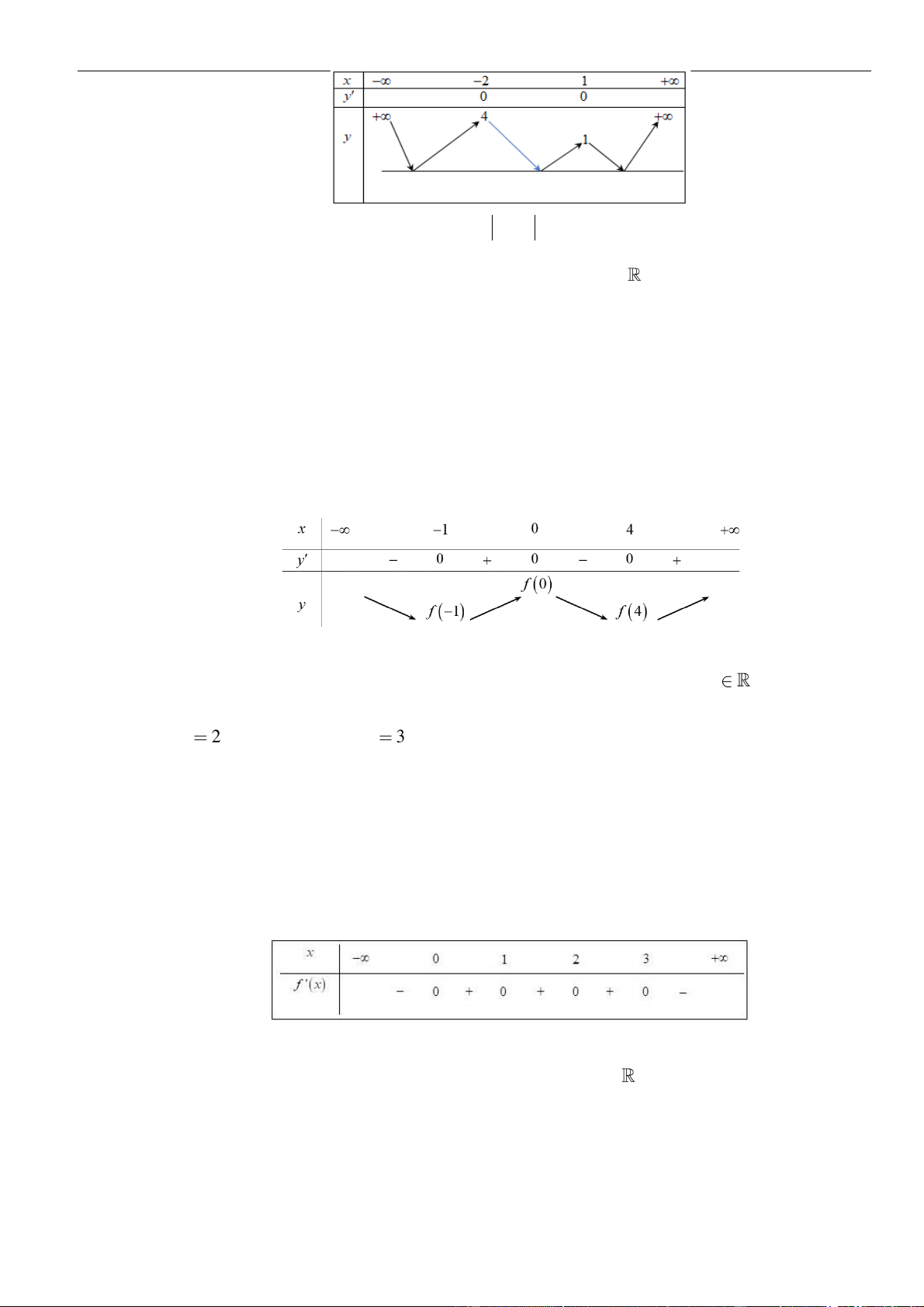
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Dựa vào bng bin thiên, ta thy hàm số
( )
y f x=
có 5 điểm cực trị.
Câu 20: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
1 4 ,f x x x x x
= + −
. Số điểm cực đại của hàm số
đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn D
( ) ( )( )
3
0
0 1 4 0 1
4
x
f x x x x x
x
=
= + − = = −
=
.
Lp bng bin thiên của hàm số
( )
fx
Vy hàm số đã cho có một điểm cực đại.
Câu 21: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
2 3 4
' 1 3 2f x x x x x= − − −
với mọi
x
. Điểm cực tiểu
của hàm số đã cho là
A.
2x
. B.
3x
. C.
0x =
. D.
1x =
.
Lời giải
Ta có
( ) ( ) ( ) ( ) ( )
2 3 4
0
1
' 1 3 2 ' 0
2
3
x
x
f x x x x x f x
x
x
=
=
= − − − =
=
=
.
Bng xét du đạo hàm.
Suy ra hàm số
( )
fx
đạt cực tiểu tại
0x =
Câu 22: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
1 2 ,f x x x x x
= − −
. Số điểm cực trị của hàm số đã
cho là
A.
1
. B.
3
. C.
5
. D.
2
.
Lời giải
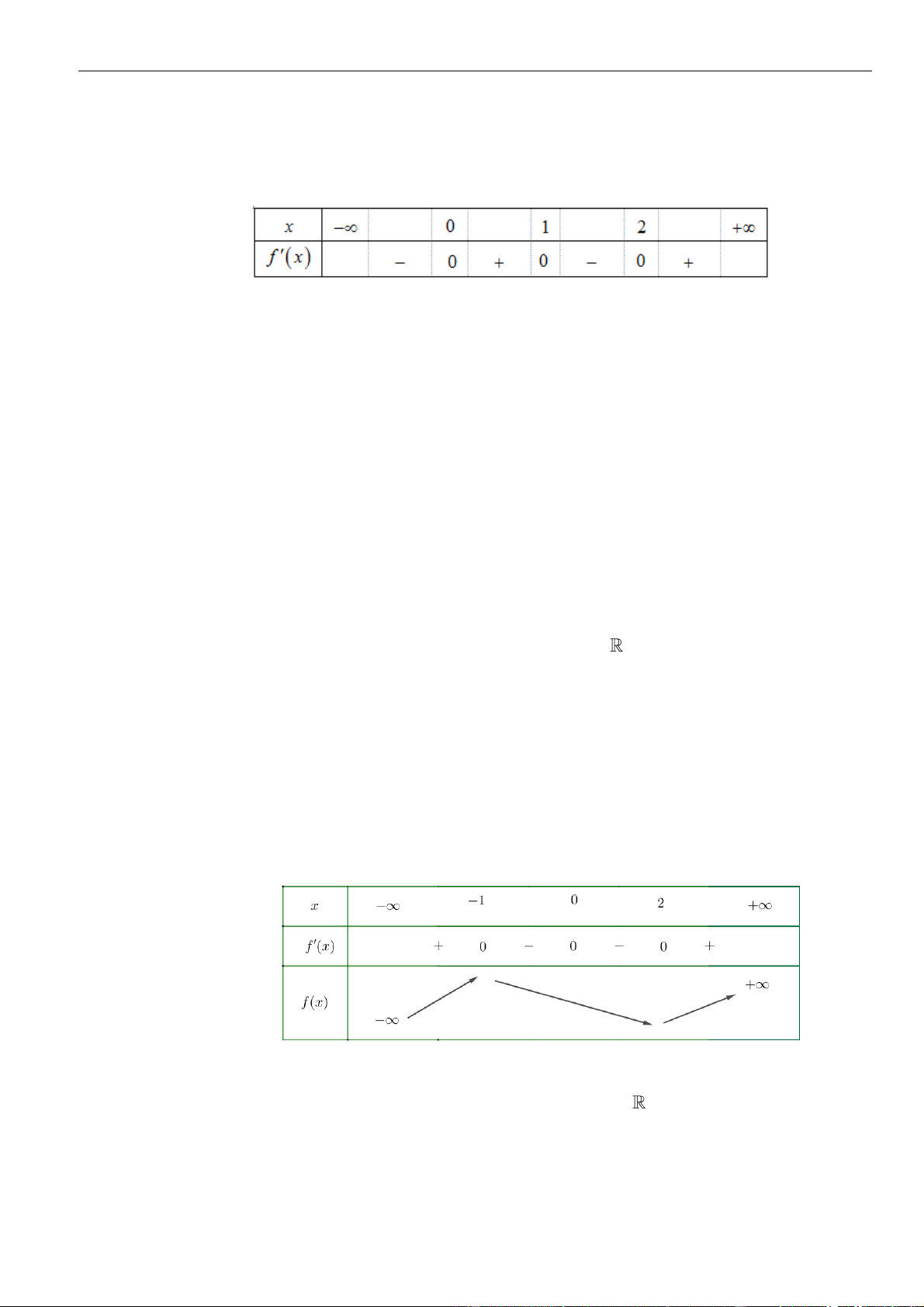
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Ta có:
( ) ( )( )
3
0
0 1 2 0 1
2
x
f x x x x x
x
=
= − − = =
=
.
Bng xét du:
Dựa vào bng xét du nhn thy hàm số
( )
fx
có
3
điểm cực trị.
Câu 23: Hàm số
( )
y f x=
có đạo hàm
( ) ( )( ) ( )
1 2 ... 2019f x x x x
= − − −
,
xR
. Hàm số
( )
y f x=
có tt c bao nhiêu điểm cực tiểu?
A.
1008
B.
1010
C.
1009
D.
1011
Lời giải
Chọn B
Ta có:
( ) ( )( ) ( )
1
2
1 2 ... 2019 0
......
2019
x
x
f x x x x
x
=
=
= − − − =
=
( )
0fx
=
có
2019
nghim bội lẻ và h số
a
dương nên có
1010
cực tiểu
Câu 24: Hàm số
( )
fx
có đạo hàm
( ) ( )( )
3
2
12f x x x x
= + −
,
x
. Hỏi
( )
fx
có bao nhiêu điểm
cực đại?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Ta có
( )
( )
2
3
00
0 1 0 1
2
20
xx
f x x x
x
x
==
= − = =
=
−=
.
Bng bin thiên
Dựa vào bng bin thiên suy ra hàm số có
1
điểm cực đại.
Câu 25: Cho hàm số
( )
fx
có đạo hàm là
( ) ( )( )
2
12f x x x x x
= − +
. Số điểm cực trị của hàm số
là?
A.
5
. B.
2
. C.
1
. D.
3
.
Lời giải

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Ta có
( )
0
01
2
x
f x x
x
=
= =
=−
. Do
0, 1xx==
là nghim đơn, còn cc nghim và
2x =−
là
nghim bội chẵn nên
( )
fx
chỉ đổi khi đi qua
0, 1xx==
.
Hàm số
( )
2
0
1 4 0 2 2
0
a
m m m
− −
có
2
điểm cực trị.
Câu 26: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( ) ( ) ( )
2 3 4
1 2 3 4 , x .f x x x x x
= − − − −
Số điểm cực trị
của hàm số đã cho là
A.
3
B.
5
C.
2
D.
4
Lời giải
Chọn C
( )
1
2
0
3
4
x
x
fx
x
x
=
=
=
=
=
Bng bin thiên:
Dựa vào bng bin thiên: Số điểm cực trị của hàm số đã cho là 2.
Câu 27: Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
2
1 2 ,f x x x x x
= − −
. Số điểm cực trị của hàm số đã
cho là
A.
5
. B.
2
. C.
1
. D.
3
.
Lời giải
Ta có
( ) ( )( )
2
0
0 1 2 0 1
2
x
f x x x x x
x
=
= − − = =
=
.
Lp bng xét du của
( )
fx
như sau:
Ta thy
( )
fx
đổi du khi đi qua cc điểm
0x =
và
1x =
, do đó hàm số
( )
y f x=
có hai điểm
cực trị.
Câu 28: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )( )
24
2 3 9f x x x x
= − − −
. Số điểm cực trị của hàm số
( )
y f x=
là
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
( ) ( )
( ) ( )
( )
( ) ( )
( )
22
2
2 2 2
2 3 3 2 3 3 3f x x x x x x x x
= − − + = − − + +
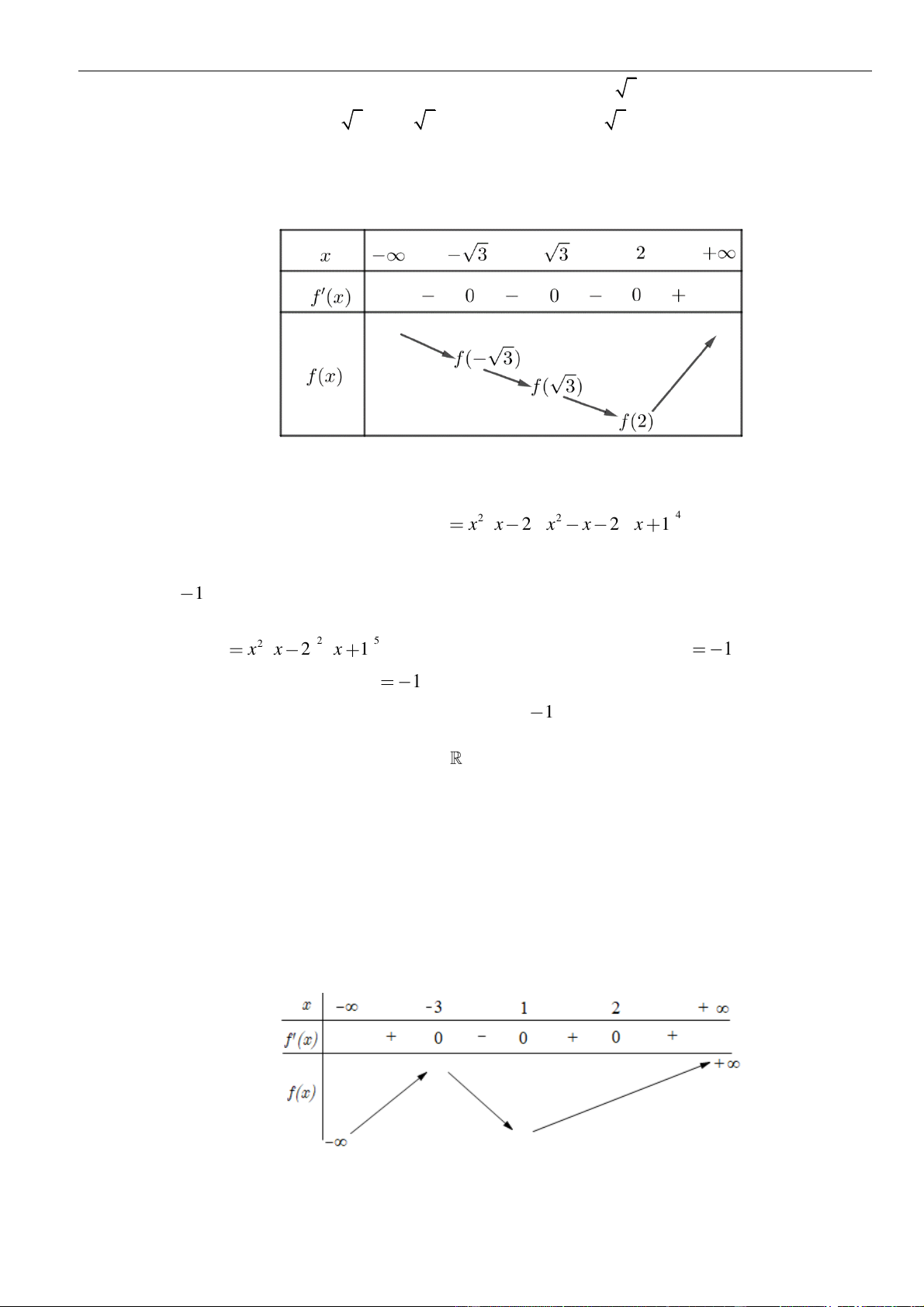
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
( ) ( )
( ) ( )
( )
22
2
0 2 3 3 3 0f x x x x x
= − + − + =
3
3
2
x
x
x
=−
=
=
.
Bng bin thiên
Từ bng bin thiên của hàm số
( )
y f x=
, ta thy hàm số
( )
y f x=
có đúng 1 điểm cực trị.
Câu 29: Nu hàm số
fx
có đạo hàm là
4
22
' 2 2 1f x x x x x x
thì tổng cc điểm cực trị
của hàm số
fx
bng
A.
1
. B.
2
. C.
1
. D.
0
.
Lời giải
Có
25
2
' 2 1f x x x x
. Ta thy
'fx
chỉ đổi du qua nghim
1x
nên hàm số
fx
có đúng một điểm cực trị là
1x
.
Vy tổng cc điểm cực trị của hàm số
fx
bng
1
.
Câu 30: Cho hàm số
( )
y f x=
có đạo hàm trên và
( ) ( )( ) ( )
2
1 2 3f x x x x
= − − +
. Số điểm cực trị của
hàm số đã cho là:
A.
3
B.
1
C.
0
D.
2
Lời giải
Chọn D
Ta có
( )
1
02
3
x
f x x
x
=
= =
=−
Bng bin thiên
Từ bng bin thiên ta thy hàm số đã cho có
2
điểm cực trị.
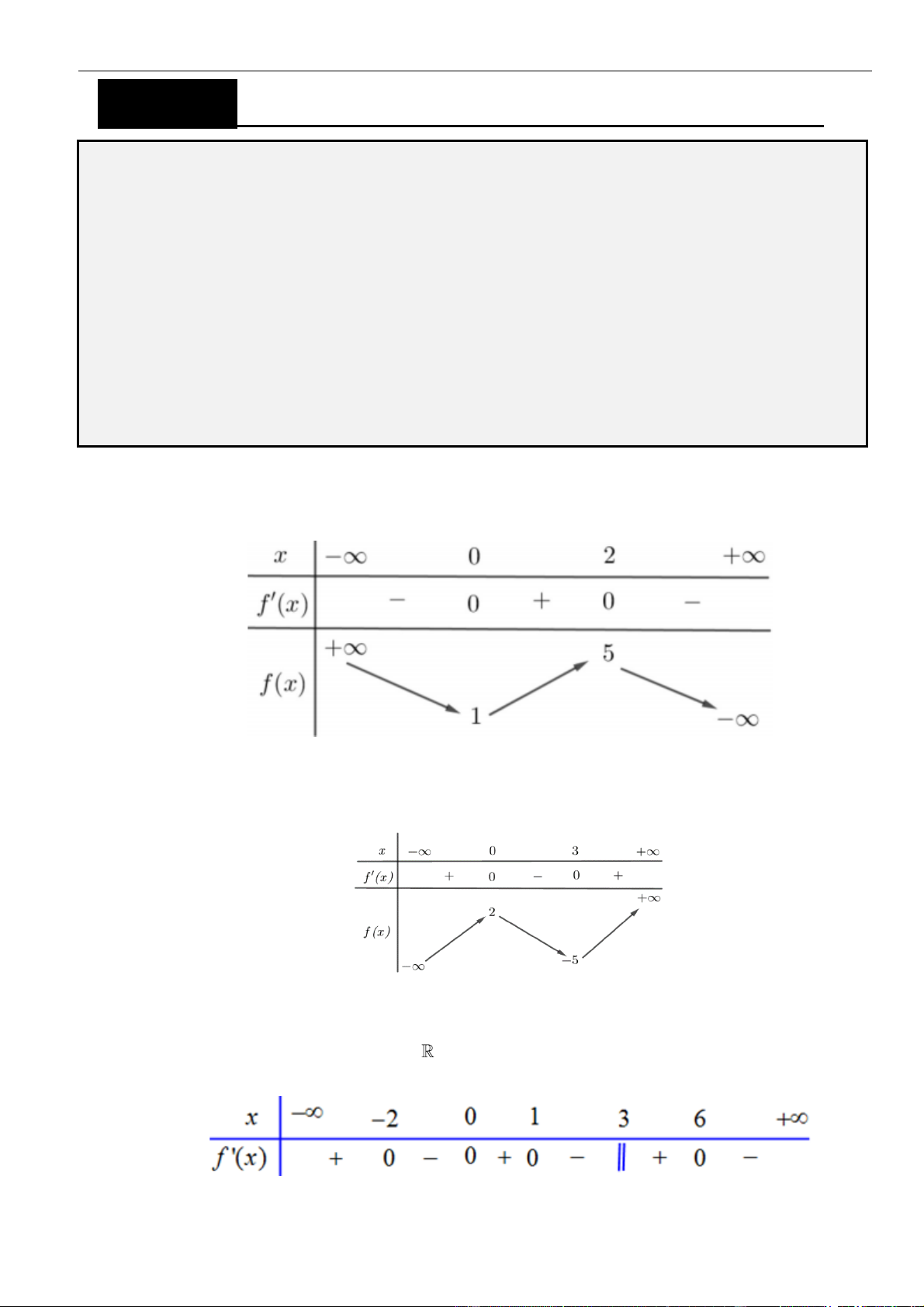
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho đặt cực đại tại điểm nào dưới đây
A.
5x =
. B.
2x =
. C.
0x =
. D.
1x =
.
Câu 2: Cho hàm
()y f x=
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
3
. B.
2
. C.
0
. D.
5−
.
Câu 3: Cho hàm số
()y f x=
liên tục trên và có bảng xét dấu đạo hàm như hình bên. Hỏi hàm số đã
cho có bao nhiêu điểm cực trị?
A.
3
. B.
4
. C.
2
. D.
5
.
Tìm cực trị của hàm tổng và hàm hợp
DẠNG 4
Phương pháp:
Bài toán: Cho hàm số
( )
y f x=
(Đề có thể cho bằng hàm, đồ thị, bảng biến thiên của
( ) ( )
,'f x f x
).
Tìm số điểm cực trị của hàm số
( )
y f u=
trong đó
u
là một hàm số đối với
x
. Ta thực hiện phương
pháp tương tự xét số điểm cực trị của hàm số
( )
y f x=
• Bước 1. Tính đạo hàm
( )
' '. 'y u f u=
• Bước 2. Giải phương trình
( )
'0
'0
'0
u
y
fu
=
=
=
• Bước 3.Tìm số nghiệm đơn và bội lẻ hoặc các điểm mà
'y
không xác định.
• Bước 4. Kết luận
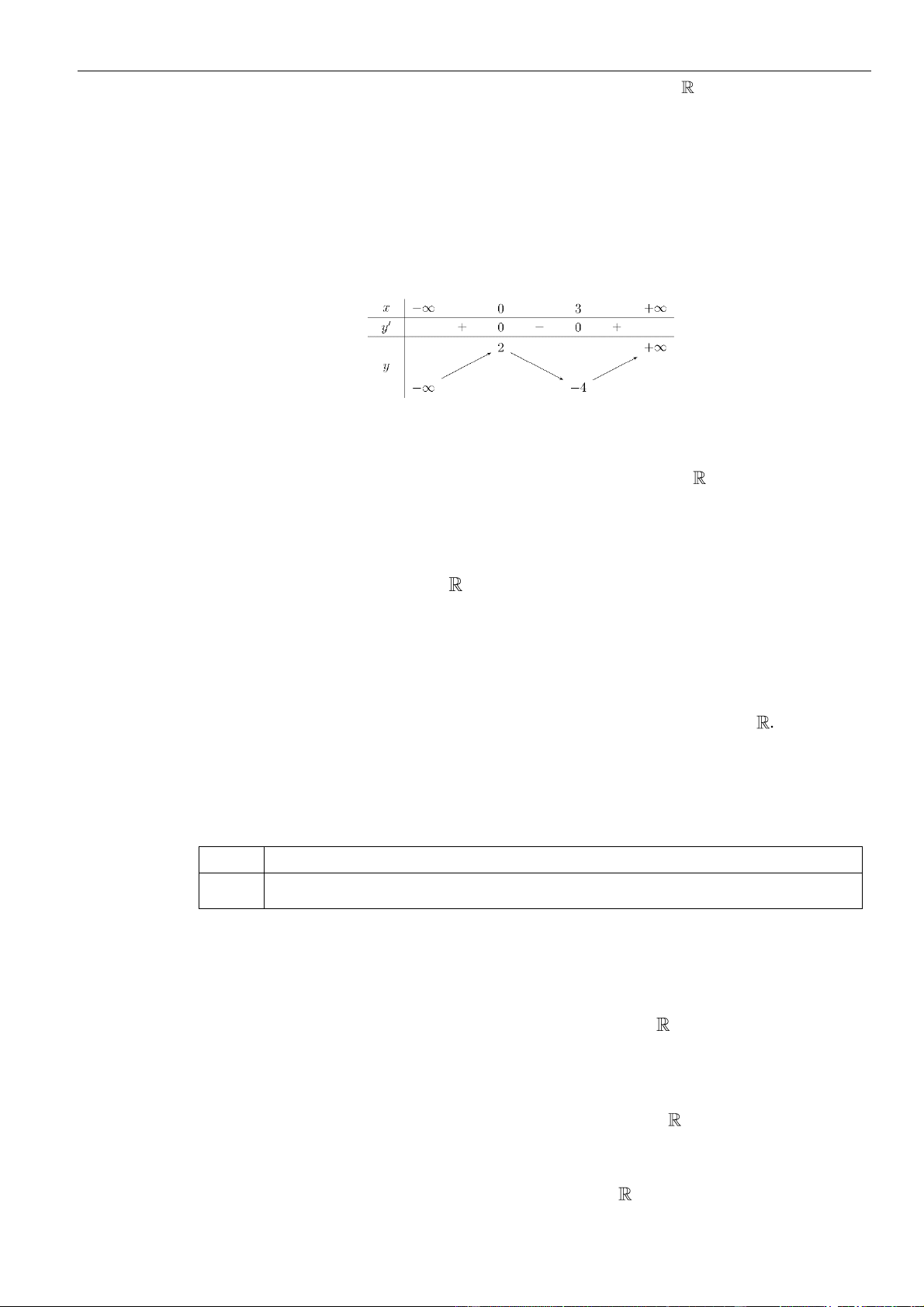
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 4: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( )
3
2
21f x x x x
= + −
với
x
. Hàm số đã cho có bao
nhiêu điểm cực trị?
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 5: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( )
2
1 2 3f x x x x
= − +
. Hàm số đã cho có bao nhiêu điểm
cực trị?
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 6: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng?
A. 2 B. 3. C. 0 D. -4
Câu 7: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
2 3 4
1 2 3f x x x x x
= − − −
,
x
. Số điểm cực trị của
hàm số
( )
fx
là
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 8: Hàm số
( )
fx
xác định và liên tục trên và có đạo hàm
( ) ( ) ( )
2
2 1 1f x x x
= − − +
. Khi đó hàm
số
( )
fx
A. đạt cực đại tại điểm
1x =−
. B. đạt cực tiểu tại điểm
1x =−
.
C. đạt cực đại tại điểm
1x =
. D. đạt cực tiểu tại điểm
1x =
.
Câu 9: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( ) ( ) ( )
3 4 5
1 2 3 5 ; .f x x x x x x
= + − − +
Hỏi hàm số
( )
y f x=
có mấy điểm cực trị?
A.
4
. B.
3
. C.
2
. D.
5
.
Câu 10: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm
( )
'fx
như sau:
x
−
2−
1−
0
2
4
+
( )
'fx
−
0
+
0
−
0
−
0
+
0
−
Hàm số đã cho có bao nhiêu điểm cực trị?
A.
3
. B.
2
. C.
5
. D.
4
.
Câu 11: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )
23
2021
' 1 2 ,f x x x x x= − +
. Số điểm cực trị của hàm
số đã cho là
A.
3
. B.
2
. C.
6
. D.
1
.
Câu 12: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
( )
2
39f x x x
= + −
với mọi
x
. Hàm số đã cho có bao
nhiêu điểm cực trị?
Câu 13: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )
3
1 2 ,
= − + f x x x x x
. Số điểm cực trị của hàm số đã
cho là
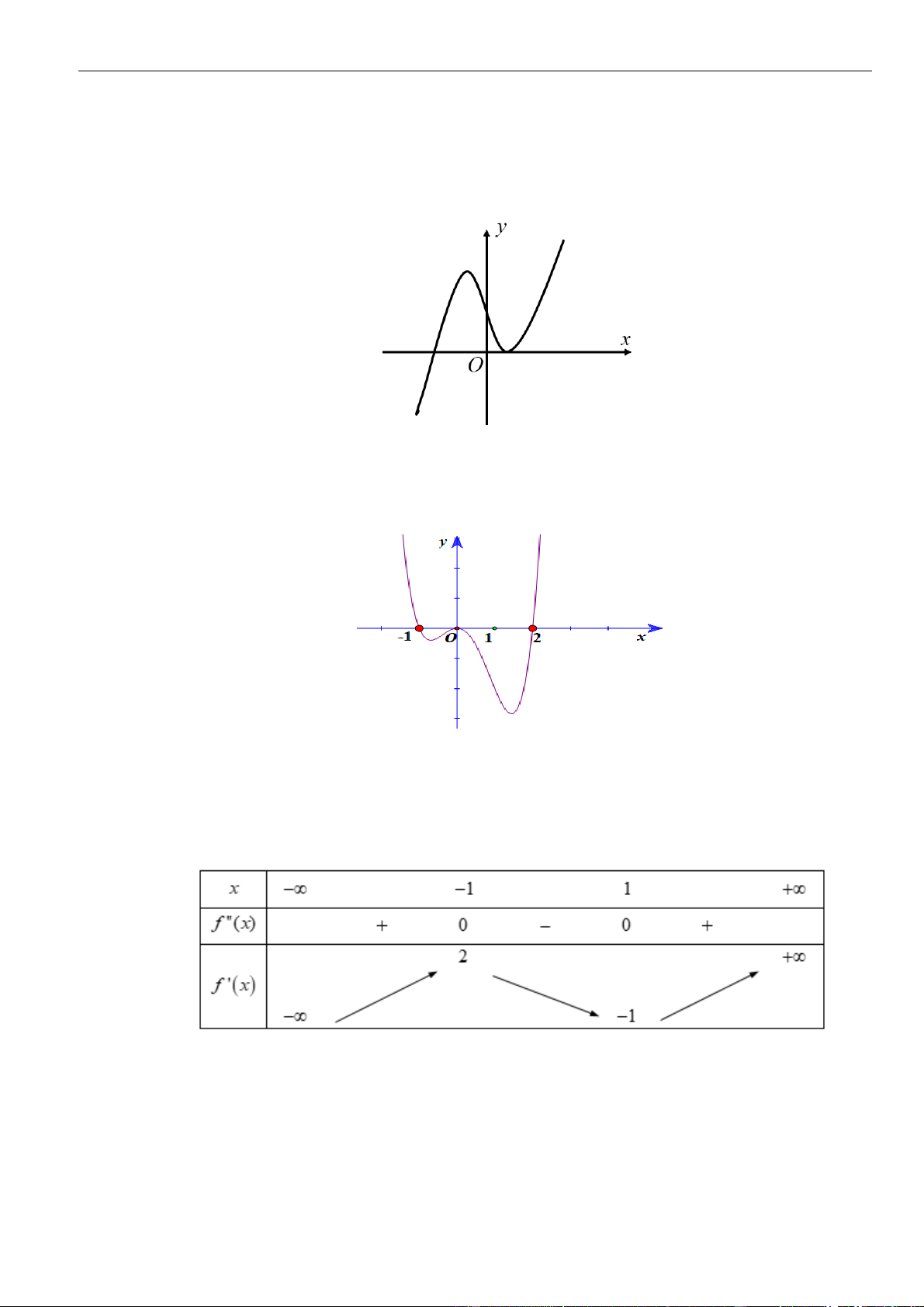
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
2
. B.
3
. C.
5
. D.
1
.
Câu 14:
Cho hàm số
f
có đạo hàm là
( ) ( ) ( )
23
13f x x x x
= − +
. Số điểm cực trị của hàm số
f
là:
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 15: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị như hình vẽ.
Số điểm cực trị của hàm số
( )
y f x=
là:
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 16: Cho hàm số
()y f x=
có đồ thị hàm
'( )fx
như hình vẽ
Số điểm cực trị của hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 17: Cho hàm số
( )
fx
liên tục trên R và hàm số
( )
'fx
có bảng biến thiên như sau. Tìm mệnh đề
đúng?
A. Hàm số
( )
y f x=
có 2 điểm cực tiểu và 1 điểm cực đại.
B. Hàm số
( )
y f x=
có 1 điểm cực tiểu và 1 điểm cực đại.
C. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
D. Hàm số
( )
y f x=
có 1 điểm cực tiểu và 2 điểm cực đại.
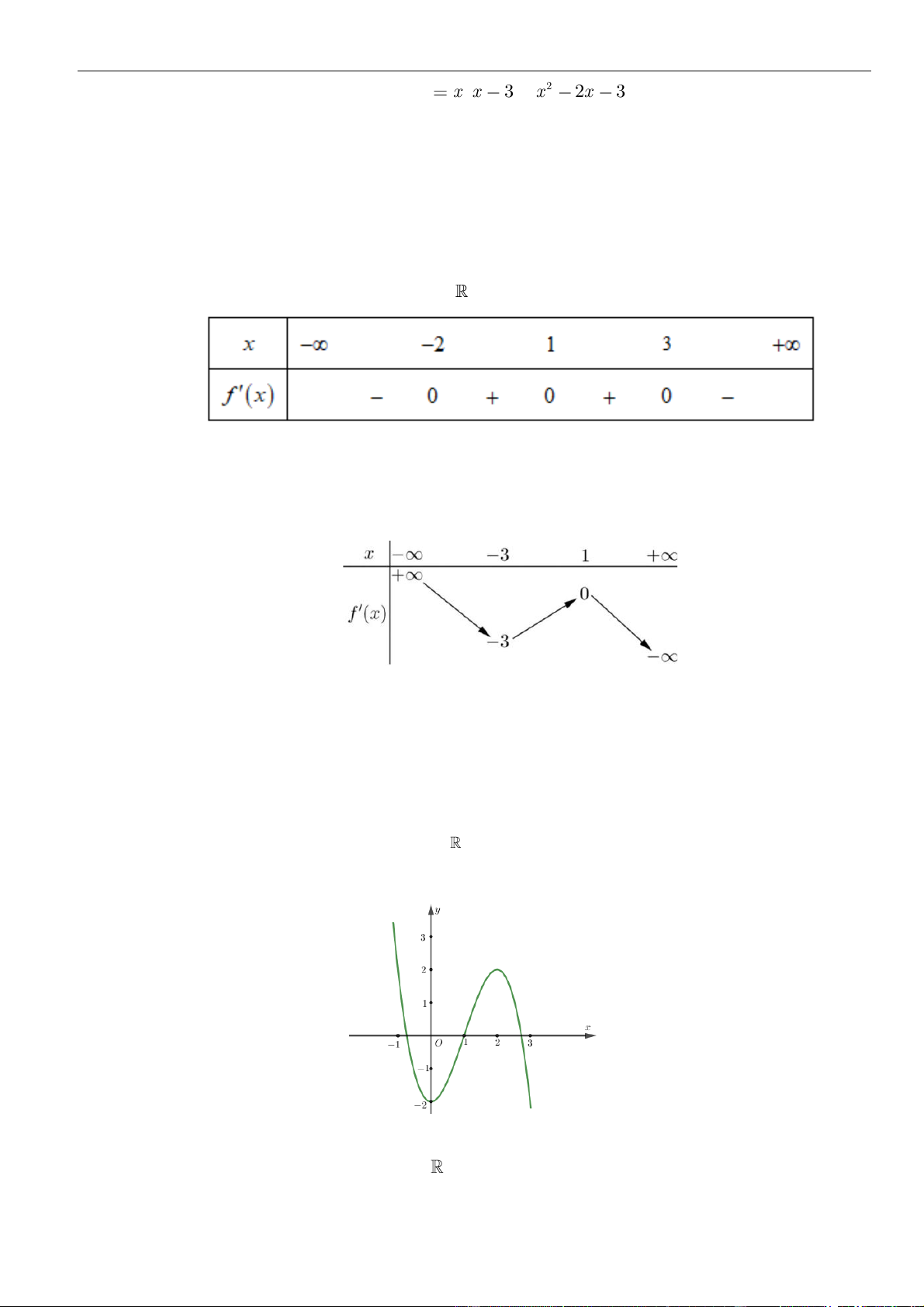
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 18: Cho hàm số
fx
có đạo hàm
2
2
' 3 2 3f x x x x x
. Số điểm cực trị của hàm số đã
cho là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 19: Cho hàm số
()y f x=
có đạo hàm
2
( ) ( 1) ( 1)(2 )f x x x x
= − + −
. Điểm cực đại của hàm số
()y f x=
là
A.
2x =
B.
1; 2xx= − =
C.
1x =−
D.
1x =
Câu 20: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu
( )
fx
như sau:
Hỏi hàm số
( )
2
2y f x x=−
có bao nhiêu điểm cực tiểu?
A. 1. B. 4. C. 3. D. 2.
Câu 21: Cho hàm số:
()y f x=
. Hàm số
'( )y f x=
có bảng biến thiên như sau:
Số điểm cực trị của hàm số
()y f x=
là :
A. 3. B. 0. C. 2. D. 1.
Câu 22: Cho hàm số
()fx
có đạo hàm
22
( ) ( 3) ( 2 3)f x x x x x
= − − −
. Số điểm cực đại của hàm số đã cho
là
A. 4. B. 3. C. 1. D. 2.
Câu 23: Cho hàm số
( )
y f x=
có đạo hàm trên . Biết rằng hàm số
( )
'y f x=
có đồ thị như hình dưới.
Đặt
( ) ( )
g x f x x=−
. Hỏi hàm số
( )
gx
có bao nhiêu điểm cực trị?
A.
1
. B.
3
. C.
1−
. D.
0
.
Câu 24: Cho hàm số
( )
=y f x
xác định trên và có đồ thị của hàm số
( )
=y f x
như hình vẽ. Hàm số
( )
=y f x
có mấy điểm cực trị?
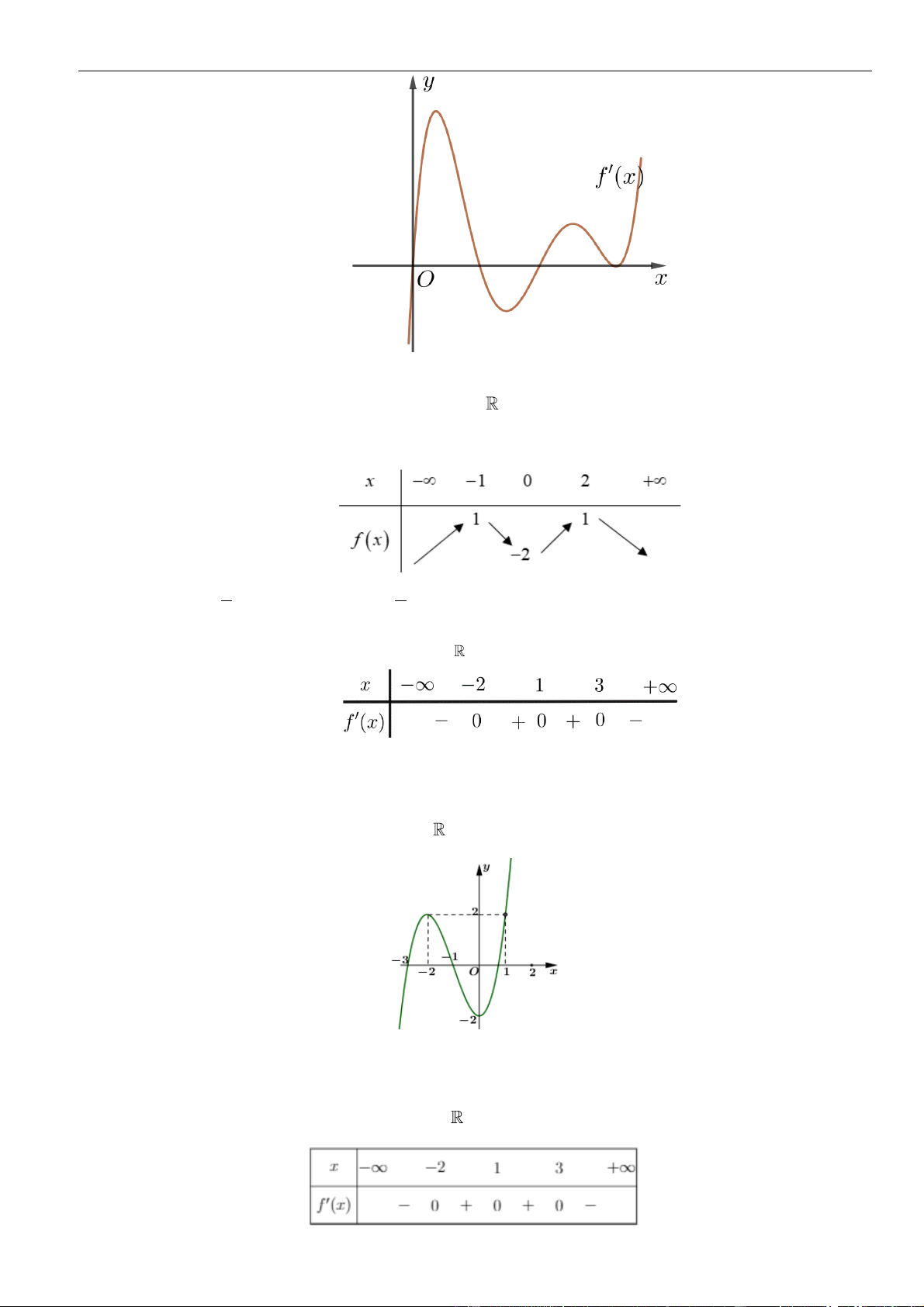
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 25: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng biến thiên như hình vẽ. Hàm số
( )
12y f x=−
đạt cực tiểu tại
A.
1
2
x =−
. B.
1
2
x =
. C.
1x =
. D.
0x =
Câu 26: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu của
( )
fx
như sau
Hỏi hàm số
( )
( )
2
2g x f x x=−
có bao nhiêu điểm cực tiểu?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 27: Cho hàm số
( )
y f x=
xác định trên và hàm số
( )
y f x
=
có đồ thị như hình vẽ bên dưới
Hỏi hàm số
( )
fx
ye=
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
Câu 28: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu
'fx
như sau biến thiên như sau:
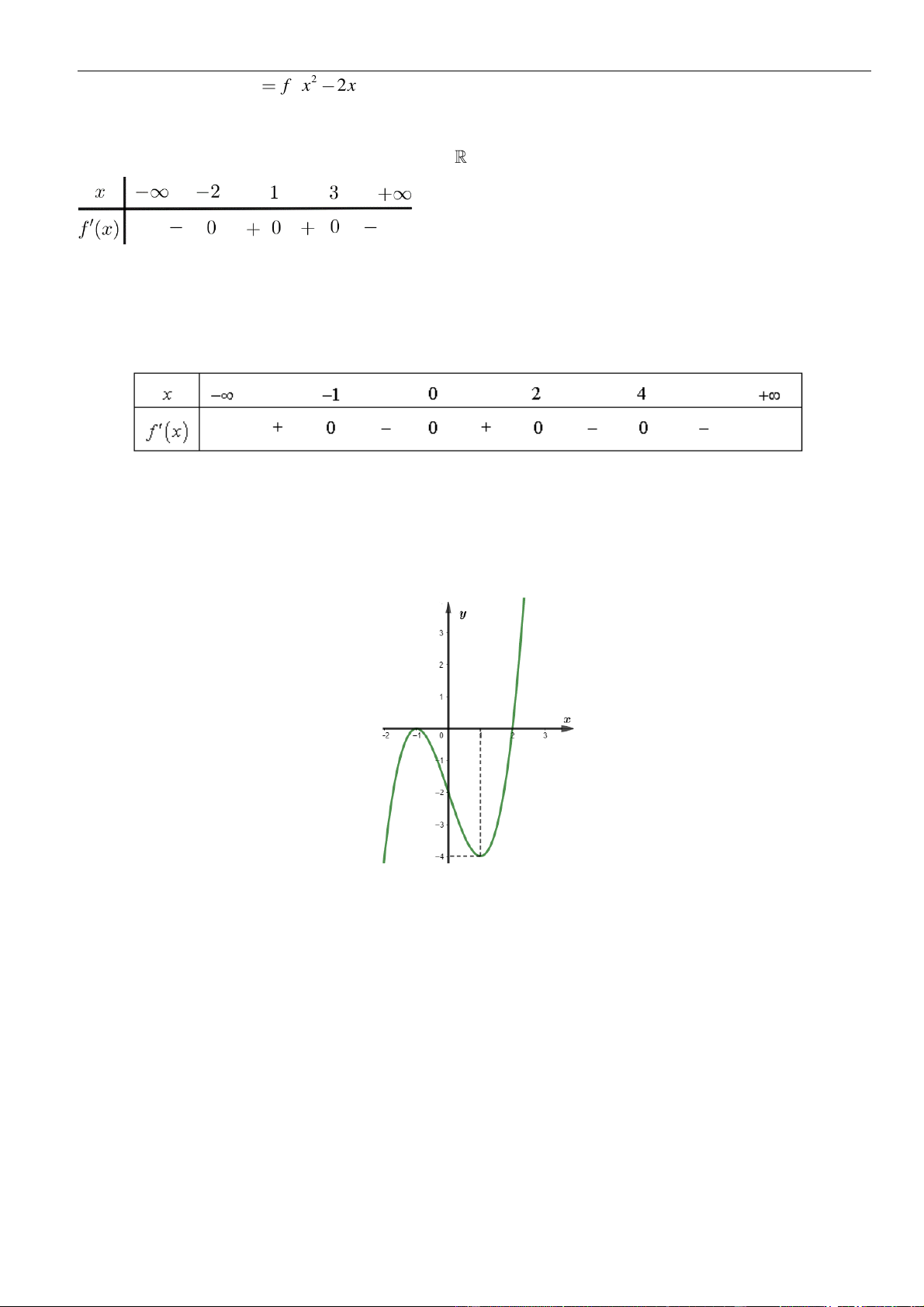
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Hỏi hàm số
2
2y f x x
có bao nhiêu điểm cực tiểu
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 29: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu của
( )
fx
như sau
Hỏi hàm số
( )
( )
2
2g x f x x=−
có bao nhiêu điểm cực tiểu?
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 30: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm
( )
'fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực đại?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 31: Cho hàm số bậc bốn
( )
y f x=
và có đồ thị
( )
fx
như sau:
Số điểm cực trị của hàm số
( )
( )
2
1g x f x=−
là
A.
1.
B.
3.
C.
2.
D.
4.
Câu 32: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Tìm số điểm cực trị của hàm số
( )
( )
2
2g x f x x=−
trên khoảng
( )
0; +
.
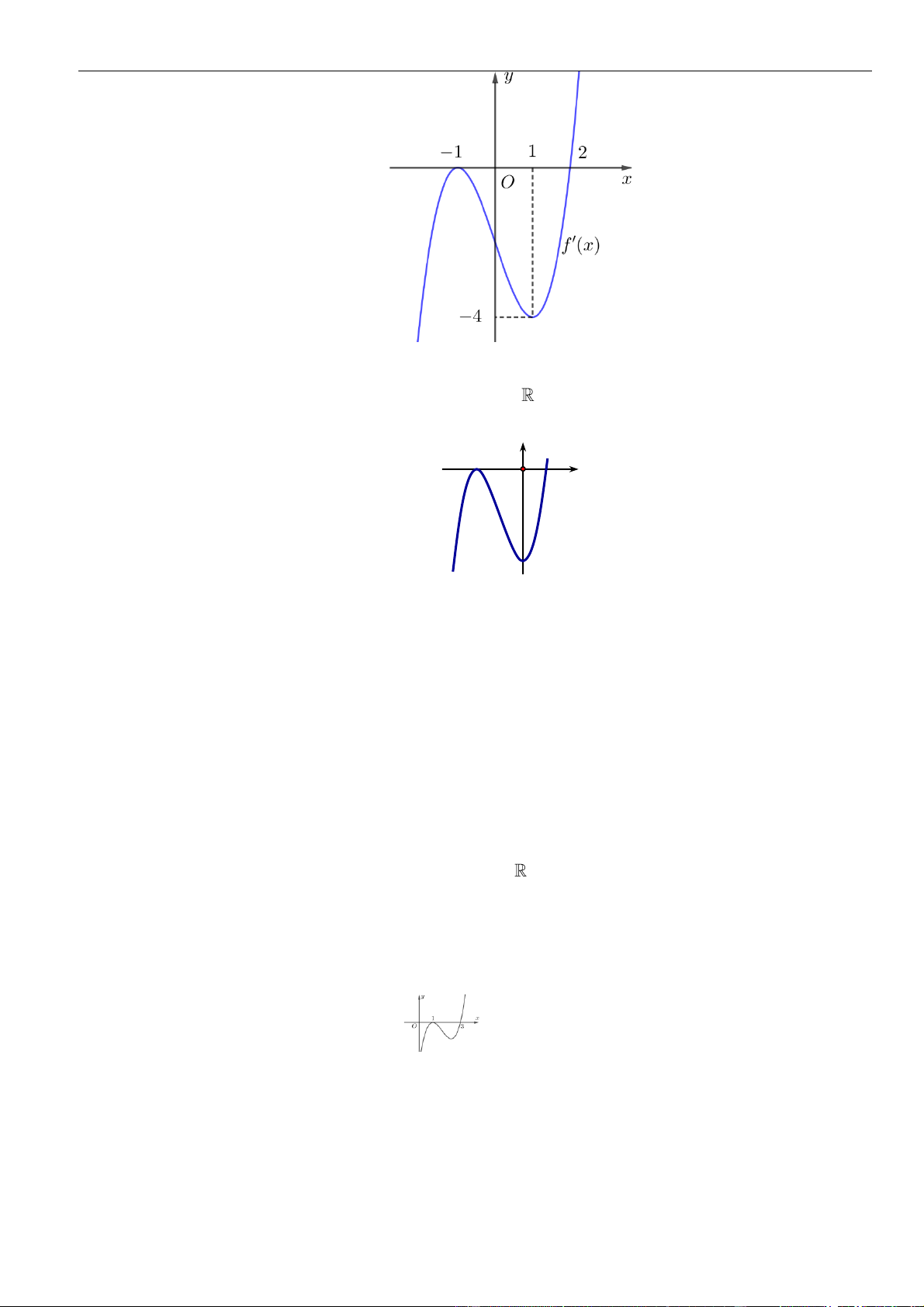
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 33: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên và có đồ thị hàm số
( )
y f x
=
như hình vẽ
bên dưới.
Xét hàm số
( )
( )
2
3g x f x=−
và các mệnh đề sau:
I. Hàm số
( )
gx
có 3 điểm cực trị.
II. Hàm số
( )
gx
đạt cực tiểu tại
0x =
.
III. Hàm số
( )
gx
đạt cực đại tại
2x =
.
IV. Hàm số
( )
gx
đồng biến trên khoảng
( )
2;0−
.
V. Hàm số
( )
gx
nghịch biến trên khoảng
( )
1;1−
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.
3
. B.
2
. C.
0
. D.
1
Câu 34: Cho hàm số
( )
y f x=
xác định và liên tục trên và có đồ thị
( )
y f x
=
như hình vẽ
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số
( )
y f x=
đạt cực đại tại
1x =
.
B. Đồ thị hàm số
( )
y f x=
có một điểm cực đại.
C. Hàm số
( )
y f x=
đạt cực tiểu tại
3x =
.
O
x
y
2−
4−
1
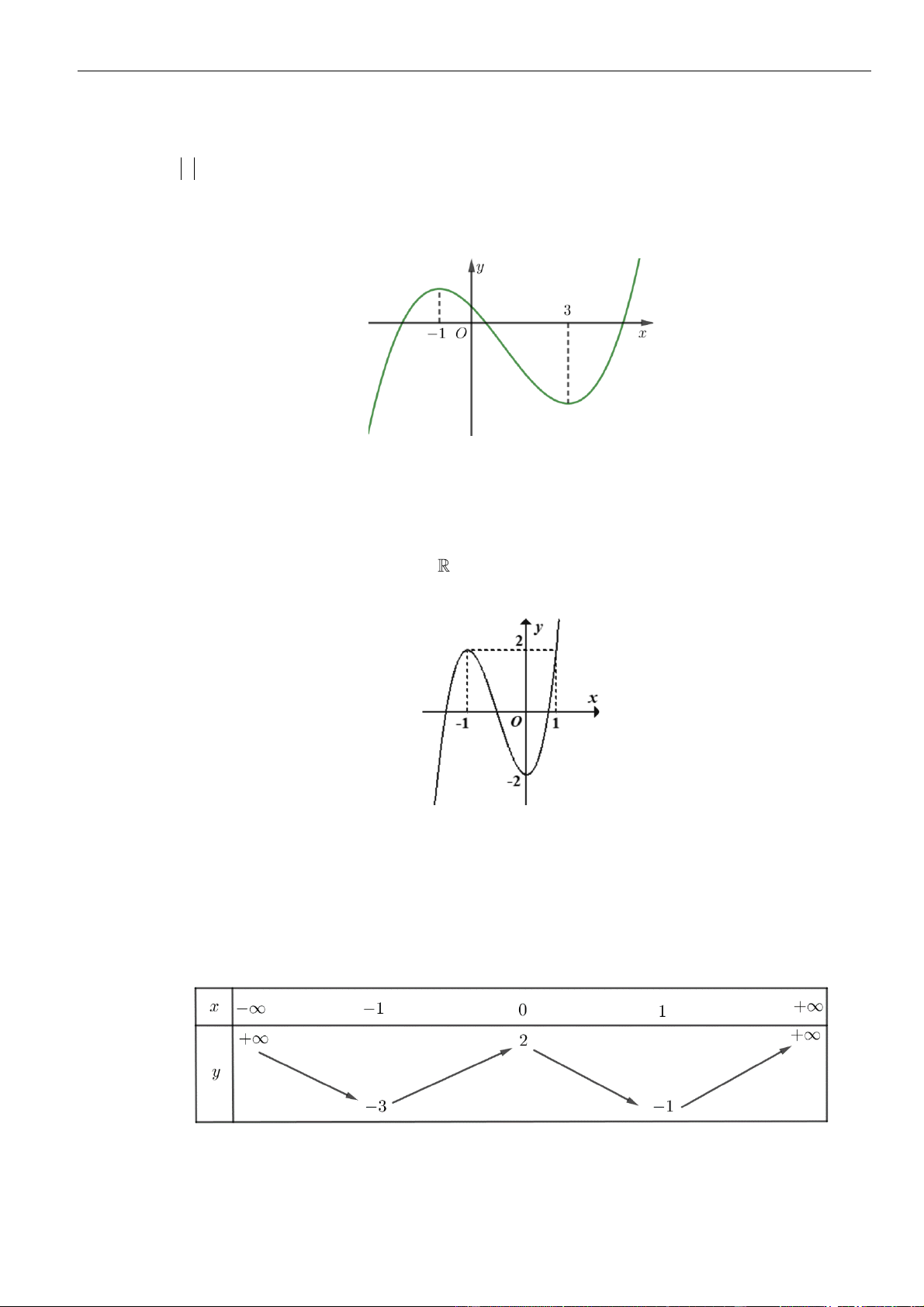
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
D. Đồ thị hàm số
( )
y f x=
có hai điểm cực trị.
Câu 35: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
4 5 3
2 3 1f x x x x
= + − +
. Số điểm cực trị của hàm số
( )
fx
là
A.
1
. B.
5
. C.
3
. D.
2
.
Câu 36: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ:
Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
( )
( )
2
1y f x m= − +
có 3
điểm cực trị. Tổng các phần tử của
S
là:
A.
2
. B.
4
. C.
8
. D.
10
.
Câu 37: Cho hàm số
( )
y f x=
xác định trên và hàm số
( )
y f x
=
có đồ thị như hình vẽ bên dưới.
Hỏi hàm số
( )
e
fx
y =
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 38: Cho hàm số
( )
=y f x
có đạo hàm
( ) ( )( )
2
23
= + −f x x x x
. Điểm cực đại của hàm số
( )
( )
2
2g x f x x=−
là
A.
0=x
. B.
1=−x
. C.
3=x
. D.
1=x
.
Câu 39: Cho hàm số
( )
fx
. Bảng biến thiên của hàm số
( )
fx
như sau:
Số điểm cực trị của hàm số
( )
2
2=−y f x x
là :
A.
7
. B.
9
. C.
3
. D.
5
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Câu 40: Cho hàm số
( )
4 3 2
y f x ax bx cx dx e= = + + + +
có đồ thị như hình vẽ bên.
Số cực trị của hàm số
( )
13y f x= + −
là
A.
3
. B.
8
. C.
7
. D.
4
.
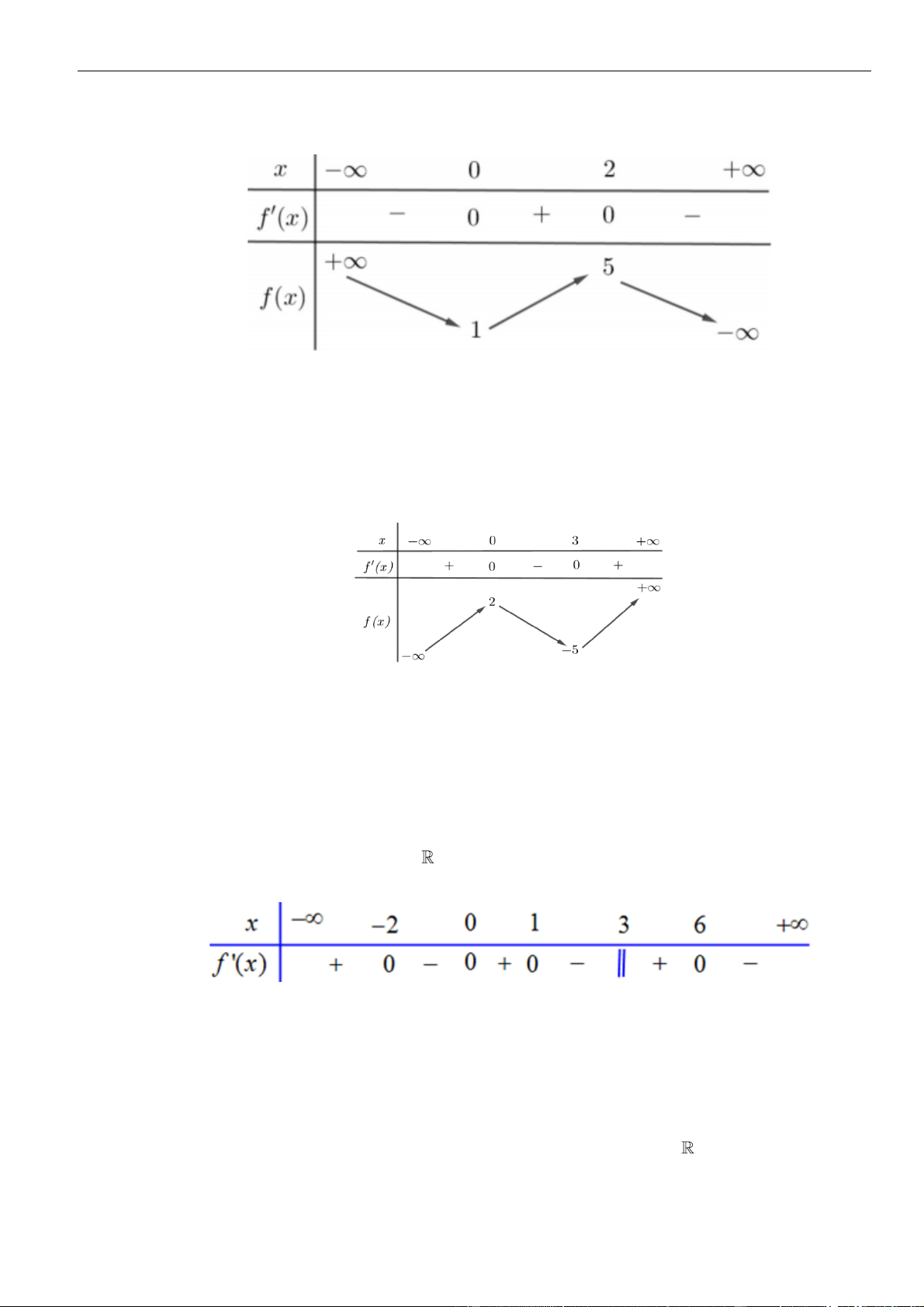
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
fx
có bảng biến thiên như sau
Hàm số đã cho đặt cực đại tại điểm nào dưới đây
A.
5x =
. B.
2x =
. C.
0x =
. D.
1x =
.
Lời giải
Chọn B
Hàm số có điểm cực đại tại
2x =
, cực tiểu tại
0x =
.
Câu 2: Cho hàm
()y f x=
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
3
. B.
2
. C.
0
. D.
5−
.
Lời giải
Chọn D
Điểm cực tiểu của hàm số là
3
CT
x =
và giá trị cực tiểu của hàm số là
5
CT
y =−
.
Điểm cực đại của hàm số là
0
CD
x =
và giá trị cực đại của hàm số là
2
CD
y =
.
Câu 3: Cho hàm số
()y f x=
liên tục trên và có bảng xét dấu đạo hàm như hình bên. Hỏi hàm số đã
cho có bao nhiêu điểm cực trị?
A.
3
. B.
4
. C.
2
. D.
5
.
Lời giải
Chọn D
Có
()fx
đổi dấu
5
lần khi đi qua các điểm
2;0;1;3;6−
nên hàm số đã cho có
5
điểm cực
trị.
Câu 4: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( )
3
2
21f x x x x
= + −
với
x
. Hàm số đã cho có bao
nhiêu điểm cực trị?
A.
2
. B.
0
. C.
3
. D.
1
.
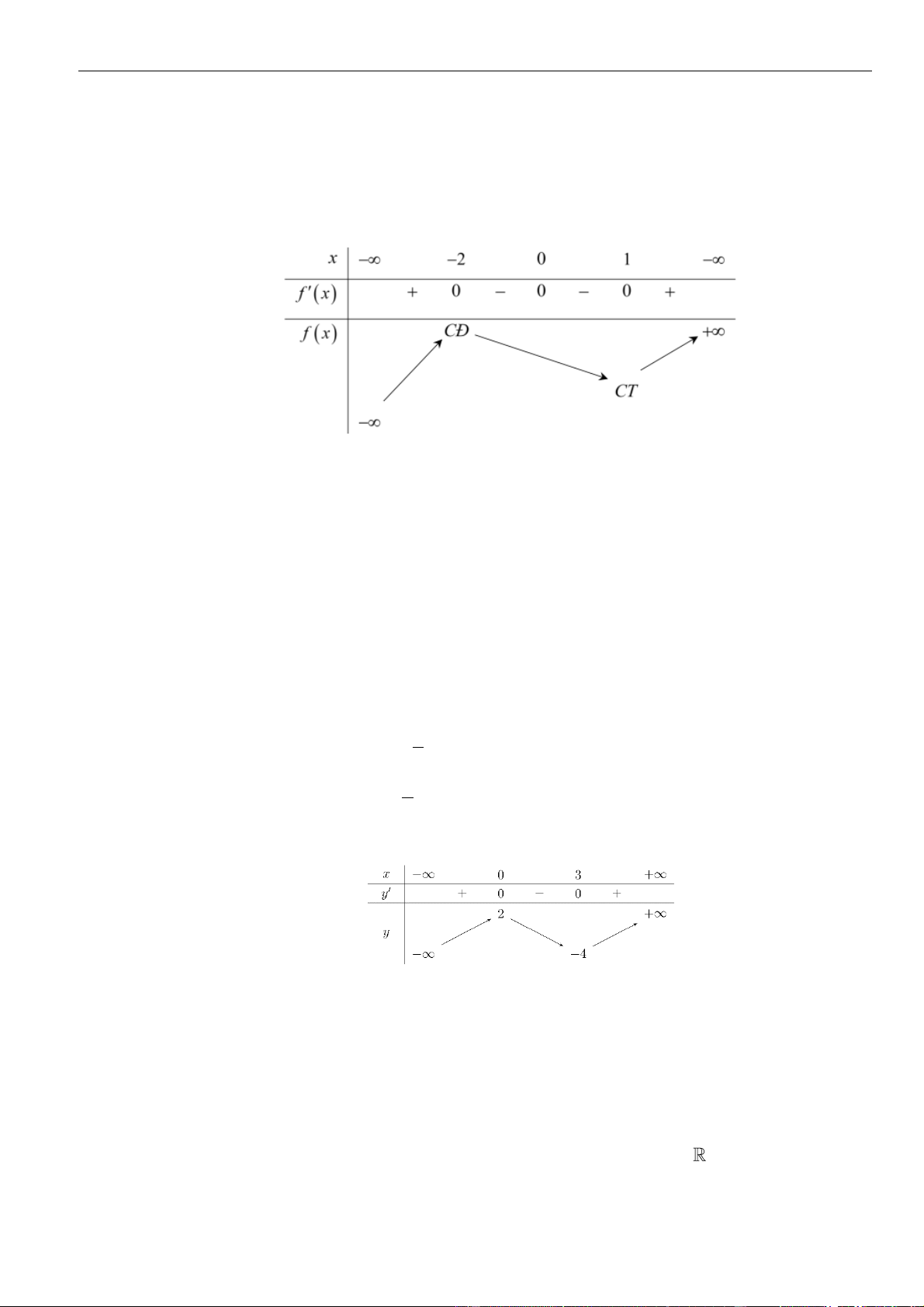
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn A
Ta có
( ) ( ) ( )
3
2
21f x x x x
= + −
,
( )
=
= = −
=
1
02
0
x
f x x
x
.
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số có hai điểm cực trị.
Câu 5: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( ) ( )
2
1 2 3f x x x x
= − +
. Hàm số đã cho có bao nhiêu điểm
cực trị?
A.
1
. B.
3
. C.
0
. D.
2
.
Lời giải
Chọn D
Số điểm cực trị của hàm số là số nghiệm đơn của
( )
0fx
=
( ) ( )
2
0
1 2 3 0 1
3
2
x
x x x x
x
=
− + = =
=−
1x =
là nghiệm kép,
3
0,
2
xx= = −
là nghiệm đơn.
Câu 6: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng?
A. 2 B. 3. C. 0 D. -4
Lời giải
Chọn D
Từ bảng biến thiên ta thấy đạo hàm của hàm số đổi dấu từ
( )
−
sang
( )
+
khi qua điểm
0
3x =
và
(3) 4y =−
Câu 7: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
2 3 4
1 2 3f x x x x x
= − − −
,
x
. Số điểm cực trị của
hàm số
( )
fx
là
A.
2
. B.
1
. C.
0
. D.
3
.
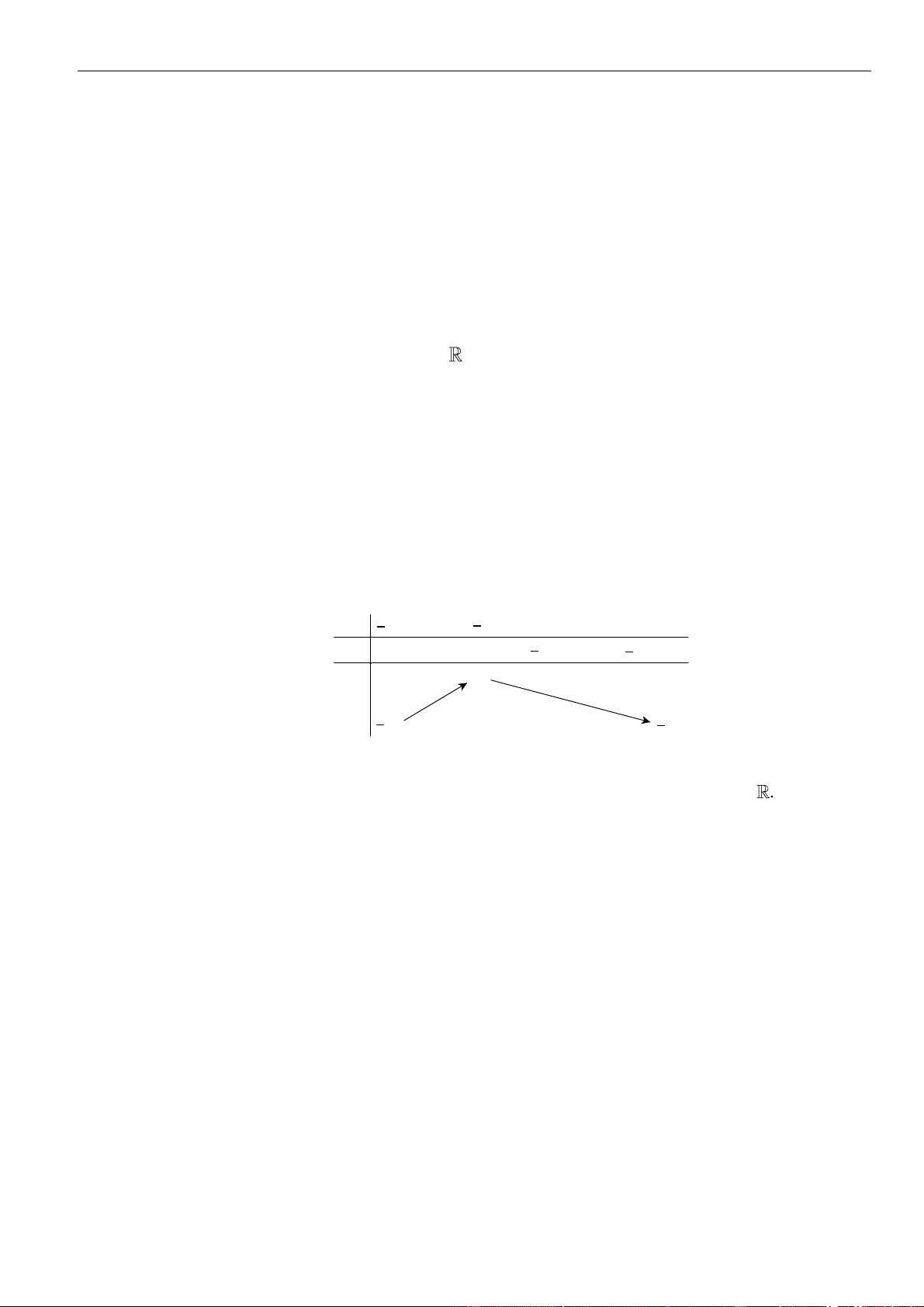
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Lời giải
Chọn A
Xét phương trình
( ) ( ) ( ) ( )
2 3 4
0 1 2 3 0f x x x x x
= − − − =
0
1
2
3
x
x
x
x
=
=
=
=
.
Nghiệm
0; 2xx==
là nghiệm bội bậc lẻ nên hàm số
( )
y f x=
có hai điểm cực trị.
(còn
1; 3xx==
là các nghiệm bội bậc chẵn nên không phải là điểm cực trị của hàm số
( )
y f x=
)
Câu 8: Hàm số
( )
fx
xác định và liên tục trên và có đạo hàm
( ) ( ) ( )
2
2 1 1f x x x
= − − +
. Khi đó hàm
số
( )
fx
A. đạt cực đại tại điểm
1x =−
. B. đạt cực tiểu tại điểm
1x =−
.
C. đạt cực đại tại điểm
1x =
. D. đạt cực tiểu tại điểm
1x =
.
Lời giải
Chọn A
Ta có
( ) ( ) ( )
2
1
' 0 2 1 1 0
1
x
f x x x
x
=−
= − − + =
=
.
Bảng biến thiên của hàm số
( )
fx
Suy ra hàm số đã cho đạt cực đại tại
1x =−
.
Câu 9: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( ) ( ) ( )
3 4 5
1 2 3 5 ; .f x x x x x x
= + − − +
Hỏi hàm số
( )
y f x=
có mấy điểm cực trị?
A.
4
. B.
3
. C.
2
. D.
5
.
Lời giải
Chọn B
Ta có:
( ) ( )( ) ( ) ( ) ( )
3 4 5
1
2
1 2 3 5 0 .
3
5
x
x
f x x x x x f x
x
x
=−
=
= + − − + =
=
=−
Mặt khác,
( )
fx
đổi dấu khi
x
qua
1; 2; 5x x x= − = = −
và
( )
fx
không đổi dấu khi
x
qua
3.x =
Vậy hàm số
( )
y f x=
có ba điểm cực trị.
+
0
+
∞
x
∞
0
∞
∞
f
(
x
)
f'
(
x
)
1
1
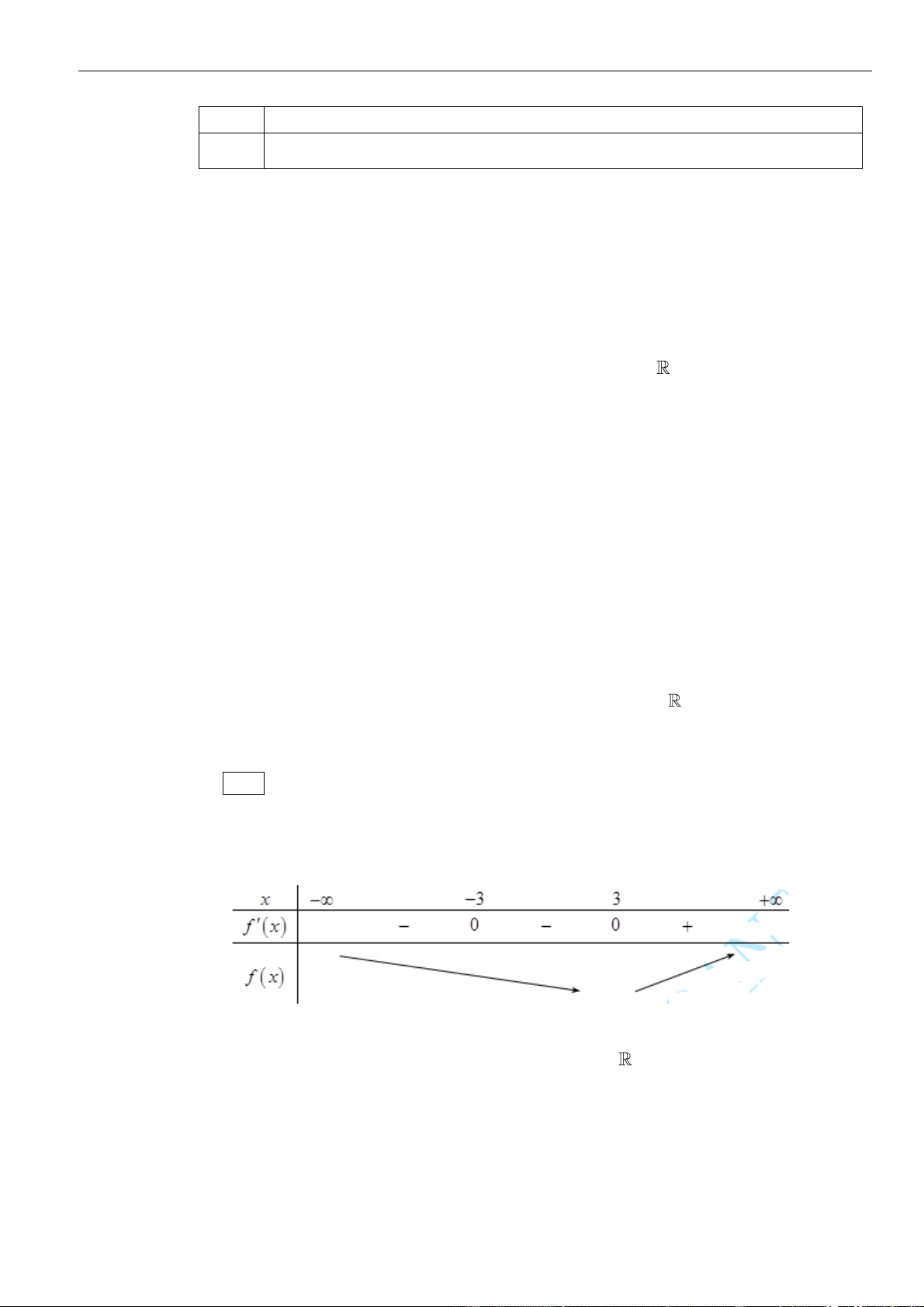
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Câu 10: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm
( )
'fx
như sau:
x
−
2−
1−
0
2
4
+
( )
'fx
−
0
+
0
−
0
−
0
+
0
−
Hàm số đã cho có bao nhiêu điểm cực trị?
A.
3
. B.
2
. C.
5
. D.
4
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy
( )
'fx
đổi dấu 4 lần khi đi qua
0
x
. Nên hàm số có bốn điểm cực
trị.
Câu 11: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )
23
2021
' 1 2 ,f x x x x x= − +
. Số điểm cực trị của hàm
số đã cho là
A.
3
. B.
2
. C.
6
. D.
1
.
Lời giải
Chọn B
Ta có:
( )
0
' 0 1
2
x
f x x
x
=
= =
=−
Do
1x =
là nghiệm bội chẵn,
0, 2xx= = −
là các nghiệm bội lẻ nên
( )
'fx
đổi dấu khi qua các
nghiệm
0, 2xx= = −
.
Vậy hàm số
( )
fx
có hai điểm cực trị.
Câu 12: Cho hàm số
( )
fx
có đạo hàm
( ) ( )
( )
2
39f x x x
= + −
với mọi
x
. Hàm số đã cho có bao
nhiêu điểm cực trị?
Lời giải
Đáp án:
1
1aa
Ta có
( )
2
30
3
0
3
90
x
x
fx
x
x
+=
=−
=
=
−=
.
Bảng biến thiên
Dựa vào bảng biến thiên ta thấy hàm số đã cho có
1
điểm cực trị.
Câu 13: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( )
3
1 2 ,
= − + f x x x x x
. Số điểm cực trị của hàm số đã
cho là
A.
2
. B.
3
. C.
5
. D.
1
.
Lời giải
Chọn B
Phương trình
( )
0
=fx
có
3
nghiệm đơn
2, 0, 1= − = =x x x
và
( )
fx
đổi dấu khi đi qua
3
nghiệm đó. Do đó, hàm số đã cho có
3
cực trị.
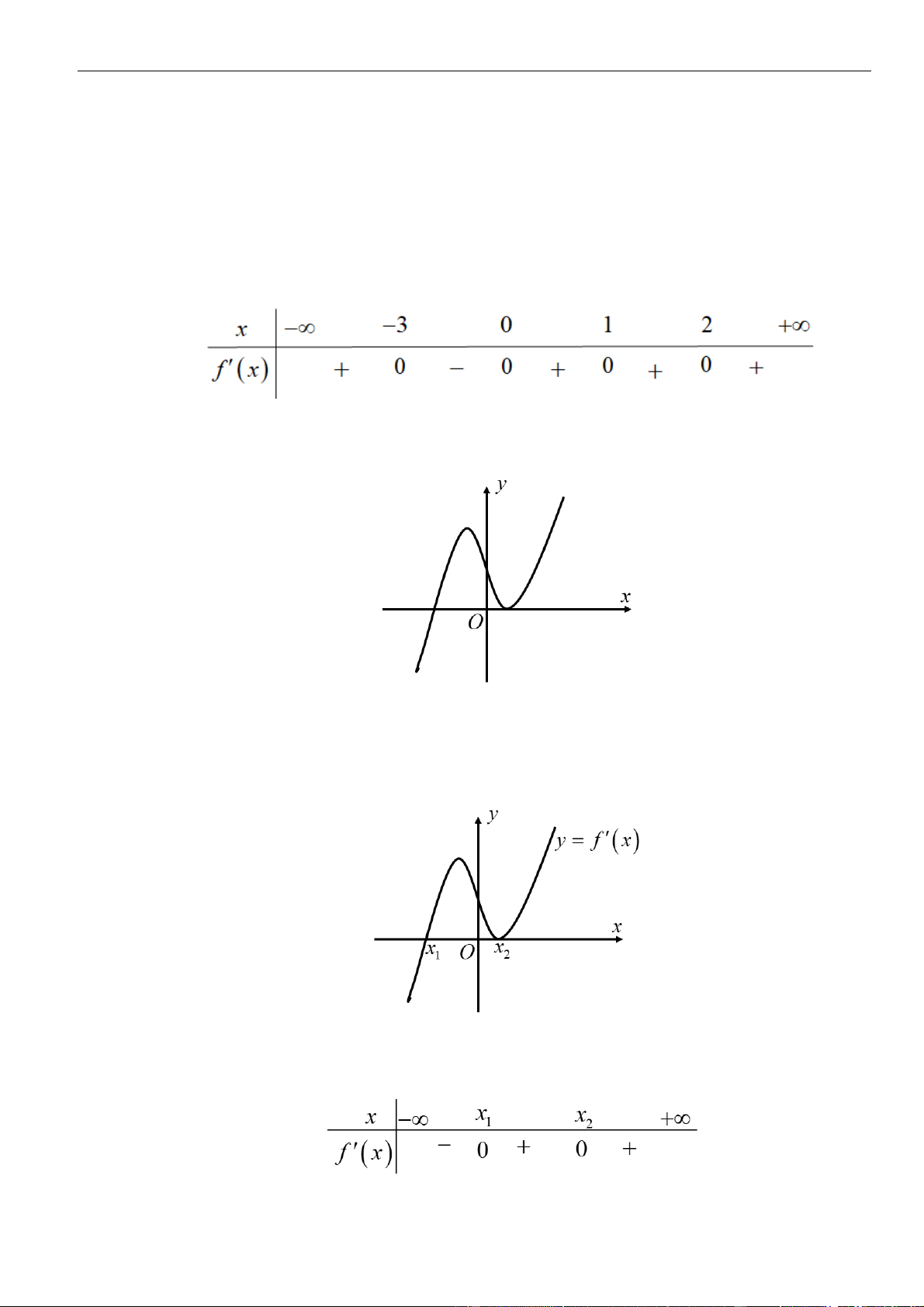
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Câu 14:
Cho hàm số
f
có đạo hàm là
( ) ( ) ( )
23
13f x x x x
= − +
. Số điểm cực trị của hàm số
f
là:
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn A
+)
( )
'
0
01
3
x
f x x
x
=
= =
=−
+) Dấu
( )
'
fx
Vậy hàm số
( )
y f x=
có 2 điểm cực trị.
Câu 15: Cho hàm số
( )
y f x=
. Hàm số
( )
y f x
=
có đồ thị như hình vẽ.
Số điểm cực trị của hàm số
( )
y f x=
là:
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
Gọi
1
x
;
2
x
là hoành độ giao điểm của đồ thị hàm số
( )
y f x
=
với trục hoành. Khi đó, ta có:
1
x
và
2
x
là hai nghiệm của
( )
fx
. Dựa vào đồ thị ta có bảng xét dấu của
( )
fx
như sau:
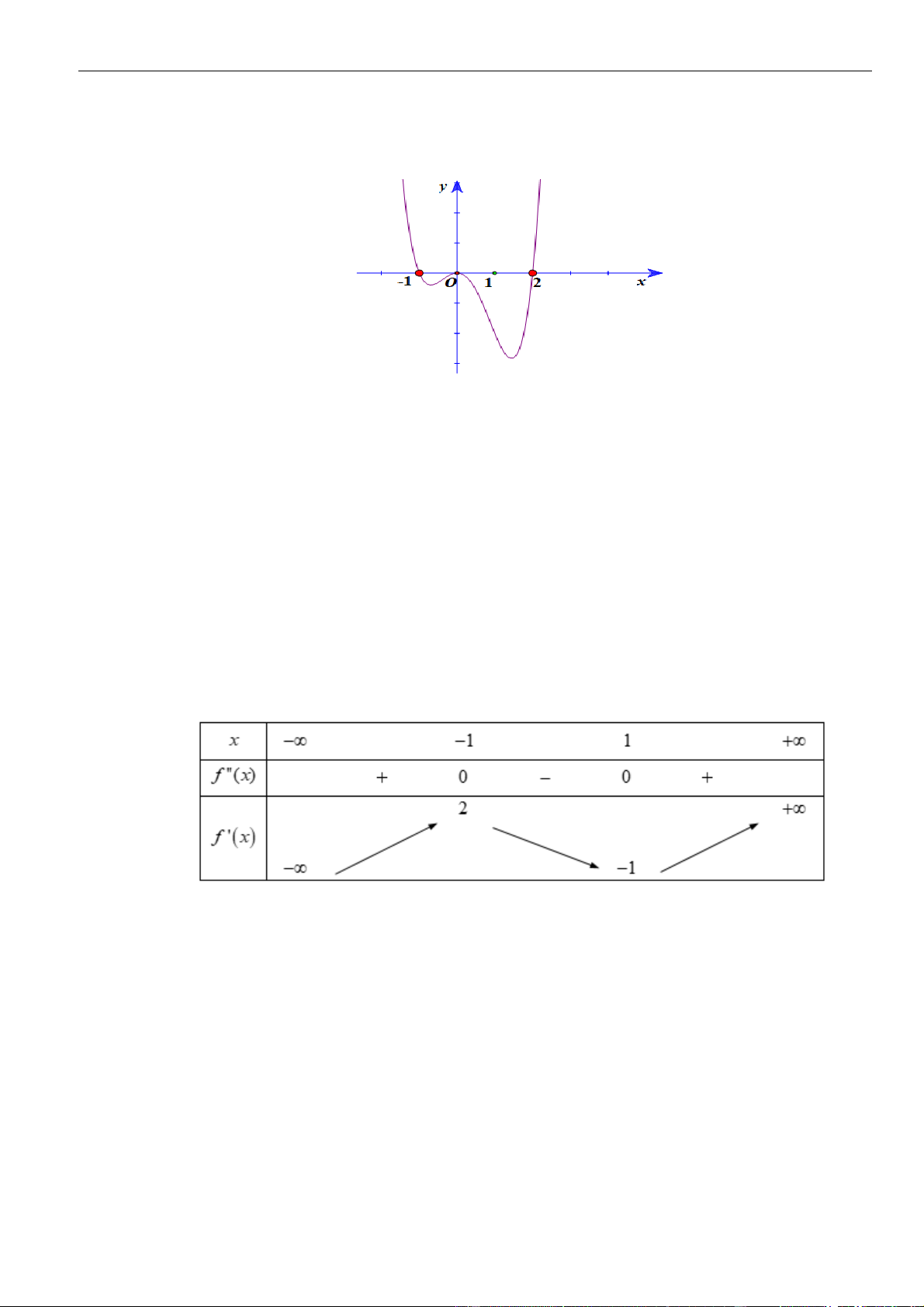
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Từ bảng xét dấu của
( )
fx
ta thấy
( )
fx
đổi dấu một lần khi qua điểm
1
x
. Vậy hàm số
( )
y f x=
có một điểm cực trị.
Câu 16: Cho hàm số
()y f x=
có đồ thị hàm
'( )fx
như hình vẽ
Số điểm cực trị của hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
( ) ( )
2
'( ) 1 2f x a x x x= + −
1
'( ) 0 0
2
x
f x x
x
=−
= =
=
Hàm số đã cho có 2 điểm cực trị.
Câu 17: Cho hàm số
( )
fx
liên tục trên R và hàm số
( )
'fx
có bảng biến thiên như sau. Tìm mệnh đề
đúng?
A. Hàm số
( )
y f x=
có 2 điểm cực tiểu và 1 điểm cực đại.
B. Hàm số
( )
y f x=
có 1 điểm cực tiểu và 1 điểm cực đại.
C. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
D. Hàm số
( )
y f x=
có 1 điểm cực tiểu và 2 điểm cực đại.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta thấy hàm số
( )
'fx
ta ta có
( )
( )
( )
( )
1
' 0 1 1
1
x a a
f x x b b
x c c
= −
= = −
=
. Từ
đây ta có bảng biến thiên của hàm số
( )
fx
như sau
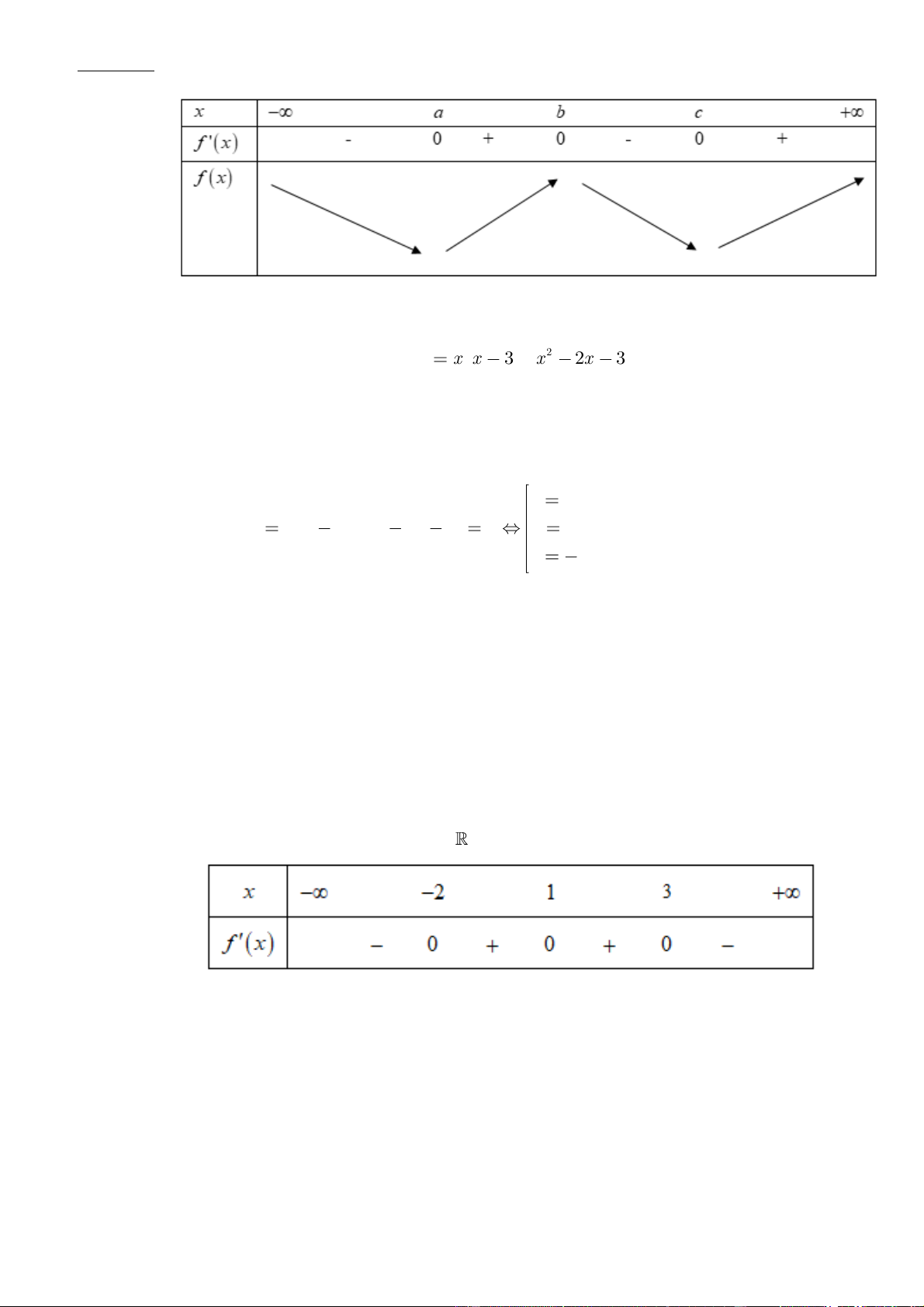
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Hàm số
( )
y f x=
có 2 điểm cực tiểu và 1 điểm cực đại.
Câu 18: Cho hàm số
fx
có đạo hàm
2
2
' 3 2 3f x x x x x
. Số điểm cực trị của hàm số đã
cho là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta có
2
2
0
' 3 2 3 0 3
1
x
f x x x x x x
x
đều là các nghiệm bội lẻ.
Số điểm cực trị của hàm số đã cho bằng
3
.
Câu 19: Cho hàm số
()y f x=
có đạo hàm
2
( ) ( 1) ( 1)(2 )f x x x x
= − + −
. Điểm cực đại của hàm số
()y f x=
là
A.
2x =
B.
1; 2xx= − =
C.
1x =−
D.
1x =
Lời giải
Chọn A
Đa thức
2
( ) ( 1) ( 1)(2 )f x x x x
= − + −
có 2 nghiệm đơn
1; 2xx= − =
. Mặt khác đạo hàm đổi dấu
từ dương sang âm tại
2x =
nên
2x =
là điểm cực đại của hàm số đã cho.
Câu 20: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu
( )
fx
như sau:
Hỏi hàm số
( )
2
2y f x x=−
có bao nhiêu điểm cực tiểu?
A. 1. B. 4. C. 3. D. 2.
Lời giải
Chọn D
Đặt
( )
( )
2
2g x f x x=−
, có
( ) ( )
( )
2
2 2 2g x x f x x
= − −
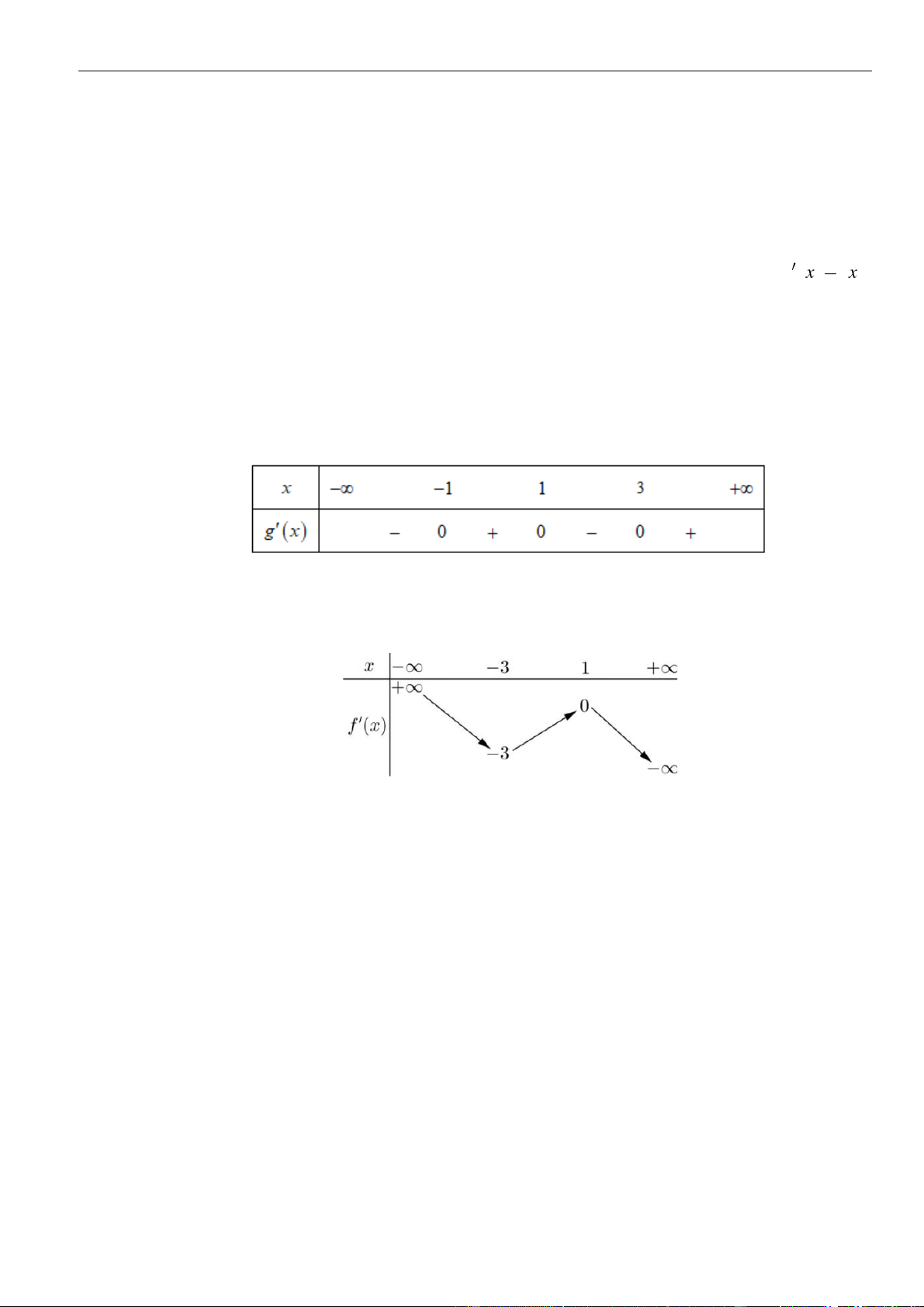
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Từ bảng xét dấu của hàm số
( )
fx
có
( )
( )
2
2
2
2
22
20
21
0
23
2 2 0
2 2 0
xx
f x x
xx
gx
xx
x
x
− = −
−=
−=
=
−=
−=
−=
(1)
(2)
(3)
(4)
Để tìm số điểm cực tiểu của hàm số
( )
gx
ta chỉ quan tâm đến những giá trị của
x
tại đó
( )
gx
đổi dấu.
Phương trình (1) vô nghiệm; phương trình (2) có hai nghiệm phân biệt nhưng vì
f x x
2
2
không đổi dấu khi đi qua nghiệm
2
21xx−=
nên hàm số
( )
gx
cũng không đổi dấu khi qua
những nghiệm này; phương trình (3):
2
1
2 3 0
3
x
xx
x
=−
− − =
=
là các nghiệm bậc lẻ nên
( )
gx
đổi dấu khi qua những nghiệm này; phương trình (4):
2 2 0 1xx− = =
nên
( )
gx
đổi dấu khi
qua những nghiệm này. Từ đó ta có bảng xét dấu của
( )
gx
như sau:
Từ bảng xét dấu trên suy ra hàm số
( )
2
2y f x x=−
có 2 điểm cực tiểu.
Câu 21: Cho hàm số:
()y f x=
. Hàm số
'( )y f x=
có bảng biến thiên như sau:
Số điểm cực trị của hàm số
()y f x=
là :
A. 3. B. 0. C. 2. D. 1.
Lời giải
Chọn D
Từ bảng biến thiên ta suy ra
0
'( ) 0
( 3)
x
fx
x a a
=
=
= −
Từ bảng biến thiên suy ra
'( )y f x=
dổi dấu khi qua
xa=
.
Suy ra hàm số đã cho có một điểm cực trị.
Câu 22: Cho hàm số
()fx
có đạo hàm
22
( ) ( 3) ( 2 3)f x x x x x
= − − −
. Số điểm cực đại của hàm số đã cho
là
A. 4. B. 3. C. 1. D. 2.
Lời giải
Chọn C
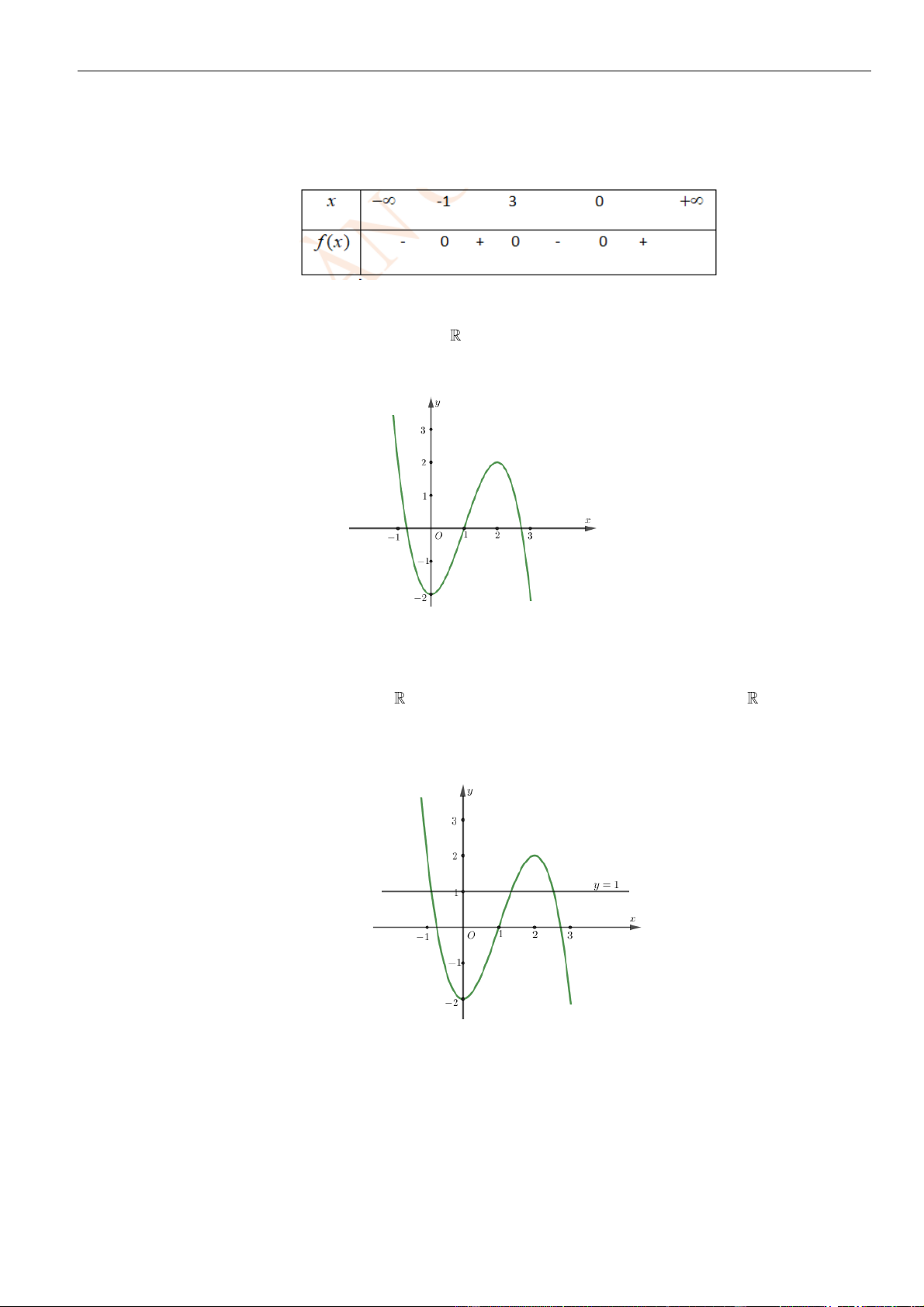
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
2 2 2
2
0
( ) ( 3) ( 2 3) 0 ( 3) 0
2 3 0
x
f x x x x x x
xx
=
= − − − = − =
− − =
0
3
13
x
x
xx
=
=
= − =
( bội 2 )
Bảng biến thiên
Vậy hàm số
()fx
có 1 điểm cực đại.
Câu 23: Cho hàm số
( )
y f x=
có đạo hàm trên . Biết rằng hàm số
( )
'y f x=
có đồ thị như hình dưới.
Đặt
( ) ( )
g x f x x=−
. Hỏi hàm số
( )
gx
có bao nhiêu điểm cực trị?
A.
1
. B.
3
. C.
1−
. D.
0
.
Lời giải
Chọn B
Hàm số
( )
fx
có đạo hàm trên nên
( ) ( )
g x f x x=−
cũng có đạo hàm trên
Ta có:
( ) ( )
' ' 1g x f x=−
( ) ( )
' 0 ' 1g x f x= =
Dựa vào đồ thị
( )
'fx
ta có
( )
( )
( )
( )
1
2
3
1;0
' 1 1;2
2;3
xx
f x x x
xx
= −
= =
=
, suy ra
1 2 3
;;x x x
là ba nghiệm phân biệt
và
1 2 3
x x x
Bảng biến thiên của hàm
( )
gx
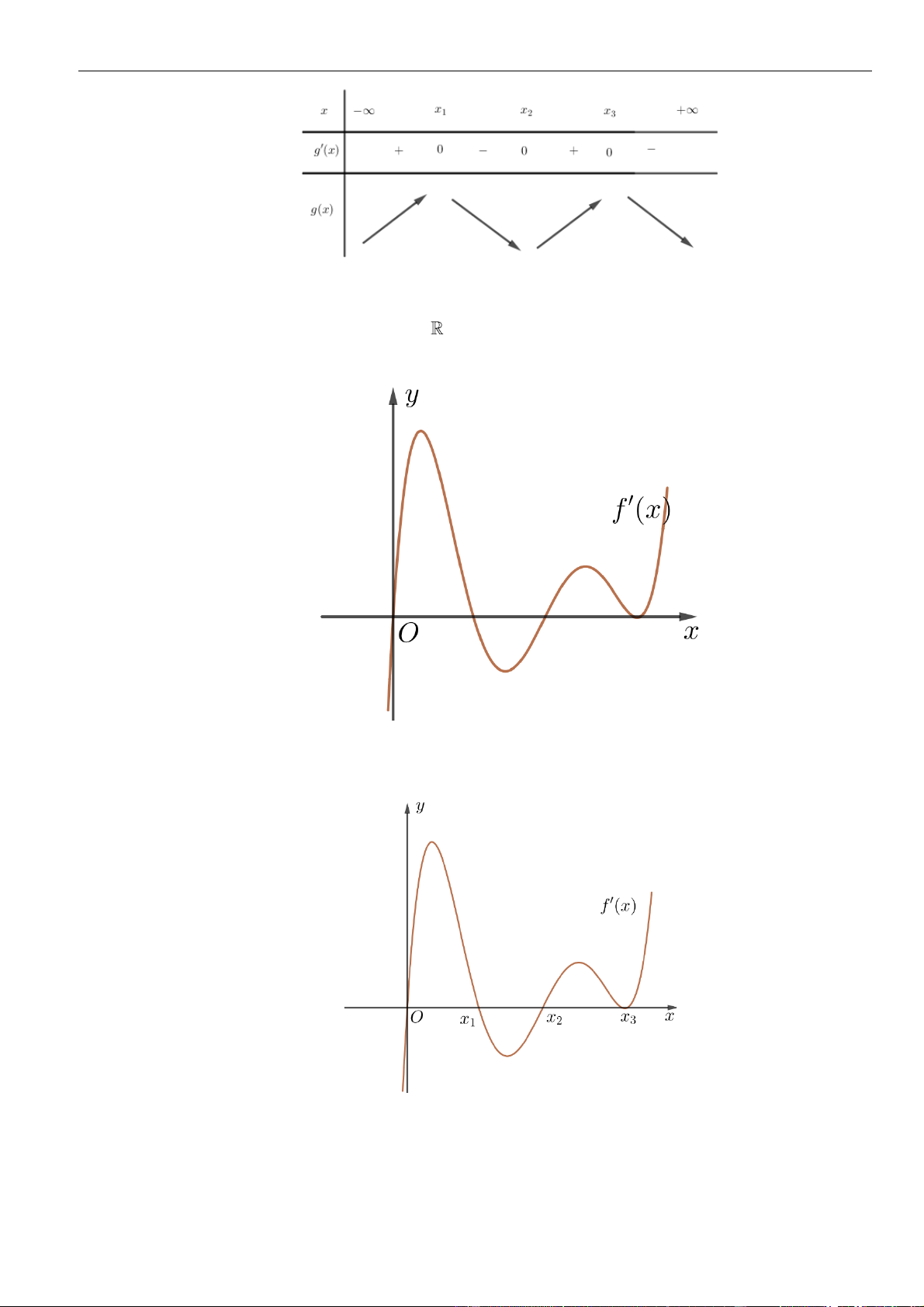
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Vậy hàm số
( ) ( )
1g x f x=−
có 3 điểm cực trị.
Câu 24: Cho hàm số
( )
=y f x
xác định trên và có đồ thị của hàm số
( )
=y f x
như hình vẽ. Hàm số
( )
=y f x
có mấy điểm cực trị?
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn A
Từ đồ thị hàm số
( )
=y f x
suy ra
( )
1
2
3
0
0
=
=
=
=
=
x
xx
fx
xx
xx
.
Bảng biến thiên
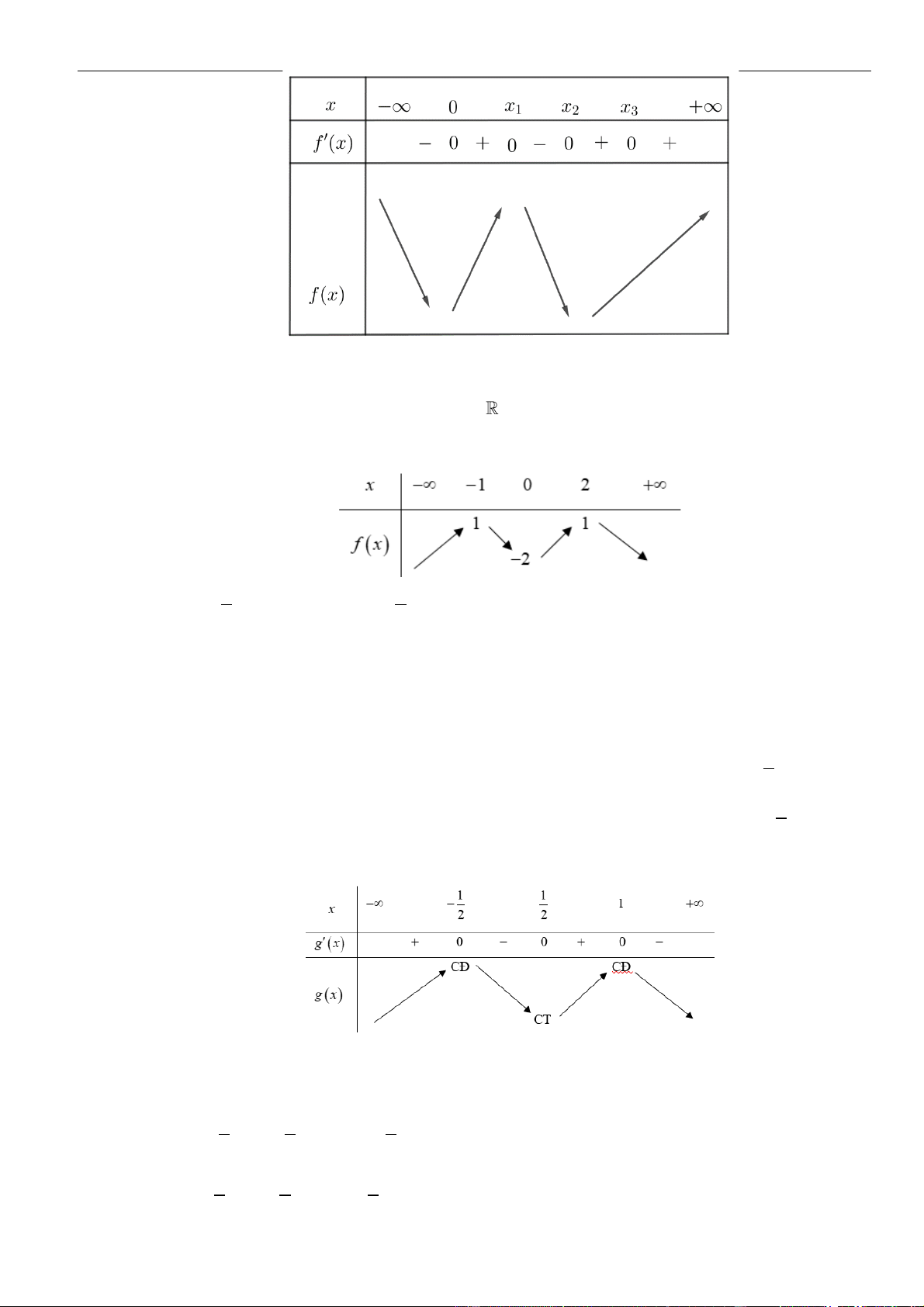
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Suy ra hàm số
( )
=y f x
có 3 điểm cực trị
Câu 25: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng biến thiên như hình vẽ. Hàm số
( )
12y f x=−
đạt cực tiểu tại
A.
1
2
x =−
. B.
1
2
x =
. C.
1x =
. D.
0x =
Lời giải
Chọn B.
( ) ( ) ( )
1
1 2 1
1
2 1 2 0 2 1 2 0 1 2 0
2
1 2 2
1
2
x
x
g x f x f x x x
x
x
=
− = −
= − − = − − = − = =
−=
=−
Ta có bảng biến thiên
Ta xét dấu bằng cách thay số
Với
( ) ( )
2 2 2 3 0x g f
= = − −
Với
3 3 1
20
4 4 2
x g f
= = − −
Với
1 1 1
20
4 4 2
x g f
= = −
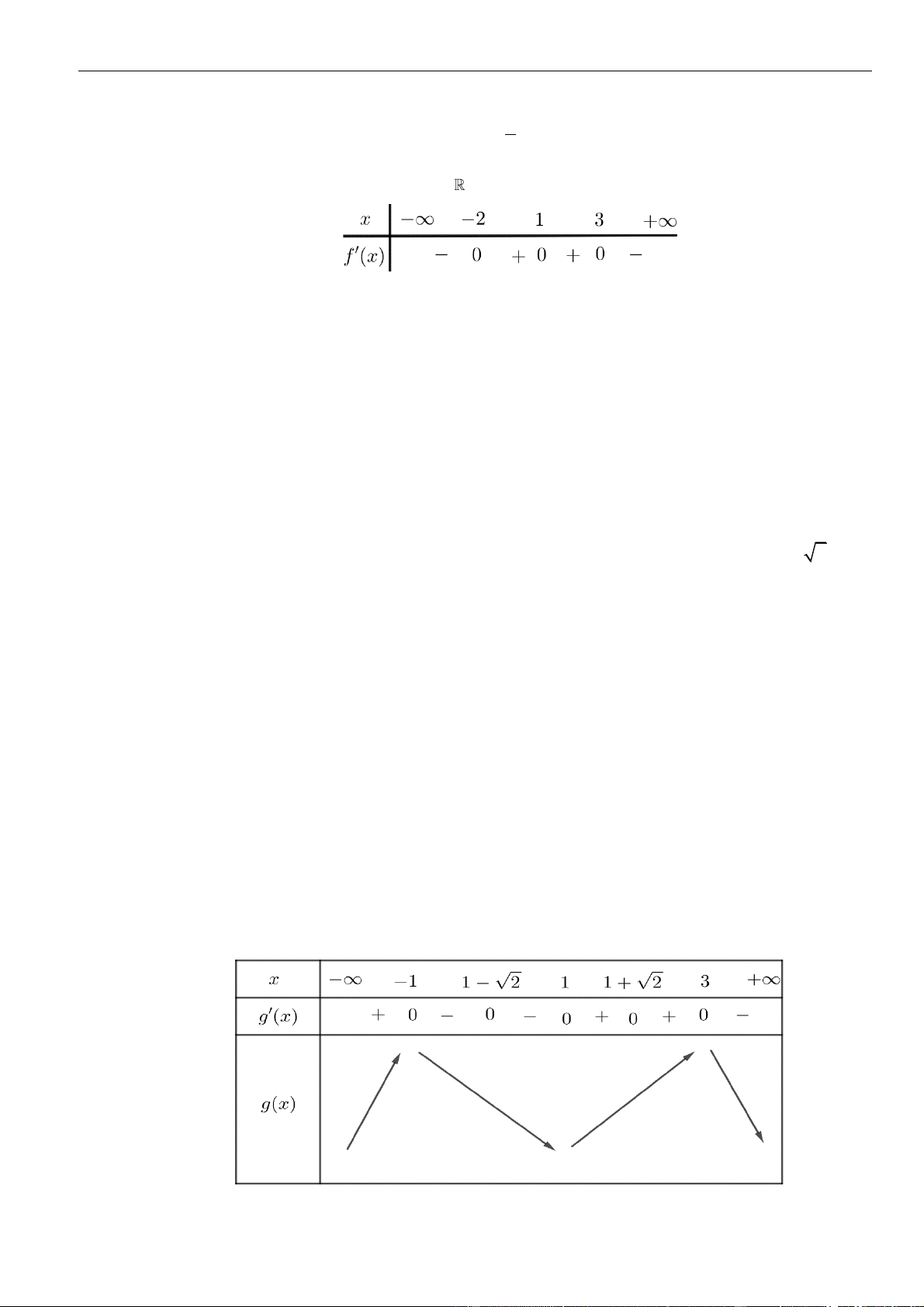
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Với
( ) ( )
1 1 2 3 0x g f
= − − = −
Vậy hàm số
( )
12y f x=−
đạt cực tiểu tại
1
2
x =
.
Câu 26: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu của
( )
fx
như sau
Hỏi hàm số
( )
( )
2
2g x f x x=−
có bao nhiêu điểm cực tiểu?
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
Ta có
( ) ( )
( )
2
2 2 2g x x f x x
= − −
.
Suy ra
( ) ( )
( )
( )
2
2
2
2
2
1
2 2 0
23
0 2 2 2 0
20
22
21
x
x
xx
g x x f x x
f x x
xx
xx
=
−=
−=
= − − =
−=
− = −
−=
1
3
1
12
x
x
x
x
=
=
=−
=
.
Xét
( )
0gx
( )
( )
2
2 2 2 0x f x x
− −
( )
( )
2
2
2 2 0
20
2 2 0
20
x
f x x
x
f x x
−
−
−
−
2
2
2
1
2 2 3
1
23
22
x
xx
x
xx
xx
− −
−
− −
2
2
2
2
1
2 2 0
2 3 0
1
2 3 0
2 2 0
x
xx
xx
x
xx
xx
− +
− −
− −
− +
1
13
1
3
1
x
x
x
x
x
−
−
13
1
x
x
−
.
Bảng biến thiên
Từ bảng biến thiên suy ra hàm số
( )
( )
2
2g x f x x=−
có 1 điểm cực tiểu.
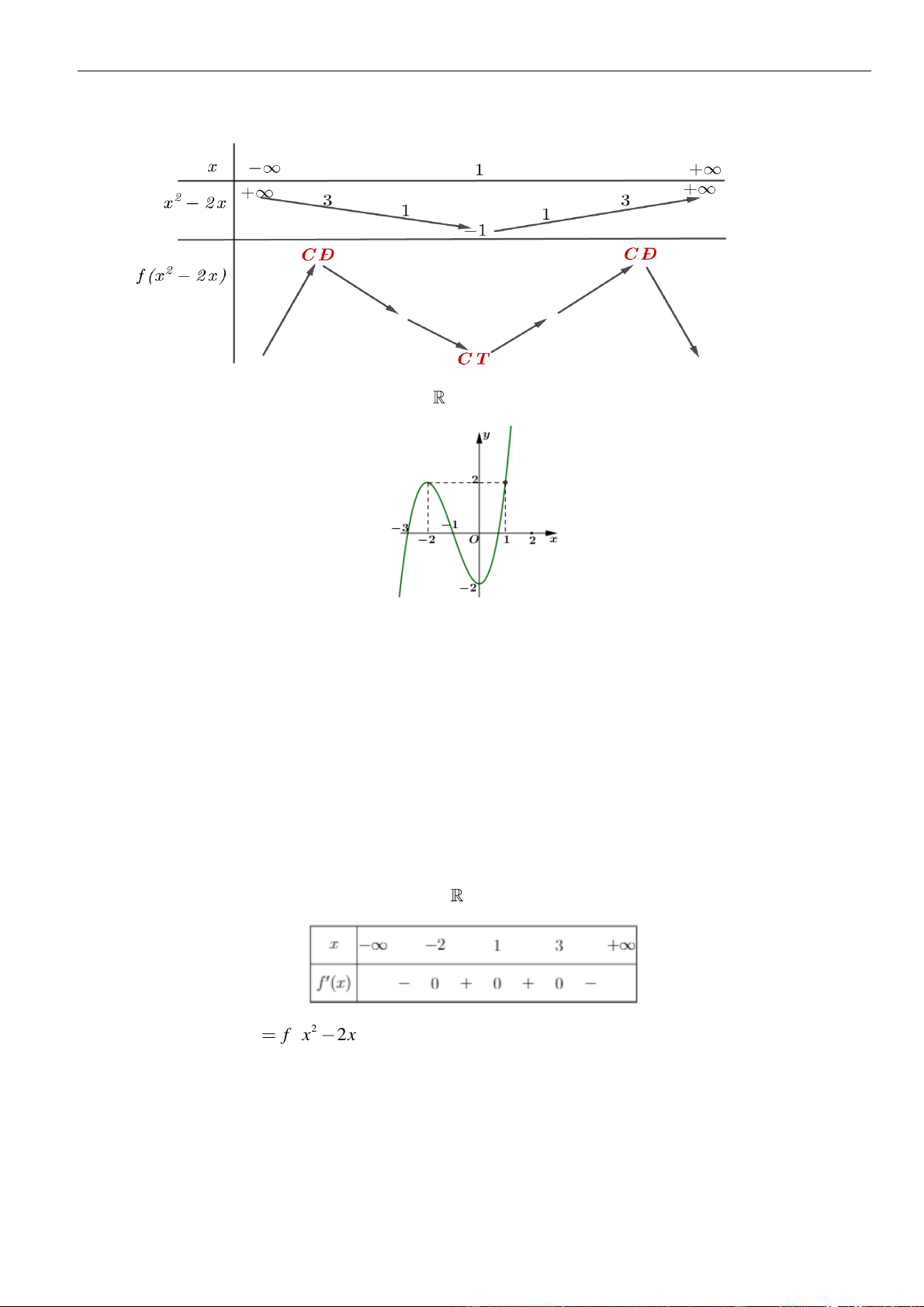
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Cách khác:
Từ BBT hàm
( )
2
2f x x−
được mô tả ở dưới ta suy ra hàm có 1 điểm cực tiểu.
Câu 27: Cho hàm số
( )
y f x=
xác định trên và hàm số
( )
y f x
=
có đồ thị như hình vẽ bên dưới
Hỏi hàm số
( )
fx
ye=
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
Lời giải
Chọn C
Ta có
( )
( )
( )
( )
.
f x f x
y e f x e
==
.
Xét phương trình
( )
( )
( )
( )
( )
. 0 0, 0,
f x f x
f x e f x e x
= =
Suy ra
( ) ( )
0 3, 1, , 0 1f x x x x a a
= = − = − =
.
Các nghiệm này là các nghiệm đơn. Do vậy hàm số
( )
fx
ye=
có 3 điểm cực trị.
Câu 28: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu
'fx
như sau biến thiên như sau:
Hỏi hàm số
2
2y f x x
có bao nhiêu điểm cực tiểu
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn D
Xét hàm số
( )
( )
2
2g x f x x=−
:
( ) ( )
( )
2
' 2 2 ' 2g x x f x x= − −

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
( )
'0gx=
2
2
2
2 2 0
22
21
23
x
xx
xx
xx
−=
− = −
−=
− =
1
12
12
3
1
x
x
x
x
x
=
=+
= −
=
=−
đều là các nghiệm bội lẻ.
Bảng xét dấu
Suy ra hàm số có hai điểm cực tiểu.
Câu 29: Cho hàm số
( )
y f x=
có đạo hàm trên và có bảng xét dấu của
( )
fx
như sau
Hỏi hàm số
( )
( )
2
2g x f x x=−
có bao nhiêu điểm cực tiểu?
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
Ta có
( ) ( )
( )
2
2 2 2g x x f x x
= − −
.
Suy ra
( ) ( )
( )
( )
2
2
2
2
2
1
2 2 0
23
0 2 2 2 0
20
22
21
x
x
xx
g x x f x x
f x x
xx
xx
=
−=
−=
= − − =
−=
− = −
−=
1
3
1
12
x
x
x
x
=
=
=−
=
.
Xét
( )
0gx
( )
( )
2
2 2 2 0x f x x
− −
( )
( )
2
2
2 2 0
20
2 2 0
20
x
f x x
x
f x x
−
−
−
−
2
2
2
1
2 2 3
1
23
22
x
xx
x
xx
xx
− −
−
− −
2
2
2
2
1
2 2 0
2 3 0
1
2 3 0
2 2 0
x
xx
xx
x
xx
xx
− +
− −
− −
− +
1
13
1
3
1
x
x
x
x
x
−
−
13
1
x
x
−
.
Bảng biến thiên
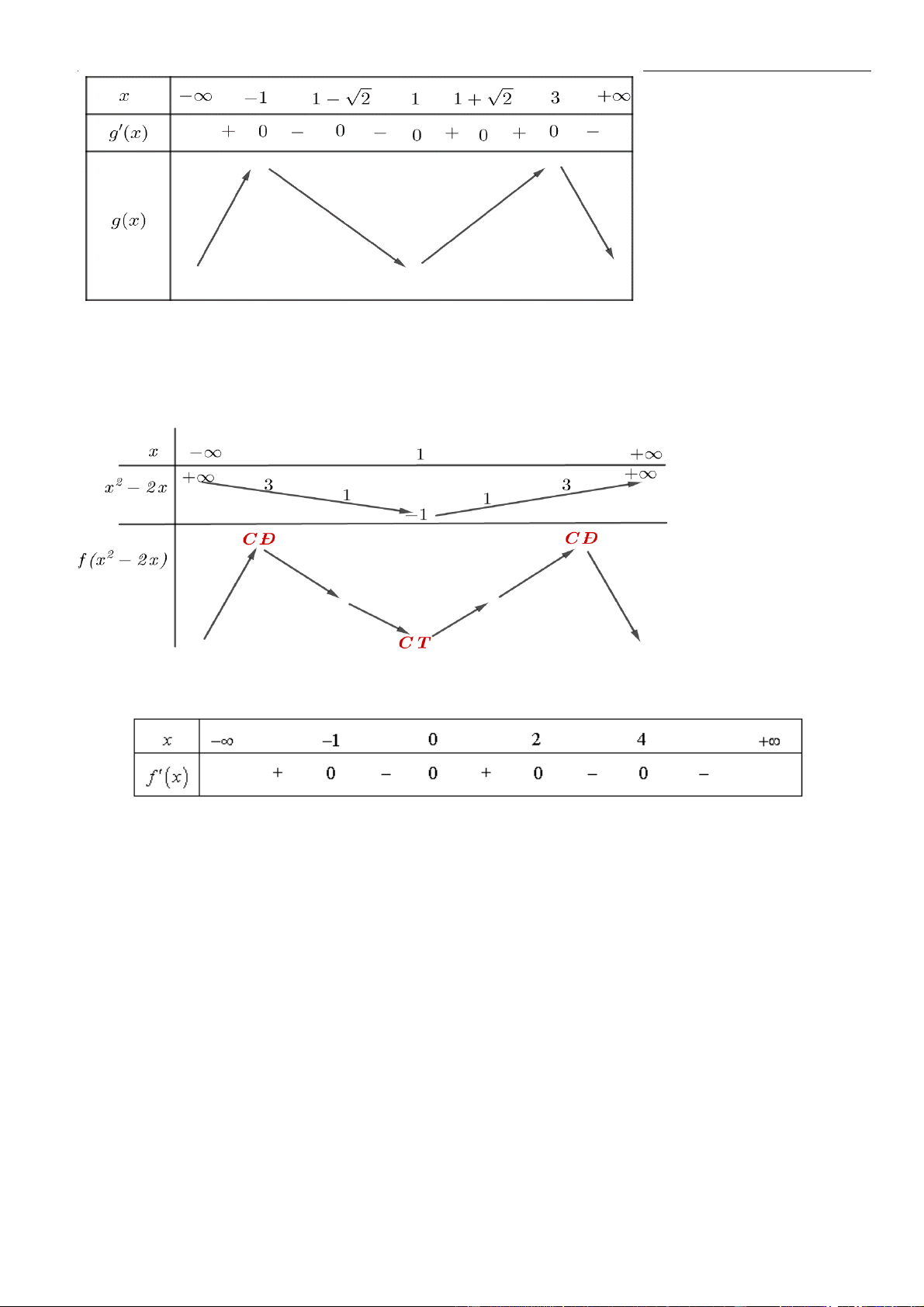
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Từ bảng biến thiên suy ra hàm số
( )
( )
2
2g x f x x=−
có 1 điểm cực tiểu.
Cách khác:
Từ BBT hàm
( )
2
2f x x−
được mô tả ở dưới ta suy ra hàm có 1 điểm cực tiểu.
Câu 30: Cho hàm số
( )
fx
có bảng xét dấu đạo hàm
( )
'fx
như sau:
Hàm số
( )
fx
có bao nhiêu điểm cực đại?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn B
Dựa vào bảng xét dấu đạo hàm
( )
'fx
ta thấy đạo hàm
( )
'fx
đổi dấu từ dương sang âm 2 lần
nên hàm số
( )
fx
có 2 điểm cực đại.
Câu 31: Cho hàm số bậc bốn
( )
y f x=
và có đồ thị
( )
fx
như sau:
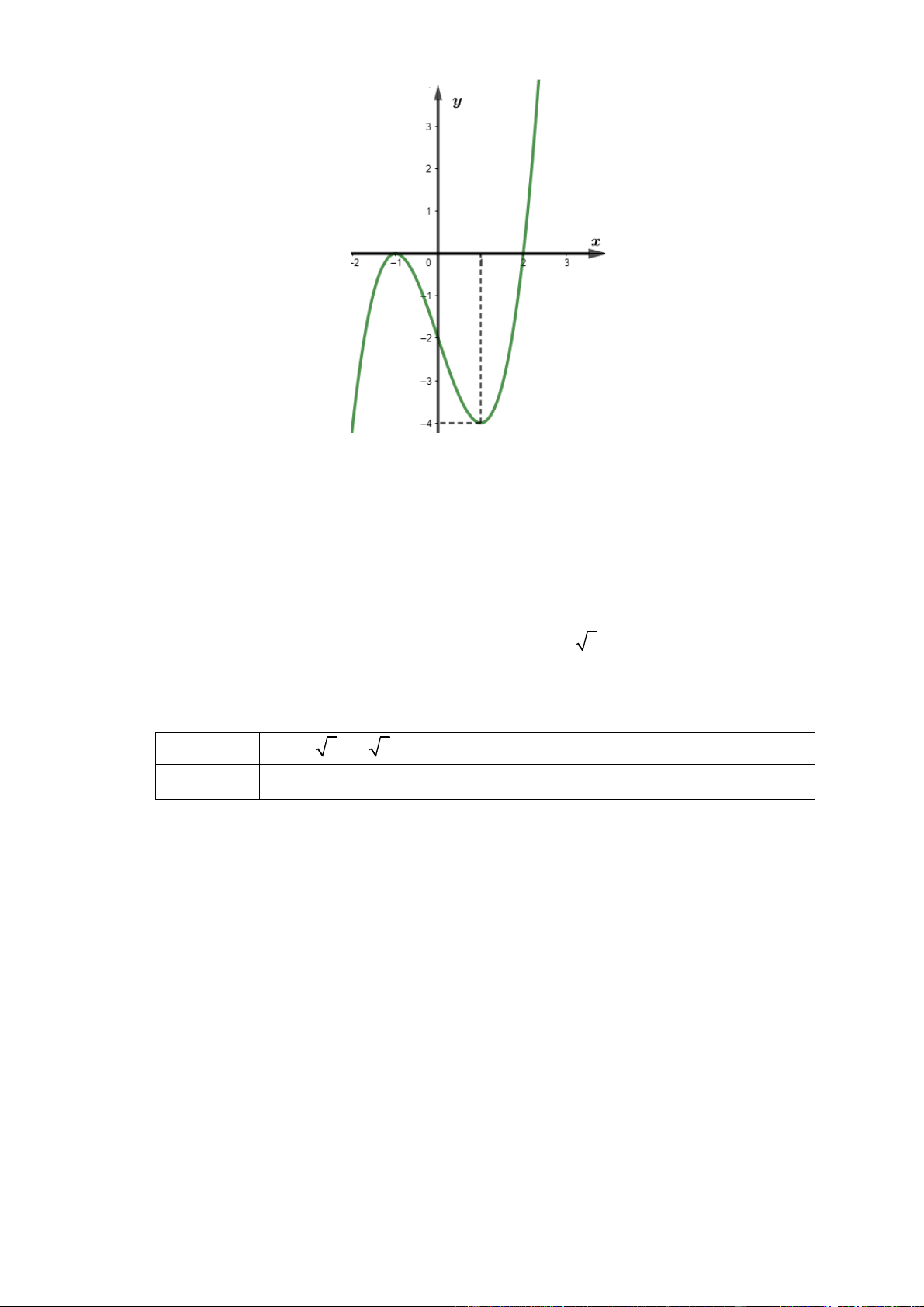
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
Số điểm cực trị của hàm số
( )
( )
2
1g x f x=−
là
A.
1.
B.
3.
C.
2.
D.
4.
Lời giải
Chọn B
Ta có
( )
( )
2
2 . 1g x x f x
=−
Xét
( )
( )
2
2
0
0
0
0
10
12
3
x
x
x
gx
fx
x
x
=
=
=
=
−=
−=
=
( ) ( )
2 4. 3 0gf
=
Ta có bảng xét dấu
( )
gx
:
x
−
3−
0
3
+
( )
gx
−
0
+
0
−
0
+
Vậy số điểm cực trị của hàm số là 3 điểm.
Câu 32: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Tìm số điểm cực trị của hàm số
( )
( )
2
2g x f x x=−
trên khoảng
( )
0; +
.
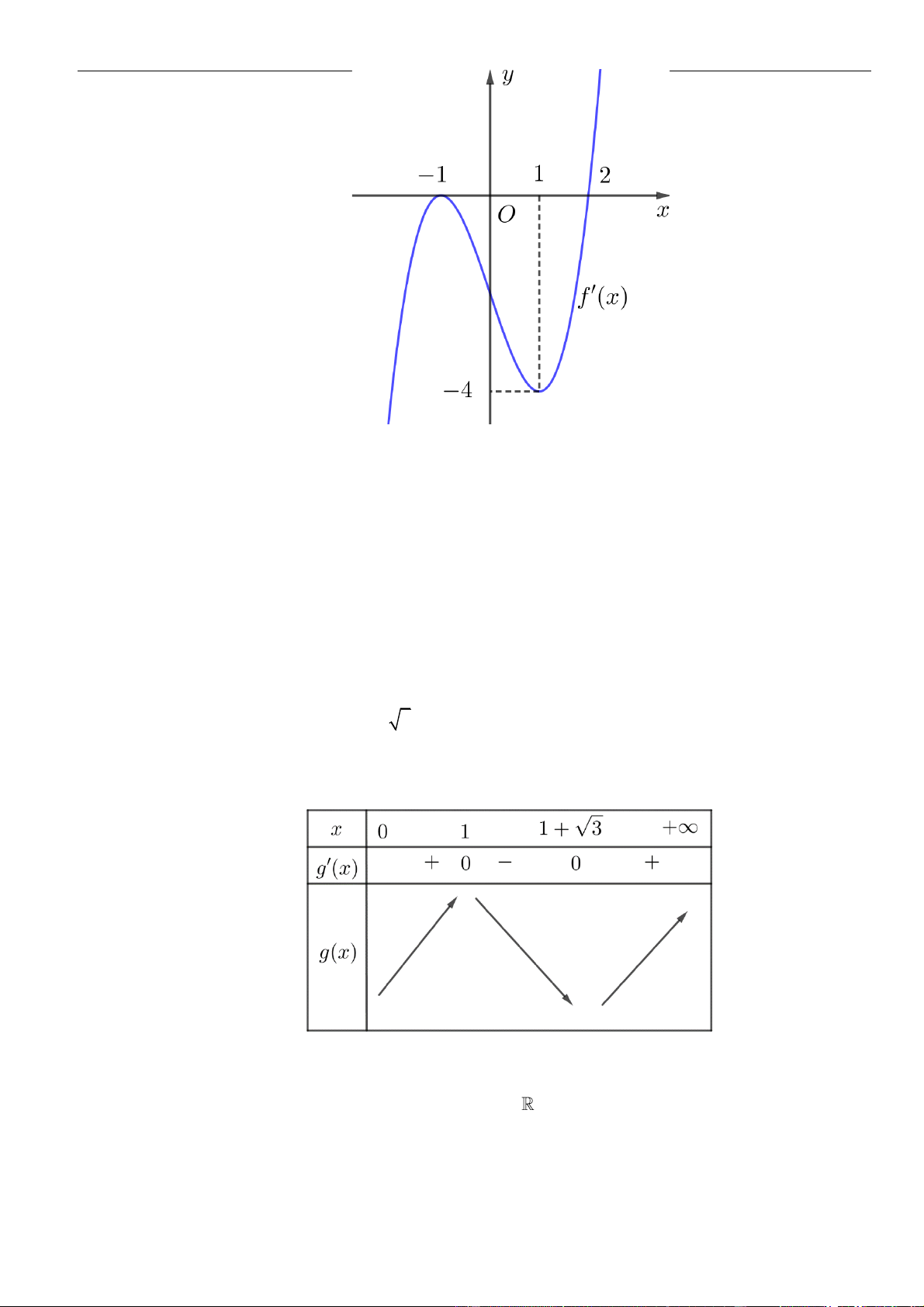
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn B
Ta có
( )
( )
2
2g x f x x=−
( ) ( )
( )
2
2 2 . 2g x x f x x
= − −
.
Suy ra
( )
0gx
=
( )
( )
2
02 2 . 2x f x x
−−=
( )
2
2
1
0f x x
x
−
=
=
2
2
2
1
12
2
xx
xx
x
=
−=
=−
−
2
2
1
102
2 2 0
xx
xx
x
=
+ =
=
−
−−
1
13
1
x
x
x
=
=
=
.
Nhận xét:
( )
2
02f x x
=−
2
21xx − = −
là nghiệm kép.
Bảng biến thiên
Từ bảng biến thiên suy ra hàm số
( )
( )
2
2g x f x x=−
có 2 điểm cực trị trên khoảng
( )
0; +
Câu 33: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên và có đồ thị hàm số
( )
y f x
=
như hình vẽ
bên dưới.
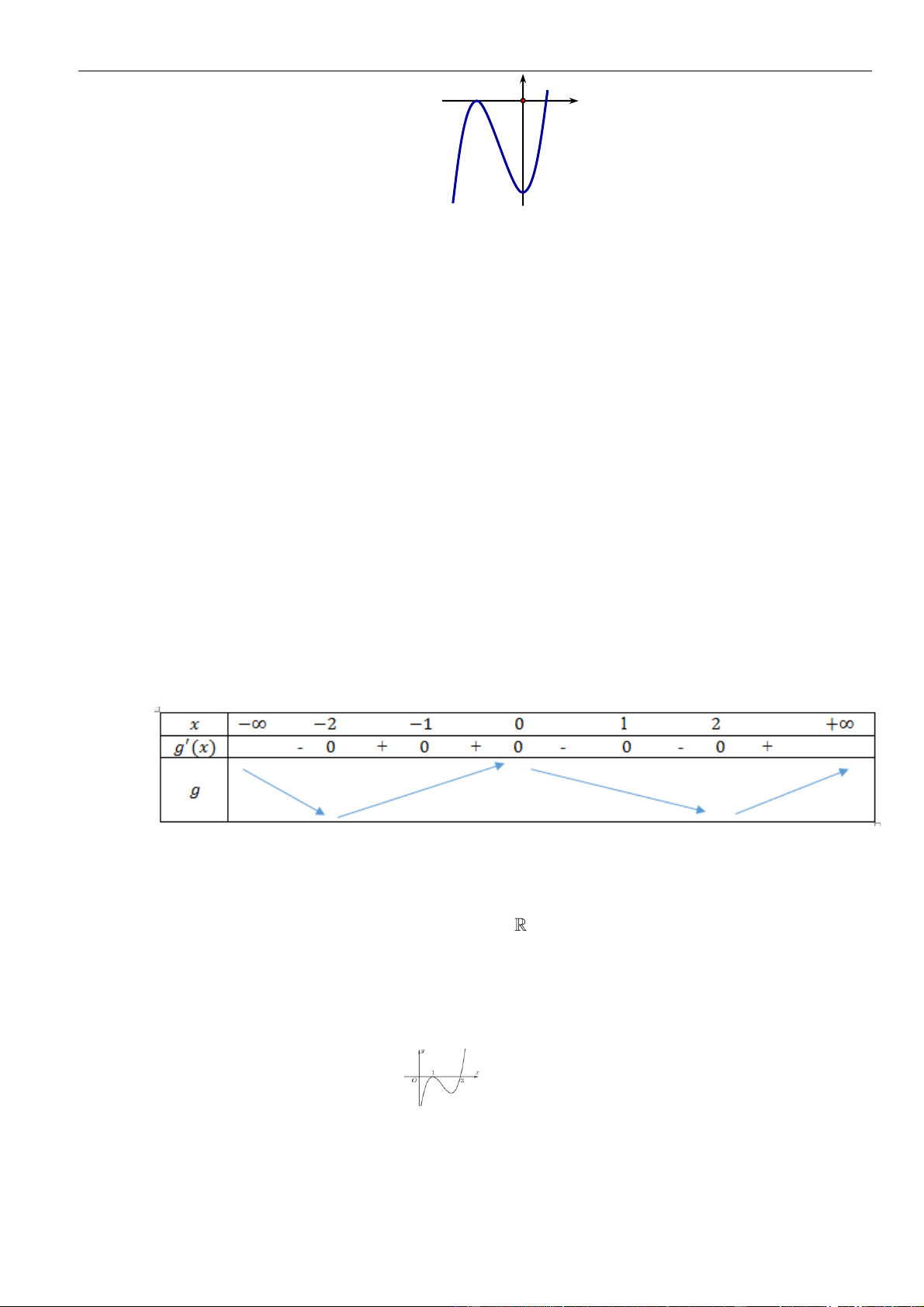
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
27 | Facebook tác giả: Phan Nhật Linh
Xét hàm số
( )
( )
2
3g x f x=−
và các mệnh đề sau:
I. Hàm số
( )
gx
có 3 điểm cực trị.
II. Hàm số
( )
gx
đạt cực tiểu tại
0x =
.
III. Hàm số
( )
gx
đạt cực đại tại
2x =
.
IV. Hàm số
( )
gx
đồng biến trên khoảng
( )
2;0−
.
V. Hàm số
( )
gx
nghịch biến trên khoảng
( )
1;1−
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.
3
. B.
2
. C.
0
. D.
1
Lời giải
Chọn B
Ta có:
( )
( )
2
2 . 3g x x f x
=−
( )
( )
22
2
22
00
0
0 3 2 1
30
3 1 4
xx
x
g x x x
fx
xx
==
=
= − = − =
−=
− = =
0
1
2
x
x
x
=
=
=
Từ đồ thị ta nhận thấy
1x =
là nghiệm kép nên ta có bảng biến thiên sau
Bảng biến thiên
Dựa vào bảng biến thiên của hàm
( )
gx
ta thấy hàm số có 3 điểm cực trị và đồng biến trên
( )
2;0−
.
Câu 34: Cho hàm số
( )
y f x=
xác định và liên tục trên và có đồ thị
( )
y f x
=
như hình vẽ
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số
( )
y f x=
đạt cực đại tại
1x =
.
B. Đồ thị hàm số
( )
y f x=
có một điểm cực đại.
O
x
y
2−
4−
1
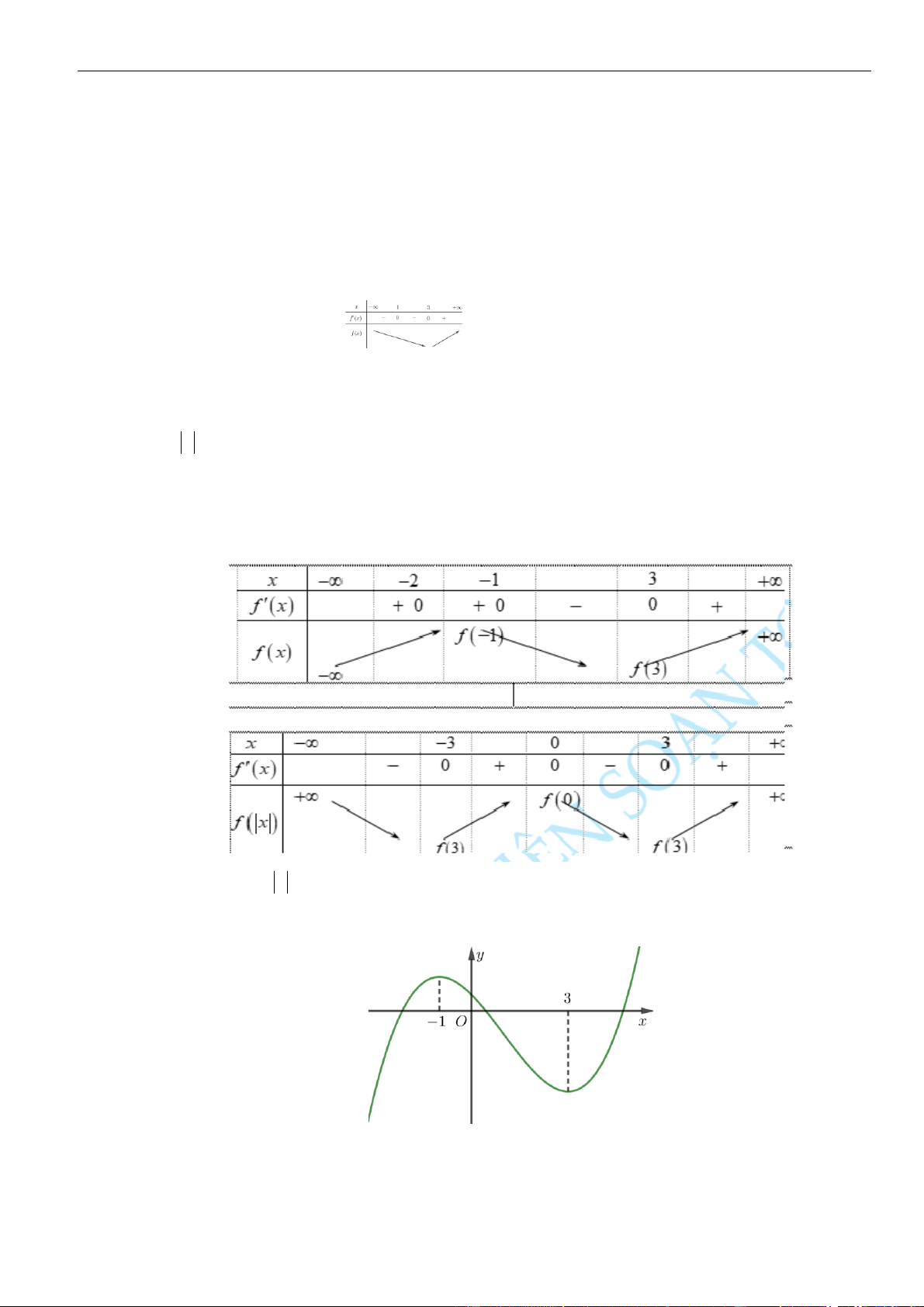
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 28
C. Hàm số
( )
y f x=
đạt cực tiểu tại
3x =
.
D. Đồ thị hàm số
( )
y f x=
có hai điểm cực trị.
Lời giải
Chọn C
Dựa vào đồ thị, ta có bảng biến thiên
Hàm số đạt cực tiểu tại điểm
3x =
.
Câu 35: Cho hàm số
( )
fx
có đạo hàm
( ) ( ) ( ) ( )
4 5 3
2 3 1f x x x x
= + − +
. Số điểm cực trị của hàm số
( )
fx
là
A.
1
. B.
5
. C.
3
. D.
2
.
Lời giải
Chọn C
Ta có bảng biến thiên:
Vậy hàm số
( )
fx
có 3 điểm cực trị.
Câu 36: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ:
Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
( )
( )
2
1y f x m= − +
có 3
điểm cực trị. Tổng các phần tử của
S
là:
A.
2
. B.
4
. C.
8
. D.
10
.
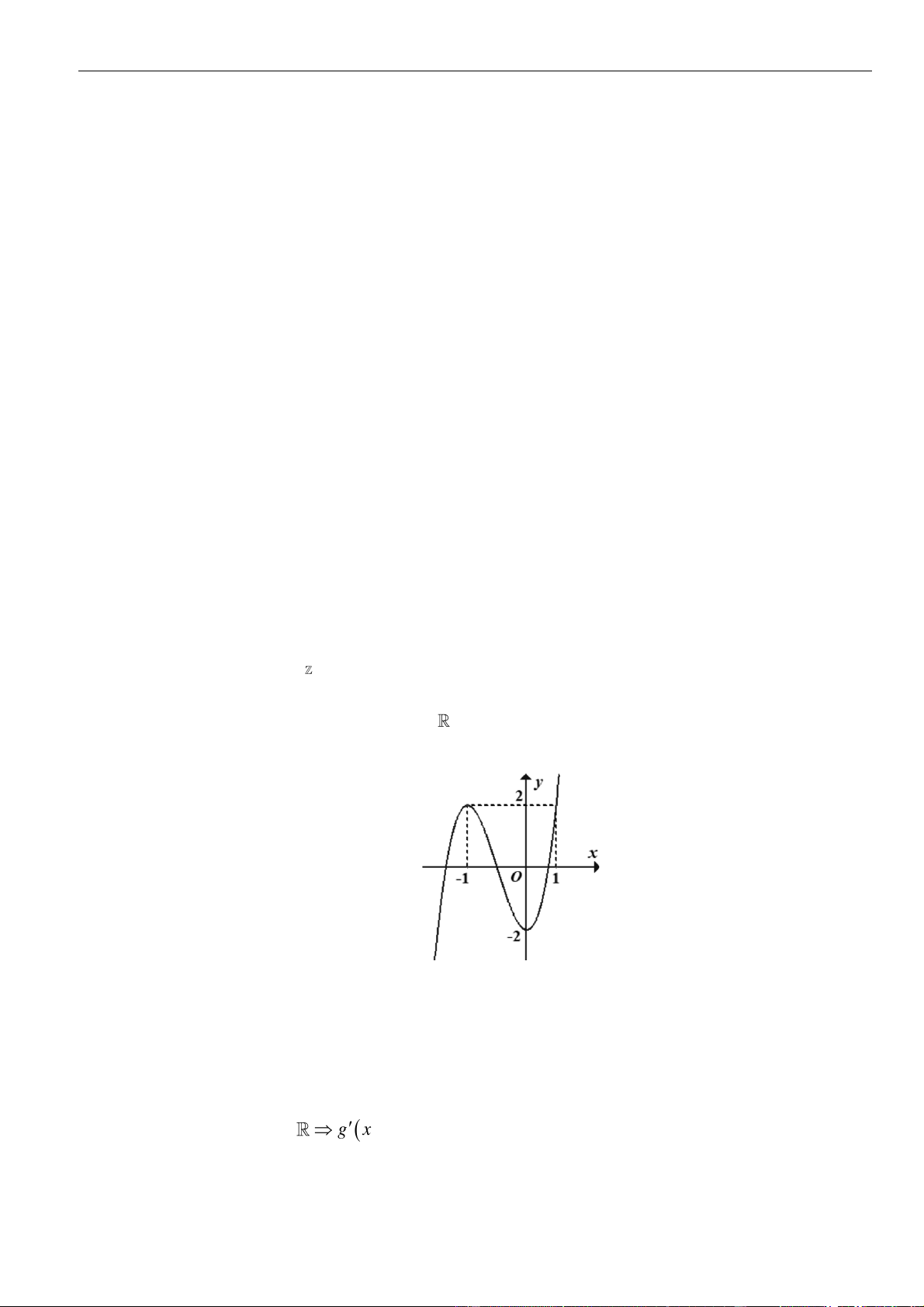
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
29 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn A
Ta có
( ) ( )
( )
2
' 2 1 ' 1y x f x m= − − +
.
( )
( )
( )
( )
( ) ( )
( ) ( )
22
2
22
11
1
' 0 1 1 1 1 1
' 1 0
1 3 1 3 2
xx
x
y x m x m
f x m
x m x m
==
=
= − + = − − = − −
− + =
− + = − = −
.
+) Nếu
1 0 1mm− − = = −
khi đó phương trình
( ) ( )
2
2 1 4x − =
có hai nghiệm phân biệt
khác
1
nên
1m =−
thỏa mãn.
+) Nếu
3 0 3mm− = =
khi đó phương trình
( ) ( )
2
1 1 4x − = −
vô nghiệm. Do đó,
3m =
không thỏa mãn.
+) Để hàm số
( )
( )
2
1y f x m= − +
có 3 điểm cực trị thì phương
( )
1
có hai nghiệm phân biệt và
( )
2
vô nghiệm; hoặc
( )
1
vô nghiệm và
( )
2
có hai nghiệm phân biệt.
1 0 1
3 0 3
13
1 0 1
3 0 3
mm
mm
m
mm
mm
− − −
−
−
− − −
−
.
Vậy
1 3 1;0;1;2
m
mm
− ⎯⎯⎯→ −
. Chọn
A
.
Câu 37: Cho hàm số
( )
y f x=
xác định trên và hàm số
( )
y f x
=
có đồ thị như hình vẽ bên dưới.
Hỏi hàm số
( )
e
fx
y =
có bao nhiêu điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn C
Từ đồ thị hàm số
( )
y f x
=
suy ra
( )
0fx
=
có 3 nghiệm đơn.
Đặt
( )
( )
( ) ( )
( )
ee
f x f x
g x g x f x
= =
.
Vì
( )
( )
e 0, 0
fx
x g x
=
có 3 nghiệm đơn chính là 3 nghiệm của
( )
0fx
=
.
Do đó hàm số
( )
e
fx
y =
có 3 điểm cực trị.
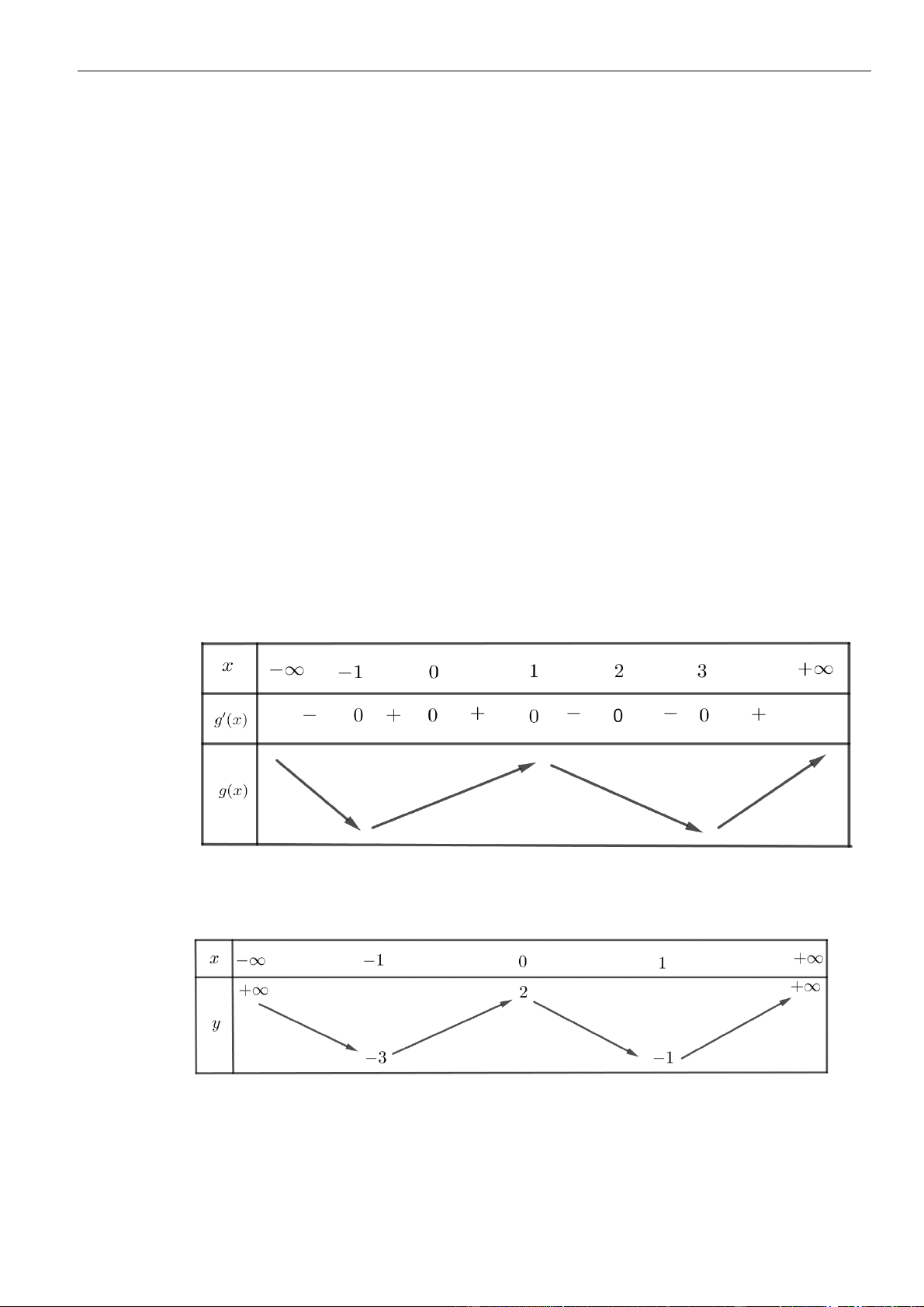
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 30
Câu 38: Cho hàm số
( )
=y f x
có đạo hàm
( ) ( )( )
2
23
= + −f x x x x
. Điểm cực đại của hàm số
( )
( )
2
2g x f x x=−
là
A.
0=x
. B.
1=−x
. C.
3=x
. D.
1=x
.
Lời giải
Chọn D
Theo giả thiết :
( )
0
02
3
=
= = −
=
x
f x x
x
(trong đó
0x =
là nghiệm kép).
Ta có
( ) ( )
( )
2
2 2 2g x x f x x
= − −
, có
( )
( )
2
2
2
2
2 2 0
2 2 0
20
0
20
2 2( )
23
−=
−=
−=
=
−=
− = −
− =
x
x
xx
gx
f x x
x x vn
xx
=
=
=
=−
=
1
0
2
1
3
x
x
x
x
x
(trong đó
0x =
và
2x =
là nghiệm kép).
Bảng biến thiên của hàm số
()gx
Dựa vào BBT, hàm số
()gx
đạt cực đại tại
1x =
.
Câu 39: Cho hàm số
( )
fx
. Bảng biến thiên của hàm số
( )
fx
như sau:
Số điểm cực trị của hàm số
( )
2
2=−y f x x
là :
A.
7
. B.
9
. C.
3
. D.
5
.
Lời giải
Chọn A
Ta có :
( )
( )
2
2 2 2
= − −y x f x x
.
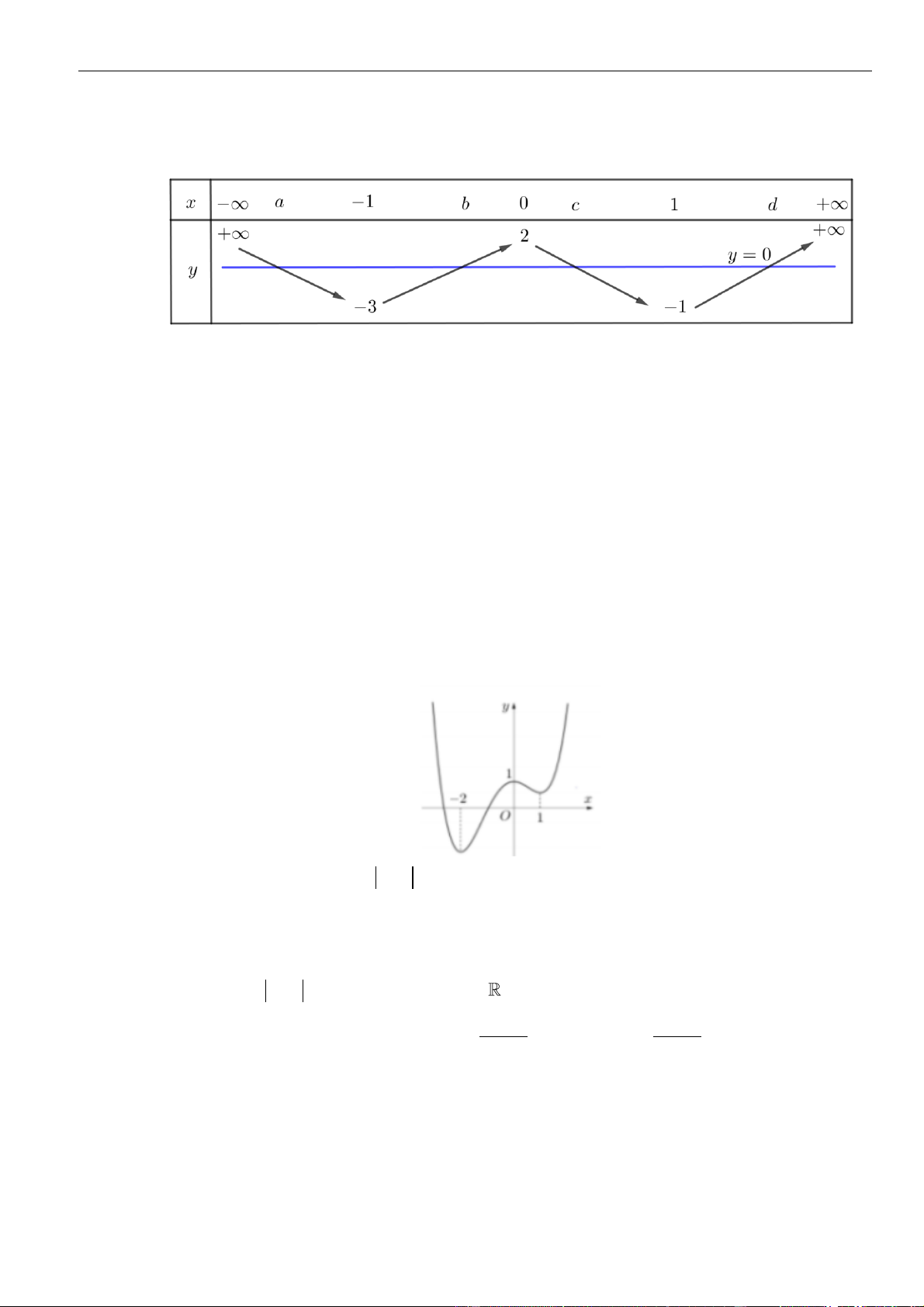
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
31 | Facebook tác giả: Phan Nhật Linh
( )
( )
( )
2
2
1
0 2 2 2 0
20
=
= − − =
−=
x
y x f x x
f x x
.
Từ bảng biến thiên của hàm số
( )
=y f x
Ta có
( )
( )
( )
( )
( )
2
2
2
2
2
2 ; 1
2 1;0
20
2 0;1
2 1;
− = − −
− = −
− =
− =
− = +
x x a
x x b
f x x
x x c
x x d
( )
*
.
Nhận xét phương trình
22
2 2 0− = − − =x x m x x m
:
+) Có 2 nghiệm phân biệt khi và chỉ khi:
1 0 1+ −mm
.
+) Có nghiệm kép khi và chỉ khi:
1 0 1+ = = −mm
khi đó nghiệm kép
1=x
.
+) Có nghiệm
1=x
khi và chỉ khi:
1 0 1− − = = −mm
.
Suy ra
( )
*
có
6
nghiệm (đơn) phân biệt và khác
1=x
. Do đó
0
=y
có
7
nghiệm đơn.
Vây:
( )
2
2=−y f x x
có
7
điểm cực trị.
Câu 40: Cho hàm số
( )
4 3 2
y f x ax bx cx dx e= = + + + +
có đồ thị như hình vẽ bên.
Số cực trị của hàm số
( )
13y f x= + −
là
A.
3
. B.
8
. C.
7
. D.
4
.
Lời giải
Chọn C
Xét
( )
( )
13g x f x= + −
. Tập xác định
D =
.
Ta có:
11
( ) (| 1| 3) (| 1| 3) (| 1| 3) ( )
| 1| | 1|
x
g x x f x f x h x
xx
+
= + − + − = + − =
++
Với
( ) ( 1) (| 1| 3)h x x f x
= + + −

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 32
1
0
1
2
1 0 | 1| 3 2
( ) 0
2
(| 1| 3) 0 | 1| 3 0
4
| 1| 3 1
3
5
x
x
x
x
xx
hx
x
f x x
x
x
x
x
=−
=
=−
=−
+ = + − = −
=
=
+ − = + − =
=−
+ − =
=
=−
bảng xét dấu
( )
gx
Vậy hàm số
( )
y g x=
có
7
cực trị.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
33 | Facebook tác giả: Phan Nhật Linh

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Có bao nhiêu giá trị của tham số
m
để hàm số
3 2 2
1
( 1) 1
2
y x m x m= + − + −
có điểm cực đại là
1x =−
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 2: Cho hàm số
( )
( )
3 2 2
3 3 1 .f x x mx m x= − + −
Tìm tất cả các giá trị của
m
để hàm số
( )
fx
đạt
cực đại tại
0
1x =
.
A.
1m =
. B.
0m =
. C.
2m =
. D.
0m =
hoặc
2m =
.
Câu 3: Có bao nhiêu số nguyên
m
để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
.
A.
0
. B.
1
. C.
2
. D. Vô số.
Câu 4: Tìm
m
để hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại
1x =
.
A.
1
2
m
m
=
=
. B.
1m =
. C.
1m =
. D.
2m =
.
Câu 5: Tìm tất cả các giá trị của tham số
m
để hàm số
32
3y x x mx= − +
có điểm cực đại là
2x =
?
A.
0m
. B.
0m =
. C.
0m
. D.
0m
.
Câu 6: Với giá trị nào của
m
thì hàm số
( )
32
1 2 1y x m x m= − + + − +
đạt cực đại tại
= 2x
A.
2m =
. B.
3m =−
C.
1m =
. D.
3m =
.
Câu 7: Cho hàm số
( )
3 2 2
11
31
32
y x m x m x= − + + +
. Có bao nhiêu số thực m để hàm số đạt cực trị tại
1x =
?
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 8: Đồ thị hàm số
42
y ax bx c= + +
có điểm cực đại là
( )
0; 3A −
và một điểm cực tiểu là
( )
1; 5B −−
. Khi đó tổng
abc++
bằng.
A.
1−
.
B.
7
. C.
5−
. D.
3
.
Câu 9: Hàm số
42
21y x mx= − + +
đạt cực tiểu tại
0x =
khi:
A.
0m
. B.
10m−
. C.
0m
. D.
1m −
.
Câu 10: Có bao nhiêu số nguyên
m
để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
.
Tìm m để hàm số đạt cực trị tại điểm x=x
0
cho trước
DẠNG 5
Phương pháp:
•
Bưc 1. Tính
( ) ( )
00
' , ''y x y x
•
Bưc 2. Giải phương trình
( )
0
' 0 ?y x m=
•
Bưc 3. Thế
m
vào
( )
0
''yx
nếu giá trị
0
0
'' 0
'' 0
y x CT
y x CD
→ =
→ =

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
0
. B.
1
. C.
2
. D. Vô số.
Câu 11: Tìm
m
đề hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại điểm
3x =
.
A.
1m =−
. B.
1m =
. C.
5m =
. D.
5m =−
.
Câu 12: Tìm tất cả các giá trị của tham số
m
để hàm số
32
23y x mx mx= − + −
đạt cực tiểu tại điểm
1x =
.
A.
1m =−
. B.
2m =
. C.
2m =−
. D.
1m =
.
Câu 13: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
12 2y x mx m x= − + + − +
đạt cực tiểu tại
1x =−
thuộc khoảng nào dưới đây?
A.
( )
5;9
. B.
( )
4;0−
. C.
( )
0;3
. D.
( )
3;6
.
Câu 14: Với giá trị nào của
m
thì hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
?
A.
0m =
. B.
0m
. C.
0m
. D.
0m
.
Câu 15: Để hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
thì tham số
m
thuộc khoảng nào sau đây?
A.
( )
3;5m
B.
( )
3; 1m − −
C.
( )
1;3m
D.
( )
1;1m−
Câu 16: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
là
A.
1m =
. B.
5m =
. C.
1m =
;
5m =
. D.
1m =−
;
5m =−
.
Câu 17: Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
A.
1m =
. B.
1m =−
. C.
1m =
hoặc
2m =
. D.
2m =
.
Câu 18: Tất cả các giá trị thực của tham số
m
để hàm số
32
35y x x mx= − + +
có hai điểm cực trị là
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Câu 19: Để hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
thì tham số
m
thuộc khoảng nào sau đây?
A.
( )
3;5m
B.
( )
3; 1m − −
C.
( )
1;3m
D.
( )
1;1m−
Câu 20: Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
A.
2m =−
. B.
1m =−
. C.
2m =
. D.
1m =
.
Câu 21: Tìm tất cả giá trị của tham số thực
m
để hàm số
3 2 2
( 1) 2 3y mx m x x= − + + −
đạt cực tiểu tại
điểm
1x =
A.
3
2
m =
. B.
2m =−
. C.
0m =
. D.
m
.
Câu 22: Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2 2
21y x mx m x= − + +
đạt cực tiểu tại
1x =
là
A.
1
. B.
1; 3−−
. C.
3
. D.
1;3
.
Câu 23: Hàm số
3 2 2
22y x mx m x= − + −
đạt cực tiểu tại
1x =
khi
A.
1m =−
. B.
3m =
. C.
1m =
. D.
3m =−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 24: Cho hàm số đạt cực tiểu tại
1x =
. Giá trị của
m
A. B. C. D.
Câu 25: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
.
A.
7m =−
. B.
1m =−
. C.
5m =
. D.
1m =
.
Câu 26: Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
A.
1m =
. B.
1m =−
. C.
1m =
hoặc
2m =
. D.
2m =
.
Câu 27: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
12 2y x mx m x= − + + − +
đạt cực tiểu tại
1x =−
thuộc khoảng nào dưới đây?
A.
( )
5;9
. B.
( )
4;0−
. C.
( )
0;3
. D.
( )
3;6
.
Câu 28: Tìm
m
đề hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại điểm
3x =
.
A.
1m =−
. B.
1m =
. C.
5m =
. D.
5m =−
.
Câu 29: Cho hàm số
32
( ) 3 1y f x x mx= = + −
. Giá trị của tham số
m
để hàm số có điểm cực đại
2x =−
là:
A.
2−
. B.
C.
1−
D.
1
Câu 30: Có bao nhiêu giá trị của tham số
m
để hàm số
( )
3 2 2
1
11
2
y x m x m= + − + −
có điểm cực đại là
1x =−
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 31: Tìm tất cả các giá trị của tham số
m
để hàm số
( ) ( )
3 2 2 2
231
1
3
y x m m x m x= − + +++
đạt cực
tiểu tại
2x =−
.
A.
3
1
m
m
=
=
. B.
3m =
. C.
1m =
. D.
3
1
m
m
=−
=−
.
Câu 32: Để hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
thì tham số thực
m
thuộc khoảng nào sau
đây?
A.
( )
3;5m
. B.
( )
3; 1m − −
. C.
( )
1;3m
. D.
( )
1;1m−
.
Câu 33: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
là
A.
1m =
. B.
5m =
. C.
1; 5mm==
. D.
1; 5mm= − = −
.
Câu 34: Có bao nhiêu số nguyên
m
để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
.
A.
0
. B.
1
. C.
2
. D. Vô số.
Câu 35: Cho hàm số
( )
32
12y x mx m x= − + − +
. Tìm
m
để hàm số đạt cực tiểu tại
1x =
.
A.
2m =−
. B.
2m =
. C.
1m =
. D.
1m =−
.
32
23y x x mx= − + +
4.
3.
2.
1.
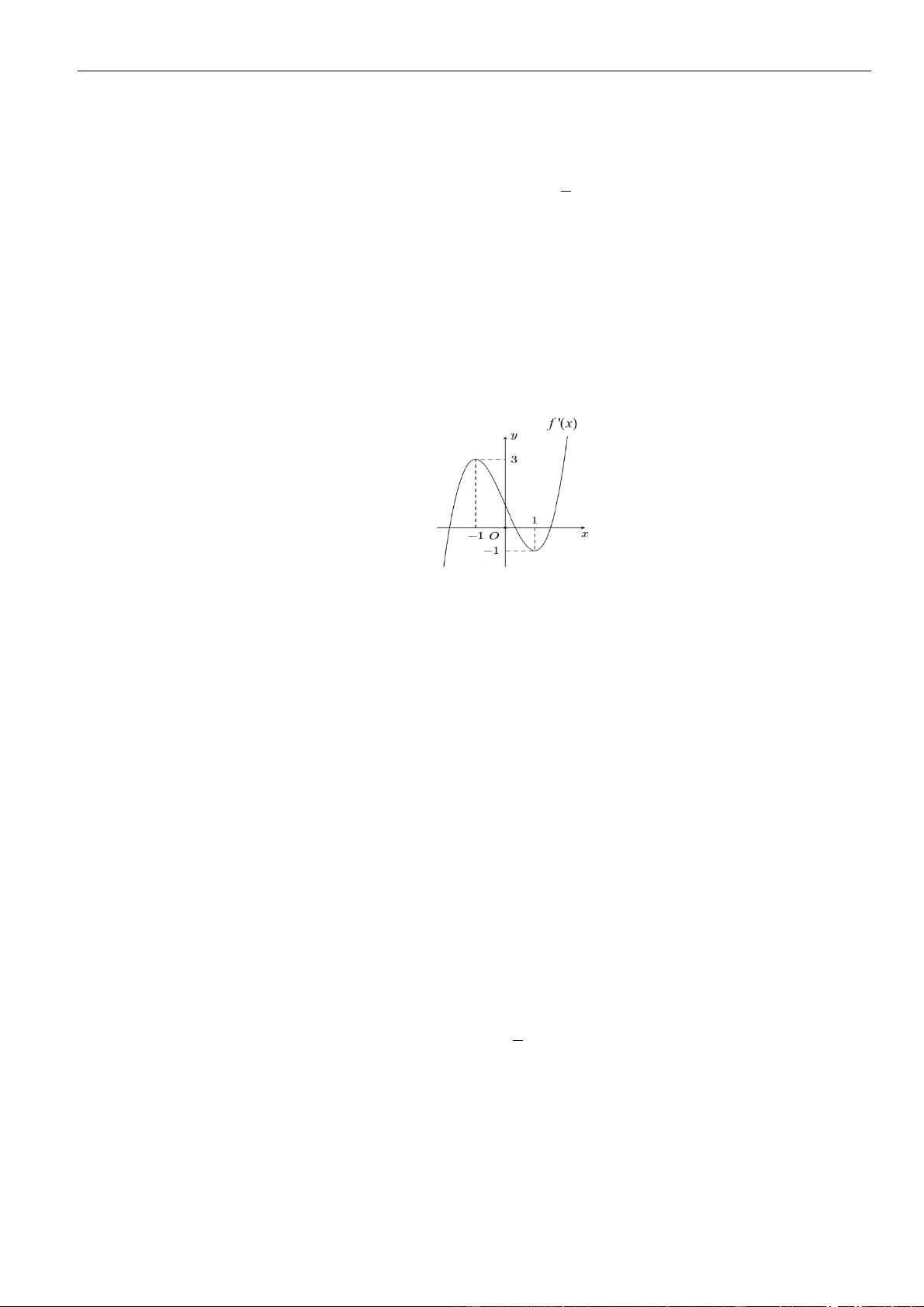
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 36: Có bao nhiêu giá trị thực của tham số m để hàm số
( )
( )
4 2 2
11x m x m x+ − + −
đạt cực tiểu tại
điểm
0x =
?
A. 3. B. 0. C. 2. D. 1.
Câu 37: Tất cả các giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
điểm
3x =
là
A.
7.m =−
B.
5.m =
C.
1.m =−
D.
1.m =
Câu 38: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
4 2 2
5 3 3 4y x m x m= − − + −
đạt cực
tiểu tại
0x =
là
A.
( )
;3−
. B.
(
;3− −
. C.
( )
3; +
. D.
)
3; +
.
Câu 39: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
fx
như sau:
Trên khoảng
( )
10;10−
có tất cả bao nhiêu số nguyên của
m
để hàm số
( ) ( )
2020g x f x mx= + +
có đúng một cực trị?
A.
16
. B.
15
. C.
14
. D.
13
.
Câu 40: Cho hàm số
32
23y x x mx= − + +
đạt cực tiểu tại
1x =
. Giá trị của
m
bằng
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 41: Tất cả các giá trị của tham số
m
để hàm số
42
( 1)y x m x= − + +
đạt cực đại tại
0x =
là
A.
1m =−
. B.
1m −
. C.
1m −
. D.
1m −
.
Câu 42: Cho hàm số
( )
3 2 2 2
3 3 1 1y x mx m x m= − + − − +
với
m
là tham số thự C. Tìm
m
để hàm số
đạt cực tiểu tại
1x =
.
A.
4m =−
. B.
0m =
. C.
2m =
. D.
0; 2mm==
.
Câu 43: Có bao nhiêu giá trị của tham số
m
để hàm số
( )
3 2 2
32y x mx m x m= − + + −
đạt cực tiểu tại
1x =
?
A.
1
. B.
0
. C.
2
. D. Vô số
Câu 44: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt giá trị cực đại tại
3x =
.
A.
1m =−
. B.
5m =
C.
7m =−
. D.
1m =
Câu 45: Có bao nhiêu giá trị thực của tham số
m
để hàm số
( )
( )
4 2 2
11y x m x m x= + − + −
đạt cực tiểu
tại điểm
0x =
A.
3
. B.
0
. C.
2
. D.
1
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Có bao nhiêu giá trị của tham số
m
để hàm số
3 2 2
1
( 1) 1
2
y x m x m= + − + −
có điểm cực đại là
1x =−
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Ta có
( )
2 2 2
3 1 , 6 1y x m x y x m
= + − = + −
.
Hàm số có điểm cực đại là
1x =−
khi
( )
( )
2
2
10
40
2
10
70
y
m
m
y
m
−=
−=
=
−
−
.
Câu 2: Cho hàm số
( )
( )
3 2 2
3 3 1 .f x x mx m x= − + −
Tìm tất cả các giá trị của
m
để hàm số
( )
fx
đạt
cực đại tại
0
1x =
.
A.
1m =
. B.
0m =
. C.
2m =
. D.
0m =
hoặc
2m =
.
Giải
Chọn C
Hàm số đạt cực đại tại
0
1x =
( )
( )
' 1 0
'' 1 0
f
f
=
Ta có
( )
( )
( )
22
' 3 6 3 1
'' 6 6
f x x mx m
f x x m
= − + −
=−
2
0
3 6 3 3 0
2.
2
6 6 0
1
m
mm
m
m
m
m
=
− + − =
=
=
−
.
Câu 3: Có bao nhiêu số nguyên
m
để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
.
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải
Chọn B
32
31y x x mx= + − +
.
2
36y x x m
= + −
.
66yx
= +
.
Để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
( )
( )
10
10
y
y
=
2
3.1 6.1 0
6.1 6 0
m
+ − =
+
.
( )
9
12 0
m
n
=
.
Câu 4: Tìm
m
để hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại
1x =
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
A.
1
2
m
m
=
=
. B.
1m =
. C.
1m =
. D.
2m =
.
Lời giải
Chọn D
TXD:
D =
Ta có
22
' 2 1y x mx m m= − + − +
Để
1x =
là điểm cực đại của hàm số thì
( )
1
' 1 0
2
m
y
m
=
=
=
Với
1m =
thì
( )
2
2
' 2 1 1 0,y x x x x= − + = −
. Vậy
1m =
không thỏa mãn
Với
2m =
thì
2
1
' 4 3 0
3
x
y x x
x
=
= − + =
=
Xét dấu
'y
ta được
1x =
là điểm cực đại của hàm số. Vậy
2m =
.
Câu 5: Tìm tất cả các giá trị của tham số
m
để hàm số
32
3y x x mx= − +
có điểm cực đại là
2x =
?
A.
0m
. B.
0m =
. C.
0m
. D.
0m
.
Lời giải
Chọn B
TXĐ:
D =
Ta có
2
36y x x m
= − +
.
* Hàm số có điểm cực đại là
2x =
khi
( )
2
2 0 3.2 6.2 0 0y m m
= − + = =
.
* Với
0m =
ta có
2
0
3 6 , 0
2
x
y x x y
x
=
= − =
=
.
Ta có bảng xét dấu
Vậy hàm số có điểm cực đại là
2x =
.
Câu 6: Với giá trị nào của
m
thì hàm số
( )
32
1 2 1y x m x m= − + + − +
đạt cực đại tại
= 2x
A.
2m =
. B.
3m =−
C.
1m =
. D.
3m =
.
Lời giải
Chọn A
( )
2
3 2 1y x m x
= − + +
( )
6 2 1y x m
= − + +
Hàm số đạt cực đại tại điểm
2x =
khi
( )
( )
20
20
y
y
=
( )
( )
12 4 1 0
12 2 1 0
m
m
− + + =
− + +
2
2
5
m
m
m
=
=
.
Câu 7: Cho hàm số
( )
3 2 2
11
31
32
y x m x m x= − + + +
. Có bao nhiêu số thực m để hàm số đạt cực trị tại
1x =
?
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
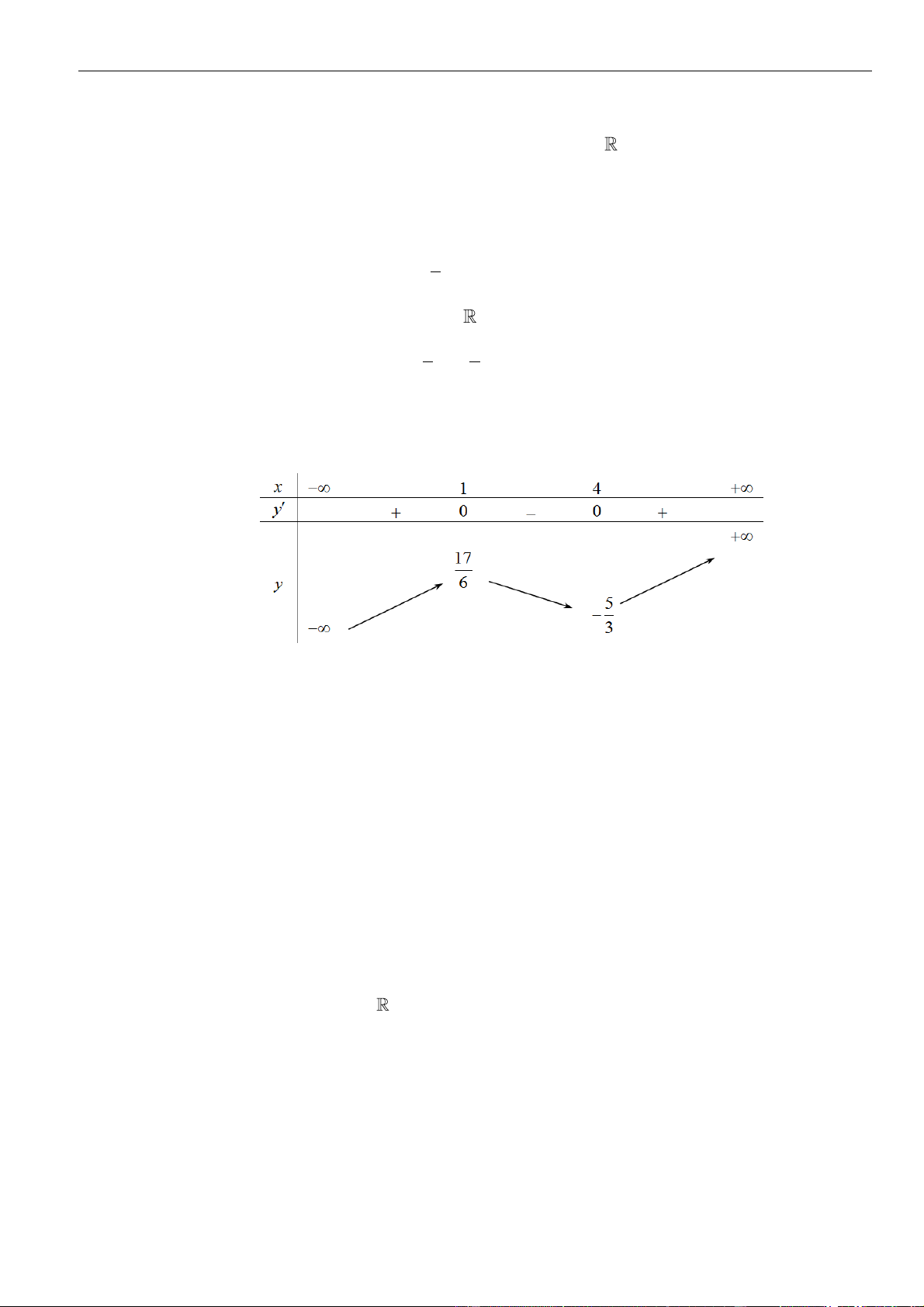
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Chọn D
Ta có:
( )
22
( ) 3y f x x m x m
= = − + +
.
Điều kiện cần: Hàm số
()y f x=
đã có đạo hàm tại
x
.
Do đó, hàm số
()y f x=
đạt cực trị tại
1x =
(1) 0f
=
2
20mm − − =
1
2
m
m
=−
=
.
Điều kiện đủ:
* Với
1m =−
hàm số trở thành:
32
1
1
3
y x x x= − + +
.
Ta có:
( )
2
2
2 1 1 0,y x x x x
= − + = −
. Do đó hàm số không có điểm cực trị.
* Với
2m =
hàm số trở thành:
32
15
41
32
y x x x= − + +
.
Ta có:
2
54y x x
= − +
;
1
0
4
x
y
x
=
=
=
.
Bảng biến thiên:
Hàm số đạt cực đại tại
1x =
. Vậy
4m =
thỏa mãn.
Câu 8: Đồ thị hàm số
42
y ax bx c= + +
có điểm cực đại là
( )
0; 3A −
và một điểm cực tiểu là
( )
1; 5B −−
. Khi đó tổng
abc++
bằng.
A.
1−
.
B.
7
. C.
5−
. D.
3
.
Lời giải
Chọn C
Do đồ thị hàm số
42
y ax bx c= + +
có và một điểm cực tiểu là
( )
1; 5B −−
nên ta có:
( )
1 5 5y a b c− = − + + = −
.
Câu 9: Hàm số
42
21y x mx= − + +
đạt cực tiểu tại
0x =
khi:
A.
0m
. B.
10m−
. C.
0m
. D.
1m −
.
Lời giải
Chọn A
Hàm số xác định với mọi
x
.
Ta có:
32
4 4 ; 12 4y x mx y x m
= − + = − +
.
Hàm số đạt cực tiểu tại
0x =
khi
( )
( )
00
0
40
00
y
m
m
m
y
=
.
Vậy
0m
.
Câu 10: Có bao nhiêu số nguyên
m
để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
.
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Chọn B
32
31y x x mx= + − +
.
2
36y x x m
= + −
.
66yx
= +
.
Để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
( )
( )
10
10
y
y
=
2
3.1 6.1 0
6.1 6 0
m
+ − =
+
.
( )
9
12 0
m
n
=
.
Câu 11: Tìm
m
đề hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại điểm
3x =
.
A.
1m =−
. B.
1m =
. C.
5m =
. D.
5m =−
.
Lời giải
Chọn C
Ta có
( )
22
24y x mx m
= − + −
,
22y x m
=−
.
Hàm số đạt cực trị tại
3x =
suy ra
( )
30y
=
2
6 5 0mm − + =
1
5
m
m
=
=
.
Với
5m =
ta có
( )
3 6 10 4 0y
= − = −
suy ra hàm số đạt cực đại tại
3x =
.
Với
1m =
ta có
( )
3 6 2 4 0y
= − =
suy ra hàm số đạt cực tiểu tại
3x =
.
Vậy
5m =
thì hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại điểm
3x =
.
Câu 12: Tìm tất cả các giá trị của tham số
m
để hàm số
32
23y x mx mx= − + −
đạt cực tiểu tại điểm
1x =
.
A.
1m =−
. B.
2m =
. C.
2m =−
. D.
1m =
.
Lời giải
Chọn D
3 2 2
2 3 3 4y x mx mx y x mx m
= − + − = − +
và
64y x m
=−
Hàm số đạt cực tiểu tại điểm
1x =
suy ra
( )
1 0 3 4 0 1y m m m
= − + = =
.
Với
1m =
có
( )
1 6.1 4.1 2 0y
= − =
suy ra
( )
( )
10
1 2 0
y
y
=
=
hay hàm số đạt cực tiểu tại
1x =
.
Câu 13: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
12 2y x mx m x= − + + − +
đạt cực tiểu tại
1x =−
thuộc khoảng nào dưới đây?
A.
( )
5;9
. B.
( )
4;0−
. C.
( )
0;3
. D.
( )
3;6
.
Lời giải
Chọn D
Tập xác định
D =
.
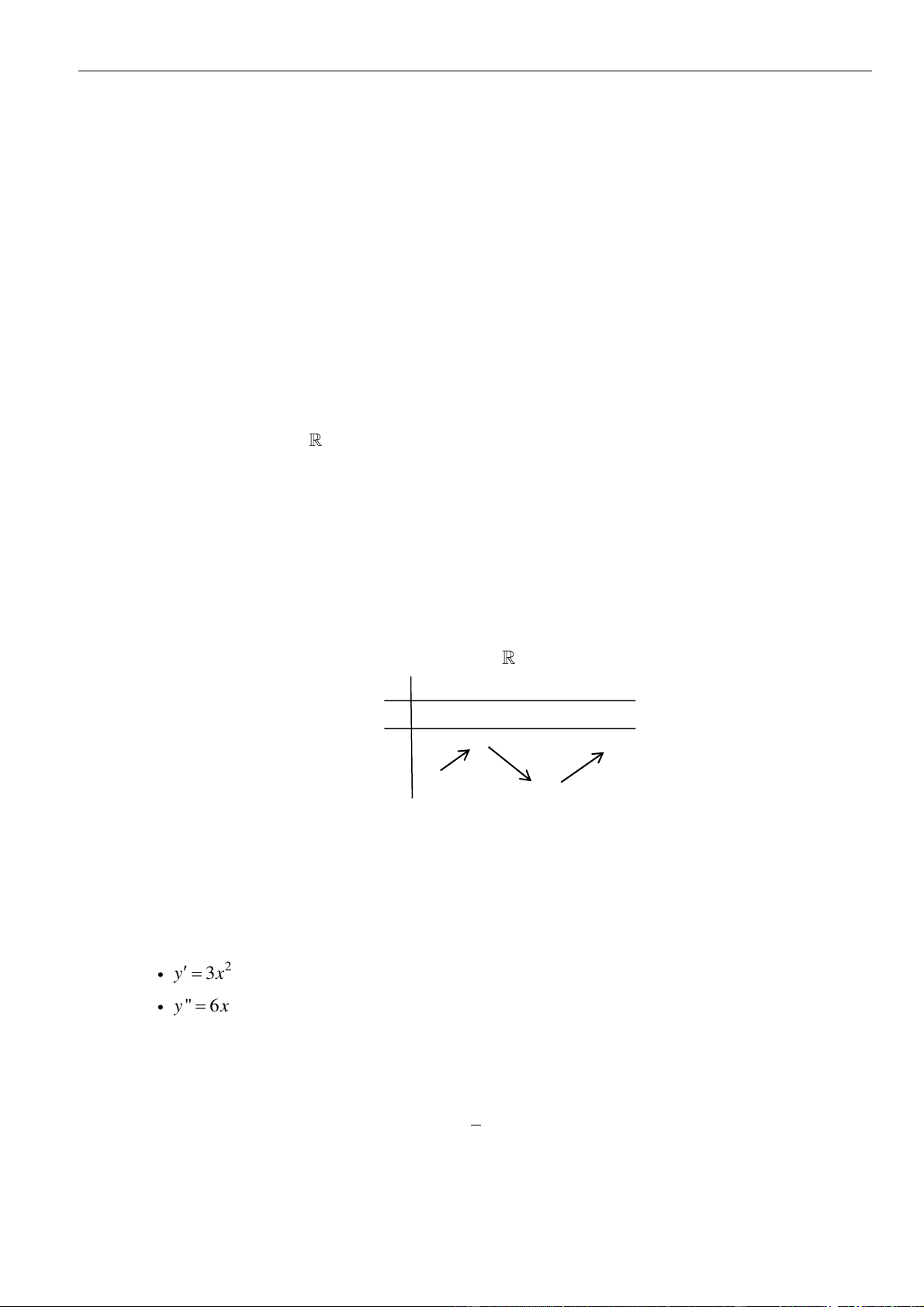
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
22
3 2 12y x mx m
= − + + −
;
62y x m
= − +
.
Để hàm số đạt cực tiểu tại
1x =−
khi
( )
( )
10
10
y
y
−=
−
( ) ( )
( )
2
2
3. 1 2 . 1 12 0
6. 1 2 0
mm
m
− − + − + − =
− − +
2
2 15 0
3
mm
m
− − =
−
( )
( )
5
3
3
m TM
mL
m
=
=−
−
5m=
.
Vậy
( )
5 3;6m =
Câu 14: Với giá trị nào của
m
thì hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
?
A.
0m =
. B.
0m
. C.
0m
. D.
0m
.
Lời giải
Chọn A
Tập xác định:
D =
.
Ta có
2
36y x x m
= − +
.
Giả sử hàm số đạt cực tiểu tại
( )
2 2 0 12 12 0x y m
= = − + =
0m=
.
Với
0m =
tacó
32
3y x x=−
.
Tacó
2
36y x x
=−
0
0
2
x
y
x
=
=
=
.
Bảng biến thiên của hàm
32
3y x x=−
với
x
Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại
2x =
.
Câu 15: Để hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
thì tham số
m
thuộc khoảng nào sau đây?
A.
( )
3;5m
B.
( )
3; 1m − −
C.
( )
1;3m
D.
( )
1;1m−
Lời giải
Chọn D
2
3 6 .
" 6 6.
y x x
yx
=−
=−
Hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
khi
( )
( )
2
20
3.2 6.2 0
0
6.2 6 0
20
y
m
m
y
=
− + =
=
−
Câu 16: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
là
A.
1m =
. B.
5m =
. C.
1m =
;
5m =
. D.
1m =−
;
5m =−
.
Lời giải
Chọn A
'y
x
y
+
+
−
0
2
0
−
0
2
+
4−
−
+

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Hàm số xác định với mọi
x
.
Ta có:
22
24y x mx m
= − + −
;
22y x m
=−
.
Để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
thì:
( )
( )
2
1
30
6 5 0
1
5
6 2 0
30
3
m
y
mm
m
m
m
y
m
=
=
− + =
=
=
−
.
Vậy
1m =
.
Câu 17: Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
A.
1m =
. B.
1m =−
. C.
1m =
hoặc
2m =
. D.
2m =
.
Lời giải
Chọn D
Có
22
21y x mx m m
= − + − +
,
22y x m
=−
Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
( )
( )
2
10
3 2 0
2
2 2 0
10
y
mm
m
m
y
=
− + =
=
−
.
Câu 18: Tất cả các giá trị thực của tham số
m
để hàm số
32
35y x x mx= − + +
có hai điểm cực trị là
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Lời giải
Chọn B
Ta có
2
36y x x m
= − +
Để hàm số có hai điểm cực trị thì
0y
=
có hai nghiệm phân biệt
9 3 0 3
y
mm
= −
.
Câu 19: Để hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
thì tham số
m
thuộc khoảng nào sau đây?
A.
( )
3;5m
B.
( )
3; 1m − −
C.
( )
1;3m
D.
( )
1;1m−
Lời giải
Chọn D
2
3 6 .
" 6 6.
y x x
yx
=−
=−
Hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
khi
( )
( )
2
20
3.2 6.2 0
0
6.2 6 0
20
y
m
m
y
=
− + =
=
−
Câu 20: Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
A.
2m =−
. B.
1m =−
. C.
2m =
. D.
1m =
.
Lời giải
Ta có
22
21y x mx m m
= − + − +
và
22y x m
=−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Hàm số đạt cực đại tại điểm
( )
( )
2
10
1 2 1 0
12
2 2 0
10
y
m m m
xm
m
y
=
− + − + =
= =
−
.
Câu 21: Tìm tất cả giá trị của tham số thực
m
để hàm số
3 2 2
( 1) 2 3y mx m x x= − + + −
đạt cực tiểu tại
điểm
1x =
A.
3
2
m =
. B.
2m =−
. C.
0m =
. D.
m
.
Lời giải
Chọn A
22
' 3 2( 1) 2y mx m x= − + +
,
2
'' 6 2( 1)y mx m= − +
Điều kiện cần
2
0
'(1) 0 2 3 0
3
2
m
y m m
m
=
= − + =
=
Điều kiện đủ
Khi
0 ''(1) 2 0 1m y x= = − =
là điểm cực đại của hàm số
Khi
35
''(1) 0 1
22
m y x= = =
là điểm cực tiểu của hàm số
Câu 22: Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2 2
21y x mx m x= − + +
đạt cực tiểu tại
1x =
là
A.
1
. B.
1; 3−−
. C.
3
. D.
1;3
.
Lời giải
Chọn A
Tập xác định
D =
Ta có :
22
34y x mx m
= − +
64y x m
=−
Để hàm số đạt cực tiểu tại
1x =
thì:
2
1
(1) 0
4 3 0
3
1
(1) 0
6 4 0
3
2
m
y
mm
m
m
y
m
m
=
=
− + =
=
=
−
Vậy tập hợp tất cả các giá trị của tham số
m
để hàm số đạt cực tiểu tại
1x =
là
1S =
.
Câu 23: Hàm số
3 2 2
22y x mx m x= − + −
đạt cực tiểu tại
1x =
khi
A.
1m =−
. B.
3m =
. C.
1m =
. D.
3m =−
.
Lời giải
Chọn C
Ta có:
' 2 2 ''
3 4 ; 6 4y x mx m y x m= − + = −
.
Hàm số đạt cực tiểu tại
1x =
( )
'2
1
1 3 4 0
3
m
y m m
m
=
= − + =
=
( )
'' 1 6 4ym=−
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Với
1m =
thì
( ) ( )
'' 1 2 0y TM=
.
Với
3m =
thì
( ) ( )
'' 1 2 6 0y ktm= −
.
Vậy
1m =
.
Câu 24: Cho hàm số đạt cực tiểu tại
1x =
. Giá trị của
m
A. B. C. D.
Lời giải
Chọn D
Tập xác định
D =
.
Ta có:
2
34y x x m
= − +
.
Hàm số đạt cực tiểu tại
1x =
suy ra
( )
10y
=
1 0 1mm − + = =
.
Với
1m =
:
3 2 2
2 3, ' 3 4 1y x x x y x x= − + + = − +
,
64yx
=−
.
'(1) 0, ''(1) 0yy=
1x=
là điểm cực tiểu của hàm số.
Vậy
1m =
là giá trị cần tìm.
Câu 25: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
.
A.
7m =−
. B.
1m =−
. C.
5m =
. D.
1m =
.
Lời giải
Chọn D
Ta có
22
2 4 ; 2 2y x mx m y x m
= − + − = −
Để hàm số đạt cực tiểu tại
3x =
khi
( )
( )
2
1
30
6 5 0
1
5
6 2 0
30
3
m
y
mm
m
m
m
y
m
=
=
− + =
=
=
−
.
Câu 26: Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
A.
1m =
. B.
1m =−
. C.
1m =
hoặc
2m =
. D.
2m =
.
Lời giải
Chọn D
Có
22
21y x mx m m
= − + − +
,
22y x m
=−
Hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại điểm
1x =
khi
( )
( )
2
10
3 2 0
2
2 2 0
10
y
mm
m
m
y
=
− + =
=
−
.
Câu 27: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
12 2y x mx m x= − + + − +
đạt cực tiểu tại
1x =−
thuộc khoảng nào dưới đây?
A.
( )
5;9
. B.
( )
4;0−
. C.
( )
0;3
. D.
( )
3;6
.
Lời giải
Chọn D
Tập xác định
D =
.
22
3 2 12y x mx m
= − + + −
;
62y x m
= − +
.
32
23y x x mx= − + +
4.
3.
2.
1.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Để hàm số đạt cực tiểu tại
1x =−
khi
( )
( )
10
10
y
y
−=
−
( ) ( )
( )
2
2
3. 1 2 . 1 12 0
6. 1 2 0
mm
m
− − + − + − =
− − +
2
2 15 0
3
mm
m
− − =
−
( )
( )
5
3
3
m TM
mL
m
=
=−
−
5m=
.
Vậy
( )
5 3;6m =
Câu 28: Tìm
m
đề hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại điểm
3x =
.
A.
1m =−
. B.
1m =
. C.
5m =
. D.
5m =−
.
Lời giải
Chọn C
Ta có
( )
22
24y x mx m
= − + −
,
22y x m
=−
.
Hàm số đạt cực trị tại
3x =
suy ra
( )
30y
=
2
6 5 0mm − + =
1
5
m
m
=
=
.
Với
5m =
ta có
( )
3 6 10 4 0y
= − = −
suy ra hàm số đạt cực đại tại
3x =
.
Với
1m =
ta có
( )
3 6 2 4 0y
= − =
suy ra hàm số đạt cực tiểu tại
3x =
.
Vậy
5m =
thì hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại điểm
3x =
.
Câu 29: Cho hàm số
32
( ) 3 1y f x x mx= = + −
. Giá trị của tham số
m
để hàm số có điểm cực đại
2x =−
là:
A.
2−
. B.
C.
1−
D.
1
Lời giải
Chọn D
Ta có:
2
' '( ) 3 6 ; ''( ) 6 6y f x x mx f x x m= = + = +
. Hàm số đạt cực đại tại
'( 2) 0 12 12 0
21
''( 2) 0 12 6 0
fm
xm
fm
− = − =
= − =
− − +
.
Câu 30: Có bao nhiêu giá trị của tham số
m
để hàm số
( )
3 2 2
1
11
2
y x m x m= + − + −
có điểm cực đại là
1x =−
?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
( )
3 2 2
1
11
2
y x m x m= + − + −
( )
22
2
' 3 1
'' 6 1
y x m x
y x m
= + −
= + −
Hàm số
( )
3 2 2
1
11
2
y x m x m= + − + −
có điểm cực đại là
1x =−

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
( )
( )
22
2
3 1 1 0 4
2
m
mm
m
=
+ − − = =
=−
Lúc này
( )
'' 1 6 4 1 0y − = − + −
nên hàm số đạt cực đại tại
1x =−
.
Vậy có 2 giá trị
m
thỏa yêu cầu bài toán.
Câu 31: Tìm tất cả các giá trị của tham số
m
để hàm số
( ) ( )
3 2 2 2
231
1
3
y x m m x m x= − + +++
đạt cực
tiểu tại
2x =−
.
A.
3
1
m
m
=
=
. B.
3m =
. C.
1m =
. D.
3
1
m
m
=−
=−
.
Lời giải
Chọn B
Xét
( ) ( )
3 2 2 2
231
1
3
y x m m x m x= − + +++
.
Tập xác định
D =
.
Ta có:
( ) ( )
2 2 2
3 122y x m m x m
= − ++++
.
Hàm số đạt cực tiểu tại
2x =−
nên
( )
2 0y
− =
.
Ta có
( )
2 2 2
144032 043 mm m m m−+ −+= ++ =−
1
3
m
m
=
=
.
( )
2
222y x m m
+
= − +
.
( )
2
22 2y m m
=−−
.
( )
2
1
2
0
2 0 2 0
m
y m m
m
−
−
Để hàm số hàm số đạt cực tiểu tại
2x =−
thì
3m =
thỏa mãn.
Câu 32: Để hàm số
32
3y x x mx= − +
đạt cực tiểu tại
2x =
thì tham số thực
m
thuộc khoảng nào sau
đây?
A.
( )
3;5m
. B.
( )
3; 1m − −
. C.
( )
1;3m
. D.
( )
1;1m−
.
Lời giải
Chọn D
Tập xác định:
D =
.
2
36y x x m
= − +
.
Hàm số đạt cực tiểu tại
( )
2
2 2 0 3.2 6.2 0 0x y m m
= = − + = =
. (Trắc nghiệm: làm đến
đây và xét các đáp án ta chọn D)
Khi
0m =
thì
2
3 6 6 6y x x y x
= − = −
.
Ta có:
( )
2 6.2 6 6 0y
= − =
hàm số đạt cực tiểu tại
2x =
.
Vậy
0m =
thì hàm số đạt cực tiểu tại
( )
2 1;1xm= −
.
Câu 33: Giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
là
A.
1m =
. B.
5m =
. C.
1; 5mm==
. D.
1; 5mm= − = −
.
Lời giải

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Chọn A
Ta có: TXĐ: R.
22
' 2 4y x mx m= − + −
.
'' 2 2y x m=−
.
Hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực tiểu tại
3x =
khi:
( )
( )
2
1
' 3 0
6 5 0
1
5
6 2 0
'' 3 0
3
m
y
mm
m
m
m
y
m
=
=
− + =
=
=
−
. Vậy
1m =
là giá trị cần tìm.
Câu 34: Có bao nhiêu số nguyên
m
để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
.
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải
Chọn B
32
31y x x mx= + − +
.
2
36y x x m
= + −
.
66yx
= +
.
Để hàm số
32
31y x x mx= + − +
đạt cực tiểu tại
1x =
( )
( )
10
10
y
y
=
2
3.1 6.1 0
6.1 6 0
m
+ − =
+
.
( )
9
12 0
m
n
=
.
Câu 35: Cho hàm số
( )
32
12y x mx m x= − + − +
. Tìm
m
để hàm số đạt cực tiểu tại
1x =
.
A.
2m =−
. B.
2m =
. C.
1m =
. D.
1m =−
.
Lời giải
Chọn B
2
3 2 1y x mx m
= − + −
62y x m
=−
Hàm số
( )
y f x=
đạt cực tiểu tại
1x =
( )
( )
10
10
f
f
=
3 2 1 0 2
2
6 2 0 3
m m m
m
mm
− + − = =
=
−
Câu 36: Có bao nhiêu giá trị thực của tham số m để hàm số
( )
( )
4 2 2
11x m x m x+ − + −
đạt cực tiểu tại
điểm
0x =
?
A. 3. B. 0. C. 2. D. 1.
Lời giải
Chọn D
Ta có:
( )
( )
32
4 2 1 1y x m x m
= + − + −
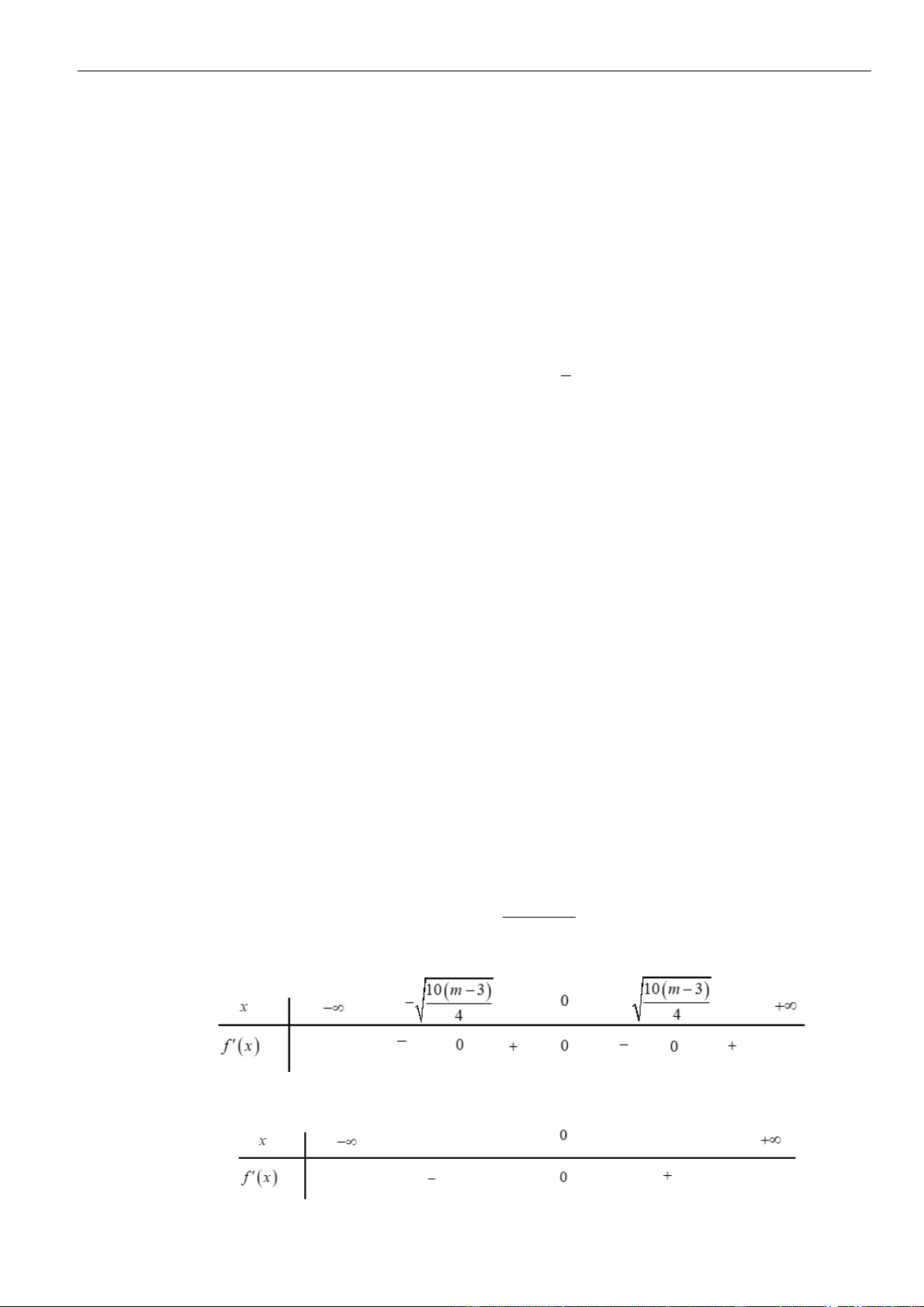
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
( )
2
12 2 1y x m
= + −
Hàm số đạt cực tiểu tại
0x =
( )
2
' 0 0 1 0 1y m m = − = =
Thử lại
- Với
1m =
ta được:
4
yx=
3
4yx
=
00yx
= =
. Hàm số đạt cực tiểu tại
0x =
(thỏa ycbt).
- Với
1m =−
ta được:
42
2y x x=−
3
44y x x
= −
0
0
1
x
y
x
=
=
=
. Hàm số đạt cực đại tại
0x =
và đạt cực tiểu tại
1x =
(không thỏa ycbt).
Vậy có 1 giá trị m thỏa yêu cầu bài toán.
Câu 37: Tất cả các giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
điểm
3x =
là
A.
7.m =−
B.
5.m =
C.
1.m =−
D.
1.m =
Lời giải
Chọn B
Ta có
22
24y x mx m
= − + −
.
Hàm số đạt cực đại tại
3x =
( )
' 3 0y =
2
6 5 0 1;5m m m − + =
.
Thử lại:
+) Với
1m =
thì
2
' 2 3; '' 2 2 ''(3) 0y x x y x y= − − = −
Hàm số đạt cực tiểu tại
1x =
(KTM)
+) Với
5m =
thì
2
' 10 21; '' 2 10 ''(3) 0y x x y x y= − + = −
Hàm số đạt cực đại tại
3x =
(TM)
Câu 38: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
( )
4 2 2
5 3 3 4y x m x m= − − + −
đạt cực
tiểu tại
0x =
là
A.
( )
;3−
. B.
(
;3− −
. C.
( )
3; +
. D.
)
3; +
.
Lời giải
Chọn B
Ta có:
( )
3
4 10 3y x m x
= − −
;
( )
2
0
0
10 3
4
x
y
m
x
=
=
−
=
.
- Trường hợp 1:
30m −
3m
. Khi đó, ta có bảng xét dấu như sau:
Dựa vào bảng biến thiên ta thấy
0x =
là điểm cực đại, nên trường hợp 1 không thỏa mãn.
- Trường hợp 2:
30m −
3m
. Khi đó, ta có bảng xét dấu như sau:
Dựa vào bảng biến thiên ta thấy
0x =
là điểm cực tiểu. Vậy
3m
thỏa mãn ycbt.
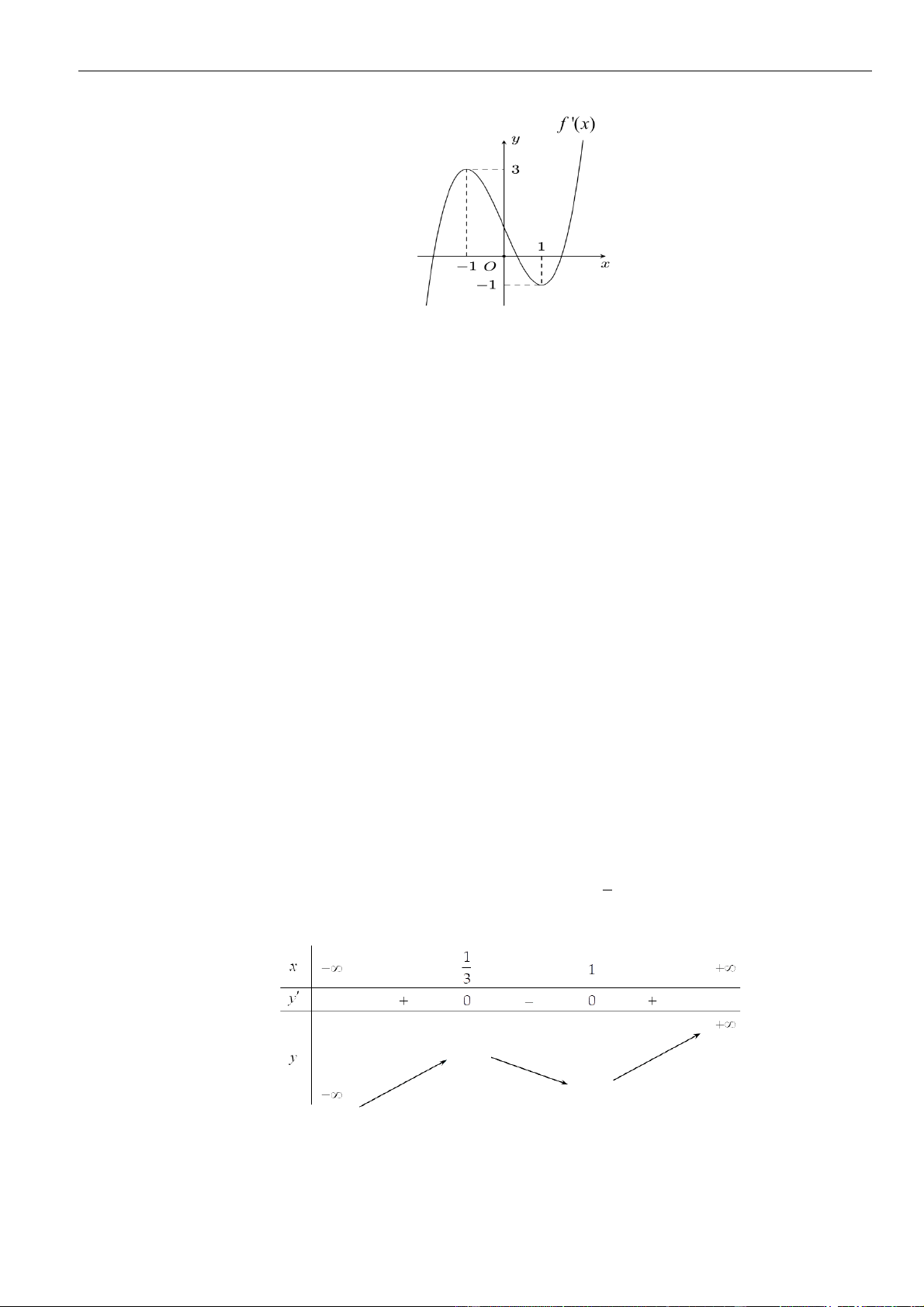
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Câu 39: Cho hàm số
( )
y f x=
có đồ thị của hàm số
( )
fx
như sau:
Trên khoảng
( )
10;10−
có tất cả bao nhiêu số nguyên của
m
để hàm số
( ) ( )
2020g x f x mx= + +
có đúng một cực trị?
A.
16
. B.
15
. C.
14
. D.
13
.
Lời giải
Chọn A
Ta có:
( ) ( )
g x f x m
=+
và
( )
0gx
=
( )
f x m
= −
.
Để hàm số
( ) ( )
2020g x f x mx= + +
có đúng một cực trị
( )
f x m
= −
có đúng một nghiệm
bội lẻ.
Dựa vào đồ thị hàm số
( )
y f x
=
suy ra:
3
1
m
m
−
− −
3
1
m
m
−
.
Câu 40: Cho hàm số
32
23y x x mx= − + +
đạt cực tiểu tại
1x =
. Giá trị của
m
bằng
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có
32
23y x x mx= − + +
. Suy ra
2
34y x x m
= − +
.
Giả sử
1x =
là điểm cực tiểu của hàm số
32
23y x x mx= − + +
thì
( )
10y
=
. Hay
( )
2
1 3.1 4.1 0 1y m m
= − + = =
.
Thay
m
ngược trở lại, ta có
2
1
3 4 1, 0
1
3
x
y x x y
x
=
= − + =
=
.
Ta có bảng biến thiên.
Vậy
1m =
.
Câu 41: Tất cả các giá trị của tham số
m
để hàm số
42
( 1)y x m x= − + +
đạt cực đại tại
0x =
là
A.
1m =−
. B.
1m −
. C.
1m −
. D.
1m −
.
Lời giải

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Chọn C
( )
4 2 3
( 1) ' 4 2 1y x m x y x m x= − + + = − + +
. Ta có
( )( )
2
0
'0
1
11
2
x
y
xm
=
=
=+
;
Ta thấy vì hệ số
10a = −
nên nếu hàm số có ba cực trị thì hàm số có 2 đại và một cực tiểu nên
không thể đạt cực đại tại
0x =
. Để hàm số đạt cực đại tại
0x =
thì hàm số có một cực trị hay
phương trình
( )
1
vô nghiệm hoặc có nghiệm kép
1 0 1mm + −
.
Câu 42: Cho hàm số
( )
3 2 2 2
3 3 1 1y x mx m x m= − + − − +
với
m
là tham số thự C. Tìm
m
để hàm số
đạt cực tiểu tại
1x =
.
A.
4m =−
. B.
0m =
. C.
2m =
. D.
0; 2mm==
.
Lời giải
Chọn B
( )
( )( )
3 2 2 2 2 2
3 3 1 1 3 6 3 3 3 1 1y x mx m x m y x mx m x m x m
= − + − − + = − + − = − + − −
66y x m
=−
.
Để hàm số đạt cực tiểu tại
1x =
( )
10y
=
2
3 6 0mm − =
0
2
m
m
=
=
.
+ Với
0m =
( )
1 6 0y
=
. Suy ra
0m =
(thỏa mãn).
+ Với
2m =
( )
1 6 0y
= −
. Suy ra
2m =
(loại).
Vậy giá trị của
m
để hàm số
( )
3 2 2 2
3 3 1 1y x mx m x m= − + − − +
đạt cực tiểu tại
1x =
là
0m =
.
Câu 43: Có bao nhiêu giá trị của tham số
m
để hàm số
( )
3 2 2
32y x mx m x m= − + + −
đạt cực tiểu tại
1x =
?
A.
1
. B.
0
. C.
2
. D. Vô số
Lời giải
Chọn B
+) Ta có
( )
2 2 2
3 6 2 1 6 5y x mx m y m m
= − + + = − +
.
Ta có
( )
2
1
1 0 6 5 0
5
m
y m m
m
=
= − + =
=
+) Với
1m =
,
2
3 6 3 0 1y x x x
= − + = =
nên hàm số không có cực trị, do đó
1m =
không
thỏa yêu cầu đề.
+) Với
5m =
,
2
9
3 30 27 0
1
x
y x x
x
=
= − + =
=
, vì
0a
nên hàm số đạt cực đại tại
1x =
và
đạt cực tiểu tại
9x =
. Do đó
5m =
không thỏa yêu cầu đề.
+) Vậy không có giá trị nào của
m
để hàm số đạt cực tiểu tại
1x =
.
Câu 44: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt giá trị cực đại tại
3x =
.
A.
1m =−
. B.
5m =
C.
7m =−
. D.
1m =

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn
B
Ta có:
22
' 2 4y x mx m= − + −
; và:
'' 2 2y x m=−
Giả sử
3x =
là điểm cực đại, khi đó ta có:
( )
( )
2
' 3 0
6 5 0
5
6 2 0
'' 3 0
y
mm
m
m
y
=
− + =
=
−
Với
5m =
, hàm số trở thành:
32
1
5 21 3
3
y x x x= − + +
,
2
' 10 21y x x= − +
Xét dấu
'y
ta thấy
3x =
là điểm cực đại của hàm số. Vậy
5m =
.
Câu 45: Có bao nhiêu giá trị thực của tham số
m
để hàm số
( )
( )
4 2 2
11y x m x m x= + − + −
đạt cực tiểu
tại điểm
0x =
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có
( )
32
4 2 1 1y x m x m
= + − + −
Vì hàm số đạt cực tiểu tại
( )
2
1
0 0 0 1 0
1
m
x y m
m
=
= = − =
=−
+) Với
1m =
thay vào hàm số ta có
43
4y x y x
= =
,
00yx
= =
hàm số đạt cực tiểu
tại
0x =
+) Với
1m =−
thay vào hàm số ta có
4 2 3
2 4 4y x x y x x
= − = −
,
0
01
1
x
yx
x
=
= =
=−
Lập BBT ta thấy hàm số đạt cực đại tại
0x =
nên
1m =−
(loại)
Vậy có 1 giá trị của tham số
m
thỏa yêu cầu bài toán.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Có bao nhiêu số thực
m
để hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại
1.x =
A.
0.
B.
2.
C.
1.
D.
3.
Câu 2: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
3.x =
A.
1m =−
. B.
5m =
. C.
7m =−
. D.
1m =
.
Câu 3: Tất cả các giá trị thực của tham số
m
để hàm số
( )
32
3 1 2y x x m x= − + + +
có hai điểm cực trị
là
A.
2m
. B.
2m
. C.
4m −
. D.
2m
.
Câu 4: Cho hàm số
3 2 2
3 4 2y x mx m= − + −
( )
1
. Tìm tất cả các giá trị của tham số
m
để hàm số
( )
1
có
hai điểm cực trị.
A.
11m−
. B.
1m −
. C.
1m
. D.
0m
.
Câu 5: Tất cả các giá trị của tham số
m
để hàm số
( ) ( )
32
3 1 3 3 7 1y x m x m x= − + + + +
có cực trị là
A.
2
3
m
m
−
. B.
3
2
m
m
−
. C.
2
3
m
m
−
. D.
23m−
.
Câu 6: Tìm tất cả các giá trị của tham số
m
để hàm số
32
32y x x mx= − − + +
có cực đại và cực tiểu?
A.
3m
. B.
3m −
. C.
3m
. D.
3m −
.
Câu 7: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
3x =
?
A.
1m =
В.
1m =−
C.
7m =−
D.
5m =
Câu 8: Có bao nhiêu số nguyên
m
để hàm số
( )
32
1
5 4 1
3
y x mx m x= − + − −
không có điểm cực trị?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 9: Tất cả các giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
điểm
3x =
là :
A.
7m =−
. B.
5m =
. C.
1m =−
D.
1m =
.
Câu 10: Tìm
m
để đồ thị của hàm số
3
32y x mx= − +
có hai điểm cực trị và khoảng cách giữa hai điểm
cực trị đó bằng
2
.
Cực trị hàm số bậc ba
DẠNG 6
Phương pháp:
Cho hàm số bậc ba
( )
32
y f x ax bx cx d= = + + +
có đạo hàm
( )
2
32y f x ax bx c
= = + +
▪ Hàm số
( )
fx
có cực trị
( )
fx
có cực đại và cực tiểu
( )
0fx
=
có hai nghiệm phân biệt
2
30b ac
= −
.
▪ Hàm số
( )
fx
không có cực trị
2
30b ac
= −

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 11: Biết
0
m
là giá trị của tham số để hàm số
32
31y x x mx= − + −
có hai điểm cực trị
12
,xx
sao cho
22
1 2 1 2
13x x x x+ − =
. Mệnh đề nào dưới đây đúng?
A.
( )
0
1;7m −
. B.
( )
0
7; 1m − −
. C.
( )
0
15; 7m − −
. D.
( )
0
7;10m
.
Câu 12: Số giá trị nguyên của tham số
m
để hàm số
32
2 5 4 2y x x x m= − − + −
có giá trị cực cực đại và
giá trị cực tiểu trái dấu là
A.
13
. B.
11
. C.
9
. D.
12
.
Câu 13: Cho hàm số
32
1
1.
3
y x mx x m= − − + +
Tìm các giá trị của tham số
m
để đồ thị hàm số có hai
điểm cực trị là
,AB
thỏa
22
2.
AB
xx+=
A.
= 0m
. B.
= 2m
. C.
=1m
. D.
=3m
.
Câu 14: Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
( )
3 2 2
1
31
32
= − − − +
m
y x x m x m
đạt cực trị tại hai điểm
12
,xx
thỏa mãn
( )
1 2 1 2
2 4 0+ + + =x x x x
. Số phần tử của
S
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 15: Gọi
1
m
,
2
m
là các giá trị của tham số
m
để đồ thị hàm số
32
2 3 1y x x m= − + −
có hai điểm cực
trị là
B
,
C
sao cho tam giác
OBC
có diện tích bằng
2
,với
O
là gốc tọa độ. Tính
12
.mm
.
A.
6
. B.
15−
. C.
12
. D.
20−
.
Câu 16: Cho biết hàm số
32
31= − + −y x x mx
đạt cực trị tại
12
,xx
thỏa mãn
22
12
3+=xx
. Khi đó
A.
( )
0;1m
. B.
( )
2;3m
. C.
( )
1;2m
. D.
1−m
.
Câu 17: Tập tất cả các giá trị của tham số
m
để đồ thị hàm số
( )
32
1
12
3
y x x m x= + + − +
có hai điểm
cực trị nằm bên trái trục tung là:
A.
( )
;1 .−
. B.
( )
1;2 .
C.
( )
;2 .−
. D.
( )
1;+
.
Câu 18: Biết rằng đồ thị hàm số
32
11
2
32
y x mx x= − + −
có giá trị tuyệt đối của hoành độ hai điểm cực
trị là độ dài hai cạnh của tam giác vuông có cạnh huyền
7
. Hỏi có mấy giá trị của
m
?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 19: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
( )
( )
3 2 2 2
2 1 2 2 4 2 4y x m x m m x m= − + + + − − +
có hai điểm cực trị nằm về hai phía của trục
hoành?
A.
3
. B.
4
. C.
6
. D.
5
.
Câu 20: Cho hàm số
32
1
( 2) 9 1
3
y x m x x= − − − +
, với
m
là tham số. Gọi
1
x
,
2
x
là các điểm cực trị của
hàm số đã cho thì giá trị nhỏ nhất của biểu thức
12
9 25xx−
bằng
A.
15
. B.
90
. C.
450
. D.
45
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 21: Cho hàm số
3 2 2
8y x mx m x= − − +
. Có bao nhiêu giá trị
m
nguyên đề hàm số có điểm cực tiểu
nằm hoàn toàn phía trên trục hoành?
A.
3
. B.
5
. C.
4
. D.
6
.
Câu 22: Có bao nhiêu giá trị thực của tham số
m
để hàm số
( )
( )
3 2 2
11
3 2 2 3 1 2
32
y x m x m m x= − + + + + −
có điểm cực đại
DC
x
và điểm cực tiểu
CT
x
thoả
mãn
2
34
CD CT
xx=
?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 23: Gọi
1
m
,
2
m
là các giá trị của tham số
m
để đồ thị hàm số
32
2 3 1y x x m= − + −
có hai điểm cực
trị là
B
,
C
sao cho tam giác
OBC
có diện tích bằng
2
,với
O
là gốc tọa độ. Tính
12
.mm
.
A.
6
. B.
15−
. C.
12
. D.
20−
.
Câu 24: Cho hàm số
( )
( )
3 2 2
1
2 4 3 6 9
3
y x m x m m x m= − + + + + + +
. Tìm giá trị của tham số
m
để đồ thị
hàm số
( )
C
có cực đại tại
1
x
, đạt cực tiểu tại
2
x
sao cho
2
12
2xx=
.
A.
4m =
. B.
2m =−
. C.
4
2
m
m
=
=−
. D.
5m =
.
Câu 25: Hàm số
32
31y x x mx= − + −
có hai điểm cực trị
12
,xx
thỏa
22
12
3xx+=
khi
A.
1
2
m =
. B.
3
2
m =
. C.
2m =−
. D.
1m =
.
Câu 26: Cho
| 0 20A n n=
và
F
là tập hợp các hàm số
3 2 2 2
( ) (2 5) 6 8f x x m x x m= + − + −
có
mA
. Chọn ngẫu nhiên một hàm số
()fx
thuộc
F
. Tính xác suất để đồ thị hàm số
()y f x=
có hai điểm cực trị nằm khác phía đối với trục
.Ox
A.
18
21
. B.
19
20
. C.
9
10
. D.
19
21
.
Câu 27: Biết
a
b
là giá trị của tham số
m
để hàm số
( )
3 2 2
2 3 6 3 1 2020y x mx m x= − − − +
có hai điểm
cực trị
12
,xx
thỏa mãn
( )
1 2 1 2
21x x x x+ + =
. Tính
2P a b=+
.
A.
6
. B.
5
. C.
8
. D.
7
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Có bao nhiêu số thực
m
để hàm số
( )
3 2 2
1
11
3
y x mx m m x= − + − + +
đạt cực đại tại
1.x =
A.
0.
B.
2.
C.
1.
D.
3.
Lời giải
Chọn C
Ta có
22
21y x mx m m
= − + − +
,
22y x m
=−
Để hàm số đạt cực đại tại
1x =
thì
( )
( )
2
1
10
3 2 0
2
2
2 2 0
10
1
m
y
mm
m
m
m
y
m
=
=
− + =
=
=
−
Câu 2: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
3.x =
A.
1m =−
. B.
5m =
. C.
7m =−
. D.
1m =
.
Lời giải
Chọn B
22
24
= − + −y x mx m
22
=−y x m
Hàm số đạt cực đại tại
3=x
( )
( )
2
30
15
6 5 0
5
3
6 2 0
30
=
= =
− + =
=
−
y
mm
mm
m
m
m
y
Câu 3: Tất cả các giá trị thực của tham số
m
để hàm số
( )
32
3 1 2y x x m x= − + + +
có hai điểm cực trị
là
A.
2m
. B.
2m
. C.
4m −
. D.
2m
.
Lời giải
Chọn B
Ta có
2
3 6 1y x x m
= − + +
Để hàm số
( )
32
3 1 2y x x m x= − + + +
có hai điểm cực trị thì
0y
=
có hai nghiệm phân biệt
( )
0 9 3. 1 0 2mm
− +
.
Vậy với
2m
thì hàm số
( )
32
3 1 2y x x m x= − + + +
có hai điểm cực trị.
Câu 4: Cho hàm số
3 2 2
3 4 2y x mx m= − + −
( )
1
. Tìm tất cả các giá trị của tham số
m
để hàm số
( )
1
có
hai điểm cực trị.
A.
11m−
. B.
1m −
. C.
1m
. D.
0m
.
Lời giải
Chọn D
Ta có
3 2 2 2
3 4 2 3 6y x mx m y x mx
= − + − = −
.
2
0
0 3 6 0
2
x
y x mx
xm
=
= − =
=
.
Để hàm số có hai cực trị thì phương trình
0y
=
có hai nghiệm phân biệt
2 0 0mm
.
Câu 5: Tất cả các giá trị của tham số
m
để hàm số
( ) ( )
32
3 1 3 3 7 1y x m x m x= − + + + +
có cực trị là

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
2
3
m
m
−
. B.
3
2
m
m
−
. C.
2
3
m
m
−
. D.
23m−
.
Lời giải
Chọn A
Ta có
( ) ( ) ( ) ( )
3 2 2
3 1 3 3 7 1 ' 3 6 1 3 3 7y x m x m x y x m x m= − + + + + = − + + +
.
Để hàm số
( ) ( )
32
3 1 3 3 7 1y x m x m x= − + + + +
có cực trị thì
'0y =
có 2 nghiệm phân biệt
2
2
' 0 9 9 54 0
3
m
mm
m
−
− −
.
Câu 6: Tìm tất cả các giá trị của tham số
m
để hàm số
32
32y x x mx= − − + +
có cực đại và cực tiểu?
A.
3m
. B.
3m −
. C.
3m
. D.
3m −
.
Lời giải
Chọn B
( )
2
' 3 6 1y x x m= − − +
.
Để hàm số có cực đại, cực tiểu thì phương trình
( )
1
có
2
nghiệm phân biệt
0 9 3 0 3mm
+ −
.
Câu 7: Tìm giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
3x =
?
A.
1m =
В.
1m =−
C.
7m =−
D.
5m =
Lời giải
Chọn D
Ta có: hàm số có TXĐ
D =
22
' 2 4y x mx m= − + −
.
Hàm số đạt cực đại tại
2
1
3 6 5 0
5
m
x m m
m
=
= − + =
=
.
32
1
1 3 3
3
m y x x x= = − − +
2
' 2 3
1
'0
3
y x x
x
y
x
= − −
=−
=
=
'' 2 2 ''(3) 4 0y x y= − =
. Suy ra
3x =
là điểm cực tiểu.
Vậy
1m =
không thỏa mãn.
32
1
5 5 21 3
3
m y x x x= = − − +
2
' 10 21
7
'0
3
y x x
x
y
x
= − +
=
=
=
'' 2 10 ''(3) 4 0y x y= − = −
. Suy ra
3x =
là điểm cực đại.
Vậy
5m =
thỏa mãn.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 8: Có bao nhiêu số nguyên
m
để hàm số
( )
32
1
5 4 1
3
y x mx m x= − + − −
không có điểm cực trị?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn B
Ta có
2
2 5 4y x mx m
= − + −
Hàm số
y
không có cực trị
0y
=
vô nghiệm hoặc có nghiệm kép
2
0 5 4 0 1 4m m m
− +
Do
m
nên
1;2;3;4m
Vậy có bốn giá trị của tham số
m
cần tìm.
Câu 9: Tất cả các giá trị thực của tham số
m
để hàm số
( )
3 2 2
1
43
3
y x mx m x= − + − +
đạt cực đại tại
điểm
3x =
là :
A.
7m =−
. B.
5m =
. C.
1m =−
D.
1m =
.
Lời giải
Chọn B
Hàm số đạt cực đại tại điểm
3x =
khi và chỉ khi
( )
( )
2 2 2
1
30
3 6 4 0 6 5 0
5
5
6 2 0 3
30
3
m
y
m m m m
m
m
mm
y
m
=
=
− + − = − + =
=
=
−
.
Thử lại với
5m =
thỏa mãn yêu cầu bài toán.
Vậy
5m =
thì hàm số đạt cực đại tại điểm
3x =
.
Câu 10: Tìm
m
để đồ thị của hàm số
3
32y x mx= − +
có hai điểm cực trị và khoảng cách giữa hai điểm
cực trị đó bằng
2
.
Lời giải
Tập xác định
D =
.
Ta có
2
33y x m
=−
. Để đồ thị của hàm số
3
32y x mx= − +
có hai điểm cực trị
0y
=
có hai
nghiệm phân biệt
00m
.
Khi đó :
22
0
22
x m y m m
y
x m y m m
= = − +
=
= − = +
Giả sử hai điểm cực trị
( ) ( )
; 2 2 , ;2 2A m m m B m m m− + − +
Ta có
( ) ( )
22
2
2 4 2 4 4AB AB m m m= = − + =
33
4 16 4 4 1 0m m m m + = + − =
( )
( )
( )
( )
2
2
2 1 0
1
2 1 2 1 0
2 1 0
2
m
m m m m TM
m m VN
−=
− + + = =
+ + =
.
Câu 11: ) Biết
0
m
là giá trị của tham số để hàm số
32
31y x x mx= − + −
có hai điểm cực trị
12
,xx
sao cho
22
1 2 1 2
13x x x x+ − =
. Mệnh đề nào dưới đây đúng?

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
A.
( )
0
1;7m −
. B.
( )
0
7; 1m − −
. C.
( )
0
15; 7m − −
. D.
( )
0
7;10m
.
Lời giải
Chọn C
3 2 2
3 1; 3 6y x x mx y x x m
= − + − = − +
. Hàm số có hai cực trị
' 9 3 0 3mm = −
12
,xx
là hai nghiệm của phương trình
2
3 6 0x x m− + =
.
Áp dụng định lí Vi – ét, ta có:
12
12
2
3
S x x
m
P x x
= + =
==
Ta có:
( ) ( )
2
22
1 2 1 2 1 2 1 2
13 3 13 4 13 9 15; 7x x x x x x x x m m+ − = + − = − = = − − −
Câu 12: Số giá trị nguyên của tham số
m
để hàm số
32
2 5 4 2y x x x m= − − + −
có giá trị cực cực đại và
giá trị cực tiểu trái dấu là
A.
13
. B.
11
. C.
9
. D.
12
.
Lời giải
Chọn D
32
2 5 4 2y x x x m= − − + −
2
2 10
6 10 4 0
1 73
3 27
x y m
y x x
x y m
= = − −
= − − =
= − = −
.
Giá trị cực cực đại và giá trị cực tiểu trái dấu
( )
73 73
10 . 0 10
27 27
m m m
− − − −
.
Mà
m
. Vậy có
12
có giá trị nguyên thỏa mãn.
Câu 13: Cho hàm số
32
1
1.
3
y x mx x m= − − + +
Tìm các giá trị của tham số
m
để đồ thị hàm số có hai
điểm cực trị là
,AB
thỏa
22
2.
AB
xx+=
A.
= 0m
. B.
= 2m
. C.
=1m
. D.
=3m
.
Lời giải
Chọn A
Ta có
( )
2
' 2 1 1 .y x mx= − −
Hàm số đã cho có hai điểm cực trị
( )
22
, ' 1. 1 1 0, .A B m m m = − − = +
Khi đó,
,
AB
xx
là hai nghiệm của tam thức
( )
1.
Suy ra
2 , . 1.
A B A B
bc
x x m x x
aa
+ = − = = = −
Ta có
( ) ( )
2
2 2 2 2
2 2 2 4 2. 1 2 4 0 0.
A B A B A B
x x x x x x m m m+ = + − = − − = = =
Vậy,
0m =
thỏa yêu cầu bài toán.
Câu 14: Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
( )
3 2 2
1
31
32
= − − − +
m
y x x m x m
đạt cực trị tại hai điểm
12
,xx
thỏa mãn
( )
1 2 1 2
2 4 0+ + + =x x x x
. Số phần tử của
S
là
A.
2
. B.
3
. C.
1
. D.
0
.
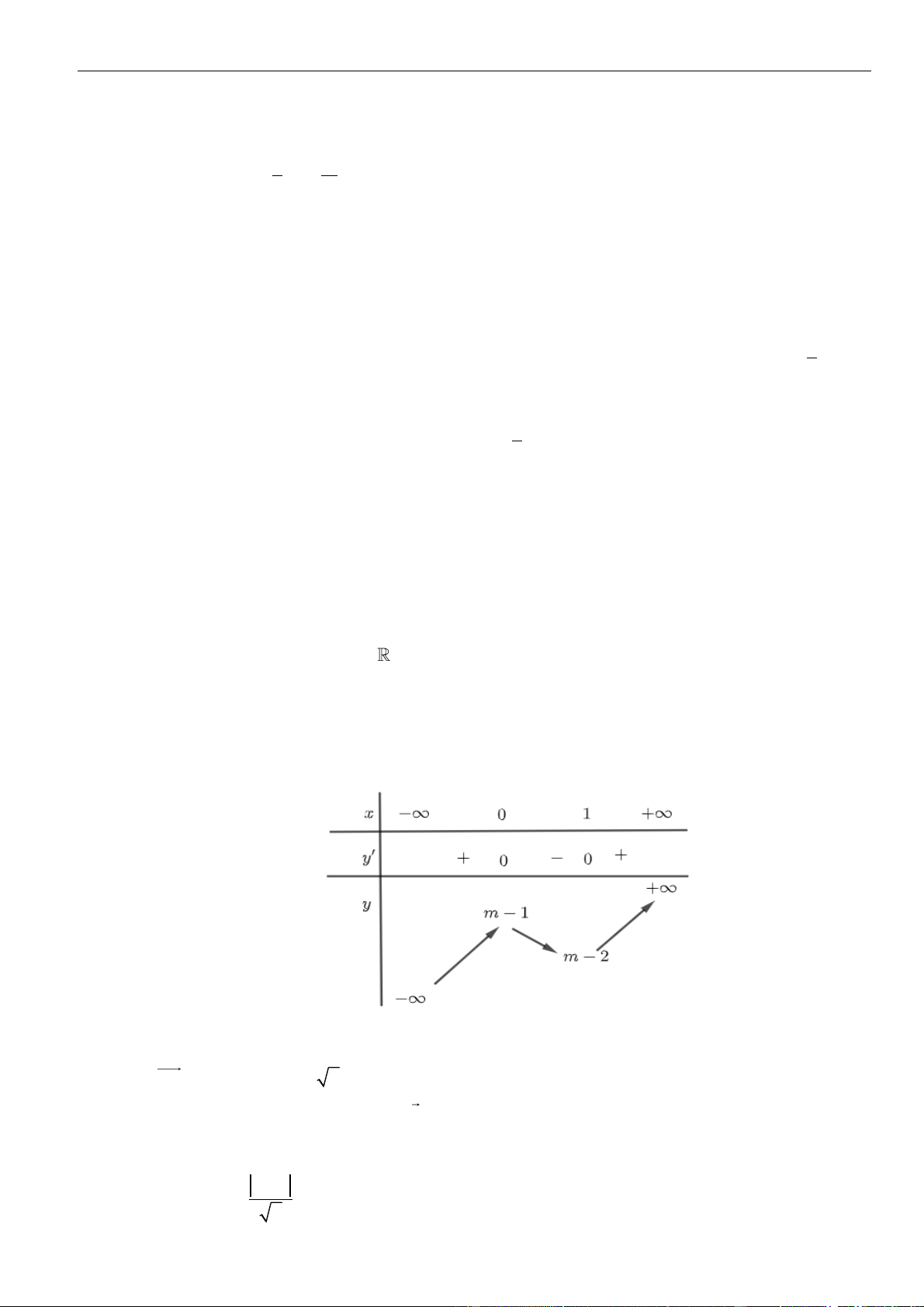
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Lời giải
Chọn A
Ta có:
22
31
= − − +y x mx m
.
Hàm số
( )
3 2 2
1
31
32
= − − − +
m
y x x m x m
đạt cực trị tại hai điểm
12
,xx
khi phương trình
0
=y
có hai nghiệm phân biệt
12
,xx
. Khi đó
( )
2 2 2
4 3 1 0 13 4 0m m m = − − + −
.
Theo định lí Vi-et ta có:
12
2
12
31
+=
= − +
x x m
x x m
.
Do đó
( )
1 2 1 2
2 4 0+ + + =x x x x
22
3 1 2 4 0 3 2 5 0 − + + + = − + + =m m m m
1
5
3
=−
=
m
m
.
Do điều kiện nên giá trị của
m
cần tìm là
1
5
3
m
m
=−
=
.
Vậy tập hợp
S
có 2 phần tử.
Câu 15: Gọi
1
m
,
2
m
là các giá trị của tham số
m
để đồ thị hàm số
32
2 3 1y x x m= − + −
có hai điểm cực
trị là
B
,
C
sao cho tam giác
OBC
có diện tích bằng
2
,với
O
là gốc tọa độ. Tính
12
.mm
.
A.
6
. B.
15−
. C.
12
. D.
20−
.
Lời giải
Chọn B
Hàm số xác định với mọi
x
.
2
66y x x
=−
.
0; 1
0
1; 2
x y m
y
x y m
= = −
=
= = −
.
Bảng biến thiên:
Vậy
( )
0; 1Bm−
,
( )
1; 2Cm−
.
( )
1; 1 2BC BC= − =
.
( )
BC
đi qua
( )
0; 1Bm−
và nhận
( )
1;1n =
làm một vectơ pháp tuyến nên có phương trình
( ) ( )
1 0 1 1 0 1 0x y m x y m− + − + = + − + =
.
( )
1
;
2
m
d O BC
−
=
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
( )
1 4 3
1
11
; . . . 2 2 1 4
1 4 5
22
2
OBC
mm
m
S d O BC BC m
mm
− = = −
−
= = = − =
− = − =
.
Vậy
12
. 15mm=−
.
Câu 16: Cho biết hàm số
32
31= − + −y x x mx
đạt cực trị tại
12
,xx
thỏa mãn
22
12
3+=xx
. Khi đó
A.
( )
0;1m
. B.
( )
2;3m
. C.
( )
1;2m
. D.
1−m
.
Lời giải
Chọn C
=D
.
2
' 3 6= − +y x x m
, hàm số có hai cực trị
12
,xx
khi và chỉ khi
0 9 3 0 3 − mm
.
Khi đó
12
12
2
.
3
+=
=
xx
m
xx
. Mặt khác
( ) ( )
2
2 2 2
1 2 1 2 1 2
23
3 2 3 2 3
32
+ = + − = − = =
m
x x x x x x m tm
.
Câu 17: Tập tất cả các giá trị của tham số
m
để đồ thị hàm số
( )
32
1
12
3
y x x m x= + + − +
có hai điểm
cực trị nằm bên trái trục tung là:
A.
( )
;1 .−
. B.
( )
1;2 .
C.
( )
;2 .−
. D.
( )
1;+
.
Lời giải
Chọn B
Ta có :
2
21y x x m
= + + −
.
Đồ thị hàm số đã cho có
2
điểm cực trị nằm bên trái trục tung khi và chỉ khi phương trình
0y
=
có hai nghiệm âm phân biệt
0
1 1 0
0 2 0 1 2
0 1 0
y
m
Sm
Pm
− +
−
−
.
Câu 18: Biết rằng đồ thị hàm số
32
11
2
32
y x mx x= − + −
có giá trị tuyệt đối của hoành độ hai điểm cực
trị là độ dài hai cạnh của tam giác vuông có cạnh huyền
7
. Hỏi có mấy giá trị của
m
?
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn B
Ta có:
2
'1y x mx= − +
.
2
' 0 1 0y x mx= − + =
.
Đồ thị hàm số có hai điểm cực trị
phương trình có hai nghiệm phân biệt
2
' 4 0m = −
.
Khi đó, gọi các nghiệm của là
12
,xx
thì
12
,xx
chính là hoành độ hai điểm cực trị. Theo Viet ta
có
1 2 1 2
; . 1x x m x x+ = =
.
Theo bài ra ta có:
( )
2
2 2 2 2
1 2 1 2 1 2
7 2 7 2 7 9 3x x x x x x m m m+ = + − = − = = =
).
Vậy có 2 giá trị của
m
thỏa mãn yêu cầu.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Câu 19: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
( )
( )
3 2 2 2
2 1 2 2 4 2 4y x m x m m x m= − + + + − − +
có hai điểm cực trị nằm về hai phía của trục
hoành?
A.
3
. B.
4
. C.
6
. D.
5
.
Lời giải
Chọn A
Xét phương trình hoành độ giao điểm:
( )
( )
3 2 2 2
2 1 2 2 4 2 4 0x m x m m x m− + + + − − + =
( )
1
.
( )
( )
22
1 2 2 4 0x x mx m − − + − =
( ) ( )
22
1
2 2 4 0 2
x
f x x mx m
=
= − + − =
.
Đồ thị hàm số
( )
( )
3 2 2 2
2 1 2 2 4 2 4y x m x m m x m= − + + + − − +
có hai điểm cực trị nằm về hai
phía của trục hoành khi và chỉ khi phương trình
( )
1
có 3 nghiệm phân biệt
( )
2
có 2 nghiệm phân biệt khác
1
( )
( )
22
2
22
2 4 0
17
1 2 2 3 0
2
m
mm
m
f m m
−
= − −
= − −
.
Vì
m
nên
1;0;1m−
.
Vậy có
3
giá trị nguyên của
m
thỏa mãn bài toán.
Câu 20: Cho hàm số
32
1
( 2) 9 1
3
y x m x x= − − − +
, với
m
là tham số. Gọi
1
x
,
2
x
là các điểm cực trị của
hàm số đã cho thì giá trị nhỏ nhất của biểu thức
12
9 25xx−
bằng
A.
15
. B.
90
. C.
450
. D.
45
.
Lời giải
Chọn B
+
( )
2
2 2 9y x m x
= − − −
;
( )
2
0 2 2 9 0y x m x
= − − − =
.
+ Có
( )
2
2 9 0,mm
= − +
nên hàm số có hai cực trị.
Theo định lý Vi-et:
( )
12
12
22
.9
x x m
xx
+ = −
=−
.
Khi đó
12
, xx
trái dấu.
+ Nếu
1
0x
thì
1 2 1 1 1
1 1 1
9 225 225
9 25 9 25. 9 2. 9 . 90x x x x x
x x x
− = − − = + =
Dấu “
=
” xảy ra khi và chỉ khi
2
1 1 1
1
225
9 25 5x x x
x
= = =
.
+ Nếu
1
0x
thì
1
0x−
, khi đó
( ) ( )
( )
1 2 1 1 1
1 1 1
9 225 225
9 25 9 25. 9 2. 9 . 90x x x x x
x x x
− = − − = − + − =
−−
Dấu “
=
” xảy ra khi và chỉ khi
2
1 1 1
1
225
9 25 5x x x
x
= = = −
.
Vậy GTNN
12
9 25xx−
là
90
. Dấu “
=
” xảy ra khi và chỉ khi
1
5x =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Câu 21: Cho hàm số
3 2 2
8y x mx m x= − − +
. Có bao nhiêu giá trị
m
nguyên đề hàm số có điểm cực tiểu
nằm hoàn toàn phía trên trục hoành?
A.
3
. B.
5
. C.
4
. D.
6
.
Lời giải
Chọn C
Ta có:
22
32y x mx m
= − −
,
0
3
xm
y
m
x
=
=
=−
.
Để hàm số có hai điểm cực trị thì
0y
=
có hai nghiệm phân biệt
0m
.
Trường hợp 1:
0m
( )
3
8 0 2
ct
y y m m m = = − +
. Vậy
02m
có 1 giá trị
nguyên
1m =
.
Trường hợp 2:
0m
3
3
56
80
3 27
5
ct
m
y y m m
= − = + −
. Vậy
3
6
0
5
m−
có 3
giá trị nguyên của
m
là
3; 2; 1− − −
.
Vậy tổng số có 4 giá trị nguyên của
m
.
Câu 22: Có bao nhiêu giá trị thực của tham số
m
để hàm số
( )
( )
3 2 2
11
3 2 2 3 1 2
32
y x m x m m x= − + + + + −
có điểm cực đại
DC
x
và điểm cực tiểu
CT
x
thoả
mãn
2
34
CD CT
xx=
?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn A
Ta có
( )
( )
3 2 2
11
3 2 2 3 1 2
32
y x m x m m x= − + + + + −
( )
( )
22
3 2 2 3 1y x m x m m
= − + + + +
có
2
0,mm =
nên
21
0
1
xm
y
xm
=+
=
=+
.
Hàm số có cực đại và cực tiểu khi và chỉ khi
0m
.
Trường hợp 1.
2 1; 1
CD CT
x m x m= + = +
.
Do
1
0
3
a =
nên suy ra
2 1 1 0
CD CT
x x m m m + +
.
Lại có
( ) ( )
2
22
27
3 4 3 2 1 4 1 12 8 1 0
6
CD CT
x x m m m m m
−
= + = + + − = =
.
Với điều kiện
0m
27
6
m
−−
=
thoả mãn.
Trường hợp 2:
1; 2 1
CD CT
x m x m= + = +
Do
1
0
3
a =
nên suy ra
1 2 1 0
CD CT
x x m m m + +
.
Lại có
( ) ( )
2
22
1
3 4 3 1 4 2 1 3 2 1 0
1
3
CD CT
m
x x m m m m
m
=
= + = + − − =
=−
.
Với điều kiện
0m
1m=
thoả mãn.
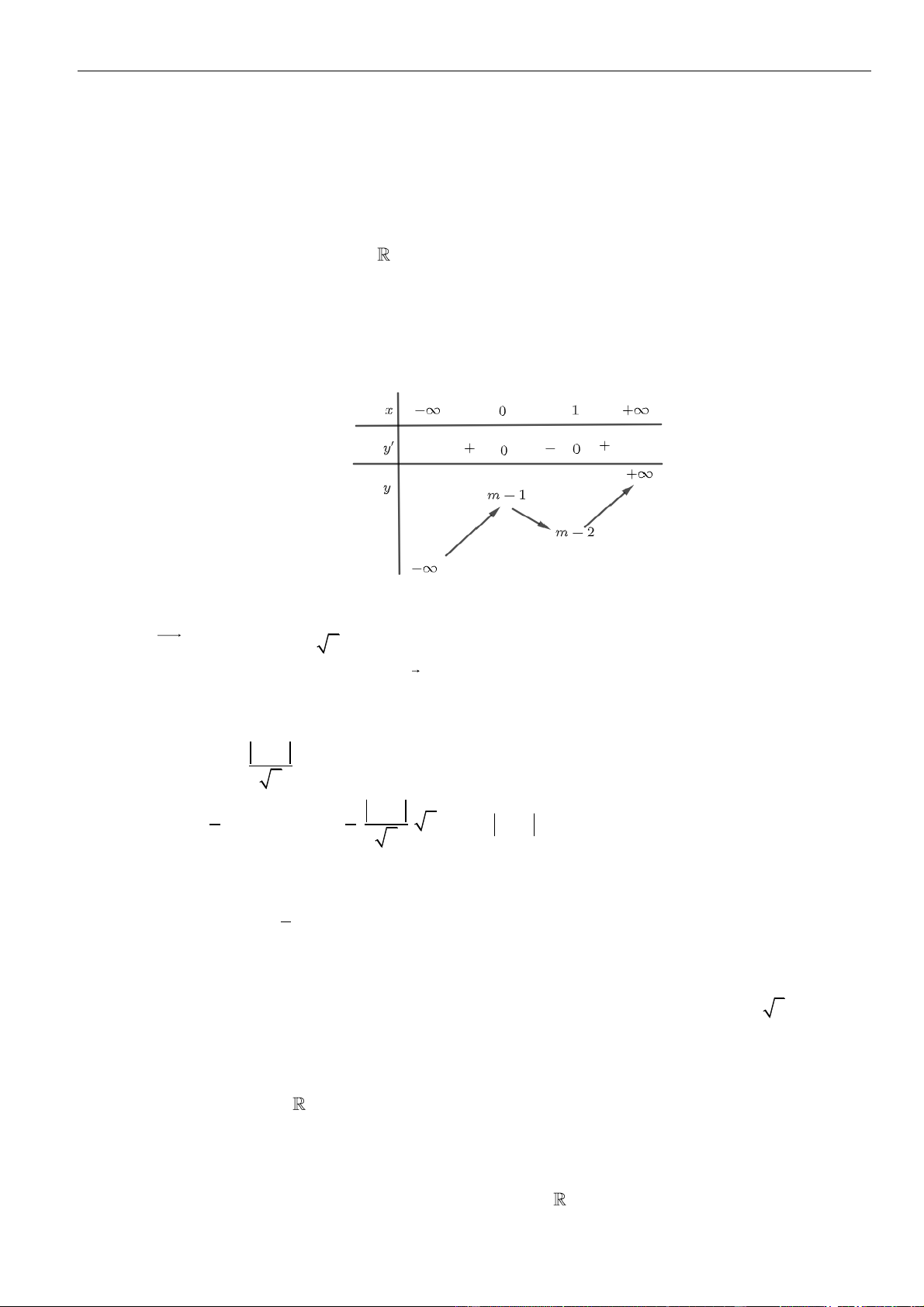
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Kết luận: vậy có 2 giá trị thực của tham số
m
thoả mãn.
Câu 23: Gọi
1
m
,
2
m
là các giá trị của tham số
m
để đồ thị hàm số
32
2 3 1y x x m= − + −
có hai điểm cực
trị là
B
,
C
sao cho tam giác
OBC
có diện tích bằng
2
,với
O
là gốc tọa độ. Tính
12
.mm
.
A.
6
. B.
15−
. C.
12
. D.
20−
.
Lời giải
Chọn B
Hàm số xác định với mọi
x
.
2
66y x x
=−
.
0; 1
0
1; 2
x y m
y
x y m
= = −
=
= = −
.
Bảng biến thiên:
Vậy
( )
0; 1Bm−
,
( )
1; 2Cm−
.
( )
1; 1 2BC BC= − =
.
( )
BC
đi qua
( )
0; 1Bm−
và nhận
( )
1;1n =
làm một vectơ pháp tuyến nên có phương trình
( ) ( )
1 0 1 1 0 1 0x y m x y m− + − + = + − + =
.
( )
1
;
2
m
d O BC
−
=
.
( )
1 4 3
1
11
; . . . 2 2 1 4
1 4 5
22
2
OBC
mm
m
S d O BC BC m
mm
− = = −
−
= = = − =
− = − =
.
Vậy
12
. 15mm=−
.
Câu 24: Cho hàm số
( )
( )
3 2 2
1
2 4 3 6 9
3
y x m x m m x m= − + + + + + +
. Tìm giá trị của tham số
m
để đồ thị
hàm số
( )
C
có cực đại tại
1
x
, đạt cực tiểu tại
2
x
sao cho
2
12
2xx=
.
A.
4m =
. B.
2m =−
. C.
4
2
m
m
=
=−
. D.
5m =
.
Lời giải
Chọn D
Tập xác định
D =
.
( )
22
2 2 4 3y x m x m m
= − + + + +
.
Hàm số đạt cực đại tại
1
x
, đạt cực tiểu tại
2
x
khi và chỉ khi
( )
( )
2
2
0 2 4 3 0 1 0m m m
+ − + +
, m
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
3
0
1
xm
y
xm
=+
=
=+
.
Theo đề bài ta có:
( ) ( )
2
22
12
5
2 1 2 3 5 0
5
m
x x m m m
m
=−
= + = + − =
=
.
Câu 25: Hàm số
32
31y x x mx= − + −
có hai điểm cực trị
12
,xx
thỏa
22
12
3xx+=
khi
A.
1
2
m =
. B.
3
2
m =
. C.
2m =−
. D.
1m =
.
Lời giải
Chọn B
Hàm số
32
31y x x mx= − + −
Tập xác định
D =
.
( )
2
3 6 , 3, 6, , 36 12y x x m a b c m m
= − + = = − = = −
.
Để hàm số có hai điểm cực trị
12
,xx
thì
03m
.
Theo đề bài
( )
2
22
1 2 1 2 1 2
23
3 2 3 4 3
32
x x x x x x m m+ = + − = − = =
.
Câu 26: Cho
| 0 20A n n=
và
F
là tập hợp các hàm số
3 2 2 2
( ) (2 5) 6 8f x x m x x m= + − + −
có
mA
. Chọn ngẫu nhiên một hàm số
()fx
thuộc
F
. Tính xác suất để đồ thị hàm số
()y f x=
có hai điểm cực trị nằm khác phía đối với trục
.Ox
A.
18
21
. B.
19
20
. C.
9
10
. D.
19
21
.
Lời giải
Chọn D
+ Không gian mẫu
21=
+ Ta có:
2 2 2
2
( ) 0
(2 3) 4 0(*)
x
fx
x m x m
=
=
+ − + =
+ Đồ thị hàm số
()y f x=
có hai điểm cực trị nằm khác phía đối với trục
Ox
có hai nghiệm phân biệt khác 2
2 2 2
2 2 2
7 2 10
2,58
2
(2 3) 16 0 0;3;4;...;20
7 2 10
2 (2 3).2 4 0
0 0,58
2
mA
mA
m
m m m
mm
m
m
+
− −
−
+ − +
Vậy xác suất là:
19
21
P =
.
Câu 27: Biết
a
b
là giá trị của tham số
m
để hàm số
( )
3 2 2
2 3 6 3 1 2020y x mx m x= − − − +
có hai điểm
cực trị
12
,xx
thỏa mãn
( )
1 2 1 2
21x x x x+ + =
. Tính
2P a b=+
.
A.
6
. B.
5
. C.
8
. D.
7
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Lời giải
Xét hàm số
( )
3 2 2
2 3 6 3 1 2020y x mx m x= − − − +
, ta có
( )
22
6 6 6 3 1y x mx m
= − − −
22
0 3 1 0y x mx m
= − − + =
( )
1
Hàm số có hai điểm cực trị
12
,xx
khi và chỉ khi phương trình
( )
1
có hai nghiệm phân biệt
( )
( )
2
2
4 3 1 0mm = − − − +
2
2
13 4 0
13
mm − −
hoặc
2
13
m
.
Khi đó, theo định lí Viet, ta có
12
2
12
. 3 1
x x m
x x m
+=
= − +
.
Theo giả thiết,
( )
1 2 1 2
21x x x x+ + =
nên
22
3 1 2 1 3 2 0m m m m− + + = − + =
0m=
hoặc
2
3
m =
.
Suy ra
2, 3ab==
. Vậy
28P a b= + =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1:
Tất cả các giá trị của tham số
m
để hàm số
( )
42
2020 1y x m x= + − +
có 3 điểm cực trị phân biệt
là
A.
2020.m
. B.
2020.m
. C.
2020.m
. D.
2020.m
Câu 2: Có bao nhiêu giá trị nguyên dương của tham số
m
không vượt quá
2020
để hàm số
( )
42
5 3 1y x m x m= − + − + −
có ba điểm cực trị
A.
2017
. B.
2019
. C.
2016
. D.
2015
.
Câu 3: Tìm số các giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
2 6 1y x m m x m= + − − + −
có ba điểm
cực trị.
A.
3
B.
4.
C.
6.
D.
5.
Câu 4: Tìm tất cả các giá trị thực của
m
để hàm số
( )
42
2 6 2020y x m x= + − −
có 3 điểm cực trị?
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Câu 5: Tìm số các giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
2 6 1y x m m x m= + − − + −
có ba điểm
cực trị.
A.
3
B.
4.
C.
6.
D.
5.
Câu 6: Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
9 2021y x m x= − − +
có 1
cực trị. Số phần tử của tập
S
là
A. Vô số. B. 7. C. 5. D. 3.
Câu 7: Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
( )
4 2 2
9 2021y x m x= − − +
có 1
cực trị. Số phần tử của tập S là
A. Vô số. B.
3
. C.
7
. D.
5
.
Cực trị hàm trùng phương
DẠNG 7
Phương pháp:
Cho hàm số bậc 4 trùng phương
( )
42
0y ax bx c a= + +
▪ Hàm số có một cực trị
0ab
.
▪ Hàm số có ba cực trị
0ab
.
▪ Hàm số có đúng một cực trị và cực trị là cực tiểu
0
0
a
b
.
▪ Hàm số có đúng một cực trị và cực trị là cực đại
0
0
a
b
.
▪ Hàm số có hai cực tiểu và một cực đại
0
0
a
b
.
▪ Hàm số có một cực tiểu và hai cực đại
0
0
a
b
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 8: Tất cả các giá trị thực của tham số
m
để hàm số
42
5y x mx m= + − −
có
3
điểm cực trị là
A.
1.m =
B.
8m
. C.
0.m
D.
4 5.m
Câu 9: Cho hàm số
( )
4 2 2
y x m m x= − + −
. Tìm
m
để hàm số có đúng một cực trị.
A.
(
)
;0 1;m − +
. B.
( ) ( )
;0 1;m − +
.
C.
0;1m
. D.
( )
0;1m
.
Câu 10: Tìm điều kiện của tham số
b
để hàm số
42
y x bx c= + +
có ba điểm cực trị.
A.
0b =
. B.
0b
. C.
0b
. D.
0b
.
Câu 11: Tìm điều kiện của tham số
b
để hàm số
42
y x bx c= + +
có ba điểm cực trị.
A.
0b =
. B.
0b
. C.
0b
. D.
0b
.
Câu 12: Tìm tất cả giá trị thực của
m
để hàm số
( )
42
26 2020y x m x= +−−
có ba điểm cực trị.
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Câu 13: Số giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
3y mx m x m= − − +
không có điểm cực đại là
A.
3
. B.
4
. C.
0
. D.
1
.
Câu 14: Tìm
m
để đồ thị hàm số
42
21y x mx= − +
có ba điểm cực trị
( )
0;1A
,
B
,
C
thỏa mãn
4BC =
A.
2m =
. B.
4m =
. C.
2m =
. D.
4m =
.
Câu 15: Tập hợp các giá trị của tham số thực m để hàm số
( )
42
2 2 3 1y x m x m= − + + −
chỉ có điểm cực
tiểu và không có điểm cực đại là
A.
( )
;2− −
. B.
2;2−
. C.
( )
2;− +
. D.
(
;2− −
.
Câu 16: Tập hợp các giá tị thực của tham số
m
để hàm số
( )
42
2 2 3 1y x m x m= − + + −
chỉ có điểm cực
tiểu, không có điểm cực đại là
A.
( )
;2− −
. B.
2;2−
. C.
( )
2;− +
. D.
(
;2−
.
Câu 17: Tập hợp các giá trị của tham số thực
m
để hàm số
( )
42
2 2 3 1y x m x m= − + + −
chỉ có điểm cực
tiểu, không có điểm cực đại là
A.
( )
;2− −
. B.
2;2−
. C.
( )
2;− +
. D.
(
;2− −
.
Câu 18: Có bao nhiêu giá trị
m
nguyên để hàm số
( )
42
3 2021y mx m x= + − +
có
2
cực tiểu và một cực
đại.
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 19: Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
42
2f x x xm=−
có đúng
3
điểm cực
trị?
A.
0m
. B.
m
. C.
0m
. D.
mR
.
Câu 20: Cho hàm số trùng phương
( )
42
21f x x mx= − −
. Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
fx
có ba điểm cực trị.
A.
1m
. B.
1m
. C.
0m
. D.
0m
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 21: Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
42
21y x m x= − −
có đúng một điểm
cực trị?
A.
1m
. B.
1m
. C.
1m
. D.
1m =
.
Câu 22: Có bao nhiêu giá trị nguyên dương của tham số
m
không vượt quá 2020 để hàm số
42
( 5) 3 1y x m x m= − + − + −
có ba điểm cực trị
A.
2017
. B.
2019
. C.
2016
. D.
2015
.
Câu 23: Tìm các giá trị của tham số
m
để đồ thị hàm số
( )
42
1 2020y mx m x= + − +
có đúng một điểm
cực đại.
A.
1
0
m
m
. B.
0m
. C.
01m
. D.
1m
.
Câu 24: Có bao nhiêu giá trị
m
nguyên để hàm số
( )
42
3 2021y mx m x= + − +
có
2
cực tiểu và một cực
đại.
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 25: Cho đồ thị hàm số
42
y ax bx c= + +
có điểm cực đại
( )
0; 3A −
và điểm cực tiểu
( )
1; 5B −−
. Tính
giá trị của
23P a b c= + +
.
A.
3P =
. B.
5P =−
. C.
9P =−
. D.
15P =−
.
Câu 26: Tìm các giá trị của tham số
m
để đồ thị hàm số
( )
42
2 1 2y mx m x m= + − + −
chỉ có một điểm
cực đại mà không có điểm cực tiểu.
A.
0
1
2
m
m
. B.
0m
. C.
0
1
2
m
m
. D.
1
2
m
.
Câu 27: Để đồ thị hàm số
42
21y x mx m= − + −
có ba điểm cực trị tạo thành một tam giác có diện tích
bằng
2
, giá trị của tham số
m
thuộc khoảng nào sau đây?
A.
( )
1;0−
. B.
( )
2;3
. C.
( )
0;1
. D.
( )
1;2
.
Câu 28: Tìm giá trị của tham số
m
để hàm số
( )
4 2 2
2 3 2y x m x= − + + +
có điểm cực trị sao cho giá
trị cực đại của hàm số đạt giá trị nhỏ nhất.
A.
0m =
. B.
3m =−
. C.
1m =−
. D.
2m =−
.
Câu 29: Cho hàm trùng phương
( ) ( )
4 2 2
2 1 8= = − + + −y f x x m x m
có đồ thị
( )
C
. Gọi
,,A B C
là ba
điểm cực trị của đồ thị
( )
C
. Để tam giác
ABC
đều thì giá trị tham số
m
nằm trong khoảng nào
sau đây?
A.
11
;
42
. B.
1
0;
4
. C.
1
;1
2
. D.
( )
1; 2
.
Câu 30: Gọi
S
là tập hợp chứa tất cả các giá trị nguyên của tham số
20; 20m−
để hàm số
42
2( 2) 1y x m x= + − +
có duy nhất một điểm cực tiểu. Số phần tử của tập
S
bằng
A. 19. B. 21. C. 20. D. 41.
3

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 31: Cho hàm số
42
22y x mx= − +
. Tổng bình phương các giá trị
m
để hàm số có ba cực trị và đường
tròn qua ba cực trị đó có bán kính bằng
4
, gần với số nguyên nào nhất trong các số nguyên sau?
A.
8
. B.
9
. C.
16
. D.
7
.
Câu 32: Cho hàm số
( )
42
22f x x mx= − +
. Tổng bình phương các giá trị
m
để hàm số có ba cực trị và
đường tròn đi qua ba điểm cực trị của đồ thị hàm số có bán kính bằng
4
, gần với số nguyên nào
nhất trong các số nguyên sau?
A.
8
. B.
9
. C.
16
. D.
7
.
Câu 33: Cho hàm số
( )
42
2 1 1y mx m x= − + +
. Tìm tất cả các giá trị của
m
để hàm số có một điểm cực
đại
A.
1
0
2
m−
. B.
1
2
m −
. C.
1
0
2
m−
. D.
1
2
m −
.
Câu 34: Tìm giá trị tham số
m
để đồ thị hàm số
( )
42
2 1 2 3y x m x m= − + + +
có ba điểm cực trị
,,A B C
sao cho trục hoành chia tam giác
ABC
thành một tam giác và một hình thang biết rằng tỉ số diện
tích tam giác nhỏ được chia ra và diện tích tam giác
ABC
bằng
4
9
A.
53
2
m
+
=
. B.
1 15
2
m
−+
=
. C.
13
2
m
−+
=
. D.
1 15
2
m
+
=
.
Câu 35: Với tất cả giá trị nào của
m
thì hàm số
( )
42
2 1 2y mx m x m= + − + +
chỉ có một cực trị:
A.
2m
. B.
02m
. C.
0
2
m
m
. D.
0m
.
Câu 36: Tìm giá trị của tham số
m
để hàm số
( )
4 2 2
2 3 2y x m x= − + + +
có điểm cực trị sao cho giá
trị cực đại của hàm số đạt giá trị nhỏ nhất.
A.
0m =
. B.
3m =−
. C.
1m =−
. D.
2m =−
.
3

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1:
Tất cả các giá trị của tham số
m
để hàm số
( )
42
2020 1y x m x= + − +
có 3 điểm cực trị phân biệt
là
A.
2020.m
. B.
2020.m
. C.
2020.m
. D.
2020.m
Lời giải
Chọn C
Để hàm số đã cho có 3 điểm cực trị khi và chỉ khi
2020 0 2020mm−
.
Câu 2: Có bao nhiêu giá trị nguyên dương của tham số
m
không vượt quá
2020
để hàm số
( )
42
5 3 1y x m x m= − + − + −
có ba điểm cực trị
A.
2017
. B.
2019
. C.
2016
. D.
2015
.
Lời giải
Chọn D
Hàm số
42
y ax bx c= + +
có ba điểm cực trị khi và chỉ khi
0ab
.
Suy ra hàm số
( )
42
5 3 1y x m x m= − + − + −
có ba điểm cực trị khi và chỉ khi
5 0 5.mm−
Mà
m
nguyên dương và không vượt quá
2020
nên
6,7,...,2019,2020m
có tất cả
2015
giá trị.
Câu 3: Tìm số các giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
2 6 1y x m m x m= + − − + −
có ba điểm
cực trị.
A.
3
B.
4.
C.
6.
D.
5.
Lời giải
Chọn B
Ta có
( )
32
' 4 4 6y x m m x= + − −
( )
32
' 0 4 4 6 0y x m m x= + − − =
22
40
6
x
x m m
=
= − + +
Hàm số có ba cực trị
2
60mm − + +
23m −
Do đó ta chọn B
Câu 4: Tìm tất cả các giá trị thực của
m
để hàm số
( )
42
2 6 2020y x m x= + − −
có 3 điểm cực trị?
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Lời giải
Chọn D
Ta có :
( )
3
4 2 2 6y x m x
= + −
( )
2
43x x m= + −
2
40
0
30
x
y
xm
=
=
+ − =
2
0
3
x
xm
=
=−
Để hàm số có ba điểm cực trị thì phương trình
0y
=
có ba nghiệm phân biệt.
phương trình
2
3xm=−
có hai nghiệm phân biệt khác 0.
30m−
3m
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 5: Tìm số các giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
2 6 1y x m m x m= + − − + −
có ba điểm
cực trị.
A.
3
B.
4.
C.
6.
D.
5.
Lời giải
Chọn B
Ta có
( )
32
' 4 4 6y x m m x= + − −
( )
32
' 0 4 4 6 0y x m m x= + − − =
22
40
6
x
x m m
=
= − + +
Hàm số có ba cực trị
2
60mm − + +
23m −
Do đó ta chọn B
Câu 6: Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
9 2021y x m x= − − +
có 1
cực trị. Số phần tử của tập
S
là
A. Vô số. B. 7. C. 5. D. 3.
Lời giải
Chọn B
Để hàm số có 1 cực trị thì
( )
22
9 0 9 0 3 3m m m− − − −
.
Vậy có 7 giá trị nguyên thỏa mãn yêu cầu bài toán.
Câu 7: Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
( )
4 2 2
9 2021y x m x= − − +
có 1
cực trị. Số phần tử của tập S là
A. Vô số. B.
3
. C.
7
. D.
5
.
Lời giải
Chọn A
Để hàm số
( )
4 2 2
9 2021y x m x= − − +
có 1 cưc trị thì
( )
32
4 2 9y x m
= − −
( )
22
2 2 9 0x x m − + =
có 1 nghiệm, suy ra:
2
2 2 2
9
2 9 0
2
m
x m x
−
− + = =
vô nghiệm hoặc
có nghiệm
0x =
nên
2
3
90
3
m
m
m
−
−
.
Câu 8: Tất cả các giá trị thực của tham số
m
để hàm số
42
5y x mx m= + − −
có
3
điểm cực trị là
A.
1.m =
B.
8m
. C.
0.m
D.
4 5.m
Lời giải
Chọn C
Để hàm số có
3
cực trị thì
. 0 1. 0 0a b m m
.
Câu 9: Cho hàm số
( )
4 2 2
y x m m x= − + −
. Tìm
m
để hàm số có đúng một cực trị.
A.
(
)
;0 1;m − +
. B.
( ) ( )
;0 1;m − +
.
C.
0;1m
. D.
( )
0;1m
.
Lời giải
Chọn C
Ta có
( )
32
42y x m m x
= − + −
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
( )
32
22
0
0 4 2 0
2
x
y x m m x
x m m
=
= − + − =
=−
.
Hàm số có đúng một điểm cực trị khi phương trình
22
2x m m=−
vô nghiệm hoặc có nghiệm
kép
0x =
.
Điều kiện là
2
0 0 1m m m−
.
Vậy
0;1m
.
Câu 10: Tìm điều kiện của tham số
b
để hàm số
42
y x bx c= + +
có ba điểm cực trị.
A.
0b =
. B.
0b
. C.
0b
. D.
0b
.
Lời giải
Chọn C
Tập xác định của hàm số:
D =
.
( )
32
4 2 2 2y x bx x x b
= + = +
.
2
0
0
2
x
y
b
x
=
=
=−
Hàm số có ba điểm cực trị
0y
=
có ba nghiệm phân biệt
2
2
b
x = −
có hai nghiệm phân biệt khác
0
00
2
b
b −
.
Câu 11: Tìm điều kiện của tham số
b
để hàm số
42
y x bx c= + +
có ba điểm cực trị.
A.
0b =
. B.
0b
. C.
0b
. D.
0b
.
Lời giải
Chọn C
Tập xác định của hàm số:
D =
.
( )
32
4 2 2 2y x bx x x b
= + = +
.
2
0
0
2
x
y
b
x
=
=
=−
Hàm số có ba điểm cực trị
0y
=
có ba nghiệm phân biệt.
2
2
b
x = −
có hai nghiệm phân biệt khác
0
00
2
b
b −
.
Câu 12: Tìm tất cả giá trị thực của
m
để hàm số
( )
42
26 2020y x m x= +−−
có ba điểm cực trị.
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Lời giải
Chọn D
Hàm số có ba điểm cực trị khi
2 6 0 3mm−
.
Câu 13: Số giá trị nguyên của tham số
m
để hàm số
( )
4 2 2
3y mx m x m= − − +
không có điểm cực đại là
A.
3
. B.
4
. C.
0
. D.
1
.
Lời giải
Chọn B
Hàm số
( )
4 2 2
3y mx m x m= − − +
không có điểm cực đại

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
( )
0
00
30
. 0 3
m
am
m
a b m
− −
03m
.
Do
0;1;2;3mm
. Vậy có bốn giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài
toán.
Câu 14: Tìm
m
để đồ thị hàm số
42
21y x mx= − +
có ba điểm cực trị
( )
0;1A
,
B
,
C
thỏa mãn
4BC =
A.
2m =
. B.
4m =
. C.
2m =
. D.
4m =
.
Lời giải
Chọn D
Tập xác định
D =
.
Ta có:
( )
32
4 4 4y x mx x x m
= − = −
.
Để hàm số có 3 cực trị thì
0m
.
( )
( )
2
0 0 1
0
1
xy
y
x m y m m
= =
=
= = −
, suy ra
( )
0;1A
,
( )
2
;1B m m−
,
( )
2
;1C m m−−
.
4 4 4 4BC m m= = =
.
Câu 15: Tập hợp các giá trị của tham số thực m để hàm số
( )
42
2 2 3 1y x m x m= − + + −
chỉ có điểm cực
tiểu và không có điểm cực đại là
A.
( )
;2− −
. B.
2;2−
. C.
( )
2;− +
. D.
(
;2− −
.
Lời giải
Chọn D
Tập xác định của hàm số đã cho là:
D =
.
Ta có:
( )
3
' 4 4 2y x m x= − +
( )
3
2
0
' 0 4 4 2 0
2
x
y x m x
xm
=
= − + =
=+
Để hàm số đã cho chỉ có điểm cực tiểu và không có điểm cực đại thì
2 0 2mm+ −
.
Câu 16: Tập hợp các giá tị thực của tham số
m
để hàm số
( )
42
2 2 3 1y x m x m= − + + −
chỉ có điểm cực
tiểu, không có điểm cực đại là
A.
( )
;2− −
. B.
2;2−
. C.
( )
2;− +
. D.
(
;2−
.
Lời giải
Chọn A
Hàm trùng phương
42
y ax bx c= + +
chỉ có điểm cực tiểu, không có điểm cực đại khi
0
0
0
0
a
b
a
ab
=
Áp dụng cho bài toán này ta được:
( )
2 2 0 2mm− + −
Câu 17: Tập hợp các giá trị của tham số thực
m
để hàm số
( )
42
2 2 3 1y x m x m= − + + −
chỉ có điểm cực
tiểu, không có điểm cực đại là
A.
( )
;2− −
. B.
2;2−
. C.
( )
2;− +
. D.
(
;2− −
.
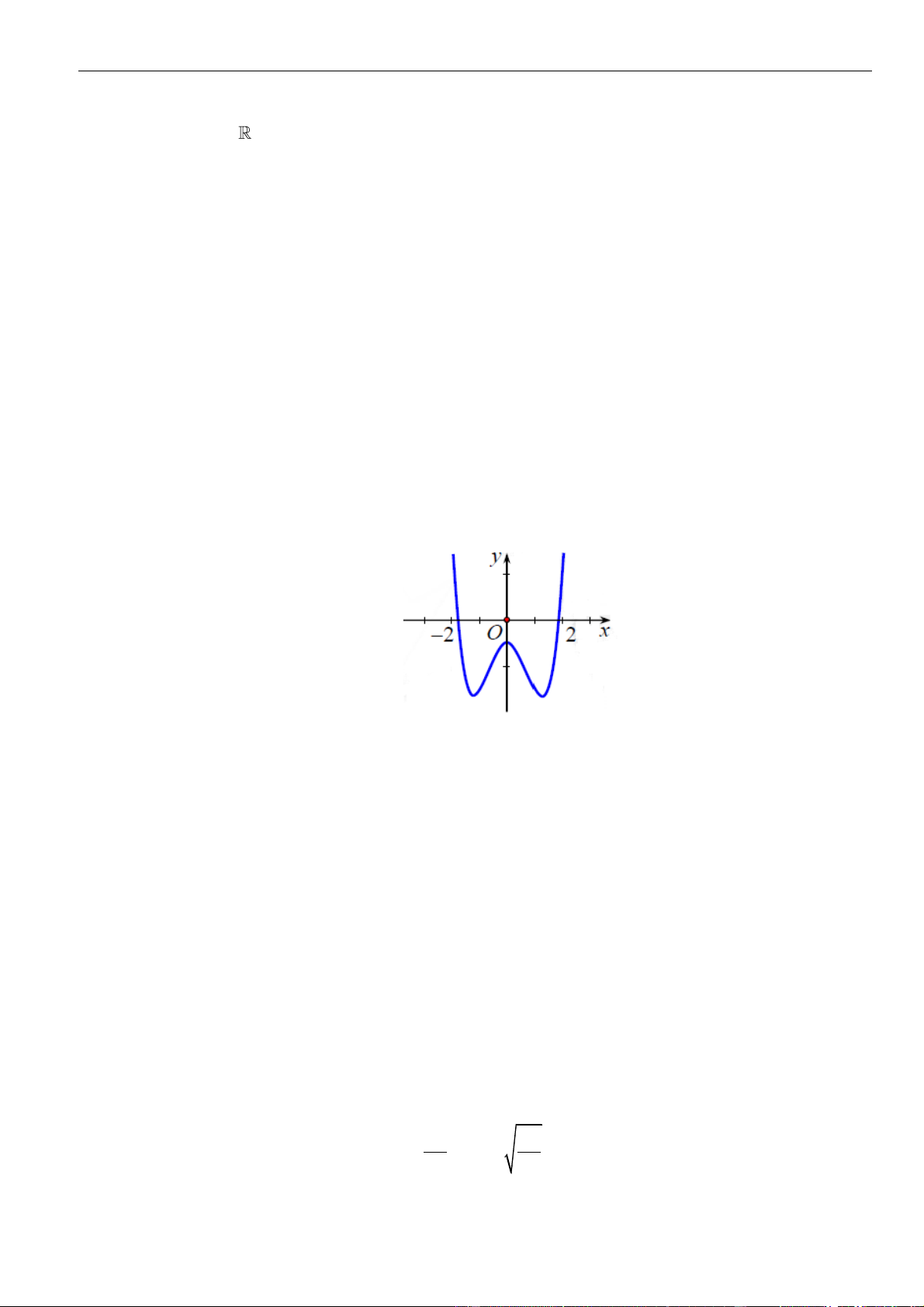
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn D
TXĐ:
D =
Ta có
( )
3
4 4 2y x m x
= − +
( )
2
42x x m= − −
Xét
2
0
0
2
x
y
xm
=
=
=+
Để hàm số chỉ có cực tiểu và không có cực đại thì
20
2
10
m
m
a
+
−
=
Vậy
(
;2m − −
thỏa mãn yêu cầu đề bài.
Câu 18: Có bao nhiêu giá trị
m
nguyên để hàm số
( )
42
3 2021y mx m x= + − +
có
2
cực tiểu và một cực
đại.
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn A
Ta có hàm số
( ) ( )
42
0y f x ax bx c a= = + +
có 3 cực trị khi
0ab
Để hàm số
( )
y f x=
có
2
cực tiểu và 1 cực đại thì đồ thị hàm số
( )
y f x=
có dạng
Ta có:
( )
lim
x
fx
→+
= +
Đồ thị nhánh ngoài của hàm số hướng lên, nên hàm số có hệ số
0a
.
Khi đó để thỏa mãn yêu cầu bài toán ta có:
0
0
a
ab
( )
0
30
m
mm
−
03m
.
Vậy có 2 giá trị
m
nguyên là
1;2m
.
Câu 19: Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
42
2f x x xm=−
có đúng
3
điểm cực
trị?
A.
0m
. B.
m
. C.
0m
. D.
mR
.
Lời giải
Chọn B
Hàm số đã cho có đúng
3
điểm cực trị
( )
'0fx=
có đúng
3
nghiệm phân biệt.
Ta có
( )
32
' 4 2f x x m=−
( )
22
3 2 3
3
' 0 4 2 0
22
mm
f x x m x x= − = = =
.
Vậy không có giá trị nào của tham số
m
để hàm số có đúng
3
điểm cực trị.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Câu 20: Cho hàm số trùng phương
( )
42
21f x x mx= − −
. Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
fx
có ba điểm cực trị.
A.
1m
. B.
1m
. C.
0m
. D.
0m
.
Lời giải
Chọn C
Ta có
( )
3
44f x x mx
=−
. Phương trình
( )
2
0
0
x
fx
xm
=
=
=
.
Hàm số
( )
fx
có ba điểm cực trị
phương trình
( )
0fx
=
có ba nghiệm phân biệt
0m
.
Vậy
0m
thỏa mãn yêu cầu bài toán.
Câu 21: Hãy tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
42
21y x m x= − −
có đúng một điểm
cực trị?
A.
1m
. B.
1m
. C.
1m
. D.
1m =
.
Lời giải
Chọn A
Hàm số
( )
42
21y x m x= − −
có đúng một điểm cực trị khi và chỉ khi
( )
2 1 0 1mm− −
.
Câu 22: Có bao nhiêu giá trị nguyên dương của tham số
m
không vượt quá 2020 để hàm số
42
( 5) 3 1y x m x m= − + − + −
có ba điểm cực trị
A.
2017
. B.
2019
. C.
2016
. D.
2015
.
Lời giải
Chọn D
Để hàm số có ba điểm cực trị thì:
1.( 5) 0 5 0 5ab m m m= − − −
(1)
Theo giả thiết:
2020m
(2)
Từ (1) và (2) suy ra có 2015 giá trị nguyên dương của m thỏa mãn là:
{6;7;...;2020}m
Câu 23: Tìm các giá trị của tham số
m
để đồ thị hàm số
( )
42
1 2020y mx m x= + − +
có đúng một điểm
cực đại.
A.
1
0
m
m
. B.
0m
. C.
01m
. D.
1m
.
Lời giải
Chọn D.
Tập xác định:
D =
Xét các trường hợp:
+TH1:
0m =
2
2020yx = − +
là hàm bậc hai có đồ thị là parabol có bề lõm hướng xuống nên
có đúng một điểm cực đại. Do đó
0m =
là một giá trị cần tìm.
+TH2:
0m
: hàm số
( )
42
1 2020y mx m x= + − +
là hàm trùng phương nên đồ thị có đúng một
điểm cực đại khi
0
10
01
0
0
10
m
m
m
m
m
m
−
−
Kết hợp
2
trường hợp trên ta được
1m
là tất cả các giá trị cần tìm.
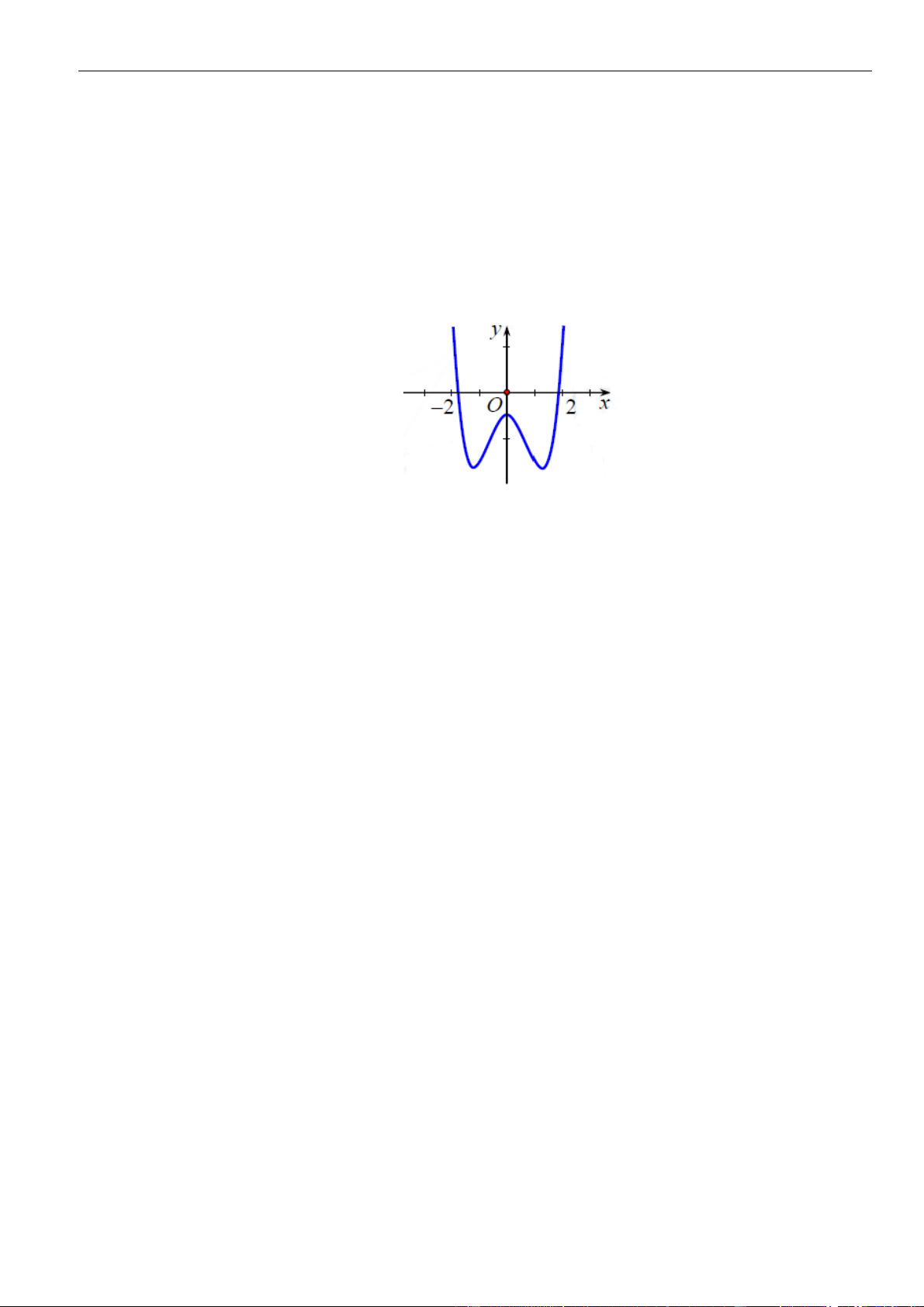
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Câu 24: Có bao nhiêu giá trị
m
nguyên để hàm số
( )
42
3 2021y mx m x= + − +
có
2
cực tiểu và một cực
đại.
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn A
Ta có hàm số
( ) ( )
42
0y f x ax bx c a= = + +
có 3 cực trị khi
0ab
Để hàm số
( )
y f x=
có
2
cực tiểu và 1 cực đại thì đồ thị hàm số
( )
y f x=
có dạng
Ta có:
( )
lim
x
fx
→+
= +
Đồ thị nhánh ngoài của hàm số hướng lên, nên hàm số có hệ số
0a
.
Khi đó để thỏa mãn yêu cầu bài toán ta có:
0
0
a
ab
( )
0
30
m
mm
−
03m
.
Vậy có 2 giá trị
m
nguyên là
1;2m
.
Câu 25: Cho đồ thị hàm số
42
y ax bx c= + +
có điểm cực đại
( )
0; 3A −
và điểm cực tiểu
( )
1; 5B −−
. Tính
giá trị của
23P a b c= + +
.
A.
3P =
. B.
5P =−
. C.
9P =−
. D.
15P =−
.
Lời giải
Chọn D
Đồ thị hàm số đi qua điểm
( )
0; 3A −
và
( )
( )
21
3
1; 5
5
3.
ab
c
B
abc
c
+ = −
=−
− −
+ + = −
=−
4 2 3
42y ax bx c y ax bx
= + + = +
.
Đồ thị hàm số có điểm cực tiểu
( )
1; 5B −−
( )
4 2 0. 2ab − − =
Từ (1) và (2) suy ra
22
4 2 0 4.
a b a
a b b
+ = − =
− − = = −
Với
4 2 3 2
2
4 2 4 3 8 8 24 8
3
a
b y x x y x x y x
c
=
= − = − − = − = −
=−
.
0
0
1.
x
y
x
=
=
=
( )
0 8 0y
= −
( )
0; 3A −
là điểm cực đại.
( )
1 16 0y
− =
( )
1; 5B −−
là điểm cực tiểu.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Vậy
2
4 2 3 15
3
a
b P a b c
c
=
= − = + + = −
=−
.
Câu 26: Tìm các giá trị của tham số
m
để đồ thị hàm số
( )
42
2 1 2y mx m x m= + − + −
chỉ có một điểm
cực đại mà không có điểm cực tiểu.
A.
0
1
2
m
m
. B.
0m
. C.
0
1
2
m
m
. D.
1
2
m
.
Lời giải
Chọn B
Xét
0m =
, khi đó
2
2yx= − −
là hàm số bậc hai có
10a = −
nên đồ thị là Parabol có bề lõm
hướng xuống nên có 1 cực đại mà không có cực tiểu. Suy ra
0m =
thỏa mãn đề bài.
Xét
0m
, khi đó
( )
42
2 1 2y mx m x m= + − + −
là hàm số bậc 4 dạng trùng phương.
Để đồ thị hàm số
( )
42
2 1 2y mx m x m= + − + −
chỉ có một điểm cực đại mà không có điểm cực
tiểu thì
( )
0
0
0
0
. 2 1 0
1
2
m
m
m
m
mm
m
−
.
Vậy
0m
.
Câu 27: Để đồ thị hàm số
42
21y x mx m= − + −
có ba điểm cực trị tạo thành một tam giác có diện tích
bằng
2
, giá trị của tham số
m
thuộc khoảng nào sau đây?
A.
( )
1;0−
. B.
( )
2;3
. C.
( )
0;1
. D.
( )
1;2
.
Lời giải
Chọn D
Tập xác định:
D =
Ta có
( )
32
4 4 4y x mx x x m
= − = −
+) Đồ thị hàm số đã cho có ba điểm cực trị
Phương trình
0y
=
có ba nghiệm phân biệt
0m
( )
*
.
+) Với
0m
, ta có
0
0
x
y
xm
=
=
=
Gọi
( )
( ) ( )
22
0; 1 , ; 1 , ; 1A m B m m m C m m m− − − + − − + −
là ba điểm cực trị của đồ thị hàm số
đã cho.
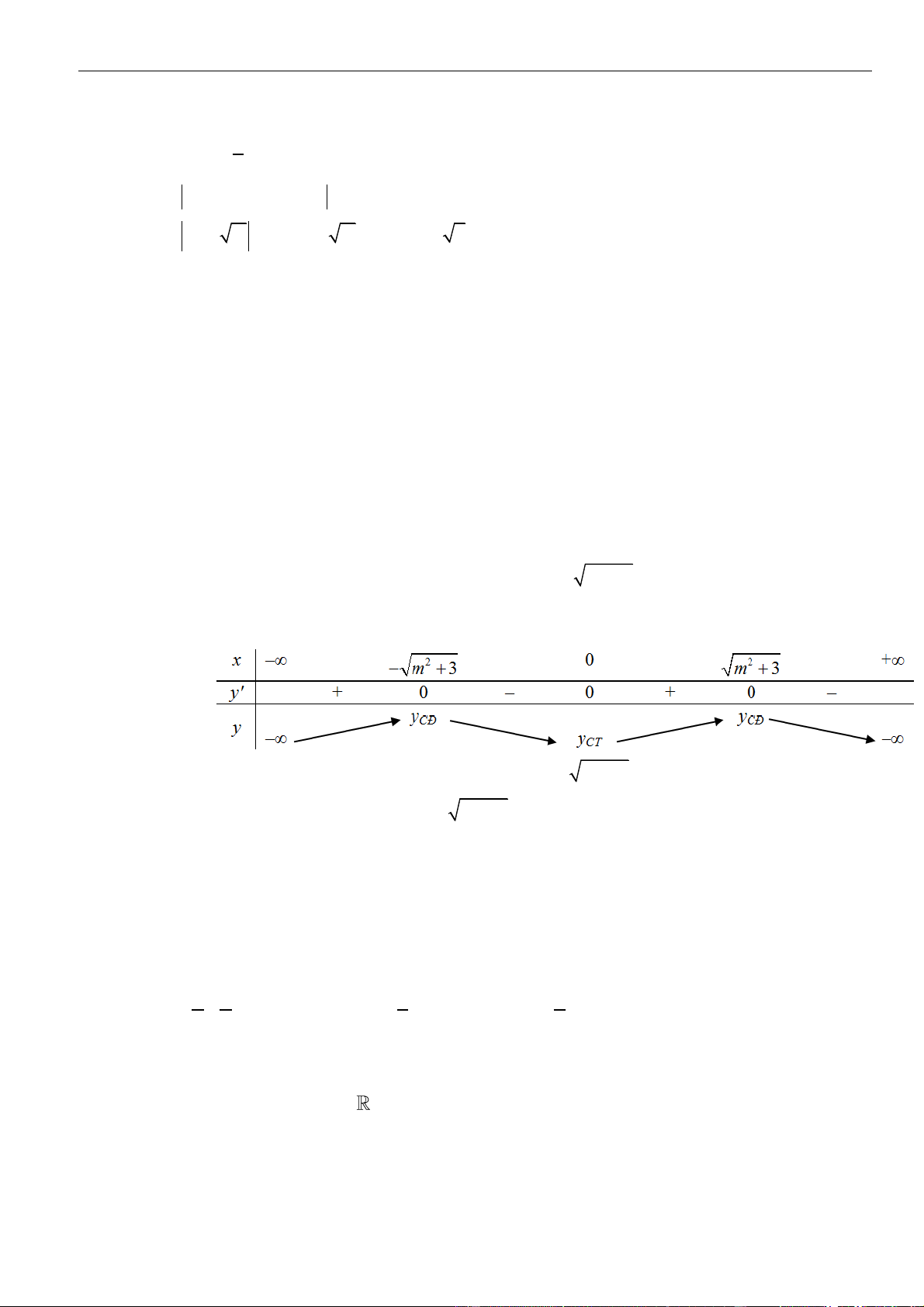
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Vì
;A Oy B
và
C
đối xứng nhau qua
Oy
nên tam giác
ABC
cân tại
A
(tham khảo hình vẽ).
Gọi
H BC Oy AH BC= ⊥
1
.2
2
ABC
S AH BC = =
( )( )
4
A H C B
y y x x − − =
(với
H B C
y y y==
)
( )
22
5
.2 4 2 4 1;2m m m m m = = =
.
Câu 28: Tìm giá trị của tham số
m
để hàm số
( )
4 2 2
2 3 2y x m x= − + + +
có điểm cực trị sao cho giá
trị cực đại của hàm số đạt giá trị nhỏ nhất.
A.
0m =
. B.
3m =−
. C.
1m =−
. D.
2m =−
.
Lời giải
Chọn A
Người làm: Côngg
Hiếnn
Xét hàm số
( )
4 2 2
2 3 2y x m x= − + + +
Ta có
( )
32
4 4 3y x m x
= − + +
.
Phương trình
( )
32
0 4 4 3 0y x m x
= − + + =
2
0
3
x
xm
=
= +
Hàm số luôn có 3 điểm cực trị với
m
Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đạt cực đại khi
2
3xm= +
.
Giá trị cực đại của hàm số:
(
)
( )
4
2
22
§
3 2 3 2
C
y m m= − + + + +
( )
2
2
32m= + +
.
§
min 11
C
y =
khi
0m =
.
Câu 29: Cho hàm trùng phương
( ) ( )
4 2 2
2 1 8= = − + + −y f x x m x m
có đồ thị
( )
C
. Gọi
,,A B C
là ba
điểm cực trị của đồ thị
( )
C
. Để tam giác
ABC
đều thì giá trị tham số
m
nằm trong khoảng nào
sau đây?
A.
11
;
42
. B.
1
0;
4
. C.
1
;1
2
. D.
( )
1; 2
.
Lời giải
Chọn A
Tập xác định:
=D
.
( )
3
4 4 1
= − +y x m x
;
( )
2
2
0
0 4 1 0
1
=
= − − =
=+
x
y x x m
xm
.
Hàm số có ba điểm cực trị khi và chỉ khi phương trình
0
=y
có ba nghiệm phân biệt
10 + m
1 −m
.
3

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Khi đó
0
=y
0
1
1
=
= +
= − +
x
xm
xm
.
Đồ thị
( )
C
có ba điểm cực trị là
( )
2
0 ; 8−Am
,
( )
( )
2
2
1; 1 8+ − + + −B m m m
và
( )
( )
2
2
1; 1 8− + − + + −C m m m
.
Ta có
( )
4
11= = + + +AB AC m m
.
Do đó tam giác
ABC
đều
( ) ( )
4
1 1 4 1 = + + + = +AB BC m m m
( ) ( )
4
1 1 4 1 + + + = +m m m
( ) ( )
4
1 3 1 0 + − + =mm
( ) ( )
3
1 . 1 3 0
+ + − =
mm
( )
3
3
10
1
1 3 0
13
+=
=−
+ − =
= − +
m
m
m
m
.
So điều kiện
1−m
ta nhận
3
13= − +m
.
Câu 30: Gọi
S
là tập hợp chứa tất cả các giá trị nguyên của tham số
20; 20m−
để hàm số
42
2( 2) 1y x m x= + − +
có duy nhất một điểm cực tiểu. Số phần tử của tập
S
bằng
A. 19. B. 21. C. 20. D. 41.
Lời giải
Chọn A
Điều kiện để hàm số
42
2( 2) 1y x m x= + − +
có duy nhất một điểm cực tiểu là
10a =
và
phương trình
'0y =
có duy nhất một nghiệm. Ta có:
3
2
2
' 4 4( 2) .
0
' 0 4 ( 2) 0
2 (*)
y x m x
x
y x x m
xm
= + −
=
= + − =
=−
Để phương trình
'0y =
có duy nhất một nghiệm
0x =
thì phương trình (*) vô nghiệm hoặc có
nghiệm duy nhất
0 2 0 2.x m m= −
Vậy
2,3,...,20m
hay có 19 giá trị của tham
số
20; 20m−
thỏa mãn.
Câu 31: Cho hàm số
42
22y x mx= − +
. Tổng bình phương các giá trị
m
để hàm số có ba cực trị và đường
tròn qua ba cực trị đó có bán kính bằng
4
, gần với số nguyên nào nhất trong các số nguyên sau?
A.
8
. B.
9
. C.
16
. D.
7
.
Lời giải
Chọn A

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Ta có
(
)
32
' 4 4 4y x mx x x m= − = −
;
2
0
'0
x
y
xm
=
=
=
.
Để hàm số có ba cực trị thì
0m
( )
1
. Khi đó ba điểm cực trị của đồ thị hàm số là
(
)
(
)
( )
22
;2 ; ;2 ; 0;2A m m B m m C− − −
. Theo giả thiết ta có
.
4
2
2sin
CA AC BC
R
CH
CBA
= = =
( )
2
( Với
H
là trung điểm của
AB
và ta có
AC BC=
)
Hay
( )
2
2 2 2
. 8 8 8AC BC CH AC CH CH AH CH= = + =
2 4 4 2
8 8 0m m m m m m= + − + =
Khi đó với
0m
sử dụng máy tính casio ta được tổng bình phương các giá trị
m
gần bằng
7,654
Câu 32: Cho hàm số
( )
42
22f x x mx= − +
. Tổng bình phương các giá trị
m
để hàm số có ba cực trị và
đường tròn đi qua ba điểm cực trị của đồ thị hàm số có bán kính bằng
4
, gần với số nguyên nào
nhất trong các số nguyên sau?
A.
8
. B.
9
. C.
16
. D.
7
.
Lời giải
Chọn A
Ta có:
( )
3
44f x x mx
=−
Hàm số có ba cực trị
0m
Khi đó đồ thị hàm số có ba điểm cực trị là
( )
0;2A
;
( )
2
;2B m m−−
;
( )
2
;2C m m−
Ta có:
4
AB m m AC= + =
;
2BC m=
2 2 2 3
3
1
cos
2 . 1
AB AC BC m
BAC
AB AC m
+ − −
==
+
2
3
2
sin 1 cos
1
mm
BAC BAC
m
= − =
+
Mà
2 sinBC R BAC=
3
2
2 2.4.
1
mm
m
m
=
+
3
8 1 0mm− + =
( )
( )
( )
2,889
2,764
0,125
m lo i
m th
m th
−
¹
áa m· n
áa m· n
Vậy tổng bình phương các giá trị
m
là
2
2,764 0,125 7,655+
.
Câu 33: Cho hàm số
( )
42
2 1 1y mx m x= − + +
. Tìm tất cả các giá trị của
m
để hàm số có một điểm cực
đại
A.
1
0
2
m−
. B.
1
2
m −
. C.
1
0
2
m−
. D.
1
2
m −
.
Lời giải
Chọn C
Ta có
( )
( )
32
2
0
4 2 2 1 2 2 2 1 ; 0
2 2 1
x
y mx m x x mx m y
mx m
=
= − + = − − =
=+
*
0m =
ta có
2
1yx= − +
. Vậy hàm số đạt cực đại tại
0x =
.
*
0m
để hàm số có một điểm cực đại khi
0
1
0
2 1 0
2
m
m
m
−
+
.
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Vậy
1
0
2
m−
thì hàm số có một điểm cực đại.
Câu 34: Tìm giá trị tham số
m
để đồ thị hàm số
( )
42
2 1 2 3y x m x m= − + + +
có ba điểm cực trị
,,A B C
sao cho trục hoành chia tam giác
ABC
thành một tam giác và một hình thang biết rằng tỉ số diện
tích tam giác nhỏ được chia ra và diện tích tam giác
ABC
bằng
4
9
A.
53
2
m
+
=
. B.
1 15
2
m
−+
=
. C.
13
2
m
−+
=
. D.
1 15
2
m
+
=
.
Lời giải
Chọn D
Xét hàm số
( )
42
2 1 2 3y x m x m= − + + +
.
( )
3
4 4 1y x m x
= − +
.
2
0
0
1
x
y
xm
=
=
=+
.
Hàm số có ba điểm cực trị
0y
=
có ba nghiệm phân biệt
1m −
.
Khi
1m −
, đồ thị hàm số có ba điểm cực trị là
( )
0;2 3Am+
,
( )
2
1; 2B m m− + − +
,
( )
2
1; 2C m m+ − +
.
Ta có
A Oy
,
,BC
đối xứng nhau qua
Oy
ABC
cân tại
A
.
Trục hoành chia tam giác
ABC
thành một tam giác và một hình thang
2
2 3 0
20
m
m
+
− +
3
2
2
2
m
m
m
−
−
2
3
2
2
m
m
− −
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Kết hợp với điều kiện
1m −
ta được
2m
.
Khi đó, gọi
,DE
lần lượt là giao điểm của trục
Ox
và các cạnh
,AB AC
,
K
là giao điểm của
BC
và
Oy
.
Ta có
2
ADE
ABC
S
AO
S AK
=
2
A
AB
y
yy
=
−
2
2
23
21
m
mm
+
=
++
.
Mà
4
9
ADE
ABC
S
S
=
2
2
2 3 4
2 1 9
m
mm
+
=
++
.
Vì
2m
( )
2
2 3 2
3
21
m
mm
+
=
++
2
2 2 7 0mm − − =
1 15
2
1 15
2
m
m
+
=
−
=
1 15
2
m
+
=
.
Vậy
1 15
2
m
+
=
thoả mãn yêu cầu đề bài.
Câu 35: Với tất cả giá trị nào của
m
thì hàm số
( )
42
2 1 2y mx m x m= + − + +
chỉ có một cực trị:
A.
2m
. B.
02m
. C.
0
2
m
m
. D.
0m
.
Lời giải
Chọn C
* Nếu
0=m
thì
2
21yx= − +
là hàm bậc hai nên chỉ có duy nhất một cực trị.
* Khi
0m
, ta có:
( ) ( )
32
' 4 2 2 2 2 2y mx m x x mx m
= + − = + −
;
2
0
'0
2
2
x
y
m
x
m
=
=
−
=
.
Để hàm số có một cực trị khi
2
2
0
0
2
m
m
m
m
−
.
Kết hợp hai trường hợp ta được
0
2
m
m
.
Câu 36: Tìm giá trị của tham số
m
để hàm số
( )
4 2 2
2 3 2y x m x= − + + +
có điểm cực trị sao cho giá
trị cực đại của hàm số đạt giá trị nhỏ nhất.
A.
0m =
. B.
3m =−
. C.
1m =−
. D.
2m =−
.
Lời giải
Chọn A
Xét hàm số
( )
4 2 2
2 3 2y x m x= − + + +
Ta có
( )
32
4 4 3y x m x
= − + +
.
Phương trình
( )
32
0 4 4 3 0y x m x
= − + + =
2
0
3
x
xm
=
= +
Hàm số luôn có 3 điểm cực trị với
m
Bảng biến thiên
3

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Từ bảng biến thiên ta thấy hàm số đạt cực đại khi
2
3xm= +
.
Giá trị cực đại của hàm số:
(
)
( )
4
2
22
§
3 2 3 2
C
y m m= − + + + +
( )
2
2
32m= + +
.
§
min 11
C
y =
khi
0m =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
32
y ax bx cx d= + + +
(
, , ,a b c d
là các hằng số thực) có đồ thị cắt trục hoành tại ba
điểm phân biệt. Số điểm cực trị của hàm số
32
y ax bx cx d= + + +
là
A.
3
. B.
5
. C.
4
. D.
1
.
Câu 2: Cho hàm số
( ) ( )
32
1 5 3 3.y m x x m x= − − + + +
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
y f x=
có đúng 3 điểm cực trị?
A.
4
. B.
3
. C.
5
. D.
1
.
Câu 3: Cho hàm số
( ) ( ) ( )
32
2 1 2 2.f x x m x m x= − − + − +
Tất cả các giá trị thực của tham số m để hàm
số
( )
y f x=
có 5 cực trị là
A.
5
2
4
m
. B.
5
2
4
m−
. C.
5
2
4
m−
. D.
5
2
4
m
.
Câu 4: Cho hàm số
( ) ( ) ( )
32
2 1 2 2f x x m x m x= − − + − +
. Tất cả các giá trị thực của tham số m để
hàm số
( )
y f x=
có 5 cực trị là
Cực trị hàm số chứa dấu giá trị tuyệt đối
DẠNG 8
Phương pháp:
a. Hàm số dạng
( )
y f x=
Để tìm cực trị của hàm số
( )
y f x=
ta sẽ lập bảng biến thiên hoặc vẽ đồ thị hàm số
( )
y f x=
từ đồ thị của hàm số
( )
y f x=
.
Chú ý: Đồ thị hàm số
( )
y f x=
gồm 2 phần:
▪ Phần đồ thị
( )
y f x=
nằm trên trục
Ox
▪ Phần đồ thị lấy đối xứng qua
Ox
của đồ thị
( )
y f x=
nằm dưới
Ox
▪ Số điểm cực trị của hàm số
( )
y f x=
bằng tổng số điểm cực trị của hàm số
( )
y f x=
và
số nghiệm bội lẻ của phương trình
( )
0fx=
.
b. Hàm số dạng
( )
y f x=
Để tìm cực trị của hàm số
( )
y f x=
ta sẽ lập bảng biến thiên hoặc vẽ đồ thị hàm số
( )
y f x=
từ đồ thị của hàm số
( )
y f x=
.
Chú ý: Đồ thị hàm số
( )
y f x=
gồm 2 phần:
▪ Phần đồ thị
( )
y f x=
nằm bên phải trục
( )
1
Oy C
▪ Phần lấy đối xứng
( )
1
C
qua
Oy
▪ Số điểm cực trị của hàm số
( )
y f x=
bằng hai lần số điểm cực trị dương của hàm số
( )
y f x=
và cộng thêm 1.
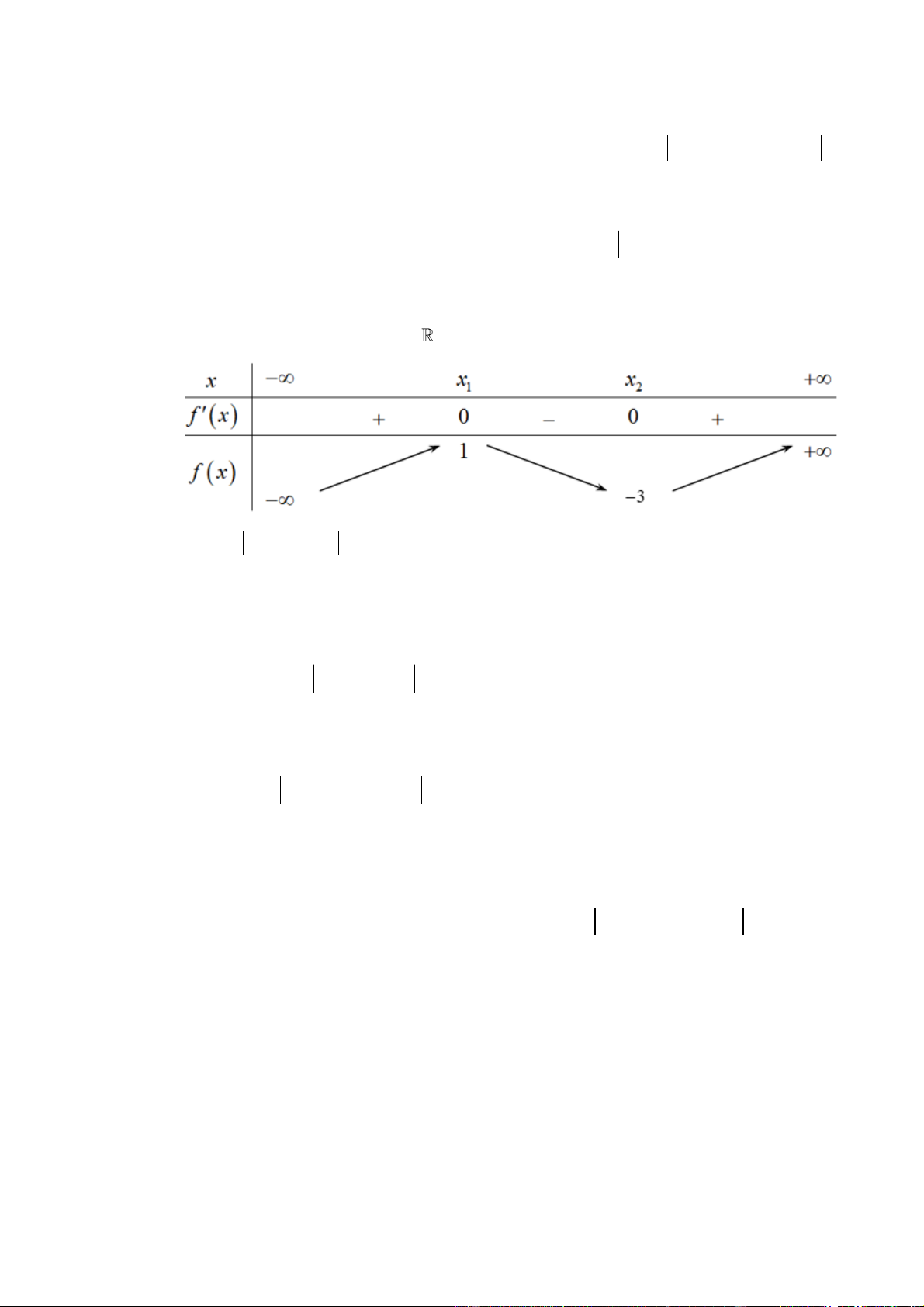
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
5
2
4
m
. B.
5
2
4
m−
. C.
5
2
4
m−
. D.
5
2
4
m
.
Câu 5: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12y x x x m= − − +
có
5
điểm cực trị
A.
26
. B.
16
. C.
27
. D.
44
.
Câu 6: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2 2
3 4 12y x x x m= − − +
có đúng 5
điểm cực trị?
A.
5
. B.
7
. C. 6. D.
4
.
Câu 7: Cho hàm số
()y f x=
liên tục trên , có bảng biến thiên như hình vẽ dưới đây:
Đặt
( )
( ) 1g x m f x= + +
(với
m
là tham số). Tìm tất cả các giá trị thực của
m
để hàm số
()y g x=
có đúng 3 điểm cực trị
A.
1
3
m
m
−
. B.
13m−
. C.
1
3
m
m
−
. D.
13m−
.
Câu 8: Cho hàm số
( )
32
3f x x x m= − +
với
4;4m−
là tham số. Có bao nhiêu giá trị nguyên của
m
để hàm số
( )
fx
có đúng 3 điểm cực trị?
A. 5. B.
8
. C.
4
. D.
6
.
Câu 9: Cho hàm số
4 3 2
44y x x x m= − + +
(
m
là tham số). Khi
m
thay đổi thì số điểm cực trị của hàm
số có thể là
a
hoặc
b
hoặc
c
. Tính tích
abc
.
A. 120. B. 105. C. 60. D. 15.
Câu 10: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong trong hình bên dưới. Tìm số giá trị nguyên
của tham số
m
thuộc đoạn
200;200−
để hàm số
( ) ( ) ( )
2
8g x f x f x m= + −
có đúng 3 điểm
cực trị.
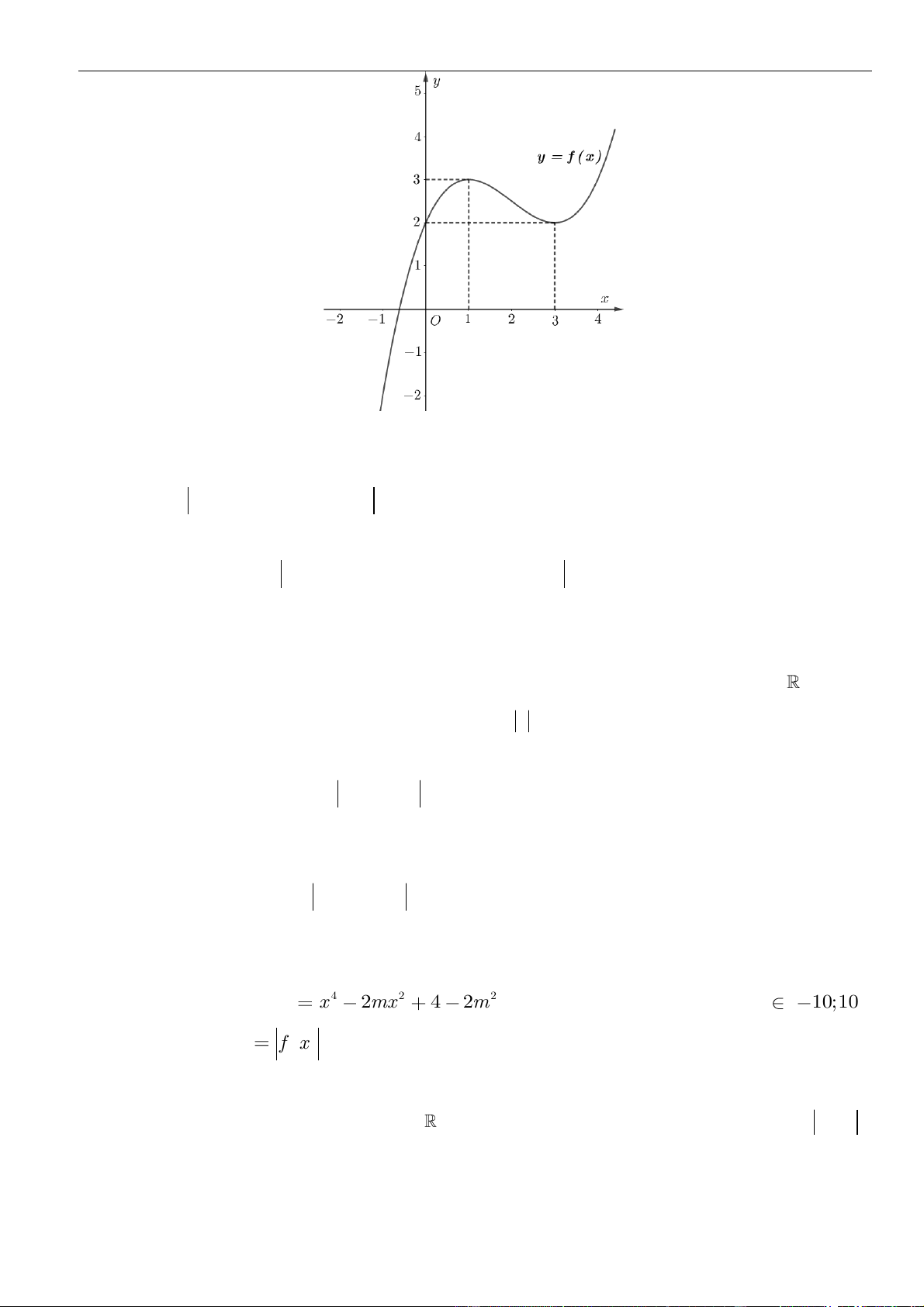
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
186
. B.
184
. C.
185
. D.
187
.
Câu 11: Gọi tập
X
là tập hợp tất cả các số nguyên
2021;2021m−
sao cho đồ thị của hàm số
( )
32
21y x m x mx m= − + + +
có 5 điểm cực trị. Tính tổng các phần tử của tập
X
.
A.
0
. B.
1−
. C.
4036
. D.
1
.
Câu 12: Cho hàm số
( )
24 3
3 3 2 3 42y x m x mxm mx + − +=+ −−
. Hỏi có bao nhiêu giá trị
nguyên của tham số
10;10m−
để đồ thị hàm số đã cho có 7 điểm cực trị?
A.
15
. B.
14
. C.
13
. D.
16
.
Câu 13: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )
22
1 2 1f x x x x mx m
= − + + +
với mọi
x
. Có bao
nhiêu số nguyên
10m −
để hàm số
( )
( )
g x f x=
có
5
điểm cực trị?
A.
6
. B.
7
. C.
9
. D.
8
.
Câu 14: Cho hàm số
2
( ) 4 3y f x x x mx= = − + +
. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để
hàm số
()y f x=
có đúng ba điểm cực trị.
A.
2
. B.
3
. C.
4
. D.
6
.
Câu 15: Cho hàm số
( )
32
3= − +f x x x m
với
4;4−m
là tham số. Có bao nhiêu giá trị nguyên của
m
để hàm số
( )
fx
có đúng 3 điểm cực trị?
A.
5
. B.
8
. C.
4
. D.
6
.
Câu 16: Cho hàm số
4 2 2
2 4 2f x x mx m
. Có tất cả bao nhiêu số nguyên
10;10m
để hàm số
y f x
có đúng
3
điểm cực trị?
A.
9
. B.
8
. C.
7
. D.
6
.
Câu 17: Cho hàm số
( )
y f x=
liên tục trên có đồ thị như hình vẽ. Đồ thị của hàm số
( ) ( )
2
g x f x=
có bao nhiêu điểm cực đại, bao nhiêu điểm cực tiểu?
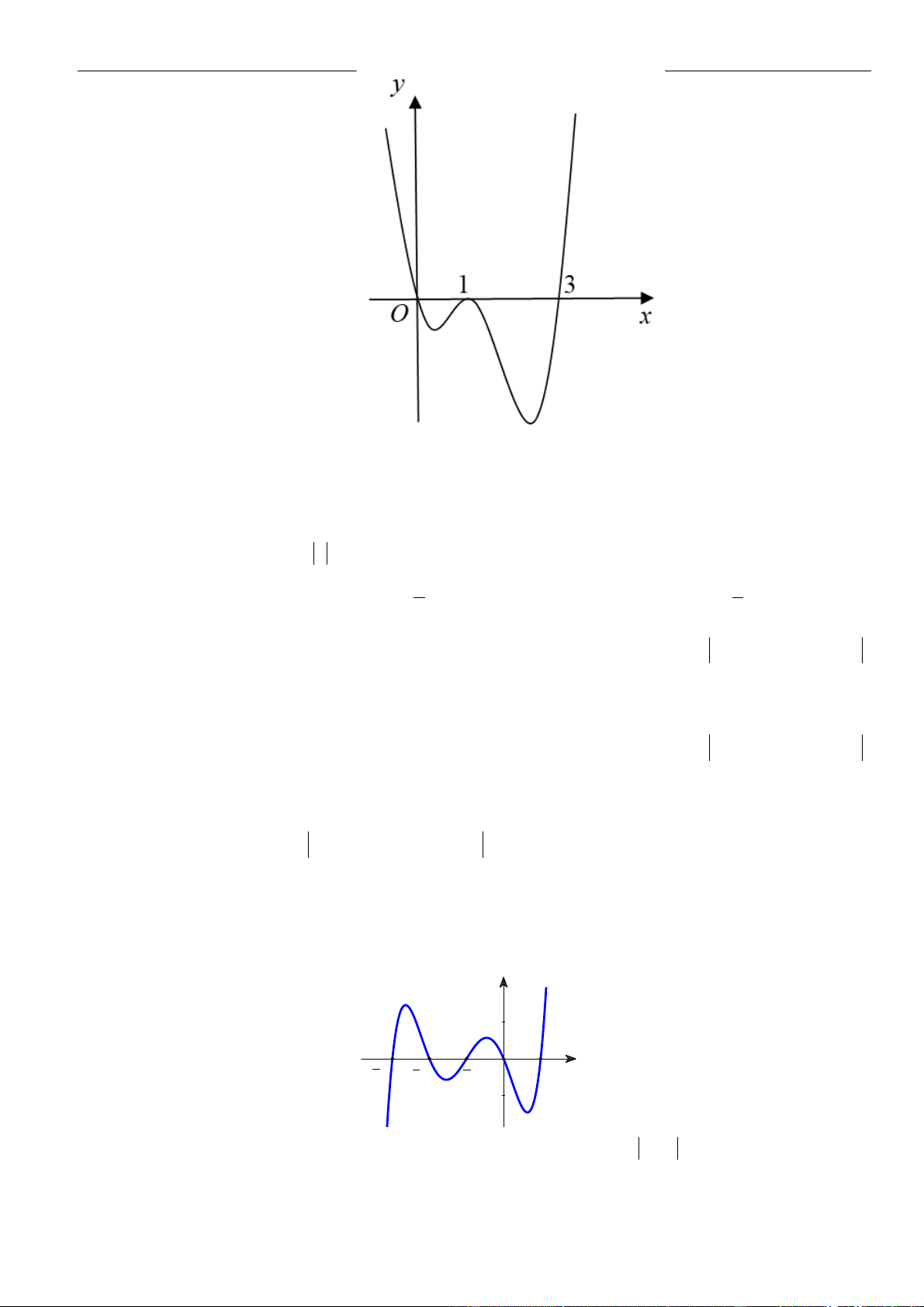
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
A.
2
điểm cực đại, 3 điểm cực tiểu. B.
3
điểm cực đại, 2 điểm cực tiểu.
C.
1
điểm cực đại, 3 điểm cực tiểu. D.
2
điểm cực đại, 2 điểm cực tiểu.
Câu 18: Cho hàm số
( ) ( ) ( )
32
2 1 3 2y f x x m x m x= = − + + − +
. Tìm tất cả các giá trị của tham số thực
m
để hàm số
( )
y f x=
có 3 điểm cực trị.
A.
3m
. B.
1
2
m −
. C.
3m
. D.
1
3
2
m−
.
Câu 19: Tìm số các giá trị nguyên của tham số
( )
2021;2021m −
để hàm số
42
4 2020y x x m= − + +
có 7 điểm cực trị.
A.
2020
. B.
1
. C.
5
. D.
3
.
Câu 20: Tìm số các giá trị nguyên của tham số
( )
2021;2021m −
để hàm số
42
4 2020y x x m= − + +
có 7 điểm cực trị.
A.
2020
. B.
1
. C.
5
. D.
3
.
Câu 21: Cho hàm số
( )
4 3 2
2 8 16 1f x x x x m= − − + −
(m là tham số). Biết rằng khi m thay đổi thì số điểm
cực trị của hàm số có thể là a hoặc b hoặc C. Giá trị
abc++
bằng
A. 12. B. 16. C. 15. D. 13.
Câu 22: Cho hàm đa thức
( )
2
2y f x x
=+
có đồ thị như hình vẽ.
Tổng giá trị nguyên của
10;10m−
để hàm số
( )
( )
2y g x f x m= = − +
có 5 điểm cực trị là
A.
52−
. B.
55
. C.
55−
. D.
56
.
x
y
1
2
3
O
1

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Câu 23: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ dưới. Tìm số các giá trị nguyên của tham số
m
thuộc
10; 10−
để hàm số
( ) ( )
g x f x m=−
có 3 điểm cực trị?
.
A.
4
. B.
5
. C.
9
. D.
8
.
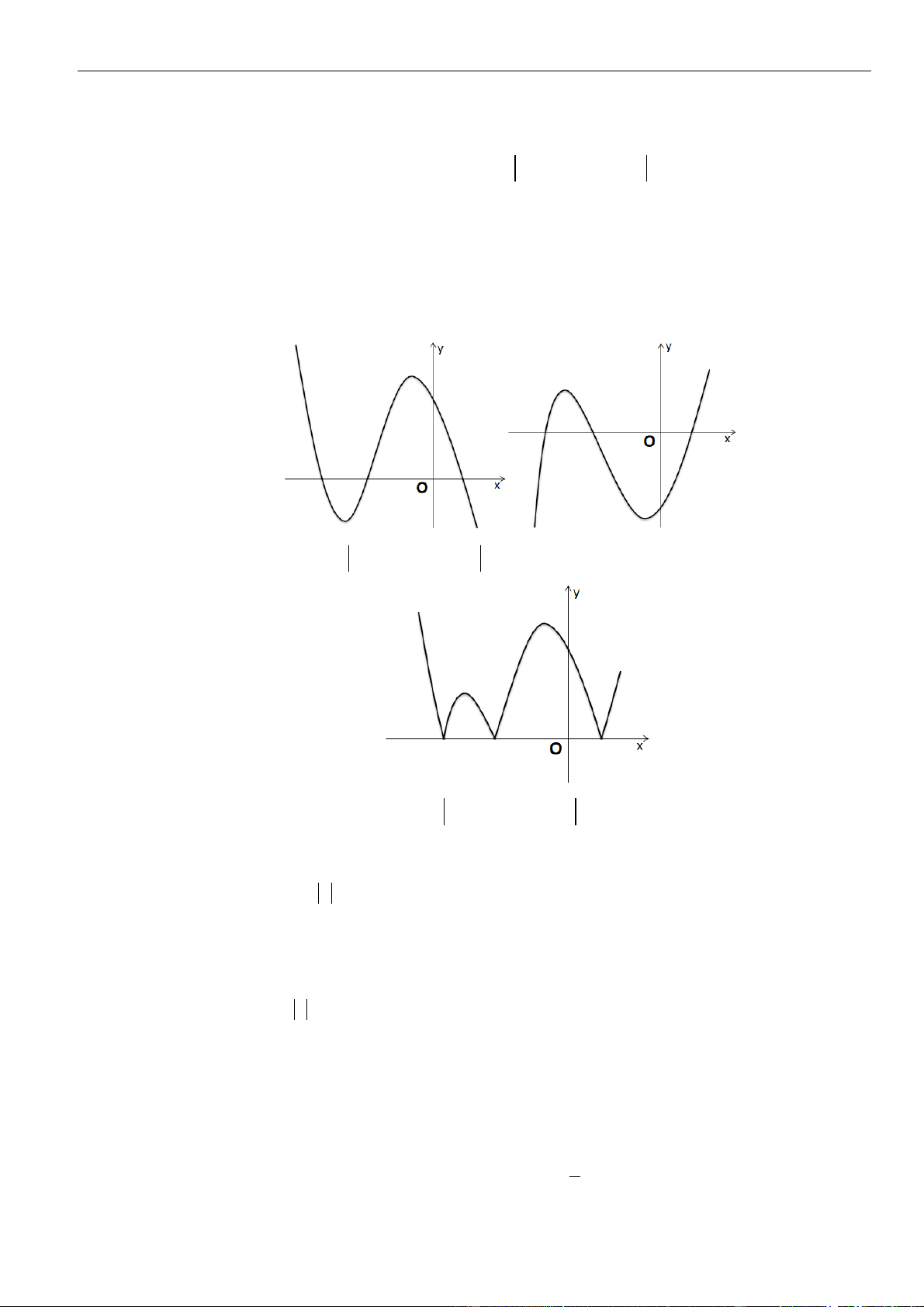
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
32
y ax bx cx d= + + +
(
, , ,a b c d
là các hằng số thực) có đồ thị cắt trục hoành tại ba
điểm phân biệt. Số điểm cực trị của hàm số
32
y ax bx cx d= + + +
là
A.
3
. B.
5
. C.
4
. D.
1
.
Lời giải
Chọn B
Ta có các trường hợp đồ thị hàm số
32
y ax bx cx d= + + +
(
, , ,a b c d
là các hằng số thực) có đồ
thị cắt trục hoành tại ba điểm phân biệt:
Khi đó đồ thị hàm số
32
y ax bx cx d= + + +
là
Suy ra số điểm cực trị của hàm số
32
y ax bx cx d= + + +
là 5.
Câu 2: Cho hàm số
( ) ( )
32
1 5 3 3.y m x x m x= − − + + +
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
y f x=
có đúng 3 điểm cực trị?
A.
4
. B.
3
. C.
5
. D.
1
.
Lời giải
Chọn A
Để hàm số
( )
y f x=
có đúng 3 điểm cực trị thì hàm số
( )
y f x=
phải có đúng 1 điểm cực trị
dương.
Xét
( ) ( ) ( )
32
1 5 3 3f x m x x m x= − − + + +
( ) ( )
2
3 1 10 3y m x x m
= − − + +
.
Lúc này, phương trình
( ) ( )
2
3 1 10 3 0y m x x m
= − − + + =
phải có tối đa 2 nghiệm bội lẻ, trong
đó có 1 nghiệm bắt buộc dương.
Trường hợp 1:
1m =
. Khi đó
2
10 4 0 0
5
y x x
= − + = =
, là nghiệm bội lẻ.
Suy ra, nhận giá trị
1m =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Trường hợp 2:
1.m
Khi đó,
( ) ( )
2
3 1 10 3 0y m x x m
= − − + + =
là hàm bậc 2.
Gọi
( )
1 2 1 2
,x x x x
là 2 nghiệm của phương trình trên, hiển nhiên hai nghiệm này bội lẻ.
12
1
0
0
0
xx
x
=
( )( )
( )
12
1 2 1
100 12 1 3 0
3
.0
1
5
03
6
mm
m
P x x
m
x m x x VL
= − − +
+
= =
−
= = − = −
( )
2
12 24 136 0
3;1
mm
m
m
+ −
−
( )
3;1m
m
−
Có
3
giá trị m nguyên khác
1
Vậy, tồn tại 4 giá trị nguyên của tham số
m
để hàm số
( )
y f x=
có đúng 3 điểm cực trị.
Câu 3: Cho hàm số
( ) ( ) ( )
32
2 1 2 2.f x x m x m x= − − + − +
Tất cả các giá trị thực của tham số m để hàm
số
( )
y f x=
có 5 cực trị là
A.
5
2
4
m
. B.
5
2
4
m−
. C.
5
2
4
m−
. D.
5
2
4
m
.
Lời giải
Chọn D
Nhận thấy rằng nếu
0
x
là điểm cực trị dương của hàm số
( )
y f x=
thì
0
x
và
0
x−
là điểm cực trị
của hàm số
( )
y f x=
.
Lại thấy vì đồ thị hàm số
( )
y f x=
nhận trục
Oy
làm trục đối xứng mà
( )
fx
là hàm đa thức
bậc ba nên
0x =
luôn là một điểm cực trị của hàm số
( )
y f x=
Khi đó, để hàm số
( )
y f x=
có 5 điểm cực trị thì hàm số
( ) ( ) ( )
32
2 1 2 2f x x m x m x= − − + − +
có hai điểm cực trị dương phân biệt.
Suy ra phương trình
( ) ( )
2
' 3 2 2 1 2 0f x x m x m= − − + − =
có hai nghiệm phân biệt dương.
( ) ( )
2
2
2 1 3 2 0
4 5 0
'0
2 1 1 5
0 0 2.
3 2 4
0
2
20
mm
mm
m
S m m
P
m
m
− − −
− −
−
−
Câu 4: Cho hàm số
( ) ( ) ( )
32
2 1 2 2f x x m x m x= − − + − +
. Tất cả các giá trị thực của tham số m để
hàm số
( )
y f x=
có 5 cực trị là
A.
5
2
4
m
. B.
5
2
4
m−
. C.
5
2
4
m−
. D.
5
2
4
m
.
Lời giải
Chọn D
Ta có
( ) ( ) ( )
2
3 2 2 1 2f x x m x m
= − − + −
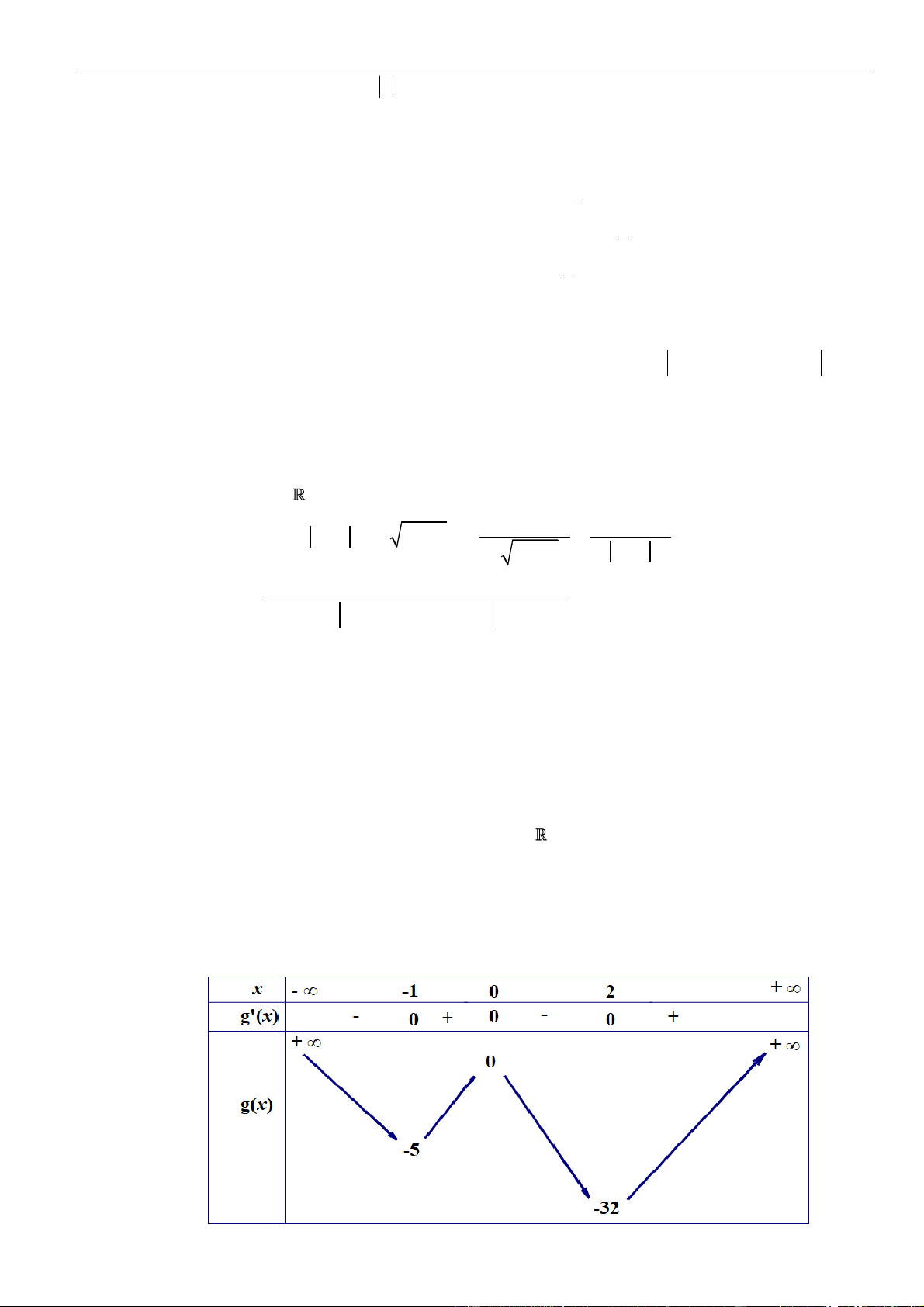
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Điều kiện để hàm số
( )
y f x=
có 5 cực trị là
( )
y f x=
có 2 cực trị dương hay phương trình
( )
0fx
=
có 2 nghiệm dương phân biệt.
Do đó ycbt
0
0
0
S
P
2
4 5 0
2 1 0
20
mm
m
m
− −
−
−
1
5
4
2
1
2
m
m
m
m
−
5
2
4
m
Câu 5: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12y x x x m= − − +
có
5
điểm cực trị
A.
26
. B.
16
. C.
27
. D.
44
.
Lời giải
Chọn C
Tập xác định
D =
.
Ta có đạo hàm của
( )
(
)
2
2
2 ( ). ( ) ( ). ( )
( ) ( )
()
2 ( )
f x f x f x f x
f x f x
fx
fx
= = =
, suy ra
Đạo hàm
3 2 4 3 2
4 3 2
(12 12 24 )(3 4 12 )
3 4 12
x x x x x x m
y
x x x m
− − − − +
=
− − +
Xét phương trình
3 2 4 3 2
(12 12 24 )(3 4 12 ) 0x x x x x x m− − − − + =
32
4 3 2
12 12 24 0
3 4 12 0
x x x
x x x m
− − =
− − + =
4 3 2
0
1
2
3 4 12 (*)
x
x
x
x x x m
=
=−
=
− − = −
Xét hàm số
4 3 2
( ) 3 4 12g x x x x= − −
trên ta có
32
( ) 12 12 24g x x x x
= − −
và
0
( ) 0 1
2
x
g x x
x
=
= = −
=
.
Bảng biến thiên của
()gx
như sau:
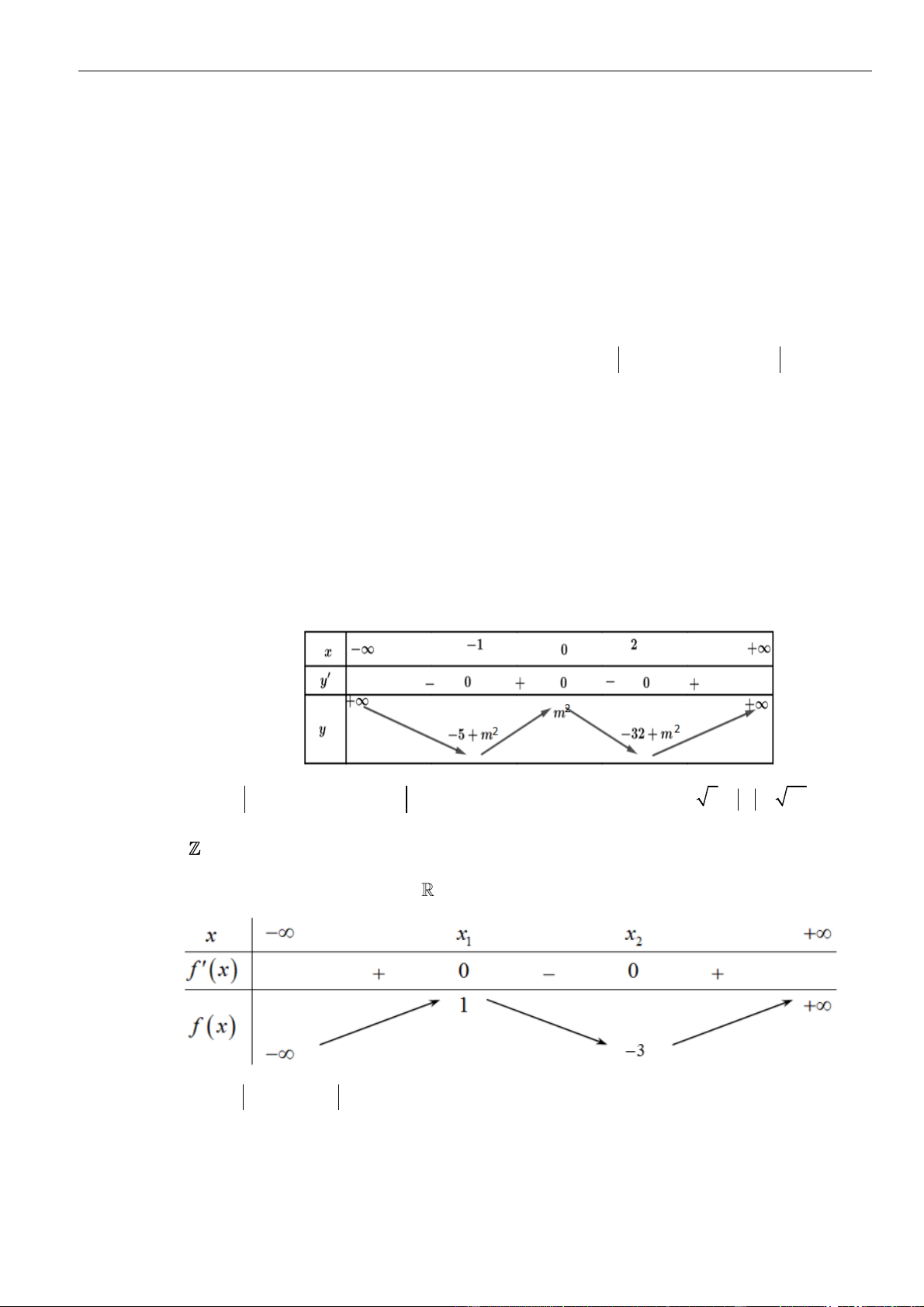
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Hàm số đã cho có
5
điểm cực trị khi và chỉ khi tổng số nghiệm bội lẻ của
0y
=
và số điểm tới
hạn của
y
là
5
, do đó ta cần có các trường hợp sau
TH1: Phương trình
(*)
có hai nghiệm phân biệt khác
1;0;2−
00
32 5 5 32
mm
mm
−
− − −
, trường hợp này có
26
số nguyên dương.
TH2: Phương trình
(*)
có
3
nghiệm trong đó có một nghiệm kép trùng với một trong các
nghiệm
1;0;2−
00
55
mm
mm
− = =
− = − =
, trường hợp này có một số nguyên dương.
Vậy có tất cả là
27
số nguyên dương thỏa mãn bài toán.
Câu 6: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2 2
3 4 12y x x x m= − − +
có đúng 5
điểm cực trị?
A.
5
. B.
7
. C. 6. D.
4
.
Lời giải
Chọn C
4 3 2 2
3 4 12y x x x m= − − +
32
12 12 24y x x x
= − −
Ta có:
32
12 12 24 0y x x x
= − − =
1
0
2
x
x
x
=−
=
=
Bảng biến thiên
Hàm số
4 3 2 2
3 4 12y x x x m= − − +
có 5 điểm cực trị
2
2
0
5 32
m
m
5 32m
m
3; 4; 5;3;4;5m − − −
.
Câu 7: Cho hàm số
()y f x=
liên tục trên , có bảng biến thiên như hình vẽ dưới đây:
Đặt
( )
( ) 1g x m f x= + +
(với
m
là tham số). Tìm tất cả các giá trị thực của
m
để hàm số
()y g x=
có đúng 3 điểm cực trị
A.
1
3
m
m
−
. B.
13m−
. C.
1
3
m
m
−
. D.
13m−
.
Lời giải
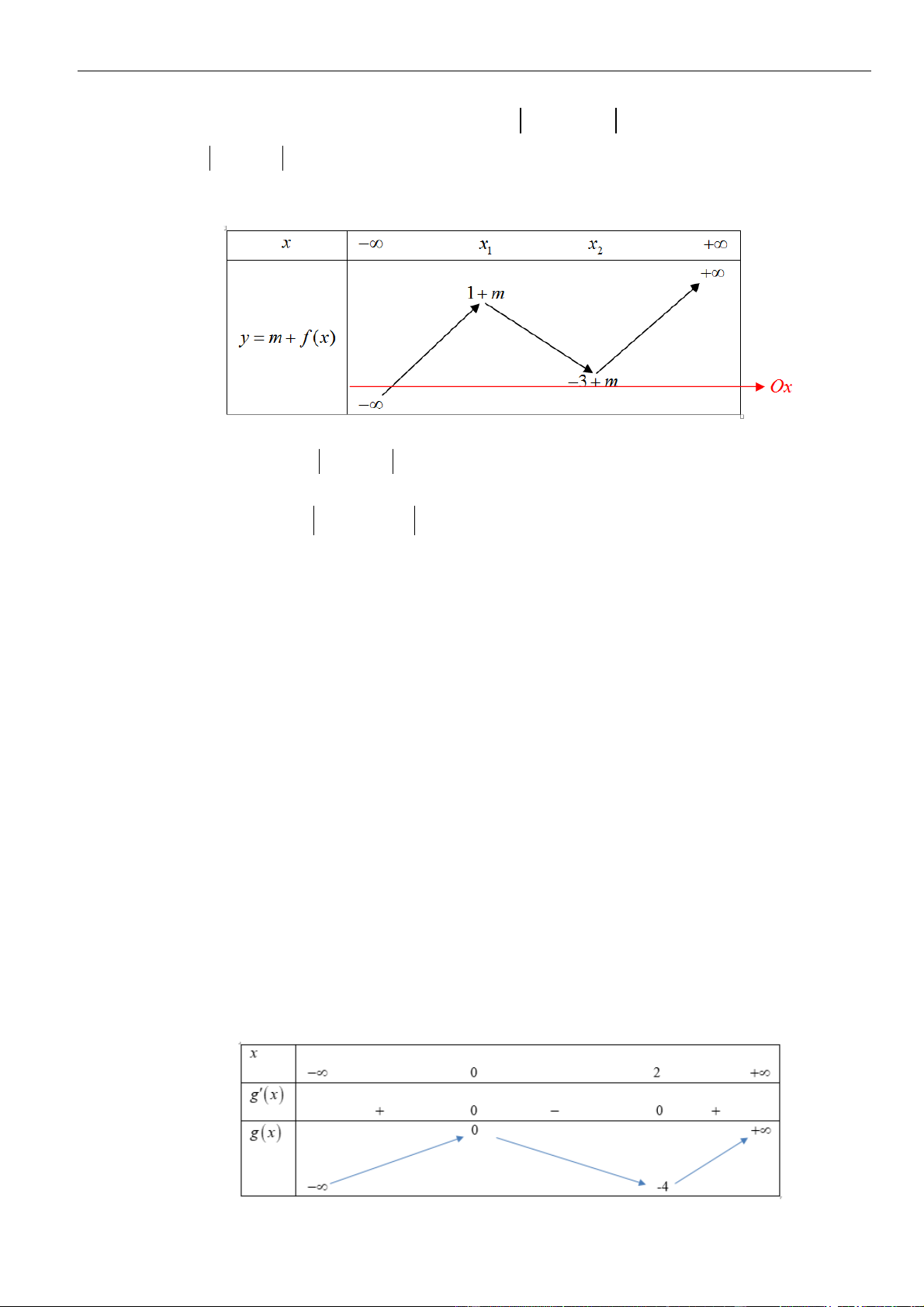
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Chọn C
Nhận xét: Số điểm cực trị của hàm số
( )
( ) 1g x m f x= + +
bằng số điểm cực trị của hàm số
( )
()h x m f x=+
.
Ta có bảng biến thiên của hàm số
()y m f x=+
như sau:
Suy ra hàm số
( )
()h x m f x=+
có đúng 3 điểm cực trị khi
3 0 3
1 0 1
mm
mm
− +
+ −
.
Câu 8: Cho hàm số
( )
32
3f x x x m= − +
với
4;4m−
là tham số. Có bao nhiêu giá trị nguyên của
m
để hàm số
( )
fx
có đúng 3 điểm cực trị?
A. 5. B.
8
. C.
4
. D.
6
.
Lời giải
Chọn D
( )
32
3g x x x m= − +
Ta có
( )
2
0
3 6 0
2
x
g x x x
x
=
= − =
=
Vậy hàm số
( )
32
3g x x x m= − +
có hai cực trị. Do đó, để hàm đã cho có 3 cực trị thì phương
trình
( )
32
30g x x x m= − + =
có nghiệm duy nhất 1 nghiệm đơn.
Ta có
( )
32
32
30
3
g x x x m
x x m
= − + =
− = −
Xét hàm số
( )
32
3g x x x=−
,
( )
2
0
3 6 0
2
x
g x x x
x
=
= − =
=
Ta có Bảng biến thiên
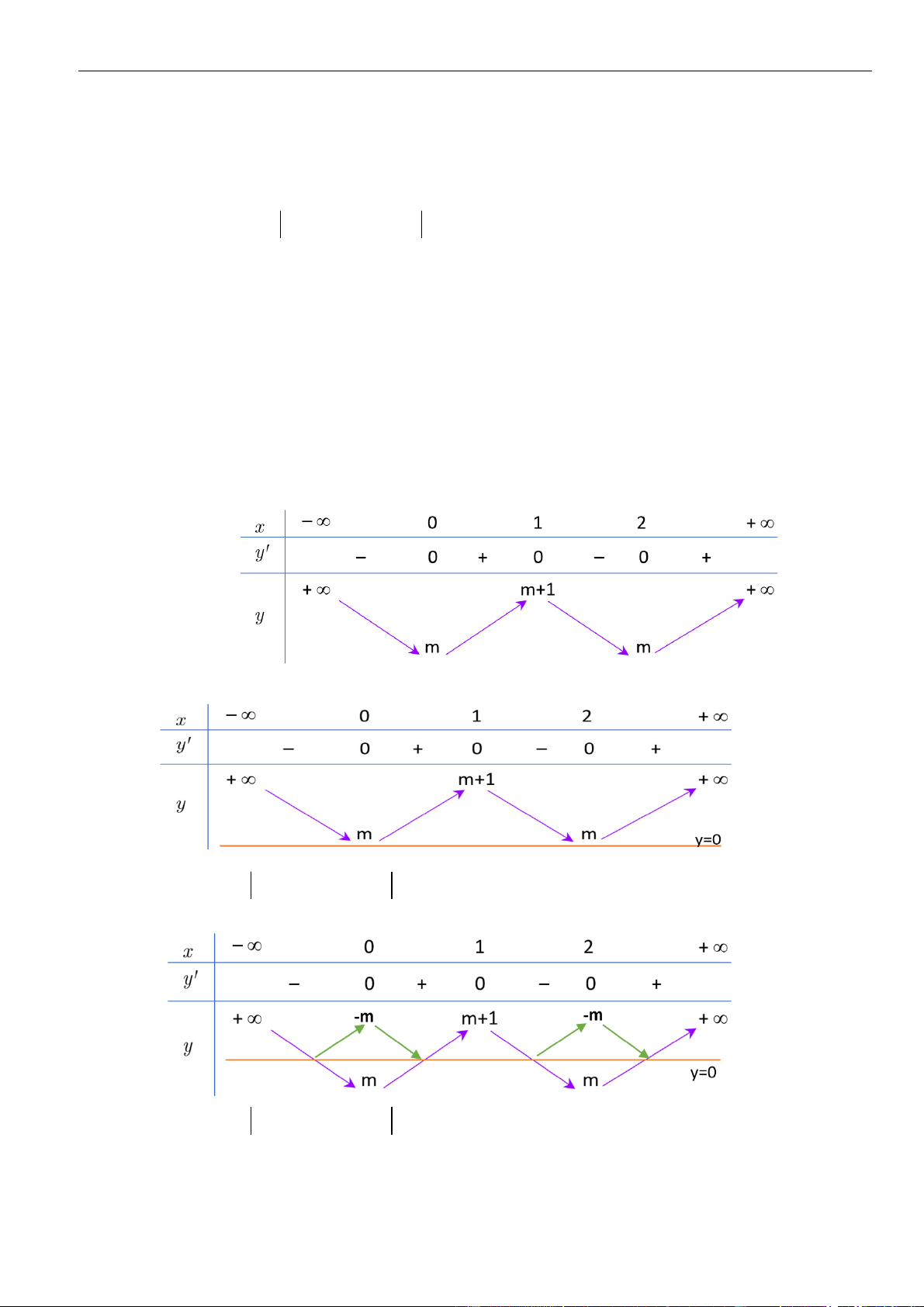
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Dựa vào bảng biến thiên suy ra phương trình
32
3x x m− = −
0
4
m
m
−
Mà
4;4m−
. Suy ra
4;0;1;2;3;4m−
Vậy có 6 giá trị của m.
Câu 9: Cho hàm số
4 3 2
44y x x x m= − + +
(
m
là tham số). Khi
m
thay đổi thì số điểm cực trị của hàm
số có thể là
a
hoặc
b
hoặc
c
. Tính tích
abc
.
A. 120. B. 105. C. 60. D. 15.
Lời giải
Chọn B
Gọi
( )
4 3 2
44g x x x x m= − + +
.
Ta có:
( )
32
4 12 8 0g x x x x
= − + =
0
1
2
x
x
x
=
=
=
.
Bảng biến thiên của hàm số
( )
y g x=
Trường hợp 1:
0m
.
Hàm số
4 3 2
44y x x x m= − + +
có 3 điểm cực trị, suy ra
3a =
.
Trường hợp 2:
10m−
.
Hàm số
4 3 2
44y x x x m= − + +
có 7 điểm cực trị, suy ra
7b =
.
Trường hợp 3:
1m −
.
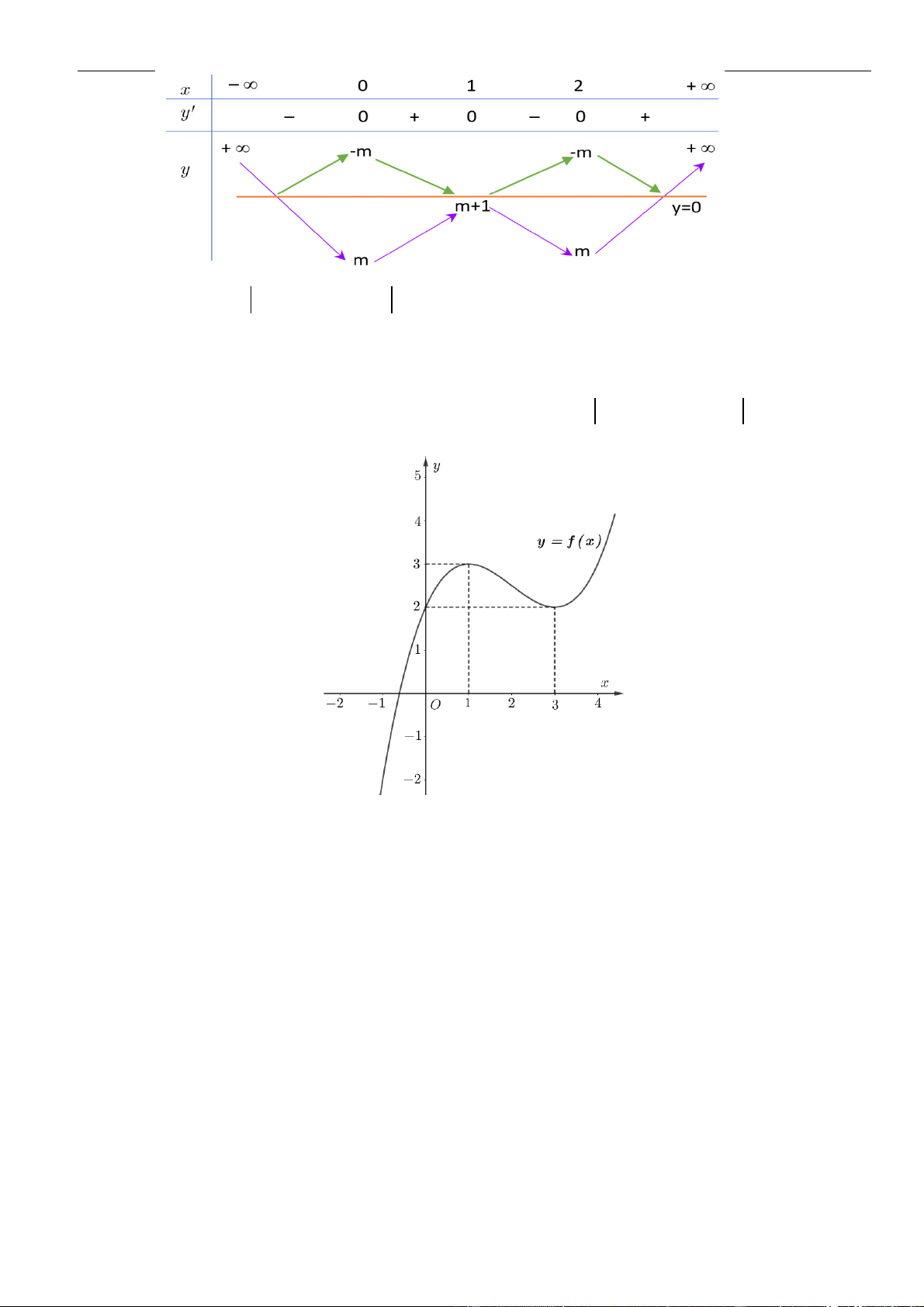
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Hàm số
4 3 2
44y x x x m= − + +
có 5 điểm cực trị, suy ra
5c =
.
Vậy tích
105abc =
.
Câu 10: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong trong hình bên dưới. Tìm số giá trị nguyên
của tham số
m
thuộc đoạn
200;200−
để hàm số
( ) ( ) ( )
2
8g x f x f x m= + −
có đúng 3 điểm
cực trị.
A.
186
. B.
184
. C.
185
. D.
187
.
Lời giải
Chọn C
Xét
( ) ( ) ( )
2
8h x f x f x m= + −
.
( ) ( )
' 2 ( ). ( ) 8 ( ) 2 ( ) ( ) 4h x f x f x f x f x f x
= + = +
.
( )
( )
( )
1
0
03
4
0
x
fx
h x x
fx
xa
=
=
= =
=−
=
.
Bảng biến thiên
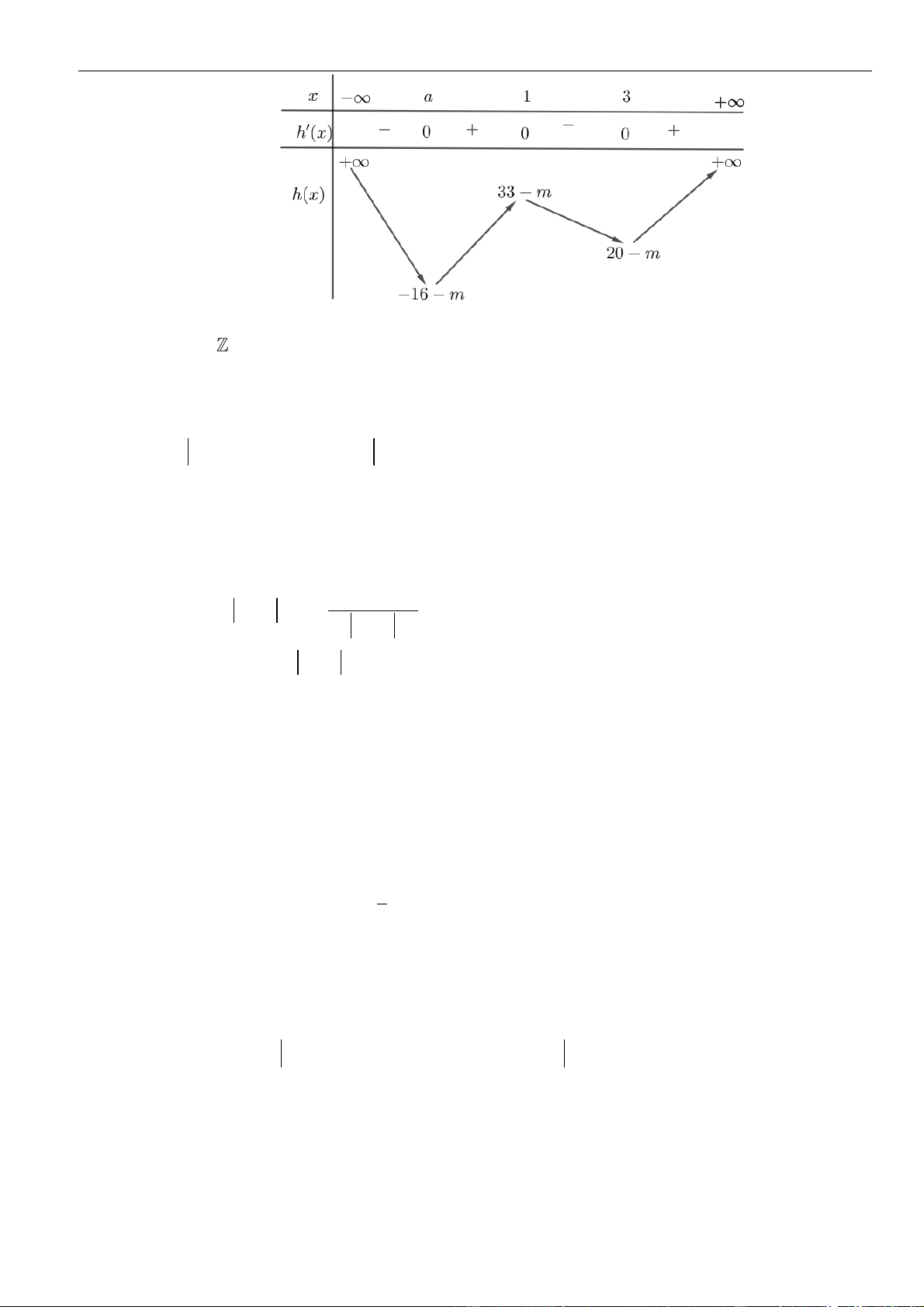
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Từ BBT, yêu cầu bài toán
16 0 16.mm − − −
Mà
m
và
200;200m−
nên
200, 199,...., 16m − − −
.
Suy ra có tất cả
185
số thỏa yêu cầu.
Câu 11: Gọi tập
X
là tập hợp tất cả các số nguyên
2021;2021m−
sao cho đồ thị của hàm số
( )
32
21y x m x mx m= − + + +
có 5 điểm cực trị. Tính tổng các phần tử của tập
X
.
A.
0
. B.
1−
. C.
4036
. D.
1
.
Lời giải
Chọn D
Đặt
( ) ( )
32
21f x x m x mx m= − + + +
.
Ta có
( )
y f x=
,
( ) ( )
( )
.f x f x
y
fx
=
(
( )
fx
là đa thức bậc 3;
( )
fx
là đa thức bậc 2).
Suy ra hàm số
( )
y f x=
có 5 điểm cực trị
( )
fx
có 3 nghiệm phân biệt và
( )
fx
có 2 nghiệm phân biệt
( )
0fx=
có 3 nghiệm phân biệt
( )
( )
2
1 2 0x x mx m − − − =
có 3 nghiệm phân biệt
2
20x mx m − − =
có 2 nghiệm phân biệt khác
1
2
1
0
0
1 2 0
1
3
m
mm
m
mm
m
−
= +
− −
.
Kết hợp điều kiện
m
nguyên và
2021;2021m−
ta được
2021; 2020;....; 3; 2;1;2;...;2021mX − − − − =
.
Tổng các phần tử của
X
bằng
1
.
Câu 12: Cho hàm số
( )
24 3
3 3 2 3 42y x m x mxm mx + − +=+ −−
. Hỏi có bao nhiêu giá trị
nguyên của tham số
10;10m−
để đồ thị hàm số đã cho có 7 điểm cực trị?
A.
15
. B.
14
. C.
13
. D.
16
.
Lời giải
Chọn B
Đặt
( )
34 2
3 3 2 3(2 4)f x m x mx mx x m= − − ++ +−
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Ta thấy
( ) ( )( )
( )
324 2
3 3 2 3 4 1 12 24) 3(f mx m x mx m x x x xx mxm+ − − + − = + − + + −=+
.
Để đồ thị hàm số
( )
24 3
3 3 2 3 42y x m x mxm mx + − +=+ −−
có 7 điểm cực trị thì đồ thị hàm số
()y f x=
có 3 cực trị và cắt trục hoành tại 4 điểm phân biệt. Vì hàm số
()y f x=
là hàm liên
tục trên nên chỉ cần điều kiện phương trình
( ) 0fx=
có 4 nghiệm phân biệt.
Khi đó phương trình
2
2 4 3 0x mx m+ + − =
có 2 nghiệm
x
phân biệt khác 1 và
1−
0
50
5 5 0
m
m
−
−
2
4
1
3 4 0
55
10;10 \ 4; 3; 2; 1;0;1;5
11
m
m
mm
m
mm
m
mm
−
+ −
= − − − − −
.
Vậy có 14 giá trị nguyên của
m
thỏa mãn.
Câu 13: Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )
( )
22
1 2 1f x x x x mx m
= − + + +
với mọi
x
. Có bao
nhiêu số nguyên
10m −
để hàm số
( )
( )
g x f x=
có
5
điểm cực trị?
A.
6
. B.
7
. C.
9
. D.
8
.
Lời giải
Chọn C
Hàm số
( )
( )
g x f x=
là hàm số chẵn nên
( )
gx
có
5
điểm cực trị khi
( )
fx
có đúng
2
điểm
cực trị dương, hay phương trình
( ) ( )
( )
22
0 1 2 1 0f x x x x mx m
= − + + + =
có đúng
2
nghiệm bội lẻ dương.
Ta có
( )
( )
2
0
01
2 1 0 *
x
f x x
x mx m
=
= =
+ + + =
Xét các trường hợp
+ Trường hợp
( )
*
có
1
nghiệm dương khác
1
và
1
nghiệm bằng
0
, hay
10
1
20
m
m
m
+=
= −
−
.
+ Trường hợp
( )
*
có hai nghiệm trái dấu, trong đó nghiệm dương khác
1
, hay
2
1 2 1 0
1
3
10
1
mm
m
m
m
m
+ + +
−
−
+
−
.
Vậy với
1m −
thì
( )
gx
có
5
điểm cực trị.
Vì
10m −
nên
9; 8;...; 1m − − −
, có
9
giá trị.
Câu 14: Cho hàm số
2
( ) 4 3y f x x x mx= = − + +
. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để
hàm số
()y f x=
có đúng ba điểm cực trị.
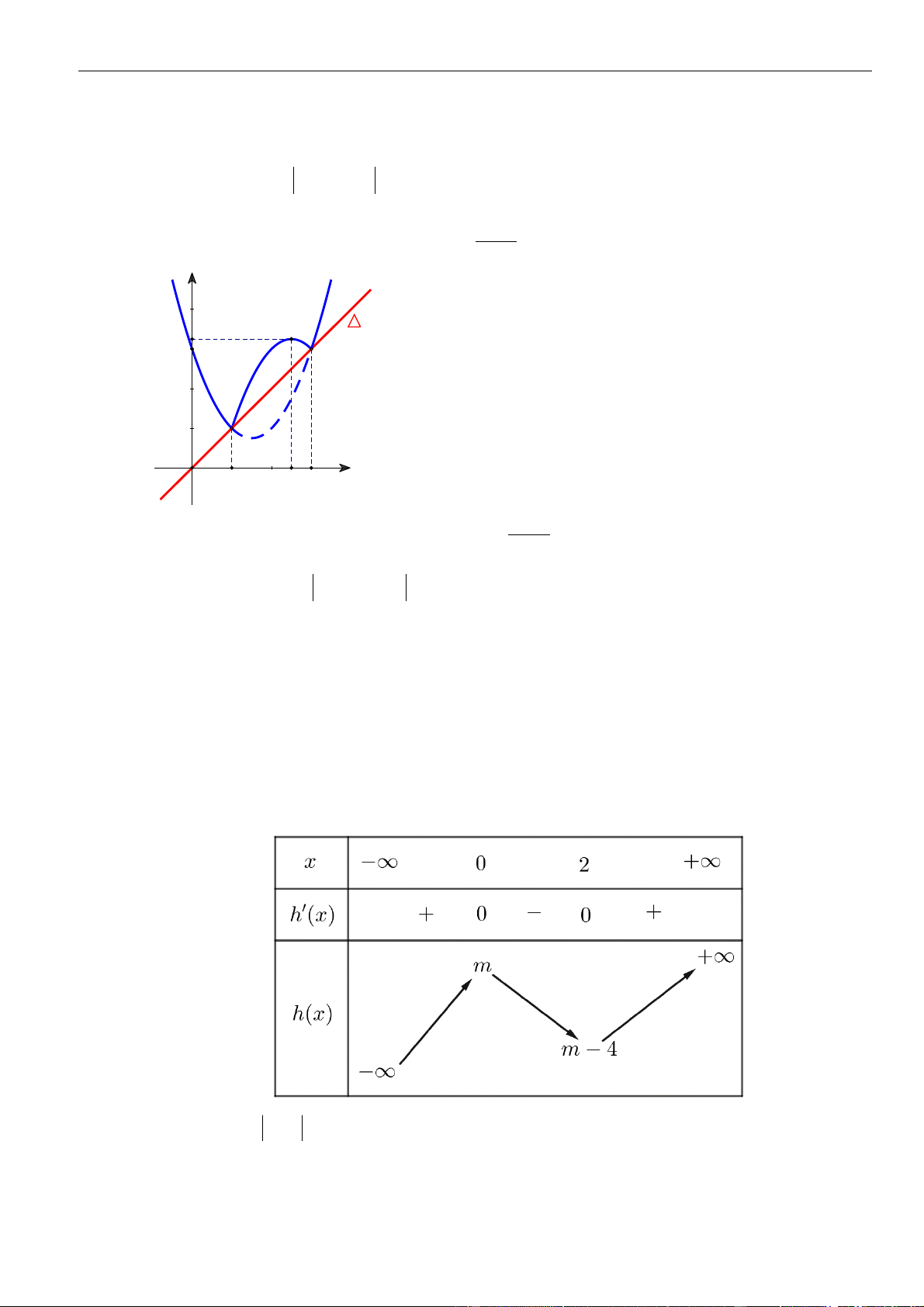
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
A.
2
. B.
3
. C.
4
. D.
6
.
Lời giải
Chọn B.
Ta có:
( ) (
)
( ) ( )
2
2
2
4 3 , ;1 3;
( ) 4 3
4 3 , 1;3
x m x x
y f x x x mx
x m x x
+ − + − +
= = − + + =
− + + −
Ta có đồ thị, đường thẳng
: y mx=
,
0
4
2
m
x
+
=
Từ đồ thị ta có hàm số có 3 điểm cực trị
4
1 3 2 2 1;0 ;1
2
m
mm
+
− −
.
Câu 15: Cho hàm số
( )
32
3= − +f x x x m
với
4;4−m
là tham số. Có bao nhiêu giá trị nguyên của
m
để hàm số
( )
fx
có đúng 3 điểm cực trị?
A.
5
. B.
8
. C.
4
. D.
6
.
Lời giải
GVSB: Quách Đăng Thăng; GVPB: Hải Hạnh Trần
Chọn D
Xét hàm số
( ) ( ) ( )
2 223
0
3 3 6 0 3 6 0
2
=
= − + = − = − =
=
x
h x x x m h x x x h x x x
x
.
Bảng biến thiên
Ta có
( ) ( )
=fx hx
nên để hàm số
( )
fx
có đúng 3 điểm cực trị thì hàm số
( )
hx
có hai điểm
cực trị
12
,xx
thoả mãn
( ) ( )
12
.0h x h x
.
x
y
y
0
x
0
3
3
(
C
)
O
1
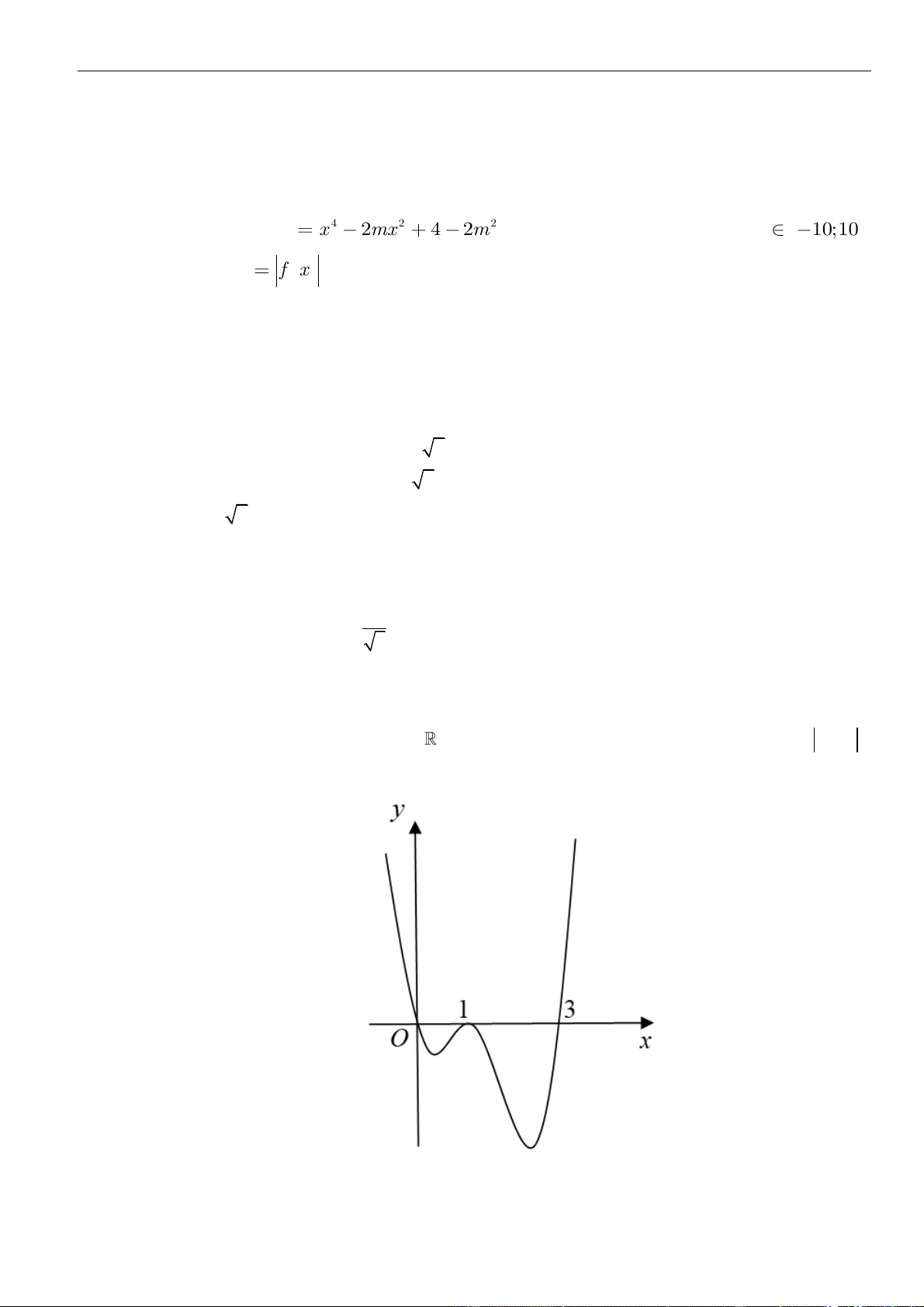
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Từ bảng biến thiên suy ra
4 0 4
00
mm
mm
−
.
Mà
4;4−m
và
m
là số nguyên nên
4; 3; 2; 1;0;4m − − − −
.
Vậy có 6 giá trị nguyên của tham số
4;4−m
thoả mãn hàm số
( )
fx
có đúng 3 điểm cực trị.
Câu 16: Cho hàm số
4 2 2
2 4 2f x x mx m
. Có tất cả bao nhiêu số nguyên
10;10m
để hàm số
y f x
có đúng
3
điểm cực trị?
A.
9
. B.
8
. C.
7
. D.
6
.
Lời giải
Chọn A
TH1:
( )
C
có một điểm cực trị và tung độ điểm cực trị nhỏ hơn
0
( )
2
0
20
2
0 4 2 0
2
2
9; 8; 7; 6; 5; 4; 3; 2
m
m
m
fm
m
m
m
−
−
= −
−
− − − − − − − −
TH2:
( )
C
có ba điểm cực trị và tung độ điểm cực tiểu lớn hơn
0
2
20
2
0
4 3 0
3
1
m
m
m
m
−
−
=
Vậy: có
9
giá trị
m
nguyên thỏa ycbt
Câu 17: Cho hàm số
( )
y f x=
liên tục trên có đồ thị như hình vẽ. Đồ thị của hàm số
( ) ( )
2
g x f x=
có bao nhiêu điểm cực đại, bao nhiêu điểm cực tiểu?
A.
2
điểm cực đại, 3 điểm cực tiểu. B.
3
điểm cực đại, 2 điểm cực tiểu.
C.
1
điểm cực đại, 3 điểm cực tiểu. D.
2
điểm cực đại, 2 điểm cực tiểu.
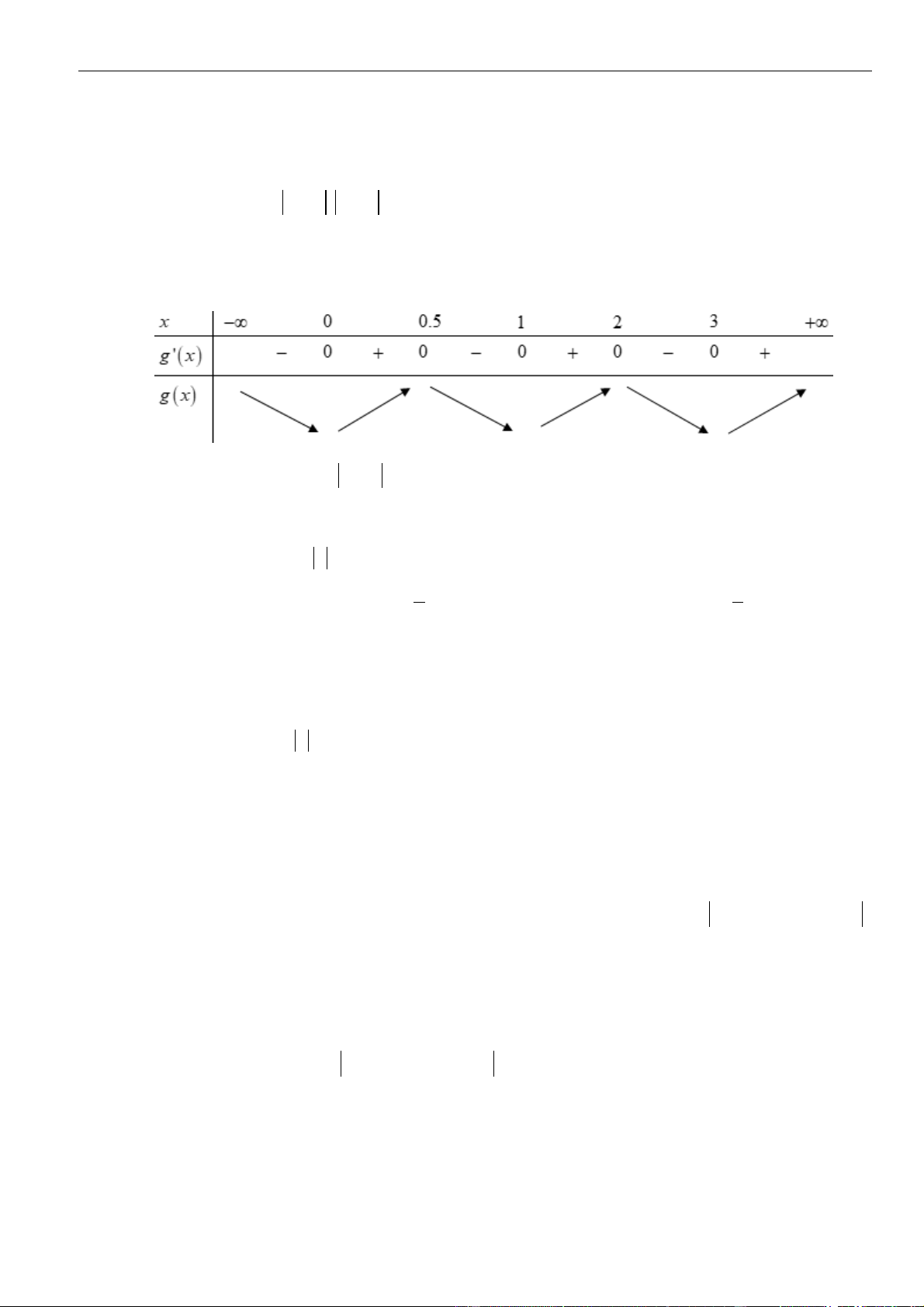
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn A
Ta có:
( ) ( ) ( ) ( )
0
0.5
' 2 ' ; ' 0 1
2
3
x
x
g x f x f x g x x
x
x
=
=
= = =
=
=
.
Ta có bảng biến thiên
Vậy của hàm số
( ) ( )
2
g x f x=
có 2 điểm cực đại, 3 điểm cực tiểu.
Câu 18: Cho hàm số
( ) ( ) ( )
32
2 1 3 2y f x x m x m x= = − + + − +
. Tìm tất cả các giá trị của tham số thực
m
để hàm số
( )
y f x=
có 3 điểm cực trị.
A.
3m
. B.
1
2
m −
. C.
3m
. D.
1
3
2
m−
.
Lời giải
Chọn C
Ta có
( ) ( )
2
3 2 2 1 3y f x x m x m
= = − + + −
;
( ) ( )
2
0 3 2 2 1 3 0f x x m x m
= − + + − =
( )
1
Để hàm số
( )
y f x=
có 3 điểm cực trị thì đồ thị hàm số
( )
y f x=
có đúng 1 cực trị nằm bên
phải trục tung
( )
1
có 1 nghiệm dương
( )
1
có 2 nghiệm
12
,xx
thỏa mãn
12
0 xx=
hoặc
12
0xx
30
3
2 1 0
30
m
m
m
m
− =
+
−
.
Câu 19: Tìm số các giá trị nguyên của tham số
( )
2021;2021m −
để hàm số
42
4 2020y x x m= − + +
có 7 điểm cực trị.
A.
2020
. B.
1
. C.
5
. D.
3
.
Lời giải
Chọn D
Nhận xét: Hàm số
42
4 2020y x x m= − + +
có 7 điểm cực trị khi và chỉ khi đồ thị hàm số
( )
42
4 2020f x x x m= − + +
có ba điểm cực trị nằm về hai phía của trục
Ox
.
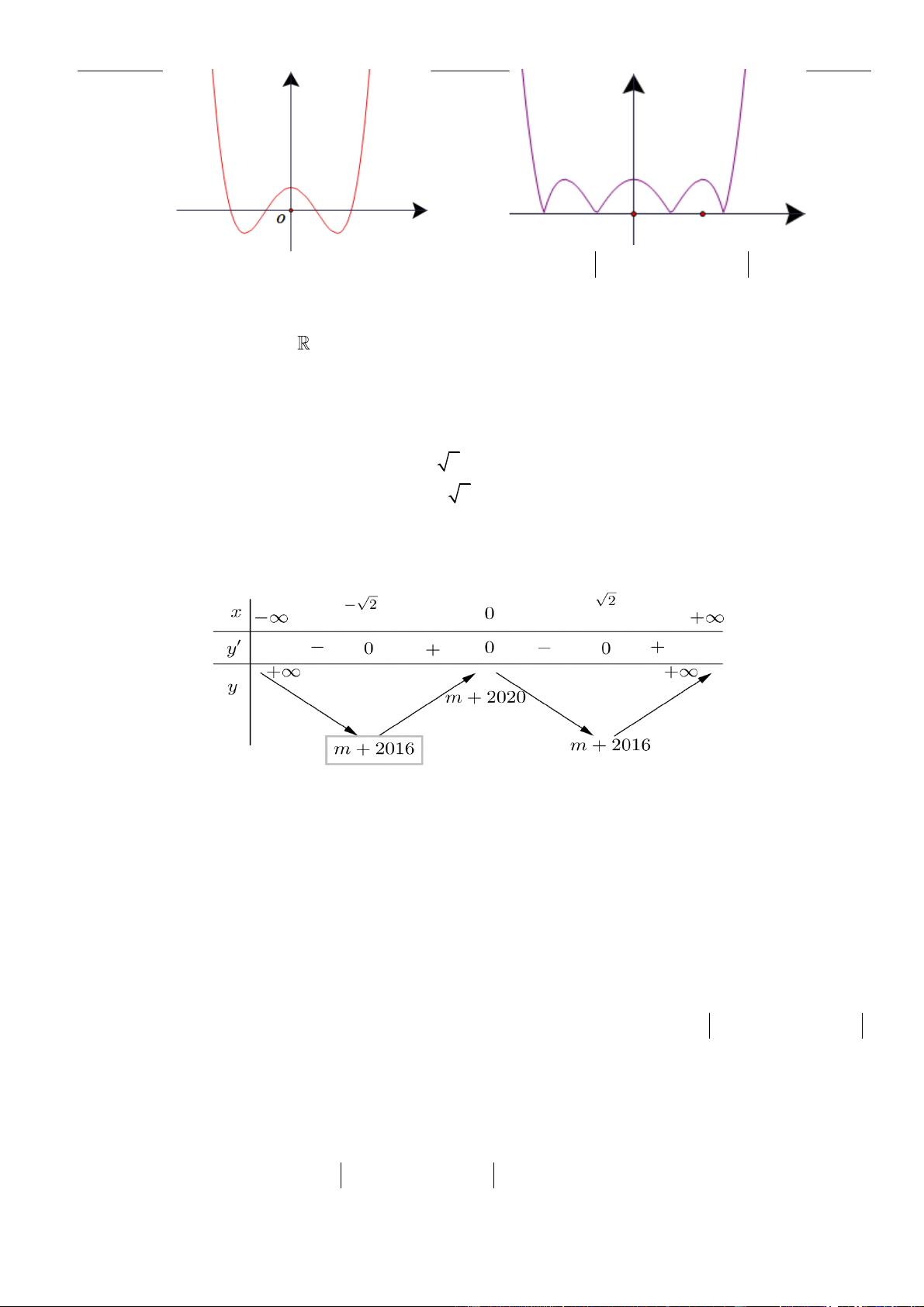
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Đồ thị
42
4 2020y x x m= − + +
Đồ thị
42
4 2020y x x m= − + +
Xét hàm số
( )
42
4 2020f x x x m= − + +
Tập xác định:
D =
.
Ta có
( )
( )
32
4 8 4 2f x x x x x
= − = −
.
( )
( )
2
0
0 4 2 0 2
2
x
f x x x x
x
=
= − = =
=−
.
Bảng biến thiên
Đồ thị hàm số
( )
42
4 2020f x x x m= − + +
có ba điểm cực trị nằm về hai phía của trục
Ox
2020 0 2020
2016 0 2016
mm
mm
+ −
+ −
.
Vậy có 3 giá trị nguyên của
m
thỏa mãn yêu cầu là:
2019
2018
2017
m
m
m
=−
=−
=−
.
Câu 20: Tìm số các giá trị nguyên của tham số
( )
2021;2021m −
để hàm số
42
4 2020y x x m= − + +
có 7 điểm cực trị.
A.
2020
. B.
1
. C.
5
. D.
3
.
Lời giải
Chọn D
Nhận xét: Hàm số
42
4 2020y x x m= − + +
có 7 điểm cực trị khi và chỉ khi đồ thị hàm số
( )
42
4 2020f x x x m= − + +
có ba điểm cực trị nằm về hai phía của trục
Ox
.
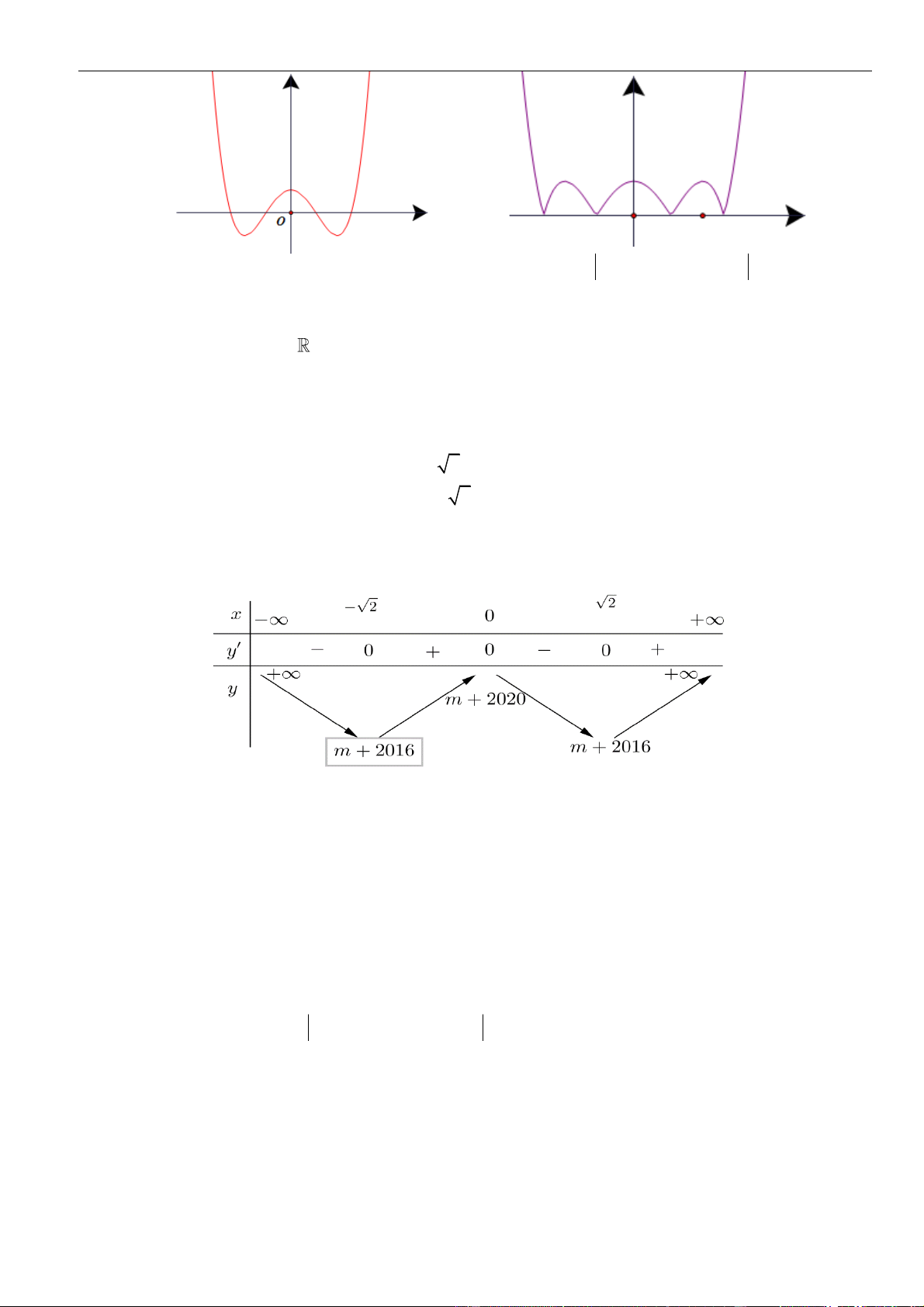
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Đồ thị
42
4 2020y x x m= − + +
Đồ thị
42
4 2020y x x m= − + +
Xét hàm số
( )
42
4 2020f x x x m= − + +
Tập xác định:
D =
.
Ta có
( )
( )
32
4 8 4 2f x x x x x
= − = −
.
( )
( )
2
0
0 4 2 0 2
2
x
f x x x x
x
=
= − = =
=−
.
Bảng biến thiên
Đồ thị hàm số
( )
42
4 2020f x x x m= − + +
có ba điểm cực trị nằm về hai phía của trục
Ox
2020 0 2020
2016 0 2016
mm
mm
+ −
+ −
.
Vậy có 3 giá trị nguyên của
m
thỏa mãn yêu cầu là:
2019
2018
2017
m
m
m
=−
=−
=−
.
Câu 21: Cho hàm số
( )
4 3 2
2 8 16 1f x x x x m= − − + −
(m là tham số). Biết rằng khi m thay đổi thì số điểm
cực trị của hàm số có thể là a hoặc b hoặc C. Giá trị
abc++
bằng
A. 12. B. 16. C. 15. D. 13.
Lời giải
GVSB: Trần Xuân Thiện; GVPB: Nguyễn Minh Luận
Chọn C
Xét hàm số
( )
4 3 2
2 8 16 1g x x x x m= − − + −
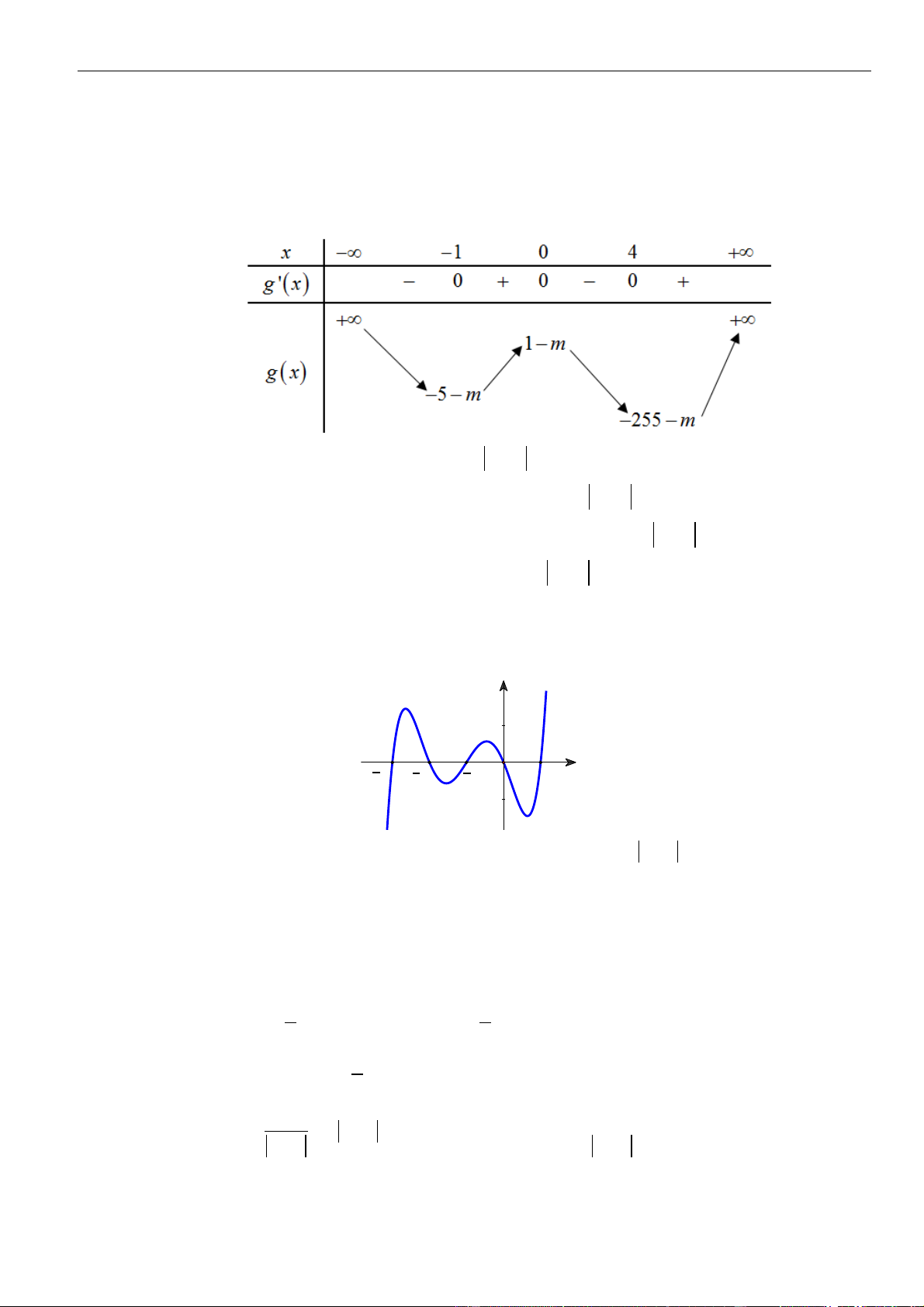
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Ta có:
( )
32
' 8 24 32g x x x x= − −
.
( )
0
' 0 1
4
x
g x x
x
=
= = −
=
.
Bảng biến thiên của hàm số
( )
y g x=
:
Trường hợp 1:
( ) ( )
1 0 1m m f x g x− =
có 5 cực trị.
Trường hợp 2:
( ) ( )
5 0 1 5 1m m m f x g x− − − − =
có 7 cực trị.
Trường hợp 3:
( ) ( )
255 0 5 255 5m m m f x g x− − − − − − =
có 5 cực trị.
Trường hợp 4:
( ) ( )
0 255 255m m f x g x − − − =
có 3 cực trị.
Vậy
15abc+ + =
.
Câu 22: Cho hàm đa thức
( )
2
2y f x x
=+
có đồ thị như hình vẽ.
Tổng giá trị nguyên của
10;10m−
để hàm số
( )
( )
2y g x f x m= = − +
có 5 điểm cực trị là
A.
52−
. B.
55
. C.
55−
. D.
56
.
Lời giải
Chọn C
Ta có:
( )
( )
( )
( )( )( ) ( ) ( )
22
2 2 2 2 3 2 1 1 0f x x x f x x a x x x x x a
+ = + + = + + + −
( )
( )( ) ( )
( )( )
2 2 2
2 3 2 1 2 3 2
22
aa
f x x x x x x x x x x
+ = + + − = + − +
Đặt
( ) ( )
2
23
2
a
t x x f t t t
= + = −
.
Ta có
( )
( )
2
20
2
x
g x f x m
x
−
= − + =
−
,
( )
( )
2
0
20
x
gx
f x m
=
=
− + =
x
y
1
2
3
O
1
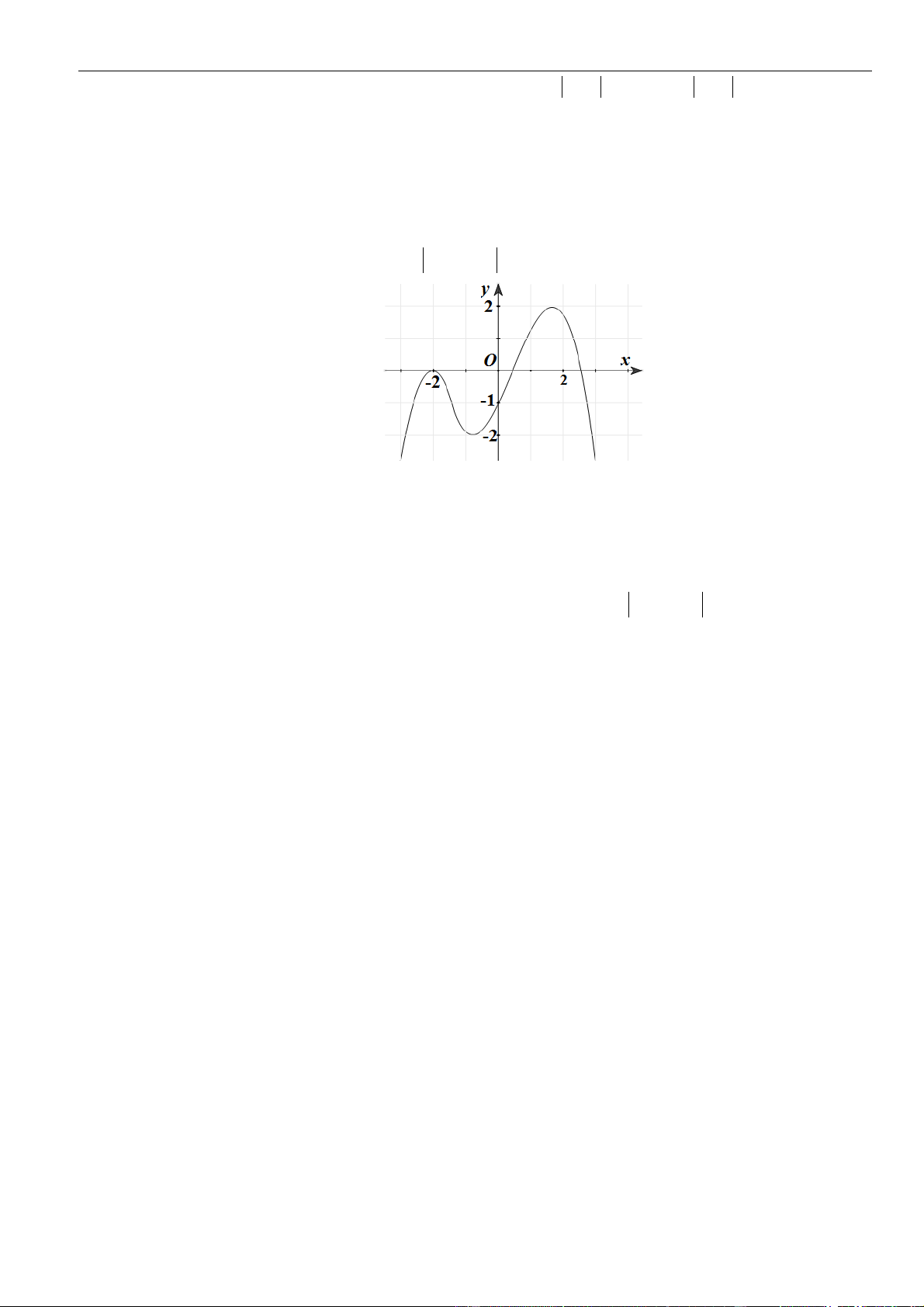
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Để hàm số
( )
y g x=
có 5 cực trị thì các phương trình
20xm− + =
và
23xm− + =
phải có 4
nghiệm phân biệt khác
2
00
0
3 0 3
mm
m
mm
−
−
.
Suy ra
10; 9;...; 1m − − −
. Tổng giá trị
m
nguyên là
55−
.
Câu 23: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ dưới. Tìm số các giá trị nguyên của tham số
m
thuộc
10; 10−
để hàm số
( ) ( )
g x f x m=−
có 3 điểm cực trị?
.
A.
4
. B.
5
. C.
9
. D.
8
.
Lời giải
Số cực trị của hàm số
( )
gx
bằng tổng số cực trị của hàm
( )
y f x m=−
và số nghiệm đơn hoặc
nghiệm bội lẻ của phương trình
( )
f x m=
.
Hàm số
( )
y f x m=−
có 3 điểm cực trị. Do đó hàm số
( ) ( )
g x f x m=−
có 3 điểm cực trị khi
và chỉ khi phương trình
( )
f x m=
vô nghiệm hoặc có nghiệm bội chẵn
2m
.
Kết hợp điều kiện ta có
2;3;4;5;6;7;8;9;10m
. Vậy có
9
giá trị của
m
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Giá trị lớn nhất của hàm số
( )
3
32f x x x=−+
trên đoạn
1;3−
bằng
A.
4
. B.
2
. C.
20
. D.
16
.
Câu 2: Giá trị nhỏ nhất của hàm số
( )
3
2
x
fx
x
−
=
+
trên đoạn
0;4
bằng:
A.
( )
0f
. B.
( )
4f
. C.
( )
2f
. D.
( )
3f
.
Câu 3: Giá trị lớn nhất của hàm số
3
( ) 48f x x x= − +
trên đoạn
7;5−
bằng
A.
127
. B.
128
. C.
115
. D.
7
.
Câu 4: Giá trị nhỏ nhất của hàm số
( )
3
3=−f x x x
trên đoạn
2;1−
bằng
A.
2
. B.
2−
. C.
3
. D.
3−
.
Câu 5: Giá trị nhỏ nhất của hàm số
2
8
yx
x
=+
trên đoạn
1
;2
2
bằng
A.
8
. B.
15
2
. C.
65
4
. D.
3
62
.
Câu 6: Giá trị lớn nhất của hàm số
( )
3
62f x x x= − + −
trên đoạn
0;2
bằng
A.
6 2 2−
. B.
4 2 2−
. C.
2
. D.
3
.
Câu 7: Giá trị nhỏ nhất của hàm số
3
34y x x= − +
trên đoạn
0;2
là
A.
0;2
min 0y =
. B.
0;2
min 2y =
. C.
0;2
min 1y =
. D.
0;2
min 4y =
.
Câu 8: Giá trị nhỏ nhất của hàm số
43yx=−
trên đoạn
0;1
bằng
A.
2
. B.
1
. C.
0
. D.
4
.
Câu 9: Giá trị lớn nhất của hàm số
42
21y x x= − + +
trên đoạn
2;5−
bằng
A.
1−
. B.
7−
. C.
5
. D.
2
.
Câu 10: Tìm giá trị nhỏ nhất m của hàm số
42
13y x x= − +
trên đoạn
[ 2;3].−
Giá trị lớn nhất, giá trị nhỏ nhất trên khoảng, đoạn
DẠNG 1
Phương pháp:
• Bước 1: Hàm số đã cho
( )
y f x=
xác định và liên tục trên đoạn
;.ab
Tìm các điểm
12
, ,...,
n
x x x
trên khoảng
( )
;ab
, tại đó
( )
0fx
=
hoặc
( )
fx
không xác định.
• Bước 2: Tính
( ) ( ) ( )
( )
( )
12
, , ,..., , .
n
f a f x f x f x f b
• Bước 3: Khi đó:
( ) ( ) ( )
( )
( ) ( )
12
,
max max , ,..., , , .
n
ab
f x f x f x f x f a f b=
( ) ( ) ( )
( )
( ) ( )
12
,
min min , ,..., , , .
n
ab
f x f x f x f x f a f b=
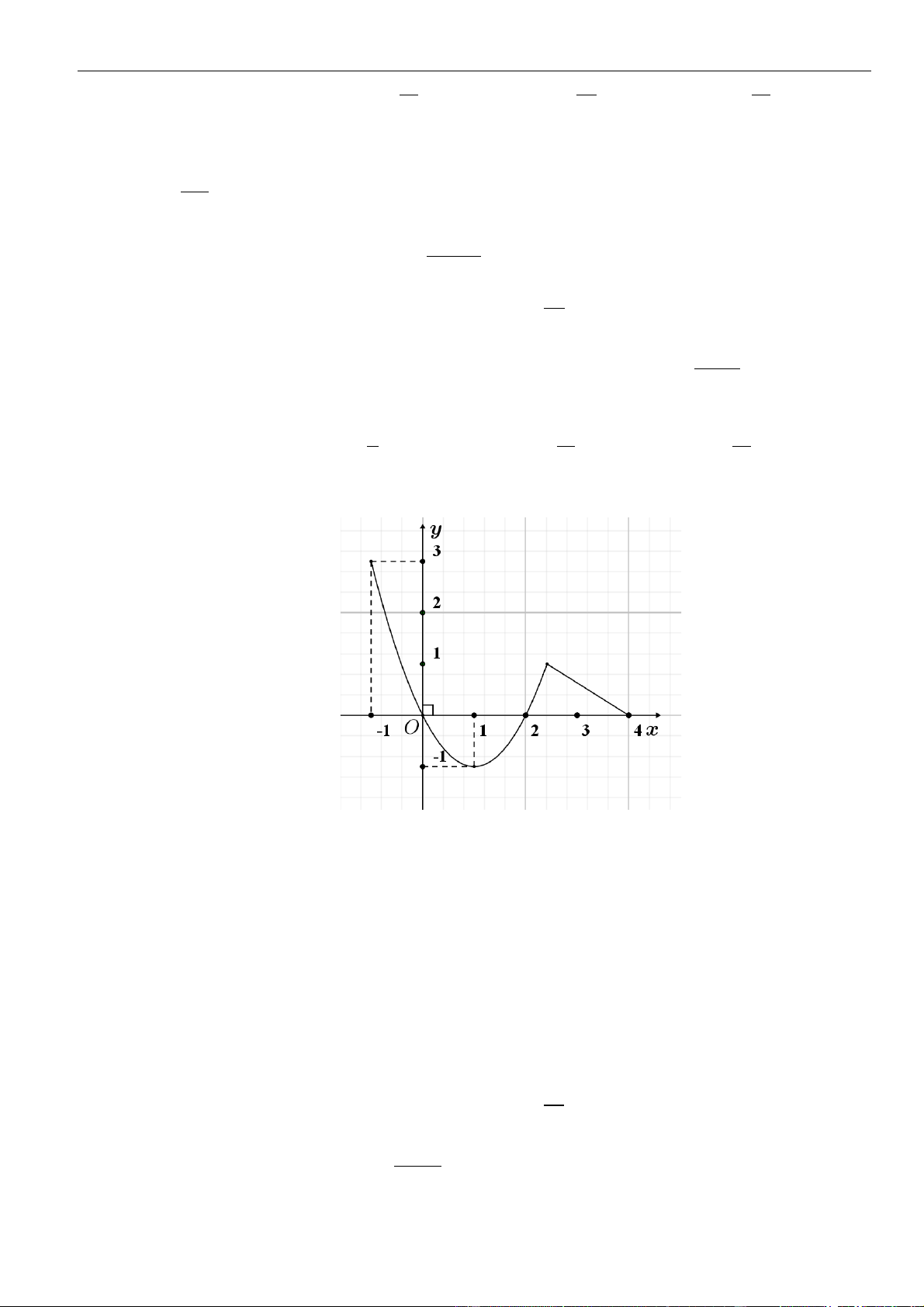
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
13.m =
B.
51
.
2
m =
C.
49
.
4
m =
D.
51
.
4
m =
Câu 11: Giá trị lớn nhất của hàm số
32
2 7 3y x x x= + − −
trên đoạn
1;2−
bằng
A.
311
27
. B.
7−
. C.
1−
. D.
5
.
Câu 12: Giá trị nhỏ nhất của hàm số
( )
2
3
1
xx
fx
x
−
=
+
trên đoạn
0;2
bằng
A.
0
. B.
9−
. C.
2
3
−
. D.
1−
.
Câu 13: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
23
2
x
y
x
+
=
−
trên đoạn
0;1
.
Tổng
Mm+
bằng
A.
2−
. B.
7
2
. C.
13
2
−
. D.
17
3
−
.
Câu 14: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;4−
và có đồ thị như hình vẽ dưới đây
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;4−
. Giá trị
Mm+
bằng
A.
2
. B.
0
. C.
1
. D.
5
.
Câu 15: Tìm giá trị nhỏ nhất của
32
7 11 2y x x x= − + −
trên
0;2
.
A.
2−
. B.
0
. C.
11
. D.
3
.
Câu 16: Cho hàm số
3
57y x x= + +
, giá trị lớn nhất của hàm số trên đoạn
[ 5;0]−
bằng bao nhiêu?
A.
7
. B.
5
. C.
80
. D.
143−
.
Câu 17: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3y x x=−
trên
1;2
bằng:
A.
0
. B.
2
. C.
14
27
. D.
7−
.
Câu 18: Giá trị lớn nhất của hàm số
3
2
x
y
x
−+
=
−
trên đoạn
2;0−
bằng

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
4
. B.
3
2
−
. C.
5
4
−
. D.
3
.
Câu 19: Giá trị lớn nhất của hàm số
2
2
yx
x
=+
trên đoạn
1
;2
2
bằng
A.
5
. B.
17
4
. C.
3
. D.
10
.
Câu 20: Giá trị nhỏ nhất của hàm số
3
35= − +y x x
trên đoạn
2;4
là
A.
2;4
min 5=y
. B.
2;4
min 0=y
. C.
2;4
min 3=y
. D.
2;4
min 7=y
.
Câu 21: Gọi
M
và
n
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
3
32y x x= − +
trên
0;2
. Khi
đó tổng
Mn+
bằng:
A.
6
. B.
2
. C.
4
. D.
16
.
Câu 22: Gọi
,MN
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
31y x x= − +
trên
0;2
. Khi đó
MN+
bằng
A.
3
. B.
4
. C.
6
. D.
2
.
Câu 23: Gọi giá trị nhỏ nhất của hàm số
1
1
x
y
x
−
=
+
trên đoạn
0;3
là
m
. Khi đó, khẳng định nào sau đây
đúng?
A.
1
2
m =
. B.
3m =−
. C.
1m =
. D.
1m =−
.
Câu 24: Giá trị lớn nhất của hàm số
2
2
yx
x
=+
trên đoạn
1
;2
2
bằng
A.
5
. B.
17
4
. C.
3
. D.
10
.
Câu 25: Giá trị nhỏ nhất của hàm số
32
3y x x=+
trên đoạn
5; 1−−
bằng
A.
0
. B.
4
. C.
2
. D.
50−
.
Câu 26: Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( ) 4= + −f x x x
lần lượt là
M
và
m
. Giá
trị của biểu thức
22
=−T M m
A.
2
. B.
4
. C.
0
. D.
3
.
Câu 27: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
31y x x x= + + −
trên đoạn
1;2−
lần lượt là:
A.
136
21;
125
−
. B.
6
21;
9
−
. C.
6
19;
9
−
. D.
46
21;
9
−
.
Câu 28: Cho hàm số
32
32y x x= − +
. Giả sử giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
1;3−
lần lượt là
,Mm
thì
Mm−
bằng
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 29: Giá trị nhỏ nhất của hàm số
2
4xx
y
x
++
=
trên đoạn
3; 1−−
bằng
A.
4−
. B.
5−
. C.
3−
. D.
5
.
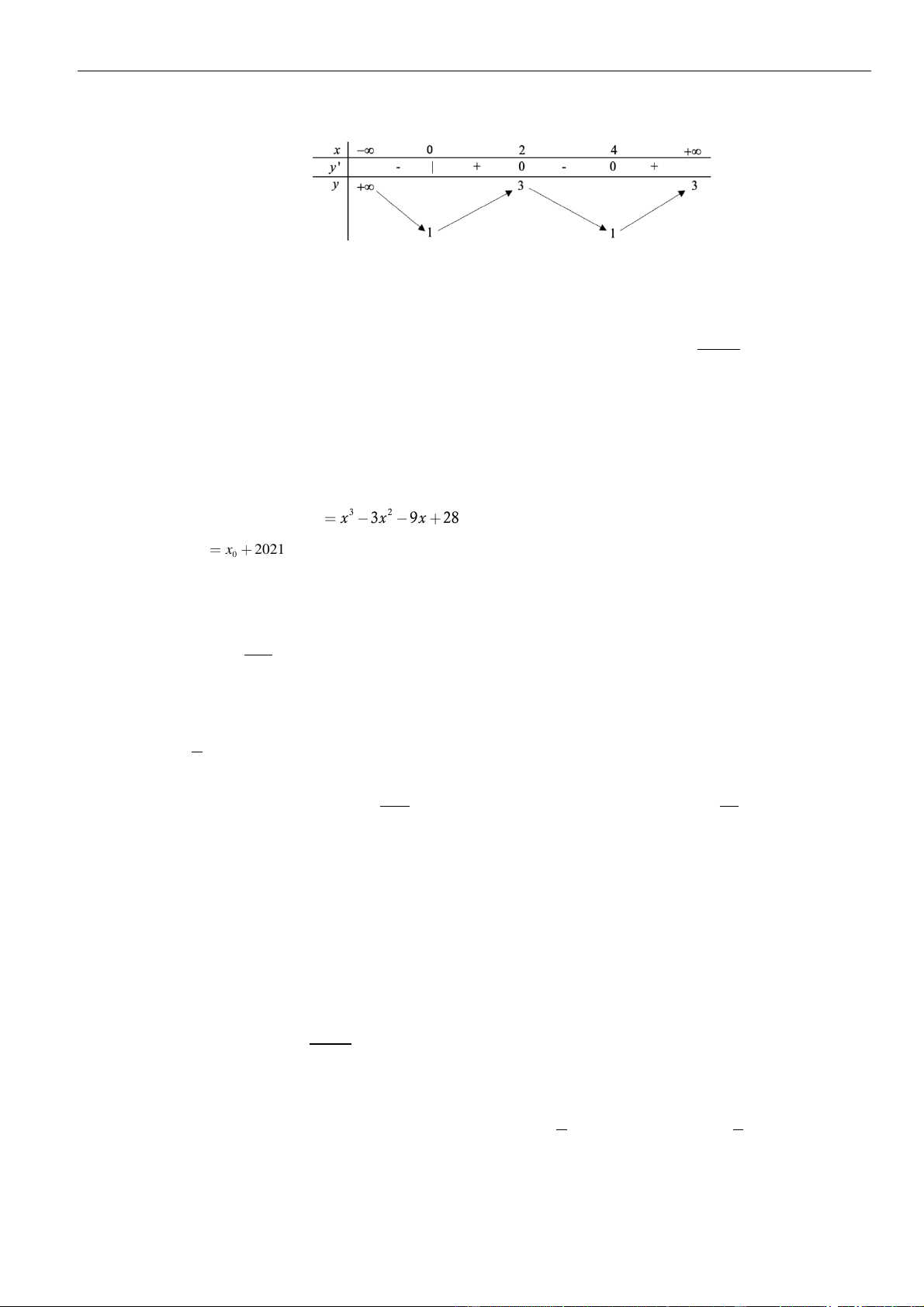
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 30: Cho hàm số
( )
y f x=
xác định và liên tục trên khoảng
( )
;− +
có bảng biến thiên như hình
sau
Giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;5
A. 2. B. 4. C. 3. D. 1.
Câu 31: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
21
2
x
fx
x
−
=
+
trên đoạn
0;2
. Tổng
24mM+
bằng
A.
7
. B.
5
. C.
4
. D.
2
.
Câu 32: Giá trị lớn nhất của hàm số
32
33y x x= − +
trên
0;3
là
A.
3
. B.
1−
. C.
2−
. D.
2
.
Câu 33: Biết rằng hàm số
32
3 9 28f x x x x
đạt giá trị nhỏ nhất trên đoạn
0;4
tại
0
.x
Tính
0
2021Px
A.
3
. B.
2021
. C.
2018
. D.
2024
.
Câu 34: Tìm giá trị lớn nhất của hàm số
32
8y x x x= − −
trên đoạn
[1;3]
.
A.
[1;3]
176
max
27
y =
. B.
[1;3]
max 8y =−
. C.
[1;3]
max 6y =−
. D.
[1;3]
max 4y =−
.
Câu 35: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
33f x x x= − +
trên đoạn
3
3;
2
−
. Tích
.Mm
bằng:
A.
5
. B.
225
8
−
. C.
75−
. D.
75
8
.
Câu 36: Tìm giá trị lớn nhất
M
của hàm số
32
2 3 12 2y x x x= + − +
trên đoạn
1;2 .−
A.
10M =
. B.
6M =
. C.
11M =
. D.
15M =
.
Câu 37: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
12f x x x=−
trên
đoạn
0;3
. Giá trị
Mm−
bằng
A.
32
. B.
4
. C.
16
. D.
64
.
Câu 38: Cho hàm số
( )
31
1
x
fx
x
−
=
+
. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
0;2
. Khi đó
2Mm+
bằng
A.
2
. B.
0
. C.
2
3
−
. D.
1
3
−
.
Câu 39: Cho hàm số
( )
3
31y f x x x− += −=
có đồ thị như hình vẽ. Giá trị nhỏ nhất của hàm số đã cho
trên đoạn
0;2
là bao nhiêu?

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
1−
. B.
3−
. C.
1
. D.
2
.
Câu 40: Giá trị nhỏ nhất của hàm số
( )
3
31f x x x= + +
trên đoạn
1;3
là
A.
5
. B.
37
. C.
3
. D.
6
.
Câu 41: Giá trị lớn nhất của hàm số
42
45y x x= − +
trên đoạn
1;2−
là
A.
3
. B.
5.
C.
2.
D.
1.
Câu 42: Giá trị nhỏ nhất của hàm số
32
3y x x=−
trên đoạn
1;5
bằng
A.
4−
. B.
50
. C.
2−
. D.
45
.
Câu 43: Giá trị nhỏ nhất của hàm số
42
( ) 10 2f x x x= − −
trên đoạn
0;9
bằng
A.
2−
. B.
11−
. C.
26−
. D.
27−
.
Câu 44: Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
31y x x= − + −
trên đoạn
[ 3;1]−
. Tổng
Mm+
bằng
A.
0
. B.
52
. C.
3−
. D.
54
.
Câu 45: Giá trị nhỏ nhất của hàm số
32
3y x x=+
trên đoạn
5; 1−−
bằng
A.
0
. B.
4
. C.
2
. D.
50−
.
Câu 46: Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( ) 4= + −f x x x
lần lượt là
M
và
m
. Giá
trị của biểu thức
22
=−T M m
A.
2
. B.
4
. C.
0
. D.
3
.
Câu 47: Gọi
m
là giá trị nhỏ nhất của hàm số
31
2
x
y
x
+
=
−
trên
1;1−
. Khi đó giá trị của
m
là
A.
2
3
m =−
. B.
4m =
. C.
4m =−
. D.
2
3
m =
.
Câu 48: Gọi
m
và
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
1
2
2
y x x= − +
trên
đoạn
1;34−
. Tổng
3S m M=+
bằng.
A.
13
2
S =
. B.
25
2
S =
. C.
63
2
S =
. D.
11
2
S =
.
Câu 49: Giá trị nhỏ nhất của hàm số
42
21y x x= + −
trên
1;1−
bằng
A.
2
. B.
1−
. C.
0
. D.
1
.
Câu 50: Giá trị lớn nhất của hàm số
32
2 7 3y x x x= + − −
trên đoạn
1;2−
bằng

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
A.
311
27
. B.
7−
. C.
1−
. D.
5
.
Câu 51: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
3
34f x x x= − +
trên đoạn
0;2
. Tổng
Mm+
bằng?
A.
8
. B.
12
. C.
6
. D.
10
.
Câu 52: Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
32
5 3 2y x x x= − + +
trên đoạn
0;2
. Tổng
Mm+
bằng
A.
122
27
−
. B.
2−
. C.
41
27
−
. D.
4−
.
Câu 53: Tính giá trị nhỏ nhất của hàm số
2
4
21
xx
y
x
−
=
+
trên đoạn
0;3
.
A.
0;3
min 0y =
. B.
0;3
7
min
3
y =−
. C.
0;3
min 4y =−
. D.
0;3
min 1.y =−
Câu 54: Tìm giá trị nhỏ nhất của hàm số
32
3 9 5y x x x= − − +
trên đoạn
2;2−
.
A.
1−
. B.
17−
. C.
22−
. D.
3
.
Câu 55: Tìm giá trị lớn nhất của hàm số
32
8y x x x= − −
trên đoạn
[1;3]
.
A.
[1;3]
176
max
27
y =
. B.
[1;3]
max 8y =−
. C.
[1;3]
max 6y =−
. D.
[1;3]
max 4y =−
.
Câu 56: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
33f x x x= − +
trên đoạn
3
3;
2
−
. Tích
.Mm
bằng:
A.
5
. B.
225
8
−
. C.
75−
. D.
75
8
.
Câu 57: Tìm giá trị lớn nhất
M
của hàm số
32
2 3 12 2y x x x= + − +
trên đoạn
1;2 .−
A.
10M =
. B.
6M =
. C.
11M =
. D.
15M =
.
Câu 58: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
12f x x x=−
trên
đoạn
0;3
. Giá trị
Mm−
bằng
A.
32
. B.
4
. C.
16
. D.
64
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Giá trị lớn nhất của hàm số
( )
3
32f x x x=−+
trên đoạn
1;3−
bằng
A.
4
. B.
2
. C.
20
. D.
16
.
Lời giải
Chọn C
Ta có
( )
2
33f x x
=−
( )
1 1;3
0
1 1;3
x
fx
x
= −
=
= − −
.
Do
( )
14f −=
;
( )
10f =
;
( )
3 20f =
nên
( )
1;3 .
20 3max f x x
−
= =
.
Câu 2: Giá trị nhỏ nhất của hàm số
( )
3
2
x
fx
x
−
=
+
trên đoạn
0;4
bằng:
A.
( )
0f
. B.
( )
4f
. C.
( )
2f
. D.
( )
3f
.
Lời giải
Chọn A
Ta có
( )
( )
2
5
'0
2
fx
x
=
+
,
0;4x
nên hàm số đồng biến trên
0;4
Do đó
( ) ( )
0;4
min 0
x
f x f
=
.
Câu 3: Giá trị lớn nhất của hàm số
3
( ) 48f x x x= − +
trên đoạn
7;5−
bằng
A.
127
. B.
128
. C.
115
. D.
7
.
Lời giải
Chọn B
Ta có:
2
( ) 3 48f x x
= − +
3
0
( ) 0 48 0 4
4
x
f x x x x
x
=
= − + = =
=−
(0) 0f=
,
( 4) 128f − = −
,
(4) 128f =
,
(5) 115f =
,
( 7) 7f −=
7;5
max ( ) 128fx
−
=
.
Câu 4: Giá trị nhỏ nhất của hàm số
( )
3
3=−f x x x
trên đoạn
2;1−
bằng
A.
2
. B.
2−
. C.
3
. D.
3−
.
Lời giải
Chọn B
Xét hàm số
( )
3
3f x x x=−
xác định trên .
Có
( )
2
33f x x
=−
;
( )
( )
1
0
1 2;1
x
fx
x
=−
=
= −
.
Ta có:
( ) ( ) ( )
1 2; 1 2; 1 2f f f− = − − = = −
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Nên giá trị nhỏ nhất của hàm số trên đoạn
2;1−
bằng
2−
, đạt được tại
1x =
hoặc
1x =−
.
Câu 5: Giá trị nhỏ nhất của hàm số
2
8
yx
x
=+
trên đoạn
1
;2
2
bằng
A.
8
. B.
15
2
. C.
65
4
. D.
3
62
.
Lời giải
Chọn D
Ta có
( )
2
8
y f x x
x
= = +
3
22
8 2 8
2
x
yx
xx
−
= − =
. Có
3
3
0 4 4y x x
= = =
.
Có
1 65
24
f
=
,
( )
28f =
,
( )
33
4 6 2f =
. Vậy
( )
3
1
;2
2
min 6 2fx
=
.
Câu 6: Giá trị lớn nhất của hàm số
( )
3
62f x x x= − + −
trên đoạn
0;2
bằng
A.
6 2 2−
. B.
4 2 2−
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
( )
2
36f x x
= − +
. Cho
( )
( )
( )
2
2 0;2
0 3 6 0
2 0;2
x
f x x
x
=
= − + =
= −
.
Khi đó
( )
02f =−
,
( )
2 2 4 2f = − +
và
( )
22f =
.
Vậy
( )
0;2
max 2 4 2 2yf= = −
.
Câu 7: Giá trị nhỏ nhất của hàm số
3
34y x x= − +
trên đoạn
0;2
là
A.
0;2
min 0y =
. B.
0;2
min 2y =
. C.
0;2
min 1y =
. D.
0;2
min 4y =
.
Lời giải
Chọn B
( )
22
3 3 3 1y x x
= − = −
;
10yx
==
.
( )
04y =
,
( )
12y =
,
( )
26y =
. Vậy
0;2
min 2y =
.
Câu 8: Giá trị nhỏ nhất của hàm số
43yx=−
trên đoạn
0;1
bằng
A.
2
. B.
1
. C.
0
. D.
4
.
Lời giải
Chọn B
TXĐ:
4
;
3
D
= −
Ta có
3
0
2 4 3
y
x
−
=
−
,
4
3
x
Trên đoạn
0;1
hàm số
43yx=−
nghịch biến
( )
0;1
min 1 1yy = =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Câu 9: Giá trị lớn nhất của hàm số
42
21y x x= − + +
trên đoạn
2;5−
bằng
A.
1−
. B.
7−
. C.
5
. D.
2
.
Lời giải
Chọn D
Ta có
( )
( )
( )
3
0
4 4 0 1
1
xn
y x x y x n
xn
=
= − + = = −
=
.
Khi đó
( )
25y − = −
,
( ) ( )
1 1 2yy− = =
,
( )
01y =
và
( )
5 574y =−
.
Vậy
( ) ( )
2;5
max 1 1 2y y y
−
= = − =
.
Câu 10: Tìm giá trị nhỏ nhất m của hàm số
42
13y x x= − +
trên đoạn
[ 2;3].−
A.
13.m =
B.
51
.
2
m =
C.
49
.
4
m =
D.
51
.
4
m =
Lời giải
Chọn D
Hàm số liên tục trên
[ 2;3].−
3
0
' 4 2 0
1
2
x
y x x
x
=
= − =
=
+)
(0) 13y =
+)
1 51
4
2
y
=
+)
( 2) 25y −=
+)
(3) 85.y =
Vậy giá trị nhỏ nhất của hàm số
51
.
4
m =
.
Câu 11: Giá trị lớn nhất của hàm số
32
2 7 3y x x x= + − −
trên đoạn
1;2−
bằng
A.
311
27
. B.
7−
. C.
1−
. D.
5
.
Lời giải
Chọn D
Ta có
2
3 4 7y x x
= + −
.
Giải
1 1;2
0
7
1;2
3
x
y
x
= −
=
= − −
.
Tính
( ) ( ) ( )
1 7, 2 1, 1 5y y y= − = − − =
.
Suy ra
( )
1;2
max 1 5yy
−
= − =
.
Câu 12: Giá trị nhỏ nhất của hàm số
( )
2
3
1
xx
fx
x
−
=
+
trên đoạn
0;2
bằng
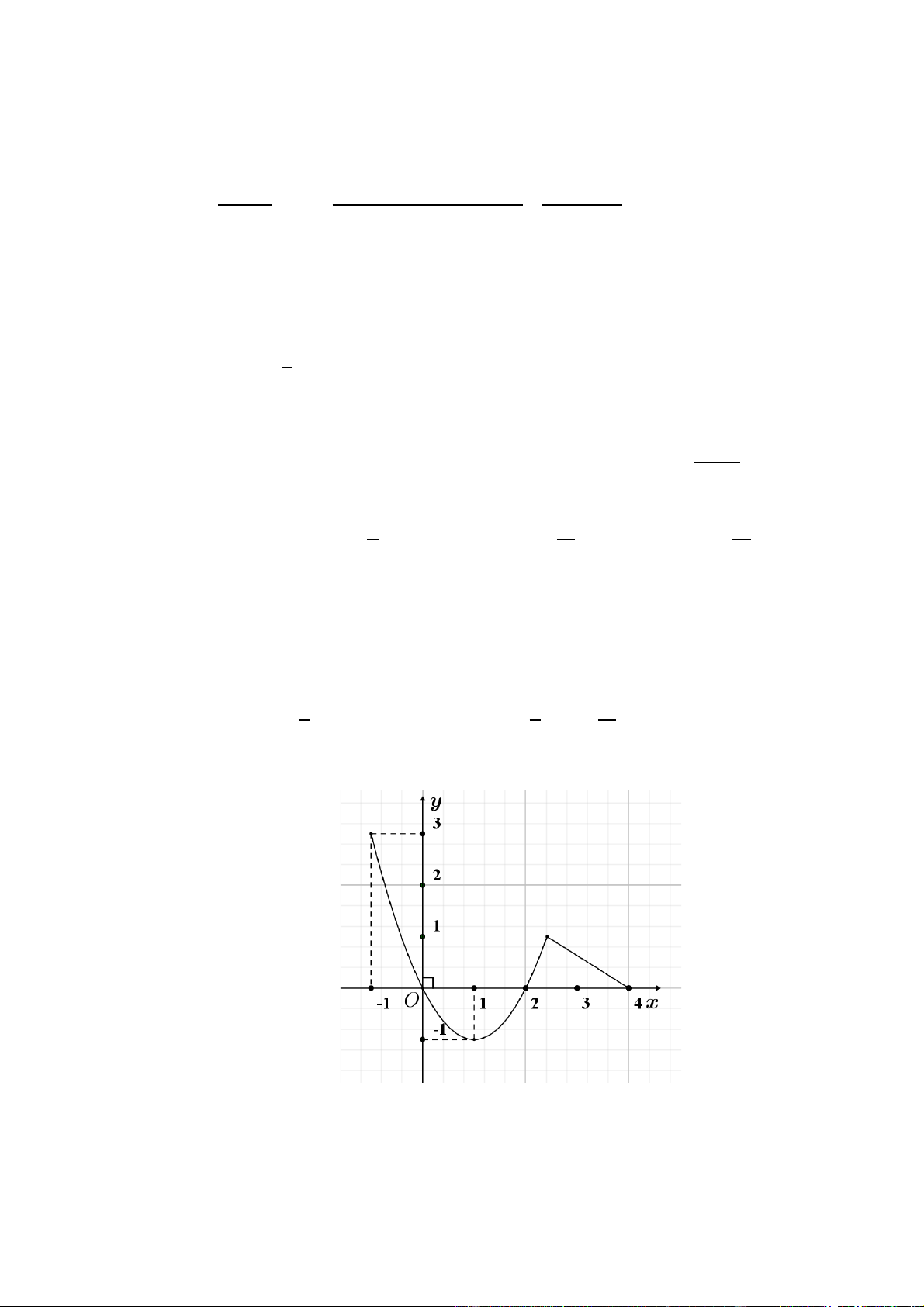
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
A.
0
. B.
9−
. C.
2
3
−
. D.
1−
.
Lời giải
Chọn D
Đặt
( )( )
( )
( ) ( )
2
22
22
2 3 1 3
3 2 3
1
11
x x x x
x x x x
yy
x
xx
− + − −
− + −
= = =
+
++
.
1 0;2
0
3 0;2
x
y
x
=
=
= −
.
Ta có
( )
( )
( )
( )
0;2
00
2
2 min 1 1
3
11
y
y y y
y
=
= − = = −
=−
Câu 13: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
23
2
x
y
x
+
=
−
trên đoạn
0;1
.
Tổng
Mm+
bằng
A.
2−
. B.
7
2
. C.
13
2
−
. D.
17
3
−
.
Lời giải
Chọn C
Ta có
( )
2
7
0
2
y
x
= −
−
trên
0;1
.
Vậy
( ) ( )
3 3 13
0 , 1 5 5
2 2 2
M y m y M m= = − = = − + = − − = −
.
Câu 14: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;4−
và có đồ thị như hình vẽ dưới đây
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;4−
. Giá trị
Mm+
bằng
A.
2
. B.
0
. C.
1
. D.
5
.
Lời giải
Chọn A

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Từ đồ thị hàm số
( )
y f x=
liên tục trên đoạn
1;4−
suy ra
3; 1Mm= = −
.
Vậy
( )
3 1 2Mm+ = + − =
.
Câu 15: Tìm giá trị nhỏ nhất của
32
7 11 2y x x x= − + −
trên
0;2
.
A.
2−
. B.
0
. C.
11
. D.
3
.
Lời giải
Chọn A
Ta có
2
' 3 14 11 0y x x= − + =
1
11
3
x
x
=
=
( )
02f =−
;
( )
13f =
;
( )
20f =
.
Vậy
( )
0;2
min 2fx=−
.
Câu 16: Cho hàm số
3
57y x x= + +
, giá trị lớn nhất của hàm số trên đoạn
[ 5;0]−
bằng bao nhiêu?
A.
7
. B.
5
. C.
80
. D.
143−
.
Lời giải
Chọn A
Hàm số xác định và liên tục trên
[ 5;0]−
.
2
35yx
=+
.
0, 5;0yx
−
Hàm số đồng biến trên
[ 5;0]−
.
Vậy
( )
5;0
max 0 7yy
−
==
.
Câu 17: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3y x x=−
trên
1;2
bằng:
A.
0
. B.
2
. C.
14
27
. D.
7−
.
Lời giải
Chọn A
2
1 1;2
' 3 3 0
1 1;2
x
yx
x
=
= − =
= −
( )
( )
12
22
y
y
=−
=
1;2
1;2
max 2
min 2
y
y
=
=−
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3y x x=−
trên
1;2
bằng 0.
Câu 18: Giá trị lớn nhất của hàm số
3
2
x
y
x
−+
=
−
trên đoạn
2;0−
bằng
A.
4
. B.
3
2
−
. C.
5
4
−
. D.
3
.
Lời giải
Chọn C

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Tập xác định:
\2D =
Ta có :
( )
2
1
0, 2
2
yx
x
−
=
−
.
Hàm số đã cho nghịch biến trên trên đoạn
2;0−
.
Do đó:
( )
( )
2;0
23
5
max 2
2 2 4
yy
−
− − +
= − = = −
−−
.
Câu 19: Giá trị lớn nhất của hàm số
2
2
yx
x
=+
trên đoạn
1
;2
2
bằng
A.
5
. B.
17
4
. C.
3
. D.
10
.
Lời giải
Chọn A
Ta có:
2
2
2yx
x
=−
.
2
21
0 2 0 1 ;2
2
y x x
x
= − = =
.
Suy ra:
1 17
24
f
=
,
( )
13f =
,
( )
25f =
Vậy
( )
1
;2
2
max 2 5yf
==
.
Câu 20: Giá trị nhỏ nhất của hàm số
3
35= − +y x x
trên đoạn
2;4
là
A.
2;4
min 5=y
. B.
2;4
min 0=y
. C.
2;4
min 3=y
. D.
2;4
min 7=y
.
Lời giải
Chọn D
Hàm số đã cho liên tục trên tập số thực, và
2
33
=−yx
, suy ra
0 1 2;4= = yx
.
Ta có
( )
27=y
và
( )
4 57=y
nên
2;4
min 7=y
.
Câu 21: Gọi
M
và
n
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
3
32y x x= − +
trên
0;2
. Khi
đó tổng
Mn+
bằng:
A.
6
. B.
2
. C.
4
. D.
16
.
Lời giải
Chọn C
Cách 1.
Ta có:
2
1 0;2
3 3 0
1 0;2
x
y x y
x
=
= − =
= −
( ) ( ) ( )
0 2; 1 0; 2 4y y y= = =
4, 0Mn = =
Khi đó
4 0 4Mn+ = + =
Cách 2. Dùng máy tính tính giá trị lớn nhất và nhỏ nhất của hàm số
Câu 22: Gọi
,MN
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
31y x x= − +
trên
0;2
. Khi đó
MN+
bằng

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
A.
3
. B.
4
. C.
6
. D.
2
.
Lời giải
Chọn D
Ta có
2
1 0;2
3 3 0
1 0;2
x
yx
x
=
= − =
= −
.
( ) ( ) ( )
0 1; 2 3; 1 1y y y= = = −
.
( )
( )
0;2 0; 2
3; 1
max min
f x M f x N= = = = −
.
Vậy
2MN+=
.
Câu 23: Gọi giá trị nhỏ nhất của hàm số
1
1
x
y
x
−
=
+
trên đoạn
0;3
là
m
. Khi đó, khẳng định nào sau đây
đúng?
A.
1
2
m =
. B.
3m =−
. C.
1m =
. D.
1m =−
.
Lời giải
Chọn D
Ta có: TXĐ:
\1D =−
.
( )
2
2
0,
1
y x D
x
=
+
.
Và
( ) ( )
1
0 1; 3
2
yy= − =
.
Vậy
0;3
min 1
x
ym
= − =
.
Câu 24: Giá trị lớn nhất của hàm số
2
2
yx
x
=+
trên đoạn
1
;2
2
bằng
A.
5
. B.
17
4
. C.
3
. D.
10
.
Lời giải
Chọn A
Ta có:
2
2
2yx
x
=−
.
2
21
0 2 0 1 ;2
2
y x x
x
= − = =
.
Suy ra:
1 17
24
f
=
,
( )
13f =
,
( )
25f =
Vậy
( )
1
;2
2
max 2 5yf
==
.
Câu 25: Giá trị nhỏ nhất của hàm số
32
3y x x=+
trên đoạn
5; 1−−
bằng
A.
0
. B.
4
. C.
2
. D.
50−
.
Lời giải
Chọn D
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Ta có:
2
' 3 6y x x=+
Cho
2
0 5; 1
' 0 3 6 0
2 5; 1
x
y x x
x
= − −
= + =
= − − −
( ) ( )
( 5) 50; 2 4; 1 2;y y y− = − − = − =
Vậy giá trị nhỏ nhất của hàm số
32
3y x x=+
trên đoạn
5; 1−−
là
50−
Câu 26: Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( ) 4= + −f x x x
lần lượt là
M
và
m
. Giá
trị của biểu thức
22
=−T M m
A.
2
. B.
4
. C.
0
. D.
3
.
Lời giải
Chọn B
Tập xác định
2; 2=−D
2
10
4
= − =
−
x
y
x
2
40 − − =xx
2
4 − =xx
22
0
0
2
4
2
x
x
x
xx
x
=
−=
=
.
( )
22=f
;
( )
22− = −f
;
( )
2 2 2=f
( )
2;2
max ( ) 2 2 2
−
= = =M f x f
,
( )
2;2
min ( ) 2 2
−
= = − = −m f x f
( )
( )
2
2
22
2 2 2 4= − = − − =T M m
Câu 27: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
31y x x x= + + −
trên đoạn
1;2−
lần lượt là:
A.
136
21;
125
−
. B.
6
21;
9
−
. C.
6
19;
9
−
. D.
46
21;
9
−
.
Lời giải
Chọn D
Trên đoạn
1;2−
Ta có
2
3 6 1y x x
= + +
2
36
1;2
3
0 3 6 1 0
36
1;2
3
x
y x x
x
−−
= −
= + + =
−+
= −
( )
1 0;y −=
3 6 4 6
39
y
−+
=−
;
( )
2 21y =
Vậy
( )
1;2
max 2 21yy
−
==
;
1;2
3 6 4 6
min
39
yy
−
−+
= = −
.
Câu 28: Cho hàm số
32
32y x x= − +
. Giả sử giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
1;3−
lần lượt là
,Mm
thì
Mm−
bằng
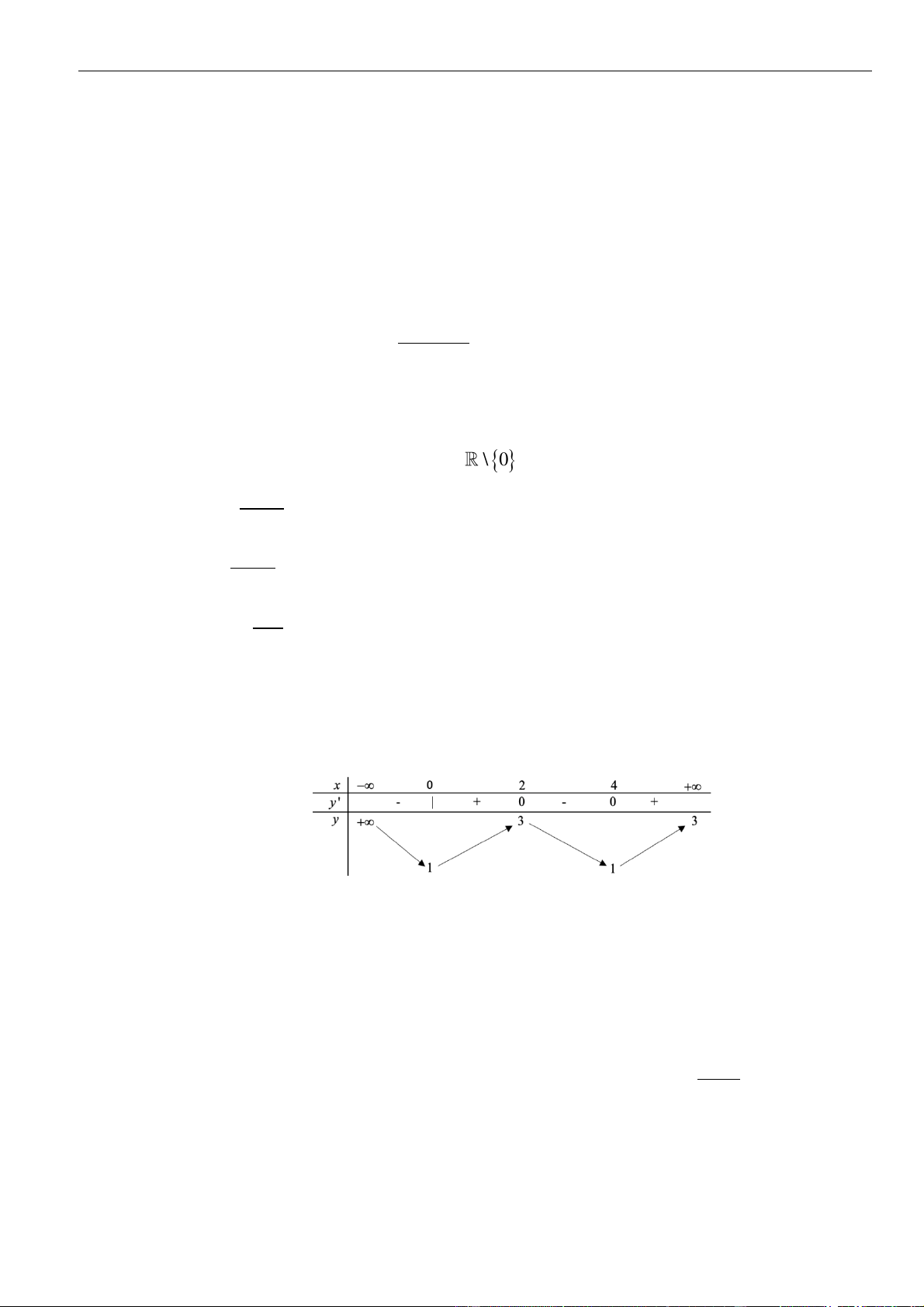
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A
Ta có
3 2 2
3 2 ' 3 6y x x y x x= − + = −
( )
2
0
' 0 3 6 0 3 2 0
2
x
y x x x x
x
=
= − = − =
=
.
( ) ( ) ( ) ( )
1 2; 0 2; 2 2; 3 2f f f f− = − = = − =
.
Vậy
2; 2 4M m M m= = − − =
.
Câu 29: Giá trị nhỏ nhất của hàm số
2
4xx
y
x
++
=
trên đoạn
3; 1−−
bằng
A.
4−
. B.
5−
. C.
3−
. D.
5
.
Lời giải
Chọn A
Hàm số xác định và liên tục trên trên tập
\0
nên xác định và liên tục trên
3; 1−−
.
Ta có
2
2
4
' , 0
x
yx
x
−
=
.
2
2
4
' 0 0
x
y
x
−
= =
.
2
40
0
x
x
−=
2 3; 1
2 3; 1
x
x
= − −
= − − −
.
Mà
( ) ( ) ( )
10
3 ; 1 4; 2 3
3
y y y
−
− = − = − − = −
.
Vậy
( )
3; 1
min 1 4yy
−−
= − = −
.
Câu 30: Cho hàm số
( )
y f x=
xác định và liên tục trên khoảng
( )
;− +
có bảng biến thiên như hình
sau
Giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;5
A. 2. B. 4. C. 3. D. 1.
Lời giải
Chọn C
Dựa vào BBT, giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;5
bằng 3.
Câu 31: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
21
2
x
fx
x
−
=
+
trên đoạn
0;2
. Tổng
24mM+
bằng
A.
7
. B.
5
. C.
4
. D.
2
.
Lời giải
Chọn D

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Ta có:
( )
( )
2
5
0, 2
2
f x x
x
= −
+
nên hàm số đồng biến
0;2
.
( ) ( )
( ) ( )
0;2
0;2
13
min 0 ; max 2
24
m f x f M f x f= = = − = = =
.
Vậy
2 4 2mM+=
.
Câu 32: Giá trị lớn nhất của hàm số
32
33y x x= − +
trên
0;3
là
A.
3
. B.
1−
. C.
2−
. D.
2
.
Lời giải
Chọn A
Hàm số
32
33y x x= − +
xác định và liên tục trên
0;3
.
2
36y x x
=−
,
0
0
2
x
y
x
=
=
=
,
( )
03y =
,
( )
21y =−
,
( )
33y =
.
Vậy giá trị lớn nhất của hàm số trên
0;3
là
3
.
Câu 33: Biết rằng hàm số
32
3 9 28f x x x x
đạt giá trị nhỏ nhất trên đoạn
0;4
tại
0
.x
Tính
0
2021Px
A.
3
. B.
2021
. C.
2018
. D.
2024
.
Lời giải
Chọn D
Ta có:
2
1 0;4
3 6 9 0 .
3 0;4
x
f x x x f x
x
0;4
0 28
3 1 min 1
48
f
f f x
f
khi
0
3 2024.x x P
Câu 34: Tìm giá trị lớn nhất của hàm số
32
8y x x x= − −
trên đoạn
[1;3]
.
A.
[1;3]
176
max
27
y =
. B.
[1;3]
max 8y =−
. C.
[1;3]
max 6y =−
. D.
[1;3]
max 4y =−
.
Lời giải
Chọn C
2
' 3 2 8y x x= − −
. Cho
2
2 (nhan)
' 0 3 2 8 0
4
(loai)
3
x
y x x
x
=
= − − =
=−
.
(1) 8y =−
,
(2) 12y =−
,
(3) 6y =−
.
Vậy
[1;3]
max (3) 6yy= = −
.
Câu 35: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
33f x x x= − +
trên đoạn
3
3;
2
−
. Tích
.Mm
bằng:
A.
5
. B.
225
8
−
. C.
75−
. D.
75
8
.
Lời giải
Chọn C

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Ta có:
( )
2
3
1 3;
2
' 3 3 0
3
1 3;
2
x
f x x
x
= −
= − =
= − −
( ) ( ) ( )
3 15
3 15; 1 5; 1 1;
28
f f f f
− = − − = = =
.
Suy ra:
( ) ( ) ( ) ( )
33
3; 3;
22
1 5, 3 15M Max f x f m Min f x f
−−
= = − = = = − = −
Do đó:
. 75Mm=−
.
Câu 36: Tìm giá trị lớn nhất
M
của hàm số
32
2 3 12 2y x x x= + − +
trên đoạn
1;2 .−
A.
10M =
. B.
6M =
. C.
11M =
. D.
15M =
.
Lời giải
Chọn D
Ta có
( )
22
6 6 12 6 2y x x x x
= + − = + −
1 1;2
0
2 1;2
x
y
x
= −
=
= − −
Ngoài ra
( ) ( ) ( )
1 15; 1 5; 2 6y y y− = = − =
nên
15.M =
Câu 37: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
12f x x x=−
trên
đoạn
0;3
. Giá trị
Mm−
bằng
A.
32
. B.
4
. C.
16
. D.
64
.
Lời giải
Chọn C
Tập xác định:
D =
.
Ta có:
( )
3
12f x x x=−
( )
2
3 12f x x
= −
.
( )
2
2 0;3
0 3 12 0
2 0;3
x
f x x
x
=
= − =
= −
.
Ta có:
( ) ( ) ( )
0 0; 2 16; 3 9f f f= = − = −
.
Khi đó:
0; 16Mm= = −
. Vậy:
( )
0 16 16Mm− = − − =
.
Câu 38: Cho hàm số
( )
31
1
x
fx
x
−
=
+
. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
0;2
. Khi đó
2Mm+
bằng
A.
2
. B.
0
. C.
2
3
−
. D.
1
3
−
.
Lời giải
Chọn D
Xét hàm số
( )
31
1
x
fx
x
−
=
+
.
TXĐ:
\1D =−
; Hàm số liên tục trên đoạn
0;2
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
( )
( )
2
4
0, 1
1
f x x
x
= −
+
;
( ) ( )
5
0 1; 2
3
ff= − =
. Khi đó
5
;1
3
Mm= = −
.
Suy ra
1
2
3
Mm+ = −
.
Câu 39: Cho hàm số
( )
3
31y f x x x− += −=
có đồ thị như hình vẽ. Giá trị nhỏ nhất của hàm số đã cho
trên đoạn
0;2
là bao nhiêu?
A.
1−
. B.
3−
. C.
1
. D.
2
.
Lời giải
Chọn B
Nhìn vào đồ thị hàm số
( )
3
31y f x x x− += −=
ta thấy giá trị nhỏ nhất của hàm số trên đoạn
0;2
là
3−
.
Câu 40: Giá trị nhỏ nhất của hàm số
( )
3
31f x x x= + +
trên đoạn
1;3
là
A.
5
. B.
37
. C.
3
. D.
6
.
Lời giải
Chọn A
Ta có
( ) ( )
32
3 1 3 3 0,f x x x f x x x
= + + = +
. Suy ra hàm số
( )
fx
đồng biến trên
đoạn
1;3
do đó
( ) ( )
1;3
min 1 5
x
f x f
==
Câu 41: Giá trị lớn nhất của hàm số
42
45y x x= − +
trên đoạn
1;2−
là
A.
3
. B.
5.
C.
2.
D.
1.
Lời giải
Chọn B
Ta có:
3
48y x x
=−
0
0
2
x
y
x
=
=
=
( ) ( )
( )
( )
1 2; 0 5; 2 1; 2 5y y y y− = = = =
Do đó giá trị lớn nhất của hàm số trên đoạn
1;2−
là
5
.
Câu 42: Giá trị nhỏ nhất của hàm số
32
3y x x=−
trên đoạn
1;5
bằng
A.
4−
. B.
50
. C.
2−
. D.
45
.
Lời giải
Chọn A

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Ta có trên đoạn
1;5
:
2
36y x x
=−
0 1;5
0
2 1;5
x
y
x
=
=
=
.
( )
12y =−
;
( )
24y =−
;
( )
5 50y =
.
Vậy
( )
1;5
min 2 4yy= = −
.
Câu 43: Giá trị nhỏ nhất của hàm số
42
( ) 10 2f x x x= − −
trên đoạn
0;9
bằng
A.
2−
. B.
11−
. C.
26−
. D.
27−
.
Lời giải
Chọn D
Hàm số
42
( ) 10 2f x x x= − −
xác định và liên tục trên đoạn
0;9
.
Ta có
3
3
'( ) 4 20
0 0;9
'( ) 0 4 20 0 5 0;9
5 0;9
f x x x
x
f x x x x
x
=−
=
= − = =
= −
( )
( )
( )
0 2; 5 27; 9 5749f f f= − = − =
.
So sánh 3 giá trị trên và kết luận
0;9
min ( ) 27
x
fx
=−
.
Câu 44: Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
32
31y x x= − + −
trên đoạn
[ 3;1]−
. Tổng
Mm+
bằng
A.
0
. B.
52
. C.
3−
. D.
54
.
Lời giải
Ta có:
2
36y x x
= − +
.
2
0 [ 3;1]
0 3 6 0
2 [ 3;1]
x
y x x
x
= −
= − + =
= −
.
Khi đó:
( )
3 53y −=
,
( )
01y =−
,
( )
11y =
.
Suy ra
( )
[ 3;1]
3 53M Max y y
−
= = − =
,
( )
[ 3;1]
01m Min y y
−
= = = −
.
Vậy
( )
53 1 52Mm+ = + − =
.
Câu 45: Giá trị nhỏ nhất của hàm số
32
3y x x=+
trên đoạn
5; 1−−
bằng
A.
0
. B.
4
. C.
2
. D.
50−
.
Lời giải
Chọn D
Ta có:
2
' 3 6y x x=+
Cho
2
0 5; 1
' 0 3 6 0
2 5; 1
x
y x x
x
= − −
= + =
= − − −
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
( ) ( )
( 5) 50; 2 4; 1 2;y y y− = − − = − =
Vậy giá trị nhỏ nhất của hàm số
32
3y x x=+
trên đoạn
5; 1−−
là
50−
Câu 46: Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( ) 4= + −f x x x
lần lượt là
M
và
m
. Giá
trị của biểu thức
22
=−T M m
A.
2
. B.
4
. C.
0
. D.
3
.
Lời giải
Chọn B
Tập xác định
2; 2=−D
2
10
4
= − =
−
x
y
x
2
40 − − =xx
2
4 − =xx
22
0
0
2
4
2
x
x
x
xx
x
=
−=
=
.
( )
22=f
;
( )
22− = −f
;
( )
2 2 2=f
( )
2;2
max ( ) 2 2 2
−
= = =M f x f
,
( )
2;2
min ( ) 2 2
−
= = − = −m f x f
( )
( )
2
2
22
2 2 2 4= − = − − =T M m
Câu 47: Gọi
m
là giá trị nhỏ nhất của hàm số
31
2
x
y
x
+
=
−
trên
1;1−
. Khi đó giá trị của
m
là
A.
2
3
m =−
. B.
4m =
. C.
4m =−
. D.
2
3
m =
.
Lời giải
Chọn C
Ta có:
31
2
x
y
x
+
=
−
( )
2
7
0
2
y
x
−
=
−
nên hàm số nghịch biến trên từng khoảng xác định.
Do đó:
( )
1;1
min 1 4m y y
−
= = = −
.
Câu 48: Gọi
m
và
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
1
2
2
y x x= − +
trên
đoạn
1;34−
. Tổng
3S m M=+
bằng.
A.
13
2
S =
. B.
25
2
S =
. C.
63
2
S =
. D.
11
2
S =
.
Lời giải
Chọn A
1 1 2 1
'
2
2 2 2 2
x
y
xx
+−
= − =
++
.
' 0 2 1 1y x x= + = = −
.
( )
3
1
2
f − = −
;
( )
34 11f =
.
3
; 11
2
mM= − =
.
3 9 13
3 11 11
2 2 2
S
−
= − + = + =
.
Câu 49: Giá trị nhỏ nhất của hàm số
42
21y x x= + −
trên
1;1−
bằng
A.
2
. B.
1−
. C.
0
. D.
1
.
Lời giải

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Chọn B
Ta có:
( )
32
' 4 4 0 4 1 0 0y x x x x x= + = + = =
Khi đó
( )
01f =−
,
( )
12f =
,
( )
12f −=
Vậy
( ) ( ) ( )
1;1
min min 0 , 1 , 1 1y f f f
−
= − = −
Câu 50: Giá trị lớn nhất của hàm số
32
2 7 3y x x x= + − −
trên đoạn
1;2−
bằng
A.
311
27
. B.
7−
. C.
1−
. D.
5
.
Lời giải
Chọn D
Ta có
2
1
3 4 7 0
7
3
x
y x x y
x
=
= + − =
=−
vì
1;2 1xx − =
.
Khi đó
( )
15y −=
;
( )
17y =−
và
( )
21y =−
. Vậy
1;2
max 5y
−
=
.
Câu 51: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
3
34f x x x= − +
trên đoạn
0;2
. Tổng
Mm+
bằng?
A.
8
. B.
12
. C.
6
. D.
10
.
Lời giải
Chọn A
Ta có:
( ) ( )
32
1
3 4 3 3 0
1 0;2
x
f x x x f x x
x
=
= − + = − =
= −
( )
( )
( )
( )
( )
0;2
0;2
04
2 6 max
1 2 min
f
f f x M
f f x m
=
= = =
= = =
8Mm + =
.
Câu 52: Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
32
5 3 2y x x x= − + +
trên đoạn
0;2
. Tổng
Mm+
bằng
A.
122
27
−
. B.
2−
. C.
41
27
−
. D.
4−
.
Lời giải
Chọn C
Xét trên đoạn
0;2
( )
( )
2
3 0;2
' 3 10 3; 0
1
0;2
3
x
y x x y
x
=
= − + =
=
( )
02y =
;
( )
24y =−
;
1 67
3 27
y
=
Vậy
( )
67 41
4
27 27
Mn+ = + − = −
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Câu 53: Tính giá trị nhỏ nhất của hàm số
2
4
21
xx
y
x
−
=
+
trên đoạn
0;3
.
A.
0;3
min 0y =
. B.
0;3
7
min
3
y =−
. C.
0;3
min 4y =−
. D.
0;3
min 1.y =−
Lời giải
Chọn D
Hàm số
2
4
21
xx
y
x
−
=
+
liên tục trên đoạn
0;3
( )
2
2
2 2 4
21
xx
y
x
+−
=
+
,
1 0;3
0
2 0;3
x
y
x
=
=
= −
.
Có:
( ) ( ) ( )
3
0 0; 1 1; 3
7
y y y= = − = −
;
( ) ( ) ( )
1 3 0y y y
nên
( )
0;3
min 1 1yy= = −
.
Câu 54: Tìm giá trị nhỏ nhất của hàm số
32
3 9 5y x x x= − − +
trên đoạn
2;2−
.
A.
1−
. B.
17−
. C.
22−
. D.
3
.
Lời giải
Chọn B
Với
2;2x−
, ta có:
2
3 6 9y x x
= − −
;
01yx
= = −
.
Ta có:
( ) ( ) ( )
2 3; 1 10; 2 17y y y− = − = = −
.
Do đó
2;2
min 17y
−
=−
tại
2x =
.
Câu 55: Tìm giá trị lớn nhất của hàm số
32
8y x x x= − −
trên đoạn
[1;3]
.
A.
[1;3]
176
max
27
y =
. B.
[1;3]
max 8y =−
. C.
[1;3]
max 6y =−
. D.
[1;3]
max 4y =−
.
Lời giải
Chọn C
2
' 3 2 8y x x= − −
. Cho
=
= − − =
=−
2
2 (nhaän)
' 0 3 2 8 0
4
(loaïi)
3
x
y x x
x
.
(1) 8y =−
,
(2) 12y =−
,
(3) 6y =−
.
Vậy
[1;3]
max (3) 6yy= = −
.
Câu 56: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
33f x x x= − +
trên đoạn
3
3;
2
−
. Tích
.Mm
bằng:
A.
5
. B.
225
8
−
. C.
75−
. D.
75
8
.
Lời giải
Chọn C

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Ta có:
( )
2
3
1 3;
2
' 3 3 0
3
1 3;
2
x
f x x
x
= −
= − =
= − −
( ) ( ) ( )
3 15
3 15; 1 5; 1 1;
28
f f f f
− = − − = = =
.
Suy ra:
( ) ( ) ( ) ( )
33
3; 3;
22
1 5, 3 15M Max f x f m Min f x f
−−
= = − = = = − = −
Do đó:
. 75Mm=−
.
Câu 57: Tìm giá trị lớn nhất
M
của hàm số
32
2 3 12 2y x x x= + − +
trên đoạn
1;2 .−
A.
10M =
. B.
6M =
. C.
11M =
. D.
15M =
.
Lời giải
Chọn D
Ta có
( )
22
6 6 12 6 2y x x x x
= + − = + −
1 1;2
0
2 1;2
x
y
x
= −
=
= − −
Ngoài ra
( ) ( ) ( )
1 15; 1 5; 2 6y y y− = = − =
nên
15.M =
Câu 58: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
3
12f x x x=−
trên
đoạn
0;3
. Giá trị
Mm−
bằng
A.
32
. B.
4
. C.
16
. D.
64
.
Lời giải
Chọn C
Tập xác định:
D =
.
Ta có:
( )
3
12f x x x=−
( )
2
3 12f x x
= −
.
( )
2
2 0;3
0 3 12 0
2 0;3
x
f x x
x
=
= − =
= −
.
Ta có:
( ) ( ) ( )
0 0; 2 16; 3 9f f f= = − = −
.
Khi đó:
0; 16Mm= = −
. Vậy:
( )
0 16 16Mm− = − − =
.
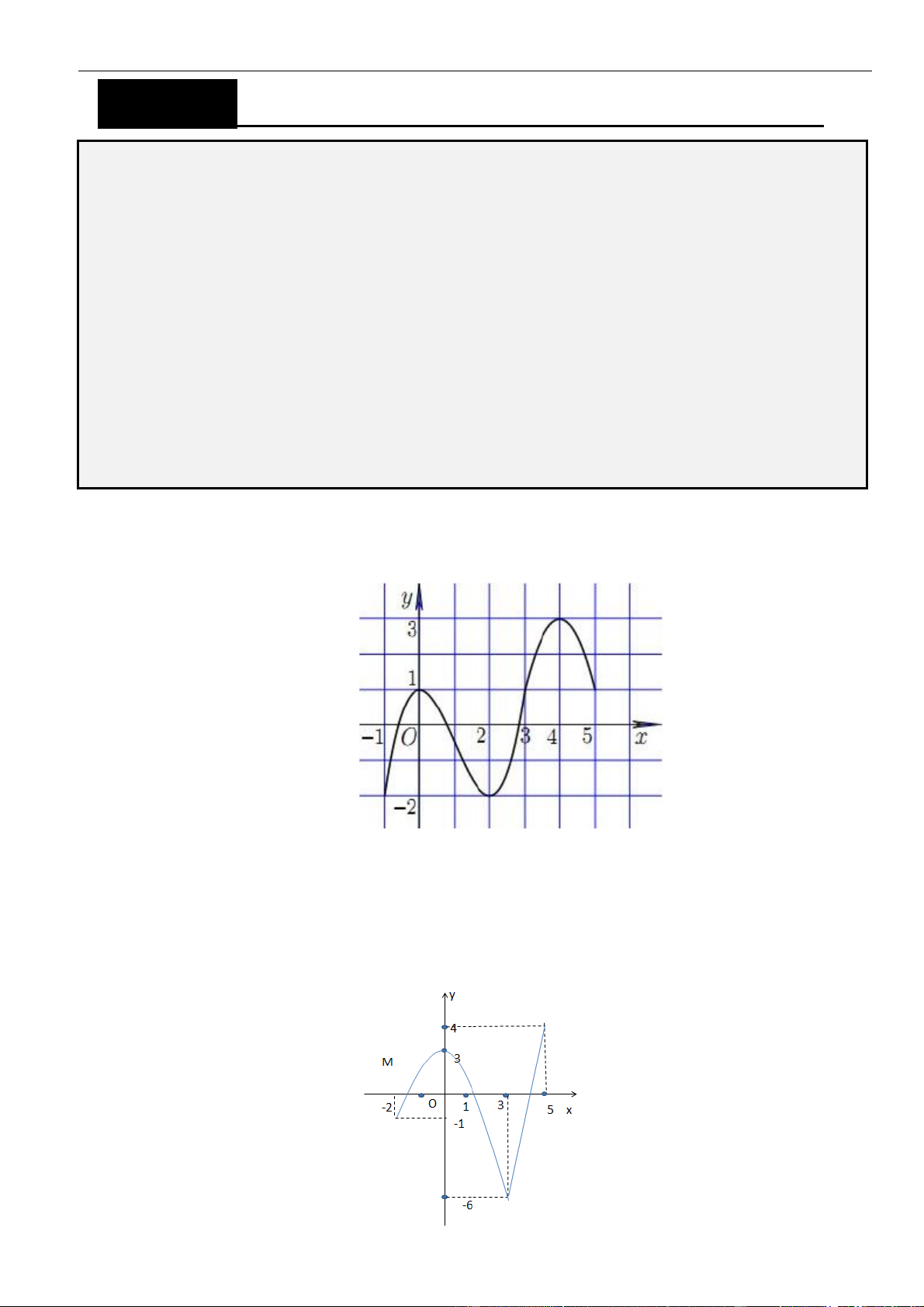
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
( )
fx
liên tục trên đoạn
1;5−
và có đồ thị như hình vẽ sau:
Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;5−
bằng
A. 2. B. 3. C. 5. D. 6.
Câu 2: Cho hàm
( )
y f x=
liên tục trên đoạn
2;5
và có đồ thị như hình vẽ bên. Gọi M và m lần lượt
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
2;5
. Giá trị của
Mm−
bằng
Xác định min-max thông qua đồ thị, bảng biến thiên
DẠNG 2
Phương pháp:
• Giá trị lớn nhất của hàm số
( )
fx
trên đoạn
;ab
Hàm số
( )
fx
liên tục trên đoạn
;ab
và
( )
0, ;
ii
f x x a b
=
. Khi đó giá trị lớn nhất của hàm số
( )
fx
là
( ) ( ) ( )
max , ,
i
M f a f b f x=
• Giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
;ab
Hàm số
( )
fx
liên tục trên đoạn
;ab
và
( )
0, ;
ii
f x x a b
=
. Khi đó giá trị nhỏ nhất của hàm số
( )
fx
là
( ) ( ) ( )
,,
i
m Min f a f b f x=
•
Hàm số
( )
y f x=
đồng biến trên đoạn
;ab
thì
( ) ( )
( ) ( )
;;
;
a b a b
Max f x f b Min f x f a==
• Hàm số
( )
y f x=
nghịch biến trên đoạn
;ab
thì
( ) ( )
( ) ( )
;;
;
a b a b
Max f x f a Min f x f b==
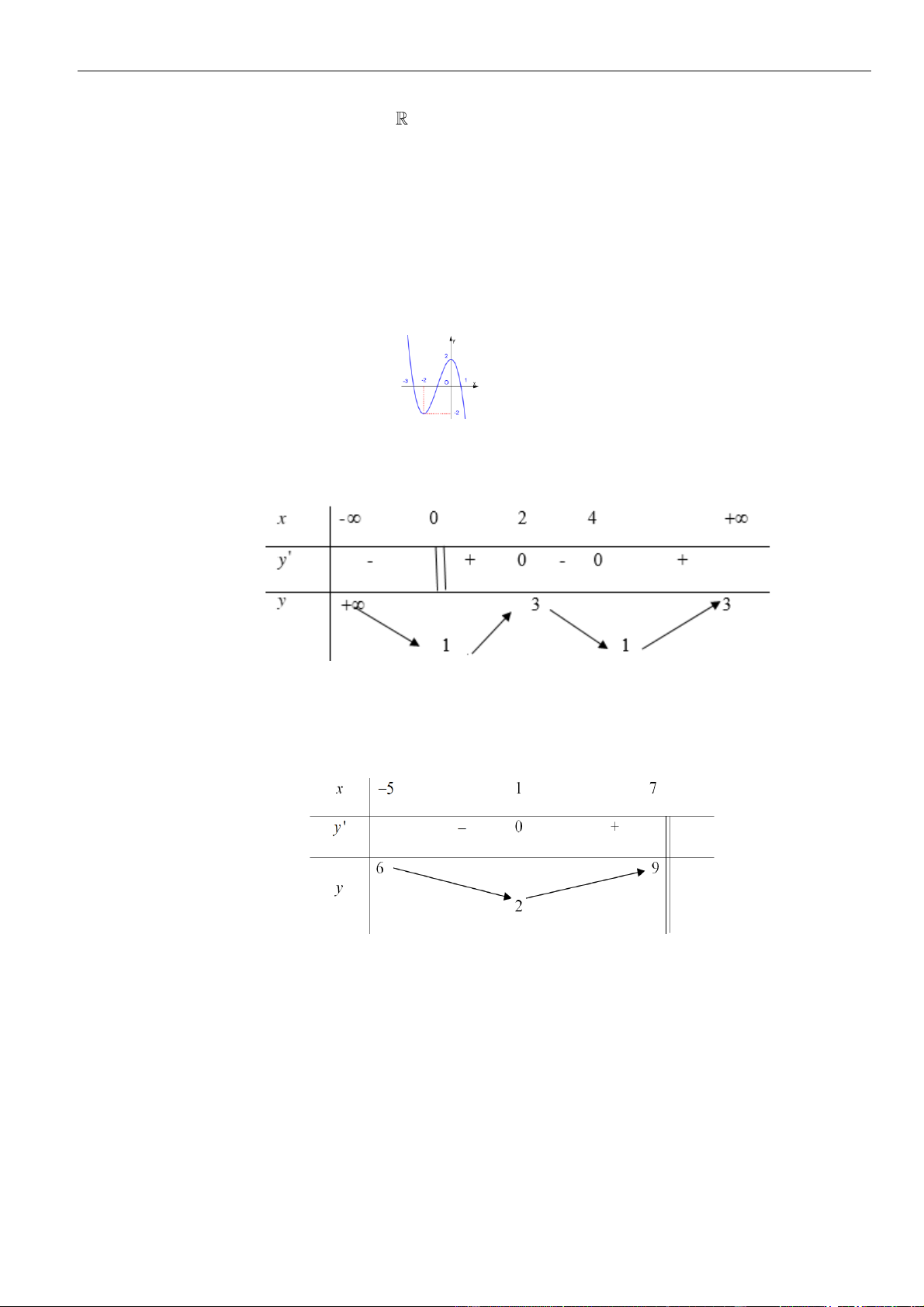
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A. 9. B. 5. C. 10. D. -10.
Câu 3: Cho hàm số
( )
fx
liên tục trên và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số đã
cho trên
2;0−
là:
A.
1−
. B.
0
. C.
2
. D.
2−
.
Câu 4: Hàm số
( )
y f x=
xác định và liên tục trên
( )
;− +
có bảng biến thiên như hình vẽ sau.
Giá trị lớn nhất của
( )
y f x=
trên
1;5
bằng
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 5: Cho hàm số
( )
y f x=
có bảng biến thiến trên đoạn
5;7−
như sau:
Mệnh đề nào dưới đây đúng?
A.
( )
5;7
1Min f x
−
=
. B.
( )
5;7
6Min f x
−
=
. C.
( )
5;7
2Min f x
−
=
. D.
( )
5;7
9Min f x
−
=
.
Câu 6: Cho hàm số
( )
fx
liên tục trên đoạn
2;2−
có đồ thị như hình vẽ
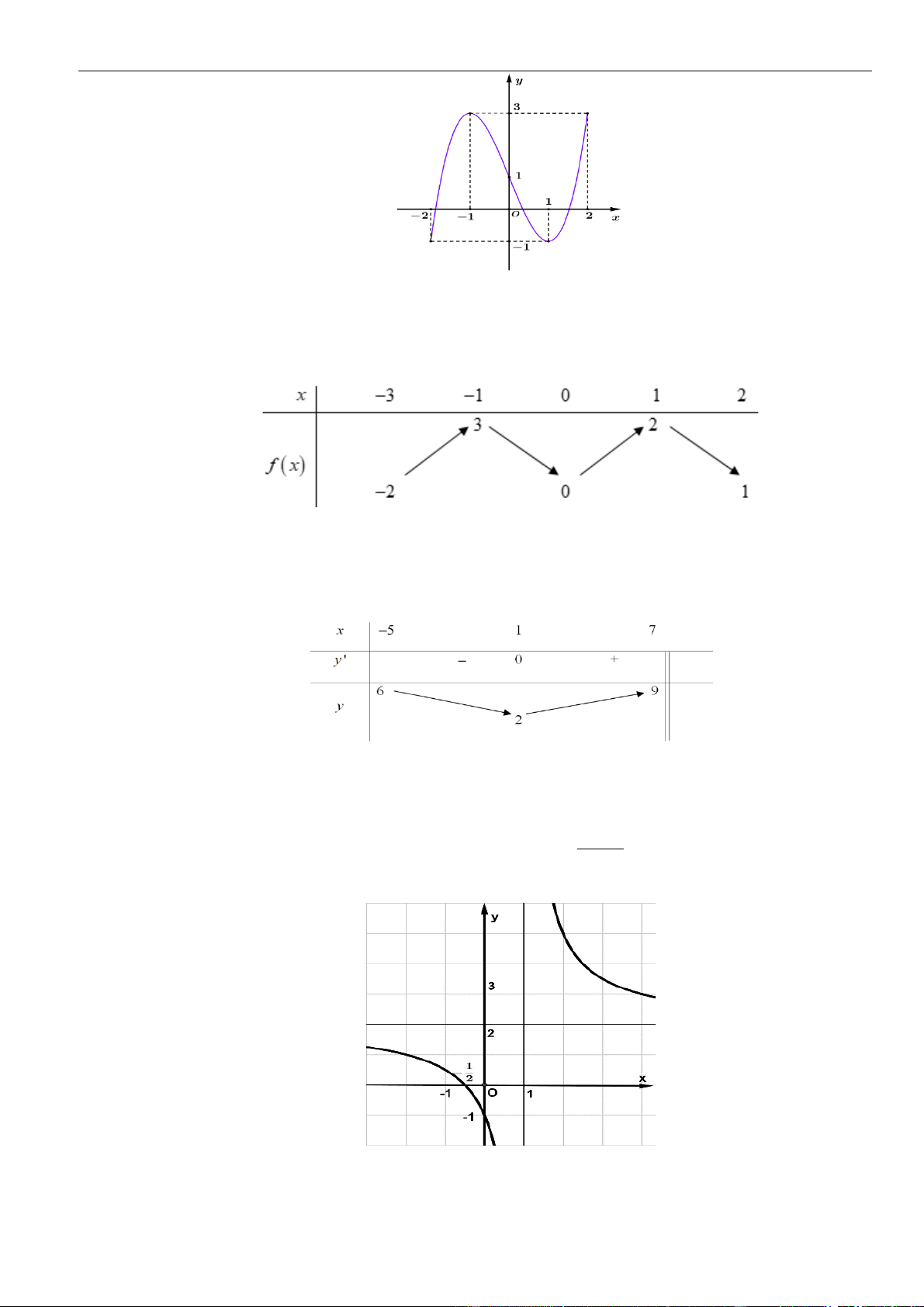
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Giá trị nhỏ nhất của hàm số trên đoạn
2;2−
là
A.
1
. B.
1−
. C.
2−
. D.
3
.
Câu 7: Cho hàm số
( )
y f x=
liên tục trên đoạn
3;2−
và có bảng biến thiên như sau.
Giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
1;2−
là
A.
2
. B.
0
. C.
1
. D.
2−
.
Câu 8: Cho hàm số
( )
y f x=
có bảng biến thiến trên đoạn
5;7−
như sau:
Mệnh đề nào dưới đây đúng?
A.
( )
5;7
1.Min f x
−
=
B.
( )
5;7
6.Min f x
−
=
C.
( )
5;7
2.Min f x
−
=
D.
( )
5;7
9.Min f x
−
=
Câu 9: Đường cong ở hình bên dưới là đồ thị của hàm số
ax b
y
cx d
+
=
+
với
a
,
b
,
c
,
d
là các số thực.
Giá trị nhỏ nhất của hàm số trên đoạn
[ 1;0]−
là
A.
1−
. B.
2
. C.
0
D.
1
.
Câu 10: Cho hàm số có đồ thị như hình vẽ
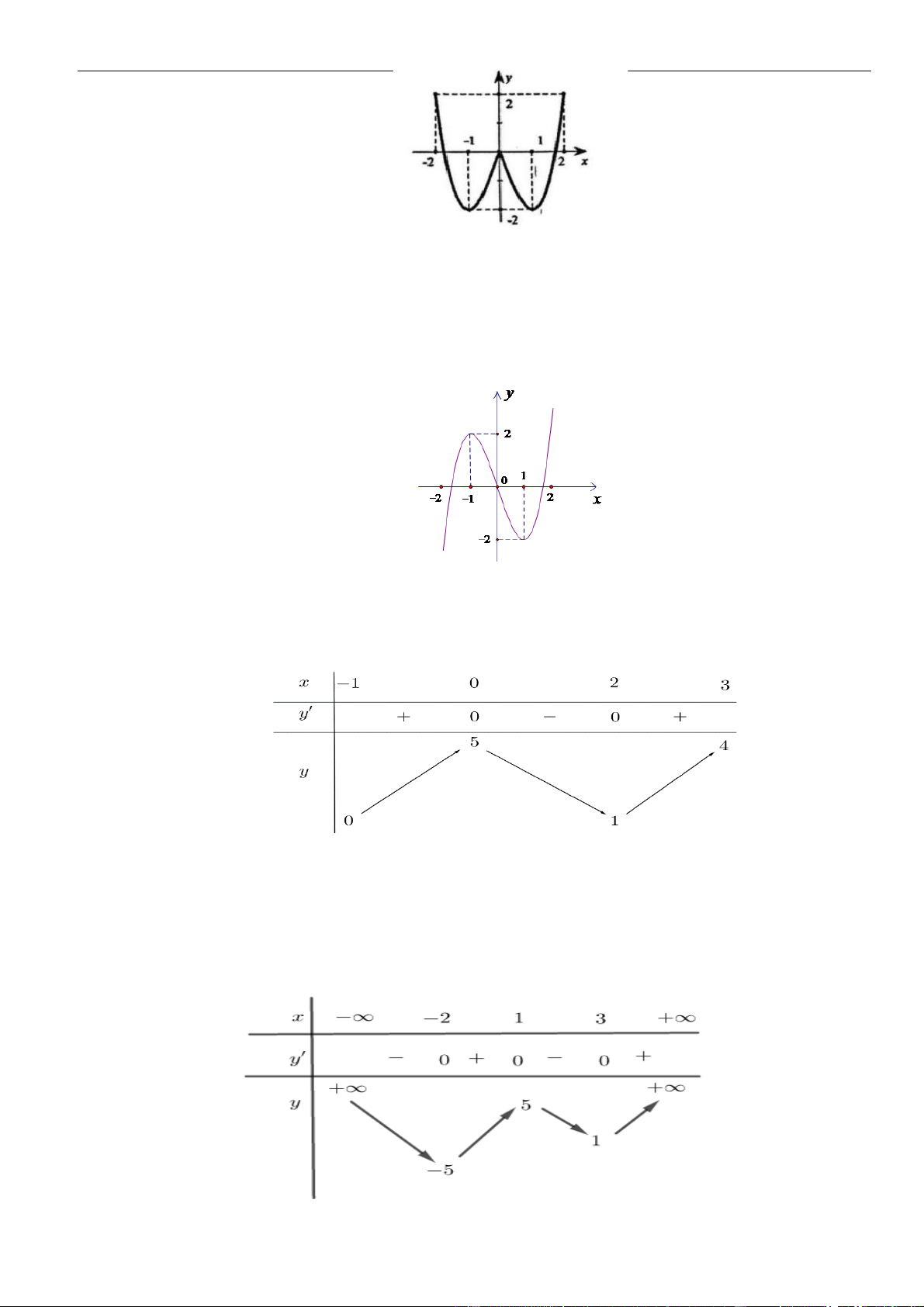
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Mệnh đề nào sau đây sai?
A.
( ) ( )
2;2
max 2f x f
−
=
. B.
( ) ( )
2;2
min 1f x f
−
=
. C.
( ) ( )
2;2
max 2f x f
−
=−
. D.
( ) ( )
2;2
min 0f x f
−
=
.
Câu 11: Cho hàm số
( )
y f x=
xác định và liên tục trên
1;1−
và có đồ thị như hình vẽ bên dưới. Tìm
giá trị
0
x
để hàm số
( )
y f x=
đạt giá trị lớn nhất trên
1;1−
.
A.
0
2x =−
. B.
0
2x =
. C.
0
1x =−
. D.
0
1x =
.
Câu 12: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có bảng biến thiên như sau.
Gọi
M
là giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;3−
. Khẳng định nào sau đây là
khẳng định đúng?
A.
( )
0Mf=
. B.
( )
3Mf=
. C.
( )
2Mf=
. D.
( )
1Mf=−
.
Câu 13: Cho hàm số
( )
y f x=
có bảng biến thiên như bên. Khẳng định nào sau đây sai?
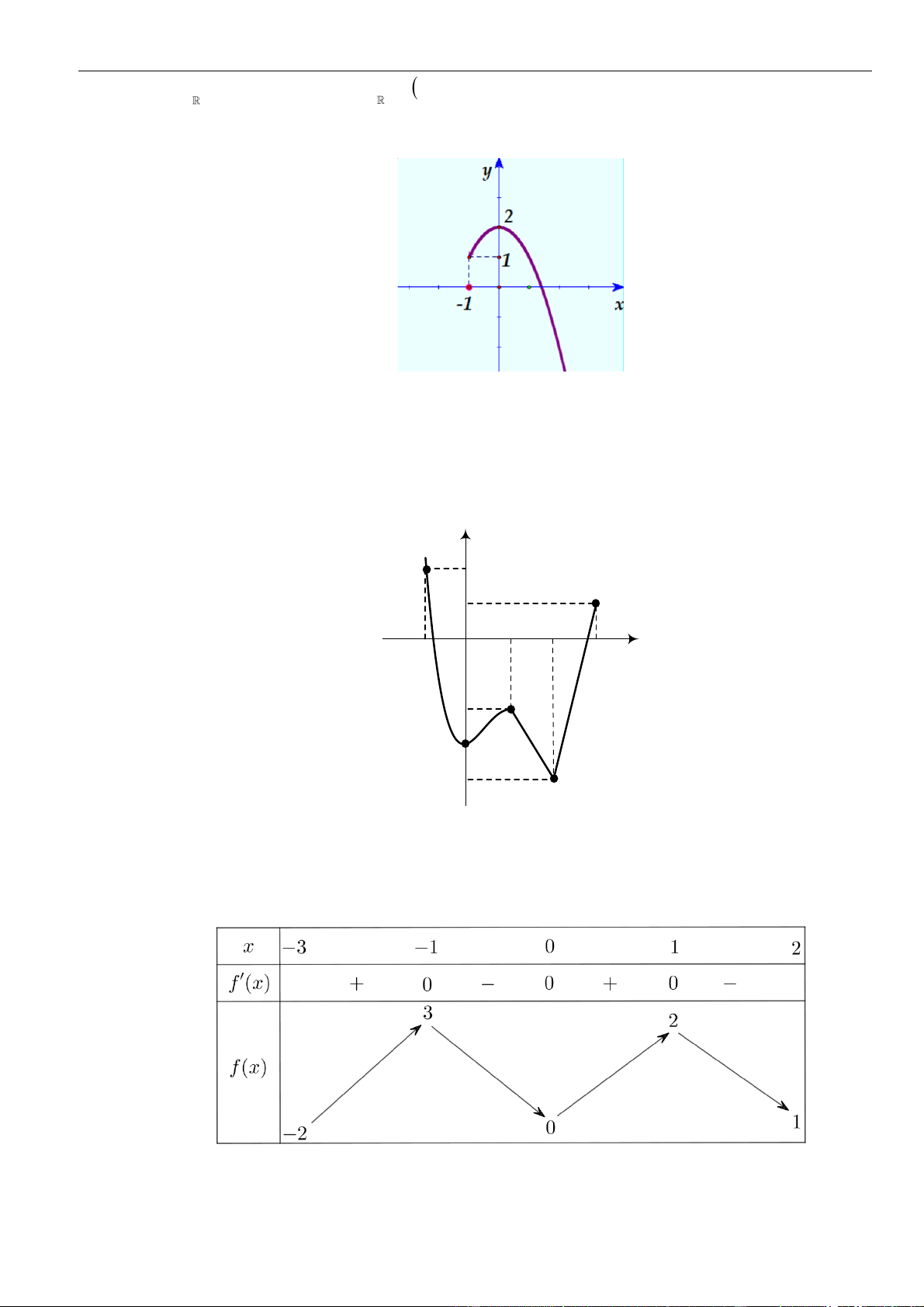
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
( )
max 5fx=
. B.
( )
min 5fx=−
. C.
( )
1;3
min 1fx=
. D.
( )
( )
2;3
max 5fx
−
=
.
Câu 14: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ bên dưới
Giá trị lớn nhất của hàm số đã cho trên đoạn
1;3−
bằng
A.
2−
. B.
1
. C.
2
. D.
3
.
Câu 15: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn
1;3−
. Khi đó, tổng
Mm+
bằng
1
2
3
1−
2−
3−
4−
x
y
O
2
1
A.
6−
. B.
2−
. C.
5−
. D.
2
.
Câu 16: Cho đồ thị hàm số
( )
y f x=
liên tục trên
3;2−
và có bảng biến thiên như hình dưới đây. Giá
trị nhỏ nhất của hàm số
( )
y f x=
trên
3;2−
là
A.
0
. B.
1
. C.
2−
. D.
3
.
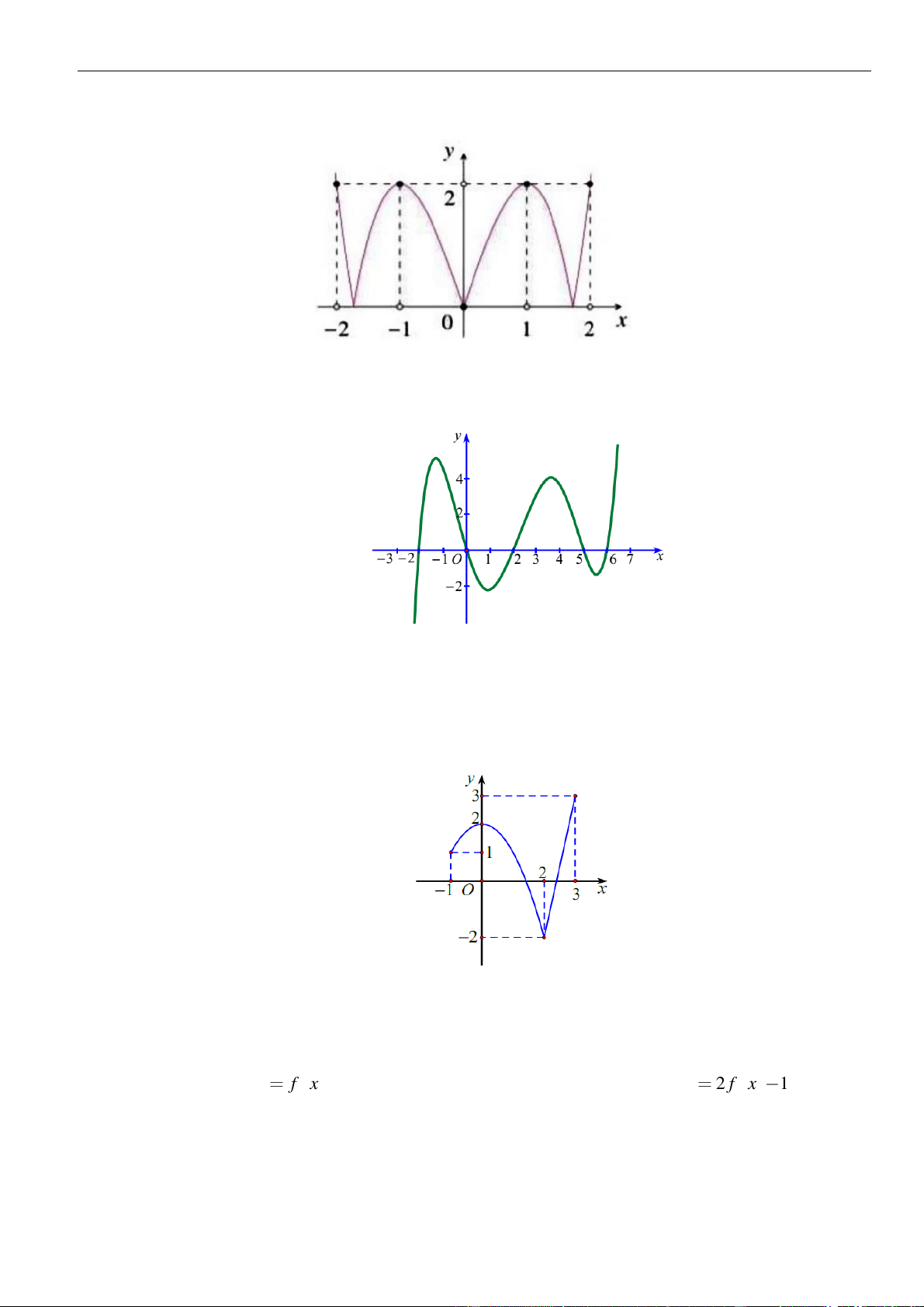
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 17: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số trên đoạn
2;1−
. Giá trị của
3
Mm−
bằng
A.
8
. B.
6
. C.
4
. D.
2
.
Câu 18: Cho hàm số
()y f x=
liên tục trên đoạn
0;6
. Đồ thị của hàm số
'( )y f x=
như hình vẽ sau:
Giá trị lớn nhất của hàm số
()y f x=
trên đoạn
0;6
bằng
A.
(2)f
. B.
(0)f
. C.
(5)f
. D.
(6)f
.
Câu 19: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình dưới đây
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3−
. Giá trị
của
2Mm+
bằng
A.
1−
. B.
1
. C.
2−
. D.
7
.
Câu 20: Cho hàm số
y f x
như hình vẽ. Giá trị lớn nhất của hàm số
21g x f x
trên đoạn
1;2−
tương ứng là
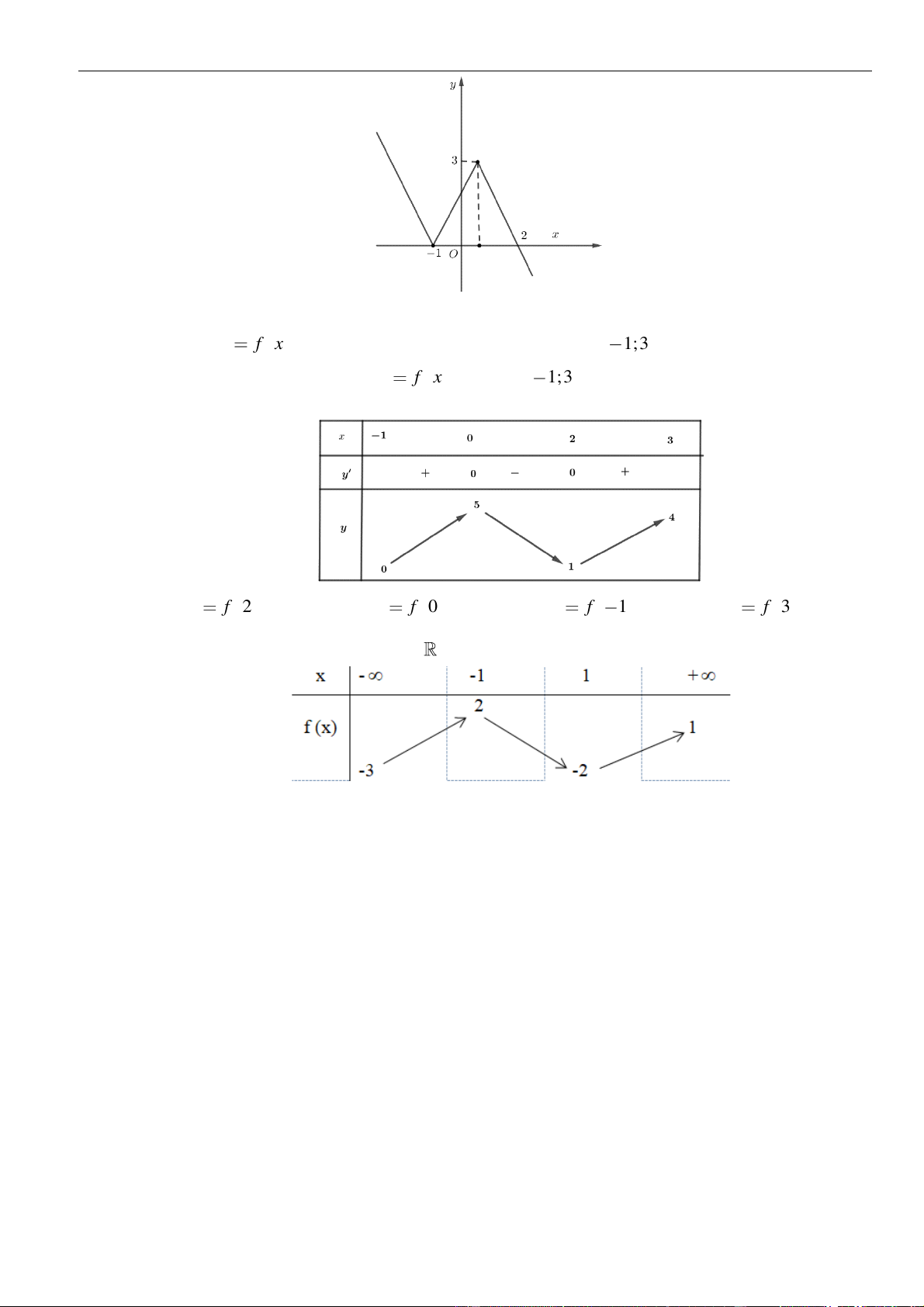
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
A.
6
. B.
5
. C.
3
. D.
2
.
Câu 21: Hàm số
y f x
liên tục và có bảng biến thiên trong đoạn
1;3
cho trong hình ben. Gọi
M
là giá trị lớn nhất của hàm số
y f x
trên đoạn
1;3
, thì
M
bằng
A.
2Mf
. B.
0Mf
. C.
1Mf
. D.
3Mf
.
Câu 22: Cho hàm số
()y f x=
liên tục trên và có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số không có GTLN và không có GTNN.
B. Hàm số có GTLN bằng 2 và GTNN bằng -3.
C. Hàm số có GTLN bằng 2 và GTNN bằng -2.
D. Hàm số có GTLN bằng 2 và không có GTNN.
Câu 23: Cho hàm số
( )
fx
liên tục trên
R
và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số đã cho
trên
2;0−
là:
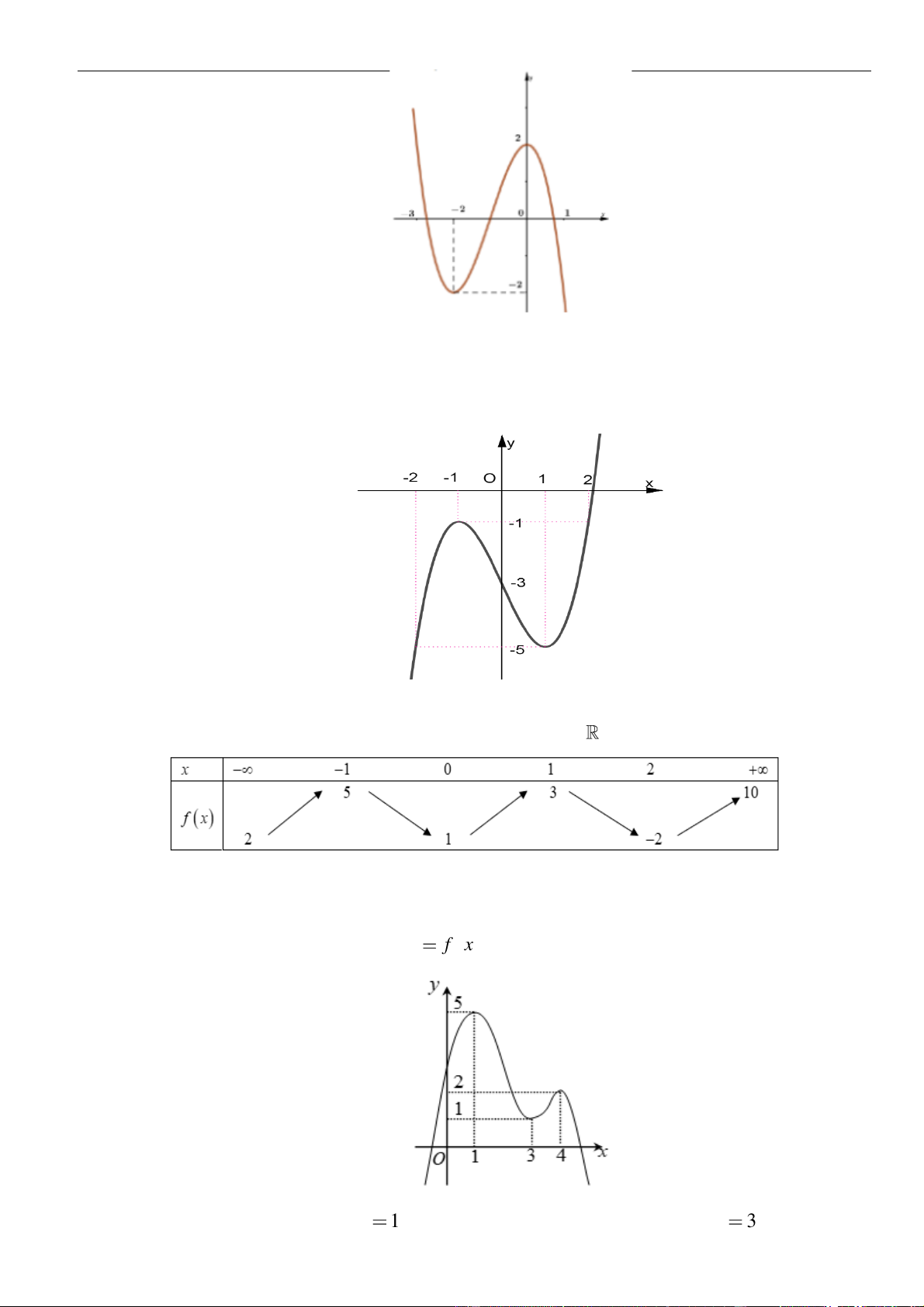
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
A.
1−
. B.
0
. C.
2
. D.
2−
.
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ. Giá trị nhỏ nhất và giá trị lớn nhất của hàm
số trên đoạn
2;2−
lần lượt là
A.
5−
và
0
. B.
5−
và
1−
. C.
1−
và
0
. D.
2−
và
2
.
Câu 25: Cho hàm số
( )
y f x=
liên tục và có bảng biến thiên trên như hình vẽ bên dưới
Giá trị lớn nhất của hàm số
( )
cosy f x=
.
A.
5
. B.
3
. C.
10
. D.
1
.
Câu 26: Hình vẽ bên là đồ thị của hàm số
y f x
. Khẳng định nào sau đây đúng
A. Hàm số đạt cực tiểu tại
1x
. B. Hàm số đạt cực đại tại
3x
.
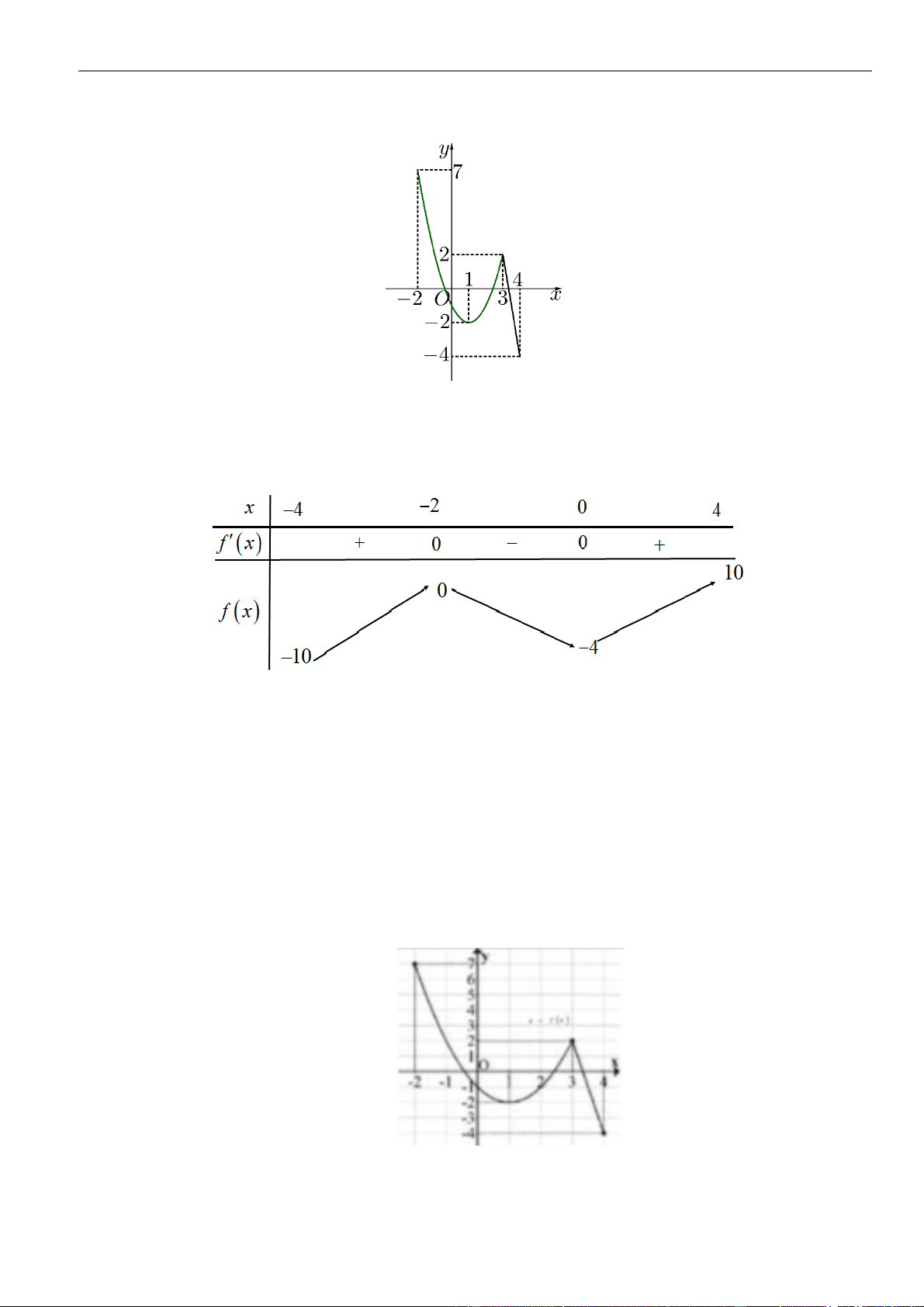
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
C. Giá trị lớn nhất của hàm số bằng
5
. D. Giá trị lớn nhất của hàm số bằng
3
.
Câu 27: Cho hàm số
( )
y f x=
liên tục và có đồ thị trên đoạn
2 ; 4−
như hình vẽ bên dưới.
Tổng giá trị lớn nhất và nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2 ; 4−
bằng
A. 5. B. 3. C.
2−
. D. 0.
Câu 28: Cho hàm số
()y f x=
xác định trên
( 4;4)−
có bảng biến thiên trên
( 4;4)−
như hình sau:
Phát biểu nào sau đây đúng:
A.
( 4;4)
min 4y
−
=−
và
( 4;4)
max 10y
−
=
.
B.
( 4;4)
max 10y
−
=
và
( 4;4)
min 10y
−
=−
.
C.
( 4;4)
max 0y
−
=
và
( 4;4)
min 4y
−
=−
.
D. Hàm số không có GTLN, GTNN trên
( 4;4)−
.
Câu 29: Cho hàm số
( )
y f x=
liên tục trên đoạn
2;4−
và có đồ thị như hình vẽ bên. Tổng giá trị nhỏ
nhất và giá trị lớn nhất của hàm số đã cho trên
2;4−
bằng
A.
3
. B.
2−
. C.
5
. D.
0
.
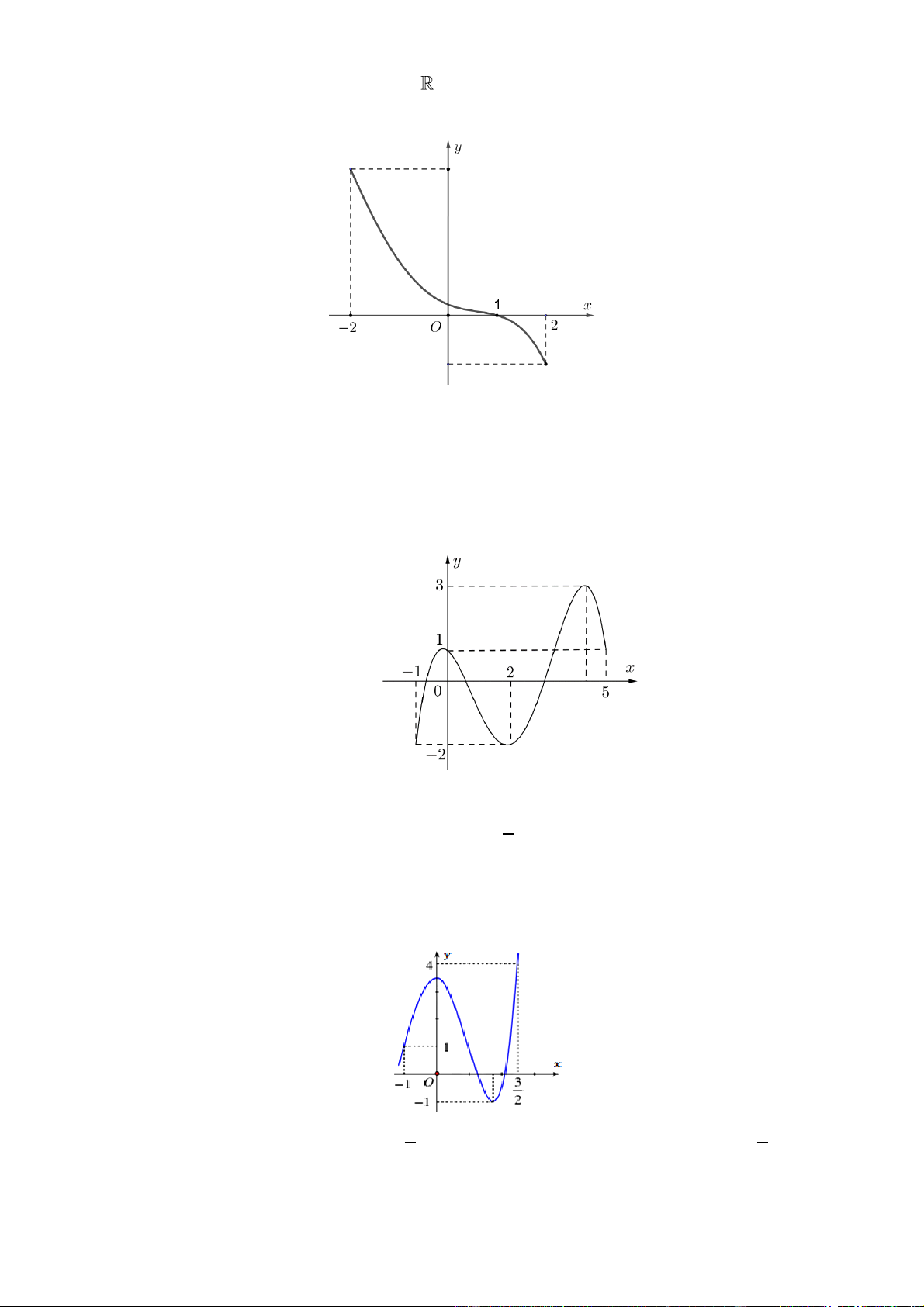
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Câu 30: Cho hàm số
( )
fx
có đạo hàm trên . Đồ thị của hàm số
( )
y f x
=
trên đoạn
2;2−
là đường
cong hình bên. Mệnh đề nào dưới đây đúng?
A.
( ) ( )
2;2
max 2f x f
−
=
. B.
( ) ( )
2;2
min 1f x f
−
=
.
C.
( ) ( )
2;2
max 1f x f
−
=
. D.
( ) ( )
2;2
max 2f x f
−
=−
.
Câu 31: Cho hàm số
( )
fx
liên tục trên
1;5−
và có đồ thị trên đoạn
1;5−
như hình vẽ bên dưới. Tổng
giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
1;5−
bằng
A.
1−
. B.
4
. C.
1
. D.
2
Câu 32: Cho hàm số
( )
y f x=
liên tục trên đoạn
3
1;
2
−
và có đồ thị là đường cong như hình vẽ. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số của hàm số
( )
y f x=
trên đoạn
3
1;
2
−
. Khi đó,
M
và
m
lần lượt là:
A.
4; 1Mm==
. B.
3
;1
2
Mm= = −
. C.
4; 1Mm= = −
. D.
3
;1
2
Mm==
.
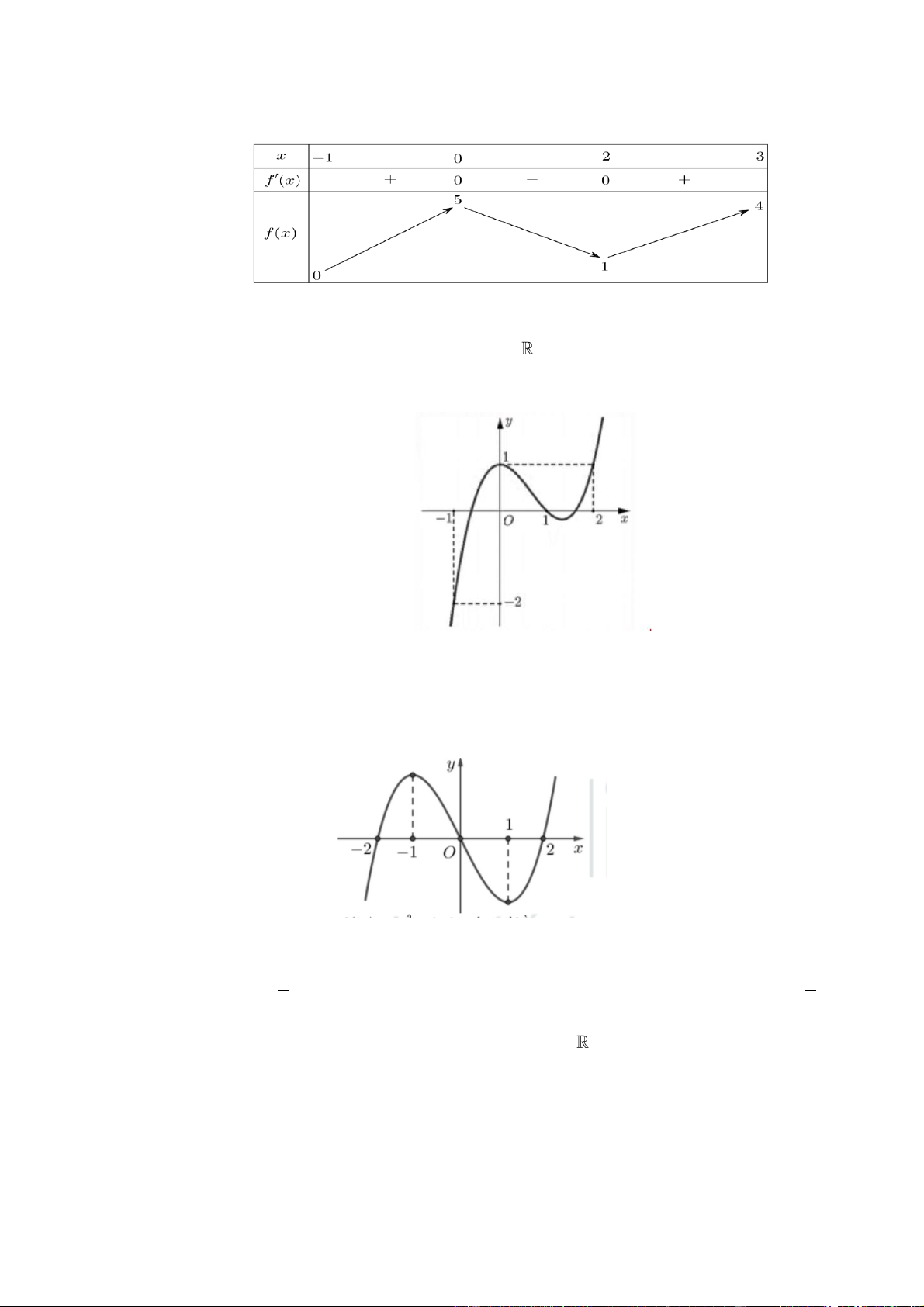
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Câu 33: Cho hàm số
( )
y f x=
liên tục và có bảng biến thiên trên đoạn
1;3−
như hình vẽ. Gọi
M
là
giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;3−
. Tìm mệnh đề đúng?
A.
( )
2Mf=
. B.
( )
3Mf=
. C.
( )
0Mf=
. D.
( )
1Mf=−
.
Câu 34: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên , đồ thị của hàm số
( )
'y f x=
như hình vẽ
bên.
Giá trị nhỏ nhất của hàm số
( ) ( ) ( )
2
21g x f x x= − −
trên đoạn
1;2−
bằng:
A.
( )
2 0 1f −
B.
( )
2 1 4.f −−
. C.
( )
2 1 .f
. D.
( )
2 2 1.f −
Câu 35: Cho hàm số
( )
fx
có đồ thị của đạo hàm như sau:
Giá trị lớn nhất của hàm số
( ) ( )
2
2 sing x f x x=−
trên đoạn
1;1−
bằng
A.
( )
2
1
1 sin
2
f −−
. B.
( )
2
2 sin 1f −
. C.
( )
0f
. D.
( )
2
1
1 sin
2
f −
.
Câu 36: Cho hàm số
( )
y f x=
có đạo hàm
( )
'fx
liên tục trên và hàm số
( )
'y f x=
có đồ thị trên
đoạn
2;3−
như hình vẽ bên dưới.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2;3−
. Khi
đó
;Mm
lần lượt là
A.
( ) ( )
2 ; 1M f m f= − =
. B.
( ) ( )
3 ; 1M f m f==
.
C.
( ) ( )
1 ; 2M f m f= = −
. D.
( ) ( )
3 ; 2M f m f= = −
.
Câu 37: Cho hàm số
( )
fx
, đồ thị của hàm số
( )
y f x
=
là đường cong trong hình bên. Giá trị nhỏ nhất
của hàm số
( ) ( )
2 2 2021g x f x x= − +
trên đoạn
1
;1
2
−
bằng
A.
( )
2 2019.f +
B.
( )
1 2022.f −+
C.
( )
0 2021.f +
D.
( )
1 2020.f +
Câu 38: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới:
Khi đó, giá trị lớn nhất của hàm số
( )
( )
2
2g x f x=−
trên đoạn
0; 2
là
A.
( ) ( )
=
0; 2
max 0g x f
. B.
( ) ( )
=
0; 2
max 1g x f
. C.
( )
( )
=
0; 2
max 2g x f
. D.
( ) ( )
=
0; 2
max 2g x f
.
Câu 39: Cho hàm số
( )
fx
liên tục trên và có đồ thị của đạo hàm
( )
y f x
=
như hình dưới đây.
x
y
4
-1
2
2
O
1
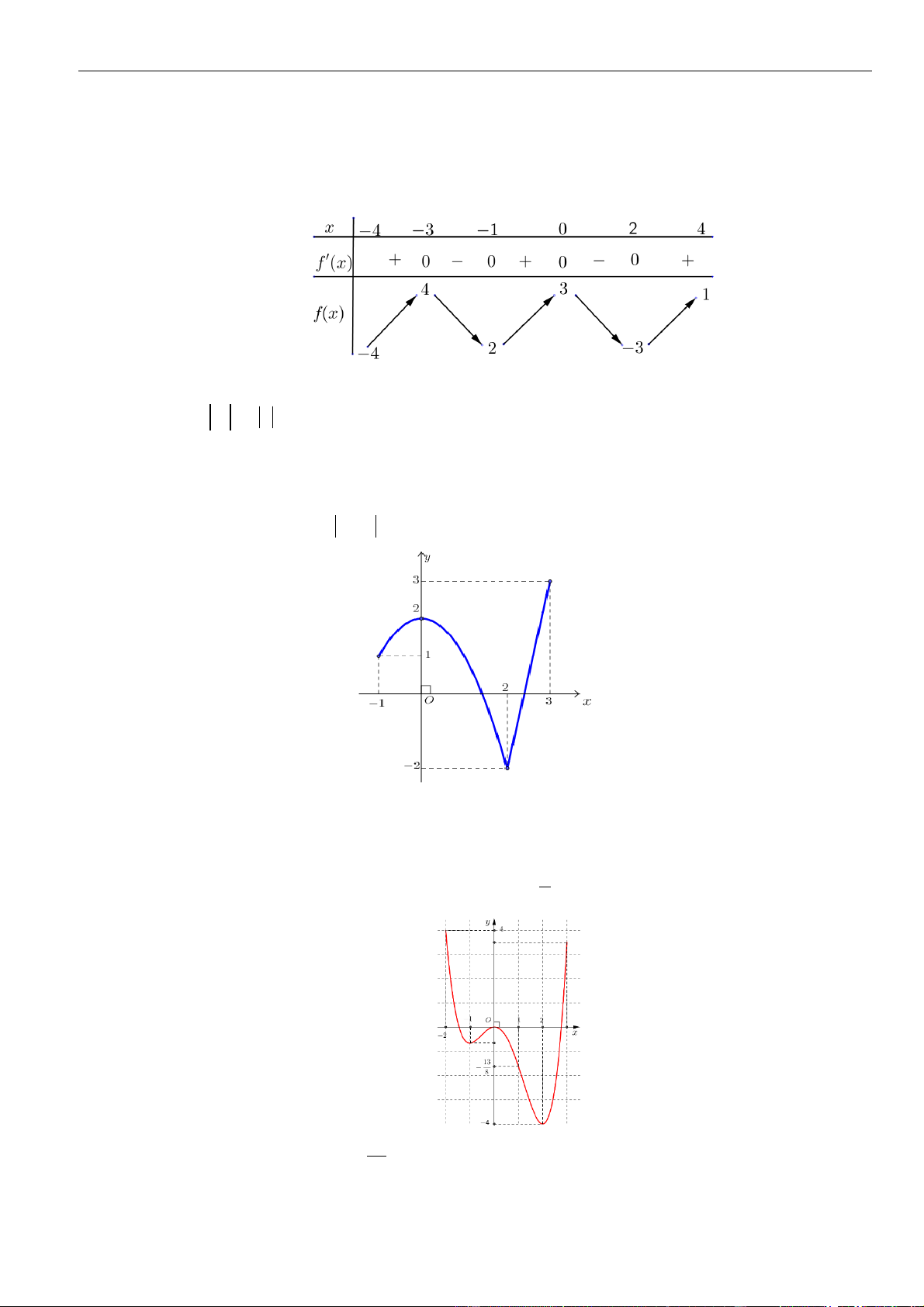
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Trên đoạn
3;4−
, hàm số
( ) ( ) ( )
2
21g x f x x= + −
đạt giá trị nhỏ nhất tại điểm nào trong các
điểm sau đây?
A.
0
4x =−
. B.
0
3x =
. C.
0
1x =−
. D.
0
3x =−
.
Câu 40: Cho hàm số
( )
y f x=
có bảng biến thiên trên đoạn
4;4−
như hình vẽ.
Có bao nhiêu giá trị của tham số
m
trên đoạn
4;4−
sao cho giá trị lớn nhất của hàm số
( )
( )
3
3y f x x f m= + +
trên đoạn
1;1−
bằng
1
?
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 41: Cho hàm số
( )
fx
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ bên. Giá trị lớn nhất của
hàm số
( )
( )
3 cos 1y g x f x= = −
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 42: Cho hàm số
( )
y f x=
có đồ thị như hình bên dưới. Gọi
,mM
lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của hàm số
( )
2y f x=−
trên đoạn
1
1;
2
−
. Giá trị của
23mM+
là
A. 0. B.
35
4
. C. 4. D.
8−
.
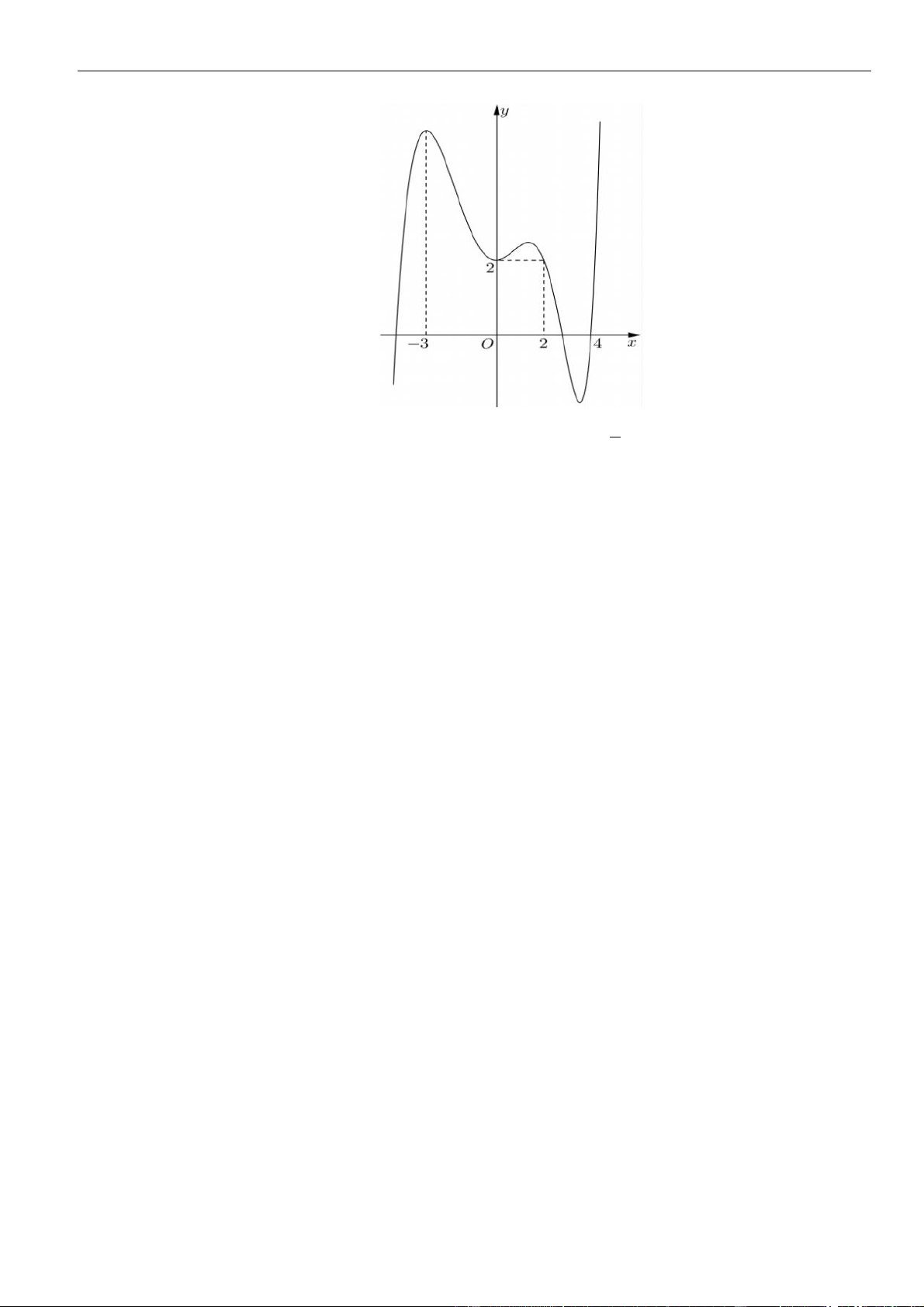
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Câu 43: Cho hàm số
( )
fx
, đồ thị của hàm số
( )
y f x
=
là đường cong trong hình bên.
Giá trị lớn nhất của hàm số
( ) ( )
24g x f x x=−
trên đoạn
3
;2
2
−
bằng
A.
( )
0f
. B.
( )
36f −+
. C.
( )
24f −
. D.
( )
48f −
.
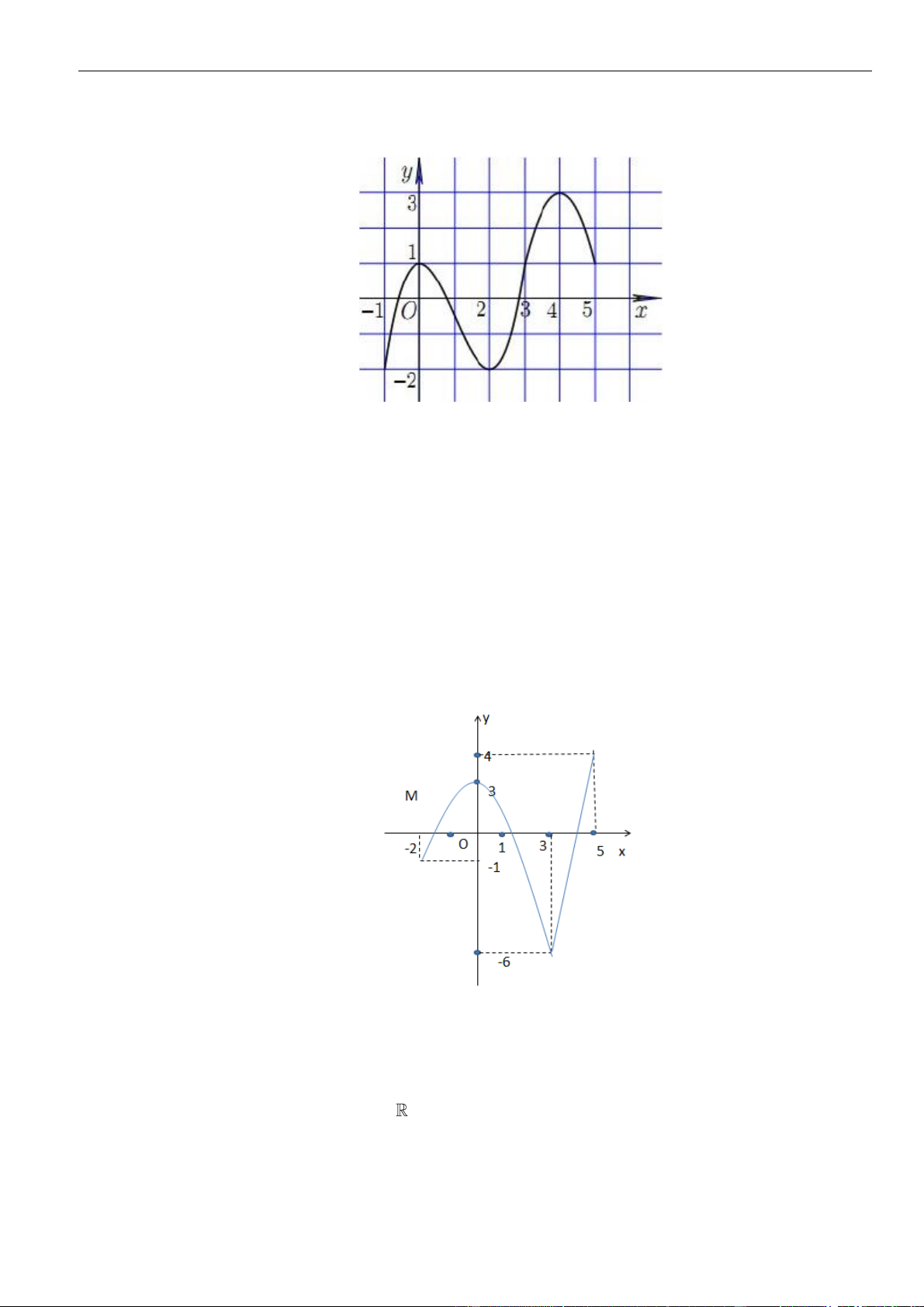
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
fx
liên tục trên đoạn
1;5−
và có đồ thị như hình vẽ sau:
Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;5−
bằng
A. 2. B. 3. C. 5. D. 6.
Lời giải
Chọn C
Từ đồ thị của hàm số đã cho ta có:
( )
1;5
3max fx
−
=
;
( )
1;5
2min fx
−
=−
.
Suy ra
( )
( )
1;5
1;5
max m 5inf x f x
−
−
−=
.
Câu 2: Cho hàm
( )
y f x=
liên tục trên đoạn
2;5
và có đồ thị như hình vẽ bên. Gọi M và m lần lượt
là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
2;5
. Giá trị của
Mm−
bằng
A. 9. B. 5. C. 10. D. -10.
Lời giải
Chọn C
4M =
;
6m =−
.Vậy
10Mm−=
.
Câu 3: Cho hàm số
( )
fx
liên tục trên và có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số đã
cho trên
2;0−
là:

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
A.
1−
. B.
0
. C.
2
. D.
2−
.
Lời giải
Chọn C
Giá trị lớn nhất của hàm số đã cho trên
2;0−
là
2
.
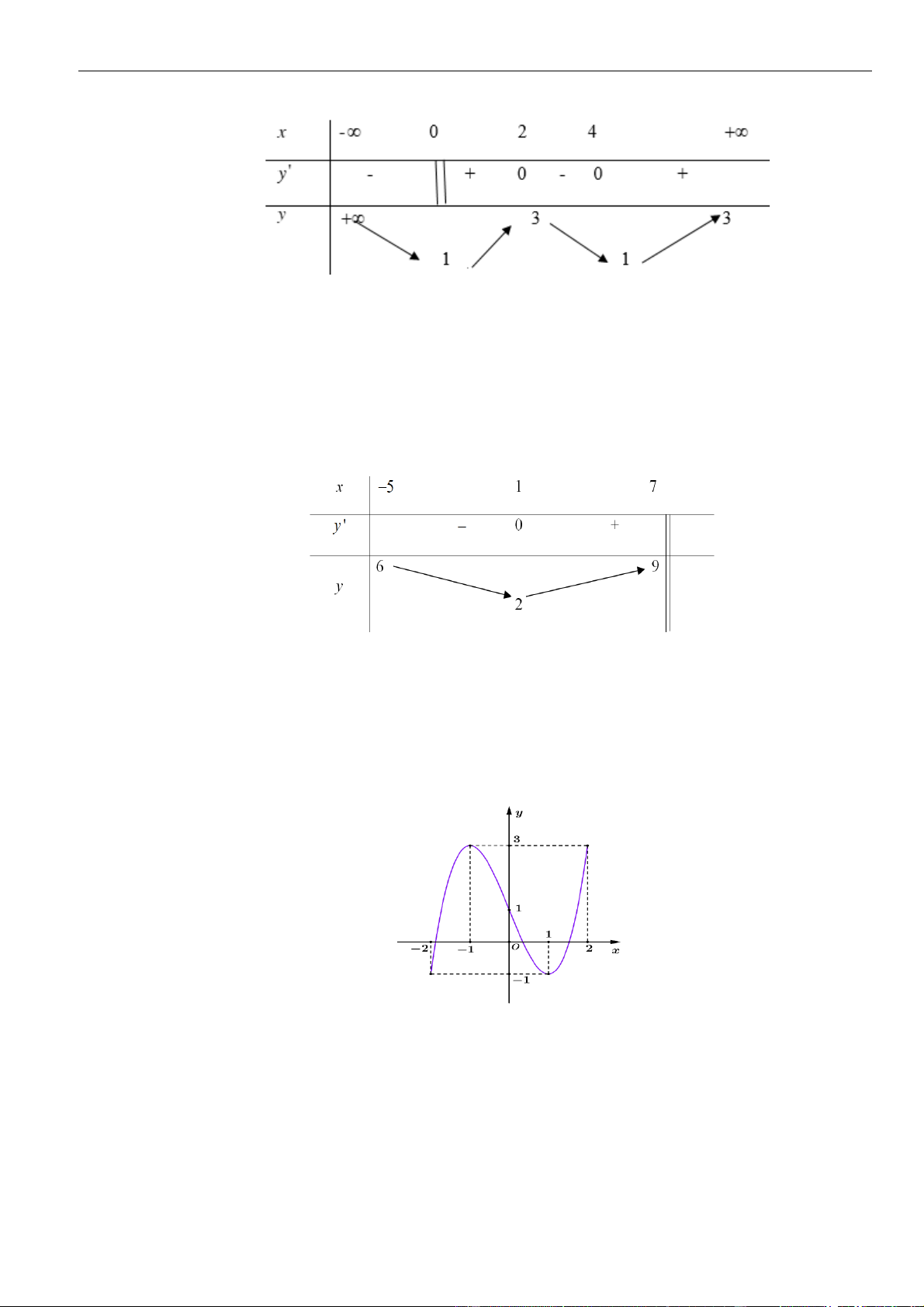
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Câu 4: Hàm số
( )
y f x=
xác định và liên tục trên
( )
;− +
có bảng biến thiên như hình vẽ sau.
Giá trị lớn nhất của
( )
y f x=
trên
1;5
bằng
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
Từ bảng biến thiên suy ra giá trị lớn nhất của
( )
y f x=
trên
1;5
bằng
3
.
Câu 5: Cho hàm số
( )
y f x=
có bảng biến thiến trên đoạn
5;7−
như sau:
Mệnh đề nào dưới đây đúng?
A.
( )
5;7
1Min f x
−
=
. B.
( )
5;7
6Min f x
−
=
. C.
( )
5;7
2Min f x
−
=
. D.
( )
5;7
9Min f x
−
=
.
Lời giải
Chọn C
Câu 6: Cho hàm số
( )
fx
liên tục trên đoạn
2;2−
có đồ thị như hình vẽ
Giá trị nhỏ nhất của hàm số trên đoạn
2;2−
là
A.
1
. B.
1−
. C.
2−
. D.
3
.
Lời giải
Chọn B
Trên đoạn
2;2−
ta có
( )
1fx−
và
( )
2
1
1
x
fx
x
=−
= −
=
Vậy
( )
2;2
min 1fx
−
=−
.
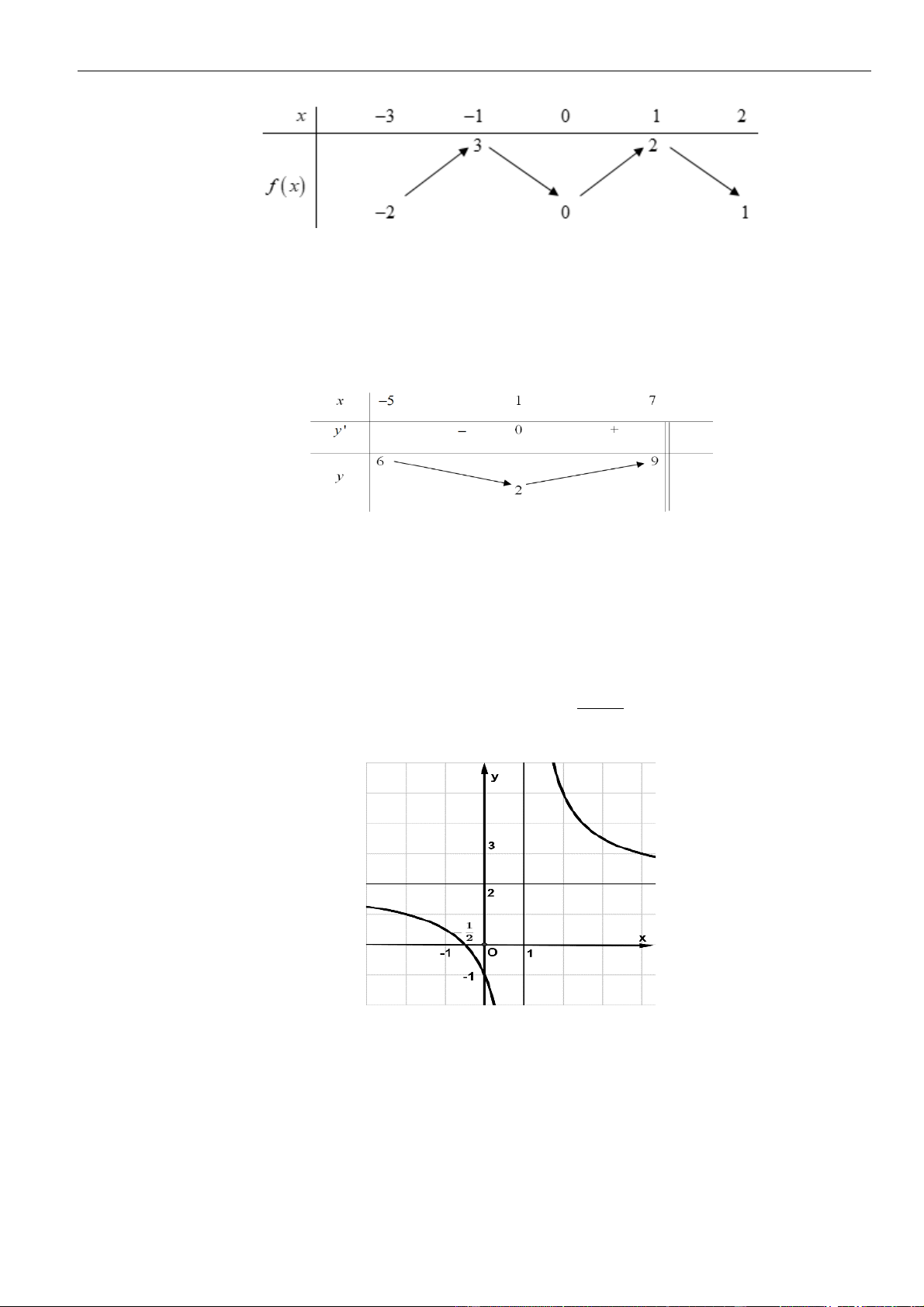
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Câu 7: Cho hàm số
( )
y f x=
liên tục trên đoạn
3;2−
và có bảng biến thiên như sau.
Giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
1;2−
là
A.
2
. B.
0
. C.
1
. D.
2−
.
Lời giải
Chọn B
Câu 8: Cho hàm số
( )
y f x=
có bảng biến thiến trên đoạn
5;7−
như sau:
Mệnh đề nào dưới đây đúng?
A.
( )
5;7
1.Min f x
−
=
B.
( )
5;7
6.Min f x
−
=
C.
( )
5;7
2.Min f x
−
=
D.
( )
5;7
9.Min f x
−
=
Lời giải
Chọn C
Từ BBT
( )
5;7
2.Min f x
−
=
Câu 9: Đường cong ở hình bên dưới là đồ thị của hàm số
ax b
y
cx d
+
=
+
với
a
,
b
,
c
,
d
là các số thực.
Giá trị nhỏ nhất của hàm số trên đoạn
[ 1;0]−
là
A.
1−
. B.
2
. C.
0
D.
1
.
Lời giải
Chọn A
Từ đồ thị, ta thấy
1;0
min 1y
−
=−
.
Câu 10: Cho hàm số có đồ thị như hình vẽ
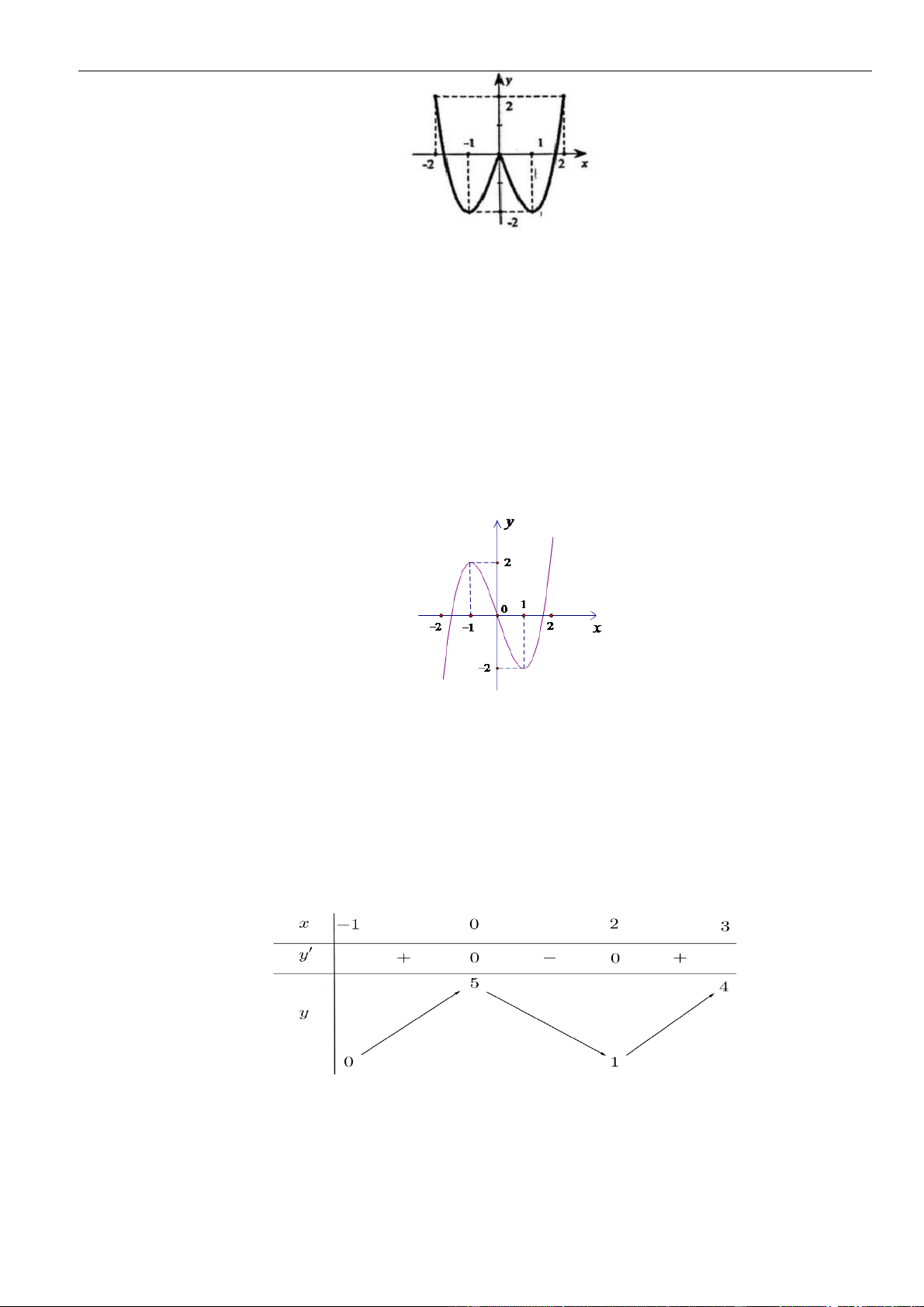
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Mệnh đề nào sau đây sai?
A.
( ) ( )
2;2
max 2f x f
−
=
. B.
( ) ( )
2;2
min 1f x f
−
=
. C.
( ) ( )
2;2
max 2f x f
−
=−
. D.
( ) ( )
2;2
min 0f x f
−
=
.
Lời giải
Chọn D
Quan sát đồ thị hàm số trên đoạn
2;2−
, ta thấy:
( ) ( ) ( )
2;2
max 2 2f x f f
−
= = −
và
( ) ( ) ( )
2;2
min 1 1f x f f
−
= = −
.
Câu 11: Cho hàm số
( )
y f x=
xác định và liên tục trên
1;1−
và có đồ thị như hình vẽ bên dưới. Tìm
giá trị
0
x
để hàm số
( )
y f x=
đạt giá trị lớn nhất trên
1;1−
.
A.
0
2x =−
. B.
0
2x =
. C.
0
1x =−
. D.
0
1x =
.
Lời giải
Chọn D
Dựa vào đồ thị ta thấy trên đoạn
1;1−
điểm có tung độ lớn nhất là số
2
đạt được khi
0
1x =
. Do
đó chọn đáp án D.
Câu 12: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có bảng biến thiên như sau.
Gọi
M
là giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;3−
. Khẳng định nào sau đây là
khẳng định đúng?
A.
( )
0Mf=
. B.
( )
3Mf=
. C.
( )
2Mf=
. D.
( )
1Mf=−
.
Lời giải
Chọn A
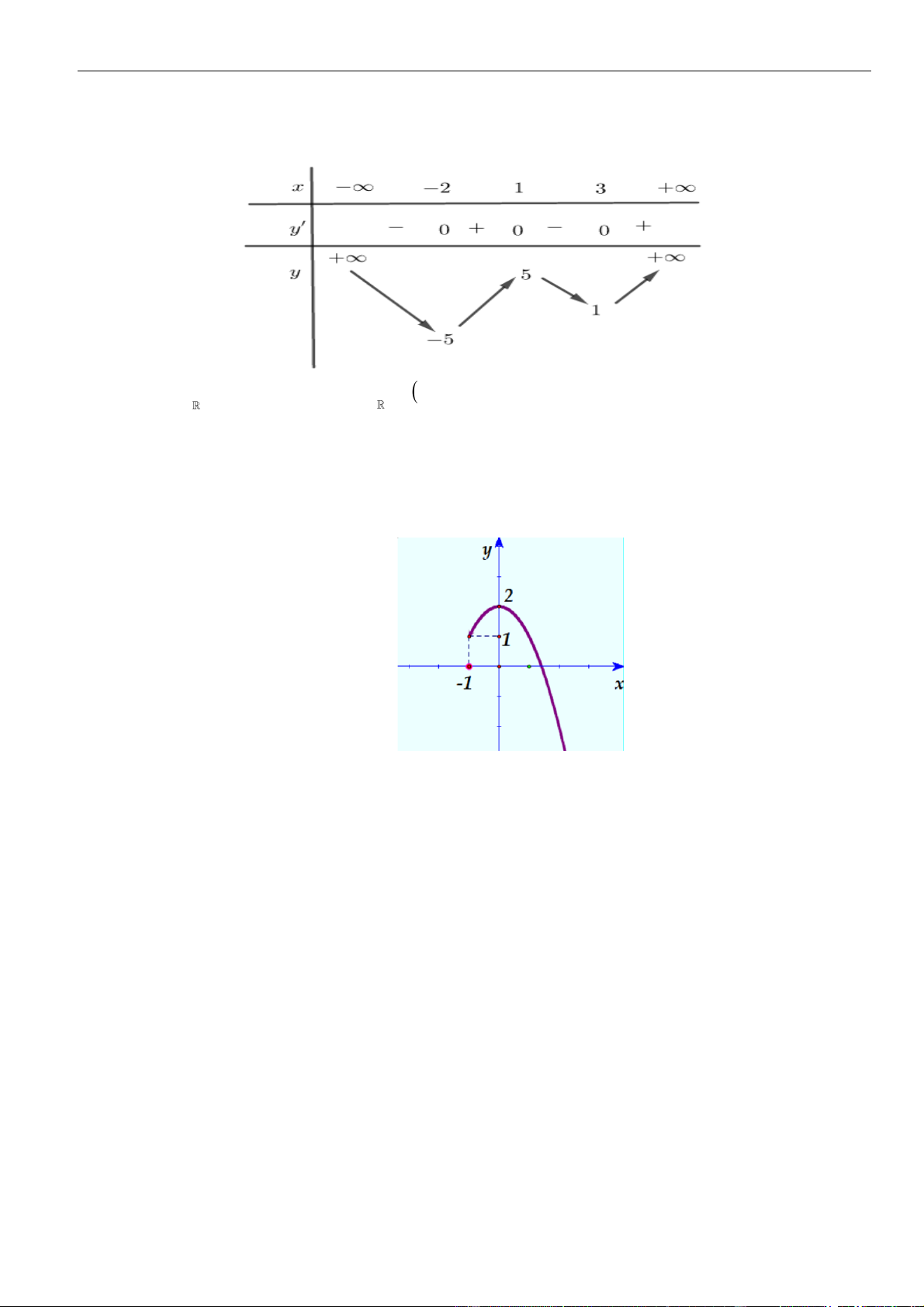
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Dựa vào bảng biến thiên, ta có giá trị lớn nhất của hàm số là
( )
05Mf==
.
Câu 13: Cho hàm số
( )
y f x=
có bảng biến thiên như bên. Khẳng định nào sau đây sai?
A.
( )
max 5fx=
. B.
( )
min 5fx=−
. C.
( )
1;3
min 1fx=
. D.
( )
( )
2;3
max 5fx
−
=
.
Lời giải
Chọn A
Từ bảng biến thiên ta có A là đáp án sai
Câu 14: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ bên dưới
Giá trị lớn nhất của hàm số đã cho trên đoạn
1;3−
bằng
A.
2−
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Dựa vào đồ thị ta có giá trị lớn nhất trên đoạn
1;3−
bằng
2
.
Câu 15: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn
1;3−
. Khi đó, tổng
Mm+
bằng
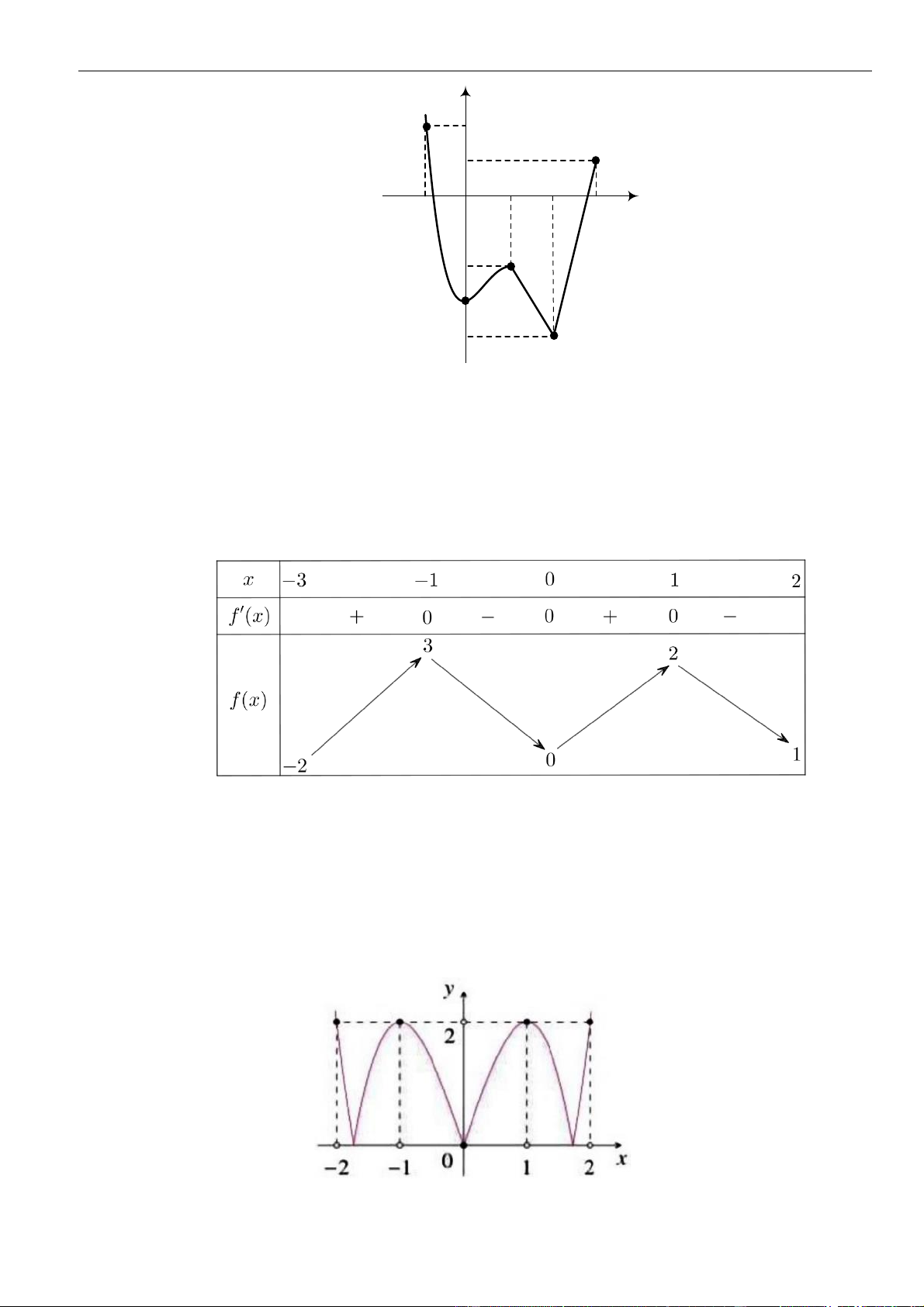
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
1
2
3
1−
2−
3−
4−
x
y
O
2
1
A.
6−
. B.
2−
. C.
5−
. D.
2
.
Lời giải
Chọn B
Theo đồ thị, ta có :
2M =
và
4m =−
2Mm + = −
.
Câu 16: Cho đồ thị hàm số
( )
y f x=
liên tục trên
3;2−
và có bảng biến thiên như hình dưới đây. Giá
trị nhỏ nhất của hàm số
( )
y f x=
trên
3;2−
là
A.
0
. B.
1
. C.
2−
. D.
3
.
Lời giải
Chọn C
( )
3;2
min 2fx
−
=−
khi
3x =−
.
Câu 17: Cho hàm số
( )
y f x=
có đồ thị như hình bên. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số trên đoạn
2;1−
. Giá trị của
3
Mm−
bằng
A.
8
. B.
6
. C.
4
. D.
2
.
Lời giải
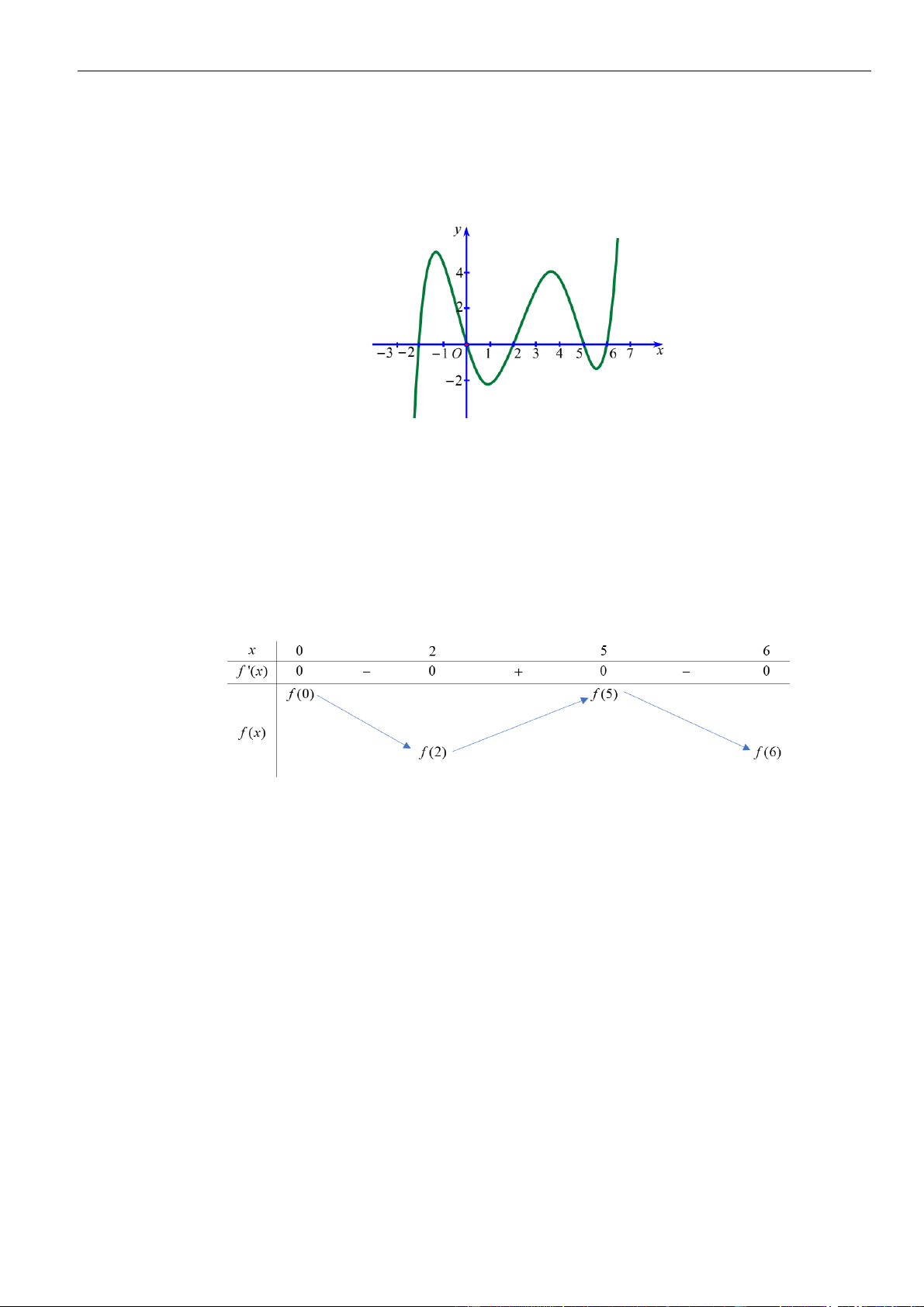
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Chọn A
Dựa vào đồ thị, ta thấy
( )
( )
2;1
2;1
max 2;min 0f x f x
−
−
==
. Suy ra
2; 0Mm==
.
Vậy
3
8Mm−=
.
Câu 18: Cho hàm số
()y f x=
liên tục trên đoạn
0;6
. Đồ thị của hàm số
'( )y f x=
như hình vẽ sau:
Giá trị lớn nhất của hàm số
()y f x=
trên đoạn
0;6
bằng
A.
(2)f
. B.
(0)f
. C.
(5)f
. D.
(6)f
.
Lời giải
Chọn C
Từ đồ thị hàm số
'( )y f x=
, ta lập được bảng biến thiên của hàm số
()y f x=
trên đoạn
0;6
như sau:
Từ bảng biến thiên trên, ta suy ra:
( ) ( ) ( )
0;6
max max 0 ; 5=f x f f
+) Gọi
1
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
'( )fx
, đường thẳng
0, 2xx==
,
ta có:
2
1
0
'( )d (0) (2)S f x x f f= − = −
.
+) Gọi
2
S
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
'( )fx
, đường thẳng
2, 5xx==
,
ta có:
5
2
2
'( )d (5) (2)S f x x f f= = −
.
+) Từ hình vẽ đồ thị hàm số ta suy ra
21
(5) (2) (0) (2) (5) (0) − − S S f f f f f f
Vậy
0;6
max ( ) (5)f x f=
.
Câu 19: Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ thị như hình dưới đây
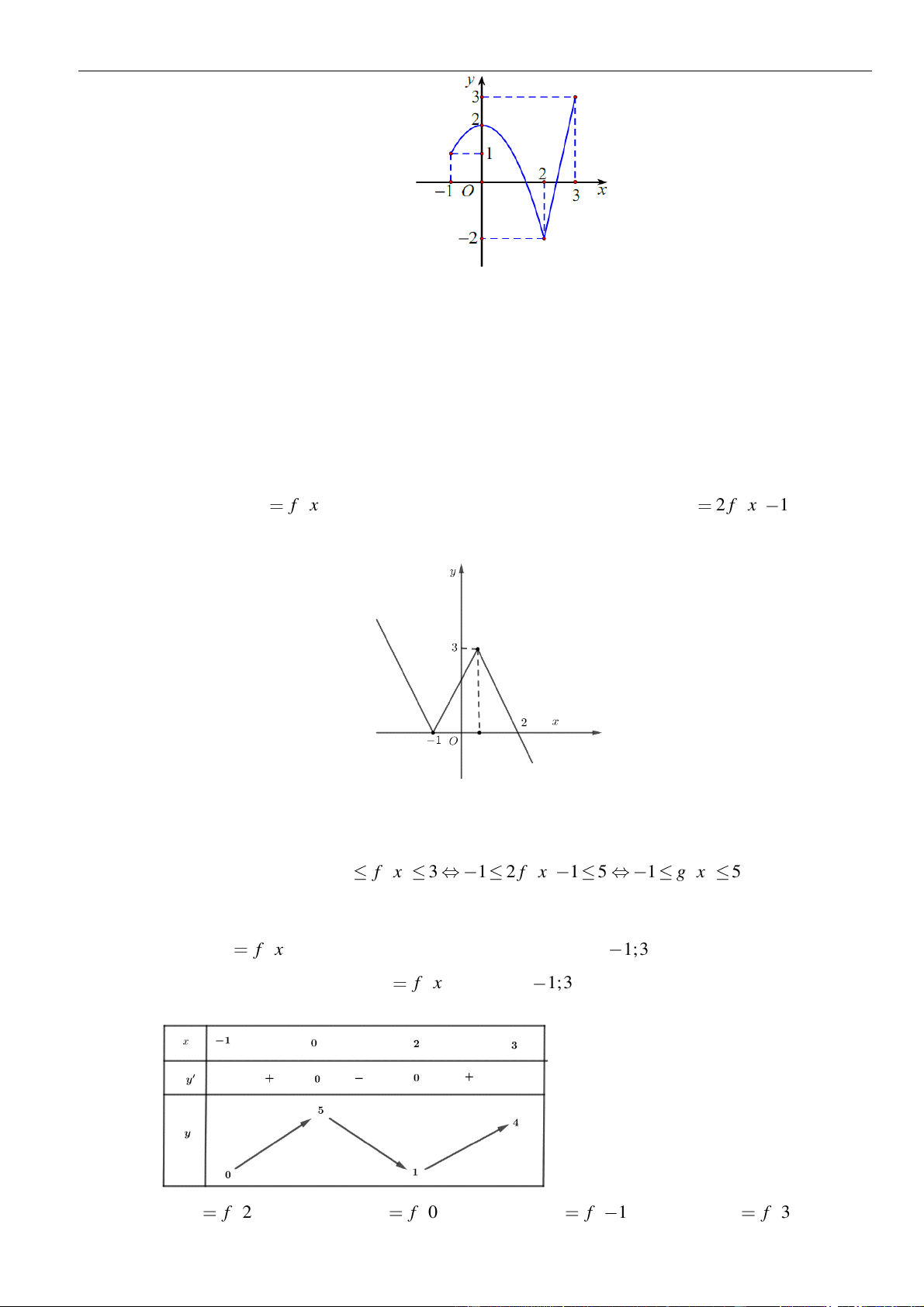
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3−
. Giá trị
của
2Mm+
bằng
A.
1−
. B.
1
. C.
2−
. D.
7
.
Lời giải
Chọn A
Ta có
( )
-1;3
max 3M f x==
và
( )
-1;3
min -2m f x==
Khi đó
2 3 2.( 2) 1Mm+ = + − = −
.
Câu 20: Cho hàm số
y f x
như hình vẽ. Giá trị lớn nhất của hàm số
21g x f x
trên đoạn
1;2−
tương ứng là
A.
6
. B.
5
. C.
3
. D.
2
.
Lời giải
Chọn B
Trên đoạn
1;2−
ta có:
0 3 1 2 1 5 1 5f x f x g x
.
Vậy giá trị lớn nhất của hàm số
( )
gx
trên đoạn
1;2−
là
5
.
Câu 21: Hàm số
y f x
liên tục và có bảng biến thiên trong đoạn
1;3
cho trong hình ben. Gọi
M
là giá trị lớn nhất của hàm số
y f x
trên đoạn
1;3
, thì
M
bằng
A.
2Mf
. B.
0Mf
. C.
1Mf
. D.
3Mf
.
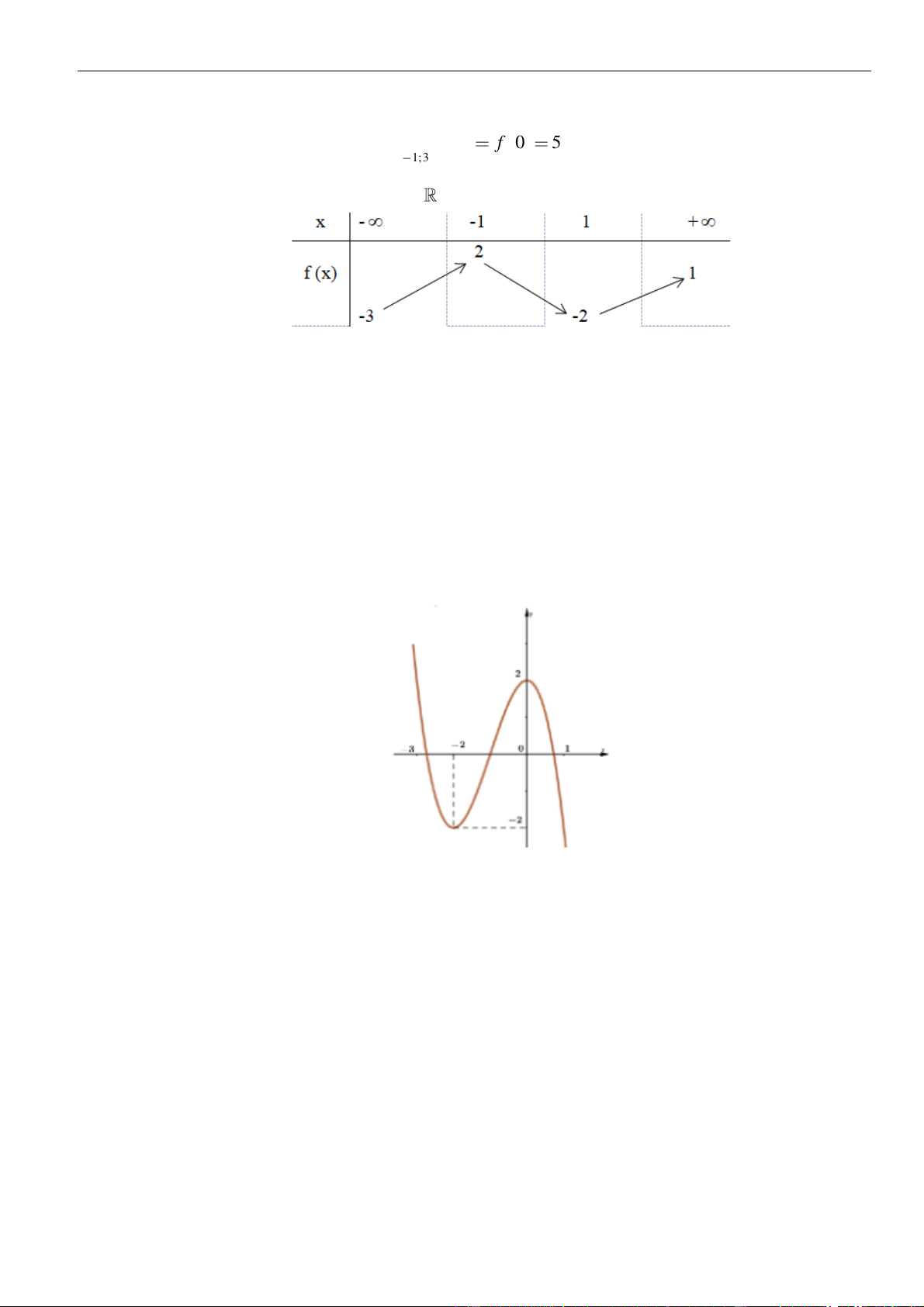
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Lời giải
Chọn B.
Dựa vào bảng biến thiên ta thấy
1;3
max 0 5f x f
.
Câu 22: Cho hàm số
()y f x=
liên tục trên và có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số không có GTLN và không có GTNN.
B. Hàm số có GTLN bằng 2 và GTNN bằng -3.
C. Hàm số có GTLN bằng 2 và GTNN bằng -2.
D. Hàm số có GTLN bằng 2 và không có GTNN.
Lời giải
Chọn D
Từ bảng biến thiên ta thây hàm số có GTLN bằng 2 và không có GTNN.
Câu 23: Cho hàm số
( )
fx
liên tục trên
R
và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số đã cho
trên
2;0−
là:
A.
1−
. B.
0
. C.
2
. D.
2−
.
Lời giải
Chọn C
Dựa vào đồ thị ta có
( )
2;0
2max f x
−
=
.
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ. Giá trị nhỏ nhất và giá trị lớn nhất của hàm
số trên đoạn
2;2−
lần lượt là
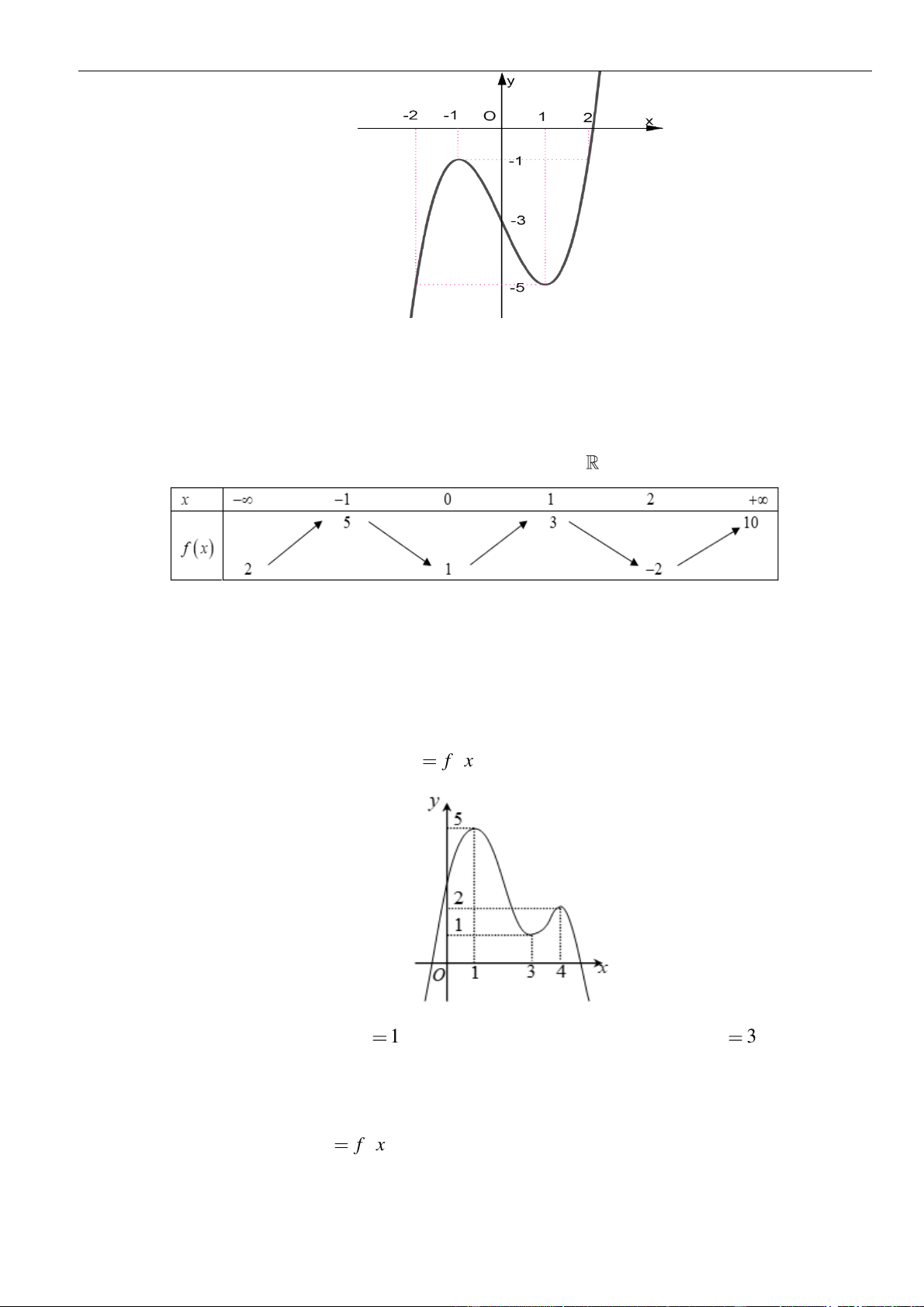
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
A.
5−
và
0
. B.
5−
và
1−
. C.
1−
và
0
. D.
2−
và
2
.
Lời giải
Chọn B
Từ đồ thị hàm số suy ra
( )
( )
2;2
2;2
min 5; max 1f x f x
−
−
= − = −
.
Câu 25: Cho hàm số
( )
y f x=
liên tục và có bảng biến thiên trên như hình vẽ bên dưới
Giá trị lớn nhất của hàm số
( )
cosy f x=
.
A.
5
. B.
3
. C.
10
. D.
1
.
Lời giải
Chọn A
Ta có
cos 1;1x−
nên giá trị lớn nhất của hàm số
( )
cosy f x=
là
5
.
Câu 26: Hình vẽ bên là đồ thị của hàm số
y f x
. Khẳng định nào sau đây đúng
A. Hàm số đạt cực tiểu tại
1x
. B. Hàm số đạt cực đại tại
3x
.
C. Giá trị lớn nhất của hàm số bằng
5
. D. Giá trị lớn nhất của hàm số bằng
3
.
Lời giải
Chọn C
Từ đồ thị của hàm số
y f x
ta có giá trị lớn nhất của hàm số bằng
5
.
Câu 27: Cho hàm số
( )
y f x=
liên tục và có đồ thị trên đoạn
2 ; 4−
như hình vẽ bên dưới.
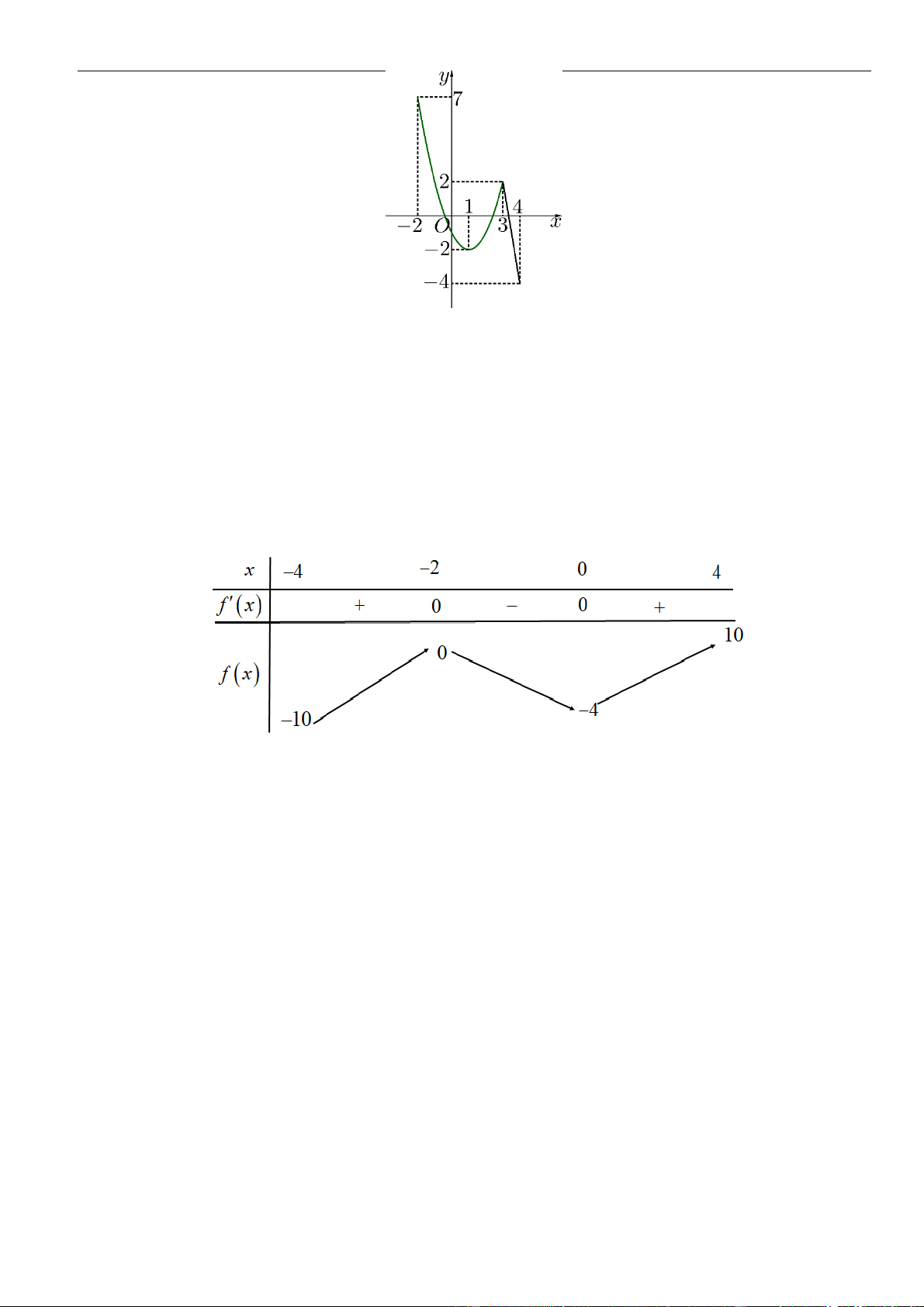
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
Tổng giá trị lớn nhất và nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2 ; 4−
bằng
A. 5. B. 3. C.
2−
. D. 0.
Lời giải
Chọn
B
Dựa vào đồ thị hàm số ta thấy
( )
2 ; 4
max 7,
x
fx
−
=
( )
2 ; 4
min 4.
x
fx
−
=−
Vậy tổng giá trị lớn nhất và nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2 ; 4−
là
( )
7 4 3.+ − =
Câu 28: Cho hàm số
()y f x=
xác định trên
( 4;4)−
có bảng biến thiên trên
( 4;4)−
như hình sau:
Phát biểu nào sau đây đúng:
A.
( 4;4)
min 4y
−
=−
và
( 4;4)
max 10y
−
=
.
B.
( 4;4)
max 10y
−
=
và
( 4;4)
min 10y
−
=−
.
C.
( 4;4)
max 0y
−
=
và
( 4;4)
min 4y
−
=−
.
D. Hàm số không có GTLN, GTNN trên
( 4;4)−
.
Lời giải
Chọn D
Dựa vào bảng biến thiên của hàm số
()y f x=
trên
( 4;4)−
ta thấy
10 ( ) 10, ( 4;4)f x x− −
.
Vậy hàm số không có GTLN, GTNN trên
( 4;4)−
.
Câu 29: Cho hàm số
( )
y f x=
liên tục trên đoạn
2;4−
và có đồ thị như hình vẽ bên. Tổng giá trị nhỏ
nhất và giá trị lớn nhất của hàm số đã cho trên
2;4−
bằng
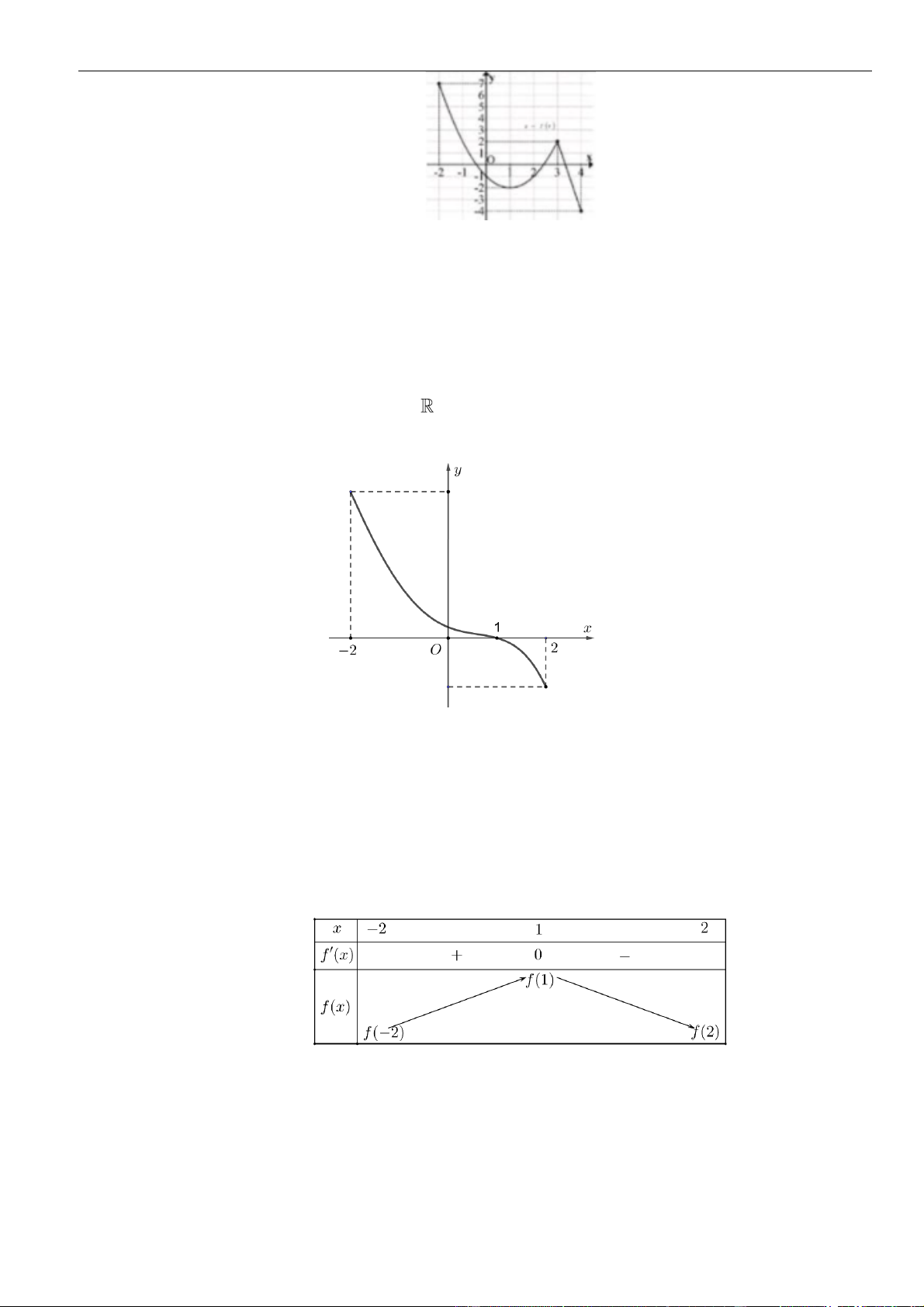
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
27 | Facebook tác giả: Phan Nhật Linh
A.
3
. B.
2−
. C.
5
. D.
0
.
Lời giải
Chọn A
Quan sát đồ thị hàm số trên đoạn
2;4−
ta thấy:
Hàm số đạt GTNN bằng
4−
tại
4x =
và đạt GTLN bằng
7
tại
2x =−
.
Vậy tổng GTNN và GTNN bằng
4 7 3− + =
.
Câu 30: Cho hàm số
( )
fx
có đạo hàm trên . Đồ thị của hàm số
( )
y f x
=
trên đoạn
2;2−
là đường
cong hình bên. Mệnh đề nào dưới đây đúng?
A.
( ) ( )
2;2
max 2f x f
−
=
. B.
( ) ( )
2;2
min 1f x f
−
=
.
C.
( ) ( )
2;2
max 1f x f
−
=
. D.
( ) ( )
2;2
max 2f x f
−
=−
.
Lời giải
Chon C
Dựa vào thị của hàm số
( )
y f x
=
trên đoạn
2;2−
ta thấy
( )
0fx
=
1x=
.
Ta có bảng BBT:
Do đó
( ) ( )
2;2
max 1f x f
−
=
.
Câu 31: Cho hàm số
( )
fx
liên tục trên
1;5−
và có đồ thị trên đoạn
1;5−
như hình vẽ bên dưới. Tổng
giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
1;5−
bằng
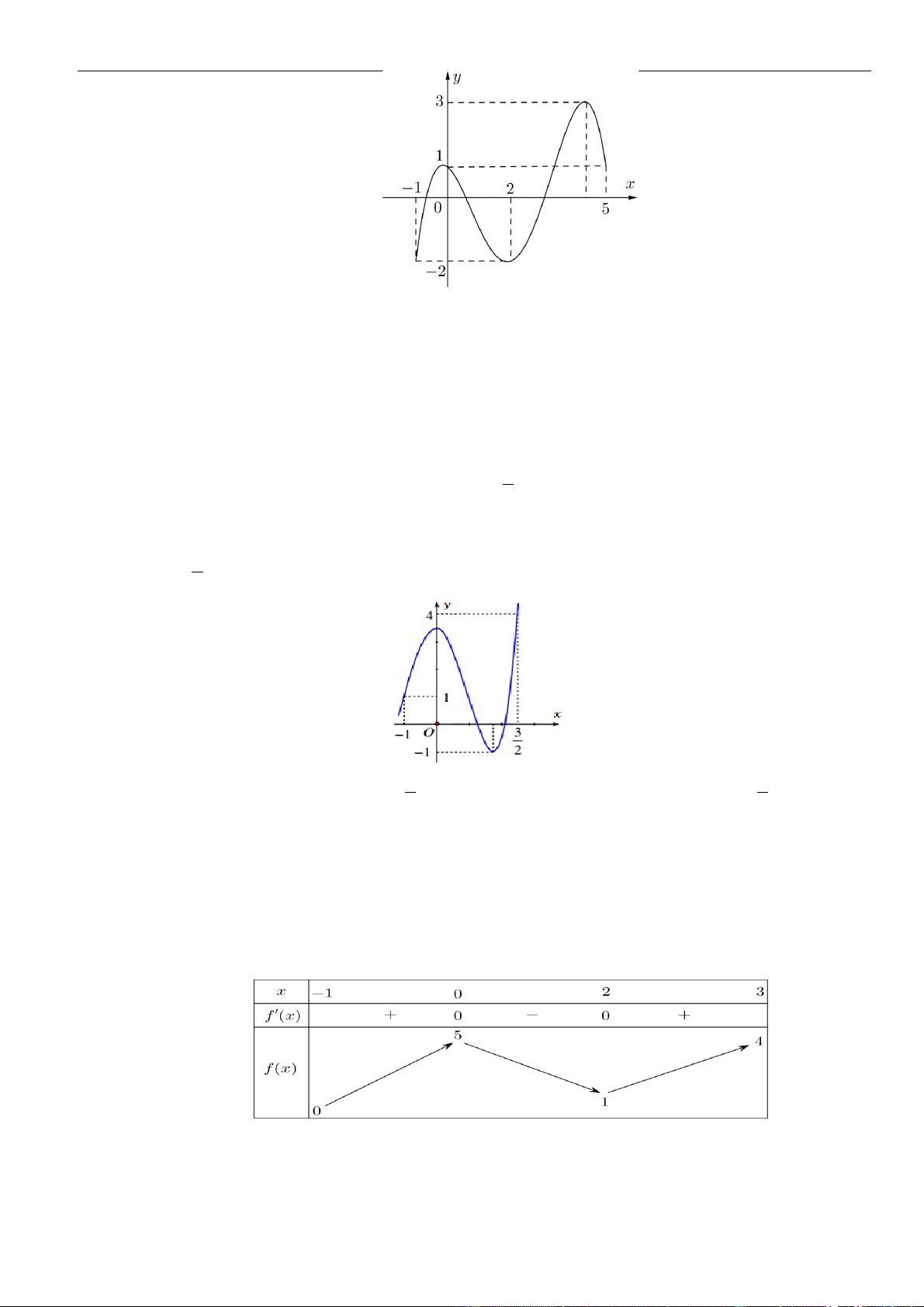
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 28
A.
1−
. B.
4
. C.
1
. D.
2
Lời giải
Chọn C
Từ đồ thị ta thấy:
( )
( )
1;5
1;5
max 3
1
min 2
M f x
Mn
n f x
−
−
==
+ =
= = −
.
Câu 32: Cho hàm số
( )
y f x=
liên tục trên đoạn
3
1;
2
−
và có đồ thị là đường cong như hình vẽ. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số của hàm số
( )
y f x=
trên đoạn
3
1;
2
−
. Khi đó,
M
và
m
lần lượt là:
A.
4; 1Mm==
. B.
3
;1
2
Mm= = −
. C.
4; 1Mm= = −
. D.
3
;1
2
Mm==
.
Lời giải
Chọn C
Dựa vào đồ thị ta thấy:
4; 1Mm= = −
.
Câu 33: Cho hàm số
( )
y f x=
liên tục và có bảng biến thiên trên đoạn
1;3−
như hình vẽ. Gọi
M
là
giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;3−
. Tìm mệnh đề đúng?
A.
( )
2Mf=
. B.
( )
3Mf=
. C.
( )
0Mf=
. D.
( )
1Mf=−
.
Lời giải
Chọn C
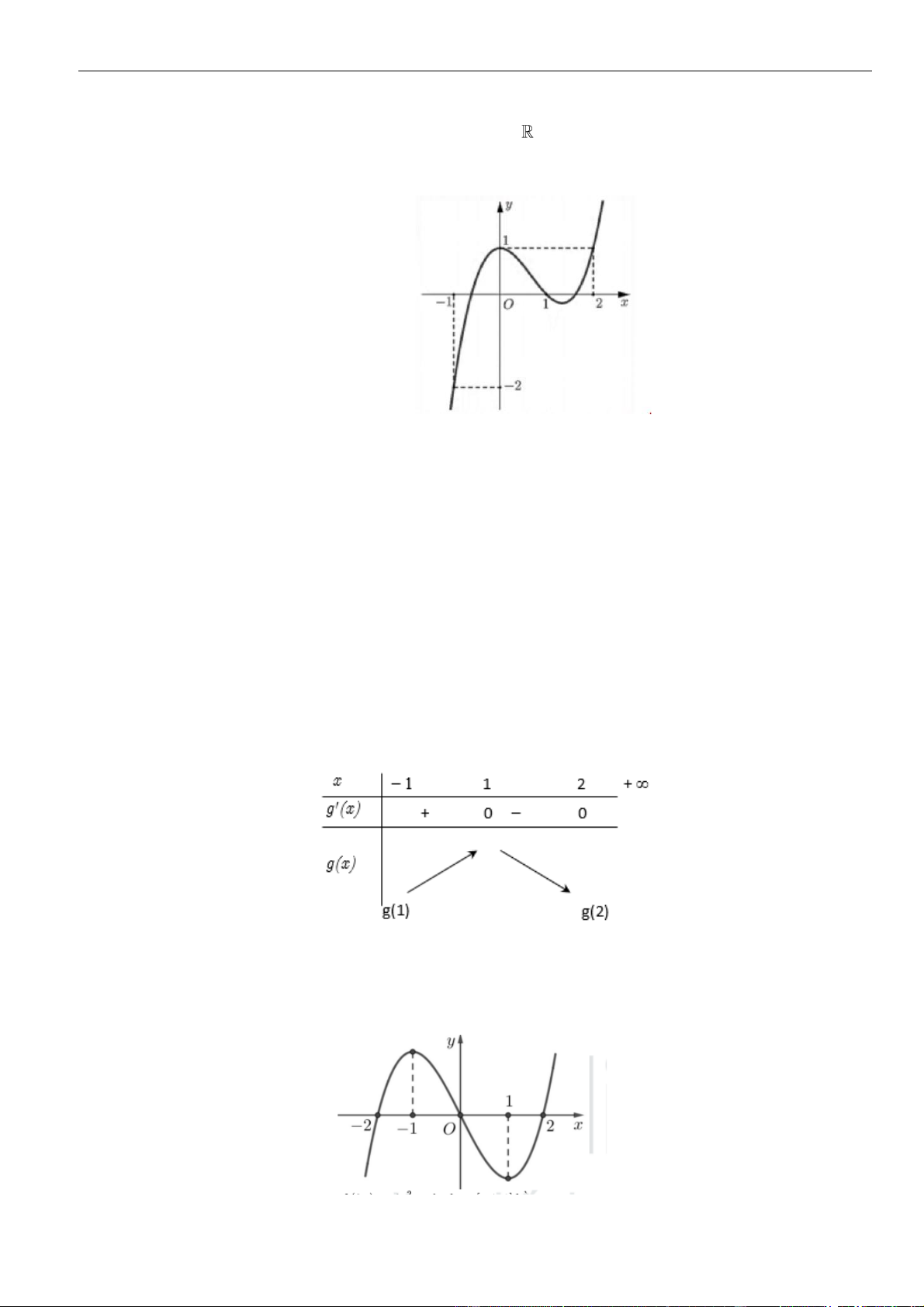
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
29 | Facebook tác giả: Phan Nhật Linh
Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
1;3−
là
( )
0Mf=
.
Câu 34: Cho hàm số
( )
y f x=
có đạo hàm liên tục trên , đồ thị của hàm số
( )
'y f x=
như hình vẽ
bên.
Giá trị nhỏ nhất của hàm số
( ) ( ) ( )
2
21g x f x x= − −
trên đoạn
1;2−
bằng:
A.
( )
2 0 1f −
B.
( )
2 1 4.f −−
. C.
( )
2 1 .f
. D.
( )
2 2 1.f −
Lời giải
Chọn B
Có:
( ) ( ) ( )
( ) ( )
' 2 ' 2 1
1
' 0 ' 1 1
2
g x f x x
x
g x f x x x
x
= − −
=−
= = − =
=
Bảng biến thiên:
( ) ( ) ( ) ( ) ( ) ( )
12
' 1 1 2 1 2 1S S g g g g g g − − − + −
( ) ( ) ( )
1 2 1 4Min g x g f = − = − −
.
Câu 35: Cho hàm số
( )
fx
có đồ thị của đạo hàm như sau:
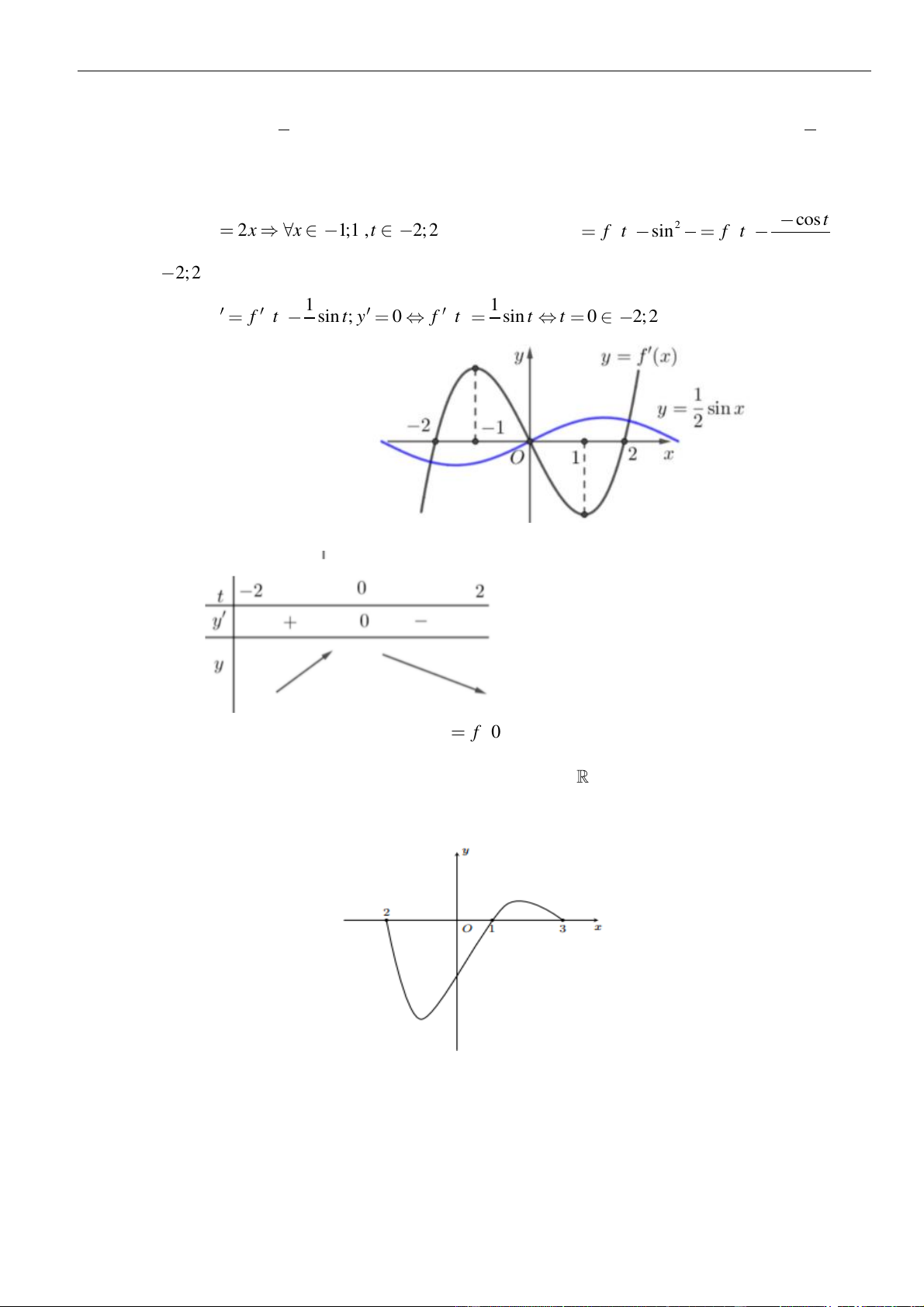
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 30
Giá trị lớn nhất của hàm số
( ) ( )
2
2 sing x f x x=−
trên đoạn
1;1−
bằng
A.
( )
2
1
1 sin
2
f −−
. B.
( )
2
2 sin 1f −
. C.
( )
0f
. D.
( )
2
1
1 sin
2
f −
.
Lời giải
Chọn C
Đặt
2 1;1 , 2;2t x x t
. Ta xét hàm số
2
1 cos
sin
22
tt
y f t f t
trên
2;2
.
Ta có:
11
sin ; 0 sin 0 2;2
22
y f t t y f t t t
.
Bảng biến thiên:
Vậy giá trị lớn nhất của hàm số là
00yf
.
Câu 36: Cho hàm số
( )
y f x=
có đạo hàm
( )
'fx
liên tục trên và hàm số
( )
'y f x=
có đồ thị trên
đoạn
2;3−
như hình vẽ bên dưới.
Gọi
M
là giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2;3−
. Khi
đó
;Mm
lần lượt là
A.
( ) ( )
2 ; 1M f m f= − =
. B.
( ) ( )
3 ; 1M f m f==
.
C.
( ) ( )
1 ; 2M f m f= = −
. D.
( ) ( )
3 ; 2M f m f= = −
.
Lời giải
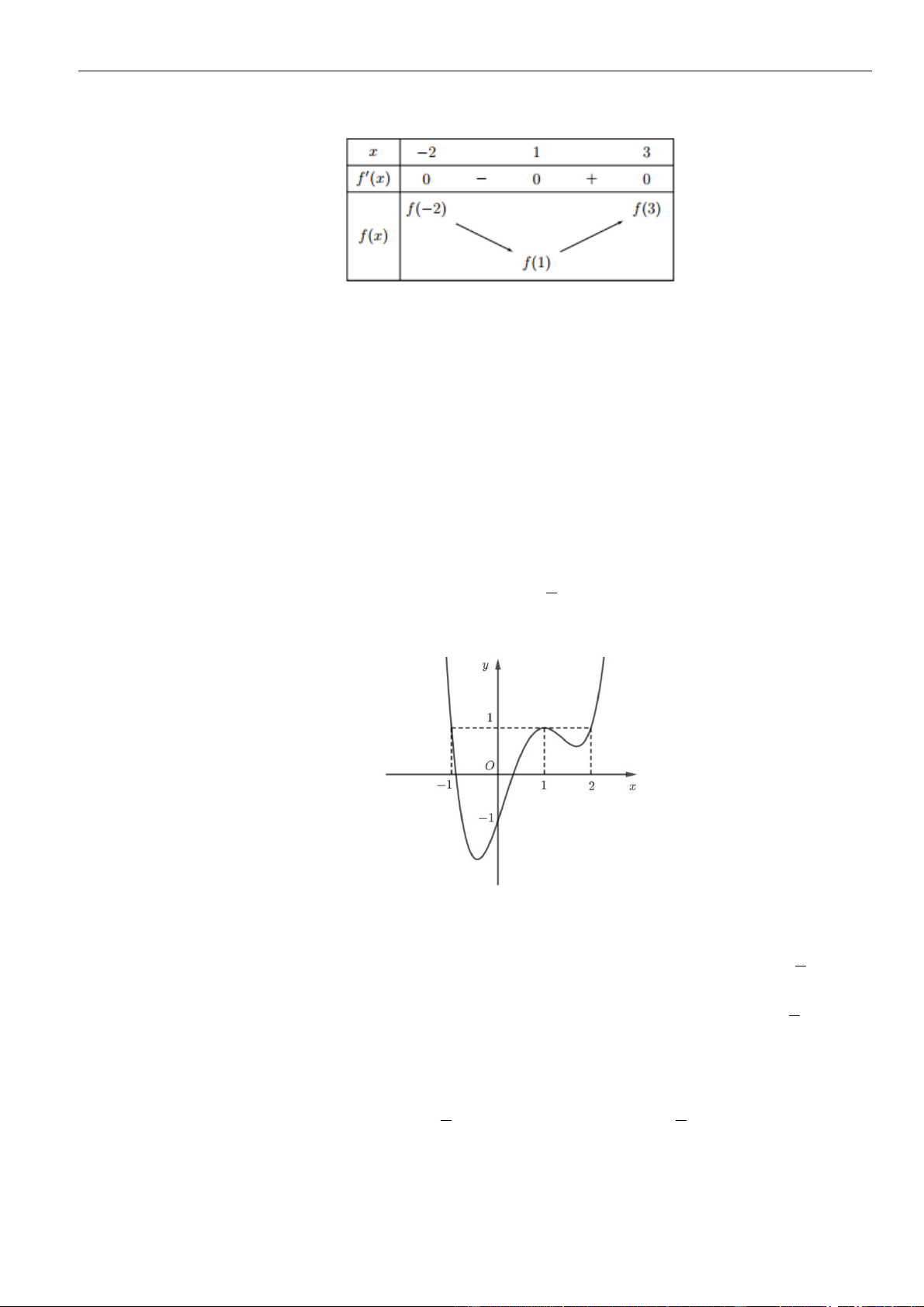
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
31 | Facebook tác giả: Phan Nhật Linh
Chọn A
Từ đồ thị hàm số
( )
'y f x=
ta suy ra bảng biến thiên như sau
Từ bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số đã cho trên đoạn
2;3−
bằng
( )
1f
. Mặt
khác, cũng từ đồ thị hàm số
( )
'y f x=
ta suy ra diện tích của hình phẳng giới hạn bởi đồ thị hàm
số
( )
'y f x=
với trục hoành trên đoạn
2;1−
lớn hơn diện tích của hình phẳng giới hạn bởi đồ
thị hàm số
( )
'y f x=
với trục hoành trên đoạn
1;3
, do đó chúng ta có
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
13
21
' ' 2 1 3 1 2 3f x dx f x dx f f f f f f
−
− − − − −
.
Vậy giá trị lớn nhất là
( )
2f −
. Vậy
( ) ( )
2 ; 1M f m f= − =
.
Câu 37: Cho hàm số
( )
fx
, đồ thị của hàm số
( )
y f x
=
là đường cong trong hình bên. Giá trị nhỏ nhất
của hàm số
( ) ( )
2 2 2021g x f x x= − +
trên đoạn
1
;1
2
−
bằng
A.
( )
2 2019.f +
B.
( )
1 2022.f −+
C.
( )
0 2021.f +
D.
( )
1 2020.f +
Lời giải
Chọn A
Ta có
( ) ( )
2. 2 2g x f x
=−
;
( ) ( )
1
2
21
1
0 2 1 2 1
2
22
1
x
x
g x f x x x
x
x
=−
=−
= = = =
=
=
Trong đó các nghiệm
1
2
x =−
và
1x =
là nghiệm đơn,
1
2
x =
là nghiệm kép.
( ) ( )
0 2 0 2 4 0gf
= − = −
nên ta có BBT của hàm
( )
gx
như sau:
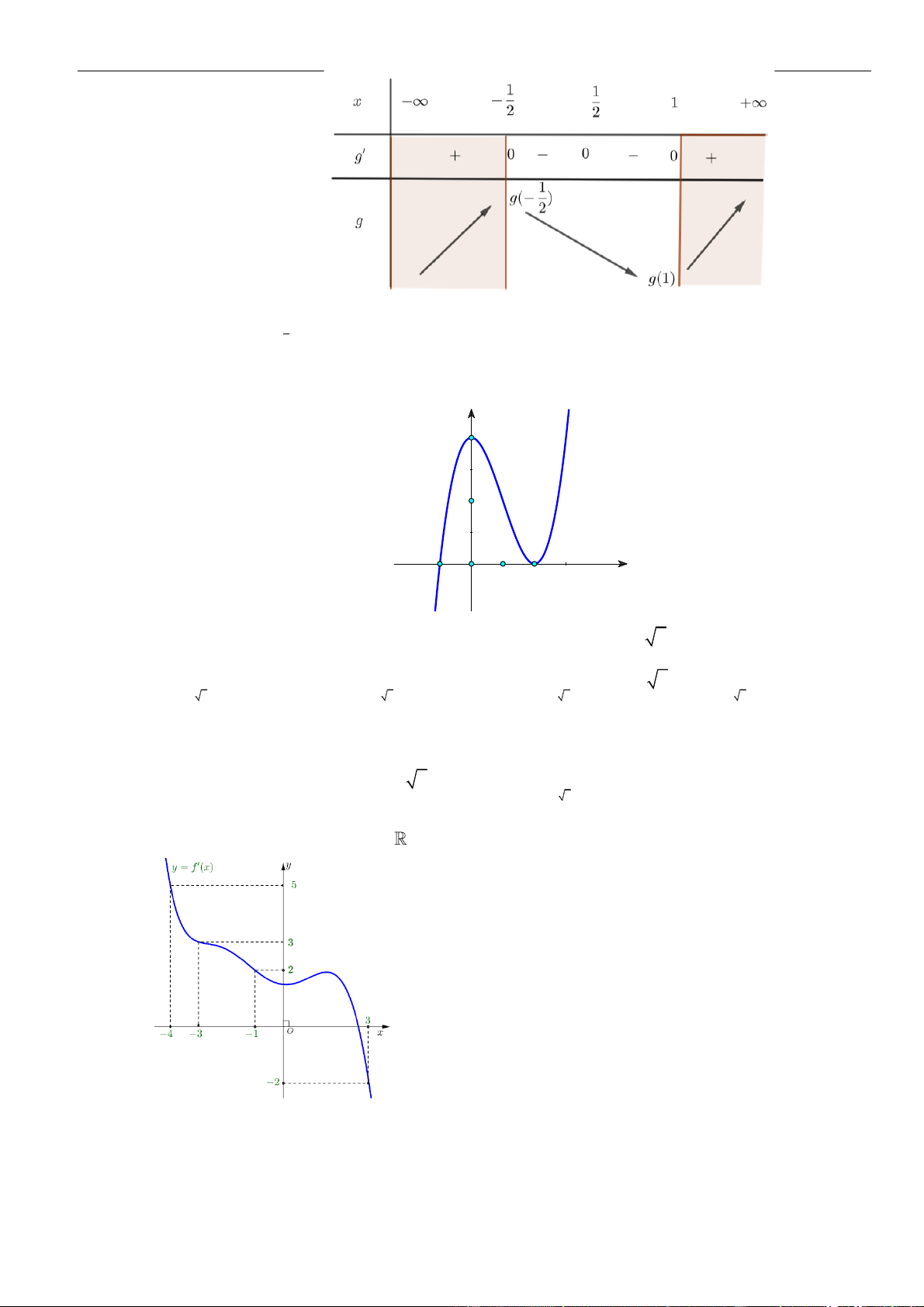
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 32
Vậy
( ) ( ) ( )
1
;1
2
Min 1 2 2019.g x g f
−
= = +
Câu 38: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên dưới:
Khi đó, giá trị lớn nhất của hàm số
( )
( )
2
2g x f x=−
trên đoạn
0; 2
là
A.
( ) ( )
=
0; 2
max 0g x f
. B.
( ) ( )
=
0; 2
max 1g x f
. C.
( )
( )
=
0; 2
max 2g x f
. D.
( ) ( )
=
0; 2
max 2g x f
.
Lời giải
Chọn A
Đặt
( ) ( ) ( )
2
0;2
0; 2
2 ; 2 0, 0; 2 0; 2 max max 0 .t x t x x t g x f t f
= − = − = =
Câu 39: Cho hàm số
( )
fx
liên tục trên và có đồ thị của đạo hàm
( )
y f x
=
như hình dưới đây.
Trên đoạn
3;4−
, hàm số
( ) ( ) ( )
2
21g x f x x= + −
đạt giá trị nhỏ nhất tại điểm nào trong các
điểm sau đây?
A.
0
4x =−
. B.
0
3x =
. C.
0
1x =−
. D.
0
3x =−
.
Lời giải
x
y
4
-1
2
2
O
1
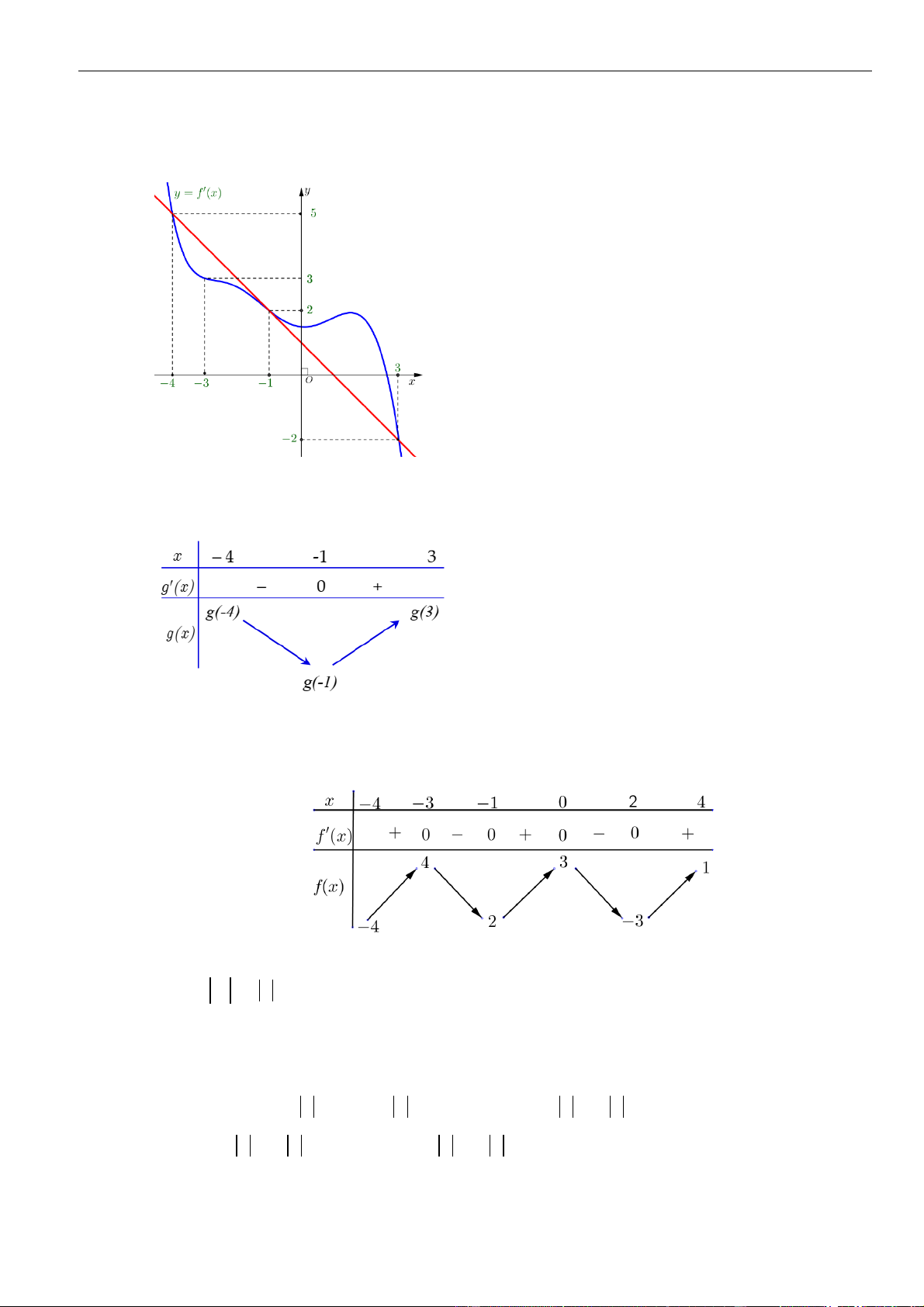
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
33 | Facebook tác giả: Phan Nhật Linh
Chọn C
Xét hàm
( ) ( ) ( )
2
21g x f x x= + −
trên đoạn
3;4−
.
( ) ( ) ( ) ( ) ( )
( )
2 2 1 2 1g x f x x f x x
= − − = − −
,
( ) ( )
01g x f x x
= = −
Đồ thị hàm
( )
y f x
=
và
1yx=−
cắt nhau tại các điểm có hoành độ
4; 1; 3x x x= − = − =
.
Bảng biến thiên:
Vậy giá trị nhỏ nhất của hàm
( ) ( ) ( )
2
21g x f x x= + −
trên đoạn
3;4−
đạt được tại
0
1x =−
.
Câu 40: Cho hàm số
( )
y f x=
có bảng biến thiên trên đoạn
4;4−
như hình vẽ.
Có bao nhiêu giá trị của tham số
m
trên đoạn
4;4−
sao cho giá trị lớn nhất của hàm số
( )
( )
3
3y f x x f m= + +
trên đoạn
1;1−
bằng
1
?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn B
Ta có
3
1;1 0;1 0;1x x x −
. Suy ra
3
3 0;4t x x= +
.
Khi đó
( )
3
3 3;3f x x+ −
hay
( )
3
3 ( ) 3 ( );3 ( )f x x f m f m f m+ + − + +
.
YCBT
3 ( ) 1 ( ) 2f m f m+ = = −
.
Nhìn vào bảng biến thiên, ta thấy phương trình
( ) 2fm=−
có ba nghiệm.
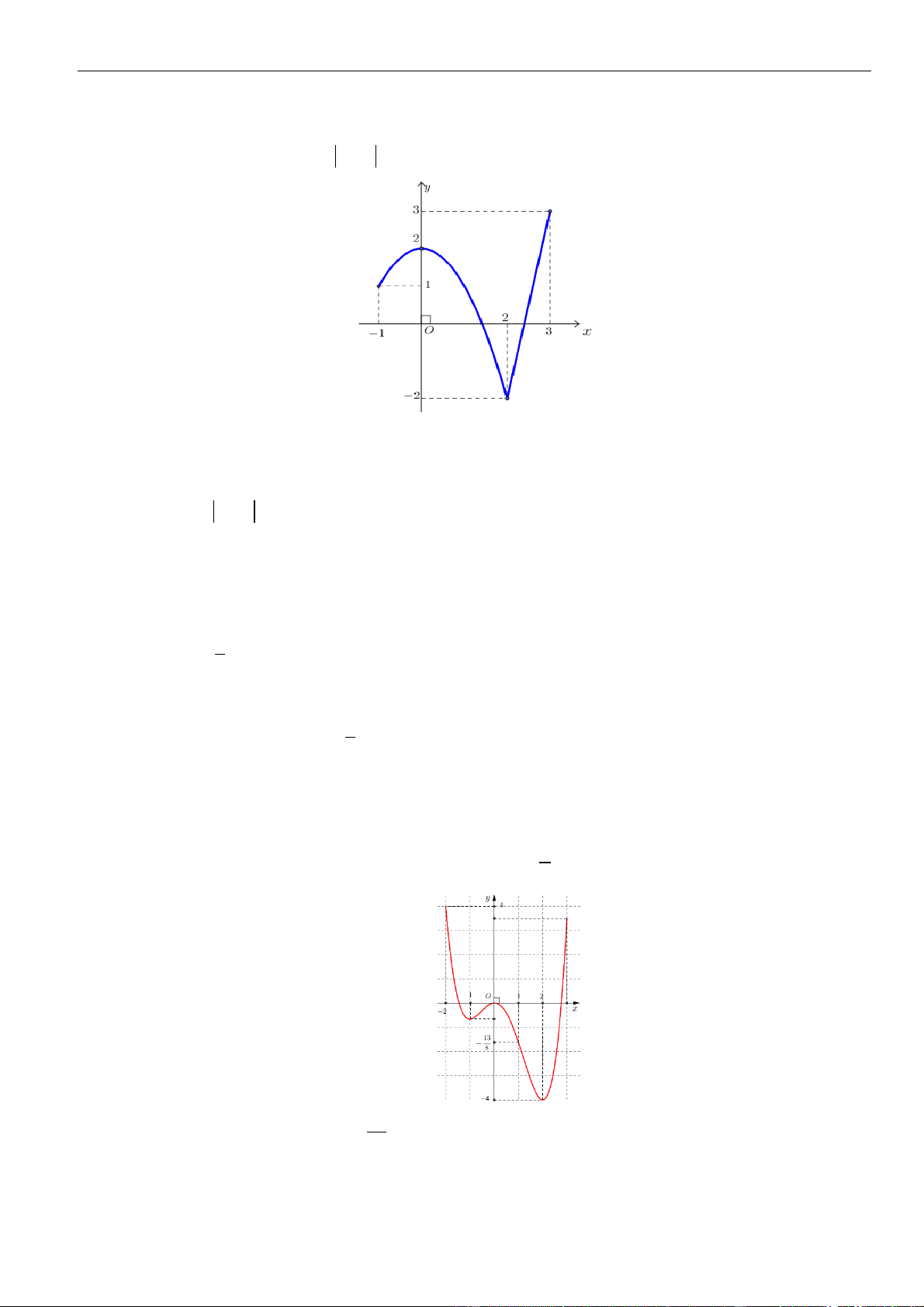
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 34
Vậy có 3 giá trị của
m
thỏa đề.
Câu 41: Cho hàm số
( )
fx
liên tục trên đoạn
1;3−
và có đồ thị như hình vẽ bên. Giá trị lớn nhất của
hàm số
( )
( )
3 cos 1y g x f x= = −
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn B
Đặt
costx=
, với
x
1;3 cos3 cos 1 0 1x x t −
.
Xét hàm số
( ) ( )
31g t f t=−
trên
0 ;1
, ta có:
+)
( ) ( )
3 1 0
3 3 1 0
3 1 2
t
g t f t
t
−=
= − =
−=
1
3
1
t
t
=
=
.
+)
( ) ( )
0 1 1gf= − =
,
( )
1
02
3
gf
==
,
( ) ( )
1 2 2gf= = −
.
Vậy giá trị lớn nhất cần tìm là
2
.
Câu 42: Cho hàm số
( )
y f x=
có đồ thị như hình bên dưới. Gọi
,mM
lần lượt là giá trị nhỏ nhất và giá
trị lớn nhất của hàm số
( )
2y f x=−
trên đoạn
1
1;
2
−
. Giá trị của
23mM+
là
A. 0. B.
35
4
. C. 4. D.
8−
.
Lời giải
Chọn D
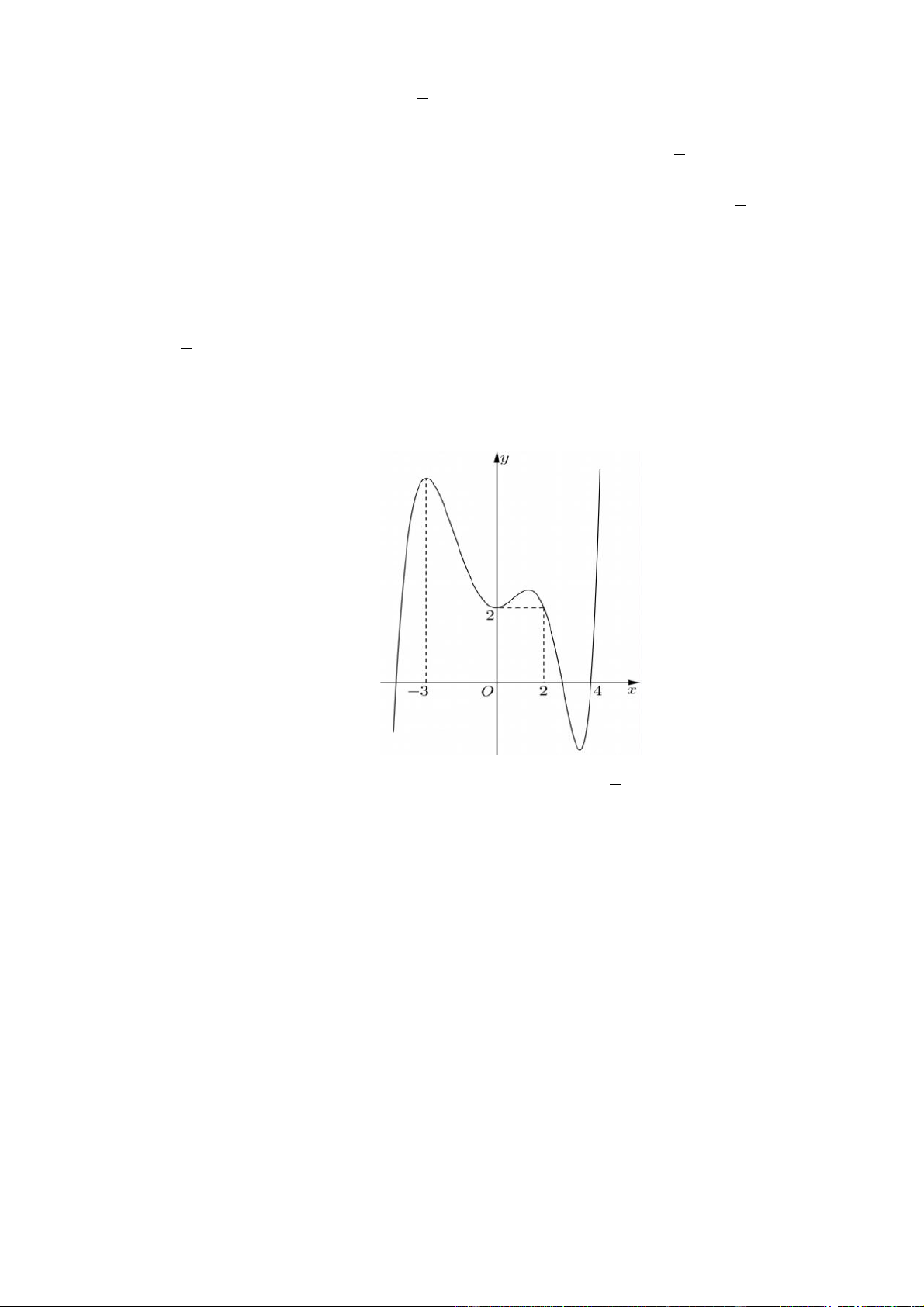
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
35 | Facebook tác giả: Phan Nhật Linh
Xét
( ) ( )
2g x f x=−
trên đoạn
1
1;
2
−
( ) ( )
' 2 ' 2g x f x= − −
,
( ) ( )
1
2
21
1
' 0 ' 2 0 2 0 0 1;
2
22
1
x
x
g x f x x x
x
x
=
− = −
= − = − = = −
−=
=−
Dựa vào đồ thị
( )
y f x=
ta tính được
( ) ( ) ( ) ( )
1 2 4, 0 0 0g f g f− = = − = =
( )
1
1
2
gf
=−
với
( )
4 1 0f− −
.
Vậy
4, 0 2 3 8m M m M= − = + = −
.
Câu 43: Cho hàm số
( )
fx
, đồ thị của hàm số
( )
y f x
=
là đường cong trong hình bên.
Giá trị lớn nhất của hàm số
( ) ( )
24g x f x x=−
trên đoạn
3
;2
2
−
bằng
A.
( )
0f
. B.
( )
36f −+
. C.
( )
24f −
. D.
( )
48f −
.
Lời giải
Chọn C
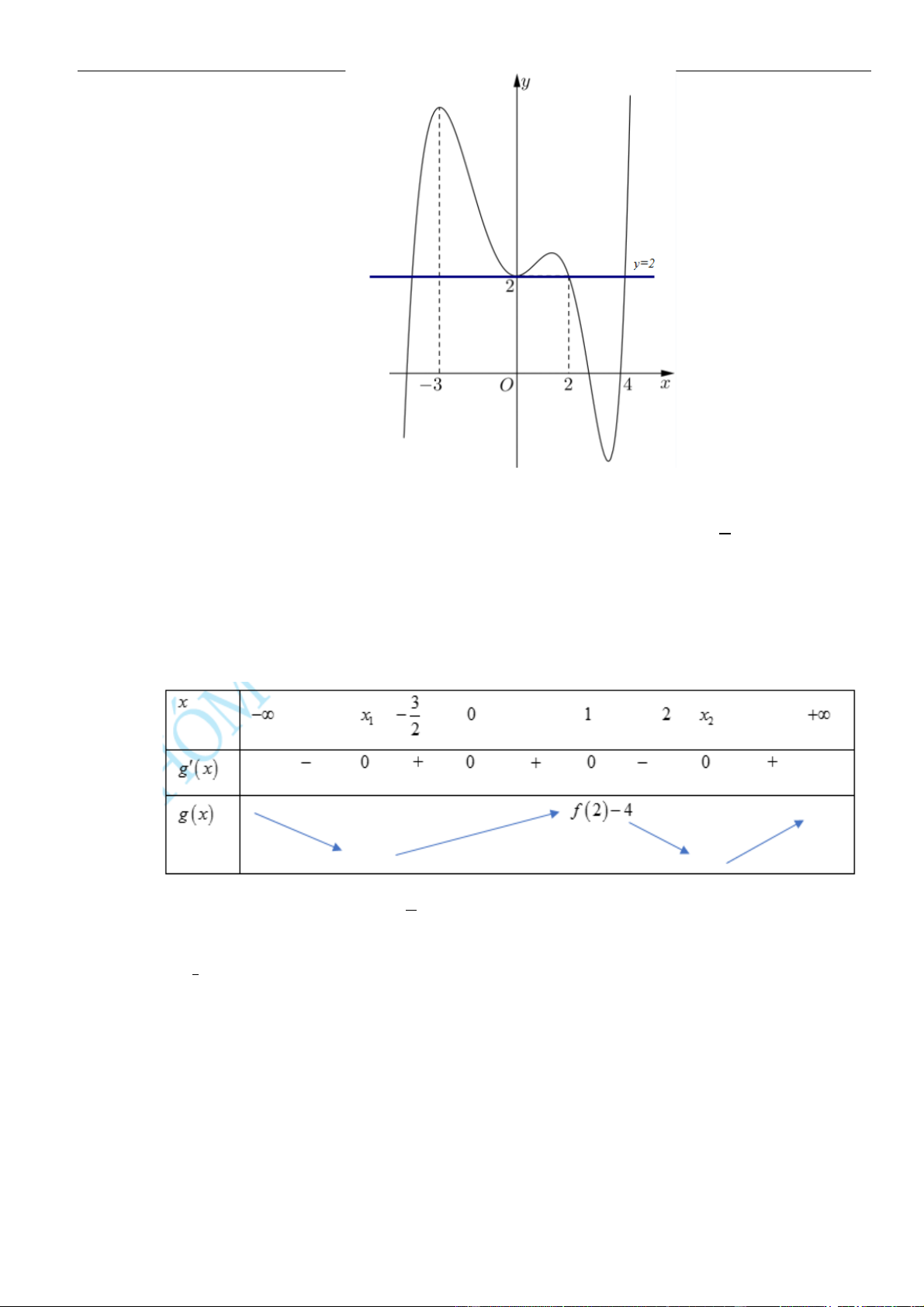
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 36
Ta có:
( ) ( )
2 2 4g x f x
=−
.
( ) ( ) ( )
1
1
2
2
3
23
2
20
0
0 2 2 4 0 2 2
22
1
24
2
xx
xx
x
x
g x f x f x
x
x
xx
x
= −
= −
=
=
= − = =
=
=
=
Ta có bảng biến thiên của hàm số
( )
y g x=
:
Từ bảng biến thiên ta có: trên
3
;2
2
−
hàm số
( ) ( )
24g x f x x=−
đạt giá trị lớn nhất tại
1x =
và
( )
3
;1
2
max 2 4yf
−
=−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
37 | Facebook tác giả: Phan Nhật Linh

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
1
xm
y
x
+
=
+
thỏa mãn
1;2 1;2
9
min max
2
yy+=
.Mệnh đề nào dưới đây đúng
A.
02m
. B.
0m
. C.
4m
. D.
24m
.
Câu 2: Gọi
S
là tập tất cả các giá trị thực của tham số m để hàm số
3 2 2
( ) 3 5f x x x m= + + −
có giá trị
lớn nhất trên
1,2−
bằng
19
. Tính tổng tất cả các phần tử của
S
.
A.
2−
. B.
2
. C.
4
. D.
0
.
Câu 3: Biết giá trị lớn nhất của hàm số
2
2
xm
y
x
+
=
−
trên đoạn
1;1−
bằng
1.−
Khẳng định nào dưới
đây đúng?
A.
( )
1;0 .m−
. B.
( )
4;3 .m−
. C.
( )
4;6 .m
. D.
( )
0;1 .m
Câu 4: Cho hàm số
1
xm
y
x
+
=
−
thỏa mãn
2;4
min 3y =
. Mệnh đề nào dưới đây là đúng?
A.
3 4.m
B.
1 3.m
C.
4.m
D.
1.m −
Câu 5: Cho hàm số
32
23y x x m= − −
. Trên
1;1−
hàm số có giá trị nhỏ nhất là
1−
. Tìm
m
.
A.
5m =−
. B.
3m =−
. C.
6m =−
. D.
4m =−
.
Câu 6: Biết
32
3;0
1
min 2
3
x x x m
−
− + − + =
, giá trị của
m
bằng
A. . B.
23
. C.
2
. D.
19−
.
Câu 7: Tìm tất cả các giá trị thực của
m
để giá trị nhỏ nhất của hàm số
( )
32
3f x x x m= − − +
trên đoạn
1;1−
bằng
0.
A.
4m =
. B.
0m =
. C.
6m =
. D.
2m =
.
Câu 8: Cho hàm số
3
(x) x 3
m
f x e= − +
, với m là tham số thực. Biết rằng giá trị nhỏ nhất của hàm số đã
cho trên [0;2] bằng 0; khi đó, giá trị lớn nhất của hàm số đã cho bằng
A.
5
. B.
6
. C.
2
. D.
4
.
2−
Tìm m để hàm số có GTLN-GTNN thỏa mãn điều kiện
DẠNG 3
Phương pháp:
• Bước 1. Tìm nghiệm
( 1,2,...)
i
xi=
của
0y
=
thuộc
;ab
• Bước 2. Tính các giá trị
( ) ( ) ( )
;;
i
f x f a f b
theo tham số
• Bước 3. So sánh các giá trị, suy ra giá trị lớn nhất, giá trị nhỏ nhất.
• Bước 4. Biện luận
m
theo giả thiết đề để kết luận bài toán.
Chú ý:
• Hàm số
( )
y f x=
đồng biến trên đoạn
;ab
thì
( ) ( )
( ) ( )
;;
;
a b a b
Max f x f b Min f x f a==
• Hàm số
( )
y f x=
nghịch biến trên đoạn
;ab
thì
( ) ( )
( ) ( )
;;
;
a b a b
Max f x f a Min f x f b==
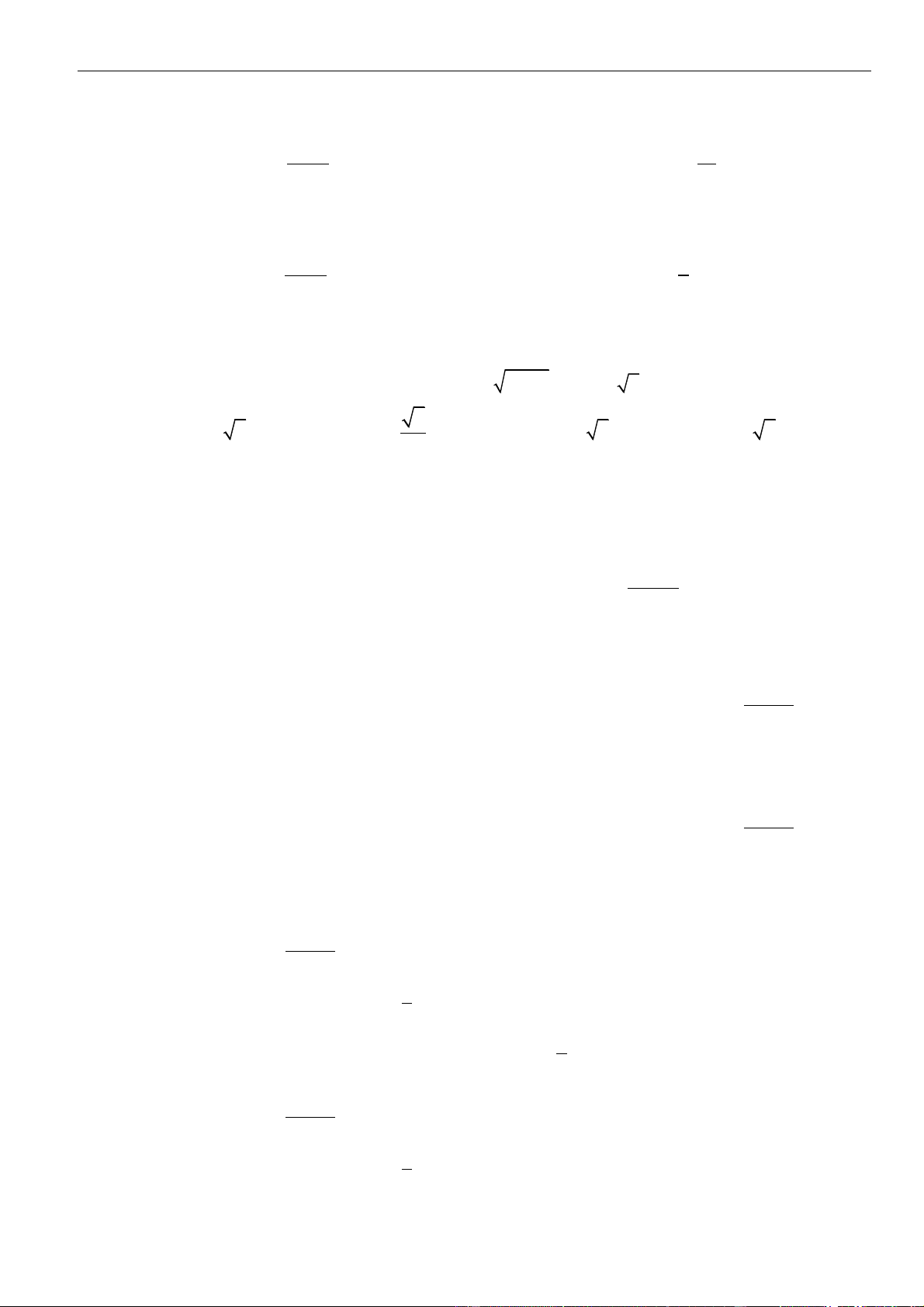
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 9: Cho hàm số
32
23y x x m= − −
. Trên
1;1−
hàm số có giá trị nhỏ nhất là
1−
. Tìm
m
.
A.
5m =−
. B.
3m =−
. C.
6m =−
. D.
4m =−
.
Câu 10: Cho hàm số
1
xm
y
x
+
=
+
(
m
là tham số thực) thỏa mãn
1;2
1;2
16
min
3
y max y+=
. Mệnh đề nào dưới
đây đúng?
A.
4m
. B.
02m
. C.
24m
. D.
0m
.
Câu 11: Cho hàm số
1
xm
y
x
+
=
+
(
m
là tham số thực) thỏa mãn
1;2
1;2
9
min max
2
yy+=
. Mệnh đề nào dưới đây
đúng?
A.
02m
. B.
0m
. C.
4m
. D.
24m
.
Câu 12: Biết rằng giá trị lớn nhất của hàm số
2
4y x x m= + − +
là
32
. Giá trị của
m
là:
A.
22m =
. B.
2
2
m =
. C.
2m =−
. D.
2m =
.
Câu 13: Biết giá trị lớn nhất của hàm số
32
23y x x m= − + +
trên đoạn
0;2
bằng 5, tìm giá trị của tham
số
m
.
A. 5. B. 6. C. 3. D. 4.
Câu 14: Tìm giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
xm
y
x
+
=
+
trên đoạn
0;4
bằng
5
.
A.
7m =
. B.
21m=
. C.
17m =
. D.
5m=
.
Câu 15: Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
xm
y
x
−
=
+
trên đoạn
1;5
bằng
4−
. Tính tổng các phần tử của
S
.
A.
0
B.
5
C.
5−
D.
10
Câu 16: Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
xm
y
x
−
=
+
trên đoạn
1;5
bằng
4−
. Tính tổng các phần tử của
S
.
A.
0
B.
5
C.
5−
D.
10
Câu 17: Cho hàm số
2
,
2
xm
ym
x
−
=
+
là tham số. Tích tất cả các giá trị của
m
để giá trị lớn nhất của hàm
số đã cho trên đoạn
1;1−
bằng
1
4
là
A. Không tồn tại. B.
1.−
C.
1
.
4
−
D.
4.−
Câu 18: Cho hàm số
2
,
2
xm
ym
x
−
=
+
là tham số. Tích tất cả các giá trị của
m
để giá trị lớn nhất của hàm
số đã cho trên đoạn
1;1−
bằng
1
4
là
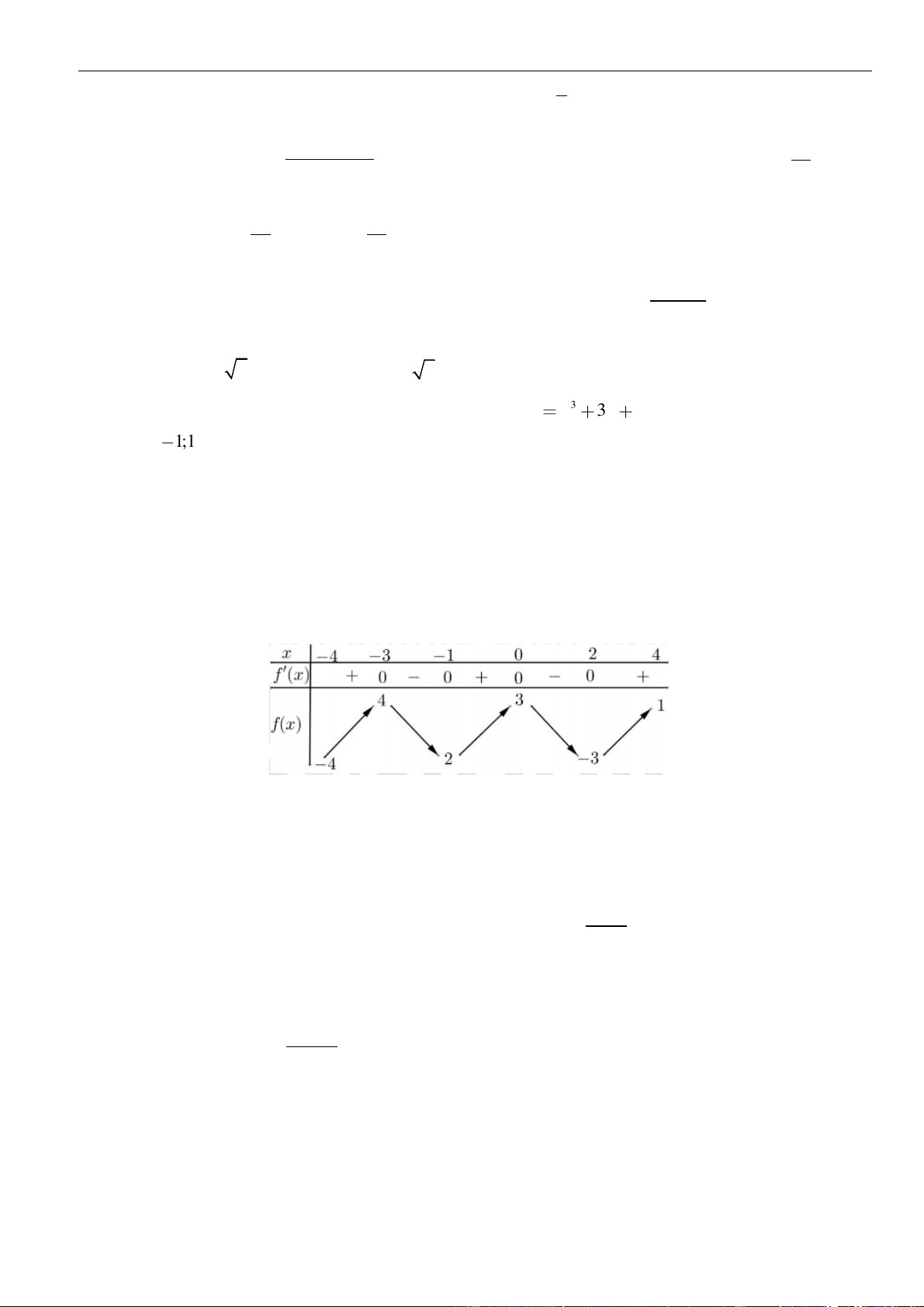
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A. Không tồn tại. B.
1.−
C.
1
.
4
−
D.
4.−
Câu 19: Cho hàm số
2
2
1
mx m
y
x
−−
=
−+
với
m
là tham số thực lớn hơn
3−
thỏa mãn
4; 2
1
max
3
−−
−
=y
. Mệnh
đề nào sau dưới đây đúng?
A.
1
3
2
m
−
−
. B.
1
0
2
m
−
. C.
4m
. D.
13m
.
Câu 20: Tìm giá trị âm của tham số
m
để giá trị lớn nhất của hàm số
2
1
2
mx
y
x
−
=
+
trên đoạn
1;3
bằng
1
.
A.
2m =−
. B.
3m =−
. C.
4m =−
. D.
2m =−
.
Câu 21: Tìm tất cả các giá trị của tham số
m
để hàm số
3
3y x x m
có giá trị lớn nhất trên đoạn
1;1
bằng
8
.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 22: Có bao nhiêu số thực dương
m
để giá trị lớn nhất của hàm số
3
31y x x= − +
trên đoạn
1; 2mm++
bằng
53
.
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 23: Cho hàm số
( )
fx
liên tục trên đoạn
4;4
−
và có bảng biến thiên như hình vẽ bên:
Có bao nhiêu số thực
4;4m
−
để giá trị lớn nhất của hàm số
( )
( )
( )
3
32g x f x x f m= − + +
trên đoạn
1;1
−
bằng
1
.
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 24: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
xm
y
x
+
=
+
trên đoạn
1;2
bằng
8
. Giá trị
của
m
thỏa mãn điều kiện trên thuộc tập hợp nào sau đây?
A.
( )
0;4 .
B.
( )
8;10 .
C.
( )
4;8 .
D.
( )
10; .+
Câu 25: Cho hàm số
2
4
xm
y
x
+
=
−
(
m
là tham số thực) thỏa mãn
0;2
max 3y =
. Mệnh đề nào dưới đây đúng
A.
11m −
B.
12m =−
C.
8m −
D.
8m −
Câu 26: Cho hàm số
32
23y x x m= − −
. Trên
[ 1;1]−
hàm số có giá trị nhỏ nhất là
1−
. Tìm
m
.
A.
5m =−
. B.
3m =−
. C.
6m =−
. D.
4m =−
.
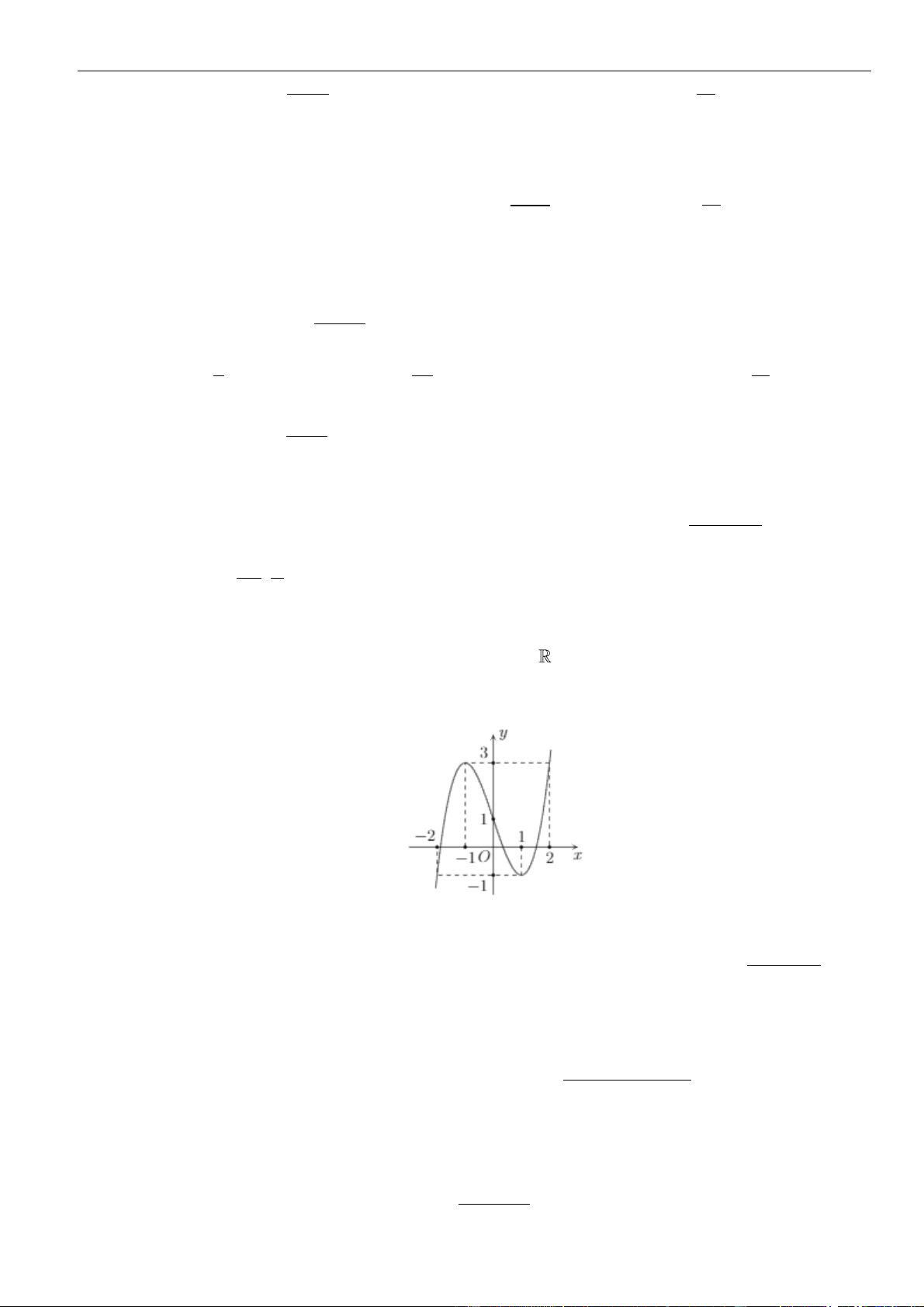
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 27: Cho hàm số
1
xm
y
x
+
=
+
(
m
là tham số thực) thỏa mãn
1;2
1;2
16
min max
3
yy+=
. Mệnh đề nào dưới
đây đúng?
A.
0m
. B.
24m
. C.
4m
. D.
02m
.
Câu 28: Biết rằng tồn tại tham số thực
m
để hàm số
1
xm
y
x
+
=
+
có
1;2
1;2
16
min max .
3
yy
+=
Mệnh đề nào dưới
đây đúng?
A.
(
2; 4m
. B.
(
0; 2m
. C.
( )
+4;m
. D.
(
−
;0m
.
Câu 29: Cho hàm số
( )
2
3
xm
fx
x
+
=
−
. Giá trị của
m
để
( )
( )
1;2
1;2
max min 8f x f x
−
−
+=
là
A.
4
5
m =
. B.
46
5
m =−
. C.
12m =−
. D.
18
5
m =
.
Câu 30: Cho hàm số
1
xm
y
x
+
=
−
thỏa mãn
2;4
min 3y =
. Mệnh đề nào sau đây là đúng?
A.
34m
. B.
13m
. C.
4m
. D.
1m −
.
Câu 31: Gọi S là tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
cos
2 sx
xm
y
co
+
=
−
có giá trị lớn
nhất trên
;
23
−
bằng 1. Số phần tử của S là:
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 32: Cho hàm số bậc ba
( )
y f x=
có đạo hàm trên và có đồ thị như hình vẽ. Xét hàm số
( )
( )
3
21g x f x x m= + − +
. Tìm
m
để
( )
0;1
max 10gx=−
.
A.
3m =
. B.
13m =−
. C.
1m =−
. D.
9m =−
.
Câu 33: Có bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
sin 1
cos 2
mx
y
x
+
=
+
nhỏ
hơn
2
?
A.
5
. B.
3
. C.
4
. D.
6
.
Câu 34: Gọi
S
là tập hợp các giá trị tham số
m
để hàm số
2
22mx m m
y
xm
+ + −
=
+
có giá trị nhỏ nhất trên
đoạn
1;4
bằng
1
. Tổng các phần tử của
S
bằng.
A.
2−
. B.
1
. C.
0
. D.
3−
.
Câu 35: Số các giá trị tham số
m
để hàm số
2
1xm
y
xm
−−
=
−
có giá trị lớn nhất trên
0;4
bằng
6−
là :

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 36: Cho hàm số
2
1
xm
y
x
+
=
+
. Biết
min 2y =−
. Mệnh đề nào dưới đây đúng?
A.
2m −
. B.
02m
. C.
2m
. D.
20m−
.
Câu 37: Hàm số
2
1
xm
y
x
−
=
+
đạt giá trị lớn nhất trên đoạn
0;1
bằng
1
khi
A.
0m =
. B.
2m =
. C.
1m =−
. D.
1m =
.
Câu 38: Cho hàm số
2
2
xm
y
x
−
=
+
với
m
là tham số,
4m −
. Biết
( )
( )
0;2
0;2
min max 8f x f x+ = −
. Giá trị
của tham số
m
bằng
A.
9
. B.
12
. C.
10
. D.
8
.
Câu 39: Biết rằng giá trị nhỏ nhất của hàm số
5
()
mx
fx
xm
+
=
−
trên đoạn
0;1
bằng −7. Mệnh đề nào sau
đây đúng.
A.
11m−
. B.
01m
. C.
02m
. D.
10m−
.
Câu 40: Số các giá trị nguyên của tham số
m
để hàm số
32
1
3 2 7
3
y x x x m= − − + +
có giá trị nhỏ nhất
trên đoạn [2; 4] thuộc khoảng
( 5;8)−
là
A. 12. B. 3. C. 7. D. 6.
Câu 41:
Vậy có 6 số nguyên cần tìm.
Cho hàm số
3 2 2
( ) 3 2f x x x m m= − + −
. Gọi
S
tập hợp tất cả các
giá trị nguyên của tham số
m
thỏa mãn
3;1
3;1
3max (| |) 2min (| |) 112f x f x
−
−
+
. Số phần tử của S
bằng
A.
12
. B.
10
. C.
11
. D.
9
.
Câu 42: Cho hàm số
3
xm
y
x
(
m
là tham số thực) thỏa mãn
1;2
min 2y
. Mệnh đề nào dưới đây
đúng?
A.
3m
. B.
11m
. C.
3m
. D.
31m
.
Câu 43: Cho hàm số
3
31f x x x m
, đặt
22
1;7
1;7
max min
x
x
P f x f x
. Có bao nhiêu giá
trị nguyên của
m
để giá trị lớn nhất của
P
không vượt quá
26
.
A.
6
. B.
7
. C.
4
. D.
5
.
Câu 44: Tìm giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm số
2
1
xm
y
x
+
=
+
trên đoạn
0;4
bằng
5
.
A.
7m =
. B.
21m =
. C.
17m =
. D.
5m =
.
Câu 45: Gọi S là tập hợp các giá trị m để giá trị nhỏ nhất của hàm số
22
()y x x m= + −
trên đoạn
2;2−
bằng 4. Tổng các phần tử của tập hợp S bằng
A.
23
4
. B.
23
4
−
. C.
41
4
. D.
23
2
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
1
xm
y
x
+
=
+
thỏa mãn
1;2 1;2
9
min max
2
yy+=
.Mệnh đề nào dưới đây đúng
A.
02m
. B.
0m
. C.
4m
. D.
24m
.
Lời giải
Chọn D
Tập xác định:
\1D =−
.Hàm số luôn đơn điệu trên đoạn
1;2
nên
( ) ( )
1;2 1;2
min max 1 2y y f f+ = +
1 2 9
4
2 3 2
mm
m
++
+ = =
.
Câu 2: Gọi
S
là tập tất cả các giá trị thực của tham số m để hàm số
3 2 2
( ) 3 5f x x x m= + + −
có giá trị
lớn nhất trên
1,2−
bằng
19
. Tính tổng tất cả các phần tử của
S
.
A.
2−
. B.
2
. C.
4
. D.
0
.
Lời giải
Chọn D
Ta có
2
0
3 6 0
2
x
y x x
x
=
= + =
=−
.
Ta có
2
1,2
maxf(x) (2) 15fm
−
= = +
Theo bài ta được
2
15 19 2 0m m S+ = = =
Câu 3: Biết giá trị lớn nhất của hàm số
2
2
xm
y
x
+
=
−
trên đoạn
1;1−
bằng
1.−
Khẳng định nào dưới
đây đúng?
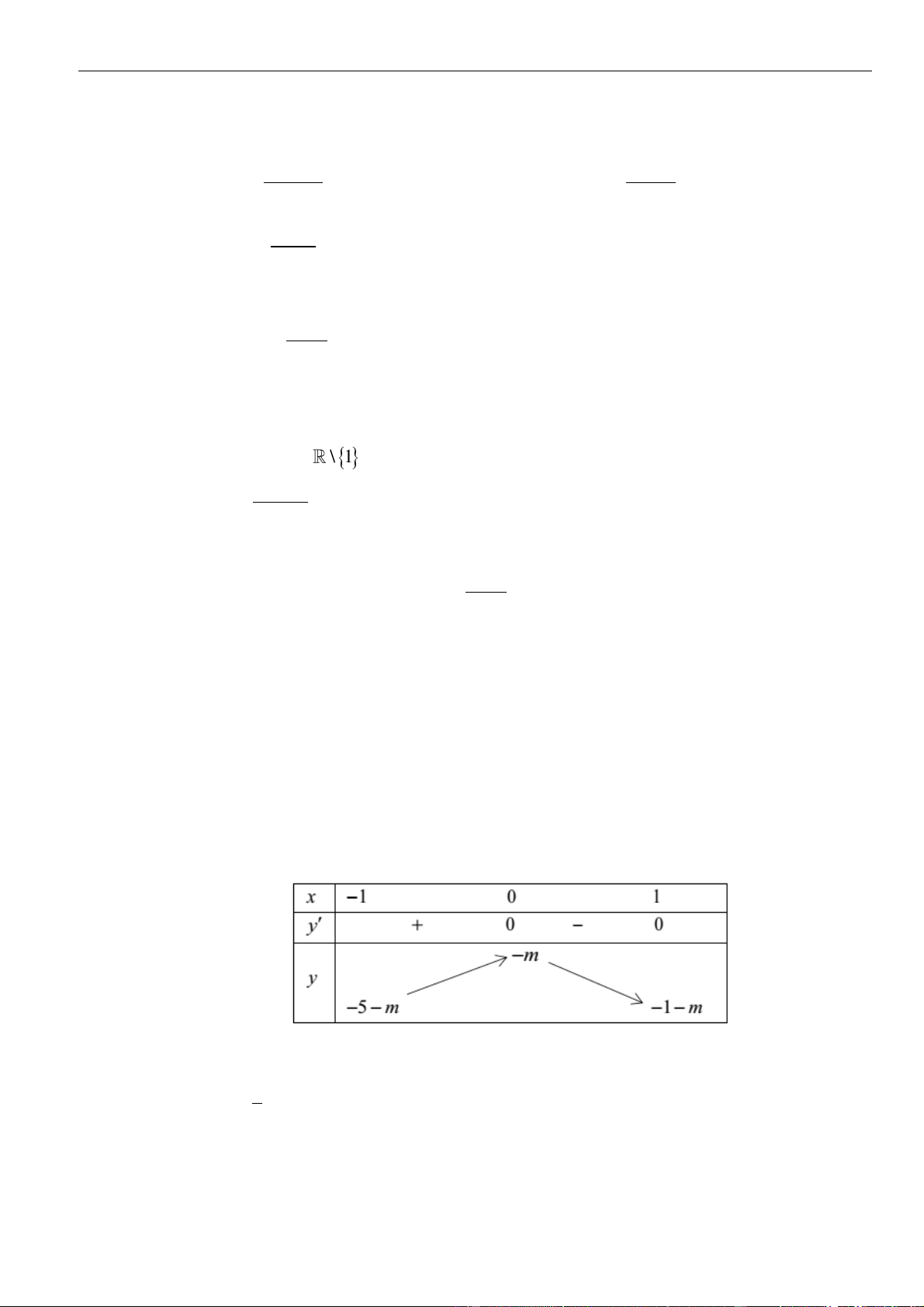
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
A.
( )
1;0 .m−
. B.
( )
4;3 .m−
. C.
( )
4;6 .m
. D.
( )
0;1 .m
Lời giải
Chọn B
Đạo hàm
( )
2
2
2
0
2
m
y
x
−−
=
−
nên giá trị lớn nhất của hàm số
2
2
xm
y
x
+
=
−
trên đoạn
1;1−
là
( )
2
22
1
1 1 1 1 3 4 2
3
m
f m m m
−
− = − = − − = = =
−
Suy ra
( )
4;3 .m−
.
Câu 4: Cho hàm số
1
xm
y
x
+
=
−
thỏa mãn
2;4
min 3y =
. Mệnh đề nào dưới đây là đúng?
A.
3 4.m
B.
1 3.m
C.
4.m
D.
1.m −
Lời giải
Chọn C
Tập xác định:
\1D =
.
Ta có
( )
2
1
'.
1
m
y
x
−−
=
−
Vì hàm số đơn điệu trên
2;4
nên
( )
( )
2;4
2;4
min 2 , 1 0
min 4 , 1 0
y y m
y y m
= − −
= − −
2;4
min 3
3 2 , 1
4
3 , 1
3
y
mm
m
m
=
= + −
⎯⎯⎯→
+
= −
1, 1
5
5, 1
mm
m
mm
= −
=
= −
Nếu
11my= − =
Hàm số không có giá trị nhỏ nhất.
Vậy
4.m
Câu 5: Cho hàm số
32
23y x x m= − −
. Trên
1;1−
hàm số có giá trị nhỏ nhất là
1−
. Tìm
m
.
A.
5m =−
. B.
3m =−
. C.
6m =−
. D.
4m =−
.
Lời giải
Chọn D
Ta có:
( )
2
6 6 6 1y x x x x
= − = −
,
( )
0
0 6 1 0
1
x
y x x
x
=
= − =
=
.
Bảng biến thiên
Từ bảng biến thiên suy ra:
1;1
min 5ym
−
= − −
1 5 4mm − = − − = −
.
Câu 6: Biết
32
3;0
1
min 2
3
x x x m
−
− + − + =
, giá trị của
m
bằng
A. . B.
23
. C.
2
. D.
19−
.
Lời giải
Chọn C
2−

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Xét hàm số
( )
32
1
3
f x x x x m= − + − +
trên
3;0−
.
Hàm số liên tục trên đoạn
3;0−
.
Ta có
( ) ( )
2
2
2 1 1 0, 3;0f x x x x x
= − + − = − − −
.
Do đó hàm số nghịch biến trên khoảng
( )
3;0−
.
( ) ( )
3;0
min 0 2f x f m m
−
= = =
.
Câu 7: Tìm tất cả các giá trị thực của
m
để giá trị nhỏ nhất của hàm số
( )
32
3f x x x m= − − +
trên đoạn
1;1−
bằng
0.
A.
4m =
. B.
0m =
. C.
6m =
. D.
2m =
.
Lời giải
Chọn A
Ta có
( )
2
3 6 .f x x x
= − −
Xét
( )
2
0 1;1
0 3 6 0 .
2 1;1
x
f x x x
x
= −
= − − =
= − −
Mà
( ) ( ) ( )
1 2, 0 , 1 4f m f m f m− = − = = −
và
42mmm− −
.
Khi đó
( ) ( )
1;1
min 1 4.
x
f x f m
−
= = −
Theo đề bài ta có
( )
1;1
min 0 4 0 4.
x
f x m m
−
= − = =
Câu 8: Cho hàm số
3
(x) x 3
m
f x e= − +
, với m là tham số thực. Biết rằng giá trị nhỏ nhất của hàm số đã
cho trên [0;2] bằng 0; khi đó, giá trị lớn nhất của hàm số đã cho bằng
A.
5
. B.
6
. C.
2
. D.
4
.
Lời giải
Chọn D
Ta có
2
1
'(x) 3x 3 0
1
x
f
x
=−
= − =
=
, do xét trên [0;2] nên nhận x=1
Vì
(1) 2; (0) ; (2) 2
m m m
f e f e f e= − = = +
nên
[0;2]
min (x) e 2 0 2
mm
fe= − = =
Từ đó
[0;2]
max (x) e 2 4
m
f = + =
.
Câu 9: Cho hàm số
32
23y x x m= − −
. Trên
1;1−
hàm số có giá trị nhỏ nhất là
1−
. Tìm
m
.
A.
5m =−
. B.
3m =−
. C.
6m =−
. D.
4m =−
.
Lời giải
Chọn D
Ta có:
( )
2
6 6 6 1y x x x x
= − = −
,
( )
0
0 6 1 0
1
x
y x x
x
=
= − =
=
.
Bảng biến thiên

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Từ bảng biến thiên suy ra:
1;1
min 5ym
−
= − −
1 5 4mm − = − − = −
.
Câu 10: Cho hàm số
1
xm
y
x
+
=
+
(
m
là tham số thực) thỏa mãn
1;2
1;2
16
min
3
y max y+=
. Mệnh đề nào dưới
đây đúng?
A.
4m
. B.
02m
. C.
24m
. D.
0m
.
Lời giải
Chọn A
Ta có:
( )
2
1
'
1
m
y
x
−
=
+
TH1:
11my= =
loại
TH2:
1m
khi đó
1;2
1;2
12
min ;
23
mm
y max y
++
==
1;2
1;2
1 2 16
min 5
2 3 3
mm
y max y m
++
+ = + = =
TH3:
1m
khi đó:
1;2
1;2
12
;min
23
mm
max y y
++
==
1;2
1;2
2 1 16
min 5
3 2 3
mm
y max y m
++
+ = + = =
Vậy
5m =
thỏa mãn
Câu 11: Cho hàm số
1
xm
y
x
+
=
+
(
m
là tham số thực) thỏa mãn
1;2
1;2
9
min max
2
yy+=
. Mệnh đề nào dưới đây
đúng?
A.
02m
. B.
0m
. C.
4m
. D.
24m
.
Lời giải
Chọn D
Điều kiện xác định:
1 0 1.xx+ −
TH1:
1m =
thì
1y =
TH2:
1m
thì hàm số
1
xm
y
x
+
=
+
luôn đồng biến hoặc nghịch biến trên
( )
;1− −
và
( )
1;− +
.
Mà
( )
1;2 1; − +
nên
( ) ( )
1;2
1;2
99
min max 1 2
22
y y y y+ = + =

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
( ) ( )
1 2 9
1 1 2 1 2
1 2 9
2 3 2
3 1 2 2 3.9
5 7 27
4.
mm
mm
mm
m
m
++
+ =
++
++
+ =
+ + + =
+ =
=
Câu 12: Biết rằng giá trị lớn nhất của hàm số
2
4y x x m= + − +
là
32
. Giá trị của
m
là:
A.
22m =
. B.
2
2
m =
. C.
2m =−
. D.
2m =
.
Lời giải
Chọn D
2
4y x x m= + − +
Tập xác định
2;2D =−
.
( )
2
1 , 2;2
4
x
yx
x
−
= + −
−
.
2
22
2
0
0 1 4 2
4
4
x
x
y x x x
xx
x
= = − = =
−=
−
.
( )
22ym=+
.
( )
22ym− = − +
.
( )
2 2 2ym=+
.
Giá trị lớn nhất
2 2 3 2 2mm+ = =
.
Câu 13: Biết giá trị lớn nhất của hàm số
32
23y x x m= − + +
trên đoạn
0;2
bằng 5, tìm giá trị của tham
số
m
.
A. 5. B. 6. C. 3. D. 4.
Lời giải
Chọn D
2
66y x x
= − +
;
0
0
1
x
y
x
=
=
=
.
Bảng biến thiên:
Theo bảng biến thiên ta có
( ) ( )
0;2
max 5 1 5 1 5 4f x f m m= = + = =
.
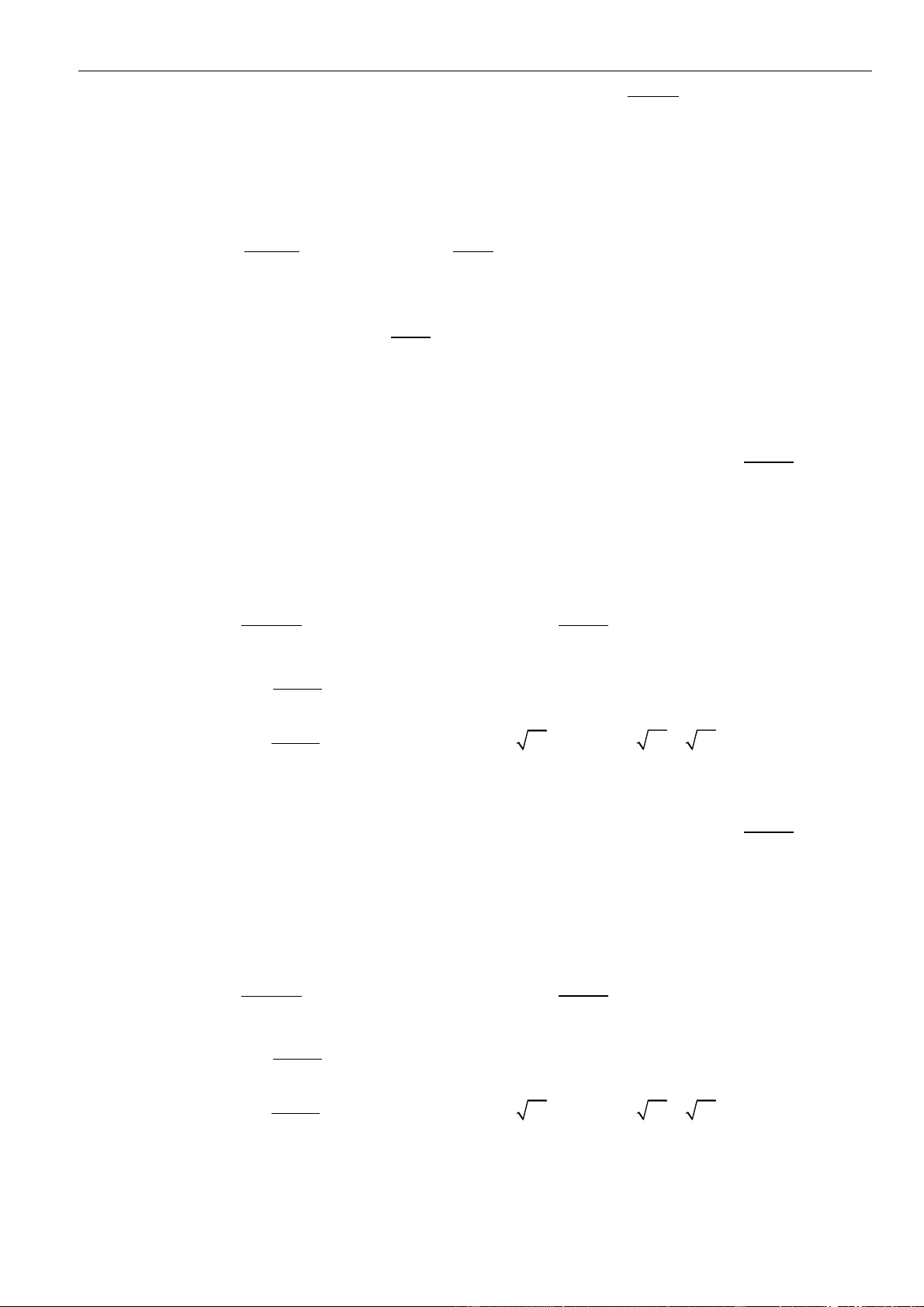
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Câu 14: Tìm giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
xm
y
x
+
=
+
trên đoạn
0;4
bằng
5
.
A.
7m =
. B.
21m=
. C.
17m =
. D.
5m=
.
Lời giải
Chọn C
Ta có:
2
2
'
( 1)
m
y
x
−
=
+
;
(0)ym=
;
( )
8
4
5
m
y
+
=
.
0;4
5min y =
'0
(4) 5
'0
(0) 5
y
y
y
y
=
=
20
8
5
5
20
5
m
m
m
m
−
+
=
−
=
2
17
2
5
m
m
m
m
=
=
17m=
.
Câu 15: Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
xm
y
x
−
=
+
trên đoạn
1;5
bằng
4−
. Tính tổng các phần tử của
S
.
A.
0
B.
5
C.
5−
D.
10
Lời giải
Chọn A
Ta có
( )
2
2
2
' 0, 2.
2
m
yx
x
+
= −
+
Suy ra hàm số
2
2
xm
y
x
−
=
+
đồng biến trên đoạn
1;5
, do đó
2
1;5
5
(5)
7
m
max y y
−
==
.
Theo giả thiết,
2
2
5
4 33 33
7
m
mm
−
= − = =
. Vậy
33; 33S =−
nên tổng các phần
tử của
S
bằng 0.
Câu 16: Gọi
S
là tập hợp các giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
xm
y
x
−
=
+
trên đoạn
1;5
bằng
4−
. Tính tổng các phần tử của
S
.
A.
0
B.
5
C.
5−
D.
10
Lời giải
Chọn A
Ta có
( )
2
2
2
' 0, 2.
2
m
yx
x
+
= −
+
Suy ra hàm số
2
2
xm
y
x
−
=
+
đồng biến trên đoạn
1;5
, do đó
2
1;5
5
(5)
7
m
max y y
−
==
.
Theo giả thiết,
2
2
5
4 33 33
7
m
mm
−
= − = =
. Vậy
33; 33S =−
nên tổng các phần
tử của
S
bằng 0.
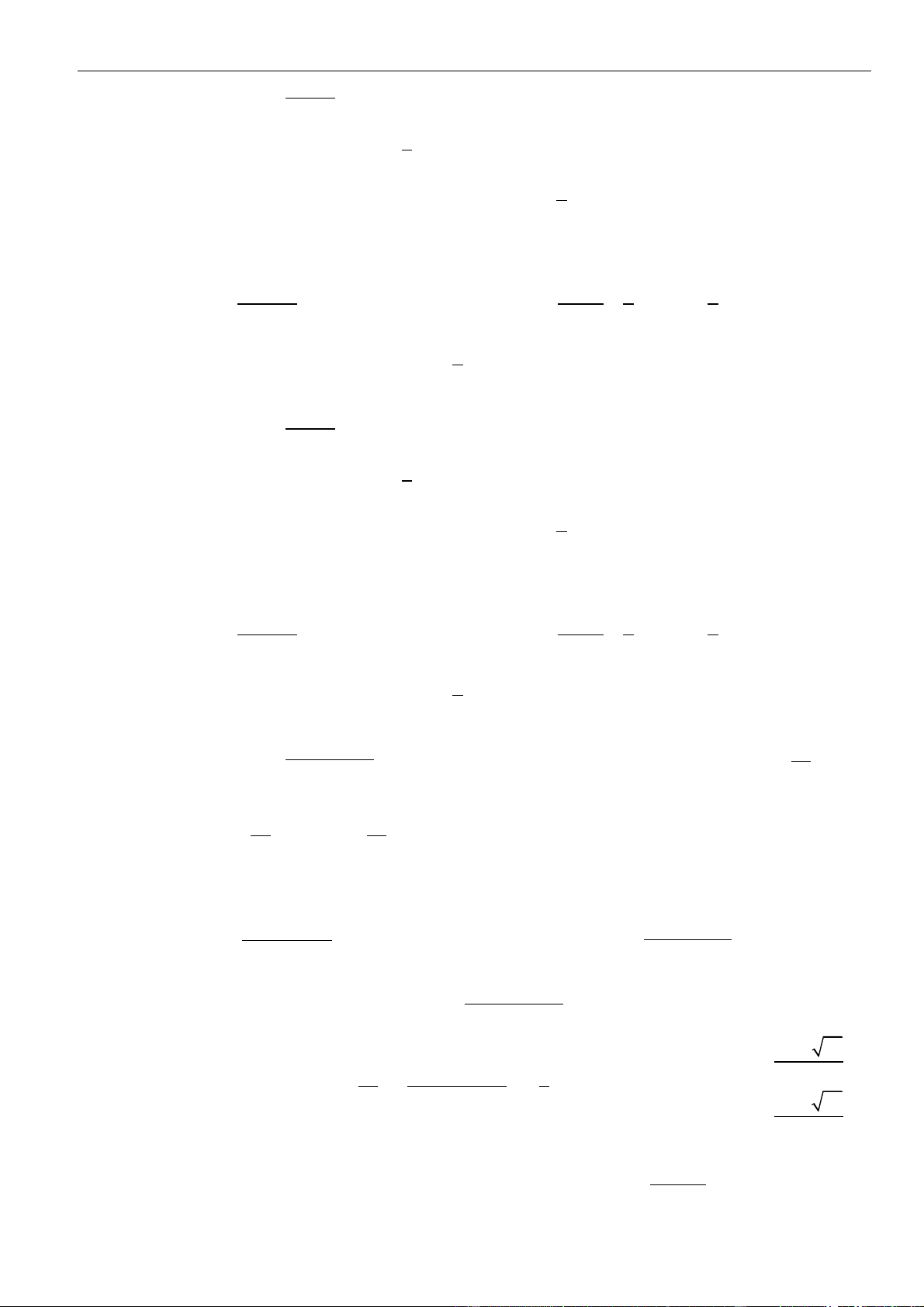
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Câu 17: Cho hàm số
2
,
2
xm
ym
x
−
=
+
là tham số. Tích tất cả các giá trị của
m
để giá trị lớn nhất của hàm
số đã cho trên đoạn
1;1−
bằng
1
4
là
A. Không tồn tại. B.
1.−
C.
1
.
4
−
D.
4.−
Lời giải
Chọn C
Ta có
( )
( )
22
2
1;1
2 1 1 1
0, 1;1 max 1 .
3 4 2
2
mm
y x y y m
x
−
+−
= − = = = =
+
Vậy tích các giá trị của tham số
m
là
1
.
4
−
Câu 18: Cho hàm số
2
,
2
xm
ym
x
−
=
+
là tham số. Tích tất cả các giá trị của
m
để giá trị lớn nhất của hàm
số đã cho trên đoạn
1;1−
bằng
1
4
là
A. Không tồn tại. B.
1.−
C.
1
.
4
−
D.
4.−
Lời giải
Chọn C
Ta có
( )
( )
22
2
1;1
2 1 1 1
0, 1;1 max 1 .
3 4 2
2
mm
y x y y m
x
−
+−
= − = = = =
+
Vậy tích các giá trị của tham số
m
là
1
.
4
−
Câu 19: Cho hàm số
2
2
1
mx m
y
x
−−
=
−+
với
m
là tham số thực lớn hơn
3−
thỏa mãn
4; 2
1
max
3
−−
−
=y
. Mệnh
đề nào sau dưới đây đúng?
A.
1
3
2
m
−
−
. B.
1
0
2
m
−
. C.
4m
. D.
13m
.
Lời giải
Chọn B
Ta có
( )
2
2
2
0
1
mm
y
x
− + −
=
−+
,
4; 2 − −x
. Do đó hàm số
2
2
1
mx m
y
x
−−
=
−+
nghịch biến trên
4; 2−−
. Từ đó suy ra
( )
2
4; 2
42
max 4
5
−−
− − −
= − =
mm
yy
.
Theo đề bài ta có
2
2
4; 2
6 33
1 4 2 1
3
max 3 12 1 0
3 5 3
6 33
3
−−
−+
=
− − − −
= = − + + =
−−
=
m
mm
y m m
m
.
Câu 20: Tìm giá trị âm của tham số
m
để giá trị lớn nhất của hàm số
2
1
2
mx
y
x
−
=
+
trên đoạn
1;3
bằng
1
.
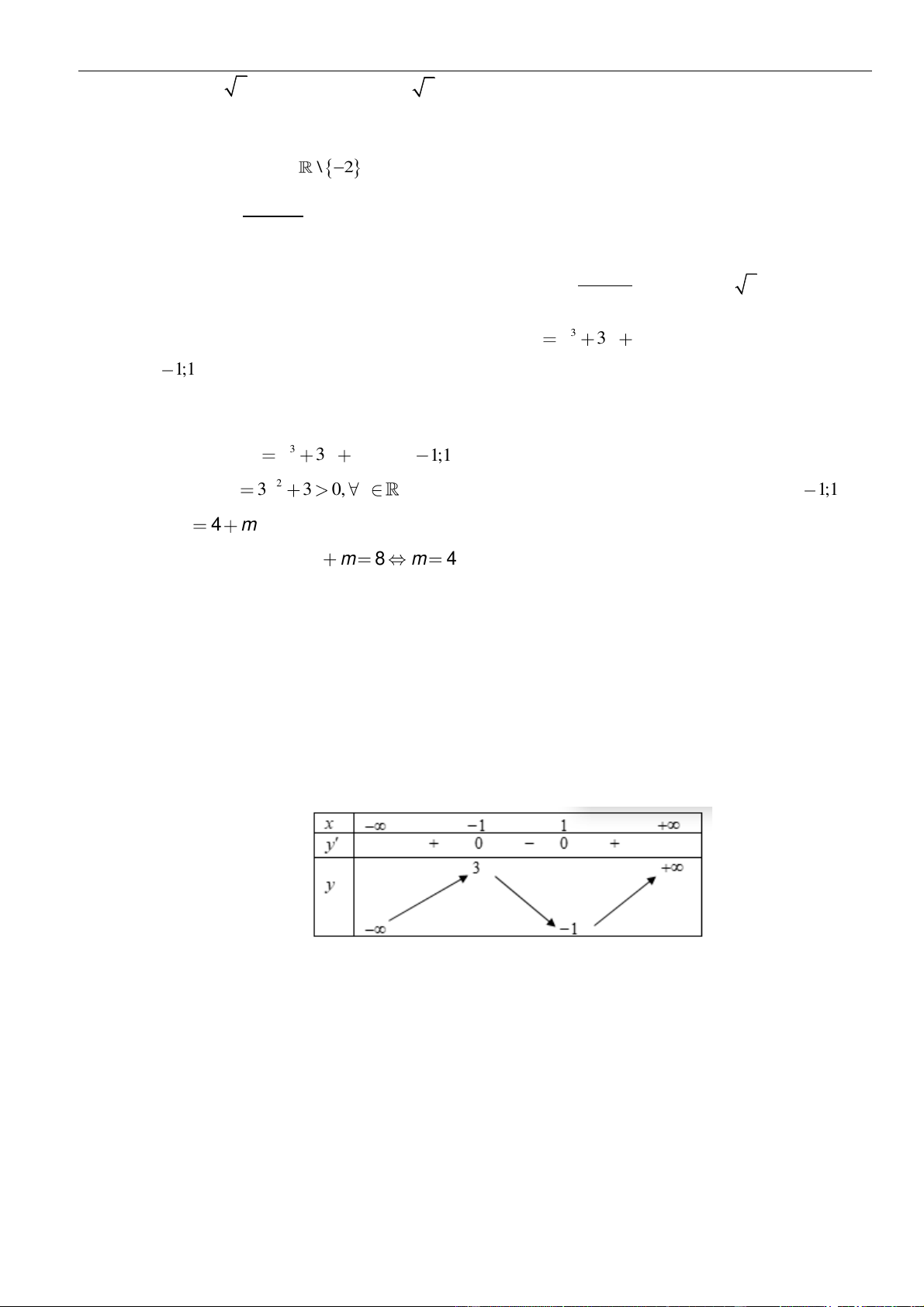
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
A.
2m =−
. B.
3m =−
. C.
4m =−
. D.
2m =−
.
Lời giải
Chọn A
Tập xác định:
\2D =−
.
Ta có:
( )
2
2
21
0, 2
2
m
yx
x
+
= −
+
.
Hàm số đồng biến trên đoạn
1;3
nên
( )
1;3
max 3yy=
2
31
1
5
m −
=
2m = −
.
Câu 21: Tìm tất cả các giá trị của tham số
m
để hàm số
3
3y x x m
có giá trị lớn nhất trên đoạn
1;1
bằng
8
.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Xét hàm số
3
3y x x m
trên
1;1
.
Ta có:
2
' 3 3 0,y x x
, nên giá trị lớn nhất của hàm số trên đoạn
1;1
là
14ym
.
Theo giả thiết ta có:
4 8 4mm
.
Câu 22: Có bao nhiêu số thực dương
m
để giá trị lớn nhất của hàm số
3
31y x x= − +
trên đoạn
1; 2mm++
bằng
53
.
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn D
Ta có
2
1
3 3 0
1
x
yx
x
=
= − =
=−
.
Ta có bảng biến thiên:
Dựa theo bảng biến thiên thì để giá trị lớn nhất của hàm số
3
31y x x= − +
trên đoạn
1; 2mm++
bằng
53
thì
1 1 0mm+
. Khi đó
( ) ( ) ( ) ( )
3
1; 2
max 2 2 3 2 1 53
mm
f x f m m m
++
= + = + − + + =
32
6 9 50 0m m m + + − =
2m=
.
Vậy có
1
giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 23: Cho hàm số
( )
fx
liên tục trên đoạn
4;4
−
và có bảng biến thiên như hình vẽ bên:

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Có bao nhiêu số thực
4;4m
−
để giá trị lớn nhất của hàm số
( )
( )
( )
3
32g x f x x f m= − + +
trên đoạn
1;1
−
bằng
1
.
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn B
Đặt
3
32t x x= − +
Ta có
( )
2
3 3 0, 1;1t x x x
= − −
Suy ra
( ) ( ) ( ) ( )
1;1
1;1
Min 1 0, 1 4t x t Maxt x t
−
−
= = = − =
Do đó
1;1x
−
thì
0;4t
nên
( ) ( )
( ) ( ) ( ) ( )
0;4 0;4
1 1 3 1 2Max f t f m Max f t f m f m f m
+ = + = + = = −
Dựa vào bảng biến thiên ta thấy trên đoạn
4;4
−
phương trình
( )
2fm=−
có ba nghiệm phân
biệt.
Câu 24: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
xm
y
x
+
=
+
trên đoạn
1;2
bằng
8
. Giá trị
của
m
thỏa mãn điều kiện trên thuộc tập hợp nào sau đây?
A.
( )
0;4 .
B.
( )
8;10 .
C.
( )
4;8 .
D.
( )
10; .+
Lời giải
Chọn.B.
( )
2
1
1
m
y
x
−
=
+
Nếu
1
11
1
x
my
x
+
= = =
+
1;2 1;2
max min 2 8yy + =
1m=
loại.
Nếu
( ) ( )
1;2 1;2
12
1 0 max min 1 2
23
mm
m y y y y y
++
+ = + = +
8=
41
5
m=
Nếu
( ) ( )
1;2 1;2
2 1 35
1 0 max min 2 1 8
3 2 6
mm
m y y y y y m
+ + −
+ = + = + = =
.
Vậy
( )
41
8;10
5
m =
.
Câu 25: Cho hàm số
2
4
xm
y
x
+
=
−
(
m
là tham số thực) thỏa mãn
0;2
max 3y =
. Mệnh đề nào dưới đây đúng
A.
11m −
B.
12m =−
C.
8m −
D.
8m −
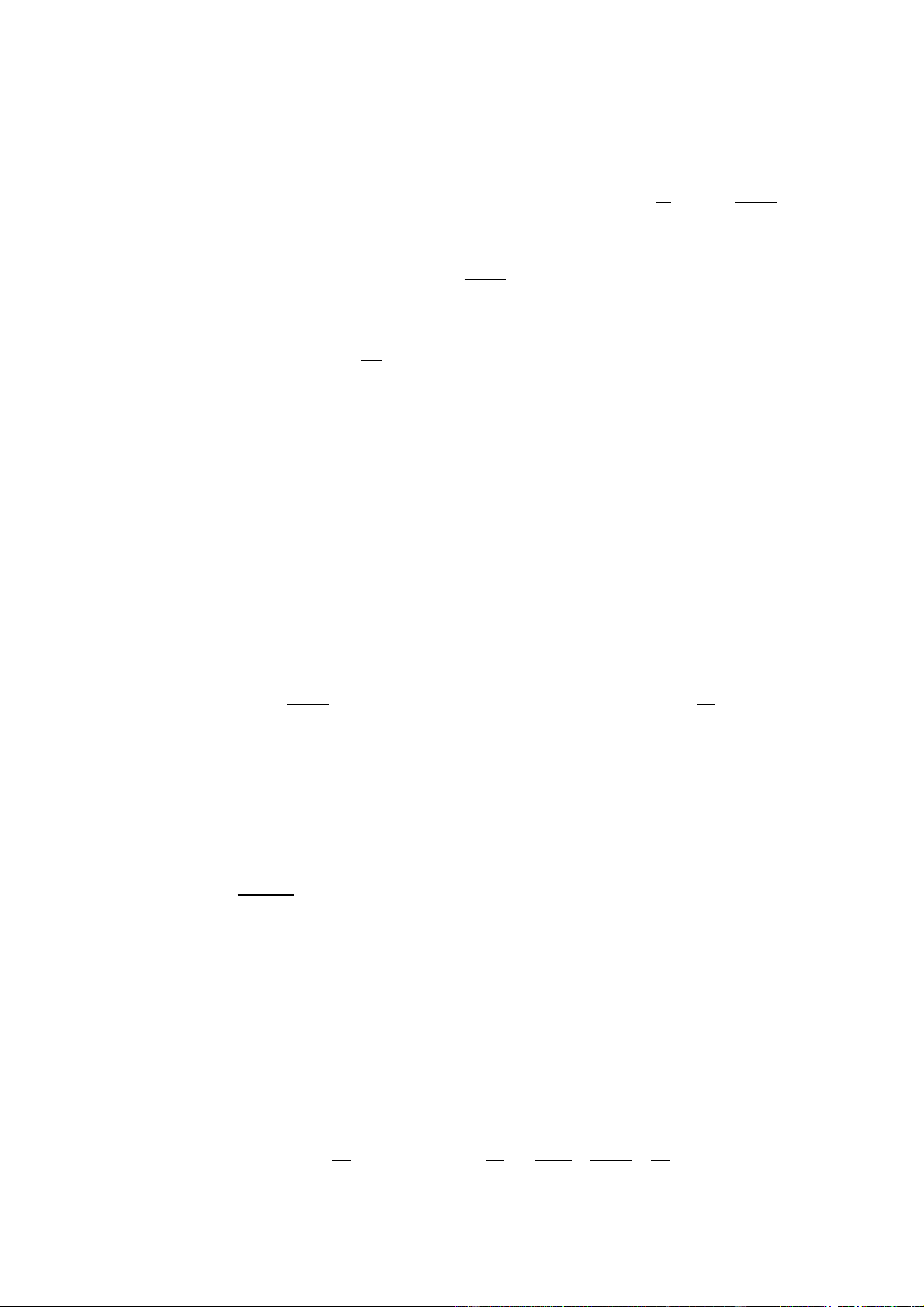
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn D
Đạo hàm
2
28
4 ( 4)
x m m
yy
xx
+ − −
= =
−−
.
Do hàm số đơn điệu trên từng khoảng xác định nên ta xét
4
(0) ; (2)
42
mm
ff
+
= − =
−
.
Hàm số đồng biến trên từng khoảng xác định khi
0;2
4
8 0 8 max (2) 3 10
2
m
m m y f m
+
− − − = = = −
−
.
Hàm số nghịch biến trên từng khoảng xác định khi
0;2
8 max (0) 3 12
4
m
m y f m − = = = −
−
.
Như vậy
10m =−
.
Câu 26: Cho hàm số
32
23y x x m= − −
. Trên
[ 1;1]−
hàm số có giá trị nhỏ nhất là
1−
. Tìm
m
.
A.
5m =−
. B.
3m =−
. C.
6m =−
. D.
4m =−
.
Lời giải
Chọn D
Ta có
2
66y x x
=−
. Xét
2
0 [ 1;1]
0 6 6 0
1 [ 1;1].
x
y x x
x
= −
= − =
= −
Mặt khác
( 1) 5ym− = − −
,
(0)ym=−
,
(1) 1ym= − −
.
Suy ra hàm số có giá trị nhỏ nhất là
5m−−
tại
1x =−
.
Theo giả thiết suy ra
5 1 4mm− − = − = −
.
Câu 27: Cho hàm số
1
xm
y
x
+
=
+
(
m
là tham số thực) thỏa mãn
1;2
1;2
16
min max
3
yy+=
. Mệnh đề nào dưới
đây đúng?
A.
0m
. B.
24m
. C.
4m
. D.
02m
.
Lời giải
Chọn C
Xét trên đoạn
1;2
hàm số liên tục
Ta có
( )
2
1
1
m
y
x
−
=
+
.
+TH1:
1 0 1mm−
Hàm số đồng biến trên
( )
1;2
.
Suy ra
( )
1;2
max 2yy=
và
( )
1;2
min 1yy=
.
Do đó
( ) ( )
1;2
1;2
16 16
min max 2 1
33
y y y y+ = + =
2 1 16
5
3 2 3
mm
m
++
+ = =
+TH2:
1 0 1mm−
Hàm số nghịch biến trên
( )
1;2
.
Suy ra
( )
1;2
max 1yy=
và
( )
1;2
min 2yy=
.
Do đó
( ) ( )
1;2
1;2
16 16
min max 1 2
33
y y y y+ = + =
1 2 16
5
2 3 3
mm
m
++
+ = =
+TH3:
1 0 1 1m m y− = = =
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Do đó
1;2 1;2
1;2 1;2
16
min max 1 min max
3
y y y y= = + =
Vậy
5m =
.
Câu 28: Biết rằng tồn tại tham số thực
m
để hàm số
1
xm
y
x
+
=
+
có
1;2
1;2
16
min max .
3
yy
+=
Mệnh đề nào dưới
đây đúng?
A.
(
2; 4m
. B.
(
0; 2m
. C.
( )
+4;m
. D.
(
−
;0m
.
Lời giải
Chọn C
Ta có
( ) ( )
1;2
1;2
16 16 1 2 16
min max 1 2 5.
3 3 2 3 3
mm
y y y y m
++
+ = + = + = =
Suy ra
( )
4; .m +
Câu 29: Cho hàm số
( )
2
3
xm
fx
x
+
=
−
. Giá trị của
m
để
( )
( )
1;2
1;2
max min 8f x f x
−
−
+=
là
A.
4
5
m =
. B.
46
5
m =−
. C.
12m =−
. D.
18
5
m =
.
Lời giải
Chọn B
Ta có
( )
2
1
4
m
f
−
−=
và
( )
24fm= − −
Khi đó
( )
( )
1;2
1;2
2 46
max min 8 4 8 5 46 0
45
m
f x f x m m m
−
−
−
+ = − − = − − = = −
.
Câu 30: Cho hàm số
1
xm
y
x
+
=
−
thỏa mãn
2;4
min 3y =
. Mệnh đề nào sau đây là đúng?
A.
34m
. B.
13m
. C.
4m
. D.
1m −
.
Lời giải
Chọn C
Tập xác định:
\1D =
. Khi đó
( )
2
1
1
m
y
x
−−
=
−
,
1x
Nếu
1 0 1mm− − −
thì
,
0, 1yx
nên
2;4
2
min (2) 2 3 1
21
m
y y m m
+
= = = + = =
−
.
Nếu
1 0 1mm− − −
thì
,
0, 1yx
nên
2;4
44
min (4) 3 5
4 1 3
mm
y y m
++
= = = = =
−
.
Chọn
4m
.
Câu 31: Gọi S là tập hợp tất cả các giá trị thực của tham số
m
để hàm số
2
cos
2 sx
xm
y
co
+
=
−
có giá trị lớn
nhất trên
;
23
−
bằng 1. Số phần tử của S là:
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn C
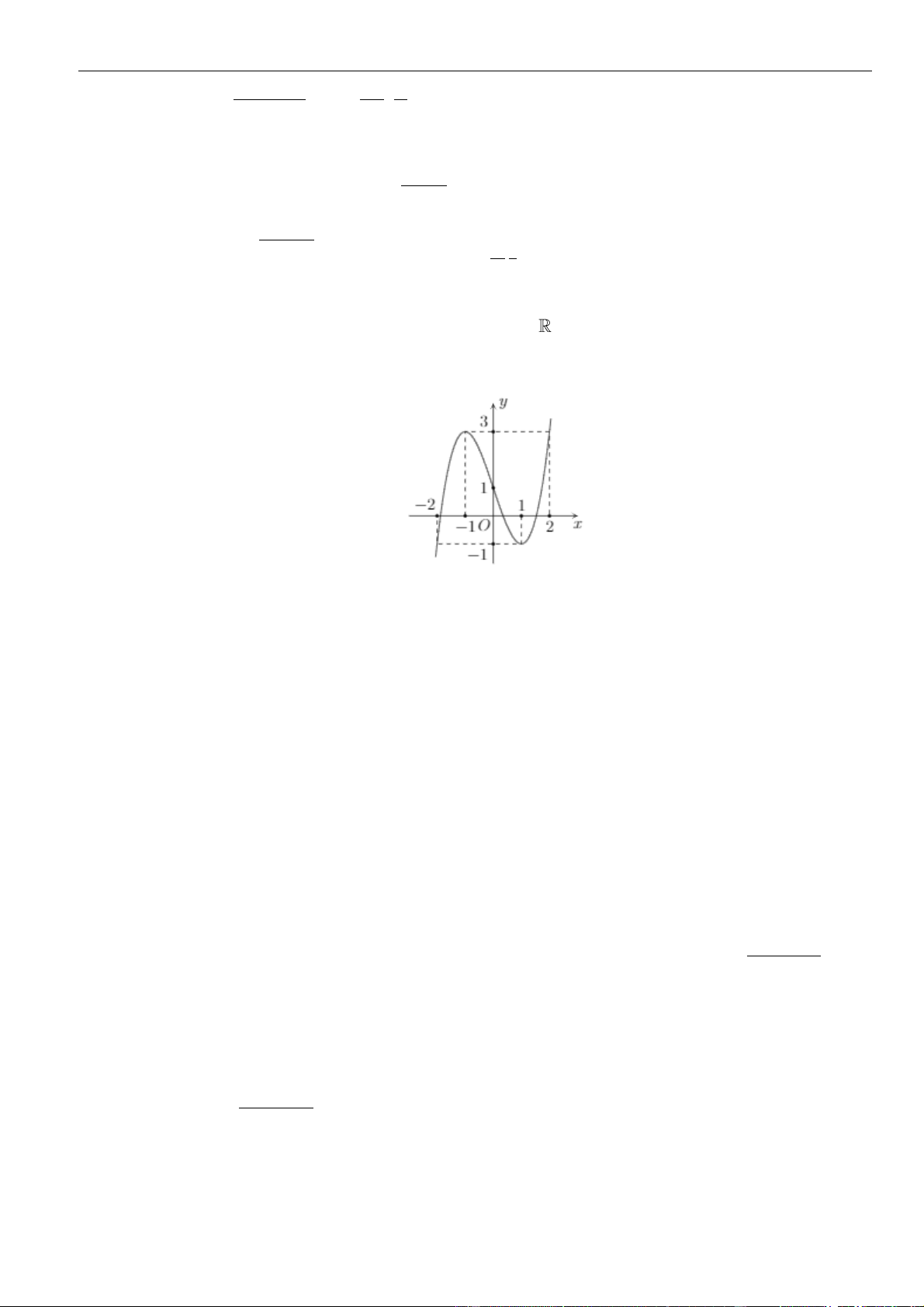
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Ta có
2
cos
2 sx
xm
y
co
+
=
−
;
23
x
−
Đặt
osx (0 t 1)tc=
.
Hàm số đã cho trở thành:
2
( ) 0;1
2
tm
f t t
t
+
=
−
Ta có:
( )
2
'
2
2
( ) 0 0;1
2
m
f t t
t
+
=
−
. Suy ra:
2
;
23
Max (1) 1 1 0y f m m
−
= = + = =
Vậy số phần tử của S là 1.
Câu 32: Cho hàm số bậc ba
( )
y f x=
có đạo hàm trên và có đồ thị như hình vẽ. Xét hàm số
( )
( )
3
21g x f x x m= + − +
. Tìm
m
để
( )
0;1
max 10gx=−
.
A.
3m =
. B.
13m =−
. C.
1m =−
. D.
9m =−
.
Lời giải
Chọn B
Ta có
( )
( ) ( )
23
' 6 1 2 1g x x f x x
= + + −
( )
( )
( )
( )
( )
3
3
3
2 1 1
0
' 0 2 1 0
0;1
2 1 1
u x x x
x
g x f x x
x
u x x x
= + − = −
=
= + − =
=
= + − =
Khi đó:
( ) ( )
( ) ( )
( ) ( )
0 1 3
11
1 2 3
g f m m
g f m m
g f m m
= − + = +
= + = −
= + = +
Vậy
( )
0;1
max 10 3 10 13.g x m m= − + = − = −
.
Câu 33: Có bao nhiêu giá trị nguyên của tham số
m
để giá trị lớn nhất của hàm số
sin 1
cos 2
mx
y
x
+
=
+
nhỏ
hơn
2
?
A.
5
. B.
3
. C.
4
. D.
6
.
Lời giải
Chọn A
Ta có:
sin 1
sin 1 cos 2
cos 2
mx
y m x y x y
x
+
= + = +
+
sin cos 2 1m x y x y − = −
Phương trình có nghiệm khi
( )
2
22
21m y y+ −
2 2 2
4 4 1m y y y + − +
22
3 4 1 0y y m − + −
Xét phương trình
22
3 4 1 0y y m− + − =
có
( )
( )
2
22
' 2 3. 1 3 1 0,m m m = − − − = +
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Suy ra phương trình
22
3 4 1 0y y m− + − =
luôn có hai nghiệm phân biệt. Do đó,
22
2 3 1 2 3 1
33
mm
y
− + + +
.
Suy ra
2
2 3 1
max
3
m
y
++
=
. Theo yêu cầu bài toán ta có:
2
2 3 1
max 2 2
3
m
y
++
2
3 1 4m +
2
3 1 16m +
55m −
.
Vậy có 5 giá trị nguyên của tham số
m
thỏa yêu cầu bài toán là:
2, 1, 0, 1, 2−−
.
Câu 34: Gọi
S
là tập hợp các giá trị tham số
m
để hàm số
2
22mx m m
y
xm
+ + −
=
+
có giá trị nhỏ nhất trên
đoạn
1;4
bằng
1
. Tổng các phần tử của
S
bằng.
A.
2−
. B.
1
. C.
0
. D.
3−
.
Lời giải
Chọn B
Điều kiện:
xm−
.
Ta có
( )
2
2
2mm
y
xm
−+
=
+
. Vì
( )
2
2
1
2 0, 0, 1;4
1 4.1.2 0
m
a
m m m y x
=
− +
= − −
.
Suy ra, giá trị nhỏ nhất trên đoạn
1;4
bằng
( )
2
2
1
32
1 1 1 1; 3
1
2 3 0
m
mm
ym
m
mm
−
+−
= = −
+
+ − =
Kết hợp điều kiện
3
1;4
xm
m
x
−
= −
loại. Vậy
1m=
.
Câu 35: Số các giá trị tham số
m
để hàm số
2
1xm
y
xm
−−
=
−
có giá trị lớn nhất trên
0;4
bằng
6−
là :
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn B
Hàm số
2
1xm
y
xm
−−
=
−
có tập xác định
\ m
Ta có:
( ) ( )
22
22
11m m m m
y
x m x m
− + + − +
==
−−
Nhận xét: với
0;4m
thì hàm số không có GTLN, GTNN trên
0;4
Với
0;4m
, Ta có
( ) ( )
22
22
11
0, 0;4
m m m m
ym
x m x m
− + + − +
= =
−−
Khi đó giá trị lớn nhất của hàm số trên
0;4
bằng
( )
2
2
9
41
4 6 24 27 0
3 0;4
4
m
m
y m m
m
m
=−
−−
= = − + − =
=
−
.
Vậy kết hợp với điều kiện ta chọn
9m =−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Câu 36: Cho hàm số
2
1
xm
y
x
+
=
+
. Biết
min 2y =−
. Mệnh đề nào dưới đây đúng?
A.
2m −
. B.
02m
. C.
2m
. D.
20m−
.
Lời giải
Chọn D
TXĐ
D =
.
Ta có
2
0
0
2
0
: 2 (1)
1
min 2
: 2 (2)
1
xm
x
x
y
xm
x
x
+
−
+
= −
+
= −
+
( )
2
2
15
(1) 2 2 2 0, 1 4.2 2 0
18
xm
x x m x m m
x
+
− + + + − + −
+
.
Từ suy ra
15
8
m =−
.
Vậy
15
8
m =−
.
Câu 37: Hàm số
2
1
xm
y
x
−
=
+
đạt giá trị lớn nhất trên đoạn
0;1
bằng
1
khi
A.
0m =
. B.
2m =
. C.
1m =−
. D.
1m =
.
Lời giải
Chọn A
+) Hàm số
2
1
xm
y
x
−
=
+
liên tục trên đoạn
0;1
và có đạo hàm là
( )
2
2
1
m
y
x
+
=
+
.
+) Hàm số
2
1
xm
y
x
−
=
+
là một hàm liên tục và đơn điệu trên đoạn
0;1
nên hàn số này đạt giá
trị lớn nhất trên đoạn
0;1
bằng
1
khi
( )
( ) ( )
( )
( ) ( )
( )
( )
2
0;1
2
0;1
2
0
2
1
2
2
2
max 1
1
11
0
11
0
2 2 2
2
0
1
1
01
1
1
max 0
m
y
m
x
m
m
m
f x f
f
m
m
m m m
m
y
mm
x
f
f x f
+
=
−
+
−
−
−
=
=
=
=
+
=
− − −
+
=
− = −
+
=
=
=
.
Câu 38: Cho hàm số
2
2
xm
y
x
−
=
+
với
m
là tham số,
4m −
. Biết
( )
( )
0;2
0;2
min max 8f x f x+ = −
. Giá trị
của tham số
m
bằng
A.
9
. B.
12
. C.
10
. D.
8
.
Lời giải
Chọn B
Ta có
( )
2
4
.
2
m
y
x
+
=
+
TH1. Nếu
4 0 4mm+ −
thì
0, \ 2 .yx
−

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Khi đó
( ) ( )
( ) ( )
0;2
0;2
min 0
2
.
4
max 2
4
x
x
m
f x f
m
f x f
= = −
−
==
Mà
( )
( )
0;2
0;2
4
min max 8 8 12
24
x
x
mm
f x f x m
−
+ = − − + = − =
.
TH2. Nếu
4 0 4mm+ −
thì
0, \ 2 .yx
−
Khi đó
( ) ( )
( ) ( )
0;2
0;2
max 0
2
.
4
min 2
4
x
x
m
f x f
m
f x f
= = −
−
==
Mà
( )
( )
0;2
0;2
4
min max 8 8 12
24
x
x
mm
f x f x m
−
+ = − − + = − =
.
Vậy
12m =
thỏa yêu cầu bài toán.
Câu 39: Biết rằng giá trị nhỏ nhất của hàm số
5
()
mx
fx
xm
+
=
−
trên đoạn
0;1
bằng −7. Mệnh đề nào sau
đây đúng.
A.
11m−
. B.
01m
. C.
02m
. D.
10m−
.
Lời giải
Chọn C
Ta có:
( )
2
2
5
' 0,
m
y x m
xm
+
= −
−
.
Suy ra hàm số luôn nghịch biến trên các khoảng
( ; )m−
và
( ; ).m +
Vì hàm số có giá trị nhỏ nhất trên đoạn
0;1
nên
0;1 .m
Hàm số có giá trị nhỏ nhất trên đoạn
0;1
bằng −7 nên suy ra:
1
1
5
()
(1) 7
2
1
2
00
()
52
(1) 7
1
m
m
m
TM
f
m
m
m
mm
L
mm
f
m
+
= = −
=
−
=
+=
= = −
−
.
Câu 40: Số các giá trị nguyên của tham số
m
để hàm số
32
1
3 2 7
3
y x x x m= − − + +
có giá trị nhỏ nhất
trên đoạn [2; 4] thuộc khoảng
( 5;8)−
là
A. 12. B. 3. C. 7. D. 6.
Lời giải
Chọn D
Xét hàm số trên [2; 4], ta có:
( ) ( ) ( )
11
2 2 ; 4 2 ; 3 2 2
33
y m y m y m= − + = + = − +
( )
( )
2
1 2;4
' 2 3, ' 0
3 2;4
x
y x x y
x
= −
= − − =
=

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
2;4
3
2 2 ( 5;8) 5 2 2 8 3 2 10 5
2
Min y m m m m
−
= − + − − − + −
1;0;1;2;3;4mm −
Câu 41:
Vậy có 6 số nguyên cần tìm.
Cho hàm số
3 2 2
( ) 3 2f x x x m m= − + −
. Gọi
S
tập hợp tất cả các
giá trị nguyên của tham số
m
thỏa mãn
3;1
3;1
3max (| |) 2min (| |) 112f x f x
−
−
+
. Số phần tử của S
bằng
A.
12
. B.
10
. C.
11
. D.
9
.
Lời giải
Chọn C
Ta có
( ) ( )
( )
( )
( )
( )
3;1 0;3
3;1 0;3
max max
min min
f
f x f x
f x f x
x f x x
−
−
=
=
=−
.
Đạo hàm
( )
( )
2
2
2
0 0 2
( ) 3 6 0
2 2 2 4
x f m m
f x x x
x f m m
= = −
= − =
= = − −
và
( )
2
32f m m=−
.
Suy ra
3;1
3;1
3max (| |) 2min (| |) 112f x f x
−
−
+
( ) ( )
22
1123 2 2 2 4m m m m+ − − −
2
0 4 6 4; 3; 2...2 24 ;5;6
m
mm mm
− − − − − −
có
11
giá trị của
.m
.
Câu 42: Cho hàm số
3
xm
y
x
(
m
là tham số thực) thỏa mãn
1;2
min 2y
. Mệnh đề nào dưới đây
đúng?
A.
3m
. B.
11m
. C.
3m
. D.
31m
.
Lời giải
Chọn B
Ta thấy
( )
2
3
'
3
m
y
x
−−
=
−
Trường hợp 1:
( )
1;2
30
3
()
min 1 2
9
m
m
VN
yy
m
−
− −
−
= − = −
=
Trường hợp 2:
( )
1;2
30
3
0
min 2 2
0
m
m
m
yy
m
−
− −
−
=
= = −
=
Câu 43: Cho hàm số
3
31f x x x m
, đặt
22
1;7
1;7
max min
x
x
P f x f x
. Có bao nhiêu giá
trị nguyên của
m
để giá trị lớn nhất của
P
không vượt quá
26
.
A.
6
. B.
7
. C.
4
. D.
5
.
Lời giải
Chọn B
Đặt
3
1 0;2tx
ta có
32
3 1 3 3 0 1; 1f t t t m f t t t t
.
Bảng biến thiên:

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Suy ra
3; 1f t m m
.
Ta có
0;2
0;2
3 1 3 1
max 1 2
2
0 3 1 0
min
1 2 3 1 0
m m m m
f t m
khi m m
ft
m khi m m
.
Trường hợp 1: Khi
3 1 0 1;3m m m
thì
2
1 2 26 1 26 2 3,09 1;0;1;2;3P m m m
.
Trường hợp 2: Khi
3 1 0 1;3m m m
thì
22
2
1 2 1 2 2 1 8 26P m m m
2
1 9 2;4 2;4m m m
.
Vậy có 7 giá trị của
m
thỏa mãn.
Câu 44: Tìm giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm số
2
1
xm
y
x
+
=
+
trên đoạn
0;4
bằng
5
.
A.
7m =
. B.
21m =
. C.
17m =
. D.
5m =
.
Lời giải
Chọn C
Hàm số đã cho xác định và liên tục trên đoạn
0;4
.
Ta có
( )
2
2
1
m
y
x
−
=
+
.
Nếu
( ) ( )
2 0 2 1 0, 0;4m m y x
−
suy ra
hàm số đồng biến trên đoạn
0;4
.
Khi đó
( )
0;4
05Miny y m= = =
.
Nếu
( ) ( )
2 0 2 2 0, 0;4m m y x
−
suy ra
hàm số nghịch biến trên đoạn
0;4
.
Khi đó
( )
0;4
8
4 5 17
5
m
Miny y m
+
= = = =
Nếu
2 0 2 2, 0;4m m y x− = = =
.
Khi đó
0;4
25Miny =
.
Vậy
17m =
.
Câu 45: Gọi S là tập hợp các giá trị m để giá trị nhỏ nhất của hàm số
22
()y x x m= + −
trên đoạn
2;2−
bằng 4. Tổng các phần tử của tập hợp S bằng
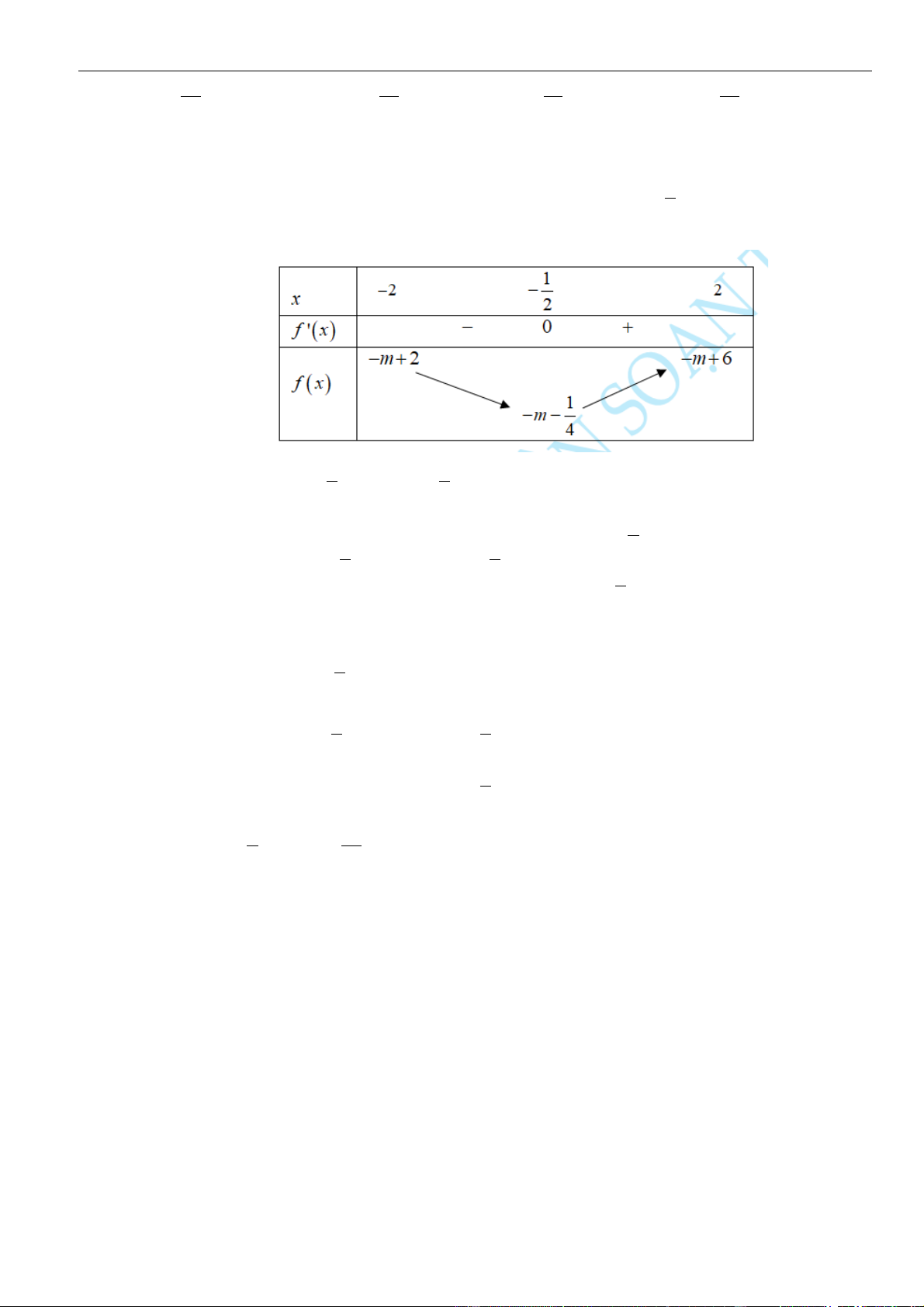
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
A.
23
4
. B.
23
4
−
. C.
41
4
. D.
23
2
.
Lời giải
Chọn A
Đặt
( )
2
f x x x m= + −
. Ta có:
( )
' 2 1f x x=+
;
( )
1
'0
2
f x x= = −
Bảng biến thiên:
Trường hợp 1:
11
0
44
mm− − −
Ta có:
( )
( )
( )
2
2;2
2;2
9
11
4
min min 4
7
44
4
x
x
mn
f x m y m
ml
−
−
=−
= − − = − − =
=
Trường hợp 2:
6 0 6mm− +
Ta có
( )
( )
( )
( )
2
2;2
2;2
4
1
min min 6 4
4
8
x
x
ml
f x m y m
mn
−
−
=
= − − = − + =
=
Trường hợp 3:
11
0 6 6
44
m m m− − − + −
Ta có
( )
2;2
2;2
min 0 min 0
x
x
f x y
−
−
= =
. Suy ra
1
6
4
m−
không thỏa yêu cầu bài toán.
Vậy
9 23
;8
44
mS
− =
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
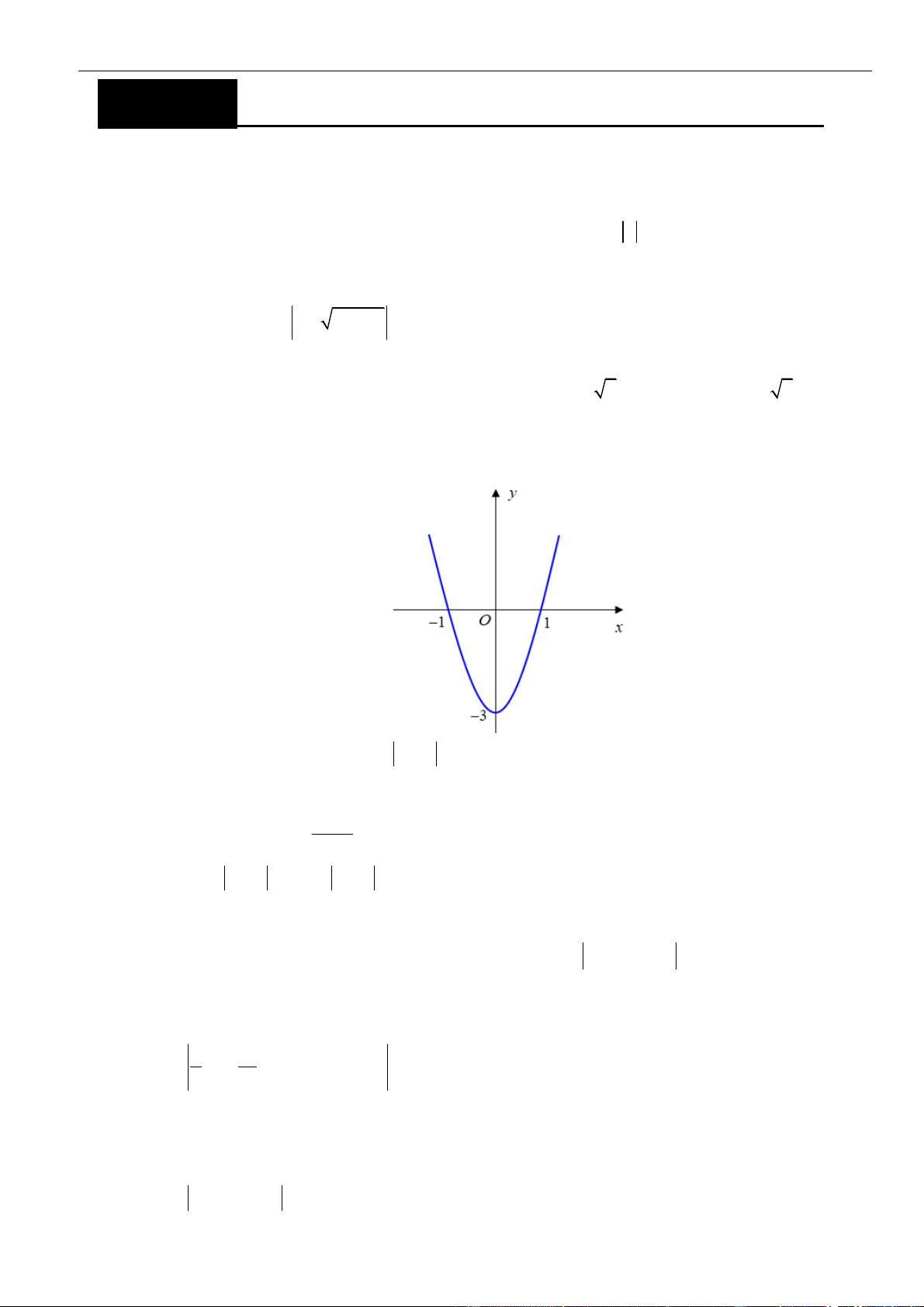
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1:
Gọi
, mn
lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
2yx=+
trên
2; 1−−
. Tính
mn+
.
A.
8
. B.
5
. C.
7
. D.
6
.
Câu 2: Cho hàm số
2
16y x x a= + − +
có giá trị lớn nhất và nhỏ nhất lần lượt là
,mM
. Biết
2
m M a+=
. Tìm tích
P
tất cả các giá trị
a
thỏa mãn đề bài
A.
4P =−
. B.
8P =−
. C.
42P =−
. D.
4 2 4P = − −
.
Câu 3: Cho hàm số
( )
32
f x ax bx cx d= + + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
tiếp xúc với đường thẳng
4y =
tại điểm có hoành độ dương và đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
0;2
bằng
A.
3
. B.
14
. C.
8
. D.
20
.
Câu 4: Cho hàm số
( )
1
xm
fx
x
+
=
+
với
m
là tham số. Có bao nhiêu giá trị nguyên của tham số
m
sao
cho
( )
( )
0;1
0;1
max 2min 200
x
x
f x f x
+
?
A.
400
. B.
301
. C.
401
. D.
200
.
Câu 5: Cho
(0;2)m
. Gọi
là giá trị lớn nhất của hàm số
32
3y x x m= − −
trên
0;3
. Tính
.
A.
2 m
=+
. B.
4m
=+
. C.
2 m
=−
. D.
4 m−
.
Câu 6: Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao cho giá trị lớn nhất của hàm số
42
1 19
30 20
42
y x x x m= − + + −
trên đoạn
0;2
không vượt quá 20. Tổng các phần tử của
S
bằng
A.
300
. B.
105
. C.
195−
. D.
210
.
Câu 7: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
42
4y x x m= − +
trên đoạn
2;1−
bằng 2020. Tính tổng các phần tử của
S
Max-min hàm số chứa dấu giá trị tuyệt đối
DẠNG 4
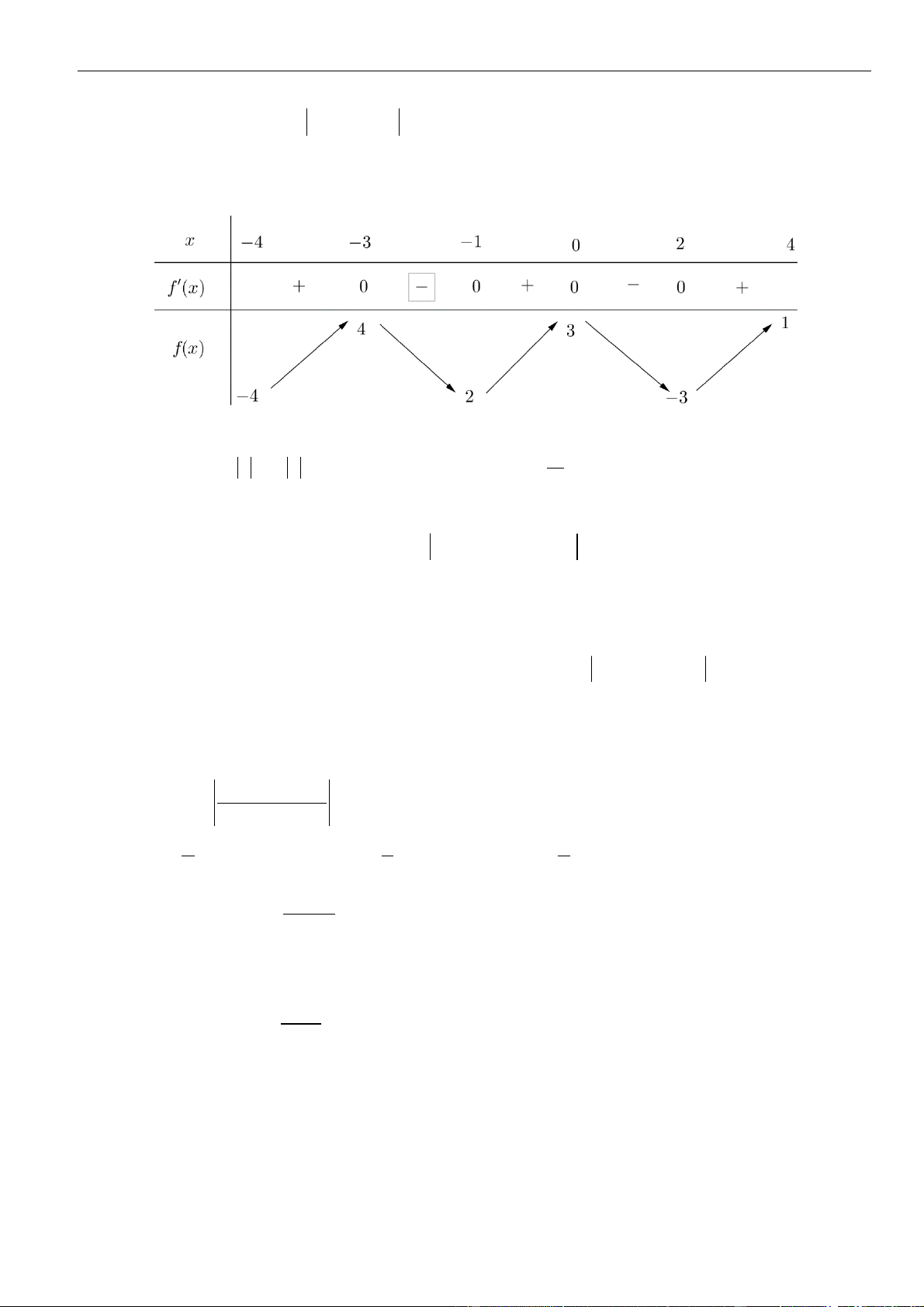
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
4
. B.
5
. C.
2020
. D.
0
.
Câu 8: Cho hàm số
32
( ) 3 .f x x x m= − +
Có bao nhiêu số nguyên
m
để
1;3
min ( ) 3fx
.
A. 4. B. 10. C. 6. D. 11.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên trên đoạn
4;4−
như sau:
Có bao nhiêu giá trị của tham số
m
thuộc đoạn
4;4−
để giá trị lớn nhất của hàm số
( )
( )
( )
3
3g x f x x f m= + +
trên đoạn
1;1−
bằng
11
2
?
A.
2
. B.
4
. C.
3
D.
5
.
Câu 10: Giá trị lớn nhất của hàm số
( )
32
3 72 90f x x x x m= + − + +
trên đoạn
5;5−
là
2020
. Trong
các khẳng định sau, khẳng định nào đúng về tham số
m
?
A.
m
là số chính phương. B.
m
là một số chẵn.
C.
m
là số nguyên âm. D.
m
là số nguyên tố.
Câu 11: Gọi
m
là tham số thực để giá trị lớn nhất của hàm số
2
24y x x m= + + −
trên đoạn
2;1−
đạt
giá trị nhỏ nhất. Giá trị của
m
là
A.
3
. B.
5
. C.
4
. D.
1
.
Câu 12: Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho giá trị lớn nhất của hàm số
2
24
()
2
x mx m
fx
x
++
=
+
trên đoạn
1;1−
bằng
3
. Tích các phần tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
3
2
−
. D.
1
.
Câu 13: Cho hàm số
2
4
xm
y
x
+
=
−
(
m
là tham số thực ) Thỏa mãn
0;2
max 3y =
. Mệnh đề nào dưới đây là
đúng?
A.
11m −
. B.
12m =−
. C.
8m −
. D.
8m −
.
Câu 14: Cho hàm số
3
xm
y
x
+
=
−
(
m
là tham số) thỏa mãn
1;2
min 2.y
−
=−
Mệnh đề nào dưới đây đúng?
A.
3.m
B.
1 1.m−
C.
3.m −
D.
3 1.m− −
Câu 15: Cho hàm số
()y f x=
có bảng biến thiên trên đoạn
4;4−
như sau:
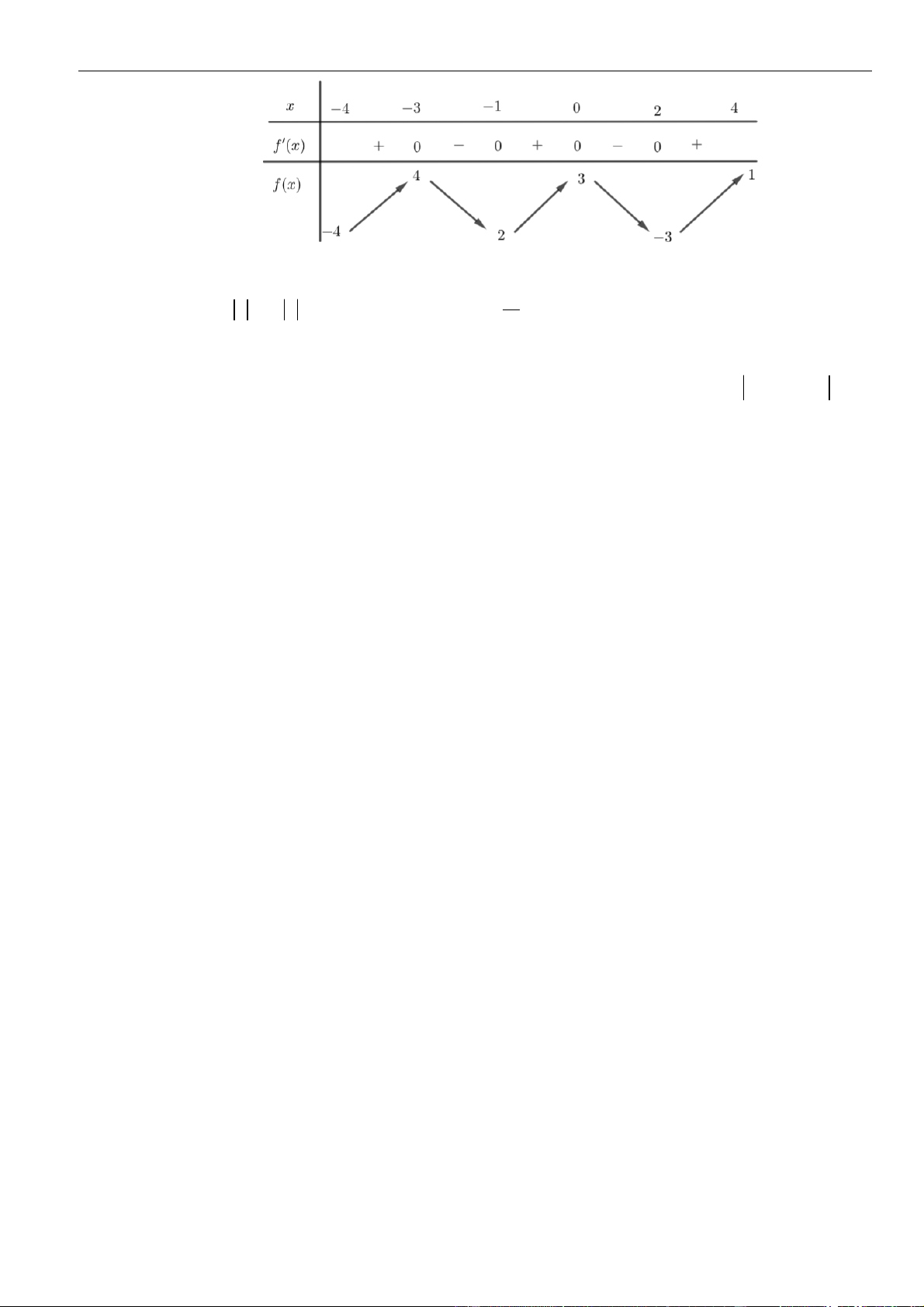
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Có bao nhiêu giá trị của tham số
4;4m−
để giá trị lớn nhất của hàm số
( )
( )
3
( ) 3g x f x x f m= + +
trên
1;1−
bằng
11
?
2
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 16: Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
y =
3
3x x m−+
trên
đoạn
0;3
bằng 20.
A.
1
. B.
2
. C.
3
. D.
31
.

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1:
Gọi
, mn
lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số
2yx=+
trên
2; 1−−
. Tính
mn+
.
A.
8
. B.
5
. C.
7
. D.
6
.
Lời giải
Chọn D
Vì trên
2; 1−−
thì
4
0 2 2 2 4 6.
2
m
x x m n
n
=
+ + =
=
.
Câu 2: Cho hàm số
2
16y x x a= + − +
có giá trị lớn nhất và nhỏ nhất lần lượt là
,mM
. Biết
2
m M a+=
. Tìm tích
P
tất cả các giá trị
a
thỏa mãn đề bài
A.
4P =−
. B.
8P =−
. C.
42P =−
. D.
4 2 4P = − −
.
Lời giải
Chọn C
Đặt
( )
2
16f x x x= + −
với
44x−
.
Ta có
( )
2
22
16
1
16 16
x x x
fx
xx
−−
= − =
−−
;
Cho
( )
2
2
16
0 0 2 2.
16
xx
f x x
x
−−
= = =
−
Ta tính
( ) ( )
( )
4 4; 4 4; 2 2 4 2f f f− = − = =
suy ra
( )
( )
min 4
max 4 2
fx
fx
= −
=
.
Ta có
( )
y f x a=+
do đó
min 0
max 4 2
m y a a
M y a
= = + =
= = +
.
2 2 2
4 242 2 0m aM a a a a a+ = + −−+ = =
.
Do đó
12
42.aPa= = −
.
Câu 3: Cho hàm số
( )
32
f x ax bx cx d= + + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
tiếp xúc với đường thẳng
4y =
tại điểm có hoành độ dương và đồ thị của hàm số
( )
y f x
=
như hình vẽ.
Giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
0;2
bằng
A.
3
. B.
14
. C.
8
. D.
20
.
Lời giải

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Chọn C
Ta có:
( )
2
32f x ax bx c
= + +
.
Đồ thị của hàm số
( )
fx
đi qua các điểm
( )
1;0
;
( )
0; 3−
và có trục đối xứng là
0x =
1
0
3
a
b
c
=
=
=−
( )
3
3f x x x d = − +
.
Đồ thị
( )
C
tiếp xúc với đường thẳng
4y =
tại điểm có hoành độ dương
( )
3
3
2
34
34
1
3 3 0
1
x x d
x x d
x
x
xl
− + =
− + =
=
−=
=−
6
1
d
x
=
=
( )
3
36f x x x = − +
Xét trên đoạn
0;2
ta có:
( )
( )
( )
06
28
14
f
f
f
=
=
=
giá trị lớn nhất của hàm số
( )
y f x=
trên đoạn
0;2
bằng
( )
28f =
.
Câu 4: Cho hàm số
( )
1
xm
fx
x
+
=
+
với
m
là tham số. Có bao nhiêu giá trị nguyên của tham số
m
sao
cho
( )
( )
0;1
0;1
max 2min 200
x
x
f x f x
+
?
A.
400
. B.
301
. C.
401
. D.
200
.
Lời giải
Chọn D
Ta có
( )
fx
liên tục trên
0;1
và có
( )
( )
2
1
1
m
fx
x
−
=
+
.
TH1:
1m =
( ) ( )
0f x f x
=
là hàm hằng
( )
( ) ( )
0;1
0;1
max min 0 1
x
x
f x f x f
= = =
Thỏa điều kiện
( )
( )
0;1
0;1
max 2min 200
x
x
f x f x
+
nên nhận
1m =
.
TH2:
( ) ( )
10m f x f x
đồng biến
0;1
Suy ra
( ) ( )
0;1
1
max 1
2
x
m
f x f
+
==
,
( )
0;1
min
x
f x m
=
.
TH2.1:
0m
.
( )
( )
0;1
0;1
max 2min 200
x
x
f x f x
+
1 399
2 200
25
m
mm
+
+
.
Suy ra
)
0;1m
.
TH2.2:
10m−
( )
( )
0;1
0;1
min 0
1
max ;
2
x
x
fx
m
f x m
=
+
, nên
( )
0;1
max 1
x
fx
.
Do đó
( )
( )
0;1
0;1
max 2min 200
x
x
f x f x
+
luôn đúng.
Nên
10m−
.
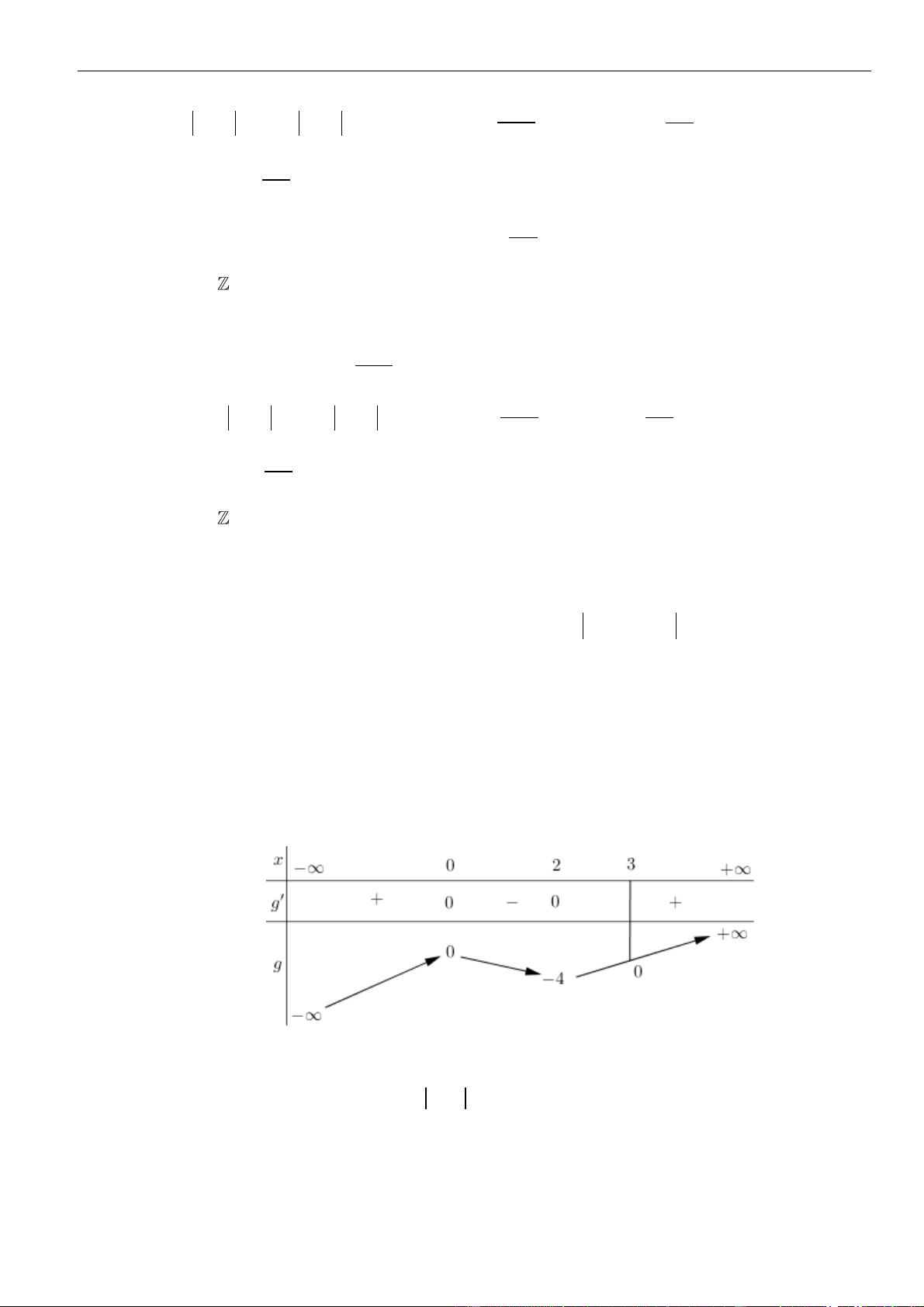
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
TH3:
1m −
( )
( )
0;1
0;1
max 2min 200
x
x
f x f x
+
1
2. 200
2
m
m
+
− + −
201
2
m −
.
Suy ra
201
;1
2
m
− −
.
Kết hợp 3 trường hợp của TH2, ta nhận
201
;1
2
m
−
.
Mà
m
nên
100; 99;...;0m − −
.
TH3:
( )
10m f x
( )
fx
nghịch biến
0;1
.
Suy ra
( ) ( )
0;1
1
min 1 1
2
x
m
f x f
+
= =
,
( ) ( )
0;1
max 0
x
f x f m
==
Nên
( )
( )
0;1
0;1
max 2min 200
x
x
f x f x
+
1 199
2. 200
22
m
mm
+
+
Suy ra
199
1;
2
m
.
Mà
m
nên
2;3;...99m
.
Kết hợp 3 trường hợp, ta được
100; 99;...;99m − −
.
Vậy có
200
giá trị nguyên của tham số
m
thỏa mãn.
Câu 5: Cho
(0;2)m
. Gọi
là giá trị lớn nhất của hàm số
32
3y x x m= − −
trên
0;3
. Tính
.
A.
2 m
=+
. B.
4m
=+
. C.
2 m
=−
. D.
4 m−
.
Lời giải
Chọn B
Đặt
32
3t x x=−
. Xét hàm số
32
( ) 3g x x x=−
trên
0;3
.
Ta có:
2
'( ) 3 6g x x x=−
. Xét
0
'( ) 0
2
x
gx
x
=
=
=
.
Ta có bảng biến thiên
Từ bảng biến thiên ta suy ra:
40t−
khi
03x
.
Từ đó bài toán trở thành
Tìm giá trị lớn nhất của hàm số
y t m=−
trên
4;0−
.
Nhận thấy hàm số
( ) t mft=−
là hàm đồng biến.
Kết hợp với điều kiện
( )
0;2m
nên ta có bảng biến thiên.
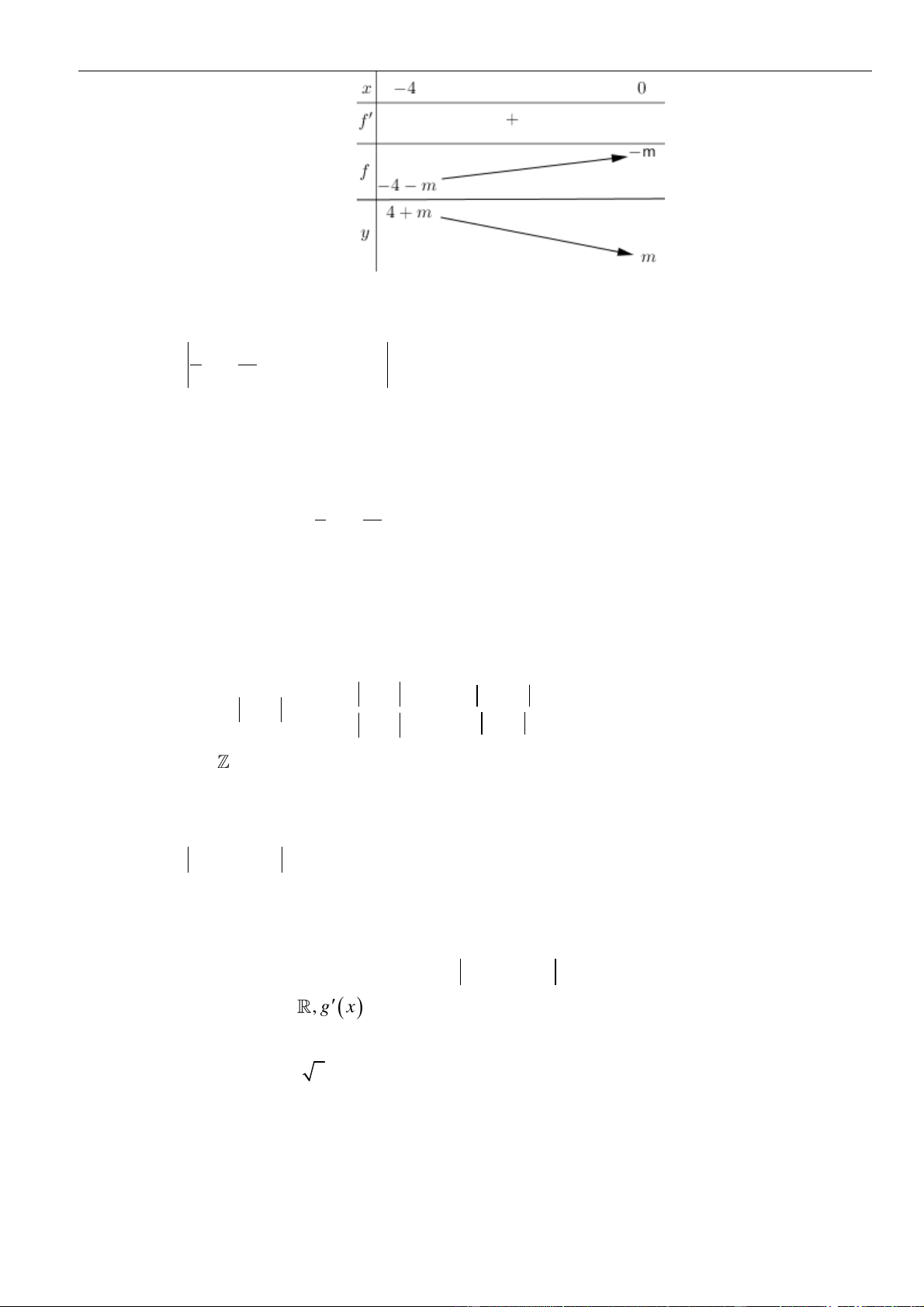
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Vậy
4 m
=+
.
Câu 6: Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao cho giá trị lớn nhất của hàm số
42
1 19
30 20
42
y x x x m= − + + −
trên đoạn
0;2
không vượt quá 20. Tổng các phần tử của
S
bằng
A.
300
. B.
105
. C.
195−
. D.
210
.
Lời giải
Chọn B
Xét hàm số
42
1 19
( ) 30 20
42
g x x x x m= − + + −
trên đoạn
0;2
Ta có:
( )
( )
( )
3
5 0;2
( ) 19 30; ( ) 0 2 0;2
3 0;2
x
g x x x g x x
x
= −
= − + = =
=
.
( ) ( )
0 20; 2 6g m g m= − = +
.
Ta có
( )
( )
( )
0;2
0 20
20 20
max 20 0 14
6 20
2 20
g
m
g x m
m
g
−
+
.
Mà
m
nên
0;1;2;...14m
.
Vậy tổng các phần tử của
S
bằng 105.
Câu 7: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
42
4y x x m= − +
trên đoạn
2;1−
bằng 2020. Tính tổng các phần tử của
S
A.
4
. B.
5
. C.
2020
. D.
0
.
Lời giải
Chọn A
Xét hàm số
( ) ( )
4 2 4 2
4 , 4g x x x m f x x x m= − + = − +
TXĐ của
( )
gx
là
( )
3
, 4 8g x x x
=−
.
( )
0
0
2
x
gx
x
=
=
=
Ta có bảng biến thiên của hàm số
( )
gx
với
2;1x−

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Ta có:
( )
2;1
max max , 4 , 3
x
f x m m m
−
= − −
(1)
- Nếu
0m
: Toàn bộ phần đồ thị trên của hàm số
( )
gx
nằm phía dưới trục hoành
( )
2;1
max 4 4 2020 2016
x
f x m m m
−
= − = − = = −
- Nếu
4 0 4mm−
: Toàn bộ phần đồ thị trên của hàm số
( )
gx
nằm phía trên trục hoành
( )
2;1
max 2020
x
f x m m
−
= = =
- Nếu
04m
: Vì có (1) nên yêu cầu của bài toán không thể thỏa mãn. Vậy có 2 giá trị của
m
thỏa mãn bài toán là:
2016
2016 2020 4
2020
m
m
=−
− + =
=
.
Câu 8: Cho hàm số
32
( ) 3 .f x x x m= − +
Có bao nhiêu số nguyên
m
để
1;3
min ( ) 3fx
.
A. 4. B. 10. C. 6. D. 11.
Lời giải
Chọn D
Xét hàm số
3 2 2
0 1;3
( ) 3 ( ) 3 6 0
2
x
g x x x m g x x x
x
=
= − + = − =
=
.
Ta có
( )
12gm=−
;
( )
24gm=−
;
( )
3gm=
. Ta thấy
( ) ( ) ( )
3 1 2g g g
.
Nếu
( ) ( ) ( )
3 . 2 0 4 0 0 4g g m m m −
thì
1;3
min ( ) 0fx=
thỏa mãn.
Nếu
( )
3 0 0gm
thì
( ) ( )
1;3
min 3 3 3 3f x g m m= = −
. Vậy
)
3;0m−
.
Nếu
( )
2 0 4gm
thì
( ) ( )
1;3
min 2 4 3 1 7f x g m m= = −
. Vậy
(
4;7m
.
Kết hợp 3 điều trên ta được
3;7
m
m
− →
có 11 giá trị
m
thỏa ycbt.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên trên đoạn
4;4−
như sau:
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Có bao nhiêu giá trị của tham số
m
thuộc đoạn
4;4−
để giá trị lớn nhất của hàm số
( )
( )
( )
3
3g x f x x f m= + +
trên đoạn
1;1−
bằng
11
2
?
A.
2
. B.
4
. C.
3
D.
5
.
Lời giải
Chọn B
1;1 1;1xx − − −
Có
( )
( )
( )
( )
( ) ( )
33
33g x f x x f m f x x f m g x− = − + − + = + + =
Suy ra
( )
gx
là hàm số chẵn trên
1;1−
.
Xét trên
0;1
, ta có:
( )
( )
( )
3
3g x f x x f m= + +
( )
( ) ( )
23
3 3 . 3g x x f x x
= + +
Cho
( )
( )
( )
3
3
3
3
3
3 3( )
33
0
0 3 0
1
30
32
x x VN
x x VN
x
g x f x x
x
xx
xx
+ = −
+ = −
=
= + =
=
+=
+=
.
( ) ( ) ( ) ( )
0 0 3g f f m f m= + = +
;
( ) ( ) ( ) ( )
1 1 0g f f m g= +
.
Từ đó:
( ) ( ) ( )
1;1
11 5
max 3
22
g x f m f m
−
= + = =
Dựa vào bảng biến thiên ta thấy có
4
giá trị của
m
thuộc đoạn
4;4−
thỏa điều kiện bài toán.
Câu 10: Giá trị lớn nhất của hàm số
( )
32
3 72 90f x x x x m= + − + +
trên đoạn
5;5−
là
2020
. Trong
các khẳng định sau, khẳng định nào đúng về tham số
m
?
A.
m
là số chính phương. B.
m
là một số chẵn.
C.
m
là số nguyên âm. D.
m
là số nguyên tố.
Lời giải
Chọn B
Ta có:
( ) ( )
f x g x m=+
với
( )
( )
2
3 2 3 2
3 72 90 3 72 90g x x x x x x x= + − + = + − +
.
( )
( ) ( )
( )
( )( )
( )
3 2 3 2 3 2 2
22
3 2 3 2
2 3 72 90 . 3 72 90 3 72 90 3 6 72
2 3 72 90 3 72 90
x x x x x x x x x x x
gx
x x x x x x
+ − + + − + + − + + −
==
+ − + + − +
.
( )
2
4 5;5
0 3 6 72 0
6 5;5
x
g x x x
x
= −
= + − =
= − −
.
( )
5 400fm− = +
,
( )
5 70fm=+
,
( )
4 86fm=+
.
Vậy
( )
5;5
max 400 2020 1620
x
f x m m
−
= + = =
.
Vậy
m
là một số chẵn.
Câu 11: Gọi
m
là tham số thực để giá trị lớn nhất của hàm số
2
24y x x m= + + −
trên đoạn
2;1−
đạt
giá trị nhỏ nhất. Giá trị của
m
là

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
A.
3
. B.
5
. C.
4
. D.
1
.
Lời giải
Chọn A
Xét hàm số
( )
2
24f x x x m= + + −
liên tục trên
2;1−
.
Ta có:
( )
22f x x
=+
;
( ) ( )
0 1 2;1f x x
= = − −
.
Ta có
( )
24fm− = −
,
( )
11fm=−
,
( )
15fm− = −
.
Khi đó
( )
2;1
max 1f x m
−
=−
,
( )
2;1
min 5f x m
−
=−
.
Khi đó
( )
2;1
max max 5 ; 1f x m m M
−
= − − =
.
Ta có:
5
2 5 1 5 1 4
11
Mm
M m m m m
M m m
−
− + − − + − =
− = −
2M
.
Dấu
""=
xảy ra
( )( )
5 1 2
3
5 1 0
mm
m
mm
− = − =
=
− −
.
Câu 12: Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho giá trị lớn nhất của hàm số
2
24
()
2
x mx m
fx
x
++
=
+
trên đoạn
1;1−
bằng
3
. Tích các phần tử của
S
bằng
A.
1
2
. B.
1
2
−
. C.
3
2
−
. D.
1
.
Lời giải
Chọn C
Xét hàm số
2
24
()
2
x mx m
gx
x
++
=
+
trên đoạn
1;1−
Ta có:
2
2
4
'( )
( 2)
xx
gx
x
+
=
+
,
0 [ 1;1]
'( ) 0
4
x
gx
x
= −
=
= − [ 1;1]
−
(0) 2 ;gm=
( 1) 2 1;gm− = +
1
( 1) 2 .
3
gm− = +
Theo đề bài
1;1 1;1 1;1
1
max ( ) max ( ) max |2m| ; |2m + |;| 2 1| 3
3
f x g x m
− − −
= = + =
.
Chỉ có thể xảy ra một trong hai trường hợp:
Th1:
3
2
| 2 | 3 ;
3
2
m
m
m
=
=
=−
*
1;1
3
max ( ) 4
2
m f x
−
= =
vì vậy ta loại trường hợp
3
2
m =
.
*
1;1
3
max ( ) 3
2
m f x
−
= − =
(nhận).
Th2:
1
| 2 1| 3 ;
2
m
m
m
=
+ =
=−
*
1;1
2 max ( ) 4m f x
−
= − =
vì vậy ta loại trường hợp
2m =−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
*
1;1
1 max ( ) 3m f x
−
= =
(nhận).
Vậy
33
.1
22
S = − = −
.
Câu 13: Cho hàm số
2
4
xm
y
x
+
=
−
(
m
là tham số thực ) Thỏa mãn
0;2
max 3y =
. Mệnh đề nào dưới đây là
đúng?
A.
11m −
. B.
12m =−
. C.
8m −
. D.
8m −
.
Lời giải
Chọn D
Ta có:
,
2
8
( 4)
m
y
x
−−
=
−
TH1:
,
8 0 8 0 4m m y x− − −
nên hàm số đồng biến trong
0;2
0;2
44
max (2) 3 10 ( )
2 4 2
mm
y y m tm
++
= = = = = −
−−
TH2:
,
8 0 8 0 4m m y x− − −
nên hàm số nghịch biến trong
0;2
0;2
max (0) 3 12 ( )
4
m
y y m L = = = = −
−
Vậy
10m =−
là giá trị cần tìm nên đáp án D là mệnh đề đúng
Câu 14: Cho hàm số
3
xm
y
x
+
=
−
(
m
là tham số) thỏa mãn
1;2
min 2.y
−
=−
Mệnh đề nào dưới đây đúng?
A.
3.m
B.
1 1.m−
C.
3.m −
D.
3 1.m− −
Lời giải
Chọn B
Hàm số
3
xm
y
x
+
=
−
liên tục trên đoạn
1;2−
và có đạo hàm
2
3
'
( 3)
m
y
x
−−
=
−
Nếu
' 0 3ym −
thì hàm số đồng biến trên đoạn
1;2−
nên
1;2
1
min ( 1) 2 9
4
m
y y m
−
−+
= − = = − =
−
không thỏa mãn.
Nếu
' 0 3ym −
hàm số nghịch biến trên đoạn
1;2−
nên
1;2
2
min (2) 2 0
1
m
y y m
−
+
= = = − =
−
thỏa mãn.
Vậy đáp án B đúng.
Câu 15: Cho hàm số
()y f x=
có bảng biến thiên trên đoạn
4;4−
như sau:

Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Có bao nhiêu giá trị của tham số
4;4m−
để giá trị lớn nhất của hàm số
( )
( )
3
( ) 3g x f x x f m= + +
trên
1;1−
bằng
11
?
2
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn B
Ta có
( ) ( )
g x g x−=
nên
()gx
chẵn hay đồ thị của hàm số
()y g x=
đối xứng qua trục tung.
( )
( )
( )
( )
33
1;1 0;1 0;1 0;1
max ( ) max ( ) max 3 max 3 .g x g x f x x f m f x x f m
−
= = + + = + +
Xét hàm số
( )
3
3y f x x=+
trên
0;1
.
Đặt
3
[0;1] 0;4
3 0;4 max max ( ) 3.t x x t y f t= + = =
Khi đó
( )
1;1
11 5
max ( ) 3 ( ) .
22
g x f m f m
−
= + = =
Vậy có 4 giá trị m thỏa mãn yêu cầu bài toán.
Câu 16: Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
y =
3
3x x m−+
trên
đoạn
0;3
bằng 20.
A.
1
. B.
2
. C.
3
. D.
31
.
Lời giải
Chọn B
Xét hàm
( )
3
3f x x x m= − +
trên
0;3
.
Ta có
( )
2
33f x x
=−
,
( )
1
0
1
x
fx
x
=
=
=−
.
Khi đó
( )
12fm=−
,
( )
0fm=
và
(3) 18fm=+
.
Do
(1) (0) (3)f f f
nên
0;3
max max (1) ; (3)y f f=
.
Nếu
0;3
max 18 20ym= + =
thì
18 20
2
18 2
m
m
mm
+ =
=
+ −
.
Nếu
0;3
max 2 20ym= − =
thì
2 20
18
2 18
m
m
mm
− =
= −
− +
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Một chất điểm chuyển động với quy luật
( )
23
6.s t t t=−
Thời điểm
t
(giây) tại vận tốc
( )
/v m s
của chuyển động đạt giá trị lớn nhất bằng
A.
12
. B.
24
. C.
2
. D.
6
.
Câu 2: Độ giảm huyết áp của một bệnh
( ) ( )
2
0,025 30G x x x=−
trong đó
x
là số miligam thuốc được
tiêm cho bệnh nhân
( )
0 30x
. Để bệnh nhân đó có huyết áp giảm nhiều nhất thì liều lượng
thuốc cần tiêm vào là
A.
( )
15x mg=
. B.
( )
20x mg=
. C.
( )
20x mg=
. D.
( )
25x mg=
.
Câu 3: Một chất điểm chuyển động với quy luật
23
( ) 6 .s t t t=−
Thời điểm
t
(giây) tại vận tốc
( )
/v m s
của chuyển động đạt giá trị lớn nhất bằng
A.
12
. B.
24
. C.
2
. D.
6
.
Câu 4:
Vận tốc của một hạt chuyển động được xác định bởi công thức
32
10 29 20v t t t t
(
t
được tính bằng giây). Vận tốc của hạt tại thời điểm gia tốc nhỏ nhất gần bằng
A.
0,88−
. B.
2,59
. C.
6,06
. D.
2,61
.
Câu 5: Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng
2mr =
, chiều cao
6mh =
. Bác thợ
mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi
V
là thể
tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Giá trị của V là:
A.
( )
3
32
m
9
V
=
. B.
( )
3
32
m
3
V
=
. C.
( )
3
32
m
27
V
=
. D.
( )
3
32
m
5
V
=
.
Câu 6: Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được
giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể
trong
t
giờ được cho bởi công thức
( ) ( )
2
/
1
t
c t mg L
t
=
+
. Sau khi tiêm thuốc bao lâu thì nồng
độ thuốc trong máu của bệnh nhân cao nhất?
A.
4
giờ. B.
3
giờ. C.
1
giờ. D.
2
giờ.
Câu 7: Một chất điểm chuyển động theo phương trình
32
12 30 10S t t t= − + − +
trong đó
t
tính bằng
( )
s
và
S
tính bằng
( )
m
. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là
A.
2ts=
. B.
4ts=
. C.
6ts=
. D.
5ts=
.
Câu 8: Ông A dự định sử dụng hết
2
8 m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng bao nhiêu?
A.
3
2.05 m
. B.
3
1.02 m
. C.
3
1.45 m
. D.
3
0.73 m
.
Các bài toán ứng dụng, tối ưu và thực tế
DẠNG 5
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 9: Một sợi dây kim loại dài
60cm
được cắt thành hai đoạn. Đoạn thứ nhất được uốn thành một hình
vuông, đoạn thứ hai được uốn thành một vòng tròn. Hỏi khi tổng diện tích của hình vuông và
hình tròn ở trên nhỏ nhất thì chiều dài đoạn dây uốn thành hình vuông bằng bao nhiêu (làm tròn
đến hàng phần trăm)?
A.
30,54cm
. B.
33,61cm
. C.
40,62cm
. D.
26,43cm
Câu 10: Sự ảnh hưởng khi sử dụng một loại độc tố với vi khuẩn
X
được một nhà sinh học mô tả bởi
hàm số
( )
2
1
4
t
Pt
tt
+
=
++
, trong đó
( )
Pt
là số lượng vi khuẩn sau
t
sử dụng độc tố. Vào thời
điểm nào thì số lượng vi khuẩn
X
bắt đầu giảm?
A. Ngay từ lúc bắt đầu sử dụng độc tố. B. Sau
0,5
giờ.
C. Sau
2
giờ. D. Sau
1
giờ.
Câu 11: Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất
8000
quả bóng
tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất
30
quả bóng trong một
giờ. Chi phí thiết lập các máy này là
200
nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt
động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát
là
192
nghìn đồng một giờ. Số máy móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động
là thấp nhất?
Câu 12: Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để
tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi
của chiến sĩ bằng một phần ba vận tốc chạy trên bộ.Hãy cho biết chiến sỹ phải bơi bao nhiêu mét
để đến được mục tiêu nhanh nhất?Biết dòng sông là thẳng,mục tiêu cách chiến sỹ 1km theo
đường chim bay và chiến sỹ cách bờ bên kia 100m.
A.
200 2
3
. B.
75 3
. C.
200 3
3
. D.
75 2
.
Câu 13: Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng
3
200m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 300 nghìn
đồng/
2
m
. Hãy xác định chi phí thấp nhất để xây bể.
A.
46
triệu đồng. B.
51
triệu đồng. C.
75
triệu đồng. D.
36
triệu đồng.
Câu 14: Ông X muốn xây một bình chứa hình trụ có thể tích
3
72m
. Đáy làm bằng bêtông giá
100
nghìn
đồng
2
/m
, thành làm bằng tôn giá
90
nghìn đồng
2
/m
, nắp bằng nhôm giá
140
nghìn đồng
2
/m
. Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?
A.
( )
3
3
m
. B.
( )
3
3
m
. C.
( )
3
2
m
. D.
( )
3
3
33
m
2
.
Câu 15: Một sợi dây kim loại dài 120cm được cắt thành hai đoạn. Đoạn dây thứ nhất được uốn thành
hình vuông, đoạn dây thứ hai được uốn thành vòng tròn (tham khảo hình bên dưới).
Tổng diện tích của hình vuông và hình tròn đạt giá trị nhỏ nhất là (làm tròn đến hàng đơn vị)
A.
462
. B.
426
. C.
498
. D.
504
.
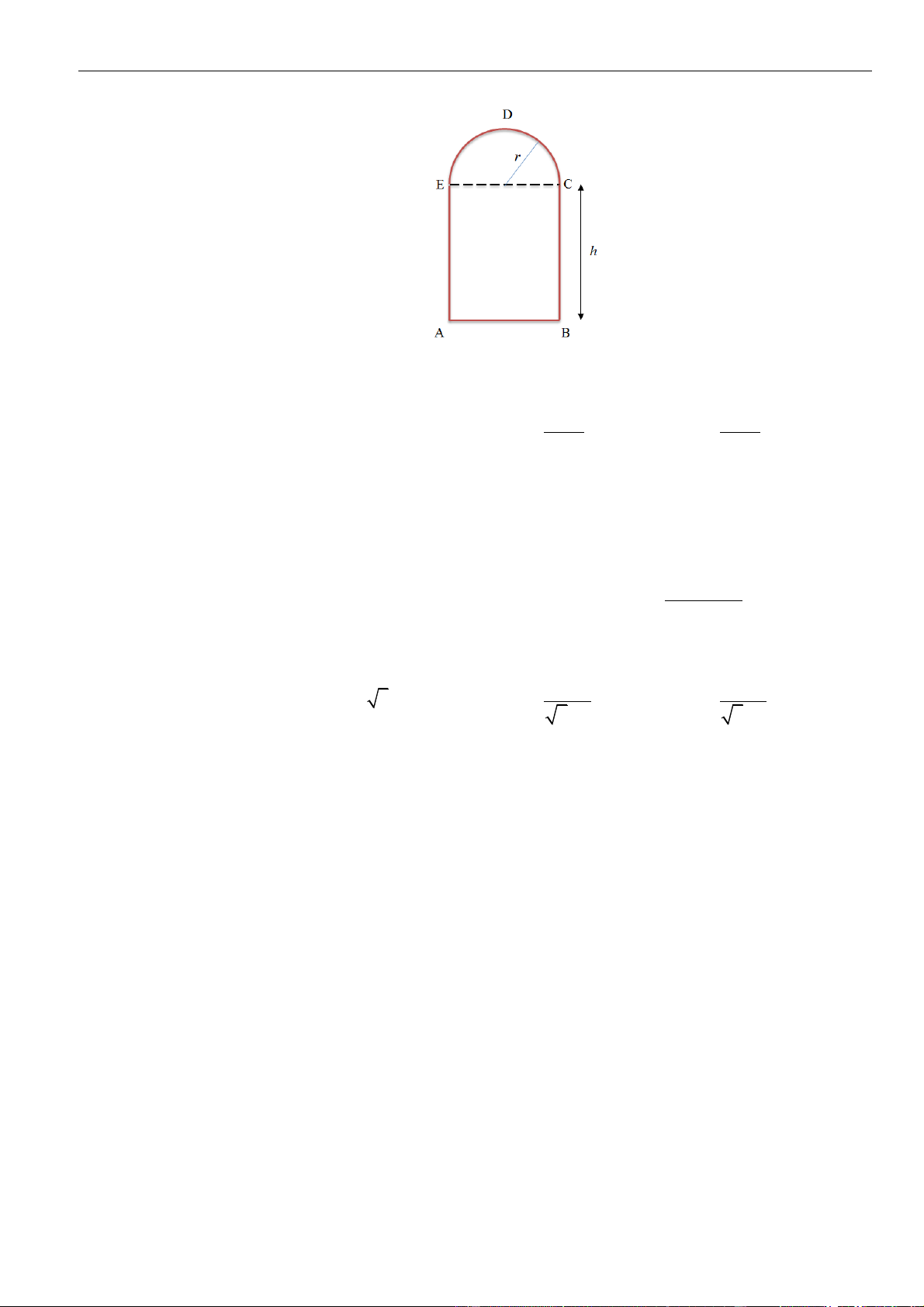
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 16: Bác thợ hàn dùng một thanh kim loại dài
4m
để uốn thành khung cửa sổ có dạng như hình vẽ.
Gọi
r
là bán kính của nửa đường tròn. Tìm
r
(theo
m
) đẻ diện tích tạo thành đạt giá trị lớn
nhất.
A. 1. B. 0,5. C.
4
4
+
. D.
2
4
+
.
Câu 17: Một công ty bất động sản có 50 căn hộ cho thuê. Nếu giá cho thuê mỗi căn là 3 000 000
đồng/tháng thì không có phòng trống, còn nếu cho thuê mỗi căn hộ thêm 200.000đ/tháng thì sẽ
có 2 căn bị bỏ trống. Hỏi công ty phải niêm yếu bao nhiêu để doanh thu là lớn nhất?
A.
3400000
. B.
3000000
. C.
5000000
. D.
4000000
.
Câu 18: Lưu lượng xe ô tô vào đường hầm được cho bởi công thức
( )
2
386
25
v
fv
vv
=
++
(xe/giây), trong
đó
v
(km/h) là vận tốc trung bình của các xe khi vào đường hầm. Tính vận tốc trung bình của
các xe khi vào đường hầm sao cho lưu lượng xe là lớn nhất
A.
5
km/h. B.
5
km/h. C.
193
51+
km/h. D.
193
51−
km/h.
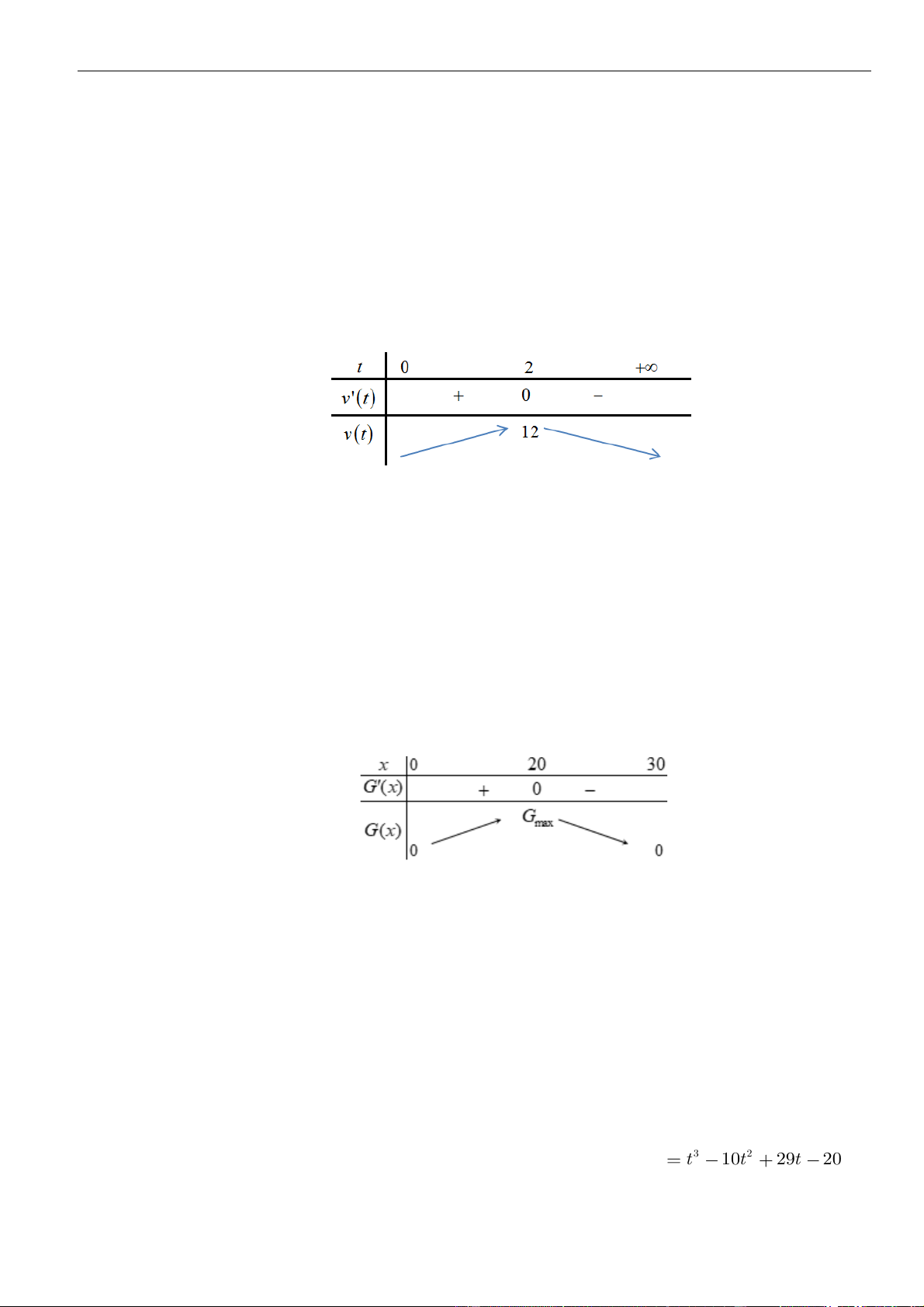
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Một chất điểm chuyển động với quy luật
( )
23
6.s t t t=−
Thời điểm
t
(giây) tại vận tốc
( )
/v m s
của chuyển động đạt giá trị lớn nhất bằng
A.
12
. B.
24
. C.
2
. D.
6
.
Lời giải
Chọn C
Ta có
( ) ( ) ( )
2 3 2
6 ' 12 3s t t t v t s t t t= − = = −
.
( )
' 12 6 0 2v t t t = − = =
.
Bảng biến thiên:
Vậy vận tốc của chuyển động đạt giá trị lớn nhất bằng
12
khi
2t =
.
Câu 2: Độ giảm huyết áp của một bệnh
( ) ( )
2
0,025 30G x x x=−
trong đó
x
là số miligam thuốc được
tiêm cho bệnh nhân
( )
0 30x
. Để bệnh nhân đó có huyết áp giảm nhiều nhất thì liều lượng
thuốc cần tiêm vào là
A.
( )
15x mg=
. B.
( )
20x mg=
. C.
( )
20x mg=
. D.
( )
25x mg=
.
Lời giải
Chọn C
( )
2
1,5 0,075G x x x
=−
( )
0 0 20G x x x
= = =
Vậy để bệnh nhân đó có huyết áp giảm nhiều nhất thì liều lượng thuốc cần tiêm vào là
( )
20x mg=
.
Câu 3: Một chất điểm chuyển động với quy luật
23
( ) 6 .s t t t=−
Thời điểm
t
(giây) tại vận tốc
( )
/v m s
của chuyển động đạt giá trị lớn nhất bằng
A.
12
. B.
24
. C.
2
. D.
6
.
Lời giải
Chọn C
Vận tốc của chuyển động là
( ) ( ) ( )
2
2
12 3 12 3 2 12,v t s t t t t t
= = − = − −
.
Vậy vận tốc đạt giá trị lớn nhất khi
2t =
.
Câu 4:
Vận tốc của một hạt chuyển động được xác định bởi công thức
32
10 29 20v t t t t
(
t
được tính bằng giây). Vận tốc của hạt tại thời điểm gia tốc nhỏ nhất gần bằng
A.
0,88−
. B.
2,59
. C.
6,06
. D.
2,61
.
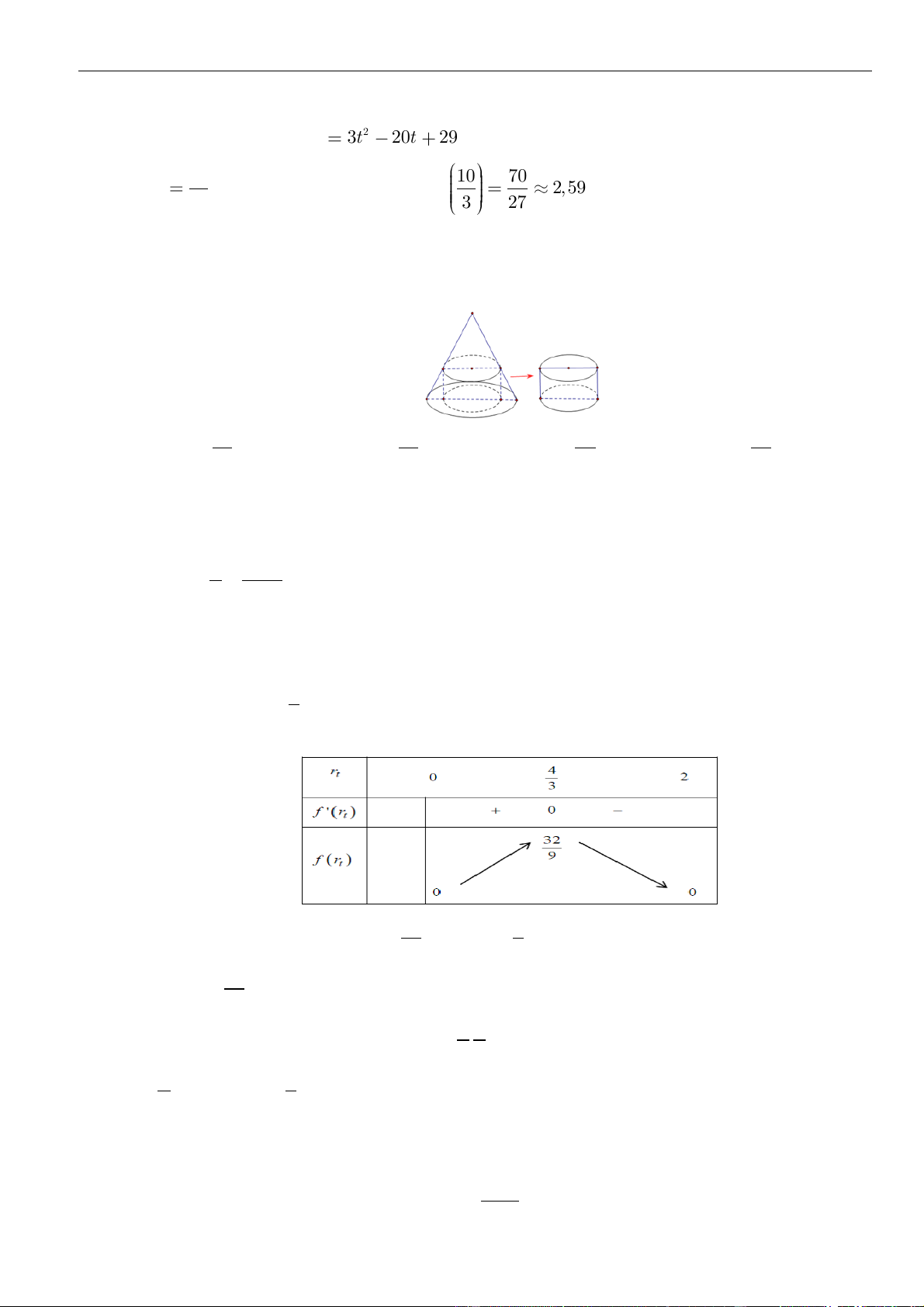
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn B
Gia tốc của hạt
2
3 20 29a t t t
, gia tốc là hàm số bậc hai ẩn
t
đạt giá trị nhỏ nhất tại
10
3
t
. Tại đó, vận tốc của hạt bằng
10 70
2,59
3 27
v
.
Câu 5: Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng
2mr =
, chiều cao
6mh =
. Bác thợ
mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi
V
là thể
tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Giá trị của V là:
A.
( )
3
32
m
9
V
=
. B.
( )
3
32
m
3
V
=
. C.
( )
3
32
m
27
V
=
. D.
( )
3
32
m
5
V
=
.
Lời giải
Chọn B
Gọi
t
r
,
t
h
lần lượt là bán kính và chiều cao của khối trụ.
Ta có:
( )
6
2 6 6 6 3
26
tt
t t t t
rh
h r h r
−
= − = = −
.
Ta lại có:
( )
( )
2 2 2 3
. 6 3 6 3
t t t t t t
V r h r r r r
= = − = −
.
Xét hàm số
( )
23
63
t t t
f r r r=−
, với
( )
0;2
t
r
có
( )
2
12 9
t t t
f r r r
=−
;
( )
4
0
3
tt
f r r
= =
.
Bảng biến thiên:
Dựa vào BBT ta có
( )
9
mx
32
a
t
fr=
đạt tại
4
3
t
r =
.
Vậy
32
9
V
=
.
Cách 2:
( ) ( )
22
. 6 3 12 2
22
tt
t t t t t
rr
V r h r r r
= = − = −
. Áp dụng BĐT Co-si, V max khi
4
2
23
t
tt
r
rr= − =
.
Câu 6: Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được
giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể
trong
t
giờ được cho bởi công thức
( ) ( )
2
/
1
t
c t mg L
t
=
+
. Sau khi tiêm thuốc bao lâu thì nồng
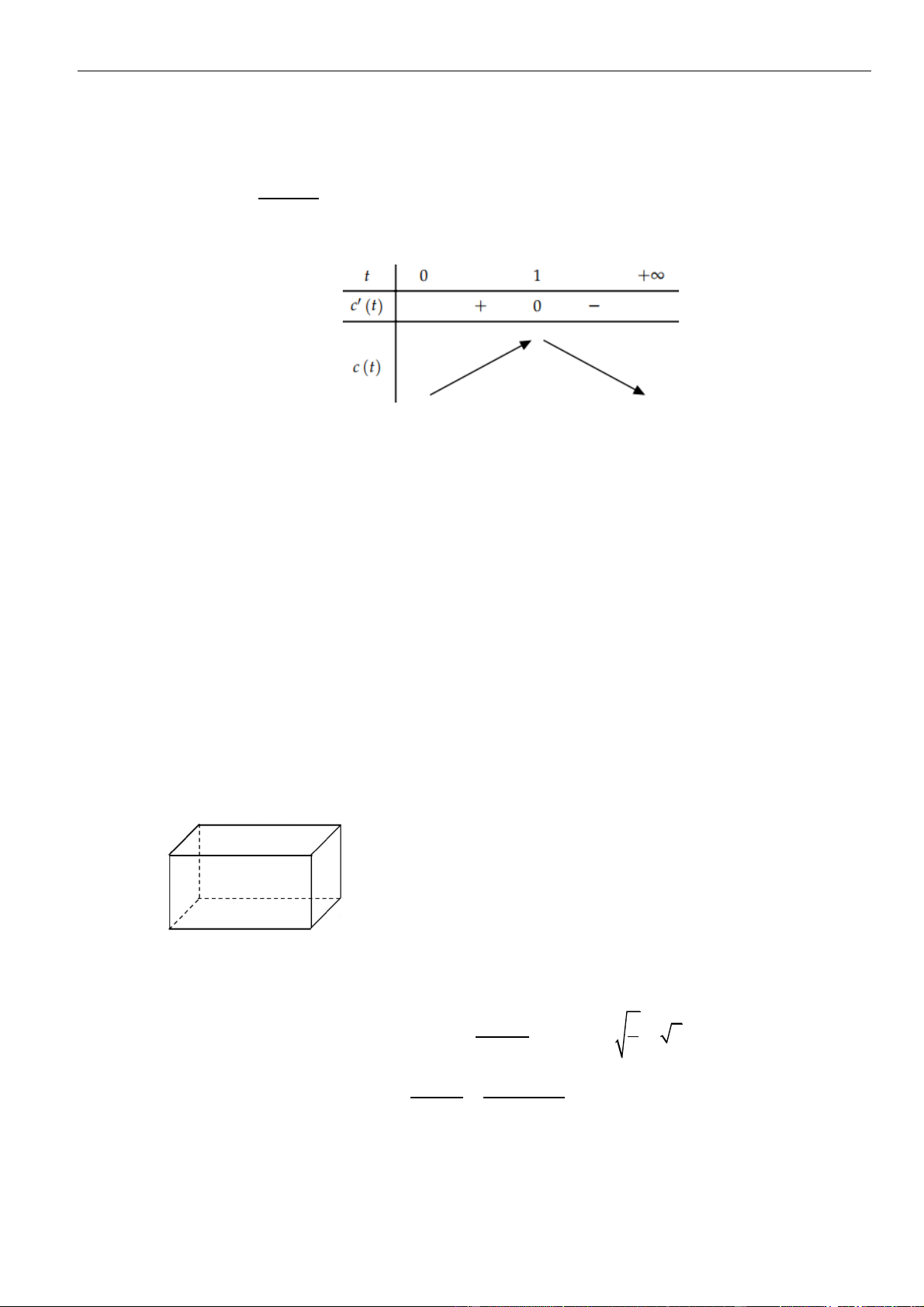
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
độ thuốc trong máu của bệnh nhân cao nhất?
A.
4
giờ. B.
3
giờ. C.
1
giờ. D.
2
giờ.
Lời giải
Chọn C
Ta có
( )
( )
( )
2
2
2
1
' , 0;
1
−+
= +
+
t
c t t
t
. Cho
( )
1
'0
1
t
ct
t
=
=
=−
.
Bảng biến thiên:
Vậy sau khi tiêm
1
giờ, nồng độ thuốc trong máu bệnh nhân cao nhất.
Câu 7: Một chất điểm chuyển động theo phương trình
32
12 30 10S t t t= − + − +
trong đó
t
tính bằng
( )
s
và
S
tính bằng
( )
m
. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là
A.
2ts=
. B.
4ts=
. C.
6ts=
. D.
5ts=
.
Lời giải
Chọn B
Ta có
( ) ( )
2
2
3 24 30 3 4 18 18v t S t t t
= = − + − = − − +
.
Khi đó
( ) ( )
max 18 4v t t s= =
.
Câu 8: Ông A dự định sử dụng hết
2
8 m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng bao nhiêu?
A.
3
2.05 m
. B.
3
1.02 m
. C.
3
1.45 m
. D.
3
0.73 m
.
Lời giải
Chọn A
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là
( )
,2 , , 0x x y x y
.
Diện tích phần lắp kính là
2
2
82
2 . 2 2.2 . 2 6 8 0
6
x
x x xy x y x xy xy
−
+ + = + = =
8
42
2
x = =
Thể tích bể cá là:
23
8 2 4 16
2 . . 2 .
66
x x x
V x x y x
− − +
= = =
với
02x
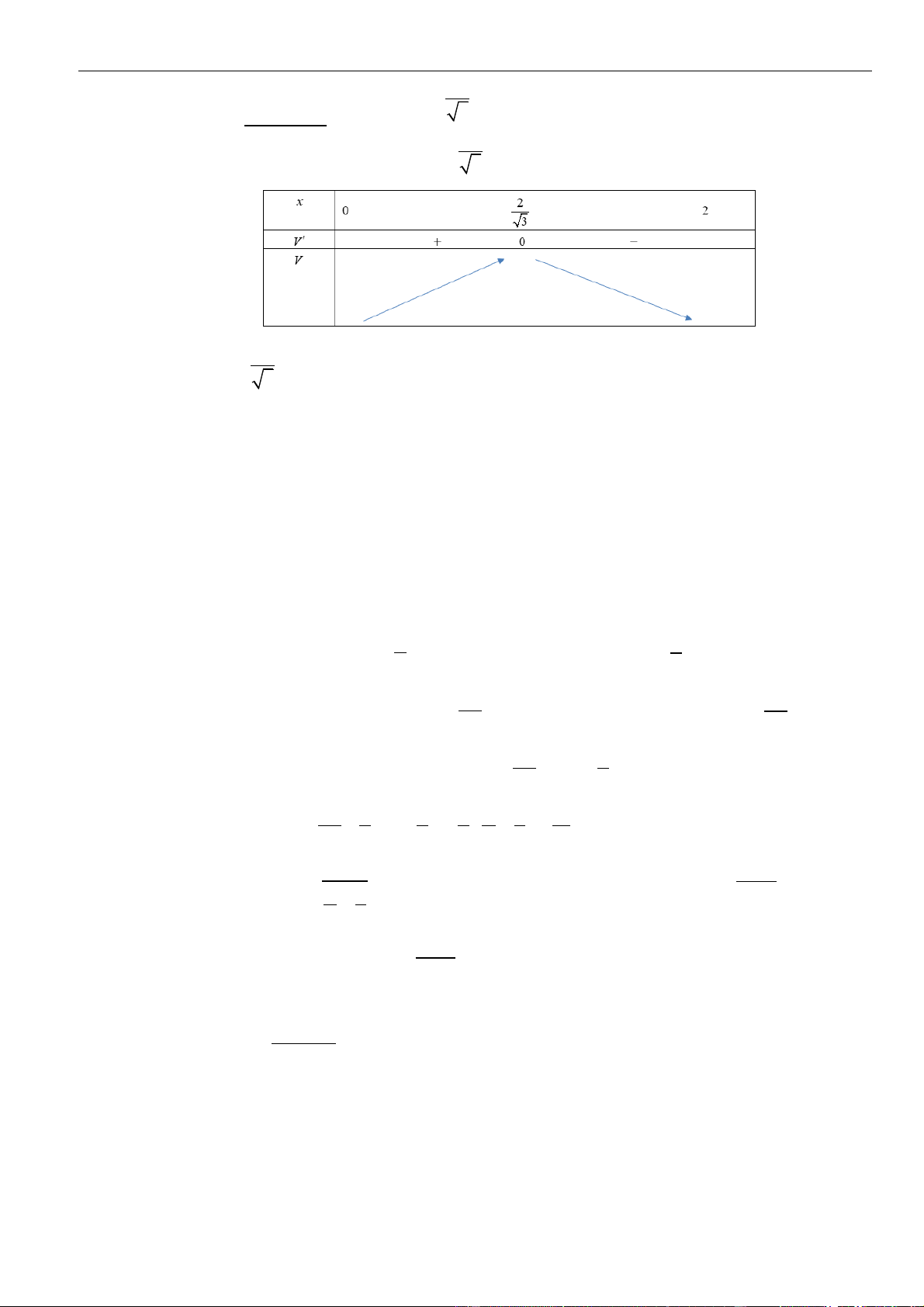
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Ta có:
( )
2
2
12 16
3
,0
2
6
3
x
x
VV
xL
=
−+
= =
=−
3
max
2
2,05
3
V V m
=
Câu 9: Một sợi dây kim loại dài
60cm
được cắt thành hai đoạn. Đoạn thứ nhất được uốn thành một hình
vuông, đoạn thứ hai được uốn thành một vòng tròn. Hỏi khi tổng diện tích của hình vuông và
hình tròn ở trên nhỏ nhất thì chiều dài đoạn dây uốn thành hình vuông bằng bao nhiêu (làm tròn
đến hàng phần trăm)?
A.
30,54cm
. B.
33,61cm
. C.
40,62cm
. D.
26,43cm
Lời giải
Chọn B
Gọi
( )
0 60 xx
là chiều dài của đoạn thứ hai, suy ra
60 x−
là độ dài đoạn thứ nhất.
Khi đó cạnh hình vuông là
15
4
x
−
nên diện tích hình vuông là
2
15
4
x
−
.
Chu vi của vòng tròn là
2
2
x
R x R
= =
. Khi đó diện tích hình tròn là
2
2
4
x
R
=
.
Khi đó tổng diện tích của hai hình sẽ là
( )
2
2
15
44
xx
fx
= + −
.
Khi đó ta có
( )
1 1 1 15
' 15
2 2 4 2 4 2
x x x
fx
= − − = + −
.
Cho
( )
15
'0
11
4
f x x
= =
+
. Suy ra tổng diện tích hai hình nhỏ nhất khi
60
4
x
=
+
.
Khi đó cạnh hình vuông sẽ là
60
60 33,61
4
−
+
.
Câu 10: Sự ảnh hưởng khi sử dụng một loại độc tố với vi khuẩn
X
được một nhà sinh học mô tả bởi
hàm số
( )
2
1
4
t
Pt
tt
+
=
++
, trong đó
( )
Pt
là số lượng vi khuẩn sau
t
sử dụng độc tố. Vào thời
điểm nào thì số lượng vi khuẩn
X
bắt đầu giảm?
A. Ngay từ lúc bắt đầu sử dụng độc tố. B. Sau
0,5
giờ.
C. Sau
2
giờ. D. Sau
1
giờ.
Lời giải
Chọn D
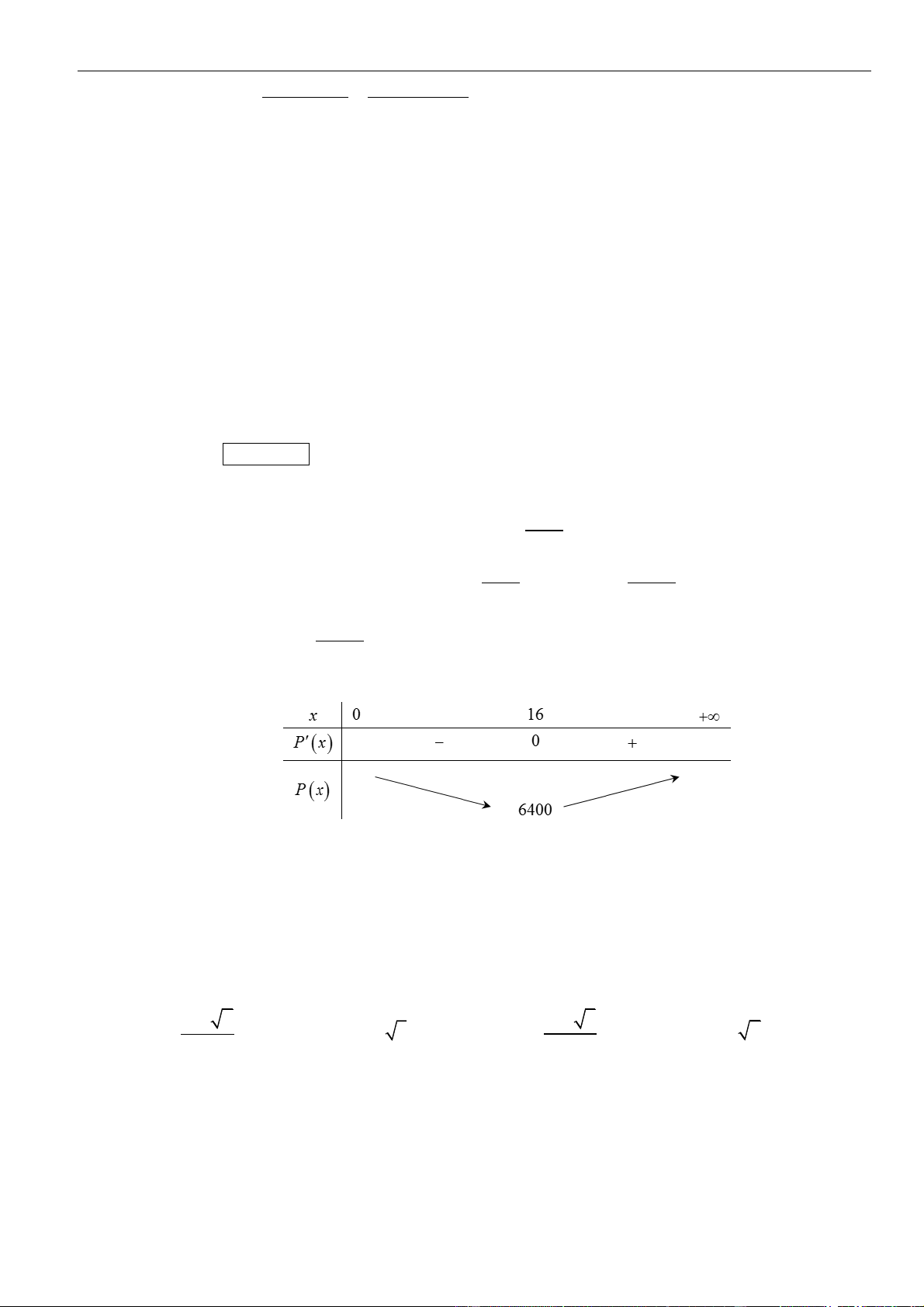
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Xét
( )
( )
( )( )
( )
2
22
22
13
23
'
44
tt
tt
Pt
t t t t
− − −
− − +
==
+ + + +
.
( )
3
'0
1
t
Pt
t
=−
=
=
.
Ta thấy hàm số đạt cực đại tại
1t =
và
( ) ( )
' 0, 1;P t t +
nên sau
( )
1 h
thì vi khuẩn bắt đầu
giảm.
Câu 11: Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất
8000
quả bóng
tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất
30
quả bóng trong một
giờ. Chi phí thiết lập các máy này là
200
nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt
động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát
là
192
nghìn đồng một giờ. Số máy móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động
là thấp nhất?
Lời giải
Đáp án: 16 máy1aa
Gọi số máy móc công ty sử dụng để sản xuất là
( )
,0x x x
.
Thời gian cần để sản xuất hết
8000
quả bóng là:
8000
30x
.
Tổng chi phí để sản xuất là:
( )
8000 51200
200 .192 200
30
P x x x
xx
= + = +
Ta có:
( )
( )
2
2
16
51200
200 0 256
16
x
P x x
xL
x
=
= − = =
=−
.
Vậy công ty nên sử dụng
16
máy để chi phí hoạt động là thấp nhất.
Câu 12: Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để
tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi
của chiến sĩ bằng một phần ba vận tốc chạy trên bộ.Hãy cho biết chiến sỹ phải bơi bao nhiêu mét
để đến được mục tiêu nhanh nhất?Biết dòng sông là thẳng,mục tiêu cách chiến sỹ 1km theo
đường chim bay và chiến sỹ cách bờ bên kia 100m.
A.
200 2
3
. B.
75 3
. C.
200 3
3
. D.
75 2
.
Lời giải
Chọn D
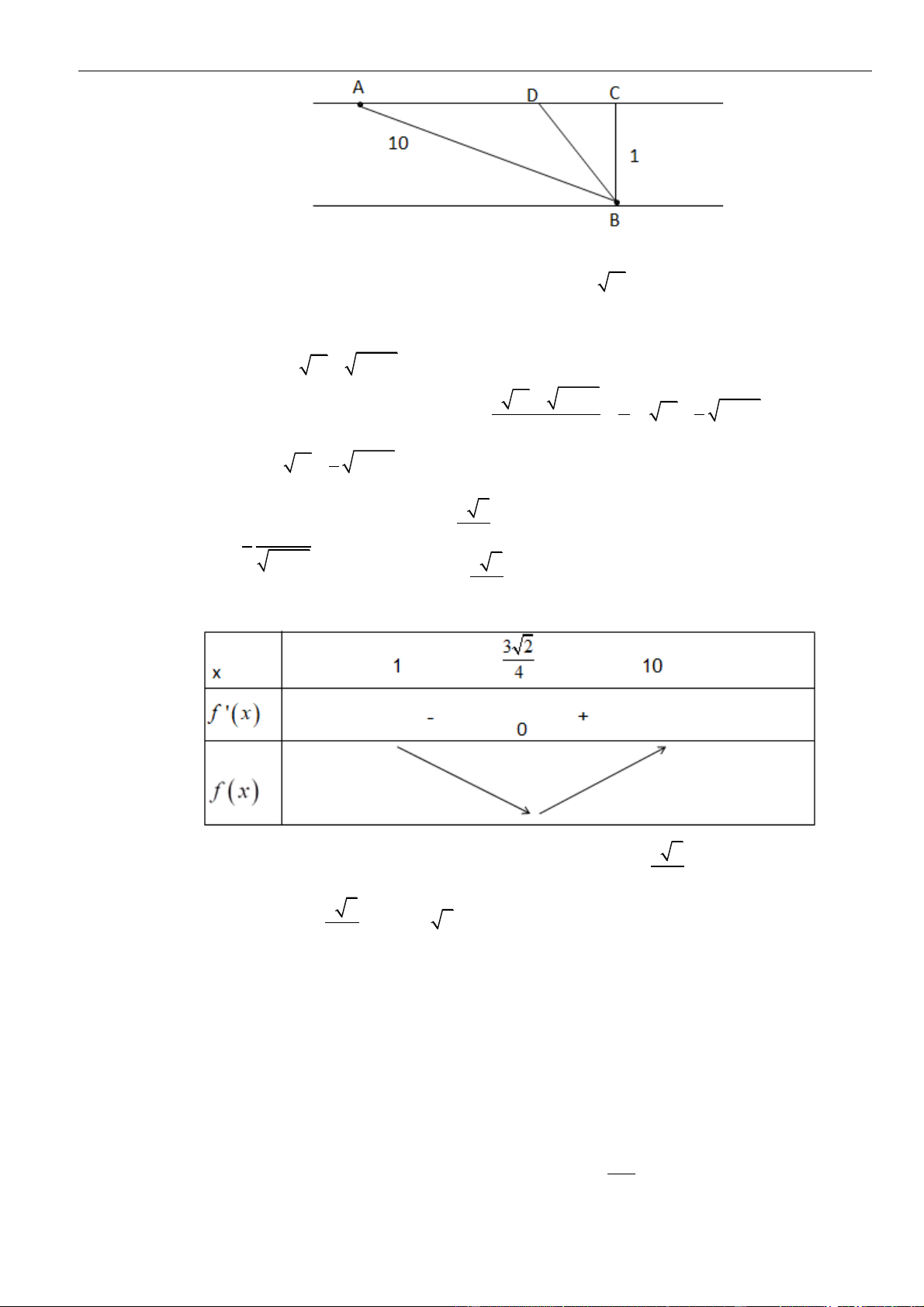
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Gọi A là mục tiêu;B là vị trí chiến sỹ,
BD
là đường bơi của chiến sỹ.
Chọn 1 đơn vị độ dài là 100m,suy ra BC=1;AB=10;
3 11AC =
Gọi vận tốc bơi của chiến sỹ là 1 đơn vị vận tốc,thì vận tốc chạy của chiến sỹ là 3 đơn vị vận tốc.
Gọi x là quãng đường chiến sỹ bơi suy ra BD=x; Vậy quãng đường chiến sỹ chạy là
2
3 11 1AD AC CD x= − = − −
Thời gian chiến sỹ đến được mục tiêu là:
2
2
3 11 1 1
11 1
3 1 3
xx
t x x
−−
= + = − − +
Xét hàm
( )
2
1
11 1
3
f x x x= − − +
có
( ) ( )
( )
( )
2
32
1
4
' 1 ; ' 0
3
1
32
4
x TM
x
f x f x
x
xL
=
= − =
−
=−
BBT
Vậy thời gian chiến sỹ đến mục tiêu ngắn nhất khi
( )
min
32
4
f x x=
Vậy chiến sỹ phải bơi
( )
32
.100 75 2
4
m=
.
Câu 13: Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng
3
200m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 300 nghìn
đồng/
2
m
. Hãy xác định chi phí thấp nhất để xây bể.
A.
46
triệu đồng. B.
51
triệu đồng. C.
75
triệu đồng. D.
36
triệu đồng.
Lời giải
Chọn B
Gọi chiều rộng của hình chữ nhật đáy bể là
( )
xm
suy ra chiều dài của hình chữ nhật là
2x
.
Gọi
h
là chiều cao của bể ta có
2
2
100
2 . 200 .V Sh x h h
x
= = = =
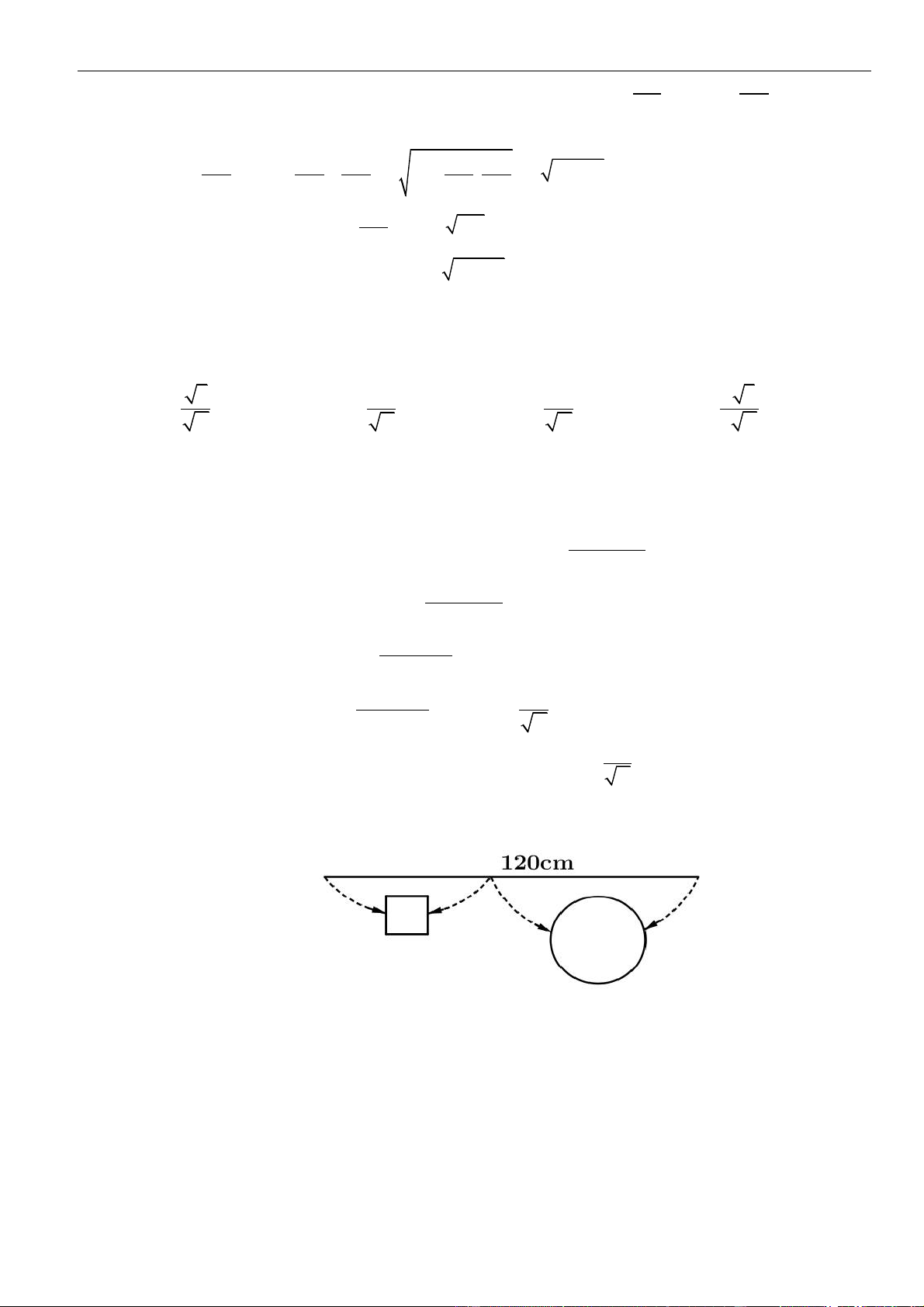
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Diện tích của bể là
2 2 2 2
2
100 600
2 . 2.2 2 2 6 2 6. . 2S h x hx x x hx x x x
xx
= + + = + = + = +
.
Theo bất đẳng thức AM – GM, ta có:
3
2 2 2 2
3
600 300 300 300 300
2 2 3 2 . . 3 2.300x x x
x x x x x
+ = + + =
.
Dấu bằng xảy ra khi
2
3
300
2 150xx
x
= =
.
Suy ra chi phí thấp nhất để xây bể là
3
2
3 2.300 .300000 51
triệu đồng.
Câu 14: Ông X muốn xây một bình chứa hình trụ có thể tích
3
72m
. Đáy làm bằng bêtông giá
100
nghìn
đồng
2
/m
, thành làm bằng tôn giá
90
nghìn đồng
2
/m
, nắp bằng nhôm giá
140
nghìn đồng
2
/m
. Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?
A.
( )
3
3
m
. B.
( )
3
3
m
. C.
( )
3
2
m
. D.
( )
3
3
33
m
2
.
Lời giải
Chọn B
Gọi
( ) ( )
,0x m x
là bán kính đáy của bình chứa hình trụ.
Khi đó tổng số tiền phải trả là :
4
4 2 5 2
144.9.10
14.10 10xx
x
++
.
Đặt
( )
4
4 2 5 2
144.9.10
14.10 10f x x x
x
= + +
.
Suy ra :
( )
4
4
2
1296.10
48.10f x x
x
=−
.
( )
4
4
2
3
1296.10 3
0 48.10 0f x x x
x
= − = =
.
Vậy để chi phí xây dựng là thấp nhất thì bán kính đáy bằng
3
3
.
Câu 15: Một sợi dây kim loại dài 120cm được cắt thành hai đoạn. Đoạn dây thứ nhất được uốn thành
hình vuông, đoạn dây thứ hai được uốn thành vòng tròn (tham khảo hình bên dưới).
Tổng diện tích của hình vuông và hình tròn đạt giá trị nhỏ nhất là (làm tròn đến hàng đơn vị)
A.
462
. B.
426
. C.
498
. D.
504
.
Lời giải
Chọn D
Gọi độ là của đoạn dây thứ hai là
x
cm. Khi đó, độ dài của đoạn dây thứ nhất là
( )
120 x−
cm
( )
0 120x
.
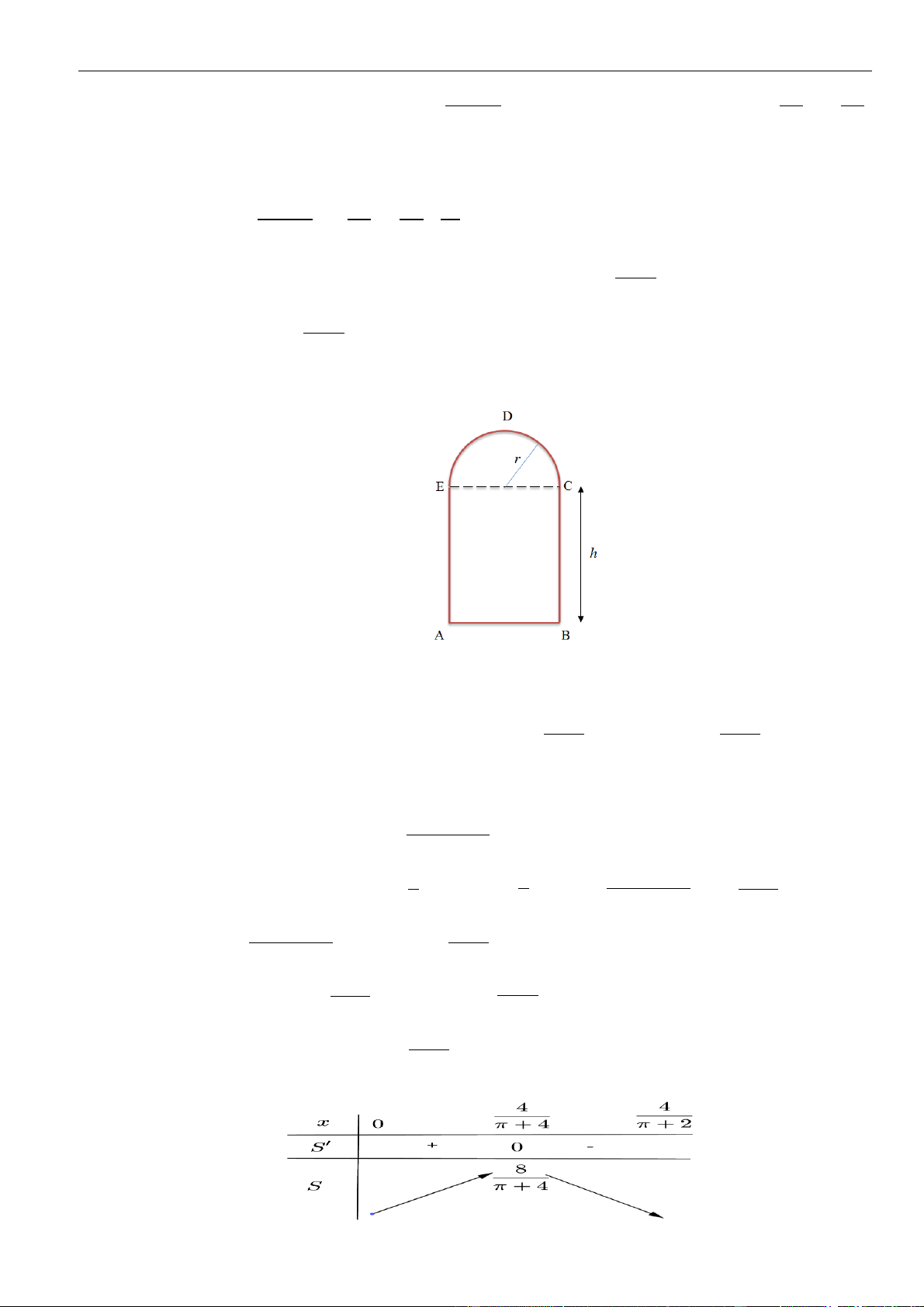
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Suy ra diện tích của hình vuông bằng
2
120
4
x
−
và diện tích của hình tròn bằng
2
2
24
xx
=
.
Tổng diện tích của hình vuông và hình tròn:
( )
2
2
2
120 1 1
15 900
4 4 4 16
xx
S x x x
−
= + = + − +
,
( )
0 120x
.
Ta có
( )
Sx
là một hàm số bậc hai, đạt giá trị nhỏ nhất tại
( )
120
0;120
4
x
=
+
.
Vậy
( )
2
120
min 504
4
S x S cm
=
+
.
Câu 16: Bác thợ hàn dùng một thanh kim loại dài
4m
để uốn thành khung cửa sổ có dạng như hình vẽ.
Gọi
r
là bán kính của nửa đường tròn. Tìm
r
(theo
m
) đẻ diện tích tạo thành đạt giá trị lớn
nhất.
A. 1. B. 0,5. C.
4
4
+
. D.
2
4
+
.
Lời giải
Chọn C
Ta có
( )
24h r r
+ + =
42
2
rr
h
−−
=
.
Diện tích của khung cửa là
2
1
2
2
S r rh
=+
2
1 4 2
2
22
rr
rr
−−
=+
2
4
.4
2
rr
+
= − +
.
Ta có
4 2 4
00
22
rr
hr
−−
=
+
.
Xét hàm số
( )
2
4
.4
2
S r r r
+
= − +
trên
4
0;
2
+
.
( ) ( )
4 4 0S r r
= − + + =
4
4
r
=
+
Bảng biến thiên
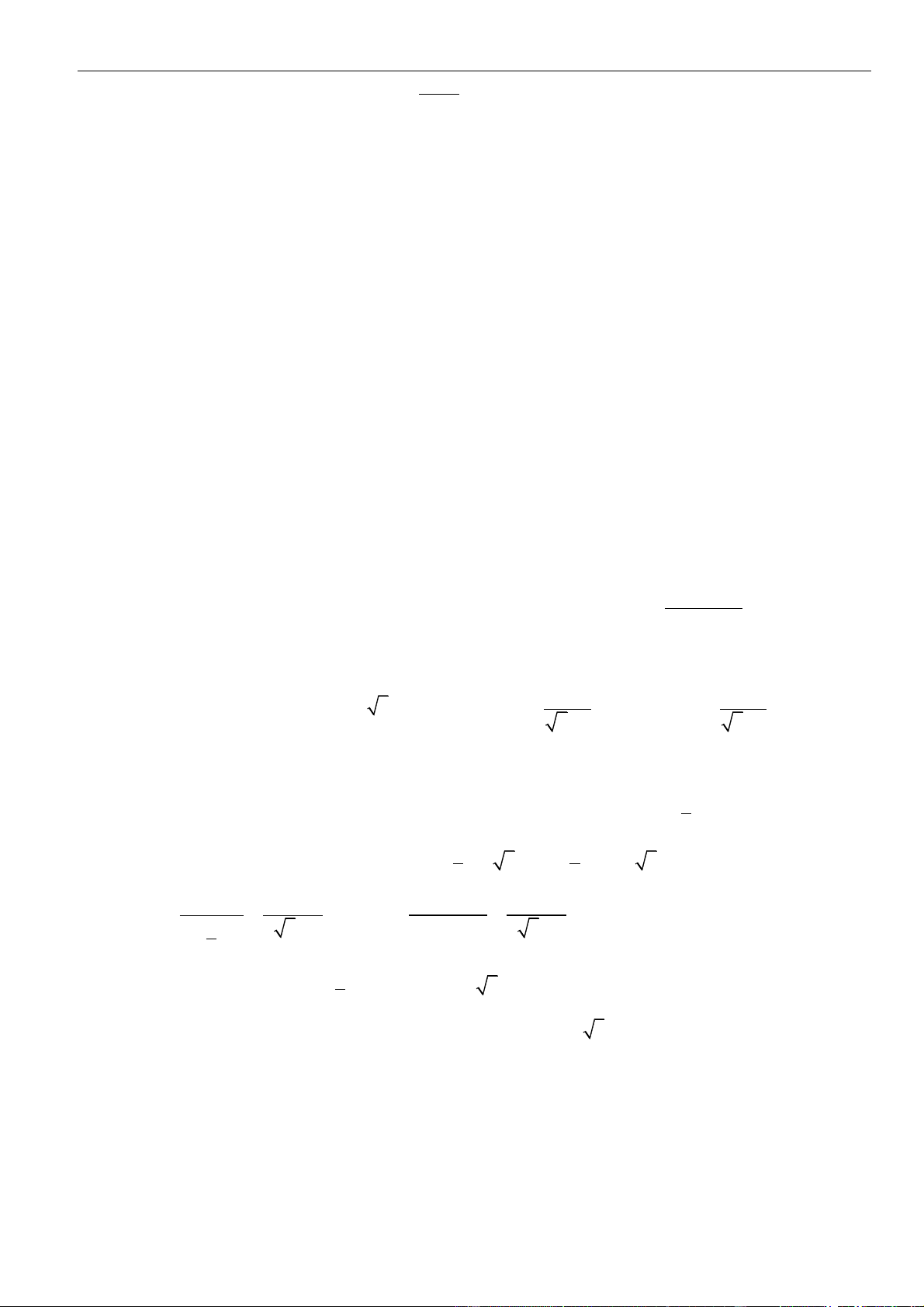
Chủ đề 02: Cực trị của hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
( )
Sr
đạt giá trị lớn nhất
4
4
r
=
+
.
Câu 17: Một công ty bất động sản có 50 căn hộ cho thuê. Nếu giá cho thuê mỗi căn là 3 000 000
đồng/tháng thì không có phòng trống, còn nếu cho thuê mỗi căn hộ thêm 200.000đ/tháng thì sẽ
có 2 căn bị bỏ trống. Hỏi công ty phải niêm yếu bao nhiêu để doanh thu là lớn nhất?
A.
3400000
. B.
3000000
. C.
5000000
. D.
4000000
.
Lời giải
Chọn D
Đặt số tiền tăng thêm là
200000x
Giá tiền mỗi căn hộ một tháng là
3000000 200000x+
(đồng)
Số căn hộ bị trống là
50 2x−
phòng
Số tiền thu được mỗi tháng là:
( )( )
3000000 200000 50 2xx+−
đồng
Đặt
( ) ( )( )
3000000 200000 50 2f x x x= + −
Để doanh thu là lớn nhất thì ta tìm giá trị lớn nhất của hàm số
( )
fx
, giá trị lớn nhất của hàm
số
( )
fx
tại đỉnh của parabol. Hay:
( ) ( ) ( )
200000 50 2 2 3000000 200000 0 5f x x x x
= − − + = =
.
Vậy công ty niêm yết giá tiền là:
3000000 200000 5 4000000+ =
đồng để được doanh thu là
lớn nhất.
Câu 18: Lưu lượng xe ô tô vào đường hầm được cho bởi công thức
( )
2
386
25
v
fv
vv
=
++
(xe/giây), trong
đó
v
(km/h) là vận tốc trung bình của các xe khi vào đường hầm. Tính vận tốc trung bình của
các xe khi vào đường hầm sao cho lưu lượng xe là lớn nhất
A.
5
km/h. B.
5
km/h. C.
193
51+
km/h. D.
193
51−
km/h.
Lời giải
Chọn B
Vì
v
là vận tốc trung bình của các xe khi vào đường hầm
0v
và
5
0
v
Theo bất đẳng thức AM-GM, ta có:
5
25v
v
+
5
2 2 5 2v
v
+ + +
386 386
5
2 5 2
2v
v
+
++
( )
2
386 386
25
2 5 2
v
fv
vv
=
++
+
Dấu
""=
xảy ra
5
v
v
=
2
5v=
5v=
(vì
0v
)
Vậy vận tốc trung bình của các xe khi vào đường hầm là
5
km/h thì lưu lượng xe là lớn nhất.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
=
−
là
A.
1.y
B.
1.x
C.
1.x
D.
0.y
Câu 2: Đồ thị của hàm số nào trong các hàm số sau đây có tiệm cận đứng?
A.
=
+
2
1
1
y
x
. B.
=
++
2
1
1
y
xx
. C.
=
+
4
1
1
y
x
. D.
=
1
y
x
.
Câu 3: Đường tiệm cận ngang của đồ thị hàm số
2
1
4
x
y
x
+
=
−
có phương trình là
A.
2y =−
. B.
2y =
. C.
0y =
. D.
1y =−
.
Câu 4: Tiệm cận ngang của đồ thị hàm số
5
1
y
x
=
−
là đường thẳng có phương trình:
A.
0y =
. B.
1x =
. C.
5y =
. D.
0x =
.
Câu 5: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
2
3
y
x
=
−+
?
A.
2x =−
. B.
2y =−
. C.
0y =
. D.
3x =
.
Câu 6: Đường thẳng nào dưới đây là đường tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
−
=
−−
.
A.
3x =
. B.
3y =−
. C.
1x =
. D.
1y =
.
Câu 7: Đồ thị hàm số
2
2
4
x
y
x
−
=
−
có đường tiệm cận ngang là
A.
2y =
. B.
0y =
. C.
1y =
. D.
2x =−
.
Tiệm cận của đồ thị hàm số phân thức hữu tỷ
DẠNG 1
Phương pháp:
1. Đường tiệm cận ngang
Cho hàm số
=y f x()
xác định trên một khoảng vô hạn (là khoảng dạng
( ) ( )
+ −ab; , ;
hoặc
( )
;− +
Đường thẳng
yy
0
=
là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số
=y f x()
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
xx
f x y f x y
00
lim ( ) , lim ( )
→+ →−
==
2. Đường tiệm cận đứng
Đường thẳng
=xx
0
được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số
()y f x=
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
+−
→→
= + = −
x x x x
f x f x
00
lim ( ) , lim ( ) ,
00
lim ( ) , li m ( )
x x x x
f x f x
+−
→→
= − = +
• Với đồ thị hàm phân thức dạng
( )
+
= −
+
ax b
y c ad bc
cx d
0; 0
luôn có tiệm cận ngang là
=
a
y
c
và tiệm cận đứng
=−
d
x
c
.

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 8: Tiệm cận ngang của đồ thị hàm số
2020
1
y
x
=
−
là đường thẳng có phương trình?
A.
2020y =
. B.
2020x =
. C.
0y =
. D.
0x =
.
Câu 9: Đồ thị hàm số
3
63
x
y
x
−
=
−
có bao nhiêu tiệm cận đứng và tiệm cận ngang?
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 10: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
x
fx
x
=
−
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 11: Cho hàm số
2
1
23
x
y
xx
+
=
−−
. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho
là:
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 12: Số đường tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
=
+
là?
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 13: Đồ thị hàm số
3
3
4
32
xx
y
xx
−
=
−−
có bao nhiêu đường tiệm cận?
A. 4. B. 3. C. 1. D. 2.
Câu 14: Đồ thị hàm số
2
3
2
x
y
xx
−
=
+−
có bao nhiêu đường tiệm cận đứng?
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 15: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
34
x
y
xx
+
=
−+
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 16: Số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
2
32
4
xx
y
x
−+
=
−
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 17: Cho hàm số
2
mx n
y
ax bx c
+
=
++
(
, , , ,m n a b c
là các tham số thực). Hỏi đồ thị hàm số có tối đa bao
nhiêu đường tiệm cận ngang và tiệm cận đứng?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 18: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
−
=
+
là
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 19: Số đường tiệm cận của đồ thị hàm số
2
1
2
x
y
xx
−
=
−
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 20: Số đường tiệm cận của đồ thị hàm số
11
2
x
y
x
−−
=
−
là

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 21: Đồ thị của hàm số
2
2
1
3 2 5
x
y
xx
−
=
−−
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 22: Tất cả các giá trị của tham số
m
để đồ thị hàm số
2
1
4
x
y
x x m
+
=
++
có duy nhất một đường tiệm
cận là
A.
4.m
. B.
4.m
. C.
4.m
. D.
4.m
Câu 23: Số đường tiệm cận của đồ thị hàm số
2
2
32
x
y
xx
−
=
−+
là
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 24: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là bao nhiêu ?
A.
2
. B.
1
. C.
3
. D.
0.
Câu 25: Đồ thị hàm số
2
4
16
x
y
x
−
=
−
có tất cả bao nhiêu đường tiệm cận?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 26: ) Đồ thị hàm số
2
2
32
32
xx
y
xx
−+
=
++
có số đường tiệm cận là?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 27: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
+
=
−
là:
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 28: Đường thẳng
20y +=
là đường tiệm cận của đồ thị hàm số nào sau đây?
A.
2
32
y
x
=
+
. B.
2
23
2
x
y
x
−
=
+
. C.
( )( )
2
21
13
xx
y
xx
+−
=
+−
. D.
2
1
21
x
y
x
+
=
−
.
Câu 29: Số đường tiệm cận của đồ thị hàm số
2
1
x
y
x
=
−
là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 30: Đường tiệm cận ngang của đồ thị hàm số
2
1
4
x
y
x
+
=
−
có phương trình là
A.
2y =−
. B.
2y =
. C.
0y =
. D.
1y =−
.
Câu 31: Một đường tiệm cận đứng của đồ thị hàm số
( )
( )
2
2
43
21
xx
y
xx
++
=
−−
là
A.
1x =−
. B.
1x =
. C.
0x =
. D.
2x =−
.
Câu 32: Đồ thị hàm số
( )
2
2
31
3
xx
fx
xx
−+
=
−
có bao nhiêu đường tiệm cận?
A.
1
. B.
3
. C.
4
. D.
2
.
2
31
4
x
y
x
+
=
−
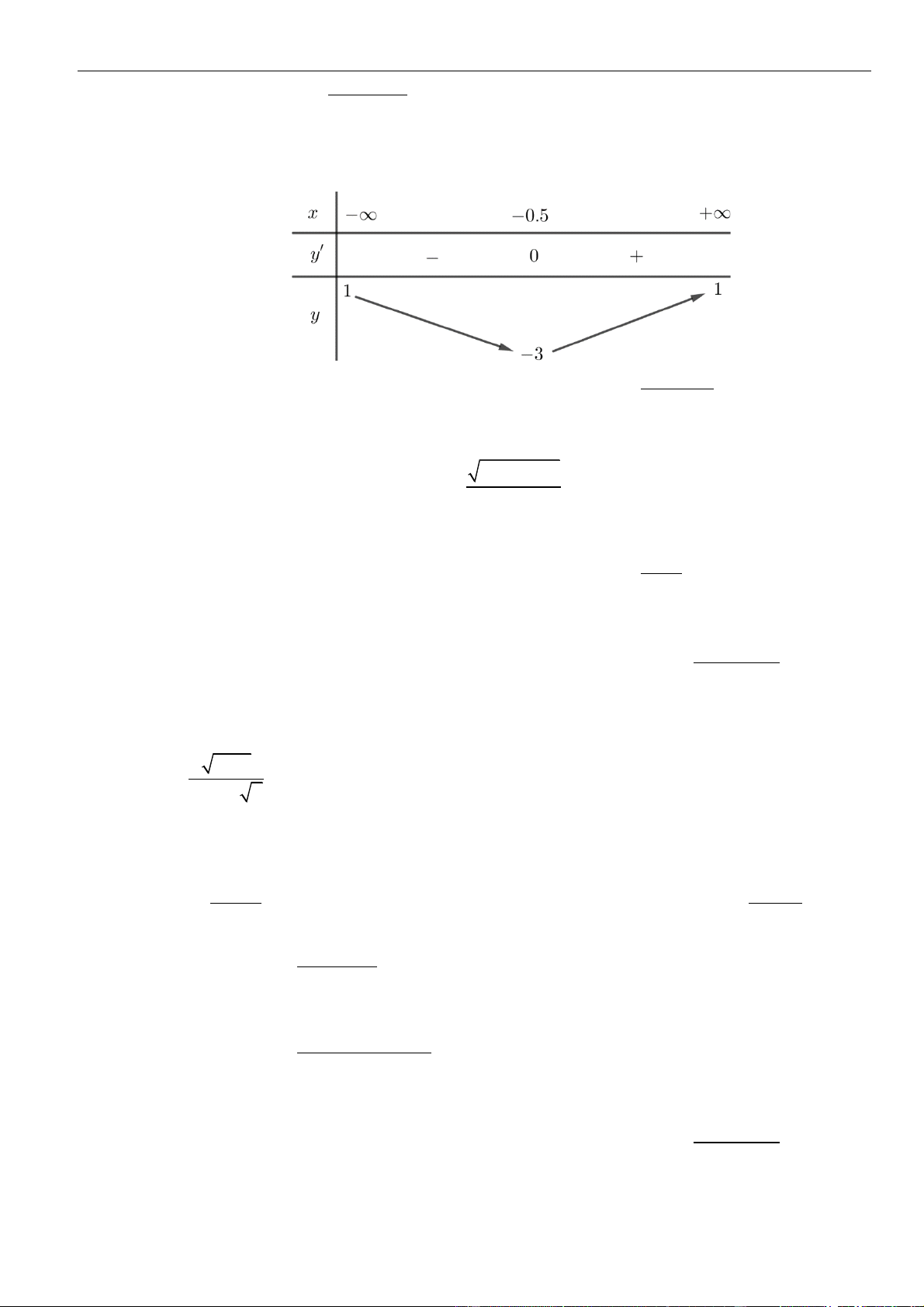
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 33: Đồ thị của hàm số
2
1
23
x
y
xx
−
=
+−
có bao nhiêu đường tiệm cận?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 34: Cho hàm số
( )
=y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
1
21
=
−
y
fx
là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 35: Số tiệm cận ngang của đồ thị hàm số
2
10000
2
−
=
−
x
y
x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 36: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
+
=
−
là
A. 2. B. 1. C. 3. D. 4
Câu 37: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
3 4 1
1
xx
y
x
−+
=
−
là
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 38: Gọi
k
và
l
lần lượt là số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
2
1
x
y
xx
−
=
−
. Khẳng định nào sau đây đúng ?
A.
0, 2kl==
. B.
1, 2kl==
. C.
1, 1kl==
. D.
0, 1kl==
.
Câu 39: Trong các hàm số sau, đồ thị hàm số nào có đường tiệm cận ngang.
A.
2
21
3
x
y
x
−
=
−
. B.
42
10 97y x x= − +
. C.
32
20 6y x x= + +
. D.
2
41
2
x
y
x
−+
=
−
.
Câu 40: Đồ thị hàm số
2
2
3
69
xx
y
xx
−
=
−+
có bao nhiêu đường tiệm cận?
A. 2. B. 3. C. 0. D. 1.
Câu 41: Đồ thị hàm số
2
1
2020 2021
x
y
xx
+
=
−−
có bao nhiêu tiệm cận đứng?
A.
3
. B.
1
. C.
2
. D.
0
Câu 42: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
3 4 1
1
xx
y
x
−+
=
−
là
A.
4
. B.
2
. C.
1
. D.
3
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
=
−
là
A.
1.y
B.
1.x
C.
1.x
D.
0.y
Lời giải
Chọn D
Ta có
2
lim 0.
1
→
=
−
x
x
x
Do đó tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
=
−
là
0.=y
Câu 2: Đồ thị của hàm số nào trong các hàm số sau đây có tiệm cận đứng?
A.
=
+
2
1
1
y
x
. B.
=
++
2
1
1
y
xx
. C.
=
+
4
1
1
y
x
. D.
=
1
y
x
.
Lời giải
Chọn D
Cách 1: Các hàm số ở các đáp án A, B, C có tập xác định
D =
nên đáp án D đúng.
Cách 2: Xét đáp án D:
Hàm số có tập xác định
( )
0; .D = +
0
lim 0
x
yx
+
→
= + =
là tiệm cận đứng của hàm số.
Câu 3: Đường tiệm cận ngang của đồ thị hàm số
2
1
4
x
y
x
+
=
−
có phương trình là
A.
2y =−
. B.
2y =
. C.
0y =
. D.
1y =−
.
Lời giải
Chọn C
Ta có
2
1
lim lim 0
4
xx
x
y
x
→ →
+
==
−
Vậy đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số.
Câu 4: Tiệm cận ngang của đồ thị hàm số
5
1
y
x
=
−
là đường thẳng có phương trình:
A.
0y =
. B.
1x =
. C.
5y =
. D.
0x =
.
Lời giải
Chọn A
Ta có:
5
lim 0
1
x
x
→
=
−
.
Vậy tiệm cận ngang của đồ thị hàm số
5
1
y
x
=
−
là đường thẳng có phương trình
0y =
.
Câu 5: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
2
3
y
x
=
−+
?
A.
2x =−
. B.
2y =−
. C.
0y =
. D.
3x =
.
Lời giải
Chọn C
Ta có:
2
lim lim 0 0
3
xx
yy
x
→ →
= = =
−+
là tiệm cận ngang của đồ thị hàm số.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 6: Đường thẳng nào dưới đây là đường tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
−
=
−−
.
A.
3x =
. B.
3y =−
. C.
1x =
. D.
1y =
.
Lời giải
Chọn B
Ta có:
3 1 3 1
lim lim 3
11
xx
xx
xx
→+ →−
−−
= = −
− − − −
.
Vậy đường tiệm cận ngang của đồ thị hàm số
31
1
x
y
x
−
=
−−
là
3y =−
.
Câu 7: Đồ thị hàm số
2
2
4
x
y
x
−
=
−
có đường tiệm cận ngang là
A.
2y =
. B.
0y =
. C.
1y =
. D.
2x =−
.
Lời giải
Chọn B
Ta có
2
2
2
12
2
lim lim lim 0
4
4
1
x x x
x
xx
y
x
x
→+ →+ →+
−
−
= = =
−
−
tiệm cận ngang là
0y =
.
Câu 8: Tiệm cận ngang của đồ thị hàm số
2020
1
y
x
=
−
là đường thẳng có phương trình?
A.
2020y =
. B.
2020x =
. C.
0y =
. D.
0x =
.
Lời giải
Chọn C
Ta có:
2020
lim lim 0
1
xx
y
x
→ →
==
−
nên
0y =
là tiệm cận ngang của đồ thị hàm số
2020
1
y
x
=
−
.
Câu 9: Đồ thị hàm số
3
63
x
y
x
−
=
−
có bao nhiêu tiệm cận đứng và tiệm cận ngang?
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn C
2
3
lim
63
x
x
x
+
→
−
= +
−
(hoặc
2
3
lim
63
x
x
x
−
→
−
= −
−
) nên đường thẳng
2x =
là TCĐ của ĐTHS.
31
lim
6 3 3
x
x
x
→
−−
=
−
nên đường thẳng
1
3
y
−
=
là TCN của ĐTHS.
Câu 10: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
x
fx
x
=
−
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Khi
( )
0, 1
1
x
x x f x
x
=
−
đồ thị hàm số có 1 tiệm cận ngang
1y =
và 1 tiệm cận đứng
1x =
.
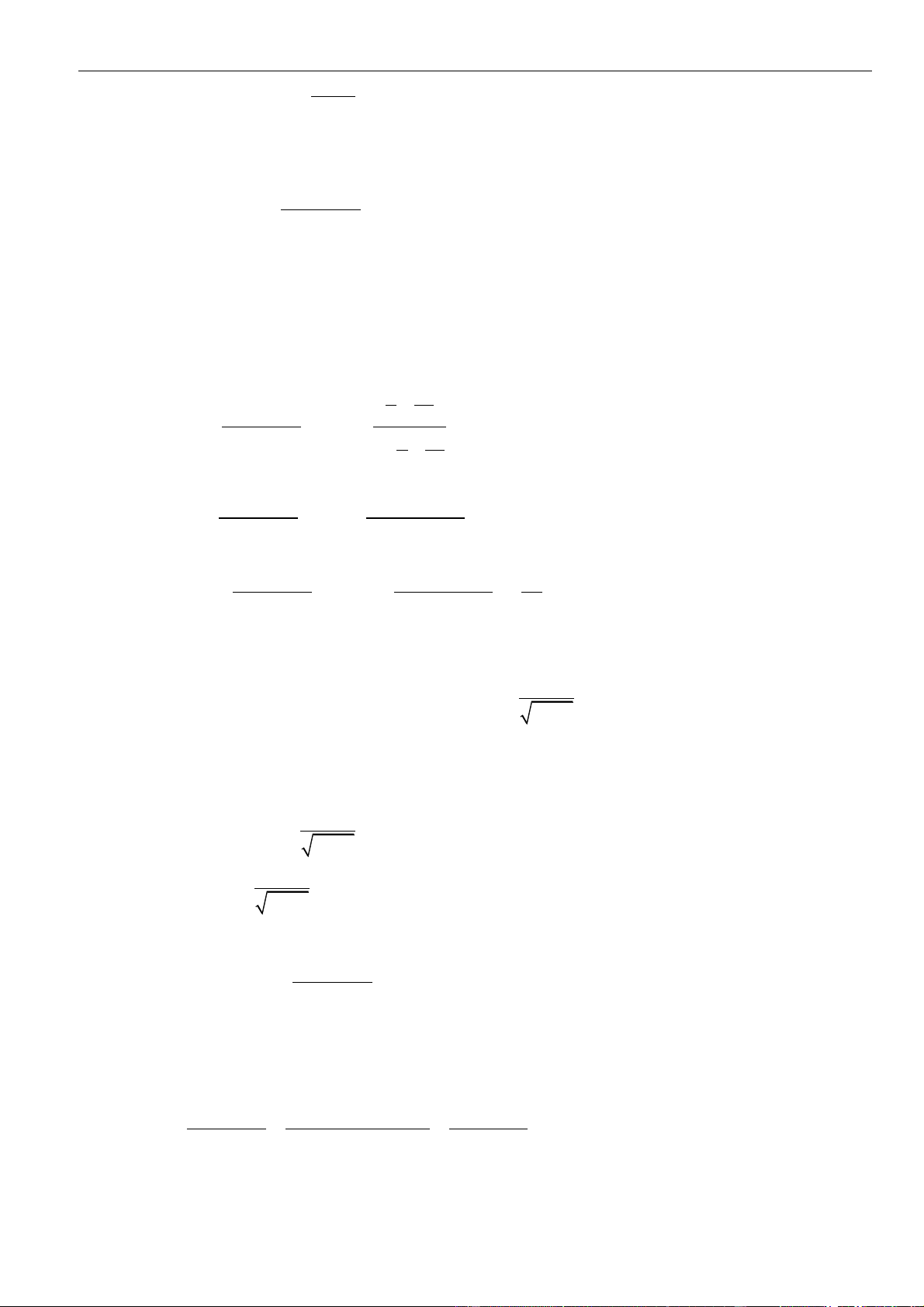
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Khi
( )
0
1
x
x f x
x
=
−−
đồ thị hàm số có 1 tiệm cận ngang
1y =−
và 1 tiệm cận đứng
1x =−
.
Vậy đồ thị hàm số có tất cả 4 đường tiệm cận.
Câu 11: Cho hàm số
2
1
23
x
y
xx
+
=
−−
. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho
là:
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn A
Ta có
+)
2
2
2
11
1
lim lim 0
23
23
1
xx
x
xx
xx
xx
→ →
+
+
==
−−
−−
: đồ thị hàm số có tiệm cận ngang
0y =
.
+)
( )( )
2
33
11
lim lim
2 3 1 3
xx
xx
x x x x
++
→→
++
= = +
− − + −
: đồ thị hàm số có tiệm cận đứng
3x =
.
+)
( ) ( )
( )( )
2
11
1 1 1
lim lim
2 3 1 3 4
xx
xx
x x x x
++
→ − → −
++
==
− − + − −
.
Vậy đồ thị hàm số có tiệm cận ngang
0y =
, tiệm cận đứng
3x =
Câu 12: Số đường tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
=
+
là?
A.
1
. B.
3
. C.
0
. D.
2
.
Lời giải
Chọn D
Ta có
2
lim lim 1 1
1
xx
x
yy
x
→+ →+
= = =
+
là một tiệm cận ngang của đồ thị hàm số.
2
lim lim 1 1
1
xx
x
yy
x
→− →−
= = − = −
+
là một tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 tiệm cận ngang.
Câu 13: Đồ thị hàm số
3
3
4
32
xx
y
xx
−
=
−−
có bao nhiêu đường tiệm cận?
A. 4. B. 3. C. 1. D. 2.
Lời giải
Chọn D.
( )
( )
( )
( )
2
32
32
2
22
42
3 2 2 1
2 2 1
x x x
x x x x
y
x x x x
x x x
−+
−+
= = =
− − + +
− + +

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Ta có:
3
2
1
lim lim 1
21
1
x
x
x
y
xx
→
→
+
= =
++
Đồ thị hàm số đã cho có một tiệm cận ngang là
1y =
( )
( )
( )
( )
2
1
1
2
lim lim
1
x
x
xx
y
x
+
+
→−
→−
+
= = −
+
Đồ thị hàm số đã cho có một tiệm cận đứng là
1x =−
Vậy đồ thị có hai đường tiệm cận.
Câu 14: Đồ thị hàm số
2
3
2
x
y
xx
−
=
+−
có bao nhiêu đường tiệm cận đứng?
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn C
Ta có
( )( )
2
33
2 1 2
xx
y
x x x x
−−
==
+ − − +
Xét
( )( )
1
3
lim
12
x
x
xx
+
→
−
= −
−+
suy ra
1x =
là đường tiệm cận đứng của đồ thị.
Xét
( )( )
2
3
lim
12
x
x
xx
+
→−
−
= +
−+
suy ra
2x =−
là đường tiệm cận đứng của đồ thị.
Vậy đồ thị hàm số
2
3
2
x
y
xx
−
=
+−
có 2 đường tiệm cận đứng.
Câu 15: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
34
x
y
xx
+
=
−+
là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn B
Tập xác định
D =
.
Đồ thị hàm số
2
1
34
x
y
xx
+
=
−+
không có tiệm cận đứng.
Ta có
2
2
11
lim lim 0 0
34
1
xx
xx
yy
xx
→ →
+
= = =
−+
là đường tiệm cận ngang.
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
34
x
y
xx
+
=
−+
là
1
.
Câu 16: Số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
2
32
4
xx
y
x
−+
=
−
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn A
TXĐ
\2D =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Ta có
2
2
32
lim lim 1
4
xx
xx
y
x
→+ →+
−+
= = −
−
;
2
2
32
lim lim 1
4
xx
xx
y
x
→− →−
−+
= = −
−
nên
1y =−
là tiệm cận
ngang.
( )( )
( )( )
2
2
2 2 2 2
12
3 2 1 1
lim lim lim lim
4 2 2 2 4
x x x x
xx
x x x
y
x x x x
→ → → →
−−
− + −
= = = = −
− − + +
( )( )
( )( )
2
2
2
2 2 2 2
32
12
32
2
lim lim lim lim
4 2 2 2
x x x x
xx
xx
xx
x
y
x x x x
+ + + +
→− →− →− →−
−+
−−
−+
−
= = = = −
− − + +
nên
2x =−
là tiệm cận
ngang.
Vậy tổng số tiệm cận đứng và tiệm cận ngang là
2
.
Câu 17: Cho hàm số
2
mx n
y
ax bx c
+
=
++
(
, , , ,m n a b c
là các tham số thực). Hỏi đồ thị hàm số có tối đa bao
nhiêu đường tiệm cận ngang và tiệm cận đứng?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
Ta có phương trình
2
0ax bx c+ + =
có nhiều nhất hai nghiệm.
Nên đồ thị hàm số có nhiều nhất hai đường tiệm cận đứng.
2
lim lim 0; lim 0 0
x x x
mx n
y y y
ax bx c
→+ →+ →−
+
= = = =
++
là tiệm cân ngang.
Vậy đồ thị hàm số có nhiều nhất 3 đường tiệm cận ngang và tiệm cận đứng.
Câu 18: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
−
=
+
là
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn B
Tập xác định
D =
. Đồ thị hàm số không có tiệm cận đứng.
Ta có
2
2
11
lim lim 0
1
1
xx
x
x
y
x
→+ →+
−
==
+
và
2
2
11
lim lim 0
1
1
xx
x
x
y
x
→− →−
−
==
+
0y=
là đường tiệm cận ngang của ĐTHS.
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
−
=
+
là
1
.
Câu 19: Số đường tiệm cận của đồ thị hàm số
2
1
2
x
y
xx
−
=
−
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Điều kiện xác định:
1
2
x
x

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Ta có
lim 0
x
y
→+
=
nên đồ thị hàm số có
1
đường tiệm cận ngang
0y =
.
2
lim
x
y
+
→
= +
nên đồ thị hàm số có 1 đường tiệm cận đứng
2x =
.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 20: Số đường tiệm cận của đồ thị hàm số
11
2
x
y
x
−−
=
−
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C
Tập xác định
) ( )
1;2 2;D = +
.
Ta có:
11
11
lim lim 1
2
xx
x
y
x
++
→→
−−
==
−
;
( )
( ) ( )
2 2 2 2
1 1 2 1 1
lim lim lim lim
22
2 1 1 1 1
x x x x
xx
y
x
x x x
− − − −
→ → → →
− − −
= = = =
−
− − + − +
.
( )
( ) ( )
2 2 2 2
1 1 2 1 1
lim lim lim lim
22
2 1 1 1 1
x x x x
xx
y
x
x x x
+ + + +
→ → → →
− − −
= = = =
−
− − + − +
.
11
lim lim 0
2
xx
x
y
x
→+ →+
−−
==
−
.
Vậy đồ thị hàm số có một tiệm cận ngang
0y =
.
Câu 21: Đồ thị của hàm số
2
2
1
3 2 5
x
y
xx
−
=
−−
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
2
1
5 2 3 0
3
5
x
xx
x
=−
− − + =
=
.
Với
1x =−
thì
2
10x −=
nên đồ thị hàm số có một tiệm cận đứng là
3
5
x =
.
Câu 22: Tất cả các giá trị của tham số
m
để đồ thị hàm số
2
1
4
x
y
x x m
+
=
++
có duy nhất một đường tiệm
cận là
A.
4.m
. B.
4.m
. C.
4.m
. D.
4.m
Lời giải
Chọn A
Ta có
lim lim 0
xx
yy
→+ →−
==
nên đồ thị hàm số luôn có 1 đường tiệm cận ngang là
0y =
.
Vậy để đồ thị hàm số
2
1
4
x
y
x x m
+
=
++
có duy nhất một đường tiệm cận thì đồ thị hàm số không
có tiệm cận đứng, hay phương trình
2
40x x m+ + =
vô nghiệm
0
4 0 4mm −
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Câu 23: Số đường tiệm cận của đồ thị hàm số
2
2
32
x
y
xx
−
=
−+
là
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn A
Ta có:
2
2
lim 0
32
x
x
xx
→
−
=
−+
nên đồ thị hàm số có 1 tiệm cận ngang
0.y =
Mặt khác
2
1
3x 2 0
2
x
x
x
=
− + =
=
và
2
22
21
lim lim 1
3 2 1
xx
x
x x x
++
→→
−
==
− + −
nên
2x =
không phải tiệm cận đứng của đồ thị hàm số;
2
11
21
lim lim
3 2 1
xx
x
x x x
++
→→
−
= = +
− + −
nên đồ thị hàm số có tiệm cận đứng là:
1x =
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 24: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là bao nhiêu ?
A.
2
. B.
1
. C.
3
. D.
0.
Lời giải
Chọn C
Tập xác định của hàm số là :
( ) ( ) ( )
; 2 2;2 2;D = − − − +
.
Ta có:
lim 0
x
y
→+
=
. Đồ thị hàm số có một đường tiệm cận ngang là
0y =
.
( ) ( )
22
lim ; lim
xx
yy
−+
→ − → −
= + = −
và
22
lim ; lim
xx
yy
−+
→→
= − = +
. Đồ thị hàm số có hai đường tiệm cận
đứng là
2x =−
và
2x =
.
Câu 25: Đồ thị hàm số
2
4
16
x
y
x
−
=
−
có tất cả bao nhiêu đường tiệm cận?
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn A
Tập xác định
\ 4; 4D =−
.
Ta có
2
2
2
14
4
lim lim lim 0
16
16
1
x x x
x
xx
y
x
x
→ → →
−
−
= = =
−
−
0y=
là đường tiệm cận ngang.
Ta có
2
4 4 4 4
4 1 1 1
lim lim lim ; lim
16 4 8 8
x x x x
x
yy
xx
+ + + −
→ → → →
−
= = = =
−+
Ta có
( ) ( ) ( ) ( )
2
4 4 4 4
41
lim lim lim ; lim
16 4
x x x x
x
yy
xx
+ + + −
→ − → − → − → −
−
= = = + = −
−+
4x = −
là đường tiệm cận
đứng.
Số đường tiệm cận của đồ thị hàm số là
2
.
Câu 26: ) Đồ thị hàm số
2
2
32
32
xx
y
xx
−+
=
++
có số đường tiệm cận là?
2
31
4
x
y
x
+
=
−
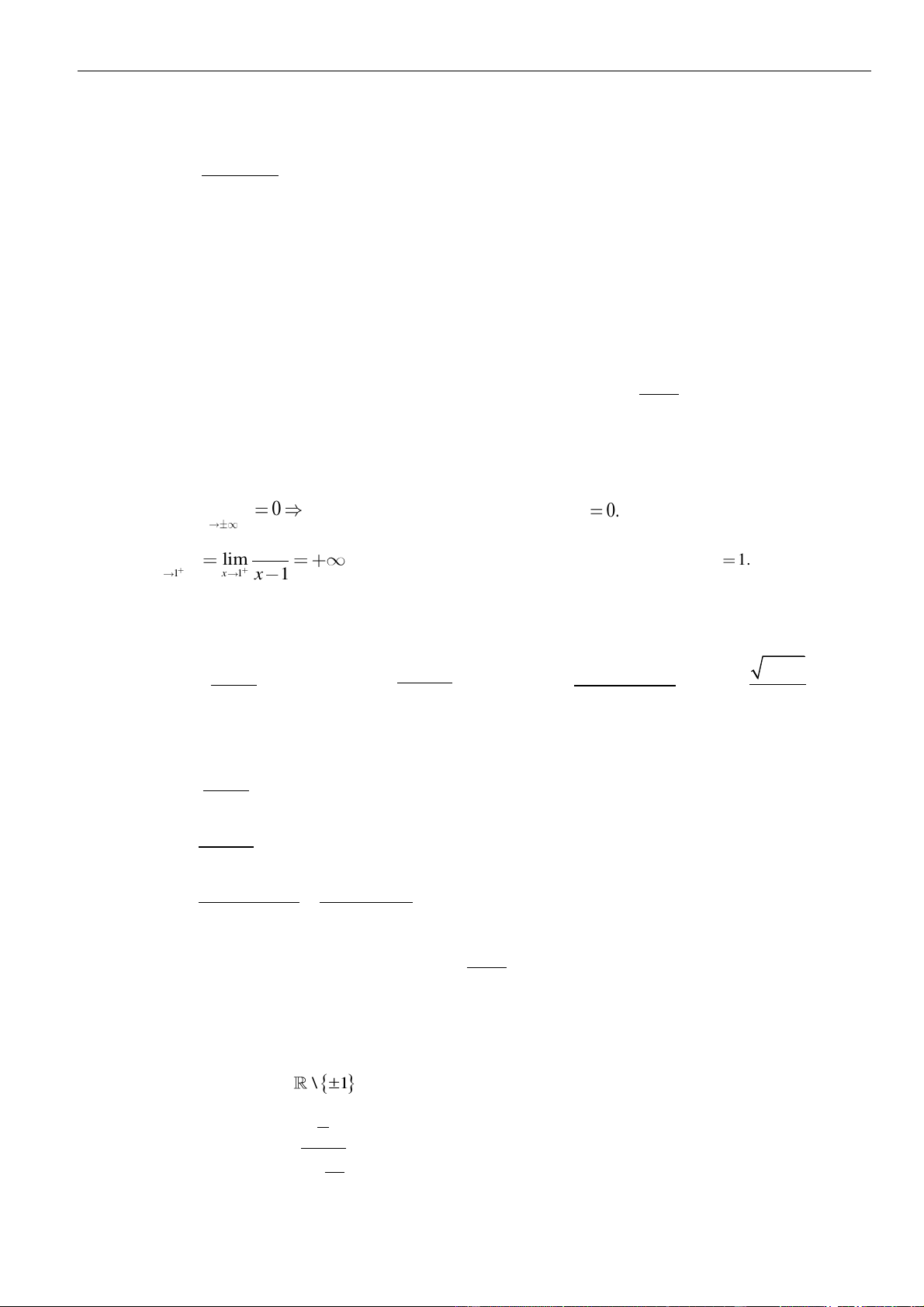
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn D
2
2
32
32
xx
y
xx
−+
=
++
Tiệm cận đứng :
1
1
lim
lim
x
x
y
y
−
+
→−
→−
= −
= +
;
2
2
lim
lim
x
x
y
y
−
+
→−
→−
= +
= −
. Vậy
1; 2xx= − = −
là hai tiệm cận đứng
Tiệm cận ngang:
lim 1 1
x
yy
→
= =
. Vậy
1y =
là tiệm cận ngang.
Câu 27: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
+
=
−
là:
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn A
Ta có
lim 0
x
y
đồ thị hàm số có tiệm cận ngang là
0.y
11
1
lim lim
1
xx
y
x
nên đồ thị hàm số có 1 đường tiệm cận đứng là
1.x
Vậy tổng số tiệm cận ngang và đứng là 2 tiệm cận.
Câu 28: Đường thẳng
20y +=
là đường tiệm cận của đồ thị hàm số nào sau đây?
A.
2
32
y
x
=
+
. B.
2
23
2
x
y
x
−
=
+
. C.
( )( )
2
21
13
xx
y
xx
+−
=
+−
. D.
2
1
21
x
y
x
+
=
−
.
Lời giải
Chọn C
2
32
y
x
=
+
có
lim 0 0
x
yy
→
= =
là tiệm cận ngang nên đáp án A sai.
2
23
2
x
y
x
−
=
+
có
lim
x
y
→
=
nên đồ thị hàm số không có tiệm cận ngang. Đáp án B sai.
( )( )
22
2
2 1 2 1
1 3 2 3
x x x x
y
x x x x
+ − + −
==
+ − − + +
có
lim 2 2
x
yy
→
= − = −
là tiệm cận ngang. Đáp án C đúng.
Câu 29: Số đường tiệm cận của đồ thị hàm số
2
1
x
y
x
=
−
là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn B
Tập xác định
\1D =
.
Ta có
2
1
lim lim 0 0
1
1
xx
x
yy
x
→ →
= = =
−
là đường tiệm cận ngang.
Ta có
11
lim ;lim 1
xx
y y x
+−
→→
= + = − =
là đường tiệm cận đứng.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Ta có
( ) ( )
11
lim ; lim 1
xx
y y x
+−
→ − → −
= − = + = −
là đường tiệm cận đứng.
Số đường tiệm cận của đồ thị hàm số
2
1
x
y
x
=
−
là
3
.
Câu 30: Đường tiệm cận ngang của đồ thị hàm số
2
1
4
x
y
x
+
=
−
có phương trình là
A.
2y =−
. B.
2y =
. C.
0y =
. D.
1y =−
.
Lời giải
Chọn C
Ta có
2
1
lim lim 0
4
xx
x
y
x
→ →
+
==
−
Vậy đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số.
Câu 31: Một đường tiệm cận đứng của đồ thị hàm số
( )
( )
2
2
43
21
xx
y
xx
++
=
−−
là
A.
1x =−
. B.
1x =
. C.
0x =
. D.
2x =−
.
Lời giải
Chọn B
( )( )
( )( )( ) ( )( )
( )( )
( )( )( ) ( )( )
1 1 1
2 2 2
13
3
lim lim lim
2 1 1 2 1
13
3
lim lim lim
2 1 1 2 1
x x x
x x x
xx
x
y
x x x x x
xx
x
y
x x x x x
+ + +
+ + +
→ → →
→ → →
++
+
= = = −
− − + − −
++
+
= = = +
− − + − −
Vậy một đường tiệm cận đứng của đồ thị hàm số là
1x =
.
Câu 32: Đồ thị hàm số
( )
2
2
31
3
xx
fx
xx
−+
=
−
có bao nhiêu đường tiệm cận?
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn A
\ 0;3D =
( )
2
2
31
3
xx
fx
xx
−+
=
−
( ) ( )
0 0 0
22
2
0
2
lim lim ; li
31
m lim
31
33
x x x x
f x f
x x x x
x x x
x
x
+ + − −
→ → → →
− + − +
−−
= = − = = +
.
Đồ thị hàm số
( )
2
2
31
3
xx
fx
xx
−+
=
−
có tiệm cận đứng là đường thẳng
0x =
.
( ) ( )
3 3 3
22
2
3
2
lim lim ; lim lim
3 1 3 1
33
x x x x
f x f
x x x x
x x x
x
x
+ + − −
→ → → →
− + − +
−−
= = + = = −
Đồ thị hàm số
( )
2
2
31
3
xx
fx
xx
−+
=
−
có tiệm cận đứng là đường thẳng
3x =
.
( )
2
2
lim lim
3
1
31
xx
xx
xx
fx
→ →
−=
−
==
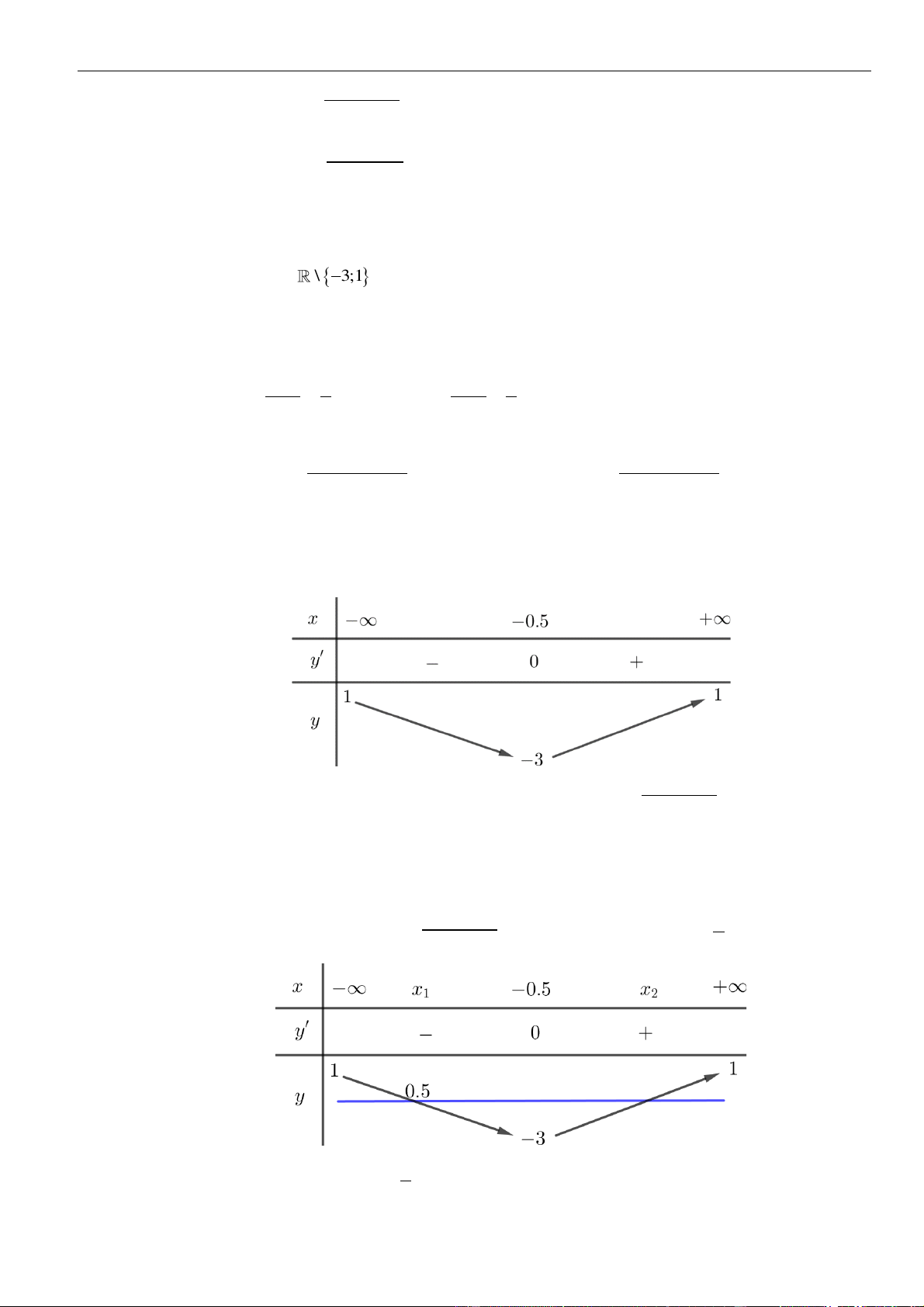
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Đồ thị hàm số
( )
2
2
31
3
xx
fx
xx
−+
=
−
có một tiệm cận ngang là đường thẳng
1y =
.
Câu 33: Đồ thị của hàm số
2
1
23
x
y
xx
−
=
+−
có bao nhiêu đường tiệm cận?
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn B
Tập xác định:
\ 3;1D =−
+)
lim 0
lim 0
x
x
y
y
→+
→−
=
=
đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số đã cho.
+)
11
11
lim lim
34
xx
y
x
++
→→
==
+
và
11
11
lim lim
34
xx
y
x
−−
→→
==
+
nên đường thẳng
1x =
không là đường tiệm
cận đứng của đồ thị hàm số đã cho.
+)
( ) ( )
( )( )
33
1
lim lim
13
xx
x
y
xx
++
→ − → −
−
= = +
−+
và
( ) ( )
( )( )
33
1
lim lim
13
xx
x
y
xx
−−
→ − → −
−
= = −
−+
nên đường
thẳng
3x =−
là đường tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có
2
đường tiệm cận.
Câu 34: Cho hàm số
( )
=y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
1
21
=
−
y
fx
là
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn B
Điều kiện xác định của hàm số
( )
1
21
=
−
y
fx
là
( ) ( )
1
2 1 0
2
− f x f x
.
Từ bảng biến thiên ta có
( )
( )
( )
1
1
; 0.5
1
2
0.5;
= − −
=
= − +
xx
fx
xx
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Tập xác định
12
\;xx
.
Có
( )
11
lim 1
2 1 2.1 1
→−
==
−−
x
fx
đồ thị hàm số có tiệm cận ngang
1=y
.
Có
( )
11
lim 1
2 1 2.1 1
→+
==
−−
x
fx
đồ thị hàm số có tiệm cận ngang
1=y
.
Có
( )
1
1
lim
21
→
=
−
xx
fx
đồ thị hàm số có tiệm cận đứng
1
=xx
.
Có
( )
2
1
lim
21
→
=
−
xx
fx
đồ thị hàm số có tiệm cận đứng
2
=xx
.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
21
=
−
y
fx
là
3
.
Câu 35: Số tiệm cận ngang của đồ thị hàm số
2
10000
2
−
=
−
x
y
x
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A
Điều kiện xác định của hàm số
2
100 100
10000 0
2
20
−
−
−
x
x
x
x
.
Tập xác định
100;100 \ 2−
.
Vì hàm số không tồn tại khi
→ −x
và
→ +x
nên đồ thị hàm số không có tiệm cận ngang.
Câu 36: Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
1
x
y
x
+
=
−
là
A. 2. B. 1. C. 3. D. 4
Lời giải
Chọn A
2
1
11
lim lim 0;lim
11
x x x
x
y y y y
xx
→+ →− →
+
= = = = =
−−
.
Do đó đồ thị hàm số có tiệm cận đứng và tiệm cận đứng lần lượt là
1; 0xy==
.
Câu 37: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
3 4 1
1
xx
y
x
−+
=
−
là
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Điều kiện xác định của hàm số là
2
1 0 1− xx
.
Tập xác định
\ 1;1−
.
2
2
3 4 1
lim 3
1
→−
−+
=
−
x
xx
x
đồ thị hàm số có tiệm cận ngang
3=y
.
2
2
3 4 1
lim 3
1
→+
−+
=
−
x
xx
x
đồ thị hàm số có tiệm cận ngang
3=y
.

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
2
2
1
3 4 1
lim
1
→−
−+
=
−
x
xx
x
đồ thị hàm số có tiệm cận đứng
1=−x
.
( )( )
( )( )
2
2
1 1 1
1 3 1
3 4 1 3 1
lim lim lim 1
1 1 1 1
→ → →
−−
− + −
= = =
− − + +
x x x
xx
x x x
x x x x
1=x
không là tiệm cận đứng.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
3 4 1
1
xx
y
x
−+
=
−
là
2
.
Câu 38: Gọi
k
và
l
lần lượt là số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
( )
2
1
x
y
xx
−
=
−
. Khẳng định nào sau đây đúng ?
A.
0, 2kl==
. B.
1, 2kl==
. C.
1, 1kl==
. D.
0, 1kl==
.
Lời giải
Chọn A
Tập xác định của hàm số: có:
(
0;2 \ 1D =
.
Đồ thị hàm số không có tiệm cận ngang.
( ) ( )
11
22
lim ;lim
11
xx
xx
x x x x
+−
→→
−−
= + = −
−−
ta có
1x =
là tiệm cận đứng.
( )
0
2
lim
1
x
x
xx
+
→
−
= −
−
ta có
0x =
là tiệm cận đứng.
Vậy
0, 2kl==
.
Câu 39: Trong các hàm số sau, đồ thị hàm số nào có đường tiệm cận ngang.
A.
2
21
3
x
y
x
−
=
−
. B.
42
10 97y x x= − +
. C.
32
20 6y x x= + +
. D.
2
41
2
x
y
x
−+
=
−
.
Lời giải
Chọn D
Ta có:
2
2
1
4
4 1 1
lim lim 0
1
lim
2
2
xxx
x
x
xx
x
→ →→
−+
−+
= =
−
−
. Khi đó, đồ thị hàm số
2
41
2
x
y
x
−+
=
−
có tiệm cận
ngang là
0y =
.
Câu 40: Đồ thị hàm số
2
2
3
69
xx
y
xx
−
=
−+
có bao nhiêu đường tiệm cận?
A. 2. B. 3. C. 0. D. 1.
Lời giải
Chọn A
TXĐ:
\3D =
.
Ta có:
lim 1
x
y
→
=
nên đồ thị có 1 đường tiệm cận ngang là
1y =
.
Và:
3
3
lim
lim
x
x
y
y
+
−
→
→
= +
= −
nên đồ thị có 1 đường tiệm cận đứng là
3x =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Câu 41: Đồ thị hàm số
2
1
2020 2021
x
y
xx
+
=
−−
có bao nhiêu tiệm cận đứng?
A.
3
. B.
1
. C.
2
. D.
0
Lời giải
Chọn B
Ta có:
2
1
2020 2021 0
2021
x
xx
x
=−
− − =
=
( )( )
2
1 1 1 1
1 1 1 1
lim lim lim lim
2020 2021 1 2021 2021 2022
x x x x
xx
y
x x x x x
→− →− →− →−
+ + −
= = = =
− − + − −
2
2021 2021
1
lim lim
2020 2021
xx
x
y
xx
++
→→
+
= = +
−−
.
2
2021 2021
1
lim lim
2020 2021
xx
x
y
xx
−−
→→
+
= = −
−−
Suy ra đường thẳng
2021x =
là tiệm cận đứng
Vậy hàm số đã cho có 1 tiệm cận đứng.
Câu 42: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
3 4 1
1
xx
y
x
−+
=
−
là
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Điều kiện xác định của hàm số là
2
1 0 1− xx
.
Tập xác định
\ 1;1−
.
2
2
3 4 1
lim 3
1
→−
−+
=
−
x
xx
x
đồ thị hàm số có tiệm cận ngang
3=y
.
2
2
3 4 1
lim 3
1
→+
−+
=
−
x
xx
x
đồ thị hàm số có tiệm cận ngang
3=y
.
2
2
1
3 4 1
lim
1
→−
−+
=
−
x
xx
x
đồ thị hàm số có tiệm cận đứng
1=−x
.
( )( )
( )( )
2
2
1 1 1
1 3 1
3 4 1 3 1
lim lim lim 1
1 1 1 1
→ → →
−−
− + −
= = =
− − + +
x x x
xx
x x x
x x x x
1=x
không là tiệm cận đứng.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
3 4 1
1
xx
y
x
−+
=
−
là
2
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Đồ thị của hàm số nào trong bốn hàm số sau có đường tiệm cận ngang?
A.
1
x
y
x
=
+
. B.
3
3y x x=−
. C.
2
logyx=
. D.
2
4y x x= + +
.
Câu 2: Đồ thị hàm số
( )
.
x
fx
xx
+
=
−−
1
23
có tất cả mấy đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 3: Số đường tiệm cận của đồ thị hàm số
2
1
1
x
y
x
+
=
+
là:
A. 2. B. 3. C. 1. D. 0.
Câu 4: Sau đây, có bao nhiều hàm số mà đồ thị có đúng một tiệm cận ngang?
1)
sin x
y
x
=
2)
2
1xx
y
x
++
=
3)
1
1
x
y
x
−
=
+
4)
2
1 1.y x x= + + −
A. 1. B. 2. C. 3. D. 4.
Câu 5: Số tiệm cận của đồ thị hàm số
( )
2
2
2 1 1
1
xx
y
x
−+
=
−
là
A.
3
. B.
1
. C.
4
. D.
2
Câu 6: Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
2
4
x
y
x
=
−
bằng
A. 3. B. 2. C. 4. D. 1.
Câu 7: Đồ thị hàm số nào dưới đây có đúng một đường tiệm cận ngang?
A.
2
23
1
x
y
x
−
=
+
. B.
2
23
x
y
x
=
+
. C.
2
31
21
x
y
xx
+
=
+−
. D.
2
42
32
x
y
xx
−
=
−+
.
Tiệm cận của đồ thị hàm số chứa căn
DẠNG 2
Phương pháp:
•
Bưc 1. Tm tập xc định của hàm số.
•
Bưc 2. Xc định cc đường tiệm cận
- Tiệm cận ngang:
+) Điều kiện cần: Để đồ thị hàm số chứa căn thức có tiệm cận ngang th trong tập xc định phải
có cc khoảng
( )
;a−
hoặc
( )
;b +
.
+) Điều kiện đủ: Tồn tại một trong cc giới hạn
lim
x
a
→−
=
hoặc
lim
x
b
→+
=
th đường thẳng
ya=
hoặc
yb=
là tiệm cận ngang của đồ thị hàm số đã cho.
- Tiệm cận đứng: Tồn tại gi trị
0
x
để một trong cc giới hạn
0
lim
xx
y
+
→
= −
hoặc
0
lim
xx
y
→−
= +
thì
0
xx=
là tiệm cận đứng của đồ thị hàm số đã cho.
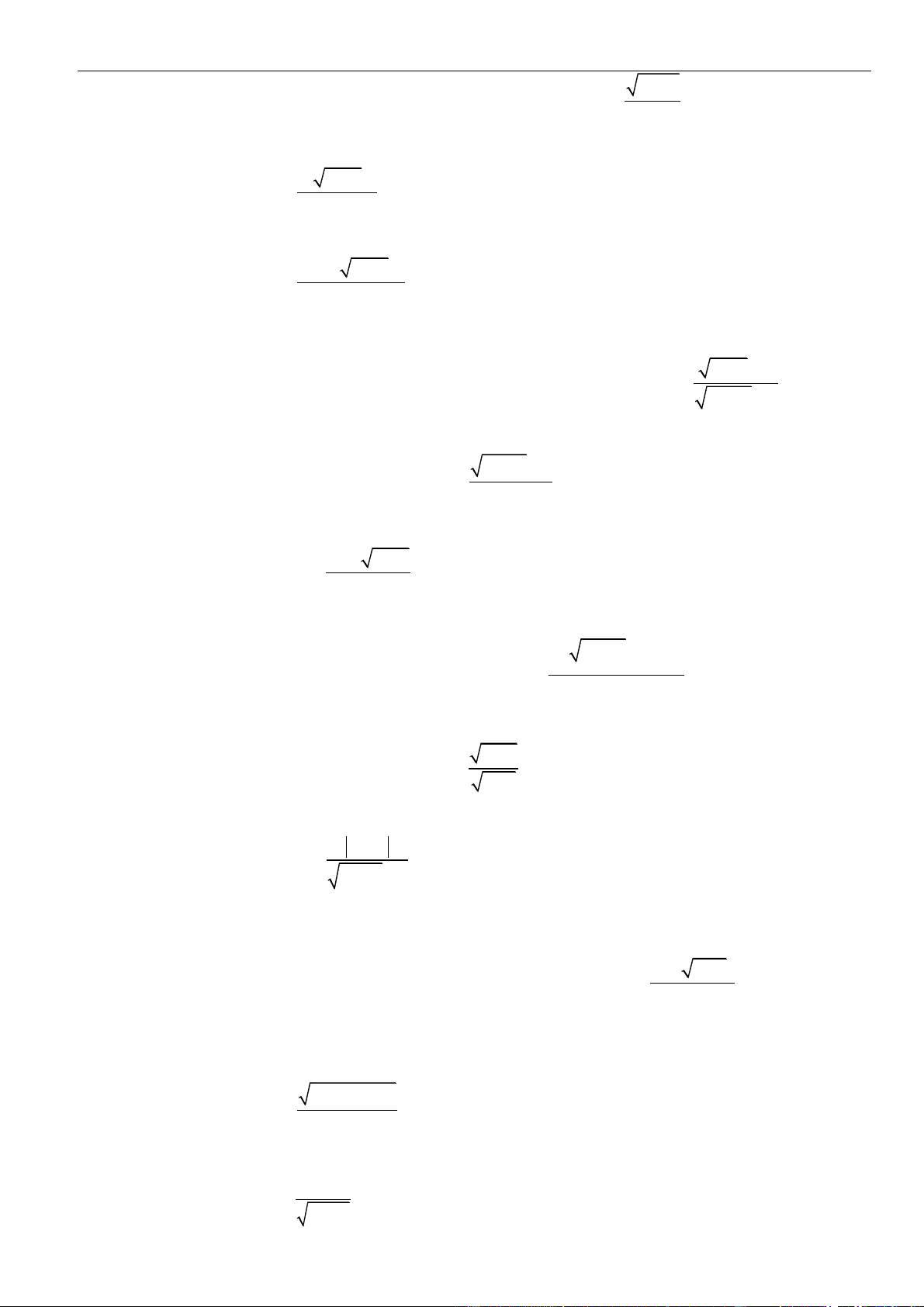
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 8: Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số
2
2
1
2
x
y
xx
−
=
+
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 9: Đồ thị hàm số
2
7
34
x
y
xx
−
=
+−
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 10: Đồ thị hàm số
( ) ( )
2
2
21
xx
y
xx
−+
=
−−
có tất cả bao nhiêu đường tiệm cận đứng?
A.
3
. B.
2
. C. 1. D.
4
.
Câu 11: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
32
xx
y
x
−−
=
+−
là
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 12: Số đường tiệm cận của đồ thị hàm số
2
53
2
x
y
x
+−
=
−
là
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 13: Hỏi đồ thị hàm số
2
2
1
xx
yx
x
−−
=−
−
có tất cả bao nhiêu đường tiệm cận?
A.
2.
B.
1.
C.
0.
D.
3.
Câu 14: Tổng số đường TCĐ và TCN của đồ thị hàm số
(
)
2
2
31
23
x x x
y
xx
++−
=
−−
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 15: Số đường tiệm cận của đồ thị hàm số
4
1
x
y
x
−
=
+
là
A. 1. B. 2. C. 3. D. 0.
Câu 16: Hỏi đồ thị hàm số
2
1
32
x
y
x
+
=
+−
có tất cả bao nhiêu đường tiệm cận (nếu ta chỉ tính đến cc
đường TCĐ và TCN)?
A. 2. B. 3. C. 4. D. 1.
Câu 17: Tập hợp tất cả cc gi trị thực của tham số
m
để đồ thị hàm số
2
11
2
x
y
x x m
++
=
−−
có đúng hai tiệm
cận đứng là
A.
1;3 .−
B.
(
1;3 .−
C.
( )
1;3 .−
D.
( )
1; .− +
Câu 18: Đồ thị hàm số
2
3 10
2
xx
y
x
−−
=
−
có bao nhiêu đường tiệm cận?
A.
0.
B.
3
. C.
1
. D.
2
.
Câu 19: Đồ thị hàm số
2
1
9
x
y
x
−
=
−
có bao nhiêu đường tiệm cận?

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
2
. B.
0
. C.
1
. D. 3.
Câu 20: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
3
9
x
y
x
−
=
−
là
A.
3.
B.
2.
C.
1.
D.
4.
Câu 21: Đồ thị của hàm số nào trong bốn hàm số sau có đường tiệm cận ngang?
A.
1
=
+
x
y
x
. B.
3
3=−y x x
. C.
2
log=yx
. D.
2
4= + +y x x
.
Câu 22: Số đường tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 23: Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
1
1
x
y
x
+
=
−
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 24: Phương trnh tất cả cc đường tiệm cận đứng của đồ thị hàm số
2
10
100
x
y
x
−
=
−
là
A.
100x =
. B.
10x =−
. C.
10x =
và
10x =−
. D.
10x =
.
Câu 25: Số đường tiệm cận của đồ thị hàm số
2
2
9
65
−
=
−+
x
y
xx
là
A. 2. B. 4. C. 1. D. 3.
Câu 26: Tìm tất cả cc đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
9 6 4
2
xx
y
x
++
=
+
A.
2x =−
và
3y =
. B.
2; 3xy= − = −
và
3y =
.
C.
2x =
và
3y =
. D.
2; 9xy= − = −
và
9y =
.
Câu 27: Tm tất cả cc đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
9 6 4
2
xx
y
x
++
=
+
.
A.
2x =−
và
3y =
. B.
2, 3xy= − = −
và
3y =
.
C.
2x =
và
3y =
. D.
2x =−
,
9y =−
và
9y =
.
Câu 28: Tính tổng số đường tiệm cận của hàm số
( )
( )
22
34
2 5 2 16
xx
y
x x x
−+
=
− + −
là
A.
2
. B.
3
. C.
5
. D.
4
.
Câu 29: Tính tổng số đường tiệm cận của hàm số
( )
( )
22
34
2 5 2 16
xx
y
x x x
−+
=
− + −
là
A.
2
. B.
3
. C.
5
. D.
4
.
Câu 30: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
2
21
1
xx
y
x
−−
=
−
bằng
A. 3. B. 2. C. 0. D. 1.

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 31: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
2
xx
y
x
+−
=
+
là :
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 32: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
2 . 3
x
fx
xx
−
=
−−
là
A. 2. B. 1. C. 4. D. 3.
Câu 33: Số đường tiệm cận đứng của đồ thị hàm số
2
1
1
x
y
x
là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 34: Số đường tiệm cận của đồ thị hàm số
2
2
9
65
x
y
xx
−
=
−+
là:
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 35: Số đường tiệm cận của đồ thị hàm số
2
1
56
x
y
xx
−
=
+−
là:
A.
4.
B.
2.
C.
1.
D.
3.
Câu 36: Cho hàm số
( )
2
4
2 1 3
,
1
mx
ym
x
++
=
+
là tham số. Tm gi trị của
m
để đường tiệm cận ngang của
đồ thị hàm số đi qua điểm
( )
1; 3 .A −
A.
= 0m
. B.
= = −1; 1mm
. C.
= 2m
. D.
2.m =−
Câu 37: Đồ thị hàm số nào trong cc hàm số dưới đây có tiệm cận đứng?
A.
1
.y
x
=
B.
4
1
.
1
y
x
=
+
C.
2
1
.
1
y
x
=
+
D.
2
1
.
1
y
xx
=
++
Câu 38: Đồ thị hàm số
2
2
42
2 3 1
xx
y
xx
−+
=
−+
có tất cả bao nhiêu đường tiệm cận?
A. 2. B. 3. C. 4. D. 1.
Câu 39: Đồ thị hàm số
2
2
4
34
x
y
xx
−
=
−−
có tất cả bao nhiêu đường tiệm cận?
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 40: Số đường tiệm cận của hàm số
2
1
2
x
y
xx
là
A.
0
. B.
1
. C.
2
. D.
3
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Đồ thị của hàm số nào trong bốn hàm số sau có đường tiệm cận ngang?
A.
1
x
y
x
=
+
. B.
3
3y x x=−
. C.
2
logyx=
. D.
2
4y x x= + +
.
Lời giải
Chọn D
Xét đp n A: Không có tiệm cận ngang v
lim
1
x
x
x
→+
= +
+
Xét đp n B: Không có tiệm cận ngang v
( )
3
lim 3
x
xx
→
− =
Xét đp n C: Không có tiệm cận ngang v
( )
2
lim log
x
x
→+
= +
Xét đp n D: Có tiệm cận ngang v
(
)
(
)
22
lim 4 ; lim 4 0
xx
x x x x
→+ →−
+ + = + + + =
Câu 2: Đồ thị hàm số
( )
.
x
fx
xx
+
=
−−
1
23
có tất cả mấy đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Hàm số xc định khi và chỉ khi
xx
x
xx
−
−
2 0 2
2
3 0 3
.
Tập xc định
( )
;D = − 2
.
Ta có
lim
x
−
→
= +
2
x=2
là tiệm cận đứng của đồ thị hàm số.
( )
lim lim lim lim
.
lim
x x x x
x
x
xx
x
fx
xx
xx
x
xx
x
xx
→− →− →− →−
→−
+
++
= = =
−−
−+
− − +
+
= = −
− − +
2
2
2
1
1
11
2 3 5 6
56
1
1
1
1
56
1
y = −1
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có
2
đường tiệm cận.
Câu 3: Số đường tiệm cận của đồ thị hàm số
2
1
1
x
y
x
+
=
+
là:
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn B
+ TXĐ
\1−
+ Vì
1
lim
x
y
+
→−
= +
nên đồ thị hàm số nhận đường thẳng
1x =−
làm đường tiệm cận đứng
( )
*
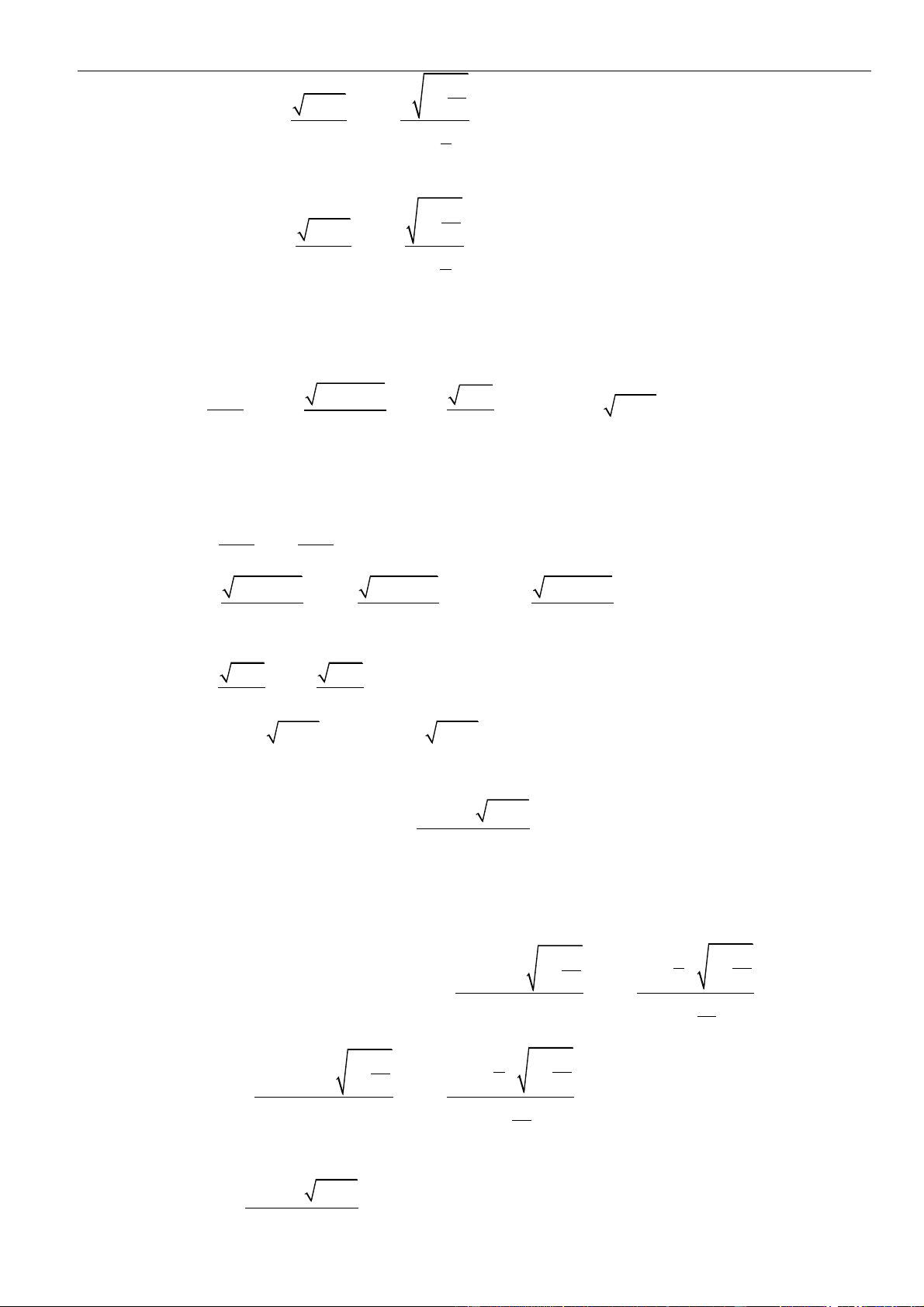
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
+ Vì
2
2
1
1
1
lim lim lim 1
1
1
1
x x x
x
x
y
x
x
→− →− →−
−+
+
= = = −
+
+
nên đồ thị hàm số nhận đường thẳng
1y =−
làm
đường tiệm cận ngang.
+ Vì
2
2
1
1
1
lim lim lim 1
1
1
1
x x x
x
x
y
x
x
→− →+ →+
+
+
= = =
+
+
nên đồ thị hàm số nhận đường thẳng
1y =
làm
đường tiệm cận ngang.
Vậy đồ thị hàm số có tổng số đường tiệm cận là 3.
Câu 4: Sau đây, có bao nhiều hàm số mà đồ thị có đúng một tiệm cận ngang?
1)
sin x
y
x
=
2)
2
1xx
y
x
++
=
3)
1
1
x
y
x
−
=
+
4)
2
1 1.y x x= + + −
A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn C
Xét
sin x
y
x
=
:
sin
lim 0
x
x
x
→
=
nên có 1 TCN là
0y =
Xét
2
1xx
y
x
++
=
:
2
1
lim 1
x
xx
x
→+
++
=
và
2
1
lim 1
x
xx
x
→−
++
=−
nên có 2 TCN là
1y =
và
1y =−
Xét
1
1
x
y
x
−
=
+
:
1
lim 0
1
x
x
x
→−
−
=
+
nên có 1 TCN là
0y =
Xét
2
11y x x= + + −
:
(
)
2
lim 1 1 1
x
xx
→−
+ + − =
nên có 1 TCN là
1y =
Vậy có 3 hàm số mà đồ thị có đứng 1 TCN.
Câu 5: Số tiệm cận của đồ thị hàm số
( )
2
2
2 1 1
1
xx
y
x
−+
=
−
là
A.
3
. B.
1
. C.
4
. D.
2
Lời giải
Chọn C
Ta có
( )
2
2
2
2
2
11
1
21
21
lim lim lim 2
1
1
1
x x x
xx
xx
x
y
x
x
→+ →+ →+
−+
−+
= = =
−
−
.
( )
2
2
2
2
2
11
1
21
21
lim lim lim 2
1
1
1
x x x
xx
xx
x
y
x
x
→− →− →−
− + +
− + +
= = = −
−
−
.
2y =
là tiệm cận ngang.
( )
2
2
11
2 1 1
lim lim 1
1
xx
xx
yx
x
→→
−+
= = =
−
là tiệm cận đứng.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
( ) ( )
( )
2
2
11
2 1 1
lim lim 1
1
xx
xx
yx
x
→ − → −
−+
= = = −
−
là tiệm cận đứng.
Câu 6: Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
2
4
x
y
x
=
−
bằng
A. 3. B. 2. C. 4. D. 1.
Lời giải
Chọn C
Tập xc định:
( ) ( )
; 2 2;D = − − +
lim 1
x
y
→+
=
Đường thẳng
1y =
là đường tiệm cận ngang của đồ thị hàm số đã cho.
lim 1
x
y
→−
= −
Đường thẳng
1y =−
là đường tiệm cận ngang của đồ thị hàm số đã cho.
( )
2
lim
x
y
−
→−
= −
Đường thẳng
2x =−
là đường tiệm cận đứng của đồ thị hàm số đã cho.
2
lim
x
y
+
→
= +
Đường thẳng
2x =
là đường tiệm cận đứng của đồ thị hàm số đã cho.
Vậy có tổng số 4 đường đường tiệm cận đứng và đường tiệm cận ngang.
Câu 7: Đồ thị hàm số nào dưới đây có đúng một đường tiệm cận ngang?
A.
2
23
1
x
y
x
−
=
+
. B.
2
23
x
y
x
=
+
. C.
2
31
21
x
y
xx
+
=
+−
. D.
2
42
32
x
y
xx
−
=
−+
.
Lời giải
Chọn D
Xét hàm số
2
42
32
x
y
xx
−
=
−+
có tập xc định
\ 1;2D =
.
Ta có
2
2
42
lim 0
32
42
lim 0
32
x
x
x
xx
x
xx
→+
→−
−
=
−+
−
=
−+
Suy ra đồ thị hàm số
2
42
32
x
y
xx
−
=
−+
chỉ có một đường tiệm cận ngang là
0y =
.
Câu 8: Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số
2
2
1
2
x
y
xx
−
=
+
là
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn C
Ta có TXĐ:
1;1 \ 0D =−
.
V TXĐ của hàm số không chứa
−
và
+
nên đồ thị hàm số không có đường tiệm cận ngang.
Lại có:
2
2
00
1
lim lim
2
xx
x
y
xx
−−
→→
−
= = −
+
và
2
2
00
1
lim lim
2
xx
x
y
xx
++
→→
−
= = +
+
.
Vậy đồ thị hàm số có đường tiệm cận đứng
0x =
.
Câu 9: Đồ thị hàm số
2
7
34
x
y
xx
−
=
+−
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
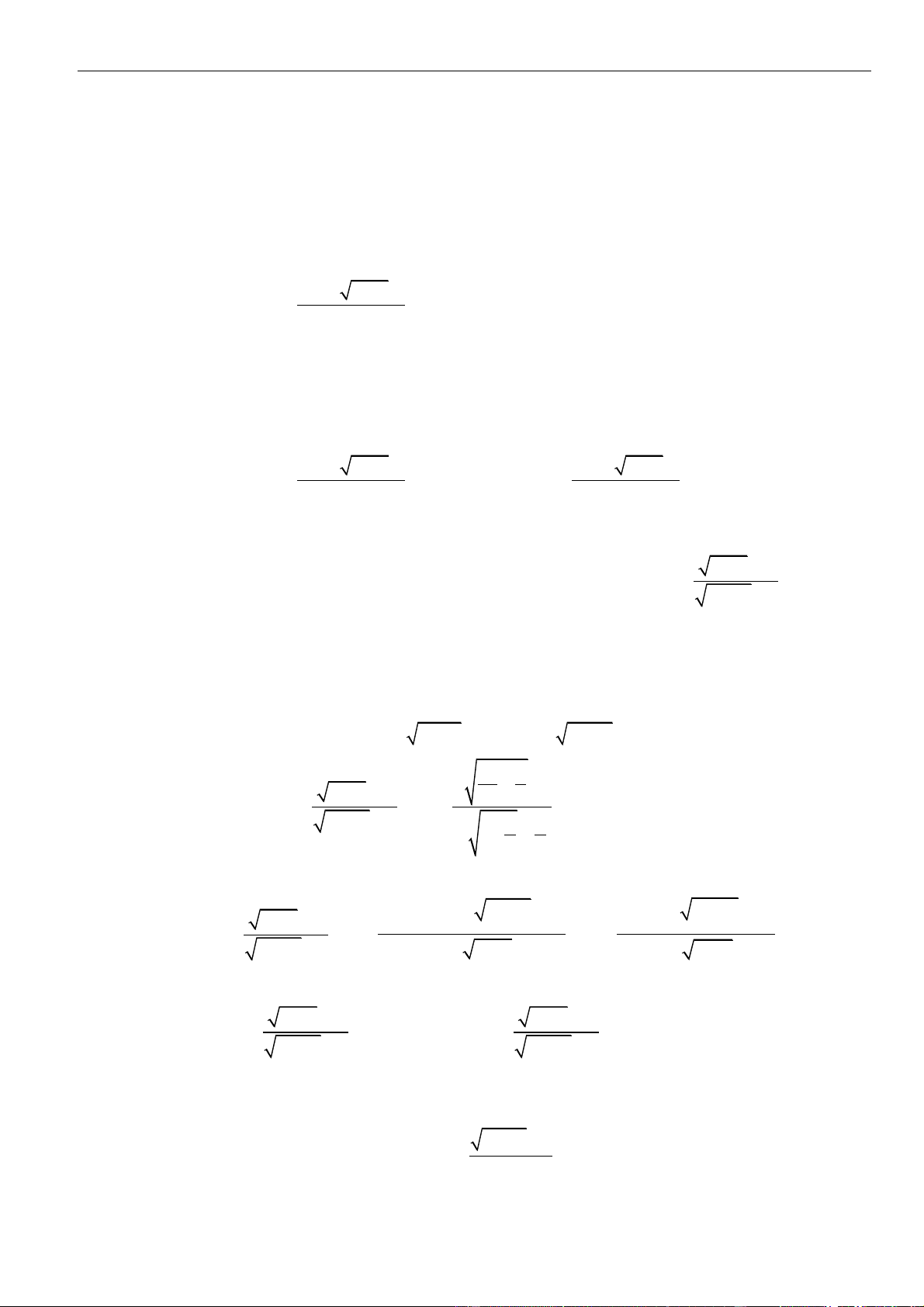
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Chọn A
Tập xc định
)
7;D = +
.
Phương trnh
)
)
2
1 7;
3 4 0
4 7;
x
xx
x
= +
+ − =
= − +
Do đó không tồn tại cc giới hạn
4 4 1 1
lim ,lim ;lim ,lim
x x x x
yyyy
− + − +
→− →− → →
. V vậy đồ thị hàm số không có đường
tiệm cận đứng.
Câu 10: Đồ thị hàm số
( ) ( )
2
2
21
xx
y
xx
−+
=
−−
có tất cả bao nhiêu đường tiệm cận đứng?
A.
3
. B.
2
. C. 1. D.
4
.
Lời giải
Chọn B
Tập xc định
)
2; \ 1;2D = − +
.
Ta có:
( ) ( )
2
11
2
lim lim
21
xx
xx
y
xx
−−
→→
−+
= = +
−−
và
( ) ( )
2
22
2
lim lim
21
xx
xx
y
xx
−−
→→
−+
= = −
−−
Suy ra đường thẳng
1x =
và
2x =
là hai đường tiệm cận đứng của đồ thị hàm số.
Câu 11: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
32
xx
y
x
−−
=
+−
là
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn A
Điều kiện xc định của hàm số:
2
20
3 2 0
x
x
−
+ −
2
2
32
x
x
+
2
1
x
x
.
Ta có:
lim
x
y
→−
2
2
lim
32
x
xx
x
→−
−−
=
+−
2
21
1
lim 1
32
1
x
xx
xx
→−
− − −
==
− + −
. Suy ra đồ thị hàm số có một đường
tiệm cận ngang là đường thẳng
1y =
.
1
lim
x
y
→
2
1
2
lim
32
x
xx
x
→
−−
=
+−
( )
(
)
( )
( )
22
2
1
2 3 2
lim
12
x
x x x
x x x
→
− − + +
=
− − +
( )
(
)
( )
( )
2
1
2 3 2
lim 3
12
x
xx
x x x
→
+ + +
= = −
+ − +
.
Suy ra đường thẳng
1x =
không phải là tiệm cận đứng của đồ thị hàm số.
1
lim
x
y
−
→−
2
1
2
lim
32
x
xx
x
−
→−
−−
= = +
+−
,
1
lim
x
y
+
→−
2
1
2
lim
32
x
xx
x
+
→−
−−
= = −
+−
.
Suy ra đường thẳng
1x =−
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Câu 12: Số đường tiệm cận của đồ thị hàm số
2
53
2
x
y
x
+−
=
−
là
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
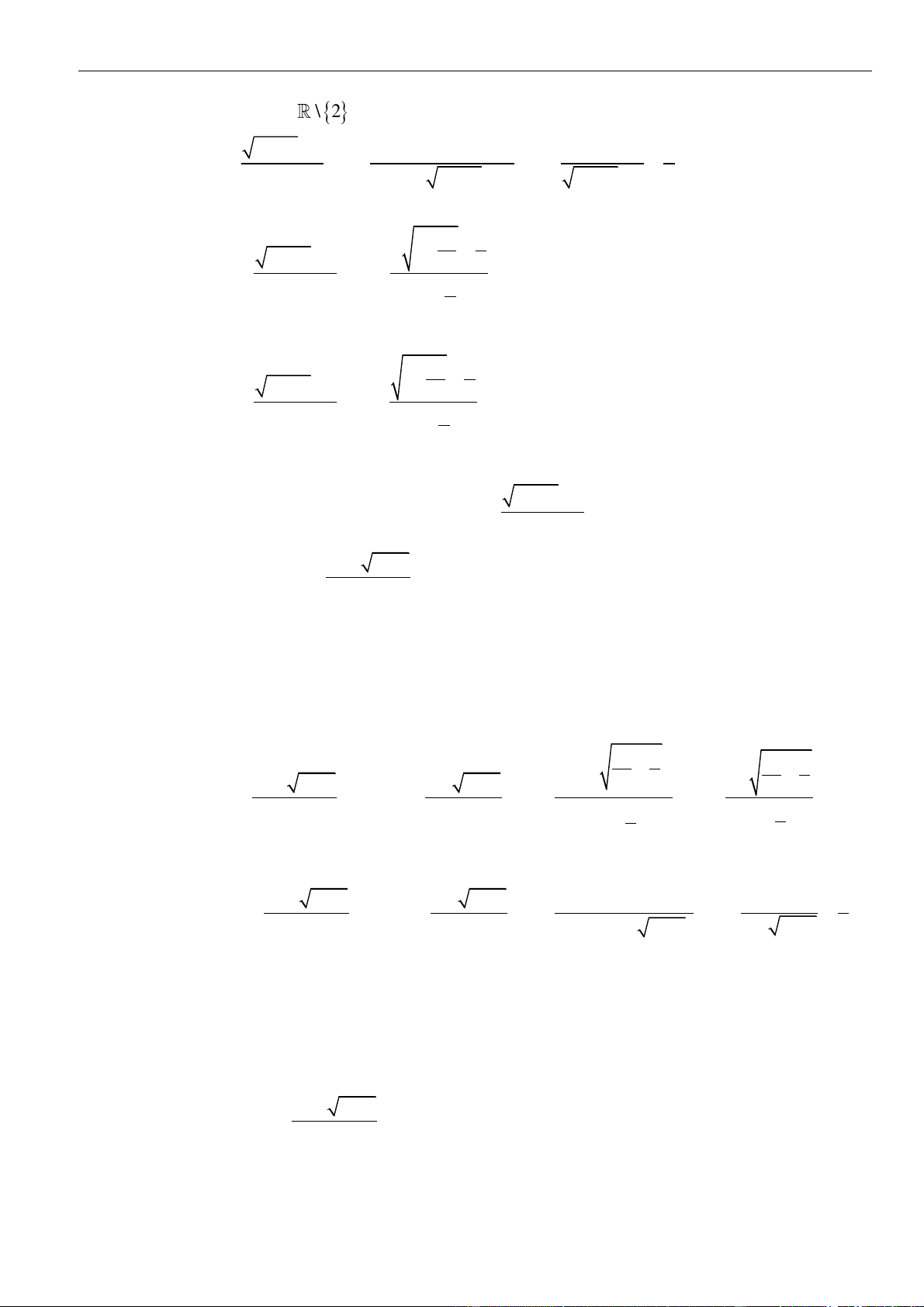
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Chọn D
Tập xc định:
\2D =
.
22
22
2 2 2 2
5 3 4 2 2
lim lim lim lim
23
( 2)( 5 3) 5 3
x x x x
x x x
y
x
x x x
→ → → →
+ − − +
= = = =
−
− + + + +
nên
2x =
không phải
tiệm cận đứng.
2
2
53
1
53
lim lim lim 1
2
2
1
x x x
x
xx
y
x
x
→− →− →−
− + −
+−
= = = −
−
−
1y = −
là một tiệm cận ngang.
2
2
53
1
53
lim lim lim 1
2
2
1
x x x
x
xx
y
x
x
→+ →+ →+
+−
+−
= = =
−
−
1y=
là một tiệm cận ngang.
Vậy số đường tiệm cận của đồ thị hàm số
2
53
2
x
y
x
+−
=
−
là 2.
Câu 13: Hỏi đồ thị hàm số
2
2
1
xx
yx
x
−−
=−
−
có tất cả bao nhiêu đường tiệm cận?
A.
2.
B.
1.
C.
0.
D.
3.
Lời giải
Chọn B
Cách 1.
TXĐ:
( )
;2 \ 1−
Ta có:
2
2
2
21
21
1
1
22
lim lim lim lim 1
1
1
11
1
1
x x x x
x
xx
x x x x
xx
x
xx
x
x
x
→− →− →− →−
+−
+−
− − − −
− = = = =
−−
−
−
Suy ra hàm số có tiệm cận ngang
1.y =
Ta lại có:
( )
( )
22
1 1 1 1
2 2 2 2 3
lim lim lim lim
1 1 2
2
12
x x x x
x x x x x x x
x
xx
xx
x x x
→ → → →
− − − − − + +
− = = = =
−−
+−
− + −
Suy ra hàm số không có tiệm cận đứng.
Vậy hàm số có 1 đường tiệm cân.
Cách 2.
Xc định tiệm cận ngang:
Tính:
lim
x
y
→+
và
lim
x
y
→+
bằng casio
+ Nhập biểu thức
2
2
1
xx
x
x
−−
−
−
+ Nhấn r rồi lần lượt nhập
9
10
và
9
10−
+ Kết quả
lim
x
y
→+
không xc định;
lim 1
x
y
→+
=
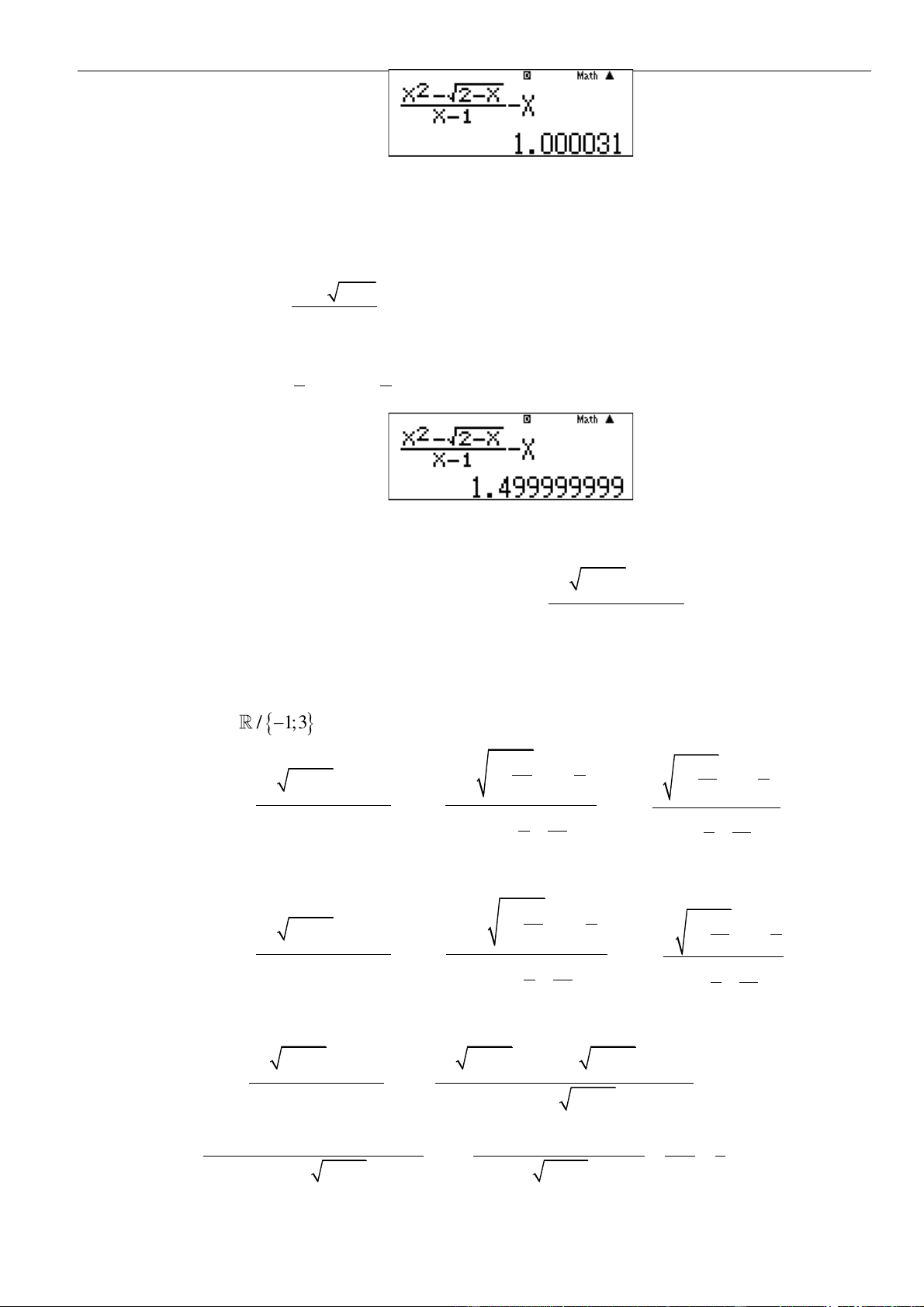
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Suy ra hàm số có 1 tiệm cận ngang
1y =
.
xc định tiệm cận đứng
Giải
1 0 1xx− = =
Tính
1
lim
x
y
−
→
và
1
lim
x
y
+
→
bằng casio
+ Nhập biểu thức
2
2
1
xx
x
x
−−
−
−
+ Nhấn r rồi lần lượt nhập
9
1 10
−
−
và
9
1 10
−
+
+ Kết quả
1
3
lim
2
x
y
−
→
=
;
1
3
lim
2
x
y
+
→
=
Suy ra hàm số không có tiệm cận đứng.
Vậy hàm số có 1 đường tiệm cận.
Câu 14: Tổng số đường TCĐ và TCN của đồ thị hàm số
(
)
2
2
31
23
x x x
y
xx
++−
=
−−
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
TXĐ:
/ 1;3D =−
.
(
)
2
2
2
2
2
2
31
11
31
lim lim lim
23
23
1
x x x
x
x x x
xx
y
xx
x
xx
→+ →+ →+
+ + −
++−
==
−−
−−
2
2
31
11
lim 2
23
1
x
xx
xx
→+
+ + −
==
−−
.
Suy ra
2y =
là TCN.
(
)
2
2
2
2
2
2
31
11
31
lim lim lim
23
23
1
x x x
x
x x x
xx
y
xx
x
xx
→− →− →−
− + + −
++−
==
−−
−−
2
2
31
11
lim 0
23
1
x
xx
xx
→−
− + + −
==
−−
.
Suy ra
0y =
là TCN.
(
)
(
)
(
)
( )
(
)
2 2 2
2
1 1 1
22
3 1 3 1 3 1
lim lim lim
23
2 3 3 1
x x x
x x x x x x x x
y
xx
x x x x
→− →− →−
+ + − + + − + − +
==
−−
− − + − +
( )
( )( )
(
)
( )
(
)
11
22
21
2 2 1
lim lim
16 8
1 3 3 1 3 3 1
xx
xx
x
x x x x x x x
→− →−
+
−
= = = =
−
+ − + − + − + − +
.
Suy ra
1x =−
không phải là TCĐ của đồ thị hàm số đã cho.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
(
)
(
)
22
22
3 3 3 3
3 1 3 1
lim lim ; lim lim
2 3 2 3
x x x x
x x x x x x
yy
x x x x
+ + − −
→ → → →
+ + − + + −
= = + = = −
− − − −
.
Suy ra
3x =
là TCĐ của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có 2 TCN và 1 TCĐ.
Câu 15: Số đường tiệm cận của đồ thị hàm số
4
1
x
y
x
−
=
+
là
A. 1. B. 2. C. 3. D. 0.
Lời giải
Chọn A
GV phản biện:Quý Nguyễn – Hoàng Thị Minh Huệ
Ta có tập xc định của hàm số là
(
1;4D = −
Đồ thị hàm số không có đường tiệm cận ngang
và đường tiệm cận xiên.
1
lim
x
y
+
→−
= +
Đồ thị nhận đường thẳng
1x =−
làm tiệm cận đứng. Vậy đồ thị hàm số có một
đường tiệm cận.
Câu 16: Hỏi đồ thị hàm số
2
1
32
x
y
x
+
=
+−
có tất cả bao nhiêu đường tiệm cận (nếu ta chỉ tính đến cc
đường TCĐ và TCN)?
A. 2. B. 3. C. 4. D. 1.
Lời giải
Chọn A
GV phản biện: Nguyễn Duy Tân – Thuy Hoang
Tập xc định của hàm số là:
\ 1;1D =−
Ta có
2
1
lim lim 1
32
xx
x
y
x
→ →
+
==
+−
nên đồ thị hàm số có tiệm cận ngang là
1y =
.
(
)
2
2
2
2
2
32
,1
1 3 2
1
1
1
32
32
,1
1
x
x
xx
x
x
y
x
x
x
x
x
++
−
+ + +
−
+
= = =
−
+−
++
− −
−
11
lim ; lim
xx
yy
+−
→→
=+ =+
nên đồ thị hàm số có tiệm cận đứng là
1x =
.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 17: Tập hợp tất cả cc gi trị thực của tham số
m
để đồ thị hàm số
2
11
2
x
y
x x m
++
=
−−
có đúng hai tiệm
cận đứng là
A.
1;3 .−
B.
(
1;3 .−
C.
( )
1;3 .−
D.
( )
1; .− +
Lời giải
Chọn B
ĐKXĐ:
1.x −
Vì
1 1 0x+ +
với
1x −
nên để đồ thị hàm số có đúng hai tiệm cận đứng th phương trnh
2
2x x m−=
(1) phải có hai nghiệm phân biệt lớn hơn -1.
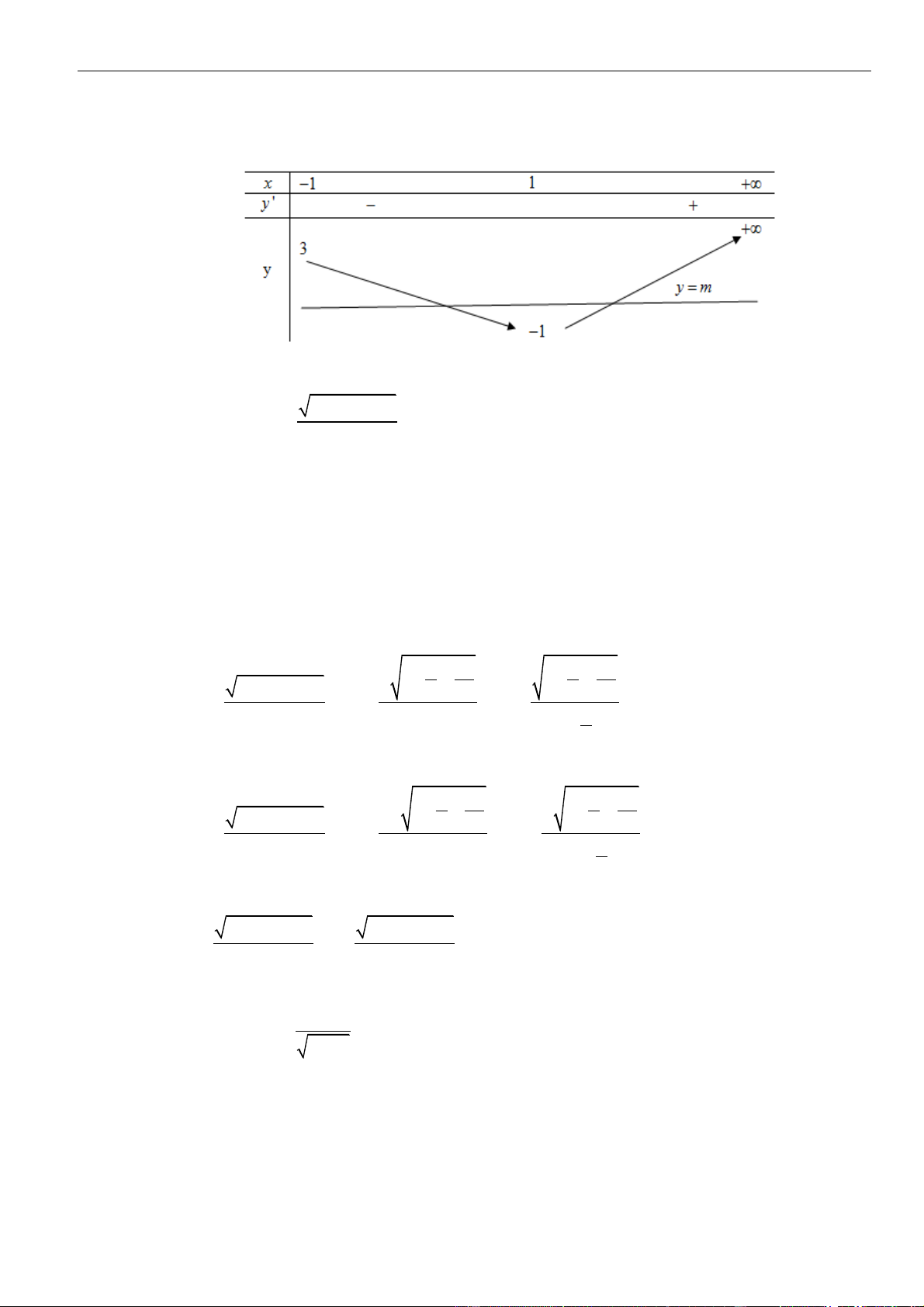
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Xét hàm số
2
( ) 2f x x x=−
trêm
)
1;− +
.
'( ) 2 2 0 1.f x x x= − = =
BBT
Phương trnh (1) có hai nghiệm phân biệt lớn hơn -1 khi
1 3.m−
Câu 18: Đồ thị hàm số
2
3 10
2
xx
y
x
−−
=
−
có bao nhiêu đường tiệm cận?
A.
0.
B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
Điều kiện:
2
2
2
3 10 0
5
5
20
2
x
x
xx
x
x
x
x
−
−
− −
−
Vậy
(
)
; 2 5;D = − − +
Xét
2
22
3 10 3 10
11
3 10
lim lim lim 1
2
22
1
x x x
x
xx
x x x x
xx
x
→+ →+ →+
− − − −
−−
= = =
−−
−
Vậy
1y =
là TCN của đồ thị hàm số
Xét
2
22
3 10 3 10
11
3 10
lim lim lim 1
2
22
1
x x x
x
xx
x x x x
xx
x
→− →− →−
− − − − − −
−−
= = = −
−−
−
Vậy
1y =−
là một TCN của đồ thị hàm số
Vì
22
22
3 10 3 10
lim ; lim
22
xx
x x x x
xx
+−
→→
− − − −
−−
không tồn tại nên đồ thị hàm số không có TCĐ.
Vậy đồ thị hàm số có 2 tiệm cận.
Câu 19: Đồ thị hàm số
2
1
9
x
y
x
−
=
−
có bao nhiêu đường tiệm cận?
A.
2
. B.
0
. C.
1
. D. 3.
Lời giải
Chọn A
Hàm số có tập xc định là
( )
3;3D =−
, do đó đồ thị hàm số không có tiệm cận ngang.
Ta có

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
+)
2
33
1
lim lim
9
xx
x
y
x
−−
→→
−
= = +
−
, suy ra đồ thị hàm số đã cho nhận đường thẳng
3x =
làm tiệm
cận đứng.
+)
( ) ( )
2
33
1
lim lim
9
xx
x
y
x
++
→ − → −
−
= = −
−
, suy ra đồ thị hàm số đã cho nhận đường thẳng
3x =−
làm
tiệm cận đứng.
Vậy đồ thị hàm số đã cho có tất cả 2 đường tiệm cận.
Câu 20: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
3
9
x
y
x
−
=
−
là
A.
3.
B.
2.
C.
1.
D.
4.
Lời giải
Chọn C
Tập xc định
( )
3;3D =−
đồ thị hàm số không có tiệm cận ngang.
( )( )
2
3 3 3
3 3 3
lim lim lim 0
3
33
9
x x x
x x x
x
xx
x
− − −
→ → →
− − − −
= = =
+
−+
−
3x =
không phải là đường tiệm cận đứng của đồ thị hàm số.
( )( )
2
3 3 3
3 3 3
lim lim lim
3
33
9
x x x
x x x
x
xx
x
+ + +
→− →− →−
− − − −
= = = −
+
−+
−
3x =−
là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
1
dường tiệm cận.
Câu 21: Đồ thị của hàm số nào trong bốn hàm số sau có đường tiệm cận ngang?
A.
1
=
+
x
y
x
. B.
3
3=−y x x
. C.
2
log=yx
. D.
2
4= + +y x x
.
Lời giải
Chọn D
Ta có:
(
)
2
2
2
4
4
lim 4 lim lim 0.
4
4
11
→− →− →−
−
−
+ + = = =
−+
++
x x x
x
xx
xx
x
Do đó đồ thị hàm số
2
4= + +y x x
có đường tiệm cận ngang là đường thẳng
0=y
.
Câu 22: Số đường tiệm cận đứng của đồ thị hàm số
2
42x
y
xx
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn A
Tập xc định:
4; \ 0;1 .D
Ta có
2
2
0 0 0
4 2 1 1
lim lim lim
4
4 2 1 4 2
x x x
xx
xx
x x x x x

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
2
2
1 1 1
4 2 1
lim lim lim
4 2 1 4 2
x x x
xx
xx
x x x x x
Vậy đồ thị hàm số
2
42x
y
xx
có một tiệm cận đứng là đường thẳng
1.x
Câu 23: Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
1
1
x
y
x
+
=
−
là
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn B
Tập xc định
)
1; \ 1D = − +
Tiệm cận đứng
1x =
vì
1
1
lim
1x
x
x
+
→
+
= +
−
Tiệm cận ngang
0y =
vì
1
lim 0
1
x
x
x
→+
+
=
−
Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
1
1
x
y
x
+
=
−
là
2.
Câu 24: Phương trnh tất cả cc đường tiệm cận đứng của đồ thị hàm số
2
10
100
x
y
x
−
=
−
là
A.
100x =
. B.
10x =−
. C.
10x =
và
10x =−
. D.
10x =
.
Lời giải
Chọn C
( )
;10 \ 10D = − −
.
( )
10
lim
x
fx
−
→
= −
nên
10x =
là tiệm cận đứng.
( )
( )
10
lim
x
fx
+
→−
= −
và
( )
( )
10
lim
x
fx
−
→−
= +
nên
10x =−
là tiệm cận đứng.
Vậy phương trnh đường tiệm cận đứng của đồ thị hàm số
2
10
100
x
y
x
−
=
−
là
10x =
và
10x =−
.
Câu 25: Số đường tiệm cận của đồ thị hàm số
2
2
9
65
−
=
−+
x
y
xx
là
A. 2. B. 4. C. 1. D. 3.
Lời giải
Chọn C
TXĐ:
3;3 \ 1=−D
.
Ta có
2
1
6 5 0
5
=
− + =
=
x
xx
x
.
Do
2
2
11
9
lim lim
65
xx
x
y
xx
++
→→
−
= = −
−+
,
2
2
11
9
lim lim
65
xx
x
y
xx
−−
→→
−
= = +
−+
nên đồ thị hàm số có một tiệm
cận đứng là
1x =
.
Do
5 3;3x
= −
nên đồ thị hàm số không nhận
5x =
là tiệm cận đứng.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
V hàm số có tập xc định là
3;3 \ 1=−D
nên đồ thị hàm số không có tiệm cận ngang.
Vậy đồ thị hàm số đã cho chỉ có 1 tiệm cận đứng là
1x =
.
Câu 26: Tìm tất cả cc đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
9 6 4
2
xx
y
x
++
=
+
A.
2x =−
và
3y =
. B.
2; 3xy= − = −
và
3y =
.
C.
2x =
và
3y =
. D.
2; 9xy= − = −
và
9y =
.
Lời giải
Chọn B
2
lim 2
x
yx
+
→−
= + = −
là tiệm cận ngang của hàm số.
lim 3 3
x
yy
→+
= =
và
lim 3
x
y
→−
=−
nên
3; 3yy= − =
là hai tiệm cận ngang của hàm số.
Câu 27: Tm tất cả cc đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
9 6 4
2
xx
y
x
++
=
+
.
A.
2x =−
và
3y =
. B.
2, 3xy= − = −
và
3y =
.
C.
2x =
và
3y =
. D.
2x =−
,
9y =−
và
9y =
.
Lời giải
Chọn B
Tập xc định:
\2D =−
.
( )
2
lim
x
y
+
→−
=+
TCĐ:
2x =−
.
lim 3 ; lim 3
xx
yy
→+ →−
= = −
TCN:
3y =
và
3y =−
.
Câu 28: Tính tổng số đường tiệm cận của hàm số
( )
( )
22
34
2 5 2 16
xx
y
x x x
−+
=
− + −
là
A.
2
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn A
Tập xc định:
( )
4;D = +
.
Ta có:
( )
( )
( )
( )
22
2
2
3 4 3 4
lim lim 0
16
2 5 2 16
2 5 2 1
xx
x x x x
x x x
x x x
x
→+ →+
− + − +
==
− + −
− + −
Đồ thị hàm số có tiệm cận ngang
0y =
.
Mặt khc
( )
( )
22
4
34
lim
2 5 2 16
x
xx
x x x
+
→
−+
= +
− + −
4x =
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
2
đường tiệm cận.
Câu 29: Tính tổng số đường tiệm cận của hàm số
( )
( )
22
34
2 5 2 16
xx
y
x x x
−+
=
− + −
là
A.
2
. B.
3
. C.
5
. D.
4
.
Lời giải
Chọn A

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Tập xc định:
( )
4;D = +
.
Ta có:
( )
( )
( )
( )
22
2
2
3 4 3 4
lim lim 0
16
2 5 2 16
2 5 2 1
xx
x x x x
x x x
x x x
x
→+ →+
− + − +
==
− + −
− + −
Đồ thị hàm số có tiệm cận ngang
0y =
.
Mặt khc
( )
( )
22
4
34
lim
2 5 2 16
x
xx
x x x
+
→
−+
= +
− + −
4x =
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
2
đường tiệm cận.
Câu 30: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
2
21
1
xx
y
x
−−
=
−
bằng
A. 3. B. 2. C. 0. D. 1.
Lời giải
Chọn B
Tập xc định
( )
1;D = +
.
Ta có
( )
( )
2
21
2
1
11
xx
x
y
x
xx
−−
−
==
−
+−
.
( )
2
lim 0
11
x
x
xx
→+
−
=
+−
. Nên đồ thị hàm số có tiệm cận ngang là
0y =
.
( )
1
2
lim
11
x
x
xx
+
→
−
= −
+−
. Nên đồ thị hàm số có tiệm cận đứng là
1x =
.
Vậy đồ thị hàm số
( )
2
21
1
xx
y
x
−−
=
−
có 2 đường tiệm cận.
Câu 31: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
1
2
xx
y
x
+−
=
+
là :
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
Tập xc định :
(
)
; 1 0; / 2D = − − + −
.
Ta có :
lim 1
x
y
→−
=−
,
lim 1
x
y
→+
=
,
( )
2
lim
x
y
−
→−
= −
,
( )
2
lim
x
y
+
→−
= +
.
Vậy đồ thị hàm số có hai tiệm cận ngang
1; 1yy= = −
và một đường tiệm cận đứng
2x =−
.
Câu 32: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
2 . 3
x
fx
xx
−
=
−−
là
A. 2. B. 1. C. 4. D. 3.
Lời giải
Chọn A

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Ta có:
( )
lim
x
fx
→+
không tồn tại.
( )
1
1
lim lim 1 1
23
1. 1
xx
x
f x y
xx
→− →−
−+
= = − = −
− + − +
là một đường tiệm cận ngang của đồ thị hàm
số đã cho.
Ta lại có :
( )
2
lim 2
x
f x x
−
→
= + =
là một đường tiệm cận đứng của đồ thị hàm số đã cho.
( ) ( )
33
lim ; lim
xx
f x f x
+−
→→
không tồn tại.
Vậy tổng số đường tiệm cận đứng và ngang của đồ thị hàm số đã cho là 2.
Câu 33: Số đường tiệm cận đứng của đồ thị hàm số
2
1
1
x
y
x
là
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn C
Có:
2
1
lim 0
1
x
x
x
→+
+
=
−
tiệm cận ngang :
= 0y
.
Và:
22
1
11
1 1 1
lim ; lim lim
11
( 1) 1
x
xx
xx
xx
xx
++
→
→− →−
++
= + = = −
−−
−+
tiệm cận đứng :
=1x
.
Câu 34: Số đường tiệm cận của đồ thị hàm số
2
2
9
65
x
y
xx
−
=
−+
là:
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn C
Ta có:
3;3 \ 1D =−
.
11
lim ;lim
xx
yy
+−
→→
= − = +
nên
1x =
là TCĐ của ĐTHS.
Câu 35: Số đường tiệm cận của đồ thị hàm số
2
1
56
x
y
xx
−
=
+−
là:
A.
4.
B.
2.
C.
1.
D.
3.
Lời giải
Chọn B
Tập xc định
\ 6;1D =−
Ta có
lim 0 0
x
yy
→
= =
là đường tiệm cận ngang.
( )( )
1 1 1
1 1 1
lim lim lim 1
1 6 6 7
x x x
x
yx
x x x
→ → →
−
= = = =
− + +
không phải là đường tiệm cận đứng
( )( )
6 6 6
11
lim lim lim 6
1 6 6
x x x
x
yx
x x x
+ + +
→− →− →−
−
= = = + = −
− + +
là đường tiệm cận đứng
Vậy đồ thị hàm số đã cho có
2
đường tiệm cận.

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Câu 36: Cho hàm số
( )
2
4
2 1 3
,
1
mx
ym
x
++
=
+
là tham số. Tm gi trị của
m
để đường tiệm cận ngang của
đồ thị hàm số đi qua điểm
( )
1; 3 .A −
A.
= 0m
. B.
= = −1; 1mm
. C.
= 2m
. D.
2.m =−
Lời giải
Chọn D
Ta có:
lim lim 2 1 : 2 1
xx
y y m d y m
→+ →−
= = + = +
là tiệm cận ngang của đồ thị hàm số đã cho.
Do
( )
1; 3 2 1 3 2.A d m m− + = − = −
Câu 37: Đồ thị hàm số nào trong cc hàm số dưới đây có tiệm cận đứng?
A.
1
.y
x
=
B.
4
1
.
1
y
x
=
+
C.
2
1
.
1
y
x
=
+
D.
2
1
.
1
y
xx
=
++
Lời giải
Chọn A
+) Xét hàm số
1
.y
x
=
TXĐ
( )
0;D = +
0
1
lim
x
x
+
→
= +
Tiệm cận đứng của đồ thị là
0x =
+) Hàm số
4
1
.
1
y
x
=
+
có TXĐ
D =
. Vậy đồ thị hàm số không có tiệm cận.
+) Hàm số
2
1
.
1
y
x
=
+
có TXĐ
D =
. Vậy đồ thị hàm số không có tiệm cận.
+) Hàm số
2
1
.
1
y
xx
=
++
có TXĐ
D =
. Vậy đồ thị hàm số không có tiệm cận.
Câu 38: Đồ thị hàm số
2
2
42
2 3 1
xx
y
xx
−+
=
−+
có tất cả bao nhiêu đường tiệm cận?
A. 2. B. 3. C. 4. D. 1.
Lời giải
Chọn A
Tập xc định
1
2;2 \ 1;
2
D
=−
( )
1
lim
x
fx
+
→
= +
suy ra tiệm cận đứng
1x =
( )
1
2
lim
x
fx
+
→
= −
suy ra tiệm cận đứng
1
2
x =
.
Hàm số không có tiệm cận ngang.
Câu 39: Đồ thị hàm số
2
2
4
34
x
y
xx
−
=
−−
có tất cả bao nhiêu đường tiệm cận?
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
Tập xc định
2;2D =−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Không tồn tại
lim
x
y
→−
và
lim
x
y
→+
, suy ra đồ thị hàm số đã cho không có tiệm cận ngang.
Lại có
( )
1
lim
x
+
→−
= −
,
( )
1
lim
x
−
→−
= +
.
Suy ra đồ thị hàm số có tiệm cận đứng là
1x =−
.
Vậy đồ thị hàm số đã cho có tất cả là
1
đường tiệm cận.
Câu 40: Số đường tiệm cận của hàm số
2
1
2
x
y
xx
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Tập xc định :
)
1; \ 2D = +
.
Ta có :
34
2
11
1
lim lim 0.
2
2
1
xx
x
xx
xx
x
Đường thẳng
0y =
là tiệm cận ngang.
22
22
11
lim ; lim
22
xx
xx
x x x x
−+
→→
−−
= − = +
−−
Đường thẳng
2x =
là tiệm cận đứng.

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
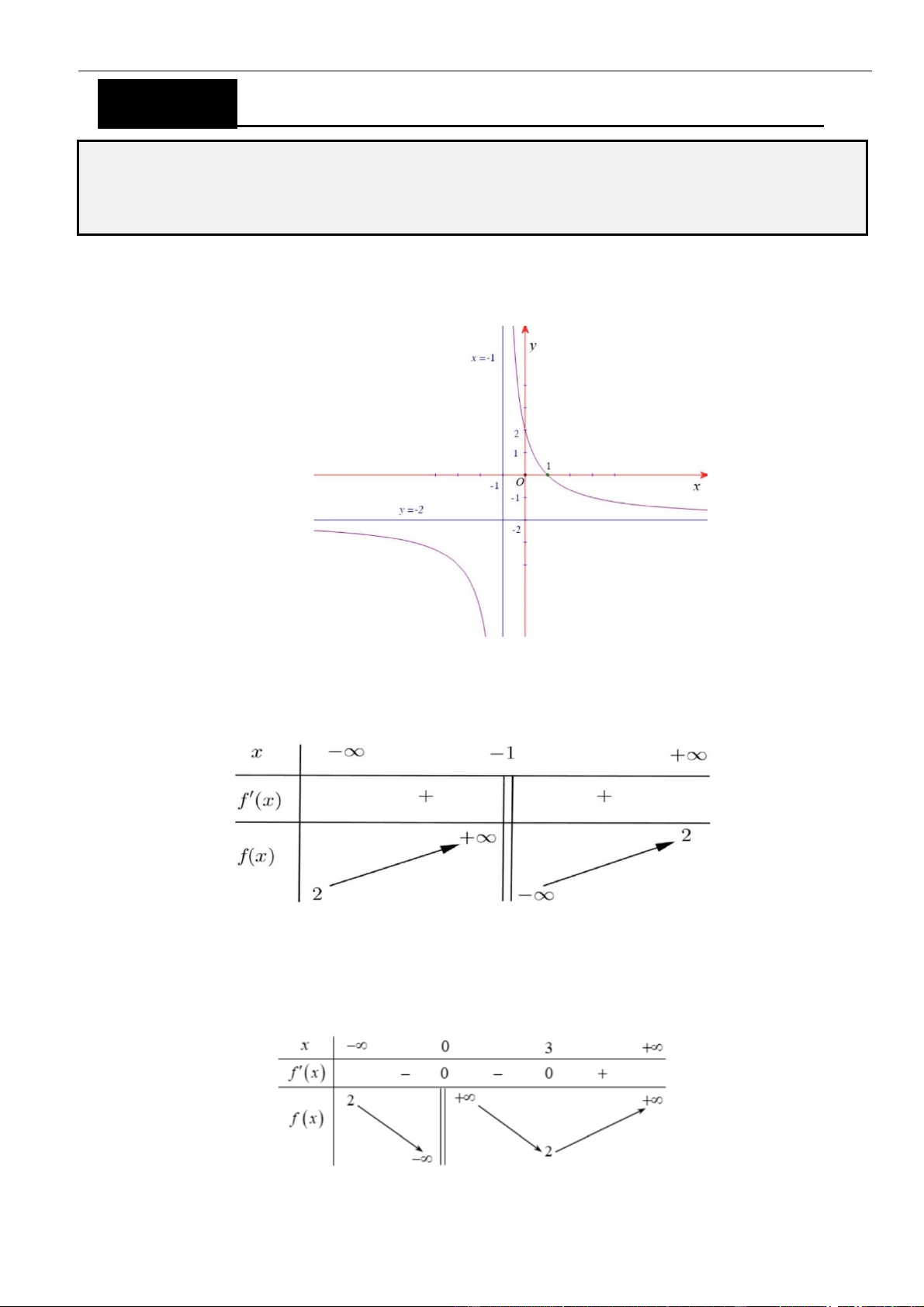
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
( )
y f x=
có đồ thị như hình sau
Đồ thị hàm số trên có đường tiệm cận đứng là
A.
1x =−
. B.
2x =−
. C.
1y =−
. D.
2y =−
.
Câu 2: Cho hàm số
()fx
có bảng biến thiên như sau
Đồ thị hàm số có đường tiệm cận ngang là
A.
2y =
. B.
2x =
. C.
1y =−
. D.
1x =−
.
Câu 3: Cho hàm số
( )
y f x=
xác định và liên tục trên
( )
;0−
và
( )
0;+
có bảng biến thiên như hình
vẽ. Mệnh đề nào sau đây đúng?
A. Đường thẳng
2x =
là tiệm cận đứng của đồ thị hàm số.
B. Đồ thị hàm số có hai đường tiệm cận ngang.
Xác định số đường tiệm cận dựa vào đồ thị, BBT
DẠNG 3
Phương pháp:
Nắm chắc được lý thuyết về cách xác định số đường tiệm cận của đồ thị hàm số, kết hợp với việc quan
sát đồ thị, bảng biến thiên để đưa ra kết luận
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
C. Đồ thị hàm số có hai đường tiệm cận.
D. Đồ thị hàm số chỉ có một đường tiệm cận.
Câu 4: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Đồ thị hàm số trên có tiệm cận ngang là
A.
1x =−
. B.
1y =−
. C.
1x =
. D.
1y =
.
Câu 5: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Đồ thị hàm số trên có tiệm cận đứng là:
A.
1y =−
. B.
1y =
. C.
1x =
. D.
1x =−
.
Câu 6: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Đồ thị hàm số có đường tiệm cận đứng là
A.
1y =−
. B.
2x =
. C.
2y =
. D.
1x =−
.
Câu 7: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 8: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
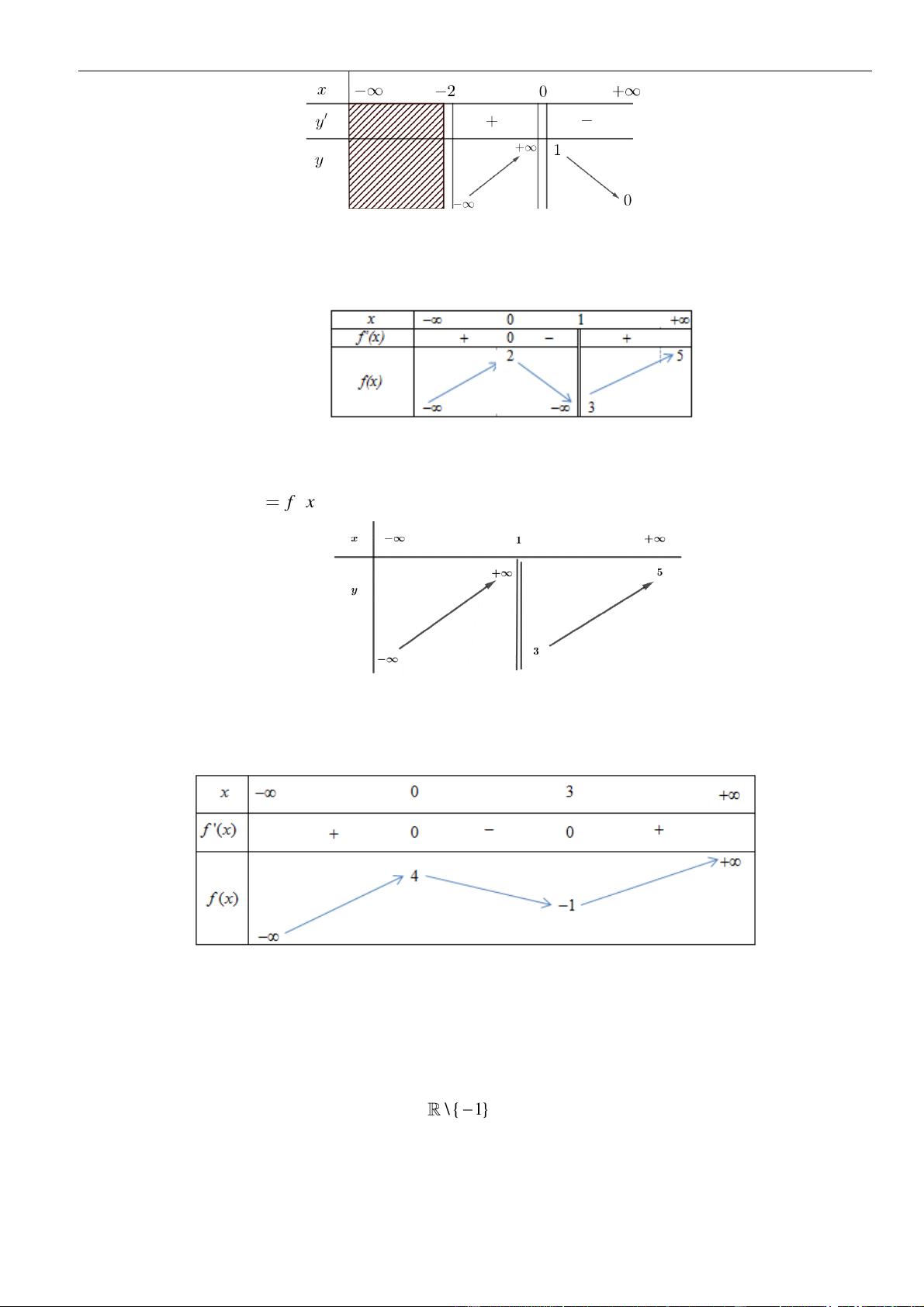
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 10: Cho hàm số
y f x
có bảng biến thiên như hình bên dưới
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 11: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số có
2
đường tiệm cận ngang.
B. Đồ thị hàm số có đường tiệm cận ngang
4y =
.
C. Đồ thị hàm số không có tiệm cận.
D. Đồ thị hàm số có đường tiệm cận đứng
0x =
.
Câu 12: Cho hàm số
()y f x=
xác định trên
}\{1−
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình sau:
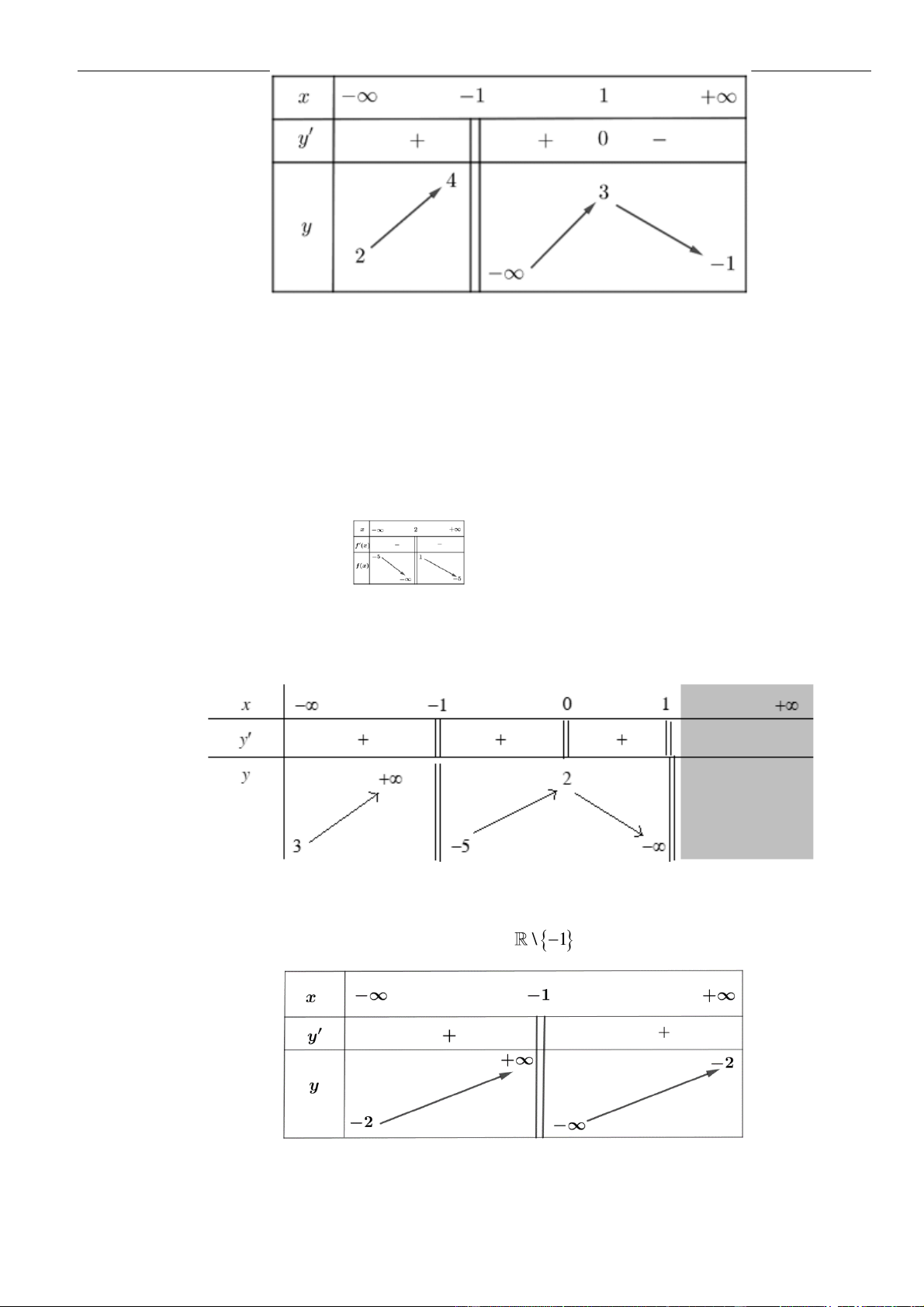
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Hỏi đồ thị hàm số có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 13: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số tiệm cận ngang của đồ thị hàm số đã cho là
A. 4. B. 2. C. 1. D. 3.
Câu 14: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ dưới đây:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
A.
1.
B.
4.
C.
0.
D.
3.
Câu 15: Cho hàm số
( )
y f x=
xác định và liên tục trên
\1−
, có bảng biến thiên như sau.
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng
1y =−
và tiệm cận ngang
2x =−
.
B. Đồ thị hàm số có duy nhất một tiệm cận.
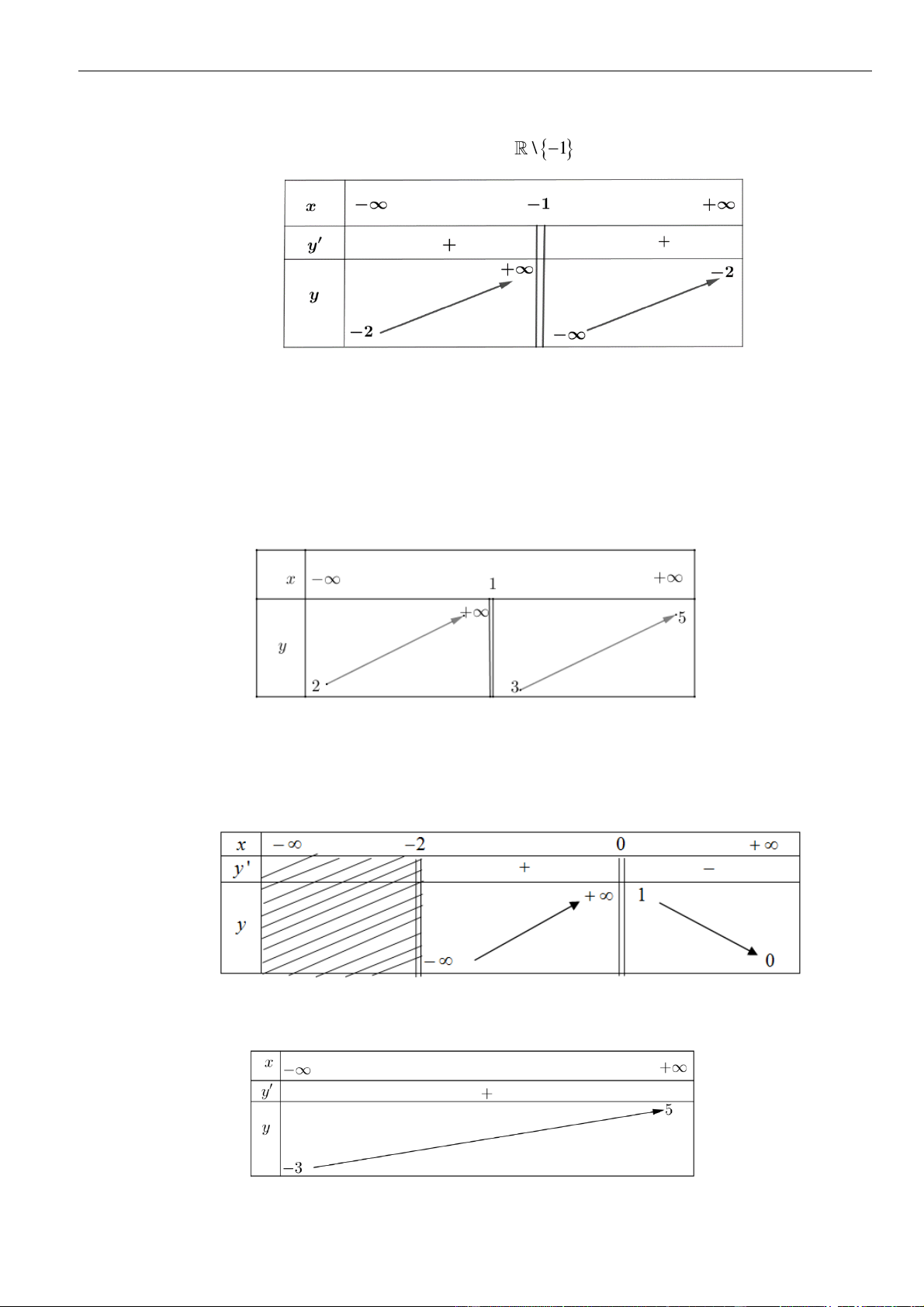
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
C. Đồ thị hàm số có ba tiệm cận.
D. Đồ thị hàm số có tiệm cận đứng
1x =−
và tiệm cận ngang
2y =−
.
Câu 16: Cho hàm số
( )
y f x=
xác định và liên tục trên
\1−
, có bảng biến thiên như sau.
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng
1y =−
và tiệm cận ngang
2x =−
.
B. Đồ thị hàm số có duy nhất một tiệm cận.
C. Đồ thị hàm số có ba tiệm cận.
D. Đồ thị hàm số có tiệm cận đứng
1x =−
và tiệm cận ngang
2y =−
.
Câu 17: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 18: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho
có bao nhiêu đường tiệm cận?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 19: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số đường tiệm cận ngang của đồ thị hàm số
( )
y f x=
là
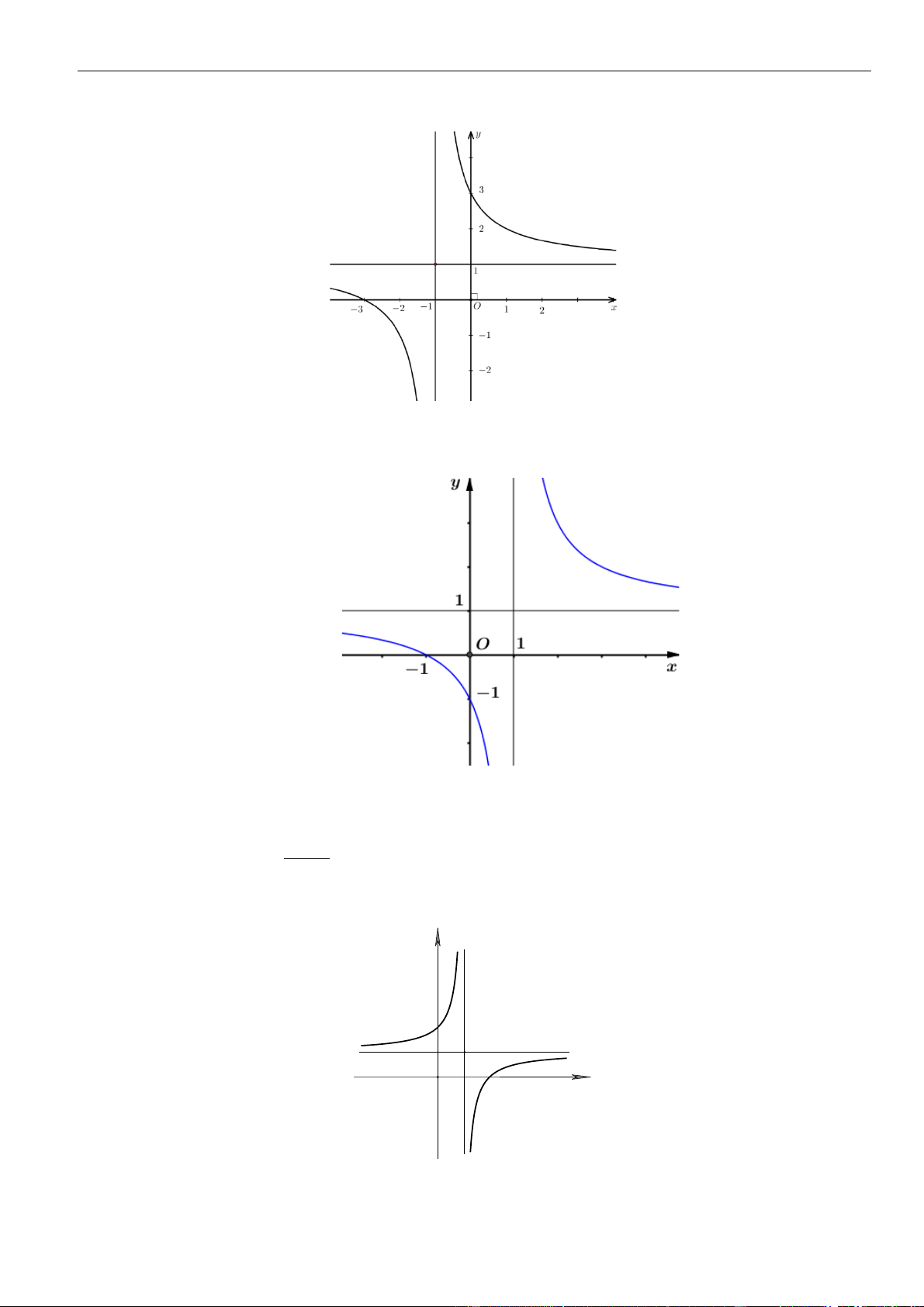
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 20: Đồ thị hàm số như hình vẽ dưới đây có tiệm cận đứng và tiệm cận ngang theo thứ tự là
A.
1x =
,
1y =
. B.
3x =−
,
3y =
. C.
1x =−
,
1y =
. D.
1x =
,
1y =−
.
Câu 21: Cho hàm số
( )
fx
có đồ thị như hình vẽ bên dưới.
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là
A.
1; 1xy= − = −
. B.
1; 1xy==
. C.
1; 1xy= = −
. D.
1; 1xy= − =
.
Câu 22: Cho hàm số
( )
0 ; 0
ax b
y ad bc ac
cx d
+
= −
+
có đồ thị như hình vẽ bên dưới. Tìm đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số?
A.
1,x =−
1y =
. B.
1,x =
2y =
. C.
1,x =
1y =
. D.
2,x =
1y =
.
2
2
1
1
O
x
y
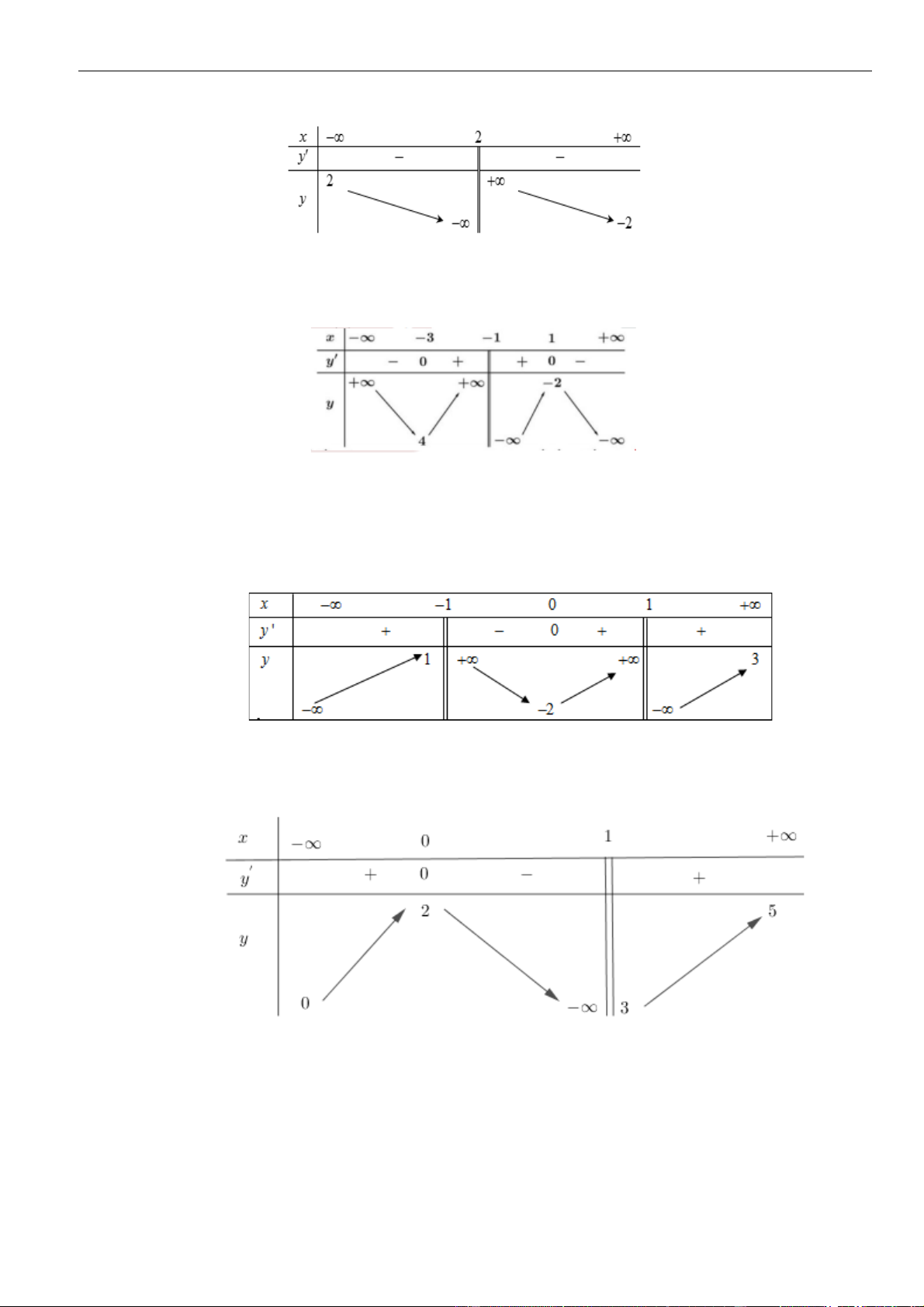
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Câu 23: Cho hàm số
( )
y f x=
có bảng biến thiên sau. Hỏi đồ thị hàm số đó có mấy tiệm cận.
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 24: Cho hàm số
( )
fx
có bảng biến thiên như hình vẽ sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 0. B.
2
. C. 3. D.
1
.
Câu 25: Cho hàm
( )
y f x=
có bảng biến thiên như hình vẽ. Đồ thị hàm số
( )
y f x=
có bao nhiêu đường
tiệm cận?
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 26: Cho hàm số
( )
fx
có bảng biến thiên như sau.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
3
B.
1
.
C.
2
. D.
4
.
Câu 27: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
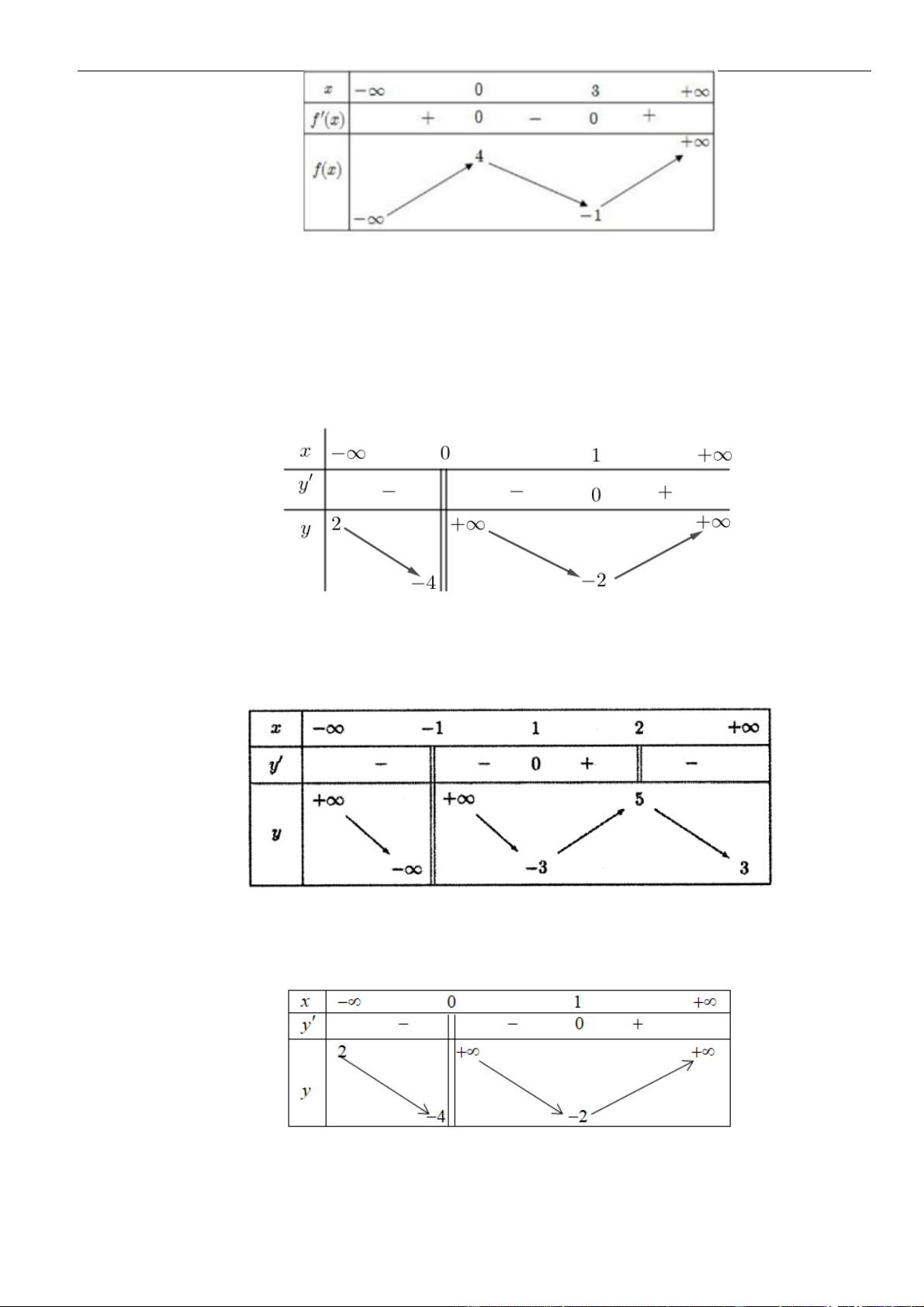
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số có
2
đường tiệm cận ngang.
B. Đồ thị hàm số có đường tiệm cận ngang
4y =
.
C. Đồ thị hàm số không có tiệm cận.
D. Đồ thị hàm số có đường tiệm cận đứng
0x =
.
Câu 28: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 29: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A.
2.
B.
3.
C.
4.
D.
1.
Câu 30: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số đường tiệm cận đứng và tiệm cận ngang của đô thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 31: Cho hàm số
()y f x=
có bảng biến thiên như hình dưới đây:
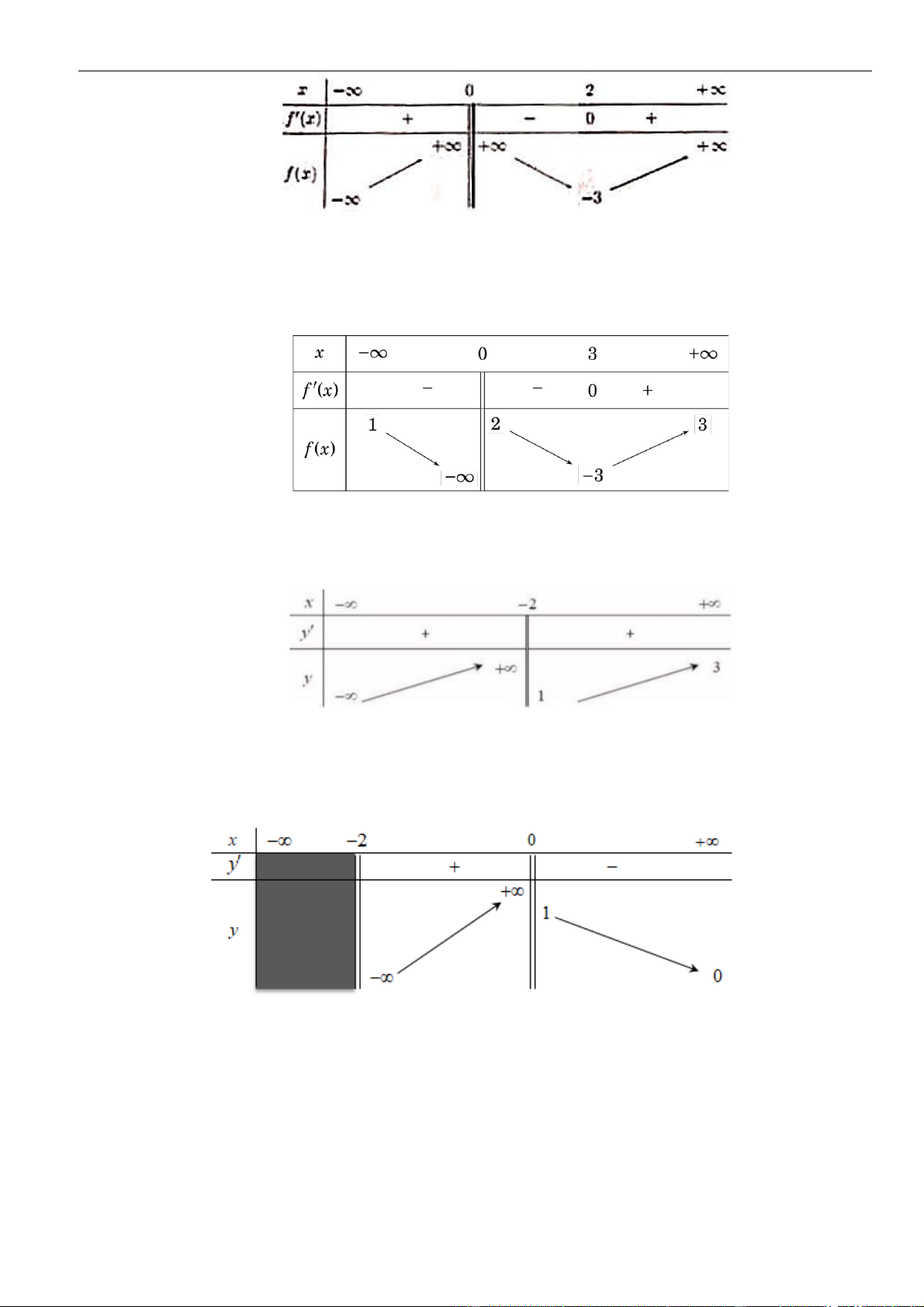
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Gọi
a
và
b
lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị
()y f x=
. Tính
ab+
.
A.
3ab+=
. B.
1ab+=
. C.
2ab+=
. D.
0ab+=
Câu 32: Cho hàm số
()fx
có bảng biến thiên như sau
Số tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 33: Cho hàm số
( )
y f x=
có bảng biến thiên như hình bên dưới
Hàm số
( )
y f x=
có đường tiệm cận đứng là
A.
3.y =
B.
1.x =
C.
2.x =−
D.
3.x =
Câu 34: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Đồ thị của hàm số đã cho có tổng số bao nhiêu tiệm cận đứng và tiệm cận ngang?
A. 1. B. 3. C. 4. D. 2.
Câu 35: Cho hàm số
()y f x=
có bảng biến thiên như sau:
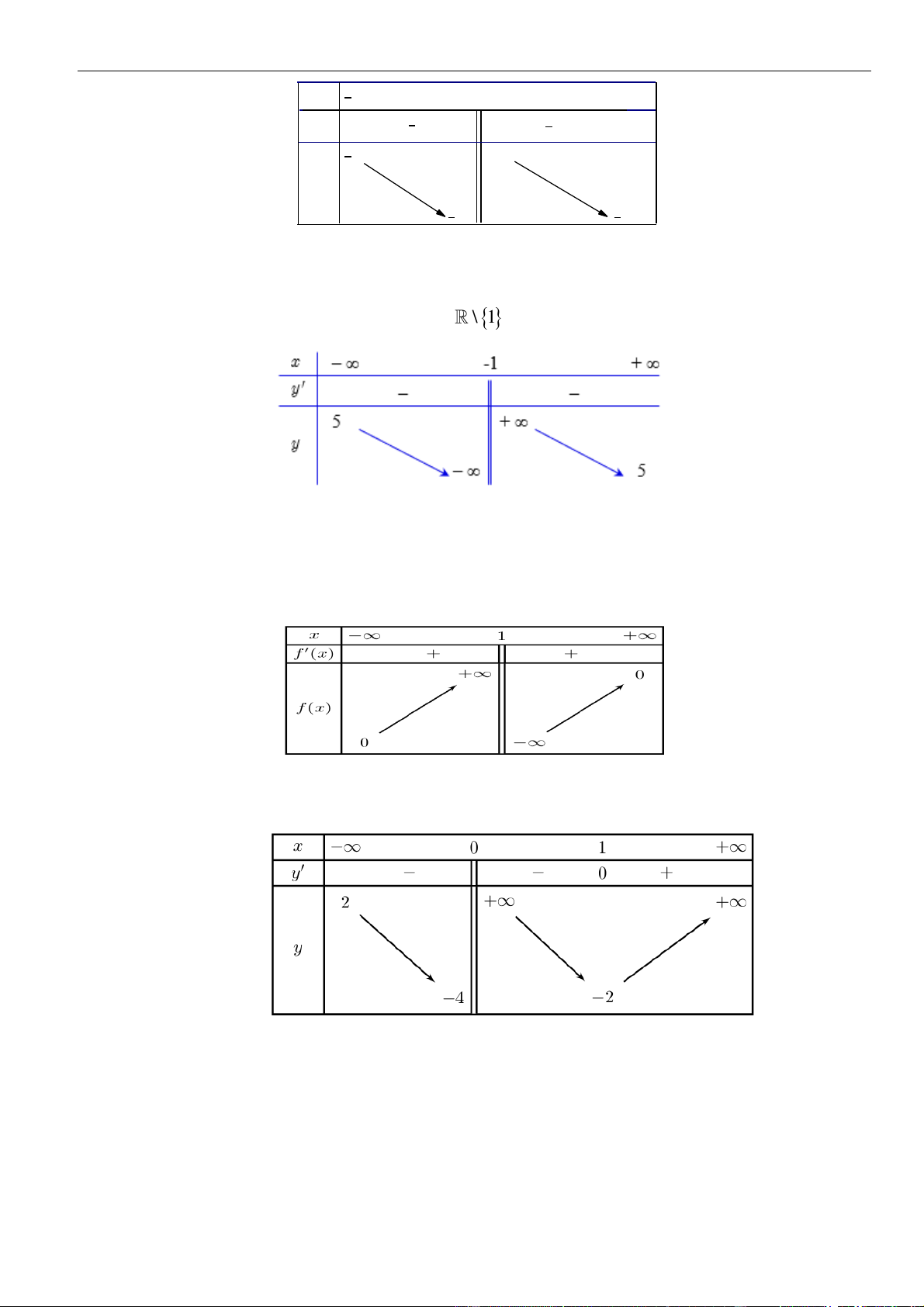
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Số tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 36: Cho hàm số
( )
y f x=
có đạo hàm trên
\1
và có bảng biến thiên
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
B.
1
C.
4
D.
2
Câu 37: Cho hàm số
( )
y f x=
có bảng biến thiên như sau. Tổng số tiệm cận ngang và tiệm cận đứng
của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 38: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 39: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
5
f(x)
f'(x)
∞
x
2
+
∞
∞
1
5
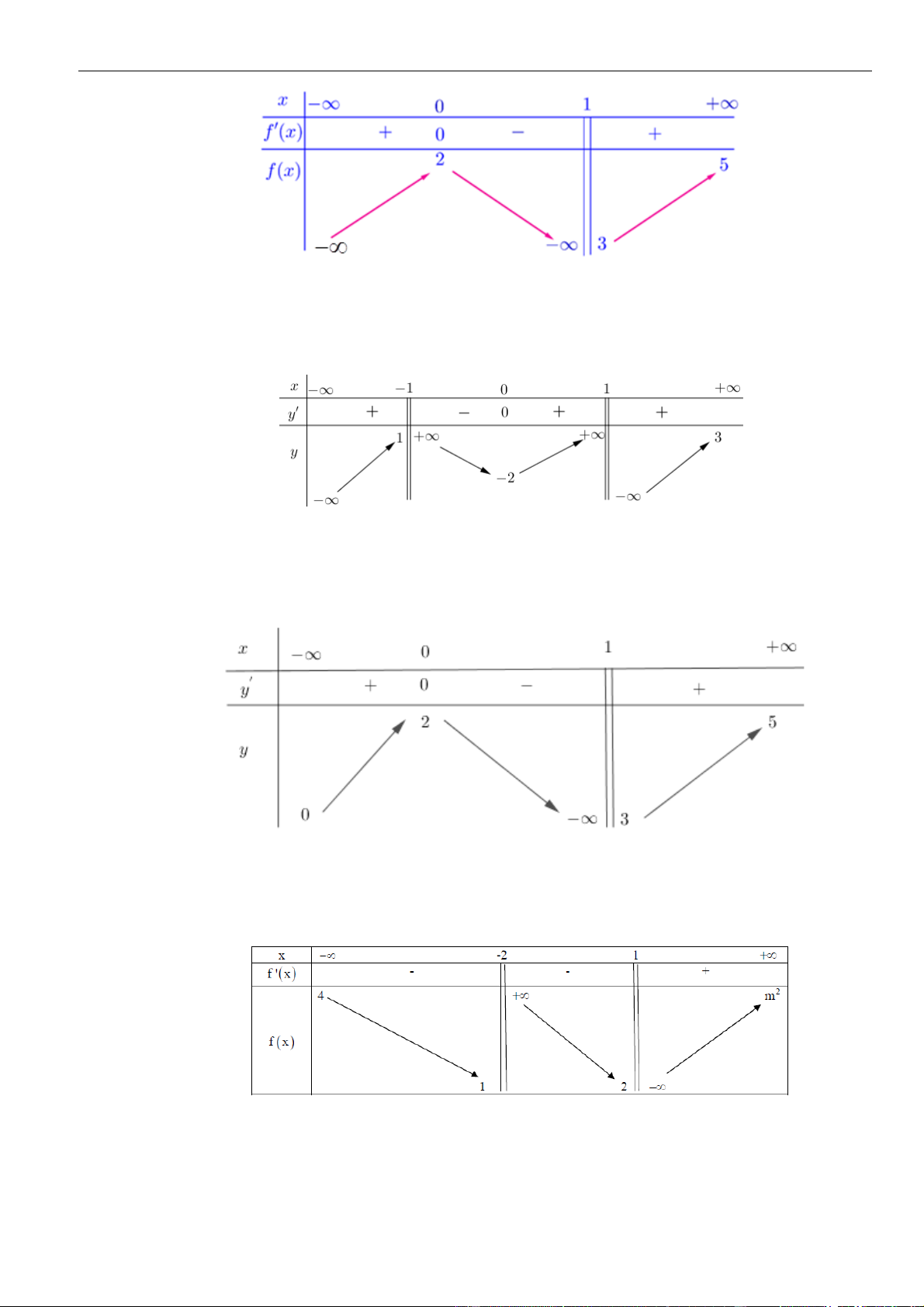
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 40: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 41: Cho hàm số
( )
fx
có bảng biến thiên như sau.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
3
B.
1
.
C.
2
. D.
4
.
Câu 42: Cho hàm số
( )
y f x=
có bảng biến thiên:
Số giá trị nguyên của
[ 4;4]m−
để đồ thị hàm số có 4 tiệm cận là
A.
7
. B.
6
. C.
5
. D.
8
.
Câu 43: Cho hàm số
( )
=y f x
có bảng biến thiên như sau
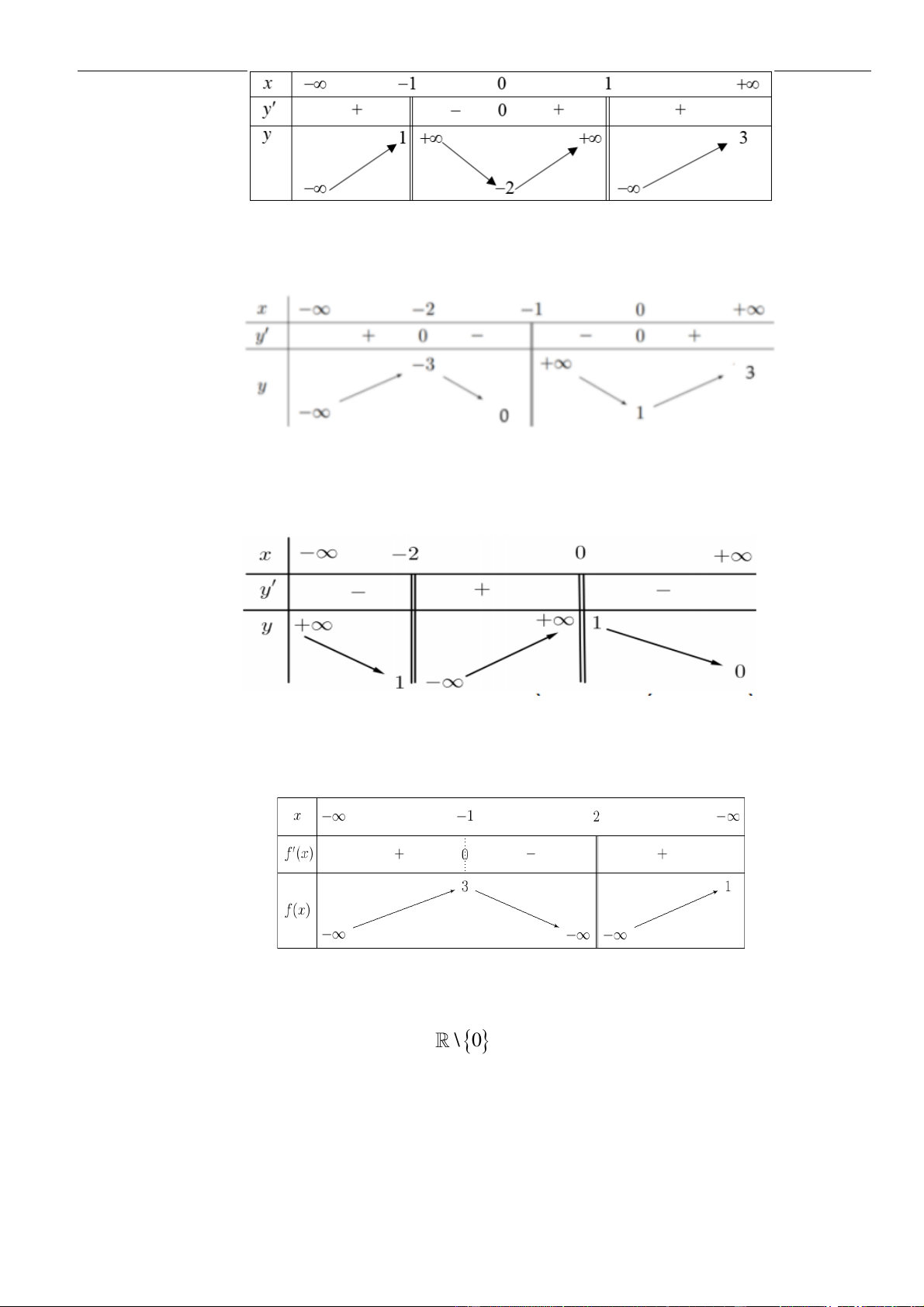
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số trên là
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 44: Cho hàm số có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 45: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 46: Cho hàm số
( )
y f x=
có bảng biến thiên
Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
y f x=
là
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 47: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau
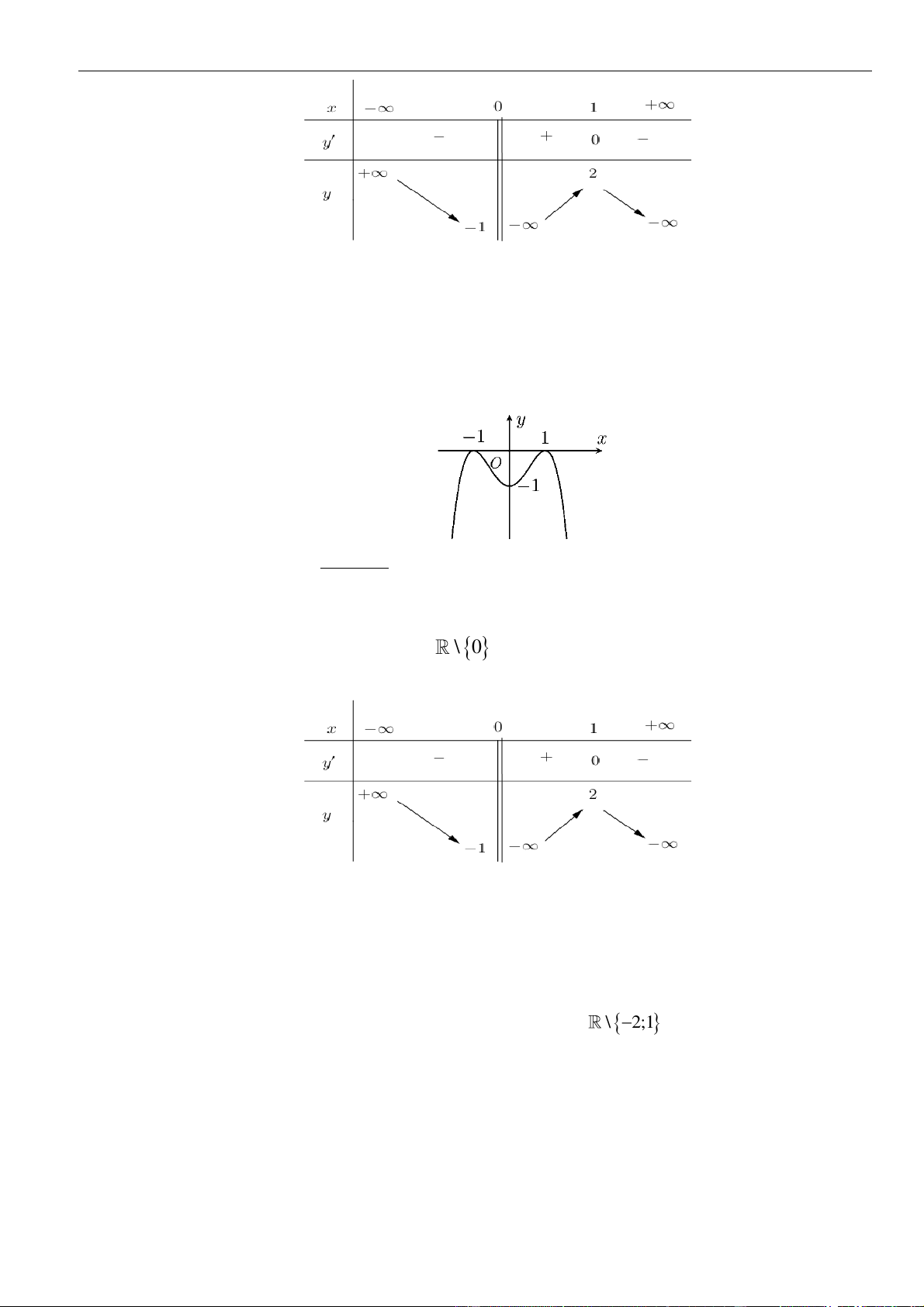
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Chọn khẳng định đúng trong các khẳng định sau
A. Đồ thị hàm số có hai đường tiệm cận ngang.
B. Đồ thị hàm số có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số có đúng một đường tiệm cận đứng.
D. Đồ thị hàm số không có đường tiệm cận đứng và tiệm cận ngang.
Câu 48: Cho hàm số
()=y f x
có đồ thị như hình sau:
Đồ thị hàm số
2020
()
2 ( ) 1
=
+
gx
fx
có số đường tiệm cận đứng là
A. 2. B. 3. C. 4. D. 5.
Câu 49: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau
Chọn khẳng định đúng trong các khẳng định sau
A. Đồ thị hàm số có hai đường tiệm cận ngang.
B. Đồ thị hàm số có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số có đúng một đường tiệm cận đứng.
D. Đồ thị hàm số không có đường tiệm cận đứng và tiệm cận ngang.
Câu 50: Cho hàm số
( )
y f x=
xác định và có đạo hàm trên trên
\ 2;1−
và có bảng biến thiên như
sau
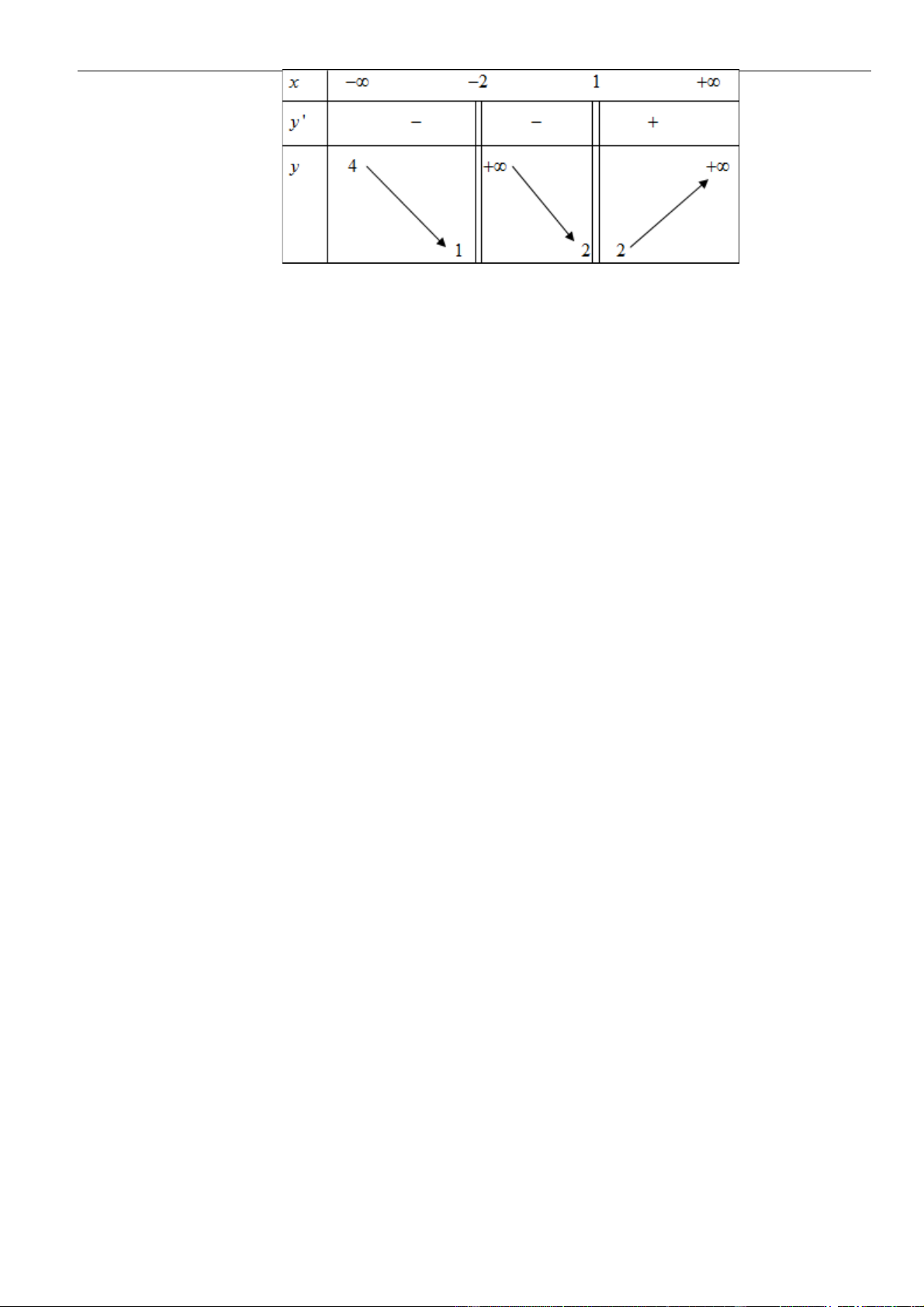
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Số đường tiệm cận của đồ thị hàm số là
A.
1
. B.
3
. C.
2
. D.
4
.
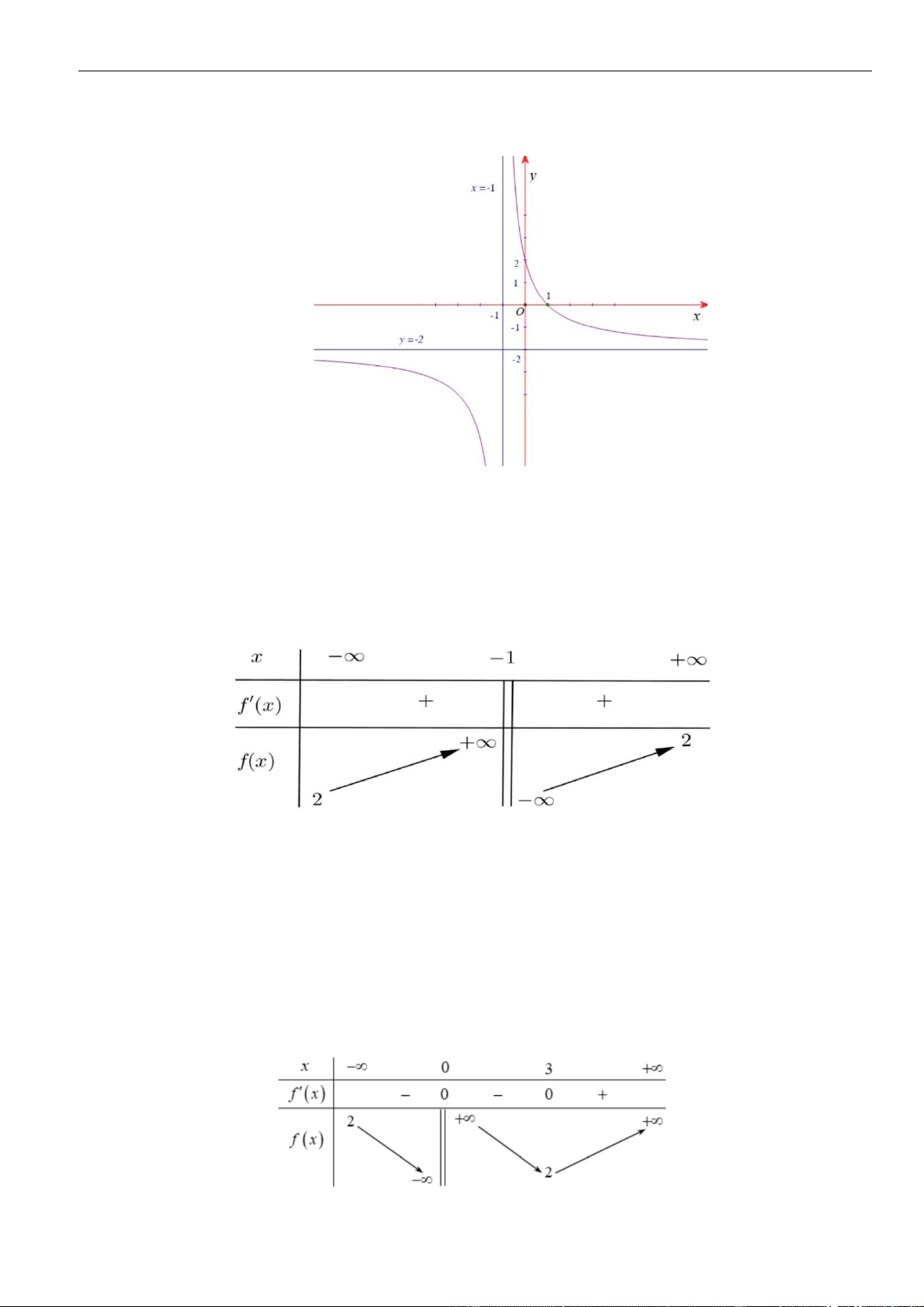
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
y f x=
có đồ thị như hình sau
Đồ thị hàm số trên có đường tiệm cận đứng là
A.
1x =−
. B.
2x =−
. C.
1y =−
. D.
2y =−
.
Lời giải
Chọn A
Dựa vào đồ thị của hàm số, đường tiệm cận đứng của đồ thị hàm số đã cho là
1x =−
.
Câu 2: Cho hàm số
()fx
có bảng biến thiên như sau
Đồ thị hàm số có đường tiệm cận ngang là
A.
2y =
. B.
2x =
. C.
1y =−
. D.
1x =−
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta có
lim ( ) 2
x
fx
→
=
nên đồ thị hàm số có đường tiệm cận ngang là
2y =
.
Câu 3: Cho hàm số
( )
y f x=
xác định và liên tục trên
( )
;0−
và
( )
0;+
có bảng biến thiên như hình
vẽ. Mệnh đề nào sau đây đúng?
A. Đường thẳng
2x =
là tiệm cận đứng của đồ thị hàm số.
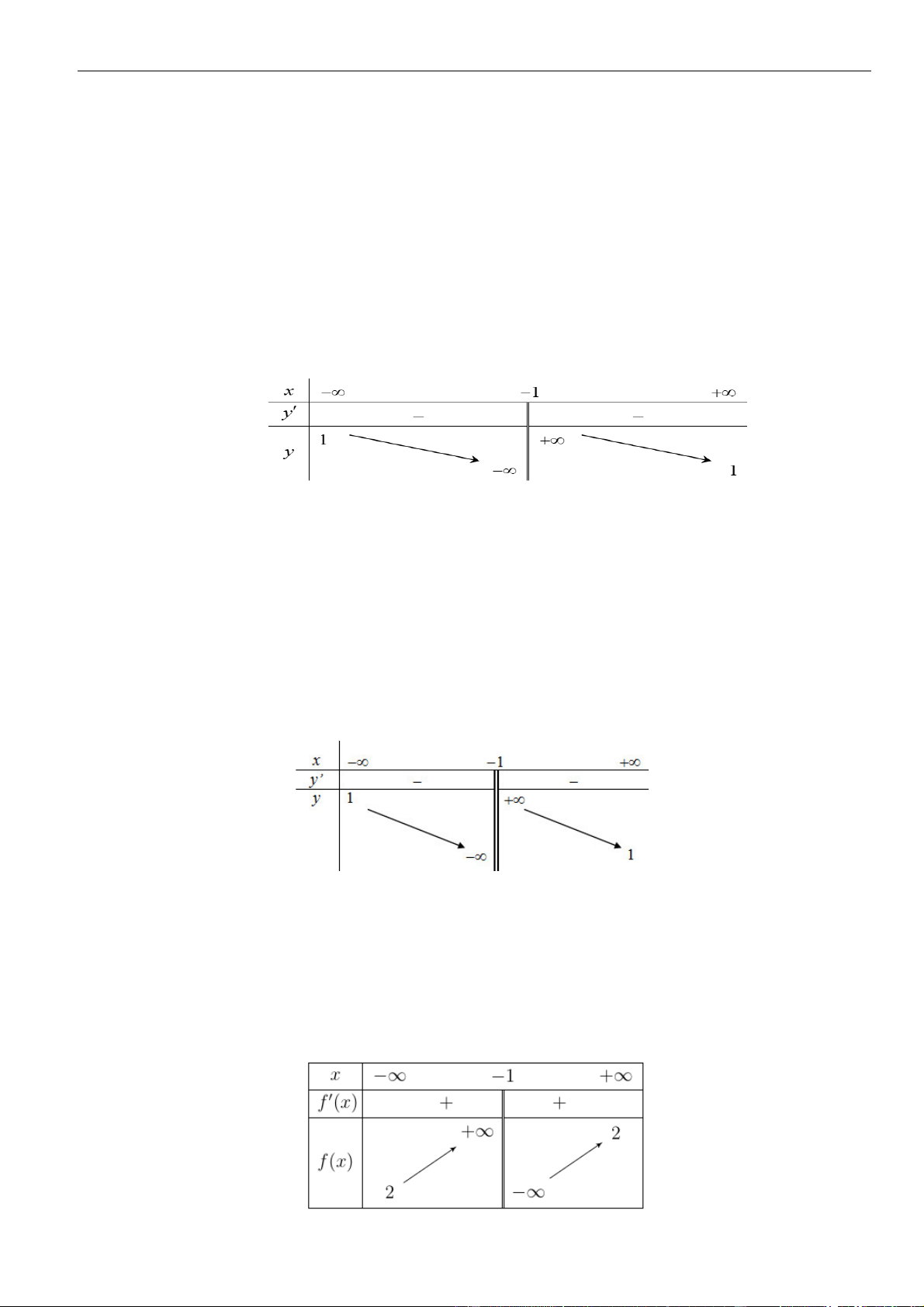
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
B. Đồ thị hàm số có hai đường tiệm cận ngang.
C. Đồ thị hàm số có hai đường tiệm cận.
D. Đồ thị hàm số chỉ có một đường tiệm cận.
Lời giải
Chọn C
Vì
lim 2
x
y
→−
=
nên
2y =
là tiệm cận ngang của đồ thị hàm số.
Vì
0
0
lim
lim
x
x
y
y
+
−
→
→
= +
= −
nên
0x =
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 4: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Đồ thị hàm số trên có tiệm cận ngang là
A.
1x =−
. B.
1y =−
. C.
1x =
. D.
1y =
.
Lời giải
GVSB: Vũ Viên; GVPB:Thuy Nguyen
Chọn D
Dựa vào bảng biến thiên ta có
lim 1
x
y
→+
=
;
lim 1
x
y
→−
=
.
Tiệm cận ngang của đồ thị hàm số là
1y =
.
Câu 5: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Đồ thị hàm số trên có tiệm cận đứng là:
A.
1y =−
. B.
1y =
. C.
1x =
. D.
1x =−
.
Lời giải
Chọn D
Từ bảng biến thiên ta có đồ thị hàm số có đường tiệm cận đứng là:
1x =−
Câu 6: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
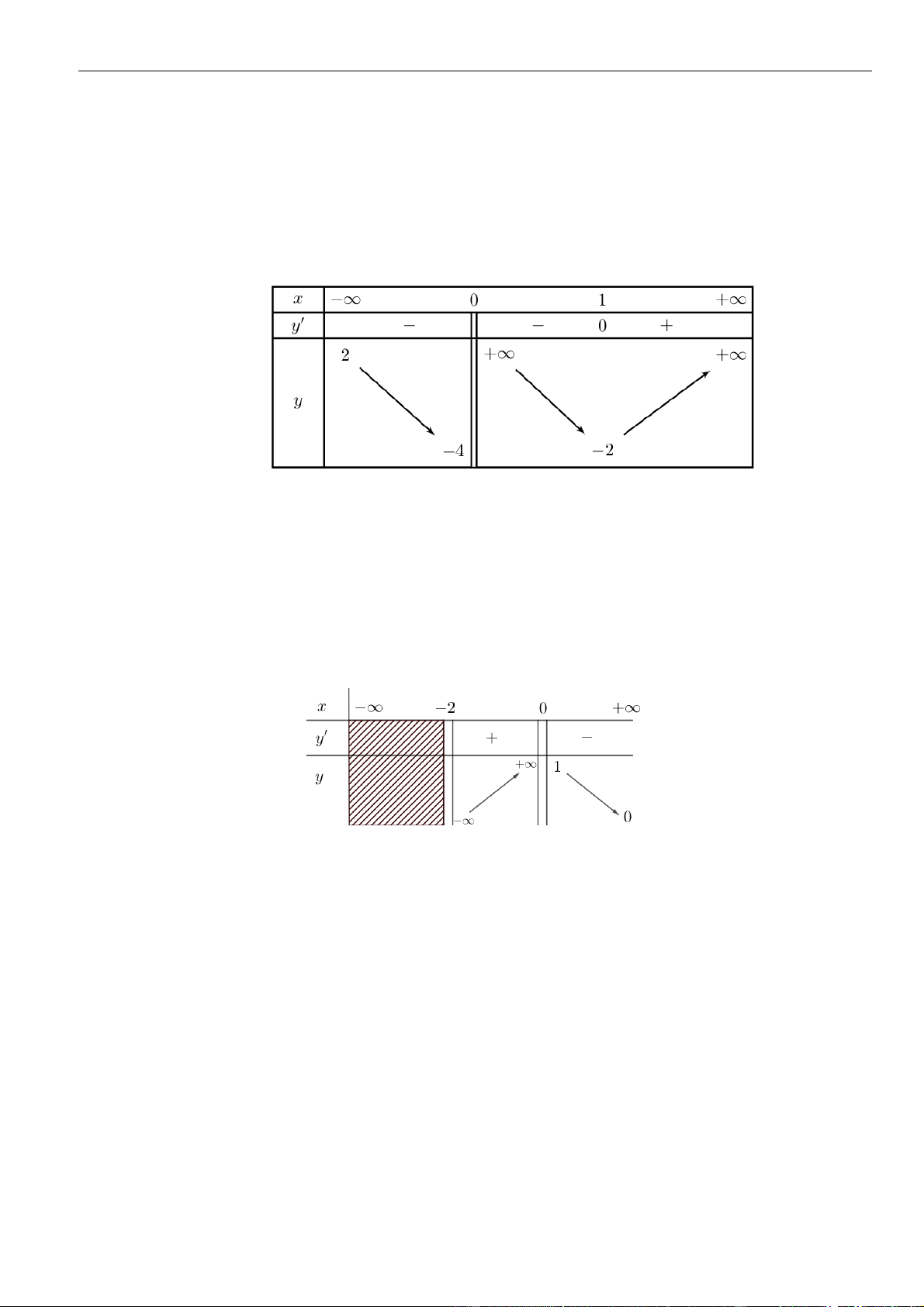
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Đồ thị hàm số có đường tiệm cận đứng là
A.
1y =−
. B.
2x =
. C.
2y =
. D.
1x =−
.
Lời giải
Chọn D
Từ bảng biến thiên ta có:
1
lim
x
−
→−
= +
và
1
lim
x
+
→−
= −
Suy ra đồ thị hàm số có tiệm cận đứng là đường thẳng
1x =−
.
Câu 7: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có
( )
0
lim 2, lim
x
x
yy
+
→−
→
= = +
nên hàm số có tiệm cận ngang là
2y =
và tiệm cận
đứng là
0x =
.
Câu 8: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta có:
1)
2
lim
x
y
+
→−
= −
và
0
lim
x
y
−
→
= +
nên đồ thị hàm số đã cho có hai tiệm cận đứng là
2x =−
và
0x =
.
2)
lim 0
x
y
→+
=
nên đồ thị hàm số đã cho có một tiệm cận ngang là
0y =
.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận
Câu 9: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
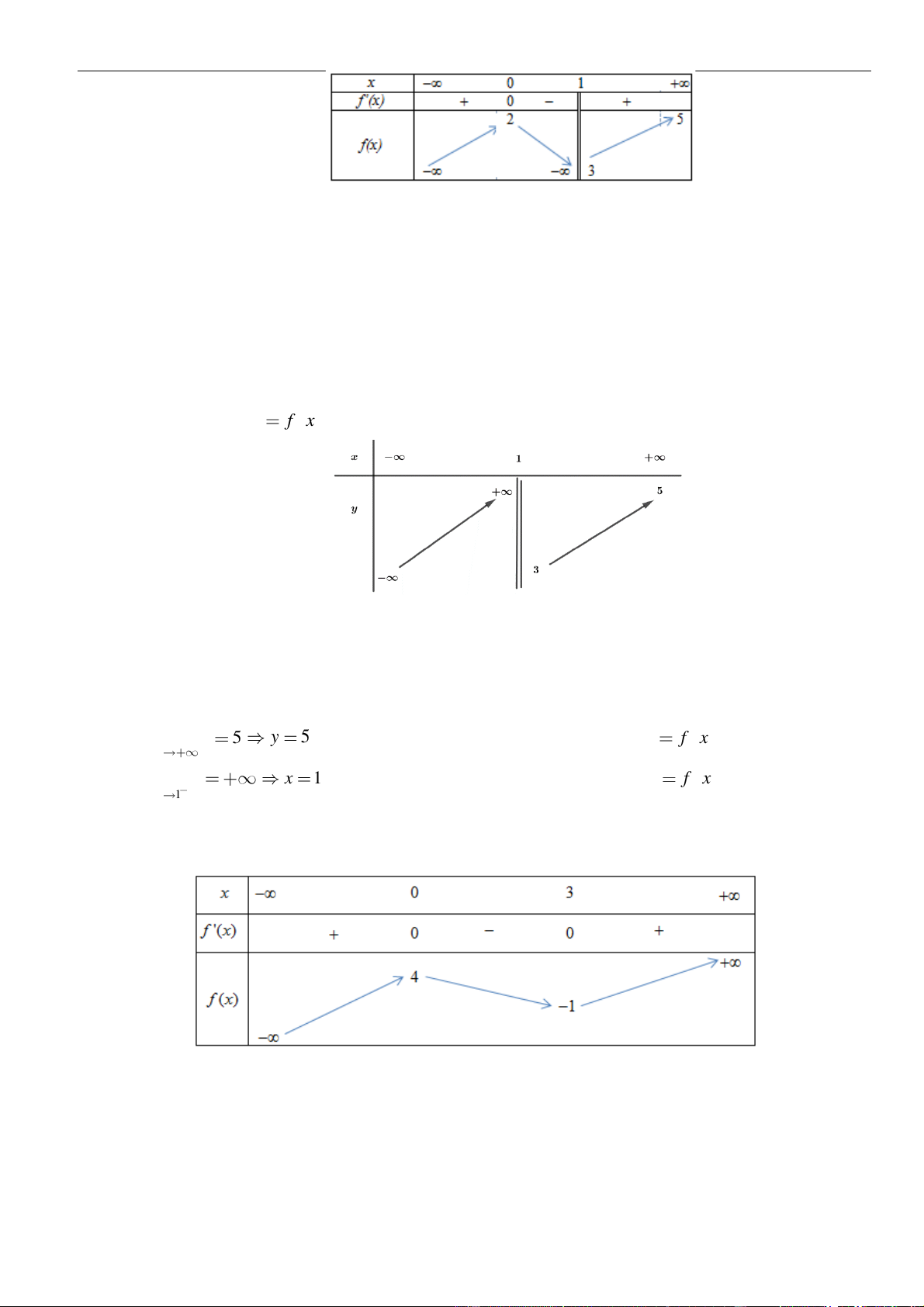
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn C
Ta có
( )
lim 5
x
fx
→+
=
nên đồ thị hàm số có tiệm cận ngang là
5y =
( )
1
lim
x
fx
−
→
= −
nên đồ thị hàm số có tiệm cận đứng là
1x =
Vậy đồ thị hàm số có tổng số đường tiệm cận ngang và đứng là 2.
Câu 10: Cho hàm số
y f x
có bảng biến thiên như hình bên dưới
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy:
lim 5
x
y
5y
là đường tiệm cận ngang của đồ thị hàm số
y f x
.
1
lim
x
y
1x
là đường tiệm cận đứng của đồ thị hàm số
y f x
.
Vậy đồ thị hàm số có
2
đường tiệm cận.
Câu 11: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số có
2
đường tiệm cận ngang.
B. Đồ thị hàm số có đường tiệm cận ngang
4y =
.
C. Đồ thị hàm số không có tiệm cận.
D. Đồ thị hàm số có đường tiệm cận đứng
0x =
.
Lời giải
Chọn C
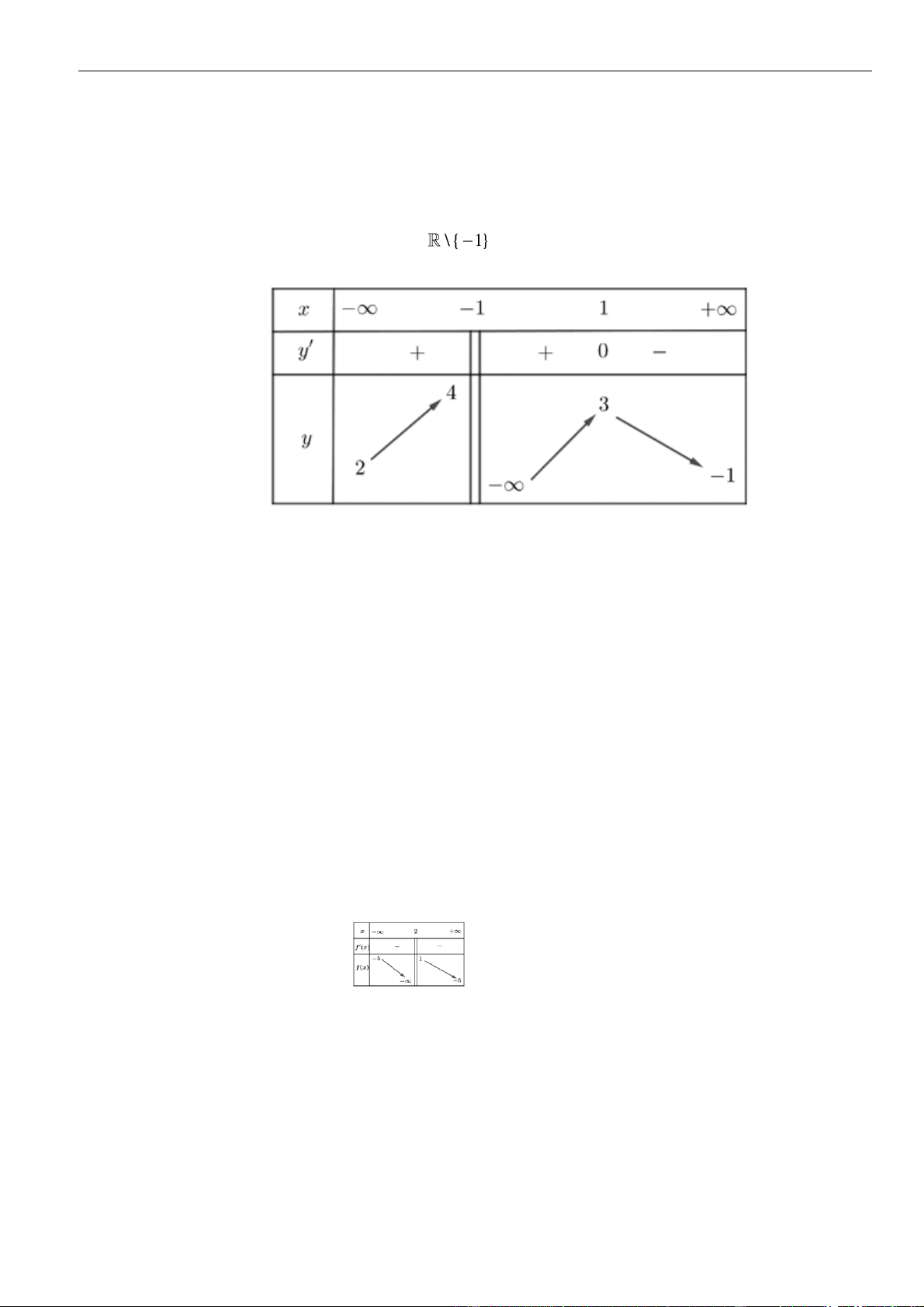
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Từ BBT của hàm số
()y f x=
ta có:
lim ( ) , lim ( )
xx
f x f x
→− →+
= − = +
nên đồ thị hàm số đã cho
không có tiệm cận ngang.
Và
0 0 3 3
lim ( ) 4, lim ( ) 4, lim ( ) 1, lim ( ) 1
x x x x
f x f x f x f x
+ − − +
→ → → →
= = = − = −
nên đồ thị hàm số đã cho không có
tiệm cận đứng.
Vậy đồ thị hàm số đã cho không có tiệm cận.
Câu 12: Cho hàm số
()y f x=
xác định trên
}\{1−
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình sau:
Hỏi đồ thị hàm số có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn C
Từ bảng biến thiên
1
lim 1
x
yx
+
→−
= − = −
là tiệm cận đứng.
lim 2 2
x
yy
→−
= =
là tiệm cận ngang.
lim 1 1
x
yy
→+
= − = −
là tiệm cận ngang.
Đồ thị hàm số có tất cả 3 đường tiệm cận.
Câu 13: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số tiệm cận ngang của đồ thị hàm số đã cho là
A. 4. B. 2. C. 1. D. 3.
Lờigiải
Người làm: Trịnh Thanh Hải
Chọn C
Dựa vào bảng biến thiên ta có:
( )
lim 5
x
fx
→+
=−
;
( )
lim 5
x
fx
→−
=−
, nên đồ thị hàm số đã cho có 1
tiệm cận ngang.
Câu 14: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ dưới đây:
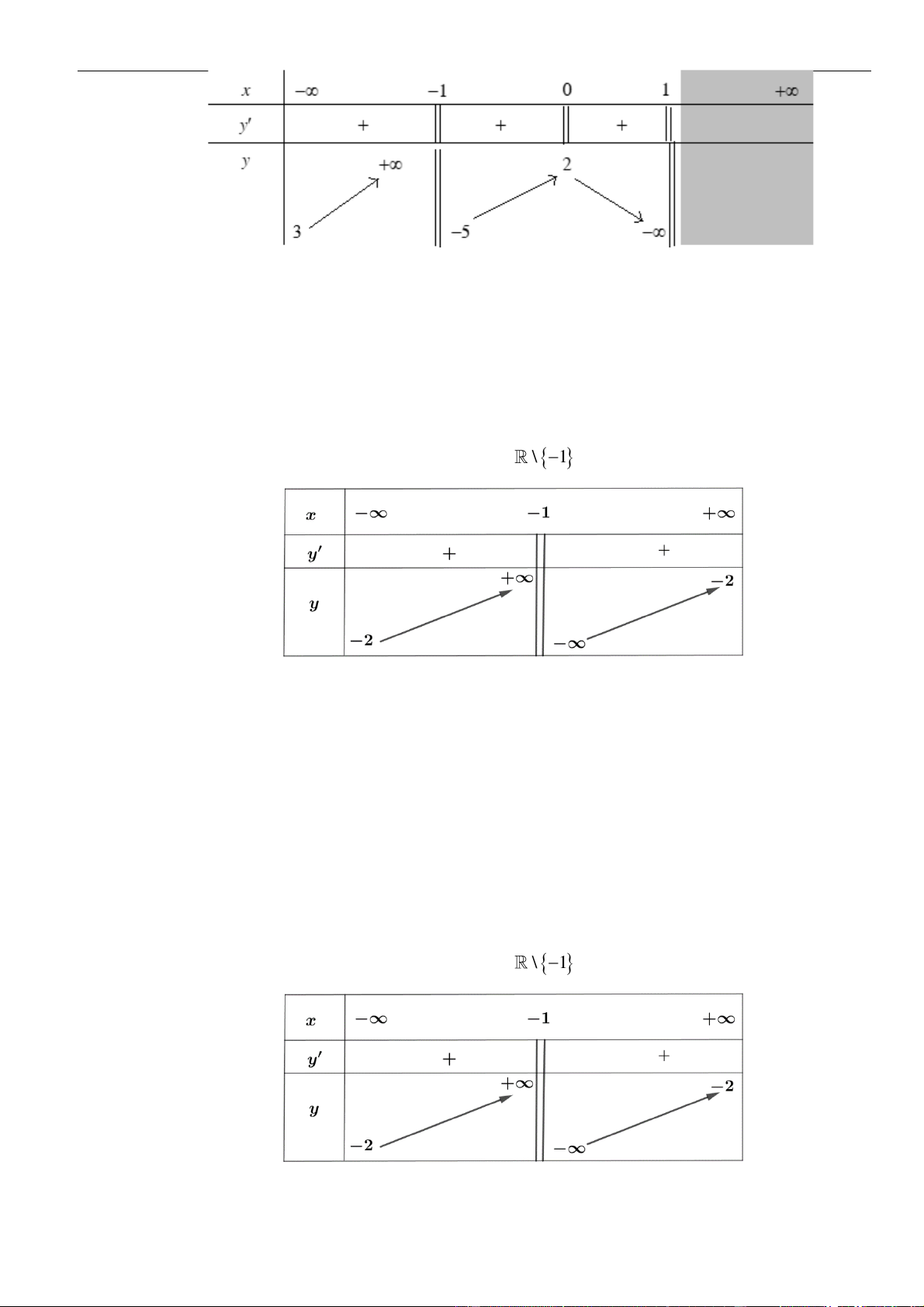
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
A.
1.
B.
4.
C.
0.
D.
3.
Lời giải
Chọn D
Tiệm cận ngang:
3.y =
Tiệm cận đứng:
1; 1.xx= − =
Vậy tổng số tiệm cận là 3.
Câu 15: Cho hàm số
( )
y f x=
xác định và liên tục trên
\1−
, có bảng biến thiên như sau.
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng
1y =−
và tiệm cận ngang
2x =−
.
B. Đồ thị hàm số có duy nhất một tiệm cận.
C. Đồ thị hàm số có ba tiệm cận.
D. Đồ thị hàm số có tiệm cận đứng
1x =−
và tiệm cận ngang
2y =−
.
Lời giải
Chọn D
Từ bảng biến thiên suy ra
lim 2
x
y
→+
= −
đồ thị hàm số có tiệm cận ngang
2y =−
.
( )
1
lim
x
y
−
→−
= +
đồ thị hàm số có tiệm cận đứng
1x =−
.
Câu 16: Cho hàm số
( )
y f x=
xác định và liên tục trên
\1−
, có bảng biến thiên như sau.
Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số có tiệm cận đứng
1y =−
và tiệm cận ngang
2x =−
.
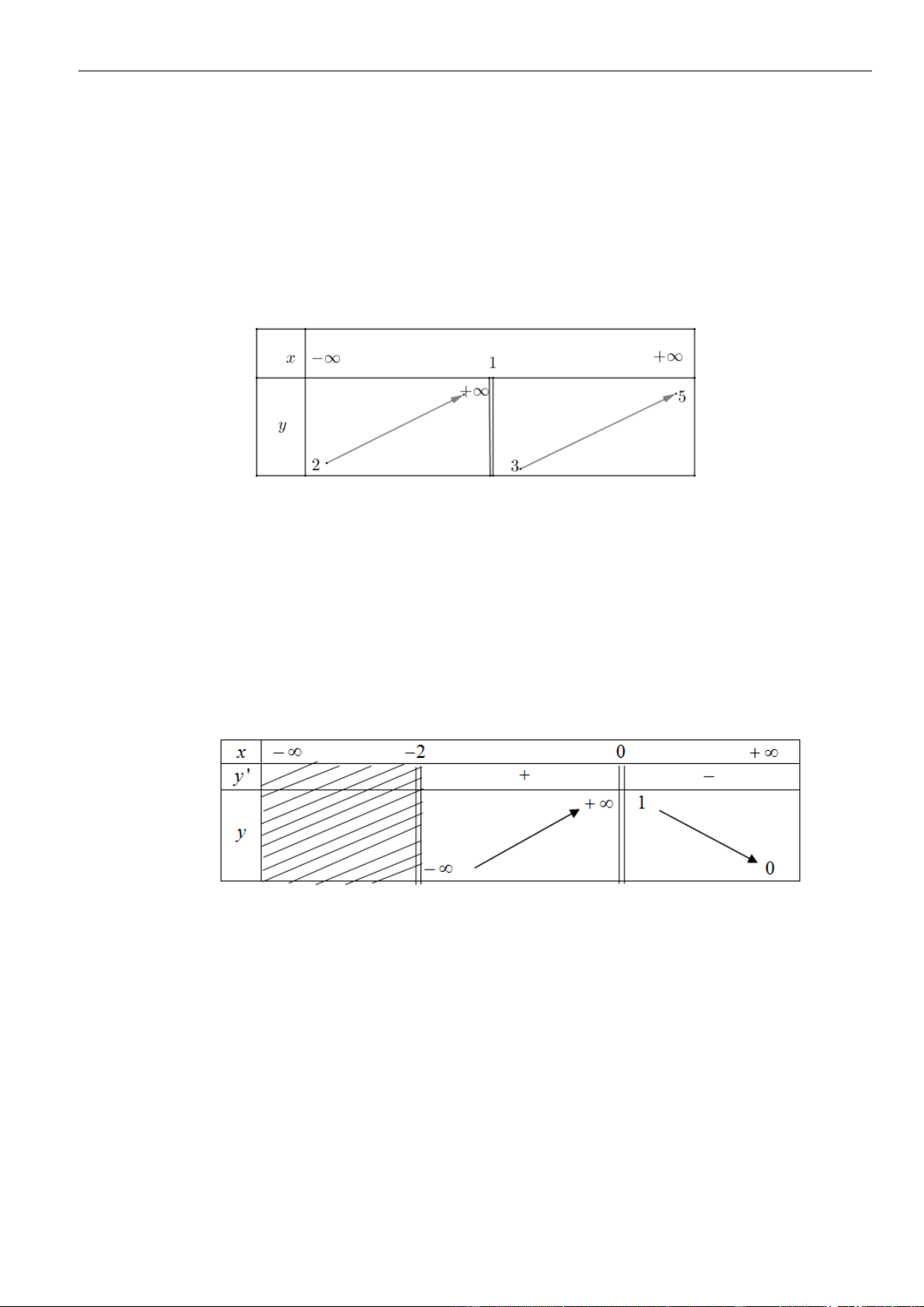
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
B. Đồ thị hàm số có duy nhất một tiệm cận.
C. Đồ thị hàm số có ba tiệm cận.
D. Đồ thị hàm số có tiệm cận đứng
1x =−
và tiệm cận ngang
2y =−
.
Lời giải
Chọn D
Từ bảng biến thiên suy ra
lim 2
x
y
→+
= −
đồ thị hàm số có tiệm cận ngang
2y =−
.
( )
1
lim
x
y
−
→−
= +
đồ thị hàm số có tiệm cận đứng
1x =−
.
Câu 17: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy đồ thị hàm số có một đường tiệm cận đứng
1x =
và hai đường
tiệm cận ngang
2; 5yy==
. Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị
hàm số là
3
đường.
Câu 18: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho
có bao nhiêu đường tiệm cận?
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
Ta có
( )
2
lim
x
y
+
→−
= −
suy ra đồ thị hàm số có tiệm cận đứng
2x =−
.
Ta có
0
lim
x
y
−
→
= +
suy ra đồ thị hàm số có tiệm cận đứng
0x =
.
Ta có
lim 0
x
y
→+
=
suy ra đồ thị hàm số có tiệm cận ngang
0y =
.
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 19: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
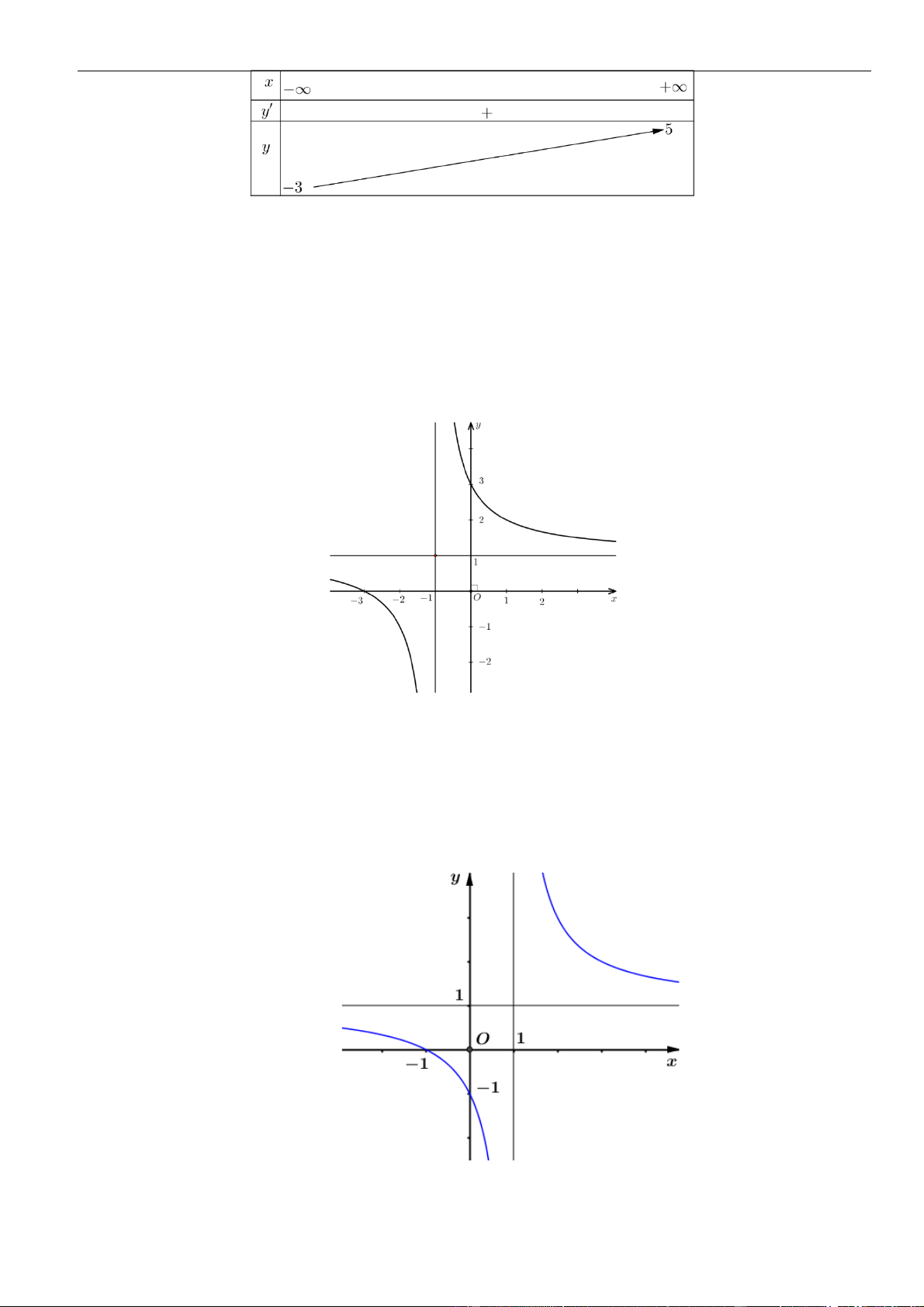
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Số đường tiệm cận ngang của đồ thị hàm số
( )
y f x=
là
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chon D
Do
lim 5
lim 3
x
x
y
y
→+
→−
=
=−
nên đồ thị hàm số
( )
y f x=
có 2 đường tiệm cận ngang là
3, 5yy= − =
.
Câu 20: Đồ thị hàm số như hình vẽ dưới đây có tiệm cận đứng và tiệm cận ngang theo thứ tự là
A.
1x =
,
1y =
. B.
3x =−
,
3y =
. C.
1x =−
,
1y =
. D.
1x =
,
1y =−
.
Lời giải
Chọn C
Dựa vào đồ thị hàm số ta thấy tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là
1x =−
,
1y =
.
Câu 21: Cho hàm số
( )
fx
có đồ thị như hình vẽ bên dưới.
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là
A.
1; 1xy= − = −
. B.
1; 1xy==
. C.
1; 1xy= = −
. D.
1; 1xy= − =
.
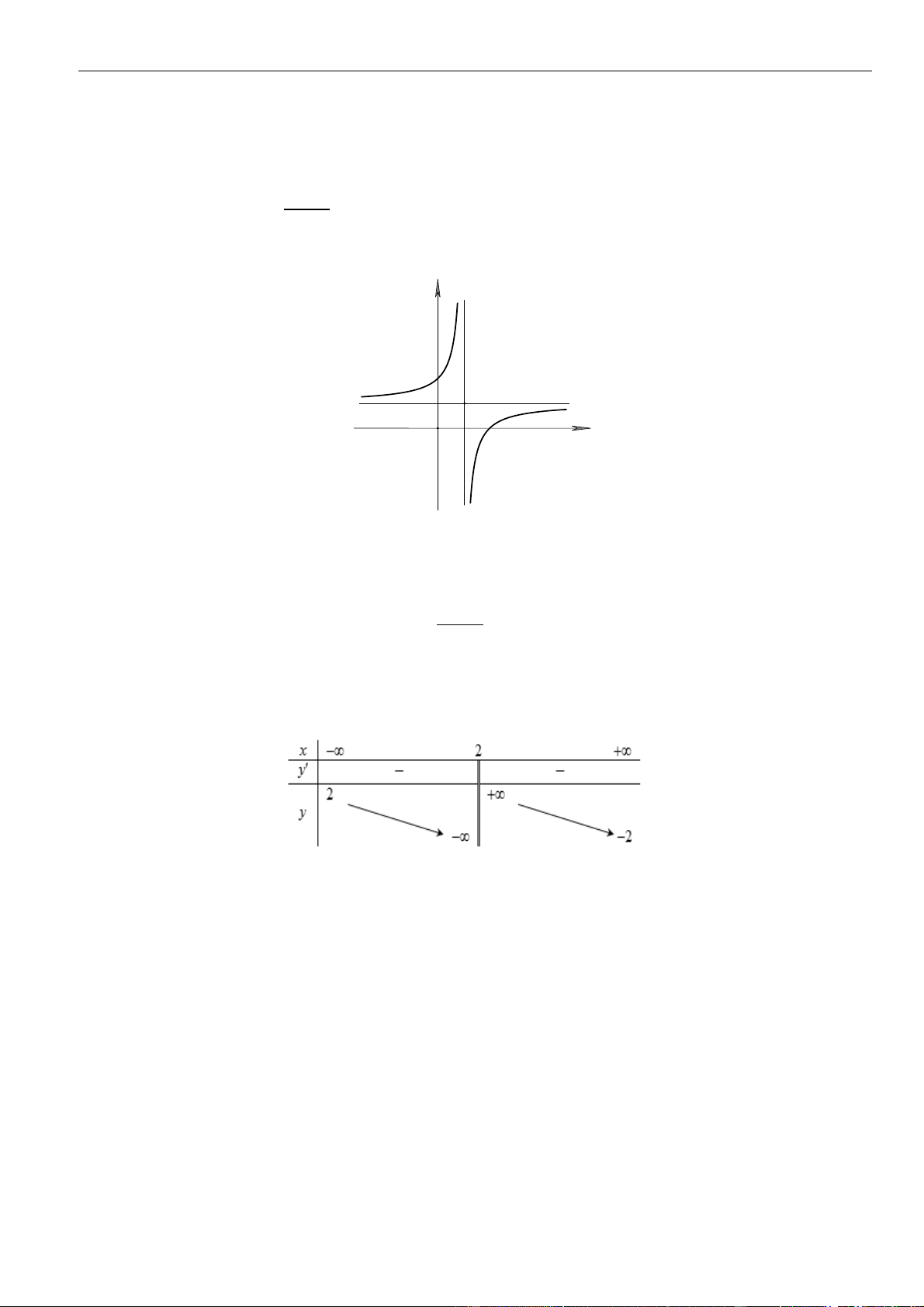
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn B
Dựa vào đồ thị hàm số ta thấy đồ thị có đường tiệm cận đứng
1x =
là và đường tiệm cận ngang
là
1y =
.
Câu 22: Cho hàm số
( )
0 ; 0
ax b
y ad bc ac
cx d
+
= −
+
có đồ thị như hình vẽ bên dưới. Tìm đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số?
A.
1,x =−
1y =
. B.
1,x =
2y =
. C.
1,x =
1y =
. D.
2,x =
1y =
.
Lời giải
Chọn C
Dựa vào hình vẽ đồ thị hàm số
ax b
y
cx d
+
=
+
ta có
1x =
là tiệm cân đứng và
1y =
là tiệm cận
ngang của đồ thị.
Câu 23: Cho hàm số
( )
y f x=
có bảng biến thiên sau. Hỏi đồ thị hàm số đó có mấy tiệm cận.
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
Từ bảng biến thiên trên
Ta có
( )
lim 2
x
fx
→−
=
2y=
là tiệm cận ngang
Ta có
( )
lim 2
x
fx
→+
=−
2y = −
là tiệm cận ngang
Ta có
( )
2
lim 2
x
f x x
+
→
= + =
là tiệm cận đứng
Vậy hàm số có 3 tiệm cận.
Câu 24: Cho hàm số
( )
fx
có bảng biến thiên như hình vẽ sau:
2
2
1
1
O
x
y
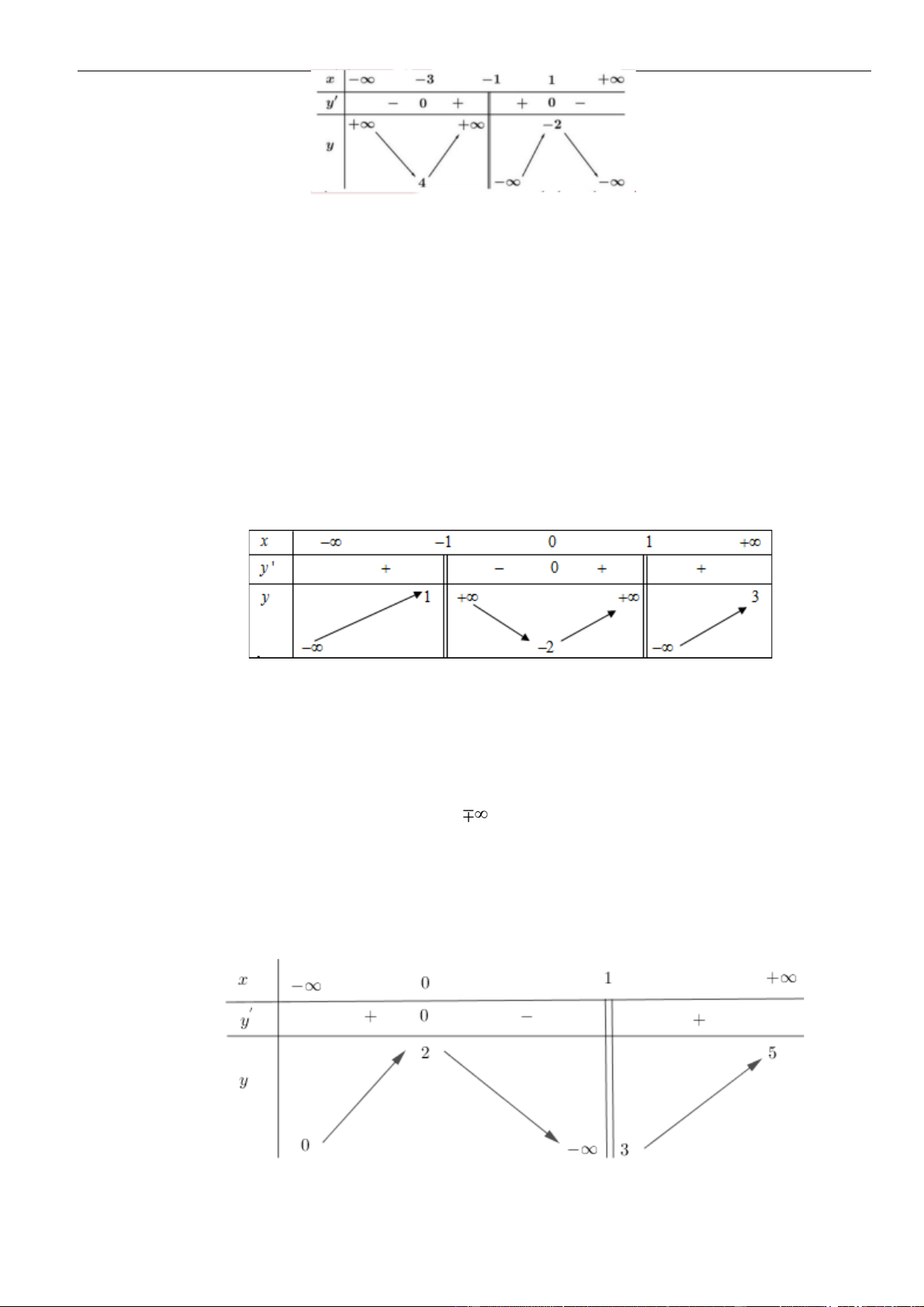
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 0. B.
2
. C. 3. D.
1
.
Lời giải
Chọn D
Ta có
( )
( )
1
lim
x
fx
+
→−
= −
và
( )
( )
1
lim
x
fx
−
→−
= +
nên đồ thị hàm số có tiệm cận đứng
1x =−
( )
lim
x
fx
→−
= +
và
( )
lim
x
fx
→+
= −
nên đồ thị hàm số không có tiệm cận ngang.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 1.
Câu 25: Cho hàm
( )
y f x=
có bảng biến thiên như hình vẽ. Đồ thị hàm số
( )
y f x=
có bao nhiêu đường
tiệm cận?
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn B
Ta có
( ) ( )
lim ; lim 3
xx
f x f x
→− →+
= − =
nên đường thẳng
3y =
là tiệm cận ngang của đồ thị hàm
số
Mặt khác,
( )
( )
( )
( )
11
lim ; lim
xx
f x f x
+
→ − →
= + =
nên đường thẳng
1x =
là tiệm cận đứng của đồ
thị hàm số.
Vậy đồ thị hàm số có tất cả 3 đường tiệm cận.
Câu 26: Cho hàm số
( )
fx
có bảng biến thiên như sau.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
3
B.
1
.
C.
2
. D.
4
.
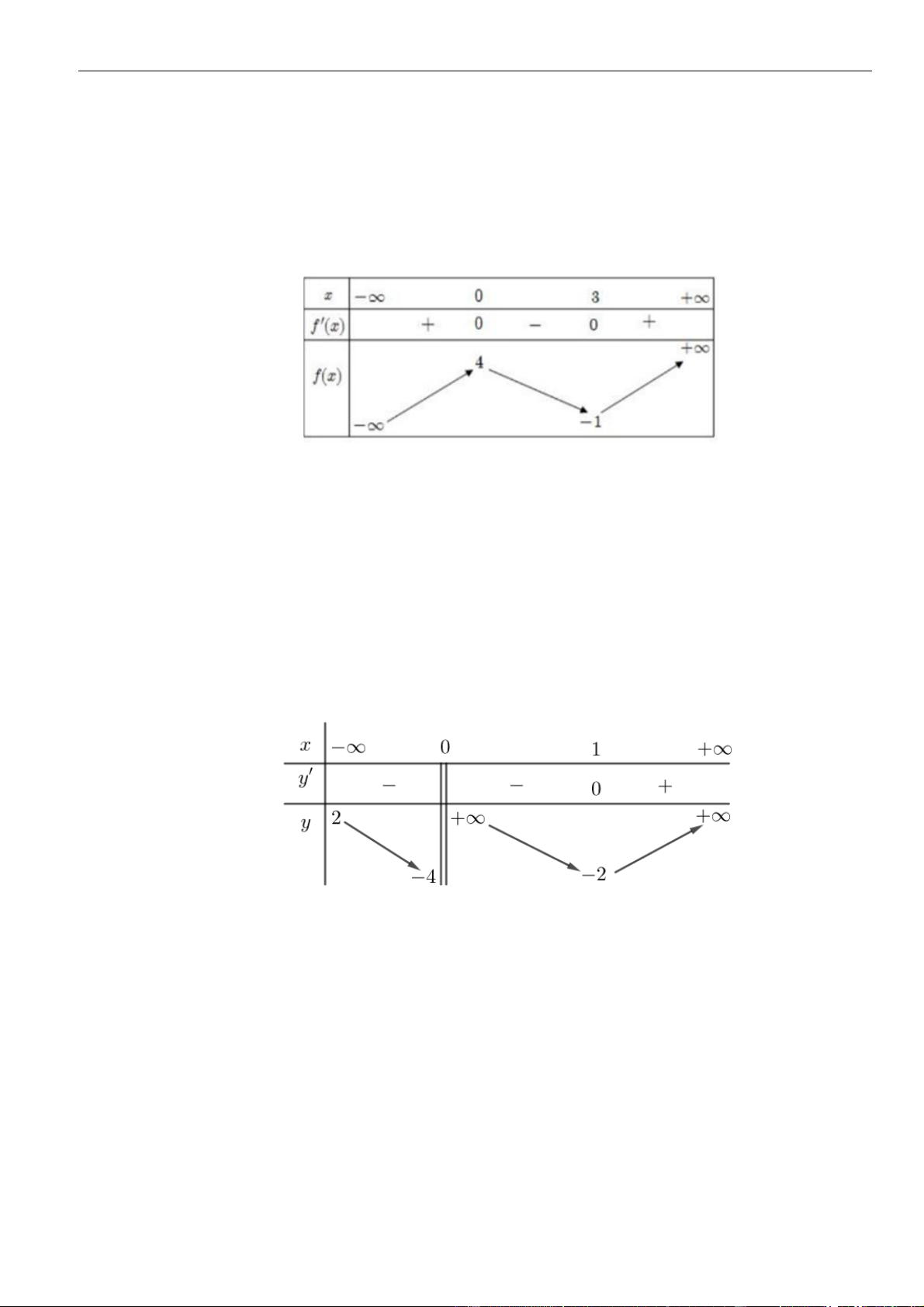
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn A
+
( )
lim 5
x
fx
→+
=
và
( )
lim 0
x
fx
→−
=
nên hàm số có 2 tiệm cận ngang.
+
( )
1
lim
x
fx
−
→
= −
nên hàm số có 1 tiệm cận đứng.
Nên hàm số đã cho có 3 tiệm cận.
Câu 27: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số có
2
đường tiệm cận ngang.
B. Đồ thị hàm số có đường tiệm cận ngang
4y =
.
C. Đồ thị hàm số không có tiệm cận.
D. Đồ thị hàm số có đường tiệm cận đứng
0x =
.
Lời giải
Chọn C
Từ bảng biến thiên suy ra đồ thị hàm số không có tiệm cận.
Câu 28: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có:
( )
0
lim 0
x
f x x
+
→
= + =
là tiệm cận đứng của đồ thị hàm số đã cho.
( )
lim 2 2
x
f x y
→−
= =
là tiệm cận ngang của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Câu 29: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
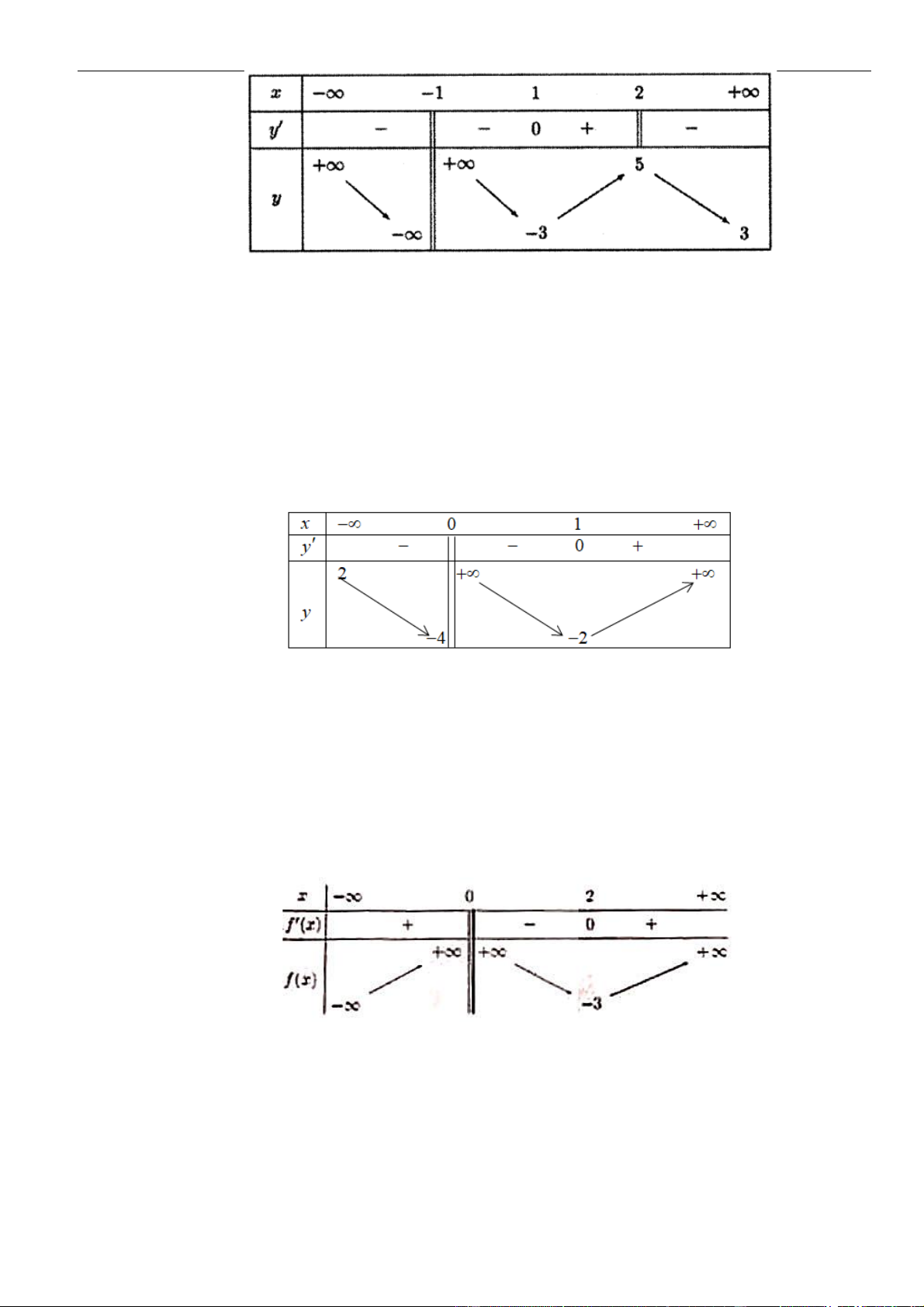
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A.
2.
B.
3.
C.
4.
D.
1.
Lời giải
Chọn A
Ta có:
( ) ( )
11
lim , lim 1
xx
f x f x x
+−
→− →−
= + = − = −
là tiệm cận đứng.
( )
lim 3 3
x
f x y
→+
= =
là tiệm cận ngang.
Vậy tổng số tiệm cận là
2.
Câu 30: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số đường tiệm cận đứng và tiệm cận ngang của đô thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Từ bảng biến thiên ta có:
0
lim
x
y
+
→
= +
,
lim 2
x
y
→−
=
Vậy đồ thị có
2
tiệm cận gồm một tiêm cận đứng
0x =
và một tiệm cận ngang
2y =
.
Câu 31: Cho hàm số
()y f x=
có bảng biến thiên như hình dưới đây:
Gọi
a
và
b
lần lượt là số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị
()y f x=
. Tính
ab+
.
A.
3ab+=
. B.
1ab+=
. C.
2ab+=
. D.
0ab+=
Lời giải
Chọn B
Dựa vào bảng biến thiên ta thấy:
lim ( ) , lim ( )
xx
f x f x
→+ →−
= + = −
, suy ra hàm số không có tiệm cận ngang.
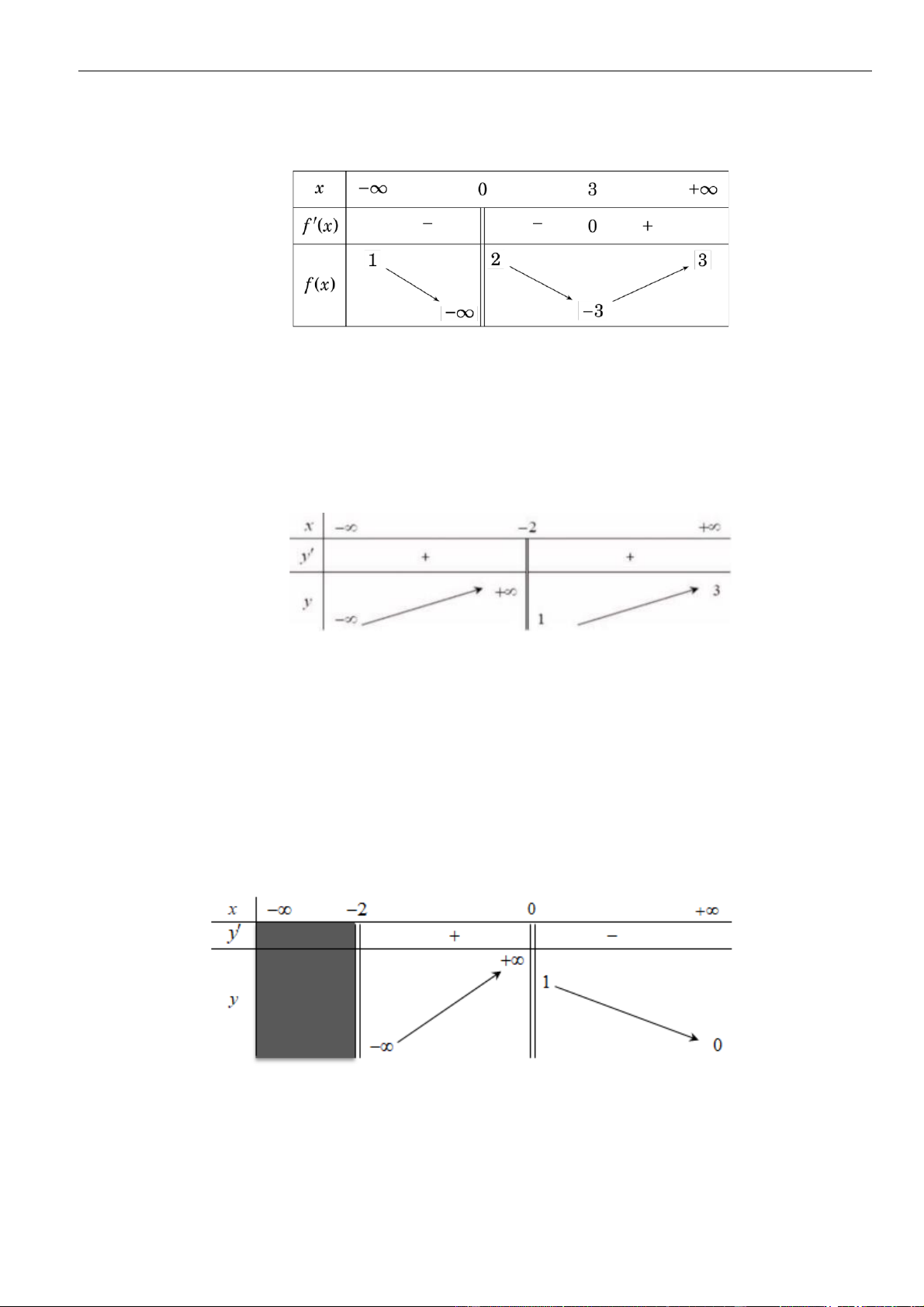
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
27 | Facebook tác giả: Phan Nhật Linh
00
lim ( ) , lim ( )
xx
f x f x
+−
→→
= + = +
, suy ra hàm số có tiệm cận đứng
0x =
.
Vậy
1ab+=
.
Câu 32: Cho hàm số
()fx
có bảng biến thiên như sau
Số tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn B
Quan sát bảng biến thiên ta có
0
lim
x
y
−
→
= −
nên đồ thị hàm số có tiệm cận đứng
0x =
.
Câu 33: Cho hàm số
( )
y f x=
có bảng biến thiên như hình bên dưới
Hàm số
( )
y f x=
có đường tiệm cận đứng là
A.
3.y =
B.
1.x =
C.
2.x =−
D.
3.x =
Lời giải
Chọn C
Ta thấy 2 giới hạn sau thông qua bảng biến thiên
2
2
lim
lim 1
x
x
y
y
−
+
→−
→−
= +
=
Suy ra
2x =−
là đường tiệm cận đứng của đồ thị hàm số. Chọn C
Câu 34: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Đồ thị của hàm số đã cho có tổng số bao nhiêu tiệm cận đứng và tiệm cận ngang?
A. 1. B. 3. C. 4. D. 2.
Lời giải
Chọn B
Từ bảng biến thiên ta có:
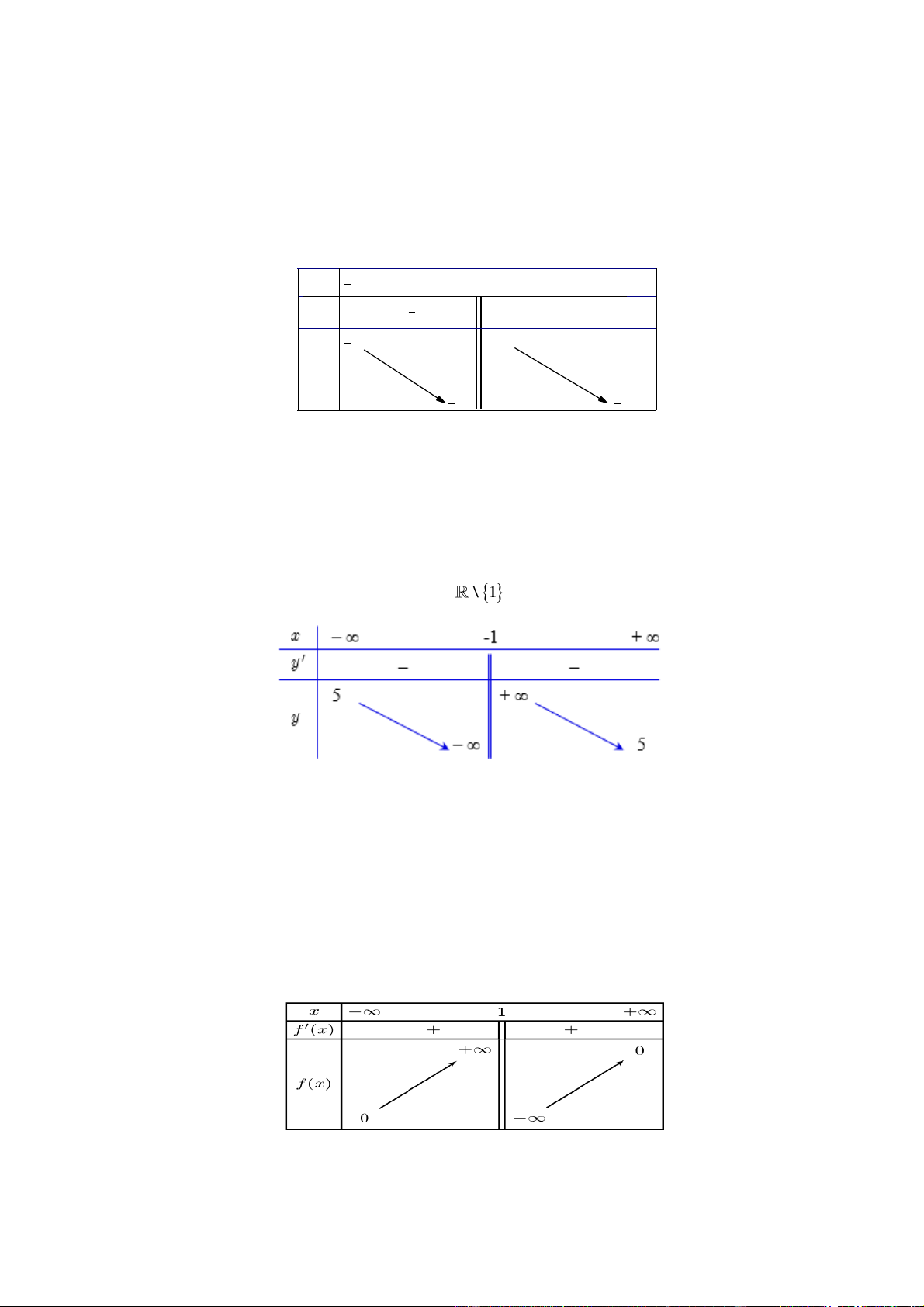
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 28
*)
( )
lim 0
x
fx
→+
=
suy ra đồ thị hàm số có tiệm cận ngang
0y =
.
*)
( )
0
lim
x
fx
−
→
= +
suy ra đồ thị hàm số có tiệm cận đứng
0x =
.
*)
( )
2
lim
x
fx
+
→−
= −
suy ra đồ thị hàm số có tiệm cận đứng
2x =−
.
Vậy đồ thị hàm số có 3 tiệm cận.
Câu 35: Cho hàm số
()y f x=
có bảng biến thiên như sau:
Số tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
Ta có
( )
lim 5
x
fx
→−
=−
và
( )
lim 5
x
fx
→+
=−
nên
5y =−
là tiệm cận ngang.
Câu 36: Cho hàm số
( )
y f x=
có đạo hàm trên
\1
và có bảng biến thiên
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
B.
1
C.
4
D.
2
Lời giải
Chọn D
Dựa vào BBT ta thấy đồ thị hàm số có 1 TCĐ
1x =−
và 1 TCN
5y =
. Nên tổng số tiệm cận
ngang và tiệm cận đứng của đồ thị hàm số đã cho là 2.
Câu 37: Cho hàm số
( )
y f x=
có bảng biến thiên như sau. Tổng số tiệm cận ngang và tiệm cận đứng
của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
5
f(x)
f'(x)
∞
x
2
+
∞
∞
1
5
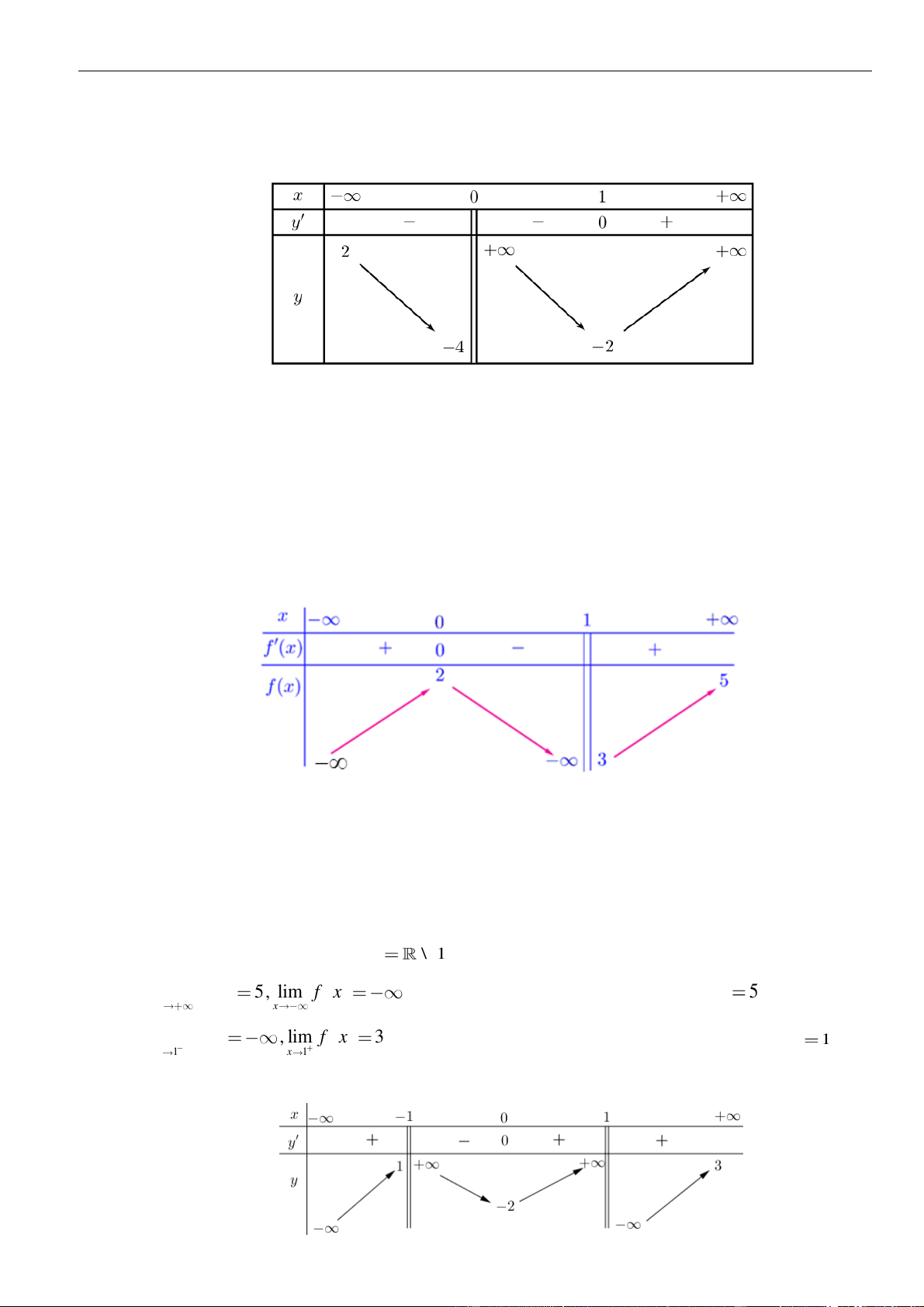
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
29 | Facebook tác giả: Phan Nhật Linh
Ta có
( ) ( )
11
lim 0, lim , lim
x
xx
y y y
−+
→
→→
= = + = −
nên hàm số có tiệm cận ngang là
0y =
và tiệm cận
đứng là
0x =
.
Câu 38: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn D
Ta có
( )
0
lim 2, lim
x
x
yy
+
→−
→
= = +
nên hàm số có tiệm cận ngang là
2y =
và tiệm cận
đứng là
0x =
.
Câu 39: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn C
Dựa vào bảng biến thiên ta có:
Tập xác định của hàm số là
\1D
.
lim 5, lim
xx
f x f x
nên đồ thị có 1 đường tiệm cận ngang là
5y
.
11
lim , lim 3
xx
f x f x
nên đồ thị có 1 đường tiệm cận đứng là đường thẳng
1x
.
Câu 40: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
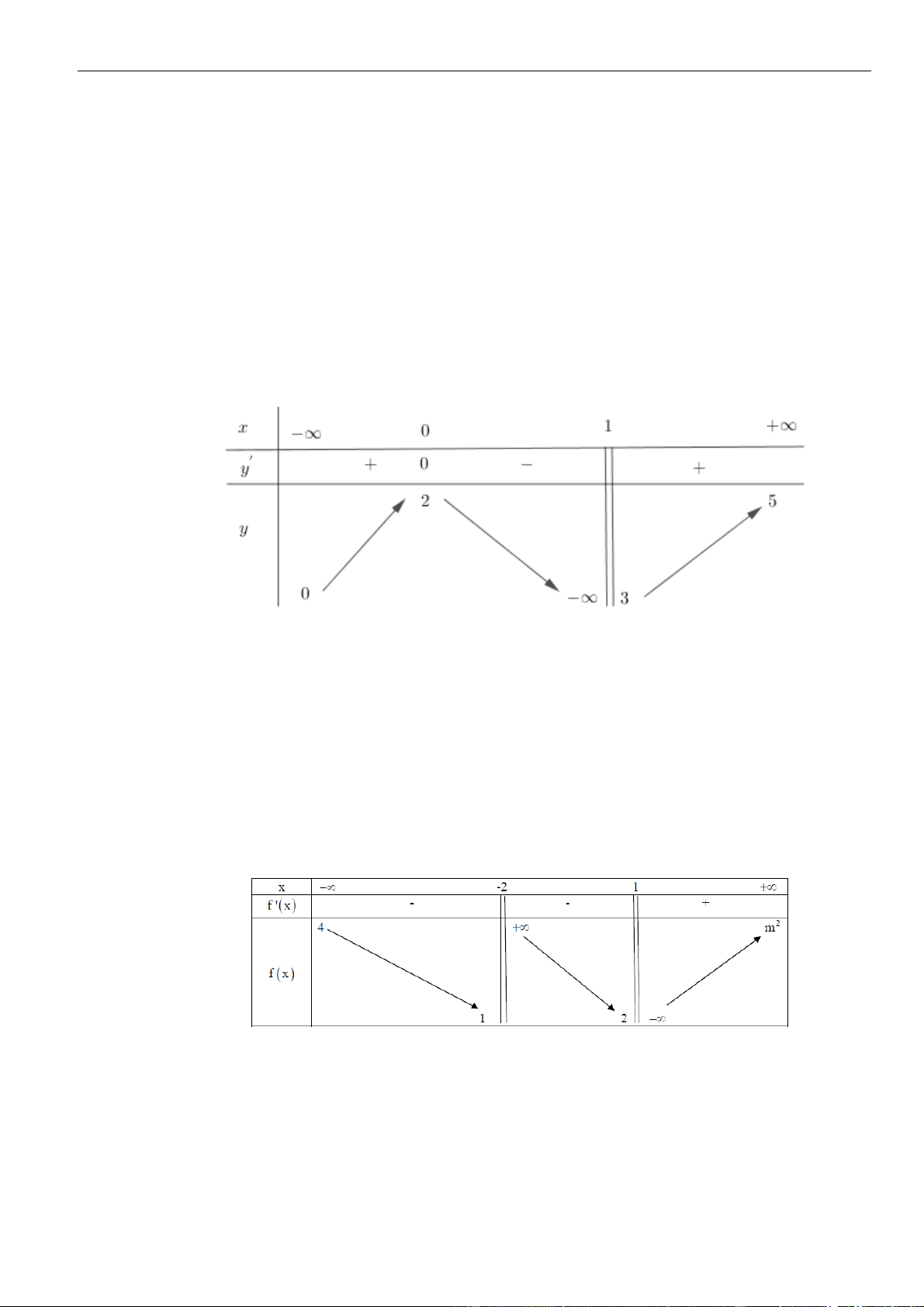
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 30
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn B
Từ bảng biến thiên, ta có
( )
1
lim 1
x
f x x
+
→−
= + = −
là tiệm cận đứng của đồ thị;
( )
1
lim 1
x
f x x
−
→
= + =
là tiệm cận đứng của đồ thị;
( )
lim 3 3
x
f x y
→+
= =
là tiệm cận ngang của đồ thị.
Vậy đồ thị hàm số có tất cả 3 tiệm cận đứng và ngang.
Câu 41: Cho hàm số
( )
fx
có bảng biến thiên như sau.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
3
B.
1
.
C.
2
. D.
4
.
Lời giải
Chọn A
+
( )
lim 5
x
fx
→+
=
và
( )
lim 0
x
fx
→−
=
nên hàm số có 2 tiệm cận ngang.
+
( )
1
lim
x
fx
−
→
= −
nên hàm số có 1 tiệm cận đứng.
Nên hàm số đã cho có 3 tiệm cận.
Câu 42: Cho hàm số
( )
y f x=
có bảng biến thiên:
Số giá trị nguyên của
[ 4;4]m−
để đồ thị hàm số có 4 tiệm cận là
A.
7
. B.
6
. C.
5
. D.
8
.
Lời giải
Chọn A
Từ bảng biến thiên ta thấy đồ thị có hai tiệm cận đứng
2; 1xx= − =
và các tiệm cận ngang
2
4;y y m==
. Suy ra đồ thị có bốn tiệm cận khi
2
42mm
.
Do
4;4m−
và
m
nguyên nên
4; 3; 1;0m
.
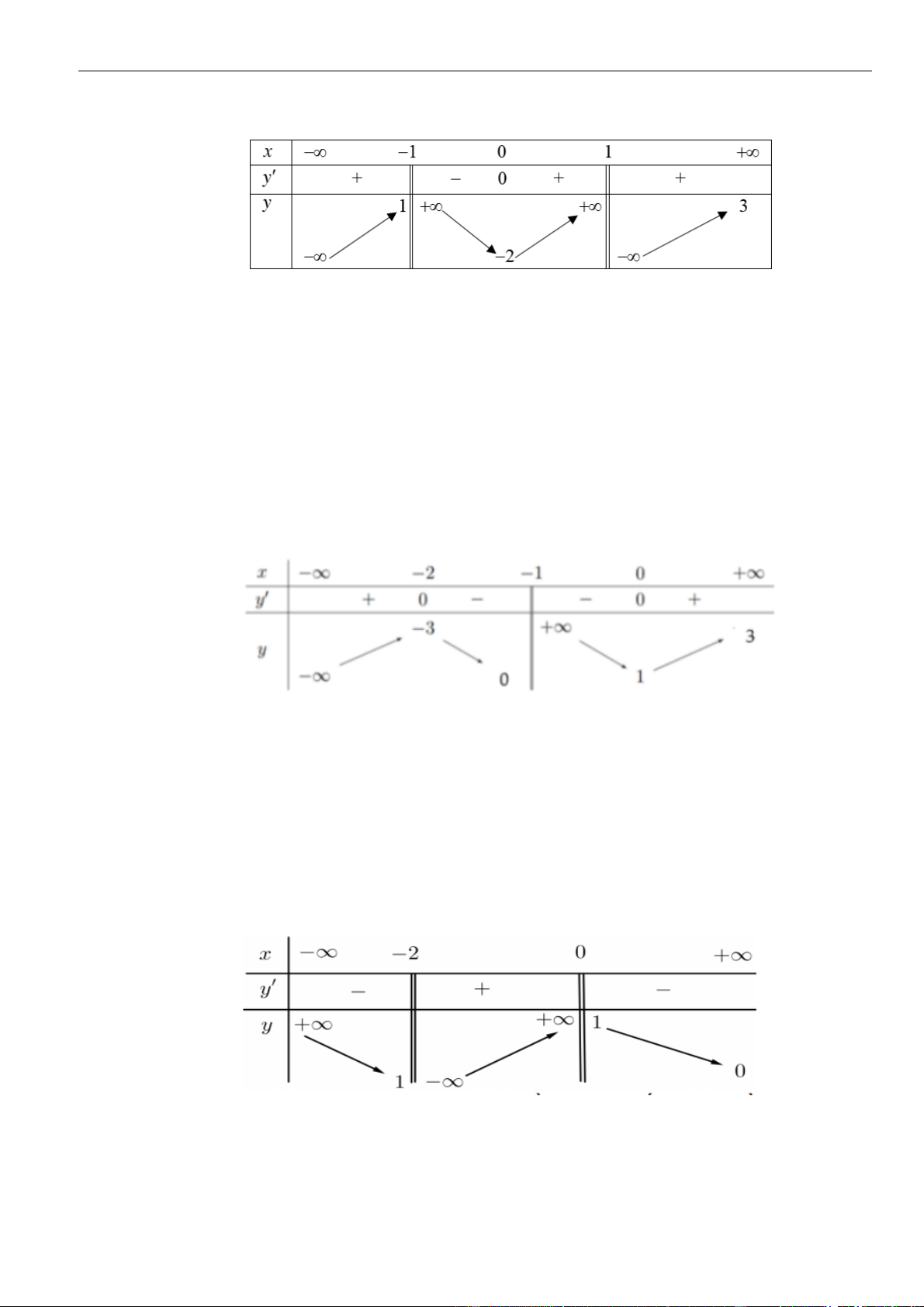
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
31 | Facebook tác giả: Phan Nhật Linh
Vậy có
7
giá trị của
m
thỏa mãn.
Câu 43: Cho hàm số
( )
=y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số trên là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn B
Ta có:
( )
1
lim 1
+
→−
= + = −
x
f x x
là tiệm cận đứng.
Ta có:
( )
1
lim 1
+
→
= − =
x
f x x
là tiệm cận đứng.
Ta có:
( )
lim 3 3
→+
= =
x
f x y
là tiệm cận ngang.
Vậy đồ thị của hàm số có 3 đường tiệm cận.
Câu 44: Cho hàm số có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn D
Do
lim 3
x
y
→+
=
nên đồ thị hàm số có một tiệm cận ngang
3y =
.
Do
1
lim
x
y
+
→−
= +
nên đồ thị hàm số có một tiệm cận đứng
1x =−
.
Câu 45: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn D
Từ bảng biến thiên ta có :
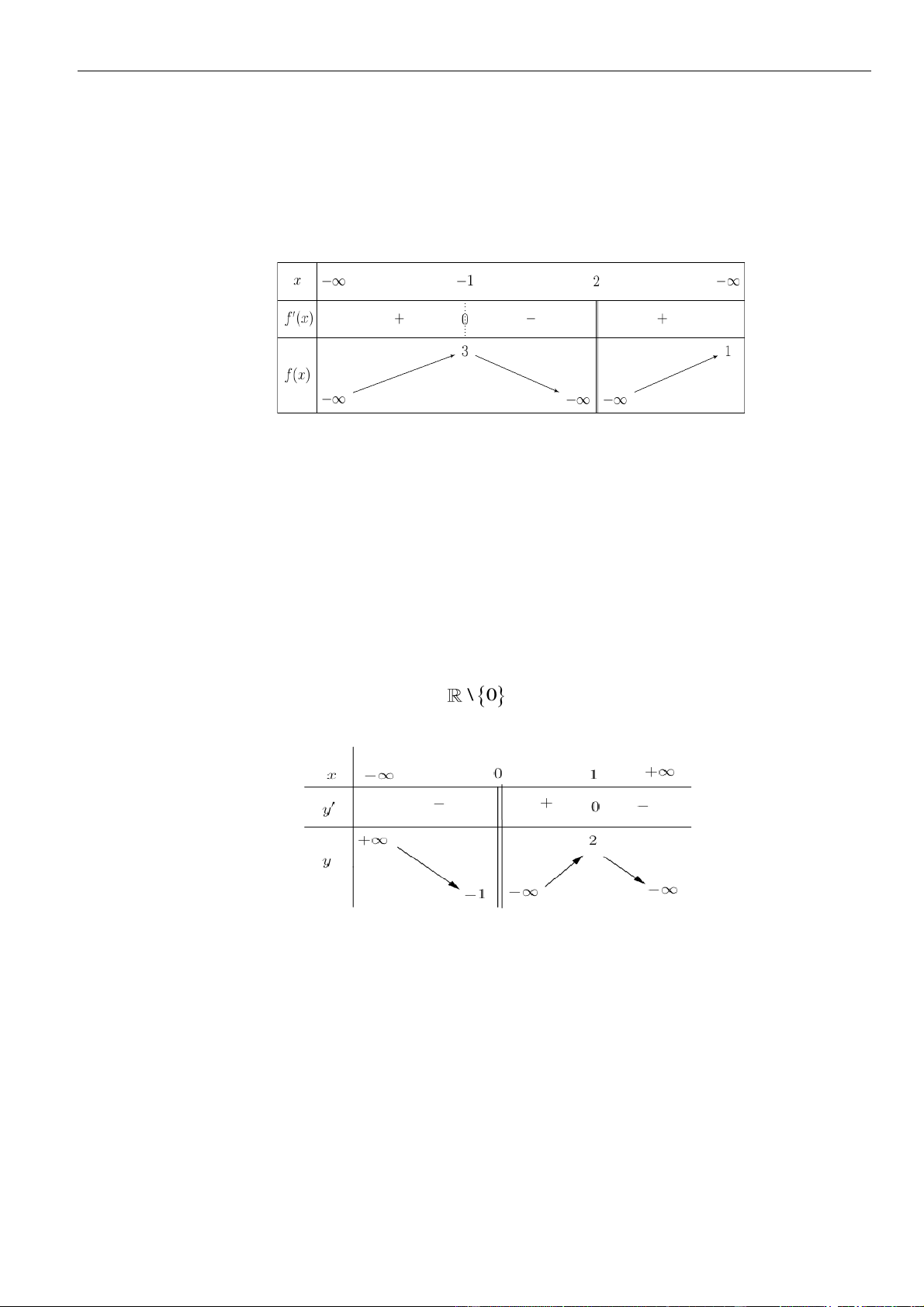
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 32
( )
2
lim
x
y
+
→−
= −
Đồ thị hàm số có đường tiệm cận đứng
2x =−
.
0
lim
x
y
−
→
= +
Đồ thị hàm số có đường tiệm cận đứng
0x =
.
lim 0
x
y
→+
=
Đồ thị hàm số có đường tiệm cận ngang
0y =
.
Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
3
.
Câu 46: Cho hàm số
( )
y f x=
có bảng biến thiên
Số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
y f x=
là
A.
3
. B.
1
. C.
0
. D.
2
.
Lời giải
Chọn D
Theo bảng biến thiên của hàm số
( )
y f x=
ta có:
( )
lim
x
fx
→−
= −
,
( )
lim 1
x
fx
→+
=
suy ra đồ thị hàm số có đường tiệm cận ngang
1y =
.
( )
2
lim
x
fx
+
→
= −
suy ra đồ thị hàm số có đường tiệm cận đứng
2x =
.
Vậy đồ thị hàm số
( )
y f x=
có tổng số tiệm cận đứng và tiệm cận ngang là
2
.
Câu 47: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng
biến thiên như sau
Chọn khẳng định đúng trong các khẳng định sau
A. Đồ thị hàm số có hai đường tiệm cận ngang.
B. Đồ thị hàm số có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số có đúng một đường tiệm cận đứng.
D. Đồ thị hàm số không có đường tiệm cận đứng và tiệm cận ngang.
Lời giải
Chọn B
Ta có:
( )
0
lim
x
fx
+
→
= −
nên đồ thị hàm số có đúng một đường tiệm cận đứng
Câu 48: Cho hàm số
()=y f x
có đồ thị như hình sau:
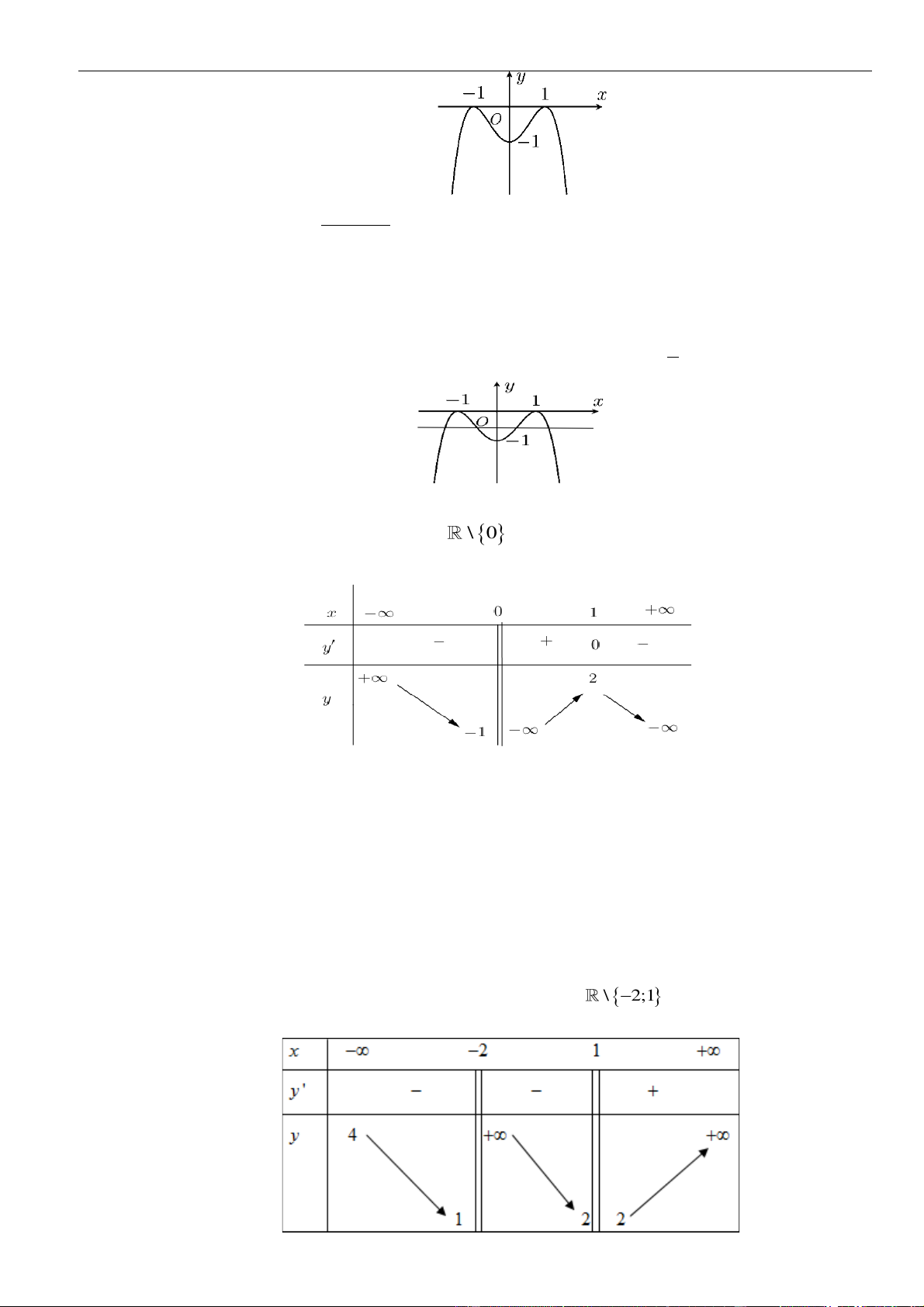
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
33 | Facebook tác giả: Phan Nhật Linh
Đồ thị hàm số
2020
()
2 ( ) 1
=
+
gx
fx
có số đường tiệm cận đứng là
A. 2. B. 3. C. 4. D. 5.
Lời giải
Chọn C
Số đường tiệm cận đứng là số nghiệm của phương trình
( )
1
2
fx=−
Nhìn vào đồ thị ta thấy phương trình trên có 4 nghiệm tương ứng với 4 đường tiệm cận đứng.
Câu 49: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng
biến thiên như sau
Chọn khẳng định đúng trong các khẳng định sau
A. Đồ thị hàm số có hai đường tiệm cận ngang.
B. Đồ thị hàm số có đúng một đường tiệm cận ngang.
C. Đồ thị hàm số có đúng một đường tiệm cận đứng.
D. Đồ thị hàm số không có đường tiệm cận đứng và tiệm cận ngang.
Lời giải
Chọn B
Ta có:
( )
0
lim
x
fx
+
→
= −
nên đồ thị hàm số có đúng một đường tiệm cận đứng
Câu 50: Cho hàm số
( )
y f x=
xác định và có đạo hàm trên trên
\ 2;1−
và có bảng biến thiên như
sau

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 34
Số đường tiệm cận của đồ thị hàm số là
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Đồ thị hàm số có một đường tiệm cận ngang là
4y =
và một đường tiệm cận đứng
2x =−

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Hai đường tiệm cận đứng và ngang của đồ thị hàm số
25
4
x
y
x
−
=
−
cắt nhau tại điểm
I
.
Tìm tọa
độ điểm
I
A.
( )
4;2−
. B.
( )
4;2
. C.
( )
4; 2−−
. D.
( )
4; 2−
.
Câu 2: Tâm đối xứng của đồ thị hàm số
31
2
x
y
x
−
=
+
là điểm nào sau đây?
A.
( )
2;3−
. B.
( )
3; 2−
. C.
( )
2; 1−
. D.
( )
1;2−
.
Câu 3: Cho các đường tiệm cận của đồ thị hàm số
3
12
y
x
x
=
−
+
tạo với hai trục tọa độ diện tích bằng
A.
6
. B.
2
. C.
3
. D.
4
.
Câu 4: Đường tiệm cận ngang của đồ thị hàm số
1
3
−−
=
+
x
y
x
cắt đường thẳng
2021=yx
tại điểm có tung
độ bằng
A.
1−
. B.
3−
. C.
0
. D.
1
2021
−
.
Câu 5: Đồ thị hàm số
3
3
3
x
y
xx
+
=
−
có bao nhiêu đường tiệm cận?
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 6: Cho hàm số
2
1
mx m
y
x
+
=
−
. Tìm tất cả các giá trị thực của tham số
m
để đường tiệm cận đứng,
tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện
tích bằng
8
.
A.
4m =
. B.
1
2
m =
. C.
4m =
. D.
2m =
.
Câu 7: Gọi S là tập các giá trị nguyên của tham số
m
để đồ thị hàm số
22
3
2 2 9
x
y
x mx m
−
=
− + −
có đúng
3
đường tiệm cận. Số phần tử của S là
A.
6
. B.
7
. C.
4
. D.
5
.
Câu 8: Đồ thị hàm số nào dưới có đường tiệm cận đứng đi qua điểm
( )
4;5M −
?
A.
47
5
x
y
x
−+
=
+
. B.
51
4
x
y
x
+
=
+
. C.
41
5
x
y
x
−+
=
−
. D.
53
4
x
y
x
+
=
−
.
Câu 9: Tìm tâm đối xứng của đồ thị hàm số
21
3
x
y
x
+
=
−
A.
( )
3;2A
. B.
( )
3;2B −
C.
( )
1;3D −
D.
( )
1; 3C −
.
Các dạng toán khác liên quan đến tiệm cận
DẠNG 4

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 10: Giao điểm hai đường tiệm cận của đồ thị hàm số
2
3
x
y
x
+
=
−
là điểm
A.
( )
3; 2G −
. B.
( )
1;3F
. C.
( )
2;3H −
. D.
( )
3;1E
.
Câu 11: Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số
2
1
8
x
y
x x m
−
=
−+
có 3 đường
tiệm cận?
A. 14. B. 16. C. 15. D. 8.
Câu 12: Cho hàm số
2
mx n
y
ax bx c
+
=
++
(
, , , ,m n a b c
là các tham số thực). Hỏi đồ thị hàm số đã cho có tối
đa bao nhiêu tiệm cận (ngang hoặc đứng)?
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 13: Số tiệm cận đứng của đồ thị hàm số
2
93x
y
xx
+−
=
+
là:
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 14: Hai đường tiệm cận đứng và ngang của đồ thị hàm số
25
4
x
y
x
−
=
−
cắt nhau tại điểm
I
. Tìm tọa
độ điểm
I
.
A.
( )
4; 2−
. B.
( )
4;2
. C.
( )
4; 2−−
. D.
( )
4;2−
.
Câu 15: Tìm tâm đối xứng của đồ thị hàm số
21
3
x
y
x
+
=
−
A.
( )
3;2A
. B.
( )
3;2B −
C.
( )
1;3D −
D.
( )
1; 3C −
.
Câu 16: Đồ thị hàm số
( )
2
31
2
m m x
y
x
−−
=
−
có đường tiệm cận ngang qua điểm
( )
12A;−
khi:
A.
1m =
hoặc
2m =−
. B.
1m =−
hoặc
2m =
.
C.
1m =−
hoặc
2m =−
. D.
1m =
hoặc
2m =
.
Câu 17: Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
24x
y
xm
−
=
−
có tiệm cận đứng.
A.
2m
. B.
2m =
. C.
2m
. D.
2m
.
Câu 18: Cho các đường tiệm cận của đồ thị hàm số
3
12
y
x
x
=
−
+
tạo với hai trục tọa độ diện tích bằng
A.
6
. B.
2
. C.
3
. D.
4
.
Câu 19: Các đường tiệm cận của đồ thị hàm số
23
1
x
y
x
+
=
−
tạo với hai trục tọa độ một hình chữ nhật có
diện tích bằng
A.
3.
B.
6.
C.
1.
D.
2.
Câu 20: Với giá trị nào của
m
thì đường tiệm cận ngang của đồ thị hàm số
3
4
mx
y
xm
−
=
−
đi qua điểm
( )
2;4A −
?
A.
1m =
. B.
2m =−
. C.
4m =
. D.
1
2
m =−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 21: Tập hợp tất cả các giá trị thực của tham số
m
để đồ thị hàm số
2
11
2
x
y
x x m
++
=
−−
có đúng hai tiệm
cận đứng là
A.
1;3−
. B.
(
1;3−
. C.
( )
1;3−
. D.
( )
1;− +
.
Câu 22: Biết đồ thị hàm số
( )
2
2
21
6
m n x mx
y
x mx n
− + +
=
+ + −
(
,mn
là tham số) nhận trục hoành và trục trung
làm hai đường tiệm cận. Tính
mn+
.
A.
8
. B.
6−
. C.
9
. D.
6
.
Câu 23: Tập hợp tất cả các giá trị của tham số
m
để đồ thị hàm số
2
1
3
x
y
x x m
−
=
−+
có đúng hai đường
tiệm cận là
A.
9
;
4
−
. B.
2
. C.
9
;
4
−
. D.
9
2;
4
.
Câu 24: (HK1 - K12 - THPT Marie - Curie - Hà Nội - 2021) Tất cả các giá trị thực của tham số
m
để
đồ thị hàm số
2
1
2 3 4
x
y
x mx m
+
=
+ + +
có đúng một đường tiệm cận đứng là
A.
1;4m−
. B.
1;4;5m−
. C.
( )
1;4m−
. D.
5; 1;4m − −
.
Câu 25: Số các giá trị nguyên của tham số
m
để đồ thị hàm số
22
1
2 2 4 12
y
x mx m m
=
− + − −
có ba
đường tiệm cận
A.
7
. B.
6
. C.
9
. D.
8
.
Câu 26: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
4
x
y
x x m
−
=
++
có đúng 3 đường
tiệm cận?
A.
9
. B.
7
. C.
10
. D.
8
.
Câu 27: Có bao nhiêu số nguyên
m
để đồ thị hàm số
22
1
2 3 1
x
y
x mx m m
−
=
+ + − −
có ba đường tiệm cận?
A.
1
. B.
0
. C.
2
. D.
7
.
Câu 28: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5−
để đồ thị hàm số
32
1
3
x
y
x x m
+
=
−−
có đúng một tiệm cận đứng?
A.
6
. B.
7
. C.
8
. D.
5
.
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Hai đường tiệm cận đứng và ngang của đồ thị hàm số
25
4
x
y
x
−
=
−
cắt nhau tại điểm
I
.
Tìm tọa
độ điểm
I
A.
( )
4;2−
. B.
( )
4;2
. C.
( )
4; 2−−
. D.
( )
4; 2−
.
Lời giải
Chọn D
Đồ thị hàm số
25
4
x
y
x
−
=
−
có đường tiệm cận đứng
4x =
và đường tiệm cận ngang
2y =−
. Do
đó giao điểm của hai đường tiệm cận là
( )
4; 2I −
.
Câu 2: Tâm đối xứng của đồ thị hàm số
31
2
x
y
x
−
=
+
là điểm nào sau đây?
A.
( )
2;3−
. B.
( )
3; 2−
. C.
( )
2; 1−
. D.
( )
1;2−
.
Lời giải
Chọn A
Đồ thị hàm số
31
2
x
y
x
−
=
+
có tiệm cận đứng
2x =−
, tiệm cận ngang
3y =
.
Tâm đối xứng
( )
2;3−
.
Câu 3: Cho các đường tiệm cận của đồ thị hàm số
3
12
y
x
x
=
−
+
tạo với hai trục tọa độ diện tích bằng
A.
6
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A
Ta có: Đồ thị hàm số
3
12
y
x
x
=
−
+
có đường tiệm cận đứng là
3x =
và đường tiệm cận ngang
là
2y =
. Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có kích thước lần lượt là
2
và
3
nên diện tích của hình chữ nhật là
2.3 6S ==
.
Câu 4: Đường tiệm cận ngang của đồ thị hàm số
1
3
−−
=
+
x
y
x
cắt đường thẳng
2021=yx
tại điểm có tung
độ bằng
A.
1−
. B.
3−
. C.
0
. D.
1
2021
−
.
Lời giải
Chọn A
Do
11
11
11
lim lim 1; lim lim 1
33
33
11
→+ →+ →− →−
− − − −
− − − −
= = − = = −
++
++
x x x x
xx
xx
xx
xx
nên đồ thị hàm số có đường
tiệm cận ngang là
1=−y
;

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Xét phương trình hoành độ giao điểm :
1
2021 1
2021
−
= − =xx
; vậy tung độ giao điểm là
1=−y
.
Câu 5: Đồ thị hàm số
3
3
3
x
y
xx
+
=
−
có bao nhiêu đường tiệm cận?
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta có
3
3
lim 0
3
x
x
xx
→
+
=
−
. Suy ra đường thẳng
0y =
là tiệm cận ngang của đồ thị hàm số.
Mặt khác
3
0
3
lim
3
x
x
xx
+
→
+
=
−
. Suy ra
0x =
là tiệm cận đứng của đồ thị hàm số.
Ta có
3
3
3
lim
3
x
x
xx
+
→
+
=
−
. Suy ra
3x =
là tiệm cận đứng của đồ thị hàm số.
Ta có
( )
3
3
3
lim
3
x
x
xx
−
→−
+
= −
−
. Suy ra
3x =−
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
4
đường tiệm cận.
Câu 6: Cho hàm số
2
1
mx m
y
x
+
=
−
. Tìm tất cả các giá trị thực của tham số
m
để đường tiệm cận đứng,
tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện
tích bằng
8
.
A.
4m =
. B.
1
2
m =
. C.
4m =
. D.
2m =
.
Lời giải
Chọn A
Điều kiện để đồ thị hàm số có tiệm cận là
2 0 0m m m− −
.
Khi đó, đồ thị hàm số có:
+) tiệm cận đứng:
1x =
, song song với
Oy
và cắt
Ox
tại điểm
( )
1;0A
.
+) tiệm cận ngang:
2ym=
, song song với
Ox
và cắt
Oy
tại điểm
( )
2 ;0Bm
.
Diện tích hình chữ nhật tạo bởi hai đường tiệm cận cùng với hai trục tọa độ là
. 1. 2 8 4S OAOB m m= = = =
.
Câu 7: Gọi S là tập các giá trị nguyên của tham số
m
để đồ thị hàm số
22
3
2 2 9
x
y
x mx m
−
=
− + −
có đúng
3
đường tiệm cận. Số phần tử của S là
A.
6
. B.
7
. C.
4
. D.
5
.
Lời giải
Chọn C
22
3
2 2 9
x
y
x mx m
−
=
− + −
có 1 đường tiệm cận ngang là
0y
Để có 3 đường tiệm cận thì
22
2 2 9 0x mx m− + − =
phải có 2 nghiệm phân biệt khác 3.

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Tức là:
2
2
22
3 3 3 3
2 9 0
0; 3 0
3 6 2 9 0
mm
mm
m m m
mm
2; 1S
.
Câu 8: Đồ thị hàm số nào dưới có đường tiệm cận đứng đi qua điểm
( )
4;5M −
?
A.
47
5
x
y
x
−+
=
+
. B.
51
4
x
y
x
+
=
+
. C.
41
5
x
y
x
−+
=
−
. D.
53
4
x
y
x
+
=
−
.
Lời giải
Chọn B
Đáp án B:
( )
4
lim
x
y
+
→−
= +
và
( )
4
lim
x
y
−
→−
= −
Suy ra:
4x =−
là tiệm cận đứng của đồ thị hàm số.
Tiệm cận đứng đi qua điểm
( )
4;5 4Mx− = −
.
Câu 9: Tìm tâm đối xứng của đồ thị hàm số
21
3
x
y
x
+
=
−
A.
( )
3;2A
. B.
( )
3;2B −
C.
( )
1;3D −
D.
( )
1; 3C −
.
Lời giải
Chọn A
Tập xác định
\3D =
1
2
21
lim lim lim 2
3
3
1
x x x
x
x
y
x
x
→+ →+ →+
+
+
= = =
−
−
Tiệm cận ngang của đồ thị hàm số
2y =
33
21
lim lim
3
xx
x
y
x
++
→→
+
= = +
−
( vì
( ) ( )
33
lim 2 1 7; lim 3 0; 3 0, 3
xx
x x x x
++
→→
+ = − = −
)
Tiệm cận đứng của đồ thị hàm số
3x =
.
Tâm đối xứng của đồ thị hàm số là
( )
3;2A
.
Câu 10: Giao điểm hai đường tiệm cận của đồ thị hàm số
2
3
x
y
x
+
=
−
là điểm
A.
( )
3; 2G −
. B.
( )
1;3F
. C.
( )
2;3H −
. D.
( )
3;1E
.
Lời giải
Chọn D
Cách 1:
Ta có:
+)
lim lim 1
xx
yy
→+ →−
==
.
Đồ thị hàm số nhận đường thẳng
1y =
là tiệm cận ngang.
+)
3
lim
x
y
−
→
= −
;
3
lim
x
y
+
→
= +
.
Đồ thị hàm số nhận đường thẳng
3x =
là tiệm cận đứng.
Như vậy giao điểm hai đường tiệm cận của đồ thị hàm số là
( )
3;1E
.
Cách 2:

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Đồ thị của hàm số
( )
0
ax b
yc
cx d
+
=
+
:
+) Nhận đường thẳng
d
x
c
=−
là tiệm cận đứng.
+) Nhận đường thẳng
a
y
c
=
là tiệm cận ngang.
Như vậy đồ thị hàm số
2
3
x
y
x
+
=
−
nhận đường thẳng
1y =
là tiệm cận ngang, nhận đường thẳng
3x =
là tiệm cận đứng.
Nên giao điểm hai đường tiệm cận của đồ thị hàm số là
( )
3;1E
.
Câu 11: Có bao nhiêu giá trị nguyên dương của tham số m để đồ thị hàm số
2
1
8
x
y
x x m
−
=
−+
có 3 đường
tiệm cận?
A. 14. B. 16. C. 15. D. 8.
Lời giải
Chọn A
Ta có:
2
1
lim 0
8
x
x
x x m
→
−
=
−+
nên suy ra hàm số có 1đường tiệm cận ngang là
0y =
.
Để đồ thị hàm số có 3 đường tiệm cận thì phải có 2 tiệm cận đứng hay phương trình
2
8x 0xm− + =
có 2 nghiệm phân biệt khác
1
2
16 0
1 8.1 0
m
m
= −
− +
16
7
m
m
.
Do
m
nguyên dương nên có 14 giá trị m thỏa mãn.
Câu 12: Cho hàm số
2
mx n
y
ax bx c
+
=
++
(
, , , ,m n a b c
là các tham số thực). Hỏi đồ thị hàm số đã cho có tối
đa bao nhiêu tiệm cận (ngang hoặc đứng)?
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
Với
0; 0ab=
thì
lim
x
mm
yy
bb
→
= =
là tiệm cận ngang.
Với
0a
thì
lim 0 0
x
yy
→
= =
là tiệm cận ngang
Vậy tối đa hàm số có
1
tiệm cận ngang.
Để hàm số có tối đa tiệm cận đứng thì phương trình
2
0ax bx c+ + =
có
2
nghiệm phân biệt
khác
n
m
−
. Nên hàm số có tối đa
2
tiệm cận đứng.
Câu 13: Số tiệm cận đứng của đồ thị hàm số
2
93x
y
xx
+−
=
+
là:
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
( )
( )
( )
( )
2
9 3 9 9 1
1 9 3 1 9 3
xx
y
xx
x x x x x
+ − + −
= = =
+
+ + + + + +
.
1
lim 1
x
yx
→−
= = −
là tiệm cận đứng của đồ thị hàm số.
Câu 14: Hai đường tiệm cận đứng và ngang của đồ thị hàm số
25
4
x
y
x
−
=
−
cắt nhau tại điểm
I
. Tìm tọa
độ điểm
I
.
A.
( )
4; 2−
. B.
( )
4;2
. C.
( )
4; 2−−
. D.
( )
4;2−
.
Lời giải
Chọn A
Đồ thị hàm số
25
4
x
y
x
−
=
−
có TCĐ:
4x =
, TCN
2y =−
.
Khi đó giao điểm
I
của tiệm cận đứng và tiệm cận ngang có tọa độ là
( )
4; 2−
.
Câu 15: Tìm tâm đối xứng của đồ thị hàm số
21
3
x
y
x
+
=
−
A.
( )
3;2A
. B.
( )
3;2B −
C.
( )
1;3D −
D.
( )
1; 3C −
.
Lời giải
Chọn A
Tập xác định
\3D =
1
2
21
lim lim lim 2
3
3
1
x x x
x
x
y
x
x
→+ →+ →+
+
+
= = =
−
−
Tiệm cận ngang của đồ thị hàm số
2y =
33
21
lim lim
3
xx
x
y
x
++
→→
+
= = +
−
( vì
( ) ( )
33
lim 2 1 7; lim 3 0; 3 0, 3
xx
x x x x
++
→→
+ = − = −
)
Tiệm cận đứng của đồ thị hàm số
3x =
.
Tâm đối xứng của đồ thị hàm số là
( )
3;2A
.
Câu 16: Đồ thị hàm số
( )
2
31
2
m m x
y
x
−−
=
−
có đường tiệm cận ngang qua điểm
( )
12A;−
khi:
A.
1m =
hoặc
2m =−
. B.
1m =−
hoặc
2m =
.
C.
1m =−
hoặc
2m =−
. D.
1m =
hoặc
2m =
.
Lời giải
Chọn D
Đồ thị hàm số
( )
2
31
2
m m x
y
x
−−
=
−
có đường tiệm cận ngang là:
2
3y m m.=−
.
Đường tiệm cận ngang đi qua
( )
12A;−
nên ta có:
22
1
3 2 3 2 0
2
m
m m m m
m
=
− = − − + =
=
.
Câu 17: Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
24x
y
xm
−
=
−
có tiệm cận đứng.
A.
2m
. B.
2m =
. C.
2m
. D.
2m
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn C
Ta có
\Dm=
.
Đồ thị hàm số có tiệm cận đứng khi
2 4 0 2mm−
.
Câu 18: Cho các đường tiệm cận của đồ thị hàm số
3
12
y
x
x
=
−
+
tạo với hai trục tọa độ diện tích bằng
A.
6
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn A
Ta có: Đồ thị hàm số
3
12
y
x
x
=
−
+
có đường tiệm cận đứng là
3x =
và đường tiệm cận ngang
là
2y =
. Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có kích thước lần lượt là
2
và
3
nên diện tích của hình chữ nhật là
2.3 6S ==
.
Câu 19: Các đường tiệm cận của đồ thị hàm số
23
1
x
y
x
+
=
−
tạo với hai trục tọa độ một hình chữ nhật có
diện tích bằng
A.
3.
B.
6.
C.
1.
D.
2.
Lời giải
Chọn D
Do
23
lim 2 2
1
x
x
y
x
→
+
= =
−
là phương trình đường tiệm cận ngang.
Do
1
23
lim 1
1
x
x
x
x
+
→
+
= + =
−
là phương trình đường tiệm cận đứng.
Khi đó hai đường tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có kích thước là
2;1 2.1 2.S = =
Câu 20: Với giá trị nào của
m
thì đường tiệm cận ngang của đồ thị hàm số
3
4
mx
y
xm
−
=
−
đi qua điểm
( )
2;4A −
?
A.
1m =
. B.
2m =−
. C.
4m =
. D.
1
2
m =−
.
Lời giải
Chọn C
Xét hàm số
3
4
mx
y
xm
−
=
−
.
Tập xác định
\4Dm=
.
Ta có
lim lim
xx
y y m
→− →+
==
.
Do đó đồ thị hàm số có tiệm cận ngang là đường thẳng
:d y m=
.
( )
2;4Ad−
nên
4m =
.

Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Câu 21: Tập hợp tất cả các giá trị thực của tham số
m
để đồ thị hàm số
2
11
2
x
y
x x m
++
=
−−
có đúng hai tiệm
cận đứng là
A.
1;3−
. B.
(
1;3−
. C.
( )
1;3−
. D.
( )
1;− +
.
Lời giải
Chọn B
Tập xác định
)
1;D = − +
.
Yêu cầu đề bài
2
20x x m − − =
có 2 nghiệm phân biệt
12
,1xx−
.
Khi đó, ta có :
( )( )
( )
12
1 2 1 2
12
' 1 0 1
1
2 2 2 1 3
2 1 0
10
1 1 0
mm
m
x x m
m
x x x x
xx
= + −
−
+ − − −
− + +
+ + +
+ +
.
Câu 22: Biết đồ thị hàm số
( )
2
2
21
6
m n x mx
y
x mx n
− + +
=
+ + −
(
,mn
là tham số) nhận trục hoành và trục trung
làm hai đường tiệm cận. Tính
mn+
.
A.
8
. B.
6−
. C.
9
. D.
6
.
Lời giải
Chọn C
Theo giả thiết ta có
20
60
mn
n
−=
−=
3
6
m
n
=
=
. Vậy
9mn+=
.
Câu 23: Tập hợp tất cả các giá trị của tham số
m
để đồ thị hàm số
2
1
3
x
y
x x m
−
=
−+
có đúng hai đường
tiệm cận là
A.
9
;
4
−
. B.
2
. C.
9
;
4
−
. D.
9
2;
4
.
Lời giải
Chọn D
+) Ta có:
22
11
lim lim 0
33
xx
xx
x x m x x m
→+ →−
−−
==
− + − +
Suy ra đồ thị hàm số
2
1
3
x
y
x x m
−
=
−+
luôn có đúng một tiệm cận ngang
0y =
. Nên đề đồ thị
hàm số có đúng hai tiệm cận thì phải có thêm đúng một tiệm cận đứng.
+) Tam thức
( )
2
3h x x x m= − +
có
94m = −
.
+) Đồ thị hàm số có đúng hai tiệm cận thì phải có thêm đúng một tiệm cận đứng khi
( )
9
9 4 0
4
9
9 4 0
9
4
2
4
10
2
m
m
m
m
m
m
h
m
=
= − =
=
= −
=
=
=
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Câu 24: (HK1 - K12 - THPT Marie - Curie - Hà Nội - 2021) Tất cả các giá trị thực của tham số
m
để
đồ thị hàm số
2
1
2 3 4
x
y
x mx m
+
=
+ + +
có đúng một đường tiệm cận đứng là
A.
1;4m−
. B.
1;4;5m−
. C.
( )
1;4m−
. D.
5; 1;4m − −
.
Lời giải
Chọn D
Để đồ thị hàm số
2
1
2 3 4
x
y
x mx m
+
=
+ + +
có đúng một đường tiệm cận đứng thì phương trình
2
2 3 4 0x mx m+ + + =
có duy nhất một nghiệm hoặc phương trình
2
2 3 4 0x mx m+ + + =
có hai
nghiệm phân biệt, trong đó có một nghiệm
1x =−
và một nghiệm
x
khác
1−
.
Trường hợp 1: Phương trình
2
2 3 4 0x mx m+ + + =
có duy nhất một nghiệm
Suy ra
0
=
2
3 4 0mm − − =
1
4
m
m
=−
=
.
Trường hợp 2: Phương trình có một nghiệm bằng
1−
, một nghiệm khác
1−
.
Khi đó ta có:
( ) ( )
2
1 2. 1 3 4 0mm− + − + + =
5m = −
.
Thử lại thấy với
5m =−
phương trình có 2 nghiệm phân biệt thỏa mãn điều kiện.
Vậy
5; 1;4m − −
.
Câu 25: Số các giá trị nguyên của tham số
m
để đồ thị hàm số
22
1
2 2 4 12
y
x mx m m
=
− + − −
có ba
đường tiệm cận
A.
7
. B.
6
. C.
9
. D.
8
.
Lời giải
Chọn A
22
1
lim 0
2 2 4 12
x
x mx m m
→
=
− + − −
nên
0y =
là tiệm cận ngang.
Theo yêu cầu bài toán:
22
2 2 4 12 0x mx m m− + − − =
phải có hai nghiệm phân biệt
'0
( )
22
2 4 12 0m m m − − −
2
4 12 0mm − + +
26m −
Vậy
1;0;1;2;3;4;5m−
.
Câu 26: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
4
x
y
x x m
−
=
++
có đúng 3 đường
tiệm cận?
A.
9
. B.
7
. C.
10
. D.
8
.
Lời giải
Chọn A
ĐK:
1 x
Do
2
1
lim lim 0
4
xx
x
y
x x m
→− →−
−
==
++
0y=
là tiệm cận ngang của đồ thị hàm số.
Để đồ thị hàm số có 3 đường tiệm cận
2
40x x m + + =
có 2 nghiệm phân biệt
12
;1xx
.
2
4x x m+ = −
. Đặt
2
4y x x=+
Ta có BBT:
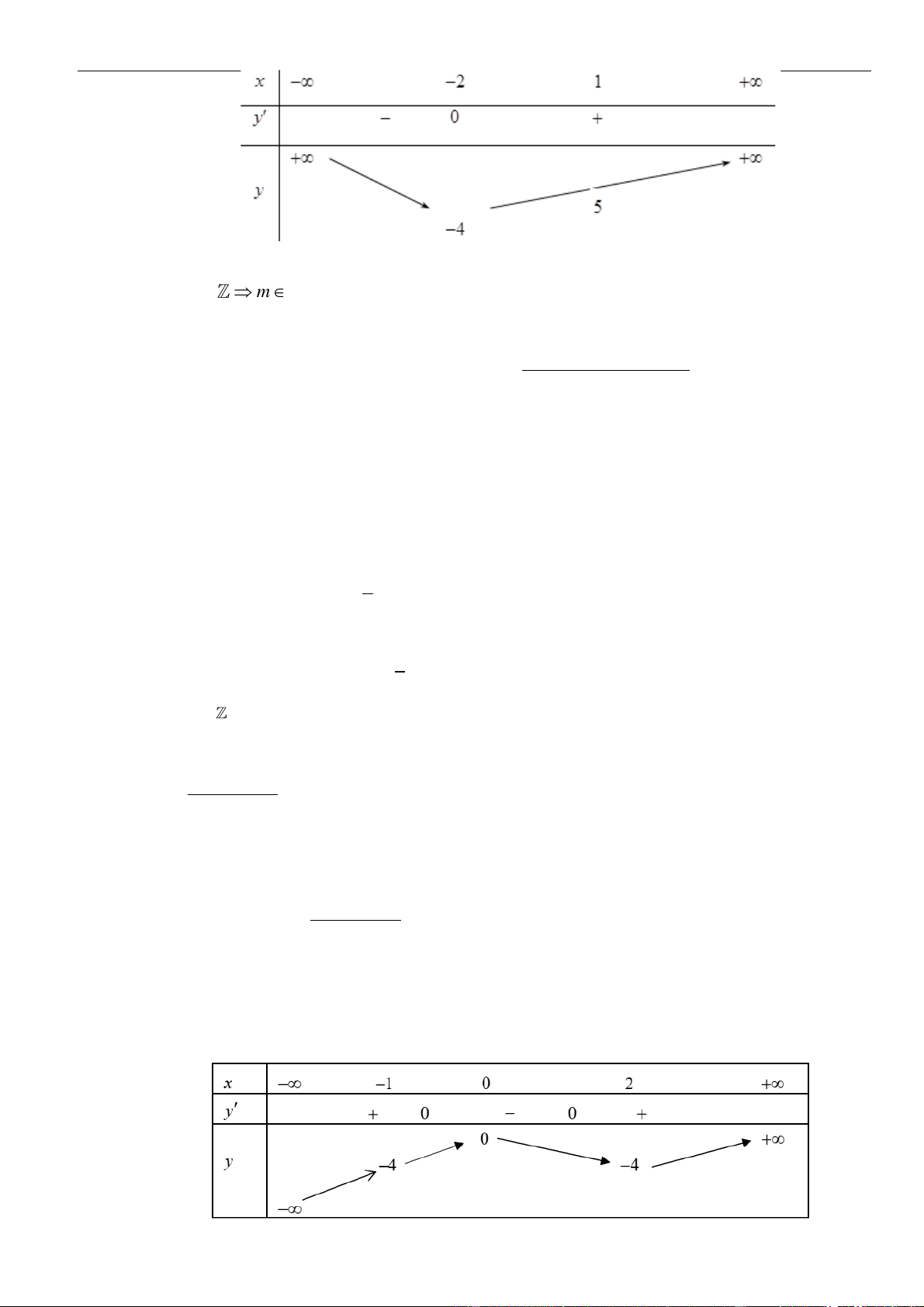
Chủ đề 04: Tiệm cận của đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Dựa vào BBT, có: Phương trình có
2
nghiệm phân biệt
12
;1xx
45m − −
45m −
Mà
5; 4; 3; 2; 1;0;1;2;3mm − − − − −
Vậy có 9 số
m
thỏa mãn.
Câu 27: Có bao nhiêu số nguyên
m
để đồ thị hàm số
22
1
2 3 1
x
y
x mx m m
−
=
+ + − −
có ba đường tiệm cận?
A.
1
. B.
0
. C.
2
. D.
7
.
Lời giải
Chọn B
Ta có:
lim 0 0
x
yy
→
= =
là một tiệm cận ngang của đồ thị hàm số.
Do đó để đồ thị hàm số có ba đường tiệm cận thì đồ thị hàm số phải có hai tiệm cận đứng.
22
2 3 1 0x mx m m + + − − =
có hai nghiệm phân biệt khác
1
.
2
2
1
1
2
2 1 0
0
30
1
3
m
mm
m
mm
m
−
− + +
+
−
.
Mà
m
nên không tồn tại giá trị nguyên
m
thỏa mãn yêu cầu đề bài.
Câu 28: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
5;5−
để đồ thị hàm số
32
1
3
x
y
x x m
+
=
−−
có đúng một tiệm cận đứng?
A.
6
. B.
7
. C.
8
. D.
5
.
Lời giải
Chọn A
Đồ thị hàm số
32
1
3
x
y
x x m
+
=
−−
có đúng một tiệm cận đứng khi và chỉ khi phương trình
32
30x x m− − =
có đúng 1 nghiệm khác
1−
.
Ta có
32
30x x m− − =
32
3m x x = −
.
Xét hàm số
( )
32
3g x x x=−
( )
2
36g x x x
= −
( )
0
0
2
x
gx
x
=
=
=

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Từ bảng biến thiên suy ra
0
4
m
m
−
.
Mà
m
là tham số nguyên thuộc đoạn
5;5−
suy ra
5;1;2;3;4;5m−
.
Vậy có 6 giá trị nguyên của tham số
m
thuộc đoạn
5;5−
thoả mãn yêu cầu bài toán.
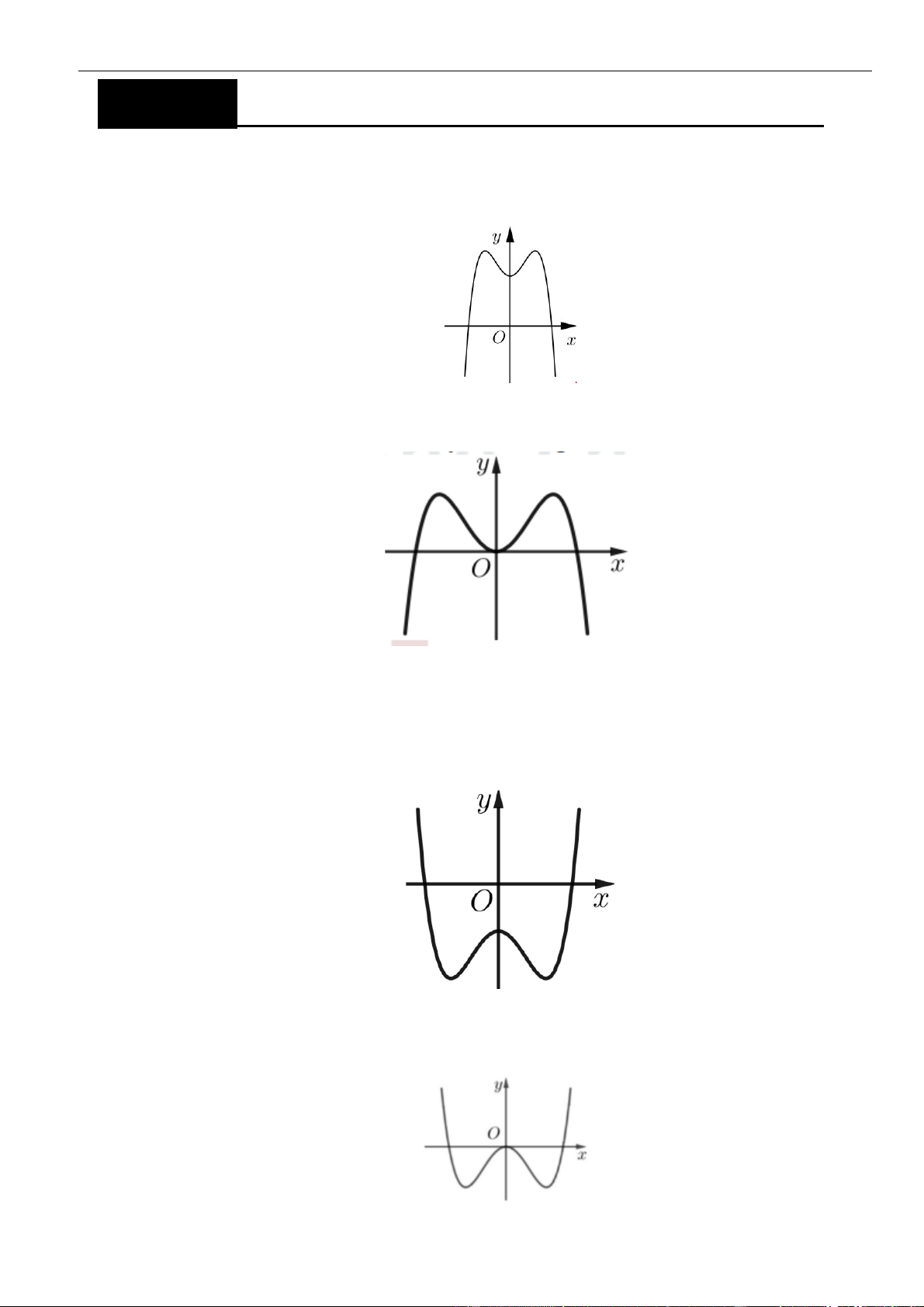
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
22y x x= − + +
. B.
42
22y x x= − +
. C.
32
32y x x= − +
. D.
32
32y x x= − + +
.
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
2y x x= − +
. B.
42
2y x x=−
. C.
32
3y x x=−
. D.
32
3y x x= − +
Câu 3: Hàm số nào dưới đây có đồ thị như hình vẽ bên?
A.
3
2 2.y x x= − + −
B.
3
22y x x= − + +
. C.
42
22y x x= − + −
. D.
42
22y x x= + −
Câu 4: Đồ thị hàm số nào dưới đây có dạng nhưng đường cong trong hình
A.
42
21y x x= − + −
. B.
42
21y x x= − −
. C.
32
31y x x= − −
. D.
32
31y x x= − + −
.
Câu 5: Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây?
Nhận diện hàm số thông qua đồ thị, BBT
DẠNG 1
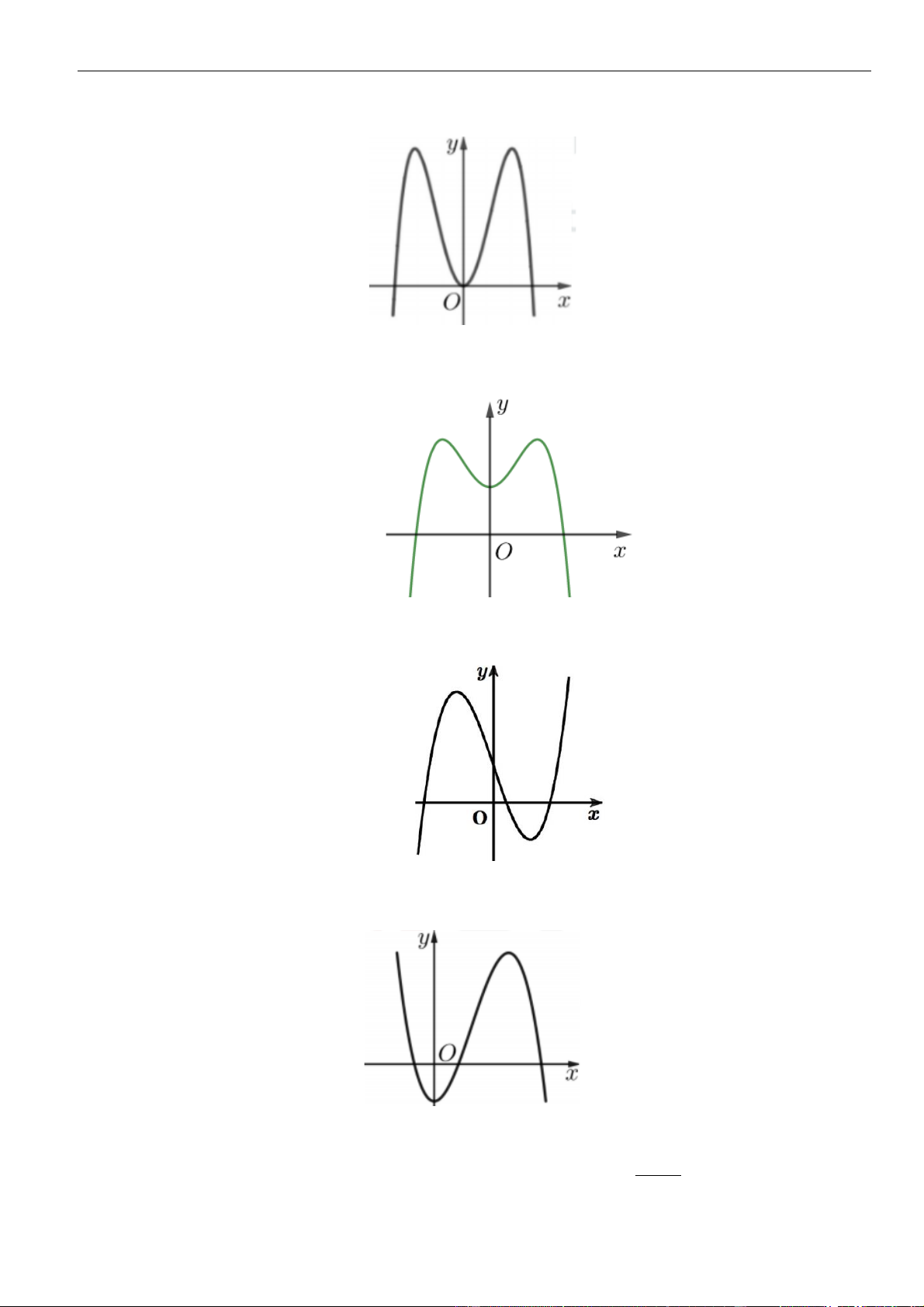
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
32
3y x x=−
. B.
42
2y x x= − +
. C.
32
3y x x= − +
. D.
42
2y x x=−
.
Câu 6: Đồ thị hàm số nào dưới đây có dạng như hình bên?
A.
42
4y x x= − −
. B.
42
4y x x= − +
. C.
3
2y x x= − +
. D.
3
2y x x=−
.
Câu 7: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên dưới?
A.
= − +
32
31y x x
. B.
= − + +
32
31y x x
. C.
= − + +
42
21y x x
. D.
= − +
42
21y x x
.
Câu 8: Đường cog ở hình dưới đây là đồ thị của hàm số nào?
A.
3
31y x x= − +
. B.
42
21y x x= − +
. C.
3
31y x x= − + +
. D.
42
21y x x= − + +
.
Câu 9: Đồ thị của hàm số nào dưới đây có dạng như hình bên?
A.
42
21y x x= − + −
. B.
42
21y x x= − −
. C.
32
3 1.y x x= − + −
D.
32
3 1.y x x= − −
Câu 10: Đường cong ở hình vẽ dưới đây là đồ thị của hàm số
ax b
y
cx d
+
=
+
với
, , ,a b c d
là các số
thực.Mệnh đề nào dưới đây đúng?
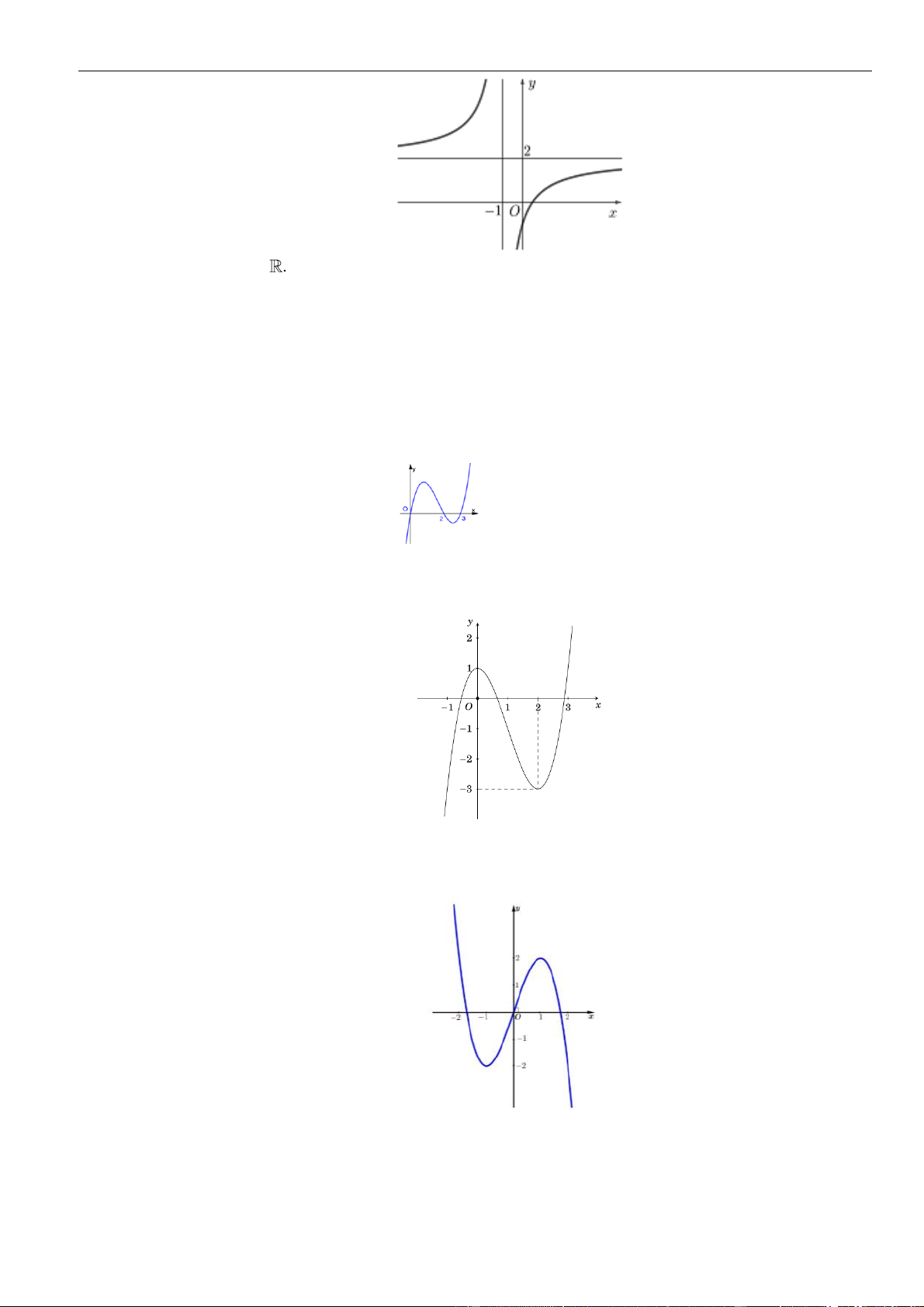
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
A.
0, .yx
B.
0, 1.yx
−
C.
0, 1.yx
−
D.
0, 2.yx
Câu 11: Biết rằng đường cong ở hình bên là đồ thị của một trong các hàm số dưới đây, đó là hàm số nào?
A.
32
36y x x x= − + −
. B.
32
2y x x=−
. C.
32
2y x x= − +
. D.
32
56y x x x= − +
.
Câu 12: Đồ thị được cho bên dưới là đồ thị của hàm số nào?
A.
3
31y x x= − + +
. B.
32
31y x x= − + +
. C.
32
31y x x= − +
. D.
3
31y x x= − +
.
Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên
A.
42
3y x x= − +
. B.
3
3y x x=−
. C.
42
32y x x=−
. D.
3
3y x x= − +
.
Câu 14: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
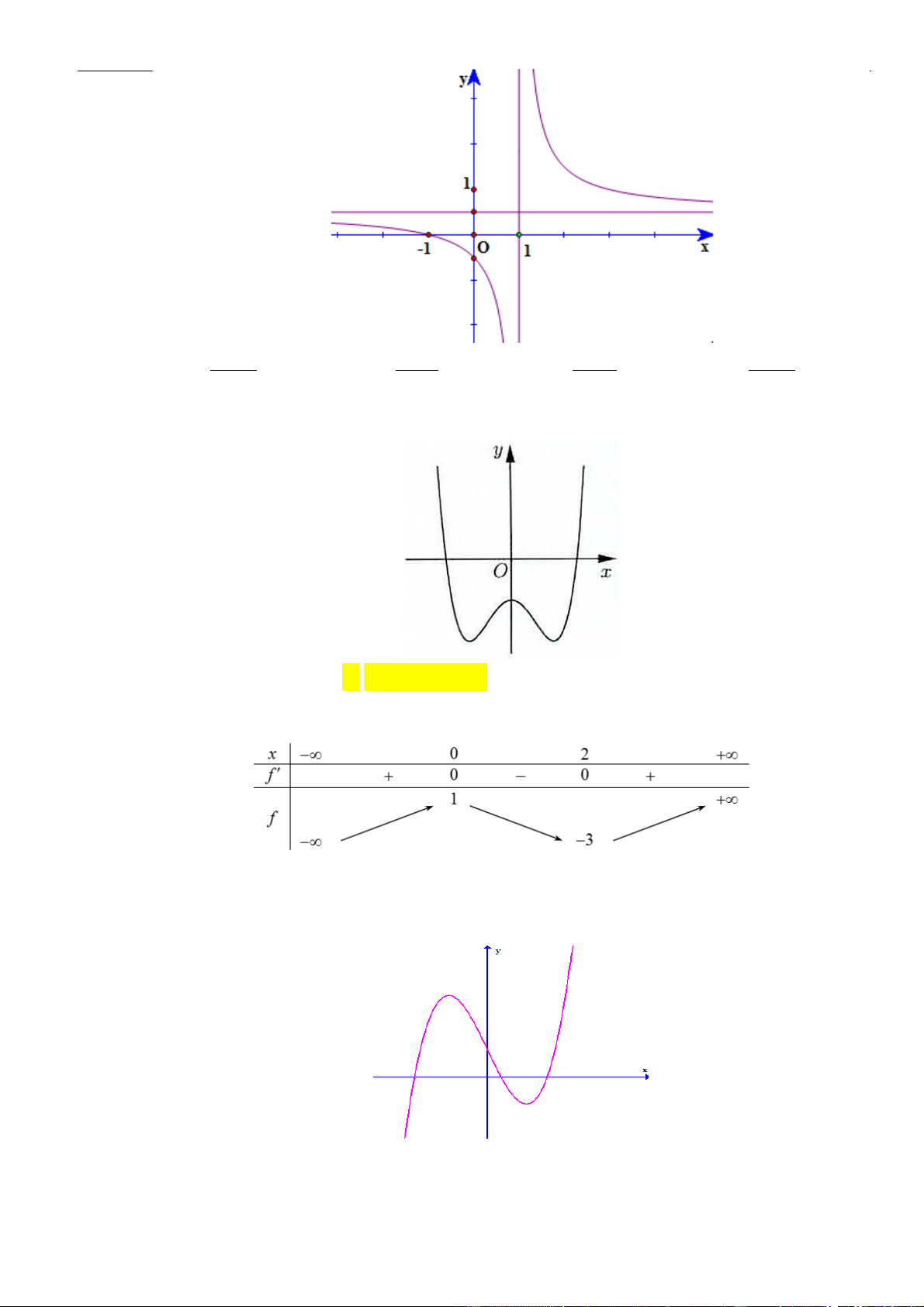
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
A.
24
.
1
x
y
x
−
=
−
B.
2
.
21
x
y
x
+
=
−
C.
2
.
33
x
y
x
=
−
D.
1
.
22
x
y
x
+
=
−
Câu 15: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
42
21= − + −y x x
. B.
42
21= − −y x x
. C.
32
31= − −y x x
. D.
32
31= − + −y x x
.
Câu 16: Hàm số nào dưới đây có bảng biến thiên như hình vẽ sau?
A.
42
21y x x= − +
. B.
32
31y x x= − + +
. C.
32
31y x x= − +
. D.
42
21y x x= − + +
.
Câu 17: Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào sau đây?
A.
42
1y x x= − +
. B.
3
31y x x= − +
. C.
3
31y x x= − + +
. D.
2
1y x x= − + −
.
Câu 18: Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ bên dưới?
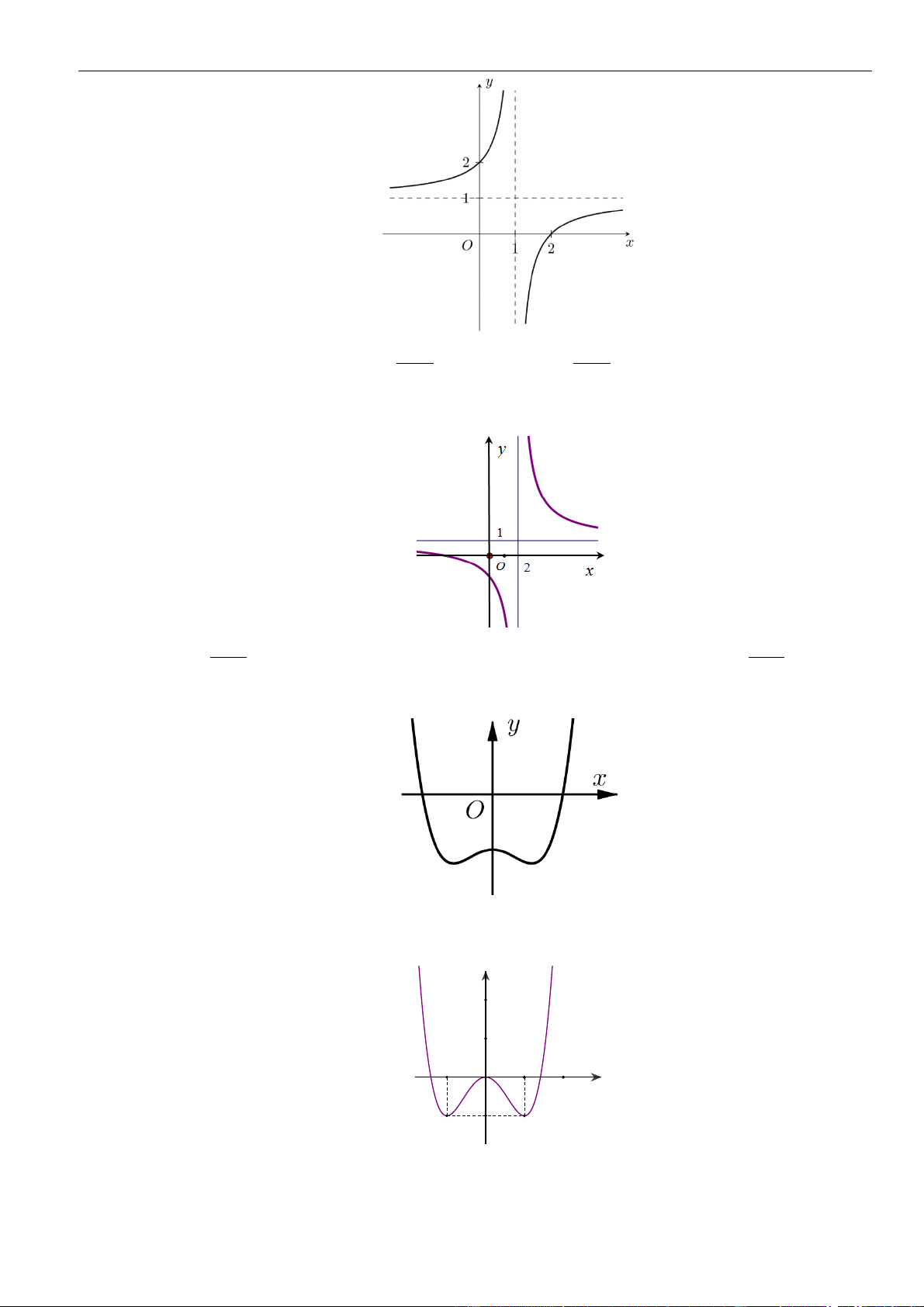
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
3
3 2.y x x= − +
B.
2
.
1
x
y
x
+
=
−
C.
2
.
1
x
y
x
−
=
−
D.
42
5 4.y x x= − + −
Câu 19: Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?
A.
3
2
x
y
x
+
=
−
. B.
3
3y x x=−
. C.
42
42y x x= − +
. D.
3
1
x
y
x
−
=
+
.
Câu 21: Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ bên?
A.
32
1= − + −y x x
. B.
42
1= − −y x x
. C.
32
1= − −y x x
. D.
42
1= − + −y x x
.
Câu 22: Đồ thị hình bên dưới là đồ thị của hàm số nào sau đây?
A.
42
2y x x= − +
. B.
32
2y x x=−
. C.
42
23y x x= − −
. D.
42
2y x x=−
.
Câu 23: Đồ thị được cho ở hình dưới là đồ thị của hàm số nào trong các hàm số dưới đây?
y
x
-1
-1
2
1
O
1
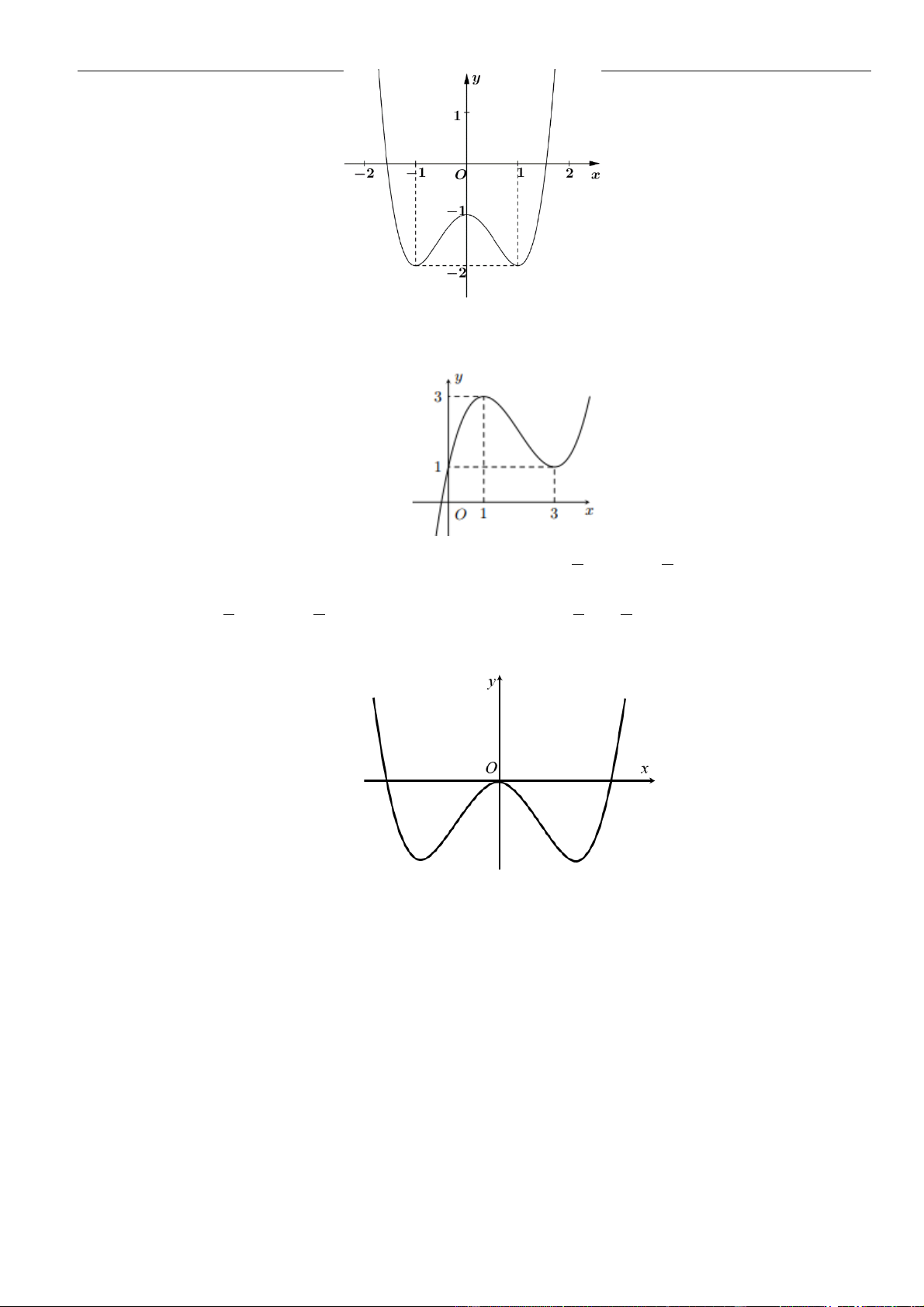
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
A.
42
2y x x=−
. B.
42
2 2 1y x x= − −
. C.
42
222y x x= − −
. D.
42
21y x x= − + +
.
Câu 24: Đường cong trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
32
31y x x= − +
. B.
32
19
31
22
y x x x= − + +
.
C.
32
19
31
22
y x x x= − + + +
. D.
32
13
21
22
y x x x= + − +
.
Câu 25: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên dưới
A.
32
3y x x= − +
. B.
32
3y x x=−
. C.
42
2y x x= − +
. D.
42
2y x x=−
.
Câu 27: Đồ thị sau đây là của hàm số nào?
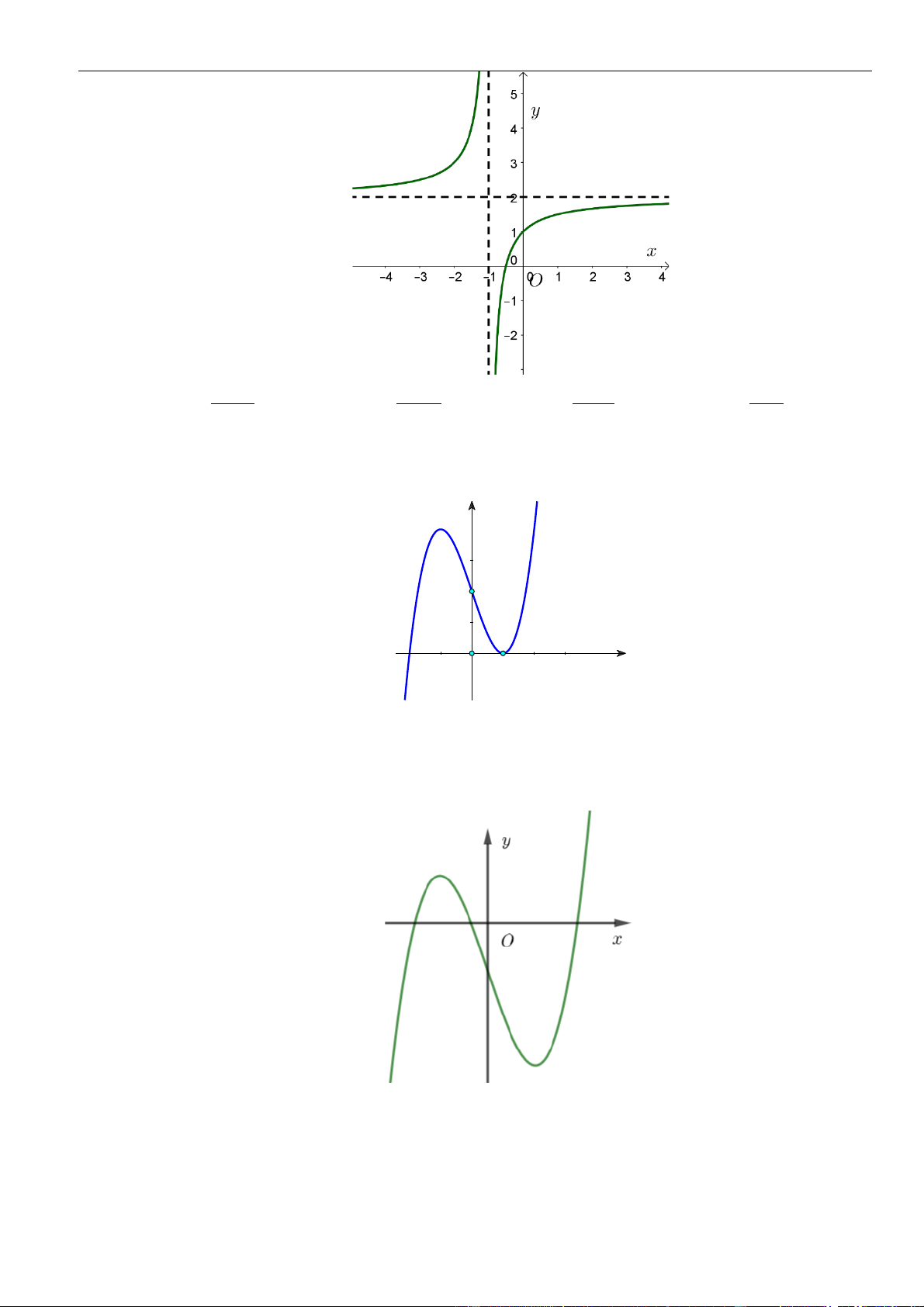
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
A.
21
1
+
=
+
x
y
x
. B.
23
1
+
=
+
x
y
x
. C.
21
1
−
=
−
x
y
x
. D.
1
1
−
=
+
x
y
x
.
Câu 28: Đường cong ở hình bên dưới là đồ thị của một hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây:
Hàm số đó là hàm số nào?
A.
= + +
42
1y x x
. B.
= − +
42
1y x x
. C.
= − + +
32
32y x x
. D.
= − +
3
32y x x
.
Câu 31: Đồ thị của hàm số nào dưới đây có dạng đường cong như hình bên?
A.
42
1y x x= − + −
. B.
3
31y x x= − + −
. C.
3
31y x x= − −
. D.
42
21y x x= − −
.
Câu 32: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số sau?
x
y
O
1
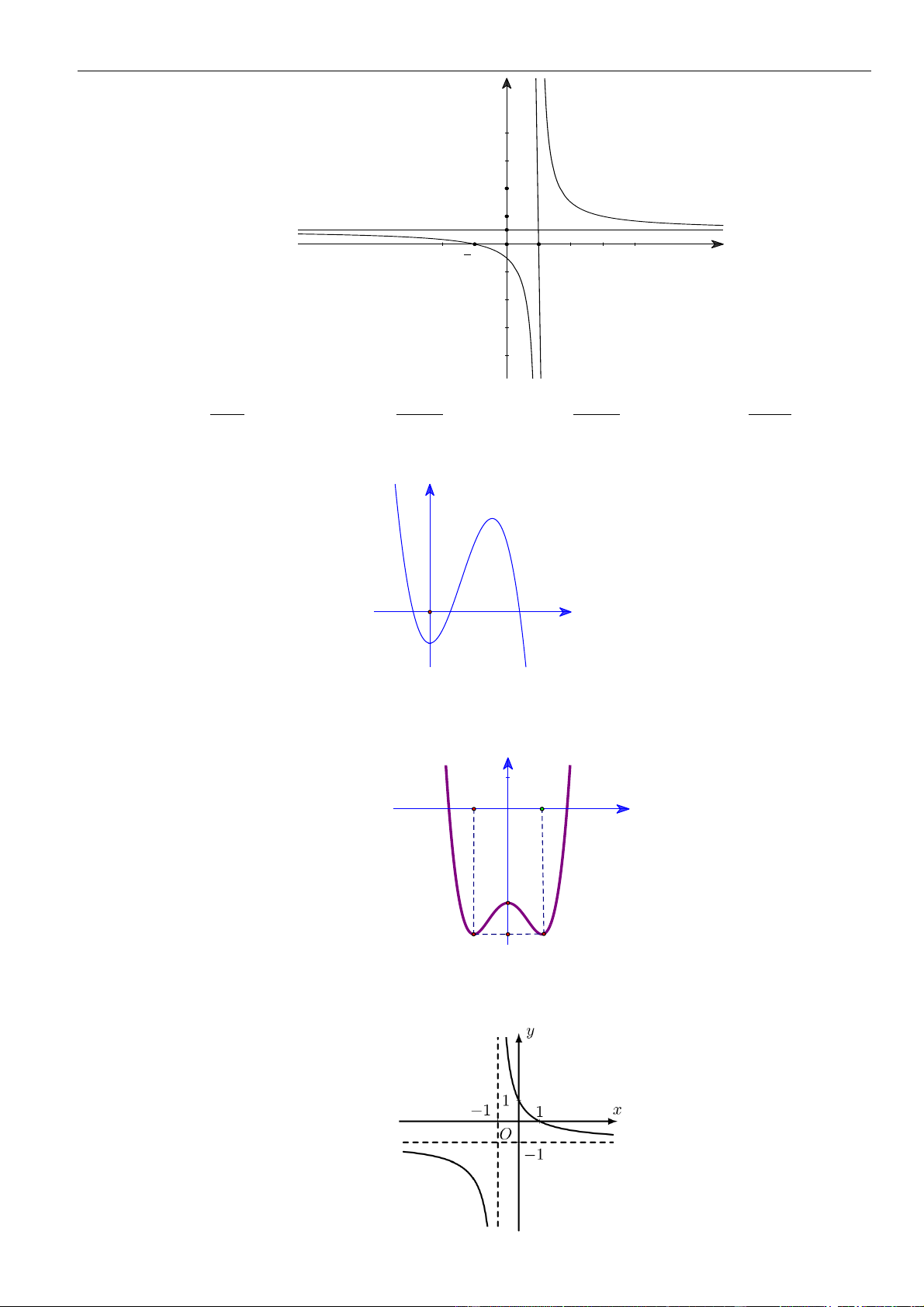
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
A.
1
1
x
y
x
+
=
−
. B.
24
1
x
y
x
−
=
−
. C.
1
22
x
y
x
+
=
−
. D.
2
33
x
y
x
=
−
.
Câu 33: Đồ thị của hàm số nào dưới đây có dạng như hình?
A.
32
31y x x= − −
. B.
43
21y x x= − −
. C.
42
21y x x= − + −
. D.
32
31y x x= − + −
.
Câu 34: Đường cong trong hình dưới đây là đồ thị của hàm số nào?
A.
42
23y x x= − − −
. B.
42
23y x x= + −
. C.
42
3y x x= − + −
. D.
42
23y x x= − −
.
Câu 35: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây.
x
y
2
1
1
1
O
x
y
O
x
y
-4
-3
-1
1
O
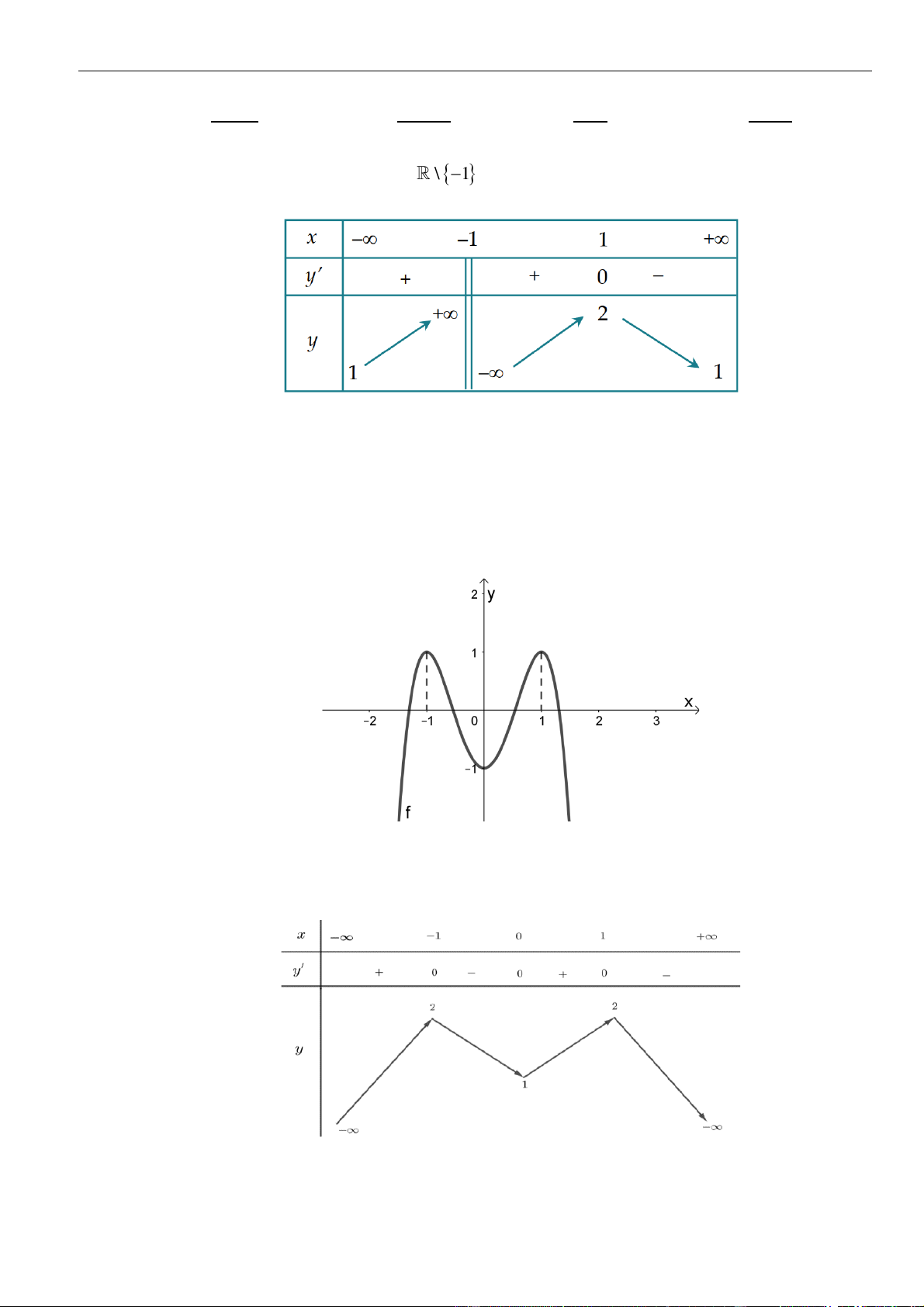
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Hàm số đó là hàm số nào?
A.
3
1
x
y
x
−+
=
+
. B.
21
21
x
y
x
−+
=
+
. C.
1
x
y
x
−
=
+
. D.
1
1
x
y
x
−+
=
+
.
Câu 36: Cho hàm số
( )
y f x=
xác định trên
\1−
, liên tục trên các khoảng xác định của nó và có bảng
biến thiên như hình vẽ.
Khẳng định nào sau đây là đúng?
A. Giá trị lớn nhất của hàm số là
2
.
B. Phương trình
( )
f x m=
có
3
nghiệm thực phân biệt khi và chỉ khi
( )
1;2m
.
C. Hàm số đồng biến trên
( )
;1−
.
D. Đồ thị hàm số có
3
đường tiệm cận.
Câu 38: Hàm số nào sau đây có đồ thị như hình vẽ.
A.
42
2y x x= − +
. B.
42
21y x x= − + −
.
C.
42
2 4 1y x x= − + −
. D.
42
21y x x= − −
.
Câu 39: Hàm số nào sau đây có bảng biến thiên như hình vẽ?
A.
42
2x 1yx= − + +
. B.
32
3x 1yx= − +
. C.
32
3x 1yx= − + +
. D.
42
2x 1yx= − +
Câu 40: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
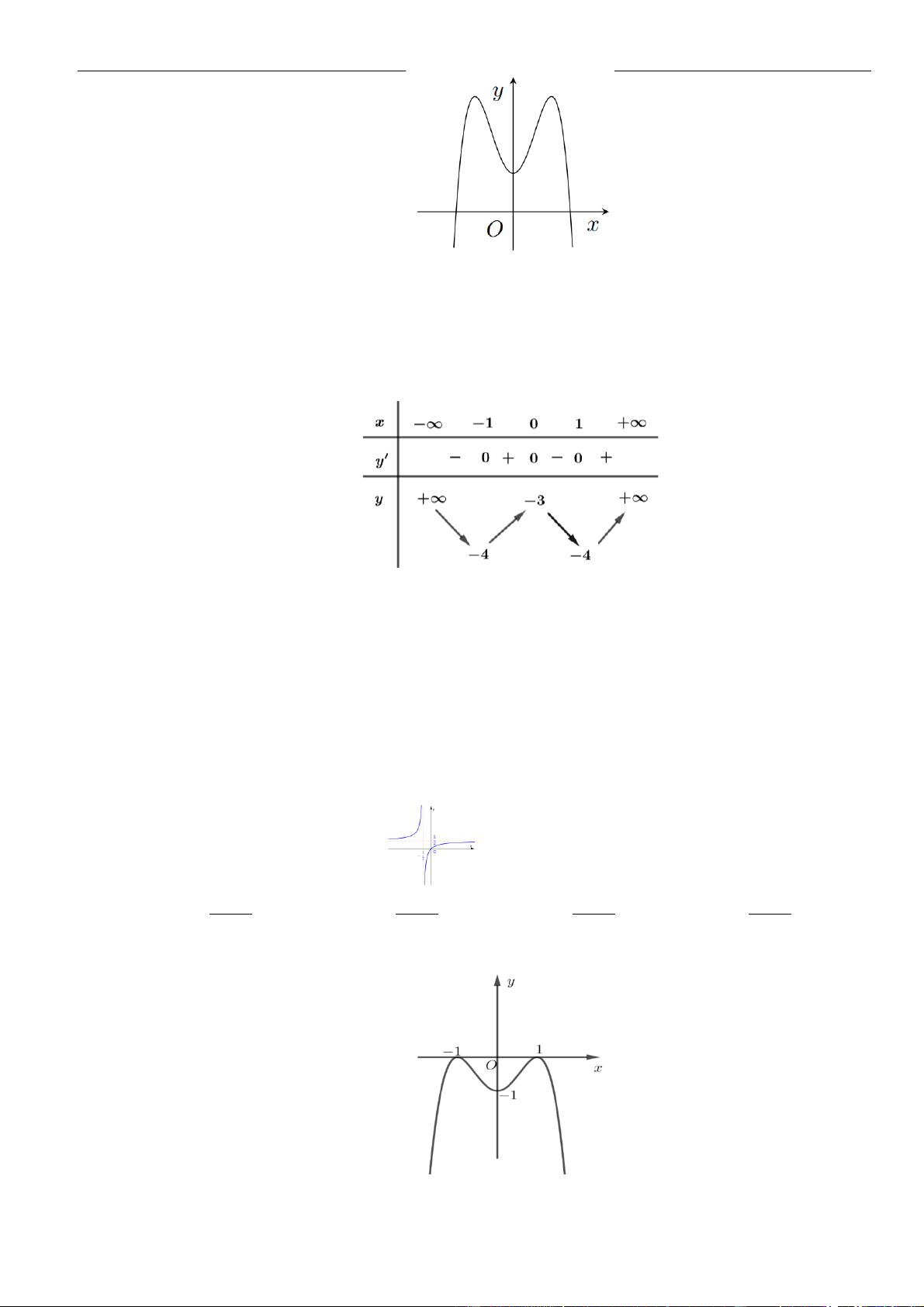
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
A.
42
2 4 1y x x= − +
. B.
42
2 4 1y x x= − + +
. C.
3
2 3 1y x x= − +
. D.
3
2 3 1y x x= − + +
.
Câu 44: Hàm số
( )
y f x=
có đạo hàm trên khoảng
( )
;− +
và có bảng biến thiên dưới đây. Hàm số
( )
y f x=
là một trong bốn hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số
đó là hàm số nào?
A.
42
2 3.y x x= + +
. B.
42
2 3.y x x= + −
. C.
42
2 3.y x x= − + −
. D.
42
2 3.y x x= − −
Câu 45: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
21
x
y
x
=
+
. B.
1
21
x
y
x
+
=
+
. C.
3
21
x
y
x
+
=
+
. D.
1
21
x
y
x
−
=
+
.
Câu 46: Đường cong trong hình bên là đồ thị của hàm số nào?
A.
42
21y x x= − + −
. B.
42
23y x x= − + −
. C.
42
31y x x= − + −
. D.
42
1y x x= − + −
.
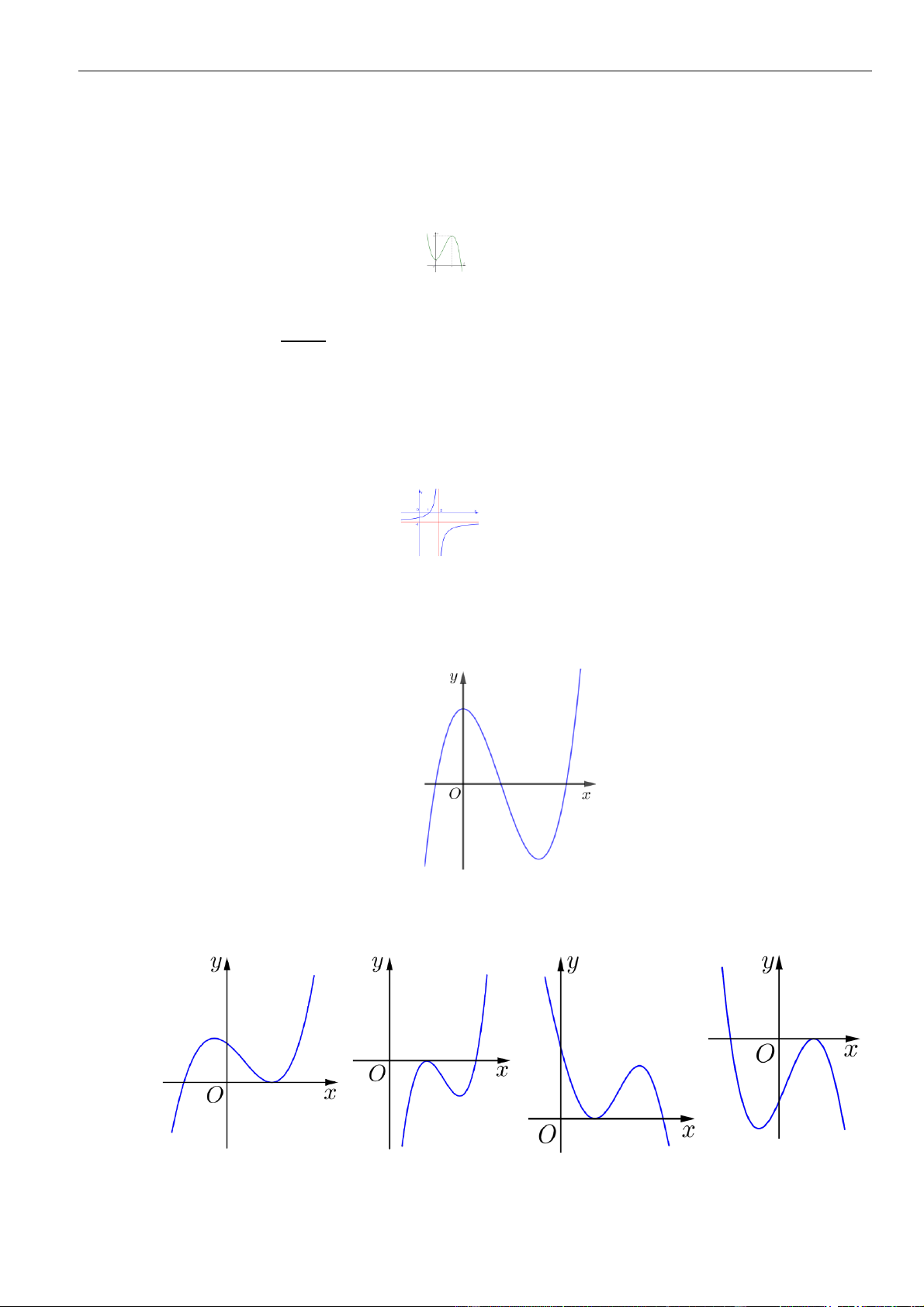
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Câu 47: Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
A.
32
34y x x= − + −
. B.
32
31y x x= − + +
. C.
32
31y x x= − +
. D.
32
21y x x= − + +
.
Câu 48: Cho hàm số
ax b
y
xc
+
=
−
có đồ thị như hình vẽ.
Khi đó tổng
abc++
bằng
A.
3
. B.
0
. C.
2−
. D.
2
.
Câu 49: Đường cong hình sau là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số
nào?
A.
32
32= − + +y x x
. B.
32
32= − +y x x
. C.
42
32= + +y x x
. D.
42
32= − +y x x
.
Câu 50: Hình vẽ nào dưới đây là đồ thị hàm số
( )( )
2
y x c d x= − −
với
0cd
.
Hình 1
Hình 2
Hình 3
Hình 4
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
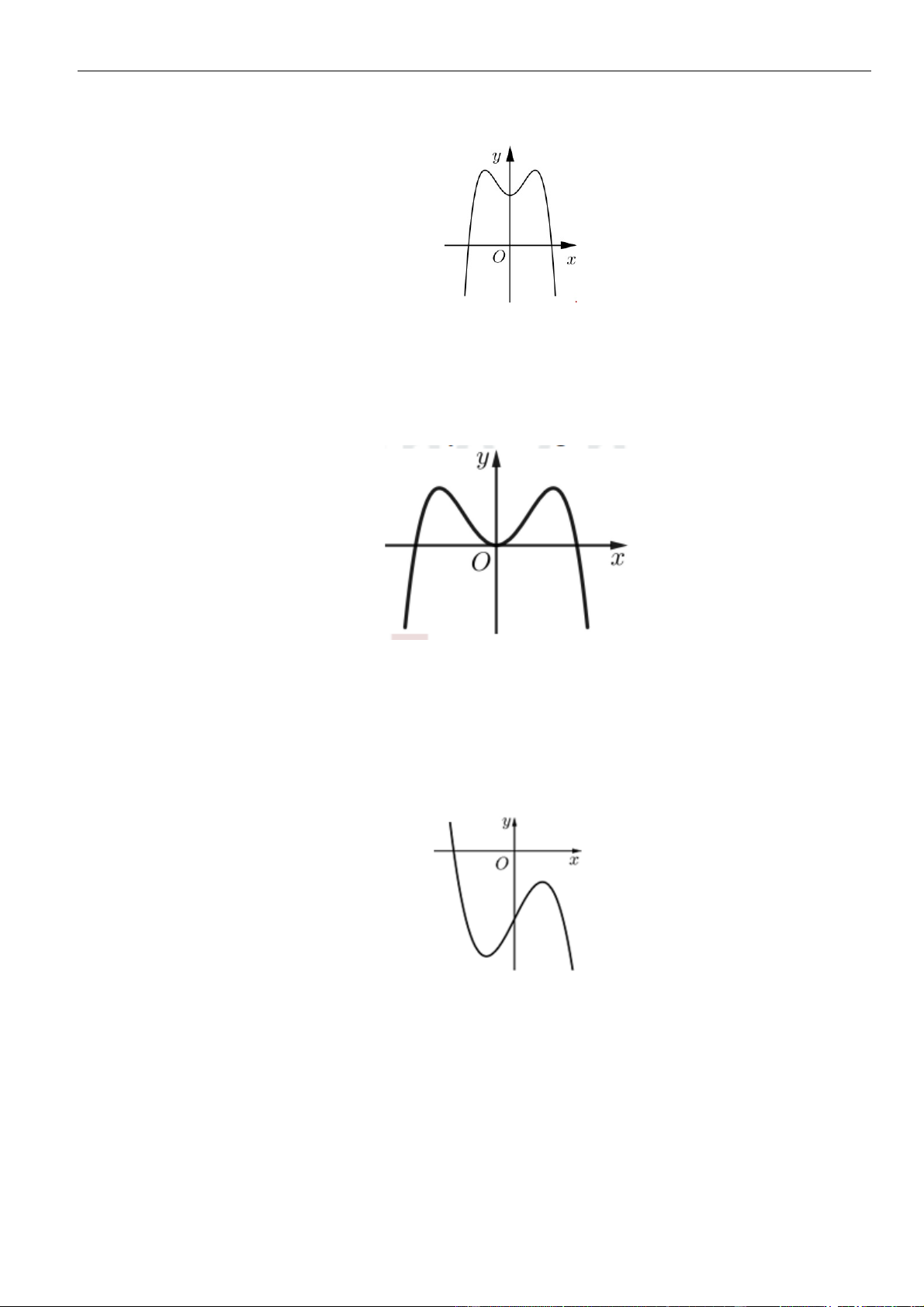
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
22y x x= − + +
. B.
42
22y x x= − +
. C.
32
32y x x= − +
. D.
32
32y x x= − + +
.
Lời giải
Chọn A
Dựa vào đồ thị đã cho, ta thấy đồ thị này là đồ thị hàm số bậc 4 có hệ số
0a
nên chọn A.
Câu 2: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
42
2y x x= − +
. B.
42
2y x x=−
. C.
32
3y x x=−
. D.
32
3y x x= − +
Lời giải
Chọn A
Đồ thị là hàm bậc 4 với a<0 và a.b<0.
Câu 3: Hàm số nào dưới đây có đồ thị như hình vẽ bên?
A.
3
2 2.y x x= − + −
B.
3
22y x x= − + +
. C.
42
22y x x= − + −
. D.
42
22y x x= + −
Lời giải
Chọn A
Nhận thấy đây là dáng đồ thị của hàm số bậc ba
( )
32
0y ax bx cx d a= + + +
nên loại C, D.
Đồ thị cắt trục tung tại điểm có tung độ âm nên chọn A.
Câu 4: Đồ thị hàm số nào dưới đây có dạng nhưng đường cong trong hình
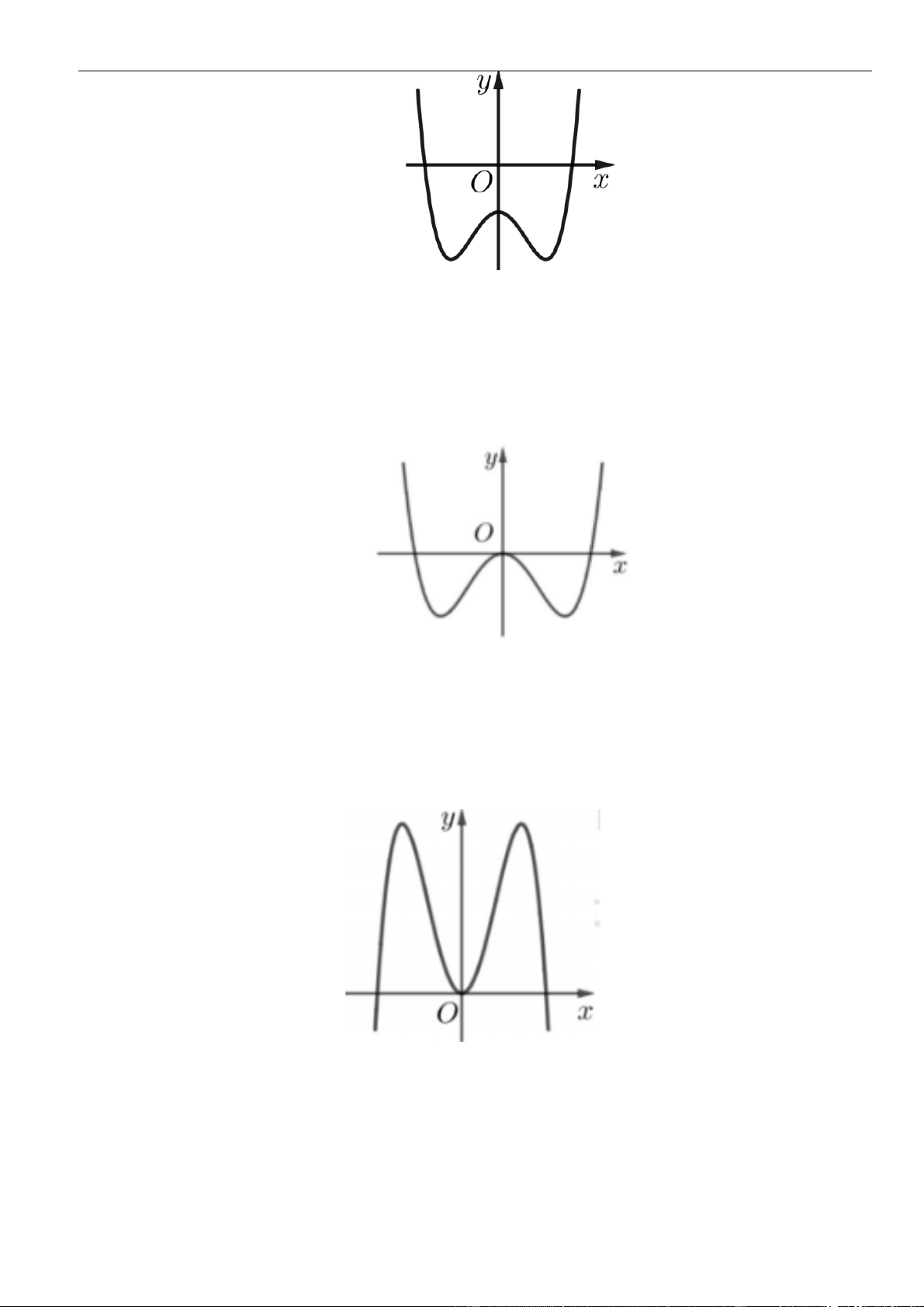
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
A.
42
21y x x= − + −
. B.
42
21y x x= − −
. C.
32
31y x x= − −
. D.
32
31y x x= − + −
.
Lời giải
Chọn B
Đồ thị hàm bậc 4 có hệ số
0a
, cắt trục tung tại điểm có tung độ lớn hơn 0.
Câu 5: Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
32
3y x x=−
. B.
42
2y x x= − +
. C.
32
3y x x= − +
. D.
42
2y x x=−
.
Lời giải
Chọn D
Đây là dáng điệu của hàm trùng phương với hệ số
0a
và hàm số có 3 điểm cực trị (
0ab
).
Câu 6: Đồ thị hàm số nào dưới đây có dạng như hình bên?
A.
42
4y x x= − −
. B.
42
4y x x= − +
. C.
3
2y x x= − +
. D.
3
2y x x=−
.
Lời giải
Chọn B
Ta thấy đồ thị hàm số cắt
Ox
tại
3
điểm phân biệt nên chọn
42
4.y x x= − +
Câu 7: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên dưới?
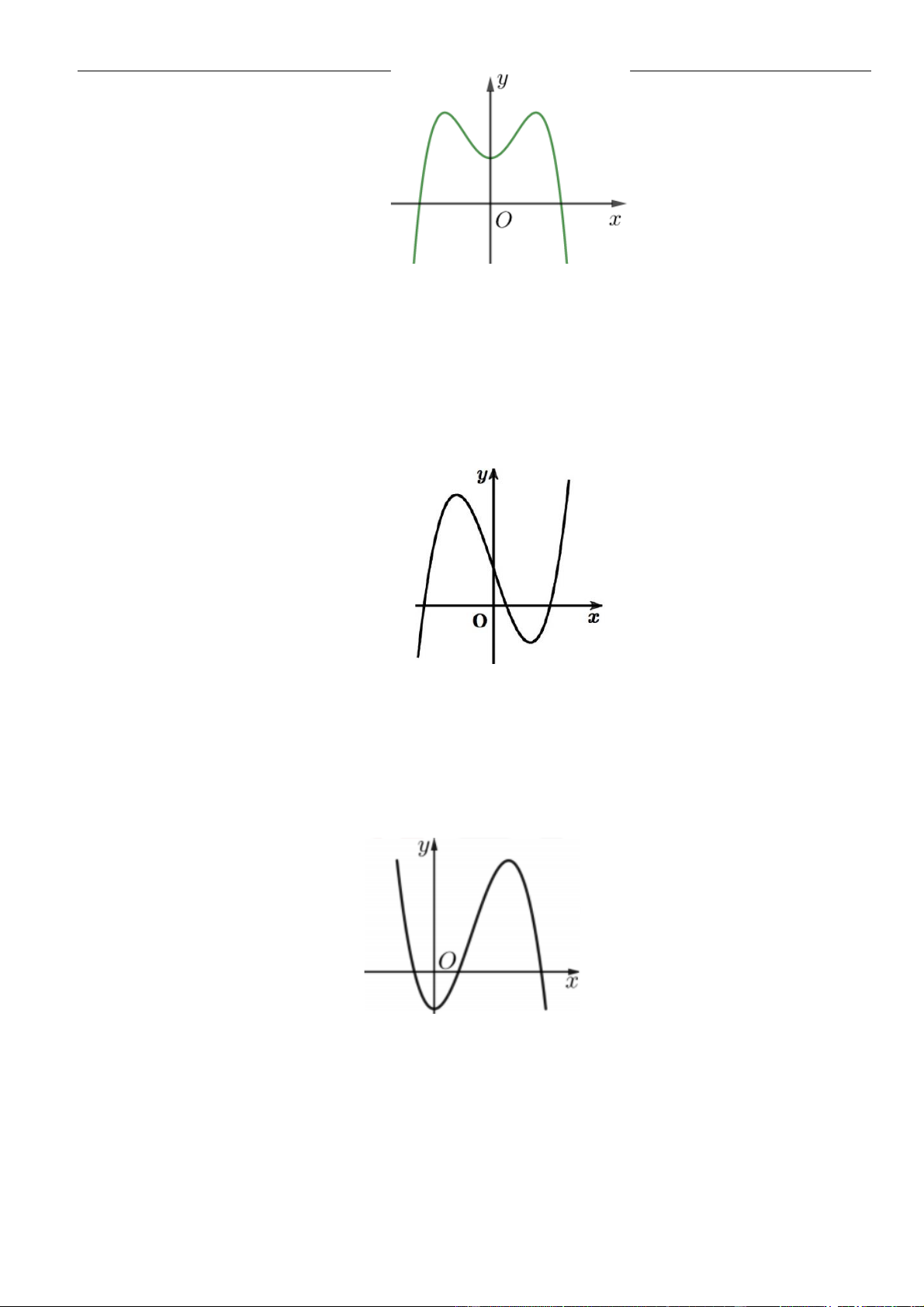
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
A.
= − +
32
31y x x
. B.
= − + +
32
31y x x
. C.
= − + +
42
21y x x
. D.
= − +
42
21y x x
.
Lời giải
Chọn C
Đồ thị đã cho không phải là đồ thị của hàm số bậc ba nên loại đáp án A, B
Mặt khác từ đồ thị ta có
lim
x
y
→
= −
nên loại đáp án D.
Vậy Chọn C
Câu 8: Đường cog ở hình dưới đây là đồ thị của hàm số nào?
A.
3
31y x x= − +
. B.
42
21y x x= − +
. C.
3
31y x x= − + +
. D.
42
21y x x= − + +
.
Lời giải
Chọn A
Dựa vào hình dạng đồ thị ta thấy đây là hàm số bậc ba dạng
32
y ax bx cx d= + + +
với
0a
nên
Chọn A
Câu 9: Đồ thị của hàm số nào dưới đây có dạng như hình bên?
A.
42
21y x x= − + −
. B.
42
21y x x= − −
. C.
32
3 1.y x x= − + −
D.
32
3 1.y x x= − −
Lời giải
Chọn C
Từ hình dáng đồ thị ta nhận ra đây là đồ thị của hàm số bậc ba.
Đồ thị hàm số bậc ba có phần ngoài cùng bên phải đi xuống nên hệ số của hạng tử bậc ba phải
âm.
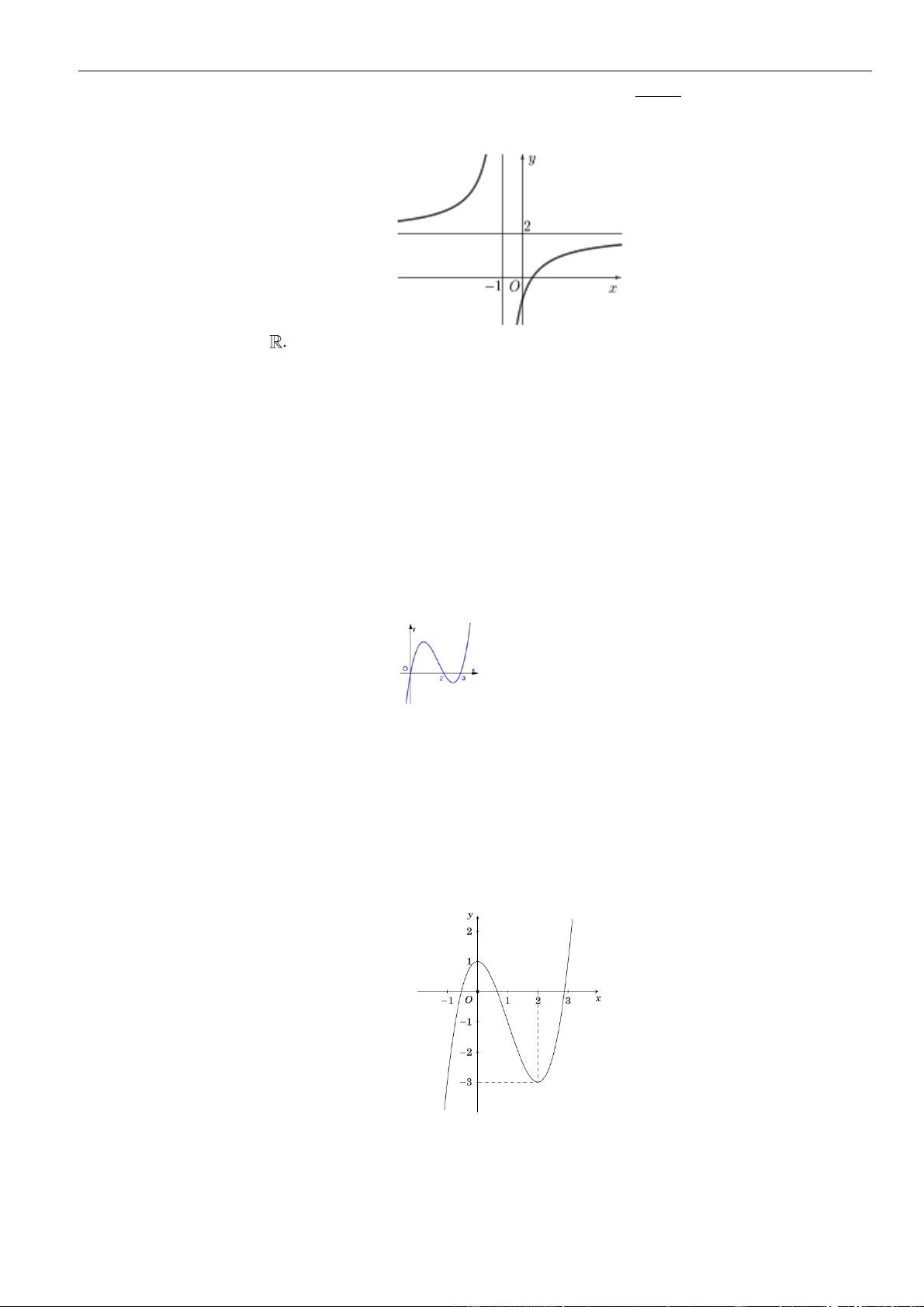
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Câu 10: Đường cong ở hình vẽ dưới đây là đồ thị của hàm số
ax b
y
cx d
+
=
+
với
, , ,a b c d
là các số
thực.Mệnh đề nào dưới đây đúng?
A.
0, .yx
B.
0, 1.yx
−
C.
0, 1.yx
−
D.
0, 2.yx
Lời giải
Chọn B
Từ đồ thị ta thấy hàm số đồng biến trên
( )
;1− −
và
( )
1;− +
, suy ra
0, 1.yx
−
Câu 11: Biết rằng đường cong ở hình bên là đồ thị của một trong các hàm số dưới đây, đó là hàm số nào?
A.
32
36y x x x= − + −
. B.
32
2y x x=−
. C.
32
2y x x= − +
. D.
32
56y x x x= − +
.
Lời giải
Chọn D
Đây là đồ thị hàm số bậc ba
32
y ax bx cx d= + + +
, với hệ số
0a
Loại đáp án A, C.
Đồ thị cắt trục hoành tại điểm
( )
3;0
Chọn đáp án D.
Câu 12: Đồ thị được cho bên dưới là đồ thị của hàm số nào?
A.
3
31y x x= − + +
. B.
32
31y x x= − + +
. C.
32
31y x x= − +
. D.
3
31y x x= − +
.
Lời giải
Chọn B
Từ đồ thị ta thấy đây là đồ thị của hàm số bậc ba với hệ số
0a
nên loại phương án A và B.
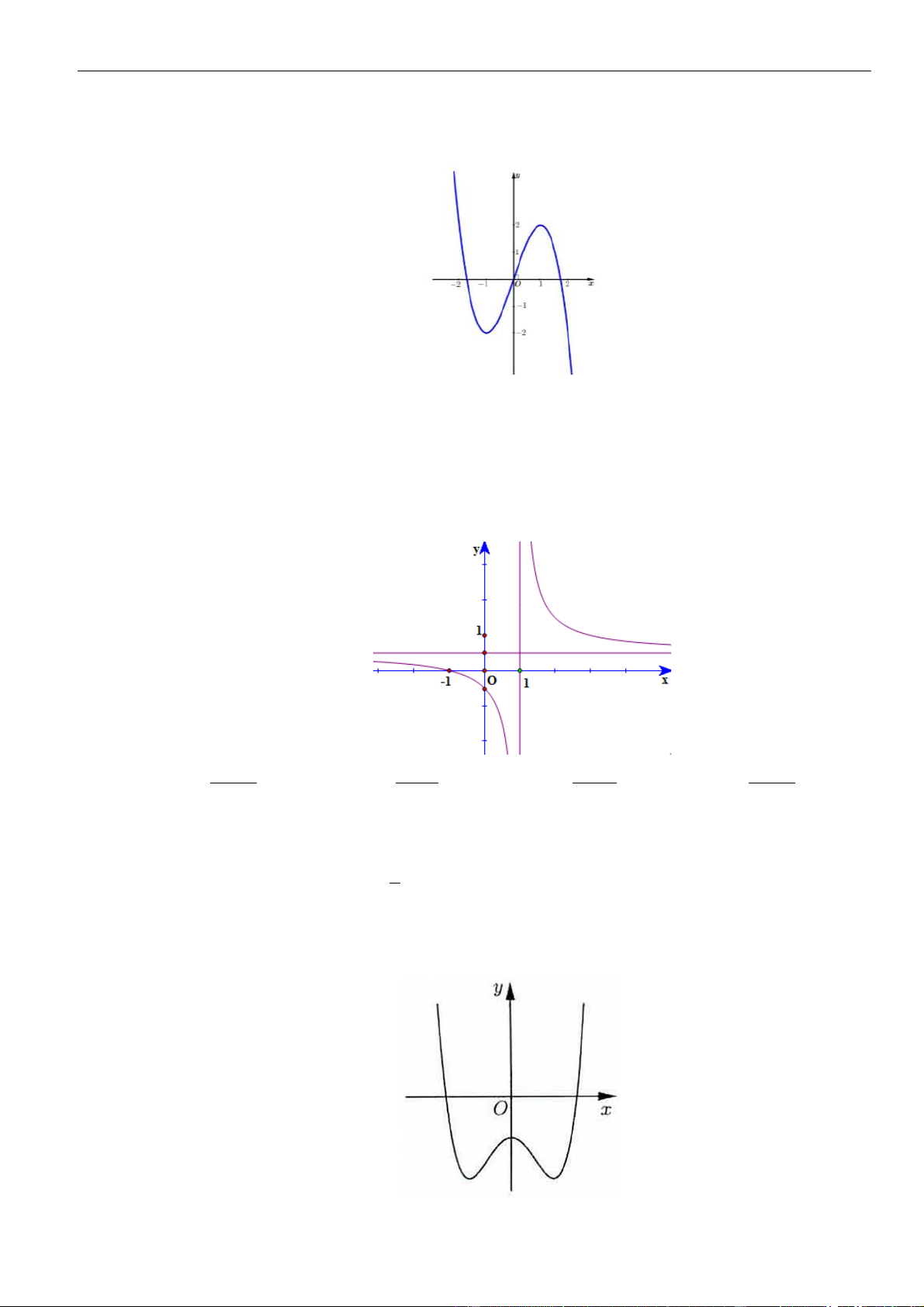
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Mặt khác ta lại thấy hàm số có hai điểm cực trị là
0x =
và
2x =
, do đó trong bốn phương án
chỉ có phương án C thỏa mãn.
Câu 13: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên
A.
42
3y x x= − +
. B.
3
3y x x=−
. C.
42
32y x x=−
. D.
3
3y x x= − +
.
Lời giải
Chọn D
Đồ thị hàm số hình chữ
N
ngược nên của hàm số bậc ba với
0a
, như vậy
3
3xyx= − +
.
Câu 14: Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
24
.
1
x
y
x
−
=
−
B.
2
.
21
x
y
x
+
=
−
C.
2
.
33
x
y
x
=
−
D.
1
.
22
x
y
x
+
=
−
Lời giải
Chọn D
Đường tiệm cận ngang:
1
2
y =
Đường tiệm cận đứng:
1x =
Câu 15: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
42
21= − + −y x x
. B.
42
21= − −y x x
. C.
32
31= − −y x x
. D.
32
31= − + −y x x
.
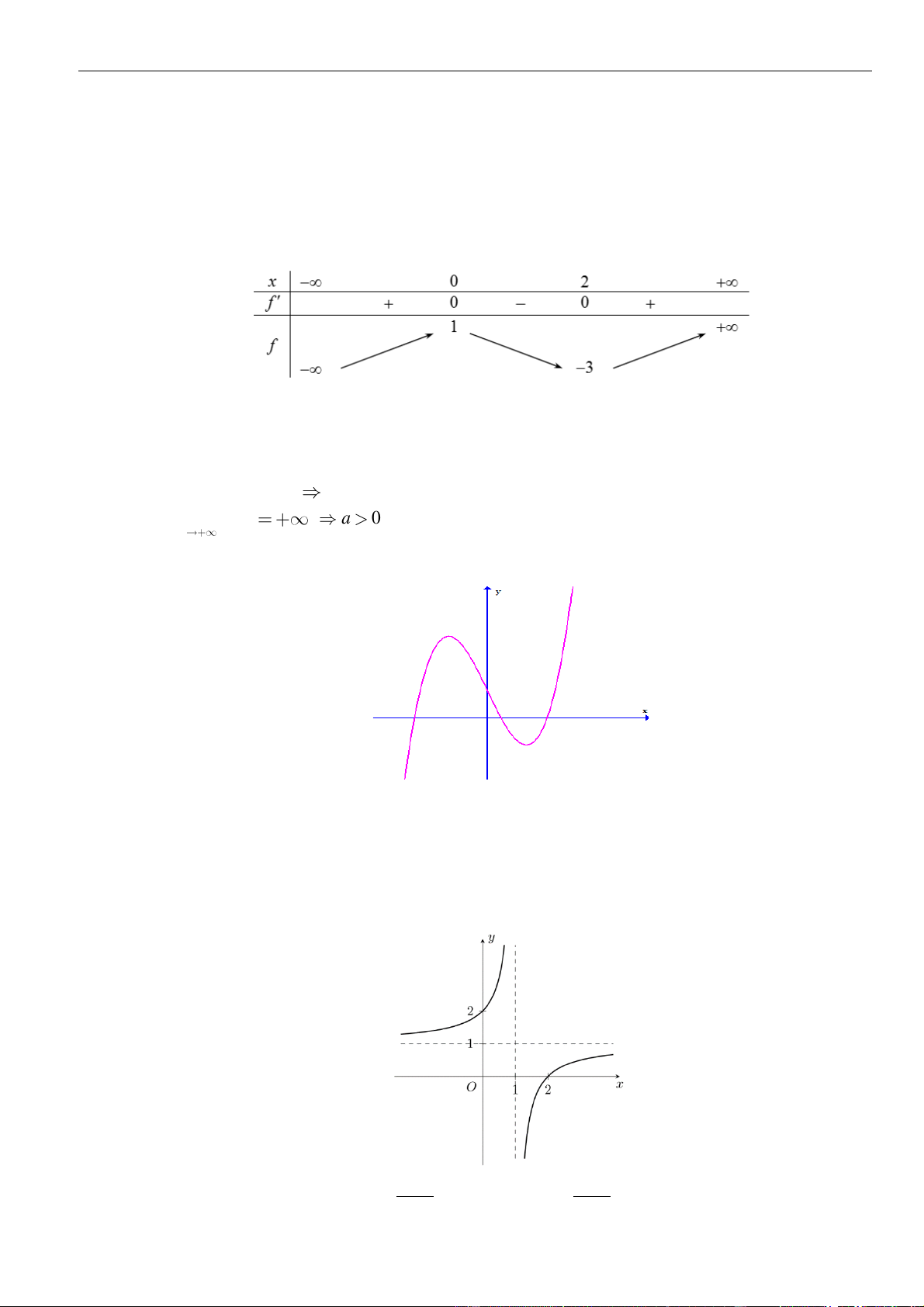
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn B
Dựa vào đồ thị có ba điểm cực trị, nhận thấy đây là đồ thị của hàm đa thức bậc bốn nên loại
phương án C và D
Vì
lim
→+
= +
x
y
nên hệ số
0a
Câu 16: Hàm số nào dưới đây có bảng biến thiên như hình vẽ sau?
A.
42
21y x x= − +
. B.
32
31y x x= − + +
. C.
32
31y x x= − +
. D.
42
21y x x= − + +
.
Lời giải
Chọn C
Từ bảng biến thiên Hàm số bậc ba nên loại câu A và D.
Vì
lim ( )
x
fx
0a
, nên loại câu B.
Câu 17: Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào sau đây?
A.
42
1y x x= − +
. B.
3
31y x x= − +
. C.
3
31y x x= − + +
. D.
2
1y x x= − + −
.
Lời giải
Chọn B
Dựa vào đồ thị ta nhận thấy đồ thị là của hàm số bậc 3 có hệ số
0a
. Nên Chọn B
Câu 18: Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ bên dưới?
A.
3
3 2.y x x= − +
B.
2
.
1
x
y
x
+
=
−
C.
2
.
1
x
y
x
−
=
−
D.
42
5 4.y x x= − + −
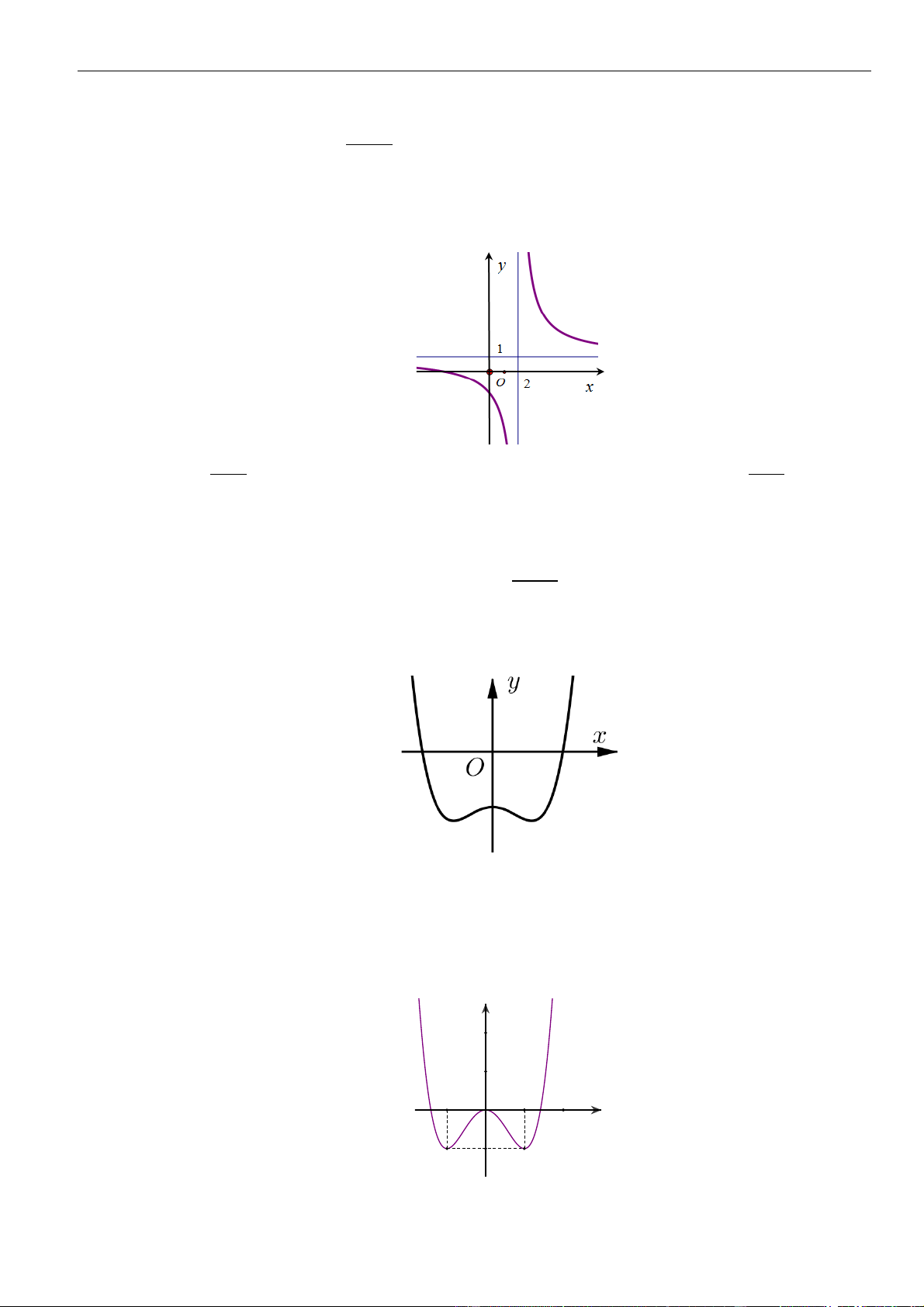
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Lời giải
Chọn C
Hàm số trên có dạng
ax b
y
cx d
+
=
+
nên loại
,AD
.
Ta có
( )
02y =
nên loại
B
.
Câu 19: Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?
A.
3
2
x
y
x
+
=
−
. B.
3
3y x x=−
. C.
42
42y x x= − +
. D.
3
1
x
y
x
−
=
+
.
Lời giải
Chọn A
Đồ thị trong hình vẽ là của hàm số có dạng
ax b
y
cx d
+
=
+
Loại B, C.
Đồ thị trong hàm vẽ nghịch biến trên từng khoảng
( )
;2−
và
( )
2;+
Chọn A
Câu 21: Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ bên?
A.
32
1= − + −y x x
. B.
42
1= − −y x x
. C.
32
1= − −y x x
. D.
42
1= − + −y x x
.
Lời giải
Chọn B
Dựa vào hình dáng đồ thị suy ra đồ thị là đồ thị của hàm số bậc bốn có hệ số
0a
.
Câu 22: Đồ thị hình bên dưới là đồ thị của hàm số nào sau đây?
A.
42
2y x x= − +
. B.
32
2y x x=−
. C.
42
23y x x= − −
. D.
42
2y x x=−
.
Lời giải
y
x
-1
-1
2
1
O
1
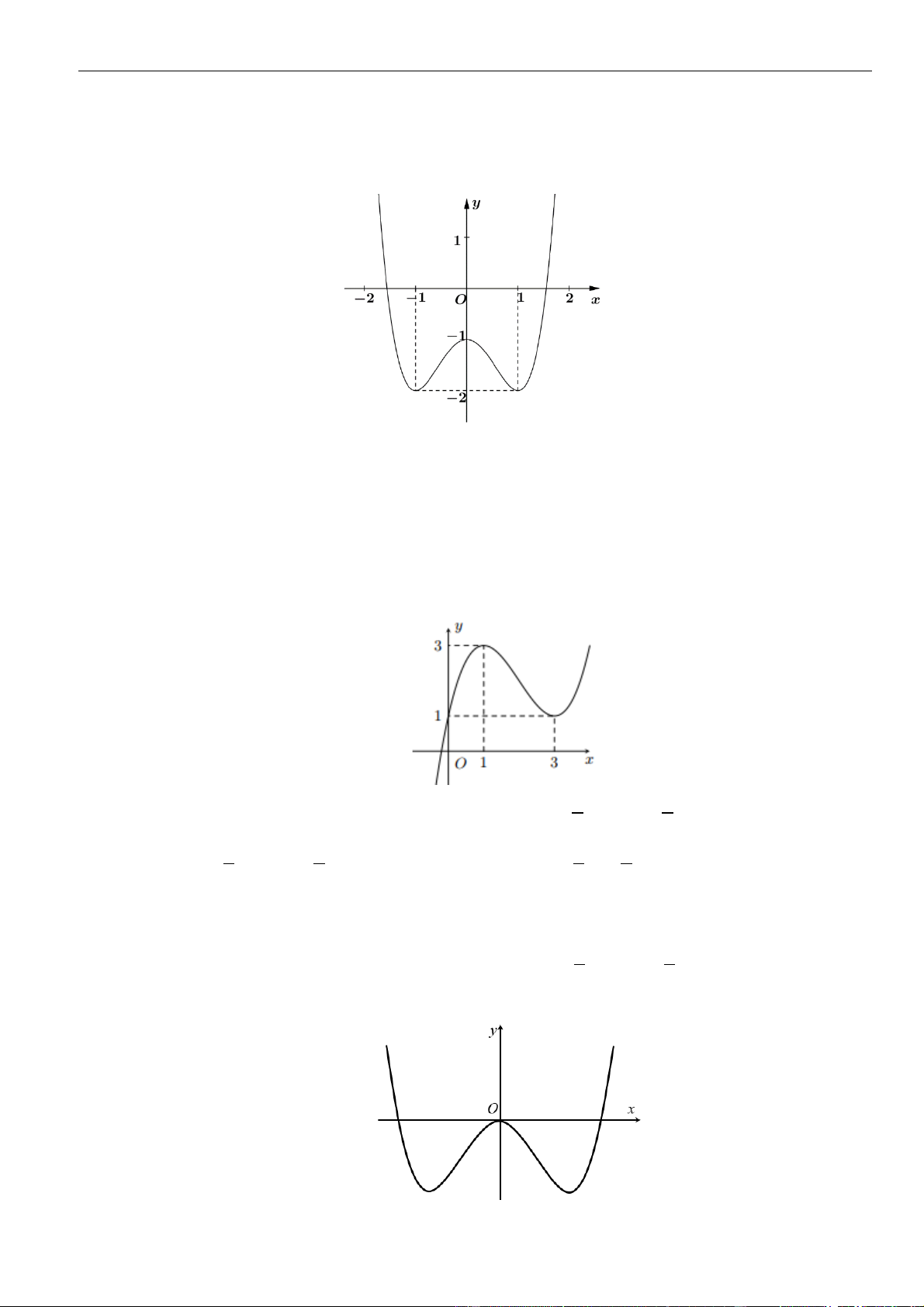
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Chọn D
Dựa vào đồ thị hàm số, ta thấy nhánh cuối của đồ thị đi lên nên hệ số
0a
và cắt trục
Oy
tại
điểm
O
suy ra
0c =
.
Câu 23: Đồ thị được cho ở hình dưới là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
42
2y x x=−
. B.
42
2 2 1y x x= − −
. C.
42
222y x x= − −
. D.
42
21y x x= − + +
.
Lời giải
Chọn B
Từ đồ thị ta thấy đây là đồ thị của hàm số trùng phương với hệ số
0a
, nên loại đáp án D.
Mặt khác hàm số đạt cực tiểu tại
1x =
và
1x =−
và giá trị cực tiểu
( ) ( )
1 1 2yy= − = −
, nên ta
Chọn B
Câu 24: Đường cong trong hình bên là đồ thị của hàm số nào trong các hàm số dưới đây?
A.
32
31y x x= − +
. B.
32
19
31
22
y x x x= − + +
.
C.
32
19
31
22
y x x x= − + + +
. D.
32
13
21
22
y x x x= + − +
.
Lời giải
Chọn B
Đồ thị hàm số đi qua điểm
( )
1;3
nên chỉ có hàm số
32
19
31
22
y x x x= − + +
thỏ mãn.
Câu 25: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên dưới
A.
32
3y x x= − +
. B.
32
3y x x=−
. C.
42
2y x x= − +
. D.
42
2y x x=−
.
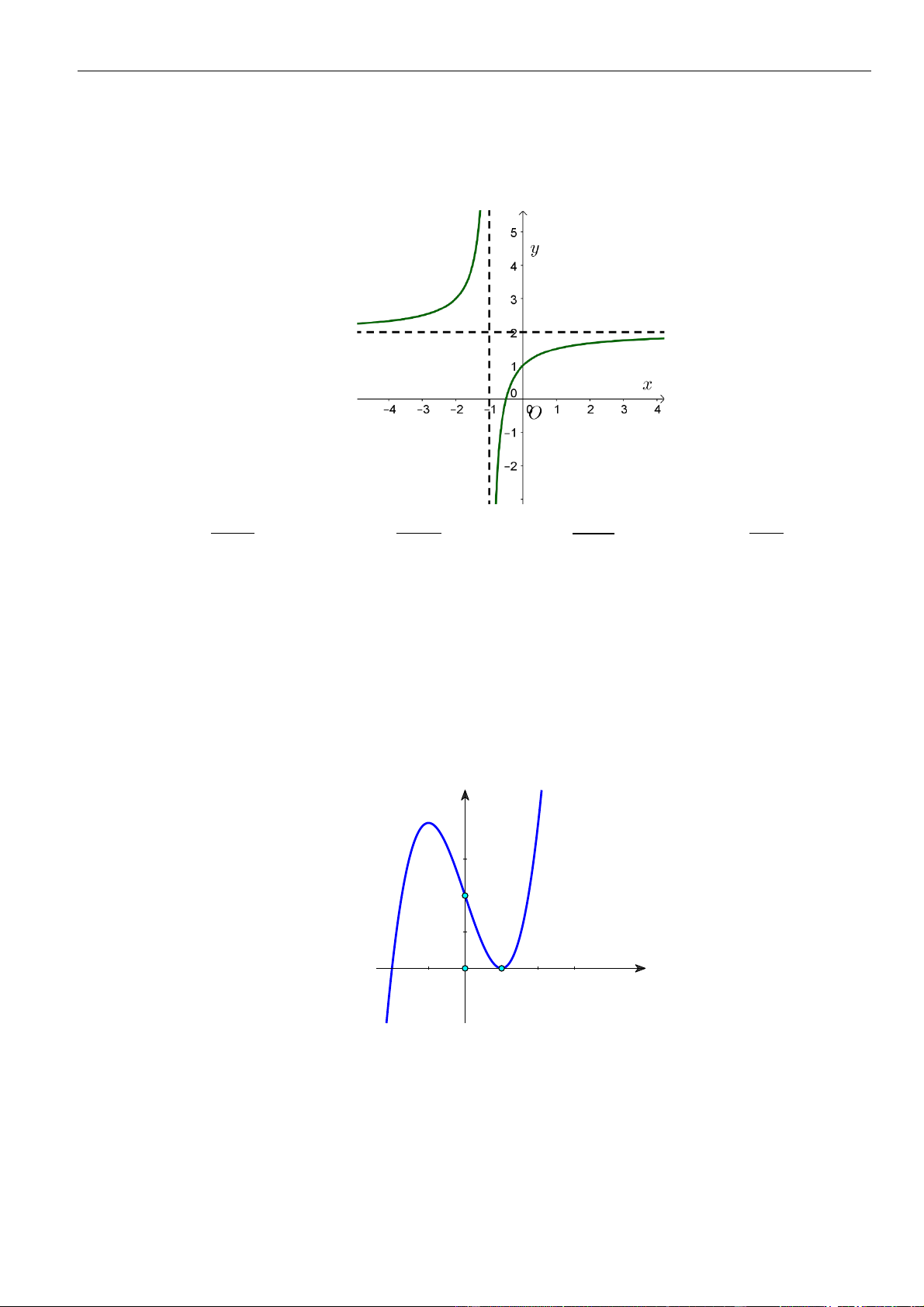
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Lời giải
Chọn D
Dựa vào đồ thị và các phương án trả lời ta có đồ thị đã cho là đồ thị của hàm số
42
y ax bx c= + +
với hệ số
0a
nên chọn D.
Câu 27: Đồ thị sau đây là của hàm số nào?
A.
21
1
+
=
+
x
y
x
. B.
23
1
+
=
+
x
y
x
. C.
21
1
−
=
−
x
y
x
. D.
1
1
−
=
+
x
y
x
.
Lời giải
Chọn A
Tiệm cận đứng:
1=−x
Tiệm cận ngang:
2=y
Đồ thị hàm số cắt trục tung tại
( )
0;1A
.
Câu 28: Đường cong ở hình bên dưới là đồ thị của một hàm số được liệt kê ở bốn phương án A, B, C, D
dưới đây:
Hàm số đó là hàm số nào?
A.
= + +
42
1y x x
. B.
= − +
42
1y x x
. C.
= − + +
32
32y x x
. D.
= − +
3
32y x x
.
Lời giải
Chọn D
Câu 31: Đồ thị của hàm số nào dưới đây có dạng đường cong như hình bên?
x
y
O
1
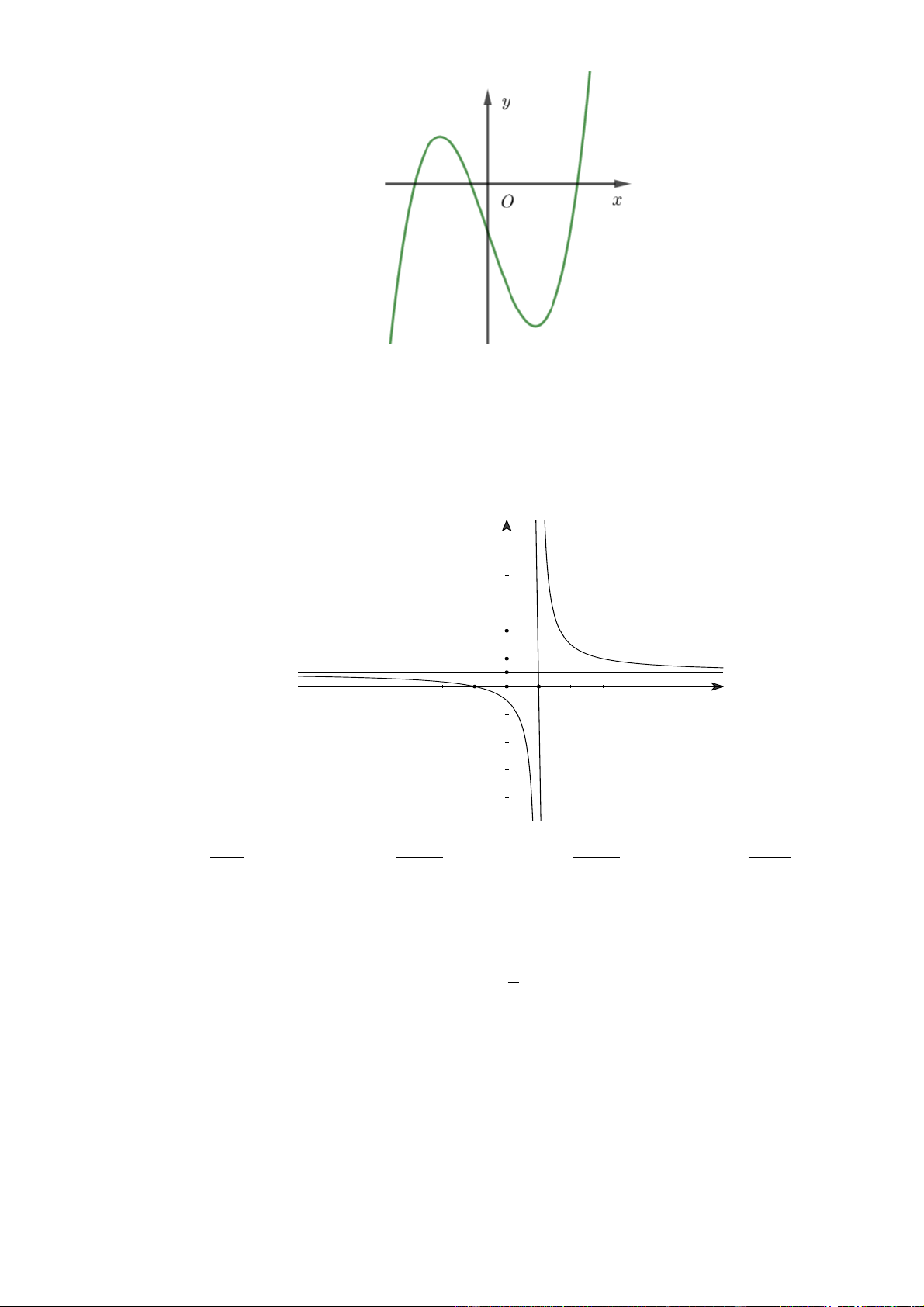
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
A.
42
1y x x= − + −
. B.
3
31y x x= − + −
. C.
3
31y x x= − −
. D.
42
21y x x= − −
.
Lời giải
Chọn C
Ta thấy hỉnh vẽ là đồ thị của hàm bậc 3, loại A, D.
Lại có nhánh cuối củng của đồ thị đi lên nên
0a
Chọn C
Câu 32: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số sau?
A.
1
1
x
y
x
+
=
−
. B.
24
1
x
y
x
−
=
−
. C.
1
22
x
y
x
+
=
−
. D.
2
33
x
y
x
=
−
.
Lời giải
Chọn C
Dựa vào đò thị hàm số ta thấy :
Đồ thị hàm số có đường tiệm cận ngang là
1
2
y =
và đường tiệm cận đứng là
1x =
.
Câu 33: Đồ thị của hàm số nào dưới đây có dạng như hình?
x
y
2
1
1
1
O
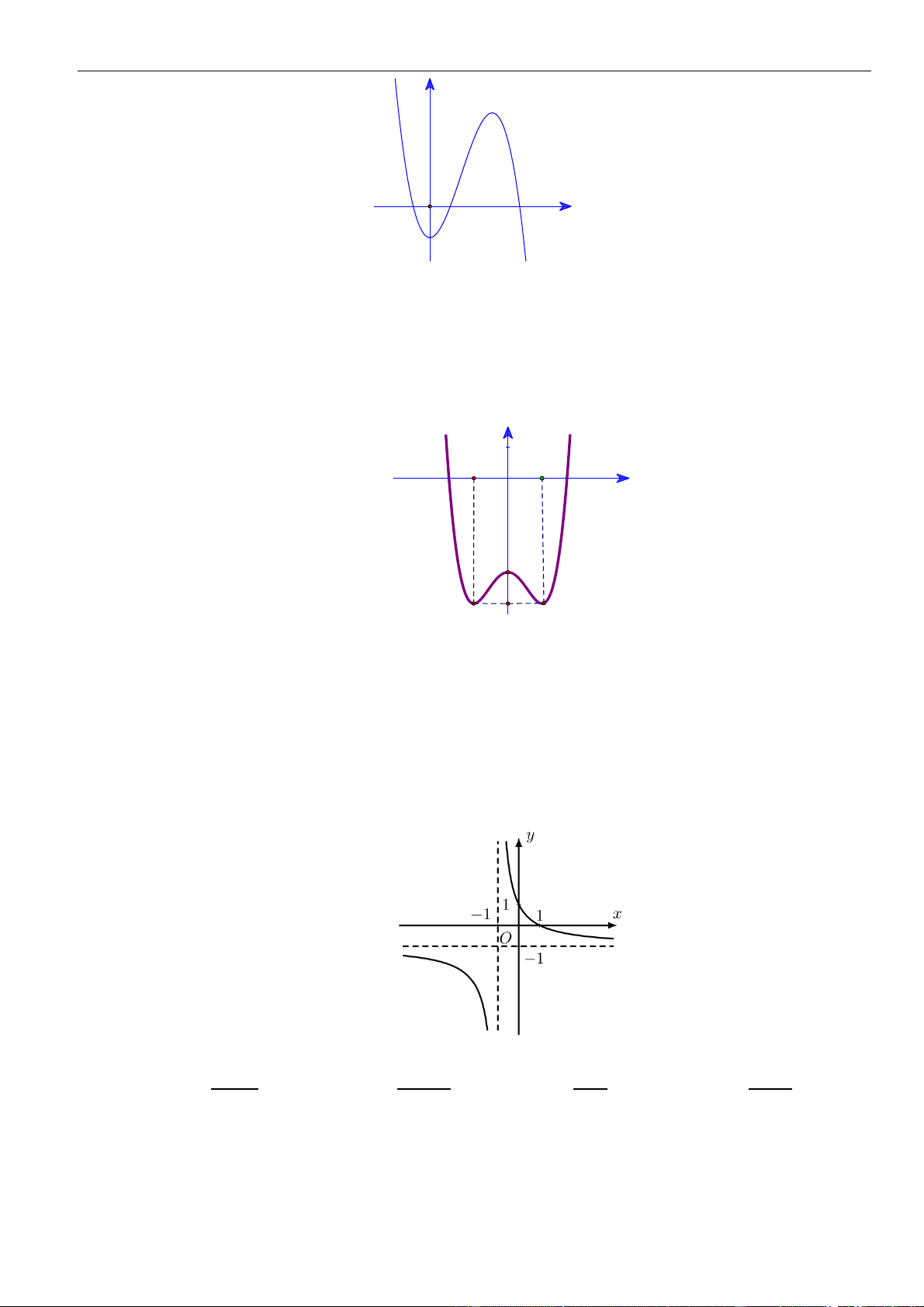
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
A.
32
31y x x= − −
. B.
43
21y x x= − −
. C.
42
21y x x= − + −
. D.
32
31y x x= − + −
.
Lời giải
Chọn D
Đồ thị có dạng của một hàm số bậc ba, nhánh cuối đi xuống nên
0a
. Do đó Chọn D
Câu 34: Đường cong trong hình dưới đây là đồ thị của hàm số nào?
A.
42
23y x x= − − −
. B.
42
23y x x= + −
. C.
42
3y x x= − + −
. D.
42
23y x x= − −
.
Lời giải
Chọn D
Từ đồ thị và các phương án trả lời ta thấy đây là đồ thị của hàm số bậc 4 trùng phương với hệ số
của
4
x
dương, đồ thị hàm số đi qua điểm
1
4
x
y
=
=−
nên ta chọn phương án. D.
Câu 35: Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây.
Hàm số đó là hàm số nào?
A.
3
1
x
y
x
−+
=
+
. B.
21
21
x
y
x
−+
=
+
. C.
1
x
y
x
−
=
+
. D.
1
1
x
y
x
−+
=
+
.
Lời giải
Chọn D
Ta có
lim lim 1
xx
yy
→+ →−
= = −
và
( ) ( )
11
lim , lim
xx
yy
+−
→ − → −
= + = −
nên đồ thị hàm số có tiệm cận đứng
và tiệm cận ngang là
1, 1xy= − = −
suy ra loại. B.
x
y
O
x
y
-4
-3
-1
1
O
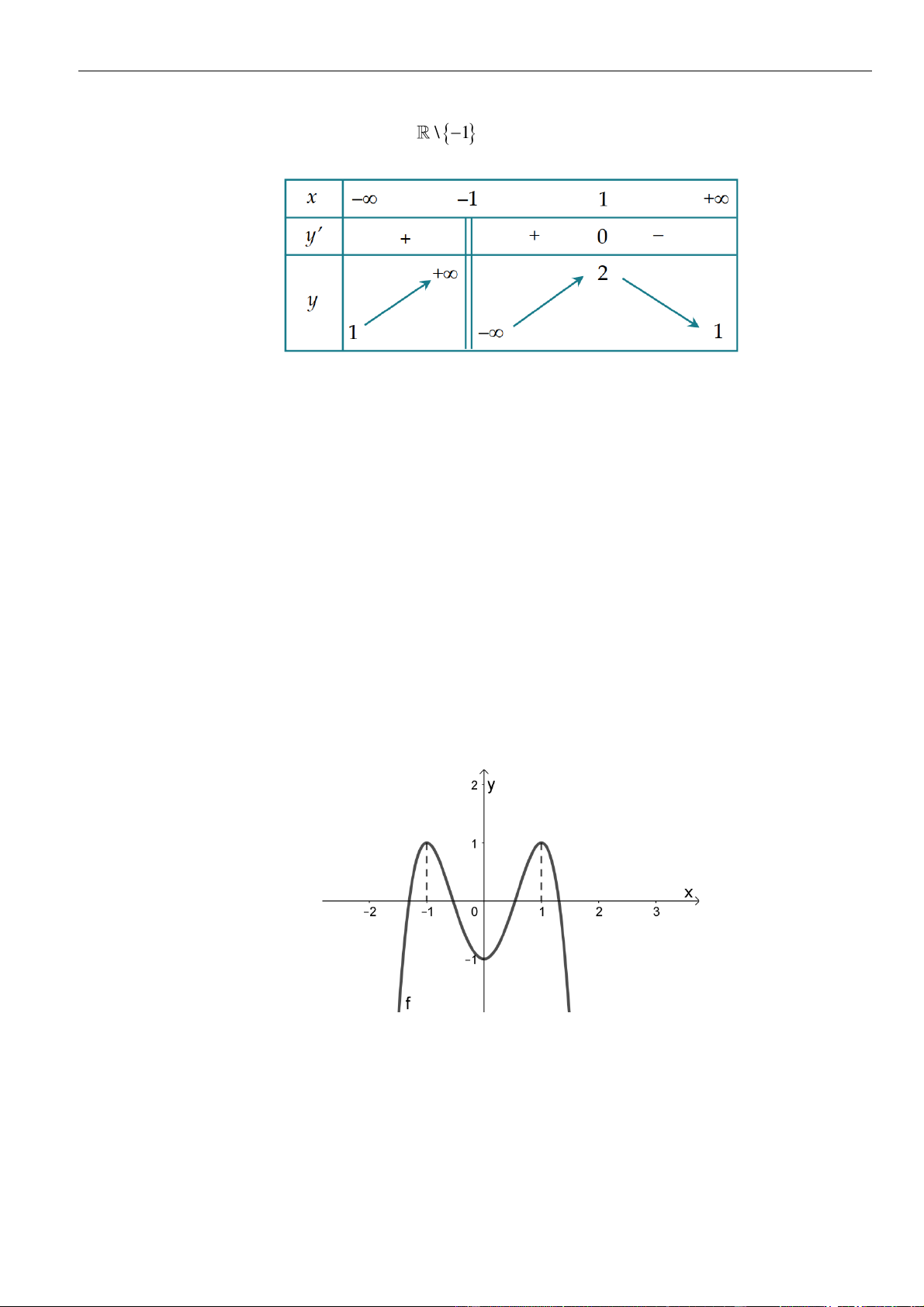
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Đồ thị hàm số đi qua điểm
( )
1;0
nên loại A,C.
Câu 36: Cho hàm số
( )
y f x=
xác định trên
\1−
, liên tục trên các khoảng xác định của nó và có bảng
biến thiên như hình vẽ.
Khẳng định nào sau đây là đúng?
A. Giá trị lớn nhất của hàm số là
2
.
B. Phương trình
( )
f x m=
có
3
nghiệm thực phân biệt khi và chỉ khi
( )
1;2m
.
C. Hàm số đồng biến trên
( )
;1−
.
D. Đồ thị hàm số có
3
đường tiệm cận.
Lời giải
Chọn B
Đáp án A sai: Hàm số không có giá trị lớn nhất, vì
1
lim
x
y
−
→−
= +
.
Đáp án B đúng: Phương trình
( )
f x m=
có
3
nghiệm thực phân biệt khi và chỉ khi
12m
.
Đáp án C sai: Hàm số đồng biến trên các khoảng
( )
;1− −
;
( )
1;1−
.
Đáp án D sai: Đồ thị hàm số có
2
đường tiệm cận là
1x =−
;
1y =
vì
lim 1
x
y
→
=
và
1
lim
x
y
−
→−
= +
;
1
lim
x
y
+
→−
= −
.
Câu 38: Hàm số nào sau đây có đồ thị như hình vẽ.
A.
42
2y x x= − +
. B.
42
21y x x= − + −
.
C.
42
2 4 1y x x= − + −
. D.
42
21y x x= − −
.
Lời giải
Chọn C
Vì đồ thị hàm số đi qua diểm có tọa độ
( )
0; 1−
nên loại A.
Vì đồ thị hàm số có điểm cực trị là
( ) ( )
1;1 ; 1;1−
nên loại B, D.
Vậy đáp án là C.
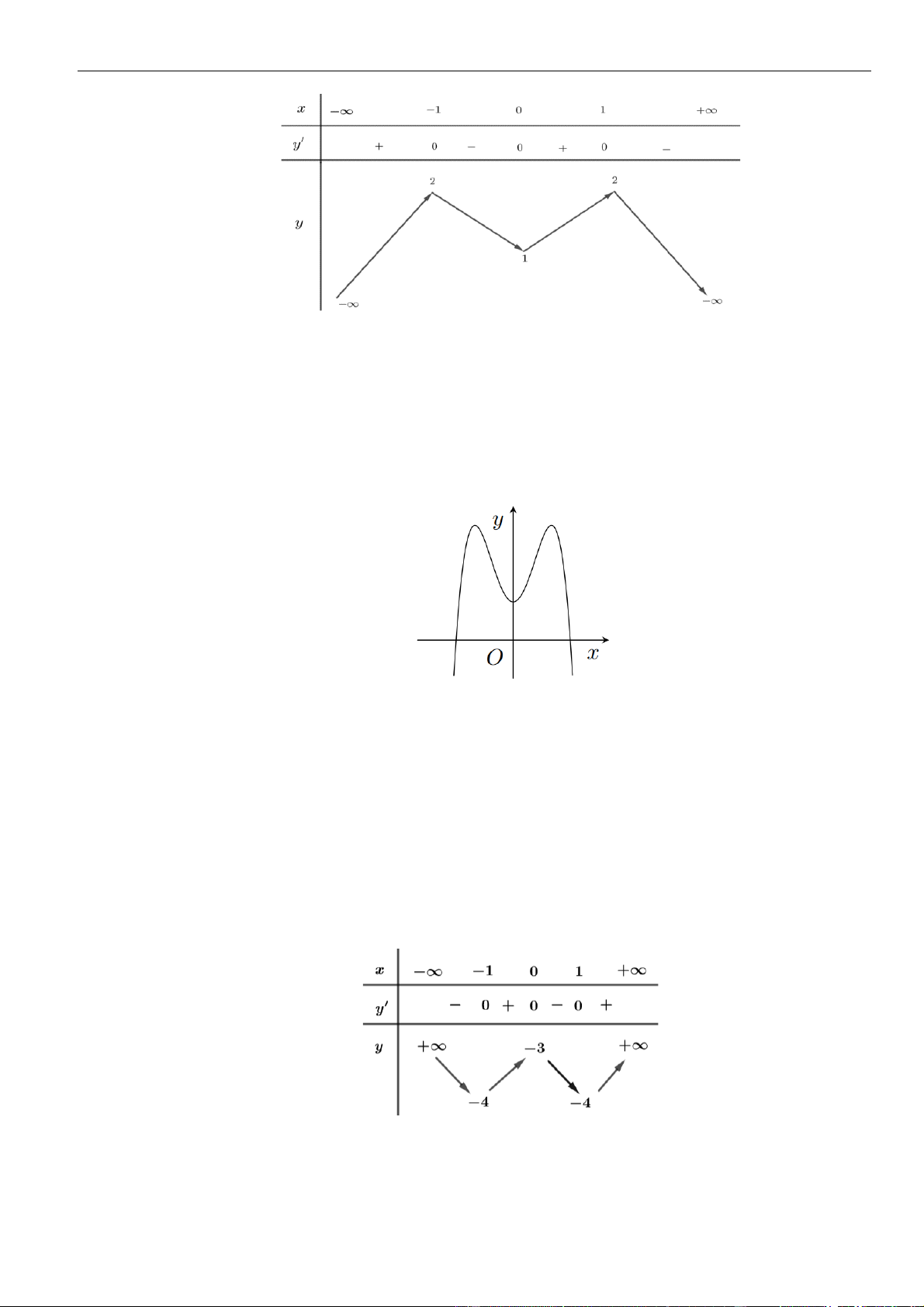
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Câu 39: Hàm số nào sau đây có bảng biến thiên như hình vẽ?
A.
42
2x 1yx= − + +
. B.
32
3x 1yx= − +
. C.
32
3x 1yx= − + +
. D.
42
2x 1yx= − +
Lời giải
Chọn A
Đồ thị hàm số dạng hình chữ M nên là hàm số trùng phương với
0a
.
Như vậy
42
2x 1yx= − + +
.
Câu 40: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
42
2 4 1y x x= − +
. B.
42
2 4 1y x x= − + +
. C.
3
2 3 1y x x= − +
. D.
3
2 3 1y x x= − + +
.
Lời giải
Chọn B
Từ hình vẽ ta thấy đây là đồ thị hàm trùng phương
42
y ax bx c= + +
nên loại C,. D.
Lại thấy
lim
x
y
→
= −
nên
0a
, suy ra loại A chọn. B.
Câu 44: Hàm số
( )
y f x=
có đạo hàm trên khoảng
( )
;− +
và có bảng biến thiên dưới đây. Hàm số
( )
y f x=
là một trong bốn hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số
đó là hàm số nào?
A.
42
2 3.y x x= + +
. B.
42
2 3.y x x= + −
. C.
42
2 3.y x x= − + −
. D.
42
2 3.y x x= − −
Lời giải
Chọn D
Nhận diện đồ thị hàm số
42
y ax bx c= + +
như sau:
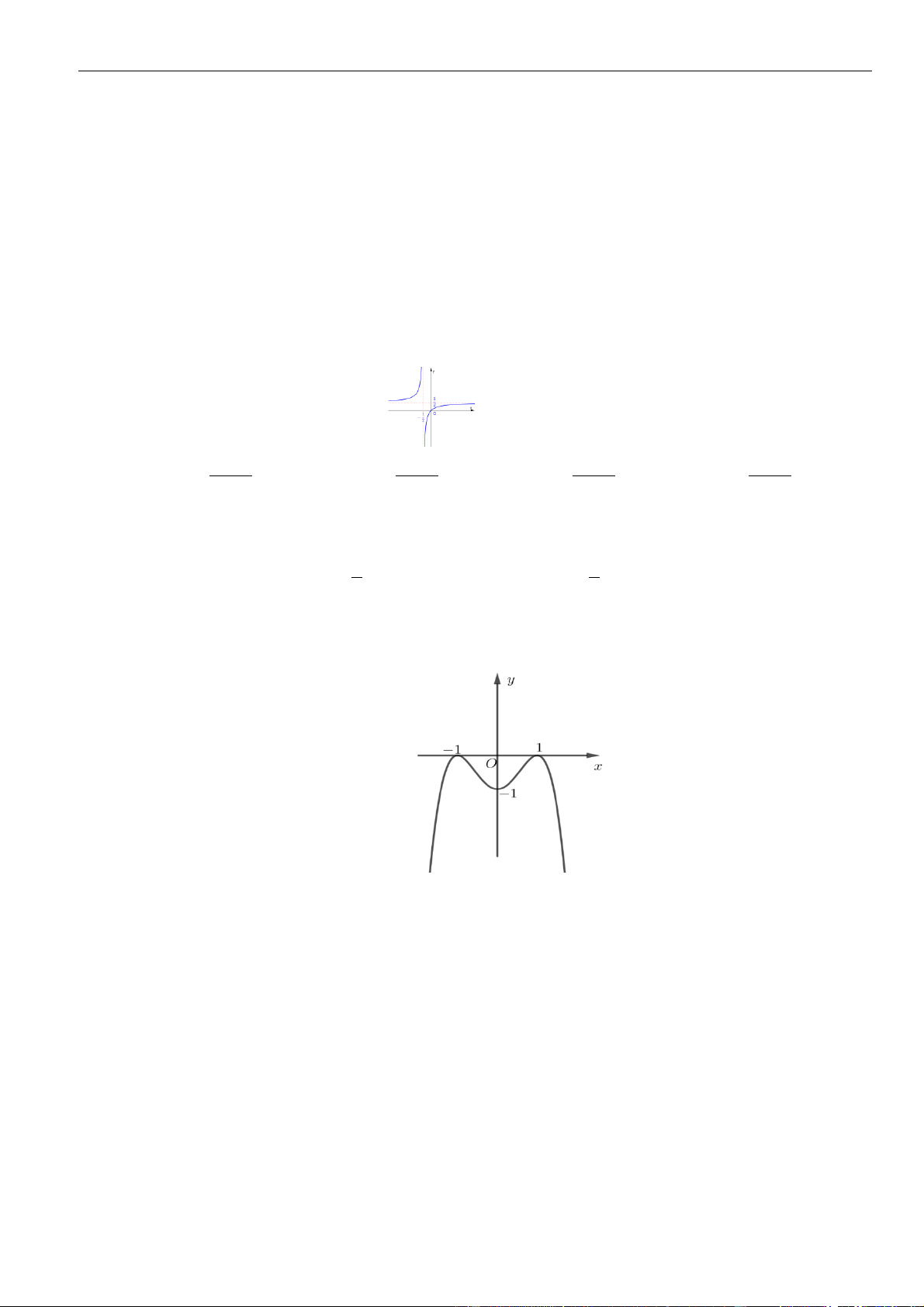
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
Hàm số đồng biến trên
( )
1; +
nên
0a
.
Hàm số có 3 cực trị nên
0ab
Do
00
03xy= =
. Vậy ta chọn đáp án D.
Câu 45: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
21
x
y
x
=
+
. B.
1
21
x
y
x
+
=
+
. C.
3
21
x
y
x
+
=
+
. D.
1
21
x
y
x
−
=
+
.
Lời giải
Chọn A
Từ đồ thị hàm số
1
2
x = −
là đường tiệm cận đứng,
1
2
y =
là đường tiệm cận ngang.
Đồ thị hàm số đi qua gốc tọa độ
( )
0;0O
Chọn đáp án A.
Câu 46: Đường cong trong hình bên là đồ thị của hàm số nào?
A.
42
21y x x= − + −
. B.
42
23y x x= − + −
. C.
42
31y x x= − + −
. D.
42
1y x x= − + −
.
Lời giải
Chọn A
Đồ thị hàm số đi qua điểm
( )
0; 1−
nên loại đáp án B
Đồ thị hàm số đi qua điểm
( ) ( )
1;0 ; 1;0−
, dễ thấy chỉ có đáp án A thỏa mãn.
Vậy đường cong trong hình vẽ trên là đồ thị của hàm số
42
21y x x= − + −
.
Câu 47: Đường cong trong hình vẽ bên là đồ thị của hàm số nào?

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
A.
32
34y x x= − + −
. B.
32
31y x x= − + +
. C.
32
31y x x= − +
. D.
32
21y x x= − + +
.
Lời giải
Chọn B
Đồ thị hàm số có hệ số
0a
và có hai điểm cực trị là
( ) ( )
0;1 , 2;5AB
nên chỉ có hàm số
32
31y x x= − + +
thoả mãn vì:
2
36y x x
= − +
.
2
0
0 3 6 0
2
x
y x x
x
=
= − + =
=
.
Khi đó
( )
0 1 0;1x y A= =
và
( )
2 5 2;5x y B= =
.
Câu 48: Cho hàm số
ax b
y
xc
+
=
−
có đồ thị như hình vẽ.
Khi đó tổng
abc++
bằng
A.
3
. B.
0
. C.
2−
. D.
2
.
Lời giải
Chọn D
Từ đồ thị hàm số, đường tiệm cận đứng
2x =
, đường tiệm cận ngang
1y =−
.
Xét hàm số
ax b
y
xc
+
=
−
, đồ thị có tiệm cận đứng
xc=
, đường tiệm cận ngang
ya=
Ta có
2; 1ca= = −
.
Đồ thị hàm số
ax b
y
xc
+
=
−
đi qua điểm
( )
.1
1;0 0 0 1
1
ab
a b b
c
+
= + = =
−
.
Ta có
1 1 2 2abc+ + = − + + =
.
Câu 49: Đường cong hình sau là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số
nào?
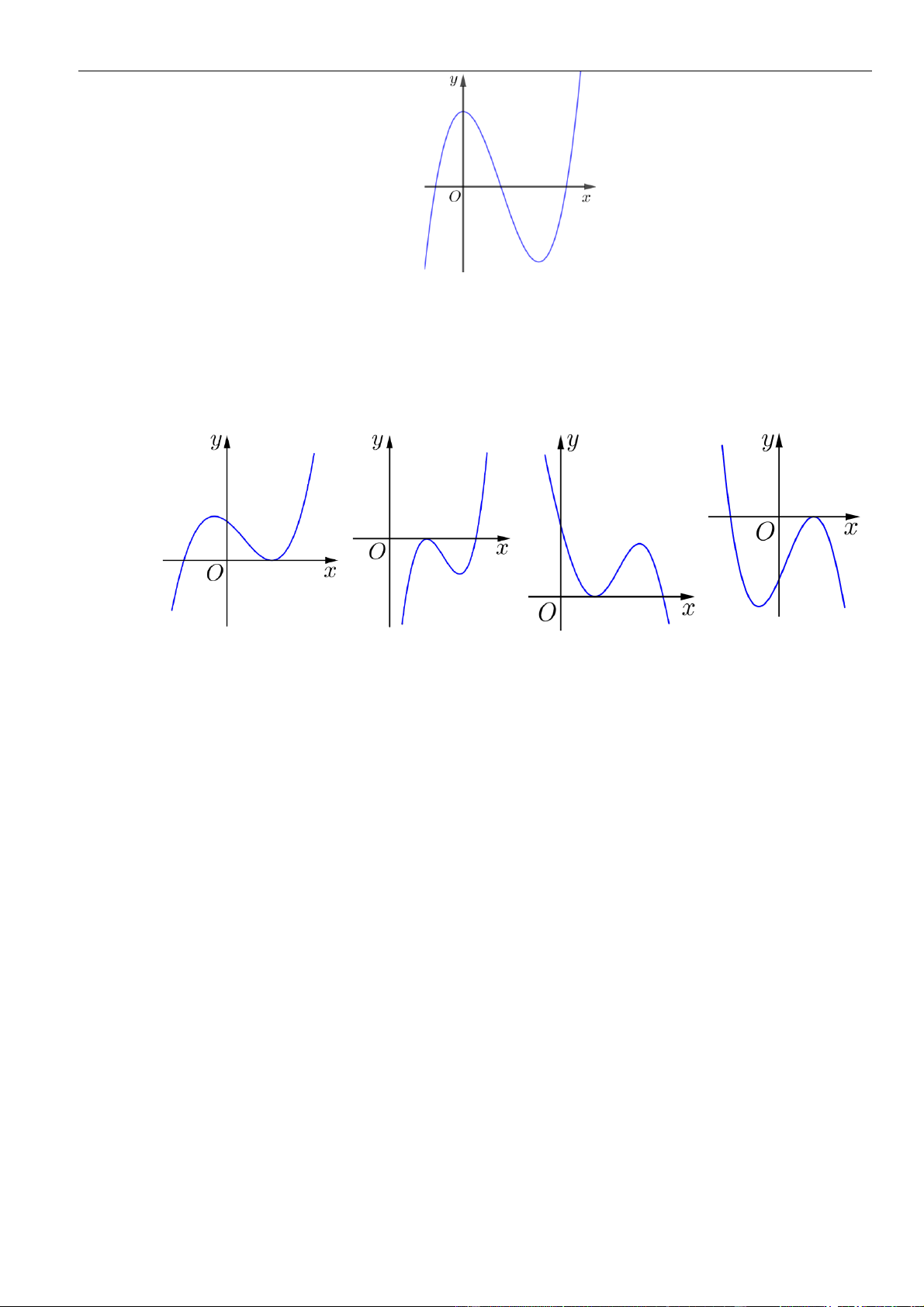
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
27 | Facebook tác giả: Phan Nhật Linh
A.
32
32= − + +y x x
. B.
32
32= − +y x x
. C.
42
32= + +y x x
. D.
42
32= − +y x x
.
Lời giải
Chọn C
Từ dạng đồ thị hàm số ta có đó là đồ thị hàm bậc ba và có hệ số
0a
.
Câu 50: Hình vẽ nào dưới đây là đồ thị hàm số
( )( )
2
y x c d x= − −
với
0cd
.
Hình 1
Hình 2
Hình 3
Hình 4
A. Hình 1. B. Hình 2. C. Hình 3. D. Hình 4.
Lời giải
Chọn B
Với
0 dc
thì đồ thị hàm số
( )( )
2
y x c d x= − −
theo thứ tự tiếp xúc với trục hoành tại điểm
có hoành độ
xd=
, cắt trục hoành tại điểm có hoành độ
xc=
.
Mặt khác: Với
xc
thì
0y
nên khi
xc
thì đồ thị hàm số nằm phía dưới trục hoành.
Vậy đồ thì hàm số là hình vẽ 2.
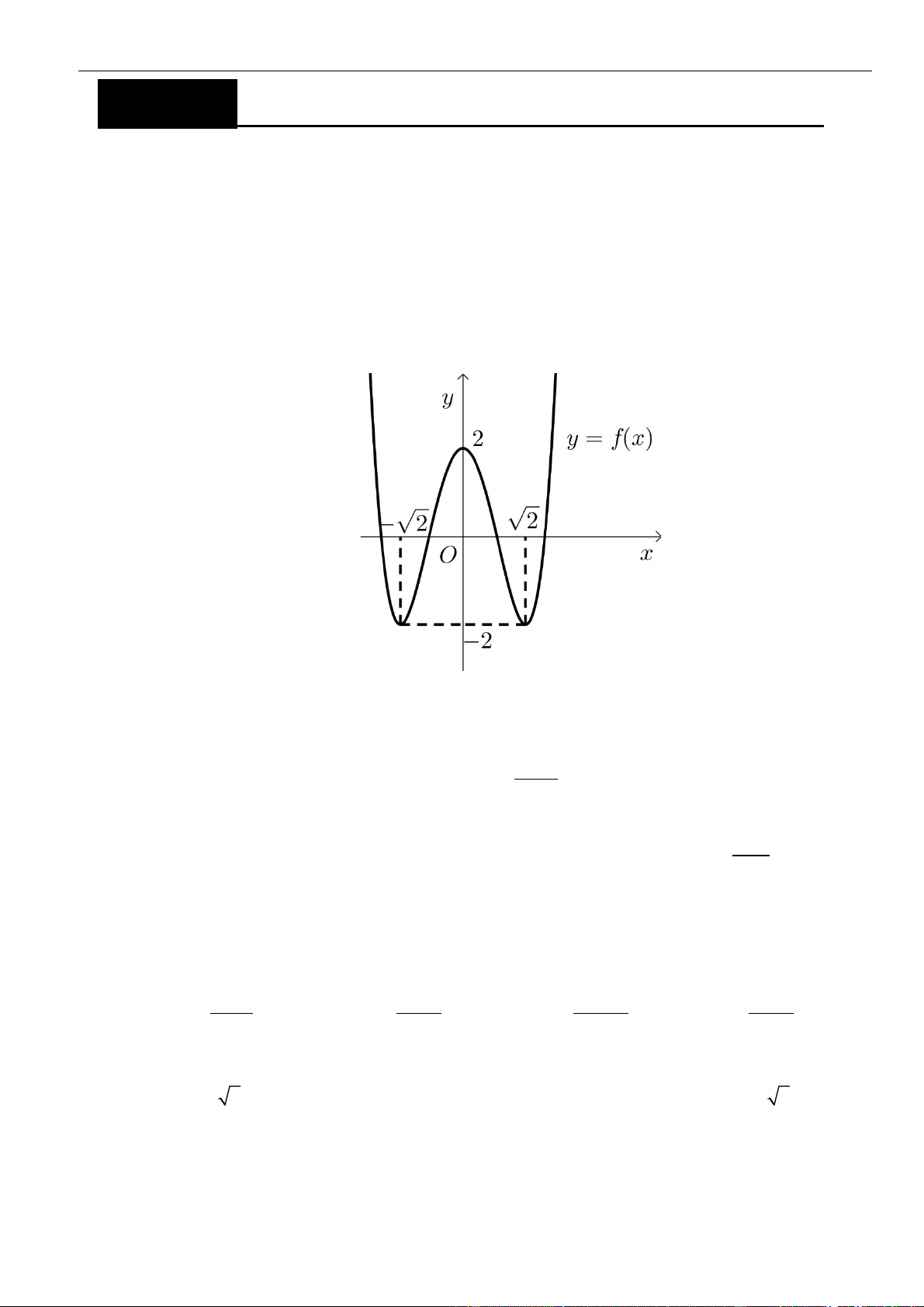
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Số giao điểm của đồ thị hàm số
42
9y x x=−
với trục hoành là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 2: Tìm số giao điểm của đồ thị hàm số
3
33= − +y x x
và đường thẳng
=yx
.
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 3: Cho hàm số
( )
=y f x
có đồ thị như hình vẽ bên dưới
Số nghiệm của phương trình
( )
2 5 0−=fx
là.
A.
4
. B.
2
. C.
0
. D.
3
.
Câu 4: Đường tiệm cận ngang của đồ thị hàm số
1
3
x
y
x
−−
=
+
cắt đường thẳng
2021yx=
tại điểm có
tung độ bằng
A.
1−
. B.
2−
. C.
0
. D.
1
2021
−
.
Câu 5: Cho hàm số
( )( )
22
2 2 1y x x= + −
có đồ thị
( )
C
, số giao điểm của đồ thị
( )
C
với trục hoành là
A.
4.
B.
1.
C.
2.
D.
3.
Câu 6: Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A.
41
2
x
y
x
+
=
+
. B.
34
1
x
y
x
+
=
−
. C.
23
1
x
y
x
−+
=
+
. D.
23
1
x
y
x
−
=
−
.
Câu 7: Đồ thị hàm số
42
2y x x= − −
cắt trục
Oy
tại điểm
A.
( )
0; 2A
. B.
( )
2;0A −
. C.
( )
0; 2A −
. D.
( )
0; 2A −
.
Câu 8: Đồ thị hàm số
32
34y x x= − +
cắt trục tung tại điểm có tung độ:
A.
0
. B.
1−
. C.
2−
. D.
4
.
Câu 9: Hàm số
( )
y f x=
có đồ thị
( )
C
như hình vẽ. Số giao điểm của
( )
C
và đường thẳng
3y =
là
Tìm tọa độ, số giao điểm của hai đồ thị không chứa tham số
DẠNG 2
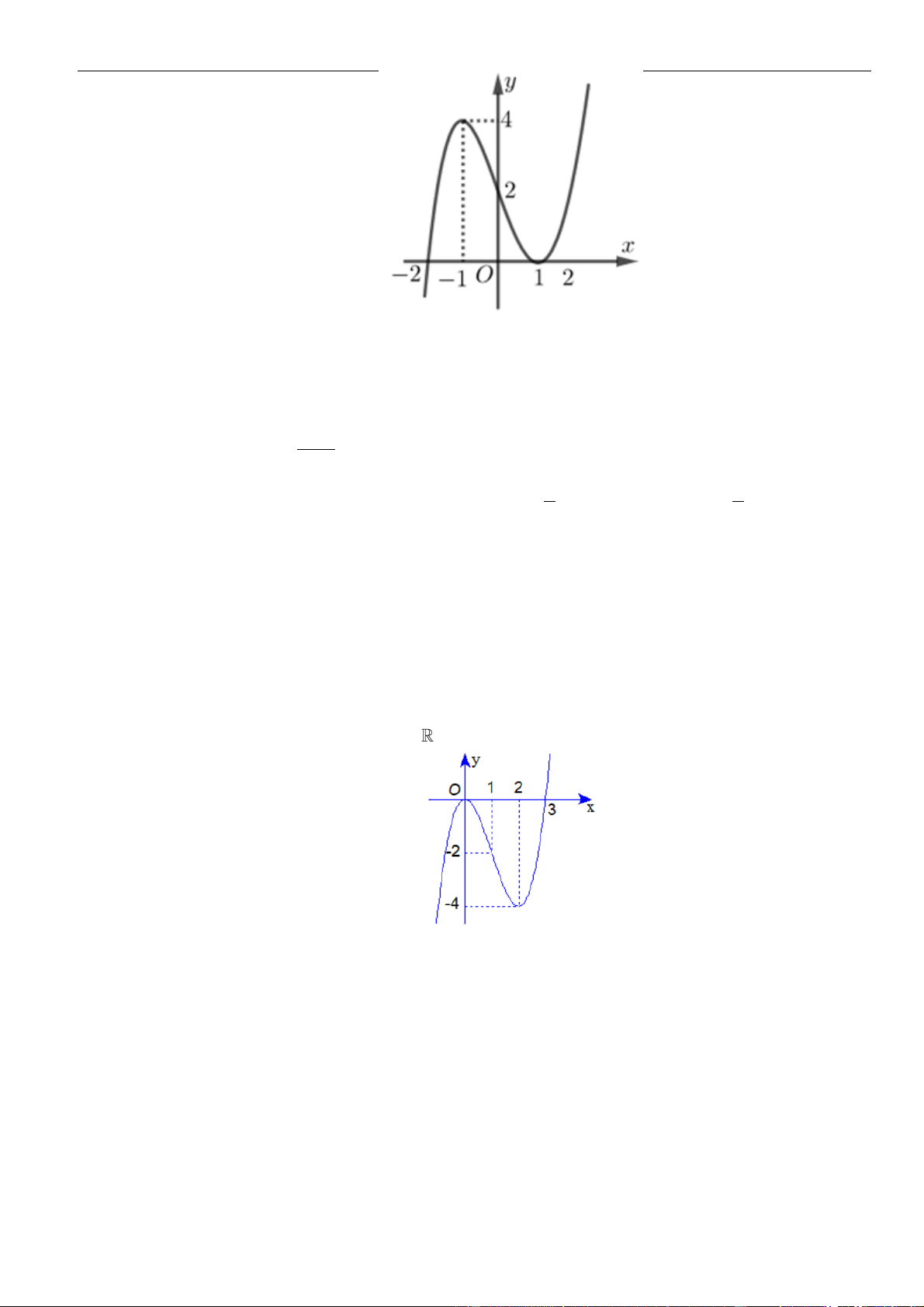
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 10: Đồ thị hàm số
42
23y x x= + −
cắt trục tung tại điểm có tọa độ là?
A.
( )
1;0
. B.
( )
0; 3−
. C.
( )
3;0−
. D.
( )
0;3
.
Câu 11: Đồ thị hàm số
2
4
x
y
x
−
=
+
cắt trục tung tại điểm có tung độ bằng?
A.
0
. B.
2
. C.
1
2
. D.
1
2
−
.
Câu 12: ) Đường thẳng
41yx=−
và đồ thị hàm số
32
31y x x= − −
có tất cả bao nhiêu điểm chung?
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 13: Số giao điểm của đồ thị hàm số
32
22y x x x= + − +
và đồ thị hàm số
2
23y x x= − +
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 14: Số giao điểm của đồ thị hàm số
32
3 9 2y x x x= − − −
với trục hoành là:
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 15: Cho hàm số
()y f x=
liên tục trên và có đồ thị như hình vẽ sau
Hỏi phương trình
( ) 0fx=
có bao nhiêu nghiệm thực phân biệt?
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 16: Đồ thị hàm số
42
2y x x= − + +
cắt trục
Oy
tại điểm nào?
A.
( )
2;0A
. B.
( )
0;0A
. C.
( )
0; 2A −
. D.
( )
0;2A
.
Câu 17: Biết rằng đường thẳng
45yx=+
cắt đồ thị hàm số
3
21y x x= + +
tại điểm duy nhất, kí hiệu
( )
00
;xy
là tọa độ của điểm đó. Tìm
0
y
.
A.
0
11y =
. B.
0
10y =
. C.
0
13y =
. D.
0
12y =
.
Câu 18: Số giao điểm của đồ thị hàm số
( )
2
2y x x x= − −
và trục hoành là
A.
2
. B.
1
. C.
0
. D.
3
.
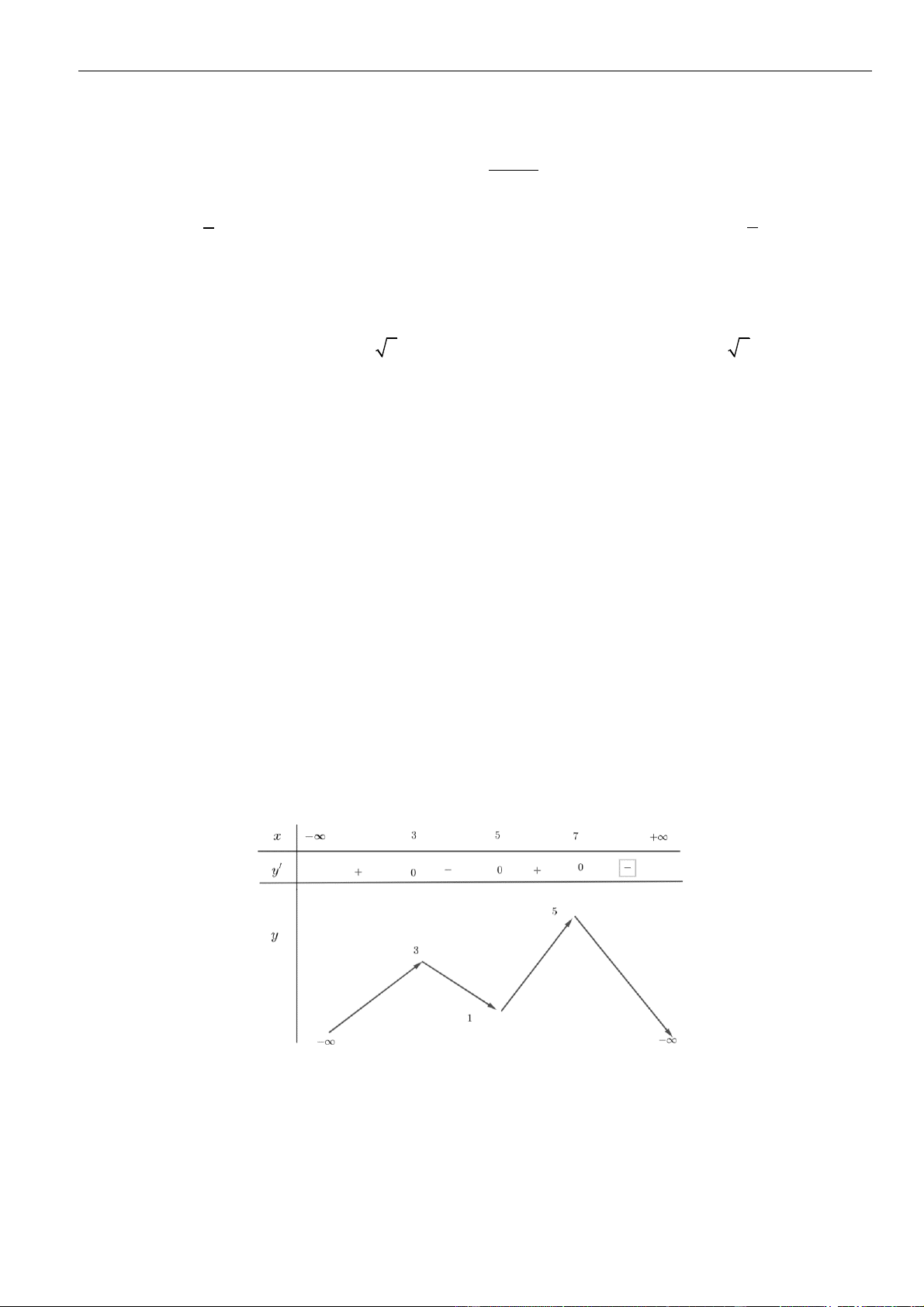
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 19: Cho hàm số
32
32= + +y x x
có đồ thị
( )
C
. Số giao điểm của
( )
C
với đường thẳng
4=y
là:
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 20: Tọa độ giao điểm
M
của đồ thị hàm số
23
2
x
y
x
+
=
+
với trục hoành là
A.
3
;0
2
−
. B.
( )
2; 0−
. C.
( )
0; 2−
. D.
3
0;
2
.
Câu 21: Cho hàm số
3
45y x x= − +
( )
1
. Đường thẳng
( )
:3d y x=−
cắt đồ thị hàm số
( )
1
tại hai điểm
phân biệt
,AB
. Độ dài đoạn thẳng
AB
bằng
A.
3
. B.
52
. C.
5
. D.
32
.
Câu 22: Số giao điểm của đồ thị hàm số
32
22y x x x= + − +
và đồ thị hàm số
2
23y x x= − +
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 23: Số giao điểm của đồ thị hàm số
42
41y x x= − +
với trục hoành là:
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 24: Biết rằng đường thẳng
23yx=−
cắt đồ thị hàm số
32
23y x x x= + + −
tại hai điểm phân biệt
A
và
B
, biết điểm
B
có hoành độ âm. Hoành độ điểm
B
bằng
A.
0
. B.
5−
. C.
1−
. D.
2−
.
Câu 25: Số giao điểm của đồ thị của hàm số
42
41y x x= − + +
và đồ thị của hàm số
2
1yx= −
là
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 26: Tìm số giao điểm của đồ thị hàm số
3
33y x x= − +
và đường thẳng
yx=
.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 27: Đồ thị của hàm số
3
32y x x= − +
cắt trục tung tại điểm có tung độ bằng
A.
0
. B.
1
. C.
2
. D.
2−
.
Câu 28: Cho hàm số
()y f x=
có bảng biến thiên như sau
Phương trình
( ) 4fx=
có bao nhiêu nghiệm thực?
A. 0. B. 3. C. 2. D. 4.
Câu 29: Cho hàm số
( )
fx
có bảng biến thiên như sau
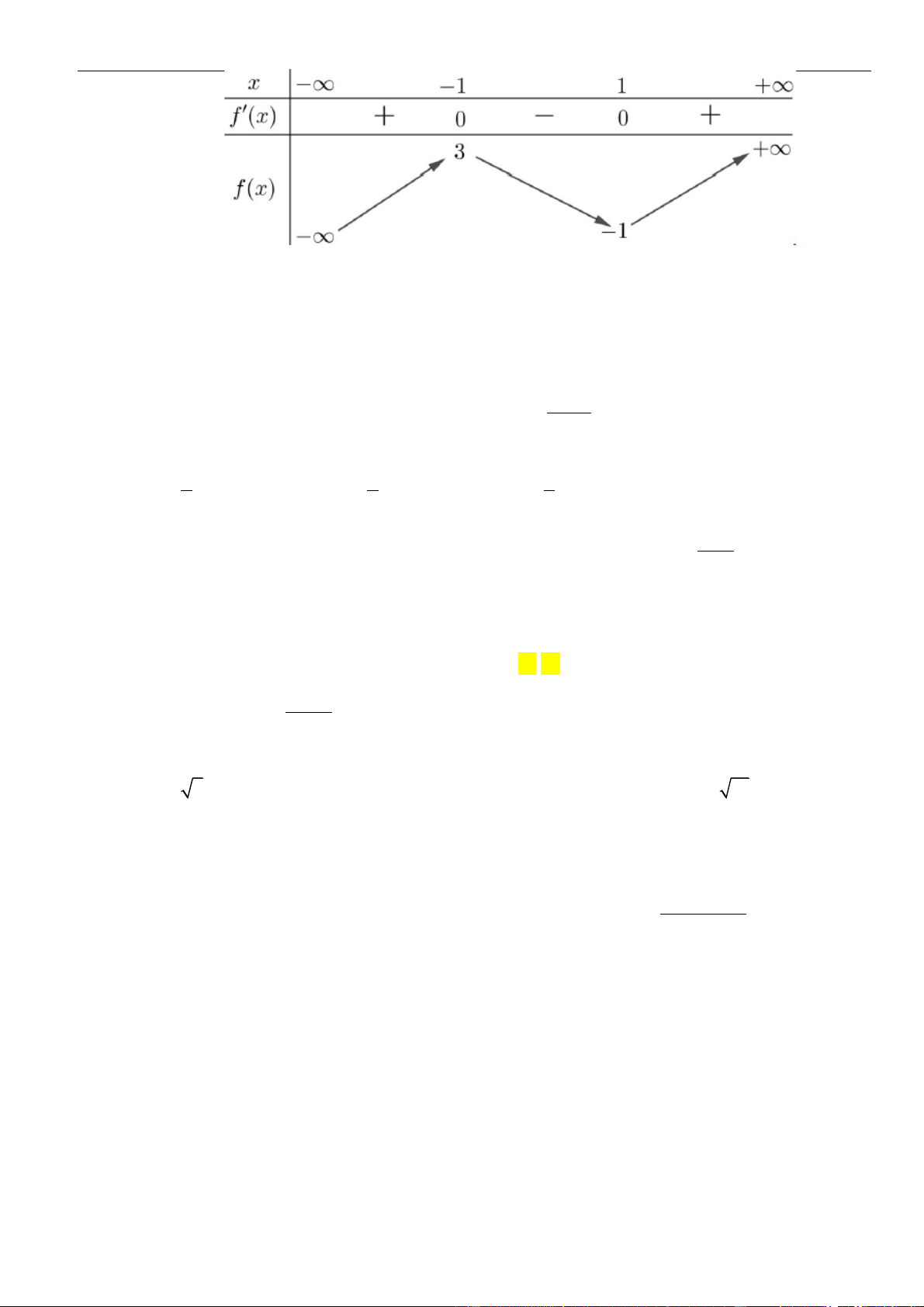
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Số nghiệm của phương trình
( )
3 2 0fx−=
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 30: Số giao điểm của hai đường cong
4
2yx=−
và
2
3yx=
là
A.
3
. B.
4
. C.
2
. D.
0
.
Câu 31: Gọi
A
,
B
là hai giao điểm của đồ thị hàm số
21
1
x
y
x
+
=
−
và đường thẳng
32yx=−
. Khi đó
trung điểm
I
của đoạn thẳng
AB
có tung độ bằng
A.
7
6
. B.
7
3
. C.
3
2
. D.
5−
.
Câu 32: ) Tìm tọa độ giao điểm của đường thẳng
1yx=+
với đồ thị hàm số
1
2
x
y
x
+
=
−
.
A.
( )
3; 1D −
. B.
( ) ( )
1;0 , 3;4IJ−
. C.
( ) ( )
4;3 , 0; 1AB−
. D.
( )
1;3C −
.
Câu 33: Đồ thị của hàm số
3
32= − +y x x
cắt trục tung tại điểm có tung độ bằng
A.
0
. B.
1
. C.
2
. D.
2−
.
Câu 34: Cho hàm số
22
1
x
y
x
−
=
+
có đồ thị
( )
C
. Gọi
,AB
là hai giao điểm của đồ thị
( )
C
với đường
thẳng
( )
: 2 10d y x=+
. Tính độ dài đoạn thẳng
AB
.
A.
5
. B.
10
. C.
5
. D.
10
.
Câu 35: Số giao điểm của đường cong
32
21y x x x= − + −
và đường thẳng
12yx=−
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 36: Gọi
( ) ( )
; , ;
A A B B
A x y B x y
là các giao điểm của đồ thị hàm số
2
43
2
xx
y
x
−+
=
−
với trục hoành.
Tìm tổng
AB
P x x=+
.
A.
1P =
. B.
2P =
. C.
3P =
. D.
4P =
.
Câu 37: Số giao điểm của đồ thị hàm số
42
23y x x= − −
và trục hoành là
A.
3
. B.
2
. C.
4
. D.
0
Câu 38: Số giao điểm của hai đồ thị các hàm số
( )
42
21f x x x= − + −
và
( )
2
g x x x= − +
là
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 39: Cho hàm số
32
32y x x= + +
có đồ thị
( )
C
. Số giao điểm của
( )
C
với đường thẳng
4y =
là
A.
1
. B.
0
. C.
2
. D.
3
.
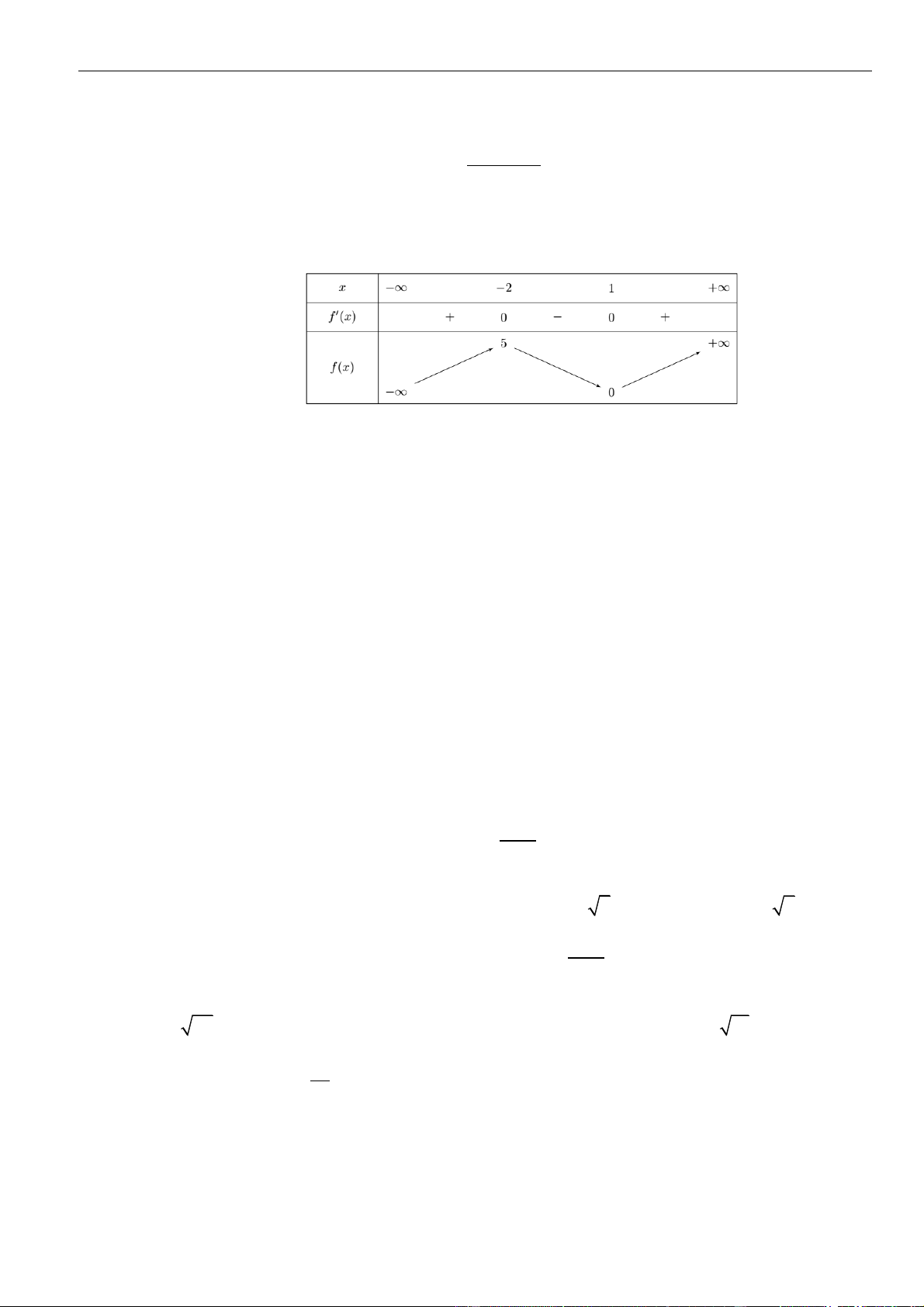
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Câu 40: Đồ thị hàm số nào trong bốn hàm số sau đây luôn nằm dưới trục hoành?
A.
32
2 1.y x x x= − − + −
B.
42
3 3.y x x= − +
C.
42
4 1.y x x= − − +
D.
42
2 2.y x x= − + −
Câu 41: Số giao điểm của đồ thị hàm số
( )
3
2
:
1
xx
Cy
x
+−
=
−
và đường thẳng
:5d y x= − +
làs
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 42: Cho hàm số
( )
fx
có bảng biến thiên như sau
Số nghiệm thực của phương trình
( )
30fx−=
là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 43: Cho hàm số
( )( )
22
2 2 1y x x= + −
có đồ thị
( )
C
, số giao điểm của đồ thị
( )
C
với trục hoành là
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 44: Số giao điểm của đồ thị
42
54y x x= − +
với trục hoành là
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 45: Cho hàm số
( )
( )
2
1 3 2y x x x x= − − +
có đồ thị
( )
C
. Mệnh đề nào dưới đây đúng?
A.
( )
C
cắt trục hoành tại
1
điểm.
B.
( )
C
cắt trục hoành tại
4
điểm phân biệt.
C.
( )
C
cắt trục hoành tại
2
điểm phân biệt.
D.
( )
C
cắt trục hoành tại
3
điểm phân biệt.
Câu 46: Đường thẳng
1yx=+
cắt đồ thị hàm số
1
2
x
y
x
−
=
−
tại hai điểm phân biệt
,AB
. Khi đó độ dài
đoạn thẳng
AB
bằng
A.
4AB =
. B.
8AB =
. C.
6AB =
. D.
22AB =
.
Câu 47: Biết rằng đường thẳng
12yx=−
cắt đồ thị hàm số
2
1
x
y
x
−
=
−
tại hai điểm phân biệt
A
và
B
. Độ
dài đoạn
AB
bằng
A.
20
. B.
20
. C.
15
. D.
15
.
Câu 48: Đồ thị hàm số
4
2
1
2
= − + +
x
yx
cắt trục hoành tại mấy điểm?
A.
2
. B.
4
. C.
3
. D.
0
.
Câu 49: Số giao điểm của đường cong
32
3 2 5y x x x= + + +
và đường thẳng
32yx=−
bằng
A. 1. B. 0 C. 3 D. 2.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 50: Số giao điểm của đồ thị hàm số
42
42y x x= − − −
và trục hoành là
A.
1
. B.
2
. C.
0
. D.
4
.
Câu 51: Biết đường thẳng
:2d y x=−
cắt đồ thị hàm số
2x 1
1
y
x
+
=
−
tại hai điểm phân biệt A và B có hoành
độ lần lượt
A
x
và
B
x
. Giá trị của biểu thức
AB
xx+
là
A. 5. B. 1. C. 3. D. 2
Câu 52: Số giao điểm của đường cong
32
21y x x x= − + −
và đường thẳng
12yx=−
là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 53: Số giao điểm của đồ thị hàm số
42
21y x x= − + −
với trục hoành là
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 54: Số giao điểm của đồ thị hàm số
3
5y x x= − +
với trục hoành là:
A.
3
. B.
2
. C.
0
. D.
1
Câu 55: Số giao điểm của đồ thị hàm số
3
43y x x= − +
và đường thẳng
3yx=+
là
A.
1
. B.
3
. C.
2
. D.
0
.
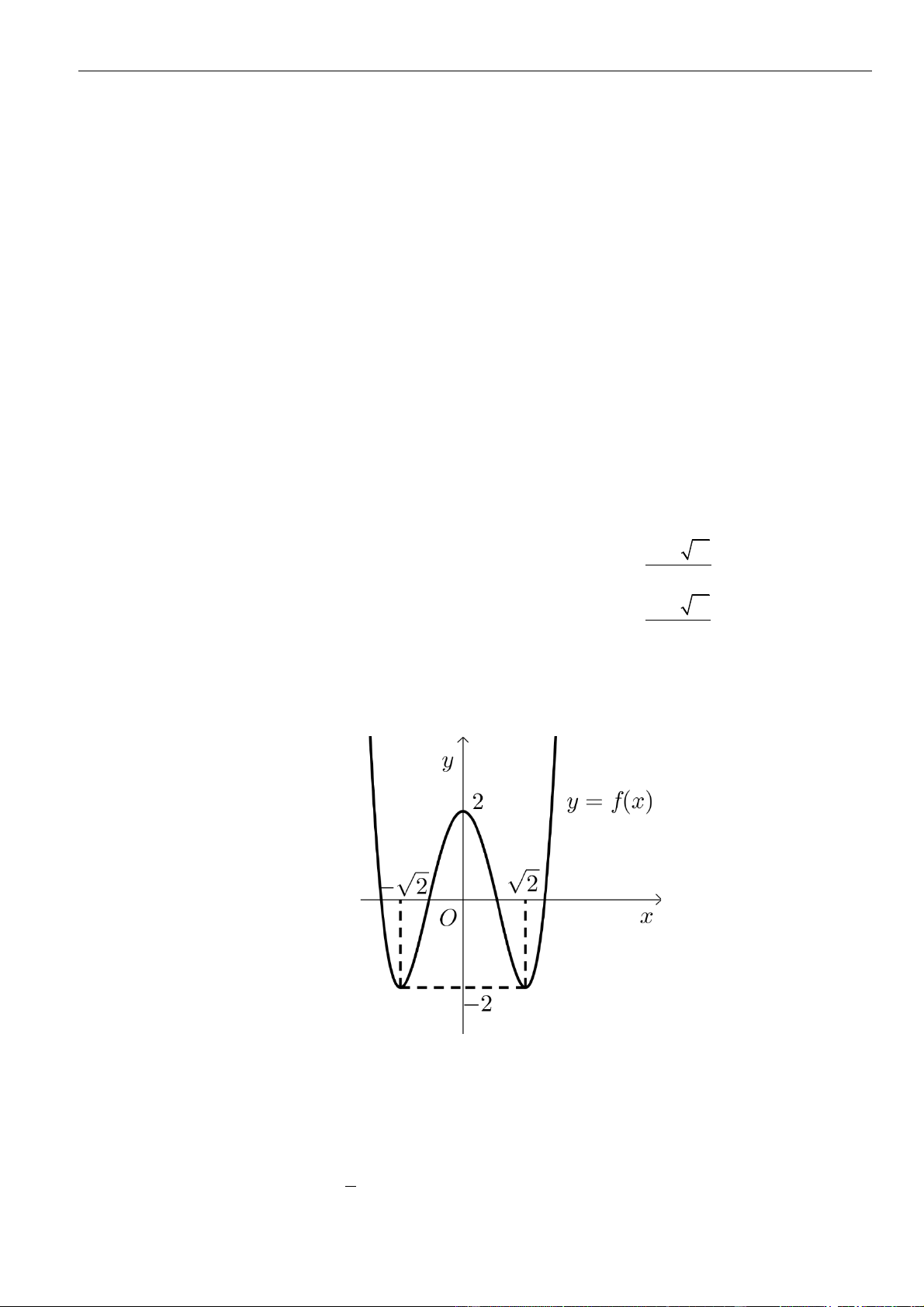
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Số giao điểm của đồ thị hàm số
42
9y x x=−
với trục hoành là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm là:
42
90xx−=
. Nghiệm của phương trình là:
3,0,3x−
.
Vậy số giao điểm của đồ thị hàm số
42
9y x x=−
với trục hoành là 3.
Câu 2: Tìm số giao điểm của đồ thị hàm số
3
33= − +y x x
và đường thẳng
=yx
.
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số
3
33= − +y x x
và đường thẳng
=yx
là
( )
( )
3 3 2
1
1 13
3 3 4 3 0 1 3 0
2
1 13
2
=
−+
− + = − + = − + − = =
−−
=
x
x x x x x x x x x
x
Vậy đồ thị hai hàm số có 3 giao điểm.
Câu 3: Cho hàm số
( )
=y f x
có đồ thị như hình vẽ bên dưới
Số nghiệm của phương trình
( )
2 5 0−=fx
là.
A.
4
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
( ) ( )
5
2 5 0
2
− = =f x f x
có hai nghiệm.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Câu 4: Đường tiệm cận ngang của đồ thị hàm số
1
3
x
y
x
−−
=
+
cắt đường thẳng
2021yx=
tại điểm có
tung độ bằng
A.
1−
. B.
2−
. C.
0
. D.
1
2021
−
.
Lời giải
Chọn A
Ta có
1
1
lim lim 1
3
1
xx
x
y
x
→+ →+
−−
= = −
+
và
1
1
lim lim 1
3
1
xx
x
y
x
→− →−
−−
= = −
+
1y = −
là đường tiệm cận ngang của ĐTHS
Đường tiệm cận ngang
1y =−
cắt đường thẳng
2021yx=
tại điểm có tung độ bằng
1−
.
Câu 5: Cho hàm số
( )( )
22
2 2 1y x x= + −
có đồ thị
( )
C
, số giao điểm của đồ thị
( )
C
với trục hoành là
A.
4.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là:
( )( )
22
1
2 2 1 0
1
x
xx
x
=
+ − =
=−
.
Vậy đồ thị
( )
C
cắt trục hoành tại hai điểm.
Câu 6: Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A.
41
2
x
y
x
+
=
+
. B.
34
1
x
y
x
+
=
−
. C.
23
1
x
y
x
−+
=
+
. D.
23
1
x
y
x
−
=
−
.
Lời giải
Chọn B
Đồ thị hàm số cắt trục tung tại điểm có hoành độ
0x =
, do đó thay
0x =
vào các hàm số đã cho
ta nhận thấy đáp án B thỏa mãn với
4y =−
.
Câu 7: Đồ thị hàm số
42
2y x x= − −
cắt trục
Oy
tại điểm
A.
( )
0; 2A
. B.
( )
2;0A −
. C.
( )
0; 2A −
. D.
( )
0; 2A −
.
Lời giải
Chọn C
Đồ thị hàm số
42
2y x x= − −
cắt trục
Oy
tại điểm
( )
0; 2A −
.
Câu 8: Đồ thị hàm số
32
34y x x= − +
cắt trục tung tại điểm có tung độ:
A.
0
. B.
1−
. C.
2−
. D.
4
.
Lời giải
Chọn D
Đồ thị hàm số cắt trục tung tại điểm có hoành độ bằng
0
suy ra
4y =
.
Câu 9: Hàm số
( )
y f x=
có đồ thị
( )
C
như hình vẽ. Số giao điểm của
( )
C
và đường thẳng
3y =
là
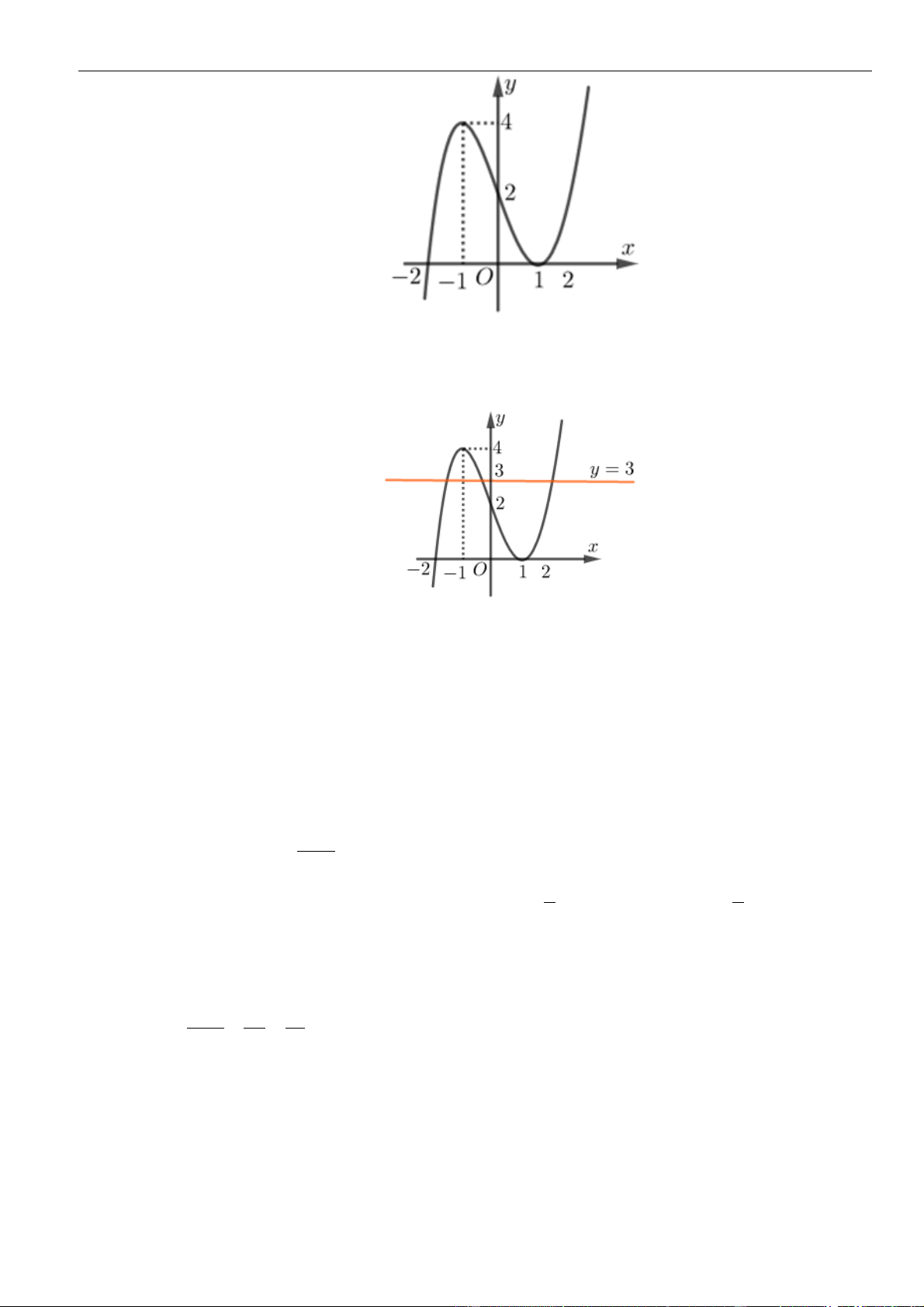
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn C
.
Câu 10: Đồ thị hàm số
42
23y x x= + −
cắt trục tung tại điểm có tọa độ là?
A.
( )
1;0
. B.
( )
0; 3−
. C.
( )
3;0−
. D.
( )
0;3
.
Lời giải
Chọn B
Thay
0x =
vào hàm số
42
23y x x= + −
ta được
3y =−
.
Suy ra đồ thị hàm số
42
23y x x= + −
cắt trục tung tại điểm có tọa độ là
( )
0; 3−
.
Câu 11: Đồ thị hàm số
2
4
x
y
x
−
=
+
cắt trục tung tại điểm có tung độ bằng?
A.
0
. B.
2
. C.
1
2
. D.
1
2
−
.
Lời giải
Chọn D
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng:
0 2 2 1
0 4 4 2
y
− − −
= = =
+
Câu 12: ) Đường thẳng
41yx=−
và đồ thị hàm số
32
31y x x= − −
có tất cả bao nhiêu điểm chung?
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn B
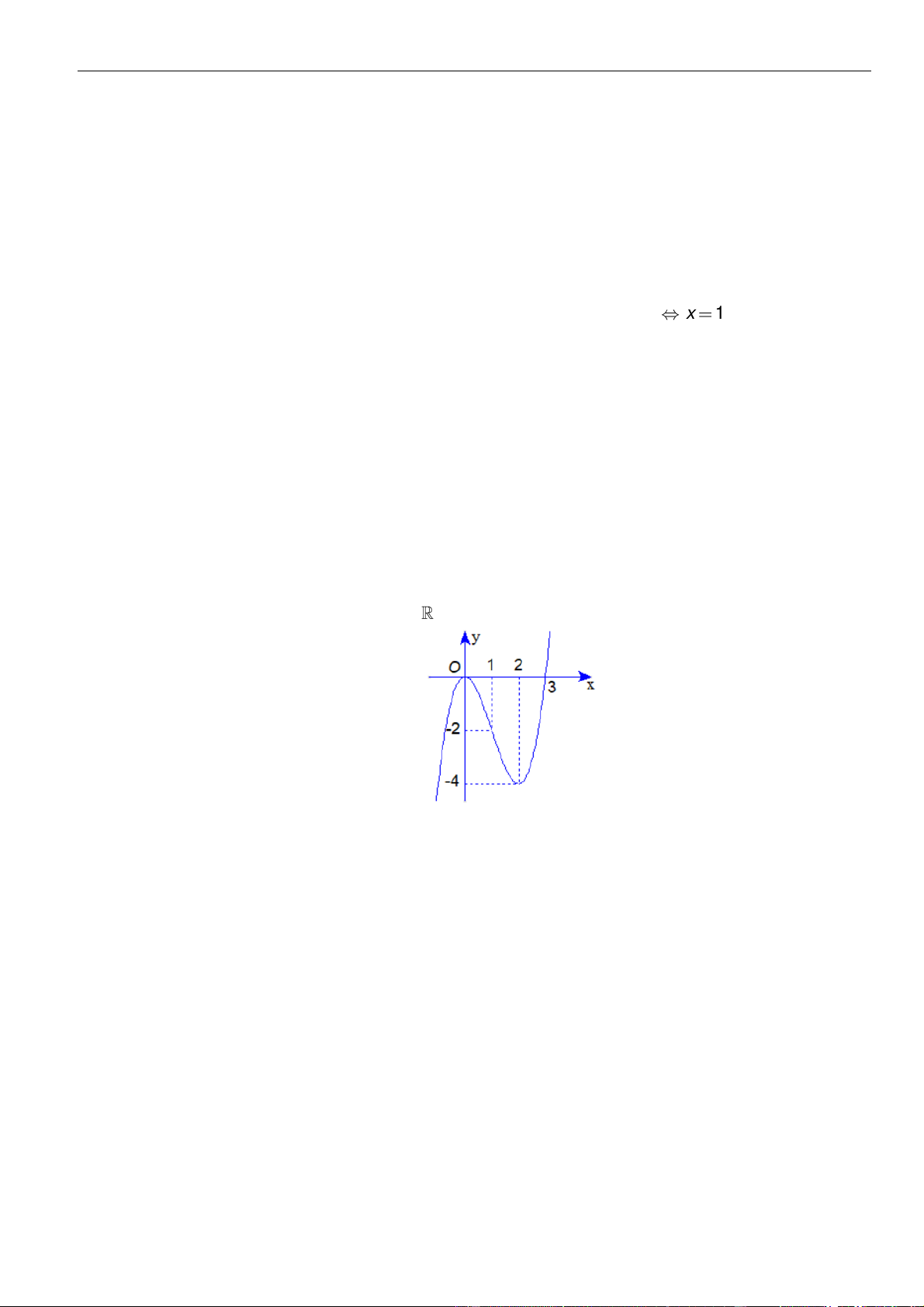
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Phương trình hoành độ giao điểm:
3 2 3 2
0
3 1 4 1 3 4 0 1
4
x
x x x x x x x
x
=
− − = − − − = = −
=
.
Suy ra số điểm chung là
3
.
Câu 13: Số giao điểm của đồ thị hàm số
32
22y x x x= + − +
và đồ thị hàm số
2
23y x x= − +
là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm:
3 2 2
2 2 2 3x x x x x+ − + = − +
1x
.
Câu 14: Số giao điểm của đồ thị hàm số
32
3 9 2y x x x= − − −
với trục hoành là:
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn D
Xét hàm số
32
3 9 2y x x x= − − −
Ta có
2
3 6 9 0y x x
= − − =
Giải
13
0
3 29
xy
y
xy
= − =
=
= = −
Ta có
D
.0
C CT
yy
đồ thị hàm số
32
3 9 2y x x x= − − −
cắt trục hoành tại
3
điểm phân biệt.
Câu 15: Cho hàm số
()y f x=
liên tục trên và có đồ thị như hình vẽ sau
Hỏi phương trình
( ) 0fx=
có bao nhiêu nghiệm thực phân biệt?
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn A
Nhìn vào đồ thị đã cho ta thấy đồ thị hàm số
()y f x=
giao với trục hoành tại hai điểm phân
biệt.
Do đó phương trình
( ) 0fx=
có hai nghiệm phân biệt.
Câu 16: Đồ thị hàm số
42
2y x x= − + +
cắt trục
Oy
tại điểm nào?
A.
( )
2;0A
. B.
( )
0;0A
. C.
( )
0; 2A −
. D.
( )
0;2A
.
Lời giải
Chọn D
Do đồ thị cắt trục
Oy
nên
02xy= =
nên tọa độ
( )
0;2A
.
Câu 17: Biết rằng đường thẳng
45yx=+
cắt đồ thị hàm số
3
21y x x= + +
tại điểm duy nhất, kí hiệu
( )
00
;xy
là tọa độ của điểm đó. Tìm
0
y
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
A.
0
11y =
. B.
0
10y =
. C.
0
13y =
. D.
0
12y =
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số
3
21y x x= + +
và đường thẳng
45yx=+
:
3
2 1 4 5x x x+ + = +
3
2 4 0 2x x x − − = =
.
Với
( )
00
;xy
là tọa độ của giao điểm đó. Khi đó
00
2 13xy= =
.
Câu 18: Số giao điểm của đồ thị hàm số
( )
2
2y x x x= − −
và trục hoành là
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số
( )
2
2y x x x= − −
và trục hoành là
( )
2
0
2 0 1
2
x
x x x x
x
=
− − = = −
=
.
Vậy số giao điểm của đồ thị hàm số
( )
2
2y x x x= − −
và trục hoành là
3
.
Câu 19: Cho hàm số
32
32= + +y x x
có đồ thị
( )
C
. Số giao điểm của
( )
C
với đường thẳng
4=y
là:
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn C
Số giao điểm của hàm số
32
32= + +y x x
với đường thẳng
4=y
là số nghiệm của phương
trình:
32
3 2 4xx+ + =
32
3 2 0xx + − =
13
13
x
x
= − −
= − +
.
Vậy đồ thị hàm số
( )
C
giao với đường thẳng
4=y
tại
2
điểm.
Câu 20: Tọa độ giao điểm
M
của đồ thị hàm số
23
2
x
y
x
+
=
+
với trục hoành là
A.
3
;0
2
−
. B.
( )
2; 0−
. C.
( )
0; 2−
. D.
3
0;
2
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm
2 3 3
0 2 3 0
22
x
xx
x
+
= + = = −
+
.
Giao điểm
3
;0
2
M
−
.
Câu 21: Cho hàm số
3
45y x x= − +
( )
1
. Đường thẳng
( )
:3d y x=−
cắt đồ thị hàm số
( )
1
tại hai điểm
phân biệt
,AB
. Độ dài đoạn thẳng
AB
bằng
A.
3
. B.
52
. C.
5
. D.
32
.
Lời giải

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Chọn D
Phương trình hoành độ giao điểm:
3
4 5 3x x x− + = −
3
3 2 0xx − + =
1
2
x
x
=
=−
.
Suy ra
( )
1;2A
và
( )
2;5B −
.
Ta có:
( )
3;3AB =−
nên
99AB =+
32AB=
.
Câu 22: Số giao điểm của đồ thị hàm số
32
22y x x x= + − +
và đồ thị hàm số
2
23y x x= − +
là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm :
3 2 2 3
2 2 2 3 1 0 1x x x x x x x+ − + = − + − = =
Vậy số giao điểm của 2 đồ thị là 1.
Câu 23: Số giao điểm của đồ thị hàm số
42
41y x x= − +
với trục hoành là:
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có:
42
23
4 1 0
23
x
xx
x
= −
− + =
= +
nên đồ thị hàm số
42
41y x x= − +
cắt trục hoành tại
4
điểm phân biệt.
Câu 24: Biết rằng đường thẳng
23yx=−
cắt đồ thị hàm số
32
23y x x x= + + −
tại hai điểm phân biệt
A
và
B
, biết điểm
B
có hoành độ âm. Hoành độ điểm
B
bằng
A.
0
. B.
5−
. C.
1−
. D.
2−
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm:
3 2 3 2
0
2 3 2 3 0
1
x
x x x x x x
x
=
+ + − = − + =
=−
Điểm
B
có hoành độ âm nên
1
B
x =−
.
Câu 25: Số giao điểm của đồ thị của hàm số
42
41y x x= − + +
và đồ thị của hàm số
2
1yx= −
là
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm:
2
4 2 2 4 2
2
3 17
3 17
22
22
4 1 1 3 2 0
3 17
3 17
0( )
22
22
x
x
x x x x x
x vn
x
=+
=+
− + + = − − + + =
= −
= − +
.
Vậy có 2 giao điểm.
Câu 26: Tìm số giao điểm của đồ thị hàm số
3
33y x x= − +
và đường thẳng
yx=
.
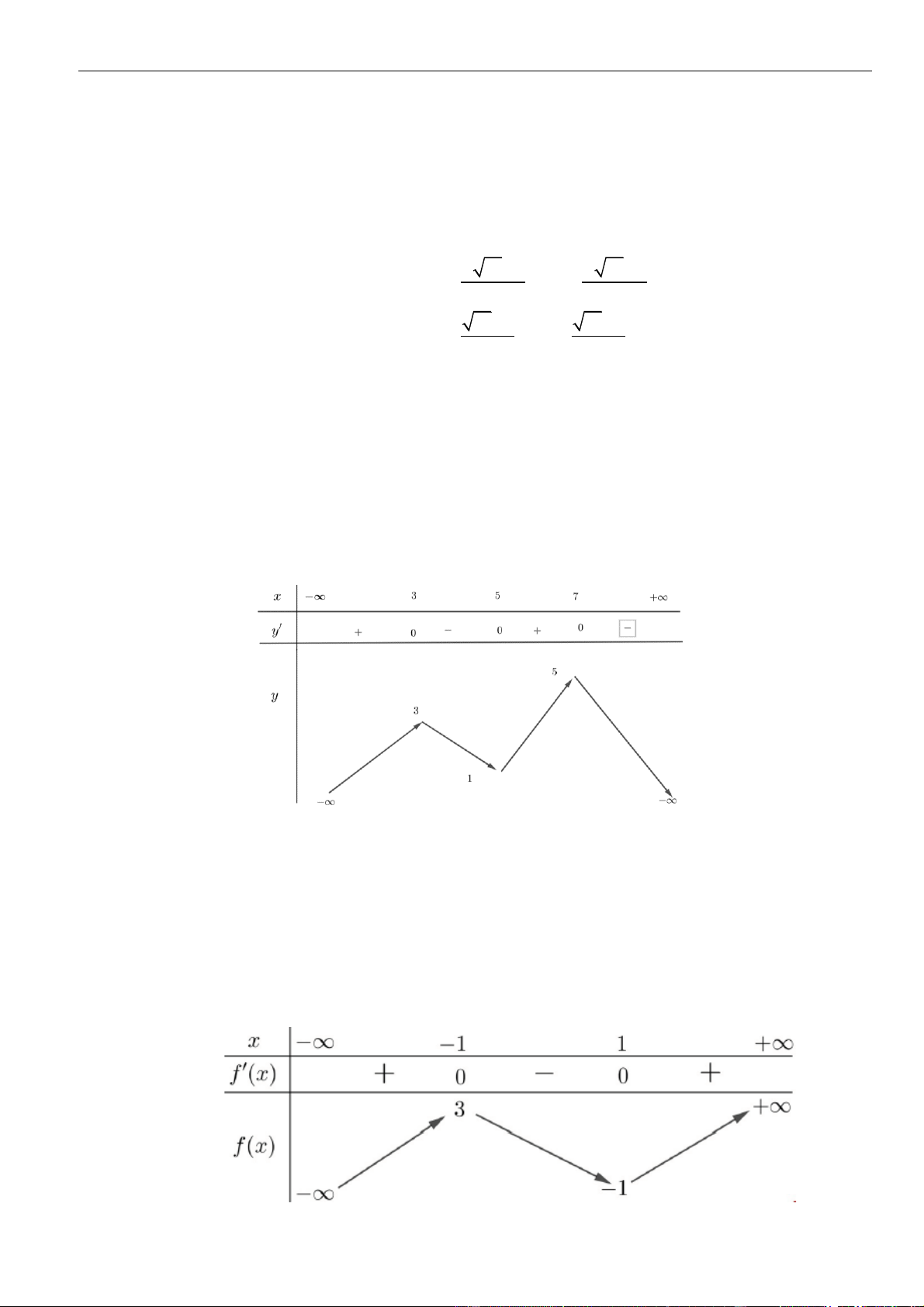
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
GVSB: Chương Huy; GVPB: Hoàng Tiến Đông
Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số
3
33y x x= − +
và đường thẳng
yx=
là
3
33x x x− + =
3
11
13 1 13 1
4 3 0
22
13 1 13 1
22
xy
x x x y
xy
= =
− − − −
− + = = =
−−
= =
.
Vậy đồ thị hàm số
3
33y x x= − +
và đường thẳng
yx=
có 3 giao điểm.
Câu 27: Đồ thị của hàm số
3
32y x x= − +
cắt trục tung tại điểm có tung độ bằng
A.
0
. B.
1
. C.
2
. D.
2−
.
Lời giải
Chọn C
Gọi
( )
00
;M x y
là giao điểm của đồ thị hàm số với trục tung. Ta có
00
02xy= =
.
Câu 28: Cho hàm số
()y f x=
có bảng biến thiên như sau
Phương trình
( ) 4fx=
có bao nhiêu nghiệm thực?
A. 0. B. 3. C. 2. D. 4.
Lời giải
Chọn C
Dựa theo bảng biến thiên ta thấy đồ thị hàm số cắt đường thẳng
4y =
tại 2 điểm phân biệt.
Do đó phương trình đã cho có 2 nghiệm thực.
Câu 29: Cho hàm số
( )
fx
có bảng biến thiên như sau
Số nghiệm của phương trình
( )
3 2 0fx−=
là

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
*Ta có
( ) ( )
2
3 2 0
3
f x f x− = =
. Đường thẳng
2
3
y =
cắt đồ thị hàm số
( )
y f x=
tại ba
điểm phân biệt, do đó phương trình
( )
3 2 0fx−=
có 3 nghiệm phân biệt.
Câu 30: Số giao điểm của hai đường cong
4
2yx=−
và
2
3yx=
là
A.
3
. B.
4
. C.
2
. D.
0
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm của hai đường cong là
( )
2
4 2 4 2
2
3 17
3 17
2
2 3 3 2 0
2
3 17
2
x
x x x x x
xL
+
=
+
− = − − = =
−
=
.
Do phương trình trên có 2 nghiệm nên số giao điểm của hai đường cong là
2
.
Câu 31: Gọi
A
,
B
là hai giao điểm của đồ thị hàm số
21
1
x
y
x
+
=
−
và đường thẳng
32yx=−
. Khi đó
trung điểm
I
của đoạn thẳng
AB
có tung độ bằng
A.
7
6
. B.
7
3
. C.
3
2
. D.
5−
.
Lời giải
Chọn C
Điều kiện:
1x
.
Ta có hoành độ giao điểm của đồ thị hàm số
21
1
x
y
x
+
=
−
và đường thẳng
32yx=−
là nghiệm
phương trình
2
21
3 2 2 1 3 5 2
1
x
x x x x
x
+
= − + = − +
−
( )
2
3 7 1 0 1xx − + =
Do
2
7 4.3.1 37 0 = − =
nên đồ thị hàm số
21
1
x
y
x
+
=
−
cắt đường thẳng
32yx=−
tại hai điểm
phân biệt
A
,
.B
Gọi là nghiệm của phương trình
( )
1.
Theo Viét ta có
12
12
7
3
1
3
xx
xx
+=
=
Khi đó
( )
11
;3 2A x x −
,
( )
12
;3 2B x x −
nên trung điểm
I
của đoạn thẳng
AB
có tọa độ bằng
1 2 1 2
3 2 3 2
73
;;
2 2 6 2
x x x x
II
+ − + −
. Vậy tung độ điểm
I
bằng
3
.
2
Câu 32: ) Tìm tọa độ giao điểm của đường thẳng
1yx=+
với đồ thị hàm số
1
2
x
y
x
+
=
−
.
12
,xx

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
A.
( )
3; 1D −
. B.
( ) ( )
1;0 , 3;4IJ−
. C.
( ) ( )
4;3 , 0; 1AB−
. D.
( )
1;3C −
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm:
1
1
2
x
x
x
+
=+
−
( )( ) ( )( )
22
1
1 1 2 1 3 0
3
xx
x
x x x x x
x
=−
+ = + − + − =
=
.
Với
( )
1 0 1;0x y I= − = −
.
Với
( )
3 4 3;4x y J= =
.
Do đó, tọa độ giao điểm của đường thẳng
1yx=+
với đồ thị hàm số
1
2
x
y
x
+
=
−
là
( ) ( )
1;0 , 3;4IJ−
.
Câu 33: Đồ thị của hàm số
3
32= − +y x x
cắt trục tung tại điểm có tung độ bằng
A.
0
. B.
1
. C.
2
. D.
2−
.
Lời giải
Chọn C
Vì đồ thị của hàm số
3
32= − +y x x
cắt trục tung
:0=Oy x
nên giao điểm có hoành độ
02= =xy
.
Câu 34: Cho hàm số
22
1
x
y
x
−
=
+
có đồ thị
( )
C
. Gọi
,AB
là hai giao điểm của đồ thị
( )
C
với đường
thẳng
( )
: 2 10d y x=+
. Tính độ dài đoạn thẳng
AB
.
A.
5
. B.
10
. C.
5
. D.
10
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm
22
2 10
1
x
x
x
−
+=
+
.
Điều kiện
1x −
.
Phương trình tương đương với
( )( )
2
2
2 10 1 2 2 5 6 0
3
x
x x x x x
x
=−
+ + = − + + =
=−
.
Hai giao điểm là
( ) ( )
2;6 , 3;4AB−−
.
Suy ra
( )
2
2
1 2 5AB = − + =
.
Câu 35: Số giao điểm của đường cong
32
21y x x x= − + −
và đường thẳng
12yx=−
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm
3 2 3 2
2 1 1 2 2 3 2 0x x x x x x x− + − = − − + − =
1x=
.
Vậy đường cong
32
21y x x x= − + −
và đường thẳng
12yx=−
có một giao điểm.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Câu 36: Gọi
( ) ( )
; , ;
A A B B
A x y B x y
là các giao điểm của đồ thị hàm số
2
43
2
xx
y
x
−+
=
−
với trục hoành.
Tìm tổng
AB
P x x=+
.
A.
1P =
. B.
2P =
. C.
3P =
. D.
4P =
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm:
2
43
0 1 3
2
xx
xx
x
−+
= = =
−
.
1 3 4
AB
P x x= + = + =
.
Câu 37: Số giao điểm của đồ thị hàm số
42
23y x x= − −
và trục hoành là
A.
3
. B.
2
. C.
4
. D.
0
Lời giải
Chọn B
Phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành là
2
4 2 2
2
1
2 3 0 3 3
3
x
x x x x
x
=−
− − = = =
=
.
Phương trình hoành độ giao điểm có hai nghiệm nên số giao điểm là 2.
Câu 38: Số giao điểm của hai đồ thị các hàm số
( )
42
21f x x x= − + −
và
( )
2
g x x x= − +
là
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn B
Số giao điểm của đồ thị các hàm số
( )
42
21f x x x= − + −
và
( )
2
g x x x= − +
là số nghiệm của
phương trình:
4 2 2 4 2
2 1 3 1 0x x x x x x x− + − = − + − + − − =
Phương trình
42
3 1 0x x x− + − − =
có 4 nghiệm phân biệt. Vậy có 4 giao điểm.
Câu 39: Cho hàm số
32
32y x x= + +
có đồ thị
( )
C
. Số giao điểm của
( )
C
với đường thẳng
4y =
là
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm
3 2 3 2
13
3 2 4 3 2 0 1
13
x
x x x x x
x
= − +
+ + = + − = = −
= − −
.
Phương trình này có ba nghiệm nên hai đồ thị đã cho cắt nhau tại ba điểm phân biệt.
Câu 40: Đồ thị hàm số nào trong bốn hàm số sau đây luôn nằm dưới trục hoành?
A.
32
2 1.y x x x= − − + −
B.
42
3 3.y x x= − +
C.
42
4 1.y x x= − − +
D.
42
2 2.y x x= − + −
Lời giải
Chọn D
Xét hàm số
42
22y x x= − + −
.
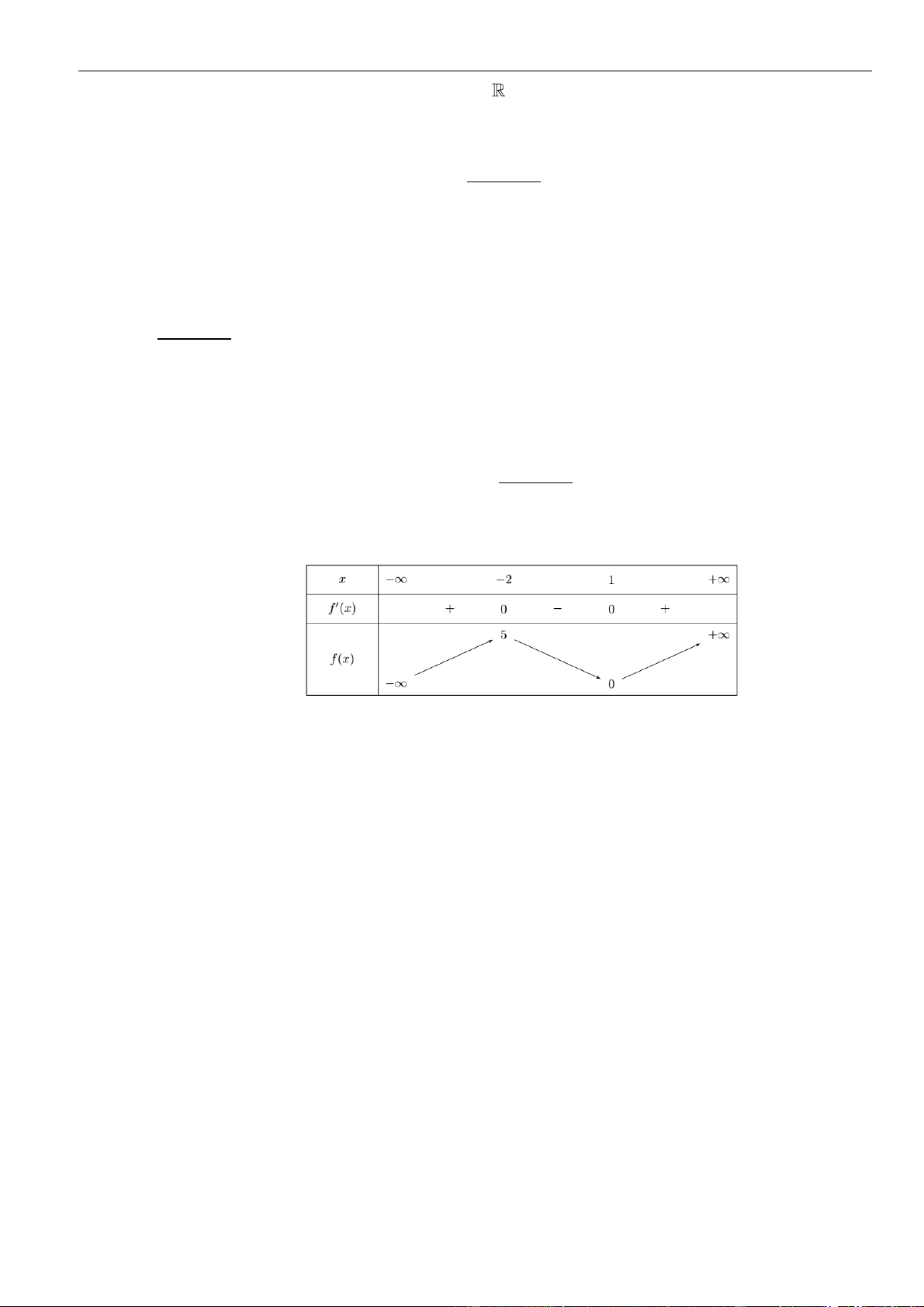
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Ta có:
( )
2
4 2 2
2 2 1 1 0,x x x x− + − = − − −
Do đó đồ thị hàm số
42
22y x x= − + −
luôn nằm dưới trục hoành.
Câu 41: Số giao điểm của đồ thị hàm số
( )
3
2
:
1
xx
Cy
x
+−
=
−
và đường thẳng
:5d y x= − +
làs
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm:
( )( )
3
3
2
5 2 1 5
1
xx
x x x x x
x
+−
= − + + − = − − +
−
( với
1x
).
32
3
5 3 0
1
x
x x x
x
=−
+ − + =
=
.
Đối chiếu với điều kiện ta được
3x =−
.
Vậy số giao điểm của đồ thị hàm số
( )
3
2
:
1
xx
Cy
x
+−
=
−
và đường thẳng
:5d y x= − +
là
1
.
Câu 42: Cho hàm số
( )
fx
có bảng biến thiên như sau
Số nghiệm thực của phương trình
( )
30fx−=
là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A
Ta
( ) ( )
3 0 3f x f x− = =
(2).
Số nghiệm của phương trình (1) bằng số giao điểm của đồ thị hàm số
( )
y f x=
và đường thẳng
3y =
.
Do đó dựa vào bảng biến thiên suy ra phương trình (1) có 3 nghiệm thực phân biệt.
Câu 43: Cho hàm số
( )( )
22
2 2 1y x x= + −
có đồ thị
( )
C
, số giao điểm của đồ thị
( )
C
với trục hoành là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Ta có:
( )( )
( )
2
22
2
2 2 0
2 2 1 0 1
10
x VN
x x x
x
+=
+ − = =
−=
Vậy đồ thị hàm số
( )( )
22
2 2 1y x x= + −
giao với trục hoành tại hai điểm phân biệt.
Câu 44: Số giao điểm của đồ thị
42
54y x x= − +
với trục hoành là
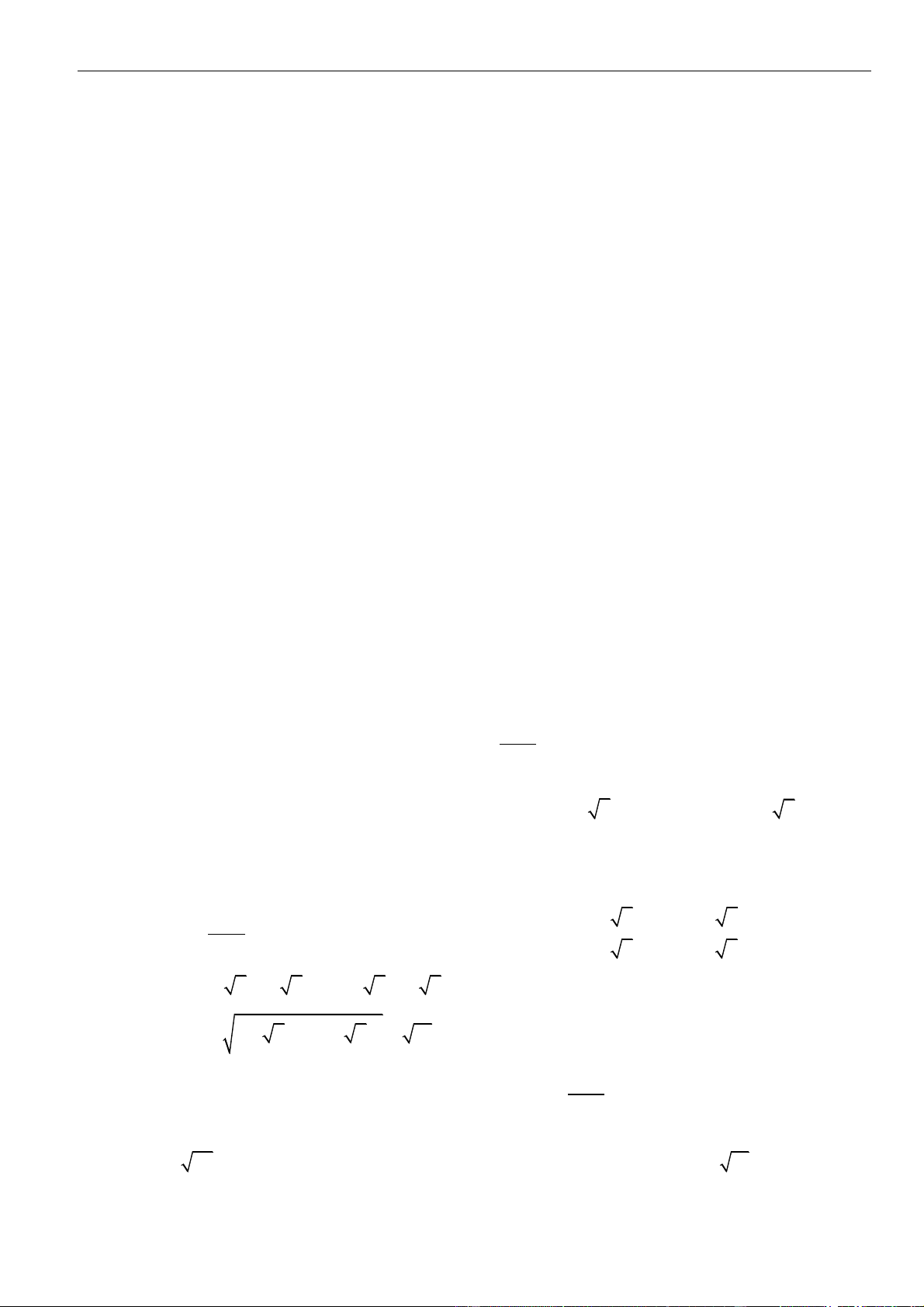
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn C
Số giao điểm của đồ thị
42
54y x x= − +
với trục hoành là số nghiệm của phương trình:
42
1
1
5 4 0
2
2
x
x
xx
x
x
=−
=
− + =
=−
=
Vậy số giao điểm của đồ thị
42
54y x x= − +
với trục hoành là
4
.
Câu 45: Cho hàm số
( )
( )
2
1 3 2y x x x x= − − +
có đồ thị
( )
C
. Mệnh đề nào dưới đây đúng?
A.
( )
C
cắt trục hoành tại
1
điểm.
B.
( )
C
cắt trục hoành tại
4
điểm phân biệt.
C.
( )
C
cắt trục hoành tại
2
điểm phân biệt.
D.
( )
C
cắt trục hoành tại
3
điểm phân biệt.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm ta có:
( )
( )
2
0
1 3 2 0 1
2
x
x x x x x
x
=
− − + = =
=
.
(trong đó
1x =
là nghiệm bội chẵn)
( )
C
cắt trục hoành tại
0x =
,
2x =
và tiếp xúc với trục
hoành tại
1x =
.
Câu 46: Đường thẳng
1yx=+
cắt đồ thị hàm số
1
2
x
y
x
−
=
−
tại hai điểm phân biệt
,AB
. Khi đó độ dài
đoạn thẳng
AB
bằng
A.
4AB =
. B.
8AB =
. C.
6AB =
. D.
22AB =
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm là:
22
1 2 2 2
1
1 2 1 2 1 0
2
1 2 2 2
xy
x
x x x x x x
x
xy
= + = +
−
+ = − − = − − − =
−
= − = −
( ) ( )
1 2;2 2 ; 1 2;2 2AB + + − −
( ) ( )
22
2 2 2 2 16 4AB = − + − = =
.
Câu 47: Biết rằng đường thẳng
12yx=−
cắt đồ thị hàm số
2
1
x
y
x
−
=
−
tại hai điểm phân biệt
A
và
B
. Độ
dài đoạn
AB
bằng
A.
20
. B.
20
. C.
15
. D.
15
.
Lời giải
Chọn D

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Phương trình hoành độ giao điểm của đường thẳng
12yx=−
cắt đồ thị hàm số
2
1
x
y
x
−
=
−
:
( )
2
2
1 2 2 2 1 0 1
1
x
x x x
x
−
− = − + + =
−
.
Giả sử
( ) ( )
1 1 2 2 1 2
;1 2 ; ;1 2 ;A x x B x x x x− −
là nghiệm của phương trình
( )
1
.
( )
( )
2 1 2 1
;2AB x x x x = − − −
( ) ( )
22
2 1 2 1 1 2
1
5 5 4 5. 1 4. 15
2
AB x x x x x x
= − = + − = − − =
.
Câu 48: Đồ thị hàm số
4
2
1
2
= − + +
x
yx
cắt trục hoành tại mấy điểm?
A.
2
. B.
4
. C.
3
. D.
0
.
Lời giải
Chọn A
Hoành độ giao điểm của đồ thị hàm số
4
2
1
2
= − + +
x
yx
với trục hoành là nghiệm phương trình :
2
4
2 4 2
2
1 3 0
1 0 2 2 0
2
1 3 0
= −
− + + = − + + =
= +
x
x
x x x
x
.
Phương trình có hai nghiệm phân biệt nên đồ thị hàm số
4
2
1
2
= − + +
x
yx
cắt trục hoành tại hai
điểm.
Câu 49: Số giao điểm của đường cong
32
3 2 5y x x x= + + +
và đường thẳng
32yx=−
bằng
A. 1. B. 0 C. 3 D. 2.
Lời giải
Chọn A
Phương trình hoành độ giao điểm
32
3 2 5 3 2
1
x x x x
x
+ + + = −
= −
Câu 50: Số giao điểm của đồ thị hàm số
42
42y x x= − − −
và trục hoành là
A.
1
. B.
2
. C.
0
. D.
4
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
42
4 2 0xx− − − =
(vô nghiệm).
Vậy số giao điểm của đồ thị hàm số
42
42y x x= − − −
và trục hoành là
0
.
Câu 51: Biết đường thẳng
:2d y x=−
cắt đồ thị hàm số
2x 1
1
y
x
+
=
−
tại hai điểm phân biệt A và B có hoành
độ lần lượt
A
x
và
B
x
. Giá trị của biểu thức
AB
xx+
là
A. 5. B. 1. C. 3. D. 2
Lời giải
Chọn A
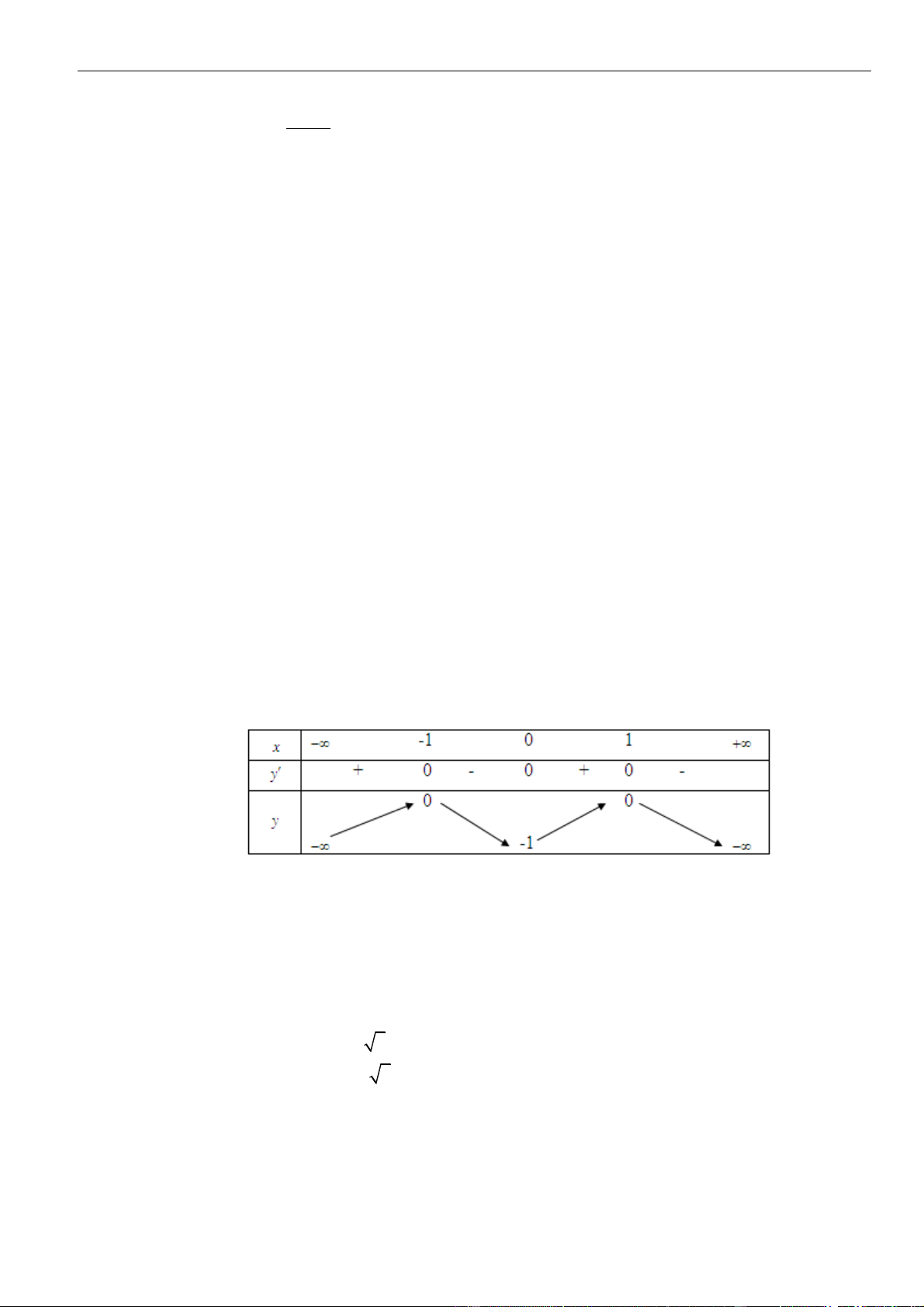
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Phương trình hoành độ giao điểm của đường thẳng
:2d y x=−
và đồ thị hàm số đã cho là
22
11
2x 1
2
1
2x 1 3x 2 5x 1 0 (1)
xx
x
x
xx
+
= −
−
+ = − + − + =
Dễ thấy (1) có 2 nghiệm phân biệt, theo Viet ta có
5
AB
xx+=
.
.
Câu 52: Số giao điểm của đường cong
32
21y x x x= − + −
và đường thẳng
12yx=−
là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của hai đường là:
3 2 3 2
2 1 1 2 2 3 2 0 1x x x x x x x x− + − = − − + − = =
Vậy số giao điểm của hai đường là
1
.
Câu 53: Số giao điểm của đồ thị hàm số
42
21y x x= − + −
với trục hoành là
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn A
Xét hàm số
42
2 1.y x x= − + −
3
4 4 .y x x
= − +
3
0
0 4 4 0 1 .
1
x
y x x x
x
=
= − + = =
=−
Bảng biến thiên:
Từ bảng biến thiên ta thấy đồ thị hàm số đã cho có 2 giao điểm với trục hoành.
Câu 54: Số giao điểm của đồ thị hàm số
3
5y x x= − +
với trục hoành là:
A.
3
. B.
2
. C.
0
. D.
1
Lời giải
Chọn A
Ta có
3
5
5 0 5
0
x
x x x
x
=
− + = = −
=
Vậy số giao điểm của đồ thị hàm số
3
5y x x= − +
với trục hoành là
3
.
Câu 55: Số giao điểm của đồ thị hàm số
3
43y x x= − +
và đường thẳng
3yx=+
là
A.
1
. B.
3
. C.
2
. D.
0
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Lời giải
Phương trình hoành độ giao điểm:
33
5
4 3 3 5 0 5
0
x
x x x x x x
x
=
− + = + − = = −
=
.
Phương trình có 3 nghiệm nên số giao điểm là 3.
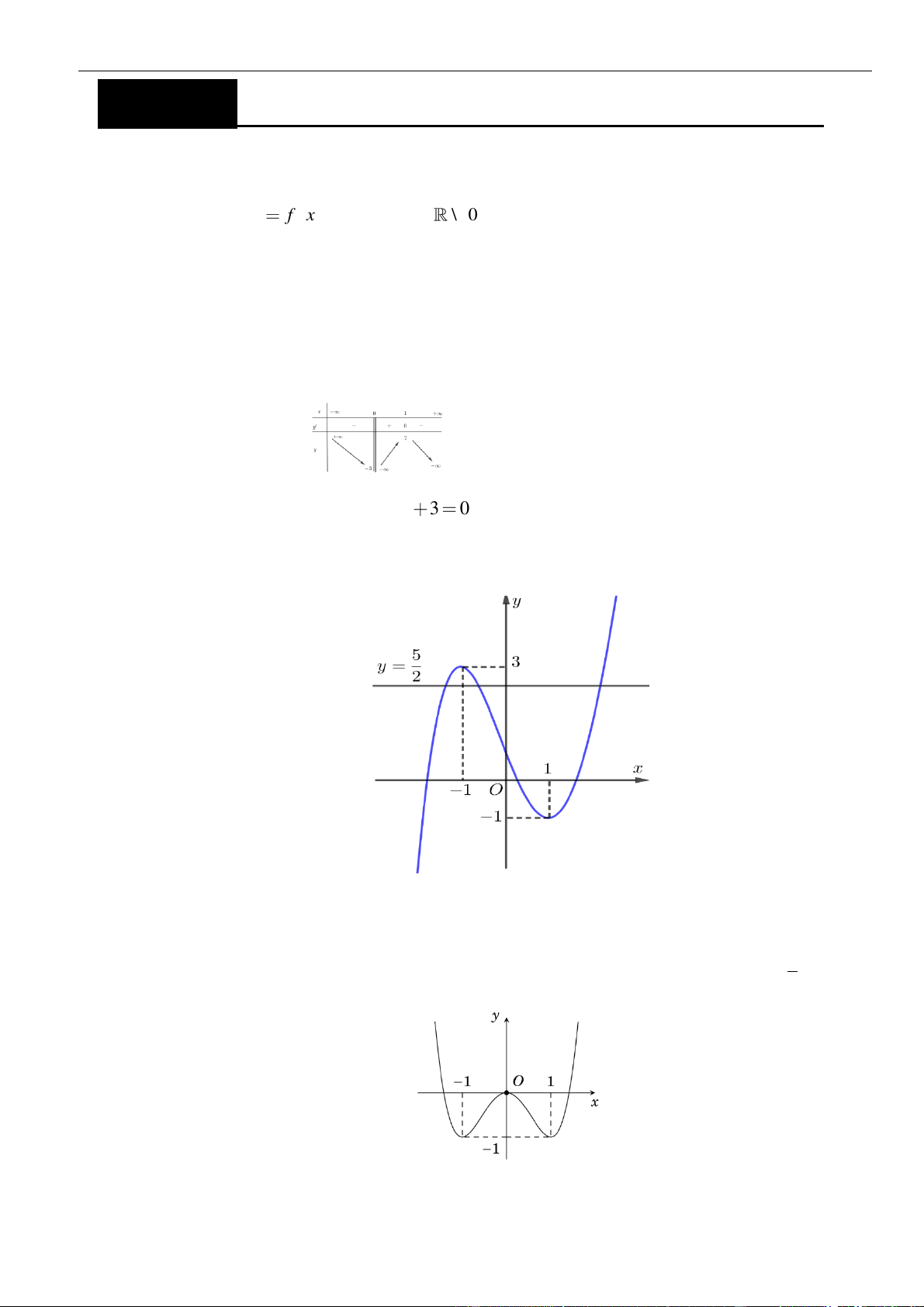
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
y f x
xác định trên
\0
có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình
( ) 3 0fx
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 2: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong như hình vẽ sau:
Số nghiệm thực của phương trình
( )
2 5 0fx−=
là.
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 3: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số nghiệm của phương trình
( )
1
3
fx=−
là
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 4: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên.
Tìm số nghiệm f(x)=g(x) khi biến đồ thị, BBT
DẠNG 3
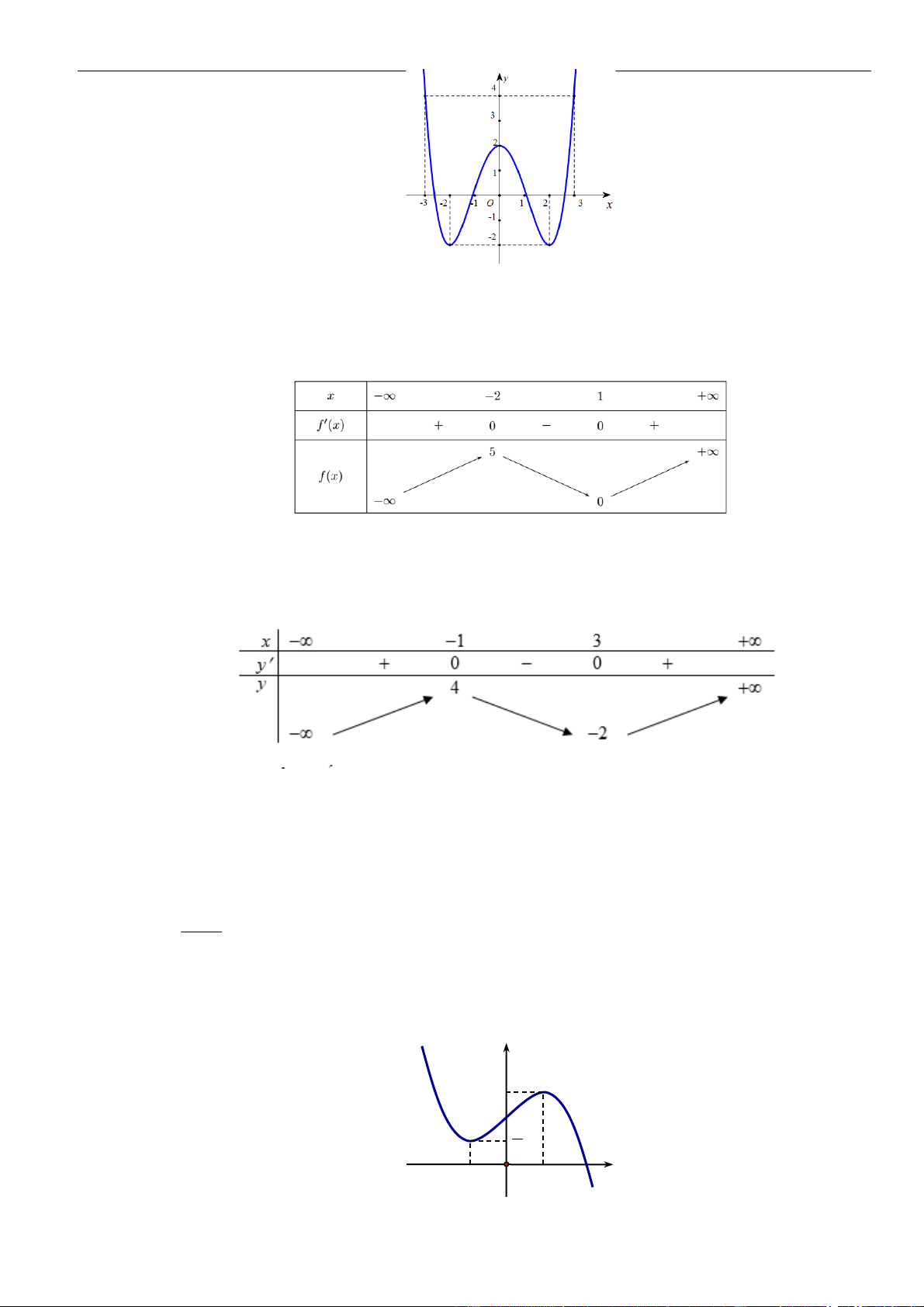
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Số nghiệm của phương trình
( )
3 5 0fx−=
là
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 5: Cho hàm số
( )
fx
có bảng biến thiên như sau
Số nghiệm thực của phương trình
( )
30fx−=
là
A. 3. B. 0. C. 2. D. 1.
Câu 6: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ
Số nghiệm của phương trình
( )
10fx−=
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 7: Số giao điểm của hai đồ thị hàm số
( )
y f x=
và
( )
y g x=
bằng số nghiệm phân biệt của phương
trình nào sau đây?
A.
( )
( )
0
fx
gx
=
. B.
( ) ( )
0f x g x+=
. C.
( ) ( )
0f x g x−=
. D.
( ) ( )
.0f x g x =
.
Câu 8: Cho hàm số
( )
y f x=
có đồ thị là đường cong trong hình vẽ bên. Tìm số nghiệm của phương
trình
( )
2 3 0fx−=
.
A.
2
. B.
1
. C.
3
. D.
4
.
O
x
y
1
1−
2
2
3
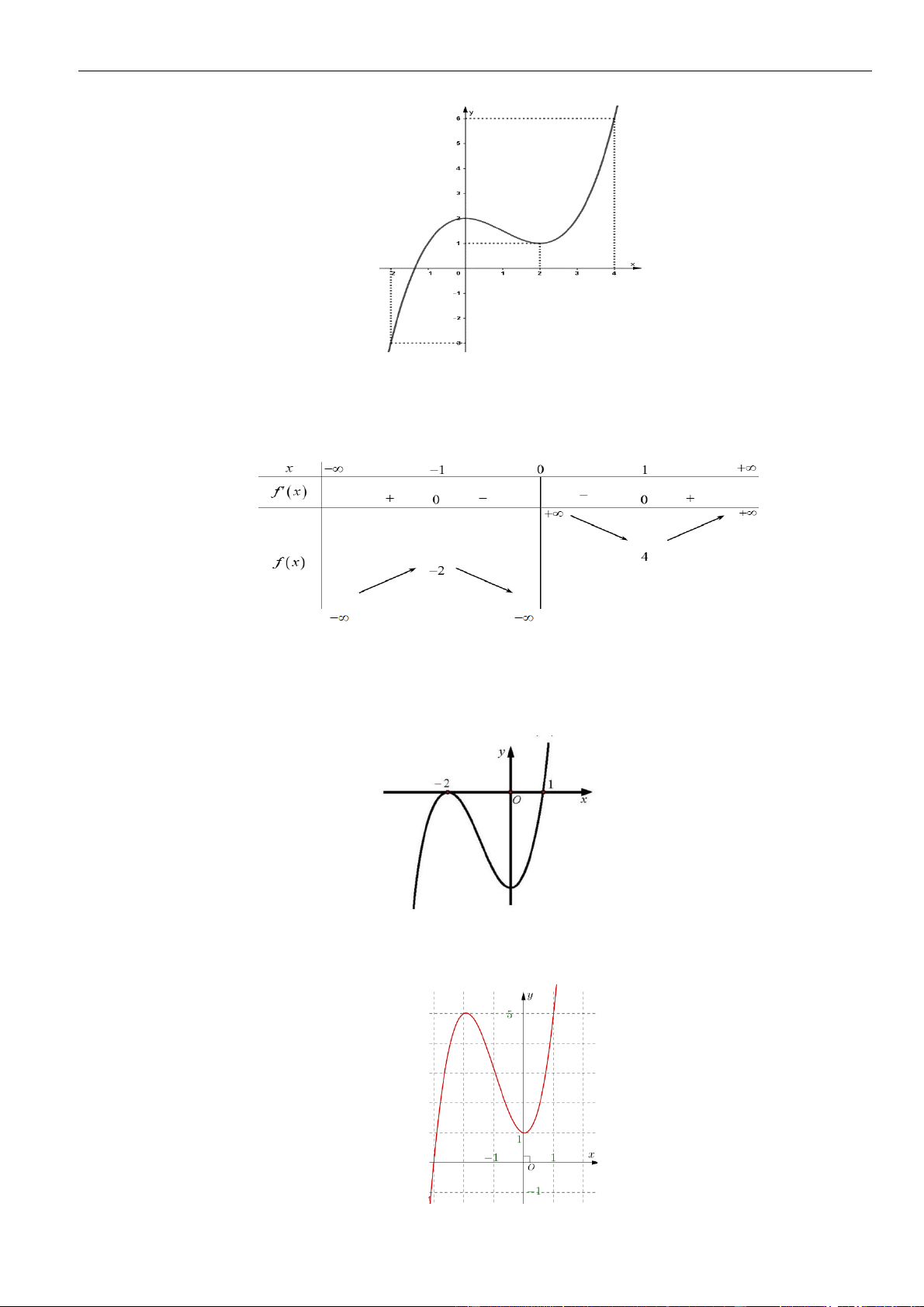
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 9: Cho hàm số
( )
y f x=
liên tục trên đoạn
2;4−
và có đồ thị như hình vẽ.
Phương trình
( )
3 4 0fx−=
có bao nhiêu nghiệm thực trên đoạn
2;4−
?
A.
3
. B.
2
C.
0
D.
1
.
Câu 10: Cho hàm số
( )
y f x=
liên tục trên từng khoảng xác định và bảng biến thiên như sau:
Số giao điểm của đồ thị hàm số
( )
y f x=
và đường thẳng
40y −=
là
A.
2
. B.
1
. C.
4
. D.
0
.
Câu 11: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số nghiệm thực phân biệt của
( )
1fx=
là
A. 1. B. 2. C. 3. D. 0.
Câu 12: Cho đồ thị hàm số bậc ba
( )
y f x=
như hình vẽ bên.
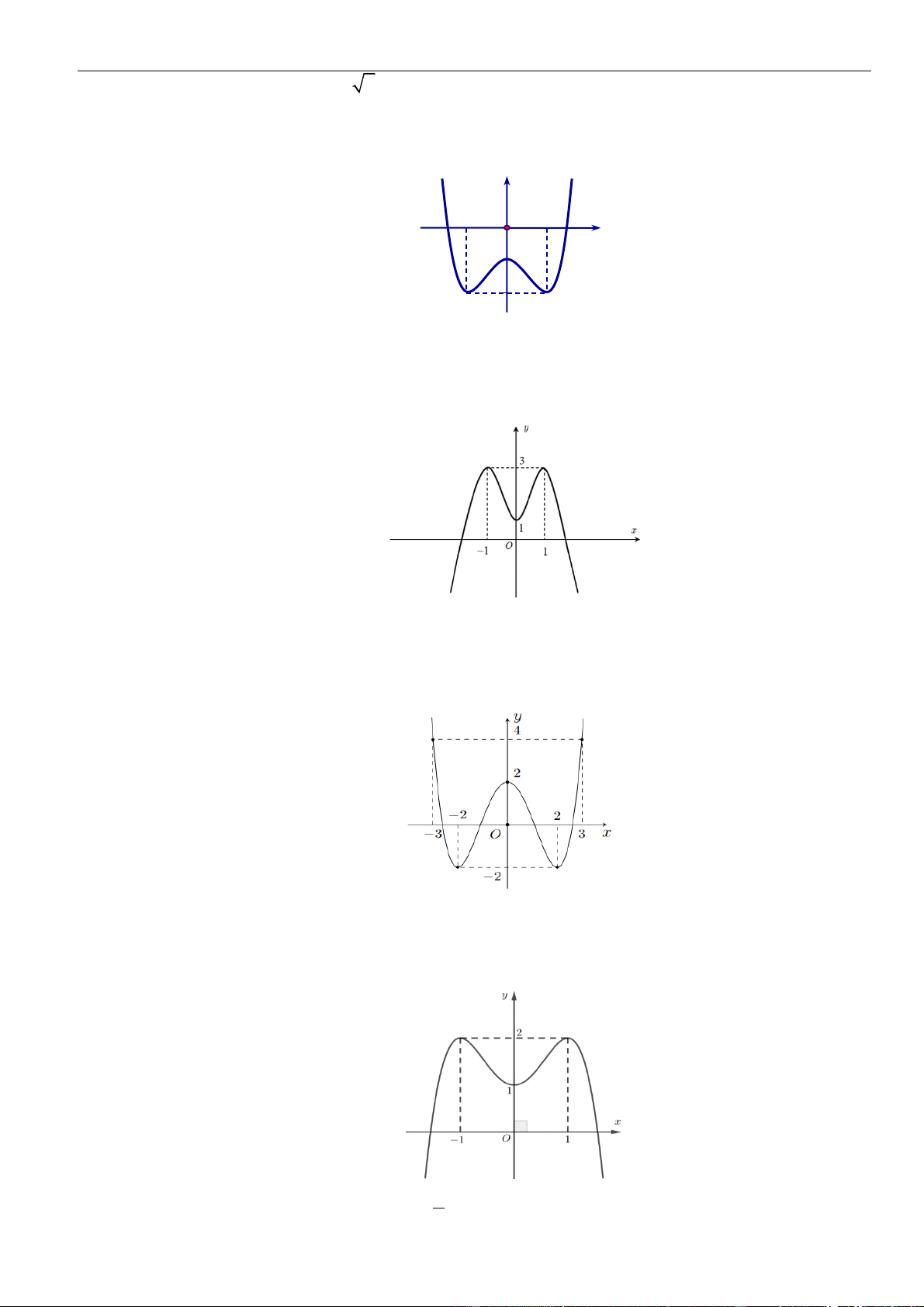
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Phương trình
( )
3 2 2fx=−
có bao nhiêu nghiệm?
A. 2 nghiệm. B. 3 nghiệm. C. 0 nghiệm. D. 1 nghiệm.
Câu 13: Cho hàm số
( )
42
y f x ax bx c= = + +
có đồ thị hình dưới đây.
Hỏi phương trình
( )
21fx=−
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 14: Cho hàm số bậc bốn
( )
y f x=
có đồ thị như hình vẽ bên dưới.
Số nghiệm của phương trình
( )
2 5 0fx+=
là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 15: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ.
Số nghiệm của phương trình
( )
3 5 0fx−=
là
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 16: Cho hàm số bậc bốn có đồ thị như hình vẽ bên dưới:
Số nghiệm của phương trình
( )
1
2
fx=
là:
O
x
y
1−
2−
1−
1
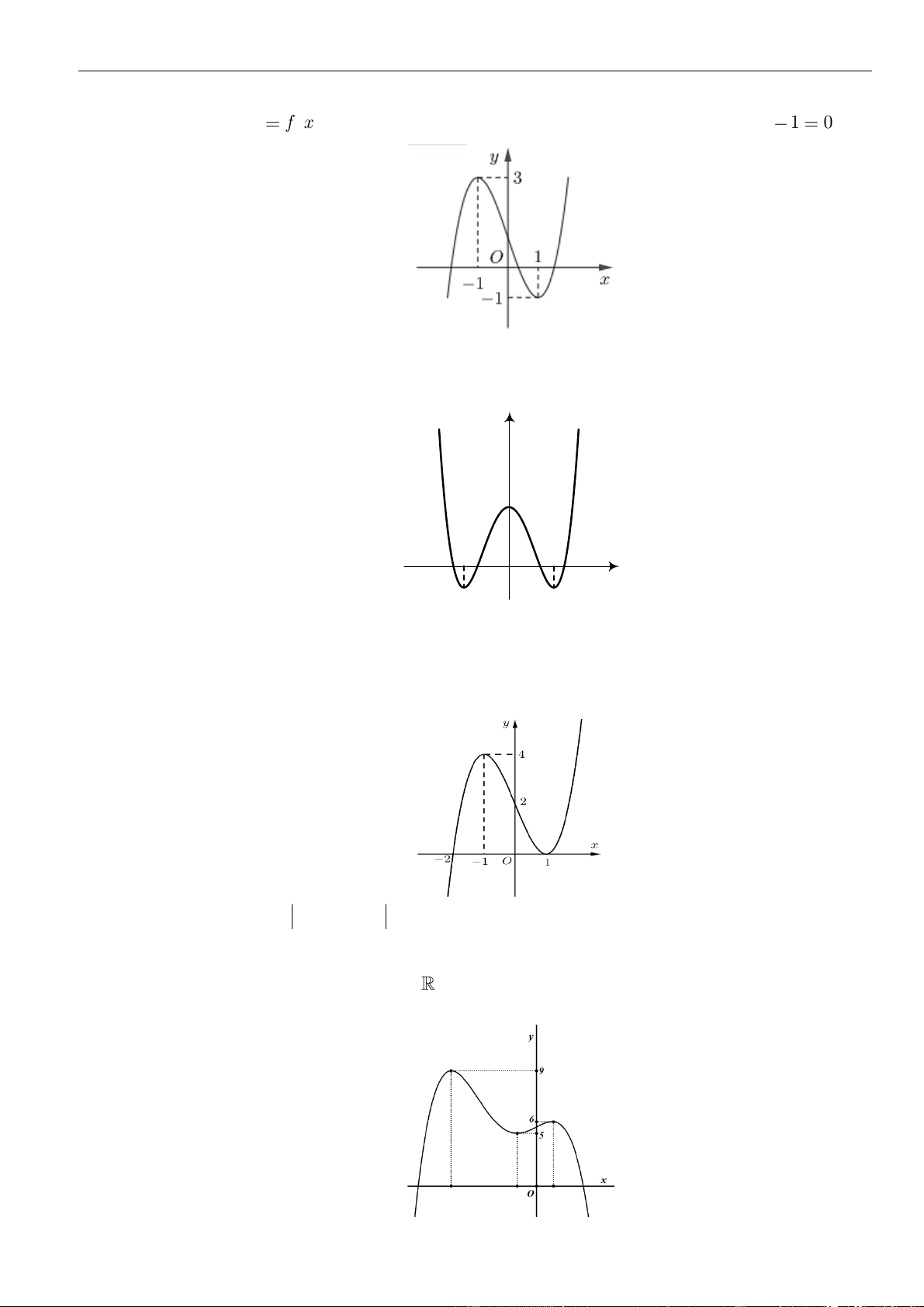
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 17: Cho hàm số
y f x
có đồ thị trong hình bên. Số nghiệm của phương trình
10fx
là
A.
0
. B.
2
.
C.
1
. D.
3
.
Câu 18: Cho hàm số
42
y ax bx c= + +
có đồ thị như hình vẽ
2−
2
x
y
O
3
Số nghiệm của phương trình
( )
2 5 0fx−=
là
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 19: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ.
Hỏi phương trình
( )
2 2 1fx− − =
có tất cả bao nhiêu nghiệm phân biệt thuộc khoảng
( )
0;+
?
A.
2
. B.
3
. C.
4
. D.
6
.
Câu 20: Cho hàm số
()y f x=
liên tục trên và có đồ thị như hình bên. Hỏi phương trình
( ) 6fx=
có
bao nhiêu nghiệm?
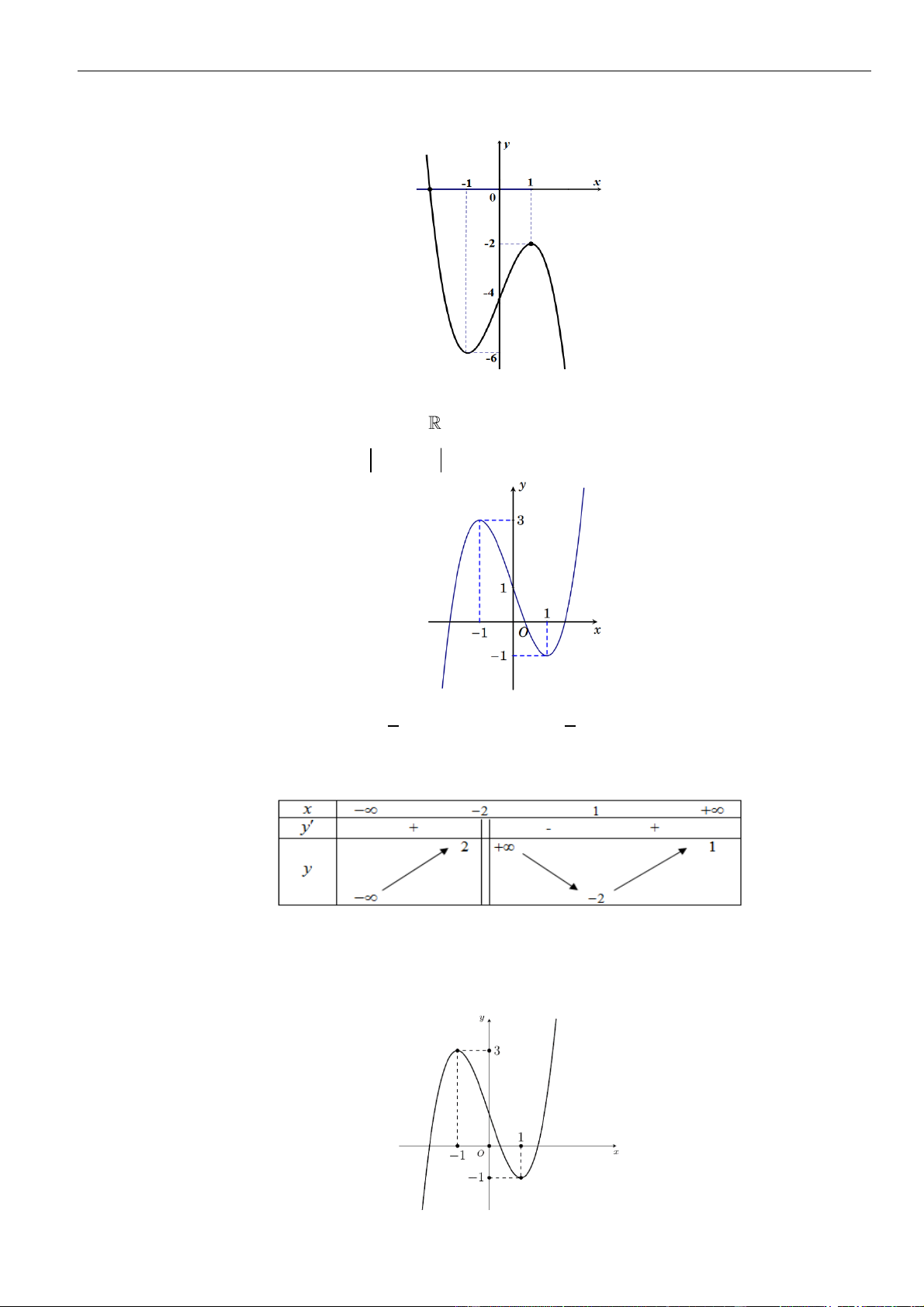
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 21: Cho hàm số
( )
fx
có đồ thị như hình vẽ. Phương trình
( )
6fx=−
có số nghiệm là
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 22: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của
tham số
m
để phương trình
( )
cos 2 3f x m= − +
có
4
nghiệm thuộc đoạn
0;2
là:
A.
1
. B.
3
1;
2
. C.
3
1;
2
. D.
( )
0;1
.
Câu 23: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Số nghiệm của phương trình
( )
2
40fx−=
là
A.
4
. B.
3
. C.
5
. D.
2
.
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong như hình vẽ
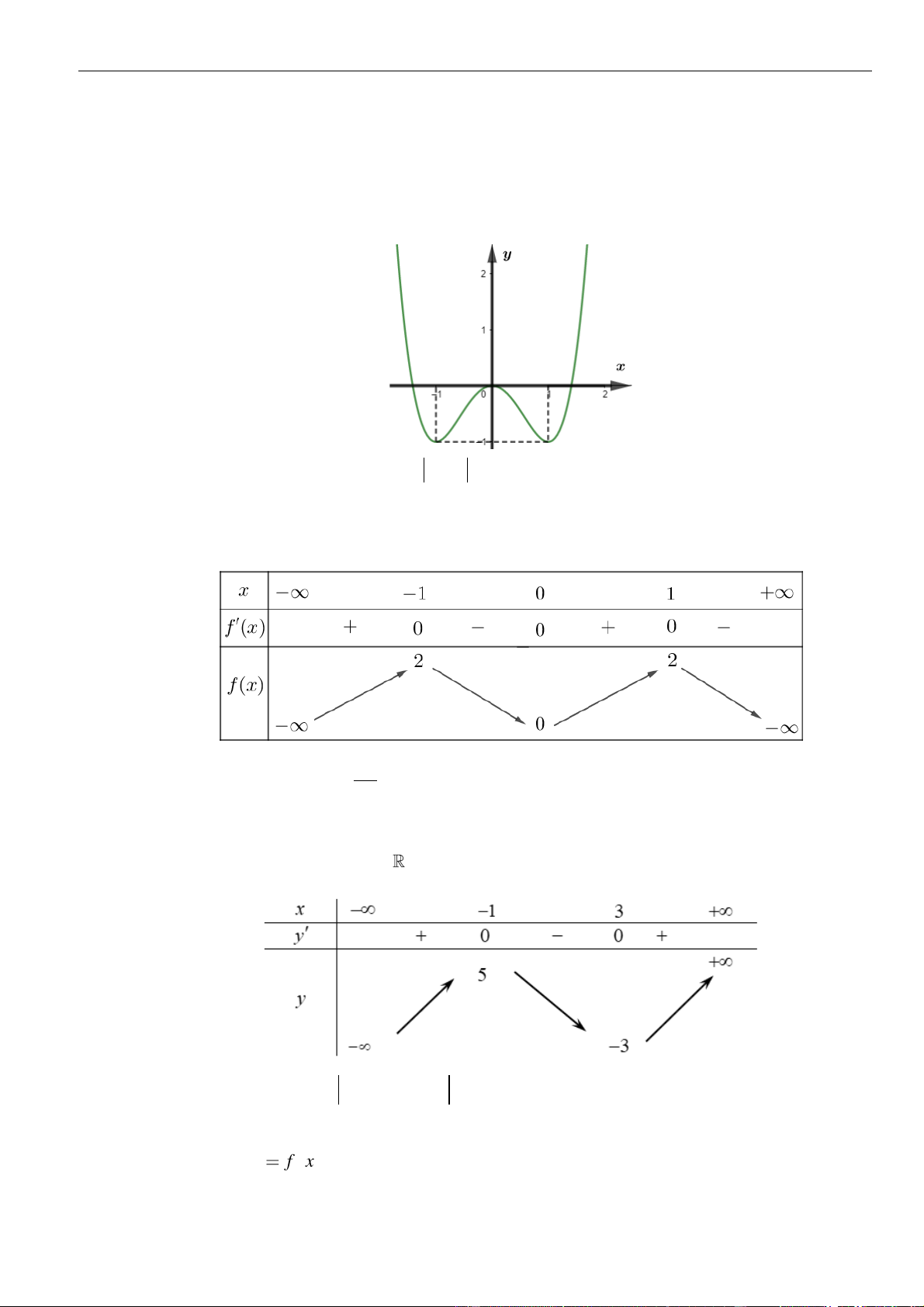
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Số nghiệm thực của phương trình
( )
2 5 0fx−=
là
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 25: Cho hàm số
( )
3
31f x x x= − +
. Số nghiệm thực phân biệt của phương trình
( )
( )
( )
2f f x f=
là
A.
1
. B.
3
. C.
5
. D.
9
.
Câu 26: Cho hàm số trùng phương
( )
y f x=
có đồ thị như hình vẽ bên dưới
Số nghiệm thực của phương trình
( )
2 1 0fx−=
là
A.
2
. B.
0
. C.
4
. D.
6
.
Câu 27: Cho hàm số
( )
fx
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
7
0;
2
của phương trình
( )
cos 1fx=
là
A.
6
. B.
4
. C.
7
. D.
5
.
Câu 28: Hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình vẽ
Phương trình
( )
2
2 3 2 5fx+ − =
có bao nhiêu nghiệm?
A.
3
. B.
5
. C.
6
. D.
4
.
Câu 29: Cho hàm số
y f x
có bảng biến thiên như hình bên.
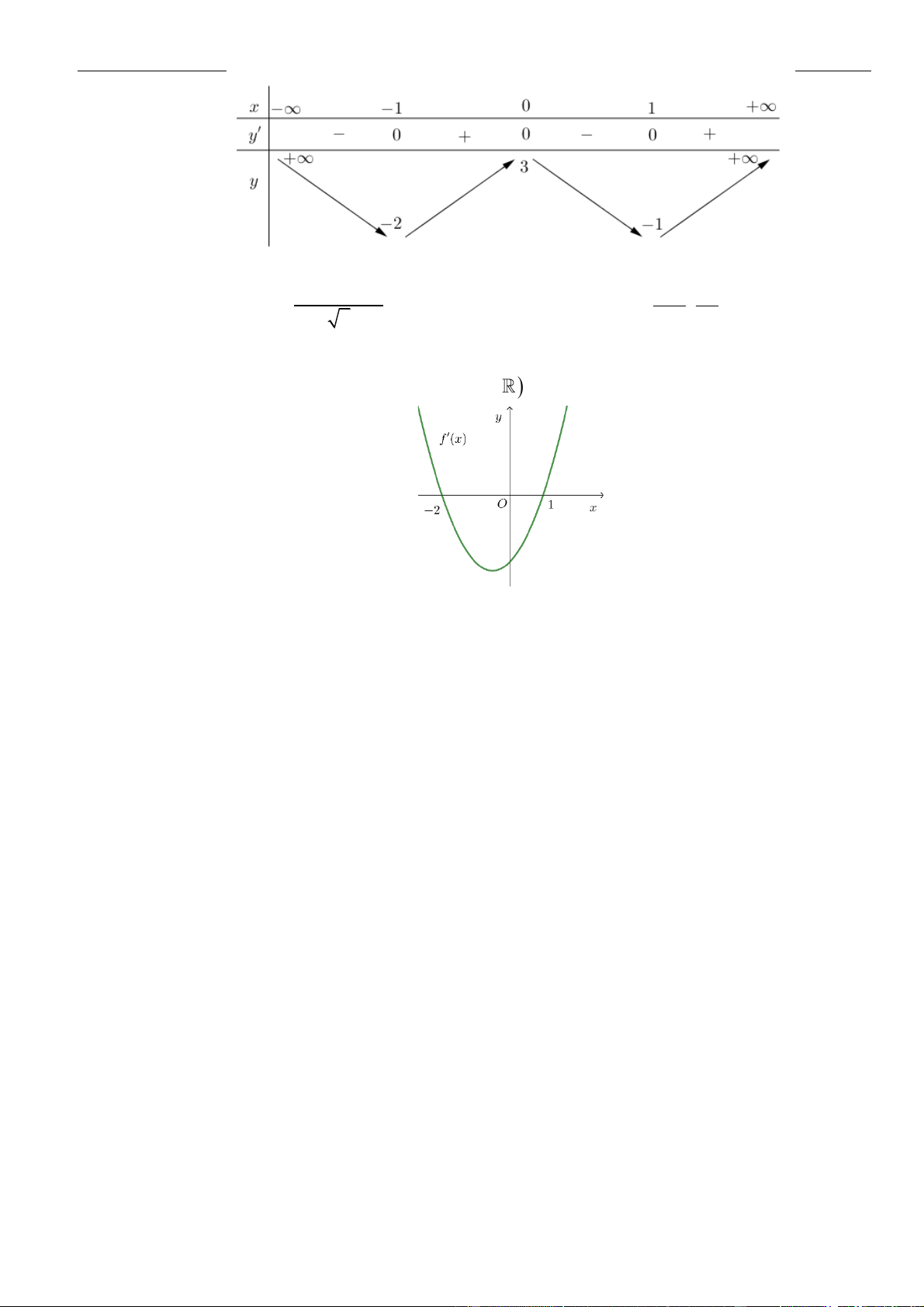
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Phương trình
sin cos
2 3 0
2
xx
f
+
+=
có bao nhiêu nghiệm trên
37
;
44
−
:
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 30: Cho hàm số
32
y ax bx cx d= + + +
( )
, , ,a b c d
. Hàm số
( )
fx
có đồ thị hàm số như sau:
Và
( ) ( )
2020 1 2021 0ff=
. Hỏi đồ thị hàm số
( )
y f x=
và đồ thị hàm số
( )
y f x
=
cắt nhau
tại bao nhiêu điểm phân biệt.
A.
0
. B.
2
. C.
3
. D.
1
.
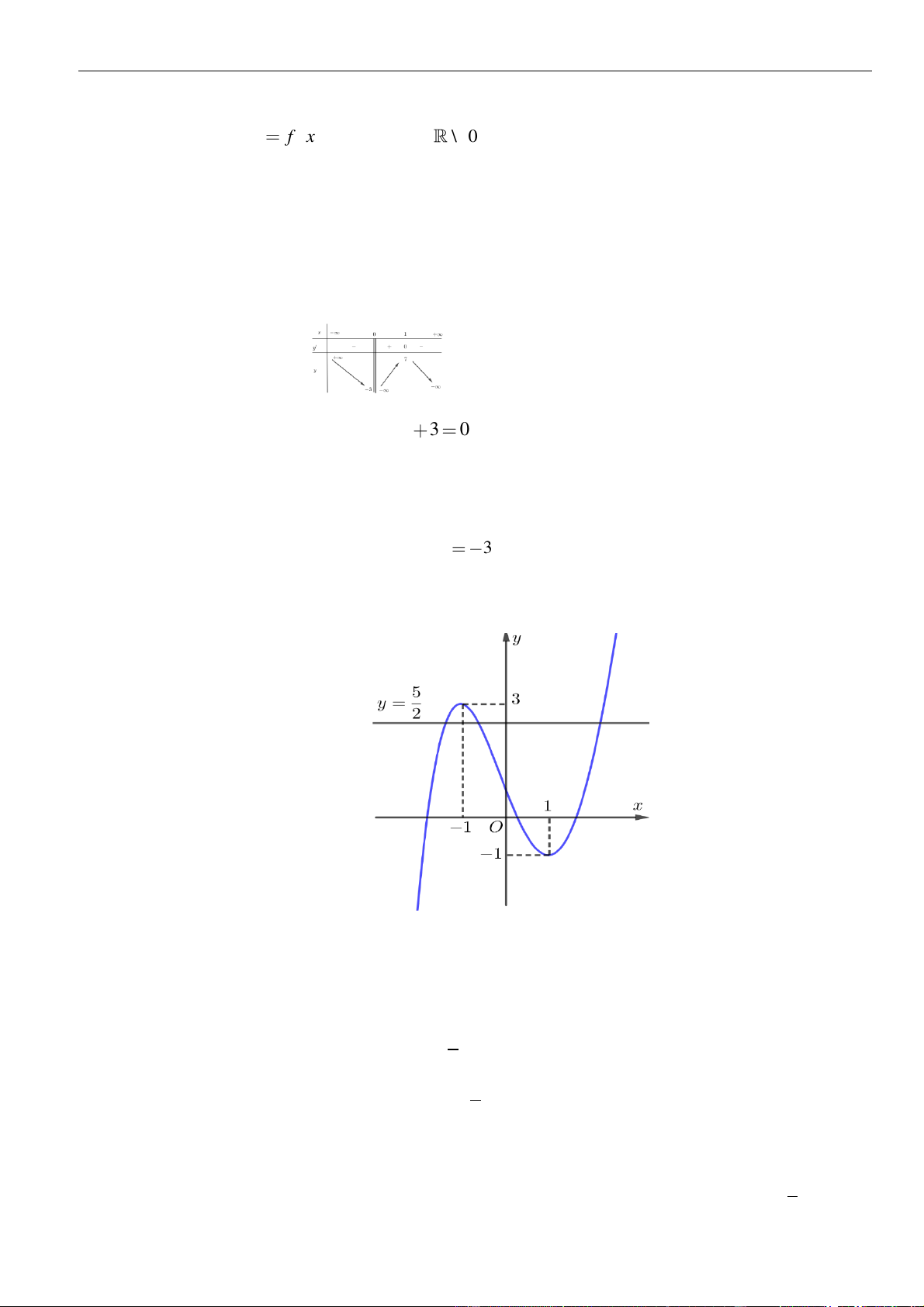
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
y f x
xác định trên
\0
có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình
( ) 3 0fx
là
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn B
Phương trình đã cho tương đương
( ) 3fx
, dựa vào bảng biến thiên suy ra phương trình có 2
nghiệm.
Câu 2: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong như hình vẽ sau:
Số nghiệm thực của phương trình
( )
2 5 0fx−=
là.
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn C
Phương trình
( ) ( )
5
2 5 0
2
f x f x− = =
.
Quan sát hình vẽ ta thấy đường thẳng
5
2
y =
cắt đồ thị hàm số
( )
y f x=
tại 3 điểm phân biệt.
Vậy phương trình
( )
2 5 0fx−=
có 3 nghiệm thực phân biệt.
Câu 3: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số nghiệm của phương trình
( )
1
3
fx=−
là
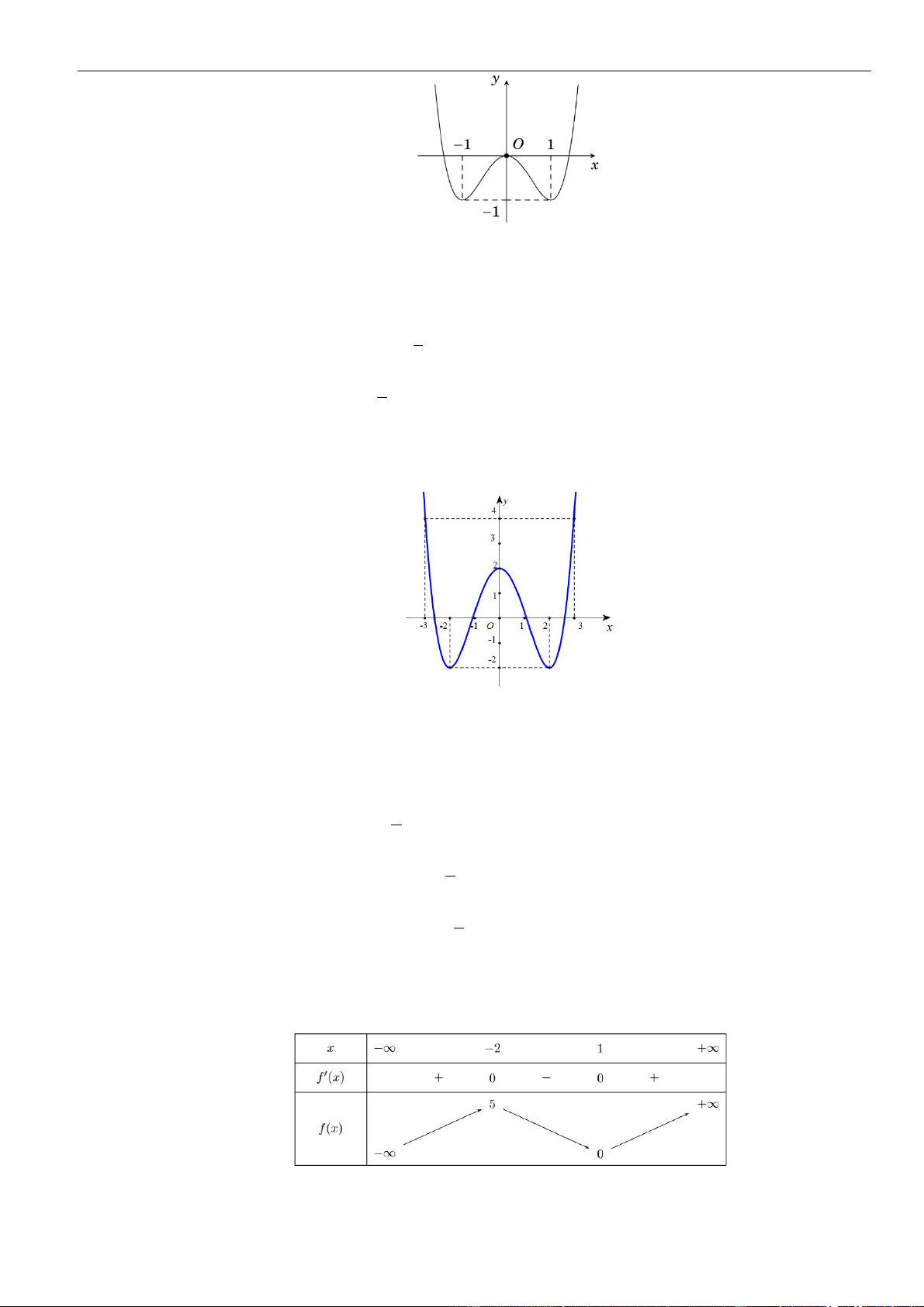
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn B
Ta xem phương trình
( )
1
3
fx=−
là phương trình hoành độ giao điểm của hai đồ thị
( ) ( )
:C y f x=
và
( )
1
:
3
dy=−
. Do
( )
d
cắt
( )
C
tại
4
điểm phân biệt nên phương trình có
4
nghiệm.
Câu 4: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên.
Số nghiệm của phương trình
( )
3 5 0fx−=
là
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn A
Ta có
( )
3 5 0fx−=
( )
5
3
fx=
nên số nghiệm của phương trình bằng số giao điểm của đồ thị
hàm số
( )
y f x=
và đường thẳng
5
3
y =
.
Từ đồ thị hàm số ta có đường thẳng
5
3
y =
cắt đồ thị hàm số tại
4
điểm nên phương trình đã cho
có
4
nghiệm phân biệt.
Câu 5: Cho hàm số
( )
fx
có bảng biến thiên như sau
Số nghiệm thực của phương trình
( )
30fx−=
là
A. 3. B. 0. C. 2. D. 1.
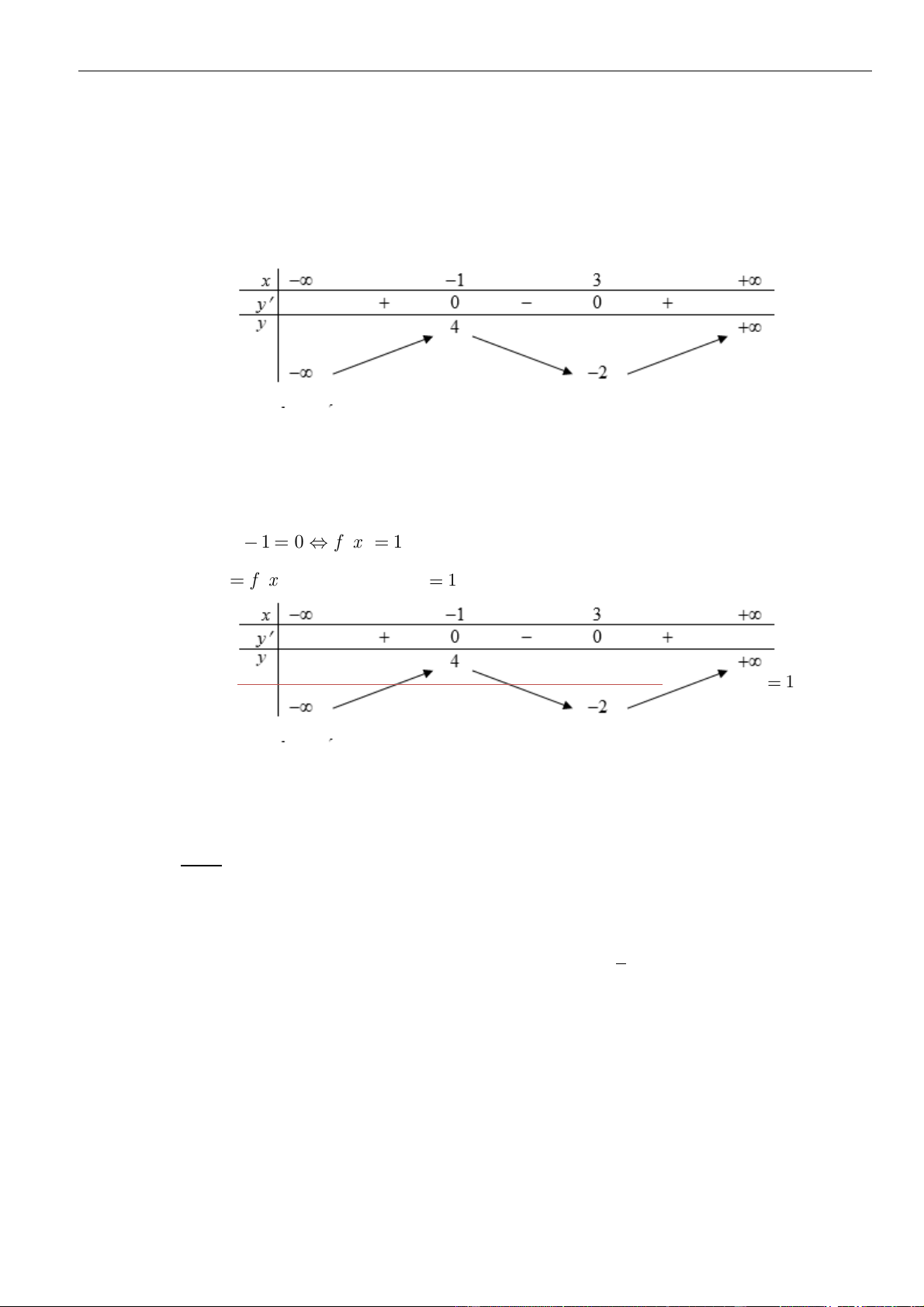
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn A
Phương trình
( ) ( )
3 0 3f x f x− = =
.
Từ bảng biến thiên ta thấy đồ thị
( )
y f x=
cắt đường thẳng
3y =
tại ba điểm.
Vậy phương trình
( )
30fx−=
có ba nghiệm phân biệt.
Câu 6: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ
Số nghiệm của phương trình
( )
10fx−=
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
Ta có
1 0 1f x f x
nên số nghiệm của phương trình là số giao điểm của đồ thị
hàm số
y f x
và đường thẳng
1y
.
Vậy phương trình đã cho có 3 nghiệm.
Câu 7: Số giao điểm của hai đồ thị hàm số
( )
y f x=
và
( )
y g x=
bằng số nghiệm phân biệt của phương
trình nào sau đây?
A.
( )
( )
0
fx
gx
=
. B.
( ) ( )
0f x g x+=
. C.
( ) ( )
0f x g x−=
. D.
( ) ( )
.0f x g x =
.
Lời giải
Chọn C
Hoành độ giao điểm của đồ thị hai hàm số
và
là nghiệm của phương trình
sau
( ) ( ) ( ) ( )
0f x g x f x g x= − =
.
Câu 8: Cho hàm số
( )
y f x=
có đồ thị là đường cong trong hình vẽ bên. Tìm số nghiệm của phương
trình
( )
2 3 0fx−=
.
R
3
4
3
VR
=
1y
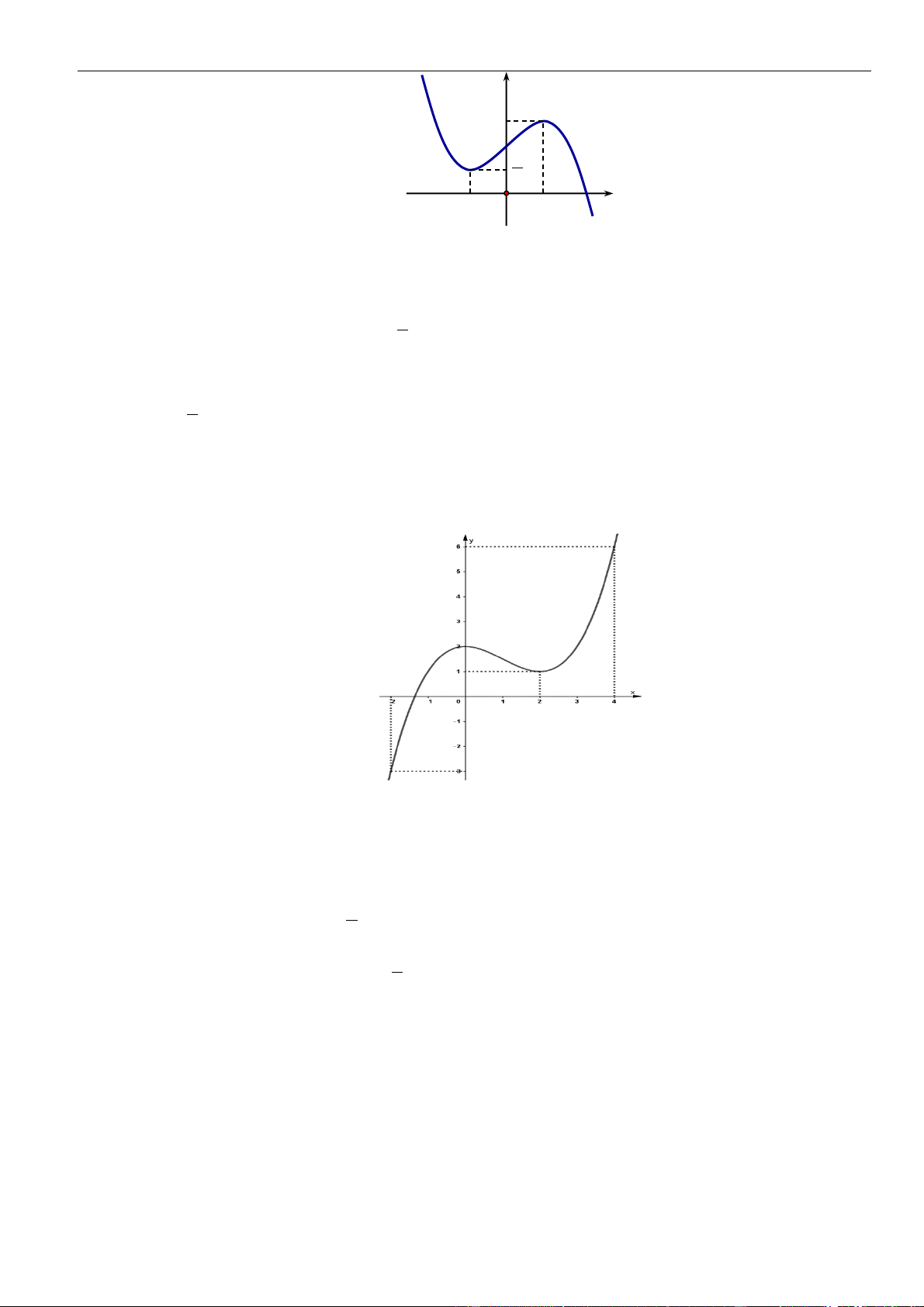
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn C
Ta có:
( ) ( )
3
2 3 0
2
f x f x− = =
.
Số nghiệm của phương trình bằng số giao điểm của hai đồ thị hàm số
( )
y f x=
và đường thẳng
3
2
y =
Quan sát đồ thị hàm số ta thấy hai đồ thị hàm số cắt nhau tại
3
điểm nên phương trình có
3
nghiệm.
Câu 9: Cho hàm số
( )
y f x=
liên tục trên đoạn
2;4−
và có đồ thị như hình vẽ.
Phương trình
( )
3 4 0fx−=
có bao nhiêu nghiệm thực trên đoạn
2;4−
?
A.
3
. B.
2
C.
0
D.
1
.
Lời giải
Chọn A
( ) ( )
4
3 4 0
3
f x f x− = =
với mọi
2;4x−
2;4x −
đường thẳng
4
3
y =
cắt đồ thị hàm số
( )
y f x=
tại 3 điểm phân biệt nên
( )
3 4 0fx−=
có 3 nghiệm phân biệt.
Câu 10: Cho hàm số
( )
y f x=
liên tục trên từng khoảng xác định và bảng biến thiên như sau:
O
x
y
1
1−
2
2
3
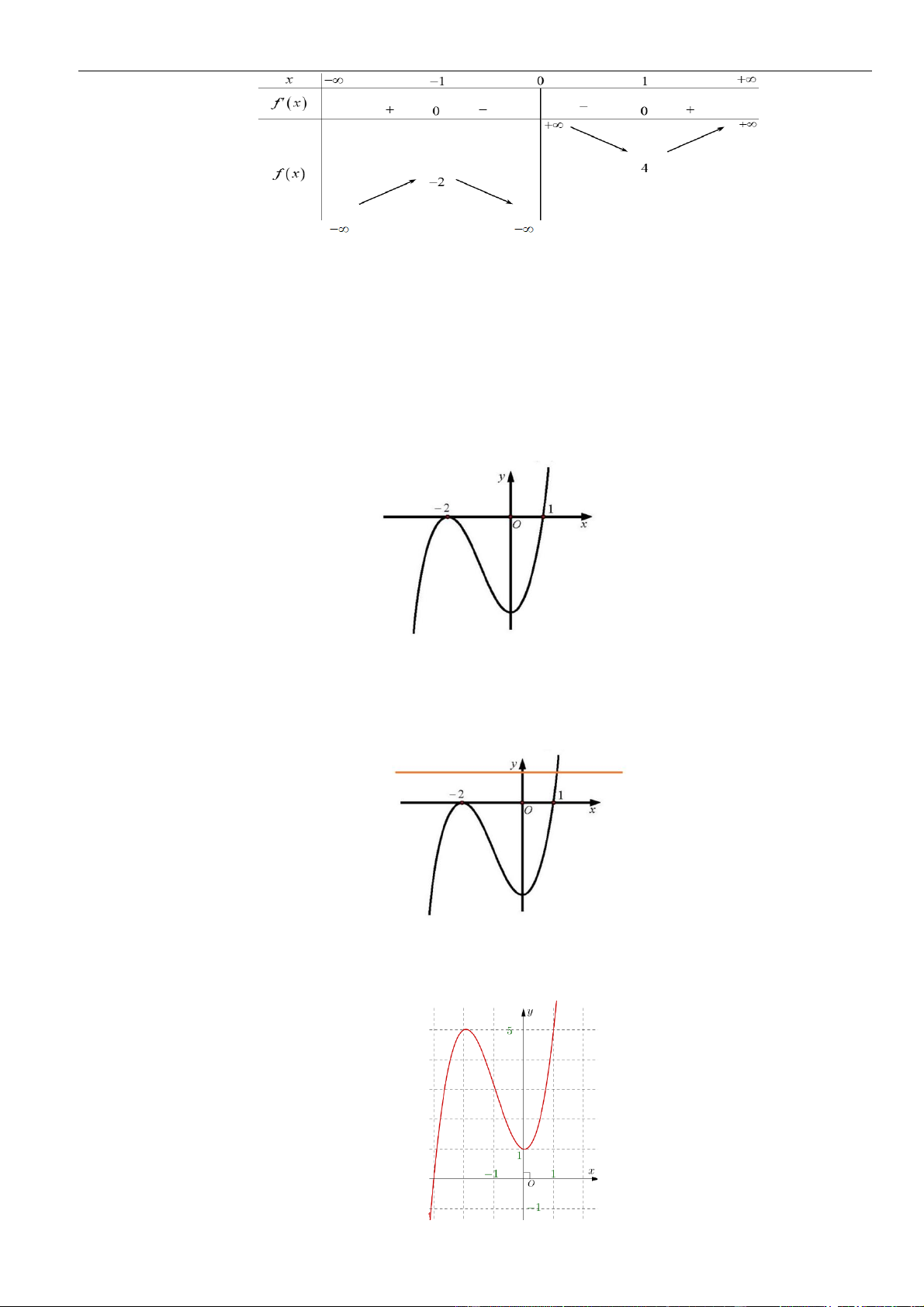
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Số giao điểm của đồ thị hàm số
( )
y f x=
và đường thẳng
40y −=
là
A.
2
. B.
1
. C.
4
. D.
0
.
Lời giải
Chọn B
Ta có: Dựa vào bảng biến thiên thấy rằng đường thẳng
4 0 4yy− = =
tiếp xúc đồ thị hàm số
( )
y f x=
tại 1 điểm.
Câu 11: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số nghiệm thực phân biệt của
( )
1fx=
là
A. 1. B. 2. C. 3. D. 0.
Lời giải
Chọn A
Số nghiệm thực phân biệt của
( )
1fx=
là số giao điểm của đồ thị hàm số
( )
y f x=
và
1y =
Dựa vào hình vẽ ta có số nghiệm thực phân biệt của
( )
1fx=
là 1.
Câu 12: Cho đồ thị hàm số bậc ba
( )
y f x=
như hình vẽ bên.
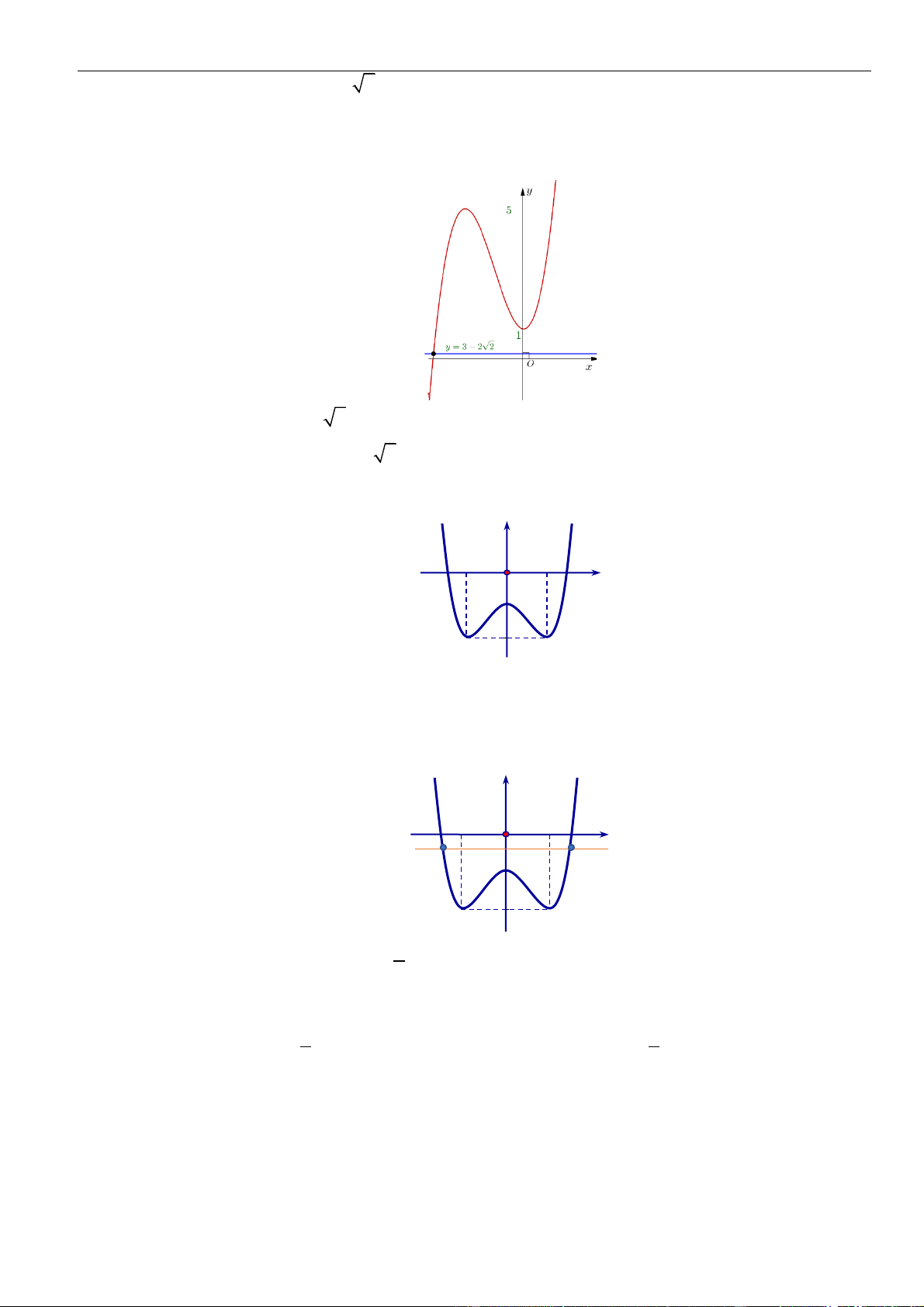
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Phương trình
( )
3 2 2fx=−
có bao nhiêu nghiệm?
A. 2 nghiệm. B. 3 nghiệm. C. 0 nghiệm. D. 1 nghiệm.
Lời giải
Chọn D
Đường thẳng
3 2 2y =−
cắt đồ thị
( )
y f x=
tại 1 điểm
phương trình
( )
3 2 2fx=−
có 1 nghiệm.
Câu 13: Cho hàm số
( )
42
y f x ax bx c= = + +
có đồ thị hình dưới đây.
Hỏi phương trình
( )
21fx=−
có bao nhiêu nghiệm?
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn A
Ta có
( )
21fx=−
( )
1
2
fx=−
.
Số nghiệm của phương trình
( )
21fx=−
chính là số giao điểm của đồ thị hàm số
( )
y f x=
với
đường thẳng
1
2
y =−
. Quan sát đồ thị ta thấy đường thẳng
1
2
y =−
cắt đồ thị tại hai điểm. Do
đó phương trình
( )
21fx=−
có
2
nghiệm.
Câu 14: Cho hàm số bậc bốn
( )
y f x=
có đồ thị như hình vẽ bên dưới.
O
x
y
1−
2−
1−
1
O
x
y
1−
2−
1−
1
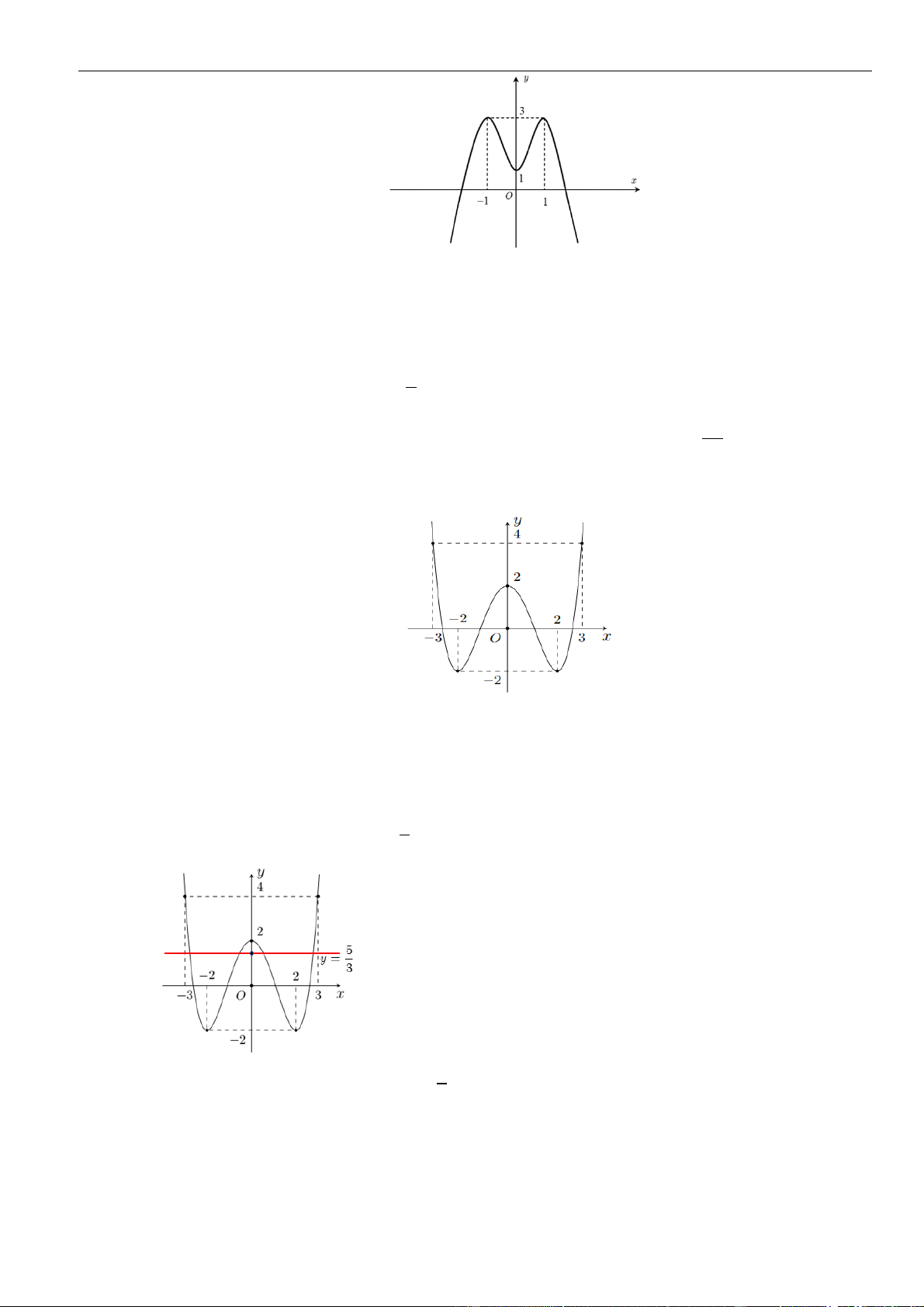
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Số nghiệm của phương trình
( )
2 5 0fx+=
là
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn B
Ta có
( ) ( )
5
2 5 0
2
f x f x+ = = −
Dựa vào đồ thị ta thầy hàm số
( )
y f x=
cắt đường thẳng nằm ngang
5
2
y
−
=
tại hai điểm.
Câu 15: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ.
Số nghiệm của phương trình
( )
3 5 0fx−=
là
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn A
Ta có:
( )
3 5 0fx−=
( )
5
3
fx=
.
Từ đồ thị, ta thấy đường thẳng
5
3
y =
cắt đồ thị tại
4
điểm phân biệt. Do đó phương trình
( )
3 5 0fx−=
có
4
nghiệm.
Câu 16: Cho hàm số bậc bốn có đồ thị như hình vẽ bên dưới:
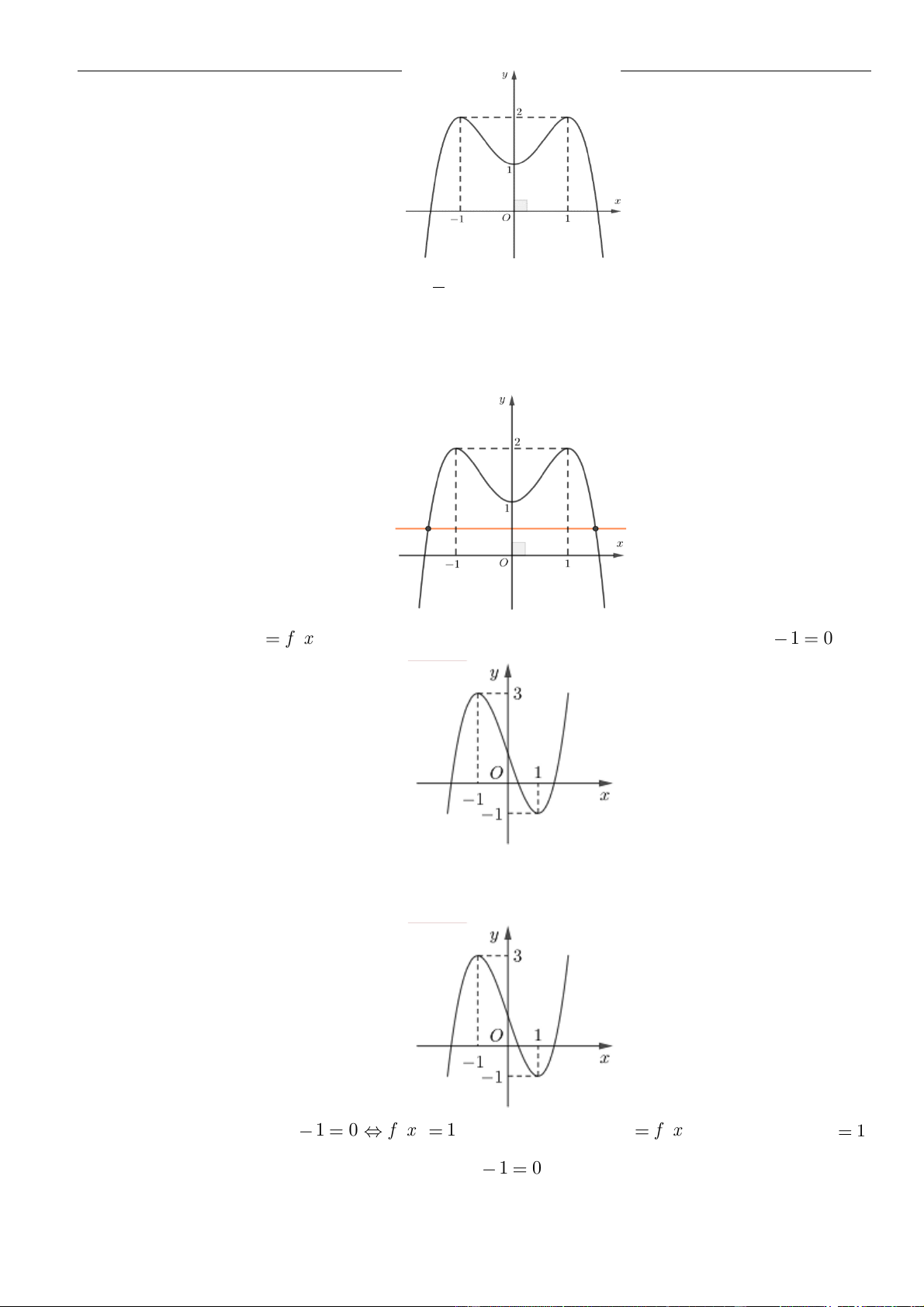
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Số nghiệm của phương trình
( )
1
2
fx=
là:
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn C
Câu 17: Cho hàm số
y f x
có đồ thị trong hình bên. Số nghiệm của phương trình
10fx
là
A.
0
. B.
2
.
C.
1
. D.
3
.
Lời giải
Chọn D
Phương trình
1 0 1f x f x
. Ta có đồ thị hàm số
y f x
cắt đường thẳng
1y
tại 3 điểm phân biệt nên phương trình
10fx
có 3 nghiệm phân biệt.
Câu 18: Cho hàm số
42
y ax bx c= + +
có đồ thị như hình vẽ
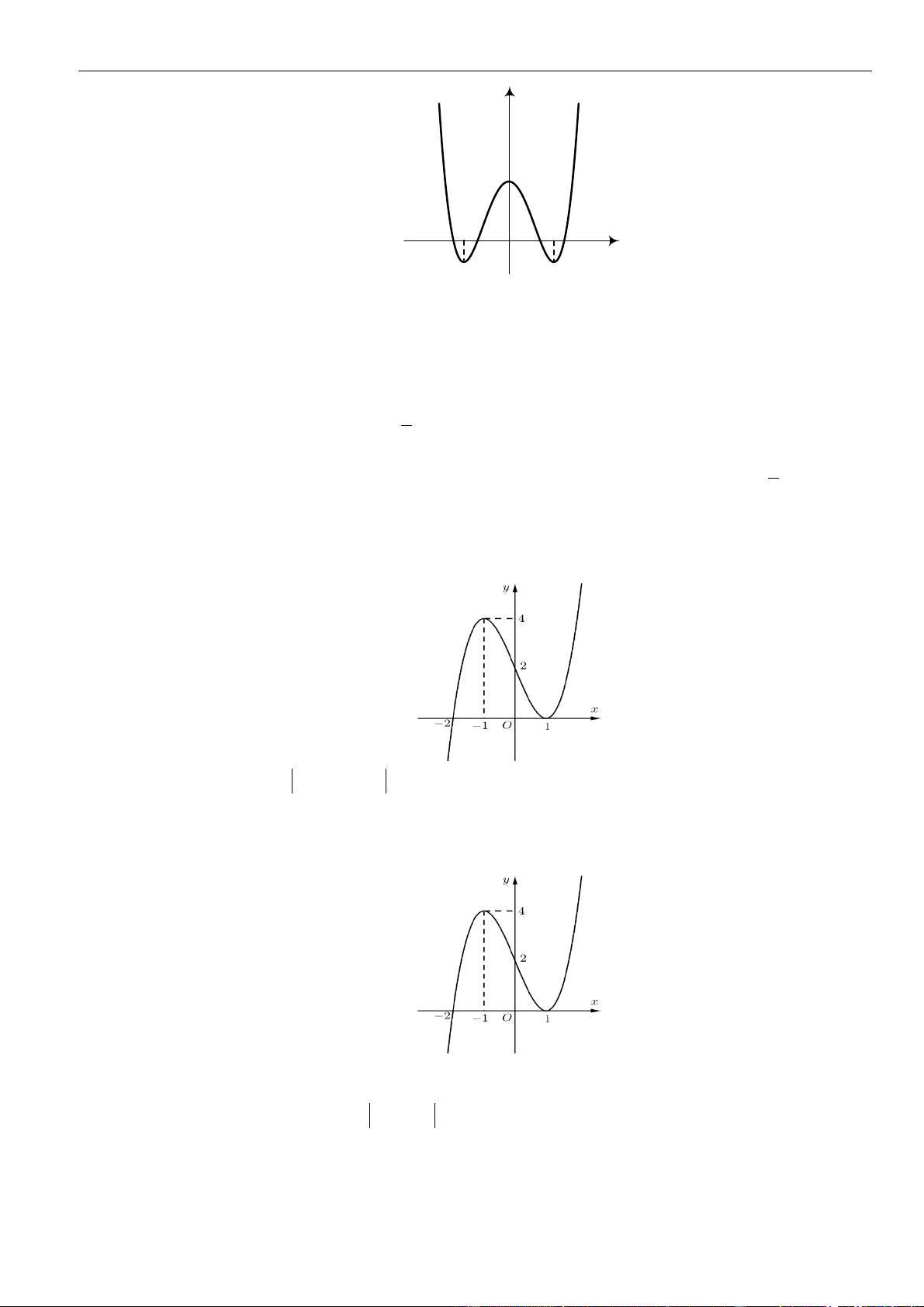
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
2−
2
x
y
O
3
Số nghiệm của phương trình
( )
2 5 0fx−=
là
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có :
( ) ( )
5
2 5 0
2
f x f x− = =
( )
1
( )
1
là phương trình hoành độ giao điểm của đồ thị
( )
y f x=
và đường thẳng
5
2
y =
.
Do hai đồ thị có
4
giao điểm nên
( )
1
có
4
nghiệm phân biệt.
Câu 19: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ.
Hỏi phương trình
( )
2 2 1fx− − =
có tất cả bao nhiêu nghiệm phân biệt thuộc khoảng
( )
0;+
?
A.
2
. B.
3
. C.
4
. D.
6
.
Lời giải
Chọn D
Đặt:
2, 2t x t= − −
.
Phương trình cho trở thành:
( )
21ft−=
( )
( )
3
1
ft
ft
=
=
Dựa vào đồ thị ta thấy phương trình có 6 nghiệm phân
( )
2;t − +
Phương trình đã cho có 6
nghiệm phân biệt thuộc
( )
0;+
.
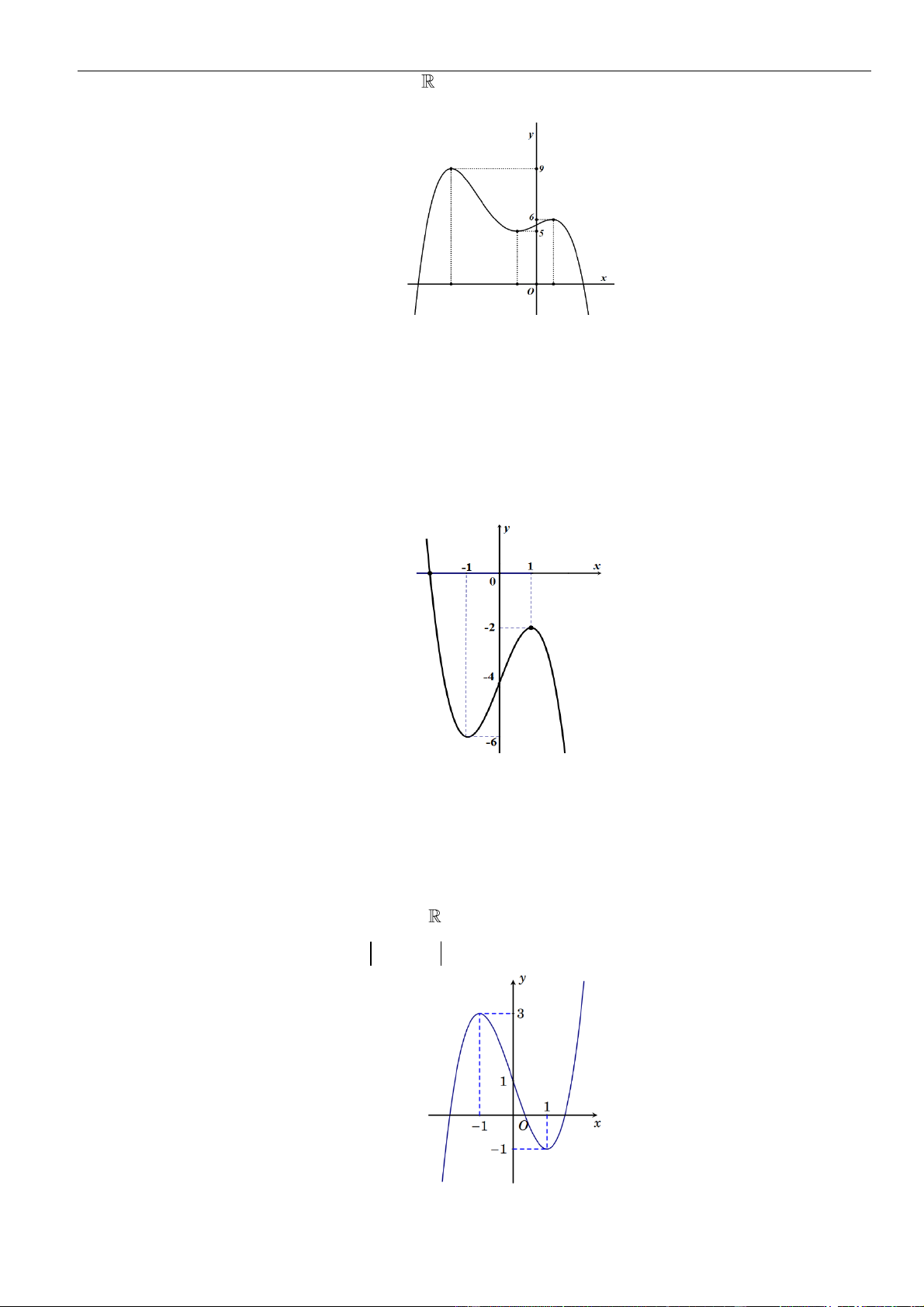
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Câu 20: Cho hàm số
()y f x=
liên tục trên và có đồ thị như hình bên. Hỏi phương trình
( ) 6fx=
có
bao nhiêu nghiệm?
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn A
Số nghiệm của phương trình
( ) 6fx=
chính là số giao điểm của đồ thị hàm số
()y f x=
với
đường thẳng
6y =
.
Dựa vào đồ thị đã cho ta thấy đường thẳng
6y =
cắt đồ thị
()y f x=
tại 3 điểm phân biệt.
Câu 21: Cho hàm số
( )
fx
có đồ thị như hình vẽ. Phương trình
( )
6fx=−
có số nghiệm là
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số
( )
y f x=
và đường thẳng
6y =−
Ta thấy hai đồ thị cắt nhau tại hai điểm phân biệt hay phương trình có hai nghiệm.
Câu 22: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của
tham số
m
để phương trình
( )
cos 2 3f x m= − +
có
4
nghiệm thuộc đoạn
0;2
là:
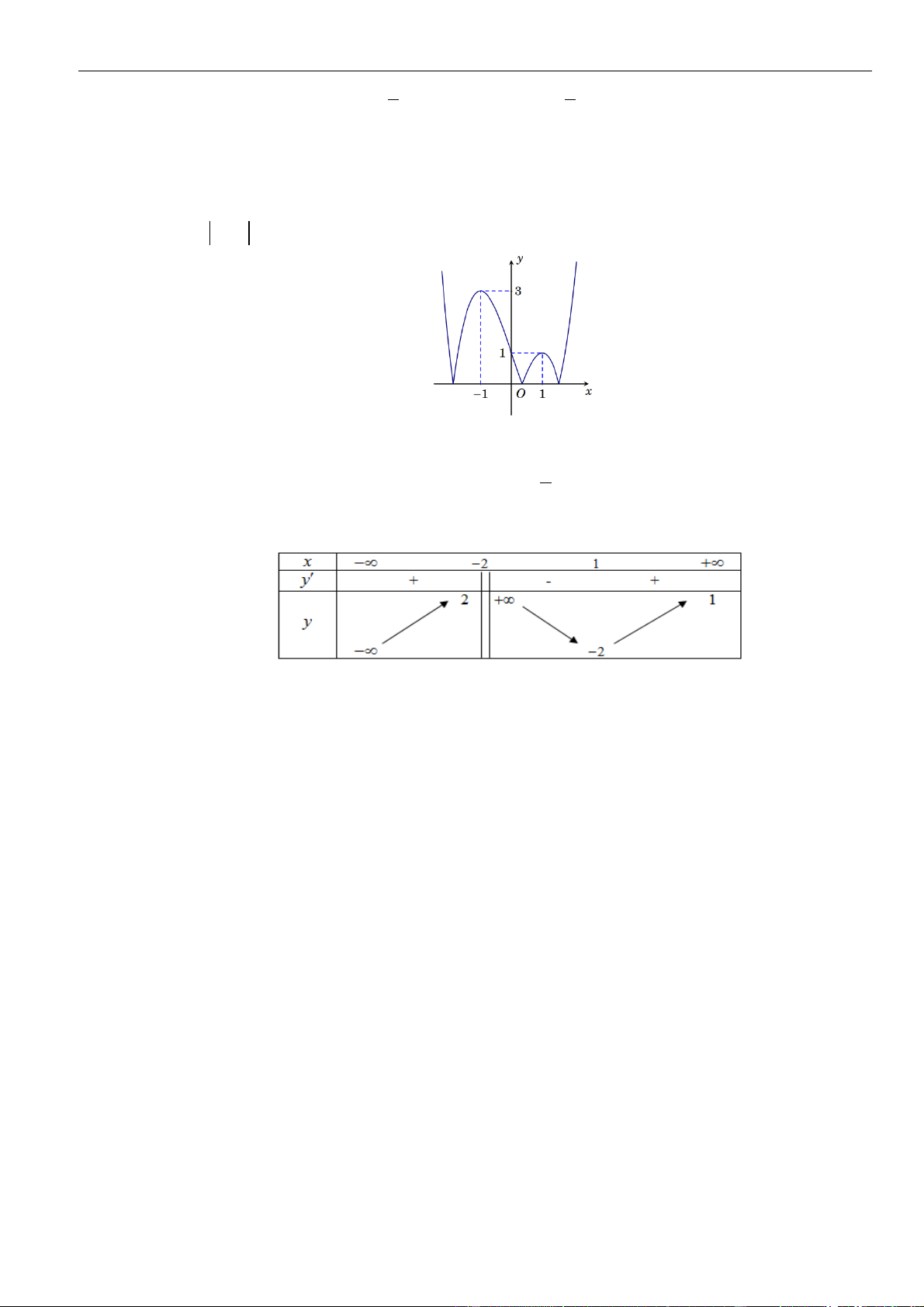
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
A.
1
. B.
3
1;
2
. C.
3
1;
2
. D.
( )
0;1
.
Lời giải
Chọn C
Đặt
costx=
,
1;1t −
Ta có:
( )
23f t m= − +
( )
*
, với
1;1t −
Dựa vào đồ thị, phương trình đã cho có
4
nghiệm thuộc đoạn
0;2
khi phương trình
( )
*
có
hai nghiệm
1;1t −
3
0 2 3 1 1
2
mm − +
.
Câu 23: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Số nghiệm của phương trình
( )
2
40fx−=
là
A.
4
. B.
3
. C.
5
. D.
2
.
Lời giải
Chọn A
Ta có
( )
( ) ( )
( ) ( )
2
21
40
22
fx
fx
fx
=
− =
=−
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số
( )
y f x=
với đường thẳng
2; 2yy= = −
.
Phương trình
( )
1
có
1
nghiệm.
Phương trình
( )
2
có
2
nghiệm.
Số nghiệm của phương trình
( )
2
40fx−=
là
3
.
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị là đường cong như hình vẽ
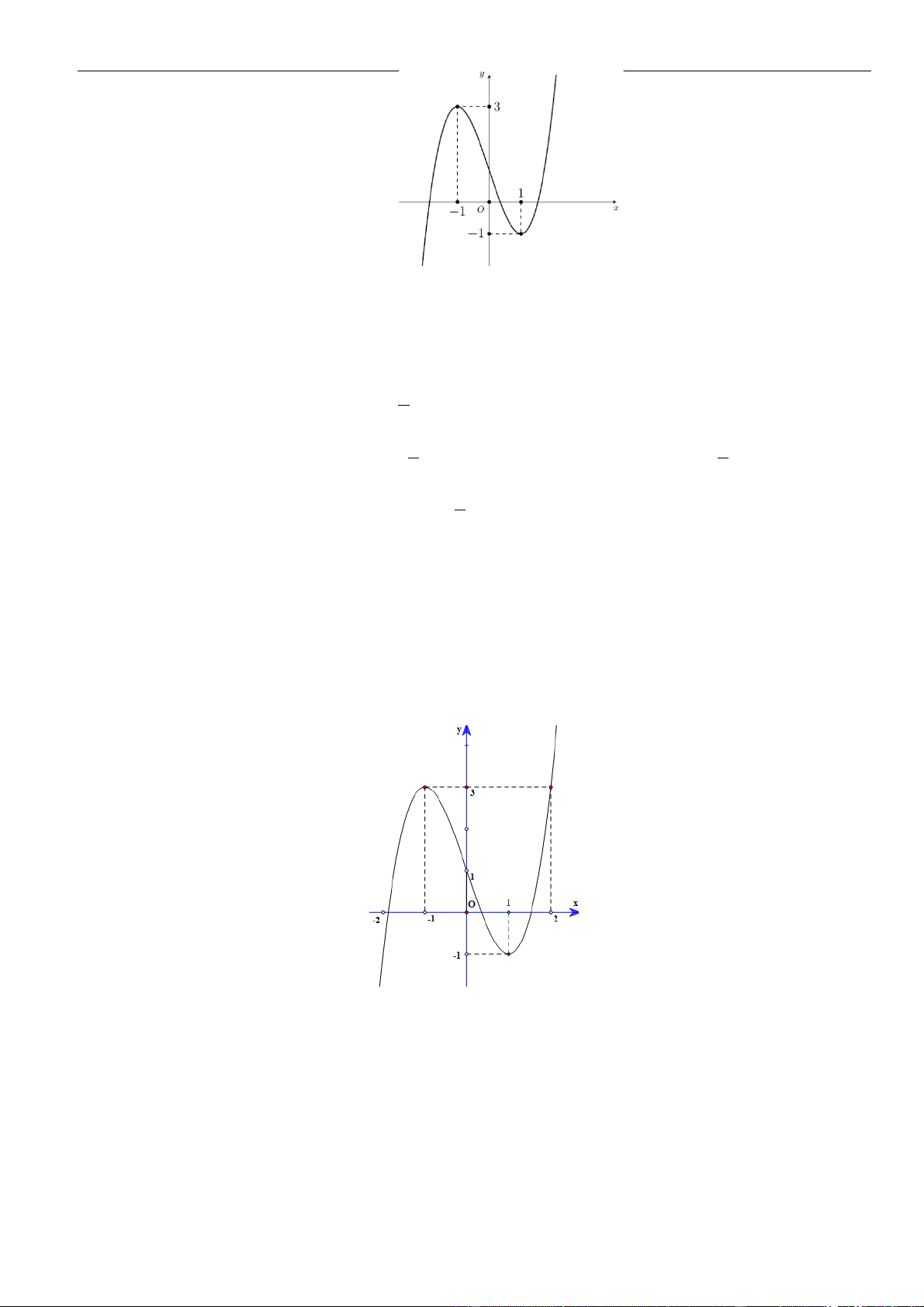
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Số nghiệm thực của phương trình
( )
2 5 0fx−=
là
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn C
Ta có:
( ) ( )
5
2 5 0
2
f x f x− = =
.
Số nghiệm phương trình
( )
5
2
fx=
là số giao điểm của đường thẳng
5
2
y =
và đồ thị hàm số
( )
y f x=
. Suy ra phương trình
( )
5
2
fx=
có
3
nghiệm phân biệt.
Câu 25: Cho hàm số
( )
3
31f x x x= − +
. Số nghiệm thực phân biệt của phương trình
( )
( )
( )
2f f x f=
là
A.
1
. B.
3
. C.
5
. D.
9
.
Lời giải
Chọn C
Ta có
( )
( )
( )
23f f x f==
.
Đồ thị của hàm số
( )
3
31f x x x= − +
như sau:
Từ đồ thị suy ra
( )
( )
( )
( )
( )
( )
3
3
33
2 3 1 0 1
3 1 2
3
1
3 1 1 3 2 0 2
f x x x
xx
f f x
fx
x x x x
= − − =
− + =
=
=−
− + = − − + =
Dùng máy tính ta thấy
( )
1
có 3 nghiệm thực,
( )
2
có 2 nghiệm thực.
Câu 26: Cho hàm số trùng phương
( )
y f x=
có đồ thị như hình vẽ bên dưới
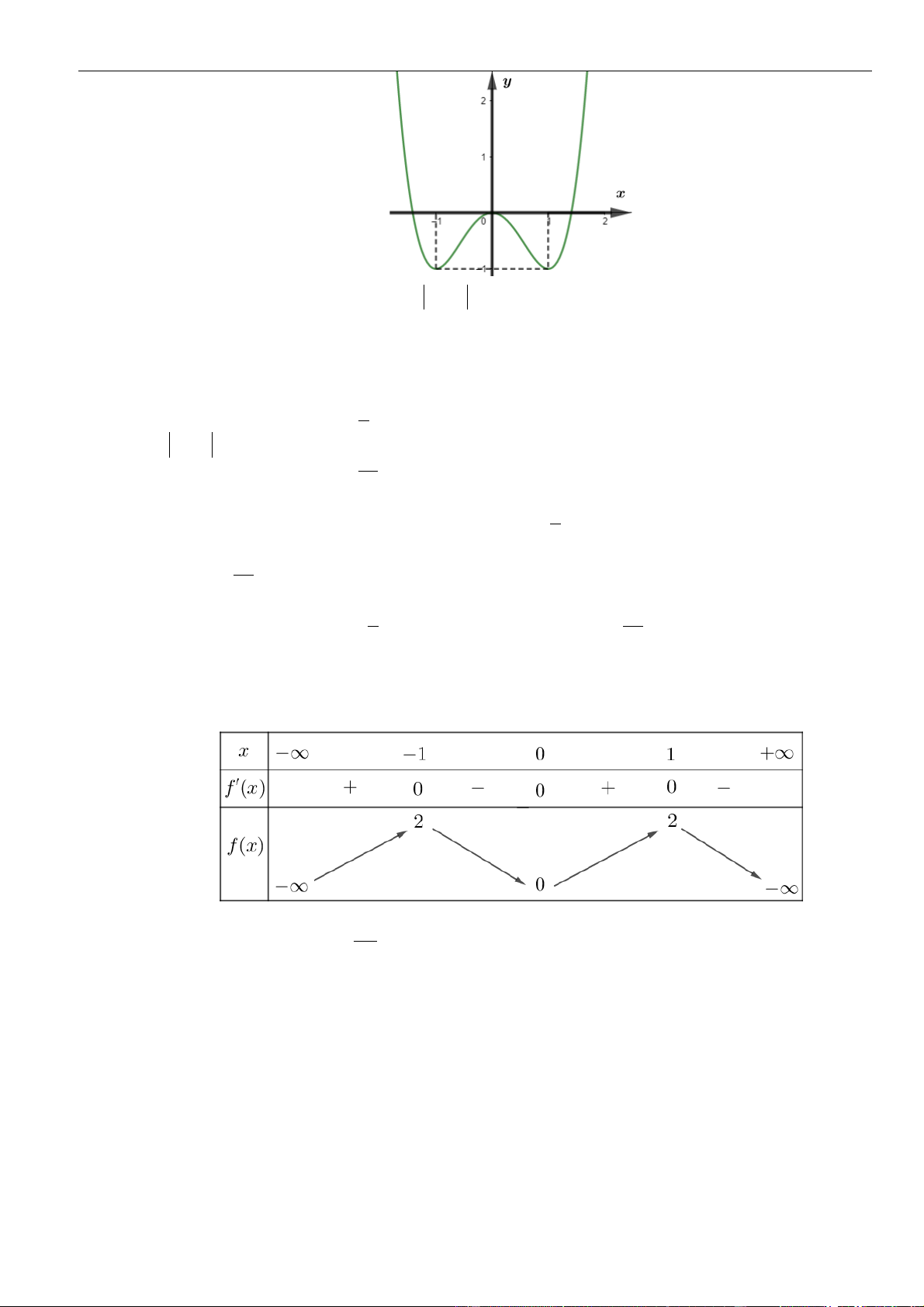
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Số nghiệm thực của phương trình
( )
2 1 0fx−=
là
A.
2
. B.
0
. C.
4
. D.
6
.
Lời giải
Chọn D
( )
( )
( )
1
2
2 1 0
1
2
fx
fx
fx
=
− =
−
=
Từ đồ thị hàm số
( )
y f x=
ta thấy đường thẳng
1
2
y =
cắt đồ thị tại hai điểm phân biệt, đường
thẳng
1
2
y
−
=
cắt đồ thị tại bốn điểm phân biệt.
Do đó phương trình
( )
1
2
fx=
có 2 nghiệm phân biệt;
( )
1
2
fx
−
=
có 4 nghiệm phân biệt.
Vậy phương trình đã cho có 6 nghiệm thực phân biệt.
Câu 27: Cho hàm số
( )
fx
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
7
0;
2
của phương trình
( )
cos 1fx=
là
A.
6
. B.
4
. C.
7
. D.
5
.
Lời giải
Chọn C
Dựa vào bảng biến thiên suy ra
( )
( )
( ) ( )
( ) ( )
( )
cos 1 1
cos 1;0 2
cos 1
cos 0;1 3
cos 1 4
xa
xb
fx
xc
xd
= −
= −
=
=
=
.
Các phương trình
( )
1
và
( )
4
vô nghiệm.
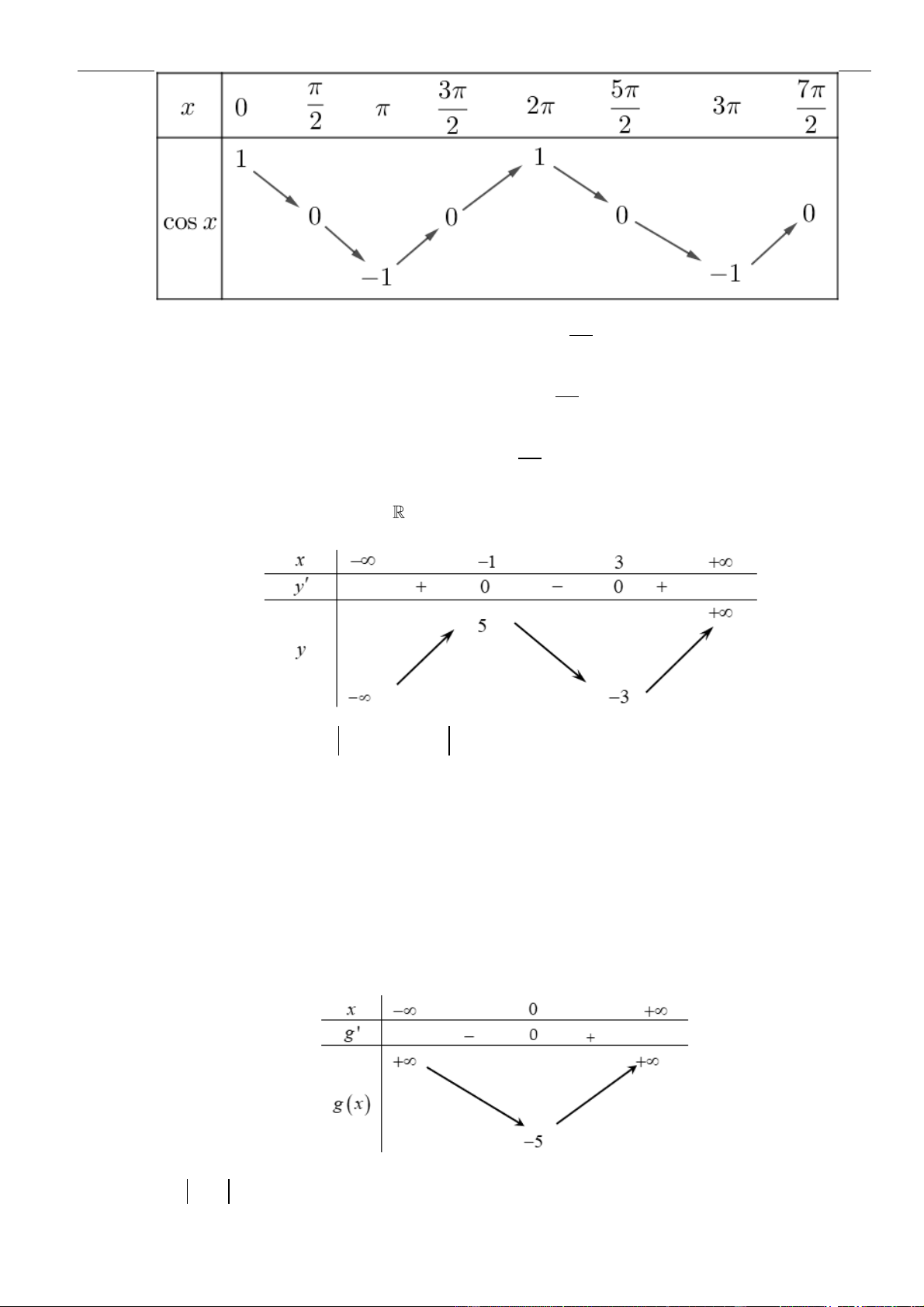
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Phương trình
( )
cos 1;0xb= −
có
4
nghiệm đoạn
7
0;
2
.
Phương trình
( )
cos 0;1xc=
có
3
nghiệm đoạn
7
0;
2
.
Vậy phương trình đã cho có
7
nghiệm đoạn
7
0;
2
.
Câu 28: Hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình vẽ
Phương trình
( )
2
2 3 2 5fx+ − =
có bao nhiêu nghiệm?
A.
3
. B.
5
. C.
6
. D.
4
.
Lời giải
Chọn A
Gọi
( )
( )
2
2 3 2g x f x= + −
. Ta có:
( )
( )
2
' 4 . ' 2 3g x x f x=+
.
( )
2
2
0
' 0 2 3 1 0
2 3 3
x
g x x x
x
=
= + = − =
+=
.
Ta có bảng biến thiên:
Mà
( )
( )
( )
5
5
5
gx
gx
gx
=
=
=−
. Từ bảng biến thiên ta thấy phương trình có 3 nghiệm.
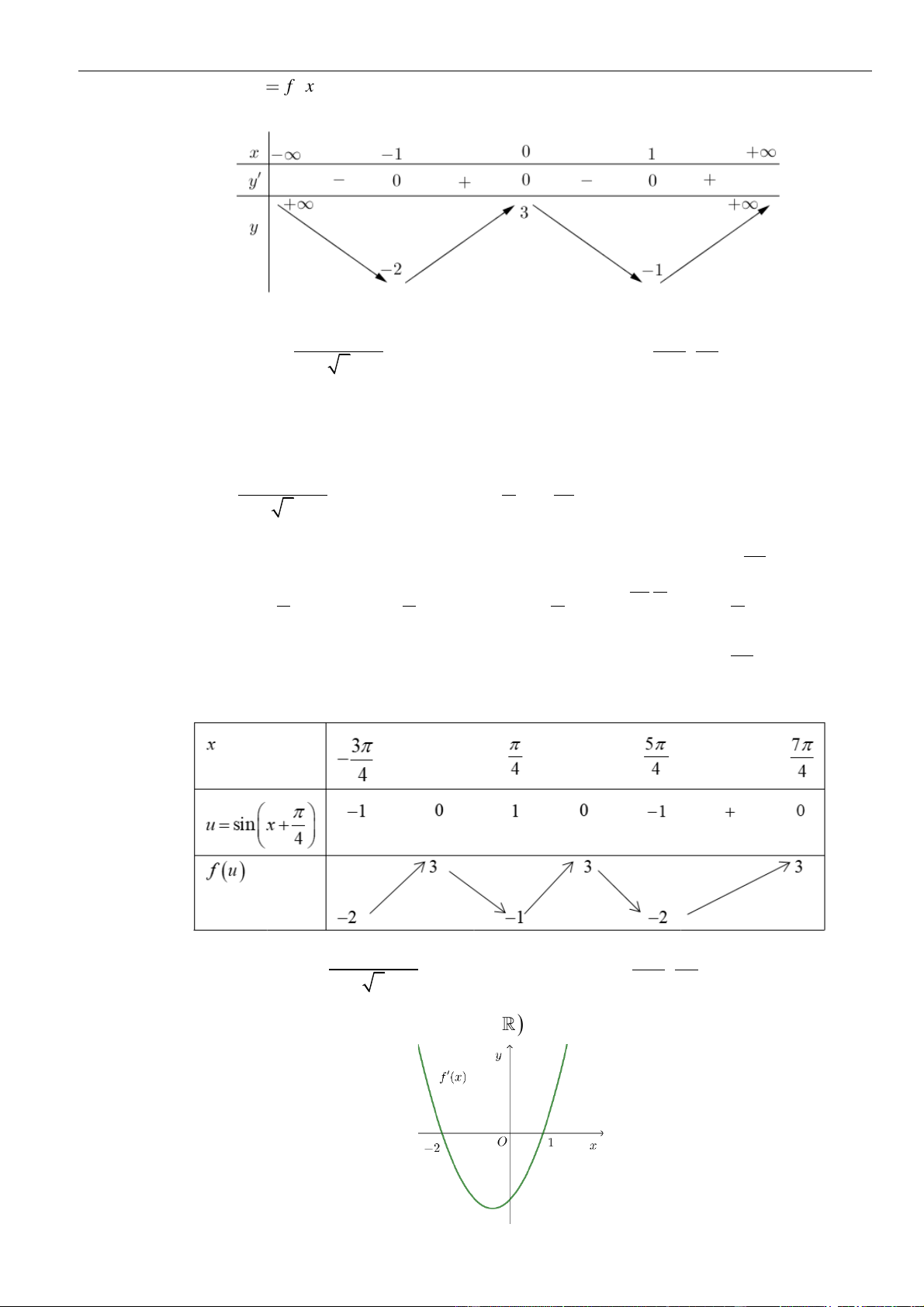
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Câu 29: Cho hàm số
y f x
có bảng biến thiên như hình bên.
Phương trình
sin cos
2 3 0
2
xx
f
+
+=
có bao nhiêu nghiệm trên
37
;
44
−
:
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn A
Ta có
( )
sin cos 3
2 3 0 sin 1
42
2
xx
f f x
+ −
+ = + =
;
Đặt
37
;
44
3
4
sin ;u' cos ' 0
4 4 4 4
5
4
x
u x x u x k x
x
−
=−
= + = + = = + ⎯⎯⎯⎯→ =
=
;
Ta có:
Vậy phương trình
sin cos
2 3 0
2
xx
f
+
+=
có ba nghiệm trên
37
;
44
−
.
Câu 30: Cho hàm số
32
y ax bx cx d= + + +
( )
, , ,a b c d
. Hàm số
( )
fx
có đồ thị hàm số như sau:

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Và
( ) ( )
2020 1 2021 0ff=
. Hỏi đồ thị hàm số
( )
y f x=
và đồ thị hàm số
( )
y f x
=
cắt nhau
tại bao nhiêu điểm phân biệt.
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Ta có :
( )
2
32f x ax bx c
= + +
( )( )
( )
2
3 2 1 3 2a x x a x x= + − = + −
( )
0a
Đồng nhất hệ số ta có:
3
2
ba=
,
6ca=−
.
Theo đề bài:
( ) ( )
2020 1 2021 0ff=
( )
2020 2021a b c d d + + + =
7070da = −
.
Phương trình hoành độ giao điểm:
( ) ( )
f x f x
=
3 2 2
32ax bx cx d ax bx c + + + = + +
3 2 2
3
6 7070 3 3 6
2
ax ax ax a ax ax a + − − = + −
32
3
9 7064 0
2
x x x − − − =
( )
*
.
Phương trình
( )
*
có một nghiệm.
Vậy đồ thị hàm số
( )
y f x=
và đồ thị hàm số
( )
y f x
=
cắt nhau tại một điểm.
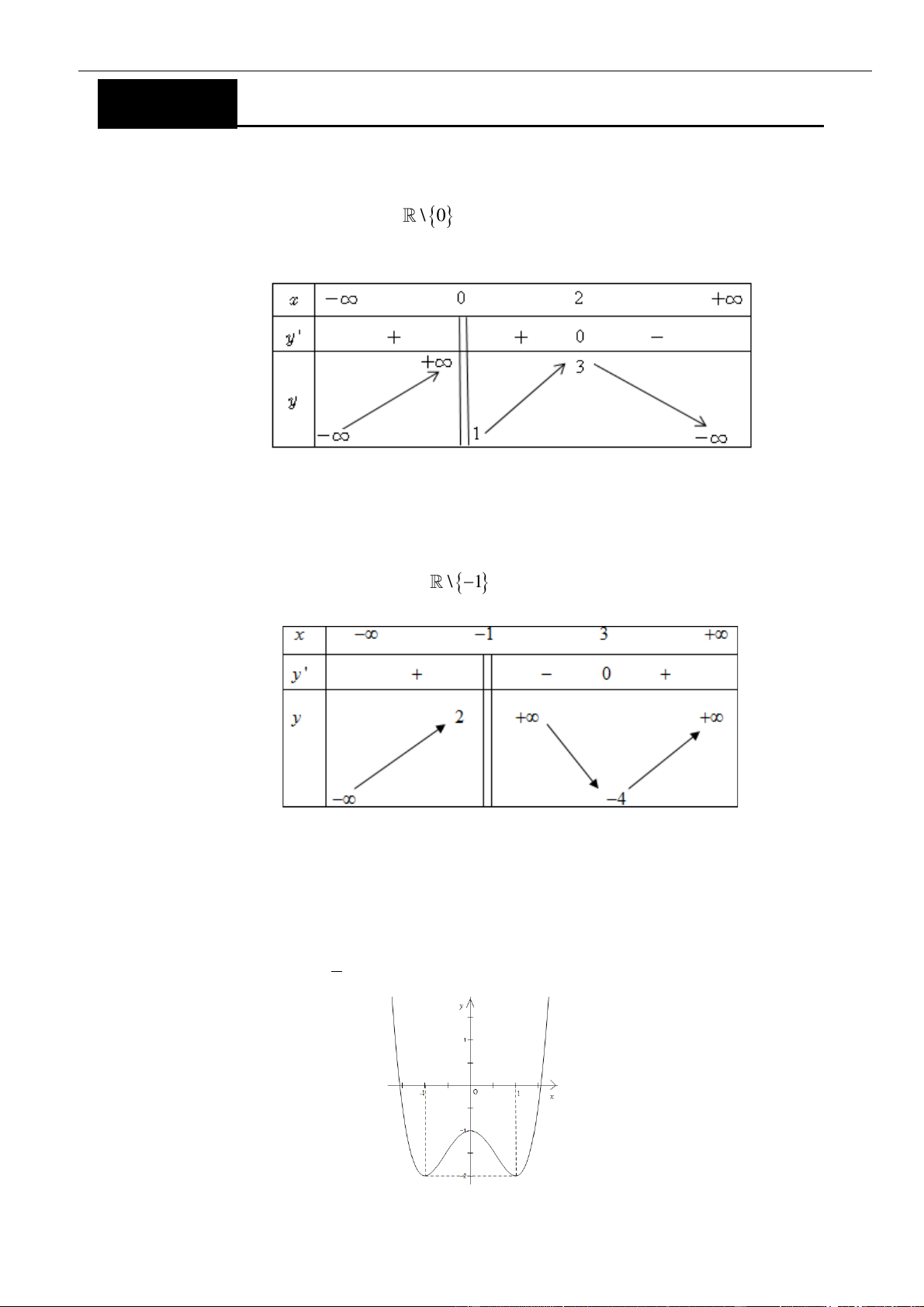
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
( )
fx
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau
Tìm tất cả các giá trị thực của tham số
m
để phương trình
( )
1f x m=−
có ba nghiệm thực phân
biệt.
A.
( )
2;4m
. B.
)
2;4m
. C.
( )
1;3m
. D.
)
1;3m
.
Câu 2: Cho hàm số
( )
y f x=
xác định trên
\1−
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình sau
Tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
( )
f x m=
có đúng 3 nghiệm thực
phân biệt.
A.
)
4;2−
. B.
(
4;2−
. C.
( )
4;2−
. D.
(
;2−
.
Câu 3: Cho hàm số bậc bốn
( )
y f x=
có đồ thị là đường cong trong hình bên. Số nghiệm thực của
phương trình
( )
1
2
fx=−
là
A.
3
. B.
4
. C.
2
. D.
1
.
Tim m để hàm số có k nghiệm khi biết đồ thị, BBT
DẠNG 4
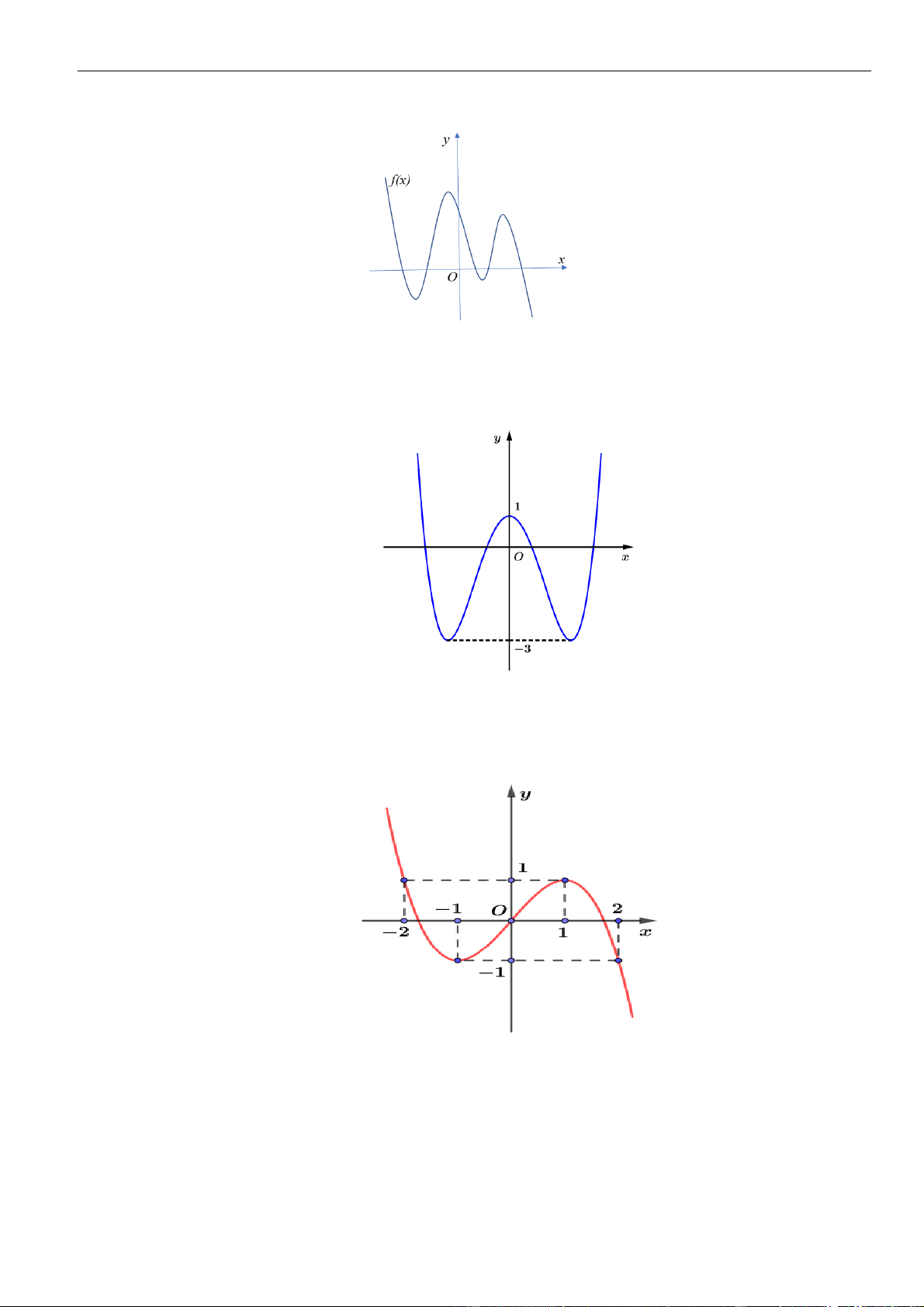
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
Câu 4: Cho đồ thị hàm số
( )
y f x=
như hình vẽ. Hỏi phương trình
( )
2 f x m=
có tối đa bao nhiêu
nghiệm thực
x
?
A.
3
. B.
6
. C.
5
. D.
4
.
Câu 5: Cho hàm trùng phương
( )
y f x=
có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham
số
m
để phương trình
( )
f x m=
có 4 nghiệm phân biệt.
A.
1m =
. B.
1m −
. C.
31m−
. D.
1m
.
Câu 6: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ dưới. Tìm tất cả các giá trị của tham số
m
để số
nghiệm dương của phương trình
( )
f x m=
bằng
1
.
A.
0m
. B.
0m
.
C.
0m
hoặc
1m =
. D.
1m −
hoặc
1m
.
Câu 7: Cho hàm số bậc ba
()fx
có đồ thị như hình vẽ bên:
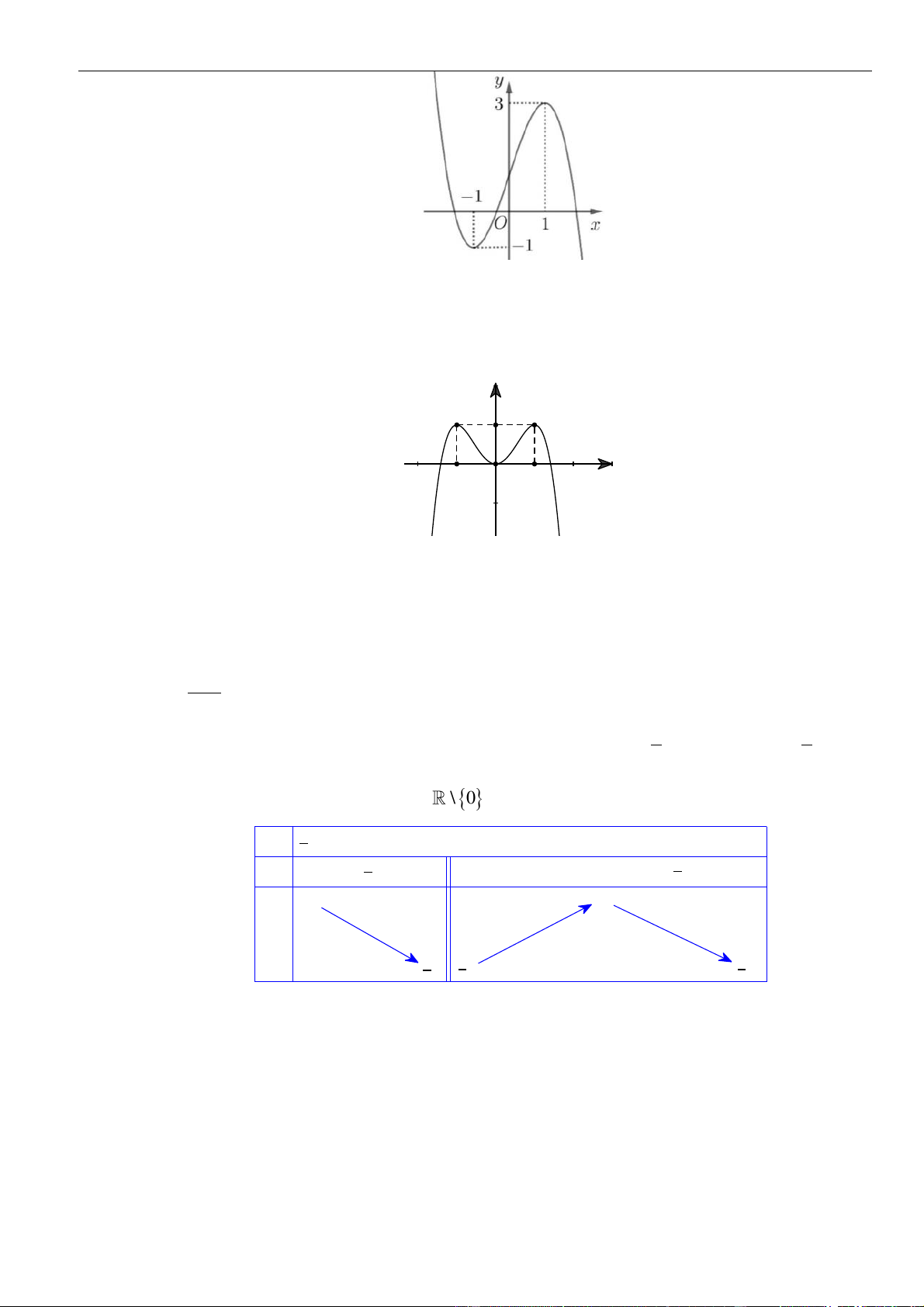
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Số giá trị nguyên của
m
để phương trình
( ) 3 0f x m+=
có ba nghiệm phân biệt là:
A.
3
. B.
5
. C.
2
. D.
1
.
Câu 8: Cho hàm số
42
2y x x= − +
có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị thực của tham số
m
để phương trình
42
2x x m− + =
có bốn nghiệm thực
phân biệt.
A.
1m
. B.
01m
. C.
0m
. D.
01m
.
Câu 9: Biết rằng có hai giá trị
12
,mm
của tham số
m
để đường thẳng
:d y m x=−
và đồ thị hàm số
1
x
y
x
=
−
có đúng một điểm chung. Khẳng định nào sau đây đúng?
A.
( )
12
10; 1mm+ − −
. B.
( )
12
7;12mm+
. C.
12
9
1;
2
mm
+ −
. D.
12
9
;7
2
mm
+
.
Câu 10: Cho hàm số
( )
y f x=
xác định trên
\0
và có bảng biến thiên như sau
Tập hợp tất cả các giá trị của
m
sao cho phương trình
( )
f x m=
có ba nghiệm thực phân biệt.
A.
( )
1;2−
. B.
(
1;2−
. C.
(
;2−
. D.
1;2−
.
Câu 11: Cho hàm số có bảng biến thiên như sau
x
y
1
1
O
-1
+
∞
∞ ∞
+
∞
x
y'
y
∞
0
1
0
+
2
1
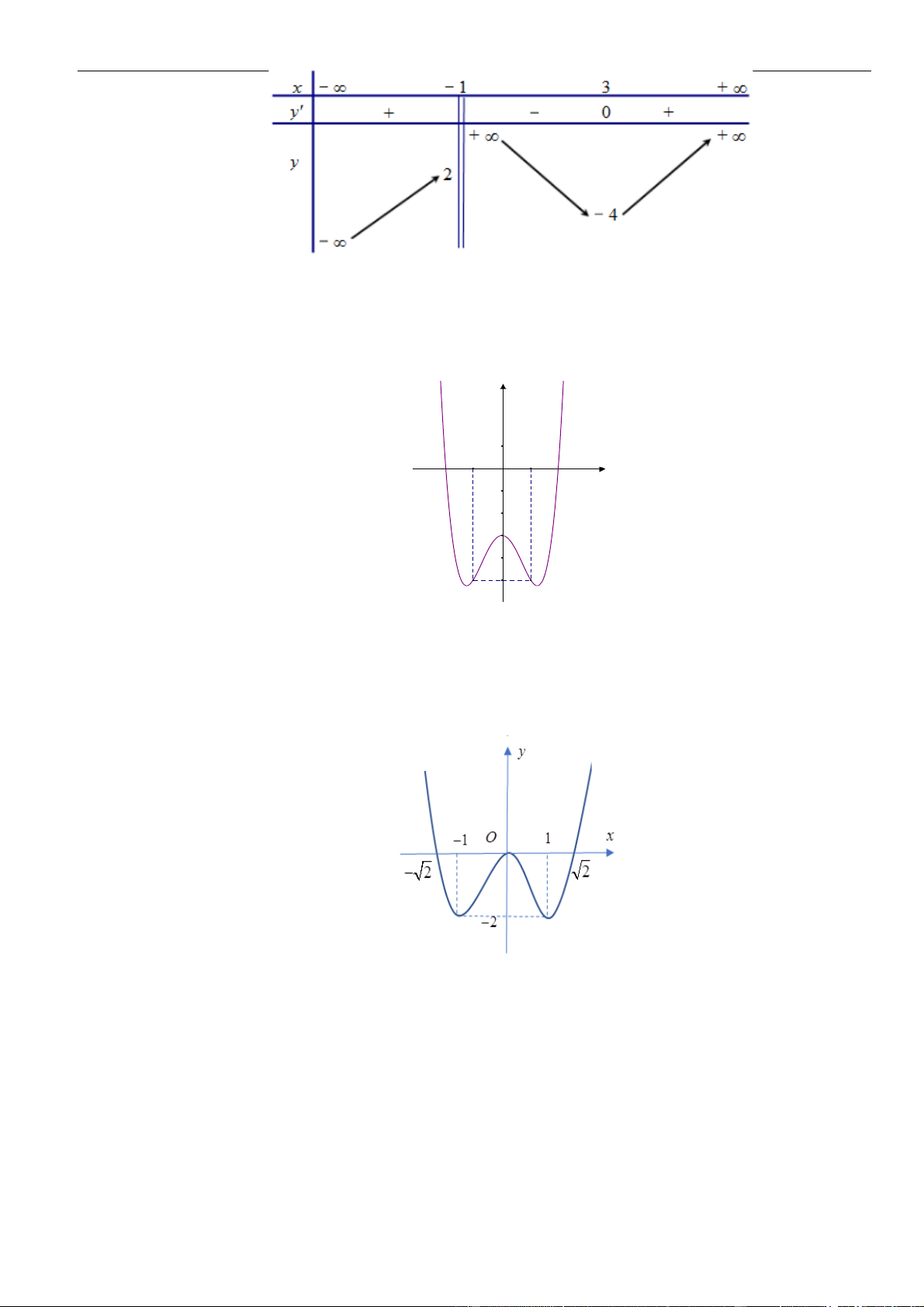
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Tổng các giá trị nguyên của
m
để đường thẳng
ym=
cắt đồ thị hàm số tại ba điểm phân biệt
bằng
A.
0
. B.
3−
. C.
5−
. D.
1−
.
Câu 12: Đồ thị bên dưới đây là của hàm số
42
33y x x= − −
Với giá trị nào của
m
thì phương trình
42
30x x m− + =
có đúng ba nghiệm phân biệt?
A.
4m =−
. B.
4m =
. C.
3m =−
. D.
0m =
.
Câu 13: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ dưới đây. Tìm
m
để phương trình
( )
f x m=
có
bốn nghiệm phân biệt.
A.
1m −
. B.
10m−
. C.
10m−
. D.
10m−
.
Câu 14: Cho hàm số
( )
y f x=
xác định, liên tục trên mỗi nửa khoảng
(
;2− −
và
)
2;+
và có bảng
biến thiên như hình dưới đây:
y
x
O
-5
-3
-1
1
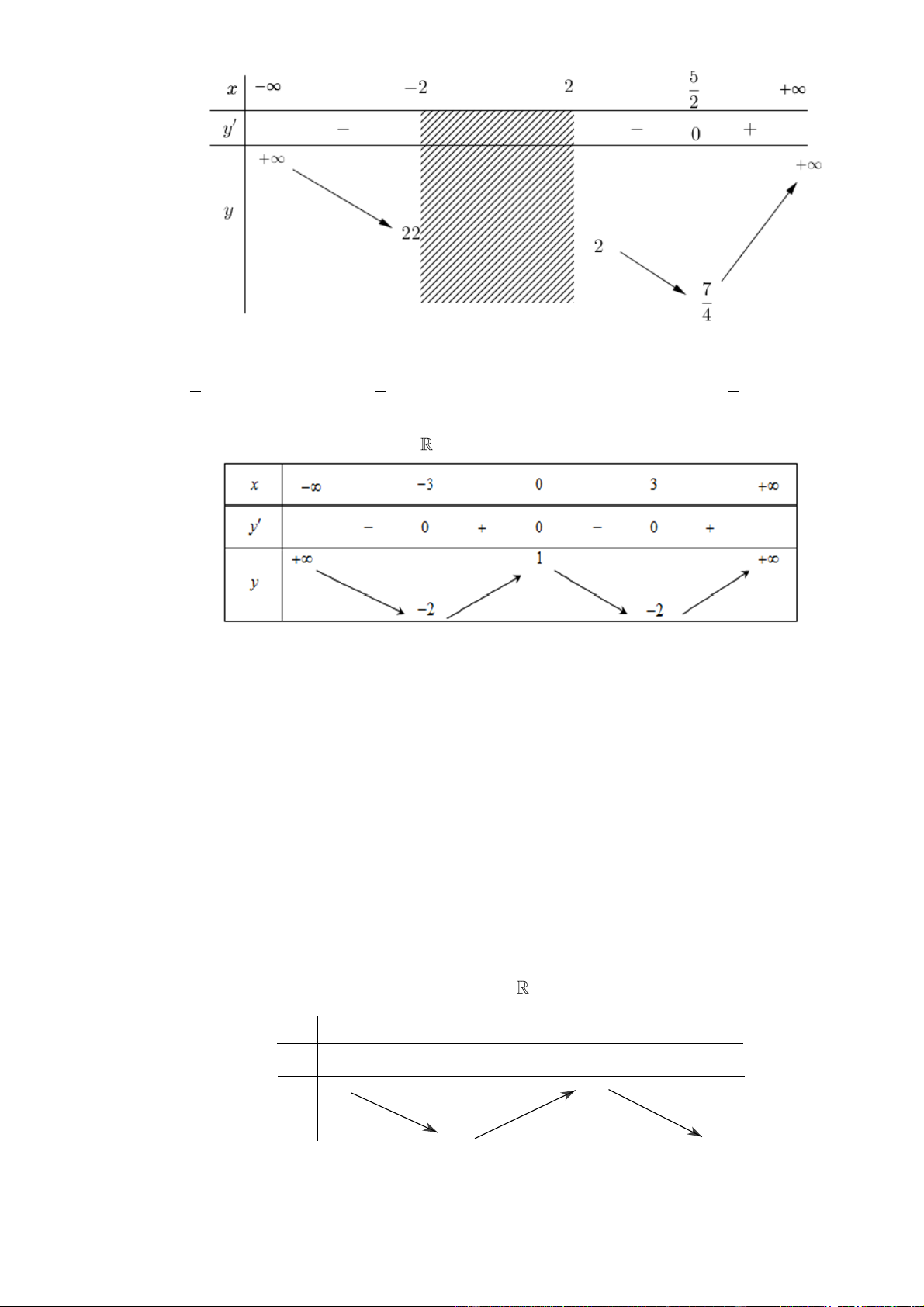
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Tìm tập hợp các giá trị thực của tham số
m
để phương trình
( )
f x m=
có hai nghiệm phân biệt.
A.
)
7
;2 22;
4
+
. B.
)
7
;2 22;
4
+
. C.
)
22;+
. D.
7
;
4
+
Câu 15: Cho hàm số
()y f x=
liên tục trên
và có bảng biến
Tìm
m
để phương trình
2 ( ) 0f x m+=
có đúng ba nghiệm phân biệt
A.
1m =−
. B.
2m =−
. C.
1m =
. D.
2m =
.
Câu 16: Cho hàm số
32
33y x x= − − +
có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
32
3 5 0x x m− − + − =
có ba nghiệm phân biệt?.
B.
4
. B.
3
. C.
1
. D.
2
.
Câu 17: Có bao nhiêu giá trị nguyên của tham số m để phương trình
3
41x x m− + + =
có ba nghiệm phân
biệt?
A. 5. B. 17. C. 7. D. 15.
Câu 18: Đồ thị sau đây là của hàm số
3
31y x x= − +
. Với giá trị nào của
m
thì phương trình
3
3x x m−−
có
3
nghiệm phân biệt?
A.
22m−
. B.
23m−
. C.
13m−
. D.
22m−
.
Câu 19: Cho hàm số
( )
y f x=
xác định và liên tục trên , có bảng biến thiên như sau:
Tìm tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
( )
f x m=
có ít nhất hai
nghiệm thực phân biệt.
+
∞
3
+
0
0
y
y'
x
–
∞
– 1
–
–
+
∞
1
– 1
–
∞
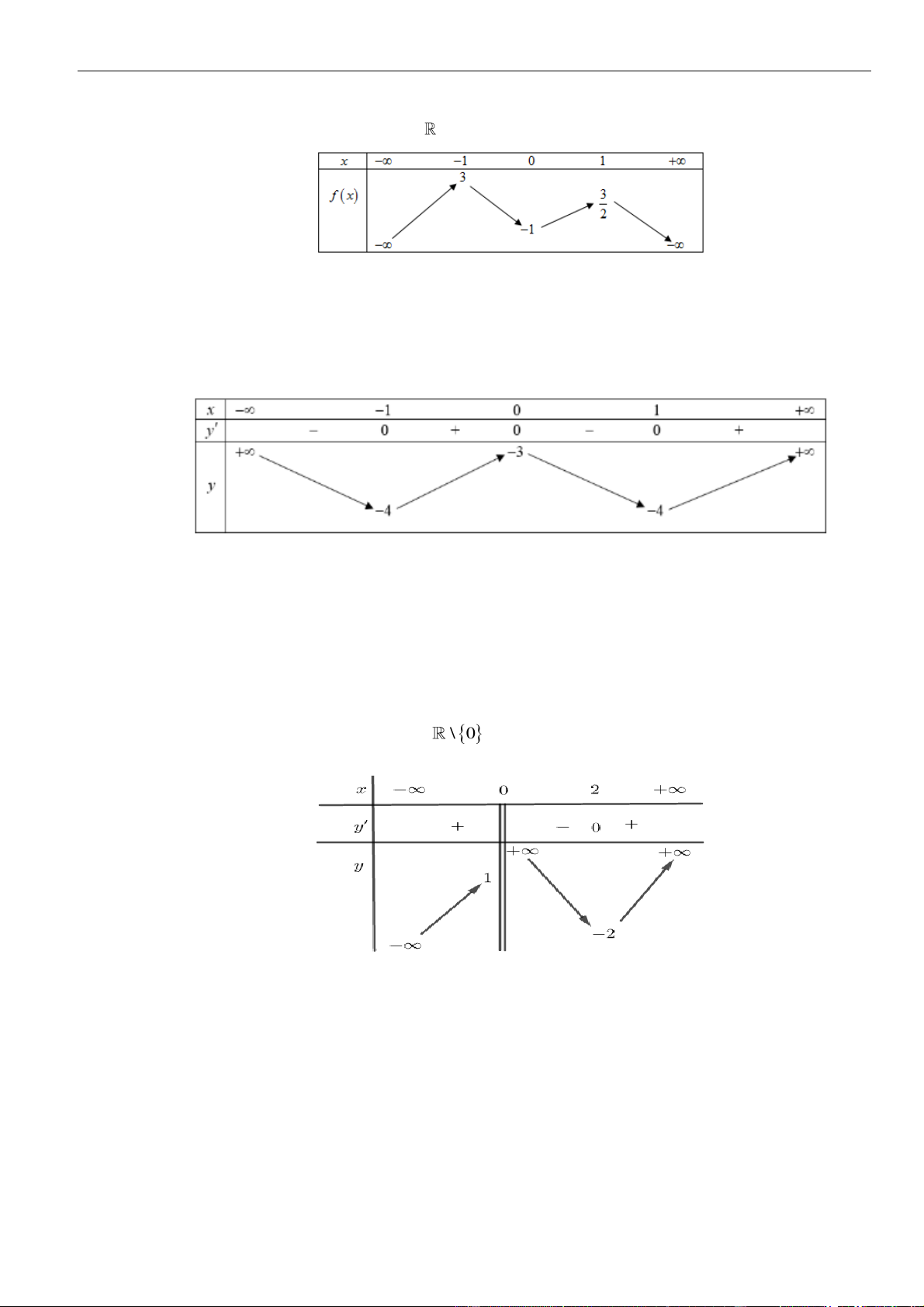
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
A.
( )
1;3−
. B.
(
1;3−
. C.
1;3−
. D.
)
1;3−
.
Câu 20: Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình vẽ sau:
Hỏi có bao nhiêu giá trị nguyên dương của
m
để phương trình
( )
2 2 0f x m− + =
có đúng 3
nghiệm phân biệt?
A. 1. B. 3. C. 2. D. 0.
Câu 21: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình
( )
2 3 0f x m+=
có ba nghiệm phân biệt?
A. Vô số. B.
1
. C.
2
. D.
3
.
Câu 22: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số giá trị nguyên dương của tham số
m
để phương
trình
( )
2020 0f x m+ − =
có 2 nghiệm là
A.
2024
. B.
2021
. C.
2020
. D.
2023
.
Câu 23: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
( )
1f x m=−
có đúng ba
nghiệm thực phân biệt là
A.
( )
2;− +
. B.
( )
1;2−
. C.
( )
1;− +
. D.
( )
2;1−
.
Câu 24: Cho hàm số
( )
fx
có đồ thị như hình vẽ. Số giá trị nguyên của tham số
m
để phương trình
( )
1f x m+=
có
3
nghiệm phân biệt là:
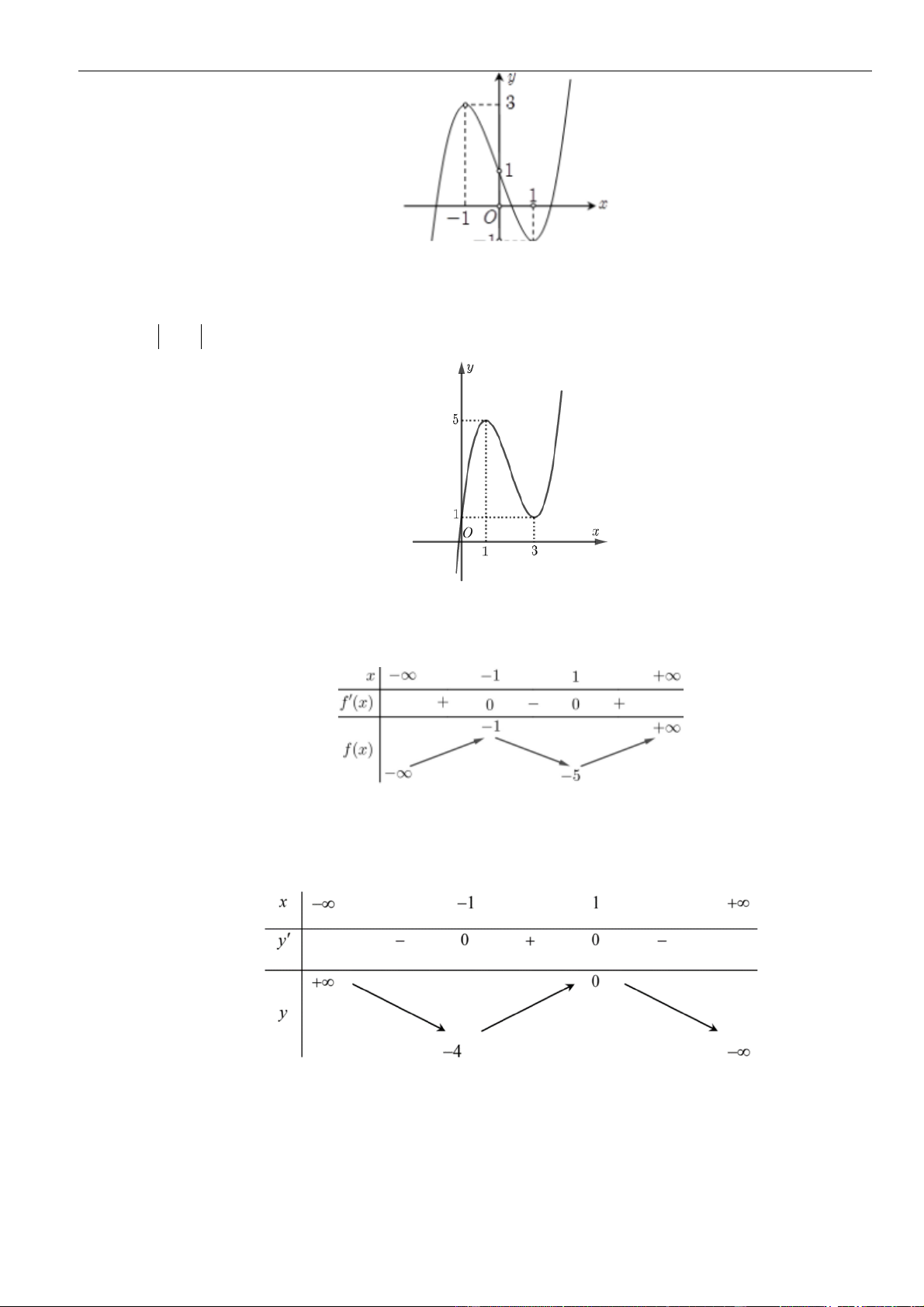
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
A.
4.
B.
5.
C.
2.
D.
3.
Câu 25: Cho hàm số
( )
y f x=
có đồ thị trong hình vẽ bên. Tìm tất cả các giá trị của
m
để phương trình
( )
f x m=
có đúng hai nghiệm phân biệt.
A.
5m
,
01m
. B.
1m
. C.
1m =
,
5m =
. D.
15m
.
Câu 26: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Số giá trị nguyên của tham số
m
để phương trình
( )
f x m=
có ba nghiệm phân biệt là
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 27: Cho hàm số
( )
=y f x
có bảng biến thiên:
Với giá trị nào của m thì phương trình
( )
0f x m+=
có
3
nghiệm phân biệt.
A.
11m−
. B.
40m−
. C.
04m
. D.
21m−
.
Câu 28: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
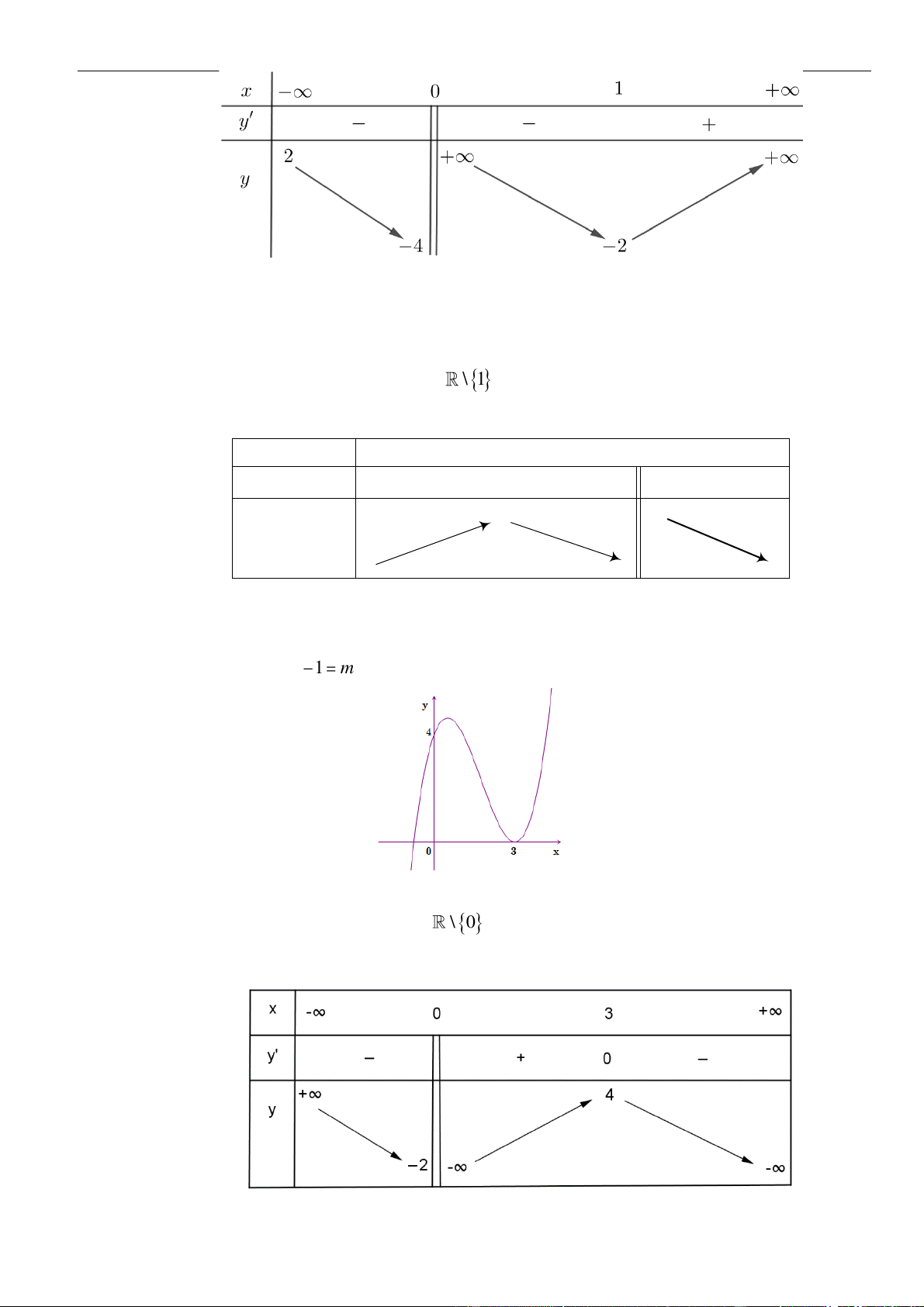
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Phương trình
( )
f x m=
có ba nghiệm thực phân biệt khi và chỉ khi
A.
42m− −
. B.
22m−
. C.
22m−
. D.
42m−
.
Câu 29: Cho hàm số
( )
y f x=
xác định trên
\1
và có bảng biến thiên như hình bên. Số giá trị
nguyên
m
để phương trình
( )
f x m=
có
3
nghiệm phân biệt là
x
−
+
+
−
y
y
0
1−
1
−
4
1
−
+
0
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 30: Cho hàm số
fx
có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số
m
để
phương trình
1f x m
có
3
nghiệm phân biệt
A.
13m−
. B.
14m
. C.
25m−
. D.
04m
.
Câu 31: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
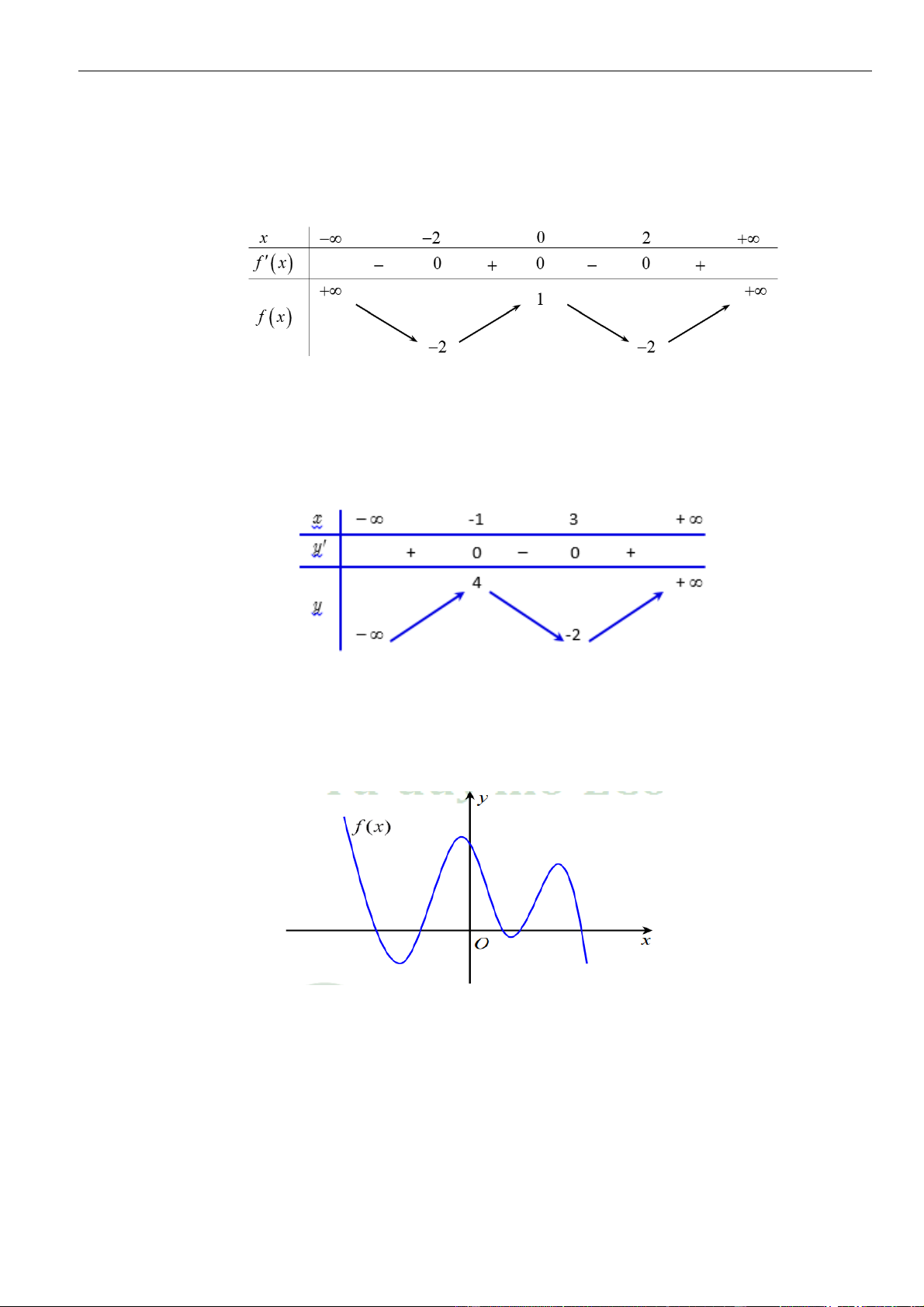
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
( )
f x m=
có hai
nghiệm thực phân biệt
A.
( )
; 2 4− −
. B.
(
;2− −
. C.
(
; 2 4− −
. D.
( )
;2− −
.
Câu 32: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình
( )
40f x m+=
có
4
nghiệm thực phân
biệt?
A.
10
. B.
11
. C.
12
. D.
9
.
Câu 33: Cho hàm số
( )
y f x=
có bảng biến thiên như sau :
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
f x m=
có ba nghiệm phân biệt.
A.
2m −
. B.
24m−
. C.
24m−
. D.
4m
.
Câu 34: Cho đồ thị hàm số
( )
y f x=
như hình vẽ. Hỏi phương trình
( )
2 f x m=
có tối đa bao nhiêu
nghiệm thực
x
?
A.
3
. B.
6
. C.
5
. D.
4
.
Câu 35: Cho đồ thị hàm số
( )
y f x=
như hình vẽ bên dưới. Số nghiệm thực của phương trình
( )
4 5 0fx−=
là:
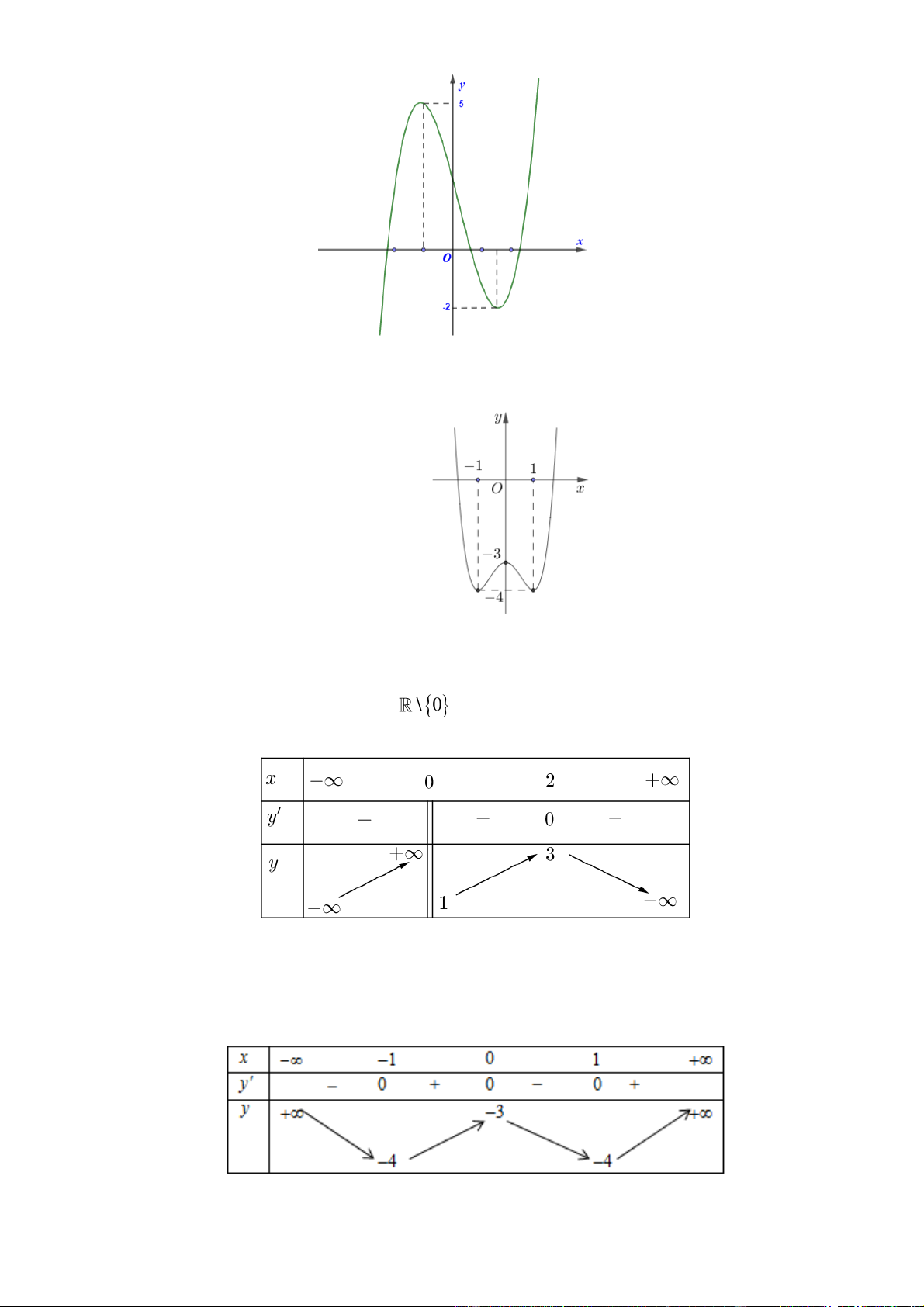
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 36: Cho hàm số
( )
y f x=
có đồ thị như hình sau:
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
f x m=
có bốn nghiệm phân biệt.
A.
43m− −
. B.
4m −
. C.
43m− −
. D.
43m− −
.
Câu 37: Cho hàm số
( )
fx
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau
Tìm tất cả các giá trị thực của tham số
m
để phương trình
( )
1f x m=−
có ba nghiệm thực phân biệt.
A.
( )
2;4m
. B.
)
2;4m
. C.
( )
1;3m
. D.
)
1;3m
.
Câu 38: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình
( )
2 3 0f x m+=
có 3 nghiệm phân biệt?
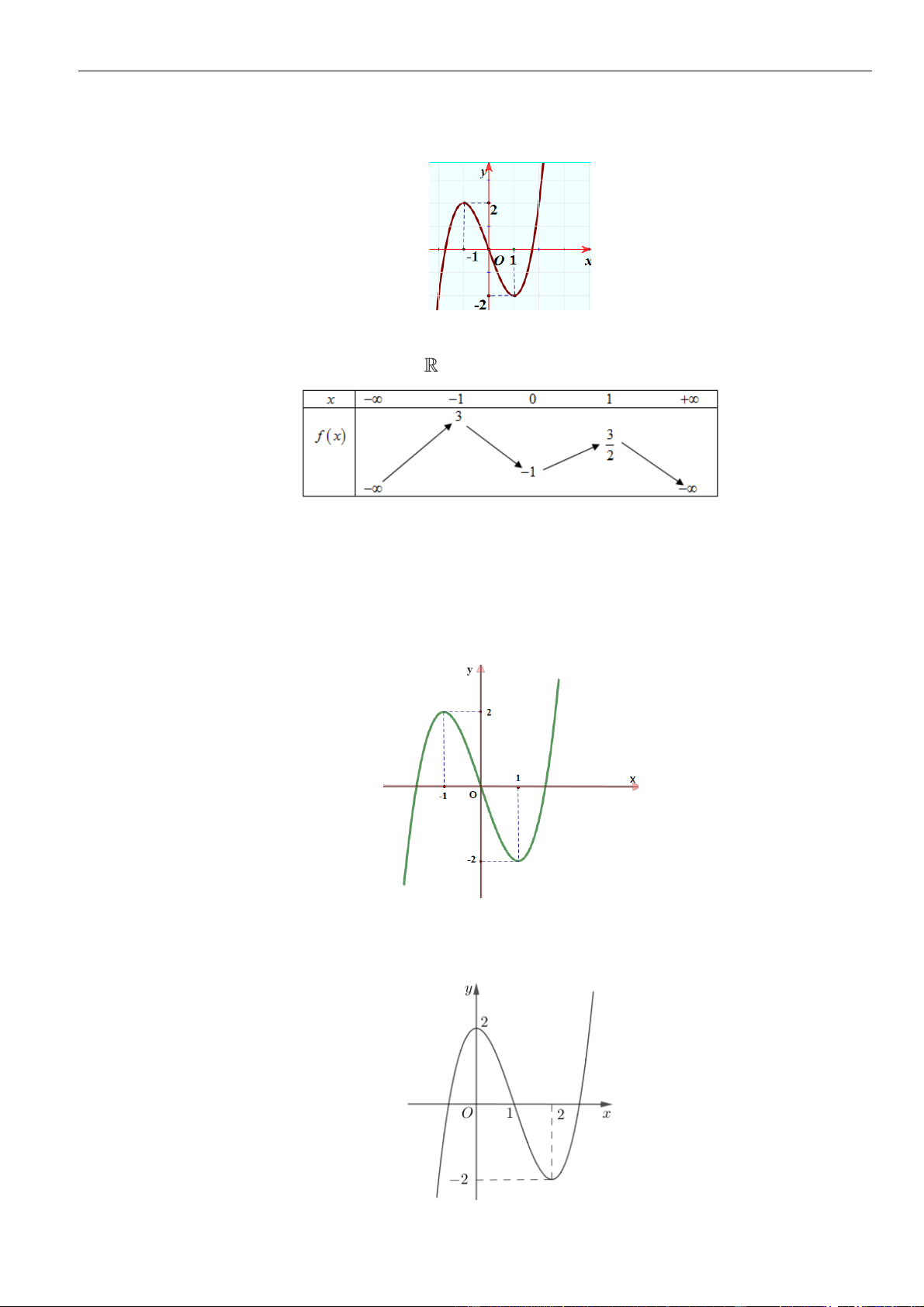
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
A. Vô số. B.
1.
C.
2.
D.
3.
Câu 39: Cho hàm số
()y f x=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
( ) 3 5 0f x m− + =
có 3 nghiệm phân biệt?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 40: Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình vẽ sau:
Hỏi có bao nhiêu giá trị nguyên dương của
m
để phương trình
( )
2 2 0f x m− + =
có đúng 3
nghiệm phân biệt?
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 41: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
( )
2 1 0f x m+ − =
có ba nghiệm phân biệt?
A.
2.
B.
3.
C.
4.
D.
1.
Câu 42: Cho hàm số
( )
32
f x ax bx cx d= + + +
và
0a
có đồ thị như hình vẽ
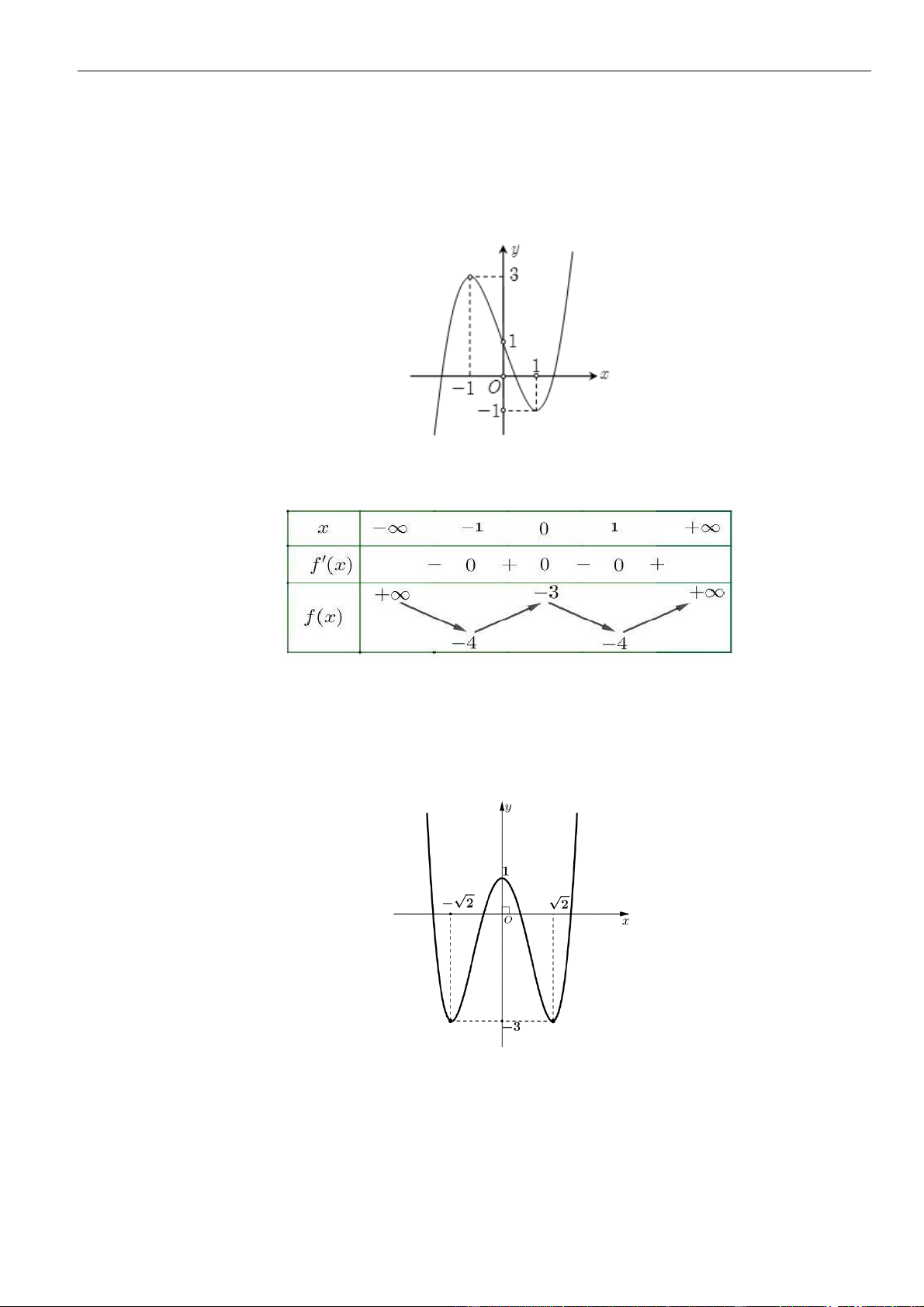
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Tập hợp tất cả các giá trị của tham số
m
để phương trình
( )
f x m m+=
có đúng
3
nghiệm phân
biệt là
A.
( )
2;2−
. B.
( )
1;1−
. C.
( )
1;2
. D.
( )
2;1−
.
Câu 43: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ. Số giá trị nguyên của tham số
m
để phương
trình
( )
1f x m+=
có
3
nghiệm phân biệt là
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 44: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
( )
50fx+=
là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 45: Cho hàm số
42
y ax bx c= + +
có đồ thị như hình vẽ. Với giá trị nào của tham số
m
thì đường
thẳng
ym=
cắt đồ thị hàm số đã cho tại
4
điểm phân biệt?
A.
31m−
. B.
1m
. C.
3m =−
. D.
31m−
.
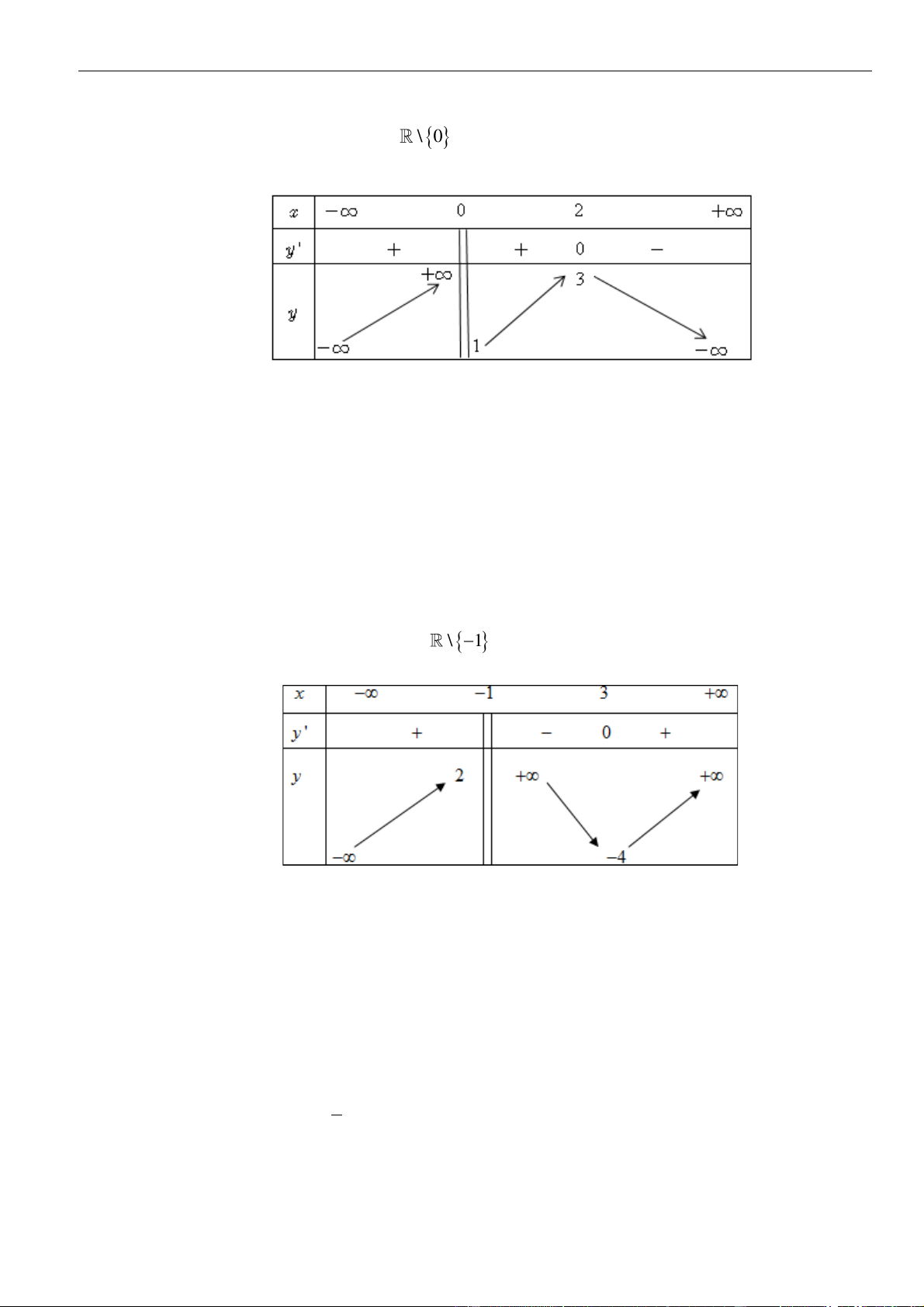
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
( )
fx
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau
Tìm tất cả các giá trị thực của tham số
m
để phương trình
( )
1f x m=−
có ba nghiệm thực phân
biệt.
A.
( )
2;4m
. B.
)
2;4m
. C.
( )
1;3m
. D.
)
1;3m
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta thấy phương trình
( )
1f x m=−
có ba nghiệm thực phân biệt khi
( )
1 1 3 2 4 2;4m m m −
Câu 2: Cho hàm số
( )
y f x=
xác định trên
\1−
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình sau
Tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
( )
f x m=
có đúng 3 nghiệm thực
phân biệt.
A.
)
4;2−
. B.
(
4;2−
. C.
( )
4;2−
. D.
(
;2−
.
Lời giải
Số nghiệm của phương trình
( )
f x m=
là số giao điểm của đồ thị hàm số
( )
y f x=
và
ym=
Vậy để phương trình có 3 nghiệm phân biệt thì
42m−
Câu 3: Cho hàm số bậc bốn
( )
y f x=
có đồ thị là đường cong trong hình bên. Số nghiệm thực của
phương trình
( )
1
2
fx=−
là
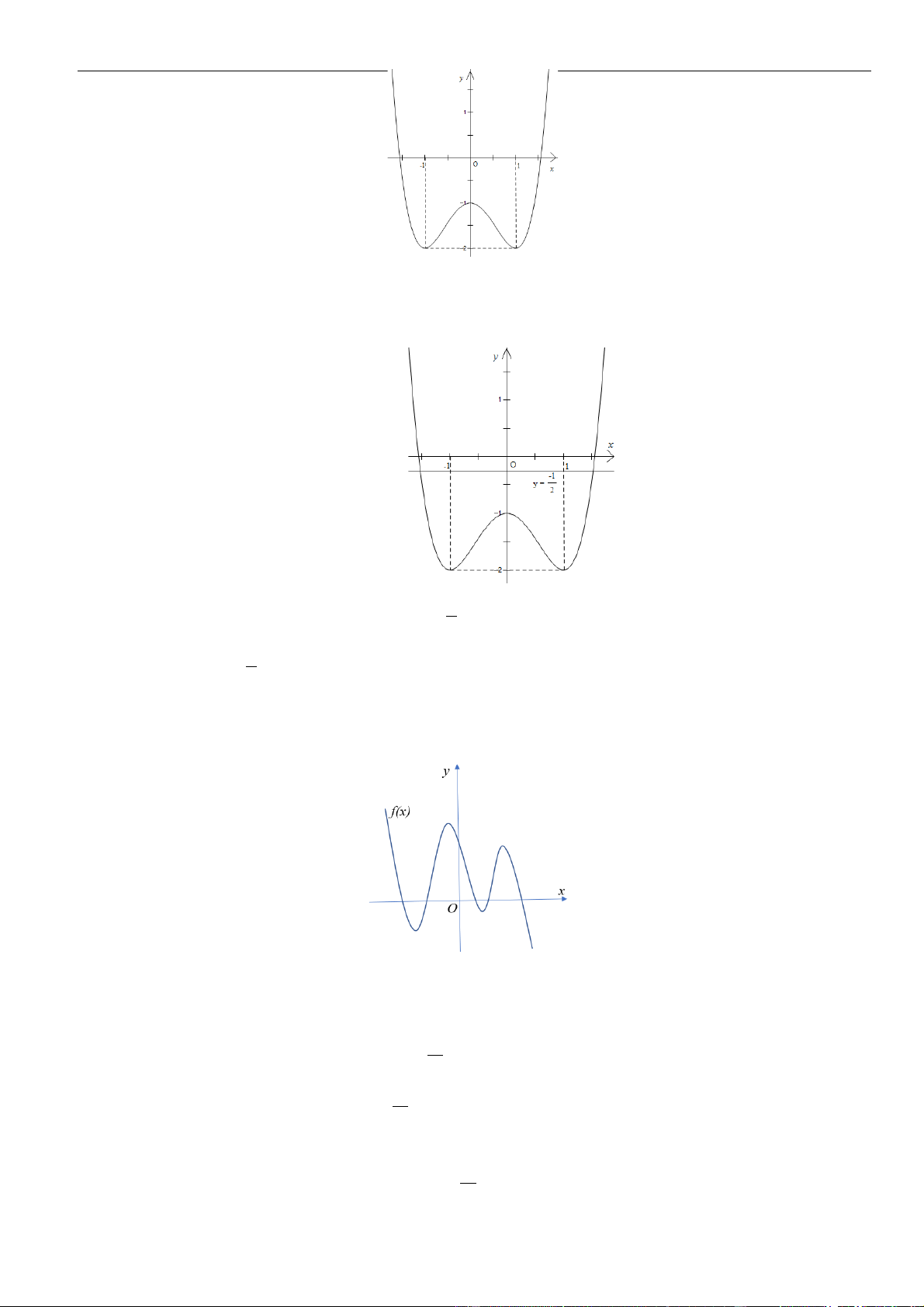
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn C
Số nghiệm của phương trình
( )
1
2
fx=−
là số giao điểm của đồ thị hàm số
( )
y f x=
và đường
thẳng
1
2
y =−
. Vậy phương trình đã cho có 2 nghiệm thực phân biệt.
Câu 4: Cho đồ thị hàm số
( )
y f x=
như hình vẽ. Hỏi phương trình
( )
2 f x m=
có tối đa bao nhiêu
nghiệm thực
x
?
A.
3
. B.
6
. C.
5
. D.
4
.
Lời giải
Chọn C
Phương trình
( ) ( )
2
2
m
f x m f x= =
là phương trình hoành độ giao điểm của đồ thị hàm số
( )
y f x=
và đường thẳng
2
m
y =
. Số giao điểm của hai đường bằng số nghiệm của phương
trình.
Dựa vào đồ thị ta thấy đường thẳng
2
m
y =
cắt đồ thị tại nhiều nhất
5
điểm. Vậy phương trình
có nhiều nhất
5
nghiệm.
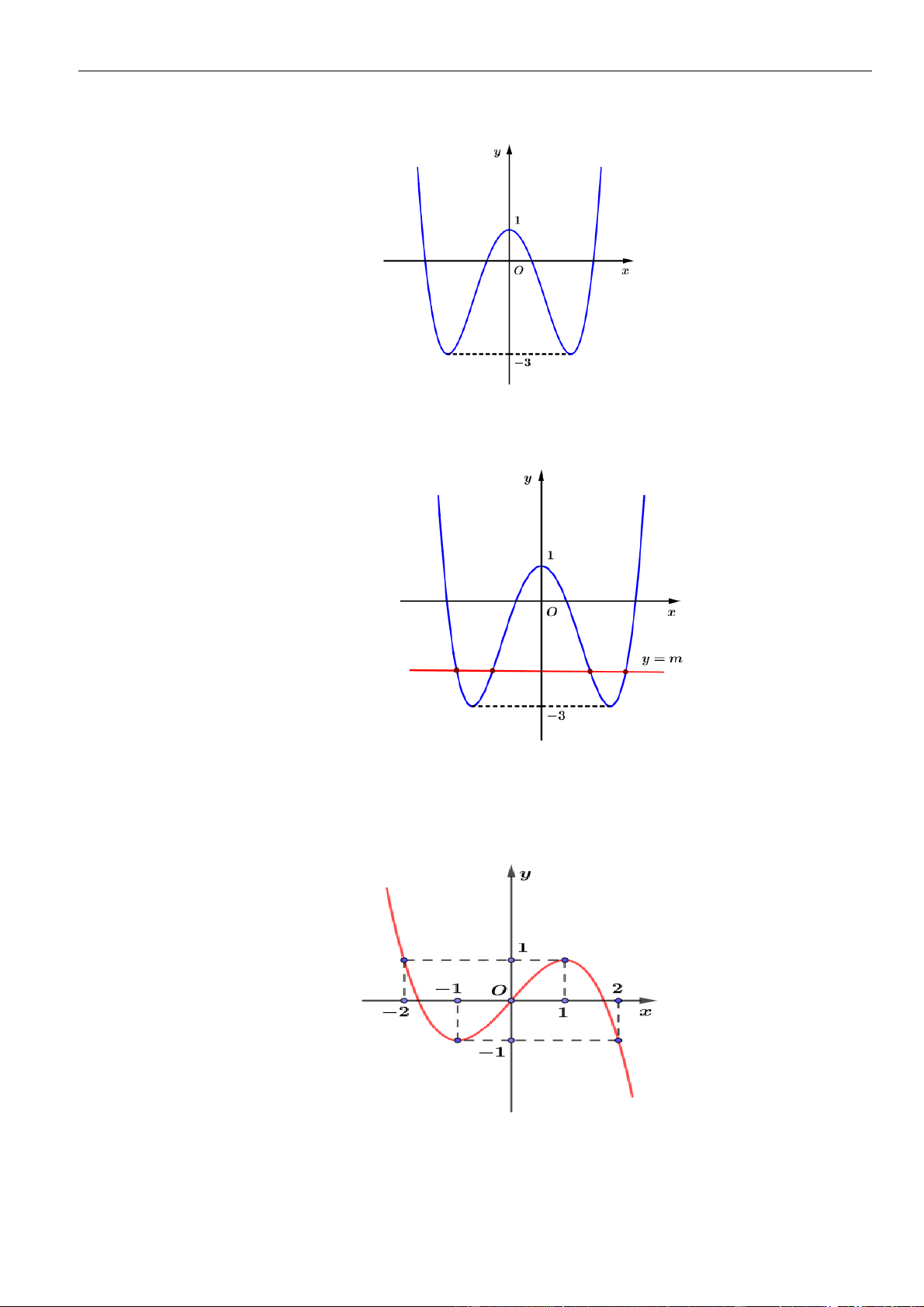
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Câu 5: Cho hàm trùng phương
( )
y f x=
có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham
số
m
để phương trình
( )
f x m=
có 4 nghiệm phân biệt.
A.
1m =
. B.
1m −
. C.
31m−
. D.
1m
.
Lời giải
Chọn C
Để phương trình
( )
f x m=
có 4 nghiệm phân biệt thì
31m−
.
Câu 6: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ dưới. Tìm tất cả các giá trị của tham số
m
để số
nghiệm dương của phương trình
( )
f x m=
bằng
1
.
A.
0m
. B.
0m
.
C.
0m
hoặc
1m =
. D.
1m −
hoặc
1m
.
Lời giải
Chọn C
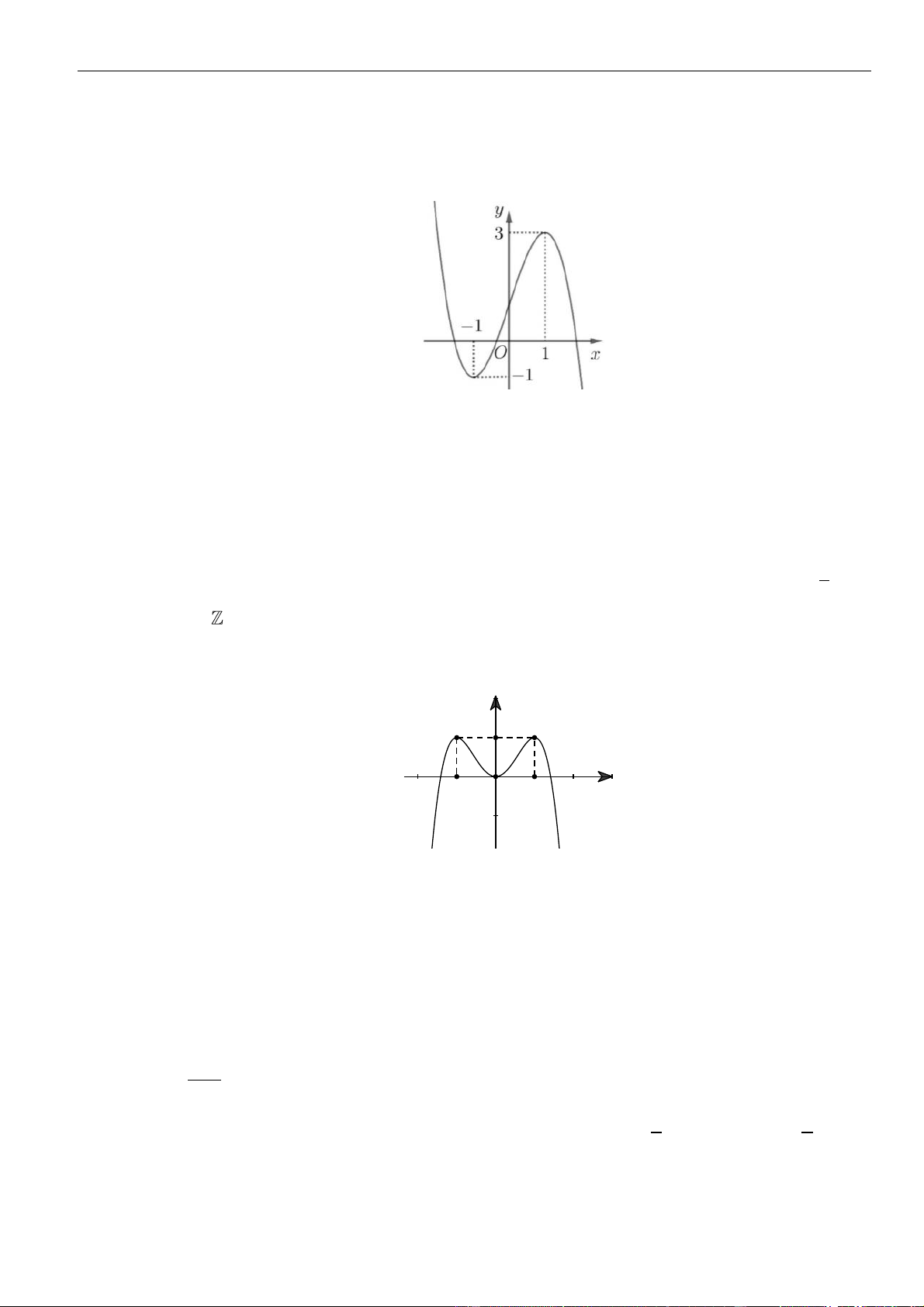
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Để số nghiệm dương của phương trình
( )
f x m=
bằng
1
thì đường thẳng
ym=
cắt đồ thị hàm
số
( )
y f x=
tại một điểm có hoành độ dương
0
1
m
m
=
.
Câu 7: Cho hàm số bậc ba
()fx
có đồ thị như hình vẽ bên:
Số giá trị nguyên của
m
để phương trình
( ) 3 0f x m+=
có ba nghiệm phân biệt là:
A.
3
. B.
5
. C.
2
. D.
1
.
Lời giải
Chọn D
Số nghiệm của phương trình
( ) 3 0f x m+=
là số giao điểm của đồ thị hàm số
()y f x=
và đường
thẳng
3ym=−
.
Để phương trình
( ) 3 0f x m+=
có ba nghiệm phân biệt thì
1 3 3m− −
1
1
3
m −
Vì
m
nên
0m =
.
Câu 8: Cho hàm số
42
2y x x= − +
có đồ thị như hình vẽ bên dưới:
Tìm tất cả các giá trị thực của tham số
m
để phương trình
42
2x x m− + =
có bốn nghiệm thực
phân biệt.
A.
1m
. B.
01m
. C.
0m
. D.
01m
.
Lời giải
Chọn B
YCBT
0 1.m
Câu 9: Biết rằng có hai giá trị
12
,mm
của tham số
m
để đường thẳng
:d y m x=−
và đồ thị hàm số
1
x
y
x
=
−
có đúng một điểm chung. Khẳng định nào sau đây đúng?
A.
( )
12
10; 1mm+ − −
. B.
( )
12
7;12mm+
. C.
12
9
1;
2
mm
+ −
. D.
12
9
;7
2
mm
+
.
Lời giải
Chọn C
x
y
1
1
O
-1
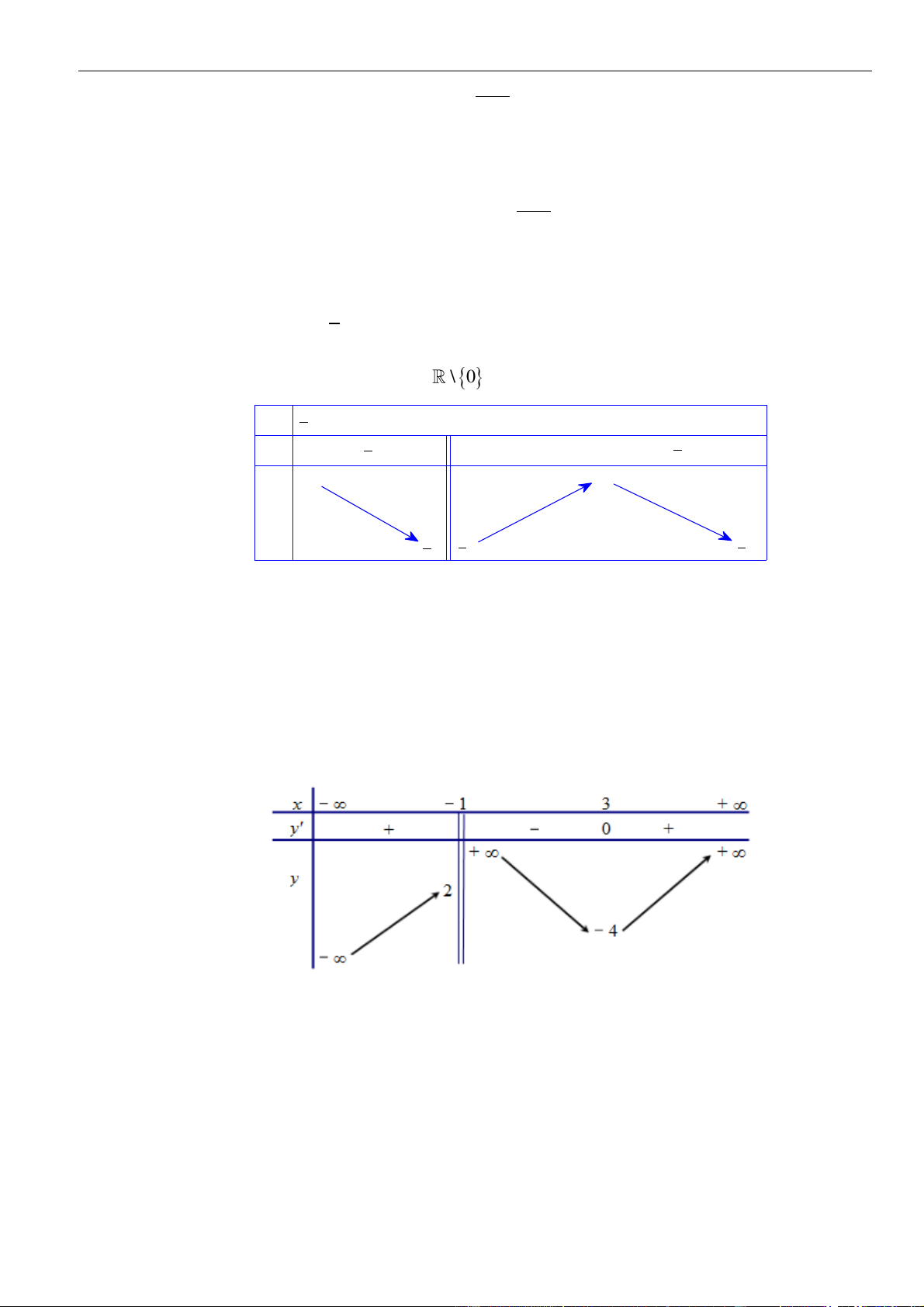
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
Phương trình hoành độ giao điểm:
1
−=
−
x
mx
x
( )( 1) − − =m x x x
.
( )
2
0 1 . − + =x mx m
Đường thẳng
:d y m x=−
và đồ thị hàm số
1
x
y
x
=
−
có một điểm chung khi và chỉ khi phương
trình có nghiệm duy nhất
2
0
0 4 0
4
=
= − =
=
m
mm
m
.
Vậy
12
9
4 1;
2
+ = −
mm
.
Câu 10: Cho hàm số
( )
y f x=
xác định trên
\0
và có bảng biến thiên như sau
Tập hợp tất cả các giá trị của
m
sao cho phương trình
( )
f x m=
có ba nghiệm thực phân biệt.
A.
( )
1;2−
. B.
(
1;2−
. C.
(
;2−
. D.
1;2−
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta được:
Phương trình
( )
f x m=
có ba nghiệm thực phân biệt khi và chỉ khi
( )
1;2m−
.
Câu 11: Cho hàm số có bảng biến thiên như sau
Tổng các giá trị nguyên của
m
để đường thẳng
ym=
cắt đồ thị hàm số tại ba điểm phân biệt
bằng
A.
0
. B.
3−
. C.
5−
. D.
1−
.
Lời giải
Chọn C
+
∞
∞ ∞
+
∞
x
y'
y
∞
0
1
0
+
2
1
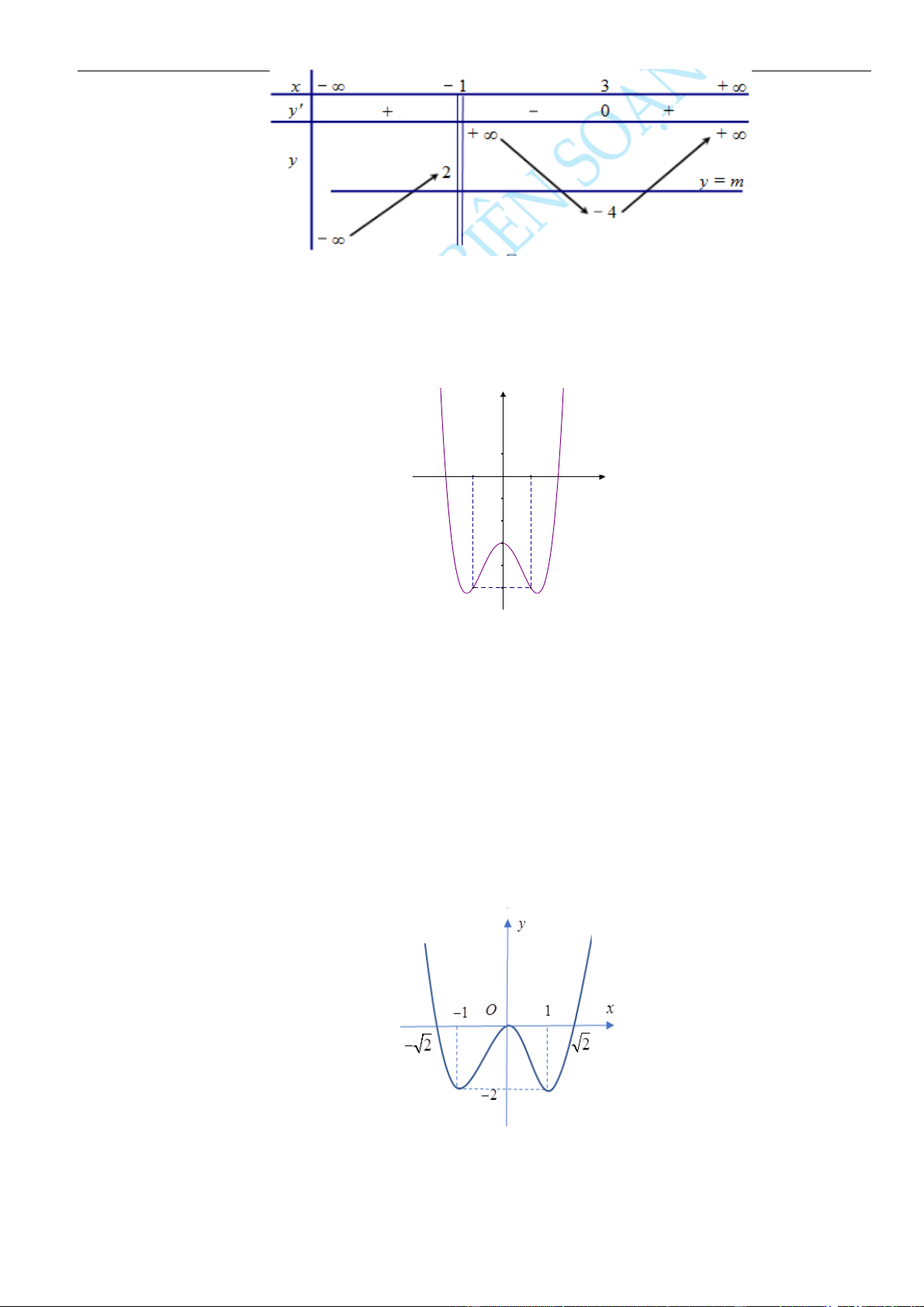
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Đường thẳng
ym=
cắt đồ thị hàm số tại ba điểm phân biệt
42m −
.
Các giá trị nguyên của
3; 2; 1;0;1m − − −
.
Tổng các giá trị nguyên của
m
bằng
5−
.
Câu 12: Đồ thị bên dưới đây là của hàm số
42
33y x x= − −
Với giá trị nào của
m
thì phương trình
42
30x x m− + =
có đúng ba nghiệm phân biệt?
A.
4m =−
. B.
4m =
. C.
3m =−
. D.
0m =
.
Lời giải
Chọn D
4 2 4 2
3 0 3 3 3x x m x x m− + = − − = − −
.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số
42
33y x x= − −
và đường thẳng
3ym=−
.
Để phương trình có đúng ba nghiệm phân biệt
3 3 0mm − − = − =
.
Câu 13: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ dưới đây. Tìm
m
để phương trình
( )
f x m=
có
bốn nghiệm phân biệt.
A.
1m −
. B.
10m−
. C.
10m−
. D.
10m−
.
Lời giải
Chọn D
y
x
O
-5
-3
-1
1
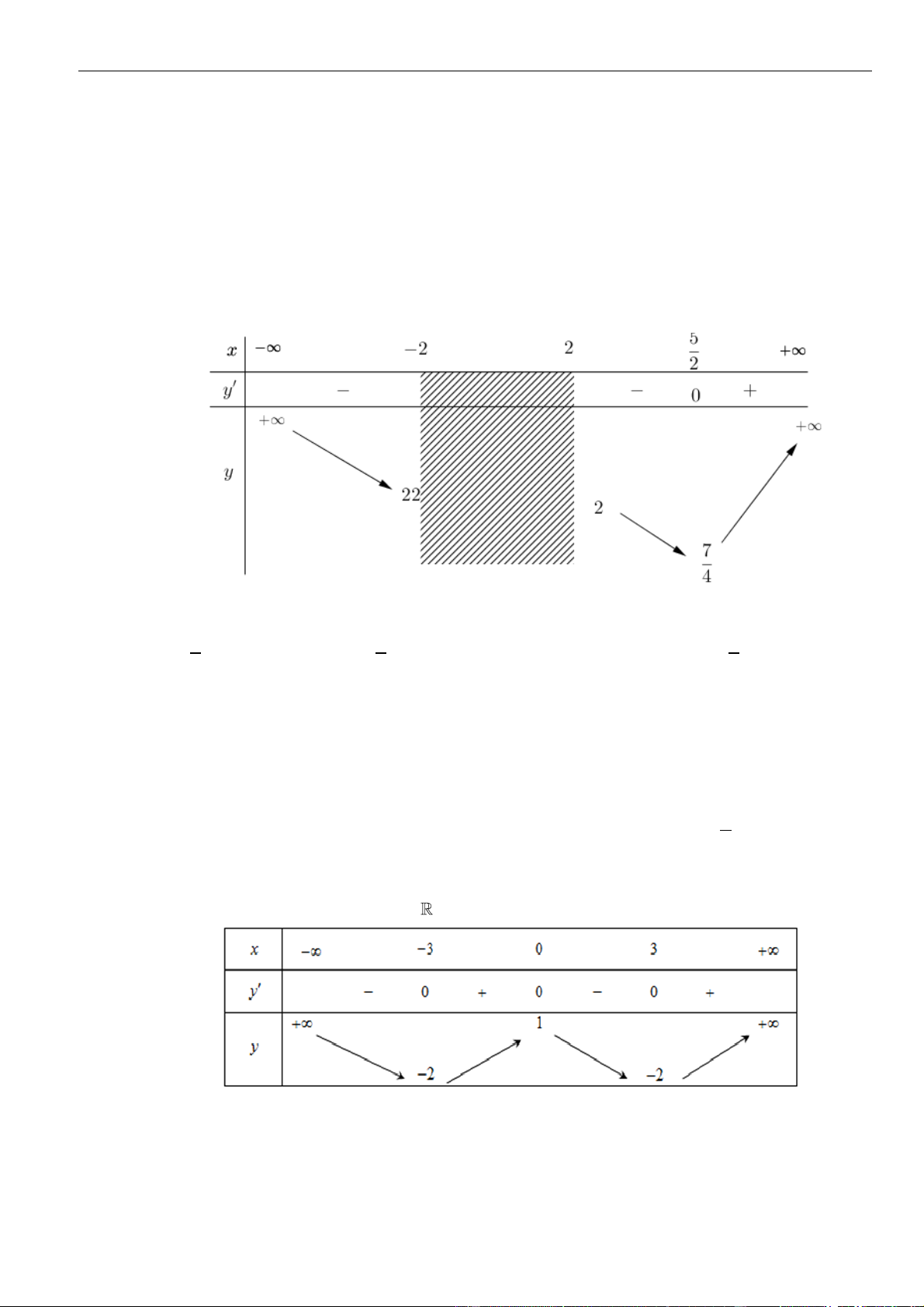
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Số nghiệm của phương trình
( )
f x m=
là số giao điểm của đồ thị hai hàm số sau:
( ) ( )
( )
1
2
y f x
ym
=
=
Đồ thị của hàm số (1) đã vẽ ở trên.
Đường thẳng
ym=
song song với trục hoành cắt trục tung tại điểm có tung độ
m
.
Vây phương trình
( )
f x m=
có 4 nghiệm phân biệt thì
10m−
.
Câu 14: Cho hàm số
( )
y f x=
xác định, liên tục trên mỗi nửa khoảng
(
;2− −
và
)
2;+
và có bảng
biến thiên như hình dưới đây:
Tìm tập hợp các giá trị thực của tham số
m
để phương trình
( )
f x m=
có hai nghiệm phân biệt.
A.
)
7
;2 22;
4
+
. B.
)
7
;2 22;
4
+
. C.
)
22;+
. D.
7
;
4
+
Lời giải
Chọn A
Số nghiệm của phương trình
( )
f x m=
là số giao điểm của đường thẳng
ym=
và đồ thị hàm
số
( )
y f x=
.
Để phương trình có hai nghiệm phân biệt, dựa vào bảng biến thiên ta thấy
7
2
4
22
m
m
.
Câu 15: Cho hàm số
()y f x=
liên tục trên
và có bảng biến
Tìm
m
để phương trình
2 ( ) 0f x m+=
có đúng ba nghiệm phân biệt
A.
1m =−
. B.
2m =−
. C.
1m =
. D.
2m =
.
Lời giải
Chọn B
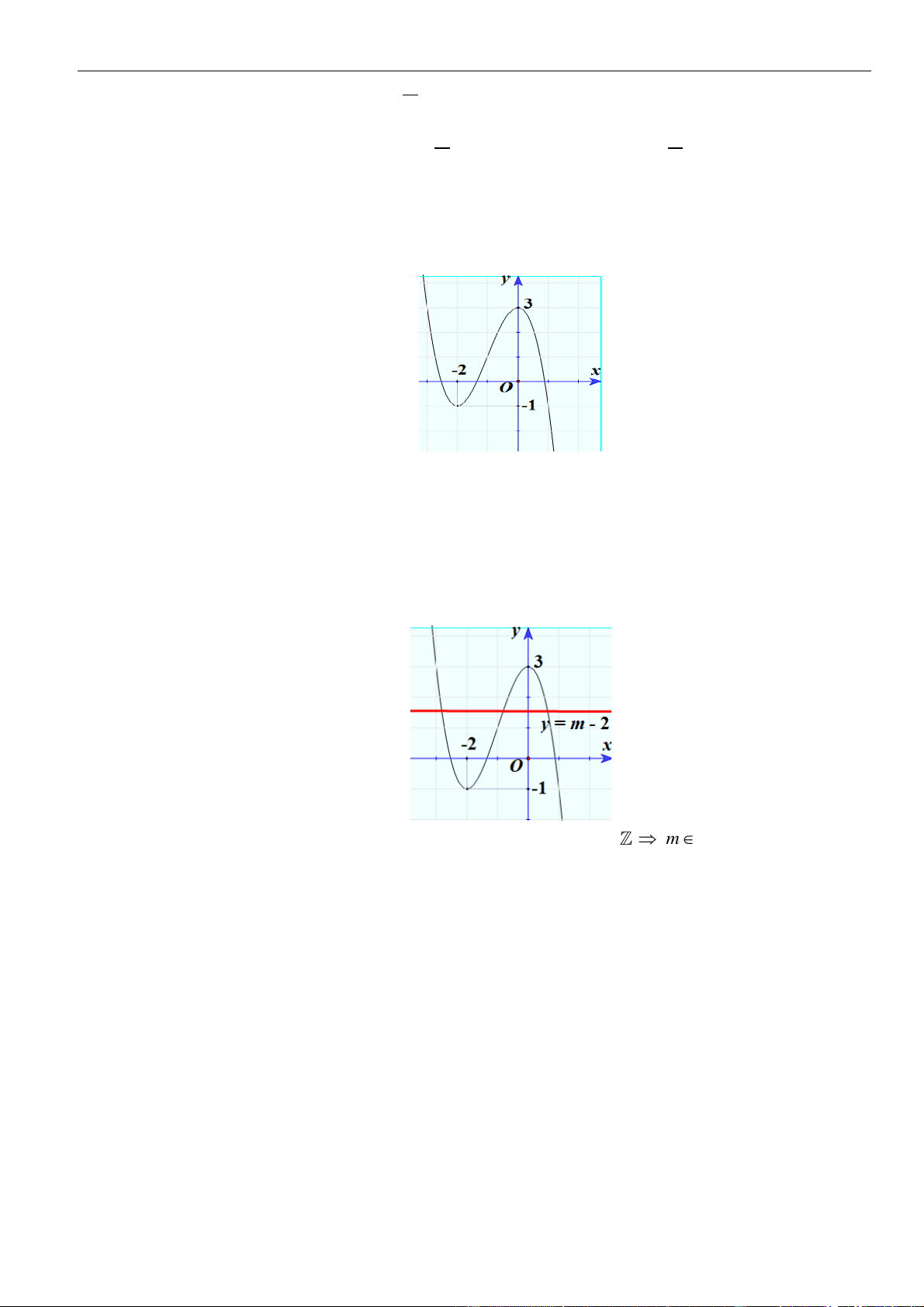
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Ta có
2 ( ) 0 ( )
2
m
f x m f x+ = = −
Dựa vào bảng biến thiến
()
2
m
fx = −
có ba ngiệm phân biệt
12
2
m
m − = = −
.
Câu 16: Cho hàm số
32
33y x x= − − +
có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
32
3 5 0x x m− − + − =
có ba nghiệm phân biệt?.
B.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta có
3 2 3 2
3 5 0 3 3 2x x m x x m− − + − = − − + = −
(1).
Để phương trình (1) có ba nghiệm phân biệt thì đồ thị hàm số
32
33y x x= − − +
phải cắt đường
thẳng
2ym=−
tại ba điểm phân biệt.
Vẽ đường thẳng
2ym=−
.
Quan sát đồ thị, suy ra
1 2 3 1 5mm− −
, mà
2;3; 4mm
.
Vậy có giá trị
3
nguyên của
m
thỏa mãn bài toán.
Câu 17: Có bao nhiêu giá trị nguyên của tham số m để phương trình
3
41x x m− + + =
có ba nghiệm phân
biệt?
A. 5. B. 17. C. 7. D. 15.
Lời giải
Chọn C
Phương trình đã cho là phương trình hoành độ giao điểm của đồ thị hàm số
( )
3
41y f x x x= = − + +
và đường thẳng
ym=
.
Xét
( )
3
41f x x x= − + +
. Ta có
( )
2
34f x x
= − +
.
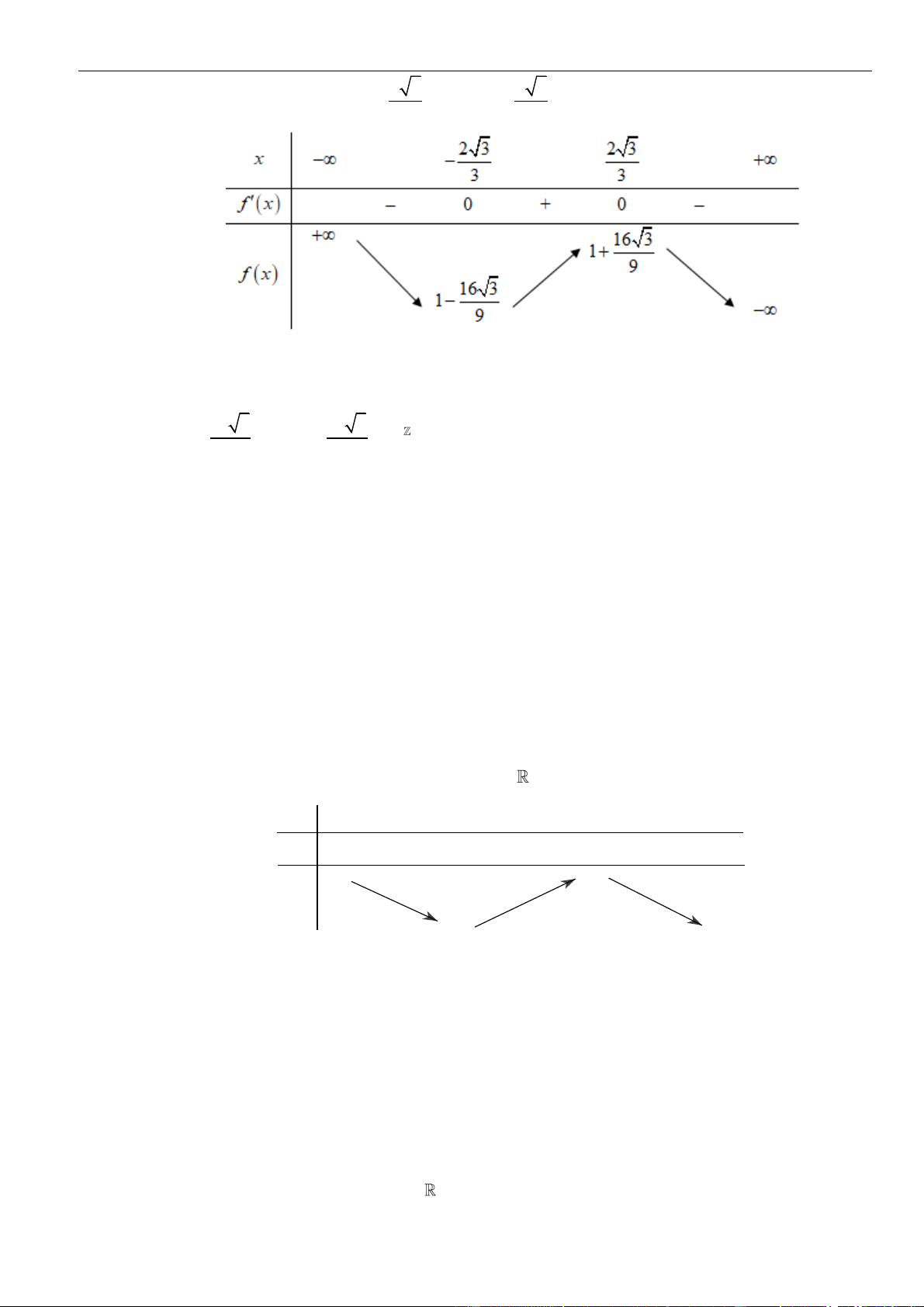
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Phương trình
( )
23
0
3
f x x
= =
hoặc
23
3
x =−
. Ta lập bảng biến thiên của hàm số
( )
fx
.
Đường thẳng
ym=
là đường thẳng cắt trục tung tại điểm
( )
0;m
và song song với trục
Ox
.
Dựa vào bảng biến thiên, ta thấy đường thẳng
ym=
cắt đồ thị
( )
y f x=
tại 3 điểm phân biệt
khi
16 3 16 3
1 1 2; 1;...;4
33
m
mm
− + ⎯⎯⎯→ − −
.
Như vậy có 7 giá trị nguyên của m thỏa mãn.
Câu 18: Đồ thị sau đây là của hàm số
3
31y x x= − +
. Với giá trị nào của
m
thì phương trình
3
3x x m−−
có
3
nghiệm phân biệt?
A.
22m−
. B.
23m−
. C.
13m−
. D.
22m−
.
Lời giải
Chọn A
Phương trình
( )
33
3 3 1 1 *x x m x x m− − − + = +
số nghiệm của phương trình
( )
*
là số giao
điểm của đồ thị hàm số với đường thẳng
1ym=+
Dựa vào đồ thị hàm số
3
31y x x= − +
, phương trình có ba nghiệm phân biệt khi
1 1 3 2 2mm− + −
.
Câu 19: Cho hàm số
( )
y f x=
xác định và liên tục trên , có bảng biến thiên như sau:
Tìm tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
( )
f x m=
có ít nhất hai
nghiệm thực phân biệt.
A.
( )
1;3−
. B.
(
1;3−
. C.
1;3−
. D.
)
1;3−
.
Lời giải
Chọn C
Phương trình
( )
f x m=
có ít nhất hai nghiệm thực phân biệt Đường thẳng
ym=
cắt đồ thị
hàm số
( )
y f x=
tại ít nhất hai điểm phân biệt
13m−
.
Câu 20: Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình vẽ sau:
+
∞
3
+
0
0
y
y'
x
–
∞
– 1
–
–
+
∞
1
– 1
–
∞
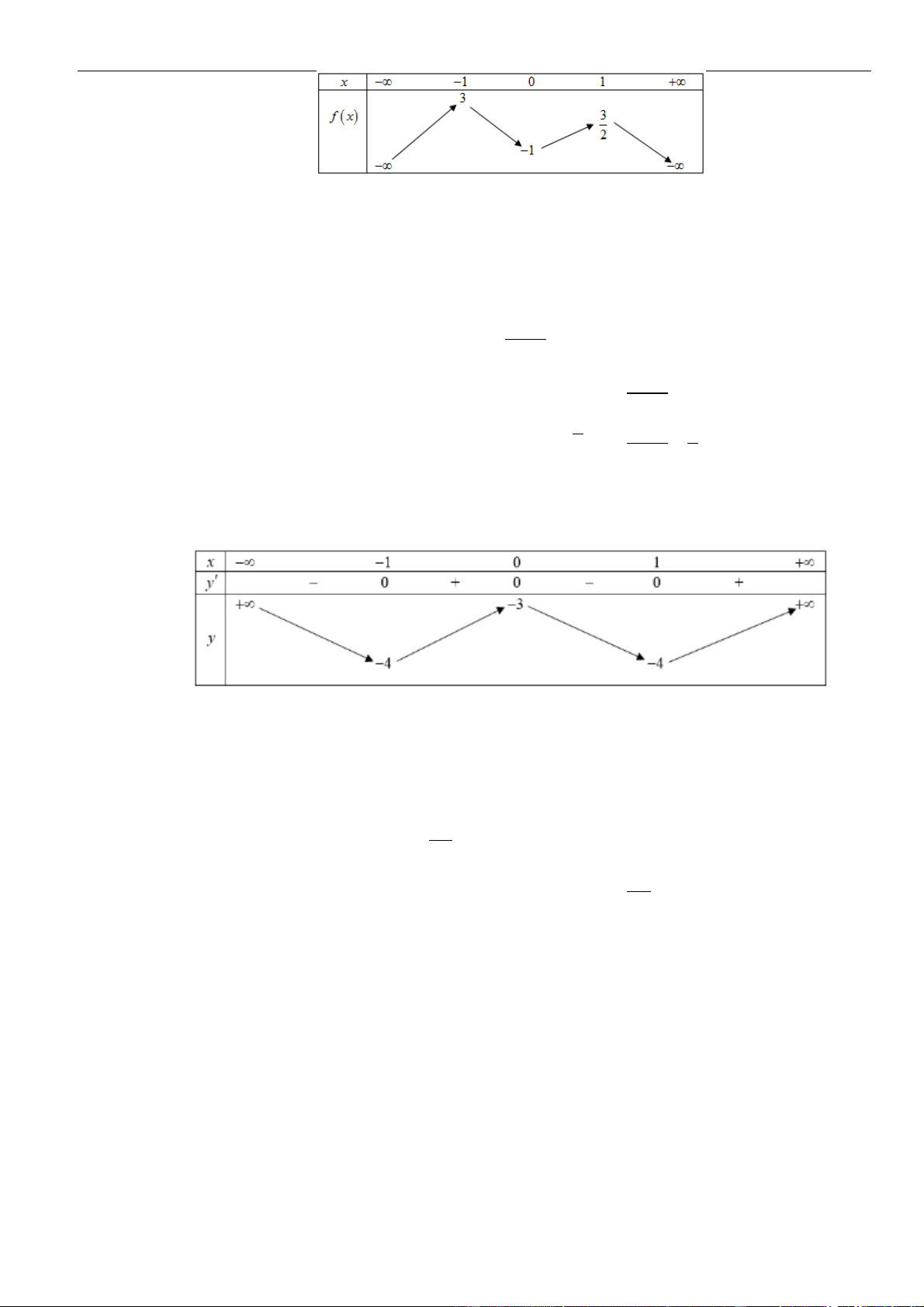
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Hỏi có bao nhiêu giá trị nguyên dương của
m
để phương trình
( )
2 2 0f x m− + =
có đúng 3
nghiệm phân biệt?
A. 1. B. 3. C. 2. D. 0.
Lời giải
Chọn A
( ) ( ) ( )
2
2 2 0 2 2
2
m
f x m f x m f x
−
− + = = − =
Để phương trình có đúng ba nghiệm phân biệt:
( )
( )
2
1
1
0
2
3
2 3 5
2
22
m
fx
m
mm
fx
−
=−
=−
=
−=
=
=
Vậy có một giá trị nguyên dương của m để phương trình có đúng ba nghiệm phân biệt.
Câu 21: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình
( )
2 3 0f x m+=
có ba nghiệm phân biệt?
A. Vô số. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Ta có :
( ) ( )
3
2 3 0
2
m
f x m f x+ = = −
.
Để phương trình
( )
2 3 0f x m+=
có ba nghiệm phân biệt thì
3
32
2
m
m− = − =
.
Câu 22: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Số giá trị nguyên dương của tham số
m
để phương
trình
( )
2020 0f x m+ − =
có 2 nghiệm là
A.
2024
. B.
2021
. C.
2020
. D.
2023
.
Lời giải
Chọn D
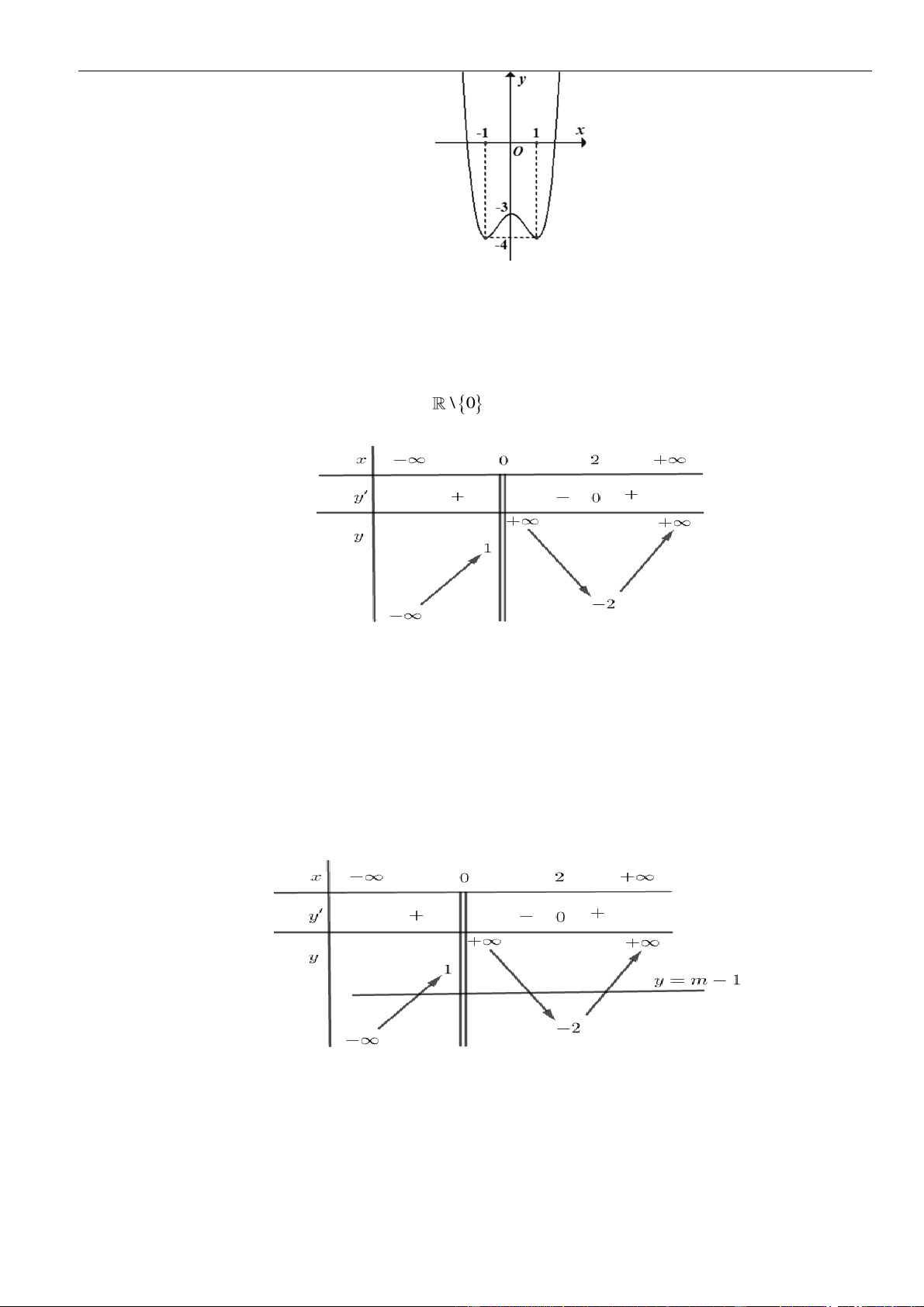
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
Ta có
( ) ( )
2020 0 2020f x m f x m+ − = = −
.
Phương trình đã cho có 2 nghiệm
2020 4 2024
2020 3 2023
mm
mm
− = − =
− −
.
Vậy có 2023 giá trị của tham số
m
.
Câu 23: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
( )
1f x m=−
có đúng ba
nghiệm thực phân biệt là
A.
( )
2;− +
. B.
( )
1;2−
. C.
( )
1;− +
. D.
( )
2;1−
.
Lời giải
Chọn B
Số nghiệm của phương trình
( )
1f x m=−
là số giao điểm của hai đồ thị
( )
1
y f x
ym
=
=−
.
Bảng biến thiên:
Phương trình
( )
1f x m=−
có đúng ba nghiệm thực phân biệt khi
2 1 1m− −
12m −
.
Câu 24: Cho hàm số
( )
fx
có đồ thị như hình vẽ. Số giá trị nguyên của tham số
m
để phương trình
( )
1f x m+=
có
3
nghiệm phân biệt là:
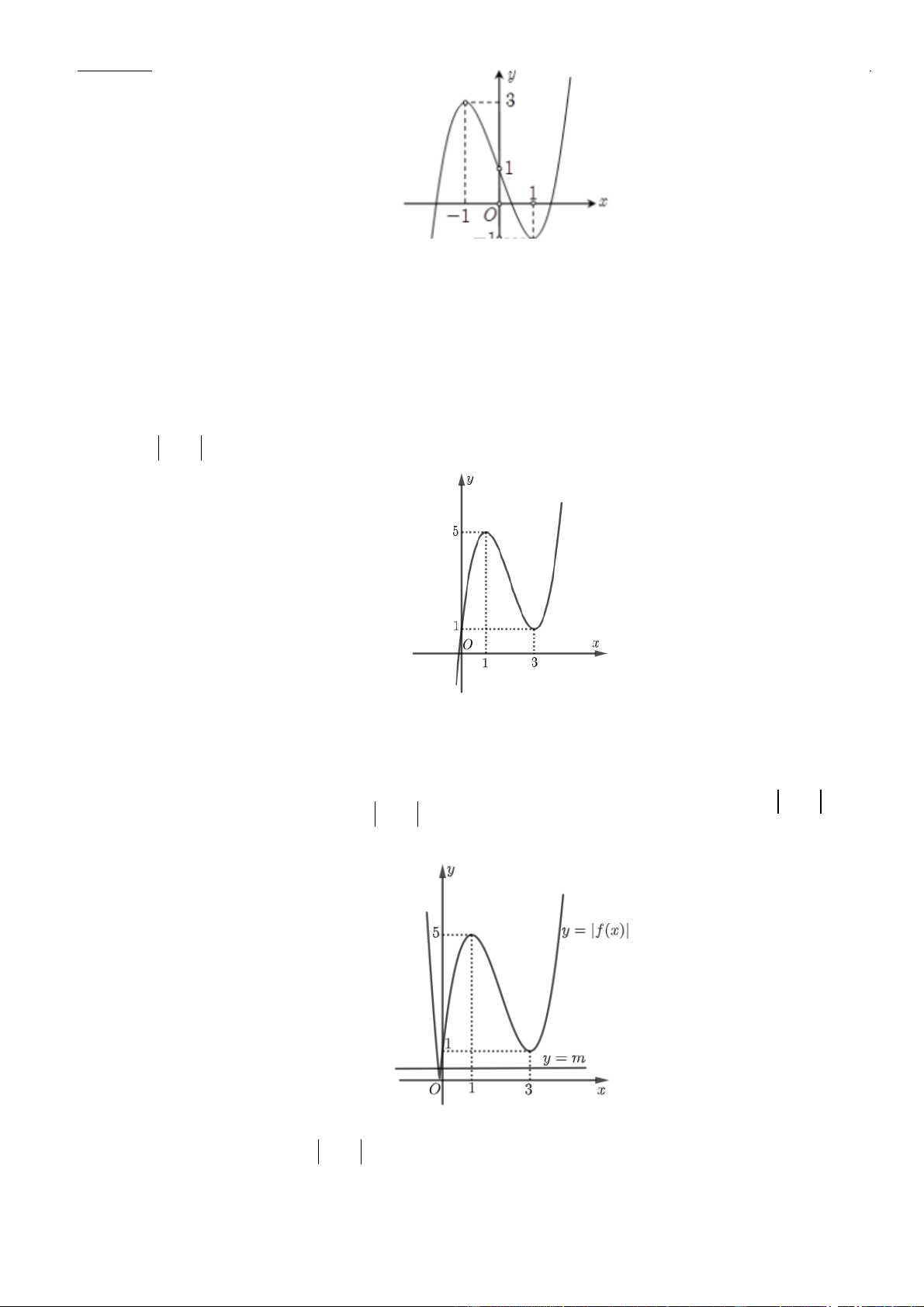
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
A.
4.
B.
5.
C.
2.
D.
3.
Lời giải
Chọn D
Để phương
( )
1f x m+=
có
3
nghiệm phân biệt thì
( )
1f x m=−
có 3 nghiệm phân biệt
1 1 3 0 4.mm − −
Vậy
1,2,3.m =
Câu 25: Cho hàm số
( )
y f x=
có đồ thị trong hình vẽ bên. Tìm tất cả các giá trị của
m
để phương trình
( )
f x m=
có đúng hai nghiệm phân biệt.
A.
5m
,
01m
. B.
1m
. C.
1m =
,
5m =
. D.
15m
.
Lời giải
Chọn A
Số nghiệm của phương trình
( )
f x m=
chính là số giao điểm của hai đồ thị:
( )
y f x
ym
=
=
.
Vậy để phương trình
( )
f x m=
có đúng hai nghiệm phân biệt thì
5m
,
01m
.
Câu 26: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
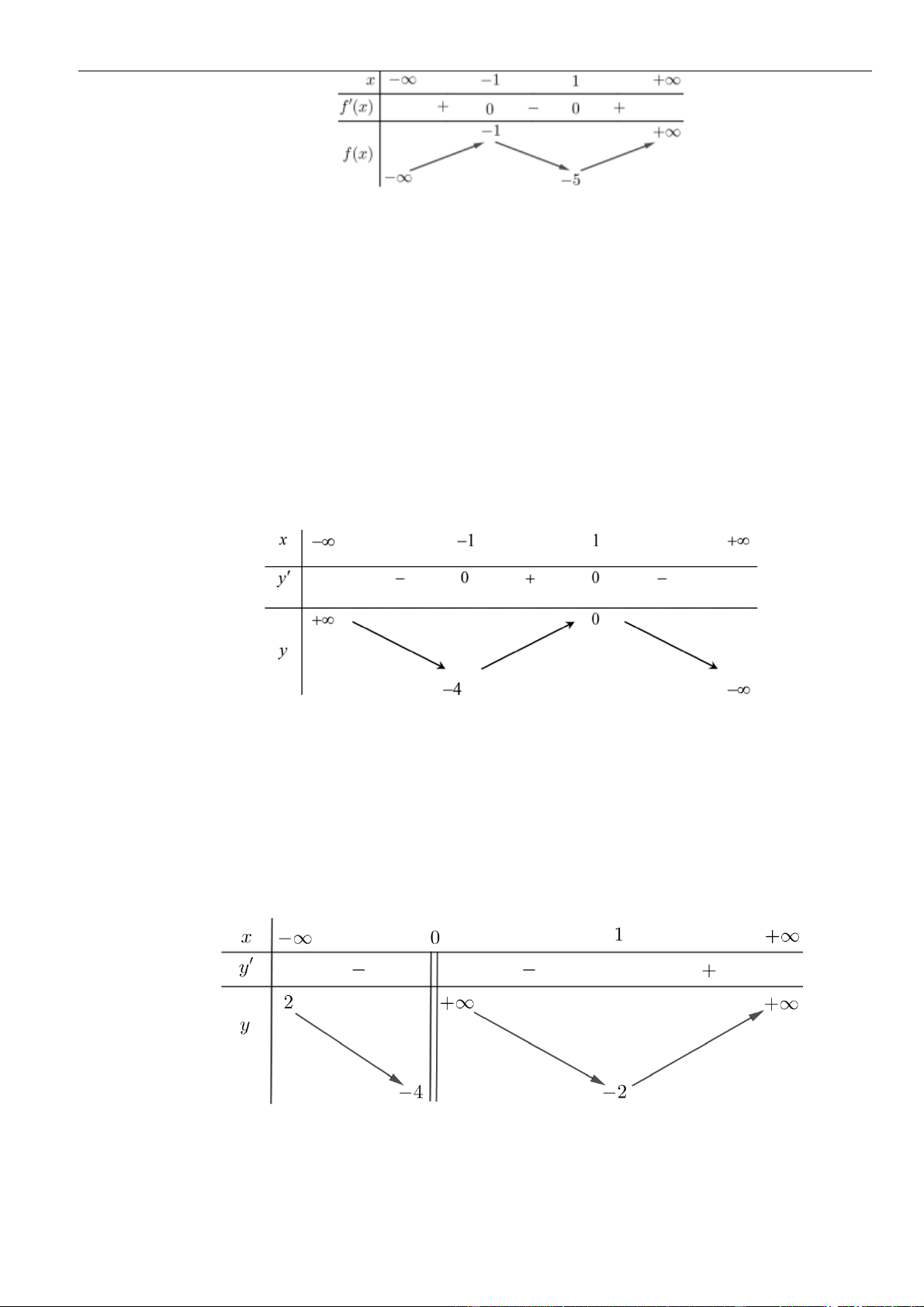
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
Số giá trị nguyên của tham số
m
để phương trình
( )
f x m=
có ba nghiệm phân biệt là
A.
3
. B.
4
. C.
2
. D.
5
.
Lời giải
Chọn A
Số nghiệm của phương trình
( )
f x m=
bằng số giao điểm của đồ thị hàm số
( )
y f x=
và đường
thẳng
ym=
.
Dựa vào bảng biến thiên, suy ra phương trình
( )
f x m=
có ba nghiệm phân biệt khi
51m− −
.
Mà
m
nguyên nên
4; 3; 2m − − −
.
Vậy số giá trị nguyên của tham số
m
là
3
.
Câu 27: Cho hàm số
( )
=y f x
có bảng biến thiên:
Với giá trị nào của m thì phương trình
( )
0f x m+=
có
3
nghiệm phân biệt.
A.
11m−
. B.
40m−
. C.
04m
. D.
21m−
.
Lời giải
Chọn C
( ) ( )
0 1f x m+=
( )
f x m = −
.
Dựa vào bảng biến thiên ta có
4 0 0 4mm− −
.
Câu 28: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Phương trình
( )
f x m=
có ba nghiệm thực phân biệt khi và chỉ khi
A.
42m− −
. B.
22m−
. C.
22m−
. D.
42m−
.
Lời giải
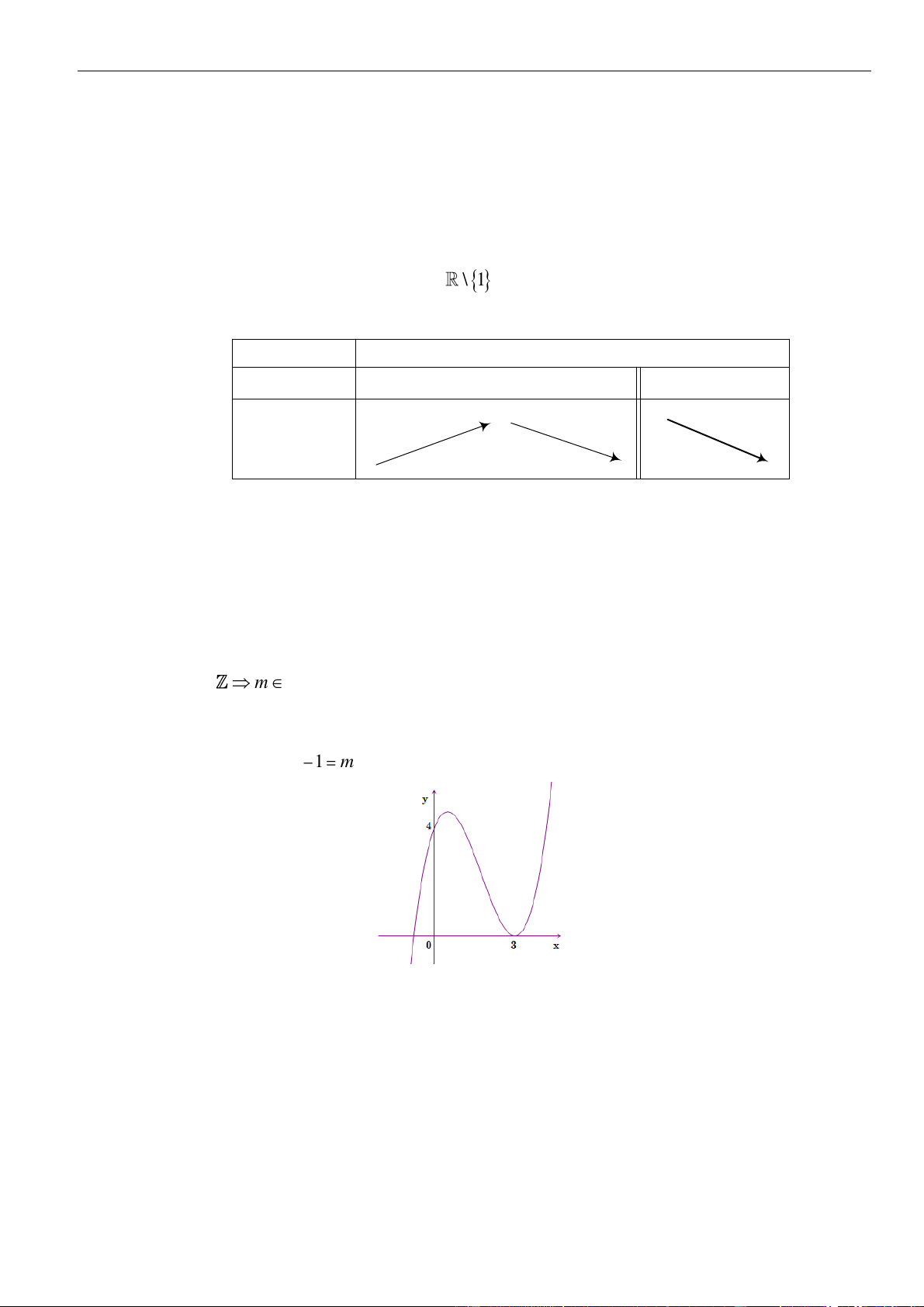
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 26
Chọn B
Số nghiệm của phương trình
( )
f x m=
bằng số giao điểm của đồ thị hàm số
( )
y f x=
và đường
thẳng
ym=
.
Dựa vào bảng biến thiên, ta có phương trình
( )
f x m=
có ba nghiệm thực phân biệt
22m −
.
Câu 29: Cho hàm số
( )
y f x=
xác định trên
\1
và có bảng biến thiên như hình bên. Số giá trị
nguyên
m
để phương trình
( )
f x m=
có
3
nghiệm phân biệt là
x
−
+
+
−
y
y
0
1−
1
−
4
1
−
+
0
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn D
Phương trình
( )
f x m=
là phương trình hoành độ giao điểm của hai đồ thị
( ) ( )
:C y f x=
và
đường thẳng
( )
:d y m=
.
Để
( )
f x m=
có ba nghiệm phân biệt
( )
C
và
( )
d
có ba giao điểm
14m
.
Do
2;3mm
.
Câu 30: Cho hàm số
fx
có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị của tham số
m
để
phương trình
1f x m
có
3
nghiệm phân biệt
A.
13m−
. B.
14m
. C.
25m−
. D.
04m
.
Lời giải
Chọn A
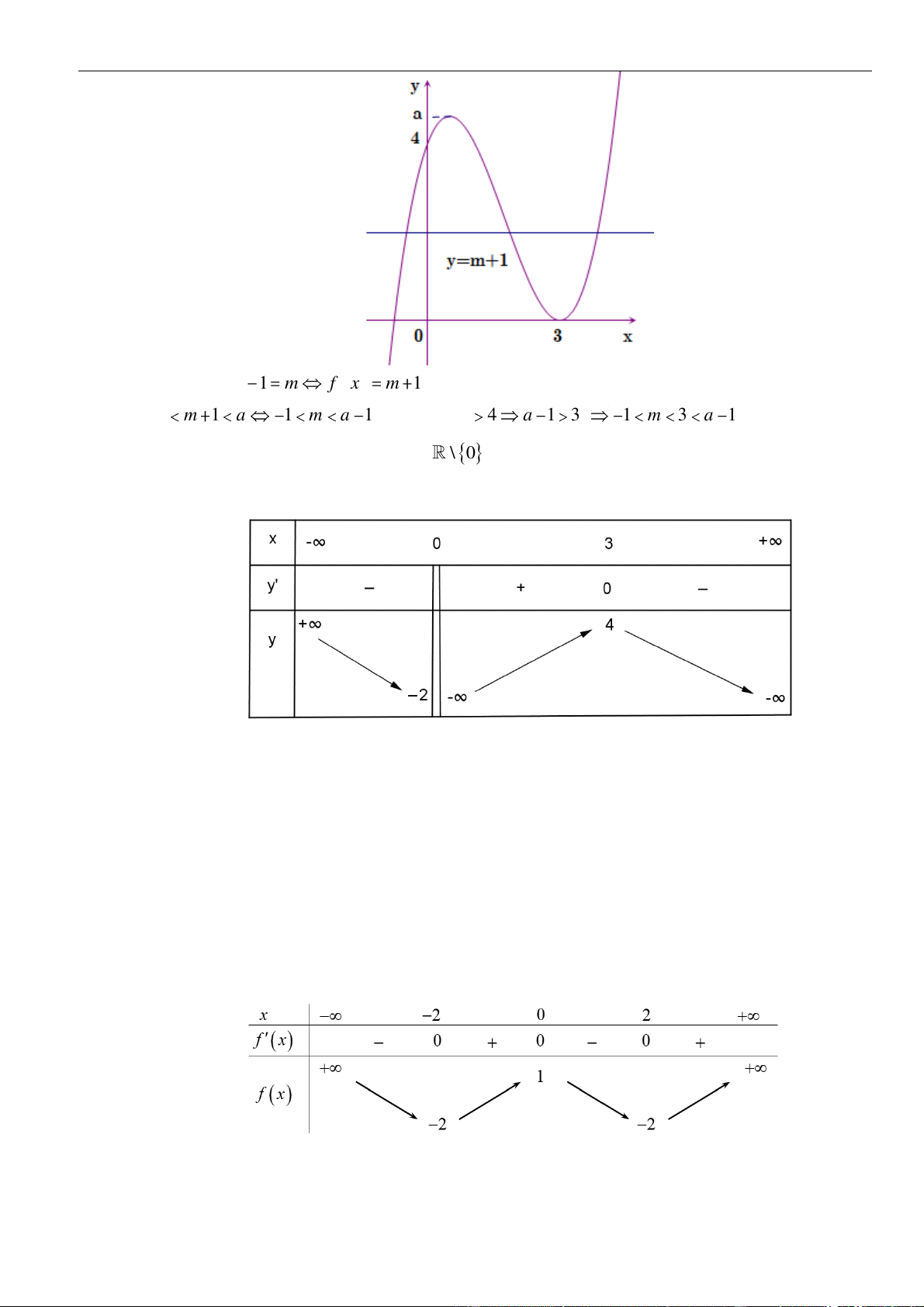
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
27 | Facebook tác giả: Phan Nhật Linh
Ta có
11f x m f x m
. Quan sát đồ thị phương trình có
3
nghiệm phân biệt khi
0 1 1 1m a m a
. Mặt khác
4 1 3aa
1 3 1ma
.
Câu 31: Cho hàm số
( )
y f x=
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
( )
f x m=
có hai
nghiệm thực phân biệt
A.
( )
; 2 4− −
. B.
(
;2− −
. C.
(
; 2 4− −
. D.
( )
;2− −
.
Lời giải
Chọn C
Phương trình có hai nghiệm thực phân biệt
4
2
m
m
=
−
.
Câu 32: Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình
( )
40f x m+=
có
4
nghiệm thực phân
biệt?
A.
10
. B.
11
. C.
12
. D.
9
.
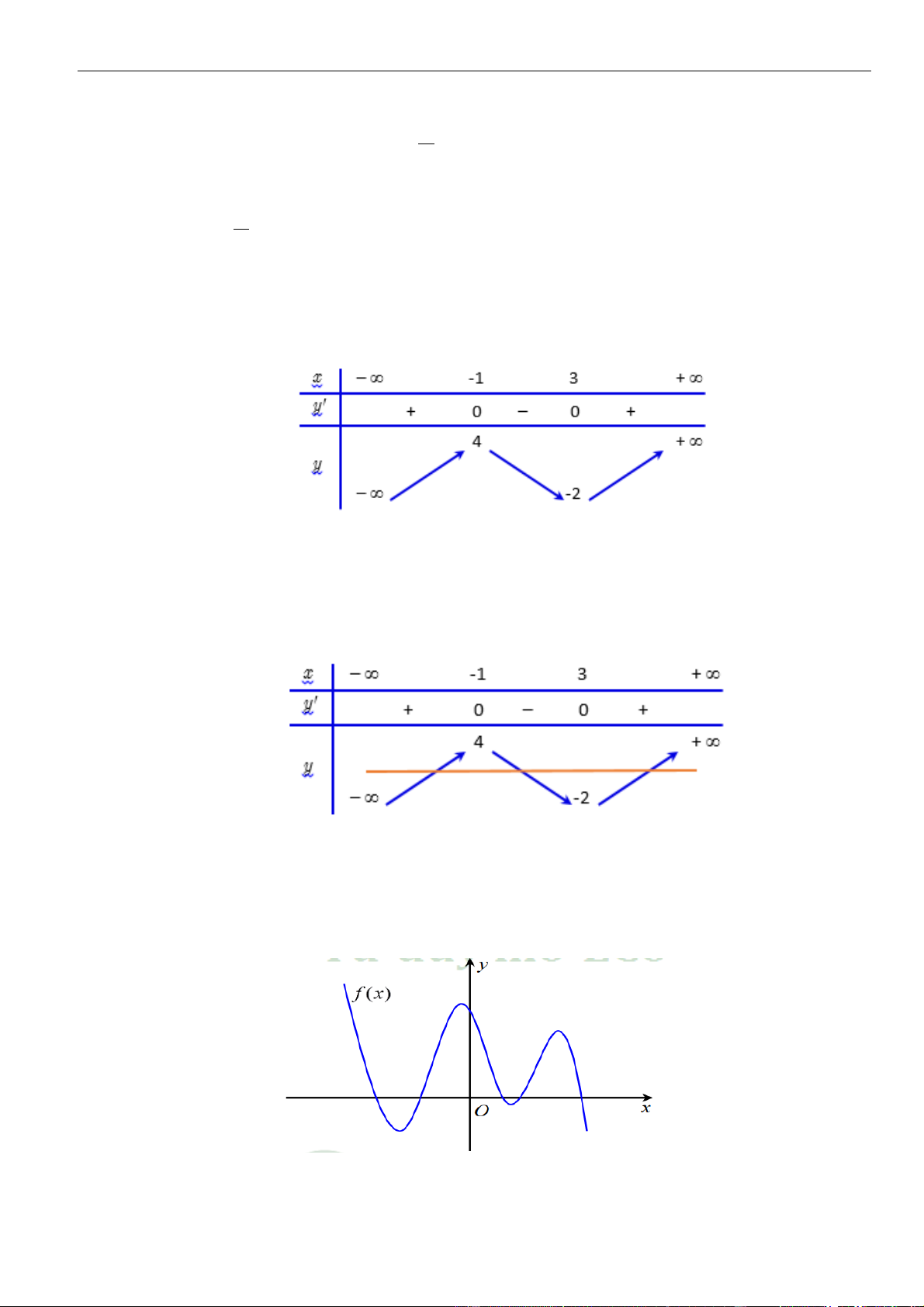
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 28
Lời giải
Chọn B
Ta có:
( )
40f x m+=
( )
4
m
fx=−
Dựa vào BBT ta có phương trình
( )
40f x m+=
có
4
nghiệm thực phân biệt
21
4
m
− −
48m−
.
Do
m
nguyên nên
3; 2;...;7m − −
.
Vậy có
11
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 33: Cho hàm số
( )
y f x=
có bảng biến thiên như sau :
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
f x m=
có ba nghiệm phân biệt.
A.
2m −
. B.
24m−
. C.
24m−
. D.
4m
.
Lời giải
Chọn B
Ta có
Phương trình
( )
f x m=
có ba nghiệm phân biệt khi và chỉ khi đường thẳng
ym=
cắt đồ thị
hàm số
( )
y f x=
tại ba điểm phân biệt
24m −
.
Câu 34: Cho đồ thị hàm số
( )
y f x=
như hình vẽ. Hỏi phương trình
( )
2 f x m=
có tối đa bao nhiêu
nghiệm thực
x
?
A.
3
. B.
6
. C.
5
. D.
4
.
Lời giải
Chọn C
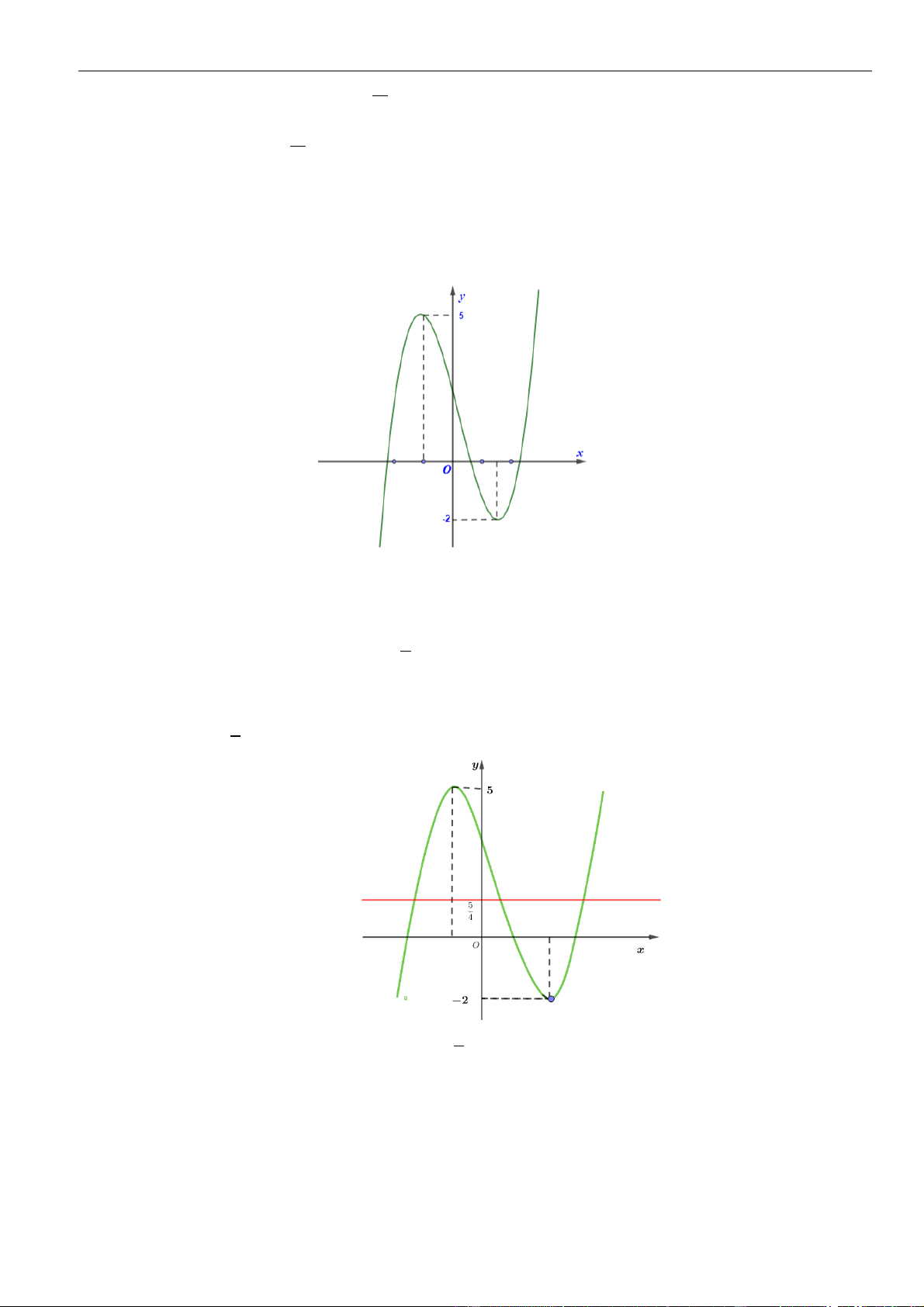
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
29 | Facebook tác giả: Phan Nhật Linh
Ta có
( ) ( )
2
2
m
f x m f x= =
.
Đường thẳng
2
m
y =
cắt đồ thị hàm số
( )
y f x=
tối đa tại
5
điểm nên phương trình
( )
2 f x m=
có tối đa 5 nghiệm thực
x
.
Câu 35: Cho đồ thị hàm số
( )
y f x=
như hình vẽ bên dưới. Số nghiệm thực của phương trình
( )
4 5 0fx−=
là:
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn A
Ta có:
( ) ( ) ( )
5
4 5 0 1
4
f x f x− = =
.
Số nghiệm của phương trình
( )
1
chính là số giao điểm của đồ thị hàm số
( )
y f x=
và đường
thẳng
5
4
y =
.
Dựa vào đồ thị ta thấy đường thẳng
5
4
y =
cắt đồ thị hàm số
( )
y f x=
tại
3
điểm phân biệt.
Vậy phương trình đã cho có 3 nghiệm phân biệt.
Câu 36: Cho hàm số
( )
y f x=
có đồ thị như hình sau:
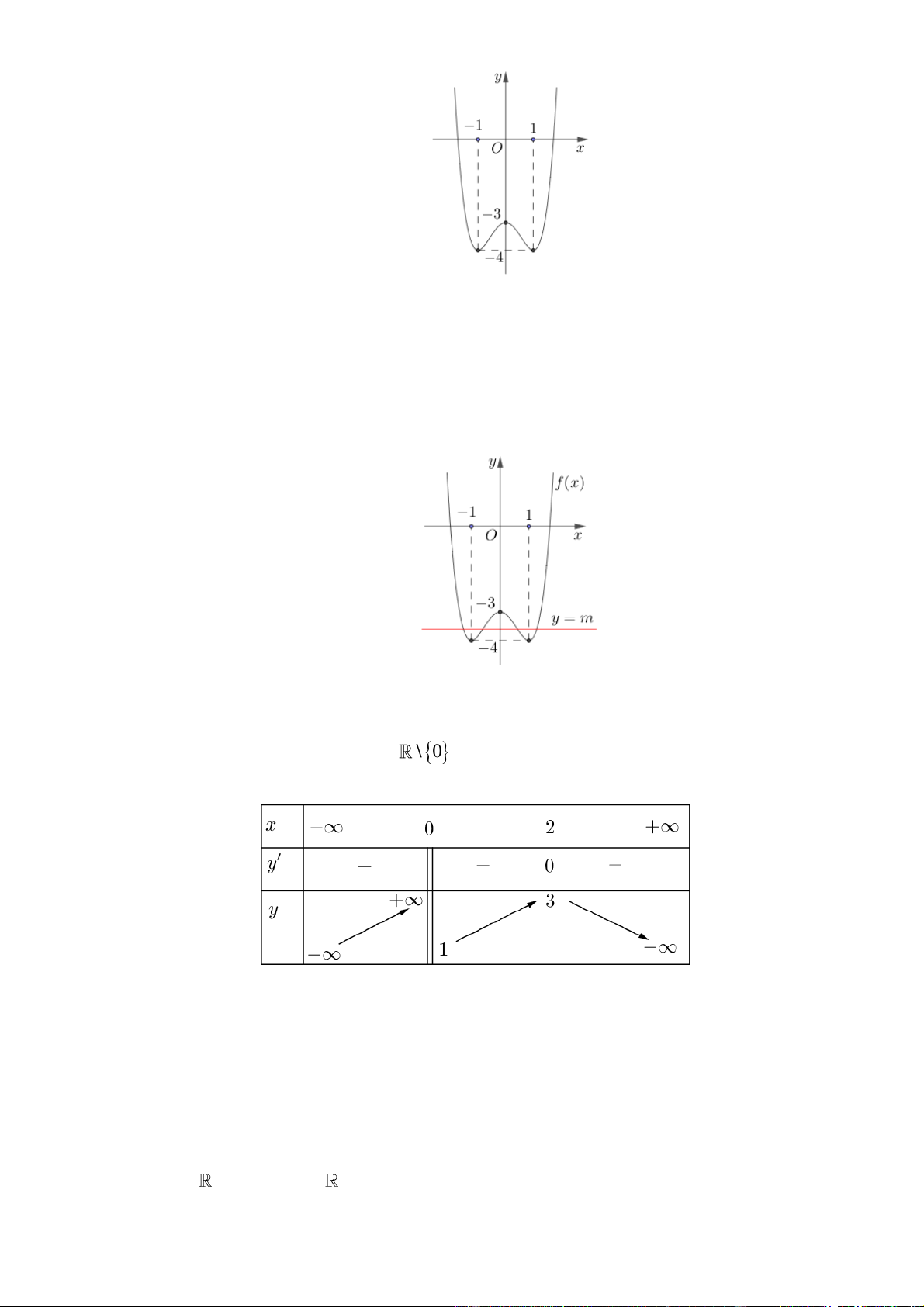
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 30
Tìm tất cả các giá trị của tham số
m
để phương trình
( )
f x m=
có bốn nghiệm phân biệt.
A.
43m− −
. B.
4m −
. C.
43m− −
. D.
43m− −
.
Lời giải
Chọn A
Số nghiệm của phương trình
( )
f x m=
bằng số giao điểm của đồ thị hàm số
( )
y f x=
và đường
thẳng
ym=
.
Quan sát đồ thị, để đường thẳng
ym=
cắt đồ thị hàm số
( )
y f x=
tại bốn điểm phân biệt
43m − −
.
Câu 37: Cho hàm số
( )
fx
xác định trên
\0
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau
Tìm tất cả các giá trị thực của tham số
m
để phương trình
( )
1f x m=−
có ba nghiệm thực phân biệt.
A.
( )
2;4m
. B.
)
2;4m
. C.
( )
1;3m
. D.
)
1;3m
.
Lời giải
Chọn A
Để phương trình
( )
1f x m=−
có ba nghiệm thực phân biệt thì đồ thị hàm số củađường thẳng
1ym=−
phải cắt đồ thị hàm số
( )
y f x=
tại ba điểm phân biệt. Do đó
1 1 3
m
m
−
24
24
m
m
m
.
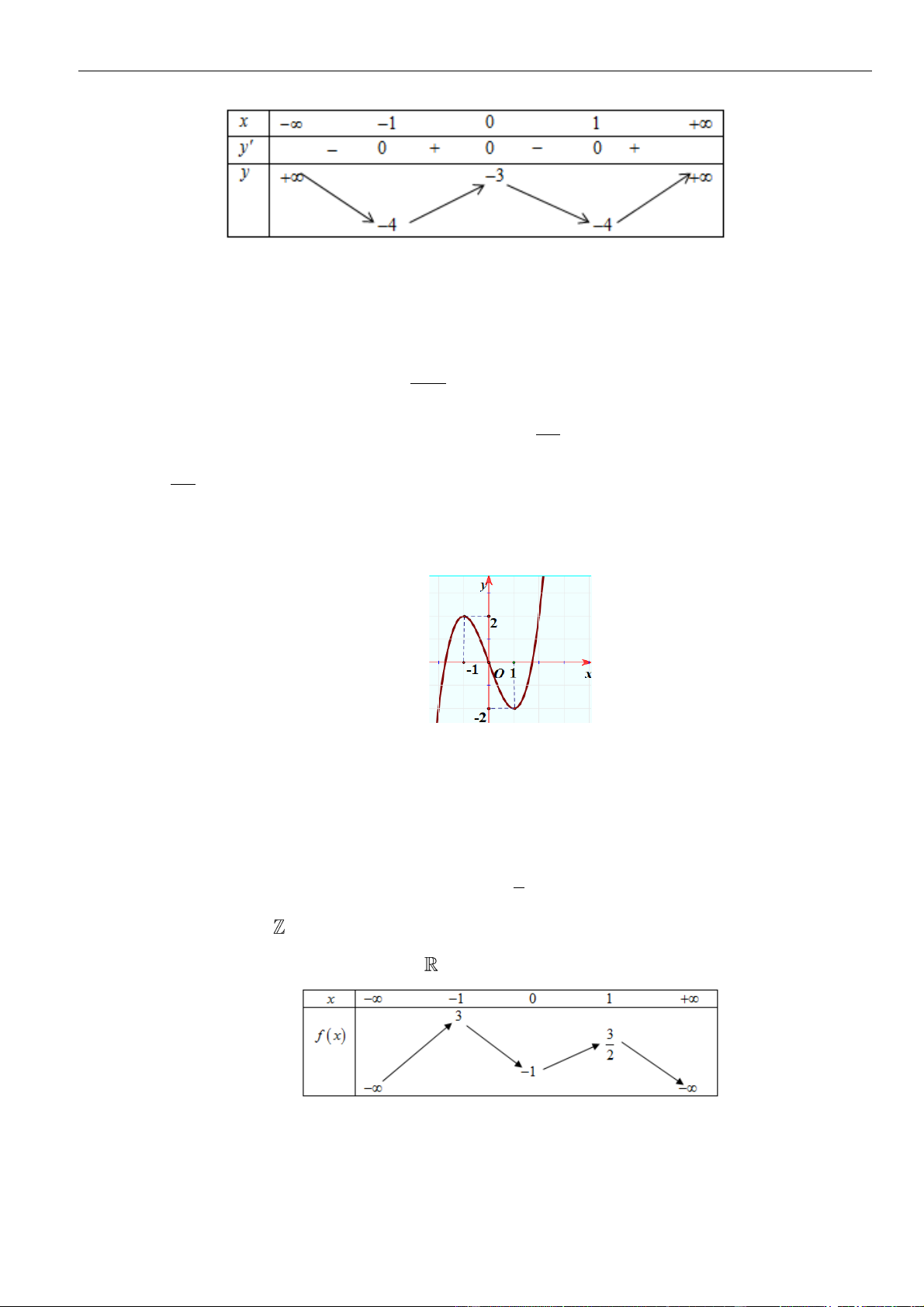
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
31 | Facebook tác giả: Phan Nhật Linh
Câu 38: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình
( )
2 3 0f x m+=
có 3 nghiệm phân biệt?
A. Vô số. B.
1.
C.
2.
D.
3.
Lời giải
Chọn B
Ta có
( ) ( )
3
2 3 0 .
2
m
f x m f x
−
+ = =
Dựa vào bảng biến thiên, phương trình
( )
3
2
m
fx=−
có ba nghiệm phân biệt khi và chỉ khi
3
3 2.
2
m
m− = − =
Câu 39: Cho hàm số
()y f x=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
( ) 3 5 0f x m− + =
có 3 nghiệm phân biệt?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Ta có
( ) 3 5 0f x m− + =
( ) 3 5f x m=−
.
Phương trình có 3 nghiệm phân biệt khi đường thẳng
35ym=−
cắt đồ thị hàm số
()y f x=
tại
ba điểm phân biệt
7
2 3 5 2 1
3
mm− −
.
Mà
m
nên
2m =
.
Câu 40: Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình vẽ sau:
Hỏi có bao nhiêu giá trị nguyên dương của
m
để phương trình
( )
2 2 0f x m− + =
có đúng 3
nghiệm phân biệt?
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn A
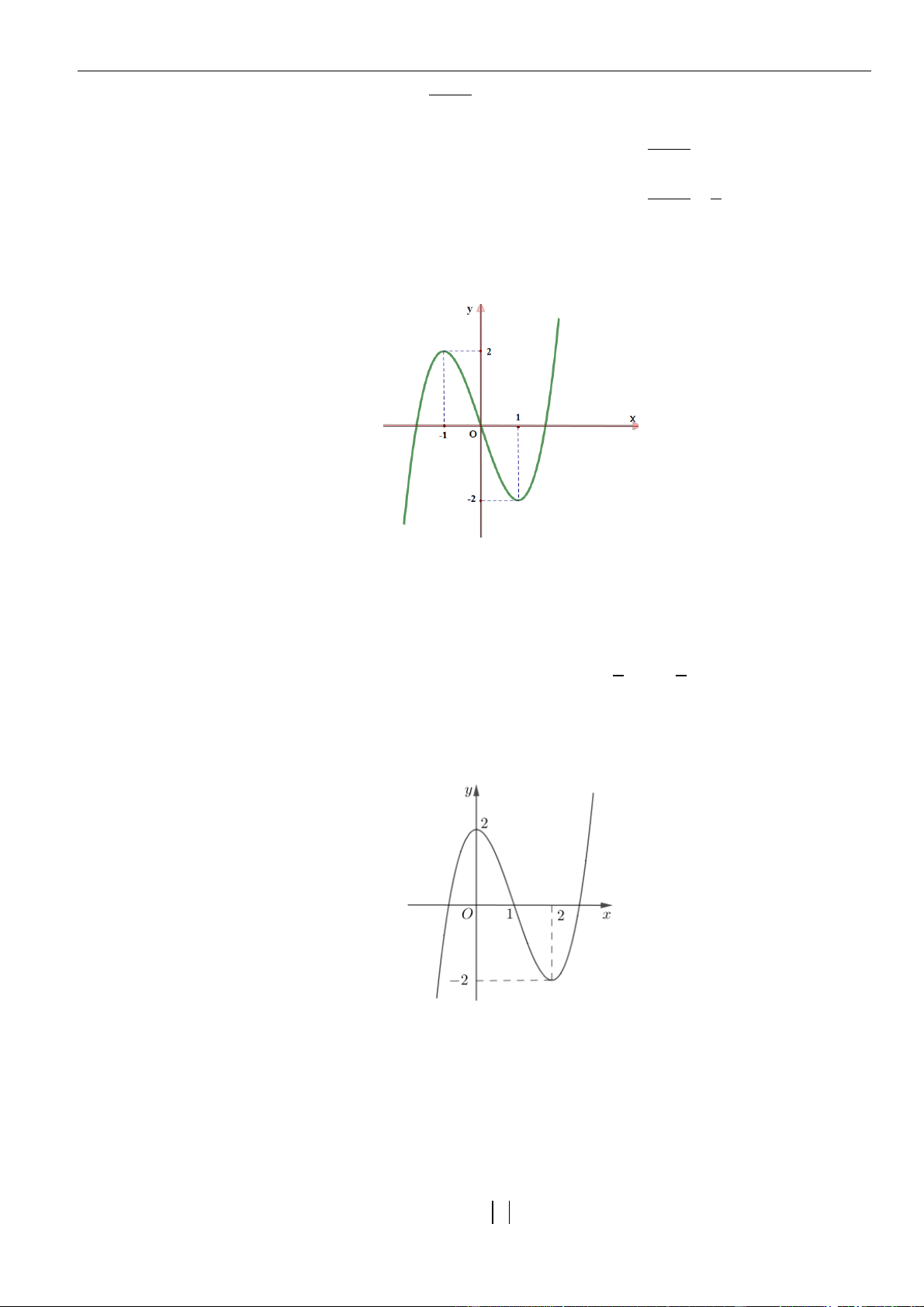
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 32
Ta có
( ) ( )
2
2 2 0
2
m
f x m f x
−
− + = =
.
Phương trình
( )
2 2 0f x m− + =
có đúng 3 nghiệm phân biệt
2
1
0
2
2 3 5.
22
m
m
mm
−
=−
=
−=
=
Câu 41: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
( )
2 1 0f x m+ − =
có ba nghiệm phân biệt?
A.
2.
B.
3.
C.
4.
D.
1.
Lời giải
Chọn A
Ta có
( ) ( )
2 1 0 1 2f x m f x m+ − = = −
Để phương trình có
3
nghiệm ta phải có
13
2 1 2 2
22
mm− − −
.
Vậy có
2
giá trị nguyên của
m
thỏa mãn đề bài.
Câu 42: Cho hàm số
( )
32
f x ax bx cx d= + + +
và
0a
có đồ thị như hình vẽ
Tập hợp tất cả các giá trị của tham số
m
để phương trình
( )
f x m m+=
có đúng
3
nghiệm phân
biệt là
A.
( )
2;2−
. B.
( )
1;1−
. C.
( )
1;2
. D.
( )
2;1−
.
Lời giải
Chọn A
Đồ thị hàm số
( )
y f x m=+
có được bằng cách tịnh tiến đồ thị hàm số
( )
y f x=
sang trái (hoặc
phải) theo phương song song với trục hoành
m
đơn vị.
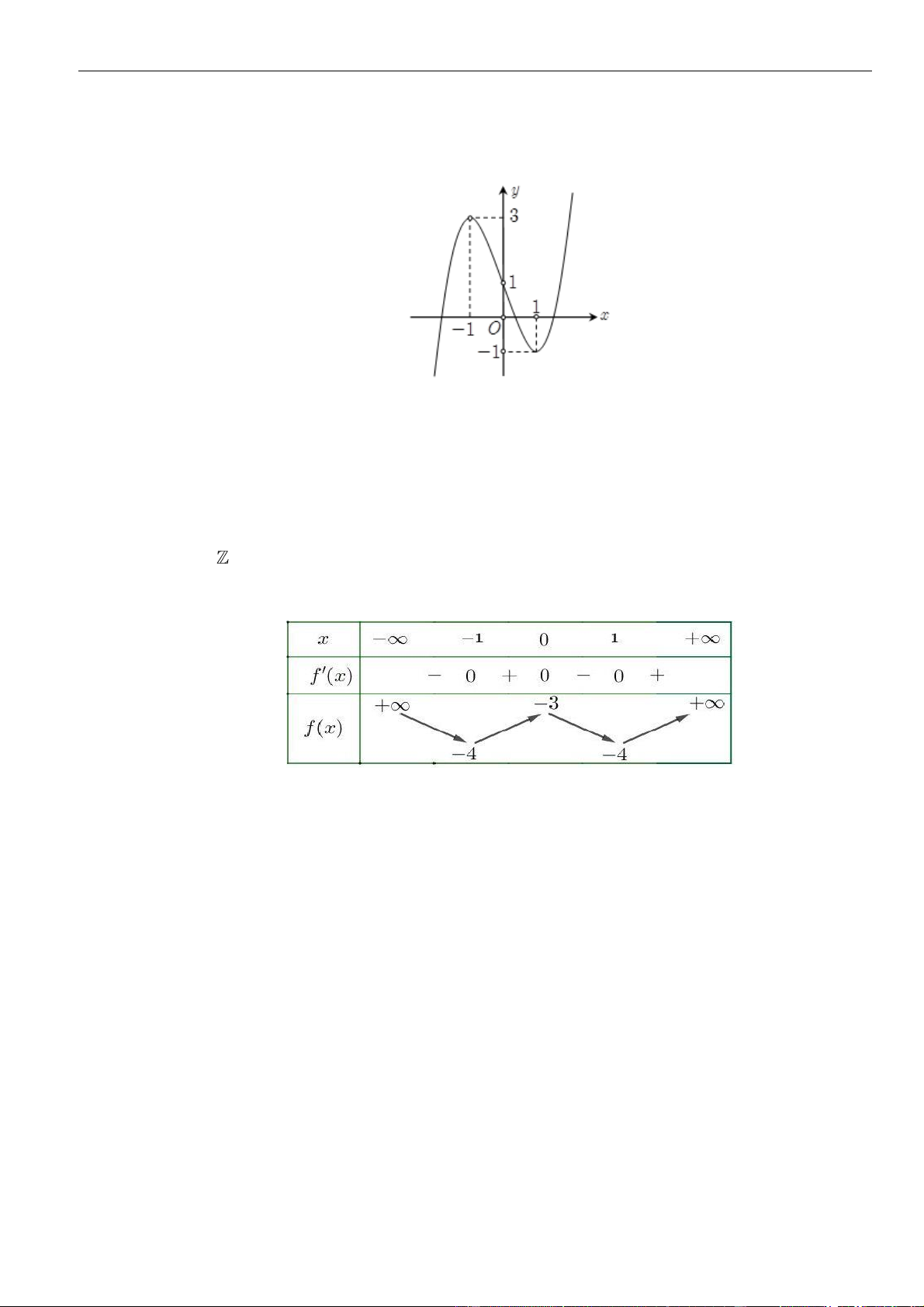
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
33 | Facebook tác giả: Phan Nhật Linh
Suy ra phương trình
( )
f x m m+=
có đúng
3
nghiệm phân biệt khi và chỉ khi
( )
2;2 .m−
Câu 43: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ. Số giá trị nguyên của tham số
m
để phương
trình
( )
1f x m+=
có
3
nghiệm phân biệt là
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn D
Phương trình
( ) ( )
11f x m f x m+ = = −
.
Từ đồ thị ta thấy để phương trình có
3
nghiệm phân biệt ta phải có
1 1 3 0 4mm− −
.
Do
m
nên ta được
1;2;3m
.
Câu 44: Cho hàm số
( )
fx
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
( )
50fx+=
là
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn B
Phương trình đã cho tương đương với
( )
5fx=−
.
Ta thấy đường thẳng
5y =−
không có điểm chung với đồ thị hàm số
( )
y f x=
nên phương
trình đã cho vô nghiệm.
Câu 45: Cho hàm số
42
y ax bx c= + +
có đồ thị như hình vẽ. Với giá trị nào của tham số
m
thì đường
thẳng
ym=
cắt đồ thị hàm số đã cho tại
4
điểm phân biệt?
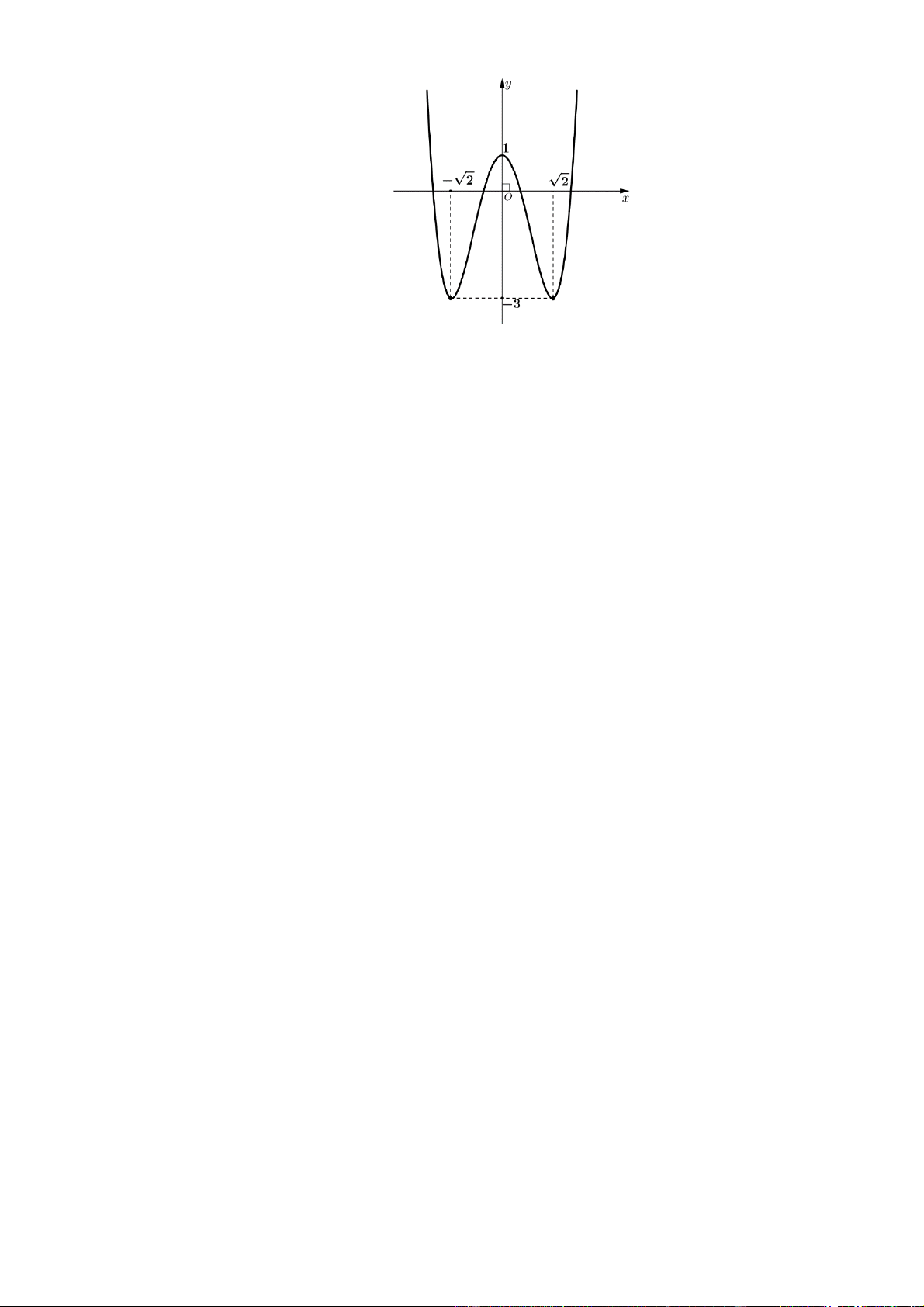
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 34
A.
31m−
. B.
1m
. C.
3m =−
. D.
31m−
.
Lời giải
Chọn A
Từ đồ thị suy ra hai đồ thị cắt nhau tại
4
điểm phân biệt
31m −
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
35 | Facebook tác giả: Phan Nhật Linh

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
32
31y x x m= − + −
. Tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm
số cắt trục hoành tại
3
điểm phân biệt là
A.
9
. B.
9−
. C.
15−
. D.
15
.
Câu 2: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Câu 3: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3
12 1y x x m= − + −
cắt trục hoành
tại
3
điểm phân biệt
?
A.
3
. B.
32
. C.
31
. D.
33
.
Câu 4: Cho hàm số
32
31y x x mx= − + +
có đồ thị
( )
C
và đường thẳng
: 2 1d y x=+
. Có bao nhiêu giá
trị nguyên dương của tham số
m
để đồ thị
( )
C
cắt đường thẳng
d
tại
3
điểm phân biệt?
A.
4
. B.
5
. C.
9
. D.
3
.
Câu 5: Với
m
là một tham số thực thì đồ thị hàm số
32
21y x x x= − + −
và đường thẳng
ym=
có nhiều
nhất bao nhiêu giao điểm?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 6: Tìm tất cả các giá trị của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
6y x x= − +
tại
ba điểm phân biệt.
A.
0 32m
. B.
16
0
m
m
. C.
0 16m
. D.
32 0m−
.
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3 2 2
3 5 0x x m m− − + =
có ba
nghiệm thực phân biệt?
A. Vô số. B.
0.
C.
5.
D.
4.
Câu 8: Cho hàm số
32
21y x x= − −
có đồ thị
(C)
, đường thẳng
( )
:1d y mx=−
và điểm
( )
4;11K
.Biết
rằng
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
( )
0; 1A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không có
m
.
Câu 9: Gọi
S
là tập tất cả các giá trị của tham số
m
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1yx=+
. Tổng các phần tử của
S
bằng
A.
0
. B.
3
. C.
2
. D.
1−
.
Câu 10: Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
( )
3
22y x m x m= − + +
cắt
trục hoành tại 3 điểm phân biệt
Tìm m liên quan đến tương giao hàm bậc ba
DẠNG 5
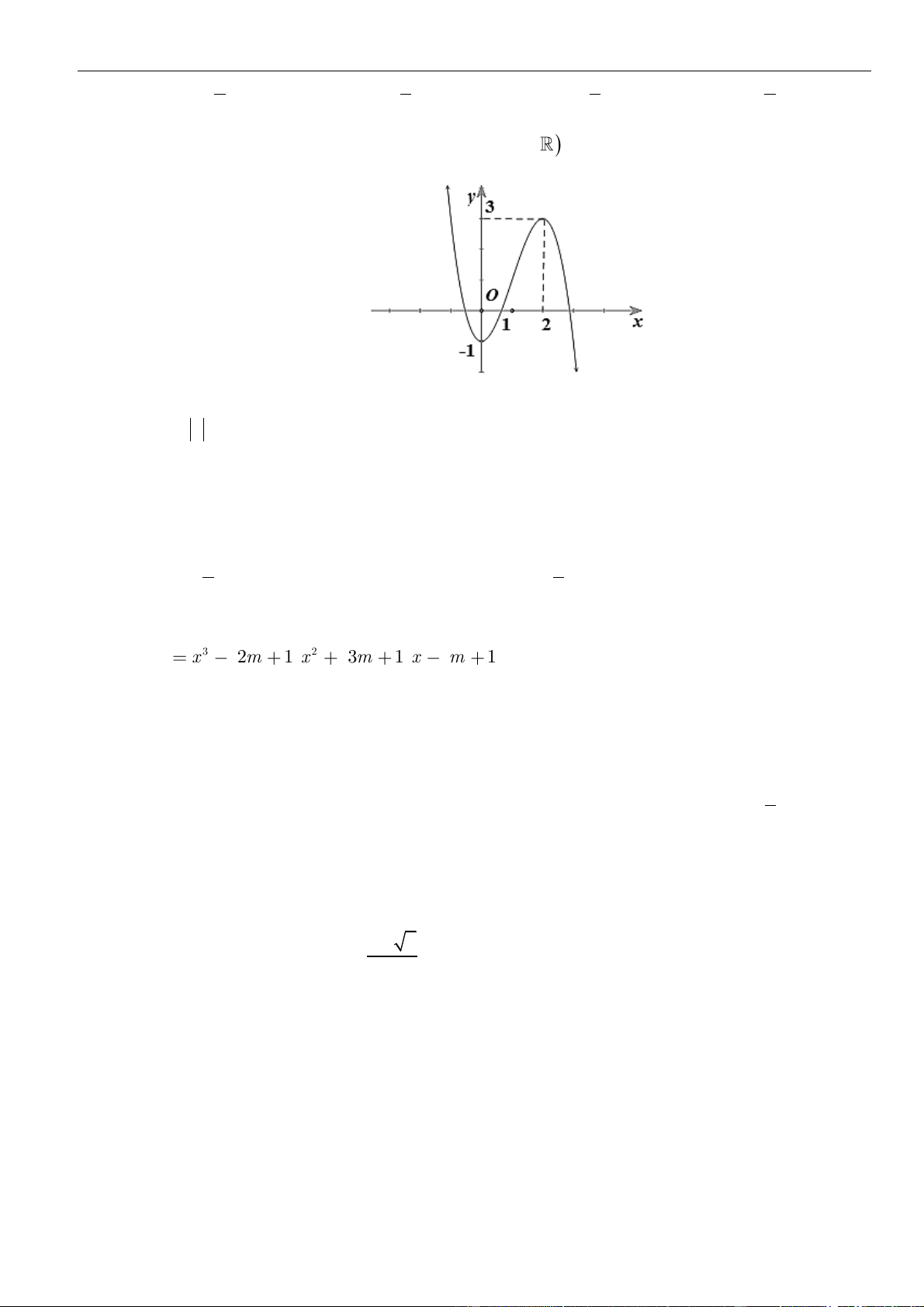
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
1
2
m
. B.
1
2
m
. C.
1
2
m −
. D.
1
; 4
2
mm −
.
Câu 11: Cho hàm số
( ) ( )
32
, , ,f x ax bx cx d a b c d= + + +
có đồ thị như hình vẽ sau.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn
2020;2020−
của tham số
m
để phương trình
( )
20f x m−=
có đúng
2
nghiệm thực phân biệt?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Câu 12: Biết đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó
m
thuộc khoảng nào dưới đây?
A.
3
1;
2
. B.
( )
0;1
. C.
3
;2
2
. D.
( )
1;0−
.
Câu 13: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
32
2 1 3 1 1y x m x m x m
cắt trục hoành tại 2 điểm phân biệt?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 14: Cho đồ thị
( ) ( )
32
: 2 1
m
C y x x m x m= − + − +
. Tìm tất cả các giá trị của tham số m để
( )
m
C
cắt
trục hoành tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thỏa
222
1 2 3
4xxx+ + =
A.
0m
. B.
( )
0;2m
. C.
1m =
. D.
1
4
−m
và
0m
.
Câu 15: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
(
B
nằm giữa
,AC
) sao cho
2AB BC=
. Tính tổng
các phần tử thuộc
S
.
A.
4−
. B.
77
7
−
. C.
2−
. D.
0
.
Câu 16: Có bao nhiêu giá trị nguyên âm của
a
để đồ thị hàm số
( )
32
10 1y x a x x= + + − +
cắt trục
hoành tại đúng một điểm?
A.
10
. B.
8
. C.
11
. D.
9
.
Câu 17: Có bao nhiêu giá trị nguyên thuộc
2020;2021−
của hàm số
m
để đường thẳng
1y mx m= − −
cắt đồ thị của hàm số
32
3y x x x= − +
tại ba điểm phân biệt
,,A B C
sao cho
AB BC=
.
A.
2021
. B.
2023
. C.
2024
. D.
2022
.
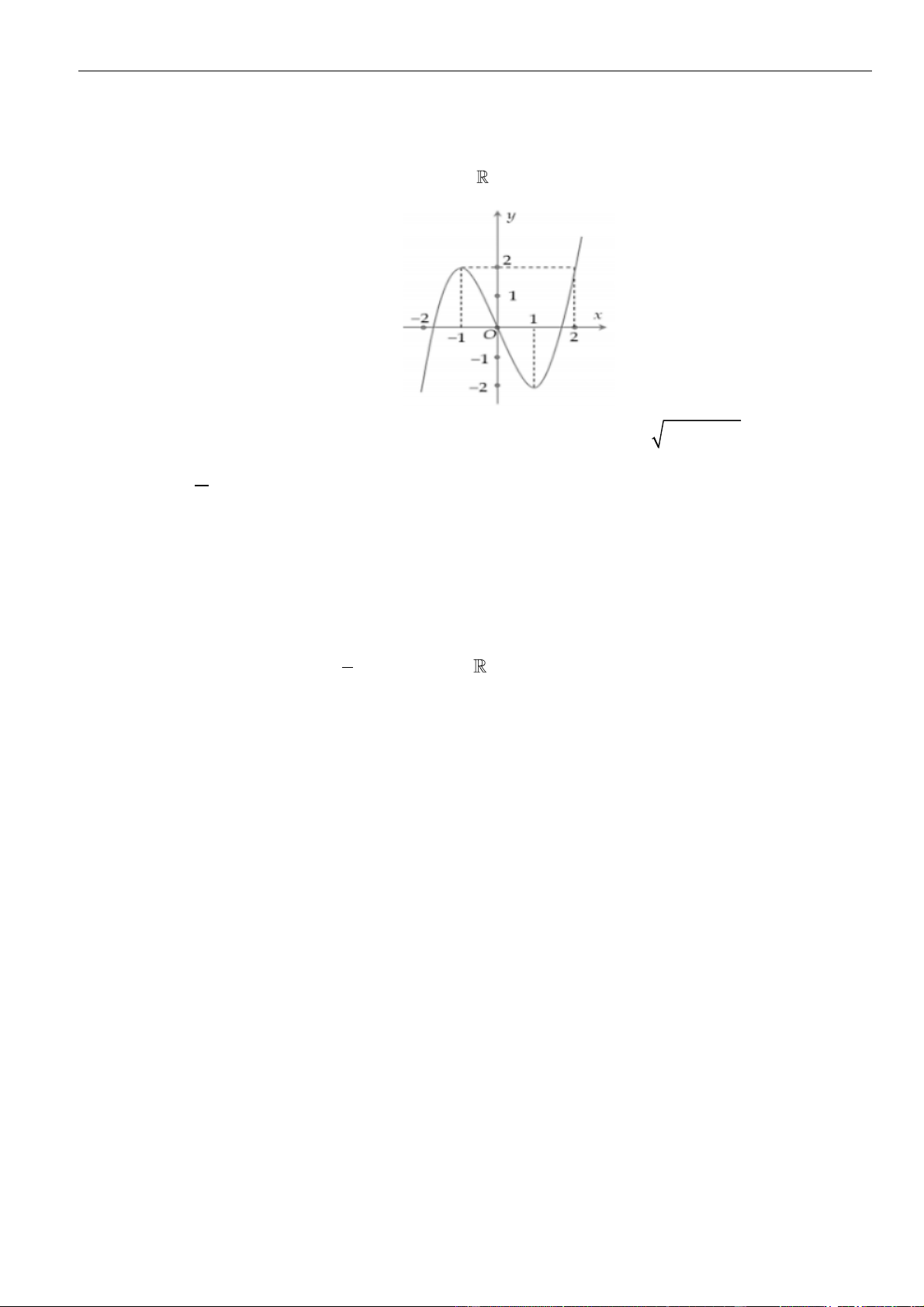
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 18: Cho bao nhiêu giá trị
m
để đồ thị hàm số
32
2y x mx m= − + −
cắt trục
Ox
tại
3
điểm phân biệt
có hoành độ lập thành cấp số cộng.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 19: Cho hàm số bậc ba
( )
y f x=
liên tục trên và có đồ thị như hình vẽ bên.
Tổng tất cả các giá trị nguyên của tham số
m
để phương trình
( )
( )
2 cosf f x m=
có nghiệm
;
2
x
A.
1−
. B.
0
. C.
1
. D.
2−
.
Câu 20: Gọi S là tập hợp các số nguyên m để phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng
A.
0
. B.
2−
. C.
3
. D.
1−
.
Câu 21: Cho hàm số
3
1
( ) 8 ,
2
f x x mx m x= − + −
với
m
là một hằng số khác
0
. Biết rằng phương
trình
( ) 0fx=
có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương
k
thỏa mãn
phương trình
()f x k=
có 3 nghiệm phân biệt?
A.
3
. B.
6
. C.
34
. D.
31
.
Câu 22: Cho hàm số
32
( 2) (2 13) 2y x m x m x m= − + − + − −
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= + +
và điểm
( )
1;4 .I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Câu 23: Gọi
d
là đường thẳng đi qua
( )
2;0A
có hệ số góc
( )
0mm
cắt đồ thị
( )
32
: 6 9 2C y x x x= − + − +
tại ba điểm phân biệt
, , .A B C
Gọi
,BC
lần lượt là hình chiếu
vuông góc của
,BC
lên trục tung. Biết rằng hình thang
BB C C
có diện tích bằng
8,
giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
5;8
. B.
( )
5;0−
. C.
( )
0;2
. D.
( )
1;5
.
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
có đúng
8
nghiệm phân biệt?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 25: Gọi
S
là tập hợp chứa tất cả các giá trị thực của tham số
m
để đồ thị hàm số
( ) ( ) ( )
32
6 1 3 2 1 2f x x m x m x= − + + + +
cắt trục
Ox
tại ba điểm phân biệt có hoành độ lớn hơn
1−
.
Biết rằng
;
a
S
b
−
= +
; trong đó
,ab
là các số nguyên dương và phân số
a
b
là tối giản. Giá trị
biểu thức
T a b=+
tương ứng bằng
A.
4
. B.
8
. C.
5
. D.
7
.
Câu 26: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị hàm số
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Câu 27: Cho hàm số
32
3y x x m= + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
. Phát biểu nào sau đây đúng?
A.
( )
4;0m−
. B.
( )
0;m +
. C.
( )
;4m − −
. D.
( )
4; 2m − −
.
Câu 28: Cho hàm số
32
21y x x= − −
có đồ thị
( )
C
, đường thẳng
( )
d
:
1y mx=−
và điểm
(4;11)K
. Biết
rằng
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
(0; 1)A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không tồn tại
m
Câu 29: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại 3 điểm phân biệt
1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Câu 30: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại
3
điểm phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
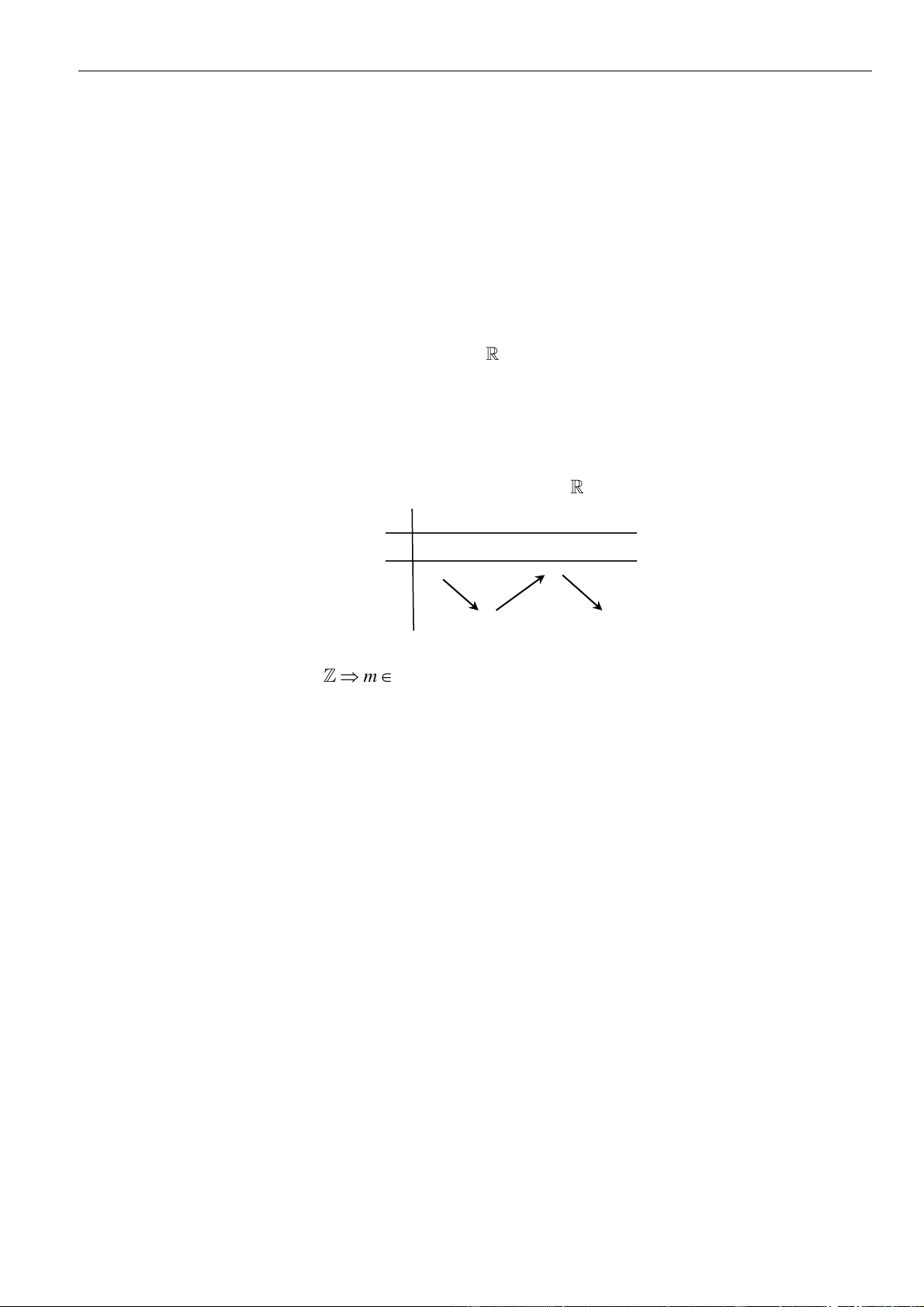
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
32
31y x x m= − + −
. Tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm
số cắt trục hoành tại
3
điểm phân biệt là
A.
9
. B.
9−
. C.
15−
. D.
15
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của đồ thị và trục hoành là
32
3 1 0x x m− + − =
32
31x x m − + + =
.
Xét hàm số
( )
32
31f x x x= − + +
với
x
.
Ta
có
( )
2
36f x x x
= − +
( )
0
0
2
x
fx
x
=
=
=
.
Bảng biến thiên của hàm
( )
32
31f x x x= − + +
với
x
Dựa vào bảng biến thiên ta thấy để đồ thị hàm số cắt trục hoành tại
3
điểm phân biệt
15m
. Do
2;3;4mm
Vậy tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số cắt trục hoành tại
3
điểm
phân biệt là
2 3 4 9S = + + =
.
Câu 2: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của hai đồ thị:
( )
3
3 2 1x m x+ − = −
32
31m x x = − +
( )
1
Nhận xét:
( )
1
là phương trình hoành độ giao điểm của hai đồ thị
( )
:d y m=
và đồ thị
( )
32
: 3 1C y x x= − +
.
Xét hàm số
32
31y x x= − +
2
36y x x
=−
,
0
0
2
x
y
x
=
=
=
.
Bảng biến thiên
( )
fx
x
( )
fx
+
−
0
0
−
2
+
−
+
−
0
1
5
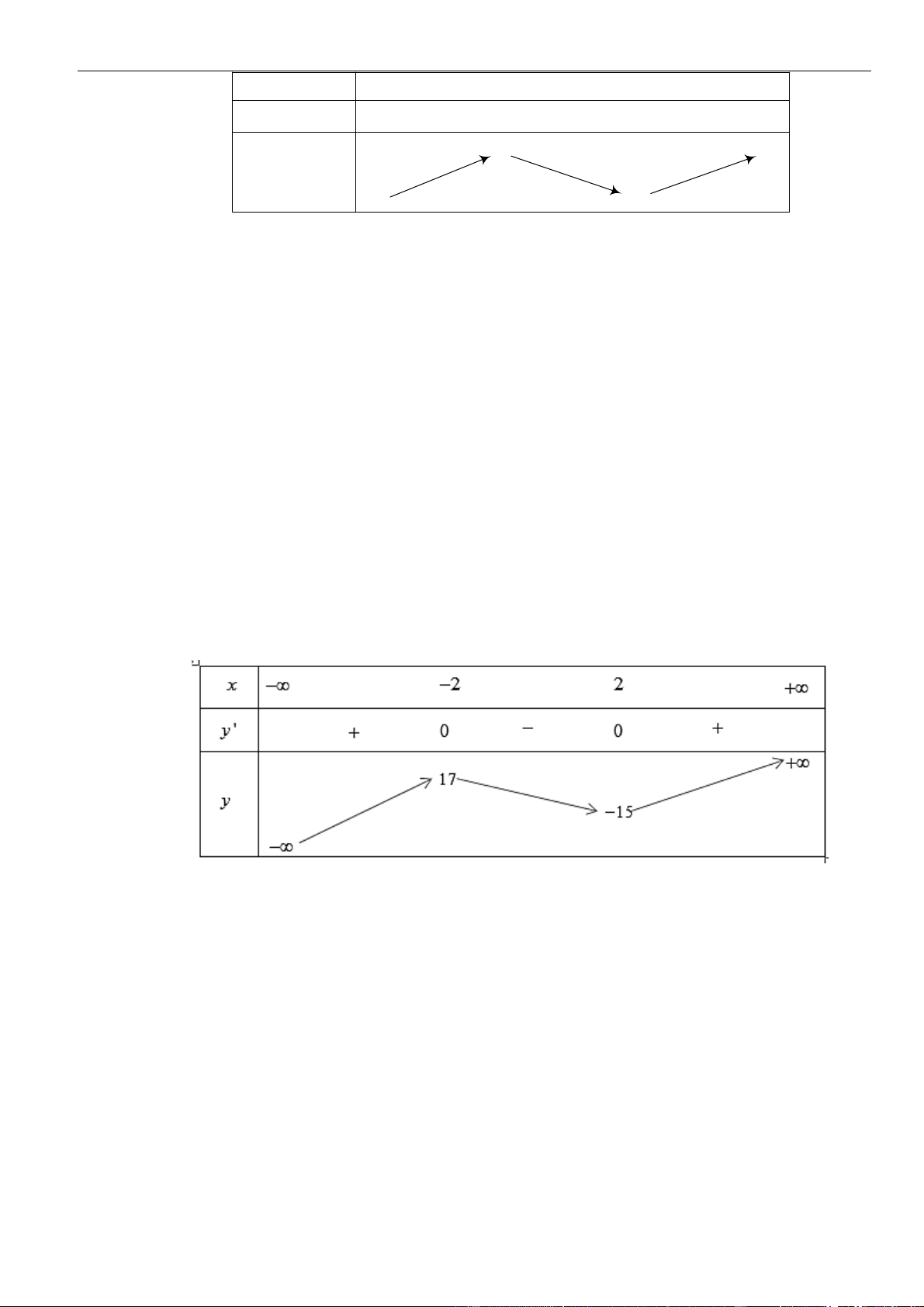
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
x
−
+
0
+
−
y
y
1
2
3−
−
0
0
+
+
Vậy: yêu cầu bài toán
31m −
.
Câu 3: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3
12 1y x x m= − + −
cắt trục hoành
tại
3
điểm phân biệt
?
A.
3
. B.
32
. C.
31
. D.
33
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục hoành là
3
12 1 0x x m− + − =
Ta có:
3
12 1 0x x m− + − =
3
12 1x x m − + =
(1)
.
Đặt
3
12 1y x x
ym
= − +
=
. Khi đó số nghiệm của phương trình
(1)
bằng số giao điểm của đồ thị hàm
số
3
12 1y x x= − +
và đường thẳng
ym=
.
Khảo sát sự biến thiên của hàm số
3
12 1y x x= − +
ta có:
2
' 3 12yx=−
.
2
' 0 3 12 0yx= − =
2
2
x
x
=−
=
.
BBT của hàm số
3
12 1y x x= − +
là:
Với
15 17m−
thì phương trình
(1)
có
3
nghiệm phân biệt. Mặt khác do
m
nguyên nên
14,...,16m−
. Vậy có 31 giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 4: Cho hàm số
32
31y x x mx= − + +
có đồ thị
( )
C
và đường thẳng
: 2 1d y x=+
. Có bao nhiêu giá
trị nguyên dương của tham số
m
để đồ thị
( )
C
cắt đường thẳng
d
tại
3
điểm phân biệt?
A.
4
. B.
5
. C.
9
. D.
3
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm
32
3 1 2 1x x mx x− + + = +
( )
32
3 2 0x x m x − + − =
( )
2
2
0
3 2 0
3 2 0
x
x x x m
x x m
=
− + − =
− + − =
.
Đặt
( )
2
32f x x x m= − + −
.
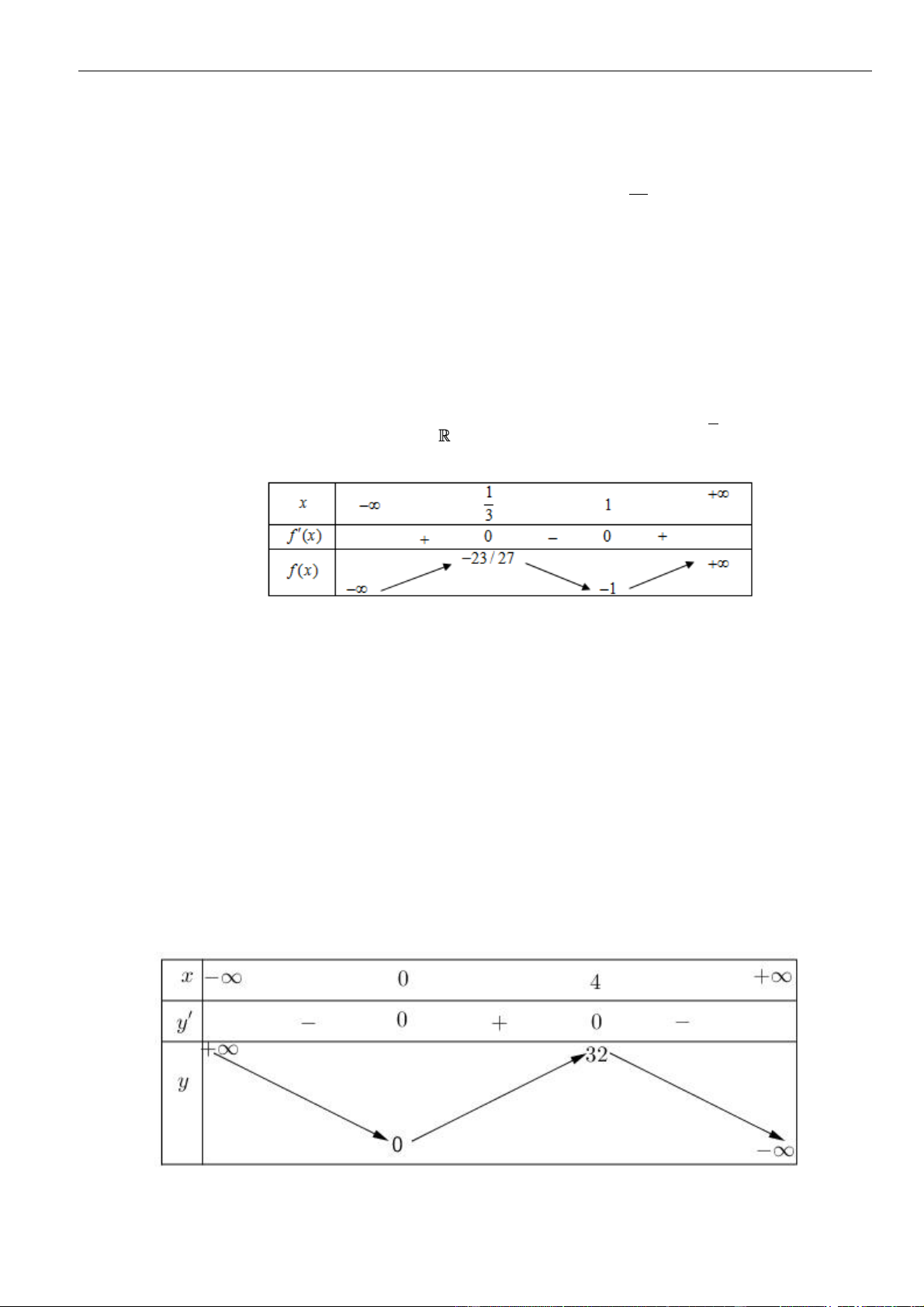
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Để đồ thị
( )
C
cắt đường thẳng
d
tại
3
điểm phân biệt thì phương trình
( )
32
3 2 0x x m x− + − =
phải có
3
nghiệm phân biệt, khi đó
( )
0fx=
phải có hai nghiệm phân biệt khác
0
.
Do đó
( )
( )
20
00
2
9 4 2 0
4 17
0
m
f
m
m
m
−
− −
− −
2
17
4
m
m
.
Do
m
là số nguyên dương nên
1,3,4m
.
Câu 5: Với
m
là một tham số thực thì đồ thị hàm số
32
21y x x x= − + −
và đường thẳng
ym=
có nhiều
nhất bao nhiêu giao điểm?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
Hàm số
32
21y x x x= − + −
có TXĐ: ;
2
3 4 1y x x
= − +
;
1
'0
3
1
x
y
x
=
=
=
.
Dựa vào BBT đồ thi hàm số
32
21y x x x= − + −
và đường thẳng
ym=
có nhiều nhất là ba giao
điểm.
Câu 6: Tìm tất cả các giá trị của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
6y x x= − +
tại
ba điểm phân biệt.
A.
0 32m
. B.
16
0
m
m
. C.
0 16m
. D.
32 0m−
.
Lời giải
Chọn A
Ta có
3 2 2
6 3 12y x x y x x
= − + = − +
.
2
0
0 3 12 0
4
x
y x x
x
=
= − + =
=
.
Ta có BBT
Để đường thẳng
ym=
cắt đồ thị hàm số
32
6y x x= − +
tại ba điểm phân biệt thì
0 32m
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3 2 2
3 5 0x x m m− − + =
có ba
nghiệm thực phân biệt?
A. Vô số. B.
0.
C.
5.
D.
4.
Lời giải
Chọn B
Đặt
( )
3 2 2
35f x x x m m= − − +
.
Để
3 2 2
3 5 0x x m m− − + =
có ba nghiệm thực phân biệt thì
( )
0fx
=
có hai nghiệm phân biệt
12
,xx
thỏa mãn:
( ) ( )
12
.0f x f x
Ta có:
( )
2
36f x x x
=−
( )
2
0
0 3 6 0
2
x
f x x x
x
=
= − =
=
.
( )
2
05f m m= − +
.
( )
2
2 5 4f m m= − + −
.
Khi đó:
( ) ( )
( )( )
22
01
0 . 2 0 5 5 4 0
45
m
f f m m m m
m
− + − + −
Vậy không có giá trị nguyên nào của
m
thỏa mãn.
Câu 8: Cho hàm số
32
21y x x= − −
có đồ thị
(C)
, đường thẳng
( )
:1d y mx=−
và điểm
( )
4;11K
.Biết
rằng
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
( )
0; 1A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không có
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
(C)
và
( )
d
là:
( )
3 2 3 2 2
2
0
2 1 1 2 0 2 0
2 0(1)
x
x x mx x x mx x x x m
x x m
=
− − = − − − = − − =
− − =
Để
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt thì (1) có hai nghiệm phân biệt khác 0. Ta có:
'
2
0 1 0 1
00
0 0 0
mm
mm
m
+ −
− −
Gọi
12
,xx
là nghiệm của (1), ta có
( ) ( )
1 1 2 2
B ; 1 ; ; 1x mx C x mx−−
. Trọng tâm G của tam giác
KBC
, ta có
12
12
4
2
3
11 2
29
33
G
G
xx
x
mx mx
m
y
++
==
+ + −
+
==
Theo giả thiết G thuộc đường thẳng
( )
: 2 1d y x=+
nên ta có:
( )
29
2.2 1 3
3
m
m tm
+
= + =
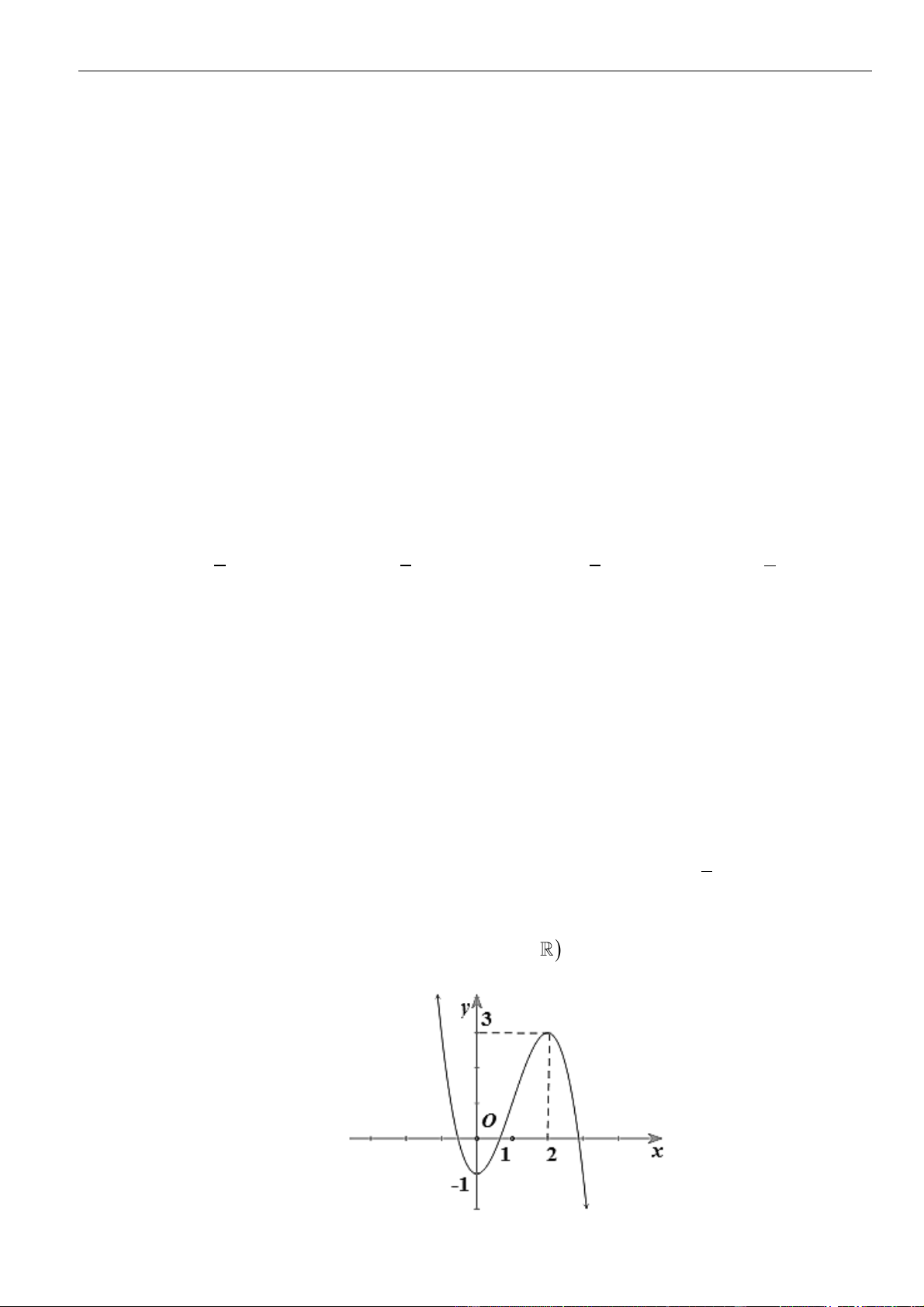
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Câu 9: Gọi
S
là tập tất cả các giá trị của tham số
m
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1yx=+
. Tổng các phần tử của
S
bằng
A.
0
. B.
3
. C.
2
. D.
1−
.
Lời giải
Chọn C
2
'3yx=
.
Giả sử đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm số
3
1yx=+
tại điểm
0
x
thì
( )
00
3 1.y x x
= =
Đk đủ:
00
12xy= =
thì PTTT là
3 2 1y x m= − = −
.
00
10xy= − =
thì PTTT là
3 3 3y x m= + =
.
Tổng các phần tử của
S
bằng
2
.
Cách 2: Điều kiện tiếp xúc
3
3
2
13
13
1; 3.
1
33
x x m
x x m
mm
x
x
+ = +
+ − =
= − =
=
=
Câu 10: Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
( )
3
22y x m x m= − + +
cắt
trục hoành tại 3 điểm phân biệt
A.
1
2
m
. B.
1
2
m
. C.
1
2
m −
. D.
1
; 4
2
mm −
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của đồ thị với trục Ox:
( )
3
2 2 0− + + =x m x m
3
2 2 0 − − + =x x mx m
( ) ( )
2
1 2 2 0 1
− + − =
x x x m
( )
2
1
2 2 0 2
=
+ − =
x
x x m
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt
( )
1
có 3 nghiệm phân biệt
( )
2
có 2 nghiệm phân biệt khác
1
( )
' 1 2 0
1 2 2 0
= +
= + −
m
gm
1
2
4
−
m
m
Câu 11: Cho hàm số
( ) ( )
32
, , ,f x ax bx cx d a b c d= + + +
có đồ thị như hình vẽ sau.
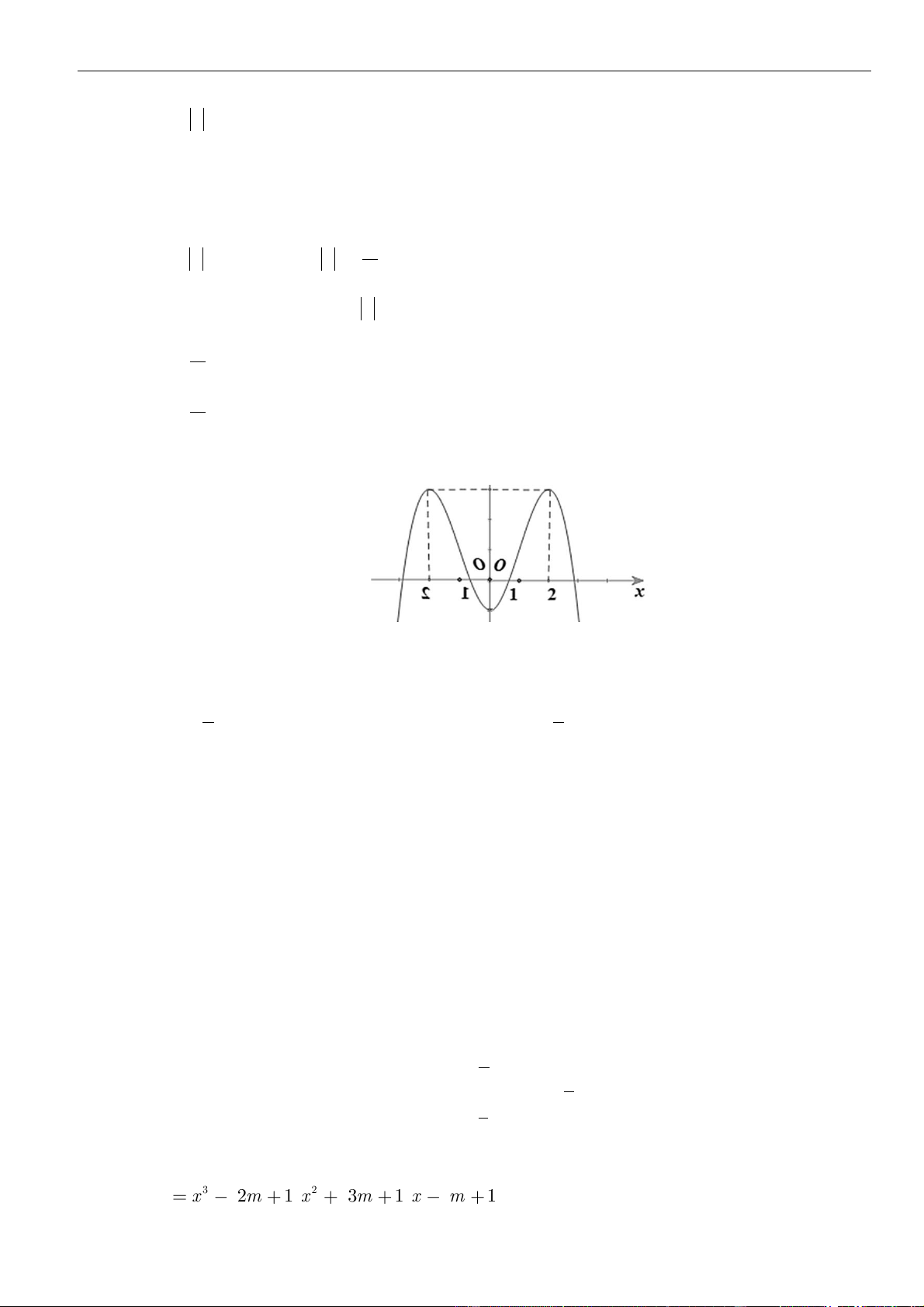
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn
2020;2020−
của tham số
m
để phương trình
( )
20f x m−=
có đúng
2
nghiệm thực phân biệt?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Lời giải
Chọn D
( )
20f x m−=
( )
( )
1
2
=
m
fx
Dựa vào đồ thị hàm
( )
=y f x
ta có: để phương trình
( )
1
có đúng 2 nghiệm thực phân biệt
3
6
2
2
1
2
=
=
−
−
m
m
mm
Vì
2020;2020−m
2020; 2019;...... 3;6 − − −m
. Vậy có 2019 số.
Câu 12: Biết đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó
m
thuộc khoảng nào dưới đây?
A.
3
1;
2
. B.
( )
0;1
. C.
3
;2
2
. D.
( )
1;0−
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm là
( )
32
3 1 6 3 3 1m x m x x− + + = − +
( ) ( )
32
3 3 1 6 2 0 1x x m x m − − − − − =
.
Xét hàm số
( ) ( ) ( )
32
3 3 1 6 2
m
g x x x m x m C= − − − − −
.
( ) ( )
2
3 6 3 1 6 6g x x x m g x x
= − − + = −
;
( )
01g x x
= =
.
Đồ thị
( )
m
C
có điểm uốn là
( )
1; 9 3Im−−
.
Để đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại
( ) ( )
( )
2
2
3 3. 3 1 0
1
3
1;0
1
3
3
m
m
m
I Ox
m
−
= − − − +
= − −
=−
.
Câu 13: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
32
2 1 3 1 1y x m x m x m
cắt trục hoành tại 2 điểm phân biệt?

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Xét phương trình
3 2 2
2
2 1 3 1 1 0 1 2 1 0
1
2 1 0 *
x m x m x m x x mx m
x
x mx m
Theo yêu cầu bài toán phương trình
*
xảy ra 2 trường hợp
TH1: phương trình có nghiệm kép khác 1, tức là
2
10
1 2 1 0
mm
mm
loại, do nghiệm không
nguyên.
TH2: phương trình có 2 nghiệm phân biệt trong đó 1 là một nghiệm, tức là
2
10
2
1 2 1 0
mm
m
mm
.
Nhận xét: cụm từ “cắt trục hoành tại 2 điểm phân biệt” được người ra đề hiểu là “có đúng 2 điểm
chung với trục hoành”. Theo ý kiến chủ quan của người giải, ta nên phát biểu rõ ràng hơn.
Câu 14: Cho đồ thị
( ) ( )
32
: 2 1
m
C y x x m x m= − + − +
. Tìm tất cả các giá trị của tham số m để
( )
m
C
cắt
trục hoành tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thỏa
222
1 2 3
4xxx+ + =
A.
0m
. B.
( )
0;2m
. C.
1m =
. D.
1
4
−m
và
0m
.
Lời giải
Chọn C
Để hàm số đã cho cắt trục hoành tại 3 điếm phàn biệt thì phưong trình hoành độ giao điểm
phải có 3 nghiệm phàn biệt:
32
2 (1 ) 0− + − + =x x m x m
( )
2
( 1) 0− − − =x x x m
Ta đặt
1
1=x
. Khi đó, đế phưong trình có 3 nghiệm phân biệt thì phương trình sau phải có 2
nghiệm phân biệt khác 1.
2
0− − =x x m
Do có nghiệm khác 1 nên
1 1 0− − m
hay
0.m
Ta có
14 = + m
Để có 2 nghiệm phàn biệt thì
0
hay
1
4
−m
.
Theo điều kiện của đề bài ta có
222
1 2 3
4+ + =xxx
( )
2
2 3 2 3
1 2 4 + + − =x x x x
( )
2
2 3 2 3
23 + − =x x x x
vói
23
,xx
là nghiệm của phương trình bậc 2 trên.
Áp dụng Viet ta có
2
1 2( ) 3− − =m
1=m
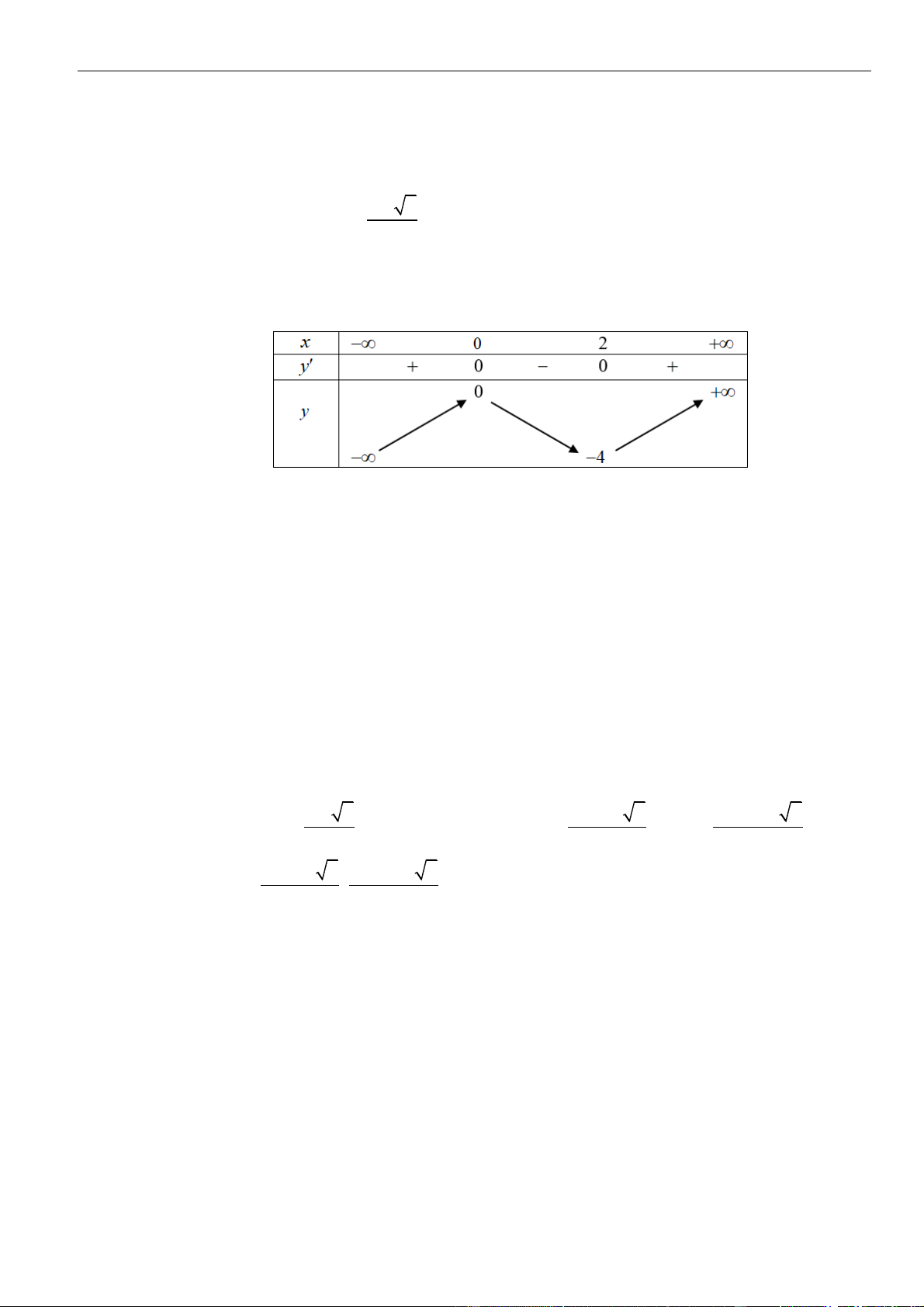
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Kết hợp các điều kiện ta có
1=m
.
Câu 15: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
(
B
nằm giữa
,AC
) sao cho
2AB BC=
. Tính tổng
các phần tử thuộc
S
.
A.
4−
. B.
77
7
−
. C.
2−
. D.
0
.
Lời giải
Chọn A
Ta có BBT của hàm số
32
3y x x=−
như sau:
Suy ra đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
40m −
.
Khi đó
3, 0,
A B C A B B C C A A B C
x x x x x x x x x x x x m+ + = + + = =
.
Để
B
nằm giữa
,AC
và
2AB BC=
thì
( )
( )
2
2
A B C
B A C B
C B A
A B B C
xxx
x x x x
x x x
x x x x
− = −
− = −
3 2 4 3 6 5
B A C B C A B
x x x x x x x = + − = = −
.
Suy ra
( ) ( ) ( ) ( )
( ) ( )
6 5 . . 4 3 4 3 . 6 5 0 (*)
4 3 . . 6 5 (**)
B B B B B B
B B B
x x x x x x
x x x m
− + − + − − =
− − =
.
Từ (*) được
77
7
B
x
=
. Thay vào (**) được
98 20 7
49
m
+
=−
và
98 20 7
49
m
−+
=
.
Vậy
98 20 7 98 20 7
;
49 49
S
+ − +
=−
.
Câu 16: Có bao nhiêu giá trị nguyên âm của
a
để đồ thị hàm số
( )
32
10 1y x a x x= + + − +
cắt trục
hoành tại đúng một điểm?
A.
10
. B.
8
. C.
11
. D.
9
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của đồ thị và trục hoành là:
( ) ( )
32
10 1 0 1x a x x+ + − + =
3 2 2
10 1x x x ax + − + = −
.
Ta thấy
0x =
không là nghiệm của phương trình nên
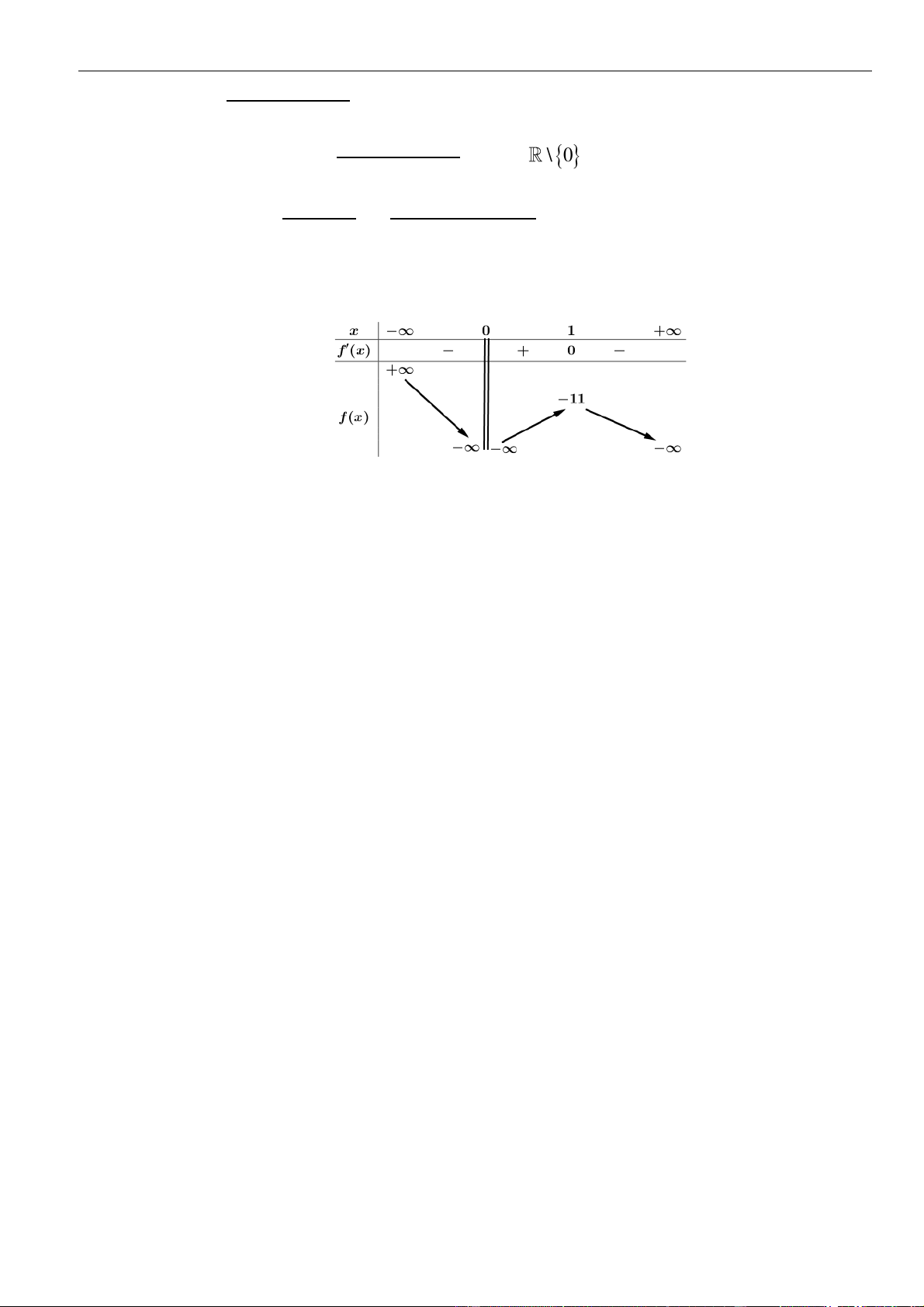
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
( )
1
32
2
10 1x x x
a
x
+ − +
− =
.
Xét hàm số
( )
32
2
10 1x x x
fx
x
+ − +
=−
với
\0x
Ta có
( )
( )
( )
2
3
33
1 . 2
2
x x x
xx
fx
xx
− + +
+−
= − = −
( )
01f x x
= =
.
Bảng biến thiên của hàm số
( )
fx
như sau:
Từ bảng biến thiên ta thấy đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm khi
( )
1
có
đúng 1 nghiệm
11a −
.
Do
a
nguyên âm nên
10, 9, 8,..., 1a − − − −
. Vậy có 10 giá trị của
a
thỏa mãn yêu cầu bài
toán
Câu 17: Có bao nhiêu giá trị nguyên thuộc
2020;2021−
của hàm số
m
để đường thẳng
1y mx m= − −
cắt đồ thị của hàm số
32
3y x x x= − +
tại ba điểm phân biệt
,,A B C
sao cho
AB BC=
.
A.
2021
. B.
2023
. C.
2024
. D.
2022
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm
( )
3 2 3 2
3 1 3 1 1 0x x x mx m x x m x m− + = − − − + − + + =
.
( )
( )
( )
2
2
1
1 2 1 0
2 1 0 1
x
x x x m
x x m
=
− − − − =
− − − =
Để để đường thẳng
1y mx m= − −
cắt đồ thị hàm số
32
3y x x x= − +
tại ba điểm phân biệt
A
,
B
,
C
thì phương trình
( )
1
có hai nghiệm phân biệt khác
1
20
2
20
m
m
m
+
−
− −
.
Khi đó phương trình
( )
1
có hai nghiệm
12
,xx
thỏa mãn
12
2xx+=
với mọi tham số
m
.
Trường hợp 1:
1
B
x =
.
Khi đó yêu cầu bài toán trở thành
( )
12
12
12
12
2
2
2
2 2 2
22
A C B
A C B
xx
x x x
xx
m x x m
y y y y y
+=
+=
+=
+ − + =
+ = + =
.
Điều này thỏa mãn với mọi
2m −
.
Trường hợp 2:
1
B
x
và giả sử
12
xx
.
Khi đó yêu cầu bài toán trở thành
( )( )
12
12
12
12
12
2
12
2 2 1 *
2 1 2
A C B
A C B
xx
x x x
xx
mx m mx m
y y y y y
+=
+=
+=
− + = − +
+ = + =
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Ta có hệ
1 2 2
1 2 1
1 2 1
21
x x x
x x x
+ = =
+ = =
không thỏa mãn yêu cầu bài toán.
Vậy giá trị
m
cần tìm là
2m −
.
Vì
, 2020;2021 1;2021m m m − −
có
2023
giá trị của
m
.
Câu 18: Cho bao nhiêu giá trị
m
để đồ thị hàm số
32
2y x mx m= − + −
cắt trục
Ox
tại
3
điểm phân biệt
có hoành độ lập thành cấp số cộng.
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm:
32
20x mx m− + − =
(*).
Giả sử phương trình (*) có
3
nghiệm phân biệt
1
x
,
2
x
,
3
x
theo thứ tự lập thành một cấp số
cộng, theo tính chất của cấp số cộng ta có:
1 3 2
2x x x+=
.
Áp dụng định lí Vi-et ta có:
1 2 3 2 2
3
3
m
x x x m x m x+ + = = =
.
Vì
2
3
m
x =
là một nghiệm của phương trình (*) nên ta có:
32
. 2 0
33
mm
mm
− + − =
3
0
2 54 0 3 3
33
m
m m m
m
=
− = =
=−
.
Thử lại:
+ Với
0m =
, phương trình trở thành:
3
00xx− = =
( loại).
+ Với
33m =
, phương trình trở thành:
1
32
2
3
33
3 3 6 3 0 3
33
x
x x x
x
= − +
− + − = =
=+
và
3
nghiệm
này lập thành 1 CSC.
+ Với
33m =−
, phương trình trở thành:
1
32
2
3
33
3 3 6 3 0 3
33
x
x x x
x
= − −
− − + = = −
=−
và
3
nghiệm
này lập thành 1 CSC.
Vậy có
2
giá trị của
m
thỏa yêu cầu bài toán là
33m =
và
33m =−
.
Câu 19: Cho hàm số bậc ba
( )
y f x=
liên tục trên và có đồ thị như hình vẽ bên.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Tổng tất cả các giá trị nguyên của tham số
m
để phương trình
( )
( )
2 cosf f x m=
có nghiệm
;
2
x
A.
1−
. B.
0
. C.
1
. D.
2−
.
Lời giải
Chọn D
Đặt
cos ,tx=
do
;
2
x
nên suy ra
(
1;0t −
.
Trên khoảng
( )
1;0−
hàm số nghịch biến nên suy ra
Với
(
1;0t −
thì
( ) ( ) ( )
01f f t f −
hay
( )
02ft
.
Đặt
( )
2 cosu f x=
thì
( )
)
2 , 0;2u f t u=
. Khi đó bài toán trở thành:
Tìm
m
để phương trình
( )
f u m=
có nghiệm
)
0;2u
.
Quan sát đồ thị ta thấy rằng với
)
0;2u
thì
( )
)
2;2 2 2f u m − −
.
Vì
2; 1;0;1 2m m m − − = −
.
Câu 20: Gọi S là tập hợp các số nguyên m để phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng
A.
0
. B.
2−
. C.
3
. D.
1−
.
Lời giải
Chọn C
Giả sử
1 2 3
,,x x x
là ba nghiệm của phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
.
Khi đó ta có
( )( )( )
32
1 2 3
(2 1) 2(3 2) 8x m x m x x x x x x x− + + − − = − − −
Ta có
( )
1 2 3
1 2 3
1 2 2 3 3 1
21
8
2 3 2
x x x m
x x x
x x x x x x m
+ + = +
=
+ + = +
Do
1 2 3
,,x x x
lập thành một cấp số nhân nên ta có
1 2 3 2
82x x x x= =
.
Thay
2
2x =
vào phuognw trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
ta có
( ) ( )
8 2 1 .4 4 3 2 8 0 4 12 3m m m m− + + − − = = =
.
Thử lại với
3m =
ta thấy thỏa mãn. Vậy
3m =
. Dó đó tổng tất cả các giá trị của
m
bằng
3
Câu 21: Cho hàm số
3
1
( ) 8 ,
2
f x x mx m x= − + −
với
m
là một hằng số khác
0
. Biết rằng phương
trình
( ) 0fx=
có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương
k
thỏa mãn
phương trình
()f x k=
có 3 nghiệm phân biệt?
A.
3
. B.
6
. C.
34
. D.
31
.
Lời giải
Chọn D
( )
2
( ) 0 2 2 4 0
2
m
pt f x x x x
= − + + − =
có đúng 2 nghiệm phân biệt
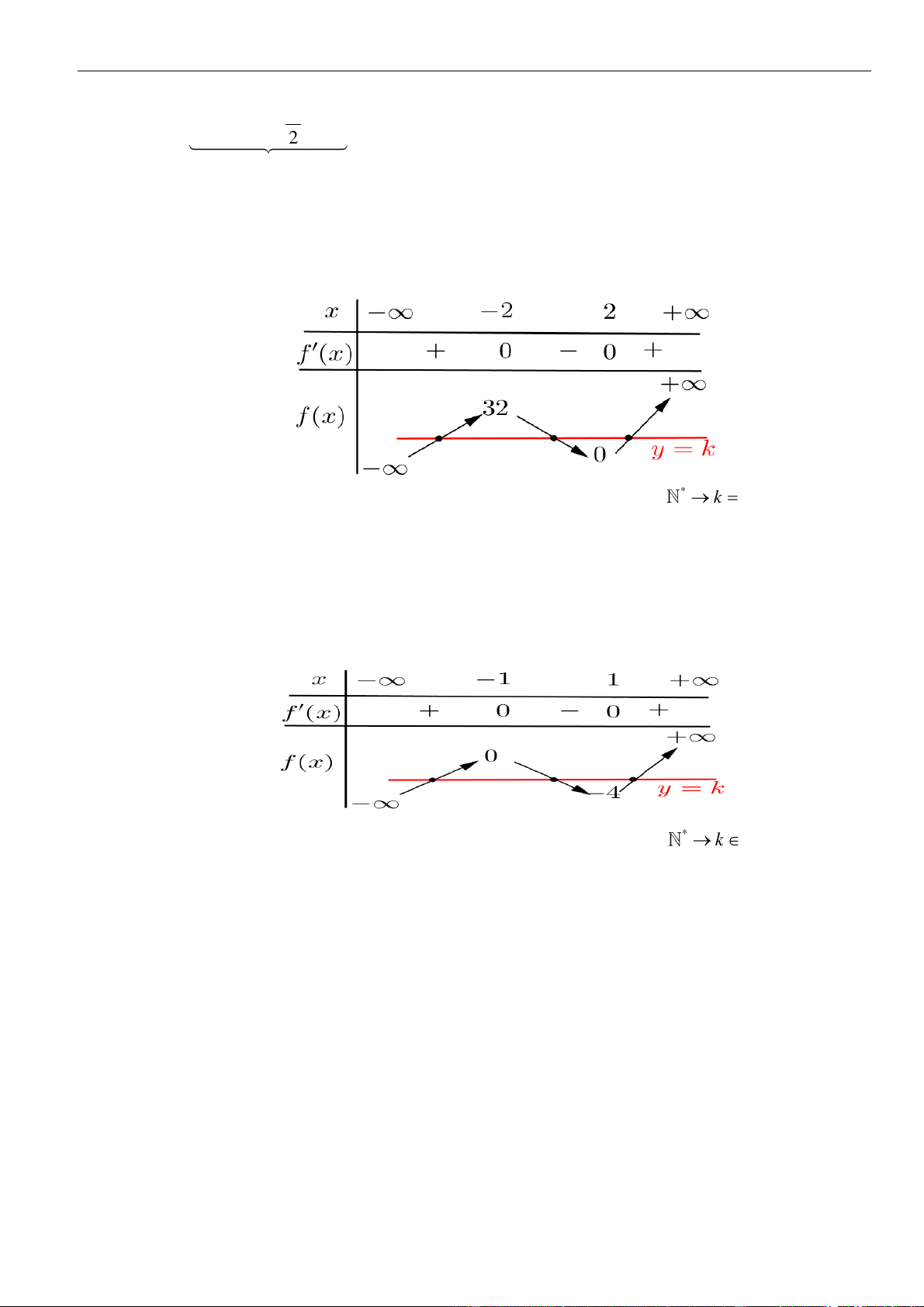
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
( )
2
()
2
2 4 0 1
2
gx
x
m
xx
=
+ + − =
có đúng 2 nghiệm phân biệt
+
(2) 0 24gm= =
( nhận )
32
( ) 12 16 '( ) 3 12f x x x f x x= − + → = −
'( ) 0 2f x x= =
BBT
Phương trình
()f x k=
có 3 nghiệm phân biệt khi
0 32k
và
*
1;2;3;....;31kk → =
+
( )
1Pt
có nghiệm kép và khác
2
0
6
(2) 0
m
g
=
=
( nhận )
32
( ) 3 2 '( ) 3 3f x x x f x x= − − → = −
'( ) 0 1f x x= =
BBT
Phương trình
()f x k=
có 3 nghiệm phân biệt khi
40k−
và
*
kk →
Vậy có
31
giá trị
k
thỏa điều kiện bài toán.
Câu 22: Cho hàm số
32
( 2) (2 13) 2y x m x m x m= − + − + − −
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= + +
và điểm
( )
1;4 .I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Lời giải
Chọn B
+ Phương trình hoành độ giao điểm của
d
và
()
m
C
là:
3
2
( 2) (3 13) 2 10 0 1
5
x
x m x m x m x
xm
=−
− + − + − − = = −
=+

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
+ Để đường thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
thì
7
6
m
m
−
−
+ Giả sử
2
( 1;8), ( 5; 6 8)B C m m m− + + +
. Để tam giác
IBC
cân tại
I
thì
2 2 2 2 2
2
20 ( 4) ( 6 4) 6( )
23
m
IB IC m m m m l
m
=−
= = + + + + = −
= −
Vậy có ba giá trị của m thỏa mãn nên tổng các giá trị của m bằng
6−
.
Câu 23: Gọi
d
là đường thẳng đi qua
( )
2;0A
có hệ số góc
( )
0mm
cắt đồ thị
( )
32
: 6 9 2C y x x x= − + − +
tại ba điểm phân biệt
, , .A B C
Gọi
,BC
lần lượt là hình chiếu
vuông góc của
,BC
lên trục tung. Biết rằng hình thang
BB C C
có diện tích bằng
8,
giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
5;8
. B.
( )
5;0−
. C.
( )
0;2
. D.
( )
1;5
.
Lời giải
Chọn D
Phương trình đường thẳng
( )
: 2 .d y m x=−
Phương trình hoành độ giao điểm
( ) ( )
( )
( )
3 2 2
2
2 2;0
6 9 2 2 2 4 1 0 .
4 1 0
xA
x x x m x x x x m
x x m
=
− + − + = − − − + + =
− + + =
Để
( )
C
cắt
d
tại 3 điểm phân biệt thì
0 4 1 0 3.mm − −
Giả sử
( ) ( )
12
1 1 2 2
12
4
, 2 , , 2 .
1
xx
B x mx m C x mx m
x x m
+=
− −
=+
Ta có
( ) ( )
12
0, 2 , 0, 2 .B mx m C mx m
−−
( ) ( )
''
1
' 8 16.
2
BB C C
S B C BB CC B C BB CC
= + = + =
Mà
( )
1 2 1 2
, , .B C m x x BB x CC x
= − = =
Do
m
dương nên
12
10x x m= +
mà
1 2 1 2
4 0 0, 0.x x x x+ =
( )
1 2 1 2 1 2 1 2 1 2
' ' , ' , ' 16 4B C m x x BB x CC x m x x x x m x x = − = = − + = − =
( ) ( ) ( )
22
2 2 2
1 2 1 2 1 2
16 4 16 16 4 4 16m x x m x x x x m m
− = + − = − − =
( )
32
1
3 4 0
2
ml
mm
m
=−
− + =
=
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ
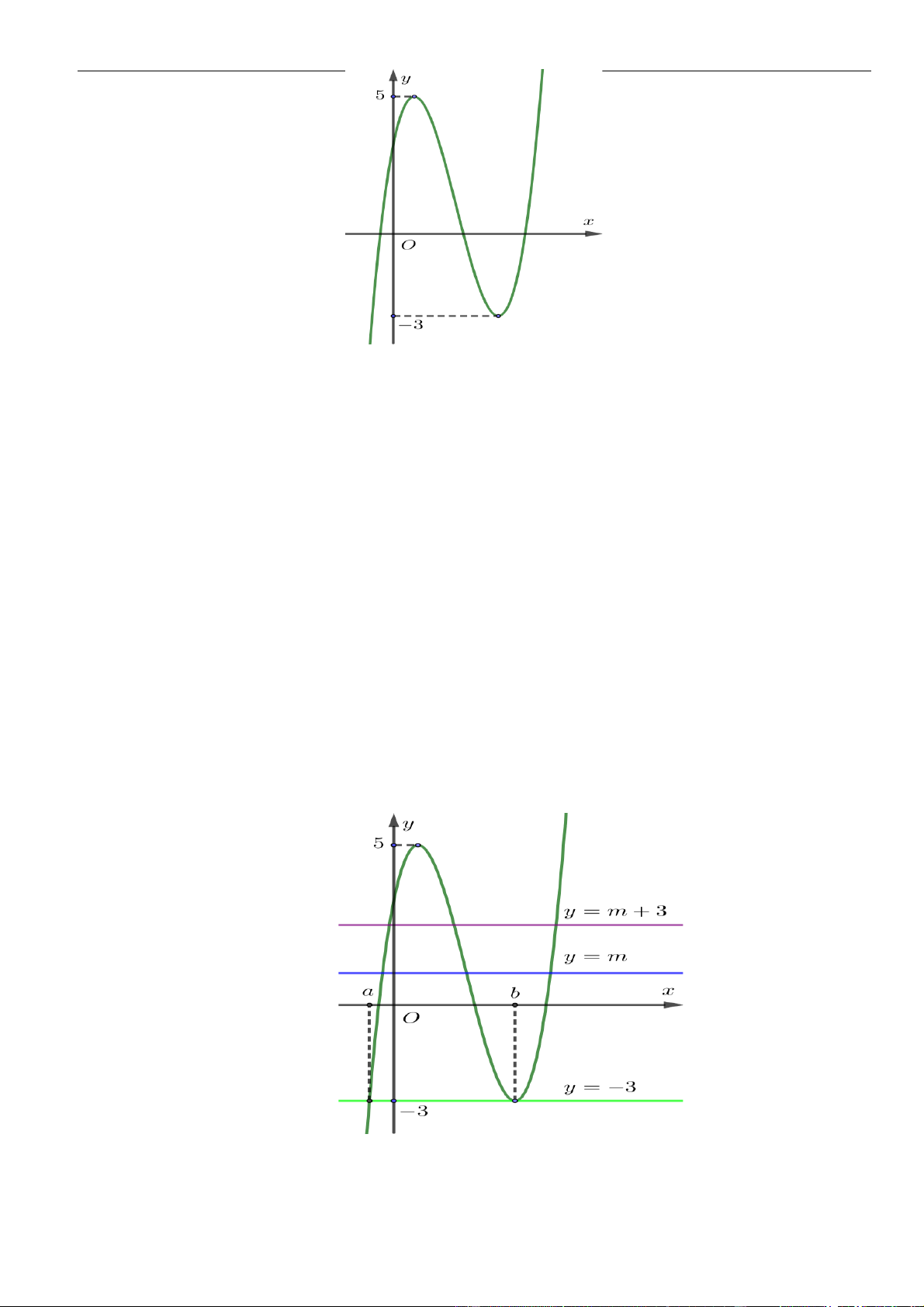
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
có đúng
8
nghiệm phân biệt?
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn B
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
Đặt
( )
t f x=
, phương trình trở thành:
( )
3 2 2 2
2 3 9 3 9 0t mt m m t m m− + − − + + =
( ) ( )
22
3 2 3 3 0t t m t m m
+ − + + + =
( )( )( )
3 3 0t t m t m + − − − =
( ) ( )
( ) ( )
( ) ( )
31
3
2
3
33
fx
t
t m f x m
tm
f x m
=−
=−
= =
=+
=+
Nhận xét các phương trình
( )
2
và
( )
3
không có nghiệm chung.
Dựa vào đồ thị, ta thấy:
( )
1
xa
xb
=
=

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
YCBT
Các phương trình
( )
2
và
( )
3
đều có 3 nghiệm phân biệt khác
,ab
3 5 2
32
33
mm
m
mm
+
−
− −
Mà
m
là số nguyên nên
2; 1;0;1m − −
.
Câu 25: Gọi
S
là tập hợp chứa tất cả các giá trị thực của tham số
m
để đồ thị hàm số
( ) ( ) ( )
32
6 1 3 2 1 2f x x m x m x= − + + + +
cắt trục
Ox
tại ba điểm phân biệt có hoành độ lớn hơn
1−
.
Biết rằng
;
a
S
b
−
= +
; trong đó
,ab
là các số nguyên dương và phân số
a
b
là tối giản. Giá trị
biểu thức
T a b=+
tương ứng bằng
A.
4
. B.
8
. C.
5
. D.
7
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm:
( ) ( )
32
6 1 3 2 1 2 0x m x m x− + + + + =
( ) ( )
( )
2
1 6 5 2 0x x m x − − + − =
( ) ( )
2
1
6 5 2 0 *
x
x m x
=
− + − =
Yêu cầu bài toán tương đương với phương trình
( )
*
có hai nghiệm phân biệt
12
;xx
lớn hơn
1−
và khác
1
.Ta có:
( )( )
( )
2
12
12
2
0
36 60 33 0
2
6 5 2
2
1 1 0
3
6 4 0
1
1 6 5 2 0
mm
xx
m
m
xx
m
m
m
+ +
+ −
+ −
−
+ +
+
−
− + −
Do đó
2; 3 5a b T a b= = = + =
Câu 26: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị hàm số
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Lời giải
Chọn B
Xét phương trình:
( )
3
32
321 31x mx m x x= + − − +− =
(*).
Đường thẳng
32y x m= + −
cắt đồ thị
( )
3
1yx=−
tại ba điểm phân biệt khi và chỉ khi phương
trình (*) có ba nghiệm phân biệt.
Đặt
( ) ( )
3 2 2
0
3 1 ' 3 6 0
2
x
f x x x f x x x
x
=
= − + = − =
=
.
Ta có bảng biến thiên

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Từ bảng biến thiên suy ra phương trình (*) có ba nghiệm phân biệt khi và chỉ khi đường thẳng
ym=
cắt đồ thị hàm số
( )
32
31f x x x= − +
tại ba điểm phân biệt. Vậy
31m−
.
Câu 27: Cho hàm số
32
3y x x m= + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
. Phát biểu nào sau đây đúng?
A.
( )
4;0m−
. B.
( )
0;m +
. C.
( )
;4m − −
. D.
( )
4; 2m − −
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là
( )
32
3 0 1x x m+ + =
.
Giả sử
( )
1
có 3 nghiệm phân biệt
( )
1 2 3 1 2 3
;;x x x x x x
thì
1 2 3
;;x x x
lần lượt là hoành độ của
,,A B C
và
( )( )( )
32
1 2 3
3x x m x x x x x x+ + = − − −
( ) ( )
3 2 3 2
1 2 3 1 2 2 3 3 1 1 2 3
3x x m x x x x x x x x x x x x x x x + + = − + + + + + −
Nên ta có
1 2 3
3x x x+ + = −
.
Để
B
là trung điểm
AC
thì
1 3 2
2x x x+=
nên
22
3 3 1xx= − = −
.
Tức là
( )
1
có 1 nghiệm là
1x =−
. Suy ra
1 3 0 2mm− + + = = −
.
Thử lại với
2m =−
thì
( )
1
trở thành
32
13
3 2 0 1
13
x
x x x
x
= − −
+ − = = −
= − +
(thỏa điều kiện bài toán).
Cách 2: Ta có
2
36y x x
=+
và
66yx
=+
nên
( )
C
có điểm uốn
( )
1; 2Im−+
.
Để
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
thì
I Ox
2 0 2mm + = = −
.
Câu 28: Cho hàm số
32
21y x x= − −
có đồ thị
( )
C
, đường thẳng
( )
d
:
1y mx=−
và điểm
(4;11)K
. Biết
rằng
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
(0; 1)A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không tồn tại
m
Lời giải

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Chọn C
Xét phương trình hoành độ:
3 2 3 2
2
0
2 1 1 2 0
2 0(1)
x
x x mx x x mx
x x m
=
− − = − − − =
− − =
Suy ra
(0; 1)A −
và hoành độ của điểm
B
và
C
là nghiệm của phương trình (1)
Để
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt khác 0
Khi và chỉ khi:
+ −
(1)
'0
1 m 0 m 1
(*)
m 0 m 0
m0
Giả sử:
11
( ;m 1)B x x −
,
22
( ;m 1)C x x −
. Theo Vi–ét ta có
12
2xx+=
Gọi
G
là trọng tâm của tam giác
KBC
:
++
=
=
+
+
+ − + −
=
=
12
G
G
12
G
G
4 x x
x2
x
2m 9
3
G 2;
2m 9
11 mx 1 mx 1
3
y
y
3
3
Trọng tâm
G
nằm trên đường thẳng
21yx=+
suy ra
29
2.2 1 3
3
m
m
+
= + =
thỏa mãn
( )
*
Câu 29: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại 3 điểm phân biệt
1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là:
( ) ( )
( )
( )
3 2 2
2
1
2 1 0 1 0
0*
x
x x m x m x x x m
x x m
=
− + − + = − − − =
− − =
.
( )
C
cắt trục hoành tại 3 điểm phân biệt
( )
*
có hai nghiệm phân biệt khác 1
2
1
1 4 0
4
1 1 0
0
m
m
m
m
+
−
− −
.
Khi đó
1
1x =
,
2
x
và
3
x
là hai nghiệm của
( )
*
.
( )
2
222
1 2 3 2 3 2 3
4 2 3 1 2 3 1x x x x x x x m m+ + + − +
.
Vậy các giá trị cần tìm của
m
là
1
1
4
0
m
m
−
.
Câu 30: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại
3
điểm phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx+ +
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm:
( ) ( )
( )
( )
3 2 2
2 1 0 1 0 1x x m x m x x x m− + − + = − − − =
( )
3
2
1
02
x
x x m
=
− − =
. Điều kiện để phương trình
( )
1
có 3 nghiệm phân biệt là phương trình
( )
2
có 2 nghiệm phân biệt khác
1
0
1
1
1 4 0
4
m
x
m
m
= +
−
.
Khi đó phương trình
( )
2
có 2 nghiệm phân biệt
12
,xx
.
Ta có
( )
2
2 2 2 2 2
1 2 3 1 2 1 2 1 2
4 3 2 3x x x x x x x x x+ + + + −
2
1 2 3 1mm +
.
Vậy
1
1
4
0
m
m
−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Cho hàm số
32
31y x x m= − + −
. Tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm
số cắt trục hoành tại
3
điểm phân biệt là
A.
9
. B.
9−
. C.
15−
. D.
15
.
Câu 2: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Câu 3: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3
12 1y x x m= − + −
cắt trục hoành
tại
3
điểm phân biệt
?
A.
3
. B.
32
. C.
31
. D.
33
.
Câu 4: Cho hàm số
32
31y x x mx= − + +
có đồ thị
( )
C
và đường thẳng
: 2 1d y x=+
. Có bao nhiêu giá
trị nguyên dương của tham số
m
để đồ thị
( )
C
cắt đường thẳng
d
tại
3
điểm phân biệt?
A.
4
. B.
5
. C.
9
. D.
3
.
Câu 5: Với
m
là một tham số thực thì đồ thị hàm số
32
21y x x x= − + −
và đường thẳng
ym=
có nhiều
nhất bao nhiêu giao điểm?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 6: Tìm tất cả các giá trị của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
6y x x= − +
tại
ba điểm phân biệt.
A.
0 32m
. B.
16
0
m
m
. C.
0 16m
. D.
32 0m−
.
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3 2 2
3 5 0x x m m− − + =
có ba
nghiệm thực phân biệt?
A. Vô số. B.
0.
C.
5.
D.
4.
Câu 8: Cho hàm số
32
21y x x= − −
có đồ thị
(C)
, đường thẳng
( )
:1d y mx=−
và điểm
( )
4;11K
.Biết
rằng
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
( )
0; 1A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không có
m
.
Câu 9: Gọi
S
là tập tất cả các giá trị của tham số
m
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1yx=+
. Tổng các phần tử của
S
bằng
A.
0
. B.
3
. C.
2
. D.
1−
.
Câu 10: Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
( )
3
22y x m x m= − + +
cắt
trục hoành tại 3 điểm phân biệt
Tìm m liên quan đến tương giao hàm bậc ba
DẠNG 5
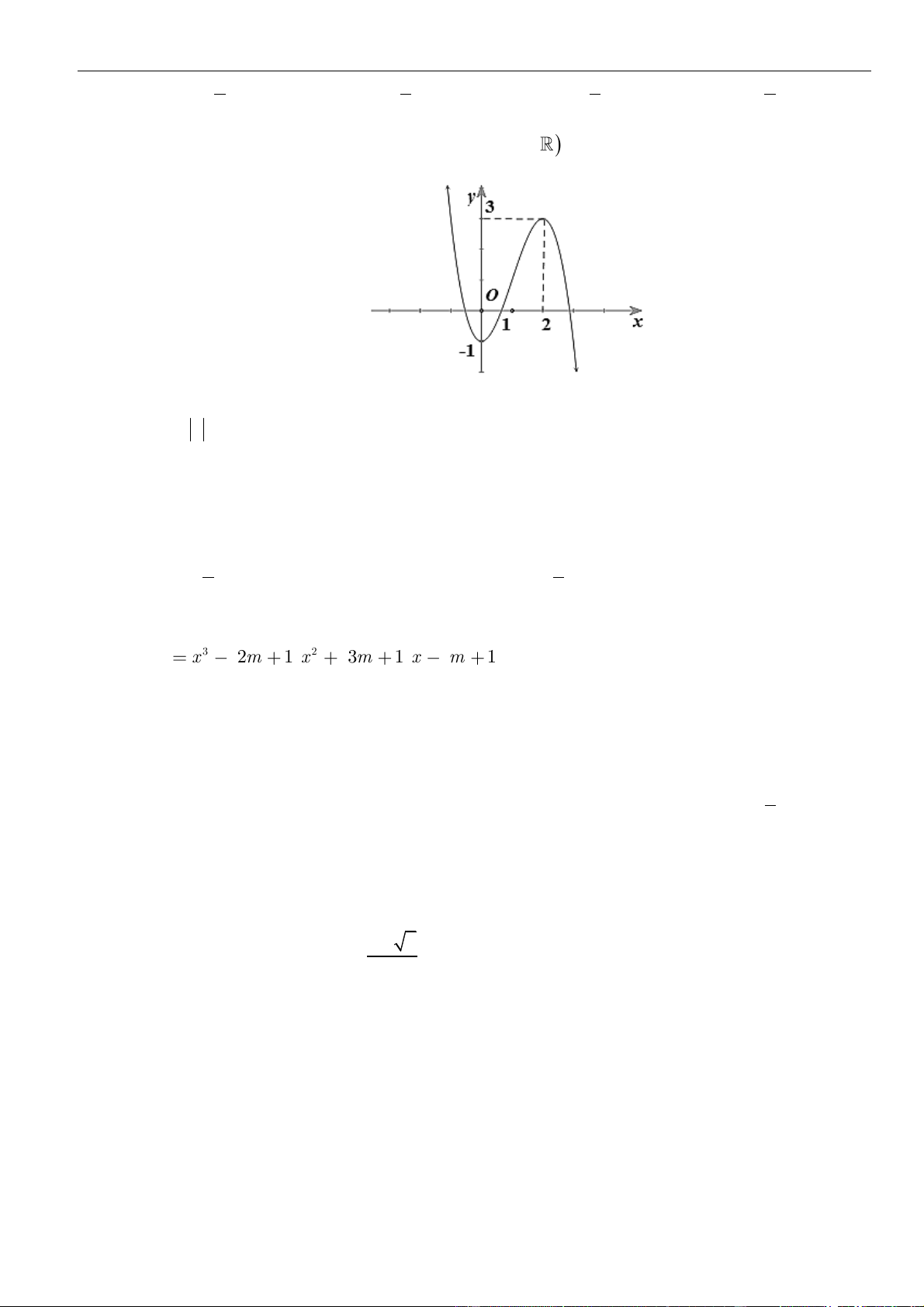
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
1
2
m
. B.
1
2
m
. C.
1
2
m −
. D.
1
; 4
2
mm −
.
Câu 11: Cho hàm số
( ) ( )
32
, , ,f x ax bx cx d a b c d= + + +
có đồ thị như hình vẽ sau.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn
2020;2020−
của tham số
m
để phương trình
( )
20f x m−=
có đúng
2
nghiệm thực phân biệt?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Câu 12: Biết đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó
m
thuộc khoảng nào dưới đây?
A.
3
1;
2
. B.
( )
0;1
. C.
3
;2
2
. D.
( )
1;0−
.
Câu 13: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
32
2 1 3 1 1y x m x m x m
cắt trục hoành tại 2 điểm phân biệt?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 14: Cho đồ thị
( ) ( )
32
: 2 1
m
C y x x m x m= − + − +
. Tìm tất cả các giá trị của tham số m để
( )
m
C
cắt
trục hoành tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thỏa
222
1 2 3
4xxx+ + =
A.
0m
. B.
( )
0;2m
. C.
1m =
. D.
1
4
−m
và
0m
.
Câu 15: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
(
B
nằm giữa
,AC
) sao cho
2AB BC=
. Tính tổng
các phần tử thuộc
S
.
A.
4−
. B.
77
7
−
. C.
2−
. D.
0
.
Câu 16: Có bao nhiêu giá trị nguyên âm của
a
để đồ thị hàm số
( )
32
10 1y x a x x= + + − +
cắt trục
hoành tại đúng một điểm?
A.
10
. B.
8
. C.
11
. D.
9
.
Câu 17: Có bao nhiêu giá trị nguyên thuộc
2020;2021−
của hàm số
m
để đường thẳng
1y mx m= − −
cắt đồ thị của hàm số
32
3y x x x= − +
tại ba điểm phân biệt
,,A B C
sao cho
AB BC=
.
A.
2021
. B.
2023
. C.
2024
. D.
2022
.
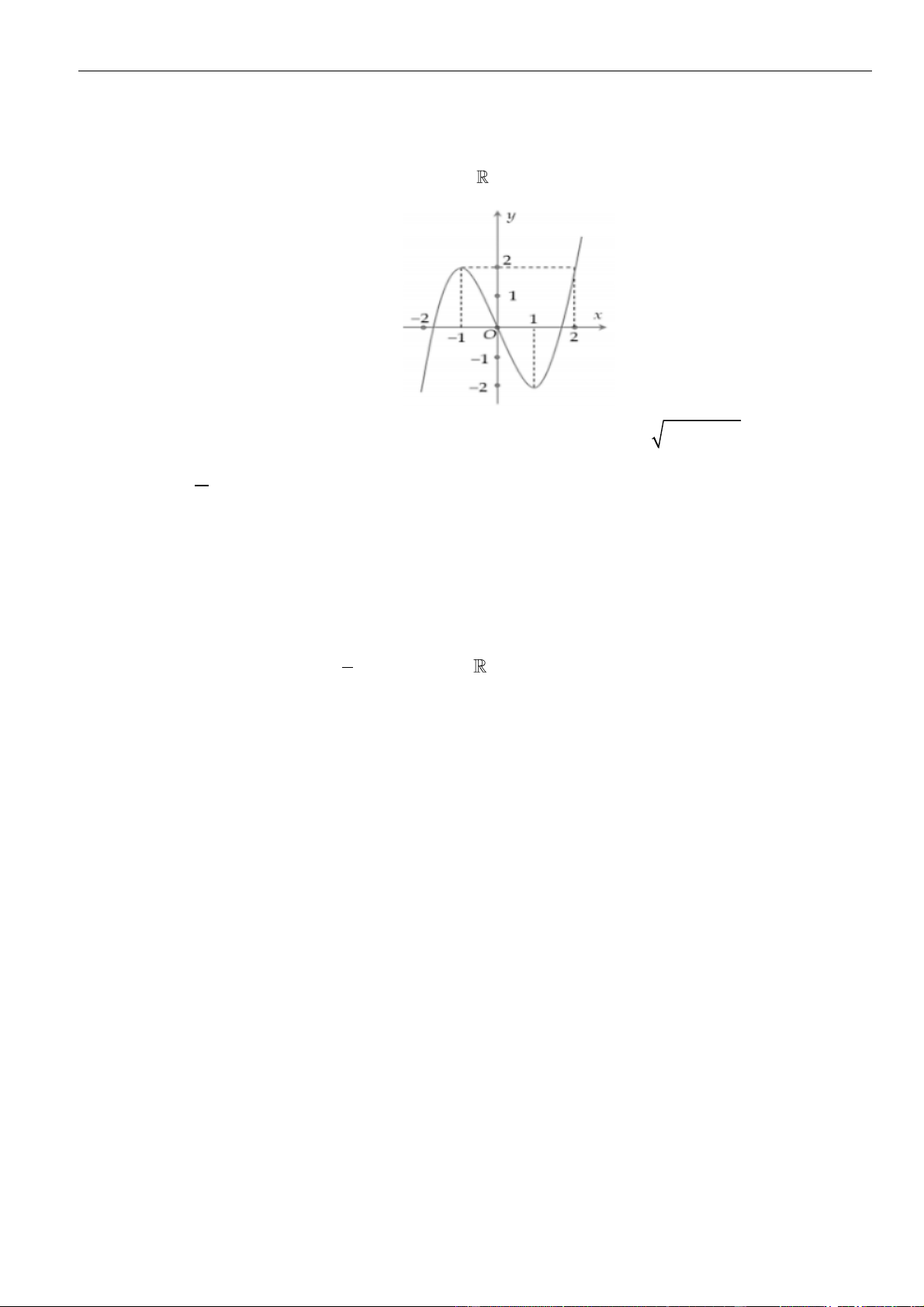
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 18: Cho bao nhiêu giá trị
m
để đồ thị hàm số
32
2y x mx m= − + −
cắt trục
Ox
tại
3
điểm phân biệt
có hoành độ lập thành cấp số cộng.
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 19: Cho hàm số bậc ba
( )
y f x=
liên tục trên và có đồ thị như hình vẽ bên.
Tổng tất cả các giá trị nguyên của tham số
m
để phương trình
( )
( )
2 cosf f x m=
có nghiệm
;
2
x
A.
1−
. B.
0
. C.
1
. D.
2−
.
Câu 20: Gọi S là tập hợp các số nguyên m để phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng
A.
0
. B.
2−
. C.
3
. D.
1−
.
Câu 21: Cho hàm số
3
1
( ) 8 ,
2
f x x mx m x= − + −
với
m
là một hằng số khác
0
. Biết rằng phương
trình
( ) 0fx=
có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương
k
thỏa mãn
phương trình
()f x k=
có 3 nghiệm phân biệt?
A.
3
. B.
6
. C.
34
. D.
31
.
Câu 22: Cho hàm số
32
( 2) (2 13) 2y x m x m x m= − + − + − −
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= + +
và điểm
( )
1;4 .I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Câu 23: Gọi
d
là đường thẳng đi qua
( )
2;0A
có hệ số góc
( )
0mm
cắt đồ thị
( )
32
: 6 9 2C y x x x= − + − +
tại ba điểm phân biệt
, , .A B C
Gọi
,BC
lần lượt là hình chiếu
vuông góc của
,BC
lên trục tung. Biết rằng hình thang
BB C C
có diện tích bằng
8,
giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
5;8
. B.
( )
5;0−
. C.
( )
0;2
. D.
( )
1;5
.
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
có đúng
8
nghiệm phân biệt?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 25: Gọi
S
là tập hợp chứa tất cả các giá trị thực của tham số
m
để đồ thị hàm số
( ) ( ) ( )
32
6 1 3 2 1 2f x x m x m x= − + + + +
cắt trục
Ox
tại ba điểm phân biệt có hoành độ lớn hơn
1−
.
Biết rằng
;
a
S
b
−
= +
; trong đó
,ab
là các số nguyên dương và phân số
a
b
là tối giản. Giá trị
biểu thức
T a b=+
tương ứng bằng
A.
4
. B.
8
. C.
5
. D.
7
.
Câu 26: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị hàm số
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Câu 27: Cho hàm số
32
3y x x m= + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
. Phát biểu nào sau đây đúng?
A.
( )
4;0m−
. B.
( )
0;m +
. C.
( )
;4m − −
. D.
( )
4; 2m − −
.
Câu 28: Cho hàm số
32
21y x x= − −
có đồ thị
( )
C
, đường thẳng
( )
d
:
1y mx=−
và điểm
(4;11)K
. Biết
rằng
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
(0; 1)A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không tồn tại
m
Câu 29: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại 3 điểm phân biệt
1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Câu 30: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại
3
điểm phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số
32
31y x x m= − + −
. Tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm
số cắt trục hoành tại
3
điểm phân biệt là
A.
9
. B.
9−
. C.
15−
. D.
15
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của đồ thị và trục hoành là
32
3 1 0x x m− + − =
32
31x x m − + + =
.
Xét hàm số
( )
32
31f x x x= − + +
với
x
.
Ta
có
( )
2
36f x x x
= − +
( )
0
0
2
x
fx
x
=
=
=
.
Bảng biến thiên của hàm
( )
32
31f x x x= − + +
với
x
Dựa vào bảng biến thiên ta thấy để đồ thị hàm số cắt trục hoành tại
3
điểm phân biệt
15m
. Do
2;3;4mm
Vậy tổng tất cả các giá trị nguyên của tham số
m
để đồ thị hàm số cắt trục hoành tại
3
điểm
phân biệt là
2 3 4 9S = + + =
.
Câu 2: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của hai đồ thị:
( )
3
3 2 1x m x+ − = −
32
31m x x = − +
( )
1
Nhận xét:
( )
1
là phương trình hoành độ giao điểm của hai đồ thị
( )
:d y m=
và đồ thị
( )
32
: 3 1C y x x= − +
.
Xét hàm số
32
31y x x= − +
2
36y x x
=−
,
0
0
2
x
y
x
=
=
=
.
Bảng biến thiên
( )
fx
x
( )
fx
+
−
0
0
−
2
+
−
+
−
0
1
5
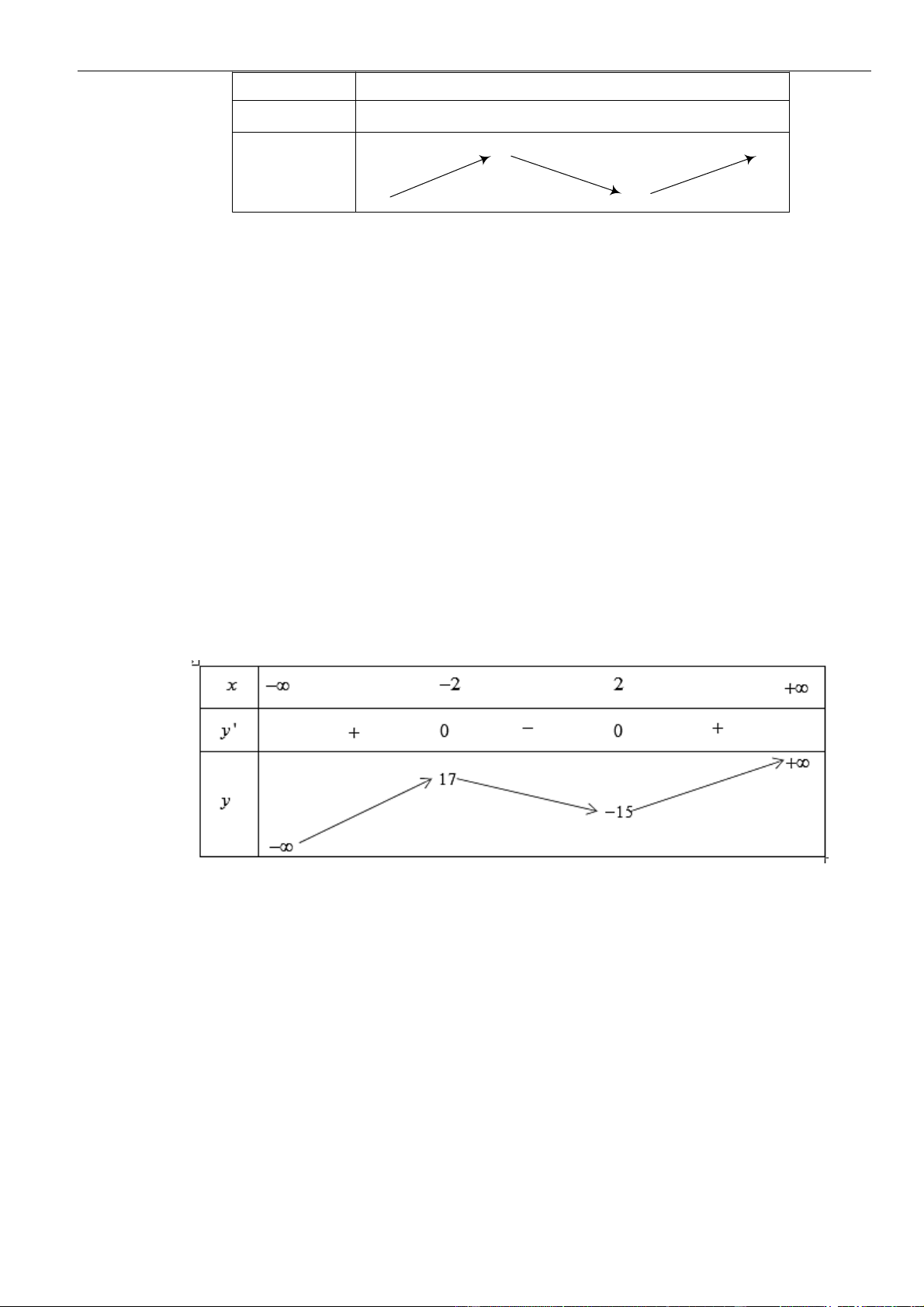
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
x
−
+
0
+
−
y
y
1
2
3−
−
0
0
+
+
Vậy: yêu cầu bài toán
31m −
.
Câu 3: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3
12 1y x x m= − + −
cắt trục hoành
tại
3
điểm phân biệt
?
A.
3
. B.
32
. C.
31
. D.
33
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho với trục hoành là
3
12 1 0x x m− + − =
Ta có:
3
12 1 0x x m− + − =
3
12 1x x m − + =
(1)
.
Đặt
3
12 1y x x
ym
= − +
=
. Khi đó số nghiệm của phương trình
(1)
bằng số giao điểm của đồ thị hàm
số
3
12 1y x x= − +
và đường thẳng
ym=
.
Khảo sát sự biến thiên của hàm số
3
12 1y x x= − +
ta có:
2
' 3 12yx=−
.
2
' 0 3 12 0yx= − =
2
2
x
x
=−
=
.
BBT của hàm số
3
12 1y x x= − +
là:
Với
15 17m−
thì phương trình
(1)
có
3
nghiệm phân biệt. Mặt khác do
m
nguyên nên
14,...,16m−
. Vậy có 31 giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 4: Cho hàm số
32
31y x x mx= − + +
có đồ thị
( )
C
và đường thẳng
: 2 1d y x=+
. Có bao nhiêu giá
trị nguyên dương của tham số
m
để đồ thị
( )
C
cắt đường thẳng
d
tại
3
điểm phân biệt?
A.
4
. B.
5
. C.
9
. D.
3
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm
32
3 1 2 1x x mx x− + + = +
( )
32
3 2 0x x m x − + − =
( )
2
2
0
3 2 0
3 2 0
x
x x x m
x x m
=
− + − =
− + − =
.
Đặt
( )
2
32f x x x m= − + −
.
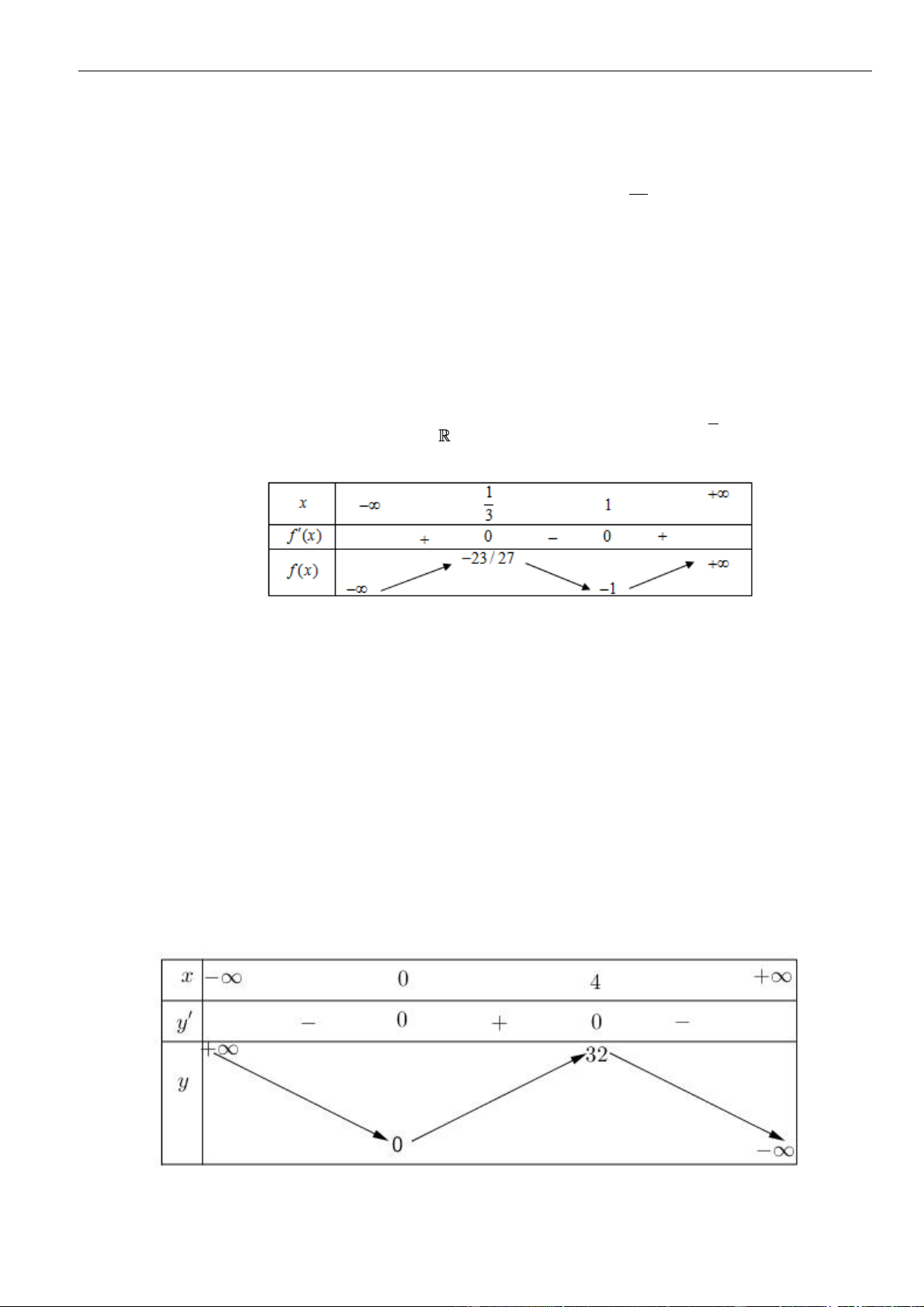
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
Để đồ thị
( )
C
cắt đường thẳng
d
tại
3
điểm phân biệt thì phương trình
( )
32
3 2 0x x m x− + − =
phải có
3
nghiệm phân biệt, khi đó
( )
0fx=
phải có hai nghiệm phân biệt khác
0
.
Do đó
( )
( )
20
00
2
9 4 2 0
4 17
0
m
f
m
m
m
−
− −
− −
2
17
4
m
m
.
Do
m
là số nguyên dương nên
1,3,4m
.
Câu 5: Với
m
là một tham số thực thì đồ thị hàm số
32
21y x x x= − + −
và đường thẳng
ym=
có nhiều
nhất bao nhiêu giao điểm?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
Hàm số
32
21y x x x= − + −
có TXĐ: ;
2
3 4 1y x x
= − +
;
1
'0
3
1
x
y
x
=
=
=
.
Dựa vào BBT đồ thi hàm số
32
21y x x x= − + −
và đường thẳng
ym=
có nhiều nhất là ba giao
điểm.
Câu 6: Tìm tất cả các giá trị của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
6y x x= − +
tại
ba điểm phân biệt.
A.
0 32m
. B.
16
0
m
m
. C.
0 16m
. D.
32 0m−
.
Lời giải
Chọn A
Ta có
3 2 2
6 3 12y x x y x x
= − + = − +
.
2
0
0 3 12 0
4
x
y x x
x
=
= − + =
=
.
Ta có BBT
Để đường thẳng
ym=
cắt đồ thị hàm số
32
6y x x= − +
tại ba điểm phân biệt thì
0 32m
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3 2 2
3 5 0x x m m− − + =
có ba
nghiệm thực phân biệt?
A. Vô số. B.
0.
C.
5.
D.
4.
Lời giải
Chọn B
Đặt
( )
3 2 2
35f x x x m m= − − +
.
Để
3 2 2
3 5 0x x m m− − + =
có ba nghiệm thực phân biệt thì
( )
0fx
=
có hai nghiệm phân biệt
12
,xx
thỏa mãn:
( ) ( )
12
.0f x f x
Ta có:
( )
2
36f x x x
=−
( )
2
0
0 3 6 0
2
x
f x x x
x
=
= − =
=
.
( )
2
05f m m= − +
.
( )
2
2 5 4f m m= − + −
.
Khi đó:
( ) ( )
( )( )
22
01
0 . 2 0 5 5 4 0
45
m
f f m m m m
m
− + − + −
Vậy không có giá trị nguyên nào của
m
thỏa mãn.
Câu 8: Cho hàm số
32
21y x x= − −
có đồ thị
(C)
, đường thẳng
( )
:1d y mx=−
và điểm
( )
4;11K
.Biết
rằng
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
( )
0; 1A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không có
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
(C)
và
( )
d
là:
( )
3 2 3 2 2
2
0
2 1 1 2 0 2 0
2 0(1)
x
x x mx x x mx x x x m
x x m
=
− − = − − − = − − =
− − =
Để
(C)
và
( )
d
cắt nhau tại ba điểm phân biệt thì (1) có hai nghiệm phân biệt khác 0. Ta có:
'
2
0 1 0 1
00
0 0 0
mm
mm
m
+ −
− −
Gọi
12
,xx
là nghiệm của (1), ta có
( ) ( )
1 1 2 2
B ; 1 ; ; 1x mx C x mx−−
. Trọng tâm G của tam giác
KBC
, ta có
12
12
4
2
3
11 2
29
33
G
G
xx
x
mx mx
m
y
++
==
+ + −
+
==
Theo giả thiết G thuộc đường thẳng
( )
: 2 1d y x=+
nên ta có:
( )
29
2.2 1 3
3
m
m tm
+
= + =
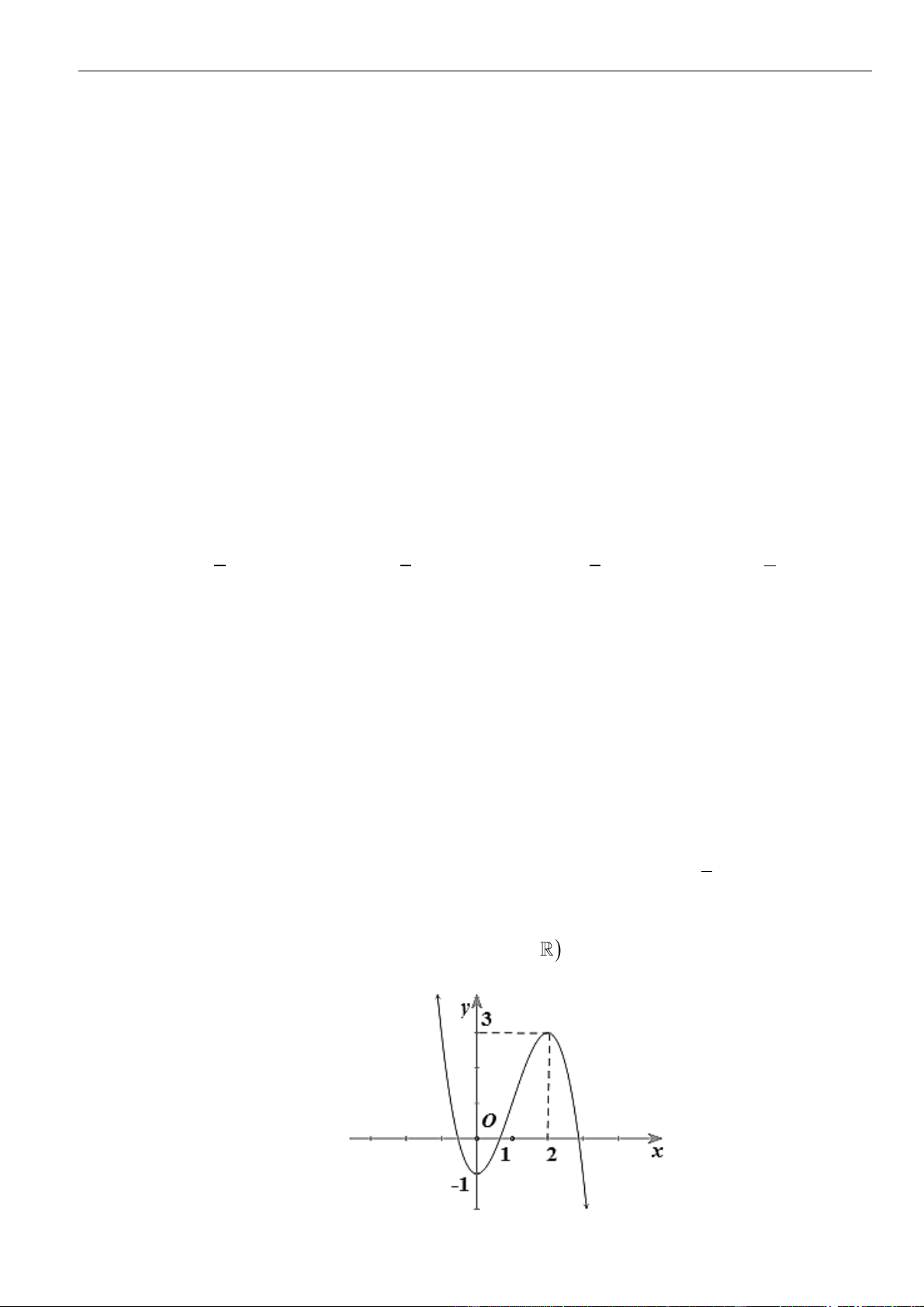
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Câu 9: Gọi
S
là tập tất cả các giá trị của tham số
m
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1yx=+
. Tổng các phần tử của
S
bằng
A.
0
. B.
3
. C.
2
. D.
1−
.
Lời giải
Chọn C
2
'3yx=
.
Giả sử đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm số
3
1yx=+
tại điểm
0
x
thì
( )
00
3 1.y x x
= =
Đk đủ:
00
12xy= =
thì PTTT là
3 2 1y x m= − = −
.
00
10xy= − =
thì PTTT là
3 3 3y x m= + =
.
Tổng các phần tử của
S
bằng
2
.
Cách 2: Điều kiện tiếp xúc
3
3
2
13
13
1; 3.
1
33
x x m
x x m
mm
x
x
+ = +
+ − =
= − =
=
=
Câu 10: Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
( )
3
22y x m x m= − + +
cắt
trục hoành tại 3 điểm phân biệt
A.
1
2
m
. B.
1
2
m
. C.
1
2
m −
. D.
1
; 4
2
mm −
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm của đồ thị với trục Ox:
( )
3
2 2 0− + + =x m x m
3
2 2 0 − − + =x x mx m
( ) ( )
2
1 2 2 0 1
− + − =
x x x m
( )
2
1
2 2 0 2
=
+ − =
x
x x m
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt
( )
1
có 3 nghiệm phân biệt
( )
2
có 2 nghiệm phân biệt khác
1
( )
' 1 2 0
1 2 2 0
= +
= + −
m
gm
1
2
4
−
m
m
Câu 11: Cho hàm số
( ) ( )
32
, , ,f x ax bx cx d a b c d= + + +
có đồ thị như hình vẽ sau.
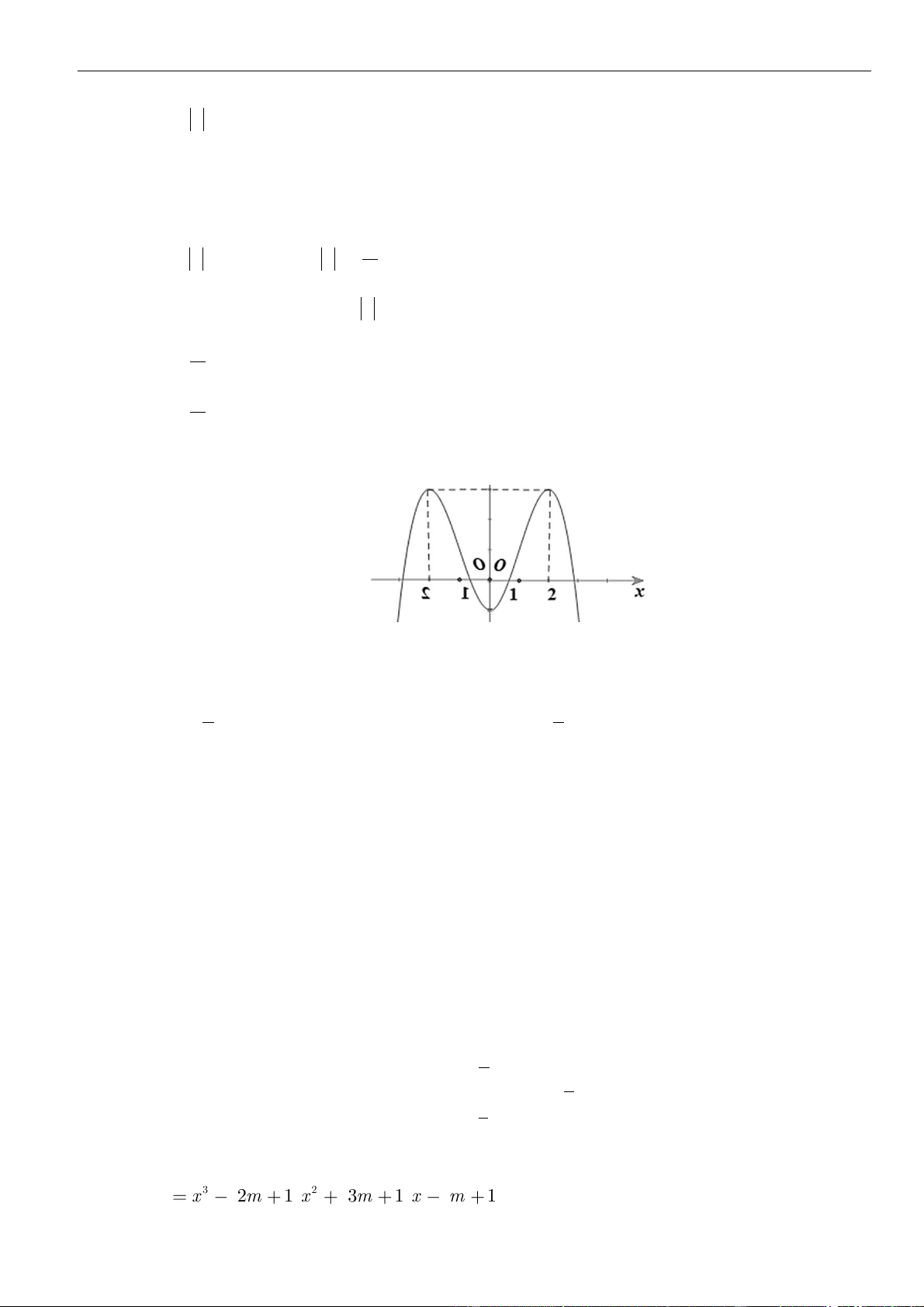
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn
2020;2020−
của tham số
m
để phương trình
( )
20f x m−=
có đúng
2
nghiệm thực phân biệt?
A.
2020
. B.
2022
. C.
2021
. D.
2019
.
Lời giải
Chọn D
( )
20f x m−=
( )
( )
1
2
=
m
fx
Dựa vào đồ thị hàm
( )
=y f x
ta có: để phương trình
( )
1
có đúng 2 nghiệm thực phân biệt
3
6
2
2
1
2
=
=
−
−
m
m
mm
Vì
2020;2020−m
2020; 2019;...... 3;6 − − −m
. Vậy có 2019 số.
Câu 12: Biết đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó
m
thuộc khoảng nào dưới đây?
A.
3
1;
2
. B.
( )
0;1
. C.
3
;2
2
. D.
( )
1;0−
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm là
( )
32
3 1 6 3 3 1m x m x x− + + = − +
( ) ( )
32
3 3 1 6 2 0 1x x m x m − − − − − =
.
Xét hàm số
( ) ( ) ( )
32
3 3 1 6 2
m
g x x x m x m C= − − − − −
.
( ) ( )
2
3 6 3 1 6 6g x x x m g x x
= − − + = −
;
( )
01g x x
= =
.
Đồ thị
( )
m
C
có điểm uốn là
( )
1; 9 3Im−−
.
Để đường thẳng
( )
3 1 6 3y m x m= − + +
cắt đồ thị hàm số
32
31y x x= − +
tại ba điểm phân biệt
sao cho một giao điểm cách đều hai giao điểm còn lại
( ) ( )
( )
2
2
3 3. 3 1 0
1
3
1;0
1
3
3
m
m
m
I Ox
m
−
= − − − +
= − −
=−
.
Câu 13: Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
32
2 1 3 1 1y x m x m x m
cắt trục hoành tại 2 điểm phân biệt?

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Xét phương trình
3 2 2
2
2 1 3 1 1 0 1 2 1 0
1
2 1 0 *
x m x m x m x x mx m
x
x mx m
Theo yêu cầu bài toán phương trình
*
xảy ra 2 trường hợp
TH1: phương trình có nghiệm kép khác 1, tức là
2
10
1 2 1 0
mm
mm
loại, do nghiệm không
nguyên.
TH2: phương trình có 2 nghiệm phân biệt trong đó 1 là một nghiệm, tức là
2
10
2
1 2 1 0
mm
m
mm
.
Nhận xét: cụm từ “cắt trục hoành tại 2 điểm phân biệt” được người ra đề hiểu là “có đúng 2 điểm
chung với trục hoành”. Theo ý kiến chủ quan của người giải, ta nên phát biểu rõ ràng hơn.
Câu 14: Cho đồ thị
( ) ( )
32
: 2 1
m
C y x x m x m= − + − +
. Tìm tất cả các giá trị của tham số m để
( )
m
C
cắt
trục hoành tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thỏa
222
1 2 3
4xxx+ + =
A.
0m
. B.
( )
0;2m
. C.
1m =
. D.
1
4
−m
và
0m
.
Lời giải
Chọn C
Để hàm số đã cho cắt trục hoành tại 3 điếm phàn biệt thì phưong trình hoành độ giao điểm
phải có 3 nghiệm phàn biệt:
32
2 (1 ) 0− + − + =x x m x m
( )
2
( 1) 0− − − =x x x m
Ta đặt
1
1=x
. Khi đó, đế phưong trình có 3 nghiệm phân biệt thì phương trình sau phải có 2
nghiệm phân biệt khác 1.
2
0− − =x x m
Do có nghiệm khác 1 nên
1 1 0− − m
hay
0.m
Ta có
14 = + m
Để có 2 nghiệm phàn biệt thì
0
hay
1
4
−m
.
Theo điều kiện của đề bài ta có
222
1 2 3
4+ + =xxx
( )
2
2 3 2 3
1 2 4 + + − =x x x x
( )
2
2 3 2 3
23 + − =x x x x
vói
23
,xx
là nghiệm của phương trình bậc 2 trên.
Áp dụng Viet ta có
2
1 2( ) 3− − =m
1=m
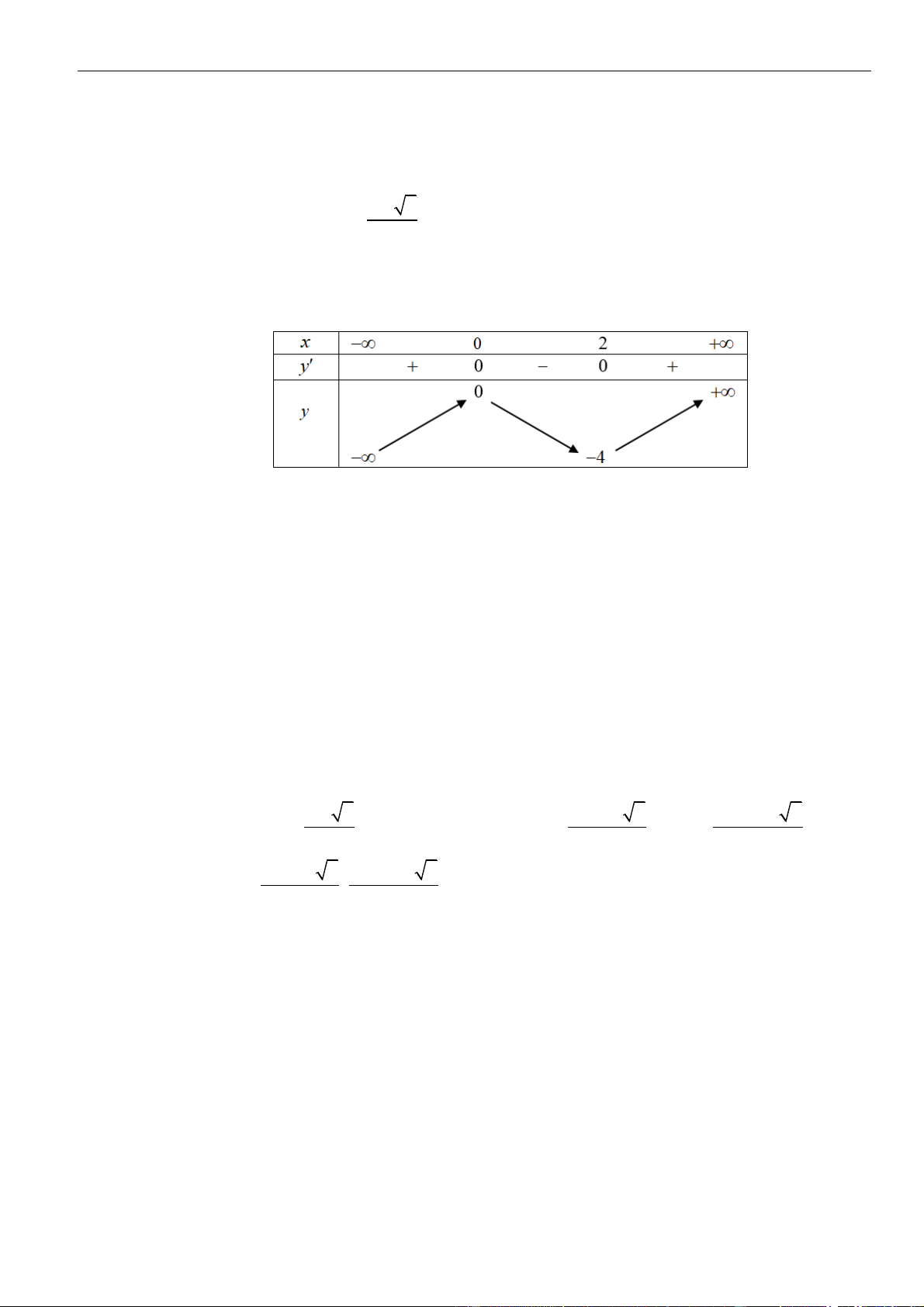
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Kết hợp các điều kiện ta có
1=m
.
Câu 15: Gọi
S
là tập tất cả các giá trị thực của tham số
m
để đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
(
B
nằm giữa
,AC
) sao cho
2AB BC=
. Tính tổng
các phần tử thuộc
S
.
A.
4−
. B.
77
7
−
. C.
2−
. D.
0
.
Lời giải
Chọn A
Ta có BBT của hàm số
32
3y x x=−
như sau:
Suy ra đường thẳng
ym=
cắt đồ thị hàm số
32
3y x x=−
tại 3 điểm phân biệt
,,A B C
40m −
.
Khi đó
3, 0,
A B C A B B C C A A B C
x x x x x x x x x x x x m+ + = + + = =
.
Để
B
nằm giữa
,AC
và
2AB BC=
thì
( )
( )
2
2
A B C
B A C B
C B A
A B B C
xxx
x x x x
x x x
x x x x
− = −
− = −
3 2 4 3 6 5
B A C B C A B
x x x x x x x = + − = = −
.
Suy ra
( ) ( ) ( ) ( )
( ) ( )
6 5 . . 4 3 4 3 . 6 5 0 (*)
4 3 . . 6 5 (**)
B B B B B B
B B B
x x x x x x
x x x m
− + − + − − =
− − =
.
Từ (*) được
77
7
B
x
=
. Thay vào (**) được
98 20 7
49
m
+
=−
và
98 20 7
49
m
−+
=
.
Vậy
98 20 7 98 20 7
;
49 49
S
+ − +
=−
.
Câu 16: Có bao nhiêu giá trị nguyên âm của
a
để đồ thị hàm số
( )
32
10 1y x a x x= + + − +
cắt trục
hoành tại đúng một điểm?
A.
10
. B.
8
. C.
11
. D.
9
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của đồ thị và trục hoành là:
( ) ( )
32
10 1 0 1x a x x+ + − + =
3 2 2
10 1x x x ax + − + = −
.
Ta thấy
0x =
không là nghiệm của phương trình nên
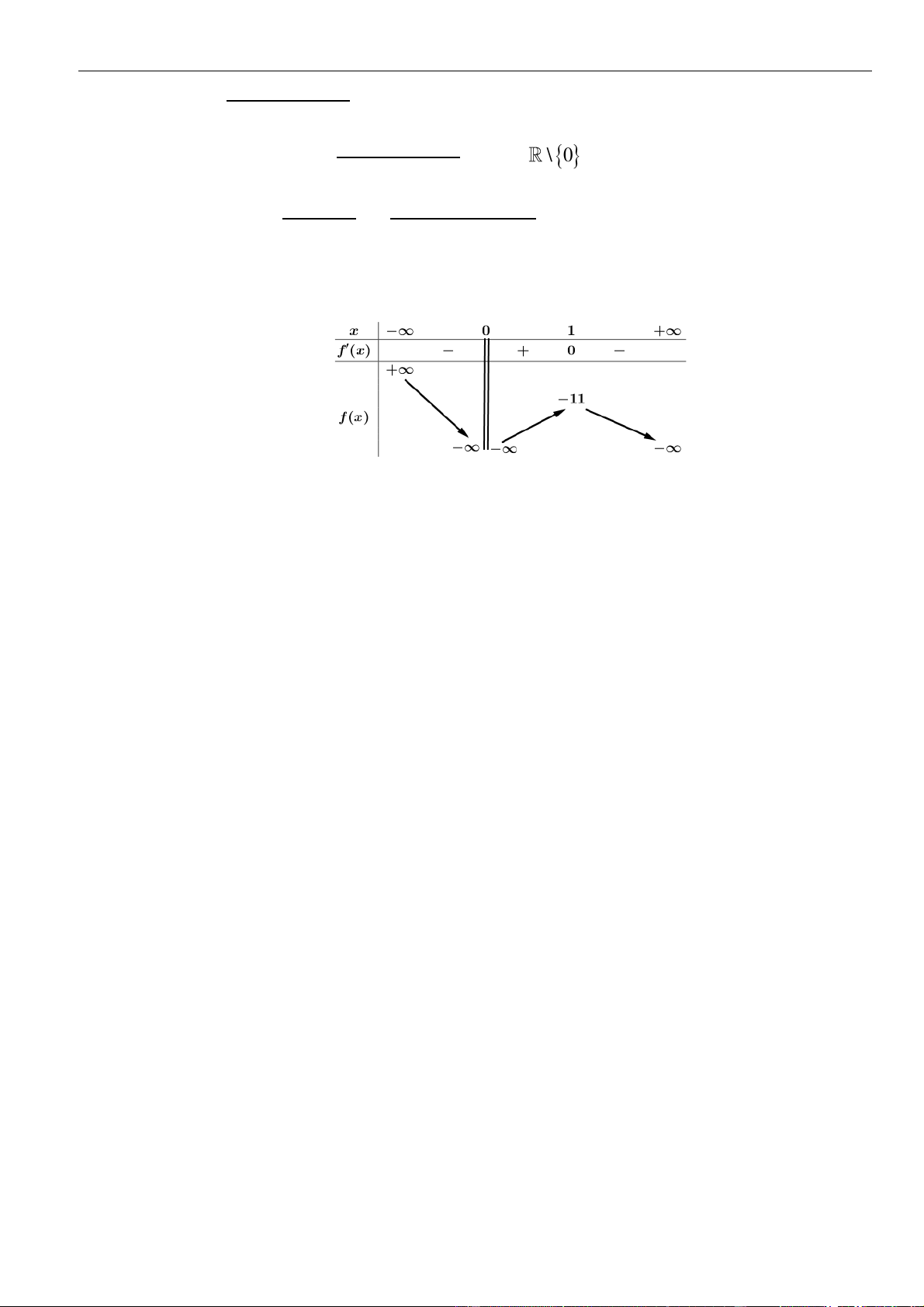
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
( )
1
32
2
10 1x x x
a
x
+ − +
− =
.
Xét hàm số
( )
32
2
10 1x x x
fx
x
+ − +
=−
với
\0x
Ta có
( )
( )
( )
2
3
33
1 . 2
2
x x x
xx
fx
xx
− + +
+−
= − = −
( )
01f x x
= =
.
Bảng biến thiên của hàm số
( )
fx
như sau:
Từ bảng biến thiên ta thấy đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm khi
( )
1
có
đúng 1 nghiệm
11a −
.
Do
a
nguyên âm nên
10, 9, 8,..., 1a − − − −
. Vậy có 10 giá trị của
a
thỏa mãn yêu cầu bài
toán
Câu 17: Có bao nhiêu giá trị nguyên thuộc
2020;2021−
của hàm số
m
để đường thẳng
1y mx m= − −
cắt đồ thị của hàm số
32
3y x x x= − +
tại ba điểm phân biệt
,,A B C
sao cho
AB BC=
.
A.
2021
. B.
2023
. C.
2024
. D.
2022
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm
( )
3 2 3 2
3 1 3 1 1 0x x x mx m x x m x m− + = − − − + − + + =
.
( )
( )
( )
2
2
1
1 2 1 0
2 1 0 1
x
x x x m
x x m
=
− − − − =
− − − =
Để để đường thẳng
1y mx m= − −
cắt đồ thị hàm số
32
3y x x x= − +
tại ba điểm phân biệt
A
,
B
,
C
thì phương trình
( )
1
có hai nghiệm phân biệt khác
1
20
2
20
m
m
m
+
−
− −
.
Khi đó phương trình
( )
1
có hai nghiệm
12
,xx
thỏa mãn
12
2xx+=
với mọi tham số
m
.
Trường hợp 1:
1
B
x =
.
Khi đó yêu cầu bài toán trở thành
( )
12
12
12
12
2
2
2
2 2 2
22
A C B
A C B
xx
x x x
xx
m x x m
y y y y y
+=
+=
+=
+ − + =
+ = + =
.
Điều này thỏa mãn với mọi
2m −
.
Trường hợp 2:
1
B
x
và giả sử
12
xx
.
Khi đó yêu cầu bài toán trở thành
( )( )
12
12
12
12
12
2
12
2 2 1 *
2 1 2
A C B
A C B
xx
x x x
xx
mx m mx m
y y y y y
+=
+=
+=
− + = − +
+ = + =
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Ta có hệ
1 2 2
1 2 1
1 2 1
21
x x x
x x x
+ = =
+ = =
không thỏa mãn yêu cầu bài toán.
Vậy giá trị
m
cần tìm là
2m −
.
Vì
, 2020;2021 1;2021m m m − −
có
2023
giá trị của
m
.
Câu 18: Cho bao nhiêu giá trị
m
để đồ thị hàm số
32
2y x mx m= − + −
cắt trục
Ox
tại
3
điểm phân biệt
có hoành độ lập thành cấp số cộng.
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm:
32
20x mx m− + − =
(*).
Giả sử phương trình (*) có
3
nghiệm phân biệt
1
x
,
2
x
,
3
x
theo thứ tự lập thành một cấp số
cộng, theo tính chất của cấp số cộng ta có:
1 3 2
2x x x+=
.
Áp dụng định lí Vi-et ta có:
1 2 3 2 2
3
3
m
x x x m x m x+ + = = =
.
Vì
2
3
m
x =
là một nghiệm của phương trình (*) nên ta có:
32
. 2 0
33
mm
mm
− + − =
3
0
2 54 0 3 3
33
m
m m m
m
=
− = =
=−
.
Thử lại:
+ Với
0m =
, phương trình trở thành:
3
00xx− = =
( loại).
+ Với
33m =
, phương trình trở thành:
1
32
2
3
33
3 3 6 3 0 3
33
x
x x x
x
= − +
− + − = =
=+
và
3
nghiệm
này lập thành 1 CSC.
+ Với
33m =−
, phương trình trở thành:
1
32
2
3
33
3 3 6 3 0 3
33
x
x x x
x
= − −
− − + = = −
=−
và
3
nghiệm
này lập thành 1 CSC.
Vậy có
2
giá trị của
m
thỏa yêu cầu bài toán là
33m =
và
33m =−
.
Câu 19: Cho hàm số bậc ba
( )
y f x=
liên tục trên và có đồ thị như hình vẽ bên.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
Tổng tất cả các giá trị nguyên của tham số
m
để phương trình
( )
( )
2 cosf f x m=
có nghiệm
;
2
x
A.
1−
. B.
0
. C.
1
. D.
2−
.
Lời giải
Chọn D
Đặt
cos ,tx=
do
;
2
x
nên suy ra
(
1;0t −
.
Trên khoảng
( )
1;0−
hàm số nghịch biến nên suy ra
Với
(
1;0t −
thì
( ) ( ) ( )
01f f t f −
hay
( )
02ft
.
Đặt
( )
2 cosu f x=
thì
( )
)
2 , 0;2u f t u=
. Khi đó bài toán trở thành:
Tìm
m
để phương trình
( )
f u m=
có nghiệm
)
0;2u
.
Quan sát đồ thị ta thấy rằng với
)
0;2u
thì
( )
)
2;2 2 2f u m − −
.
Vì
2; 1;0;1 2m m m − − = −
.
Câu 20: Gọi S là tập hợp các số nguyên m để phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
có ba
nghiệm lập thành một cấp số nhân. Tổng các phần tử của S bằng
A.
0
. B.
2−
. C.
3
. D.
1−
.
Lời giải
Chọn C
Giả sử
1 2 3
,,x x x
là ba nghiệm của phương trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
.
Khi đó ta có
( )( )( )
32
1 2 3
(2 1) 2(3 2) 8x m x m x x x x x x x− + + − − = − − −
Ta có
( )
1 2 3
1 2 3
1 2 2 3 3 1
21
8
2 3 2
x x x m
x x x
x x x x x x m
+ + = +
=
+ + = +
Do
1 2 3
,,x x x
lập thành một cấp số nhân nên ta có
1 2 3 2
82x x x x= =
.
Thay
2
2x =
vào phuognw trình
32
(2 1) 2(3 2) 8 0x m x m x− + + − − =
ta có
( ) ( )
8 2 1 .4 4 3 2 8 0 4 12 3m m m m− + + − − = = =
.
Thử lại với
3m =
ta thấy thỏa mãn. Vậy
3m =
. Dó đó tổng tất cả các giá trị của
m
bằng
3
Câu 21: Cho hàm số
3
1
( ) 8 ,
2
f x x mx m x= − + −
với
m
là một hằng số khác
0
. Biết rằng phương
trình
( ) 0fx=
có đúng 2 nghiệm phân biệt thì có bao nhiêu giá trị nguyên dương
k
thỏa mãn
phương trình
()f x k=
có 3 nghiệm phân biệt?
A.
3
. B.
6
. C.
34
. D.
31
.
Lời giải
Chọn D
( )
2
( ) 0 2 2 4 0
2
m
pt f x x x x
= − + + − =
có đúng 2 nghiệm phân biệt
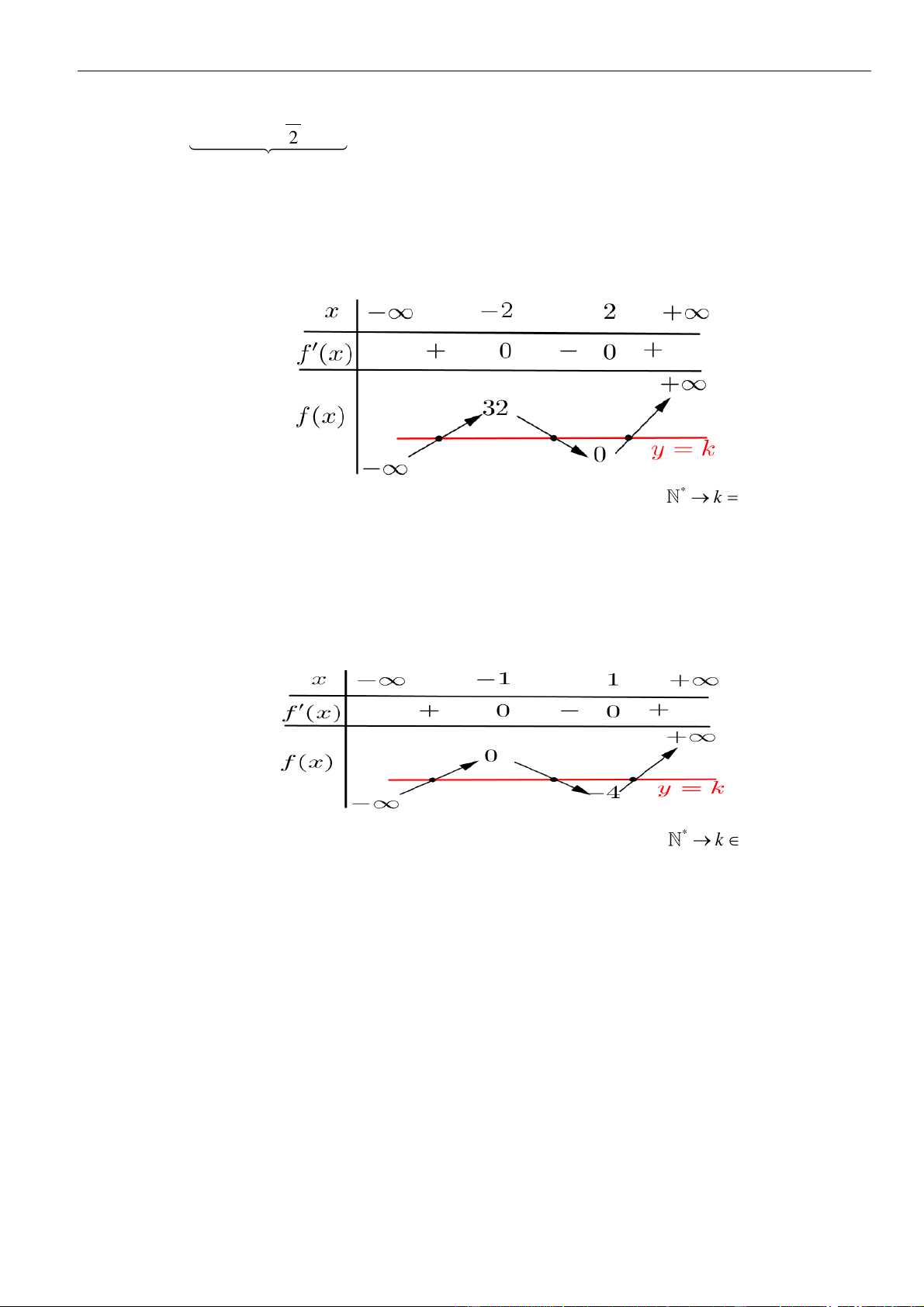
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
( )
2
()
2
2 4 0 1
2
gx
x
m
xx
=
+ + − =
có đúng 2 nghiệm phân biệt
+
(2) 0 24gm= =
( nhận )
32
( ) 12 16 '( ) 3 12f x x x f x x= − + → = −
'( ) 0 2f x x= =
BBT
Phương trình
()f x k=
có 3 nghiệm phân biệt khi
0 32k
và
*
1;2;3;....;31kk → =
+
( )
1Pt
có nghiệm kép và khác
2
0
6
(2) 0
m
g
=
=
( nhận )
32
( ) 3 2 '( ) 3 3f x x x f x x= − − → = −
'( ) 0 1f x x= =
BBT
Phương trình
()f x k=
có 3 nghiệm phân biệt khi
40k−
và
*
kk →
Vậy có
31
giá trị
k
thỏa điều kiện bài toán.
Câu 22: Cho hàm số
32
( 2) (2 13) 2y x m x m x m= − + − + − −
có đồ thị
( ),
m
C
đường thẳng
:8d y mx m= + +
và điểm
( )
1;4 .I
Tính tổng tất cả các giá trị của tham số
,m
biết rằng đường
thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
với
A
có hoành độ bằng
2−
và tam giác
IBC
cân tại
.I
A.
12−
. B.
6−
. C.
4−
. D.
10−
.
Lời giải
Chọn B
+ Phương trình hoành độ giao điểm của
d
và
()
m
C
là:
3
2
( 2) (3 13) 2 10 0 1
5
x
x m x m x m x
xm
=−
− + − + − − = = −
=+

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
+ Để đường thẳng
d
cắt đồ thị
()
m
C
tại ba điểm phân biệt
,,A B C
thì
7
6
m
m
−
−
+ Giả sử
2
( 1;8), ( 5; 6 8)B C m m m− + + +
. Để tam giác
IBC
cân tại
I
thì
2 2 2 2 2
2
20 ( 4) ( 6 4) 6( )
23
m
IB IC m m m m l
m
=−
= = + + + + = −
= −
Vậy có ba giá trị của m thỏa mãn nên tổng các giá trị của m bằng
6−
.
Câu 23: Gọi
d
là đường thẳng đi qua
( )
2;0A
có hệ số góc
( )
0mm
cắt đồ thị
( )
32
: 6 9 2C y x x x= − + − +
tại ba điểm phân biệt
, , .A B C
Gọi
,BC
lần lượt là hình chiếu
vuông góc của
,BC
lên trục tung. Biết rằng hình thang
BB C C
có diện tích bằng
8,
giá trị của
m
thuộc khoảng nào sau đây?
A.
( )
5;8
. B.
( )
5;0−
. C.
( )
0;2
. D.
( )
1;5
.
Lời giải
Chọn D
Phương trình đường thẳng
( )
: 2 .d y m x=−
Phương trình hoành độ giao điểm
( ) ( )
( )
( )
3 2 2
2
2 2;0
6 9 2 2 2 4 1 0 .
4 1 0
xA
x x x m x x x x m
x x m
=
− + − + = − − − + + =
− + + =
Để
( )
C
cắt
d
tại 3 điểm phân biệt thì
0 4 1 0 3.mm − −
Giả sử
( ) ( )
12
1 1 2 2
12
4
, 2 , , 2 .
1
xx
B x mx m C x mx m
x x m
+=
− −
=+
Ta có
( ) ( )
12
0, 2 , 0, 2 .B mx m C mx m
−−
( ) ( )
''
1
' 8 16.
2
BB C C
S B C BB CC B C BB CC
= + = + =
Mà
( )
1 2 1 2
, , .B C m x x BB x CC x
= − = =
Do
m
dương nên
12
10x x m= +
mà
1 2 1 2
4 0 0, 0.x x x x+ =
( )
1 2 1 2 1 2 1 2 1 2
' ' , ' , ' 16 4B C m x x BB x CC x m x x x x m x x = − = = − + = − =
( ) ( ) ( )
22
2 2 2
1 2 1 2 1 2
16 4 16 16 4 4 16m x x m x x x x m m
− = + − = − − =
( )
32
1
3 4 0
2
ml
mm
m
=−
− + =
=
Câu 24: Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình vẽ
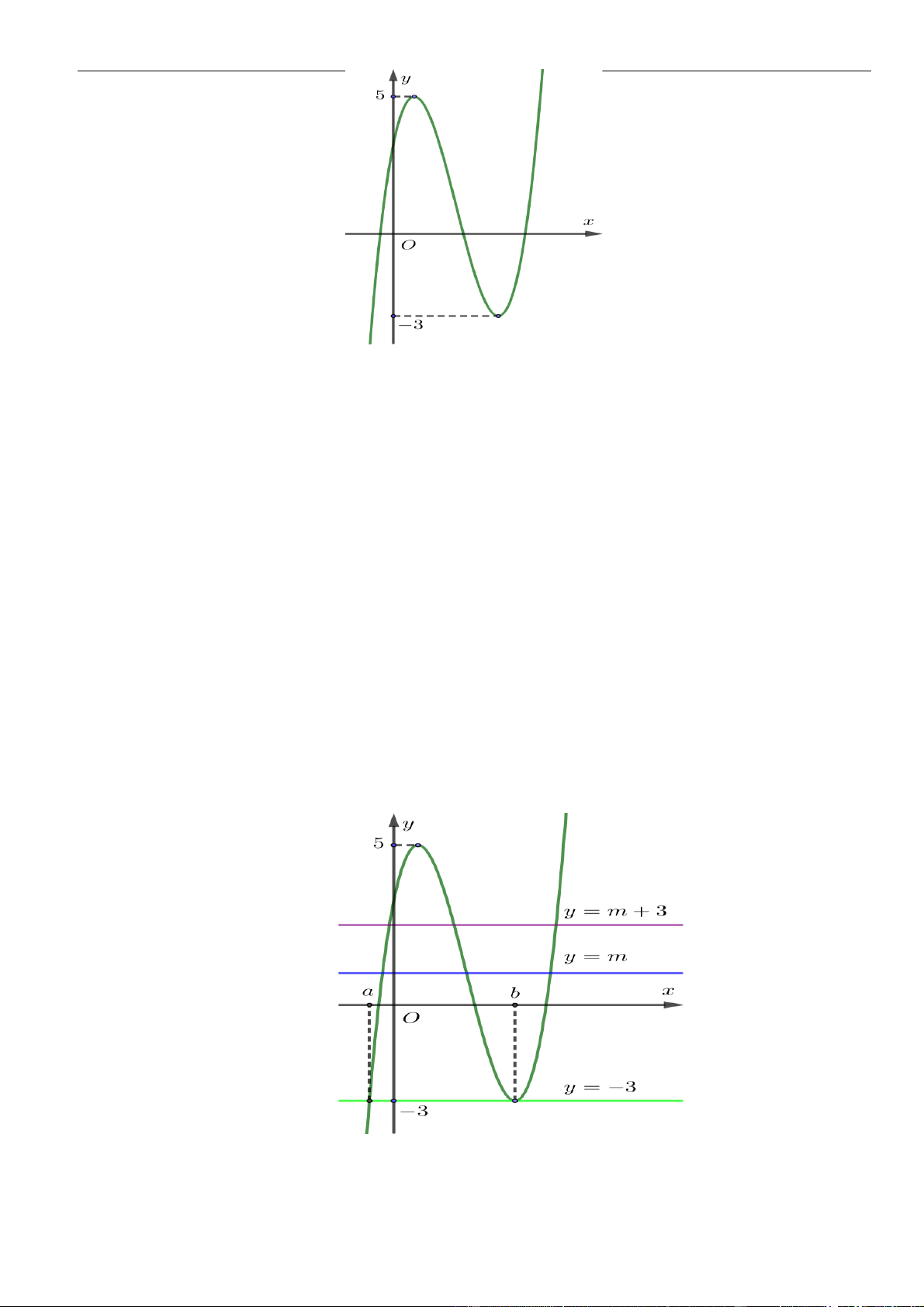
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
có đúng
8
nghiệm phân biệt?
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn B
( ) ( )
( )
( )
3 2 2 2
2 3 9 3 9 0f x mf x m m f x m m− + − − + + =
Đặt
( )
t f x=
, phương trình trở thành:
( )
3 2 2 2
2 3 9 3 9 0t mt m m t m m− + − − + + =
( ) ( )
22
3 2 3 3 0t t m t m m
+ − + + + =
( )( )( )
3 3 0t t m t m + − − − =
( ) ( )
( ) ( )
( ) ( )
31
3
2
3
33
fx
t
t m f x m
tm
f x m
=−
=−
= =
=+
=+
Nhận xét các phương trình
( )
2
và
( )
3
không có nghiệm chung.
Dựa vào đồ thị, ta thấy:
( )
1
xa
xb
=
=

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
YCBT
Các phương trình
( )
2
và
( )
3
đều có 3 nghiệm phân biệt khác
,ab
3 5 2
32
33
mm
m
mm
+
−
− −
Mà
m
là số nguyên nên
2; 1;0;1m − −
.
Câu 25: Gọi
S
là tập hợp chứa tất cả các giá trị thực của tham số
m
để đồ thị hàm số
( ) ( ) ( )
32
6 1 3 2 1 2f x x m x m x= − + + + +
cắt trục
Ox
tại ba điểm phân biệt có hoành độ lớn hơn
1−
.
Biết rằng
;
a
S
b
−
= +
; trong đó
,ab
là các số nguyên dương và phân số
a
b
là tối giản. Giá trị
biểu thức
T a b=+
tương ứng bằng
A.
4
. B.
8
. C.
5
. D.
7
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm:
( ) ( )
32
6 1 3 2 1 2 0x m x m x− + + + + =
( ) ( )
( )
2
1 6 5 2 0x x m x − − + − =
( ) ( )
2
1
6 5 2 0 *
x
x m x
=
− + − =
Yêu cầu bài toán tương đương với phương trình
( )
*
có hai nghiệm phân biệt
12
;xx
lớn hơn
1−
và khác
1
.Ta có:
( )( )
( )
2
12
12
2
0
36 60 33 0
2
6 5 2
2
1 1 0
3
6 4 0
1
1 6 5 2 0
mm
xx
m
m
xx
m
m
m
+ +
+ −
+ −
−
+ +
+
−
− + −
Do đó
2; 3 5a b T a b= = = + =
Câu 26: Điều kiện cần và đủ của tham số thực
m
để đường thẳng
32y x m= + −
cắt đồ thị hàm số
( )
3
1yx=−
tại ba điểm phân biệt là
A.
31m−
. B.
31m−
. C.
13m−
. D.
13m−
.
Lời giải
Chọn B
Xét phương trình:
( )
3
32
321 31x mx m x x= + − − +− =
(*).
Đường thẳng
32y x m= + −
cắt đồ thị
( )
3
1yx=−
tại ba điểm phân biệt khi và chỉ khi phương
trình (*) có ba nghiệm phân biệt.
Đặt
( ) ( )
3 2 2
0
3 1 ' 3 6 0
2
x
f x x x f x x x
x
=
= − + = − =
=
.
Ta có bảng biến thiên

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Từ bảng biến thiên suy ra phương trình (*) có ba nghiệm phân biệt khi và chỉ khi đường thẳng
ym=
cắt đồ thị hàm số
( )
32
31f x x x= − +
tại ba điểm phân biệt. Vậy
31m−
.
Câu 27: Cho hàm số
32
3y x x m= + +
có đồ thị
( )
C
. Biết đồ thị
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
. Phát biểu nào sau đây đúng?
A.
( )
4;0m−
. B.
( )
0;m +
. C.
( )
;4m − −
. D.
( )
4; 2m − −
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là
( )
32
3 0 1x x m+ + =
.
Giả sử
( )
1
có 3 nghiệm phân biệt
( )
1 2 3 1 2 3
;;x x x x x x
thì
1 2 3
;;x x x
lần lượt là hoành độ của
,,A B C
và
( )( )( )
32
1 2 3
3x x m x x x x x x+ + = − − −
( ) ( )
3 2 3 2
1 2 3 1 2 2 3 3 1 1 2 3
3x x m x x x x x x x x x x x x x x x + + = − + + + + + −
Nên ta có
1 2 3
3x x x+ + = −
.
Để
B
là trung điểm
AC
thì
1 3 2
2x x x+=
nên
22
3 3 1xx= − = −
.
Tức là
( )
1
có 1 nghiệm là
1x =−
. Suy ra
1 3 0 2mm− + + = = −
.
Thử lại với
2m =−
thì
( )
1
trở thành
32
13
3 2 0 1
13
x
x x x
x
= − −
+ − = = −
= − +
(thỏa điều kiện bài toán).
Cách 2: Ta có
2
36y x x
=+
và
66yx
=+
nên
( )
C
có điểm uốn
( )
1; 2Im−+
.
Để
( )
C
cắt trục hoành tại 3 điểm phân biệt
,,A B C
sao cho
B
là trung điểm
AC
thì
I Ox
2 0 2mm + = = −
.
Câu 28: Cho hàm số
32
21y x x= − −
có đồ thị
( )
C
, đường thẳng
( )
d
:
1y mx=−
và điểm
(4;11)K
. Biết
rằng
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
trong đó
(0; 1)A −
còn trọng tâm tam
giác
KBC
nằm trên đường thẳng
21yx=+
. Mệnh đề nào sau đây đúng?
A.
4m =
. B.
2m =
. C.
3m =
. D. Không tồn tại
m
Lời giải

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Chọn C
Xét phương trình hoành độ:
3 2 3 2
2
0
2 1 1 2 0
2 0(1)
x
x x mx x x mx
x x m
=
− − = − − − =
− − =
Suy ra
(0; 1)A −
và hoành độ của điểm
B
và
C
là nghiệm của phương trình (1)
Để
( )
C
và
( )
d
cắt nhau tại ba điểm phân biệt
,,A B C
khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt khác 0
Khi và chỉ khi:
+ −
(1)
'0
1 m 0 m 1
(*)
m 0 m 0
m0
Giả sử:
11
( ;m 1)B x x −
,
22
( ;m 1)C x x −
. Theo Vi–ét ta có
12
2xx+=
Gọi
G
là trọng tâm của tam giác
KBC
:
++
=
=
+
+
+ − + −
=
=
12
G
G
12
G
G
4 x x
x2
x
2m 9
3
G 2;
2m 9
11 mx 1 mx 1
3
y
y
3
3
Trọng tâm
G
nằm trên đường thẳng
21yx=+
suy ra
29
2.2 1 3
3
m
m
+
= + =
thỏa mãn
( )
*
Câu 29: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại 3 điểm phân biệt
1
x
,
2
x
,
3
x
sao cho
222
1 2 3
4xxx+ +
.
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
( )
C
và trục hoành là:
( ) ( )
( )
( )
3 2 2
2
1
2 1 0 1 0
0*
x
x x m x m x x x m
x x m
=
− + − + = − − − =
− − =
.
( )
C
cắt trục hoành tại 3 điểm phân biệt
( )
*
có hai nghiệm phân biệt khác 1
2
1
1 4 0
4
1 1 0
0
m
m
m
m
+
−
− −
.
Khi đó
1
1x =
,
2
x
và
3
x
là hai nghiệm của
( )
*
.
( )
2
222
1 2 3 2 3 2 3
4 2 3 1 2 3 1x x x x x x x m m+ + + − +
.
Vậy các giá trị cần tìm của
m
là
1
1
4
0
m
m
−
.
Câu 30: Cho hàm số
( )
32
21y x x m x m= − + − +
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để
( )
C
cắt trục hoành tại
3
điểm phân biệt
1 2 3
,,x x x
sao cho
222
1 2 3
4xxx+ +
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
A.
1
1
4
0
m
m
−
. B.
1m
. C.
1
1
4
m−
. D.
1
1
4
m
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm:
( ) ( )
( )
( )
3 2 2
2 1 0 1 0 1x x m x m x x x m− + − + = − − − =
( )
3
2
1
02
x
x x m
=
− − =
. Điều kiện để phương trình
( )
1
có 3 nghiệm phân biệt là phương trình
( )
2
có 2 nghiệm phân biệt khác
1
0
1
1
1 4 0
4
m
x
m
m
= +
−
.
Khi đó phương trình
( )
2
có 2 nghiệm phân biệt
12
,xx
.
Ta có
( )
2
2 2 2 2 2
1 2 3 1 2 1 2 1 2
4 3 2 3x x x x x x x x x+ + + + −
2
1 2 3 1mm +
.
Vậy
1
1
4
0
m
m
−
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Tìm giá trị tham số của
m
để đồ thị hàm số
42
(3 ) 7y x m x= − − −
đi qua
( )
2;1A −
.
A.
5m =
. B.
0m =
. C.
1m =
. D.
1m =−
.
Câu 2: Cho hàm số
42
42y x x= − −
có đồ thị
( )
C
và đường thẳng
:d y m=
. Tất cả các giá trị của tham
số
m
để
d
cắt
( )
C
tại bốn điểm phân biệt là
A.
26m
. B.
62m− −
. C.
62m− −
. D.
26m
.
Câu 3: Cho hàm số
42
42y x x= − −
có đồ thị
( )
C
và đường thẳng
:d y m=
. Tất cả các giá trị của tham
số
m
để
d
cắt
( )
C
tại bốn điểm phân biệt là
A.
26m
. B.
62m− −
. C.
62m− −
. D.
26m
.
Câu 4: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
30x x m− + =
có
4
nghiệm thực
phân biệt?
A.
1
. B.
4
. C.
2
. D.
0
.
Câu 5: Biết đồ thị hàm số
( )( )
( )
2
1 1 7y x x x m= − + − −
cắt trục hoành tại 4 điểm phân biệt có hoành độ
là
1 2 3 4
, , , .x x x x
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để
1 2 3 4
1 1 1 1
1.
1 1 1 1x x x x
+ + +
− − − −
A.
9
. B.
8
. C.
6
. D.
7
.
Câu 6: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho tam
giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Câu 7: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
2 3 2 0x x m− + − =
có
nghiệm thuộc
( )
2;2−
?
A.
4
. B.
3
. C.
5
. D.
6
.
Câu 8: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho
tam giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Câu 9: Đồ thị của hàm số
( )
42
2 1 2 1y x m x m= − + + +
cắt trục hoành tại bốn điểm phân biệt có hoành
độ lập thành một cấp số cộng. Mệnh đề nào dưới đây đúng?
A.
( )
6;9m
. B.
( )
6; 3m − −
. C.
( )
3;2m−
. D.
( )
2;6m
.
Câu 10: Cho hàm số
( )
42
3 2 3y x m x m= − + +
có đồ thị
( )
m
C
. Xác định tất cả các giá trị của tham số
thực
m
để
( )
m
C
cắt đường thẳng
1y =−
tại bốn điểm phân biệt
Tìm m liên quan đến tương giao hàm trùng phương
DẠNG 6
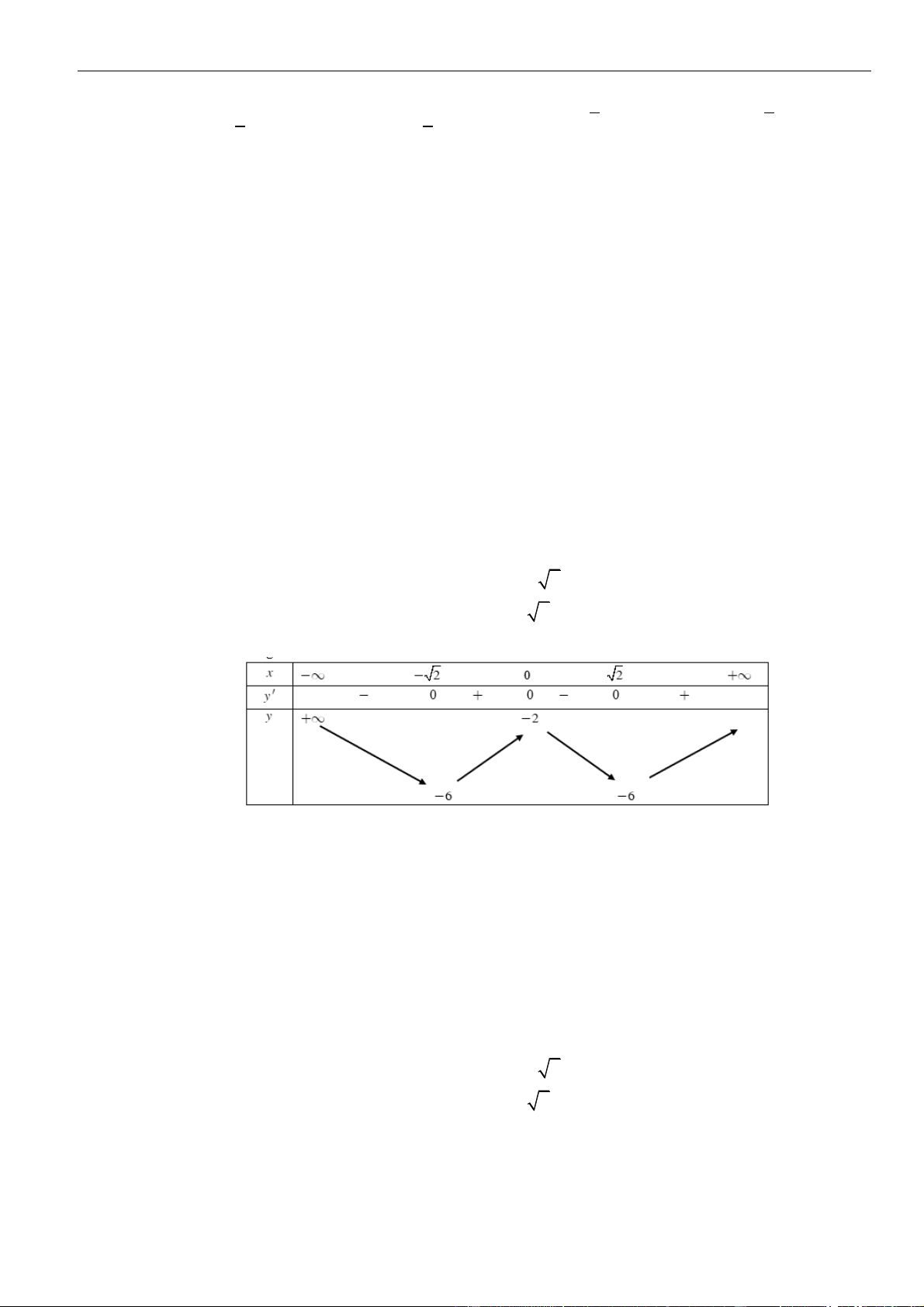
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
0
1
3
m
m
−
. B.
0
1
3
m
m
−
. C.
1
3
m −
. D.
1
3
m −
.
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Tìm giá trị tham số của
m
để đồ thị hàm số
42
(3 ) 7y x m x= − − −
đi qua
( )
2;1A −
.
A.
5m =
. B.
0m =
. C.
1m =
. D.
1m =−
.
Lời giải
Chọn C
Đồ thị hàm số đi qua điểm
( )
2;1A −
nên ta có
42
1 ( 2) (3 )( 2) 7 4 4 1m m m= − − − − − = =
.
Câu 2: Cho hàm số
42
42y x x= − −
có đồ thị
( )
C
và đường thẳng
:d y m=
. Tất cả các giá trị của tham
số
m
để
d
cắt
( )
C
tại bốn điểm phân biệt là
A.
26m
. B.
62m− −
. C.
62m− −
. D.
26m
.
Lời giải
Chọn B
42
42y x x= − −
có
32
48y x x
=−
;
0
02
2
x
yx
x
=
= = −
=
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy để đồ thị hàm số
42
42y x x= − −
cắt đường thẳng
:d y m=
tại 4
điểm phân biệt
62m − −
.
Câu 3: Cho hàm số
42
42y x x= − −
có đồ thị
( )
C
và đường thẳng
:d y m=
. Tất cả các giá trị của tham
số
m
để
d
cắt
( )
C
tại bốn điểm phân biệt là
A.
26m
. B.
62m− −
. C.
62m− −
. D.
26m
.
Lời giải
Chọn B
42
42y x x= − −
có
32
48y x x
=−
;
0
02
2
x
yx
x
=
= = −
=
.
Bảng biến thiên:
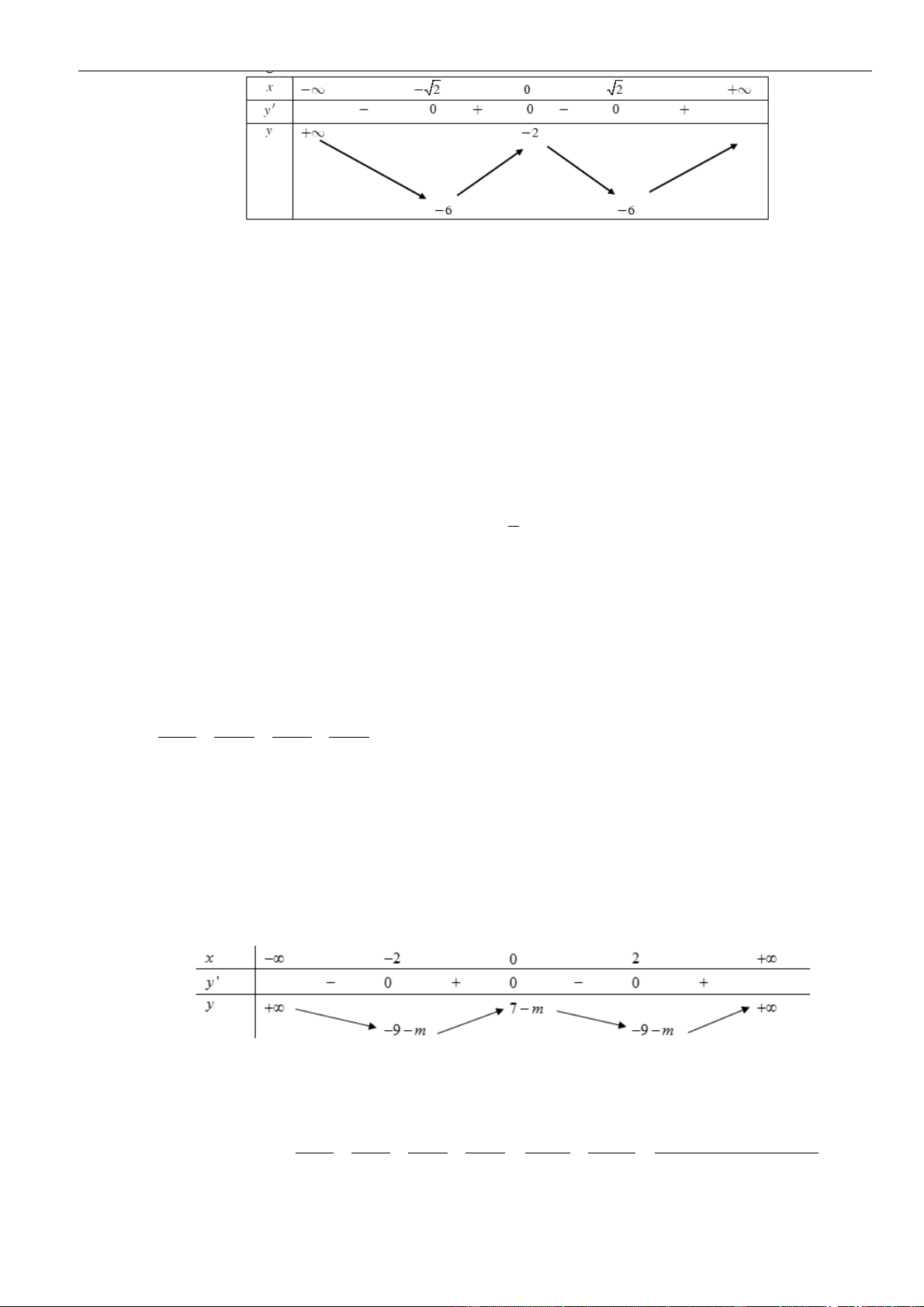
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Từ bảng biến thiên ta thấy để đồ thị hàm số
42
42y x x= − −
cắt đường thẳng
:d y m=
tại 4
điểm phân biệt
62m − −
.
Câu 4: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
30x x m− + =
có
4
nghiệm thực
phân biệt?
A.
1
. B.
4
. C.
2
. D.
0
.
Lời giải
Chọn C
Đặt
( )
2
0t x t=
. Ta được phương trình
( )
2
3 0, 1t t m− + =
.
Phương trình đã cho có
4
nghiệm thực phân biệt khi và chỉ khi phương trình có 2 nghiệm dương
phân biệt
0 9 4 0
9
0 3 0 0
4
00
m
Sm
Pm
−
.
Do
m
nguyên nên
1;2m
.
Vậy có 2 giá trị nguyên của tham số
m
thoả mãn yêu cầu bài toán.
Câu 5: Biết đồ thị hàm số
( )( )
( )
2
1 1 7y x x x m= − + − −
cắt trục hoành tại 4 điểm phân biệt có hoành độ
là
1 2 3 4
, , , .x x x x
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để
1 2 3 4
1 1 1 1
1.
1 1 1 1x x x x
+ + +
− − − −
A.
9
. B.
8
. C.
6
. D.
7
.
Lời giải
Chọn C
Ta có
( )( )
( )
2 4 2
1 1 7 8 7y x x x m x x m= − + − − = − + −
.
Mặc khác ta có
3
0
' 4 16 0
2
x
y x x
x
=
= − =
=
. Ta có bảng biến thiên như sau:
Để phương trình có 4 nghiệm phân biệt thì
97m−
. Vì hàm số chẵn nên có 2 cặp nghiệm đối
xứng. Giả sử
12
0xx+=
và
34
0xx+=
.
Theo đề bài ta có:
( )
( )
22
31
22
2 2 2 2
1 1 3 3 1 3
3 1 3 1
42
1 1 1 1 2 2
1
1 1 1 1 1 1
1.
xx
x x x x x x
x x x x
−+
+ + + = + =
− + − + − −
− + +
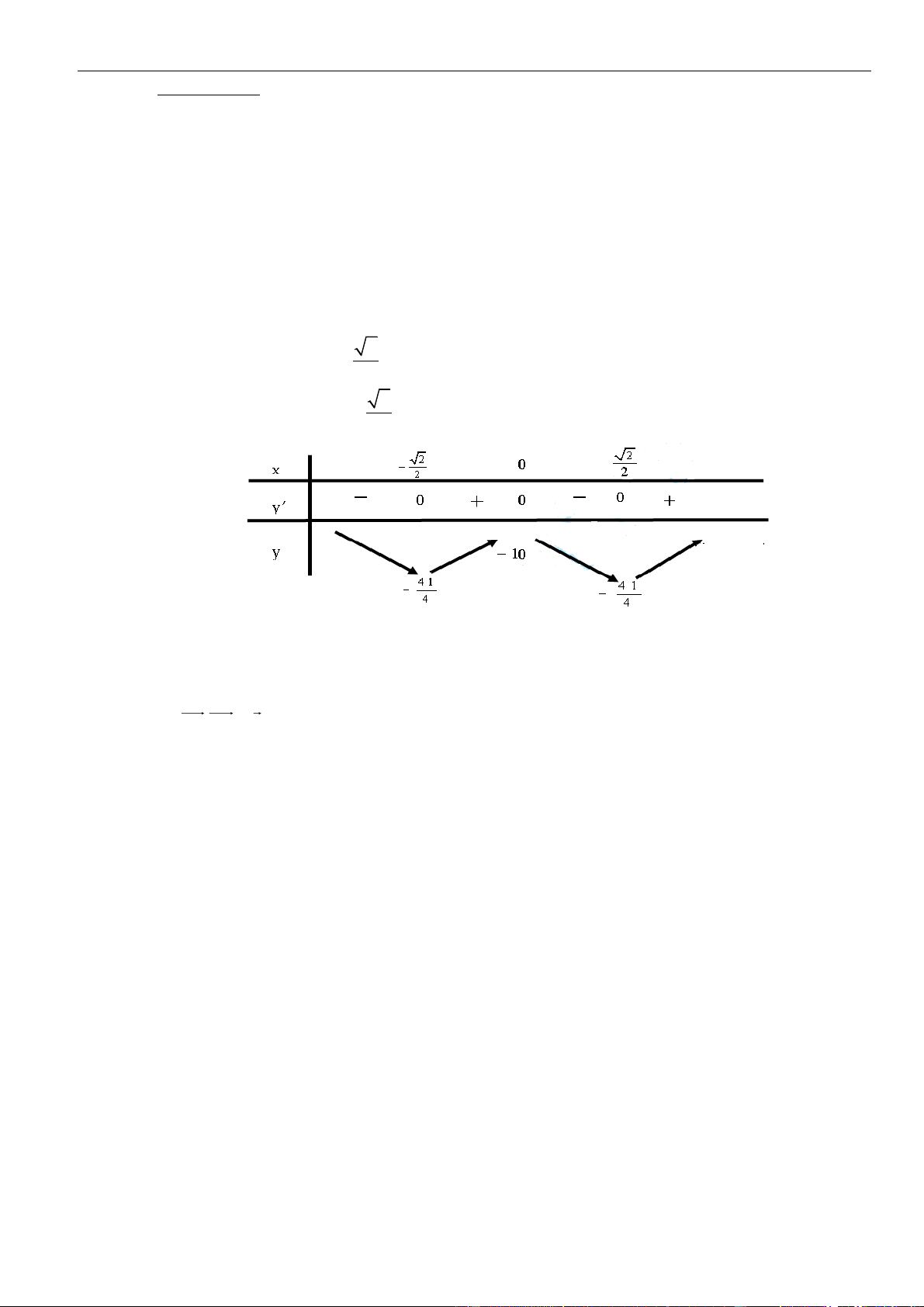
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
( )
4 2.8
1 0 12.
1 8 7
m
m
−
− + −
Kết hợp điều kiện suy ra
0 7 1;2;3;4;5;6mm
.
Câu 6: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho tam
giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Lời giải
Chọn D
Xét:
42
10y x x− −=
3
0
2
' 4 2 0
2
2
2
x
y x x x
x
=
= − = =
=−
Vì
2
0m
với mọi
m
nên từ bảng biến thiên thấy đường thẳng
2
ym=
luôn cắt đồ thị hàm số
42
10y x x− −=
tại những cặp điểm đối xứng nhau qua
Oy
. Giả sử
( ) ( )
22
11
; ; ;A x m B x m−
.Tam giác
OAB
vuông (với
O
là gốc tọa độ)
2 4 2 4 2
1 1 1
. 0 0OAOB x m x m x m = − + = = =
( )
22
;A m m
vì
( )
22
;A m m
thuộc đồ thị hàm số nên
8 4 2 2
10 2m m m m− − = =
.
Câu 7: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
2 3 2 0x x m− + − =
có
nghiệm thuộc
( )
2;2−
?
A.
4
. B.
3
. C.
5
. D.
6
.
Lời giải
Chọn C
4 2 4 2
2 3 2 0 2 3 2x x m x x m− + − = − + =
Xét
( ) ( )
42
2 3, 2;2f x x x x= − + −
( )
3
1
4 4 3 0 0
1
x
f x x x x
x
=−
= − + = =
=
Bảng biến thiên
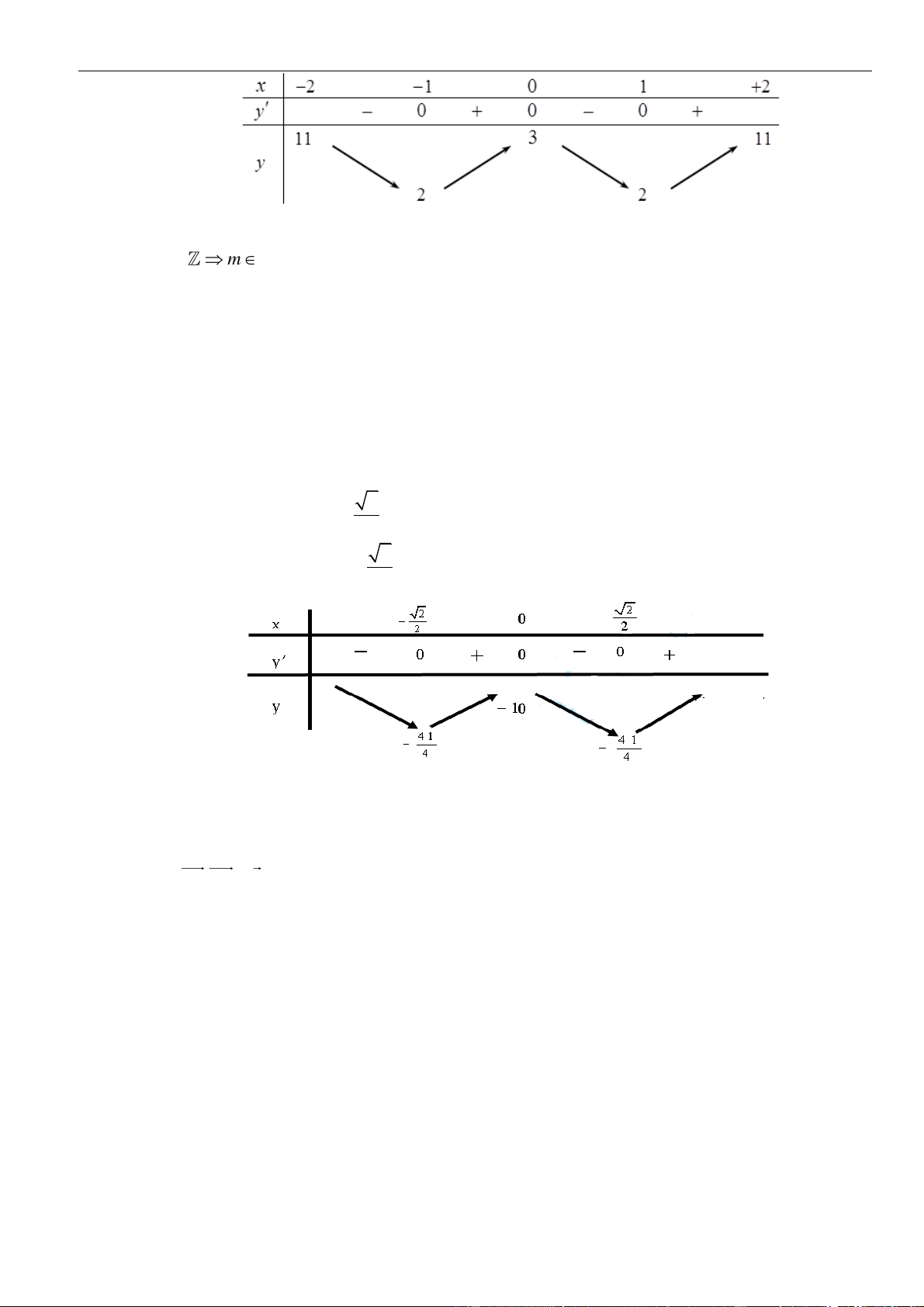
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
Theo yêu câu bài toán, có:
2 2 11 1 5,5mm
1,2,3,4,5mm
.
Câu 8: Đường thẳng
2
ym=
cắt đồ thị hàm số
42
10y x x− −=
tại hai điểm phân biệt
,AB
sao cho
tam giác
OAB
vuông (với
O
là gốc tọa độ). Mệnh đề nào sau đây đúng?
A.
( )
2
5;7m
. B.
( )
2
3;5m
. C.
( )
2
0;1m
. D.
( )
2
1;3m
.
Lời giải
Chọn D
Xét:
42
10y x x− −=
3
0
2
' 4 2 0
2
2
2
x
y x x x
x
=
= − = =
=−
Vì
2
0m
với mọi
m
nên từ bảng biến thiên thấy đường thẳng
2
ym=
luôn cắt đồ thị hàm số
42
10y x x− −=
tại những cặp điểm đối xứng nhau qua
Oy
. Giả sử
( ) ( )
22
11
; ; ;A x m B x m−
.Tam giác
OAB
vuông (với
O
là gốc tọa độ)
2 4 2 4 2
1 1 1
. 0 0OAOB x m x m x m = − + = = =
( )
22
;A m m
vì
( )
22
;A m m
thuộc đồ thị hàm số nên
8 4 2 2
10 2m m m m− − = =
.
Câu 9: Đồ thị của hàm số
( )
42
2 1 2 1y x m x m= − + + +
cắt trục hoành tại bốn điểm phân biệt có hoành
độ lập thành một cấp số cộng. Mệnh đề nào dưới đây đúng?
A.
( )
6;9m
. B.
( )
6; 3m − −
. C.
( )
3;2m−
. D.
( )
2;6m
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm:
( )
42
2 1 2 1 0x m x m− + + + =
. (1)
Đặt
2
,0t x t=
. Phương trình trở thành
( )
2
2 1 2 1 0t m t m− + + + =
. (2)

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Phương trình (1) có bốn nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm dương
phân biệt, nghĩa là
( ) ( )
2
1 2 1 0
00
1
0 1 0 1
2
0
0 2 1 0 1
2
mm
m
m
S m m
m
Pm
m
+ − +
−
+ −
+
−
.
Cách 1. Gọi
( )
1 2 3 4 1 2 3 4
, , ,x x x x x x x x
là nghiệm của phương trình (1) và
( )
1 2 1 2
,t t t t
là
nghiệm của phương trình (2).
Theo giả thiết, ta có
4 3 3 2 2 1 4 3 3 2
2 1 1 1 2 1
90
x x x x x x x x x x
t t t t t t
− = − = − − = −
− = + =
Ta có hệ
( )
1
12
1 2 2
21
12
1
55
21
4
9 9 1 9 9
2 1 2 1
4
5 5 5 5 5 5
9
9
21
m
t
t t m
m
m m m
t t m t m
m
tt
t t m
=+
+ = +
=
= + = + + + = +
=−
=
=+
(nhận)
Cách 2. Với
0
, phương trình (1) có nghiệm
12
1, 2 1t t m= = +
. Biện luận như trên, ta có hai
trường hợp
21
12
4
9
4
9
9
m
tt
tt
m
=
=
=
=−
(nhận).
Câu 10: Cho hàm số
( )
42
3 2 3y x m x m= − + +
có đồ thị
( )
m
C
. Xác định tất cả các giá trị của tham số
thực
m
để
( )
m
C
cắt đường thẳng
1y =−
tại bốn điểm phân biệt
A.
0
1
3
m
m
−
. B.
0
1
3
m
m
−
. C.
1
3
m −
. D.
1
3
m −
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm
( )
42
3 2 3 1x m x m− + + = −
( )
4 2 2
2 1 3 1 0x x m x − + − − =
( ) ( )
2
22
1 3 1 0x m x − − − =
( )( )
2
22
2
2
1, 1
10
1 3 1 0
31
3 1 0
xx
x
x x m
xm
xm
= = −
−=
− − − =
=+
− − =
Đồ thị
( )
m
C
cắt
1y =−
tại bốn điểm phân biệt khi và chỉ khi
2
31xm=+
có hai nghiệm phân
biệt khác
1
và
1−
.
Khi đó, ta có
1
3 1 0
3
3 1 1
0
m
m
m
m
+
−
+
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
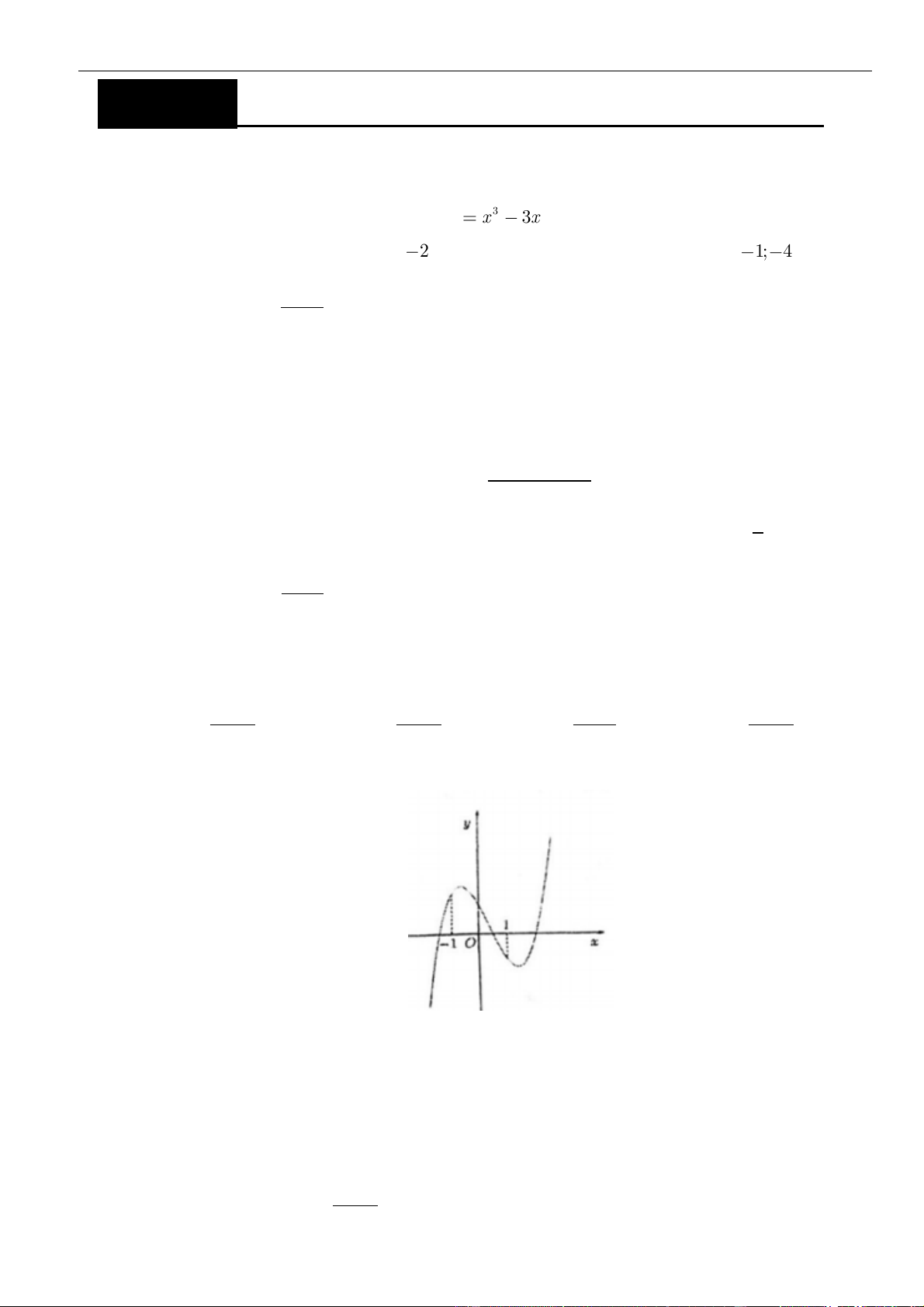
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Điểm nào sau đây thuộc đồ thị hàm số
3
3y x x
là
A.
3; 0N
. B.
1; 2M
. C.
2;14Q
. D.
1; 4P
.
Câu 2: Cho hàm số
31
2
x
y
x
−
=
+
có đồ thị
( )
H
. Điểm nào sau đây thuộc
( )
H
?
A.
( )
3;7Q −
. B.
( )
0; 1M −
. C.
( )
1; 4N −−
. D.
( )
1;1P
.
Câu 3: Điểm nào sau đây thuộc đồ thị hàm số
3
3y x x=−
?
A.
( )
3;0N
. B.
( )
1; 2M −
. C.
( )
2;14Q
. D.
( )
1; 4P −−
.
Câu 4: Với giá trị nào của
m
thì đồ thị hàm số
2
2 6 4
2
x mx
y
mx
++
=
+
đi qua điểm
( )
1;4A −
.
A.
2m =
. B.
1m =
. C.
1m =−
. D.
1
2
m =
.
Câu 5: Cho hàm số
31
2
x
y
x
−
=
+
có đồ thị
( )
H
. Điểm nào sau đây thuộc
( )
H
?
A.
( )
3;7Q −
. B.
( )
0; 1M −
. C.
( )
1; 4N −−
. D.
( )
1;1P
.
Câu 6: Đồ thị hàm số nào sau đây nhận điểm
( )
1;3I
làm tâm đối xứng
A.
23
1
x
y
x
−
=
−
. B.
34
1
x
y
x
+
=
−
. C.
41
2
x
y
x
+
=
+
. D.
32
1
x
y
x
−
=
+
.
Câu 7: Hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây là đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Câu 8: Tọa độ tâm đối xứng của đồ thị hàm số
3
32y x x= − +
.
A.
( )
0;2
. B.
( )
1;0
. C.
( )
0;0
. D.
( )
1;4−
.
Câu 9: Trên đồ thị hàm số
21
34
x
y
x
−
=
+
có bao nhiêu điểm có tọa độ nguyên?
Điểm đặc biệt của đồ thị hàm số
DẠNG 7

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
1
. B.
0
. C.
2
. D.
4
.
Câu 10: Biết rằng đồ thị hàm số
42
y ax bx c= + +
có hai điểm cực trị là
( )
0;2A
và
( )
2; 14B −
. Khi đó
( )
3f
bằng
A.
60
. B.
28−
. C.
11
. D.
155
.
Câu 11: Đồ thị hàm số nào sau đây nhận điểm
(1;3)I
làm tâm đối xứng?
A.
23
1
x
y
x
−
=
−
. B.
34
1
x
y
x
+
=
−
C.
41
2
x
y
x
+
=
+
. D.
32
1
x
y
x
−
=
+
.
Câu 12: Đồ thị hàm số
42
2y x x= − −
cắt trục
Oy
tại điểm
A.
( )
0; 2A
. B.
( )
2;0A −
. C.
( )
0; 2A −
. D.
( )
0; 2A −
.
Câu 13: Cho hàm số
42
y x mx m= − +
có đồ thị
( )
C
. Tìm tham số
m
để
( )
C
đi qua điểm
( )
2;16A
.
A.
2m =−
. B.
2m =
. C.
1m =
. D.
0m =
.
Câu 14: Cho hàm số
21
2
x
y
x
+
=
−
có đồ thị là
()C
. Số điểm thuộc
()C
có hoành độ và tung độ đều là các
số nguyên là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 15: Tìm tọa độ tâm đối xứng của đồ thị hàm số
3
32= − +y x x
.
A.
( )
0;2
. B.
( )
1;0
. C.
( )
0;0
. D.
( )
1;4−
.
Câu 16: Cho hàm số
2
1
x
y
x
+
=
−
có đồ thị
( )
C
. Tâm đối xứng của đồ thị
( )
C
là điểm có tọa độ
A.
( )
1;2
. B.
( )
2;1−
. C.
( )
3; 2−
. D.
( )
1;1
.
Câu 17: Tâm đối xứng của đồ thị hàm số
31
2
x
y
x
−
=
+
là điểm có tọa độ nào sau đây?
A.
( )
2;3−
. B.
( )
3; 2−
. C.
( )
2; 1−
. D.
( )
1;2−
.
Câu 18: Cho hàm số
32x
y
x
−
=
có đồ thị
( )
C
. Có tất cả bao nhiêu đường thẳng cắt
( )
C
tại hai điểm
phân biệt mà hoành độ và tung độ của hai giao điểm này đều là các số nguyên?
A.
10
. B.
4
. C.
6
. D.
2
.
Câu 19: Cho hàm số
32
( ) 3 3y f x x x= = − +
có độ thị
( )
C
. Gọi
A
và
B
là hai điểm nằm trên
( )
C
và
đối xứng nhau qua gốc tọa độ
O
. Độ dài
AB
bằng
A.
22
. B.
4
. C.
23
. D.
42
.
Câu 20: Cho hàm số
32
1
x
y
x
có đồ thị là
C
và
2
điểm
4;2 ; 2; 8AB
. Điểm
;M a b C
sao cho trực tâm
H
của tam giác
MAB
thuộc vào đường thẳng
: 5 4 3 0d x y
. Tính giá trị của biểu thức
2
43S a b
?
A.
9S
. B.
6S
. C.
10S
. D.
12S
.
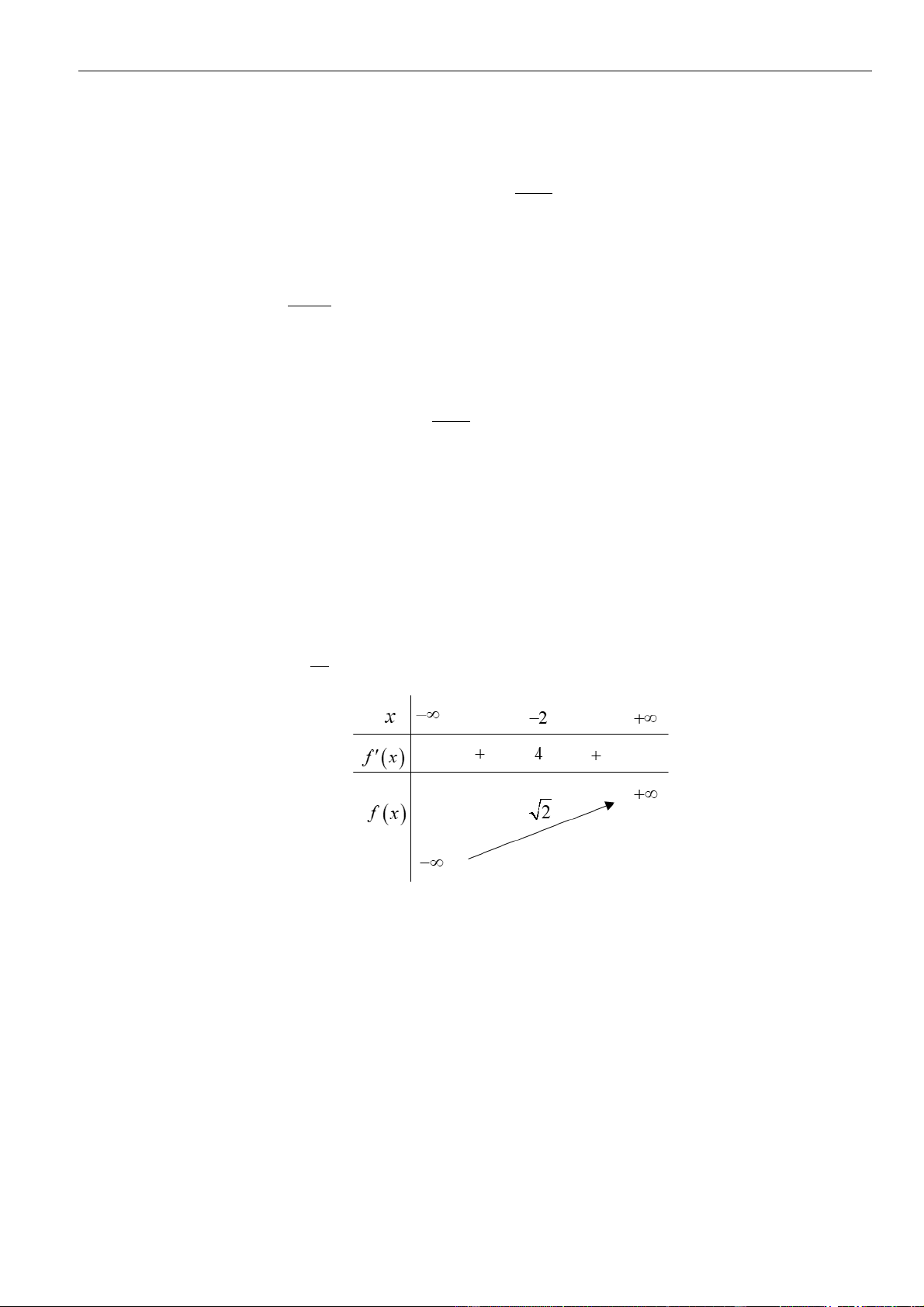
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Câu 21: Cho hàm số
32
4y x x= + −
có đồ thị
( )
C
. Có bao nhiêu cặp điểm
,AB
thuộc
( )
C
sao cho ba
điểm
,,O A B
thẳng hàng và
2OA OB=
(
O
là gốc tọa độ).
A. Vô số. B.
1
. C.
2
. D.
4
.
Câu 22: Có bao nhiêu điểm
M
thuộc đồ thị hàm số
2
1
x
y
x
+
=
−
sao cho khoảng cách từ điểm
M
đến trục
tung bằng hai lần khoảng cách từ điểm
M
đến trục hoành
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 23: Cho hàm số
21
2
x
y
x
+
=
+
có đồ thị
( )
C
. Gọi
( )
;M a b
là điểm trên
( )
C
có khoảng cách đến
đường thẳng
: 3 6d y x=+
nhỏ nhất. Khẳng định nào sau đây đúng
A.
2ab−=
. B.
2ab+=
. C.
2ab+ = −
. D.
2ab− = −
.
Câu 24: Tịnh tiến liên tiếp đồ thị hàm số
5
2
y
x
−
=
+
theo trục
Oy
lên trên 2 đơn vị và theo
Ox
sang trái
3 đơn vị ta được đồ thị hàm số
( )
y g x=
. Có bao nhiêu điểm trên đồ thị
( )
y g x=
có các tọa độ
đều là số nguyên?
A.
4
. B.
2
. C.
1
. D.
0
.
Câu 25: Cho hàm số
32
4y x x= + −
có đồ thị
( )
C
. Có bao nhiêu cặp điểm
A
,
B
thuộc
( )
C
sao cho ba
điểm
O
,
A
,
B
thẳng hàng và
2OA OB=
(
O
là gốc tọa độ)?
A. Vô số. B.
1
. C.
2
. D.
4
.
Câu 26: Cho hàm số
( )
3
2
3
x
f x ax bx c= + + +
có bảng biến thiên như sau
Hỏi có bao nhiêu số dương trong các hệ số
,,abc
?
A.
2
. B.
0
. C.
3
. D.
1
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Điểm nào sau đây thuộc đồ thị hàm số
3
3y x x
là
A.
3; 0N
. B.
1; 2M
. C.
2;14Q
. D.
1; 4P
.
Lời giải
Chọn B
Ta có:
3
1 3.1 2 1; 2M
thuộc đồ thị hàm số.
Câu 2: Cho hàm số
31
2
x
y
x
−
=
+
có đồ thị
( )
H
. Điểm nào sau đây thuộc
( )
H
?
A.
( )
3;7Q −
. B.
( )
0; 1M −
. C.
( )
1; 4N −−
. D.
( )
1;1P
.
Lời giải
Chọn C
Ta thấy
( ) ( )
4 ;41 1 HxyN= − = − − −
Câu 3: Điểm nào sau đây thuộc đồ thị hàm số
3
3y x x=−
?
A.
( )
3;0N
. B.
( )
1; 2M −
. C.
( )
2;14Q
. D.
( )
1; 4P −−
.
Lời giải
Chọn B
Thế
1x =
vào
3
3y x x=−
, ta được
3
1 3.1 2y = − = −
.
Nên
( )
1; 2M −
thuộc đồ thị hàm số
3
3y x x=−
.
Câu 4: Với giá trị nào của
m
thì đồ thị hàm số
2
2 6 4
2
x mx
y
mx
++
=
+
đi qua điểm
( )
1;4A −
.
A.
2m =
. B.
1m =
. C.
1m =−
. D.
1
2
m =
.
Lời giải
Chọn C
Thay
1; 4xy= − =
vào hàm số
2
2 6 4
2
x mx
y
mx
++
=
+
ta có
2 6 4
4
2
m
m
−+
=
−+
6 6 4 8 2 2 1m m m m − = − + = − = −
.
Câu 5: Cho hàm số
31
2
x
y
x
−
=
+
có đồ thị
( )
H
. Điểm nào sau đây thuộc
( )
H
?
A.
( )
3;7Q −
. B.
( )
0; 1M −
. C.
( )
1; 4N −−
. D.
( )
1;1P
.
Lời giải
Chọn C
Thay tọa độ điểm
( )
1; 4N −−
vào
31
2
x
y
x
−
=
+
ta được:
( )
( )
3 1 1
4
12
−−
−=
−+
(luôn đúng).
Suy ra điểm
( )
1; 4N −−
thuộc
( )
H
.
Câu 6: Đồ thị hàm số nào sau đây nhận điểm
( )
1;3I
làm tâm đối xứng

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
23
1
x
y
x
−
=
−
. B.
34
1
x
y
x
+
=
−
. C.
41
2
x
y
x
+
=
+
. D.
32
1
x
y
x
−
=
+
.
Lời giải
GVSB: Chương Huy; GVPB: Hoàng Tiến Đông
Chọn B
Đồ thị hàm số
34
1
x
y
x
+
=
−
nhận giao điểm
( )
1;3I
của 2 tiệm cận làm tâm đối xứng.
Câu 7: Hàm số
32
y ax bx cx d= + + +
có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây là đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải
ChọnB
Phần cuối đồ thị hướng lên nên
0a
.
Giao điểm của đồ thị với trục tung nằm phía trên trục hoành nên
0d
.
Hai điểm cực trị của hàm số trái dấu nên
0ac
. Suy ra
0c
.
Từ đồ thị thấy tổng hai điểm cực trị của hàm số mang dấu dương nên
0ab−
. Suy ra
0b
.
Vậy mệnh đề đúng là
0, 0, 0, 0a b c d
.
Câu 8: Tọa độ tâm đối xứng của đồ thị hàm số
3
32y x x= − +
.
A.
( )
0;2
. B.
( )
1;0
. C.
( )
0;0
. D.
( )
1;4−
.
Lời giải
Chọn A
32
3 2 3 3y x x y x
= − + = −
6yx
=
.
0 0 2y x y
= = =
.
Tọa độ tâm đối xứng của đồ thị hàm số
( )
0;2
.
Câu 9: Trên đồ thị hàm số
21
34
x
y
x
−
=
+
có bao nhiêu điểm có tọa độ nguyên?
A.
1
. B.
0
. C.
2
. D.
4
.
Lời giải
Chọn A

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Ta có
1
3 4 1
5
()
3 4 1
6 3 11 11
3
32
3 4 11 7
3 4 3 4 3 4
()
3
3 4 11
5
x
x
xL
x
x
yy
x
x x x
xL
x
x
=−
+=
=−
+ = −
−
= −
+=
+ + +
=
+ = −
=−
.
Với
1
1 ( )
7
x y L= =
.
Với
5 1 ( )x y tm= − =
.
Vậy đồ thị hàm số
21
34
x
y
x
−
=
+
có một điểm có tọa độ nguyên.
Câu 10: Biết rằng đồ thị hàm số
42
y ax bx c= + +
có hai điểm cực trị là
( )
0;2A
và
( )
2; 14B −
. Khi đó
( )
3f
bằng
A.
60
. B.
28−
. C.
11
. D.
155
.
Lời giải
Chọn C
Ta có
3
42y ax bx
=+
.
Đồ thị hàm số
42
y ax bx c= + +
có hai điểm cực trị là
( )
0;2A
và
( )
2; 14B −
ta có
( )
( )
( )
02
21
2 14 16 4 14 8
32 4 0 2
20
y
ca
y a b c b
a b c
y
=
==
= − + + = − = −
+ = =
=
Vậy
42
82y x x= − +
. Suy ra
( )
3 11f =
.
Câu 11: Đồ thị hàm số nào sau đây nhận điểm
(1;3)I
làm tâm đối xứng?
A.
23
1
x
y
x
−
=
−
. B.
34
1
x
y
x
+
=
−
C.
41
2
x
y
x
+
=
+
. D.
32
1
x
y
x
−
=
+
.
Lời giải
Chọn B
Ta có đồ thị hàm số
34
1
x
y
x
+
=
−
có tiệm cận đứng là
1=x
, tiệm cận ngang là
3=y
.
Vậy nên đồ thị hàm đó nhận
(1;3)I
làm tâm đối xứng.
Câu 12: Đồ thị hàm số
42
2y x x= − −
cắt trục
Oy
tại điểm
A.
( )
0; 2A
. B.
( )
2;0A −
. C.
( )
0; 2A −
. D.
( )
0; 2A −
.
Lời giải
Chọn C
Đồ thị hàm số
42
2y x x= − −
cắt trục
Oy
tại điểm
( )
0; 2A −
.
Câu 13: Cho hàm số
42
y x mx m= − +
có đồ thị
( )
C
. Tìm tham số
m
để
( )
C
đi qua điểm
( )
2;16A
.
A.
2m =−
. B.
2m =
. C.
1m =
. D.
0m =
.
Lời giải
Chọn D

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
( )
2;16A
( )
C
42
16 2 .2 16 16 .4 3 0 0m m m m m m = − + = − + = =
.
Vậy để
( )
C
đi qua điểm
( )
2;16A
thì
0m =
.
Câu 14: Cho hàm số
21
2
x
y
x
+
=
−
có đồ thị là
()C
. Số điểm thuộc
()C
có hoành độ và tung độ đều là các
số nguyên là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn A
Ta có:
21
2
x
y
x
+
=
−
5
2
2
y
x
= +
−
()C
.
Gọi
00
( ; ) ( )M x y C
với
0
00
0
0
,
5
2
2
xZ
x y Z
yZ
x
= +
−
0
2 1; 5x −
.
Với
0 0 0
2 1 3 7 (3;7) ( )x x y M TM− = = =
.
Với
0 0 0
2 1 1 3 (1; 3) ( )x x y M TM− = − = = − −
.
Với
0 0 0
2 5 7 3 (7;3) ( )x x y M TM− = = =
.
Với
0 0 0
2 5 3 1 ( 3;1) ( )x x y M TM− = − = − = −
.
Vậy có 4 điểm thỏa mãn yêu cầu bài toán.
Câu 15: Tìm tọa độ tâm đối xứng của đồ thị hàm số
3
32= − +y x x
.
A.
( )
0;2
. B.
( )
1;0
. C.
( )
0;0
. D.
( )
1;4−
.
Lời giải
Chọn A
Ta có:
2
33
=−yx
,
6
=yx
.
Cho
0 6 0 0
= = =y x x
.
Với
02= =xy
.
Vậy tọa độ tâm đối xứng của đồ thị hàm số
3
32= − +y x x
là
( )
0;2
.
Câu 16: Cho hàm số
2
1
x
y
x
+
=
−
có đồ thị
( )
C
. Tâm đối xứng của đồ thị
( )
C
là điểm có tọa độ
A.
( )
1;2
. B.
( )
2;1−
. C.
( )
3; 2−
. D.
( )
1;1
.
Lời giải
Chọn D
Tiệm cận đứng của đồ thị
( )
C
:
1x =
.
Tiệm cận ngang của đồ thị
( )
C
:
1y =
.
Tâm đối xứng của đồ thị
( )
C
là giao điểm của đường tiệm cận đứng và tiệm cận ngang do đó
có tọa độ
( )
1;1
.
Câu 17: Tâm đối xứng của đồ thị hàm số
31
2
x
y
x
−
=
+
là điểm có tọa độ nào sau đây?

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
A.
( )
2;3−
. B.
( )
3; 2−
. C.
( )
2; 1−
. D.
( )
1;2−
.
Lời giải
Chọn A
Đồ thị hàm số
31
2
x
y
x
−
=
+
nhận giao của hai tiệm cận làm tâm đối xứng.
Tiệm cận đứng
2x =−
vì
2
31
lim
2x
x
x
−
→−
−
= +
+
Tiệm cận ngang
3y =
vì
31
lim 3
2
x
x
x
→+
−
=
+
Do đó đồ thị hàm số nhận
( )
2;3I −
làm tâm đối xứng.
Câu 18: Cho hàm số
32x
y
x
−
=
có đồ thị
( )
C
. Có tất cả bao nhiêu đường thẳng cắt
( )
C
tại hai điểm
phân biệt mà hoành độ và tung độ của hai giao điểm này đều là các số nguyên?
A.
10
. B.
4
. C.
6
. D.
2
.
Lời giải
Chọn C
Ta có:
3 2 2
3
x
y
xx
−
= = −
.
Điểm
( )
MC
có tọa độ nguyên ( hoành độ và tung độ nguyên ) khi
( )
2 2; 1;1;2x U x − −
.
Các điểm thuộc
( )
C
có tọa độ nguyên thuộc tập
( ) ( ) ( ) ( )
1;5 , 1;1 , 2;2 , 2;4B = − −
.
Mỗi cặp hai điểm thuộc tập
B
xác định một đường thẳng cắt
( )
C
tại hai điểm có tọa độ nguyên,
do đó số đường thẳng là
2
4
6C =
.
Câu 19: Cho hàm số
32
( ) 3 3y f x x x= = − +
có độ thị
( )
C
. Gọi
A
và
B
là hai điểm nằm trên
( )
C
và
đối xứng nhau qua gốc tọa độ
O
. Độ dài
AB
bằng
A.
22
. B.
4
. C.
23
. D.
42
.
Lời giải
Chọn A
Gọi
( )
;A x y
và
( )
;B x y−−
là hai điểm đối xứng nhau qua gốc tọa độ
O
(ĐK
0x
).
Vì
A
và
B
là hai điểm nằm trên
( )
C
nên
( ) ( )
32
3 2 2
1( )
3 3 3 3 1
1(khôngTMĐK)
x TMĐK
x x x x x
x
=
− + = − − − − + =
=−
.
Với
11xy= =
khi đó
( )
1;1A
và
( )
1; 1B −−
.
Vậy độ dài
( ) ( )
22
1 1 1 1 2 2AB = + + + =
.
Câu 20: Cho hàm số
32
1
x
y
x
có đồ thị là
C
và
2
điểm
4;2 ; 2; 8AB
. Điểm
;M a b C
sao cho trực tâm
H
của tam giác
MAB
thuộc vào đường thẳng
: 5 4 3 0d x y
. Tính giá trị của biểu thức
2
43S a b
?
A.
9S
. B.
6S
. C.
10S
. D.
12S
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
Lời giải
Chọn D
Nhận xét: hai điểm
,AB
thuộc đồ thị của hàm số đã cho
Phương trình tham số của đường thẳng
( )
14
:
25
= − +
= − +
xt
dt
yt
Gọi
( )
1 4 ; 2 5− + − + M t t d
và
32
;
1
m
Hm
m
−
+
4; 2mm −
( ) ( )
6;6 ; 4 5;5 4
32
1 4 ; 2 5
1
5 10
2;
1
AB AM t t
m
HM t m t
m
m
BH m
m
= − = − −
−
= − + − − + −
+
−−
=+
+
Theo giả thiết, ta có:
( )
( )( )
( )( )
5
1 4 5 0
.0
1
5 4 5 10
.0
2 4 5 0
1
m
t m t
AB HM
m
tm
AM BH
mt
m
− − + − + − =
=
+
−+
=
+ − − =
+
5
10
1
2
25 20
4 5 0
1
m
tm
m
m
t
t
m
+ + − =
+
=−
−
− − =
+
* Giải hệ phương trình
2
2
5
11
10
1
m
m
m
t
tm
m
=−
=−
=
+ + − =
+
(không thỏa vì
MB
)
* Giải hệ phương trình:
2
5
31
10
1
1
25 20
25 20
4 5 0
4 5 0
1
1
m
mm
tm
t
m
m
t
t
t
t
m
m
−+
+ + − =
=−
+
+
−
−
− − =
− − =
+
+
2
2
32
31
31
1
1
4
4 28 57 36 0
3
2
mm
t
mm
m
t
m
m
m m m
m
−+
=−
−+
+
=−
+
=
− + − =
=
3
2
1
2
m
t
=
=
Vậy
3
;1
2
M
Vậy
2
3
4 3.1 12
2
= + =
S

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Câu 21: Cho hàm số
32
4y x x= + −
có đồ thị
( )
C
. Có bao nhiêu cặp điểm
,AB
thuộc
( )
C
sao cho ba
điểm
,,O A B
thẳng hàng và
2OA OB=
(
O
là gốc tọa độ).
A. Vô số. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
Gọi
d
đường thẳng đi qua ba điểm
,,O A B
, khi đó
d
có phương trình
y kx=
. Khi đó hoành độ
của
,,O A B
là nghiệm của phương trình
32
4x x kx+ − =
.
Giả sử
( ) ( )
1 1 2 2
; , ;A x kx B x kx
, khi đó ta có
32
1 1 1
32
2 2 2
4
4
x x kx
x x kx
+ − =
+ − =
.
Do
2OA OB=
nên
12
22OA OB x x= =
.
Nếu
12
2xx=
thế vào ta được
32
2 2 2
32
2 2 2
32
2 2 2
8 4 4 2
6 2 4 0 1
4
x x kx
x x x
x x kx
+ − =
+ + = = −
+ − =
.
Khi đó
4k =
suy ra
( ) ( )
2; 8 , 1; 4AB− − − −
.
Nếu
12
2xx=−
thế vào ta được
32
2 2 2
32
2 2 2
32
2 2 2
8 4 4 2
6 6 12 0 1
4
x x kx
x x x
x x kx
− + − = −
− + − = = −
+ − =
.
Khi đó
4k =
suy ra
( ) ( )
2;8 , 1; 4AB−−
.
Vậy có hai cặp điểm
,AB
thỏa mãn đề bài.
Câu 22: Có bao nhiêu điểm
M
thuộc đồ thị hàm số
2
1
x
y
x
+
=
−
sao cho khoảng cách từ điểm
M
đến trục
tung bằng hai lần khoảng cách từ điểm
M
đến trục hoành
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Gọi
2
;
1
a
Ma
a
+
−
,
1a
là điểm thuộc đồ thị hàm số
2
1
x
y
x
+
=
−
.
Ta có
( )
;d M Oy a=
,
( )
2
;
1
a
d M Ox
a
+
=
−
.
Theo đề bài ta có
( ) ( )
2
; 2 ; 2
1
a
d M Oy d M Ox a
a
+
= =
−
2
2
2
2.
3 4 0 1
1
24
40
2.
1
a
a
a a a
a
aa
aa
a
a
+
=
− − = = −
−
+=
+ + =
=−
−
.
Với
1
1 1;
2
aM
= − − −
.
Với
( )
4 4;2aM=
.
Vậy có hai điểm
M
thỏa mãn.
Câu 23: Cho hàm số
21
2
x
y
x
+
=
+
có đồ thị
( )
C
. Gọi
( )
;M a b
là điểm trên
( )
C
có khoảng cách đến
đường thẳng
: 3 6d y x=+
nhỏ nhất. Khẳng định nào sau đây đúng
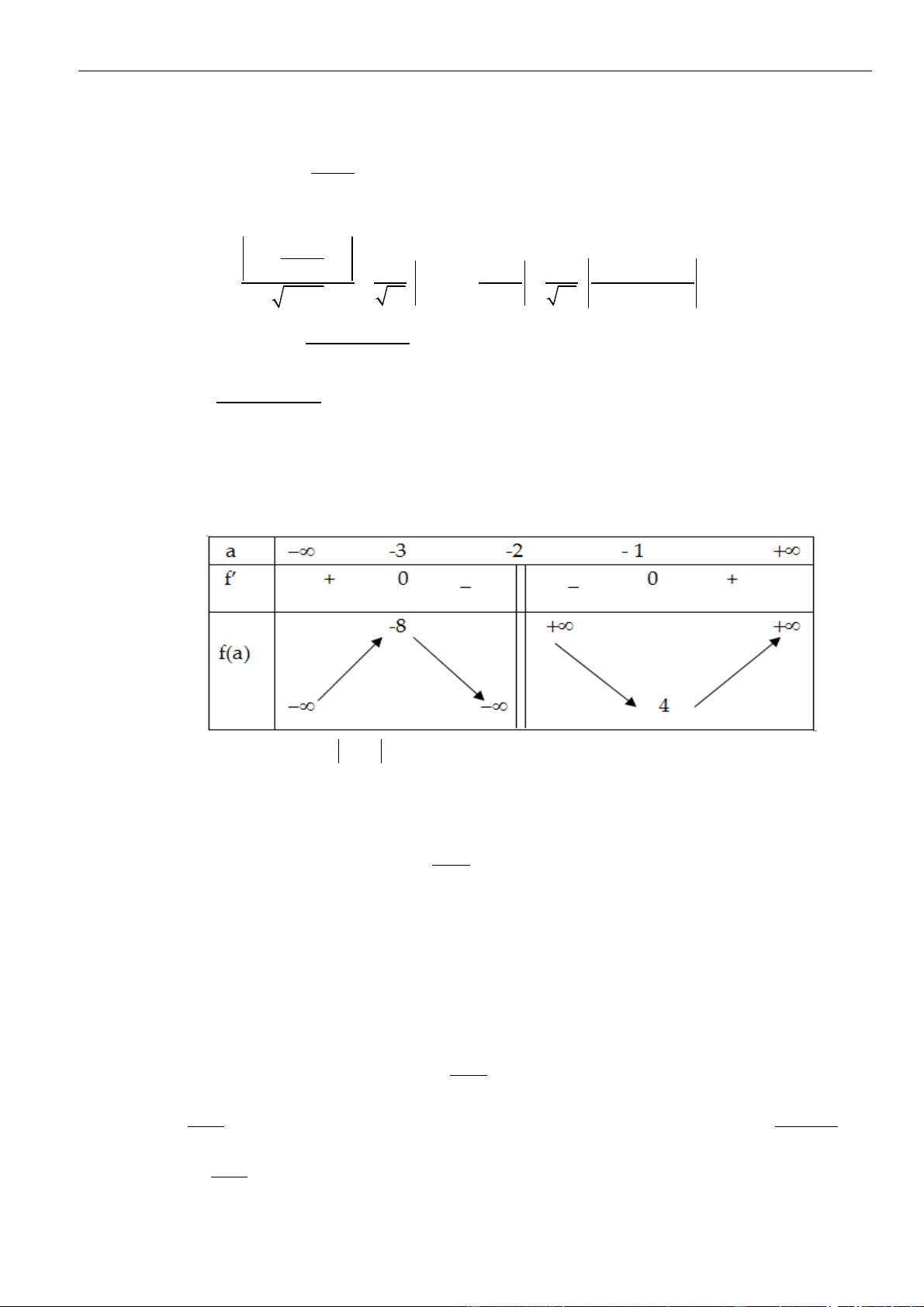
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
A.
2ab−=
. B.
2ab+=
. C.
2ab+ = −
. D.
2ab− = −
.
Lời giải
Chọn C
( )
21
;
2
a
M C M a
a
+
+
.
Khoảng cách từ
M
đến
: 3 6d y x=+
bằng:
( )
2
2
1 3 10 11
2
6
6
1
21
3
1 2 1
2
; . 3
2
10
3
0
1
a
a
a
a
dd
a
Ma
a
a
a
+
−+
+
+
++
+
= = − =
+
+
+
.
Xét hàm số
( )
2
3 10 11
2
f
aa
a
a =
++
+
với
2a −
.
( )
( )
2
2
3 4 3
1
( ) 0
3
2
aa
a
fa
a
a
++
=−
= =
=−
+
.
Ta có:
( ) ( )
1 4; 3 8;ff− = − = −
.
22
lim ( ) ; lim ( ) ; lim ( ) ; lim ( )
xx
xx
f a f a f a f a
−+
→− →+
→− →−
= − = + = − = +
BBT
Vậy GTNN của hàm số
( )
4fa=
tại
1a =−
Vậy
1
2
1
a
ab
b
=−
+ = −
=−
.
Câu 24: Tịnh tiến liên tiếp đồ thị hàm số
5
2
y
x
−
=
+
theo trục
Oy
lên trên 2 đơn vị và theo
Ox
sang trái
3 đơn vị ta được đồ thị hàm số
( )
y g x=
. Có bao nhiêu điểm trên đồ thị
( )
y g x=
có các tọa độ
đều là số nguyên?
A.
4
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn A
Điều kiện xác định
2x −
.
Tịnh tiến liên tiếp đồ thị hàm số
5
2
y
x
−
=
+
theo trục
Oy
lên trên 2 đơn vị ta được hàm số
5
2
2
y
x
−
=+
+
, rồi tịnh tiến theo
Ox
sang trái 3 đơn vị ta được hàm số
5
2
32
y
x
−
=+
++
5
2
5
y
x
−
= +
+
.
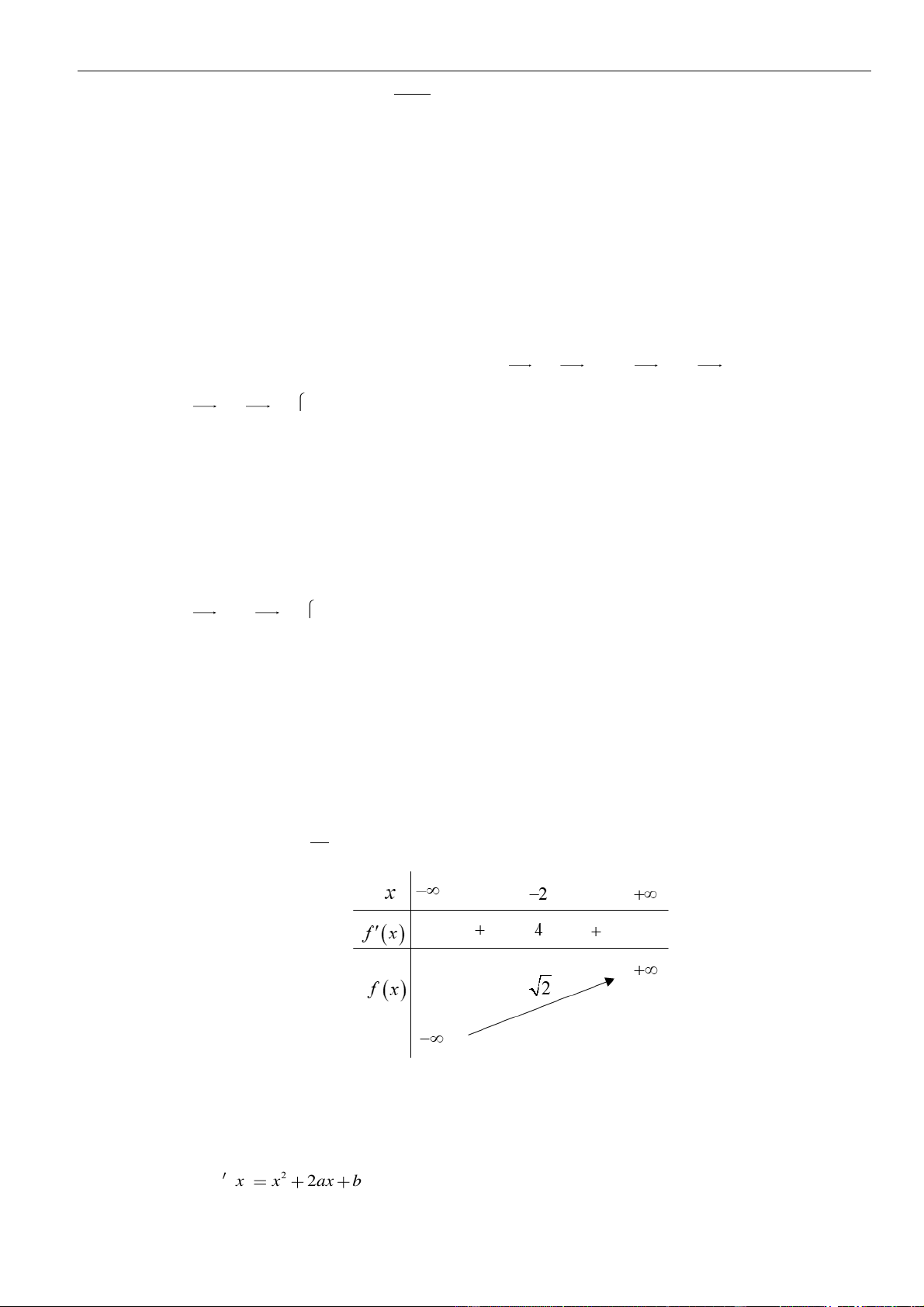
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Để điểm trên đồ thị hàm số
5
2
5
y
x
−
=+
+
có tọa độ đều nguyên thì
5x +
phải là ước của
5−
.
Ta có
( )
5 5; 1;1;5U − = − −
suy ra
10; 6; 4;0x − − −
(thỏa mãn so với điều kiện).
Vậy có 4 điểm thỏa mãn đề bài.
Câu 25: Cho hàm số
32
4y x x= + −
có đồ thị
( )
C
. Có bao nhiêu cặp điểm
A
,
B
thuộc
( )
C
sao cho ba
điểm
O
,
A
,
B
thẳng hàng và
2OA OB=
(
O
là gốc tọa độ)?
A. Vô số. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
Gọi
( )
00
;B x y
thuộc
( )
C
, suy ra:
32
0 0 0
4y x x= + −
( )
*
.
Từ
O
,
A
,
B
thẳng hàng và
2OA OB=
suy ra:
2OA OB=
hoặc
2OA OB=−
.
Nếu
0
0
22
2
22
AB
AB
xxx
OA OB
yyy
==
=
==
.
Điểm
( )
AC
, suy ra:
( ) ( )
32
32
0 0 0 0 0 0
2 2 2 4 4 2 2y x x y x x= + − = + −
( )
**
.
Từ
( )
*
và
( )
**
suy ra:
3 2 3 2 3 2
0 0 0 0 0 0
4 2 2 4 3 2 0x x x x x x+ − = + − + + =
( )
( )
2
0 0 0
1 3 2 2 0x x x + − + =
0
1x = −
.
Suy ra:
( )
2; 8A −−
,
( )
1; 4B −−
.
Nếu
0
0
22
2
22
AB
AB
xxx
OA OB
yyy
= − = −
= −
= − = −
.
Điểm
( )
AC
, suy ra:
( ) ( )
32
32
0 0 0 0 0 0
2 2 2 4 4 2 2y x x y x x− = − + − − = − +
( )
***
.
Từ
( )
*
và
( )
***
suy ra:
3 2 3 2 3 2
0 0 0 0 0 0
4 2 2 4 2 0x x x x x x− + = + − − + =
( )
( )
2
0 0 0
1 2 2 0x x x + − + =
0
1x = −
.
Suy ra:
( )
2;8A
,
( )
1; 4B −−
.
Câu 26: Cho hàm số
( )
3
2
3
x
f x ax bx c= + + +
có bảng biến thiên như sau
Hỏi có bao nhiêu số dương trong các hệ số
,,abc
?
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn C
Ta có:
2
2f x x ax b
.
Từ bảng biến thiên ta thấy, hàm số
fx
luôn đồng biến trên khoảng
( )
;− +
.
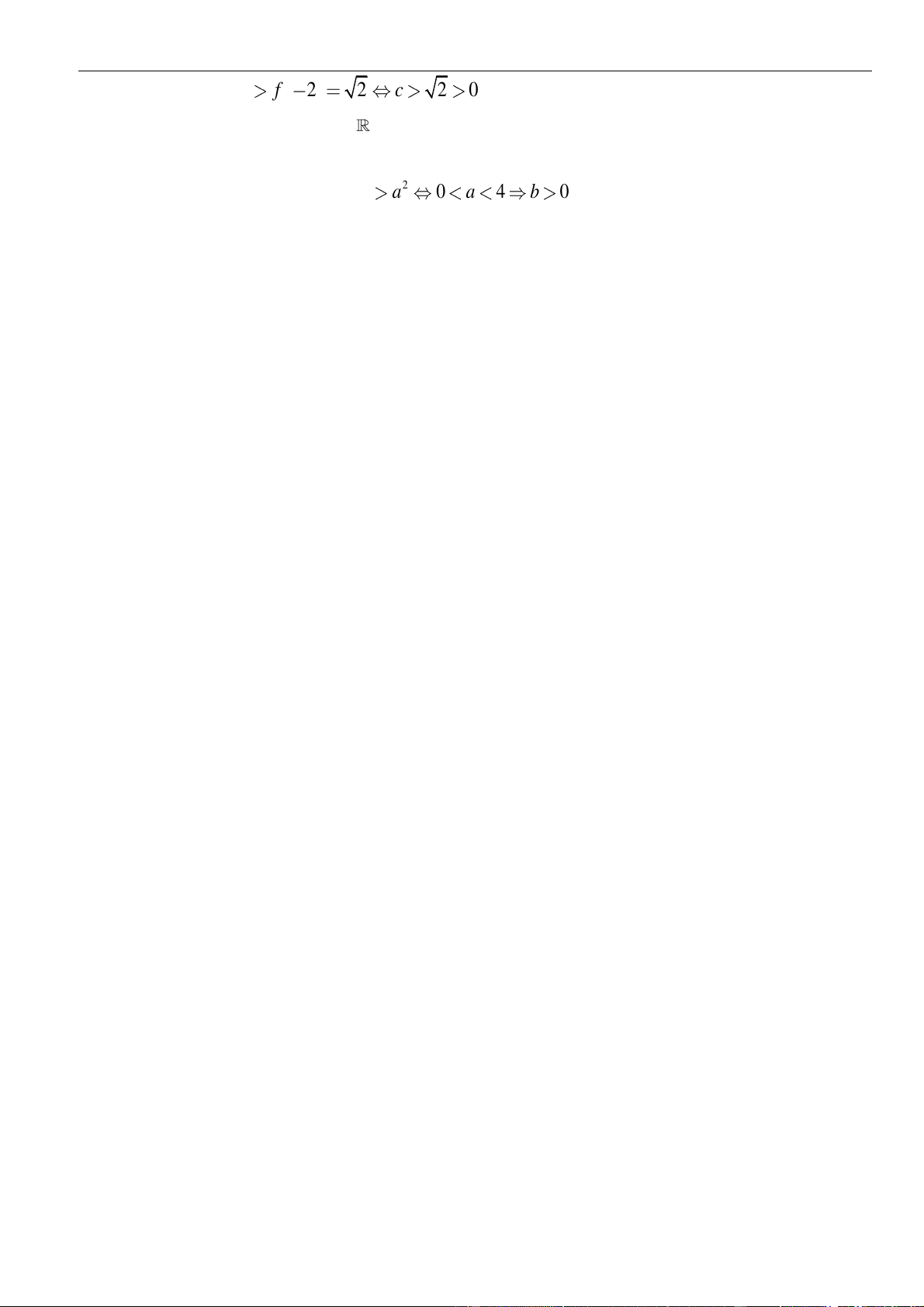
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Do đó:
0 2 2 2 0f f c
.
Đồng thời
( )
0,f x x
nên
( )
22
'
01
y
a b b a
= −
.
( ) ( )
2 4 4 4 4 4 2f a b b a
− = − + = =
Thế
2
vào
1
, ta được
2
4 0 4 0a a a b
.
Vậy cả ba hệ số
,,abc
đều dương.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
1 | Facebook tác giả: Phan Nhật Linh
PHẦN I. ĐỀ BÀI
Câu 1: Phương trình tiếp tuyến của đồ thị hàm số
3
23y x x= − +
tại điểm có hoành đô
2x =
là
A.
77yx=−
. B.
5yx=+
. C.
10 27yx=−
. D.
10 13yx=−
.
Câu 2: Cho hàm số
( )
1
2
x
fx
x
+
=
−
có đồ thị
( )
C
. Viết phương trình tiếp tuyến với đồ thị
( )
C
tại điểm
M
thuộc đồ thị có hoành độ
3x =
?
A.
3 13yx= − +
. B.
3 13yx=+
. C.
35yx=−
. D.
35yx=+
.
Câu 3: Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
32y x x= − + +
song song với đường thẳng
9 18 0xy− + =
?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 4: Tiếp tuyến của đồ thị hàm số
1
23
x
y
x
+
=
−
tại điểm có hoành độ
0
1x =−
có hệ số góc bằng bao
nhiêu?
A.
5
. B.
1
5
. C.
1
5
−
. D.
5−
.
Câu 5: Hàm số
( )
32
34f x x x= − +
có đồ thị
( )
C
. Viết phương trình tiếp tuyến với
( )
C
tại điểm
A
có
hoành độ
1
A
x =
nằm trên
( )
C
.
A.
35yx= − +
. B.
35yx=−
. C.
53yx= − +
. D.
53yx=−
.
Câu 6: Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
3
31y x x= − + −
là
A.
6
. B.
1−
. C.
6−
. D.
0
.
Câu 7: Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
3
31y x x= − + −
là
A.
6
. B.
1−
. C.
6−
. D.
0
.
Câu 8: Phương trình tiếp tuyến của đồ thị
3
( ): 3 4C y x x=−
tại điểm có hoành độ
0x =
là:
A.
3yx=
. B.
0y =
. C.
32yx=−
. D.
12yx=−
.
Câu 9: Tìm tất cả các điểm
M
trên đồ thị hàm số
2
1
x
y
x
−
=
+
mà tiếp tuyến của đồ thị tại điểm đó song
song với đường thẳng
: 3 10d y x=+
.
A.
1
3;
4
M
. B.
( )
0; 2M −
.
C.
( )
0; 2M −
và
( )
2;4M −
. D.
5
;3
2
M
−
.
Câu 10: Cho hàm số
1
1
x
y
x
+
=
−
và điểm
( )
1; 1I −
. Tìm tất cả các điểm
M
nằm trên đồ thị hàm số sao cho
tiếp tuyến tại
M
vuông góc với
IM
.
Tiếp tuyến của đồ thị hàm số
DẠNG 8

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 2
A.
( )
1 2; 1 2M + − −
và
( )
1 2; 1 2M − − +
.
B.
( )
1;0M −
và
( )
3; 2M −
.
C.
( )
2; 3 2 2M −−
.
D.
( )
2; 3M −
và
( )
0;1M
.
Câu 11: Qua điểm
( )
2;0M
kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số
42
4y x x=−
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 12: Biết tiếp tuyến của đồ thị hàm số
42
2y ax bx= + +
tại điểm
( )
1;1A −
vuông góc với đường
thẳng
2 3 0xy− + =
. Tính
22
ab−
A.
22
2ab− = −
. B.
22
10ab−=
. C.
22
13ab−=
. D.
22
5ab− = −
.
Câu 13: Viết phương tình tiếp tuyến của đồ thị hàm số
3
23y x x= − +
tại điểm
( )
1;2M
.
A.
22yx=+
. B.
31yx=−
. C.
1yx=+
. D.
2yx=−
.
Câu 14: Tiếp tuyến của đồ thị hàm số
32
23y x x x= + − −
tại điểm
( )
1; 3M −
có phương trình là
A.
3yx=−
. B.
36yx= − +
. C.
58yx=−
. D.
36yx=−
.
Câu 15: Viết phương trình tiếp tuyến của đồ thị hàm số
21
2
x
y
x
−
=
−
, biết tiếp tuyến có hệ số góc
3k =−
.
A.
34yx= − +
. B.
3 14yx= − +
và
32yx= − +
.
C.
3 14yx= − −
và
32yx= − −
. D.
34yx= − −
.
Câu 16:
Cho hàm số
()y f x=
có đạo hàm cấp một liên tục trên . Biết phương trình tiếp tuyến của hàm
số tại điểm
0
1x =
có dạng:
34yx=+
. Giá trị của
(1)f
bằng:
A.
4
. B.
3
. C.
7
. D.
0
.
Câu 17: [2D1-5.18-2] (TMD - Đề IMC10 - 2020 - 2021) Cho hàm số
32
( ) 3 4f x x x= − +
có đồ thị
( )
C
. Viết phương trình tiếp tuyến của
( )
C
tại điểm
A
có hoành độ
1
A
x =
nằm trên
( )
C
.
A.
35yx= − +
. B.
35yx=−
. C.
53yx= − +
. D.
53yx=−
.
Câu 18: Cho đồ thị
( )
C
của hàm số
32
32= − +y x x
. Có bao nhiêu tiếp tuyến với đồ thị
( )
C
song song
với trục hoành?
A.
3
. B.
2
. C. Không có. D.
1
.
Câu 19: Cho hàm số
42
63y x x= − −
có đồ thị
( )
C
. Tiếp tuyến của đồ thị hàm số
( )
C
tại điểm
A
(có
hoành độ
1
A
x =
) cắt đồ thị hàm số
( )
C
tại điểm
B
(
B
khác
A
). Hoành độ điểm
B
là
A.
1
. B.
3−
. C.
1−
. D.
3
.
Câu 20: Tiếp tuyến của đồ thị hàm số
lnyx=
tại điểm có hoành độ
1x =
có phương trình là
A.
yx=
B.
1yx=−
C.
yx=−
B.
1yx= − +
Lời giải
Chọn B
Ta có
1
y
x
=
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
3 | Facebook tác giả: Phan Nhật Linh
Khi đó, tiếp tuyến của đồ thị hàm số
( )
lny f x x==
tại điểm có hoành độ
1x =
có phương trình
là
( )( ) ( ) ( )
1
1 1 1 1 ln1 1
1
y f x f x x
= − + = − + = −
.
Câu 21: Hệ số góc của tiếp tuyến với đồ thị hàm số
21
3
x
y
x
−
=
−
tại điểm có hoành độ
4x =
là
A.
3k =−
. B.
5k =−
. C.
7k =
. D.
2k =
.
Câu 22: Phương trình tiếp tuyến của đồ thị hàm số
lny x x=
tại điểm có hoành độ bằng
e
là
A.
23y x e=+
. B.
2y x e=−
. C.
2y ex e=−
. D.
y x e=+
.
Câu 23: Phương trình tiếp tuyến với đồ thị hàm số
42
22= + −y x x
tại điểm có hoành độ
0
2x =−
là
A.
40 102= − −yx
. B.
40 58= − −yx
. C.
40 102= − +yx
. D.
40 58= − +yx
.
Câu 24: Phương trình tiếp tuyến với đồ thị hàm số
42
22= + −y x x
tại điểm có hoành độ
0
2x =−
là
A.
40 102= − −yx
. B.
40 58= − −yx
. C.
40 102= − +yx
. D.
40 58= − +yx
.
Câu 25: Tiếp tuyến của đồ thị hàm số
32
32y x x= − −
có hệ số góc
3k =−
có phương trình là
A.
31yx= − +
. B.
31yx= − −
. C.
37yx= − −
. D.
37yx= − +
.
Câu 26: Cho đường cong (C) có phương trình
1
1
x
y
x
−
=
+
. Gọi M là giao điểm của (C) và trục tung. Tiếp
tuyến của (C) tại M có phương trình là
A.
2yx=−
. B.
21yx=+
. C.
21yx= − −
. D.
21yx=−
.
Câu 27: Tìm tất cả các giá trị thực của tham số
m
để tiếp tuyến của đồ thị hàm số
( )
42
( ): 2 1 8C y m x mx= − − +
tại điểm có hoành độ
1x =
vuông góc với đường thẳng
:2 3 0d x y− − =
.
A.
9
2
m =
. B.
1
2
m =−
. C.
7
12
m =
. D.
2m =
.
Câu 28: Tiếp tuyến của đường cong
( )
21
:
1
x
Cy
x
+
=
−
tại điểm
( )
2;5M
và cắt trục tọa độ
Ox
,
Oy
lần
lượt tại
A
và
B
. Tính diện tích tam giác
OAB
.
A.
121
6
. B.
121
3
. C.
121
6
−
. D.
121
3
−
.
Câu 29: Cho hàm số
3
=−y x x
có đồ thị
( )
C
. Gọi
,MN
là hai điểm phân biệt trên
( )
C
và các tiếp
tuyến của
( )
C
tại các điểm
,MN
song song với nhau. Tính
+
MN
xx
.
A.
1
. B.
2
. C.
0
. D.
2−
.
Câu 30: Tiếp tuyến của đồ thị hàm số
32
23y x x x= + − −
tại điểm
( )
1; 3M −
có phương trình là
A.
3yx=−
. B.
36yx= − +
. C.
58yx=−
. D.
36yx=−
.
Câu 31: Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
32y x x= − +
song song với đường thẳng
9 18 0xy− + =
?
A.
2
. B.
0
. C.
1
. D.
3
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 4
Câu 32: Cho hàm số
2
1
x
y
x
+
=
+
có đồ thị
( )
C
. Phương trình tiếp tuyến với đồ thị hàm số tại giao điểm của
đồ thị
( )
C
với trục tung là
A.
1yx= − +
B.
2yx= − −
C.
2yx=−
D.
2yx= − +
Câu 33: Cho hàm số
( )
32
1 3 2 1y x m x mx m= + − − + +
có đồ thị
( )
m
C
, biết rằng đồ thị
( )
m
C
luôn đi qua
hai điểm cố định
,AB
. Có bao số nguyên dương
m
thuộc
2020;2020−
để
( )
m
C
có tiếp tuyến
vuông góc với đường thẳng
AB
?
A.
4041
. B.
2021
. C.
2019
D.
2020
.
Câu 34: Cho biết tiếp tuyến của đồ thị hàm số
( )
y f x=
tại điểm có hoành độ
1x =
là
21yx=−
.
Phương trình tiếp tuyến của đồ thị hàm số
( )
2
21y f x=−
tại điểm có hoành độ
1x =
là
A.
43yx=−
. B.
54yx=−
. C.
87yx=−
. D.
65yx=−
.
Câu 35: Cho đồ thị
(C )
của hàm số
21
1
x
y
x
−
=
−
. Viết tất cả các phương trình tiếp tuyến của
(C )
, biết
khoảng cách từ điểm
( )
12I;
đến tiếp tuyến bằng
2
.
A.
50xy+ − =
. B.
10xy+ − =
và
50xy+ − =
.
C.
10xy+ + =
và
50xy+ + =
. D.
10xy+ − =
.
Câu 36: Cho hàm số
( )
( )
21
0
m x m
ym
xm
−−
=
+
có đồ thị
( )
m
C
. Biết rằng tồn tại duy nhất một đường
thẳng
( )
d
có phương trình
y ax b=+
sao cho
( )
m
C
luôn tiếp xúc với
( )
d
. Giá trị của
ab+
là
A.
3−
. B.
1
. C.
1−
. D.
2
.
Câu 37: Cho hàm số
( )
y f x=
xác định và có đạo hàm trên , thỏa mãn:
( ) ( )
3
1 2. 1 21 3 0f x f x x+ + + − − =
. Viết phương trình tiếp tuyến của đồ thị
( )
y f x=
tại
điểm có hoành độ
0
1x =
.
A.
31yx=+
. B.
32yx=+
. C.
32yx=−
. D.
31yx=−
.
Câu 38: Xét điểm
M
có hoành độ là số nguyên thuộc đồ thị
( )
21
:
1
x
Cy
x
+
=
−
. Tiếp tuyến của đồ thị
( )
C
tại điểm
M
cắt đường tiệm cận ngang của
( )
C
tại điểm
A
. Hỏi có bao nhiêu điểm
M
thỏa
điều kiện
A
cách gốc tọa độ một khoảng cách nhỏ hơn
2 10
?
A.
6
. B.
5
. C.
7
. D.
4
.
Câu 39: Cho hàm số
( )
y f x=
có đồ thị
( )
P
như hình bên và đường thẳng
: 2 2yx = −
là tiếp tuyến
của
( )
P
tại điểm
A
. Xét hàm số
( )
( )
fx
gx
x
=
. Tính
( )
'2g
.
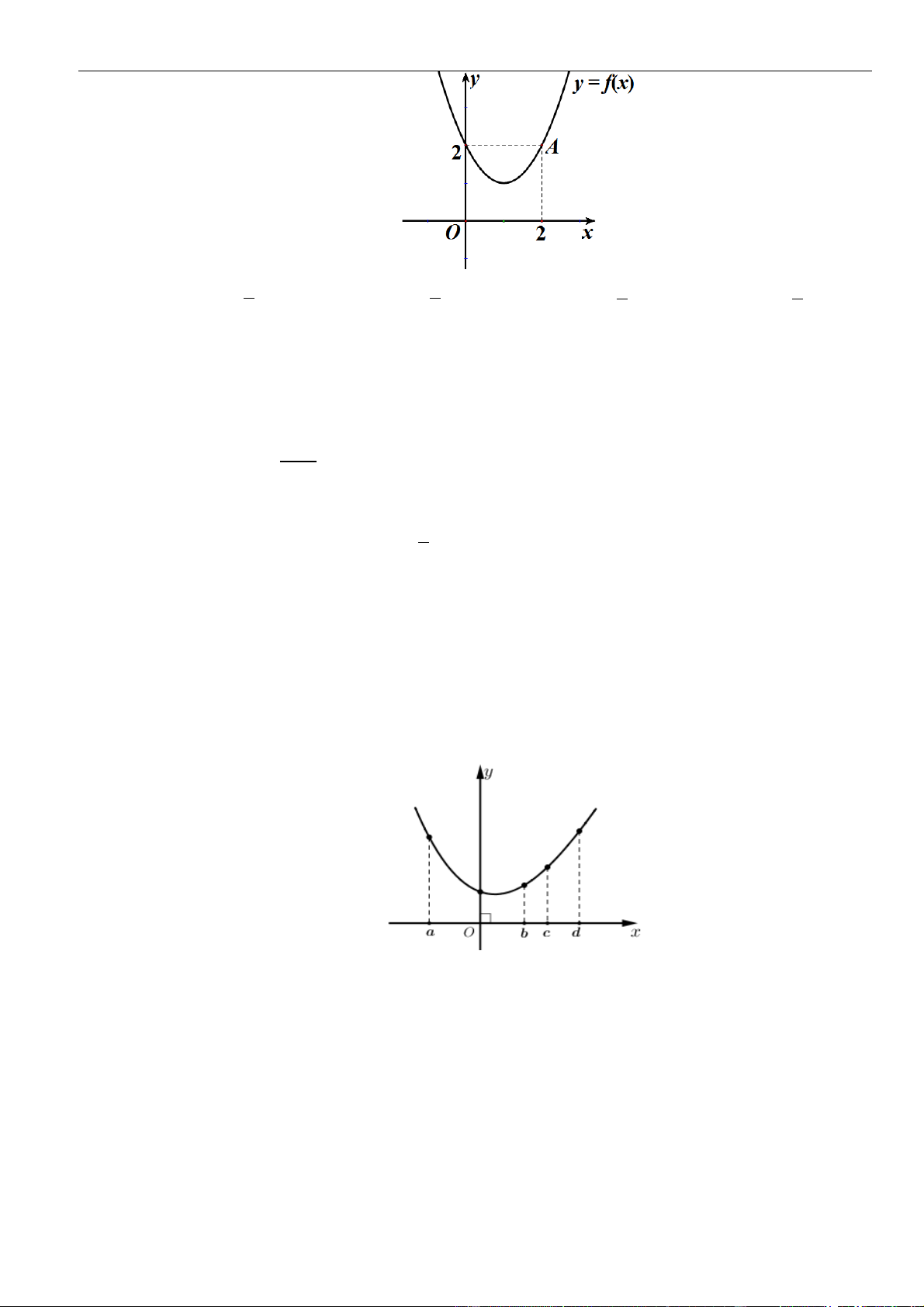
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
5 | Facebook tác giả: Phan Nhật Linh
A.
( )
1
'2
2
g =
. B.
( )
1
'2
4
g =
. C.
( )
1
'2
4
g =−
. D.
( )
1
'2
2
g =−
.
Câu 40: Cho hàm số
( )
3
3y f x x x= = −
có đồ thị
( )
C
và hàm số
( )
2
y g x x==
có đồ thị
( )
P
. Hỏi hai
đồ thị
( )
C
và
( )
P
có tất cả bao nhiêu tiếp tuyến chung?
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 41: Cho hàm số
1
2
x
y
x
+
=
+
có đồ thị
()C
và đường thẳng
: 2 1d y x m= − + −
(
m
là tham số thực). Gọi
12
,kk
là hệ số góc của tiếp tuyến của
()C
tại giao điểm của
d
và
()C
. Tính tích
12
.kk
.
A.
12
.2kk =
. B.
12
1
.
4
kk =
. C.
12
.4kk =
. D.
12
.3kk =
.
Câu 42: Gọi
S
là tập tất cả các giá trị của tham số
m
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1.yx=+
Tổng tất cả các phần tử của
S
bằng
A.
0
. B.
2
. C.
1−
. D.
3
.
Câu 43: Cho
( )
fx
là hàm đa thức có đồ thị như hình vẽ bên. Gọi
( ) ( ) ( ) ( ) ( )
, , , , 0S f a f b f c f d f
=
. Phần tử lớn nhất trong tập hợp
S
là:
A.
( )
fa
. B.
( )
fb
. C.
( )
0f
. D.
( )
fd
.
Câu 44: Cho biết tiếp tuyến của đồ thị hàm số
( )
y f x=
tại điểm có hoành độ
1x =
là
21yx=−
.
Phương trình tiếp tuyến của đồ thị hàm số
( )
2
21y f x=−
tại điểm có hoành độ
1x =
là
A.
43yx=−
. B.
54yx=−
. C.
87yx=−
. D.
65yx=−
.
Câu 45: Cho hàm số
42
2y x x=−
có đồ thị
( )
C
. Tiếp tuyến của
( )
C
tại
A
cắt
( )
C
tại
( )
22
;B x y
với
B
khác
A
thỏa
( )
2 1 2 1
24y y x x− = − −
. Số điểm
A
thỏa mãn là
A.
1
. B.
3
. C.
2
. D.
0
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 6
Câu 46: Cho hàm số
2
1
x
y
x
+
=
−
có đồ thị
( )
C
và điểm
( )
0;Aa
. Có tất cả bao nhiêu giá trị nguyên của
a
trong đoạn
2018;2018−
để từ
A
kẻ được hai tiếp tuyến đến
( )
C
sao cho hai tiếp điểm nằm
về hai phía của trục hoành
A.
2019
. B.
2020
. C.
2017
. D.
2018
.
Câu 47: Cho hàm số
42
2y x x=−
có đồ thị
( )
C
. Tiếp tuyến của
( )
C
tại
A
cắt
( )
C
tại
( )
22
;B x y
với
B
khác
A
thỏa
( )
2 1 2 1
24y y x x− = − −
. Số điểm
A
thỏa mãn là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 48: Tìm điểm
M
có hoành độ âm trên đồ thị
( )
3
12
:
33
C y x x= −+
sao cho tiếp tuyến tại
M
vuông
góc với đường thẳng
12
:
33
d y x= − +
.
A.
( )
2; 4M −−
. B.
4
1;
3
M
−
. C.
( )
2;0M −
. D.
4
2;
3
M
−
.
Câu 49: Cho đa thức
( )
fx
với hệ số thực và thỏa mãn điều kiện
( ) ( )
2
2 1 , .f x f x x x+ − =
Biết
tiếp tuyến tại điểm có hoành độ
1x =
của đồ thị hàm số
( )
y f x=
tạo với hai trục tọa độ một
tam giác. Tính diện tích của tam giác đó?
A.
1
.
6
B.
3
2
. C.
1
3
. D.
2
3
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
7 | Facebook tác giả: Phan Nhật Linh
PHẦN II. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Phương trình tiếp tuyến của đồ thị hàm số
3
23y x x= − +
tại điểm có hoành đô
2x =
là
A.
77yx=−
. B.
5yx=+
. C.
10 27yx=−
. D.
10 13yx=−
.
Lời giải
Chọn D
( )
2
3 2 2 10y x y
= − =
.
00
27xy= =
.
Vậy phương trình tiếp tuyến của đồ thị hàm số tại
0
2x =
là:
( )
10 2 7 10 13y x y x= − + = −
.
Câu 2: Cho hàm số
( )
1
2
x
fx
x
+
=
−
có đồ thị
( )
C
. Viết phương trình tiếp tuyến với đồ thị
( )
C
tại điểm
M
thuộc đồ thị có hoành độ
3x =
?
A.
3 13yx= − +
. B.
3 13yx=+
. C.
35yx=−
. D.
35yx=+
.
Lời giải
Chọn A
Tập xác định:
\2D =
.
Ta có:
( )
( )
( )
2
3
33
2
f x k f
x
−
= = = −
−
.
Vì
34
MM
xy= =
.
Vậy phương trình tiếp tuyến cần tìm là:
( )
3 3 4 3 13y x x= − − + = − +
.
Câu 3: Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
32y x x= − + +
song song với đường thẳng
9 18 0xy− + =
?
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta có
2
33yx
= − +
.
Giả sử
0
x
là hoành độ tiếp điểm của tiếp tuyến
với đồ thị
( )
3
: 3 2C y x x= − + +
.
Do
song song với đường thẳng
:9 18 0 9 18d x y y x− + = = +
nên ta có
( )
0
9yx
=
22
00
3 3 9 2xx − + = = −
( vô nghiệm).
Vậy không có tiếp tuyến nào thỏa mãn yêu cầu bài toán.
Câu 4: Tiếp tuyến của đồ thị hàm số
1
23
x
y
x
+
=
−
tại điểm có hoành độ
0
1x =−
có hệ số góc bằng bao
nhiêu?
A.
5
. B.
1
5
. C.
1
5
−
. D.
5−
.
Lời giải
Chọn C

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 8
Ta có :
( )
2
15
23
23
x
yy
x
x
+−
= =
−
−
Vậy hệ số góc của tiếp tuyến tại điểm có hoành độ
0
1x =−
là:
( )
1
1
5
y
− = −
.
Câu 5: Hàm số
( )
32
34f x x x= − +
có đồ thị
( )
C
. Viết phương trình tiếp tuyến với
( )
C
tại điểm
A
có
hoành độ
1
A
x =
nằm trên
( )
C
.
A.
35yx= − +
. B.
35yx=−
. C.
53yx= − +
. D.
53yx=−
.
Lời giải
Chọn A
+ Tung độ của điểm
A
là
2
A
y =
+
( )
32
34f x x x= − +
( )
2
36f x x x
=−
( )
13f
=−
.
+ Phương trình tiếp tuyến cần tìm là:
( )
2 3 1yx− = − −
35yx= − +
.
Câu 6: Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
3
31y x x= − + −
là
A.
6
. B.
1−
. C.
6−
. D.
0
.
Lời giải
Chọn D
Ta có
2
( ) 3 3y x x
= − +
.
Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
đã cho là:
( )
2
(1) 3 1 3 0y
= − + =
.
Câu 7: Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
3
31y x x= − + −
là
A.
6
. B.
1−
. C.
6−
. D.
0
.
Lời giải
Chọn D
Ta có
2
( ) 3 3y x x
= − +
.
Hệ số góc của tiếp tuyến tại
( )
1;0A
của đồ thị hàm số
đã cho là:
( )
2
(1) 3 1 3 0y
= − + =
.
Câu 8: Phương trình tiếp tuyến của đồ thị
3
( ): 3 4C y x x=−
tại điểm có hoành độ
0x =
là:
A.
3yx=
. B.
0y =
. C.
32yx=−
. D.
12yx=−
.
Lời giải
Chọn A
Ta có
2
3 12 (0) 3
= − =y x y
.
Phương trình tiếp tuyến của
()C
tại điểm có hoành độ
0x =
là:
( ) ( ) ( )
0 . 0 0y y x y
= − +
3=yx
.
Câu 9: Tìm tất cả các điểm
M
trên đồ thị hàm số
2
1
x
y
x
−
=
+
mà tiếp tuyến của đồ thị tại điểm đó song
song với đường thẳng
: 3 10d y x=+
.
A.
1
3;
4
M
. B.
( )
0; 2M −
.
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
9 | Facebook tác giả: Phan Nhật Linh
C.
( )
0; 2M −
và
( )
2;4M −
. D.
5
;3
2
M
−
.
Lời giải
Chọn B
Gọi
3
;1
1
Ma
a
−
+
là điểm thuộc đồ thị.
Ta có
( )
( )
( )
22
33
11
y y M
xa
= =
++
. Tiếp tuyến song song với đường thẳng
: 3 10d y x=+
nên ta suy ra
( )
( )
2
0
3
33
2
1
a
yM
a
a
=
= =
=−
+
.
Với
0a =
, ta có phương trình tiếp tuyến
32yx=−
(nhận).
Với
2a =−
, ta có phương trình tiếp tuyến
3 10yx=+
(loại).
Vậy
( )
0; 2M −
.
Câu 10: Cho hàm số
1
1
x
y
x
+
=
−
và điểm
( )
1; 1I −
. Tìm tất cả các điểm
M
nằm trên đồ thị hàm số sao cho
tiếp tuyến tại
M
vuông góc với
IM
.
A.
( )
1 2; 1 2M + − −
và
( )
1 2; 1 2M − − +
.
B.
( )
1;0M −
và
( )
3; 2M −
.
C.
( )
2; 3 2 2M −−
.
D.
( )
2; 3M −
và
( )
0;1M
.
Lời giải
Chọn A
Ta có
1 1 2 2
1
1 1 1
xx
y
x x x
+ − +
= = = − +
− − −
.
Gọi
2
;1
1
Ma
a
−+
−
là điểm thuộc đồ thị. Ta có
( )
2
22
1;
1
1
IM
IM a k
a
a
−
= − =
−
−
.
Ta có
( )
( )
( )
22
22
11
y y M
xa
= =
−−
. Tiếp tuyến vuông góc với
IM
nên ta có
( )
( ) ( )
( )
( )
22
1 2; 1 2
12
22
. 1 1
11
12
1 2; 1 2
IM
M
a
y M k
aa
a
M
− − +
=−
−
= − = −
−−
=+
+ − −
.
Câu 11: Qua điểm
( )
2;0M
kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số
42
4y x x=−
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Gọi đồ thị hàm số
42
4y x x=−
là
( )
C
.
Ta có
3
48y x x
=−

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 10
Gọi
( ) ( )
00
;A x y C
là tiếp điểm. Suy ra phương trình tiếp tuyến với
( )
C
tại
A
là
( )
( )
3 4 2
0 0 0 0 0
4 8 4y x x x x x x= − − + −
(d).
Vì (d) đi qua điểm
( )
2;0M
nên
( )
( )
3 4 2
0 0 0 0 0
4 8 2 4 0x x x x x− − + − =
( )
( ) ( )( )
22
0 0 0 0 0 0
4 8 2 2 2 0x x x x x x − − + − + =
( )
( )
2
0 0 0 0
2 3 2 8 0x x x x − − − =
0
0
0
0
2
4
3
x
x
x
=
=
=−
.
Suy ra có
3
tiếp tuyến với
( )
C
đi qua điểm
M
.
Câu 12: Biết tiếp tuyến của đồ thị hàm số
42
2y ax bx= + +
tại điểm
( )
1;1A −
vuông góc với đường
thẳng
2 3 0xy− + =
. Tính
22
ab−
A.
22
2ab− = −
. B.
22
10ab−=
. C.
22
13ab−=
. D.
22
5ab− = −
.
Lời giải
Chọn D
Vì điểm
( )
1;1A −
thuộc đồ thị hàm số
42
2y ax bx= + +
nên
1ab+ = −
( )
1
.
Ta có:
3
42y ax bx
=+
và
13
2 3 0
22
x y y x− + = = +
.
Vì tiếp tuyến của đồ thị tại
( )
1;1A −
vuông góc với đường thẳng
13
22
yx=+
nên
( ) ( )
1
1 . 1 1 2
2
yy
− = − − = −
4 2 2ab − − = −
21ab + =
( )
2
.
Từ
( )
1
,
( )
2
ta được hệ phương trình
12
2 1 3
a b a
a b b
+ = − =
+ = = −
.
Vậy
( )
2
2 2 2
2 3 5ab− = − − = −
.
Câu 13: Viết phương tình tiếp tuyến của đồ thị hàm số
3
23y x x= − +
tại điểm
( )
1;2M
.
A.
22yx=+
. B.
31yx=−
. C.
1yx=+
. D.
2yx=−
.
Lời giải
Chọn C
( )
32
2 3 3 2 1 1y x x y x y
= − + = − =
Phương trình tiếp tuyến của đồ thị hàm số
3
23y x x= − +
tại điểm
( )
1;2M
là
( )( ) ( )
0 0 0
2 1. 1 1y y y x x x y x y x
− = − − = − = +
.
Câu 14: Tiếp tuyến của đồ thị hàm số
32
23y x x x= + − −
tại điểm
( )
1; 3M −
có phương trình là
A.
3yx=−
. B.
36yx= − +
. C.
58yx=−
. D.
36yx=−
.
Lời giải
Chọn D
Ta có
( )
2
3 2 2 1 3y x x y
= + − =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
11 | Facebook tác giả: Phan Nhật Linh
Phương trình tiếp tuyến tại
( )
1; 3M −
là
( )
3 1 3yx= − −
hay
36yx=−
.
Câu 15: Viết phương trình tiếp tuyến của đồ thị hàm số
21
2
x
y
x
−
=
−
, biết tiếp tuyến có hệ số góc
3k =−
.
A.
34yx= − +
. B.
3 14yx= − +
và
32yx= − +
.
C.
3 14yx= − −
và
32yx= − −
. D.
34yx= − −
.
Lời giải
Chọn B
TXĐ:
\2D =
.
( )
2
3
2
y
x
−
=
−
.
Gọi
( )
00
;M x y
là tiếp điểm.
Tiếp tuyến có hệ số góc
3k =−
( )
0
3yx
= −
( )
( )
2
0
0
2
0
0
3
3
3 2 1
1
2
x
x
x
x
=
−
= − − =
=
−
.
Với
00
35xy= =
. Phương trình tiếp tuyến tại
( )
3;5M
là:
( )
3 3 5 3 14y x x= − − + = − +
.
Với
00
11xy= = −
. Phương trình tiếp tuyến tại
( )
1; 1M −
là:
( )
3 1 1 3 2y x x= − − − = − +
.
Vậy phương trình tiếp tuyến cần tìm là
3 14yx= − +
và
32yx= − +
.
Câu 16:
Cho hàm số
()y f x=
có đạo hàm cấp một liên tục trên . Biết phương trình tiếp tuyến của hàm
số tại điểm
0
1x =
có dạng:
34yx=+
. Giá trị của
(1)f
bằng:
A.
4
. B.
3
. C.
7
. D.
0
.
Lời giải
Chọn C
Ta có PT tiếp tuyến của hàm số tại điểm
0
x
là
0 0 0
'( )( ) ( )y f x x x f x= − +
.
Do
0
1x =
nên
'(1)( 1) (1)y f x f= − +
Suy ra
'(1) '(1) (1) 3 4y f x f f x= − + = +
Suy ra
'(1) 3 '(1) 3
'(1) (1) 4 (1) 7
ff
f f f
==
− + = =
Vậy
(1) 7.f =
Câu 17: [2D1-5.18-2] (TMD - Đề IMC10 - 2020 - 2021) Cho hàm số
32
( ) 3 4f x x x= − +
có đồ thị
( )
C
. Viết phương trình tiếp tuyến của
( )
C
tại điểm
A
có hoành độ
1
A
x =
nằm trên
( )
C
.
A.
35yx= − +
. B.
35yx=−
. C.
53yx= − +
. D.
53yx=−
.
Lời giải
Chọn A
Ta có
3 2 ' 2 '
( ) 3 4 ( ) 3 6 (1) 3f x x x f x x x f= − + = − = −
.
Điểm
( )
AC
có
1 (1;2)
A
xA=
.
Phương trình tiếp tuyến của
( )
C
tại điểm
A
là :
3( 1) 2 3 5y x y x= − − + = − +
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 12
Câu 18: Cho đồ thị
( )
C
của hàm số
32
32= − +y x x
. Có bao nhiêu tiếp tuyến với đồ thị
( )
C
song song
với trục hoành?
A.
3
. B.
2
. C. Không có. D.
1
.
Lời giải
Chọn B
Ta có:
3 2 2
3 2 3 6
= − + = −y x x y x x
.
Tiếp tuyến với đồ thị
( )
C
song song với trục hoành (nếu có) có hệ số góc bằng 0.
Gọi
0
x
là hoành độ tiếp tuyến của tiếp tuyến. Ta có
( )
0
2
0 0 0
0
0
0 3 6 0
2
=
= − =
=−
x
y x x x
x
.
TH1:
( )
0
0 0 2= =xy
PTTT:
( )
0 0 2 2= − + =y x y
(thỏa mãn).
TH2:
( )
0
2 2 2= = −xy
PTTT:
( ) ( )
0 2 2 2= − + − = −y x y
(thỏa mãn).
Vậy có hai tiếp tuyến song song với trục hoành có phương trình là
2=y
và
2=−y
.
Câu 19: Cho hàm số
42
63y x x= − −
có đồ thị
( )
C
. Tiếp tuyến của đồ thị hàm số
( )
C
tại điểm
A
(có
hoành độ
1
A
x =
) cắt đồ thị hàm số
( )
C
tại điểm
B
(
B
khác
A
). Hoành độ điểm
B
là
A.
1
. B.
3−
. C.
1−
. D.
3
.
Lời giải
Chọn B
Tiếp tuyến của đồ thị hàm số
( )
C
tại điểm
( )
;
AA
A x y
có dạng
( )( )
'= − +
A A A
y y x x x y
.
Ta có
1 8= = −
AA
xy
và
( ) ( )
' ' 1 8= = −
A
y x y
.
Vậy phương trình tiếp tuyến là
8yx=−
.
Khi đó hoành độ điểm
B
là nghiệm của phương trình
4 2 4 2
3
6 3 8 6 8 3 0
1
=−
− − = − − + − =
=
x
x x x x x x
x
.
Mà
B
khác
A
nên hoành độ điểm
B
là
3x =−
.
Câu 20: Tiếp tuyến của đồ thị hàm số
lnyx=
tại điểm có hoành độ
1x =
có phương trình là
A.
yx=
B.
1yx=−
C.
yx=−
B.
1yx= − +
Lời giải
Chọn B
Ta có
1
y
x
=
.
Khi đó, tiếp tuyến của đồ thị hàm số
( )
lny f x x==
tại điểm có hoành độ
1x =
có phương trình
là
( )( ) ( ) ( )
1
1 1 1 1 ln1 1
1
y f x f x x
= − + = − + = −
.
Câu 21: Hệ số góc của tiếp tuyến với đồ thị hàm số
21
3
x
y
x
−
=
−
tại điểm có hoành độ
4x =
là
A.
3k =−
. B.
5k =−
. C.
7k =
. D.
2k =
.
Lời giải

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
13 | Facebook tác giả: Phan Nhật Linh
Chọn B
( ) ( )
( ) ( )
22
2 3 1 1
5
33
y
xx
− − −
−
==
−−
Hệ số góc của tiếp tuyến với đồ thị hàm số
21
3
x
y
x
−
=
−
tại điểm có hoành độ
4x =
là
( )
( )
2
5
45
43
ky
−
= = = −
−
.
Câu 22: Phương trình tiếp tuyến của đồ thị hàm số
lny x x=
tại điểm có hoành độ bằng
e
là
A.
23y x e=+
. B.
2y x e=−
. C.
2y ex e=−
. D.
y x e=+
.
Lời giải
Chọn B
Ta có
1 lnyx
=+
.
Hệ số góc của tiếp tuyến là
( )
2k y e=
=
.
Phương trình tiếp tuyến cần tìm là:
( )
2y x e e= − +
hay
2y x e=−
.
Câu 23: Phương trình tiếp tuyến với đồ thị hàm số
42
22= + −y x x
tại điểm có hoành độ
0
2x =−
là
A.
40 102= − −yx
. B.
40 58= − −yx
. C.
40 102= − +yx
. D.
40 58= − +yx
.
Lời giải
Chọn B
Với
00
2 22= − =xy
.
Ta có
3
44y x x
=+
( )
2 40y
− = −
.
Phương trình tiếp tuyến tại điểm có hoành độ
0
2x =−
là
( )
40 2 22= − + +yx
hay
40 58= − −yx
.
Câu 24: Phương trình tiếp tuyến với đồ thị hàm số
42
22= + −y x x
tại điểm có hoành độ
0
2x =−
là
A.
40 102= − −yx
. B.
40 58= − −yx
. C.
40 102= − +yx
. D.
40 58= − +yx
.
Lời giải
Chọn B
Với
00
2 22= − =xy
.
Ta có
3
44y x x
=+
( )
2 40y
− = −
.
Phương trình tiếp tuyến tại điểm có hoành độ
0
2x =−
là
( )
40 2 22= − + +yx
hay
40 58= − −yx
.
Câu 25: Tiếp tuyến của đồ thị hàm số
32
32y x x= − −
có hệ số góc
3k =−
có phương trình là
A.
31yx= − +
. B.
31yx= − −
. C.
37yx= − −
. D.
37yx= − +
.
Lời giải
Chọn B
Đạo hàm
2
36y x x
=−
.
Theo đề ta có phương trình
22
3 6 3 2 1 0 1 4x x x x x y− = − − + = = = −
.
Phương trình tiếp tuyến:
( )
3 1 4 3 1y x y x= − − − = − −
.

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 14
Câu 26: Cho đường cong (C) có phương trình
1
1
x
y
x
−
=
+
. Gọi M là giao điểm của (C) và trục tung. Tiếp
tuyến của (C) tại M có phương trình là
A.
2yx=−
. B.
21yx=+
. C.
21yx= − −
. D.
21yx=−
.
Lời giải
Chọn D
TXĐ:
\1D =−
.
Ta có:
( )
2
2
()
1
y f x
x
==
+
.
Cho
( )
0 1 0; 1x y M= = − −
.
Phương trình tiếp tuyến của (C) tại M là:
( )
: (0) 0 1y f x
= − −
: 2 1yx = −
.
Câu 27: Tìm tất cả các giá trị thực của tham số
m
để tiếp tuyến của đồ thị hàm số
( )
42
( ): 2 1 8C y m x mx= − − +
tại điểm có hoành độ
1x =
vuông góc với đường thẳng
:2 3 0d x y− − =
.
A.
9
2
m =
. B.
1
2
m =−
. C.
7
12
m =
. D.
2m =
.
Lời giải
Chọn C
Tập xác định:
D =
.
Ta có:
( )
3
4 2 1 2y m x mx
= − −
.
Hệ số góc của tiếp tuyến
của đồ thị hàm số (C) tại điểm có hoành độ
1x =
là:
(1) 6 4k y m
= = −
. Hệ số góc của đường thẳng d là
2
d
k =
.
Ta có:
( )
7
. 1 6 4 .2 1
12
d
d k k m m
⊥ = − − = − =
.
Câu 28: Tiếp tuyến của đường cong
( )
21
:
1
x
Cy
x
+
=
−
tại điểm
( )
2;5M
và cắt trục tọa độ
Ox
,
Oy
lần
lượt tại
A
và
B
. Tính diện tích tam giác
OAB
.
A.
121
6
. B.
121
3
. C.
121
6
−
. D.
121
3
−
.
Lời giải
Chọn A
Phương trình tiếp tuyến có dạng :
( )( )
0 0 0
y y f x x x
− = −
Ta có
( )
2
3
1
y
x
−
=
−
và
( )
23y
=−
.
Khi đó phương trình tiếp tuyến là :
( )
5 3 2yx− = − −
3 11yx = − +
( )
d
.
A Ox d=
nên tọa độ
A
là nghiệm của hệ:
3 11
0
yx
y
= − +
=
11
3
0
x
y
=
=
nên
11
;0
3
A
.
B Oy d=
nên tọa độ
B
là nghiệm của hệ:
3 11
0
yx
x
= − +
=
0
11
x
y
=
=
nên
( )
0;11B
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
15 | Facebook tác giả: Phan Nhật Linh
1
.
2
OAB
S OAOB=
1 11 121
. .11
2 3 6
==
.
Câu 29: Cho hàm số
3
=−y x x
có đồ thị
( )
C
. Gọi
,MN
là hai điểm phân biệt trên
( )
C
và các tiếp
tuyến của
( )
C
tại các điểm
,MN
song song với nhau. Tính
+
MN
xx
.
A.
1
. B.
2
. C.
0
. D.
2−
.
Lời giải
Chọn C
Ta có
2
31
=−yx
.
Vì các tiếp tuyến của
( )
C
tại các điểm
,MN
song song với nhau nên
( ) ( ) ( )( )
22
3 1 3 1 0 0
= − = − − + = + =
M N M N M N M N M N
y x y x x x x x x x x x
(vì
,MN
là
hai điểm phân biệt).
Câu 30: Tiếp tuyến của đồ thị hàm số
32
23y x x x= + − −
tại điểm
( )
1; 3M −
có phương trình là
A.
3yx=−
. B.
36yx= − +
. C.
58yx=−
. D.
36yx=−
.
Lời giải
Chọn D
Ta có
( )
2
3 2 2 1 3y x x y
= + − =
.
Phương trình tiếp tuyến tại
( )
1; 3M −
là
( )
3 1 3yx= − −
hay
36yx=−
.
Câu 31: Có bao nhiêu tiếp tuyến của đồ thị hàm số
3
32y x x= − +
song song với đường thẳng
9 18 0xy− + =
?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Chọn C
2
33yx
=−
.
Vì tiếp tuyến song song với đường thẳng
9 18 0xy− + =
nên hệ số góc bằng 9
22
3 3 9 4 2x x x − = = =
.
Với
2x =
ta được phương trình tiếp tuyến
9 14 0xy− − =
.
Với
2x =−
ta được phương trình tiếp tuyến
9 18 0xy− + =
.
Vậy có 1 tiếp tuyến thỏa mãn.
Câu 32: Cho hàm số
2
1
x
y
x
+
=
+
có đồ thị
( )
C
. Phương trình tiếp tuyến với đồ thị hàm số tại giao điểm của
đồ thị
( )
C
với trục tung là
A.
1yx= − +
B.
2yx= − −
C.
2yx=−
D.
2yx= − +
Lời giải
Chọn D
Đạo hàm
2
1
( 1)
y
x
=−
+
.
Đồ thị cắt trục tung tại điểm
( )
;M x y
thỏa mãn
0
0
2
(0) 1
2
1
x
x
x
y k f
y
x
=
=
+
= = = −
=
+

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 16
Phương trình tiếp tuyến của đồ thị tại điểm M là
1( 0) 2 2y x x= − − + = − +
.
Câu 33: Cho hàm số
( )
32
1 3 2 1y x m x mx m= + − − + +
có đồ thị
( )
m
C
, biết rằng đồ thị
( )
m
C
luôn đi qua
hai điểm cố định
,AB
. Có bao số nguyên dương
m
thuộc
2020;2020−
để
( )
m
C
có tiếp tuyến
vuông góc với đường thẳng
AB
?
A.
4041
. B.
2021
. C.
2019
D.
2020
.
Lời giải
Chọn C
Ta tìm toạ độ hai điểm cố định
,AB
.
Ta có
( )
( )
3 2 2 3 2
1 3 2 1 3 2 1 0y x m x mx m m x x x x y= + − − + + − + + − + − =
. Toạ độ hai điểm
cố định
,AB
là nghiệm hệ
( ) ( )
2
32
3 2 0 1, 1
1;1 , 2;5
2, 5
1
x x x y
AB
xy
x x y
− + = = =
==
− + =
.
Khi đó ta có:
( ) ( )
: 4 3 0 : 4 3AB x y AB y x− + + = = −
.
Hệ số góc của tiếp tuyến với
( )
m
C
tại
( )
00
;M x y
là
( ) ( )
2
0 0 0
3 2 1 3y x x x m m
= + − −
.
Vì tiếp tuyến vuông góc với
AB
nên
( )
0
.4 1yx
=−
.
Suy ra:
( )
( )
( ) ( )
22
0 0 0 0
4. 3 2 1 3 1 12 8 1 12 1 0 *x x m m x m x m+ − − = − + − − + =
Để phương trình
( )
*
có nghiệm thì
( ) ( )
2
2
6,69
4 1 12 1 12 0 16 112 4 0
0,036
m
m m m m
m
−
= − − − + +
−
Vì
2020;2020m−
và
m
+
nên
1 2020m
.
Vậy có 2019 giá trị
m
nguyên dương.
Câu 34: Cho biết tiếp tuyến của đồ thị hàm số
( )
y f x=
tại điểm có hoành độ
1x =
là
21yx=−
.
Phương trình tiếp tuyến của đồ thị hàm số
( )
2
21y f x=−
tại điểm có hoành độ
1x =
là
A.
43yx=−
. B.
54yx=−
. C.
87yx=−
. D.
65yx=−
.
Lời giải
Chọn C
Vì tiếp tuyến của đồ thị hàm số
( )
y f x=
tại
1x =
có phương trình là
21yx=−
( )
( )
12
11
f
f
=
=
.
Đặt
( )
( )
2
21g x f x=−
;
( )
( )
2
4 . 2 1g x x f x
=−
;
( ) ( )
1 4. 1 4.2 8gf
= = =
;
( ) ( )
1 1 1gf==
Phương trình tiếp tuyến cần tìm là:
( )( ) ( )
1 1 1y g x g
= − +
( )
8 1 1yx = − +
87yx = −
.
Câu 35: Cho đồ thị
(C )
của hàm số
21
1
x
y
x
−
=
−
. Viết tất cả các phương trình tiếp tuyến của
(C )
, biết
khoảng cách từ điểm
( )
12I;
đến tiếp tuyến bằng
2
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
17 | Facebook tác giả: Phan Nhật Linh
A.
50xy+ − =
. B.
10xy+ − =
và
50xy+ − =
.
C.
10xy+ + =
và
50xy+ + =
. D.
10xy+ − =
.
Lời giải
Chọn B
Ta có
( )
2
1
1
y
x
−
=
−
.
Phương trình tiếp tuyến của
(C )
có dạng:
( )
( ) ( )
2
2
0
0 0 0 0
2
0
0
21
1
1 2 2 1 0
1
1
x
y x x x x y x x
x
x
−
−
= − + + − − + − =
−
−
Theo đề
( )
( )
( )
2
2
0 0 0
4
0
1 2 1 2 2 1
22
11
x x x
d I ,
x
+ − − + −
= =
+−
( ) ( ) ( )
4 2 2
0
0 0 0
0
2
1 2 1 1 0 1 1
0
x
x x x
x
=
− − − + = − =
=
.
Với
0
2x =
ta có phương trình tiếp tuyến:
( )
23yx= − − +
50xy + − =
.
Với
0
0x =
ta có phương trình tiếp tuyến:
( )
01yx= − − +
10xy + − =
.
Câu 36: Cho hàm số
( )
( )
21
0
m x m
ym
xm
−−
=
+
có đồ thị
( )
m
C
. Biết rằng tồn tại duy nhất một đường
thẳng
( )
d
có phương trình
y ax b=+
sao cho
( )
m
C
luôn tiếp xúc với
( )
d
. Giá trị của
ab+
là
A.
3−
. B.
1
. C.
1−
. D.
2
.
Lời giải
Chọn B
Ta có:
( )
2
2
2m
y
xm
=
+
.
Đường thẳng
( )
d
luôn tiếp xúc với đồ thị
( )
m
C
suy ra hệ phương trình sau luôn có nghiệm với
mọi giá trị
0m
.
( )
( )
( )
( )
( )( )
2
2
2
2
2
2
2 1 2
21
m
m
a
a x m
xm
xm
m x m m
m x m
ax b
ax b
xm
xm
=
=+
+
+
− + −
−−
=+
=+
+
+
( )
( )
( ) ( )
2
2
2
1
2
2 1 2
m
ax am
xm
m
m ax b
xm
=+
+
− − = +
+
Lấy
( )
1
trừ
( )
2
theo vế ta được:
( )
2
4
21
m
m am b
xm
− − + = −
+
( )
21
4
a m b
m
x m m
+ − −
=
+
Thay vào
( )
1
ta được:
( ) ( )
2
21
42
a m b
a
m
+ − +
=
( ) ( )
( )
2
2
2 1 8a m b am + − + =
( ) ( )( ) ( )
22
2
2 2 1 2 1 0a m b a m b − − + + + + =
( )
*
Vì đồ thị
( )
m
C
luôn tiếp xúc với đường thẳng
( )
d
nên
( )
*
luôn xảy ra với mọi giá trị
0m

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 18
( )
( )( )
( )
2
2
20
2
2 1 2 0
1
10
a
a
ba
b
b
−=
=
+ + =
=−
+=
.
Vậy
1ab+=
.
Câu 37: Cho hàm số
( )
y f x=
xác định và có đạo hàm trên , thỏa mãn:
( ) ( )
3
1 2. 1 21 3 0f x f x x+ + + − − =
. Viết phương trình tiếp tuyến của đồ thị
( )
y f x=
tại
điểm có hoành độ
0
1x =
.
A.
31yx=+
. B.
32yx=+
. C.
32yx=−
. D.
31yx=−
.
Lời giải
Chọn C
Xét phương trình:
( ) ( )
3
1 2. 1 21 3 0f x f x x+ + + − − =
(1).
Từ (1) cho
0x =
ta có:
( ) ( ) ( )
3
1 2. 1 3 0 1 3f f f+ − = =
.
Đạo hàm hai vế của (1) ta có
( ) ( ) ( )
2
3 1 1 4 1 2 21 0f x f x f x
+ + + + − =
(2).
Từ (2) cho
0x =
ta được:
( ) ( ) ( )
2
3 1 1 4 1 21 0f f f
+ − =
( ) ( ) ( )
3 1 4 1 21 0 1 3f f f
+ − = =
.
Vậy phương trình tiếp tuyến của đồ thị
( )
y f x=
tại điểm có hoành độ
0
1x =
là:
( ) ( ) ( ) ( )
1 . 1 1 3. 1 1 3 2y f x f x x
= − + = − + = −
.
Câu 38: Xét điểm
M
có hoành độ là số nguyên thuộc đồ thị
( )
21
:
1
x
Cy
x
+
=
−
. Tiếp tuyến của đồ thị
( )
C
tại điểm
M
cắt đường tiệm cận ngang của
( )
C
tại điểm
A
. Hỏi có bao nhiêu điểm
M
thỏa
điều kiện
A
cách gốc tọa độ một khoảng cách nhỏ hơn
2 10
?
A.
6
. B.
5
. C.
7
. D.
4
.
Lời giải
Chọn B
Ta có
( )
2
3
,1
1
yx
x
= −
−
.
Giả sử
( ) ( )
;M a b C
. Khi đó
21
1
a
b
a
+
=
−
với
,1aa
.
Tiếp tuyến với
( )
C
tại điểm
M
có phương trình là
( )
( )
2
3 2 1
:.
1
1
a
y x a
a
a
+
= − − +
−
−
.
Đồ thị
( )
C
có TCN là đường thẳng
:2dy=
.
Ta có
( )
2 1;2d A a = −
.
Theo bài ra ta có
( )
2
2 10 2 1 4 40OA a − +
2
57
4 4 35 0 ;
22
a a a
− − −
.
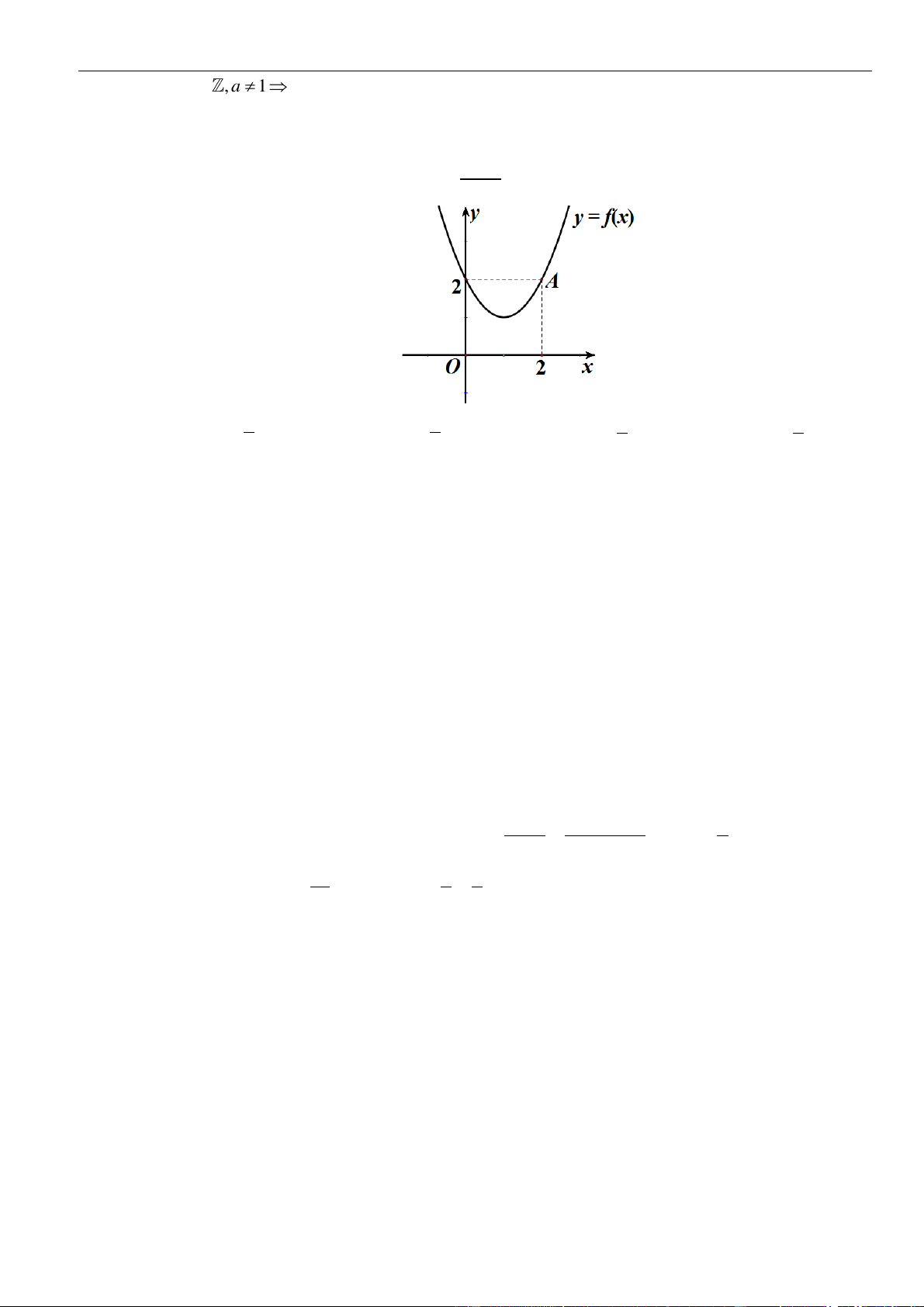
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
19 | Facebook tác giả: Phan Nhật Linh
Do
, 1 2; 1;0;2;3a a a − −
. Vậy có 5 điểm
M
thỏa mãn yêu cầu bài toán.
Câu 39: Cho hàm số
( )
y f x=
có đồ thị
( )
P
như hình bên và đường thẳng
: 2 2yx = −
là tiếp tuyến
của
( )
P
tại điểm
A
. Xét hàm số
( )
( )
fx
gx
x
=
. Tính
( )
'2g
.
A.
( )
1
'2
2
g =
. B.
( )
1
'2
4
g =
. C.
( )
1
'2
4
g =−
. D.
( )
1
'2
2
g =−
.
Lời giải
Chọn A
Đặt
( )
2
,y f x ax bx c= = + +
với
,,abc
là các số thực và
0a
.
Vì
( )
P
đi qua các điểm
( ) ( )
2;2 , 0;2AB
nên ta có hệ phương trình
( )
2 4 2 2 0
,1
22
a b c a b
cc
= + + + =
==
.
Vì đường thẳng
: 2 2yx = −
là tiếp tuyến của
( )
P
tại điểm
A
nên ta có
( ) ( )
' 2 2 4 2, 2f a b= + =
.
Từ
( )
1
và
( )
2
suy ra
1
2
2
a
b
c
=
=−
=
.
Ta có
( )
2
22y f x x x= = − +
suy ra
( )
( )
2
2 2 2
2
fx
xx
g x x
x x x
−+
= = = − +
.
Ta có
( ) ( )
2
2 2 1
' 1 ' 2 1
42
g x g
x
= − = − =
.
Câu 40: Cho hàm số
( )
3
3y f x x x= = −
có đồ thị
( )
C
và hàm số
( )
2
y g x x==
có đồ thị
( )
P
. Hỏi hai
đồ thị
( )
C
và
( )
P
có tất cả bao nhiêu tiếp tuyến chung?
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn D
Gọi
( )
2
;A a a
thuộc đồ thị
( )
P
. Phương trình tiếp tuyến tại
A
có dạng
( )( )
2
y g a x a a
= − +
.
Hay
( )
22
22y a x a a ax a= − + = −
( )
d
.
Để
( )
d
là tiếp tuyến của
( )
C
thì
( )
d
và
( )
C
phải tiếp xúc với nhau.
Ta có điều kiện tiếp xúc:
( )
( )
32
2
3 2 1
3 3 2 2
x x ax a
xa
− = −
−=
.
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 20
Thế
( )
2
vào
( )
1
ta được
( )
2
2 4 2
3 2 3 3
3 3 9 18 9
3 3 3 3 3 3
24
x x x
x x x x x x x x
− − +
− = − − − = − −
4 3 2
1,82
9 8 18 9 0
0,68
x
x x x
x
− − + =
.
Vậy hai đồ thị
( )
C
và
( )
P
có tất cả hai tiếp tuyến chung.
Câu 41: Cho hàm số
1
2
x
y
x
+
=
+
có đồ thị
()C
và đường thẳng
: 2 1d y x m= − + −
(
m
là tham số thực). Gọi
12
,kk
là hệ số góc của tiếp tuyến của
()C
tại giao điểm của
d
và
()C
. Tính tích
12
.kk
.
A.
12
.2kk =
. B.
12
1
.
4
kk =
. C.
12
.4kk =
. D.
12
.3kk =
.
Lời giải
Chọn C
Xét phương trình
2
1
2 1 2 (6 ) 3 2 0( 2)(1)
2
x
x m x m x m x
x
+
= − + − + − + − = −
+
Đặt
2
( ) 2 (6 ) 3 2f x x m x m= + − + −
. Ta có
( 2) 1 0f − = −
.
2
4 12 0,m m m = + +
.
Vậy phương trình (1) luôn có 2 nghiệm phân biệt
12
,xx
. Theo Viet ta có
12
12
6
2
32
.
2
m
xx
m
xx
−
+=
−
=
Từ
1
2
x
y
x
+
=
+
ta có
2
1
( 2)
y
x
=
+
. Do đó ta có
12
22
12
11
;
( 2) ( 2)
kk
xx
==
++
.
12
2
22
12
1 2 1 2
11
.
( 2) ( 2)
. 2( ) 4
kk
xx
x x x x
= = =
++
+ + +
Mà
2
2
1 1 2
3 2 2 12 1
. 2( ) 4 4
2 2 4
mm
x x x x
−−
+ + + = + + =
.
Vậy
12
. 4.kk =
Câu 42: Gọi
S
là tập tất cả các giá trị của tham số
m
để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm
số
3
1.yx=+
Tổng tất cả các phần tử của
S
bằng
A.
0
. B.
2
. C.
1−
. D.
3
.
Lời giải
Chọn B
Để đường thẳng
3y x m=+
tiếp xúc với đồ thị hàm số
3
1yx=+
khi và chỉ khi
3
2
13
33
x x m
x
+ = +
=
(1) có nghiệm.
Giải hệ ( 1)
3
3
2
31
1 3 1
1
3
33
1
m x x
x x m m
x
m
x
x
= − +
+ = + = −
=
=
=
=−
Vậy tổng các giá trị
m
là:
1 3 2− + =
.
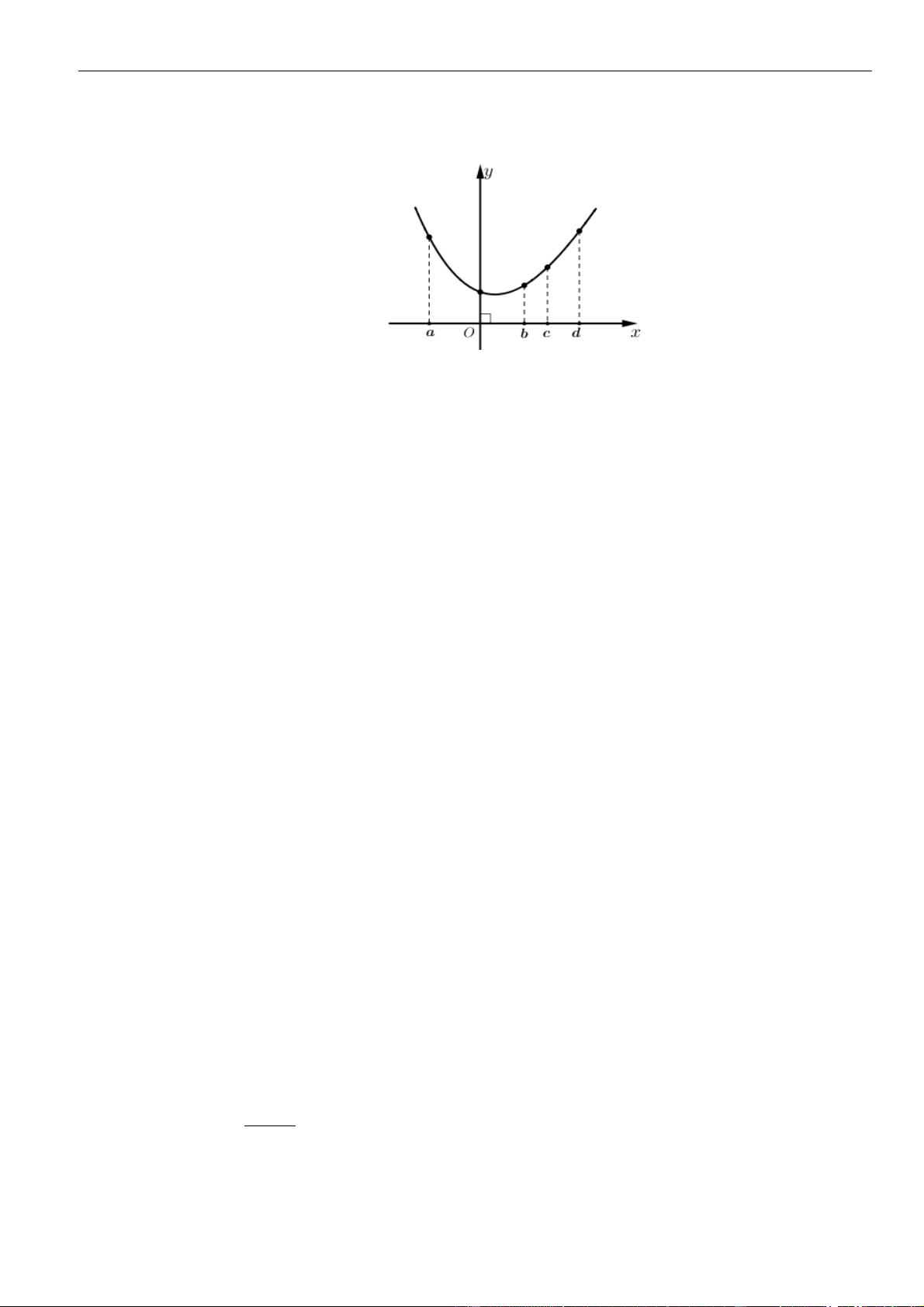
Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
21 | Facebook tác giả: Phan Nhật Linh
Câu 43: Cho
( )
fx
là hàm đa thức có đồ thị như hình vẽ bên. Gọi
( ) ( ) ( ) ( ) ( )
, , , , 0S f a f b f c f d f
=
. Phần tử lớn nhất trong tập hợp
S
là:
A.
( )
fa
. B.
( )
fb
. C.
( )
0f
. D.
( )
fd
.
Lời giải
Gọi
,
lần lượt là góc tạo bởi tiếp tuyến tại
,cd
.
( )
( ) ( ) ( )
tan
tan 0
fc
f d f c f d
=
=
.
Vậy phần tử lớn nhất trong tập hợp
S
là:
( )
fd
.
Câu 44: Cho biết tiếp tuyến của đồ thị hàm số
( )
y f x=
tại điểm có hoành độ
1x =
là
21yx=−
.
Phương trình tiếp tuyến của đồ thị hàm số
( )
2
21y f x=−
tại điểm có hoành độ
1x =
là
A.
43yx=−
. B.
54yx=−
. C.
87yx=−
. D.
65yx=−
.
Lời giải
Chọn C
Theo đề, ta có
( )
12f
=
và tiếp tuyến tại điểm có hoành độ
1x =
là
( ) ( ) ( )
2 1 1 2 1 2y x f x f= − + = + −
, suy ra
( )
1 1.f =
Xét hàm số
( )
2
21y f x=−
. Ta có
( )
2
4 2 1 .y xf x
=−
Suy ra
( ) ( )
1 4 1 8.yf
==
Từ đây ta loại ba đáp án A, B, D.
Câu 45: Cho hàm số
42
2y x x=−
có đồ thị
( )
C
. Tiếp tuyến của
( )
C
tại
A
cắt
( )
C
tại
( )
22
;B x y
với
B
khác
A
thỏa
( )
2 1 2 1
24y y x x− = − −
. Số điểm
A
thỏa mãn là
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn A
Tiếp tuyến của
( )
C
tại
A
có phương trình
( ) ( )
1 1 1
.y y y x x x
− = −
Do
B
thuộc tiếp tuyến của
( )
C
tại
A
nên
( )( )
2 1 1 2 1
y y y x x x
− = −
( )
21
1
21
24
yy
yx
xx
−
= = −
−
.
Do đó
1
x
là nghiệm của phương trình
33
4 4 24 6 0 2x x x x x− = − − + = = −
Từ đó suy ra có duy nhất điểm
A
thỏa mãn bài toán.
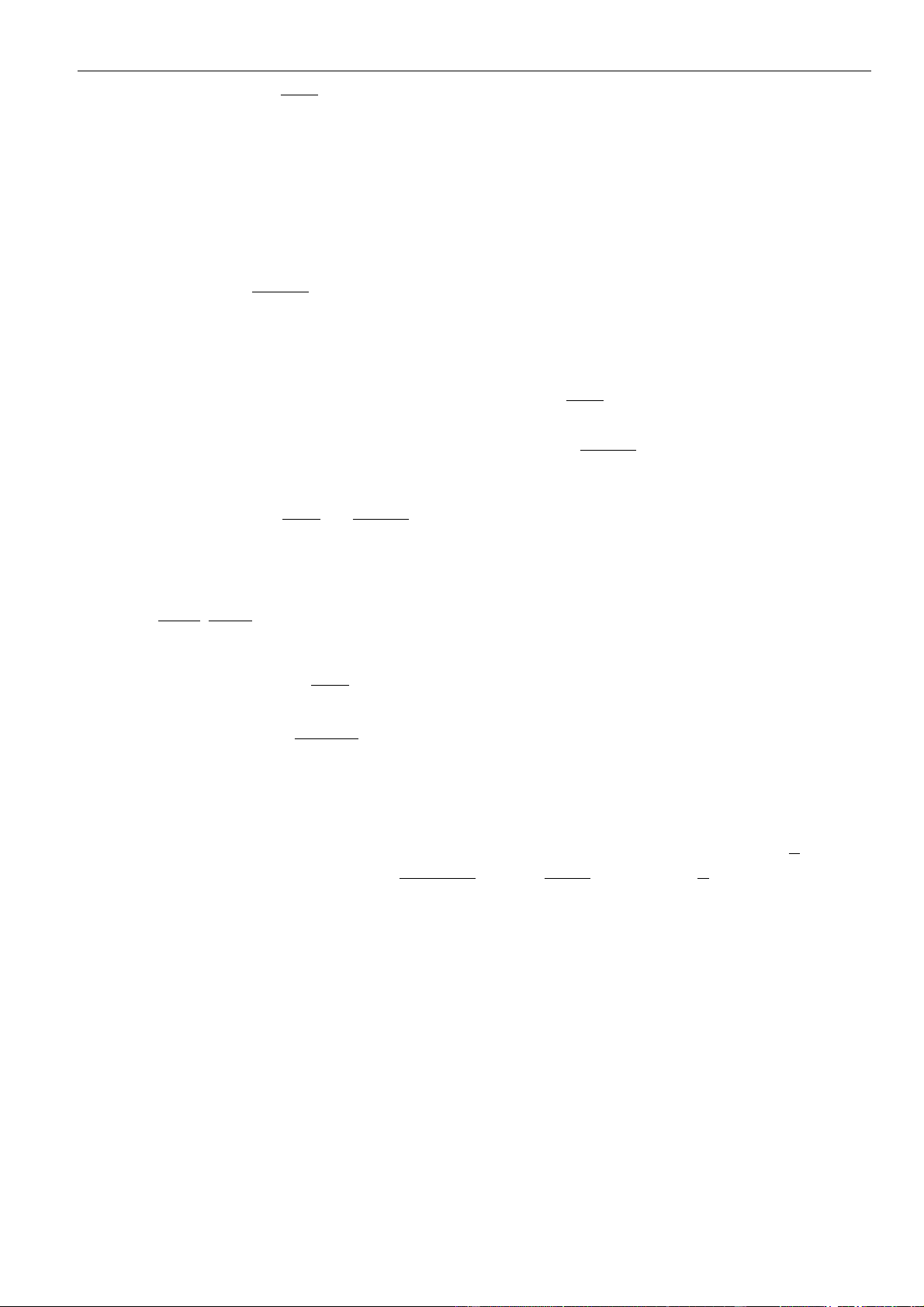
Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 22
Câu 46: Cho hàm số
2
1
x
y
x
+
=
−
có đồ thị
( )
C
và điểm
( )
0;Aa
. Có tất cả bao nhiêu giá trị nguyên của
a
trong đoạn
2018;2018−
để từ
A
kẻ được hai tiếp tuyến đến
( )
C
sao cho hai tiếp điểm nằm
về hai phía của trục hoành
A.
2019
. B.
2020
. C.
2017
. D.
2018
.
Lời giải
Chọn D
Ta có
( )
2
3
1
y
x
=−
−
.
Tiếp tuyến với đồ thị
( )
C
qua
( )
0;Aa
là
( )
Δ :y kx a=+
.
( )
Δ
tiếp xúc với
( )
C
khi và chỉ khi hệ phương trình
( )
( )
2
2
1
*
3
1
x
kx a
x
k
x
+
=+
−
−=
−
có nghiệm.
Từ hệ
( )
*
ta có
( )
( ) ( ) ( )
2
2
23
1 2 2 2 0 **
1
1
xx
a a x a x a
x
x
+
= − + − − + + + =
−
−
.
Yêu cầu bài toán là tìm
a
để phương trình
( )
**
có
2
nghiệm phân biệt
12
,xx
thỏa
12
12
22
.0
11
xx
xx
++
−−
.
Ta có
( )
12
12
2
1
22
1
Sx
a
a
a
P
a
x
xx
+
−
+
= + =
−
==
.
Yêu cầu bài toán tương đương
1
0
24
0
1
a
PS
PS
++
−+
11
1
3 6 0 2
2
9 6 2
3
0
33
aa
a
aa
a
a
a
+ −
−
+
−
−
.
Do
m
nguyên thuộc đoạn nên
0;2;3;4; ;2018 .m
Vậy có
2018
giá trị thỏa yêu cầu bài toán.
Câu 47: Cho hàm số
42
2y x x=−
có đồ thị
( )
C
. Tiếp tuyến của
( )
C
tại
A
cắt
( )
C
tại
( )
22
;B x y
với
B
khác
A
thỏa
( )
2 1 2 1
24y y x x− = − −
. Số điểm
A
thỏa mãn là
A.
1
. B.
3
. C.
2
. D.
0
.
Lời giải
Chọn A
Tiếp tuyến của
( )
C
tại
A
có phương trình
( ) ( )
1 1 1
.y y y x x x
− = −
Do
B
thuộc tiếp tuyến của
( )
C
tại
A
nên
( )( )
2 1 1 2 1
y y y x x x
− = −
2018;2018−

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
23 | Facebook tác giả: Phan Nhật Linh
( )
21
1
21
24
yy
yx
xx
−
= = −
−
.
Do đó
1
x
là nghiệm của phương trình
33
4 4 24 6 0 2x x x x x− = − − + = = −
Từ đó suy ra có duy nhất điểm
A
thỏa mãn bài toán.
Câu 48: Tìm điểm
M
có hoành độ âm trên đồ thị
( )
3
12
:
33
C y x x= −+
sao cho tiếp tuyến tại
M
vuông
góc với đường thẳng
12
:
33
d y x= − +
.
A.
( )
2; 4M −−
. B.
4
1;
3
M
−
. C.
( )
2;0M −
. D.
4
2;
3
M
−
.
Lời giải
Chọn C
Đường thẳng
12
:
33
d y x= − +
có hệ số góc
1
3
−
cho nên tiếp tuyến có hệ số góc bằng
3
.
Gọi tọa độ của
M
là
( )
00
;M x y
thì hệ số góc của tiếp tuyến tại
M
bằng
( )
2
00
'1y x x=−
.
Từ đó ta có
0
2
0
0
2
1
2
3
x
x
x
− =
=−
=
.
Theo giả thiết, điểm
M
có hoành độ âm nên
0
2x =−
. Vậy tọa độ
( )
2;0M −
.
Câu 49: Cho đa thức
( )
fx
với hệ số thực và thỏa mãn điều kiện
( ) ( )
2
2 1 , .f x f x x x+ − =
Biết
tiếp tuyến tại điểm có hoành độ
1x =
của đồ thị hàm số
( )
y f x=
tạo với hai trục tọa độ một
tam giác. Tính diện tích của tam giác đó?
A.
1
.
6
B.
3
2
. C.
1
3
. D.
2
3
.
Lời giải
Chọn A
Ta có:
( ) ( ) ( )
2
2 1 , 1 .f x f x x x+ − =
Đặt
( ) ( ) ( ) ( ) ( ) ( ) ( )
22
1 2 1 1 , 2 1 1 , 2 .t x f t f t t t f t f x x t= − − + = − − + = −
Từ (1) và (2) ta có:
( ) ( )
( ) ( ) ( )
( )
2
2
2
21
1
( ) 2 1 .
3
2 1 1
f x f x x
f x x x
f x f x x
+ − =
= + −
− + = −
Suy ra:
24
(1) ; '(1)
33
ff==
Suy ra phương trình tiếp tuyến với đồ thị hàm số
( )
y f x=
tại điểm có hoành độ
1x =
là:
( )
4 2 4 2
1
3 3 3 3
y x y x= − + = −
Tiếp tuyến cắt trục hoành tại
1
;0
2
A
và cắt trục tung tại
2
0;
3
B
−

Chủ đề 05: Khảo sát hàm số và vẽ đồ thị hàm số
Tài liệu luyện thi THPT 03 mức độ: Nhận biết -Thông hiểu và Vận dụng | 24
Suy ra diện tích tam giác
OAB
là:
1 1 1 2 1
. . .
2 2 2 3 6
S OAOB= = − =
.

Phan Nhật Linh Fanpage: Tài liệu luyện thi Đại học 2023 – Giáo viên và Học sinh
25 | Facebook tác giả: Phan Nhật Linh
Bấm Tải xuống để xem toàn bộ.