Toàn tập về phương pháp ghép trục Toán 12

Toàn tập về phương pháp ghép trục Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

55 28 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

 Cơ sở của phương pháp ghép trục giải quyết bài toán hàm hợp

 





g f u x

. Ta thực hiện theo

các bước sau đây:

 Bước 1: Tìm tập xác định của hàm

 

g f u x

. Giả sử tập xác định tìm được như sau:

     

1 2 3 4 1

; ; .... ;

n n

D a a a a a a



   

, ở đây có thể

;

a a   

 Bước 2: Xét sự biến thiên của hàm

 

u u x

và hàm

 

y f x

Lập bảng biến thiên kép, xét sự tương quan giữa

 

;x u u x

 



 

và

 

;u g f u

 



 

(Bảng biến thiên này thường có 3 dòng)

 Dòng 1: Xác định các điểm đặc biệt của hàm

 

u u x

, sắp xếp các điểm này theo thứ tự

tăng dần từ trái qua phải, giải sử như sau:

1 2 1

....

n n

a a a a



   

(xem chú ý số 1).

 Dòng 2: Điền các giá trị

 

i i

u u a

, với

 

1,.....,i n

Trên mỗi khoảng

 

;

i i

u u



, với

 

1, 1i n 

cần bổ sung các điểm kì dị

1 2

, ,....

b b b

của hàm

số

 

y f x

Trên mỗi khoảng

 

;

i i

u u



, với

 

1, 1i n 

, sắp xếp các điểm

;

i k

u b

theo thứ tự, chẳng hạn:

1 2 1

....

i k i

u b b b u



    

hoặc

1 2 1

....

i k i

u b b b u



    

(xem chú ý số 2).

 Dòng 3: Xét chiều biến thiên của hàm dựa vào bảng biến thiên của hàm

 

y f x

bằng cách hoán đổi

đóng vai trò của

;

 

f u

đóng vai trò của

 

f x

Sau khi hoàn thiện bảng biến thiên

 

g f u x

ta sẽ thấy được hình dạng của đồ thị hàm

số này.

 Bước 4: Dùng bẳng biến thiên hàm hợp

 

g f u x

để giải quyết các yêu cầu của bài toán

và đưa ra kết luận.









g f u x



LÍ THUY

ẾT

 Một số chú ý quan trọng khi sử dụng phương pháp ghép trục để giải quyết các bài toán về hàm hợp.

 CHÚ Ý 1:

 Các điểm đặc biệt của





u u x



gồm: các điểm biên của tập xác định

, các điểm cực

trị của hàm số





u u x



 Nếu xét hàm





u u x

 thì ở dòng 1 các điểm đặc biệt còn có nghiệm của phương trình





u x



( là hoành độ giao điểm của hàm số





u u x



với trục

 Nếu xét hàm





u u x

 thì ở dòng 1 các điểm đặc biệt còn có số

( là hoành độ giao

điểm của





u u x



và trục

 CHÚ Ý 2:

 Có thể dùng thêm các mũi tên để thể hiện chiều biến thiên của





u u x



 Điểm đặc biệt của hàm số





y f x



gồm: các điểm tại đó





f x

và





f x



không xác

định, các điểm cực trị của hàm số





y f x



 Nếu xét hàm









g f u x



thì trong dòng 2 các điểm đặc biệt còn có nghiệm của phương

trình





f x



 Nếu xét hàm









g f u x



thì trong dòng 2 các điểm đặc biệt còn có số

Lời giải

Chọn B

Tiến hành đặt

os osu c x c x 

. Đạo hàm

 

2.cos .sin sin sin 1 2cosu x x x x x



    

Giải phương trình:

sin 0 0; ; 2

1 5 7

cos 2 ; ;

2 3 3 3 3

x x k x

  

   



     





 



       





Sử dụng phương pháp ghép trục:

Từ bảng biến thiên ta có phương trình

 

f u 

có tất cả

nghiệm phân biệt.

VÍ DỤ MINH HỌA

VÍ DỤ 1: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Số nghiệm thuộc đoạn

;

2 2

 

 



 

 

của hàm số

 

5 cos cos 1f x x 

là

Lời giải

Chọn D

Đặt

 

2u f x 

. Từ đồ thị ta thấy hàm số đạt cực trị tại

2x 

và

5x 

Sử dụng phương pháp ghép trục:

Từ bảng biến thiên, phương trình có

nghiệm phân biệt

11 2

8 26

22 4

4 13

m m



   



  

 



   





 





Vậy có

giá trị của

thỏa mãn.

VÍ DỤ 2: Cho hàm số

 

y f x

có đồ thị như hình vẽ

Gọi

là tập hợp các giá trị nguyên của tham số

để phương trình

 

f f x  

có

nghiệm phân biệt. Số phần tử của tập

là?

. B.

. C.

. D.

Lời giải

Chọn B

Đặt

 

  

 

3 2

3 3

3 3 3

3 3

x x x

u x x x x u

x x

 



     



Giải phương trình đạo hàm

  

 

3 2

3 3 3

0 1

x x x

u x

x x





 





    





 



Sử dụng phương pháp ghép trục:

Từ bảng biến thiên, suy ra hàm số

2 ; 2  

 

có

điểm cực trị.

VÍ DỤ 3: Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình vẽ.

Hỏi phương trình

 

3f x x

có bao nhiêu điểm cực trị thuộc đoạn

2; 2 

 

Lời giải

Phương trình đã cho tướng tương với

 

3 10

5 2 1 3 cos

f x



  

Đặt

3sin

5 2 1 3cos

1 3cos

u x u



    



Giải phương trình đạo hàm

3sin

0 0

1 3cos

u x



   



Sử dụng phương pháp ghép trục:

Từ bảng biến thiên, yêu cầu bài toán

3 10 4

7 3



     

VÍ DỤ 4: Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình vẽ.

Hỏi có bao nhiêu giá trị nguyên của tham số

để phương trình

 

7 5 2 1 3 cos 3 10f x m   

có đúng ba nghiệm phân biệt thuộc

;

2 2

 

 



 

 

. B.

. C.

. D.

Câu 1: Cho hàm số

 

3 2

y f x ax bx cx d    

có đồ thị như hình vẽ

Số nghiệm thuộc khoảng



 



 

 

của phương trình

   

sin 5 sin 6 0f x f x  

là

. B.

. C.

. D.

Câu 2: Cho hàm số

 

5 4 3 2

y f x ax bx cx dx ex f      

có đồ thị như hình vẽ

Số nghiệm thực phân biệt của phương trình

 

4 5 2 3 0f x    

là:

. B.

. C. 10. D. 6

Câu 3: Cho hàm số

 

f x

có bảng biến thiên như sau:

Hỏi phương trình

 

1 2 1 1f x x   

có bao nhiêu nghiệm thực?

. B.

. C.

. D.

BÀI TẬP RÈN LUYỆN

Câu 4: Cho bảng biến thiên hàm số

 

5 2f x

như hình vẽ dưới.

Hỏi phương trình

 

2 4 3 1 3f x x    có bao nhiêu nghiệm thực

tương ứng?

. B.

. C.

. D.

Câu 5: Cho bảng biến thiên của hàm số

 

3 2f x

như hình vẽ. Biết

   

4 3; 0 0f f 

. Hỏi có bao

nhiêu giá trị nguyên của tham số

để phương trình

 

3 2 2f x x m    có nhiều nghiệm

nhất?

. B.

. C.

. D.

Câu 6: Cho hàm số

 

f x

liên tục trên



, thỏa mãn

   

  1 2 5f f

và có bảng biến thiên như sau:

Số nghiệm của phương trình

 





   

2cos 2 cos 5 2 cos 2f x x x

trên khoảng



 

 

 

là?

. B.

. C.

. D.

Câu 7: Cho hàm số

 

f x

liên tục trên



và có bảng biến thiên như hình bên.

Số giá trị nguyên của tham số

để phương trình

     

cos 3 cos 2 10 0f x m f x m    

có

đúng 4 nghiệm phân biệt thuộc đoạn

;



 



 

 

là

. B.

. C.

. D.

Câu 8: Cho

( )f x

là hàm đa thức bậc

và có đồ thị hàm số

( )y f x





như hình vẽ dưới đây

Hỏi hàm số

 

( ) 4 5y g x f x x   

có bao nhiêu điểm cực trị?

. B.

. C.

. D.

Câu 9: Cho hàm số

 

y f x

có đạo hàm liên tục trên



và có bảng xét đấu đạo hàm

 

f x



như hình

vẽ bên dưới. Hàm số

 

4 4g x f x  

đồng biến trên:

 

0;1

. B.

 

1;2

. C.

 

1; 0

. D.

 

3; 1 

Câu 10: Cho hàm số

 

y f x

có đạo hàm liên tục trên



và có bảng xét đấu đạo hàm

 

f x



như hình

vẽ bên dưới. Hàm số

 

1 7 6g x f x x    

nghịch biến trên:

 

5;6

. B.

 

1;2

. C.

 

2; 3

. D.

 

3;5

BẢNG ĐÁP ÁN

1.A 2.D 3.C 4.D 5.D 6.A 7.B 8.C 9.C 10.D

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Cho hàm số

 

3 2

y f x ax bx cx d    

có đồ thị như hình vẽ

Số nghiệm thuộc khoảng



 



 

 

của phương trình

   

sin 5 sin 6 0f x f x  

là

. B.

. C.

. D.

Bài làm:

Chọn A

Ta giải phương trình:

   

 

sin 3

sin 5 sin 6 0

sin 2

f x

f x f x

f x











 



    



 













Bảng biến thiên:

Kết hợp bảng biến thiên và đồ thị tương giao:

Ta thấy:

Với mọi

 

1;1x 

thì phương trình luôn có

nghiệm.

Với mọi

 

0;1x

thì phương trình có duy nhất

nghiệm.

Vậy số nghiệm của phương trình thuộc khoảng



 



 

 

là

3.4 1 13 

Câu 2: Cho hàm số

 

5 4 3 2

y f x ax bx cx dx ex f      

có đồ thị như hình vẽ

Số nghiệm thực phân biệt của phương trình

 

4 5 2 3 0f x    

là:

. B.

. C. 10. D. 6

Bài làm:

Đặt

     

 

4 4 5

4 5 2 4 5 2

4 5

g x x x g x





       



Giải phương trình

 

4 4 5

4 5

g x x





    



Ta lập bảng biến thiên của hàm số

 

g x

như sau:

Yêu cầu bài toán trở thành: tìm số nghiệm phân biết của phương trình

 

3 0f g x  

Kẻ đường thẳng

3y 

lên đồ thị như sau:

Từ bảng biến thiên ta thấy, số nghiệm của phương trình thuộc





 

bằng số nghiệm của

phương trình thuộc





; 2

 

. Mà trên





 

phương trình có

nghiệm nên trên





; 2

 

cũng có

nghiệm. Vậy phương trình có

3 3 6

 

nghiệm phân biệt.

Câu 3: Cho hàm số





f x

có bảng biến thiên như sau:

Hỏi phương trình





1 2 1 1

f x x

   

có bao nhiêu nghiệm thực?

. B.

. C.

. D.

Lời giải

Chọn C

Điều kiện xác định:



. Ta có:

 





 

1 2 1 1

f x x



   



    



    





Đặt

1 2 1 1 0 2.

u x x u x



         



Sử dụng phương pháp ghép trục:

Từ bảng biến thiên suy ra phương trình có

nghiệm phân biệt.

Câu 4: Cho bảng biến thiên hàm số





5 2

f x



như hình vẽ dưới.

Hỏi phương trình

 

2 4 3 1 3f x x    có bao nhiêu nghiệm thực

tương ứng?

. B.

. C.

. D.

Lời giải

Chọn D

Đặt

5 2x t 

, đưa bảng biến thiên hàm số

 

5 2f x

về bảng biến thiên hàm số

 

f x

Ta có bảng biến thiên của hàm số

 

f x

như sau:

Đặt

4 3u x x  

, phương trình trở thành

 

2 1 3

f u



  



 





Sử dụng phương pháp ghép trục:

Từ bảng biến thiên suy ra, phương trình có tất cả

nghiệm thực

Câu 5: Cho bảng biến thiên của hàm số

 

3 2f x

như hình vẽ. Biết

   

4 3; 0 0f f 

. Hỏi có bao

nhiêu giá trị nguyên của tham số

để phương trình

 

3 2 2f x x m    có nhiều nghiệm

nhất?

. B.

. C.

. D.

Lời giải

Chọn D

Đưa về bảng biến thiên của hàm số

 

f x

bằng cách đặt

   

3 2 3 2x t f x f t    

Bảng biến thiên của hàm số

 

f x

như sau:

Đặt

3 2u x x  

thì phương trình trở thành

 

f u m

 

  



 





Sử dụng phương pháp ghép trục

Để phương trình có nhiều nghiệm nhất

 

3 2 8

2 5 3;4

0 2 3

m m

  



     



  



Câu 6: Cho hàm số

 

f x

liên tục trên



, thỏa mãn

   

  1 2 5f f

và có bảng biến thiên như sau:

Số nghiệm của phương trình

 





   

2cos 2 cos 5 2 cos 2f x x x

trên khoảng



 

 

 

là?

. B.

. C.

. D.

Lời giải

Chọn A

Ta đặt

 

 

 

 

       

 

 

 

3cos 1

2cos 2cos 5 2cos ' sin 2 0

2cos 2cos 5

u x x x u x

x x

Giải phương trình

 



 

 



 

 





  







 



 



 



sin 0 ;2 .

3cos 1

2 0

2cos 2 cos 5

voi x

x x

vo nghiem

x x

Sử dụng phương pháp ghép trục:

Từ bảng biến thiên suy ra phương trình có 2 nghiệm phân biệt.

Câu 7: Cho hàm số

 

f x

liên tục trên



và có bảng biến thiên như hình bên.

Số giá trị nguyên của tham số

để phương trình

     

cos 3 cos 2 10 0f x m f x m    

có

đúng 4 nghiệm phân biệt thuộc đoạn

;



 



 

 

là

. B.

. C.

. D.

Lời giải

Chọn B

Đặt

cos sin 0

u x u x









     







( với

;



 

 

 

 

Khi đó phương trình đã cho trở thành

     

 

3 2 10 0

f u

f u m f u m

f u m



     



 





Sử dụng phương pháp ghép trục:

Do phương trình

 

2f u 

có 3 nghiệm nên yêu cầu bài toán tương đương với phương trình

 

5f u m 

có duy nhất một nghiệm

4 5 2 1 7m m      

 

1;2;3;4;5;6



 



Câu 8: Cho

( )f x

là hàm đa thức bậc

và có đồ thị hàm số

( )y f x





như hình vẽ dưới đây

Hỏi hàm số

 

( ) 4 5y g x f x x   

có bao nhiêu điểm cực trị?

. B.

. C.

. D.

Lời giải

Chọn C

Đặt

4 5 2 4 0 2.u x x u x x



         

Sử dụng phương pháp ghép trục:

Từ bảng biến thiên, suy ra hàm số có

điểm cực trị.

Câu 9: Cho hàm số





y f x



có đạo hàm liên tục trên



và có bảng xét đấu đạo hàm





f x



như hình

vẽ bên dưới. Hàm số

 





4 4

g x f x

  

đồng biến trên:





0;1

. B.





1; 2

. C.





1; 0



. D.





3; 1

 

Lời giải

Đặt

 





 

2 2

4 4 , 4 4

g x f x f u u x

      

, với





2;2

x  

Sử dụng phương pháp ghép trục:

Suy ra hàm số đồng biến trên khoảng





2;0

 .

Câu 10: Cho hàm số





y f x



có đạo hàm liên tục trên



và có bảng xét đấu đạo hàm





f x



như hình

vẽ bên dưới. Hàm số

 





1 7 6

g x f x x

    

nghịch biến trên:





5;6

. B.







1; 2

. C.





2; 3

. D.





3;5

Lời giải

Đặt:

 





 

1 7 6

g x f x x f u

     

với

1 7 6

u x x

    

và





2;2

x  

Sử dụng phương pháp ghép trục:

Vậy hàm số nghịch biến trên các khoảng





1;3 7

 

và





3;3 7



Câu 1: Cho hàm số

 

f x

có đạo hàm liên tục trên



 

2 7f  

và có bảng biến thiên như dưới đây

Có tất cả bao nhiêu giá trị nguyên của tham số

để phương trình

 

1 2f x m  

có đúng 6

nghiệm thực phân biệt?

. B.

. C.

. D.

Câu 2: Cho hàm số bậc bốn

 

y f x

có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham

số

để phương trình

 

3 1 logf x x m  

có ít nhất năm nghiệm phân biệt?

990

. B.

991

. C.

989

. D.

913

Câu 3: Cho hàm số

 

3 2

3, ,y f x x ax bx a b    

là các tham số thực thỏa mãn

 

2 0

24 3 3 0

a b

  







  





. Hỏi phương trình

     

2. . '' 'f x f x f x  

 

có bao nhiêu nghiệm?

. B.

. C.

. D.

Câu 4: Cho hàm số

 

y f x

có đồ thị như hình vẽ

Số nghiệm thực của phương trình

 

2 6 2 2f x x   là

A. 15. B. 14. C. 12. D. 13.

Câu 5: Cho hàm số

 

y f x

xác định và liên tục trên



,có đồ thị

 

'f x

như hình vẽ.

Có bao nhiêu giá trị nguyên của

 

10;10m  

để hàm số

 

4 2

(2 1)( 2 2019)

g x f m x x

 



    

 

 

đồng biến trên khoảng

 

0;  

. B.

. C.

. D.

Câu 6: Cho hàm số bậc bốn

 

y f x

có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của

tham số

để phương trình

 

3 1 logf x x m  

có ít nhất năm nghiệm phân biệt ?

990

. B.

991

. C.

989

. D.

913

Câu 7: Cho hàm số

 

y f x

có đạo hàm trên



và có bảng biến thiên như sau

Số điểm cực đại của hàm số

 

2 2

8 7 3    g x f x x x

là

. B.

. C.

. D.

Câu 8: Cho hàm số

 

y f x

có đồ thị như hình vẽ. Số nghiệm thuộc đoạn

2 ;



 



 

 

của phương trình

 

2 sin 2 5 0  f x

là

. B.

. C.

. D.

Câu 9: Cho hàm sô

 

4 3 2

, , , ,y ax bx cx dx e a b c d e     



, biết

 





và đồ thị hàm số

 

y f x





như hình vẽ. Hàm số

   

2 2g x f x x x  

đồng biến trên khoảng

 

2;

. B.

 

1;1

. C.

 

1;2

. D.

 

; 1 

Câu 10: Cho hàm số bậc bốn

   

4 3 2

, , , ,f x ax bx cx dx e a b c d e     



, biết

 

f  

và đồ thị

hàm số

 

'y f x

như hình vẽ. Hàm số

   

2 2g x f x x x  

đồng biến trên khoảng

 

2;

. B.

 

1;1

. C.

 

1;2

. D.

 

; 1 

Câu 11: Cho hàm số

 

y f x



có đạo hàm liên tục trên



và có đồ thị hàm số

 

2y f x x



 

như

hình vẽ. Hỏi hàm số

 

2 3

1 1

y f x x

   

đồng biến trên khoảng nào?

 

3; 2

 

. B.

 

1;2

. C.

 

2; 1

 

. D.

 

1;0



Câu 12: Cho hàm số

 

y f x

liên tục trên



và có đồ thị là đường cong trơn (không bị gãy khúc),

tham khảo hình vẽ bên. Gọi hàm số

   

g x f f x  

 

. Hỏi phương trình

 

' 0g x 

có bao nhiêu

nghiệm phân biệt?

. B.

. C.

. D.

Câu 13: Cho hàm số

 

f x

thỏa mãn

 

0 0f 

. Đồ thị hàm số

 

'y f x

cho bởi hình vẽ dưới đây.

Hàm số

 

3g x f x x 

có bao nhiêu điểm cực tiểu?

. B.

. C.

. D.

Câu 14: Cho hàm số

( )

9 3

y f x 



. Tìm m để phương trình

3 sin (cos ) 1

f m x f x

 

  

 

 

có đúng

nghiệm phân biệt thuộc

 

0;3



Câu 15: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Số nghiệm thuộc đoạn



 

 

 

phương trình

 

cos 2f f x 

là

. B.

. C.

. D.

Câu 16: Cho hàm số

 

4 3 2

bx cx dx ey f x ax    

với

0a 

có đồ thị như hình vẽ. Phương trình

 

logf f x m

(với

là tham số thực dương), có tối đa bao nhiêu nghiệm?

. B.

. C.

. D.

Câu 17: Cho hàm số

 

y f x

có đồ thị như hình dưới. Có bao nhiêu số nguyên

để phương trình

 

2 6 2 2 1f x x m    có 6 nghiệm phân biện thuộc đoạn

1; 2

 



 

A. 2. B. 3. C. 0. D. 1.

Câu 18: Cho hàm số

 

y f x

, hàm số

 

y f x





có đồ thị như hình bên. Hàm số

 

5sin 1

2 3

2 4

g x f



 

  

 

 

có bao nhiêu điểm cực trị trên khoảng

 

0;2



A. 9. B. 7. C. 6. D. 8.

Câu 19: Cho

 

f x

là hàm số bậc bốn thỏa mãn

 

0 0f 

. Hàm số

 

f x



có bảng biến thiên như sau:

Hàm số

 

3g x f x x  có bao nhiêu điểm cực trị

A. 5. B. 4. C. 2. D. 3

Câu 20: Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt

của phương trình

 

f f x x

là

A. 6. B. 7. C. 8. D. 9.

Câu 21: Cho hàm số

 

f x

bậc bốn có đồ thị như hình vẽ dưới đây. Tìm số điểm cực trị của hàm số

 

g x

, biết

 

2 2

1g x x f x

 



 

 

A. 5. B. 6. C. 9. D. 10.

Câu 22: Cho hàm số bậc ba

 

y f x

có đồ thị như hình vẽ sau. Có bao nhiêu giá trị nguyên của tham

số

thuộc đoạn

 

20;20

để hàm số

 

1g x f x m  

có 5 điểm cực trị?

A. 14. B. 15. C. 16. D. 17.

Câu 23: Cho hàm số

 

y f x

có đồ thị hàm số

 

'y f x

như hình vẽ dưới đây.

Hàm số

 

1g x f x x  

có bao nhiêu điểm cực đại?

. B.

. C.

. D.

Câu 24: Cho hàm số

 

y f x

liên tục trên



và có đồ thị như hình bên dưới.

Số giá trị nguyên của tham số

sao cho phương trình

   

2sinf x f m

có 5 nghiệm phân

biệt thuộc đoạn



 

 

 

là

. B.

. C.

. D.

Câu 25: Cho hàm số bậc ba

 

y f x

có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m

thuộc đoạn

 

20;20

để hàm số

 

1g x f x m  

có 5 điểm cực trị.

. B.

. C.

. D.

Câu 26: Cho hàm số

( ) 3y f x x x   . Số điểm cực tiểu của hàm số

sin 3 (sin 3 cos )

f x x x

 

 

 

 

trên

;

6 6

 

 



 

 

là?

. D.

Câu 27: Cho hàm số

( )y f x

có đạo hàm liên tục trên



( 2) 7f  

và có bảng biến thiên như hình

dưới đây.

Có tất cả bao nhiêu giá trị nguyên của tham số

để phương trình





1 2

f x m

  

có đúng 6

nghiệm thực phân biệt?

. B.

. C.

. D.

Câu 28: Cho hàm số bậc ba





y f x



và hàm số bậc nhất





y g x



có đồ thị như hình dưới đây

Hàm số

   





f x

h x g t dt





nghịch biến trên khoảng nào dưới đây?





3; 2 .

 





2; 1 .

 





1;1 .







1;3 .

Câu 1: Đặt





2 1

1 2 '

x x

u x u



    



với

 

Ta có:

' 0 1

u x







  



 



Ghép trục ta được:

Để phương trình





1 2

f x m

  

có đúng 6 nghiệm thực phân biệt thì

1 7

  

Suy ra





0;1;2;3;4;5;6

m 

Câu 2: Ta có bảng biến thiên của hàm số





y f x



Đặt

     

3 1 3 . 1

u x x x x

     

 

   









 

2 2

3 2 2

' . 1 3

3 3

x x

u x x

x x

 



     

 

Ta có bảng biến thiên của hàm số





u u x



Ghép trục ta được:





log

f u m



có ít nhất 5 nghiệm phân biệt

4 log 0

1 log 3

  







 



10 1

10 10





 





 



và m









1;10;11;...;999

m 

Câu 3: Ta có





 

   

 

lim

1 2 0

3 9 3 24 24 3 3 0

lim

f x

f a b

f a b a b

f x





 





   





      



 





Suy ra





f x



có 3 nghiệm phân biệt

1 2 3

1 3

x x x

   

Mặt khác:

           

2 2

2. . '' ' 2. . '' ' 0

f x f x f x f x f x f x

   

   

   

Xét

       

2. . '' '

g x f x f x f x

 

 

 









































' 2. ' . '' 2 . ''' 2 ' . '' 2 . ''' 12 .

g x f x f x f x f x f x f x f x f x f x

     

Khi đó

     





 

' 0 12 0 0 1;3 .

x x

g x f x f x x x

x x

  



       



  



Bảng biến thiên

         

2 2

2 2 2 2 2

2. . '' ' ' 0g x f x f x f x f x       

   

nên

 

0g x 

có hai nghiệm phân

biệt.

Câu 4:

Ta có:

 

   

3 3

2 6 2 2 2 6 2 0

2 6 2 2

2 6 2 2 2 6 2 0

f x x khi f x x

f x x

f x x khi f x x



     



   



      





Theo đồ thị:

   

2 2 1f  

     

2 0 3 2f a a  

     

2 3 6 3f b b  

     

2 6 4f c c 

Với

 

thì

3 3

2 6 2 2 2 6 4 0 2; 1x x x x x x            (2 nghiệm).

Với

 

thì

3 3

2 6 2 2 6 2 0x x a x x a       

(3 nghiệm).

Với

 

thì

3 3

2 6 2 2 6 2 0x x b x x b       

(3 nghiệm).

Với

 

thì

2 6 2x x c  

(1 nghiệm).

Vậy

 

2 6 2 2f x x  

có 2+3+3+1 = 9 nghiệm.

Với

 

2 6 2 2f x x   

thì có 3 trường hợp là

 

2f d  

với

2d  

;

 

2f e  

với

3 6e 

và

 

2f f  

với

6f 

Với

2d  

thì

2 6 2x x d  

có 1 nghiệm.

Với

3 6e 

thì

2 6 2x x e  

có 3 nghiệm.

Với

6f 

thì

2 6 2x x f  

có 1 nghiệm.

Trường hợp

 

2 6 2 2f x x   

có 1+3+1 = 5 nghiệm.

Vậy tổng cộng

 

2 6 2 2f x x   có 9 + 5 = 14 nghiệm.

Câu 5: Chọn C

Ta có

 

2 3

3 1

' ' (2 1)(4 4 )

2 2

g x x f m x x

 



   

 

 

Hàm số đồng biến trên





 

khi và chỉ khi









' 0, 0;g x x  

 

 

2 3

3 1

' (2 1)(4 4 ) 0,

2 2

3 1

2 1 . '

;

0;,

8 8 2

x f m x x x

x x

m f x

 

 



      

 

 

 



    

 



 

 

Với



thì

3 3

1 1

0 ' 2.

2 2

x x

 

 

   

 

 

Đẳng thức xảy ra khi

1 1.



  

Mặt khác,

3 3 3

8 8 16

8( )

  



Suy ra

3 3

2 2

3 1 3 3 1 3

. ' ( 2). . ' .

8 8 2 16 8 8 2 8

x x x x

f f

x x

   

  

   

   

 

   

Đẳng thức xảy ra khi



. Như vậy:

3 5

2 1 .

8 16

m m



   

Vì m





và





10;10

m  

nên





10; 9; 8;... 1;0

m      . Có 11 giá trị.

Câu 6: Đặt

       

3 1 3 1

     

u x x x x x

 

  

 

    

 

  

 

2 2 2

3 1 3 1 3 3 2x+2

' 3

3 3 3

      

    

  

x x x x x x

u x x

x x x

 

' 0

u x



 

 



 



Bảng biến thiên

Từ bảng biến thiên ta thấy, phương trình đã cho có ít nhất năm nghiệm khi :

4 log 0 1

10 1

1 log 3 10,11,12,....,999

10 10

m m





 

   

 

 



 

  

 

 



Vậy có

991

giá trị nguyên của

thỏa mãn.

Câu 7: Xét hàm số

2 2

8 7 3

    

y x x x

Tập xác định của hàm số là



Ta có

2 2

2 8 4, 1 7

8 7 3

8 10, 1 7



    

     



  



x x x x

y x x x

x x

4 8, 1 7

8 , 1 7

x x x

   







 



Đặt

2 2

8 7 3    t x x x

. Khi đó bảng biến thiên của hàm số

 

y f t

là

Dựa vào bảng biến thiên suy ra hàm số

 

y f t

cho có 7 điểm cực đại.

Câu 8: Đặt

sin 2,1 3   t x t

Phương trình

 

2 sin 2 5 0  f x

trở thành:

 

0;1

1;2

2;3

3;4

  



 



 



 



  



t t PTVN

t t

f t

t t

t t PTVN

BBT:

Dựa vào bảng biến thiên ta có:

t t

có 3 nghiệm phân biệt

thuộc

2 ;



 



 

 

t t

có 4 nghiệm phân biệt

thuộc

2 ;



 



 

 

Vậy phương trình đã cho có 7 nghiệm phân biệt.

Câu 9: Xét hàm số

       

2 2 2 2 2h x f x x x h x f x x

 

      

     

0 1 1h x f x x

 

   

Vẽ đường thẳng

y x

 

. Từ đồ thị hàm số ta thấy đường thẳng

y x

 

cắt đồ thị hàm số





y f x





tại ba điểm. Khi đó phương trình

 

1 1

 





 















1 2 1 2 0

h f x x

   

Ta có bảng biến thiên của hàm số





h x

như sau:

Khi đó ta có bảng biến thiên của hàm số









g x h x



Câu 10: Xét









2 2

h x f x x x

  









' 2 ' 2 2

h x f x x

   













' 0 2 ' 2 2 0 ' 1

h x f x x f x x

       

Dựa vào đồ thị ta thấy, đồ thị hàm số

 

'y f x

và đường thẳng

1y x 

cắt nhau tại 3 điểm có

hoành độ là

1; 1; 2x x x   

Do đó phương trình

 

' 1 1

f x x x

 





   







Bảng biến thiên

Bảng biến thiên của hàm số

   

g x h x

Vậy hàm số

   

2 2g x f x x x  

đồng biến trên khoảng

 

1;2

Câu 11: Xét hàm số

 

2 3

1 1

g x f x x

   

Ta có:

 

   

2 2 2

' 2 . ' 1 2 2 ' 1g x x f x x x f x x

 

     

 

 

 

' 0

' 1 1

g x

f x x







 



 





Xét

 

: Đặt

1x t

 

Khi đó ta có:

 

0;1

' 2 1

2;3

t a a

f t t t

t b b



 



 



    







 





 

1 1 1;0

1 1 1;2

x a a

x b b



 



    











   





Ta có:

Từ bảng xét dấu trên ta thấy hàm số

 

g x

đồng biến trên khoảng

 

2; 1

 

Câu 12: Ta có

 

2; 1

' 0

1;2

x a

f x

x b

   







 



 









Từ đồ thị ta có

 

, 3f a M M 

và

   

, 0;1f b m m 

Đặt

 

u f x

, ta có hàm số

   

g x f u

Số nghiệm phân biệt của phương trình

 

' 0g x 

chính là số cực trị của hàm số

   

g x f u

Dựa vào đồ thi hàm số

 

y f x

ta có bảng biến thiên sau:

Từ bảng biến thiên ta thấy hàm số

   

g x f u

có 12 cực trị.

Vậy phương trình

 

' 0g x 

có 12 nghiệm phân biệt.

Câu 13: Đặt:

         

3 ' ' 3h x f x x h x f x     

Từ đồ thị hàm

 

'y f x

ta có BBT:

Số điểm cực trị dương của hàm

 

h x

là

Do đó số điểm cực tiểu của

 

g x

là:

2.2 1 5 

Câu 14: Ta có

9 9 9 3

( ) (1 ) 1

9 3 9 3 9 3 9 3

x x x

x x x x

f x f x x



       

   

Do đó

2 2

3 sin (cos ) 1

1 1

3 sin cos 1 3 sin sin .

4 4

f m x f x

m x x m x x

 

  

 

 

      

Kết luận:

1 1

3 0 0

64 192

m m

 

    

Câu 15: Đặt

cosu x

 

t f u

Phương trình trở thành:

( ) 2f t 

Ta có bảng biến thiên hàm số

( )y f t

Số nghiệm phương trình

 

cos 2f f x 

bằng số giao điểm của đường thẳng

2y 

và đồ thị

hàm số

( )y f t

, từ bảng biến thiên  phương trình

( ) 2f t 

có 9 nghiệm.

Vậy phương trình

 

cos 2f f x 

có 9 nghiệm.

Câu 16: Đặt

 

t f x

Phương trình trở thành:

 

logf t m

Số nghiệm phương trình

 

logf f x m

bằng số giao điểm của đường thẳng

logy m

và

đồ thị hàm số

( )y f t

, từ bảng biến thiên  phương trình có tối đa 18 nghiệm.

Câu 17: Đặt

2 6 2t x x  

Khi đó

6 6t x



 







 



 



 

2 6 2 2 1f x x m    có 6 nghiệm phân biệt

0 2 1 2m   

1 3

2 2

m  

Lại có

1m m  



. Vậy có duy nhất 1 số nguyên

thoả mãn bài toán.

Câu 18: Đặt

5sin 1





. Suy ra

   

2 3g t f t t  

Ta có

     

2 2 0g t f t t f t t

  

     

 





 



 



Bảng biến thiên:

Suy ra:

Câu 19: Đặt

t x x t   .Ta có

 

   

3 3h x f x x h t f t t    

Dựa vào bảng biến thiên ta suy ra

   

0h x f t t a

 

     

t a x a  

Suy ra hàm số





( )

g x h x



có 3 cực trị

Câu 20: Xét phương trình









f f x x







Nhận xét:





















2 2 1

x f x x f f x f x x        không có nghiệm























2 2 1

x f x x f f x f x x          không có nghiệm

 

Ta xét bảng biến thiên của









f f x

với

2 2

  

như sau:

Dựa vào bảng biến thiên, ta thấy phương trình









f f x x



có 9 nghiệm.

Câu 21:

 

1 0

g x

f x







 



 





0 0

x x

  

(nghiệm kép, loại).

 





 

1 1

1 1 0

1 0 1

1 1

x l

x a

x a a

f x x b

x b b



  



  



    



      



   



 







 



. Vậy





g x

có 6 cực trị.

Câu 22:





f x

có hai cực trị là

     

3 2

0, 2 2 .

x x f x ax x f x x ax C



        













3 2

0 2, 1 4 3, 2 3 2

f f a c f x x x

           

 





 

1 , khi 0

3 4, khi 0

1 1

1 , khi 0

3 4, khi 0

f x x

x x x

f x f x

f x x

x x x

 



   

 

    

 

 

  





Ta có đồ thị của





f x



như sau:

Đặt









1 .

h x f x m

  

Ta có









g x h x







g x

có 5 cực trị



phương trình





h x



có 2 nghiệm đơn

 

Vậy có 17 giá trị

thỏa yêu cầu bài toán.

Câu 23: Dựa vào đồ thị ta thấy hàm số





y f x

 có 3 điểm cực trị là

1; 1; 2

x x x

   

Đặt

 

1, 1

1, 0 1

1, 1 0

1, 1

x x x

u x x x

x x x



  



    



   



     



   



;

 

' 0

u x







 



 





Bảng biến thiên ghép trục

Hàm số













g x f u x

 có

điểm cực đại và

điểm cực tiểu.

Câu 24: Từ đồ thị hàm số





y f x



ta thấy hàm số có các cực trị

1; 1

x x

  

Đặt

2sin ' 2cos

t x t x

  

;

' 0 , .

t x k k



    



Ta có bảng ghép trục.

Phương trình









2sin

f x f m



có 5 nghiệm phân biệt thuộc đoạn



 

 

 

khi









3 0 .

f m f  

Từ đồ thị hàm số





y f x



ta thấy









3 0

f m f  









 

2; 1

0;1 .

1;2

m a

m b

m c

   





  



 



Vì m





nên



Câu 25: Đặt









1 1

t x f x f t

    

Bảng ghép trục:

Phương trình





g x

trở thành









g t f t m

 

YCBT trở thành:





f t m

 

có 2 nghiệm phân biệt

Để





f t m

 

có 2 nghiệm phân biệt thì:

 

20;20

8 8

m m



 

     



có 13 giá trị m

Câu 26: Ta có:

sin(3 ) 3sin 4sin 6sin

3 3 3

y f x x f x x

  



   

     

        

     



  

     

   

Vậy hàm số trên có 6 điểm cực tiểu.

Câu 27: Đặt





2 . 1

1 2 '

x x

u x u



    



Ta có bảng biến thiên như sau

Từ bảng biến thiên để phương trình có đúng 6 nghiệm thực phân biệt khi

1 7

  

Suy ra





0,1,2,3,4,5,6

m

Câu 28: Đặt









. 2 , 0

g x k x k

  

   

 

2 2 .

2 2

f x

h x g t dt k x k f x

 

     

 

 



f(-2)=7

f(0)=-1

f(-1)=-2

f(1)=-2

f(-1)=-2

+∞

-1

+∞

-2

-1

1-1

+∞

-∞

f(u)

     

 





 

3 1

4 2

2;0

' 0 0;2

' . ' 2 ' 0

2 2;

x x

f x x x

h x k f x f x h x

f x x x x

x x x





 





  



      



   







 



Bảng biến thiên

Dưạ vào bảng biến thiên suy ra hàm số h(x) nghịch biến trên khoảng





3; 2 .

 

+ +0

-2



h(x)

h'(x)

Bấm Tải xuống để xem toàn bộ.

| 1/42

| | Tải xuống

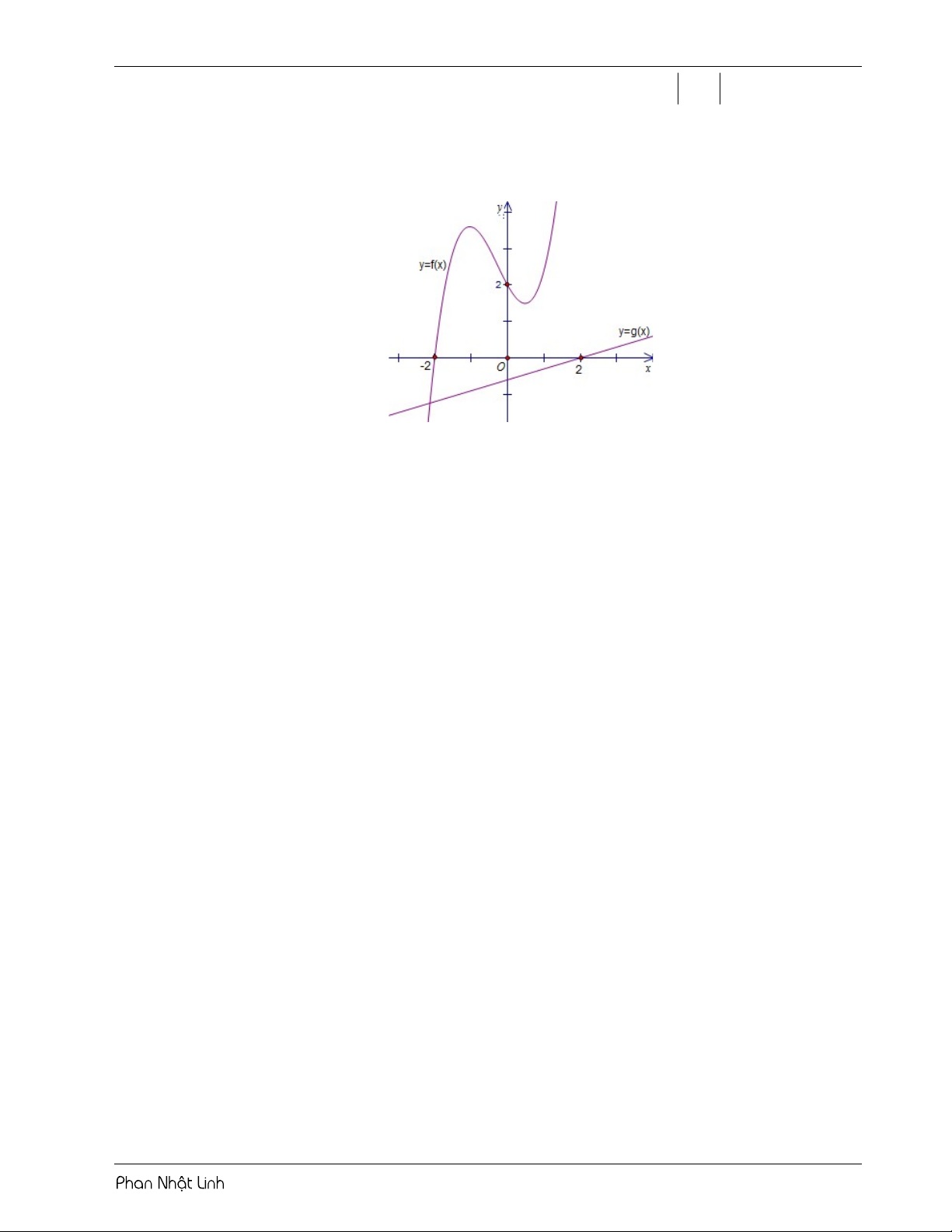
Preview text:

LÍ THUYẾT
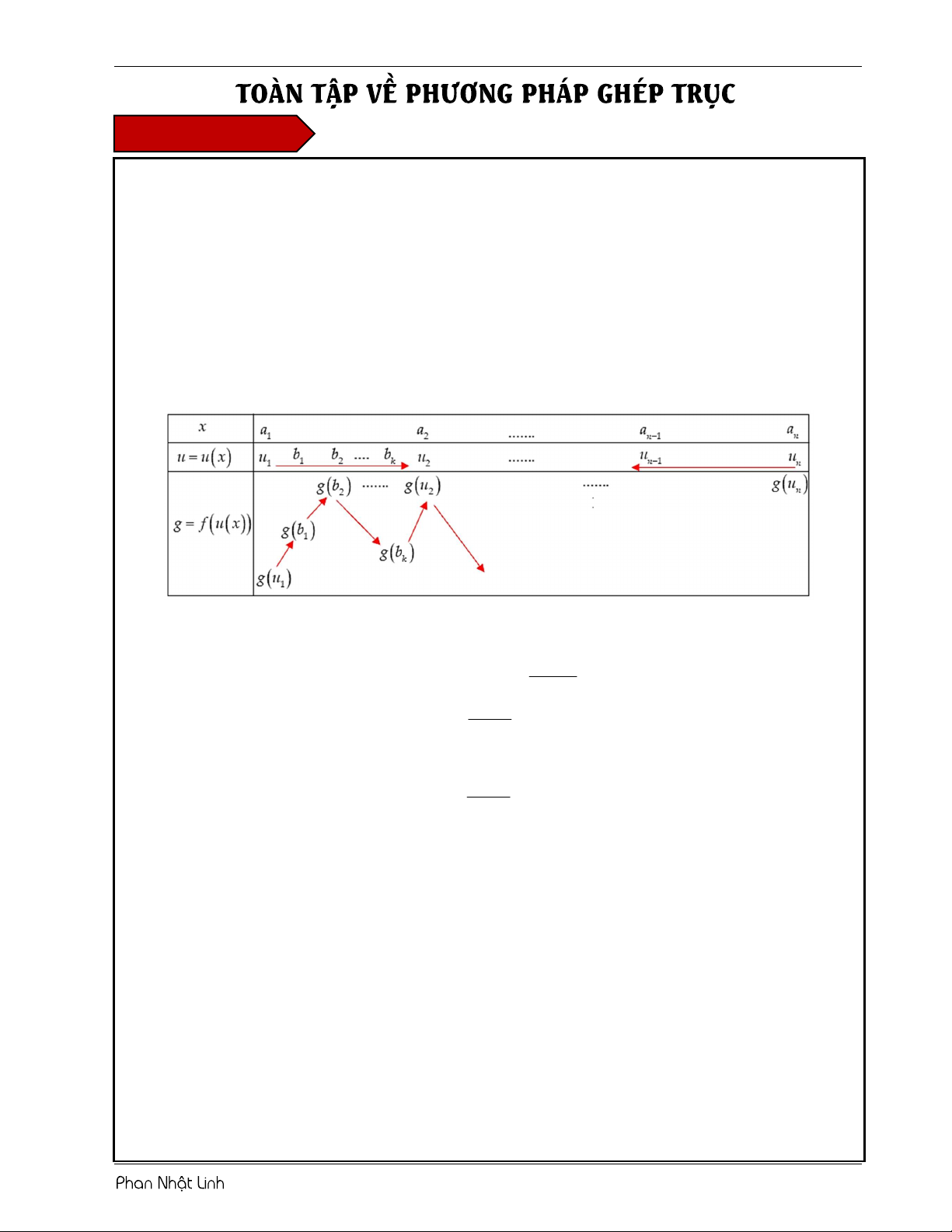
 Cơ sở của phương pháp ghép trục giải quyết bài toán hàm hợp g  f ux. Ta thực hiện theo các bước sau đây: 
Bước 1: Tìm tập xác định của hàm g  f ux. Giả sử tập xác định tìm được như sau:
D  a ;a  a ;a .... a
, ở đây có thể a  ; a    ; a 1 2   3 4  n 1 n 1 n 
Bước 2: Xét sự biến thiên của hàm u  ux và hàm y  f x
Lập bảng biến thiên kép, xét sự tương quan giữa x;u  u 
x và  ;ug  f  u
(Bảng biến thiên này thường có 3 dòng) 
Dòng 1: Xác định các điểm đặc biệt của hàm u  ux , sắp xếp các điểm này theo thứ tự
tăng dần từ trái qua phải, giải sử như sau: a  a  ....  a  (xem chú ý số 1).  a 1 2 n 1 n 
Dòng 2: Điền các giá trị u  u a , với i  1,. ...,n . i  i Trên mỗi khoảng u ;u
, với i  1,n 1 cần bổ sung các điểm kì dị b ,b ,....b của hàm i i 1   1 2 k số y  f x . Trên mỗi khoảng u ;u
, với i  1,n1 , sắp xếp các điểm u ;b theo thứ tự, chẳng hạn: i i 1   i k
u  b  b  . ..  b  u hoặc u  b  b  . ..  b  u (xem chú ý số 2). i 1 2 k i1 i 1 2 k i1 
Dòng 3: Xét chiều biến thiên của hàm g  f ux dựa vào bảng biến thiên của hàm
y  f x bằng cách hoán đổi u đóng vai trò của x ; f u đóng vai trò của f x .
Sau khi hoàn thiện bảng biến thiên g  f ux ta sẽ thấy được hình dạng của đồ thị hàm số này. 
Bước 4: Dùng bẳng biến thiên hàm hợp g  f ux để giải quyết các yêu cầu của bài toán và đưa ra kết luận.
 Một số chú ý quan trọng khi sử dụng phương pháp ghép trục để giải quyết các bài toán về hàm hợp.  CHÚ Ý 1:
 Các điểm đặc biệt của u  ux gồm: các điểm biên của tập xác định D , các điểm cực
trị của hàm số u  ux .
 Nếu xét hàm u  ux thì ở dòng 1 các điểm đặc biệt còn có nghiệm của phương trình
ux  0 ( là hoành độ giao điểm của hàm số u  ux với trục Ox ).
 Nếu xét hàm u  u x  thì ở dòng 1 các điểm đặc biệt còn có số 0 ( là hoành độ giao
điểm của u  ux và trục Oy ).  CHÚ Ý 2:
 Có thể dùng thêm các mũi tên để thể hiện chiều biến thiên của u  ux .
 Điểm đặc biệt của hàm số y  f x gồm: các điểm tại đó f x và f x không xác
định, các điểm cực trị của hàm số y  f x .
 Nếu xét hàm g  f ux thì trong dòng 2 các điểm đặc biệt còn có nghiệm của phương trình f x  0 .
 Nếu xét hàm g  f u x  thì trong dòng 2 các điểm đặc biệt còn có số 0 . VÍ DỤ MINH HỌA
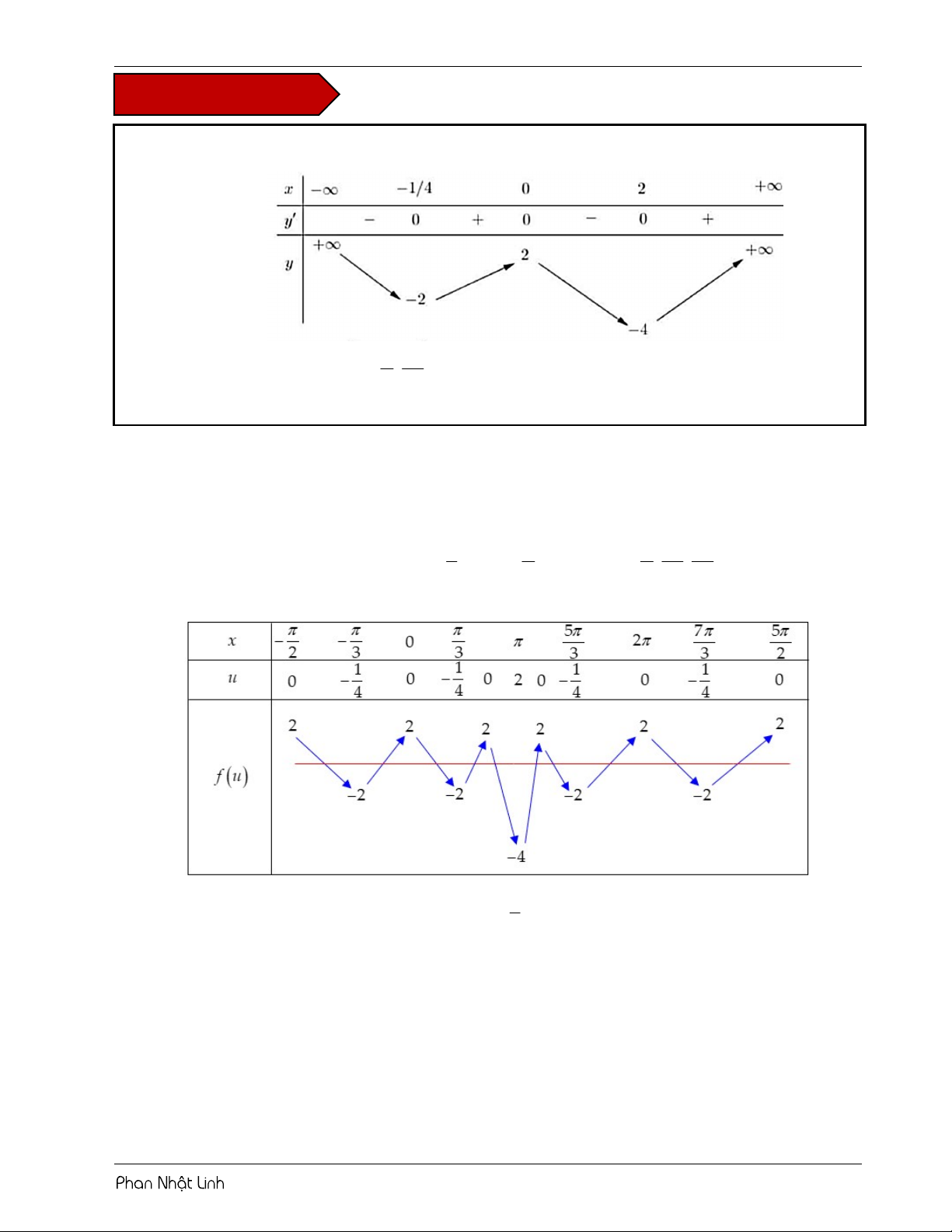
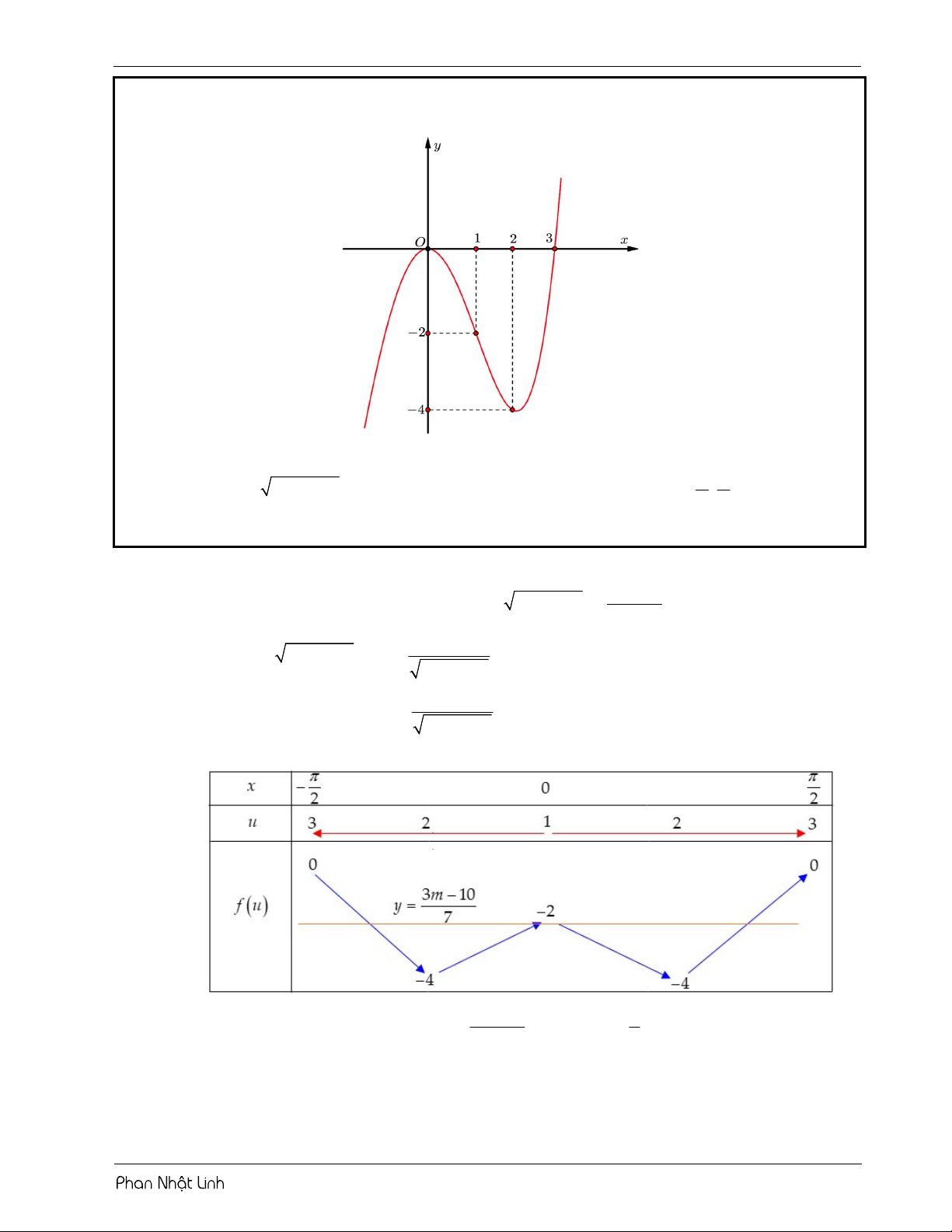
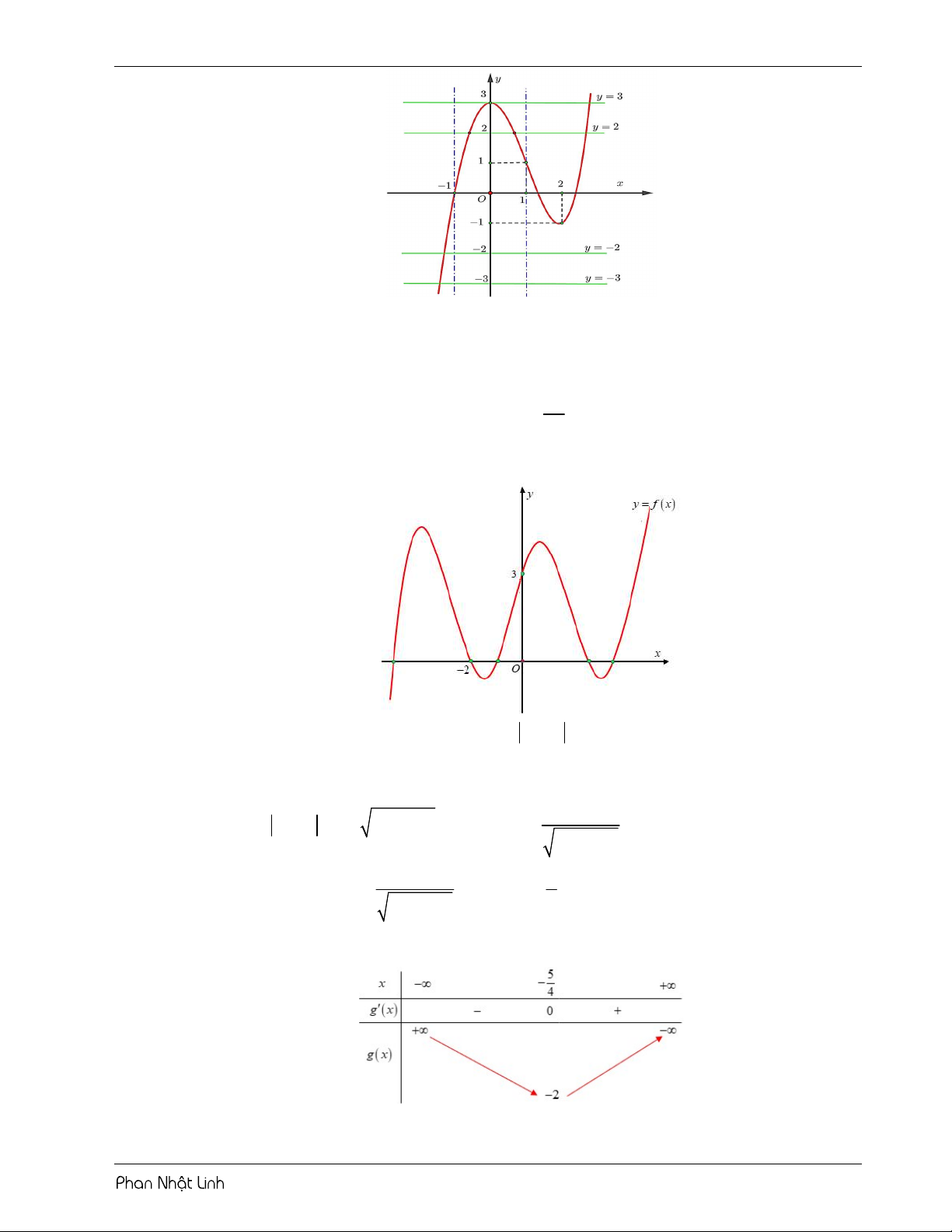
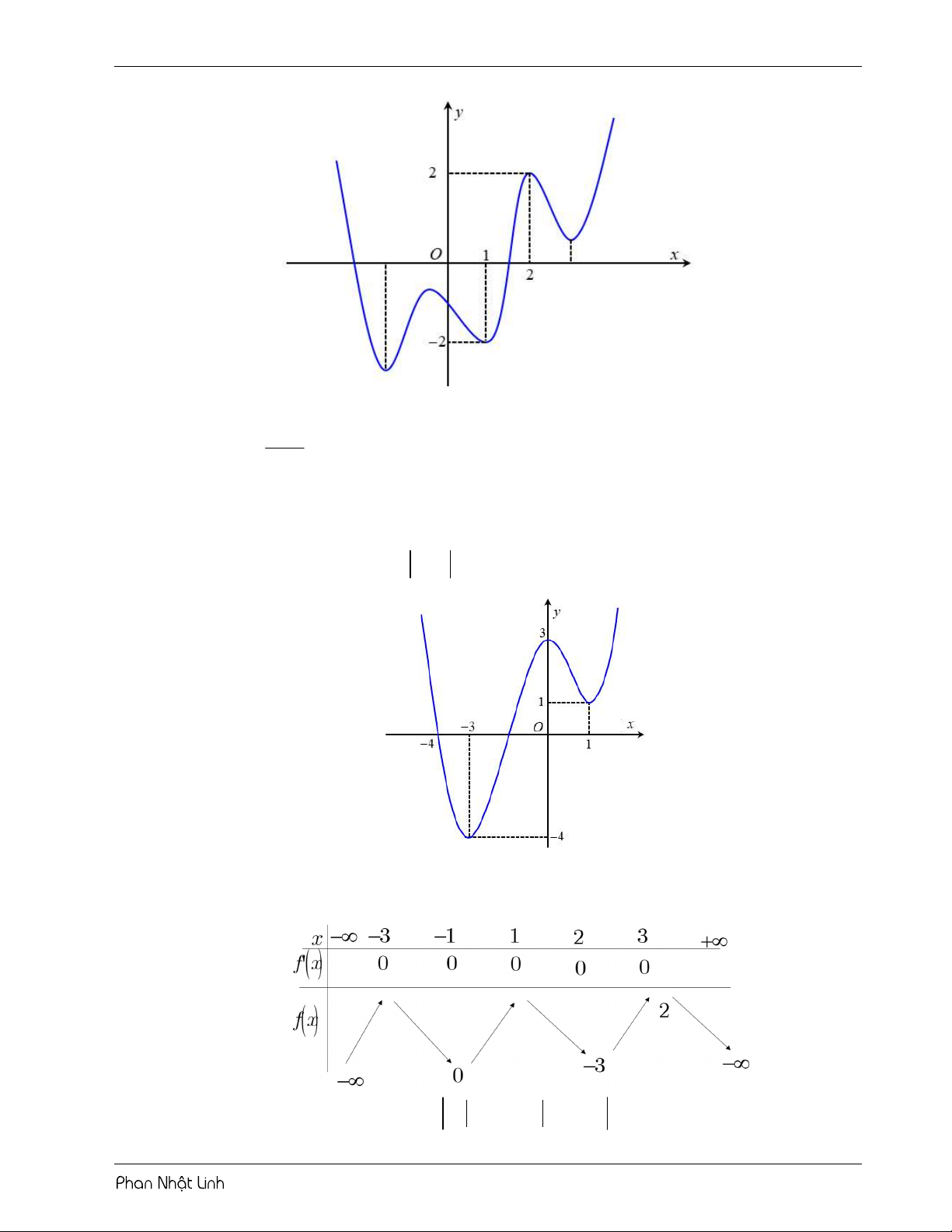
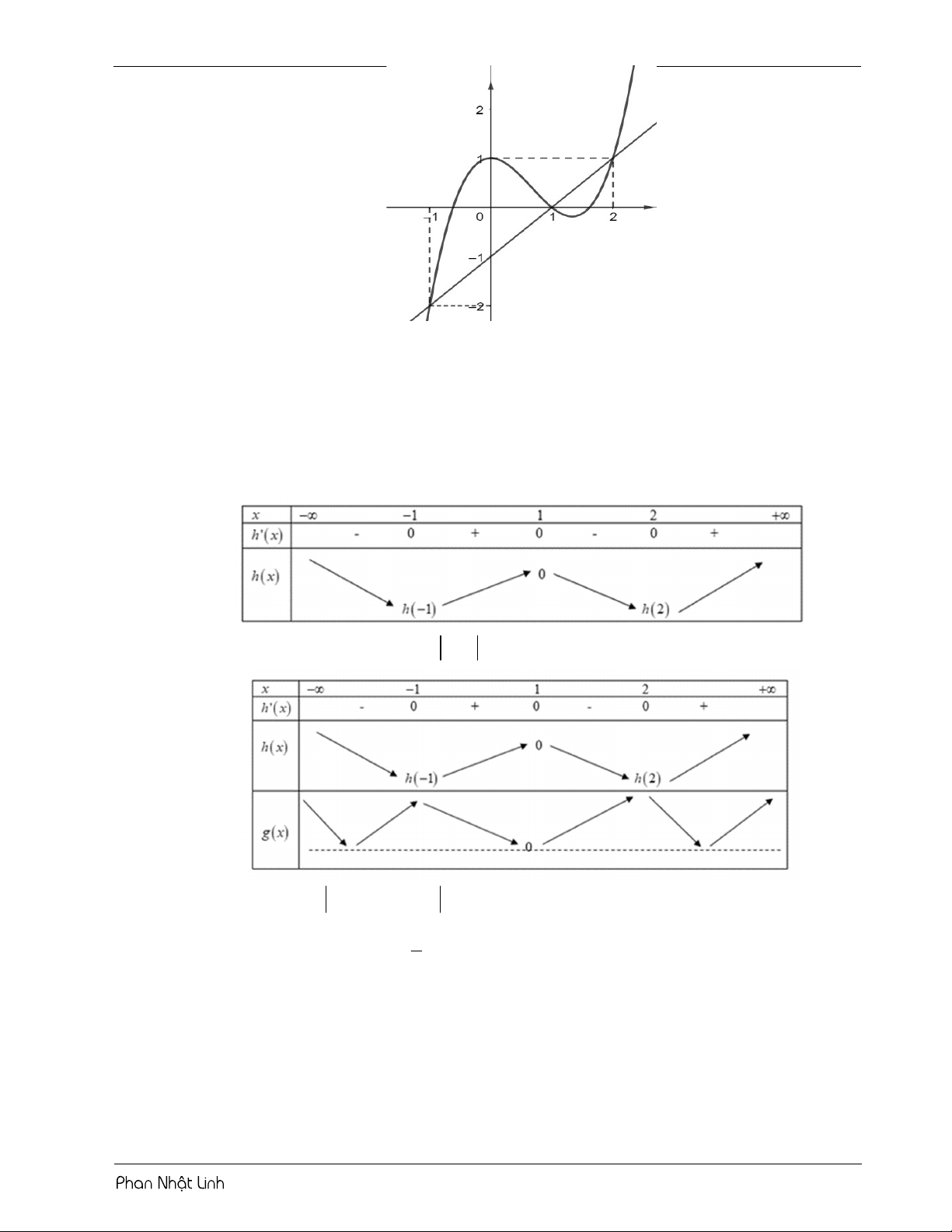
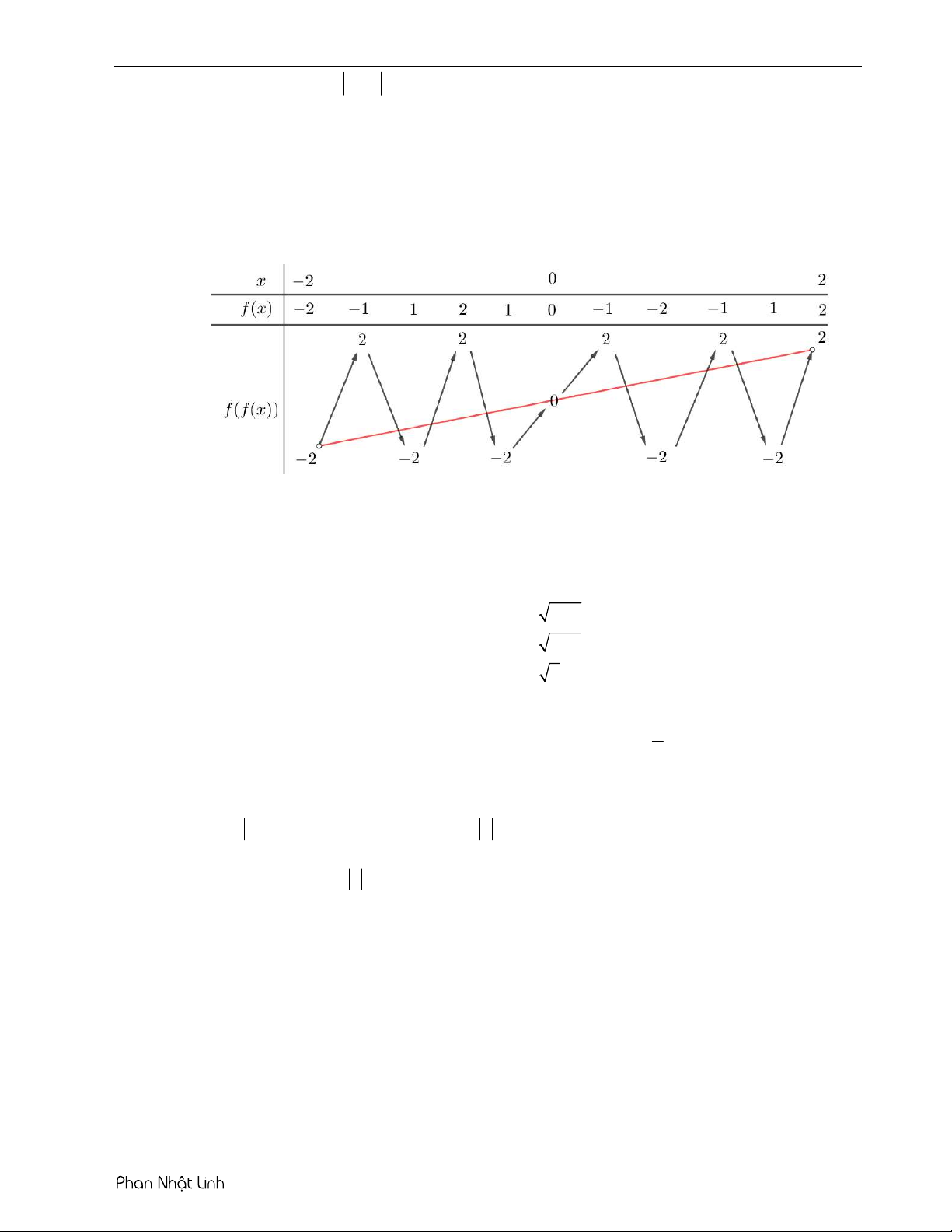
VÍ DỤ 1: Cho hàm số y  f x có bảng biến thiên như sau:   5 
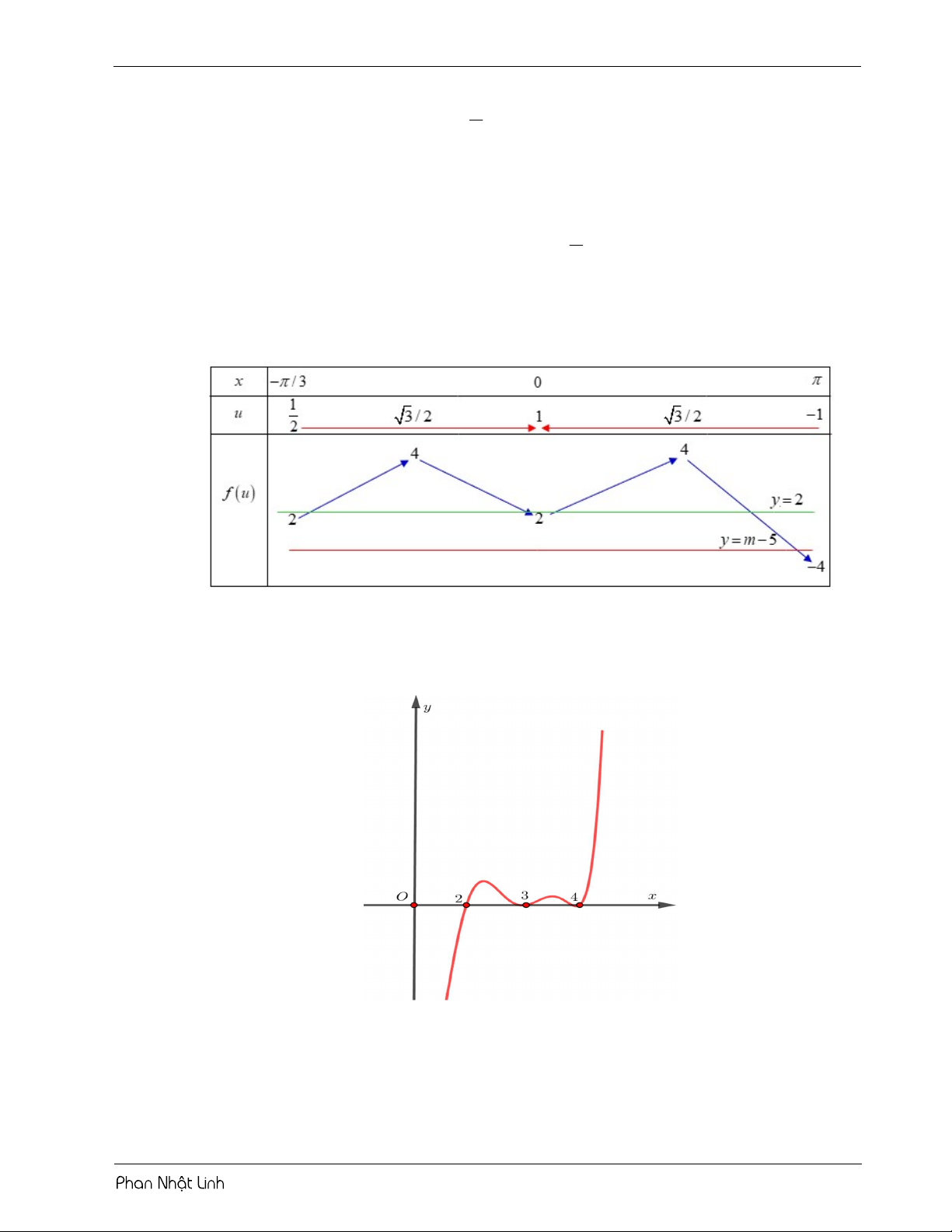
Số nghiệm thuộc đoạn   ; của hàm số f  2 5 cos x  cosx  1 là 2 2    A. 11. B. 10 . C. 9 . D. 12 . Lời giải Chọn B Tiến hành đặt 2 u  cos x o c sx . Đạo hàm u  2  .cos .
x sin x  sin x  sin x1 2cosx .
sin x  0  x  k  x  0; ;2 Giải phương trình: u 0     1   5 7
cosx   x    2k  x   ; ;  2 3 3 3 3
Sử dụng phương pháp ghép trục:
Từ bảng biến thiên ta có phương trình f u 1
 có tất cả 10 nghiệm phân biệt. 5
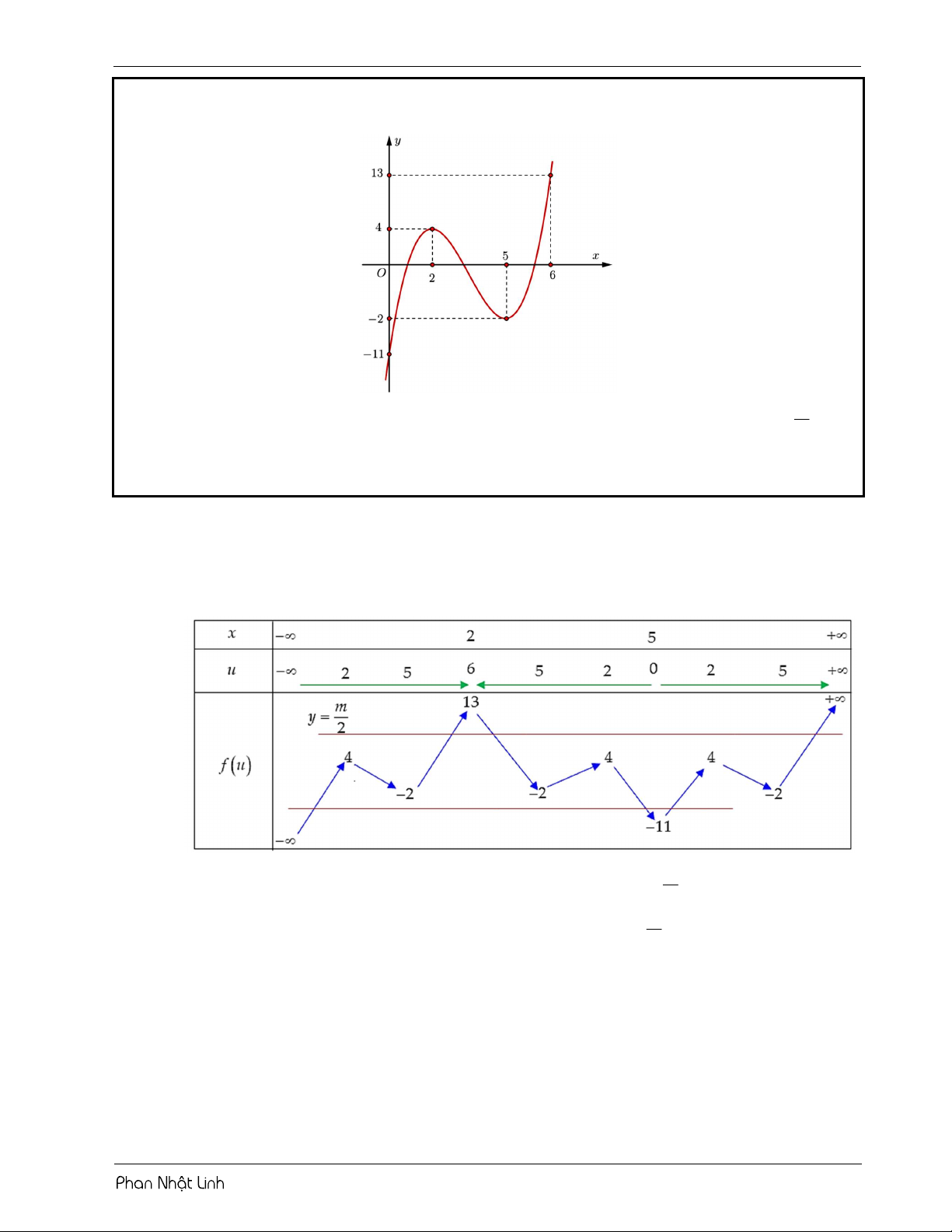
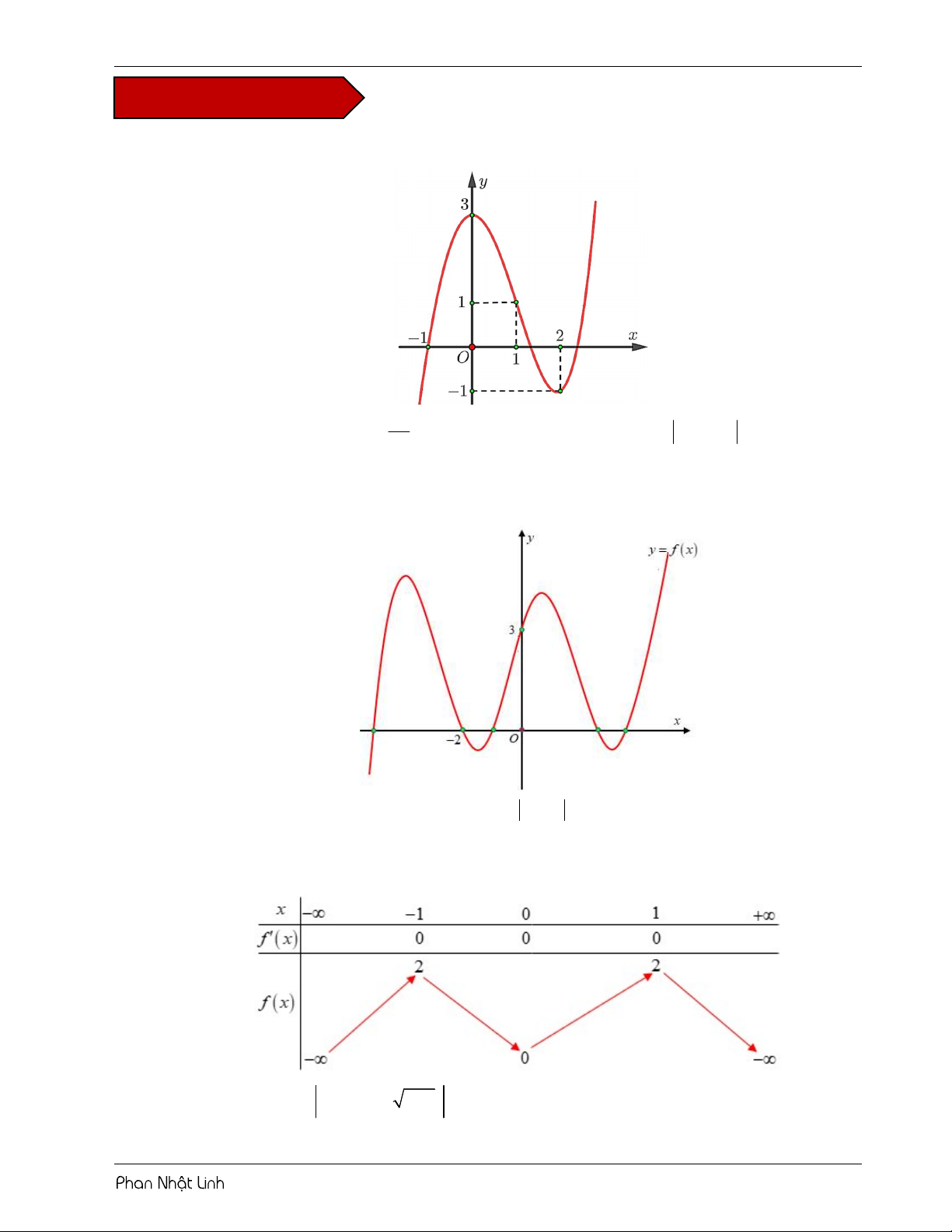
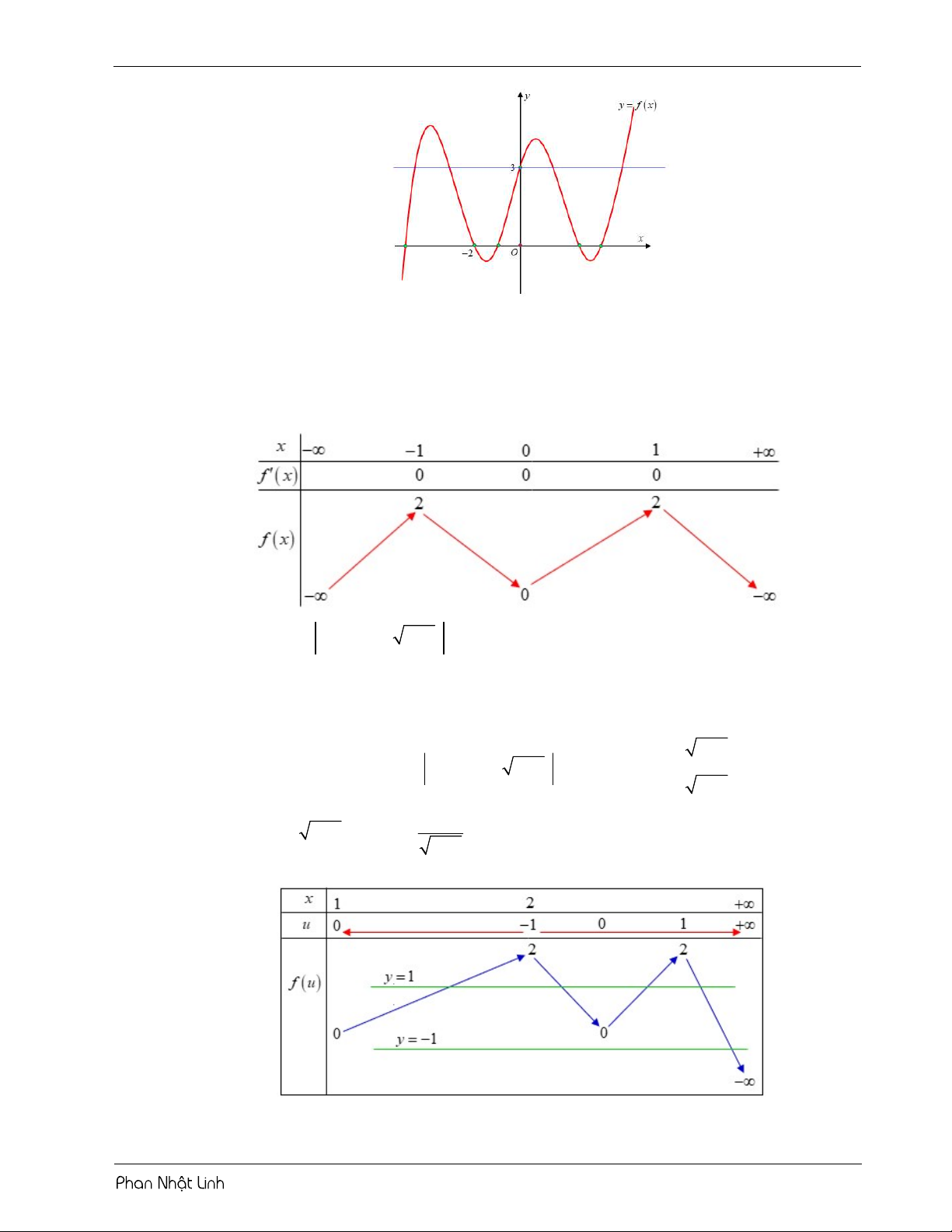
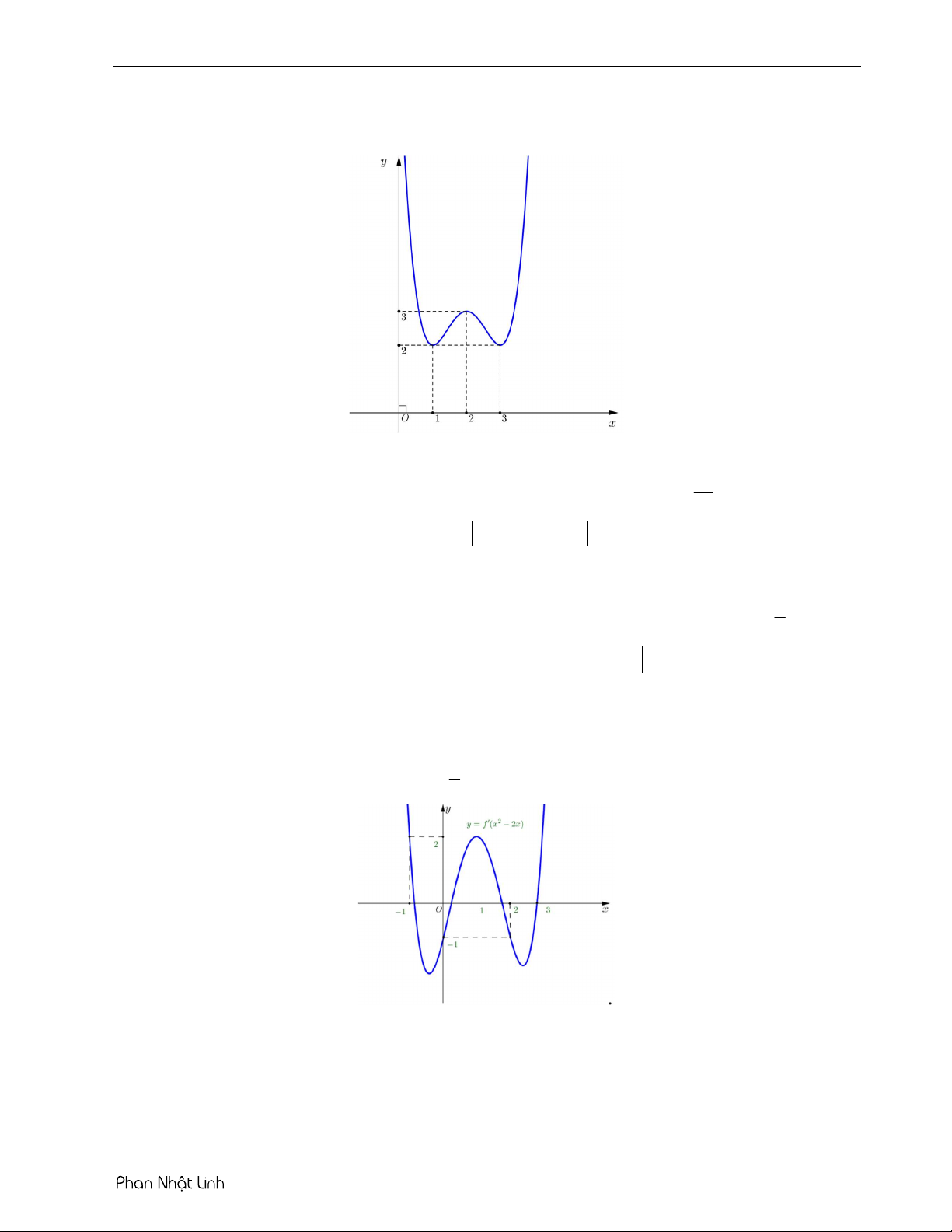
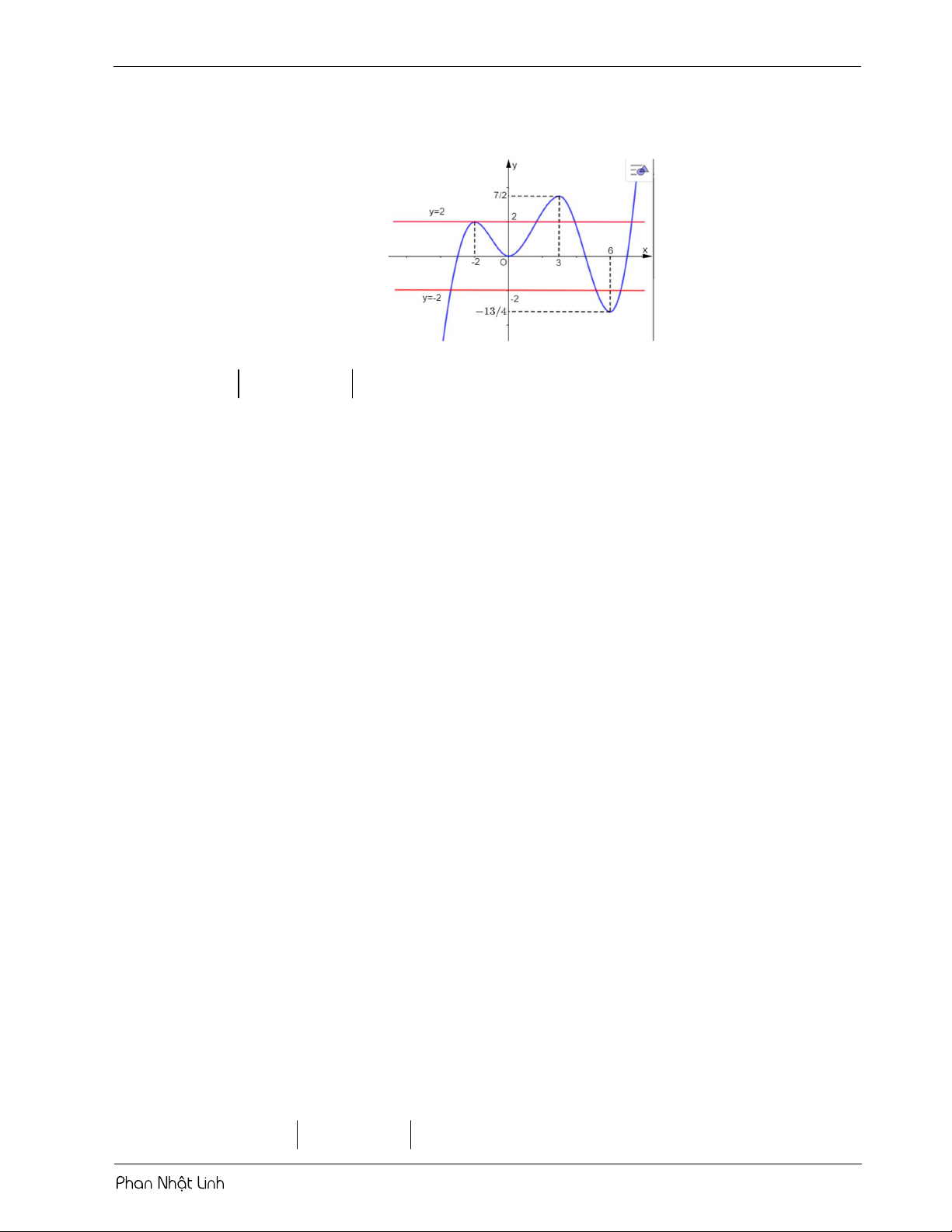
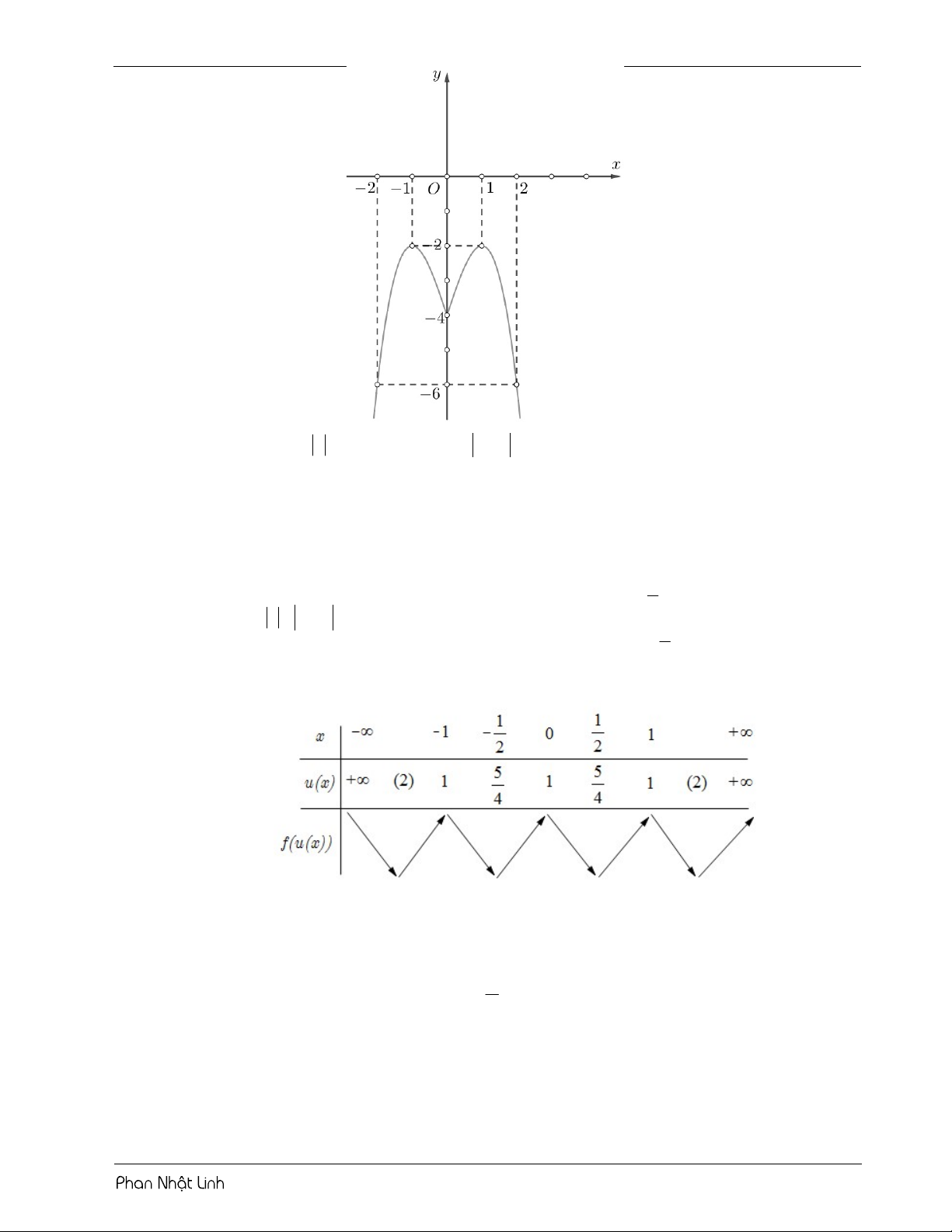
VÍ DỤ 2: Cho hàm số y  f x có đồ thị như hình vẽ m
Gọi S là tập hợp các giá trị nguyên của tham số m để phương trình f  f x  2  có 3 2
nghiệm phân biệt. Số phần tử của tập S là? A. 10 . B. 32 . C. 9 . D. 34 . Lời giải Chọn D
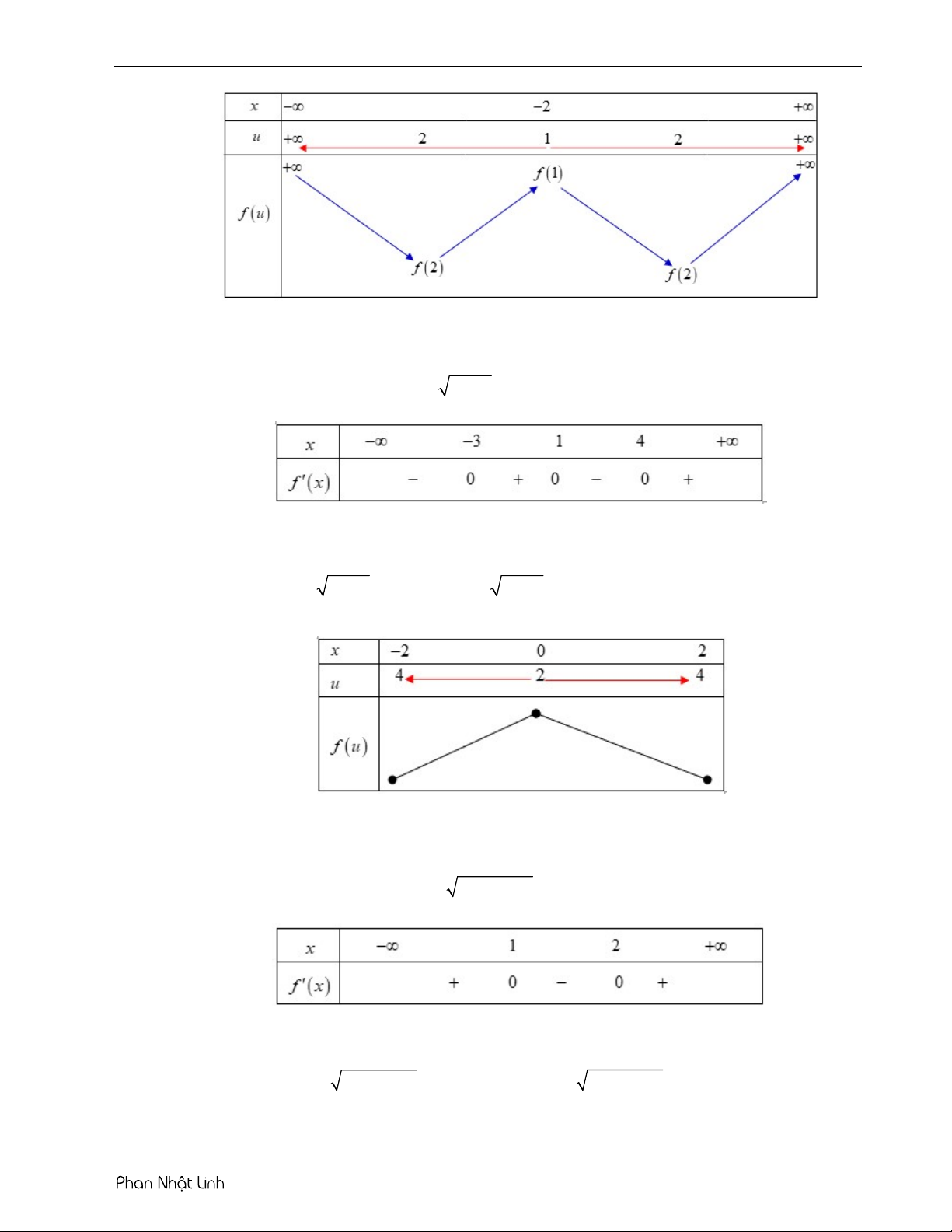
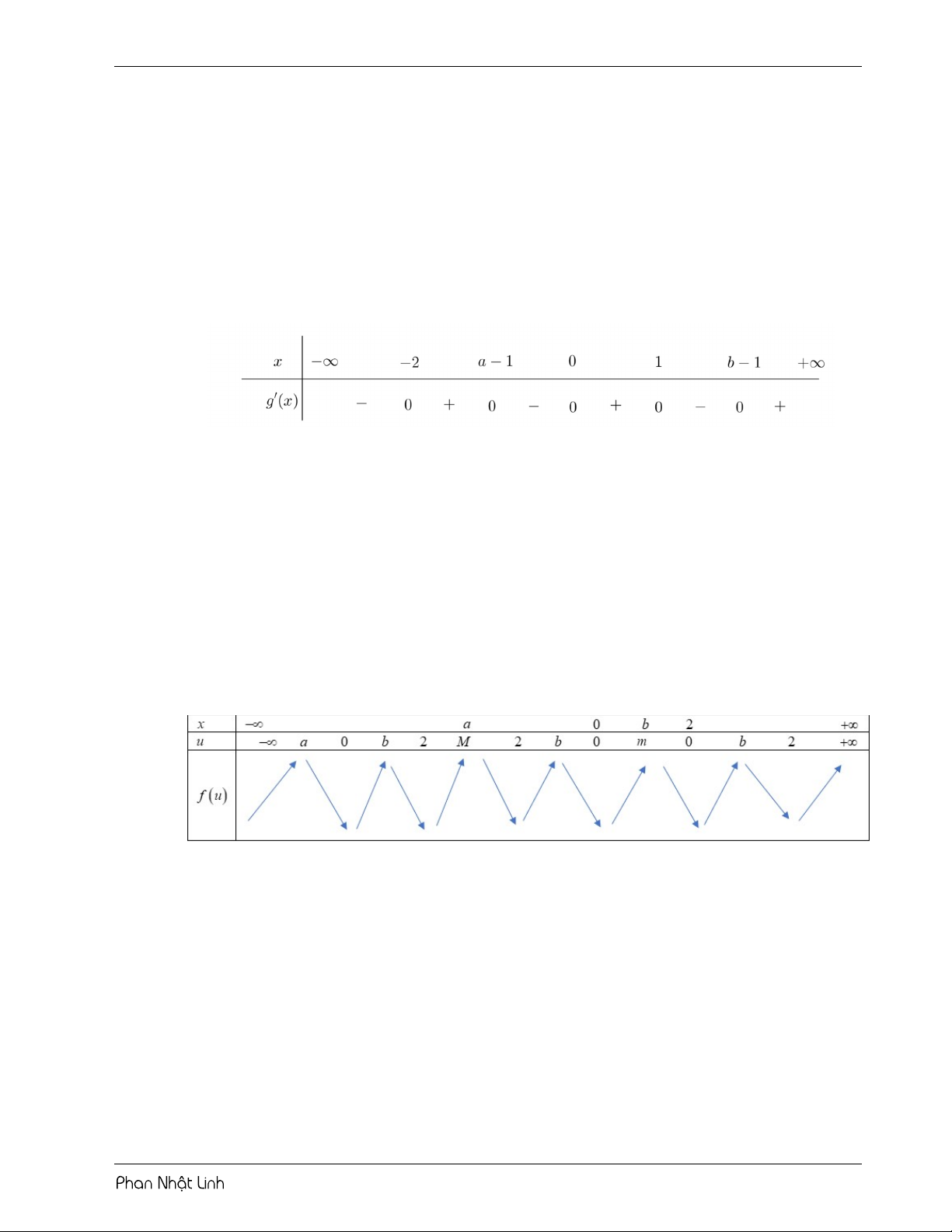
Đặt u  f x  2 . Từ đồ thị ta thấy hàm số đạt cực trị tại x  2 và x  5 .
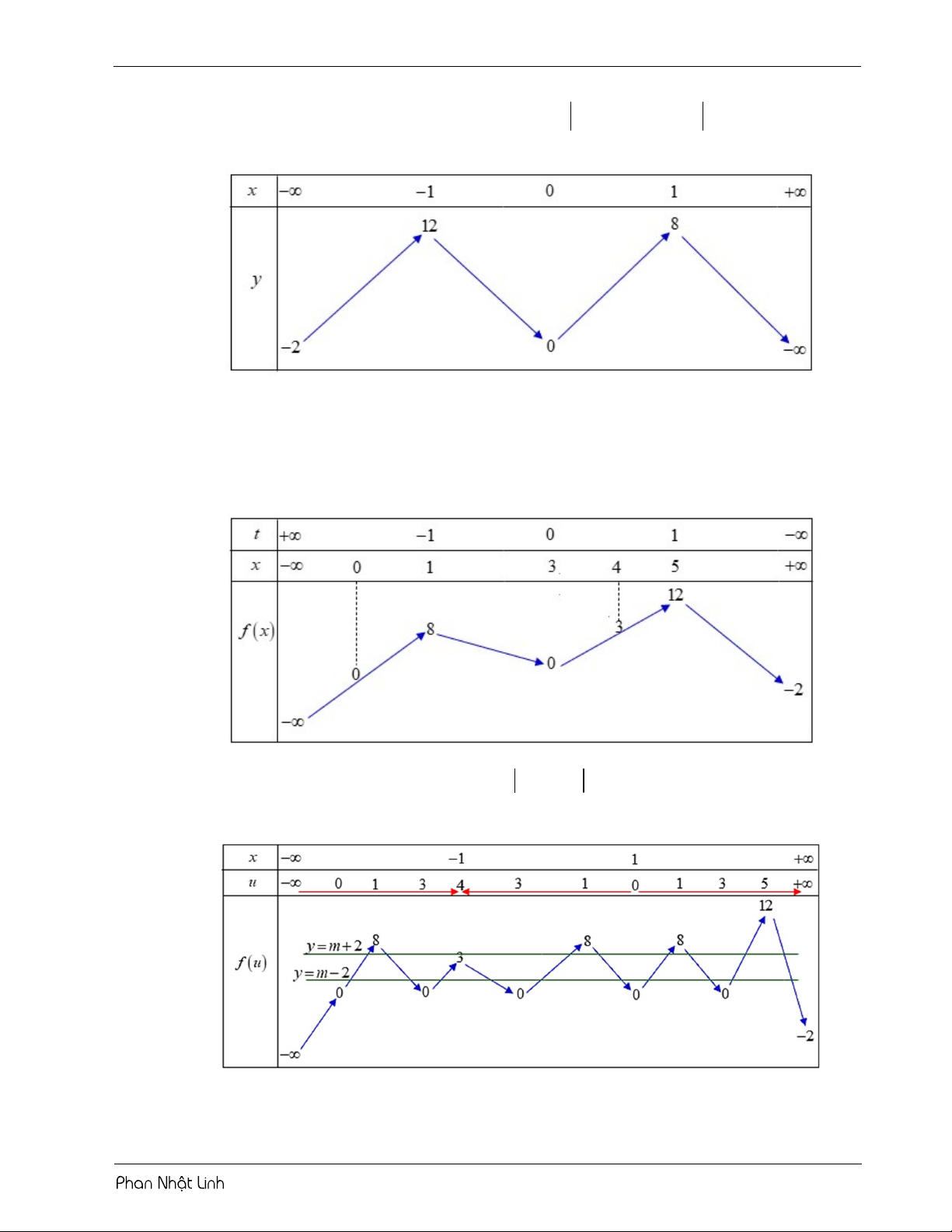
Sử dụng phương pháp ghép trục:  11 m      2 8  m  26
Từ bảng biến thiên, phương trình có 3 nghiệm phân biệt 2     m   22   m  4 4   13  2
Vậy có 34 giá trị của m thỏa mãn.
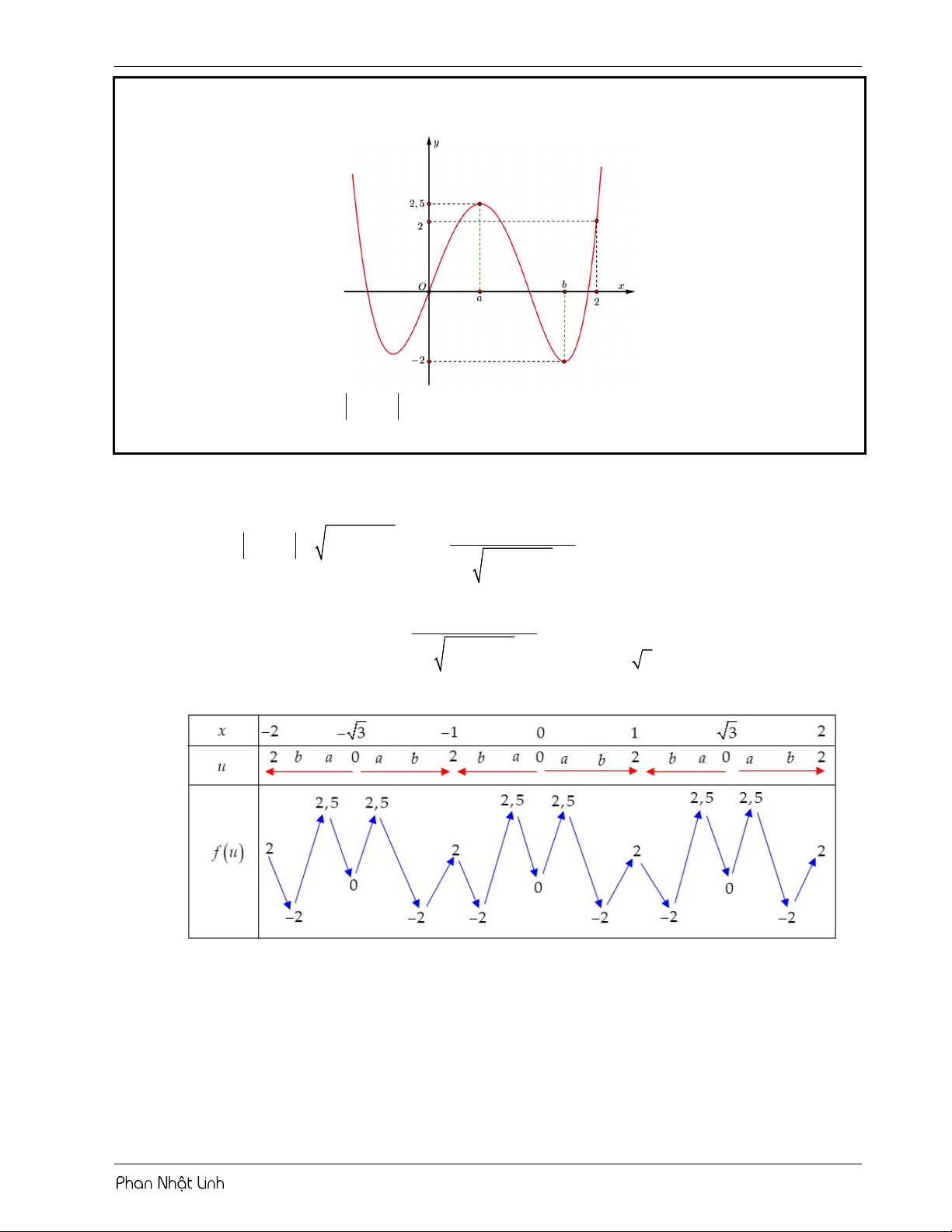
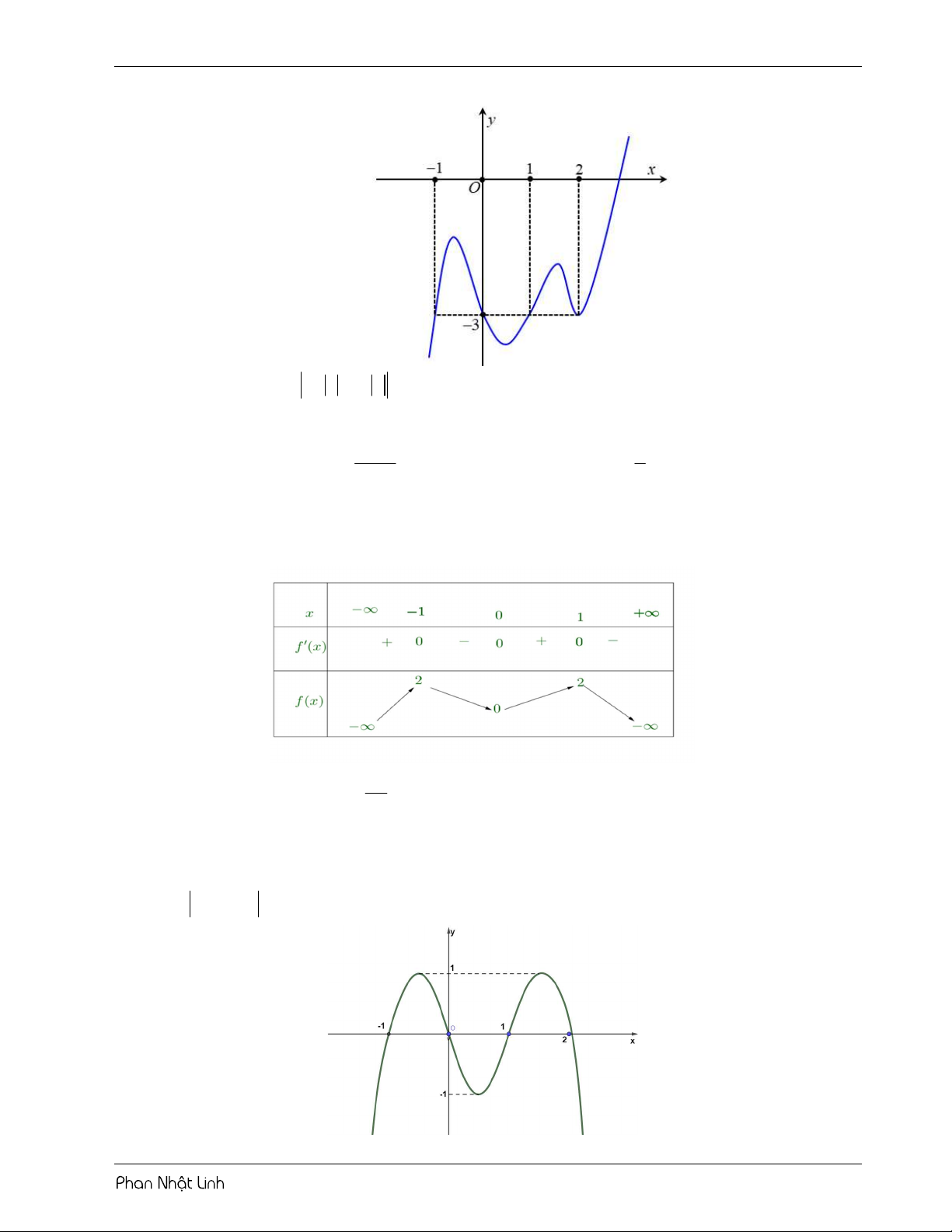
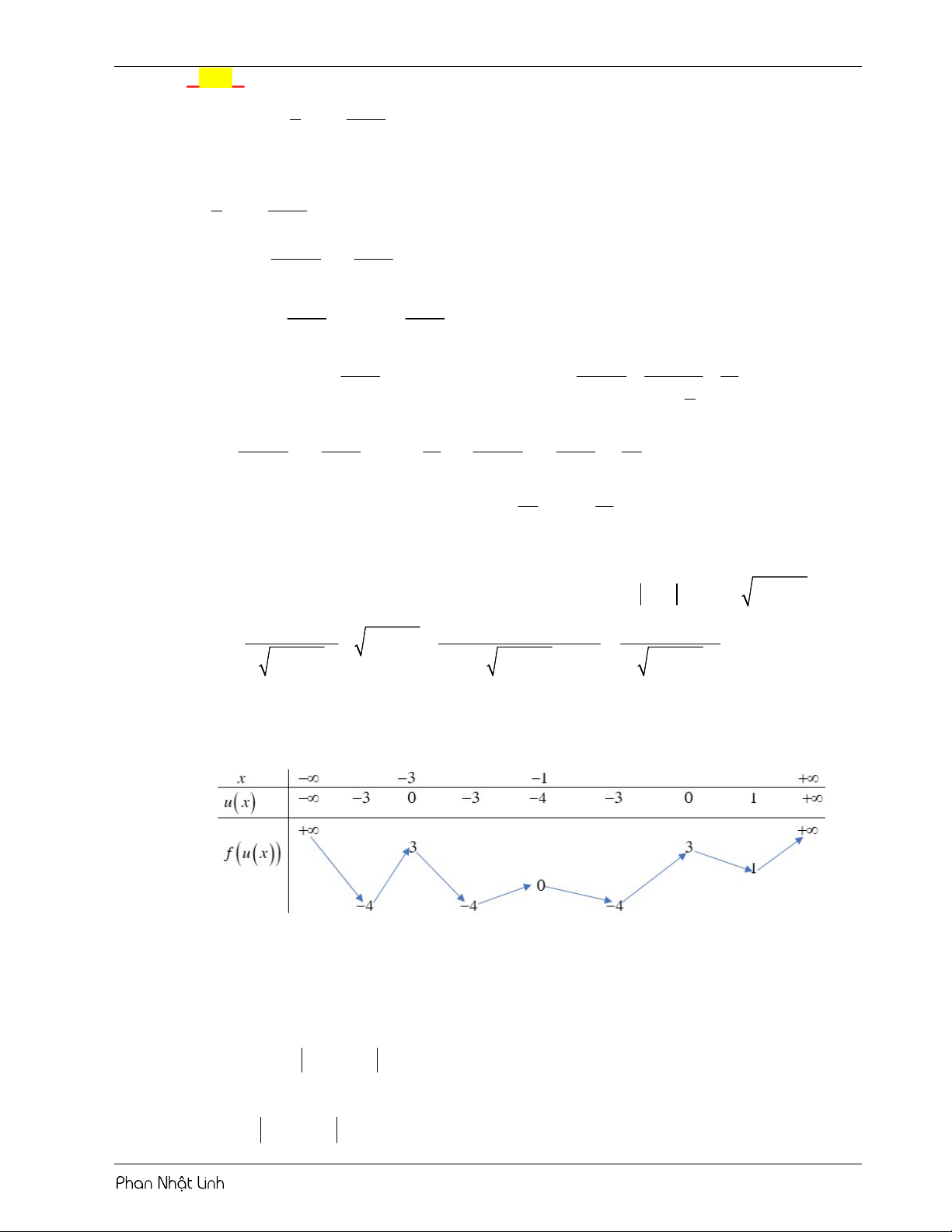
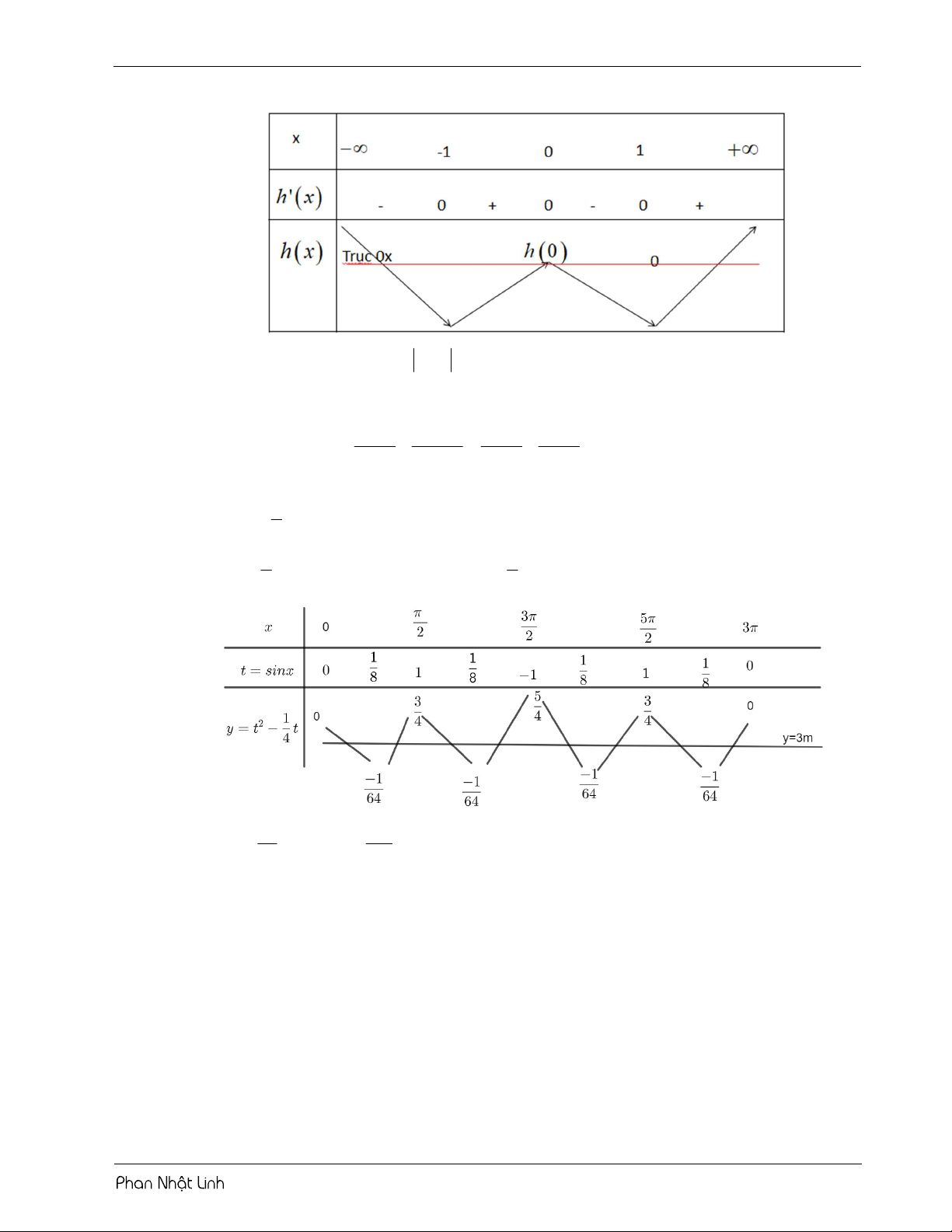
VÍ DỤ 3: Cho hàm số y  f x liên tục trên  và có đồ thị như hình vẽ. Hỏi phương trình f  3
x  3x  có bao nhiêu điểm cực trị thuộc đoạn 2;2   ? A. 10 . B. 17 . C. 12 . D. 15 . Lời giải Chọn B 3 2 2 x  3x 3x  3 Đặt 3 u  x  3x   3 x  3x     u  . x 3x2 3   3 x  x 2 x   x  0 3 3 3 
Giải phương trình đạo hàm u   0  x  1 . x 3x2 3 x    3
Sử dụng phương pháp ghép trục:
Từ bảng biến thiên, suy ra hàm số   2 ; 2  
 có 17 điểm cực trị.
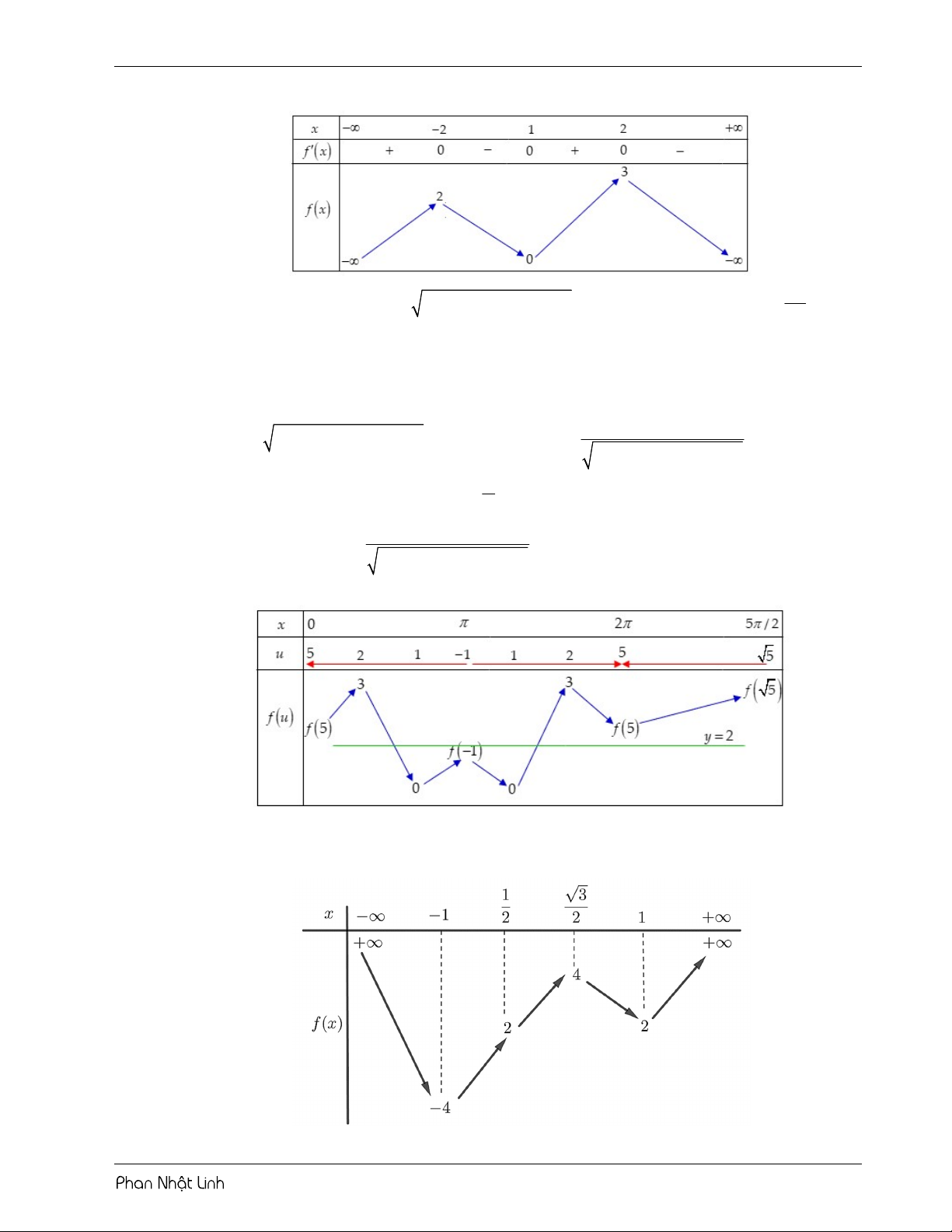
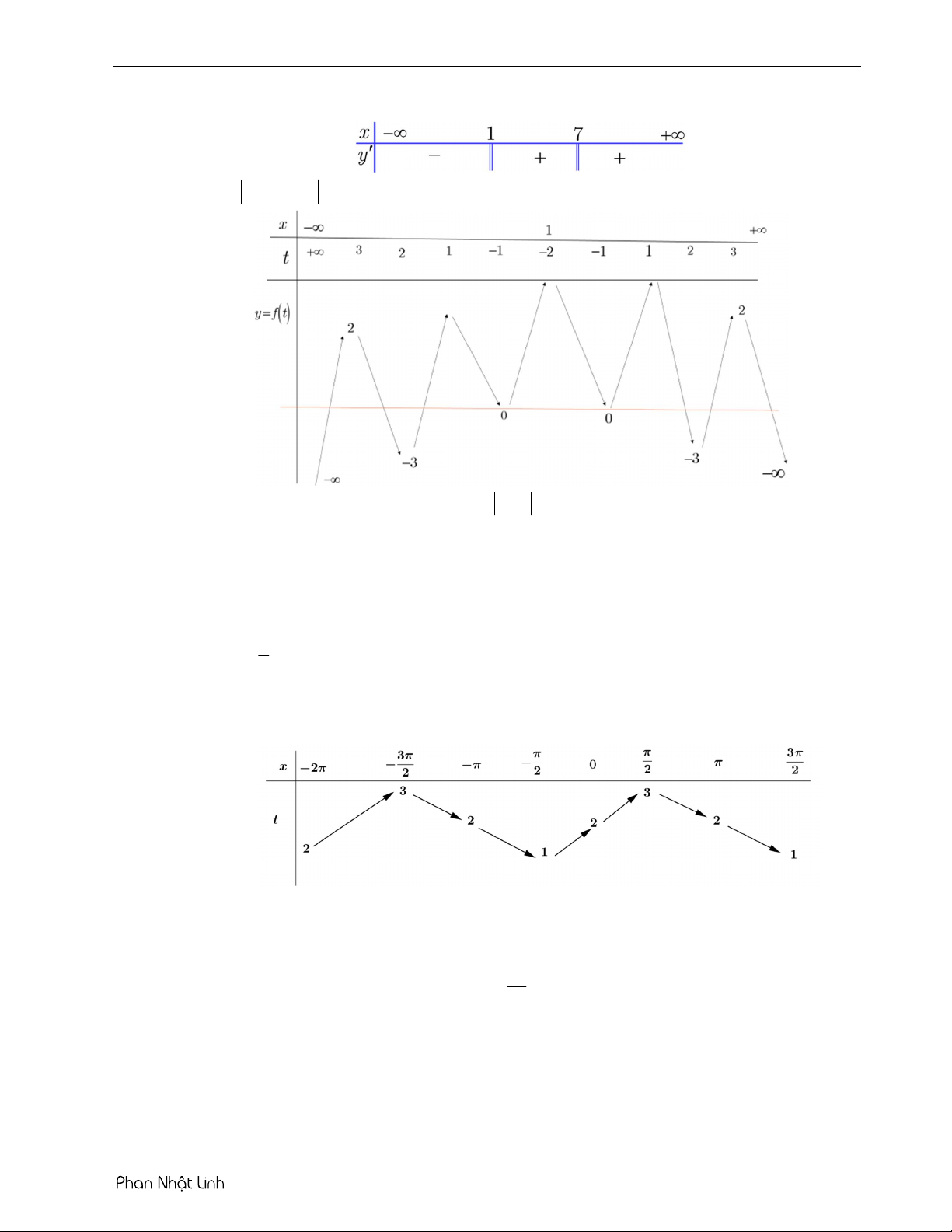
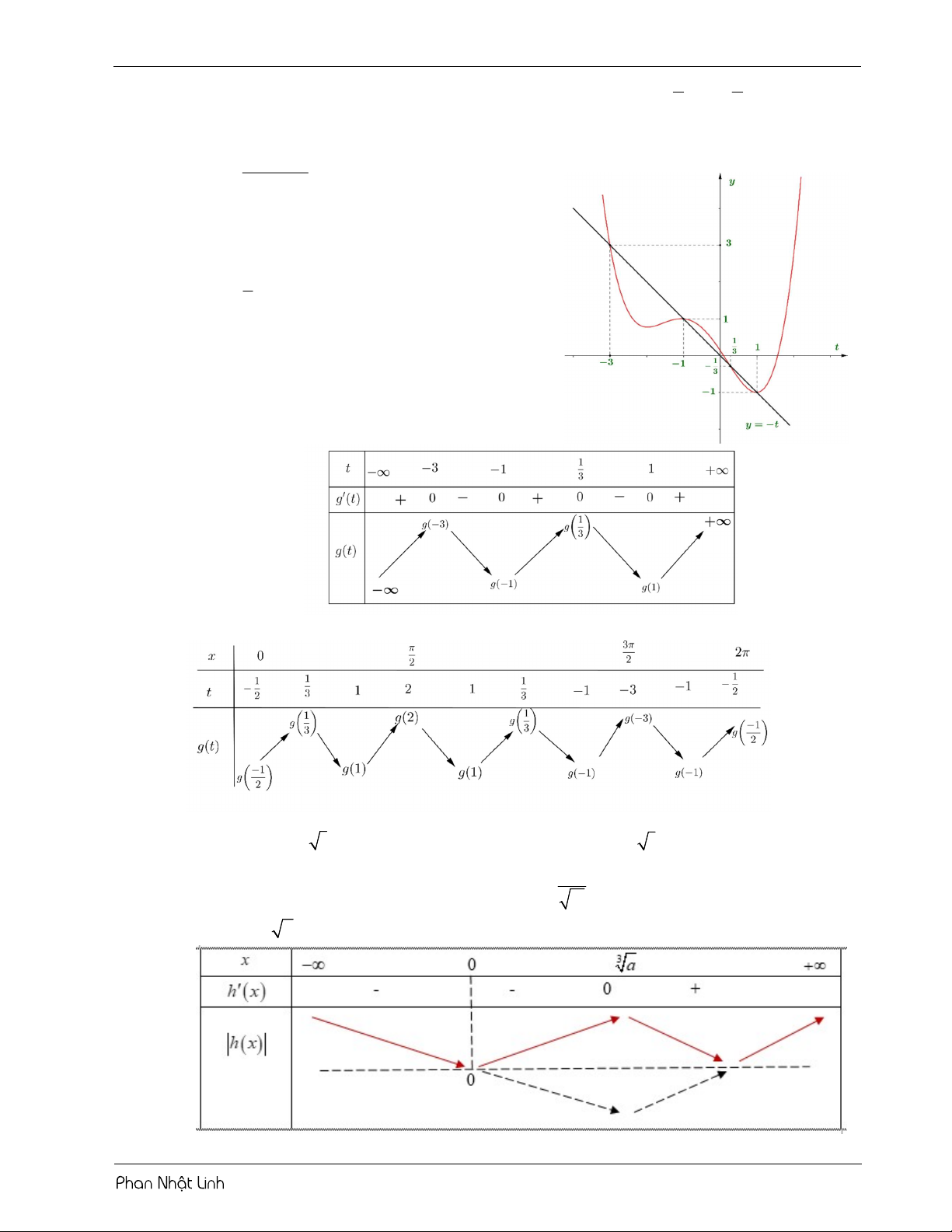
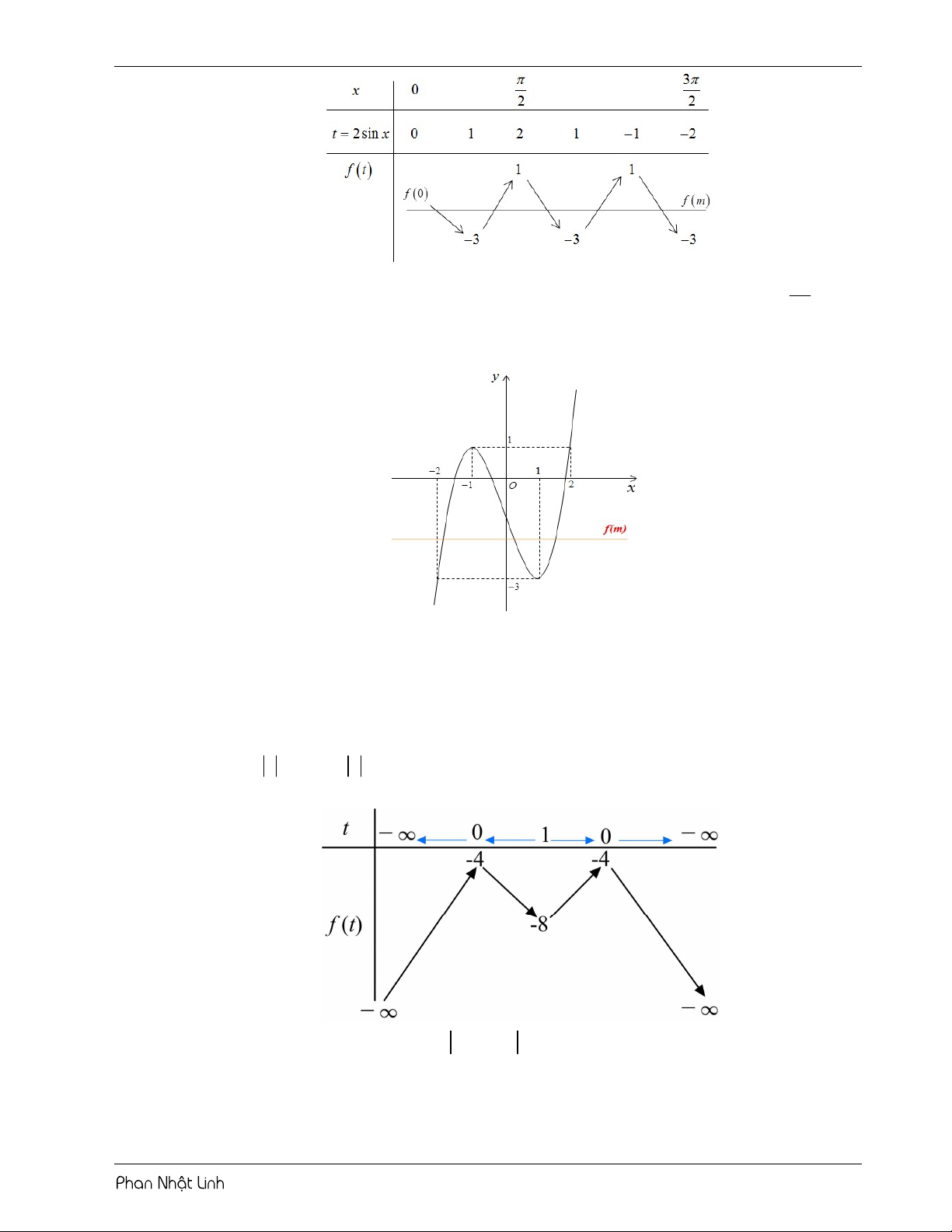
VÍ DỤ 4: Cho hàm số y  f x liên tục trên  và có đồ thị như hình vẽ.
Hỏi có bao nhiêu giá trị nguyên của tham số m để phương trình    7 f 5 
 2 1 3cos x   3m10 có đúng ba nghiệm phân biệt thuộc   ; 2 2    A. 10 . B. 1. C. 15 . D. 2 . Lời giải m 
Phương trình đã cho tướng tương với f    x  3 10 5 2 1 3cos  . 7 3sin x
Đặt u  5  2 1 3cos x  u  . 1 3cos x 3sin x
Giải phương trình đạo hàm u   0  x  0 . 1 3cos x
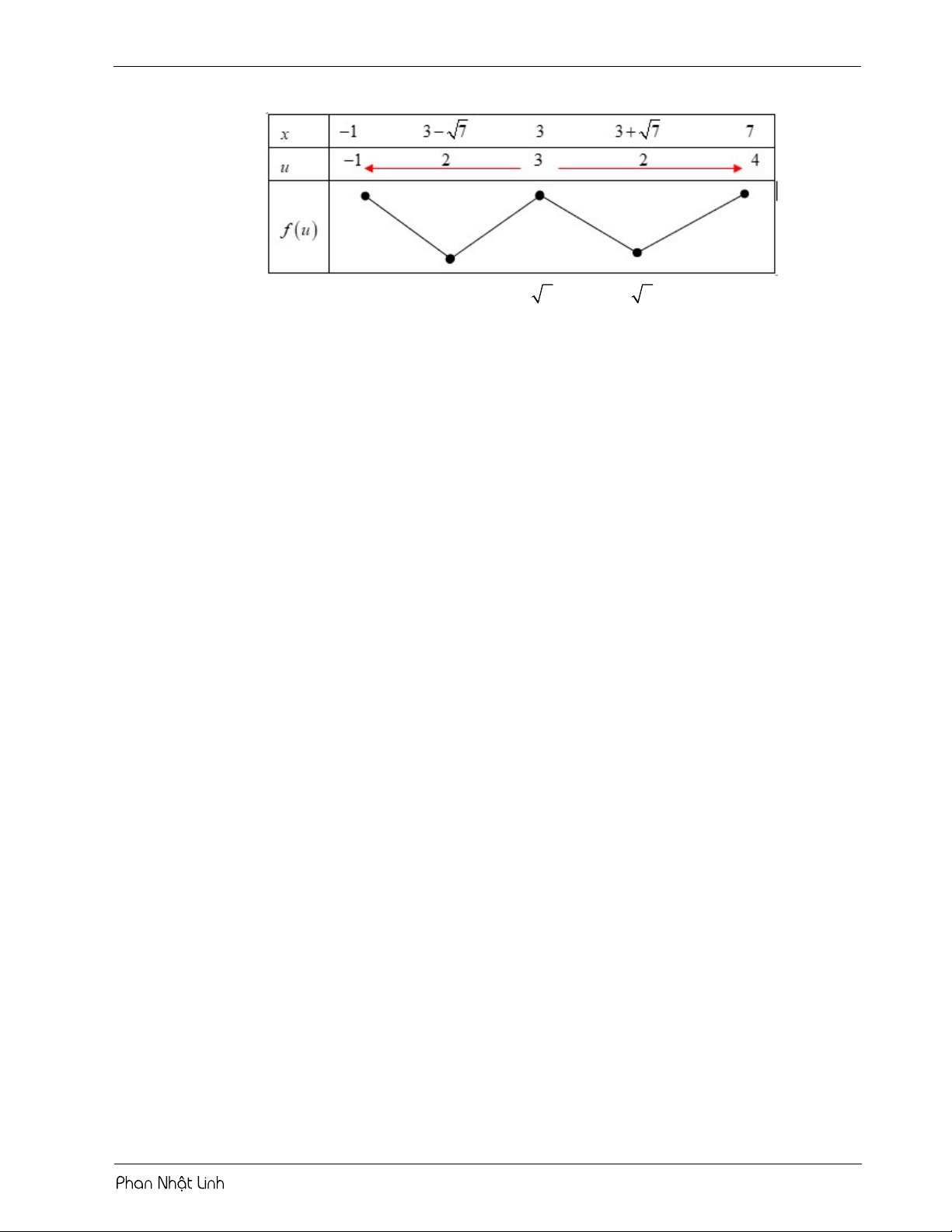
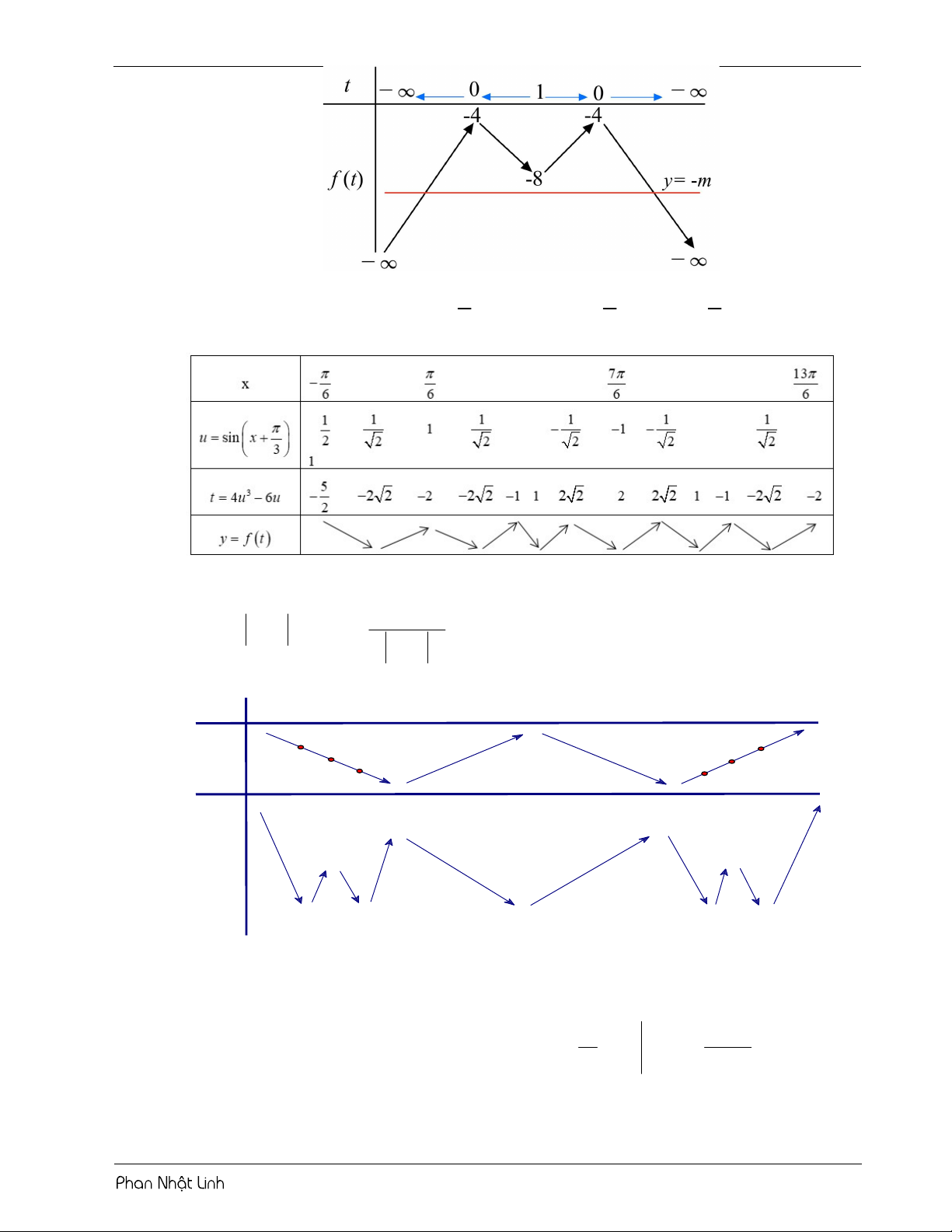
Sử dụng phương pháp ghép trục: 3m  10 4
Từ bảng biến thiên, yêu cầu bài toán   2   m   7 3 BÀI TẬP RÈN LUYỆN
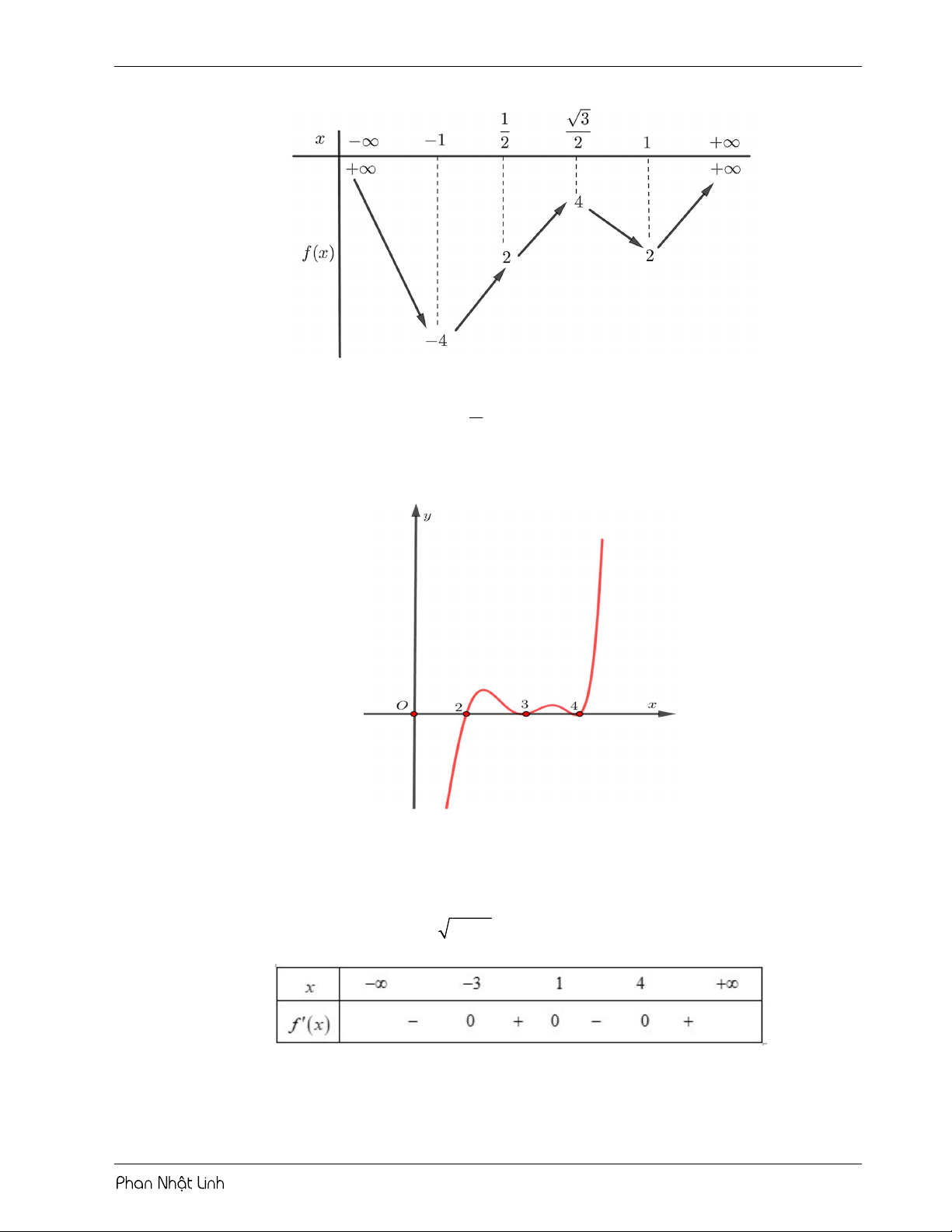
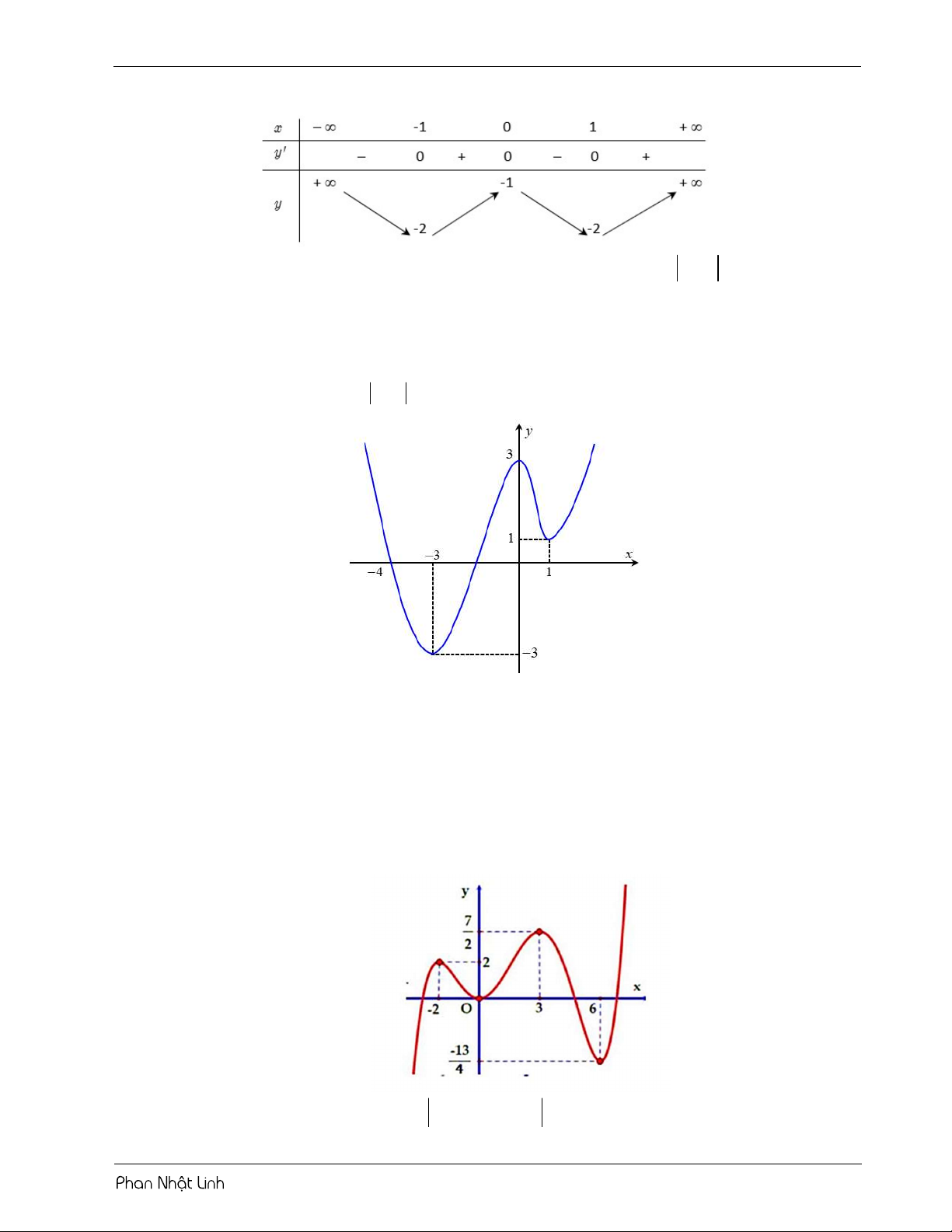
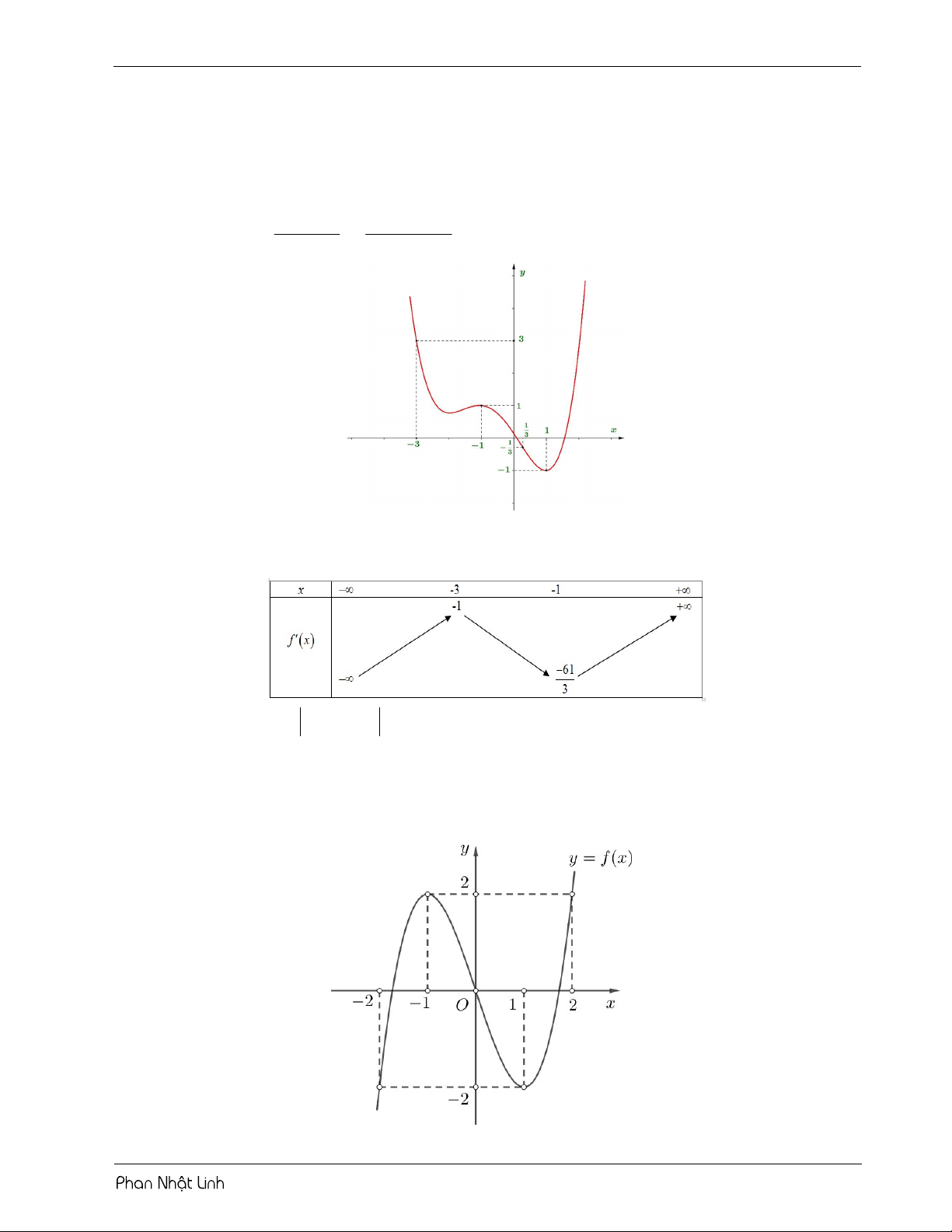
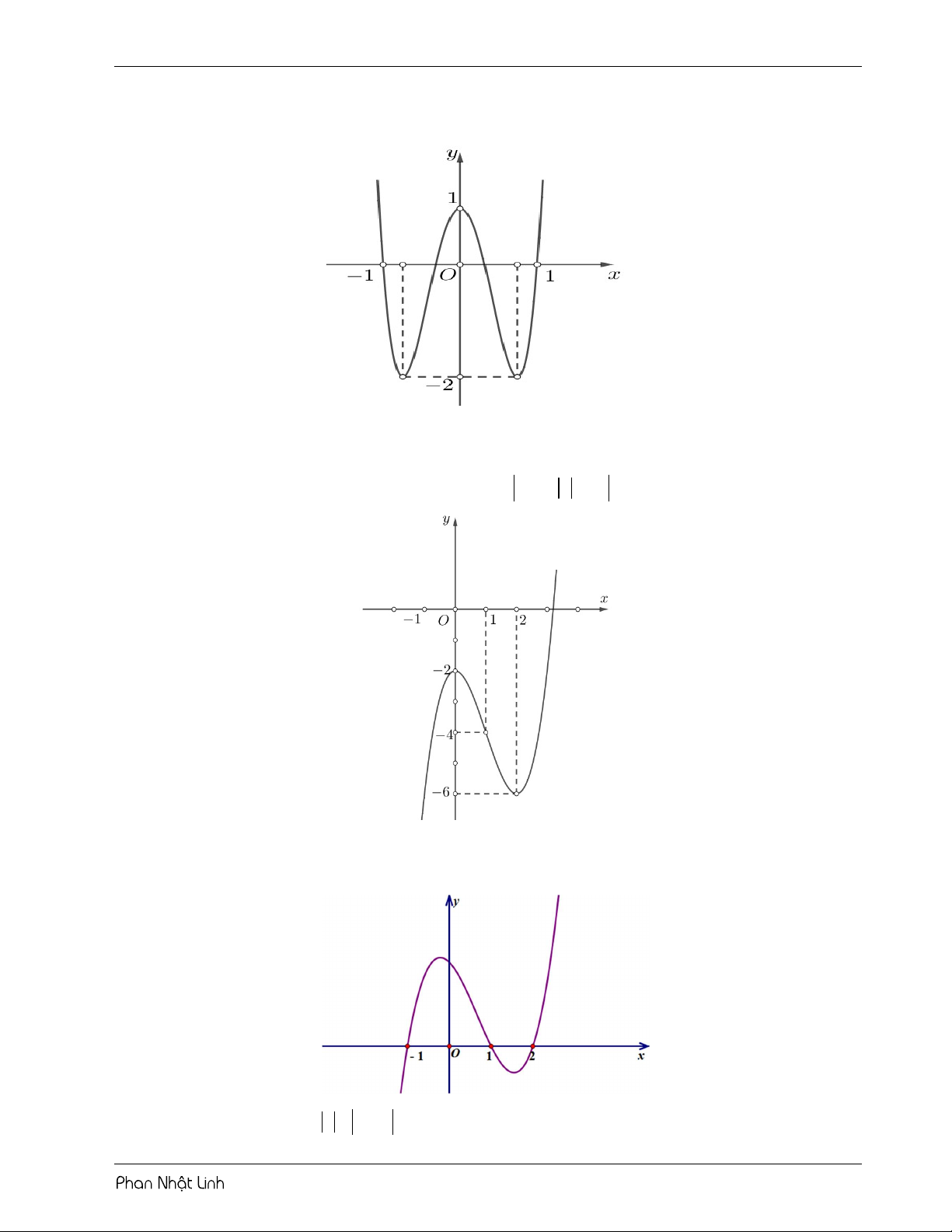
Câu 1: Cho hàm số    3 2 y
f x  ax  bx  cx  d có đồ thị như hình vẽ  3 
Số nghiệm thuộc khoảng  ;3   của phương trình 2
f sin x  5 f sin x  6  0 là  2  A. 13 . B. 12 . C. 11. D. 10
Câu 2: Cho hàm số    5 4 3 2 y
f x  ax  bx  cx  dx  ex  f có đồ thị như hình vẽ
Số nghiệm thực phân biệt của phương trình f  4x  5  2  3  0 là: A. 8 . B. 4 . C. 10. D. 6
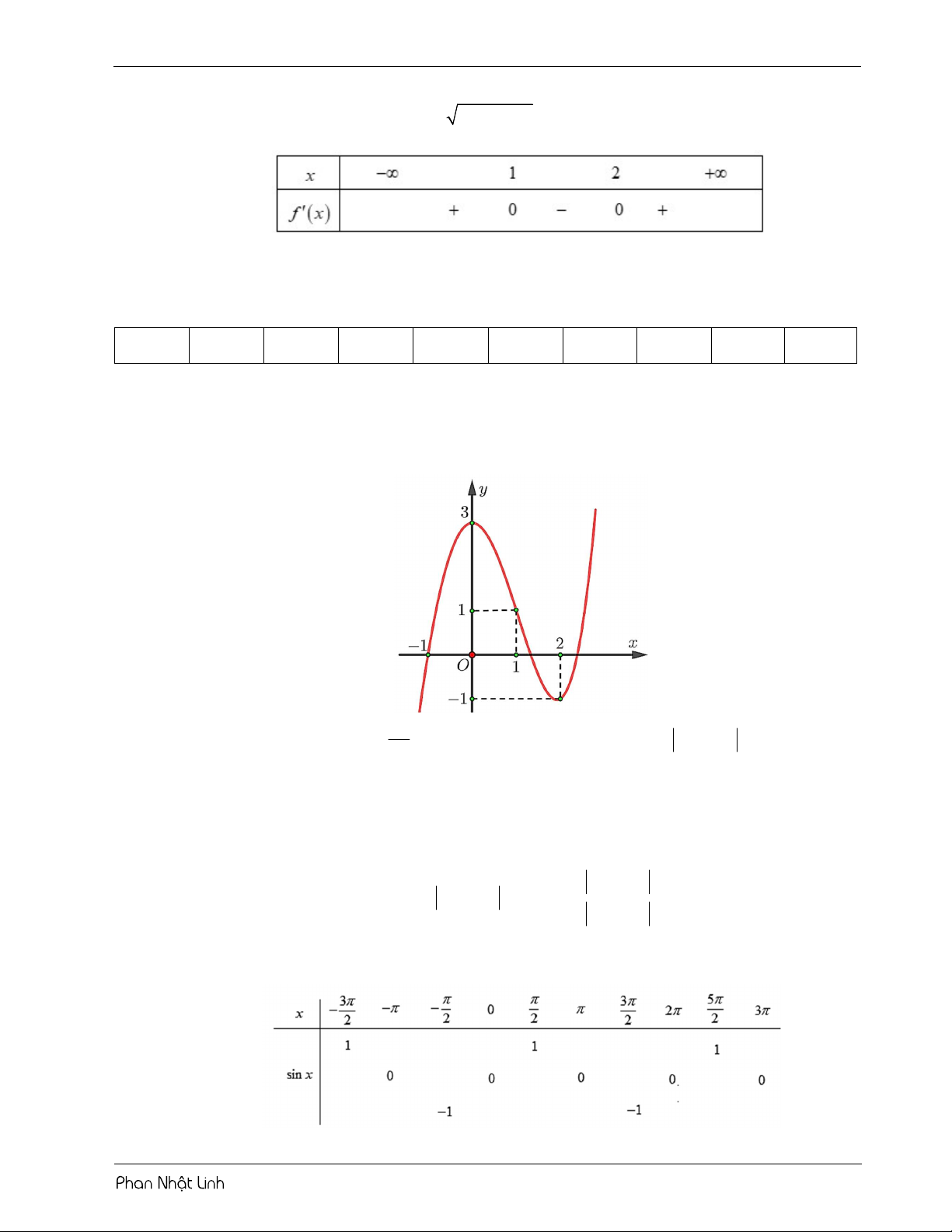
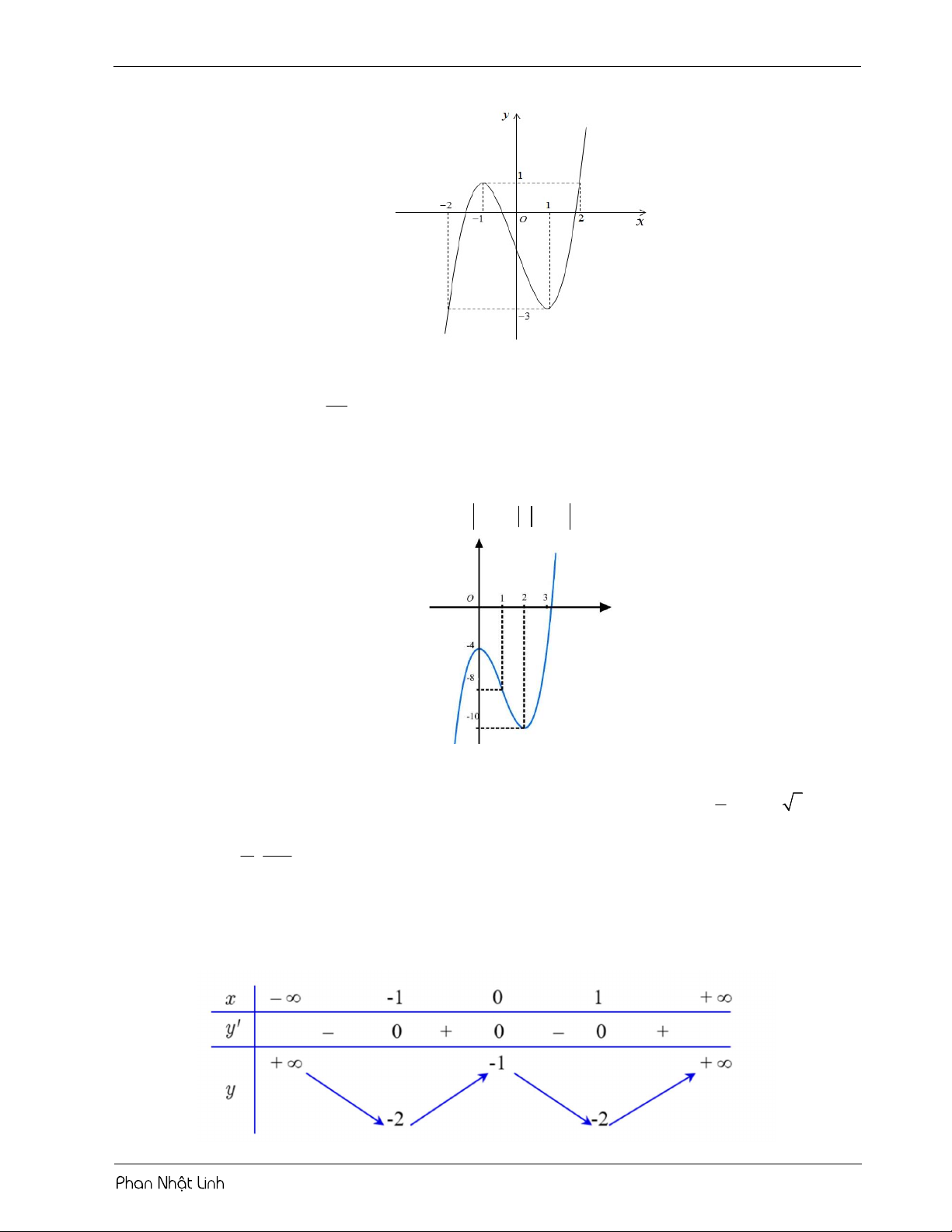
Câu 3: Cho hàm số f  x có bảng biến thiên như sau:
Hỏi phương trình f x 1 2 x 1 1 có bao nhiêu nghiệm thực? A. 12 . B. 4 . C. 5 . D. 8
Câu 4: Cho bảng biến thiên hàm số f 5  2x như hình vẽ dưới. Hỏi phương trình f  2 2
x  4x  3 1  3 có bao nhiêu nghiệm thực x tương ứng? A. 6 . B. 5 . C. 7 . D. 4
Câu 5: Cho bảng biến thiên của hàm số f 3 2x như hình vẽ. Biết f 4  3; f 0  0 . Hỏi có bao
nhiêu giá trị nguyên của tham số m để phương trình f  3
x  3x  2  m  2 có nhiều nghiệm nhất? A. 7 . B. 6 . C. 5 . D. 2
Câu 6: Cho hàm số f x liên tục trên  , thỏa mãn f  
1  2  f 5 và có bảng biến thiên như sau:   5 
Số nghiệm của phương trình f  3
2cos x  2cosx  5  2cosx  2 trên khoảng 0;  là?  2  A. 2 . B. 1. C. 5 . D. 3
Câu 7: Cho hàm số f  x liên tục trên  và có bảng biến thiên như hình bên.
Số giá trị nguyên của tham số m để phương trình 2
f cos x  3  m f cos x  2m 10  0 có   
đúng 4 nghiệm phân biệt thuộc đoạn  ;  là 3    A. 5 . B. 6 . C. 7 . D. 4 .
Câu 8: Cho f (x) là hàm đa thức bậc 6 và có đồ thị hàm số y  f (x) như hình vẽ dưới đây
Hỏi hàm số y  g x  f  2 ( )
x  4x  5 có bao nhiêu điểm cực trị? A. 2 . B. 5 . C. 3 . D. 1.
Câu 9: Cho hàm số y  f  x có đạo hàm liên tục trên  và có bảng xét đấu đạo hàm f  x như hình
vẽ bên dưới. Hàm số g  x  f  2
4  4  x  đồng biến trên: A. 0;1 . B. 1;2. C. 1;0 . D. 3;1 .
Câu 10: Cho hàm số y  f  x có đạo hàm liên tục trên  và có bảng xét đấu đạo hàm f  x như hình
vẽ bên dưới. Hàm số g  x  f  2
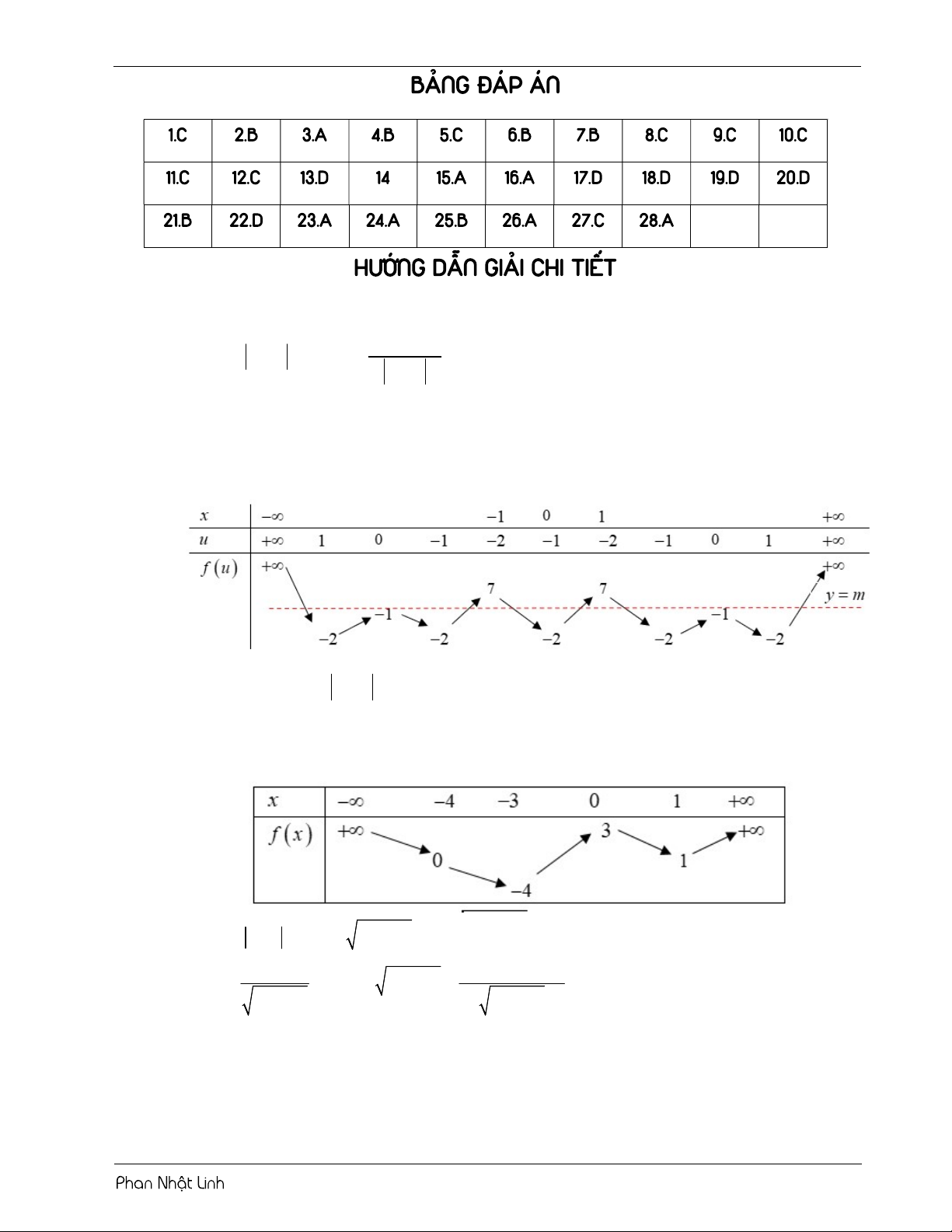
1 7  6x  x  nghịch biến trên: A. 5;6 . B. 1;2 . C. 2;3 . D. 3;5 . BẢNG ĐÁP ÁN 1.A 2.D 3.C 4.D 5.D 6.A 7.B 8.C 9.C 10.D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho hàm số    3 2 y
f x  ax  bx  cx  d có đồ thị như hình vẽ  3 
Số nghiệm thuộc khoảng  ;3   của phương trình 2
f sin x  5 f sin x  6  0 là  2  A. 13 . B. 12 . C. 11. D. 10 Bài làm: Chọn A  f sin x  3   f sin x  3  f sin x  3  Ta giải phương trình: 2
f sin x  5 f sin x  6  0     .  f sin x  2 f sin x  2     f  sin x  2 Bảng biến thiên:
Kết hợp bảng biến thiên và đồ thị tương giao: Ta thấy: Với mọi x  1  ; 
1 thì phương trình luôn có 3 nghiệm. Với mọi x 0; 
1 thì phương trình có duy nhất 1 nghiệm.  3 
Vậy số nghiệm của phương trình thuộc khoảng  ;3   là 3.4 113.  2 
Câu 2: Cho hàm số    5 4 3 2 y
f x  ax  bx  cx  dx  ex  f có đồ thị như hình vẽ
Số nghiệm thực phân biệt của phương trình f  4x  5  2  3  0 là: A. 8 . B. 4 . C. 10. D. 6 Bài làm: 4 4x  5
Đặt g x  4x  5  2  4x  52  2  gx    . 4x 52 4 4x  5 5
Giải phương trình g x     0  x   .  x  2 4 4 5
Ta lập bảng biến thiên của hàm số g  x như sau:
Yêu cầu bài toán trở thành: tìm số nghiệm phân biết của phương trình f g x  3  0 .
Kẻ đường thẳng y  3 lên đồ thị như sau:
Từ bảng biến thiên ta thấy, số nghiệm của phương trình thuộc  2
 ; bằng số nghiệm của
phương trình thuộc  ;  2   . Mà trên  2
 ; phương trình có 3 nghiệm nên trên  ;  2  
cũng có 3 nghiệm. Vậy phương trình có 3 3  6 nghiệm phân biệt.
Câu 3: Cho hàm số f  x có bảng biến thiên như sau:
Hỏi phương trình f x 1 2 x 1 1 có bao nhiêu nghiệm thực? A. 12 . B. 4 . C. 5 . D. 8 Lời giải Chọn C  f x 1 2 x 1 1
Điều kiện xác định: x 1. Ta có: f x 1 2 x 1   1        .
f x 1 2 x 1  1   1
Đặt u  x 1 2 x 1  u  1  0  x  2. x 1
Sử dụng phương pháp ghép trục:
Từ bảng biến thiên suy ra phương trình có 5 nghiệm phân biệt.
Câu 4: Cho bảng biến thiên hàm số f 5  2x như hình vẽ dưới. Hỏi phương trình f  2 2
x  4x  3 1  3 có bao nhiêu nghiệm thực x tương ứng? A. 6 . B. 5 . C. 7 . D. 4 Lời giải Chọn D
Đặt x  5  2t , đưa bảng biến thiên hàm số f 5  2x về bảng biến thiên hàm số f  x .
Ta có bảng biến thiên của hàm số f  x như sau:  f u  2 Đặt 2
u  x  4x  3 , phương trình trở thành 2 f u 1  3   .  f  u  1 
Sử dụng phương pháp ghép trục:
Từ bảng biến thiên suy ra, phương trình có tất cả 4 nghiệm thực x .
Câu 5: Cho bảng biến thiên của hàm số f 3 2x như hình vẽ. Biết f 4  3; f 0  0 . Hỏi có bao
nhiêu giá trị nguyên của tham số m để phương trình f  3
x  3x  2  m  2 có nhiều nghiệm nhất? A. 7 . B. 6 . C. 5 . D. 2 Lời giải Chọn D
Đưa về bảng biến thiên của hàm số f  x bằng cách đặt x  3 2t  f x  f 3 2t .
Bảng biến thiên của hàm số f  x như sau:  f u  m  2 Đặt 3
u  x  3x  2 thì phương trình trở thành f u  m  2   .  f  u  m  2
Sử dụng phương pháp ghép trục 3  m  2  8
Để phương trình có nhiều nghiệm nhất   2  m  5  m   3;  4 . 0  m  2  3
Câu 6: Cho hàm số f x liên tục trên  , thỏa mãn f  
1  2  f 5 và có bảng biến thiên như sau:   5 
Số nghiệm của phương trình f  3
2cos x  2cosx  5  2cosx  2 trên khoảng 0;  là?  2  A. 2 . B. 1. C. 5 . D. 3 Lời giải Chọn A  2  3 3cos x  1 Ta đặt u 2cos x   
 2cosx  5  2cos x  u'  sin x  2  0  3 2cos x   2cos x   5   5   voi  x 0;   2  sin x  0   x   ;  2 . Giải phương trình   u  0  2 3cos x   1  2  0  vo nghiem  3 2cos x  2cosx   5
Sử dụng phương pháp ghép trục:
Từ bảng biến thiên suy ra phương trình có 2 nghiệm phân biệt.
Câu 7: Cho hàm số f  x liên tục trên  và có bảng biến thiên như hình bên.
Số giá trị nguyên của tham số m để phương trình 2
f cos x  3  m f cos x  2m 10  0 có   
đúng 4 nghiệm phân biệt thuộc đoạn  ;  là 3    A. 5 . B. 6 . C. 7 . D. 4 . Lời giải Chọn B x  0   
Đặt u  cos x  u  sin x  0   ( với x   ; ). x     3     f u  2 2  
Khi đó phương trình đã cho trở thành f u  3  m f u   2m 10  0   .  f  u   m  5
Sử dụng phương pháp ghép trục:
Do phương trình f u  2 có 3 nghiệm nên yêu cầu bài toán tương đương với phương trình
f u  m 5 có duy nhất một nghiệm 4  m  5  2  1 m  7 m  m1;2;3;4;5;  6 .
Câu 8: Cho f (x) là hàm đa thức bậc 6 và có đồ thị hàm số y  f (
 x) như hình vẽ dưới đây
Hỏi hàm số y  g x  f  2 ( )
x  4x  5 có bao nhiêu điểm cực trị? A. 2 . B. 5 . C. 3 . D. 1. Lời giải Chọn C Đặt 2
u  x  4x  5  u  2x  4  0  x  2.
Sử dụng phương pháp ghép trục:
Từ bảng biến thiên, suy ra hàm số có 3 điểm cực trị.
Câu 9: Cho hàm số y  f  x có đạo hàm liên tục trên  và có bảng xét đấu đạo hàm f  x như hình
vẽ bên dưới. Hàm số g  x  f  2
4  4  x  đồng biến trên: A. 0;1 . B. 1;2. C. 1;0 . D. 3;1 . Lời giải Đặt g  x  f  2   x   f u 2 4 4
,u  4  4  x , với x 2;2
Sử dụng phương pháp ghép trục:
Suy ra hàm số đồng biến trên khoảng 2;0 .
Câu 10: Cho hàm số y  f  x có đạo hàm liên tục trên  và có bảng xét đấu đạo hàm f  x như hình
vẽ bên dưới. Hàm số g  x  f  2
1 7  6x  x  nghịch biến trên: A. 5;6 . B. 1;2 . C. 2;3. D. 3;5 . Lời giải Đặt: g  x  f  2
1 7  6x  x   f u với 2
u  1 7  6x  x và x 2;2
Sử dụng phương pháp ghép trục:
Vậy hàm số nghịch biến trên các khoảng  1
 ;3  7  và 3;3 7.
Câu 1: Cho hàm số f  x có đạo hàm liên tục trên  , f 2  7 và có bảng biến thiên như dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f  2
x 1  2  m có đúng 6 nghiệm thực phân biệt? A. 9 . B. 8 . C. 7 . D. 6 .
Câu 2: Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham
số m để phương trình f  x  3  x  
1   log m có ít nhất năm nghiệm phân biệt? A. 990 . B. 991. C. 989 . D. 913 . a  b  2  0 
Câu 3: Cho hàm số y  f  x 3 2
 x  ax  bx  3, a,b là các tham số thực thỏa mãn 243  3a  b  0
. Hỏi phương trình f  x f  x   f  x 2 2. . ' '    có bao nhiêu nghiệm? A. 2 . B. 4 . C. 3 . D. 1.
Câu 4: Cho hàm số y  f  x có đồ thị như hình vẽ
Số nghiệm thực của phương trình f  3 2x  6x  2  2 là A. 15. B. 14. C. 12. D. 13.
Câu 5: Cho hàm số y  f  x xác định và liên tục trên  ,có đồ thị f 'x như hình vẽ. Có bao nhiêu giá trị nguyên của m 10;10 để hàm số 3    g  x x 1 4 2  f 
  (2m 1)(x  2x  2019) đồng biến trên khoảng 0;  ? 2   A. 8 . B. 9 . C. 11. D. 10.
Câu 6: Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của
tham số m để phương trình f  x  3 x  
1   logmcó ít nhất năm nghiệm phân biệt ? A. 990 . B. 991. C. 989 . D. 913 .
Câu 7: Cho hàm số y  f  x có đạo hàm trên  và có bảng biến thiên như sau
Số điểm cực đại của hàm số g  x  f  2 2 x 8x  7  x   3 là A. 6 . B. 7 . C. 8 . D. 9 .  3 
Câu 8: Cho hàm số y  f  x có đồ thị như hình vẽ. Số nghiệm thuộc đoạn 2  ;  của phương trình 2   
2 f sin x  2 5  0 là A. 11. B. 15. C. 7 . D. 9 .  Câu 9: Cho hàm sô 4 3 2
y  ax  bx  cx  dx  ea, ,
b c, d,e  , biết f   1 1  và đồ thị hàm số 2
y  f x như hình vẽ. Hàm số g x  f  x 2 2
 x  2x đồng biến trên khoảng A. 2; . B.  1  ;  1 . C. 1;2 . D. ;  1 .
Câu 10: Cho hàm số bậc bốn f  x 4 3 2
 ax  bx  cx  dx  ea,b, ,
c d,e , biết f   1 1   và đồ thị 2
hàm số y  f ' x như hình vẽ. Hàm số g  x  f  x 2 2
 x  2x đồng biến trên khoảng A. 2; . B.  1  ;  1 . C. 1;2 . D.  ;    1 .
Câu 11: Cho hàm số y  f x có đạo hàm liên tục trên  và có đồ thị hàm số y  f  2x 2x như 2
hình vẽ. Hỏi hàm số y  f  2x   3
1  x 1 đồng biến trên khoảng nào? 3 A.  3  ;  2 . B. 1;2. C.  2  ;  1 . D.  1  ;  0 .
Câu 12: Cho hàm số y  f  x liên tục trên  và có đồ thị là đường cong trơn (không bị gãy khúc),
tham khảo hình vẽ bên. Gọi hàm số g  x  f  f  x 
 . Hỏi phương trình g ' x  0 có bao nhiêu nghiệm phân biệt? A. 14 . B. 10 . C. 12 . D. 8 .
Câu 13: Cho hàm số f  x thỏa mãn f 0  0 . Đồ thị hàm số y  f ' x cho bởi hình vẽ dưới đây.
Hàm số g  x  f  x   3 x có bao nhiêu điểm cực tiểu? A. 2 . B. 3 . C. 4 . D. 5 . 9x  1 
Câu 14: Cho hàm số y  f (x) 
. Tìm m để phương trình 2
f 3m  sin x  f (cos x)  1 có đúng 9x  3    4 
8 nghiệm phân biệt thuộc 0;3 
Câu 15: Cho hàm số y  f  x có bảng biến thiên như sau:  9 
Số nghiệm thuộc đoạn 0; 
phương trình f  f cos x  2 là 2    A. 9 . B. 6 . C. 5. D. 7 .
Câu 16: Cho hàm số y  f  x 4 3 2
 ax  bx  cx  dx  e với a  0 có đồ thị như hình vẽ. Phương trình
f  f  x  log m (với m là tham số thực dương), có tối đa bao nhiêu nghiệm? 2 A. 18 . B. 3. C. 5. D. 7 .
Câu 17: Cho hàm số y  f x có đồ thị như hình dưới. Có bao nhiêu số nguyên m để phương trình f  3
2x  6x  2  2m1 có 6 nghiệm phân biện thuộc đoạn 1;2   ? A. 2. B. 3. C. 0. D. 1.
Câu 18: Cho hàm số y  f  x , hàm số y  f x có đồ thị như hình bên. Hàm số     g  x 5sin x 1  x 2 5sin 1  2 f   3  
có bao nhiêu điểm cực trị trên khoảng 0;2  ?  2  4 A. 9. B. 7. C. 6. D. 8.
Câu 19: Cho f  x là hàm số bậc bốn thỏa mãn f 0  0. Hàm số f  x có bảng biến thiên như sau:
Hàm số g x  f  3
x  3x có bao nhiêu điểm cực trị A. 5. B. 4. C. 2. D. 3
Câu 20: Cho hàm số y  f  x liên tục trên  và có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt
của phương trình f  f  x  x là A. 6. B. 7. C. 8. D. 9.
Câu 21: Cho hàm số f  x bậc bốn có đồ thị như hình vẽ dưới đây. Tìm số điểm cực trị của hàm số g  x
, biết gx  x  f x    3 2 2 1  . A. 5. B. 6. C. 9. D. 10.
Câu 22: Cho hàm số bậc ba y  f  x có đồ thị như hình vẽ sau. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  2
 0;20 để hàm số g x  f 1 x   m có 5 điểm cực trị? A. 14. B. 15. C. 16. D. 17.
Câu 23: Cho hàm số y  f  x có đồ thị hàm số y  f 'x như hình vẽ dưới đây. Hàm số g  x  f  2
x  x 1  có bao nhiêu điểm cực đại? A. 3 . B. 4 . C. 5 . D. 7 .
Câu 24: Cho hàm số y  f x liên tục trên  và có đồ thị như hình bên dưới.
Số giá trị nguyên của tham số m sao cho phương trình f 2sin x  f m có 5 nghiệm phân  3  biệt thuộc đoạn 0;  là 2    A. 1. B. 3 . C. 2 . D. 0 .
Câu 25: Cho hàm số bậc ba y  f  x có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  2  0;2 
0 để hàm số g x  f 1 x   m có 5 điểm cực trị. A. 14 . B. 13 . C. 11. D. 12.  3 Câu 26: Cho hàm số 3
y  f (x)  x  3x . Số điểm cực tiểu của hàm số 
f sin 3x  (sin x  3 cos x)    2    13 trên   ;  là? 6 6    A. 6 . B. 5 . C. 7 . D. 8
Câu 27: Cho hàm số y  f (x) có đạo hàm liên tục trên  , f ( 2
 )  7 và có bảng biến thiên như hình dưới đây.
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f  2
x 1  2  m có đúng 6 nghiệm thực phân biệt? A. 9 . B. 8 . C. 7 . D. 6
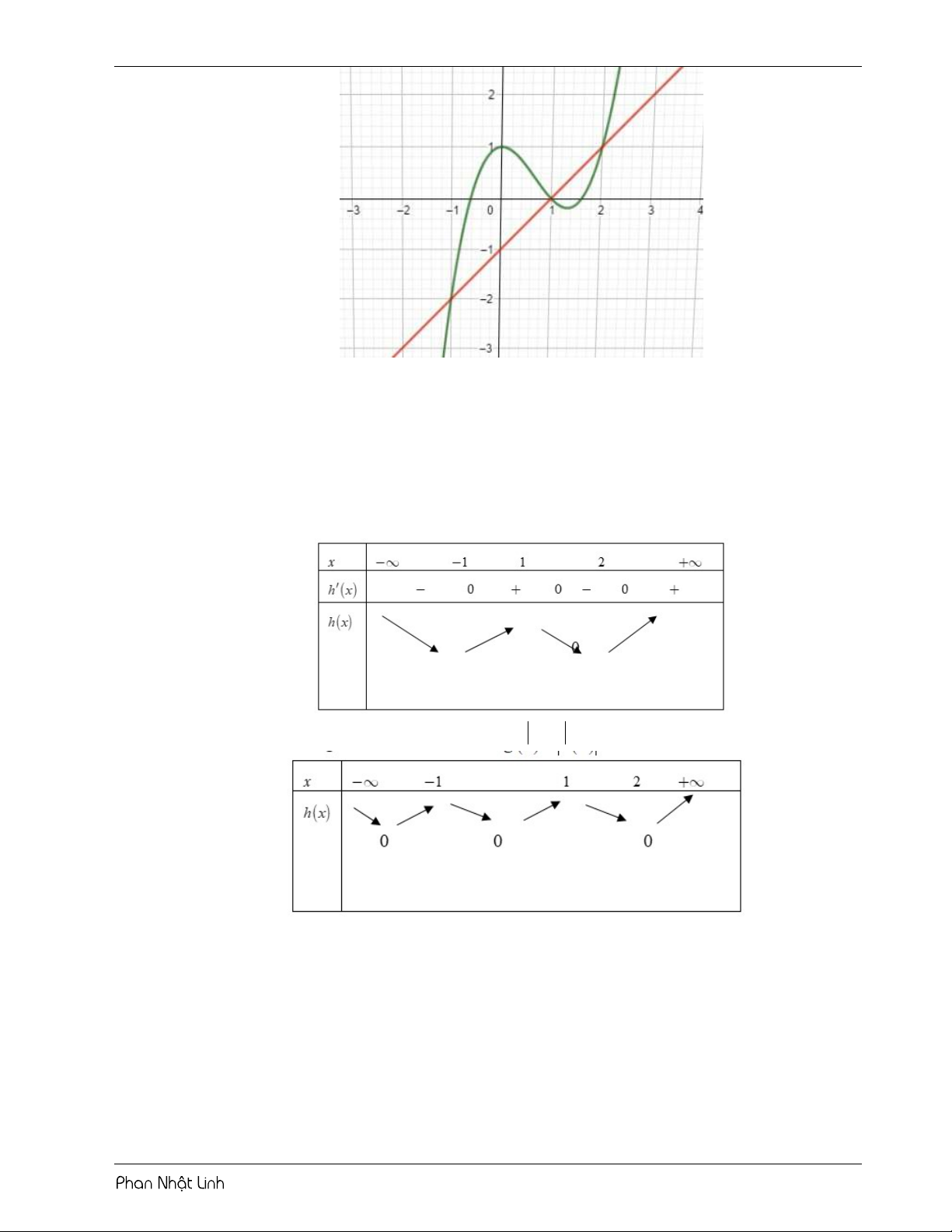
Câu 28: Cho hàm số bậc ba y  f  x và hàm số bậc nhất y  g  x có đồ thị như hình dưới đây f  x Hàm số h  x  g
 tdt nghịch biến trên khoảng nào dưới đây? 0 A. 3;2. B. 2;  1 . C. 1;  1 . D. 1;3. 2x  2 x 1 2 
Câu 1: Đặt u  x 1  2  u '  với x  1. 2 x 1 x  0 Ta có: u ' 0    x  1  . x  1   Ghép trục ta được: Để phương trình f  2
x 1  2  m có đúng 6 nghiệm thực phân biệt thì 1 m  7 .
Suy ra m 0;1;2;3;4;5;  6 .
Câu 2: Ta có bảng biến thiên của hàm số y  f  x
Đặt u  x   x     x  2 3 1 3 . x   1 x  3 x  x   u '  . x   1   x  32  32 2  x 32 x 32
Ta có bảng biến thiên của hàm số u  u  x Ghép trục ta được: 4  log m  0
f u  log m có ít nhất 5 nghiệm phân biệt  1 logm 3 4 1  0  m  1  
và m   m 1;10;11;...;99  9 . 3 1  0  m  10  lim f x   x   f    1  a  b  2  0 Câu 3: Ta có  f
 3  9a  3b  24  24  33a  b  0  lim f x   x
Suy ra f  x  0 có 3 nghiệm phân biệt x 1  x  3  x . 1 2 3
Mặt khác: f  x f  x   f   x 2   f  x f x  f  x 2 2. . ' ' 2. . ' '   0 
Xét g  x  f  x f  x   f  x 2 2. . ' '   
 g 'x  2. f 'x. f ' x  2 f  x. f ''x  2 f 'x. f ' x  2 f x. f ''x12 f x. x  x   ;  1 1   
Khi đó g ' x  0  12 f  x  0  f  x  0  x  x  1;3 .  2   x  x  3;  3   Bảng biến thiên
Do g  x   2. f  x . f '  x    f '   x  2     f '    x  2   0 g x  có hai nghiệm phân 2 2 2 2 2  nên   0 biệt. Câu 4:  f   3
2x  6x  2  2 khi f  3 2x  6x  2  0 Ta có: f  3
2x  6x  2  2  f  3 2x  6x  2  2  khi f  3 2x  6x  2  0
Theo đồ thị: f 2  2   1
f a  2 0  a  3 2
f b  2 3  b  6 3
f c  2 c  6 4 Với   1 thì 3 3 2x  6x  2  2
  2x  6x  4  0  x  2  ; x 1 (2 nghiệm). Với 2 thì 3 3
2x  6x  2  a  2x  6x  2  a  0 (3 nghiệm). Với 3 thì 3 3
2x  6x  2  b  2x  6x  2  b  0 (3 nghiệm). Với 4 thì 3
2x  6x  2  c (1 nghiệm). Vậy f  3
2x  6x  2  2 có 2+3+3+1 = 9 nghiệm. Với f  3
2x  6x  2  2 thì có 3 trường hợp là f d   2  với d  2  ; f e  2  với
3  e  6 và f  f   2 với f  6 . Với d  2  thì 3
2x  6x  2  d có 1 nghiệm. Với 3  e  6 thì 3
2x  6x  2  e có 3 nghiệm. Với f  6 thì 3
2x  6x  2  f có 1 nghiệm. Trường hợp f  3
2x  6x  2  2 có 1+3+1 = 5 nghiệm. Vậy tổng cộng f  3
2x  6x  2  2 có 9 + 5 = 14 nghiệm. Câu 5: Chọn C 3 3  x 1 Ta có g ' x 2 3  x f '
  (2m 1)(4x  4x) . 2  2 
Hàm số đồng biến trên 0;  khi và chỉ khi g ' x  0, x  0;  3 3  x 1 2 3  x f '
 (2m 1)(4x  4x)  0, x     0; 2  2  3 3x  x 1  2m 1 . f ' , x   0;  2   8x  8  2  3 3 x 1  x 1 Với x  0 thì  0  f '   2  . 2  2  3 x 1 3x 3 3 Đẳng thức xảy ra khi
 1  x  1. Mặt khác, 0    2 2 8x  8 1 16 8(x  ) x 3 3 3x  x 1 3 3x  x 1 3  Suy ra . f '   ( 2  ).  . f '   . 2 2 8x  8  2  16 8x  8  2  8 3 5
Đẳng thức xảy ra khi x  1. Như vậy: 2m 1   m  . 8 16
Vì m và m 10;10 nên m10;9;8;...1;  0 . Có 11 giá trị. Câu 6: Đặt
u  x  x   x     x  2 3 1 3  x   1 2 x  x  x  x   x  x  u ' x  3 1   x  32  3 1  3  32x+2   x 32 x 32 x 32    u x x 3 '  0  x 1 Bảng biến thiên
Từ bảng biến thiên ta thấy, phương trình đã cho có ít nhất năm nghiệm khi : 4 4  logm 0 10   m  1 m  1      3  1 logm  3 1  0  m  10 m  10,11,12,....,999
Vậy có 991 giá trị nguyên của m thỏa mãn. Câu 7: Xét hàm số 2 2
y  x  8x  7  x  3
Tập xác định của hàm số là  2
2x 8x  4, x 1 x  7 Ta có 2 2
y  x  8x  7  x  3  8x10, 1 x  7 4x 8, x  1 x  7 y '  8  , 1  x  7 Đặt 2 2
t  x  8x  7  x  3 . Khi đó bảng biến thiên của hàm số y  f t là
Dựa vào bảng biến thiên suy ra hàm số y  f t cho có 7 điểm cực đại.
Câu 8: Đặt t  sin x  2,1 t  3
Phương trình 2 f sin x  2 5  0 trở thành: t  t  0;1  PTVN 1    5 t  t  1;2 2   f t   2 t t  2;3 3    t  t  3;4   PTVN 4   BBT:
Dựa vào bảng biến thiên ta có:  
+. t  t có 3 nghiệm phân biệt x thuộc 3    2 2 ;  2     
+. t  t có 4 nghiệm phân biệt x thuộc 3    3 2 ;  2   
Vậy phương trình đã cho có 7 nghiệm phân biệt.
Câu 9: Xét hàm số h x  f  x 2 2
 x  2x  hx  2 f x  2x  2
h x  0  f x  x 1   1
Vẽ đường thẳng y  x 1. Từ đồ thị hàm số ta thấy đường thẳng y  x 1 cắt đồ thị hàm số x  1
y  f  x tại ba điểm. Khi đó phương trình   1   x  1  x  2  h   f   2 1 2 1  x  2x  0
Ta có bảng biến thiên của hàm số h x như sau:
Khi đó ta có bảng biến thiên của hàm số g  x  h  x .
Câu 10: Xét h x  f  x 2 2  x  2x
 h'x  2 f ' x  2x  2
h ' x  0  2 f ' x  2x  2  0  f ' x  x 1
Dựa vào đồ thị ta thấy, đồ thị hàm số y  f ' x và đường thẳng y  x 1 cắt nhau tại 3 điểm có hoành độ là x  1  ; x 1; x  2 x  1 
Do đó phương trình f ' x x 1     x  1  x  2  Bảng biến thiên
Bảng biến thiên của hàm số g  x  h x
Vậy hàm số g  x  f  x 2 2
 x  2x đồng biến trên khoảng 1;2 . 2
Câu 11: Xét hàm số g x f  2x   3 1  x 1 3 Ta có: g x x f  2x  2 x x  f   2 ' 2 . ' 1 2 2 ' x 1 x          x  0 g 'x 0     f '
  2x  1x  1 Xét   1 : Đặt x  t 1   t  1 t a a 0;1 2   Khi đó ta có: f 't 2t  t 1       t2 t b b2; 3   x 2
xa1a11;0  1    x1  xb1  b11;2 Ta có:
Từ bảng xét dấu trên ta thấy hàm số g x đồng biến trên khoảng  2  ;  1 . x  a  2  ;  1 x  0 Câu 12: Ta có f 'x 0    x b1;2  x  2
Từ đồ thị ta có f a  M , M  3 và f b  m, m  0;1 .
Đặt u  f  x , ta có hàm số g  x  f u .
Số nghiệm phân biệt của phương trình g ' x  0 chính là số cực trị của hàm số g  x  f u .
Dựa vào đồ thi hàm số y  f  x ta có bảng biến thiên sau:
Từ bảng biến thiên ta thấy hàm số g  x  f u có 12 cực trị.
Vậy phương trình g ' x  0 có 12 nghiệm phân biệt.
Câu 13: Đặt: h x  f  x  3x  h ' x  f ' x  3
Từ đồ thị hàm y  f ' x ta có BBT:
Số điểm cực trị dương của hàm h  x là 2 .
Do đó số điểm cực tiểu của g  x là: 2.2 1 5 . x 1 9 9 x 9x 3
Câu 14: Ta có f (x)  f (1 x)     1 x  x 1
9  3 9 x  3 9x  3 9x  3 Do đó  1  2
f 3m  sin x  f (cos x)  1    4  1 1 2 2
 3m  sin x  cos x 1  3m  sin x  sin . x 4 4 1  1  Kết luận:  3m  0   m  0 . 64 192
Câu 15: Đặt u  cos x , t  f u
Phương trình trở thành: f (t)  2 .
Ta có bảng biến thiên hàm số y  f (t)
Số nghiệm phương trình f  f cos x  2 bằng số giao điểm của đường thẳng y  2 và đồ thị
hàm số y  f (t) , từ bảng biến thiên  phương trình f (t)  2 có 9 nghiệm.
Vậy phương trình f  f cos x  2 có 9 nghiệm.
Câu 16: Đặt t  f  x
Phương trình trở thành: f t  log m 2
Số nghiệm phương trình f  f  x  log m bằng số giao điểm của đường thẳng y  log m và 2 2
đồ thị hàm số y  f (t) , từ bảng biến thiên  phương trình có tối đa 18 nghiệm. Câu 17: Đặt 3 t  2x  6x  2 x  1 Khi đó 2
t  6x  6, t  0  x  1 f  3
2x  6x  2  2m1 có 6 nghiệm phân biệt 0  2m1 1 3 2   m  2 2
Lại có m   m  1. Vậy có duy nhất 1 số nguyên m thoả mãn bài toán. 5sin x 1 Câu 18: Đặt t 
. Suy ra g t  f t 2 2  t  3 2
Ta có gt  2 f t  2t  0  f t   t  t  1   1  t   3  t  3  Bảng biến thiên: Suy ra: . Câu 19: Đặt 3 3
t  x  x  t .Ta có h x  f  3
x   x  ht  f t 3 3  3 t
 hx  f t 1   0  t  a
Dựa vào bảng biến thiên ta suy ra 3 2 t 3 t  a  x  a
Suy ra hàm số g(x)  h  x có 3 cực trị
Câu 20: Xét phương trình f  f  x  x   1 Nhận xét:
x  2  f  x  x  2  f  f x  f x  x   
1 không có nghiệm x  2 . x  2   f x  x  2
  f  f x  f  x  x   
1 không có nghiệm x  2 .
Ta xét bảng biến thiên của f  f  x với 2  x  2 như sau:
Dựa vào bảng biến thiên, ta thấy phương trình f  f  x  x có 9 nghiệm. 2 x  0
Câu 21: g x  0   . 2
x  0  x  0 (nghiệm kép, loại).  f   2 x   1  0 2 x 1  1 l   x   a 1        f x   2 x 1 a 1 a 0 2   1  0   x   b 1 
. Vậy g  x có 6 cực trị. 2
x 1  b 0  b   1   x   2   2 x 1  1  a
Câu 22: f  x có hai cực trị là x  x   f  x  ax x    f  x 3 2 0, 2 2  x  ax  C. 3 f    
f      a  c    f  x 3 2 0 2, 1 4 3, 2  x  3x  2 .     f  1 x, khi x  0     x  x  x  f x f 1 x  3 3 4, khi 0 1   .  f  1 x 3 , khi x  0
x 3x  4, khi x  0
Ta có đồ thị của f 1 x  như sau:
Đặt h  x  f 1 x   .
m Ta có g  x  h x .
g  x có 5 cực trị  phương trình h x  0 có 2 nghiệm đơn  m  4 .
Vậy có 17 giá trị m thỏa yêu cầu bài toán.
Câu 23: Dựa vào đồ thị ta thấy hàm số y  f  x có 3 điểm cực trị là x  1  ; x  1; x  2 . 2 x  x 1, x 1   1 2  x   x  x 1, 0  x 1  Đặt u x 2  x  x 1  2  ; u ' x  0   . 2
x  x 1, 1 x  0  1 x    2  x  x 1, x  1   2
Bảng biến thiên ghép trục
Hàm số g  x  f u x có 3 điểm cực đại và 4 điểm cực tiểu.
Câu 24: Từ đồ thị hàm số y  f  x ta thấy hàm số có các cực trị x  1  ; x 1. 
Đặt t  2sin x  t '  2 cos x ; t '  0  x   k ,k  .  2 Ta có bảng ghép trục.  3 
Phương trình f 2sin x  f m có 5 nghiệm phân biệt thuộc đoạn 0;  khi 2    3
  f m  f 0.
Từ đồ thị hàm số y  f  x ta thấy m  a  2  ;  1  3
  f m  f 0  m  b0;  1 . Vì m nên m  0. m  c  1;2
Câu 25: Đặt t  1 x  f 1 x   f t Bảng ghép trục:
Phương trình g  x trở thành g t   f t   m
YCBT trở thành: f t  m  0 có 2 nghiệm phân biệt
Để f t  m  0 có 2 nghiệm phân biệt thì: m  8  m  8 m      có 13 giá trị m m  20;20            Câu 26: Ta có: 3
y  f sin(3x   )  3sin x   f 4sin x   6sin x           3   3 3       
Vậy hàm số trên có 6 điểm cực tiểu. 2 . x  2 x 1 2 
Câu 27: Đặt u  x 1  2  u '  2 x 1
Ta có bảng biến thiên như sau x -∞ -1 0 1 +∞ +∞ 1 -1 +∞ 1 0 0 u -1 -1 -2 -2 +∞ +∞ f(-2)=7 f(-2)=7 f(u) f(0)=-1 f(0)=-1 f(1)=-2 f(-1)=-2 f(-1)=-2 f(-1)=-2 f(1)=-2
Từ bảng biến thiên để phương trình có đúng 6 nghiệm thực phân biệt khi 1   m  7 Suy ra m   0,1,2,3,4,5,  6 .   f  x f x  2 2  x   f x 
Câu 28: Đặt g  x  k. x  2, k  0  hx  g
 tdt  k 2x  k  2 f x. 2  2  0   0   x  x  2  ;0 1     f 'x  0 x  x  0;2 2  
 h'x  k. f ' x f x  2  h'x  0      f   x  2 x  x  2  ; x  3  1  x  x  x ;2  4  2  Bảng biến thiên x - -2 x3 x1 0 x2 x4 2 - _ h'(x) 0 + _ _ 0 0 + 0 0 + h(x)
Dưạ vào bảng biến thiên suy ra hàm số h(x) nghịch biến trên khoảng  3  ;2. . .

Toàn tập về phương pháp ghép trục Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số