30 trang 1 lượt tải

Tối Ưu Hóa Lựa Chọn Đồ Vật Trong Bài Toán Balo | Tối ưu rời rạc | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội

2

Thuật toán nhánh cận là một trong các phương pháp chủ yếu giải bài toán tối ưu tổ hợp. Tư tưởng cơ bản của nó là trong quá trình tìm kiếm ta phân hoạch các phương án của bài toán ra thành hai hay nhiều tập con như các nút, loại bỏ những nhánh mà ta biết chắc chắn là không chứa phương án tối ưu. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Môn: Tối ưu rời rạc (HUS) 10 tài liệu

Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 687 tài liệu

Tác giả:

Profile

Mai Nguyệt

1 tuần trước
Danh sách Quiz
/30
3
MỤC L C Ụ
DANH MỤC B NG ................................................................................................... 5 Ả
DANH MỤC HÌNH NH .......................................................................................... 5 Ả
CHƯƠNG 1: CƠ SỞ LÝ THUYẾT ........................................................................... 6
1.1. Thu t toán nhánh c n ........................................................................................ 6 ậ ậ
1.2. Nguyên lý .......................................................................................................... 6
1.3. Ưu điể ợc điểm và như m của thuật toán nhánh cận .......................................... 6
1.3.2. Nhược điểm ................................................................................................ 7
1.4. Các bước chính của thuật toán .......................................................................... 7
1.5. Mô t thu t toán ................................................................................................ 7 ả ậ
1.6. Áp d ng gi i bài toán ........................................................................................ 9 ụ ả
CHƯƠNG 2: PHÂN TÍCH ỐI ƯU HÓA LỰ- XÂY DỰNG THUẬT TOÁN T A
CHỌ ỒN Đ V T TRONG BÀI TOÁN BALO (KNAPSACK) ............................... 14 Ậ
2.1. Mô t bài toán ................................................................................................. 14 ả
2.1.1. Xây d ng bài toán thự ực thế ...................................................................... 14
2.1.2. Phát bi i d ng t ng quátểu bài toán dướ ạ ổ .................................................. 14
2.2. Xây d ng thu t toán ........................................................................................ 15 ự ậ
2.2.2. Xây d ng gi mã ...................................................................................... 16 ự ả
2.3. Ví d minh h tìm ki m nhánh c n trên và thu t toán backtrack ............ 18 ụ ọa về ế ậ ậ
CHƯƠNG 3: CÀI ĐẶT THUẬT TOÁN BẰNG NGÔN NGỮ LẬP TRÌNH
PYTHON ................................................................................................................... 19
3.1. Cài đặt thuật toán ............................................................................................ 19
3.1.1. Cài đặt class Item ..................................................................................... 19
3.1.4. Cài đặt thuật toán backtrack .................................................................... 20
3.2. Ki m th ......................................................................................................... 24 ể ử
3.2.1. D li u vàoữ ệu đầ ........................................................................................ 24
4
3.2.2. D li u raữ ệu đầ .......................................................................................... 25
3.2.3. Ki các ch a thu t toánểm thử ức năng củ ậ ................................................... 25
3.3. Đánh giá và so sánh ........................................................................................ 27
3.3.2. So sánh th i gian th n thu t toánờ ực hiệ ậ .................................................... 28
TỔNG KẾT ............................................................................................................... 30
ĐÁNH GIÁ NỘI BỘ ................................................................................................ 31
TÀI LI U THAM KH O ......................................................................................... 32Ệ Ả
5
DANH M C BỤ ẢNG
Bảng 1. B ng d li u vào. .................................................................................. 25 ả ữ ệu đầ
Bảng 2. B i bảng đánh giá nộ ội. ................................................................................. 31
DANH M C HÌNH Ụ ẢNH
Ảnh 1. Xây dựng cây tìm kiếm cho bài toán cái túi. ................................................. 11
Ả ịnh 2. Xây dựng cây tìm ki i du lếm cho bài toán ngườ ch. ..................................... 12
Ả ọnh 3. Ví dụ minh h a tìm kiếm nhánh trên và thuật toán backtrack. ..................... 18
6
CHƯƠNG 1: CƠ SỞ LÝ THUYẾT
1.1. Thu t toán nhánh c n ậ ậ
Thuật toán nhánh c n là m y u gi i bài toán t i ậ ột trong các phương pháp chủ ế ả ố
ưu tổ ợp. Tư tưởng cơ bả h n của nó là trong quá trình tìm kiếm ta phân hoạch các
phương án củ ập con như các nút, loạa bài toán ra thành hai hay nhiều t i bỏ những
nhánh mà ta bi t ch c ch n là không ch ế ắ ắ ứa phương án tối ưu.
Kỹ thu t nhánh c n phát tri n t ậ ậ ể ừ ý tưởng c a thu t toán quay lui. Thay vì duy t ủ ậ ệ
tất c ng hả các trườ ợp, n n m t vếu ta đế ộ ị trí mà giá trị c a hàm m c tiêu tủ ụ ại đó và các
điểm về sau chắc chắn không tốt nhất thì quay lại luôn.
1.2. Nguyên lý
Nhánh (Branch): Thu t toán chia nh bài toán l n thành các bài toán con nh ậ ỏ ớ ỏ
hơn, tứ ỗi nhánh đạc là tạo ra các nhánh trong quá trình giải. M i diện cho một trạng
thái ho c m t t p con c a không gian tìm ki m. Quá trình này ti p t n khi ặ ộ ậ ủ ế ế ục cho đế
đạ ợ ợt đư c một giải pháp h p lệ hoặc không thể tìm thêm nhánh con nào nữa.
Cận (Bound): Cận là bước quan tr ng trong thu t toán nhánh c n, giúp lo i b ọ ậ ậ ạ ỏ
các nhánh không c n thi t trong quá trình tìm ki m. M i nhánh s có m t giá tr "c n" ầ ế ế ỗ ẽ ộ ị ậ
tính toán được, và thu t toán ch ti p t c tìm ki m trong các nhánh mà giá tr c n c a ậ ỉ ế ụ ế ị ậ ủ
chúng h a h n mang l i gi i pháp tứ ẹ ạ ả ốt hơn so vớ ải pháp đã tìm được trước đó. Nếi gi u
giá tr c n c a m t nhánh không th tị ậ ủ ộ ể ốt hơn giải pháp hi n tệ ại, nhánh đó sẽ bị loại b . ỏ
1.3. Ưu điểm và nhược điểm của thuật toán nhánh cận
1.3.1. Ưu điểm
- Tìm ki m gi i pháp tế ả ối ưu: Thuật toán nhánh cận luôn đả ảo tìm đượm b c giải
pháp t u không gian tìm ki c duy t trong nhối ưu nế ếm đượ ệt đầy đủ. Đây là mộ ững ưu
điể ớ ỉm quan trọng nhất khi so v i các thuật toán “tham lam” (Greedy) hoặ ấc x p x .
- Gi m thi u không gian tìm ki m: Thu t toán s d c l c nhánh lo i ả ể ế ậ ử ụng bướ ọ để ạ
bỏ các nhánh không kh thi ho c không có tiả ặ ềm năng mang lại gi i pháp tả ốt hơn, giúp
giảm đáng kể số lượng trạng thái cần kiểm tra.
- Linh ho t v i nhi u bài toán: Thu t toán có th áp d ng cho nhi u bài toán ạ ớ ề ậ ể ụ ề
tối ưu hóa rờ ạc như bài toán cái balo, bài toán đi đười r ng ngắn nhất (Traveling
Salesman Problem), bài toán phân ho ch, bài toán l p l ch và nhi u bài toán khác. ạ ậ ị ề
- Kh n d ng chi c c n: S d ng các k thu t tính toán c n hi u ả năng tậ ụ ến lượ ậ ử ụ ỹ ậ ậ ệ
quả (upper bound - c n trên ho c lower bound - cậ ặ ận dưới) giúp nâng cao hi u qu c a ệ ả ủ
thuật toán và gi m thả ời gian tính toán.
- Kh ả năng dừng sớm: Khi tìm được m t gi i pháp mà giá tr c n c a các nhánh ộ ả ị ậ ủ
còn l i không th t i pháp hi n t i, thu t toán có th d ng s m mà không ạ ể ốt hơn giả ệ ạ ậ ể ừ ớ
cần duy t toàn b không gian. ệ ộ
7
1.3.2. Nhược điểm
- T n kém v b nh : Do c t t c các nhánh và thông tin liên quan ố ề ộ ớ ần lưu trữ ấ ả
(như trạ ớ, đặ ệt đống thái, giá trị cận), thuật toán có thể yêu cầu rất nhiều bộ nh c bi i
với các bài toán có không gian tìm ki m lế ớn.
- Độ ph c t p tính toán cao: M c dù thu t toán lo i b ứ ạ ặ ậ ạ ỏ được nhi u nhánh không ề
cần thi t, vi c tính toán c n và qu n lý các nhánh v n tiêu t n th i gian và tài nguyên, ế ệ ậ ả ẫ ố ờ
đặc biệt với các bài toán có kích thước lớn.
- Ph thu c vào chi c c n: Hi u qu c a thu t toán ph thu c r t nhi u ụ ộ ến lượ ậ ệ ả ủ ậ ụ ộ ấ ề
vào cách tính toán c n trên ho c cậ ặ ận dưới. Nếu cận không chính xác ho c không ch t ặ ặ
chẽ, thu t toán có th ph i duy t qua nhi u nhánh không c n thi t, làm gi m hi u qu . ậ ể ả ệ ề ầ ế ả ệ ả
- Không phù h p v i không gian tìm ki m quá l n: Khi không gian tìm ki m ợ ớ ế ớ ế
quá r ng ho c không th d dàng tính toán c n, thu t toán có th tr nên ch m và ộ ặ ể ễ ậ ậ ể ở ậ
kém hi u qu so v p x . ệ ả ới các phương pháp xấ ỉ
- Khó khăn trong triển khai: Vi c tri n khai thu t toán nhánh c n yêu c u hi u ệ ể ậ ậ ầ ể
rõ bài toán và các k thu t tính toán cỹ ậ ận, điều này có th ph c tể ứ ạp hơn so với các thu t ậ
toán tham lam ho c quy ho ng. ặ ạch độ
1.4. Các bước chính của thuật toán
- Kh i t o: B u v i m t gi u (có th là gi i pháp x p x ho c ở ạ ắt đầ ớ ộ ải pháp ban đầ ể ả ấ ỉ ặ
giải pháp hợp l nh t), tính toán c i (ho c c n trên) c c ệ ấ ận dướ ặ ậ ủa bài toán. Đây là bướ
khởi t o không gian tìm ki m. ạ ế
- Chia nhánh (Branching): T o ra các nhánh con b ng cách chia bài toán l n ạ ằ ớ
thành các bài toán con nh n không gian tìm ki m. M i nhánh có ỏ hơn, từ đó phát triể ế ỗ
thể đại di n cho m t t p con c a các l n ho ng thái. ệ ộ ậ ủ ựa chọ ặc các trạ
- Tính c n (Bounding): V i m i nhánh, tính toán giá tr c ng là c n ậ ớ ỗ ị ận (thườ ậ
dưới đố ận trên đố ối đa). Cậi với bài toán tối thiểu hoặc c i với bài toán t n này là một
ướ ợ ủ ịc lư ng c a giá tr t ối ưu trong nhánh đó.
- L i b c n c ọc nhánh (Pruning): Loạ ỏ các nhánh mà giá trị ậ ủa chúng không thể
tốt hơn giả năng tìm ra mộ ốt hơn. Điềi pháp hiện tại hoặc không có khả t giải pháp t u
này giúp gi m thi u không gian tìm ki m và ti t ki m th i gian. ả ể ế ế ệ ờ
- Ti n hành tìm ki m: Ti p t c m r ng các nhánh còn l n khi tìm ế ế ế ụ ở ộ ại cho đế
được giải pháp t kiối ưu hoặc không còn nhánh nào để ểm tra.
1.5. Mô t thu t toán ả ậ
Ta s mô t thu t toán trên mô hình bài toán t ng quát sau: ẽ ả ậ ối ưu tổ
min { f(x) : x D }, ∈
Trong đó D là tập h u h n ph n t . ữ ạ ầ ử
Gi
ả
thi t r ng t c mô t ế ằ ập D đượ ả như sau:
8
D={x = (x , x , ... , x )
1 2 n
∈ A × A × ... × A : x tho mãn tính ch t P},
1 2 n
ả ấ
Với A , A , ... , A là các t p h u h n, còn P là tính ch -các
1 2 n
ậ ữ ạ ất cho trên tích Đề
A
1
× A
2
... . × × A
n
Với gi thi t v t p D nêu trên, chúng ta có th s d ng thu ả ế ề ậ ể ử ụ ật toán quay lui để
liệt kê các phương án của bài toán. Trong quá trình li t kê theo thu t toán quay lui, ta ệ ậ
sẽ xây d ng d n các thành ph n c t b g m k thành ph n (a , a , a , ự ầ ầ ủa phương án. Mộ ộ ồ ầ
1 2 3
… ọi là phương án bộ, a ) xu
k
ất hiện trong trong quá trình thuật toán sẽ g phận cấp k.
Thuật toán nhánh c n có th áp d giậ ể ụng để ải bài toán đặ ếu như có thểt ra n tìm
được m nh trên trên tột hàm g xác đị ập tất cả phương án bộ phận của bài toán thỏa
mãn b ng thất đẳ ức sau:
g(a
1
, a , ... , a
2 k
) ≤ min {f(x): x ∈ D, x = a , i = 1, 2, ..., k}
i i
(*)
Bất đẳ ức (*) có nghĩa là giá trị ại phương án bộng th của hàm g t phận (a , a ,
1 2
… , a
k
) là không vượt quá giá tr nh nh t c a hàm m c tiêu c a bài toán trên t p con ị ỏ ấ ủ ụ ủ ậ
các phương án.
D(a
1
, a , a )={ x
2
, …
k
∈ D : x =a , i = 1, 2, ... , k}
1 i
Hay nói m t cách khác, g(a , a , a ) là c i c a giá tr hàm m c tiêu ộ
1 2
, …
k
ận dướ ủ ị ụ
trên t p D(a , a ). Vì l ậ
1 2
, … , a
k
ẽ đó, hàm g được gọi là hàm c i và giá tr g(a , a , ận dướ ị
1 2
… ọ đồ , a c g
k
) đượ i là c i cận dướ ủa tập D(a , a ). Do có th
1 2
, … , a
k
ể ng nhất tập D(a ,
1
a
2
, … , a
k
) v ph n (a , a i giá tr g(a , a , aới phương án bộ ậ
1 2
, … , a
k
), nên ta cũng gọ ị
1 2 3,
… , a ) là c i c ph
k
ận dướ ủa phương án bộ ận (a , a ).
1 2
, … , a
k
Giả s xét cách s d gi m bử đã có hàm g. Ta ử ụng hàm này để ả ớt kh ng ối lượ
duyệt trong quá trình duy t t t c t toán quay lui. Trong quá ệ ấ ả các phương án theo thuậ
trình li t s a bài toán. G i ệt kê các phương án có thể đã thu được mộ ố phương án củ ọ x
là phương án vớ các phương án đã tìm đượi giá trị hàm mục tiêu nhỏ nhất trong số c,
kí hi u = f(ệ f
x
). Ta sẽ g i ọ x
là phương án tố đã t nh t hi n có, còn là k l c. Gi sấ ệ f
ỷ ụ ả ử
có f
, khi đó nếu:
g(a
1
, a ) > ,
2
, … , a
k
f󰋀
Thì t b ng th c (*) suy ra ừ ất đẳ ứ
f󰋀 < g(a , a
1 2
, … , a
k
) ≤ min {f(x): x ∈ D : x = a , i= 1, 2, ... , k}
1 i
Vì th tế ập con các phương án ấy c a bài toán Dủ (a
1
, a
2
, … , a
k
) chắc ch n không ắ
chứa phương án tối ưu. Trong trường hợp này ta không cần tiếp tục phát triển các
phương án bộ các phương án phận ( nói cách khác là ta có th(a
1
, a ),
2
, … , a
k
ể loại bỏ
trong t p D i quá trình tìm ki m. ậ (a
1
, a )
2
, … , a
k
khỏ ế
9
1.6. Áp d ng gi i bài toán ụ ả
1.6.1. Bài toán cái túi
Đưa ra giả thi t r ng có n lo v t và s v t m i lo i là không h n ế ằ ại đồ ậ ố lượng đồ ậ ỗ ạ ạ
ch biế. Khi đó ta có mô hình bài toán cái túi ến nguyên sau đây: Có n loại đồ ật, đồ v
vật th j có tr ng a và giá tr s d ng là c (j = 1, 2, ... , n). C n ch v t ứ ọng lượ
j
ị ử ụ
j
ầ ất các đồ ậ
này vào m t cái túi có tr ng là b sao cho t ng giá tr s d ng c v t ộ ọng lượ ổ ị ử ụ ủa các đồ ậ
chất trong túi là l n nh t. ớ ấ
Mô hình c a bài toán s có d ủ ẽ ạng như sau:
Tìm:
𝑓 = 𝑚𝑎𝑥
{𝑓
(
𝑥
)
= ∑ 𝑐
𝑗
𝑥
𝑗
𝑛
𝑗=1
; ∑ 𝑎
𝑗
𝑥
𝑗
𝑛
𝑗=1
≤ 𝑏, 𝑥
𝑗
∈ 𝑍
+
, 𝑗 = 1, 2, . .. , 𝑛}(1)
Trong đó Z
+
là t p các s nguyên không âm. ậ ố
𝐷 = {𝑥 = (𝑥
1
, 𝑥
2
, . .. ,𝑥
𝑛
; ∑ 𝑎
𝑗
𝑥
𝑗
𝑛
𝑗=1
≤ 𝑏, 𝑥
𝑗
∈ 𝑍
+
,𝑗 = 1, 2, . .. , 𝑛}
Không gian t ng quát ta gi thi t r v sao cho b t ổ ả ế ằng các đồ ật được đánh số ấ
đẳng thức sau được thoả mãn:
𝑐
1
𝑎
1
≥
𝑐
2
𝑎
2
≥ . . . ≥
𝑐
𝑛
𝑎
𝑛
(2)
Để ti p t c xây d ng hàm tính c i, cùng v i bài toán cái túi (1) ta xét bài ế ụ ự ận dướ ớ
toán cái túi bi n liên tế ục sau:
Tìm:
𝑔 = 𝑚𝑎𝑥 𝑓
{
(
𝑥
)
=
∑
𝑐
𝑗
𝑥
𝑗
𝑛
𝑗=1
:
∑
𝑎
𝑗
𝑥
𝑗
𝑛
𝑗=1
≤ 𝑏, 𝑥
𝑗
≥ 0, 𝑗 = 1, 2, . .. , 𝑛} (3)
Mệnh đề: Phương án tối ưu của bài toán (3) là vectơ x
= (x
1
, x
2
, ... , x
n
) v i ớ
các thành ph nh b i công th c: ần được xác đị ở ứ
𝑥
1
=
𝑏
𝑎
1
, 𝑥 𝑥 𝑥
2
=
3
= . . . =
𝑛
= 0.
Và giá trị tối ưu là 𝑔 =
𝑐
1
𝑏
1
𝑎
1
Chứng minh: Thực v y, xét x = (x , x , ... , x ) là m ý c a ậ
1 2 n
ột phương án tuỳ ủ
bài toán (3). Khi đó từ bất đẳng thức (3) và do x
1
≥ 0, ta suy ra:
𝑐
𝑗
𝑥
𝑗
≥ (𝑐
1
/𝑎
1
) 𝑎
𝑗
𝑥
𝑗
, 𝑗 = 1, 2, . .. ,𝑛
Suy ra:
10
∑ 𝑐
𝑗
𝑥
𝑗
𝑛
𝑗=1
≤ ∑(𝑐
1 1
/𝑎 )𝑎
𝑗
𝑥
𝑗
𝑛
𝑗=1
= (𝑐
1 1
𝑎 ) ∑ 𝑎
𝑗
𝑥
𝑗
𝑛
𝑗=1
≤ (𝑐
1
/𝑎
1
)𝑏 = 𝑔
∗
.
M nh c ch ng minh. ệ đề đượ ứ
Bây gi , gi s ph n c p k: (u , u , ... , u ờ ả ử ta có phương án bộ ậ ấ
1 2 k
). Khi đó giá trị
sử d ng c v ụ ủa các đồ ật đang có trong túi là:
𝜎
𝑘
= 𝑐
1
𝑢
1
+ 𝑐
2 2
𝑢 + . . .+𝑐
𝑘
𝑢
𝑘
Và tr ng còn l i cọng lượ ạ ủa túi là:
𝑏
𝑘
= 𝑏 − 𝑎
1 2 2
𝑢
1
+ 𝑎 𝑢 + . .. +𝑎
𝑘
𝑢
𝑘
.
Ta có:
𝑚𝑎𝑥{ 𝑓(𝑥): 𝑥 ∈ 𝐷, 𝑥
𝑗
= 𝑢
𝑗
, 𝑗 = 1, 2, . .. , 𝑘}
= 𝑚𝑎𝑥{ 𝜎
𝑘
+ ∑ 𝑐
𝑗
𝑥
𝑗
𝑛
𝑗=𝑘+1
: ∑ 𝑎
𝑗
𝑥
𝐽
𝑛
𝑗=𝑘+1
≤ 𝑏
𝑘
, 𝑥
𝑗
∈ 𝑍
+
, 𝑗 = 𝑘 + 1, 𝑘 + 2, . .. , 𝑛}
≤ 𝜎
𝑘
+ 𝑚𝑎𝑥{ ∑ 𝑐
𝑗
𝑥
𝑗
𝑛
𝑗=𝑘+1
: ∑ 𝑎
𝑗
𝑥
𝐽
𝑛
𝑗=𝑘+1
≤ 𝑏
𝑘
, 𝑥
𝑗
≥ 0, 𝑗 = 𝑘 + 1, 𝑘 + 2, .. . , 𝑛}
(Theo m : Giá tr s h ng th hai là ) ệnh đề ị ố ạ ứ 𝑐 𝑏 /𝑎
𝑘+𝑗 𝑘 𝑘+𝑗
V y ta có th tính c ph n (u , u ) b i công ậ ể ận trên cho phương án bộ ậ
1 2
, … , u
k
ở
thức:
𝑔(𝑢 ,𝑢
1 2
, . . ., 𝑢
𝑘
) = 𝜎
𝑘
+ 𝑐
𝑘+1
𝑏
𝑘
/𝑎
𝑘+1
Chú ý: Khi ti p t c xây d ng thành ph n th k + 1 c i gi i, các giá tr ế ụ ự ầ ứ ủa lờ ả ị đề
cử cho x ]. Do có k t qu c , khi ch n giá tr cho
k+1
sẽ là 0, 1, … , [b
k
a
k+1
ế ả ủa mệnh đề ọ ị
x
k+1
ta s duy t các giá trẽ ệ ị đề c theo th t gi m d n. ử ứ ự ả ầ
Ví d ng d ng: ụ ứ ụ Giải bài toán cái túi theo thu t toán nhánh c n v a trình bày. ậ ậ ừ
𝑓
(
𝑥
)
= 10𝑥
1
+ 5𝑥
2
+ 3𝑥
3
+ 6𝑥
4
→ 𝑚𝑎𝑥,
5𝑥
1
+ 3𝑥
2
+ 2𝑥
3
+ 4𝑥
4
≤ 8,
𝑥
𝑗
∈ 𝑍
+
,𝑗 = 1, 2, 3,4.
Gi i: ả
11
Ảnh 1. Xây dựng cây tìm kiếm cho bài toán cái túi.
Quá trình gi c mô t trong cây tìm ki m trong hình trên. Thông ải bài toán đượ ả ế
tin v mề ột phương án bộ phận trên cây được ghi trong các ô trên hình tương ứng theo
thứ t u tiên là các thành ph n c c v t ự: đầ ầ ủa phương án, tiếp đến σ là giá trị ủa các đồ ậ
đang chấ ọng lượt trong túi, w – tr ng còn lại củ –a túi và g cận trên.
K t thúc thu t i ế ật toán, ta thu được phương án tối ưu là x=(1,1,0,0), và giá trị ố
ưu là f=15.
1.6.2. Bài toán người du lịch
Cố định thành ph xu t phát là ố ấ 𝑇
1
, bài toán người du l n v bài toán: ịch dẫ ề
Tìm cực ti a hàm: ểu củ
𝑓
(
𝑥 ,𝑥 , … ,𝑥
2 3 𝑛
)
= 𝑐 1, 𝑥
[
2
]
+ 𝑐 𝑥 ,𝑥
[
2 3
]
+ ⋯ + 𝑐 𝑥 , 𝑥
[
𝑛−1 𝑛
]
+ 𝑐
[
𝑥
𝑛
, 1 → min,
]
V
ới điều ki n: ệ
(
𝑥 ,𝑥 ,… , 𝑥
2 3 𝑛
)
là hoán v c . ị ủa các số 2,3, …, 𝑛
Ký hi u:
ệ 𝑐
𝑚𝑖𝑛
= min{𝑐 𝑖, 𝑗
[ ]
, 𝑖, 𝑗 = 1,2, … , 𝑛, 𝑖 𝑘ℎá𝑐 𝑗} là chi phí đi lại nh nh t ỏ ấ
giữa các thành phố.
Để có được thu t toán nhánh c n giậ ậ ải bài toán người du l c h t cịch, trướ ế ần đưa
ra cách đánh giá cận dưới cho phương án bộ ph n. Gi s ậ ả ử đang có phương án bộ ph n ậ
(
𝑢
1
,𝑢
2
,… , 𝑢
𝑘
)
. Phương án này tương ứng v i hành trình b ph n qua k thành ph : ớ ộ ậ ố
𝑇
1
→ 𝑇
(
𝑢
2
)
→ ⋯ → 𝑇
(
𝑢
𝑘−1
)
→ 𝑇(𝑢
𝑘
)
Vì vậy chi phí ph i tr theo hành trình b ph n này s là: ả ả ộ ậ ẽ
𝜎 = 𝑐 1, 𝑢
[
2
]
+ 𝑐 , 𝑢
[
𝑢
2 3
]
+ ⋯ + 𝑐[𝑢 , 𝑢
𝑘−1 𝑘
]
12
Để phát tri n hành trình b ph , ta còn phể ộ ận này thành hành trình đầy đủ ải đi
qua thành ph còn l i r i quay tr l i thành ph𝑛 − 𝑘 ố ạ ồ ở ạ ố 𝑇
1
, t c là còn phứ ải đi qua 𝑛 −
𝑘 + 1 đoạn đường nữa. Do chi phí ph i tr cho viả ả ệc đi qua mỗi một trong s ố 𝑛 − 𝑘 +
1 đoạn đườ ếu không ít hơn ng còn lại n 𝑐
𝑚𝑖𝑛
, nên c ph n ận dưới cho phương án bộ ậ
(
𝑢
1
,𝑢
2
,… , 𝑢
𝑘
)
có th tính theo công th c ể ứ
𝑔
(
𝑢 ,𝑢 ,… , 𝑢
1 2 𝑘
)
= 𝜎 + 𝑛 − 𝑘 + 1 𝑐
( )
𝑚𝑖𝑛
Sử d ng cách cụ ận dưới vừa nêu ta có th áp d ng thu t toán nhánh c gi i ể ụ ậ ận để ả
bài toán người du lịch.
Ví dụ: Giải bài toán ngườ ị ới du l ch v i ma trận chi phí sau:
0
3
14
18
15
3
0
4
22
20
C
=
17
9
0
16
4
6
2
7
0
12
9
15
11
5
0
Ta có . Quá trình th c hi n thu c mô t b i cây tìm ki m 𝑐 = 3
𝑚𝑖𝑛
ự ệ ật toán đượ ả ở ế
dưới đây:
Ảnh 2. Xây dựng cây tìm ki i du lếm cho bài toán ngườ ịch.
Thông tin v m t b ph ng ề ộ ộ ận trên cây đuọc ghi trong các ô trên hình tương ứ
theo th tứ ự: đầu tiên là các thành phần c a ủ phương án, tiếp đến là chi phí tương theo
hành trình b ph n và g - c i. ộ ậ ận dướ
13
Kết thúc thu ng ật toán, ta thu được phương án tối ưu (1, 2 , 3, 5, 4, 1) tương ứ
với hành trình:
𝑇
1
→ 𝑇
2
→ 𝑇
3
→ 𝑇
5
→ 𝑇
4
→ 𝑇
1
,
Và chi phí nhỏ nh t là 25. ấ
Hiệu qu c t toán nhánh c n ph thu c vào vi ng hàm tính c n ả ủa thuậ ậ ụ ộ ệc xây dự ậ
dưới. Vi c xây d ng hàm tính c i l i ph thu c vào cách xây d ng th t c duy t ệ ự ận dướ ạ ụ ộ ự ủ ụ ệ
các phương án của bài toán (đượ ục phân nhánh). Trên đây chúng ta đã c gọi là thủ t
trình bày cách xây d ng c n cho bài toán n i ti ng c a t ự ận dưới khá đơn giả ổ ế ủ ối ưu tổ
hợp. Các chương trình được cài đặ ật toán đó, tuy rằ ốt hơn t theo các thu ng làm việc t
nhiều so với duy t toàn b có th áp d gi i các bài toán vệ ộ, nhưng cũng chỉ ể ụng để ả ới
kích thướ ải được các bài toán đặ ới kích thước lơn hơn cầc nhỏ. Muốn gi t ra v n có
cách đánh giá cận t ốt hơn.
14
CHƯƠNG 2: PHÂN TÍCH - XÂY DỰNG THU T TOÁN T Ậ ỐI ƯU HÓA
LỰA CH VỌN ĐỒ ẬT TRONG BÀI TOÁN BALO (KNAPSACK)
2.1. Mô t bài toán ả
2.1.1. Xây d ng bài toán th ự ực thế
B n là m t nhà thám hi n b cho m t chuy n có ạ ộ ểm và đang chuẩ ị ộ ến đi dài. Bạ
một balo với tr ng t n có m t sọng lượ ối đa cho phép là X Kilogram (KG). Bạ ộ ố đồ v t ậ
cần mang theo, mỗi đồ vật có m t tr ng và m t giá tr khác nhau. M c tiêu c a ộ ọng lượ ộ ị ụ ủ
bạn là t v t ng giá tr mang theo mà không ối ưu hóa việc l a chự ọn đồ ật để ối đa hóa tổ ị
vượ ủt quá tr ng tọng lượ ối đa c a balo.
Yêu c u vào c a bài toán bao g m: ầu đầ ủ ồ
- Tr ng t t s ọng lượ ối đa của balo: Mộ ố nguyên dương.
- v t: M t danh sách ch a thông tin v t v Danh sách đồ ậ ộ ứ ề ừng đồ ật như ID đồ
vật, tr ng (KG), giá trọng lượ ị ti n t ). (đơn vị ề ệ
Yêu c u ra c a bài toán bao g m: ầu đầ ủ ồ
- v c ch n: M t danh sách các ID c a t v c Danh sách đồ ật đượ ọ ộ ủ ừng đồ ật đã đượ
chọn mang đi.
- T ng giá tr : M t s nguyên th hi n t ng giá tr cổ ị ộ ố ể ệ ổ ị ủa các đồ vật đã được ch n. ọ
- T ng tr ng: M t s nguyên th hi n t ng tr ng c v t ổ ọng lượ ộ ố ể ệ ổ ọng lượ ủa các đồ ậ
đã được chọn.
Nhi m v c th : ệ ụ ụ ể
- Phát tri n thu t toán: S dể ậ ử ụng phương pháp nhánh cận để tìm ki m gi i pháp ế ả
tối ưu cho bài toán balo.
- Th c hi n ki m tra ràng bu m b o r ng t ng tr ng c ự ệ ể ộc: Đả ả ằ ổ ọng lượ ủa các đồ
vật không vượt quá tr ng t a balo. ọng lượ ối đa củ
- In ra k t qu : Hi n th v c ch n, t ng giá tr và t ng ế ả ể ị danh sách các đồ ật đượ ọ ổ ị ổ
trọng lượng.
- Phân tích và so sánh: So sánh k t qu v ế ả ới các phương pháp khác (nếu có) để
đánh giá hiệu quả của thuật toán nhánh cận.
2.1.2. Phát bi i d ng t ng quát ểu bài toán dướ ạ ổ
T c xây d ng t i , ta có th phát bi i d ng t ng ừ bài toán đượ ự ạ Mục 2.1.1. ể ểu dướ ạ ổ
quát như sau:
Cho n đồ vật khác nhau, trong đó, đồ v t th i có mã , tr ng ậ ứ ID
i
ọng lượ w
i
và giá
trị . B n mang theo m t chi c balo có t i tr ng t , nhi m v v
i
ạ ộ ế ả ọ ối đa là W ệ ụ đặt ra là ch n ọ
các đồ v cho vào balo sao cho t ng giá tr ật để ổ ị các đồ v t lậ ấy được là l n nh t có th ? ớ ấ ể
Yêu c u vào c a bài toán là m t tầu đầ ủ ộ ập tin định dạng .xlsx, trong đó bao gồm:
15
- Tr ng t t s ọng lượ ối đa của balo: Mộ ố nguyên dương.
- v t: M t danh sách ch a thông tin v t v Danh sách đồ ậ ộ ứ ề ừng đồ ật như ID đồ
vật, tr ng (KG), giá trọng lượ ị ti n t ). (đơn vị ề ệ
Yêu c u ra c a bài toán: ầu đầ ủ
- u tiên: M t danh sách ID c v n. Dòng đầ ộ ủ ồa đ ật đã được chọ
- Dòng th hai: M t s nguyên th hi n t ng giá tr c v c ứ ộ ố ể ệ ổ ị ủa các đồ ật đã đượ
chọn.
- Dòng th ba: M t s nguyên th hi n t ng tr ng c vứ ộ ố ể ệ ổ ọng lượ ủa các đồ ật đã
được chọn.
2.2. Xây d ng thu t toán ự ậ
2.2.1. ng Ý tưở
Bài toán balo yêu c u tìm ki m giá tr t t t p h v t trong ầ ế ị ối ưu của mộ ậ ợp các đồ ậ
một balo có tr ng t . M v t chọng lượ ối đa W ỗi đồ ậ ỉ có th ể được ch c không chọn hoặ ọn
một l n duy nh u vào g m tr ng t c a balo và m t danh sách các ầ ất. Đầ ồ ọng lượ ối đa W ủ ộ
đồ ộ vật, m v có các thuỗi đồ ật đề c tính là ID tr, ọng lượng (w - weight) giá tr và ị (v -
value).
Bước đầu tiên, thực hiện tính tỷ lệ
giá ịtr
tr
ọng ng lượ
=
v
w
của m vỗi đồ ật. Sau đó, ta
s
ắp x v theo th t gi m d n c a t lếp danh sách các đồ ật đã cho ứ ự ả ầ ủ ỷ ệ
v
w
, vì vi c l a ệ ự
ch
ọn các đồ vật có tỷ lệ
v
w
cao s mang l i giá tr t ẽ ạ ị ối ưu hơn.
Ti p theo, ta áp d ng thu t toán nhánh và cế ụ ậ ận (branch and bound) để tính toán
giá tr t ị ối ưu. Công thức tính cận trên (upper bound) như sau:
𝑢𝑏
= 𝑣 + 𝑊 − 𝑤
( )
∗
vi + 1
wi + 1
Trong đó:
-
v
: T ng giá tr c v n. ổ ị ủa các đồ ật đã chọ
-
W
: Tr ng tọng lượ ối đa của balo.
-
w
: Tr ng hi n t i cọng lượ ệ ạ ủa balo.
-
v
i+1
: Giá tr c ti p x p. ị ủa món đồ ếp theo trong danh sách đã sắ ế
-
w
i+1
: Tr ng c ti p x p. ọng lượ ủa món đồ ếp theo trong danh sách đã sắ ế
Thu t toán b u v i tr ng và giá trậ ắt đầ ớ ọng lượ w = 0 ị v = 0. Sau đó, ta tính giá
trị c n trên ậ ubMax và ti n hành duy t qua t v t. T i m i l n duy t, n u tr ng ế ệ ừng đồ ậ ạ ỗ ầ ệ ế ọ
lượng c hiủa món đồ ện tại i (1 n) t quá ≤ i ≤ không vượ W (w
i
≤ W), ta ch vọn đồ ật đó
và c p nh t l i giá tr ậ ậ ạ ị vMax += v
i
(giá tr t t nh t hi n t i) và ị ố ấ ệ ạ wMax += w
i
(trọng lượng
16
tối đa hiệ ọn món đồ vì vượ ọng lượn tại). Nếu không ch đó t quá tr ng tối đa (w
i
> W),
ta b qua nó. ỏ
Quá trình này ti p t n khi không th ch nào vào balo ế ục cho đế ể ọn thêm món đồ
mà không vượ ọng lượ ối đa ( các món đồ đã t quá tr ng t wMax ≥ W), hoặc khi tất cả
được xét qua.
Cu i cùng, thu t toán quay lui c s d tìm ki m các gi i ố ậ backtrack đượ ử ụng để ế ả
pháp t t toán b u b ng vi c tính toán ch s i di n ối ưu hơn. Thuậ backtrack ắt đầ ằ ệ ỉ ố r, đạ ệ
cho ch s c c thêm vào túi do tr t quá ỉ ố ủa món hàng đầu tiên không đượ ọng lượng vượ
khả năng chứa của túi w
r
> - W w
r
. Sau đó, tính toán giá trị giới hạn trên theo công
thức:
𝑢𝑏 =
∑
v + vr
𝑟−1
𝑗
(n y) ếu balo chưa đầ
Nếu giá tr t quá hi n t i, thu t toán s quay l i m t ị ub này không vượ ubMax ệ ạ ậ ẽ ạ ộ
bướ ớc trư c đó trong quá trình tìm kiế ể ếm đ tìm ki m các giải pháp t ốt hơn.
“Quay l i m t tình ạ ột bước trước đó” có nghĩa là khi thuật toán đang trong mộ
huống mà nó đã chọn hoặc bỏ qua một món đồ, thuật toán sẽ quay lại và thử một lựa
chọn khác. Ví d , thay vì b t toán s th ch xem có tìm ra giá ụ ỏ món đồ đó, thuậ ẽ ử ọn để
trị t ốt hơn không.
2.2.2. Xây d ng gi mã ự ả
function knapsack_backtrack(W, items):
# W: Trọng lượng tối đa của balo
# items: Danh sách các đồ vật, mỗi đồ vật có ID, trọng lượng, giá trị
# Sắp xếp đồ vật theo giá trị/trọng lượng (v/w) theo thứ tự giảm dần
sort items by v/w descending
# Khởi tạo các biến cần thiết
vMax = 0 # Giá trị tối ưu hiện tại
wMax = 0 # Trọng lượng tối đa mang được
current_weight = 0 # Trọng lượng hiện tại trong balo
current_value = 0 # Giá trị hiện tại trong balo
solution = [] # Danh sách các đồ vật được chọn
# Hàm tính cận trên
function upper_bound(index, current_weight, current_value):
remaining_weight = W current_value -
bound = current_value
while index (items) items[index]< len and .weight <=
remaining_weight:
remaining_weight -= items[index] weight .
bound += items[index] weight .
index += 1
if index (items) < len
bound += items[index] value (remaining_weight . * /
items[index].weight)
return bound
17
# Hàm backtracking
function backtrack(index, current_weight, current_value, solution):
nonlocal vMax, wMax
# Cập nhật giá trị tối ưu nếu có
if current_value vMax: >
vMax = current_value
wMax = current_weight
best_solution = solution[:]
# Nếu không thể chọn thêm đồ vật (quá trọng lượng hoặc hết đồ
vật)
if index (items) current_weight >= len or >= W:
ret urn
# Tính cận trên
bound = upper_bound(index, current_weight, current_value)
# Nếu cận trên không thể vượt qua giá trị tối ưu, quay lui
if bound vMax: <=
ret urn
# Chọn đồ vật tại index
solution.append(items[index].ID)
backtrack(index + 1 , current_weight + items[index].weight,
current_value + items[index] value, solution) .
# Quay lại, không chọn đồ vật tại index
solution.pop()
backtrack(index + 1 , current_weight, current_value, solution)
# Bắt đầu thuật toán backtracking từ index 0
backtrack(0, 0 0, , [])
return vMax, wMax, best_solution
18
2.3. Ví d minh h a v tìm ki m nhánh c n trên và thu t toán backtrack ụ ọ ề ế ậ ậ
Ảnh 3. Ví dụ ậ minh họa tìm kiếm nhánh trên và thu t toán backtrack.
19
CHƯƠNG 3: CÀI ĐẶT THUẬT TOÁN B NG Ằ
NGÔN NG LỮ ẬP TRÌNH PYTHON
3.1. Cài đặt thuật toán
3.1.1. Cài đặt class Item
Class Item bao g m m t c kh i t c g i khi m t ồ ộ phương thứ ở ạo (__init__), đượ ọ ộ
đối tượ ớp Item đượ ạo ra. Phương thứng mới của l c t c này nhận vào ba tham số bao
gồm: ID, tr ng (ọng lượ w) và giá trị ( ). Các tham sv ố này l c gán cho các ần lượt đượ
thuộc tính tương ứng củ ợa đối tư ng bao g m và . Ngoài ồ self.ID, self.weight self.value
ra, t l
ỷ ệ
giá ịtr
tr
ọng ng lượ
=
v
w
c tính toán và gán cho thu c tính cũng đượ ộ self.ratio. T l này ỷ ệ
dùng để ếp danh sách các món đồ ối ưu hóa. sắp x , phụ ục v cho bài toán t
class Item:
def (__init__ self, ID, weight, value):
self.ID ID =
self.weight weight =
self.value value =
self.ratio value weight = /
3.1.2. Cài đặ ệp tin địt đọc dữ liệu đầu vào từ t nh dạng .xlsx
Một hàm knapsack_from_excel được định nghĩa để đọc d li u t m t t p tin ữ ệ ừ ộ ệ
Excel có định d ng và tạ .xlsx ạo ra các đối tượng Item t d liừ ữ ệu đó. Đầu tiên, hàm m ở
file Excel t ng d n thông qua vi c s d n ại đườ ẫ file_path ệ ử ụng thư việ openpyxl, sau đó
lấy sheet đang hoạt động (active sheet) trong workbook. Sau đó, nó lấy giá trị tại ô
A1, trích xu t s nguyên t giá tr c a ô này và gán nó cho bi n (tr ng t i ấ ố ừ ị ủ ế W ọng lượ ố
đa củ 6 đếa balo). Hàm lặp qua các dòng từ dòng thứ n dòng thứ n chứa thông tin các
đồ ỗ ị vật thông qua một vòng lặp for. Trong m i lần lặp, hàm lấy ra giá tr các cột A, B
và C tương ứ ủa đồ ọng lượng với ba thông tin c vật bao gồm ID, tr ng và giá trị. Các
giá tr t ng m i v i các thu c tính , ị này được dùng để ạo ra các đối tượ Item ớ ớ ộ ID weight
và . N u các giá tr này t n t ng s trong value ế ị ồ ại, đối tượ Item ẽ được thêm vào lưu trữ
danh sách c khai báo s ch a t t c ng c items. Danh sách items đượ ẽ ứ ấ ả đối tượ Item đượ
tạo ra t d li u c a t p tin Excel. ừ ữ ệ ủ ệ
# Hàm đọc dữ liệu từ file Excel
def knapsack_from_excel(file_path):
# Đọc dữ liệu từ file Excel
wb = openpyxl load_workbook(file_path) .
sheet = wb active .
# Lấy trọng lượng tối đa từ ô A1
cell_value = sheet[ value 'A1'].
W = int(re.search(r'\d+', cell_value) group()) .
# Đọc các đồ vật từ các ô
items = [] # Mảng lưu trữ thông tin đồ vật
for row , sheet max_row ): in range(6 . + 1
ID = sheet[f value 'A{row}'].
weight = sheet[f value 'B{row}'].
value sheet[f value = 'C{row}'].
if ID weight value: and and
20
items append(Item(ID, weight, value)) .
3.1.3. Cài đặt tìm kiếm cận trên
Ý tưở đểng xây dựng hàm upper_bound là tính toán giá trị cận trên của bài
toán. Đầu tiên hàm nhận vào các tham số:
- : Tr ng hi n t i c v n. w ọng lượ ệ ạ ủ ồa các đ ật đã chọ
- : Giá tr hi n t i c v n. v ị ệ ạ ủa các đồ ật đã chọ
- index : Ch s b v t ti p theo. ỉ ố ắt đầu để xem xét các đồ ậ ế
- items : Danh sách các đồ v t, m v t là m ng Item. ậ ỗ ồi đ ậ ột đối tượ
- : Tr ng tW ọng lượ ối đa của balo.
Sau đó hàm ọng lượ ại đã vượkiểm tra ràng buộc, nếu tr ng hiện t t quá trọng
lượng tối đa (w ≥ W) thì trả về 0, vì không thể l vấy thêm đồ ật nào nữa. Nếu chưa
vượ ởt quá (w < W), hàm kh i tạo biến:
- : Kh i t o giá tr t ng giá tr hi n t i . bound = v ở ạ ị ối đa bằ ị ệ ạ v
- : Kh i t o t ng tr ng b ng tr ng hi n t i . total_weight = w ở ạ ổ ọng lượ ằ ọng lượ ệ ạ w
Ti p theo hàm s d ng m t vòng l p duy t qua t t c v t có ch ế ử ụ ộ ặ for để ệ ấ ả các đồ ậ ỉ
số từ index đến h t danh sách ế items. Trong m i l n l p, hàm th c hi n so sánh gi a ỗ ầ ặ ự ệ ữ
trọng lượ ọng lượng đồ đang xétng hiện tại cộng tr vật tại vị trí trong danh sách với
trọng lượ ối đa củ hơn trọng lượ ối đa củng t a balo. Nếu tổng trên vẫn nhỏ ng t a balo,
trọng lượ ật đó đượng của v c cập nhật thêm vào tr ng hi n t i và giá tr c a v t ọng lượ ệ ạ ị ủ ậ
đó cũng đượ ớn hơn trọng lược cập nhật thêm vào giá trị hiện tại. Nếu tổng trên l ng
tối đa của balo, hàm s d ng vì không th v t nào n a. ẽ ừ ể thêm đồ ậ ữ
# Hàm tính cận trên
def upper_bound(w, v, index, items, W):
if w W: >
return 0
bound v =
total_weight = w
# Tính giá trị tối đa có thể đạt được từ index hiện tại
for i (index, (items)): in range len
if total_weight items[i] weight W: + . <=
total_weight += items[i] weight .
bound = items[i] value .
else:
bre ak
return bound
3.1.4. Cài đặt thuật toán backtrack
Hàm nh n vào các tham s bao g m: knapsack_backtrack ậ ố ồ
- : Ch s hi n t i. index ỉ ố ệ ạ
- : Tr ng hi n t i. current_weight ọng lượ ệ ạ
21
- : Giá tr hi n t i. current_value ị ệ ạ
- v t. items : Danh sách các đồ ậ
- : Tr ng tW ọng lượ ối đa của balo.
- v t hi c ch n. current_solution : Danh sách các đồ ậ ện đã đượ ọ
Hai bi n toàn c c giá tr t c) và ế ụ vMax (lưu trữ ị ối đa tìm đượ best_solution (lưu
trữ gi i pháp t t nh c). ả ố ất tìm đượ
Đầu tiên, thu t toán ki m tra n u tr ng hi n t i t quá tr ng ậ ể ế ọng lượ ệ ạ không vượ ọ
lượ ịng t a balo và tối đa củ ổng giá tr của giải pháp hiện tại l tớn hơn giá trị ối đa đã
biết ( ). NvMax ếu điều đó đúng, thuật toán c p nh t giá tr tậ ậ ị ối đa mới cho vMax và sao
chép giải pháp hi n t i vào . ệ ạ best_solution
Ti p theo, n t t t c v t trong danh sách, t c là ch s ế ếu đã xét hế ấ ả các đồ ậ ứ ỉ ố index
lúc này vượt quá độ dài c a danh sách ủ items, thu t toán s d ng l i. c khi th xét ậ ẽ ừ ạ Trướ ử
nhánh hi n t i, thu t toán tính c n trên b ng cách g i hàm ệ ạ ậ ậ ằ ọ upper_bound. N u c n trên ế ậ
của nhánh hi n t i không l , thu t toán s c t b nhánh này vì không th ệ ạ ớn hơn vMax ậ ẽ ắ ỏ ể
mang l i giá tr t ạ ị ốt hơn.
Sau đó, thuật toán sẽ thử hai lựa chọn:
- L a ch n 1: Không ch v t hi n t i và g ti p t ự ọ ọn đồ ậ ệ ạ ọi đệ quy để ế ục xét các đồ
vật ti i tr ng và giá trếp theo mà không thay đổ ọng lượ ị.
- L n 2: Ch v t hi n t i n t quá tr ng t a ựa chọ ọn đồ ậ ệ ạ ếu không vượ ọng lượ ố ủi đa c
balo. Trong trườ ọng lượ ị, sau đó tiếng hợp này, thuật toán sẽ cập nhật tr ng và giá tr p
tục gọi đệ tìm xem li u còn gi i pháp t quy để ệ ả ốt hơn không.
# Hàm backtracking
def knapsack_backtrack(index, current_weight, current_value, items, W,
current_solution):
global vMax, best_solution
# Cập nhật giá trị tối ưu nếu tìm được giải pháp tốt hơn
if current_weight W current_value vMax: <= and >
vMax = current_value
best_solution = current_solution[:]
# Nếu đã xét hết các đồ vật, dừng lại
if index (items): >= len
return
# Tính cận trên để kiểm tra xem có nên tiếp tục không
vMax:
return # Cắt nhánh vì không thể đạt giá trị tốt hơn vMax
# Bỏ qua đồ vật hiện tại
knapsack_backtrack(index + 1 , current_weight, current_value, items,
W, current_solution)
22
# Thêm đồ vật hiện tại nếu không vượt quá trọng lượng tối đa
if current_weight items[index] weight W: + . <=
current_solution.append(items[index])
knapsack_backtrack(index + 1, current_weight +
items[index].weight, current_value items[index]+ .value, items, W,
current_solution)
current_solution.pop()
3.1.5. Cài đặt chương trình hoàn chỉnh
import re
import time
import openpyxl
start = time time() .
# Khởi tạo lớp Item đại diện cho mỗi đồ vật
class Item:
def (__init__ self, ID, weight, value):
self.ID ID =
self.weight weight =
self.value value =
self.ratio value weight = /
# Hàm tính cận trên
def upper_bound(w, v, index, items, W):
if w W: >=
return 0
bound = v
total_weight = w
# Tính giá trị tối đa có thể đạt được từ index hiện tại
for i (index, (items)): in range len
if total_weight items[i] weight W: + . <=
total_weight += items[i] weight .
bound += items[i] value .
else:
bre ak
return bound
# Hàm backtracking
def knapsack_backtrack(index, current_weight, current_value, items, W,
current_solution):
global vMax, best_solution
# Cập nhật giá trị tối ưu nếu tìm được giải pháp tốt hơn
if current_weight W current_value vMax: <= and >
vMax = current_value
best_solution = current_solution[:]
# Nếu đã xét hết các đồ vật, dừng lại
if index (items): >= len
return
# Tính cận trên để kiểm tra xem có nên tiếp tục không
vMax:

Tài liệu khác của Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội

Preview text:

MỤC LỤC
DANH MỤC BẢNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
DANH MỤC HÌNH ẢNH . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
CHƯƠNG 1: CƠ SỞ LÝ THUYẾT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.1. Thuật toán nhánh cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.2. Nguyên lý . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3. Ưu điểm và nhược điểm của thuật toán nhánh cận . . . . . . . . . . . . . . . . . . . . . 6
1.3.1. Ưu điểm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3.2. Nhược điểm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.4. Các bước chính của thuật toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.5. Mô tả thuật toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.6. Áp dụng giải bài toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.6.1. Bài toán cái túi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.6.2. Bài toán người du lịch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
CHƯƠNG 2: PHÂN TÍCH - XÂY DỰNG THUẬT TOÁN TỐI ƯU HÓA LỰA
CHỌN ĐỒ VẬT TRONG BÀI TOÁN BALO (KNAPSACK) . . . . . . . . . . . . . . . . 14
2.1. Mô tả bài toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.1.1. Xây dựng bài toán thực thế . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.1.2. Phát biểu bài toán dưới dạng tổng quát . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.2. Xây dựng thuật toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.2.1. Ý tưởng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.2.2. Xây dựng giả mã . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.3. Ví dụ minh họa về tìm kiếm nhánh cận trên và thuật toán backtrack . . . . . . 18
CHƯƠNG 3: CÀI ĐẶT THUẬT TOÁN BẰNG NGÔN NGỮ LẬP TRÌNH
PYTHON . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.1. Cài đặt thuật toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.1.1. Cài đặt class Item . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.1.2. Cài đặt đọc dữ liệu đầu vào từ tệp tin định dạng .xlsx . . . . . . . . . . . . . . 19
3.1.3. Cài đặt tìm kiếm cận trên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.1.4. Cài đặt thuật toán backtrack . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.1.5. Cài đặt chương trình hoàn chỉnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.2. Kiểm thử . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.2.1. Dữ liệu đầu vào . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 3
3.2.2. Dữ liệu đầu ra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.2.3. Kiểm thử các chức năng của thuật toán . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.3. Đánh giá và so sánh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.3.1. Độ phức tạp của thuật toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.3.2. So sánh thời gian thực hiện thuật toán . . . . . . . . . . . . . . . . . . . . . . . . . . 28
TỔNG KẾT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
ĐÁNH GIÁ NỘI BỘ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
TÀI LIỆU THAM KHẢO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 4
DANH MỤC BẢNG
Bảng 1. Bảng dữ liệu đầu vào. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Bảng 2. Bảng đánh giá nội bội. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
DANH MỤC HÌNH ẢNH
Ảnh 1. Xây dựng cây tìm kiếm cho bài toán cái túi. . . . . . . . . . . . . . . . . . . . . . . . . . 11
Ảnh 2. Xây dựng cây tìm kiếm cho bài toán người du lịch. . . . . . . . . . . . . . . . . . . . 12
Ảnh 3. Ví dụ minh họa tìm kiếm nhánh trên và thuật toán backtrack. . . . . . . . . . . . 18 5
CHƯƠNG 1: CƠ SỞ LÝ THUYẾT
1.1. Thuật toán nhánh cận
Thuật toán nhánh cận là một trong các phương pháp chủ yếu giải bài toán tối
ưu tổ hợp. Tư tưởng cơ bản của nó là trong quá trình tìm kiếm ta phân hoạch các
phương án của bài toán ra thành hai hay nhiều tập con như các nút, loại bỏ những
nhánh mà ta biết chắc chắn là không chứa phương án tối ưu.
Kỹ thuật nhánh cận phát triển từ ý tưởng của thuật toán quay lui. Thay vì duyệt
tất cả các trường hợp, nếu ta đến một vị trí mà giá trị của hàm mục tiêu tại đó và các
điểm về sau chắc chắn không tốt nhất thì quay lại luôn. 1.2. Nguyên lý
Nhánh (Branch): Thuật toán chia nhỏ bài toán lớn thành các bài toán con nhỏ
hơn, tức là tạo ra các nhánh trong quá trình giải. Mỗi nhánh đại diện cho một trạng
thái hoặc một tập con của không gian tìm kiếm. Quá trình này tiếp tục cho đến khi đạt đ ợ
ư c một giải pháp hợp lệ hoặc không thể tìm thêm nhánh con nào nữa.
Cận (Bound): Cận là bước quan trọng trong thuật toán nhánh cận, giúp loại bỏ
các nhánh không cần thiết trong quá trình tìm kiếm. Mỗi nhánh sẽ có một giá trị "cận"
tính toán được, và thuật toán chỉ tiếp tục tìm kiếm trong các nhánh mà giá trị cận của
chúng hứa hẹn mang lại giải pháp tốt hơn so với giải pháp đã tìm được trước đó. Nếu
giá trị cận của một nhánh không thể tốt hơn giải pháp hiện tại, nhánh đó sẽ bị loại bỏ.
1.3. Ưu điểm và nhược điểm của thuật toán nhánh cận
1.3.1. Ưu điểm
- Tìm kiếm giải pháp tối ưu: Thuật toán nhánh cận luôn đảm bảo tìm được giải
pháp tối ưu nếu không gian tìm kiếm được duyệt đầy đủ. Đây là một trong những ưu
điểm quan trọng nhất khi so với các thuật toán “tham lam” (Greedy) hoặc xấp xỉ.
- Giảm thiểu không gian tìm kiếm: Thuật toán sử dụng bước lọc nhánh để loại
bỏ các nhánh không khả thi hoặc không có tiềm năng mang lại giải pháp tốt hơn, giúp
giảm đáng kể số lượng trạng thái cần kiểm tra.
- Linh hoạt với nhiều bài toán: Thuật toán có thể áp dụng cho nhiều bài toán
tối ưu hóa rời rạc như bài toán cái balo, bài toán đi đường ngắn nhất (Traveling
Salesman Problem), bài toán phân hoạch, bài toán lập lịch và nhiều bài toán khác.
- Khả năng tận dụng chiến lược cận: Sử dụng các kỹ thuật tính toán cận hiệu
quả (upper bound - cận trên hoặc lower bound - cận dưới) giúp nâng cao hiệu quả của
thuật toán và giảm thời gian tính toán.
- Khả năng dừng sớm: Khi tìm được một giải pháp mà giá trị cận của các nhánh
còn lại không thể tốt hơn giải pháp hiện tại, thuật toán có thể dừng sớm mà không
cần duyệt toàn bộ không gian. 6
1.3.2. Nhược điểm
- Tốn kém về bộ nhớ: Do cần lưu trữ tất cả các nhánh và thông tin liên quan
(như trạng thái, giá trị cận), thuật toán có thể yêu cầu rất nhiều bộ nhớ, đặc biệt đối
với các bài toán có không gian tìm kiếm lớn.
- Độ phức tạp tính toán cao: Mặc dù thuật toán loại bỏ được nhiều nhánh không
cần thiết, việc tính toán cận và quản lý các nhánh vẫn tiêu tốn thời gian và tài nguyên,
đặc biệt với các bài toán có kích thước lớn.
- Phụ thuộc vào chiến lược cận: Hiệu quả của thuật toán phụ thuộc rất nhiều
vào cách tính toán cận trên hoặc cận dưới. Nếu cận không chính xác hoặc không chặt
chẽ, thuật toán có thể phải duyệt qua nhiều nhánh không cần thiết, làm giảm hiệu quả.
- Không phù hợp với không gian tìm kiếm quá lớn: Khi không gian tìm kiếm
quá rộng hoặc không thể dễ dàng tính toán cận, thuật toán có thể trở nên chậm và
kém hiệu quả so với các phương pháp xấp xỉ.
- Khó khăn trong triển khai: Việc triển khai thuật toán nhánh cận yêu cầu hiểu
rõ bài toán và các kỹ thuật tính toán cận, điều này có thể phức tạp hơn so với các thuật
toán tham lam hoặc quy hoạch động.
1.4. Các bước chính của thuật toán
- Khởi tạo: Bắt đầu với một giải pháp ban đầu (có thể là giải pháp xấp xỉ hoặc
giải pháp hợp lệ nhất), tính toán cận dưới (hoặc cận trên) của bài toán. Đây là bước
khởi tạo không gian tìm kiếm.
- Chia nhánh (Branching): Tạo ra các nhánh con bằng cách chia bài toán lớn
thành các bài toán con nhỏ hơn, từ đó phát triển không gian tìm kiếm. Mỗi nhánh có
thể đại diện cho một tập con của các lựa chọn hoặc các trạng thái.
- Tính cận (Bounding): Với mỗi nhánh, tính toán giá trị cận (thường là cận
dưới đối với bài toán tối thiểu hoặc cận trên đối với bài toán tối đa). Cận này là một
ước lượng của giá trị tối ưu trong nhánh đó.
- Lọc nhánh (Pruning): Loại bỏ các nhánh mà giá trị cận của chúng không thể
tốt hơn giải pháp hiện tại hoặc không có khả năng tìm ra một giải pháp tốt hơn. Điều
này giúp giảm thiểu không gian tìm kiếm và tiết kiệm thời gian.
- Tiến hành tìm kiếm: Tiếp tục mở rộng các nhánh còn lại cho đến khi tìm
được giải pháp tối ưu hoặc không còn nhánh nào để kiểm tra.
1.5. Mô tả thuật toán
Ta sẽ mô tả thuật toán trên mô hình bài toán tối ưu tổng quát sau: min { f(x) : x ∈ D },
Trong đó D là tập hữu hạn phần tử.
Giả thiết rằng tập D được mô tả như sau: 7
D={x = (x1, x2, ... , xn) ∈ A1 × A2 × ... × An: x thoả mãn tính chất P},
Với A1, A2, . . , An là các tập hữu hạn, còn P là tính chất cho trên tích Đề-các A1 × A2 × . . × An.
Với giả thiết về tập D nêu trên, chúng ta có thể sử dụng thuật toán quay lui để
liệt kê các phương án của bài toán. Trong quá trình liệt kê theo thuật toán quay lui, ta
sẽ xây dựng dần các thành phần của phương án. Một bộ gồm k thành phần (a1, a2, a3,
… , ak) xuất hiện trong trong quá trình thuật toán sẽ gọi là phương án bộ phận cấp k.
Thuật toán nhánh cận có thể áp dụng để giải bài toán đặt ra nếu như có thể tìm
được một hàm g xác định trên trên tập tất cả phương án bộ phận của bài toán thỏa
mãn bất đẳng thức sau:
g(a1, a2, ... , ak) ≤ min {f(x): x ∈ D, xi = ai, i = 1, 2, ..., k} (*)
Bất đẳng thức (*) có nghĩa là giá trị của hàm g tại phương án bộ phận (a1, a2,
… , ak) là không vượt quá giá trị nhỏ nhất của hàm mục tiêu của bài toán trên tập con các phương án.
D(a1, a2, … , ak)={ x ∈ D : x1 =ai, i = 1, 2, ... , k}
Hay nói một cách khác, g(a1, a2, … , ak) là cận dưới của giá trị hàm mục tiêu
trên tập D(a1, a2, … , ak). Vì lẽ đó, hàm g được gọi là hàm cận dưới và giá trị g(a1, a2,
… , ak) được gọi là cận dưới của tập D(a1, a2, … , ak). Do có thể đồng nhất tập D(a1,
a2, … , ak) với phương án bộ phận (a1, a2, … , ak), nên ta cũng gọi giá trị g(a1, a2, a3,
… , ak) là cận dưới của phương án bộ phận (a1, a2, … , ak).
Giả sử đã có hàm g. Ta xét cách sử dụng hàm này để giảm bớt khối lượng
duyệt trong quá trình duyệt tất cả các phương án theo thuật toán quay lui. Trong quá
trình liệt kê các phương án có thể đã thu được một số phương án của bài toán. Gọi x
là phương án với giá trị hàm mục tiêu nhỏ nhất trong số các phương án đã tìm được,
kí hiệu f = f(x). Ta sẽ gọi x là phương án tốt nhất hiện có, còn f là kỷ lục. Giả sử đã có f, khi đó nếu:
g(a1, a2, … , ak) > f󰋀,
Thì từ bất đẳng thức (*) suy ra
f󰋀 < g(a1, a2, … , ak) ≤ min {f(x): x ∈ D : x1 = ai, i= 1, 2, ... , k}
Vì thế tập con các phương án ấy của bài toán D(a1, a2, … , ak) chắc chắn không
chứa phương án tối ưu. Trong trường hợp này ta không cần tiếp tục phát triển các
phương án bộ phận ((a1, a2, … , ak), nói cách khác là ta có thể loại bỏ các phương án
trong tập D(a1, a2, … , ak) khỏi quá trình tìm kiếm. 8
1.6. Áp dụng giải bài toán
1.6.1. Bài toán cái túi
Đưa ra giả thiết rằng có n loại đồ vật và số lượng đồ vật mỗi loại là không hạn
chế. Khi đó ta có mô hình bài toán cái túi biến nguyên sau đây: Có n loại đồ vật, đồ
vật thứ j có trọng lượng aj và giá trị sử dụng là cj (j = 1, 2, . . , n). Cần chất các đồ vật
này vào một cái túi có trọng lượng là b sao cho tổng giá trị sử dụng của các đồ vật
chất trong túi là lớn nhất.
Mô hình của bài toán sẽ có dạng như sau: Tìm: 𝑛 𝑛
𝑓 = 𝑚𝑎𝑥 {𝑓(𝑥) = ∑ 𝑐𝑗𝑥𝑗 ; ∑ 𝑎𝑗𝑥𝑗 ≤ 𝑏, 𝑥𝑗 ∈ 𝑍+, 𝑗 = 1, 2, . .. , 𝑛} (1) 𝑗=1 𝑗=1
Trong đó Z+ là tập các số nguyên không âm. 𝑛
𝐷 = {𝑥 = (𝑥1, 𝑥2, . .. ,𝑥𝑛; ∑ 𝑎𝑗𝑥𝑗 ≤ 𝑏, 𝑥𝑗 ∈ 𝑍+,𝑗 = 1, 2,. .. , 𝑛} 𝑗=1
Không gian tổng quát ta giả thiết rằng các đồ vật được đánh số sao cho bất
đẳng thức sau được thoả mãn: 𝑐1 𝑐2 𝑐𝑛 𝑎 ≥ ≥ . . . ≥ (2) 1 𝑎2 𝑎𝑛
Để tiếp tục xây dựng hàm tính cận dưới, cùng với bài toán cái túi (1) ta xét bài
toán cái túi biến liên tục sau: Tìm:
𝑔 = 𝑚𝑎𝑥 { 𝑓(𝑥) = ∑ 𝑛 𝑛
𝑗=1𝑐𝑗𝑥𝑗 : ∑𝑗=1 𝑎𝑗𝑥𝑗 ≤ 𝑏, 𝑥𝑗 ≥ 0, 𝑗 = 1, 2, . . . , 𝑛} (3)
Mệnh đề: Phương án tối ưu của bài toán (3) là vectơ x = (x1, x2, ... , xn) với
các thành phần được xác định bởi công thức: 𝑏
𝑥 1 =𝑎 ,𝑥 2 = 𝑥 3 = ...= 𝑥 𝑛 = 0. 1
Và giá trị tối ưu là 𝑔 = 𝑐1𝑏1 𝑎1
Chứng minh: Thực vậy, xét x = (x1, x2, . . , xn) là một phương án tuỳ ý của
bài toán (3). Khi đó từ bất đẳng thức (3) và do x1 ≥ 0, ta suy ra:
𝑐𝑗𝑥𝑗 ≥ (𝑐1/𝑎1) 𝑎𝑗𝑥𝑗, 𝑗 = 1, 2,. .. ,𝑛 Suy ra: 9 𝑛 𝑛 𝑛
∑ 𝑐𝑗𝑥𝑗 ≤ ∑(𝑐1/𝑎1)𝑎𝑗𝑥𝑗 = (𝑐1𝑎1) ∑ 𝑎𝑗𝑥𝑗 ≤ (𝑐1/𝑎1)𝑏 = 𝑔∗. 𝑗=1 𝑗=1 𝑗=1
Mệnh đề được chứng minh.
Bây giờ, giả sử ta có phương án bộ phận cấp k: (u1, u2, . . , uk). Khi đó giá trị
sử dụng của các đồ vật đang có trong túi là:
𝜎𝑘 = 𝑐1𝑢1 + 𝑐2𝑢2+ .. .+𝑐𝑘𝑢𝑘
Và trọng lượng còn lại của túi là:
𝑏𝑘 = 𝑏 − 𝑎1𝑢1 + 𝑎2𝑢2+ . .. +𝑎𝑘𝑢𝑘. Ta có:
𝑚𝑎𝑥{ 𝑓(𝑥): 𝑥 ∈ 𝐷, 𝑥𝑗 = 𝑢𝑗, 𝑗 = 1, 2,. .. , 𝑘} 𝑛 𝑛
= 𝑚𝑎𝑥{ 𝜎𝑘 + ∑ 𝑐𝑗𝑥𝑗 : ∑ 𝑎𝑗𝑥𝐽 ≤ 𝑏𝑘, 𝑥𝑗 ∈ 𝑍+, 𝑗 = 𝑘 + 1, 𝑘 + 2, . .., 𝑛} 𝑗=𝑘+1 𝑗=𝑘+1 𝑛 𝑛
≤ 𝜎𝑘 + 𝑚𝑎𝑥{ ∑ 𝑐𝑗𝑥𝑗 : ∑ 𝑎𝑗𝑥𝐽 ≤ 𝑏𝑘, 𝑥𝑗 ≥ 0, 𝑗 = 𝑘 + 1, 𝑘 + 2, .. . ,𝑛} 𝑗=𝑘+1 𝑗=𝑘+1
(Theo mệnh đề: Giá trị số hạng thứ hai là 𝑐𝑘+𝑗𝑏𝑘/𝑎 ) 𝑘+𝑗
Vậy ta có thể tính cận trên cho phương án bộ phận (u1, u2, … , uk) bởi công thức:
𝑔(𝑢1,𝑢2, . . . , 𝑢𝑘) = 𝜎𝑘 + 𝑐𝑘+1𝑏𝑘/𝑎𝑘+1
Chú ý: Khi tiếp tục xây dựng thành phần thứ k + 1 của lời giải, các giá trị đề
cử cho xk+1 sẽ là 0, 1, … , [bkak+1]. Do có kết quả của mệnh đề, khi chọn giá trị cho
xk+1 ta sẽ duyệt các giá trị đề cử theo thứ tự giảm dần.
Ví dụ ứng dụng: Giải bài toán cái túi theo thuật toán nhánh cận vừa trình bày.
𝑓(𝑥) = 10𝑥1 + 5𝑥2 + 3𝑥3 + 6𝑥4 → 𝑚𝑎𝑥,
5𝑥1 + 3𝑥2 + 2𝑥3 + 4𝑥4 ≤ 8,
𝑥𝑗 ∈ 𝑍+,𝑗 = 1,2, 3,4. Giải: 10
Ảnh 1. Xây dựng cây tìm kiếm cho bài toán cái túi.
Quá trình giải bài toán được mô tả trong cây tìm kiếm trong hình trên. Thông
tin về một phương án bộ phận trên cây được ghi trong các ô trên hình tương ứng theo
thứ tự: đầu tiên là các thành phần của phương án, tiếp đến σ là giá trị của các đồ vật
đang chất trong túi, w – trọng lượng còn lại của túi và g – cận trên.
Kết thúc thuật toán, ta thu được phương án tối ưu là x=(1,1,0,0), và giá trị tối ưu là f=15.
1.6.2. Bài toán người du lịch
Cố định thành phố xuất phát là 𝑇1, bài toán người du lịch dẫn về bài toán: Tìm cực tiểu của hàm:
𝑓(𝑥2,𝑥3,… ,𝑥𝑛) = 𝑐[1, 𝑥2] + 𝑐[𝑥2,𝑥3] + ⋯ + 𝑐[𝑥𝑛−1, 𝑥𝑛] + 𝑐[𝑥𝑛, 1] → min,
Với điều kiện: (𝑥2,𝑥3,… , 𝑥𝑛) là hoán vị của các số 2,3, …, 𝑛.
Ký hiệu: 𝑐𝑚𝑖𝑛 = min{𝑐[𝑖, 𝑗], 𝑖,𝑗 = 1,2, …, 𝑛, 𝑖 𝑘ℎá𝑐 𝑗} là chi phí đi lại nhỏ nhất giữa các thành phố.
Để có được thuật toán nhánh cận giải bài toán người du lịch, trước hết cần đưa
ra cách đánh giá cận dưới cho phương án bộ phận. Giả sử đang có phương án bộ phận
(𝑢1,𝑢2,… , 𝑢𝑘). Phương án này tương ứng với hành trình bộ phận qua k thành phố:
𝑇1 → 𝑇(𝑢2) → ⋯ → 𝑇(𝑢𝑘−1) → 𝑇(𝑢𝑘)
Vì vậy chi phí phải trả theo hành trình bộ phận này sẽ là:
𝜎 = 𝑐[1, 𝑢2] + 𝑐[𝑢2, 𝑢3] + ⋯ + 𝑐[𝑢𝑘−1,𝑢𝑘] 11
Để phát triển hành trình bộ phận này thành hành trình đầy đủ, ta còn phải đi
qua 𝑛 − 𝑘 thành phố còn lại rồi quay trở lại thành phố 𝑇1, tức là còn phải đi qua 𝑛 −
𝑘 + 1 đoạn đường nữa. Do chi phí phải trả cho việc đi qua mỗi một trong số 𝑛 − 𝑘 +
1 đoạn đường còn lại nếu không ít hơn 𝑐𝑚𝑖𝑛, nên cận dưới cho phương án bộ phận
(𝑢1,𝑢2,… , 𝑢𝑘) có thể tính theo công thức
𝑔(𝑢1,𝑢2,… , 𝑢𝑘) = 𝜎 + (𝑛 − 𝑘 + 1)𝑐𝑚𝑖𝑛
Sử dụng cách cận dưới vừa nêu ta có thể áp dụng thuật toán nhánh cận để giải
bài toán người du lịch.
Ví dụ: Giải bài toán người du lịch với ma trận chi phí sau: 0 3 14 18 15 3 0 4 22 20 C = 17 9 0 16 4 6 2 7 0 12 9 15 11 5 0
Ta có 𝑐𝑚𝑖𝑛 = 3. Quá trình thực hiện thuật toán được mô tả bởi cây tìm kiếm dưới đây:
Ảnh 2. Xây dựng cây tìm kiếm cho bài toán người du lịch.
Thông tin về một bộ phận trên cây đuọc ghi trong các ô trên hình tương ứng
theo thứ tự: đầu tiên là các thành phần của phương án, tiếp đến là chi phí tương theo
hành trình bộ phận và g - cận dưới. 12
Kết thúc thuật toán, ta thu được phương án tối ưu (1, 2 , 3, 5, 4, 1) tương ứng với hành trình:
𝑇1 → 𝑇2 → 𝑇3 → 𝑇5 → 𝑇4 → 𝑇1,
Và chi phí nhỏ nhất là 25.
Hiệu quả của thuật toán nhánh cận phụ thuộc vào việc xây dựng hàm tính cận
dưới. Việc xây dựng hàm tính cận dưới lại phụ thuộc vào cách xây dựng thủ tục duyệt
các phương án của bài toán (được gọi là thủ tục phân nhánh). Trên đây chúng ta đã
trình bày cách xây dựng cận dưới khá đơn giản cho bài toán nổi tiếng của tối ưu tổ
hợp. Các chương trình được cài đặt theo các thuật toán đó, tuy rằng làm việc tốt hơn
nhiều so với duyệt toàn bộ, nhưng cũng chỉ có thể áp dụng để giải các bài toán với
kích thước nhỏ. Muốn giải được các bài toán đặt ra với kích thước lơn hơn cần có
cách đánh giá cận tốt hơn. 13
CHƯƠNG 2: PHÂN TÍCH - XÂY DỰNG THUẬT TOÁN TỐI ƯU HÓA
LỰA CHỌN ĐỒ VẬT TRONG BÀI TOÁN BALO (KNAPSACK)
2.1. Mô tả bài toán
2.1.1. Xây dựng bài toán thực thế
Bạn là một nhà thám hiểm và đang chuẩn bị cho một chuyến đi dài. Bạn có
một balo với trọng lượng tối đa cho phép là X Kilogram (KG). Bạn có một số đồ vật
cần mang theo, mỗi đồ vật có một trọng lượng và một giá trị khác nhau. Mục tiêu của
bạn là tối ưu hóa việc lựa chọn đồ vật để tối đa hóa tổng giá trị mang theo mà không
vượt quá trọng lượng tối đa ủ c a balo.
Yêu cầu đầu vào của bài toán bao gồm:
- Trọng lượng tối đa của balo: Một số nguyên dương.
- Danh sách đồ vật: Một danh sách chứa thông tin về từng đồ vật như ID đồ
vật, trọng lượng (KG), giá trị (đơn vị tiền tệ).
Yêu cầu đầu ra của bài toán bao gồm:
- Danh sách đồ vật được chọn: Một danh sách các ID của từng đồ vật đã được chọn mang đi.
- Tổng giá trị: Một số nguyên thể hiện tổng giá trị của các đồ vật đã được chọn.
- Tổng trọng lượng: Một số nguyên thể hiện tổng trọng lượng của các đồ vật đã được chọn. Nhiệm vụ cụ thể:
- Phát triển thuật toán: Sử dụng phương pháp nhánh cận để tìm kiếm giải pháp
tối ưu cho bài toán balo.
- Thực hiện kiểm tra ràng buộc: Đảm bảo rằng tổng trọng lượng của các đồ
vật không vượt quá trọng lượng tối đa của balo.
- In ra kết quả: Hiển thị danh sách các đồ vật được chọn, tổng giá trị và tổng trọng lượng.
- Phân tích và so sánh: So sánh kết quả với các phương pháp khác (nếu có) để
đánh giá hiệu quả của thuật toán nhánh cận.
2.1.2. Phát biểu bài toán dưới dạng tổng quát
Từ bài toán được xây dựng tại Mục 2.1.1., ta có thể phát biểu dưới dạng tổng quát như sau:
Cho n đồ vật khác nhau, trong đó, đồ vật thứ i có mã IDi, trọng lượng wi và giá
trị vi. Bạn mang theo một chiếc balo có tải trọng tối đa là W, nhiệm vụ đặt ra là chọn
các đồ vật để cho vào balo sao cho tổng giá trị các đồ vật lấy được là lớn nhất có thể?
Yêu cầu đầu vào của bài toán là một tập tin định dạng .xlsx, trong đó bao gồm: 14
- Trọng lượng tối đa của balo: Một số nguyên dương.
- Danh sách đồ vật: Một danh sách chứa thông tin về từng đồ vật như ID đồ
vật, trọng lượng (KG), giá trị (đơn vị tiền tệ).
Yêu cầu đầu ra của bài toán:
- Dòng đầu tiên: Một danh sách ID của đồ vật đã được chọn.
- Dòng thứ hai: Một số nguyên thể hiện tổng giá trị của các đồ vật đã được chọn.
- Dòng thứ ba: Một số nguyên thể hiện tổng trọng lượng của các đồ vật đã được chọn.
2.2. Xây dựng thuật toán
2.2.1. Ý tưởng
Bài toán balo yêu cầu tìm kiếm giá trị tối ưu của một tập hợp các đồ vật trong
một balo có trọng lượng tối đa W. Mỗi đồ vật chỉ có thể được chọn hoặc không chọn
một lần duy nhất. Đầu vào gồm trọng lượng tối đa W của balo và một danh sách các
đồ vật, mỗi đồ vật đề có các thuộc tính là ID, trọng lượng (w - weight) và giá trị (v - value).
Bước đầu tiên, thực hiện tính tỷ lệ giá t ịr = v của mỗi đồ vật. Sau đó, ta trọng lượng w
sắp xếp danh sách các đồ vật đã cho theo thứ tự giảm dần của tỷ lệ v , vì việc lựa w
chọn các đồ vật có tỷ lệ v cao sẽ mang lại giá trị tối ưu hơn. w
Tiếp theo, ta áp dụng thuật toán nhánh và cận (branch and bound) để tính toán
giá trị tối ưu. Công thức tính cận trên (upper bound) như sau: vi + 1
𝑢𝑏 = 𝑣 + (𝑊 − 𝑤) ∗ wi + 1 Trong đó: - v
: Tổng giá trị của các đồ vật đã chọn.
- W : Trọng lượng tối đa của balo.
- w : Trọng lượng hiện tại của balo.
- vi+1 : Giá trị của món đồ tiếp theo trong danh sách đã sắp xếp.
- wi+1 : Trọng lượng của món đồ tiếp theo trong danh sách đã sắp xếp.
Thuật toán bắt đầu với trọng lượng w = 0 và giá trị v = 0. Sau đó, ta tính giá
trị cận trên ubMax và tiến hành duyệt qua từng đồ vật. Tại mỗi lần duyệt, nếu trọng
lượng của món đồ hiện tại i (1 ≤ i ≤ n) không vượt quá W (wi ≤ W), ta chọn đồ vật đó
và cập nhật lại giá trị vMax += vi (giá trị tốt nhất hiện tại) và wMax += wi (trọng lượng 15
tối đa hiện tại). Nếu không chọn món đồ đó vì vượt quá trọng lượng tối đa (wi > W), ta bỏ qua nó.
Quá trình này tiếp tục cho đến khi không thể chọn thêm món đồ nào vào balo
mà không vượt quá trọng lượng tối đa (wMax ≥ W), hoặc khi tất cả các món đồ đã được xét qua.
Cuối cùng, thuật toán quay lui backtrack được sử dụng để tìm kiếm các giải
pháp tối ưu hơn. Thuật toán backtrack bắt đầu bằng việc tính toán chỉ số r, đại diện
cho chỉ số của món hàng đầu tiên không được thêm vào túi do trọng lượng vượt quá
khả năng chứa của túi wr > W - wr. Sau đó, tính toán giá trị giới hạn trên theo công thức: 𝑢𝑏 = ∑𝑟−1 𝑗
v + vr (nếu balo chưa đầy)
Nếu giá trị ub này không vượt quá ubMax hiện tại, thuật toán sẽ quay lại một
bước trước đó trong quá trình tìm kiếm ể
đ tìm kiếm các giải pháp tốt hơn.
“Quay lại một bước trước đó” có nghĩa là khi thuật toán đang trong một tình
huống mà nó đã chọn hoặc bỏ qua một món đồ, thuật toán sẽ quay lại và thử một lựa
chọn khác. Ví dụ, thay vì bỏ món đồ đó, thuật toán sẽ thử chọn để xem có tìm ra giá trị tốt hơn không.
2.2.2. Xây dựng giả mã
function knapsack_backtrack(W, items):
# W: Trọng lượng tối đa của balo
# items: Danh sách các đồ vật, mỗi đồ vật có ID, trọng lượng, giá trị
# Sắp xếp đồ vật theo giá trị/trọng lượng (v/w) theo thứ tự giảm dần sort items by v/w descending
# Khởi tạo các biến cần thiết vMax = 0
# Giá trị tối ưu hiện tại wMax = 0
# Trọng lượng tối đa mang được
current_weight = 0 # Trọng lượng hiện tại trong balo
current_value = 0 # Giá trị hiện tại trong balo solution = []
# Danh sách các đồ vật được chọn # Hàm tính cận trên
function upper_bound(index, current_weight, current_value):
remaining_weight = W - current_value bound = current_value
while index < len(items) and items[index].weight <= remaining_weight:
remaining_weight -= items[index].weight bound += items[index].weight index += 1
if index < len(items)
bound += items[index].value * (remaining_weight / items[index].weight) return bound 16
# Hàm backtracking
function backtrack(index, current_weight, current_value, solution): nonlocal vMax, wMax
# Cập nhật giá trị tối ưu nếu có
if current_value > vMax: vMax = current_value wMax = current_weight best_solution = solution[:]
# Nếu không thể chọn thêm đồ vật (quá trọng lượng hoặc hết đồ vật)
if index >= len(items) or current_weight >= W: return # Tính cận trên
bound = upper_bound(index, current_weight, current_value)
# Nếu cận trên không thể vượt qua giá trị tối ưu, quay lui if bound <= vMax: return
# Chọn đồ vật tại index
solution.append(items[index].ID)
backtrack(index + 1, current_weight + items[index].weight,
current_value + items[index].value, solution)
# Quay lại, không chọn đồ vật tại index solution.pop()
backtrack(index + 1, current_weight, current_value, solution)
# Bắt đầu thuật toán backtracking từ index 0 backtrack(0, 0, 0, [])
return vMax, wMax, best_solution 17
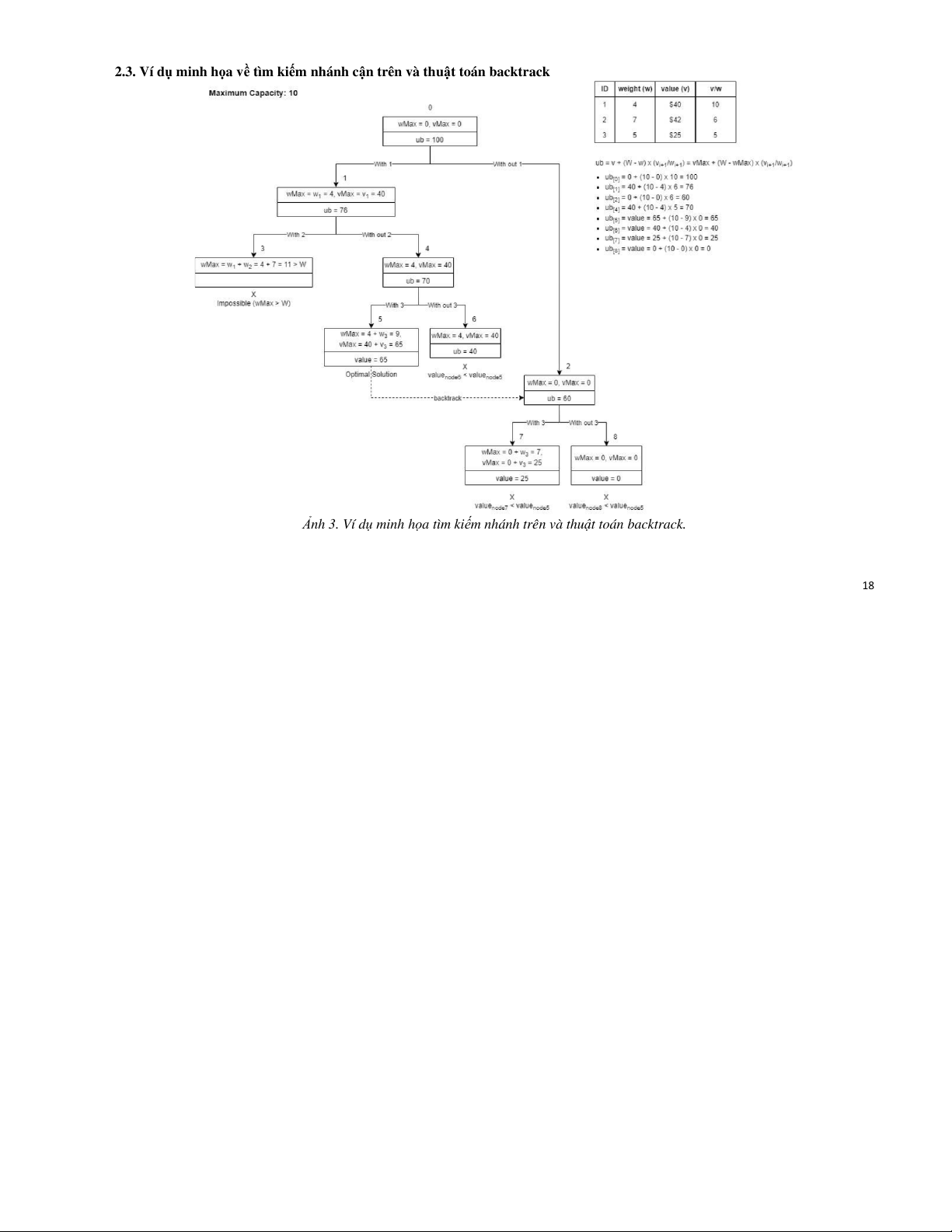
2.3. Ví dụ minh họa về tìm kiếm nhánh cận trên và thuật toán backtrack
Ảnh 3. Ví dụ minh họa tìm kiếm nhánh trên và thuật toán backtrack. 18
CHƯƠNG 3: CÀI ĐẶT THUẬT TOÁN BẰNG
NGÔN NGỮ LẬP TRÌNH PYTHON
3.1. Cài đặt thuật toán
3.1.1. Cài đặt class Item
Class Item bao gồm một phương thức khởi tạo (__init__), được gọi khi một
đối tượng mới của lớp Item được tạo ra. Phương thức này nhận vào ba tham số bao
gồm: ID, trọng lượng (w) và giá trị (v). Các tham số này lần lượt được gán cho các
thuộc tính tương ứng của đối tượng bao gồm self.ID, self.weight và self.value. Ngoài
ra, tỷ lệ giá t ịr = v cũng được tính toán và gán cho thuộc tính self.ratio. Tỷ lệ này trọng lượng w
dùng để sắp xếp danh sách các món đồ, phục vụ cho bài toán tối ưu hóa. class Item:
def __init__(self, ID, weight, value): self.ID = ID self.weight = weight self.value = value self.ratio = value / weight
3.1.2. Cài đặt đọc dữ liệu đầu vào từ tệp tin định dạng .xlsx
Một hàm knapsack_from_excel được định nghĩa để đọc dữ liệu từ một tệp tin
Excel có định dạng .xlsx và tạo ra các đối tượng Item từ dữ liệu đó. Đầu tiên, hàm mở
file Excel tại đường dẫn file_path thông qua việc sử dụng thư viện openpyxl, sau đó
lấy sheet đang hoạt động (active sheet) trong workbook. Sau đó, nó lấy giá trị tại ô
A1, trích xuất số nguyên từ giá trị của ô này và gán nó cho biến W (trọng lượng tối
đa của balo). Hàm lặp qua các dòng từ dòng thứ 6 đến dòng thứ n chứa thông tin các
đồ vật thông qua một vòng lặp for. Trong mỗi lần lặp, hàm lấy ra giá trị các cột A, B
và C tương ứng với ba thông tin của đồ vật bao gồm ID, trọng lượng và giá trị. Các
giá trị này được dùng để tạo ra các đối tượng Item mới với các thuộc tính ID, weight
và value. Nếu các giá trị này tồn tại, đối tượng Item sẽ được thêm vào lưu trữ trong
danh sách items. Danh sách items được khai báo sẽ chứa tất cả đối tượng Item được
tạo ra từ dữ liệu của tệp tin Excel.
# Hàm đọc dữ liệu từ file Excel
def knapsack_from_excel(file_path):
# Đọc dữ liệu từ file Excel
wb = openpyxl.load_workbook(file_path) sheet = wb.active
# Lấy trọng lượng tối đa từ ô A1
cell_value = sheet['A1'].value
W = int(re.search(r'\d+', cell_value).group())
# Đọc các đồ vật từ các ô
items = [] # Mảng lưu trữ thông tin đồ vật
for row in range(6, sheet.max_row + 1): ID = sheet[f'A{row}'].value
weight = sheet[f'B{row}'].value
value = sheet[f'C{row}'].value
if ID and weight and value: 19
items.append(Item(ID, weight, value))
3.1.3. Cài đặt tìm kiếm cận trên
Ý tưởng xây dựng hàm upper_bound là để tính toán giá trị cận trên của bài
toán. Đầu tiên hàm nhận vào các tham số: - w
: Trọng lượng hiện tại của các đồ vật đã chọn. - v
: Giá trị hiện tại của các đồ vật đã chọn. - index
: Chỉ số bắt đầu để xem xét các đồ vật tiếp theo. - items
: Danh sách các đồ vật, mỗi ồ
đ vật là một đối tượng Item. - W
: Trọng lượng tối đa của balo.
Sau đó hàm kiểm tra ràng buộc, nếu trọng lượng hiện tại đã vượt quá trọng
lượng tối đa (w ≥ W) thì trả về 0, vì không thể lấy thêm đồ vật nào nữa. Nếu chưa
vượt quá (w < W), hàm khởi tạo biến: - bound = v
: Khởi tạo giá trị tối đa bằng giá trị hiện tại v.
- total_weight = w : Khởi tạo tổng trọng lượng bằng trọng lượng hiện tại w.
Tiếp theo hàm sử dụng một vòng lặp for để duyệt qua tất cả các đồ vật có chỉ
số từ index đến hết danh sách items. Trong mỗi lần lặp, hàm thực hiện so sánh giữa
trọng lượng hiện tại cộng trọng lượng đồ vật tại vị trí đang xét trong danh sách với
trọng lượng tối đa của balo. Nếu tổng trên vẫn nhỏ hơn trọng lượng tối đa của balo,
trọng lượng của vật đó được cập nhật thêm vào trọng lượng hiện tại và giá trị của vật
đó cũng được cập nhật thêm vào giá trị hiện tại. Nếu tổng trên lớn hơn trọng lượng
tối đa của balo, hàm sẽ dừng vì không thể thêm đồ vật nào nữa. # Hàm tính cận trên
def upper_bound(w, v, index, items, W): if w > W: return 0 bound = v total_weight = w
# Tính giá trị tối đa có thể đạt được từ index hiện tại
for i in range(index, len(items)):
if total_weight + items[i].weight <= W:
total_weight += items[i].weight bound = items[i].value else: break return bound
3.1.4. Cài đặt thuật toán backtrack
Hàm knapsack_backtrack nhận vào các tham số bao gồm: - index : Chỉ số hiện tại. - current_weight
: Trọng lượng hiện tại. 20 - current_value : Giá trị hiện tại. - items
: Danh sách các đồ vật. - W
: Trọng lượng tối đa của balo.
- current_solution : Danh sách các đồ vật hiện đã được chọn.
Hai biến toàn cục vMax (lưu trữ giá trị tối đa tìm được) và best_solution (lưu
trữ giải pháp tốt nhất tìm được).
Đầu tiên, thuật toán kiểm tra nếu trọng lượng hiện tại không vượt quá trọng
lượng tối đa của balo và tổng giá trị của giải pháp hiện tại lớn hơn giá trị tối đa đã
biết (vMax). Nếu điều đó đúng, thuật toán cập nhật giá trị tối đa mới cho vMax và sao
chép giải pháp hiện tại vào best_solution.
Tiếp theo, nếu đã xét hết tất cả các đồ vật trong danh sách, tức là chỉ số index
lúc này vượt quá độ dài của danh sách items, thuật toán sẽ dừng lại. Trước khi thử xét
nhánh hiện tại, thuật toán tính cận trên bằng cách gọi hàm upper_bound. Nếu cận trên
của nhánh hiện tại không lớn hơn vMax, thuật toán sẽ cắt bỏ nhánh này vì không thể
mang lại giá trị tốt hơn.
Sau đó, thuật toán sẽ thử hai lựa chọn:
- Lựa chọn 1: Không chọn đồ vật hiện tại và gọi đệ quy để tiếp tục xét các đồ
vật tiếp theo mà không thay đổi trọng lượng và giá trị.
- Lựa chọn 2: Chọn đồ vật hiện tại nếu không vượt quá trọng lượng tối đa ủ c a
balo. Trong trường hợp này, thuật toán sẽ cập nhật trọng lượng và giá trị, sau đó tiếp
tục gọi đệ quy để tìm xem liệu còn giải pháp tốt hơn không.
# Hàm backtracking
def knapsack_backtrack(index, current_weight, current_value, items, W, current_solution):
global vMax, best_solution
# Cập nhật giá trị tối ưu nếu tìm được giải pháp tốt hơn
if current_weight <= W and current_value > vMax: vMax = current_value
best_solution = current_solution[:]
# Nếu đã xét hết các đồ vật, dừng lại
if index >= len(items): return
# Tính cận trên để kiểm tra xem có nên tiếp tục không
if upper_bound(current_weight, current_value, index, items, W) <= vMax:
return # Cắt nhánh vì không thể đạt giá trị tốt hơn vMax
# Bỏ qua đồ vật hiện tại
knapsack_backtrack(index + 1, current_weight, current_value, items, W, current_solution) 21
# Thêm đồ vật hiện tại nếu không vượt quá trọng lượng tối đa
if current_weight + items[index].weight <= W:
current_solution.append(items[index])
knapsack_backtrack(index + 1, current_weight +
items[index].weight, current_value + items[index].value, items, W, current_solution) current_solution.pop()
3.1.5. Cài đặt chương trình hoàn chỉnh
import re import time import openpyxl start = time.time()
# Khởi tạo lớp Item đại diện cho mỗi đồ vật class Item:
def __init__(self, ID, weight, value): self.ID = ID self.weight = weight self.value = value self.ratio = value / weight # Hàm tính cận trên
def upper_bound(w, v, index, items, W): if w >= W: return 0 bound = v total_weight = w
# Tính giá trị tối đa có thể đạt được từ index hiện tại
for i in range(index, len(items)):
if total_weight + items[i].weight <= W:
total_weight += items[i].weight bound += items[i].value else: break return bound
# Hàm backtracking
def knapsack_backtrack(index, current_weight, current_value, items, W, current_solution):
global vMax, best_solution
# Cập nhật giá trị tối ưu nếu tìm được giải pháp tốt hơn
if current_weight <= W and current_value > vMax: vMax = current_value
best_solution = current_solution[:]
# Nếu đã xét hết các đồ vật, dừng lại
if index >= len(items): return
# Tính cận trên để kiểm tra xem có nên tiếp tục không
if upper_bound(current_weight, current_value, index, items, W) <= vMax: 22

Tài liệu liên quan: