Tóm tắt lý thuyết và bài tập trắc nghiệm góc và khoảng cách Toán 12

Tóm tắt lý thuyết và bài tập trắc nghiệm góc và khoảng cách Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

44 22 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

31 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Trang 1/31
CHỦ ĐỀ 6. GÓC VÀ KHOẢNG CÁCH
A. KIẾN THỨC CƠ BẢN
I. GOC:
1. Góc giữa hai mặt phẳng.
Góc giữa hai mặt phẳng (P):
0
+ + +=
Ax By Cz D
, (Q):
’ ’ ’ ’ 0Ax By Cz D+++=
được ký
hiệu:
0 (( ),( )) 90
oo
PQ
≤≤
, xác định bởi hệ thức
222 222
cos(( ),( )) .
AA' BB' CC'
PQ
A B C . A' B' C'
++
=
++ + +
Đặc biệt:
.0''')()( =++⇔⊥ CCBBAAQP
2. Góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng.
a) Góc giữa hai đường thẳng (d) và (d’) có vectơ chỉ phương
);;( cbau =
và
)
';';'(' cbau =
la
222 2 2 2
'''
cos
.' ' '
aa bb cc
abca b c
φ
++
=
++ ++
).900(
oo
≤≤
ϕ
Đặc biệt:
.0
'
''
)'
(
)(
=+
+
⇔⊥
cc
bbaa
dd
b) Góc giữa đường thẳng d có vectơ chỉ phương
);;( cbau =
và mp
)(
α
có vectơ pháp
tuyến
).C;B;A(n =
222222
cb
a.CBA
CcBbAa
)u,ncos(sin
++++
++
==ϕ
).900(
oo
≤≤
ϕ
Đặc biệt:
)//()d
( α
hoặc
)()(
α
⊂d
.0
=++⇔ Cc
BbAa
II. KHOANG CACH
1. Khoảng cách từ một điểm đến mặt phẳng, khoảng cách giữa hai mặt phẳng song song.
a) Khoảng cách từ
);
;(
000
z
yxM
đến mặt phẳng
)(
α
có phương trình
0Ax by Cz D+ + +=
là:
.
222
000
CBA
DCzByAx
d(M,(P))
++
+++
=
b) Khoảng cách giữa hai mp song song là khoảng cách từ một điểm thuộc mặt phẳng này đến
mặt phẳng kia.
2. Khoảng cách từ một điểm đến một đường thẳng - khoảng cách giữa hai đường thẳng.
a) Khoảng cách từ điểm M đến một đường thẳng dqua điểm M
o
có vectơ chỉ phương
u
:
MM u
dMd
u
0
;
(,) .


=

b) Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường
thẳng này đến đường thẳng kia.
c) Khoảng cách giữa hai đường thẳng chéo nhau:
dđi qua điểm M và có vectơ chỉ phương
u
và d’ đi qua điểm M’ và có vectơ chỉ phương
'u
là:
uu MM
ddd
uu
0
; '.
( , ') .
;'


=




Trang 2/31
d) Khoảng cách từ giữa đường thẳng và mặt phẳng song song là khoảng cách từ một điểm
thuộc đường thẳng đến mặt phẳng hoặc khoảng cách từ một điểm thuộc mặt phẳng đến
đường thẳng.
B. KY NĂNG CƠ BAN
- Nhớ và vận dụng được công thức tính khoảng cách từ môt điểm đến mặt phẳng; biêt cach khoảng
cách giữa hai mặt phẳng song song.
- Nhớ và vận dụng được công thức tính khoảng cách từ một điểm đến một đường thẳng; biêt cach
tính khoảng cách giữa hai đường thẳng song song; khoảng cách giưa hai đương thăng cheo nhau;
khoang cach tư đương thăng đên măt phăng song song.
- Nhớ và vận dụng được công thưc góc giữa hai đường thẳng; góc giữa đường thẳng và măt phăng;
goc giưa hai măt phăng.
- Ap dụngđươc goc va khoang cach vao các bài toán khác.
C. BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong không gian Oxyz, khoang cach tư điêm
( )
1; 2; 2A
đên măt phăng
()
α
:
2 2 40xyz+ − −=
bằng:
A.
3.
B.
1.
C.
13
.
3
D.
1
.
3
Câu 2. Tinh khoang cach giưa hai măt phăng song song
()
α
:
2 2 40xy z−− −=
va
( ):
β
2 2 20xy z−− +=
.
A. 2. B. 6. C.
10
.
3
D.
4
.
3
Câu 3. Khoang cach tư điêm
( )
3; 2; 1M
đên măt phăng (P):
0
Ax Cz D+ +=
,
.. 0AC D ≠
. Chon khăng
đinh đungtrong cac khăng đinh sau:
A.
22
3
( ,( ))
AC D
dM P
AC
++
=
+
B.
222
23
( ,( )) .
A B CD
dM P
ABC
+++
=
++
C.
22
3
( ,( )) .
AC
dM P
AC
+
=
+
D.
22
3
( ,( )) .
31
AC D
dM P
++
=
+
Câu 4. Tinh khoang cach giưa măt phăng
()
α
:
2 2 40xy z−− −=
va đương thăng d:
1
24
xt
yt
zt
= +
= +
= −
.
A.
1
.
3
B.
4
.
3
C. 0. D. 2.
Câu 5. Khoang cach tư điêm
( )
2; 4; 3A
đên măt phăng
()
α
:
2 2 10xy z+ + +=
va
()
β
:
0x =
lân
lươt la
( ,( ))dA
α
,
( ,( ))dA
β
. Chon khăng đinh đung trong cac khăng đinh sau:
A.
(
)
,( )dA
α
3=
.
( )
,( ) .dA
β
B.
( )
,( )dA
α
>
( )
,( ) .dA
β
C.
( )
,( )dA
α
=
( )
,( ) .dA
β
D. 2.
( )
,( )dA
α
=
(
)
,( ) .
dA
β
Câu 6. Tim toa đô điêm Mtrên truc Oy sao cho khoang cach tư điêm M đên măt phăng (P):
2 3 40xy z−+ −=
nho nhât?
A.
( )
0; 2;0 .M
B.
( )
0; 4;0 .M
C.
( )
0; 4; 0 .M −
D.
4
0; ; 0
3
M



.
Câu 7. Khoang cach tư điêm
( )
4; 5; 6M −−
đên măt phăng (Oxy), (Oyz) lân lươt băng:
A. 6 va 4. B. 6 va 5. C. 5 va 4. D. 4 va 6.
Trang 3/31
Câu 8. Tinh khoang cach tư điêm
(
)
0 00
;;Ax y z
đến mặt phẳng
( ): 0P Ax By Cz D+ + +=
, vơi
... 0ABC D≠
. Chon khăng đinh đungtrong cac khăng đinh sau:
A.
( )
000
,( ) .d A P Ax By Cz=++
B.
( )
000
222
,( ) .
Ax By Cz
dAP
ABC
++
=
++
C.
( )
000
22
,( ) .
Ax By Cz D
dAP
AC
+++
=
+
D.
( )
000
222
,( ) .
Ax By Cz D
dAP
ABC
+++
=
++
Câu 9. Tinh khoang cach tư điêm
( )
0 00
;;Bx y z
đên măt phăng (P): y + 1 = 0. Chon khăng đinh
đungtrong cac khăng đinh sau:
A.
0
.
y
B.
0
.
y
C.
0
1
.
2
y +
D.
0
1.y +
Câu 10. Khoang cach tư điêm
(
)
2; 0; 0
C −
đên măt phăng (Oxy) băng:
A. 0. B. 2. C. 1. D.
2.
Câu 11. Khoang cach tư điêm
(
)
1; 2; 0
M
đên măt phăng (Oxy), (Oyz), (Oxz). Chon khăng đinh saitrong
cac khăng đinh sau:
A.
(
)
,( ) 2.
d M Oxz
=
B.
( )
,( ) 1.d M Oyz =
C.
( )
,( ) 1.d M Oxy
=
D.
( ) ( )
,( ) ,( ) .d M Oxz d M Oyz>
Câu 12. Khoang cach tư điêm
( )
0 00
;;Ax y z
đên măt phăng (P):
0Ax By Cz D+ + +=
, vơi
0D ≠
băng 0 khi va chi khi:
A.
000
.
Ax By Cz D
+ + ≠−
B.
( ).AP∉
C
000
.Ax By Cz D++=−
D.
000
.Ax By Cz++
= 0.
Câu 13. Khoang cach tư điêm
O
đên măt phăng (Q) băng 1. Chon khăng đinh đungtrong cac khăng
đinh sau:
A. (Q):
– 3 0.xyz
++ =
B. (Q):
2 2 – 3 0.xy z++ =
C. (Q):
2 – 2 6 0.xy z+ +=
D. (Q):
– 3 0.xyz++ =
Hương dân giai
Dung công thưc khoang cach tư 1 điêm đên măt phăng, sau đo tinh khoang cach lân lươt trong
môi trương hơp va chon đap an đung.
Câu 14. Khoang cach tư điêm H
(1;0;3)
đên đương thăng
1
1
:2
3
xt
dyt
zt
= +
=
= +
,
tR∈
va măt phăng
(P):
30z −=
lân lươt la
1
(,)dHd
va
( ,( ))dH P
. Chon khăng đinh đungtrong cac khăng đinh
sau:
A
( ) ( )
1
, ,( ) .dHd dH P>
B.
( ) ( )
1
,( ) , .dH P dHd>
C.
( )
( )
1
, 6. ,( ) .dHd dH P=
D.
( )
,( ) 1dH P =
.
Câu 15. Tinh khoang cach tư điêm E
(1;1; 3)
đên đương thăng
2
: 43
25
xt
dy t
zt
= +
= +
=−−
,
tR
∈
băng:
A
1
.
35
B.
4
.
35
C.
5
.
35
D. 0
Câu 16. Cho vectơ
( )
( )
uv2; 2; 0 ; 2; 2; 2−−

. Góc giữa vectơ
u
và vectơ
v
bằng:
Trang 4/31
A.
135°
. B.
45°
. C.
60°
. D.
150°
.
Câu 17. Cho hai đường thẳng
xt
dy t
z
1
2
:1
3
= +
=−+
=
và
xt
dy
zt
2
1
:2
2
= −
=
=−+
. Góc giữa hai đường thẳng d
1
và d
2
là:
A
30°
. B.
120
°
. C.
150°
. D.
60°
.
Câu 18. Cho đường thẳng
xyz
:
1 21
∆
= =
−
và mặt phẳng (P):
x yz511240+ + −=
. Góc giữa đường
thẳng
∆
và mặt phẳng (P) là:
A.
60°
. B.
30−°
. C.
30°
. D.
60−°
.
Câu 19. Cho mặt phẳng
xy z x y z( ):2 2 1 0;( ): 2 2 3 0
αβ
− + −= + − −=
. Cosin góc giữa mặt phẳng
()
α
và mặt phẳng
()
β
băng:
A.
4
9
B.
−
4
.
9
C.
4
.
33
D.
−
4
.
33
Câu 20. Cho mặt phẳng
Px yz( ):3 4 5 2 0+ + +=
và đường thẳng d là giao tuyến của hai mặt phẳng
xy xz( ): 2 1 0;( ): 2 3 0
αβ
− += − −=
. Gọi
ϕ
là góc giữa đường thẳng d và mặt phẳng (P).
Khi đó:
A.
60
°
. B.
45
°
. C.
30°
. D.
90
°
.
Câu 21. Cho mặt phẳng
xyz( ):3 2 2 5 0
α
− + −=
. Điểm A(1; – 2; 2). Có bao nhiêu mặt phẳng đi qua
A và tạo với mặt phẳng
()
α
một góc
45 .°
A. Vô số. B. 1. C. 2. D. 4.
Câu 22. Hai mặt phẳng nào dưới đây tạo với nhau một góc
60°
A.
Px yz
( ): 2 11 5 3 0+ − +=
và
Qx yz( ): 2 2 0+ −−=
.
B.
Px yz
( ): 2 11 5 3 0+ − +=
và
Q x yz( ): 2 5 0−+ +−=
.
C.
Px yz( ): 2 11 5 21 0
− +−=
và
Q xyz( ):2 2 0++−=
.
D.
Pxy z
( ): 2 5 11 6 0− + −=
và
Q x yz( ): 2 5 0−+ +−=
.
Câu 23. Cho vectơ
u vm(1; 1; 2), (1; 0; )−

. Tìm m để góc giữa hai vectơ
uv,

có số đo bằng
45°
.
Một học sinh giải như sau:
Bước 1: Tính
( )
m
uv
m
2
12
cos ,
6. 1
−
=
+

Bước 2: Góc giữa
uv,

có số đo bằng
45°
nên
m
m
2
12 1
2
6. 1
−
=
+
mm
2
1 2 3( 1)⇔− = +
(*)
Bước 3: Phương trình
mm
22
(*) (1 2 ) 3( 1)⇔− = +
m
mm
m
2
26
4 20
2 6.
= −
⇔ − −=⇔
= +
Bài giải đúng hay sai? Nếu sai thì sai ở bước nào?
A. Sai ở bước 3. B. Sai ở bước 2. C. Sai ở bước 1. D. Đúng.
Câu 24. Cho hai điểm
A(1; 1; 1); B(2; 2; 4)−−
. Có bao nhiêu mặt phẳng chứa A, Bvà tạo với mặt phẳng
x yz( ): 2 7 0
α
− +−=
một góc
60°
.
A. 1. B. 4. C. 2. D. Vô số.
Trang 5/31
Câu 25. Gọi
α
là góc giữa hai đường thẳng AB, CD. Khẳng định nào sau đây là khẳng định đúng:
A.
α
=
 
 
AB CD
AB CD
.
cos .
.
B.
α
=
 
 
AB CD
AB CD
.
cos .
.
C.
α
=


 
 
AB CD
AB CD
.
cos .
,
D.
α


=
 
 
AB CD
AB CD
.
cos .
.
Câu 26. Cho hình lập phương
ABCD A B C D.''' '
có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm các
cạnh
BB CD A D', , ' '
. Góc giữa hai đường thẳng MP và C’N là:
A. 30
o
. B. 120
o
. C. 60
o
. D. 90
o
.
Câu 27. Cho hình chóp A.BCD có các cạnh AB, AC, AD đôi một vuông góc.
ABC
∆
cân, cạnh bên bằng
a,
AD a
2
=
. Cosin góc giữa hai đường thẳng BD và DC là:
A.
.
4
5
B.
−
.
2
5
C.
.
4
5
D.
.
1
5
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2, AC =
5
.
SAC
∆
vuông cân
tại A. K là trung điểm của cạnh SD. Hãy xác định cosin góc giữa đường thẳng CK và AB?
A.
4
.
17
B.
2
.
11
C.
4
.
22
D.
2
.
22
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm điểm
−−A( 3; 4; 5);
B(2; 7; 7);
C(3; 5; 8);
−
D( 2; 6; 1)
. Cặp đường thẳng nào tạo với nhau một góc
60°
?
A. DB và AC. B. AC và CD. C. AB và CB. D.CB và CA.
Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào dưới đây đi qua A(2; 1; – 1) tạo với trục
Oz một góc
30°
?
A.
xyz2( 2) ( 1) ( 2) 3 0.
− + − − − −=
B.
x yz( 2) 2( 1) ( 1) 2 0.− + − − + −=
C.
xyz
2( 2) ( 1) ( 2) 0.
−+ −−− =
D.
xyz2( 2) ( 1) ( 1) 2 0.−+ −−−−=
Câu 31. Cho mặt phẳng
Px y z
( ):3 4 5 8 0+ + +=
. Đường thẳng d là giao tuyến của hai mặt phẳng
xy xz( ): 2 1 0;( ): 2 3 0
αβ
− += − −=
. Góc giữa d và (P) là:
A.
°120 .
B.
°60 .
C.
°150 .
D.
°30 .
Câu 32. Gọi
α
là góc giữa hai vectơ
AB CD,
 
. Khẳng định nào sau đây là đúng:
A.
AB CD
AB CD
.
cos
.
α


=
 
 
. B.
α
=
 
 
AB CD
AB CD
.
cos .
.
C.
=
 
 
α
AB CD
AB CD
.
sin .
.
D.
AB DC
AB DC
.
cos
.
α
=
 
 
Câu 33. Cho ba mặt phẳng
P xy z Qxyz Rx y z( ):2 2 3 0;( ): 2 1;( ): 2 2 2 0−+ += −−−= + + −=
.
Gọi
123
;;
ααα
lần lượt là góc giữa hai mặt phẳng (P) và (Q), (Q) và (R), (R) và (P). Khẳng định
nào sau đây là khẳng định đúng.
A.
ααα
>>
1 32
.
B.
α αα
>>
2 31
.
C.
α αα
>>
3 21
.
D.
ααα
>>
1 23
.
Câu 34. Trong không gian với hệ tọa độOxyz, cho mặt phẳng
( )
:22 0x y zm
α
+ + +=
vàđiểm
( )
1;1; 1A
.
Khi đó
m
nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng
( )
α
bằng 1?
A.
−
2. B.
−
8. C.
−
2 hoặc
8−
. D. 3.
Trang 6/31
Câu 35. Trong không gian với hệ tọa độOxyz, mặt phẳng
( )
α
cắt các trục
,,Ox Oy Oz
lần lượt tại 3
điểm
( )
2; 0; 0A −
,
( )
0; 3; 0B
,
( )
0; 0; 4
C
. Khi đó khoảng cách từ gốc tọa độ
O
đến mặt phẳng
( )
ABC
là
A.
61
.
12
B.4. C.
12 61
.
61
D.3.
Câu 36. Trong không gian với hệ tọa độ
0
2 2 20
y
xy z
=
−− −=
Oxyz
cho điểm
( )
1;0;0M
và
(
)
0; 0; 1
N
−
,
mặt phẳng
( )
P
qua điểm
,MN
và tạo với mặt phẳng
( )
: 40Q xy−−=
môt góc băng
O
45
.
Phương trình mặt phẳng
(
)
P
là
A.
0
2 2 20
y
xy z
=
−− −=
. B.
0
2 2 20
y
xy z
=
−− + =
.
C.
2 2 20
2 2 20
xy z
xy z
−− +=
−− −=
. D.
2 2 20
.
2 2 20
xz
xz
− +=
− −=
Câu 37. Trong không gian
Oxyz
, cho điểm
( )
2; 0; 1A −
, đường thẳng
d
qua điểm
A
và tạo với trục
Oy
góc
O
45
. Phương trình đường thẳng
d
là
A.
21
21
5
21
21
5
x yz
x yz
+−
= =
−
+−
= =
−
−
. B.
21
21
5
21
21
5
x yz
x yz
−+
= =
−
−+
= =
−
−
C.
21
21
5
21
21
5
x yz
x yz
+−
= =
−
−+
= =
−
D.
21
21
5
21
21
5
x yz
x yz
+−
= =
−
−
−+
= =
−
Câu 38. Trong không gian
Oxyz
cho mặt phẳng
( )
: 30Pxyz++−=
và mặt
phẳng
( )
: 10Qxyz
− +−=
. Khi đó mặt phẳng
( )
R
vuông góc với mặt phẳng
( )
P
và
( )
Q
sao
cho khoảng cách từ
O
đến mặt phẳng
( )
R
bằng
2
, có phương trình là
A.
2 2 22 0−− =xz
. B.
22 0xz−− =
.
C.
22 0xz
−+ =
. D.
22 0
22 0
xz
xz
−+ =
−− =
.
Câu 39. Tập hợp các điểm
( )
;;
M xyz
trong không gian
Oxyz
cách đều hai mặt phẳng
( )
: 2 30Pxy z+− −=
và
( )
: 2 50Qxy z+− +=
thoả mãn:
A.
2 10xy z+ − +=
. B.
2 40
xy z+− +=
.
C.
2 20xy z+− +=
. D.
2 40xy z+− −=
.
Câu 40. Tập hợp các điểm
( )
;;M xyz
trong không gian
Oxyz
cách đều hai mặt phẳng
( )
: 2 2 70Px y z− − −=
và mặt phẳng
( )
:2 2 1 0Q xy z+ + +=
thoả mãn:
A.
3 4 8 0.xyz+ + +=
B.
3 4 80
3 60
+ + +=
−−=
xyz
xy
.
C.
3 6 0.xy−−=
D.
3 3 4 8 0.+ + +=xyz
Trang 7/31
Câu 41. Trong không gian
Oxyz
cho điêm
M
thuôc truc Oxcách đều hai mặt phẳng
( )
: 2 30Pxy z+− −=
và
( )
Oyz
.Khitọa độ điểm
M
là
A.
3
;0;0
16


+

và
3
;0;0 .
61


−

B.
3
;0;0
16


+

và
3
;0;0 .
16


−

C.
61
;0;0
3

−



và
61
;0;0 .
3

+



D.
16
;0;0
3

+



và
16
;0;0 .
3

−



Câu 42. Trong không gian
Oxyz
cho điểm
( )
3; 2; 4A −
và đường thẳng
512
:
23 2
x yz
d
− −−
= =
−
.
Điểm
M
thuộc đường thẳng
d
sao cho
M
cách
A
một khoảng bằng
17
. Tọa độ điểm
M
là
A.
( )
5; 1; 2
và
( )
6; 9; 2
. B.
( )
5; 1; 2
và
( )
1;8;4.−−−
C.
( )
5; 1; 2
−
và
( )
1; 5; 6 .−
D.
(
)
5; 1; 2
và
( )
1; 5; 6 .−
Câu 43. Trong không gian
Oxyz
cho tứ diện
ABCD
có các đỉnh
( )
1; 2; 1A
,
( )
2; 1; 3B −
,
(
)
2; 1; 1C −
và
( )
0; 3;1D
. Phương trình mặt phẳng
(
)
P
đi qua 2 điểm
,AB
sao cho khoảng cách từ
C
đến
( )
P
bằng khoảng cách từ
D
đến
( )
P
la
A.
4 2 7 10
.
2 3 50
x yz
xz
− + −=
+ −=
B.
2 3 5 0.
xz+ −=
C.
4 2 7 15 0.xyz+ +−=
D.
4 2 7 15 0
.
2 3 50
xyz
xz
+ +−=
+ −=
Câu 44. Trong không gian với hệ trục toạ độ
,Oxyz
gọi
( )
P
là mặt phẳng chứa đường thẳng
12
:
1 12
xy z
d
−+
= =
−−
và tạo với trục
Oy
góc có số đo lớn nhất. Điểm nào sau đây thuộc
( )
mp P
?
A.
( )
3; 0; 4 .E −
B.
( )
3; 0; 2 .M
C.
( )
1;2;1.N −−−
D.
( )
1; 2;1 .F
Câu 45. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( ) ( )
0; 1; 2 , 1; 1; 3−−MN
. Gọi
( )
P
là
mặt phẳng đi qua
, MN
và tạo với mặt phẳng
( )
:2 2 2 0Q xy z−− −=
góc có số đo nhỏ nhất.
Điểm
( )
1; 2; 3A
cách mp
( )
P
một khoảng là
A.
3.
B.
53
.
3
C.
7 11
.
11
D.
43
.
3
Câu 46. Trong không gian với hệ trục toạ độ
,Oxyz
cho
( )
: 2 2 10Px y z− + −=
và 2 đường thẳng
12
1 9 131
: ;:
116 2 1 2
x yz x y z+ + −−+
∆== ∆==
−
.
Gọi
M
là điểm thuộc đường thẳng
1
∆
,
M
có toạ độ là các số nguyên,
M
cách đều
2
∆
và
( )
.P
Khoảng cách từ điểm
M
đến
( )
mp Oxy
là
A.
3.
B.
2 2.
C.
3 2.
D.
2.
Câu 47. Trong không gian với hệ trục toạ độ
,Oxyz
cho 2 điểm
( ) ( )
1; 5; 0 ; 3; 3; 6AB
và đường thẳng
11
:
2 12
xyz
d
+−
= =
−
. Gọi
C
là điểm trên đường thẳng
d
sao cho diện tích tam giác
ABC
nhỏ
nhất. Khoảng cách giữa 2 điểm
A
và
C
là
A.
29.
B.
29.
C.
33.
D.
7.
Trang 8/31
Câu 48. Trong không gian với hệ trục toạ độ Oxyz, cho điểm
(
)
10; 2;1
A
và đường thẳng
11
:
213
x yz
d
−−
= =
. Gọi
(
)
P
là mặt phẳng đi qua điểm
A
, song song với đường thẳng
d
sao
cho khoảng cách giữa
d
và
(
)
P
lớn nhất. Khoảng cách từ điểm
( )
1; 2; 3M −
đến mp
( )
P
là
A.
97 3
.
15
B.
76 790
.
790
C.
2 13
.
13
D.
3 29
.
29
Câu 49. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( )
2;5;3A
và đường thẳng
12
:
212
x yz
d
−−
= =
. Gọi
( )
P
là mặt phẳng chứa đường thẳng
d
sao cho khoảng cách từ
A
đến
( )
P
lớn nhất. Tính khoảng cách từ điểm
( )
1; 2; 1M −
đến mặt phẳng
( )
P
.
A.
11 18
.
18
B.
3 2.
C.
11
.
18
D.
4
.
3
Câu 50. Trong không gian với hệ trục toạ độ
,Oxyz
cho mặt phẳng
( )
: 20Pxyz+−+=
và hai đường
thẳng
1
:
22
xt
d yt
zt
= +
=
= +
;
3
': 1 .
12
xt
dy t
zt
′
= −
′
= +
′
= −
Biết rằng có 2 đường thẳng có các đặc điểm: song song với
( )
P
; cắt
, dd
′
và tạo với
d
góc
O
30 .
Tính cosin góc tạo bởi hai đường thẳng đó.
A.
1
.
5
B.
1
.
2
C.
2
.
3
D.
1
.
2
Câu 51. Trong không gian với hệ trục toạ độ
,
Oxyz
cho 3 điểm
( ) ( ) ( )
1; 0;1 ; 3; 2; 0 ; 1; 2; 2AB C−−
. Gọi
( )
P
là mặt phẳng đi qua
A
sao cho tổng khoảng cách từ
B
và
C
đến
( )
P
lớn nhất biết rằng
( )
P
không cắt đoạn
BC
. Khi đó, điểm nào sau đây thuộc mặt phẳng
(
)
P
?
A.
(
)
2; 0; 3 .
G −
B.
( )
3; 0; 2 .F −
C.
( )
1; 3;1 .
E
D.
(
)
0; 3;1H
Câu 52. Trong không gian với hệ trục toạ độ
,Oxyz
cho các điểm
( )
( ) ( )
1; 0; 0 , 0; ; 0 , 0; 0;A Bb C c
trong
đó
,bc
dương và mặt phẳng
( )
: 10
Pyz−+=
. Biết rằng
( )
mp ABC
vuông góc với
( )
mp P
và
( )
( )
1
,
3
d O ABC =
, mệnh đề nào sau đây đúng?
A.
1.bc+=
B.
2 1.bc+=
C.
3 1.bc−=
D.
3 3.
bc+=
Câu 53. Trong không gian với hệ trục toạ độ
,Oxyz
cho 3 điểm
( ) ( ) ( )
1; 2; 3 ; 0; 1; 1 ; 1; 0; 2A BC−
.
Điểm
( )
: 20M Pxyz∈ +++=
sao cho giá trị của biểu thức
222
23T MA MB MC=++
nhỏ nhất.
Khi đó, điểm
M
cách
( )
:2 2 3 0Q xy z−− +=
một khoảng băng
A.
121
.
54
B.
24.
C.
25
.
3
D.
101
.
54
Câu 54. Cho mặt phẳng
xy z x y z( ): 2 1 0;( ):5 2 11 3 0
αβ
+ − −= + + −=
. Góc giữa mặt phẳng
()
α
và mặt phẳng
()
β
băng
A.
120 .°
B.
30 .°
C.
150 .°
D.
60 .°
Trang 9/31
Câu 55. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) có phương trình
xy3 0.+−=
Điểm H(2; 1; 2) là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa
hai mặt phẳng (P) và (Q) bằng
A.
45 .°
B.
30 .°
C.
60 .°
D.
120 .°
Câu 56. Cho vectơ
(
)
u v uv2; 1; ,
3
π
= = =

. Gócgiữa vectơ
v
và vectơ
uv−

bằng:
A.
60 .°
B.
30 .°
C.
90 .°
D.
45 .°
Câu 57. Trong không gian với hệ trục toạ độ Oxyz, cho đường thẳng
x yz
d
3 11
:,
951
− +−
= =
xyz
x yz
2 3 3 90
:
2 30
− − +=
∆
− ++=
. Góc giữa đường thẳng d và đường thẳng
∆
bằng
A.
90 .°
B.
30 .
°
C.
0.
°
D.
180 .°
Câu 58. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng
xy z( ) : 2 2 10 0;
α
−−−=
đường
thẳng
x yz
d
11 3
:
123
−− +
= =
. Góc giữa đường thẳng d và mặt phẳng
()
α
bẳng
A.
30 .°
B.
90 .°
C.
60 .°
D.
45 .°
Câu 59. Trong không gian với hệ trục toạ độ Oxyz, phương trình các đường thẳng qua A(3; – 1;1), nằm
trong (P):
– –5 0
+=xyz
và hợp với đường thẳngd:
2
122
−
= =
xy z
một góc 45
0
là
A.

=+=+

∆ =−+ ∈ ∆ =−− ∈


= = −

xt x t
y ttR y ttR
z zt
12
3 33
:1,;:12,.
1 15
B.

=+=+

∆ =−+ ∈ ∆ =−+ ∈


= = +

xt x t
y ttR y ttR
z zt
12
3 2 3 15
:12,;:138,.
1 1 23
C.

=+=+

∆ =−+ ∈ ∆ =−− ∈


= = −

xt x t
y ttR y ttR
z zt
12
3 3 15
:1,;:18,.
1 1 23
D.

=−=+

∆ =−− ∈ ∆ =−− ∈


=+=−

xt x t
y ttR y ttR
zt z t
12
3 3 15
:1,;:18,.
1 1 23
Câu 60. Cho hình lập phương
ABCD A B C D.''' '
có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm các
cạnh
A B BC DD' ', , '
. Góc giữa đường thẳng AC’ và mặt phẳng (MNP) là
A.
30 .
°
B.
°120 .
C.
60 .°
D.
90 .°
Câu 61. Trong không gian với hệ trục toạ độ
,Oxyz
gọi(P) là mặt phẳng chứa đường thẳng
12
:2
3
xt
dy t
zt
= +
= −
=
và tạo với trục
Ox
góc có số đo lớn nhất.Khi đó, khoảng cách từ điểm
( )
1; 4; 2A −
đến
( )
mp P
là
A.
12 35
.
35
B.
43
.
3
C.
20 6
.
9
D.
26
.
3
Trang 10/31
Câu 62. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( ) ( )
2;1; 12 , 3; 0; 2MN−
. Gọi
(
)
P
là mặt
phẳng đi qua
,
MN
và tạo với mặt phẳng
( )
:2 2 3 4 0Qx yz+ − +=
góc có số đo nhỏ nhất. Điểm
( )
3;1; 0A
cách mp
( )
P
một khoảng là
A.
6 13
.
13
B.
22
.
11
C.
6
.
2
D.
1
.
22
Câu 63. Trong không gian với hệ trục toạ độ
,Oxyz
cho
( )
: 70Pxyz+−−=
và hai đường thẳng
12
112 2 34
: ;:
111 2 3 5
xyz x yz−−− − −+
∆==∆ ==
−
.
Gọi
M
là điểm thuộc đường thẳng
1
∆
,
M
có toạ độ là các số dương,
M
cách đều
2
∆
và
( )
.P
Khoảng cách từ điểm
M
đến mp(
P
) là
A.
2 3.
B.
2.
C.
7.
D.
2
.
3
Câu 64. Trong không gian với hệ trục toạ độ
,Oxyz
cho 2 điểm
( ) ( )
1; 4; 3 ; 1; 0; 5AB−
và đường thẳng
3
: 3 2.
2
xt
dy t
z
= −
= +
= −
Gọi
C
là điểm trên đường thẳng
d
sao cho diện tích tam giác
ABC
nhỏ nhất.
Khoảng cách giữa điểm
C
và gốc toạ độ
O
là
A.
6.
B.
14.
C.
14.
D.
6.
Câu 65. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( )
2;5;3A
và đường thẳng
12
:.
212
x yz
d
−−
= =
Gọi
( )
P
là mặt phẳng đi qua điểm
A
, song song với đường thẳng
d
sao
cho khoảng cách giữa
d
và
( )
P
lớn nhất. Khoảng cách từ điểm
( )
2; 0; 3B −
đến mp
( )
P
là
A.
72
.
3
B.
52
.
3
C.
7.
D.
18
.
18
Câu 66. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( )
4; 3; 2A −
và đường thẳng
43
: 2 2.
2
xt
dy t
zt
= +
= +
=−−
Gọi
( )
P
là mặt phẳng chứa đường thẳng
d
sao cho khoảng cách từ
A
đến
( )
P
lớn nhất. Tính
khoảng cách từ điểm
( )
2; 1; 3B −−
đến mặt phẳng
( )
P
đó.
A.
2 3.
B.
2.
C.
0.
D.
38.
Câu 67. Trong không gian với hệ trục toạ độ
,Oxyz
cho 3 điểm
( )
( ) ( )
1; 1; 2 ; 1; 2; 1 ; 3; 4; 1
−− −
ABC
. Gọi
( )
P
là mặt phẳng đi qua
A
sao cho tổng khoảng cách từ
B
và
C
đến
( )
P
lớn nhất biết rằng
(P) không cắt đoạn
BC
. Khi đó, điểm nào sau đây thuộc mặt phẳng
( )
P
?
A.
( )
1; 2; 0 .F −
B.
( )
2; 2;1 .E −
C.
( )
2;1; 3 .G −
D.
( )
1; 3;1 .H −
Câu 68. Trong không gian với hệ trục toạ độ
,Oxyz
cho các điểm
( ) ( ) ( )
; 0; 0 , 0; 2; 0 , 0; 0;Aa B C c
trong
đó
,ac
dương và mặt phẳng
( )
:2 3 0P xz−+=
. Biết rằng
( )
mp ABC
vuông góc với
( )
mp P
và
( )
( )
2
,
21
d O ABC =
, mệnh đề nào sau đây đúng?
A.
4 3.ac+=
B.
2 5.ac
+=
C.
1.ac−=
D.
4 3.ac−=
Trang 11/31
Câu 69. Trong không gian với hệ trục toạ độ
,Oxyz
cho 3 điểm
( ) ( ) ( )
2; 2; 3 ; 1; 1; 3 ; 3; 1; 1− −−A BC
.
Điểm
( )
: 2 80M Px z∈ + −=
sao cho giá trị của biểu thức
22 2
23T MA MB MC= ++
nhỏ nhất.
Khi đó, điểm
M
cách
( )
: 2 2 60
Q xyz−+ − −=
một khoảng băng
A.
2
.
3
B.2. C.
4
.
3
D. 4.
Câu 70. Tinh khoang cach tư điêm H(3; – 1;– 6) đên măt phăng
()
α
:
10xyz+ −+=
.
A.
83
.
3
B. 9. C.
3 3.
D. 3.
Câu 71. Tinh khoang cach giưa hai măt phăng song song (P):
2 20xy z
++ =
va (Q)
2 2 70xy z++ +=
.
A.
7
.
9
B. 7. C.
7
.
3
D. 2.
Câu 72. Khoang cach tư điêm K(1;2;3) đên măt phăng (Oxz) băng
A. 2. B. 1. C. 3. D. 4.
Câu 73. Tinh khoang cach giưa măt phăng
()
α
:
2 2 40xy z++ +=
va đương thăng d:
15
22
4
xt
yt
zt
= +
= −
= −
.
A.
8
.
3
B. 0. C.
4
.
3
D. 4.
Câu 74. Khoang cach tư giao điêm A cua măt phăng
( ): 3 0Rxyz++−=
vơi truc Oz đên măt phăng
()
α
:
2 2 10
xy z
+ + +=
băng
A.
7
.
3
B.
5
.
3
C.
4
.
3
D. 0.
Câu 75. Cho hai măt phăng
( ): 2 1 0, ( ):2 0Pxy z Q xyz++ −= ++=
va đương thăng d:
13
2.
1
= −
= +
=−+
xt
yt
zt
Goi
( ,( ))dd P
,
( ,( ))dd Q
,
(( ),( ))dP Q
lân lươt la khoang cach giưa đương thăng d va (P), d va
(Q), (P) va (Q). Trong cac mênh đê sau, tim mênh đê sai:
A.
( ,( )) 0.dd P =
B.
6
( ,( )) .
2
dd Q =
C.
(( ),( )) 0.dP Q=
D.
( ,( )) 0.dd Q =
Câu 76. Khoang cach tư điêm
( 2;1; 0)C
−
đên măt phăng (Oyz) va đên đương thăng
∆
:
1
4
62
xt
yt
zt
= +
= +
= +
lân
lươt la
1
d
va
2
d
. Chon khăng đinh đung trong cac khăng đinh sau:
A.
1
d
>
2
.d
B.
1
d
=
2
.d
C.
1
d
0.
=
D.
2
d
=1.
Câu 77. Khoang cach tư điêm
(1;1;1)B
đên măt phăng (P) băng 1. Chon khăng đinh đungtrong cac
khăng đinh sau:
A. (P):
2 – 2 6 0.
xy z+ +=
B. (P):
– 3 0.++ =xyz
B. (P):
2 2 – 2 0.xy z++ =
D. (P):
– 3 0++ =xyz
.
Câu 78. Trong không gian
Oxyz
cho mặt phẳng
( )
:2 2 1 0xy z
α
− + +=
và mặt phẳng
( )
:2 2 5 0xy z
β
−+ +=
. Tập hợp các điểm M cách đều mặt phẳng
( )
α
và
( )
β
là
A.
2 2 3 0.xy z−+ +=
B.
2 2 3 0.xy z−− +=
Trang 12/31
C.
2 2 3 0.
xy z
−+ −=
D.
2 2 3 0.xy z
++ +=
Câu 79. Trong không gian
Oxyz
cho mặt phẳng
( )
: 2 2 10
xyz
α
− + +=
và mặt
phẳng
( )
:2 2 1 0xy z
β
− + +=
. Tập hợp các điểm cách đều mặt phẳng
( )
α
và
( )
β
là
A.
20
.
3 3 4 40
xy
xyz
−+=
+ + +=
B.
20
.
3 3 4 40
xy
xyz
−+=
− + +=
C.
20
.
3 3 4 40
xy
xyz
−+=
− + +=
D.
20
.
3 3 4 40
xy
xyz
++=
− + +=
D. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN 8.5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
B
A
A
B
D
C
A
D
D
A
C
C
B
C
D
A
D
C
A
A
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
A
B
A
C
A
D
A
C
C
A
B
D
A
C
C
A
A
D
A
B
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
B
D
D
C
A
A
C
A
A
D
C
A
D
D
A
C
C
B
C
D
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
A
D
A
C
A
A
B
A
D
C
C
A
A
A
B
A
C
A
D
A
Trang 13/31
II –HƯỚNG DẪN GIẢI
Câu 1. Trong không gian Oxyz, khoang cach tư điêm
( )
1; 2; 2A
đên măt phăng
()
α
:
2 2 40xyz+ − −=
bằng:
A.
3.
B.
1.
C.
13
.
3
D.
1
.
3
Hương dân giai
22 2
1. 2.y 2. 4
( ,( )) 1.
1 2 ( 2)
A AA
xz
dA
α
+−−
= =
+ +−
Câu 2. Tinh khoang cach giưa hai măt phăng song song
()
α
:
2 2 40xy z−− −=
va
( ):
β
2 2 20xy z−− +=
.
A. 2. B. 6. C.
10
.
3
D.
4
.
3
Hương dân giai
Khoang cach giưa hai măt phăng song song băng khoang cach tư môt điêm bât ky cua măt
phăng nay đên măt phăng kia.
Ta lây điêm H(2; 0; 0) thuôc
()
α
. Khi đo
( ) ( )
22 2
2.2 1.0 2.0 2
( ),( ) ,( ) 2
2 (1) (2)
αβ β
−−+
= = =
+− +−
d dH
.
Câu 3. Khoang cach tư điêm
( )
3; 2; 1M
đên măt phăng (P):
0Ax Cz D+ +=
,
.. 0AC D ≠
. Chon khăng
đinh đungtrong cac khăng đinh sau:
A.
22
3
( ,( ))
AC D
dM P
AC
++
=
+
B.
222
23
( ,( )) .
A B CD
dM P
ABC
+++
=
++
C.
22
3
( ,( )) .
AC
dM P
AC
+
=
+
D.
22
3
( ,( )) .
31
AC D
dM P
++
=
+
Câu 4. Tinh khoang cach giưa măt phăng
()
α
:
2 2 40xy z
−− −=
va đương thăng d:
1
24
xt
yt
zt
= +
= +
= −
.
A.
1
.
3
B.
4
.
3
C. 0. D. 2.
Hương dân giai
Đương thăng d song song vơi măt phăng
()
α
.
Khoang cach giưa đương thăng va măt phăng song song băng khoang cach tư môt điêm bât ky
cua đương thăng đên măt phăng.
Ta lây điêm
( )
1; 2; 0H
thuôc đương thăng d. Khi đo:
22 2
2.1 1.2 2.0 4
4
( ,( )) ( ,( )) .
3
2 (1) (2)
dd dH
αα
−−−
= = =
+− +−
Câu 5. Khoang cach tư điêm
( )
2; 4; 3A
đên măt phăng
()
α
:
2 2 10xy z+ + +=
va
()
β
:
0x =
lân
lươt la
( ,( ))dA
α
,
( ,( ))dA
β
. Chon khăng đinh đung trong cac khăng đinh sau:
A.
( )
,( )dA
α
3=
.
( )
,( ) .dA
β
B.
( )
,( )dA
α
>
( )
,( ) .dA
β
C.
( )
,( )dA
α
=
( )
,( ) .dA
β
D. 2.
( )
,( )dA
α
=
( )
,( ) .dA
β
Hương dân giai
Trang 14/31
( )
22 2
2. y 2. 1
,( ) 1
212
AA A
xz
dA
α
++ +
= =
++
;
( )
2
,( ) 2.
1
A
x
dA
β
= =
Kêt luân:
(
) (
)
,( ) 2. ,( )dA dA
βα
=
.
Câu 6. Tim toa đô điêm Mtrên truc Oy sao cho khoang cach tư điêm M đên măt phăng (P):
2 3 40
xy z−+ −=
nho nhât?
A.
(
)
0; 2;0 .M
B.
(
)
0; 4;0 .M
C.
( )
0; 4; 0 .M −
D.
4
0; ; 0
3
M



.
Hương dân giai
Khoang cach tư M đên (P) nho nhât khi M thuôc (P). Nên M la giao điêm cua truc Oy vơi măt
phăng (P). Thay x = 0, z = 0 vao phương trinh (P) ta đươc y =
−
4. Vây M(0;
−
4;0).
Cach giai khac
Tinh khoang cach tư điêm M trong cac đap an đên măt phăng (P) sau đo so sanh chon đap an.
Câu 7. Khoang cach tư điêm
( )
4; 5; 6M −−
đên măt phăng (Oxy), (Oyz) lân lươt băng:
A. 6 va 4. B. 6 va 5. C. 5 va 4. D. 4 va 6.
Hương dân giai
(
)
( )
,6
M
d M Oxy z= =
;
( ,( )) 4.
M
d M Oyz x
= =
Câu 8. Tinh khoang cach tư điêm
( )
0 00
;;Ax y z
đến mặt phẳng
( ): 0P Ax By Cz D+ + +=
, vơi
... 0ABC D≠
. Chon khăng đinh đungtrong cac khăng đinh sau:
A.
(
)
000
,( ) .
d A P Ax By Cz
=++
B.
( )
000
222
,( ) .
Ax By Cz
dAP
ABC
++
=
++
C.
( )
000
22
,( ) .
Ax By Cz D
dAP
AC
+++
=
+
D.
( )
000
222
,( ) .
Ax By Cz D
dAP
ABC
+++
=
++
Câu 9. Tinh khoang cach tư điêm
( )
0 00
;;Bx y z
đên măt phăng (P): y + 1 = 0. Chon khăng đinh
đungtrong cac khăng đinh sau:
A.
0
.y
B.
0
.y
C.
0
1
.
2
y +
D.
0
1.y +
Câu 10. Khoang cach tư điêm
(
)
2; 0; 0C −
đên măt phăng (Oxy) băng:
A. 0. B. 2. C. 1. D.
2.
Hương dân giai
Điêm C thuôc măt phăng (Oxy) nên
( )
,( ) 0d C Oxy =
Câu 11. Khoang cach tư điêm
( )
1; 2; 0M
đên măt phăng (Oxy), (Oyz), (Oxz). Chon khăng đinh saitrong
cac khăng đinh sau:
A.
( )
,( ) 2.d M Oxz =
B.
( )
,( ) 1.d M Oyz =
C.
( )
,( ) 1.d M Oxy =
D.
( )
( )
,( ) ,( ) .
d M Oxz d M Oyz>
Câu 12. Khoang cach tư điêm
( )
0 00
;;
Ax y z
đên măt phăng (P):
0Ax By Cz D+ + +=
, vơi
0D ≠
băng 0 khi va chi khi:
A.
000
.Ax By Cz D+ + ≠−
B.
( ).AP∉
C
000
.Ax By Cz D++=−
D.
000
.Ax By Cz++
= 0.
Câu 13. Khoang cach tư điêm
O
đên măt phăng (Q) băng 1. Chon khăng đinh đungtrong cac khăng
đinh sau:
A. (Q):
– 3 0.
xyz++ =
B. (Q):
2 2 – 3 0.xy z++ =
Trang 15/31
C. (Q):
2 – 2 6 0.xy z+ +=
D. (Q):
– 3 0.xyz++ =
Hương dân giai
Dung công thưc khoang cach tư 1 điêm đên măt phăng, sau đo tinh khoang cach lân lươt trong
môi trương hơp va chon đap an đung.
Câu 14. Khoang cach tư điêm H
(1;0;3)
đên đương thăng
1
1
:2
3
xt
dyt
zt
= +
=
= +
,
tR∈
va măt phăng
(P):
30z −=
lân lươt la
1
(,)dHd
va
( ,( ))
dH P
. Chon khăng đinh đungtrong cac khăng đinh
sau:
A
( ) ( )
1
, ,( ) .dHd dH P>
B.
(
) (
)
1
,( ) , .dH P dHd
>
C.
( ) ( )
1
, 6. ,( ) .dHd dH P=
D.
( )
,( ) 1dH P =
.
Hương dân giai
Vi H thuôc đương thăng
1
d
va H thuôc măt phăng (P) nên khoang cach tư điêm H đên đương
thăng
1
d
băng 0 va khoang cach tư điêm H đên măt phăng (P) băng 0.
Câu 15. Tinh khoang cach tư điêm E
(1;1; 3)
đên đương thăng
2
: 43
25
xt
dy t
zt
= +
= +
=−−
,
tR∈
băng:
A
1
.
35
B.
4
.
35
C.
5
.
35
D. 0
Hương dân giai
+ Goi (P) la măt phăng đi qua E va vuông goc vơi (P). Viêt phương trinh (P)
+ Goi H la giao điêm cua đương thăng d va (P). Tim toa đô H
+ Tinh đô dai EH.
Khoang cach tư điêm E
(1;1; 3)
đên đương thăng d băng EH.
Cach giai khac:
Vi E thuôc đương thăng d nên khoang cach tư điêm E
(1;1; 3)
đên đương thăng d băng 0.
Câu 16. Cho vectơ
( )
( )
uv2; 2; 0 ; 2; 2; 2−−

. Góc giữa vectơ
u
và vectơ
v
bằng:
A.
135°
. B.
45°
. C.
60°
. D.
150°
.
Hướng dẫn giải
Ta có
( ) ( )
uv
uv
uv
22
22 2
. 2. 2 2. 2 2.0 1
co s( , )
2
.
( 2) ( 2) . 2 2 2
−− +
= = = −
− +− + +



uv( , ) 135⇒=°

.
Câu 17. Cho hai đường thẳng
xt
dy t
z
1
2
:1
3
= +
=−+
=
và
xt
dy
zt
2
1
:2
2
= −
=
=−+
. Góc giữa hai đường thẳng d
1
và d
2
là:
A
30°
. B.
120°
. C.
150
°
. D.
60°
.
Hướng dẫn giải
Gọi
uu
12
;

lần lượt là vectơ chỉ phương của đường thẳng d
1
; d
2
.
uu
12
(1; 1; 0); ( 1; 0; 1)= = −

Trang 16/31
Áp dụng công thức ta có
(
)
( )
−
= = = =
++

 
 
uu
dd uu
uu
12
12 1 2
12
.
1
1
cos , cos ,
2
11.11
.
.
( )
⇒=°dd
12
, 60
.
Câu 18. Cho đường thẳng
xyz
:
1 21
∆
= =
−
và mặt phẳng (P):
x yz511240+ + −=
. Góc giữa đường
thẳng
∆
và mặt phẳng (P) là:
A.
60°
. B.
30−°
. C.
30°
. D.
60−°
.
Hướng dẫn giải
Gọi
un;

lần lượt là vectơ chỉ phương, pháp tuyến của đường thẳng
∆
và mặt phẳng (P).
( ) ( )
=−=

un1; 2; 1 ; 5; 11; 2
Áp dụng công thức ta có
(
)
( )
∆
−+
= = = =
+ + ++



un
P un
un
2 22222
.
1.5 11.2 1.2
1
sin ,( ) cos , .
2
.
5112.121
( )
( )
∆
⇒=°P, 30 .
Câu 19. Cho mặt phẳng
xy z x y z
( ):2 2 1 0;( ): 2 2 3 0
αβ
− + −= + − −=
. Cosin góc giữa mặt phẳng
()
α
và mặt phẳng
()
β
băng:
A.
4
9
B.
−
4
.
9
C.
4
.
33
D.
−
4
.
33
Hướng dẫn giải
Goi
α

n
,
β

n
lân lươt la vectơ phap tuyên cua măt phăng
α
()
va
β
()
.
Ta có
nn(2; 1; 2); (1; 2; 2)
αβ
−−
 
.
Áp dụng công thức:
αβ
αβ
αβ
αβ
−−
= = = =
+− + + +−
 
 
 
nn
nn
nn
2 2222 2
.
2.1 1.2 2.2
4
cos(( ),( )) cos( , ) .
9
.
2 (1) 2.(1 2 (2)
Câu 20. Cho mặt phẳng
Px yz( ):3 4 5 2 0+ + +=
và đường thẳng d là giao tuyến của hai mặt phẳng
xy xz
( ): 2 1 0;( ): 2 3 0
αβ
− += − −=
. Gọi
ϕ
là góc giữa đường thẳng d và mặt phẳng (P).
Khi đó:
A.
60°
. B.
45°
. C.
30°
. D.
90°
.
Hướng dẫn giải
Đường thẳng d có phương trình:
xt
y t tR
zt
2
1
,
2
3
2
=
=+∈
=−+
. Suy ra VTCP cua d la
d
u (2;1;1)

Ta có
( )
( )
++
= = = =
++ + +



d
d
d
un
dP u n
un
2222 2 2
.
2.3 1.4 1.5
3
sin ,( ) cos ,
2
.
2 1 1. 3 4 5
.
dP( ,( )) 60⇒=°
.
Trang 17/31
Câu 21. Cho mặt phẳng
xyz( ):3 2 2 5 0
α
− + −=
. Điểm A(1; – 2; 2). Có bao nhiêu mặt phẳng đi qua
A và tạo với mặt phẳng
()
α
một góc
45 .°
A. Vô số. B. 1. C. 2. D. 4.
Hướng dẫn giải
[Phương pháp tự luận]
Gọi
( )
β

n abc;;
là vectơ pháp tuyến của mặt phẳng
()
β
cần lập.
( )
( )
αβ
αβ
αβ
αβ
−+
= = = =
+− + + +
 
 
 
nn
b
nn
nn
b
2 2 22 2 2
.
3.a 2. 2.c
2
cos ( ),( ) cos ,
2
.
3 ( 2) 2 . a c
abc abc
2 222
2(3 2 2 ) 17( )⇒ −+ = ++
Phương trình trên có vô số nghiệm.
Suy ra có vô số vectơ
n abc(; ; )
β

là vec tơ pháp tuyến của
()
β
. Suy ra có vô số mặt phẳng
()
β
thoa mãn điều kiện bài toán
[Phương pháp trắc nghiệm]
Dựng hình.
Giả sử tồn tại mặt phẳng
()
β
thoa mãn điều kiện bài toán. (Đi qua A và tạo với mặt phẳng
()
α
một góc
45°
). Gọi
∆
là đường thẳng đi qua A và vuông góc với mặt phẳng
()
α
. Sử dụng phép
quay theo trục
∆
với mặt phẳng
()
β
. Ta được vô số mặt phẳng
( ')
β
thoa mãn điều kiện bài
toán.
Câu 22. Hai mặt phẳng nào dưới đây tạo với nhau một góc
60°
A.
Px yz
( ): 2 11 5 3 0+ − +=
và
Qx yz( ): 2 2 0+ −−=
.
B.
Px yz
( ): 2 11 5 3 0+ − +=
và
Q x yz( ): 2 5 0−+ +−=
.
C.
Px yz( ): 2 11 5 21 0− +−=
và
Q xyz( ):2 2 0
++−=
.
D.
Pxy z( ): 2 5 11 6 0
− + −=
và
Q x yz( ): 2 5 0−+ +−=
.
Hướng dẫn giải
Áp dụng công thức tính góc giữa hai mặt phẳng.
(
)
= = °=
 
 
PQ
PQ
nn
PQ
nn
.
1
cos ( ),( ) cos60
2
.
Xác định các vectơ pháp tuyến của mặt phẳng (P) và (Q). Thay các giá trị vào biểu thức để tìm
giá trị đúng.
Dùng chức năng CALC trong máy tính bỏ túi để hỗ trợ việc tính toán nhanh nhất.
Câu 23. Cho vectơ
u vm(1; 1; 2), (1; 0; )−

. Tìm m để góc giữa hai vectơ
uv,

có số đo bằng
45°
.
Một học sinh giải như sau:
Bước 1: Tính
( )
m
uv
m
2
12
cos ,
6. 1
−
=
+

Bước 2: Góc giữa
uv
,

có số đo bằng
45°
nên
m
m
2
12 1
2
6. 1
−
=
+
mm
2
1 2 3( 1)⇔− = +
(*)
Bước 3: Phương trình
mm
22
(*) (1 2 ) 3( 1)⇔− = +
Trang 18/31
m
mm
m
2
26
4 20
2 6.
= −
⇔ − −=⇔
= +
Bài giải đúng hay sai? Nếu sai thì sai ở bước nào?
A. Sai ở bước 3. B. Sai ở bước 2. C. Sai ở bước 1. D. Đúng.
Hướng dẫn giải
Phương trình (*) chỉ bình phương được hai vế khi biến đổi tương đương nếu thỏa mãn
m12 0−≥
. Bài toán đã thiếu điều kiện để bình phương dẫn đến sai nghiệm
m
26
= +
.
Câu 24. Cho hai điểm
A
(1; 1; 1); B(2; 2; 4)−−
. Có bao nhiêu mặt phẳng chứa A, Bvà tạo với mặt phẳng
x yz
( ): 2 7 0
α
− +−=
một góc
60°
.
A. 1. B. 4. C. 2. D. Vô số.
Hướng dẫn giải
[Phương pháp tự luận]
AB n
(1; 1; 3), (1; 2; 1)
α
−−
 
Gọi
n abc
(; ; )
β

là vectơ pháp tuyến của mặt phẳng
()
β
cần lập.
( )
( )
αβ
αβ
αβ
αβ
= =
−+
= =
+− + + +
 
 
 
nn
nn
nn
b
b
2 2 22 2 2
.
cos ( ),( ) cos ,
.
1.a 2. 1.c
1
.
2
1 ( 2) 1 . a c
a bc a b c
2 222
2( 2 ) 3( )
⇒ −+ = ++
(1)
Mặt khác vì mặt phẳng
()
β
chứa A, B nên:
nAB ab c ab c. 0 30 3
β
=⇔−+ =⇔=−
 
Thế vào (1) ta được:
b bc c
22
2 13 11 0−+=
(2)
Phương trình (2) có 2 nghiệm phân biệt. Suy ra có 2 vectơ
( )
β

n abc;;
thoa mãn.
Suy ra có 2 mặt phẳng.
[Phương pháp trắc nghiệm]
Dựng hình
Câu 25. Gọi
α
là góc giữa hai đường thẳng AB, CD. Khẳng định nào sau đây là khẳng định đúng:
A.
α
=
 
 
AB CD
AB CD
.
cos .
.
B.
α
=
 
 
AB CD
AB CD
.
cos .
.
C.
α
=


 
 
AB CD
AB CD
.
cos .
,
D.
α


=
 
 
AB CD
AB CD
.
cos .
.
Hướng dẫn giải
Áp dụng công thức ở lý thuyết.
Câu 26. Cho hình lập phương
ABCD A B C D.''' '
có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm các
cạnh
BB CD A D', , ' '
. Góc giữa hai đường thẳng MP và C’N là:
A. 30
o
. B. 120
o
. C. 60
o
. D. 90
o
.
Hướng dẫn giải
Chọn hệ trục tọa độ sao cho
AO(0; 0; 0)≡
Trang 19/31
Suy ra
Ba Ca a D a
( ;0;0); ( ; ;0); (0; ;0)
A a B a a C aaa D aa'(0; 0; ); '( ; 0; ); '( ; ; ); '(0; ; )



aa a
Ma N a P a
; 0; ; ; ; 0 ; 0; ;
22 2
Suy ra

=− = ⇒=


   
aa a
MP a NC a MP NC; ; ; ' ; 0; . ' 0
22 2
MP NC
( , ') 90
⇒=°
Câu 27. Cho hình chóp A.BCD có các cạnh AB, AC, AD đôi một vuông góc.
ABC
∆
cân, cạnh bên bằng
a,
AD a2=
. Cosin góc giữa hai đường thẳng BD và DC là:
A.
.
4
5
B.
− .
2
5
C.
.
4
5
D.
.
1
5
Hướng dẫn giải
[Phương pháp tự luận]
Chọn hệ trục tọa độ sao cho
AO
(0; 0; 0)≡
Suy ra
Ba C a D a( ; 0; 0); (0; ; 0); (0; 0; 2 )
Ta có
DB a a DC a a( ; 0; 2 ); (0; ; 2 )−−
 
= = =
 
 
 
DB DC
DB DC DB DC
DB DC
.
4
cos( , ) cos( ; ) .
5
.
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2, AC =
5
.
SAC
∆
vuông cân
tại A. K là trung điểm của cạnh SD. Hãy xác định cosin góc giữa đường thẳng CK và AB?
A.
4
.
17
B.
2
.
11
C.
4
.
22
D.
2
.
22
Hướng dẫn giải
Vì ABCD là hình chữ nhật nên
= −=
AD AC CD
22
1
Chọn hệ trục tọa độ sao cho
AO
(0; 0; 0)≡
Suy ra
BCD(0; 2; 0); (1; 2; 0); (1; 0; 0)
(
)




SK
15
0; 0; 5 ; ; 0;
22
Suy ra
( )

−−



 
CK AB
15
; 2; ; 0; 2; 0
22
( )
( )
= = =
 
 
 
CK AB
CK AB CK AB
CK AB
.
4
cos , cos ; .
22
.
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm điểm
−−A( 3; 4; 5);
B(2; 7; 7);
C(3; 5; 8);
−D( 2; 6; 1)
. Cặp đường thẳng nào tạo với nhau một góc
60°
?
A. DB và AC. B. AC và CD. C. AB và CB. D.CB và CA.
Hướng dẫn giải
Tính tọa độ các vectơ sau đó thay vào công thức:
=
 
dd
dd u u
'
cos( , ') cos( ,
để kiểm tra.
Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào dưới đây đi qua A(2; 1; – 1) tạo với trục
Oz một góc
30°
?
C
D
A
B
S
z
x
y
K
Trang 20/31
A.
xyz
2( 2) ( 1) ( 2) 3 0.− + − − − −=
B.
x yz
( 2) 2( 1) ( 1) 2 0.
− + − − + −=
C.
xyz2( 2) ( 1) ( 2) 0.
−+ −−− =
D.
xyz2( 2) ( 1) ( 1) 2 0.
−+ −−−−=
Hướng dẫn giải
Gọi phương trình mặt phẳng
()
α
cần lập có dạng
Ax By Cz nA BC( 2) ( 1) ( 1) 0; ( ; ; )− + −+ + =
Oz có vectơ chỉ phương là
k(0; 0; 1)
.
Áp dụng công thức
nk
Oz
nk
.
sin(( ), ) sin30
.
α
= = °

 
Sau khi tìm được các vectơ pháp tuyến thỏa mãn, thay giá trị của A vào để viết phương trình
mặt phẳng.
Câu 31. Cho mặt phẳng
Px y z
( ):3 4 5 8 0
+ + +=
. Đường thẳng d là giao tuyến của hai mặt phẳng
xy xz( ): 2 1 0;( ): 2 3 0
αβ
− += − −=
. Góc giữa d và (P) là:
A.
°120 .
B.
°60 .
C.
°150 .
D.
°
30 .
Hướng dẫn giải
Ta có
P
n
(3; 4; 5)

d
n nn, (2;1;1)
αβ

= =

  
Áp dụng công thức
Pd
Pd
nu
Pd
nu
.
3
sin(( ), )
2
.
= =


.
Câu 32. Gọi
α
là góc giữa hai vectơ
AB CD
,
 
. Khẳng định nào sau đây là đúng:
A.
AB CD
AB CD
.
cos
.
α


=
 
 
. B.
α
=
 
 
AB CD
AB CD
.
cos .
.
C.
α
=
 
 
AB CD
AB CD
.
sin .
,
D.
AB DC
AB DC
.
cos
.
α
=
 
 
Hướng dẫn giải
Áp dụng công thức ở lý thuyết.
Câu 33. Cho ba mặt phẳng
P xy z Qxyz Rx y z( ):2 2 3 0;( ): 2 1;( ): 2 2 2 0−+ += −−−= + + −=
.
Gọi
123
;;
ααα
lần lượt là góc giữa hai mặt phẳng (P) và (Q), (Q) và (R), (R) và (P). Khẳng định
nào sau đây là khẳng định đúng.
A.
ααα
>>
1 32
.
B.
α αα
>>
2 31
.
C.
α αα
>>
3 21
.
D.
ααα
>>
1 23
.
Hướng dẫn giải
Áp dụng công thức tính góc giữa hai mặt phẳng. Sử dụng máy tính bỏ túi để tính góc rồi so
sánh các giá trị đó với nhau.
VẬN DỤNG
Câu 34. Trong không gian với hệ tọa độOxyz, cho mặt phẳng
( )
:22 0x y zm
α
+ + +=
vàđiểm
( )
1;1; 1
A
.
Khi đó
m
nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng
( )
α
bằng 1?
A.
−
2. B.
−
8. C.
−
2 hoặc
8−
. D. 3.
Hướng dẫn giải:
( )
( )
53 2
5
,1
53 8
3
mm
m
dA
mm
α
+= =−
+

==⇔⇔

+=− =−

Trang 21/31
Câu 35. Trong không gian với hệ tọa độOxyz, mặt phẳng
( )
α
cắt các trục
,,Ox Oy Oz
lần lượt tại 3
điểm
( )
2; 0; 0A −
,
( )
0; 3; 0B
,
( )
0; 0; 4
C
. Khi đó khoảng cách từ gốc tọa độ
O
đến mặt phẳng
( )
ABC
là
A.
61
.
12
B.4. C.
12 61
.
61
D.3.
Hướng dẫn giải
Cách 1:
( )
: 1 6 4 3 12 0
234
x yz
xyz
α
++=⇔ − − + =
−
;
( )
( )
12 61
,
61
d O ABC =
Cách 2: Tứ diện
OABC
có
,,OA OB OC
đôi một vuông góc, khi
đó
( )
( )
( )
( )
22 2
2
1 1 1 1 61 12 61
,
144 61
,
d O ABC
OA OB OC
d O ABC
=++ =⇒ =
Câu 36. Trong không gian với hệ tọa độ
0
2 2 20
y
xy z
=
−− −=
Oxyz
cho điểm
( )
1;0;0M
và
( )
0; 0; 1N −
,
mặt phẳng
( )
P
qua điểm
,MN
và tạo với mặt phẳng
(
)
: 40Q xy
−−=
môt góc băng
O
45
.
Phương trình mặt phẳng
( )
P
là
A.
0
2 2 20
y
xy z
=
−− −=
. B.
0
2 2 20
y
xy z
=
−− + =
.
C.
2 2 20
2 2 20
xy z
xy z
−− +=
−− −=
. D.
2 2 20
.
2 2 20
xz
xz
− +=
− −=
Hướng dẫn giải
Gọi vectơ pháp tuyến của mp
( )
P
va
( )
Q
lân lươt là
(
)
;;
P
n abc

( )
222
0
abc++≠
,
Q
n

( ) ( ) ( ) ( )
qua 1;0;0 : 1 0P M P a x by cz⇒ −+ + =
(
)
P
qua
( )
0; 0; 1
N −
0ac⇒+=
( )
P
hợp với
(
)
Q
góc
O
45
( )
O
22
0
1
, 45
2
2
22
PQ
a
ab
cos n n cos
ab
ab
=
−
⇒=⇔ =⇔
= −
+
 
Với
00ac=⇒=
chọn
1b =
phương trình
( )
:0Py=
Với
2ab= −
chọn
12ba=−⇒ =
phương trình mặt phẳng
( )
:2 2 2 0P xy z
−− −=
.
Câu 37. Trong không gian
Oxyz
, cho điểm
( )
2; 0; 1A −
, đường thẳng
d
qua điểm
A
và tạo với trục
Oy
góc
O
45
. Phương trình đường thẳng
d
là
A.
21
21
5
21
21
5
x yz
x yz
+−
= =
−
+−
= =
−
−
. B.
21
21
5
21
21
5
x yz
x yz
−+
= =
−
−+
= =
−
−
C.
21
21
5
21
21
5
x yz
x yz
+−
= =
−
−+
= =
−
D.
21
21
5
21
21
5
x yz
x yz
+−
= =
−
−
−+
= =
−
Hướng dẫn giải
Trang 22/31
Cách 1: Điểm
( )
0; ; 0M m Oy∈
,
( )
0; 1; 0j
là vectơ chỉ phương của trục
.
Oy
,
(
)
2; ; 1AM m−−

( )
O
2
1
cos , cos 45 5
2
5
m
AM j m
m
= ⇔ = ⇔=±
+

nên có 2 đường
thẳng:
2 12 1
;
2 12 1
55
x yz x y z+ −+ −
= = = =
−−
−
Cách 2:
(
)
( )
11
1
2; 5; 1 cos ,
2
u uj−⇒ =
 
;
( )
( )
22
1
2; 5; 1 cos ,
2
u uj− −⇒ =
 
Đường thẳng d đi qua điểm
( )
2; 0;1A −
nên chọn đáp án A.
Câu 38. Trong không gian
Oxyz
cho mặt phẳng
( )
: 30Pxyz++−=
và mặt
phẳng
( )
: 10Qxyz
− +−=
. Khi đó mặt phẳng
( )
R
vuông góc với mặt phẳng
( )
P
và
( )
Q
sao
cho khoảng cách từ
O
đến mặt phẳng
( )
R
bằng
2
, có phương trình là
A.
2 2 22 0−− =xz
. B.
22 0xz−− =
.
C.
22 0xz−+ =
. D.
22 0
22 0
xz
xz
−+ =
−− =
.
Hướng dẫn:
( )
( ) ( )
1;1;1 , 1; 1; 1 , 2; 0; 2
P Q PQ
n n nn

−⇒ = −

   
Mặt phẳng
( ) ( )
( )
42
:2 2 0 , 2
8
42
D
D
R x z D dO R
D
=
−+=⇒ = =⇒
= −
Vậy phương trình mp
(
)
: 22 0; 22 0
Rxz xz−+ = −− =
Câu 39. Tập hợp các điểm
( )
;;
M xyz
trong không gian
Oxyz
cách đều hai mặt phẳng
(
)
: 2 30
Pxy z+− −=
và
( )
: 2 50
Qxy z
+− +=
thoả mãn:
A.
2 10xy z
+ − +=
. B.
2 40xy z+− +=
.
C.
2 20xy z+− +=
. D.
2 40xy z+− −=
.
Hướng dẫn:
( )
;;M xyz
. Ta có
( )
( )
( )
( )
23 25
,,
66
xy z xy z
dM P dM Q
+− − +− +
=⇔=
2 3 2 5 2 10xy z xy z xy z⇔ +− −= +− +⇔+− +=
Câu 40. Tập hợp các điểm
( )
;;
M xyz
trong không gian
Oxyz
cách đều hai mặt phẳng
( )
: 2 2 70Px y z− − −=
và mặt phẳng
( )
:2 2 1 0Q xy z+ + +=
thoả mãn:
A.
3 4 8 0.xyz+ + +=
B.
3 4 80
3 60
+ + +=
−−=
xyz
xy
.
C.
3 6 0.xy
−−=
D.
3 3 4 8 0.+ + +=xyz
Hướng dẫn giải
Cho điểm
( )
;; ,M xyz
( )
( )
( )
( )
2 27 2 21
,,
33
x y z xy z
dM P dM Q
− − − ++ +
=⇔=
3 4 80
3 60
xyz
xy
+ + +=
⇔
−−=
.
Trang 23/31
Câu 41. Trong không gian
Oxyz
cho điêm
M
thuôc truc Oxcách đều hai mặt phẳng
( )
: 2 30Pxy z+− −=
và
( )
Oyz
.Khitọa độ điểm
M
là
A.
3
;0;0
16


+

và
3
;0;0 .
61


−

B.
3
;0;0
16


+

và
3
;0;0 .
16


−

C.
61
;0;0
3

−



và
61
;0;0 .
3

+



D.
16
;0;0
3

+



và
16
;0;0 .
3

−



Hướng dẫn giải: Điểm
(
)
;0;0M m Ox∈
;
( )
( )
( )
( )
3
,,
6
m
dM P dM P m
−
= ⇔=
3
36
16
3
36
16
m
mm
mm
m
=
−=
+
⇔⇔
−=−
=
−
Câu 42. Trong không gian
Oxyz
cho điểm
( )
3; 2; 4A −
và đường thẳng
512
:
23 2
x yz
d
− −−
= =
−
.
Điểm
M
thuộc đường thẳng
d
sao cho
M
cách
A
một khoảng bằng
17
. Tọa độ điểm
M
là
A.
( )
5; 1; 2
và
( )
6; 9; 2
. B.
( )
5; 1; 2
và
( )
1;8;4.−−−
C.
(
)
5; 1; 2−
và
( )
1; 5; 6 .−
D.
( )
5; 1; 2
và
(
)
1; 5; 6 .−
Hướng dẫn giải
Cách 1:
( )
52;13;22M t t td+ + −∈
;
( )
2 2 ;3 3 ; 2 2
AM m m m+ + −−

( )
( )
( )
2
5; 1; 2
0
17 17 1 17
2
1; 5; 6
M
m
AM m
m
M
=
⇒ =⇔ +=⇔ ⇒
= −
−
Cách 2: Kiểm tra các điểm thuộc đường thẳng
d
có 2 cặp điểm trong đáp án B và C
thuộcđường thẳng
d
. Dùng công thức tính độ dài
AM
suy ra đáp án C thỏa mãn.
Câu 43. Trong không gian
Oxyz
cho tứ diện
ABCD
có các đỉnh
( )
1; 2; 1A
,
( )
2; 1; 3B −
,
( )
2; 1; 1C −
và
( )
0; 3;1D
. Phương trình mặt phẳng
( )
P
đi qua 2 điểm
,AB
sao cho khoảng cách từ
C
đến
( )
P
bằng khoảng cách từ
D
đến
( )
P
la
A.
4 2 7 10
.
2 3 50
x yz
xz
− + −=
+ −=
B.
2 3 5 0.xz
+ −=
C.
4 2 7 15 0.xyz+ +−=
D.
4 2 7 15 0
.
2 3 50
xyz
xz
+ +−=
+ −=
Hướng dẫn giải:
Trường hợp 1:
( )
P
qua
AB
và song song với
CD
, khi đó:
( )
P
có vectơ pháp tuyến là
( )
, 8;4;14AB CD

=−−−

 
và
( )
CP∉
( )
: 4 2 7 15 0.Pxyz⇒ + +−=
Trường hợp 2:
( )
P
qua
AB
cắt
CD
tại trung điểm
I
của đoạn
CD
. Ta
có
( ) ( )
1;1; 1 0; 1; 0I AI⇒−

, vectơ pháp tuyến của
( )
P
là
( )
, 2; 0; 3AB AI

=

 
nên phương trình
( )
:2 3 5 0P xz+ −=
.
VẬN DỤNG CAO
Trang 24/31
Câu 44. Trong không gian với hệ trục toạ độ
,Oxyz
gọi
( )
P
là mặt phẳng chứa đường thẳng
12
:
1 12
xy z
d
−+
= =
−−
và tạo với trục
Oy
góc có số đo lớn nhất. Điểm nào sau đây thuộc
(
)
mp P
?
A.
(
)
3; 0; 4 .E −
B.
( )
3; 0; 2 .M
C.
( )
1;2;1.N −−−
D.
( )
1; 2;1 .F
Hướng dẫn giải:
Gọi
(
)
;; ; 0n abc n≠

là VTPT của
(
)
P
;
α
là góc tạo bởi
( )
P
và
Oy
,
α
lớn nhất khi
sin
α
lớn
nhất. Ta có
n
vuông góc với
d
u
nên
( )
2; ;n b cbc+
(
)
22
sin cos ,
254
α
= =
++

b
nj
b c bc
Nếu
0b =
thì
sin = 0.
α
Nếu
0b
≠
thì
2
1
sin
52 6
5
5
c
b
α
=

++


. Khi đó,
sin
α
lớn nhất khi
2
5
c
b
= −
⇒
chọn
5; 2bc= = −
Vậy, phương trình mp
( )
P
là
5 2 90xyz+ − +=
. Do đó ta có
(
)
NP∈
.
Câu 45. Trong không gian với hệ trục toạ độ
,
Oxyz
cho điểm
( )
( )
0; 1; 2 , 1; 1; 3−−
MN
. Gọi
( )
P
là
mặt phẳng đi qua
, MN
và tạo với mặt phẳng
(
)
:2 2 2 0
Q xy z
−− −=
góc có số đo nhỏ nhất.
Điểm
( )
1; 2; 3A
cách mp
( )
P
một khoảng là
A.
3.
B.
53
.
3
C.
7 11
.
11
D.
43
.
3
Hướng dẫn giải:
( )
P
có VTPT
n
vuông góc với
( )
1; 2;1MN −

nên
( )
2 ;;+n b cbc
.
Gọi
α
là góc tạo bởi
( )
P
và
( )
Q
,
α
nhỏ nhất khi
cos
α
lớn nhất.
Ta có
22
cos
524
b
b c bc
=
++
α
Nếu
0b =
thì
cos = 0.
α
Nếu
0b ≠
thì
2
1
cos
2 13
c
b
=

++


α
. Khi đó,
cos
α
lớn nhất khi
1
c
b
=−⇒
chọn
1; 1bc= = −
Vậy, phương trình mp
( )
P
là
30xyz+−+=
. Do đó
( )
( )
,3dAP =
.
Câu 46. Trong không gian với hệ trục toạ độ
,Oxyz
cho
( )
: 2 2 10Px y z− + −=
và 2 đường thẳng
12
1 9 131
: ;:
116 2 1 2
x yz x y z+ + −−+
∆== ∆==
−
.
Gọi
M
là điểm thuộc đường thẳng
1
∆
,
M
có toạ độ là các số nguyên,
M
cách đều
2
∆
và
( )
.P
Khoảng cách từ điểm
M
đến
( )
mp Oxy
là
A.
3.
B.
2 2.
C.
3 2.
D.
2.
Hướng dẫn giải:
Trang 25/31
C
A
B
H
Gọi
( )
1; ; 6 9 ,Mt t t t− −∈
.
Ta có
( )
( )
(
)
( )
( )
0
2
,
,, ,


∆= ⇔ =
MMu
dM dM P dM P
u

2
11 20
29 88 68
3
t
tt
−
⇔ − +=
với
( )
02
1; 3; 1M − ∈∆
1
1
53
35
t
t
t
t
∈
=
⇔ → =
=
Vậy,
( ) ( )
0; 1; 3 , (Ox ) 3.M dM y−⇒ =
Câu 47. Trong không gian với hệ trục toạ độ
,Oxyz
cho 2 điểm
( ) ( )
1; 5; 0 ; 3; 3; 6AB
và đường thẳng
11
:
2 12
xyz
d
+−
= =
−
. Gọi
C
là điểm trên đường thẳng
d
sao cho diện tích tam giác
ABC
nhỏ
nhất. Khoảng cách giữa 2 điểm
A
và
C
là
A.
29.
B.
29.
C.
33.
D.
7.
Hướng dẫn giải:
Ta có 2 đường thẳng
AB
và
d
chéo nhau.
Gọi
C
là điểm trên
d
và
H
là hình chiếu vuông góc
của
C
trên đường thẳng
AB
.
Vì
1
11
2
ABC
S AB CH CH= ⋅=⋅
nên
ABC
S
nhỏ nhất khi
CH
nhỏ nhất
CH⇔
là đoạn vuông góc chung của 2
đường thẳng
AB
và
d
.
Ta có
( )
1; 0; 2 29⇒=C AC
.
Câu 48. Trong không gian với hệ trục toạ độ Oxyz, cho điểm
( )
10; 2;1A
và đường thẳng
11
:
213
x yz
d
−−
= =
. Gọi
( )
P
là mặt phẳng đi qua điểm
A
, song song với đường thẳng
d
sao
cho khoảng cách giữa
d
và
( )
P
lớn nhất. Khoảng cách từ điểm
( )
1; 2; 3M
−
đến mp
( )
P
là
A.
97 3
.
15
B.
76 790
.
790
C.
2 13
.
13
D.
3 29
.
29
Hướng dẫn giải:
( )
P
là mặt phẳng đi qua điểm
A
và song song với
đường thẳng
d
nên
( )
P
chứa đường thẳng
d
′
đi qua
điểm
A
và song song với đường thẳng
d
.
Gọi
H
là hình chiếu của
A
trên
d
,
K
là hình chiếu của
H
trên
(
)
P
.
Ta có
( )
( )
, d d P HK AH
= ≤
(
AH
không đổi)
⇒
GTLN của
( , ( ))dd P
là
AH
⇒
( )
( )
, dd P
lớn nhất khi
AH
vuông góc với
( )
P
.
Khi đó, nếu gọi
( )
Q
là mặt phẳng chứa
A
và
d
thì
( )
P
vuông góc với
( )
Q
.
P
d'
d
H
K
A
Trang 26/31
( )
(
)
( )
( )
, 98;14; 70
97 3
:7 5 77 0 , .
15
P dQ
n un
P x y z dM P

⇒= = −

⇒ +− − =⇒ =

Câu 49. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( )
2;5;3A
và đường thẳng
12
:
212
x yz
d
−−
= =
. Gọi
(
)
P
là mặt phẳng chứa đường thẳng
d
sao cho khoảng cách từ
A
đến
( )
P
lớn nhất. Tính khoảng cách từ điểm
( )
1; 2; 1M −
đến mặt phẳng
( )
P
.
A.
11 18
.
18
B.
3 2.
C.
11
.
18
D.
4
.
3
Hướng dẫn giải:
Gọi
H
là hình chiếu của
A
trên
d
;
K
là hình chiếu
của
A
trên
(
)
P
.
Ta có
(
)
( )
, d A P AK AH= ≤
(Không đổi)
⇒
GTLN của
( , ( ))dd P
là
AH
( )
( )
, dAP
lớn nhất khi
KH≡
.
Ta có
(
)
3;1; 4H
,
( )
P
qua
H
và
⊥
AH
( )
: 4 30Px yz⇒ − +−=
Vậy
( )
( )
11 18
,
18
dM P =
.
Câu 50. Trong không gian với hệ trục toạ độ
,Oxyz
cho mặt phẳng
( )
: 20Pxyz+−+=
và hai đường
thẳng
1
:
22
xt
d yt
zt
= +
=
= +
;
3
': 1 .
12
xt
dy t
zt
′
= −
′
= +
′
= −
Biết rằng có 2 đường thẳng có các đặc điểm: song song với
( )
P
; cắt
, dd
′
và tạo với
d
góc
O
30 .
Tính cosin góc tạo bởi hai đường thẳng đó.
A.
1
.
5
B.
1
.
2
C.
2
.
3
D.
1
.
2
Hướng dẫn giải:
Goi
∆
la đương thăng cân tim,
P
n

la VTPT cua măt phăng
( )
P
.
Gọi
( )
1 ; ;2 2M tt t++
là giao điểm của
∆
và
d
;
( )
3 ;1 ;1 2M tt t
′ ′′ ′
−+−
là giao điểm của
∆
và
'd
Ta có:
( )
' 2 ;1 ; 1 2 2MM tt tt t t
′′ ′
− − + − −− −

MM
′
//
( )
( )
( )
2 4 ; 1 ;3 2
P
MP
P t MM t t t
MM n
∉
′′
⇔ ⇔ =− ⇒ − −− −
′
⊥

 
Ta có
(
)
O
2
4
69
3
cos30 cos ,
1
2
36 108 156
d
t
t
MM u
t
tt
=
−+
′
= ⇔= ⇔
= −
−+

P
d'
A
K
H
Trang 27/31
Vậy, có 2 đường thẳng thoả mãn là
12
5
: 4 ;: 1
10
x xt
yt y
z t zt
′
= =


∆ =+∆ =−


′
=+=

.
Khi đó,
( )
12
1
cos , .
2
∆∆ =
Câu 51. Trong không gian với hệ trục toạ độ
,Oxyz
cho 3 điểm
( ) ( ) ( )
1; 0;1 ; 3; 2; 0 ; 1; 2; 2AB C−−
. Gọi
( )
P
là mặt phẳng đi qua
A
sao cho tổng khoảng cách từ
B
và
C
đến
( )
P
lớn nhất biết rằng
( )
P
không cắt đoạn
BC
. Khi đó, điểm nào sau đây thuộc mặt phẳng
( )
P
?
A.
(
)
2; 0; 3 .G
−
B.
( )
3; 0; 2 .F
−
C.
( )
1; 3;1 .E
D.
(
)
0; 3;1H
Hướng dẫn giải:
Gọi
I
là trung điểm đoạn
BC
; các điểm
, , BCI
′′′
lần lượt là hình chiếu của
, ,BC I
trên
( )
P
.
Ta có tứ giác
BCC B
′′
là hình thang và
II
′
là đường
trung bình.
( )
( )
( )
( )
, , 2 .d B P d C P BB CC II
′
⇒ + =+=
′′
Mà
II IA
′
≤
(với
IA
không đổi)
Do vậy,
( )
( )
( )
( )
, , dB P dC P+
lớn nhất khi
IA
′
≡
( )
P
⇒
đi qua
A
và vuông goc
IA

với
( )
2;0; 1 .I −
( ) (
) ( )
: 2 1 0 1; 3;1 .Pxz E P⇒ −+ −= ⇒ ∈
Câu 52. Trong không gian với hệ trục toạ độ
,Oxyz
cho các điểm
( )
( ) ( )
1; 0; 0 , 0; ; 0 , 0; 0;
A Bb C c
trong
đó
,
bc
dương và mặt phẳng
(
)
: 10Pyz−+=
. Biết rằng
( )
mp ABC
vuông góc với
( )
mp P
và
( )
( )
1
,
3
d O ABC =
, mệnh đề nào sau đây đúng?
A.
1.bc+=
B.
2 1.bc
+=
C.
3 1.bc−=
D.
3 3.bc
+=
Hướng dẫn giải:
Ta có phương trình mp(
)ABC
là
1
1
xyz
bc
++=
( ) ( )
11
0 (1)ABC P b c
bc
⊥ ⇒ − =⇒=
Ta có
(
)
( )
22
22
1 1 1 11
, 8(2)
33
11
1
d O ABC
bc
bc
=⇔ =⇔+=
++
Từ (1) và (2)
1
1
2
bc bc⇒== ⇒+=
.
Câu 53. Trong không gian với hệ trục toạ độ
,
Oxyz
cho 3 điểm
( ) ( ) ( )
1; 2; 3 ; 0; 1; 1 ; 1; 0; 2A BC−
.
Điểm
( )
: 20M Pxyz∈ +++=
sao cho giá trị của biểu thức
222
23T MA MB MC=++
nhỏ nhất.
Khi đó, điểm
M
cách
( )
:2 2 3 0Q xy z−− +=
một khoảng băng
A.
121
.
54
B.
24.
C.
25
.
3
D.
101
.
54
P
B
C
B'
C'
A
I'
I
Trang 28/31
Hướng dẫn giải:
Gọi
( )
;;M xyz
. Ta có
2 22
6 6 6 8 8 6 31
T x y z xyz
= + + −−++
2 22
2 2 1 145
6
3 3 26
Tx y z


⇒= − + − + +





2
145
6
6
T MI
⇒= +
với
22 1
;;
33 2
I

−


T⇒
nhỏ nhất khi
MI
nhỏ nhất
M⇒
là hình chiếu vuông góc của
I
trên
( )
P
5 5 13
;;
18 18 9
M

⇒−−−


.
BÀI TẬP TỔNG HỢP
Câu 54. Cho mặt phẳng
xy z x y z( ): 2 1 0;( ):5 2 11 3 0
αβ
+ − −= + + −=
. Góc giữa mặt phẳng
()
α
và mặt phẳng
()
β
băng
A.
120 .°
B.
30 .°
C.
150 .°
D.
60 .°
Câu 55. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) có phương trình
xy
3 0.+−=
Điểm H(2; 1; 2) là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa
hai mặt phẳng (P) và (Q) bằng
A.
45 .°
B.
30 .°
C.
60 .°
D.
120 .
°
Câu 56. Cho vectơ
(
)
u v uv
2; 1; ,
3
π
= = =

. Gócgiữa vectơ
v
và vectơ
uv
−

bằng:
A.
60 .
°
B.
30 .
°
C.
90 .
°
D.
45 .°
Câu 57. Trong không gian với hệ trục toạ độ Oxyz, cho đường thẳng
x yz
d
3 11
:,
951
− +−
= =
xyz
x yz
2 3 3 90
:
2 30
− − +=
∆
− ++=
. Góc giữa đường thẳng d và đường thẳng
∆
bằng
A.
90 .°
B.
30 .°
C.
0.°
D.
180 .°
Câu 58. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng
xy z( ) : 2 2 10 0;
α
−−−=
đường
thẳng
x yz
d
11 3
:
123
−− +
= =
. Góc giữa đường thẳng d và mặt phẳng
()
α
bẳng
A.
30 .°
B.
90 .°
C.
60 .°
D.
45 .
°
Câu 59. Trong không gian với hệ trục toạ độ Oxyz, phương trình các đường thẳng qua A(3; – 1;1), nằm
trong (P):
– –5 0+=xyz
và hợp với đường thẳngd:
2
122
−
= =
xy z
một góc 45
0
là
A.

=+=+

∆ =−+ ∈ ∆ =−− ∈


= = −

xt x t
y ttR y ttR
z zt
12
3 33
:1,;:12,.
1 15
B.

=+=+

∆ =−+ ∈ ∆ =−+ ∈


= = +

xt x t
y ttR y ttR
z zt
12
3 2 3 15
:12,;:138,.
1 1 23
C.

=+=+

∆ =−+ ∈ ∆ =−− ∈


= = −

xt x t
y ttR y ttR
z zt
12
3 3 15
:1,;:18,.
1 1 23
Trang 29/31
D.

=−=+

∆ =−− ∈ ∆ =−− ∈


=+=−

xt x t
y ttR y ttR
zt z t
12
3 3 15
:1,;:18,.
1 1 23
Câu 60. Cho hình lập phương
ABCD A B C D.''' '
có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm các
cạnh
A B BC DD
' ', , '
. Góc giữa đường thẳng AC’ và mặt phẳng (MNP) là
A.
30 .
°
B.
°
120 .
C.
60 .°
D.
90 .
°
Câu 61. Trong không gian với hệ trục toạ độ
,Oxyz
gọi(P) là mặt phẳng chứa đường thẳng
12
:2
3
xt
dy t
zt
= +
= −
=
và tạo với trục
Ox
góc có số đo lớn nhất.Khi đó, khoảng cách từ điểm
( )
1; 4; 2A
−
đến
( )
mp P
là
A.
12 35
.
35
B.
43
.
3
C.
20 6
.
9
D.
26
.
3
Câu 62. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( ) ( )
2;1; 12 , 3; 0; 2MN−
. Gọi
( )
P
là mặt
phẳng đi qua
, MN
và tạo với mặt phẳng
( )
:2 2 3 4 0Qx yz+ − +=
góc có số đo nhỏ nhất. Điểm
( )
3;1; 0A
cách mp
( )
P
một khoảng là
A.
6 13
.
13
B.
22
.
11
C.
6
.
2
D.
1
.
22
Câu 63. Trong không gian với hệ trục toạ độ
,Oxyz
cho
( )
: 70Pxyz+−−=
và hai đường thẳng
12
112 2 34
: ;:
111 2 3 5
xyz x yz−−− − −+
∆==∆ ==
−
.
Gọi
M
là điểm thuộc đường thẳng
1
∆
,
M
có toạ độ là các số dương,
M
cách đều
2
∆
và
( )
.
P
Khoảng cách từ điểm
M
đến mp(
P
) là
A.
2 3.
B.
2.
C.
7.
D.
2
.
3
Câu 64. Trong không gian với hệ trục toạ độ
,Oxyz
cho 2 điểm
( )
( )
1; 4; 3 ; 1; 0; 5AB−
và đường thẳng
3
: 3 2.
2
xt
dy t
z
= −
= +
= −
Gọi
C
là điểm trên đường thẳng
d
sao cho diện tích tam giác
ABC
nhỏ nhất.
Khoảng cách giữa điểm
C
và gốc toạ độ
O
là
A.
6.
B.
14.
C.
14.
D.
6.
Câu 65. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( )
2;5;3A
và đường thẳng
12
:.
212
x yz
d
−−
= =
Gọi
( )
P
là mặt phẳng đi qua điểm
A
, song song với đường thẳng
d
sao
cho khoảng cách giữa
d
và
( )
P
lớn nhất. Khoảng cách từ điểm
( )
2; 0; 3
B −
đến mp
( )
P
là
A.
72
.
3
B.
52
.
3
C.
7.
D.
18
.
18
Trang 30/31
Câu 66. Trong không gian với hệ trục toạ độ
,Oxyz
cho điểm
( )
4; 3; 2A −
và đường thẳng
43
: 2 2.
2
xt
dy t
zt
= +
= +
=−−
Gọi
( )
P
là mặt phẳng chứa đường thẳng
d
sao cho khoảng cách từ
A
đến
( )
P
lớn nhất. Tính
khoảng cách từ điểm
(
)
2; 1; 3B −−
đến mặt phẳng
( )
P
đó.
A.
2 3.
B.
2.
C.
0.
D.
38.
Câu 67. Trong không gian với hệ trục toạ độ
,Oxyz
cho 3 điểm
( ) (
)
( )
1; 1; 2 ; 1; 2; 1 ; 3; 4; 1−− −ABC
. Gọi
( )
P
là mặt phẳng đi qua
A
sao cho tổng khoảng cách từ
B
và
C
đến
( )
P
lớn nhất biết rằng
(P) không cắt đoạn
BC
. Khi đó, điểm nào sau đây thuộc mặt phẳng
( )
P
?
A.
( )
1; 2; 0 .F −
B.
(
)
2; 2;1 .
E
−
C.
(
)
2;1; 3 .
G
−
D.
( )
1; 3;1 .H −
Câu 68. Trong không gian với hệ trục toạ độ
,Oxyz
cho các điểm
( ) ( )
( )
; 0; 0 , 0; 2; 0 , 0; 0;Aa B C c
trong
đó
,
ac
dương và mặt phẳng
( )
:2 3 0P xz−+=
. Biết rằng
( )
mp ABC
vuông góc với
( )
mp P
và
( )
( )
2
,
21
d O ABC =
, mệnh đề nào sau đây đúng?
A.
4 3.
ac+=
B.
2 5.
ac
+=
C.
1.ac−=
D.
4 3.ac
−=
Câu 69. Trong không gian với hệ trục toạ độ
,Oxyz
cho 3 điểm
( ) ( ) ( )
2; 2; 3 ; 1; 1; 3 ; 3; 1; 1− −−
A BC
.
Điểm
( )
: 2 80M Px z∈ + −=
sao cho giá trị của biểu thức
22 2
23T MA MB MC= ++
nhỏ nhất.
Khi đó, điểm
M
cách
( )
: 2 2 60Q xyz−+ − −=
một khoảng băng
A.
2
.
3
B.2. C.
4
.
3
D. 4.
Câu 70. Tinh khoang cach tư điêm H(3; – 1;– 6) đên măt phăng
()
α
:
10
xyz+ −+=
.
A.
83
.
3
B. 9. C.
3 3.
D. 3.
Câu 71. Tinh khoang cach giưa hai măt phăng song song (P):
2 20xy z++ =
va (Q)
2 2 70
xy z++ +=
.
A.
7
.
9
B. 7. C.
7
.
3
D. 2.
Câu 72. Khoang cach tư điêm K(1;2;3) đên măt phăng (Oxz) băng
A. 2. B. 1. C. 3. D. 4.
Câu 73. Tinh khoang cach giưa măt phăng
()
α
:
2 2 40xy z++ +=
va đương thăng d:
15
22
4
xt
yt
zt
= +
= −
= −
.
A.
8
.
3
B. 0. C.
4
.
3
D. 4.
Câu 74. Khoang cach tư giao điêm A cua măt phăng
( ): 3 0Rxyz++−=
vơi truc Oz đên măt phăng
()
α
:
2 2 10xy z+ + +=
băng
A.
7
.
3
B.
5
.
3
C.
4
.
3
D. 0.
Câu 75. Cho hai măt phăng
( ): 2 1 0, ( ):2 0Pxy z Q xyz++ −= ++=
va đương thăng d:
13
2.
1
= −
= +
=−+
xt
yt
zt
Trang 31/31
Goi
( ,( ))dd P
,
( ,( ))dd Q
,
(( ),( ))
dP Q
lân lươt la khoang cach giưa đương thăng d va (P), d va
(Q), (P) va (Q). Trong cac mênh đê sau, tim mênh đê sai:
A.
( ,( )) 0.dd P =
B.
6
( ,( )) .
2
dd Q =
C.
(( ),( )) 0.dP Q=
D.
( ,( )) 0.
dd Q
=
Câu 76. Khoang cach tư điêm
( 2;1; 0)C −
đên măt phăng (Oyz) va đên đương thăng
∆
:
1
4
62
xt
yt
zt
= +
= +
= +
lân
lươt la
1
d
va
2
d
. Chon khăng đinh đung trong cac khăng đinh sau:
B.
1
d
>
2
.
d
B.
1
d
=
2
.d
C.
1
d
0.=
D.
2
d
=1.
Câu 77. Khoang cach tư điêm
(1;1;1)B
đên măt phăng (P) băng 1. Chon khăng đinh đungtrong cac
khăng đinh sau:
A. (P):
2 – 2 6 0.xy z+ +=
B. (P):
– 3 0.++ =xyz
B. (P):
2 2 – 2 0.
xy z++ =
D. (P):
– 3 0++ =xyz
.
Câu 78. Trong không gian
Oxyz
cho mặt phẳng
(
)
:2 2 1 0xy z
α
− + +=
và mặt phẳng
( )
:2 2 5 0xy z
β
−+ +=
. Tập hợp các điểm M cách đều mặt phẳng
( )
α
và
( )
β
là
A.
2 2 3 0.xy z−+ +=
B.
2 2 3 0.
xy z−− +=
C.
2 2 3 0.xy z−+ −=
D.
2 2 3 0.
xy z
++ +=
Câu 79. Trong không gian
Oxyz
cho mặt phẳng
( )
: 2 2 10xyz
α
− + +=
và mặt
phẳng
( )
:2 2 1 0xy z
β
− + +=
. Tập hợp các điểm cách đều mặt phẳng
( )
α
và
( )
β
là
A.
20
.
3 3 4 40
xy
xyz
−+=
+ + +=
B.
20
.
3 3 4 40
xy
xyz
−+=
− + +=
C.
20
.
3 3 4 40
xy
xyz
−+=
− + +=
D.
20
.
3 3 4 40
xy
xyz
++=
− + +=
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

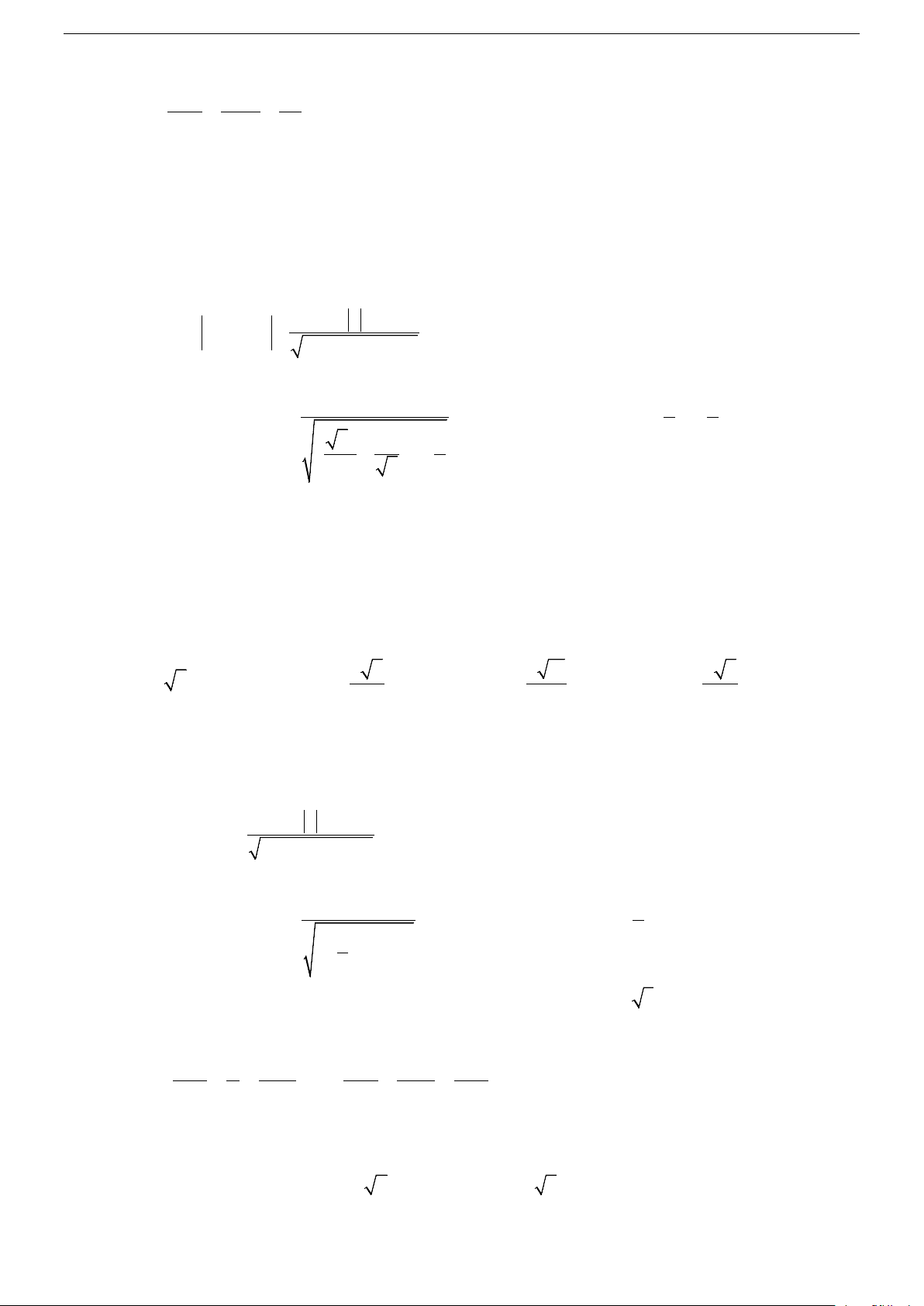
Preview text:


CHỦ ĐỀ 6. GÓC VÀ KHOẢNG CÁCH
A. KIẾN THỨC CƠ BẢN I. GÓC:
1. Góc giữa hai mặt phẳng.
Góc giữa hai mặt phẳng (P): Ax + By + Cz + D = 0 , (Q): ’ A x + ’ B y + C’z + ’ D = 0 được ký
hiệu: 0o ≤ (( ),( )) ≤ 90o P Q
, xác định bởi hệ thức
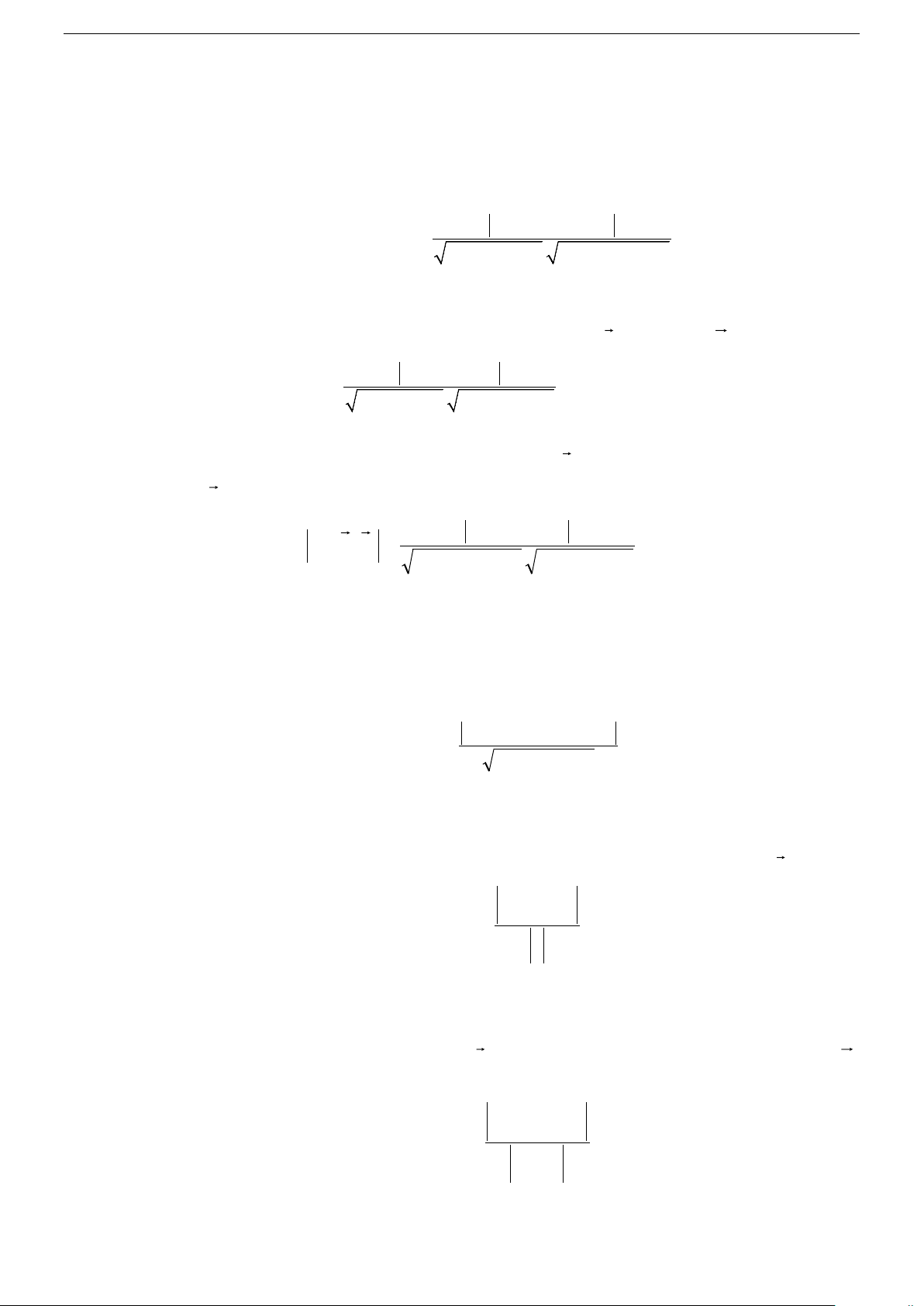
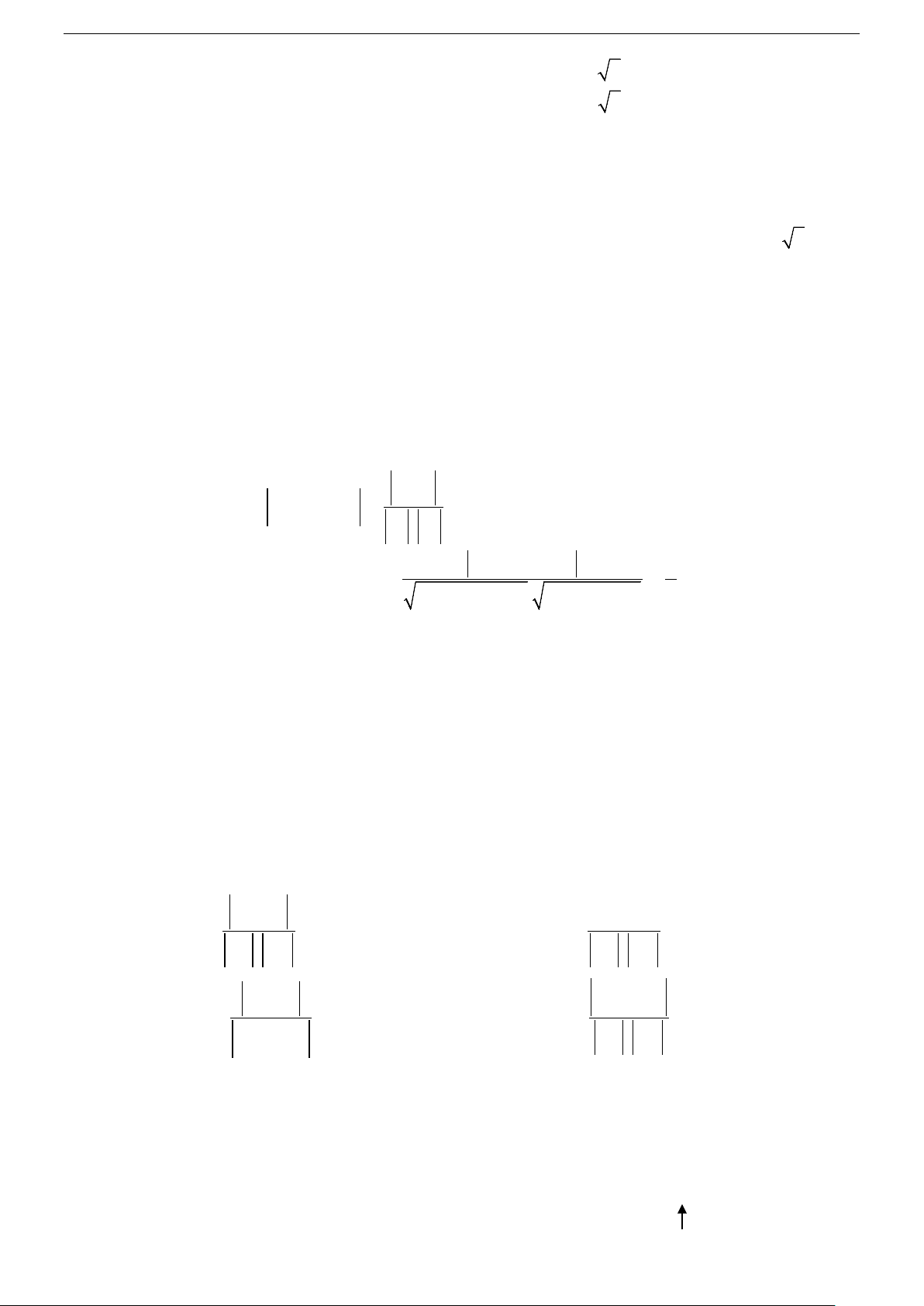
AA' + BB' + CC' cos((P),(Q)) = . 2 2 2 2 2 2
A + B + C . A' + B' + C'
Đặc biệt: (P) ⊥ (Q) ⇔ '
AA +BB'+CC'= . 0
2. Góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng.
a) Góc giữa hai đường thẳng (d) và (d’) có vectơ chỉ phương u = (a; ;
b c) và u' = (a';b';c') là φ
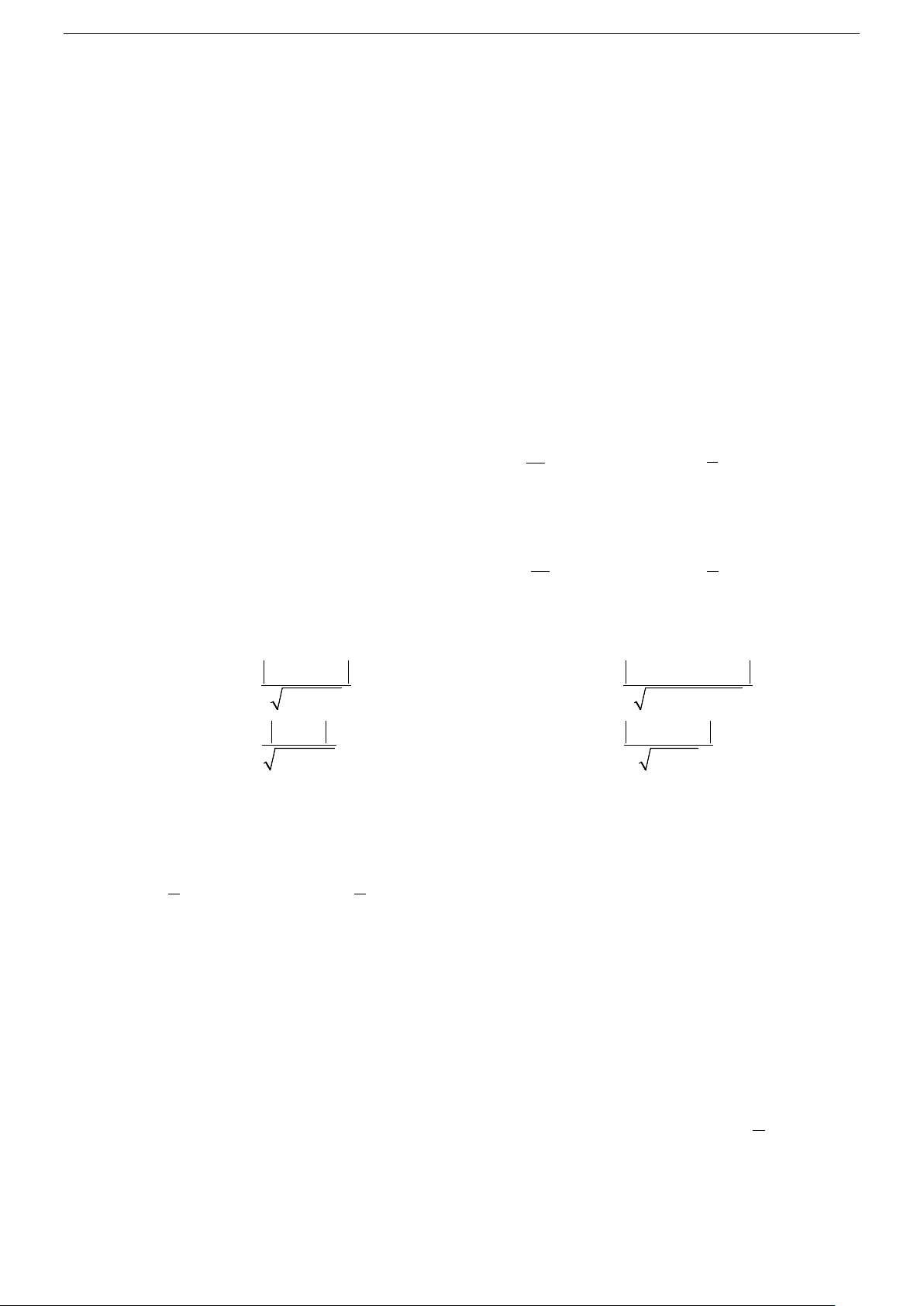
aa '+ bb'+ cc ' cosφ =
(0o ≤ ϕ ≤ 90o). 2 2 2 2 2 2
a + b + c . a ' + b' + c '
Đặc biệt: (d) ⊥ (d') ⇔ aa'+bb'+cc'= . 0
b) Góc giữa đường thẳng d có vectơ chỉ phương u = (a; ;
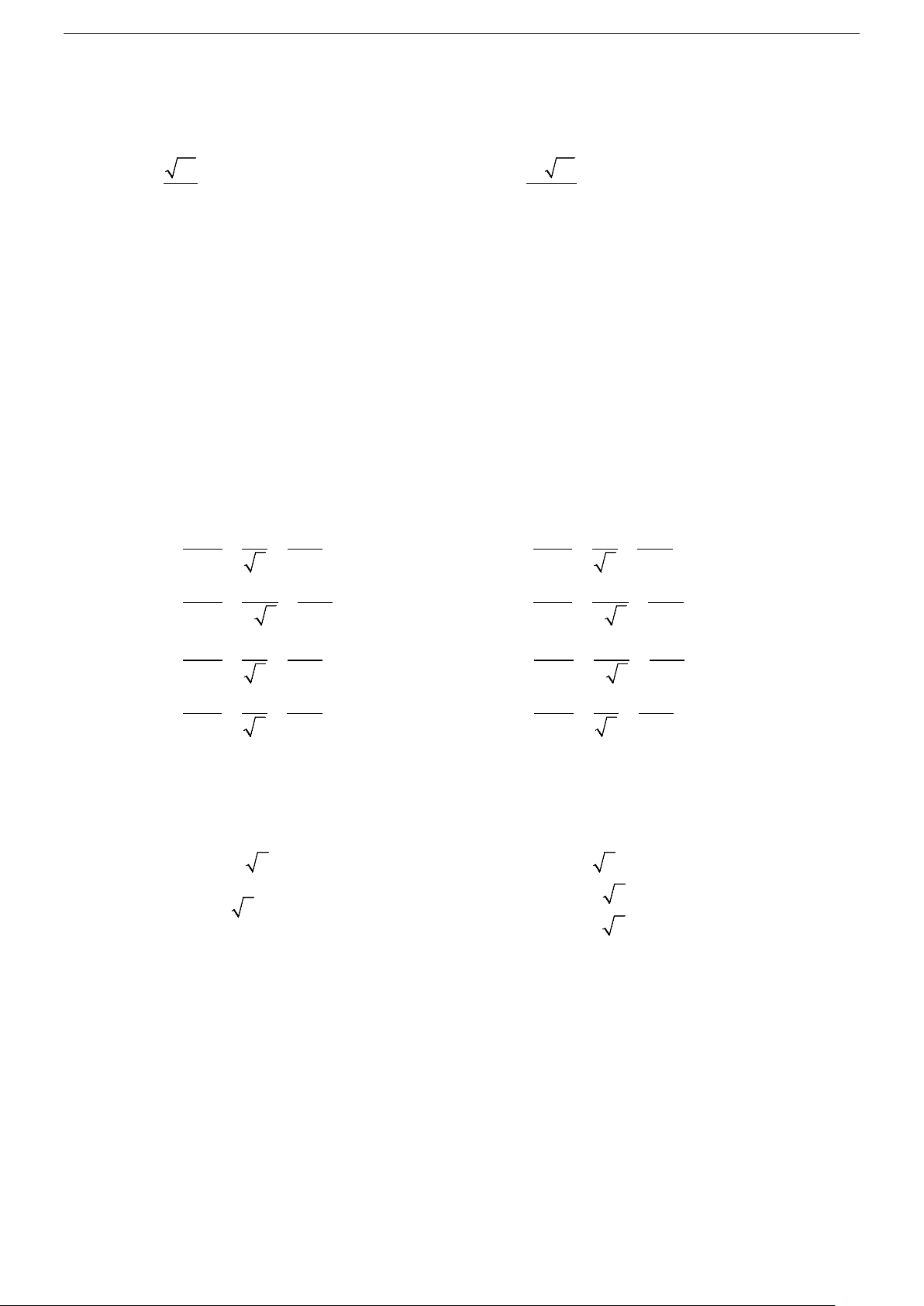
b c) và mp(α) có vectơ pháp tuyến n = ( ; A ; B C). Aa + Bb + Cc sin ϕ = cos(n, u) =
(0o ≤ ϕ ≤ 90o). 2 2 2 2 2 2 A + B + C . a + b + c
Đặc biệt: (d) //(α) hoặc (d) ⊂ (α) ⇔ Aa + Bb + Cc = . 0 II. KHOẢNG CÁCH
1. Khoảng cách từ một điểm đến mặt phẳng, khoảng cách giữa hai mặt phẳng song song.
a) Khoảng cách từ M (x y z đến mặt phẳng có phương trình 0 ; 0; 0 ) (α) Ax + by + Cz + D = 0 là:
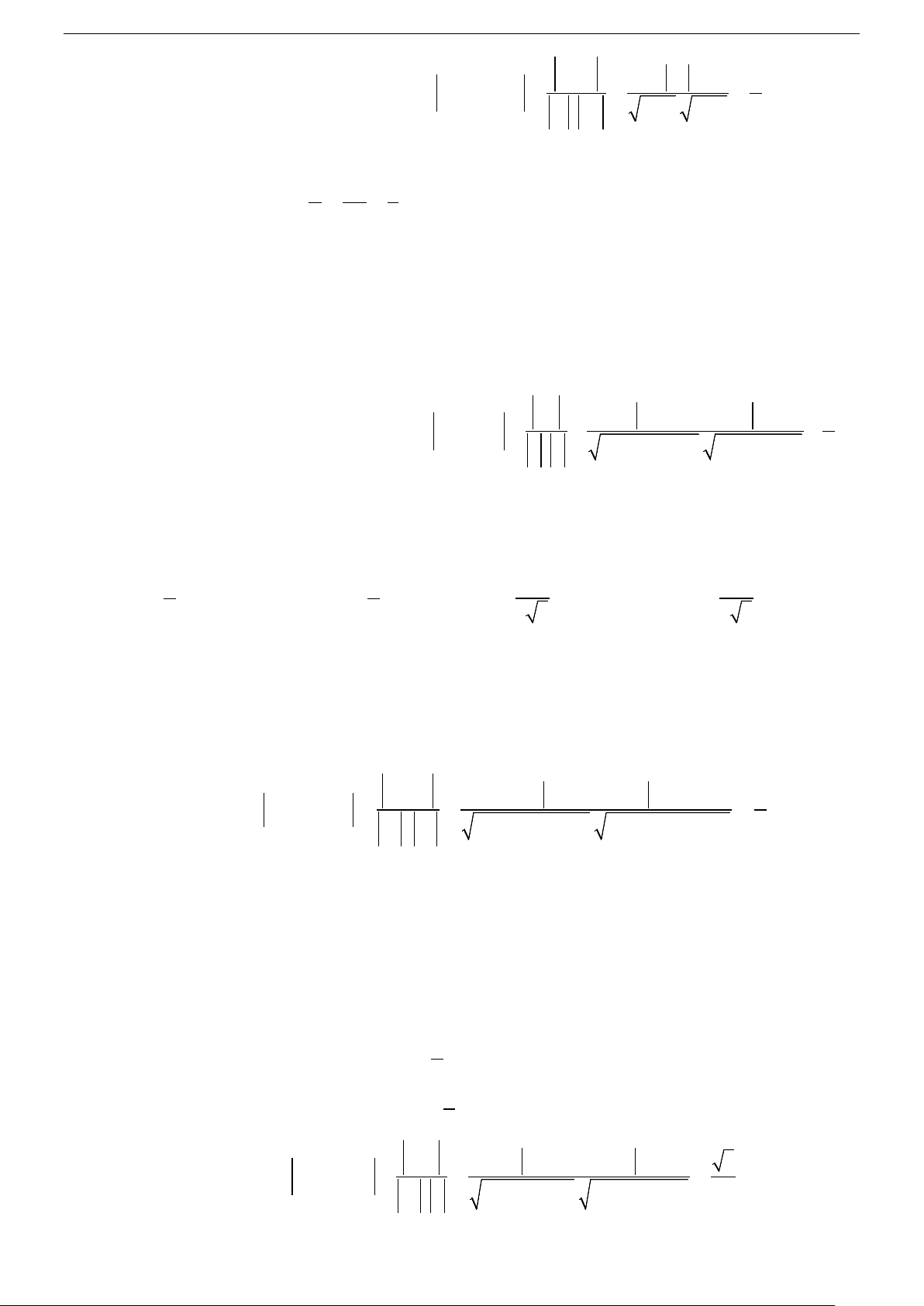
Ax + By + Cz + D 0 0 0 d(M,(P)) = . 2 2 2 A + B + C
b) Khoảng cách giữa hai mp song song là khoảng cách từ một điểm thuộc mặt phẳng này đến mặt phẳng kia.
2. Khoảng cách từ một điểm đến một đường thẳng - khoảng cách giữa hai đường thẳng.
a) Khoảng cách từ điểm M đến một đường thẳng dqua điểm Mocó vectơ chỉ phương u :   M M; ud(M, d 0 )   =  . u
b) Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường
thẳng này đến đường thẳng kia.
c) Khoảng cách giữa hai đường thẳng chéo nhau:
dđi qua điểm M và có vectơ chỉ phương u và d’ đi qua điểm M’ và có vectơ chỉ phương u' là:   
u; u'.M M d(d, d 0 ')   =   . u; u'   Trang 1/31
d) Khoảng cách từ giữa đường thẳng và mặt phẳng song song là khoảng cách từ một điểm
thuộc đường thẳng đến mặt phẳng hoặc khoảng cách từ một điểm thuộc mặt phẳng đến đường thẳng.
B. KỸ NĂNG CƠ BẢN
- Nhớ và vận dụng được công thức tính khoảng cách từ một điểm đến mặt phẳng; biết cách khoảng
cách giữa hai mặt phẳng song song.
- Nhớ và vận dụng được công thức tính khoảng cách từ một điểm đến một đường thẳng; biết cách
tính khoảng cách giữa hai đường thẳng song song; khoảng cách giữa hai đường thẳng chéo nhau;
khoảng cách từ đường thẳng đến mặt phẳng song song.
- Nhớ và vận dụng được công thức góc giữa hai đường thẳng; góc giữa đường thẳng và mặt phẳng;
góc giữa hai mặt phẳng.
- Áp dụngđược góc và khoảng cách vào các bài toán khác.
C. BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong không gian Oxyz, khoảng cách từ điểm A(1; 2; 2) đến mặt phẳng (α) :
x + 2y − 2z − 4 = 0 bằng: 1 A. 3. B. 1. C.13. D. . 3 3
Câu 2. Tính khoảng cách giữa hai mặt phẳng song song (α) : 2x − y − 2z − 4 = 0 và
(β ) : 2x − y − 2z + 2 = 0 . A 10 4 . 2. B. 6. C. . D. . 3 3
Câu 3. Khoảng cách từ điểm M (3; 2; )
1 đến mặt phẳng (P): Ax + Cz + D = 0 , .
AC.D ≠ 0 . Chọn khẳng
định đúngtrong các khẳng định sau:
3A + C + D
A + 2B + 3C + D
A. d(M ,(P)) =
B. d(M ,(P)) = . 2 2 A + C 2 2 2 A + B + C 3A + C
3A + C + D
C. d(M ,(P)) = .
D. d(M ,(P)) = . 2 2 A + C 2 2 3 +1 x =1+ t
Câu 4. Tính khoảng cách giữa mặt phẳng 
(α) : 2x − y − 2z − 4 = 0 và đường thẳng d: y = 2 + 4t . z = t−  A 1 4 . . B. . C. 0. D. 2. 3 3
Câu 5. Khoảng cách từ điểm A(2; 4; 3) đến mặt phẳng (α) : 2x + y + 2z +1 = 0 và (β): x = 0 lần lượt là d( , A (α)) , d( ,
A (β )) . Chọn khẳng định đúng trong các khẳng định sau: A. d ( ,(
A α)) = 3. d ( ,( A β )). B. d ( ,(
A α)) > d ( ,( A β )). C. d ( ,( A α)) = d ( ,( A β )). D. 2. d ( ,( A α)) = d ( ,( A β )).
Câu 6. Tìm tọa độ điểm Mtrên trục Oy sao cho khoảng cách từ điểm M đến mặt phẳng (P):
2x − y + 3z − 4 = 0 nhỏ nhất? A. M (0;2;0). B. M (0;4;0). C. M (0; 4; − 0). D. 4 M 0; ;0  . 3   
Câu 7. Khoảng cách từ điểm M ( 4 − ; 5;
− 6) đến mặt phẳng (Oxy), (Oyz) lần lượt bằng: A. 6 và 4. B. 6 và 5. C. 5 và 4. D. 4 và 6. Trang 2/31
Câu 8. Tính khoảng cách từ điểm A(x ; y ; z đến mặt phẳng (P) : Ax + By + Cz + D = 0 , với 0 0 0 ) . A .
B C.D ≠ 0 . Chọn khẳng định đúngtrong các khẳng định sau:
Ax + By + Cz A. d ( ,
A (P)) = Ax + By + Cz . d A P = 0 0 0 B. ( ,( )) 0 0 0 . 2 2 2 A + B + C
Ax + By + Cz + D
Ax + By + Cz + D C. d ( , A (P)) 0 0 0 = . D. d ( , A (P)) 0 0 0 = . 2 2 A + C 2 2 2 A + B + C
Câu 9. Tính khoảng cách từ điểm B(x ; y ;z 0 0
0 ) đến mặt phẳng (P): y + 1 = 0. Chọn khẳng định
đúngtrong các khẳng định sau: y +1 A. y .0 B. y . C. 0 . D. y +1 . 0 2 0
Câu 10. Khoảng cách từ điểm C( 2;
− 0; 0) đến mặt phẳng (Oxy) bằng: A. 0. B. 2. C. 1. D. 2.
Câu 11. Khoảng cách từ điểm M (1;2;0) đến mặt phẳng (Oxy), (Oyz), (Oxz). Chọn khẳng định saitrong các khẳng định sau:
A. d (M ,(Oxz)) = 2.
B. d (M ,(Oyz)) =1.
C. d (M ,(Oxy)) =1.
D. d (M ,(Oxz)) > d (M ,(Oyz)).
Câu 12. Khoảng cách từ điểm A(x ; y ;z + + + = 0 0
0 ) đến mặt phẳng (P): Ax By Cz D 0 , với
D ≠ 0 bằng 0 khi và chỉ khi:
A. Ax + By + Cz ≠ − . D 0 0 0
B. A∉(P).
C Ax + By + Cz = − . D
Ax + By + Cz . 0 0 0 D. 0 0 0 = 0.
Câu 13. Khoảng cách từ điểm O đến mặt phẳng (Q) bằng 1. Chọn khẳng định đúngtrong các khẳng định sau:
A. (Q): x + y + z – 3 = 0.
B. (Q): 2x + y + 2z – 3 = 0.
C. (Q): 2x + y – 2z + 6 = 0.
D. (Q): x + y + z – 3 = 0. Hướng dẫn giải
Dùng công thức khoảng cách từ 1 điểm đến mặt phẳng, sau đó tính khoảng cách lần lượt trong
mỗi trường hợp và chọn đáp án đúng. x =1+ t
Câu 14. Khoảng cách từ điểm H
(1;0;3) đến đường thẳng d : y = 2t , ∈ và mặt phẳng 1 t Rz = 3+  t
(P): z − 3 = 0 lần lượt là d(H,d )
1 và d (H , (P)) . Chọn khẳng định đúngtrong các khẳng định sau:
A d (H,d > d H,(P) . > 1 ) ( )
B. d (H,(P)) d (H,d . 1 )
C. d (H,d = 6.d H,(P) . = 1 ) ( )
D. d (H,(P)) 1. x = 2 + t
Câu 15. Tính khoảng cách từ điểm E
(1;1;3) đến đường thẳng d : y = 4 + 3t , t ∈ R bằng: z = 2 − −  5t A 1 . B. 4 . C. 5 . D. 0 35 35 35    
Câu 16. Cho vectơ u( 2;
− −2; 0); v( 2; 2; 2) . Góc giữa vectơ u và vectơ v bằng: Trang 3/31 A.135° . B. 45° . C. 60° . D. 150° . x = 2 + tx = 1 − t Câu 17.  
Cho hai đường thẳng d : y = −1 + t 1 và d : y 2 = 2
. Góc giữa hai đường thẳng d1 và d2 z = 3   z = − 2 + t  là: A30°. B. 120° . C. 150° . D. 60° . x y z
Câu 18. Cho đường thẳng ∆ : =
= và mặt phẳng (P): 5x + 1 y
1 + 2z − 4 = 0 . Góc giữa đường 1 −2 1
thẳng ∆ và mặt phẳng (P) là: A. 60° . B. −30°. C.30°. D. − 60° .
Câu 19. Cho mặt phẳng (α) : 2x − y + 2z − 1 = 0; (β) : x + 2y − 2z − 3 = 0 . Cosin góc giữa mặt phẳng
(α) và mặt phẳng (β ) bằng: 4 4 4 A 4 . B. − . C. . D. − . 9 9 3 3 3 3
Câu 20. Cho mặt phẳng (P) : 3x + 4y + 5z + 2 = 0 và đường thẳng d là giao tuyến của hai mặt phẳng
(α) : x − 2y + 1 = 0; (β ) : x − 2z − 3 = 0 . Gọi ϕ là góc giữa đường thẳng d và mặt phẳng (P). Khi đó: A. 60° . B. 45° . C. 30°. D. 90° .
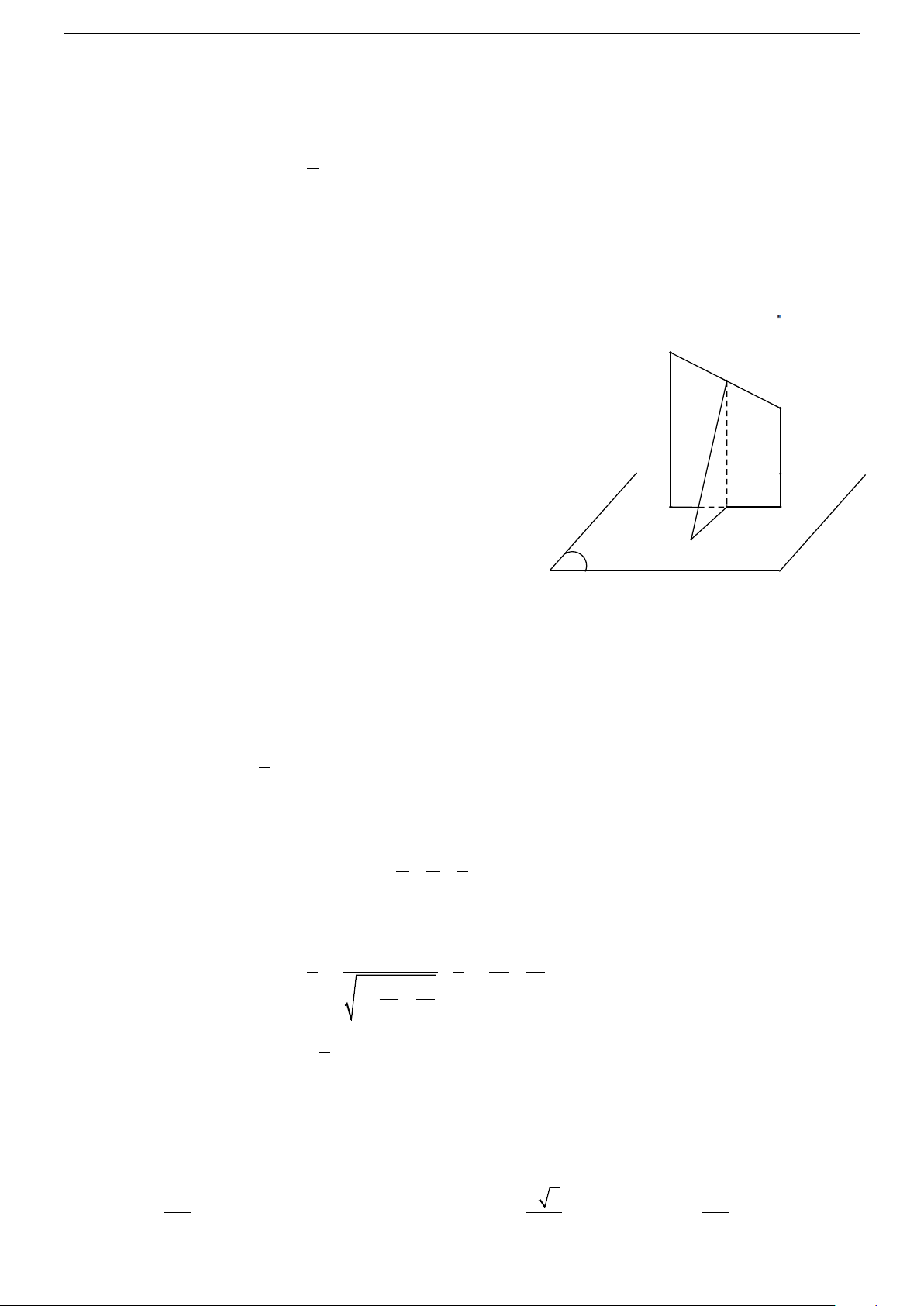
Câu 21. Cho mặt phẳng (α) : 3x − 2y + 2z − 5 = 0 . Điểm A(1; – 2; 2). Có bao nhiêu mặt phẳng đi qua
A và tạo với mặt phẳng (α) một góc 45 .° A. Vô số. B. 1. C. 2. D. 4.
Câu 22. Hai mặt phẳng nào dưới đây tạo với nhau một góc 60°
A. (P) : 2x + y
11 − 5z + 3 = 0 và Q
( ) : x + 2y − z − 2 = 0 .
B.(P) : 2x + y
11 − 5z + 3 = 0 và Q
( ) : − x + 2y + z − 5 = 0 .
C. (P) : 2x − y
11 + 5z − 21 = 0 và Q
( ) : 2x + y + z − 2 = 0 .
D. (P) : 2x − 5y + z 11 − 6 = 0 và Q
( ) : − x + 2y + z − 5 = 0 .    
Câu 23. Cho vectơ u(1; 1; −2), v(1; 0; m) . Tìm m để góc giữa hai vectơ u, v có số đo bằng 45° .
Một học sinh giải như sau:   1 − 2 Bước 1: Tính cos( , ) m u v = 6. m2 + 1   1 − 2m 1
Bước 2: Góc giữa u, v có số đo bằng 45° nên = 6. m2 + 1 2 ⇔ − m = m2 1 2 3( + 1) (*) Bước 3: Phương trình ⇔ − m 2 = m2 (*) (1 2 ) 3( + 1) m = 2 − 6
⇔ m2 − 4m − 2 = 0 ⇔  m = 2 + 6.
Bài giải đúng hay sai? Nếu sai thì sai ở bước nào? A. Sai ở bước 3. B. Sai ở bước 2. C. Sai ở bước 1. D. Đúng.
Câu 24. Cho hai điểm A(1; − 1; 1); B(2; − 2; 4) . Có bao nhiêu mặt phẳng chứa A, Bvà tạo với mặt phẳng
(α) : x − 2y + z − 7 = 0 một góc 60° . A. 1. B. 4. C. 2. D. Vô số. Trang 4/31
Câu 25. Gọi α là góc giữa hai đường thẳng AB, CD. Khẳng định nào sau đây là khẳng định đúng:   AB CD .   A AB CD . cosα . =   .
B. cosα =   . AB . CD AB . CD     AB CD . AB CD .  C. cosα =     .
D. cosα =   . AB,CDAB . CD  
Câu 26. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm các
cạnh BB', CD, A'D'. Góc giữa hai đường thẳng MP và C’N là: A. 30o. B. 120o. C. 60o. D. 90o.
Câu 27. Cho hình chóp A.BCD có các cạnh AB, AC, AD đôi một vuông góc. ∆ABC cân, cạnh bên bằng
a, AD = 2a . Cosin góc giữa hai đường thẳng BD và DC là: 4 2 4 1 A. . B. − . C. . D. . 5 5 5 5
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2, AC = 5 . ∆SAC vuông cân
tại A. K là trung điểm của cạnh SD. Hãy xác định cosin góc giữa đường thẳng CK và AB? 4 2 4 2 A. . B. . C. . D. . 17 11 22 22
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm điểm
A(−3; − 4; 5); B(2; 7; 7); C(3; 5; 8); D(−2; 6; 1) . Cặp đường thẳng nào tạo với nhau một góc 60° ?
A. DB và AC.
B. AC và CD.
C. AB và CB.
D.CB và CA.
Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào dưới đây đi qua A(2; 1; – 1) tạo với trục Oz một góc 30° ?
A. 2(x − 2) + (y − 1) − (z − 2) − 3 = 0.
B.(x − 2) + 2(y − 1) − (z + 1) − 2 = 0.
C. 2(x − 2) + (y − 1) − (z − 2) = 0.
D. 2(x − 2) + (y − 1) − (z − 1) − 2 = 0.
Câu 31. Cho mặt phẳng (P):3x + 4y + 5z + 8 = 0 . Đường thẳng d là giao tuyến của hai mặt phẳng
(α) : x − 2y + 1 = 0; (β ) : x − 2z − 3 = 0 . Góc giữa d và (P) là: A. 120°. B. 60°. C.150°. D.30°.  
Câu 32. Gọi α là góc giữa hai vectơ AB, CD . Khẳng định nào sau đây là đúng:      AB CD .  AB CD . A. cosα   =   .
B. cosα =   . AB . CD AB . CD   AB CD .   C AB DC .
. sinα =   .
D. cosα =   AB . CD AB . DC
Câu 33. Cho ba mặt phẳng (P): 2x − y + 2z + 3 = 0; Q
( ) : x − y − z − 2 = 1; (R) : x + 2y + 2z − 2 = 0 .
Gọi α ; α ; α lần lượt là góc giữa hai mặt phẳng (P) và (Q), (Q) và (R), (R) và (P). Khẳng định 1 2 3
nào sau đây là khẳng định đúng. A.α > α >α . B. α > α >α . C.α > α >α . D.α > α >α . 1 3 2 2 3 1 3 2 1 1 2 3
Câu 34. Trong không gian với hệ tọa độOxyz, cho mặt phẳng(α ) : x + 2y + 2z + m = 0 vàđiểm A(1;1; ) 1 .
Khi đó m nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng (α ) bằng 1? A. − 2. B. − 8. C. − 2 hoặc 8 − . D. 3. Trang 5/31
Câu 35. Trong không gian với hệ tọa độOxyz, mặt phẳng (α ) cắt các trục Ox, Oy, Oz lần lượt tại 3 điểm A( 2;
− 0;0), B(0;3;0) ,C (0;0;4) . Khi đó khoảng cách từ gốc tọa độ O đến mặt phẳng ( ABC) là A. 61 . B.4. C.12 61 . D.3. 12 61  y = 0
Câu 36. Trong không gian với hệ tọa độ 
Oxyz cho điểm M (1;0;0) và N (0;0;− ) 1 ,
2x − y − 2z − 2 = 0
mặt phẳng (P) qua điểm M , N và tạo với mặt phẳng (Q) : x − y − 4 = 0 một góc bằng O 45 .
Phương trình mặt phẳng (P) là  y = 0  y = 0 A.  . B.  .
2x − y − 2z − 2 = 0
2x − y − 2z + 2 = 0
2x − y − 2z + 2 = 0
2x − 2z + 2 = 0 C.  . D.  .
2x − y − 2z − 2 = 0
2x − 2z − 2 = 0
Câu 37. Trong không gian Oxyz , cho điểm A( 2; − 0; )
1 , đường thẳng d qua điểm A và tạo với trục Oy góc O
45 . Phương trình đường thẳng d là  x + 2 y z −1  − + = = x 2 y z 1  = = 2 5 1 −  2 5 1 − A.  . B.   x + 2 y z −1  − + = = x 2 y z 1  = =  2 − 5 1 −  2 − 5 1 −  x + 2 y z −1  + − = = x 2 y z 1  = = 2 5 1 −  2 − 5 1 − C.  D.   x − 2 y z +1  − + = = x 2 y z 1  = =  2 5 1 −  2 5 1 −
Câu 38. Trong không gian Oxyz cho mặt phẳng (P) : x + y + z − 3 = 0 và mặt
phẳng(Q) : x − y + z −1 = 0. Khi đó mặt phẳng (R) vuông góc với mặt phẳng (P) và (Q) sao
cho khoảng cách từ O đến mặt phẳng (R) bằng 2 , có phương trình là
A. 2x − 2z − 2 2 = 0 .
B. x − z − 2 2 = 0 .
x − z + 2 2 = 0
C. x − z + 2 2 = 0 . D.  .
x − z − 2 2 = 0
Câu 39. Tập hợp các điểm M ( ;
x y; z) trong không gian Oxyz cách đều hai mặt phẳng
(P) :x + y − 2z − 3 = 0 và (Q) :x + y − 2z + 5 = 0 thoả mãn:
A. x + y − 2z +1 = 0.
B. x + y − 2z + 4 = 0 .
C. x + y − 2z + 2 = 0 .
D. x + y − 2z − 4 = 0 .
Câu 40. Tập hợp các điểm M ( ;
x y; z) trong không gian Oxyz cách đều hai mặt phẳng
(P) :x − 2y − 2z − 7 = 0 và mặt phẳng (Q) :2x + y + 2z +1 = 0 thoả mãn:
x + 3y + 4z + 8 = 0
A. x + 3y + 4z + 8 = 0. B.  .
3x − y − 6 = 0
C. 3x − y − 6 = 0.
D.3x + 3y + 4z + 8 = 0. Trang 6/31
Câu 41. Trong không gian Oxyz cho điểm M thuộc trục Oxcách đều hai mặt phẳng
(P) : x + y − 2z − 3 = 0 và (Oyz) .Khitọa độ điểm M là     A     . 3  ;0;0 và 3  ;0;0. B. 3  ;0;0 và 3  ;0;0. 1 6  +   6 −1  1+ 6  1− 6   −   +   +   −  C. 6 1  ;0;0  và 6 1  ;0;0. D. 1 6  ;0;0 và 1 6  ;0;0. 3          3   3   3  
Câu 42. Trong không gianOxyz cho điểm A(3; 2 − ;4) và đường thẳng
x 5 y 1 z 2 d − − − : = = . 2 3 2 −
Điểm M thuộc đường thẳng d sao cho M cách A một khoảng bằng 17 . Tọa độ điểm M là
A.(5;1;2) và (6; 9; 2). B.(5;1;2) và ( 1 − ; 8 − ; 4 − ). C.(5; 1; − 2) và(1; 5 − ;6). D.(5;1;2) và (1; 5 − ;6).
Câu 43. Trong không gian Oxyz cho tứ diện ABCD có các đỉnh A(1;2; ) 1 , B( 2 − ;1;3) ,C (2; 1; − ) 1 và D(0;3; )
1 . Phương trình mặt phẳng (P) đi qua 2 điểm ,
A B sao cho khoảng cách từ C đến
(P) bằng khoảng cách từ D đến (P) là
4x − 2y + 7z −1 = 0 A.  .
B. 2x + 3z − 5 = 0.
2x + 3z − 5 = 0
4x + 2y + 7z −15 = 0
C. 4x + 2y + 7z −15 = 0. D.  .
2x + 3z − 5 = 0
Câu 44. Trong không gian với hệ trục toạ độ Oxyz, gọi(P) là mặt phẳng chứa đường thẳng x 1 y 2 : z d − + = =
và tạo với trục Oy góc có số đo lớn nhất. Điểm nào sau đây thuộc 1 1 − 2 − mp(P)? A. E ( 3 − ;0;4). B. M (3;0;2). C. N ( 1 − ; 2 − ;− ) 1 . D. F (1;2; ) 1 .
Câu 45. Trong không gian với hệ trục toạ độ Oxyz, cho điểm M (0; −1; 2), N ( 1;
− 1; 3) . Gọi (P) là
mặt phẳng đi qua M , N và tạo với mặt phẳng (Q) :2x − y − 2z − 2= 0 góc có số đo nhỏ nhất.
Điểm A(1;2;3) cách mp(P) một khoảng là A. 3. B. 5 3 . C. 7 11 . D. 4 3 . 3 11 3
Câu 46. Trong không gian với hệ trục toạ độ Oxyz, cho (P):x − 2 y + 2z −1=0 và 2 đường thẳng x +1 y z + 9
x −1 y − 3 z +1 ∆ : = = ; ∆ : = = . 1 2 1 1 6 2 1 2 −
Gọi M là điểm thuộc đường thẳng ∆ , M có toạ độ là các số nguyên, M cách đều ∆ và 1 2
(P). Khoảng cách từ điểm M đến mp(Oxy) là A.3. B. 2 2. C.3 2. D. 2.
Câu 47. Trong không gian với hệ trục toạ độ Oxyz, cho 2 điểm A(1;5;0); B(3;3;6) và đường thẳng x 1 y 1 : z d + − =
= . Gọi C là điểm trên đường thẳng d sao cho diện tích tam giác ABC nhỏ 2 1 − 2
nhất. Khoảng cách giữa 2 điểm A và C là A. 29. B. 29. C. 33. D. 7. Trang 7/31
Câu 48. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(10;2; ) 1 và đường thẳng x 1 y z 1 d − − : = =
. Gọi (P) là mặt phẳng đi qua điểm A , song song với đường thẳng d sao 2 1 3
cho khoảng cách giữa d và (P) lớn nhất. Khoảng cách từ điểm M ( 1;
− 2;3) đến mp(P) là A. 97 3 . B. 76 790 . C. 2 13 . D. 3 29 . 15 790 13 29
Câu 49. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(2;5;3) và đường thẳng x 1 y z 2 d − − : = =
. Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A 2 1 2
đến (P) lớn nhất. Tính khoảng cách từ điểm M (1;2;− )
1 đến mặt phẳng (P) . A.11 18 . B.3 2. C. 11 . D. 4 . 18 18 3
Câu 50. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) :x + y − z + 2 = 0 và hai đường x =1+ t
x = 3 − t′  
thẳng d :y = t
; d ':y =1+ t′ . z = 2+   2t z =1−  2t′
Biết rằng có 2 đường thẳng có các đặc điểm: song song với (P) ; cắt d, d′ và tạo với d góc O
30 . Tính cosin góc tạo bởi hai đường thẳng đó. A. 1 . B. 1 . C. 2. D. 1 . 5 2 3 2
Câu 51. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1;0; ) 1 ; B(3; 2; − 0);C (1;2; 2 − ) . Gọi
(P) là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) lớn nhất biết rằng
(P) không cắt đoạn BC . Khi đó, điểm nào sau đây thuộc mặt phẳng(P)? A. G ( 2; − 0; 3). B. F (3; 0; 2 − ). C. E (1;3; ) 1 . D. H ( 0;3; ) 1
Câu 52. Trong không gian với hệ trục toạ độ Oxyz, cho các điểm A(1;0;0), B(0; ;
b 0),C (0;0;c) trong đó ,
b c dương và mặt phẳng (P) : y − z +1= 0. Biết rằng mp( ABC) vuông góc với mp(P) và
d (O ( ABC)) 1 ,
= , mệnh đề nào sau đây đúng? 3
A.b + c =1.
B. 2b + c =1.
C.b − 3c =1.
D.3b + c =3.
Câu 53. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1;2;3); B(0;1; ) 1 ;C (1;0;− 2) .
Điểm M ∈(P) :x + y + z + 2 = 0 sao cho giá trị của biểu thức 2 2 2
T = MA + 2MB +3MC nhỏ nhất.
Khi đó, điểm M cách (Q) :2x − y − 2z + 3 = 0 một khoảng bằng A.121. B. 24. C. 2 5 . D.101. 54 3 54
Câu 54. Cho mặt phẳng (α) : x + y − 2z − 1 = 0; (β) : 5x + 2y + 1 z
1 − 3 = 0 . Góc giữa mặt phẳng
(α) và mặt phẳng (β ) bằng A. 120 .° B. 30 .° C.150 .° D. 60 .° Trang 8/31
Câu 55. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) có phương trình x + y − 3 = 0.
Điểm H(2; 1; 2) là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa
hai mặt phẳng (P) và (Q) bằng A. 45 .° B. 30 .° C. 60 .° D. 120 .°     π   
Câu 56. Cho vectơ u = 2; v = 1; (u, v) = . Gócgiữa vectơvvà vectơ u − v bằng: 3 A. 60 .° B. 30 .° C. 90 .° D. 45 .°
Câu 57. Trong không gian với hệ trục toạ độ Oxyz, cho đường thẳng x − y + z
2x − 3y − 3z + 9 = 0 d 3 1 − 1 : = = , ∆ :
. Góc giữa đường thẳng d và đường thẳng 9 5 1 
x − 2y + z + 3 = 0 ∆ bằng A. 90 .° B. 30 .° C. 0 .° D. 180 .°
Câu 58. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (α) : 2x − y − 2z − 10 = 0; đường x − − y z + thẳng d 1 1 3 : = =
. Góc giữa đường thẳng d và mặt phẳng (α) bẳng 1 2 3 A. 30 .° B. 90 .° C. 60 .° D. 45 .°
Câu 59. Trong không gian với hệ trục toạ độ Oxyz, phương trình các đường thẳng qua A(3; – 1;1), nằm x y − 2 z
trong (P): x – y + z – 5 = 0và hợp với đường thẳngd: = = một góc 45 0 là 1 2 2 x = 3 + tx = 3 + t 3 A.   ∆ : 1 , ; : 1 2 , . 1
y = − + t t ∈ R ∆2 y = − − t t ∈ R   z = 1 z = 1 −   t 5 x = 3 + 2tx = 3 + t 15 B.   ∆ : 1 2 , ; : 1 38 , . 1
y = − + t t ∈ R ∆2 y = − + t t ∈ R   z = 1 z = 1 +   t 23 x = 3 + tx = 3 + t 15 C.   ∆ : 1 , ; : 1 8 , . 1
y = − + t t ∈ R ∆2 y = − − t t ∈ R   z = 1 z = 1 −   t 23 x = 3 − tx = 3 + t 15 D.   ∆ : 1 , ; : 1 8 , . 1
y = − − t t ∈ R ∆2 y = − − t t ∈ R   z = 1 + t z = 1 −   t 23
Câu 60. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm các
cạnh A'B', BC, DD'. Góc giữa đường thẳng AC’ và mặt phẳng (MNP) là A. 30 .° B. 120°. C. 60 .° D. 90 .°
Câu 61. Trong không gian với hệ trục toạ độ Oxyz, gọi(P) là mặt phẳng chứa đường thẳng x = 1+ 2t
d : y = 2 −t và tạo với trục Ox góc có số đo lớn nhất.Khi đó, khoảng cách từ điểm z =  3t A(1; 4
− ;2) đến mp(P)là 12 35 A. . B. 4 3 . C. 20 6 . D. 2 6 . 35 3 9 3 Trang 9/31
Câu 62. Trong không gian với hệ trục toạ độ Oxyz, cho điểm M (2;1; 1
− 2), N ( 3;0;2) . Gọi (P) là mặt
phẳng đi qua M , N và tạo với mặt phẳng (Q) :2x + 2y −3z + 4= 0 góc có số đo nhỏ nhất. Điểm
A(3;1;0) cách mp(P) một khoảng là 1 A. 6 13 . B. 22 . C. 6 . D. . 13 11 2 22
Câu 63. Trong không gian với hệ trục toạ độOxyz, cho (P) :x + y − z − 7 =0 và hai đường thẳng
x −1 y −1 z − 2
x − 2 y − 3 z + 4 ∆ : = = ;∆ : = = . 1 2 1 1 1 2 3 5 −
Gọi M là điểm thuộc đường thẳng ∆ , M có toạ độ là các số dương, M cách đều ∆ và 1 2
(P). Khoảng cách từ điểm M đến mp( P ) là A. 2 3. B. 2. C. 7. D. 2 . 3
Câu 64. Trong không gian với hệ trục toạ độ Oxyz, cho 2 điểm A(1; 4
− ;3); B(1;0;5) và đường thẳng x = 3 − t
d : y = 3+ 2t.Gọi C là điểm trên đường thẳng d sao cho diện tích tam giác ABC nhỏ nhất. z = 2 − 
Khoảng cách giữa điểm C và gốc toạ độ O là A. 6. B. 14. C. 14. D. 6.
Câu 65. Trong không gian với hệ trục toạ độOxyz, cho điểm A(2;5;3) và đường thẳng x 1 y z 2 d − − : = =
.Gọi (P) là mặt phẳng đi qua điểm A , song song với đường thẳng d sao 2 1 2
cho khoảng cách giữa d và (P) lớn nhất. Khoảng cách từ điểm B(2;0;−3) đến mp(P) là A. 7 2 . B. 5 2 . C. 7. D. 18 . 3 3 18 x = 4 + 3t
Câu 66. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(4; 3
− ;2)và đường thẳng d :y = 2 + 2t. z = 2 − −  t
Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A đến (P) lớn nhất. Tính
khoảng cách từ điểm B( 2 − ;1; 3
− ) đến mặt phẳng (P) đó. A. 2 3. B. 2. C. 0. D. 38.
Câu 67. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1; 1;− 2);B( 1; − 2; ) 1 ;C ( 3 − ; 4; ) 1 . Gọi
(P) là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) lớn nhất biết rằng
(P) không cắt đoạn BC . Khi đó, điểm nào sau đây thuộc mặt phẳng (P) ? A. F ( 1; − 2;0). B. E (2; 2; − ) 1 . C. G (2;1; 3 − ). D. H (1; 3 − ; ) 1 .
Câu 68. Trong không gian với hệ trục toạ độOxyz, cho các điểm A( ;
a 0;0), B(0;2;0),C (0;0;c) trong
đó a,c dương và mặt phẳng (P) :2x − z + 3= 0. Biết rằng mp( ABC) vuông góc với mp(P) và
d (O ( ABC)) 2 , =
, mệnh đề nào sau đây đúng? 21
A. a + 4c =3.
B. a + 2c =5.
C. a −c =1.
D. 4a −c =3. Trang 10/31
Câu 69. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A( 2
− ; 2; 3);B(1; −1; 3);C (3; 1; − ) 1 .
Điểm M ∈(P) :x + 2z −8 = 0 sao cho giá trị của biểu thức 2 2 2
T = 2MA + MB +3MC nhỏ nhất.
Khi đó, điểm M cách (Q) :− x + 2y − 2z − 6 = 0 một khoảng bằng A. 2 . B.2. C. 4 . D. 4. 3 3
Câu 70. Tính khoảng cách từ điểm H(3; – 1;– 6) đến mặt phẳng (α) : x + y − z +1 = 0 . A 8 3 . . B. 9. C. 3 3. D. 3. 3
Câu 71. Tính khoảng cách giữa hai mặt phẳng song song (P): 2x + y + 2z = 0 và (Q) 2x + y + 2z + 7 = 0 . A 7 7 . . B. 7. C. . D. 2. 9 3
Câu 72. Khoảng cách từ điểm K(1;2;3) đến mặt phẳng (Oxz) bằng A. 2. B. 1. C. 3. D. 4. x =1+ 5t
Câu 73. Tính khoảng cách giữa mặt phẳng 
(α) : 2x + y + 2z + 4 = 0 và đường thẳng d: y = 2 − 2t . z = 4 −  t A 8 4 . . B. 0. C. . D. 4. 3 3
Câu 74. Khoảng cách từ giao điểm A của mặt phẳng (R) : x + y + z −3 = 0 với trục Oz đến mặt phẳng
(α) : 2x + y + 2z +1 = 0 bằng A 7 5 4 . . B. . C. . D. 0. 3 3 3 x = 1− 3t
Câu 75. Cho hai mặt phẳng (P) : x + y + 2z −1 = 0, (Q) : 2x + y + z = 0 và đường thẳng d: y = 2 + t . z = 1 − +  t
Gọi d(d,(P)) , d(d,(Q)) , d((P),(Q)) lần lượt là khoảng cách giữa đường thẳng d và (P), d và
(Q), (P) và (Q). Trong các mệnh đề sau, tìm mệnh đề sai:
A. d(d,(P)) = 0. B. 6
d(d,(Q)) = .
C. d((P),(Q)) = 0.
D. d(d,(Q)) = 0. 2 x =1+ t
Câu 76. Khoảng cách từ điểm  C( 2
− ;1;0) đến mặt phẳng (Oyz) và đến đường thẳng ∆ : y = 4 + t lần z = 6+  2t
lượt là d và d . Chọn khẳng định đúng trong các khẳng định sau: 1 2
A. d > d .
B. d = d . C. d = D. d =1. 1 2 1 2 1 0. 2
Câu 77. Khoảng cách từ điểm B(1;1;1) đến mặt phẳng (P) bằng 1. Chọn khẳng định đúngtrong các khẳng định sau:
A. (P): 2x + y – 2z + 6 = 0.
B. (P): x + y + z – 3 = 0.
B. (P): 2x + y + 2z – 2 = 0.
D. (P): x + y + z – 3 = 0 .
Câu 78. Trong không gian Oxyz cho mặt phẳng(α ) :2x − y + 2z +1 = 0 và mặt phẳng
(β ) :2x − y + 2z + 5 = 0. Tập hợp các điểm M cách đều mặt phẳng (α )và (β ) là
A. 2x − y + 2z + 3 = 0.
B. 2x − y − 2z + 3 = 0. Trang 11/31
C. 2x − y + 2z − 3 = 0.
D. 2x + y + 2z + 3 = 0.
Câu 79. Trong không gian Oxyz cho mặt phẳng (α ) :x − 2y + 2z +1 = 0 và mặt
phẳng(β ) : 2x − y + 2z +1 = 0 . Tập hợp các điểm cách đều mặt phẳng (α ) và (β ) là
x − y + 2 = 0
x − y + 2 = 0 A.  . B.  .
3x + 3y + 4z + 4 = 0
3x − 3y + 4z + 4 = 0
x − y + 2 = 0 x + y + 2 = 0 C.  . D.  .
3x − 3y + 4z + 4 = 0
3x − 3y + 4z + 4 = 0
D. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 8.5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
B A A B D C A D D A C C B C D A D C A A
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
A B A C A D A C C A B D A C C A A D A B
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
B D D C A A C A A D C A D D A C C B C D
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
A D A C A A B A D C C A A A B A C A D A Trang 12/31
II –HƯỚNG DẪN GIẢI
Câu 1. Trong không gian Oxyz, khoảng cách từ điểm A(1; 2; 2) đến mặt phẳng (α) :
x + 2y − 2z − 4 = 0 bằng: A 1 . 3. B. 1. C.13. D. . 3 3
Hướng dẫn giải 1.x + − z − A 2.yA 2. A 4 d( , A (α)) = =1. 2 2 2 1 + 2 + ( 2) −
Câu 2. Tính khoảng cách giữa hai mặt phẳng song song (α) : 2x − y − 2z − 4 = 0 và
(β ) : 2x − y − 2z + 2 = 0 . A 10 4 . 2. B. 6. C. . D. . 3 3 Hướng dẫn giải
Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kỳ của mặt
phẳng này đến mặt phẳng kia. 2.2 −1.0 − 2.0 + 2
Ta lấy điểm H(2; 0; 0) thuộc (α) . Khi đó d ((α),(β )) = d (H,(β )) = = 2 . 2 2 2 2 + ( 1 − ) + ( 2 − )
Câu 3. Khoảng cách từ điểm M (3; 2; )
1 đến mặt phẳng (P): Ax + Cz + D = 0 , .
AC.D ≠ 0 . Chọn khẳng
định đúngtrong các khẳng định sau:
3A + C + D
A + 2B + 3C + D
A. d(M ,(P)) =
B. d(M ,(P)) = . 2 2 A + C 2 2 2 A + B + C 3A + C
3A + C + D
C. d(M ,(P)) = .
D. d(M ,(P)) = . 2 2 A + C 2 2 3 +1 x =1+ t
Câu 4. Tính khoảng cách giữa mặt phẳng 
(α) : 2x − y − 2z − 4 = 0 và đường thẳng d: y = 2 + 4t . z = t−  1 4 A. . B. . C. 0. D. 2. 3 3 Hướng dẫn giải
Đường thẳng d song song với mặt phẳng (α) .
Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm bất kỳ
của đường thẳng đến mặt phẳng.
Ta lấy điểm H (1; 2; 0) thuộc đường thẳng d. Khi đó: 2.1−1.2 − 2.0 − 4 4
d(d,(α)) = d(H,(α)) = = . 2 2 2 2 + ( 1 − ) + ( 2 − ) 3
Câu 5. Khoảng cách từ điểm A(2; 4; 3) đến mặt phẳng (α) : 2x + y + 2z +1 = 0 và (β): x = 0 lần lượt là d( , A (α)) , d( ,
A (β )) . Chọn khẳng định đúng trong các khẳng định sau: A. d ( ,(
A α)) = 3. d ( ,( A β )). B. d ( ,(
A α)) > d ( ,( A β )). C. d ( ,( A α)) = d ( ,( A β )). D. 2. d ( ,( A α)) = d ( ,( A β )).
Hướng dẫn giải Trang 13/31 + + + x
d ( A α ) 2.x z A yA 2. A 1 ,( ) = =1 ; d ( , A (β )) A = = 2. 2 2 2 2 +1 + 2 2 1 Kết luận: d ( ,(
A β )) = 2.d ( ,( A α)) .
Câu 6. Tìm tọa độ điểm Mtrên trục Oy sao cho khoảng cách từ điểm M đến mặt phẳng (P):
2x − y + 3z − 4 = 0 nhỏ nhất? A. M (0;2;0). B. M (0;4;0). C. M (0; 4; − 0). D. 4 M 0; ;0  . 3    Hướng dẫn giải
Khoảng cách từ M đến (P) nhỏ nhất khi M thuộc (P). Nên M là giao điểm của trục Oy với mặt
phẳng (P). Thay x = 0, z = 0 vào phương trình (P) ta được y = − 4. Vậy M(0; −4;0). Cách giải khác
Tính khoảng cách từ điểm M trong các đáp án đến mặt phẳng (P) sau đó so sánh chọn đáp án.
Câu 7. Khoảng cách từ điểm M ( 4 − ; 5;
− 6) đến mặt phẳng (Oxy), (Oyz) lần lượt bằng: A. 6 và 4. B. 6 và 5. C. 5 và 4. D. 4 và 6.
Hướng dẫn giải
d (M ,(Oxy)) = z = d M Oyz = x = M 6 ; ( ,( )) M 4.
Câu 8. Tính khoảng cách từ điểm A(x ; y ; z đến mặt phẳng (P) : Ax + By + Cz + D = 0 , với 0 0 0 ) . A .
B C.D ≠ 0 . Chọn khẳng định đúngtrong các khẳng định sau:
Ax + By + Cz A. d ( ,
A (P)) = Ax + By + Cz . d , A (P) = . 0 0 0 B. ( ) 0 0 0 2 2 2 A + B + C
Ax + By + Cz + D
Ax + By + Cz + D C. d ( , A (P)) 0 0 0 = . D. d ( , A (P)) 0 0 0 = . 2 2 A + C 2 2 2 A + B + C
Câu 9. Tính khoảng cách từ điểm B(x ; y ;z 0 0
0 ) đến mặt phẳng (P): y + 1 = 0. Chọn khẳng định
đúngtrong các khẳng định sau: y +1 A. y .0 B. y . C. 0 . D. y +1 . 0 2 0
Câu 10. Khoảng cách từ điểm C( 2;
− 0; 0) đến mặt phẳng (Oxy) bằng: A. 0. B. 2. C. 1. D. 2. Hướng dẫn giải
Điểm C thuộc mặt phẳng (Oxy) nên d (C,(Oxy)) = 0
Câu 11. Khoảng cách từ điểm M (1;2;0) đến mặt phẳng (Oxy), (Oyz), (Oxz). Chọn khẳng định saitrong các khẳng định sau:
A. d (M ,(Oxz)) = 2.
B. d (M ,(Oyz)) =1.
C. d (M ,(Oxy)) =1.
D. d (M ,(Oxz)) > d (M ,(Oyz)).
Câu 12. Khoảng cách từ điểm A(x ; y ;z + + + = 0 0
0 ) đến mặt phẳng (P): Ax By Cz D 0 , với
D ≠ 0 bằng 0 khi và chỉ khi:
A. Ax + By + Cz ≠ − . D 0 0 0
B. A∉(P).
C Ax + By + Cz = − . D
Ax + By + Cz . 0 0 0 D. 0 0 0 = 0.
Câu 13. Khoảng cách từ điểm O đến mặt phẳng (Q) bằng 1. Chọn khẳng định đúngtrong các khẳng định sau:
A. (Q): x + y + z – 3 = 0.
B. (Q): 2x + y + 2z – 3 = 0. Trang 14/31
C. (Q): 2x + y – 2z + 6 = 0.
D. (Q): x + y + z – 3 = 0. Hướng dẫn giải
Dùng công thức khoảng cách từ 1 điểm đến mặt phẳng, sau đó tính khoảng cách lần lượt trong
mỗi trường hợp và chọn đáp án đúng. x = 1+ t
Câu 14. Khoảng cách từ điểm H
(1;0;3) đến đường thẳng d : y = 2t , ∈ và mặt phẳng 1 t Rz = 3+  t
(P): z − 3 = 0 lần lượt là d(H,d )
1 và d (H , (P)) . Chọn khẳng định đúngtrong các khẳng định sau:
A d (H,d > d H,(P) . > 1 ) ( )
B. d (H,(P)) d (H,d . 1 )
C. d (H,d = 6.d H,(P) . = 1 ) ( )
D. d (H,(P)) 1. Hướng dẫn giải
Vì H thuộc đường thẳng d1 và H thuộc mặt phẳng (P) nên khoảng cách từ điểm H đến đường
thẳng d1 bằng 0 và khoảng cách từ điểm H đến mặt phẳng (P) bằng 0. x = 2 + t
Câu 15. Tính khoảng cách từ điểm E
(1;1;3) đến đường thẳng d : y = 4 + 3t , t ∈ R bằng: z = 2 − −  5t A 1 . B. 4 . C. 5 . D. 0 35 35 35 Hướng dẫn giải
+ Gọi (P) là mặt phẳng đi qua E và vuông góc với (P). Viết phương trình (P)
+ Gọi H là giao điểm của đường thẳng d và (P). Tìm tọa độ H
+ Tính độ dài EH.
Khoảng cách từ điểm E (1;1;3) đến đường thẳng d bằng EH. Cách giải khác:
Vì E thuộc đường thẳng d nên khoảng cách từ điểm E(1;1;3) đến đường thẳng d bằng 0.    
Câu 16. Cho vectơ u( 2;
− −2; 0); v( 2; 2; 2) . Góc giữa vectơ u và vectơ v bằng: A.135° . B. 45° . C. 60° . D. 150° .
Hướng dẫn giải     u.v 2. − 2 − 2. 2 + 2.0 1   Ta có co u s( , v) =   = = − ⇒ u ( , v) = 135°. u . v ( 2) − + ( 2) − . ( 2)2 + ( 2)2 2 2 2 2 + 2 x = 2 + tx = 1 − t Câu 17.  
Cho hai đường thẳng d : y = −1 + t 1 và d : y 2 = 2
. Góc giữa hai đường thẳng d1 và d2 z = 3   z = − 2 + t  là: A30°. B. 120° . C. 150° . D. 60° . Hướng dẫn giải  
Gọi u ; u lần lượt là vectơ chỉ phương của đường thẳng d 1 2 1; d2.  
u =(1; 1; 0); u = (−1; 0; 1) 1 2 Trang 15/31     u .u 1 1
Áp dụng công thức ta có cos(d ,d 1 2 ) cos(u , u 1 2 ) 1 2 − = =   = = . u . u 1 + 1. 1 + 1 2 1 2 ⇒ (d ,d 1 2 ) = 60° . x y z
Câu 18. Cho đường thẳng ∆ : =
= và mặt phẳng (P): 5x + 1 y
1 + 2z − 4 = 0 . Góc giữa đường 1 −2 1
thẳng ∆ và mặt phẳng (P) là: A. 60° . B. −30°. C.30°. D. − 60° . Hướng dẫn giải  
Gọi u; n lần lượt là vectơ chỉ phương, pháp tuyến của đường thẳng ∆ và mặt phẳng (P).   u = (1; − 2; ) 1 ; n = (5; 11; 2)     u n . 1.5 −11.2 +1.2 1
Áp dụng công thức ta có sin(∆,(P)) = cos(u,n) =   = = . u . n 2 5 + 2 11 + 2 2 2 . 1 + 2 2 + 2 2 1 ⇒ (∆,(P)) = 30°.
Câu 19. Cho mặt phẳng (α) : 2x − y + 2z − 1 = 0; (β) : x + 2y − 2z − 3 = 0 . Cosin góc giữa mặt phẳng
(α) và mặt phẳng (β ) bằng: 4 4 4 A 4 . B. − . C. . D. − . 9 9 3 3 3 3 Hướng dẫn giải  
Gọi n , n lần lượt là vectơ pháp tuyến của mặt phẳng α ( ) và (β ) . α β  
Ta có n (2; − 1; 2); n (1; 2; − 2) . α β Áp dụng công thức:     n . n α β 2.1−1.2 − 2.2 α β 4
cos(( ),( )) = cos(n , n ) =   = = . α β n . n 2 2 + (− 2 1) + 2 2 2 . (1 + 2 2 + (− 2 9 2) α β
Câu 20. Cho mặt phẳng (P) : 3x + 4y + 5z + 2 = 0 và đường thẳng d là giao tuyến của hai mặt phẳng
(α) : x − 2y + 1 = 0; (β ) : x − 2z − 3 = 0 . Gọi ϕ là góc giữa đường thẳng d và mặt phẳng (P). Khi đó: A. 60° . B. 45° . C. 30°. D. 90° . Hướng dẫn giải  x = 2t   1 
Đường thẳng d có phương trình: y = + t , t ∈ R . Suy ra VTCP của d là u (2; 1; 1) 2 d  z 3 = − + t  2     u n . 2.3 1.4 1.5 3
Ta có sin(d,(P)) cos( d u , n) d + + = =   = = . 2 2 2 2 2 . 2 d u n 2 2 + 1 + 1 . 3 + 4 + 5
⇒ (d,(P)) = 60° . Trang 16/31
Câu 21. Cho mặt phẳng (α) : 3x − 2y + 2z − 5 = 0 . Điểm A(1; – 2; 2). Có bao nhiêu mặt phẳng đi qua
A và tạo với mặt phẳng (α) một góc 45 .° A. Vô số. B. 1. C. 2. D. 4. Hướng dẫn giải
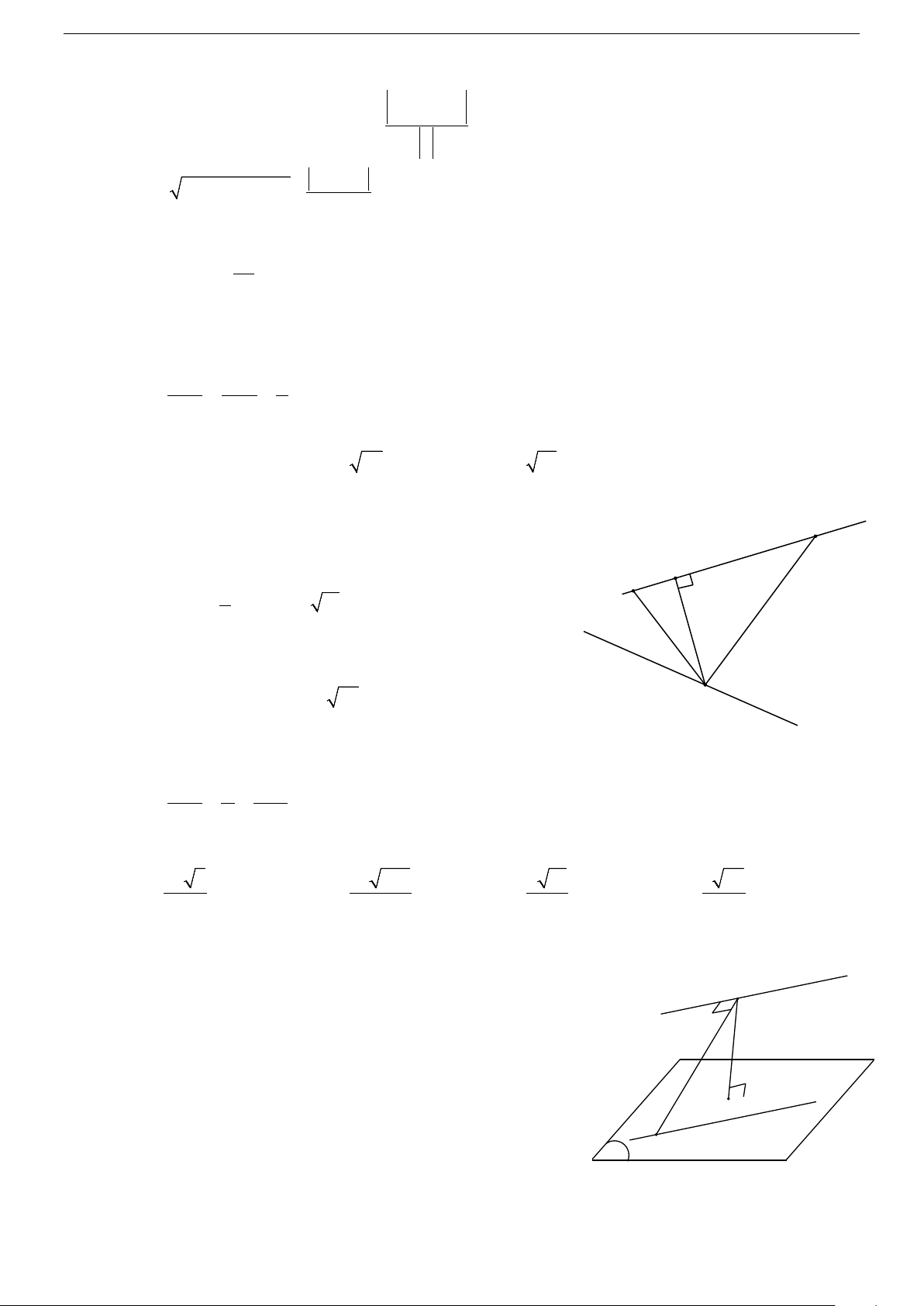
[Phương pháp tự luận] 
Gọi n a; b; c là vectơ pháp tuyến của mặt phẳng (β ) cần lập. β ( )   n . n (   3.a− b 2. + 2.c α β ) 2
cos ( ),( ) = cos(n , n ) α β =   = = α β n . n 2 3 + (− 2 2) + 2 2 2 . a + b2 + 2 c 2 α β ⇒
a − b + c 2 =
a2 + b2 + c2 2(3 2 2 ) 17( )
Phương trình trên có vô số nghiệm. 
Suy ra có vô số vectơ n (a; b; c) là véc tơ pháp tuyến của (β ) . Suy ra có vô số mặt phẳng β
(β ) thỏa mãn điều kiện bài toán
[Phương pháp trắc nghiệm] Dựng hình.
Giả sử tồn tại mặt phẳng (β ) thỏa mãn điều kiện bài toán. (Đi qua A và tạo với mặt phẳng (α)
một góc 45° ). Gọi ∆ là đường thẳng đi qua A và vuông góc với mặt phẳng (α) . Sử dụng phép
quay theo trục ∆ với mặt phẳng (β ) . Ta được vô số mặt phẳng (β ') thỏa mãn điều kiện bài toán.
Câu 22. Hai mặt phẳng nào dưới đây tạo với nhau một góc 60°
A. (P) : 2x + y
11 − 5z + 3 = 0 và Q
( ) : x + 2y − z − 2 = 0 .
B.(P) : 2x + y
11 − 5z + 3 = 0 và Q
( ) : − x + 2y + z − 5 = 0 .
C. (P) : 2x − y
11 + 5z − 21 = 0 và Q
( ) : 2x + y + z − 2 = 0 .
D. (P) : 2x − 5y + z 11 − 6 = 0 và Q
( ) : − x + 2y + z − 5 = 0 . Hướng dẫn giải
Áp dụng công thức tính góc giữa hai mặt phẳng.   n n . ( P Q ) 1 cos ( ),( ) = P Q
  = cos60° = . 2 P n Q n
Xác định các vectơ pháp tuyến của mặt phẳng (P) và (Q). Thay các giá trị vào biểu thức để tìm giá trị đúng.
Dùng chức năng CALC trong máy tính bỏ túi để hỗ trợ việc tính toán nhanh nhất.    
Câu 23. Cho vectơ u(1; 1; −2), v(1; 0; m) . Tìm m để góc giữa hai vectơ u, v có số đo bằng 45° .
Một học sinh giải như sau:   1 − 2 Bước 1: Tính cos( , ) m u v = 6. m2 + 1   1 − 2m 1
Bước 2: Góc giữa u, v có số đo bằng 45° nên = 6. m2 + 1 2 ⇔ − m = m2 1 2 3( + 1) (*) Bước 3: Phương trình ⇔ − m 2 = m2 (*) (1 2 ) 3( + 1) Trang 17/31 m = 2 − 6
⇔ m2 − 4m − 2 = 0 ⇔  m = 2 + 6.
Bài giải đúng hay sai? Nếu sai thì sai ở bước nào? A. Sai ở bước 3. B. Sai ở bước 2. C. Sai ở bước 1. D. Đúng. Hướng dẫn giải
Phương trình (*) chỉ bình phương được hai vế khi biến đổi tương đương nếu thỏa mãn
1 − 2m ≥ 0 . Bài toán đã thiếu điều kiện để bình phương dẫn đến sai nghiệm m = 2 + 6 .
Câu 24. Cho hai điểm A(1; − 1; 1); B(2; − 2; 4) . Có bao nhiêu mặt phẳng chứa A, Bvà tạo với mặt phẳng
(α) : x − 2y + z − 7 = 0 một góc 60° . A. 1. B. 4. C. 2. D. Vô số. Hướng dẫn giải
[Phương pháp tự luận]  
AB(1; − 1; 3), n (1; − 2; 1) α 
Gọi n (a; b; c) là vectơ pháp tuyến của mặt phẳng (β ) cần lập. β   n n . cos(   α
( ),(β )) = cos(n , n ) α β = α β   n . n α β 1.a− b 2. + 1.c 1 = = . 2 + − 2 + 2 2 + b2 + 2 2 1 ( 2) 1 . a c
⇒ a − b + c 2 = a2 + b2 + c2 2( 2 ) 3( ) (1)
Mặt khác vì mặt phẳng (β ) chứa A, B nên:  
n .AB = 0 ⇔ a − b + c
3 = 0 ⇔ a = b − c 3 β
Thế vào (1) ta được: b2 − bc + c2 2 13 11 = 0 (2) 
Phương trình (2) có 2 nghiệm phân biệt. Suy ra có 2 vectơ n a; b; c thỏa mãn. β ( ) Suy ra có 2 mặt phẳng.
[Phương pháp trắc nghiệm] Dựng hình
Câu 25. Gọi α là góc giữa hai đường thẳng AB, CD. Khẳng định nào sau đây là khẳng định đúng:   AB CD .   A AB CD . cosα . =   .
B. cosα =   . AB . CD AB . CD     AB CD . AB CD .  C. cosα =     .
D. cosα =   . AB,CDAB . CD   Hướng dẫn giải
Áp dụng công thức ở lý thuyết.
Câu 26. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm các
cạnh BB', CD, A'D'. Góc giữa hai đường thẳng MP và C’N là: A. 30o. B. 120o. C. 60o. D. 90o. Hướng dẫn giải
Chọn hệ trục tọa độ sao cho A ≡ O(0; 0; 0) Trang 18/31
Suy ra B(a; 0; 0); C(a; a; 0); D(0; a; 0)
A'(0; 0; a); B'(a; 0; a); C '(a; a; a); D'(0; a; a)  a   a   a
M a; 0; ; N  ; a; 0; P0; ; a  2   2   2   
a a    a   
Suy ra MP = − a; ; ; NC ' =
; 0; a ⇒ MP.NC ' =     0  2 2   2 
⇒ (MP,NC ') = 90°
Câu 27. Cho hình chóp A.BCD có các cạnh AB, AC, AD đôi một vuông góc. ∆ABC cân, cạnh bên bằng
a, AD = 2a . Cosin góc giữa hai đường thẳng BD và DC là: 4 2 4 1 A. . B. − . C. . D. . 5 5 5 5 Hướng dẫn giải
[Phương pháp tự luận]
Chọn hệ trục tọa độ sao cho A ≡ O(0; 0; 0)
Suy ra B(a; 0; 0); C(0; a; 0); D(0; 0; 2a)  
Ta có DB(a; 0; − 2a); DC(0; a;−2a)     DB. DC DB DC 4 cos( ,
) = cos(DB; DC) =   = . DB . DC 5
Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2, AC = 5 . ∆SAC vuông cân
tại A. K là trung điểm của cạnh SD. Hãy xác định cosin góc giữa đường thẳng CK và AB? 4 2 4 2 A. . B. . C. . D. . 17 11 22 22 Hướng dẫn giải
Vì ABCD là hình chữ nhật nên AD = AC2 − CD2 = 1
Chọn hệ trục tọa độ sao cho A ≡ O(0; 0; 0) z
Suy ra B(0; 2; 0); C(1; 2; 0); D(1; 0; 0) S S( )   K 1 5 0; 0; 5 ;  ; 0;   2 2      1 5 
Suy ra CK  − ;−2; ; AB(0; 2; 0) K  2 2    A B y   CK. AB (CK AB)   4 cos ,
= cos(CK; AB) =   = . CK . AB 22 D C x
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm điểm
A(−3; − 4; 5); B(2; 7; 7); C(3; 5; 8); D(−2; 6; 1) . Cặp đường thẳng nào tạo với nhau một góc 60° ?
A. DB và AC.
B. AC và CD.
C. AB và CB.
D.CB và CA. Hướng dẫn giải  
Tính tọa độ các vectơ sau đó thay vào công thức: cos(d,d ') = cos u
( ,u để kiểm tra. d d '
Câu 30. Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào dưới đây đi qua A(2; 1; – 1) tạo với trục Oz một góc 30° ? Trang 19/31
A. 2(x − 2) + (y − 1) − (z − 2) − 3 = 0.
B.(x − 2) + 2(y − 1) − (z + 1) − 2 = 0.
C. 2(x − 2) + (y − 1) − (z − 2) = 0.
D. 2(x − 2) + (y − 1) − (z − 1) − 2 = 0. Hướng dẫn giải
Gọi phương trình mặt phẳng (α) cần lập có dạng A(x − 2) + B(y − 1) + C(z + 1) = 0; n(A; B; C) 
Oz có vectơ chỉ phương là k(0; 0; 1) .   n k .
Áp dụng công thức sin((α), Oz) =   = sin30° n . k
Sau khi tìm được các vectơ pháp tuyến thỏa mãn, thay giá trị của A vào để viết phương trình mặt phẳng.
Câu 31. Cho mặt phẳng (P):3x + 4y + 5z + 8 = 0 . Đường thẳng d là giao tuyến của hai mặt phẳng
(α) : x − 2y + 1 = 0; (β ) : x − 2z − 3 = 0 . Góc giữa d và (P) là: A. 120°. B. 60°. C.150°. D.30°. Hướng dẫn giải  Ta có n (3; 4; 5) P    nn , n  = = (2; 1; 1) d α β     n u . Áp dụng công thức P d 3
sin((P), d) =   = . n u 2 . P d  
Câu 32. Gọi α là góc giữa hai vectơ AB, CD . Khẳng định nào sau đây là đúng:      AB CD .  AB CD . A. cosα   =   .
B. cosα =   . AB . CD AB . CD   AB CD .   C AB DC .
. sinα =   .
D. cosα =   AB , CD AB . DC Hướng dẫn giải
Áp dụng công thức ở lý thuyết.
Câu 33. Cho ba mặt phẳng (P): 2x − y + 2z + 3 = 0; Q
( ) : x − y − z − 2 = 1; (R) : x + 2y + 2z − 2 = 0 .
Gọi α ; α ; α lần lượt là góc giữa hai mặt phẳng (P) và (Q), (Q) và (R), (R) và (P). Khẳng định 1 2 3
nào sau đây là khẳng định đúng. A.α > α >α . B. α > α >α . C.α > α >α . D.α > α >α . 1 3 2 2 3 1 3 2 1 1 2 3 Hướng dẫn giải
Áp dụng công thức tính góc giữa hai mặt phẳng. Sử dụng máy tính bỏ túi để tính góc rồi so
sánh các giá trị đó với nhau. VẬN DỤNG
Câu 34. Trong không gian với hệ tọa độOxyz, cho mặt phẳng(α ) : x + 2y + 2z + m = 0 vàđiểm A(1;1; ) 1 .
Khi đó m nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng (α ) bằng 1? A. − 2. B. − 8. C. − 2 hoặc 8 − . D. 3. 5 + mm + = m = −
Hướng dẫn giải: d ( , A (α )) 5 3 2 = =1 ⇔ ⇔ 3  m 5 3  + = − m = 8 − Trang 20/31
Câu 35. Trong không gian với hệ tọa độOxyz, mặt phẳng (α ) cắt các trục Ox, Oy, Oz lần lượt tại 3 điểm A( 2;
− 0;0), B(0;3;0) ,C (0;0;4) . Khi đó khoảng cách từ gốc tọa độ O đến mặt phẳng ( ABC) là A. 61 . B.4. C.12 61 . D.3. 12 61 Hướng dẫn giải x y z Cách 1: (α ) :
+ + =1 ⇔ 6x − 4y − 3z +12 = 0 ; d (O ( ABC)) 12 61 , = 2 − 3 4 61 Cách 2: Tứ diệnOABC có , OA OB, OC đôi một vuông góc, khi đó 1 1 1 1 61 12 61 = + + = ⇒ d O, ABC = 2 d ( 2 2 2 ( ) O,( ABC)) ( ) OA OB OC 144 61  y = 0
Câu 36. Trong không gian với hệ tọa độ 
Oxyz cho điểm M (1;0;0) và N (0;0;− ) 1 ,
2x − y − 2z − 2 = 0
mặt phẳng (P) qua điểm M , N và tạo với mặt phẳng (Q) : x − y − 4 = 0 một góc bằng O 45 .
Phương trình mặt phẳng (P) là  y = 0  y = 0 A.  . B.  .
2x − y − 2z − 2 = 0
2x − y − 2z + 2 = 0
2x − y − 2z + 2 = 0
2x − 2z + 2 = 0 C.  . D.  .
2x − y − 2z − 2 = 0
2x − 2z − 2 = 0 Hướng dẫn giải 
Gọi vectơ pháp tuyến của mp(P) và (Q) lần lượt là n a b c ( 2 2 2
a + b + c ≠ 0), P ( ; ; ) 
n (P) qua M (1;0;0) ⇒ (P) : a(x − ) 1 + by + cz = 0 Q
(P) qua N (0;0;− ) 1 ⇒ a + c = 0 (   a − b 1 a = 0
P) hợp với (Q) góc O
45 ⇒ cos(n n = cos ⇔ = ⇔ P , Q ) O 45  2 2 2a + b 2 2 a = 2 − b
Với a = 0 ⇒ c = 0 chọn b =1 phương trình (P) : y = 0 Với a = 2
− b chọn b = 1
− ⇒ a = 2 phương trình mặt phẳng (P) : 2x − y − 2z − 2 = 0 .
Câu 37. Trong không gian Oxyz , cho điểm A( 2; − 0; )
1 , đường thẳng d qua điểm A và tạo với trục Oy góc O
45 . Phương trình đường thẳng d là  x + 2 y z −1  − + = = x 2 y z 1  = = 2 5 1 −  2 5 1 − A.  . B.   x + 2 y z −1  − + = = x 2 y z 1  = =  2 − 5 1 −  2 − 5 1 −  x + 2 y z −1  + − = = x 2 y z 1  = = 2 5 1 −  2 − 5 1 − C.  D.   x − 2 y z +1  − + = = x 2 y z 1  = =  2 5 1 −  2 5 1 − Hướng dẫn giải Trang 21/31
Cách 1: Điểm M (0; ; m 0)∈Oy ,
j (0;1;0) là vectơ chỉ phương của trục    m 1
.Oy , AM (2;− ; m − ) 1 cos( AM, j) O = cos 45 ⇔ =
⇔ m = ± 5 nên có 2 đường 2 m + 5 2 thẳng: x + 2 y z −1 x + 2 y z −1 = = ; = = 2 5 1 − 2 − 5 1 −       Cách 2: 1 u 2; 5; 1
− ⇒ cos u , j = ; 1 u 2;− 5; 1
− ⇒ cos u , j = 2 ( ) ( 2 ) 1 ( ) ( 1 ) 2 2
Đường thẳng d đi qua điểm A( 2; − 0; )
1 nên chọn đáp án A.
Câu 38. Trong không gian Oxyz cho mặt phẳng (P) : x + y + z − 3 = 0 và mặt
phẳng(Q) : x − y + z −1 = 0. Khi đó mặt phẳng (R) vuông góc với mặt phẳng (P) và (Q) sao
cho khoảng cách từ O đến mặt phẳng (R) bằng 2 , có phương trình là
A. 2x − 2z − 2 2 = 0 .
B. x − z − 2 2 = 0 .
x − z + 2 2 = 0
C. x − z + 2 2 = 0 . D.  .
x − z − 2 2 = 0 Hướng dẫn:     n n − ⇒ n n  = − P (1;1; ) 1 , Q (1; 1; ) 1 P , Q (2;0; 2)   DD =
Mặt phẳng (R) x − z + D = ⇒ d (O (R)) 4 2 : 2 2 0 , = = 2 ⇒  8 D = 4 − 2
Vậy phương trình mp (R) : x − z + 2 2 = 0; x − z − 2 2 = 0
Câu 39. Tập hợp các điểm M ( ;
x y; z) trong không gian Oxyz cách đều hai mặt phẳng
(P) :x + y − 2z − 3 = 0 và (Q) :x + y − 2z + 5 = 0 thoả mãn:
A. x + y − 2z +1 = 0.
B. x + y − 2z + 4 = 0 .
C. x + y − 2z + 2 = 0 .
D. x + y − 2z − 4 = 0 . Hướng dẫn: M ( ;
x y; z) . Ta có
x + y − z −
x + y − z +
d (M (P)) = d (M (Q)) 2 3 2 5 , , ⇔ = 6 6
⇔ x + y − 2z − 3 = x + y − 2z + 5 ⇔ x + y − 2z +1 = 0
Câu 40. Tập hợp các điểm M ( ;
x y; z) trong không gian Oxyz cách đều hai mặt phẳng
(P) :x − 2y − 2z − 7 = 0 và mặt phẳng (Q) :2x + y + 2z +1 = 0 thoả mãn:
x + 3y + 4z + 8 = 0
A. x + 3y + 4z + 8 = 0. B.  .
3x − y − 6 = 0
C. 3x − y − 6 = 0.
D.3x + 3y + 4z + 8 = 0. Hướng dẫn giải
x − y − z −
x + y + z + Cho điểm M ( ;
x y; z), d (M (P)) = d (M (Q)) 2 2 7 2 2 1 , , ⇔ = 3 3
x + 3y + 4z + 8 = 0 ⇔  .
3x − y − 6 = 0 Trang 22/31
Câu 41. Trong không gian Oxyz cho điểm M thuộc trục Oxcách đều hai mặt phẳng
(P) : x + y − 2z − 3 = 0 và (Oyz) .Khitọa độ điểm M là     A     . 3  ;0;0 và 3  ;0;0. B. 3  ;0;0 và 3  ;0;0. 1 6  +   6 −1  1+ 6  1− 6   −   +   +   −  C. 6 1  ;0;0  và 6 1  ;0;0. D. 1 6  ;0;0 và 1 6  ;0;0. 3          3   3   3   m −
Hướng dẫn giải: Điểm M ( ;0
m ;0) ∈Ox ; d (M (P)) = d (M (P)) 3 , , ⇔ = m 6  3 m = m − 3 = m 6  1+ 6 ⇔  ⇔ 
m − 3 = −m 6  3 m =  1− 6
Câu 42. Trong không gianOxyz cho điểm A(3; 2 − ;4) và đường thẳng
x 5 y 1 z 2 d − − − : = = . 2 3 2 −
Điểm M thuộc đường thẳng d sao cho M cách A một khoảng bằng 17 . Tọa độ điểm M là
A.(5;1;2) và (6; 9; 2). B.(5;1;2) và ( 1 − ; 8 − ; 4 − ). C.(5; 1; − 2) và(1; 5 − ;6). D.(5;1;2) và (1; 5 − ;6). Hướng dẫn giải 
Cách 1: M (5 + 2t;1+ 3t;2 − 2t) ∈ d ; AM (2 + 2 ; m 3 + 3 ; m 2 − − 2m) m = 0 M 5;1;2 2 ( )
⇒ AM = 17 ⇔ 17(1+ m) = 17 ⇔ ⇒   m = 2 − M  (1; 5 − ;6)
Cách 2: Kiểm tra các điểm thuộc đường thẳng d có 2 cặp điểm trong đáp án B và C
thuộcđường thẳng d . Dùng công thức tính độ dài AM suy ra đáp án C thỏa mãn.
Câu 43. Trong không gian Oxyz cho tứ diện ABCD có các đỉnh A(1;2; ) 1 , B( 2 − ;1;3) ,C (2; 1; − ) 1 và D(0;3; )
1 . Phương trình mặt phẳng (P) đi qua 2 điểm ,
A B sao cho khoảng cách từ C đến
(P) bằng khoảng cách từ D đến (P) là
4x − 2y + 7z −1 = 0 A.  .
B. 2x + 3z − 5 = 0.
2x + 3z − 5 = 0
4x + 2y + 7z −15 = 0
C. 4x + 2y + 7z −15 = 0. D.  .
2x + 3z − 5 = 0 Hướng dẫn giải:
Trường hợp 1: (P) qua AB và song song với CD , khi đó: (  
P) có vectơ pháp tuyến là AB,CD = ( 8 − ; 4 − ; 1 − 4)  
và C ∉(P) ⇒ (P) : 4x + 2y + 7z −15 = 0.
Trường hợp 2: (P) qua AB cắt CD tại trung điểm I của đoạn CD . Ta    có I (1;1; ) 1 ⇒ AI (0; 1;
− 0) , vectơ pháp tuyến của (P) là AB, AI  = (2;0;3)   nên phương trình
(P) : 2x + 3z − 5 = 0. VẬN DỤNG CAO Trang 23/31
Câu 44. Trong không gian với hệ trục toạ độ Oxyz, gọi(P) là mặt phẳng chứa đường thẳng x 1 y 2 : z d − + = =
và tạo với trục Oy góc có số đo lớn nhất. Điểm nào sau đây thuộc 1 1 − 2 − mp(P)? A. E ( 3 − ;0;4). B. M (3;0;2). C. N ( 1 − ; 2 − ;− ) 1 . D. F (1;2; ) 1 .
Hướng dẫn giải:    Gọi n(a; ;
b c);n≠0là VTPT của (P) ; α là góc tạo bởi (P) và Oy , α lớn nhất khi sinα lớn   
nhất. Ta có n vuông góc với ud nên n(b + 2 ; c ; b c)   b sinα = cos( ,n j) = 2 2
2b + 5c + 4bc
Nếu b =0 thì sinα = 0. Nếu 1 c b ≠ 0 thì sinα =
. Khi đó, sinα lớn nhất khi 2 = − 2  5c 2  6 b 5  +  + b  5 5 
⇒ chọn b =5;c = − 2
Vậy, phương trình mp(P) là x +5y − 2z +9=0 . Do đó ta có N∈(P) .
Câu 45. Trong không gian với hệ trục toạ độ Oxyz, cho điểm M (0; −1; 2), N ( 1;
− 1; 3) . Gọi (P) là
mặt phẳng đi qua M , N và tạo với mặt phẳng (Q) :2x − y − 2z − 2= 0 góc có số đo nhỏ nhất.
Điểm A(1;2;3) cách mp(P) một khoảng là A. 3. B. 5 3 . C. 7 11 . D. 4 3 . 3 11 3
Hướng dẫn giải:   ( 
P) có VTPT n vuông góc với MN ( 1; − 2; ) 1 nên n(2b+ ; c ; b c) .
Gọiα là góc tạo bởi (P) và(Q),α nhỏ nhất khi cosα lớn nhất. b Ta có cosα = 2 2
5b + 2c + 4bc
Nếu b =0 thì cosα = 0. Nếu 1 c b ≠ 0 thì cosα =
. Khi đó, cosα lớn nhất khi = −1⇒ chọn b =1;c = −1 2 b 2 c 1 + +   3  b
Vậy, phương trình mp(P) là x + y − z +3=0 . Do đó d ( , A (P)) = 3 .
Câu 46. Trong không gian với hệ trục toạ độ Oxyz, cho (P):x − 2 y + 2z −1=0 và 2 đường thẳng x +1 y z + 9
x −1 y − 3 z +1 ∆ : = = ; ∆ : = = . 1 2 1 1 6 2 1 2 −
Gọi M là điểm thuộc đường thẳng ∆ , M có toạ độ là các số nguyên, M cách đều ∆ và 1 2
(P). Khoảng cách từ điểm M đến mp(Oxy) là A.3. B. 2 2. C.3 2. D. 2.
Hướng dẫn giải: Trang 24/31
Gọi M (t −1;t;6t − 9),t ∈.   M M ,u
Ta có d (M , ) d (M ,(P)) 0   ∆ = ⇔  = d M , P 2 ( ( )) u 11t − 20 2
⇔ 29t −88t + 68 =
với M 1;3;−1 ∈∆ 0 ( ) 3 2 t =1  ⇔ 53 t∈ → t =1 t =  35
Vậy, M (0;−1;3)⇒ d (M ,(Oxy))=3.
Câu 47. Trong không gian với hệ trục toạ độ Oxyz, cho 2 điểm A(1;5;0); B(3;3;6) và đường thẳng x 1 y 1 : z d + − =
= . Gọi C là điểm trên đường thẳng d sao cho diện tích tam giác ABC nhỏ 2 1 − 2
nhất. Khoảng cách giữa 2 điểm A và C là A. 29. B. 29. C. 33. D. 7. Hướng dẫn giải:
Ta có 2 đường thẳng AB và d chéo nhau. B
Gọi C là điểm trên d và H là hình chiếu vuông góc H
của C trên đường thẳng AB . A Vì 1 S = AB ⋅CH = ⋅CH nên S nhỏ nhất khi ABC 11 2 ABC
CH nhỏ nhất ⇔ CH là đoạn vuông góc chung của 2
đường thẳng AB và d .
Ta có C (1; 0; 2)⇒ AC = 29 . C
Câu 48. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(10;2; ) 1 và đường thẳng x 1 y z 1 d − − : = =
. Gọi (P) là mặt phẳng đi qua điểm A , song song với đường thẳng d sao 2 1 3
cho khoảng cách giữa d và (P) lớn nhất. Khoảng cách từ điểm M ( 1;
− 2;3) đến mp(P) là A. 97 3 . B. 76 790 . C. 2 13 . D. 3 29 . 15 790 13 29
Hướng dẫn giải:
(P) là mặt phẳng đi qua điểm A và song song với d
đường thẳng d nên (P) chứa đường thẳng d′ đi qua H
điểm A và song song với đường thẳng d .
Gọi H là hình chiếu của A trên d , K là hình chiếu của H trên (P) . d' K
Ta có d (d,(P))
= HK ≤ AH ( AH không đổi)
⇒ GTLN của d(d, (P)) là AH P A
⇒ d (d,( P)) lớn nhất khi AH vuông góc với (P) .
Khi đó, nếu gọi (Q) là mặt phẳng chứa A và d thì (P) vuông góc với (Q). Trang 25/31   
⇒ nP = ud ,nQ  =(98;14;− 70)  
⇒(P) x + y − z −
= ⇒ d (M (P)) 97 3 :7 5 77 0 , = . 15
Câu 49. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(2;5;3) và đường thẳng x 1 y z 2 d − − : = =
. Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A 2 1 2
đến (P) lớn nhất. Tính khoảng cách từ điểm M (1;2;− )
1 đến mặt phẳng (P) . A.11 18 . B.3 2. C. 11 . D. 4 . 18 18 3 Hướng dẫn giải:
Gọi H là hình chiếu của A trên d ; K là hình chiếu A
của A trên (P) . Ta có d ( , A (P))
= AK ≤ AH (Không đổi)
⇒ GTLN của d(d, (P)) là AH d ( ,
A ( P)) lớn nhất khi K ≡ H . d' K
Ta có H (3;1;4) , (P) qua H và ⊥ AH
⇒(P) :x − 4y + z −3 = 0 P H
Vậy d (M (P)) 11 18 , = . 18
Câu 50. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) :x + y − z + 2 = 0 và hai đường x =1+ tx = 3− t′  
thẳng d :y = t
; d ':y =1+ t′ . z = 2+   2t z =1−  2t′
Biết rằng có 2 đường thẳng có các đặc điểm: song song với (P) ; cắt d, d′ và tạo với d góc O
30 . Tính cosin góc tạo bởi hai đường thẳng đó. A. 1 . B. 1 . C. 2. D. 1 . 5 2 3 2
Hướng dẫn giải: 
Gọi ∆ là đường thẳng cần tìm, n là VTPT của mặt phẳng (P) . P
Gọi M (1+ t;t;2 + 2t) là giao điểm của ∆ và d ; M ′(3− t ;1 ′ + t ;1
′ − 2t′) là giao điểm của ∆ và d ' 
Ta có: MM '(2 − t′ − t;1+ t′ − t;−1− 2t′ − 2t) M ∉  (P) 
MM ′ // (P)⇔   ⇔t′=− 2⇒ MM ′(4 −t; 1
− − t;3− 2t)
MM ′⊥ nP   3 6 − t + 9 t = 4 Ta có O
cos30 =cos(MM ,′ud )⇔ = ⇔  2 2 36t −108t +156 t = 1 − Trang 26/31 x = 5 x = t′  
Vậy, có 2 đường thẳng thoả mãn là ∆ :y = 4 + t ;∆ :y = 1 − 1 2 . z =10+tz =   t′ Khi đó, ( 1 cos ∆ ,∆ = . 1 2 ) 2
Câu 51. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1;0; ) 1 ; B(3; 2; − 0);C (1;2; 2 − ) . Gọi
(P) là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) lớn nhất biết rằng
(P)không cắt đoạn BC . Khi đó, điểm nào sau đây thuộc mặt phẳng(P)? A. G ( 2; − 0; 3). B. F (3; 0; 2 − ). C. E (1;3; ) 1 . D. H ( 0;3; ) 1 Hướng dẫn giải:
Gọi I là trung điểm đoạn BC ; các điểm B ,′ C ,′ I′ B I
lần lượt là hình chiếu của B,
C, I trên (P) . C Ta có tứ giác BCC B
′ ′ là hình thang và II′là đường trung bình.
⇒ d (B,( P)) + d (C,( P)) = BB′+ CC′ = 2II .′
Mà II′ ≤ IA (với IA không đổi) B' I' C'
Do vậy, d (B,(P)) + d ( C,(P))
lớn nhất khi I′ ≡ A A  P
⇒ (P) đi qua A và vuông góc IA với I (2;0; − ) 1 .
⇒ (P) : −x + 2z −1 = 0 ⇒ E (1;3; ) 1 ∈(P).
Câu 52. Trong không gian với hệ trục toạ độ Oxyz, cho các điểm A(1;0;0), B(0; ;
b 0),C (0;0;c) trong đó ,
b c dương và mặt phẳng (P) : y − z +1= 0. Biết rằng mp( ABC) vuông góc với mp(P) và
d (O ( ABC)) 1 ,
= , mệnh đề nào sau đây đúng? 3
A.b + c =1.
B. 2b + c =1.
C.b − 3c =1.
D.3b + c =3. Hướng dẫn giải:
Ta có phương trình mp( ABC) là x y z + + = 1 1 b c ( ABC)⊥(P) 1 1
⇒ − = 0⇒b = c (1) b c
Ta có d (O ( ABC)) 1 1 1 1 1 , = ⇔ = ⇔ + = 8(2) 2 2 3 1 1 3 b c 1+ + 2 2 b c Từ (1) và (2) 1
⇒ b =c = ⇒b + c =1. 2
Câu 53. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1;2;3); B(0;1; ) 1 ;C (1;0;− 2) .
Điểm M ∈(P) :x + y + z + 2 = 0 sao cho giá trị của biểu thức 2 2 2
T = MA + 2MB +3MC nhỏ nhất.
Khi đó, điểm M cách (Q) :2x − y − 2z + 3 = 0 một khoảng bằng A.121. B. 24. C. 2 5 . D.101. 54 3 54 Trang 27/31 Hướng dẫn giải: Gọi M ( ;
x y; z) . Ta có 2 2 2
T = 6x + 6y + 6z −8x −8y + 6z + 31 2 2 2  2 2 1        145
⇒ T = 6  x − + 
y −   z +   +  3   3   2    6  2 145 ⇒T = 6MI + với 2 2 1 I  ; ;  − 6 3 3 2   
⇒ T nhỏ nhất khi MI nhỏ nhất ⇒ M là hình chiếu vuông góc của I trên (P) 5 5 13 M  ; ;  ⇒ − − −  . 18 18 9   
BÀI TẬP TỔNG HỢP
Câu 54. Cho mặt phẳng (α) : x + y − 2z − 1 = 0; (β) : 5x + 2y + 1 z
1 − 3 = 0 . Góc giữa mặt phẳng
(α) và mặt phẳng (β ) bằng A. 120 .° B. 30 .° C.150 .° D. 60 .°
Câu 55. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) có phương trình x + y − 3 = 0.
Điểm H(2; 1; 2) là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa
hai mặt phẳng (P) và (Q) bằng A. 45 .° B. 30 .° C. 60 .° D. 120 .°     π   
Câu 56. Cho vectơ u = 2; v = 1; (u, v) = . Gócgiữa vectơvvà vectơ u − v bằng: 3 A. 60 .° B. 30 .° C. 90 .° D. 45 .°
Câu 57. Trong không gian với hệ trục toạ độ Oxyz, cho đường thẳng x − y + z
2x − 3y − 3z + 9 = 0 d 3 1 − 1 : = = , ∆ :
. Góc giữa đường thẳng d và đường thẳng 9 5 1 
x − 2y + z + 3 = 0 ∆ bằng A. 90 .° B. 30 .° C. 0 .° D. 180 .°
Câu 58. Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (α) : 2x − y − 2z − 10 = 0; đường x − − y z + thẳng d 1 1 3 : = =
. Góc giữa đường thẳng d và mặt phẳng (α) bẳng 1 2 3 A. 30 .° B. 90 .° C. 60 .° D. 45 .°
Câu 59. Trong không gian với hệ trục toạ độ Oxyz, phương trình các đường thẳng qua A(3; – 1;1), nằm x y − 2 z
trong (P): x – y + z – 5 = 0và hợp với đường thẳngd: = = một góc 45 0 là 1 2 2 x = 3 + tx = 3 + t 3 A.   ∆ : 1 , ; : 1 2 , . 1
y = − + t t ∈ R ∆2 y = − − t t ∈ R   z = 1 z = 1 −   t 5 x = 3 + 2tx = 3 + t 15 B.   ∆ : 1 2 , ; : 1 38 , . 1
y = − + t t ∈ R ∆2 y = − + t t ∈ R   z = 1 z = 1 +   t 23 x = 3 + tx = 3 + t 15 C.   ∆ : 1 , ; : 1 8 , . 1
y = − + t t ∈ R ∆2 y = − − t t ∈ R   z = 1 z = 1 −   t 23 Trang 28/31 x = 3 − tx = 3 + t 15 D.   ∆ : 1 , ; : 1 8 , . 1
y = − − t t ∈ R ∆2 y = − − t t ∈ R   z = 1 + t z = 1 −   t 23
Câu 60. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm các
cạnh A'B', BC, DD'. Góc giữa đường thẳng AC’ và mặt phẳng (MNP) là A. 30 .° B. 120°. C. 60 .° D. 90 .°
Câu 61. Trong không gian với hệ trục toạ độ Oxyz, gọi(P) là mặt phẳng chứa đường thẳng x = 1+ 2t
d : y = 2 −t và tạo với trục Ox góc có số đo lớn nhất.Khi đó, khoảng cách từ điểm z =  3t A(1; 4
− ;2) đến mp(P)là 12 35 A. . B. 4 3 . C. 20 6 . D. 2 6 . 35 3 9 3
Câu 62. Trong không gian với hệ trục toạ độ Oxyz, cho điểm M (2;1; 1
− 2), N ( 3;0;2) . Gọi (P) là mặt
phẳng đi qua M , N và tạo với mặt phẳng (Q) :2x + 2y −3z + 4= 0 góc có số đo nhỏ nhất. Điểm
A(3;1;0) cách mp(P) một khoảng là 1 A. 6 13 . B. 22 . C. 6 . D. . 13 11 2 22
Câu 63. Trong không gian với hệ trục toạ độOxyz, cho (P) :x + y − z − 7 =0 và hai đường thẳng
x −1 y −1 z − 2
x − 2 y − 3 z + 4 ∆ : = = ;∆ : = = . 1 2 1 1 1 2 3 5 −
Gọi M là điểm thuộc đường thẳng ∆ , M có toạ độ là các số dương, M cách đều ∆ và 1 2
(P). Khoảng cách từ điểm M đến mp( P ) là A. 2 3. B. 2. C. 7. D. 2 . 3
Câu 64. Trong không gian với hệ trục toạ độ Oxyz, cho 2 điểm A(1; 4
− ;3); B(1;0;5) và đường thẳng x = 3 − t
d : y = 3+ 2t.Gọi C là điểm trên đường thẳng d sao cho diện tích tam giác ABC nhỏ nhất. z = 2 − 
Khoảng cách giữa điểm C và gốc toạ độ O là A. 6. B. 14. C. 14. D. 6.
Câu 65. Trong không gian với hệ trục toạ độOxyz, cho điểm A(2;5;3) và đường thẳng x 1 y z 2 d − − : = =
.Gọi (P) là mặt phẳng đi qua điểm A , song song với đường thẳng d sao 2 1 2
cho khoảng cách giữa d và (P) lớn nhất. Khoảng cách từ điểm B(2;0;−3) đến mp(P) là A. 7 2 . B. 5 2 . C. 7. D. 18 . 3 3 18 Trang 29/31 x = 4 + 3t
Câu 66. Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(4; 3
− ;2)và đường thẳng d :y = 2 + 2t. z = 2 − −  t
Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A đến (P) lớn nhất. Tính
khoảng cách từ điểm B( 2 − ;1; 3
− ) đến mặt phẳng (P) đó. A. 2 3. B. 2. C. 0. D. 38.
Câu 67. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1; 1;− 2);B( 1; − 2; ) 1 ;C ( 3 − ; 4; ) 1 . Gọi
(P) là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) lớn nhất biết rằng
(P) không cắt đoạn BC . Khi đó, điểm nào sau đây thuộc mặt phẳng (P) ? A. F ( 1; − 2;0). B. E (2; 2; − ) 1 . C. G (2;1; 3 − ). D. H (1; 3 − ; ) 1 .
Câu 68. Trong không gian với hệ trục toạ độOxyz, cho các điểm A( ;
a 0;0), B(0;2;0),C (0;0;c) trong
đó a,c dương và mặt phẳng (P) :2x − z + 3= 0. Biết rằng mp( ABC) vuông góc với mp(P) và
d (O ( ABC)) 2 , =
, mệnh đề nào sau đây đúng? 21
A. a + 4c =3.
B. a + 2c =5.
C. a −c =1.
D. 4a −c =3.
Câu 69. Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A( 2
− ; 2; 3);B(1; −1; 3);C (3; 1; − ) 1 .
Điểm M ∈(P) :x + 2z −8 = 0 sao cho giá trị của biểu thức 2 2 2
T = 2MA + MB +3MC nhỏ nhất.
Khi đó, điểm M cách (Q) :− x + 2y − 2z − 6 = 0 một khoảng bằng A. 2 . B.2. C. 4 . D. 4. 3 3
Câu 70. Tính khoảng cách từ điểm H(3; – 1;– 6) đến mặt phẳng (α) : x + y − z +1 = 0 . A 8 3 . . B. 9. C. 3 3. D. 3. 3
Câu 71. Tính khoảng cách giữa hai mặt phẳng song song (P): 2x + y + 2z = 0 và (Q) 2x + y + 2z + 7 = 0 . A 7 7 . . B. 7. C. . D. 2. 9 3
Câu 72. Khoảng cách từ điểm K(1;2;3) đến mặt phẳng (Oxz) bằng A. 2. B. 1. C. 3. D. 4. x =1+ 5t
Câu 73. Tính khoảng cách giữa mặt phẳng 
(α) : 2x + y + 2z + 4 = 0 và đường thẳng d: y = 2 − 2t . z = 4 −  t A 8 4 . . B. 0. C. . D. 4. 3 3
Câu 74. Khoảng cách từ giao điểm A của mặt phẳng (R) : x + y + z −3 = 0 với trục Oz đến mặt phẳng
(α) : 2x + y + 2z +1 = 0 bằng A 7 5 4 . . B. . C. . D. 0. 3 3 3 x = 1− 3t
Câu 75. Cho hai mặt phẳng (P) : x + y + 2z −1 = 0, (Q) : 2x + y + z = 0 và đường thẳng d: y = 2 + t . z = 1 − +  t Trang 30/31
Gọi d(d,(P)) , d(d,(Q)) , d((P),(Q)) lần lượt là khoảng cách giữa đường thẳng d và (P), d và
(Q), (P) và (Q). Trong các mệnh đề sau, tìm mệnh đề sai:
A. d(d,(P)) = 0. B. 6
d(d,(Q)) = .
C. d((P),(Q)) = 0.
D. d(d,(Q)) = 0. 2 x =1+ t
Câu 76. Khoảng cách từ điểm  C( 2
− ;1;0) đến mặt phẳng (Oyz) và đến đường thẳng ∆ : y = 4 + t lần z = 6+  2t
lượt là d và d . Chọn khẳng định đúng trong các khẳng định sau: 1 2
B. d > d .
B. d = d . C. d = D. d =1. 1 2 1 2 1 0. 2
Câu 77. Khoảng cách từ điểm B(1;1;1) đến mặt phẳng (P) bằng 1. Chọn khẳng định đúngtrong các khẳng định sau:
A. (P): 2x + y – 2z + 6 = 0.
B. (P): x + y + z – 3 = 0.
B. (P): 2x + y + 2z – 2 = 0.
D. (P): x + y + z – 3 = 0 .
Câu 78. Trong không gian Oxyz cho mặt phẳng(α ) :2x − y + 2z +1 = 0 và mặt phẳng
(β ) :2x − y + 2z + 5 = 0. Tập hợp các điểm M cách đều mặt phẳng (α )và (β ) là
A. 2x − y + 2z + 3 = 0.
B. 2x − y − 2z + 3 = 0.
C. 2x − y + 2z − 3 = 0.
D. 2x + y + 2z + 3 = 0.
Câu 79. Trong không gian Oxyz cho mặt phẳng (α ) :x − 2y + 2z +1 = 0 và mặt
phẳng(β ) : 2x − y + 2z +1 = 0 . Tập hợp các điểm cách đều mặt phẳng (α ) và (β ) là
x − y + 2 = 0
x − y + 2 = 0 A.  . B.  .
3x + 3y + 4z + 4 = 0
3x − 3y + 4z + 4 = 0
x − y + 2 = 0 x + y + 2 = 0 C.  . D.  .
3x − 3y + 4z + 4 = 0
3x − 3y + 4z + 4 = 0 Trang 31/31
Document Outline

  • DS_C8_GOC - KHOANG CACH
    • A. KIẾN THỨC CƠ BẢN
    • B. KỸ NĂNG CƠ BẢN
    • C. BÀI TẬP TRẮC NGHIỆM
    • D. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM