Tóm tắt lý thuyết và bài tập trắc nghiệm khối đa diện và thể tích khối đa diện Toán 12

Giới thiệu đến các em tài liệu tóm tắt lý thuyết và bài tập trắc nghiệm khối đa diện và thể tích khối đa diện, một chủ đề rất quan trọng trong chương trình Hình học 12 chương 1. Bên cạnh tài liệu khối đa diện và thể tích khối đa diện dạng PDF dành cho học sinh.Mời bạn đọc đón xem.

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

34 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/35
Chọn góc nhọn là
α
sin ;

α=


caïnh oái i
caïnh uyeà ïc
ñ
ohn
ñ
h
cos ;

α=


kk
h
caïnh eà hoâng
caïnh uyeàn öh
tan ;
α=
caïnh oái oaøn
caïnh
ññ
tkeà ek á
cot ;
α=
kk
ñ
caïnh eà eát
caïnh oái oaønñ
A
B
C
c
a
222
2 22
2 22
2 22
222
2 22
2 cos cos
2
2 cos cos
2
2 cos cos
2
bca
a b c bc A A
bc
acb
b a c ac B B
ac
abc
c a b ab C C
ab






Chọn góc nhọn là
α
sin ;

α=


caïnh oái i
caïnh uyeà ïc
ñ
ohn
ñ
h
cos ;

α=


kk
h
caïnh eà hoâng
caïnh uyeàn öh
tan ;

α=


caïnh oái oaøn
caïnh
ññ
tk
eà ek á
cot ;

α=


kk
ñ
caïnh eà eát
caïnh oái oaønñ
α
Cạnh
đối
Cạnh kề
Cạnh huyền
CHỦ ĐỀ 1. KHỐI ĐA DIỆN VÀ THỂ TÍCH KHỐI ĐA DIỆN
A. KIẾN THỨC CƠ BẢN
a. HÌNH HỌC PHẲNG
1. Các hệ thức lượng trong tam giác vuông:
Cho tam giác
ABC
vuông tại
A
,
AH
là đường cao,
AM
là đường trung tuyến. Ta có:
2. Các tỉ số lượng giác của góc nhọn trong tam giác vuông:
3. Các hệ thức lượng trong tam giác thường:
a. Định lý cosin:
b. Định lý sin:
B
A
B
C
H
M
222
BC AB AC
..AH BC AB AC
22
., .AB BH BC AC CH CB
2
222
1 11
,.AH HB HC
AH AB AC

2AM BC
Trang 2/35
c. Công thức tính diện tích tam giác:
d. Công thức tính độ dài đường trung tuyến:
4. Định lý Thales:
A
B
C
c
a
b
- nửa chu vi
- bán kính đường tròn nội tiếp
p
r
1 11
...
2 22
ABC a b c
S ah bh ch

1 11
sin sin sin
2 22
ABC
S ab C bc A ac B

,.
4
ABC ABC
abc
S S pr
R


(
)( )( )
p pp a p b p c= −−−
222
2
24
AB AC BC
AM

22 2
2
24
BA BC AC
BN

22 2
2
24
CA CB AB
CK

A
B
C
N
K
M
A
B
C
N
M
2
2
//
AMN
ABC
AM AN MN
MN BC k
AB AC BC
S
AM
k
S AB




(Tỉ diện tích bằng tỉ bình phương đồng dạng)
2
sin sin sin
abc
R
ABC

(R là bán kính đường tròn ngoại tiếp ∆ABC)
A
B
C
c
b
a
R
Trang 3/35
5. Diện tích đa giác:
a. Diên tich tam giac vuông:
Diên tich tam giac vuông băng ½ tich 2 ca
nh
goc vuông.
b. Diên tich tam giac đêu:
Diên tich tam giac đêu:
.
3
4
S
Chiêu cao tam giac đêu:
. 3
2
h
c. Diê n tich hinh vuông va hinh chư nhât:
Diên tich hinh vuông băng canh binh phương.
Đương cheo hinh vuông băng canh nhân
2
.
Diên tich hinh chư nhât băng dai nhân rông.
d. Diên tich hinh thang:
S
Hinh Thang
1
2
.(đay lơn + đay be) x chiêu cao
e. Diê n tich tư giac co hai đương cheo vuông
goc:
Diên tich tư giac co hai đương cheo vuông go
c
nhau băng ½ tich hai đương cheo.
Hinh thoi co hai đương cheo vuông goc nhau
tai trung điêm cua môi đương.
b. CAC PHƯƠNG PHAP CHƯNG MINH HINH HOC
1. Chưng minh đương thăng song song với mặt phẳng :
()
()
()
d
dd d
d

(Định lý 1, trang 61, SKG HH11)
()
()
()
d
d

(Hệ quả 1, trang 66, SKG HH11)
A
B
H
C
D
.
2
AD BC AH
S

A
C
B
1
.
2
ABC
S AB AC

A
B
C
a
h
2
3
4
3
2
ABC
a
S
a
h
A
B
C
D
a
O
2
2
HV
Sa
AC BD a

A
B
D
C
.
1
.
2
H Thoi
S AC BD
(cạnh)
2
đều
(cạnh)
đều
Trang 4/35
'
() ' ()
()
d
dd


d
d
(Tính chất 3b, trang 101, SKG HH11)
2. Chưng minh hai mặt phẳng song song:
() , ()
() , () ( ) ()
aa
bb
ab O





(Định lý 1, trang 64, SKG HH11)
() ()
() ()
() ()
Q
Q

(Hệ quả 2, trang 66, SKG HH11)
() ()
() () ()
()
d
d



. (Tính chất 2b, trang 101, SKG HH11)
3. Chưng minh hai đương thăng song song: Ap dung môt trong cac đinh li sau
Hai mặt phẳng
( ),

co điêm chung S va lân lươt chưa 2 đương thăng song song
,ab
thi giao
tuyến của chúng đi qua điểm S cùng song song với a,B.
(
()
() , () ).
S
a b Sx a b
ab





(Hệ quả trang 57, SKG HH11)
Cho đường thẳng a song song với mặt phẳng
()
. Nếu mặt phẳng
()
chứa a và cắt
()
theo
giao tuyến b thì b song song với a.
( ),
()
a
b
b



a
a.
(Định lý 2, trang 61, SKG HH11)
Hai măt phăng cung song song vơi môt đương thăng thi giao tuyên cua chung song song vơi
đương thăng đo.
() ()
() ()
() ()
P
Pd




=d ,d d
. (Định lý 3, trang 67, SKG HH11)
Hai đương thăng phân biệt cung vuông goc vơi môt măt phăng thi song song vơi nhau.
()
()
dd
d
d

d d
(Tính chất 1b, trang 101, SKG HH11)
Sư dung phương phap hinh hoc phăng: Đương trung binh, đinh li Talet đao, …
4. Chưng minh đương thăngvuông góc với mặt phẳng:
Định lý (Trang 99 SGK HH11). Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau
nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
{
()
()
}
da
db d
ab O




.
Tính chất 1a (Trang 101 SGK HH11). Cho hai đường thẳng song song. Mặt phẳng nào vuông
Trang 5/35
góc với đường thẳng này thì vuông góc với đường thẳng kia.
()
d
d

dd
.
Tính chất 2a (Trang 101 SGK HH11). Cho hai mặt phẳng song song. Đường thẳng nào vuông
góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
d
d


.
Định lý 2 (Trang 109 SGK HH11). Nếu hai măt phăng căt nhau và cung vuông goc vơi măt
phăng thư ba thi giao tuyên cua chung vuông goc vơi măt phăng thư ba đó.
P
P dP
d



.
Định lý 1 (Trang 108 SGK HH11). Nếu hai măt phăng vuông goc thì bất cứ đường thẳng nào
nao năm trong măt phăng nay va vuông goc vơi giao tuyên đều vuông goc vơi măt phăng kiA.
,
P
a P dP
d da


5. Chưng minh hai đương thăng vuông góc:
Cách 1: Dùng định nghĩa:
0
, 90 .a b ab
Hay
. 0 .. , 0a b a b a b a b cos a b


Cách 2: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì phải
vuông góc với đường kia.
b//c
ab
ac

.
Cách 3: Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường
thẳng nằm trong mặt phẳng đó.
.
a
ab
b

Cách 4: (Sư dung Đinh ly Ba đương vuông goc) Cho đường thẳng b nằm trong mặt phẳng
P
và a là đường thẳng không thuộc
P
đồng thời không vuông góc với
P
. Gọi a’ là hình chiếu
vuông góc của a trên
P
. Khi đó b vuông góc với a khi và chỉ khi b vuông góc với a’.
' ()
'.
a hch P
ba ba
bP

Cách khác: Sư dung hinh hoc phăng (nếu được).
6. Chưng minh
mp mp
:
Cách 1: Theo định nghĩa:
0
, 90 . 
Chưng to goc giưa hai măt phăng băng
90
.
Cách 2: Theo định lý 1 (Trang 108 SGK HH11):
c. HINH CHOP ĐÊU
Trang 6/35
A
B
1. Đinh nghia: Môt hinh chop đươc goi la hinh chop đêu nêu co đay la môt đa giac đêu vaco chân
đương cao trung vơi tâm cua đa giac đay.
Nhân xet:
Hinh chop đêu co cac măt bên la nhưng tam giac cân băng nhau.
Cac măt bên tao vơi đay cac goc băng nhau.
Cac canh bên cua hinh chop đêu tao vơi măt đay cac goc băng
nhau.
2. Hai hinh chop đêu thương găp:
a. Hinh chop tam giac đêu: Cho hinh chop tam giac đêu
.S ABC
. Khi
đo:
Đay
ABC
la tam giac đêu.
Cac măt bên la cac tam giac cân tai
S
.
Chiêu cao:
SO
.
Goc giưa canh bên va măt đay:
SAO SBO SCO
.
Goc giưa măt bên va măt đay:
SHO
.
Tinh chât:
21 3
,,
33 2
AB
AO AH OH AH AH
.
Lưu y: Hinh chop tam giac đêu khac vơi tư diên đêu.
Tư diên đêu cocac măt lacac tam giac đêu.
Tư diên đêu la hinh chop tam giac đêu cocanh bên
băng canh đay.
b. Hinh chop tư giac đêu: Cho hinh chop tam giac đêu
.S ABCD
.
Đay
ABCD
la hinh vuông.
Cac măt bên la cac tam giac cân tai
S
.
Chiêu cao:
SO
.
Goc giưa canh bên va măt đay:
SAO SBO SCO SDO
.
Goc giưa măt bên va măt đay:
SHO
.
d. THÊ TICH KHÔI ĐA DIÊN
1. Thê tich khôi chop:
1
.
3
V Bh
:B
Diên tich măt đay.
:h
Chiêu cao cua khôi chop.
C
D
S
O
B
A
C
D
S
O
I
B
A
C
S
O
Trang 7/35
2. Thê tich khôi lăng tru:
.
V Bh
:B
Diên tich măt đay.
:h
Chiêu cao cua khôi chop.
Lưu y: Lăng tru đưng co chiêu cao cung la
canh bên.
3. Thê tich hinh hôp chư nhât:
..V abc
Thê tich khôi lâp phương:
3
Va
4. Ti sô thê tich:
.
.
..
SABC
S ABC
V
SA SB SC
V SA SB SC


5. Hinh chop cut
.
ABC A B C
′′′
3
h
V B B BB


Vơi
,,BB h
la diên tich hai đay va chiêu cao.
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho hình chóp
.S ABC
có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích
.S ABC
tăng lên bao nhiêu lần?
A.
4
. B.
2
. C.
3
. D.
1
2
.
Câu 2. Có bao nhiêu khối đa diện đều?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 3. Cho khối đa diện đều
{ }
;pq
, chỉ số
p
là
A. Số các cạnh của mỗi mặt. B. Số mặt của đa diện.
C. Số cạnh của đa diện. D. Số đỉnh của đa diện.
Câu 4. Cho khối đa diện đều
{ }
;
pq
, chỉ số
q
là
A. Số đỉnh của đa diện. B. Số mặt của đa diện.
C. Số cạnh của đa diện. D. Số các mặt ở mỗi đỉnh.
Câu 5. Tính thể tích khối tứ diện đều cạnh
a
.
A.
3
2
12
a
⋅
B.
3
2
4
a
⋅
C.
3
a
. D.
3
6
a
⋅
Câu 6. Cho
.S ABCD
là hình chóp đều. Tính thể tích khối chóp
.S ABCD
biết
AB a=
,
SA a=
.
A.
3
a
B.
3
2
2
a
C.
3
2
6
a
. D.
3
3
a
Câu 7. Cho hình chóp
.S ABC
có
( )
SA ABC⊥
, đáy
ABC
là tam giác đều. Tính thể tích khối chóp
.S ABC
biết
AB a=
,
SA a
=
.
C
A
B
B’
A’
C’
A
B
C
A’
B’
C’
a
b
c
a
a
a
S
A’
B’
C’
A
B
C
Trang 8/35
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
a
. D.
3
3
a
Câu 8. Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
, đáy
ABCD
là hình chữ nhật. Tính thể tích
.S ABCD
biết
AB a
=
,
2
AD a=
,
3SA a=
.
A.
3
a
. B.
3
6
a
. B.
3
2a
. D.
3
3
a
⋅
Câu 9. Thể tích khối tam diện vuông
.O ABC
vuông tại
O
có
, 2OA a OB OC a= = =
là
A.
3
2
3
a
⋅
B.
3
2
a
⋅
C.
3
6
a
⋅
D.
3
2
a
.
Câu 10. Cho hình chóp
.S ABC
có
SA
vuông góc mặt đáy, tam giác
ABC
vuông tại
, 2A SA cm=
,
4 , 3AB cm AC cm= =
. Tính thể tích khối chóp.
A.
3
12
3
cm
. B.
3
24
5
cm
. C.
3
24
3
cm
. D.
3
24cm
.
Câu 11. Cho hình chóp
.
S ABCD
đáy hình chữ nhật,
SA
vuông góc đáy,
, 2AB a AD a= =
. Góc giữa
SB
và đáy bằng
0
45
. Thể tích khối chóp là
A.
3
2
3
a
⋅
B.
3
2
3
a
⋅
C.
3
3
a
⋅
D.
3
2
6
a
⋅
Câu 12. Hinh chop
.S ABCD
đáy hình vuông,
SA
vuông góc với đáy,
3, 2ASA
Caa
= =
. Khi đó thê
tich khôi chop
.S ABCD
la
A.
3
2
2
a
⋅
B.
3
2
3
a
⋅
C.
3
3
2
a
⋅
D.
3
3
3
a
⋅
Câu 13. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
. Biết
SAB∆
là tam giác đều và
thuộc mặt phẳng vuông góc với mặt phẳng
( )
ABC
. Tính thể tích khối chóp
.S ABC
biết
AB a=
,
3AC a=
.
A.
3
6
12
a
⋅
B.
3
6
4
a
⋅
C.
3
2
6
a
⋅
D.
3
4
a
⋅
Câu 14. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi. Mặt bên
( )
SAB
là tam giác vuông cân tại
S
và thuộc mặt phẳng vuông góc với mặt phẳng
( )
ABCD
. Tính thể tích khối chóp
.S ABCD
biết
BD a=
,
3AC a=
.
A.
3
a
. B.
3
3
4
a
⋅
C.
3
3
12
a
⋅
D.
3
3
a
⋅
Câu 15. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
. Hình chiếu của
S
lên mặt phẳng
( )
ABC
là trung điểm
H
của
BC
. Tính thể tích khối chóp
.S ABC
biết
AB a=
,
3AC a=
,
2SB a=
.
A.
3
6
6
a
⋅
B.
3
3
2
a
⋅
C.
3
3
6
a
⋅
D.
3
6
2
a
⋅
Câu 16. Cho hình chóp
.S ABCD
có đáy
ABCD
hình vuông cạnh
a
. Hình chiếu của
S
lên mặt phẳng
(
)
ABCD
là trung điểm
H
của
AD
. Tính thể tích khối chóp
.S ABCD
biết
3
2
a
SB =
.
A.
3
3
a
⋅
B.
3
a
. C.
3
2
a
⋅
D.
3
3
2
a
⋅
Trang 9/35
Câu 17. Hình chóp
.S ABCD
đáy là hình vuông cạnh
1
,
3
2
a
SD
a
=
. Hình chiếu của S lên
(
)
ABCD
là
trung điểm
H
của
AB
. Thể tích khối chóp là
A.
3
2
3
a
⋅
B.
3
2
3
a
⋅
C.
3
12a
. D.
3
3
a
⋅
Câu 18. Hinh chop
.S ABCD
đáy hình thoi,
2AB a=
, góc
BAD
bằng
0
120
. Hình chiếu vuông góc của
S
lên
( )
ABCD
là
I
giao điểm của 2 đường chéo, biết
2
SI
a
=
. Khi đó thê tich khôi chop
.S ABCD
la
A.
3
2
9
a
⋅
B.
3
3
9
a
⋅
C.
3
2
3
a
⋅
D.
3
3
3
a
⋅
Câu 19. Cho hình chóp
.S ABC
, gọi
M
,
N
lần lượt là trung điểm của
,SA SB
. Tính tỉ số
.
.
S ABC
S MNC
V
V
.
A.
4
. B.
1
2
⋅
C.
2
. D.
1
4
⋅
Câu 20. Cho khối chop
.O ABC
. Trên ba cạnh
,,OA OB OC
lần lượt lấy ba điểm
’, ,ABC
′′
sao cho
2 , 4 , 3OA OA OB OB OC OC
′′′
= = =
. Tính tỉ số
.'''
.
OABC
O ABC
V
V
A.
1
12
. B.
1
24
. C.
1
16
. D.
1
32
.
Câu 21. Cho hình chóp S.ABC. Gọi
(
)
α
là mặt phẳng qua
A
và song song với
BC
.
( )
α
cắt
SB
,
SC
lần lượt tại
,
MN
. Tính tỉ số
SM
SB
biết
(
)
α
chia khối chóp thành 2 phần có thể tích bằng nhau.
A.
1
2
. B.
1
2
. C.
1
4
. D.
1
22
.
Câu 22. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
là:
A.
3
3
4
a
⋅
B.
3
3
3
a
⋅
C.
3
2
3
a
⋅
D.
3
2
2
a
⋅
Câu 23. Cho lăng trụ
.'' ' 'ABCD A B C D
có
ABCD
là hình chữ nhật,
'''
AA AB AD
= =
. Tính thể tích
khối lăng trụ
.'' ' 'ABCD A B C D
biết
AB a=
,
3AD a=
,
'2AA a=
.
A.
3
3
a
. B.
3
a
. C.
3
3a
. D.
3
33
a
.
Câu 24. Cho lăng trụ
.'' 'ABC A B C
có
ABC
là tam giác vuông tại
A
. Hình chiếu của
'A
lên
( )
ABC
là
trung điểm của
BC
. Tính thể tích khối lăng trụ
.'' 'ABC A B C
biết
AB a=
,
3AC a=
,
'2
AA a=
.
A.
3
2
a
⋅
B.
3
3
2
a
⋅
C.
3
3a
. D.
3
33a
.
Câu 25. Cho lăng trụ
.'' ' 'ABCD A B C D
có
ABCD
là hình thoi. Hình chiếu của
'A
lên
( )
ABCD
là
trọng tâm của tam giác
ABD
. Tính thể tích khối lăng trụ
'''ABCA B C
biết
AB a=
,
0
120ABC =
,
'AA a=
.
A.
3
2a
. B.
3
2
6
a
⋅
C.
3
2
3
a
⋅
D.
3
2
2
a
⋅
Câu 26. Cho lăng trụ
.'' 'ABC A B C
. Tính tỉ số
''
'''
ABB C
ABCA B C
V
V
.
Trang 10/35
A.
1
2
⋅
B.
1
6
⋅
C.
1
3
⋅
D.
2
3
.
Câu 27. Cho khối lăng trụ tam giác đều
.’’’
ABC A B C
có tất cả các cạnh đều bằng
a
. Thể tích khối tứ
diện
’ ’’
A BB C
là
A.
3
3
12
a
⋅
B.
3
3
4
a
⋅
C.
3
3
6
a
⋅
D.
3
12
a
⋅
Câu 28. Lăng trụ tam giác
.
ABC A B C
′′′
có đáy tam giác đều cạnh
a
, góc giữa cạnh bên và mặt đáy bằng
30
0
. Hình chiếu
A
′
lên
( )
ABC
là trung điểm
I
cua
BC
. Thể tích khối lăng trụ là
A.
3
3
6
a
⋅
B.
3
3
2
a
⋅
C.
3
3
12
a
⋅
D.
3
3
8
a
⋅
Câu 29. Lăng trụ đứng
.’’’
ABC A B C
có đáy
ABC
là tam giác vuông tại
, 2 ,
A BC a AB a= =
. Mặt bên
( )
’’BB C C
là hình vuông. Khi đó thê tich lăng trụ là
A.
3
3
3
a
. B.
3
2a
. C.
3
23a
.
D.
3
3a
.
Câu 30. Cho lăng trụ
.'' 'ABC A B C
. Gọi
M
,
N
lần lượt là trung điểm của
'CC
và
'BB
. Tính tỉ số
.'''
ABCMN
ABC A B C
V
V
.
A.
1
3
. B.
1
6
. C.
1
2
. D.
2
3
.
Câu 31. Cho khối lăng trụ
.ABC A B C
′′′
. Tỉ số thể tích giữa khối chóp
.
A ABC
′
và khối lăng trụ đó là
A.
1
4
. B.
1
2
. C.
1
3
. D.
1
6
.
Câu 32. Cho khối lập phương
.ABCD A B C D
′′′′
. Tỉ số thể tích giữa khối
.A ABD
′
và khối lập phương là:
A.
1
4
. B.
1
8
. C.
1
6
. D.
1
3
.
Câu 33. Cho hình chóp tứ giác đều
.S ABCD
có chiều cao bằng
h
, góc giữa hai mặt phẳng
()
SAB
và
()ABCD
bằng
α
. Tính thể tích của khối chóp
.S ABCD
theo
h
và
α
.
A.
3
2
3
4 tan
h
α
. B.
3
2
4
3tan
h
α
. C.
3
2
8
3tan
h
α
. D.
3
2
3
8tan
h
α
.
Câu 34. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
, cạnh
SB
vuông góc với đáy
và mặt phẳng
( )
SAD
tạo với đáy một góc
60°
. Tính thể tích khối chóp
.S ABCD
.
A.
3
33
4
a
V =
. B.
3
33
8
a
V
=
. C.
3
83
3
a
V =
. D.
3
43
3
a
V =
.
Câu 35. Cho hình lăng trụ đứng
.'' 'ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
BC a=
, mặt
phẳng
( )
'A BC
tạo với đáy một góc
30°
và tam giác
'A BC
có diện tích bằng
2
3a
. Tính thể
tích khối lăng trụ
.'' 'ABC A B C
.
A.
3
3
8
a
. B.
3
33
4
a
. C.
3
33
8
a
. D.
3
33
2
a
.
Câu 36. Cho hình lăng trụ
.'' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh bằng
a
. Hình chiếu vuông
góc của
'A
trên
( )
ABC
là trung điểm của
AB
. Mặt phẳng
( )
''AA C C
tạo với đáy một góc
bằng
45°
. Tính thể tích V của khối lăng trụ
.'' 'ABC A B C
.
A.
3
3
16
a
V =
. B.
3
3
8
a
V =
. C.
3
3
4
a
V =
. D.
3
3
2
a
V =
.
Trang 11/35
Câu 37. Cho hình chóp đều
.S ABC
, góc giữa mặt bên và mặt phẳng đáy
( )
ABC
bằng
0
60
, khoảng
cách giưa hai đương thăng
SA
va
BC
băng
3
27
a
. Thê tich cua khôi chóp
.
S ABC
theo
a
bằng
A.
3
3
12
a
. B.
3
3
18
a
. C.
3
3
16
a
. D.
3
3
24
a
.
Câu 38. Cho hình chóp đều
.
S ABCD
co đáy
ABCD
là hình thoi tâm
O
,
23
AC a=
,
2BD a=
, hai
mặt phẳng
( )
SAC
và
( )
SBD
cùng vuông góc với mặt phẳng
( )
ABCD
. Biết khoảng cách từ
điểm
O
đến mặt phẳng
(
)
SAB
bằng
3
4
a
. Tính thê tich cua khôi chóp
.S ABCD
theo
a
.
A.
3
3
16
a
. B.
3
3
18
a
. C.
3
3
3
a
. D.
3
3
12
a
.
Câu 39. Cho hinh chop tứ giác đều
.S ABCD
,
O
là giao điểm của
AC
và
BD
. Biết mặt bên của hình
chóp là tam giác đều và khoảng từ
O
đến mặt bên là
a
. Tính thể tích khối chóp
.S ABCD
theo
a
.
A.
3
23a
. B.
3
43a
. C.
3
63a
. D.
3
83a
.
Câu 40. Cho hinh chop tứ giác
.S ABCD
có
( )
SA ABCD⊥
.
ABCD
là hình thang vuông tại
A
và
B
biết
2AB a=
.
33
AD BC a
= =
. Tính thể tích khối chóp
.S ABCD
theo
a
biết góc giữa
( )
SCD
và
( )
ABCD
bằng
0
60
.
A.
3
26a
. B.
3
66a
. C.
3
23a
. D.
3
63a
.
Câu 41. Cho hinh chop tứ giác
.S ABCD
có
( )
SA ABCD⊥
,
ABCD
là hình thang vuông tại
A
và
B
biết
2AB a=
.
33AD BC a= =
. Tính thể tích khối chóp
.S ABCD
theo
a
, biết khoảng cách từ
A đến mặt phẳng
()
SCD
bằng
36
4
a
.
A.
3
66
a
. B.
3
26
a
. C.
3
23a
. D.
3
63a
.
Câu 42. Cho lăng tru tam giac
.'' 'ABC A B C
co
'BB a=
, goc giưa đương thăng
'BB
va
( )
ABC
băng
60
°
, tam giac
ABC
vuông tai
C
va goc
60BAC = °
. Hinh chiêu vuông goc cua điêm
'B
lên
( )
ABC
trung vơi trong tâm cua
ABC∆
. Thê tich cua khôi tư diên
'.A ABC
theo
a
bằng
A.
3
13
108
a
. B.
3
7
106
a
. C.
3
15
108
a
. D.
3
9
208
a
.
Câu 43. Cho hình lăng trụ đứng
.'' 'ABC A B C
, biết đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách từ
tâm
O
của tam giác
ABC
đến mặt phẳng
( )
'A BC
bằng
6
a
.Tính thể tích khối lăng trụ
.'' 'ABC A B C
.
A.
3
32
8
a
. B.
3
32
28
a
. C.
3
32
4
a
. D.
3
32
16
a
.
Câu 44. Cho hình chóp tam giác
.S ABC
có
M
là trung điểm của
SB
,
N
là điểm trên cạnh
SC
sao cho
2NS NC=
. Kí hiệu
12
,VV
lần lượt là thể tích của các khối chóp
.A BMNC
và
.S AMN
. Tính tỉ
số
1
2
V
V
.
A.
1
2
2
3
V
V
=
B.
1
2
1
2
V
V
=
C.
1
2
2.
V
V
=
D.
1
2
3
V
V
=
Trang 12/35
Câu 45. ho
2NS NC
=
,
P
là điểm trên cạnh
SA
sao cho
2PA PS
=
. Kí hiệu
12
,
VV
lần lượt là thể tích
của các khối tứ diện
BMNP
và
SABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
1
9
V
V
=
. B.
1
2
3
4
V
V
=
. C.
1
2
2
3
V
V
=
. D.
1
2
1
3
V
V
=
.
Câu 46. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
, góc giữa hai mặt phẳng
()
SAB
và
()ABCD
bằng
45°
,
,MN
và
P
lần lượt là trung điểm các cạnh
,SA SB
và
AB
. Tính thể tích
V
của khối tứ diện
DMNP
.
A.
3
6
a
V =
B.
3
4
a
V
=
C.
3
12
a
V =
D.
3
2
a
V =
Câu 47. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
B
,
2AC a
=
; cạnh bên
2AA a
′
=
. Hình chiếu vuông góc của
A
′
trên mặt phẳng
()ABC
là trung điểm cạnh
AC
.
Tính thể tích
V
của khối lăng trụ
.ABC A B C
′′′
.
A.
3
1
2
Va=
. B.
3
3
a
V =
. C.
3
Va=
. D.
3
2
3
a
V
=
.
Câu 48. Cho tứ diện
ABCD
có các cạnh
,AB AC
và
AD
đôi một vuông góc với nhau. Gọi
123
,,GGG
và
4
G
lần lượt là trọng tâm các mặt
,,ABC ABD ACD
và
BCD
. Biết
6,
AB a=
9AC a=
,
12
AD a=
. Tính theo a thể tích khối tứ diện
1234
GGGG
.
A.
3
4a
B.
3
a
C.
3
108a
D.
3
36a
Câu 49. Cho tứ diện
ABCD
có
11AB CD m= =
,
20BC AD m= =
,
21BD AC m= =
. Tính thể tích khối
tứ diện
ABCD
.
A.
3
360m
B.
3
720m
C.
3
770m
D.
3
340m
Câu 50. Cho hình chóp tứ giác
.S ABCD
có đáy là vuông; mặt bên
()SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm
A
đến mặt phẳng
()SCD
bằng
37
7
a
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
1
3
Va=
. B.
3
Va=
. C.
3
2
3
Va=
. D.
3
3
2
a
V =
.
Câu 51. Cho tứ diện
.
S ABC
,
M
và
N
là các điểm thuộc các cạnh
SA
và
SB
sao cho
2MA SM=
,
2SN NB=
,
()
α
là mặt phẳng qua
MN
và song song với
SC
. Kí hiệu
1
()H
và
2
()H
là các
khối đa diện có được khi chia khối tứ diện
.S ABC
bởi mặt phẳng
()
α
, trong đó,
1
()H
chứa
điểm
S
,
2
()H
chứa điểm
A
;
1
V
và
2
V
lần lượt là thể tích của
1
()H
và
2
()H
. Tính tỉ số
1
2
V
V
.
A.
4
5
B.
5
4
C.
3
4
D.
4
3
Câu 52. Cho hình chóp
.S ABC
có chân đường cao nằm trong tam giác
ABC
; các mặt phẳng
()SAB
,
()SAC
và
()SBC
cùng tạo với mặt phẳng
()ABC
các góc bằng nhau. Biết
25AB =
,
17BC =
,
26AC
=
; đường thẳng
SB
tạo với mặt đáy một góc bằng
45°
. Tính thể tích
V
của khối chóp
.S ABC
.
A.
408V =
. B.
680V
=
. C.
578V =
. D.
600V
=
.
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN 7.4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Trang 13/35
A
B
A
D
A
C
A
C
A
A
B
D
A
C
C
A
A
D
A
B
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
B
A
A
B
D
C
A
D
D
A
C
C
B
C
D
A
D
C
A
A
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
B
D
D
C
A
A
C
A
A
D
A
B
II –HƯỚNG DẪN GIẢI
NHẬN BIẾT – THÔNG HIỂU
Câu 1. Cho hình chóp
.S ABC
có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích
.S ABC
tăng lên bao nhiêu lần?
A.
4
. B.
2
. C.
3
. D.
1
2
.
Hướng dẫn giải:
Khi độ dài cạnh đáy tăng lên
2
lần thì diện tích đáy tăng lên 4 lần.
⇒
Thể tích khối chóp tăng lên 4 lần.
Câu 2. Có bao nhiêu khối đa diện đều?
A.
4
. B.
5
. C.
3
. D.
2
.
Hướng dẫn giải:
Có 5 khối đa diện đều là: tứ diện đều, hình lập phương, khối
8
mặt đều, khối
12
mặt đều, khối
20
mặt đều.
Câu 3. Cho khối đa diện đều
{ }
;pq
, chỉ số
p
là
A. Số các cạnh của mỗi mặt. B. Số mặt của đa diện.
C. Số cạnh của đa diện. D. Số đỉnh của đa diện.
Câu 4. Cho khối đa diện đều
{
}
;pq
, chỉ số
q
là
A. Số đỉnh của đa diện. B. Số mặt của đa diện.
C. Số cạnh của đa diện. D. Số các mặt ở mỗi đỉnh.
Câu 5. Tính thể tích khối tứ diện đều cạnh
a
.
A.
3
2
12
a
⋅
B.
3
2
4
a
⋅
C.
3
a
. D.
3
6
a
⋅
Hướng dẫn giải:
Gọi tứ diện
ABCD
đều cạnh
a
.
Gọi
H
là hình chiếu của
A
lên
( )
BCD
.
Ta có:
3
3
a
BH =
22
6
3
a
AH AB BH⇒= − =
2
3
4
BCD
a
S
∆
=
3
2
12
ABCD
a
V⇒=
.
Câu 6. Cho
.S ABCD
là hình chóp đều. Tính thể tích khối chóp
.S ABCD
biết
AB a=
,
SA a=
.
A.
3
a
B.
3
2
2
a
C.
3
2
6
a
. D.
3
3
a
Hướng dẫn giải:
B
A
C
S
O
Trang 14/35
Gọi
H
là hình chiếu của
S
lên
( )
ABCD
Ta có:
2
2
a
AH
=
22
2
2
a
SH SA AH⇒= − =
2
ABCD
Sa=
3
.
2
6
S ABCD
a
V⇒=
Câu 7. Cho hình chóp
.S ABC
có
( )
SA ABC⊥
, đáy
ABC
là tam giác đều. Tính thể tích khối chóp
.S ABC
biết
AB a=
,
SA a=
.
A.
3
3
12
a
. B.
3
3
4
a
. C.
3
a
. D.
3
3
a
Hướng dẫn giải:
2
3
4
ABC
a
S
∆
=
3
.
3
12
S ABC
a
V⇒=
.
Câu 8. Cho hình chóp
.S ABCD
có
( )
SA ABCD⊥
, đáy
ABCD
là hình chữ nhật. Tính thể tích
.S ABCD
biết
AB a=
,
2
AD a=
,
3SA a=
.
A.
3
a
. B.
3
6a
. B.
3
2a
. D.
3
3
a
⋅
Hướng dẫn giải:
2
2. 2
ABCD
S aa a
∆
= =
3
.
2
S ABC
Va⇒=
Câu 9. Thể tích khối tam diện vuông
.O ABC
vuông tại
O
có
, 2OA a OB OC a= = =
là
A.
3
2
3
a
⋅
B.
3
2
a
⋅
C.
3
6
a
⋅
D.
3
2a
.
Hướng dẫn giải:
2
3
.
1
.2
2
12
33
OBC
O ABC OBC
S OB OC a
h OA a
a
V OA S
= =
= =
⇒ = ⋅=
B
A
C
D
S
H
B
A
C
D
S
A
B
C
S
O
B
C
A
Trang 15/35
Câu 10. Cho hình chóp
.
S ABC
có
SA
vuông góc mặt đáy, tam giác
ABC
vuông tại
, 2A SA cm=
,
4 , 3AB cm AC cm= =
. Tính thể tích khối chóp.
A.
3
12
3
cm
. B.
3
24
5
cm
. C.
3
24
3
cm
. D.
3
24cm
.
Hướng dẫn giải:
2
3
.
1
.6
2
2
1 12
33
ABC
S ABC ABC
S AB AC cm
h SA cm
V SA S cm
= =
= =
⇒ =⋅=
Câu 11. Cho hình chóp
.S ABCD
đáy hình chữ nhật,
SA
vuông góc đáy,
, 2AB a AD a= =
. Góc giữa
SB
và đáy bằng
0
45
. Thể tích khối chóp là
A.
3
2
3
a
⋅
B.
3
2
3
a
⋅
C.
3
3
a
⋅
D.
3
2
6
a
⋅
Hướng dẫn giải:
( )
0
2
3
.
.tan 45
.2 2
12
.
33
ABCD
S ABCD ABCD
SA AB a
S aa a
a
V SA S
= =
= =
⇒= =
Câu 12. Hinh chop
.S ABCD
đáy hình vuông,
SA
vuông góc với đáy,
3, 2ASA Caa= =
. Khi đó thê
tich khôi chop
.S ABCD
la
A.
3
2
2
a
⋅
B.
3
2
3
a
⋅
C.
3
3
2
a
⋅
D.
3
3
3
a
⋅
Hướng dẫn giải:
(
)
02
3
.
3
.cos 45
13
.
33
ABCD
S ABCD ABCD
SA a
AB AC a S a
a
V SA S
=
= =⇒=
⇒= =
Câu 13. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
. Biết
SAB∆
là tam giác đều và
thuộc mặt phẳng vuông góc với mặt phẳng
( )
ABC
. Tính thể tích khối chóp
.S ABC
biết
AB a=
,
3AC a=
.
A.
3
6
12
a
⋅
B.
3
6
4
a
⋅
C.
3
2
6
a
⋅
D.
3
4
a
⋅
Hướng dẫn giải:
B
A
C
D
S
B
A
C
D
S
0
45
A
B
C
S
Trang 16/35
ABC∆
vuông tại
B
22
2BC AC AB a⇒= − =
.
2
12
.
22
ABC
a
S BA BC
∆
= =
Gọi
H
là trung điểm
AB
3
2
a
SH⇒=
Ta có:
SAB∆
đều
SH AB
⇒⊥
( )
SH ABC⇒⊥
(vì
(
)
( )
SAB ABC⊥
).
3
.
16
.
3 12
S ABC ABC
a
V SH S
∆
⇒= =
Câu 14. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi. Mặt bên
( )
SAB
là tam giác vuông cân tại
S
và thuộc mặt phẳng vuông góc với mặt phẳng
( )
ABCD
. Tính thể tích khối chóp
.S ABCD
biết
BD a=
,
3AC a=
.
A.
3
a
. B.
3
3
4
a
⋅
C.
3
3
12
a
⋅
D.
3
3
a
⋅
Hướng dẫn giải:
Gọi
O
là giao điểm của
AC
và
BD
.
ABCD
là hình thoi
AC BD⇒⊥
,
O
là trung điểm của
AC
,
BD
.
ABO
∆
vuông tại
O
22
AB AO OB a⇒= + =
.
2
13
.
22
ABCD
a
S AC BD= =
.
Gọi
H
là trung điểm
AB
.
SAB
∆
vuông cân tại
S
cạnh
AB a=
2
a
SH
⇒=
.
Ta có:
SAB∆
cân
( )
SH AB SH ABCD
⇒⊥⇒⊥
(vì
( )
( )
SAB ABC
⊥
).
3
.
13
.
3 12
S ABCD ABCD
a
V SH S⇒= =
.
Câu 15. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
. Hình chiếu của
S
lên mặt phẳng
( )
ABC
là trung điểm
H
của
BC
. Tính thể tích khối chóp
.S ABC
biết
AB a
=
,
3AC a=
,
2
SB a=
.
A.
3
6
6
a
⋅
B.
3
3
2
a
⋅
C.
3
3
6
a
⋅
D.
3
6
2
a
⋅
Hướng dẫn giải:
ABC∆
vuông tại
A
22
2BC AC AB a⇒= + =
.
2
13
.
22
ABC
a
S AB AC
∆
= =
.
22
SH SB BH a= −=
.
B
A
C
S
H
S
B
C
D
A
H
C
B
A
S
H
Trang 17/35
3
.
13
.
36
S ABC ABC
a
V SH S
∆
⇒= =
.
Câu 16. Cho hình chóp
.
S ABCD
có đáy
ABCD
hình vuông cạnh
a
. Hình chiếu của
S
lên mặt phẳng
( )
ABCD
là trung điểm
H
của
AD
. Tính thể tích khối chóp
.S ABCD
biết
3
2
a
SB =
.
A.
3
3
a
⋅
B.
3
a
. C.
3
2
a
⋅
D.
3
3
2
a
⋅
Hướng dẫn giải:
ABH∆
vuông tại
A
22
5
2
a
BH AH AB⇒= + =
.
22
SH SB BH a= −=
.
2
ABCD
Sa=
.
3
.
1
.
33
S ABCD ABCD
a
V SH S⇒= =
.
Câu 17. Hình chóp
.S ABCD
đáy là hình vuông cạnh
1
,
3
2
a
SDa =
. Hình chiếu của S lên
( )
ABCD
là
trung điểm
H
của
AB
. Thể tích khối chóp là
A.
3
2
3
a
⋅
B.
3
2
3
a
⋅
C.
3
12a
. D.
3
3
a
⋅
Hướng dẫn giải:
2
2
2 22
22
22
5
4
13 5
2
44
ABCD
Sa
a
HD AH AD
aa
SH SD HD a
=
=+=
⇒= − = − =
3
.
12
.S
33
S ABCD ABCD
a
V SH⇒= =
.
Câu 18. Hinh chop
.S ABCD
đáy hình thoi,
2AB a=
, góc
BAD
bằng
0
120
. Hình chiếu vuông góc của
S
lên
( )
ABCD
là
I
giao điểm của 2 đường chéo, biết
2
SI
a
=
. Khi đó thê tich khôi chop
.S ABCD
la
A.
3
2
9
a
⋅
B.
3
3
9
a
⋅
C.
3
2
3
a
⋅
D.
3
3
3
a
⋅
Hướng dẫn giải:
2
3
.
2
. .sin 2 3
13
.
33
ABCD
S ABCD ABCD
a
SI
S AB AD BAD a
a
V SI S
=
= =
⇒= =
S
B
C
D
A
H
S
D
C
B
A
H
B
A
C
D
S
I
Trang 18/35
Câu 19. Cho hình chóp
.S ABC
, gọi
M
,
N
lần lượt là trung điểm của
,SA SB
. Tính tỉ số
.
.
S ABC
S MNC
V
V
.
A.
4
. B.
1
2
⋅
C.
2
. D.
1
4
⋅
Hướng dẫn giải:
.
.
.4
S ABC
S MNC
V
SA SB
V SM SN
= =
Câu 20. Cho khối chop
.O ABC
. Trên ba cạnh
,,OA OB OC
lần lượt lấy ba điểm
’, ,ABC
′′
sao cho
2 , 4 , 3OA OA OB OB OC OC
′′′
= = =
. Tính tỉ số
.'''
.
OABC
O ABC
V
V
A.
1
12
. B.
1
24
. C.
1
16
. D.
1
32
.
Hướng dẫn giải:
Ta co:
. ’’
.
111
; ;
243
111 1
2 4 3 24
O
A
ABC
O BC
OA OB OC
OA OB OC
V
OA OB OC
V OA OB OC
′
′′′
= = =
′′′
⇒ = ⋅ ⋅ =⋅⋅=
Câu 21. Cho hình chóp S.ABC. Gọi
( )
α
là mặt phẳng qua
A
và song song với
BC
.
( )
α
cắt
SB
,
SC
lần lượt tại
,
MN
. Tính tỉ số
SM
SB
biết
( )
α
chia khối chóp thành 2 phần có thể tích bằng nhau.
A.
1
2
. B.
1
2
. C.
1
4
. D.
1
22
.
Hướng dẫn giải:
O
A
B
C
C
′
B
′
A
′
S
A
B
C
N
M
Trang 19/35
Ta co:
//
SM SN
MN BC
SB SC
⇒=
Ta có:
2
.
.
.
S AMN
S ABC
V
SM SN SM
V SB SC SB

= =


Ta có:
.
.
11
2
2
S AMN
S ABC
V
SM
V SB
=⇒=
Câu 22. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng
a
là:
A.
3
3
4
a
⋅
B.
3
3
3
a
⋅
C.
3
2
3
a
⋅
D.
3
2
2
a
⋅
Hướng dẫn giải:
3
2
3
.
3
4
4
ha
a
V hS
a
S
=
⇒= =
=
Câu 23. Cho lăng trụ
.'' ' 'ABCD A B C D
có
ABCD
là hình chữ nhật,
'''AA AB AD= =
. Tính thể tích
khối lăng trụ
.'' ' '
ABCD A B C D
biết
AB a=
,
3AD a=
,
'2AA a=
.
A.
3
3a
. B.
3
a
. C.
3
3a
. D.
3
33a
.
Hướng dẫn giải:
Gọi
O
là giao điểm của
AC
và
BD
.
ABCD
là hình chữ nhật
OA OB OD⇒==
Mà
AA AB AD
′′′
= =
nên
( )
'
A O ABD⊥
(vì
'AO
là trực tâm giác
ABD
)
ABD∆
vuông tại
A
22
2BD AB AD a⇒= + =
OA OB OD a⇒== =
'AA O∆
vuông tại
O
22
'' 3A O AA AO a⇒= −=
2
.3
ABCD
S AB AD a= =
3
''''
'. 3
ABCDA B C D ABCD
V A OS a= =
.
Câu 24. Cho lăng trụ
.'' 'ABC A B C
có
ABC
là tam giác vuông tại
A
. Hình chiếu của
'A
lên
( )
ABC
là
trung điểm của
BC
. Tính thể tích khối lăng trụ
.'' 'ABC A B C
biết
AB a=
,
3AC a=
,
'2AA a=
.
A.
3
2
a
⋅
B.
3
3
2
a
⋅
C.
3
3a
. D.
3
33a
.
Hướng dẫn giải:
S
A
B
C
N
M
A
B
C
A'
B'
C'
O
D
B
C
A
'D
'C
'B
'A
Trang 20/35
Gọi
H
là trung điểm của
BC
(
)
'A H ABC
⇒⊥
.
ABC
là tam giác vuông tại
A
22
2BC AB AC a
⇒= + =
1
2
AH BC a⇒= =
'
A AH∆
vuông tại
H
22
'' 3A H AA AH a⇒= −=
2
13
.
22
ABC
a
S AB AC
∆
= =
3
'''
3
'.
2
ABCA B C ABC
a
V AHS
= =
.
Câu 25. Cho lăng trụ
.'' ' 'ABCD A B C D
có
ABCD
là hình thoi. Hình chiếu của
'
A
lên
( )
ABCD
là
trọng tâm của tam giác
ABD
. Tính thể tích khối lăng trụ
'''
ABCA B C
biết
AB a=
,
0
120ABC =
,
'AA a=
.
A.
3
2a
. B.
3
2
6
a
⋅
C.
3
2
3
a
⋅
D.
3
2
2
a
⋅
Hướng dẫn giải:
Gọi
H
là trọng tâm của tam giác
ABD
( )
'A H ABCD⇒⊥
.
Ta có:
00
180 60
BAD ABC=−=
.
Tam giác
ABD
cân có
0
60BAD =
nên tam giác
ABD
đều.
ABD
là tam giác đều cạnh
a
3
3
a
AH⇒=
'A AH∆
vuông tại
H
22
6
''
3
a
A H AA AH⇒= −=
22
33
2 2.
42
ABCD ABD
aa
SS= = =
;
3
''''
2
'.
2
ABCDA B C D ABC
a
V AHS= =
Câu 26. Cho lăng trụ
.'' 'ABC A B C
. Tính tỉ số
''
'''
ABB C
ABCA B C
V
V
.
A.
1
2
⋅
B.
1
6
⋅
C.
1
3
⋅
D.
2
3
.
Hướng dẫn giải:
Ta có:
''BB C C
là hình bình hành
'' ''
1
2
BB C BB C C
SS⇒=
. '' . ''
1
2
A BB C A BB C C
VV⇒=
Ta có:
.''' '''
1
3
AABC ABCABC
VV=
. '' ''' .''' '''
2
3
A BB C C ABCA B C A A B C ABCA B C
VV V V⇒ = −=
A
C
H
B
'C
'B
'A
A
B
C
A'
B'
C'
'A
'
B
'C
'D
A
B
C
D
H
Trang 21/35
''
'' '''
'''
11
33
ABB C
ABB C ABCA B C
ABCA B C
V
VV
V
⇒= ⇒ =
Câu 27. Cho khối lăng trụ tam giác đều
.’’’ABC A B C
có tất cả các cạnh đều bằng
a
. Thể tích khối tứ
diện
’ ’’
A BB C
là
A.
3
3
12
a
⋅
B.
3
3
4
a
⋅
C.
3
3
6
a
⋅
D.
3
12
a
⋅
Hướng dẫn giải:
2
3
3
4
13
.
3 12
ABC
ABBC ABC
h BB a
a
S
a
V BB S
′′′
′ ′′ ′′′
′
= =
=
′
⇒= =
Câu 28. Lăng trụ tam giác
.ABC A B C
′′′
có đáy tam giác đều cạnh
a
, góc giữa cạnh bên và mặt đáy bằng
30
0
. Hình chiếu
A
′
lên
(
)
ABC
là trung điểm
I
cua
BC
. Thể tích khối lăng trụ là
A.
3
3
6
a
⋅
B.
3
3
2
a
⋅
C.
3
3
12
a
⋅
D.
3
3
8
a
⋅
Hướng dẫn giải:
( )
0
2
3
.’’’
33
.tan 30
232
3
4
3
.
8
ABC
AB
B
C
AAC BC
aa
A I AI
a
S
a
V AIS
′
= = ⋅=
=
′
⇒==
Câu 29. Lăng trụ đứng
.’’’ABC A B C
có đáy
ABC
là tam giác vuông tại
, 2 , A BC a AB a
= =
. Mặt bên
( )
’’BB C C
là hình vuông. Khi đó thê tich lăng trụ là
A.
3
3
3
a
. B.
3
2a
. C.
3
23a
.
D.
3
3a
.
Hướng dẫn giải:
22
2
.’’
3
’
2
3
13
.
22
.3
ABC A B
ABC
ABCC
h BB a
AC BC AB a
a
S AB AC
V BB S a
′
= =
= −=
⇒= =
′
⇒==
Câu 30. Cho lăng trụ
.'' 'ABC A B C
. Gọi
M
,
N
lần lượt là trung điểm của
'CC
và
'BB
. Tính tỉ số
.'''
ABCMN
ABC A B C
V
V
.
A
B
C
A'
B'
C'
A
B
C
A'
B'
C'
A
C
I
B
'C
'
B
'A
Trang 22/35
A.
1
3
. B.
1
6
. C.
1
2
. D.
2
3
.
Hướng dẫn giải:
Ta có:
''BB C C
là hình bình hành
''
1
2
BCMN BB C C
SS
⇒=
. . ''
1
2
A BCMN A BB C C
VV⇒=
Ta có:
.''' '''
1
3
AABC ABCABC
VV=
. '' ''' .''' '''
2
3
A BB C C ABCA B C A A B C ABCA B C
VV V V⇒ = −=
.
. '''
'''
11
.
33
A BCMN
A BCMN ABCA B C
ABCA B C
V
VV
V
⇒= ⇒ =
Câu 31. Cho khối lăng trụ
.ABC A B C
′′′
. Tỉ số thể tích giữa khối chóp
.A ABC
′
và khối lăng trụ đó là
A.
1
4
. B.
1
2
. C.
1
3
. D.
1
6
.
Hướng dẫn giải:
.
.
11
.
33
1
3
A ABC ABC ABC A B C
A ABC
ABC A B C
V AA S V
V
V
′ ′′′
′
′′′
′
= =
⇒=
Câu 32. Cho khối lập phương
.ABCD A B C D
′′′′
. Tỉ số thể tích giữa khối
.A ABD
′
và khối lập phương là:
A.
1
4
. B.
1
8
. C.
1
6
. D.
1
3
.
Hướng dẫn giải:
’.
.’’’ ’
’.
.’’’ ’
1
.
3
11 1
.. .
32 6
1
6
1
.
6
ABD
ABCD
A ABD
ABCD A B C D
A ABD
ABCD A B C D
V AA S
AA AB AD AA S
V
V
V
′
=
′′
= =
=
⇒=
VẬN DỤNG THẤP
Câu 33. Cho hình chóp tứ giác đều
.S ABCD
có chiều cao bằng
h
, góc giữa hai mặt phẳng
()SAB
và
()ABCD
bằng
α
. Tính thể tích của khối chóp
.S ABCD
theo
h
và
α
.
A.
3
2
3
4 tan
h
α
. B.
3
2
4
3tan
h
α
. C.
3
2
8
3tan
h
α
. D.
3
2
3
8tan
h
α
.
Hướng dẫn giải:
Gọi O là tâm của mặt đáy thì
A
B
C
A'
B'
C'
'
A
'B
'C
A
C
B
M
N
B
A
C
D
A'
B'
C'
D'
Trang 23/35
( )
SO mp ABCD⊥
. Từ đó,
SO
là đường
cao của hình chóp.Gọi M là trung điểm
đoạn CD.
Ta có:
()
()
( )( )
CD SM SCD
CD OM ABCD SMO
CD SCD ABCD
α
⊥⊂
⊥⊂ ⇒ =
= ∩
.
V =
1
3
.S
ABC
D.
SO; B = S
ABCD
= AB
2
; Tìm AB: AB = 2OM
Tam giác SOM vuông tại tại O, ta có: tan
α
=
SO
OM
=
h
OM
⇒
OM =
tan
h
α
.
⇒
AB =
2
tan
h
α
. Suy ra: B = S
ABCD
=
2
2
4
tan
h
α
. SO = h.
Vậy V
S.ABCD
=
1
3
.
2
2
4
tan
h
α
.h =
3
2
4
3tan
h
α
.
Câu 34. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
, cạnh
SB
vuông góc với đáy
và mặt phẳng
( )
SAD
tạo với đáy một góc
60°
. Tính thể tích khối chóp
.S ABCD
.
A.
3
33
4
a
V
=
. B.
3
33
8
a
V =
. C.
3
83
3
a
V =
. D.
3
43
3
a
V =
.
Hướng dẫn giải:
Ta có:
AD AB
AD SB
⊥
⊥
⇒
AD
⊥
(SAB)
⇒
AD
⊥
SA.
0
60
SAB⇒=
.
S
ABCD
= 4a
2
.
Xét tam giác SAB tại vuông tại B, ta có:
0
tan 60 2 3SB AB a
= =
.
Vậy V =
1
3
.4a
2
. 2a
3
=
3
83
3
a
.
Câu 35. Cho hình lăng trụ đứng
.'' 'ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
BC a=
, mặt
phẳng
( )
'A BC
tạo với đáy một góc
30°
và tam giác
'A BC
có diện tích bằng
2
3a
. Tính thể
tích khối lăng trụ
.'' 'ABC A B C
.
A.
3
3
8
a
. B.
3
33
4
a
. C.
3
33
8
a
. D.
3
33
2
a
.
Hướng dẫn giải:
α
B
S
A
D
C
2a
S
A
O
α
h
M
B
D
C
Trang 24/35
V= Bh = S
AB
C.
A’B’C’
.AA’.
Do
BC AB
BC A B
BC AA
⊥
′
⇒⊥
′
⊥
.
Và
()
'( )
( ) (' )
BC AB ABC
BC A B A BC
BC ABC A BC
⊥⊂
′
⊥⊂
= ∩
( )
( )
( ),( ' ) , ' 'ABC A BC AB A B ABA⇒==
Ta có:
2
1
.
2
2.
2. 3
23
A BC
A BC
S A B BC
S
a
AB a
BC a
′
∆
′
∆
′
=
′
⇒= = =
.
00
.cos 2 3.cos30 3 ; .sin 2 3.sin 30 3AB A B ABA a a AA A B ABA a a
′ ′ ′′ ′
= = = = = =
.'''
1
. . ...
2
ABC A B C ABC
V B h S AA AB BC AA
′′
= = =
3
1 33
.3 . . 3
22
a
aaa= =
.
Câu 36. Cho hình lăng trụ
.'' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh bằng
a
. Hình chiếu vuông
góc của
'A
trên
( )
ABC
là trung điểm của
AB
. Mặt phẳng
( )
''AA C C
tạo với đáy một góc
bằng
45°
. Tính thể tích V của khối lăng trụ
.'' '
ABC A B C
.
A.
3
3
16
a
V =
. B.
3
3
8
a
V =
. C.
3
3
4
a
V =
. D.
3
3
2
a
V =
.
Hướng dẫn giải:
Goi H, M, I lân lươt la trung điêm
cua cac đoan thăng AB, AC, AM.
.'''
.'
ABC A B C ABC
V S AH
∆
=
.
2
3
4
ABC
a
S
∆
=
.
Ta có IH la đương trung binh của tam giác
AMB
, MB la trung tuyên của tam giác đều
ABC.
Do đo:
// IH MB
IH AC
MB A C
⇒⊥
⊥
( )
'
''
AC A H
AC A HI AC A I
AC IH
⊥
⇒⊥ ⇒⊥
⊥
Ma:
()
' ( ' ')
( ) ( ' ')
AC IH ABC
AC A I ACC A
ABC AC C A AC
⊥⊂
⊥⊂
∩=
'A IH⇒
là góc gữa hai mặt phẳng
( )
''AA C C
và
( )
ABCD
' 45A IH⇒=°
Trong tam giác
'A HI
vuông tai H, ta co:
o
'
tan 45 ' .tan 45
AH
A H IH
HI
°= ⇒ =
.
13
24
a
IH MB= = =
. Vậy
23
3 33
.
4 4 16
aa a
V = =
B
A’
C’
B’
A
C
30
o
a
A’
B’
C’
A
B
C
M
I
H
a
Trang 25/35
Câu 37. Cho hình chóp đều
.S ABC
, góc giữa mặt bên và mặt phẳng đáy
( )
ABC
bằng
0
60
, khoảng
cách giưa hai đương thăng
SA
va
BC
băng
3
27
a
. Thê tich cua khôi chóp
.
S ABC
theo
a
bằng
A.
3
3
12
a
. B.
3
3
18
a
. C.
3
3
16
a
. D.
3
3
24
a
.
Hướng dẫn giải:
Goi
M
la trung điêm cua
BC
.
Trong mp(SAM), Kẻ
,( )MH SA H SA
⊥∈
.
Ta có:
( )
BC AM
BC SAM BC MH
BC SO
⊥
⇒⊥ ⇒⊥
⊥
.
Do đó
MH
là đường vuông góc chung của
SA
và
BC
.
Suy ra
3
27
a
MH =
. Ta có:
( ) ( )
( )
0
, 60SM BC SBC ABC SMA⊥⇒ = =
.
Đặt
3, 2OM x AM x OA x
=⇒= =
.
0
.tan 60 3SO OM x⇒= =
và
( )
( )
2
2
32 7SA x x x= +=
.
Trong
SAM
ta có:
..
3
7. 3.3
27 23
SA MH SO AM
aa
x x xx
=
⇔ = ⇔=
.
Khi
đó:
3
3 3.
2
23
aa
AM x AB a== = ⇒=
.
22
.
1 13 3
.. . .
3 3 4 2 24
S ABC ABC
a aa
V S SO
∆
= = =
Câu 38. Cho hình chóp đều
.S ABCD
co đáy
ABCD
là hình thoi tâm
O
,
23
AC a=
,
2BD a=
, hai
mặt phẳng
( )
SAC
và
( )
SBD
cùng vuông góc với mặt phẳng
( )
ABCD
. Biết khoảng cách từ
điểm
O
đến mặt phẳng
( )
SAB
bằng
3
4
a
. Tính thê tich cua khôi chóp
.S ABCD
theo
a
.
A.
3
3
16
a
. B.
3
3
18
a
. C.
3
3
3
a
. D.
3
3
12
a
.
Hướng dẫn giải
Ta có tam giác ABO vuông tại O và
3AO a=
,
BO a=
. Do đó
00
3 tan 60 60
AO
ABO
BO
== ⇒=
.
Suy ra
ABD∆
đều.
Ta
có:
B
A
C
S
O
N
H
S
C
B
D
A
O
I
23a
Trang 26/35
A
M
A
( ) ( )
( ) (
)
(
) (
)
(
SAC ABCD
SBD ABCD SO ABCD
SAC SBD SO
⊥
⊥ ⇒⊥
∩=
.
Trong tam giác đều
ABD
, gọi H là
trung điểm AB,
K là trung điểm BH,
suy ra
DH AB⊥
và
3DH a=
;
//OK DH
và
13
22
a
OK DH= =
.
Suy ra
(
)
OK AB AB SOK⊥⇒⊥
.
Gọi I là hình chiếu của O lên SK, ta
có:
( )
;OI SK AB OI OI SAB⊥ ⊥⇒⊥
.
( )
;OI d O SAB⇒=


.
Tam giác SOK vuông tại O, OI là đường cao:
2 22
111
2
a
SO
OI OK SO
= + ⇒=
.
3
.
1 1 11 3
. . .4. . .4. . . .
3 3 32 3
S ABCD ABCD ABO
a
V S SO S SO OA OB SO
∆∆
= = = =
Câu 39. Cho hinh chop tứ giác đều
.S ABCD
,
O
là giao điểm của
AC
và
BD
. Biết mặt bên của hình
chóp là tam giác đều và khoảng từ
O
đến mặt bên là
a
. Tính thể tích khối chóp
.S ABCD
theo
a
.
A.
3
23a
. B.
3
43a
. C.
3
63
a
. D.
3
83
a
.
Hướng dẫn giải:
Goi
M
la trung điêm cua
CD
,
trong
SOM∆
kẻ đường cao
OH
.
( )
OH SCD OH a⇒⊥ ⇒=
.
Đặt
CM x=
. Khi đó
OM x=
,
3SM x=
,
22
2SO SM x x= −=
.
Ta có:
..SM OH SO OM=
6
3. 2.
2
a
x ax x x⇔ = ⇒=
6, 3CDa SOa⇒= =
a
x
O
D
B
C
S
H
2 23
.
1 11
.....6.323
3 33
S ABCD ABCD
V S SO CD SO a a a= = = =
.
Câu 40. Cho hinh chop tứ giác
.S ABCD
có
( )
SA ABCD⊥
.
ABCD
là hình thang vuông tại
A
và
B
biết
2AB a=
.
33AD BC a= =
. Tính thể tích khối chóp
.S ABCD
theo
a
biết góc giữa
( )
SCD
và
( )
ABCD
bằng
0
60
.
A.
3
26a
. B.
3
66a
. C.
3
23a
. D.
3
63a
.
Hướng dẫn giải:
Trang 27/35
Dựng
AM CD⊥
tại
M
.
Ta có:
0
60
SMA =
.
2
.4
2
ABCD
AD BC
S AB a
+
= =
( )
2
2
22
CD AD BC AB a= − +=
2
1
.
2
ABC
S AB BC a
= =
2
3
ACD ABCD ABC
SS S a= −=
2
1 32
.
22
ACD
ACD
S
S AM CD AM a
CD
= ⇒= =
Ta có:
36
.tan
2
SA AM SMA a= =
.
3
.
1
. 26
3
S ABCD ABCD
V SA S a= =
.
Câu 41. Cho hinh chop tứ giác
.
S ABCD
có
( )
SA ABCD⊥
,
ABCD
là hình thang vuông tại
A
và
B
biết
2AB a=
.
33
AD BC a= =
. Tính thể tích khối chóp
.S ABCD
theo
a
, biết khoảng cách từ
A đến mặt phẳng
()SCD
bằng
36
4
a
.
A.
3
66a
. B.
3
26a
. C.
3
23a
. D.
3
63a
.
Hướng dẫn giải:
Dựng
AM CD⊥
tại
M
.
Dựng
AH SM⊥
tại
H
.
Ta có:
36
4
AH a=
.
2
.4
2
ABCD
AD BC
S AB a
+
= =
( )
2
2
22CD AD BC AB a= − +=
2
1
.
2
ABC
S AB BC a= =
2
3
ACD ABCD ABC
SS S a= −=
2
1 32
.
22
ACD
ACD
S
S AM CD AM a
CD
= ⇒= =
Ta có:
2 22
22
1 1 1 . 36
2
AH AM
AS a
AH AM AS
AM AH
= + ⇒= =
−
3
.
1
. 26
3
S ABCD ABCD
V SA S a= =
Câu 42. Cho lăng tru tam giac
.'' 'ABC A B C
co
'BB a=
, goc giưa đương thăng
'BB
va
( )
ABC
băng
60°
, tam giac
ABC
vuông tai
C
va goc
60BAC = °
. Hinh chiêu vuông goc cua điêm
'
B
lên
( )
ABC
trung vơi trong tâm cua
ABC∆
. Thê tich cua khôi tư diên
'.A ABC
theo
a
bằng
A.
3
13
108
a
. B.
3
7
106
a
. C.
3
15
108
a
. D.
3
9
208
a
.
Hướng dẫn giải:
B
A
C
D
S
M
B
A
C
D
S
M
H
Trang 28/35
Goi
,MN
la trung điêm cua
,AB AC
và
G
la trong tâm cua
ABC∆
.
( )
'B G ABC⊥
( )
(
)
0
', ' 60BB ABC B BG⇒==
.
'.
11
. .' . . .'
36
A ABC ABC
V S B G AC BC B G
∆
= =
Xét
'B BG∆
vuông tai
G
, co
0
' 60B BG =
3
'
2
a
BG⇒=
. (nửa tam giac đêu)
C'
A'
G
M
N
B
A
C
B'
Đăt
2AB x
=
. Trong
ABC∆
vuông tai
C
co
0
60BAC =
⇒
tam giác
ABC
la nưa tam giac đêu
, 3
2
AB
AC x BC x
⇒== =
Do
G
la trong tâm
ABC
∆
33
24
a
BN BG⇒= =
.
Trong
BNC∆
vuông tai
C
:
2 22
BN NC BC= +
22 2
22
3
2 13
9 93
3
16 4 52
2 13
33
2 13
a
AC
ax a a
xx x
a
BC
=
⇔ = + ⇔ = ⇒= ⇒
=
Vậy,
3
'
13 33 39
...
6 2 208
2 13 2 13
A ABC
aa a a
V = =
.
Câu 43. Cho hình lăng trụ đứng
.'' 'ABC A B C
, biết đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách từ
tâm
O
của tam giác
ABC
đến mặt phẳng
( )
'A BC
bằng
6
a
.Tính thể tích khối lăng trụ
.'' '
ABC A B C
.
A.
3
32
8
a
. B.
3
32
28
a
. C.
3
32
4
a
. D.
3
32
16
a
.
Hướng dẫn giải:
Goi
M
la trung điêm cua
BC
,
ta có
( ) ( )
''A AM A BC⊥
theo giao tuyến
'AM
.
Trong
( )
'
A AM
kẻ
'( ')OH AM H AM⊥∈
.
( )
'OH A BC⇒⊥
Suy ra:
( )
( )
,'
6
a
d O A BC OH= =
.
2
3
4
ABC
a
S
∆
=
.
Xét hai tam giác vuông
'
A AM
và
OHM
có
góc
M
chung nên chúng đồng dạng.
O
H
A'
A
C
C'
B
B'
M
60°
60°
Trang 29/35
Suy ra:
22 2
2
13
.
13
6 32
'' ' '
'
3
'
2
aa
OH OM
AA AM AA AA
A A AM
a
AA
= ⇒= ⇒=
+

+


.
6
'
4
a
AA⇒=
. Thể tích:
23
.'''
6 33 2
.' .
4 4 16
ABC A B C ABC
aa a
V S AA
∆
= = =
.
VẬN DỤNG CAO
Câu 44. Cho hình chóp tam giác
.
S ABC
có
M
là trung điểm của
SB
,
N
là điểm trên cạnh
SC
sao cho
2NS NC
=
. Kí hiệu
12
,VV
lần lượt là thể tích của các khối chóp
.A BMNC
và
.S AMN
. Tính tỉ
số
1
2
V
V
.
A.
1
2
2
3
V
V
=
B.
1
2
1
2
V
V
=
C.
1
2
2.
V
V
=
D.
1
2
3
V
V
=
Hướng dẫn giải
.
.
12 1
23 3
S AMN
S ABC
V
SM SN
V SB SC
= ⋅ =⋅=
;
.. .S AMN A BMNC S ABC
VV V+=
.
Suy ra,
.
.
2
A BMNC
S AMN
V
V
=
.
Câu 45. Cho hình chóp tam giác
.S ABC
có
M
là trung điểm của
SB
,
N
là điểm trên cạnh
SC
sao cho
2NS NC=
,
P
là điểm trên cạnh
SA
sao cho
2PA PS=
. Kí hiệu
12
,VV
lần lượt là thể tích của
các khối tứ diện
BMNP
và
SABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
1
9
V
V
=
. B.
1
2
3
4
V
V
=
. C.
1
2
2
3
V
V
=
. D.
1
2
1
3
V
V
=
.
Hướng dẫn giải
N
M
A
B
C
S
Trang 30/35
.
.
1
( ,( ))
3
1
(C,( ))
3
BMP
N BMP
C SAB
SAB
d N SAB S
V
V
d SAB S
⋅⋅
=
⋅⋅
;
( ,( )) 2
(C,( )) 3
d N SAB NS
d SAB CS
= =
,
1 11
2 23
BPM BPS SAB
SS S= = ⋅
Suy ra,
.
.
21 1
36 9
N BMP
C SAB
V
V
=⋅=
.
P
N
M
A
B
C
S
Câu 46. Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
, góc giữa hai mặt phẳng
()SAB
và
()ABCD
bằng
45°
,
,MN
và
P
lần lượt là trung điểm các cạnh
,SA SB
và
AB
. Tính thể tích
V
của khối tứ diện
DMNP
.
A.
3
6
a
V =
B.
3
4
a
V
=
C.
3
12
a
V =
D.
3
2
a
V =
Hướng dẫn giải
Ta có:
1
4
SMN
SAB
S
SM SN
S SA SB
= ⋅=
.
Tương tự,
11
,
44
BNP
AMP
SAB SAB
S
S
SS
= =
.
Suy ra
1
4
MNP
SAB
S
S
=
(có thể khẳng định
1
4
MNP
SAB
S
S
=
nhờ hai tam giác MNP và BAS
là hai tam giác đồng dạng với tỉ số
1
2
k =
).
Do đó
.
.
1
4
D MNP
D SAB
V
V
=
(1)
45
°
M
N
P
O
D
A
B
C
S
.. .
1
2
D SAB S DAB S ABCD
VV V= =
. (2)
3
.
11 4
. .tan 45 .
33 3
S ABCD ABCD ABCD
a
V SO S OP S= = °=
(3). Từ (1), (2) và (3):
33
114
..
42 3 6
DMNP
aa
V = =
.
Câu 47. Cho lăng trụ
.ABC A B C
′′′
có đáy
ABC
là tam giác vuông cân tại
B
,
2AC a=
; cạnh bên
2AA a
′
=
. Hình chiếu vuông góc của
A
′
trên mặt phẳng
()ABC
là trung điểm cạnh
AC
.
Tính thể tích
V
của khối lăng trụ
.
ABC A B C
′′′
.
A.
3
1
2
Va=
. B.
3
3
a
V =
. C.
3
Va=
. D.
3
2
3
a
V =
.
Hướng dẫn giải
Trang 31/35
Vì ABC là tam giác vuông cân tại B nên trung
tuyến BH cũng là đường cao của nó, và
1
2
HB HA HC AC a= = = =
.
2 2 22
2AH AA AH a a a
′′
= − = −=
.
3
.
1
2
ABC A B C ABC
V A H S A H BH AC a
′′′
′′
= ⋅ = ⋅ ⋅=
a
a
a
a
2
B'
C'
H
A
C
B
A'
Câu 48. Cho tứ diện
ABCD
có các cạnh
,AB AC
và
AD
đôi một vuông góc với nhau. Gọi
123
,,
GGG
và
4
G
lần lượt là trọng tâm các mặt
,,ABC ABD ACD
và
BCD
. Biết
6,AB a=
9AC a=
,
12AD a=
. Tính theo a thể tích khối tứ diện
1234
GGGG
.
A.
3
4a
B.
3
a
C.
3
108a
D.
3
36a
Hướng dẫn giải
Trong trường hợp tổng quát, ta
chứng
minh được
1234
1
27
G G G G ABCD
VV=
.
Thật vậy,
ta có
234
( )( )G G G CBA
và
234
)G G G CBA 
(tỉ số đồng dạng
1
3
k =
) . Từ đó:
234
2
1
9
GGG
CBA
S
k
S
= =
và
1 234 4
4
( ,( )) ( ,( ))
11
( ,( )) (do )
33
d G G G G d G ABC
d D ABC G M DM
=
= =
G
1
G
3
G
4
G
2
M
A
B
C
D
Suy ra
1234 234
1 234
( ,( ))
11 1
( ,( )) 3 9 27
GGGG GGG
ABCD CBA
VS
d G GGG
V d D ABC S
= ⋅ =⋅=
1234
3
1 11
... 4
27 27 6
G G G G ABCD
V V AB AC AD a⇒= =⋅ =
Câu 49. Cho tứ diện
ABCD
có
11AB CD m= =
,
20BC AD m= =
,
21BD AC m= =
. Tính thể tích khối
tứ diện
ABCD
.
A.
3
360m
B.
3
720m
C.
3
770m
D.
3
340m
Hướng dẫn giải
Trang 32/35
Dựng tam giác MNP sao cho C,
B, D lần lượt là trung điểm các
cạnh MN, MP, NP.
Do BD là đường trung bình tam
giác MNP nên
1
2
BD MN=
hay
1
2
AC MN=
.
Tam giác AMN vuông tại A (do
có trung tuyến bằng một nửa
cạnh tương ứng), hay
AM AN⊥
. Tương tự,
AP AN⊥
và
AM AP⊥
.
x
y
z
21
11
20
20
11
21
D
B
C
A
M
P
N
Ta có
1
4
MBC MNP
SS=
,
1
4
NCD MNP
SS
=
,
1
4
BPD MNP
SS=
.Suy ra
1
4
BCD MNP
SS
=
.
Từ đó,
1
4
ABCD AMNP
VV=
. Đặt
,,
AM AN AP
x yz
m mm
= = =
. Ta có
22 2
22 2
22 2
4.20
4.21
4.11
xy
yz
xz
+=
+=
+=
,
suy ra
2
23
2
160
11
1440 1440 360
64
324
ABCD AMNP
x
y xyz V V m
z
=
=⇒=⇒= =
=
(AM, AN, AP đôi một vuông góc nên
1
..
6
AMNP
V AM AN AP=
)
222222 222
2
( )( )( )
12
V abcabc abc= +− −+ −++
Câu 50. Cho hình chóp tứ giác
.S ABCD
có đáy là vuông; mặt bên
()SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm
A
đến mặt phẳng
()SCD
bằng
37
7
a
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
1
3
Va=
. B.
3
Va=
. C.
3
2
3
Va=
. D.
3
3
2
a
V =
.
Hướng dẫn giải
Gọi H là trung điểm AB, suy ra SH là
chiều cao khối chóp đã cho.
Kí hiệu
x
là độ dài cạnh đáy.
Ta có
3
2
SH x=
và
3
.
3
6
S ABCD
Vx=
.
Kẻ
()
HK CD K CD⊥∈
;
Kẻ
(L )HL SK SK⊥∈
.
Suy ra
()HL SCD⊥
và
Trang 33/35
22
( ,( )) ( ,( ))
21
7
d A SCD d H SCD
HS HK
HL x
HS HK
=
⋅
= = =
+
X
K
H
D
A
B
C
S
L
Theo gt,
21 3 7
3
77
a
x xa= ⇒=
. Suy ra
3 33
.
33 3
( 3)
66 2
S ABCD
V xa a= = =
Câu 51. Cho tứ diện
.S ABC
,
M
và
N
là các điểm thuộc các cạnh
SA
và
SB
sao cho
2MA SM=
,
2SN NB=
,
()
α
là mặt phẳng qua
MN
và song song với
SC
. Kí hiệu
1
()H
và
2
()H
là các
khối đa diện có được khi chia khối tứ diện
.S ABC
bởi mặt phẳng
()
α
, trong đó,
1
()H
chứa
điểm
S
,
2
()H
chứa điểm
A
;
1
V
và
2
V
lần lượt là thể tích của
1
()H
và
2
()H
. Tính tỉ số
1
2
V
V
.
A.
4
5
B.
5
4
C.
3
4
D.
4
3
Hướng dẫn giải
Kí hiệu
V
là thể tích khối tứ diện
SABC
.
Gọi
P
,
Q
lần lượt là giao điểm của
()
α
với các đường thẳng
BC
,
AC
.
Ta có
// //NP MQ SC
. Khi chia khối
1
()
H
bởi mặt phẳng
()QNC
, ta được hai khối chóp
.N SMQC
và
.N QPC
.
Ta có:
.
.
( ,( ))
(B,( ))
N SMQC SMQC
B ASC SAC
VS
d N SAC
V d SAC S
= ⋅
;
( ,( )) 2
(B,( )) 3
d N SAC NS
d SAC BS
= =
;
2
45
99
AMQ SMQC
ASC ASC
SS
AM
S AS S

= =⇒=


.
Suy ra
.
.
2 5 10
3 9 27
N SMQC
B ASC
V
V
=⋅=
.QP
.
( ,(QP ))
(S,(A ))
112 2
3 3 3 27
QPC
NC
S ABC ABC
S
V
dN C
V d BC S
NB CQ CP
SB CA CB
= ⋅
=⋅⋅==⋅⋅=
P
N
Q
M
A
B
C
S
.
.QP
11
12
. . 12
10 2 4 4
54
27 27 9 9
N SMQC
NC
B ASC S ABC
V
V
VV
VV
V V V VV
= + =+=⇒ =⇒=
+
1
2
4
5
V
V
⇒=
Câu 52. Cho hình chóp
.S ABC
có chân đường cao nằm trong tam giác
ABC
; các mặt phẳng
()SAB
,
()SAC
và
()SBC
cùng tạo với mặt phẳng
()ABC
các góc bằng nhau. Biết
25AB =
,
17BC =
,
26AC =
; đường thẳng
SB
tạo với mặt đáy một góc bằng
45°
. Tính thể tích
V
của khối chóp
.S ABC
.
Trang 34/35
A.
408
V
=
. B.
680V =
. C.
578
V
=
. D.
600
V
=
.
Hướng dẫn giải
Gọi J là chân đường cao của hình chóp
S.ABC; H, K và L lần lượt là hình chiếu của
J trên các cạnh AB, BC và
CA
. Suy ra,
SHJ
,
SLJ
và
SKJ
lần lượt là góc tạo bởi
mặt phẳng
()ABC
với các mặt phẳng
(S )AB
,
()
SBC
và
()SAC
. Theo giả thiết, ta
có
SHJ SLJ SKJ= =
, suy ra các tam giác
vuông
,SJH SJL
và
SJK
bằng nhau. Từ đó,
JH JL JK= =
. Mà J nằm trong tam giác
ABC nên J là tâm đường tròn nội tiếp tam
giác ABC.
Áp dụng công thức Hê-rông, ta tính được
diện tích S của tam giác ABC là
204S =
.
z=17
z=17
y=9
y=9
x=8
x=8
A
B
C
S
J
H
L
K
Kí hiệu
p
là nửa chu vi tam giác ABC,
r
là
bán kính đường tròn nội tiếp của ABC. Ta có
204
6
34
S
r
p
= = =
. Đặt
x BH BL= =
,
y CL CK= =
,
z AH AK
= =
.
Ta có hệ phương trình
17
25
26
xy
xz
yz
+=
+=
+=
.
z
z
y
y
x
x
L
K
H
J
A
B
C
Giải ra được
( ; ; ) (8; 9;17)xyz =
2 2 22
6 8 10
JB JH BH= + = +=
.
Ta có
( ,( )) 45SBJ SB ABC= = °
, suy ra SJB là tam giác vuông cân tại J.
10SJ JB= =
.
Thể tích V của khối chóp S.ABC là
1
. 680
3
ABC
V SJ S= =
| 1/34
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHỦ ĐỀ 1. KHỐI ĐA DIỆN VÀ THỂ TÍCH KHỐI ĐA DIỆN
A. KIẾN THỨC CƠ BẢN a. HÌNH HỌC PHẲNG
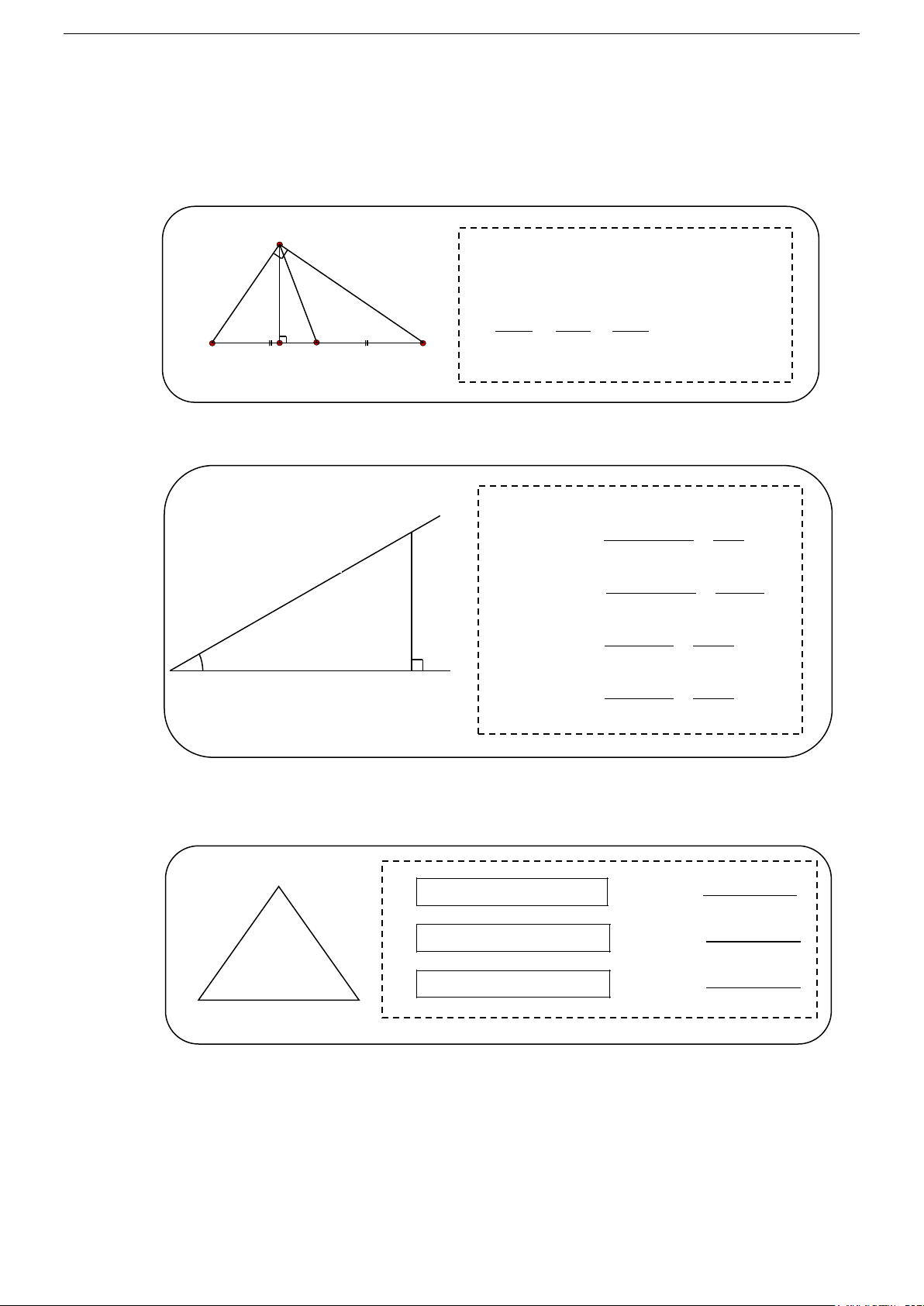
1. Các hệ thức lượng trong tam giác vuông:
Cho tam giác ABC vuông tại A , AH là đường cao, AM là đường trung tuyến. Ta có: B A 2 2 2
BC AB AC
AH.BC AB.AC 2 2
AB BH.BC, AC CH.CB 1 1 1   , 2
AH HB.HC B 2 2 2 AH AB AC H M C
2AM BC
2. Các tỉ số lượng giác của góc nhọn trong tam giác vuông: Ch C ọn góc n họn góc họn l nhọn là à α caïnh oá ñ nh oá i ñi ñsin ;  α = ; α =   Cạnh huyền caïnh uy h
nh uy eàn ïo h c caï k nh eà khoâng Cạnh  cos ;  α = ; α =   caï h nh uyeàn ö h  đối caïnh oá ñ nh oá i ñoaø ñ ntan ;  α = ; α =   α
caïnh keà keát c aï k nh eà keát Cạnh kề  cot ;  α = ; α =   caï ñ
nh oái ñoaø ñ n
3. Các hệ thức lượng trong tam giác thường: a. Định lý cosin: A 2 2 2    2 2 2 b c a
a b c  2bc cos A  cos A 2bc c b 2 2 2    2 2 2 a c b
b a c  2ac cos B  cos B  2ac 2 2 2
a b c a  2 2 2
c a b  2ab cosC  cosC B C 2ab b. Định lý sin: Trang 1/35 A a b c    2R c b sin A sin B sinC
(R là bán kính đường tròn ngoại tiếp ∆ABC) R B a C
c. Công thức tính diện tích tam giác: A  1 1 1 Sa.h  . b h  . c h ABC 2 a 2 b 2 c c  1 1 1 S
ab sinC bc sin A ac sin B b ABC 2 2 2 abcS  , Sp r ABC . 4 ABC R B a C
p = p ( p − a)( p − b)( p − c) p - nửa chu vi
r - bán kính đường tròn nội tiếp
d. Công thức tính độ dài đường trung tuyến: A 2 2 2   2 AB AC BC AM   2 4 K N 2 2 2  2 BA BC ACBN   2 4 B C 2 2 2 M   2 CA CB AB CK   2 4
4. Định lý Thales: A AM AN MN MN / /BC     k AB AC BC M N 2 S    AM AMN   2     k S  AB   B C ABC
(Tỉ diện tích bằng tỉ bình phương đồng dạng) Trang 2/35
5. Diện tích đa giác: B
a. Diện tích tam giác vuông: 1  SAB.AC ABC
Diện tích tam giác vuông bằng ½ tích 2 cạnh 2 góc vuông. A C
b. Diện tích tam giác đều: B 2  .  a 3 (cạnh)2 3 S  
Diện tích tam giác đều: SABC   đều  4 4 a   h  a 3 . (cạnh) 3 h  
Chiều cao tam giác đều: h   2  A C đều 2
c. Diện tích hình vuông và hình chữ nhật: A B 2 
Diện tích hình vuông bằng cạnh bình phương. S   a HVa  
Đường chéo hình vuông bằng cạnh nhân 2 . O A
 C BD a 2 
Diện tích hình chữ nhật bằng dài nhân rộng. D C
d. Diện tích hình thang: A D 1
AD BC .AH
SHình Thang  .(đáy lớn + đáy bé) x chiều cao  S  2 2 B H C
e. Diện tích tứ giác có hai đường chéo vuông góc: B 1
Diện tích tứ giác có hai đường chéo vuông góc A C  SAC.BD H .Thoi 2
nhau bằng ½ tích hai đường chéo.
Hình thoi có hai đường chéo vuông góc nhau D
tại trung điểm của mỗi đường.
b. CÁC PHƯƠNG PHÁP CHỨNG MINH HÌNH HỌC
1. Chứng minh đường thẳng song song với mặt phẳng :
d  ()   d d
   d  () (Định lý 1, trang 61, SKG HH11)  d ()   
() 
  d () (Hệ quả 1, trang 66, SKG HH11)
d  ()  Trang 3/35 d d '   () d '
   d  () (Tính chất 3b, trang 101, SKG HH11)  d ()   
2. Chứng minh hai mặt phẳng song song:
()  a,a  ()  () , b b  () 
  ()  () (Định lý 1, trang 64, SKG HH11)  a b O    
()  (Q) 
  ()() (Hệ quả 2, trang 66, SKG HH11)
()  (Q) 
()  ()  () d  
  ()  () . (Tính chất 2b, trang 101, SKG HH11)  () d   
3. Chứng minh hai đường thẳng song song: Áp dụng một trong các định lí sau
 Hai mặt phẳng (), có điểm chung S và lần lượt chứa 2 đường thẳng song song a,b thì giao
tuyến của chúng đi qua điểm S cùng song song với a,B. S  ( )
   ( )
a,b 
   ()    Sx ( a b). (Hệ quả trang 57, SKG HH11)  a b 
 Cho đường thẳng a song song với mặt phẳng (). Nếu mặt phẳng () chứa a và cắt () theo
giao tuyến b thì b song song với a. a  ( ),
 a   b a . (Định lý 2, trang 61, SKG HH11) ( )
   b 
 Hai mặt phẳng cùng song song với một đường thẳng thì giao tuyến của chúng song song với đường thẳng đó. ()  ()
(P)() =d,dd . (Định lý 3, trang 67, SKG HH11)
(P)  ()  d
 Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau. d d   
d  ()   d d (Tính chất 1b, trang 101, SKG HH11)  d ()   
 Sử dụng phương pháp hình học phẳng: Đường trung bình, định lí Talét đảo, …
4. Chứng minh đường thẳngvuông góc với mặt phẳng:
Định lý (Trang 99 SGK HH11). Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau
nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
d a  () d b ()  
  d   .  a b {O}   
Tính chất 1a (Trang 101 SGK HH11). Cho hai đường thẳng song song. Mặt phẳng nào vuông Trang 4/35
góc với đường thẳng này thì vuông góc với đường thẳng kia.
d d  d   .
d  ()
Tính chất 2a (Trang 101 SGK HH11). Cho hai mặt phẳng song song. Đường thẳng nào vuông
góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
  . d  d   
Định lý 2 (Trang 109 SGK HH11). Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt
phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
  P     P  
  d  P .  
    d
Định lý 1 (Trang 108 SGK HH11). Nếu hai mặt phẳng vuông góc thì bất cứ đường thẳng nào
nào nằm trong mặt phẳng này và vuông góc với giao tuyến đều vuông góc với mặt phẳng kiA.
  P  a
 P   
  d  P 
d  ,d a
5. Chứng minh hai đường thẳng vuông góc:
Cách 1: Dùng định nghĩa: 
a b  a b 0 ,  90 .        
Hay a b a b a.b  0  a . b .cos a,b   0
Cách 2: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì phải
vuông góc với đường kia.
b//c  a b. a c
Cách 3: Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường
thẳng nằm trong mặt phẳng đó.
a        a . b b 
Cách 4: (Sử dụng Định lý Ba đường vuông góc) Cho đường thẳng b nằm trong mặt phẳng P
và a là đường thẳng không thuộc P đồng thời không vuông góc với P. Gọi a’ là hình chiếu
vuông góc của a trên P. Khi đó b vuông góc với a khi và chỉ khi b vuông góc với a’.
a '  hch (P)      b  Pb a b a '. 
Cách khác: Sử dụng hình học phẳng (nếu được).
6. Chứng minh mp  mp:
Cách 1: Theo định nghĩa:        0 ,
 90 . Chứng tỏ góc giữa hai mặt phẳng bằng 90 .
Cách 2: Theo định lý 1 (Trang 108 SGK HH11):
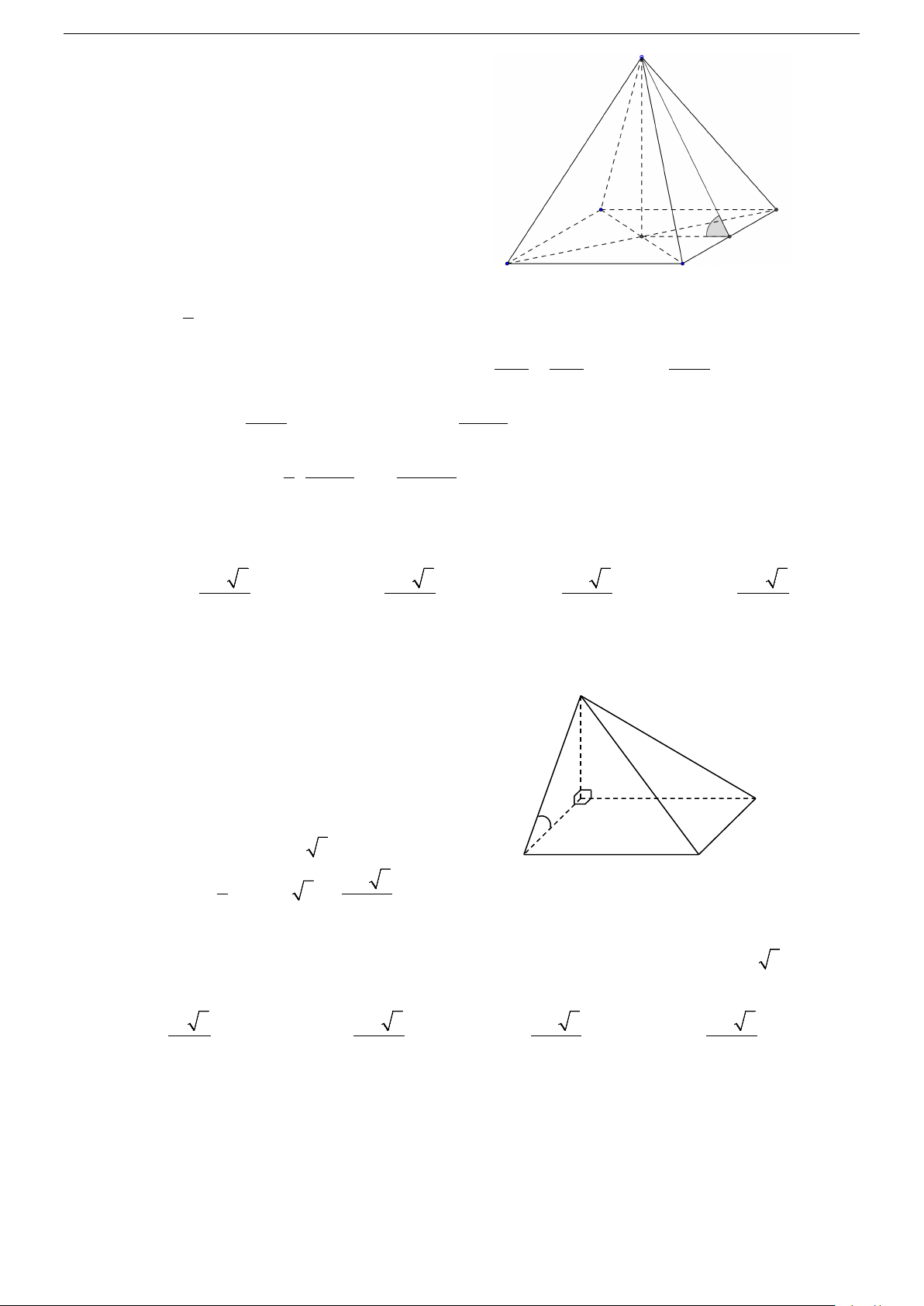
c. HÌNH CHÓP ĐỀU Trang 5/35
1. Định nghĩa: Một hình chóp được gọi là hình chóp đều nếu có đáy là một đa giác đều và có chân
đường cao trùng với tâm của đa giác đáy. Nhận xét: S
 Hình chóp đều có các mặt bên là những tam giác cân bằng nhau.
Các mặt bên tạo với đáy các góc bằng nhau.
 Các cạnh bên của hình chóp đều tạo với mặt đáy các góc bằng nhau.
2. Hai hình chóp đều thường gặp: A C
a. Hình chóp tam giác đều: Cho hình chóp tam giác đều S.ABC . Khi đó: O
 ĐáyABC là tam giác đều. B
 Các mặt bên là các tam giác cân tại S .  Chiều cao: SO .
 Góc giữa cạnh bên và mặt đáy:   
SAO SBO SCO .
 Góc giữa mặt bên và mặt đáy:  SHO . 2 1 AB 3
 Tính chất: AO AH,
OH AH, AH  . 3 3 2 S
Lưu ý: Hình chóp tam giác đều khác với tứ diện đều.
Tứ diện đều có các mặt là các tam giác đều.
Tứ diện đều là hình chóp tam giác đều có cạnh bên bằng cạnh đáy. I
b. Hình chóp tứ giác đều: Cho hình chóp tam giác đềuS.ABCD . A D
 ĐáyABCDlà hình vuông. O
 Các mặt bên là các tam giác cân tại S . B C  Chiều cao: SO .
 Góc giữa cạnh bên và mặt đáy:    
SAO SBO SCO SDO .
 Góc giữa mặt bên và mặt đáy:  SHO .
d. THỂ TÍCH KHỐI ĐA DIỆN S
1. Thể tích khối chóp: 1
V B.h 3 D
B : Diện tích mặt đáy.
h : Chiều cao của khối chóp. A O B C Trang 6/35 A C A C
2. Thể tích khối lăng trụ: V B.h B B
B : Diện tích mặt đáy.
h : Chiều cao của khối chóp. A’ C’ A’ C’
Lưu ý: Lăng trụ đứng có chiều cao cũng là B’ B’ cạnh bên. c
3. Thể tích hình hộp chữ nhật: V a. . b c a a a
 Thể tích khối lập phương: 3 V a b a V    S
4. Tỉ số thể tích:    SA SB SC S .A B C  . . V SA SB SC S .ABC A’ B’
5. Hình chóp cụt ABC.A′B C ′ ′ C’ h
V  B B  BB A B 3 Với ,
B B ,h là diện tích hai đáy và chiều cao. C
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần? A. 4 . B. 2 . C. 3. D. 1 . 2
Câu 2. Có bao nhiêu khối đa diện đều? A. 4 . B. 5. C. 3. D. 2 .
Câu 3. Cho khối đa diện đều { ; p }
q , chỉ số p là
A. Số các cạnh của mỗi mặt.
B. Số mặt của đa diện.
C. Số cạnh của đa diện.
D. Số đỉnh của đa diện.
Câu 4. Cho khối đa diện đều { ; p }
q , chỉ số q là
A. Số đỉnh của đa diện.
B. Số mặt của đa diện.
C. Số cạnh của đa diện.
D. Số các mặt ở mỗi đỉnh.
Câu 5. Tính thể tích khối tứ diện đều cạnh a . 3 3 3 A. a 2 ⋅ B. a 2 ⋅ C. 3 a . D. a ⋅ 12 4 6
Câu 6. Cho S.ABCD là hình chóp đều. Tính thể tích khối chóp S.ABCD biết AB = a , SA = a . 3 3 3 A. 3 a B. a 2 C. a 2 . D. a 2 6 3
Câu 7. Cho hình chóp S.ABC có SA ⊥ ( ABC) , đáy ABC là tam giác đều. Tính thể tích khối chóp
S.ABC biết AB = a , SA = a . Trang 7/35 3 3 3 A. a 3 . B. a 3 . C. 3 a . D. a 12 4 3
Câu 8. Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình chữ nhật. Tính thể tích
S.ABCD biết AB = a , AD = 2a , SA = 3a . 3 A. 3 a . B. 3 6a . B. 3 2a . D. a ⋅ 3
Câu 9. Thể tích khối tam diện vuông .
O ABC vuông tại O có OA = a, OB = OC = 2a là 3 3 3 A. 2a ⋅ B. a ⋅ C. a ⋅ D. 3 2a . 3 2 6
Câu 10. Cho hình chóp S.ABC có SA vuông góc mặt đáy, tam giác ABC vuông tại ,
A SA = 2cm, AB = 4c ,
m AC = 3cm . Tính thể tích khối chóp. A. 12 3 cm . B. 24 3 cm . C. 24 3 cm . D. 3 24cm . 3 5 3
Câu 11. Cho hình chóp S.ABCD đáy hình chữ nhật, SA vuông góc đáy, AB = a, AD = 2a . Góc giữa SB và đáy bằng 0
45 . Thể tích khối chóp là 3 3 3 3 A. a 2 ⋅ B. 2a ⋅ C. a ⋅ D. a 2 ⋅ 3 3 3 6
Câu 12. Hình chóp S.ABCD đáy hình vuông, SAvuông góc với đáy, SA = a 3, AC = a 2 . Khi đó thể
tích khối chóp S.ABCD là 3 3 3 3 A. a 2 ⋅ B. a 2 ⋅ C. a 3 ⋅ D. a 3 ⋅ 2 3 2 3
Câu 13. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B . Biết S
∆ AB là tam giác đều và
thuộc mặt phẳng vuông góc với mặt phẳng ( ABC). Tính thể tích khối chóp S.ABC biết
AB = a , AC = a 3 . 3 3 3 3 A. a 6 ⋅ B. a 6 ⋅ C. a 2 ⋅ D. a ⋅ 12 4 6 4
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại
S và thuộc mặt phẳng vuông góc với mặt phẳng ( ABCD) . Tính thể tích khối chóp S.ABCD
biết BD = a , AC = a 3 . 3 3 3 A. 3 a . B. a 3 ⋅ C. a 3 ⋅ D. a ⋅ 4 12 3
Câu 15. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A . Hình chiếu của S lên mặt phẳng
( ABC)là trung điểm H của BC . Tính thể tích khối chóp S.ABC biết AB = a , AC = a 3 , SB = a 2 . 3 3 3 3 A. a 6 ⋅ B. a 3 ⋅ C. a 3 ⋅ D. a 6 ⋅ 6 2 6 2
Câu 16. Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a . Hình chiếu của S lên mặt phẳng
( ABCD) là trung điểm H của AD . Tính thể tích khối chóp S.ABCD biết 3a SB = . 2 3 3 3 A. a ⋅ B. 3 a . C. a ⋅ D. 3a ⋅ 3 2 2 Trang 8/35
Câu 17. Hình chóp S.ABCD đáy là hình vuông cạnh a 1 a, 3 SD =
. Hình chiếu của S lên ( ABCD) là 2
trung điểm H của AB . Thể tích khối chóp là 3 3 3 A. a 2 ⋅ B. a 2 ⋅ C. 3 a 12 . D. a ⋅ 3 3 3
Câu 18. Hình chóp S.ABCD đáy hình thoi, AB = 2a , góc  BAD bằng 0
120 . Hình chiếu vuông góc của
S lên ( ABCD) là I giao điểm của 2 đường chéo, biết SI a
= . Khi đó thể tích khối chóp 2 S.ABCD là 3 3 3 3 A. a 2 ⋅ B. a 3 ⋅ C. a 2 ⋅ D. a 3 ⋅ 9 9 3 3
Câu 19. Cho hình chóp S.ABC , gọi M , N lần lượt là trung điểm của ,
SA SB . Tính tỉ số VS.ABC . VS.MNC A. 4 . B. 1 ⋅ C. 2 . D. 1 ⋅ 2 4
Câu 20. Cho khối chop .
O ABC . Trên ba cạnh ,
OA OB,OC lần lượt lấy ba điểm ’,
A B ,′C′ sao cho 2OA′ = ,
OA 4OB′ = OB, 3OC′ = OC . Tính tỉ số VO.A'B'C' VO.ABC A. 1 . B. 1 . C. 1 . D. 1 . 12 24 16 32
Câu 21. Cho hình chóp S.ABC. Gọi (α ) là mặt phẳng qua A và song song với BC . (α ) cắt SB , SC
lần lượt tại M , N . Tính tỉ số SM biết (α ) chia khối chóp thành 2 phần có thể tích bằng nhau. SB A. 1 . B. 1 . C. 1 . D. 1 . 2 2 4 2 2
Câu 22. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là: 3 3 3 3
A. a 3 ⋅
B. a 3 ⋅
C. a 2 ⋅ D. a 2 ⋅ 4 3 3 2
Câu 23. Cho lăng trụ ABC .
D A'B 'C 'D ' có ABCD là hình chữ nhật, A' A = A' B = A' D . Tính thể tích
khối lăng trụ ABC .
D A' B 'C ' D ' biết AB = a , AD = a 3 , AA' = 2a . A. 3 3a . B. 3 a . C. 3 a 3 . D. 3 3a 3 .
Câu 24. Cho lăng trụ ABC.A'B'C ' có ABC là tam giác vuông tại A . Hình chiếu của A' lên ( ABC) là
trung điểm của BC . Tính thể tích khối lăng trụ ABC.A' B 'C ' biết AB = a , AC = a 3 , AA' = 2a . 3 3 A. a ⋅ B. 3a ⋅ C. 3 a 3 . D. 3 3a 3 . 2 2
Câu 25. Cho lăng trụ ABC .
D A'B 'C 'D ' có ABCD là hình thoi. Hình chiếu của A' lên ( ABCD) là
trọng tâm của tam giác ABD . Tính thể tích khối lăng trụ ABCA' B 'C ' biết AB = a ,  0
ABC =120 , AA' = a . 3 3 3 A. 3 a 2 . B. a 2 ⋅ C. a 2 ⋅ D. a 2 ⋅ 6 3 2
Câu 26. Cho lăng trụ ABC.A'B'C '. Tính tỉ số VABB'C' .
VABCA'B'C' Trang 9/35 A. 1 ⋅ B. 1 ⋅ C. 1 ⋅ D. 2 . 2 6 3 3
Câu 27. Cho khối lăng trụ tam giác đều ABC. ’ A ’
B C’ có tất cả các cạnh đều bằng a . Thể tích khối tứ diện ’ A B ’ B C’ là 3 3 3 3 A. a 3 ⋅ B. a 3 ⋅ C. a 3 ⋅ D. a ⋅ 12 4 6 12
Câu 28. Lăng trụ tam giác ABC.A′B C
′ ′có đáy tam giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng
300. Hình chiếu A′ lên ( ABC)là trung điểm I của BC . Thể tích khối lăng trụ là 3 3 3 3 A. a 3 ⋅ B. a 3 ⋅ C. a 3 ⋅ D. a 3 ⋅ 6 2 12 8
Câu 29. Lăng trụ đứng ABC. ’ A ’
B C’ có đáy ABC là tam giác vuông tại ,
A BC = 2a, AB = a . Mặt bên (B ’
B C’C) là hình vuông. Khi đó thể tích lăng trụ là 3 A. a 3 . B. 3 a 2 . C. 3 2a 3 . a . 3 D. 3 3
Câu 30. Cho lăng trụ ABC.A'B'C '. Gọi M , N lần lượt là trung điểm của CC ' và BB'. Tính tỉ số VABCMN .
VABC.A'B'C' A. 1 . B. 1 . C. 1 . D. 2 . 3 6 2 3
Câu 31. Cho khối lăng trụ ABC.A′B C
′ ′. Tỉ số thể tích giữa khối chóp A .′ABC và khối lăng trụ đó là A. 1 . B. 1 . C. 1 . D. 1 . 4 2 3 6
Câu 32. Cho khối lập phương ABC . D A′B C ′ D
′ ′ . Tỉ số thể tích giữa khối A .′ABD và khối lập phương là: A. 1 . B. 1 . C. 1 . D. 1 . 4 8 6 3
Câu 33. Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng h , góc giữa hai mặt phẳng (SAB) và
(ABCD) bằng α . Tính thể tích của khối chóp S.ABCD theo h và α . 3 3 3 3 A. 3h 4h 8h 3h . B. . C. . D. . 2 4 tan α 2 3tan α 2 3tan α 2 8tan α
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh SB vuông góc với đáy
và mặt phẳng (SAD) tạo với đáy một góc 60°. Tính thể tích khối chóp S.ABCD . 3 3 3 3 A. 3a 3 3a 3 8a 3 4a 3 V = . B. V = . C. V = . D. V = . 4 8 3 3
Câu 35. Cho hình lăng trụ đứng ABC.A'B'C ' có đáy ABC là tam giác vuông tại B , BC = a , mặt
phẳng ( A'BC) tạo với đáy một góc 30° và tam giác A'BC có diện tích bằng 2 a 3 . Tính thể
tích khối lăng trụ ABC.A' B 'C '. 3 3 3 3 A. a 3 . B. 3a 3 . C. 3a 3 . D. 3a 3 . 8 4 8 2
Câu 36. Cho hình lăng trụ ABC.A'B'C ' có đáy ABC là tam giác đều cạnh bằng a . Hình chiếu vuông
góc của A' trên ( ABC) là trung điểm của AB . Mặt phẳng ( AA'C 'C) tạo với đáy một góc
bằng 45°. Tính thể tích V của khối lăng trụ ABC.A' B 'C '. 3 3 3 3 A. 3a V = . B. 3a V = . C. 3a V = . D. 3a V = . 16 8 4 2 Trang 10/35
Câu 37. Cho hình chóp đều S.ABC , góc giữa mặt bên và mặt phẳng đáy ( ABC) bằng 0 60 , khoảng
cách giữa hai đường thẳng SA và BC a
bằng 3 . Thể tích của khối chóp S.ABC 2 7 theo a bằng 3 3 3 3 A. a 3 . B. a 3 . C. a 3 . D. a 3 . 12 18 16 24
Câu 38. Cho hình chóp đều S.ABCD có đáy ABCD là hình thoi tâm O, AC = 2 3a , BD = 2a , hai
mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng ( ABCD) . Biết khoảng cách từ
điểm O đến mặt phẳng (SAB) bằng a 3 . Tính thể tích của khối chóp S.ABCD 4 theo a . 3 3 3 3 A. a 3 . B. a 3 . C. a 3 . D. a 3 . 16 18 3 12
Câu 39. Cho hình chóp tứ giác đều S.ABCD , O là giao điểm của AC và BD. Biết mặt bên của hình
chóp là tam giác đều và khoảng từ O đến mặt bên là a . Tính thể tích khối chóp S.ABCD theo a . A. 3 2a 3 . B. 3 4a 3 . C. 3 6a 3 . D. 3 8a 3 .
Câu 40. Cho hình chóp tứ giác S.ABCD có SA ⊥ ( ABCD) . ABCD là hình thang vuông tại A và B
biết AB = 2a . AD = 3BC = 3a . Tính thể tích khối chóp S.ABCD theo a biết góc giữa
(SCD)và ( ABCD) bằng 0 60 . A. 3 2 6a . B. 3 6 6a . C. 3 2 3a . D. 3 6 3a .
Câu 41. Cho hình chóp tứ giác S.ABCD có SA ⊥ ( ABCD) , ABCD là hình thang vuông tại A và B
biết AB = 2a . AD = 3BC = 3a . Tính thể tích khối chóp S.ABCD theo a , biết khoảng cách từ
A đến mặt phẳng (SCD) bằng 3 6 a . 4 A. 3 6 6a . B. 3 2 6a . C. 3 2 3a . D. 3 6 3a .
Câu 42. Cho lăng trụ tam giác ABC.A'B'C ' có BB' = a , góc giữa đường thẳng BB' và ( ABC) bằng
60°, tam giác ABC vuông tại C và góc 
BAC = 60° . Hình chiếu vuông góc của điểm B ' lên
( ABC) trùng với trọng tâm của A
∆ BC . Thể tích của khối tứ diện A'.ABC theo a bằng 3 3 3 3 A. 13a . B. 7a . C. 15a . D. 9a . 108 106 108 208
Câu 43. Cho hình lăng trụ đứng ABC.A'B'C ', biết đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm O a
của tam giác ABC đến mặt phẳng ( A' BC) bằng .Tính thể tích khối lăng trụ 6
ABC.A'B 'C ' . 3 3 3 3 A. 3a 2 . B. 3a 2 . C. 3a 2 . D. 3a 2 . 8 28 4 16
Câu 44. Cho hình chóp tam giác S.ABC có M là trung điểm của SB , N là điểm trên cạnh SC sao cho
NS = 2NC . Kí hiệu V ,V lần lượt là thể tích của các khối chóp .
A BMNC và S.AMN . Tính tỉ 1 2 số V1 . V2 A. V 2 V 1 V V 1 = B. 1 = C. 1 = 2. D. 1 = 3 V 3 V 2 V V 2 2 2 2 Trang 11/35
Câu 45. ho NS = 2NC , P là điểm trên cạnh SAsao cho PA = 2PS . Kí hiệu V ,V lần lượt là thể tích 1 2
của các khối tứ diện BMNP và SABC . Tính tỉ số V1 . V2 A. V 1 V 3 V 2 V 1 1 = . B. 1 = . C. 1 = . D. 1 = . V 9 V 4 V 3 V 3 2 2 2 2
Câu 46. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a , góc giữa hai mặt phẳng (SAB) và
(ABCD) bằng 45°, M , N và P lần lượt là trung điểm các cạnh ,
SA SB và AB . Tính thể tích
V của khối tứ diện DMNP . 3 3 3 3 A. a V = B. a V = C. a V = D. a V = 6 4 12 2
Câu 47. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông cân tại B , AC = 2a ; cạnh bên
AA′ = 2a . Hình chiếu vuông góc của A′ trên mặt phẳng (ABC) là trung điểm cạnh AC .
Tính thể tích V của khối lăng trụ ABC.A′B C ′ ′. 3 3 A. 1 3 V = a . B. a V = . C. 3 V = a . D. 2a V = . 2 3 3
Câu 48. Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau. Gọi G ,G ,G và 1 2 3
G lần lượt là trọng tâm các mặt ABC, ABD, ACD và BCD . Biết AB = 6a, AC = 9a , 4
AD =12a . Tính theo a thể tích khối tứ diện G G G G . 1 2 3 4 A. 3 4a B. 3 a C. 3 108a D. 3 36a
Câu 49. Cho tứ diện ABCD có AB = CD =11m , BC = AD = 20m, BD = AC = 21m . Tính thể tích khối tứ diện ABCD . A. 3 360m B. 3 720m C. 3 770m D. 3 340m
Câu 50. Cho hình chóp tứ giác S.ABCD có đáy là vuông; mặt bên (SAB) là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng (SCD) bằng
3 7a . Tính thể tích V của khối chóp S.ABCD 7 . 3 A. 1 3 V = a . B. 3 V = a . C. 2 3 V = a . D. 3a V = . 3 3 2
Câu 51. Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA = 2SM ,
SN = 2NB , (α) là mặt phẳng qua MN và song song với SC . Kí hiệu (H )và (H ) là các 1 2
khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng (α) , trong đó, (H ) chứa 1
điểm S , (H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . Tính tỉ số V1 . 2 1 2 1 2 V2 A. 4 B. 5 C. 3 D. 4 5 4 4 3
Câu 52. Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC ; các mặt phẳng (SAB) ,
(SAC) và (SBC) cùng tạo với mặt phẳng (ABC) các góc bằng nhau. Biết AB = 25, BC =17 ,
AC = 26 ; đường thẳng SB tạo với mặt đáy một góc bằng 45°. Tính thể tích V của khối chóp S.ABC . A.V = 408 . B.V = 680 . C.V = 578. D.V = 600 .
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 7.4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Trang 12/35
A B A D A C A C A A B D A C C A A D A B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B A A B D C A D D A C C B C D A D C A A
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 B D D C A A C A A D A B
II –HƯỚNG DẪN GIẢI
NHẬN BIẾT – THÔNG HIỂU
Câu 1. Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài
đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần? A. 4 . B. 2 . C. 3. D. 1 . 2 Hướng dẫn giải:
Khi độ dài cạnh đáy tăng lên 2 lần thì diện tích đáy tăng lên 4 lần.
⇒ Thể tích khối chóp tăng lên 4 lần.
Câu 2. Có bao nhiêu khối đa diện đều? A. 4 . B. 5. C. 3. D. 2 . Hướng dẫn giải:
Có 5 khối đa diện đều là: tứ diện đều, hình lập phương, khối 8 mặt đều, khối 12 mặt đều, khối 20 mặt đều.
Câu 3. Cho khối đa diện đều { ; p }
q , chỉ số p là
A. Số các cạnh của mỗi mặt.
B. Số mặt của đa diện.
C. Số cạnh của đa diện.
D. Số đỉnh của đa diện.
Câu 4. Cho khối đa diện đều { ; p }
q , chỉ số q là
A. Số đỉnh của đa diện.
B. Số mặt của đa diện.
C. Số cạnh của đa diện.
D. Số các mặt ở mỗi đỉnh.
Câu 5. Tính thể tích khối tứ diện đều cạnh a . 3 3 3 A. a 2 ⋅ B. a 2 ⋅ C. 3 a . D. a ⋅ 12 4 6 Hướng dẫn giải:
Gọi tứ diện ABCD đều cạnh a . S
Gọi H là hình chiếu của A lên (BCD) . Ta có: a 3 BH = 3 2 2 a 6
⇒ AH = AB − BH = A C 3 2 a 3 3 O S = a 2 ⇒ V = . BC ∆ D 4 ABCD 12 B
Câu 6. Cho S.ABCD là hình chóp đều. Tính thể tích khối chóp S.ABCD biết AB = a , SA = a . 3 3 3 A. 3 a B. a 2 C. a 2 . D. a 2 6 3 Hướng dẫn giải: Trang 13/35
Gọi H là hình chiếu của S lên ( ABCD) S Ta có: a 2 AH = 2 2 2 a 2
⇒ SH = SA − AH = A D 2 3 H 2 S = a a 2 ⇒ V = ABCD S.ABCD 6 B C
Câu 7. Cho hình chóp S.ABC có SA ⊥ ( ABC) , đáy ABC là tam giác đều. Tính thể tích khối chóp
S.ABC biết AB = a , SA = a . 3 3 3 A. a 3 . B. a 3 . C. 3 a . D. a 12 4 3 Hướng dẫn giải: 2 a 3 S S = ABC ∆ 4 3 a 3 ⇒ V = . S.ABC 12 A C B
Câu 8. Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình chữ nhật. Tính thể tích
S.ABCD biết AB = a , AD = 2a , SA = 3a . 3 A. 3 a . B. 3 6a . B. 3 2a . D. a ⋅ 3 Hướng dẫn giải: S 2 S = = 3 ⇒ V = a S ABC 2 ∆ a a a ABCD 2 . 2 . D A B C
Câu 9. Thể tích khối tam diện vuông .
O ABC vuông tại O có OA = a, OB = OC = 2a là 3 3 3 A. 2a ⋅ B. a ⋅ C. a ⋅ D. 3 2a . 3 2 6 Hướng dẫn giải: A  1 2 S = OB OC = a OBC . 2  2
h = OA = a 3 1 2a O C ⇒ V = OA⋅ S = O.ABC 3 OBC 3 B Trang 14/35
Câu 10. Cho hình chóp S.ABC có SA vuông góc mặt đáy, tam giác ABC vuông tại ,
A SA = 2cm, AB = 4c ,
m AC = 3cm . Tính thể tích khối chóp. A. 12 3 cm . B. 24 3 cm . C. 24 3 cm . D. 3 24cm . 3 5 3 Hướng dẫn giải: S  1 2 S = AB AC = cm ABC . 6  2
h = SA = 2cm A C 1 12 3 ⇒ V = SA⋅ S = cm S.ABC 3 ABC 3 B
Câu 11. Cho hình chóp S.ABCD đáy hình chữ nhật, SA vuông góc đáy, AB = a, AD = 2a . Góc giữa SB và đáy bằng 0
45 . Thể tích khối chóp là 3 3 3 3 A. a 2 ⋅ B. 2a ⋅ C. a ⋅ D. a 2 ⋅ 3 3 3 6 Hướng dẫn giải: S SA = A . B tan ( 0 45 ) =  a  2 S = a a = a ABCD .2 2 3 1 2a D ⇒ V = SA S = A S ABCD . . 3 ABCD 3 0 45 B C
Câu 12. Hình chóp S.ABCD đáy hình vuông, SAvuông góc với đáy, SA = a 3, AC = a 2 . Khi đó thể
tích khối chóp S.ABCD là 3 3 3 3 A. a 2 ⋅ B. a 2 ⋅ C. a 3 ⋅ D. a 3 ⋅ 2 3 2 3 Hướng dẫn giải: S SA =  a 3 AB = AC.cos  ( 0 45 ) 2 = a ⇒ S =  a ABCD 3 1 a 3 D ⇒ V = SA S = A S ABCD . . 3 ABCD 3 B C
Câu 13. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B . Biết S
∆ AB là tam giác đều và
thuộc mặt phẳng vuông góc với mặt phẳng ( ABC). Tính thể tích khối chóp S.ABC biết
AB = a , AC = a 3 . 3 3 3 3 A. a 6 ⋅ B. a 6 ⋅ C. a 2 ⋅ D. a ⋅ 12 4 6 4 Hướng dẫn giải: Trang 15/35 A
∆ BC vuông tại B 2 2
⇒ BC = AC − AB = a 2 . S 2 1 a 2 S = = ∆ BA BC ABC . 2 2
Gọi H là trung điểm AB a 3 ⇒ SH = 2 A C Ta có: S
∆ AB đều ⇒ SH ⊥ AB
⇒ SH ⊥ ( ABC)(vì (SAB) ⊥ ( ABC) ). H B 3 1 a 6 ⇒ V = SH S = S ABC . . 3 ABC ∆ 12
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại
S và thuộc mặt phẳng vuông góc với mặt phẳng ( ABCD) . Tính thể tích khối chóp S.ABCD
biết BD = a , AC = a 3 . 3 3 3 A. 3 a . B. a 3 ⋅ C. a 3 ⋅ D. a ⋅ 4 12 3 Hướng dẫn giải:
Gọi O là giao điểm của AC và BD . S
ABCD là hình thoi ⇒ AC ⊥ BD ,
O là trung điểm của AC , BD . A
∆ BO vuông tại O A 2 2
⇒ AB = AO + OB = a . D 2 1 a 3 S H = AC BD = . ABCD . 2 2 B C
Gọi H là trung điểm AB . S
∆ AB vuông cân tại S cạnh AB = a a ⇒ SH = . 2 Ta có: S
∆ AB cân ⇒ SH ⊥ AB ⇒ SH ⊥ ( ABCD) (vì (SAB) ⊥ ( ABC) ). 3 1 a 3 ⇒ V = SH S = . S ABCD . . 3 ABCD 12
Câu 15. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A . Hình chiếu của S lên mặt phẳng
( ABC)là trung điểm H của BC . Tính thể tích khối chóp S.ABC biết AB = a , AC = a 3 , SB = a 2 . 3 3 3 3 A. a 6 ⋅ B. a 3 ⋅ C. a 3 ⋅ D. a 6 ⋅ 6 2 6 2 Hướng dẫn giải: S A
∆ BC vuông tại A 2 2
⇒ BC = AC + AB = 2a . 2 1 a 3 S = = . ∆ AB AC ABC . B 2 2 A 2 2
SH = SB − BH = a . H C Trang 16/35 3 1 a 3 ⇒ V = SH S = . S ABC . . 3 ABC ∆ 6
Câu 16. Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a . Hình chiếu của S lên mặt phẳng
( ABCD) là trung điểm H của AD . Tính thể tích khối chóp S.ABCD biết 3a SB = . 2 3 3 3 A. a ⋅ B. 3 a . C. a ⋅ D. 3a ⋅ 3 2 2 Hướng dẫn giải: A
∆ BH vuông tại A S 2 2 a 5
⇒ BH = AH + AB = . 2 2 2
SH = SB − BH = a . A B 2 S = a . ABCD H 3 1 a ⇒ V = SH S = . D C S ABCD . . 3 ABCD 3
Câu 17. Hình chóp S.ABCD đáy là hình vuông cạnh a 1 a, 3 SD =
. Hình chiếu của S lên ( ABCD) là 2
trung điểm H của AB . Thể tích khối chóp là 3 3 3 A. a 2 ⋅ B. a 2 ⋅ C. 3 a 12 . D. a ⋅ 3 3 3 Hướng dẫn giải: 2 S = a S ABCD 2 2 2 2 5a
HD = AH + AD = 4 2 2 2 2 13a 5a
⇒ SH = SD − HD = − = a 2 A 4 4 D 3 1 a 2 ⇒ V = SH = . H S ABCD .S . 3 ABCD 3 B C
Câu 18. Hình chóp S.ABCD đáy hình thoi, AB = 2a , góc  BAD bằng 0
120 . Hình chiếu vuông góc của
S lên ( ABCD) là I giao điểm của 2 đường chéo, biết SI a
= . Khi đó thể tích khối chóp 2 S.ABCD là 3 3 3 3 A. a 2 ⋅ B. a 3 ⋅ C. a 2 ⋅ D. a 3 ⋅ 9 9 3 3 Hướng dẫn giải: S  a SI =   2  =  2 S AB AD BAD =  a ABCD . .sin 2 3 A D 3 1 a 3 ⇒ V = SI S = S ABCD . . 3 ABCD 3 I B C Trang 17/35
Câu 19. Cho hình chóp S.ABC , gọi M , N lần lượt là trung điểm của ,
SA SB . Tính tỉ số VS.ABC . VS.MNC A. 4 . B. 1 ⋅ C. 2 . D. 1 ⋅ 2 4 Hướng dẫn giải: S M V SA SB S.ABC = . = 4 V SM SN N S.MNC A C B
Câu 20. Cho khối chop .
O ABC . Trên ba cạnh ,
OA OB,OC lần lượt lấy ba điểm ’,
A B ,′C′ sao cho 2OA′ = ,
OA 4OB′ = OB, 3OC′ = OC . Tính tỉ số VO.A'B'C' VO.ABC A. 1 . B. 1 . C. 1 . D. 1 . 12 24 16 32 Hướng dẫn giải: O Ta có: B′ C′
OA′ 1 OB′ 1 OC′ 1 A′ = ; ; = =
OA 2 OB 4 OC 3 V ′ ′ ′ ′ OA OB OC O A B C 1 1 1 1 . ’ ’ ⇒ = ⋅ ⋅ = ⋅ ⋅ = A C V OA OB OC O ABC 2 4 3 24 . B
Câu 21. Cho hình chóp S.ABC. Gọi (α ) là mặt phẳng qua A và song song với BC . (α ) cắt SB , SC
lần lượt tại M , N . Tính tỉ số SM biết (α ) chia khối chóp thành 2 phần có thể tích bằng nhau. SB A. 1 . B. 1 . C. 1 . D. 1 . 2 2 4 2 2 Hướng dẫn giải: Trang 18/35 S Ta có: // SM SN MN BC ⇒ = SB SC M 2 Ta có: V SM SN SM S.AMN .  = = V
SB SC  SB N S.ABCA C Ta có: V SM S AMN 1 1 . = ⇒ = V SB S ABC 2 . 2 B
Câu 22. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là: 3 3 3 3
A. a 3 ⋅
B. a 3 ⋅
C. a 2 ⋅ D. a 2 ⋅ 4 3 3 2 Hướng dẫn giải: A ' C' B' h = a 3  a 3 2  ⇒ V = . 3 h S a = S = 4  4 A C B
Câu 23. Cho lăng trụ ABC .
D A'B 'C 'D ' có ABCD là hình chữ nhật, A' A = A' B = A' D . Tính thể tích
khối lăng trụ ABC .
D A'B 'C 'D ' biết AB = a , AD = a 3 , AA' = 2a . A. 3 3a . B. 3 a . C. 3 a 3 . D. 3 3a 3 . Hướng dẫn giải:
Gọi O là giao điểm của AC và BD . A' B '
ABCD là hình chữ nhật ⇒ OA = OB = OD
Mà A′A = A′B = A′D nên A'O ⊥ ( ABD) (vì
A'O là trực tâm giác ABD ) D ' C A
∆ BD vuông tại A ' 2 2
⇒ BD = AB + AD = 2a A B
⇒ OA = OB = OD = a O A
∆ A'O vuông tại O 2 2
⇒ A'O = AA' − AO = a 3 D C 2 S = AB AD = a ABCD . 3 3 V = A O S = a . ABCDA B C D ' . ABCD 3 ' ' ' '
Câu 24. Cho lăng trụ ABC.A'B'C ' có ABC là tam giác vuông tại A . Hình chiếu của A' lên ( ABC) là
trung điểm của BC . Tính thể tích khối lăng trụ ABC.A' B 'C ' biết AB = a , AC = a 3 , AA' = 2a . 3 3 A. a ⋅ B. 3a ⋅ C. 3 a 3 . D. 3 3a 3 . 2 2 Hướng dẫn giải: Trang 19/35
Gọi H là trung điểm của BC A' B '
⇒ A' H ⊥ ( ABC) .
ABC là tam giác vuông tại A C ' 2 2
⇒ BC = AB + AC = 2a 1
⇒ AH = BC = a 2 A B A
∆ ' AH vuông tại H H 2 2
⇒ A' H = AA' − AH = a 3 C 2 1 a 3 S = = ∆ AB AC ABC . 2 2 3 3a V = A H S = . ABCA B C ' . ' ' ' ABC 2
Câu 25. Cho lăng trụ ABC .
D A' B 'C ' D ' có ABCD là hình thoi. Hình chiếu của A' lên ( ABCD) là
trọng tâm của tam giác ABD . Tính thể tích khối lăng trụ ABCA' B 'C ' biết AB = a ,  0
ABC =120 , AA' = a . 3 3 3 A. 3 a 2 . B. a 2 ⋅ C. a 2 ⋅ D. a 2 ⋅ 6 3 2 Hướng dẫn giải: A'
Gọi H là trọng tâm của tam giác ABD B'
⇒ A' H ⊥ ( ABCD) . C ' D' Ta có:  0 = −  0 BAD 180 ABC = 60 .
Tam giác ABD cân có  0 BAD = 60
nên tam giác ABD đều. A B
ABD là tam giác đều cạnh a a 3 ⇒ AH = H 3 D C A
∆ ' AH vuông tại H 2 2 a 6
⇒ A' H = AA' − AH = 3 2 2 a 3 a 3 3 S = S = = ; a 2 V = A H S = ABCDA B C D ' . ABCD 2 ABD 2. 4 2 ' ' ' ' ABC 2
Câu 26. Cho lăng trụ ABC.A'B'C '. Tính tỉ số VABB'C' .
VABCA'B'C' A. 1 ⋅ B. 1 ⋅ C. 1 ⋅ D. 2 . 2 6 3 3 Hướng dẫn giải:
Ta có: BB 'C 'C là hình bình hành A' C' 1 ⇒ S = S 1 ⇒ V = V B' BB'C ' BB'C ' 2 C . A BB'C ' . A BB'C ' 2 C Ta có: 1 V = V . A A'B'C '
ABCA'B'C ' 3 A C 2 ⇒ V = V −V = V . A BB'C 'C
ABCA'B'C ' . A A'B'C '
ABCA'B'C ' B 3 Trang 20/35 1 VABB C 1 ' ' ⇒ V = V ⇒ = ABB'C '
ABCA'B'C ' 3 VABCA B C 3 ' ' '
Câu 27. Cho khối lăng trụ tam giác đều ABC. ’ A ’
B C’ có tất cả các cạnh đều bằng a . Thể tích khối tứ diện ’ A B ’ B C’ là 3 3 3 3 A. a 3 ⋅ B. a 3 ⋅ C. a 3 ⋅ D. a ⋅ 12 4 6 12 Hướng dẫn giải: A ' C'
h = BB′ = a B'  2  a 3 S = A′B C ′ ′  4 3 1 a 3 A C ⇒ V = ′ = ′ ′ ′ BB S A BB C . 3 A′B C ′ ′ 12 B
Câu 28. Lăng trụ tam giác ABC.A′B C
′ ′có đáy tam giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng
300. Hình chiếu A′ lên ( ABC)là trung điểm I của BC . Thể tích khối lăng trụ là 3 3 3 3 A. a 3 ⋅ B. a 3 ⋅ C. a 3 ⋅ D. a 3 ⋅ 6 2 12 8 Hướng dẫn giải: A' B '   ′ = ( 0) a 3 3 .tan 30 a A I AI = ⋅ =  2 3 2  C ' 2  a 3 S = ABC  4 3 a 3 A ⇒ V = A′I S = B ABC A B C . . ’ ’ ’ ABC 8 I C
Câu 29. Lăng trụ đứng ABC. ’ A ’
B C’ có đáy ABC là tam giác vuông tại ,
A BC = 2a, AB = a . Mặt bên (B ’
B C’C) là hình vuông. Khi đó thể tích lăng trụ là 3 A. a 3 . B. 3 a 2 . C. 3 2a 3 . a . 3 D. 3 3 Hướng dẫn giải: A' C'
h = BB′ = 2a  B' 2 2
AC = BC − AB = a 3 2 1 a 3 ⇒ S = AB AC = ABC . 2 2 A C 3 ⇒ V = BB′ S = a ABC A B C . ABC 3 . ’ ’ ’ B
Câu 30. Cho lăng trụ ABC.A'B'C '. Gọi M , N lần lượt là trung điểm của CC ' và BB'. Tính tỉ số VABCMN .
VABC.A'B'C' Trang 21/35 A. 1 . B. 1 . C. 1 . D. 2 . 3 6 2 3 Hướng dẫn giải:
Ta có: BB 'C 'C là hình bình hành A' B ' 1 ⇒ S = S BCMN BB'C ' 2 C 1 ⇒ V = V . A BCMN . A BB'C ' 2 C C ' M Ta có: 1 V = V . A A'B'C '
ABCA'B'C ' 3 2 N ⇒ V = V −V = V A . A BB'C 'C
ABCA'B'C ' . A A'B'C '
ABCA'B'C ' 3 B 1 VA BCMN 1 . ⇒ V = V ⇒ = A BCMN ABCA B C . . ' ' ' 3 VABCA B C 3 ' ' ' C
Câu 31. Cho khối lăng trụ ABC.A′B C
′ ′. Tỉ số thể tích giữa khối chóp A .′ABC và khối lăng trụ đó là A. 1 . B. 1 . C. 1 . D. 1 . 4 2 3 6 Hướng dẫn giải: A' C' 1 1 B' V = ′ = ′ AA S V A ABC . ABC ABC. 3 3 A B ′ C ′ ′ V A′ABC 1 ⇒ = V A C ABC A′B C ′ ′ 3 . B
Câu 32. Cho khối lập phương ABC . D A′B C ′ D
′ ′ . Tỉ số thể tích giữa khối A .′ABD và khối lập phương là: A. 1 . B. 1 . C. 1 . D. 1 . 4 8 6 3 Hướng dẫn giải: 1 A ' V = AA′ S D' A ABD . ’. 3 ABD B' C' 1 1 1 = AA .′ A .
B AD = AA .′S 3 2 6 ABCD 1 = V A D ABCD. ’
A B’C’D’ 6 B C VA ABD 1 ’. ⇒ = . VABCD A B C D 6 . ’ ’ ’ ’ VẬN DỤNG THẤP
Câu 33. Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng h , góc giữa hai mặt phẳng (SAB) và
(ABCD) bằng α . Tính thể tích của khối chóp S.ABCD theo h và α . 3 3 3 3 A. 3h 4h 8h 3h . B. . C. . D. . 2 4 tan α 2 3tan α 2 3tan α 2 8tan α Hướng dẫn giải:
Gọi O là tâm của mặt đáy thì Trang 22/35
SO ⊥ mp( ABCD) . Từ đó, SO là đường S
cao của hình chóp.Gọi M là trung điểm đoạn CD. Ta có: C
D ⊥ SM ⊂ (SCD) h   ⊥ ⊂ ⇒  CD OM (ABCD) SMO = α . CD  
= (SCD) ∩ (ABCD) A D O α M B C V = 1 .S
3 ABCD.SO; B = SABCD = AB2; Tìm AB: AB = 2OM
Tam giác SOM vuông tại tại O, ta có: tanα = SO = h ⇒ OM = h . OM OM tanα 2
⇒ AB = 2h . Suy ra: B = S 4h . SO = h. tanα ABCD = 2 tan α 2 3 Vậy V 4h 4h S.ABCD = 1 . .h = . 3 2 tan α 2 3tan α
Câu 34. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh SB vuông góc với đáy
và mặt phẳng (SAD) tạo với đáy một góc 60°. Tính thể tích khối chóp S.ABCD . 3 3 3 3 A. 3a 3 3a 3 8a 3 4a 3 V = . B. V = . C. V = . D. V = . 4 8 3 3 Hướng dẫn giải: AD ⊥ AB S Ta có:  AD ⊥ SB
⇒ AD ⊥ (SAB)⇒ AD ⊥ SA. ⇒  0 SAB = 60 . A D SABCD = 4a2.
Xét tam giác SAB tại vuông tại B, ta có: α 0
SB = AB tan 60 = 2a 3 . 2a B C 3
Vậy V = 1 .4a2. 2a 3 = 8a 3 . 3 3
Câu 35. Cho hình lăng trụ đứng ABC.A'B'C ' có đáy ABC là tam giác vuông tại B , BC = a , mặt
phẳng ( A'BC) tạo với đáy một góc 30° và tam giác A'BC có diện tích bằng 2 a 3 . Tính thể
tích khối lăng trụ ABC.A' B 'C '. 3 3 3 3 A. a 3 . B. 3a 3 . C. 3a 3 . D. 3a 3 . 8 4 8 2 Hướng dẫn giải: Trang 23/35
V= Bh = SABC.A’B’C’.AA’. A’ C’ BC ⊥ AB Do 
⇒ BC ⊥ A′B . BC ⊥ AA′ B’
BC ⊥ AB ⊂ (ABC)
Và BC ⊥ A'B ⊂ (A′BC) 
BC = (ABC) ∩ (A' BC) ⇒  ( ABC A BC )=  (AB A B)=  ( ),( ' ) , ' ABA' A C Ta có: 30o 1 a S = ′ ∆ ′ A B BC A BC . 2 . B 2 2.S∆ ′ a A BC 2. 3 ⇒ A′B = = = 2a 3 BC a = ′  0 ′ = = ′ = ′  0 AB A .
B cos ABA 2a 3.cos30 3 ; a AA A .
B sin ABA′ = 2a 3.sin 30 = a 3 1 3 V = B h = S
AA′ = AB BC AA′ 1 3a 3 = .3 . a . a a 3 = . ABC A B C . ABC . . . . . ' ' ' 2 2 2
Câu 36. Cho hình lăng trụ ABC.A'B'C ' có đáy ABC là tam giác đều cạnh bằng a . Hình chiếu vuông
góc của A' trên ( ABC) là trung điểm của AB . Mặt phẳng ( AA'C 'C) tạo với đáy một góc
bằng 45°. Tính thể tích V của khối lăng trụ ABC.A' B 'C '. 3 3 3 3 A. 3a V = . B. 3a V = . C. 3a V = . D. 3a V = . 16 8 4 2 Hướng dẫn giải:
Gọi H, M, I lần lượt là trung điểm A’ B’
của các đoạn thẳng AB, AC, AM. V = S . ∆ A H ABC A B C ABC . ' . ' ' ' 2 a 3 C’ S = . ABC ∆ 4
Ta có IH là đường trung bình của tam giác
AMB , MB là trung tuyến của tam giác đều H A B ABC. I IH // MB M a Do đó:  ⇒ IH ⊥ AC MB ⊥ AC C
AC ⊥ A' H
⇒ AC ⊥ ( A'HI ) ⇒ AC ⊥ A'I AC ⊥ IH
AC ⊥ IH ⊂ (ABC)
Mà: AC ⊥ A'I ⊂ (ACC ' A') ⇒ 
A'IH là góc gữa hai mặt phẳng ( AA'C 'C) và
(ABC)∩(ACC ' A') =  AC ( ABCD) ⇒  A'IH = 45°
Trong tam giác A' HI vuông tại H, ta có: A'H o tan 45° =
⇒ A' H = IH.tan 45 . HI 1 a 3 2 3 = IH = MB = . Vậy a 3 a 3 3 . a V = = 2 4 4 4 16 Trang 24/35
Câu 37. Cho hình chóp đều S.ABC , góc giữa mặt bên và mặt phẳng đáy ( ABC) bằng 0 60 , khoảng
cách giữa hai đường thẳng SA và BC a
bằng 3 . Thể tích của khối chóp S.ABC 2 7 theo a bằng 3 3 3 3 A. a 3 . B. a 3 . C. a 3 . D. a 3 . 12 18 16 24 Hướng dẫn giải:
Gọi M là trung điểm của BC .
Trong mp(SAM), Kẻ MH ⊥ ,( SA H ∈ ) SA . BC ⊥ AM Ta có: 
⇒ BC ⊥ (SAM ) ⇒ BC ⊥ MH . BC ⊥ SO
Do đó MH là đường vuông góc chung của SA và BC . Suy ra 3a MH =
. Ta có: SM ⊥ BC ⇒ ((SBC) ( ABC))  =  0 , SMA = 60 . 2 7
Đặt OM = x ⇒ AM = 3x,OA = 2x . 0
⇒ SO = OM.tan 60 = x 3 và S
SA = (x )2 +( x)2 3 2 = x 7 . Trong SAM ta có: . SA MH = . SO AM H 3 . ⇔ 7. a = 3.3 a x x x ⇔ x = 2 7 2 3 A C Khi O N đó: a a 3 AM = 3x = 3. = ⇒ AB = a . 2 3 2 B 2 2 1 1 a 3 a a 3 V = S = = ∆ SO S ABC . ABC. . . . 3 3 4 2 24
Câu 38. Cho hình chóp đều S.ABCD có đáy ABCD là hình thoi tâm O, AC = 2 3a , BD = 2a , hai
mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng ( ABCD) . Biết khoảng cách từ
điểm O đến mặt phẳng (SAB) bằng a 3 . Tính thể tích của khối chóp S.ABCD 4 theo a . 3 3 3 3 A. a 3 . B. a 3 . C. a 3 . D. a 3 . 16 18 3 12 Hướng dẫn giải
Ta có tam giác ABO vuông tại O và S AO = a 3 ,
BO = a . Do đó AO 0 = = ⇒  0 3 tan 60 ABO = 60 . I BO Suy ra A ∆ BD D A đều. Ta 2a 3 có: O C B Trang 25/35 (
SAC) ⊥ ( ABCD) ( 
SBD) ⊥ ( ABCD)
⇒ SO ⊥ ( ABCD (  SAC  )∩(SBD) = SO .
Trong tam giác đều ABD , gọi H là trung điểm AB, K là trung điểm BH,
suy ra DH ⊥ AB và DH = a 3 ; OK / /DH và 1 a 3 OK = DH = . 2 2
Suy ra OK ⊥ AB ⇒ AB ⊥ (SOK ) .
Gọi I là hình chiếu của O lên SK, ta
có:OI ⊥ SK; AB ⊥ OI ⇒ OI ⊥ (SAB) .⇒ OI = d  ; O (SAB)   .
Tam giác SOK vuông tại O, OI là đường cao: 1 1 1 a = + ⇒ SO = . 2 2 2 OI OK SO 2 3 1 1 1 1 a 3 V = S = = = ∆ SO S∆ SO OAOB SO S ABCD . ABCD. .4. ABO. .4. . . . . 3 3 3 2 3
Câu 39. Cho hình chóp tứ giác đều S.ABCD , O là giao điểm của AC và BD. Biết mặt bên của hình
chóp là tam giác đều và khoảng từ O đến mặt bên là a . Tính thể tích khối chóp S.ABCD theo a . A. 3 2a 3 . B. 3 4a 3 . C. 3 6a 3 . D. 3 8a 3 . Hướng dẫn giải:
Gọi M là trung điểm của CD , S trong S
∆ OM kẻ đường cao OH .
⇒ OH ⊥ (SCD) ⇒ OH = a .
Đặt CM = x . Khi đó OM = x , A SM = x 3 , H 2 2
SO = SM − x = x 2 . A a
Ta có: SM.OH = S . O OM D a 6
⇔ x 3.a = x 2.x ⇒ x = M 2 O x
⇒ CD = a 6, SO = a 3 B C 1 1 2 1 2 3 V = S SO = CD SO = a a = a . S ABCD . ABCD. . . .6 . 3 2 3 . 3 3 3
Câu 40. Cho hình chóp tứ giác S.ABCD có SA ⊥ ( ABCD) . ABCD là hình thang vuông tại A và B
biết AB = 2a . AD = 3BC = 3a . Tính thể tích khối chóp S.ABCD theo a biết góc giữa
(SCD)và ( ABCD) bằng 0 60 . A. 3 2 6a . B. 3 6 6a . C. 3 2 3a . D. 3 6 3a . Hướng dẫn giải: Trang 26/35
Dựng AM ⊥ CD tại M . S Ta có:  0 SMA = 60 . AD + BC 2 S = AB = a ABCD . 4 2
CD = ( AD − BC)2 2 + AB = 2a 2 A D 1 2 S = AB BC = a ABC . 2 M 2 S = S − S = a ACD ABCD ABC 3 B C 1 2SACD 3 2 S = AM CD ⇒ AM = = a ACD . 2 CD 2 Ta có: =  3 6 SA AM.tan SMA = a . 1 3 V = SA S = a . S ABCD . ABCD 2 6 2 . 3
Câu 41. Cho hình chóp tứ giác S.ABCD có SA ⊥ ( ABCD) , ABCD là hình thang vuông tại A và B
biết AB = 2a . AD = 3BC = 3a . Tính thể tích khối chóp S.ABCD theo a , biết khoảng cách từ
A đến mặt phẳng (SCD) bằng 3 6 a . 4 A. 3 6 6a . B. 3 2 6a . C. 3 2 3a . D. 3 6 3a . Hướng dẫn giải:
Dựng AM ⊥ CD tại M . S
Dựng AH ⊥ SM tại H . Ta có: 3 6 AH = a . 4 AD + BC 2 S = AB = a ABCD . 4 H 2 A D
CD = ( AD − BC)2 2 + AB = 2a 2 1 M 2 S = AB BC = a ABC . 2 B C 2 S = S − S = a ACD ABCD ABC 3 1 2SACD 3 2 S = AM CD ⇒ AM = = a ACD . 2 CD 2 Ta có: 1 1 1 AH.AM 3 6 = + ⇒ AS = = a 2 2 2 2 2 AH AM AS AM − AH 2 1 3 V = SA S = a S ABCD . ABCD 2 6 . 3
Câu 42. Cho lăng trụ tam giác ABC.A'B'C ' có BB' = a , góc giữa đường thẳng BB' và ( ABC) bằng
60°, tam giác ABC vuông tại C và góc 
BAC = 60° . Hình chiếu vuông góc của điểm B ' lên
( ABC) trùng với trọng tâm của A
∆ BC . Thể tích của khối tứ diện A'.ABC theo a bằng 3 3 3 3 A. 13a . B. 7a . C. 15a . D. 9a . 108 106 108 208 Hướng dẫn giải: Trang 27/35
Gọi M , N là trung điểm của AB, AC B' C'
và G là trọng tâm của A ∆ BC . A'
B 'G ⊥ ( ABC) ⇒ BB ( ABC)  ( )=  0 ', B 'BG = 60 . 1 1 V = S = ∆ B G AC BC B G A ABC . ABC. ' . . . ' '. 3 6 60° Xét B
∆ ' BG vuông tại G , có  0 B 'BG = 60 B C a 3 G ⇒ B 'G =
. (nửa tam giác đều) M N 2 60° A
Đặt AB = 2x . Trong A
∆ BC vuông tại C có  0 BAC = 60
⇒ tam giác ABC là nữa tam giác đều AB ⇒ AC = = x, BC = x 3 2
Do G là trọng tâm A ∆ BC 3 3a ⇒ BN = BG = . 2 4 Trong B
∆ NC vuông tại C : 2 2 2
BN = NC + BC  3a AC = 2 2 2 9a x 9a 3a  2 13 2 2 ⇔ = + 3x ⇔ x = ⇒ x = ⇒ 16 4 52  2 13  3a 3 BC =  2 13 3 Vậy,
1 3a 3a 3 a 3 9a V = = . A ABC . . . ' 6 2 13 2 13 2 208
Câu 43. Cho hình lăng trụ đứng ABC.A'B'C ', biết đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm O a
của tam giác ABC đến mặt phẳng ( A' BC) bằng .Tính thể tích khối lăng trụ 6
ABC.A'B 'C ' . 3 3 3 3 A. 3a 2 . B. 3a 2 . C. 3a 2 . D. 3a 2 . 8 28 4 16 Hướng dẫn giải:
Gọi M là trung điểm của BC , A' C'
ta có ( A' AM ) ⊥ ( A'BC) theo giao tuyến A'M .
Trong ( A' AM ) kẻ OH ⊥ A'M (H ∈ A'M ). B'
⇒ OH ⊥ ( A'BC) Suy ra: ( ,( ' )) a
d O A BC = OH = . 6 2 a 3 A C S = . H ABC ∆ 4 O
Xét hai tam giác vuông A' AM và OHM có M góc 
M chung nên chúng đồng dạng. B Trang 28/35 a 1 a 3 . Suy ra: OH OM 6 3 2 1 3 = ⇒ = ⇒ = . 2 2 2 A' A A'M A' A A' A + AM A' A   2 a 3 A' A +  2    a 6 2 3 ⇒ A' A = . Thể tích:
a 6 a 3 3a 2 V = S = = . ∆ A A ABC A B C ABC . ' . 4 . ' ' ' 4 4 16 VẬN DỤNG CAO
Câu 44. Cho hình chóp tam giác S.ABC có M là trung điểm của SB , N là điểm trên cạnh SC sao cho
NS = 2NC . Kí hiệu V ,V lần lượt là thể tích của các khối chóp .
A BMNC và S.AMN . Tính tỉ 1 2 số V1 . V2 A. V 2 V 1 V V 1 = B. 1 = C. 1 = 2. D. 1 = 3 V 3 V 2 V V 2 2 2 2 Hướng dẫn giải S V SM SN S AMN 1 2 1 . = ⋅ = ⋅ = ; V SB SC S ABC 2 3 3 . V +V = V . M N S.AMN . A BMNC S.ABC
Suy ra, V .ABMNC = 2 . V C S.AMN A B
Câu 45. Cho hình chóp tam giác S.ABC có M là trung điểm của SB , N là điểm trên cạnh SC sao cho
NS = 2NC , P là điểm trên cạnh SA sao cho PA = 2PS . Kí hiệu V ,V lần lượt là thể tích của 1 2
các khối tứ diện BMNP và SABC . Tính tỉ số V1 . V2 A. V 1 V 3 V 2 V 1 1 = . B. 1 = . C. 1 = . D. 1 = . V 9 V 4 V 3 V 3 2 2 2 2 Hướng dẫn giải Trang 29/35 1 S
⋅ d(N,(SAB))⋅ SBMP VN.BMP 3 = V 1 ; C.SAB
⋅ d(C,(SAB))⋅ S 3 SAB P
d(N,(SAB)) NS 2 = =
d(C,(SAB)) CS 3 , M N 1 1 1 S = S = ⋅ S BPM 2 BPS 2 3 SAB C V A N BMP 2 1 1 Suy ra, . = ⋅ = V . C SAB 3 6 9 . B
Câu 46. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a , góc giữa hai mặt phẳng (SAB) và
(ABCD) bằng 45°, M , N và P lần lượt là trung điểm các cạnh ,
SA SB và AB . Tính thể tích
V của khối tứ diện DMNP . 3 3 3 3 A. a V = B. a V = C. a V = D. a V = 6 4 12 2 Hướng dẫn giải Ta có: S SM SN SMN 1 = ⋅ = . S SA SB SAB 4 S Tương tự, S S BNP 1 AMP 1 = , = . S S SAB 4 SAB 4 M Suy ra SMNP 1 = (có thể khẳng định SSAB 4 N SMNP 1
= nhờ hai tam giác MNP và BAS A S D SAB 4 P 45°
là hai tam giác đồng dạng với tỉ số 1 k = ). O 2 B Do đó VD MNP 1 C . = (1) VD SAB 4 . 1 V = V = V . (2) D.SAB S.DAB S. 2 ABCD 3 1 1 4a 3 3 V = SO S = OP ° S = (3). Từ (1), (2) và (3): 1 1 4a a V = = . DMNP . . S ABCD . ABCD .tan 45 . . 3 3 ABCD 3 4 2 3 6
Câu 47. Cho lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông cân tại B , AC = 2a ; cạnh bên
AA′ = 2a . Hình chiếu vuông góc của A′ trên mặt phẳng (ABC) là trung điểm cạnh AC .
Tính thể tích V của khối lăng trụ ABC.A′B C ′ ′. 3 3 A. 1 3 V = a . B. a V = . C. 3 V = a . D. 2a V = . 2 3 3 Hướng dẫn giải Trang 30/35 A' B'
Vì ABC là tam giác vuông cân tại B nên trung
tuyến BH cũng là đường cao của nó, và C' 1
HB = HA = HC = AC = a . a 2 2 2 2 2 2
A′H = A′A − AH = 2a − a = a . B 1 A 3 V = ′ ⋅ = ′ ⋅ ⋅ = a ′ ′ ′ A H S A H BH AC a a ABC.A B C ABC 2 H a C
Câu 48. Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau. Gọi G ,G ,G và 1 2 3
G lần lượt là trọng tâm các mặt ABC, ABD, ACD và BCD . Biết AB = 6a, AC = 9a , 4
AD =12a . Tính theo a thể tích khối tứ diện G G G G . 1 2 3 4 A. 3 4a B. 3 a C. 3 108a D. 3 36a Hướng dẫn giải
Trong trường hợp tổng quát, ta chứng D minh được 1 V = V . 1 G 2 G 3 G 4 G 27 ABCD Thật vậy,
ta có (G G G )  (CB ) A và G 2 3 4 3 GG G ) C
 BA (tỉ số đồng dạng 2 3 4 G2 G4 A C 1 S
k = ) . Từ đó: 2G 3G 4G 2 1 = k = và 3 S G CBA 9 1 M
d(G ,(G G G )) = d(G ,(ABC)) 1 2 3 4 4 1 1
= d(D,(ABC)) (do G M = DM ) B 4 3 3 V d G G G G S Suy ra G G G G ( ,( )) G G G 1 1 1 1 2 3 4 1 2 3 4 2 3 4 = ⋅ = ⋅ = V d D ABC S ABCD ( ,( )) CBA 3 9 27 1 1 1 3 ⇒ V = V =
⋅ AB AC AD = a G G G G ABCD . . . 4 1 2 3 4 27 27 6
Câu 49. Cho tứ diện ABCD có AB = CD =11m , BC = AD = 20m, BD = AC = 21m . Tính thể tích khối tứ diện ABCD . A. 3 360m B. 3 720m C. 3 770m D. 3 340m Hướng dẫn giải Trang 31/35
Dựng tam giác MNP sao cho C,
B, D lần lượt là trung điểm các A cạnh MN, MP, NP.
Do BD là đường trung bình tam giác MNP nên 1 BD = MN hay z 2 x 11 1 21 AC = MN . 20 2 y
Tam giác AMN vuông tại A (do B
có trung tuyến bằng một nửa M P 21 20 cạnh tương ứng), hay 11 AM ⊥ AN . Tương tự, C D AP ⊥ AN và N AM ⊥ AP . Ta có 1 S = S , 1 S = S , 1 S = S .Suy ra 1 S = S . MBC 4 MNP NCD 4 MNP BPD 4 MNP BCD 4 MNP 2 2 2 x + y = 4.20  Từ đó, 1 V = V . Đặt AM = , AN = , AP x y z = . Ta có 2 2 2
y + z = 4.21 , ABCD 4 AMNP m m m  2 2 2 x + z = 4.11  2 x =160  suy ra 2 1 1 3
y = 1440 ⇒ xyz = 1440 ⇒ V = V = m ABCD AMNP 360 6 4  2 z = 324 
(AM, AN, AP đôi một vuông góc nên 1 V = AM AN AP ) AMNP . . 6 2 2 2 2 2 2 2 2 2 2 V =
(a + b − c )(a − b + c )(−a + b + c ) 12
Câu 50. Cho hình chóp tứ giác S.ABCD có đáy là vuông; mặt bên (SAB) là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng (SCD) bằng
3 7a . Tính thể tích V của khối chóp S.ABCD 7 . 3 A. 1 3 V = a . B. 3 V = a . C. 2 3 V = a . D. 3a V = . 3 3 2 Hướng dẫn giải
Gọi H là trung điểm AB, suy ra SH là
chiều cao khối chóp đã cho.
Kí hiệu x là độ dài cạnh đáy. Ta có 3 SH = x và 3 3 V = x . 2 S.ABCD 6
Kẻ HK ⊥ CD (K ∈CD) ;
Kẻ HL ⊥ SK (L∈ SK) .
Suy ra HL ⊥ (SCD) và Trang 32/35 d( ,
A (SCD)) = d(H,(SCD)) S HS ⋅ HK 21 = HL = = x 2 2 HS + HK 7 L A D H K X B C Theo gt, 21 3 7a x =
⇒ x = a 3 . Suy ra 3 3 3 3 3 3 V = x = a = a S ABCD ( 3) 7 7 . 6 6 2
Câu 51. Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA = 2SM ,
SN = 2NB , (α) là mặt phẳng qua MN và song song với SC . Kí hiệu (H )và (H ) là các 1 2
khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng (α) , trong đó, (H ) chứa 1
điểm S , (H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . Tính tỉ số V1 . 2 1 2 1 2 V2 A. 4 B. 5 C. 3 D. 4 5 4 4 3 Hướng dẫn giải
Kí hiệu V là thể tích khối tứ diện SABC .
Gọi P , Q lần lượt là giao điểm của (α) với các đường thẳng BC , AC .
Ta có NP//MQ//SC . Khi chia khối (H )bởi mặt phẳng (QNC) , ta được hai khối chóp 1
N.SMQC và N.QPC . V d N SAC S Ta có: N.SMQC ( ,( )) SMQC = ⋅ ; V d SAC S S B ASC (B,( )) . SAC
d(N,(SAC)) NS 2 = = ; d(B,(SAC)) BS 3 M 2 SAM S AMQ 4 SMQC 5 = = ⇒ = . SAS    S ASC 9 ASC 9 V N
Suy ra N.SMQC 2 5 10 = ⋅ = VB ASC 3 9 27 . C V d N C S A Q N.QPC ( ,(QP )) QPC = ⋅ P V d BC S B S ABC (S,(A )) . ABC NB CQ CP 1 1 2 2 = ⋅ ⋅ == ⋅ ⋅ = SB CA CB 3 3 3 27 V V V N SMQC N C 10 2 4 V 4 V 4 1 . .QP 1 = + = + = ⇒ = ⇒ 5V = 4V 1 ⇒ = 1 2 V V V V +V V 5 B ASC S ABC 27 27 9 9 . . 1 2 2
Câu 52. Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC ; các mặt phẳng (SAB) ,
(SAC) và (SBC) cùng tạo với mặt phẳng (ABC) các góc bằng nhau. Biết AB = 25, BC =17 ,
AC = 26 ; đường thẳng SB tạo với mặt đáy một góc bằng 45°. Tính thể tích V của khối chóp S.ABC . Trang 33/35 A.V = 408 . B.V = 680 . C.V = 578. D.V = 600 . Hướng dẫn giải
Gọi J là chân đường cao của hình chóp S
S.ABC; H, K và L lần lượt là hình chiếu của
J trên các cạnh AB, BC và CA . Suy ra,  SHJ ,  SLJ và 
SKJ lần lượt là góc tạo bởi
mặt phẳng (ABC) với các mặt phẳng
(S AB) , (SBC) và (SAC) . Theo giả thiết, ta có  =  = 
SHJ SLJ SKJ , suy ra các tam giác z=17 K y=9
vuông SJH, SJL và SJK bằng nhau. Từ đó, A C
JH = JL = JK . Mà J nằm trong tam giác z=17 J y=9
ABC nên J là tâm đường tròn nội tiếp tam H L giác ABC. x=8 x=8
Áp dụng công thức Hê-rông, ta tính được B
diện tích S của tam giác ABC là S = 204 .
Kí hiệu p là nửa chu vi tam giác ABC, r là z y K C
bán kính đường tròn nội tiếp của ABC. Ta có A S 204 r = = = 6 . Đặt p 34 y J
x = BH = BL , y = CL = CK , z
z = AH = AK . Lx + y =17 H x
Ta có hệ phương trình x + z = 25 . x y + z =  26 B Giải ra được ( ;
x y; z) = (8;9;17) 2 2 2 2
JB = JH + BH = 6 + 8 =10 . Ta có  = 
SBJ (SB,(ABC)) = 45° , suy ra SJB là tam giác vuông cân tại J. SJ = JB =10 .
Thể tích V của khối chóp S.ABC là 1 V = SJ.S = 680 3 ABC Trang 34/35
Document Outline

  • DS_C7_THE TICH KHOI CHOP
    • A. KIẾN THỨC CƠ BẢN
    • B. BÀI TẬP TRẮC NGHIỆM
    • C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM