Tóm tắt lý thuyết và bài tập trắc nghiệm phương trình bậc hai với hệ số thực trên tập số phức Toán 12

Tóm tắt lý thuyết và bài tập trắc nghiệm phương trình bậc hai với hệ số thực trên tập số phức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

20 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Trang 1/21
CHỦ ĐỀ 2. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC TRÊN TẬP SỐ PHỨC
A. KIẾN THỨC CƠ BẢN
1. Căn bậc hai của số phức: Cho số phức
w
. Mỗi số phức
z
thỏa mãn
2
zw=
được gọi là một căn
bậc hai của
w
.
• .
2. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai
(
)
2
0 ,, ; 0
ax bx c a b c a
+ += ∈ ≠
. Xét
2
4b ac∆= −
, ta có
•
0:∆=
phương trình có nghiệm thực
2
b
x
a
= −
.
•
: phương trình có hai nghiệm thực được xác định bởi công thức:
1,2
2
b
x
a
−± ∆
=
.
•
: phương trình có hai nghiệm phức được xác định bởi công thức:
1,2
||
2
bi
x
a
−± ∆
=
.
Chú ý.
Mọi phương trình bậc
n
:
1
11
... 0
nn
o nn
Az Az A z A
−
−
+ ++ + =
luôn có
n
nghiệm phức (không
nhất thiết phân biệt).
Hệ thức Vi–ét đối với phương trình bậc hai với hệ số thực: Cho phương trình bậc hai
( )
2
00ax bx c a+ += ≠
có hai nghiệm phân biệt
12
,xx
(thực hoặc phức). Ta có hệ thức Vi–ét
12
12
.
b
Sxx
a
c
P xx
a
=+=−
= =
B. KỸ NĂNG CƠ BẢN
1. Dạng 1: Tìm căn bậc hai của một số phức
• Trường hợp
w
là số thực: Nếu
a
là một số thực
+
0,a
<
a
có các căn bậc hai là
||ia±
.
+
0
a =
,
a
có đúng một căn bậc hai là 0.
+
0a >
,
a
có hai căn bậc hai là
a±
.
Ví dụ 1: Ta có hai căn bậc hai của – 1 là
i
và
i−
. Hai căn bậc hai của
2
a−
(
a
là số thực khác 0) là
ai
và
ai−
.
• Trường hợp
( )
, ,0w a bi a b b=+ ∈≠
Gọi
( )
,z x yi x y=+∈
là một căn bậc hai của
w
khi và chỉ khi
2
zw=
, tức là
( )
22
2
22
2
2
xya
x yi a bi x y xyi a bi
xy b
−=
+ =+⇔−+ =+⇔
=
Mỗi cặp số thực
( )
;xy
nghiệm đúng hệ phương trình trên cho ta một căn bậc hai
x yi+
của số
phức
w a bi= +
.
Ví dụ 2: Tìm các căn bậc hai của
5 12wi
=−+
.
Gọi
( )
,z x yi x y=+∈
là một căn bậc hai của số phức
5 12wi=−+
.
Ta có
( )
2
22
2
2
2
4
3
5
5 12
6
2 12
2
3
x
x
y
xy
z w x yi i
xy
x
y
x
y
=
=
=
−=−

= ⇔ + =−+ ⇔ ⇔ ⇔

=
= −
=
= −
Vậy
5 12wi=−+
có hai căn bậc hai là
và
23i−−
.
2. Dạng 2: Giải phương trình bậc hai với hệ số thực và các dạng toán liên quan
Trang 2/21
• Giải các phương trình bậc hai với hệ số thực
Ví dụ 3: Giải phương trình bậc hai sau:
2
10zz−+=
Ta có
2
4 30b ac∆= − =− <
Phương trình có hai nghiệm phức phân biệt là
1,2
13
2
i
x
±
=
.
• Giải phương trình quy về phương trình bậc hai với hệ số thực
Phương pháp 1: Phân tích đa thức thành nhân tử:
– Bước 1: Nhẩm 1 nghiệm đặc biệt của phương trình.
+ Tổng các hệ số trong phương trình là 0 thì phương trình có một nghiệm
1x =
.
+ Tổng các hệ số biến bậc chẵn bằng tổng các hệ số biến bậc lẻ thì phương trình có một nghiệm
1x = −
.
+ Định lý Bơdu:
Phần dư trong phép chia đa thức
(
)
fx
cho
xa−
bằng giá trị của đa thức
tại
.xa
=
Tức là
( ) ( )
( )
( )
f x x agx f a
=−−
Hệ quả: Nếu
(
)
0
fa=
thì
( )
( )
fx xa
−
Nếu
( ) ( )
fx xa−
thì
(
)
0
fa
=
hay
(
)
0
fx
=
có một nghiệm
.xa=
– Bước 2: Đưa phương trình về phương trình bậc nhất hoặc bậc hai bằng cách hân tích đa thức ở
vế trái của phương trình thành nhân tử (dùng hẳng đảng thức, chia đa thức hoặc sử dụng lược đồ
Hoocne) như sau:
Với đa thức
( )
1
1 10
...
nn
nn
f x ax a x ax a
−
−
= + ++ +
chia cho
xa−
có thương là
( )
12
1 2 10
...
nn
nn
g x b x b x bx b
−−
−−
= + ++ +
dư
r
n
a
1n
a
−
2n
a
−
2
a
1
a
0
a
a
1nn
ba
−
=
2 12n nn
b ab a
− −−
= +
3 23n nn
b ab a
− −−
= +
1 22
baba= +
0 11
b ab a= +
00
r ab b= +
– Bước 3: Giải phương trình bậc nhất hoặc bậc hai, kết luận nghiệm
Phương pháp 2: Đặt ẩn phụ:
– Bước 1: Phân tích phương trình thành các đại lượng có dạng giống nhau.
– Bước 2: Đặt ẩn phụ, nêu điều kiện của ẩn phụ (nếu có).
– Bước 3: Đưa phương trình ban đầu về phương trình bậc nhất, bậc hai với ẩn mới.
– Bước 4: Giải phương trình, kết luận nghiệm.
C. KỸ NĂNG SỬ DỤNG MÁY TÍNH
1. Chọn chế độ tính toán với số phức: MODE 2 màn hình hiện CMPLX.
Nhập số thuần ảo
i
: Phím ENG
2. Tìm các căn bậc hai của một số phức
Ví dụ 5: Khai căn bậc hai số phức
34zi=−−
có kết quả:
Cách 1:
– Mode 2 (CMPLX)
– Nhập hàm
2
X
– Sử dụng phím CALC, nhập từng giá trị vào, giá trị nào ra kết quả bằng
z
thì ta nhận.
Cách 2:
– Mode 1 (COMP)
– Nhấn Shift + (Pol), ta nhập
( )
3; 4Pol
−
– Nhấn Shift – (Rec), ta nhập
(
)
Re , : 2c XY
, ta thu được kết quả
1; 2XY= =
.
– Vậy 2 số phức cần tìm là
12i+
và
12i−−
.
Trang 3/21
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong
, phương trình
2
2 10++=xx
có nghiệm là:
A.
( )
( )
12
11
1 7; 1 7
44
x ix i= −− = −+
B.
( ) ( )
12
11
1 7; 1 7
44
x ix i=+=−
C.
( ) ( )
12
11
1 7; 1 7
44
x ix i= −+ = −
D.
( )
(
)
12
11
1 7; 1 7
44
x ix i
= + = −−
Câu 2. Khai căn bậc hai số phức
34=−+zi
có kết quả:
A.
12
1 2; 1 2z iz i
=+ =−−
B.
12
1 2; 1 2z iz i=+=−
C.
12
12; 12
z iz i
=+ =−+
D.
12
1 2; 1 2z iz i=−+ =−−
.
Câu 3. Trong
, nghiệm của phương trình
3
80−=
z
là:
A.
12 3
2; 1 3 ; 1 3z z iz i==+=−
B.
12 3
2; 1 3 ; 1 3z z iz i= =−+ =−−
C.
12 3
2; 1 3 ; 1 3z z iz i
=− =−+ =−−
D.
12 3
2; 1 3 ; 1 3z z iz i=−=+ =−
Câu 4. Trong
, phương trình
24+=+zz i
có nghiệm là:
A.
34=−+zi
B.
24=−+zi
C.
44=−+zi
D.
54=−+zi
Câu 5. Hai giá trị
12
;=+=−x a bi x a bi
là hai nghiệm của phương trình:
A.
2 22
20+ ++=x ax a b
B.
2 22
20+ +−=x ax a b
C.
2 22
20− ++=x ax a b
D.
2 22
20− +−=x ax a b
Câu 6. Trong
, phương trình z
2
+ 3iz + 4 = 0 có nghiệm là:
A.
3
4
=
=
zi
zi
B.
4
=
= −
zi
zi
C.
1
3
= +
= −
zi
zi
D.
23
1
= −
= +
zi
zi
Câu 7. Trong
, phương trình
2
10
zz−+=
có nghiệm là:
A.
35
35
= +
= −
zi
zi
B.
23
2
23
2
+
=
−
=
i
z
i
z
C.
15
2
15
2
+
=
−
=
i
z
i
z
D.
13
2
13
2
+
=
−
=
i
z
i
z
Câu 8. Tính căn bậc hai của số phức
86= +zi
ra kết quả:
A.
3
3
zi
zi
= −
= +
B.
3
3
zi
zi
= +
=−−
C.
3
3
zi
zi
=−+
= −
D.
3
3
zi
zi
= −
=−−
Câu 9. Trong
, nghiệm của phương trình
2
50+=z
là:
A.
5
5
z
z
=
= −
B.
4
4
5
5
zi
zi
=
= −
C.
5i
D.
5− i
Câu 10. Trong
, nghiệm của phương trình
2
5 12
zi=−+
là:
A.
23
23
zi
zi
= +
=−−
B.
23= +zi
C.
23= −zi
D.
23
23
zi
zi
= −
=−+
Câu 11. Trong
, nghiệm của phương trình
2
4 50+ +=
zz
là:
A.
2= −zi
B.
2=−−zi
C.
2
2
zi
zi
=−−
=−+
D.
2
=−+zi
Câu 12. Trong
, nghiệm của phương trình
2
2120− +− =zz i
là
A.
1
2
2= −
= −
zi
zi
B.
1
2
2= −
= −
zi
zi
C.
1
2
2
2
= +
= −
zi
zi
D.
1
2
2= +
= −
zi
zi
Câu 13. Cho
34= +zi
. Tìm căn bậc hai của
z
.
A.
2−+i
và
2 −i
B.
2 + i
và
2 −
i
Trang 4/21
C.
2 + i
và
2−−i
D.
32+ i
và
32−−i
Câu 14. Cho
1= −zi
. Tìm căn bậc hai dạng lượng giác của
z
:
A.
4
2 cos sin
88
−−

+


ππ
i
và
4
77
2 cos sin
88
i
ππ

+


B.
2 cos sin
44

+


ππ
i
C.
2 cos sin
44
−−

+


ππ
i
D.
4
2 cos sin
88

+


ππ
i
và
4
2 cos sin
88
−−

+


ππ
i
Câu 15. Trong
, phương trình
(
)(
)
22
2 10+ − −=
z i z iz
có nghiệm là:
C.
( )
3
12
2
− i
;
( )
3
2
2
−+i
; 4i B.
1 i−
;
1 i−+
;
2i
A.
( )
21
2
−i
,
(
)
2
1
2
−+
i
, i D.
12i−
;
15i−
;
3i
Câu 16. Trong
, phương trình
42
6 25 0− +=zz
có nghiệm là:
A.
8; 5±±i
B.
3; 4±±i
C.
5; 2±±i
D.
( ) ( )
2 ;2ii±+±−
Câu 17. Trong
, phương trình
1
2+=zi
z
có nghiệm là:
A.
( )
13± i
B.
( )
52± i
C.
( )
12±
i
D.
(
)
25
± i
Câu 18. Trong
, phương trình
3
10+=z
có nghiệm là:
A.
1−
;
23
2
± i
B.
1−
;
13
2
± i
C.
1−
;
15
4
± i
D.
1−
;
53
4
±
i
Câu 19. Trong
, phương trình
4
10−=z
có nghiệm là:
A
1; 2±±i
B.
2; 2±±i
C.
3; 4±±
i
D.
1;±±i
Câu 20. Trong
, căn bậc hai của
121−
là:
A.
11i−
B.
11
i
C.
11−
D.
11
i
và
11i−
Câu 21. Phương trình
2
8 4 10zz− +=
có nghiệm là:
A
12
11 51
;
44 44
z iz i=+=−
B.
12
11 13
;
44 44
z iz i=+=−
C.
12
11 11
;
44 44
z iz i=+=−
D.
12
21 11
;
44 44
z iz i
=+=−
Câu 22. Biết
12
;zz
là hai nghiệm của phương trình
2
2 3 30zz+ +=
. Khi đó giá trị của
22
12
zz+
là:
A.
9
4
B.
9
C.
4
D.
9
4
−
Câu 23. Phương trình
2
0z az b+ +=
có một nghiệm phức là
12zi= +
. Tổng 2 số
a
và
b
bằng:
A.
0
B.
3−
C. 3 D.
4−
Câu 24. Gọi
12
;zz
là hai nghiệm phức của phương trình
2
4 50zz− +=
. Khi đó phần thực của
22
12
zz+
là:
A. 5 B. 6 C. 4 D. 7
Câu 25. Gọi
12
;zz
là hai nghiệm phức của phương trình
2
2 40zz
+ +=
. Khi đó
22
12
|| ||Az z= +
có giá
trị là
A.
7−
B. – 8 C.
4−
D. 8
Câu 26. Phương trình
3
8z =
có bao nhiêu nghiệm phức với phần ảo âm?
Trang 5/21
A. 1 B. 2 C. 3 D. 0
Câu 27. Biết
12
,
zz
là hai nghiệm của phương trình
2
2 3 30zz+ +=
. Khi đó giá trị của
22
12
zz
+
là:
A. 4 B.
9
4
C. 9 D.
9
4
−
Câu 28. Phương trình sau có mấy nghiệm thực:
2
2 20zz+ +=
A. 0 B. 1 C. 2 D. Vô số nghiệm.
Câu 29. Tìm các căn bậc hai của
9
−
.
A.
3i
±
B. 3 C.
3i
D.
3−
Câu 30. Trong
, phương trình
4
40
+=
z
có nghiệm là:
A.
( ) ( )
14; 14±− ±+ii
B.
(
)
12
±−
i
;
( )
12±+i
C.
( ) ( )
13; 13±− ±+ii
D. ±
( )
1− i
;
( )
1±+i
Câu 31. Giải phương trình
2
2 70
zz− +=
trên tập số phức ta được nghiệm là:
A.
1 22zi= ±
B.
16zi= ±
C.
12zi= ±
D.
17zi= ±
Câu 32. Căn bậc hai của số phức
4 65i+
là:
A.
(
)
35i−+
B.
( )
35i+
C.
(
)
35
i
±+
D. 2
Câu 33. Gọi z là căn bậc hai có phần ảo âm của
33 56
i−
. Phần thực của z là:
A. 6 B. 7 C. 4 D. –4
Câu 34. Tập nghiệm trong
của phương trình
32
10zzz+ ++=
là:
A.
{
}
;i;1; 1i
−−
B.
{ }
; ;1ii−
C.
{ }
;1i−−
D.
{ }
;; 1ii−−
Câu 35. Trên tập số phức, phương trình bậc hai có hai nghiệm
4 3; 2= + =−+
αβ
ii
là:
A.
( ) ( )
2
2 4 11 2 0
++ − + =
z iz i
B.
(
) ( )
2
2 4 11 2 0−+ − + =z iz i
C.
( ) ( )
2
2 4 11 2 0−+ + + =
z iz i
D.
( ) ( )
2
2 4 11 2 0++ + + =z iz i
Câu 36. Có bao nhiêu số phức thỏa mãn điều kiện
22
||zzz= +
?
A. 3 B. 0 C. 1 D. 2
Câu 37. Phương trình
( )
( )
2
2 0,i z az b a b
+ + += ∈
có hai nghiệm là
3
i+
và
12i
−
. Khi đó
?a =
A.
92i−−
B.
15 5i
+
C.
92i+
D.
15 5i−
Câu 38. Cho số phức z thỏa mãn
2
6 13 0zz−+=
. Tính
6
z
zi
+
+
A.
17
và 4 B.
17
và 5 C.
17
và 3 D.
17
và 2
Câu 39. Gọi
12
,zz
là các nghiệm phức của phương trình
( ) ( )
2
1 3 21 0z iz i+− − +=
. Khi đó
22
1 2 12
3w z z zz=+−
là số phức có môđun là:
A. 2 B.
13
C.
2 13
D.
20
Câu 40. Số nghiệm của phương trình với ẩn số phức z:
22
4 8|z| 3 0z + −=
là:
A. 3 B. 2 C. 4 D. 1
Câu 41. Tìm số phức z để
2
zz z−=
.
A
0; 1zz i= = −
B.
0; 1zz i= = +
C.
0;1;1z z iz i= =+=−
D.
1; 1z iz i
=+=−
Câu 42. Với mọi số ảo z, số
22
|z|z +
là:
A. Số thực âm B. Số 0 C. Số thực dương D. Số ảo khác 0
Câu 43. Trong trường số phức phương trình
3
10z +=
có mấy nghiệm?
A. 2 B. 3 C. 1 D. 0
Câu 44. Giá trị của các số thực b, c để phương trình
2
0z bz c+ +=
nhận số phức
1zi= +
làm một
nghiệm là:
Trang 6/21
A.
2
2
b
c
=
= −
B.
2
2
b
c
= −
= −
C.
2
2
b
c
= −
=
D.
2
2
b
c
=
=
Câu 45. Trên tập hợp số phức, phương trình
2
7 15 0zz++=
có hai nghiệm
12
,zz
. Giá trị biểu thức
1 2 12
z z zz++
là:
A. –7 B. 8 C. 15 D. 22
Câu 46. Tìm số nguyên x, y sao cho số phức
z x yi= +
thỏa mãn
3
18 26
zi= +
A.
3
1
x
y
=
= ±
B.
3
1
x
y
=
= −
C.
3
1
x
y
=
=
D.
3
1
x
y
= −
= ±
Câu 47. Trên tập số phức, cho phương trình sau:
( )
4
2
40
zi z++ =
. Có bao nhiêu nhận xét đúng trong
số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực
.
2. Phương trình vô nghiệm trên trường số phức
.
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0 B. 1 C. 3 D. 2
Câu 48. Phương trình
63
9 80zz
− +=
có bao nhiêu nghiệm trên tập số phức?
A. 3 B. 4 C. 2 D. 6
Câu 49. Giả sử
12
,zz
là hai nghiệm của phương trình
2
2 50zz− +=
và A, B là các điểm biểu diễn của
12
,zz
. Tọa độ trung điểm I của đoạn thẳng AB là:
A.
( )
1;1I
B.
( )
1; 0
I
−
C.
( )
0;1I
D.
( )
1; 0I
Câu 50. Cho phương trình
2
60z mz i+ −=
. Để phương trình có tổng bình phương hai nghiệm bằng 5
thì m có dạng
( )( )
,m a bi a b=±+ ∈
. Giá trị
2ab+
là:
A. 0 B. 1 C.
2
−
D.
1−
Câu 51. Gọi
1224
,,,zzzz
là các nghiệm phức của phương trình
4
1
1
2
z
zi
−

=

−

. Giá trị của
( )
( )(
)( )
2222
1 234
1111Pzzzz=++++
là:
A.
17
8
B.
17
9
C.
9
17
D.
17
9
i
Câu 52. Trong tập số phức, giá trị của m để phương trình bậc hai
2
0z mz i+ +=
có tổng bình phương
hai nghiệm bằng
4i−
là:
A.
(
)
1 i
±−
B.
( )
1 i−
C.
( )
1 i±+
D.
1 i
−−
Câu 53. Cho phương trình
2
2 10z mz m− + −=
trong đó m là tham số phức. Giá trị của m để phương
trình có hai nghiệm
12
,zz
thỏa mãn
22
12
10zz+=−
là:
A.
2 22mi= ±
B.
2 22mi= +
C.
2 22mi= −
D.
2 22
mi=−−
Câu 54. Gọi
12
,zz
là hai nghiệm của phương trình
2
2 80zz+ +=
, trong đó
1
z
có phần ảo dương. Giá
trị của số phức
( )
1 21
2w z zz= +
là:
A.
12 6
i+
B. 10 C. 8 D.
12 6
i−
Câu 55. Tổng bình phương các nghiệm của phương trình
4
10z −=
trên tập số phức là bao nhiêu?
A. 3 B. 1 C. 2 D. 0
Câu 56. Gọi
12
,zz
là hai nghiệm của phương trình
2
2 60zz− +=
. Trong đó
1
z
có phần ảo âm. Giá trị
biểu thức
1 12
| | |3 |Mz zz=+−
là:
Trang 7/21
A.
6 2 21−
B.
6 2 21+
C.
6 4 21+
D.
6 4 21−
Câu 57. Phương trình
42
2 24 72 0xx x+ − +=
trên tập số phức có các nghiệm là:
A.
22
i±
hoặc
222
i−±
B.
22
i±
hoặc
12 2i±
C.
12 2i±
hoặc
222i
−±
D.
12 2i
−±
hoặc
222i−±
Câu 58. Gọi
12
,zz
là các nghiệm phức của phương trình
2
3 70zz
+ +=
. Khi đó
44
12
Az z= +
có giá trị
là:
A. 23 B.
23
C. 13 D.
13
Trang 8/21
E. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN 1.2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
A
B
A
C
B
D
B
B
A
C
D
C
A
C
D
C
B
D
D
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
C
D
C
B
D
A
D
A
A
D
B
C
B
D
B
A
A
B
C
C
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
C
B
B
C
B
C
D
D
D
D
B
A
A
C
D
B
A
A
II –HƯỚNG DẪN GIẢI
Câu 1. Trong
, phương trình
2
2 10++=xx
có nghiệm là:
A.
( ) ( )
12
11
1 7; 1 7
44
x ix i= −− = −+
B.
(
)
( )
12
11
1 7; 1 7
44
x ix i=+=−
C.
( )
( )
12
11
1 7; 1 7
44
x ix i= −+ = −
D.
( )
(
)
12
11
1 7; 1 7
44
x ix i= + = −−
Hướng dẫn giải:
Ta có:
22 2
4 1 4.2.1 7 7 0b ac i
∆= − = − =− = <
nên phương trình có hai nghiệm phức là:
1,2
17
4
i
x
−±
==
Vậy ta chọn đáp án A.
Câu 2. Khai căn bậc hai số phức
34=−+zi
có kết quả:
A.
12
1 2; 1 2z iz i=+ =−−
B.
12
1 2; 1 2z iz i=+=−
C.
12
12; 12z iz i=+ =−+
D.
12
1 2; 1 2z iz i=−+ =−−
.
Hướng dẫn giải:
Giả sử
( )
,w x yi x y=+∈
là một căn bậc hai của số phức
34=−+zi
.
Ta có:
(
)
2
22
2
2
1
1
2
3
34
2
24
1
2
x
x
y
xy
w z x yi i
xy
x
y
x
y
=
=
=
−=−

= ⇔ + =−+ ⇔ ⇔ ⇔

=
= −
=
= −
Do đó z có hai căn bậc hai là:
1
2
12
12
zi
zi
= +
=−−
Ta chọn đáp án A.
Câu 3. Trong
, nghiệm của phương trình
3
80−=z
là:
A.
12 3
2; 1 3 ; 1 3z z iz i==+=−
B.
12 3
2; 1 3 ; 1 3
z z iz i= =−+ =−−
C.
12 3
2; 1 3 ; 1 3z z iz i=− =−+ =−−
D.
12 3
2; 1 3 ; 1 3z z iz i=−=+ =−
Hướng dẫn giải:
Sử dụng hằng đẳng thức số 7, ta có:
( )
( )
( )
32
2
2
2
2
80 2 2 4 0
2 40
13
22
13 13
1 3 13
z
z
z z zz
zz
z
zz
z iz i
z iz i
=
=
−=⇔ − + + =⇔ ⇔
+ +=
+=−
= =


⇔ += ⇔ =−+


+=− =−−

Trang 9/21
Ta chọn đáp án A.
Câu 4. Trong
, phương trình
24+=+zz i
có nghiệm là:
A.
34=−+zi
B.
24=−+zi
C.
44=−+zi
D.
54=−+zi
Hướng dẫn giải:
Đặt
( )
22
,z a bi a b z a b=+ ∈ ⇒= +
.
Thay vào phương trình:
22
24+ ++ =+a b a bi i
Suy ra
22
3
2
4
4
= −
+ +=
⇔

=
=
a
aba
b
b
Ta chọn đáp án A.
Câu 5. Hai giá trị
12
;=+=−x a bi x a bi
là hai nghiệm của phương trình:
A.
2 22
20+ ++=x ax a b
B.
2 22
20+ +−=x ax a b
C.
2 22
20− ++=x ax a b
D.
2 22
20− +−=x ax a b
Hướng dẫn giải:
Áp dụng định lý đảo Viet :
12
22
12
2
.
=+=
= = +
Sxx a
P xx a b
.
Do đó
12
,xx
là hai nghiệm của phương trình:
2 2 22
02 0x Sx P x ax a b− +=⇔ − + + =
Ta chọn đáp án A.
Câu 6. Trong
, phương trình z
2
+ 3iz + 4 = 0 có nghiệm là:
A.
3
4
=
=
zi
zi
B.
4
=
= −
zi
zi
C.
1
3
= +
= −
zi
zi
D.
23
1
= −
= +
zi
zi
Hướng dẫn giải:
( )
2
2
4 3 4.1.4 25 0b ac i∆= − = − =− <
Nên phương trình có hai nghiệm phức là:
1
2
35
2
35
4
2
ii
zi
ii
zi
−+
= =
−−
= = −
Ta chọn đáp án A.
Câu 7. Trong
, phương trình
2
10
zz−+=
có nghiệm là:
A.
35
35
= +
= −
zi
zi
B.
23
2
23
2
+
=
−
=
i
z
i
z
C.
15
2
15
2
+
=
−
=
i
z
i
z
D.
13
2
13
2
+
=
−
=
i
z
i
z
Hướng dẫn giải:
( )
2
2
4 1 4.1.1 3 0b ac∆= − = − − =− <
Nên phương trình có hai nghiệm phức là:
1
2
13
2
13
2
i
x
i
x
+
=
−
=
Ta chọn đáp án A.
Câu 8. Tính căn bậc hai của số phức
86= +zi
ra kết quả:
Trang 10/21
A.
3
3
zi
zi
= −
= +
B.
3
3
zi
zi
= +
=−−
C.
3
3
zi
zi
=−+
= −
D.
3
3
zi
zi
= −
=−−
Hướng dẫn giải:
Giả sử
( )
,w x yi x y=+∈
là một căn bậc hai của số phức
86= +zi
.
Ta có:
( )
2
22
2
2
3
9
1
8
86
3
26
3
1
x
x
y
xy
w z x yi i
xy
x
y
x
y
=
=
=
−=

=⇔+ =+⇔ ⇔ ⇔

=
= −
=
= −
Do đó z có hai căn bậc hai là
1
2
3
3
zi
zi
= +
=−−
Ta chọn đáp án A.
Câu 9. Trong
, nghiệm của phương trình
2
50
+=z
là:
A.
5
5
z
z
=
= −
B.
4
4
5
5
zi
zi
=
= −
C.
5i
D.
5−
i
Hướng dẫn giải:
22
4
50 5 5z z zi+ =⇔ =− ⇔=±
Ta chọn đáp án A.
Câu 10. Trong
, nghiệm của phương trình
2
5 12zi=−+
là:
A.
23
23
zi
zi
= +
=−−
B.
23= +
zi
C.
23
= −zi
D.
23
23
zi
zi
= −
=−+
Hướng dẫn giải:
Giả sử
( )
,z x yi x y=+∈
là một nghiệm của phương trình.
( )
2
2 22
2
22
5 12 5 12 2 5 12
2
4
3
5
6
2 12
2
3
z i x yi i x y xy i
x
x
y
xy
xy
x
y
x
y
=−+ ⇔ + =−+ ⇔ − + =−+
=
=
=
−=−

⇔ ⇔⇔

=
= −
=

= −
Do đó phương trình có hai nghiệm là
23
23
zi
zi
= +
=−−
Ta chọn đáp án A.
Câu 11. Trong
, nghiệm của phương trình
2
4 50+ +=zz
là:
A.
2
= −zi
B.
2
=−−zi
C.
2
2
zi
zi
=−−
=−+
D.
2=−+zi
Hướng dẫn giải:
( )
2
2
4 50 2 1 2 2z z z z iz i+ + = ⇔ + =−⇔ + =±⇔ =−±
Ta chọn đáp án A.
Câu 12. Trong
, nghiệm của phương trình
2
2120− +− =zz i
là
A.
1
2
2= −
= −
zi
zi
B.
1
2
2= −
= −
zi
zi
C.
1
2
2
2
= +
= −
zi
zi
D.
1
2
2= +
= −
zi
zi
Hướng dẫn giải:
Trang 11/21
( )
(
)
2
2
11 2
2120 1 2 1 1
11
z ii
z z i z iz i
z ii
=++= +
− +− = ⇔ − = ⇔ −=± + ⇔
=−−=−
Ta chọn đáp án A.
Câu 13. Cho
34= +zi
. Tìm căn bậc hai của
z
.
A.
2
−+i
và
2 −i
B.
2 + i
và
2 −
i
C.
2 + i
và
2−−i
D.
32+ i
và
32−−
i
Hướng dẫn giải:
Giả sử
(
)
,
w x yi x y
=+∈
là một căn bậc hai của số phức
34= +zi
.
Ta có:
( )
2
22
2
2
2
4
1
3
34
2
24
2
1
x
x
y
xy
w z x yi i
xy
x
y
x
y
=
=
=
−=

=⇔+ =+⇔ ⇔ ⇔

=
= −
=
= −
Do đó z có hai căn bậc hai là
2
2
zi
zi
= +
=−−
Ta chọn đáp án A.
Câu 14. Cho
1= −zi
. Tìm căn bậc hai dạng lượng giác của
z
:
A.
4
2 cos sin
88
−−

+


ππ
i
và
4
77
2 cos sin
88
i
ππ

+


B.
2 cos sin
44

+


ππ
i
C.
2 cos sin
44
−−

+


ππ
i
D.
4
2 cos sin
88

+


ππ
i
và
4
2 cos sin
88
−−

+


ππ
i
Hướng dẫn giải:
Ta có
1 2 cos sin
44
zi i
ππ

 
=−= − + −
 

 

có các căn bậc hai là:
44
12
77
2 cos sin ; 2 cos sin
88 88
w iw i
ππ ππ
−−

=+=+


Ta chọn đáp án A.
Câu 15. Trong
, phương trình
( )( )
22
2 10+ − −=z i z iz
có nghiệm là:
C.
( )
3
12
2
− i
;
( )
3
2
2
−+i
; 4i B.
1 i
−
;
1 i−+
;
2
i
A.
( )
21
2
−i
,
( )
2
1
2
−+i
, i D.
12i−
;
15i−
;
3i
Hướng dẫn giải:
( )( )
( )
( )
2
22
2
1
2 10
2
0
i
zi
z
z i z iz
zi
zi
±−
= −
=
+ − −=⇔ ⇔
−=
=
Ta chọn đáp án A.
Câu 16. Trong
, phương trình
42
6 25 0− +=zz
có nghiệm là:
A.
8; 5±±i
B.
3; 4±±i
C.
5; 2±±i
D.
( ) (
)
2 ;2ii±+±−
Hướng dẫn giải:
Trang 12/21
( )
( )
( )
2
42 2 2 2
2
6 25 0 3 16 0 3 4 3 4
2
zi
z z z z iz i
zi
=±+
− + =⇔ − + =⇔ −=± ⇔ =± ⇔
=±−
Ta chọn đáp án A.
Câu 17. Trong
, phương trình
1
2+=zi
z
có nghiệm là:
A.
( )
13± i
B.
( )
52± i
C.
( )
12± i
D.
(
)
25
±
i
Hướng dẫn giải:
( )
( )
( )
2
2
0
0
0
0
1
2 12
21
2 10
20
2
z
z
z
z
zi z i
zi
z
z iz
zi
zi i
≠
≠
≠
≠

+= ⇔ ⇔ ⇔ ⇔ ⇔=±

=±+
− +=
− +=
−=±
Ta chọn đáp án A.
Câu 18. Trong
, phương trình
3
10+=z
có nghiệm là:
A.
1−
;
23
2
± i
B.
1−
;
13
2
± i
C.
1−
;
15
4
± i
D.
1−
;
53
4
± i
Hướng dẫn giải:
( )
( )
32
2
1
1
10 1 1 0
13
10
2
z
z
z z zz
zz
z
= −
= −
+= ⇔ + −+ = ⇔ ⇔
±
−+=
=
Ta chọn đáp án A
Câu 19. Trong
, phương trình
4
10−=z
có nghiệm là:
A
1; 2±±i
B.
2; 2±±
i
C.
3; 4±±i
D.
1;±±i
Hướng dẫn giải:
(
)(
)
( )
42
2
11
10 1 1 1 0 1 1
10
zz
z zzz z z
zi
z
= =
−=⇔− + +=⇔=− ⇔=−
= ±
+=
Ta chọn đáp án A.
Câu 20. Trong
, căn bậc hai của
121
−
là:
A.
11i−
B.
11i
C.
11−
D.
11i
và
11i−
Hướng dẫn giải:
Ta có:
( )
2
121 11z zi=− ⇔=
. Do đó z có hai căn bậc hai là
11 ; 11z iz i= = −
Ta chọn đáp án A.
Câu 21. Phương trình
2
8 4 10zz− +=
có nghiệm là:
A
12
11 51
;
44 44
z iz i
=+=−
B.
12
11 13
;
44 44
z iz i=+=−
C.
12
11 11
;
44 44
z iz i=+=−
D.
12
21 11
;
44 44
z iz i=+=−
Hướng dẫn giải:
2
1,2
22 1
' ' 48 4 0
8 44
ii
b ac z
±
∆= − = − =− < ⇒ = = ±
Ta chọn đáp án A.
Câu 22. Biết
12
;zz
là hai nghiệm của phương trình
2
2 3 30zz+ +=
. Khi đó giá trị của
22
12
zz+
là:
A.
9
4
B.
9
C.
4
D.
9
4
−
Hướng dẫn giải:
Trang 13/21
Theo Viet, ta có:
12
12
3
2
3
.
2
b
Szz
a
c
P zz
a
=+ =−=−
= = =
22 2
12
39
23
44
zzS P+ = − = −=−
Ta chọn đáp án A.
Câu 23. Phương trình
2
0z az b+ +=
có một nghiệm phức là
12zi= +
. Tổng 2 số
a
và
b
bằng:
A.
0
B.
3
−
C. 3 D.
4−
Hướng dẫn giải:
Vì
12zi= +
là một nghiệm của phương trình
2
0z az b+ +=
nên ta có:
( ) ( )
2
12 12 0 2 34 3i a i b ab ai i ab+ + + +=⇔++ =− ⇔+=
Ta chọn đáp án A.
Câu 24. Gọi
12
;zz
là hai nghiệm phức của phương trình
2
4 50zz− +=
. Khi đó phần thực của
22
12
zz+
là:
A. 5 B. 6 C. 4 D. 7
Hướng dẫn giải:
Theo Viet, ta có:
12
12
4
.5
b
Szz
a
c
P zz
a
=+ =−=
= = =
22 2
12
2 16 2.5 6zzS P
+=− =− =
Ta chọn đáp án A.
Câu 25. Gọi
12
;zz
là hai nghiệm phức của phương trình
2
2 40zz+ +=
. Khi đó
22
12
|| ||
Az z
= +
có giá
trị là
A.
7−
B. – 8 C.
4−
D. 8
Hướng dẫn giải:
( )
2
2
22
12
2 40 1 30 1 3
|| ||8
zz z z i
Az z
+ + = ⇔ + + = ⇔ =−±
⇒= + =
Ta chọn đáp án A.
Câu 26. Phương trình
3
8z =
có bao nhiêu nghiệm phức với phần ảo âm?
A. 1 B. 2 C. 3 D. 0
Hướng dẫn giải:
( )
( )
( ) (
)
2
32
8 2 240 2 1 30
2
13
z z zz z z
z
zi

=⇔− ++=⇔− + +=

=
⇔
=−±
Do đó phương trình chỉ có một nghiệm phức có phần ảo âm.
Ta chọn đáp án A.
Câu 27. Biết
12
,zz
là hai nghiệm của phương trình
2
2 3 30
zz+ +=
. Khi đó giá trị của
22
12
zz+
là:
A. 4 B.
9
4
C. 9 D.
9
4
−
Hướng dẫn giải:
Trang 14/21
Áp dụng định lý Viet, ta có:
12
12
3
2
3
2
b
Szz
a
c
P zz
a
=+ =−=−
= = =
22 2
12
39
23
44
zzS P+ = − = −=−
Ta chọn đáp án A.
Câu 28. Phương trình sau có mấy nghiệm thực:
2
2 20zz
+ +=
A. 0 B. 1 C. 2 D. Vô số nghiệm.
Hướng dẫn giải:
2
' b' 1 2 1 0ac
∆= − = − =−<
nên phương trình vô nghiệm trên tập số thực.
Ta chọn đáp án A.
Câu 29. Tìm các căn bậc hai của
9−
.
A.
3i±
B. 3 C.
3
i
D.
3−
Hướng dẫn giải:
Ta có
2
9 9.i−=
nên
9−
có các căn bậc hai là
3
i
và
3i−
.
Ta chọn đáp án A.
Câu 30. Trong
, phương trình
4
40+=z
có nghiệm là:
A.
( ) ( )
14; 14±− ±+ii
B.
( )
12±−i
;
( )
12±+i
C.
( ) ( )
13; 13±− ±+ii
D. ±
( )
1− i
;
( )
1±+i
Hướng dẫn giải:
( )
(
)
2
4
2
1
2
40
1
2
=±+
=
+=⇔ ⇔
=±−
= −
zi
zi
z
zi
zi
Ta chọn đáp án A.
Câu 31. Giải phương trình
2
2 70zz− +=
trên tập số phức ta được nghiệm là:
A.
1 22zi= ±
B.
16zi= ±
C.
12zi= ±
D.
17zi= ±
Hướng dẫn giải:
( )
2
2
2 70 1 60 1 6zz z z i− +=⇔ − +=⇔=±
Ta chọn đáp án A.
Câu 32. Căn bậc hai của số phức
4 65i+
là:
A.
( )
35i−+
B.
( )
35i+
C.
( )
35
i±+
D. 2
Hướng dẫn giải:
Giả sử
w
là một căn bậc hai của
4 65i+
. Ta có:
( ) ( )
2
22
465 35 35w iw i w i=+ ⇔ =+ ⇔=±+
.
Ta chọn đáp án A.
Câu 33. Gọi z là căn bậc hai có phần ảo âm của
33 56i−
. Phần thực của z là:
A. 6 B. 7 C. 4 D. –4
Hướng dẫn giải:
Ta có:
( )
2
33 56 7 4ii−=−
74zi⇒=−
Do đó phần thực của z là 7.
Ta chọn đáp án A.
Câu 34. Tập nghiệm trong
của phương trình
32
10zzz+ ++=
là:
A.
{ }
;i;1; 1i−−
B.
{ }
; ;1ii−
C.
{ }
;1i−−
D.
{ }
;; 1ii−−
Hướng dẫn giải:
Trang 15/21
( )
( )
32 2
1
10 1 1 0
z
zzz z z
zi
= −
+ ++= ⇔ + + = ⇔
= ±
Ta chọn đáp án A.
Câu 35. Trên tập số phức, phương trình bậc hai có hai nghiệm
4 3; 2= + =−+
αβ
ii
là:
A.
( ) ( )
2
2 4 11 2 0++ − + =z iz i
B.
( ) ( )
2
2 4 11 2 0−+ − + =z iz i
C.
(
) ( )
2
2 4 11 2 0−+ + + =z iz i
D.
( ) ( )
2
2 4 11 2 0++ + + =z iz i
Hướng dẫn giải:
Áp dụng định lý Viet, ta có:
24
. 11 2
Si
Pi
αβ
αβ
=+=+
= =−−
.
Do đó
,
αβ
là hai nghiệm của phương trình:
(
) (
)
22
0 2 4 11 2 0z Sz P z i z i
− +=⇔ −+ − + =
Ta chọn đáp án A.
Câu 36. Có bao nhiêu số phức thỏa mãn điều kiện
22
||zzz= +
?
A. 3 B. 0 C. 1 D. 2
Hướng dẫn giải:
Gọi
( )
,
z a bi a b=+∈
là số phức thỏa mãn điều kiện trên. Ta có:
( )
( )
( )
2
2 2 22 2 2
2
2
|| 2 2 0 2 2 0
0
20
1
20
0
2
20
1
1
2
2
z z z a bi a b a bi a b bi abi a b b ab i
ab
ab
ab
a
b
b ab
a
b
= + ⇔ + = + + − ⇔ + − − = ⇔ + +−− =
= =
+=
+=
= −
=
⇔⇔⇔

+=
= −
= ±
Vậy có 3 số phức thỏa mãn yêu cầu bài toán.
Ta chọn đáp án A.
Câu 37. Phương trình
( ) ( )
2
2 0,i z az b a b+ + += ∈
có hai nghiệm là
3 i+
và
12i−
. Khi đó
?a
=
A.
92i−−
B.
15 5i+
C.
92i+
D.
15 5i−
Hướng dẫn giải:
Theo Viet, ta có:
( )( )
12
4 4 2 92
2
a
Szz i a i i a i
i
=+ =− =−⇔=− + ⇔=−−
+
Ta chọn đáp án A.
Câu 38. Cho số phức z thỏa mãn
2
6 13 0zz−+=
. Tính
6
z
zi
+
+
A.
17
và 4 B.
17
và 5 C.
17
và 3 D.
17
và 2
Hướng dẫn giải:
( )
2
2
6 13 0 3 4 0 3 2zz z z i− + =⇔ − +=⇔=±
+) Nếu
32zi= +
:
6 6 9 15 18 72
32 14
33 33 18
6
1 4 17
ii
zi i
zi i i
zi
zi
+ −+
+ = + + = = =−+
+ ++
⇒ + =−+ =
+
+) Nếu
32zi= −
:
6 6 13 9 30 40
32 34
3 3 10
6
34 5
ii
zi i
zi i i
zi
zi
−−
+ =−+ = = =−
+ −−
⇒+ =− =
+
Trang 16/21
Ta chọn đáp án A.
Câu 39. Gọi
12
,
zz
là các nghiệm phức của phương trình
( ) ( )
2
1 3 21 0z iz i
+− − +=
. Khi đó
22
1 2 12
3w z z zz=+−
là số phức có môđun là:
A. 2 B.
13
C.
2 13
D.
20
Hướng dẫn giải:
Theo Viet, ta có:
(
)
12
12
13
. 21
b
Szz i
a
c
P zz i
a
= + =− =−+
= ==−+
( ) ( )
2
22 2
1 2 12
3 5 1 3 10 1 2 4
| | 4 16 20
w z z zz S P i i i
w
= + − = − =−+ + + = +
⇒= +=
Ta chọn đáp án A.
Câu 40. Số nghiệm của phương trình với ẩn số phức z:
22
4 8|z| 3 0z + −=
là:
A. 3 B. 2 C. 4 D. 1
Hướng dẫn giải:
Gọi
( )
,z a bi a b=+∈
là nghiệm của phương trình. Ta có:
( )
( )
( )
( )
2
22 2 2 2 2
22
4 8a 30 4 2 8 30
12 4 8 3 0
a bi b a b abi a b
a b abi
+ + + −=⇔ − + + + −=
⇔ + + −=
2 2 22
12 4 3 4 1
00
a b ab
ab ab

+ = +=
⇒⇔

= =

( )
2
22
0
21
1
44 1
0
1
0
4
0
0
a
ab
b
a ab b
a
ab
a
b
b
=
+=
= ±
+ +=
⇒ ⇔⇔

=
=
= ±

=
=
Vậy phương trình có 4 nghiệm phức
Ta chọn đáp án A.
Câu 41. Tìm số phức z để
2
zz z−=
.
A
0; 1
zz i= = −
B.
0; 1
zz i= = +
C.
0;1;1z z iz i= =+=−
D.
1; 1z iz i
=+=−
Hướng dẫn giải:
Gọi
( )
,z a bi a b=+∈
là số phức thỏa mãn đẳng thức trên. Ta có:
( )
22
22
2
2
1
0
1
0
1
22
0
0
0
a
ab
b
ab
z z z a bi a bi a bi
a
ab b
a
b
b
=
−=
= ±
−=
−=⇔+−+=+⇔⇔⇔
=

=
=
=
=
0
1
1
z
zi
zi
=
⇒=+
= −
Ta chọn đáp án A.
Câu 42. Với mọi số ảo z, số
22
|z|z +
là:
A. Số thực âm B. Số 0 C. Số thực dương D. Số ảo khác 0
Hướng dẫn giải:
Trang 17/21
Do z là số ảo nên z có dạng:
( )
z bi b= ∈
.
Ta có:
(
)
2
2 2 2 22
|| 0z z bi b b b
+ = +=−+=
.
Ta chọn đáp án A.
Câu 43. Trong trường số phức phương trình
3
10z +=
có mấy nghiệm?
A. 2 B. 3 C. 1 D. 0
Hướng dẫn giải:
( )
( )
32
1
10 1 1 0
13
2
z
z z zz
i
z
=
+= ⇔ + −+ = ⇔
±
=
Vậy phương trình có ba nghiệm trong trường số phức.
Ta chọn đáp án A.
Câu 44. Giá trị của các số thực b, c để phương trình
2
0z bz c
+ +=
nhận số phức
1zi= +
làm một
nghiệm là:
A.
2
2
b
c
=
= −
B.
2
2
b
c
= −
= −
C.
2
2
b
c
= −
=
D.
2
2
b
c
=
=
Hướng dẫn giải:
Do
1zi= +
là một nghiệm của
2
0z bz c
+ +=
nên ta có:
( ) (
)
2
02
1 1 0 20
22
bc b
i b i c b c bi i
bc
+= =−

+ + + += ⇔++ + =⇒ ⇔

=−=

Ta chọn đáp án A.
Câu 45. Trên tập hợp số phức, phương trình
2
7 15 0zz++=
có hai nghiệm
12
,zz
. Giá trị biểu thức
1 2 12
z z zz++
là:
A. –7 B. 8 C. 15 D. 22
Hướng dẫn giải:
Theo Viet, ta có:
12
12
7
15
b
Szz
a
c
P zz
a
=+ =−=−
= = =
1 2 12
7 15 8z z zz S P⇒ + + = + =−+ =
Ta chọn đáp án A.
Câu 46. Tìm số nguyên x, y sao cho số phức
z x yi= +
thỏa mãn
3
18 26zi= +
A.
3
1
x
y
=
= ±
B.
3
1
x
y
=
= −
C.
3
1
x
y
=
=
D.
3
1
x
y
= −
= ±
Hướng dẫn giải:
( )
( )
( )
( )
3
3 3 2 23
3 2 23
22
32
23
22
18 26 18 26 3 3 18 26
( 3 ) 3 18 26
3 18
3 18
3 26
3 26
z i x yi i x x yi xy y i i
x xy x y y i i
xx y
x xy
xy y
yx y
=+⇔+ =+⇔+ − −=+
⇔− + − =+
−=
−=

⇒⇔

−=
−=
Do x, y nguyên nên
( )
( )
22
22
22
3
3
1
36
3 18
6
6
loai
11
33
x
x
y
xy
xx y
x
x
y
xy
=
=
= ±
−=
−=⇔ ⇔
=
=
= ±
−=
Mà
( )
22
3 26 3; 1yx y x y− = ⇒= =
Trang 18/21
Ta chọn đáp án A.
Câu 47. Trên tập số phức, cho phương trình sau:
( )
4
2
40zi z++ =
. Có bao nhiêu nhận xét đúng trong
số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực
.
2. Phương trình vô nghiệm trên trường số phức
.
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0 B. 1 C. 3 D. 2
Hướng dẫn giải:
( ) ( )
( )
( )
( )
( )
44
22
2
2
2
22
40 4
1
1
2
10
23
2 30
4 10
2
zi z zi z
z
z
z i iz
z
zi
zi
z iz
z i iz
+ + =⇔+ =−
= ±
= ±
+=
−=
⇔⇔⇔ ⇔
=−±
+ +=
+ −=
+=−
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Ta chọn đáp án A.
Câu 48. Phương trình
63
9 80zz
− +=
có bao nhiêu nghiệm trên tập số phức?
A. 3 B. 4 C. 2 D. 6
Hướng dẫn giải:
Ta có:
( )
( )
(
)( )
63 2 2
3
9 80 1 2 1 2 4 0
1
2
1
13
z z z z zz z z
z
z
z
i
− +=⇔ − − ++ + + =
=
=
⇔
=±−
−±
Ta chọn đáp án A.
Câu 49. Giả sử
12
,zz
là hai nghiệm của phương trình
2
2 50
zz− +=
và A, B là các điểm biểu diễn của
12
,zz
. Tọa độ trung điểm I của đoạn thẳng AB là:
A.
( )
1;1I
B.
( )
1; 0I −
C.
( )
0;1I
D.
( )
1; 0I
Hướng dẫn giải:
( )
2
2
2 5 0 1 4 0 12zz z z i− +=⇔ − +=⇔=±
( ) ( )
1; 2 ; 1; 2AB⇒−
Do đó tọa độ trung điểm I của đoạn thẳng AB là
( )
1; 0I
.
Ta chọn đáp án A.
Câu 50. Cho phương trình
2
60z mz i
+ −=
. Để phương trình có tổng bình phương hai nghiệm bằng 5
thì m có dạng
( )( )
,m a bi a b=±+ ∈
. Giá trị
2ab+
là:
A. 0 B. 1 C.
2−
D.
1−
Hướng dẫn giải:
Gọi
12
,zz
là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
12
12
.6
b
Szz m
a
c
P zz i
a
=+ =−=−
= = = −
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
Trang 19/21
( )
(
)
2
22 2 2 2 2
12
2 12 5 5 12 3 2
32
z z S Pm i m i m i
mi
+=−=+=⇔=−⇔=−
⇒=±−
3; 2 2 3 4 1a b ab⇒ = =−⇒ + = − =−
Ta chọn đáp án A.
Câu 51. Gọi
1224
,,,zzzz
là các nghiệm phức của phương trình
4
1
1
2
z
zi
−

=

−

. Giá trị của
(
)(
)( )( )
2222
1 234
1111
Pzzzz=++++
là:
A.
17
8
B.
17
9
C.
9
17
D.
17
9
i
Hướng dẫn giải:
Với mọi
2
i
z ≠
, ta có:
4
1
11
1
1
23
1
1 24
2
25
0
zi
zi
z
z
zi
zi
zi
iz
zi
z
=−+
−+
=±=
−

−
=⇔⇔

−+
−

=±=
−
=
( )( )( )( )
( )
( ) ( )
( )
22
2
2222
1 234
1 24
1111 1 1 1 1
9 25
9 2 13 16 425 17
12 .
9 25 9.25 9
ii
Pzzzz i
ii
i

++

⇒=++++=−++ + +




++
=−==
Ta chọn đáp án A.
Câu 52. Trong tập số phức, giá trị của m để phương trình bậc hai
2
0z mz i+ +=
có tổng bình phương
hai nghiệm bằng
4
i−
là:
A.
(
)
1 i
±−
B.
( )
1 i−
C.
( )
1
i±+
D.
1 i−−
Hướng dẫn giải:
Gọi
12
,zz
là hai nghiệm của phương trình.
Theo Viet, ta có:
12
12
.
b
Szz m
a
c
P zz i
a
=+ =−=−
= = =
22 2 2
12
22z z S Pm i⇒+=− = −
Ta có:
( )
( )
2
2 22
24 2 1 1m i im im i m i− =−⇔ =−⇔ =− ⇔ =±−
Ta chọn đáp án A.
Câu 53. Cho phương trình
2
2 10z mz m− + −=
trong đó m là tham số phức. Giá trị của m để phương
trình có hai nghiệm
12
,zz
thỏa mãn
22
12
10zz+=−
là:
A.
2 22
mi= ±
B.
2 22mi
= +
C.
2 22mi= −
D.
2 22mi=−−
Hướng dẫn giải:
Theo Viet, ta có:
12
12
. 21
b
Szz m
a
c
P zz m
a
=+ =−=
= = = −
( )
( )
22 2 2 2
12
2
10 2 10 2 2 1 10 4 12 0
2 8 0 2 22
zz S P m m m m
m mi
+=−⇔ − =−⇔ − −=−⇔ − +=
⇔ − +=⇔ =±
Trang 20/21
Ta chọn đáp án A.
Câu 54. Gọi
12
,
zz
là hai nghiệm của phương trình
2
2 80zz+ +=
, trong đó
1
z
có phần ảo dương. Giá
trị của số phức
( )
1 21
2w z zz
= +
là:
A.
12 6i+
B. 10 C. 8 D.
12 6i−
Hướng dẫn giải:
(
)
2
1
2
2
17
2 80 1 70 1 7
17
zi
zz z z i
zi
=−+
+ + = ⇔ + + = ⇔ =−± ⇒
= −
( )
( )
( ) ( )( )
1 21
2 21717 17 17 17 178w z zz i i i i i

= + = −+ +− −− =−+ −− =+ =

Câu 55. Tổng bình phương các nghiệm của phương trình
4
10z −=
trên tập số phức là bao nhiêu?
A. 3 B. 1 C. 2 D. 0
Hướng dẫn giải:
4
1
10
z
z
zi
= ±
−= ⇔
= ±
Do đó tổng bình phương các nghiệm của phương trình là
11 0−=
Ta chọn đáp án A.
Câu 56. Gọi
12
,zz
là hai nghiệm của phương trình
2
2 60zz− +=
. Trong đó
1
z
có phần ảo âm. Giá trị
biểu thức
1 12
| | |3 |Mz zz=+−
là:
A.
6 2 21−
B.
6 2 21+
C.
6 4 21+
D.
6 4 21−
Hướng dẫn giải:
( )
2
2
12
1 12
2 60 1 50 1 5
1 5; 1 5
| | | 3 | 1 5 2 4 5 6 84 6 2 21
zz z z i
z iz i
Mz zz i i
− +=⇔ − +=⇔=±
⇒=− =+
⇒ = + − =− +− = + = +
Ta chọn đáp án A.
Câu 57. Phương trình
42
2 24 72 0xx x+ − +=
trên tập số phức có các nghiệm là:
A.
22i±
hoặc
222i−±
B.
22i±
hoặc
12 2i±
C.
12 2i±
hoặc
222i−±
D.
12 2i−±
hoặc
222i−±
Hướng dẫn giải:
( )
( )
( )
(
)
42 2 2
2
2
22
2 24 72 0 4 6 4 12 0
2 20
4 60 2 2
4 12 0
2 22
2 80
xx x xx xx
x
xx x i
xx
xi
x
+ − +=⇔ −+ ++ =
− +=
− += =±
⇔ ⇔⇔
++=
=−±
+ +=
Ta chọn đáp án A.
Câu 58. Gọi
12
,zz
là các nghiệm phức của phương trình
2
3 70zz+ +=
. Khi đó
44
12
Az z= +
có giá trị
là:
A. 23 B.
23
C. 13 D.
13
Hướng dẫn giải:
Theo Viet, ta có:
12
12
3
.7
b
Szz
a
c
P zz
a
=+ =−=−
= = =
( )
( )
2
2
44 2 2
12
2 2 3 2.7 2.49 23Az z S P P=+= − − =− − =
Ta chọn đáp án A.
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

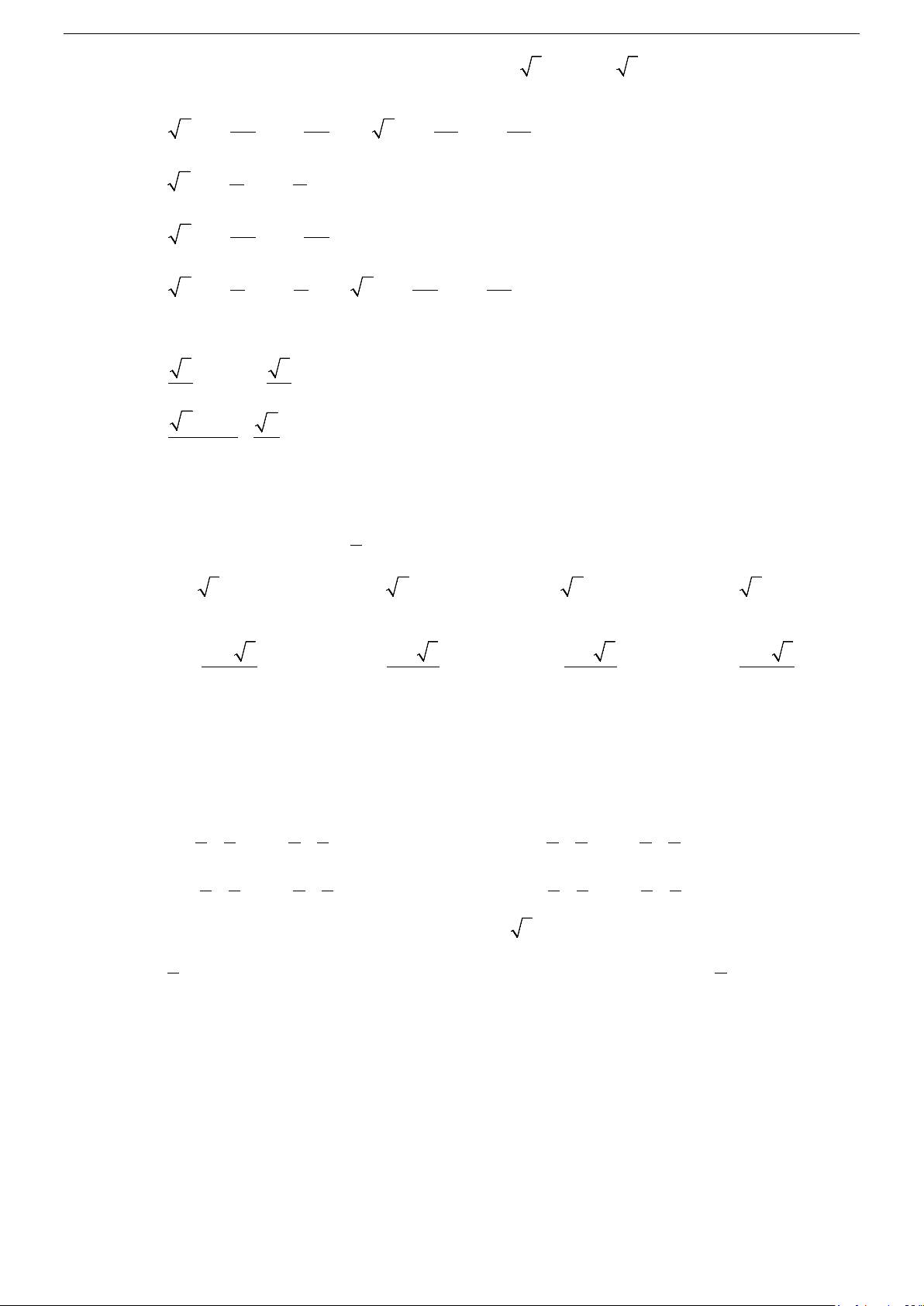
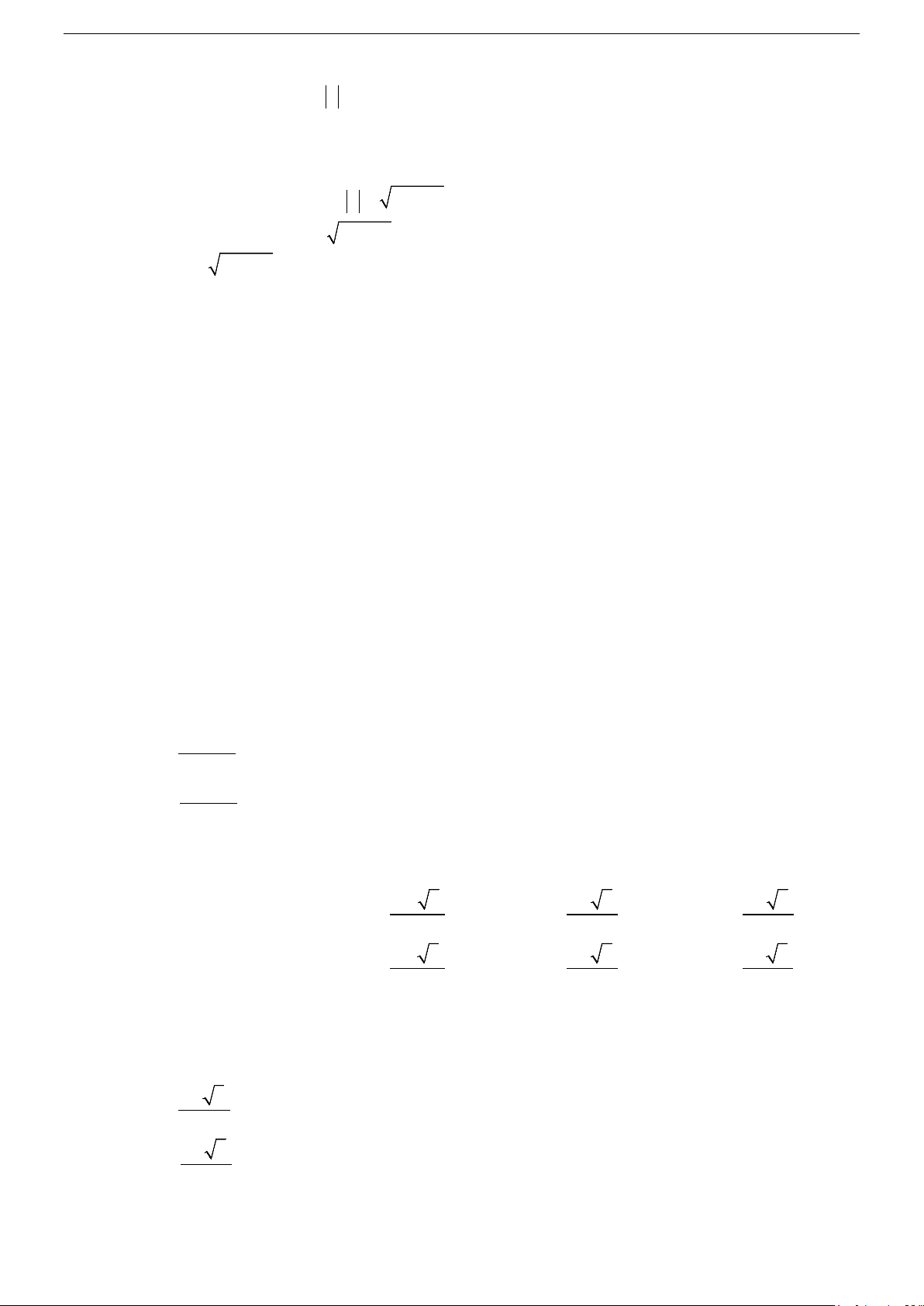
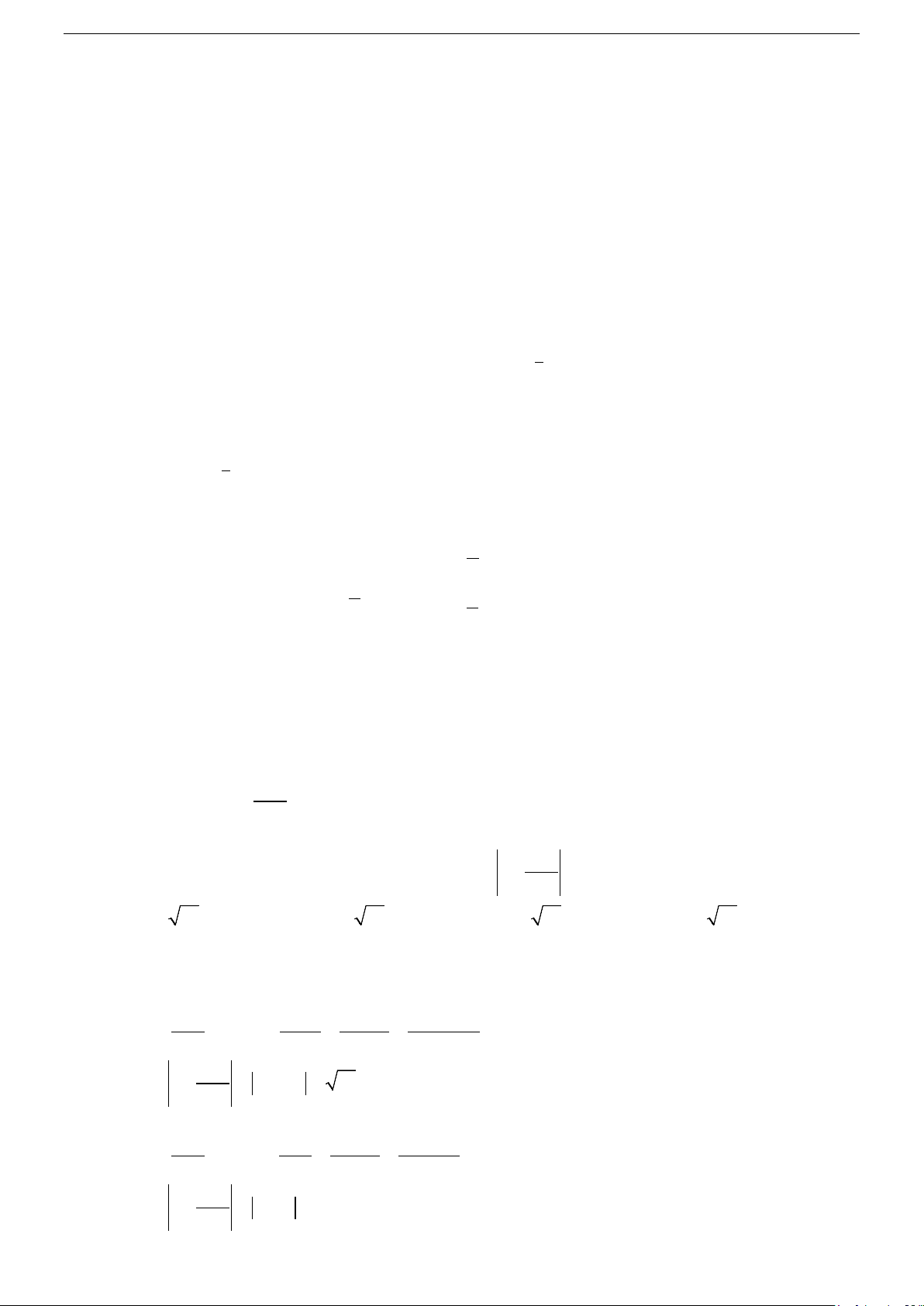
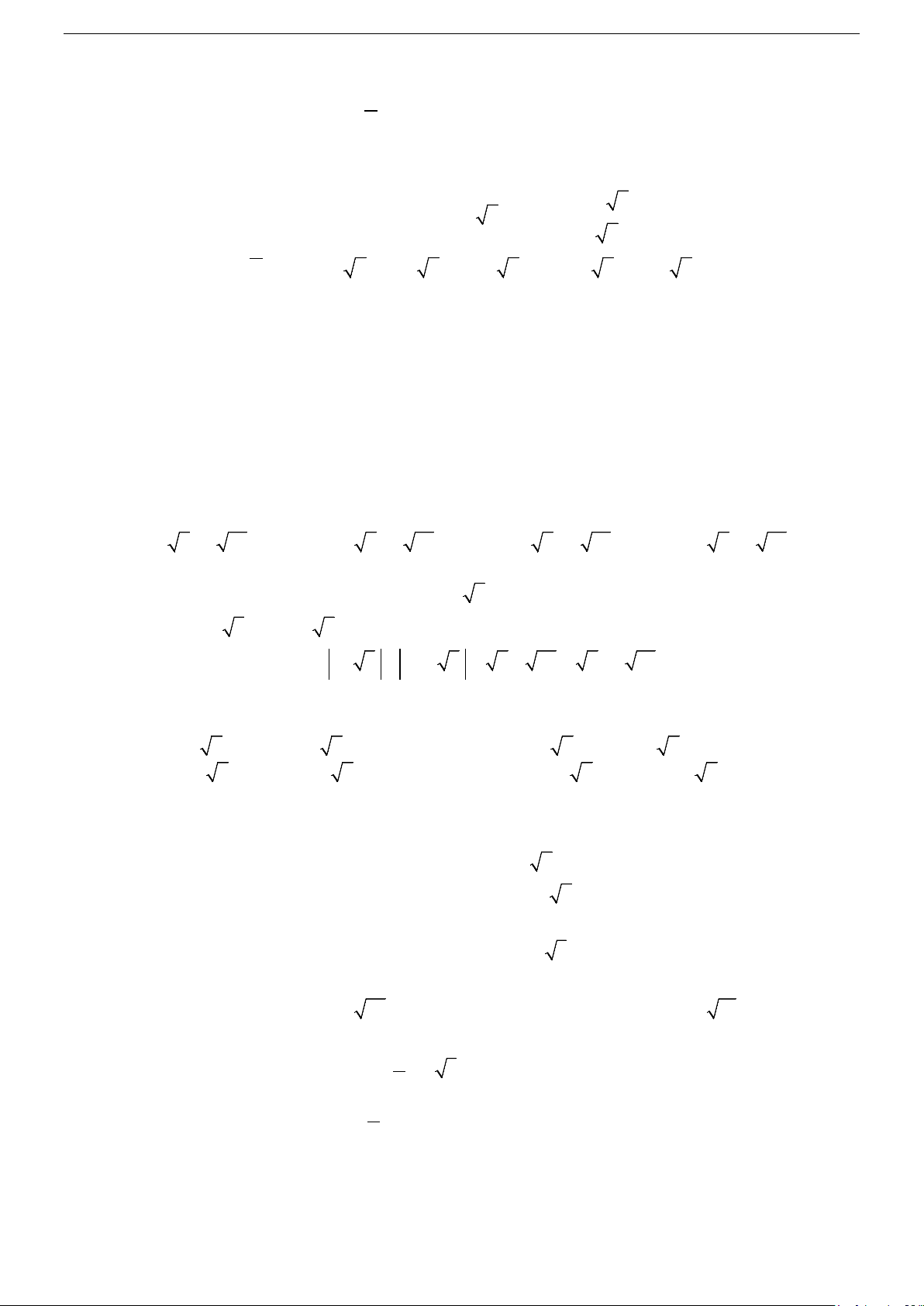
Preview text:


CHỦ ĐỀ 2. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC TRÊN TẬP SỐ PHỨC
A. KIẾN THỨC CƠ BẢN
1. Căn bậc hai của số phức: Cho số phức w . Mỗi số phức z thỏa mãn 2
z = w được gọi là một căn bậc hai của w . • .
2. Phương trình bậc hai với hệ số thực
Cho phương trình bậc hai 2
ax + bx + c = 0 (a,b,c∈ ;  a ≠ 0) . Xét 2
∆ = b − 4ac , ta có
• ∆ = 0 : phương trình có nghiệm thực b x = − . 2a − ± ∆
• ∆ > 0 : phương trình có hai nghiệm thực được xác định bởi công thức: b x = . 1,2 2a b − ± i | ∆ |
• ∆ < 0 : phương trình có hai nghiệm phức được xác định bởi công thức: x = . 1,2 2a Chú ý.
 Mọi phương trình bậc n : n n 1
A z + A z − + + A +
= luôn có n nghiệm phức (không − z A o ... n n 0 1 1 nhất thiết phân biệt).
Hệ thức Vi–ét đối với phương trình bậc hai với hệ số thực: Cho phương trình bậc hai 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm phân biệt x , x (thực hoặc phức). Ta có hệ thức Vi–ét 1 2  b
S = x + x = −  1 2  a  = . c P x x = 1 2  a
B. KỸ NĂNG CƠ BẢN
1. Dạng 1: Tìm căn bậc hai của một số phức
• Trường hợp w là số thực: Nếu a là một số thực
+ a < 0, a có các căn bậc hai là ±i | a | .
+ a = 0 , a có đúng một căn bậc hai là 0.
+ a > 0 , a có hai căn bậc hai là ± a .
Ví dụ 1: Ta có hai căn bậc hai của – 1 là i và i
− . Hai căn bậc hai của 2
−a ( a là số thực khác 0) là ai và −ai .
• Trường hợp w = a + bi (a,b∈,b ≠ 0)
Gọi z = x + yi (x, y ∈) là một căn bậc hai của w khi và chỉ khi 2
z = w , tức là 2 2 ( + )2  − = 2 2 x y a
x yi = a + bi ⇔ x − y + 2xyi = a + bi ⇔  2xy = b Mỗi cặp số thực ( ;
x y) nghiệm đúng hệ phương trình trên cho ta một căn bậc hai x + yi của số
phức w = a + bi .
Ví dụ 2: Tìm các căn bậc hai của w = 5 − +12i .
Gọi z = x + yi (x, y ∈) là một căn bậc hai của số phức w = 5 − +12i . x = 2 2  =  2 2 x 4 x − y = 5 −  y = 3 Ta có 2
z = w ⇔(x + yi)2 = 5 − +12i ⇔  ⇔  6 ⇔ 2xy 12 y  = = x = 2 −  x  y = 3 − Vậy w = 5
− +12i có hai căn bậc hai là 2 + 3i và 2
− − 3i .
2. Dạng 2: Giải phương trình bậc hai với hệ số thực và các dạng toán liên quan Trang 1/21
• Giải các phương trình bậc hai với hệ số thực
Ví dụ 3: Giải phương trình bậc hai sau: 2 z − z +1 = 0 Ta có 2
∆ = b − 4ac = 3 − < 0
Phương trình có hai nghiệm phức phân biệt là 1 i 3 x ± = . 1,2 2
• Giải phương trình quy về phương trình bậc hai với hệ số thực
Phương pháp 1: Phân tích đa thức thành nhân tử:
– Bước 1: Nhẩm 1 nghiệm đặc biệt của phương trình.
+ Tổng các hệ số trong phương trình là 0 thì phương trình có một nghiệm x =1.
+ Tổng các hệ số biến bậc chẵn bằng tổng các hệ số biến bậc lẻ thì phương trình có một nghiệm x = 1 − . + Định lý Bơdu:
Phần dư trong phép chia đa thức f (x) cho x − a bằng giá trị của đa thức f (x) tại x = . a
Tức là f (x) = (x − a) g (x) − f (a)
Hệ quả: Nếu f (a) = 0 thì f (x)(x − a)
Nếu f (x)(x − a)thì f (a) = 0 hay f (x) = 0 có một nghiệm x = . a
– Bước 2: Đưa phương trình về phương trình bậc nhất hoặc bậc hai bằng cách hân tích đa thức ở
vế trái của phương trình thành nhân tử (dùng hẳng đảng thức, chia đa thức hoặc sử dụng lược đồ Hoocne) như sau: Với đa thức f (x) n n 1
= a x + a x − + +
+ chia cho x − a có thương là − a x a n n ... 1 1 0 g (x) n 1 − n−2 = b + + + + dư r − x b − x b x b n n ... 1 2 1 0 a a a a a a n n 1 − n−2 2 1 0
a b = b = + b = +
b = ab + a b = ab + a r = ab + b − ab − a − ab − a − a n 1 n n 2 n 1 n−2 n 3 n 2 n−3 1 2 2 0 1 1 0 0
– Bước 3: Giải phương trình bậc nhất hoặc bậc hai, kết luận nghiệm
Phương pháp 2: Đặt ẩn phụ:
– Bước 1: Phân tích phương trình thành các đại lượng có dạng giống nhau.
– Bước 2: Đặt ẩn phụ, nêu điều kiện của ẩn phụ (nếu có).
– Bước 3: Đưa phương trình ban đầu về phương trình bậc nhất, bậc hai với ẩn mới.
– Bước 4: Giải phương trình, kết luận nghiệm.
C. KỸ NĂNG SỬ DỤNG MÁY TÍNH
1. Chọn chế độ tính toán với số phức: MODE 2 màn hình hiện CMPLX.
Nhập số thuần ảo i : Phím ENG
2. Tìm các căn bậc hai của một số phức
Ví dụ 5: Khai căn bậc hai số phức z = 3
− − 4i có kết quả: Cách 1: – Mode 2 (CMPLX) – Nhập hàm 2 X
– Sử dụng phím CALC, nhập từng giá trị vào, giá trị nào ra kết quả bằng z thì ta nhận. Cách 2: – Mode 1 (COMP)
– Nhấn Shift + (Pol), ta nhập Pol ( 3 − ;4)
– Nhấn Shift – (Rec), ta nhập Rec( X ,Y : 2) , ta thu được kết quả X =1;Y = 2 .
– Vậy 2 số phức cần tìm là 1+ 2i và 1 − − 2i . Trang 2/21
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong , phương trình 2
2x + x +1 = 0 có nghiệm là: A. 1 1 x = 1 − − 7i ; x = 1 − + 7i B. 1 1
x = 1+ 7i ; x = 1− 7i 1 ( ) 2 ( ) 1 ( ) 2 ( ) 4 4 4 4 C. 1 1 x = 1
− + 7i ; x = 1− 7i D. 1 1
x = 1+ 7i ; x = 1 − − 7i 1 ( ) 2 ( ) 1 ( ) 2 ( ) 4 4 4 4
Câu 2. Khai căn bậc hai số phức z = 3
− + 4i có kết quả:
A. z =1+ 2i; z = 1 − − 2i
B. z =1+ 2i; z =1− 2i 1 2 1 2
C. z =1+ 2i; z = 1 − + 2i D. z = 1 − + 2i; z = 1 − − 2i . 1 2 1 2
Câu 3. Trong , nghiệm của phương trình 3 z −8 = 0 là:
A. z = 2; z =1+ 3i; z =1− 3i
B. z = 2; z = 1 − + 3i; z = 1 − − 3i 1 2 3 1 2 3 C. z = 2; − z = 1 − + 3i; z = 1 − − 3i D. z = 2;
− z =1+ 3i; z =1− 3i 1 2 3 1 2 3
Câu 4. Trong , phương trình z + z = 2 + 4i có nghiệm là: A. z = 3 − + 4i B. z = 2 − + 4i C. z = 4 − + 4i D. z = 5 − + 4i
Câu 5. Hai giá trị x = a + bi; x = a −bi là hai nghiệm của phương trình: 1 2 A. 2 2 2
x + 2ax + a + b = 0 B. 2 2 2
x + 2ax + a − b = 0 C. 2 2 2
x − 2ax + a + b = 0 D. 2 2 2
x − 2ax + a − b = 0
Câu 6. Trong , phương trình z2 + 3iz + 4 = 0 có nghiệm là: z = 3iz = iz =1+ iz = 2 − 3i A. B. C. D.  z = 4iz = 4 − iz = 3 − iz =1+ i
Câu 7. Trong , phương trình 2
z − z +1 = 0 có nghiệm là:  2 + 3i  1+ 5i  1+ 3iz = z = z = z = 3 + 5i A. 2 2 2  B. C. D.  z = 3 − 5i  2 − 3i  1− 5i  1− 3iz = z = z =  2  2  2
Câu 8. Tính căn bậc hai của số phức z = 8 + 6i ra kết quả: z = 3 − iz = 3 + iz = 3 − + iz = 3 − i A. B.C. D.  z = 3 + iz = 3 − − iz = 3 − iz = 3 − − i
Câu 9. Trong , nghiệm của phương trình 2 z + 5 = 0 là: z = 5 4 z = 5i A.B.C. 5i D. − 5i z = − 5 4 z = − 5i
Câu 10. Trong , nghiệm của phương trình 2 z = 5 − +12i là: z = 2 + 3iz = 2 − 3i A.
B. z = 2 + 3i
C. z = 2 − 3i D.  z = 2 − − 3iz = 2 − + 3i
Câu 11. Trong , nghiệm của phương trình 2
z + 4z + 5 = 0 là: z = 2 − − i
A. z = 2 − i B. z = 2 − − i C. D. z = 2 − + i z = 2 − + i
Câu 12. Trong , nghiệm của phương trình 2
z − 2z +1− 2i = 0 là z = 2 − iz = i − 2 z = 2 + iz = 2 + i A. 1  B. 1 C. 1 D. 1 z = −     i z = −i z =  2 − i z = −i 2  2 2  2
Câu 13. Cho z = 3+ 4i . Tìm căn bậc hai của z . A. 2
− + i và 2 − i
B. 2 + i và 2 − i Trang 3/21 C. 2 + i và 2 − − i
D. 3 + 2i và − 3 − 2i
Câu 14. Cho z =1−i . Tìm căn bậc hai dạng lượng giác của z : π π  π π A.  − − 4 2 cos isin  +   và 4 7 7 2 cos +  isin 8 8      8 8  π π B. 2 cos isin  +  4 4    π π C.  − − 2 cos isin  +  4 4    π π π π D.  − − 4 2 cos isin  +   và 4 2 cos +  isin 8 8      8 8 
Câu 15. Trong , phương trình ( 2z + i)( 2z − 2iz − ) 1 = 0 có nghiệm là:
C. 3 (1− 2i) ; 3 ( 2 − + i) ; 4i B. 1− i ; 1 − + i ; 2i 2 2 2 (1− i) A. , 2 ( 1 − + i) , i D. 1− 2i ; 15 − i ; 3i 2 2
Câu 16. Trong , phương trình 4 2
z − 6z + 25 = 0 có nghiệm là: A. 8 ± ;± 5i B. 3; ± ± 4i C. 5 ± ;± 2i
D. ±(2 + i);± (2 −i)
Câu 17. Trong , phương trình 1
z + = 2i có nghiệm là: z A. (1± 3)i B. (5± 2)i C. (1± 2)i D. (2± 5)i
Câu 18. Trong , phương trình 3
z +1 = 0 có nghiệm là: A. ± ± ± ± 1 − ; 2 i 3 B. 1 − ; 1 i 3 C. 1 − ; 1 i 5 D. 1 − ; 5 i 3 2 2 4 4
Câu 19. Trong , phương trình 4
z −1 = 0 có nghiệm là: A 1; ± ± 2i B. 2; ± ± 2i C. 3; ± ± 4i D. 1; ± ± i
Câu 20. Trong , căn bậc hai của 121 − là: A. 11 − i B. 11i C. 11 − D. 11i và 11 − i
Câu 21. Phương trình 2
8z − 4z +1 = 0 có nghiệm là: A 1 1 5 1
z = + i; z = − i B. 1 1 1 3
z = + i; z = − i 1 2 4 4 4 4 1 2 4 4 4 4 C. 1 1 1 1
z = + i; z = − i D. 2 1 1 1
z = + i; z = − i 1 2 4 4 4 4 1 2 4 4 4 4
Câu 22. Biết z ; z là hai nghiệm của phương trình 2
2z + 3z + 3 = 0 . Khi đó giá trị của 2 2 z + z là: 1 2 1 2 A. 9 B.9 C. 4 D. 9 − 4 4
Câu 23. Phương trình 2
z + az + b = 0 có một nghiệm phức là z =1+ 2i . Tổng 2 số a và b bằng: A. 0 B. 3 − C. 3 D. 4 −
Câu 24. Gọi z ; z là hai nghiệm phức của phương trình 2
z − 4z + 5 = 0 . Khi đó phần thực của 2 2 z + z 1 2 1 2 là: A. 5 B. 6 C. 4 D. 7
Câu 25. Gọi z ; z là hai nghiệm phức của phương trình 2
z + 2z + 4 = 0 . Khi đó 2 2 A |
= z | + | z | có giá 1 2 1 2 trị là A. 7 − B. – 8 C. 4 − D. 8
Câu 26. Phương trình 3
z = 8 có bao nhiêu nghiệm phức với phần ảo âm? Trang 4/21 A. 1 B. 2 C. 3 D. 0
Câu 27. Biết z , z là hai nghiệm của phương trình 2
2z + 3z + 3 = 0 . Khi đó giá trị của 2 2 z + z là: 1 2 1 2 A. 4 B. 9 C. 9 D. 9 − 4 4
Câu 28. Phương trình sau có mấy nghiệm thực: 2 z + 2z + 2 = 0 A. 0 B. 1 C. 2 D. Vô số nghiệm.
Câu 29. Tìm các căn bậc hai của 9 − . A. 3 ± i B. 3 C. 3i D. 3 −
Câu 30. Trong , phương trình 4
z + 4 = 0 có nghiệm là:
A. ±(1− 4i);± (1+ 4i)
B. ±(1− 2i) ; ±(1+ 2i)
C. ±(1−3i);± (1+ 3i)
D. ±(1−i) ; ±(1+ i)
Câu 31. Giải phương trình 2
z − 2z + 7 = 0 trên tập số phức ta được nghiệm là:
A. z =1± 2 2i
B. z =1± 6i
C. z =1± 2i
D. z =1± 7i
Câu 32. Căn bậc hai của số phức 4 + 6 5i là: A. −(3+ 5i)
B. (3+ 5i) C. ±(3+ 5i) D. 2
Câu 33. Gọi z là căn bậc hai có phần ảo âm của 33−56i . Phần thực của z là: A. 6 B. 7 C. 4 D. –4
Câu 34. Tập nghiệm trong  của phương trình 3 2
z + z + z +1 = 0 là: A. { i − ;i;1;− } 1 B. { i − ;i } ;1 C. { i − ;− } 1 D. { i − ;i;− } 1
Câu 35. Trên tập số phức, phương trình bậc hai có hai nghiệm α = 4 + 3i;β = 2 − + i là: A. 2
z + (2 + 4i) z −(11+ 2i) = 0 B. 2
z − (2 + 4i) z −(11+ 2i) = 0 C. 2
z − (2 + 4i) z + (11+ 2i) = 0 D. 2
z + (2 + 4i) z + (11+ 2i) = 0
Câu 36. Có bao nhiêu số phức thỏa mãn điều kiện 2 2 z | = z | +z ? A. 3 B. 0 C. 1 D. 2
Câu 37. Phương trình ( + i) 2 2
z + az + b = 0(a,b∈) có hai nghiệm là 3+ i và 1− 2i . Khi đó a = ? A. 9 − − 2i B. 15 + 5i C. 9 + 2i D. 15 − 5i
Câu 38. Cho số phức z thỏa mãn 2
z − 6z +13 = 0 . Tính 6 z + z + i A. 17 và 4 B. 17 và 5 C. 17 và 3 D. 17 và 2
Câu 39. Gọi z , z là các nghiệm phức của phương trình 2
z + (1−3i) z − 2(1+ i) = 0 . Khi đó 1 2 2 2
w = z + z − 3z z là số phức có môđun là: 1 2 1 2 A. 2 B. 13 C. 2 13 D. 20
Câu 40. Số nghiệm của phương trình với ẩn số phức z: 2 2 4z + 8 | z | 3 − = 0 là: A. 3 B. 2 C. 4 D. 1
Câu 41. Tìm số phức z để 2
z − z = z .
A z = 0; z =1− i
B. z = 0; z =1+ i
C. z = 0; z =1+ i; z =1− i
D. z =1+ i; z =1− i
Câu 42. Với mọi số ảo z, số 2 2 z + | z | là:
A. Số thực âm B. Số 0 C. Số thực dương D. Số ảo khác 0
Câu 43. Trong trường số phức phương trình 3
z +1 = 0 có mấy nghiệm? A. 2 B. 3 C. 1 D. 0
Câu 44. Giá trị của các số thực b, c để phương trình 2
z + bz + c = 0 nhận số phức z =1+ i làm một nghiệm là: Trang 5/21 b  = 2 b  = 2 − b  = 2 − b  = 2 A. B. C. D.  c = 2 − c = 2 − c = 2 c = 2
Câu 45. Trên tập hợp số phức, phương trình 2
z + 7z +15 = 0 có hai nghiệm z , z . Giá trị biểu thức 1 2
z + z + z z là: 1 2 1 2 A. –7 B. 8 C. 15 D. 22
Câu 46. Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn 3 z =18 + 26i x = 3 x = 3 x = 3 x = 3 − A.B.C.D.  y = 1 ± y = 1 − y = 1 y = 1 ±
Câu 47. Trên tập số phức, cho phương trình sau: (z + i)4 2
+ 4z = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực  .
2. Phương trình vô nghiệm trên trường số phức  .
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực A. 0 B. 1 C. 3 D. 2
Câu 48. Phương trình 6 3
z − 9z + 8 = 0 có bao nhiêu nghiệm trên tập số phức? A. 3 B. 4 C. 2 D. 6
Câu 49. Giả sử z , z là hai nghiệm của phương trình 2
z − 2z + 5 = 0 và A, B là các điểm biểu diễn của 1 2
z , z . Tọa độ trung điểm I của đoạn thẳng AB là: 1 2 A. I (1; ) 1 B. I ( 1; − 0) C. I (0; ) 1 D. I (1;0)
Câu 50. Cho phương trình 2
z + mz − 6i = 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5
thì m có dạng m = ±(a + bi)(a,b∈) . Giá trị a + 2b là: A. 0 B. 1 C. 2 − D. 1 − 4 Câu 51.  −
Gọi z , z , z , z là các nghiệm phức của phương trình z 1  =   1. Giá trị của 1 2 2 4  2z − i P = ( 2 z + ) 1 ( 2 z + ) 1 ( 2 z + ) 1 ( 2 z +1 là: 1 2 3 4 ) A. 17 B. 17 C. 9 D. 17i 8 9 17 9
Câu 52. Trong tập số phức, giá trị của m để phương trình bậc hai 2
z + mz + i = 0 có tổng bình phương hai nghiệm bằng 4 − i là: A. ±(1−i) B. (1−i) C. ±(1+ i) D. 1 − − i
Câu 53. Cho phương trình 2
z − mz + 2m −1 = 0 trong đó m là tham số phức. Giá trị của m để phương
trình có hai nghiệm z , z thỏa mãn 2 2 z + z = 10 − là: 1 2 1 2
A. m = 2 ± 2 2i
B. m = 2 + 2 2i
C. m = 2 − 2 2i D. m = 2 − − 2 2i
Câu 54. Gọi z , z là hai nghiệm của phương trình 2
z + 2z + 8 = 0 , trong đó z có phần ảo dương. Giá 1 2 1
trị của số phức w = (2z + z z là: 1 2 ) 1
A.12 + 6i B. 10 C. 8 D. 12 − 6i
Câu 55. Tổng bình phương các nghiệm của phương trình 4
z −1 = 0 trên tập số phức là bao nhiêu? A. 3 B. 1 C. 2 D. 0
Câu 56. Gọi z , z là hai nghiệm của phương trình 2
z − 2z + 6 = 0. Trong đó z có phần ảo âm. Giá trị 1 2 1 biểu thức M |
= z | + | 3z − z | là: 1 1 2 Trang 6/21 A. 6 − 2 21 B. 6 + 2 21 C. 6 + 4 21 D. 6 − 4 21
Câu 57. Phương trình 4 2
x + 2x − 24x + 72 = 0 trên tập số phức có các nghiệm là:
A. 2 ± i 2 hoặc 2 − ± 2i 2
B. 2 ± i 2 hoặc 1± 2i 2
C. 1± 2i 2 hoặc 2 − ± 2i 2 D. 1 − ± 2i 2 hoặc 2 − ± 2i 2
Câu 58. Gọi z , z là các nghiệm phức của phương trình 2
z + 3z + 7 = 0 . Khi đó 4 4
A = z + z có giá trị 1 2 1 2 là: A. 23 B. 23 C. 13 D. 13 Trang 7/21
E. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 1.2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A A B A C B D B B A C D C A C D C B D D
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
C D C B D A D A A D B C B D B A A B C C
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58
C B B C B C D D D D B A A C D B A A
II –HƯỚNG DẪN GIẢI
Câu 1. Trong , phương trình 2
2x + x +1 = 0 có nghiệm là: A. 1 1 x = 1 − − 7i ; x = 1 − + 7i B. 1 1
x = 1+ 7i ; x = 1− 7i 1 ( ) 2 ( ) 1 ( ) 2 ( ) 4 4 4 4 C. 1 1 x = 1
− + 7i ; x = 1− 7i D. 1 1
x = 1+ 7i ; x = 1 − − 7i 1 ( ) 2 ( ) 1 ( ) 2 ( ) 4 4 4 4 Hướng dẫn giải: Ta có: 2 2 2
∆ = b − 4ac =1 − 4.2.1 = 7
− = 7i < 0 nên phương trình có hai nghiệm phức là: 1 i 7 x − ± == 1,2 4 Vậy ta chọn đáp án A.
Câu 2. Khai căn bậc hai số phức z = 3
− + 4i có kết quả:
A. z =1+ 2i; z = 1 − − 2i
B. z =1+ 2i; z =1− 2i 1 2 1 2
C. z =1+ 2i; z = 1 − + 2i D. z = 1 − + 2i; z = 1 − − 2i . 1 2 1 2 Hướng dẫn giải:
Giả sử w = x + yi (x, y ∈) là một căn bậc hai của số phức z = 3 − + 4i . Ta có: x =1 2  =  2 2 x 1 x − y = 3 −  y = 2 2
w = z ⇔(x + yi)2 = 3 − + 4i ⇔  ⇔  2 ⇔ 2xy 4 y  = = x = 1 −  x  y = 2 −
Do đó z có hai căn bậc hai là: z =1+ 2i 1z = 1 − − 2i 2 Ta chọn đáp án A.
Câu 3. Trong , nghiệm của phương trình 3 z −8 = 0 là:
A. z = 2; z =1+ 3i; z =1− 3i
B. z = 2; z = 1 − + 3i; z = 1 − − 3i 1 2 3 1 2 3 C. z = 2; − z = 1 − + 3i; z = 1 − − 3i D. z = 2;
− z =1+ 3i; z =1− 3i 1 2 3 1 2 3 Hướng dẫn giải:
Sử dụng hằng đẳng thức số 7, ta có: z = 2 z = 2 3
z −8 = 0 ⇔ (z − 2)( 2
z + 2z + 4) = 0 ⇔  ⇔  2
z + 2z + 4 = 0 (z + )2 1 = 3 − z = 2 z = 2  
⇔ z +1 = 3i ⇔ z = 1 − +   3iz 1 3i  + = − z = 1 − −   3i Trang 8/21 Ta chọn đáp án A.
Câu 4. Trong , phương trình z + z = 2 + 4i có nghiệm là: A. z = 3 − + 4i B. z = 2 − + 4i C. z = 4 − + 4i D. z = 5 − + 4i Hướng dẫn giải:
Đặt z = a + bi(a b∈) 2 2 ,
⇒ z = a + b . Thay vào phương trình: 2 2
a + b + a + bi = 2 + 4i  2 2
a + b + a = 2 a = 3 − Suy ra  ⇔  b = 4 b = 4 Ta chọn đáp án A.
Câu 5. Hai giá trị x = a + bi; x = a −bi là hai nghiệm của phương trình: 1 2 A. 2 2 2
x + 2ax + a + b = 0 B. 2 2 2
x + 2ax + a − b = 0 C. 2 2 2
x − 2ax + a + b = 0 D. 2 2 2
x − 2ax + a − b = 0 Hướng dẫn giải:
S = x + x = 2a
Áp dụng định lý đảo Viet : 1 2  . 2 2
P = x .x = a +  b 1 2
Do đó x , x là hai nghiệm của phương trình: 2 2 2 2
x − Sx + P = 0 ⇔ x − 2ax + a + b = 0 1 2 Ta chọn đáp án A.
Câu 6. Trong , phương trình z2 + 3iz + 4 = 0 có nghiệm là: z = 3iz = iz =1+ iz = 2 − 3i A. B. C. D.  z = 4iz = 4 − iz = 3 − iz =1+ i Hướng dẫn giải: 2
∆ = b − 4ac = (3i)2 − 4.1.4 = 25 − < 0
Nên phương trình có hai nghiệm phức là: 3 − i + 5i z = = i 1 2 3 − i − 5i z = = 4 − i 2 2 Ta chọn đáp án A.
Câu 7. Trong , phương trình 2
z − z +1 = 0 có nghiệm là:  2 + 3i  1+ 5i  1+ 3iz = z = z = z = 3 + 5i A. 2 2 2  B. C. D.  z = 3 − 5i  2 − 3i  1− 5i  1− 3iz = z = z =  2  2  2 Hướng dẫn giải: 2
∆ = b − 4ac = (− )2 1 − 4.1.1 = 3 − < 0
Nên phương trình có hai nghiệm phức là: 1+ 3i x = 1 2 1− 3i x = 2 2 Ta chọn đáp án A.
Câu 8. Tính căn bậc hai của số phức z = 8 + 6i ra kết quả: Trang 9/21 z = 3 − iz = 3 + iz = 3 − + iz = 3 − i A. B.C. D.  z = 3 + iz = 3 − − iz = 3 − iz = 3 − − i
Hướng dẫn giải:
Giả sử w = x + yi (x, y ∈) là một căn bậc hai của số phức z = 8 + 6i . x = 3 2  =  2 2 x 9
x − y = 8  y = 1 2 2
Ta có: w = z ⇔( x + yi) = 8 + 6i ⇔  ⇔  3 ⇔ 2xy 6 y  = = x = 3 −  x  y = 1 − z = 3 + i
Do đó z có hai căn bậc hai là 1 z = 3 − −  i 2 Ta chọn đáp án A.
Câu 9. Trong , nghiệm của phương trình 2 z + 5 = 0 là: z = 5 4 z = 5i A.B.C. 5i D. − 5i z = − 5 4 z = − 5i Hướng dẫn giải: 2 2 4
z + 5 = 0 ⇔ z = − 5 ⇔ z = ±i 5 Ta chọn đáp án A.
Câu 10. Trong , nghiệm của phương trình 2 z = 5 − +12i là: z = 2 + 3iz = 2 − 3i A.
B. z = 2 + 3i
C. z = 2 − 3i D.  z = 2 − − 3iz = 2 − + 3i Hướng dẫn giải:
Giả sử z = x + yi (x, y ∈) là một nghiệm của phương trình. 2 z = 5
− +12i ⇔ (x + yi)2 2 2 = 5
− +12i ⇔ x − y + 2xy = 5 − +12i x = 2 2  =  2 2 x 4 x − y = 5  −   y = 3 ⇔  ⇔  6 ⇔  2xy = 12 y = x = 2 −  x   y = 3 − z = 2 + 3i
Do đó phương trình có hai nghiệm là z = 2 − − 3i Ta chọn đáp án A.
Câu 11. Trong , nghiệm của phương trình 2
z + 4z + 5 = 0 là: z = 2 − − i
A. z = 2 − i B. z = 2 − − i C. D. z = 2 − + i z = 2 − + i Hướng dẫn giải: 2
z + 4z + 5 = 0 ⇔ (z + 2)2 = 1
− ⇔ z + 2 = ±i ⇔ z = 2 − ± i Ta chọn đáp án A.
Câu 12. Trong , nghiệm của phương trình 2
z − 2z +1− 2i = 0 là z = 2 − iz = i − 2 z = 2 + iz = 2 + i A. 1  B. 1 C. 1 D. 1 z = −     i z = −i z =  2 − i z = −i 2  2 2  2 Hướng dẫn giải: Trang 10/21
z =1+1+ i = 2 + i 2
z − 2z +1− 2i = 0 ⇔ (z − )2
1 = 2i ⇔ z −1 = ±(1+ i) ⇔ 
z = 1−1− i = i − Ta chọn đáp án A.
Câu 13. Cho z = 3+ 4i . Tìm căn bậc hai của z . A. 2
− + i và 2 − i
B. 2 + i và 2 − i C. 2 + i và 2 − − i
D. 3 + 2i và − 3 − 2i Hướng dẫn giải:
Giả sử w = x + yi (x, y ∈) là một căn bậc hai của số phức z = 3+ 4i . Ta có: x = 2 2  =  2 2 x 4
x − y = 3  y = 1 2
w = z ⇔(x + yi)2 = 3+ 4i ⇔  ⇔  2 ⇔ 2xy 4 y  = = x = 2 −  x  y = 1 − z = 2 + i
Do đó z có hai căn bậc hai là z = 2 − − i Ta chọn đáp án A.
Câu 14. Cho z =1−i . Tìm căn bậc hai dạng lượng giác của z : π π  π π A.  − − 4 2 cos isin  +   và 4 7 7 2 cos +  isin 8 8      8 8  π π B. 2 cos isin  +  4 4    π π C.  − − 2 cos isin  +  4 4    π π π π D.  − − 4 2 cos isin  +   và 4 2 cos +  isin 8 8      8 8  Hướng dẫn giải:   π   π 
Ta có z =1− i = 2 cos − +  i sin −  có các căn bậc hai là:  4  4       π π   π − π − 4 7 7 4 w 2 cos isin ; w 2 cos isin  = + = + 1 2 8 8 8 8      Ta chọn đáp án A.
Câu 15. Trong , phương trình ( 2z + i)( 2z − 2iz − ) 1 = 0 có nghiệm là:
C. 3 (1− 2i) ; 3 ( 2 − + i) ; 4i B. 1− i ; 1 − + i ; 2i 2 2 2 (1− i) A. , 2 ( 1 − + i) , i D. 1− 2i ; 15 − i ; 3i 2 2 Hướng dẫn giải: 2  ± (1− i) ( z = i − z = 2 z + i)( 2 z − 2iz − ) 1 = 0 ⇔  ⇔ (z i)2 2 0  − = z = i Ta chọn đáp án A.
Câu 16. Trong , phương trình 4 2
z − 6z + 25 = 0 có nghiệm là: A. 8 ± ;± 5i B. 3; ± ± 4i C. 5 ± ;± 2i
D. ±(2 + i);± (2 −i) Hướng dẫn giải: Trang 11/21 z = ± 2 + i 4 2
z − 6z + 25 = 0 ⇔ ( 2 z − 3)2 ( ) 2 2 +16 = 0 ⇔ z − 3 = 4
± i ⇔ z = 3± 4i ⇔ z = ±  (2−i) Ta chọn đáp án A.
Câu 17. Trong , phương trình 1
z + = 2i có nghiệm là: z A. (1± 3)i B. (5± 2)i C. (1± 2)i D. (2± 5)i Hướng dẫn giải: 1 z ≠ 0 z ≠ 0  z ≠ 0 z ≠ 0 z 2i  + = ⇔  ⇔  ⇔  ⇔  ⇔ z = 1± 2 i 2 z
z − 2iz +1 = 0 (  z − i
)2 + 2 = 0 z −i = ± 2i z =  (± 2 + ) ( ) 1 i Ta chọn đáp án A.
Câu 18. Trong , phương trình 3
z +1 = 0 có nghiệm là: A. ± ± ± ± 1 − ; 2 i 3 B. 1 − ; 1 i 3 C. 1 − ; 1 i 5 D. 1 − ; 5 i 3 2 2 4 4 Hướng dẫn giải: z = 1 − z = 1 − 3 z 1 0 (z ) 1 ( 2 z z ) 1 0  + = ⇔ + − + = ⇔  ⇔ 2 1±  3
z − z +1 = 0 z =  2 Ta chọn đáp án A
Câu 19. Trong , phương trình 4
z −1 = 0 có nghiệm là: A 1; ± ± 2i B. 2; ± ± 2i C. 3; ± ± 4i D. 1; ± ± i Hướng dẫn giải: z =1 z =1 4 z 1 0 (z ) 1 (z ) 1 ( 2 z )1 0 z 1  − = ⇔ − + + = ⇔ = − ⇔ z = 1 −    2 z +1 = 0 z = ±i Ta chọn đáp án A.
Câu 20. Trong , căn bậc hai của 121 − là: A. 11 − i B. 11i C. 11 − D. 11i và 11 − i Hướng dẫn giải: Ta có: z = − ⇔ z = ( i)2 121
11 . Do đó z có hai căn bậc hai là z =11i; z = 11 − i Ta chọn đáp án A.
Câu 21. Phương trình 2
8z − 4z +1 = 0 có nghiệm là: A 1 1 5 1
z = + i; z = − i B. 1 1 1 3
z = + i; z = − i 1 2 4 4 4 4 1 2 4 4 4 4 C. 1 1 1 1
z = + i; z = − i D. 2 1 1 1
z = + i; z = − i 1 2 4 4 4 4 1 2 4 4 4 4 Hướng dẫn giải: 2 2 2i 1 ' ' 4 8 4 0 i b ac z ± ∆ = − = − = − < ⇒ = = ± 1,2 8 4 4 Ta chọn đáp án A.
Câu 22. Biết z ; z là hai nghiệm của phương trình 2
2z + 3z + 3 = 0 . Khi đó giá trị của 2 2 z + z là: 1 2 1 2 A. 9 B.9 C. 4 D. 9 − 4 4 Hướng dẫn giải: Trang 12/21 b 3
S = z + z = − = − 1 2 Theo Viet, ta có:  a 2   c 3
P = z .z = = 1 2  a 2 2 2 2 3 9
z + z = S − 2P = − 3 = − 1 2 4 4 Ta chọn đáp án A.
Câu 23. Phương trình 2
z + az + b = 0 có một nghiệm phức là z =1+ 2i . Tổng 2 số a và b bằng: A. 0 B. 3 − C. 3 D. 4 − Hướng dẫn giải:
Vì z =1+ 2i là một nghiệm của phương trình 2
z + az + b = 0 nên ta có: ( + i)2
1 2 + a(1+ 2i) + b = 0 ⇔ a + b + 2ai = 3− 4i ⇔ a + b = 3 Ta chọn đáp án A.
Câu 24. Gọi z ; z là hai nghiệm phức của phương trình 2
z − 4z + 5 = 0 . Khi đó phần thực của 2 2 z + z 1 2 1 2 là: A. 5 B. 6 C. 4 D. 7 Hướng dẫn giải:b
S = z + z = − = 4  1 2 Theo Viet, ta có:  a   = . c P z z = = 5 1 2  a 2 2 2
z + z = S − 2P =16 − 2.5 = 6 1 2 Ta chọn đáp án A.
Câu 25. Gọi z ; z là hai nghiệm phức của phương trình 2
z + 2z + 4 = 0 . Khi đó 2 2 A |
= z | + | z | có giá 1 2 1 2 trị là A. 7 − B. – 8 C. 4 − D. 8 Hướng dẫn giải: 2
z + 2z + 4 = 0 ⇔ (z + )2 1 + 3 = 0 ⇔ z = 1 − ± 3i 2 2 ⇒ A |
= z | + | z | = 8 1 2 Ta chọn đáp án A.
Câu 26. Phương trình 3
z = 8 có bao nhiêu nghiệm phức với phần ảo âm? A. 1 B. 2 C. 3 D. 0 Hướng dẫn giải: 3
z = ⇔ (z − )( 2 8
2 z + 2z + 4) = 0 ⇔ (z − 2)(z + )2 1 + 3 = 0   z = 2
⇔ z = 1−± 3i
Do đó phương trình chỉ có một nghiệm phức có phần ảo âm. Ta chọn đáp án A.
Câu 27. Biết z , z là hai nghiệm của phương trình 2
2z + 3z + 3 = 0 . Khi đó giá trị của 2 2 z + z là: 1 2 1 2 A. 4 B. 9 C. 9 D. 9 − 4 4 Hướng dẫn giải: Trang 13/21 b 3
S = z + z = − = − 1 2
Áp dụng định lý Viet, ta có:  a 2   c 3 P = z z = = 1 2  a 2 2 2 2 3 9
z + z = S − 2P = − 3 = − 1 2 4 4 Ta chọn đáp án A.
Câu 28. Phương trình sau có mấy nghiệm thực: 2 z + 2z + 2 = 0 A. 0 B. 1 C. 2 D. Vô số nghiệm. Hướng dẫn giải: 2
∆ ' = b' − ac =1− 2 = 1
− < 0 nên phương trình vô nghiệm trên tập số thực. Ta chọn đáp án A.
Câu 29. Tìm các căn bậc hai của 9 − . A. 3 ± i B. 3 C. 3i D. 3 − Hướng dẫn giải: Ta có 2 9 − = 9.i nên 9
− có các căn bậc hai là 3i và 3 − i . Ta chọn đáp án A.
Câu 30. Trong , phương trình 4
z + 4 = 0 có nghiệm là:
A. ±(1− 4i);± (1+ 4i)
B. ±(1− 2i) ; ±(1+ 2i)
C. ±(1−3i);± (1+ 3i)
D. ±(1−i) ; ±(1+ i) Hướng dẫn giải: 2 z = 2iz = ±(1+ i) 4 z + 4 = 0 ⇔  ⇔  2 z = 2 − iz = ±  (1−i) Ta chọn đáp án A.
Câu 31. Giải phương trình 2
z − 2z + 7 = 0 trên tập số phức ta được nghiệm là:
A. z =1± 2 2i
B. z =1± 6i
C. z =1± 2i
D. z =1± 7i Hướng dẫn giải: 2
z − 2z + 7 = 0 ⇔ (z − )2
1 + 6 = 0 ⇔ z =1± 6i Ta chọn đáp án A.
Câu 32. Căn bậc hai của số phức 4 + 6 5i là: A. −(3+ 5i)
B. (3+ 5i) C. ±(3+ 5i) D. 2 Hướng dẫn giải:
Giả sử w là một căn bậc hai của 4 + 6 5i . Ta có: w = +
i ⇔ w = ( + i)2 2 2 4 6 5 3
5 ⇔ w = ±(3+ 5)i. Ta chọn đáp án A.
Câu 33. Gọi z là căn bậc hai có phần ảo âm của 33−56i . Phần thực của z là: A. 6 B. 7 C. 4 D. –4 Hướng dẫn giải:
Ta có: − i = ( − i)2 33 56
7 4 ⇒ z = 7 − 4i
Do đó phần thực của z là 7. Ta chọn đáp án A.
Câu 34. Tập nghiệm trong  của phương trình 3 2
z + z + z +1 = 0 là: A. { i − ;i;1;− } 1 B. { i − ;i } ;1 C. { i − ;− } 1 D. { i − ;i;− } 1 Hướng dẫn giải: Trang 14/21 z = 1 − 3 2
z + z + z +1 = 0 ⇔ (z + ) 1 ( 2 z + ) 1 = 0 ⇔  z = ±i Ta chọn đáp án A.
Câu 35. Trên tập số phức, phương trình bậc hai có hai nghiệm α = 4 + 3i;β = 2 − + i là: A. 2
z + (2 + 4i) z −(11+ 2i) = 0 B. 2
z − (2 + 4i) z −(11+ 2i) = 0 C. 2
z − (2 + 4i) z + (11+ 2i) = 0 D. 2
z + (2 + 4i) z + (11+ 2i) = 0 Hướng dẫn giải:
S = α + β = 2 + 4i
Áp dụng định lý Viet, ta có:  . P = α.β = 11 − − 2i
Do đó α, β là hai nghiệm của phương trình: 2 2
z − Sz + P = 0 ⇔ z − (2 + 4i) z − (11+ 2i) = 0 Ta chọn đáp án A.
Câu 36. Có bao nhiêu số phức thỏa mãn điều kiện 2 2 z | = z | +z ? A. 3 B. 0 C. 1 D. 2 Hướng dẫn giải:
Gọi z = a + bi(a,b∈) là số phức thỏa mãn điều kiện trên. Ta có: 2 2 z |
= z | +z ⇔ (a + bi)2 2 2 2
= a + b + a − bi ⇔ a + 2b − bi − 2abi = 0 ⇔ ( 2
a + 2b ) + ( b
− − 2ab)i = 0  = = 2 a b 0 a + 2b = 0  2   1 a + 2b = 0 b = 0  a = − ⇔  ⇔  ⇔    2 b  + 2ab = 0  1  a   = − 1  2  b  = ±   2
Vậy có 3 số phức thỏa mãn yêu cầu bài toán. Ta chọn đáp án A.
Câu 37. Phương trình ( + i) 2 2
z + az + b = 0(a,b∈) có hai nghiệm là 3+ i và 1− 2i . Khi đó a = ? A. 9 − − 2i B. 15 + 5i C. 9 + 2i D. 15 − 5i Hướng dẫn giải: Theo Viet, ta có: a
S = z + z = −
= 4 − i ⇔ a = i − 4 i + 2 ⇔ a = 9 − − 2i 1 2 ( )( ) 2 + i Ta chọn đáp án A.
Câu 38. Cho số phức z thỏa mãn 2
z − 6z +13 = 0 . Tính 6 z + z + i A. 17 và 4 B. 17 và 5 C. 17 và 3 D. 17 và 2 Hướng dẫn giải: 2
z − 6z +13 = 0 ⇔ (z −3)2 + 4 = 0 ⇔ z = 3± 2i
+) Nếu z = 3+ 2i : 6 6 9 +15i 18 − + 72 + = 3+ 2 i z i + = = = 1 − + 4i z + i 3+ 3i 3+ 3i 18 6 ⇒ z + = 1 − + 4i = 17 z + i
+) Nếu z = 3− 2i : 6 6 13− 9i 30 − 40 + = 3− 2 i z i + = = = 3− 4i z + i 3− i 3− i 10 6 ⇒ z + = 3− 4i = 5 z + i Trang 15/21 Ta chọn đáp án A.
Câu 39. Gọi z , z là các nghiệm phức của phương trình 2
z + (1− 3i) z − 2(1+ i) = 0 . Khi đó 1 2 2 2
w = z + z − 3z z là số phức có môđun là: 1 2 1 2 A. 2 B. 13 C. 2 13 D. 20 Hướng dẫn giải: b
S = z + z = − = 1 − + 3i  1 2 Theo Viet, ta có:  a   = . c P z z = = 2 − 1+ i 1 2 ( )  a 2 2 2
w = z + z − 3z z = S − 5P = 1
− + 3i +10 1+ i = 2 + 4i 1 2 1 2 ( )2 ( ) | ⇒ w |= 4 +16 = 20 Ta chọn đáp án A.
Câu 40. Số nghiệm của phương trình với ẩn số phức z: 2 2 4z + 8 | z | 3 − = 0 là: A. 3 B. 2 C. 4 D. 1 Hướng dẫn giải:
Gọi z = a + bi(a,b∈) là nghiệm của phương trình. Ta có:
4(a + bi)2 + 8( 2 2
a + b ) −3 = 0 ⇔ 4( 2 2
a − b + 2abi) +8( 2 2
a + b ) −3 = 0 2 2
⇔ 12a + 4b + 8abi − 3 = 0 2 2 2 2 12  a + 4b = 3 4a + b =1 ⇒  ⇔  ab = 0 ab = 0 a = 0 (
 2a + b)2 =1  b = 1 ± 2 2
4a + 4ab + b =1   ⇒  ⇔ a = 0 ⇔  1 ab = 0   a = ± b 0  = 4  b = 0
Vậy phương trình có 4 nghiệm phức Ta chọn đáp án A.
Câu 41. Tìm số phức z để 2
z − z = z .
A z = 0; z =1− i
B. z = 0; z =1+ i
C. z = 0; z =1+ i; z =1− i
D. z =1+ i; z =1− i Hướng dẫn giải:
Gọi z = a + bi(a,b∈) là số phức thỏa mãn đẳng thức trên. Ta có: a =1 2 2 a − b = 0  2 2 a − b = 0  b  = 1 ± 2
z − z = z ⇔ a + bi − a + bi = (a + bi)2 ⇔  ⇔ a =1 ⇔ 2ab 2b  =  a = 0 b = 0   b   = 0 z = 0  ⇒ z =1+ i  z =1−  i Ta chọn đáp án A.
Câu 42. Với mọi số ảo z, số 2 2 z + | z | là:
A. Số thực âm B. Số 0 C. Số thực dương D. Số ảo khác 0 Hướng dẫn giải: Trang 16/21
Do z là số ảo nên z có dạng: z = bi(b∈) . Ta có: 2 2
z + z = (bi)2 2 2 2 | | + b = b − + b = 0 . Ta chọn đáp án A.
Câu 43. Trong trường số phức phương trình 3
z +1 = 0 có mấy nghiệm? A. 2 B. 3 C. 1 D. 0 Hướng dẫn giải: z =1 3 z 1 0 (z ) 1 ( 2 z z ) 1 0  + = ⇔ + − + = ⇔ 1±  3i z =  2
Vậy phương trình có ba nghiệm trong trường số phức. Ta chọn đáp án A.
Câu 44. Giá trị của các số thực b, c để phương trình 2
z + bz + c = 0 nhận số phức z =1+ i làm một nghiệm là: b  = 2 b  = 2 − b  = 2 − b  = 2 A. B. C. D.  c = 2 − c = 2 − c = 2 c = 2 Hướng dẫn giải:
Do z =1+ i là một nghiệm của 2
z + bz + c = 0 nên ta có: (  + =  = −
+ i)2 + b( + i) b c 0 b 2 1 1
+ c = 0 ⇔ b + c + bi + 2i = 0 ⇒  ⇔ b  2  = − c = 2 Ta chọn đáp án A.
Câu 45. Trên tập hợp số phức, phương trình 2
z + 7z +15 = 0 có hai nghiệm z , z . Giá trị biểu thức 1 2
z + z + z z là: 1 2 1 2 A. –7 B. 8 C. 15 D. 22 Hướng dẫn giải: b
S = z + z = − = 7 −  1 2 Theo Viet, ta có:  a
⇒ z + z + z z = S + P = 7 − +15 = 8 c 1 2 1 2 P = z z = =15 1 2  a Ta chọn đáp án A.
Câu 46. Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn 3 z =18 + 26i x = 3 x = 3 x = 3 x = 3 − A.B.C.D.  y = 1 ± y = 1 − y = 1 y = 1 ± Hướng dẫn giải: 3
z =18 + 26i ⇔ (x + yi)3 3 2 2 3
= 18 + 26i ⇔ x + 3x yi − 3xy − y i =18 + 26i 3 2
⇔ (x − 3xy ) + ( 2 3
3x y − y )i =18+ 26i
x −3xy =18 x  ( 2 2 3 2 x − 3y ) =18 ⇒  ⇔  2 3 3
 x y − y = 26 y  ( 2 2 3x − y ) = 26 Do x, y nguyên nên x = 3 x = 3   2 2  − =  = ± x( x 3y 6 y 1 2 2
x − 3y ) =18 ⇔ ⇔  x = 6 x = 6     (loai) 2 2
x −3y = 3 y = ± 11 Mà y ( 2 2
3x − y ) = 26 ⇒ x = 3; y =1 Trang 17/21 Ta chọn đáp án A.
Câu 47. Trên tập số phức, cho phương trình sau: (z + i)4 2
+ 4z = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực  .
2. Phương trình vô nghiệm trên trường số phức  .
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực A. 0 B. 1 C. 3 D. 2 Hướng dẫn giải: (z +i)4 2
+ 4z = 0 ⇔ (z + i)4 2 = 4 − z (z +i)2 2 = 2izz −1 = 0 z = 1 ± z = 1 ± ⇔  ⇔  ⇔  ⇔  (z +i) = 2 − iz
z + 4iz −1 = 0 (z + 2i)2 2 2 + 3 = 0 z =  ( 2−± 3)i
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng. Ta chọn đáp án A.
Câu 48. Phương trình 6 3
z − 9z + 8 = 0 có bao nhiêu nghiệm trên tập số phức? A. 3 B. 4 C. 2 D. 6 Hướng dẫn giải: Ta có: 6 3
z − 9z + 8 = 0 ⇔ (z − ) 1 (z − 2)( 2 z + z + ) 1 ( 2 z + 2z + 4) = 0 z =1 z = 2  ⇔  3 z = ± 1 −    1 − ± i 3 Ta chọn đáp án A.
Câu 49. Giả sử z , z là hai nghiệm của phương trình 2
z − 2z + 5 = 0 và A, B là các điểm biểu diễn của 1 2
z , z . Tọa độ trung điểm I của đoạn thẳng AB là: 1 2 A. I (1; ) 1 B. I ( 1; − 0) C. I (0; ) 1 D. I (1;0) Hướng dẫn giải: 2
z − 2z + 5 = 0 ⇔ (z − )2
1 + 4 = 0 ⇔ z =1± 2i
⇒ A(1;2); B(1; 2 − )
Do đó tọa độ trung điểm I của đoạn thẳng AB là I (1;0) . Ta chọn đáp án A.
Câu 50. Cho phương trình 2
z + mz − 6i = 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5
thì m có dạng m = ±(a + bi)(a,b∈) . Giá trị a + 2b là: A. 0 B. 1 C. 2 − D. 1 − Hướng dẫn giải:
Gọi z , z là hai nghiệm của phương trình đã cho 1 2  b
S = z + z = − = −m  1 2 Theo Viet, ta có:  a   = . c P z z = = 6 − i 1 2  a
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có: Trang 18/21 2 2 2 2 2 2
z + z = S − 2P = m +12i = 5 ⇔ m = 5 −12i ⇔ m = 3− 2i 1 2 ( )2
⇒ m = ±(3− 2i) ⇒ a = 3;b = 2
− ⇒ a + 2b = 3− 4 = 1 − Ta chọn đáp án A. 4 Câu 51.  −
Gọi z , z , z , z là các nghiệm phức của phương trình z 1  =   1. Giá trị của 1 2 2 4  2z − i P = ( 2 z + ) 1 ( 2 z + ) 1 ( 2 z + ) 1 ( 2 z +1 là: 1 2 3 4 ) A. 17 B. 17 C. 9 D. 17i 8 9 17 9 Hướng dẫn giải: Với mọi i z ≠ , ta có: 2 z = 1 − + iz 1  − 1+ i = ±  4 1 z =  z 1  −  2z − i  3 =   1 ⇔  ⇔  2z − i   z 1  − 2 + 4i = ±iz = 2z −i  5 z = 0 2 2  +   +  ⇒ P = ( 1 i 2 4i 2 z + ) 1 ( 2 z + ) 1 ( 2 z + ) 1 ( 2 z +1 =  1 − + i +1  +1  +1 1 2 3 4 ) ( )2 ( ) ( )    9   25     
= ( − i) 9 + 2i 13+16i 425 17 1 2 . = = 9 25 9.25 9 Ta chọn đáp án A.
Câu 52. Trong tập số phức, giá trị của m để phương trình bậc hai 2
z + mz + i = 0 có tổng bình phương hai nghiệm bằng 4 − i là: A. ±(1−i) B. (1−i) C. ±(1+ i) D. 1 − − i Hướng dẫn giải:
Gọi z , z là hai nghiệm của phương trình. 1 2  b
S = z + z = − = −m  1 2 Theo Viet, ta có:  a  2 2 2 2
⇒ z + z = S − 2P = m − 2i 1 2  = . c P z z = = i 1 2  a Ta có: 2 2 2 m − 2i = 4 − i ⇔ m = 2
− i ⇔ m = (1− i)2 ⇔ m = ±(1− i) Ta chọn đáp án A.
Câu 53. Cho phương trình 2
z − mz + 2m −1 = 0 trong đó m là tham số phức. Giá trị của m để phương
trình có hai nghiệm z , z thỏa mãn 2 2 z + z = 10 − là: 1 2 1 2
A. m = 2 ± 2 2i
B. m = 2 + 2 2i
C. m = 2 − 2 2i D. m = 2 − − 2 2i Hướng dẫn giải: b
S = z + z = − = m  1 2 Theo Viet, ta có:  a   = . c
P z z = = 2m −1 1 2  a 2 2 2 2 z + z = 10
− ⇔ S − 2P = 10
− ⇔ m − 2(2m − ) 2 1 = 10
− ⇔ m − 4m +12 = 0 1 2
⇔ (m − 2)2 + 8 = 0 ⇔ m = 2 ± 2 2i Trang 19/21 Ta chọn đáp án A.
Câu 54. Gọi z , z là hai nghiệm của phương trình 2
z + 2z + 8 = 0 , trong đó z có phần ảo dương. Giá 1 2 1
trị của số phức w = (2z + z z là: 1 2 ) 1
A.12 + 6i B. 10 C. 8 D. 12 − 6i Hướng dẫn giải: z = 1 − + 7i 2
z + 2z + 8 = 0 ⇔ (z + )2 1 1 + 7 = 0 ⇔ z = 1 − ± 7i ⇒  z =1− 7i 2
w = (2z + z z = 2 1
− + 7i +1− 7i 1 − − 7i = 1 − + 7i 1 − − 7i =1+ 7 = 8 1 2 ) 1  ( )  ( ) ( )( )
Câu 55. Tổng bình phương các nghiệm của phương trình 4
z −1 = 0 trên tập số phức là bao nhiêu? A. 3 B. 1 C. 2 D. 0 Hướng dẫn giải: z = 1 ± 4 z −1 = 0 ⇔  z = ±i
Do đó tổng bình phương các nghiệm của phương trình là 1−1 = 0 Ta chọn đáp án A.
Câu 56. Gọi z , z là hai nghiệm của phương trình 2
z − 2z + 6 = 0. Trong đó z có phần ảo âm. Giá trị 1 2 1 biểu thức M |
= z | + | 3z − z | là: 1 1 2 A. 6 − 2 21 B. 6 + 2 21 C. 6 + 4 21 D. 6 − 4 21 Hướng dẫn giải: 2
z − 2z + 6 = 0 ⇔ (z − )2
1 + 5 = 0 ⇔ z =1± 5i
⇒ z =1− 5i; z =1+ 5i 1 2 ⇒ M |
= z | + | 3z − z |= 1− 5i + 2 − 4 5i = 6 + 84 = 6 + 2 21 1 1 2 Ta chọn đáp án A.
Câu 57. Phương trình 4 2
x + 2x − 24x + 72 = 0 trên tập số phức có các nghiệm là:
A. 2 ± i 2 hoặc 2 − ± 2i 2
B. 2 ± i 2 hoặc 1± 2i 2
C. 1± 2i 2 hoặc 2 − ± 2i 2 D. 1 − ± 2i 2 hoặc 2 − ± 2i 2 Hướng dẫn giải: 4 2
x + 2x − 24x + 72 = 0 ⇔ ( 2 x − 4x + 6)( 2 x + 4x +12) = 0
x − 4x + 6 = 0 (x − 2)2 2 + 2 = 0 x = 2 ± 2i ⇔  ⇔  ⇔  2
x + 4x +12 = 0
(x + 2)2 +8 = 0 x = 2 − ± 2 2i Ta chọn đáp án A.
Câu 58. Gọi z , z là các nghiệm phức của phương trình 2
z + 3z + 7 = 0 . Khi đó 4 4
A = z + z có giá trị 1 2 1 2 là: A. 23 B. 23 C. 13 D. 13 Hướng dẫn giải: b
S = z + z = − = − 3  1 2 Theo Viet, ta có:  a   = . c P z z = = 7 1 2  a 4 4
A = z + z = ( 2 S − 2P)2 2
− 2P = 3− 2.7 − 2.49 = 23 1 2 ( )2 Ta chọn đáp án A. Trang 20/21
Document Outline

  • DS_C4_PHUONG TRINH TREN TAP SO PHUC
    • CHỦ ĐỀ 2. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC TRÊN TẬP SỐ PHỨC
      • A. KIẾN THỨC CƠ BẢN
      • B. KỸ NĂNG CƠ BẢN
      • C. KỸ NĂNG SỬ DỤNG MÁY TÍNH
      • D. BÀI TẬP TRẮC NGHIỆM
      • E. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM