Tóm tắt lý thuyết và bài tập trắc nghiệm tọa độ trong không gian Toán 12

Tóm tắt lý thuyết và bài tập trắc nghiệm tọa độ trong không gian Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

51 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Phương pháp tọa độ trong không gian

Môn: Toán 12

Thông tin:

22 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Trang 1/22
CHỦ ĐỀ 1. TỌA ĐỘ TRONG KHÔNG GIAN
A. LÝ THUYẾT
1. Hệ trục tọa độ trong không gian
Trong không gian, xét ba trục tọa độ
,,Ox Oy Oz
vuông góc với nhau từng đôi một và chung một
điểm gốc O. Gọi
,,i jk

là các vectơ đơn vị, tương ứng trên các trục
,,Ox Oy Oz
. Hệ ba trục như vậy
gọi là hệ trục tọa độ vuông góc trong không gian.
Chú ý:
222
1i jk
= = =

và
. . .0i j ik k j= = =
 
.
2. Tọa độ của vectơ
a) Định nghĩa:
( )
;;
u x y z u xi y j zk= ⇔= + +

b) Tính chất: Cho
1 2 3 123
( ; ; ), ( ; ; ),a aa a b bbb k= = ∈

•
1 12 23 3
(; ; )
a b a ba ba b±= ± ± ±
•
•
11
22
33
ab
ab a b
ab
=
=⇔=
=

•
0 (0; 0; 0), (1;0;0), (0;1;0), (0;0;1)i jk= = = =

•
a
cùng phương
( 0)bb≠
⇔
()a kb k= ∈

11
3
12
2 2 123
123
33
, ( , , 0)
a kb
a
aa
a kb b b b
bbb
a kb
=
⇔ = ⇔== ≠
=
•
11 2 2 3 3
.. . .ab a b a b a b=++
•
11 2 2 33
0a b ab a b ab⊥⇔ + + =

•
2 222
1 23
a aaa=++
•
222
122
a aaa
= ++
•
11 2 2 3 3
222222
1 2 31 23
.
cos( , )
.
.
ab ab ab
ab
ab
ab
aaabbb
++
= =
++ ++
(với
,0ab≠
)
3. Tọa độ của điểm
a) Định nghĩa:
(; ; ) . . .M x y z OM x i y j z k⇔ =++

(x : hoành độ, y : tung độ, z : cao độ)
Chú ý:
•
(
) ( )
( )
0; 0; 0
M Oxy z M Oyz x M Oxz y∈⇔=∈⇔=∈⇔=
•
0; 0; 0M Ox y z M Oy x z M Oz x y∈ ⇔== ∈ ⇔== ∈ ⇔==
.
b) Tính chất: Cho
(; ; ), (; ; )
A AA B BB
Axyz Bxyz
•
(; ;)
B A B AB A
AB x x y y z z=−−−

•
2 22
( )( )( )
BA B A BA
AB x x y y z z= − +− +−
• Toạ độ trung điểm
M
của đoạn thẳng
AB
:
;;
222
A B A BA B
x xy yz z
M
+++



• Toạ độ trọng tâm
G
của tam giác
ABC
:
;;
333
A B C A B CA B C
xxxyyyzzz
G
++ ++ ++



• Toạ độ trọng tâm
G
của tứ diện
ABCD
:
;;
444
A B C D A B C DA B C C
xxxxyyyyzzzz
G
+++ +++ +++



4. Tích có hướng của hai vectơ
a) Định nghĩa: Trong không gian
Oxyz
cho hai vectơ
123
(; ; )a aa a=
,
123
(; ; )
b bb b=
. Tích có hướng
của hai vectơ
a
và
,b
kí hiệu là
,ab



, được xác định bởi
Trang 2/22
( )
23 31
12
23 32 31 13 12 21
23 31
12
, ;; ; ;
aa aa
aa
a b ab ab ab ab ab ab
bb bb
bb


= =−−−



Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.
b) Tính chất:
•
[, ] ; [, ]ab a ab b⊥⊥
 
•
,,a b ba

= −


•
,; ,; ,
i j k jk i ki j


= = =




•
(
)
[ , ] . .sin ,ab a b ab=



(Chương trình nâng cao)
•
,ab

cùng phương
[, ] 0ab⇔=

(chứng minh 3 điểm thẳng hàng)
c) Ứng dụng của tích có hướng: (Chương trình nâng cao)
• Điều kiện đồng phẳng của ba vectơ:
,ab

và
c
đồng phẳng ⇔
[ , ]. 0abc=

• Diện tích hình bình hành
ABCD
:
,
ABCD
S AB AD

=

 
•
Diện tích tam giác
ABC
:
1
,
2
ABC
S AB AC
∆

=

 
•
Thể tích khối hộp
ABCDA B C D
′′′′
:
.''' '
[ , ].
ABCD A B C D
V AB AD AA
′
=
  
•
Thể tích tứ diện
ABCD
:
1
[ , ].
6
ABCD
V AB AC AD=
  
Chú ý:
– Tích vô hướng của hai vectơ thường sử dụng để chứng minh hai đường thẳng vuông góc, tính
góc giữa hai đường thẳng.
– Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ
diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các
vectơ cùng phương.
[ ]
[ ]
0
0
0
a b ab
a vaø b cuøng phöông a b
a b c ñoàng phaúng a b c
.
,
,, , .
⊥⇔ =
⇔=
⇔=






5. Một vài thao tác sử dụng máy tính bỏ túi (Casio Fx570 Es Plus, Casio Fx570 Vn Plus, Vinacal
570 Es Plus )
Trong không gian
Oxyz
cho bốn điểm
( ) (
) ( ) ( )
;y ; , ; ;z , ; ;z , ; ;z
A AA B BB C CC D DD
Ax z Bx y Cx y Dx y
w 8 1 1 (nhập vectơ
AB

)
q 5 2 2 2 (nhập vectơ
AC

)
q 5 2 3 1 (nhập vectơ
AD

)
C q53q54= (tính
,AB AC


 
)
C q53q54q57q55= (tính
[ , ].AB AC AD
  
)
Cqc(Abs) q53q54q57q55= (tính
[ , ].AB AC AD
  
)
C1a6qc(Abs) q53q54q57q55=
(tính
1
[ , ].
6
ABCD
V AB AC AD=
  
Trang 3/22
B. BÀI TẬP TRẮC NGHIỆM
Câu 1. Gọi
ϕ
là góc giữa hai vectơ
a
và
b
, với
a
và
b
khác
0
, khi đó
cos
ϕ
bằng
A.
.
.
ab
ab


. B.
.
.
ab
ab


. C.
.
.
ab
ab
−


. D.
.
ab
ab
+


.
Câu 2. Gọi
ϕ
là góc giữa hai vectơ
( )
1; 2; 0a =
và
( )
2;0; 1b = −
, khi đó
cos
ϕ
bằng
A. 0. B.
2
5
. C.
2
5
. D.
2
5
−
.
Câu 3. Cho vectơ
( )
1; 3; 4a =
, tìm vectơ
b
cùng phương với vectơ
a
A.
( )
2; 6; 8 .b =−−−
B.
( )
2; 6;8 .b =−−
C.
( )
2;6;8 .b = −
D.
( )
2; 6; 8 .b = −−
Câu 4. Tích vô hướng của hai vectơ
( ) ( )
2; 2;5 , 0;1; 2ab
=−=

trong không gian bằng
A. 10. B. 13. C. 12. D. 14.
Câu 5. Trong không gian cho hai điểm
( )
( )
1; 2; 3 , 0;1;1AB−
, độ dài đoạn
AB
bằng
A.
6.
B.
8.
C.
10.
D.
12.
Câu 6. Trong không gian
Oxyz
, gọi
,,
i jk

là các vectơ đơn vị, khi đó với
( )
;;M xyz
thì
OM

bằng
A.
.xi y j zk−− −

B.
.xi y j zk−−

C.
.x j yi zk
++

D.
.xi y j zk++

Câu 7. Tích có hướng của hai vectơ
123
(; ; )
a aa a=
,
123
(; ; )b bb b=
là một vectơ, kí hiệu
,ab


, được
xác định bằng tọa độ
A.
( )
23 32 31 13 12 21
;; .ab ab ab ab ab a b−−−
B.
( )
23 32 31 13 12 21
;; .ab ab ab ab ab ab+++
C.
( )
23 32 31 13 12 21
;; .a b ab ab ab ab ab−+−
D.
( )
2 2 3 3 3 3 11 11 2 2
;; .
ab ab ab ab ab ab
− −−
Câu 8. Cho các vectơ
( )
123
;;u uuu=
và
( )
123
;;v vvv
=
,
.0uv=

khi và chỉ khi
A.
11 2 2 33
1uv u v uv++=
. B.
11 2 2 3 3
0
uvu v uv
+++++=
.
C.
11 2 2 33
0uv uv uv++=
. D.
12 2 3 31
1uv u v uv++=−
.
Câu 9. Cho vectơ
( )
1; 1; 2a = −
, độ dài vectơ
a
là
A.
6
. B. 2. C.
6−
. D. 4.
Câu 10. Trong không gian
Oxyz
, cho điểm
M
nằm trên trục
Ox
sao cho
M
không trùng với gốc tọa
độ, khi đó tọa độ điểm
M
có dạng
A.
( )
;0;0 , 0Ma a≠
. B.
( )
0; ;0 , 0Mb b≠
. C.
( )
0;0; , 0M cc≠
. D.
( )
;1;1 , 0Ma a
≠
.
Câu 11. Trong không gian
Oxyz
, cho điểm
M
nằm trên mặt phẳng
( )
Oxy
sao cho
M
không trùng với
gốc tọa độ và không nằm trên hai trục
,Ox Oy
, khi đó tọa độ điểm
M
là (
,, 0abc≠
)
A.
( )
0; ; .ba
B.
( )
; ;0 .ab
C.
( )
0;0; .c
D.
( )
;1;1a
Câu 12. Trong không gian
Oxyz
, cho
( )
0; 3; 4a =
và
2
ba=

, khi đó tọa độ vectơ
b
có thể là
A.
( )
0; 3; 4 .
B.
( )
4;0;3 .
C.
( )
2;0;1 .
D.
( )
8; 0; 6 .−−
Câu 13. Trong không gian
Oxyz
cho hai vectơ
u
và
v
, khi đó
,uv



bằng
A.
( )
. .sin , .u v uv

B.
( )
. .cos , .u v uv

C.
( )
. .cos , .uv u v

D.
( )
. .sin , .uv u v

Câu 14. Trong không gian
Oxyz
cho ba vectơ
( ) ( ) ( )
1; 1; 2 , 3; 0; 1 , 2; 5;1abc=− = −=−

, vectơ
mabc=+−

có tọa độ là
A.
( )
6;0; 6−
. B.
( )
6;6;0−
. C.
( )
6; 6; 0−
. D.
(
)
0;6; 6−
.
Trang 4/22
Câu 15. Trong không gian
Oxyz
cho ba điểm
( ) ( ) (
)
1;0; 3 , 2; 4; 1 , 2; 2;0
AB C− −−
. Độ dài các cạnh
,,
AB AC BC
của tam giác
ABC
lần lượt là
A.
21, 13, 37
. B.
11, 14, 37
. C.
21, 14, 37
. D.
21, 13, 35
.
Câu 16. Trong không gian
Oxyz
cho ba điểm
( )
(
) (
)
1;0; 3 , 2; 4; 1 , 2; 2;0
AB C
− −−
. Tọa độ trọng tâm
G
của tam giác
ABC
là
A.
52 4
;;
33 3

−


. B.
524
;;
333



. C.
( )
5;2;4
. D.
5
;1; 2
2

−


.
Câu 17. Trong không gian
Oxyz
cho ba điểm
( ) ( ) ( )
1; 2; 0 , 1;1; 3 , 0; 2; 5
AB C−−
. Để 4 điểm
,,,ABC D
đồng phẳng thì tọa độ điểm
D
là
A.
( )
2; 5; 0D −
. B.
( )
1; 2; 3D
. C.
(
)
1; 1; 6
D
−
. D.
( )
0;0; 2D
.
Câu 18. Trong không gian
Oxyz
, cho ba vecto
123 201 101
(;;), ( ;;), ( ;;)ab c
= =−=−

. Tìm tọa độ của
vectơ
23nab c i=++ −

A.
( )
6; 2; 6n =
. B.
( )
6; 2; 6n = −
. C.
( )
0; 2; 6n =
. D.
( )
6; 2; 6n = −
.
Câu 19. Trong không gian
Oxyz
, cho tam giác
ABC
có
(1;0; 2), ( 2;1;3), (3;2; 4)AB C−
. Tìm tọa độ
trọng tâm G của tam giác
ABC
A.
2
;1; 3
3
G



. B.
(
)
2;3;9G
. C.
( )
6;0; 24G −
. D.
1
2; ;3
3
G



.
Câu 20. Cho 3 điểm
( ) ( ) ( )
2;0;0 , 0; 3;0 , 0;0;4 .MN P−
Nếu
MNPQ
là hình bình hành thì tọa độ của
điểm
Q
là
A.
( )
Q 2; 3; 4−−
B.
( )
2; 3; 4Q
C.
( )
3;4;2Q
D.
( )
Q 2;3;4−−−
Câu 21. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) ( ) ( )
1;1; 1 , 2; 3; 4 , 7; 7; 5MN P
. Để tứ giác
MNPQ
là hình bình hành thì tọa độ điểm
Q
là
A.
( )
6; 5; 2Q −
. B.
( )
6; 5; 2Q
. C.
( )
6; 5; 2Q −
. D.
( )
6;5;2Q −−−
.
Câu 22. Cho 3 điểm
( ) ( ) ( )
1; 2; 0 , 1; 0; 1 , 0; 1; 2 .AB C−−
Tam giác
ABC
là
A. tam giác có ba góc nhọn. B. tam giác cân đỉnh
A
.
C. tam giác vuông đỉnh
A
. D. tam giác đều.
Câu 23. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) (
) ( )
1; 2; 2 , 0;1;3 , 3; 4; 0
A BC−−
. Để tứ giác
ABCD
là hình bình hành thì tọa độ điểm
D
là
A.
(
)
4; 5; 1D
−−
. B.
(
)
4; 5; 1
D −
. C.
( )
4;5;1D −−−
. D.
( )
4; 5;1D −
.
Câu 24. Cho hai vectơ
a
và
b
tạo với nhau góc
0
60
và
2; 4
ab= =

. Khi đó
ab+

bằng
A.
8 3 20.+
B.
2 7.
C.
2 5.
D.
2
.
Câu 25. Cho điểm
( )
1; 2; 3M −
, khoảng cách từ điểm
M
đến mặt phẳng
( )
Oxy
bằng
A. 2. B.
3−
. C. 1. D. 3.
Câu 26. Cho điểm
( )
2; 5; 0M −
, hình chiếu vuông góc của điểm
M
trên trục
Oy
là điểm
A.
(
)
2; 5; 0M
′
. B.
( )
0; 5;0M
′
−
. C.
( )
0; 5; 0M
′
. D.
( )
2;0;0M
′
−
.
Câu 27. Cho điểm
( )
1; 2; 3M −
, hình chiếu vuông góc của điểm
M
trên mặt phẳng
( )
Oxy
là điểm
A.
( )
1; 2; 0M
′
. B.
( )
1; 0; 3M
′
−
. C.
( )
0; 2; 3M
′
−
. D.
( )
1; 2; 3M
′
.
Câu 28. Cho điểm
( )
2; 5;1M
−
, khoảng cách từ điểm
M
đến trục
Ox
bằng
A.
29
. B.
5
. C. 2. D.
26
.
Câu 29. Cho hình chóp tam giác
.S ABC
với
I
là trọng tâm của đáy
ABC
. Đẳng thức nào sau đây là
đẳng thức đúng
Trang 5/22
A.
.
IA IB IC
= +
  
B.
0.IA IB CI++=
  
C.
0.
IA BI IC++=
  
D.
0.
IA IB IC++ =
  
Câu 30. Trong không gian
Oxyz
, cho 3 vectơ
( )
1;1; 0a
→
= −
;
( )
1;1; 0b
→
=
;
(
)
1;1; 1c
→
=
. Trong các mệnh
đề sau, mệnh đề nào sai:
A.
.
bc⊥

B.
2.a =

C.
3.
c
=

D.
.ab⊥

Câu 31. Cho điểm
(
)
3; 2; 1M −
, điểm đối xứng của
M
qua mặt phẳng
( )
Oxy
là điểm
A.
(
)
3; 2;1
M
′
−
. B.
( )
3;2;1M
′
−−
. C.
( )
3; 2;1M
′
. D.
(
)
3; 2; 0
M
′
.
Câu 32. Cho điểm
( )
3; 2; 1M −
, điểm
( )
;;M abc
′
đối xứng của M qua trục
Oy
, khi đó
abc++
bằng
A.
6.
B.
4.
C.
0.
D.
2.
Câu 33. Cho
( )
1;1; 1u =
và
( )
0;1; mv =
. Để góc giữa hai vectơ
,uv

có số đo bằng
0
45
thì
m
bằng
A.
3±
. B.
23
±
. C.
13±
. D.
3
.
Câu 34. Cho
( ) ( ) ( ) ( )
1; 2; 0 , 3; 3; 2 , 1; 2; 2 , 3;3;1A BC D−−
. Thể tích của tứ diện
ABCD
bằng
A. 5. B. 4. C. 3. D. 6.
Câu 35. Trong không gian
Oxyz
cho tứ diện
ABCD
. Độ dài đường cao vẽ từ
D
của tứ diện
ABCD
cho bởi công thức nào sau đây:
A.
,.
1
.
3
.
AB AC AD
h
AB AC


=


  
 
B.
,.
1
.
3
.
AB AC AD
h
AB AC


=
  
 
C.
,.
..
.
AB AC AD
h
AB AC


=
  
 
D.
,.
.
.
AB AC AD
h
AB AC


=


  
 
Câu 36. Trong không gian tọa độ
Oxyz
, cho bốn điểm
( ) ( ) (
) ( )
1; 2; 0 , 3;3; 2 , 1; 2; 2 , 3;3;1
A BC D−−
. Độ
dài đường cao của tứ diện
ABCD
hạ từ đỉnh
D
xuống mặt phẳng
(
)
ABC
là
A.
9
72
. B.
9
7
. C.
9
2
. D.
9
14
.
Câu 37. Trong không gian
Oxyz
, cho tứ diện
ABCD
có
(1;0; 2), ( 2;1;3), (3; 2; 4), (6;9; 5)AB C D−−
. Tìm
tọa độ trọng tâm G của tứ diện
ABCD
A.
18
9; ; 30
4
G

−−


. B.
( )
8;12; 4G
. C.
14
3; 3;
4
G



. D.
( )
2; 3;1G
.
Câu 38. Trong không gian
Oxyz
, cho hai điểm
(1; 2;1), ( 2; 1; 2)AB−
. Điểm
M
trên trục
Ox
và cách đều
hai điểm
,AB
có tọa độ là
A.
113
;;
222
M



. B.
1
;0;0
2
M



. C.
3
;0;0
2
M



. D.
13
0; ;
22
M



.
Câu 39. Trong không gian
Oxyz
, cho hai điểm
(1; 2; 1), (3; 1; 2)AB−
. Điểm
M
trên trục
Oz
và cách đều
hai điểm
,AB
có tọa độ là
A.
( )
0;0; 4M
. B.
( )
0;0; 4M −
. C.
3
0;0;
2
M



. D.
313
;;
222
M



.
Câu 40. Trong không gian
Oxyz
cho ba điểm
( 1; 2;3), (0;3;1), (4; 2; 2)A BC−−
. Cosin của góc
BAC
là
A.
9
2 35
. B.
9
35
. C.
9
2 35
−
. D.
9
35
−
.
Câu 41. Tọa độ của vecto
n
vuông góc với hai vecto
(2; 1; 2), (3; 2;1)ab=−=−

là
A.
( )
3; 4;1n =
. B.
( )
3; 4; 1n = −
. C.
( )
3; 4; 1n =−−
. D.
( )
3;4;1n = −−
.
Câu 42. Cho
2; 5,ab= =

góc giữa hai vectơ
a
và
b
bằng
2
3
π
,
; 2.u ka b v a b=−=+

Để
u
vuông
góc với
v
thì
k
bằng
Trang 6/22
A.
6
.
45
−
B.
45
.
6
C.
6
.
45
D.
45
.
6
−
Câu 43. Cho
( ) ( )
( )
2; 1;1 , m; 3; 1 , w 1; 2;1uv=− = −=

. Với giá trị nào của m thì ba vectơ trên đồng phẳng
A.
3
8
. B.
3
8
−
. C.
8
3
. D.
8
3
−
.
Câu 44. Cho hai vectơ
( ) ( )
35
1; log 5; , 3; log 3; 4a mb= =

. Với giá trị nào của m thì
ab⊥

A.
1; 1mm
= = −
. B.
1m =
. C.
1m = −
. D.
2; 2mm= = −
.
Câu 45. Trong không gian
Oxyz
cho ba điểm
(2;5;3), (3;7; 4), ( ; ;6)
A B Cxy
. Giá trị của
,xy
để ba điểm
,,ABC
thẳng hàng là
A.
5; 11xy= =
. B.
5; 11xy
=−=
. C.
11; 5xy=−=−
. D.
11; 5xy= =
.
Câu 46. Trong không gian
Oxyz
cho ba điểm
(1;0;0), (0;0;1), (2;1;1)ABC
. Tam giác
ABC
là
A. tam giác vuông tại
A
. B. tam giác cân tại
A
.
C. tam giác vuông cân tại
A
. D. Tam giác đều.
Câu 47. Trong không gian
Oxyz
cho tam giác
ABC
có
(1;0;0), (0;0;1), (2;1;1)ABC
. Tam giác
ABC
có
diện tích bằng
A.
6
. B.
6
3
. C.
6
2
. D.
1
2
.
Câu 48. Ba đỉnh của một hình bình hành có tọa độ là
( ) ( ) ( )
1;1; 1 , 2; 3; 4 , 7; 7; 5
. Diện tích của hình bình
hành đó bằng
A.
2 83
. B.
83
. C.
83
. D.
83
2
.
Câu 49. Cho 3 vecto
( )
1; 2; 1 ;a =
( )
1;1; 2b = −
và
(
)
;3 ; 2c x xx
= +
. Tìm
x
để 3 vectơ
,,
abc

đồng
phẳng
A.
2.
B.
1.
−
C.
2.
−
D.
1.
Câu 50. Trong không gian
Oxyz
cho ba vectơ
( )
3; 2; 4 ,
a = −
( )
5; 1; 6b
→
=
,
( )
3; 0; 2c
→
= −
. Tìm vectơ
x
sao cho vectơ
x
đồng thời vuông góc với
,,abc

A.
( )
1;0;0 .
B.
( )
0;0;1 .
C.
( )
0;1; 0 .
D.
(
)
0;0;0 .
Câu 51. Trong không gian
Oxyz
, cho 2 điểm
(1; 2; 3)B −
,
(7; 4; 2)
C −
. Nếu
E
là điểm thỏa mãn đẳng
thức
2CE EB=
 
thì tọa độ điểm
E
là
A.
88
3; ; .
33

−


B.
88
3; ; .
33



C.
8
3; 3; .
3

−


D.
1
1; 2; .
3



Câu 52. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
(1; 2; 1)A −
,
(2; 1;3)B −
,
( 2; 3; 3)C −
.
Điêm
( )
;;
M abc
la đinh thư tư cua hinh binh hanh
ABCM
, khi đó
222
Pa b c=+−
có giá trị
bằng
A.
43.
. B.
44.
. C.
42.
. D.
45.
Câu 53. Trong không gian với hệ trục tọa độ
Oxyz
cho ba điểm
(1; 2; 1)A −
,
(2; 1;3)B −
,
( 2; 3; 3)C −
. Tìm
tọa độ điêm
D
la chân đương phân giac trong goc
A
cua tam giac
ABC
A.
(0;1;3)D
. B.
(0; 3;1)D
. C.
(0; 3;1)D −
. D.
(0; 3; 1)D −
.
Câu 54. Trong không gian với hệ toạ độ
Oxyz
, cho các điểm
A
( 1; 3; 5)−
,
B( 4; 3; 2)−
,
C(0;2;1)
. Tìm tọa
độ điêm
I
tâm đường tròn ngoại tiếp tam giác
ABC
A.
858
(;;)
333
I
. B.
588
(;;)
333
I
. C.
588
( ; ; ).
333
I −
D.
885
(;;)
333
I
.
Câu 55. Trong không gian
Oxyz
, cho 3 vectơ
( ) ( ) ( )
1;1; 0 , 1;1; 0 , 1;1;1a bc=−= =

. Cho hình hộp
.OABC O A B C
′′′ ′
thỏa mãn điều kiện
, , 'OA a OB b OC c= = =
  

. Thể tích của hình hộp nói trên
bằng:
Trang 7/22
A.
1
3
B. 4 C.
2
3
D. 2
Câu 56. Trong không gian với hệ trục
Oxyz
cho tọa độ 4 điểm
( ) ( )
2; 1;1 , 1; 0; 0 ,AB−
( ) ( )
3;1;0 , 0;2;1CD
. Cho các mệnh đề sau:
1) Độ dài
2
AB =
.
2) Tam giác
BCD
vuông tại
B
.
3) Thể tích của tứ diện
ABCD
bằng
6
.
Các mệnh đề đúng là:
A. 2). B. 3). C. 1); 3). D. 2), 1)
Câu 57. Trong không gian
Oxyz
, cho ba vectơ
( ) ( )
1,1, 0 ; (1,1, 0); 1,1,1a bc=−= =

. Trong các mệnh đề
sau, mệnh đề nào đúng:
A.
( )
6
cos , .
3
bc
=

B.
0.abc++=

A.
,,abc

đồng phẳng. D.
. 1.ab=

Câu 58. Trong không gian với hệ tọa độ
Oxyz
, cho tư diên
ABCD
, biết
(1; 0;1)A
,
( 1; 1; 2)B −
,
( 1;1; 0)C −
,
(2;1;2)
D −−
. Đô dai đương cao
AH
cua tư diên
ABCD
bằng:
A.
2
.
13
B.
1
.
13
C.
13
.
2
D.
3 13
.
13
Câu 59. Cho hình chóp tam giác
.S ABC
với
I
là trọng tâm của đáy
ABC
. Đẳng thức nào sau đây là
đẳng thức đúng
A.
( )
1
.
2
SI SA SB SC= ++
   
B.
( )
1
.
3
SI SA SB SC= ++
   
C.
.SI SA SB SC=++
   
D.
0.SI SA SB SC+++ =
   
Câu 60. Trong không gian
Oxyz
, cho tứ diện
ABCD
có
(1;0;0), (0;1;0), (0;0;1), ( 2;1; 1)ABC D−−
. Thể
tích của tứ diện
ABCD
bằng
A.
3
2
. B.
3
. C.
1
. D.
1
2
.
Câu 61. Cho hình chóp
.S ABC
có
00
, 3 , 60 , 90SA SB a SC a ASB CSB CSA= = = = = =
. Gọi G là trọng
tâm tam giác
ABC
. Khi đó khoảng cách
SG
bằng
A.
15
3
a
. B.
5
3
a
. C.
7
3
a
. D.
3a
.
Câu 62. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) (
) (
)
2;5;1 , 2; 6; 2 , 1; 2; 1AB C−− −
và điểm
( )
;;M mmm
, để
2MB AC−
 
đạt giá trị nhỏ nhất thì
m
bằng
A. 2. B. 3 . C. 1. D. 4.
Câu 63. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) (
) ( )
2;5;1 , 2; 6; 2 , 1; 2; 1AB C−− −
và điểm
( )
;;M mmm
, để
22 2
MA MB MC−−
đạt giá trị lớn nhất thì
m
bằng
A. 3. B. 4. C. 2. D. 1.
Câu 64. Cho hình chóp
.S ABCD
biết
( ) ( ) (
) ( )
2; 2; 6 , 3;1;8 , 1; 0; 7 , 1; 2;3A BC D
− −−
. Gọi
H
là trung
điểm của
,CD
( )
SH ABCD⊥
. Để khối chóp
.S ABCD
có thể tích bằng
27
2
(đvtt) thì có hai
điểm
12
,SS
thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm
I
của
12
SS
A.
( )
0;1;3−−I
. B.
( )
1; 0; 3I
C.
( )
0;1; 3I
. D.
( )
1; 0; 3 .−−I
Câu 65. Trong không gian
Oxyz
, cho hai điểm
(2; 1;7), (4; 5; 2)AB−−
. Đường thẳng
AB
cắt mặt phẳng
()Oyz
tại điểm
M
. Điểm
M
chia đoạn thẳng
AB
theo tỉ số nào
A.
1
2
. B.
2
. C.
1
3
. D.
2
3
.
Trang 8/22
Câu 66. Trong không gian
Oxyz
, cho tứ diện
ABCD
có
(2;1; 1), (3;0;1),C(2; 1;3)AB−−
và
D
thuộc
trục
Oy
. Biết
5
ABCD
V
=
và có hai điểm
( ) ( )
11 2 2
0; ; 0 , 0; ; 0Dy Dy
thỏa mãn yêu cầu bài toán.
Khi đó
12
yy
+
bằng
A.
0.
B.
1
. C.
2
. D.
3
.
Câu 67. Trong không gian
Oxyz
, cho tam giác
ABC
có
( 1;2;4), (3;0; 2),C(1;3;7)AB−−
. Gọi
D
là
chân đường phân giác trong của góc
A
. Tính độ dài
.OD

A.
207
.
3
B.
203
3
C.
201
.
3
D.
205
.
3
Câu 68. Trong không gian với hệ toạ độ
Oxyz
, cho tam giac
ABC
, biêt
(1;1;1)A
,
(5; 1; 2)
B
−
,
(7; 9;1)C
.
Tinh đô dai phân giac trong
AD
cua goc
A
A.
2 74
.
3
B.
3 74
.
2
C.
2 74.
D.
3 74.
Câu 69. Trong không gian với hệ toạ độ
Oxyz
, cho 4 điểm
(2; 4; 1)A −
,
(1; 4; 1)B −
,
(2; 4; 3)C
(2; 2; 1)D
−
. Biết
( )
;;M xyz
, để
22 2 2
MA MB MC MD+++
đạt giá trị nhỏ nhất thì
++xyz
bằng
A.
7.
B.
8.
C.
9.
D.
6.
Câu 70. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
(2; 3;1)A
,
( 1; 2; 0)B −
,
(1;1; 2)C −
.
H
là
trực tâm tam giác
ABC
, khi đó, độ dài đoạn
OH
bằng
A.
870
.
12
B.
870
.
14
C.
870
.
16
D.
870
.
15
Câu 71. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
(3;1; 0)A
,
B
nằm trên mặt
phẳng
()Oxy
và có hoành độ dương,
C
nằm trên trục
Oz
và
(2;1;1)H
là trực tâm của tam giác
ABC
. Toạ độ các điểm
B
,
C
thỏa mãn yêu cầu bài toán là:
A.
3 177 17 177 3 177
; ; 0 , 0; 0; .
42 4
BC

−+ − −


B.
3 177 17 177 3 177
; ;0 , 0;0; .
42 4
BC

−− + +


C.
3 177 17 177 3 177
; ; 0 , 0; 0; .
42 4
BC

−+ − +


D.
3 177 17 177 3 177
; ;0 , 0;0; .
42 4
BC

−+ + −


Câu 72. Trong không gian với hệ tọa độ
Oxyz
, cho hình vuông
ABCD
,
(3; 0;8)B
,
( 5; 4; 0)
D −−
. Biêt
đỉnh
A
thuộc mặt phẳng (
Oxy
) va co toa đô la nhưng sô nguyên, khi đó
CA CB+
 
bằng:
A.
5 10.
B.
6 10.
C.
10 6.
D.
10 5.
Câu 73. Trong không gian với hệ tọa độ
Oxyz
, cho tam giac
ABC
, biết
(5; 3; 1)A −
,
(2; 3; 4)B −
,
(3; 1; 2)C −
. Ban kinh đương tron nôi tiêp tam giac
ABC
bằng:
A.
9 2 6.−
B.
9 3 6.−
C.
9 3 6.+
D.
9 2 6.+
Câu 74. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
( ) ( ) ( )
3; 0; 0 , , , 0 , 0;0;M N mn P p
. Biết
0
13, 60MN MON
= =
, thể tích tứ diện
OMNP
bằng 3. Giá trị của biểu thức
22
2Am n p=++
bằng
A.
29.
B.
27.
C.
28.
D.
30.
Câu 75. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
(2; 3;1)A
,
( 1; 2; 0)
B −
,
(1;1; 2)C −
. Gọi
( )
;;I abc
là tâm đường tròn ngoại tiếp tam giác
ABC
. Tính giá trị biểu thức
15 30 75Pabc=++
A.
48.
B.
50.
C.
52.
D.
46.
Trang 9/22
Trang 10/22
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM
I – ĐÁP ÁN 8.1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
A
B
A
C
A
D
A
C
A
A
B
D
A
C
C
A
A
D
A
B
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
B
A
A
B
D
C
A
D
D
A
C
C
B
C
D
A
D
C
A
A
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
B
D
D
C
A
A
C
A
A
D
A
B
A
C
D
A
A
B
B
D
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
A
A
B
C
A
B
D
A
A
D
A
B
B
A
B
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
II –HƯỚNG DẪN GIẢI
Câu 1. Gọi
ϕ
là góc giữa hai vectơ
a
và
b
, với
a
và
b
khác
0
, khi đó
cos
ϕ
bằng
A.
.
.
ab
ab


. B.
.
.
ab
ab


. C.
.
.
ab
ab
−


. D.
.
ab
ab
+


.
Câu 2. Gọi
ϕ
là góc giữa hai vectơ
( )
1; 2; 0a =
và
(
)
2;0; 1b
= −
, khi đó
cos
ϕ
bằng
A. 0. B.
2
5
. C.
2
5
. D.
2
5
−
.
Câu 3. Cho vectơ
( )
1; 3; 4a =
, tìm vectơ
b
cùng phương với vectơ
a
A.
( )
2; 6; 8 .b =−−−
B.
(
)
2; 6;8 .b
=−−
C.
(
)
2;6;8 .b
= −
D.
( )
2; 6; 8 .b = −−
Câu 4. Tích vô hướng của hai vectơ
( ) ( )
2; 2;5 , 0;1; 2ab=−=

trong không gian bằng
A. 10. B. 13. C. 12. D. 14.
Câu 5. Trong không gian cho hai điểm
( ) ( )
1; 2; 3 , 0;1;1AB−
, độ dài đoạn
AB
bằng
A.
6.
B.
8.
C.
10.
D.
12.
Câu 6. Trong không gian
Oxyz
, gọi
,,i jk

là các vectơ đơn vị, khi đó với
( )
;;M xyz
thì
OM

bằng
A.
.xi y j zk−− −

B.
.xi y j zk−−

C.
.x j yi zk++

D.
.xi y j zk
++

Câu 7. Tích có hướng của hai vectơ
123
(; ; )a aa a=
,
123
(; ; )b bb b=
là một vectơ, kí hiệu
,ab


, được
xác định bằng tọa độ
A.
( )
23 32 31 13 12 21
;; .a b ab ab ab ab a b−−−
B.
( )
23 32 31 13 12 21
;; .ab ab ab ab ab ab+++
C.
( )
23 32 31 13 12 21
;; .a b ab ab ab ab ab−+−
D.
( )
2 2 3 3 3 3 11 11 2 2
;; .a b ab ab ab ab ab− −−
Câu 8. Cho các vectơ
(
)
123
;;u uuu=
và
( )
123
;;v vvv=
,
.0uv=

khi và chỉ khi
A.
11 2 2 33
1uv u v uv++=
. B.
11 2 2 3 3
0uvu v uv+++++=
.
C.
11 2 2 33
0uv uv uv++=
. D.
12 2 3 31
1uv u v uv++=−
.
Câu 9. Cho vectơ
( )
1; 1; 2a = −
, độ dài vectơ
a
là
A.
6
. B. 2. C.
6−
. D. 4.
Trang 11/22
Câu 10. Trong không gian
Oxyz
, cho điểm
M
nằm trên trục
Ox
sao cho
M
không trùng với gốc tọa
độ, khi đó tọa độ điểm
M
có dạng
A.
( )
;0;0 , 0Ma a≠
. B.
( )
0; ;0 , 0Mb b≠
. C.
( )
0;0; , 0M cc≠
. D.
( )
;1;1 , 0
Ma a≠
.
Câu 11. Trong không gian
Oxyz
, cho điểm
M
nằm trên mặt phẳng
(
)
Oxy
sao cho
M
không trùng với
gốc tọa độ và không nằm trên hai trục
,Ox Oy
, khi đó tọa độ điểm
M
là (
,, 0abc≠
)
A.
( )
0; ; .ba
B.
( )
; ;0 .
ab
C.
( )
0;0; .c
D.
( )
;1;1a
Câu 12. Trong không gian
Oxyz
, cho
( )
0; 3; 4a =
và
2
ba
=

, khi đó tọa độ vectơ
b
có thể là
A.
( )
0; 3; 4 .
B.
(
)
4;0;3 .
C.
( )
2;0;1 .
D.
( )
8; 0; 6 .−−
Câu 13. Trong không gian
Oxyz
cho hai vectơ
u
và
v
, khi đó
,uv



bằng
A.
( )
. .sin , .u v uv

B.
( )
. .cos , .u v uv

C.
( )
. .cos , .uv u v

D.
( )
. .sin , .uv u v

Câu 14. Trong không gian
Oxyz
cho ba vectơ
( ) ( ) ( )
1; 1; 2 , 3; 0; 1 , 2; 5;1abc=− = −=−

, vectơ
mabc=+−

có tọa độ là
A.
( )
6;0; 6−
. B.
( )
6;6;0−
. C.
( )
6; 6; 0−
. D.
( )
0;6; 6−
.
Câu 15. Trong không gian
Oxyz
cho ba điểm
( ) ( ) ( )
1;0; 3 , 2; 4; 1 , 2; 2;0AB C− −−
. Độ dài các cạnh
,,
AB AC BC
của tam giác
ABC
lần lượt là
A.
21, 13, 37
. B.
11, 14, 37
. C.
21, 14, 37
. D.
21, 13, 35
.
Câu 16. Trong không gian
Oxyz
cho ba điểm
(
) (
) (
)
1;0; 3 , 2; 4; 1 , 2; 2;0AB C
− −−
. Tọa độ trọng tâm
G
của tam giác
ABC
là
A.
52 4
;;
33 3

−


. B.
524
;;
333



. C.
( )
5;2;4
. D.
5
;1; 2
2

−


.
Câu 17. Trong không gian
Oxyz
cho ba điểm
( ) ( ) (
)
1; 2; 0 , 1;1; 3 , 0; 2; 5
AB C−−
. Để 4 điểm
,,,
ABC D
đồng phẳng thì tọa độ điểm
D
là
A.
( )
2; 5; 0D −
. B.
( )
1; 2; 3D
. C.
( )
1; 1; 6D −
. D.
(
)
0;0; 2D
.
Hướng dẫn giải
Cách 1:Tính
,. 0AB AC AD

=

  
Cách 2: Lập phương trình (ABC) và thế toạ độ D vào phương trình tìm được.
Câu 18. Trong không gian
Oxyz
, cho ba vecto
123 201 101(;;), ( ;;), ( ;;)ab c
= =−=−

. Tìm tọa độ của
vectơ
23nab c i=++ −

A.
( )
6; 2; 6n =
. B.
( )
6; 2; 6n = −
. C.
( )
0; 2; 6n =
. D.
( )
6; 2; 6n = −
.
Câu 19. Trong không gian
Oxyz
, cho tam giác
ABC
có
(1;0; 2), ( 2;1;3), (3; 2; 4)AB C−
. Tìm tọa độ
trọng tâm G của tam giác
ABC
A.
2
;1; 3
3
G



. B.
( )
2;3;9
G
. C.
( )
6;0; 24G −
. D.
1
2; ;3
3
G



.
Câu 20. Cho 3 điểm
( ) ( ) ( )
2;0;0 , 0; 3;0 , 0;0;4 .MN P−
Nếu
MNPQ
là hình bình hành thì tọa độ của
điểm
Q
là
A.
( )
Q 2; 3; 4−−
B.
( )
2; 3; 4Q
C.
( )
3;4;2Q
D.
( )
Q 2;3;4−−−
Hướng dẫn giải
Gọi
(;;)Qxyz
,
MNPQ
là hình bình hành thì
MN QP=
 
⇔
2
3
40
x
y
z
=
=
−=
Trang 12/22
Câu 21. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) ( ) ( )
1;1; 1 , 2; 3; 4 , 7; 7; 5MN P
. Để tứ giác
MNPQ
là hình bình hành thì tọa độ điểm
Q
là
A.
( )
6; 5; 2Q −
. B.
( )
6; 5; 2Q
. C.
( )
6; 5; 2Q −
. D.
( )
6;5;2Q −−−
.
Hướng dẫn giải
Điểm
( )
;;Q xyz
( )
1; 2; 3MN =

,
(
)
7 ;7 ;5
QP x y z=−−−

Vì
MNPQ
là hình bình hành nên
( )
6; 5; 2MN QP Q= ⇒
 
Câu 22. Cho 3 điểm
( )
(
) (
)
1; 2; 0 , 1; 0; 1 , 0; 1; 2 .AB C−−
Tam giác
ABC
là
A. tam giác có ba góc nhọn. B. tam giác cân đỉnh
A
.
C. tam giác vuông đỉnh
A
. D. tam giác đều.
Hướng dẫn giải
(0;2;1); (1;3;2)AB AC= −− =−−
 
. Ta thấy
.0AB AC ≠⇒
 
ABC∆
không vuông.
AB AC≠
 
ABC
⇒∆
không cân.
Câu 23. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) ( ) ( )
1; 2; 2 , 0;1;3 , 3; 4;0A BC−−
. Để tứ giác
ABCD
là hình bình hành thì tọa độ điểm
D
là
A.
( )
4; 5; 1D −−
. B.
( )
4; 5; 1D −
. C.
( )
4;5;1D −−−
. D.
( )
4; 5;1
D
−
.
Hướng dẫn giải
Điểm
(
)
;;D xyz
( )
1; 1; 1AB
= −

,
(
)
3 ;4 ;
DC x y z
=−− − −

Vì
ABCD
là hình bình hành nên
( )
4; 5; 1AB DC D
= ⇒− −
 
Câu 24. Cho hai vectơ
a
và
b
tạo với nhau góc
0
60
và
2; 4ab= =

. Khi đó
ab+

bằng
A.
8 3 20.+
B.
2 7.
C.
2 5.
D.
2
.
Hướng dẫn giải
Ta có
( )
2 22
2 .cos , 4 16 8 28 2 7.
ab a b ab ab ab+ = + + =+ += ⇒ + =
 
Câu 25. Cho điểm
( )
1; 2; 3M
−
, khoảng cách từ điểm
M
đến mặt phẳng
( )
Oxy
bằng
A. 2. B.
3−
. C. 1. D. 3.
Hướng dẫn giải
Với
( ) ( )
( )
;; ,M abc d M Oxy c⇒=
Câu 26. Cho điểm
( )
2; 5; 0M −
, hình chiếu vuông góc của điểm
M
trên trục
Oy
là điểm
A.
( )
2; 5; 0M
′
. B.
( )
0; 5;0M
′
−
. C.
( )
0; 5; 0M
′
. D.
( )
2;0;0M
′
−
.
Hướng dẫn giải
Với
( )
;;M abc
⇒
hình chiếu vuông góc của
M
lên trục
Oy
là
( )
1
0; ;0Mb
Câu 27. Cho điểm
( )
1; 2; 3M −
, hình chiếu vuông góc của điểm
M
trên mặt phẳng
( )
Oxy
là điểm
A.
( )
1; 2; 0M
′
. B.
( )
1; 0; 3M
′
−
. C.
( )
0; 2; 3M
′
−
. D.
( )
1; 2; 3M
′
.
Hướng dẫn giải
Với
( )
;;M abc ⇒
hình chiếu vuông góc của
M
lên mặt phẳng
( )
Oxy
là
( )
1
; ;0M ab
Câu 28. Cho điểm
( )
2; 5;1M −
, khoảng cách từ điểm
M
đến trục
Ox
bằng
A.
29
. B.
5
. C. 2. D.
26
.
Hướng dẫn giải
Trang 13/22
Với
(
) ( )
22
;; ,
M abc d MOx b c
⇒=+
Câu 29. Cho hình chóp tam giác
.S ABC
với
I
là trọng tâm của đáy
ABC
. Đẳng thức nào sau đây là
đẳng thức đúng
A.
.
IA IB IC= +
  
B.
0.
IA IB CI++=
  
C.
0.IA BI IC++=
  
D.
0.
IA IB IC++ =
  
Câu 30. Trong không gian
Oxyz
, cho 3 vectơ
( )
1;1; 0a
→
= −
;
( )
1;1; 0b
→
=
;
( )
1;1; 1c
→
=
. Trong các mệnh
đề sau, mệnh đề nào sai:
A.
.bc⊥

B.
2.
a =

C.
3.c =

D.
.ab
⊥

Hướng dẫn giải
Vi
. 2 0.bc= ≠

Câu 31. Cho điểm
( )
3; 2; 1M −
, điểm đối xứng của
M
qua mặt phẳng
( )
Oxy
là điểm
A.
( )
3; 2;1
M
′
−
. B.
( )
3;2;1M
′
−−
. C.
( )
3; 2;1M
′
. D.
( )
3; 2; 0M
′
.
Hướng dẫn giải
Với
( )
;;M abc ⇒
điểm đối xứng của
M
qua mặt phẳng
( )
Oxy
là
( )
;;M ab c−
Câu 32. Cho điểm
( )
3; 2; 1M −
, điểm
(
)
;;
M abc
′
đối xứng của M qua trục
Oy
, khi đó
abc++
bằng
A.
6.
B.
4.
C.
0.
D.
2.
Hướng dẫn giải
Với
( )
;;
M abc ⇒
điểm đối xứng của
M
qua trục
Oy
là
(
)
;;M ab c
′
−−
( )
3; 2;1 0.M abc
′
⇒ − ⇒++=
Câu 33. Cho
( )
1;1; 1u =
và
( )
0;1; mv =
. Để góc giữa hai vectơ
,uv

có số đo bằng
0
45
thì
m
bằng
A.
3
±
. B.
23±
. C.
13±
. D.
3
.
Hướng dẫn giải
( )
( )
(
)
2
2
2
2
1
1.0 1.1 1. 1
cos 2 1 3 1
3 12 1
2
3. 1
23
m
m
mm
mm
m
m
ϕ
≥−
++
= = ⇔ + = +⇔
+= +
+
⇔=±
Câu 34. Cho
( ) ( ) ( ) ( )
1; 2; 0 , 3; 3; 2 , 1; 2; 2 , 3; 3;1A BC D−−
. Thể tích của tứ diện
ABCD
bằng
A. 5. B. 4. C. 3. D. 6.
Hướng dẫn giải
Tính
( ) ( ) ( )
2;5; 2 , 2; 4; 2 , 2;5;1AB AC AD= =−=
  
1
,. 3
6
V AB AC AD

= =

  
Sử dụng Casio
w 8 1 1 (nhập vectơ
AB

)
q 5 2 2 2 (nhập vectơ
AC

)
q 5 2 3 1 (nhập vectơ
AD

)
C1a6qc(abs) q53q54q57q55= (tính
V
)
Câu 35. Trong không gian
Oxyz
cho tứ diện
ABCD
. Độ dài đường cao vẽ từ
D
của tứ diện
ABCD
cho bởi công thức nào sau đây:
A.
,.
1
.
3
.
AB AC AD
h
AB AC


=


  
 
B.
,.
1
.
3
.
AB AC AD
h
AB AC


=
  
 
C.
,.
..
.
AB AC AD
h
AB AC


=
  
 
D.
,.
.
.
AB AC AD
h
AB AC


=


  
 
Hướng dẫn giải
Trang 14/22
Vi
11 1
. . ,.
32 6
ABCD
V h AB AC AB AC AD

= =

    
nên
,.
.
.
AB AC AD
h
AB AC


=


  
 
Câu 36. Trong không gian tọa độ
Oxyz
, cho bốn điểm
(
)
(
)
(
)
(
)
1; 2; 0 , 3; 3; 2 , 1; 2; 2 , 3; 3;1
A BC D−−
. Độ
dài đường cao của tứ diện
ABCD
hạ từ đỉnh
D
xuống mặt phẳng
( )
ABC
là
A.
9
72
. B.
9
7
. C.
9
2
. D.
9
14
.
Hướng dẫn giải
Tính
( ) ( ) ( )
2;5; 2 , 2; 4; 2 , 2;5;1AB AC AD−
  
1
,. 3
6
V AB AC AD

= =

  
1
.
3
V Bh
=
, với
1
, 72
2
ABC
B S AB AC
∆

= = =

 
,
( )
( )
,h d D ABC=
3 3.3 9
72 72
V
h
B
⇒= = =
Câu 37. Trong không gian
Oxyz
, cho tứ diện
ABCD
có
(1;0; 2), ( 2;1;3), (3; 2; 4), (6;9; 5)AB C D−−
. Tìm
tọa độ trọng tâm G của tứ diện
ABCD
A.
18
9; ; 30
4
G

−−


. B.
( )
8;12; 4G
. C.
14
3; 3;
4
G



. D.
( )
2; 3;1G
.
Câu 38. Trong không gian
Oxyz
, cho hai điểm
(1; 2;1), ( 2; 1; 2)AB−
. Điểm
M
trên trục
Ox
và cách đều
hai điểm
,AB
có tọa độ là
A.
113
;;
222
M



. B.
1
;0;0
2
M



. C.
3
;0;0
2
M



. D.
13
0; ;
22
M



.
Hướng dẫn giải
( )
;0;0
M Ox M a∈⇒
M
cách đều hai điểm
,AB
nên
( ) (
)
22
2 2 22 22
1 21 2 21MA MB a a= ⇔− ++=− ++
3
23
2
aa⇔ =⇔=
Câu 39. Trong không gian
Oxyz
, cho hai điểm
(1; 2; 1), (3; 1; 2)
AB−
. Điểm
M
trên trục
Oz
và cách đều
hai điểm
,AB
có tọa độ là
A.
(
)
0;0; 4M
. B.
( )
0;0; 4M −
. C.
3
0;0;
2
M



. D.
313
;;
222
M



.
Câu 40. Trong không gian
Oxyz
cho ba điểm
( 1; 2;3), (0;3;1), (4; 2; 2)A BC
−−
. Cosin của góc
BAC
là
A.
9
2 35
. B.
9
35
. C.
9
2 35
−
. D.
9
35
−
.
Câu 41. Tọa độ của vecto
n
vuông góc với hai vecto
(2; 1; 2), (3; 2;1)
ab=−=−

là
A.
( )
3; 4;1n =
. B.
(
)
3; 4; 1n = −
. C.
( )
3; 4; 1n =−−
. D.
( )
3;4;1n = −−
.
Câu 42. Cho
2; 5,ab= =

góc giữa hai vectơ
a
và
b
bằng
2
3
π
,
; 2.u ka b v a b=−=+

Để
u
vuông
góc với
v
thì
k
bằng
A.
6
.
45
−
B.
45
.
6
C.
6
.
45
D.
45
.
6
−
Hướng dẫn giải
Trang 15/22
( )
( )
( )
2
. 2 4 50 2 1 cos
3
6 45
uv ka b a b k k a b
k
π
= − + = −+ −
=−−

Câu 43. Cho
( ) (
) (
)
2; 1;1 , m; 3; 1 , w 1; 2;1uv=− = −=

. Với giá trị nào của m thì ba vectơ trên đồng phẳng
A.
3
8
. B.
3
8
−
. C.
8
3
. D.
8
3
−
.
Hướng dẫn giải
Ta có:
( )
, 2; 2; 6 , , .w 3 8uv m m uv m
 
=−+ + =+
 
 
, ,wuv

đồng phẳng
8
, .w 0
3
uv m

⇔ =⇔=−


Câu 44. Cho hai vectơ
( ) ( )
35
1; log 5; , 3; log 3; 4a mb= =

. Với giá trị nào của m thì
ab⊥

A.
1; 1mm
= = −
. B.
1m =
. C.
1m
= −
. D.
2; 2mm
= = −
.
Câu 45. Trong không gian
Oxyz
cho ba điểm
(2;5;3), (3;7; 4), ( ; ;6)A B Cxy
. Giá trị của
,
xy
để ba điểm
,,
ABC
thẳng hàng là
A.
5; 11xy= =
. B.
5; 11xy=−=
. C.
11; 5xy=−=−
. D.
11; 5xy= =
.
Hướng dẫn giải
( ) ( )
1; 2;1 , 2; 5;3AB AC x y= =−−
 
,,ABC
thẳng hàng
,AB AC⇔
 
cùng phương
2 53
5; 11
1 21
xy
xy
−−
⇔ = =⇔= =
Câu 46. Trong không gian
Oxyz
cho ba điểm
(1;0;0), (0;0;1), (2;1;1)
ABC
. Tam giác
ABC
là
A. tam giác vuông tại
A
. B. tam giác cân tại
A
.
C. tam giác vuông cân tại
A
. D. Tam giác đều.
Hướng dẫn giải
( ) ( ) ( )
1; 0; 1 , 1; 1; 1 , 2; 1; 0BA CA CB= − =−−− =−−
  
.0BA CA = ⇒
 
tam giác vuông tại
A
,
AB AC
≠
.
Câu 47. Trong không gian
Oxyz
cho tam giác
ABC
có
(1;0;0), (0;0;1), (2;1;1)ABC
. Tam giác
ABC
có
diện tích bằng
A.
6
. B.
6
3
. C.
6
2
. D.
1
2
.
Hướng dẫn giải
(
) ( )
1; 0;1 , 1;1;1AB AC
=−=
 
.
16
.
22
ABC
S AB AC
∆

= =

 
Câu 48. Ba đỉnh của một hình bình hành có tọa độ là
(
) ( ) (
)
1;1; 1 , 2; 3; 4 , 7; 7; 5
. Diện tích của hình bình
hành đó bằng
A.
2 83
. B.
83
. C.
83
. D.
83
2
.
Hướng dẫn giải
Gọi 3 đỉnh theo thứ tự là
,,ABC
( ) ( )
1; 2; 3 , 6; 6; 4AB AC= =
 
( ) ( )
22
2
, 10 14 6 2 83
hbh
S AB AC

= = − + +− =

 
Câu 49. Cho 3 vecto
( )
1; 2; 1 ;
a =
( )
1;1; 2b = −
và
( )
;3 ; 2
c x xx= +
. Tìm
x
để 3 vectơ
,,abc

đồng
phẳng
A.
2.
B.
1.−
C.
2.−
D.
1.
Hướng dẫn giải
,,abc

đồng phẳng thì
, . 0 2.ab c x

=⇒=




Trang 16/22
Câu 50. Trong không gian
Oxyz
cho ba vectơ
( )
3; 2; 4 ,
a = −
( )
5; 1; 6b
→
=
,
( )
3; 0; 2
c
→
= −
. Tìm vectơ
x
sao cho vectơ
x
đồng thời vuông góc với
,,abc

A.
(
)
1;0;0 .
B.
( )
0;0;1 .
C.
( )
0;1; 0 .
D.
( )
0;0;0 .
Hướng dẫn giải
Dê thây chi co
(0;0;0)
x =
thoa man
. . . 0.xa xb xc= = =

Câu 51. Trong không gian
Oxyz
, cho 2 điểm
(1; 2; 3)
B −
,
(7; 4; 2)C −
. Nếu
E
là điểm thỏa mãn đẳng
thức
2CE EB
=
 
thì tọa độ điểm
E
là
A.
88
3; ; .
33

−


B.
88
3; ; .
33



C.
8
3; 3; .
3

−


D.
1
1; 2; .
3



Hướng dẫn giải
(; ;)Exyz
, tư
3
8
2.
3
8
3
x
CE EB y
z
=
= ⇒=
= −
 
Câu 52. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
(1; 2; 1)A −
,
(2; 1;3)
B
−
,
( 2; 3; 3)
C
−
.
Điêm
( )
;;M abc
la đinh thư tư cua hinh binh hanh
ABCM
, khi đó
222
Pa b c=+−
có giá trị
bằng
A.
43.
. B.
44.
. C.
42.
. D.
45.
Hướng dẫn giải
(; ;)M xyz
,
ABCM
la hinh binh hanh thi
1 22
2 3 1 ( 3;6; 1) P 44.
133
x
AM BC y M
z
−=−−
= ⇒ −=+ ⇒ − −⇒ =
+=−
 
.
Câu 53. Trong không gian với hệ trục tọa độ
Oxyz
cho ba điểm
(1; 2; 1)A −
,
(2; 1;3)B −
,
( 2; 3; 3)
C
−
. Tìm
tọa độ điêm
D
la chân đương phân giac trong goc
A
cua tam giac
ABC
A.
(0;1;3)D
. B.
(0; 3;1)D
. C.
(0; 3;1)D −
. D.
(0; 3; 1)D −
.
Hướng dẫn giải
Ta co
26, 26AB AC= = ⇒
tam giac
ABC
cân ơ
A
nên
D
la trung điêm
BC
(0;1;3).
D⇒
Câu 54. Trong không gian với hệ toạ độ
Oxyz
, cho các điểm
A( 1; 3; 5)−
,
B( 4; 3; 2)−
,
C(0;2;1)
. Tìm tọa
độ điêm
I
tâm đường tròn ngoại tiếp tam giác
ABC
A.
858
(;;)
333
I
. B.
588
(;;)
333
I
. C.
588
( ; ; ).
333
I −
D.
885
(;;)
333
I
.
Hướng dẫn giải
Ta có:
32AB BC CA
= = =
⇒
ABC∆
đều. Do đó tâm
I
của đường tròn ngoại tiếp
ABC∆
là trọng tâm của nó. Kết luận:
588
;;
333
I

−


.
Câu 55. Trong không gian
Oxyz
, cho 3 vectơ
( )
( ) ( )
1;1; 0 , 1;1; 0 , 1;1;1a bc=−= =

. Cho hình hộp
.OABC O A B C
′′′ ′
thỏa mãn điều kiện
, , 'OA a OB b OC c= = =
  

. Thể tích của hình hộp nói trên
bằng:
A.
1
3
B. 4 C.
2
3
D. 2
Hướng dẫn giải
, ( 1;1; 0 ), (1;1; 0 ), ' '(1;1;1)OA a A OB b B OC c C=⇒− =⇒ =⇒
  

Trang 17/22
( 2; 0; 0) ' ( 1;1;1) 'AB OC C CC OO
=⇒ ⇒=− =
   
.''''
,'
OABC O A B C
V OA OB OO

⇒=

  
Câu 56. Trong không gian với hệ trục
Oxyz
cho tọa độ 4 điểm
( ) ( )
2; 1;1 , 1; 0; 0 ,AB
−
( ) ( )
3;1;0 , 0;2;1CD
. Cho các mệnh đề sau:
1) Độ dài
2AB
=
.
2) Tam giác
BCD
vuông tại
B
.
3) Thể tích của tứ diện
ABCD
bằng
6
.
Các mệnh đề đúng là:
A. 2). B. 3). C. 1); 3). D. 2), 1)
Câu 57. Trong không gian
Oxyz
, cho ba vectơ
( ) ( )
1,1, 0 ; (1,1, 0); 1,1,1a bc=−= =

. Trong các mệnh đề
sau, mệnh đề nào đúng:
A.
( )
6
cos , .
3
bc =

B.
0.abc++=

A.
,,abc

đồng phẳng. D.
. 1.ab
=

Hướng dẫn giải
.
cos( , )
.
bc
bc
bc
=



Câu 58. Trong không gian với hệ tọa độ
Oxyz
, cho tư diên
ABCD
, biết
(1; 0;1)A
,
( 1; 1; 2)B −
,
( 1;1; 0)C −
,
(2;1;2)D −−
. Đô dai đương cao
AH
cua tư diên
ABCD
bằng:
A.
2
.
13
B.
1
.
13
C.
13
.
2
D.
3 13
.
13
Hướng dẫn giải
Sư dung công thưc
,.
1
.
13
.
AB AC AD
h
AB AC


= =
  
 
Câu 59. Cho hình chóp tam giác
.S ABC
với
I
là trọng tâm của đáy
ABC
. Đẳng thức nào sau đây là
đẳng thức đúng
A.
( )
1
.
2
SI SA SB SC= ++
   
B.
(
)
1
.
3
SI SA SB SC= ++
   
C.
.SI SA SB SC
=++
   
D.
0.SI SA SB SC+++ =
   
Hướng dẫn giải
( )
3
SI SA AI
SI SB BI SI SA SB SB AI BI CI
SI SC CI
= +
=+ ⇒ =+++ ++
= +
  
         
  
Vì I là trọng tâm tam giác
( )
1
0.
3
ABC AI BI CI SI SA SB SC⇒++=⇒= ++
      
Câu 60. Trong không gian
Oxyz
, cho tứ diện
ABCD
có
(1;0;0), (0;1;0), (0;0;1), ( 2;1; 1)ABC D−−
. Thể
tích của tứ diện
ABCD
bằng
A.
3
2
. B.
3
. C.
1
. D.
1
2
.
Hướng dẫn giải
Thể tích tứ diện:
1
, .
6
ABCD
V AB AC AD

=

  
Câu 61. Cho hình chóp
.S ABC
có
00
, 3 , 60 , 90SA SB a SC a ASB CSB CSA= = = = = =
. Gọi G là trọng
tâm tam giác
ABC
. Khi đó khoảng cách
SG
bằng
A.
15
3
a
. B.
5
3
a
. C.
7
3
a
. D.
3a
.
Trang 18/22
Hướng dẫn giải
Áp dụng công thức tổng quát: Cho hình chóp
.S ABC
có
,,
SA a SB b SC c= = =
và có
,,ASB BSC CSA
α βγ
= = =
. Gọi G là trọng tâm tam giác ABC, khi đó
222
1
2 cos 2 cos 2
3
SG a b c ab ac bc
α γβ
= +++ + +
Chứng minh:
Ta có:
( )
1
3
SG SA SB SC= ++
   
( )
2
22 2
2. 2. 2.SA SB SC SA SB SC SA SB SA SC SB SC++ = + + + + +
           
Khi đó
222
1
2 cos 2 cos 2
3
SG a b c ab ac bc
α γβ
= +++ + +
Áp dụng công thức trên ta tính được
15
3
a
SG =
Câu 62. Trong không gian tọa độ
Oxyz
cho ba điểm
(
) (
)
( )
2;5;1 , 2; 6; 2 , 1; 2; 1AB C
−− −
và điểm
( )
;;M mmm
, để
2
MB AC−
 
đạt giá trị nhỏ nhất thì
m
bằng
A. 2. B. 3 . C. 1. D. 4.
Hướng dẫn giải
(
) ( )
1;3;2, 2 ; 6 ;2
AC MB m m m−− − −− − − −
 
( )
( )
22
22 2
2 6 3 12 36 3 2 24MB AC m m m m m m− = ++− = − += − +
 
Để
2MB AC
−
 
nhỏ nhất thì
2m =
Câu 63. Trong không gian tọa độ
Oxyz
cho ba điểm
( ) ( ) ( )
2;5;1 , 2; 6; 2 , 1; 2; 1AB C−− −
và điểm
( )
;;M mmm
, để
22 2
MA MB MC−−
đạt giá trị lớn nhất thì
m
bằng
A. 3. B. 4. C. 2. D. 1.
Hướng dẫn giải
( ) ( ) ( )
2;5;1 , 2;6;2 , 1;2;1MA m m m MB m m m MC m m m= − − − =−− −− − = − − −−
  
( )
2
22 2 2
3 24 20 28 3 4 28MA MB MC m m m− − =− − −=− − ≤
Để
22 2
MA MB MC−−
đạt giá trị lớn nhất thì
4m =
Câu 64. Cho hình chóp
.S ABCD
biết
( ) ( ) ( ) ( )
2; 2; 6 , 3;1;8 , 1; 0; 7 , 1; 2;3A BC D− −−
. Gọi
H
là trung
điểm của
,CD
( )
SH ABCD⊥
. Để khối chóp
.S ABCD
có thể tích bằng
27
2
(đvtt) thì có hai
điểm
12
,SS
thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm
I
của
12
SS
A.
( )
0;1;3
−−I
. B.
( )
1; 0; 3I
C.
( )
0;1; 3I
. D.
( )
1; 0; 3 .−−
I
Hướng dẫn giải
Ta có
( ) ( )
1 33
1; 1; 2 , 1; 2; 1 ,
22
ABC
AB AC S AB AC

=−− = − ⇒ = =

   
( ) ( )
2; 2; 4 , 1; 1; 2 2.DC AB DC AB=−− =−− ⇒ =
   
ABCD⇒
là hình thang và
93
3
2
ABCD ABC
SS= =
Vì
.
1
. 33
3
S ABCD ABCD
V SH S SH= ⇒=
Lại có
H
là trung điểm của
( )
0;1; 5CD H⇒
Gọi
( ) ( ) ( ) ( )
; ; ;1 ;5 , 3;3;3 3 ;3 ;3S a b c SH a b c SH k AB AC k k k k

⇒=−−−⇒= = =

   
Trang 19/22
Suy ra
222
33999 1kkk k= + + ⇒=±
+) Với
(
)
(
)
1 3; 3; 3 3; 2; 2
k SH S
=⇒ = ⇒ −−

+) Với
( ) ( )
1 3; 3; 3 3; 4; 8k SH S=−⇒ =−−− ⇒

Suy ra
( )
0;1; 3I
Câu 65. Trong không gian
Oxyz
, cho hai điểm
(2; 1;7), (4; 5; 2)
AB
−−
. Đường thẳng
AB
cắt mặt phẳng
()Oyz
tại điểm
M
. Điểm
M
chia đoạn thẳng
AB
theo tỉ số nào
A.
1
2
. B.
2
. C.
1
3
. D.
2
3
.
Hướng dẫn giải
Đường thẳng
AB
cắt mặt phẳng
()
Oyz
tại điểm
(0; ; )M M yz⇒
(2; 1 ; 7 ), (4; 5 ; 2 )MA y z MB y z⇒ = −− − = − −−
 
Từ
MA k MB=
 
ta có hệ
( )
( )
2 .4
1
15
2
72
k
yk y k
zk z
=
−− = − ⇒ =
− = −−
Câu 66. Trong không gian
Oxyz
, cho tứ diện
ABCD
có
(2;1; 1), (3;0;1),C(2; 1;3)AB−−
và
D
thuộc
trục
Oy
. Biết
5
ABCD
V =
và có hai điểm
( ) ( )
11 2 2
0; ; 0 , 0; ;0Dy Dy
thỏa mãn yêu cầu bài toán.
Khi đó
12
yy+
bằng
A.
0.
B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
(0; ;0)D Oy D y∈⇒
Ta có:
( ) ( ) ( )
1; 1; 2 , 2; 1;1 , 0; 2; 4AB AD y AC=− =−− =−
  
( )
. 0; 4; 2 . . 4 2AB AC AB AC AD y
 
⇒ = −− ⇒ =− +
 
    
1
5 4 2 5 7; 8
6
ABCD
V y yy=⇔ − +=⇔=− =
(
) ( )
1 2 12
0; 7;0 , 0;8;0 1D D yy⇒ − ⇒+=
Câu 67. Trong không gian
Oxyz
, cho tam giác
ABC
có
( 1;2;4), (3;0; 2),C(1;3;7)AB−−
. Gọi
D
là
chân đường phân giác trong của góc
A
. Tính độ dài
.OD

A.
207
.
3
B.
203
3
C.
201
.
3
D.
205
.
3
Hướng dẫn giải
Gọi
( )
; y; zDx
2 14
2
14
DB AB
DC AC
= = =
Vì D nằm giữa B, C (phân giác trong) nên
( )
( )
( )
5
3 21
3
2 23 2
4
2 27
x
xx
DB DC y y y
z
zz
=
−=− −
=− ⇔−=− − ⇔ =


=
−− =− −
 
Suy ra
5 205
;2;4
33

⇒=



D OD
Câu 68. Trong không gian với hệ toạ độ
Oxyz
, cho tam giac
ABC
, biêt
(1;1;1)A
,
(5; 1; 2)B −
,
(7; 9;1)C
.
Tinh đô dai phân giac trong
AD
cua goc
A
A.
2 74
.
3
B.
3 74
.
2
C.
2 74.
D.
3 74.
Hướng dẫn giải
Trang 20/22
(; ;)Dxyz
la chân đương phân giac trong goc
A
cua tam giac
ABC
.
Ta co
1 17 11 2 74
2 ( ; ; 1) .
2 33 3
DB AB
DC DB D AD
DC AC
= =⇒ =− ⇒ −⇒ =
 
Câu 69. Trong không gian với hệ toạ độ
Oxyz
, cho 4 điểm
(2; 4; 1)A −
,
(1; 4; 1)B −
,
(2; 4; 3)C
(2; 2; 1)D −
. Biết
(
)
;;
M xyz
, để
22 2 2
MA MB MC MD+++
đạt giá trị nhỏ nhất thì
++xyz
bằng
A.
7.
B.
8.
C.
9.
D.
6.
Hướng dẫn giải
Gọi
G
là trọng tâm của
ABCD
ta có:
7 14
; ;0
33
G



.
Ta có:
2 2 2 2 222 2 2
4
MA MB MC MD MG GA GB GC GD+ + + = ++++
≥
22 2 2
GA GB GC GD+++
. Dấu bằng xảy ra khi
M
≡
7 14
; ;0 7
33
G xyz

⇒++=


.
Câu 70. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
(2; 3;1)A
,
( 1; 2; 0)
B
−
,
(1;1; 2)C −
.
H
là
trực tâm tam giác
ABC
, khi đó, độ dài đoạn
OH
bằng
A.
870
.
12
B.
870
.
14
C.
870
.
16
D.
870
.
15
Hướng dẫn giải
(; ;)Hxyz
là trực tâm của ∆ABC ⇔
, ,( )BH AC CH AB H ABC⊥ ⊥∈
.0
2 29 1
.0 ; ;
15 15 3
,. 0
BH AC
CH AB x y z
AB AC AH
=
⇔ = ⇔= = =−


=

 
 
  
⇒
2 29 1 870
;;
15 15 3 15
H OH

−⇒ =


.
Câu 71. Trong không gian với hệ tọa độ
Oxyz
, cho tam giác
ABC
có
(3;1; 0)A
,
B
nằm trên mặt
phẳng
()Oxy
và có hoành độ dương,
C
nằm trên trục
Oz
và
(2;1;1)
H
là trực tâm của tam giác
ABC
. Toạ độ các điểm
B
,
C
thỏa mãn yêu cầu bài toán là:
A.
3 177 17 177 3 177
; ; 0 , 0; 0; .
42 4
BC

−+ − −


B.
3 177 17 177 3 177
; ;0 , 0;0; .
42 4
BC

−− + +


C.
3 177 17 177 3 177
; ; 0 , 0; 0; .
42 4
BC

−+ − +


D.
3 177 17 177 3 177
; ;0 , 0;0; .
42 4
BC

−+ + −


Hướng dẫn giải
Giả sử
( ; ;0) ( ), (0; 0; )B x y Oxy C z Oz∈∈
.
H
là trực tâm của tam giác
ABC
⇔
,,
⊥
⊥
 
 
  
AH BC
CH AB
AB AC AH ñoàng phaúng
⇔
.0
.0
,. 0
AH BC
CH AB
AB AH AC
=
=

=

 
 
  
⇔
0
2x 7 0
3x 3 0
xz
y
y yz z
+=
+−=
− + −=
⇔
3 177 17 177 3 177
;;
4 24
x yz
−− + +
= = =
⇒
3 177 17 177 3 177
; ;0 , 0;0; .
42 4
BC

−− + +


Trang 21/22
Câu 72. Trong không gian với hệ tọa độ
Oxyz
, cho hình vuông
ABCD
,
(3; 0;8)B
,
( 5; 4; 0)D −−
. Biêt
đỉnh
A
thuộc mặt phẳng (
Oxy
) va co toa đô la nhưng sô nguyên, khi đó
CA CB+
 
bằng:
A.
5 10.
B.
6 10.
C.
10 6.
D.
10 5.
Hướng dẫn giải
Ta có trung điểm
BD
là
( 1; 2; 4)I −−
,
12BD =
và điểm
A
thuộc mặt phẳng
()Oxy
nên
( ; ;0)Aab
.
ABCD
là hình vuông
⇒
22
2
2
1
2
AB AD
AI BD
=

=


222 2 2
2 22
(3) 8(5)(4)
( 1) ( 2) 4 36
ab a b
ab
− ++=+ ++
⇔
+ ++ + =
22
42
( 1) (6 2 ) 20
ba
aa
= −
⇔
+ +− =
1
2
a
b
=
⇔
=
hoặc
17
5
14
5
a
b
=
−
=
⇒
A(1; 2; 0) hoặc
17 14
; ;0
55
A
−



(loai). Với
(1; 2; 0)A
⇒
( 3; 6; 8)C −−
.
Câu 73. Trong không gian với hệ tọa độ
Oxyz
, cho tam giac
ABC
, biết
(5; 3; 1)A −
,
(2; 3; 4)B −
,
(3; 1; 2)C
−
. Ban kinh đương tron nôi tiêp tam giac
ABC
bằng:
A.
9 2 6.
−
B.
9 3 6.−
C.
9 3 6.+
D.
9 2 6.
+
Hướng dẫn giải
Ta co
22 2
99AC BC AB
+ =+= ⇒
tam giac
ABC
vuông tai
C
.
Suy ra:
( )
1
CA.CB
3.3 2
2
9 36
1
32 3 3
2
ABC
S
r
p
AB BC CA
= = = = −
++
++
Câu 74. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
( ) ( ) ( )
3; 0; 0 , , , 0 , 0; 0;M N mn P p
. Biết
0
13, 60MN MON= =
, thể tích tứ diện
OMNP
bằng 3. Giá trị của biểu thức
22
2Am n p=++
bằng
A.
29.
B.
27.
C.
28.
D.
30.
Hướng dẫn giải
(
) ( )
3;0;0 , ; ;0 . 3
OM ON m n OM ON m= =⇒=
   
0
22
.1 1
. . cos60
22
.
OM ON m
OM ON OM ON
OM ON
mn
= ⇒ =⇒=
+
 
   
 
( )
2
2
3 13MN m n= − +=
Suy ra
2; 2 3mn= = ±
1
, . 63 63 3 3
6
OM ON OP p V p p

= ⇒= =⇒=±

  
Vậy
2 2.12 3 29.A
=+ +=
Câu 75. Trong không gian với hệ trục tọa độ
Oxyz
, cho ba điểm
(2; 3;1)A
,
( 1; 2; 0)B −
,
(1;1; 2)C −
. Gọi
( )
;;I abc
là tâm đường tròn ngoại tiếp tam giác
ABC
. Tính giá trị biểu thức
15 30 75Pabc=++
A.
48.
B.
50.
C.
52.
D.
46.
Hướng dẫn giải
(; ;)Ixyz
là tâm đường tròn ngoại tiếp tam giac
ABC
⇔
,( )AI BI CI I ABC
= = ∈
Trang 22/22
22
22
,0
AI BI
CI BI
AB AC AI
=
⇔=

=

  
14 61 1 14 61 1
; ; ; ; 50.
15 30 3 15 30 3
xyz I P

⇔ = = =−⇒ − ⇒ =


| 1/22
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHỦ ĐỀ 1. TỌA ĐỘ TRONG KHÔNG GIAN A. LÝ THUYẾT
1. Hệ trục tọa độ trong không gian
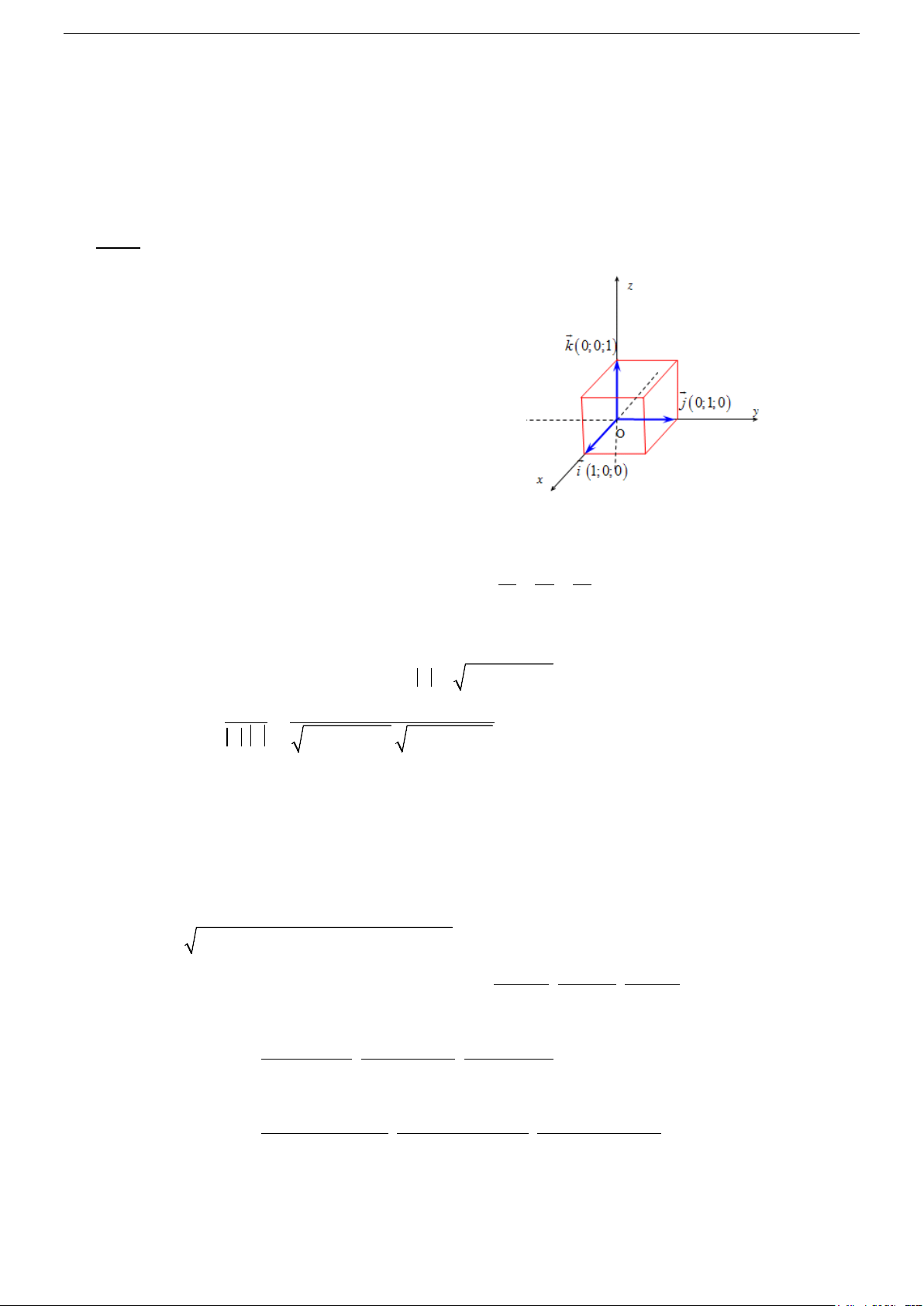
Trong không gian, xét ba trục tọa độ Ox,Oy,Oz vuông góc với nhau từng đôi một và chung một   
điểm gốc O. Gọi i, j, k là các vectơ đơn vị, tương ứng trên các trục Ox,Oy,Oz . Hệ ba trục như vậy
gọi là hệ trục tọa độ vuông góc trong không gian.          Chú ý: 2 2 2
i = j = k =1 và .i j = .ik = k. j = 0 .
2. Tọa độ của vectơ     
a) Định nghĩa: u = ( ;
x y; z) ⇔ u = xi + y j + zk  
b) Tính chất: Cho a = (a ;a ;a ), b = (b ;b ;b ), k ∈ 1 2 3 1 2 3   
• a ± b = (a ± b ; a ± b ; a ± b ) 1 1 2 2 3 3
• ka = (ka ; ka ; ka ) 1 2 3 a = b 1 1   • a b  = ⇔ a = b 2 2 a =  b 3 3    
• 0 = (0;0;0), i = (1;0;0), j = (0;1;0), k = (0;0;1)      
• a cùng phương b(b ≠ 0) ⇔ a = kb (k ∈) a = kb 1 1  a a a 1 2 3 ⇔ a = kb ⇔ = =
, (b , b , b ≠ 0) 2 2 1 2 3 b b b  1 2 3 a =  kb 3 3    
• a.b = a .b + a .b + a .b
• a ⊥ b ⇔ a b + a b + a b = 0 1 1 2 2 3 3 1 1 2 2 3 3 • 2 2 2 2
a = a + a + a •  2 2 2
a = a + a + a 1 2 3 1 2 2     + +    • a.b a b a b a b 1 1 2 2 3 3
cos(a, b) =   =
(với a, b ≠ 0 ) 2 2 2 2 2 2 a . b
a + a + a . b + b + b 1 2 3 1 2 3
3. Tọa độ của điểm    
a) Định nghĩa: M ( ;
x y; z) ⇔ OM = . x i + .
y j + z.k
(x : hoành độ, y : tung độ, z : cao độ)
Chú ý: • M ∈(Oxy) ⇔ z = 0;M ∈(Oyz) ⇔ x = 0;M ∈(Oxz) ⇔ y = 0
• M ∈Ox ⇔ y = z = 0;M ∈Oy ⇔ x = z = 0;M ∈Oz ⇔ x = y = 0 . b) Tính chất: Cho ( A x y z B x y z A; A; A ),
( B; B; B) 
• AB = (x − x y − y z − z B A; B A; B A ) • 2 2 2
AB = (x − x + y − y + z − z B A ) ( B A ) ( B A )  + + +
• Toạ độ trung điểm M của đoạn thẳng AB : x x y y z z A B M ; A B ; A B     2 2 2 
• Toạ độ trọng tâm G của tam giác ABC :  + + + + + + x x x y y y z z z A B C G ; A B C ; A B C   3 3 3   
• Toạ độ trọng tâmG của tứ diện ABCD :  + + + + + + + + + x x x x y y y y z z z z A B C D G ; A B C D ; A B C C     4 4 4 
4. Tích có hướng của hai vectơ  
a) Định nghĩa: Trong không gian Oxyz cho hai vectơ a = (a ;a ;a ) , b = (b ;b ;b ) . Tích có hướng 1 2 3 1 2 3    
của hai vectơ a và ,
b kí hiệu là a,b 
 , được xác định bởi Trang 1/22    a a a a a a  2 3 3 1 1 2
a,b =  ; ;
 = (a b − a b ;a b − a b ;a b − a b 2 3 3 2 3 1 1 3 1 2 2 1 ) b b b b b b  2 3 3 1 1 2 
Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số. b) Tính chất:       • [a, b] ⊥ ; a
[a, b] ⊥ b    
• a, b  = − b,a             
• i , j= k;
 j,k  = i ;
k,i  = j      
• [a,b] = a . b .sin (a,b )(Chương trình nâng cao)     
• a, b cùng phương ⇔ [a, b] = 0 (chứng minh 3 điểm thẳng hàng)
c) Ứng dụng của tích có hướng: (Chương trình nâng cao)      
• Điều kiện đồng phẳng của ba vectơ: a, b và c đồng phẳng ⇔ [a, b].c = 0  
• Diện tích hình bình hành ABCD : S =   AB ADABCD ,   
• Diện tích tam giác ABC : 1 S =   ∆ AB AC ABC , 2 
  
• Thể tích khối hộp ABCDA′B C ′ D ′ ′ : V = AB AD AA′ ABCD A B C D [ , ]. . ' ' ' '
  
• Thể tích tứ diện ABCD : 1 V = AB AC AD ABCD [ , ]. 6 Chú ý:
– Tích vô hướng của hai vectơ thường sử dụng để chứng minh hai đường thẳng vuông góc, tính
góc giữa hai đường thẳng.
– Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ
diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.    
a ⊥ b ⇔ a b . = 0     
a vaø b cuøng phöông ⇔ [a,b] = 0     
a, b, c ñoàng phaúng ⇔ [a,b] c . = 0
5. Một vài thao tác sử dụng máy tính bỏ túi (Casio Fx570 Es Plus, Casio Fx570 Vn Plus, Vinacal 570 Es Plus )
Trong không gian Oxyz cho bốn điểm A(x z B x y C x y D x y
A; y A; A ) ,
( B; B;zB ), ( C; C;zC ), ( D; D;zD ) 
w 8 1 1 (nhập vectơ AB ) 
q 5 2 2 2 (nhập vectơ AC ) 
q 5 2 3 1 (nhập vectơ AD )  
C q53q54= (tính AB, AC   )
  
C q53q54q57q55= (tính [AB, AC].AD )
  
Cqc(Abs) q53q54q57q55= (tính [AB, AC].AD ) C1a6qc(Abs) q53q54q57q55=
   (tính 1 V = AB AC AD ABCD [ , ]. 6 Trang 2/22
B. BÀI TẬP TRẮC NGHIỆM     
Câu 1. Gọi ϕ là góc giữa hai vectơ a và b , với a và b khác 0 , khi đó cosϕ bằng    . a b     A. . a b −a b a + b   . B.   . C. .   . D.   . a . b a . b a . b a . b  
Câu 2. Gọi ϕ là góc giữa hai vectơ a = (1;2;0) và b = (2;0;− ) 1 , khi đó cosϕ bằng A. 0. B. 2 . C. 2 . D. 2 − . 5 5 5   
Câu 3. Cho vectơ a = (1;3;4) , tìm vectơ b cùng phương với vectơ a     A. b = ( 2; − 6; − 8 − ). B. b = ( 2; − 6; − 8). C. b = ( 2; − 6;8). D. b = (2; 6; − 8 − ).  
Câu 4. Tích vô hướng của hai vectơ a = ( 2;
− 2;5),b = (0;1;2) trong không gian bằng A. 10. B. 13. C. 12. D. 14.
Câu 5. Trong không gian cho hai điểm A( 1; − 2;3), B(0;1; )
1 , độ dài đoạn AB bằng A. 6. B. 8. C. 10. D. 12.    
Câu 6. Trong không gian Oxyz , gọi i, j,k là các vectơ đơn vị, khi đó với M ( ;
x y; z) thì OM bằng            
A. −xi − y j − zk.
B. xi − y j − zk.
C. x j + yi + zk.
D. xi + y j + zk.    
Câu 7. Tích có hướng của hai vectơ a = (a ;a ;a ) ,b = (b ;b ;b ) là một vectơ, kí hiệu a,b , được 1 2 3 1 2 3 
xác định bằng tọa độ
A. (a b − a b ;a b − a b ;a b − a b .
B. (a b + a b ;a b + a b ;a b + a b . 2 3 3 2 3 1 1 3 1 2 2 1 ) 2 3 3 2 3 1 1 3 1 2 2 1 )
C. (a b − a b ;a b + a b ;a b − a b .
D. (a b − a b ;a b − a b ;a b − a b . 2 2 3 3 3 3 1 1 1 1 2 2 ) 2 3 3 2 3 1 1 3 1 2 2 1 )    
Câu 8. Cho các vectơ u = (u ;u ;u và v = (v ;v ;v , .
u v = 0 khi và chỉ khi 1 2 3 ) 1 2 3 )
A. u v + u v + u v =1.
B. u + v + u + v + u + v = 0 . 1 1 2 2 3 3 1 1 2 2 3 3
C. u v + u v + u v = 0 .
D.u v + u v + u v = 1 − . 1 1 2 2 3 3 1 2 2 3 3 1  
Câu 9. Cho vectơ a = (1; 1;
− 2), độ dài vectơ a là A. 6 . B. 2. C. − 6 . D. 4.
Câu 10. Trong không gian Oxyz , cho điểm M nằm trên trục Ox sao cho M không trùng với gốc tọa
độ, khi đó tọa độ điểm M có dạng A. M ( ;0
a ;0),a ≠ 0. B. M (0; ;
b 0),b ≠ 0 . C. M (0;0;c),c ≠ 0. D. M ( ;1 a ) ;1 ,a ≠ 0 .
Câu 11. Trong không gian Oxyz , cho điểm M nằm trên mặt phẳng (Oxy)sao cho M không trùng với
gốc tọa độ và không nằm trên hai trục Ox,Oy , khi đó tọa độ điểm M là ( a,b,c ≠ 0 ) A. (0; ; b a). B. ( ; a ;0 b ).
C. (0;0;c). D. ( ;1 a ) ;1    
Câu 12. Trong không gian Oxyz , cho a = (0;3;4) và b = 2 a , khi đó tọa độ vectơ b có thể là A. (0;3;4). B. (4;0;3). C. (2;0; ) 1 . D. ( 8; − 0; 6 − ).    
Câu 13. Trong không gian Oxyz cho hai vectơ u và v , khi đó u,v   bằng                
A. u . v .sin (u,v).
B. u . v .cos(u,v). C. . u .
v cos(u,v). D. . u .
v sin (u,v).   
Câu 14. Trong không gian Oxyz cho ba vectơ a = (1; 1; − 2),b = (3;0;− ) 1 ,c = ( 2 − ;5; ) 1 , vectơ    
m = a + b − c có tọa độ là A. (6;0; 6 − ) . B. ( 6; − 6;0) . C. (6; 6; − 0) . D. (0;6; 6 − ) . Trang 3/22
Câu 15. Trong không gian Oxyz cho ba điểm A(1;0; 3 − ), B(2;4;− ) 1 ,C (2; 2;
− 0) . Độ dài các cạnh
AB, AC, BC của tam giác ABC lần lượt là A. 21, 13, 37 . B. 11, 14, 37 . C. 21, 14, 37 . D. 21, 13, 35 .
Câu 16. Trong không gian Oxyz cho ba điểm A(1;0; 3 − ), B(2;4;− ) 1 ,C (2; 2;
− 0) . Tọa độ trọng tâm G
của tam giác ABC là A.  5 2 4 ; ;  −      . B. 5 2 4  ; ; . C. (5;2;4) . D. 5  ;1; 2 − . 3 3 3       3 3 3   2 
Câu 17. Trong không gian Oxyz cho ba điểm A(1;2;0), B( 1; − 1;3),C (0; 2 − ;5). Để 4 điểm ,
A B,C, D
đồng phẳng thì tọa độ điểm D là A. D( 2 − ;5;0) .
B. D(1;2;3). C. D(1; 1; − 6) .
D. D(0;0;2) .   
Câu 18. Trong không gian Oxyz , cho ba vecto a = 1 ( ;2;3),b = ( 2 − ;0 1 ; ),c = ( 1 − ;0 1 ; ). Tìm tọa độ của     
vectơ n = a + b + 2c − 3i    
A. n = (6;2;6). B. n = (6;2; 6 − ) .
C. n = (0;2;6). D. n = ( 6; − 2;6) .
Câu 19. Trong không gian Oxyz , cho tam giác ABC có ( A 1;0;2), B( 2;
− 1;3),C(3;2;4). Tìm tọa độ
trọng tâm G của tam giác ABC A. 2 G  ;1;3   .
B. G (2;3;9) . C. G ( 6; − 0;24) . D. 1 G 2; ;3 . 3      3 
Câu 20. Cho 3 điểm M (2;0;0), N (0;−3;0), P(0;0;4). Nếu MNPQ là hình bình hành thì tọa độ của điểm Q là A. Q( 2 − ; 3 − ;4)
B. Q(2;3;4)
C. Q(3;4;2) D. Q( 2 − ; 3 − ; 4 − )
Câu 21. Trong không gian tọa độ Oxyz cho ba điểm M (1;1; )
1 , N (2;3;4), P(7;7;5) . Để tứ giác MNPQ
là hình bình hành thì tọa độ điểm Q là A. Q( 6 − ;5;2) .
B. Q(6;5;2) . C. Q(6; 5; − 2) . D. Q( 6 − ; 5 − ; 2 − ) .
Câu 22. Cho 3 điểm A(1;2;0), B(1;0;− )
1 , C (0;−1;2). Tam giác ABC là
A. tam giác có ba góc nhọn.
B. tam giác cân đỉnh A .
C. tam giác vuông đỉnh A . D. tam giác đều.
Câu 23. Trong không gian tọa độ Oxyz cho ba điểm A( 1
− ;2;2), B(0;1;3),C ( 3 − ;4;0) . Để tứ giác
ABCD là hình bình hành thì tọa độ điểm D là A. D( 4 − ;5;− ) 1 . B. D(4;5;− ) 1 . C. D( 4 − ; 5 − ;− ) 1 . D. D(4; 5; − ) 1 .      
Câu 24. Cho hai vectơ a và b tạo với nhau góc 0
60 và a = 2; b = 4 . Khi đó a + b bằng A. 8 3 + 20. B. 2 7. C. 2 5. D. 2 .
Câu 25. Cho điểm M (1;2; 3
− ) , khoảng cách từ điểm M đến mặt phẳng (Oxy) bằng A. 2. B. 3 − . C. 1. D. 3.
Câu 26. Cho điểm M ( 2
− ;5;0) , hình chiếu vuông góc của điểm M trên trục Oy là điểm
A. M ′(2;5;0) . B. M ′(0; 5; − 0) .
C. M ′(0;5;0) . D. M ′( 2; − 0;0) .
Câu 27. Cho điểm M (1;2; 3
− ) , hình chiếu vuông góc của điểm M trên mặt phẳng (Oxy) là điểm
A. M ′(1;2;0). B. M ′(1;0; 3 − ) . C. M ′(0;2; 3 − ) .
D. M ′(1;2;3) .
Câu 28. Cho điểm M ( 2 − ;5; )
1 , khoảng cách từ điểm M đến trục Ox bằng A. 29 . B. 5 . C. 2. D. 26 .
Câu 29. Cho hình chóp tam giác S.ABC với I là trọng tâm của đáy ABC . Đẳng thức nào sau đây là đẳng thức đúng Trang 4/22   
   
   
   
A. IA = IB + IC.
B. IA + IB + CI = 0.
C. IA + BI + IC = 0. D. IA + IB + IC = 0. → → →
Câu 30. Trong không gian Oxyz , cho 3 vectơ a = ( 1;
− 1;0) ; b = (1;1;0) ; c = (1;1; ) 1 . Trong các mệnh
đề sau, mệnh đề nào sai:      
A. b ⊥ .c
B. a = 2.
C. c = 3.
D. a ⊥ .b
Câu 31. Cho điểm M (3;2;− )
1 , điểm đối xứng của M qua mặt phẳng (Oxy) là điểm A. M ′(3; 2 − ; ) 1 . B. M ′(3; 2 − ;− ) 1 . C. M ′(3;2; ) 1 .
D. M ′(3;2;0) .
Câu 32. Cho điểm M (3;2;− ) 1 , điểm M ′( ; a ;
b c) đối xứng của M qua trục Oy , khi đó a + b + c bằng A. 6. B. 4. C. 0. D. 2.    
Câu 33. Cho u = (1;1; )
1 và v = (0;1;m) . Để góc giữa hai vectơ u,v có số đo bằng 0 45 thì m bằng A. ± 3 . B. 2 ± 3 . C. 1± 3 . D. 3 .
Câu 34. Cho A(1; 2
− ;0), B(3;3;2),C ( 1 − ;2;2), D(3;3; )
1 . Thể tích của tứ diện ABCD bằng A. 5. B. 4. C. 3. D. 6.
Câu 35. Trong không gian Oxyz cho tứ diện ABCD . Độ dài đường cao vẽ từ D của tứ diện ABCD
cho bởi công thức nào sau đây:
  
  
AB, AC.AD
AB, AC.AD A. 1 h   = 1     . B. h =   . 3 A . B AC 3 A . B AC  
  
  
AB, AC.AD
AB, AC.AD C. h   =   .. D. h   =   . A . B ACA . B AC  
Câu 36. Trong không gian tọa độ Oxyz , cho bốn điểm A(1; 2
− ;0), B(3;3;2),C ( 1 − ;2;2), D(3;3; ) 1 . Độ
dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống mặt phẳng ( ABC) là A. 9 . B. 9 . C. 9 . D. 9 . 7 2 7 2 14
Câu 37. Trong không gian Oxyz , cho tứ diện ABCD có ( A 1;0;2), B( 2;
− 1;3),C(3;2;4), D(6;9; 5 − ) . Tìm
tọa độ trọng tâm G của tứ diện ABCD A. 18 G  9; ; 30 − −   .
B. G (8;12;4) . C. 14 G 3;3; . D. G (2;3; ) 1 . 4      4 
Câu 38. Trong không gian Oxyz , cho hai điểm (
A 1;2;1), B(2; 1;
− 2) . Điểm M trên trục Ox và cách đều hai điểm ,
A B có tọa độ là A. 1 1 3 M  ; ;      . B. 1 M  ;0;0 . C. 3 M  ;0;0 . D. 1 3 M 0; ; . 2 2 2        2   2   2 2 
Câu 39. Trong không gian Oxyz , cho hai điểm (
A 1;2;1), B(3; 1;
− 2) . Điểm M trên trục Oz và cách đều hai điểm ,
A B có tọa độ là
A. M (0;0;4) . B. M (0;0; 4 − ). C. 3 M 0;0;    . D. 3 1 3 M  ; ; . 2      2 2 2 
Câu 40. Trong không gian Oxyz cho ba điểm ( A 1 − ; 2;
− 3), B(0;3;1),C(4;2;2) . Cosin của góc  BAC là A. 9 . B. 9 . C. 9 − . D. 9 − . 2 35 35 2 35 35   
Câu 41. Tọa độ của vecto n vuông góc với hai vecto a = (2; 1 − ;2),b = (3; 2; − 1) là     A. n = (3;4; ) 1 .
B. n = (3;4;− ) 1 . C. n = ( 3 − ;4;− ) 1 . D. n = (3; 4 − ;− ) 1 .     π       
Câu 42. Cho a = 2; b = 5, góc giữa hai vectơ a và b bằng 2 , u = ka − ; b v = a + 2 .
b Để u vuông 3 
góc với v thì k bằng Trang 5/22 A. 6 − . B. 45. C. 6 . D. 45 − . 45 6 45 6   
Câu 43. Cho u = (2; 1; − ) 1 ,v = (m;3;− ) 1 , w = (1;2; )
1 . Với giá trị nào của m thì ba vectơ trên đồng phẳng A. 3 . B. 3 − . C. 8 . D. 8 − . 8 8 3 3    
Câu 44. Cho hai vectơ a = (1;log 5;m , b = 3;log 3;4 . Với giá trị nào của m thì a ⊥ b 3 ) ( 5 )
A. m =1;m = 1 − . B. m =1. C. m = 1 − .
D. m = 2;m = 2 − .
Câu 45. Trong không gian Oxyz cho ba điểm (
A 2;5;3), B(3;7;4),C( ;
x y;6) . Giá trị của x, y để ba điểm ,
A B,C thẳng hàng là
A. x = 5; y =11. B. x = 5; − y =11. C. x = 1 − 1; y = 5 − .
D. x =11; y = 5.
Câu 46. Trong không gian Oxyz cho ba điểm (
A 1;0;0), B(0;0;1),C(2;1;1) . Tam giác ABC là
A. tam giác vuông tại A .
B. tam giác cân tại A .
C. tam giác vuông cân tại A . D. Tam giác đều.
Câu 47. Trong không gian Oxyz cho tam giác ABC có (
A 1;0;0), B(0;0;1),C(2;1;1) . Tam giác ABC có diện tích bằng A. 6 . B. 6 . C. 6 . D. 1 . 3 2 2
Câu 48. Ba đỉnh của một hình bình hành có tọa độ là(1;1; )
1 ,(2;3;4),(7;7;5). Diện tích của hình bình hành đó bằng A. 2 83 . B. 83 . C. 83 . D. 83 . 2      
Câu 49. Cho 3 vecto a = (1;2; ) 1 ; b = ( 1; − 1;2) và c = ( ; x 3 ;
x x + 2) . Tìm x để 3 vectơ a,b,c đồng phẳng A. 2. B. 1. − C. 2. − D. 1.  → → 
Câu 50. Trong không gian Oxyz cho ba vectơ a = (3; 2
− ;4), b = (5;1;6) , c = ( 3
− ;0;2) . Tìm vectơ x    
sao cho vectơ x đồng thời vuông góc với a,b,c A. (1;0;0). B. (0;0; )1. C. (0;1;0). D. (0;0;0).
Câu 51. Trong không gianOxyz , cho 2 điểm B(1;2; 3) − ,C(7;4; 2
− ) . Nếu E là điểm thỏa mãn đẳng  
thức CE = 2EB thì tọa độ điểm E là A.  8 8 3; ;  −  8 8   8   1   . B. 3; ; . C. 3;3;−  . D. 1;2; .  3 3   3 3   3   3 
Câu 52. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm ( A 1;2; 1 − ) , B(2; 1 − ;3) ,C( 2; − 3;3) . Điểm M (a; ;
b c) là đỉnh thứ tư của hình bình hành ABCM , khi đó 2 2 2
P = a + b − c có giá trị bằng A. 43.. B. 44.. C. 42.. D. 45.
Câu 53. Trong không gian với hệ trục tọa độ Oxyz cho ba điểm ( A 1;2; 1 − ) , B(2; 1 − ;3) ,C( 2; − 3;3) . Tìm
tọa độ điểm D là chân đường phân giác trong góc A của tam giác ABC
A. D(0;1;3) .
B. D(0;3;1) . C. D(0; 3 − ;1) . D. D(0;3; 1) − .
Câu 54. Trong không gian với hệ toạ độ Oxyz , cho các điểm A( 1; − 3;5) , B( 4
− ;3;2) , C(0;2;1) . Tìm tọa
độ điểm I tâm đường tròn ngoại tiếp tam giác ABC A. 8 5 8 I( ; ; ) . B. 5 8 8 I( ; ; ) . C. 5 8 8 I(− ; ; ). D. 8 8 5 I( ; ; ) . 3 3 3 3 3 3 3 3 3 3 3 3  
Câu 55. Trong không gian Oxyz , cho 3 vectơ a = (−1;1;0), b = (1;1;0), c = (1;1; ) 1 . Cho hình hộp
     OABC.O A ′ B ′ C
′ ′ thỏa mãn điều kiện OA = a, OB = b, OC ' = c . Thể tích của hình hộp nói trên bằng: Trang 6/22 A. 1 B. 4 C. 2 D. 2 3 3
Câu 56. Trong không gian với hệ trục Oxyz cho tọa độ 4 điểm A(2;−1; ) 1 , B(1;0;0),
C (3;1;0), D(0;2; )
1 . Cho các mệnh đề sau: 1) Độ dài AB = 2 .
2) Tam giác BCD vuông tại B .
3) Thể tích của tứ diện ABCD bằng 6.
Các mệnh đề đúng là: A. 2). B. 3). C. 1); 3). D. 2), 1)   
Câu 57. Trong không gianOxyz , cho ba vectơ a = ( 1,
− 1,0);b = (1,1,0);c = (1,1, ) 1 . Trong các mệnh đề
sau, mệnh đề nào đúng:       A. (b c) 6 cos , = .
B. a +b + c = 0. 3     
A. a,b,c đồng phẳng.
D. .ab =1.
Câu 58. Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD , biết ( A 1;0;1) , B( 1; − 1;2) , C( 1; − 1;0) , D(2; 1 − ; 2
− ) . Độ dài đường cao AH của tứ diện ABCD bằng: A. 2 . B. 1 . C. 13 . D. 3 13 . 13 13 2 13
Câu 59. Cho hình chóp tam giác S.ABC với I là trọng tâm của đáy ABC . Đẳng thức nào sau đây là đẳng thức đúng 
   
   A. 1
SI = (SA+ SB + SC). B. 1
SI = (SA+ SB + SC). 2 3
   
    
C. SI = SA + SB + SC.
D. SI + SA + SB + SC = 0.
Câu 60. Trong không gian Oxyz , cho tứ diện ABCD có (
A 1;0;0), B(0;1;0),C(0;0;1), D( 2; − 1; 1 − ) . Thể
tích của tứ diện ABCD bằng A. 3 . B. 3. C. 1. D. 1 . 2 2
Câu 61. Cho hình chóp S.ABC có = = =  =  0 =  0
SA SB a, SC 3a, ASB CSB 60 ,CSA = 90 . Gọi G là trọng
tâm tam giác ABC . Khi đó khoảng cách SG bằng
A. a 15 .
B. a 5 .
C. a 7 . D. a 3 . 3 3 3
Câu 62. Trong không gian tọa độ Oxyz cho ba điểm A(2;5; ) 1 , B( 2; − 6; − 2),C (1;2;− ) 1 và điểm   M ( ; m ;
m m) , để MB − 2AC đạt giá trị nhỏ nhất thì m bằng A. 2. B. 3 . C. 1. D. 4.
Câu 63. Trong không gian tọa độ Oxyz cho ba điểm A(2;5; ) 1 , B( 2; − 6; − 2),C (1;2;− ) 1 và điểm M ( ; m ; m m) , để 2 2 2
MA − MB − MC đạt giá trị lớn nhất thì m bằng A. 3. B. 4. C. 2. D. 1.
Câu 64. Cho hình chóp S.ABCD biết A( 2; − 2;6), B( 3 − ;1;8),C ( 1
− ;0;7), D(1;2;3) . Gọi H là trung
điểm của CD, SH ⊥ ( ABCD). Để khối chóp S.ABCD có thể tích bằng 27 (đvtt) thì có hai 2
điểm S , S thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm I của S S 1 2 1 2 A. I (0; 1 − ; 3 − ).
B. I (1;0;3)
C. I (0;1;3) . D. I ( 1; − 0; 3 − ).
Câu 65. Trong không gian Oxyz , cho hai điểm ( A 2; 1 − ;7), B(4;5; 2
− ) . Đường thẳng AB cắt mặt phẳng
(Oyz) tại điểm M . Điểm M chia đoạn thẳng AB theo tỉ số nào A. 1 . B. 2 . C. 1 . D. 2 . 2 3 3 Trang 7/22
Câu 66. Trong không gian Oxyz , cho tứ diện ABCD có ( A 2;1; 1 − ), B(3;0;1),C(2; 1 − ;3) và D thuộc
trục Oy . Biết V
= và có hai điểm D 0; y ;0 , D 0; y ;0 thỏa mãn yêu cầu bài toán. 1 ( 1 ) 2 ( 2 ) ABCD 5
Khi đó y + y bằng 1 2 A. 0. B. 1. C. 2 . D. 3.
Câu 67. Trong không gian Oxyz , cho tam giác ABC có ( A 1 − ;2;4), B(3;0; 2
− ),C(1;3;7) . Gọi D là 
chân đường phân giác trong của góc A . Tính độ dài OD . A. 207 . B. 203 C. 201 . D. 205 . 3 3 3 3
Câu 68. Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC , biết (
A 1;1;1) , B(5;1; 2 − ) ,C(7;9;1) .
Tính độ dài phân giác trong AD của góc A A. 2 74 . B. 3 74 . C. 2 74. D. 3 74. 3 2
Câu 69. Trong không gian với hệ toạ độ Oxyz , cho 4 điểm ( A 2;4; 1 − ), B(1;4; 1 − ) , C(2;4;3) D(2;2; 1 − ) . Biết M ( ; x y; z) , để 2 2 2 2
MA + MB + MC + MD đạt giá trị nhỏ nhất thì x + y + z bằng A. 7. B. 8. C. 9. D. 6.
Câu 70. Tr ong không gian với hệ tr ục tọa độ Oxyz , cho ba điểm ( A 2;3;1) , B( 1; − 2;0) ,C(1;1; 2 − ) . H là
trực tâm tam giác ABC , khi đó, độ dài đoạn OH bằng A. 870 . B. 870 . C. 870 . D. 870 . 12 14 16 15
Câu 71. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có (
A 3;1;0) , B nằm trên mặt
phẳng (Oxy) và có hoành độ dương, C nằm trên trục Oz và H (2;1;1) là trực tâm của tam giác
ABC . Toạ độ các điểm B , C thỏa mãn yêu cầu bài toán là:  − + −   −  A. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4   − − +   +  B. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4   − + −   +  C. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4   − + +   −  D. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4 
Câu 72. Trong không gian với hệ tọa độ Oxyz , cho hình vuông ABCD , B(3;0;8) , D( 5; − 4 − ;0) . Biết  
đỉnh A thuộc mặt phẳng (Oxy ) và có tọa độ là những số nguyên, khi đó CA + CB bằng: A. 5 10. B. 6 10. C. 10 6. D. 10 5.
Câu 73. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC , biết ( A 5;3; 1) − , B(2;3; 4 − ) , C(3;1; 2
− ) . Bán kính đường tròn nội tiếp tam giác ABC bằng: A. 9 − 2 6. B. 9 − 3 6. C. 9 + 3 6. D. 9 + 2 6.
Câu 74. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm M (3;0;0), N ( ,
m n,0), P(0;0; p). Biết =  0 MN
13, MON = 60 , thể tích tứ diện OMNP bằng 3. Giá trị của biểu thức 2 2
A = m + 2n + p bằng A. 29. B. 27. C. 28. D. 30.
Câu 75. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm ( A 2;3;1) , B( 1; − 2;0) ,C(1;1; 2 − ) . Gọi I ( ; a ;
b c) là tâm đường tròn ngoại tiếp tam giác ABC . Tính giá trị biểu thức
P =15a + 30b + 75c A. 48. B. 50. C. 52. D. 46. Trang 8/22 Trang 9/22
C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM I – ĐÁP ÁN 8.1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A B A C A D A C A A B D A C C A A D A B
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
B A A B D C A D D A C C B C D A D C A A
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
B D D C A A C A A D A B A C D A A B B D
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 A A B C A B D A A D A B B A B
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
II –HƯỚNG DẪN GIẢI     
Câu 1. Gọi ϕ là góc giữa hai vectơ a và b , với a và b khác 0 , khi đó cosϕ bằng    . a b     A. . a b −a b a + b   . B.   . C. .   . D.   . a . b a . b a . b a . b  
Câu 2. Gọi ϕ là góc giữa hai vectơ a = (1;2;0) và b = (2;0;− ) 1 , khi đó cosϕ bằng A. 0. B. 2 . C. 2 . D. 2 − . 5 5 5   
Câu 3. Cho vectơ a = (1;3;4) , tìm vectơ b cùng phương với vectơ a     A. b = ( 2; − 6; − 8 − ). B. b = ( 2; − 6; − 8). C. b = ( 2; − 6;8). D. b = (2; 6; − 8 − ).  
Câu 4. Tích vô hướng của hai vectơ a = ( 2;
− 2;5),b = (0;1;2) trong không gian bằng A. 10. B. 13. C. 12. D. 14.
Câu 5. Trong không gian cho hai điểm A( 1; − 2;3), B(0;1; )
1 , độ dài đoạn AB bằng A. 6. B. 8. C. 10. D. 12.    
Câu 6. Trong không gian Oxyz , gọi i, j,k là các vectơ đơn vị, khi đó với M ( ;
x y; z) thì OM bằng            
A. −xi − y j − zk.
B. xi − y j − zk.
C. x j + yi + zk.
D. xi + y j + zk.    
Câu 7. Tích có hướng của hai vectơ a = (a ;a ;a ) ,b = (b ;b ;b ) là một vectơ, kí hiệu a,b , được 1 2 3 1 2 3 
xác định bằng tọa độ
A. (a b − a b ;a b − a b ;a b − a b .
B. (a b + a b ;a b + a b ;a b + a b . 2 3 3 2 3 1 1 3 1 2 2 1 ) 2 3 3 2 3 1 1 3 1 2 2 1 )
C. (a b − a b ;a b + a b ;a b − a b .
D. (a b − a b ;a b − a b ;a b − a b . 2 2 3 3 3 3 1 1 1 1 2 2 ) 2 3 3 2 3 1 1 3 1 2 2 1 )    
Câu 8. Cho các vectơ u = (u ;u ;u và v = (v ;v ;v , .
u v = 0 khi và chỉ khi 1 2 3 ) 1 2 3 )
A. u v + u v + u v =1.
B. u + v + u + v + u + v = 0 . 1 1 2 2 3 3 1 1 2 2 3 3
C. u v + u v + u v = 0 .
D.u v + u v + u v = 1 − . 1 1 2 2 3 3 1 2 2 3 3 1  
Câu 9. Cho vectơ a = (1; 1;
− 2), độ dài vectơ a là A. 6 . B. 2. C. − 6 . D. 4. Trang 10/22
Câu 10. Trong không gian Oxyz , cho điểm M nằm trên trục Ox sao cho M không trùng với gốc tọa
độ, khi đó tọa độ điểm M có dạng A. M ( ;0
a ;0),a ≠ 0. B. M (0; ;
b 0),b ≠ 0 . C. M (0;0;c),c ≠ 0. D. M ( ;1 a ) ;1 ,a ≠ 0 .
Câu 11. Trong không gian Oxyz , cho điểm M nằm trên mặt phẳng (Oxy)sao cho M không trùng với
gốc tọa độ và không nằm trên hai trục Ox,Oy , khi đó tọa độ điểm M là ( a,b,c ≠ 0 ) A. (0; ; b a). B. ( ; a ;0 b ).
C. (0;0;c). D. ( ;1 a ) ;1    
Câu 12. Trong không gian Oxyz , cho a = (0;3;4) và b = 2 a , khi đó tọa độ vectơ b có thể là A. (0;3;4). B. (4;0;3). C. (2;0; ) 1 . D. ( 8; − 0; 6 − ).    
Câu 13. Trong không gian Oxyz cho hai vectơ u và v , khi đó u,v   bằng                
A. u . v .sin (u,v).
B. u . v .cos(u,v). C. . u .
v cos(u,v). D. . u .
v sin (u,v).   
Câu 14. Trong không gian Oxyz cho ba vectơ a = (1; 1; − 2),b = (3;0;− ) 1 ,c = ( 2 − ;5; ) 1 , vectơ    
m = a + b − c có tọa độ là A. (6;0; 6 − ) . B. ( 6; − 6;0) . C. (6; 6; − 0) . D. (0;6; 6 − ) .
Câu 15. Trong không gian Oxyz cho ba điểm A(1;0; 3 − ), B(2;4;− ) 1 ,C (2; 2;
− 0) . Độ dài các cạnh
AB, AC, BC của tam giác ABC lần lượt là A. 21, 13, 37 . B. 11, 14, 37 . C. 21, 14, 37 . D. 21, 13, 35 .
Câu 16. Trong không gian Oxyz cho ba điểm A(1;0; 3 − ), B(2;4;− ) 1 ,C (2; 2;
− 0) . Tọa độ trọng tâm G
của tam giác ABC là A.  5 2 4 ; ;  −      . B. 5 2 4  ; ; . C. (5;2;4) . D. 5  ;1; 2 − . 3 3 3       3 3 3   2 
Câu 17. Trong không gian Oxyz cho ba điểm A(1;2;0), B( 1; − 1;3),C (0; 2 − ;5). Để 4 điểm ,
A B,C, D
đồng phẳng thì tọa độ điểm D là A. D( 2 − ;5;0) .
B. D(1;2;3). C. D(1; 1; − 6) .
D. D(0;0;2) . Hướng dẫn giải
  
Cách 1:Tính AB, AC.AD = 0  
Cách 2: Lập phương trình (ABC) và thế toạ độ D vào phương trình tìm được.   
Câu 18. Trong không gian Oxyz , cho ba vecto a = 1 ( ;2;3),b = ( 2 − ;0 1 ; ),c = ( 1 − ;0 1 ; ). Tìm tọa độ của     
vectơ n = a + b + 2c − 3i    
A. n = (6;2;6). B. n = (6;2; 6 − ) .
C. n = (0;2;6). D. n = ( 6; − 2;6) .
Câu 19. Trong không gian Oxyz , cho tam giác ABC có ( A 1;0;2), B( 2;
− 1;3),C(3;2;4). Tìm tọa độ
trọng tâm G của tam giác ABC A. 2 G  ;1;3   .
B. G (2;3;9) . C. G ( 6; − 0;24) . D. 1 G 2; ;3 . 3      3 
Câu 20. Cho 3 điểm M (2;0;0), N (0;−3;0), P(0;0;4). Nếu MNPQ là hình bình hành thì tọa độ của điểm Q là A. Q( 2 − ; 3 − ;4)
B. Q(2;3;4)
C. Q(3;4;2) D. Q( 2 − ; 3 − ; 4 − ) Hướng dẫn giải x = 2   Gọi Q( ;
x y;z) , MNPQ là hình bình hành thì MN = QP ⇔  y = 3 z − 4 =  0 Trang 11/22
Câu 21. Trong không gian tọa độ Oxyz cho ba điểm M (1;1; )
1 , N (2;3;4), P(7;7;5) . Để tứ giác MNPQ
là hình bình hành thì tọa độ điểm Q là A. Q( 6 − ;5;2) .
B. Q(6;5;2) . C. Q(6; 5; − 2) . D. Q( 6 − ; 5 − ; 2 − ) . Hướng dẫn giải Điểm Q( ; x y; z)  
MN = (1;2;3) , QP = (7 − ;
x 7 − y;5 − z)  
Vì MNPQ là hình bình hành nên MN = QP ⇒ Q(6;5;2)
Câu 22. Cho 3 điểm A(1;2;0), B(1;0;− )
1 , C (0;−1;2). Tam giác ABC là
A. tam giác có ba góc nhọn.
B. tam giác cân đỉnh A .
C. tam giác vuông đỉnh A . D. tam giác đều. Hướng dẫn giải    
AB = (0;−2;−1); AC = (−1;−3;2) . Ta thấy .
AB AC ≠ 0 ⇒ ∆ABC không vuông.  
AB ≠ AC ⇒ ∆ABC không cân.
Câu 23. Trong không gian tọa độ Oxyz cho ba điểm A( 1
− ;2;2), B(0;1;3),C ( 3 − ;4;0) . Để tứ giác
ABCD là hình bình hành thì tọa độ điểm D là A. D( 4 − ;5;− ) 1 . B. D(4;5;− ) 1 . C. D( 4 − ; 5 − ;− ) 1 . D. D(4; 5; − ) 1 . Hướng dẫn giải Điểm D( ; x y; z)   AB = (1; 1; − ) 1 , DC = ( 3 − − ;4
x − y;− z)  
Vì ABCD là hình bình hành nên AB = DC ⇒ D( 4 − ;5;− ) 1      
Câu 24. Cho hai vectơ a và b tạo với nhau góc 0
60 và a = 2; b = 4 . Khi đó a + b bằng A. 8 3 + 20. B. 2 7. C. 2 5. D. 2 . Hướng dẫn giải           Ta có 2 2 2
a + b = a + b + 2 a b .cos(a,b) = 4+16+8 = 28 ⇒ a +b = 2 7.
Câu 25. Cho điểm M (1;2; 3
− ) , khoảng cách từ điểm M đến mặt phẳng (Oxy) bằng A. 2. B. 3 − . C. 1. D. 3. Hướng dẫn giải Với M (a; ;
b c) ⇒ d (M ,(Oxy)) = c
Câu 26. Cho điểm M ( 2
− ;5;0) , hình chiếu vuông góc của điểm M trên trục Oy là điểm
A. M ′(2;5;0) . B. M ′(0; 5; − 0) .
C. M ′(0;5;0) . D. M ′( 2; − 0;0) . Hướng dẫn giải Với M (a; ;
b c) ⇒ hình chiếu vuông góc của M lên trục Oy là M 0; ; b 0 1 ( )
Câu 27. Cho điểm M (1;2; 3
− ) , hình chiếu vuông góc của điểm M trên mặt phẳng (Oxy) là điểm
A. M ′(1;2;0). B. M ′(1;0; 3 − ) . C. M ′(0;2; 3 − ) .
D. M ′(1;2;3) . Hướng dẫn giải Với M (a; ;
b c) ⇒ hình chiếu vuông góc của M lên mặt phẳng(Oxy) là M ; a ;0 b 1 ( )
Câu 28. Cho điểm M ( 2 − ;5; )
1 , khoảng cách từ điểm M đến trục Ox bằng A. 29 . B. 5 . C. 2. D. 26 . Hướng dẫn giải Trang 12/22
Với M (a b c) ⇒ d (M Ox) 2 2 ; ; , = b + c
Câu 29. Cho hình chóp tam giác S.ABC với I là trọng tâm của đáy ABC . Đẳng thức nào sau đây là đẳng thức đúng   
   
   
   
A. IA = IB + IC.
B. IA + IB + CI = 0.
C. IA + BI + IC = 0. D. IA + IB + IC = 0. → → →
Câu 30. Trong không gian Oxyz , cho 3 vectơ a = ( 1;
− 1;0) ; b = (1;1;0) ; c = (1;1; ) 1 . Trong các mệnh
đề sau, mệnh đề nào sai:      
A. b ⊥ .c
B. a = 2.
C. c = 3.
D. a ⊥ .b Hướng dẫn giải   Vì . b c = 2 ≠ 0.
Câu 31. Cho điểm M (3;2;− )
1 , điểm đối xứng của M qua mặt phẳng (Oxy) là điểm A. M ′(3; 2 − ; ) 1 . B. M ′(3; 2 − ;− ) 1 . C. M ′(3;2; ) 1 .
D. M ′(3;2;0) . Hướng dẫn giải Với M (a; ;
b c) ⇒ điểm đối xứng của M qua mặt phẳng (Oxy) là M (a; ; b −c)
Câu 32. Cho điểm M (3;2;− ) 1 , điểm M ′( ; a ;
b c) đối xứng của M qua trục Oy , khi đó a + b + c bằng A. 6. B. 4. C. 0. D. 2. Hướng dẫn giải Với M (a; ;
b c) ⇒ điểm đối xứng của M qua trục Oy là M ′(− ; a ; b −c) ⇒ M ′( 3 − ;2; )
1 ⇒ a + b + c = 0.    
Câu 33. Cho u = (1;1; )
1 và v = (0;1;m) . Để góc giữa hai vectơ u,v có số đo bằng 0 45 thì m bằng A. ± 3 . B. 2 ± 3 . C. 1± 3 . D. 3 . Hướng dẫn giải m ≥ 1 1.0 +1.1+1.m 1 − cosϕ 2 (m ) 2 1 3 m 1  = = ⇔ + = + ⇔  3. m +1 2 3  ( 2 2 m + ) 1 = 2(m + )2 1 ⇔ m = 2 ± 3
Câu 34. Cho A(1; 2
− ;0), B(3;3;2),C ( 1 − ;2;2), D(3;3; )
1 . Thể tích của tứ diện ABCD bằng A. 5. B. 4. C. 3. D. 6. Hướng dẫn giải   
Tính AB = (2;5;2), AC = ( 2; − 4;2), AD = (2;5; ) 1
1   
V = AB, AC.AD = 3 6   Sử dụng Casio 
w 8 1 1 (nhập vectơ AB ) 
q 5 2 2 2 (nhập vectơ AC ) 
q 5 2 3 1 (nhập vectơ AD )
C1a6qc(abs) q53q54q57q55= (tính V )
Câu 35. Trong không gian Oxyz cho tứ diện ABCD . Độ dài đường cao vẽ từ D của tứ diện ABCD
cho bởi công thức nào sau đây:
  
  
AB, AC.AD
AB, AC.AD A. 1 h   = 1     . B. h =   . 3 A . B AC 3 A . B AC  
  
  
AB, AC.AD
AB, AC.AD C. h   =   .. D. h   =   . A . B ACA . B AC   Hướng dẫn giải Trang 13/22
    
  
AB, AC.AD Vì 1 1 1 V
= h AB AC = AB ACAD nên h   =   . ABCD . . , . 3 2   6   A . B AC  
Câu 36. Trong không gian tọa độ Oxyz , cho bốn điểm A(1; 2
− ;0), B(3;3;2),C ( 1 − ;2;2), D(3;3; ) 1 . Độ
dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống mặt phẳng ( ABC) là A. 9 . B. 9 . C. 9 . D. 9 . 7 2 7 2 14 Hướng dẫn giải   
Tính AB(2;5;2), AC ( 2; − 4;2), AD(2;5; ) 1
1   
V = AB, AC.AD = 3 6   1   V = . B h , với 1 B = S =   =
, h = d (D,( ABC)) ∆ AB AC ABC , 7 2 3 2   3V 3.3 9 ⇒ h = = = B 7 2 7 2
Câu 37. Trong không gian Oxyz , cho tứ diện ABCD có ( A 1;0;2), B( 2;
− 1;3),C(3;2;4), D(6;9; 5 − ) . Tìm
tọa độ trọng tâm G của tứ diện ABCD A. 18 G  9; ; 30 − −   .
B. G (8;12;4) . C. 14 G 3;3; . D. G (2;3; ) 1 . 4      4 
Câu 38. Trong không gian Oxyz , cho hai điểm (
A 1;2;1), B(2; 1;
− 2) . Điểm M trên trục Ox và cách đều hai điểm ,
A B có tọa độ là A. 1 1 3 M  ; ;      . B. 1 M  ;0;0 . C. 3 M  ;0;0 . D. 1 3 M 0; ; . 2 2 2        2   2   2 2  Hướng dẫn giải
M ∈Ox ⇒ M ( ;0 a ;0)
M cách đều hai điểm , A B nên 2 2
MA = MB ⇔ ( − a)2 2 2 + + = ( − a)2 2 2 1 2 1 2 + 2 +1 3
⇔ 2a = 3 ⇔ a = 2
Câu 39. Trong không gian Oxyz , cho hai điểm (
A 1;2;1), B(3; 1;
− 2) . Điểm M trên trục Oz và cách đều hai điểm ,
A B có tọa độ là
A. M (0;0;4) . B. M (0;0; 4 − ). C. 3 M 0;0;    . D. 3 1 3 M  ; ; . 2      2 2 2 
Câu 40. Trong không gian Oxyz cho ba điểm ( A 1 − ; 2;
− 3), B(0;3;1),C(4;2;2) . Cosin của góc  BAC là A. 9 . B. 9 . C. 9 − . D. 9 − . 2 35 35 2 35 35   
Câu 41. Tọa độ của vecto n vuông góc với hai vecto a = (2; 1 − ;2),b = (3; 2; − 1) là     A. n = (3;4; ) 1 .
B. n = (3;4;− ) 1 . C. n = ( 3 − ;4;− ) 1 . D. n = (3; 4 − ;− ) 1 .     π       
Câu 42. Cho a = 2; b = 5, góc giữa hai vectơ a và b bằng 2 , u = ka − ; b v = a + 2 .
b Để u vuông 3 
góc với v thì k bằng A. 6 − . B. 45. C. 6 . D. 45 − . 45 6 45 6 Hướng dẫn giải Trang 14/22         π
u v = (ka −b )(a + b) = k − +( k − ) 2 . 2 4 50 2 1 a b cos 3 = 6 − k − 45   
Câu 43. Cho u = (2; 1; − ) 1 ,v = (m;3;− ) 1 , w = (1;2; )
1 . Với giá trị nào của m thì ba vectơ trên đồng phẳng A. 3 . B. 3 − . C. 8 . D. 8 − . 8 8 3 3 Hướng dẫn giải     
Ta có: u,v = ( 2
− ;m + 2;m + 6), u,v.w = 3m + 8          
u,v, w đồng phẳng 8
⇔ u,v.w = 0 ⇔ m = −   3    
Câu 44. Cho hai vectơ a = (1;log 5;m , b = 3;log 3;4 . Với giá trị nào của m thì a ⊥ b 3 ) ( 5 )
A. m =1;m = 1 − . B. m =1. C. m = 1 − .
D. m = 2;m = 2 − .
Câu 45. Trong không gian Oxyz cho ba điểm (
A 2;5;3), B(3;7;4),C( ;
x y;6) . Giá trị của x, y để ba điểm ,
A B,C thẳng hàng là
A. x = 5; y =11. B. x = 5; − y =11. C. x = 1 − 1; y = 5 − .
D. x =11; y = 5. Hướng dẫn giải   AB = (1;2; )
1 , AC = (x − 2; y − 5;3)   − − ,
A B,C thẳng hàng ⇔ AB, AC cùng phương x 2 y 5 3 ⇔ =
= ⇔ x = 5; y =11 1 2 1
Câu 46. Trong không gian Oxyz cho ba điểm (
A 1;0;0), B(0;0;1),C(2;1;1) . Tam giác ABC là
A. tam giác vuông tại A .
B. tam giác cân tại A .
C. tam giác vuông cân tại A . D. Tam giác đều. Hướng dẫn giải    BA = (1;0;− ) 1 ,CA = ( 1; − 1; − − ) 1 ,CB = ( 2 − ; 1; − 0)   B .
ACA = 0 ⇒tam giác vuông tại A , AB ≠ AC .
Câu 47. Trong không gian Oxyz cho tam giác ABC có (
A 1;0;0), B(0;0;1),C(2;1;1) . Tam giác ABC có diện tích bằng A. 6 . B. 6 . C. 6 . D. 1 . 3 2 2 Hướng dẫn giải     AB = ( 1; − 0; ) 1 , AC = (1;1; ) 1 . 1 6 S =   = ∆ AB AC ABC . 2   2
Câu 48. Ba đỉnh của một hình bình hành có tọa độ là(1;1; )
1 ,(2;3;4),(7;7;5). Diện tích của hình bình hành đó bằng A. 2 83 . B. 83 . C. 83 . D. 83 . 2 Hướng dẫn giải
Gọi 3 đỉnh theo thứ tự là , A B,C  
AB = (1;2;3), AC = (6;6;4)  
S = AB AC = − + + − = hbh ( )2 2 , 10 14 ( 6)2 2 83        
Câu 49. Cho 3 vecto a = (1;2; ) 1 ; b = ( 1; − 1;2) và c = ( ; x 3 ;
x x + 2) . Tìm x để 3 vectơ a,b,c đồng phẳng A. 2. B. 1. − C. 2. − D. 1. Hướng dẫn giải        a,b,c  
đồng phẳng thì a,b .c = 0 ⇒ x = 2.    Trang 15/22  → → 
Câu 50. Trong không gian Oxyz cho ba vectơ a = (3; 2
− ;4), b = (5;1;6) , c = ( 3
− ;0;2) . Tìm vectơ x    
sao cho vectơ x đồng thời vuông góc với a,b,c A. (1;0;0). B. (0;0; )1. C. (0;1;0). D. (0;0;0). Hướng dẫn giải       
Dễ thấy chỉ có x = (0;0;0) thỏa mãn . x a = . x b = . x c = 0.
Câu 51. Trong không gianOxyz , cho 2 điểm B(1;2; 3) − ,C(7;4; 2
− ) . Nếu E là điểm thỏa mãn đẳng  
thức CE = 2EB thì tọa độ điểm E là A.  8 8 3; ;  −  8 8   8   1   . B. 3; ; . C. 3;3;−  . D. 1;2; .  3 3   3 3   3   3  Hướng dẫn giải  x = 3    E( ; x y; z) , từ  8
CE = 2EB ⇒ y = . 3   8 z = −  3
Câu 52. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm ( A 1;2; 1 − ) , B(2; 1 − ;3) ,C( 2; − 3;3) . Điểm M (a; ;
b c) là đỉnh thứ tư của hình bình hành ABCM , khi đó 2 2 2
P = a + b − c có giá trị bằng A. 43.. B. 44.. C. 42.. D. 45. Hướng dẫn giải M ( ;
x y; z) , ABCM là hình bình hành thì x −1 = 2 − − 2   AM BC  =
⇒ y − 2 = 3+1 ⇒ M ( 3 − ;6; 1 − ) ⇒ P = 44.. z +1= 3−  3
Câu 53. Trong không gian với hệ trục tọa độ Oxyz cho ba điểm ( A 1;2; 1 − ) , B(2; 1 − ;3) ,C( 2; − 3;3) . Tìm
tọa độ điểm D là chân đường phân giác trong góc A của tam giác ABC
A. D(0;1;3) .
B. D(0;3;1) . C. D(0; 3 − ;1) . D. D(0;3; 1) − . Hướng dẫn giải
Ta có AB = 26, AC = 26 ⇒ tam giác ABC cân ở A nên D là trung điểm BC ⇒ D(0;1;3).
Câu 54. Trong không gian với hệ toạ độ Oxyz , cho các điểm A( 1; − 3;5) , B( 4
− ;3;2) , C(0;2;1) . Tìm tọa
độ điểm I tâm đường tròn ngoại tiếp tam giác ABC A. 8 5 8 I( ; ; ) . B. 5 8 8 I( ; ; ) . C. 5 8 8 I(− ; ; ). D. 8 8 5 I( ; ; ) . 3 3 3 3 3 3 3 3 3 3 3 3 Hướng dẫn giải
Ta có: AB = BC = CA = 3 2 ⇒ A
∆ BC đều. Do đó tâm I của đường tròn ngoại tiếp A ∆ BC
là trọng tâm của nó. Kết luận: 5 8 8 I  ; ;  −  . 3 3 3     
Câu 55. Trong không gian Oxyz , cho 3 vectơ a = (−1;1;0), b = (1;1;0), c = (1;1; ) 1 . Cho hình hộp
     OABC.O A ′ B ′ C
′ ′ thỏa mãn điều kiện OA = a, OB = b, OC ' = c . Thể tích của hình hộp nói trên bằng: A. 1 B. 4 C. 2 D. 2 3 3 Hướng dẫn giải      OA = a, ⇒ (
A −1;1;0),OB = b ⇒ B(1;1;0), OC ' = c ⇒ C '(1;1;1) Trang 16/22    
  
AB = OC ⇒ C(2;0;0) ⇒ CC ' = (−1;1;1) = OO' ⇒V = OAOBOO OABC O A B C , ' . ' ' ' '  
Câu 56. Trong không gian với hệ trục Oxyz cho tọa độ 4 điểm A(2;−1; ) 1 , B(1;0;0),
C (3;1;0), D(0;2; )
1 . Cho các mệnh đề sau: 1) Độ dài AB = 2 .
2) Tam giác BCD vuông tại B .
3) Thể tích của tứ diện ABCD bằng 6.
Các mệnh đề đúng là: A. 2). B. 3). C. 1); 3). D. 2), 1)   
Câu 57. Trong không gianOxyz , cho ba vectơ a = ( 1,
− 1,0);b = (1,1,0);c = (1,1, ) 1 . Trong các mệnh đề
sau, mệnh đề nào đúng:       A. (b c) 6 cos , = .
B. a +b + c = 0. 3     
A. a,b,c đồng phẳng.
D. .ab =1. Hướng dẫn giải     . cos( , ) b c b c =   b . c
Câu 58. Trong không gian với hệ tọa độ Oxyz , cho tứ diện ABCD , biết ( A 1;0;1) , B( 1; − 1;2) , C( 1; − 1;0) , D(2; 1 − ; 2
− ) . Độ dài đường cao AH của tứ diện ABCD bằng: A. 2 . B. 1 . C. 13 . D. 3 13 . 13 13 2 13 Hướng dẫn giải
  
AB, AC.AD Sử dụng công thức   1 h =   = . A . B AC 13
Câu 59. Cho hình chóp tam giác S.ABC với I là trọng tâm của đáy ABC . Đẳng thức nào sau đây là đẳng thức đúng 
   
   A. 1
SI = (SA+ SB + SC). B. 1
SI = (SA+ SB + SC). 2 3
   
    
C. SI = SA + SB + SC.
D. SI + SA + SB + SC = 0. Hướng dẫn giải   
SI = SA + AI
   
       SI SB BI  = +
 ⇒ 3SI = SA + SB + SB + ( AI + BI + CI )
   SI SC CI  = + 
    
  
Vì I là trọng tâm tam giác 1
ABC ⇒ AI + BI + CI = 0 ⇒ SI = (SA+ SB + SC). 3
Câu 60. Trong không gian Oxyz , cho tứ diện ABCD có (
A 1;0;0), B(0;1;0),C(0;0;1), D( 2; − 1; 1 − ) . Thể
tích của tứ diện ABCD bằng A. 3 . B. 3. C. 1. D. 1 . 2 2 Hướng dẫn giải
   Thể tích tứ diện: 1 V
=  AB ACAD ABCD , . 6  
Câu 61. Cho hình chóp S.ABC có = = =  =  0 =  0
SA SB a, SC 3a, ASB CSB 60 ,CSA = 90 . Gọi G là trọng
tâm tam giác ABC . Khi đó khoảng cách SG bằng
A. a 15 .
B. a 5 .
C. a 7 . D. a 3 . 3 3 3 Trang 17/22 Hướng dẫn giải
Áp dụng công thức tổng quát: Cho hình chóp S.ABC có SA = a, SB = ,
b SC = c và có  = α  = β  ASB , BSC
,CSA = γ . Gọi G là trọng tâm tam giác ABC, khi đó 1 2 2 2 SG =
a + b + c + 2abcosα + 2ac cosγ + 2bcβ 3 Chứng minh: 
   Ta có: 1
SG = (SA+ SB + SC) 3
(           
SA + SB + SC)2 2 2 2
= SA + SB + SC + 2 . SA SB + 2 . SA SC + 2 . SB SC Khi đó 1 2 2 2 SG =
a + b + c + 2abcosα + 2ac cosγ + 2bcβ 3
Áp dụng công thức trên ta tính được a 15 SG = 3
Câu 62. Trong không gian tọa độ Oxyz cho ba điểm A(2;5; ) 1 , B( 2; − 6; − 2),C (1;2;− ) 1 và điểm   M ( ; m ;
m m) , để MB − 2AC đạt giá trị nhỏ nhất thì m bằng A. 2. B. 3 . C. 1. D. 4. Hướng dẫn giải   AC ( 1 − ; 3 − ; 2 − ), MB( 2 − − ; m − 6 − ;
m 2 − m)   2 2
MB − AC = m + m + (m − )2 2 2
6 = 3m −12m + 36 = 3(m − 2)2 + 24  
Để MB − 2AC nhỏ nhất thì m = 2
Câu 63. Trong không gian tọa độ Oxyz cho ba điểm A(2;5; ) 1 , B( 2; − 6; − 2),C (1;2;− ) 1 và điểm M ( ; m ; m m) , để 2 2 2
MA − MB − MC đạt giá trị lớn nhất thì m bằng A. 3. B. 4. C. 2. D. 1. Hướng dẫn giải    MA = (2 − ; m 5 − ;
m 1− m), MB = ( 2 − − ; m 6 − − ;
m 2 − m), MC = (1− ; m 2 − ; m 1 − − m) 2 2 2 2
MA − MB − MC = 3
− m − 24m − 20 = 28 − 3(m − 4)2 ≤ 28 Để 2 2 2
MA − MB − MC đạt giá trị lớn nhất thì m = 4
Câu 64. Cho hình chóp S.ABCD biết A( 2; − 2;6), B( 3 − ;1;8),C ( 1
− ;0;7), D(1;2;3) . Gọi H là trung
điểm của CD, SH ⊥ ( ABCD). Để khối chóp S.ABCD có thể tích bằng 27 (đvtt) thì có hai 2
điểm S , S thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm I của S S 1 2 1 2 A. I (0; 1 − ; 3 − ).
B. I (1;0;3)
C. I (0;1;3) . D. I ( 1; − 0; 3 − ). Hướng dẫn giải    
Ta có AB = (− − ) AC = ( − ) 1 3 3 1; 1;2 , 1; 2;1 ⇒ S = AB AC = ABC , 2   2     DC = ( 2 − ; 2 − ;4), AB = ( 1; − 1;
− 2) ⇒ DC = 2.AB ⇒ ABCD là hình thang và 9 3 S = S = ABCD 3 ABC 2 Vì 1 V = SH S ⇒ SH = S ABCD . ABCD 3 3 . 3
Lại có H là trung điểm của CD ⇒ H (0;1;5)     Gọi S ( ; a ;
b c) ⇒ SH = (− ; a 1− ;
b 5 − c) ⇒ SH = k AB, AC = k (3;3;3) = (3k;3k;3k )   Trang 18/22 Suy ra 2 2 2
3 3 = 9k + 9k + 9k ⇒ k = 1 ± 
+) Với k =1⇒ SH = (3;3;3) ⇒ S ( 3 − ; 2 − ;2)  +) Với k = 1 − ⇒ SH = ( 3 − ; 3 − ; 3 − ) ⇒ S (3;4;8) Suy ra I (0;1;3)
Câu 65. Trong không gian Oxyz , cho hai điểm ( A 2; 1 − ;7), B(4;5; 2
− ) . Đường thẳng AB cắt mặt phẳng
(Oyz) tại điểm M . Điểm M chia đoạn thẳng AB theo tỉ số nào A. 1 . B. 2 . C. 1 . D. 2 . 2 3 3 Hướng dẫn giải
Đường thẳng AB cắt mặt phẳng (Oyz) tại điểm M ⇒ M (0; y; z)   ⇒ MA = (2; 1
− − y;7 − z), MB = (4;5 − y; 2 − − z) 2 = k.4   
Từ MA = kMB ta có hệ − − y = k ( − y) 1 1 5 ⇒ k = 2 7− z = k  ( 2 − − z)
Câu 66. Trong không gian Oxyz , cho tứ diện ABCD có ( A 2;1; 1 − ), B(3;0;1),C(2; 1 − ;3) và D thuộc
trục Oy . Biết V
= và có hai điểm D 0; y ;0 , D 0; y ;0 thỏa mãn yêu cầu bài toán. 1 ( 1 ) 2 ( 2 ) ABCD 5
Khi đó y + y bằng 1 2 A. 0. B. 1. C. 2 . D. 3. Hướng dẫn giải
D ∈Oy ⇒ D(0; y;0)    Ta có: AB = (1; 1; − 2), AD = ( 2 − ; y −1; ) 1 , AC = (0; 2 − ;4)  
   ⇒ A . B AC = (0; 4; − 2 − ) ⇒ A . B AC.AD = 4 − y + 2     1 V
= ⇔ − y + = ⇔ y = − y = ⇒ D 0; 7
− ;0 , D 0;8;0 ⇒ y + y =1 1 ( ) 2 ( ) ABCD 5 4 2 5 7; 8 6 1 2
Câu 67. Trong không gian Oxyz , cho tam giác ABC có ( A 1 − ;2;4), B(3;0; 2
− ),C(1;3;7) . Gọi D là 
chân đường phân giác trong của góc A . Tính độ dài OD . A. 207 . B. 203 C. 201 . D. 205 . 3 3 3 3 Hướng dẫn giải Gọi D( ; x y;z) DB AB 2 14 = = = 2 DC AC 14  5 3  2(1 ) x x x = − = − −  3    
Vì D nằm giữa B, C (phân giác trong) nên DB = 2
− DC ⇔ −y = 2 − (3− y) ⇔ y = 2  2 − − z = 2 − 
(7 − z) z = 4    Suy ra  5  205 D ;2;4 ⇒ OD =  3    3
Câu 68. Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC , biết (
A 1;1;1) , B(5;1; 2 − ) ,C(7;9;1) .
Tính độ dài phân giác trong AD của góc A A. 2 74 . B. 3 74 . C. 2 74. D. 3 74. 3 2 Hướng dẫn giải Trang 19/22 D( ;
x y; z) là chân đường phân giác trong góc A của tam giác ABC .   Ta có DB AB 1 17 11 2 74 = = ⇒ DC = 2
− DB ⇒ D( ; ; 1) − ⇒ AD = . DC AC 2 3 3 3
Câu 69. Trong không gian với hệ toạ độ Oxyz , cho 4 điểm ( A 2;4; 1 − ), B(1;4; 1 − ) , C(2;4;3) D(2;2; 1 − ) . Biết M ( ; x y; z) , để 2 2 2 2
MA + MB + MC + MD đạt giá trị nhỏ nhất thì x + y + z bằng A. 7. B. 8. C. 9. D. 6.
Hướng dẫn giải
Gọi G là trọng tâm của ABCD ta có: 7 14 G  ; ;0  . 3 3    Ta có: 2 2 2 2 2 2 2 2 2
MA + MB + MC + MD = 4MG + GA + GB + GC + GD ≥ 2 2 2 2
GA + GB + GC + GD . Dấu bằng xảy ra khi M ≡  7 14
G  ; ;0 ⇒ x + y + z = 7.  3 3 
Câu 70. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm ( A 2;3;1) , B( 1; − 2;0) ,C(1;1; 2 − ) . H là
trực tâm tam giác ABC , khi đó, độ dài đoạn OH bằng A. 870 . B. 870 . C. 870 . D. 870 . 12 14 16 15 Hướng dẫn giải H ( ;
x y; z) là trực tâm của ∆ABC ⇔ BH ⊥ AC,CH ⊥ AB, H ∈(ABC)   BH.AC = 0
   2 29 1 ⇔ C    H.AB = 0 ⇔ x = ; y = ; z = − ⇒ 2 29 1 870
H  ; ;−  ⇒ OH = .
     15 15 3 15 15 3  15 
AB, AC.AH = 0
Câu 71. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có (
A 3;1;0) , B nằm trên mặt
phẳng (Oxy) và có hoành độ dương, C nằm trên trục Oz và H (2;1;1) là trực tâm của tam giác
ABC . Toạ độ các điểm B , C thỏa mãn yêu cầu bài toán là:  − + −   −  A. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4   − − +   +  B. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4   − + −   +  C. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4   − + +   −  D. 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4  Hướng dẫn giải Giả sử B( ;
x y;0)∈(Oxy),C(0;0; z)∈Oz .     AH ⊥ BCAH.BC = 0    
H là trực tâm của tam giác ABC ⇔ CH ⊥ AB ⇔ CH.AB = 0
  
   
AB, AC, AH ñoàng phaúng 
AB, AH .AC = 0 x + z = 0 − − + +
⇔ 2x + y − 7 = 0 ⇔ 3 177 17 177 3 177 x = ; y = ; z = 4 2 4 3x 
 − 3y + yz − z = 0  − − +   +  ⇒ 3 177 17 177 3 177 B ; ;0,C 0;0; .  4 2   4  Trang 20/22
Câu 72. Trong không gian với hệ tọa độ Oxyz , cho hình vuông ABCD , B(3;0;8) , D( 5; − 4 − ;0) . Biết  
đỉnh A thuộc mặt phẳng (Oxy ) và có tọa độ là những số nguyên, khi đó CA + CB bằng: A. 5 10. B. 6 10. C. 10 6. D. 10 5. Hướng dẫn giải
Ta có trung điểm BD là I( 1; − 2
− ;4) , BD =12 và điểm A thuộc mặt phẳng (Oxy) nên ( A a; ; b 0) . 2 2 AB = AD 2 2 2 2 2
(a −3) + b +8 = (a + 5) + (b + 4)
ABCD là hình vuông ⇒  2  ⇔  2  1 AI BD =   2 2 2
(a +1) + (b + 2) + 4 = 36   2   17 b  = 4 − 2a = a =1 a  ⇔  5  ⇔  hoặc  ⇒ A(1; 2; 0) hoặc 2 2
(a +1) + (6 − 2a) = 20 b  = 2 14 b −  =  5 17 14 A − ; ;0  (loại). Với ( A 1;2;0) ⇒C( 3 − ; 6 − ;8) . 5 5   
Câu 73. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC , biết ( A 5;3; 1) − , B(2;3; 4 − ) , C(3;1; 2
− ) . Bán kính đường tròn nội tiếp tam giác ABC bằng: A. 9 − 2 6. B. 9 − 3 6. C. 9 + 3 6. D. 9 + 2 6. Hướng dẫn giải Ta có 2 2 2
AC + BC = 9 + 9 = AB ⇒ tam giác ABC vuông tại C . 1 CA.CB Suy ra: SABC 2 3.3 2 r = = = = 9 − 3 6 p
1 (AB+ BC +CA) 3 2 + 3 + 3 2
Câu 74. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm M (3;0;0), N ( ,
m n,0), P(0;0; p). Biết =  0 MN
13, MON = 60 , thể tích tứ diện OMNP bằng 3. Giá trị của biểu thức 2 2
A = m + 2n + p bằng A. 29. B. 27. C. 28. D. 30. Hướng dẫn giải    
OM = (3;0;0),ON = ( ; m ;0
n ) ⇒ OM.ON = 3m  
    0 OM.ON 1 m 1
OM.ON = OM . ON cos60 ⇒   = ⇒ = 2 2 OM . ON 2 m + n 2 MN = (m − )2 2 3 + n = 13
Suy ra m = 2;n = 2 ± 3
   1
OM ,ON .OP = 6 3p ⇒V = 6 3p = 3 ⇒ p = ± 3   6
Vậy A = 2 + 2.12 + 3 = 29.
Câu 75. Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm ( A 2;3;1) , B( 1; − 2;0) ,C(1;1; 2 − ) . Gọi I ( ; a ;
b c) là tâm đường tròn ngoại tiếp tam giác ABC . Tính giá trị biểu thức
P =15a + 30b + 75c A. 48. B. 50. C. 52. D. 46. Hướng dẫn giải I( ;
x y; z) là tâm đường tròn ngoại tiếp tam giác ABC ⇔ AI = BI = CI, I ∈(ABC) Trang 21/22 2 2 AI = BI  2 2 ⇔ C     I = BI 14 61 1 14 61 1 ⇔ x = ; y =
; z = − ⇒ I  ; ;− ⇒  P = 50.
     15 30 3 15 30 3  
AB, AC AI = 0 Trang 22/22
Document Outline

  • DS_C8_HE TOA DO TRONG KHONG GIAN
    • A. LÝ THUYẾT
    • B. BÀI TẬP TRẮC NGHIỆM
    • C. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM