Tóm tắt lý thuyết và giải nhanh Toán 12 – Nguyễn Chiến, Nguyễn Hồng Quân

Tóm tắt lý thuyết và giải nhanh Toán 12 – Nguyễn Chiến, Nguyễn Hồng Quân được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

53 27 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

- : 0973.514.674

Page | 1

 TOÁN 12





1. 

x x K x x

1 2 1 2

,,  

( K là khong hon hoc na khong).

   

f x f x



 

y f x

 trên K n 

   

f x f x



 

y f x

 trên K  

Chú ý: u

   



   f x x a b0, ;

hà

 

ng bin 

 

ab;.

u

   

0, ;f x x a b



   

hà

 

nghn trên khong

 

ab;.

u

   



  f x x a b0, ;



hà

 

i trên khong

 

ab;.

u

 

ng bin trên khong

     



   a b f x x a b; 0, ; .

+ Nu

 

nghn trên khong

     

a b f x x a b; 0, ; .



   

2. Quy tc và công tho hàm

Quy to hàm: Cho

   

u u x v v x C; ; :

là hng s .

Tng, hiu:

 





  u v u v .

Tích:

   



  

   u v u v v u C u C u. . . . . .



 



   

  



    

   

   

u u v v u C C u

. . .

o hàm hàm hp: Nu

   

  

   

x u x

y f u u u x y y u,.

Bng công tho hàm:





 



C 0



 









xx

 









xx





  





( 0)





 



xx

 

..u u u











 







  









 





 



xxsin cos

 



u u usin .cos

 



xxcos sin

 



u u ucos .sin

- 

- : 0973.514.674

Page | 2

 



x

tan

cos

 





tan

cos

 



x

cot

sin

 





cot

sin

 





 





e u e.

 





a a a.ln

 





a u a a. .ln

 



x

 





 

log





 





log

.ln

Công tho hàm hàm phân thc:

 

















ax b ad bc

cx d

;

 

c b c

f e f

a b a

d e d

ax bx c

dx ex f

  

  





















o hàm cp 2 :

+ 

   

f x f x





 





+ c: Gia tc tc thi ca chuyng

 

s f t

ti thm

là:

   



a t f t

* 

 

 

và

 

K 

   

f x g x



   

f x g x

 

 

và

 



K thì h

   

f x g x.





   

f x g x,

g trên K.

 

 

u u x



 

x a b;

và

   

u x c d;



 

f u x







 

x a b;

Quy tu ca hàm s.

Gi s hàm s

o hàm trên

 Nu

 

fx'0

vi mi

xK

và

 

fx'0

ch ti mt s hu hm

xK

thì

hàm s

ng bin trên

 Nu

 

fx'0

vi mi

xK

và

 

fx'0

ch ti mt s hu hm

xK

thì hàm s

nghch bin trên

- : 0973.514.674

Page | 3

Chú ý:

* i vi hàm phân thc hu t

ax b d

y x

cx d c





  







thì du

""

khi xét do

hàm



không xy ra.

Gi s

   

y f x ax bx cx d f x ax bx c

3 2 2

3 2 .



        

Hàm s ng bin trên

 

f x x

0; .



























    

























Hàm s nghch bin trên

 

f x x

0; .



























    

























ng hp 2 thì h s

khác

vì khi

a b c 0  

thì

 

f x d

ng thng song song hoc trùng vi trc Ox u)

* Vi dng toán tìm tham s  hàm su mt chiu trên kho

dài bng

ta gi

 c 1: Tính

 

y f x m ax bx c



   

 c 2: Hàm s u trên

 

x x y





có

nghim phân bit

















 

 c 3: Hàm s u trên kho dài bng

 

x x l x x x x l

1 2 1 2 1 2

4      

4  S P l

 

 c 4: Gii

 

và giao vi

 

 suy ra giá tr m cn tìm.



1. nh 





xK

là  



 

;ab



sao cho

 

;a b K

và

       

  f x f x x a b x

, ; \



 

 

là  



 

ab;



sao cho

 

;a b K

và

       

  f x f x x a b x

, ; \



 

 

+ .

+ .

+ m cm cc tic gi chung là m cc tr ca hàm s m

cc tr phi là mm trong tp hp K.

- : 0973.514.674

Page | 4

+ Giá tr ci và giá tr cc tic gi chung là giá tr cc tr (hay cc tr)

ca hàm s.





 

x f x

; ( )





2. u kin c hàm s t cc tr

nh lí 1: Gi s hàm s

 

y f x

t cc tr tm

u

 

y f x

o hàm

tm

thì

 



fx

Chú ý:

 o hàm

 



có th bng

tm



t cc tr ti

m

 Hàm s có th t cc tr ti mm mà t o hàm.

 Hàm s ch có th t cc tr ti mm mà to hàm ca hàm s bng

hoc t o hàm.

3. 

 



. 





thì

 

'0fx

. u

 



fx 0



 

x h x

;

và

 



fx 0

trên g

 

x x h

;

thì

làt im cc m s

 

fx.

 u

 



fx 0

trên khong

 

x h x

;

và

 



fx 0

trên khong

 

;x x h

thì

làt im cc tiu ca hàm

 

fx.





 c 1: Tìm tp xác nh. Tìm

 



fx.

 c 2: m

 

i 1;2;...

mà to hàm ca hàm s bng 0 hoc

hàm s liên to hàm.

 c 3: Lp bng bin thiên hoc bng xét du

 



. Nu

 



i d

qua

thì hàm s t cc tr ti

nh lí 3: Gi s

 

y f x

có o hàp 2 trong khong

 

x h x h

;

vi

h 0.

 Nu

 



fx

 



fx

thì hàm s

t ci ti

 Nu

 

0,fx





 



fx

thì hàm s

t cc tiu ti





 c 1: Tìm tnh. Tìm

 



fx.

 c 2: Tìm các nghim

 

i 1;2;...

c

 



fx 0.

 c 3: Tính

 



và tính

 



fx.

 Nu

 





fx 0

thì hàm s

t ci tm

x .

 Nu

 





fx 0

thì hàm s

t cc tiu tm

- : 0973.514.674

Page | 5



I. CC TR CC BC BA:

1. u ki hàm s có cc i, cc tiu th c

t: Cho hàm s

 

y f x m ax bx cx d

;.    

Tìm tham s m  hàm

s có ci, cc tiu ti

thu kin

c.

:

 c 1:

 Tnh:

D .

 o hàm:

y ax bx c Ax Bx C



     

 c 2:

Hàm s có cc tr (hay có hai cc tr, hai cc tr phân bit hay có ci và cc tiu)

y 0





có hai nghim phân bit và



i du qua 2 nghi





y 0





có hai nghim phân bit

A a a

B AC b ac b ac

2 2 2

3 0 0

4 4 12 0 3 0





  



   



       





 c 3: Gi

là hai nghim c

y 0.









    













c 4:n i iu kin

ng tng

ch

. T ó gii ra tìm c

.

c 5: t lun các giá tr m tha mãn:

m D D

.

* Chú ý: Hàm s bc ba:

 

y ax bx cx d a

0.    

Ta có:

y ax bx c

' 3 2 .  





b ac

30



b ac

30



 u ki hàm s có cc tr cùng du, trái du.

 Hàm s có 2 cc tr trái du





y 0





có hai nghim phân bit trái du

ac 0.

 Hàm s có hai cc tr cùng du





y 0





có hai nghim phân bit cùng du

P x x













  





 Hàm s có hai cc tr cùng d





y 0





có hai nghit

S x x

P x x









     





  





- : 0973.514.674

Page | 6

 Hàm s có hai cc tr cùng du âm





y 0





có hai nghim âm phân bit

S x x

P x x







     





  





 u ki hàm s có hai cc tr

tha mãn:





 Hai cc tr

tha mãn





    

x x x x x x

1 2 1 2 1 2

0 . 0

   

        

 Hai cc tr

tha mãn





    

x x x x x x

x x x x

1 2 1 2 1 2

1 2 1 2

0 . 0

   





      







   





 Hai cc tr

tha mãn





    

x x x x x x

x x x x

1 2 1 2 1 2

1 2 1 2

0 . 0

   





      







   





 c 3 có 3 nghim lp thành cp s cng

khi có 1 nghim là





, có 3 nghim lp thành cp s nhân khi có 1 nghim là



2. u ki   th hàm s   m c i, cc tiu nm cùng phía,

khác phía so vi mng thng

i gia 2 im vi ng thng:

m

   

A A B B

A x y B x y; , ;

ng thng

ax by c: 0.   

u

  

A A B B

ax by c ax by c 0    

 

A B,

m v

hai phía so vi ng thng

.

u

  

A A B B

ax by c ax by c 0    

 m

A B,

ng

phía so vi ng thng

.

Mt sng hp c bit:

m cc tr c th nm cùng v i vi trc Oy



hàm s có 2 cc tr cùng du





y 0





có hai nghim phân bit cùng du

m cc tr c th nm cùng v i vi trc Oy



hàm s có 2 cc tr trái du





y 0





có hai nghim trái du

m cc tr c th nm cùng v i vi trc Ox





y 0





có hai nghim phân bit và

CC T

yy.0

- : 0973.514.674

Page | 7

c bit:

+ m cc tr c th nm cùng v i vi trc Ox





y 0





có hai nghim phân bit và

CTC















m cc tr c th nm cùng v i vi trc Ox





y 0





có hai nghim phân bit và

CTC















+ m cc tr c th nm v i vi trc Ox





y 0





có hai nghim phân bit và

CC T

yy.0

(ám c nghim và ving th

m cc tr c th hàm s)

Hom cc tr c th nm v i vi trc Ox



 th ct trc Ox tm phân bit



nh hoành  giao im

 

fx 0

m phân bit (á

m c nghim)

3. Png thm cc tr

 

c b bc

g x x d

3 9 9



   





hoc

 

 



g x ay

hoc

 

g x y

 







4 16





b ac





II. CC TR CA HÀM B

 

y ax bx c a

0   

MT S KT QU CN NH

 Hàm s có mt cc tr

ab 0.

 Hàm s có ba cc tr

ab 0.

 Hàm s t cc tr và cc tr là cc tiu

















 Hàm s t cc tr và cc tr là ci

















 Hàm s có hai cc tiu và mt ci

















 Hàm s có mt cc tiu và hai ci



















y ax bx c

  

có



A c B C

a a a a

(0; ), ; , ;

2 4 2 4

   



   

    

   

   



ABC



ab 0

- : 0973.514.674

Page | 8



Tng quát:

cot











ab 0



ABC



8



ABC



24



ABC



ABC

0



a S b

3 2 5

32 ( ) 0



ABC



max S

()



 

ABC

      

ABC

0



4 1 1













 

ABC

      

ABC











ABC



BC m



am b

20



ABC



AB AC n



a n b ab

2 2 4

16 8 0  



ABC



B C Ox, 

b ac

4



ABC





b a b

(8 ) 0



ABC



b ac

6



ABC



b a ac

8 4 0  



ABC





b ac

2



ABC





b a abc

8 4 0  



ABC





b a abc

8 8 0  



ABC



BC kAB kAC

b k a k

3 2 2

. 8 ( 4) 0  



ABC





b ac

42

Tam giác

ABC



b ac

8



 

C y ax bx c

:   







b ac

100



          

 

C y ax bx c

:   

     



b ac





ABC

x y c y c

b a b a

   



      

   

   

- : 0973.514.674

Page | 9

GIÁ TR LN NHT - GIÁ TR NH NHT



Cho hàm s

 

y f x

nh trên tp

 S M gi là giá tr ln nht ca hàm s

 

y f x

trên

nu:

f x M x D

x D f x M

( ) ,

, ( )



  





  





Kí hiu:

max ( )

M f x





 S

gi là giá tr nh nht ca hàm s

 

y f x

trên

nu:

f x m x D

x D f x m

( ) ,

, ( )



  





  





Kí hiu:

m f xmin ( )





2. 

* Tìm GTLN, GTNN ca hàm s bng cách kho sát trc tip

 c 1: Tính

 



m



x x x D

, ,...,

mà t

 



fx 0

hoc hàm s

o hàm.

+ : 

* Tìm GTL

 c 1:

 Hàm s 

 

y f x

nh và liên tn





ab;.

 m

x x x

, ,...,

trên khong

 

ab;

, t

 



fx 0

hoc

 



nh.

 c 2: Tính

         

f a f x f x f x f b

, , ,..., , .

 c 3: 



           

 

max f x max f x f x f x f a f b

, ,..., , , .









           

 







min f x min f x f x f x f a f b

, ,..., , , .



 : 

fx()



 : 

x a b( ; )



fx( ) 0







ab( ; )





làm cho

fx()





  Tính

A f xlim ( )







B f xlim ( )







fx()

f ()



  

M f x

( ; )

max ( )

m f x

( ; )

min ( )

 

+ u

 

y f x

ng bin trên

ab;





thì

   

f x f a

f x f b

;

min

max























+ u

 

y f x

n trên

ab;





thì

 























f x f b

f x f a

;

min ( )

max ( )

- : 0973.514.674

Page | 10

NG TIM CN C TH HÀM S

ng tim cn ngang

Cho hàm s

y f x()

 nh trên mt khong vô hn (là khong dng

   

 ab; , ;

hoc

 

; 

ng thng



ng tim cn ngang (hay tim

cn ngang) c th hàm s

y f x()

nu ít nht mu kin sau tha mãn:

 



f x y f x y

lim ( ) , lim ( )

ng tim cng

ng thng

xx

c gng tim cng (hay tim cng) c

th hàm s

()y f x

nu ít nht mu kic tha mãn:





   

x x x x

f x f x

lim ( ) , lim ( ) ,

lim ( ) , lim ( )

x x x x

f x f x





   

     

 



   



ax b

y c ad bc

cx d

0; 0

  

ngang là













 

y f x

 

 

 Ch

i. Tính

y '

ii. 

y '0



y '

không



iii. 

y '



 Tìm ).

 

   ,





 ).

 

 

  

 Ox, Oy ().

 

- : 0973.514.674

Page | 11





 

    y ax bx cx d a



a 0

0a 



y

có





y

có





0y 

vô





 

   y ax bx c a



a 0

0a 



y

có



- : 0973.514.674

Page | 12



y

có





 

0, 0

ax b

y c ad bc

cx d



   



  D ad bc 0

  D ad bc 0



: 

   

C y f x:



 



C y f x:

Ta có

 

f x khi x

y f x

f x khi x

















và

 

y f x

là  

 



Oy 



 





 

+  Oy 

   

C y f x:

+ bên trái Oy 

 

,  qua Oy.

Ví d: T  th

   

  C y f x x x

 th

 



C y x x

Bii

 

+ B ph th ca

 

bên trái

Oy,

gi nguyên

 

bên phi

.Oy

+ Li xng ph th c

gi qua

-2

-1

 



C y x x

 

C y x x

-2

-1

- : 0973.514.674

Page | 13

: 

   

C y f x:



   



C y f x:

 dung: Ta có:

 

   

















f x khi f x

y f x

f x khi f x



 





 

+  Ox 

 

y f x

+ Ox  qua Ox.

Ví d: T  th

   

:3C y f x x x  

 th

y x x

Bii

 

+ B ph th ca

 

i

,Ox

gi nguyên

 

phía trên

.Ox

+ Li xng ph th b b

qua

-2

-1

Chú ý 

 

y f x



 

y f x

và

 

y f x

Ví d: T  th

   

  C y f x x x

 th

y x x

. Bii

 

 

th

 



C y x x

. Bii

 



C y x x

 th

 



C y x x

-1

: 

     

C y u x v x:.



     



C y u x v x:.

Ta có:

   

       

u x v x f x khi u x

y u x v x

u x v x f x khi u x











  







 





 

+  

 

ux 0



   

C y f x:

+ 

 

ux 0



 

,  qua Ox.

 

:3C y x x

 



C y x x

 



C y x x

- : 0973.514.674

Page | 14





   

   C y f x x x

: 2 3 1



 



   C y x x x

: 1 2 1



   





C y f x

suy



 







 







    









f x khi x

y x x x

f x khi x

1 2 1





1x 



x 1



 qua Ox.

(C)

(C')

 

 

 Ox, Oy

 



 













  





khi x





 



x 1



 



1.x 



Ox.

: 

 



chính xác.



1.  : 

 

y f x

C).  

C

 

M x y C

0 0 0

; ( )



  



  y y x x x y

0 0 0

 

 

M x y C

0 0 0

; ( )



 

y f x

 

k f x

là  

2. : 

   

C y f x:

và

   

C y g x': 



 

và

 



 

   















f x g x







y f x()



()

và

y g x()



()C



()

và

()C

là

 

f x g x ( ) ( ) 1



- : 0973.514.674

Page | 15

 

()C

và

()





 

 



 

chính là





 



vào

 

y f x



 

y g x

 

 

;M x y



()

và

()



1. 



C()



y f x m( , )



là 





 m không quá 2. T





 

+  

( , )y f x m







Am B 0



  Am Bm C

+ : 

,  

































+  :

- 

C()



- 

C()

2. 



C()



y f x()





         



 

+  

+  

3.  

  

()C

  

y f x()

        



Bài toán 1: 

 

   C y Ax Bx Cx D



 





I x y( , )

 

+ 

   

     M a Aa Ba Ca D N b Ab Bb Cb D

3 2 3 2

; , ;



 





- : 0973.514.674

Page | 16

+ Ta có

 









      





a b x

A a b B a b C a b D y

3 3 2 2

( ) 2 2



ab,

M, N.

       

 

   C y Ax Bx Cx D

   

 

tìm



 

 

   

     M a Aa Ba Ca D N b Ab Bb Cb D

3 2 3 2

, , ,

   

 



 Ta có

 









      





A a b B a b C a b D

3 3 2 2

( ) 2 0

 

ab,



MN,

Bài toán 3: C

 

   C y Ax Bx Cx D



 





d y Ax B

 

 

   

3 2 3 2

; , ;M a Aa Ba Ca D N b Ab Bb Cb D     

   

 





 Ta có:















MN u

(1)

. 0 (2)





và





). M, N.

4. 

 Lý 

+ 

   

A x y B x y

1 1 2 2

; ; ;

   

    AB x x y y

2 1 2 1

 

 

M x y

;

 

:0d Ax By C  

  



là

 







Ax By C

h M d

;



ax b

cx d







M  TCN A và B thì M là trung

AB.



IAB



IAB

S ad bc



 

Bài toán 1: 

 



   



ax b

c ad bc

cx d

y 0, 0



 

. Hãy tìm trên

C()



và





 

 





hai phía







- : 0973.514.674

Page | 17

 

:



       

d d d

c c c

;



y f x()

 





       

d d d

c c c

;



y f x()

 

         





         



B A B A B A

AB x x y y a a y y

2 2 2

 Cauchy 

Bài toán 2: 

 



y f x()





()C





 

 

 

M x y;





thì

d x y

 







  







 



Bài toán 3: 

C()



()y f x



trên

C()

sao cho









 



 







  









y kx f x kx

y k x

y kx

f x kx

Bài toán 4:     

C()

  

 

( ) 0, 0

ax b

y f x c ad bc

cx d



    





trên

()C







 

 









 









;



 

 

Mx y;



 

   

    

   

   

M M M

IM x y g x

 m GTLN - 



Bài toán 5:     

C()

  

y f x()

  

  d Ax By C:0



trên

C()







 

 



C()

 

I x y y f x

0 0 0 0

; ; ( )

 



là

 







Ax By C

g x h I d

( ) ;

 

y g x()





- : 0973.514.674

Page | 18



A VÀ HÀM S A.

1. KHÁI NIA.

 a vi s 

Cho













a a a a. ......

(





a 0.











và

n





 

   



a a a ;











;

   

aa

( ) ;

  

ab a b( ) ;











;





   



   

   

 

a 1

thì



  aa

;



a01

thì



  aa

 

ab0

, ta có:

  

a b m 0

;

  

a b m 0

 Chú ý:













 



xb.

Ta có kt qu bin lun s nghim c

xb



 ng hp n l:

Vi mi s thc

m duy nht.

 ng hp n chn:

+ Vi

0b 

m.

+ Vi

b 0

, t nghim

x 0.

+ Vi

b 0

, m trái du, kí hiu giá tr 

, còn

giá tr âm là







ab

, ;n

, ta có:



a a a

;



 

a a a

   

ab a b ab

;

  

  

n n n

ab a b a b

2 1 2 1 2 1



   



ab b

, 0, 0

;



   

- : 0973.514.674

Page | 19

 

  

a a a,0



nguyên.

  

m nm

a a a,0







thì

  

a a a m n, 0, ,



pq,

nguyên.







2. HÀM S A.

 Khái nim.

Xét hàm s



yx

, vi



là s thc.

Hàm s



yx

, vi





c gi là hàm s a.

Chú ý.

Tnh ca hàm s a



yx

tùy thuc vào giá tr ca



. C th.

 Vi



nh là

 Vi



nguyên âm hoc bng

, tnh là

 

\ 0 .

 Vi



không nguyên, tnh

 

0; .

 Kho sát hàm s a.

 Tnh ca hàm s a



yx

luôn cha khong

 

0; 

vi mi





ng hp tng quát, ta kho sát hàm s



yx

trên khong này.



yx, 0.



yx, 0.

1. Tnh:

 

0; .

2. S bin thiên





   y x x

' . 0 0.

Gii hc bit:









  

lim 0, lim .

Tim cn: không có.

3. Bng bin thiên.









1. Tnh:

 

0; .

2. S bin thiên





   y x x

' . 0 0.

Gii hc bit:

lim , lim 0.









  

Tim cn:

Ox là tim cn ngang.

Oy là tim cng.

3. Bng bin thiên.









- : 0973.514.674

Page | 20

 th ca hàm s.

 th ca hàm s a





m

 

I 1;1 .

 Kho sát hàm s 

 

, 0, 1

y a a a  

 



y a a,1

 

y a a

1. Tnh:

2. S bin thiên.

' ln 0, .

y a a x  

Gii hc bit:

 

  

aalim 0, lim .

Tim cn:

Ox là tim cn ngang.

3. Bng bin thiên.



0 1



y '





 th 

1. Tp xánh:

2. S bin thiên.

  

y a a x' ln 0,

Gii hc bit:

 

  

aalim , lim 0.

Tim cn:

Ox là tim cn ngang.

3. Bng bin thiên.



0 1



y '





 th 

- : 0973.514.674

Page | 21



1. KHÁI NIM TÍNH CHT VÀ QUY TT TÍNH LOGARIT.

 Khái nim Logarit.



ab,



1a 









ab







blog

log .

b a b



  



Bng tóm tt công th-ng gp:



 

aa

1, 0 .



 

aa



 





a



 













     

.a b a

   







     

  

a b a b..



 













   

 





aa



 







aa



 



  

a b blog



 

  

alog 1 0, 0 1



 

  

aalog 1, 0 1



 



  

aalog , 0 1



 

log , 0 1



  



 

log .log , , 0, 1

b b a b a



  







log .log



log .log











 



a a a

b c bclog log log











a a a

log log log





log

2. B

 Bn.

Bn có dng



(hoc

xxx

a b a b a b

) vi

aa0, 1.

Ta xét bng



ab.

 Nu

b 0

, tp nghim ca b , vì

  

a b x,.

 Nu

b 0

thì bi



log

Vi

a 1

, nghim ca b

xblog .

Vi

a01

, nghim ca b

xblog .

- : 0973.514.674

Page | 22

Ta minh ha b th sau:

 Vi

a 1

 th

 Vi

a01

 th

 Bn.

Bn có dng

log

xb

(hoc

log ,log ,log

aaa

x b x b x b

)

vi

aa0, 1.

Xét b



xblog .

 ng hp

a 1

, ta có:

  

x b x alog .

 ng hp

a01

, ta có:

log 0 .

x b x a   



 Vi

a 1

 th sau.

 Vi

a01

, ta  th sau.

 th, ta thy rng:

 ng hp

a 1

log

xb

khi và ch khi



xa.

 ng hp

01a



xblog

khi và ch khi



xa0

- : 0973.514.674

Page | 23



1. là s tin lãi ch tính trên s tin gc mà không tính trên s tin lãi do s tin

g



 







kì 

n *

) là:

 

S A nAr A nr1   

2. Lãi kép: 



 









n *

) là:

 

log











 

S A r1

%1

 







  

lãi

kép



tháng (

n *

) (



 

log 1















   

1 1 1





  







 









tháng là bao

nhiêu?

n là





          





tháng.

 







   

S r r

1 1 1



   







 

S A r X



  

 

X A r S



  







- : 0973.514.674

Page | 24

 

S A r X



  





S 0

nên

 

A r X



  

 

A r r















th

 là bao nhiêu ?

 

tháng là

 

S Ak

11







 

X X r m n m n1 , , ,





   















8. 









 



là:

 

S A r1









:











m  





S Ae





- : 0973.514.674

Page | 25

PHN III.

NGUYÊN HÀM - TÍCH PHÂN - NG DNG TÍCH PHÂN

I. NGUYÊN HÀM

1. Nguyên hàm

   

 

 

(

    



 



 

trên



   

F x f x'



xK



   





f x dx F x C





 



 

trên





   

G x F x C



 

trên



 



 

trên



 

trên



 

F x C







 

F x C C,



 

trên





 







f x dx f x

và

   





f x dx f x C'

;

 





d f x f xdx dx

 No hàm thì:

 





d F x F x C( ) ( )



   





kf x dx k f x dx

vi

là hng s khác



       



  



  

f x g x dx f x dx g x dx

 Công thi bin s: Cho

 

y f u

và

 

u g x .

Nu





f x dx F x C( ) ( )

thì

 





f g x g x dx f u du( ) '( ) ( )

F u C()



 

 



ên







dx C0





dx x C

 







   





x dx x C

16.

 









    









ax b

ax b c

dx , 1

  



dx C

17.





x x x





dx x C

18.

  





ax b c

ax b a

dx 1





e dx e C

19.







ax b ax b

e dx e C





a dx C

aln

20.







kx b

a dx C

- : 0973.514.674

Page | 26





xdx x Ccos sin

21.

   

   



ax b dx ax b C

cos sin

xdx x Csin co s  



22.

   

    



ax b dx ax b C

sin cos

10.

  



x dx x Ctan . ln | cos |

23.

   

ax b ax b c

tan dx ln cos    



11.





x dx x Ccot . ln | sin |

24.

   

   



ax b ax b c

cotg dx ln sin

12.





dx x C

tan

cos

25.

 

  





dx ax b C

ax b

tan

cos

13.

  



dx x C

cot

sin

26.

 

   





dx ax b C

ax b

cot

sin

14.

 

  



x dx x C

1 tan tan

27.

 

    



ax b dx ax b C

1 tan tan

15.

 

   



x dx co x C

1 cot t

28.

 

     



ax b dx co ax b C

1 cot t









dx 1

arctg

   



x a x c

arcsin dx arcsin









a a x

dx 1

   



x a x c

arccos dx arccos

 

   





x x a c

 

x x a

x a x c

arctan dx arctan ln

   









arcsin

 

x x a

x a x c

arc cot dx arccot ln

   









x x a

dx 1

arccos

 









ax b

dx 1

ln tg

sin



  





a x a

x x a

dx 1

 

ax b

dx 1

ln tan

sin









   



     







ax b x ax b x c

ln dx ln

 









e a bx b bx

e bx c

cos sin

cos dx



   



x a x a x

a x c

2 2 2

dx arcsin

 









e a bx b bx

e bx c

sin cos

sin dx

- : 0973.514.674

Page | 27













f x F x C( ) ( )



 

u t











f u du F u C( ) ( )



 

 







 





 

 



dx t dt'

 

     









f x dx f t t dt g t dt( ) '

 

  



f x dx g t dt G t C( ) ( ) ( )







ax



x a sint













t ;.



x a cost











t 0; .

xa





sint

; v

 











t ; \ 0





cost

















t 0; \ .

ax



x a tant













t ;.



x a tcot



 



t 0; .













x acos t2

  

x a b x



x a b a sin t

–()

ax



x atant













t ;.





 



xt



 





(

 





   





   



  

f x dx f t t dt g t dt G t C( ) ' ( ) ( )

- : 0973.514.674

Page | 28

.

 

 





 





 

 



dt t dt'

 

   









f x dx f t t dt g t dt( ) ' ( )

 

   



I f x dx g t dt G t C( ) ( ) ( )













 



f x x;

 



tx

Hàm

 



a inx+b.cosx

c inx+d.cosx+e









t cos

tan ; 0

Hàm

 

  





x a x b



xa 0

và

xb 0

 

   t x a x b



xa0

và

xb0



    t x a x b



 





u x v x dx u x v x v x u x dx( ). '( ) ( ). ( ) ( ). '( )

Hay





udv uv vdu



   

du u x dx dv v x dx’ , ’

)



 





I f x dx f x f x dx

( ) ( ). ( )

 



















du f x dx

u f x

dv f x

v f x dx

' ( )

()

 





u dv u v v du. . .























I P x x dx

sin

( ) cos .































u P x

dv x dx

()

sin

cos .

































u du P x dx

'. '( )

cos

sin

I = P(x)













cos

sin















x P x dx

cos

sin . '( )

- : 0973.514.674

Page | 29

:





I P x xdx( ).ln

















dv P x dx

()



















du dx

v P x dx Q x

( ) ( )

I = lnx.Q(x) -



Q x dx

( ).





















I e dx

sin

cos





























dv dx

sin

cos































du e dx

cos

sin

I =

















cos

sin



















e dx

cos

sin





















e dx

cos

sin



TÍCH PHÂN

1.  tích phân

  



f x dx F x F b F a( ) ( ) ( ) ( )

: 

a b 



f x dx()

hay



f t dt( ) .

Tích

f a, b mà khô









f x dx( ) 0





f x dx f x dx( ) ( )



  

b c b

a a c

f x dx f x dx f x dx( ) ( ) ( )



  



  

b b b

a a a

f x g x dx f x dx g x dx( ) ( ) ( ) ( )





kf x dx k f x dx( ) . ( )

6. 



  



x a b0;

thì :



  





f x dx x a b( ) 0 ;



x a b f x g x f x dx g x dx; : ( ) ( ) ( ) ( )



    















x a b;



M f x N()

thì

   

   



M b a f x dx N b a()

- : 0973.514.674

Page | 30







 

x u t()









;



f u t( ( ))









;



u a u b( ) , ( )











I f x dx f u t u t dt

( ) ( ( )) ( )



  

 

x u t

   :

  x u t dx u t dt( ) '( )













x b t

x a t

  









  



  

I f x dx f u t u t dt g t dt( ) ( ) '( ) ( )







  G t G G( ) ( ) ( )



: 

u u x()

       





ab;

sao cho

 

f x dx g u x u x dx g u du( ) ( ) '( ) ( )

thì:





a u a

I f x dx g u du

()

( ) ( )



 : 

  u u x du u x dx

( ) ( )

 







x b u u b

x a u u a

()

 : 





  



  

a a u a

I f x dx g u x u x dx g u du

()

( ) ( ) . '( ) ( )



. 





ab;

thì:

 





u x v x dx u x v x v x u x dx

( ) ( ) ( ) ( ) ( ) ( )

Hay



udv







vdu



  

udv uv dx





dv v x dx'( )

  Tính

du u dx'

và





v dv





v x dx'( )

  Tính



vu x dx'( )

và

- : 0973.514.674

Page | 31





tiên:

---



P x e dx()



P x xdx( )ln



P x xdx( )cos



e xdxcos

P(x)

lnx

P(x)

e dx

P(x)dx

cosxdx

Chú ý

dv vdx





TÍCH PHÂN CÁC HÀM S N

1. Tích phân hàm hu t

 I =









  





dx adx

ax b

ax b a ax b a

0)











  

   







ax b adx ax b

a a k

ax b

( ) . .( )

(1 )

()

:

 











ax bx c

(

  ax bx c











x ;

)

Xét

  b ac





> 0:

     



;



  



    





a x x x x a x x x x x x

ax bx c

1 2 1 2 1 2

1 1 1 1 1

( )( ) ( )

thì :















      







     





I dx x x x x

a x x x x x x a x x a x x x x

1 2 1 2 1 2 1 2 2

1 1 1 1 1

ln ln ln

( ) ( ) ( )





= 0:









  



ax bx c a x x

()

thì I =









  



  



dx dx

a a x x

ax bx c x x

()



0

thì































dx dx

ax bx c



 

 

    

x t dx t dt

tan 1 tan

:

 













mx n

I dx a

ax bx c









mx n

ax bx c

()









;

)



- : 0973.514.674

Page | 32

  



     

mx n A ax bx c B

ax bx c ax bx c ax bx c

2 2 2

( )'





   

A ax b B

ax bx c ax bx c

(2 )

+)Ta có I=















     



mx n A ax b B

dx dx dx

ax bx c ax bx c ax bx c

2 2 2

(2 )

. Tích phân











A ax b

ax bx c

(2 )





A ax bx c

Tích phân









ax bx c



Tính tích phân





I dx

()



 

 



  

n12

, ,...,



  

   

  

A A A

Q x x x x

()

...

()



 



       Q x x x px q p q

( ) , 4 0













P x A Bx C

Q x x

x px q

()

+ Khi Q(x) 



  Q x x x

( ) ( )( )

   

 





  





P x B C

Q x x x

()



  Q x x x

( ) ( ) ( )

   



    

    



    

P x A B C D E

x x x x x

2 3 2 3 2

()

( ) ( ) ( ) ( ) ( )

2. Tích phân hàm vô t



R x f x dx( , ( ))

 













x acos t2

t [0; ]









R x a x

, 



x a tsin



x a tcos

ax b

cx d













ax b

cx d







 

R x f x

ax b x x

, ( )

()

  



  



 

x x k ax b

  



   



t x x

  

  



ax b





- : 0973.514.674

Page | 33





R x a x

, 



attan

t ;















R x x a

, 



xcos



t 0; \



















n n n

R x x x

; ;...;



 

k BSCNN n n n

; ; ...;



xt



 











I dx a

ax bx c



















       





















f(x)=ax bx c a x du dx

có :

- 

 

        a f x a u k f x a u k

2 2 2 2

0, 0 ( ) ( ) .

(1)

- 









     





  







f x a x

f x a x a u

0 ( )

( ) .

(2)

- 

0



     

      f x a x x x x f x a x x x x

1 2 1 2

( ) ( ) .

(3)



     

        f x a x x x x f x a x x x x

1 2 1 2

( ) ( ) .

(4)



 



 

        a f x a u k f x a u k

2 2 2 2

0, 0 ( ) ( ) .



   

ax bx c t a x.



















  









     







  







x dx tdt

bx c t ax

x t t x t t

t a x t a

;











     





  







f x a x

f x a x a u

0 ( )

( ) .



















  









  









   











I dx dx

a x x

ln : 0

1 1 1

ln : 0



  a0, 0

- 

  

 







     







x x t

ax bx c a x x x x

x x t

- : 0973.514.674

Page | 34



  a0, 0

- 

  

 







     







x x t

ax bx c a x x x x

x x t



 













mx n

I dx a

ax bx c

 

 Phân tích





 





  

     

2 2 2

Ad ax bx c

mx n B

ax bx c ax bx c ax bx c

( ) 1

  

 

 Tính I =













  





A ax bx c B dx

ax bx c

(2)



 











dx a

ax bx c





 







  



I dx a

mx n ax bx c

 

 Phân tích :

 





  





mx n ax bx c

m x ax bx c

. (1)

 





    











  



   



         

   



   



y t dy dx

x t m x t

x t ax bx c a t b t c

y y y

1 1 1

 











Ly My N

 :

 

I R x y dx R x dx

;;



























 

R x y;

: 

   

, , ,



 

 











 Tính x theo t 

 



xt

 

 



dx t dt'



 Tính :

 



























R x dx R t t t dt

; ; '

- : 0973.514.674

Page | 35







a b a b a bcos cos .cos sin() .sin

a b a b b asin sin .cos sin .) os( c  

atan tan

()

1 tan .tan

tan 



b

a a a a

2 2 2

cos2 cos – sin 2 cos – 1

1 tan

1 – 2 sin

1 tan

  







a a a

sin2 2 sin .cos

2 tan

1 tan



;





2 tan

tan2

1 tan

c os 3 4 c os 3cos

  



;

sin3 3sin 4 sin

  



c. 

1 cos2

sin





;

1 cos2

cos





;







1 cos2

tan

1 cos2









3sin sin 3

sin

;

cos 3 3cos

cos









d. 

t tan



sin





cos







tan







     



   





   





   



cos .cos cos( ) cos( )

sin .sin cos( ) cos( )

sin .cos sin( ) sin( )



   



   



   



   









  

















cos cos 2 cos .cos

cos cos 2 sin .sin

sin sin 2 sin .cos

sin sin 2 cos .sin

sin( )

tan tan

cos cos

sin( )

tan tan

cos cos

H qu:



   



   

   

    

   

   

   

     

   

   

cos sin 2 cos 2 sin

Công thng dùng:

















3 cos 4

cos sin

5 3 cos 4

cos sin

- : 0973.514.674

Page | 36



 Nu gp

 





sin .cos

I f x xdx

t

 sintx

 Nu gp dng

 





cos .sin

I f x xdx

t

 costx

 Nu gp dng

 





tan

cos

I f x

t

 tantx

 Nu gp dng

 





cot

sin

I f x

t

 cottx



   

= sinx dx ; cosx dxII



ng pháp

2.1. 

2.2.  

2.3.    2p 

   

 

n 2p+1

= sinx dx = sinx dx    

   

I x xdx x d x

sin sin 1 cos cos

 

p p p p

C C x C x C x d x

C x C x C x C x C

0 1 2 2 2

2 1 2 1

0 1 3

cos ... 1 cos ... 1 cos cos

1 1 1

cos cos ... cos ... cos

3 2 1 2 1





        











       









   

 

n 2p+1

= cosx dx = cosx dx   

   

I x xdx x d x

cos cos 1 sin sin

 

p p p p

C C x C x C x d x

C x C x C x C x C

0 1 2 2 2

2 1 2 1

0 1 3

sin ... 1 sin ... 1 sin sin

1 1 1

sin sin ... sin ... sin

3 2 1 2 1





       











      











I = sin x cos x dx



(m, n







a. 

b. 2p  

   

     

 

m 2p+1

I = sinx cosx dx   

  

m p m

x x xdx x x d x

sin cos cos sin 1 sin sin

   

 

   

 

m k p

p p p p

m m k m p m

p p p p

x C C x C x C x d x

x x x x

C C C C C

m m k m p m

0 1 2 2 2

1 3 2 1 2 1

sin sin ... 1 sin ... 1 sin sin

sin sin sin sin

... 1 ... 1

1 3 2 1 2 1

     



        









       

     







c. 2p 

   

     

 

2p+1 n

I = sinx cosx dx    

  

n p n

x x xdx x x d x

cos sin sin cos 1 cos cos

   

 

   

 

n k p

p p p p

n n k n p n

p p p p

x C C x C x C x d x

x x x x

C C C C C

n n k n p n

0 1 2 2 2

1 3 2 1 2 1

cos cos ... 1 cos ... 1 cos cos

cos cos cos cos

... 1 ... 1

1 3 2 1 2 1

     



         









        

     







- : 0973.514.674

Page | 37

d. 

 



sinx ta có:

 

   



   

  

m n m

B x xdx x x xdx u u du

sin cos sin cos cos 1

(*)

  

  m n m k11

;;

2 2 2





   

= tan x dx ; = cot x dx



(nN). :



 

    

  

x dx d x x c

1 tan tan tan

cos



 

       

  

x dx d x x C

1 cot cot cot

sin



 

     

  

x d x

xdx dx x C

sin cos

tan ln cos

cos cos



 

   

  

x d x

xdx dx x C

cos sin

cot ln sin

sin sin





a) 

y f x()







ab;



xa

xb







S f x dx()

b) 

y f x()

y g x()







ab;



xa

xb







S f x g x dx( ) ( )

- 

[a b];



fx()







f x dx f x dx( ) ( )

- 

- 

x g y()

x h y()





yc

yd







S g y h y dy( ) ( )





















( ): ( )

()

C y f x

()C





S f x f x dx

( ) ( )





















()

y f x

 ()y f x





S f x dx()

- : 0973.514.674

Page | 38



a) 



 Ox 

a và b;

Sx()

Ox



a x b()



Sx()



[a b];

b) 

           

y f x()

g

xa

xb

Ox:

-         

x g y()



yc

yd

Oy:

- 

y f x()

y g x()



xa

xb

Ox:

V f x g x dx

( ) ( )







( ): ( )

( ):





















C y f x

Ox y 0

 

()

V f x dx



 ()y f x





S x dxV ()

()

S(x)

( ): ( )

( ):





















C x g y

Oy x 0

 

()

V g y dy



- : 0973.514.674

Page | 39

PHN IV. S PHC





) :

 

z a bi a b;,  

 :







1.

 .







g

 

b 0







 

a 0







Hai s phc

 

z a bi a b

,  

và

 

z c di c d

,  

bàng nhau khi phn thc và

phn o cng nhau.



z z a bi c di







     











 

 

z a bi a b,  

    

 

M a b;



 

u a b;



Oxy





 

z a bi a b,  

là

z a bi



z z z z z z z z z z z z a b

; ' ' ; . ' . '; ; . .



       







zz

;



zz



 dài c

c gi là a s phc

và kí hiu là

Vy

z OM

hay

z a bi OM a b

    



z a b zz OM

   

;

zz

zz0, ;  

zz00  

z z z z

1 2 1 2

..

;



;

z z z

1 1 2

.

z z z z z z

1 2 1 2 1 2

    

M (a;b)

- : 0973.514.674

Page | 40







 

z a bi a b

,  

và

 

z c di c d

,  



   

z z a c b d i

    



z a bi

là

z a bi   

+ Tng ca mt s phc vi s phc liên hp ca nó bng hai ln phn thc ca s thc



z a bi z z a,2   





 

z a bi a b

,  

và

 

z c di c d

,  



      

z z a bi c di ac bd ad bc i

–     





 

z a bi a b,  

, ta có

 

k z k a bi ka kbi. . .   



z0. 0





i i i i i i i i

0 1 2 3 2

1, , 1, .      

n n n n

i i i i i i n

4 4 1 4 2 4 3

1, , 1, ,

   

       





khác









z '

và

z 0

là

z z z z z

z z z

' '. '.



  





ax by c 0   



x 0

g Oy

y 0

Ox

   

x a y b R

    

hình tròn tâm

 

I a b;,

bán kính

   

x a y b R

x y ax by c

2 2 0



   







    



 có

tâm

 

I a b;,

bán kính

R a b c

  

0x 



y 0

h

x 0



y 0



y ax bx c

   



1  



1  



- : 0973.514.674

Page | 41





+ Cho s

, nu có s phc

sao cho



thì ta nói

là mc hai ca

+ Mi s phc

z 0

c hai.

c hai ca s thc

âm là

iz



âm là

ia



c hai

ax bx c a b c a

0, , , , 0     

. Xét bit s

b ac

4  

ca

y:

+ Khi

0

t nghim thc



+ Khi

0

m thc phân bit

1,2

  



+ Khi

0

m phc

1,2

  



 





 

. , 0z z z r r  

max

min





















 

1 2 1 1

. , 0z z z r r  

max   

và

min   





 

z z z z z z k k

1 2 1 2

. . , 0    

max



và

min





- : 0973.514.674

Page | 42



I- 



 









 





 



                







 





Ñieåm ngoaøi

Ñieåm trong

Mieàn ngoaøi

III- 

ng gian:





M '











a) 

      



M '

sao cho

MM v' 

- : 0973.514.674

Page | 43

b) 

 

 

 







 

th

M '

sao cho

 



MM '



 



 





 



 

c) 

     

    





 

M '

sao cho

  

MM '





 





 

d) 







 





 





 

M '

sao

cho





MM '







 







 

* :









 



 

H '



 





 

H '

2. Hai h



- : 0973.514.674

Page | 44



I. 

 A B 

AB 





II. 

1. :  

 n 

 p 



 

np,

2. 



h











 

3;3



 

4; 3



 

3;4



 

5;3



 

3;5

K

 

np,



C nMp 2.Đ

- : 0973.514.674

Page | 45





áy

V S h



áy





 

S.ABCD ABCD

S, ABCD

V d .S





áy

V S h.

áy









V a b c..







 



a 2

 



a 3

  

a b c,,



a b c

2 2 2



 



a 3

- : 0973.514.674

Page | 46



S A B C

S ABC

SA SB SC

V SA SB SC

  





ABC A B C.

  





V B B BB



  



B B h,,









a) Cho

ABC

AAH.



AB AC BC

2 2 2





AB BH BC

.



AC CH BC

.



AH BC AB AC..



AH BH HC

.



AH AB AC

2 2 2

1 1 1





AB BC C BC B AC C AC B.sin .cos .tan .cot   

b) Cho

ABC



a b c

m m m, , 





 

a b c bc A b c a ca B c a b ab C

2 2 2 2 2 2 2 2 2

- 2 .cos ; 2 .cos ; 2 .cos       

  sin:

a b c

A B C

sin sin sin



  n:

a b c

b c a c a b a b c

mmm

2 2 2 2 2 2 2 2 2

222

;;

2 4 2 4 2 4

  

     



:



a b c

S a h b h c h

1 1 1

. . .

2 2 2

  



S bc A ca B ab C

1 1 1

sin .sin sin

2 2 2

  



abc





S pr

 CT He-ron:

   

S p p a p b p c   



ABC

i A:

AB AC BC AH





ABC

u, cnh a:









- : 0973.514.674

Page | 47

:



(a: c

 nht:

S ab

c)

 



cao

AB AD BAD. .sin



S AB AD BAD AC BD

. .sin .





 

S a b h



u cao)

g) T 

S AC BD









Cho hSABC 

     

SAB SBC SAC,,



SAB SBC SAC,,



1 2 3

,S ,S



S ABC

1 2 3

2 .S .S



 S.ABC 



 

ABC





 

SAB



 

SBC



BSC ASB,







S ABC

.sin 2 .tan





S.ABC ABC  a,





S ABC

a b a

2 2 2





S.ABC a 







S ABC

tan





- : 0973.514.674

Page | 48

S.ABC b 







S ABC

3 .sin cos





S.ABC a







S ABC

.tan





 S.ABCD ABCD 

 a

SA SB SC SD b   



S ABC

a b a

2 2 2





 S.ABCD  a







S ABCD

.tan





S.ABCD  a,

SAB







;















S ABCD

tan 1







Cho S.ABCD  a





















 

S ABCD

4 .tan

3 2 tan







- : 0973.514.674

Page | 49

S.ABC a. 

 



A BC 

 

SBC



 







S ABCD

cot







a.





a   







C BIT TH  DIN :

U KIN T DIN

C

SA a SB b SC c

ASB BSC CSA

  









  





S ABC

abc

2 2 2

1 cos cos cos 2 cos cos cos

     

    

t 3 c nh 1 t din

   

AB a CD b

d AB CD d AB CD

, , ,

















ABCD

V abd

sin





t 2 ci, kho

   

 

SAB SAC

S S S S SA a

SAB SAC







  











SABC

2 sin





t mt cnh, dia 2 mt k

   

 

SA a SB b SC c

SAB SAC

ASB ASC























S ABC

abc

sin sin sin

  



t 3 c  din

T diu

tt c nh bng

ABCD



T din gu

AB CD a

AC BD b

AD BC c

















   

ABCD

V a b c b c a a c b

2 2 2 2 2 2 2 2 2

      

- : 0973.514.674

Page | 50

-  - 



1) 













0 90





 

mp P





 

  











h













2) 







        

    





u cao hng sinh l 

 Di c

S rl .





 

áy





 Din: c

S rl r





+ Th :

V r h





3) 

 i mp

Q()

a mt nn.

mp Q()

ng sinh.

mp Q()

i mng sinh.

n.

Q()



 i mp

Q()

a mt nn.

mp Q()



mp Q()



mp Q()



ng parabol.





- : 0973.514.674

Page | 51









 









 



 

xung quanh



 

 



 





 









a) 

ABCD



ABCD





ADCB



.

+ Khi quay quanh

,AB















 

khi

quay xung quanh















 



 u cao hng sinh l 

 Di

S rl2.





 Din:

S rl r

2 2 .





 Th 

V r h





 

1. M





 M  

 I   R     I,

R.



 

S I R;.



 

 

S I R M IM R ; 



- : 0973.514.674

Page | 52

2. 



 

S I R;



 

H I 

 

d IH

I 

 



dR

dR

dR



g.



 



H: 





 





r R IH



 Khi m

 

I 

 



 

3. 



 

S I R;





H I 





IH R

IH R

IH R











 

 

H:













 

tA, B R 

 

d I IH

R IH AH IH

2 2 2

;











   











- : 0973.514.674

Page | 53



  





+ Giao 





        



kinh tuyeán

vó tuyeán















 





S ABCD.



OA OB OC OD OS r    



 

S I R;













- : 0973.514.674

Page | 54

 



 

 





 





 











M AC



 

AC SMI

 

 

SAC



 

ABC



SMI.

 

 

SAC





MSI.



 

d I SAC IH d,.



td SAC

h d h d

S S SM AC SI IM AI IM r h

h d h d

2 2 2 2

2 2 2 2 2 2

2 2 2 2

. .2 .



       





 

S ABCD.





   



ABCD





r IM





h SI



l SM.

 

S ABCD.

- : 0973.514.674

Page | 55

     

S ABCD.

 







ABCD



 

AC AB

r IA

  

 

h SI.

 

l SA.



S ABCD.

    

S ABC.

  

 

     



ABC.



 

AM AB

r IM

  

 

h SI.

 

l SM.



S ABC.

 

S ABC.









ABC.



 

AM AB

r IA

  

 o:

h SI.

 

l SA.



S ABC.





.

 



 



    

R r h,,







 

 

S l R r .







 

áy

S r R









  











- : 0973.514.674

Page | 56



  

 

OR;

  

 

AmB

   

AnB



   



  

   



≡



r x r

h l r









  











 



  



 

ABCD



AB R2



AD h





hR2

song so 

  

BGHC

     

 

d OO BGHC OM'; 











 

ABCD

V ABCDOO AB CD

. . '.sin ,









ABCD

V ABCDOO

. . '



 

 

S l R r r R

  

   



 

V h R r Rr



  

- : 0973.514.674

Page | 57







OO '





AB OO A AB; ' '





OO '

 

d AB OO OM;'

 

ABCD

  

        





AB R h

24





Mt khi tr  i.

         din

n nh nht:

min





















         din

ng vi di nht:

min





























(T)







ABCD A B C D. ' ' ' '









- : 0973.514.674

Page | 58







1/ 

 









 









 









2/ 

 





 

3/ 

a/ .

- 







trung

AC '

- 







b/ .



AA A A AA A A

' ' ' '

1 2 3 1 2 3

... . ...



AA A A

1 2 3

...



AA A A

' ' ' '

1 2 3

...



 





 

O '





- :





OO '

- :

R IA IA IA

...   

c/ 

 .

- 

S ABC.



SAC SBC

90

+ 



+ 

R IA IB IC

   













- : 0973.514.674

Page | 59

- 

S ABCD.



SAC SBC SDC

90  

+ 



+ 

R IA IB IC ID

    

d/ .



S ABC. ...

- 



SO



- 





 

mp SAO















I



- 



SM SI

SMI SOA

SO SA

    



SM SA SA

R IS IA IB IC

SO SO

...

      

e/ .



S ABC. ...



SA 



 

ABC...



ABC...







S ABC. ...





- 







 

mp ABC...



- Trong

 

mp d SA,











t





I







R IA IB IC IS ...    

- :



MIOB





MAI





R AI MI MA AO

2 2 2



    





f/ 

- 





- 

 





 



   



- 





- : 0973.514.674

Page | 60

g/ 

K





Ch

S AA A

. ...





: 







: 

()





- 

 

mp( O)



  

- 

 

R SA SO

g



 









M MA MB MC :   

Suy ra:

MA MB MC M     



-  

-  





























- : 0973.514.674

Page | 61



  



SMO



SO SM

SIA

SA SI

  

4. :

MA MB MC

M S SM

SA SB SC



















ABC





S AA A

. ...

 



  



  



 d 



I 

 

dI  

+  

 

R IA IS

.   

.



- : 0973.514.674

Page | 62

 

Loi 1: C

vi 

ABC

90







m

Loi 2: C

t k 

ch ci tip c







   

abc

p p a p b p c4



  

(

: na chu vi).

 Nu



ABC

i



 

R AB AC AS

2 2 2 2

  

     nh





, n     u cnh





Loi 3: ng nhau:

SA SB SC SD  





ABCD

    nh  







ABC



m cnh huyn.



ABC



c 

Loi 4: Hai mt phng

 

SAB



 

ABC

i

n

i

l

i ti

SAB



ABC

t cu ngoi tip:

R R R

2 2 2

  

Loi 5 : 

S.ABCD

ng cao

i ti

. Ki



 

SH x OH x R

2 2 2

   

. V



R x R

2 2 2



Loi 6: t cu ni tip:



- : 0973.514.674

Page | 63

TNG HC BIT V KH

Chm cu:

 

S Rh r h

h R h r

2 2 2







  







  











 ct:

(phin tr)

 

S R h h



























i 1:

tan





i 2:

tan













Parabol bc hai.

Parabol 

xoay.

parabol

tru

S x a

S Rh

S h R

V R h V

;











  





























elip

xoay

uanh a

quaoay nh b

S ab

V ab

V a b

2





















n

Di



 

S R r





Th n (phao)

R r R r



  





  

  

- : 0973.514.674

Page | 64

VII



1. Ox, Oy, Oz 

O, trc hoành OxOyOzOxy, Oyz,Ozx.

i j k,,



Chú ý:

i j k

i j ik jk

2 2 2

  



  

2. 

u x y z u x y z u xi yj zk( ; ; ) ( ; ; )     

3. 

M x y z OM xi y j zk( ; ; )    

4.  Cho

u a b c v a b c( ; ; ), ( ; ; )

  



u v b b











  











 

u v a a b b c c;;

  

   

ku ka kb kc( ; ; )

u v u v u v aa bb cc. . .cos( , )

  

   

u v aa bb cc

u v u v

cos( , )

  





u u a b c

2 2 2

   

u v u v.0  

 

B A B A B A

AB x x y y z z;;   

     

B A B A B A

AB AB x x y y z z

2 2 2

      

5. Chú ý: 





uv,

là góc h 

trong 















u v u v

sin , 1 cos , 0  

6. : M chia AB k 

MA kMB



x kx

y ky

z kz





































- : 0973.514.674

Page | 65



MA MB 0





























7. 

GA GB GC 0  

A B C

x x x

y y y

z z z





























8. 

GA GB GC GD 0   

A B C D

x x x x

y y y y

z z z z



  





  









  









9.  

u a b c( ; ; )

và

v a b c( ; ; )

  







uv,





hay

uv



b c c a a b

, ; ;











     





 

bc b c ca ac ab ba;;

     

   

10. 

uv,





vuông góc 

và

u v u v u v, . .sin( , )







uv,0









uv,



11. 

a. :

S AB AD,







b. 

S AB AC







c. 

u v w,,



u v w, . 0







d.          ABCD    :

V AB AD AA,.









e. 

V AB AC SA

. , .







- : 0973.514.674

Page | 66





 

 

 



 trong



 

 

 

A B C,,



AB AC,



AB k AC  

AB AC,0







ABCD



AB DC



Cho

ABC



E F,

 



ABC





EB EC

.

FB FC

.

A B C D, , ,



AB AC AD,,

kh

AB AC AD, . 0











 

S ,









 



 

I a b c;;



R :

(S):

x a y b z c R

2 2 2 2

( ) ( ) ( )     



 



 

I a b c;;



A :



R IA.



 









AB :

A B A B A B

I I I

x x y y z z

x y z;;

2 2 2

  

  

 h





 



A B C D, , ,



ABCD

 

 



x y z ax by cz d

2 2 2

2 2 2 0      

 

* .

- : 0973.514.674

Page | 67

 

A B C D, , ,



 

* ,



 

a b c d,,,





 



 



A B C,,





 







 





 



 



R '



 

T .

 



 

S .





 

S :

x y z ax by cz d

2 2 2

2 2 2 0      



a b c d

2 2 2

0   



 



 

I a b c;;  



R a b c d

2 2 2

  





 

S I R

1 1 1



 

S I R

2 2 2



I I R R

1 2 1 2



   

S S

,

trong nhau



I I R R

1 2 1 2



   

S S

,





I I R R

1 2 1 2



   

S S

,





I I R R

1 2 1 2



   

S S

,





R R I I R R

1 2 1 2 1 2

   

   

S S

,



 

1. 





 



 

x y z,,



x a y b z c R

2 2 2 2

( ) ( ) ( )     



x y z ax by cz d

2 2 2

2 2 2 0      

 

2. 

 



 

x f t

y g t

z h t

()

*

















 

 



 

- : 0973.514.674

Page | 68







2. 



kn k( 0)



3.  qua

M x y z

0 0 0

( ; ; )



n A B C( ; ; )



A x x B y y C z z

0 0 0

( ) ( ) ( ) 0     

4. 

Ax By Cz D 0   



5. 

  D=0

 (Oxy)



A=B=0

 (Oyz)



B=C=0

 (Ozx)



A=C=0

 Ox



A=0

 Oy



B=0

 (P) 



C=0

 A(a;0;0), B(0;b;0) Oz C(0;0;c)

 

x y z

a b c

1  

6. 

Cho

 

M x y z

0 0 0

;;



P Ax By Cz D( :0)    

;

Ax By Cz D

d M P

A B C

0 0 0

222

( ,( ))

  







 



 





()





 

 



 

Ax B y C z D

1 1 1 1



   



 

A x B y C z D

2 2 2 2



   



 



 



 





 

P m Ax B y C z D n A x B y C z D m n

1 1 1 1 2 2 2 2

: .( ) .( ) 0, 0         







 





 







 





 

M x y z

0 0 0

;;



 

n A B C;;

       

A x x B y y C z z

0 0 0



     



 





 

M x y z

0 0 0

;;



ab,



 





n a b,







 

 



  

 

M x y z

0 0 0

;;

     





- : 0973.514.674

Page | 69

 

Ax By Cz D : 0 :



   

       

A x x B y y C z z

0 0 0



     



 





A B C,,



 





n AB AC,









 







 



 

 



v

 

 





n AM u,









 







 

VTCP



 



 





 





d d

, :

 

ab,

 

d d

 

 





n a b,







 

1 

 

d M







 







d d



) :

 

ab,



d d

 

 



l

n a b,







 



 

d M





:

 







 

ab,



d d

 

 





n a b,









 





 

 

 



 



 







 



 

 





n u n,









 



 

d M .







 







   

 , :



 TPT

nn,





 





 



 

 





n u n,











 





 

cho t





 



) 

Ax By Cz+D 0  

 

A B C

222

0  

 

   

A B d A B, , (



  



   

1 , 2 ).

- : 0973.514.674

Page | 70

 

d M k( ,( ))







 

 

     

1 , 2 , 3





 





 



H :

 

 





 

 





n IH





 

:0P A B DxyCz   



 

: 0.xA zP B Cy D













 



 



: : : .:A B C A B C

  



   

// PP



A B C D







  

   





A B C D







  

   





       

. 0 0.

P P P P

n n n n AA BB CC





  

     













 

M x y z

0 0 0 0

;;



Ax By Cz D():0



   

 

Ax By Cz D

A B C

0 0 0

222

,( )



  







  













 

MH n cung phuong

()



















M '



qua

 

MM MHP 2









   





 

Ax B y C z D

1 1 1 1



   

 

A x B y C z D

2 2 2 2



   



   





 

n n AA B B C C

A B C A B C

1 2 1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

cos ( ),( )







   



 

0 ( ),( ) 90





;

AA B B C C

1 2 1 2 1 2

( ) ( ) 0



    

- : 0973.514.674

Page | 71







 

Ax By Cz D:0



   



 

S x a y b z c R

2 2 2 2

: ( ) ( ) ( )     



 





 



d I R( ,( ))







 





 

d I R( ,( ))





 







 





 



 



 





 





 



 





 





 



d I R( ,( ))







v



 





 



 



 





 





 



 



nh



r R IH









 



a 0











a a a a

1 2 3

( ; ; )

 





ka.

k( 0)







A B,









ai(1;0;0)





aj(0;1;0)





ak(0;0;1)





()



M x y z

0 0 0 0

( ; ; )



a a a a

1 2 3

( ; ; )



 

x x ta

y y ta t

z z ta

( ) :







   











)(

),,( zyxM



- : 0973.514.674

Page | 72



()



M x y z

0 0 0 0

( ; ; )



a a a a

1 2 3

( ; ; )



x x y y z z

a a a

0 0 0

1 2 3

( ) :

  

  







: Trong

 

Kg Oxyz



x x a t

y y a t

z z a t

(1)

( ) : (2)

(3)







  











a a a a

1 2 3

( ; ; )



M x y z

0 0 0 0

( ; ; )



Ax By Cz D ( ) : 0



   



n A B C( ; ; )



cat ( ) a n Aa Ba Ca

Aa Ba Ca

// ( )

Ax By Cz D

Aa Ba Ca

( )

Ax By Cz D

0 0 0

( ) . 0 0

()



      



  





  



   









  





   



   









( ) ( )











a a a A B C

: : : :

 

 





 





()

















x y z, , .

Suy ra:

 

M x y z, , 



     

1 , 2 , 3



 

mp P



at b 0 (*)





 

mp P



 

Pt *







   

P Pt *







   

P Pt *







 

a



 



C











)(



)(



)(



- : 0973.514.674

Page | 73







  

1 2 1

, , 0.u u u MN



    





// 

u MN



  



























, . 0

u u MN



  









  

















, . 0.u u MN   



 

va (

( ) )



()

















x y z, , .

Suy ra:

 

M x y z, , 

 



x x a t

y y a t

z z a t

(1)

(2)

(3)



















 

x a y bS z c R

2 2 2 2

( ) ) ( ): (     





I a b c( ; ; )









 





IM a

h d I d

( , )









d I d( , )







d I d R( , ) 





 



d I d R( , ) 





 



d I d R( , ) 





 



M N,







 

     

1 , 2 , 3



 



hai theo

 

t *

nh

 





 



 





 



 





 



M N,



M N,





- : 0973.514.674

Page | 74





Trong

 

Kg Oxyz









Ax B y C z D

A x B y C z D

1 1 1 1

2 2 2 2

( ) : 0





   







( ) & ( )





AA B B C C

A B C A B C

1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

cos







   





x x y y z z

a b c

0 0 0

( ) :

  

  



Ax By Cz D ( ) : 0



   







( ) &( )







Aa Bb Cc

A B C a b c

2 2 2 2 2 2

sin







   



C

x x y y z z

a b c

x x y y z z

a b c

0 0 0

' ' '

( ) :

  

  

  

  







( ) & ( )



aa bb cc

a b c a b c

' ' '

2 2 2 '2 '2 '2

cos







   





C

Ax By Cz D( ) : 0



   



M x y z

0 0 0 0

( ; ; )





()





Ax By Cz D

A B C

0 0 0

222

( ; )

  





);;(

2222

CBAn 



);;(

1111

CBAn 



900 



);;( CBAn 



)(

);;( cbaa 



900 



);;(

cbaa 





)';';'(

cbaa 



900 



);;(

0000

zyxM

- : 0973.514.674

Page | 75



C

()



M x y z

0 0 0 0

( ; ; )



u a b c( ; ; )



1 

()



M M u

;

( , )









 Trong

 

Kg Oxyz



co VTCP u a b c va qua M x y z

1 0 0 0

' ' ' ' ' ' '

2 0 0 0

( ) ( ; ; ) ( ; ; )





va (

( ) )



u u M M

, ' .

( , )





  

















 

M x y z

0 0 0 0

( ; ; )



a a a a

1 2 3

( ; ; )

x x a t

d y y a t t R

z z a t

( ) : ( )







  













A B,:









M x y z

0 0 0 0

( ; ; )







d //











M x y z

0 0 0 0

( ; ; )



 



 

dP



 



ng 5:



   

,:PQ





 

Ad:



()















 

a n nd ,:











A B,









M x y z

0 0 0 0

( ; ; )





);;(

0000

zyxM

)(





- : 0973.514.674

Page | 76



d d d d

,





a a a











M x y z

0 0 0 0

( ; ; )















M H u

0 



















M H





 





 







   

d P Q 





M x y z

0 0 0 0

( ; ; )







M d M d

1 1 2 2

,.



M M M



M M





  

 

MdP

( , )

 

MdQ

( , )

  

   

d P Q . 

   





a n n,







 

   

 

    

  

   

A d P B d P

,.





AB.









   

 







 

 







 

   

d P Q . 





d d







M d M d

1 1 2 2

,.



MN d

















M N,.







MN.





 











a a a







 

 













 



n a a







 

 







   

d P Q . 









 



L

 







 



 

M  

 

 







 



n a n,









- : 0973.514.674

Page | 77



   

d P Q . 



















MN d

,









MN.





 

 

qua



 

 







   

d P Q . 







  









 













 











1. 











M M a

d M d

( , )









 







 

d M d MH,.



  

 

N x y z d; ; .



theo

t t(





d).

 





 

NH.



 

d M d MH,.

2. Kh







1 



- : 0973.514.674

Page | 78



a a M M

d d d

1 2 1 2

( , )













d d





 







3. 





4. 





 











 





1. 



d d





d d

b

 

cos ,



2. 

 



a a a a

1 2 3

( ; ; )

 

 





n A B C( ; ; )







 







d '



 



 

dsin ,( )





Aa Ba Ca

A B C a a a

1 2 3

2 2 2 2 2 2

123



   









 



 

I a b c; ; ,





 

S x a y b z c R

2 2 2 2

( ) : ( ) ( ) ( ) 1     



 

 

 Khi

IO



C x y z R

2 2 2 2

( ) :   





x y z ax by cz d

2 2 2

2 2 2 0      



a b c d

2 2 2

0   





 



 

I a b c; ; ,



R a b c d

2 2 2

   





()





 



Ax By Cz D

S x a y b z c R

2 2 2 2

( ) : 0

( ) : ( ) ( ) ( )



   

     

- : 0973.514.674

Page | 79



dI( ; )





 

 



  

 

;S I R

  

 

.  H       I 

 

,.d IH d I P  

dR

dR

dR







 





H: 

 

 







r R IH



 



 

I a b c;;



 

S x a y b z c R

2 2 2 2

: ( ) ( ) ( )     



 



 

I a b c;;





R IA



 







 



A B A B A B

I I I

x x y

A yB

y z z

xz;;:

2 2 2

  

  

 

R IA





 



A B C D, , , (





 

 



 

x y z ax by cz d

2 2 2

22 *20.      

 

A B C D,,,



 



 

a b c d, , , 



 



 



A B C,,





 







 





 





 



R '



 

  



 



- : 0973.514.674

Page | 80

 

 

S x y z ax by cz d

2 2 2

: 2 2 2 0      



a b c d

2 2 2

0   



 



 

I a b c– ; – ; –



R a b c d

2 2 2

   



 

S I R

1 1 1



 

S I R

2 2 2



I I R R

1 2 1 2



   

S S

,

trong nhau



I I R R

1 2 1 2



   

S S

,





I I R R

1 2 1 2



   

S S

,





I I R R

1 2 1 2



   

S S

,





R R I I R R

1 2 1 2 1 2

   

   

S S

,





 



 

I a b c;;



 





 

R d I P;

  

 



 

I a b c;;



 







 





    





  

Pr2









 

 

d d I P,

 

R d r



 

 

 



 

I a b c;;



 



giao tuy



 

 

R d I P;

 



 







 

I a b c;;











 



 

R d I,

      

 

     



  

 

o o o

M x y z,,













 

 







 

 

IP  



- : 0973.514.674

Page | 81

 

 

R IM d I,  

  

 

 

 



 

I a b c;;







AB,









IAB





IAB







 

d I IH, 



IAB









R IH HB





sin 45





sin 60





Cho

 

và hA, B.

Tìm

 

MP



 

MA MB

min



A và B 

 

M A B,,



 

M AB P  

A và B 

 

Tìm

B '



qua

 

M A B, , '



 

M AB P'  

Cho

 

A, B.

Tìm

 

MP



MA MB

max



 A và B 

 

M A B,,



 

M AB P  

A và B 

 

Tìm

B '



qua

 

MA MB AB''  



 

M M M

M x y z;;







 

qua



Ox Oy Oz,,



A B C,,

sao cho

O ABC



 

M M M

x y z

3 3 3

  



 









Md



 



 

P d d

Qua A d

n u AM u

























 

qua

và cách



 

Qua A

n AM















- : 0973.514.674

Page | 82



 





, sao cho

 





(









 

P d d

Qua A d

n u u u

























Cho

 

P//









và

cách





L

A 







trên

 

QuaA





























 

 sao cho







không vuông góc



 

) ?

 

Qua A d

u n AM































 









không vuông góc



 

) ?

   

d P P

Qua A d

u n AM n























    



 

 

AP

    

 

 

   





    







 

   

d P P

Qua A d

u n AM n























Bấm Tải xuống để xem toàn bộ.

| 1/82

| | Tải xuống

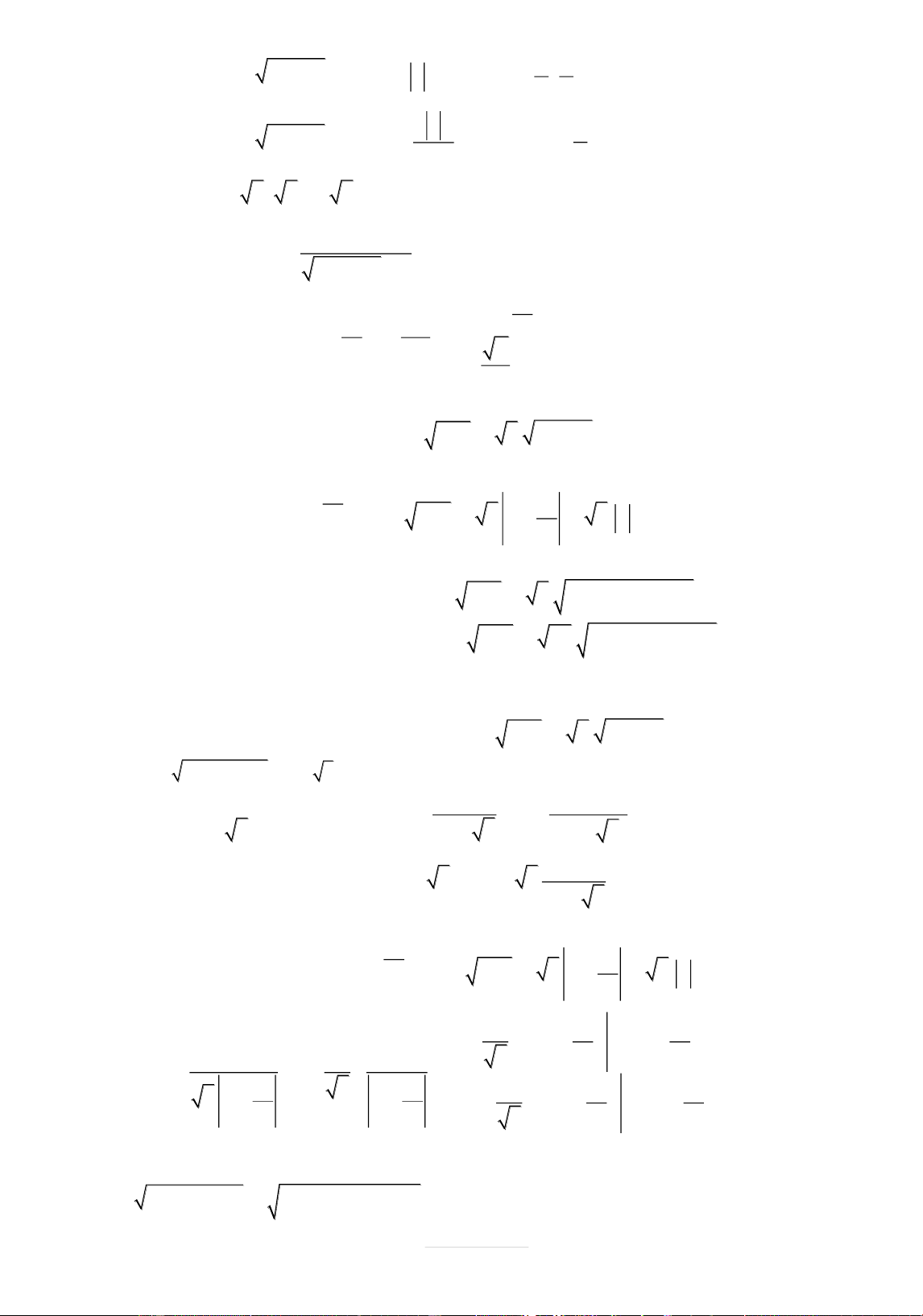
Preview text:

TÓM TẮT LÝ THUYẾT VÀ GIÂI NHANH TOÁN 12
Nguyễn Chiến - Nguyễn Hồng Quân PHÆN 1. HÀM SỐ
SỰ ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ 1. Đðnh nghïa x
 ,x K,x  x ( K là khoâng hoặc đoạn hoặc nửa khoâng). 1 2 1 2
f x   f x  y  f x đồng biến trên K đồ thð đi lên tÿ trái sang phâi. 1 2 
f x   f x  y  f x nghðch biến trên K đồ thð đi xuống tÿ trái sang phâi. 1 2 
Chú ý: + N u f x   0, x  a b
;   hàm s f x  đ ng bi n tr n khoâng a;b.
+ N u f x  0, x
  ;ab  hàm s f x  nghðch bi n trên khoâng a;b.
+ N u f x   0, x  a b
;   hàm s f x  h ng đ i trên khoâng a;b.
+ N u f x  đ ng bi n trên khoâng a;b  f x   0, x  a b ; .
+ Nếu f x  nghðch bi n trên khoâng a;b  f x   0, x
  a;b.
2. Quy tắc và công thức tính đäo hàm
Quy tắc tính đạo hàm: Cho u  u x ; v  v x ; C : là hìng số .
Tổng, hiệu: u  v  u  v.
Tích: u v.  u v.  v u. C u.    C u . . 
 u  uv .  vu . C  C u . 
Thương:    , 0 2
v         v  v  u  u2
Đạo hàm hàm hợp: Nếu y  f u, u  u x   y  y u .  . x u x
Bâng công thức tính đäo hàm:
Đäo hàm của hàm sơ cçp
Đäo hàm của hàm hợp  
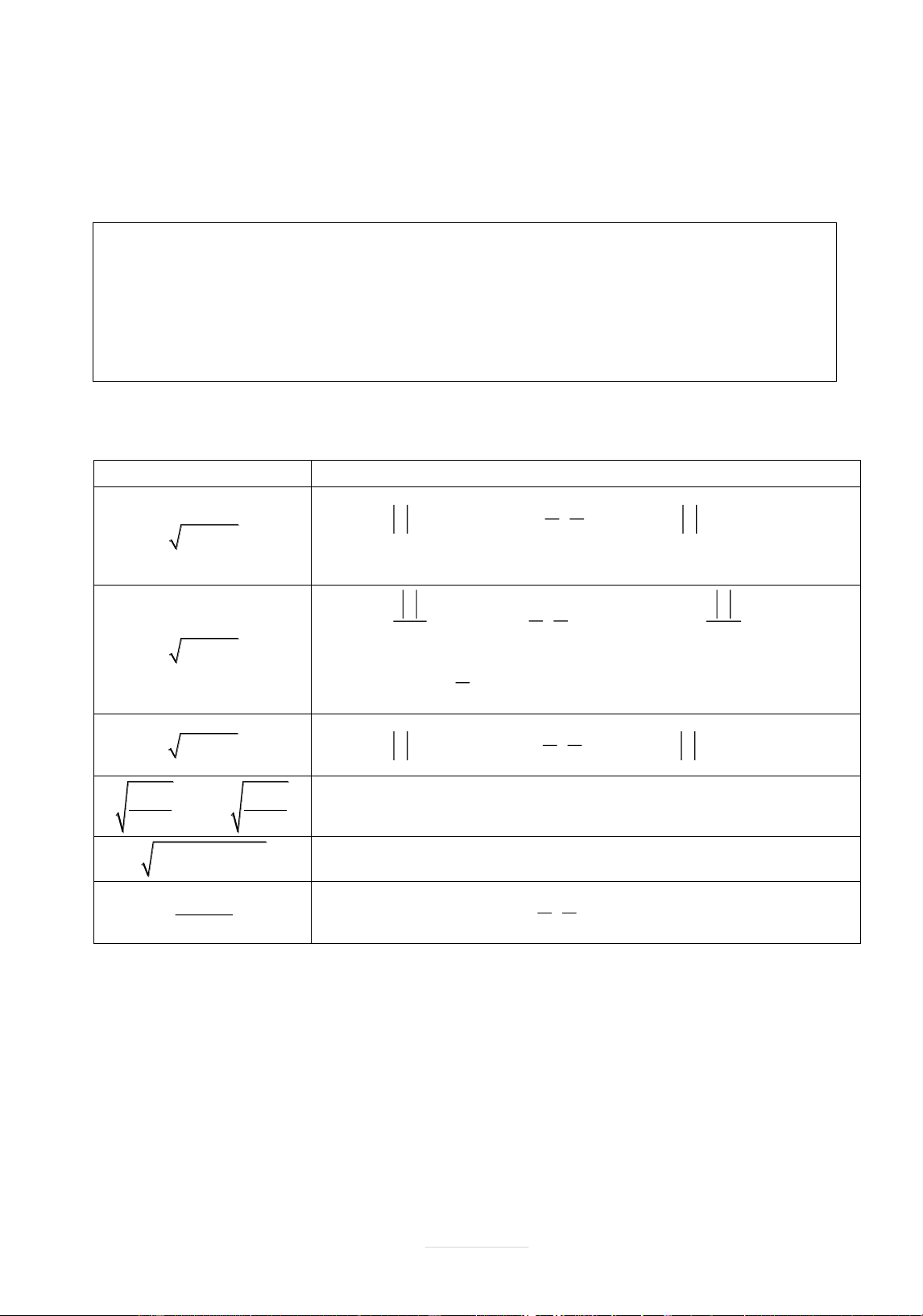
C   0 (C là hìng số).  x      x 1 .    x      x 1 . u   1
.u  .u    1  1  1  u     x (  0)     u  0  x  x2  u  u2  1  u x   x  0
 u  u  0 2 x 2 u
sinx cosx
sinu u.cosu
cosx  sinx
cosu  u.sinu
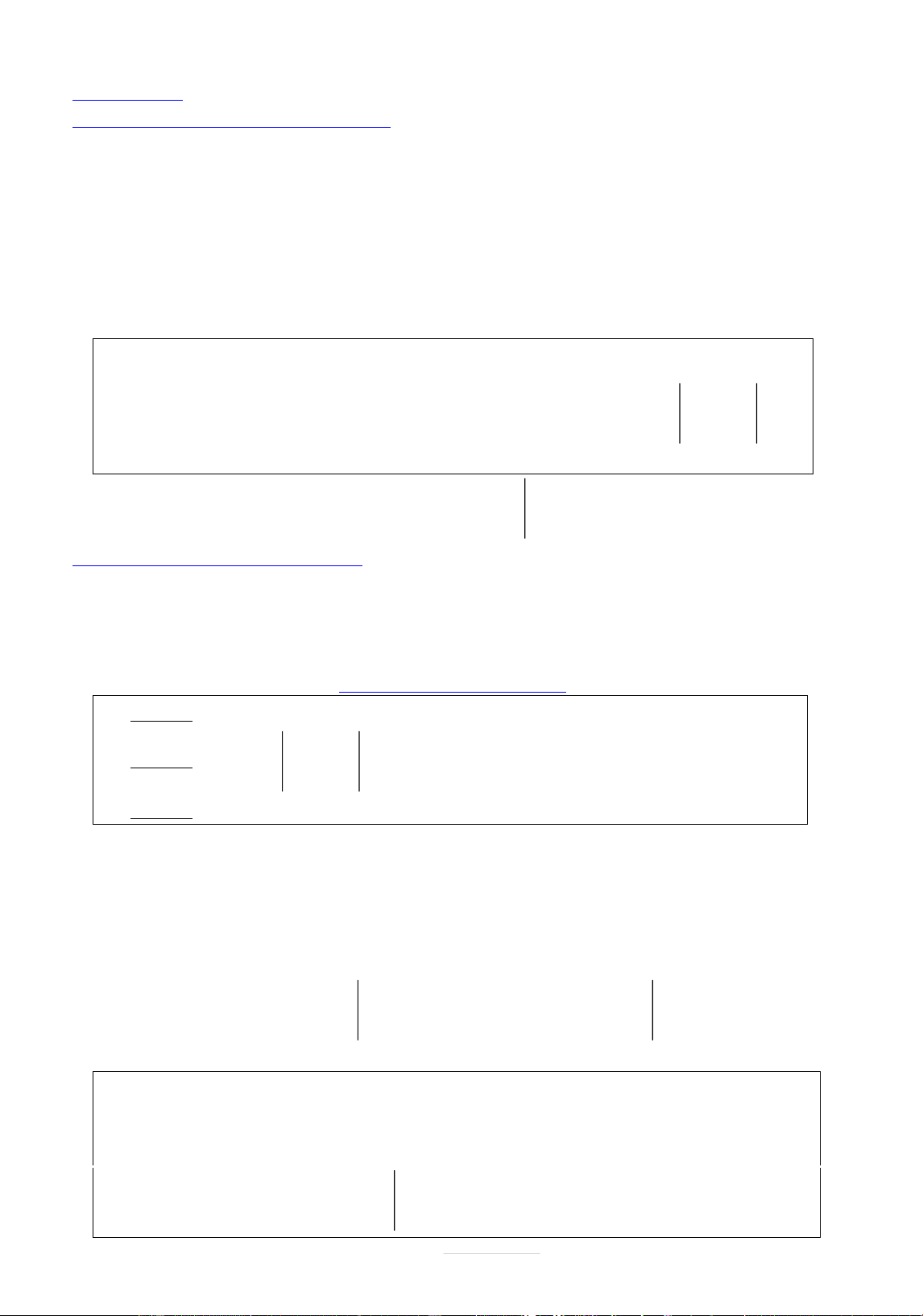
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 1 |  1  tan x   tan    u u 2 cos x 2 cos u  1  cotx    cot     u u 2 sin x 2 sin u
 x   x e e
 u   u e u e .
 x  x a a .lna
 u   u a u a . .lna  1  ln x   ln    u u x u    u x  log u a    a  1 log x ln a u.lna
Công thức tính nhanh đạo hàm hàm phân thức: a b a c b c 2  x  2 x    ax  b  ad  bc 2     d e d f e f ax bx c    . ;    . cx   d   2 2 2 cx  d 
dx  ex  f  
dx2 ex  f  Đạo hàm cấp 2 :
+ Đðnh nghïa: 
f  x   f   x
+ Ý nghïa cơ học: Gia tốc tĀc thąi cûa chuyển động s  f t täi thąi điểm t là: 0
a t   f  t . 0 0  * Một số chú ý:
 Nếu hàm số f x  và g x  cùng đồng biến (nghðch biến) tr n K thì hàm số
f x   g x 
cüng đồng biến (nghðch biến) tr n K. Tính chçt này cò thể kh ng đúng đối vĆi hiệu
f x   g x  .
 Nếu hàm số f x  và g x  là các hàm số dþĄng và cùng đồng biến (nghðch biến) tr n
K thì hàm số f x  g. x  cüng đồng biến (nghðch biến) tr n K. Tính chçt này cò thể
kh ng đúng khi các hàm số f x ,g x  kh ng là các hàm số dþĄng trên K.
 Cho hàm số u  u x , xác đðnh vĆi x  a;b và u x   c;d . Hàm số f ux  
cüng xác đðnh vĆi x  a;b .
Quy tắc xét tính đơn điệu của hàm số.
Giâ sā hàm số f cò đäo hàm trên K
 Nếu f ' x   0 vĆi mọi x  K và f 'x   0 chî täi một số hĂu hän điểm xK thì
hàm số f đồng biến trên K .
 Nếu f ' x   0 vĆi mọi x  K và f 'x   0 chî täi một số hĂu hän điểm x  K
thì hàm số f nghðch biến trên K .
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 2 | Chú ý: ax  b  d 
* Đối vĆi hàm phân thĀc hĂu tî y 
x    thì dçu "  " khi xét dçu đäo cx  d c  
hàm y không xây ra.
Giâ sā y  f x   ax3 bx2  cx  d  f x   ax2 3  b 2 x  c.
Hàm số đồng biến trên
Hàm số nghðch biến trên  a   0  a   0     0    0 
 f x   0; x      a   0 . 
 f x   0; x    a   0 .     b   0  b   0   c   0   c  0 
Trþąng hợp 2 thì hệ số c khác 0 vì khi a  b  c  0thì f x   d
(Đþąng thîng song song hoðc trùng vĆi trýc Ox thì kh ng đĄn điệu)
* Với dạng toán tìm tham số m để hàm số c a đơn điệu một chiều trên khoâng cò độ
dài bằng l ta giâi như sau:
 BþĆc 1: Tính y  f x m  ax2 ;  bx  c.
 BþĆc 2: Hàm số đĄn điệu trên x ;x   y  0 có 2 nghiệm phân biệt 1 2   0   * a  0 
 BþĆc 3: Hàm số đĄn điệu trên khoâng cò độ dài bìng l 2
 x  x  l  x  x   x 4 x  l2 2 2
 S  4P  l * * 1 2 1 2 1 2
 BþĆc 4: Giâi * và giao vĆi * * để suy ra giá trð m cæn tìm. CỰC TRỊ HÀM SỐ 1. Đðnh nghïa
Giâ sā hàm số f xác đðnh tr n têp K và x  K . 0
+ x là điểm cực tiểu cûa hàm số f nếu tồn täi một khoâng a;b chĀa x sao cho 0 0
 ;ab  K và f x  f x ,x a;b\x . 0 0
Khi đò f x đþợc gọi là giá trð cực tiểu cûa hàm số f . 0 
+ x là điểm cực đäi cûa hàm số f nếu tồn täi một khoâng a;b chĀa x sao cho 0 0
 ;ab  K và f x  f x ,x a;b\x . 0 0
Khi đò f x đþợc gọi là giá trð cực đäi cûa hàm số f . 0 
+ Điểm căc đäi và điểm căc tiểu gọi chung là điểm cực trð.
+ Giá trð căc đäi và giá trð căc tiểu gọi chung là cực trð.
+ Điểm căc đäi và điểm căc tiểu đþợc gọi chung là điểm cực trð của hàm số và điểm
căc trð phâi là một điểm trong têp hợp K.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 3 |
+ Giá trð căc đäi và giá trð căc tiểu đþợc gọi chung là giá trð cực trð (hay cực trð)
của hàm số.
+ Nếu x là điểm căc trð cûa hàm số thì điểm x ; f x
( ) đþợc gọi là điểm cực trð 0 0  0
của đồ thð hàm số f .
2. Điều kiện cæn để hàm số đät cực trð
Đðnh lí 1: Giâ sā hàm số y  f x  đät căc trð täi điểm x . Khi đò, nếu y  f x  cò đäo hàm 0
täi điểm x thì f x 0. 0   0 Chú ý:
 Đäo hàm f x có thể bìng 0 täi điểm x nhþng hàm số f kh ng đät căc trð täi 0 điểm x . 0
 Hàm số có thể đät căc trð täi một điểm mà täi đò hàm số kh ng cò đäo hàm.
 Hàm số chî có thể đät căc trð täi một điểm mà täi đò đäo hàm cûa hàm số bìng 0
hoðc täi đò hàm số kh ng cò đäo hàm.
3. Điều iện đủ để hàm số đät cực trð
Đðnh lí 2: Giâ sā hàm số f đät căc trð täi điểm x . Khi đò, nếu hàm số f cò đäo hàm täi 0
điểm x thì f 'x  0. N u f x   0 tr n khoâng x  h;x và f x   0 trên khoâng 0 0  0  0
x ;x h thì x là m t đi m cþ c đa i cûa hàm s f x. 0 0  0
 N u f x   0 trên khoâng x  h;x và f x   0 trên khoâng x ; x  h thì 0 0  0 0 
x là m t đi m cþ c ti u cûa hàm s f x . 0
Quy tắc tìm cực trð Quy tắc 1:
 Bước 1: Tìm têp xác đðnh. Tìm f x .
 Bước 2: Tìm các điểm x i  1;2;... mà täi đò đạo hàm của hàm số bằng 0 hoðc i
hàm số liên tục nhưng không cò đạo hàm.
 Bước 3: Lêp bâng biến thiên hoðc bâng xét dçu f x  . Nếu f x  đổi dấu khi đi
qua x thì hàm số đät căc trð täi x . i i
Đðnh lí 3: Giâ sā y  f x  có đäo hàm cå p 2 trong khoâng x  h;x  h vĆi h  0. 0 0 
 Nếu f x 0, f  x
0 thì hàm số f đät căc đäi täi x . 0   0   0
 Nếu f x  0, f  x
0 thì hàm số f đät căc tiểu täi x . 0   0  0
Từ đðnh lí trên, ta cò một quy tắc khác để tìm cực trð của hàm số Quy tắc 2:
 Bước 1: Tìm têp xác đðnh. Tìm f x .
 Bước 2: Tìm các nghiệm x i  1;2;... cûa phþĄng trình f x   0. i
 Bước 3: Tính f  x  và tính f  x . i 
 Nếu f  x   0 thì hàm số f đät căc đäi täi điểm x . i i
 Nếu f  x   0 thì hàm số f đät căc tiểu täi điểm x . i i
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 4 |
MỘT SỐ DÄNG TOÁN LIÊN QUAN ĐẾN CỰC TRỊ HÀM SỐ
I. CỰC TRỊ CỦA HÀM ĐA THỨC BẬC BA:
1. Tìm điều kiện để hàm số có cực đại, cực tiểu thỏa mãn hoành độ cho trước
ài to n t ng qua t: Cho hàm số y  f x m  ax3 bx2 ;
 cx  d. Tìm tham số m để hàm
số có căc đäi, căc tiểu täi x ,x thóa mãn điều kiện K cho trþĆc. 1 2 Phương ph p:  ước 1:
 Têp xác đðnh: D  .  2 2
Đäo hàm: y  a 3 x  b
2 x  c  Ax  Bx C  ước 2:
Hàm số có căc trð (hay có hai căc trð, hai căc trð phân biệt hay có căc đäi và căc tiểu)
 y  0 có hai nghiệm phân biệt vày đổi dçu qua 2 nghiệm đò
 phþĄng trình y  0 có hai nghiệm phân biệt A   a 3  0 a   0        m  D .   B2  A 4 C  b2 4  1 a 2 c  0 b2  a 3 c 1  0  y  
 ước 3: Gọi x ,x là hai nghiệm cûa phþĄng trình y  0. 1 2  B b 2 x  x      Khi đò: 1 2 A a 3  . C c x  x.   1 2  A a 3
ước 4: Bi n đ i đi u ki n K v da ng t ng S và ti ch P . Tÿ đó giâi ra tìm đþĄ c m  D . 2
ước 5: K t luå n các giá trð m thóa mãn: m  D  D . 1 2
* Chú ý: Hàm số bêc ba: y  ax3  bx2  cx  d a  0.
Ta có: y  ax2 ' 3  b 2 x  c. Điều kiện Kết luận b2  a 3 c  0
Hàm số kh ng cò căc trð. b2  a 3 c  0
Hàm số cò hai điểm căc trð.
 Điều kiện để hàm số có cực trð cùng dấu, trái dấu.
 Hàm số có 2 cực trð trái dấu
 phþĄng trình y  0 có hai nghiệm phân biệt trái dçu  ac  0.
 Hàm số có hai cực trð cùng dấu   0 y  
phþĄng trình y  0 có hai nghiệm phân biệt cùng dçu   C P  x x .   0  1 2  A
 Hàm số có hai cực trð cùng dấu dương    0 y    B
phþĄng trình y  0 có hai nghiệm dþĄng phån biệt  S
  x  x    0 1 2 A  C P   x x.   0 1 2  A
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 5 |
 Hàm số có hai cực trð cùng dấu âm    0 y '   phþĄng trình  B
y  0 có hai nghiệm âm phân biệt  S
  x  x    0 1 2 A  C P   x x.   0 1 2  A
 Tìm điều kiện để hàm số có hai cực trð x ,x thỏa mãn: 1 2 x    x 1 2
x  x   1 2   x  x 1 2
 Hai căc trð x ,x thóa mãn x    x 1 2 1 2
 x  x    0  x x.   x  x  2    0 1 2 1 2 1 2
 Hai căc trð x ,x thóa mãn x  x   1 2 1 2
x x   0 x
 x.   x  x  2    0 1 2 1 2 1 2     x  x  2 x  x  2  1 2   1 2 
 Hai căc trð x ,x thóa mãn   x  x 1 2 1 2
x x   0 x
 x.   x  x  2    0 1 2 1 2 1 2     x  x  2 x  x  2  1 2   1 2 
 PhþĄng trình bêc 3 có 3 nghiệm lêp thành cçp số cộng b  d
khi có 1 nghiệm là x 
, có 3 nghiệm lêp thành cçp số nhân khi có 1 nghiệm là x 3   . a 3 a
2. Tìm điều kiện để đồ thð hàm số có c c điểm cực đại, cực tiểu nằm cùng phía,
khác phía so với một đường thẳng
i tri tương đ i giư a 2 điê m vơ i đươ ng th ng:
Cho 2 đi m Ax ;y , B x ;y và đþąng thë ng  : ax by  c  0. A A   B B
N u ax  by  c ax  by  c  0 thi hai điểm A, B në m v A A  B B 
hai phía so vĄ i đþĄ ng thë ng . 
N u ax  by  c ax  by  c  0 thi hai điểm A, B në m cu ng A A  B B 
phía so vĆi đþĄ ng thîng . 
Một số trươ ng hơ p đ c biê t:
+ Các điểm căc trð cûa đồ thð nìm cùng về 1 phía đối với trục Oy
 hàm số có 2 căc trð cùng dçu
 phþĄng trình y  0 có hai nghiệm phân biệt cùng dçu
+ Các điểm căc trð cûa đồ thð nìm cùng về 2 phía đối với trục Oy
 hàm số có 2 căc trð trái dçu
 phþĄng trình y  0 có hai nghiệm trái dçu
+ Các điểm căc trð cûa đồ thð nìm cùng về 1 phía đối với trục Ox
 phþĄng trình y  0 có hai nghiệm phân biệt và y y .  0 C Đ CT
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 6 |
Đặc biệt:
+ Các điểm căc trð cûa đồ thð nìm cùng về phía trên đối với trục Ox y  y .  0
 phþĄng trình y  0 có hai nghiệm phân biệt và CĐ T C  y  y  0  CĐ CT 
Các điểm căc trð cûa đồ thð nìm cùng về phía dưới đối với trục Ox y  y .  0
 phþĄng trình y  0 có hai nghiệm phân biệt và CĐ T C  . y  y  0  CĐ CT 
+ Các điểm căc trð cûa đồ thð nìm về 2 phía đối với trục Ox
 phþĄng trình y  0 có hai nghiệm phân biệt và y y .  0 C Đ CT
(áp du ng khi không nh m đươ c nghiê m và viết được phương trình đường thẳng đi qua hai
điểm cực trð của đồ thð hàm số)
Hoðc: Các điểm căc trð cûa đồ thð nìm về 2 phía đối với trục Ox
 đồ thð cít trýc Ox täi 3 điểm phân biệt
 phþĄng tri nh hoành đ giao đi m f x   0 co 3 nghi m phân bi t (áp du ng khi
nh m được nghiê m)
3. Phương trình đường thẳng qua c c điểm cực trð 2   .    c 2 b 2 bc y y g x    x  d  hoặc gx    ay  . 9 hoặc   y y g x  y  3 a 9 a 9   2 y 3 
Khoâng cách giữa hai điểm cực trð của đồ thð hàm số ậc 3 là e  e3 4 16 b2  a 3 c AB  vĆi e  a a 9
II. CỰC TRỊ CỦA HÀM BẬC 4 TRÙNG PHƯƠNG y  ax 4  bx2  c a  0
MỘT SỐ KẾT QUÂ CÆN NHỚ
 Hàm số có một căc trð  ab  0.
 Hàm số có ba căc trð  ab  0. a   0
 Hàm số cò đúng một căc trð và căc trð là căc tiểu   . b  0  a   0
 Hàm số cò đúng một căc trð và căc trð là căc đäi   . b  0  a   0
 Hàm số có hai căc tiểu và một căc đäi   . b  0  a   0
 Hàm số có một căc tiểu và hai căc đäi   . b  0   b   b    Giâ sā hàm số y ax4 bx2  
 c có 3 căc trð: A(0;c),B    ;   C ,   ;    a 2 a 4   a 2 a 4     
täo thành tam giác ABC thóa mãn dĂ kiện: ab  0 .
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 7 |
MỘT SỐ CÔNG THỨC GIẢI NHANH y  b3  2 A Tổng quát: cot  2 a 8 O x B C Dữ kiện
Công thức thỏa mãn ab  0
Tam gi{c ABC vuông c}n tại A b3  a 8 Tam gi{c ABC đều b3  a 24
Tam gi{c ABC có diện tích S  S 3 a3 2 S 2 ( )  b5  0 A  BC 0 0
Tam gi{c ABC có diện tích max S ( ) 5 0 b S   0 a3 32
Tam gi{c ABC có b{n kính đường tròn nội tiếp b2 r  r r  A  BC 0  b3  4 a 1  1    a 8   
Tam gi{c ABC có b{n kính đường tròn ngoại tiếp b3  a 8 R  R R  A  BC 8 a b
Tam gi{c ABC có độ d|i cạnh BC  m am2  b 2  0 0 0
Tam gi{c ABC có độ d|i AB  AC  n 1 a 6 n 2 2  b4  a 8 b  0 0 0
Tam gi{c ABC có cực trị B C , Ox b2  a 4 c
Tam gi{c ABC có 3 góc nhọn b a  b3 (8 )  0
Tam gi{c ABC có trọng t}m O b2  a 6 c
Tam gi{c ABC có trực t}m O b3  a 8  a 4 c  0
Tam gi{c ABC cùng điểm O tạo th|nh hình thoi b2  a 2 c
Tam gi{c ABC có O l| t}m đường tròn nội tiếp b3  a 8  a 4 bc  0
Tam gi{c ABC có O l| t}m đường tròn ngoại tiếp b3  a 8  a 8 bc  0
Tam gi{c ABC có cạnh BC  kAB  kAC
b3 k2  a k2 . 8 (  4)  0
Trục ho|nh chia tam gi{c ABC th|nh b2  4 2 ac
hai phần có diện tích bằng nhau
Tam giác ABC cò điểm căc trð cách đều trýc hoành b2  a 8 c
Đồ thð hàm số C  y ax4 bx2 :  
 c cít trýc Ox täi 100 b2  ac
4 điểm phån biệt lêp thành cçp số cộng 9
Đðnh tham số để hình phîng giĆi hän bći đồ thð
C y ax4 bx2 :    c 36
và trýc hoành cò diện tích b2  ac 5
phæn tr n và phæn dþĆi bìng nhau.  2    2  
PhþĄng trình đþąng trñn ngoäi tiếp ABC 
: x2  y2   
 c y  c     0 b a 4 b a 4    
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 8 |
GIÁ TRỊ LỚN NHÇT - GIÁ TRỊ NHỎ NHÇT I. Đðnh nghïa.
Cho hàm số y  f x  xác đðnh trên têp . D f x ( )  M, x   D
 Số M gọi là giá trð lớn nhất cûa hàm số y  f x  trên D nếu:  x   D, f x ( )  M  0 0 
Kí hiệu: M  max f (x) . x D  f x ( )  m, x   D
 Số m gọi là giá trð nhỏ nhất cûa hàm số y  f x  trên D nếu:  x   D, f x ( )  m  0 0 
Kí hiệu: m  minf x ( ) . x D 
2. Phương pháp tìm GTLN,GTNN
* Tìm GTLN, GTNN của hàm số bằng cách khâo sát trực tiếp
 Bước 1: Tính f x và tìm các điểm x ,x ,...,x D mà täi đò f x   0 hoðc hàm số 1 2 n kh ng cò đäo hàm.
+ Bước 2: Lêp bâng biến thi n và rồi suy ra giá trð lĆn nhçt, giá trð nhó nhçt cûa hàm số.
* Tìm GTLN, GTNN của hàm số tr n một đoän  Bước 1:
 Hàm số đã cho y  f x  xác đðnh và liên týc tr n đoän a;b  .
 Tìm các điểm x ,x ,...,x trên khoâng a;b , täi đò f x   0 hoðc f x  1 2 n kh ng xác đðnh.
 Bước 2: Tính f a, f x , f x ,..., f x , f b . 1 2 n   
 Bước 3: Khi đò:
 max f x   max  
f x ,f x ,...,f x ,f a ,f b . 1 2 n      a b ,  
 min f x   min f x , f x ,..., f x , f a , f b . a b ,    1  2
 n      
* Tìm GTLN, GTNN của hàm số tr n một hoâng
 Bước 1: Tính đäo hàm f  x ( ) .
 Bước 2: Tìm tçt câ các nghiệm x  a
( ;b) cûa phþĄng trình i f  x
( )  0 và tçt câ các điểm   a
( ;b) làm cho f  x ( ) kh ng xác đðnh. i
 Bước 3. Tính A  lim f x
( ), B  lim f x ( ), f x ( ), f ( ) . i i x a  x b 
 Bước 4. So sánh các giá trð tính đþợc và kết luên M  maxf x
( ), m  minf x ( ) . a ( b ; ) a ( b ; )
Nếu giá trð lớn nhất (nhó nhất) là A hoặc B thì kết luận không cò giá trð lớn nhất (nhó nhất).
min f x  f a  + N  
u y  f x  đ ng bi n trên a  ;b a b ;   thì    . max f 
x  f b a  b ;     min f x
( )  f b  + N a b ; 
u y  f x  nghi ch bi n trên a  ;b   thì    . max f x ( )   f a a b ;    
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 9 |
ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
1. Đường tiệm cận ngang
Cho hàm số y  f x
( ) xác đðnh trên một khoâng vô hän (là khoâng däng
a;,;b hoðc ;). Đþąng thîng y  y là đþąng tiệm cận ngang (hay tiệm 0
cên ngang) cûa đồ thð hàm số y  f x
( ) nếu ít nhçt một trong các điều kiện sau thóa mãn: lim f x
( )  y , lim f x ( )  y x  0 x 0
2. Đường tiệm cận đứng
Đþąng thîng x  x đþợc gọi là đþąng tiệm cận đứng (hay tiệm cên đĀng) cûa đồ 0
thð hàm số y  f ( )
x nếu ít nhçt một trong các điều kiện sau đþợc thóa mãn: lim f x ( )  , lim f x
( )  , lim f ( )
x  , lim f ( ) x     x x x x     0 0 x x x x 0 0 ax  b
Lưu ý: VĆi đồ thð hàm phån thĀc däng y 
c  0; ad bc  0 lu n cò tiệm cên cx  d ngang là  a y
và tiệm cên đĀng   d x . c c
KHÂO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ
1. Sơ đồ hâo sát hàm số
Cho hàm số y  f x .
 Tìm tập xác đðnh của hàm số.
 Sự biến thi n  Chiều biến thi n. i. Tính y ' .
ii. Tìm các nghiệm cûa phþĄng trình y '  0 và các điểm täi đò y ' không xác đðnh.
iii. Xét dçu y ' và suy ra các khoâng biến thi n cûa hàm số.
 Tìm căc trð (nếu cò).
 Tìm các giĆi v căc; các giĆi hän täi ,   và täi các điểm mà hàm số kh ng xác đðnh.
 Tìm các đþąng tiệm cên cûa hàm số (nếu cò).  Lêp bâng biến thi n.  Đồ thð.
 Liệt k các điểm đðc biệt ( điểm căc đäi, điểm căc tiểu, tåm đối xĀng,…)
 Xác đðnh giao điểm cûa (C) vĆi Ox, Oy (nếu cò).  Vẽ đồ thð.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 10 |
2. KHÂO SÁT MỘT SỐ HÀM ĐA THỨC VÀ PHÅN THỨC:
a) HÀM SỐ BẬC BA y  ax3  bx2  cx  d a  0 TRƯỜNG HỢP a  0 a  0
Phương trình y/  0 có y y 2 nghiệm ph n iệt 1 1 O x 1 1 O x
Phương trình y/  0 có y y nghiệm kép 1 1 1 O x 1 O x Phương trình / y  0 vô y y nghiệm 1 O 1 1 x 1 O x
b) HÀM SỐ TRÙNG PHƯƠNG y  ax4  bx2  c a  0 TRƯỜNG HỢP a  0 a  0
Phương trình y/  0 có y y 3 nghiệm ph n iệt 1 1 1 1 O O x x
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 11 |
Phương trình y/  0 có y y 1 nghiệm. 1 1 1 O x 1 O x 
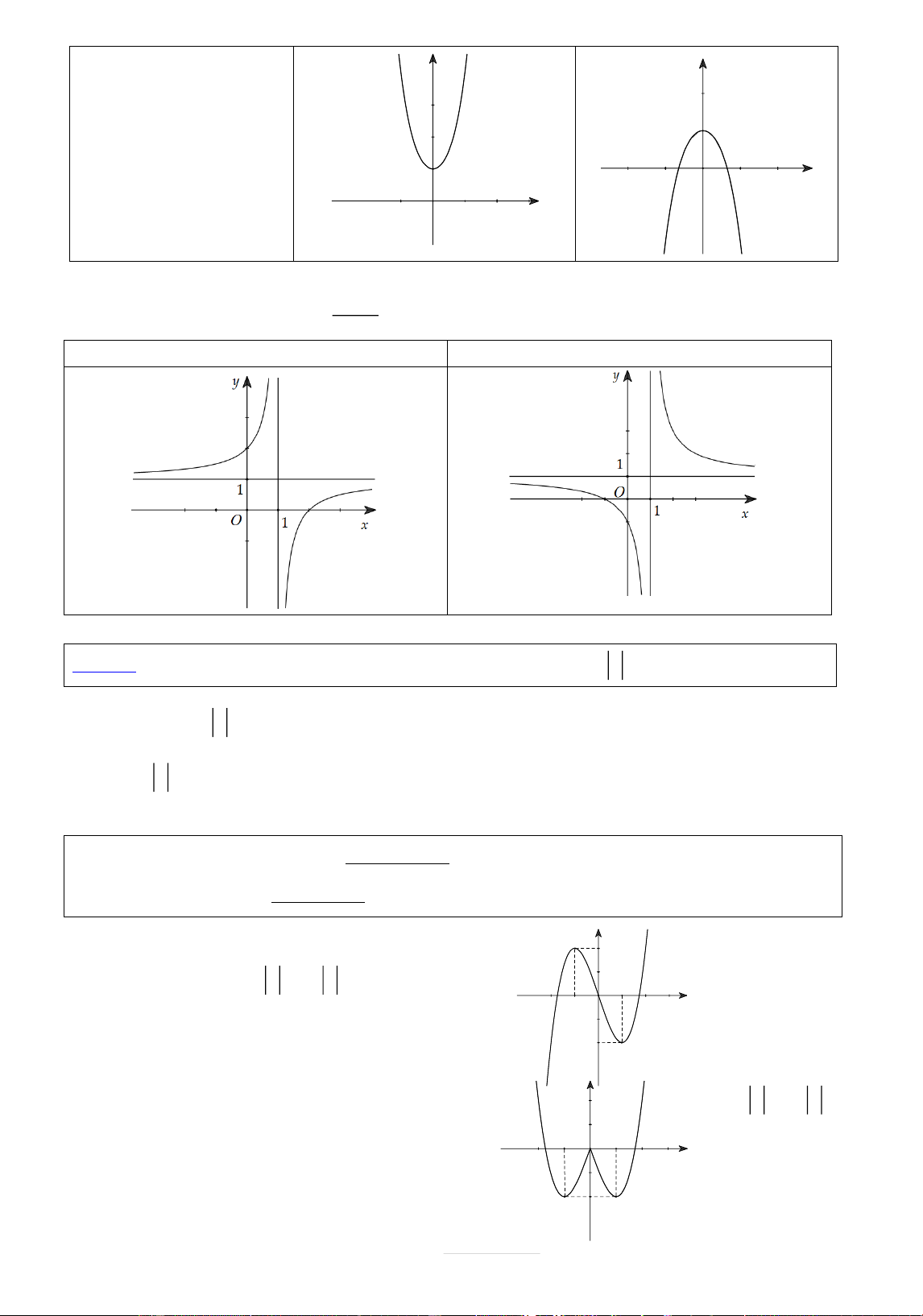
c) HÀM SỐ NHÇT BIẾN ax b y 
c  0, ad  bc  0 cx  d
D  ad  bc  0
D  ad  bc  0
MỘT SỐ PHÉP BIẾN ĐỔI ĐỒ THỊ Däng 1:
Tÿ đồ thð C  : y  f x  suy ra đồ thð C : y  f  x  . f x khi x  0
Ta có y  f  x      f   x   khi x  0
và y  f  x  là hàm chẵn n n đồ thð C nhên Oy làm trýc đối xĀng.
* Cách vẽ C từ C  :
+ Giữ nguyên phæn đồ thð b n phâi Oy cûa đồ thð C  : y  f x  .
+ Bó phæn đồ thð bên trái Oy cûa C  , lçy đối xứng phæn đồ thð được giữ qua Oy.
Ví dụ: Tÿ đồ thð C  y  f x   x3 :  x 3 y 2
C y  x3 :  x 3 suy ra đồ thð  3
C  : y  x  3 x . 1 O
Biến đổi C  : -1 x
+ Bó phæn đồ thð cûa  -2 C  bên trái y
Oy, giĂ nguyên C  bên phâi 3 . Oy
C :y  x  3 x
+ Lçy đối xĀng phæn đồ thð đþợc -1 giĂ qua 1 Oy . O x -2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 12 | Däng 2:
Tÿ đồ thð C  : y  f x  suy ra đồ thð C : y  f x  . f x khi f x  0 Nội dung:
Ta có: y  f x       
f x  khi f x    0
* Cách vẽ C từ C :
+ Giữ nguyên phæn đồ thð phía tr n Ox cûa đồ thð (C):y  f x  .
+ Bó phæn đồ thð phía dþĆi Ox cûa (C), lçy đối xứng phæn đồ thð bð bỏ qua Ox.
Ví dụ: Tÿ đồ thð C y  f x 3 :  x  3x y 2 C 3  
suy ra đồ thð y  x3  x 3 . : y x 3x 1
Biến đổi C : O -1 x
+ Bó phæn đồ thð cûa C  dþĆi -2
Ox, giĂ nguyên C  phía trên . Ox y
+ Lçy đối xĀng phæn đồ thð bð bó
C y  x3 :  x 3 qua Ox . 2 -1 O 1 x
Chú ý vĆi däng: y  f  x  ta læn lþợt biến đổi 2 đồ thð y  f  x  và y  f x 
Ví dụ: Tÿ đồ thð y
C y  f x  x3 :  x 3 suy ra đồ thð  3
C  : y  x  3 x 2 3
y  x  3 x . Biến đổi C  để đþợc đồ thð  3
C  : y  x  3 x . Biến đổi  3
C  : y  x  3 x ta đþợc đồ thð -1 O 1 x  3
C  : y  x  3 x . Däng 3:
Tÿ đồ thð C  : y  u x  v. x  suy ra đồ thð C : y  u x  v. x  . u
 x v. x  f x khi u x  0
Ta có: y  u x  v. x            u 
 x  v. x   f x  khi u x   0
* Cách vẽ C từ C :
+ Giữ nguyên phæn đồ thð tr n miền u x   0 cûa đồ thð C  : y  f x  .
+ Bó phæn đồ thð tr n miền u x   0 cûa C  , lçy đối xứng phæn đồ thð bð bỏ qua Ox.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 13 | Ví dụ
a) Tÿ đồ thð C  y  f x   x3  x2 : 2 3  1 x
b) Tÿ đồ thð C  : y  f x   suy x  1
suy ra đồ thð C y  x   x2 : 1 2  x   1
ra đồ thð   :  x C y x  1 f x khi x 1  x
y  x  1  x2 2
 x       1   khi x  x 1;  
f x  khi x   x  1  1 y    . x  1
 x khi x     ;1  x  1 Đồ thð (C’): Đồ thð (C’):
+ GiĂ nguy n (C) vĆi x  1.
+ Bó phæn đồ thð cûa C  vĆi x  1,
+ Bó (C) vĆi x  1. Lçy đối xứng phần
đồ thð ð ó qua Ox.
giĂ nguy n C  vĆi x  1. y
+ Lçy đối xĀng phæn đồ thð bð bó qua (C') Ox. y 1 O 1 1 x O 1 x (C)
Nhên xét: Trong quá trình thăc hiện phép
Nhên xét: Đối vĆi hàm phån thĀc thì n n
suy đồ thð n n lấy đối xứng các điểm đặc
lấy đối xứng các đường tiệm cận để thăc
iệt cûa (C): giao điểm vĆi Ox, Oy, CĐ, CT… hiện phép suy đồ thð một cách tþĄng đối chính xác. TIẾP TUYẾN
1. Tiếp tuyến : Cho hàm số y  f x , cò đồ thð (C). Tiếp tuyến cûa
đồ thð (C) täi điểm M x ;y   C
( ) cò däng: y  yx .
0  x  x0   y 0 0 0 0
Trong đò: Điểm M x ;y   C
( ) đþợc gọi là tiếp điểm. ( vĆi y  f x ). 0 0  0 0 0
k  f ' x là hệ số góc cûa tiếp tuyến. 0 
2. Điều iện tiếp xúc: Cho hai hàm số C  : y  f x  và C ' : y  g x 
f x   g x 
Đồ thð C  và C  tiếp xúc nhau khi chî khi hệ phþĄng trình:  cò nghiệm. f / x    /  g x  y
TƯƠNG GIAO ĐỒ THỊ y0
Cho hàm số y  f x ( ) cò đồ thð C
( ) và y  g x
( ) cò đồ thð (C ) . 1 2
PhþĄng trình hoành độ giao điểm cûa C ( ) và x (C ) x 1 2 0 O là f x ( )  g x ( )   1 . Khi đò:
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 14 |
 Số giao điểm cûa (C ) và C ( ) bìng vĆi số nghiệm 1 2 cûa phþĄng trình   1 .
 Nghiệm x cûa phþĄng trình 1 chính là 0
hoành độ x cûa giao điểm. 0
 Để tính tung độ y cûa giao điểm, ta thay hoành độ x vào 0 0
y  f x  hoðc y  g x .
 Điểm M x ; y là giao điểm cûa C ( ) và C ( ) . 0 0  1 2
ĐIỂM ĐẶC BIỆT CỦA HỌ ĐƯỜNG CONG
1. Bài toán tìm điểm cố đðnh của họ đường cong
Xét họ đþąng cong C (
) cò phþĄng trình y  f x
( ,m), trong đò f là hàm đa thĀc theo m
biến x vĆi m là tham số sao cho bêc cûa m không quá 2. Tìm nhĂng điểm cố đðnh thuộc họ
đþąng cong khi m thay đổi?
 Phương pháp giâi:
+ Bước 1: Đþa phþĄng trình y  f (x, )
m về däng phþĄng trình
theo èn m cò däng sau: Am  B  0 hoðc Am2  Bm C  0 .
+ Bước 2: Cho các hệ số bìng 0 , ta thu đþợc hệ phþĄng trình và giâi hệ phþĄng trình: A   0 A  0   hoðc B  0 . B   0 C   0
+ Bước 3: Kết luên:
- Nếu hệ v nghiệm thì họ đþąng cong C (
) kh ng cò điểm cố đðnh. m
- Nếu hệ cò nghiệm thì nghiệm đò là điểm cố đðnh cûa C ( ). m
2. Bài toán tìm điểm cò tọa độ nguy n: Cho đþąng cong C
( ) cò phþĄng trình y  f x
( ) (hàm phån thĀc). Hãy tìm nhĂng điểm
cò tọa độ nguy n cûa đþąng cong?
Những điểm cò tọa độ nguyên là những điểm sao cho câ hoành độ và tung độ của
điểm đò đều là số nguyên.
 Phương pháp giâi:
+ Bước 1: Thăc hiện phép chia đa thĀc chia tā số cho méu số.
+ Bước 2: Lêp luên để giâi bài toán.
3. Bài toán tìm điểm cò tính chçt đối xứng:
Cho đþąng cong (C) cò phþĄng trìnhy  f x
( ). Tìm nhĂng điểm đối xĀng nhau qua một điểm, qua đþąng thîng.
Bài toán 1: Cho đồ thð C  y  Ax3  Bx2 :
Cx  D trên đồ thð C  tìm những cặp điểm
đối xứng nhau qua điểmI x ( ,y ) . I I
 Phương pháp giâi:
+ Gọi M a Aa3  Ba2 Ca  D N b Ab3  Bb2 ; , ;
Cb  D là hai điểm tr n C  đối
xĀng nhau qua điểm I .
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 15 |
a  b  x 2 + Ta có  I . A a3 (
 b3)  B a2 b2 C a b  D 2   y 2 I
Giâi hệ phþĄng trình tìm đþợc a,b tÿ đò tìm đþợc toä độ M, N.
Trường hợp đặc biệt : Cho đồ thð C  y  Ax3  Bx2 :
Cx  D . Trên đồ thð C  tìm
những cặp điểm đối xứng nhau qua gốc tọa độ.
 Phương pháp giâi:
 Gọi M a Aa3  Ba2 Ca  D N b Ab3  Bb2 , , ,
Cb  D là hai điểm tr n C
đối xĀng nhau qua gốc tọa độ. a  b   0  Ta có  . A a3 (
 b3)  B a2  b2  C a b  D 2   0
 Giâi hệ phþĄng trình tìm đþợca,b tÿ đò tìm đþợc toä độ M,N .
Bài toán 3: Cho đồ thð C  y  Ax3  Bx2 :
Cx  D trên đồ thð C  tìm những cặp điểm
đối xứng nhau qua đường thẳng d : y  Ax  B . 1 1
 Phương pháp giâi:  Gọi M 3 2
a Aa  Ba  Ca  D N  3 2 ; , ;
b Ab  Bb  Cb  D là hai điểm tr n C đối
xĀng nhau qua đþąng thîng d . I   d (1)  Ta có: 
(vĆi I là trung điểm cûa MN và u là vectĄ chî phþĄng MN u d .   d 0 (2)
cûa đþąng thîng d ). Giâi hệ phþĄng trình tìm đþợc M, N.
4. Bài toán tìm điểm đặc biệt, hoâng cách  Lý thuyết: 2 2
+ Cho hai điểm Ax ;y ;B x ;y  AB  x  x 2
1   y  y 2 1  1 1 2 2 
Cho điểm M x ;y và đþąng thîng d : Ax By C  0 , thì khoâng cách tÿ M đến d là 0 0 
 ;  Ax  By C h M d  0 0 . A2  B2 ax  b
+ Cho hàm phån thĀc: y 
tiếp tuyến täi M cít TCĐ, TCN ć A và B thì M là trung cx  d điểm cûa AB. 2
Diện tích tam giác IAB kh ng đổi: S  ad  bc . IAB c2 
Các bài toán thường gặp: ax  b
Bài toán 1: Cho hàm số y 
c  0, ad bc  0 cò đồ thð C. Hãy tìm trên C() cx  d
hai điểm A và B thuộc hai nhánh đồ thð hàm số sao cho khoâng cách AB ngắn nhất.
 Phương pháp giâi:
+ C  cò tiệm cên đĀng   d x
do tính chçt cûa hàm phån thĀc, đồ thð nìm về hai phía c
cûa tiệm cên đĀng. N n gọi hai số ,  là hai số dþĄng.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 16 | d d d 
Nếu A thuộc nhánh trái: x    x       ; y  f x ( ) . A A c c c A A d d d 
Nếu B thuộc nhánh phâi: x    x       ; y  f x ( ) . B B c c c B B 2 2 2 2 
Sau đò tính: AB2  x  x y y a a y y . B A     B A 
               B A  
Áp dýng bçt đîng thĀc Cauchy sẽ tìm ra kết quâ.
Bài toán 2: Cho đồ thð hàm số C  cò phương trình y  f x
( ). Tìm tọa độ điểm M
thuộc (C) để tổng khoâng cách từ M đến hai trục tọa độ nhó nhất.
 Phương pháp giâi:
 Gọi M x;yvà tổng khoâng cách tÿ M đến hai trýc tọa độ là d thì d  x  y .
 Xét các khoâng cách tÿ M đến hai trýc tọa độ khi M nìm ć các vð trí đðc biệt:
Tr n trýc hoành, tr n trýc tung.
 Sau đò xét tổng quát, nhĂng điểm M cò hoành độ, hoðc tung độ lĆn hĄn hoành độ
hoðc tung độ cûa M khi nìm tr n hai trýc thì loäi đi kh ng xét đến.
 NhĂng điểm cñn läi ta đþa về tìm giá trð nhó nhçt cûa đồ thi hàm số dăa vào đäo
hàm rồi tìm đþợc giá trð nhó nhçt cûa d .
Bài toán 3: Cho đồ thð C
( ) cò phương trình y  f ( )
x . Tìm điểm M trên C ( ) sao cho
khoâng cách từ M đến Ox ằng k lần khoâng cách từ M đến trụcOy .
 Phương pháp giâi: y  kx
f x  kx
Theo đæu bài ta cò y  k x     . y    kx  
f x   kx Bài toán 4: Cho đồ thð hàm số C ( ) cò phương trình ax  b
y  f (x) 
c  0, adbc  0. Tìm tọa độ điểm M trên (C) sao cho độ dài MI ngắn cx  d
nhất (với I là giao điểm hai tiệm cận).
 Phương pháp giâi:  
Tiệm cên đĀng  d x
; tiệm cên ngang  a y . c c  d a  
Ta tìm đþợc tọa độ giao điểm I  ;  cûa hai tiệm cên.  c c   2 2 2 d   a  
Gọi M x ;y là điểm cæn tìm. Khi đò: IM  x  y g x M     M    M  M M   c   c  
Sā dýng phþĄng pháp tìm GTLN - GTNN cho hàm số g để thu đþợc kết quâ.
Bài toán 5: Cho đồ thð hàm số C
( ) cò phương trình y  f x
( ) và đường thẳng
d : Ax  By C  0 . Tìm điểm I trên C
( ) sao cho khoâng cách từ I đến d là ngắn nhất.
 Phương pháp giâi:
 Gọi I thuộc C
( )  I x ;y ; y  f x ( ) . 0 0 0 0 Ax By C  0 0
Khoâng cách tÿ I đến d là g x ( ) h ; 0 I d     A2  B2
 Khâo sát hàm số y  g x
( ) để tìm ra điểm I thóa mãn y u cæu.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 17 |
PHÆN II. MŨ VÀ LOGARIT
LŨY THỪA VÀ HÀM SỐ LŨY THỪA.
1. KHÁI NIỆM LŨY THỪA.
 Lũy thừa với số mũ nguyên.
Cho n là một số nguy n dþĄng.
VĆi a là số thăc tùy ý, lüy thÿa bêc n cûa a là tích cûa n thÿa số a . n a  a a . .... a .. ( n thÿa số). n VĆi a  0. 1 0  a  n 1 a  n a
Ta gọi a là cĄ số, m là mü số. Và chú ý 0
0 và 0n kh ng cò nghïa.
+ Một số tính chất của lũy thừa
 Giâ thuyết rìng mỗi biểu thĀc đþợc xét đều cò nghïa:      a
a  a  a ;    a ;     a  a . ( ) ;    a
( b)  a b ;  a      a  a a   b     ;         b  b  b  a 
 Nếu a  1 thì  
a  a     ;
Nếu 0  a  1 thì  
a  a     .
 VĆi mọi 0  a  b , ta có: m  m a b  m  0 ; m  m a b  m  0  Chú ý:
+ Các tính chçt tr n đúng trong trþąng hợp số mü nguy n hoðc kh ng nguy n.
+ Khi xét lüy thÿa vĆi số mü 0 và số mü nguy n åm thì cĄ số a phâi khác 0 .
+ Khi xét lüy thÿa vĆi số mü kh ng nguy n thì cĄ số a phâi dþĄng.
 Phương trình n x  b.
Ta có kết quâ biện luên số nghiệm cûa phþĄng trình n
x  b nhþ sau:  Trþąng hợp n lẻ:
VĆi mọi số thăc b , phþĄng trình cò nghiệm duy nhçt.  Trþąng hợp n chïn:
+ Với b  0 , phþĄng trình v nghiệm.
+ Với b  0 , phþĄng trình cò một nghiệm x  0.
+ Với b  0 , phþĄng trình cò hai nghiệm trái dçu, kí hiệu giá trð dþĄng là n b , còn
giá trð âm là n b .
Một số tính chçt của căn bậc n VĆi a b   * , ;n , ta có: n 2 n 2 n 2 1 n 2 1 + a  a  a ; + a  aa . n 2 n 2 n 2 n 2 1 2n1 2n1 + ab   a  
b ,ab  0 ; + ab  a  ba b , . a 2  n a n 2  a 1 a + n 2 
,ab  0,b  0 ; + n 2 1 
a,b  0 . b 2  n b 2n  b 1 b
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 18 | m n m n +
a   a  ,a  0 , n nguy n dþĄng, m nguyên. n m nm + a 
a,a  0 , n , m nguy n dþĄng. p q n p m q + Nếu 
thì a  a ,a  0,m,n nguy n dþĄng p,q nguyên. n m Đðc biệt: n   m n m a a . 2. HÀM SỐ LŨY THỪA.
 Khái niệm. Xét hàm số 
y  x , vĆi  là số thăc cho trþĆc. Hàm số 
y  x , vĆi   , đþợc gọi là hàm số lüy thÿa. Chú ý.
Têp xác đðnh cûa hàm số lüy thÿa 
y  x tùy thuộc vào giá trð cûa  . Cý thể.
 VĆi  nguy n dþĄng, têp xác đðnh là .
 VĆi  nguyên âm hoðc bìng 0 , têp xác đðnh là  \  0 .
 VĆi  không nguyên, têp xác đðnh 0; .
 Khảo sát hàm số lũy thừa.
 Têp xác đðnh cûa hàm số lüy thÿa 
y  x luôn chĀa khoâng 0;
vĆi mọi   . Trong trþąng hợp tổng quát, ta khâo sát hàm số 
y  x trên khoâng này. 
y  x ,  0. 
y  x ,  0.
1. Têp xác đðnh: 0;.
1. Têp xác đðnh: 0;. 2. Să biến thiên 2. Să biến thiên  y    x 1 ' .  0 x  0.  y    x 1 ' .  0 x  0. GiĆi hän đðc biệt: GiĆi hän đðc biệt:  
lim x  0, lim x  .
lim x   , lim x  0.  x 0 x   x 0  x Tiệm cên: không có. Tiệm cên: 3. Bâng biến thiên. Ox là tiệm cên ngang. x 0  Oy là tiệm cên đĀng. y’  3. Bâng biến thiên. y x 0   y’  y  0 0
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 19 |
Đồ thð của hàm số.
Đồ thð cûa hàm số lüy thÿa y x 
lu n đi qua điểm I 1;1.
 Khâo sát hàm số mü x y  a ,
a  0,a  1.  x y a ,a   1 x
y  a ,a   1
1. Têp xác đðnh: .
1. Têp xác đðnh: . 2. Să biến thiên. 2. Să biến thiên. ' x
y  a ln a  0, . x '  x y
a lna  0,x GiĆi hän đðc biệt: GiĆi hän đðc biệt: x lim a  0, lim a  . x lim a   x , lim a  0. x  x  x  x  Tiệm cên: Tiệm cên:
Ox là tiệm cên ngang.
Ox là tiệm cên ngang.
3. Bâng biến thiên. 3. Bâng biến thiên.  0 1  0 1 x  x 
y '    y '    a  1
y  y 1 a 0 0 Đồ thð nhþ hình sau. Đồ thð nhþ hình sau.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 20 |
LOGARIT VÀ HÀM SỐ LOGARIT
1. KHÁI NIỆM –TÍNH CHÇT VÀ QUY TẮT TÍNH LOGARIT.
 Khái niệm Logarit.
Cho hai số dþĄng a,b vĆi a  1. Số  thóa mãn đîng thĀc 
a  b đþợc gọi là logarit cĄ số
a cûa b và đþợc kí hiệu là log b . a      log b a . b a
Không cò logarit của số m và số 0.
Bâng tóm tắt công thức Mũ-loarrit thường gặp:
 a0  1,a  0.
 log 1  0,0  a  1 a  1
 a  a
 log a  1,0  a  1 a    1
 log a  ,0  a  1 a   a    a 1   log     a ,0 a 1 a  a      a     
 log b  .log b, a b  a  a a  , 0, 1 a  1       log b  .log b
a .b  a  a  a   
 a .b  a b.    log   b .log b a a     a    a
 log b  log c  log bc    ,  a a a    b 0    b b  b  
 log b  log c  log a a a       c
a   a    * ,    1      log b  .
a   a  a log a b
 a  b    log b a
2. BÇT PHƯƠNG TRÌNH MŨ VÀ LOGARIT.
 Bất phương trình mũ cơ bản.
Bçt phþĄng trình mü cĄ bân có däng x
a  b (hoðc x  , x  , x a b a
b a  b ) vĆi a  0,a  1.
Ta xét bçt phþĄng trình cò däng x a  b.  x
Nếu b  0, têp nghiệm cûa bçt phþĄng trình là
, vì a  b,x  . .  x b
Nếu b  0 thì bçt phþĄng trình tþĄng đþĄng vĆi a  a alog .
VĆi a  1, nghiệm cûa bçt phþĄng trình là x  log b. a
VĆi 0  a  1, nghiệm cûa bçt phþĄng trình là x  log b. a
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 21 |
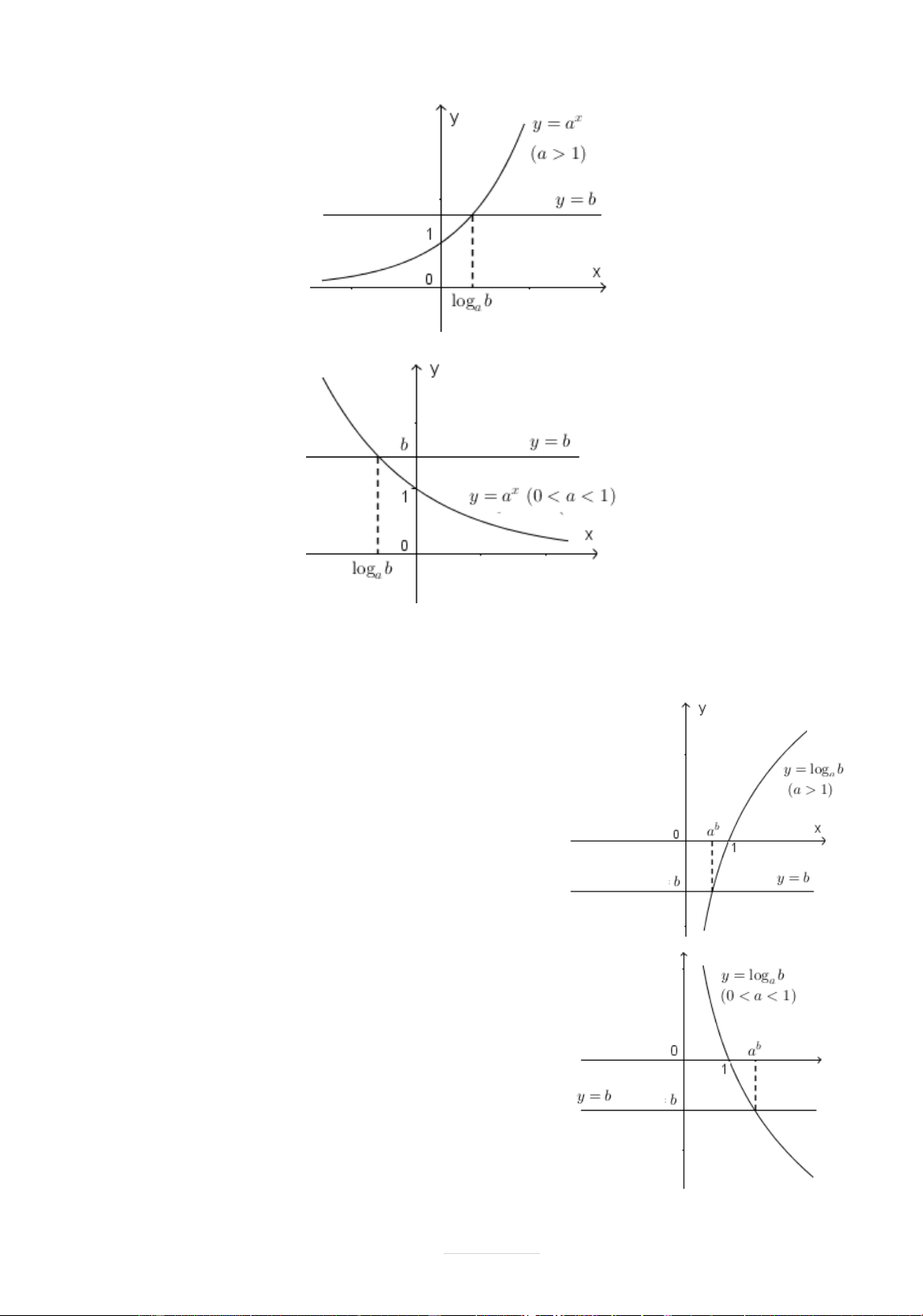
Ta minh họa bìng đồ thð sau:
 VĆi a  1, ta cò đồ thð
 VĆi 0  a  1, ta cò đồ thð
 Bất phương trình logarit cơ bản.
Bçt phþĄng trình logarit cĄ bân có däng log x  b (hoðc log x  , b log x  ,
b log x  b ) a a a a
vĆi a  0,a  1.
Xét bçt phþĄng trình log x  b. a
 Trþąng hợp a  1, ta có: log x  b  x  b a . a
 Trþąng hợp 0  a  1, ta có: log x  b  0 b  x  a . a
Ta minh họa bìng đồ thð nhþ sau.
 VĆi a  1, ta cò đồ thð sau.
 VĆi 0  a  1, ta cò đồ thð sau.
Quan sát đồ thð, ta thçy rìng:
 Trþąng hợp a  1: log x  b a khi và chî khi  b x a .
 Trþąng hợp 0  a  1:
log x  b khi và chî khi 0   b x a . a
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 22 |
BÀI TOÁN LÃI SUÇT NGÅN HÀNG
1. Lãi đơn: là số tiền lãi chî tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền
gốc sinh ra, tĀc là tiền lãi cûa kì hän trþĆc kh ng đþợc tính vào vốn để tính lãi cho kì hän
kế tiếp, cho dù đến kì hän ngþąi gāi kh ng đến gāi tiền ra.
a) C ng thức tính: Khách hàng gāi vào ngån hàng A đồng vĆi lãi đĄn r% /kì hän thì số
tiền khách hàng nhên đþợc câ vốn lén lãi sau n kì hän ( n  * ) là:
S  A  nAr  A 1  nr n  
2. Lãi kép: tiền lãi cûa kì hän trþĆc nếu ngþąi gāi kh ng rút ra thì đþợc tính vào vốn để tính lãi cho kì hän sau.
a) C ng thức tính: Khách hàng gāi vào ngån hàng A đồng vĆi lãi kép r% /kì hän thì số
tiền khách hàng nhên đþợc câ vốn lén lãi sau n kì hän ( n  * ) là:  S  n n  log  
1r   A    S
S  A1  r n n n r%   1  n A S n A  1 rn
3. Tiền gửi hàng tháng: Mỗi tháng gāi đúng cùng một số tiền vào 1 thąi gian cố đðnh.
a) C ng thức tính: Đæu mỗi tháng khách hàng gāi vào ngån hàng số tiền A đồng vĆi lãi
kép r% /tháng thì số tiền khách hàng nhên đþợc câ vốn lén lãi sau n tháng ( n  * ) (
nhên tiền cuối tháng, khi ngån hàng đã tính lãi) là S . n  S r.  n n  log     1 1r   A n  1  r    A  S  1 r 1    1  r n     r   S r . n A 
1 r1 rn 1       
4. Gửi ngån hàng và rút tiền gửi hàng tháng:
a) C ng thức tính: Gāi ngån hàng số tiền là A đồng vĆi lãi suçt r% /tháng. Mỗi tháng vào
ngày ngån hàng tính lãi, rút ra số tiền là X đồng. Tính số tiền cñn läi sau n tháng là bao nhiêu? n   r 1   1 X  A
 1  r   S
S  A1  r   rn n  X n  n   n 1 r r   1
5. Vay vốn trâ gòp: Vay ngån hàng số tiền là A đồng vĆi lãi suçt r% /tháng. Sau đúng một
tháng kể tÿ ngày vay, bít đæu hoàn nợ; hai læn hoàn nợ cách nhau đúng một tháng, mỗi
hoàn nợ số tiền là X đồng và trâ hết tiền nợ sau đúng n tháng.
a) C ng thức tính: Cách tính số tiền cñn läi sau n tháng giống hoàn toàn c ng thĀc tính
gāi ngån hàng và rút tiền hàng tháng n n ta cò
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 23 | 1  r  1
S  A1  r   n n  X n r
Để sau đúng n tháng trâ hết nợ thì S  0 nên n 1   1 1   n n r A r  X  0 r
A1  r n r. X 
1 rn 1
6. Bài toán tăng lương: Một ngþąi đþợc lãnh lþĄng khći điểm là A đồng/tháng. CĀ sau n
tháng thì lþĄng ngþąi đò đþợc tëng th m r% /tháng. Hói sau kn tháng ngþąi đò lïnh đþợc
tçt câ là bao nhiêu tiền?
1 rk 1
C ng thức tính: Tổng số tiền nhên đþợc sau kn tháng là S  Ak kn r
7. Bài toán tăng trưởng dån số:
C ng thĀc tính tëng trþćng dån số  X
X 1 r m n , m,n     ,m  n m n   Trong đò:
r % là tî lệ tëng dån số tÿ nëm n đến nëm m
X dån số nëm m m
X dån số nëm n n X
Tÿ đò ta cò c ng thĀc tính tî lệ tëng dån số là m r%  m n   1 Xn
8. Lãi ép li n tục:
Gāi vào ngån hàng A đồng vĆi lãi kép r% /nëm thì số tiền nhên đþợc câ vốn lén lãi sau n nëm n * 
 là: S  A1rn . Giâ sā ta chia mỗi nëm thành m kì hän để tính n r
lãi và lãi suçt mỗi kì hän là
% thì số tiền thu đþợc sau n nëm là: m m n .  r  S  A1   n m  
Khi tëng số kì hän cûa mỗi nëm l n v căc, tĀc là m   , gọi là hình thĀc lãi kép ti n
týc thì ngþąi ta chĀng minh đþợc số tiền nhên đþợc câ gốc lén lãi là: n r S Ae . 
( c ng thĀc tëng trþćng mü)
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 24 | PHÆN III.
NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN I. NGUYÊN HÀM 1. Nguyên hàm
Đðnh nghïa: Cho hàm số f x  xác đðnh tr n K (K là khoâng, đoän hay nāa khoâng).
Hàm số F x  đþợc gọi là nguy n hàm cûa hàm số f x  trên K nếu F 'x   f x  vĆi mọi
x  K . Kí hiệu:        f x dx F x C . Đðnh lí:
1) Nếu F x  là một nguy n hàm cûa f x  trên K thì vĆi mỗi hìng số C , hàm số
G x   F x  C cüng là một nguy n hàm cûa f x  trên K .
2) Nếu F x  là một nguy n hàm cûa hàm số f x  trên K thì mọi nguy n hàm cûa
f x  trên K đều cò däng F x  C , vĆi C là một hìng số.
Do đò F x  C C
,  là họ tçt câ các nguy n hàm cûa f x  trên K .
2. Tính chçt của nguy n hàm         f x dx f x  và '      
 f x dx f x C ; d  f x dx   f x dx
 Nếu F(x) cò đäo hàm thì: d F x (  )  F x ( )  C
 kf x dx  
k  f xdx vĆi k là hìng số khác 0 .  
 f x  g xdx   f xdx   
g xdx
 Công thức đổi biến số: Cho y  f u và u  g x . Nếu ( )  ( ) 
 f x dx F x C thì  f g x( )g x '( d ) x  f u ( d ) u  F u ( )  C 
3. Sự tồn täi của nguy n hàm
Đðnh lí: Mọi hàm số f x  li n týc tr n K đều cò nguy n hàm trên K .
Bâng nguy n hàm các hàm số thường gặp 1. 0   dx C 2.   dx x C  1 3.  1    1  x dx x C     1  1      16.    1 dx   ax b ax b    c,  1 a    1  4. 1 2 3   1   dx C 17. 3   x2 x  x x x dx x 5. 1  dx 1 ln   dx x C 18.  ln    ax b c x ax  b a 6.    x x e dx e C 19.  1     ax b ax b e dx e C a x kx b 7. a 1 a x a dx    C 20. kxb a dx    C lna k lna
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 25 | 8. cos  sin   xdx x C 21.     1 cos sin      ax b dx ax b C a
9. sinxdx  cosx C  22.      1 sin cos      ax b dx ax b C a
10. tan .  ln | cos |   x dx x C 23.  1
tan ax  b dx   ln cos ax  b  c  a 11. cot .  ln | sin |   x dx x C 24.     1 cotg dx ln sin      ax b ax b c a 12. 1  1 1 tan   dx x C 25.  tan    dx ax b C 2 cos x 2
cos ax  b   a 13. 1   1 1 cot   dx x C 26.   cot    dx ax b C 2 sin x 2
sin ax  b   a 14.   2 1 tan   tan   x dx x C 27. 1  1 2 tan     tan      ax b dx ax b C a 15.   2 1 cot    t   x dx co x C 28. 1  1 2 cot      t     ax b dx co ax b C a
Bâng nguy n hàm mở rộng dx  1 arctg   x c   2  2 arcsin dx arcsin   x x x a x c a2  x2 a a a a dx 1   ln   a x c   2  2 arccos dx arccos   x x x a x c a2  x2 a 2 a  x a a dx  ln   2  2    x x a c x x a  x  a2  x2 arctan dx arctan ln   c  x2  a2 a a 2 dx  arcsin   x c x x a  x  a2  x2 arc cot dx arc cot ln   c  a2  x2 a a a 2 dx  1 dx 1  arccos   x c  ln tg   ax b c 2  2 a a x x a
sin ax  b a 2 dx 1  2  2    dx 1 ax b ln   a x a c  ln tan  c  2  2 a x x x a
sin ax  b a 2 ax
e a cosbx b sinbx ax   ln      dx   b ax b x  ln  
ax  b  x  c e cosbx dx    c  a  a2  b2 2 2  2 2 2  dx   arcsin   x a x a x a x c ax
e a sinbx b cosbx ax   2 2 a e sinbx dx    c a2  2 b
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 26 |
CÁC PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
1. PHƯƠNG PHÁP ĐỔI BIẾN a. Đổi biến däng 1: Nếu : ( )  ( ) 
 f x F x C và vĆi u   tlà hàm số cò đäo hàm thì : ( )  ( )   f u du F u C PHƯƠNG PHÁP CHUNG
 BþĆc 1: Chọn x   t , trong đò  t là hàm số mà ta chọn thích hợp .
 BþĆc 2: Lçy vi phån hai vế : dx   ' tdt
 BþĆc 3: Biến đổi : f x ( d ) x  f 
 t 'tdt   
g tdt
 BþĆc 4: Khi đò tính : f x ( d ) x  g t ( d ) t  G t ( )    C .
* Các dçu hiệu đổi biến thường gặp : Dçu hiệu Cách chọn    
Đðt x  a sint ; vĆi t   
; . hoðc x  a cost ; vĆi a2  x2  2 2  t  0;   . a     a Đðt x  .; vĆi t    ;  \   0 hoðc x  sint  2 2  cost x2  a2  
vĆi t  0;  \     .  2      a2  x2
Đðt x  a tant ; vĆi t   ; . hoðc x  a cott vĆi t  0; .  2 2  a  x a  x . hoðc
. Đðt x  acos t 2 a  x a  x
x ab x
Đðt x  a  b ( a s ) in t 2 – 1    
Đðt x  atant ; vĆi t   ; . a2  x2  2 2 
b. Đổi biến däng 2:
Nếu hàm số f(x) li n týc thì đðt x   t . Trong đò  t cùng vĆi đäo hàm cûa nò
( ' t là nhĂng hàm số li n týc) thì ta đþợc : f x ( d ) x  f    
t'tdt  g t( d)t G t()    C .
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 27 | PHƯƠNG PHÁP CHUNG. 
BþĆc 1: Chọn t= x . Trong đò  x  là hàm số mà ta chọn thích hợp . 
BþĆc 2: Tính vi phån hai vế : dt   ' tdt . 
BþĆc 3: Biểu thð : f x ( d ) x  f 
 t 'tdt    g t ( d ) t . 
BþĆc 4: Khi đò : I  f x ( d ) x  g t ( d ) t  G t ( )    C
* Các dçu hiệu đổi biến thường gặp : Dçu hiệu Cách chọn Hàm số méu số cò t là méu số
Hàm số : f x;  x
t   x  .s x  x 
Hàm    a inx+b.cosx f x
t  tan ;cos  0 c  .sinx+d.cosx+e 2  2  1
VĆi : x  a  0 và x  b  0 .
Hàm f x   
x  a x  b 
Đðt : t  x  a  x  b
VĆi x  a  0 và x  b  0 .
Đðt : t  x  a  x  b
2. NGUYÊN HÀM TỪNG PHÆN
Nếu u(x) , v(x) là hai hàm số cò đäo hàm li n týc tr n K: u x ( ) v . x '( d ) x  u x ( ) v . x ( )  
v x()u. x '( d ) x
Hay udv  uv  
vdu ( vĆi du  u’xdx, d v  v’xdx ) PHƯƠNG PHÁP CHUNG
 BþĆc 1: Ta biến đổi tích phån ban đæu về däng : I  f x ( d ) x  
 f x() f. x( d)x 1 2 u  f x ( ) du  ' ( ) 1  f x dx  1 BþĆc 2: Đðt :    dv  f x ( ) v   ( ) 2   f x dx 2
 BþĆc 3: Khi đò : u d . v  u v .   vd.u sinx   
Däng I: I  P x()cosx dx .  x  e  u  P x ( ) u ' du .  P ' x ( dx )    cosx   cosx  sinx      cosx      Đðt         
Vêy I = P(x) sin x  -  sinx  P . ' x ( dx ) dv   cosx  dx . v   sin x   x   x    e e x  e   x  e          
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 28 |
Däng II: I  P x().lnxdx u  lnx   1 du  dx 1 Đðt    x
Vêy I = lnx.Q(x) - Q x(). dx  x dv  v  P x ( dx )  Q x ( )  P x ( dx )   sinx  Däng III   I   xe  dx cosx    x u e   x du e dx    cosx cosx x   Đðt    sin x       
 cos x  Vêy I = e   -    x e dx dv     dx . v     sinx  sinx   cos x sin x         cosx
Bìng phþĄng pháp tþĄng tă ta tính đþợc     x
e dx sau đò thay vào I sinx  TÍCH PHÂN
1. C ng thức tính tích phân b f x ( d ) x  b F x ( )  F b ( )   F a ( ) . a a b b
* Nhận xét: Tích phån cûa hàm số f tÿ a đến b cò thể kí hiệu bći  f x( dx ) hay  f t( dt ) . Tích a a
phån đò chî phý thuộc vào f và các cên a, b mà không phý thuộc vào cách ghi biến số.
2. Tính chçt của tích phån
Giâ sā cho hai hàm số f(x) và g(x) li n týc tr n K , a,b,c là ba số bçt kỳ thuộc K. Khi đò ta cò : a 1. f x ( dx )   0 a b a 2. f x ( d ) x   
 f x( d)x . a b b c b 3. f x ( d ) x  f x ( d ) x   
 f x( d)x a a c b b b 4. f x ( )  g x (  ) dx  f x ( d ) x     
g x( d)x . a a a b b 5. kf x ( d ) x   k . f x ( d ) x . a a b 6. Nếu f(x)  
0 x  a;b   thì : f x ( d ) x  
0 x  a;b    a b b 7. Nếu x   a  ;b : f x ( )  g x ( )  f x ( d ) x  g x ( d ) x    
. (Bçt đîng thĀc trong tích phån ) a a b
8. Nếu x  a;b 
 Nếu M  f x
( )  N thì M b  a  f x ( d
) x  N b   a . a
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 29 |
PHƯƠNG PHÁP TÍNH TÍCH PHÅN I. ĐỔI BIẾN
a. Phương pháp đổi biến số däng 1.
Đðnh lí . Nếu 1) Hàm x  u t
( ) cò đäo hàm li n týc tr n đoän   ;     , 2) Hàm hợp f u ( t
( )) đþợc xác đðnh tr n   ;     , 3) u 
( )  a, u()  b , b 
Khi đò: I  f x dx    f u t u' ( ) ( ( )) t ( d ) t . a  PHƯƠNG PHÁP CHUNG
 Bước 1: Đðt x  u t x  b t  
 Bước 2: Tính vi phån hai vế : x  u t
( )  dx  u t '( d ) t Đổi cên:  x  a t  
 Bước 3: Chuyển tích phån đã cho sang tích phån theo biến t b    Vêy: I  f x ( d
) x  f u t (  ) u t '( d ) t     
g t( d)t G t() G() G   ( ) a  
b. Phương ph p đổi biến dạng 2
Đðnh lí: Nếu hàm số u  u x
( )đĄn điệu và cò đäo hàm li n týc tr n đoän a;b   sao cho b u b ( ) f x ( d
) x  g u x (  ) u x '( d ) x  g u ( d
) u thì: I  f x ( d ) x  
 g u( d)u . a u a ( ) PHƯƠNG PHÁP CHUNG  '
Bước 1: Đðt u  u x
( )  du  u x ( d ) x x  b u  u b ( )
 Bước 2: Đổi cên :  x  a u  u a ( )
 Bước 3: Chuyển tích phån đã cho sang tích phån theo biến u b b u b ( ) Vêy: I  f x ( d
) x  g u x (  ) u . x '( d ) x     
 g u( d)u a a u a ( )
II. TÍCH PHÅN TỪNG PHÆN
Đðnh lí . Nếu u(x) và v(x) là các hàm số cò đäo hàm li n týc tr n a;b   thì: b b b b b b
u x v' x dx  u x v x    v x u' ( ) ( ) ( ) ( ) ( ) x ( d
) x Hay udv  uv vdu a a a a a a PHƯƠNG PHÁP CHUNG
 Bước 1: Viết f(x)dx dþĆi däng udv  uv d
' x bìng cách chọn một phæn thích hợp
cûa f(x) làm u(x) và phæn cñn läi dv  v x '( d ) x
 Bước 2: Tính du  u 'dx và v  dv  v x '( d ) x b b
 Bước 3: Tính vu ' x ( dx ) và uv a a
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 30 |
*Cách đặt u và dv trong phương pháp tích phån từng phæn.
Đðt u theo thĀ tă þu b b b b x x tiên:
P x( e) dx P x()lnxdx P x()cosxdx e cosxdx
Lốc-đa-mũ-lượng a a a a u P(x) lnx P(x) x e dv x e dx P(x)dx cosxdx cosxdx
Chú ý: N n chọn u là phæn cûa f(x) mà khi lçy đäo hàm thì đĄn giân, chọn dv  v d ' x là phæn
cûa f(x)dx là vi phån một hàm số đã biết hoðc cò nguy n hàm dễ tìm.
TÍCH PHÂN CÁC HÀM SỐ SƠ CÇP CƠ BÂN
1. Tích phân hàm hữu tî    dx 1 adx 1 Däng 1: I =   ln ax    b . (vĆi a≠0) ax  b a ax  b a      dx 1 1 Chú ý: Nếu I =   1   a
( x  b) a . dx  . a ( x    k k b) k  a ( x  b) a a(1  k)    Däng 2:   dx I
0 (ax2  bx  c  0 vĆi mọi x    ;   ) 2 a   ax  bx     c
Xét   b2  a 4 c . b   b  
+ Nếu  > 0: x  ;x  1 a 2 2 a 2 1 1 1  1 1       thì : 2  
ax  bx  c a x (  x ) x (  x ) a x
(  x ) x  x x  1 2 1 2  x 1 2   1  1 1  1 1   1    x x I   dx 
ln x  x  ln x  x      ln 1 2  a x (  x ) x  x x  x a x (  x )  a x (  x ) x  x  1 2   1 2  1 2 1 2 2 1 1  b  + Nếu  = 0:  2 2 x  0 
ax  bx  c a x (  x ) 2 0  a    dx 1 dx 1 thì I =      2  2 
ax  bx  c a x (  x ) a x (  x )   0 0   dx dx
+ Nếu   0thì I    2 
ax  bx  c  2 2     b       a x       a  a2 2 4          b  1  Đðt x   tant  dx  1 tan 2 2   2 t dt a 2 a 4 2 a  
Däng 3:   mx n I dx, 0 . 2 a   ax  bx   c mx  n (trong đò f x ( )  li n týc tr n đoän   ;   )
ax2  bx  c  
+) Bìng phþĄng pháp đồng nhçt hệ số, ta tìm A và B sao cho:
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 31 | mx  n A a
( x2  bx  c)' B A( a 2 x  b) B    
ax2  bx  c
ax2  bx  c
ax2  bx  c
ax2  bx  c
ax2  bx  c    mx  n A( a 2 x  b) B +)Ta có I=  dx  dx  2  2  dx
ax  bx  c
ax  bx  c ax2  bx     c  (2  ) 
. Tích phân  A ax b dx = A ax2 ln  bx  c ax2  bx    c  Tích phân  dx thuộc däng 2. ax2  bx   c b P x ( )
Tính tích phân I  
dx với P(x) và Q(x) là đa thức của x. Q x ( ) a
 Nếu bêc cûa P(x) lĆn hĄn hoðc bìng bêc cûa Q(x) thì dùng phép chia đa thĀc.
 Nếu bêc cûa P(x) nhó hĄn bêc cûa Q(x) thì cò thể xét các trþąng hợp:
+ Khi Q(x) chî cò nghiệm đĄn  , ,..., thì đðt 1 2 n P x ( ) A A A  1  2  ...  n . Q x ( ) x   x   x   1 2 n
+ Khi Q(x) cò nghiệm đĄn và v nghiệm
Q x  x   x2  px  q   p2 ( ) ,  q 4  0 thì đðt P x ( ) A Bx    C . Q x ( ) x  
x2  px  q + Khi Q(x) cò nghiệm bội
Q x  x   x   2 ( ) ( )( ) vĆi    thì đðt P x ( ) A   B  C . Q x ( ) x   x    2 x   
Q x  x   2 x   3 ( ) ( ) ( ) vĆi    thì đðt P x ( )  A  B  C  D  E x (   2 ) x (   3 ) x (   2 ) x (  ) x (   3 ) x (   2 ) x  
2. Tích phân hàm vô tî b
R x(,f x() dx )
Trong đò R(x, f(x)) có dạng: a  a x    +) R x,
 Đðt x  acos t ,   2 t [0; ] a  x    2
+) R x a2 x2 , 
Đðt x  a sint hoðc x  a cost  ax b   ax  b +) n R x,  Đðt n   t cx  d    cx  d +) 1 
R x, f x (  )  VĆi  x2
  x     k ax b a
( x  b) x2  x   1 Đðt t  x2
  x   , hoðc Đðt t  ax  b
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 32 |    
+) R x a2 x2 , 
 Đðt x = a tant, t   ;   2 2   a  
+) R x x2 a2 , 
 Đðt x  , t 0;\  cos x   2   +) R n n n 1 2 i
x ; x ;...; x  Gọi k  BSCNN n ; n ; ...; n Đðt k x  t 1 2 i   1
a. Tích phån däng : I   dx a  0 2 
ax  bx  c  b  2  x      u b 2  Tÿ :            a f(x)=ax bx c a x 2  du  dx  a 2  a2 4        K  a 2 Khi đò ta có :
- Nếu   a   f x  a u2  k2  f x  a u2  k2 0, 0 ( ) ( ) . (1) 2 a  0  b  
- Nếu :   0  f x
( )  a x     (2) a 2 ( )   b f x a x     a. u  a 2 - Nếu :   0. + VĆi a>0 : f x
( )  a x  x x  x   f x
( )  a. x  x x  x (3) 1 2 1 2  + VĆi a<0 : f x
( )  a x  x x  x   f x
( )  a. x  x x  x (4) 1 2 1 2 
Cën cĀ vào phån tích tr n , ta cò một số cách giâi sau :  Phương pháp :
* Trþąng hợp :   a   f x  a u2  k2  f x  a u2  k2 0, 0 ( ) ( ) . Khi đò đðt : 2
ax  bx  c  t  a x .  t2  c 2 x  ;dx  tdt
bx  c  t2  2 ax  b  2 a  b 2 a      x  t t ,x        t   t  t2 0 1  t  a x .  t  c  a  b  2 a 2 a  0  b  
* Trþąng hợp :   0  f x
( )  a x     a 2 ( )   b f x a x     a. u  a 2  1  b    b ln x   : x   0   1 1 1 a a 2   a 2 Khi đò :   I  dx  dx     b a b 1  b     a x  x   b ln x   : x   0 a 2 a 2  a 2     a a 2
* Trþąng hợp :   0,a  0  x  x t - Đðt : 2
ax  bx  c  a x  x
1  x  x2   1 
 x x2t
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 33 |
* Trþąng hợp :   0,a  0  x  x t - Đðt : 2
ax  bx  c  a x  x 1 x  x 2   1 
 x x 2 t  
b. Tích phån däng :   mx n I dx a  0 2 
ax  bx  c  Phương pháp : Ad .  2 ax  bx   c mx n  B
+Bước 1: Phân tích f x ( )     1 2 ax  bx  2 c ax  bx  2 c
ax  bx  c
+Bước 2: Quy đồng méu số , sau đò đồng nhçt hệ số hai tā số để suy ra hệ hai èn số A,B
+Bước 3: Giâi hệ tìm A,B thay vào (1)  +Bước4 : Tính I = 1 A 2  2
ax  bx  c    (2)  B dx 2 
ax  bx  c  1 Trong đò  dx
a  0 đã biết cách tính ć tr n 2 
ax  bx  c  1
a. Tích phån däng : I   dx a  0 2
 mx  n  ax  bx  c  Phương pháp : 1 1
+Bước 1: Phân tích :  . (1) mx n   2  ax bx c n     m x   2
ax  bx  c  m   1  n  1 y  t    dy   dx 1 n  x  t m x  t +Bước 2: Đðt :    x    y m 1  1 2  1 
x   t  2
ax  bx  c  a   t   b   t    c  y  y   y   '
+Bước 3: Thay tçt câ vào (1) thì I cò däng :    dy I . 2  '
Ly  My  N    x   
d. Tích phån däng : I  R
 x;ydx  R x;m d  x   x       
Trong đò R x;y : là hàm số hĂu tỷ đối vĆi hai biến số x,y và , ,, là các hìng số đã biết
 Phương ph p : x  
+Bước 1: Đðt : t  m  x  
+Bước 2: Tính x theo t : Bìng cách nång lüy thÿa bêc m hai vế ta cò däng x   t
+Bước 3: Tính vi phån hai vế : dx   ' tdt và đổi cên    x    '
+Bước 4: Tính : R x;m dx  
 R t;t 't  dt x        '
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 34 |
3. Tích phån hàm lượng giác
Một số c ng thức lượng giác a. C ng thức cộng: cos a
(  b)  cosa.cosb sina.sinb sin a
(  b)  sina.cosb  sinb. os c a tana  tanb tan a (  b)  1 tana.tanb b. C ng thức nhån: 2 1  tan 2 2 2 2 a cos a
2  cos a – sin a  2 cos a – 1  1 – 2 sin a  2 1  tan a 2 tana 2 tana sin a
2  2 sina.cosa  ; tan a 2  2 1  tan a 1  2 tan a 3
cos 3  4 cos  3cos  ; 3
sin 3  3 sin  4 sin 
c. C ng thức hä bậc: 1  cos2 1  cos 2 1 cos 2 2  a 2 a 2 a sin a  ; cos a  ; tan a  2 2 1  cos a 2 3 sin sin 3 cos 3 3 cos 3   sin    ; 3 cos    4 4 a
d. C ng thức tính theo t : t  tan 2 t 2 1  t2 t 2 sina  cosa  tana  1  t2 1  t2 1  t2
e.C ng thức biến đổi tích thành tổng:    1 cos .cos cos  (  )  cos  (      ) 2    1 sin .sin cos  (  )  cos  (      ) 2    1 sin .cos sin  (  )  sin  (      ) 2
f. C ng thức biến đổi tổng thành tích:       Hệ quâ: cos  cos   2 cos .cos 2 2            
cos  sin  2 cos     2 sin   
cos  cos   2 sin .sin  4   4  2 2            
cos  sin  2 cos      2 sin   sin  sin   2 sin .cos  2 2  4   4        sin  sin   2 cos .sin
Công thức thường dùng: 2 2 3 cos 4 4 4   sin  (   cos   sin       ) tan tan 4 cos cos  5 3 cos 4 6 6   sin  (   cos   sin       ) tan tan 8 cos cos 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 35 |
Một số däng tích phån lượng giác b
 Nếu gặp I   f sinx.cos xdx ta đặt t  sinx . a b
 Nếu gặp dạng I   f cosx.sinxdx ta đặt t  cosx. a b  dx
Nếu gặp dạng I   f tanx
ta đặt t  tan x . 2 cos x a b  dx
Nếu gặp dạng I   f cot x
ta đặt t  cot x . 2 sin x a
I. Däng 1: I = sinxn dx ; I cosxn dx   1 2 2. Phương pháp
2.1. Nếu n chïn thì sā dýng c ng thĀc hä bêc
2.2. Nếu n  3 thì sā dýng c ng thĀc hä bêc hoðc biến đổi theo 2.3.
2.3. Nếu 3  n lẻ (n  2p 1) thì thăc hiện biến đổi: 2p
I = sinxn dx = sinx2p+1 dx   x  xdx     2 sin sin
1 cos x  d cosx      p 1 C  0 C1 2     cos x  ...   1  k C  2
cos x k  ...   1  p k p C  2
cos x p d cos x    p p p p   1  k p 1   2 1  1  2 1    C 0  cos x  C 1 3 cos x  ... 
C cos x  k    ... 
C cos x  p k p  C p p p p  3 k 2  1 2p  1  2p
I = cosxn dx = cosx2p+1 dx   x  xdx    2 cos cos
1 sin x  d sin x      p 2    C 0  C 1 2 sin x  ...   1  k C  2
sin x k  ...   1  p k p C  2
sin x p d sin x    p p p p   1  k p 1   2 1  1  2 1   C 0  sin x  C 1 3 sin x  ... 
C sin x  k    ... 
C sin x  p k p  C p p p p  3 k 2  1 2p  1  II. Däng 2: m n I = sin x cos x dx  (m, nN) 1. Phương pháp:
1.1. Trường hợp 1: m, n là c c số nguyên
a. Nếu m chïn, n chïn thì sā dýng c ng thĀc hä bêc, biến đổi tích thành tổng.
b. Nếu m chïn, n lẻ (n 2p 1) thì biến đổi:  m  2p+1 m 2p m I = sinx cosx dx   x   x  xdx   x    2 sin cos cos sin
1 sin x  d sin x     p    
sin x m C 0 C 1 2 sin x  ...   1  k C  2
sin x k  ...   1  p k p C  2
sin x p d sin x     p p p p    1  3 2 1   2 1   sin sin sin sin  0 x m  1 x m k m p m C  C  ...   k  x  x k 1 C  ...   1  p   p C  C p p p p  m  1 m  3 k 2  1  m
2p  1  m 
c. Nếu m chïn, n lẻ (n 2p 1) thì biến đổi:  2p+1  n n 2p n I = sinx cosx dx   x   x  xdx    x    2 cos sin sin cos
1 cos x  d cosx     p   
  cosx n C 0 C 1 2 cos x  ...   1  k C  2
cos x k  ...   1  p k p C  2
cos x p d cos x     p p p p    1  3 2 1   2 1   cos cos cos cos  0 x n  1 x n k n p n  C  C  ...   k  x  x k 1 C  ...   1  p   p C  C p p p p  n  1 n  3 k 2  1  n
2p  1  n 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 36 |
d. Nếu m lẻ, n lẻ thì sā dýng biến đổi 1.2. hoðc 1.3. cho số mü lẻ bé hĄn.
1.2. Nếu m, n là c c số hữu tî thì biến đổi và đặt u  sinx ta có: n1 m1    m m n  2  2  m B x xdx x x xdx u   u2     2 sin cos sin cos cos 1 du (*)
m  1 n  1 m  k
• Tích phån (*) tính đþợc  1 trong 3 số ; ; là số nguy n 2 2 2
III. Däng 3: I = tan xn dx ; I = cot xn dx  
(nN). Công thức sử dụng: 1 2 2 dx
• 1  tan x dx 
 d tanx   tanx    2  c cos x 2 dx
• 1  cot x dx  
  d cotx    cotx    2  C sin x sin x d cos x  • tan xdx  dx     ln cosx     C cosx cosx cos x d sin x  • cotxdx  dx   ln sinx     C sin x sin x
ỨNG DỤNG TÍCH PHÅN
1. Diện tích hình phẳng
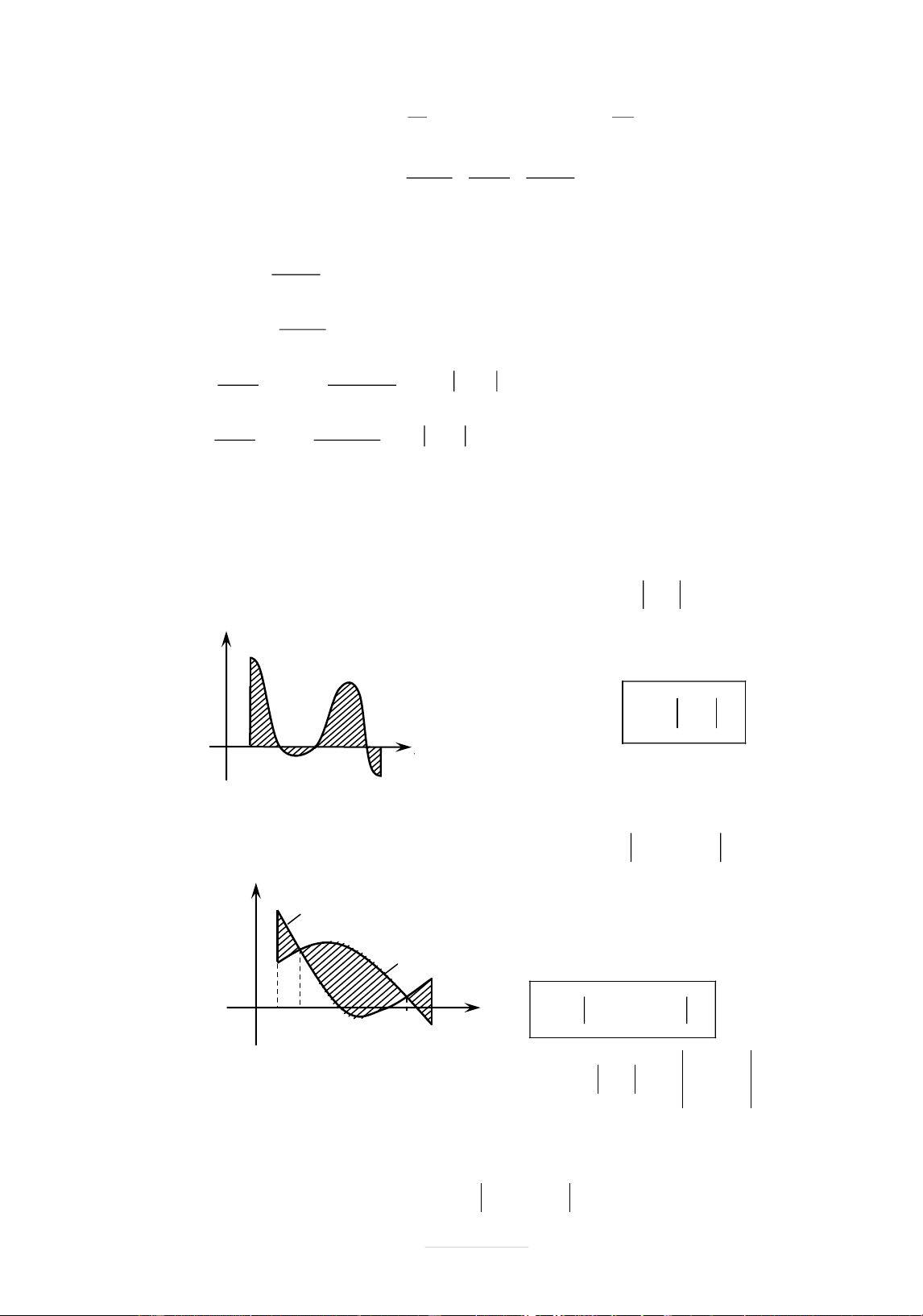
a) Diện tích hình phîng giĆi hän bći đồ thð hàm số y  f x
( ) li n týc tr n đoän a;b   , b
trýc hoành và hai đþąng thîng x  a , x  b đþợc xác đðnh: S   f x() dx a y
y  f (x)
y  f (x)  b y  0 (H) S   f x ( ) dx x   a a O a c c c b x 1 2 3  x  b
b) Diện tích hình phîng giĆi hän bći đồ thð hàm số y  f x ( ), y  g x ( ) li n týc tr n đoän b a;b 
 và hai đþąng thîng x  a , x  b đþợc xác đðnh: S  f x ( )   g x ( ) dx a y
(C ) : y  f (x) (C ) 1  1 1
(C ) : y  f (x) (H) 2 2 x  a (C ) 2 x  b b S  f x ( )  a c O c 1 b x 2  f x ( ) dx 1 2 a b b
- Nếu tr n đoän [a;b] , hàm số f x
( ) kh ng đổi dçu thì: f x ( ) dx  
 f x( d)x a a
- Ním vĂng cách tính tích phån cûa hàm số cò chĀa giá trð tuyệt đối
- Diện tích cûa hình phîng giĆi hän bći các đþąng x  g y ( ), x  h y ( ) và hai đþąng d
thîng y  c , y  d đþợc xác đðnh: S  g y ( )   h y ( ) dy c
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 37 |
2. Thể tích vật thể và thể tích hối trñn xoay a) Thể tích vêt thể:
Gọi B là phæn vêt thể giĆi hän bći hai mðt phîng vu ng gòc vĆi trýc Ox täi các điểm
a và b; S x
( ) là diện tích thiết diện cûa vêt thể bð cít bći mðt phîng vu ng gòc vĆi trýc Ox
täi điểm x , a
(  x  b) . Giâ sā S x
( ) là hàm số li n týc tr n đoän [a;b] . ( ) b x V  a b S x( dx ) O x a S(x)
b) Thể tích khối trñn xoay:
Thể tích khối trñn xoay đþợc sinh ra khi quay hình phîng giĆi hän bći các đþąng y  f x
( ), trýc hoành và hai đþąng thîng x  a , x  b quanh trýc Ox: y
y  f (x) (
 C) : y  f (x) ( 
 Ox) : y  0 b  V   f x dx a  x  ( )2 O b x x   a a  x  b
- Thể tích khối trñn xoay đþợc sinh ra khi quay hình phîng giĆi hän bći các đþąng x  g y
( ), trýc hoành và hai đþąng thîng y  c , y  d quanh trýc Oy: y d (
 C) : x  g(y)  (
 Oy) : x  0 d  V   g y dy  y  ( )2 y  c  c  c y  d x
- Thể tích khối trñn xoay
O đþợc sinh ra khi quay hình phîng giĆi hän bći các đþąng y  f x ( ), y  g x
( ) và hai đþąng thîng x  a , x  b quanh trýc Ox: b
V   f 2 x  g2 ( ) x ( ) dx  a
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 38 | PHÆN IV. SỐ PHỨC I. SỐ PHỨC 1. Khái niệm số phức
+ Số phĀc (däng đäi số) : z  a  bi; a,b   . Trong đò : a là phæn thăc,
b là phæn âo, i là đĄn vð âo, i2  1. 
+ Têp hợp số phĀc kí hiệu: .
+ z là số thăc  phæn âo cûa z bìng 0 b  0 .
+ z là số âo (hay cñn gọi là thuæn âo)  phæn thăc bìng 0 a  0 .
Số 0 vÿa là số thăc vÿa là số âo.
2. Hai số phức bằng nhau
Hai số phĀc z  a  bi a, b 
và z  c  di c, d  bàng nhau khi phæn thăc và 2  1 
phæn âo cûa chúng tþĄng đþĄng bìng nhau. a   c
Khi đò ta viết z  z  a  bi  c  di   1 2 b  d 
3. Biểu diễn hình học số phức
Số phĀc z  a  bi a, b   đþợc biểu diễn bći điểm M a;b y
hay bći u  a;b trong mðt phîng phĀc vĆi hệ tọa độ Oxy . M (a;b) 4. Số phức li n hợp O x
Số phĀc li n hợp cûa z  a  bi a, b   là z  a bi . Một số tính chçt:  z  z + z  z ;
z  z '  z  z ' ; z z . '  z z 1 1 . ';    ; z z .  a2  b2.  z  z  2  2
+ z là số thăc  z  z ; z là số âo z  z  .
5. M đun của số phức
Độ dài cûa vectĄ OM đþợc gọi là m đun của số phức z và kí hiệu là z .
Vêy z  OM hay z a bi OM a2 b2      . Một số tính chçt: + z a2 b2  
 zz  OM ; z  z + z  0, z
  ; z  0  z  0. z z z z z + z z .  z . z ; 1 1  ; 1 1 2  . 1 2 1 2 z z z 2 2 2 2 z2
+ z  z  z  z  z  z . 1 2 1 2 1 2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 39 |
II. PHÉP CỘNG TRỪ NHÅN CHIA SỐ PHỨC
1. Phép cộng và phép trừ số phức
Cho hai số phĀc z  a  bi a, b 
và z  c  di c, d  . Khi đò: 2  1 
+ z  z  a  c  b  di 1 2
+ Số đối cûa số phĀc z  a  bi là z   a   bi .
+ Tổng cûa một số phĀc vĆi số phĀc liên hợp cûa nó bìng hai læn phæn thăc cûa số thăc
đò: z  a  bi,z  z  a 2 . 2. Phép nhån số phức
+ Cho hai số phĀc z  a  bi a, b 
và z  c  di c, d  . Khi đò 2  1 
z z  a  bic  di  ac – bd  ad  bci . 1 2
+ VĆi mọi số thăc k và mọi số phĀc z  a  bi a, b  , ta có k z
.  k.a  bi  ka  kbi.
Đặc iệt: 0 z
.  0 vĆi mọi số phĀc z .
+ Lüy thÿa cûa i : i0  i1  i i2   i3  i2 1, , 1, i.  i  n 4 n 4 1  n 4 2  4n i i i i i 3 1, , 1, i, n          .
3. Chia hai số phức  1
Số phĀc nghðch đâo cûa z khác 0 là số z 1  z . 2 z z '  '. '. 1 z z z z
Phép chia hai số phĀc z ' và z  0 là  z 'z   . z 2 z z z .
III. TẬP HỢP ĐIỂM BIỂU DIỄN SỐ PHỨC
Một số têp hợp điểm biểu diễn số phĀc z thþąng gðp:
+ ax  by  c  0 têp hợp điểm là đþąng thîng
+ x  0  têp hợp điểm là trýc tung Oy
+ y  0  têp hợp điểm là trýc hoành Ox +  2 2 x a  y b R2    
 têp hợp điểm là hình tròn tâm I a;b, bán kính R   2 2
x  a   y  b  R2 +
 têp hợp điểm là đường trñn có x2   y2  a 2 x  b 2 y  c  0 
tâm I a;b, bán kính R a2 b2    c
+ x  0  têp hĄp điểm là miền b n phâi trýc tung
+ y  0  têp hợp điểm là miền phía dþĆi trýc hoành
+ x  0  têp hợp điểm là miền b n trái trýc tung
+ y  0  têp hợp điểm là phía tr n trýc hoành + y ax2 
 bx  c  têp hợp điểm là đþąng Parabol x2 y2 + 
 1 têp hợp điểm là đþąng Elip a2 b2 x2 y2 + 
 1  têp hợp điểm là đþąng Hyperbol a2 b2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 40 |
IV. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
a. Căn bậc hai của số thực åm
+ Cho số z , nếu có số phĀc z sao cho z 2  z thì ta nói z là một cën bêc hai cûa z . 1 1 1
+ Mọi số phĀc z  0 đều cò hai cën bêc hai.
+ Cën bêc hai cûa số thăc z âm là i  z .
Tổng quát, các cën bêc hai cûa số thăc a âm là i  a .
b. Phương trình bậc hai với hệ số thực
Cho phþĄng trình bêc hai ax2  bx  c  0, a
 ,b,c  ,a  0 . Xét biệt số   b2  a 4 c cûa phþĄng trình. Ta thçy: b
+ Khi   0, phþĄng trình cò một nghiệm thăc x   . a 2 b   
+ Khi   0, phþĄng trình cò hai nghiệm thăc phân biệt x  . 1,2 a 2 b   i 
+ Khi   0, phþĄng trình cò hai nghiệm phĀc x  . 1,2 a 2
BÀI TOÁN LIÊN QUAN ĐẾN MAX – MIN MÔ ĐUN SỐ PHỨC  z r max z 2   z  z + Cho số phĀc 1 1
z thóa mãn z .z  z  r, r  0  . 1 2   z  r min z 2    z z 1 1 
+ Cho số phĀc z thóa mãn z .z  z  r , r  0 . 1 2 1  1  z r z r max P 2   z 1  và min P 2   z 1  z 3 z z 3 z 1 1 1 1
+ Cho số phĀc z thóa mãn z z .  z  z z
.  z  k, k  0 . 1 2 1 2  2 2 k k  4 z max z  và min z 2  2 z 2 z 1 1
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 41 |
PHẦN V. KHỐI ĐA DIỆN
I- KH[I NIỆM VỀ HÌNH ĐA DIỆN V\ KHỐI ĐA DIỆN:
1. Khái niệm về hình đa diện:
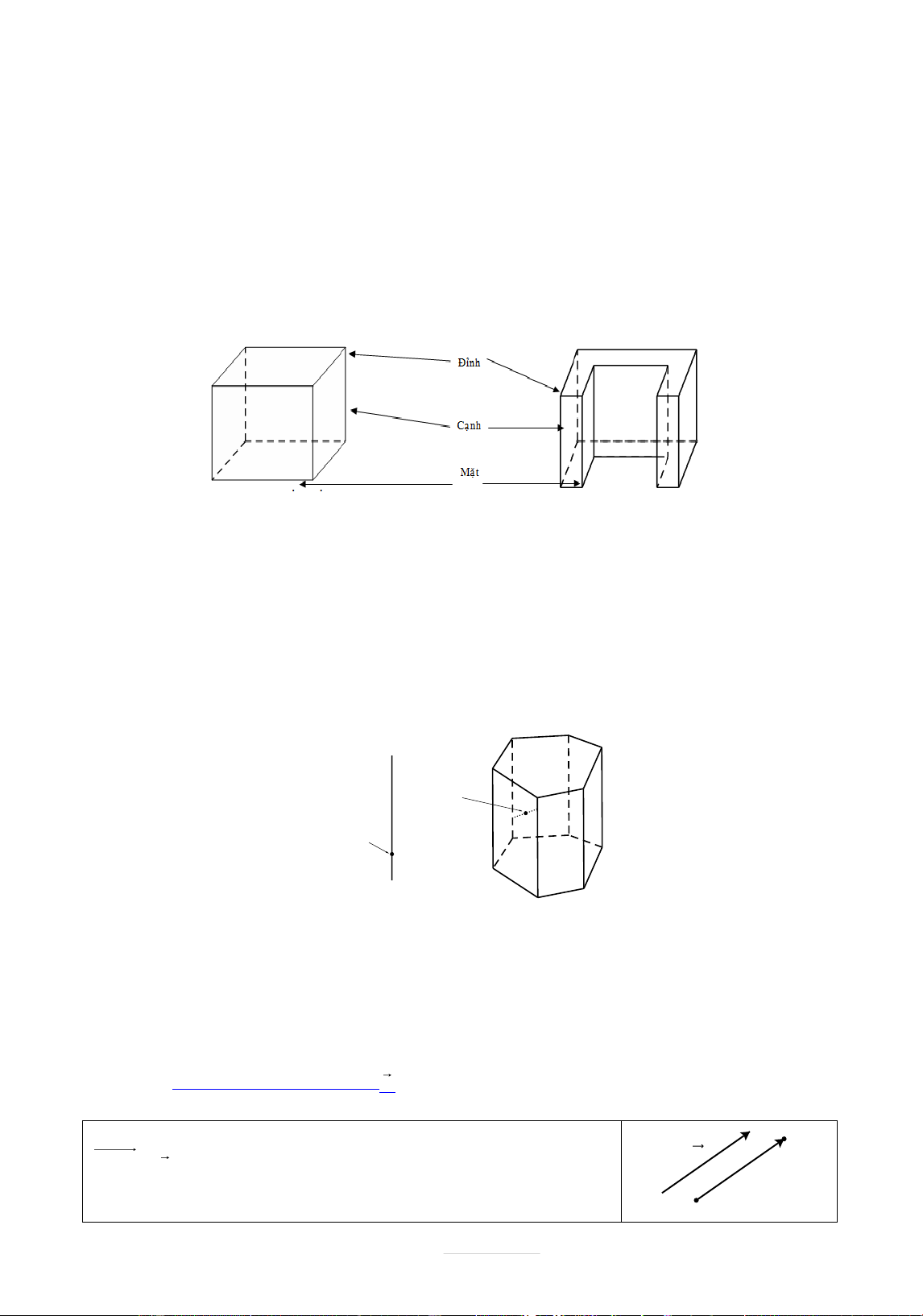
 Hình đa diện (gọi tắt l| đa diện) l| hình được tạo bởi một số hữu hạn c{c đa gi{c thỏa mãn hai tính chất:
a) Hai đa gi{c ph}n biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh
chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa gi{c n|o cũng l| cạnh chung của đúng hai đa gi{c.
 Mỗi đa gi{c gọi l| một mặt của hình đa diện. C{c đỉnh, cạnh của c{c đa gi{c ấy theo thứ
tự được gọi l| c{c đỉnh, cạnh của hình đa diện.
2. Khái niệm về khối đa diện:
 Khối đa diện l| phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
 Những điểm không thuộc khối đa diện được gọi l| điểm ngo|i của khối đa diện.
Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện đó được gọi l| điểm trong của
khối đa diện. Tập hợp c{c điểm trong được gọi l| miền trong, tập hợp những điểm ngo|i được
gọi l| miền ngo|i của khối đa diện.
 Mỗi hình đa diện chia c{c điểm còn lại của không gian th|nh hai miền không giao nhau
l| miền trong v| miền ngo|i của hình đa diện, trong đó chỉ có miền ngo|i l| chứa ho|n to|n một đường thẳng n|o đó. d Mieàn ngoaøi Ñieåm trong N Ñieåm ngoaøi M
III- HAI ĐA DIỆN BẰNG NHAU:
1. Phép dời hình trong không gian:
Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M ' x{c định duy nhất
được gọi l| một phép biến hình trong không gian.
Phép biến hình trong không gian được gọi l| phép dời hình nếu nó bảo to|n khoảng c{ch giữa hai điểm tùy ý.
* Một số phép dời hình trong không gian:
a) Phép tịnh tiến theo vectơ v :
L| phép biến hình biến mỗi điểm M th|nh M ' sao cho M' MM '  v v . M
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 42 |
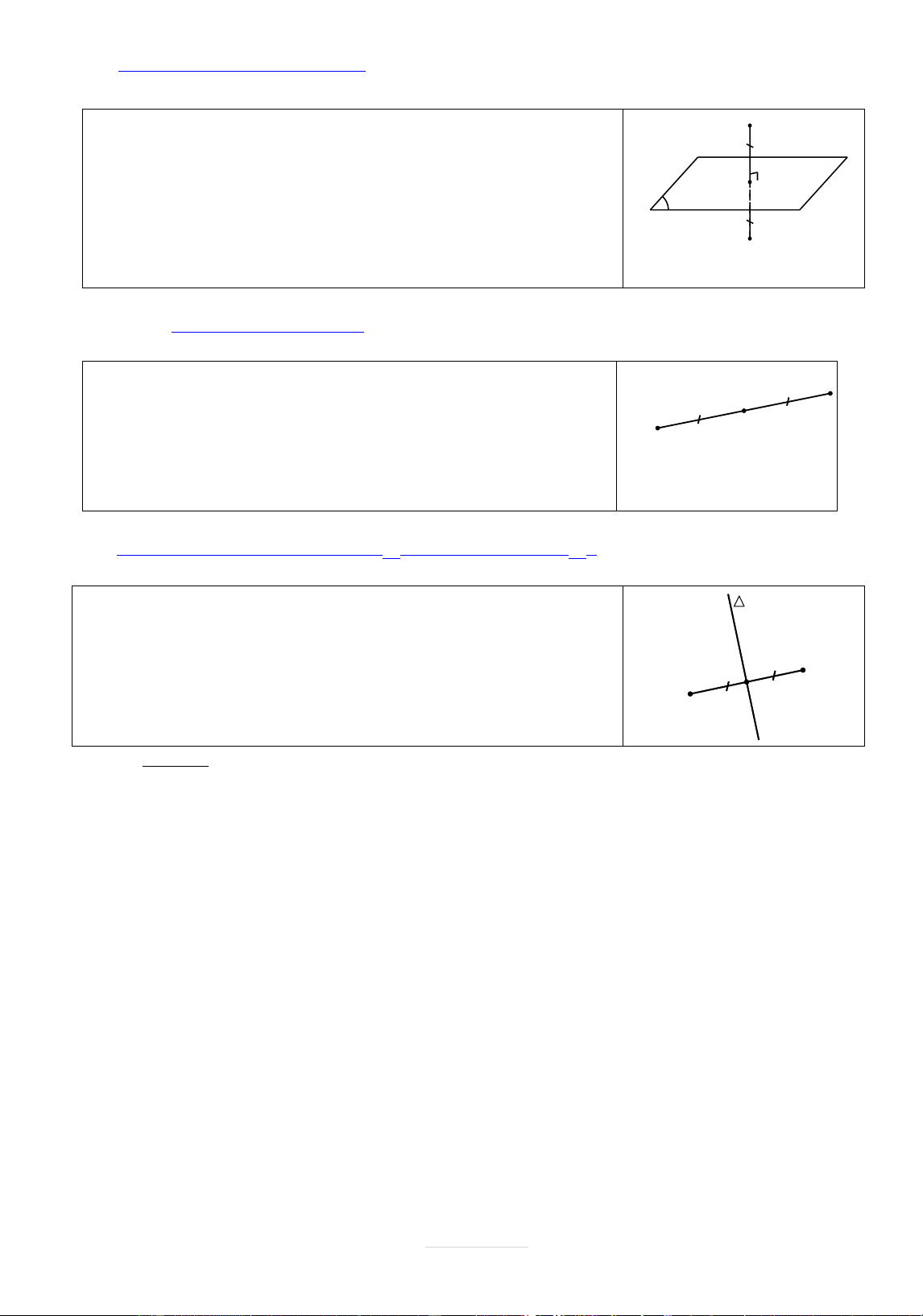
b) Phép đối xứng qua mặt phẳng P  : M
L| phép biến hình biến mỗi điểm thuộc P  th|nh chính nó,
biến mỗi điểm M không thuộc P  th|nh điểm M ' sao cho P  I
l| mặt phẳng trung trực của MM ' . P
Nếu phép đối xứng qua mặt phẳng P  biến hình H  th|nh M'
chính nó thì P  được gọi l| mặt phẳng đối xứng của H  .
c) Phép đối xứng qua tâm O :
L| phép biến hình biến điểm O th|nh chính nó, biến mỗi
điểm M kh{c O th|nh điểm M ' sao cho O l| trung điểm M' MM ' . O M
Nếu phép đối xứng t}m O biến hình H  th|nh chính nó thì
O được gọi l| t}m đối xứng của H 
d) Phép đối xứng qua đường thẳng  (phép đối xứng trục  ):
L| phép biến hình biến mọi điểm thuộc đường thẳng  th|nh
chính nó, biến mỗi điểm M không thuộc  th|nh điểm M ' sao
cho  l| đường trung trực của MM ' .
Nếu phép đối xứng trục  biến hình H  th|nh chính nó thì  I M' M
được gọi l| trục đối xứng của H  * Nhận xét:
 Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
 Phép dời hình biến đa diện H  thành đa diện H ' , biến đỉnh, cạnh, mặt của H  thành
đỉnh, cạnh, mặt tương ứng của H ' . 2. Hai hình bằng nhau:
Hai hình được gọi l| bằng nhau nếu có một phép dời hình biến hình n|y th|nh hình kia.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 43 |
KHỐI ĐA DIỆN LỒI
I. Khối đa diện lồi
Khối đa diện được gọi l| khối đa diện lồi nếu với bất kì hai điểm A v| B n|o của nó thì
mọi điểm của đoạn AB cũng thuộc khối đó.
Khối đa diện lồi
Khối đa diện không lồi II.
Khối đa diện đều
1. Định nghĩa: Khối đa diện đều l| một khối đa diện lồi có hai tính chất sau đ}y:
 C{c mặt l| những đa gi{c đều n cạnh.
 Mỗi đỉnh l| đỉnh chung của đúng p cạnh.
Khối đa diện đều như vậy gọi l| khối đa diện đều loại n,  p .
2. Bảng tóm tắt của năm loại khối đa diện đều
Khối đa diện đều Số đỉnh Số cạnh
Số mặt Loại Số MPĐX Tứ diện đều 4 6 4 3; 3 6 Khối lập phương 8 12 6 4; 3 9 Bát diện đều 6 12 8 3; 4 9
Mười hai mặt đều 20 30 12 5; 3 15
Hai mươi mặt đều 12 30 20 3; 5 15
Khối đa diện đều loại n, 
p có Đ đỉnh, C cạnh v| M mặt: pĐ  C 2  nM .
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 44 |
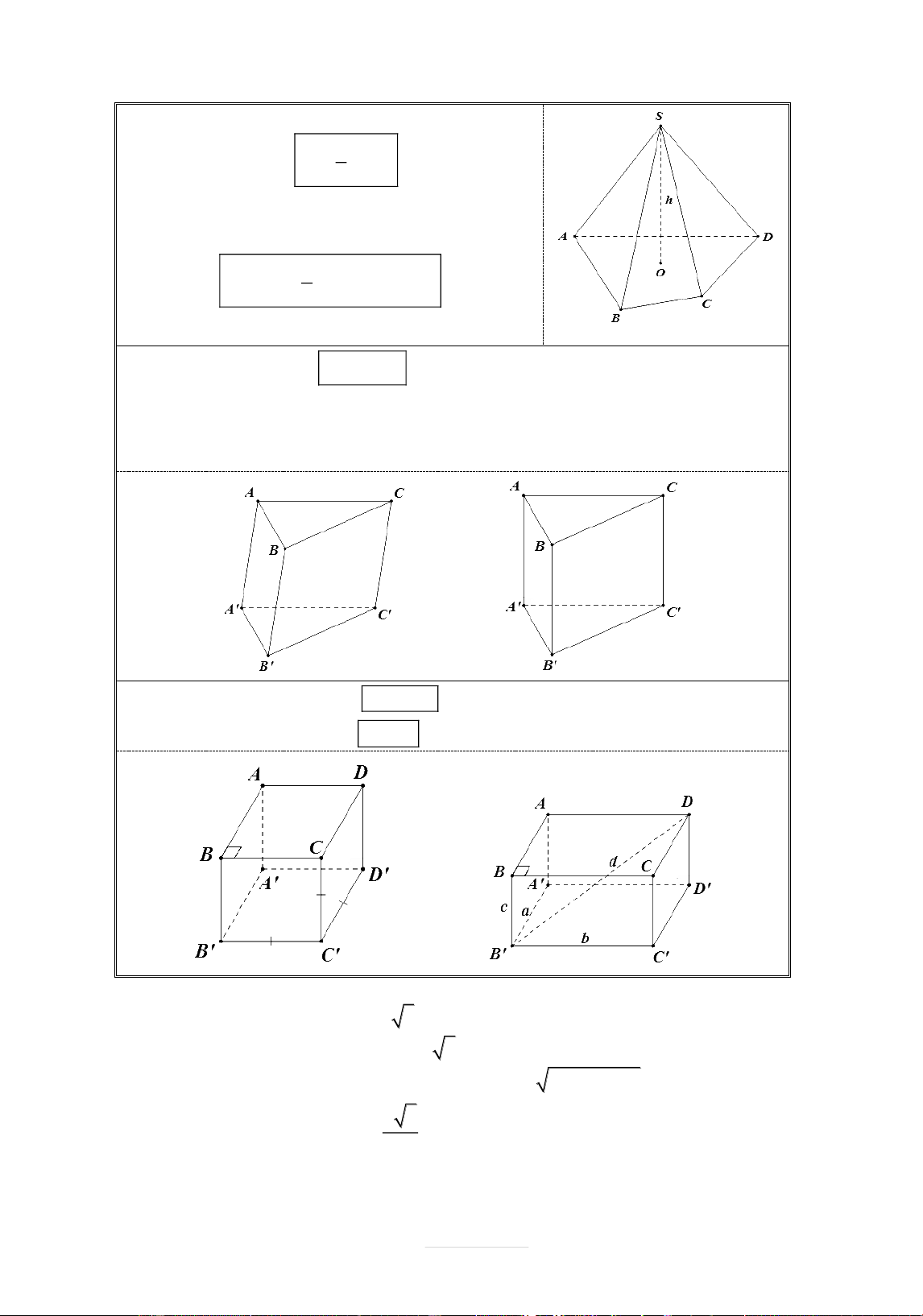
THỂ TÍCH KHỐI ĐA DIỆN 1
Thể t ch khối chóp: V  S h . áy 3 đ + S : Diện tích mặt đ{y. áy đ
+ h : Độ d|i chiều cao khối chóp. 1 V  d .S S.ABCD
3 S ,ABCD ABCD
Thể t ch khối lăng trụ: V  S h . áy đ + S : Diện tích mặt đ{y. áy đ
+ h : Chiều cao của khối chóp.
Lưu : L ng trụ đứng có chiều cao chính l| cạnh b n.
Thể t ch khối h p chữ nh t: V  a b . c .
Thể t ch khối l p phương: V a3  * Chú ý:
 Đường chéo của hình vuông cạnh a là a 2
 Đường chéo của hình lập phương cạnh a là : a 3  2 2 2
Đường chéo của hình hộp chữ nhật có 3 kích thước a,b,c là : a  b  c a 3
 Đường cao của tam giác đều cạnh a là: 2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 45 |
ỉ số th t ch: S V
SA SB SC  S A . B C    . . V SA SB SC S A . BC A’ B’
nh ch p c t ABC A . B C   C’ h V 
B B BB A B 3
ới B,B ,h l| diện tích hai đ{y v| chiều cao. C
C[C CÔNG THỨC HÌNH PHẲNG
1. Hệ thức lượng trong tam giác a) Cho A
 BC vuông tại A, đường cao AH. A B C H  AB2 AC 2 BC 2    AB2  BH B . C
 AC 2  CH B . C  AH B . C  AB A . C 1 1 1
 AH 2  BH H . C    AH 2 AB2 AC 2
 AB  BC.sinC  BC.cosB  AC. ta C n  AC.cotB b) Cho A
 BC có độ d|i ba cạnh l|: a, b, c độ dài các trung tuyến là m ,m ,m bán kính đường tròn a b c
ngoại tiếp R; bán kính đường tròn nội tiếp r nửa chu vi p.
 Định lí h|m số cosin:
a2  b2  c2 bc
A b2  c2  a2  ca
B c2  a2  b2 - 2 .cos ; 2 .cos ;  a
2 b.cosC a b c
 Định lí h|m số sin:    R 2 sin A sin B sinC    2 b2 c2 a2 2 c2 a2 b2 2 a2 b2 c2
 Độ d|i trung tuyến: m   ; m   ; m   a b c 2 4 2 4 2 4
2. Các công thức t nh diện t ch a) Tam giác: 1 1 1 1 1 1  S  a h .  b h .  c h
.  S  bc sinA  ca.sinB  ab sinC a b c 2 2 2 2 2 2 abc  S   S  pr R 4
 CT He-ron: S  p p  ap bp  c AB A . C BC A . H  A
 BC vuông tại A: S   2 2 a 3 a2 3  A
 BC đều, cạnh a: AH  , S  2 4
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 46 |
b) Hình vuông: S a2 
(a: cạnh hình vuông) c) Hình chữ nh t: S  ab
(a, b: hai kích thước)
d) Hình bình hành: S = đáy  cao  AB A . D.sin BAD 1 e) Hình thoi: S  AB A
. D.sin BAD  AC B . D 2 1 f) Hình thang:
S  a  bh (a, b: hai đáy, h: chiều cao) 2 1
g) Tứ giác có hai đường chéo vuông góc: S  AC B . D 2
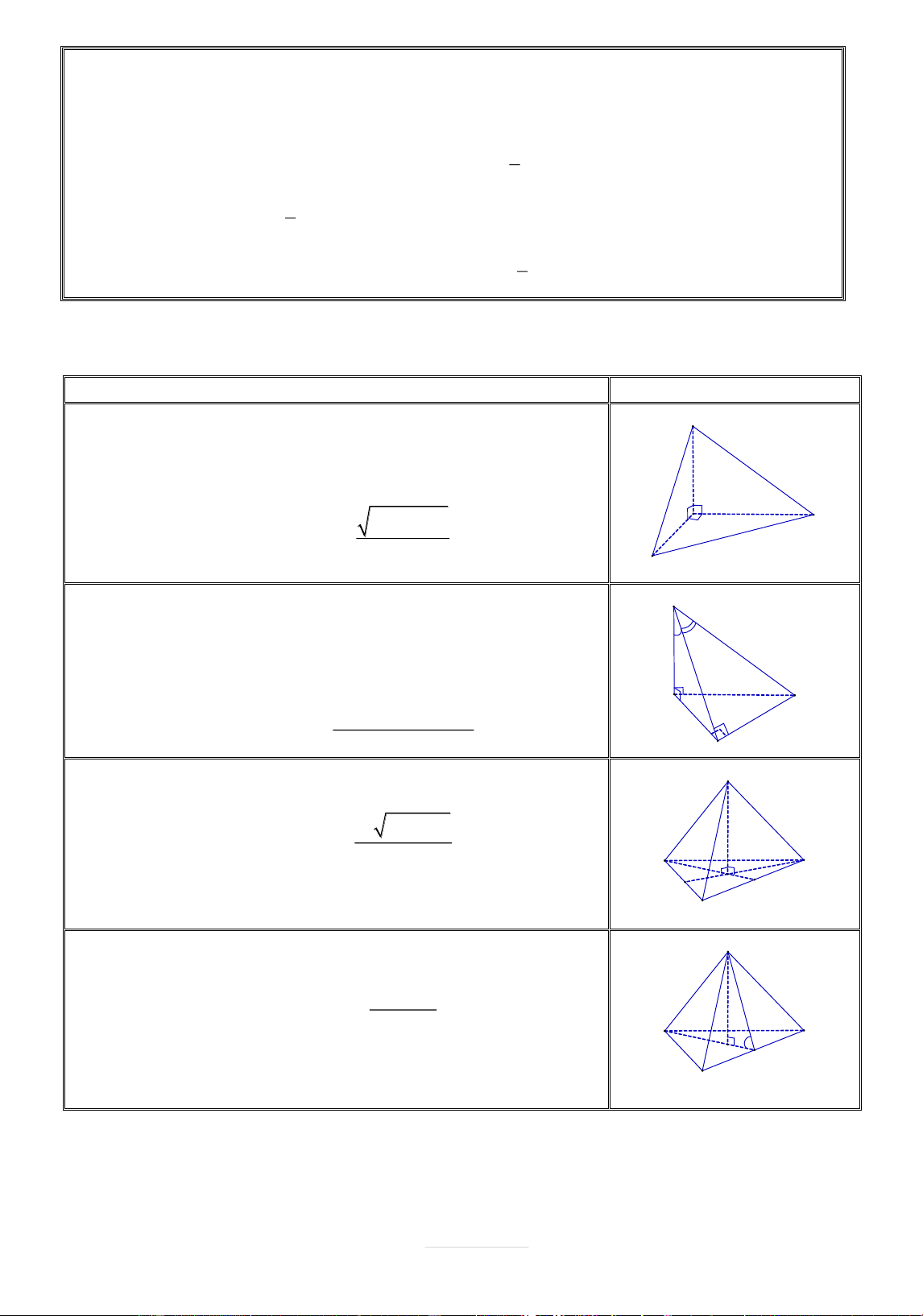
MỘT SỐ CÔNG THỨC TÍNH NHANH THỂ TÍCH KHỐI CHÓP THƯỜNG GẶP TÍNH CHẤT HÌNH VẼ
Cho hình chóp SABC với c{c mặt phẳng SAB,SBC ,SAC  A
vuông góc với nhau từng đôi một, diện tích c{c tam gi{c
SAB,SBC,SAC lần lượt l| S ,S ,S . 1 2 3 S S 2 .S .S C Khi đó: V 1 2 3  S A . BC 3 B
Cho hình chóp S.ABC có SA vuông góc với ABC  , hai mặt S
phẳng SAB v| SBC  vuông góc với nhau,
BSC  ,ASB   . A C SB3.sin 2.tan  Khi đó: V  S A . BC 12 B
Cho hình chóp đều S.ABC có đ{y ABC l| tam gi{c đều cạnh bằng a, S cạnh b n bằng b . a2 b2 3  a2 Khi đó: V  S A . BC 12 C A G M B
Cho hình chóp tam gi{c đều S.ABC có cạnh đ{y bằng a v| mặt b n S
tạo với mặt phẳng đ{y góc  . a3 tan Khi đó: V  S A . BC 24 C A G M B
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 47 |
Cho hình chóp tam gi{c đều S.ABC có c{c cạnh b n bằng b v| cạnh S
b n tạo với mặt phẳng đ{y góc  . b3 2 3 .sin  cos  Khi đó: V  S A . BC 4 A C G M B
Cho hình chóp tam gi{c đều S.ABC có c{c cạnh đ{y bằng a, cạnh S
b n tạo với mặt phẳng đ{y góc  . a3.tan  Khi đó: V  S A . BC 12 A C G M B
Cho hình chóp tứ gi{c đều S.ABCD có đ{y ABCD l| hình vuông S
cạnh bằng a, v| SA  SB  SC  SD  b . a2 b2 4  a2 2 Khi đó: V  S A . BC 6 D A O M C B
Cho hình chóp tứ gi{c đều S.ABCD có cạnh đ{y bằng a, góc tạo S
bởi mặt b n v| mặt phẳng đ{y l|  . a3.tan Khi đó: V  S A . BCD 6 A D O M B C
Cho hình chóp tứ gi{c đều S.ABCD có cạnh đ{y bằng a, SAB   , S     với    ;  4 2   D a3 2 tan   1 A Khi đó: V  O M S A . BCD 6 C B
Cho hình chóp tứ gi{c đều S.ABCD có c{c cạnh b n bằng a, góc tạo S   
bởi mặt b n v| mặt đ{y l|  với    0;  . 2   a3 4 .tan A D Khi đó: V  S A . BCD O M 3 2  tan  3 2 B C
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 48 |
Cho hình chóp tam gi{c đều S.ABC có cạnh đ{y bằng a. Gọi P  l| S F
mặt phẳng đi qua A song song với BC v| vuông góc với SBC  , N A E a3 cot C x
góc giữa P  với mặt phẳng đ{y l|  . Khi đó: V  G S A . BCD 24 M B
Khối t{m mặt đều có đỉnh l| t}m c{c mặt của hình lập phương A' B' O' cạnh a. D' O1 C' a3 Khi đó: V  O4 O2 6
A O3 B O D C
Cho khối t{m mặt đều cạnh a. Nối t}m của c{c mặt b n ta được S khối lập phương. G2 a3 2 2 D
A G1 Khi đó: V  N 27 M B C S'
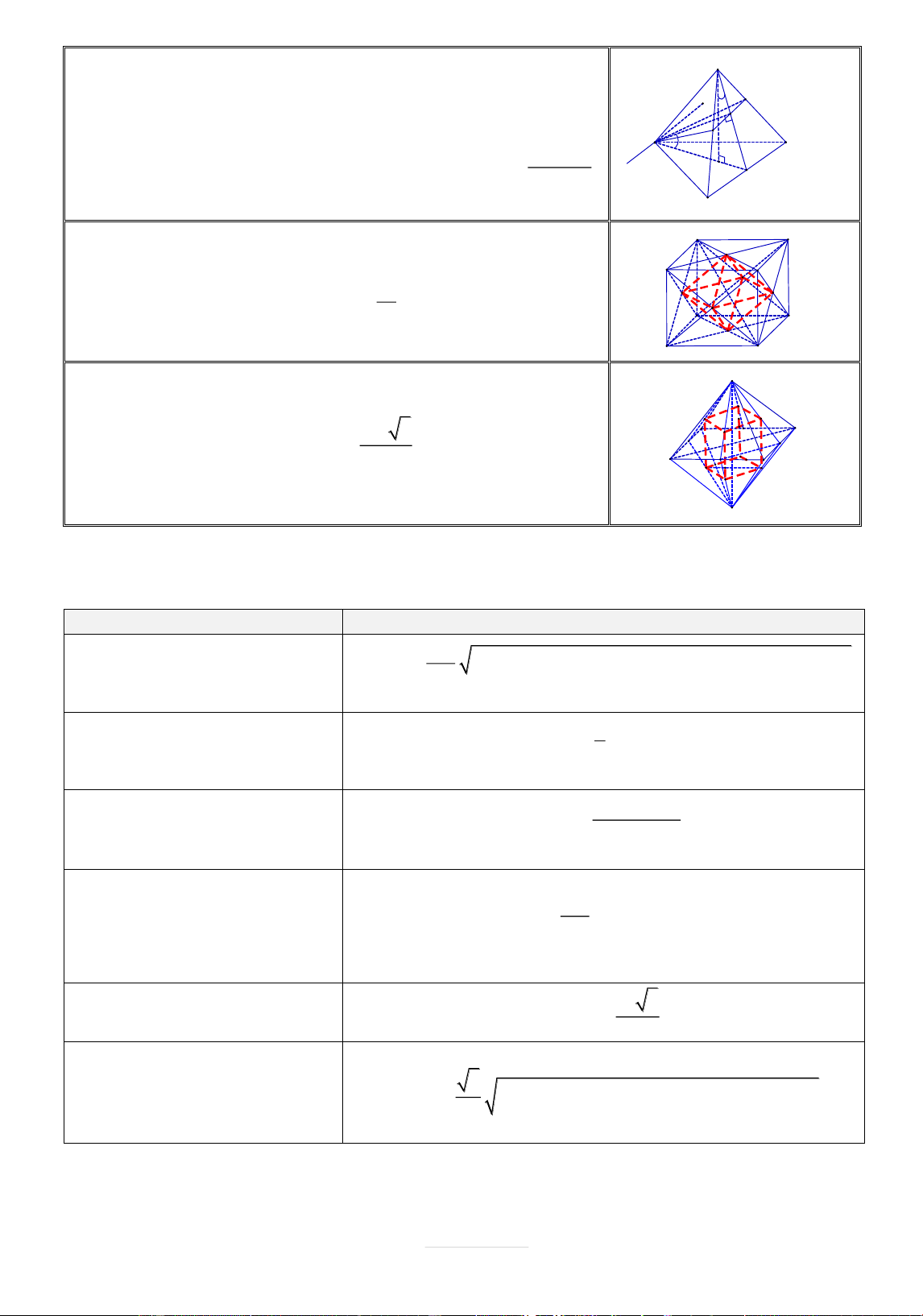
C[C CÔNG THỨC ĐẶC BIỆT THỂ TÍCH TỨ DIỆN (ĐTD):
ĐIỀU KIỆN TỨ DIỆN CÔNG THỨC S
 A  a,SB  b,SC  c  abc             V 2 2 2 1 cos cos cos 2 cos cos cos S A . BC
ASB  ,BSC   C , SA   6  
Công thức tính khi biết 3 cạnh, 3 góc ở đỉnh 1 tứ diện A  B  a C , D  b  1 V  abd sin  ABCD d 6  AB C
, D   d,AB C , D   
Công thức tính khi biết 2 cạnh đối, khoảng cách và góc 2 cạnh đó S   S ,S
 S ,SA  a   S 2 S sin 1 2
 SAB 1 SAC 2   V SABC a 3
 SAB,SAC    
Công thức tính khi biết một cạnh, diện tích và góc giữa 2 mặt kề S
 A  a,SB  b,SC  c  abc V  sin sin  sin
 SAB,SAC    S A . BC 6
ASB  ,ASC   
Công thức tính khi biết 3 cạnh, 2 góc ở đỉnh và 1 góc nhị diện 
Tứ diện đều a3 2 V 
tất cả c{c cạnh bằng a ABCD 12 AB   CD  a  2
Tứ diện gần đều AC 
 BD  b V 
a2  b2  c2 b2  c2  a2 a2  c2  b2 ABCD     AD   BC  c 12 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 49 |
MẶT NÓN - MẶT TRỤ - MẶT CẦU
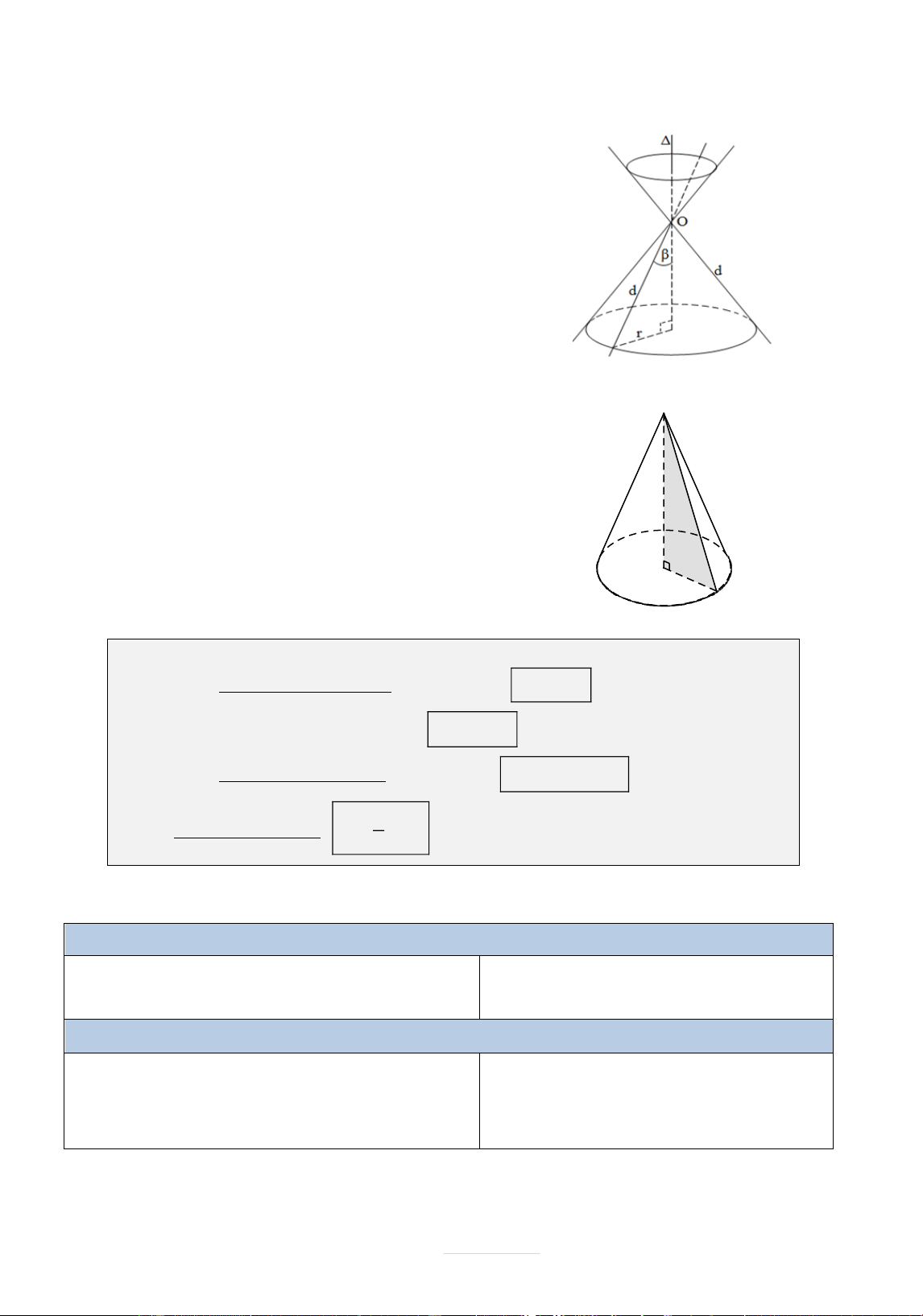
I. MẶT NÓN TRÒN XOAY V\ KHỐI NÓN
1) Mặt n n tr n oa
Đường thẳng d ,  cắt nhau tại O v| tạo th|nh góc  với 0 0
0    90 , mp P  chứa d ,  . P  quay quanh trục
 với góc  không đổi
 mặt nón tròn xoay đỉnh O. +  gọi l| trục.
+ d được gọi l| đường sinh.
Góc 2 gọi l| góc ở đỉnh. 2) Khối n n
L| phần không gian được giới hạn bởi một hình nón O
tròn xoay kể cả hình nón đó. Những điểm không thuộc
khối nón gọi l| những điểm ngo|i của khối nón.
Những điểm thuộc khối nón nhưng không thuộc
hình nón tương ứng gọi l| những điểm trong của khối h l
nón. Đỉnh, mặt đ{y, đường sinh của một hình nón cũng
l| đỉnh, mặt đ{y, đường sinh của khối nón tương ứng. I r M
Cho hình nón có chiều cao h, đường sinh l v| b{n kính đ{yr . 
Diện t ch ung quanh: của hình nón: S  rl . xq 
Diện t ch đá (h nh tr n): S  r2 . áy đ 
Diện t ch toàn phần: của hình nón: S
 rl  r2 . tp 1
+ Th t ch khối n n: V  r h 2 . 3
3) hiết diện khi cắt bởi mặt phẳng
 Cắt mặt nón tr n xoa b i mp Q
( ) đi qua đ nh của mặt nón. mp Q
( ) cắt mặt nón theo đường sinh.
Thiết diện l| tam gi{c c}n. mp Q
( ) tiếp xúc với mặt nón theo một đường sinh. Q
( ) l| mặt phẳng tiếp diện của hình nón.
 Cắt mặt nón tr n xoa b i mp Q
( ) không đi qua đ nh của mặt nón. mp Q
( ) vuông góc với trục hình nón.
Giao tuyến l| đường parabol. mp Q
( ) song song với đường sinh hình nón.
Giao tuyến l| nh{nh của hypebol. mp Q
( ) song song với đường sinh hình nón.
Giao tuyến l| một đường tròn.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 50 | II. MẶT TRỤ TRÒN XOAY 1. Mặt trụ:
Trong mặt phẳng P cho hai đường thẳng  v| l song song với nhau,
c{ch nhau một khoảng bằng r . Khi quay mặt phẳng P xung quanh  r
thì đường thẳng l sinh ra một mặt tròn xoay được gọi l| mặt trụ tròn
xoay, gọi tắt l| mặt trụ. l
 Đường thẳng  gọi l| trục.
 Đường thẳng l l| đường sinh. r
 r l| b{n kính của mặt trụ đó. 
2. Hình trụ tr n xoa và khối trụ tr n xoa :
a) Ta xét hình chữ nhật ABCD . Khi quay hình chữ nhật ABCD
xung quanh đường thẳng chứa một cạnh n|o đó, chẳng hạn cạnh AB
thì đường gấp khúc ADCB sẽ tạo th|nh một hình gọi l| hình trụ tròn
xoay, hay gọi tắt l| hình trụ. r A D + Khi quay quanh ,
AB hai cạnh AD v| BC sẽ vạch ra hai hình
tròn bằng nhau gọi l| hai đ{y của hình trụ, b{n kính của chúng gọi l| h b{n kính của hình trụ. l
Độ d|i đoạn CD gọi l| độ d|i đường sinh của hình trụ.
Phần mặt tròn xoay được sinh ra bởi c{c điểm tr n cạnh CD khi r B
quay xung quanh AB gọi l| mặt xung quanh của hình trụ. C
Khoảng c{ch AB giữa hai mặt phẳng song song chứa hai đ{y 
l| chiều cao của hình trụ.
b) Khối trụ tròn xoay hay khối trụ l| phần không gian được giới hạn bởi một hìn h trụ
tròn xoay kể cả hình trụ tròn xoay đó. Những điểm không thuộc khối trụ gọi l| những
điểm ngo|i của khối trụ. Những điểm thuộc khối trụ nhưng không thuộc hình trụ tương
ứng gọi l| những điểm trong của khối trụ. Mặt đ{y, chiều cao, đường sinh, b{n kính của
một hình trụ cũng l| mặt đ{y, chiều cao, đường sinh, b{n kính của khối trụ tương ứng.
Hình trụ có chiều cao h, đường sinh l v| b{n kính đ{y r. 
Diện t ch ung quanh: S
 2rl . xq 
Diện t ch toàn phần: S
 rl  r2 2 2 . tp 
Th t ch: V  r h 2 .
III. MẶT CẦU – KHỐI CẦU 1. Mặt cầu
Cho điểm I cố định v| một số thực dương R .
Tập hợp tất cả những điểm M trong không gian
c{ch I một khoảng R được gọi l| mặt cầu t}m I,
b{n kính R.
K hiệu: S I;R. Khi đó:
S I;R  M IM   R
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 51 |
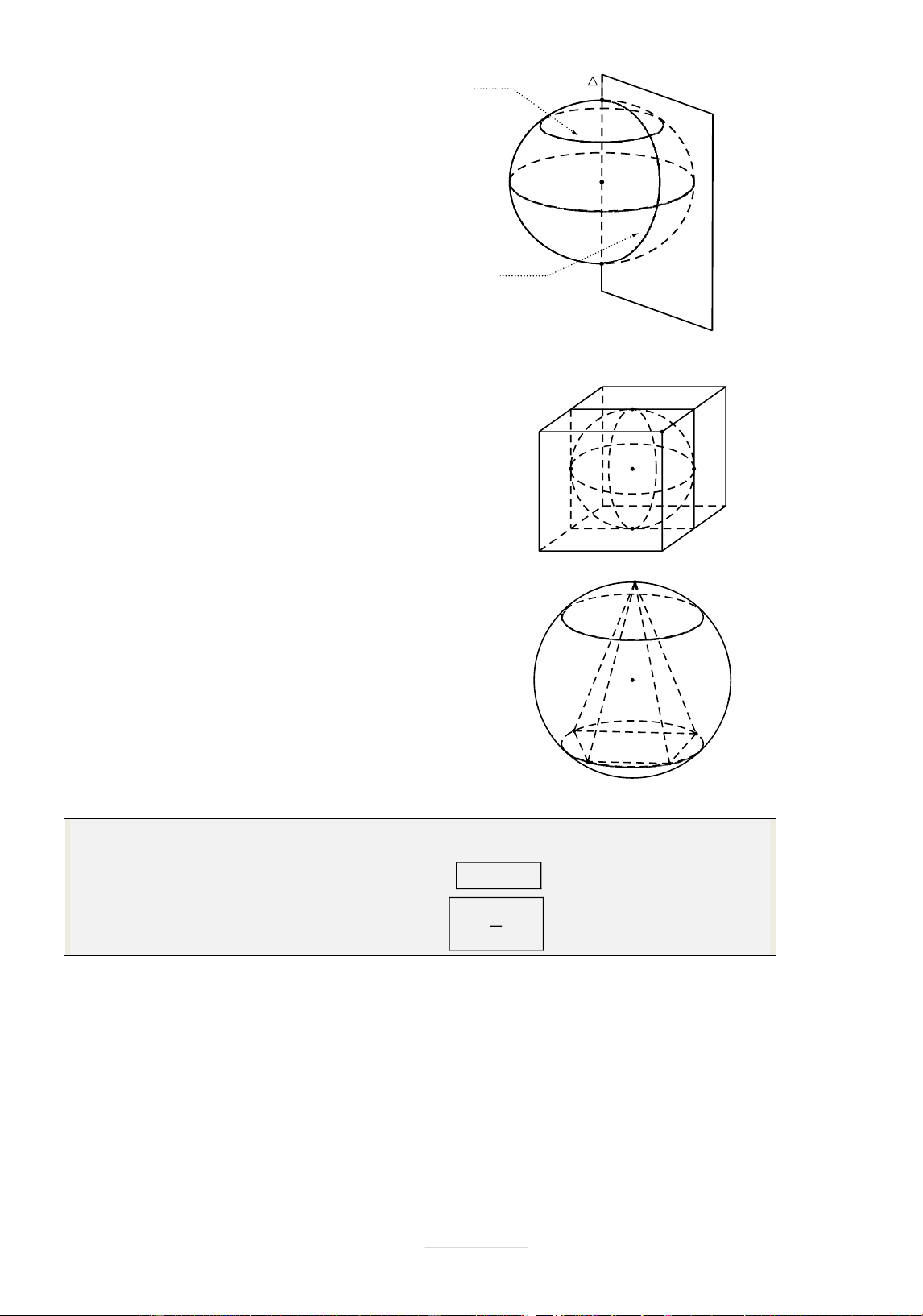
2. Vị tr tương đối giữa mặt cầu và mặt phẳng
Cho mặt cầu S I;R v| mặt phẳng P  . Gọi H l| hình chiếu vuông góc của I l n
P d  IH l| khoảng c{ch từ I đến mặt phẳng P. Khi đó: d  R d  R d  R Mặt cầu v| mặt phẳng
Mặt phẳng tiếp xúc mặt cầu:
Mặt phẳng cắt mặt cầu không có điểm chung.
P l| mặt phẳng tiếp diện theo thiết diện l| đường tròn có t}m
của mặt cầu v| H: tiếp điểm.
I  v| b{n kính r R2 IH 2  
Lưu ý: Khi mặt phẳng P  đi qua t}m I của mặt cầu thì mặt phẳng P  được gọi
l| mặt phẳng k nh v| thiết diện lúc đó được gọi l| đường tr n lớn.
3. Vị tr tương đối giữa mặt cầu và đường thẳng
Cho mặt cầu S I;R v| đường thẳng  . Gọi H l| hình chiếu của I l n  . Khi đó: IH  R IH  R IH  R  không cắt mặt cầu.
 tiếp xúc với mặt cầu.  :  cắt mặt cầu tại hai điểm
Tiếp tu ến của S  v| H: ph}n biệt. tiếp điểm. d
 I;  IH  
cắt S  tại điểm A, B thì b{n kính R của S  :  2  .   2 2 2 AB R
  IH  AH  IH    2   
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 52 |
4. Đường kinh tu ến và vĩ tu ến của mặt cầu:
Giao tuyến của mặt cầu với nửa mặt vó tuyeán A
phẳng có bờ l| trục của mặt cầu được gọi l| kinh tuyến.
+ Giao tuyến (nếu có) của mặt cầu với
c{c mặt phẳng vuông góc với trục được gọi O
l| vĩ tuyến của mặt cầu.
Hai giao điểm của mặt cầu với trục
được gọi l| hai cực của mặt cầu kinh tuyeán B
* Mặt cầu nội tiếp, ngoại tiếp hình đa diện:
Mặt cầu nội tiếp hình đa diện nếu mặt cầu
đó tiếp xúc với tất cả c{c mặt của hình đa diện.
Còn nói hình đa diện ngoại tiếp mặt cầu.
Mặt cầu ngoại tiếp hình đa diện nếu tất cả c{c S
đỉnh của hình đa diện đều nằm tr n mặt cầu.
Còn nói hình đa diện nội tiếp mặt cầu.
Mặt cầu tâm O bán kính r ngoại tiếp hình chóp S A
. BCD khi và chỉ khi: O
OA  OB  OC  OD  OS  r A B D C
Cho mặt cầu S I;R
+ Diện t ch mặt cầu: S  R2 4 . 4
+ h t ch khối cầu: V  R3 . 3
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 53 |
MỘT SỐ DẠNG TO[N V\ CÔNG THỨC GIẢI B\I TO[N MẶT NÓN
Dạng 1 hiết diện của h nh n n cắt bởi một mặt phẳng S
hiết diện qua tr c của hình nón là tam giác cân. A I B
hiết diện qua đỉnh của hình nón là những tam giác cân có hai S
cạnh bên là hai đường sinh của hình nón. A I B
hiết diện vuông g c với tr c của hình nón là những đường S
tròn có tâm nằm trên trục của hình nón. A I B
Dạng 2 Bài toán liên quan đến thiết diện qua đỉnh của h nh n n
Cho hình nón có chiều cao l| h , b{n kính đ{y r v| đường sinh l .
Một thiết diện đi qua đỉnh của hình nón có khoảng c{ch từ t}m của đ{y đến mặt phẳng chứa thiết diện l| d.
Gọi M l| trung điểm của AC. Khi đó: S
 AC  SMI 
 Góc giữa SAC  v| ABC  l| góc SMI.
 Góc giữa SAC  v| SI l| góc MSI. H I  A
d I,SAC   IH  d. B M C
Diện t ch thiết diện: 1 1 2 2 2 2 2 h d 2 2 2 h d 2 2 S  S  SM A . C 
SI  IM .2 AI  IM  r  . h  td S  AC 2 2 h2  d2 h2  d2
Dạng 3 Bài toán h nh n n ngoại tiếp và nội tiếp h nh ch p
Hình nón nội tiếp hình chóp S A
. BCD đều l| hình Hình chóp tứ gi{c đều S A . BCD
nón có đỉnh l| S , đ{y l| đường tròn nội tiếp hình S vuông ABCD . Khi đó hình nón có: AB
B{n kính đ{y r  IM  , 2 A D
Đường cao h  SI , đường sinh l  SM. I M B C
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 54 |
Hình nón ngoại tiếp hình chóp S A . BCD đều l|
Hình chóp tứ gi{c đều S A . BCD
hình nón có đỉnh l| S , đ{y l| đường tròn ngoại tiếp S hình vuông ABCD . Khi đó hình nón có: AC AB 2
 B{n kính đ{y: r  IA   . 2 2 A D
 Chiều cao: h  SI.  I
Đường sinh: l  SA. B C
Hình nón nội tiếp hình chóp S A . BC đều l| hình
Hình chóp tam gi{c đều S A . BC
nón có đỉnh l| S , đ{y l| đường tròn nội tiếp tam S gi{c ABC. Khi đó hình nón có AM AB 3
 B{n kính đ{y: r  IM   . 3 6  A C
Chiều cao: h  SI. I
 Đường sinh: l  SM. M B
Hình nón ngoại tiếp hình chóp S A . BC đều l| hình
Hình chóp tam gi{c đều S A . BC
nón có đỉnh l| S , đ{y l| đường tròn ngoại tiếp tam S gi{c ABC. Khi đó hình nón có: A 2 M AB 3
 B{n kính đ{y: r  IA   . 3 3 C
 Chiều cao: h  SI. A  M
Đường sinh: l  SA. I B
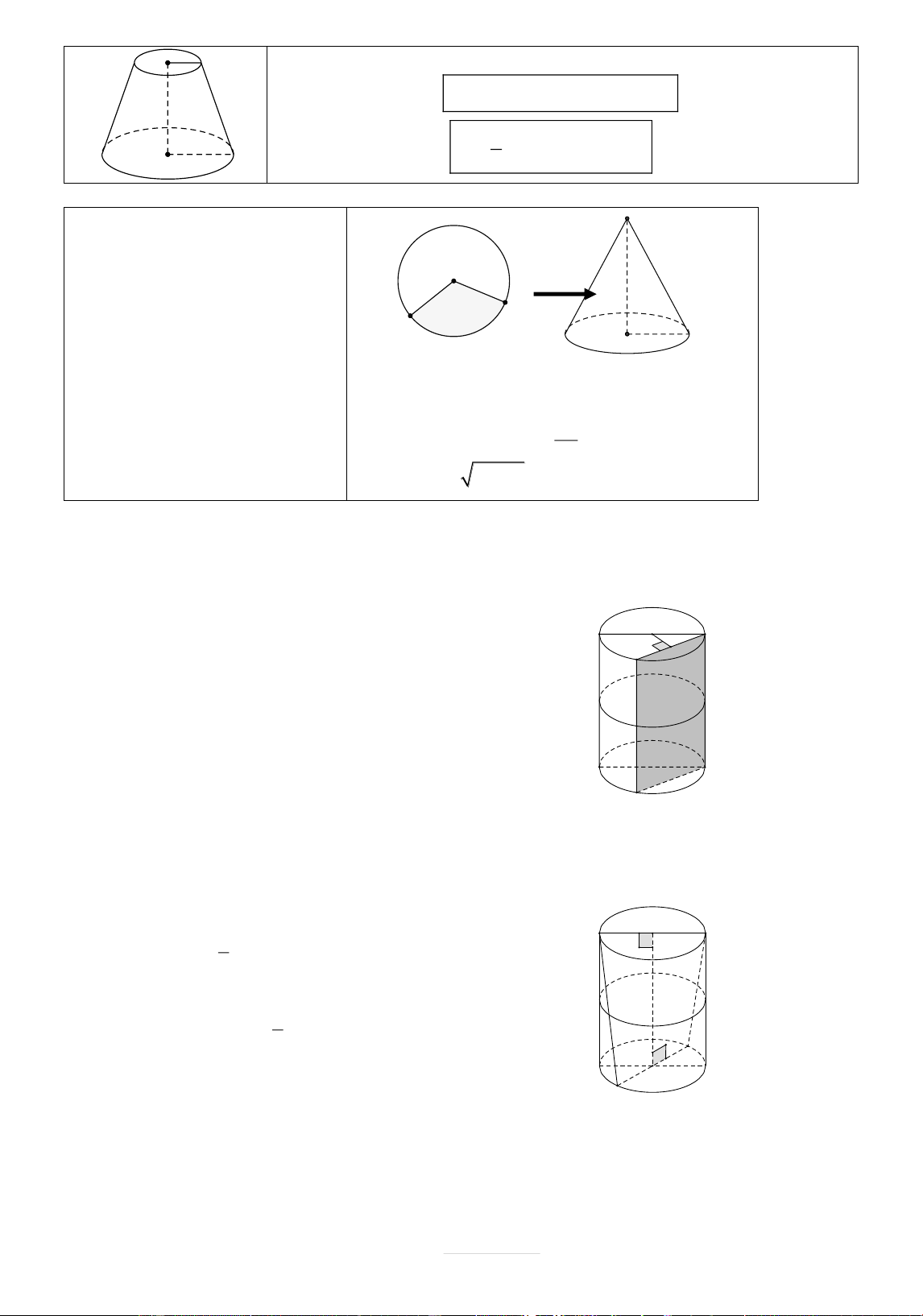
Dạng 4 Bài toán h nh n n c t
Khi cắt hình nón bởi một mặt phẳng song song với đ{y thì phần mặt phẳng nằm trong hình nón l|
một hình tròn. Phần hình nón nằm giữa hai mặt phẳng nói tr n được gọi l| h nh n n c t.
 Khi cắt hình nón cụt bởi một mặt phẳng song song với
đ{y thì được mặt cắt l| một hình tròn.
 Khi cắt hình nón cụt bởi một mặt phẳng song song với
trục thì được mặt cắt l| một hình thang c}n.
Cho hình nón cụt có Diện tích xung quanh của hình nón cụt: S  l R  r . xq  
R, r, h lần lượt l| b{n kính đ{y lớn, b{n kính 2 đ{y nhỏ v| chiều cao. S   r áy đ 1 2 2
Diện tích đ{y (hình tròn): 
 S   r  R . 2 áy đ   S  R  áy đ 2 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 55 | r
Diện tích toàn phần của hình nón cụt:
S  l R  r  r2  R2 . tp   h 1 R
Thể tích khối nón cụt: V 
h R2  r2  Rr. 3
Dạng 5 Bài toán h nh n n tạo bởi phần c n lại của h nh tr n sau khi cắt bỏ đi h nh quạt n
Từ hình tròn O;R cắt bỏ đi O
hình quạt AmB . Độ d|i cung R
AnB bằng x . Phần còn lại của R h O
hình tròn ghép lại được một hình B A r
nón. Tìm b{n kính, chiều cao v| A ≡ B m
độ d|i đường sinh của hình nón
Hình nón được tạo th|nh có đó. l   R   2 2
 r  x  r  . x
h  l2 r2 
MỘT SỐ DẠNG TO[N V\ CÔNG THỨC GIẢI B\I TO[N MẶT TRỤ
Dạng 1 hiết diện của h nh tr cắt bởi một mặt phẳng
Thiết diện vuông g c tr c l| một đường tròn b{n kính R . O A B
Thiết diện chứa tr c l| một hình chữ nhật ABCD M G
trong đó AB  R
2 v| AD  h . Nếu thiết diện qua trục
l| một hình vuông thì h  R 2 .
Thiết diện song song với tr c v| không chứa tr c l|
hình chữ nhật BGHC có khoảng c{ch tới trục l|:
d OO ';BGHC   OM D C H
Dạng 2 h t ch khối tứ diện c 2 cạnh là đường k nh 2 đá
Nếu như AB v| CD l| hai đường kính bất kỳ tr n hai đ{y của hình trụ thì: O A B 1 V  ABC . DO . O '.sin AB C , D ABCD   6
* Đặc biệt: Nếu AB v| CD vuông góc nhau thì: 1 V  ABC . DO . O ' . ABCD 6 C O' D
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 56 |
Dạng 3 Xác định g c khoảng cách
Góc giữa AB v| trục OO ' :  A O O O AB O
; O '  A'AB B . A A I O' O' O' B D B M A' A' C
Khoảng c{ch giữa AB v| trục OO ' : A d AB O ; O '  OM O O O . B A A I O' O' O' B D B M A' A' C
Nếu ABCD l| một hình vuông nội tiếp trong hình A O O O
trụ thì đường chéo của hình vuông cũng bằng đường B A A chéo của hình trụ.
Nghĩa l| cạnh hình vuông: AB  R2  h2 2 4 . I O' O' O' B D B M A' A' C
Dạng 4 Xác định mối liên hệ giữa diện t ch ung quanh, toàn phần và th t ch khối tr trong bài toán tối ưu
Một khối trụ có thể tích không đổi.
Tìm b{n kính đ{y v| chiều cao hình trụ để diện
tích to|n phần nhỏ nhất:  V R 3    S 2 min    r tp  V 4 h 3    l
Tìm b{n kính đ{y v| chiều cao hình trụ để diện
tích xung quanh cộng với diện tích đ{y v| nhỏ nhất:  V R 3   r  S min     V  h 3   
Dạng 5 nh tr ngoại tiếp, nội tiếp một h nh lăng tr đứng
+ Cho hình lăng trụ tam giác đêu nội tiếp trong một hình trụ. Thể tích khối lăng trụ là V thì 4 V 
thể tích khối trụ là V  (T) 9
+ Cho hình lăng trụ tứ giác đêu ABCD A
. 'B 'C 'D ' ngoại tiếp trong một hình trụ. Diện S 2
tích xung quanh hình trụ là S thì diện tích xung quanh của hình lăng trụ là S  xq 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 57 |
MỘT SỐ DẠNG TO[N V\ CÔNG THỨC GIẢI B\I TO[N MẶT CẦU
I. Mặt cầu ngoại tiếp khối đa diện
1/ Các khái niệm cơ bản
 Trục của đa giác đá : l| đường thẳng đi qua t}m đường tròn ngoại tiếp của đa gi{c đ{y v|
vuông góc với mặt phẳng chứa đa gi{c đ{y  Bất kì một điểm n|o nằm tr n trục của đa
gi{c thì c{ch đều c{c đỉnh của đa gi{c đó.
 Đường trung trực của đoạn thẳng: l| đường thẳng đi qua trung điểm của đoạn thẳng v|
vuông góc với đoạn thẳng đó  Bất kì một điểm n|o nằm tr n đường trung trực thì c{ch
đều hai đầu mút của đoạn thẳng.
 Mặt trung trực của đoạn thẳng: l| mặt phẳng đi qua trung điểm của đoạn thẳng v| vuông
góc với đoạn thẳng đó  Bất kì một điểm n|o nằm tr n mặt trung trực thì c{ch đều hai
đầu mút của đoạn thẳng.
2/ Tâm và bán k nh mặt cầu ngoại tiếp hình chóp
 Tâm mặt cầu ngoại tiếp hình chóp: l| điểm c{ch đều c{c đỉnh của hình chóp. Hay nói c{ch
kh{c, nó chính l| giao điểm I của trục đường tròn ngoại tiếp mặt ph ng đáy v| mặt ph ng
trung trực của một cạnh bên hình chóp.
 Bán k nh: l| khoảng c{ch từ I đến c{c đỉnh của hình chóp.
3/ Cách xác định tâm và bán k nh mặt cầu của m t số hình đa diện
a/ Hình h p chữ nh t hình l p phương.
- Tâm: trùng với t}m đối xứng của hình hộp chữ nhật (hình lập phương)  T}m l| I l|
trung điểm của AC ' .
- Bán k nh: bằng nửa độ d|i đường chéo hình hộp chữ nhật (hình lập phương).  AC ' A B B{n kính: R  . 2 D C I
b/ Hình lăng trụ đứng có đá n i tiếp đường tr n. A’ B’
ét hình l ng trụ đứng A A A .. A . A'
. A'A' .. A' . , 1 2 3 n 1 2 3 n D’ C’ An A1
trong đó có đ{y A A A A
... v| A'A'A' A'
... nội tiếp đường tròn O 1 2 3 n 1 2 3 n O A2 A3
v| O ' . Lúc đó, I
mặt cầu nội tiếp hình l ng trụ đứng có: A’n
- Tâm: I với I l| trung điểm của OO ' . A’1 O
- Bán k nh: R  IA  IA  ...  IA' . A’2 ’ 1 2 n A’3 S S
c/ Hình chóp có các đ nh nhìn đoạn thẳng nối 2 đ nh
c n lại dưới 1 góc vuông. - Hình chóp S A
. BC có SAC  SBC 0  90 . I
+ T}m: I l| trung điểm củaSC . I SC A D + B{n kính: R 
 IA  IB  IC . A C D 2 B B C
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 58 | - Hình chóp S A . BCD có
SAC  SBC  SDC 0  90 .
+ T}m: I l| trung điểm củaSC . SC + B{n kính: R 
 IA  IB  IC  ID . 2 d/ Hình chóp đều.
Cho hình chóp đềuS A . BC... S
- Gọi O l| t}m của đ{y  SO l| trục của đ{y.
- Trong mặt phẳng x{c định bởi SO v| một cạnh b n,
chẳng hạn như mp SAO , ta vẽ đường trung trực của cạnhSA M I
l|  cắt SA tại M v| cắt SO tại I  I l| t}m của mặt cầu. A - B{n kính: O SM SI D Ta có: S  MI S  OA    B{n kính l|: B SO SA C SM SA SA2 . R  IS  
 IA  IB  IC  ... SO S 2 O
e/ Hình chóp có cạnh b n vuông góc với mặt phẳng đá . Cho hình chóp S A
. BC... có cạnh b n SA  đ{y ABC... v| đ{y ABC... nội tiếp được
trong đường tròn t}m O . T}m v| b{n kính mặt cầu ngoại tiếp hình chóp S A . BC... được x{c định như sau: S
- Từ t}m O ngoại tiếp của đường tròn d
đ{y, ta vẽ đường thẳng d vuông góc với mp ABC... tại O .
- Trong mp d,SA, ta dựng đường trung M ∆ I
trực  của cạnhSA, cắtSAtạiM , cắt d tại I  I l| t}m mặt
cầu ngoại tiếp hình chóp A O
v| b{n kính R  IA  IB  IC  IS  ... C - Tìm b{n kính:
Ta có: MIOB l| hình chữ nhật. B ét M
 AI vuông tại M có: 2   2 2 2 SA
R  AI  MI  MA  AO    . 2   f/ Hình chóp khác.
- Dựng trục  của đ{y.
- Dựng mặt phẳng trung trực   của một cạnh b n bất kì.
-      I  I l| t}m mặt cầu ngoại tiếp hình chóp.
- B{n kính: khoảng c{ch từ I đến c{c đỉnh của hình chóp.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 59 | -
g/ Đường tr n ngoại tiếp m t số đa giác thường gặp.
Khi x{c định t}m mặt cầu, ta cần x{c định trục của mặt phẳng đ{y, đó chính l| đường
thẳng vuông góc với mặt phẳng đ{y tại t}m O của đường tròn ngoại tiếp đ{y. O O O Hình vuông: O l| giao Hình chữ nhật: O l| giao
đều: O l| giao điểm của điểm đường chéo.
điểm của hai đường chéo. đường trung tuyến (trọng t}m). O O vuông: O l| trung điểm
thường: O l| giao điểm của hai của cạnh huyền.
đường trung trực của hai cạnh .
II. KỸ THUẬT X[C ĐỊNH MẶT CẦU NGOẠI TIẾP CHÓP Cho hình chóp S A . A .. A
. (thoả mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường, để xác 1 2 n
định mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước: S
Bước 1: {c định t}m của đường tròn ngoại tiếp đa
gi{c đ{y. Dựng  : trục đường tròn ngoại tiếp đa gi{c đ{y. 
Bước 2: Lập mặt phẳng trung trực () của một cạnh b n. I
Lúc đó : - T}m O của mặt cầu:   mp()    O O D
- B{n kính: R  SA SO . Tuỳ v|o từng A H C trường hợp. B
Lưu ý: Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy. 
1. Trục đường tr n ngoại tiếp đa giác đá : l| đường M
thẳng đi qua t}m đường tròn ngoại tiếp đ{y v| vuông góc với mặt phẳng đ{y.
nh chất: M
   : MA  MB  MC A
Suy ra: MA  MB  MC  M   C H
2. Các bước xác định trục: B
- Bước : {c định t}m H của đường tròn ngoại tiếp đa gi{c đ{y.
- Bước : Qua H dựng  vuông góc với mặt phẳng đ{y.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 60 |
Một số trường hợp đặc biệt Tam gi{c vuông Tam gi{c đều Tam gi{c bất kì    B B H B C C H C H A A A S
3. Kỹ năng tam giác đồng dạng SO SM S
 MO đồng dạng với S  IA   . M SA SI O 4. Nh n xét: I A M
 A  MB  MC M  ,S : 
 SM l| trục đường tròn ngoại tiếp A  BC .
SA  SB  SC 
* KỸ THUẬT SỬ DỤNG HAI TRỤC X[C ĐỊNH T]M MẶT CẦU NGOẠI TIẾP ĐA DIỆN Cho hình chóp S A . A .. A
. (thõa mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường 1 2 n
để xác định mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước:
Bước 1: {c định t}m của đường tròn ngoại tiếp đa gi{c đ{y. Dựng  : trục đường tròn ngoại tiếp đa gi{c đ{y.
Bước 2: {c định trục d của đường tròn ngoại tiếp một mặt b n (dễ xác định) của khối chóp. Lúc đó: Δ
T}m I của mặt cầu:   d  I S
+ B{n kính: R  IA IS  . Tuỳ vào từng R
trường hợp. I d D C A B
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 61 |
TỔNG KẾT C[C DẠNG TÌM T]M V\ B[N KÍNH MẶT CẦU (ĐTD) SC
Loại 1: Cạnh b n SA vuông góc với đ{y v| ABC 0  90 khi đó R  v| t}m l| trung 2 điểm SC . S S A C A D B C B
Loại 2: Cạnh b n SA vuông góc đ{y v| bất kể đ{y l| hình gì, S
chỉ cần tìm được b{n kính đường tròn ngoại tiếp của đ{y l| R , D K 2 2 SA2
khi đó : R  R  . I D 4 A C abc  R  ( p : nửa chu vi). O D
4 p p  ap  bp  c B 1
 Nếu  ABC vuông tại A thì: R2  AB2  AC2  AS2  . 4 a 2
 Đ{y l| hình vuông cạnh a thì R 
, nếu đ{y l| tam gi{c đều cạnh a thì D 2 a 3 R  . D 3
Loại 3: Chóp có c{c cạnh b n bằng nhau: S SA2
SA  SB  SC  SD : R  . SO 2
 ABCD l| hình vuông, hình chữ nhật, khi đó O l| giao hai đường chéo. A D  A
 BC vuông, khi đó O l| trung điểm cạnh huyền.  A
 BC đều, khi đó O l| trọng t}m, trực t}m. B C
Loại 4: Hai mặt phẳng SAB v| ABC  vuông góc với S
nhau v| có giao tuyến AB . Khi đó ta gọi R ,R lần lượt l| 1 2 O
b{n kính đường tròn ngoại tiếp c{c tam gi{c SAB v| ABC . I A C
B{n kính mặt cầu ngoại tiếp: J K 2 2 2 AB2
R  R  R  1 2 4 B
Loại 5 : Chóp S.ABCD có đường cao SH , t}m đường tròn ngoại tiếp đ{y l| O . Khi đó ta giải 2 2 2 2
phương trình: SH x  OH 2 x2 R2    
. Với gi{ trị x tìm được ta có: R  x  R . D D V 3
Loại 6: B{n kính mặt cầu nội tiếp: r  . Stp
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 62 |
TỔNG HỢP C[C CÔNG THỨC ĐẶC BIỆT VỀ KHỐI TRÒN XOAY S 
 2Rh   r2  h2 xq    h r Chỏm cầu:     2 h h V  h  R    h2  r2 3  3 6    R S   R h  h xq  1 2 Hình trụ cụt:    h  h  h2 (phiến tr ) V  R2 1 2     h1 2     R 2 Hình n m loại 1: V  R3 tan 3   2  Hình n m loại 2:
V    R3 tan 2 3   3  3 4 S '  x   a  S   Rh;     Parabol b c hai.    parabol 3 S  h  R R R      Parabol tr n  1 1 h xoay. V   R h 2  Vtru  2 2     Diện t ch Elip và S ab elip  b Thể t ch khối  4 V   ab2 a a tr n xoa sinh xoay q uanh a 2 3  b b i Elip 4 V   a b 2 xoay q uanh b 2  3 R Diện tích hình v|nh r kh nS  R2 r2   Hình xu ến
Thể tích hình xuyến (phao) 2      2 R r R r V  2    r 2 2    R
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 63 |
PHẦN VII. HỆ TRỤC TỌA ÐỘ TRONG KHÔNG GIAN OXYZ
A. HỆ TỌA ĐỘ KHÔNG GIAN
1. Trong kh ng gian cho ba trýc Ox, Oy, Oz phån biệt và vu ng gòc tÿng đ i một.
Gốc tọa độ O, trýc hoành Ox, trýc tung Oy, trýc cao Oz, các mðt tọa độ Oxy, Oyz,Ozx.
i, j,k là các vecto đĄn vð 2 2 2
i  j  k  1 2 2
Chú ý: a  a
i j  ik  jk  0
2. Tọa độ véc tơ: u  x
( ;y;z)  u x
( ;y;z)  u  xi  y j  zk
3. Tọa độ điểm: M x
( ;y;z)  OM  xi  y j  zk
4. Các c ng thức tọa độ cæn nhớ: Cho u  a ( ;b;c), v  a ( ;b ;c )  a   a 
a) u  v  b   b c   c 
b) u v  a  a ;b b ;c  c c) ku  k
( a;kb;kc) d) u v
.  u . v .cos u ( v
, )  aa  bb  cc u v .
aa  bb  cc e) cos u ( v , )   u . v u . v 2 f) u u a2 b2 c2    
g) u  v  u v .  0
h) AB  x  x ;y  y ;z  z B A B A B A  2 2 2
i) AB  AB  x  x  y  y  z  z B A 
 B A  B A
5. Chú ý: gòc cûa 2 véc tĄ u,v là góc hình học (nhó) giĂa 2 tia mang vectĄ cò giá trð trong đoän 0;  2 
 . sin u,v  1  cos u,v  0
6. Chia tî lệ đoän thẳng: M chia AB theo tî số k nghïa là MA  kMB  x  kx A B x   M 1  k   y  ky
Công thức tọa độ của M là : A B y   M 1  k  z  kz  A B z  M  1  k 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 64 |  x  x A B x   M 2   y  y
M là trung điểm AB: MA  MB  0 A B  y   M 2  z  z  A B z  M  2 
7. G là trọng tåm tam giác ABC: 
x  x  x A B C x   G 3  
y  y  y
GA GB  GC  0 A B C  y   G 3 
z  z  z  A B C z  G  3 
8. G là trọng tåm tứ diện ABCD: 
x  x  x  x A B C D x   G 4  
y  y  y  y
GA GB GC GD  0 A B C D  y   G 4 
z  z  z  z  A B C D z  G  4 
9. Tích cò hướng 2 véc tơ: Cho 2 véc tĄ u  a
( ;b;c) và v  a ( ;b ;c )  ta đðnh nghïa tích
cò hþĆng cûa 2 véc tĄ đò là một véc tĄ, kí hiệu u
 ,v hay  cò toä độ:   u v  b c c a a b  u  ,v   ; ;
  bc b c;ca ac ;ab ba 
  b c c a a b   
10. Tính chçt tích cò hướng 2 véc tơ: a. u
 ,v vuông góc vĆi   u và v b.  
u,v  u . v .sin u ( ,v)   c.   u,v  0 cùng phþĄng    u,v
11. Ứng dụng tích cò hướng 2 véc tơ: a.  
Diện tích hình bình hành ABCD: S  AB,AD   1 b.  
Diện tích tam giác ABC: S  . AB,AC 2   c.  
Ba véc tĄ u,v,w đồng phîng: u, v w .  0  
d. Thể tích khối hộp cò đáy hình bình hành ABCD và cänh b n AA’: V  A
 B,AD A . A   1 e.  
Thể tích khối tĀ diện S.ABC: V  . AB,AC S . A 6  
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 65 |
MỘT SỐ DÄNG TOÁN THƯỜNG GẶP
VẤN ĐỀ 1: Các phép toán về toạ đ của vectơ và của điểm
– Sử dụng các công thức về toạ độ của vectơ và của điểm trong không gian.
– Sử dụng các phép toán về vectơ trong không gian.
VẤN ĐỀ 2: Xác định điểm trong không gian. Chứng minh t nh chất hình học. Diện t ch – Thể t ch.
– Sử dụng các công thức về toạ độ của vectơ và của điểm trong không gian.
– Sử dụng các phép toán về vectơ trong không gian.
– Công thức xác định toạ độ của các điểm đặc biệt.
– Tính chất hình học của các điểm đặc biệt:
 A, B, C th ng hàng  AB,AC cùng phương
 AB  k AC  A
 B,AC   0
 ABCD là hình bình hành  AB  DC  Cho A
 BC có các chân E, F của các đường phân giác trong và ngoài của góc A của A
 BC trên BC . AB AB Ta có: EB   E . C , FB  F . C AC AC
 A, B, C, D  , , không đồng ph ng
AB AC AD không đồng ph ng A  B,AC    A . D  0
VẤN ĐỀ 3: Phương trình mặt cầu
Để viết phương trình mặt cầu S ,ta cần xác định tâm I và bán kính R của mặt cầu.
Dạng 1: S  có t}m I a; b; c v| b{n kính R : 2 2 2 2 (S): x (  a)  y (  b)  z (  c)  R
Dạng 2: S  có t}m I a; b; c v| đi qua điểm A :
Khi đó bán kính R  IA.
Dạng 3: S  nhận đoạn thẳng AB cho trước l|m đường kính:
–Tâm I là trung điểm của đoạn th ng AB : x  x y  y z  z A B A B A B x  ; y  ; z  . I I I 2 2 2 B A
– Bán kính R  IA  . 2
Dạng 4: S  đi qua bốn điểm A, B, C, D (mặt cầu ngoại tiếp tứ diện ABCD ):
– Giả sử phương trình mặt cầu S  có dạng: 2 2 2
x  y  z  a 2 x  b 2 y  c
2 z  d  0  *.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 66 |
– Thay lần lượt toạ độ của các điểm A, B, C, D vào  *, ta được 4 phương trình.
– Giải hệ phương trình đó, ta tìm được a, b, c, d  Phương trình mặt cầu S  .
Dạng 5: S  đi qua ba điểm A, B, C v| có t}m I nằm tr n mặt phẳng P  cho trước: Giải
tương tự như dạng 4.
Dạng 6: S  có t}m I v| tiếp xúc với mặt cầu T  cho trước:
– Xác định tâm J và bán kính R ' của mặt cầu T .
– Sử dụng điều kiện tiếp xúc của hai mặt cầu để tính bán kính R của mặt cầu S .
(Xét hai trường hợp tiếp xúc trong và tiếp xúc ngoài)
Chú ý: Với phương trình mặt cầu S  :
x2  y2  z2  a 2 x  b 2 y  c 2 z  d  0
với a2  b2  c2  d  0 2 2 2
thì S  có t}m I  a  ; b  ; c
  v| b{n kính R  a b  c d .
VẤN ĐỀ 4: Vị tr tương đối giữa hai mặt cầu mặt cầu
Cho hai mặt cầu S I , R và S I , R . 2 2 2  1 1 1 
 I I  R  R
 S , S trong nhau 1 2  1 2 1 2
 I I  R  R
 S , S ngoài nhau 1 2  1 2 1 2
 I I  R  R
 S , S tiếp xúc trong 1 2  1 2 1 2
 I I  R  R
 S , S tiếp xúc ngoài 1 2  1 2 1 2
 R  R  I I  R  R
 S , S cắt nhau theo một đường tròn. 1 2  1 2 1 2 1 2
VẤN ĐỀ 5: T p hợp điểm là mặt cầu – T p hợp tâm mặt cầu
1. ập hợp đi m là mặt cầu
Giả sử tìm tập hợp điểm M thoả tính chất P  nào đó.
– Tìm hệ thức giữa các toạ độ x, y, z của điểm M. 2 2 2 2 x (  a)  y (  b)  z (  c)  R 2 2 2
hoặc: x  y  z  a 2 x  b 2 y  c 2 z  d  0
– Tìm giới hạn quĩ tích (nếu có). 2.
m tập hợp tâm mặt cầu x   f t() 
– Tìm toạ độ của tâm I , ch ng hạn: y   g t ( )  * z   h t() 
– Khử t trong * ta có phương trình tập hợp điểm.
– Tìm giới hạn quĩ tích (nếu có).
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 67 | MẶT PHẲNG
1. n kh{c 0 v| có gi{ vuông góc mp(P) được gọi l| véc tơ ph{p tuyến của (P).
2. Nếu n l| véc tơ ph{p tuyến của (P) thì kn k
(  0) cũng l| véc tơ ph{p tuyến của (P).
3. Phương trình tổng quát của mp(P): qua M x
( ;y ;z ) có véc tơ ph{p tuyến n  A ( ;B C ; ) l|: 0 0 0 A x
(  x )  B y (  y ) C z (  z )  0 0 0 0
4. Khai triển của phương trình tổng quát:
Ax  By Cz  D  0
(A,B,C không đồng thời bằng 0)
5. Những trường hợp ri ng của phương trình tổng quát:
 (P) qua gốc tọa độ  D=0
 (P) song song hoặc trùng (Oxy)  A=B=0
 (P) song song hoặc trùng (Oyz)  B=C=0
 (P) song song hoặc trùng (Ozx)  A=C=0
 (P) song song hoặc chứa Ox  A=0
 (P) song song hoặc chứa Oy  B=0
 (P) song song hoặc chứa Oz  C=0
 (P) cắt Ox tại A(a;0;0), cắt Oy tại B(0;b;0) v| cắt Oz tại C(0;0;c) x y z  (P) có phương trình    1 a b c
6. Khoảng cách từ 1 điểm đến mặt phẳng:
Ax  By  Cz  D 0 0 0
Cho M x ;y ;z v| P
( ) : Ax  By Cz  D  0 ; d M ( , P ( ))  0 0 0 
A2  B2  C 2 8. Chùm mặt phẳng
 Tập hợp tất cả cc mặt phẳng qua giao tuyến của hai
mặt phẳng   v| () được gọi l| một chùm mặt phẳng
 Gọi d  l| giao tuyến của hai mặt phẳng d
 : Ax  By C z  D  0 v|  : Ax  B y C z  D  0. 1 1 1 1 2 2 2 2
Khi đó nếu P  l| mặt phẳng chứa d  thì mặt phẳng P  có   P dạng
P :m. A
( x  B y C z  D )  n. A
( x  B y C z  D )  0, m2  n2  0 1 1 1 1 2 2 2 2
C[C DẠNG TO[N THƯỜNG GẶP
VẤN ĐỀ 1: Viết phương trình mặt phẳng
Để lập phương trình mặt ph ng   ta cần xác định một điểm thuộc   và một VTPT của nó.
Dạng 1:   đi qua điểm M x ;y ;z có TPT n  A;B C ;  : 0 0 0 
 : Ax x   By y  C z z  0 0 0 0 
Dạng 2:   đi qua điểm M x ;y ;z có cặp TCP a,b : 0 0 0 
Khi đó một VTPT của   là n  a
 ,b  . Dạng 3:
 đi qua điểm M x ;y ;z v| song song với mặt phẳng 0 0 0 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 68 |
 : Ax  By Cz  D  0 :
 : Ax x   By y  C z z  0 0 0 0 
Dạng 4:   đi qua 3 điểm không thẳng h|ng A,B C ,
Khi đó ta có thể xác định một VTPT của   là: n A  B,AC    
Dạng 5:   đi qua một điểm M v| một đường thẳng d  không chứa M :
– Trên d  lấy điểm A và VTCP u .
– Một VTPT của   là: n A  M,u   
Dạng 6:   đi qua một điểm M , vuông góc với đường thẳng d  :
VTCP u của đường th ng d  là một VTPT của   .
Dạng 7:   đi qua đường thẳng cắt nhau d , d : 1 2
– Xác định các VTCP a,b của các đường th ng d , d . . 1 2
– Một VTPT của   là: n  a
 ,b  .
– Lấy một điểm M thuộc d1 hoặc d  M   . 2  
Dạng 8:   chứa đường thẳng d v| song song với đường thẳng d ( d , d chéo nhau) : 1 2 1 2
– Xác định các VTCP a,b của các đường th ng d , d . 1 2
– Một VTPT của   là: n  a
 ,b  .
– Lấy một điểm M thuộc d  M   . 1  
Dạng 9:   đi qua điểm M v| song song với hai đường thẳng chéo nhau d , d : 1 2
– Xác định các VTCP a,b của các đường th ng d , d . 1 2
– Một VTPT của   là: n  a
 ,b  .
Dạng 10:   đi qua một đường thẳng d v| vuông góc với một mặt phẳng   :
– Xác định VTCP u của d và VTPT n   của  .
– Một VTPT của   là: n  u  ,n     .
– Lấy một điểm M thuộc d  M   .
Dạng 11:   đi qua điểm M v| vuông góc với hai mặt phẳng cắt nhau   ,   :
– Xác định các VTPT n ,n     của 
 và  .
– Một VTPT của   là: n  u  ,n      .
Dạng 12:   đi qua đường thẳng d cho trước v| c{ch điểm M cho trước một khoảng k cho trước:
– Giả sử () có phương trình: Ax  By  Cz+D  0 A2  B2 C 2  0 .
– Lấy 2 điểm A, B  d   A, B    ( ta được hai phương trình   1 , 2).
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 69 |
– Từ điều kiện khoảng cách d M
( ,())  k , ta được phương trình 3.
– Giải hệ phương trình  
1 , 2, 3 (bằng cách cho giá trị một ẩn, tìm các ẩn còn lại).
Dạng 13:   l| tiếp xúc với mặt cầu S tại điểm H :
– Giả sử mặt cẩu S có tâm I và bán kính R.
– Một VTPT của   là: n  IH
VẤN ĐỀ 2: Vị tr tương đối của hai mặt phẳng
Cho hai mặt phẳng P : Ax  By  Cz  D  0 v| P : A x   B y
 C z  D  0.
Khi đó: P cắt P  A : B : C  A : B : C . A B C D
P // P     . A B C D  A B C D
P  P     . A B C D
P  P          n   n      n .  n  0 AA BB CC 0. P P P P
VẤN ĐỀ 3: Khoảng cách từ m t điểm đến m t mặt phẳng.
Khoảng c{ch giữa hai mặt phẳng song song.
Hình chiếu của một điểm tr n mặt phẳng .
Điểm đối xứng của một điểm qua mặt phẳng.
 Khoảng cách từ điểm M x ; y ; z đến mặt ph ng () : Ax  By Cz  D  0 0 0 0 0     0 0 0  ,()  0  Ax By Cz D d M
A2  B2  C 2
 Khoảng cách giữa hai mặt ph ng song song bằng khoảng cách từ một điểm bất kì trên mặt
ph ng này đến mặt ph ng kia.
Chú ý: Nếu hai mặt ph ng không song song thì khoảng cách giữa chúng bằng 0.  ,
 Điểm H là hình chiếu của điểm M trên P MH n cung phuong   H  P ( ) 
 Điểm M ' đối xứng với điểm M qua P  MM  M 2 H
VẤN ĐỀ 4: Góc giữa hai mặt phẳng
Cho hai mặt ph ng  ,   có phương trình:
  : Ax  B y C z  D  0   : A x  B y C z  D  0 1 1 1 1 2 2 2 2
Góc giữa  ,   bằng hoặc bù với góc giữa hai VTPT n ,n . 1 2 .   cos (),() n n A A B B C C 1 2 1 2 1 2 1 2   n . n
A2  B2  C 2 . A2  B2  C 2 1 2 1 1 1 2 2 2 0      Chú ý: 0 0
( ),( )  90 ; ()  ()  AA  B B  C C  0 1 2 1 2 1 2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 70 |
VẤN ĐỀ 5: Vị tr tương đối giữa mặt phẳng và mặt cầu.
Phương trình mặt phẳng tiếp xúc với mặt cầu
Cho mặt ph ng   : Ax  By Cz  D  0 và mặt cầu S  x  a 2  y  b 2  z  c 2  R2 : ( ) ( ) ( )
   và S  không có điểm chung  d I(,())  R
   tiếp xúc với S   d I ( ,())  R
 là tiếp diện
Để tìm toạ độ tiếp điểm ta có thể thực hiện như sau:
– Viết phương trình đường th ng d đi qua tâm I của S  và vuông góc với   .
– Tìm toạ độ giao điểm H của d và   . H là tiếp điểm của S  với   .
   cắt S  theo một đường tròn  d I(,())  R
Để xác định tâm H và bán kính r của đường tròn giao tuyến ta có thể thực hiện như sau:
– Viết phương trình đường th ng d đi qua tâm I của S  và vuông góc với   .
– Tìm toạ độ giao điểm H của d và   .
H là tâm của đường tròn giao tuyến của S  với   .
Bán kính r của đường tròn giao tuyến: r R2 IH 2   ĐƯỜNG THẲNG
I. Phương trình của đường thẳng:
1) Vect ch phương của đường thẳng:
Ðịnh nghĩa: Cho đường thẳng d . Nếu vectơ a  0 v| có gi{ song song hoặc trùng với
đường phẳng d thì vect a được gọi l| vectơ chỉ phương của đường phẳng d . Kí hiệu: a  a ( ;a ;a ) 1 2 3  Chú :
1) a l| TCP của d thì k a . k
(  0) cũng l| TCP của d
) Nếu d đi qua hai điểm A, B thì AB l| một TCP của d
3) Trục Ox có vectơ chỉ phương a  i  (1; 0; 0)
4) Trục Oy có vectơ chỉ phương a  j  (0;1; 0)
5) Trục Oz có vectơ chỉ phương a  k  (0; 0;1)
2.Phương trình tham số của đường thẳng:
Phương trình tham số của đường thẳng ( )  đi qua điểm M x
( ;y ;z ) v| nhận a  a ( ;a ;a ) 0 0 0 0 1 2 3  l|m TCP l| : z a () x   x  ta 0 1 M 0 
M (x, y, z) y ( )  : y
  y  ta  0 2 t  O z   z  ta 0 3  x
3. Phương trình ch nh tắc của đường thẳng:
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 71 |
Phương trình chính tắc của đường thẳng ( )  đi qua điểmM x
( ;y ;z ) v| nhận a  a ( ;a ;a ) 0 0 0 0 1 2 3 l|m TCP l| : x  x y  y z  z 0 0 0 ( )  :   a a a 1 2 3
II. Vị tr tương đối của đường thẳng và mặt phẳng :
1.Vị tr tương đối của đường thẳng và mặt phẳng : PP HÌNH HỌC  M a () ()   a n  n n M M  () a a a a x
  x  a t (1) 0 1 
Định l : Trong Kg Oxyz  cho: đường thẳng ( )  : y
  y  a t (2) có TCP a  a ( ;a ;a ) 0 2 1 2 3 z
  z  a t (3) 0 3  v| qua M x
( ;y ;z ) v| mặt phẳng () : Ax  By Cz  D  0 có TPT n  A ( ;B C ; ) 0 0 0 0 Khi đó : (
) cat ( )  a n .  0
 Aa  Ba  Ca  0 1 2 3 a  n.  0 Aa 
 Ba  Ca  0 1 (
) // ( )    2 3  M  P ( )
Ax  By  Cz  D  0  0  0 0 0   a  n.  0 Aa 
 Ba  Ca  0 1 (
)  ( )    2 3  M  P ( )
Ax  By  Cz  D  0  0  0 0 0    a n
Đặc biệt: ( )  ()  a v| n cùng phương
 a : a : a  A : B : C 1 2 3 a pt( ) 
PP ĐẠI SỐ: Muốn tìm giao điểm M của  v|   ta giải hệ phương trình: 
tìm x,y,z. pt() 
Suy ra: M x,y,z  Thế  
1 ,2,3 v|o phương trình mp P v| rút gọn dưa về dạng: at  b  0 (*)
 d cắt mp P  tại một điểm  Pt * có một nghiệm t .
 d song song với P  Pt * vô nghiệm.
 d nằm trong P  Pt * có vô số nghiệm t .
 d vuông góc P   a v| n cùng phương
2. Vị tr tương đối của hai đường thẳng: PP HÌNH HỌC
Vị tr tương đối của hai đường thẳng trong không gian
Cho hai đường thẳng:  đi qua M v| có một vectơ chỉ phương u . 1 1
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 72 |
 đi qua N v| có một vectơ chỉ phương u . 2 2
     u ,u   u  ,MN  0. 1 2  1 2  1  
u ,u   0    1 2  //    . 1 2 
 u , MN  0 1  
u ,u    0     1 2 cắt    . 1 2
u ,u .MN  0  1 2 
  v|  chéo nhau  u
 ,u .MN  0. 1 2  1 2  pt( )
PP ĐẠI SỐ: Muốn tìm giao điểm M của (
) va (  ) ta giải hệ phương trình : 1  tìm 1 2 pt( )  2 
x,y,z.Suy ra: M x,y,z 
3) Vị tr tương đối giữa đường thẳng và mặt cầu: x
  x  a t (1) 0 1 
Cho đường thẳng d: y
  y  a t (2) v| mặt cầu S  : x  a 2  y
(  b 2  z  c 2  R2 ( ) ) ( ) có 0 2 z
  z  a t (3) 0 3  t}m I a
( ;b;c) , b{n kính R. PP HÌNH HỌC IM  a .  0  
B . Tính khoảng c{ch từ t}m I của mặt cầu S  đến đường thẳng d l|h  d I ( d , )  a B . So s{nh d I
( ,d) với b{n kính R của mặt cầu: ● Nếu d I
( ,d)  R thì d không cắt S  ● Nếu d I
( ,d)  R thì d tiếp xúc S  ● Nếu d I
( ,d)  R thì d cắt S tại hai điểm ph}n biệt M, N v| MN vuông góc với
đường kính (b{n kính) mặt cầu
PP ĐẠI SỐ: Thế  
1 , 2, 3 v|o phương trình S v| rút gọn đưa về phương trình bậc hai theo t *
● Nếu phương trình * vô nghiệm thì d khơng cắt S 
● Nếu phương trình * có một nghiệm thì d tiếp xc S 
● Nếu phương trình * có hai nghiệm thì d cắt S  tại hai điểm ph}n biệt M, N
Chú ý: Ðể tìm tọa độ M, N ta thay gi{ trị t v|o phương trình đường thẳng d
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 73 |
III. Góc trong không gian:
n  (A ;B ;C )
1. Góc giữa hai mặt phẳng: 1 1 1 1
Định l : Trong Kg Oxyz  cho hai mặt
n  (A ;B ;C ) 2 2 2 2
phẳng ,  x{c định bởi phương trình :
() : A x  B y  C z  D  0 1 1 1 1
() : A x  B y  C z  D  0 a 2 2 2 2 0 0  
Gọi  l| góc giữa hai mặt phẳng () & () ta có công thức: 0  90 b
A A  B B  C C 1 2 1 2 1 2 cos  ()
A2  B2  C 2 . A2  B2  C 2 1 1 1 2 2 2  a  (a; ; b c) 
2. Góc giữa đường thẳng và mặt phẳng: n  ( ; A ; B C) x  x y  y z  z Cho đường thẳng 0 0 0 ( )  :   a b c a
v| mặt phẳng () : Ax  By  Cz  D  0 0 0 0    90
Gọi  l| góc giữa hai mặt phẳng ( )
 & ()ta có công thức:
Aa  Bb  Cc sin 
A2  B2  C 2 . a2  b2  c2
3.Góc giữa hai đường thẳng : 
Cho hai đường thẳng : a  (a; ; b c) 1 x  x y  y z  z 0 0 0 ( ) :   1  a b c x  x y  y z  z 1 0 0 0 ( ) :   2 a' b' c'   2
a  (a';b'; c') 2 0 0 0    90
Gọi  l| góc giữa hai mặt phẳng ( ) & ( ) ta có công thức: 1 2
aa'  bb'  cc' cos 
a2  b2  c2 . a'2  b'2  c'2 IV. Khoảng cách:
1. Khoảng cách từ m t điểm đến m t mặt phẳng:
Cho mặt phẳng () : Ax  By  Cz  D  0 v| điểm M x
( ;y ;z ) 0 0 0 0
Khoảng c{ch từ điểm M đến mặt phẳng () được tính bởi : 0
M (x ; y ; z ) 0 0 0 0
Ax  By  Cz  D 0 0 0 d M ( ; )   0
A2  B2  C 2 H a
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 74 |
2. Khoảng cách từ m t điểm đến m t đường thẳng: Cho đường thẳng ( )  đi qua điểm M x
( ;y ;z ) v| có TCP u  a
( ;b;c). Khi đó khoảng c{ch 0 0 0 0 từ điểm M1 đến ( )
 được tính bởi công thức: M1 M  M ;u 0 1    d M ( , )   u () 1 u
M (x ; y ; z ) H 0 0 0 0
3. Khoảng cách giữa hai đường thẳng chéo nhau:
Định l : Trong Kg Oxyz  cho hai đường thẳng chéo nhau : (
) co VTCP u  a ( ;b;c ) va qua M x ( ;y ;z ) 1 0 0 0 0 ' ' ' ' ' (
) co VTCP u  a ( ;b ;c ) va qua M x ' ( ;y' ;z ' ) 2 0 0 0 0 u  ,u ' M . M ' 0 0  
Khi đó khoảng c{ch giữa (
) va (  ) được tính bởi công thứcd( ,  )  1 2 1 2  u  ;u ' u 1   M 0  u ' ' M  0 2
C[C DẠNG THƯỜNG GẶP
VẤN ĐỀ 1: L p phương trình đường thẳng
Để lập phương trình đường th ng d ta cần xác định một điểm thuộc d và một VTCP của nó.
Dạng 1: d đi qua điểm M x
( ;y ;z ) v| có TCP a  a ( ;a ;a ): 0 0 0 0 1 2 3 x
  x  a t o 1  d ( ) : y
  y  a t (t  R) o 2 z
  z  a t o 3 
Dạng 2: d đi qua hai điểm A, B : Một VTCP của d là AB .
Dạng 3: d đi qua điểm M x
( ;y ;z ) v| song song với đường thẳng  cho trước: Vì d / / 0 0 0 0
nên VTCP của  cũng là VTCP của d .
Dạng 4: d đi qua điểm M x
( ;y ;z ) v| vuông góc với mặt phẳng P  cho trước: Vì d  P 0 0 0 0
nên VTPT của P  cũng là VTCP của d .
Dạng 5: d l| giao tuyến của hai mặt phẳng P, Q :
 Cách 1: Tìm một điểm và một VTCP.  P ( )
– Tìm toạ độ một điểm A d : bằng cách giải hệ phương trình 
(với việc chọn giá Q ( )  trị cho một ẩn)
– Tìm một VTCP của d : a  n  ,n   P Q 
 Cách 2: Tìm hai điểm A, B thuộc d , rồi viết phương trình đường th ng đi qua hai điểm đó.
Dạng 6: d đi qua điểm M x
( ;y ;z ) v| vuông góc với hai đường thẳng d ,d : 0 0 0 0 1 2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 75 |
Vì d  d , d  d nên một VTCP của d là: a  a  ,a  1 2 d d   1 2
Dạng 7: d đi qua điểm M x
( ;y ;z ) , vuông góc v| cắt đường thẳng  . 0 0 0 0
 Cách 1: Gọi H là hình chiếu vuông góc của M trên đường th ng  . 0 H      M H  u  0  
Khi đó đường th ng d là đường th ng đi qua M , H. 0
 Cách 2: Gọi P  là mặt ph ng đi qua A và vuông góc với d ; Q là mặt ph ng đi qua A và chứa d.
Khi đó d  P   Q
Dạng 8: d đi qua điểm M x
( ;y ;z ) v| cắt hai đường thẳng d ,d : 0 0 0 0 1 2
 Cách 1: Gọi M d , M d . Từ điều kiện M, M , M th ng hàng ta tìm được M , M . 1 1 2 2 1 2 1 2
Từ đó suy ra phương trình đường th ng d .
 Cách 2: Gọi P  M (
,d ) , Q  M (
,d ). Khi đó d  P  Q. Do đó, một VTCP 0 1 0 2
củad có thể chọn là a  n  ,n   P Q  .
Dạng 9: d nằm trong mặt phẳng P  v| cắt cả hai đường thẳng d ,d : Tìm các giao điểm 1 2
A  d  P, B  d  P . Khi đód chính là đường th ng AB. 1 2 
Dạng 10: d song song với  v| cắt cả hai đường thẳng d ,d : 1 2
Viết phương trình mặt ph ng P  chứa  và d , mặt ph ng Q  chứa  và d . Khi đó 1 2
d  P  Q.
Dạng 11: d l| đường vuông góc chung của hai đường thẳng d , d chéo nhau: 1 2 M  N  d
 Cách 1: Gọi M d , M d . Từ điều kiện 1 
, ta tìm được M, N. 1 1 2 2 MN  d 
Khi đó, d là 2 
đường th ng MN.  Cách 2:
– Vì d  d và d  d nên một VTCP của d có thể là: a  a  ,a  1 2 d d   . 1 2
– Lập phương trình mặt ph ng P  chứad và d , bằng cách: 1
+ Lấy một điểm A trên d . 1
+ Một VTPT của P  có thể là: n  a  ,a  P d   . 1
– Tương tự lập phương trình mặt ph ng Q  chứad và d . 2
Khi đó d  P   Q.
Dạng 12: d l| hình chiếu của đường thẳng  l n mặt phẳng P :
 Lập phương trình mặt ph ng Q chứa  và vuông góc với mặt ph ng P  bằng cách:
– Lấy M   .
– Vì Q  chứa  và vuông góc với P  nên n  a  ,n  Q   P  .
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 76 |
Khi đó d  P   Q.
Dạng 13: d đi qua điểm ,
M vuông góc với d v| cắt d : 1 2
 Cách 1: Gọi N là giao điểm củad và d . Từ điều kiện MN  d , ta tìm được N. Khi đó, d là 2 1
đường th ng MN.  Cách 2:
– Viết phương trình mặt ph ng P  qua M và vuông góc với d . 1
– Viết phương trình mặt ph ng Q  chứa M và d . 2
Khi đó d  P   Q.
VẤN ĐỀ 2: Vị tr tương đối giữa hai đường thẳng
Để xét VTTĐ giữa hai đường th ng, ta có thể sử dụng một trong các phương pháp sau:
 Phương pháp hình học: Dựa vào mối quan hệ giữa các VTCP và các điểm thuộc các đường th ng.
 Phương pháp đại số: Dựa vào số nghiệm của hệ phương trình các đường th ng.
VẤN ĐỀ 3: Vị tr tương đối giữa đường thẳng và mặt phẳng
Để xét VTTĐ giữa đường th ng và mặt ph ng, ta có thể sử dụng một trong các phương pháp sau:
 Phương pháp hình học: Dựa vào mối quan hệ giữa VTCP của đường th ng và VTPT của mặt ph ng.
 Phương pháp đại số: Dựa vào số nghiệm của hệ phương trình đường th ng và mặt ph ng.
VẤN ĐỀ 4: Vị tr tương đối giữa đường thẳng và mặt cầu
Để xét VTTĐ giữa đường th ng và mặt cầu ta có thể sử dụng các phương pháp sau:
 Phương pháp hình học: Dựa vào khoảng cách từ tâm mặt cầu đến đường th ng và bán kính.
 Phương pháp đại số: Dựa vào số nghiệm của hệ phương trình đường th ng và mặt cầu.
VẤN ĐỀ 5: Khoảng cách 1.
Khoảng cách từ đi m M đến đường thẳng d
 Cách 1: Cho đường th ngd đi qua M và có VTCP a . 0 M  M,a   0  d M ( ,d)  a
 Cách 2: – Tìm hình chiếu vuông góc H của M trên đường th ng d.
– d M,d   MH.  Cách 3:
– Gọi N x; y; z  d. Tính MN 2 theo t t
( tham số trong phương trình đường th ng d).
– Tìm t để MN 2 nhỏ nhất.
– Khi đó N  H. Do đó d M,d   MH. 2.
Khoảng cách giữa hai đường thẳng chéo nhau
Cho hai đường th ng chéo nhau d và d . Biết d đi qua điểm M , d đi qua điểm M 1 2 1 1 và có VTCP a1 2 2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 77 | a  ,a  M . M  1 2  1 2 và có VTCP a d d ( ,d )  2 1 2 a  ,a   1 2 
Chú ý: Khoảng cách giữa hai đường th ng chéo nhau d , d bằng khoảng cách giữa d với mặt ph ng 1 2 1
 chứa d và song song với d . 2 1 3.
Khoảng cách giữa hai đường thẳng song song
Khoảng cách giữa hai đường th ng song song bằng khoảng cách từ một điểm thuộc đường th ng này
đến đường th ng kia. 4.
Khoảng cách giữa một đường thẳng và một mặt phẳng song song
Khoảng cách giữa đường th ng d với mặt ph ng   song song với nó bằng khoảng cách từ một
điểm M bất kì trênd đến mặt ph ng   . VẤN ĐỀ 6: Góc 1.
G c giữa hai đường thẳng
Cho hai đường th ng d , d lần lượt có các VTCP a ,a . 1 2 1 2
Góc giữa d , d bằng hoặc bù với góc giữa a ,a . 1 2 1 2 . cos  ,  a a a a 1 2  1 2 a . a 1 2 2.
G c giữa một đường thẳng và một mặt phẳng
Cho đường th ng d có VTCP a  a
( ;a ;a ) và mặt ph ng   có VTPT n  A ( ;B C ; ).Góc giữa 1 2 3
đường th ng d và mặt ph ng   bằng góc giữa đường th ng d với hình chiếu d ' của nó trên   .
Aa  Ba  Ca sin d,()  1 2 3
A2  B2  C 2 . a2  a2  a2 1 2 3 MẶT CẦU
I. Phương trình mặt cầu:
1. Phương trình ch nh tắc:
Phương trình của mặt cầu S  t}m I a;b;c, b{n kính R l|: S
x  a 2  y  b 2  z  c 2  R2 ( ) : ( ) ( ) ( )  1
Phương trình 1 được gọi l| phương trình chính tắc của mặt cầu 2 2 2 2
Đặc biệt: Khi I  O thì C
( ) : x  y  z  R
2. Phương trình tổng quát: 2 2 2 Phương trình : 2 2 2
x  y  z  a 2 x  b 2 y  c
2 z  d  0 với a  b  c  d  0 l| phương 2 2 2
trình của mặt cầu S  có t}m I a;b;c, b{n kính R  a b  c d .
II. Giao của mặt cầu và mặt phẳng:
Cho mặt phẳng () v| mặt cầu S  có phương trình :
() : Ax  By  Cz  D  0 S ( ) : x (  a 2 )  y (  b 2 )  z (  c 2 )  R2
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 78 | Gọi d I
( ;) l| khoảng c{ch từ t}m mặt cầu S  đến mặt phẳng 
Cho mặt cầu SI; R v| mặt phẳng P . Gọi H l| hình chiếu vuông góc của I l n
P d  IH  dI,P. d  R d  R d  R
Mặt phẳng tiếp xúc mặt cầu.
P l| mặt phẳng tiếp diện Mặt phẳng cắt mặt cầu theo
Mặt cầu v| mặt phẳng không
thiết diện l| đường tròn có của mặt cầu v| có điểm chung.
t}m I v| b{n kính
H: tiếp điểm. 2 2
r  R  IH
Dạng 1: S  có t}m I a;b;c v| b{n kính R : S  x  a 2  y  b 2  z  c 2  R2 : ( ) ( ) ( )
Dạng 2: S  có t}m I a;b;c v| đi qua điểm A :
Phương pháp: Khi đó b{n kính R  IA.
Dạng 3: S  nhận đoạn thẳng AB cho trước l|m đường kính: Phương pháp: 
T}m I l| trung điểm của đoạn thẳng x  x y  y z  z A B A B A B AB : x  ; y  ; z  . I I I 2 2 2 AB 
B{n kính R  IA  . 2
Dạng 4: S  đi qua bốn điểm A,B C
, ,D ( mặt cầu ngoại tiếp tứ diện) Phương pháp: 
Giả sử S  có dạng: x2  y2  z2  a 2 x  b 2 y  c
2 z  d  0 *. 
Thay lần lượt toạ độ của c{c điểm A,B C
, ,D v|o *, ta được 4 phương trình. 
Giải hệ phương trình đó, ta tìm được a,b,c,d  Phương trình mặt cầu S  .
Dạng 5: S  đi qua ba điểm A,B C
, v| có t}m I nằm tr n mặt phẳng P  cho trước:
Phương pháp: Giải tương tự như dạng 4.
Dạng 6: S  có t}m I v| tiếp xúc với mặt cầu T  cho trước: Phương pháp: 
{c định t}m I v| b{n kính R ' của mặt cầu T  . 
Sử dụng điều kiện tiếp xúc của hai mặt cầu để tính b{n kính R
của mặt cầu S  . ( ét hai trường hợp tiếp xúc trong v| ngo|i)
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 79 |
Chú : ới phương trình mặt cầu S  x2  y2  z2 :  a 2 x  b 2 y  c 2 z  d  0
với a2  b2  c2  d  0 thì S  có t}m I  a – ; b – ; c –  v| b{n kính R a2 b2 c2     d .
Cho hai mặt cầu S I , R v| S I , R . 2 2 2  1 1 1 
 I I  R  R
 S , S trong nhau 1 2  1 2 1 2
 I I  R  R
 S , S ngo|i nhau 1 2  1 2 1 2
 I I  R  R
 S , S tiếp xúc trong 1 2  1 2 1 2
 I I  R  R
 S , S tiếp xúc ngo|i 1 2  1 2 1 2
 R  R  I I  R  R
 S , S cắt nhau theo một đường tròn 1 2  1 2 1 2 1 2
Dạng 7: iết phương trình mặt cầu S  có t}m I a;b;c , tiếp xúc với mặt phẳng P  cho trước.
Phương pháp: B{n kính mặt cầu R  d I;P 
Dạng 8: iết phương trình mặt cầu S  có t}m I a;b;c , cắt mặt phẳng P  cho trước theo
giao tuyến l| một đường tròn thoả điều kiện .
a. Đường tròn có diện tích cho trước.
b. Đường tròn có chu vi cho trước.
c. Đường tròn có b{n kính cho trước. Phương pháp:
 Từ công thức diện tích đường tròn S  r2
 hoặc chu vi đường tròn P  2r ta tìm
được b{n kính đường tròn giao tuyến r .
 Tính d  d I,P  2 2
Tính b{n kính mặt cầu R  d  r
 Kết luận phương trình mặt cầu.
Dạng 8: iết phương trình mặt cầu S  có t}m I a;b;c , cắt mặt phẳng P  cho trước theo
giao tuyến l| một đường tròn thoả điều kiện. Phương pháp:
 Ta có b{n kính mặt cầu R  d I;P
 Kết luận phương trình mặt cầu.
Dạng 10: iết phương trình mặt cầu S  tiếp xúc với một đường thẳng  cho trước v| có t}m
I a;b;c cho trước. Phương pháp
Đường thẳng  tiếp xúc với mặt cầu S  ta có R  d I,  .
Dạng 11: iết phương trình mặt cầu S  tiếp xúc với một đường thẳng  tại tiếp điểm
M x ,y ,z thuộc  v| có t}m I thuộc đường thẳng d cho trước. o o o  Phương pháp
 iết phương trình mặt phẳng P  đi qua điểm M v| vuông góc với đường thẳng  .
 Toạ độ t}m I  P   l| nghiệm của phương trình.
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 80 |
 B{n kính mặt cầu R  IM  d I, .
 Kết luận về phương trình mặt cầu S 
Dạng 12: iết phương trình mặt cầu S  có t}m I a;b;c v| cắt đường thẳng  tại hai điểm
A,B thoả mãn điều kiện:
a. Độ d|i AB l| một hằng số.
b. Tam gi{c IAB l| tam gi{c vuông.
c. Tam gi{c IAB l| tam gi{c đều. Phương pháp AB
{c định d I,   IH , vì I
 AB c}n tại I n n HB  2 2 2
a. B{n kính mặt cầu R  IH  HB IH
b. B{n kính mặt cầu R  o sin 45 IH
c. B{n kính mặt cầu R  o sin 60
MỘT SỐ DẠNG GIẢI NHANH CỰC TRỊ KHÔNG GIAN
Cho P  và hai điểm A, B.
+ Nếu A và B trái phía so vĆi P 
Tìm M  Pđể MA  MB ?
 M,A,B thîng hàng  M  AB  P min
+ Nếu A và B cùng phía so vĆi P 
Tìm B ' là đối xĀng cûa B qua P 
 M,A,B ' thîng hàng  M  AB ' P
Cho P  và hai điểm A, B.
+ Nếu A và B cùng phía so vĆi P 
Tìm M  Pđể MA  MB ?
 M,A,B thîng hàng  M  AB  P max
+ Nếu A và B trái phía so vĆi P 
Tìm B ' là đối xĀng cûa B qua P 
 MA  MB '  AB '
Cho điểm M x ;y ;z kh ng thuộc  M M M 
các trýc và mðt phîng tọa độ. Viết   x y z P :    1
phþĄng trình P  qua M và cít 3 tia x 3 y 3 z 3 M M M Ox O , y O
, z læn lþợt täi A,B C , sao cho V nhó nhçt? O A . BC
Viết phþĄng trình mðt phîng P  chĀa     QuaA d  P : đþąng thîng 
d , sao cho khoâng cách tÿ n    P   ud,AM ,ud      
điểm M d đến P  là lĆn nhçt?
Viết phþĄng trình mðt phîng P    Q  ua A  P : 
qua A và cách M một khâng lĆn nhçt n
 P  AM 
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 81 |
Viết phþĄng trình mðt phîng P  chĀa     QuaA d  P : 
đþąng thîng d , sao cho P  täo vĆi  n    P  
ud,u ud      
(  kh ng song song vĆi d ) một gòc lĆn nhçt là lĆn nhçt ?
Cho  / /P. Viết phþĄng trình
Lçy A   gọi Alà hình chiếu vu ng gòc cûa   đþąng thîng Qua A
d song song vĆi  và 
A trên P  d : 
cách  một khoâng nhó nhçt ? ud  u 
Viết phþĄng trình đþąng thîng d đi Q  ua A  d 
qua điểm A cho trþĆc và nìm trong d :  u  
d  n P, AM
mðt phîng P  cho trþĆc sao cho   
khoâng cách tÿ điểm M cho trþĆc đến
d là lĆn nhçt ( AM không vuông góc vĆi P  ) ?
Viết phþĄng trình đþąng thîng d đi Q  ua A  d 
qua điểm A cho trþĆc và nìm trong d :  u  n  ,AM   ,n  mðt phîng  d P P
P  cho trþĆc sao cho      
khoâng cách tÿ điểm M cho trþĆc đến
d là nhó nhçt ( AM không vuông góc vĆi P  ) ?
Viết phþĄng trình đþąng thîng d đi Q  ua A  d 
qua điểmA  P cho trþĆc , sao cho d :  u    d 
nP,AM ,nP      
d nìm trong P  và täo vĆi đþąng
thîng  một gòc nhó nhçt vĆi  cít
nhþng kh ng vu ng gòc vĆi P  ?
Nguyễn Chiến - Hồng Quân: 0973.514.674 Page 82 |

Tóm tắt lý thuyết và giải nhanh Toán 12 – Nguyễn Chiến, Nguyễn Hồng Quân

Thông tin :

Tài liệu liên quan:

Bộ đề tham khảo tốt nghiệp THPT 2025 môn Toán sở GD&ĐT Vĩnh Phúc

Đề minh họa chọn học sinh giỏi Toán 12 năm 2024 – 2025 sở GD&ĐT Vĩnh Phúc

Đề học sinh giỏi Toán 12 THPT cấp tỉnh năm 2024 – 2025 sở GD&ĐT Hải Dương

Đề học sinh giỏi Toán 12 GDTX cấp tỉnh năm 2024 – 2025 sở GD&ĐT Hải Dương

Chuyên đề toán thực tế thống kê môn Toán 11