ÔN TẬP LÝ THUYẾT XÁC SUẤT THỐNG KÊ
1. Định nghĩa xác suất m : P(A) A  . Tính chất ( P A)  1  ( P A) n
Tính n trước, là số tất cả khả năng có thể xảy ra hay số phần tử của không gian mẫu.
2. Công thức cộng (hoặc, hay):
Xung khắc là biến cố này xảy ra thì biến cố kia không xảy ra.
Nếu A, B là hai biến cố bất kỳ thì:
P A  B  ( P ) A  ( P )
B  P(A ) B .
Nếu A, B là hai biến cố xung khắc thì: P A   B  (
P A)  P(B) .
3. Công thức nhân (và):
Độc lập là biến cố này xảy ra không ảnh hưởng đến việc xảy ra của biến cố kia.
Nếu A , A , A là các biến cố bất kỳ thì: (
P A A A )  P(A ).P(A |A ).P(A |A A ). 1 2 3 1 2 3 1 2 1 3 1 2
Nếu các biến cố A , A , A là độc lập thì: P A A A   P A .P A .P A . 1 2 3  1   2   3  1 2 3
4. Công thức Bayes
Các biến cố A , A , A được gọi là họ đầy đủ nếu xung khắc và chắc chắn có một biến cố trong họ 1 2 3 xảy ra.
B là một biến của phép thử. Khi đó: ( P ) B  ( P A ).P  | B A   ( P A ).P  | B A   (
P A ).P B|A . 1 1 2 2 3  3   P A P B A P A .P | B A P A .P | B A P A |B  .  |   1 1
, P A |B
, P A |B . 3       3 3 2       2 2 1 P B PB P B
Chú ý. Công thức Bayes thường được sử dụng khi đề bài cho biết một sự việc đã xảy ra rồi .
(ta đặt đó là biến cố B và tính P(B)).
5. Một số tính chất P A   B  P . A  B và P  .
A B  PA  B .
6. Phân phối nhị thức X  ( B ; n )
p , n là số lần thử, p là xác suất không đổi.
Dấu hiệu nhận biết phân phối nhị thức là “xác suất xảy ra của 1 sự kiện A nào đó luôn bằng p
không thay đổi”, ví dụ tỷ lệ phần tử A chiếm 70%, hay trong 1000 sản phẩm có 200 sản phẩm loại A,...vv.
X có phân phối nhị thức thì X là số tự nhiên nhỏ nhất bằng 0 và lới nhất bằng n.
Công thức tính xác suất: Bam may k n-k X nX
1) P X  k  k k C p p nCX p p n 1      1    x k Bam may a X n
2) P X  a 
nCXp  X 1   p  x 0 Bam may n X nX
3) P X  a 
nCXp    1 p  x a
7. Phân phối Poisson X  ( P )
λ , λ là trung bình số lần biến cố A xảy ra trong 1 khoảng thời gian hay trên 1 miền.
Dấu hiệu nhận biết phân phối Poisson là “1 sự kiện A nào đó xảy ra trong 1 khoảng thời gian,
hay trên một vùng, trên một miền nào đó”.
Công thức tính xác suất: λ e . k Bam may k λ λ e . X λ
1) P X  k      , k! x  X! k Bam may a  λ e . X λ
2) P X  a   x  X ! 0 Bam may a λ e . X λ
3) P X  a  1 P X  a   1   x 0 X!
X có phân phối Poisson thì X là số tự nhiên nhỏ nhất bằng 0 và lới nhất không bị giới hạn.
8. Phân phối siêu bội X  H(N; N ; ) n A
Một tập hợp có N phần tử, trong đó có N phần tử có tính chất A, lấy ra n phần tử . A k n -k C C N -
Công thức tính xác suất: ( P X  ) N N A A k  . n CN
9. Phân phối chuẩn X Nμ σ  2 ~ ;
, µ là trung bình, σ là độ lệch chuẩn và σ2 là phương sai. Công thức tính xác suất: a μ
1) P X      a     σ  a μ
2) P X  a      1     σ  b μ a μ
3) P a  X b               σ   σ  a
4) P  X μ a       2     σ  α
Tra bảng phân phối chuẩn tắc tìm giá trị tới hạn: z z α . α    α   / 2 2
Bảng phân phối chuẩn tắc dương thì
z  , còn âm thì z  .
10. Ước lượng trung bình
a. Bài toán 1: Ước lượng khoảng trung bình (hay tính độ chính xác ε):
 Biết độ tin cậy  , ta tính được  1   .  Từ bảng ta tìm được z . /2 z .s
 Tính độ chính xác (sai số ước lượng):  /2   . n
 Ước lượng khoảng cho trung bình tổng thể là:   X  ; X   
b. Bài toán tính kích thước mẫu và độ tin cậy của ước lượn g trung bình
Bài toán 3: Ước lượng trung bình biết  và độ chính xác (hay sai số)  , tìm kích thước mẫu n?  Tính s.  Từ độ tin cậy 
Tra bảng tìm được z . /2 2  z .s   Kích thước mẫu là: /2 n       
Bài toán 4: Ước lượng trung bình biết n và độ chính xác (hay sai số)  , tìm độ tin cậy  ?  Tính n, s.   n Tính z   . /2 s
 Độ tin cậy đạt được là:   2. z 1  /2 
11. Ước lượng tỷ lệ
a. Bài toán 2: Ước lượng khoảng tỷ lệ (hay tính độ chính xác ε)
Từ một mẫu có kích thước n ta tính số lần m biến cố A xuất hiện trong mẫu đó, từ đó tính được m
tỷ lệ mẫu là f  . n  Từ độ tin cậy 
Tra bảng tìm được z .  /2 f 1  f 
 Tính độ chính xác ( sai số ước lượng ):   z .  . /2 n
 Ước lượng khoảng cho tỷ lệ tổng thể là: p f  ; f   
b. Tính kích thước mẫu và độ tin cậy của ước lượng
Bài toán 5: Ước lượng tỷ lệ biết  và độ chính xác (hay sai số)  , tìm kích thước mẫu n? m  Tính f  . n  Từ độ tin cậy 
Tra bảng tìm được z .  /2  z   2 . f 1 f / 2  
 Kích thước mẫu là: n  2 
Bài toán 6: Ước lượng tỷ lệ biết n và độ chính xác (hay sai số)  , tìm độ tin cậy  ?  m Tính n , m , f  . n n  Tính z    /2 f 1 . f 
 Độ tin cậy đạt được là:   2. z 1  /2 
13. Kiểm định
a. Bài toán đặt giả thuyết kiểm định:
Giả thuyết H0 là câu văn thể hiện: một tuyên bố; một kết luận có sẵn; một báo cáo đã nói; một
quy định; một nghiên cứu; một đ ề
i u bình thường hiểu là như vậy.
Ký hiệu dùng trong giả thuyết H0 phải là một trong 3 dấu sau: ;  ;   .
Giả thuyết H1 là câu văn thể hiện: một điều nghi ngờ; một điều gì đó ta đang muốn chứng
minh; đánh giá sự hiệu quả của một phương pháp mới; một giả thuyết đang muốn kiểm định.
Ký hiệu dùng trong giả thuyết H0 phải là một trong 3 dấu sau: ;  ;   .
b. Bài toán kiểm định trung bình
Tính các tham số mẫu: ; n x; s . x   n 0 
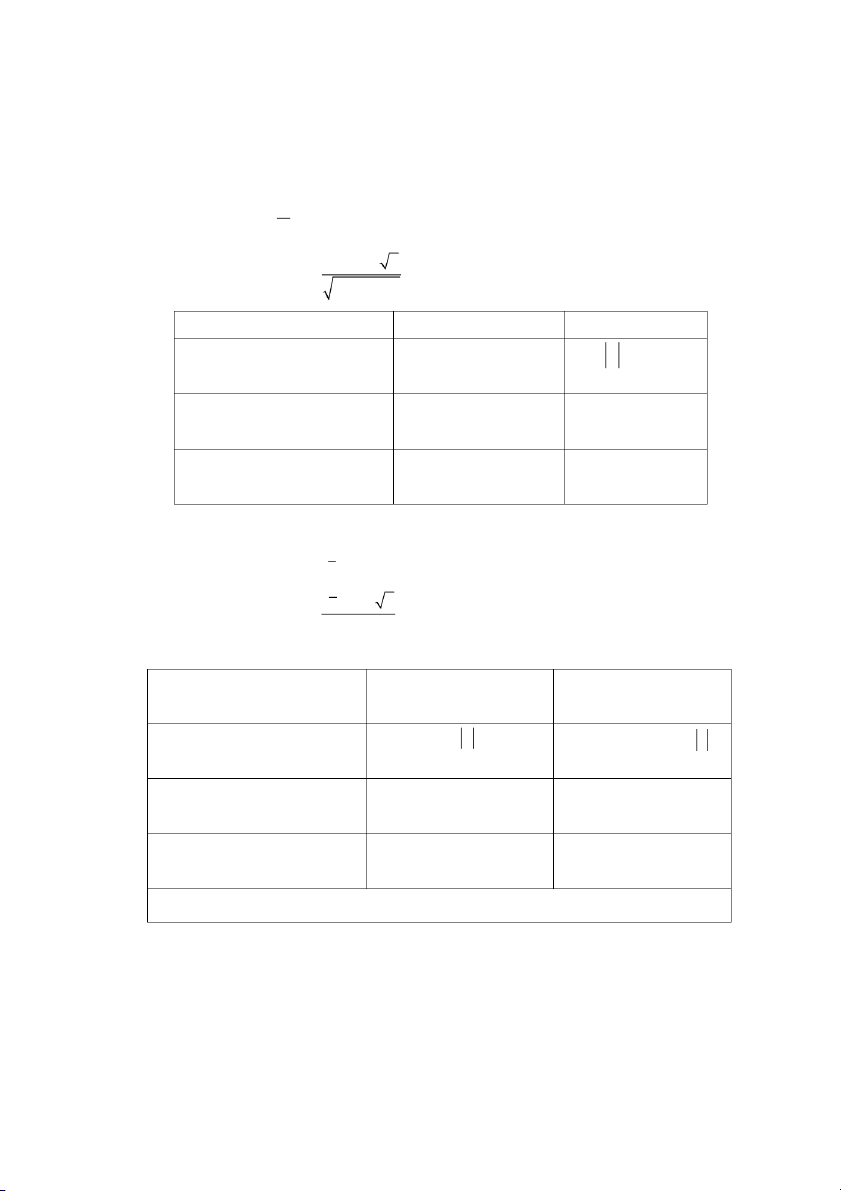
Tính giá trị kiểm định: z  . s
Giả thuyết kiểm địn h
Tra bảng giá trị tới hạn Quy tắc bác bỏ H0 H :   0 0 z  I :   z z /2 /  2 H :     1 0  H :    H :     0 0 z z II :  ; 0 0  z  H :     H :     1 0 1 0 H :    H :      0 0 z z III :  ; 0 0  z  H :     H :    1 0  1 0
c. Bài toán Kiểm định tỷ lệ m
Tính tỷ lệ mẫu: f  . n  f  p n 0 
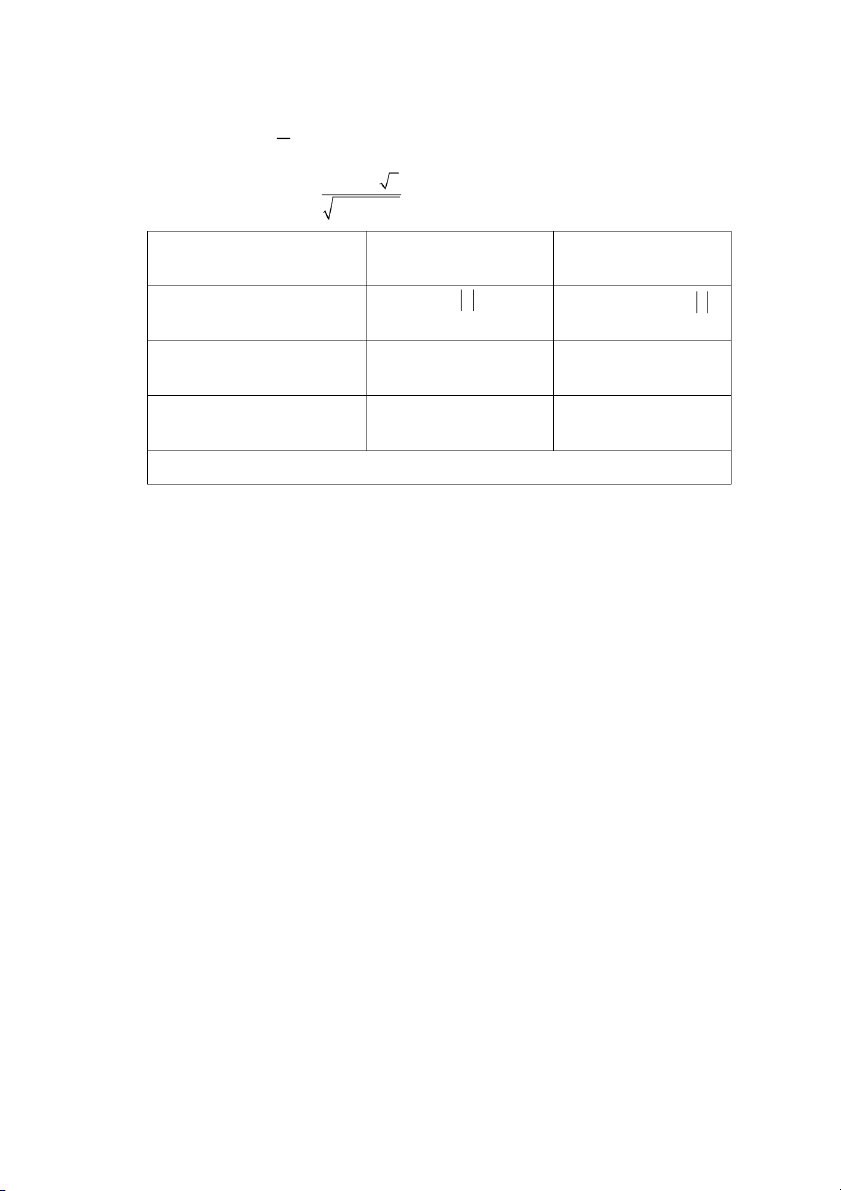
Tính giá trị kiểm định: z  . p 1  p 0  0
Giả thuyết kiểm địn h
Tra bảng giá trị tới hạn Quy tắc bác bỏ H0
H : p  p 0 0 z  I :   z z /2 /  2
H : p  p  1 0
 H : p  p
H : p  p  0 0 z z II :  ; 0 0  z 
H : p  p 
H : p  p  1 0 1 0
H : p  p
H : p  p   0 0 z z III :  ; 0 0  z 
H : p  p 
H : p  p 1 0  1 0
d. Bài toán tính p-value của kiểm định trung bình
Tính các tham số mẫu: ; n x; s . x   n 0 
Tính giá trị kiểm định: z  . s
Giả thuyết kiểm địn h
Tra bảng phân phối
Tính giá trị p-value
chuẩn tắc dương hoặc âm  H :     z        0 0 I p value 2 1 z :      H :     1 0  H :    H :     z     0 0 p value 1 z II :  ; 0 0  H :     H :     1 0 1 0 H :    H :     z    0 0 p value z III :  ; 0 0  H :     H :    1 0  1 0
Quy tắc kiểm định: Nếu p  value   thì Bác bỏ H0 .
e. Bài toán tính p-value của kiểm định tỷ lệ m
Tính tỷ lệ mẫu: f  . n  f  p n 0 
Tính giá trị kiểm định: z  . p 1  p 0  0
Giả thuyết kiểm địn h
Tra bảng phân phối
Tính giá trị p-value
chuẩn tắc dương hoặc âm
 H : p  p   z        0 0 I :  p value 2 1  z   
H : p  p  1 0
 H : p  p
H : p  p  z     0 0 p value 1 z II :  ; 0 0  H  : p  p
H : p  p 1 0  1 0
H : p  p
H : p  p  z    0 0 p value z III :  ; 0 0 
H : p  p 
H : p  p 1 0  1 0
Quy tắc kiểm định: Nếu p  value   thì Bác bỏ H0 .