TỐI ƯU HÓA QUÁ TRÌNH
T R O N G C N S H - C N T P
Giảng viên: TS Nguyễn Trường Giang
Bộ môn CNSH, Viện CNSH và CNTP
Đại học Bách Khoa Hà Nội LOGO N Ộ I D U N G 1. MỞ ĐẦU
2. TỐI ƯU HÓA QUÁ TRÌNH MỘT MỤC TIÊU ĐA YẾU TỐ
2.1. PHƯƠNG PHÁP GAUSS-SEIDENT
2.2. PHƯƠNG PHÁP BOX-WILLSON
3. TỐI ƯU HÓA QUÁ TRÌNH ĐA MỤC TIÊU ĐA YẾU TỐ
4. ỨNG DỤNG QUY HOẠCH TUYẾN TÍNH TRONG QUẢN LÝ SẢN XUẤT, CNTP VÀ CNSH
5. GIẢI QUY HOẠCH TUYẾN TÍNH BẲNG PHƯƠNG PHÁP CHUYỂN VỊ
6.GIẢI QUY HOẠCH TUYẾN TÍNH BẰNG PHƯƠNG PHÁP ĐƠN HÌNH
7. GIẢI QUY HOẠCH TUYẾN TÍNH BẲNG PHƯƠNG PHÁP ĐỔI HÌNH DẠNG BẢNG
8. ỨNG DỤNG QUY HOẠCH TUYẾN TÍNH TRONG KỸ THUẬT PHA ĐẤU THỰC PHẨM
9. BÀI TOÁN VẬN TẢI 10. ÔN TẬP LOGO
Tối ưu hóa quá trình một mục tiêu, đa yếu tố
Quá trình một mục tiêu đa yếu tố X1 X2 Y1 X QT 3 Xn
Ví dụ: Hoạt lực enzyme của nấm nấm mốc Aspergillus oryzae
phụ thuộc vào các yếu tố (x ): độ ẩm cơ chất, độ ẩm tương đối i
không khí, nhiệt độ nuôi cấy, bề dày của lớp cơ chất trên
khay… Tìm x để hoạt lực α-enzyme amylaza đạt cao nhất. i LOGO
Tối ưu hóa quá trình một mục tiêu, đa yếu tố
I. Phương pháp Gauss- Seident
Bản chất Phương pháp:
+ Cho 1 yếu tố thay đổi, cố định tất cả yếu
tố còn lại  tìm được giá trị làm y cực trị (max or min)
+ lặp lại quá trình trên nhưng thay đổi liên
tục các yếu tố khác nhau  tìm được tập giá
trị các yếu tố ảnh hưởng làm y max or min LOGO I. PP Gauss - Seident
 Phương pháp do hai nhà toán học người Đức Carl
Friedrich Gauss và Phillipp Ludwig von Seidel đề ra.
 Bản chất của phương pháp: Cố định các trục tại
một điểm khởi phát nào đó x yếu tố ảnh hưởng i-1
còn cho yếu tố x di chuyển. Trong quá trình di i
chuyển sẽ tìm được yếu tố mà tại đó mục tiêu đạt
cực đại hoặc cực tiểu. LOGO I. PP Gauss - Seident
• Trình tự tiến hành:
1) Làm thí nghiệm sơ bộ để xác định khoảng xác định
có ý nghĩa công nghệ của x (i số yếu tố ảnh hưởng) i
2) Tối ưu hóa quá trình bằng phương pháp Gauss-Seidel
+ Vòng tính 1: Cho n-1 yếu tố nhận một giá trị khởi
phát nào đó trong khoảng xác định có ý nghĩa công
nghệ của chúng còn yếu tố thứ k nào đó di động trong
khoảng xác định có ý nghĩa công nghệ của nó. Từ đây
xác định được giá trị của yếu tố mà mục tiêu đạt cực trị,
xác định x 1 optimal  y 1 max. k 1
Lặp lại quá trình như trên cho x để tìm ra x 1 optimal k+1 k+1 LOGO I. PP Gauss - Seident
Nếu có n yếu tố ta có n đợt thí nghiệm và nhận được y 1 max i (i = 1÷n)
+ Vòng tính 2: Ta lặp lại giống vòng 1 nhưng các điểm khởi phát thay đổi.
Sau vòng 2 ta nhận được y 2 max (i = 1÷n) i
+ Vòng tính 3: Ta lặp lại giống vòng 1 và 2 nhưng thay đổi
điểm cố định ban đầu
Sau vòng 3 ta nhận được y 3 max (i = 1÷n) i Cần tìm:
Lim y 1, y 2, y 3 , và đưa ra kết luận. i i i số vòng lặp  LOGO I. PP Gauss - Seident
 Ứng dụng trong trường hợp cụ thể:
 Ví dụ nuôi cấy nấm mốc thu enzyme, hoạt lực enzyme (y)
thu được phụ thuộc vào điều kiện nuôi cấy: độ ẩm cơ chất
(50-60%), độ ẩm tương đối không khí (65-85%), nhiệt độ nuôi cấy (25-35oC).
 Yêu cầu: Tìm điều kiện nuôi cấy để hoạt lực enzyme thu
được là cao nhất.
 Giải thích ý tưởng Gauss-Seident với bài toán này: cố
định 2 trong 3 yếu tố còn cho 1 yếu tố thay đổi. LOGO I. PP Gauss - Seident  Vòng 1:
 Bước 1: Gọi x là độ ẩm cơ chất, x là độ ẩm tương đối 1 2
không khí, x là nhiệt độ nuôi cấy. Cố định x = 52%, x = 3 1 2
70%, còn cho x thay đổi ở các mốc 25, 27, 29, 31, 33, 35 3 oC.
 Thảo luận ta phải tiến hành thực nghiệm như thế nào?
 Làm 6 mẫu thí nghiệm và phân tích hoạt lực enzyme và
ghi lại kết quả, chọn ra nhiệt độ tương ứng với hoạt lực
enzyme cao nhất. Chẳng hạn x = 29oC, y 1max = 75 U/g 3 1 LOGO I. PP Gauss - Seident
Bước 2: Ta cố định x = 52%, x = 29 oC, còn cho 1 3
x thay đổi ở các mốc 65, 69, 73, 77, 81, 85 % 2
(khoảng biến thiên 4%)
Cũng tiến hành thí nghiệm tương tự như vòng 1
và chọn ra giá trị x tương ứng với giá trị y 1max = 2 2
81 U/g. Chẳng hạn x = 77%. 2 LOGO I. PP Gauss - Seident
Bước 3: Cố định x = 77%, x = 29oC và cho x 2 3 1
thay đổi ở các mốc 50, 52, 54, 56, 58, 60%.
Tìm được kết quả: x = 54%, y = 89. 1 max
Như vậy thu được: y 1max = 75, y 1max = 77, y 1max 1 2 3
= 89  y1max = 89
bài toán đến đây đã được giải chưa? LOGO I. PP Gauss - Seident
 Vòng 2: Cố định x = 54%, x = 72% cho x thay đổi. Tiến 1 2 3
hành thí nghiệm như vòng 1
 Thu được kết quả y2max = 92 U/g
 Vòng 3: x = 56%, x = 74% và cho x thay đổi. Tiến hành 1 2 3
thí nghiệm như vòng 1 và 2
 Thu được kết quả y3max = 91 U/g
 Tiến hành tiếp các vòng và kết luận.
 Nếu sau vòng 4: y2max < y4max < y3max, ta có thể kết luận giá
trị cực đại nằm trong khoảng [y2max, y3max] LOGO I. PP Gauss - Seident Kết luận chung:
+ Hạn chế của phương pháp Gauss-Seidel là
không tính đến đồng tác động của các yếu tố ảnh
hưởng, từ đó có thể dẫn tới sai số trong kết quả.
+ Kết quả chỉ tiệm cận được vào vùng tối ưu. Nếu
muốn tìm được chính xác thì phải làm rất nhiều
vòng lặp thí nghiệm, tốn thời gian công sức và tiền bạc. LOGO I. PP Gauss - Seident
Ví dụ về sự không tính đến đồng tác
động của các yếu tố:
- Nhiệt độ thủy phân tinh bột tối ưu bởi enzyme amylase: + Khi pH=4,8 là 70 oC + Khi pH =5,2 là 73 oC LOGO
TỐI ƯU HÓA QUÁ TRÌNH MỘT MỤC TIÊU ĐA YẾU TỐ
II. PHƯƠNG PHÁP DÙNG GRADIENT
PHƯƠNG PHÁP BOX – WILLSON Năm 1952.
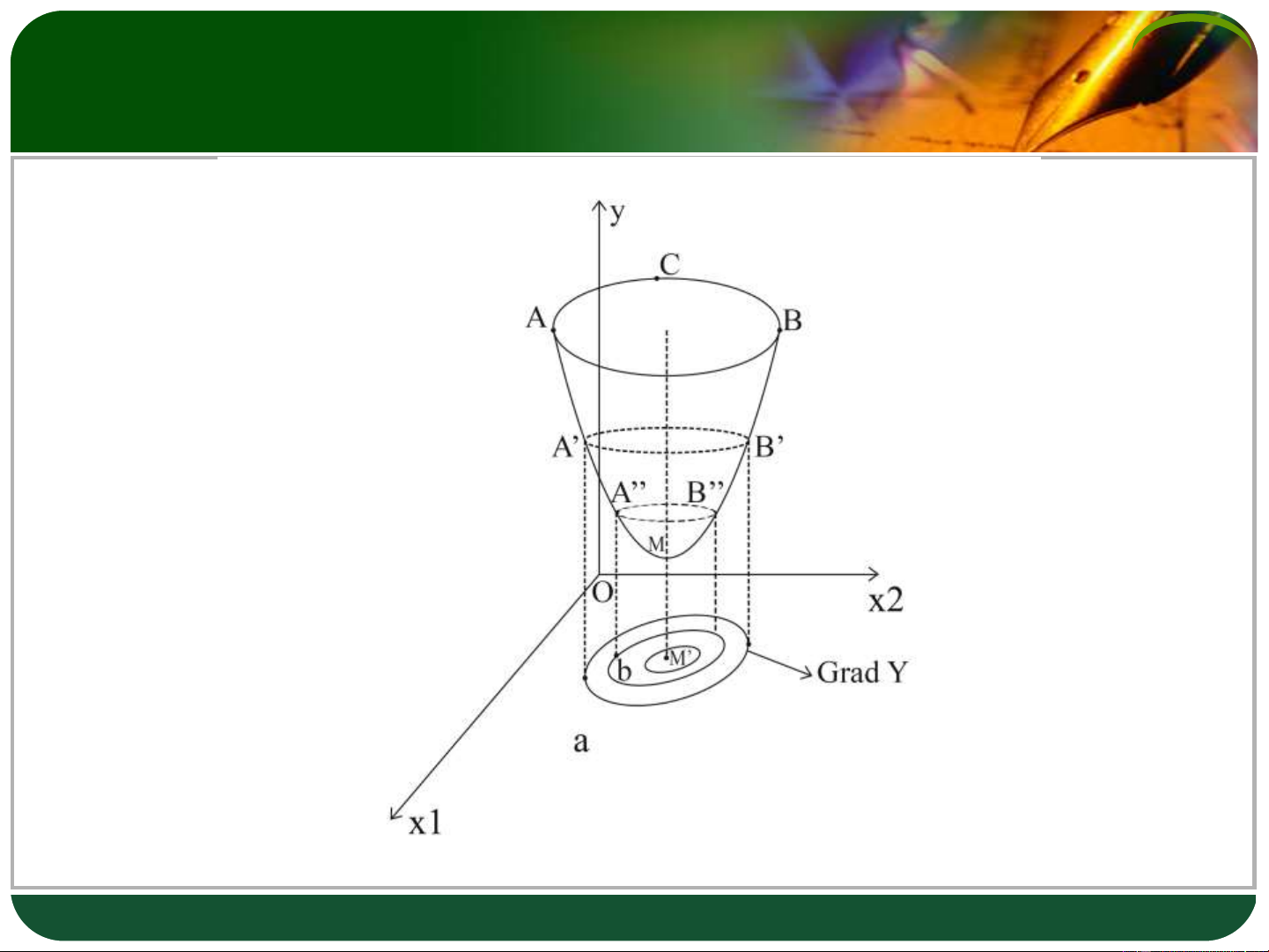
Ý tưởng: Biết được dáng điệu của 1 đường đồng mức thì có thể
chỉ ra các yếu tố chuyển địch đồng thời một lúc như thế nào để sau
một số bước nhảy thì mục tiêu đạt tối ưu. (Mô tả như hình vẽ) LOGO
PHƯƠNG PHÁP BOX – WILLSON
 Khái niệm Gradient: Trong giải tích vectơ gradient của 1
trường vô hướng là 1 trường vectơ có chiều hướng về phía
mức độ tăng lớn nhất của trường vô hướng và có độ lớn là
mức độ thay đổi lớn nhất.
 Giả sử f là 1 hàm số từ Rn đến R nghĩa là y = f(x ,x ,..,x ) 1 2 n
theo định nghĩa gradient là 1 vectơ cột mà thành phần là
đạo hàm theo các biến của f.       f= y y y 1 2  , ,..., n  x  x  x   1 2 n 
(Gradient của đường cong tại điểm M là véc tơ vuông góc với tiếp tuyến tại M).
Phương pháp Box-Willson LOGO
Phương pháp Box-Willson LOGO
 Ý tưởng của Box-Willson:
 Nếu biết dáng điệu của đường đồng mức thì có thể chỉ ra các yếu tố x , 1
x thay đổi như thế nào để sau một số lần thay đổi (bước nhảy) thì hàm 2
y đạt cực trị (tọa độ của điểm trên bề mặt đáp ứng sẽ trùng với điểm M).
 Giải quyết vấn đề
 Phương pháp Box-Willson chia làm 2 giai đoạn:
 + Mô tả đường đồng mức
 + Đưa ra chiến thuật dịch chuyển x sao cho y đạt điểm cực trị i extrimum
Phương pháp Box-Willson LOGO
Phương pháp Box-Willson chia làm 2 bước:
1) Bước 1: Mô tả đường đồng mức
y = b + b x + b x + …+ b x (1) 0 1 1 2 2 n n hoặc
y = b + b x +…+ b x + b x x + b x x …+ b x x (2) 0 1 1 n n 12 1 2 13 1 3 (n-1)n n-1 n Ở đây:
y -chỉ tiêu cần tối ưu b – hệ số tự do 0
b – các hệ số của các biến tương ứng i x
~i – các biến số mã (biến số code) của các yếu tố ảnh hưởng
Phương pháp Box-Willson LOGO