Tổng hợp câu hỏi trắc nghiệm hay chương tọa độ không gian – Nguyễn Quang Hưng, Nguyễn Thành Tiến Toán 12

Tổng hợp câu hỏi trắc nghiệm hay chương tọa độ không gian – Nguyễn Quang Hưng, Nguyễn Thành Tiến được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

49 25 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 1

Nhóm PI

Phương pháp tọa độ trong không gian

Năm 2017 – Tháng 5 – Ngày 10 – Thứ tư

Tổng hợp

câu hỏi trắc nghiệm hay

môn Toán

Nguyễn Quang Hưng – Nguyễn Thành Tiến

Phần Hình họ

c 12

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 2

Lời mở đầu

u tiên do các thành viên NHÓM PI thc hin .

Các bài t      yu là nh  c ly

 thi th,bài gii cách chi tit, nên có mt

s ch ng .

Nu mi ai có góp ý gì v bài gii hay phát hin sai sót nào

trong tài lin trong group NHÓM PI .

Link group : https://www.facebook.com/groups/NhomPI/

D gng làm rt cn thi sai sót, mong

các bn thông cm .

Cc tài liu .

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 3

Câu 1 : Trong không gian vi h trc t

Oxyz

, cho mt phng

 

qua

 

2;3;5M

và ct các tia

,,Ox Oy Oz

lt ti

,,A B C

sao cho giá tr ca

,,OA OB OC

theo th t lp thành cp s nhân có

công bi bng 3 . Khong cách t

n mt phng

 

là :

Giải :

Theo gi thuyt ta có :

 

2 3 5

:1P

abc

  

,,abc

theo th t là mt cp s nhân có công bi là

2 1 5 32

a a a





      







 

;

d I P





----------------------------------------------------------------------------------------------------------------------------------

Câu 2 : Trong không gian vi h trc to 

Oxyz

, cho

 

1;2;3M

, gi

   

: 1 0 , ,P px qy rz q p r    

là mt phng qua

và ct các trc to 

,,Ox Oy Oz

ti

,,A B C

sao cho

là trng tâm

ABC

. Tính

T p q r  

T 

18T 

T 

18T 

Giải :

 

ct các trc to 

,,Ox Oy Oz

ti

     

, , ;0;0 , 0; ;0 , 0;0;A B C A a B b C c

vi

. . 0abc

 

x y z

a b c

   

là trng tâm

A B c M

A B C G

x x x x

ABC y y y y b T

z z z z

  







         







  



----------------------------------------------------------------------------------------------------------------------------------

Câu 3 : Trong không gian vi h trc to 

Oxyz

, cho

 

1;2;3M

, gi

   

: 1 0 , ,P px qy rz q p r    

là mt phng qua

và ct các trc to 

,,Ox Oy Oz

ti

,,A B C

sao cho

là trc tâm

ABC

. Tính

T p q r  

T 

T 

Giải :

 

ct các trc to 

,,Ox Oy Oz

ti

     

, , ;0;0 , 0; ;0 , 0;0;A B C A a B b C c

vi

. . 0abc

 

x y z

a b c

    

n ca mt phng

 

là

 

1 1 1

;;

abc









Ta có

OABC

là mt t din vuông ti

có

là trc tâm

ABC

AH BC

Mc khác :

 

OA BC OA OBC

Vy

 

BC O A H BC OH  

. Ch ta có

AB OH

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 4

 

OH ABC

. Vy t 

 

OM v











    













----------------------------------------------------------------------------------------------------------------------------------

Câu 4 : Trong không gian vi h trc t

Oxyz

cho

 

3; 2; , 120a b a b  

. Gi 2 vecto

   

2 ; 2p a b q a b   

. Tính

 

cos ,pq

4 39

2 39

3 39

Giải :

Ta có :

  

2 0 2

. 2 2 2 3 2 2.3 3.3.2.cos120 2.2 1p q a b a b a ab b         

2 2 2

2 0 2

4 4 4.3 4.3.2.cos120 2 48p a ab b      

2 2 2

2 0 2

4 4 3 4.3.2.cos120 4.2 13q a ab b      

 

cos ,

4 39

p q A

   

----------------------------------------------------------------------------------------------------------------------------------

Câu 5 : Trong không gian vi h trc t

Oxyz

m và mt phng

 

: 2 3 4 0P x y z   

Bit

,MN

i xng nhau qua mt phng

 

,PM

mt cu

   

: 4 5C x y z   

. Hi

thuc mt c

2 2 2

8 40 24 45

7 7 7 7

x y z x y z      

2 2 2

8 40 24 45

7 7 7 7

x y z x y z      

2 2 2

8 40 24 45

7 7 7 7

x y z x y z      

2 2 2

8 40 24 45

7 7 7 7

x y z x y z      

Giải :

Gi

là tâm ca mt cu

   

0; 4;0CI

Gi

i xng

qua

 

4 20 12

' ; ;

7 7 7









Theo yêu cu bài toán ta có :

 

MC

có tâm

 

0; 4;0I 

và bán kính

 

5R N S  

có tâm

4 20 12

' ; ;

7 7 7









bán kính

5R 

 

2 2 2

8 40 24 45

7 7 7 7

S x y z x y z       

----------------------------------------------------------------------------------------------------------------------------------

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 5

Câu 6 : Trong không gian vi h trc t 

Oxyz

, cho mt phng

   

: 1 0, 1;1;1 ,P x y z A   

 

0;1;2 ,B

 

2;0;1C 

và

   

;;M a b c P

sao cho

2 2 2

2S MA MB MC  

t giá tr nh nh ca

32T a b c  

là :

T 

T 

Giải :

Gi

m tha

2 0 0; ;

IA IB IC I



   





Ta có :

     

2 2 2

22S MA MB MC MI IA MI IB MI IC        

 

2 2 2 2 2 2 2 2

4 2 2 2 4 2MI IA IB IC MI IA IB IC MI IA IB IC          

2 2 2

2IA IB IC const  

nên

min min

S MI M

là hình chiu ca

trên

 

3 3 1 25

;;

2 4 4 4



      





----------------------------------------------------------------------------------------------------------------------------------

Câu 7 : Trong không gian vi h trc

Oxyz

  m

   

1;0;2 , 3;1; 1AB

và mt phng

 

: 1 0P x y z   

. Gm

   

;;

o o o

M x y z P

sao cho

32MA MB

t giá tr nh nht . Tính

9 3 6

o o o

A x y z  

Giải.

Gi

m tha

 

3 2 0 3, 2,8IA IB I    

Ta có

   

3 2 3 2 3 2MA MB IA IM IB IM IA IB IM IM IM         

Vì

c nh,

 

MP

nên

32MA MB

t giá tr nh nht

IM

t giá tr nh nht.

M

là hình chiu ca

trên mt phng

 

Gi

 

ng thng qua

và vuông góc vi mt phng

 

   

 

1,1,1

P vtcpa vtpt n  

 

: 3 , 2 , 8d x t y t z t        

   

11 8 22

, , 3

3 3 3

M d P M A





    





----------------------------------------------------------------------------------------------------------------------------------

Câu 8 : Trong không gian vi h t

Oxyz

cho mt phng

 

: 2 2 7 0P x y z   

m

     

1;2; 1 , 3;1; 2 , 1; 2;1ABC  

m

   

;;M a b c P

sao cho

2 2 2

MA MB MC

t giá tr ln

nhng

A a b c  

bng bao nhiêu ?

A 

A 

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 6

Giải:

Ta có:

     

2 2 2

1 2 1

3 1 2

1 2 1

MA a b c

MB a b c

MC a b c



     



     





     





   

2 2 2 2 2 2 2

6 6 26 44 3 3MA MB MC a a b b c a b c



               



Vy

 

   

2 2 2 2

min

max

min

33MA MB MC a b c MI



       



vi

 

3; 3;0I 

Mà

 

3; 3;0I 

c nh nên

min

MI M

là hình chiu ca

trên mt phng

 

Gi

 

ng thng qua

 

3; 3;0I 

và vuông góc vi mt phng

 

, ta có:

 

: 3 2

d y t







  









Vì

   

3 ; 3 2 ;2M d M t t t    

       

4 23 35 8

3 2 3 2 2 2 7 0 ; ;

9 9 9 9

M P t t t t M

  



           





abc



   

----------------------------------------------------------------------------------------------------------------------------------

Câu 9 : Trong không gian vi h t

Oxyz

m

     

1;1;0 , 0;1;1 , 1;0;1A B C

. Tìm

hp tt c m

trên mt phng

Oxz

sao cho

.2MAMB MC

A. Mng thng

B. Mng tròn

C. Mng elip

D. c

Giải:

 

1;0;1 2AB AB   

Gi

m ca

;1;

AB I









c nh và

IC 

Ta có:

     

2 2 2 2

. . .

MA MB IA IM IB IM IA IM IA IB IM IM IM             

Vy

MA MB MC MI MC    

Gi

m ca

3 1 3

;;

424

IC J









c dnh và

ng trung tuyn ca

MIC

2 2 2 2 2

5 3 7 14

2 2 4 8 4

MI MC MJ JM JM JM const           

Mà

c nh nên

ng trên mt cu

 

tâm

vi bán kính

R 

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 7

Mt phng

Oxz



     

1 14

y d J Oxz R S Oxz      





là mng

tròn

 

Vy

ng tròn

 

----------------------------------------------------------------------------------------------------------------------------------

Câu 10 : Trong không gian

Oxyz

m

     

2 ;2 ;0 , 0;0; , 0A t t B t t 

ng

tha:

. . . 3OP AP OP BP AP BP  

. Tìm giá tr

sao cho

max

3OP 

t 

Giải:

       

. . . 3 . . . 3OP AP OP BP AP BP OP OP OA OP OP OB OP OA OP OB          

 

3 2 . 3OP OP OA OB   

. (Vì

.0OAOB 

)

3 2 . 3OP OPOI  

(vi

m th a hình bình hành

 

2 ;2 ;AOBI I t t t

3 3 . 3OP OPOJ  

(vi

tha

2 4 4 2

;;

3 3 3 3

ttt

OJ OI J









     

. 1 . 1 . 1 . 1OP OPOJ OP OP OJ OP JP MP MO MP MJ           

(vi

là

m ca

;;

3 3 3

t t t

OJ M









2 2 2 2 2 2 2

. 1 1 1 1 1MP MO MJ MP MO MP MO t MP t             

Vy

ng trên mt cu

 

tâm

vi bán kính

1Rt

Nên

 

max

OP P OM S  

và

,OM OP

ng.



2 2 2

max

3 3 3

t t t

OP OM R t t t

     

         

     

     

max

3 1 3 1 3

1 9 6

OP t t t t

t t t











          





   







----------------------------------------------------------------------------------------------------------------------------------

Câu 11 :Trong không gian vi h trc t

Oxyz

m

   

2; 2;1 , 1;2; 3MA  

ng

thng

2 2 1

x y z







 

cng thng





, vuông góc vi

ng thng

ng thi cách

mt khong cách ln nht .

 

4; 5; 2u   

 

1;0;2u 

 

3;4; 4u 

 

2;2; 1u 

Giải :

Gi

 

là mt phng vuông góc vi

và qua

Gi

là hình chiu ca

trên

 

. Gi

là hình chiu ca

trên

 

AN  

ng vuông góc )

 

;d A AN  





Tổng hợp trắc nghiệm 12 – NHÓM PI Page 8

Ta có :

AN AM

. Du

""

xy ra khi

NM  

ng thng qua

và

MH

Tính toán ta có :

 

4; 5; 2u   

----------------------------------------------------------------------------------------------------------------------------------

Câu 12 :Trong không gian vi h trc t

Oxyz

m

   

2; 2;1 , 1;2; 3MA  

ng

thng

2 2 1

x y z







 

cng thng





, vuông góc vi

ng thng

ng thi cách

mt khong cách bé nht .

 

2;1;6u 

 

1;0;2u 

 

3;4; 4u 

 

2;2; 1u 

Giải :

Gi

 

là mt phng vuông góc vi

và qua

Gi

là hình chiu ca

trên

 

. Gi

là hình chiu ca

trên

 

AN  

ng vuông góc )

 

;d A AN  





Ta có :

AN AH

. Du

""

xy ra khi

NH  

ng thng qua

,MH

Tính toán ta có :

 

1;0;2u 

----------------------------------------------------------------------------------------------------------------------------------

Câu 13 : Trong không gian vi h t    

 

1;2; 3A 

    

 

:2 2 9 0P x y z   

 

 

 

3;4; 4u 



 







 

sao cho











 

3;2;7J 

 

2; 1;3H 

 

3;0;15K

 

1; 2;3I 

Giải :

Gi

là hình chiu

trên

   

P AH P AH MB   

Vì





nên

AM MB

Vy

 

MB AHM MB HM  

M

chạy tung tăng ng kính

 

MH M B

Vy

max

khi

MH

c :

 

MB y MB

  





  









qua

 

1; 2;3I 

----------------------------------------------------------------------------------------------------------------------------------

Câu 14 : Trong không gian vi h t

Oxyz

ng thng

 

3 2 5

2 2 5

x y z

  



và

 

2 4 4

1 4 4

x y z

  



. Gi

 



ng phân giác trong ca góc tù to bng

thng

   

,dd

 





Tổng hợp trắc nghiệm 12 – NHÓM PI Page 9

 

















 







  









 

















 

















Giải:

Xét h:

5 2 0 0

x y x

y z y

y z z









  







  

     

  

  

  













. Ta nhn thy

   

1;0;0















Vy

     

1;0;0A d d

 

có

 

2;2;5vtcpa 

 

có

 

1;4;4vtcpa 

Ta có:

   

1 2 1 2 1 2

. 30 0 ; 90 ;a a a a a a    

là góc nhn

 

;aa

là góc tù.

Gi

m tha

   

3;2;5AB a B d  

m tha

   

0; 4; 4AC a C d     

Vy

BAC

là góc tù to bng thng

   

,dd



 



ng phân giác trong ca

BAC

Ta có:

33, 33AB a AC a AB AC ABC       

cân ti

 



ng trung tuyn t

ca

ABC

 



 

 

1;0;0 , ; 1;









  m ca

 

BC 

có

 

; 1;

vtcp a AM





  





 



có

 

1; 2;1a





và qua

   

1;0;0 : 2

A y t







    









----------------------------------------------------------------------------------------------------------------------------------

Câu 15 : Trong không gian vi h trc t

Oxyz

 m

   

1;2; 1 , 0;4;0AB

và mt phng

 

:2 2 2015 0P x y z   

. Gi



là góc nh nht gia mt phng

 

m

,AB

và to

vi

 

. Tính

cos



Giải :

Theo cách hình học :

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 10

Gi

là hình chiu ca

trên mt phng

 

là

giao tuyn ca

   

,PQ

m ca

và mt

phng

 

là hình chiu ca

trên



Góc ca 2 mt phng

   

,PQ

là góc

AJH

vi

sin

AJH





Góc ca

và mt phng

 

là góc

AIH

vi

sin

AIH



D dàng chc

 

d AJH IJ AJ AI J    

vuông ti

sin sinAJ AI AJH AIH   

Du

""

xy ra khi

d IH

Vy

   

min ;P Q AI H







là góc gia

và mt phng

 

Cách đại số :

Ta có :

 

1;2;1

; ; . 0 2

vtcp u

vtpt n a b c u n a c b

AB Q







     











 

2; 1; 2

vtpt n   

Ta có

cos



là góc ca

   

2 2 2 2 2

, cos

9 2 4 5

a b c b

a b c a ab b





  

   

cos

2 4 5

a ab b







Xét

0 cos 0b



  

Xét

0 cos

2 4 5

t t b





   







c :

0 cos

2 4 5 3tt



  



cos



   

Nói tóm li

max cos





----------------------------------------------------------------------------------------------------------------------------------

Câu 16 : Cho

       

1,2,3 , ,0,0 , 0, ,0 , 0,0,M A a B b C c

,b,c là các s t

phng

 



, , ,A B C M

sao cho

OABC

t giá tr nh nht.

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 11

 

:6 3 2 18 0P x y z   

 

:6 3 2 0P x y z  

 

:6 3 2 9 0P x y z   

 

:6 3 2 36 0P x y z   

Giải.

Ptmp qua

,,A B C

có dng:

x y z

a b c

  

Vì

 

1 2 3

1M ABC

abc

    

Áp d

1 2 3

abc

không âm, ta có:

1 2 3 1.2.3 27.6

1 3 1 162 27 27

. . 6

OABC

abc

abc V

a b c a b c abc

           

ng thc xy ra

1 2 3 1

3, 6, 9

a b c

abc

       

   

: 1 : 6 3 2 18 0

3 6 9

x y z

ABC ABC x y z        

----------------------------------------------------------------------------------------------------------------------------------

Câu 17 : Trong không gian vi h trc t

Oxyz

, cho

     

;0;0 , 0; ;0 , 0;0;A a B b C c

vi

, , 0abc

sao cho

12OA OB OC AB BC CA      

. Tìm giá tr ln nht ca

.O ABC

max

O ABC

V 

max

162

O ABC

V 

max

486

O ABC

V 

max

108

O ABC

V 

Giải :

Ta có :

O ABC

V abc

Theo gia thuyt ta có :

2 2 2 2 2 2

OA OB OC AB BC CA a b c a b b c c a             

Theo nhà toán hc Cauchy ta có :



3a b c abc  



 

2 2 2 2 2 2

2 3 2.a b b c c a ab bc ca abc        

 

1 2 3 1 2OA OB OC AB BC CA abc         

1 1 1

3 6 162

O ABC

abc V abc    

. Du

""

xy ra khi và ch khi

abc  

----------------------------------------------------------------------------------------------------------------------------------

Câu 18 : Trong không gian vi h trc t 

Oxyz

    ng

. ' ' 'ABC A B C

có

   

;0;0 , ;0;0A a B a

   

, 0; 1;0 , ' ;0;C B a b

vi











. Khong cách ln nht ging

thng

'BC

và

'AC

là:

A. 1 B. 2 C.

Giải.

Gi

i xng ca

qua

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 12

Ta có:

AIBC

là hình bình hành

/ / / / ' '

AI BC B C

AIB C

AI BC B C











là

hình bình hành.

 

'/ / ' 'AC B I B CI

     

' , ' ', ' , 'd B C AC d AC B CI d A B CI  

   

   

Mà

,AB

i xng vi nhau qua

nên

   

, ' , 'd A B CI d B B CI

   

   

Ta có

     

' ' 'CI OBB B CI OBB  

V ng cao

ca tam giác vuông

'OBB

   

' ' 'BJ OB B CI OBB   

   

' , 'BJ B CI BJ d B B CI   





ng cao ca tam giác vuông

'OBB

, ta có:

 

2 2 2 2

BO BB ab ab

BO BB a b

a b a b



    



ng thc xy ra

2ab  

Vy

 

' , '

d B C AC

Max Max  

----------------------------------------------------------------------------------------------------------------------------------

Câu 19 : Trong không gian vi h trc t 

Oxyz

, cho mt phng

 

:3 5 1 4 20 0

P mx m y mz    

vi



 



1;0 0;1m  

luôn ct mt phng

 

Oxz

theo giao tuyn

ng thng



. Khi

i thì các giao tuyn



có kt qu 

A. Ct nhau B. Song song C. Chéo nhau D. Trùng nhau

Giải :

 

3 5 1 4 20 0

m m

mx m y mz

Oxz





    









  

3 4 20 0:

mx mz  

vi



trong mt phng

 

Oxz

Gi

1 1 2 2

3 4 20 0, 3 4 20 0::

m x m z m x m z     

ng thng vi



 



, 1;0 0;1mm  

bt kì và

mm

Ta có :









3 4 20

    

----------------------------------------------------------------------------------------------------------------------------------

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 13

Câu 20 : Trong không gian

Oxyz

m

; ;0







và mt cu

 

2 2 2

: 8.S x y z  

ng

thng

m

ct mt cu

 

tm phân bit

,AB

. Tính din tích ln

nht

ca tam giác

OAB

7S 

. B.

4S 

. C.

27S 

. D.

22S 

Giải :

Mt cu

 

có tâm

 

0;0;0O

và bán kính

22R 

Ta có :

1OM R M  

thuc min trong ca mt cu

 

Gi

m cng thng vi mt cu. Gi

ng cao h t

ca tam giác

OAB

Gi

 

0 1x OH x OM 

2 2 2

8OH R xHA   

. . 8

OAB

S OH AB OH HA x x   

Xét :

( ) 8f x x x

vi





0;1x

 

' 8 0

f x x



     



vi





0;1x





   

0;1

max 1 7

OAB

S f x f



   

----------------------------------------------------------------------------------------------------------------------------------

Câu 21 : Trong không gian vi h trc t 

Oxyz

, cho mt phng

 

   

 

: 1 2 1 2 2P m m x m y m z     

10mm   

luôn ch ng thng



c nh khi

i. Tính khong cách t gc t n



 

dO





 

dO





 

dO





 

dO





Giải:

Ta có:

   

 

2 2 2

1 2 1 2 2 1 0m m x m y m z m m m           

     

2 1 2 1 2 4 1 0x y m x z m x y z m            

 

   

2 1 0 1

2 1 0

2 1 0 2 2 1 0

2 4 2 0 3 1

2 4 1 0 3

x z x z

x y z

  



  



       





   

   



2 1 0

2 1 0 2 1 0

2 1 0

2 1 0 0

2 1 0

x y x y

x z y z

  



     





     

  

    





  



Tổng hợp trắc nghiệm 12 – NHÓM PI Page 14

t

zt

, ta có:

2 1 0 2 1

x y x t

y t y t

z t z t

    





    









Vy

 

luôn chng thng c nh

 







  









có

 

2; 1;1vtcpa 

m

 

1;0;0A 

Ta có

   

;

; 0; 1; 1 ,

a OA

a OA d O







       





----------------------------------------------------------------------------------------------------------------------------------

Câu 22 : ng thng

4 3 2 3 8 7 3 1

: 1; ;

2 1 1 4 3 4 2

x m y m z m

m m m

        



   





  





và

 

1;1;1A

Bit

luôn nm trong mt mt phng

 

c i. Tính

 

;d A P





115

110

105

115

Giải :

ng thng



 

4 3; 2 3;8 7A m m m  

và có VTCP

 

2 1; 1;4 3u m m m   

Gi s

 

: 0 1; ;

d ax by cz d m



  



       











 

     

 

2 1 1 4 3 0 2 4 3 0

4 3 2 3 8 7 0 4 2 8 3 3 7 0

a m b m c m a b c m a b c

a m b m c m a b c m a b c d





           



  



  



            









 h có nghii mi m thì :

2 4 0

4 2 8 0

3 3 7 0

a b c

a b c d

  









   



  



  









    



Ta chn :







   









Vy

 

: 10 3 6 0 1; ;

d x y z m



  



       









Cách 2 : p trc nghim.

Ta chn 2 s

tha yêu cu bài toán



ng thng

d 

vic mp

 





xong bài .

----------------------------------------------------------------------------------------------------------------------------------

Câu 23: Trong không gian vi h trc t 

Oxyz

cho mt cu

     

: 2 5 4 1 0S x m y m z m m       

. Bit khi

i thì

 

luôn giao vi mt phng

 

c nh vi giao tuyn là mng tròn

 

c nh . Tính bán kính c

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 15

1R 

R 

Giải :

   

2 2 2

: 1 2 2 2 0S x y z m x y      



Vi mi

thì mt cu

 

luôn giao vi mt phng

 

: 2 2 0P x y  

   

 

     

2 2 2

' : 1

: 2 2 0

S x y z

S P C S P

P x y



  



     



  





Gi

 

0;0;0I

là tâm mt cu

   

S d I P





   

 

;

R R d I P   





----------------------------------------------------------------------------------------------------------------------------------

Câu 24 : im phân bit

,AB

c nh . Tp hm

trong không

gian là mt cu c nh

bán kính

R AB

a mãn

 

MAMB AB m n



là

phân s ti gin. Tính

 

2P m n mn  

A. 49 B. 64 C. 36 D. 81

Giải :

Chn h trc

Oxyz

sao cho

,A B Ox

và

 

0;0;0O

m



 

;0;0

a AB a





  









. Gi

 

;;

M M M

MA a x y z

M x y z

MB a x y z



   







    





Ta có :

MA MB a



     

2 2 2 2 2

2 2 2

0 0 0 1

M M M

x a y z a

x y z a

    



       





Do v phi là 1 hng s

M

thuc tp hng tròn tâm

có









Ta có

a AB a



  







----------------------------------------------------------------------------------------------------------------------------------

Câu 25 : Trong không gian vi h trc t

Oxyz

, cho bng thng

 

112

2 1 3

x y z

  



     

2 3 4

3 2 4 2 4 1 2

: ; : ; :

2 1 3 7 1 1 1 5 2

x y z x y z x y z

d d d

      

     

  

. Gi

 



ng thng ct

c

ng th a

 



là

 

; ;1u a b





. Tính

37T a b

5T 

5T 

4T 

4T 

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 16

Giải :

Ta có :

 

2;1;3

vtcp u 

và

 

qua

 

1; 1;2M 

 

2;1;3

vtcp u 

và

 

qua

 

3;2;4N 

Ta thy

uu

và

   

2 1 2

//M d d d

Gi

 

là mt phng cha

 

, [ , ] 7;16; 10

d d vtpt n MN u   

và

 

m

 

1; 1;2M 

 

:7 16 10 29 0P x y z    

Gi

     

7 2 0

0 5;1;1

7 1 1

7 16 10 29 0

x y z

E d P y z E

x y z

  











       







   



Gi

     

5 21 0

4 1 2

2 5 8 0 5; 4;0

1 5 2

7 16 10 29 0

x y z

F d P y z F

x y z

  



  







        







   



 

10; 5; 1EF EF    

không song song

,dd

         

,d d P    

. Mà

       

,dd   

qua

 

, 10;5;1E F u



  

5T  

----------------------------------------------------------------------------------------------------------------------------------

Câu 26 : Trong không gian

Oxyz

m

     

;0;0 ; 0; ;0 ; 0;0;A a B b C c

vi

, , 0abc

. Gi s

,,abc

a

2 2 2 2

a b c k  

vi

c thì

ABC

có din tích ln nht là :

max

S 

max

S 

max

S 

max

S 

Giải:

Gi

là hình chiu ca

trên

2 2 2 2

2 2 2 2 2 2 2

1 1 1 . .OA OB a b

AB OI

OI OA OB OA OB a b

     



OAI

vuông ti

2 2 2 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2

2 2 2 2 2 2

.a b a b b c c a a b b c c a

O IC OI OC c OI

a b a b a b

   

       

  

OAB

vuông ti

2 2 2 2 2

O AB a b AB a b     

2 2 2 2 2 2

ABC

S AB IC a b b c c a   

Ta có:

2 2 2 2 4 4 4 2 2 2 2 2 2 4

2 2 2a b c k a b c a b b c c a k         

 

4 4 4 4

2 2 2 2 2 2

k a b c

a b b c c a

  

   

Mà

 

2 2 2

4 4 4

abc



   

nên

 

4 4 4 4

k a b c

  



Vy

4 2 2

2 2 2 2 2 2

3 2 3

ABC

k k k

a b b c c a S     

ng thc xy ra

abc   

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 17

----------------------------------------------------------------------------------------------------------------------------------

Câu 27 : Trong không gian vi h trc t

Oxyz

m

     

1;0;0 , 0;1;0 , 0;0;1A B C

. Có bao

nhiêu mt cu có tâm nm trên mt phng

 

:0z y z



  

và tip xúc v  ng thng

,,AB BC CA

A. 1 B. 2 C. 3 D. 4

Giải.

Gi mt cu

 

có tâm

là mt cu tip xúc 3 cnh

,,AB BC CA

     

, , ,d I AB d I BC d I CA  

Gi

là hình chiu ca

trên mt phng

 

ABC

,,M P C

lt là hình chiu ca ca

trên

,,AB BC CA

Ta có:

IHM IHN IHP    

(cnh huyn_cnh góc

vuông).

HM HN HP H   

m thuc mt phng

 

ABC

u 3 cnh

,,AB BC CA

H

có th ng tròn ni tip hay mng tròn bàng tip ca

ABC

Mà

 

IH ABC

nên tp hm

là nh ng thng tròn ni tip hay mt

ng tròn bàng tip ca

ABC

và vuông góc vi mt phng

 

ABC 

ng

th.

Ta có

           

1;0;0 , 0;1;0 , 0;0;1 : 1 0 / /A B C PTMP ABC x y z ABC



     

Vy tn tm ca tp hm

nêu trên và mt phng

 



t cu tha yêu cu bài toán



Có 4 mt cu tha ycbt.

----------------------------------------------------------------------------------------------------------------------------------

Câu 28 : Trong không gian vi h trc t 

Oxyz

, cho hai mt cu

 

2 2 2

: 4 2 0S x y z x y z     

và

 

2 2 2

: 2 0S x y z x y z     

  m

     

1;0;0 , 0;2;0 , 0;0;3A B C

. Gi

 

là mt phng cha giao tuyn ca

   

,SS

. Hi có bao

nhiêu mt cu có tâm thuc

 

và tip xúc vng thng

,,AB BC CA

A. Không có mt cu B. 1 C. 4 D. Vô s mt cu

Bài tập tương tự, bạn đọc tự làm :)))))

----------------------------------------------------------------------------------------------------------------------------------

Câu 29 : Trong không gian vi h trc t

Oxyz

, cho hai mt cu

     

: 2 1 11S x y z    

và

       

2 2 2

: 1 3 1 17S x y z     

  m

   

3;0;0 , 0;4;0AB

. Gi

 

là mt phng

cha giao tuyn ca

   

,SS

. Hi có bao nhiêu mt cu có tâm thuc

 

và tip xúc vng

thng

,,AO OB BA

A. Không có mt cu B. 1 C. 4 D. Vô s mt cu

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 18

Giải :

 

có tâm

 

2;0;1I 

và bán kính

11R 

Ta có h:

   

     

 

2 2 2

2 1 11

2 1 11 1

1 3 1 17

x y z





    









     





 

chít phng

 

:0Q x y

Vy h

 



a mt cu

 

và mt phng

 

; 2 11

d I Q R



   







Vy

 

ct

 

vi giao tuyn là mng tròn

 

chính là giao tuyn ca

   

,SS

   

:0P Q x y   

. Mà

     

:0OAB z P OAB  

Tp hp tâm ca nhng mt cu tip xúc v  ng thng

,,AO OB BA

là b ng thng

1 2 3 4

, , ,d d d d

vuông góc mt phng

 

OAB

ng tròn tip hong tròn bàng

tip ca

OAB

Vy mt trong bng trên có th song song hay cha trong

 

Gi

       

:0P OAB x y      

v

 



trong mt phng

 

Oxy

Trong mt phng

Oxy

, ta có

 

:0xy  

ng phân giác ngoài ca góc

ca

OAB

Vy

 



p góc

,AB

Vy hai trong bng

1 2 3 4

, , ,d d d d

cha trong

 

P 

có vô s tâm mt cu có tâm thuc

 

và

tip xúc vng thng

,,AO OB BA

----------------------------------------------------------------------------------------------------------------------------------

Câu 30 : Trong không gian vi h trc t 

Oxyz

, cho hai mt cu

     

: 2 1 17S x y z    

và

       

2 2 2

: 1 3 1 11S x y z     

  m

   

3;0;0 , 0;4;0AB

. Gi

 

là mt phng cha giao tuyn ca

   

,SS

. Hi có bao nhiêu mt

cu có tâm thuc

 

và tip xúc vng thng

,,AO OB BA

A. Không có mt cu B. 1 C. 4 D. Vô s mt cu

Giải :

 

có tâm

 

2;0;1I 

và bán kính

17R 

Ta có h:

   

     

 

2 2 2

2 1 17

2 1 17 1

1 3 1 11

x y z





    









     





 

 trình mt phng

 

: 2 0Q x y  

Vy h

 



a mt cu

 

và mt phng

 

; 2 2 17

d I Q R



   







Tổng hợp trắc nghiệm 12 – NHÓM PI Page 19

Vy

 

ct

 

vi giao tuyn là mng tròn

 

chính là giao tuyn ca

   

,SS

   

: 2 0P Q x y    

. Mà

     

:0OAB z P OAB  

Tp hp tâm ca nhng mt cu tip xúc v  ng thng

,,AO OB BA

là b ng thng

1 2 3 4

, , ,d d d d

vuông góc mt phng

 

OAB

ng tròn tip hong tròn bàng

tip ca

OAB

Vy mt trong bng trên có th song song hay cha trong

 

Gi

       

: 2 0P OAB x y       

v

 



trong mt phng

 

Oxy

Trong mt phng

 

Oxy

, gi

   

: 0, ' : 0d x y d x y   

lng phân giác trong, phân

giác ngoài tnh

ca

OAB

Ta có

     

/ / 'd  

ng tròn bàng tip góc

,AB

Gi

     

1,1I d I   

Ta có

   

: 0, : 0, 4 3 12 0OA y OB x x y    

Ta xét thy

     

, , , 1d I OA d I OB d I AB I   

u ba cnh

ABC I

có th là tâm mt

cu ni tip hay tâm bàng tip góc

ca

OAB

Vy mt trong bng

1 2 3 4

, , ,d d d d

cha trong

 

P 

có vô s tâm mt cu có tâm thuc

 

và

tip xúc vng thng

,,AO OB BA

----------------------------------------------------------------------------------------------------------------------------------

Câu 31 : Trong không gian vi h trc t 

Oxyz

cho mt cu

 

  

 

2 2 2

50 0 1x y z z   

và mt cong

 



 

25 16

z

. Bit

   

SP

có giao

tuyng tròn. Tính bán kính c

A. 20 B. 45 C. 15 D. 25

Giải :

T

 

2 50

z x y  

thay vào

 

ta có :

 

3 4 0











  









. Kt hp vi

 

c 2 mt phng giao vi 1 mt cu.

 

có tâm là

 

0;0;25I

và bán kính

25R 

Ta có :



     

; 20 1d I R



   





là mng tròn có

 

; 15R R d I



  







     

; 20 1d I R



   





là mng tròn có

 

; 15R R d I



  





Vy

   

15RR





Tổng hợp trắc nghiệm 12 – NHÓM PI Page 20

----------------------------------------------------------------------------------------------------------------------------------

Câu 32 :Trong không gian vi h trc

Oxyz

,cho các

m

       

1;0;0 , 2;0;3 , 0;0;1 , 0,3,1A B M N

,mt phng

 

   m

,MN

sao

   

; 2 ;d B P d A P

   

   

,có bao nhiêu mp th bài.

A. 1 B. 2 C. vô s D. không có mt phng nào .

Giải :

m

, , ,A B M N

ng phng ,

không song song

Gi

 

I P AB

( do

không song song

 

)

Trường hợp 1 :

nm ngoài

, mà

   

; 2 ;d B P d A P AI AB  

   

   

( ta-let)

 

4;0; 3I

Trường hợp 2 :

nn

, mà

   

; 2 ; 2d B P d A P IB IB  

   

   

( ta-let)

 

0;0;1I

 

P

luôn đi qua 1 trong 2 điểm cố định trên.

, , , ,M N A B I

ng phng nên

,,I MN I M N

thng hàng



có vô số mặt phẳng ( trường hợp 2 ) .

----------------------------------------------------------------------------------------------------------------------------------

Câu 33 : Trong không gian vi h trc t

Oxyz

cho

     

2;5; 3 , 2;1;1 , 2;0;1A B C

và mt phng

 

:3 4 5 1 0x y z



   

. Gm

   

; ; 0

D D D D

D x y z y 

thuc

 



sao cho có vô s mt phng

 

qua

,CD

tha khong cách t

n

 

gp 3 ln khong cách t

n

 

. Tính

D D D

P x y z  

2P 

1P 

1P 

2P 

Giải :

 bài ta có

   

, 3 ,d A P d B B AB

   

   

không song song vi

 

Xét

 

AB P

, ta có

   

 

d A P

I AB P AI BI

d A B





       





 

4; 1;3

1;2;0

AI BI









  











     m c nh

 

4; 1;3I 

hay

 

1;2;0I 

Nu

   

AB P P

m c nh trên.

Vy  có

   

, 3 ,d A P d B B

   

   

thì

 



 

4; 1;3I 

hay

 

1;2;0I 

  bài, thì có vô s mt phng

 

qua

,CD

tha

   

, 3 ,d A P d B B

   

   

,,ICD

thng hàng. Nói cách khác

D IC

Vi

 

4; 1;3I 

, ta có

   

: 2 6 ; ; 1 2 2 6 ; ;1 2IC x t y t z t D t t t       

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 21

Mà

   

1 4; 1;3D t D



      

loi vì

y   

Vi

 

1;2;0I 

, ta có

   

: 2 3 ; 2 ; 1 2 3 ; 2 ;1IC x t y t z t D t t t         

Mà

   

2 4;4; 1D t D



      

nhn vì

4 0 1

yP    

----------------------------------------------------------------------------------------------------------------------------------

Câu 34 : Trong không gian vi h trc t 

Oxyz

, cho

     

;0;0 , 0; ;0 , 0;0;1A a B b C

vi

,0ab

và

1ab

. Tìm giá tr nh nht ca bán kính

mt cu ngoi tip t din

OABC

R 

6R 

R 

Giải :

Gi

là tâm mt cu ngoi tip t din

OABC

T cách dng hình ta có :

;;

2 2 2







, mà

1 ; ;

2 2 2

b a I





  





1 1 1 6

4 2 4 2 2 2 4

a a a a





       





. Du

""

xy ra khi

1 1 1 1

;;

2 4 4 2









----------------------------------------------------------------------------------------------------------------------------------

Câu 35 : 

Oxyz

, cho

       

;0;0 , 0; ;0 , 0;0; , , , 0A a B b C c a b c 



 

2 2 2

, , 0a b c k k k const

     

       

. Khi

,,abc

      



OABC



 

:0P x y z k

  

   

 

P x y z

  

   

 

P x y z

  

   

 

:0P x y z k

  

   

Giải :

Gi

là tâm mt cu ngoi tip t din

;;

2 2 2

a b c

OABC I









( bng cách dng hình ta d dàng tìm

c )

I I I

a b c k

x y z

  



    

Vy tâm

ca mt cu ngoi tip t din

OABC

  ng trên mt phng c nh

 

P x y z

  

   

----------------------------------------------------------------------------------------------------------------------------------

Câu 36 : 

Oxyz



 



 

2; 2;5A 





     

: 1 0; : 1 0; : 1 0x y z

  

     



D. 3

Giải :

Gi tâm mt cu

 

là

 

;;

I I I

I x y z

Ta có

 

1; 1;1B 

là t m ca 3 mt phng .

Do 3 mt phng

     

;;

  

t ct nhau



3 mt phng này chia không gian làm 8 phn



Tâm

m

cùng thuc 1 phn .

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 22







    









     

2 2 2

1 1 1

1 2 2 5

I I I

I I I I

x y z

x x y z

x x x x







     







      





       





 

4 4; 4;4 3

8 16 0

I I I

x y x

x z y I IA



  





        







  



----------------------------------------------------------------------------------------------------------------------------------

Câu 37 : Trong không gian vi h trc t

Oxyz

, cho

       

3;0;0 , 0;2;0 , 0;0;6 , 6;0; 6A B C D 

Gi



ng thng qua

sao cho tng khong cách t

,,A B C

n



t giá tr ln nht . Vy



m



 

8;3; 4M 

 

8;3; 3M 

 

4; 3; 7M 

 

4; 3; 6M 

Giải :

t phng qua

,,A B C

có dng:

3 2 6

x y z

  

Ta nhn thm

 

D ABC

Gi

', ', 'A B C

là hình chiu ca

,,A B C

trên



, ta có:

'ADA

vuông ti

''A AA AD const  

ng thc xy ra

AD  

Lp lu ta có:

BB BD const

CC CD const











ng thc xy ra













Vy

' ' 'AA BB CC D A DB D C c o nst     

ng thc xy ra

 

BD ABCD







     









 

   

2,3,1 : 3

ABCD

vtcp a vtpt n y t t









       





  



Qua

 

4; 3; 7M 

----------------------------------------------------------------------------------------------------------------------------------

Câu 38 : Trong không gian vi h t

Oxyz

, cho mt cu

   

: 4 5S x y z   

. Tìm t

m

thuc tia

. Bit rng ba mt phng phân bit qua

t vuông góc ct mt cu theo

thit din là ba hình tròn có tng din tích là



0; 2; 0

0; 6; 0

0; 0; 0

0; 8; 0

0; 6; 0

0; 0; 0

0; 2; 0

0; 8; 0

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 23

Gii:

Gi ba mt phng phân bit qua

t vuông góc lt là

     

,,Atm Amp Apt

Mt cu

 

ct

     

,,Atm Amp Apt

theo ba hình tròn

   

 

1 2 3

,,C C C

có

bán kính

1 2 3

,,R R R

Mt cu

 

có tâm

 

0;4;0I

và bán kính

5R 

Gi

,,B C D

lt là hình chiu ca

trên

     

,,Atm Amp Apt

,,B C D

lt là tâm ca

   

 

1 2 3

,,C C C

Ta có:

2 2 2 2 2 2 2 2 2

1 2 3

,,R R IB R R IC R R ID     

Tng din tích ba hình tròn

   

 

1 2 3

,,C C C

là:

   

2 2 2 2 2 2 2 2 2 2

1 2 3 1 2 3

3R R R R R R R IB IC ID

    



        



 

2 2 2

15 11IB IC ID





    



 

2 2 2 2

4 4 2 1IB IC ID IA IA       

Vì

thuc tia

nên

  

0; ;0 0A a a 

 

0;2;0

2 4 4

0;6;0

IA a







     











Ta chng minh

2 2 2 2

IB IC ID IA  

Gi

là hình chiu ca

trên

, chc

'IDA C

là hình ch nht.

2 2 2

'IA IC ID  

ng thc

'A BIA

là hình ch nht

2 2 2

'IA AB

AB IB IA

















Vng minh xong

2 2 2 2

IB IC ID IA  

----------------------------------------------------------------------------------------------------------------------------------

Câu 39 : Trong không gian vi h trc t

Oxyz

ng thng

1 2 1

1 1 1

x y z  

  

và mt

cu

       

2 2 2

: 1 2 3 27S x y z     

m

M 

k ng thng tip xúc vi

 

lt ti

,,A B C

sao cho

ABC

và

AMB CMA

 

1; 2;1

1 2 7

;;

3 3 3





















 

1;2;1

1 2 7

;;

3 3 3



















 

1; 2;1

127

;;

3 3 3



















 

1; 2;1

1 2 7

;;

3 3 3





















Giải :

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 24

Gi

là tâm ca

 

Vì

,,MA MB MC

là tip tuyn nên

,,MA IA MB IB MC IC  

,,MAI MBI MCI   

là các tam giác vuông có chung cnh huyn

Ta có :

 

IA IB IC R MAI MBI MCI MA MB MC           

M

trng tròn ngoi tip

ABC

và

     

, , ,A B C C M MA S  

vi

 

,M MA

là mt cu

tâm

, bán kính

Gi

m ca

AC J

ng tròn ngoi tip

ABC

IA IB IC R I    

trng tròn ngoi tip

ABC

,,M J I

thng hàng

,MI AC

ng phng.

Xét trong mt phng

 

AICM

, gng tròn

     

'C S AICM

có tâm

, ta có:

,MA MC

là tip tuyn ca

 

' 60

C IMA CMA  

IAM

vuông ti

có

sin60

.cot60

IA R

IMA

AM IA



















MAI

vuông ti

có

ng cao

 

AJ R  

AMB

cân ti

có

60AMB AMB  

u

AB AM  

Vì

 

AB R R











  





tn tm

tha

60AMB 

Vy vi

IM 

s tha yêu c bài .

----------------------------------------------------------------------------------------------------------------------------------

Câu 40 : Trong không gian vi h t

Oxyz

, cho các mt phng

 

: 2 1 0P x y z   

và

 

:2 1 0Q x y z   

. Gi

 

là mt cu có tâm thuc trng thi

 

ct mt phng

 

theo giao tuyn là mng tròn có bán kính bng

và

 

ct mt phng

 

theo

giao tuyn là mng tròn có bán kính bng

nh

sao cho ch t mt cu

 

tha mãn yêu cu.

r 

Giải:

Gi

 

;0;0Ia

và

0R 

lt là tâm và bán kính ca mt cu

 

d I P









và

 









Tổng hợp trắc nghiệm 12 – NHÓM PI Page 25

Ta có:

 

   

2 1 1

d I P R

d I Q r R















  





    





















 

2 2 8 0 1a a r    

 

c hai vi

là n s và

là tham s.

 t mt cu

 

tha mãn yêu ct tâm

 

;0;0Ia



 

có mt nghim duy nht:

 

' 0 1 2 8 0 0

r r r r          

Vy

r 

tha yêu cu bài toán.

----------------------------------------------------------------------------------------------------------------------------------

Câu 41 : Trong không gian vi h trc t

Oxyz

cho

       

0; ; , 0; ; , 1;0;0 , 1;0;0

A A B B

A y z B y z C D



; ; ;

A B A B

y y z z

i tha

2 2 2 2

A A B B

y z y z   

. Bit rng

,AC BD

luôn tip xúc vi mt mt cu c nh bán kính

. Xác

nh bán kính mt c

R 

Giải :

Ta có :



x x A B  

thuc mt phng

 

yOz



           

2 2 2 2 2 2

0 0 0 0 0 0 0 0 3

A A B B

y z y z           

,AB

thuc mt cu tâm

,bán kính

3R 

T u trên ta có :

,AB

thung tròn tâm

, bán kính

3R 

 

3OA OB

CD AB do CD yOz

















Ta thy :

 

..OAC OBD c g c  



ng cao h t nh

ca 2 tam giác ca bng nhau .

Gi

,HK

lt là hình chiu ca

trên

AC BD OH OK const   

Vy

,AC BD

luôn tip xúc mt cu tâm

, bán kính

RA

----------------------------------------------------------------------------------------------------------------------------------

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 26

Câu 42 : Trong không gian vi h trc t 

Oxyz

 m

   

4;0;0 , 0;0; ,A B m m

và

 

2;4;0C

. Gi

là hình chiu vuông góc ca

 

0;0;0O

ng thng

. Bit rng có mt

mt cu luôn luôn tip xúc vng thng

tm D. Tính bán kính mt c

Giải.

Ta có

90OD AB ODA  

Mà

 

D AB Oxz

nên

ng tròn

 

cha trong mt

phng

 

Oxz

có tâm

m ca

và bán kính

 

R JA

m

   

2,0,0 0,4,0OA J JC  

   

JC Oxz C JC   

là trc cng tròn

 

và

4JC 

Gi

là tâm mt cu

 

mà

luôn tip xúc ti

I JC

ID CD













IDC

vuông ti

, có

ng cao

.1JD JI JC JI   

Mà

IJD

vuông ti

5J ID JD JI   

----------------------------------------------------------------------------------------------------------------------------------

Câu 43 : Trong không gian vi h 

Oxyz

, cho hình l

. ' ' ' 'ABCD A B C D

cnh



AO

 

;0;0Ba

 

0; ;0Da

m

,MN

lng trên hai cnh

,'BD B A

sao cho

'BM B N

. Gi



lt là góc to bi ng thng

vng thng

,'BD B A

. Gi tr ca

cos cosA





bng bao nhiêu?

A 

1A 

A 

Giải:

Gi cnh ca hình l  

, ta có:

'AD AB BB b  

Ta có

'ABB

vuông cân ti

và

ABD

vuông cân ti

' ' 45

B AB AB B ABD ADB

BD B A b



   













Nu

'0BM B N



,'M B N B

, thì ta có:

cos cos ' cos90 0

cos cos

cos cos ' cos45

B BD

AB B









  



  



  







Đến đây ta có thể chọn được đáp án :)))))))

Nu

'2BM B N b



,M D N A

, thì ta có:

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 27

cos cos cos45

cos cos

cos cos ' cos90 0

ADB

DAB









  



  





  



Nu

'2BM B N x

vi

 

0;xb

, Gi

là hình chiu ca

trên

, ta có:

 

' ' 2

/ / ' ' , '

AN AB B N b x IA IN b x

BI B N BM

NI BB B N BM B A BD

BA B A BD



       





    





//MI AD

o)

 

AB MNI AB MN

MI AB

IM IB x

  





  









Gi

là hình chiu ca

trên

 

BH HM

MN MN IH MN AHB

AH HN





    







 

cos cos

MH MH MH

NH NH NH







   









   







MIN

vuông ti

có

ng cao

 

MH MN IM x

MH NH

NH NM IN b x







  





  





Vy

 

2 2 2

2 2 2 2 2

1 . 1

cos cos . .

2 2 2

MH NH MH MH MN x

MH NH

x x x x



       



Kt lun:

cos cos





----------------------------------------------------------------------------------------------------------------------------------

Câu 44: Trong không gian vi h trc

Oxyz

m

   

1;2;0 , 2; 3;2AB

. Gi

 

mt cng kính

.; ,AB Ax By

là hai tip tuyn mt cu

 

và

Ax By

. Gi

,MN

lt

ng trên

,Ax By

ng thng

luôn tip xúc vi mt cu

 

. Tính giá tr

.AM BN

. 19AM BN 

. 24AM BN 

. 38AM BN 

. 48AM BN 

Giải:

Gi

là tâm ca mt cu

 

và

là tim ca

và mt

cu..

Ta có

IMO AMO

OI OA OB

INO BNO

  



   



  



MA MI

MN AM BN

NB NI





   







,AM BN

là các tip tuyn ca mt c ng kính

và

AM B N

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 28

 

AM ABN AM AN AMN     

vuông ti

 

2 2 2 2 2 2

MN AM AN AM BA BN     

(

ABN

vuông ti

)

 

2 2 2 2

2.AM BN AM BN AB AM BN AB      

AM BN

Ta có

   

1;2;0 , 2; 3;2 38 . 19A B AB AM BN     

----------------------------------------------------------------------------------------------------------------------------------

Câu 45 : Trong không gian vi h trc to 

Oxyz

, cho mt phng

 

: 2 2 18 0,P x y z M   

là

m di chuyn trên mt phng

 

m nm trên tia

sao cho

. 24OM ON 

. Tính giá tr

nh nht ca khong cách t m

n mt phng

 

min ; 2d N P 





 

min ; 3d N P 





 

min ; 1d N P 





 

min ; 4d N P 





Giải :

Gi

là hình chiu ca

trên mt phng

 

2; 4; 4

OH const

















Gi

m nm trên tia

sao cho

. 24

4 8 8

;;

3 3 3

OI const

OH OI













  









Ta có :

OM OH

OM ON OH OI

OI ON

  

và góc

MOH ION

nên

 

MOH ION c g c   ∽



Góc

MHO INO

, mà

 

OH P OH MH   

góc

90MOH 



Góc

90INO N

thuc mt cu

 

ng kính

c nh vi tâm

244

;;

333









m ca

và bán kính

R 

Ta có :

 

;4d K P 





Mt cu

 

không giao vi mt phng

 

   

min ; ; 2d N P d K P R   

   

   

----------------------------------------------------------------------------------------------------------------------------------

Câu 46 : Trong không gian vi h trc

Oxyz

m

     

2;1; 4 , 6;2;3 , 1;1;3A B M

. Gi

 

là mt phng qua

sao cho tng khong cách t

,AB

n

 

là ln nht . Bit rng mt

phng

 

0P x ay bz c   

vi

,,abc

. Tính giá tr ca

A a b c  

A 

A 

A 

Giải :

Ta có:

 

1;0; 7

7;1;0

MA MB

MAMB



















MAB

cân ti

và có

AMB

là góc tù.

Gi

2; ;









là tn

AB MI AB

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 29

Gi

,HT

lt là hình chiu ca

,AB

lên mt phng

 

Trường hợp 1:

 

không cn

Gi

là hình chiu ca

lên mt phng

 

. Ta chc:

 

IL AH BT

IML

vuông ti

L IL IM const  

ng thc xy ra

 

P IM

ti



 

//P AB

nên

 

không cn

(thu king hp 1).

Vy

   

max

2A H BT I M P IM   

ti

Trường hợp 2:

 

cn

   

AB J AB P   

vi

n thng.

Ta có:

 

AH AJ

AH BT AJ BJ AB const

BT BJ





     







ng thc xy ra

     

P AB P IM I P     



 

cn

ti

(thu king hp 2 ).

Vy

   

max

A H BT AB P A B   

Vì

AMB

có

AMB

là góc tù nên

2AB IM

Vy tng khong cách t

,AB

n mt phng

 

ln nht là

khi

 

P AB

 

P

nhn

 

8;1;7 / / 1; ;



   





làm vtpt.

 

qua

   

1 7 7 1 7 7 3

1;1;3 : 0 ; ;

8 8 4 8 8 4 4

M P x y z a b c A



          

----------------------------------------------------------------------------------------------------------------------------------

Câu 47:Trong không gian vi h trc

Oxyz

,cho mt cu

       

2 2 2

: cos .sin sin .sin cos

S x y z

    

     

vi



    i luôn tha

mãn

 

, 0;2

  



. Bit

 

luôn tip xúc vi hai mt cu c nh

   

,SS

. Tng th tích ca hai

khi cu

   

,SS

là :



Giải :

Gi

là tâm mt cu

 

cos .sin

: sin .sin

cos

S I d y











  









 

2 2 2 2 2 2 2

sin cos .sin cos 1x y z

   

      



Vy

 

2 2 2

I S x y z    

Khong cách t tâm

ca mt cu

 

n gc t

là c

nh .



Vy mt cu

 

s tip xúc ngoài và tip xúc trong vi 2 mt cu

   

,SS

c nh có tâm là

Tổng hợp trắc nghiệm 12 – NHÓM PI Page 30

   

 

1 2 1 2

4 4 14

3 3 3

R R R

V V R R dvtt

R R R







    



     





    





----------------------------------------------------------------------------------------------------------------------------------

Câu 48 : Trong không gian vi h trc to 

Oxyz

, tp h  m

 

;;M a b c

tho mãn bt



   

2sin 2cos

a b c



    

là mt khi tròn xoay th tính bng :

















Giải :

m

   

2sin ;2cos ;0 4

A A Oxy x y



    

Vy tp hm

là mng tròn

 

tâm

 

0;0;0O

có bán kính

2R 

trong mt phng

 

Oxy

Vi mi

 

;;M a b c

ta luôn có

MA MA  



m

chng tròn

 

thì tp hm

to thành hình mt cái phao

ng tròn ln

R R MA  

ng tròn nh là

R R MA  

Áp dng công thc th tích cái phao ta có :

  

1 2 1 2

V R R R R



   

----------------------------------------------------------------------------------------------------------------------------------

Câu 49 : Trong không gian vi h trc t 

Oxyz

, cho mt phng

 

: 1 2 2 1 0

P m x mz m m     

. Bit rng khi

i thì

 

luôn tip xúc vi 1 mt

cu có bán kính c nh và có tâm

 

;;I a b c

thuc mt phng

 

: 2 0Qy

. Tính

23P a b c  

0P 

1P 

2P 

3P 

Giải :

Ta có:

 

;;I a b c

là tâm mt cu c nh luôn tip vi

 

     

 

1 2 2 1 0

2 1 2 1

;

m a mc m m

a m c m a

d I P

     

    

  











 

;

d I P





là mt hng s thì các h s ng t l vi nhau :

 

;;













   



















Tổng hợp trắc nghiệm 12 – NHÓM PI Page 31

 

: 2 0 2 ; 2; 3

I Q y b I P



           





----------------------------------------------------------------------------------------------------------------------------------

Câu 50 : Trong không gian vi h trc t 

Oxyz

, cho mt phng

 

   

: 2 1 1 10 0

P mx m y m z     

 m

 

2;11; 5A 

. Bit rng khi

 i thì

 

luôn tip xúc vi 2 mt cu có bán kính c 

. Tng bán kính 2 mt c

12 2

Giải :

Gi

 

;;I a b c

là tâm mt cu c nh luôn tip vi

 

   

 

2 2 2

2 1 1 10

2 10

;

4 1 1

ma m b m c

b c m ma b c

d I P

m m m

    

  







   



 

;

d I P





là mt hng s thì các h s ng t l vi nhau :

 

0; ; 5

b c b c











   



  











   

 

0;9; 5

; 4 11 12 2

0;25; 5

d I P b IA R R











          

















----------------------------------------------------------------------------------------------------------------------------------

Câu 51 : Trong không gian vi h trc

Oxyz

ng thng

 



là giao tuyn ca 2 mt phng

   

: 0 , : 1 0P x my z m Q mx y mz       

gi

 



là hình chiu ca

 



trên mt phng

 

Oxy

. Bit rng

 



luôn tip xúc vi mng tròn c nh. Tìm bán kính

c

1r 

1,5R 

2r 

3r 

Giải.

 

có

 

1, ,1

vtpt n m

 

có

 

;1;

vtpt n m m

 



có

     

 

, 1 ;2 ; 1

vtcp a n n m m m





   



Với

0m 

. Gi

 

;0;











Gi

 



là mt phng qua

 



và vuông góc vi mt phng

 

Oxy

có

(0,0,1)vtpt n 

 





có

   

 

, 2 ,1 ,0 :2 . 1 . 0 0

vtpt n a n m m m x m y











        







 

   

:2 1 1 0mx m y m



     

Vy

 





   

2 1 1 0mx m y m    

trong mt phng

 

Oxy

Xét trong mt phng

 

Oxy

, ta có:

m

   

 

0,0 , 1

O d O const



    







Tổng hợp trắc nghiệm 12 – NHÓM PI Page 32

Vy trong mt phng

 

Oxy

ta luôn có

 



luôn tip xúc vi mng tròn

 

c nh có tâm

 

0;0;0O

vi

 

Rm  

Với

0m 

, ta có :

     

: 1 / /

y t R Oxz











      













Vy

 



có dng

1y 

trong mt phng

 

Oxy

Mà

 

d O R  





nên

 



tip xúc vi

 

Kt lun:

 



luôn ting tròn

 

có bán kính là

mR

----------------------------------------------------------------------------------------------------------------------------------

Câu 52 : Trong không gian vi h trc to 

Oxyz

cho

       

0;0;1 , ;0;0 , 0; ;0 , 1;1;1A B m C n D

vi

0m 

0n 

và

1mn

. Bit rng khi

,mn

i thì tn ti mt mt cu c nh tip xúc vi

mt phng

 

ABC



. Tính bán kính

ca mt c

1R 

R 

2R 

R 

Giải :

Ta có :

 

: 1 0

x y z

ABC nx my mnz mn

       

Gi

 

;;I a b c

là tâm mt cu tho mãn yêu cu bài toán :

 

     

2 2 2 2

;

na mb c mn b a m a c mn

na mb mnc mn

d I ABC

mn mn

m n m n

      

  

   











 

;d I ABC





là mt hng s thì các h s ng t l vi nhau :

 

; ;1

a b b a

I a a a

a c c a











    

  



   









       

2 2 2

; 1 1 1 1d I ABC a a a a ID a R            





----------------------------------------------------------------------------------------------------------------------------------

---HẾT---

Bấm Tải xuống để xem toàn bộ.

| 1/32

| | Tải xuống

Preview text:

Nhóm PI
Tổng hợp câu hỏi trắc nghiệm hay môn Toán
Nguyễn Quang Hưng – Nguyễn Thành Tiến
Phần Hình học 12
Phương pháp tọa độ trong không gian
Năm 2017 – Tháng 5 – Ngày 10 – Thứ tư
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 1
Lời mở đầu
Đây là tài liệu đầu tiên do các thành viên NHÓM PI thực hiện .
Các bài tập được trích trong đây chủ yếu là những bài được lấy
trong các đề thi thử,bài giải được làm dưới cách chi tiết, nên có một
số chỗ dài hơn so với bình thường .
Nếu mọi người ai có góp ý gì về bài giải hay phát hiện sai sót nào
trong tài liệu thì xin đưa lên ý kiến trong group NHÓM PI .
Link group : https://www.facebook.com/groups/NhomPI/
Dẫu đã cố gắng làm rất cẩn thận nhưng khó tranh khỏi sai sót, mong các bạn thông cảm .
Cảm ơn các bạn đã đọc tài liệu .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 2
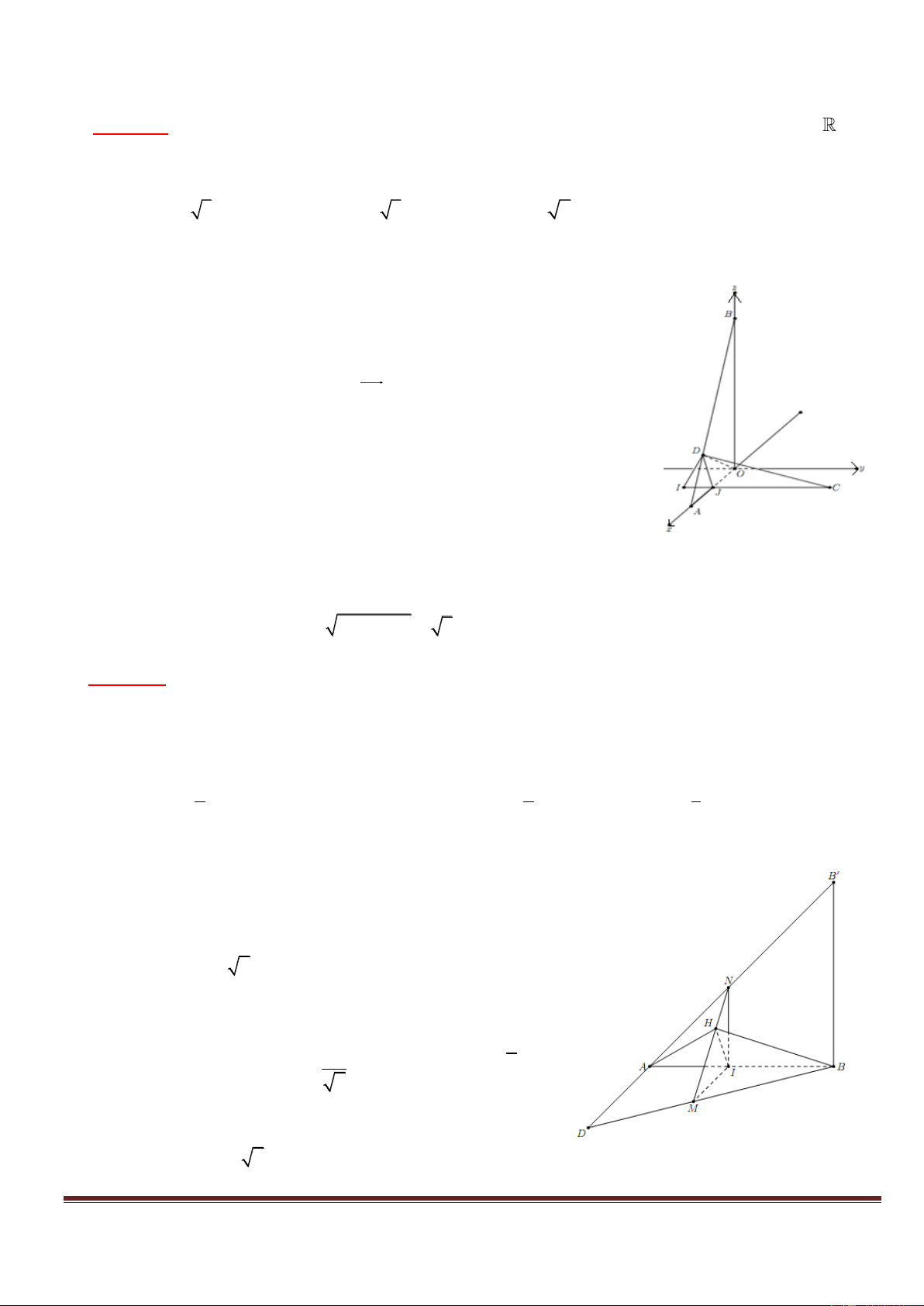
Câu 1 : Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng  P qua M 2;3;5 và cắt các tia O ,
x Oy,Oz lần lượt tại , A ,
B C sao cho giá trị của O , A O ,
B OC theo thứ tự lập thành cấp số nhân có
công bội bằng 3 . Khoảng cách từ O đến mặt phẳng  P là : 18 24 16 32 A. B. C. D. 91 91 91 91 Giải :
Theo giả thuyết ta có :  P 2 3 5 :    1 . a b c b   3a 2 1 5 32 Do a, ,
b c theo thứ tự là một cấp số nhân có công bội là 3      1 a  . c  9a a a 9a 9  d I  P 32 ;    . 91
----------------------------------------------------------------------------------------------------------------------------------
Câu 2 : Trong không gian với hệ trục toạ độ Oxyz , cho M 1; 2;3 , gọi
P: px  qy  rz 1 0  ,q ,pr  là mặt phẳng qua M và cắt các trục toạ độ O ,xOy,Oz tại , A ,
B C sao cho M là trọng tâm ABC 
. Tính T  p  q  r : 11 11 A. T   B. T  18 C. T  D. T  18  18 18 Giải :
Do  P cắt các trục toạ độ O , x Oy,Oz tại ,
A B, C  A ;
a 0; 0, B 0; ;
b 0,C 0;0;c với . a . b c  0 .    x y z P :    1 . a b c
x  x  x  3x a  3 A B c M   11
Do M là trọng tâm A
 BC  y  y  y  3y  b   6  T   . A B C G 18  
z  z  z  3z c  9   A B C G
----------------------------------------------------------------------------------------------------------------------------------
Câu 3 : Trong không gian với hệ trục toạ độ Oxyz , cho M 1; 2;3 , gọi
P: px  qy  rz 1 0  ,q ,pr  là mặt phẳng qua M và cắt các trục toạ độ O ,xOy,Oz tại , A ,
B C sao cho M là trực tâm ABC 
. Tính T  p  q  r : 77 3 77 3 A. T  B. T  C. T   D. T   3 7 3 7 Giải :
Do  P cắt các trục toạ độ O , x Oy,Oz tại ,
A B, C  A ;
a 0; 0, B 0; ;
b 0,C 0;0;c với . a . b c  0 .    x y z  1 1 1  P :
  1 véctơ pháp tuyến của mặt phẳng P là v     . P ; ; a b c  a b c 
Ta có OABC là một tứ diện vuông tại O có H là trực tâm ABC 
 AH  BC .
Mặc khác : OA  BC OA  OBC .
Vậy BC  OAH   BC OH . Chứng minh tương tự ta có AB  OH .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 3    M P a 14    3
OH   ABC  . Vậy từ đó ta có :   b   7  T   . OM / /   v P 7  14 c   3
----------------------------------------------------------------------------------------------------------------------------------
Câu 4 : Trong không gian với hệ trục tọa độ Oxyz cho a  b  a b 0 3; 2; , 120 . Gọi 2 vecto
p  2a  b; q  a  2b . Tính cos p, q . 1 1 1 1 A. B. C. D. 4 39 39 2 39 3 39 Giải :
Ta có : p q   a  ba  b 2 2 2 0 2 . 2 2
 2 a  3ab  2 b  2.3  3.3.2.cos120  2.2 1 2 2 2 2 0 2
p  4 a  4ab  b  4.3  4.3.2.cos120  2  48 . 2 2 2 2 0 2
q  a  4ab  4 b  3  4.3.2.cos120  4.2  13 .  p q .pq 1 cos ,    A . p q 4 39
----------------------------------------------------------------------------------------------------------------------------------
Câu 5 : Trong không gian với hệ trục tọa độ Oxyz cho điểm và mặt phẳng  P : x  2y  3z  4  0 .
Biết M , N là 2 điểm đối xứng nhau qua mặt phẳng  P, M mặt cầu C  x   y  2 2 2 : 4  z  5 . Hỏi
N thuộc mặt cầu nào dưới đây : 8 40 24 45 A. 2 2 2
x  y  z  x  y  z   0 7 7 7 7 8 40 24 45 B. 2 2 2
x  y  z  x  y  z   0 7 7 7 7 8 40 24 45 C. 2 2 2
x  y  z  x  y  z   0 7 7 7 7 8 40 24 45 D. 2 2 2
x  y  z  x  y  z   0 7 7 7 7 Giải :
Gọi I là tâm của mặt cầu C   I 0; 4  ;0 .  
Gọi I ' đối xứng I qua  P 4 20 12  I ' ;  ;   .  7 7 7 
Theo yêu cầu bài toán ta có :  4 20 12 
M  C  có tâm I 0; 4
 ;0 và bán kính R  5  N S có tâm I ' ; ;   bán kính R  5  7 7 7  .  S  8 40 24 45 2 2 2
: x  y  z  x  y  z   0 . 7 7 7 7
----------------------------------------------------------------------------------------------------------------------------------
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 4 Câu 6 : Trong không gian với hệ trục tọa
độ Oxyz , cho mặt phẳng
P: x  y  z 1 0, A1;1;  1 , B 0;1; 2, C  2  ;0  ;1 và M  ; a ;
b c P sao cho 2 2 2
S  2MA  MB  MC đạt giá trị nhỏ nhất . Khi đó giá trị của T  3a  2b  c là : 25 25 25 25 A. T  B. T  C. T   D. T   4 2 4 2 Giải :  3 5 
Gọi I là điểm thỏa 2IA  IB  IC  0  I 0; ;   .  4 4  2 2 2 Ta có : 2 2 2
S  2MA  MB  MC  2 MI  IA  MI  IB  MI  IC  2 2 2 2
 MI  IA  IB  IC  MI  IA IB  IC 2 2 2 2 4 2 2 2
 4MI  2IA  IB  IC . Do 2 2 2
2IA  IB  IC  const nên S  MI
 M là hình chiếu của I trên P . min min  3 3 1  25  M  ; ;  T     .  2 4 4  4
----------------------------------------------------------------------------------------------------------------------------------
Câu 7 : Trong không gian với hệ trục Oxyz cho 2 điểm A1;0; 2, B 3;1;  1 và mặt phẳng
P: x  y  z 1 0 . Gọi điểm M x ; y ;z  P sao cho 3MA 2MB đạt giá trị nhỏ nhất . Tính o o o   
A  9x  3y  6z . o o o A. 2 B. 1 C. 3 D. 4 Giải.
Gọi I là điểm thỏa 3IA  2IB  0  I  3  , 2  ,8 .
Ta có 3MA  2MB  3IA  IM   2IB  IM   3IA  2IB  IM  IM  IM .
Vì I cố định, M   P nên 3MA  2MB đạt giá trị nhỏ nhất  IM đạt giá trị nhỏ nhất.
 M là hình chiếu của I trên mặt phẳng P .
Gọi d  là đường thẳng qua I và vuông góc với mặt phẳng  P  vtcp a
 vtpt n  1,1,      1 . d P
 d  : x  3
  t, y  2
  t, z  8  t .    
M  d    P 11 8 22  M , ,  A  3   .  3 3 3 
----------------------------------------------------------------------------------------------------------------------------------
Câu 8 : Trong không gian với hệ tọa độ Oxyz cho mặt phẳng  P : x  2y  2z  7  0 và ba điểm A1; 2; 
1 , B 3;1;2 , C 1;2  ;1 . Điểm M  ; a ;
b cP sao cho 2 2 2
MA  MB  MC đạt giá trị lớn
nhất. Khi đó tổng A  a  b  c bằng bao nhiêu ? 20 14 20 14 A. A  B. A  C. A   D. A   9 9 9 9
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 5 Giải:
MA  a  2
1  b  22  c  2 2 1  2 2 2 Ta có: 2
MB  a  3  b   1  c  2 . 
MC  a  2
1  b  22  c  2 2 1 
 MA  MB  MC  a  a  b  b  c  
 a  2  b  2 2 2 2 2 2 2 2 6 6 26 44 3 3  c    . 2 2 Vậy  2 2 2
MA  MB  MC 
 a  3 b   2 3  c   MI I 3; 3  ;0 . min max   với   min Mà I 3; 3
 ;0 cố định nên MI  M là hình chiếu của I trên mặt phẳng P . min
Gọi d  là đường thẳng qua I 3; 3
 ;0 và vuông góc với mặt phẳng P , ta có: x  3 t  
d  :  y  3   2t . z  2t 
Vì M d   M 3  t; 3
  2t;2t .     
M  P    t     t    t  4 23 35 8 3 2 3 2
2 2  7  0  t   M ; ;   . 9  9 9 9  20 
 a  b  c  . 9
----------------------------------------------------------------------------------------------------------------------------------
Câu 9 : Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1;1;0, B0;1;1, C 1;0;1 . Tìm 2
hợp tất cả các điểm M trên mặt phẳng Oxz sao cho M .
A MB  MC  2 . A. Một đường thẳng B. Một đường tròn C. Một đường elip
D. Không xác định được Giải: AB   1  ;0;  1  AB  2 .  1 1  3
Gọi I là trung điểm của AB  I ;1;   cố định và 2 IC  .  2 2  2 AB 1 Ta có: M .
A MB  IA  IM .IB  IM   IA  IM.IA  IB 2 2 2 2 2  IM  
 IM    IM . 4 2 2 5 Vậy 2 2 M .
A MB  MC  2  MI  MC  . 2  3 1 3 
Gọi J là trung điểm của IC  J ; ; 
 cố dịnh và MJ là đường trung tuyến của M  IC .  4 2 4  2 5 IC 3 7 14 2 2 2 2 2
  MI  MC  2MJ 
 2JM   JM   JM   const . 2 2 4 8 4 14
Mà J cố định nên M di động trên mặt cầu S  tâm J với bán kính R  . 4
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 6 1 14
Mặt phẳng Oxz có phương trình y  0  d J ,
 Oxz    R  
SOxz là một đường 2 4 tròn C  .
Vậy M di động trên đường tròn C  .
----------------------------------------------------------------------------------------------------------------------------------
Câu 10 : Trong không gian Oxyz cho hai điểm A2t; 2t;0, B 0;0;t ,t  0 . Cho điểm P di động thỏa: O . P AP  O . P BP  A .
P BP  3 . Tìm giá trị t sao cho OP  3. max 3 4 2 3 A. t  B. t  C. t  D. t  4 3 3 2 Giải: O . P AP  O . P BP  A .
P BP  3  O .
P OP  OA  O .
P OP  OB  OP  OA.OP  OB  3 . 2  3OP  2O .
P OA OB  3. (Vì O . A OB  0 ) 2  3OP  2O .
P OI  3 (với I là điểm thứ tư của hình bình hành AOBI  I 2t; 2t;t  ). 2  2
 4t 4t 2t  3OP  3O .
P OJ  3 (với J thỏa OJ  OI  J ; ;  . 3  3 3 3  2  OP O .
P OJ  1  O .
P OP OJ  1 O .
P JP  1  MP  MO.MP  MJ  1 (với M là   trung điể 2t 2t t m của OJ  M ; ;   .  3 3 3  2 2 2 2 2 2 2  MP  M .
O MJ  1  MP  MO  1  MP  1 MO  1 t  MP  1 t .
Vậy P di động trên mặt cầu S  tâm M với bán kính 2 R  1 t . Nên OP
 P  OM  S và OM,OP cùng hướng. max   2 2 2       Khi đó 2t 2t t 2 2 OP  OM  R   
 1 t  t  1 t . max        3   3   3  t   3 t   3  2 2 OP
 3  t  1 t  3  1 t  3 t     . max 4 2 2 1
  t  9  6t  t t   3
----------------------------------------------------------------------------------------------------------------------------------
Câu 11 :Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm M  2  ; 2   ;1 , A1; 2;  3 và đường x 1 y  5 z thẳng d :  
.Tìm véctơ chỉ phương u của đường thẳng  đi qua M , vuông góc với 2 2 1 
đường thẳng d đồng thời cách A một khoảng cách lớn nhất . A. u  4; 5  ; 2   B. u  1;0;2 C. u  3;4; 4   D. u  2;2;  1 Giải :
Gọi  P là mặt phẳng vuông góc với d và qua M .
Gọi H là hình chiếu của A trên  P . Gọi N là hình chiếu của H trên d .
 AN   ( định lí 3 đường vuông góc )  d  ; A    AN  .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 7
Ta có : AN  AM . Dấu "  " xảy ra khi N  M   là đường thẳng qua M và   MH .
Tính toán ta có : u  4; 5  ; 2   .
----------------------------------------------------------------------------------------------------------------------------------
Câu 12 :Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm M  2  ; 2   ;1 , A1; 2;  3 và đường x 1 y  5 z thẳng d :  
.Tìm véctơ chỉ phương u của đường thẳng  đi qua M , vuông góc với 2 2 1 
đường thẳng d đồng thời cách A một khoảng cách bé nhất . A. u  2;1;6 B. u  1;0;2 C. u  3;4; 4   D. u  2;2;  1 Giải :
Gọi  P là mặt phẳng vuông góc với d và qua M .
Gọi H là hình chiếu của A trên  P . Gọi N là hình chiếu của H trên d .
 AN   ( định lí 3 đường vuông góc )  d  ; A    AN  .
Ta có : AN  AH . Dấu "  " xảy ra khi N  H   là đường thẳng qua M , H .
Tính toán ta có : u  1;0;2 .
----------------------------------------------------------------------------------------------------------------------------------
Câu 13 : Trong không gian với hệ tọa độ xyz, cho điểm A1; 2; 3
  và cắt mặt phẳng
P:2x  2y  z 9  0 . Đường thẳng đi qua A và có véctơ chỉ phương u  3;4; 4
  cắt P tại B
. Điểm M thay đổi trong  P sao cho M luôn nhìn đoạn AB dưới một góc 0 90 . Khi độ dài MB
lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau : A. J  3  ;2;7 B. H  2  ; 1  ;3
C. K 3;0;15 D. I  1  ; 2  ;3 Giải :
Gọi H là hình chiếu A trên  P  AH   P  AH  MB .
Vì M luôn nhìn đoạn AB dưới một góc 0
90 nên AM  MB .
Vậy MB   AHM   MB  HM .
 M chạy tung tăng trên đường tròn đường kính MH M  B . Vậy MB khi M  H . max x  2   t 
Tính toán ta có được : MB : y  2 
 MB qua I  1  ; 2  ;3 . z 1 2t 
---------------------------------------------------------------------------------------------------------------------------------- x  3 y  2 z  5
Câu 14 : Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d :   1  2 2 5 x  2 y  4 z  4 và d :  
. Gọi  là đường phân giác trong của góc tù tạo bởi hai đường 2  1 4 4
thẳng d , d .  có phương trình là: 1   2 
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 8 x 1 5t x  1 t x  1 t x 1 5t    
A.  :  y  6t
B.  :  y  2  t
C.  :  y  2t
D.  :  y  6t     z  9t  z  t  z  t  z  9t  Giải:
 x  3 y  2   2 2  x  y 1 x 1
 y  2 z  5   A
 1;0;0 d1 Xét hệ:    5
 y  2z  0  y  0 . Ta nhận thấy  . 2 5    A
 1;0;0 d2 y  z  0 z  0  
 y  4 z  4   4 4
Vậy A1;0;0  d  d . 1   2
d có vtcpa  2;2;5 , d có vtcpa  1;4;4 . 2   2  1   1 
Ta có: a .a  30  0  a ;a  0
 90  a ;a là góc nhọn  a ;a là góc tù. 1 2  1 2 1 2  1 2
Gọi B là điểm thỏa AB  a  B 3; 2;5  d . 1    1
C là điểm thỏa AC  a   C 0; 4  ; 4   d . 2    2
Vậy BAC là góc tù tạo bởi hai đường thẳng d , d . 1   2 
Do đó  chính là đường phân giác trong của BAC .
Ta có: AB  a  33, AC  a  33  AB  AC  A
 BC cân tại A . 1 2
  cũng là đường trung tuyến từ A của ABC  .   đi qua   A  3 1 1; 0; 0 , M ; 1  ;   là trung điểm của BC   có  2 2   1 1  vtcp  a     AM ; 1;   .  2 2  x 1 t   có a          1; 2    ;1 và qua A1;0;0
 : y 2t B . z  t 
----------------------------------------------------------------------------------------------------------------------------------
Câu 15 : Trong không gian với hệ trục tọa độ Oxyz cho điểm A1; 2; 
1 , B 0; 4;0 và mặt phẳng
P:2x  y 2z  2015  0 . Gọi  là góc nhỏ nhất giữa mặt phẳng Q đi qua 2 điểm , A B và tạo
với  P . Tính cos . 1 1 2 1 A. B. C. D. 9 6 3 3 Giải :
Theo cách hình học :
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 9
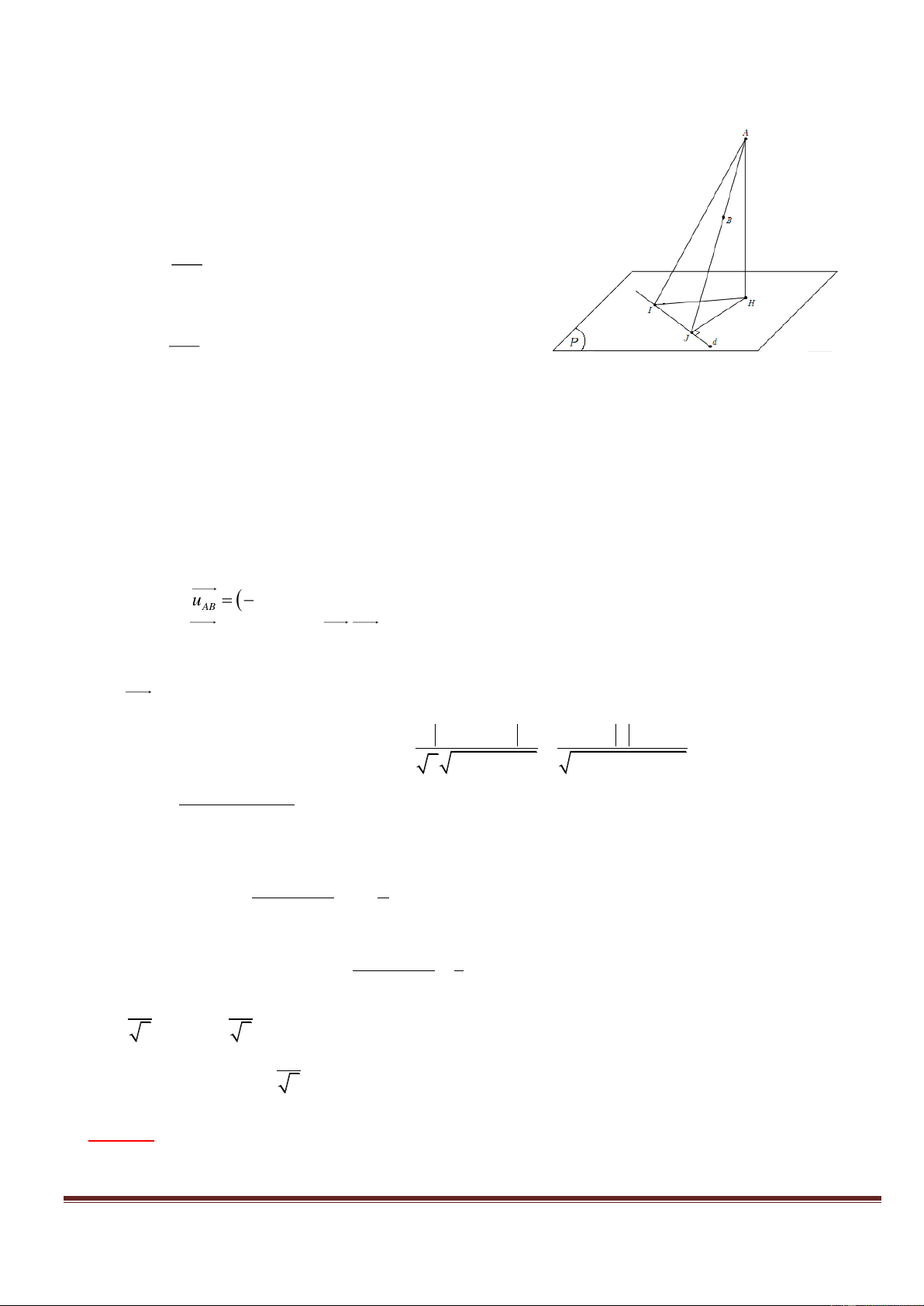
Gọi H là hình chiếu của A trên mặt phẳng  P , d là
giao tuyến của  P,Q , I là giao điểm của AB và mặt
phẳng  P , J là hình chiếu của H trên d .
 Góc của 2 mặt phẳng P,Q là góc AJH với AH sin AJH  . AJ
 Góc của AB và mặt phẳng P là góc AIH với AH sin AIH  . AI
Dễ dàng chứng minh được d   AJH   IJ  AJ  A
 IJ vuông tại J .
 AJ  AI  sin AJH  sin AIH .
Dấu "  " xảy ra khi d  IH .  
Vậy min  P;Q  AIH  
là góc giữa AB và mặt phẳng  P . Cách đại số : vtcp u   AB  1;2  ;1  Ta có : vtpt n
 a b c  u n   a  c  b . Q  ; ;    . AB Q 0 2 AB   Q  vtpt n  2; 1  ; 2  . P   
2a  b  2c b
Ta có cos là góc của  P,Q  cos   2 2 2 2 2
9 a  b  c
2a  4ab  5b 2 b 2  cos   2 2 2a  4ab  . 5b
Xét b  0  cos  0 1 a Xét 2 b 0 cos       t    . 2
2t  4t  5  b  Tính toán ta có đượ 1 1 c : 2 0  cos    2 2t  4t  . 5 3 1 1    cos  3 3 1 Nói tóm lại max cos  . 3
----------------------------------------------------------------------------------------------------------------------------------
Câu 16 : Cho M 1, 2,3, Aa,0,0, B 0, ,
b 0,C 0, 0, c trong đó a,b,c là các số dương. Tìm mặt
phẳng  P đi qua , A ,
B C, M sao cho V
đạt giá trị nhỏ nhất. OABC
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 10
A.  P : 6x  3y  2z 18  0
B.  P : 6x  3y  2z  0 B.
P:6x 3y  2z 9  0
D.  P : 6x  3y  2z  36  0 Giải. x y z Ptmp qua , A , B C có dạng:    1. a b c
Vì M   ABC  1 2 3     1 . a b c 1 2 3
Áp dụng BĐT Cauchy cho 3 số , , không âm, ta có: a b c 1 2 3 1.2.3 27.6 abc 3 1     3  1  abc  162   27  V  27 . a b c . a . b c abc 6 OABC Đẳ 1 2 3 1 ng thức xảy ra 
    a  3,b  6,c  9 . a b c 3    x y z ABC :
  1   ABC: 6x  3y  2z 18  0 . 3 6 9
----------------------------------------------------------------------------------------------------------------------------------
Câu 17 : Trong không gian với hệ trục tọa độ Oxyz , cho A ;
a 0;0, B 0; ;
b 0, C 0;0;c với a, ,
b c  0 sao cho OA  OB  OC  AB  BC  CA  1 2 . Tìm giá trị lớn nhất của V . O.ABC 1 1 1 1 A. maxV  B. maxV  C. maxV  D. maxV  O. ABC 54 O. ABC 162 O. ABC 486 O. ABC 108 Giải : 1 Ta có : V  abc . O. ABC 6 Theo gia thuyết ta có : 2 2 2 2 2 2
OA  OB  OC  AB  BC  CA  a  b  c  a  b  b  c  c  a .
Theo nhà toán học Cauchy ta có :  3
a  b  c  3 abc .  2 2 2 2 2 2
a  b  b  c  c  a 
 ab  bc  ca 3 2  3 2. abc .
 OA  OB  OC  AB  BC  CA       3 1 2 3 1 2 abc . 1 1 1 1 3
 abc   V  abc 
. Dấu "  " xảy ra khi và chỉ khi a  b  c  . O. 3 ABC 6 162 3
----------------------------------------------------------------------------------------------------------------------------------
Câu 18 : Trong không gian với hệ trục tọa độ Oxyz , cho lăng trụ đứng AB .
C A' B 'C ' có a,b  0 A ;
a 0;0, B  ;
a 0;0 , ,C 0; 1  ;0, B' ;
a 0;b với 
. Khoảng cách lớn nhất giữa 2 đường a  b  4
thẳng B 'C và AC ' là: 2 A. 1 B. 2 C. 2 D. 2 Giải.
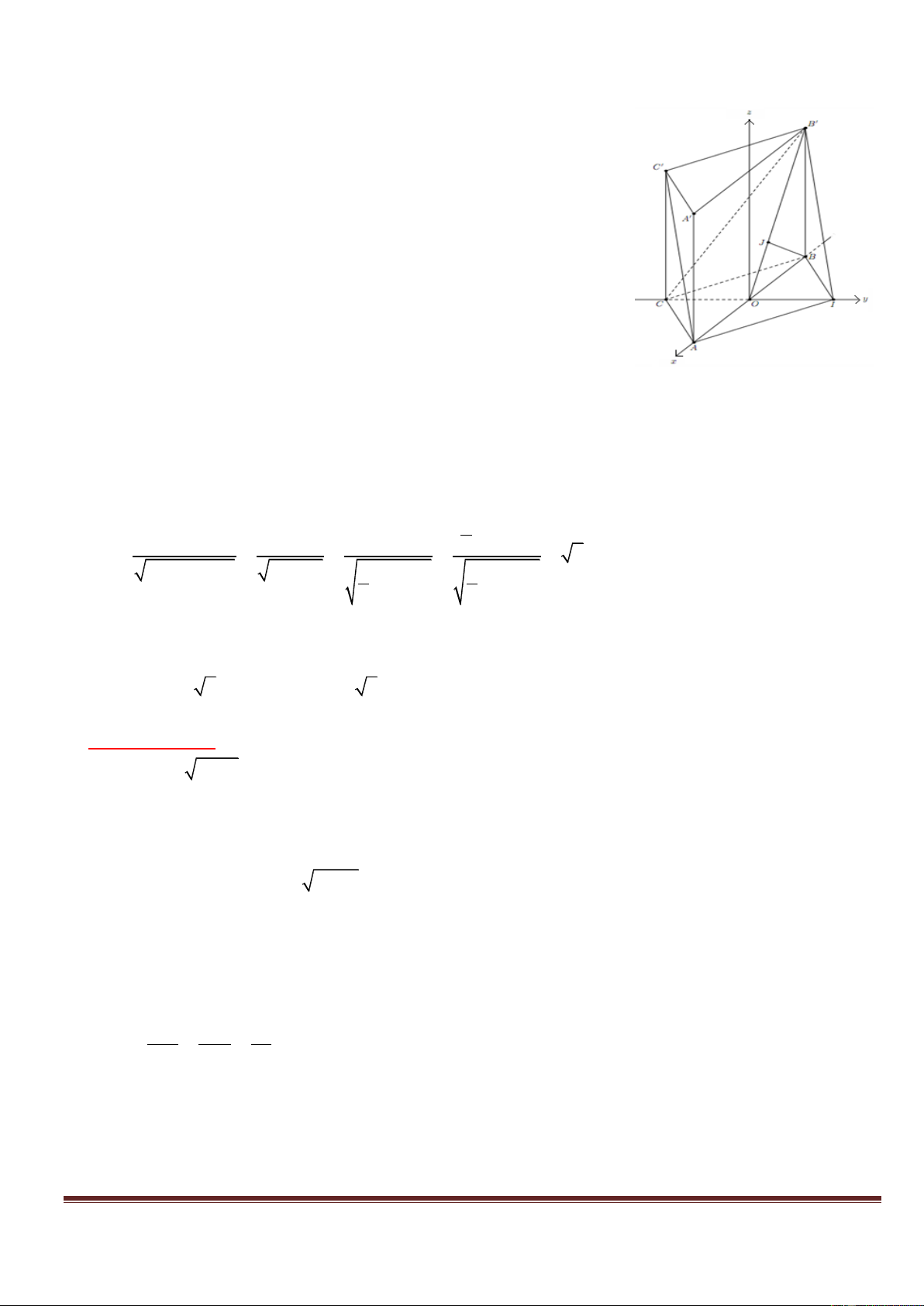
Gọi I là đối xứng của C qua O .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 11
AI / /BC / /B'C '
Ta có: AIBC là hình bình hành    AIB'C ' là
AI  BC  B'C ' hình bình hành.
 AC '/ /B'I  B'CI .
 d B'C, AC '  d AC ',B'CI   d  ,
A  B 'CI      . Mà ,
A B đối xứng với nhau qua O nên d  ,
A  B 'CI   d B, B 'CI      .
Ta có CI  OBB '   B 'CI   OBB ' .
Vẽ đường cao BJ của tam giác vuông OBB '
 BJ  OB'  B'CI   OBB'
 BJ  B'CI   BJ  d B,B'CI    .
BJ là đường cao của tam giác vuông OBB ' , ta có: 1 a  b2 B . O BB ' ab ab 4 BJ      2 . 2 2 2 2 BO  BB ' a  b 1 a  b2 1 a  b2 2 2
Đẳng thức xảy ra  a  b  2 . Vậy Max  2  Max   2 . BJ
d B ' C, AC '
---------------------------------------------------------------------------------------------------------------------------------- Câu 19 : Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P  2
: 3mx  5 1  m y  4mz  20  0 với m  1  ;00 
;1 luôn cắt mặt phẳng Oxz theo giao tuyến m
là đường thẳng  . Khi m thay đổi thì các giao tuyến  có kết quả nào sau đây : m m A. Cắt nhau B. Song song C. Chéo nhau D. Trùng nhau Giải :    mx 
 m y  mz  
P  Oxz    m    2 3 5 1 4 20 0 m y  0 
  :3mx  4mz  20  0 với  trong mặt phẳng Oxz . m m Gọi 
: 3m x  4m z  20  0, 
:3m x  4m z  20  0 là hai đường thẳng với m m 1 1 1 2 2 2 m , m  1
 ;0  0;1 bất kì và m  m . 1 2     1 2 3m 4m 20 Ta có : 1 2     / /  . 1   2  3m 4m 20 m m 2 2
----------------------------------------------------------------------------------------------------------------------------------
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 12  1 3 
Câu 20 : Trong không gian Oxyz , cho điểm M  ; ; 0  
 và mặt cầu S  2 2 2
: x  y  z  8. Đường 2 2  
thẳng d thay đổi, đi qua điểm M , cắt mặt cầu S  tại hai điểm phân biệt ,
A B . Tính diện tích lớn
nhất S của tam giác OAB : A. S  7 . B. S  4 . C. S  2 7 . D. S  2 2 . Giải :
Mặt cầu S  có tâm O 0;0;0 và bán kính R  2 2 .
Ta có : OM 1  R  M thuộc miền trong của mặt cầu S  .
Gọi A , B là giao điểm của đường thẳng với mặt cầu. Gọi H là chân đường cao hạ từ O của tam giác OAB .
Gọi x  OH 0  x  OM   1 2 2 2
 HA  R  OH  8  x . 1 2  S
 OH.AB  OH.HA  x 8  x . OAB 2 Xét : 2
f (x)  x 8  x với x 0  ;1 .    x 2 2 2 x 8 2x f '  8  x  
 0 với x 0  ;1 . 2 2 8  x 8  x  S
 max f x  f    1  7 . OAB 0; 1
---------------------------------------------------------------------------------------------------------------------------------- Câu 21 : Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P  2
m  m   x   2 : 1 2 m  
1 y  2 m  2 z 2
m  m 1  0 luôn chứa đường thẳng  cố định khi
m thay đổi. Tính khoảng cách từ gốc tọa độ đến  . A. d O   1 ,    B. d O   2 ,    C. d O   4 ,    D. d O   5 ,    3 3 3 3 Giải: Ta có:  2
m  m   x   2
m   y  m   2 1 2 1 2
2 z  m  m 1  0 m  
 x  y   2 2
1 m   x  2z  
1 m   x  2y  4z   1  0 m   .
x  2y 1  0   1
x  2y 1 0  
 x  2z 1 0 2
 x  2z 1 0  
x  2 y  4z 1  0  3
2x  4z  2  0  3  1
x  2y 1  0 
x  2y 1  0
x  2y 1  0
 x  2z 1 0     
x  2z 1  0 y  z  0
x  2z 1  0 
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 13
x  2y 1  0 x  2t 1  
Đặt z  t , ta có: y  t  0  y  t  .   z  t z  t   x  2t 1 
Vậy  P luôn chứa đường thẳng cố định  :  y  t  có vtcp a  2; 1  ;  1 và qua điểm z  t  A 1  ;0;0. a OA  
Ta có a OA       d O     ; 2 1 ; 0; 1; 1 ,      . a 6 3
---------------------------------------------------------------------------------------------------------------------------------- x  4m  3 y  2m  3
z  8m  7   3  1 
Câu 22 : Cho đường thẳng d :   m    1  ; ;  và A1;1  ;1 . m  2m 1 m 1 4m  3   4 2  Biết d
luôn nằm trong một mặt phẳng  P cố định khi m thay đổi. Tính d  A;  P m  . 115 110 105 115 A. B. C. D. 55 55 55 60 Giải :
Đường thẳng d đi qua A4m 3; 2m  3;8m  7 và có VTCP u  2m 1;m 1;4m  3 . m   Giả sử d     
ax  by  cz  d  m      . Khi đó ta có : m   3 1 : 0 1; ;    4 2  A  a   2m  
1  b m  
1  c 4m  3  0 
 2a  b  4c 
ma b 3c  0      u .n  0 
a m   b m   c m    
 a  b  c m  a  b  c  d  d 
4 3 2 3 8 7 0 4 2 8     3 3 7 0 m
2a  b  4c  0 b   10a
a  b  3c  0 
Để hệ có nghiệm đúng với mọi m thì :   c  3  a .
4a  2b  8c  0  d  6  a   3
 a  3b  7c  d  0 b   10 
Ta chọn : a  1  c  3  . d  6     Vậy d      x  y  z   m      . m   3 1 : 10 3 6 0 1; ;    4 2 
Cách 2 : đơn gian phù hợp trắc nghiệm.
Ta chọn 2 số m thỏa yêu cầu bài toán  có đường thẳng d  viết được mp    xong bài .
---------------------------------------------------------------------------------------------------------------------------------- Câu 23: Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu
S xm2 y 2 2 2 :
2m  z 5m  4m 1 0 . Biết khi m thay đổi thì S  luôn giao với mặt phẳng  P
cố định với giao tuyến là một đường tròn C  cố định . Tính bán kính của đường tròn đó
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 14 4 2 1 A. R  1 B. R  C. R  D. R  5 5 5 Giải : S 2 2 2
: x  y  z 1 2m  x  2y  2  0 .
 Với mọi m thì mặt cầu S  luôn giao với mặt phẳng P : x  2y  2  0   S ' 2 2 2     
S    P : x y z 1  
 C  S 'P  .  P
  : x  2y  2  0
Gọi I 0;0;0 là tâm mặt cầu S   d I  P 2 ' ;    . 5  R  R
 d I P   . C  1 ; S ' 2    2     5
----------------------------------------------------------------------------------------------------------------------------------
Câu 24 : Trong không gian cho 2 điểm phân biệt ,
A B cố định . Tập hợp các điểm M trong không 3 m m
gian là mặt cầu cố định 2 bán kính R 
AB . Khi đó thỏa mãn M . A MB  AB  , m n   , là 2 n n
phân số tối giản. Tính P  m  n  mn2 2 . A. 49 B. 64 C. 36 D. 81 Giải :
Chọn hệ trục Oxyz sao cho ,
A B Ox và O 0;0;0 là trung điểm AB . Khi đó ta có : A  a;0;0 MA  
a  x ;y ;z M M M   a  0
. Gọi M  x ; y ; z   . M M M      a  AB 2a B ; 0; 0 MB  
a  x ;y ;z M M M  4m Ta có : 2 M . A MB  a n 4m 2 2 2 2 2
 x  a  y  z  a M M M n 2 .   m      x   y   z    a    M 2  M 2  M 2 4 0 0 0 1  n       4m 
Do vế phải là 1 hằng số  M thuộc tập hợp điểm đường tròn tâm O có R  1 a   .  n   4m  3 m 2 Ta có
1 a  AB  3a     .  n  2 n 1
---------------------------------------------------------------------------------------------------------------------------------- x 1 y 1 z  2
Câu 25 : Trong không gian với hệ trục tọa độ Oxyz , cho bốn đường thẳng d :   ; 1  2 1 3  x  3 y  2 z  4 x  2 y z x  4 y 1 z  2 d :   ; d :   ; d :  
 là đường thẳng cắt 2   3  4 2 1 3 7  1 1 1 5  2  . Gọi  
cả 4 đường thẳng đã cho . Biết véctơ chỉ phương của  là u  a; ; b       1 . Tính T 3a 7b . A. T  5  B. T  5 C. T  4  D. T  4
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 15 Giải :
Ta có : vtcp u  2;1;3 và d qua M 1; 1
 ;2 , vtcp u  2;1;3 và d qua N  3  ;2;4. 2  d  1  d  1 2 Ta thấy u u
và M  d  d / / d . 2  1  2 1 d d2
Gọi  P là mặt phẳng chứa d , d  vtpt n  [MN,u ]  7;16; 1
 0 và P qua điểm M 1; 1  ;2 . 1 2 P d   1
 P : 7x 16y 10z  29  0 .  x  2 y z
x  7 y  2  0    
Gọi E  d  P   7  1 1
 y  z  0  E 5;1;1 . 3     
7x 16y 10z  29  0 7x 16y 10z  29  0   x  4 y 1 z  2 5
 x  y  21  0    
Gọi F  d  P   1 5  2 
 2y 5z  8  0  F 5; 4  ;0 . 4     
7x 16y 10z  29  0 7x 16y 10z  29  0   EF  10; 5  ; 
1  EF không song song d , d . 1 2
Do   d , d    P . Mà   d , d   qua E, F  u        10;5  ;1 T 5 . 3   4    1   2       
----------------------------------------------------------------------------------------------------------------------------------
Câu 26 : Trong không gian Oxyz cho ba điểm A ;
a 0;0; B 0; ;
b 0; C 0;0;c với a, , b c  0 . Giả sử a, ,
b c thay đổi nhưng luôn thỏa 2 2 2 2
a  b  c  k với k cho trước thì ABC 
có diện tích lớn nhất là : 2 k 2 k 2 k 2 k A. S  B. S  C. S  D. S  max max max max 2 3 3 2 2 2 Giải: 2 2 2 2 1 1 1 OA .OB a .b
Gọi I là hình chiếu của O trên 2 AB     OI   2 2 2 2 2 2 2 OI OA OB OA  OB a  . b O  AI vuông tại 2 2 2 2 2 2 2 2 2 2 2 2 2 2 a .b
a b  b c  c a
a b  b c  c a 2 2 2 2
O  IC  OI  OC   c   OI  2 2 2 2 2 2 a  b a  b a  . b O  AB vuông tại 2 2 2 2 2
O  AB  a  b  AB  a  b . 1 1 2 2 2 2 2 2 S  A . B IC 
a b  b c  c a . ABC 2 2 Ta có: 2 2 2 2 4 4 4 2 2 2 2 2 2 4
a  b  c  k  a  b  c  2a b  2b c  2c a  k . 4 k   4 4 4
a  b  c 2 2 2 2 2 2 
 a b  b c  c a  2
a  b  c 4 k   4 4 4
a  b  c  k 4 k 4 4 4  2 2 2 2 4
Mà a  b  c   nên  . 3 3 2 3 4 2 2 k 1 k k Vậy 2 2 2 2 2 2
a b  b c  c a   S  .  . 3 ABC 2 3 2 3 Đẳ k
ng thức xảy ra  a  b  c  . 3
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 16
----------------------------------------------------------------------------------------------------------------------------------
Câu 27 : Trong không gian với hệ trục tọa độ Oxyz cho điểm A1;0;0, B 0;1;0 ,C 0;0  ;1 . Có bao
nhiêu mặt cầu có tâm nằm trên mặt phẳng   : z  y  z  0 và tiếp xúc với 3 dường thẳng A , B BC,CA . A. 1 B. 2 C. 3 D. 4 Giải.
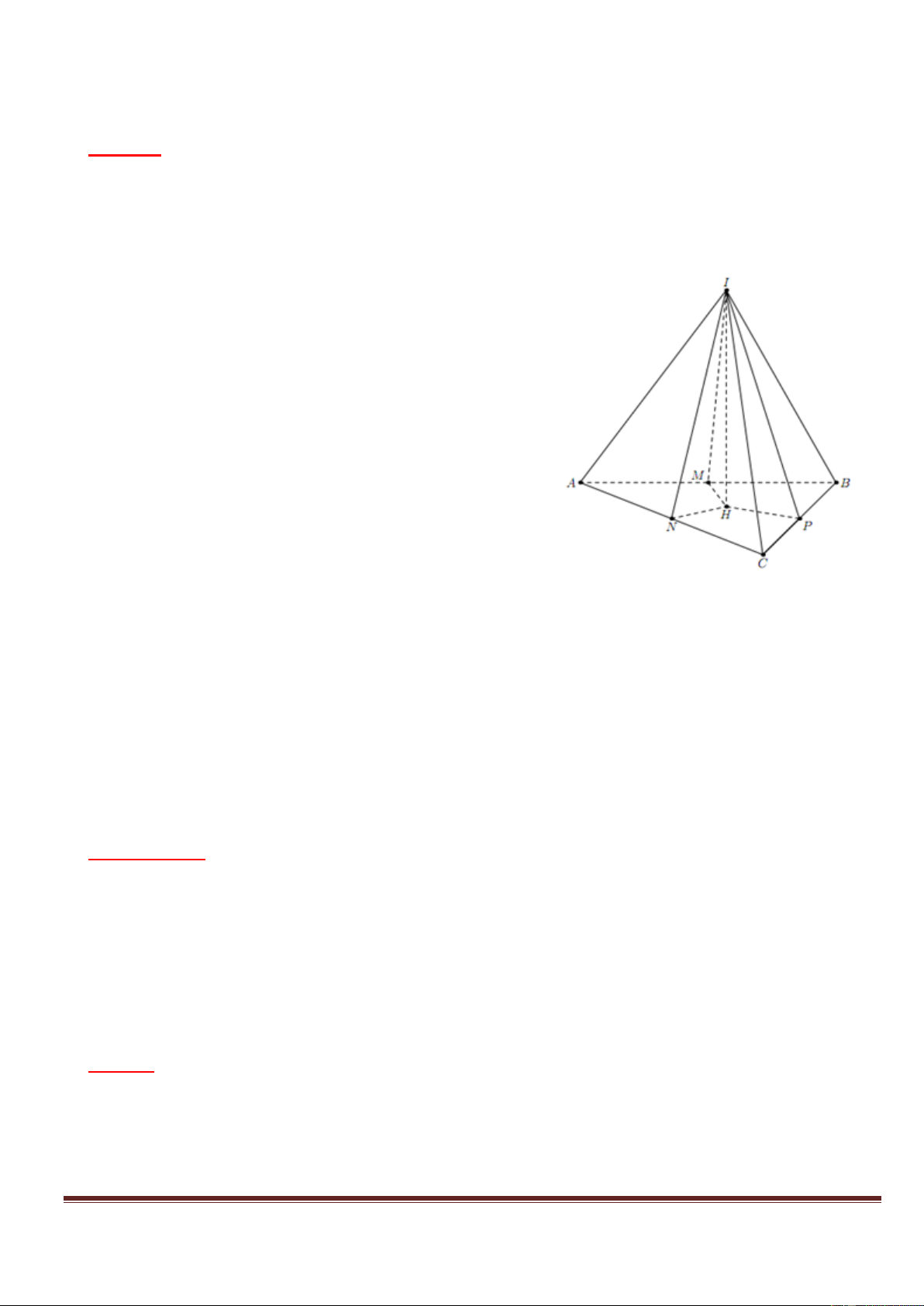
Gọi mặt cầu S  có tâm I là mặt cầu tiếp xúc 3 cạnh A , B BC,CA .
 d I, AB  d I, BC  d I,CA .
Gọi H là hình chiếu của I trên mặt phẳng  ABC .
M , P,C lần lượt là hình chiếu của của H trên A , B BC,CA . Ta có: I  HM  I  HN  I
 HP (cạnh huyền_cạnh góc vuông).
 HM  HN  HP  H là điểm thuộc mặt phẳng  ABC
và cách đều 3 cạnh A , B BC,CA .
 H có thể là tâm đường tròn nội tiếp hay một trong ba tâm đường tròn bàng tiếp của ABC  .
Mà IH   ABC  nên tập hợp điểm I là những đường thẳng qua tâm đường tròn nội tiếp hay một
trong ba tâm đường tròn bàng tiếp của ABC 
và vuông góc với mặt phẳng  ABC   Có 4 đường thẳng như thế.
Ta có A1;0;0, B 0;1;0,C 0;0 
;1  PTMP  ABC  : x  y  z 1  0   ABC  / /   .
Vậy tồn tại 4 giao điểm của tập hợp điểm I nêu trên và mặt phẳng   .
4 giao điểm đó chính là 4 tâm mặt cầu thỏa yêu cầu bài toán  Có 4 mặt cầu thỏa ycbt.
----------------------------------------------------------------------------------------------------------------------------------
Câu 28 : Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt cầu S  2 2 2
: x  y  z  4x  2 y  z  0 và
S : x  y  z 2x  y  z  0 và ba điểm 2  2 2 2 1
A1;0;0, B 0; 2;0,C 0;0; 
3 . Gọi  P là mặt phẳng chứa giao tuyến của S , S . Hỏi có bao 1   2 
nhiêu mặt cầu có tâm thuộc  P và tiếp xúc với ba đường thẳng A , B BC,CA . A. Không có mặt cầu B. 1 C. 4 D. Vô số mặt cầu
Bài tập tương tự, bạn đọc tự làm :)))))
---------------------------------------------------------------------------------------------------------------------------------- 2 2
Câu 29 : Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt cầu S  :  x  2 2
 y  z 1 11 1   2 2 2
và S : x 1  y  3  z 1  17 và hai điểm A3;0;0, B 0; 4;0 . Gọi  P là mặt phẳng 2       
chứa giao tuyến của S , S
. Hỏi có bao nhiêu mặt cầu có tâm thuộc  P và tiếp xúc với ba đường 1   2  thẳng A , O O , B BA . A. Không có mặt cầu B. 1 C. 4 D. Vô số mặt cầu
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 17 Giải :
S có tâm I 2
 ;0;1 và bán kính R  11 . 1   1  1   x  2  2 2
 y  z  2 1 11   x  22 2
 y  z  2 1 11   1 Ta có hệ:      .   x   2 1
  y 32  z  2 1 17 x  y  0  2
2 chính là phương trình mặt phẳng Q: x  y  0.
Vậy hệ   chính là tương giao giữa mặt cầu  S
và mặt phẳng Q 1  2 
d I ; Q    2  11  R  . 1   1 2 2 1 1
Vậy Q cắt  S
với giao tuyến là một đường tròn C  chính là giao tuyến của S , S . 1   2  1 
 P  Q : x  y  0 . Mà OAB: z  0  P  OAB .
Tập hợp tâm của những mặt cầu tiếp xúc với ba đường thẳng A , O O ,
B BA là bốn đường thẳng
d , d , d , d vuông góc mặt phẳng OAB và qua tâm đường tròn tiếp hoặc ba tâm đường tròn bàng 1 2 3 4 tiếp của O  AB .
Vậy một trong bốn đường trên có thể song song hay chứa trong  P .
Gọi    P  OAB   : x  y  0 với ptđt  trong mặt phẳng Oxy .
Trong mặt phẳng Oxy , ta có  : x  y  0 là đường phân giác ngoài của góc O của O  AB .
Vậy  đi qua hai tâm bàng tiếp góc , A B .
Vậy hai trong bốn đường d , d , d , d chứa trong  P  có vô số tâm mặt cầu có tâm thuộc  P và 1 2 3 4
tiếp xúc với ba đường thẳng A , O O , B BA .
---------------------------------------------------------------------------------------------------------------------------------- Câu
30 : Trong không gian với hệ trục tọa độ Oxyz , cho hai mặt cầu  2 2 2
S  :  x  22  y   z  2 2 1  17 và
S : x 1  y 3  z 1 11 và hai điểm 2        1
A3;0;0, B 0; 4;0 . Gọi  P là mặt phẳng chứa giao tuyến của S , S . Hỏi có bao nhiêu mặt 1   2 
cầu có tâm thuộc  P và tiếp xúc với ba đường thẳng A , O O , B BA . A. Không có mặt cầu B. 1 C. 4 D. Vô số mặt cầu Giải :
S có tâm I 2
 ;0;1 và bán kính R  17 . 1   1  1   x  2  2 2
 y  z  2 1 17   x  22 2
 y  z  2 1 17   1 Ta có hệ:      .   x   2 1
  y 32  z  2 1 11 x  y  2  2
2 chính là phương trình mặt phẳng Q: x  y 2  0 .
Vậy hệ   chính là tương giao giữa mặt cầu  S
và mặt phẳng Q 1  2   2
d I ; Q    2 2  17  R  . 1   1 2 2 1 1
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 18
Vậy Q cắt  S
với giao tuyến là một đường tròn C  chính là giao tuyến của S , S . 1   2  1 
 P  Q: x  y  2  0 . Mà OAB: z  0  P  OAB .
Tập hợp tâm của những mặt cầu tiếp xúc với ba đường thẳng A , O O ,
B BA là bốn đường thẳng
d , d , d , d vuông góc mặt phẳng OAB và qua tâm đường tròn tiếp hoặc ba tâm đường tròn bàng 1 2 3 4 tiếp của O  AB .
Vậy một trong bốn đường trên có thể song song hay chứa trong  P .
Gọi    P  OAB   : x  y  2  0 với ptđt  trong mặt phẳng Oxy .
Trong mặt phẳng Oxy , gọi d  : x  y  0,d ' : x  y  0 lần lượt là đường phân giác trong, phân
giác ngoài tại đỉnh A của O  AB .
Ta có  / / d '   không đi qua tâm đường tròn bàng tiếp góc , A B .
Gọi I    d   I 1,  1 .
Ta có OA : y  0, OB : x  0, 4x  3y 12  0 .
Ta xét thấy d I ,OA d I ,OB  d I ,AB  1 I
 cách đều ba cạnh A
 BC  I có thể là tâm mặt
cầu nội tiếp hay tâm bàng tiếp góc O của O  AB .
Vậy một trong bốn đường d , d , d , d chứa trong  P  có vô số tâm mặt cầu có tâm thuộc  P và 1 2 3 4
tiếp xúc với ba đường thẳng A , O O , B BA .
----------------------------------------------------------------------------------------------------------------------------------
Câu 31 : Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S  có phương trình 2 2 2 2 2 x y
x  y  z  50z  0  
1 và mặt cong  P có phương trình 
 2z 2 . Biết S P có giao 25 16
tuyến là đường tròn. Tính bán kính của đường tròn đó . A. 20 B. 45 C. 15 D. 25 Giải : 25 Từ 2 2 2
 50z  x  y thay vào   1 ta có : 16 
3y  4z  0 9   2 2
y  z  0   . Kết hợp với  
1 thì ta có được 2 mặt phẳng giao với 1 mặt cầu. 16
3y  4z  0   
 1 có tâm là I 0;0;25 và bán kính R  25 . Ta có :  d I;
    20  R  
 1 là một đường tròn có R  R       d I;   2 2   15 .  d I;
    20  R  
  1 là một đường tròn có R  R       d I;   2 2   15 . Vậy  R    R    15 .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 19
---------------------------------------------------------------------------------------------------------------------------------- Câu 32 :Trong không gian với hệ trục Oxyz ,cho các
điểm A1;0;0, B 2
 ;0;3, M 0;0  ;1 , N 0,3, 
1 ,mặt phẳng  P đi qua các điểm M , N sao d  ;
B  P  2d  ; A  P   
 ,có bao nhiêu mp thỏa mãn đề bài. A. 1 B. 2 C. vô số
D. không có mặt phẳng nào . Giải : Ta có 4 điểm , A ,
B M , N là 4 điểm đồng phẳng , MN không song song AB .
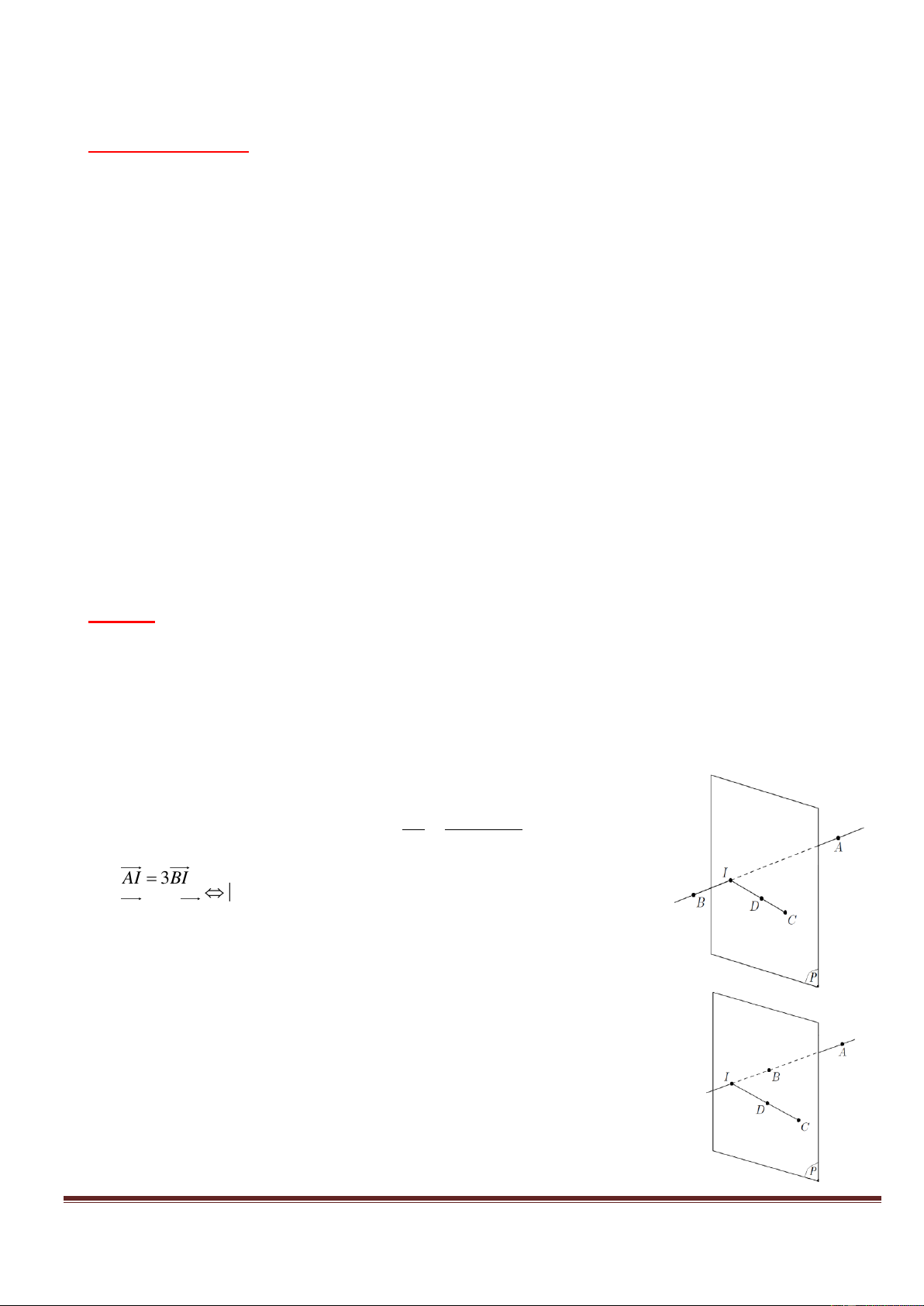
Gọi I   P  AB ( do AB không song song  P )
Trường hợp 1 :
I nằm ngoài AB , mà d  ; B
 P  2d  ; A 
 P  AI  AB 
( ta-let)  I 4;0; 3  
Trường hợp 2 :
I nằm trong đoạn AB , mà d  ; B
 P  2d  ; A 
 P  IB  2IB 
( ta-let)  I 0;0  ;1 .
 P luôn đi qua 1 trong 2 điểm cố định trên. Do M , N, , A ,
B I đồng phẳng nên I  MN  I, M , N thẳng hàng
 có vô số mặt phẳng ( trường hợp 2 ) .
----------------------------------------------------------------------------------------------------------------------------------
Câu 33 : Trong không gian với hệ trục tọa độ Oxyz cho A2;5; 3  , B 2  ;1  ;1 , C 2;0  ;1 và mặt phẳng
:3x  4y 5z 1 0 . Gọi điểm Dx ; y ;z   y  0 thuộc   sao cho có vô số mặt phẳng D D D D 
P quaC,D thỏa khoảng cách từ A đến P gấp 3 lần khoảng cách từ B đến P . Tính
P  x  y  z . D D D A. P  2  B. P  1  C. P  1 D. P  2 . Giải :
Theo đề bài ta có d  , A
 P  3d B, 
 B  AB 
không song song với  P . AI d  , A P   
Xét AB   P , ta có 
 I  AB P        . A B 3 AI 3BI BI d ,    AI  3BI I  4  ; 1  ;3    
 P đi qua một trong hai điểm cố định AI  3  BI I   1  ;2;0 I  4  ; 1  ;3 hay I  1  ;2;0.
Nếu AB   P   P đi qua hai điểm cố định trên. Vậy để có d  ,
A  P  3d B, B   
 thì  P đi qua I  4  ; 1  ;3 hay I  1  ;2;0.
Theo để bài, thì có vô số mặt phẳng  P qua C, D thỏa d  ,
A  P  3d B,B     .
 I,C, D thẳng hàng. Nói cách khác DIC . Với I  4  ; 1
 ;3 , ta có IC :x  2  6t; y  t; z 1 2t  D2  6t;t;1 2t .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 20
Mà D    t  1   D 4  ; 1
 ;3 loại vì y  1   0 . D Với I  1
 ;2;0, ta có IC :x  2  3t; y  2
 t; z 1 t  D2  3t; 2
 t;1 t  .
Mà D    t  2   D 4  ;4; 
1 nhận vì y  4  0  P  1  . D
----------------------------------------------------------------------------------------------------------------------------------
Câu 34 : Trong không gian với hệ trục tọa độ Oxyz , cho A ;
a 0;0, B0; ;
b 0,C 0;0;  1 với
a,b  0 và a  b  1 . Tìm giá trị nhỏ nhất của bán kính R mặt cầu ngoại tiếp tứ diện OABC . 6 6 6 A. R  B. R  6 C. R  D. R  3 2 4 Giải :
Gọi I là tâm mặt cầu ngoại tiếp tứ diện OABC .  a b 1 
 a 1 a 1 
Từ cách dụng hình ta có : I ; ; 
 , mà b 1 a  I ; ;    2 2 2   2 2 2  2 2 2 a 1 a  1 a a 1 6  1  1 1 1  OI         
. Dấu "  " xảy ra khi a   I ; ;   . 4  2  4 2 2 2 4 2  4 4 2 
----------------------------------------------------------------------------------------------------------------------------------
Câu 35 : Trong không gian với hệ trục tọa độ Oxyz , cho A ;
a 0; 0, B 0; ;
b 0,C 0;0;c,a, , b c  0
thỏa a  b  c  k k  k  const 2 2 2 ,
,      0 . Khi a, ,
b c thay đổi thì quỹ tích tâm mặt
cầu ngoại tiếp tứ diện OABC luôn thuộc 1 mặt phẳng cố định. Tìm phương trình mặt phẳng đó . k
A.  P : x   y   z  k  0
C.  P : x   y   z   0 2 k
B.  P : x   y   z   0
D.  P : x   y   z  k  0 2 Giải :  a b c 
Gọi I là tâm mặt cầu ngoại tiếp tứ diện OABC  I ; ; 
 ( bằng cách dựng hình ta dễ dàng tìm  2 2 2  được )
a b c k  x  y       z   . I I I 2 2
Vậy tâm I của mặt cầu ngoại tiếp tứ diện OABC luôn di động trên mặt phẳng cố định   k
P : x   y   z   0 . 2
----------------------------------------------------------------------------------------------------------------------------------
Câu 36 : Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu  S  đi qua điểm A2; 2  ;5 và tiếp
xúc với 3 mặt phẳng   : x 1  0;  : y 1  0;  : z 1  0 . Tính bán kính mặt cầu đó . A. 33 B. 1 C. 3 2 D. 3 Giải :
Gọi tâm mặt cầu  S  là I  x ; y ; z . I I I  Ta có B 1; 1  
;1 là tọa độ giao điểm của 3 mặt phẳng .
Do 3 mặt phẳng  ; ;  đôi một cắt nhau  3 mặt phẳng này chia không gian làm 8 phần
 Tâm I và điểm A cùng thuộc 1 phần .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 21 x  1 x  1 A I   Do  y  1   y  1 A I   z  1 z  1  A  I   
 x 1  y 1  z 1 x y  I I I I I     x  z I I  x 1  x   y   z   I  2 I 2  2 I 2  5 I 2   x 1  x   x   x  I  2 I 2  2 I 2  5 I 2  x  y x  4 I I I    x  z  y  4   I   IA  . I I I 4; 4;4 3   2
x  8x 16  0 z  4   I I I
----------------------------------------------------------------------------------------------------------------------------------
Câu 37 : Trong không gian với hệ trục tọa độ Oxyz , cho A3;0;0, B 0; 2;0,C 0;0;6, D 6;0; 6   .
Gọi  là đường thẳng qua D sao cho tổng khoảng cách từ ,
A B,C đến  đạt giá trị lớn nhất . Vậy
 đi qua điểm M nào sau đây : A. M 8;3; 4   B. M 8;3; 3   C. M 4; 3  ; 7   D. M 4; 3  ; 6   Giải : Phương trình mặ x y z t phẳng qua , A , B C có dạng:    1 . 3 2 6
Ta nhận thấy điểm D  ABC  .
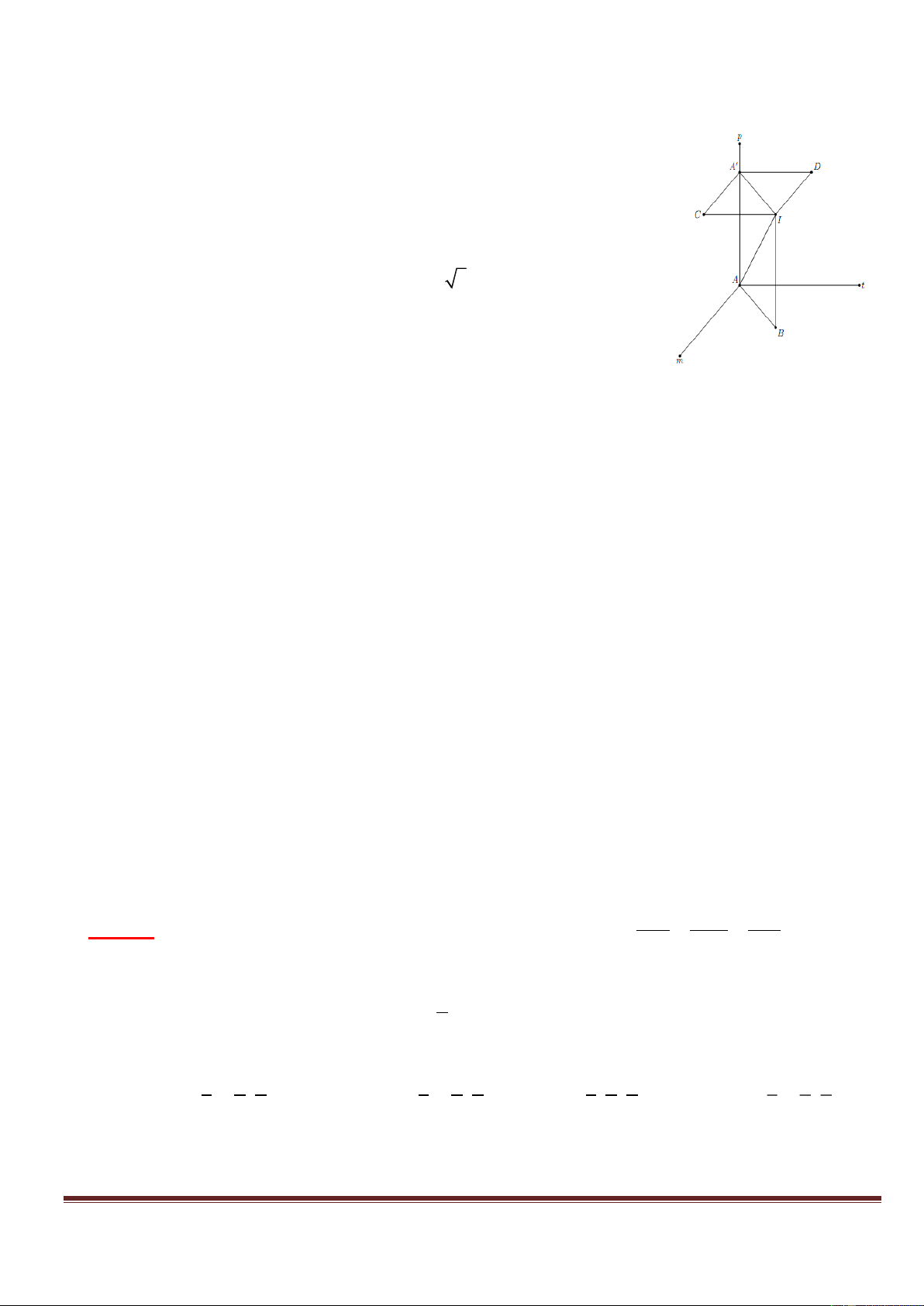
Gọi A', B ',C ' là hình chiếu của , A ,
B C trên  , ta có: A
 DA' vuông tại A'  AA'  AD  const .
Đẳng thức xảy ra    AD .
BB '  BD  const
Lập luận tương tự ta có:  . C
 C '  CD  const   BD
Đẳng thức xảy ra   CD
Vậy AA' BB 'CC '  DA DB DC const .   AD 
Đẳng thức xảy ra    BD     ABCD .   CD 
x  6  2t 
 vtcp a  vtpt n 
  y  t t      Qua M 4; 3; 7 . ABCD 2,3,  1 : 3     z  6   t 
----------------------------------------------------------------------------------------------------------------------------------
Câu 38 : Trong không gian với hệ tọa độ Oxyz , cho mặt cầu S  x   y  2 2 2 : 4
 z  5 . Tìm tọa độ
điểm A thuộc tia Oy . Biết rằng ba mặt phẳng phân biệt qua A và đôi một vuông góc cắt mặt cầu theo
thiết diện là ba hình tròn có tổng diện tích là 11 . A 0; 2; 0 A 0; 0; 0 A 0; 6; 0 A 0; 2; 0 A. B. C. D. A 0; 6; 0 A 0; 8; 0 A 0; 0; 0 A 0; 8; 0
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 22 Giải:
Gọi ba mặt phẳng phân biệt qua A và đôi một vuông góc lần lượt là
Atm,Amp,Apt .
Mặt cầu S  cắt  Atm, Amp, Apt  theo ba hình tròn C , C , C có 1   2   3 
bán kính R , R , R . 1 2 3
Mặt cầu S  có tâm I 0; 4;0 và bán kính R  5 . Gọi ,
B C, D lần lượt là hình chiếu của I trên  Atm, Amp, Apt  .  ,
B C, D lần lượt là tâm của C , C , C . 1   2   3  Ta có: 2 2 2 2 2 2 2 2 2
R  R  IB ,
R  R  IC ,
R  R  ID . 1 2 3
Tổng diện tích ba hình tròn C , C , C là: 1   2   3  2 2 2
 R  R  R    2 2 2
R  R  R  2   3R    2 2 2
IB  IC  ID  1 2 3 1 2 3        2 2 2 15
IB  IC  ID   11  . 2 2 2 2
 IB  IC  ID  4  IA  4  IA  2  1 .
Vì A thuộc tia Oy nên A0; ;
a 0a  0 . a  2 A 0;2;0 2  
IA  2  a  4  4     . a  6 A  0;6;0 Ta chứng minh 2 2 2 2
IB  IC  ID  IA .
Gọi A' là hình chiếu của I trên Ap , chứng minh được IDA'C là hình chữ nhật. 2 2 2
 IA'  IC  ID . IA'  AB 
Đồng thời ta cũng chứng minh được ABIA' là hình chữ nhật   . 2 2 2
AB  IB  IA
Vậy ta đã chứng minh xong 2 2 2 2
IB  IC  ID  IA .
---------------------------------------------------------------------------------------------------------------------------------- x 1 y  2 z 1
Câu 39 : Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng  :   và mặt 1 1 1 2 2 2
cầu S  :  x  
1   y  2   z  3  27 . Tìm điểm M  kẻ được 3 đường thẳng tiếp xúc với S  1 lần lượt tại , A , B C sao cho ABC  và 0 AMB  CMA  60 . 2 M 1;2;  1 M 1;2;  1 M  1  ; 2   ;1 M  1  ; 2   ;1     A.   1 2 7  B.   1 2 7  C.   1 2 7  D.   1 2 7  M ;  ;    M ;  ;   M ; ;   M  ;  ;     3 3 3    3 3 3    3 3 3    3 3 3  Giải :
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 23
Gọi I là tâm của S  . Vì M , A M ,
B MC là tiếp tuyến nên MA  I , A MB  I , B MC  IC .  M  AI, M  BI, M
 CI là các tam giác vuông có chung cạnh huyền MI .
Ta có : IA  IB  IC   R  M  AI  M  BI  M
 CI  MA  MB  MC . S 
 M  trục đường tròn ngoại tiếp ABC  và ,
A B, C C   M , MA  S  với M , MA là mặt cầu
tâm M , bán kính MA .
Gọi J là trung điểm của AC  J là tâm dường tròn ngoại tiếp ABC  .
IA  IB  IC  R  I  trục đường tròn ngoại tiếp ABC  .
 M , J, I thẳng hàng  MI, AC đồng phẳng.
Xét trong mặt phẳng  AICM  , gọi đường tròn C '  S    AICM  có tâm I , ta có: 1 M ,
A MC là tiếp tuyến của C ' 0
 IMA  CMA  60 . 2  IA 2R IM    0  sin 60 3 I
 AM vuông tại A có 0 IMA  60   . R 0 AM  I . A cot 60   3 R M
 AI vuông tại A có AJ là đường cao AJ   R  . 2 C R A
 MB cân tại M có 0 AMB  60  A
 MB đều  AB  AM  . 3 B C  Vì  R
 tồn tại hai điểm B thỏa 0 AMB  60 . AB   R  2   R C  3 2R Vậy với IM 
sẽ thỏa yêu cầu đề bài . 3
----------------------------------------------------------------------------------------------------------------------------------
Câu 40 : Trong không gian với hệ tọa độ Oxyz , cho các mặt phẳng  P : x  y  2z 1  0 và
Q:2x  y  z 1 0 . Gọi S là mặt cầu có tâm thuộc trục hoành đồng thời S cắt mặt phẳng
P theo giao tuyến là một đường tròn có bán kính bằng 2 và S cắt mặt phẳng Q theo
giao tuyến là một đường tròn có bán kính bằng r . Xác định r sao cho chỉ có đúng một mặt cầu
S thỏa mãn yêu cầu. 1 2 3 4 A. r  B. r  C. r  D. r  2 2 2 2 Giải: Gọi I  ;
a 0; 0 và R  0 lần lượt là tâm và bán kính của mặt cầu S  .  a  d I  P a 1 ,   
và d  Q 2 1 I,    . 6 6
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 24 2   a 1 2         2 2 2     4 , 2  R d I P R  2a  2 1  a  2 1 6 Ta có: 2         r 4 0
 d I,Q  
2  r  R  a  2 2 2 6 2 1 2 2  r  R  6 2 2
 a  2a  2r 8  0   1 .
 1 là phương trình bậc hai với a là ẩn số và r là tham số.
Để có đúng một mặt cầu S  thỏa mãn yêu cầu thì có đúng một tâm I  ; a 0; 0 . Khi đó   9 3
1 có một nghiệm duy nhất:  '  0  1  2 2r  8 2
 0  r   r  r  0 . 1     2 2 3 Vậy r 
thỏa yêu cầu bài toán. 2
----------------------------------------------------------------------------------------------------------------------------------
Câu 41 : Trong không gian với hệ trục tọa độ Oxyz cho
A0; y ; z , B0; y ; z ,C  1
 ;0;0, D1;0;0 trong đó y ; y ; z ; z thay đổi thỏa A A B B  A B A B 2 2 2 2
y  z  y  z  3 . Biết rằng AC, BD luôn tiếp xúc với một mặt cầu cố định bán kính R . Xác A A B B
định bán kính mặt cầu đó . 3 2 1 5 A. R  B. R  C. R  D. R  2 2 2 2 Giải : Ta có :
 x  x  0  ,
A B thuộc mặt phẳng  yOz . A B  2 2 2 2 2 2
0  0  0  y   0  z   0  0  0  y   0  z   3 A A B B  ,
A B thuộc mặt cầu tâm O ,bán kính R  3 .
Từ 2 điều trên ta có : ,
A B thuộc đường tròn tâm O , bán kính R  3 . O
 A  OB  3   . CD  AB  do CD   yOz Ta thấy : O  AC  O
 BD  .cg.c .
 Đường cao hạ từ đỉnh O của 2 tam giác của bằng nhau . 3
Gọi H, K lần lượt là hình chiếu của O trên AC, BD  OH  OK   const . 2 3
Vậy AC, BD luôn tiếp xúc mặt cầu tâm O , bán kính R   A . 2
----------------------------------------------------------------------------------------------------------------------------------
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 25
Câu 42 : Trong không gian với hệ trục tọa độ Oxyz cho điểm A4;0;0, B 0;0;m , m  và
C 2;4;0 . Gọi D là hình chiếu vuông góc của O 0;0;0 lên đường thẳng AB . Biết rằng có một
mặt cầu luôn luôn tiếp xúc với đường thẳng CD tại điểm D. Tính bán kính mặt cầu đó . A. 3 B. 5 C. 7 D. 3 Giải. Ta có 0
OD  AB  ODA  90 .
Mà D  AB  Oxz nên D di động trên đường tròn C  chứa trong mặt
phẳng Oxz có tâm J là trung điểm của OA và bán kính 
R   JA  2 . C
J là trung điểm OA  J 2,0,0  JC  0, 4,0 .
 JC  Oxz  C  JC là trục của đường tròn C  và JC  4 I  JC
Gọi I là tâm mặt cầu S  mà CD luôn tiếp xúc tại D   . ID  CD I
 DC vuông tại D , có JD là đường cao 2
 JD  JI.JC  JI  1 . 2 2 Mà I
 JD vuông tại J  ID  JD  JI  5 .
----------------------------------------------------------------------------------------------------------------------------------
Câu 43 : Trong không gian với hệ toa độ Oxyz , cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a
trong đó A  O, B ;
a 0; 0 , D 0; ;
a 0 . Hai điểm M , N lần lượt di động trên hai cạnh B , D B ' A
sao cho BM  B ' N . Gọi ,  lần lượt là góc tạo bởi đường thẳng MN với các đường thẳng B ,
D B ' A . Giả trị của 2 2
A  cos   cos  bằng bao nhiêu? 1 1 1 A. A  B. A  1 C. A  D. A  2 4 3 Giải:
Gọi cạnh của hình lập phương là b , ta có:
AD  AB  BB '  b . Ta có ABB 
' vuông cân tại B và ABD  vuông cân tại A . 0
B' AB  AB'B  ABD  ADB  45   .
BD  B ' A  b 2
Nếu BM  B ' N  0 nghĩa là M  ,
B N  B ' , thì ta có: 0
cos  cos B'BD  cos90  0  2 2 1   cos   cos   . 0 1
cos   cos AB ' B  cos 45  2   2
 Đến đây ta có thể chọn được đáp án :)))))))
Nếu BM  B ' N  b 2 nghĩa là M  ,
D N  A , thì ta có:
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 26  0 1
cos  cos ADB  cos 45   2 2 1  2  cos   cos   . 2  0
cos   cos DAB '  cos90  0
Nếu BM  B ' N  x 2 với x 0;b , Gọi I là hình chiếu của N trên AB , ta có:
AN  AB' B' N  b  x 2  IA  IN  b  x   BI B ' N BM .
NI / /BB '   
B'N  BM,B' A  BD  BA B ' A BD
AB  MNI     AB MN
MI / / AD (Thalès đảo)  MI  AB   .
IM  IB  x  
Gọi H là hình chiếu của I trên       BH HM MN MN IH MN AHB   . AH  HN 2  MH MH 2 MH cos    cos   2 MB  x 2 2x   . 2 NH NH  2 NH cos        NA b  x cos 2 2  b  x2 2 2
MH.MN  IM  x  MH NH M
 IN vuông tại I có IH là đường cao     . 2
NH.NM  IN   b x2 2 x b x2 2 2 2 MH NH 1 MH MH.MN x 1 Vậy 2 2 cos   cos     .
.MH  NH     . 2 2x 2 b  x2 2 2 2 2 x 2x 2x 2 Kết luận: 2 2 1 cos   cos   . 2
----------------------------------------------------------------------------------------------------------------------------------
Câu 44: Trong không gian với hệ trục Oxyz , cho các điểm A 1  ;2;0, B2; 3
 ;2  . Gọi S 
mặt cầu đường kính AB.; A ,
x By là hai tiếp tuyến mặt cầu S  và Ax  By . Gọi M , N lần lượt
là điểm di động trên A ,
x By sao đường thẳng MN luôn tiếp xúc với mặt cầu S  . Tính giá trị AM.BN . A. AM.BN  19 B. AM.BN  24 C. AM.BN  38 D. AM.BN  48 Giải:
Gọi O là tâm của mặt cầu S  và I là tiếp điểm của MN và mặt cầu.. AB  I  MO  A  MO
Ta có OI  OA  OB    . 2  I  NO  B  NO MA  MI  
 MN  AM  BN NB  NI AM , BN
là các tiếp tuyến của mặt cầu đường kính AB và AM  BN .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 27
 AM   ABN   AM  AN  A
 MN vuông tại A . 2 2 2 2       2 2 MN AM AN AM
BA  BN  ( ABN  vuông tại B )
  AM  BN 2 2 2 2 2
 AM  BN  AB  2AM.BN  AB . 2 AB  AM.BN  . 2 Ta có A  B   2 1; 2;0 ,
2; 3; 2  AB  38  AM.BN  19.
----------------------------------------------------------------------------------------------------------------------------------
Câu 45 : Trong không gian với hệ trục toạ độ Oxyz , cho mặt phẳng  P : x  2 y  2z 18  0, M là
điểm di chuyển trên mặt phẳng  P , N là điểm nằm trên tia OM sao cho OM.ON  24 . Tính giá trị
nhỏ nhất của khoảng cách từ điểm N đến mặt phẳng  P . A. min d N;  P  2  B. min d N;  P  3  C. min d N;  P 1  D. min d N;  P  4  Giải : H 2  ; 4  ; 4 
Gọi H là hình chiếu của O trên mặt phẳng  P     . O
 H  6  const O
 I  4  const 
Gọi I là điểm nằm trên tia OH sao cho OH.OI  24    4 8 8  . I  ;  ;       3 3 3  OM OH
Ta có : OM .ON  OH.OI  
và góc MOH  ION nên M  OH ∽ I
 ON c  g  c . OI ON
 Góc MHO  INO , mà OH  P  OH  MH  góc 0 MOH  90 .   2 4 4  Góc 0
INO  90  N thuộc mặt cầu S  đường kính OI cố định với tâm K  ;  ;     3 3 3  là trung điể OI
m của OI và bán kính R   2 . 2 Ta có : d K;
 P  4  
Mặt cầu S  không giao với mặt phẳng  P .  min d N;
 P  d K; 
 P  R  2  .
----------------------------------------------------------------------------------------------------------------------------------
Câu 46 : Trong không gian với hệ trục Oxyz , cho các điểm A2;1; 4
 , B6;2;  3 , M 1;1;  3 . Gọi
P là mặt phẳng qua M sao cho tổng khoảng cách từ ,
A B đến  P là lớn nhất . Biết rằng mặt
phẳng đó có dạng  P x  ay  bz  c  0 với a, , b c 
. Tính giá trị của A  a  b  c . 10 3 4 6 A. A   B. A  C. A  D. A   3 4 7 5 Giải : MA   1;0; 7  
MA  MB  50 Ta có:     M
 AB cân tại M và có AMB là góc tù. MB    7  ;1;0 M . A MB  7   3 1  Gọi I 2  ; ; 
 là trung điểm đoạn AB  MI  AB.  2 2 
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 28
Gọi H ,T lần lượt là hình chiếu của ,
A B lên mặt phẳng  P .
Trường hợp 1: P không cắt đoạn AB . 1
Gọi L là hình chiếu của I lên mặt phẳng  P . Ta chứng minh được: IL   AH  BT  . 2 IML 
vuông tại L  IL  IM  const . Đẳng thức xảy ra   P  IM tại M .
Khi đó P / / AB nên P không cắt đoạn AB (thỏa điều kiện trường hợp 1).
Vậy  AH  BT 
 2IM  P   IM tại M . max
Trường hợp 2: P cắt đoạn AB  
 J  AB P với AB là đoạn thẳng. AH  AJ Ta có: 
  AH  BT   AJ  BJ  AB  const . BT  BJ
Đẳng thức xảy ra  P  AB  P  IM  I P .
Khi đó P cắt đoạn AB tại I (thỏa điều kiện trường hợp 2 ).
Vậy  AH  BT 
 AB  P  AB . max Vì AM 
B có AMB là góc tù nên AB  2IM .
Vậy tổng khoảng cách từ ,
A B đến mặt phẳng  P lớn nhất là AB khi  P  AB .    
P nhận AB    1 7 8;1;7 / / 1;  ;    làm vtpt.  8 8     P qua M    P 1 7 7 1 7 7 3 1;1;3 : x  y  z   0  a  ;b  ;c   A  . 8 8 4 8 8 4 4
---------------------------------------------------------------------------------------------------------------------------------- Câu 47:Trong không gian với hệ trục Oxyz ,cho mặt cầu
S x  
 2  y    2  z   2 1 : cos .sin sin .sin cos
 với ,  là các góc thay đổi luôn thỏa 4
mãn  ,  0; 2  . Biết S  luôn tiếp xúc với hai mặt cầu cố định S , S
. Tổng thể tích của hai 1   2 
khối cầu S , S là : 1   2  21 14 76 A. B. C. 12 D. 8 3 3 Giải : x  cos.sin  
Gọi I là tâm mặt cầu S   I  d :  y  sin.sin  . z  cos  2 2 2
 x  y  z   2 2     2 2 sin cos .sin   cos   1
 Vậy I S  2 2 2
  : x  y  z  1  Khoảng cách từ tâm I của mặt cầu  S  đến gốc tọa độ O là cố O định .
 Vậy mặt cầu S  sẽ tiếp xúc ngoài và tiếp xúc trong với 2 mặt cầu S , S cố định có tâm là O 1   2  .
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 29  1 3 R  R  R 1   1 O S  2 2 4 4 14 3 3  
 V V   R   R  dvtt . 1 2 1 2   1 1 3 3 3
R  R  R 1  2 O S  2 2
----------------------------------------------------------------------------------------------------------------------------------
Câu 48 : Trong không gian với hệ trục toạ độ Oxyz , tập hợp các điểm M  ; a ;
b c thoả mãn bất
phương trình a  2sin 2  b  2cos 2 1 2
 c  là một khối tròn xoay thể tính bằng : 4 2  A. 2 V  2 B. 2 V   C. 2 V  3 D. V  3 Giải : Xét điểm A 
   AOxy 2 2 2sin ; 2 cos ; 0
 x  y  4 . A A
Vậy tập hợp điểm A là một đường tròn C  tâm O 0;0;0 có bán kính R  2 trong mặt phẳng Oxy . 1 1 Với mọi M  ; a ; b c ta luôn có 2 MA   MA  . 4 2
 Khi điểm A chạy tung tăng trên đường tròn C thì tập hợp điểm M tạo thành hình một cái phao có bán kính đườ 5 3
ng tròn lớn R  R  MA 
và bán kính đường tròn nhỏ là R  R  MA  . 1 2 2 2 1
Áp dụng công thức thể tích cái phao ta có : V 
 R  R R  R 2 2 2   . 1 2 1 2 4
---------------------------------------------------------------------------------------------------------------------------------- Câu 49 : Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P   2 m   2 :
1 x  2mz  2m  m 1  0 . Biết rằng khi m thay đổi thì  P
luôn tiếp xúc với 1 mặt m  m
cầu có bán kính cố định và có tâm I  ; a ;
b c thuộc mặt phẳng Q : y  2  0 . Tính P  a  2b  3c A. P  0 B. P  1  C. P  2  D. P  3  Giải : Ta có: I  ; a ;
b c là tâm mặt cầu cố định luôn tiếp với  P . m   2 m   2
1 a  2mc  2m  m 1  0 a  2 2
m  1 2c m  a    d I  P    . m  1 ;       2 2 2 2 m  m m 1 1 4
Để d I;P  
m  là một hằng số thì các hệ số tương ứng tỉ lệ với nhau :  1  1 c  a      2  2  1 1       I  b   . a  2   a   ; ; 1 1   2 2   c   1 1  2
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 30   I Q 1 1
: y  2  0  b  2   I  ; 2  ;  P  3    .  2 2 
---------------------------------------------------------------------------------------------------------------------------------- Câu 50 : Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng
P  mx   2
m   y   2 : 2 1 m   1 z 10  0
và điểm A2;11;5 . Biết rằng khi m thay đổi thì Pm  m
luôn tiếp xúc với 2 mặt cầu có bán kính cố định và cùng đi qua A . Tổng bán kính 2 mặt cầu đó là : A. 2 2 B. 5 2 C. 7 2 D. 12 2 Giải : Gọi I  ; a ;
b c là tâm mặt cầu cố định luôn tiếp với  P . m  2ma   2 m   1 b   2 m   1 c 10 b c 2
m  2ma  b  c 10  d I;  P    . m          2 2 2 2 2 2 m  m m m 1 2 4 1 1
Để d I;P  
m  là một hằng số thì các hệ số tương ứng tỉ lệ với nhau : a  0  a  0
 b  c b  c 10    I 0; ; b 5   .   c  5   1 1 b  5 b  9 I  0;9; 5  2 1    d I;  P     b   IA       R  R  . m  4   11 2 b  25 I   0;25; 5   12 2 1 2 2
----------------------------------------------------------------------------------------------------------------------------------
Câu 51 : Trong không gian với hệ trục Oxyz , cho đường thẳng  là giao tuyến của 2 mặt phẳng
P: x  my  z  m  0 ,Q:mx  y mz 1 0 gọi  là hình chiếu của  trên mặt phẳng 1 
Oxy. Biết rằng  luôn tiếp xúc với một đường tròn cố định. Tìm bán kính r của đường tròn đó. 1  A. r  1 B. R  1,5 C. r  2 D. r  3 Giải.
P có vtpt n  1, , m  vtpt n   ;1 m ; m Q    1 , Q có P  
 cóvtcp a  n n    2 2 ,
m 1 ; 2m ; m           1 P Q  . 2 2  m 1 m 1 
Với m  0 . Gọi A ; 0;  .  2m 2m 
Gọi   là mặt phẳng qua  và vuông góc với mặt phẳng Oxy có vtpt n  (0,0,1) . 2       m 1 có vtpt n
 a ,n               2 2 , m 1 m , 0  :2 . m x  2
1 m . y 0      0  .  2m 
   mx   2
 m  y  2 : 2 1 m   1  0 . Vậy 
có phương trình là: mx   2
 m  y  2 2 1 m  
1  0 trong mặt phẳng Oxy . 1 
Xét trong mặt phẳng Oxy , ta có:  2 m   1
Xét điểm O 0,0  d O,     1  const 1  2 m  . 1
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 31
Vậy trong mặt phẳng Oxy ta luôn có 
luôn tiếp xúc với một đường tròn C  cố định có tâm 1  O 0;0;0 với  R   1 m   0 . C x  t x  z  0 
Với m  0, ta có :  :   y 1 t
  R   / / Oxz . y 1 z  t   Vậy 
có dạng y  1 trong mặt phẳng Oxy . 1  Mà d O,
   1  R nên  tiếp xúc với C  . 1  1  C
Kết luận:  luôn tiếp xúc đường tròn C  có bán kính là 1 m  R . 1 
----------------------------------------------------------------------------------------------------------------------------------
Câu 52 : Trong không gian với hệ trục toạ độ Oxyz cho A0;0  ;1 , B  ;
m 0;0,C 0; ;
n 0, D 1;1  ;1 với
m  0 , n  0 và m  n  1 . Biết rằng khi m, n thay đổi thì tồn tại một mặt cầu cố định tiếp xúc với
mặt phẳng  ABC và đi qua D . Tính bán kính R của mặt cầu đó . 3 3 A. R  1 B. R  C. R  2 D. R  2 2 Giải : x y z Ta có :  ABC  :
  1  nx  my  mnz  mn  0 . m n 1 Gọi I  ; a ;
b c là tâm mặt cầu thoả mãn yêu cầu bài toán :            d I   ABC na mb mnc mn na mb c  1 mn
b am a c  1 mn ;      . 2 2 2 2   1 mn 1 mn m n m n
Để d I; ABC 
 là một hằng số thì các hệ số tương ứng tỉ lệ với nhau : b   a  0  a  b b   a  a c 1      I  ; a ;1 a  a .    a  c 1 c  1 a 1 1  d I
  ABC  a  
a  2 a  2 a2 ; 1 1
 ID  a  1  R  1 .
---------------------------------------------------------------------------------------------------------------------------------- ---HẾT---
Tổng hợp trắc nghiệm 12 – NHÓM PI Page 32

Tổng hợp câu hỏi trắc nghiệm hay chương tọa độ không gian – Nguyễn Quang Hưng, Nguyễn Thành Tiến Toán 12

Thông tin :

Tài liệu liên quan:

Bài giảng vectơ và hệ trục tọa độ trong không gian Toán 12 KNTTVCS

Toán ứng dụng thực tế vectơ và hệ trục toạ độ trong không gian

Chuyên đề hình học giải tích không gian – Lưu Huy Thưởng Toán 12

Chuyên đề HH giải tích không gian – Trung tâm LTĐH Vĩnh Viễn Toán 12

Bài tập tọa độ không gian phân theo dạng có lời giải chi tiết – Trần Sĩ Tùng Toán 12