







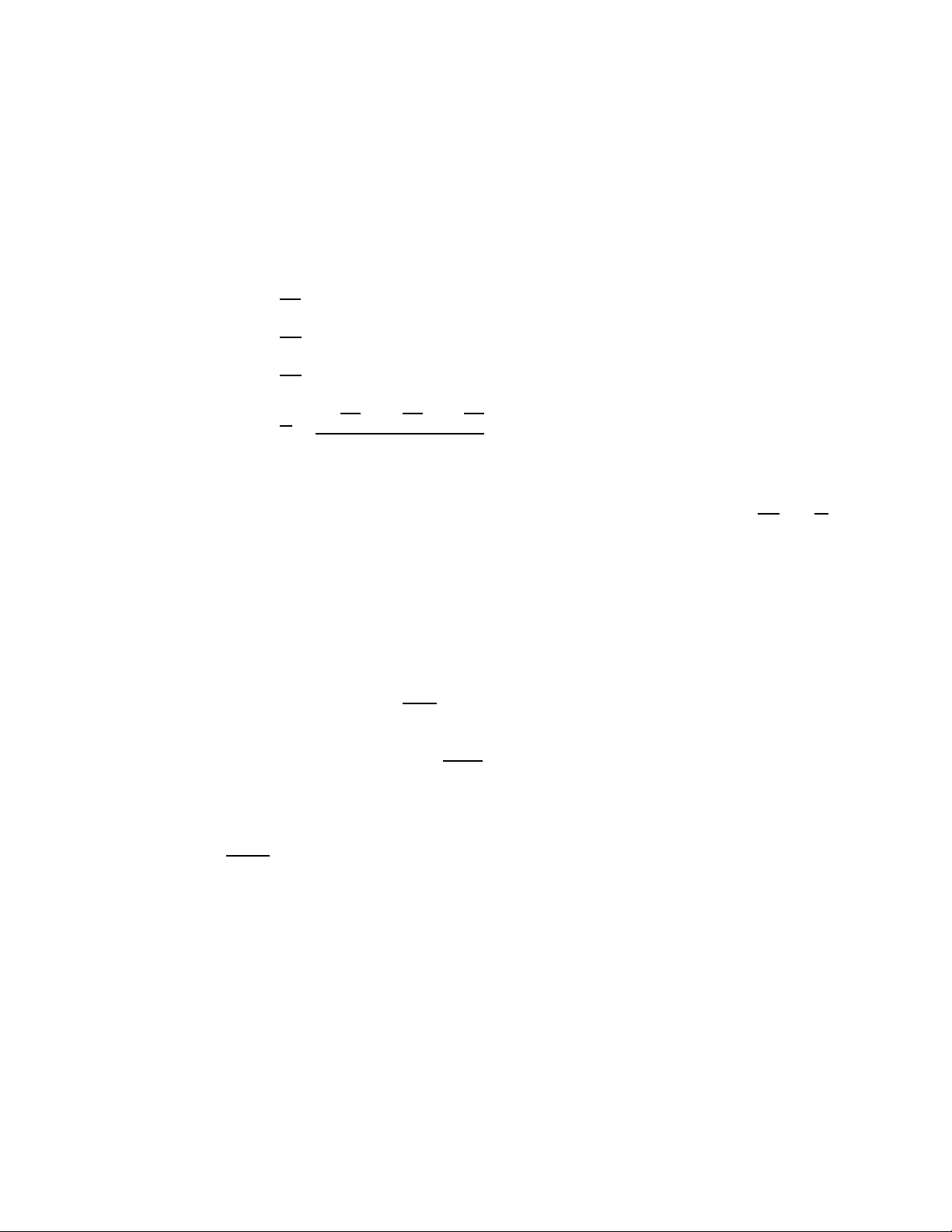


Preview text:
lOMoARcPSD|40342981
CHƯƠNG 2 – THU THẬP DỮ LIỆU VÀ TRÌNH BÀY DỮ LIỆU
Trong trường hợp phân nhóm/tổ có khoảng cách tổ đều nhau: 𝟏 𝟑 + Sổ tổ:
𝒌 = 𝟐𝒏𝟑 = √𝟐𝒏
𝑿𝒎𝒂𝒙− 𝑿𝒎𝒊𝒏 + Khoảng cách tổ: 𝒉 = 𝒌
CHƯƠNG 3 – TÓM TẮT DỮ LIỆU
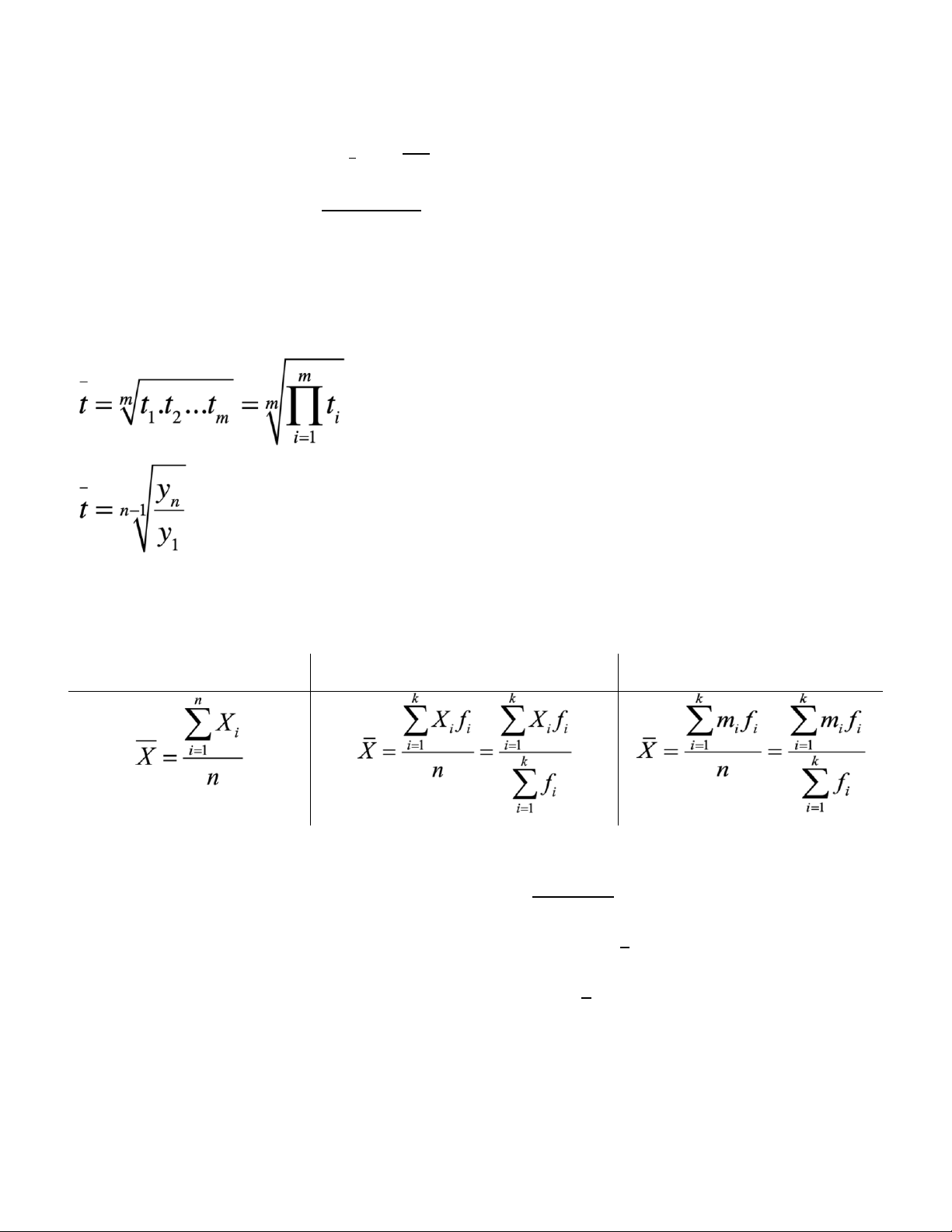
1. Số trung bình nhân (số trung bình hình học): Trong đó:
+ ti: tốc độ phát triển liên hoàn thứ i.
+ m: tốc độ phát triển liên hoàn.
+ y1: mức độ kỳ gốc (đầu tiên) trong dãy số.
+ yn: mức độ cuối cùng trong dãy số. + n: số mức độ. 2. Trung bình: Dạng liệt kê
Phân tổ không có khoảng cách
Phân tổ có khoảng cách
Cách tính trị số giữa: + Đố 𝑮𝑯𝑫+ 𝑮𝑯𝑻
i với tổ có giới hạn dưới và giới hạn trên: 𝒎𝒊 = 𝟐 + Đố 𝒉
i với tổ đầu tiên (không có giới hạn dưới): 𝒎𝒊 = 𝑮𝑯𝑻 − 𝟐 + Đố 𝒉
i với tổ cuối (không có giới hạn trên): 𝒎𝒊 = 𝑮𝑯𝑻 + 𝟐 lOMoARcPSD|40342981 3. MODE: 3.1 Dạng liệt kê:
+ M0 là lượng biến xuất hiện nhiều nhất trong dữ liệu.
+ Vì fi max = … => M0 = …
3.2 Phân tổ có khoảng cách đều:
+ fi max = … => M0 = … Trong đó: + 𝑥𝑀
: giới hạn dưới của tổ chứa mốt. 0 (min)
+ ℎ𝑀 : trị số khoảng cách tổ của tổ chứa mốt. 0
+ 𝑓𝑀 : tần số của tổ chứa M 0 0.
+ 𝑓𝑀0−1: tần số của tổ đứng trước tổ chứa M0.
+ 𝑓𝑀0+1: tần số của tổ đứng sau tổ chứa M0.
3.3 Phân tổ có khoảng cách không đều: 𝒇 + 𝒅 𝒊 𝒊 = 𝒉𝒊 Trong đó: + 𝑥𝑀
: giới hạn dưới của tổ chứa mốt. 0 (min)
+ ℎ𝑀 : trị số khoảng cách tổ của tổ chứa mốt. 0
+ 𝑑𝑀 : mật độ phân phối của tổ chứa M 0 0.
+ 𝑑𝑀0−1: mật độ phân phối của tổ đứng trước tổ chứa M0.
+ 𝑑𝑀0+1: mật độ phân phối của tổ đứng sau tổ chứa M0. lOMoARcPSD|40342981
4. Giá trị bất thường:
+ Theo biểu đồ hộp: 𝒙𝒊 < GHD 𝒙
+ Giá trị chuẩn hoá: 𝒛 𝒊− 𝒙 𝒊 = 𝑺 5. Tứ phân vi: 5.1 Dạng liệt kê:
𝑄1 = 𝑥 1.(𝑛+1) 𝑀 1.(𝑛+1) 𝑄 3.(𝑛+1) 𝑒 = 𝑄2 = 𝑥 3 = 𝑥 4 2 4
5.2 Phân tổ không có khoảng cách: 𝒏+𝟏
+ Q1: trị số tổ có tần số tích luỹ nhỏ nhất nhưng ≥ 𝟒 𝒏+𝟏
+ Q2: trị số tổ có tần số tích luỹ nhỏ nhất nhưng ≥ 𝟐 𝟑.(𝒏+𝟏)
+ Q3: trị số tổ có tần số tích luỹ nhỏ nhất nhưng ≥ 𝟒
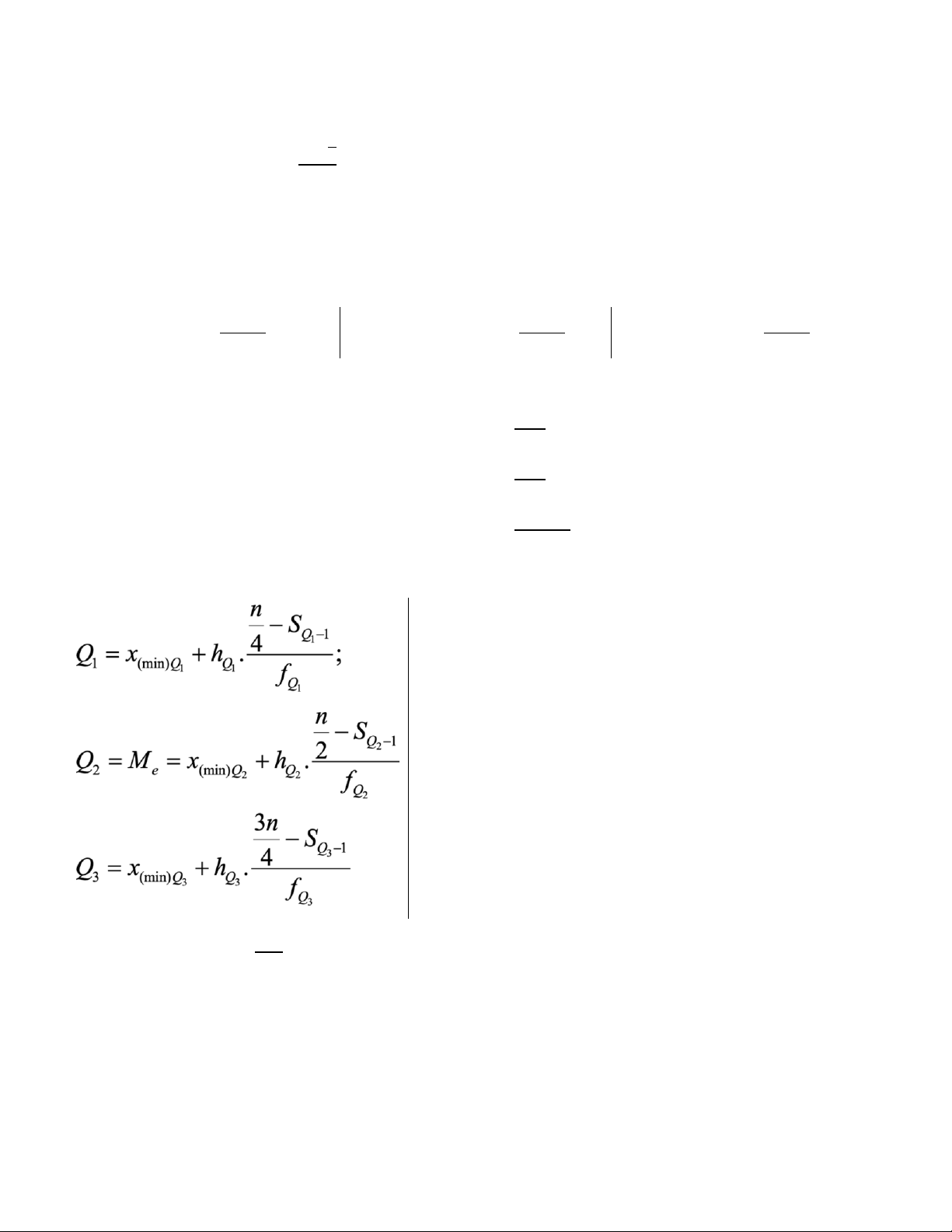
5.3 Phân tổ có khoảng cách tổ: Trong đó:
+ 𝑥𝑄1 (min): giới hạn dưới của tổ chứa nhất vị.
+ ℎ𝑄 : khoảng cách tổ chứa nhất vị. 1
+ 𝑓𝑄 : tần số tổ chứa nhất vị. 1
+ 𝑆𝑄1−1: tần số tích luỹ liền trước tổ nhất vị. 𝑷 + Phân vị thứ n: 𝒊 = . 𝒏 𝟏𝟎𝟎
+ Khoảng biến thiên: 𝑹 = 𝑿𝒎𝒂𝒙 − 𝑿𝒎𝒊𝒏
+ Độ trải giữa: 𝑰𝑸𝑹 = 𝑹𝑸 = 𝑸𝟑 − 𝑸𝟏
+ Giới hạn dưới: 𝑮𝑯𝑫 = 𝑸𝟏 − 𝟏, 𝟓. 𝑰𝑸𝑹
+ Giới hạn trên: 𝑮𝑯𝑻 = 𝑸𝟑 + 𝟏, 𝟓. 𝑰𝑸𝑹
Downloaded by Mai Nguy?t (nguyetmai131203@gmail.com) lOMoARcPSD|40342981
6. Độ lệch chuẩn tuyệt đối bình quân: Dạng liệt kê
Phân tổ không có khoảng cách
Phân tổ có khoảng cách 7. Phương sai: Dạng liệt kê
Phân tổ không có khoảng cách
Phân tổ có khoảng cách
+ Độ lệch chuẩn: 𝑺 = 𝜹 = √𝑺𝟐 𝑺
+ Hệ số biến thiên: 𝑪𝑽 = 𝒙
8. Hình dáng phân phối tổng thể: Cách 1:
+ 𝑥 < 𝑀𝑒 => hình dáng phân phối lệch trái.
+ 𝑥 = 𝑀𝑒 => hình dáng phân phối đối xứng.
+ 𝑥 > 𝑀𝑒 => hình dáng phân phối lệch phải. Cách 2: 𝟑.(𝒙− 𝑴 Hệ số lệch: 𝑺 𝒆) 𝒌 = 𝑺
+ Hệ số lệch có giá trị gần – 3 => phân phối lệch trái.
+ Hệ số lệch có giá trị gần = 0 => phân phối đối xứng.
+ Hệ số lệch có giá trị gần + 3 => phân phối lệch phải.
CHƯƠNG 4 – XÁC SUẤT CỦA BIẾN CỐ Tổ hợp Chỉnh hợp
Xác suất cổ điển Xác suất bằng tần suất 𝑛! 𝑛! 𝑛(𝐴) 𝑘 𝐶𝑘 𝑘 𝑘 𝑛 = 𝐴 = = 𝐶 . 𝑘! 𝑃(𝐴) = 𝑃 = 𝑘! (𝑛 − 𝑘)! 𝑛 (𝑛 − 𝑘)! 𝑛 𝑛(Ω) 𝑛
1. Công thức cộng:
+ A và B là hai biến cố xung khắc khi 𝑨 ∩ 𝑩 = ∅ => 𝑷(𝑨 + 𝑩) = 𝑷(𝑨) + 𝑷(𝑩)
+ A và B là hai biến cố bất kỳ => 𝑷(𝑨 + 𝑩) = 𝑷(𝑨) + 𝑷(𝑩) − 𝑷(𝑨. 𝑩)
+ A, B và C là ba biến cố bất kỳ:
=> 𝑷(𝑨 + 𝑩) = 𝑷(𝑨) + 𝑷(𝑩) + 𝑷(𝑪) − 𝑷(𝑨. 𝑩) − 𝑷(𝑨. 𝑪) − 𝑷(𝑩. 𝑪) − 𝑷(𝑨. 𝑩. 𝑪)
2. Công thức nhận:
+ A và B là hai biến cố bất kỳ => 𝑷(𝑨. 𝑩) = 𝑷(𝑨|𝑩). 𝑷(𝑩) = 𝑷(𝑩|𝑨). 𝑷(𝑨)
+ A và B là hai biến cố độc lập => 𝑷(𝑨. 𝑩) = 𝑷(𝑨). 𝑷(𝑩)
3. Công thức xác suất đầy đủ:
=> 𝑷(𝑩) = 𝑷(𝑨𝟏). 𝑷(𝑩|𝑨𝟏) + 𝑷(𝑨𝟐). 𝑷(𝑩|𝑨𝟐) + ⋯ + 𝑷(𝑨𝒏). 𝑷(𝑩|𝑨𝒏) 4. Công thức Bayes: 𝑷(𝑨 => 𝑷(𝑨 𝒊).𝑷(𝑩|𝑨𝒊) 𝒊|𝑩) = 𝑷(𝑩) lOMoARcPSD|4034981
CHƯƠNG 5 – BIẾN NGẪU NHIÊN VÀ PHÂN PHỐI XÁC SUẤT THÔNG DỤNG
1. Phân phối xác suất biến ngẫu nhiên rời rạc:
+ Hàm phân phối xác suất tích luỹ: F(x) = P (X ≤ x) 𝑥2 ≤ 𝑥 < 𝑥3 => Trung bình: 𝝁 = 𝝁 𝒏 𝒙 = 𝑬(𝒙) = ∑ 𝒙 𝒊=𝟏 𝒊 . 𝒑𝒊 => Phương sai:
𝜹𝟐 = 𝑽𝒂𝒓(𝒙) = 𝑫(𝒙) = ∑𝒏 (𝒙 𝒊=𝟏
𝒊 − 𝝁𝒙)𝟐 . 𝒑𝒊 => Độ lệch chuẩn: 𝜹 = √𝜹𝟐
2. Phân phối xác suất biến ngẫu nhiên liên tục:
+ Hàm mật độ xác suất:
+ Hàm mật độ xác suất f(x) của biến ngẫu nhiên X có tính chất: 𝒇(𝒙) ≥ 𝟎 +∞ ∫
𝒇(𝒙)𝒅𝒙 = 𝟏 −∞ +∞ => Trung bình:
𝝁 = 𝝁𝒙 = 𝑬(𝒙) = ∫ 𝒇(𝒙)𝒅𝒙 −∞ => Phương sai: +∞
𝜹𝟐 = 𝑽𝒂𝒓(𝒙) = 𝑫(𝒙) = ∫
(𝒙 − 𝝁𝒙)𝟐. 𝒇(𝒙)𝒅𝒙 −∞ => Độ lệch chuẩn: 𝜹 = √𝜹𝟐
3. Phân phối nhị thức: + Công thức Bernoulli: 𝑷 𝒌
𝒏(𝒌) = 𝑷𝒏(𝒌; 𝒑) = 𝑪𝒏. 𝒑𝒌. (𝟏 − 𝒑)𝒏− 𝒌 , 𝒗ớ𝒊 𝒌 = 𝟎, 𝒏
=> Xác suất có từ k1 đến k2 lần thành công: lOMoARcPSD|40342981
+ Tính chất: Nếu X ~ B (n, p) thì: E(x) = n.p Var(x) = n.p.(1 – p)
4. Phân phối chuẩn: 𝒂 𝟏 − (𝒙− 𝝁)𝟐 + 𝒇(𝒙) = ∫ . 𝒆 𝟐.𝜹𝟐 𝒃 𝜹.√𝟐𝝅
+ Tính chất: X ~ N (𝜇, 𝛿2) => E(x) = Mod(x) = Me(x) = 𝜇 => Var(x) = 𝛿2
5. Phân phối chuẩn tắc: x− μ
+ Nếu X ~ N (𝜇, 𝛿2) thì biến ngẫu nhiên z = có phân phối N (0, 1). δ 𝒂 𝟏 − 𝒙𝟐 + 𝒇(𝒙) = ∫ . 𝒆 𝟐 𝒃 √𝟐𝝅 lOMoARcPSD|40342981
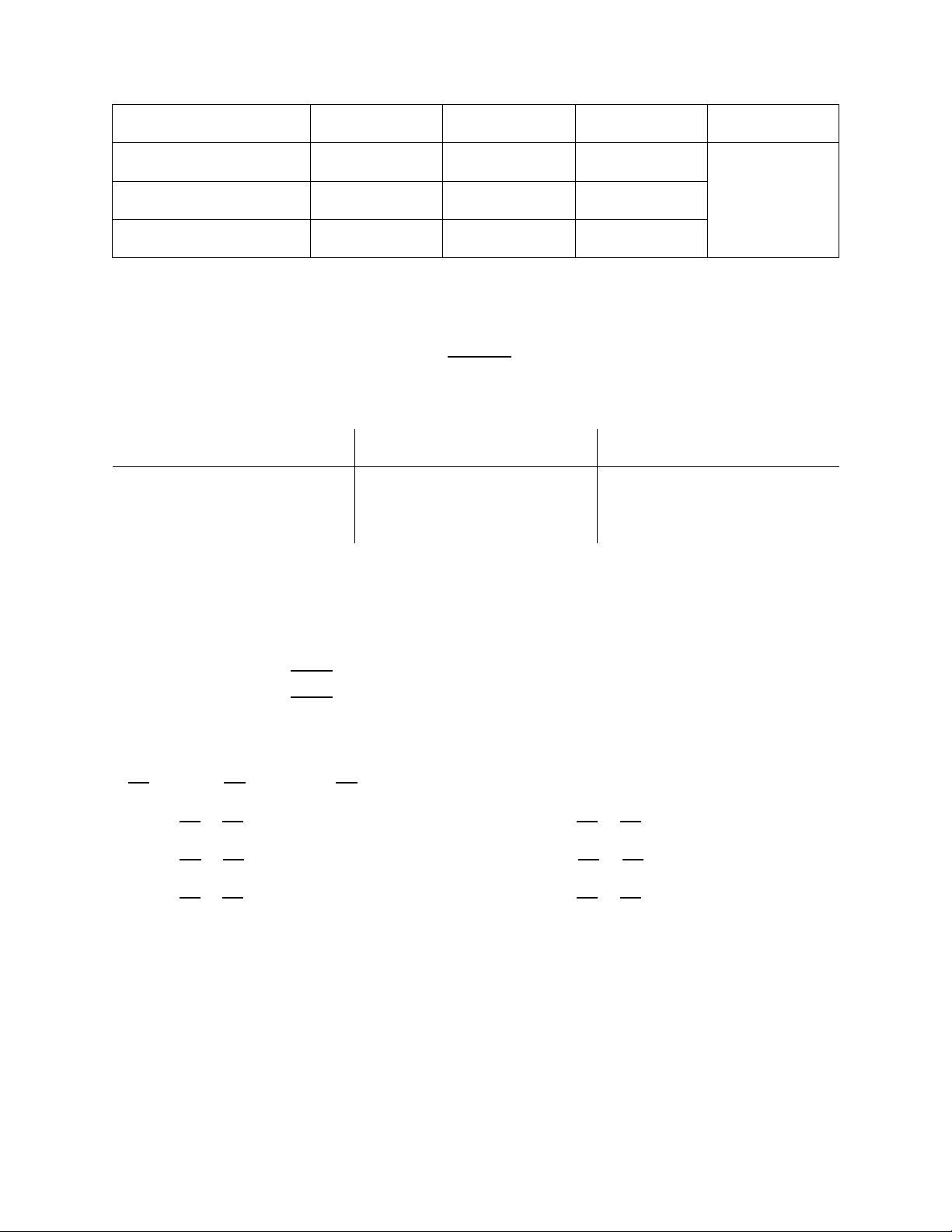
CHƯƠNG 6 – ƯỚC LƯỢNG THAM SỐ Tổng thể Mẫu Kích thước N n Trung bình 𝜇 𝑥 Độ lệch chuẩn 𝛿 S Tỷ lệ p Fn
1. Ước lượng khoảng cho trung bình (kỳ vọng):
+ Dữ liệu cần có: n, 𝑥, 𝛿 hoặc S và 1 – 𝛼 hoặc 𝛼 TH1 – Tổng thể TH2 – Mẫu TH3 – Tổng thể TH4 – Mẫu
n ≥ 30, 𝜹𝟐 đã biết
n ≥ 30, 𝜹𝟐 chưa biết
n ≤ 30, 𝜹𝟐 đã biết
n ≤ 30, 𝜹𝟐 chưa biết 𝜹 𝑺 𝜹 𝑺 𝜺 = 𝒁𝜶. 𝜺 = 𝒁𝜶. 𝜺 = 𝒁𝜶. 𝜺 = 𝒕 𝜶 . 𝒏−𝟏, 𝟐 √𝒏 𝟐 √𝒏 𝟐 √𝒏 𝟐 √𝒏 𝛂 𝛂 𝛂
Với 𝛗𝐙 = 𝟎, 𝟓 − Với 𝛗 = 𝟎, 𝟓 − Với 𝛗 = 𝟎, 𝟓 − Với 𝒕 𝜶 = … 𝛂 𝟐 𝐙𝛂 𝟐 𝐙𝛂 𝟐 𝒏−𝟏, 𝟐 𝟐 𝟐 𝟐
=> 𝒁𝜶 = …
=> 𝒁𝜶 = …
=> 𝒁𝜶 = … (Bảng student) 𝟐 𝟐 𝟐 (Hàm ngược Laplace) (Hàm ngược Laplace) (Hàm ngược Laplace)
+ Khoảng ước lượng: 𝒙 − 𝜺 ≤ 𝝁 ≤ 𝒙 − 𝜺
2. Ước lượng khoảng cho tỉ lệ:
+ Dữ liệu cần có: n, Fn và 1 – 𝛼 hoặc 𝛼 𝛂
+ Sai số: 𝜺 = 𝒁𝜶 . √𝐅𝐧.(𝟏− 𝐅𝐧) , với 𝛗𝐙 = 𝟎, 𝟓 − => Hàm ngược Laplace. 𝛂 𝟐 𝒏 𝟐 𝟐
+ Khoảng ước lượng: 𝑭𝒏 − 𝜺 ≤ 𝒑 ≤ 𝑭𝒏 + 𝜺
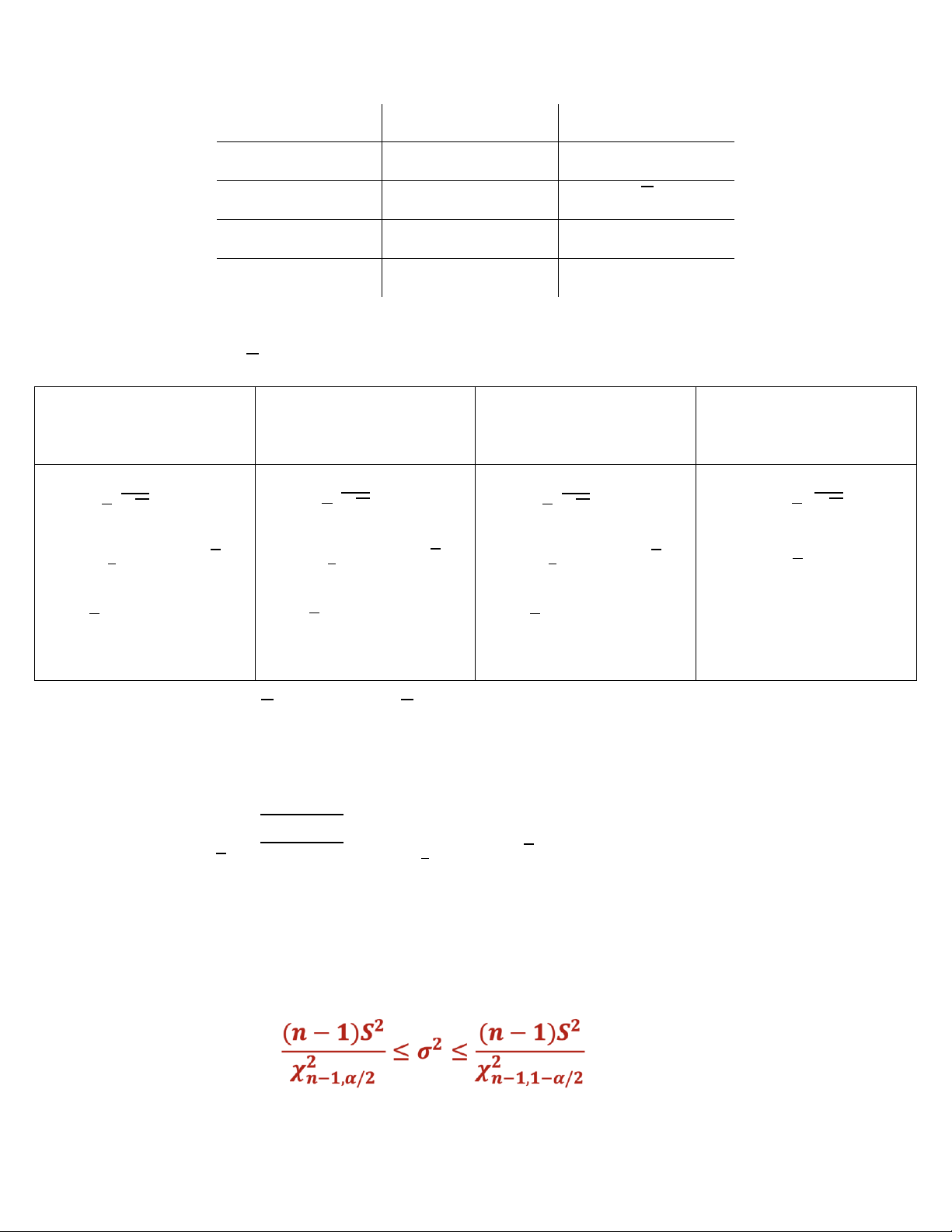
3. Ước lượng khoảng cho phương sai của tổng thể:
+ Dữ liệu cần có: n, S và 1 – 𝛼 hoặc 𝛼 + Khoảng ước lượng:
=> Bảng chi bình phương. lOMoARcPSD|40342981
CHƯƠNG 7 – KIỂM ĐỊNH GIẢ THUYẾT
1. Kiểm định giả thuyết về trung bình:
+ Cách đặt giả thuyết: Phía trái Phía phải Hai phía H0: 𝜇 ≥ 𝜇0 H0: 𝜇 ≤ 𝜇0 H0: 𝜇 = 𝜇0 H1: 𝜇 < 𝜇0 H1: 𝜇 > 𝜇0 H1: 𝜇 ≠ 𝜇0
Cách 1: Kiểm định giả thuyết hai phía.
(1) Đặt giả thuyết hai phía H0: 𝜇 = 𝜇0 H1: 𝜇 ≠ 𝜇0
(2) Kiểm định giả thuyết hai phía
TH1 – Tổng thể, 𝜹𝟐 đã biết (𝒙 − 𝝁𝟎).√𝒏 + B1: Tính 𝒕 = 𝜹
và n ≥ 30 hoặc n < 30 𝛂
+ B2: Với 𝛗𝐙 = 𝟎, 𝟓 − => 𝒁𝜶 = … (Hàm ngược Laplace) 𝛂 𝟐 𝟐 𝟐
+ B3: Khi | 𝒕 | ≤ 𝒁𝜶 => Chấp nhận H0; ngược lại thì bác bỏ H0 𝟐
TH2 – Mẫu, 𝜹𝟐 chưa biết (𝒙 − 𝝁𝟎).√𝒏 + B1: Tính 𝒕 = 𝑺 và n ≥ 30 𝛂
+ B2: Với 𝛗𝐙 = 𝟎, 𝟓 − => 𝒁𝜶 = … (Hàm ngược Laplace) 𝛂 𝟐 𝟐 𝟐
+ B3: Khi | 𝒕 | ≤ 𝒁𝜶 => Chấp nhận H0; ngược lại thì bác bỏ H0 𝟐
TH3 – Mẫu, 𝜹𝟐 chưa biết (𝒙 − 𝝁𝟎).√𝒏 + B1: Tính 𝒕 = 𝑺 và n < 30 + B2: Với 𝒕 𝜶 = … 𝒏−𝟏,
(Bảng phân phối student, n – 1 bậc tự do) 𝟐 + B3: Khi | 𝒕 | ≤ 𝒕 𝜶
𝒏−𝟏, => Chấp nhận H0; ngược lại thì bác bỏ H0 𝟐
+ 𝒙 > 𝝁𝟎 => 𝝁 > 𝝁𝟎
(3) Nếu bác bỏ H0 thì ta tiếp tục so sánh 𝒙 và 𝝁𝟎 như sau:
+ 𝒙 < 𝝁𝟎 => 𝝁 < 𝝁𝟎 lOMoARcPSD|40342981
Cách 2: Kiểm định giả thuyết một phía.
(1) Đặt giả thuyết một phía Phía trái Phía phải H0: 𝜇 ≥ 𝜇0 H0: 𝜇 ≤ 𝜇0 H1: 𝜇 < 𝜇0 H1: 𝜇 > 𝜇0
(2) Kiểm định giả thuyết một phía
TH1 – Tổng thể, 𝜹𝟐 đã biết (𝒙 − 𝝁𝟎).√𝒏 + B1: Tính 𝒕 = 𝜹
và n ≥ 30 hoặc n < 30
+ B2: Với 𝛗𝐙 = 𝟎, 𝟓 − 𝛂 => 𝐙 𝛂
𝛂 = … (Hàm ngược Laplace)
+ B3: Khi | 𝒕 | ≤ 𝐙𝛂=> Chấp nhận H0; ngược lại thì bác bỏ H0
TH2 – Mẫu, 𝜹𝟐 chưa biết (𝒙 − 𝝁𝟎).√𝒏 + B1: Tính 𝒕 = 𝑺 và n ≥ 30
+ B2: Với 𝛗𝐙 = 𝟎, 𝟓 − 𝛂 => 𝐙 𝛂
𝛂 = … (Hàm ngược Laplace)
+ B3: Khi | 𝒕 | ≤ 𝐙𝛂=> Chấp nhận H0; ngược lại thì bác bỏ H0
TH3 – Mẫu, 𝜹𝟐 chưa biết (𝒙 − 𝝁𝟎).√𝒏 + B1: Tính 𝒕 = 𝑺 và n < 30
+ B2: Với 𝒕𝒏−𝟏,𝛂 = … (Bảng phân phối student, n – 1 bậc tự do)
+ B3: Khi | 𝒕 | ≤ 𝒕𝒏−𝟏,𝛂 => Chấp nhận H0; ngược lại thì bác bỏ H0 lOMoARcPSD|40342981
2. Kiểm định giả thuyết về tỉ lệ: Một phía Hai phía Phía trái Phía phải
(1) Đặt giả thuyết H0: 𝑝 = 𝑝0 H0: 𝜇 ≥ 𝜇0 H0: 𝜇 ≤ 𝜇0 H1: 𝑝 ≠ 𝑝0 H1: 𝜇 < 𝜇0 H1: 𝜇 > 𝜇0
(2) Kiểm định giả thuyết (𝑭𝒏− 𝒑𝟎).√𝒏 (𝑭𝒏− 𝒑𝟎).√𝒏 + B1: 𝒕 = + B1: 𝒕 = √𝒑𝟎.(𝟏− 𝒑𝟎) √𝒑𝟎.(𝟏− 𝒑𝟎) 𝛂 + B2: Với 𝛗 + B2: Với 𝛗 = 𝟎, 𝟓 − 𝛂 𝐙 = 𝟎, 𝟓 − 𝛂 𝐙 𝟐 𝛂 𝟐 => 𝐙 => 𝒁 𝛂 =… 𝜶 =… 𝟐
(Hàm ngược Laplace) (Hàm ngược Laplace)
+ B3: Khi | 𝒕 | ≤ 𝒁𝜶 hoặc 𝒁𝜶 𝟐
=> Chấp nhận H0; ngược lại thì bác bỏ H0 lOMoARcPSD|40342981
CHƯƠNG 8 – PHÂN TÍCH PHƯƠNG SAI MỘT YẾU TỐ ANOVA KIỂM ĐỊNH TURKEY
1. Phân tích phương sai ANOVA:
(1) Đặt giả thuyết:
H0: … (μ1 = μ2 = ⋯ = μk)
H1: … (μ1 ≠ μ2 ≠ ⋯ ≠ μk)
(2) Kiểm định giả thuyết: + Bước 1: n 2 1 = …; 𝑥1 = …; S1 = … n 2 2 = …; 𝑥2 = …; S2 = … n 2 3 = …; 𝑥3 = …; S3 = …
𝑛1.𝑥1+ 𝑛2.𝑥2+ 𝑛3.𝑥3 => n = …; 𝑥 = 𝑛 + Bước 2:
Tổng độ lệch chuẩn bình phương được sinh ra bơi yếu tố cột: 𝑺𝑺𝑮 = ∑𝒌 (𝒙 𝒊=𝟏
𝒊 − 𝒙). 𝒏𝒊
Tổng độ lệch chuẩn của k cột: 𝑺𝑺𝑾 = ∑𝒌 (𝒏 𝟐 𝒊=𝟏
𝒊 − 𝟏). 𝑺𝒊
=> Tổng độ lệch chuẩn bình phương chung: 𝑺𝑺𝑻 = 𝑺𝑺𝑮 + 𝑺𝑺𝑾 + Bước 3: 𝑺𝑺𝑮
Phương sai giữa các nhóm: 𝑴𝑺𝑮 = 𝒌−𝟏 𝑺𝑺𝑾
Phương sai trong nội bộ nhóm: 𝑴𝑺𝑾 = 𝒏− 𝒌 + Bước 4: 𝑴𝑺𝑮 Kiểm định: 𝑭 = 𝑴𝑺𝑾 + Bước 5:
𝑭𝒌−𝟏, 𝒏− 𝒌, 𝜶 = … (Bảng phân vi Fisher với k – 1: tử, n – k: mẫu)
Nếu 𝑭 > 𝑭𝒌−𝟏, 𝒏− 𝒌, 𝜶 => Bác bỏ H0. lOMoARcPSD|40342981
BẢNG TỔNG QUÁT PHÂN TÍCH ANOVA Source of variation SS df MS F Between groups SSG k – 1 MSG Within groups SSW n – k MSW F Total SST n – 1
2. Kiểm định Turkey (phân tích hậu định): 𝒌.(𝒌−𝟏)
+ Bước 1: Số cặp trung bình cần so sánh = 𝟐 Đặt giả thuyết: (1) (2) (3) H0: 𝜇1 = 𝜇2 H0: 𝜇2 = 𝜇3 H0: 𝜇1 = 𝜇3 H1: 𝜇1 ≠ 𝜇2 H1: 𝜇2 ≠ 𝜇3 H1: 𝜇1 ≠ 𝜇3 + Bước 2:
Ta có: 𝛂 = ⋯ => 𝐪𝛂, 𝐤, 𝐧−𝐤 = ⋯ (Bảng phân phối Turkey). 𝐌𝐒𝐖
=> 𝐓 = 𝐪𝛂, 𝐤, 𝐧−𝐤 . √ 𝐧𝐢 + Bước 3:
Ta có: 𝑥1 = …; 𝑥2 = …; 𝑥3 = …
o D1 = | 𝑥1 – 𝑥2 | = … > T: bác bỏ H0 => 𝜇1 ≠ 𝜇2. Vì 𝑥1 > 𝑥2 => 𝜇1 > 𝜇2
o D2 = | 𝑥2 – 𝑥3 | = … > T: bác bỏ H0 => 𝜇2 ≠ 𝜇3. Vì 𝑥2 > 𝑥3 => 𝜇2 > 𝜇3
o D1 = | 𝑥1 – 𝑥3 | = … > T: bác bỏ H0 => 𝜇1 ≠ 𝜇3. Vì 𝑥1 > 𝑥3 => 𝜇1 > 𝜇3
CHƯƠNG 9 – TƯƠNG QUAN VÀ HỒI QUY HAI BIẾN
1. Hệ số tương quan – Pearson:
+ Hệ số tương quan tổng thể: Trong đó: + +
+ Hệ số tương quan mẫu: X – độc lập, Y – phụ thuộc. 𝑝̂ = 𝑟 = Tính chất của r:
– 1 ≤ r < 1
=> r > 0: X và Y có tương quan thuận.
=> r < 0: X và Y có tương quan nghịch.
=> r = 0: X và Y không có tương quan tuyến tính.
2. Kiểm định hệ số tương quan:
(1) Đặt giả thuyết hai phía: H0: 𝑝 = 0 (X và Y không có liên hệ tương quan).
H1: 𝑝 ≠ 0 (X và Y có liên hệ tương quan).
(2) Kiểm định giả thuyết hai phía: Ta có: 𝛂 = ⋯ => 𝒕 𝜶 = ⋯ 𝒏−𝟐,
(Bảng phân phối student). 𝟐
Nếu 𝒕 < − 𝒕 𝜶 𝜶
𝒏−𝟐, hay 𝒕 > 𝒕𝒏−𝟐, => Bác bỏ H0. 𝟐 𝟐 lOMoARcPSD|40342981
3. Phương trình hồi quy mẫu:
+ Phương trình hồi quy mẫu:
Trong đó: 𝒂 = 𝒚 − 𝒃. 𝒙
∑ 𝒙𝒊.𝒚𝒊− 𝒏.𝒙.𝒚 𝒃 = ∑ 𝟐 𝒙𝟐𝒊− 𝒏.𝒙
=> Ý nghĩa của hệ số góc (b): Khi X tăng lên một đơn vị thì Y sẽ tăng (giảm) một lượng là b.
=> Hệ số góc của phương trình hồi quy mẫu cùng dấu với hệ số tương quan.
+ Hệ số xác định: R2 = r2 = …
=> Ý nghĩa của hệ số xác định: Mức độ ảnh hưởng của X lên Y là …
+ Dự báo điểm: Cho 𝒙 = … => 𝒚 ̂ = …



