
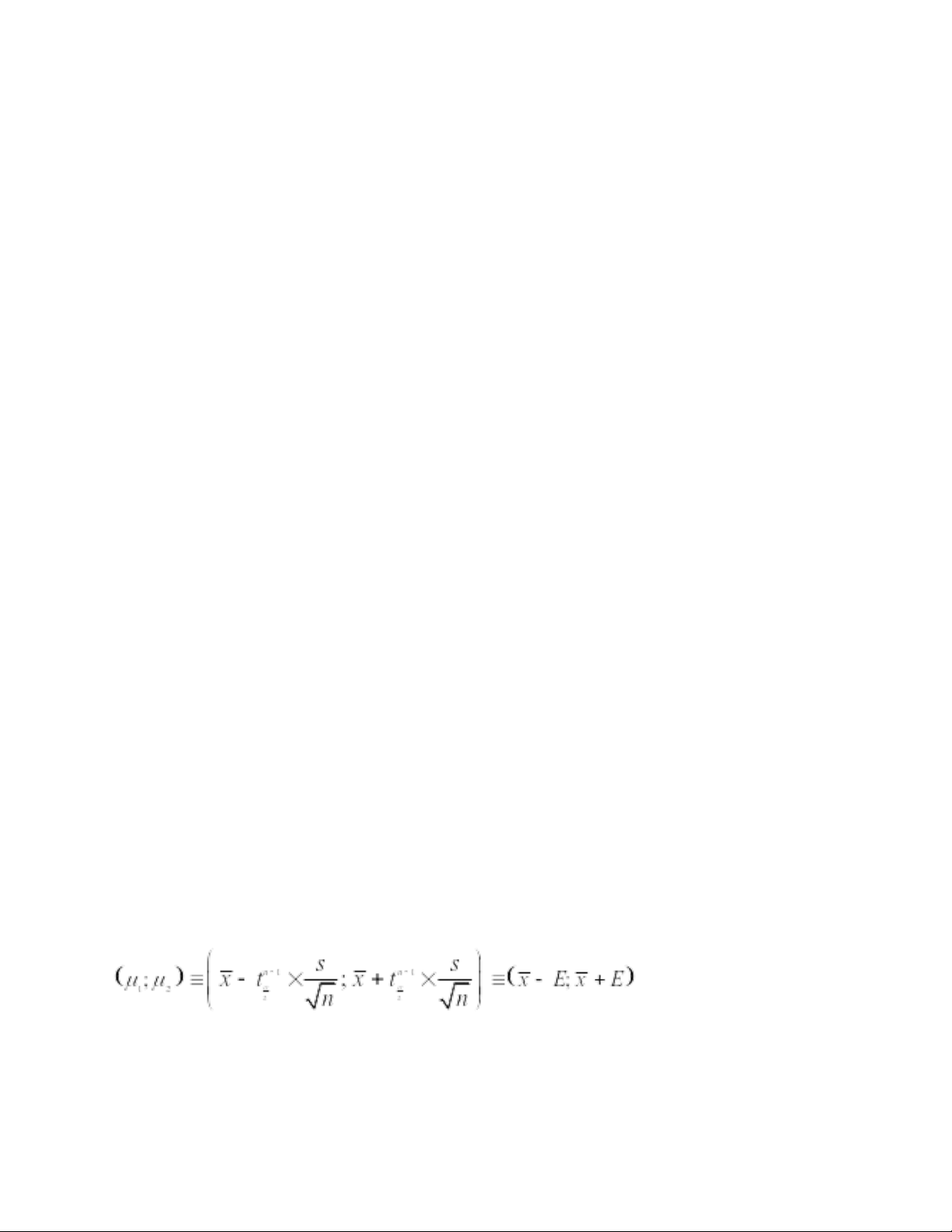

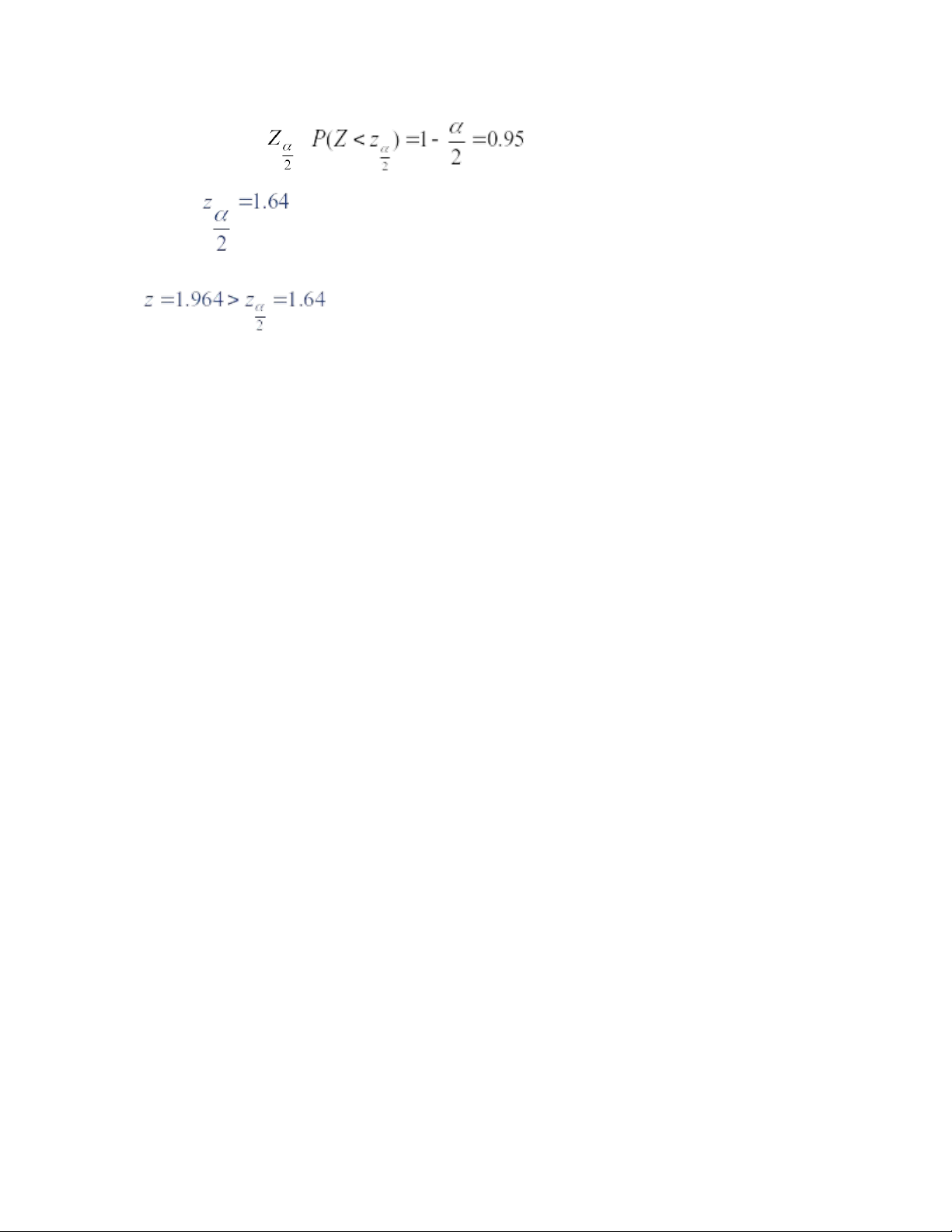





Preview text:
lOMoAR cPSD| 40342981 ÔN TẬP CUỐI KỲ Chương 5.
Bài 1: Một cuộc khảo sát môi giới báo cáo rằng 30% nhà đầu tư cá nhân đã sử dụng
chiết khấu nhà môi giới. Trong một mẫu ngẫu nhiên gồm 10 nhà đầu tư cá nhân. a/
Tính xác suất để có nhiều nhất 1 nhà đầu tư cá nhân sử dụng chiết khấu. b/ Tính số
nhà đầu tư sử dụng chiết khấu với nhiều khả năng nhất. Mod(X)=??
c/ Nếu chọn ngẫu nhiên 100 nhà đầu tư, hãy ước tính trung bình có bao nhiêu nhà
đầu tư sử dụng chiết khấu.
Bài 2: Tỷ lệ mắc bệnh nghề nghiệp trong một ngành công nghiệp đến mức người lao
động có 20% khả năng bị nó. Chọn ngẫu nhiên 3 lao động từ ngành công nghiệp trên.
Gọi X là số lao động bị mắc bệnh nghề nghiệp trong 3 lao động. a/ Lập bảng phân
phối xác suất của X. b/ Xác suất để có nhiều nhất 1 người mắc bệnh nghề nghiệp. c/
Số người mắc bệnh nghề nghiệp với nhiều khả năng nhất.
d/ Chọn ngẫu nhiên 100 lao động thuộc ngành công nghiệp trên. Theo bạn trung bình
có khoảng bao nhiêu lao động mắc bệnh nghề nghiệp.
Bài 3: Tuổi thọ của một số loại thiết bị điện tử có tuổi thọ trung bình là 300 giờ và độ lệch
chuẩn là 25 giờ. Giả sử tuổi thọ của loại thiết bị này có phân phối chuẩn.
a/ Xác định tỷ lệ thiết bị có tuổi thọ ít hơn 280 giờ. b/ Chọn ngẫu nhiên 200 thiết bị điện
tử trên, trung bình có bao nhiêu thiết bị có tuổi thọ ít hơn 300 giờ?
Bài 4: Giả sử rằng điểm kiểm tra từ kỳ thi tuyển sinh đại học có phân phối chuẩn
với giá trị trung bình là 4.5 và độ lệch chuẩn là 1.
a/ Bao nhiêu phần trăm số người làm bài thi đạt điểm từ 4 đến 5?
b/ Giả sử ai đó nhận được số điểm là 6.3. Tỉ lệ người làm bài thi có điểm cao hơn là
bao nhiêu? Điểm kém hơn bao nhiêu phần trăm?
c/ Tìm mức điểm thi để có 98,5% thí sinh có điểm thi dưới mức điểm đó. lOMoAR cPSD| 40342981
d/ Nếu một trường đại học cụ thể sẽ không thừa nhận bất kỳ điểm nào dưới 4.8, phần
trăm số người tham gia bài kiểm tra sẽ được trường đại học chấp nhận là bao nhiêu?
Bài 5: Mức lương khởi điểm trung bình của sinh viên tốt nghiệp năm nay của một
trường đại học lớn là 25.000 đô la với độ lệch chuẩn là 5.000 đô la. Hơn nữa,
được biết rằng mức lương khởi điểm có phân phối chuẩn.
a/ Chọn ngẫu nhiên một sinh viên tốt nghiệp được từ một trường đại học lớn, tính
xác suất để sinh viên này sẽ có mức lương khởi điểm ít nhất là $ 31,000? b/
Những cá nhân có mức lương khởi điểm dưới 12.200 đô la được giảm thuế thu
nhập thấp. Bao nhiêu phần trăm sinh viên tốt nghiệp sẽ được giảm thuế?
c/ Trong số 5% những người tốt nghiệp có mức lương cao nhất, hãy tìm mức lương tối thiểu.
Chương 6 và chương 7.
Bài 1: Một công ty tuyên bố rằng những cốc sữa chua ít béo (nặng 8 ounce) chứa
trung bình là 150 calo mỗi cốc. Một cơ quan người tiêu dùng muốn kiểm tra xem
tuyến bố này có đúng hay không. Lấy mẫu ngẫu nhiên 10 cốc sữa chua, cho thấy
lượng calo trong mỗi cốc như sau:
147; 159; 153; 146; 144; 161; 163; 153; 143; 158
Giả sử lượng calo trong mỗi cốc sữa chua có phân phối chuẩn.
Tìm khoảng tin cậy 99% lượng calo trung bình trong mỗi cốc sữa. 2 lOMoAR cPSD| 40342981
Bài 2: Trong một cuộc khảo sát được thực hiện tại một thành phố lớn, 170 hộ gia
đình trong số 250 mẫu ngẫu nhiên sở hữu ít nhất một con vật cưng. Tìm khoảng tin
cậy 95% cho tỷ lệ hộ gia đình ở thành phố sở hữu ít nhất một con vật cưng.
Kết quả có đúng như tuyên bố của nhà sản xuất thức ăn vật cưng rằng 75%
tổng số hộ gia đình có ít nhất một con vật cưng?
Bài 3: Một thiết bị đóng gói được thiết lập để đổ đầy các gói bột giặt có trọng lượng trung
bình là 5 kg, với độ lệch chuẩn là 0,21 kg. Trọng lượng của các gói có thể được giả định là
phân phối chuẩn. Một mẫu ngẫu nhiên gồm 100 gói được lấy và cân. Mẫu này có trọng
lượng trung bình là 5,03kg. Chúng ta có thể kết luận rằng trọng lượng trung bình do máy
tạo ra đã tăng lên không? Sử dụng mức ý nghĩa 5%.
Bài 4: Năm ngoái, thị phần một nhà sản xuất nước giải khát chiếm 21% trên thị trường. Để
tăng thị phần của họ trên thị trường, nhà sản xuất đã giới thiệu một hương vị mới trong
nước giải khát của họ. Một mẫu gồm 400 người tham gia thử nghiệm mùi vị và 100 người
chỉ ra rằng họ thích hương vị đó.
Với mức ý nghĩa 10%, hãy kiểm tra xem tỷ lệ người tiêu dùng thích hương vị đó có khác 21% hay không? Giả thuyết: H0: p = 0.21 Ha: p khác 0.21 b/ Giá trị thống kê lOMoAR cPSD| 40342981 Giá trị tới hạn: , we have bảng 1. Vì
, nên bác bỏ Ho . Kết luận: Tỷ lệ người tiêu dùng
thích hương vị mới khác 21%.
Bài 5. Một công ty tuyên bố rằng những cốc sữa chua ít béo (nặng 8 ounce) chứa
trung bình là 150 calo mỗi cốc. Một cơ quan người tiêu dùng muốn kiểm tra xem
tuyến bố này có đúng hay không. Lấy mẫu ngẫu nhiên 10 cốc sữa chua, cho thấy
lượng calo trong mỗi cốc như sau:
147; 159; 153; 146; 144; 161; 163; 153; 143; 158
Giả sử lượng calo trong mỗi cốc sữa chua có phân phối chuẩn. Với mức ý nghĩa
5%, hãy cho kết luận về lời tuyên bố của công ty.
Bài 6: Trong một cuộc khảo sát được thực hiện tại một thành phố lớn, 170 hộ gia đình
trong số 250 mẫu ngẫu nhiên sở hữu ít nhất một con vật cưng.
a/ Tìm khoảng tin cậy 95% cho tỷ lệ hộ gia đình trong thành phố sở hữu ít nhất
một con vật cưng. Đáp số: (0.622; 0.7378)
b/ Kết quả câu a) có hỗ trợ tuyên bố của nhà sản xuất thức ăn vật nuôi rằng 75% hộ gia
đình sở hữu ít nhất một con vật cưng?
Kết quả câu a) không hỗ trợ lới tuyên bố vì khoảng ước lượng không chứa tỷ lệ 75% của
nhà sản suất tuyên bố. Chương 8. 4 lOMoAR cPSD| 40342981
Một nhà nghiên cứu muốn thử ba kỹ thuật khác nhau để giảm huyết áp của những người
được chẩn đoán mắc bệnh cao huyết áp. Các đối tượng được chọn ngẫu nhiên vào ba
nhóm; nhóm thứ nhất uống thuốc, nhóm thứ hai tập thể dục, và nhóm thứ ba tuân theo
chế độ ăn kiêng đặc biệt. Sau bốn tuần, mức giảm huyết áp của người đó được ghi lại. Dùng thuốc Ăn kiêng Tập thể dục 10 6 5 12 8 9 9 3 12 15 0 8 13 2 4 a/ Hãy lập bảng ANOVA.
b/ Với mức ý nghĩa 5%, có thể kết luận các phương pháp làm giảm huyết áp có hiệu quả như nhau không?
Bài 2: Mười lăm học sinh lớp bốn được phân ngẫu nhiên vào ba nhóm để thử nghiệm ba
phương pháp dạy học toán khác nhau. Vào cuối học kỳ, bài kiểm tra tương tự đã được
đưa ra cho tất cả 15 học sinh. Bảng dưới đây cho điểm của học sinh trong ba nhóm. Phương pháp A Phương pháp B Phương pháp C lOMoAR cPSD| 40342981 48 55 84 73 85 68 51 70 95 65 69 74 87 90 67 a/ Lập bảng ANOVA.
b/ Với mức ý nghĩa 5%, có thể kết luận hiệu quả 3 phương pháp giảng dạy trên là như nhau?
Chương 9: Hồi qui đơn
Bài 1: Sau đây là thông tin về thu nhập và chi tiêu thực phẩm của 7 hộ gia đình ở
một thành phố nhỏ trong một tháng trước đó. Thu nhập (100 $)(X) Chi tiêu thực phẩm(Y) (100$) 55 14 83 24 38 13 61 16 33 9 49 15 6 lOMoAR cPSD| 40342981 67 17
a/ Xác định hệ số tương quan. Cho nhận xét về mối tương quan giữa thu nhập và
chi tiêu thực phẩm của các hộ gia đình. X_Tb = 55.143; y_Tb = 15.429;
S(x) = 17.189; S(y) = 4.577; sum(xy) = 6403;
. Tương quan thuận và khá chặt chẽ.
b/ Viết phương trình hồi qui tuyến tính thể hiện mối liên hệ giữa thu nhập và chi
tiêu thực phẩm hàng tháng. Giải thích ý nghĩa hệ số góc tìm được.
Phương trình hồi qui ước lượng được là: E(Y) = = 1.507 + 0.252*X
Giải thích ý nghĩa của = 0.252:
Khi thu nhập của hộ gia đình tăng 100$/tháng thì trung bình chi tiêu thực phẩm sẽ tăng 0.252*100$/tháng.
c/ Tìm hệ số xác định. Giải thích ý nghĩa hệ số xác định tìm được.
Khoảng 89.87% chi tiêu của các hộ gia đình được giải thích bởi thu nhập.
d/ Hãy cho biết chi tiêu thực phẩm trung bình là bao nhiêu nếu mức thu nhập là 7000$? lOMoAR cPSD| 40342981
E(Y) = 1.507 + 0.252*X = 1.507 + 0.252*70 (100$)
Bài 2: Bảng sau đây cung cấp thông tin về lượng đường (tính bằng gam) và lượng calo
trong một khẩu phần gồm 13 loại ngũ cốc của Kellogg. Đường (g) 4 15 12 11 8 6 7 2 7 14 20 3 13 calo 120 200 140 110 120 80 190 100 120 190 190 110 120
Calo: Y- phụ thuộc; Đường, X: Độc lập.
a/ Tìm hệ số tương quan tuyến giữa lượng đường và lượng calo. Cho nhận xét về mối liên hệ này.
b/ Tìm phương trình hồi qui tuyến tính thể hiện mối liên hệ giữa lượng đường và
lượng calo. Giải thích ý nghĩa hệ số góc.
PT hồi qui ước lượng được có dạng: E(Y) = b0 +b1*X Trong đó b1 =
b0 c/ Tính hệ số xác định và giải thích ý nghĩa. 8 lOMoAR cPSD| 40342981 Hết.



