Tổng hợp định nghĩa, tính chất, dấu hiệu nhận biết các hình học phẳng

Tổng hợp định nghĩa, tính chất, dấu hiệu nhận
biết các hình học phẳng 1. Hình tam giác
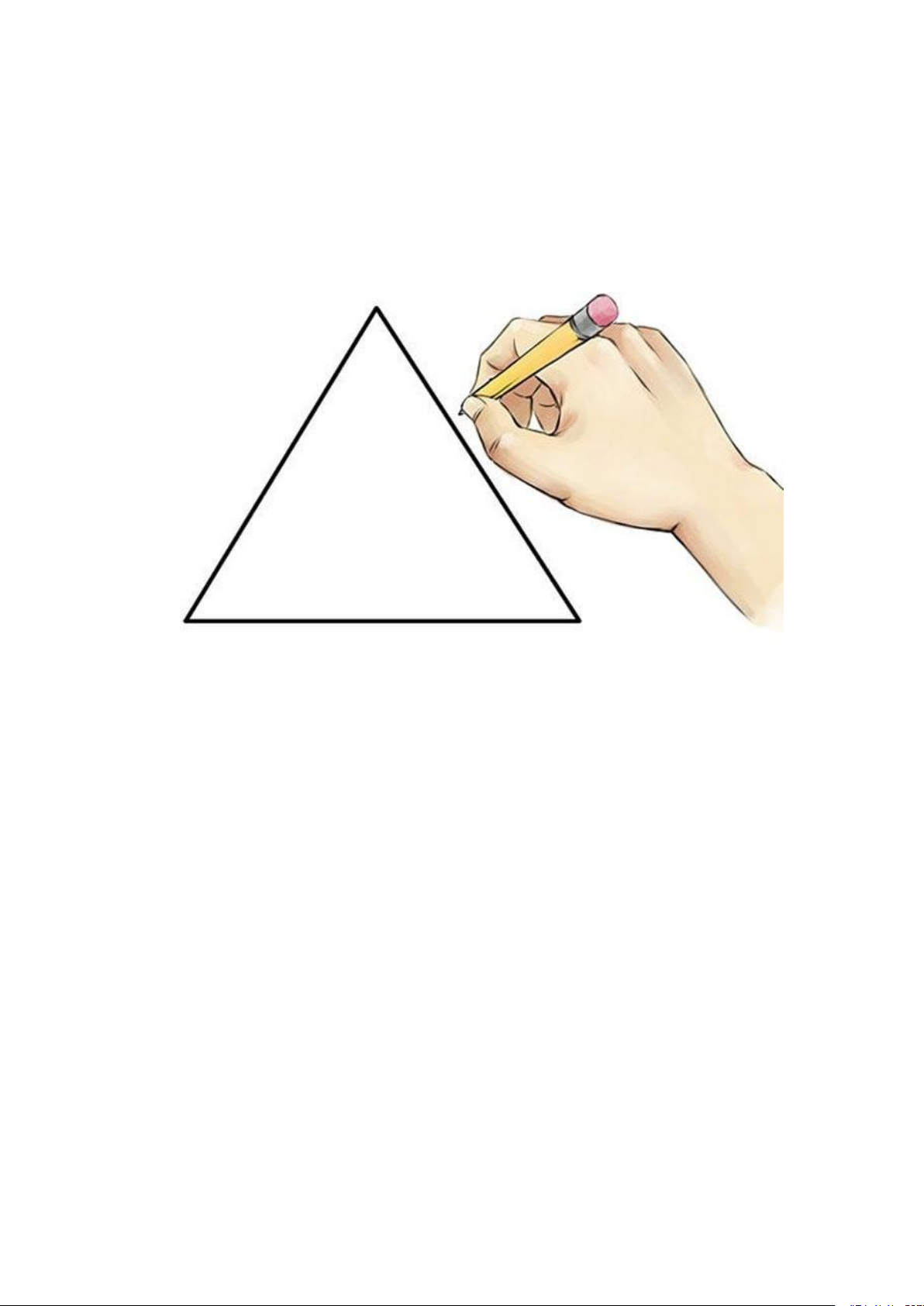
Tam giác là một hình học có ba đỉnh, ba cạnh và ba góc. Dưới đây là một số
đặc điểm và tính chất của hình tam giác:
Tính chất cơ bản: Tam giác có ba đỉnh, ba cạnh và ba góc. Tổng độ dài của
ba cạnh của tam giác phải luôn lớn hơn 0.
Dấu hiệu nhận biết: Tổng độ dài hai cạnh bất kỳ của tam giác phải lớn hơn
chiều dài cạnh còn lại. Điều này được gọi là nguyên tắc tam giác. Nếu tổng
độ dài hai cạnh bất kỳ bằng hoặc nhỏ hơn chiều dài cạnh còn lại, thì không
thể tạo thành một tam giác. Tổng độ lớn của hai góc bất kỳ trong tam giác
phải lớn hơn 180 độ. Nếu tổng độ lớn của hai góc này bằng 180 độ, thì tam
giác đó là một tam giác phẳng.
Phân loại tam giác dựa trên độ dài các cạnh:
Tam giác đều: Các cạnh và góc của tam giác đều có cùng độ dài và góc bằng 60 độ.
Tam giác vuông: Có một góc vuông, tức là một góc bằng 90 độ. Độ dài hai
cạnh gần góc vuông được gọi là cạnh góc vuông
Tam giác cân: Hai cạnh đối diện với hai góc bằng nhau có cùng độ dài. Nếu
các góc đối diện không bằng nhau, tam giác cân cũng có thể là tam giác vuông cân.
Tam giác nhọn: Tất cả các góc trong tam giác đều nhọn (ít hơn 90 độ).
Tam giác tù: Có ít nhất một góc tù (lớn hơn 90 độ).
Phân loại tam giác dựa trên độ đối xứng:
Tam giác đều có độ đối xứng cao.
Tam giác cân có ít nhất một độ đối xứng. 2. Hình vuông
Hình vuông là một loại hình học có đặc điểm sau:
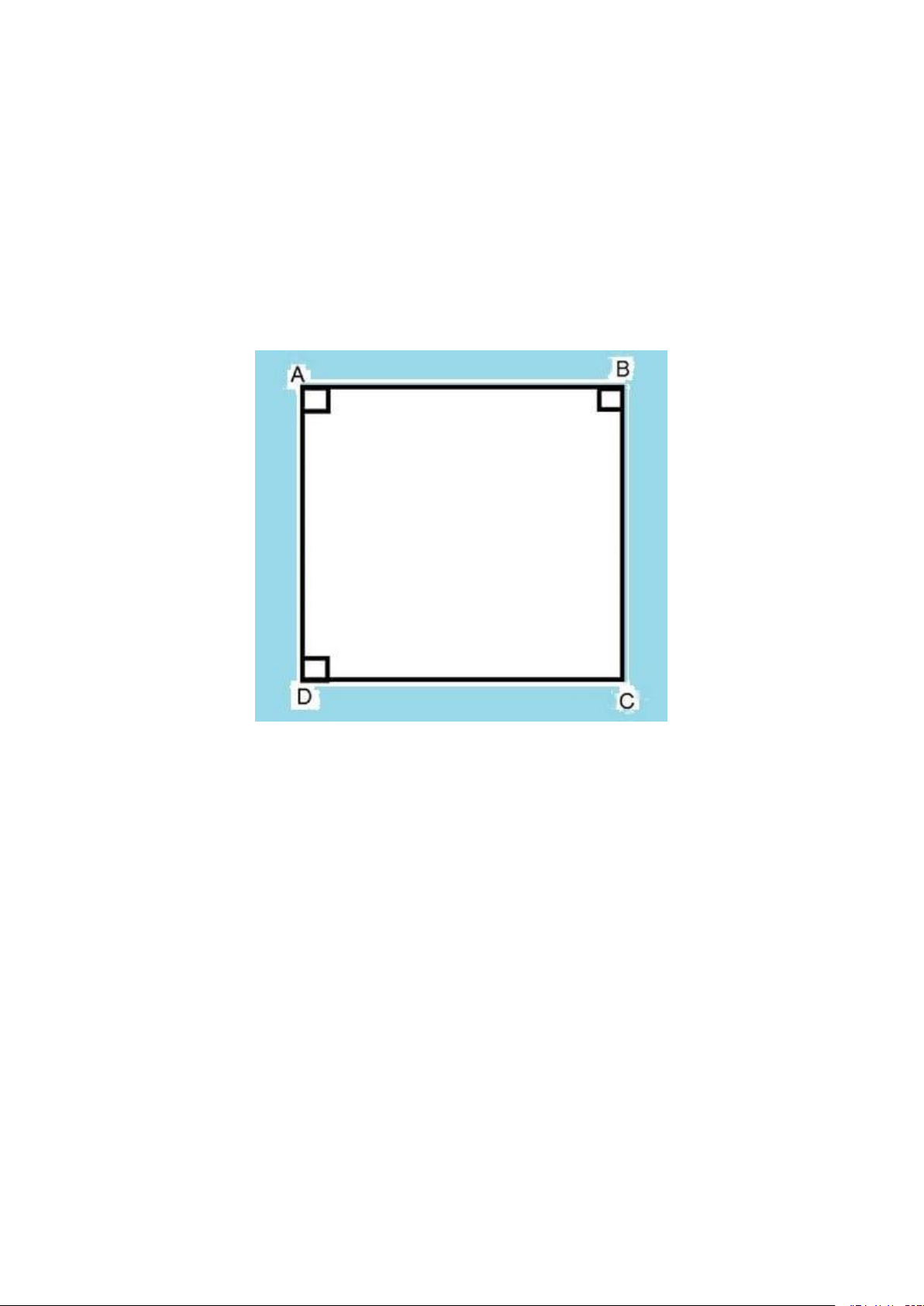
Định nghĩa: Hình vuông là một hình tứ giác có bốn cạnh có cùng độ dài và
bốn góc bằng nhau, mỗi góc bằng 90 độ. Các cạnh của hình vuông đồng
đẳng và song song với nhau. Tính chất:
- Bốn cạnh bằng nhau: Các cạnh của hình vuông có cùng độ dài. Bốn góc
bằng nhau: Các góc của hình vuông đều có độ lớn bằng 90 độ.
- Tất cả các đường chéo có cùng độ dài: Đường chéo của hình vuông là đoạn
thẳng nối hai đỉnh không kề nhau của hình vuông, và tất cả các đường chéo
trong hình vuông có cùng độ dài, bằng nửa độ dài của một cạnh.
- Có ít nhất hai trục đối xứng: Hình vuông có ít nhất hai trục đối xứng: một là
đường kết nối hai đỉnh đối diện, và hai là đường kết nối hai điểm giữa hai cạnh đối diện.
- Có tính đối xứng tâm: Hình vuông có một tâm đối xứng là giao điểm của các
đường trục đối xứng.
Dấu hiệu nhận biết: Dấu hiệu nhận biết hình vuông đơn giản nhất là kiểm tra
độ dài của các cạnh và các góc của hình. Nếu tất cả bốn cạnh bằng nhau và
bốn góc bằng 90 độ, thì bạn có thể xác định. 3. Hình thang
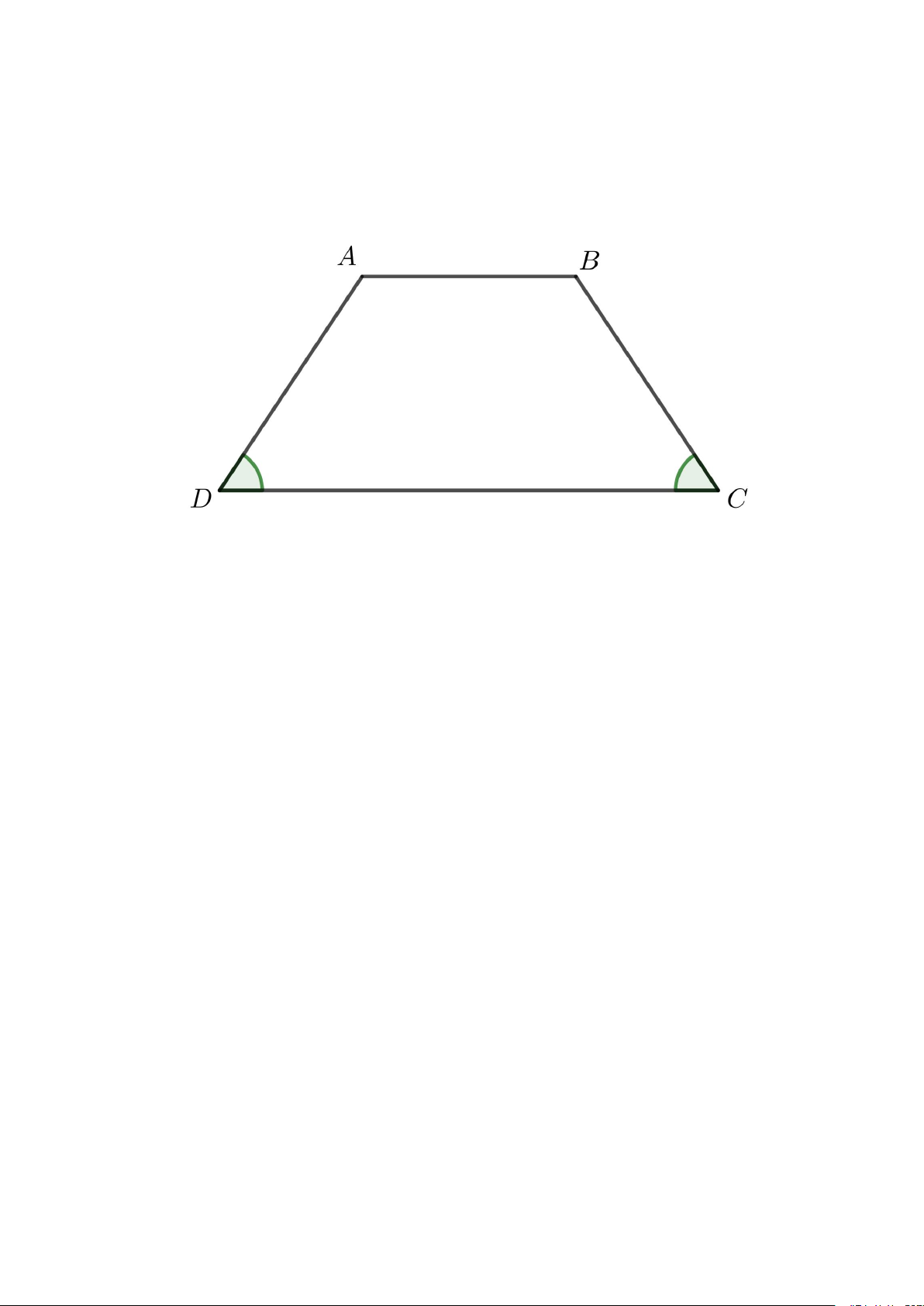
Định nghĩa: Hình thang là một hình tứ giác có hai cạnh song song (gọi là
cạnh đáy) và hai cạnh còn lại không song song (gọi là cạnh hai bên). Các
cạnh hai bên có thể có độ dài khác nhau, và các góc của hình thang không
nhất thiết phải bằng nhau. Tính chất:
- Cạnh đáy song song: Hai cạnh đáy của hình thang là hai đoạn thẳng song song với nhau.
- Cạnh hai bên không song song: Hai cạnh hai bên không song song và gặp
nhau tại hai đỉnh không kề nhau.
- Có thể có các góc khác nhau: Góc giữa hai cạnh đáy có thể khác nhau tùy
thuộc vào độ dài của cạnh hai bên.
- Đường chéo có thể có: Một số hình thang có đường chéo nối hai đỉnh không
kề nhau. Đường chéo này có thể cắt nhau tại một điểm bên trong hình thang.
Dấu hiệu nhận biết: Để nhận biết một hình thang, bạn có thể kiểm tra các đặc điểm sau:
- Các cạnh song song: Kiểm tra xem hai cạnh đáy của hình có song song với
nhau hay không. Nếu hai cạnh này không song song, đó không phải là hình thang.
- Các cạnh không song song: Kiểm tra xem hai cạnh hai bên có không song
song và gặp nhau tại hai đỉnh không kề nhau hay không. Nếu hai cạnh này
song song, đó cũng không phải là hình thang.
- Kiểm tra các độ dài cạnh và góc giữa các cạnh: Đôi khi, bạn có thể xác định
một hình thang bằng cách kiểm tra độ dài của các cạnh và góc giữa các cạnh.
Tuy nhiên, đối với những hình thang không có tất cả các cạnh và góc bằng
nhau, điều này có thể khó khăn hơn. 4. Hình thoi
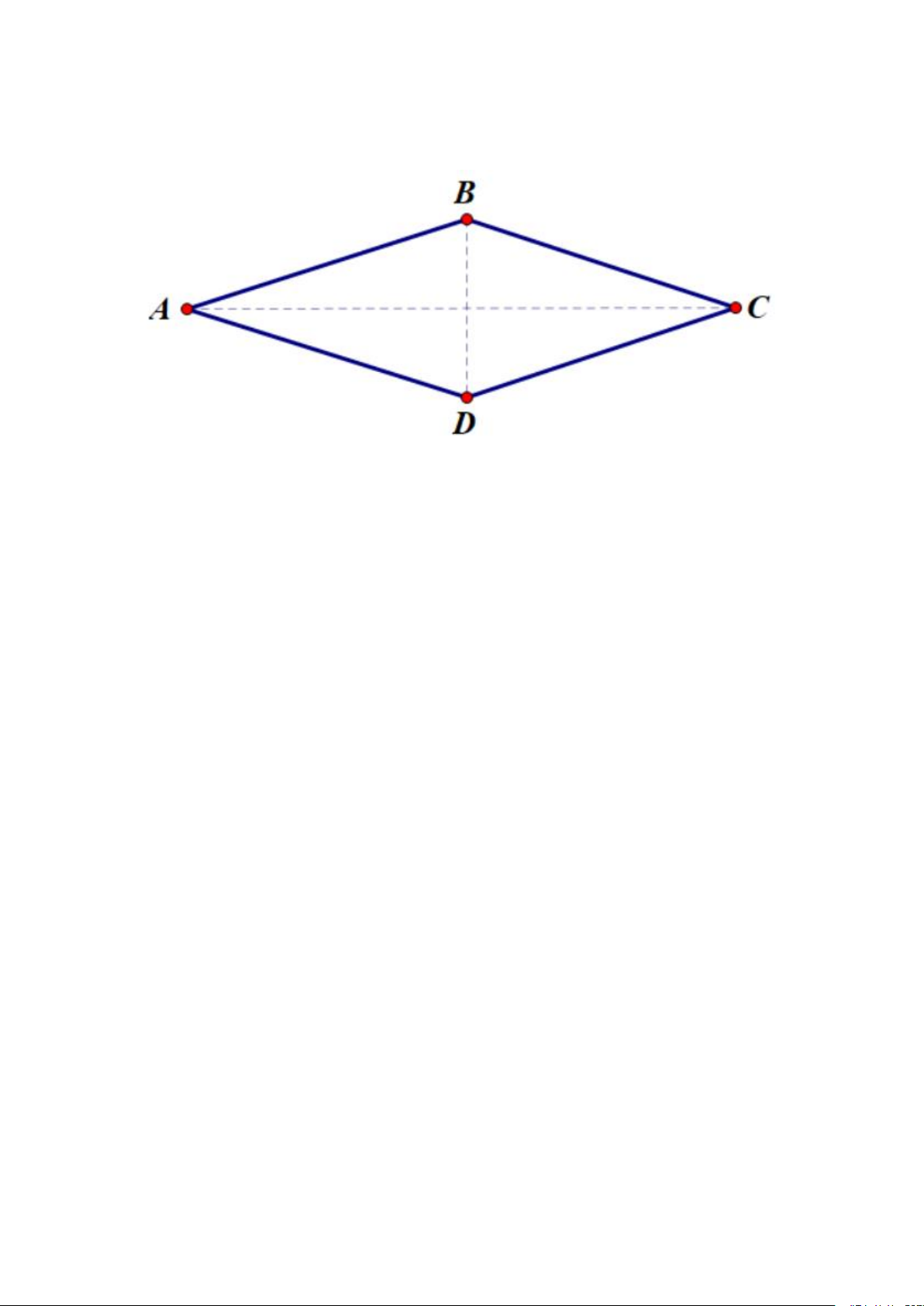
Định nghĩa: Hình thoi là một hình tứ giác có tất cả các cạnh có độ dài bằng
nhau. Nó cũng có các đặc điểm sau:
- Các góc của hình thoi không nhất thiết phải bằng 90 độ (như hình vuông).
- Cặp đối diện của các góc của hình thoi bằng nhau.
- Cặp đối diện của các cạnh của hình thoi song song và có cùng độ dài. Tính chất:
- Các cạnh bằng nhau: Tất cả bốn cạnh của hình thoi có độ dài bằng nhau.
- Các góc bằng nhau: Tất cả các góc của hình thoi không nhất thiết phải bằng
90 độ, nhưng cặp đối diện của các góc bằng nhau
- Các đường chéo chia hình thoi thành bốn tam giác bằng nhau: Hai đường
chéo của hình thoi chia nó thành bốn tam giác bằng nhau. Điều này có nghĩa
là diện tích của mỗi tam giác con là bằng nhau.
- Các cạnh đối diện song song và cùng độ dài: Hai cạnh đối diện của hình thoi
luôn song song và có độ dài bằng nhau.
- Tâm đối xứng: Hình thoi có một tâm đối xứng, là giao điểm của hai đường chéo. Dấu hiệu nhận biết:
Để nhận biết một hình tứ giác là hình thoi, bạn có thể kiểm tra các đặc điểm sau:
- Các cạnh bằng nhau: Kiểm tra xem tất cả bốn cạnh của hình tứ giác có độ dài bằng nhau không.
- Các góc đối diện bằng nhau: Xác định xem có cặp đối diện nào trong bốn
góc của hình tứ giác có bằng nhau hay không.
- Kiểm tra đường chéo: Hình thoi luôn có hai đường chéo cắt nhau tại một
điểm duy nhất. Kiểm tra xem hai đường chéo này cắt nhau tại một điểm và có cùng độ dài không.
Nếu hình tứ giác thỏa mãn các điều kiện trên, nó có thể được xem xét là một hình thoi. 5. Hình tròn
Định nghĩa: Hình tròn là một loại hình học trong mặt phẳng hai chiều được
xác định bởi tập hợp các điểm nằm cách một điểm tọa độ (gọi là tâm) ở cùng
một khoảng cách cố định. Tất cả các điểm trên bề mặt của hình tròn có
khoảng cách bằng nhau đến tâm. Tính chất:
Bán kính: Bán kính của hình tròn là khoảng cách từ tâm của nó đến bất kỳ
điểm nào trên bề mặt của hình tròn. Kí hiệu bán kính thường là "r."
Đường kính: Đường kính của hình tròn là hai lần bán kính. Kí hiệu đường
kính thường là "d" hoặc "2r."
Diện tích: Diện tích của hình tròn được tính bằng công thức A = πr^2, trong
đó π (pi) là một số xấp xỉ khoảng 3.14159.
Chu vi: Chu vi của hình tròn được tính bằng công thức C = 2πr hoặc C = πd, với d là đường kính.
Tâm đối xứng: Hình tròn có một tâm đối xứng, là điểm nằm ở giữa của hình
tròn và có độ dài bán kính đến tất cả các điểm trên bề mặt của nó bằng nhau. Dấu hiệu nhận biết:
Để nhận biết một hình là hình tròn, bạn có thể kiểm tra các điều kiện sau:
- Có một điểm tâm: Hình tròn phải có một điểm tâm xác định từ đó tính toán bán kính.
- Tất cả các điểm trên bề mặt cách tâm cùng một khoảng cách: Để kiểm tra
điều này, bạn có thể chọn hai điểm bất kỳ trên bề mặt của hình và kiểm tra
khoảng cách của chúng đến tâm. Nếu khoảng cách này bằng nhau, hình có thể là hình tròn.
- Bán kính đồng nhất: Bạn cũng có thể kiểm tra xem bán kính tính từ tâm đến
bất kỳ điểm nào trên bề mặt có giống nhau không. Nếu bán kính này không
thay đổi, thì đó là hình tròn.
- Công thức diện tích và chu vi đúng: Nếu hình này thỏa mãn các công thức
tính diện tích và chu vi của hình tròn (A = πr^2 và C = 2πr hoặc C = πd), thì đó là hình tròn.
Document Outline

• Tổng hợp định nghĩa, tính chất, dấu hiệu nhận biết
  • 1. Hình tam giác
  • 2. Hình vuông
  • 3. Hình thang
  • 4. Hình thoi
  • 5. Hình tròn