




















Preview text:
TÀ T I À I L I L Ệ I U Ệ U D À D N À H N H C H C O H O K H K ỐI Ố 1 2 1 Mục lục
Chủ đề 01. HÌNH ĐA DIỆN – KHỐI ĐA DIỆN
Chủ đề 02. THỂ TÍCH KHỐI CHÓP
Dạng 1.1. Chóp có cạnh bên vuông góc với đáy ................................................................. 9
Dạng 1.2. Chóp có mặt bên vuông góc với đáy ................................................................. 10
Dạng 1.3. Chóp đều ..................................................................................................................... 11
Dạng 1.4. Tỷ số thể tích ............................................................................................................. 13
Dạng 1.5. Tổng hiệu thể tích .................................................................................................... 16
Chủ đề 03. THỂ TÍCH KHỐI LĂNG TRỤ
Dạng 2.1. Thể tích lăng trụ đứng ............................................................................................ 19
Dạng 2.2. Thể tích lăng trụ xiên ............................................................................................. 20
Dạng 2.3. Thể tích khối lập phương – khối hộp ................................................................... 21
Dạng 2.4. Khối đa diện được cắt ra từ khối lăng trụ ........................................................ 22
Dạng 2.5. Max – min thể tích ................................................................................................... 25
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 KHỐI ĐA DIỆN
HÌNH ĐA DIỆN – KHỐI ĐA DIỆN A. LÝ THUYẾT CHUNG.
1. Khái niệm về hình đa diện – khối đa diện.
Hình lăng trụ, hình chóp ta thấy chúng là những hình không gian được tạo bởi hữu hạn đa giác.
Các đa giác ấy có tính chất:
Hai đa giác phân biệt chỉ có thể:
hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Mỗi đa giác như thế được gọi là một mặt của hình đa diện H .
Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là các đỉnh, cạnh của hình đa diện H
2. Khái niệm về khối đa diện.
Khối đa diện là phần không gian được giới hạn bởi 1 hình đa diện, kể cả hình đa diện đó.
Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Điểm trong:
Những điểm thuộc khối đa diện nhưng không
thuộc hình đa diện giới hạn khối đa diện ấy.
Miền trong khối đa diện:
Là tập hợp các điểm trong.
Miền ngoài khối đa diện:
Là tập hợp các điểm ngoài.
Mỗi đa diện chia các điểm còn lại của không gian thành hai
miền không giao nhau: miền trong và miền ngoài.
Trong đó chỉ có duy nhất miền ngoài là chứa hoàn toàn một
đường thẳng d nào đấy.
Khối đa diện H là hợp của hình đa diện H và miền trong của nó.
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 2
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 3. Phép biến hình.
Phép biến hình trong không gian:
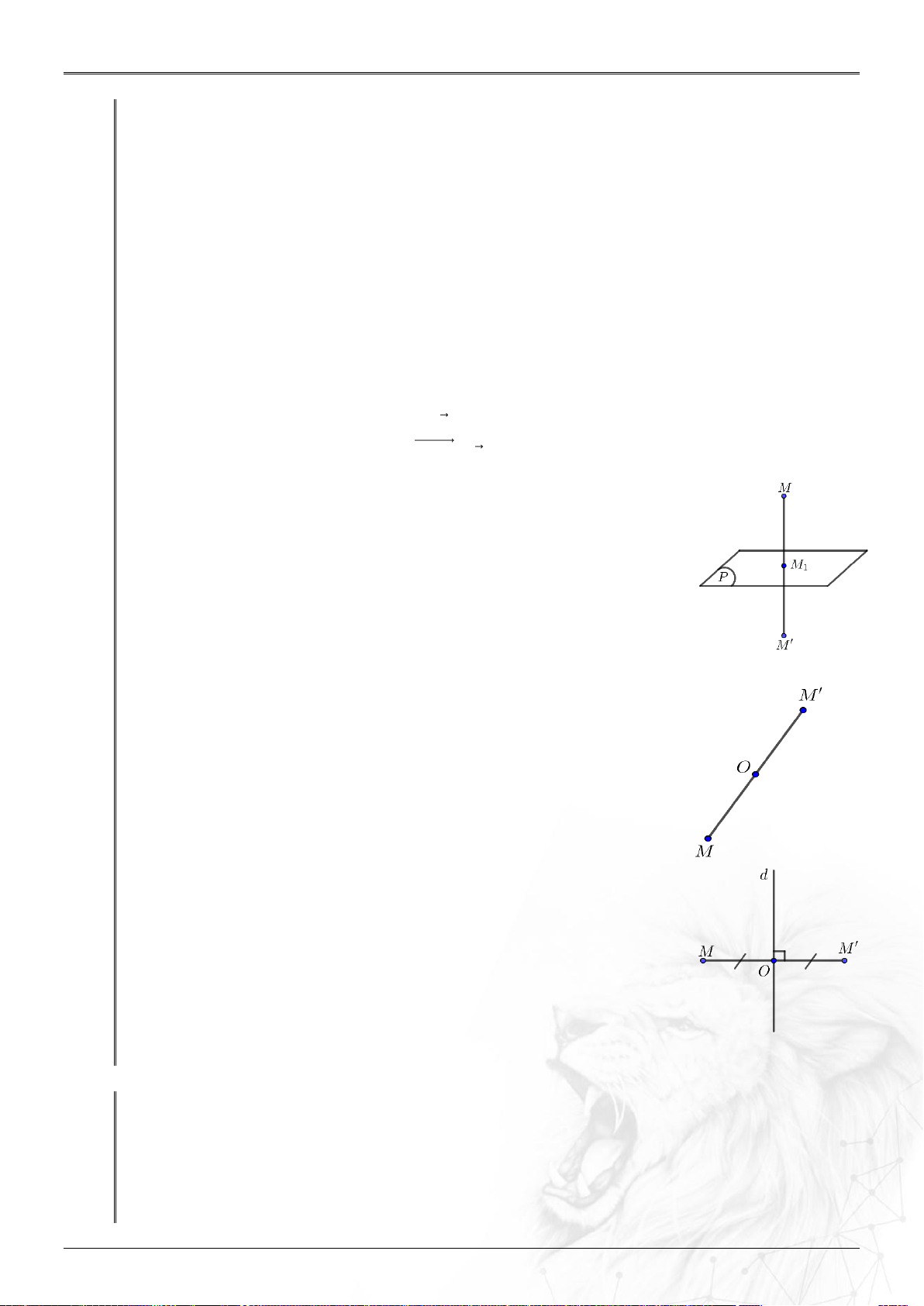
Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định
duy nhất được gọi là một phép biến hình trong không gian.
Phép dời hình :
Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo
toàn khoảng cách giữa hai điểm tùy ý. Nhận xét:
Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
Phép dời hình biến:
(+) Một đa diện H thành một đa diện H ,
(+) Các đỉnh, cạnh, mặt của H thành đỉnh, cạnh, mặt tương ứng của H .
Phép dời hình tịnh tiến theo vector v : là phép biến hình
biến điểm M thành M sao cho MM v .
Phép đối xứng qua mặt phẳng P : là phép biến hình
biến mọi điểm thuộc P thành chính nó,
biến điểm M P thành điểm M
sao cho P là mặt phẳng trung trực của MM .
Nếu phép đối xứng qua mặt phẳng P biến hình H thành chính nó
thì P được gọi là mặt phẳng đối xứng của H .
Phép đối xứng tâm O : là phép biến hình
biến điểm O thành chính nó,
biến điếm M khác O thành điểm M
sao cho O là trung điểm của MM .
Nếu phép đối xứng tâm O biến hình H thành chính nó
thì O được gọi là tâm đối xứng của H .
Phép đối xứng qua đường thẳng d : là phép biến hình
biến mọi điểm thuộc d thành chính nó,
biến điểm M d thành điểm M
sao cho d là trung trực của MM .
Nếu phép đối xứng qua đường thẳng d biến hình H thành chính nó
thì d được gọi là trục đối xứng của H .
Phép đối xứng qua đường thẳng d còn được gọi là phép đối xứng qua trục d .
4. Hai hình bằng nhau.
Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia. Nhận xét:
Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình đa diện này thành hình đa diện kia.
Hai tứ diện có các cạnh tương ứng bằng nhau thì bằng nhau.
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 3
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
5. Phân chia và lắp ghép khối đa diện.
Nếu khối đa diện H là hợp của hai khối đa diện H ; H , sao cho H và H 2 1 1 2
không có điểm trong chung thì ta nói:
(+) có thể chia được khối đa diện H thành hai khối đa diện H và H , 2 1
(+) có thể lắp ghép được hai khối đa diện H và H với nhau để được khối đa diện H . 2 1 Ví dụ.
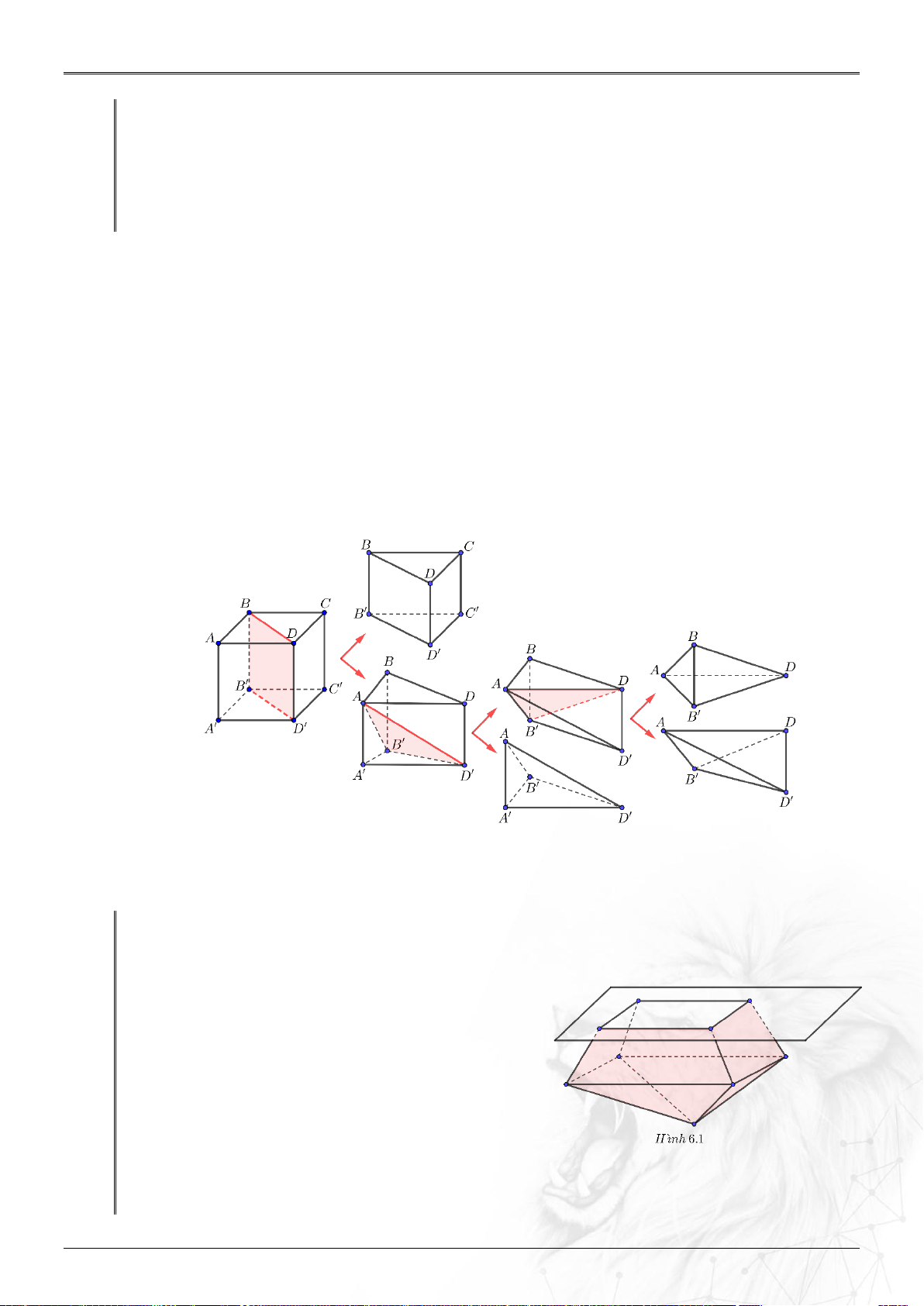
Xét khối lập phương ABC . D A B C D . Mặt BDD B
cắt khối lập phương đó theo một thiết diện là hình chữ nhật BDD B .
Thiết diện này chia các điểm còn lại của khối lập phương ra làm hai phần.
Mỗi phần cùng với hình chữ nhật BDD B
tạo thành khối lăng trụ, như vậy có hai khối lăng trụ: AB . D A B D và BC . D B C D .
Khi đó ta nói mặt phẳng P chia khối lập phương ABC . D A B C D thành hai khối lăng trụ AB . D A B D và BC . D B C D .
Tương tự trên ta có thể chia tiếp khối trụ AB . D A B D
thành ba khối tứ diện: ADBB , ADB D và AA B D . Nhận xét:
Một khối đa diện bất kì luôn có thể phân chia được thành các khối tứ diện.
6. Khối đa diện lồi.
Khối đa diện H được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của
H luôn thuộc H. Khi đó đa diện giới hạn H được gọi là đa diện lồi. Lưu ý:
Một khối đa diện là khối đa diện lồi khi
và chỉ khi miền trong của nó luôn nằm
về một phía đối với mỗi mặt phẳng đi
qua một mặt của nó. (Hình 6.1)
Công thức ƠLE:
Trong một đa diện lồi nếu gọi Đ là số
đỉnh, C là số cạnh, M là số mặt
Tức là: Đ – C + M=2
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 4
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
7. Khối đa diện đều. Định nghĩa:
Khối đa diện đều là khối đa diện lồi có các tính chất sau:
(1) Mỗi mặt của nó là một đa giác đều p cạnh.
(2) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại p; q . Nhận xét:
Các mặt của khối đa diện đều là những đa giác đều và bằng nhau. Định lý:
Chỉ có năm loại khối đa diện đều. loại 3; 3 , loại 3; 4 , loại 4; 3 , loại 5; 3 , và loại 3; 5 . Nhận xét:
Hai khối đa diện đều có cùng số mặt và có cạnh bằng nhau thì bằng nhau.
Hai khối đa diện đều có cùng số mặt thì đồng dạng với nhau. Ví dụ.
Quan sát khối tứ diện đều (Hình 7.1),
ta thấy các mặt của nó là những tam giác đều,
mỗi đỉnh của nó là đỉnh chung của đúng 3 mặt.
Quan sát khối lập phương (Hình 7.2),
ta thấy các mặt của nó là những hình vuông,
mỗi đỉnh của nó là đỉnh chung đúng 3 mặt.
Những khối đa diện nói trên được gọi là khối đa diện đều
Bảng tóm tắt của năm loại khối đa diện đều
Khối đa diện đều
Số đỉnh Số cạnh Số mặt Ký hiệu p; q Tứ diện đều 4 6 4 3; 3 Khối Lập Phương 8 12 6 4; 3
Khối Tám Mặt Đều 6 12 8 3; 4
Khối Mười Hai Mặt Đều 20 30 12 5; 3
Khối Hai Mươi Mặt Đều 12 30 20 3; 5
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 5
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 KHỐI ĐA DIỆN
THỂ TÍCH KHỐI CHÓP A. LÝ THUYẾT CHUNG. 1. Định nghĩa:
Hình chóp là hình có đáy là một đa giác, các mặt bên là tam giác có chung một đỉnh.
2. Thể tích khối chóp.
Công thức tính thể tích khối chóp: Trong đó: 1 S V . S h là diện tích đáy 3
h là chiều cao khối chóp
(khoảng cách từ đỉnh đến mặt đáy).
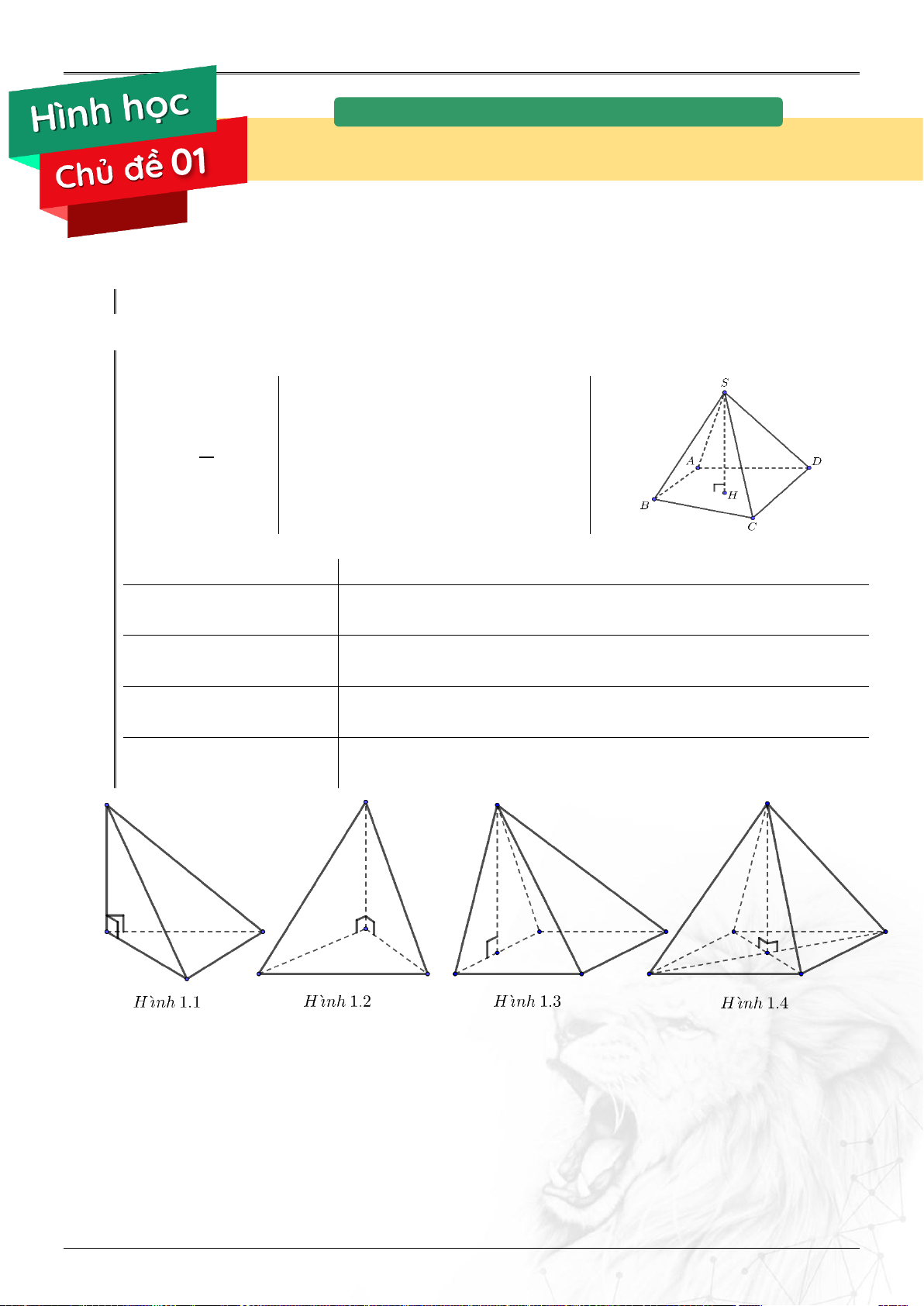
Cách xác định đường cao khối chóp: Loại Đường cao Cạnh bên vuông đáy
Đường cao chính là cạnh bên. Hình 1.1
Hai mặt bên vuông đáy Đường cao là giao tuyến của hai mặt bên vuông góc đáy. Hình 1.2 Mặt bên vuông đáy
Đường cao của mặt bên vuông góc đáy. Hình 1.3 Chóp đều
Đường cao hạ từ đỉnh đến tâm đa giác đáy. Hình 1.4
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 6
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
4. Công thức tính diện tích đáy.
Ta có các đa giác thường gặp sau: 1 1 1 S . a h . b h . c h 2 a 2 b 2 c 1 1 1 S . a h . b h . c h 2 a 2 b 2 c Tam giác 1 1 1 S b . a sin A c . a sin B b . a sin C 2 2 2 abc 2 S 2R .sin A.sin . B sinC 4R
với R là bán kính đường tròn ngoại tiếp ABC . S . p r p r
với là nửa chu vi và là bán kính đường tròn nội tiếp ΔABC
a b c
S pp ap bp c với p 2 1 2 2 hoặc S a b 2 2 c c a b 4
Tam giác vuông ΔABC vuông tại A : 1 1 S A . B AC BC.AH . 2 2 Tam giác đều
ΔABC đều, cạnh AB : S AB2 3 . ; 4 3
Chiều cao tam giác đều h A . B . 2 Hình vuông cạnh AB
Diện tích hình vuông ABCD : 2 S AB Hình chữ nhật
Diện tích hình chữ nhật ABCD :S A . BCD Hình bình hành
Diện tích hình bình hành ABCD :S A . B A . D sin BAD Hình thoi 1
Diện tích hình thoi ABCD :S A . B A . D sin BAD AC.BD 2 Hình thang 1
Diện tích hình thang ABCD :S AB CD.h 2 1
Tứ giác có hai đường chéo vuông góc: S AC.BD 2
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 7
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
5. Tỷ số diện tích.
Ta có các tỷ số thường gặp sau:
AM trung tuyến, S đặt S S
S S . ABC 1 2 2 G là trọng tâm, S đặt S S
S S S . ABC 1 2 3 3
BM MN NC S đặt S S
S S S . ABC 1 2 3 3
M; N; F lần lượt là trung điểm A ; B AC; BC S đặt S S
S S S S . ABC 1 2 3 4 4 S S S
S S S S ABCD 1 2 3 4 4 S AM AN AMN . S AB AC ABC
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 8
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
Dạng 1.1. Chóp có cạnh bên vuông góc với đáy
Đây là dạng dễ xác định được đường cao (h). 1
Áp dụng công thức: V . S h 3 Ví dụ 1.1.1 Cho khối chóp .
S ABCD có đáy ABCD là hình vuông cạnh a . Biết SA vuông góc
với ABCD và SA a 3 . Thể tích của khối chóp . S ABCD là: 3 a 3 a 3 A. . B. 3 a 3 . C. . D. 3 3a . 4 3 Lời giải Chọn C S 3 1 a 3
Thể tích khối chóp V .S .SA 3 ABCD 3 A D B C Ví dụ 1.1.2 Cho khối chóp .
S ABCD có đáy ABCD là hình chữ nhật AB a, BC 2a . Cạnh
bên SA vuông góc với đáy và SA a 2 . Thể tích của khối chóp . S ABCD là: 3 2a 3 3 a 2 3 2a 2 A. . B. 3 a 2 2 . C. . D. . 3 2 3 Lời giải Chọn D Diện tích đáy: 2 S A . D BC 2a . ABCD 3 1 2a 2
Thể tích: V .S .SA . 3 ABCD 3 Ví dụ 1.1.3 Cho khối chóp .
S ABCD có đáy ABCD là hình vuông canh a . Cạnh bên SA
vuông góc với đáy và SA 2a. Thể tích của khối chóp . S BCD là: 3 a 5 3 a 3 a 3 2a A. . B. . C. . D. . 3 3 2 3 Lời giải Chọn B 2 1 a Ta có: S S . BCD 2 ABCD 2 3 1 a Suy ra V .S .SA . 3 BCD 3
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 9
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 1.2. Chóp có mặt bên vuông góc với đáy
Khối chóp có mặt bên vuông góc mặt phẳng đáy. 1
Áp dụng công thức: V . S h . 3
Chiều cao khối chóp là đoạn thẳng từ đỉnh của chóp ta kẻ vuông góc vào giao tuyến
của mặt bên và mặt đáy.
Một số kiểu thường gặp:
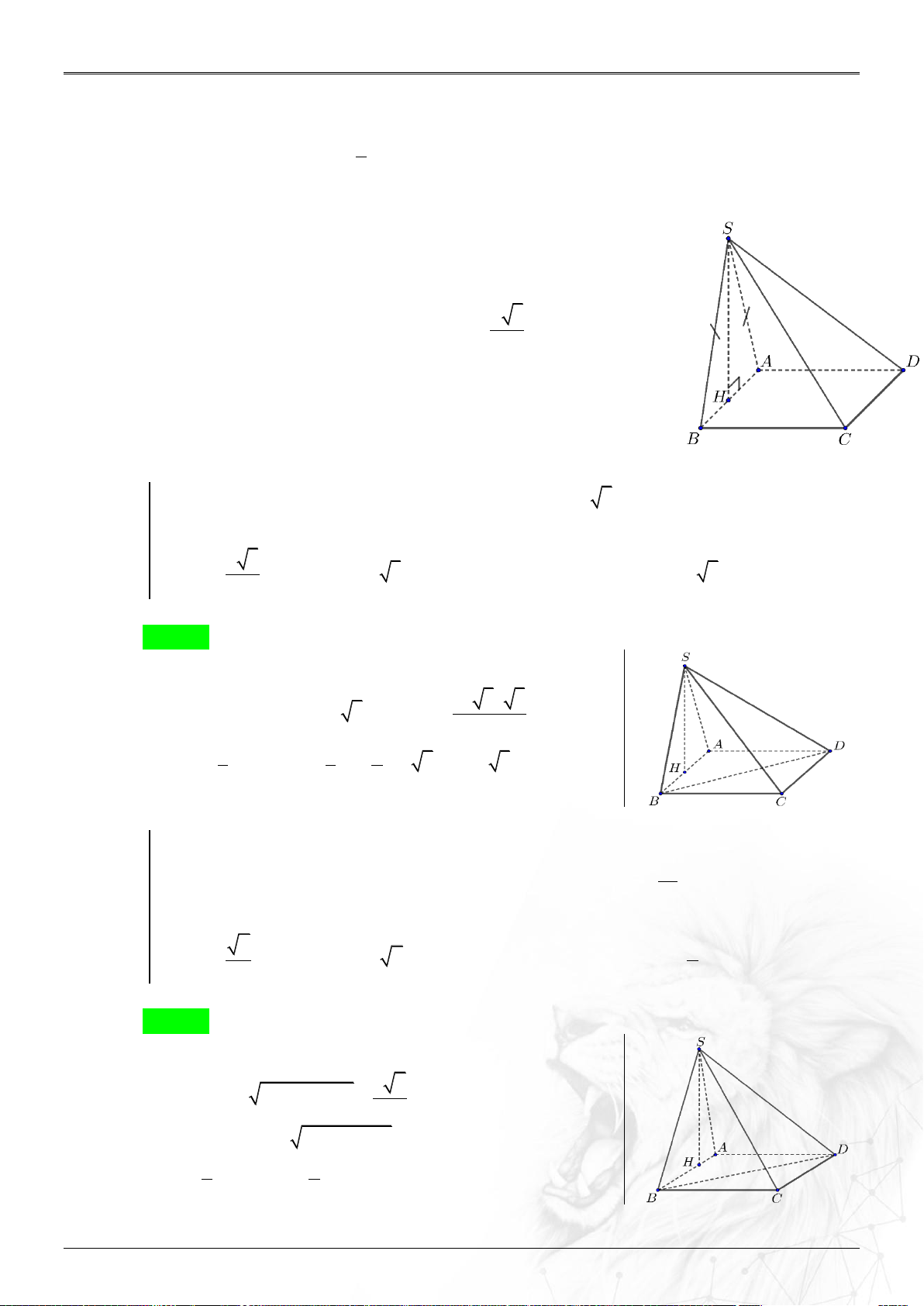
Mặt bên SAB vuông với đáy ABCD và SAB là tam giác x 3
đều cạnh x SH ABCD h SH với H là trung 2 điểm AB .
Mặt bên SAB vuông với đáy ABCD và SAB là tam giác
cân tại S SH ABCD h SH với H là trung điểm AB . Ví dụ 1.2.1 Hình chóp .
S ABCD đáy là hình chữ nhật có AB 2a 3; AD 2a . Mặt bên SAB
là Δ đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối . S ABD là. 2 3 A. 3 a . B. 3 4 3a . C. 3 4a . D. 3 2 3a . 3 Lời giải Chọn D
Gọi H là trung diểm của AB SH ABCD . 2a 3 3
ΔSABlà Δ đều cạnh 2a 3 nên SH 3a . 2 1 1 1 Vậy 3
V SH S
3a 2a 3 2a 2 3a . 3 ABD 3 2 Ví dụ 1.2.2 Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a; hình chiếu của S trên 3a
ABCD trùng với trung điểm của cạnh ;
AB cạnh bên SD . Thể tích của khối 2 chóp .
S ABCD tính theo a bằng: 2 1 A. 3 a . B. 3 2 2a . C. 3 a . D. 3 a . 3 3 Lời giải Chọn D
Gọi H là trung điểm của AB nên SH ABCD . a Lại có 2 2 5
DH AD AH . 2 Xét ΔSDH : 2 2
SH SH DH a 1 1 3 V .S .SH a 3 ABCD 3
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 10
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 1.3. Chóp đều
Khối chóp có các cạnh bên bằng nhau. 1
Áp dụng công thức: V . S h . 3
Chiều cao khối chóp là đoạn thẳng từ đỉnh chóp hạ vuông góc xuống tâm mặt đáy.
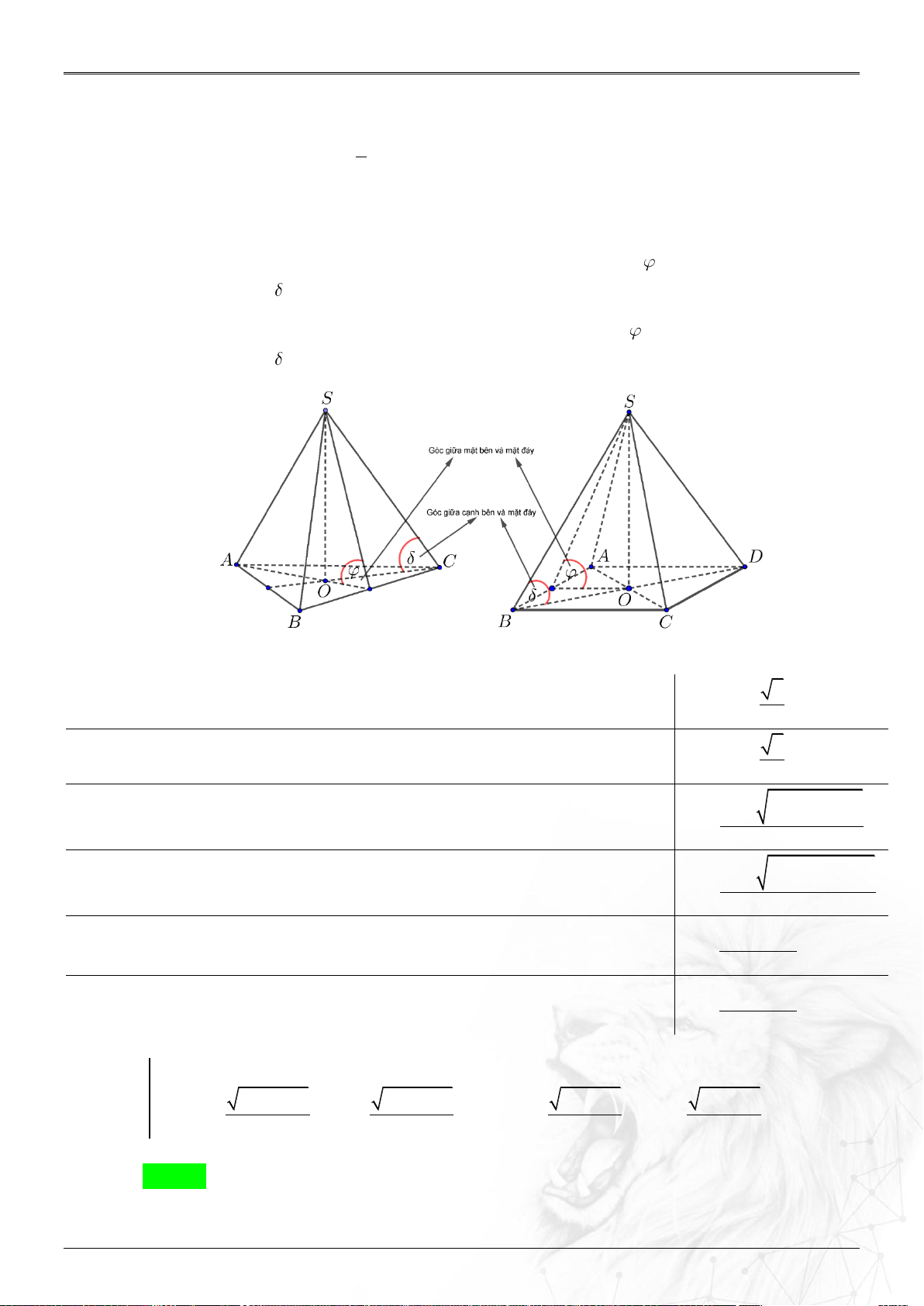
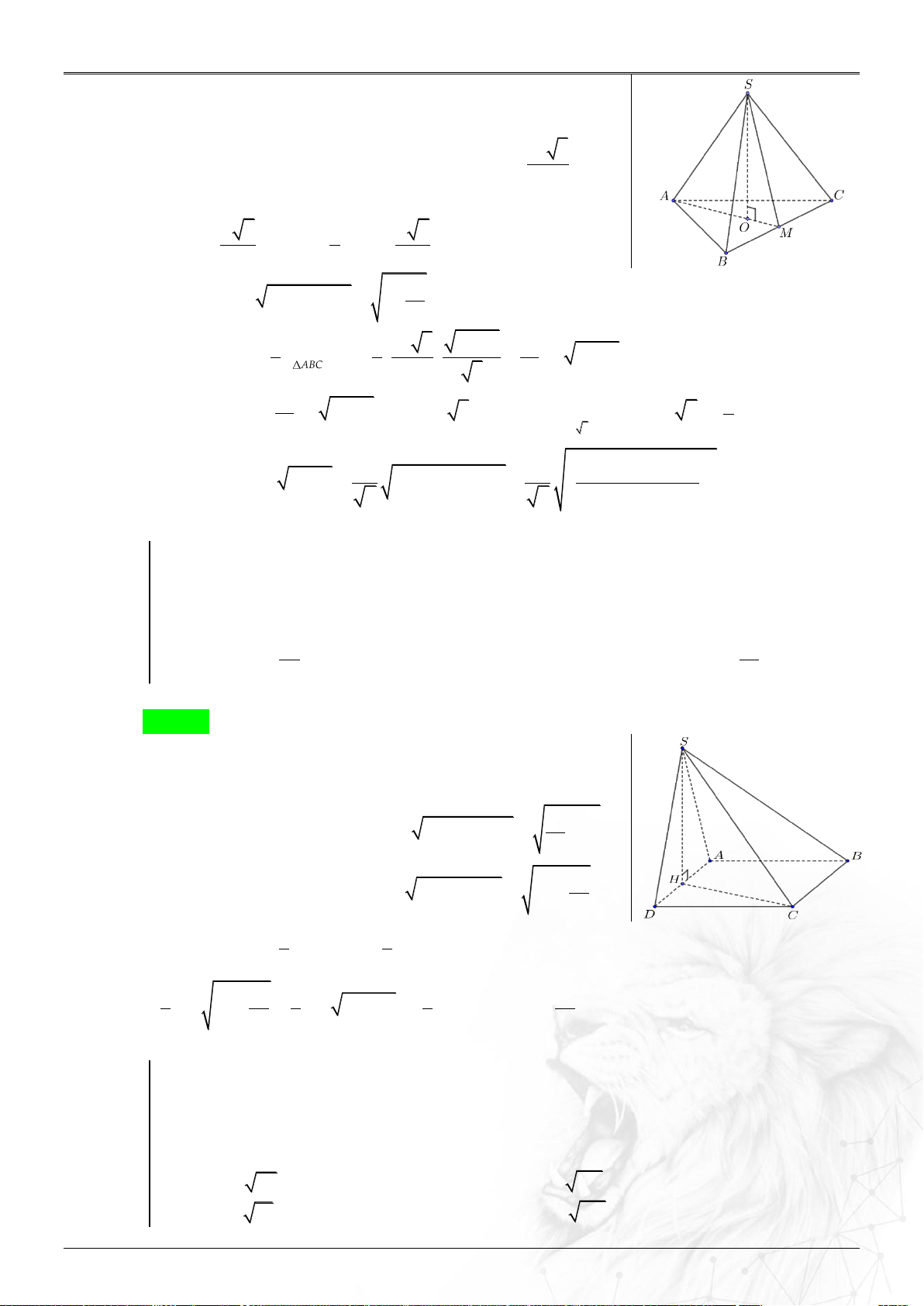
Một số kiểu thường gặp: Chóp đều .
S ABCD, góc giữa mặt phẳng bên và mặt đáy là
hoặc góc giữa cạnh bên và mặt đáy là . Chóp đều .
S ABC , góc giữa mặt phẳng bên và mặt đáy là hoặc góc giữa cạnh bên và mặt đáy là .
Một số công thức tính nhanh:
Chóp đều cạnh x , đáy là tam giác V x3 2 . 12
Chóp đều cạnh x , đáy là tứ giác V x3 2 . 6
y2 3x2 y2
Chóp đều, cạnh bên bằng x , đáy là tam giác cạnh y . V 12
y2 4x2 2y2
Chóp đều, cạnh bên bằng x , đáy là tứ giác cạnh y . V 6 x3
Chóp đều, các mặt bên cùng tạo với đáy góc φ , đáy là tam giác cạnh x . tan φ V 24 x3
Chóp đều, các mặt bên cùng tạo với đáy góc φ , đáy là tứ giác cạnh x . tan φ V 6 Ví dụ 1.3.1
Tính chiều cao của hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng b? 2 2 4b 2a 2 2 4b 2a 2 2 4b a 2 2 4b a A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn B
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 11
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Gọi H là tâm hình vuông ABCD ,
Do S.ABCD là hình chóp tứ giác đều nên SH ABCD . 2 2 2 a 4b 2a Ta có 2 2 2
SH SC HC b . 2 2 Ví dụ 1.3.2
Tính thể tích của khối chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng b là: 2 2 2 a 4b 2a 2 2 2 a b 2a 2 2 2 a 4b 2a 2 2 2 a 4b a A. . B. . C. . D. . 6 6 6 6 Lời giải Chọn A .
S ABCD là chóp tứ giác đều nên SO ABCD .
BD là đường chéo hình vuông cạnh a nên a 2
BD a 2 OB . 2 2 2 2 a 4b 2a Ta có 2 2 2
SO SB OB b . 2 2 2 2 2 2 2 1 1 4b 2a a 4b 2a 2
V .SH.S . .a . 3 ABCD 3 2 6 Ví dụ 1.3.3
Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng
đáy một góc . Thể tích của hình chóp đó là 3 3 A. 3 b cos sin . B. 3 2 b sin cos . 4 4 3 3 C. 3 2 b cos sin . D. 3 2 b cos sin . 4 4 Lời giải Chọn D S
H SAsin bsin
Xét SHA vuông tại H :
AH SA cos b cos 3 3
AM AH bcos . 2 2 AB 3 2AM Mà: AM AB 3 cos . 2 3 1 V .SH.S S.ABC 3 ABC 3 3 . b cos 1 α2 3 3 2 . b sin . α b cos . α sin α 3 4 4
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 12
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 1.4. Tỷ số thể tích
Khối chóp có các cạnh bên bằng nhau. 1
Áp dụng công thức: V . S h . 3
A. Cho khối chóp .
S ABC có A; B;C lần lượt là nằm trên SA;SB;SC khi đó:
1. Nếu A A; B B;C C thì V S S.A B C A B C
(Hai khối chóp chung đỉnh và chung mặt đáy). V S S.ABC ABC
2. Định lý SIMSON cho khối chóp tam giác V SA SB SC S.A B C . . V SA SB SC S.ABC SB
3. Cắt khối chóp bởi mặt phẳng song song với đáy sao cho 1 k thì SA1
VS.B B ...B 1 2 n 3 k
VS.A A ...A 1 2 n
B. Mặt phẳng cắt các cạnh của khối chóp tứ giác .
S ABCD có đáy là hình bình hành SM SN SP SQ
lần lượt tại M; N; P;Q : α; β; γ; λ : SA SB SC SD V S.MNPQ . α . β . γ λ 1 1 1 1 1 1 1 1
và . V 4 α β γ λ α γ β λ S.ABCD
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 13
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Ví dụ 1.4.1 Cho hình chóp .
S ABC . Gọi M, N, P lần lượt là trung điểm của S ; A S ; B SC . Tỉ số V
thể tích S.ABC bằng VS.MNP A. 12 . B. 2 . C. 8 . D. 3 . Lời giải Chọn C V SA SB SC Ta có S.ABC . . 2 2 . 2 . 8 . V SM SN SP S.MNP Ví dụ 1.4.2
Cho khối tứ diện có thể tích bằng V . Gọi V là thể tích của khối đa diện có V
các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính . V V 2 V 5 V 1 V 1 A. . B. . C. . D. . V 3 V 8 V 2 V 4 Lời giải Chọn B Cách 1.
Đặc biệt hóa tứ diện cho là tứ diện đều cạnh a .
Hình đa diện cần tính có được bằng cách cắt 4 góc
của tứ diện, mỗi góc cũng là một tứ diện đều có a cạnh bằng . 2 V V
Do đó thể tích phần cắt bỏ là V 4. . 8 2 V V 1 Vậy V . 2 V 2 Cách 2.
Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. 1 1 1
Suy ra V 2V 4.V 4.V
4. . V V N.MEPF N.MEP P.MNE 2 4 2 Cách 3. V ' V V V V V Ta có A.QEP B.QMF C.MNE D.NPF V V V V V V 1 A.QEP B.QMF C.MNE D.NPF 1 1 1 1 1 1 1 1 1 1 1 1 1
1 . . . . . . . . . V V V V 2 2 2 2 2 2 2 2 2 2 2 2 2
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 14
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Ví dụ 1.4.3 Cho hình chóp .
S ABCD . Gọi A , B , C , D theo thứ tự là trung điểm của
SA , SB, SC , SD. Tính tỉ số thể tích của hai khối chóp . S A B C D và . S ABCD A. 1 . B. 1 . C. 1 . D. 1 . 16 4 8 2 Lời giải Chọn C V SA SB SD 1 V
Ta có S.A B D . . 1 S.A B D . V SA SB SD 8 V 16 S.ABD S.ABCD V SB SD SC 1 V Và S.B D C . . 1 S.B D C . V SB SD SC 8 V 16 S.BDC S.ABCD
V V 1 1 1 V Suy ra S.A B D S. BDC 1 S.A B C D . V V 16 16 8 V 8 S.ABCD S.ABCD S.ABCD Ví dụ 1.4.4
Cho hình chóp SABCD có đáy là hình bình hành. Gọi M, N, P,Q lần lượt là
trọng tâm của các tam giác SAB,SBC,SCD,SDA . Gọi O là điểm bất kỳ trên
mặt phẳng đáy ABCD . Biết thể tích khối chóp OMNPQ bằng V . Tính thể
tích khối chóp SABCD . 27 27 9 27 A. V . B. V . C. V . D. V . 8 2 4 4 Lời giải Chọn C
Ta có MNPQ// ABCD
dS,MNPQ 2dO,MNPQ V 2V 2V S.MNPQ O.MNPQ VSMNQ SM SN SQ 2 2 2 8 8 . . . . V V . V SE SF SK 3 3 3 27 SMNQ 27 SEFK SEFK VSNPQ SN SP SQ 2 2 2 8 8 . . . . V V . V SF SG SK 3 3 3 27 SNPQ 27 SFGK SFGK 8 8 8 27 27 V V V V V V V V V . SMNQ SNPQ 27 SEFK 27 SFGK SMNPQ 27 SEFGK SEFGK 8 SMNPQ 4 1 B . E BF.sin B S 1 1 1 Ta có: EBF 2 S S S EBF ABC ABCD . S 1 4 4 8 ABC B . A BC.sin B 2 Khi đó, S S S S S S S 1 S S S EFGK ABCD ABF FCG GDK KAE 4 ABCD EBF EFGK 2 ABCD
1 dS,EFGKSEFGK V 1 27 Nên SEFGK 3 V 2V V SABCD SEFGK . V 1 SABCD
dS,ABCD 2 2 S 3 ABCD
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 15
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 1.5. Tổng hiệu thể tích
Trong quá trình tính thể tích một khối đa diện lồng ghép trong khối chóp ta gặp khó khăn
với cách tính thực tiếp thì khi đó:
Ta có thể tách khối chóp ra thành các khối nhỏ và tính trực tiếp từng khối đã tách.
Phần cần tính sẽ là phần khối chóp bỏ đi những khối nhỏ đã tính.
Ví dụ: Cho khối chóp .
S ABCD , chia khối chóp thành V V V 1 ; 2 . Tính thể tích khối 2 . Giải:
Để tính trực tiếp thể tích khối V2 ta sẽ khó áp dụng công thức vì thế ta sẽ
cắt khối chóp thành hai phần: + V S 1 là phần chứa đỉnh . + V
2 là phần dưới mặt phẳng .
Gọi thể tích khối chóp .
S ABCD là V , vậy V V V V V V . 1 2 2 1 Ví dụ 1.5.1
Cho tứ diện đều ABCD có cạnh bằng 1 . Trên AB và CD lần lượt lấy các điểm
M và N sao cho MA MB 0 và NC 2
ND . Mặt phẳng P chứa MN và
song song với AC chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối
đa diện chứa đỉnh A có thể tích là V . Tính V . 2 A. V 11 2 . B. V 7 2 . C. V 2 . D. V . 18 216 216 108 Lời giải Chọn B
Từ N kẻ NP//AC , N AD
M kẻ MQ//AC , Q BC . Mặt phẳng P là MPNQ 1 2 Ta có V AH.S ABCD ABCD 3 12 V V V V V ACMPNQ AMPC MQNC MPNC AM AP Ta có V 1 2 1 . .V . V V AMPC ABCD AB AD 2 3 ABCD 3 ABCD 1 1 CQ CN V V 1 1 2 1 . .V . V V MQNC 2 AQNC 2 ABCD CB CD 2 2 3 ABCD 2 ABCD 2 2 1 AM V V 2 1 . V 2 1 1 1 . .V . V V MPNC 3 MPCD 3 3 MACD 3 3 ABCD AB 3 3 2 ABCD 9 ABCD 1 1 1 11 11 2 Vậy V V V V . 3 6 9 ABCD 18 ABCD 216
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 16
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Ví dụ 1.5.2 Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA a và
SA ABCD . Gọi M là trung điểm SB , N là điểm thuộc cạnh SD sao cho
SN 2ND. Tính thể tích V của tứ diện ACMN . 3 a 3 a 3 a 3 a A. V . B. V . C. V . D. V . 12 6 8 36 Lời giải Chọn A
M là trung điểm SB, N là điểm thuộc cạnh SD: SN 2ND S SM 1 SN 2 nên , SB 2 SD 3 Ta có: M V 2V 2 V V V V C.AMN O.AMN
S.ABD S.AMN M.AOB N.AOD Lại có: 3 A 1 a 3 3 a a N B V . . SA A . B AD V ; V V ABCD 3 3 S.ABD 6 S.AOB S.AOD 12 O 3 V SM SN 1 2 1 1 a S.AMN . . V V V SB SD 2 3 3 S.AMN 3 S.ABD 18 S.ABD D C 3 V MB 1 1 a M.AOB V V V SB 2 M.AOB 2 S.AOB 24 S.AOB 3 V ND 1 1 a N.AOD V V V SD 3 N.AOD 3 S.AOD 36 S.AOD 3 3 3 3 3 a a a a a Do đó: V 2V 2 C.AMN O.AMN . 6 18 24 36 12
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 17
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 KHỐI ĐA DIỆN
THỂ TÍCH KHỐI LĂNG TRỤ A. LÝ THUYẾT CHUNG. 1. Định nghĩa:
Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song
song với nhau và các mặt bên đều là các hình bình hành.
Hình hộp là hình lăng trụ có đáy là hình bình hành.
2. Thể tích khối lăng trụ.
Công thức tính thể tích khối chóp: Trong đó: V . S h
S là diện tích đáy
h là chiều cao khối chóp
(khoảng cách từ đỉnh đến mặt đáy).
Cách xác định đường cao lăng trụ: Loại Đường cao Cạnh bên vuông đáy
Đường cao chính là cạnh bên. Hình 2.1 Lăng trụ đứng
Đường cao chính là cạnh bên. Hình 2.1 Lăng trụ xiên
Đường cao hạ từ đỉnh xuống mặt đáy. Hình 2.2 Lăng trụ có hình chiếu
Đường cao là hình chiếu vuông góc của 1 đỉnh xuống đáy. Hình 2.3
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 18
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 B. CÁC DẠNG BÀI TẬP.
Dạng 2.1. Thể tích lăng trụ đứng
Áp dụng công thức chính: V . S h .
Tính được diện tích đáy ta xem lại “Công thức tính diện tích đáy”
Lăng trụ đứng sẽ có các đường cao song song nhau, tùy vào trường hợp đề ra ta sẽ sử
dụng đường cao hợp lý. Định nghĩa Tính chất
Hình lăng trụ
Là hình lăng trụ có cạnh
Các mặt bên của hình lăng trụ đứng là các đứng
bên vuông góc với mặt đáy. hình chữ nhật và vuông góc với mặt đáy.
Các mặt bên của hình lăng trụ đều là các
Là hình lăng trụ đứng có
Hình lăng trụ đều
hình chữ nhật bằng nhau và vuông góc đáy là đa giác đều. với mặt đáy. Ví dụ 2.1.1
Khối lăng trụ có đáy là hình vuông cạnh a, đường cao bằng a 3 có thể tích bằng 3 a 3 3 a 3 A. . B. 3 a 3 . C. 3 2a 3 . D. . 3 6 Lời giải Chọn B Ta có 2 3 V .
S h a .a 3 a 3. Ví dụ 2.1.2
Cho hình lăng trụ đứng AB . C A B C
có AA a. Đáy ABC là tam giác vuông cân
tại A và AB a . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. V . B. V . C. V . D. 3
V a . 3 6 2 Lời giải Chọn C Theo giả thiết AB . C A B C
là lăng trụ đứng có đáy là tam
giác ABC vuông cân tại A .
Suy ra thể tích của khối lăng trụ là 3 1 a
V AA .S AA . .A . B AC . ABC 2 2 Ví dụ 2.1.3
Cho lăng trụ đứng AB . C A B C
có ABC là tam giác vuông tại A ; BC 2a; 0
ABC 30 . Biết cạnh bên của lăng trụ bằng 2a 3 . Thể tích khối lăng trụ là. A. 3 2a 3 . B. 3 3a . C. 3 3a . D. 3 6a . Lời giải Chọn C
Xét ABC : AC 2 . a s 3
in 0 a; AB 2 . a co 3 s 0 a 3.
Ta có: V h S . lt
Trong đó h AA 2a 3. . 1 3 2 S AB AC a . ABC . 2 2
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 19
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 2.2. Thể tích lăng trụ xiên
Áp dụng công thức chính: V . S h .
Tính được diện tích đáy ta xem lại “Công thức tính diện tích đáy”
Lăng trụ xiên sẽ có các đường cao đề ra cụ thể. Ví dụ 2.2.1
Cho lăng trụ tứ giác ABC . D A B C D
có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
3a . Tính chiều cao h của lăng trụ đã cho. a
A. h 9a . B. h .
C. h a .
D. h 3a . 3 Lời giải Chọn D V 3 3a Ta có: V ABCD.A B C D S .h h 3a . ABC . D A B C D ABCD S 2 a ABCD Ví dụ 2.2.2 Cho lăng trụ AB . C A B C
, đáy là tam giác đều cạnh a . Độ dài cạnh bên bằng 4a. Mặt phẳng BCC B
vuông góc với đáy và B B
C 30 . Thể tích khối . A CC B là: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 12 18 6 Lời giải Chọn D
Gọi H là hình chiếu của B trên BC .
Từ giả thiết suy ra: B H ABC . 1 1 S 2 BB .B . C sin B BC 4 . a . a sin 30 a . BB C 2 2 1 2S 2 2a Mặt khác: S BB C B H.BC B H 2a . BB C 2 BC a 2 a 3 3 a 3 V B . H S 2 . a . LT ABC 4 2 3 3 1 1 a 3 a 3 V 1 2 1 . V . V V . A.CC B 2 A.CC B B 2 3 LT 3 LT 3 2 6 Ví dụ 2.2.3 Cho lăng trụ AB . C A B C
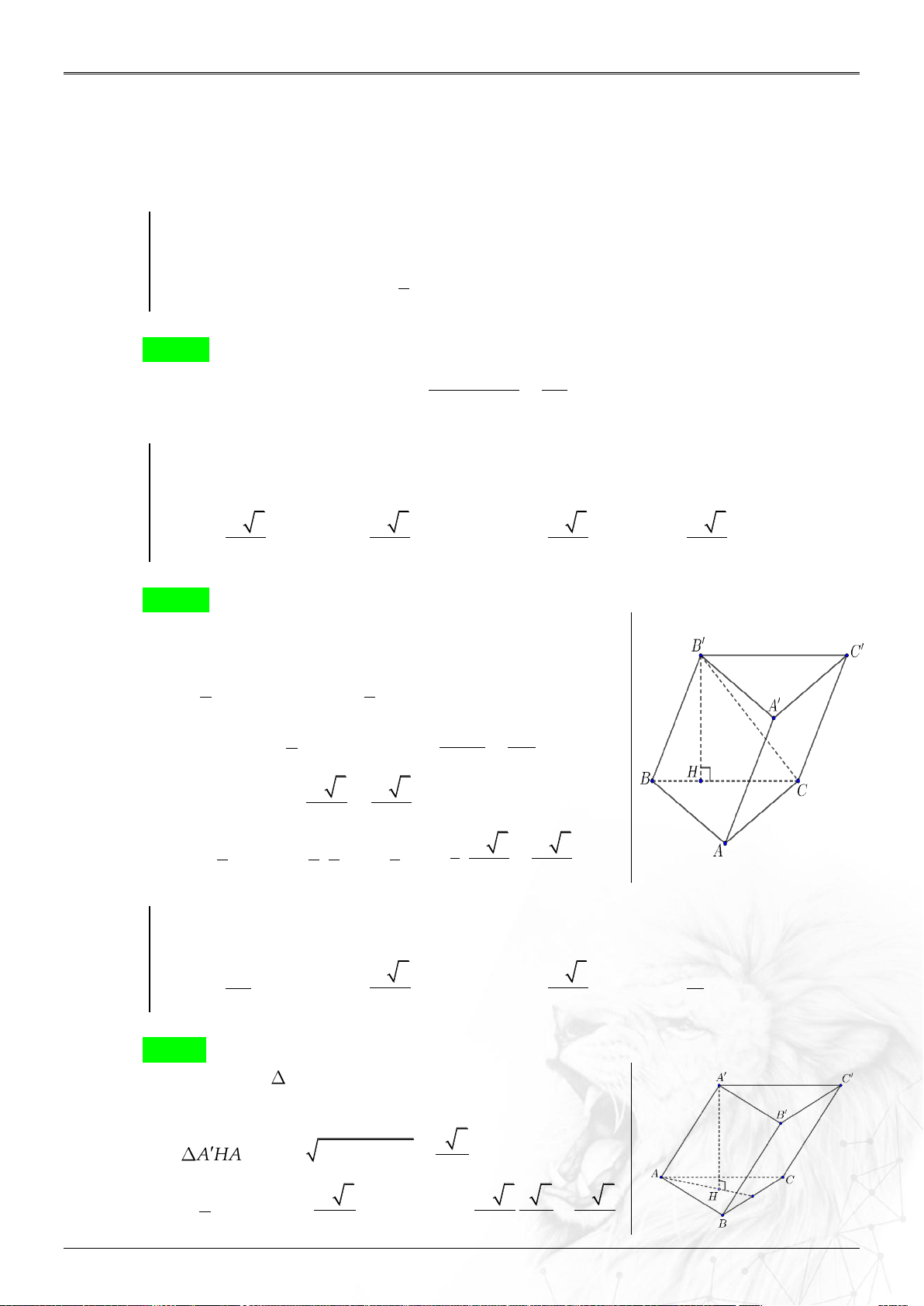
có đáy ABC là tam giác đều cạnh bằng a có H là trọng tâm, biết A A A B A C
a. Tính thể tích khối lăng trụ AB . C A B C ? 3 3a 3 a 2 3 a 3 3 a A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn B
Ta có ABC là đều cạnh a và A A A B A C a
Nên A .ABC là tứ diện đều cạnh a A H ABC a Xét A H A : 2 2 A H A A 6 AH . 3 2 2 3 1 a 3 a 3 a 6 a 2 S . a . a sin 60 V ABC.A B C ABC 2 4 4 3 4
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 20
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 2.3. Thể tích khối lập phương – khối hộp
Áp dụng công thức chính: V . S h . Định nghĩa Tính chất
Là hình hộp có cạnh bên vuông
Có 2 đáy là hình bình hành, 4 mặt xung
Hình hộp đứng góc với mặt đáy
quanh là 4 hình chữ nhật.
Là hình hộp đứng có đáy là hình
Hình hộp chữ nhật
Có 6 mặt là 6 hình chữ nhật. chữ nhật.
Là hình hộp chữ nhật 2 đáy và 4
Hình lập phương
Có 6 mặt đều là hình vuông.
mặt bên đều là hình vuông
Đường chéo hình hộp 2 2 2
d r c với d;r ;c là ba kích thước của hình hộp.
Hệ quả: Đường chéo hình lập phương a 3 với a là cạnh của hình lập phương. Ví dụ 2.3.1
Tổng diện tích các mặt của một hình lập phương bằng 150. Thể tích của khối lập phương đó là. A. 200 . B. 100 . C. 625. D. 125 . Lời giải Chọn D
Gọi cạnh hình lập phương là a . Ta có 2
6a 150 a 5 3
V a 125 . Ví dụ 2.3.2
Tính theo a thể tích V của khối lập phương ABC . D A B C D
biết AC .a 3 a 3 3a 3 3a A. V . B. V . C. 3
V 3 3a . D. V . 27 3 9 Lời giải Chọn D a
Ta có AC AB 3 AB . 3 3 3 3 a a a 3 3 V AB . 3 3 3 9 Ví dụ 2.3.3
Cho hình lập phương ABC . D A B C D
có diện tích tam giác ACD bằng 2 a 3 .
Tính thể tích V của hình lập phương. A. 3
V 3 3a . B. 3
V 2 2a . C. 3
V a . D. 3
V 8a . Lời giải Chọn B
Giả sử cạnh của hình lập phương có độ dài là x . x 6
Ta có AC x 2 , 2 2
OD OD A A 2 2 1 1 x 6 x 3 S OD .AC x 2. ACD . 2 2 2 2 2 2 x 3 x 2 2 a 3 a
x a 2 3 3
V x 2a 2 . 2 2
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 21
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 2.4. Khối đa diện được cắt ra từ khối lăng trụ
A. Một số mối liên hệ thường gặp giữa chóp – lăng trụ và chóp – thể tích:
Mối liên hệ giữa Công thức
Hình minh họa 2 V V 5d 3 L.Tr C
4 điểm thuộc mặt đáy ụ p tr g Chó Lăn 1 V V 4d 3 L.Tr C
3 điểm thuộc mặt đáy 1 V V 4d 6 Hop C
Với 3 điểm thuộc đáy và 1 điểm thuộc mặt bên 1 V V 4d 3 Hop C
Với 3 điểm thuộc mặt chéo p p ộ h Chó Hình 1 V V 5d 3 Hop C
Với 4 điểm thuộc mặt bên hoặc mặt đáy 1 V V 5d 3 Hop C
Với 4 điểm thuộc mặt chéo
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 22
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
B. Mặt phẳng cắt các cạnh của khối lăng trụ tam giác AB . C A B C
lần lượt tại M;N;P sao cho AM BN CP ; ; : AA BB CC V ABC.MNP V 3 ABC.A B C
C. Mặt phẳng cắt các cạnh của khối hộp ABC . D A B C D
lần lượt tại M;N;P;Q sao cho AM BN CP DQ ; ; ; : AA BB CC DD V ABCD.MNPQ V 4 ABCD.A B C D và . Ví dụ 2.4.1
Hình lập phương ABCDA B C D
cạnh a . Tính thể tích khối tứ diện ACB D . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 2 6 3 Lời giải Chọn D V V V
V V V . ACB D ABCDA B C D
B.ABC C.BCD D.ACD A.ABD Mà 3 V a ABCD.A B C D V
V V V B .ABC C.B C D D .ACD A.A B D 1 1 1 2 1 3 AA .S . . a a a . 3 A B D 3 2 6 3 4 a 3 3 V a a . V ACB D
V V V B .ABC C.B C D D .ACD A.A B D 6 3 Ví dụ 2.4.2
Cho hình lập phương ABC . D A B C D
cạnh bằng a . Gọi O là giao điểm của AC
và BD . Thể tích của tứ diện OA B C bằng 3 a 3 a 3 a 3 a A. B. C. D. 6 4 12 24 Lời giải Chọn C 3 1 1 a 2 a 2 a V V AA .O . B OC . . a . O.A BC A'.OBC 6 6 2 2 12
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 23
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Ví dụ 2.4.3
Cho khối lăng trụ AB . C A B C
có thể tích bằng V . Tính thể tích khối đa diện ABCB C . 2V V V 3V A. B. C. D. 3 2 4 4 Lời giải Chọn D V V 2V Ta có: V V V ABCB C B ABC C B AC 3 3 3 Ví dụ 2.4.4
Cho khối lăng trụ AB . C A B C
có thể tích là V . Gọi M là điểm bất kỳ trên đường
thẳng CC . Tính thể tích khối chóp V theo V . M.ABB A V 2V 2V V A. B. C. D. 2 9 3 3 Lời giải Chọn A
Gọi h , h là đường cao của . M ABC , . M A B C 1 2
thì h h h là đường cao của AB . C A B C . 1 2 V V V V M.ABC M.ABB A M.A B C 1 1 h .S V S h 1 ABC M.ABB A A B C 2 3 3 1 2V S
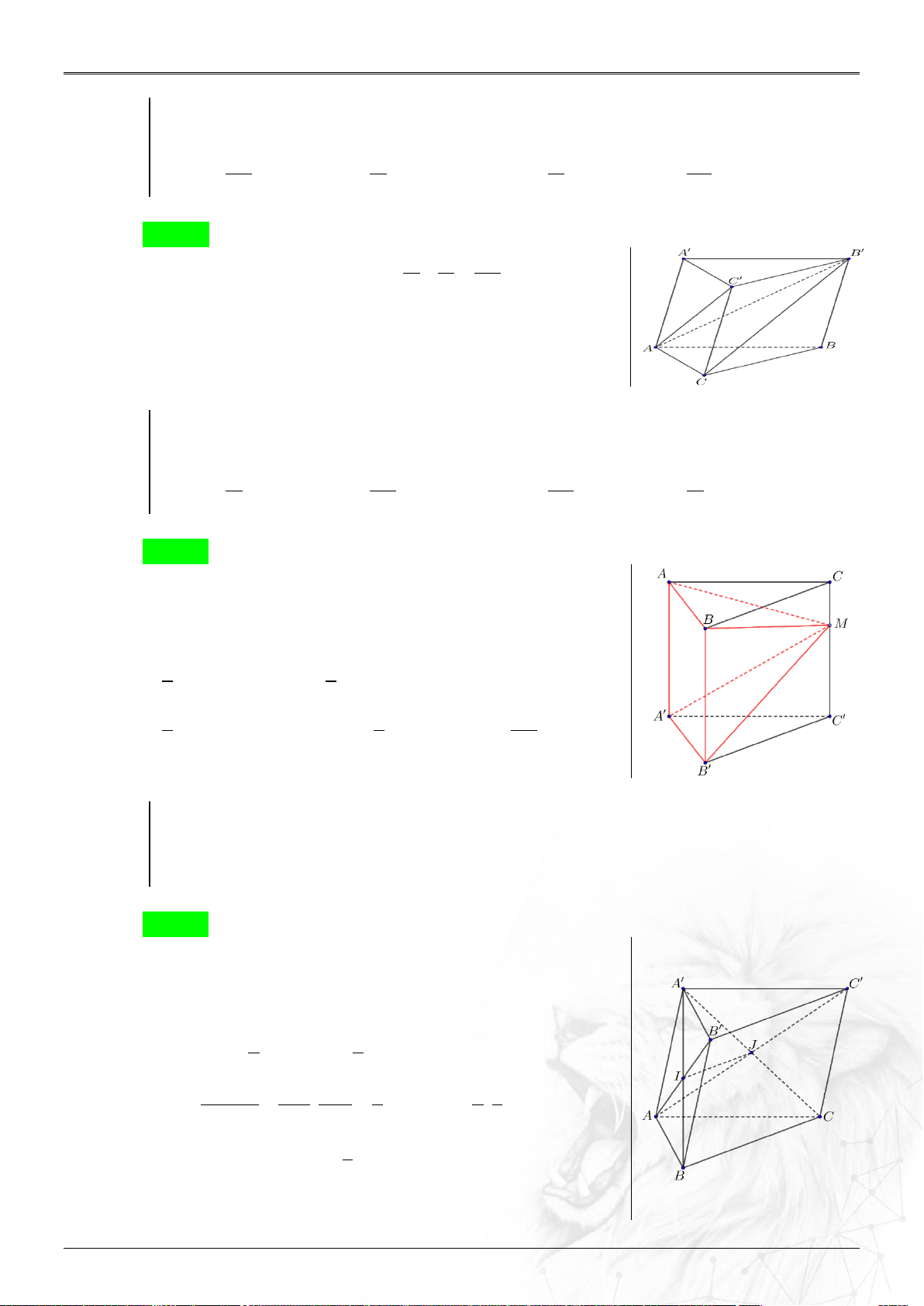
h h V a V ABC 1 3 1 2 M. 3 ABB A 6 M.ABB A 3 Ví dụ 2.4.5 Khối lăng trụ AB . C A B C có 3
V 36 cm . Mặt AB C và A B
C chia khối lăng
trụ thành 4 khối đa diện. Tính thể tích khối chứa mặt là hình bình hành BCC B A. 3 15 cm B. 3 9 cm C. 3 12 cm D. 3 18 cm Lời giải Chọn A
Gọi I AB A B , J A C AC . Ta có V V V . IJBB'C 'C
A.BB'C 'C A.BCIJ V V V . A A B C . A BCC B ABC.A B C 2 V 2 V V 24 . A.BCC B 3 ABC.A B C 3 VA.IJA AI AJ 1 1 1 Lại có . V . 3 . 6 3 . V AB AC 4 A.IJA 4 3 A.A B C 1 V V V 3 . 6 3 9 . A.IJBC A .ABC A.IJA 3 Vậy V C C 3 24 9 15 cm IJBB' ' .
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 24
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Dạng 2.5. Max – min thể tích Dạng
Dấu “=” xảy ra khi a b BĐT 2 2 2 2 2 a b c d ac bd c d Bunyakovsky a a a
a a ... a
b b ... b
a b a b ... a b 1 2 ... n 1 2 n 1 2 n 1 1 2 2 n n 2 2 2 2 2 2 2 b b b 1 2 n
a b ab a b BĐT 2 AM – GM
a a ... a 1 2 n n
a .a .....a n 1
a a ... a 1 2 n n 1 2 n
Khảo sát hàm
số trên khoảng Tính đạo hàm rồi lập BBT, từ đó kết luận theo yêu cầu bài toán. xác định Ví dụ 2.5.1 Cho hình chóp .
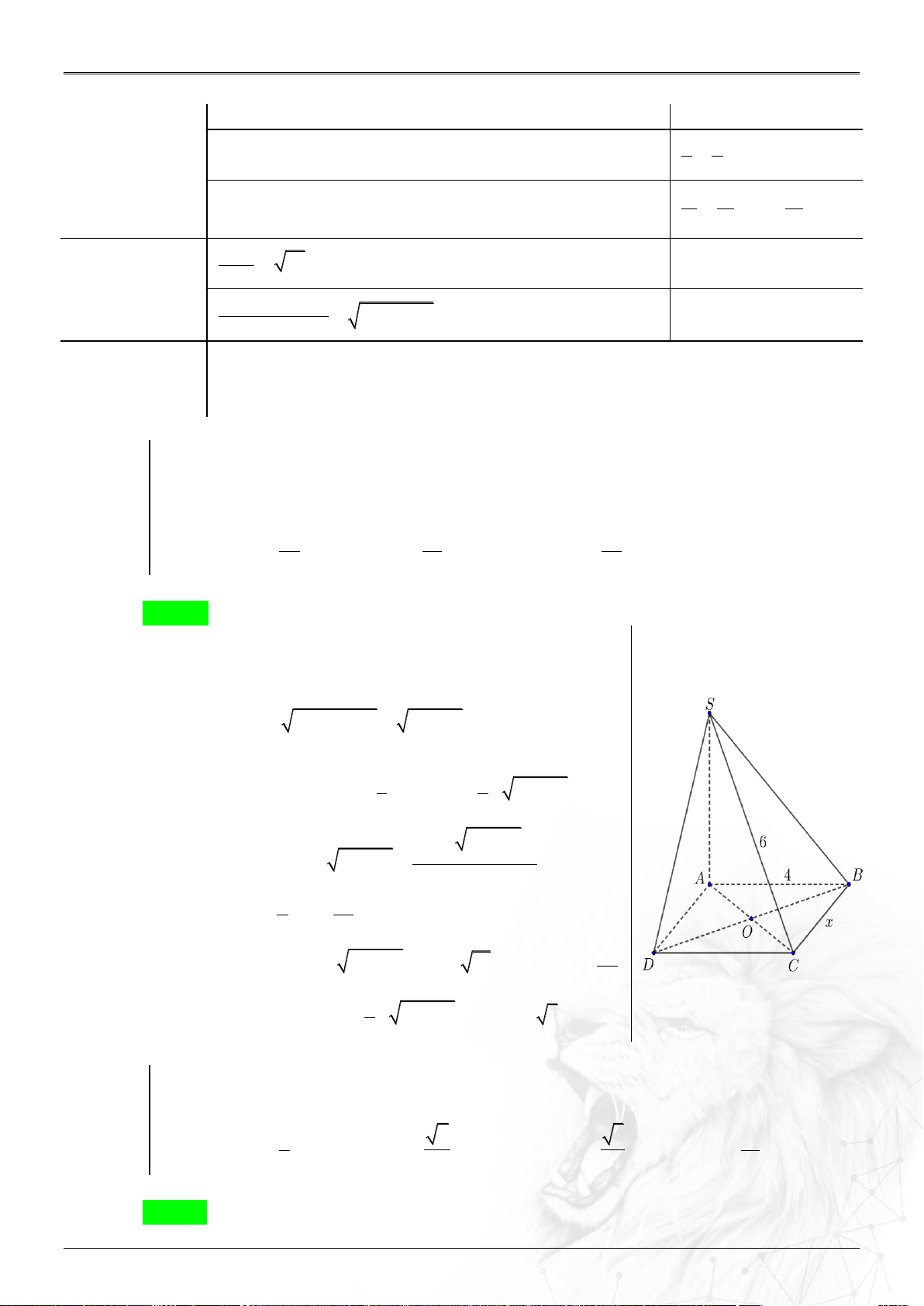
S ABCD có đáy ABCD là hình chữ nhật với AB 4 , cạnh bên
SA vuông góc với mặt phẳng đáy ABCD và SC 6. Tính thể tích lớn nhất V max của khối chóp đã cho. 40 A. V 80 . B. V 20 . C. V . D. V 24. max 3 max 3 max 3 max Lời giải Chọn A Cách 1.
Đặt cạnh BC x 0. Δ ABC, có 2 2
AC 16 x . Δ SAC, có 2 2 2
SA SC AC 20 x .
Diện tích hình chữ nhật S A . B BC 4 . x ABCD 1 4 Thể tích khối chóp 2 V S
.SA x 20 x . S.ABCD 3 ABCD 3 x 20 x 2 2 2 2 Áp dụng BĐT Côsi: . x 20 x 10 . 2 4 40 Suy ra V 10 . . S.ABCD 3 3 Dấu " " xảy ra 2
x 20 x x 40 10 . Vậy V max 3 4
Cách 2. Xét hàm số f x 2
x 20 x trên 0;2 5. 3 Ví dụ 2.5.2 Cho hình chóp .
S ABC có đáy ABC là tam giác đều và có SA SB SC 1. Tính
thể tích lớn nhất V của khối chóp đã cho. max 1 A. V 2 . B. V 3 . C. V 1 . D. V . max 6 max 12 max 12 max 12 Lời giải Chọn C
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 25
Tổng Hợp Lý Thuyết
Năm học: 2023-2024
Gọi O là tâm đường tròn ngoại tiếp tam giác đều AB . C Vì .
S ABC là hình chóp đều SO ABC. 2 x 3
Đặt AB x 0. Diện tích tam giác đều S . ABC 4
Gọi M là trung điểm BC x 3 2 x 3 AM
OA AM 2 3 3 2 x ΔSOA : 2 2
SO SA OA 1 . 3 2 2 1 1 x 3 3 x 1 Khi đó 2 2 V S .SO . . .x 3 x S.ABC 3 ABC 3 4 3 12 1 1
Xét hàm f x 2 2 .x
3 x trên 0; 3 , ta được max f x f 2 . 12 0; 3 6 3 2 2 2 1 1
x x 6 2x
Cách 2. Ta có 2 2 2 2 x 3 x x .x . 2 6 2x 2. 2 2 3 Ví dụ 2.5.3 Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật với AB 4, SC 6 và
mặt bên SAD là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy.
Tính thể tích lớn nhất V của khối chóp đã cho. max 40 A. V . B. V 40. C. V 80 80. D. V . max 3 max max max 3 Lời giải Chọn D
Gọi H là trung điểm của AD SH A . D
Mà SAD ABCD SH ABCD. 2 x
Giả sử AD x 0 . Suy ra 2 2
HC HD CD 16. 4 2 x
Tam giác vuông SHC, có 2 2
SH SC HC 20 . 4 1 1 Khi đó V S .SH A . B A . D SH S.ABCD 3 ABCD 3 2 1 x 1 4 . .x 20 1 80 2
2x 80 x 2 2
x 80 x . 3 4 3 3 3 Ví dụ 2.5.4
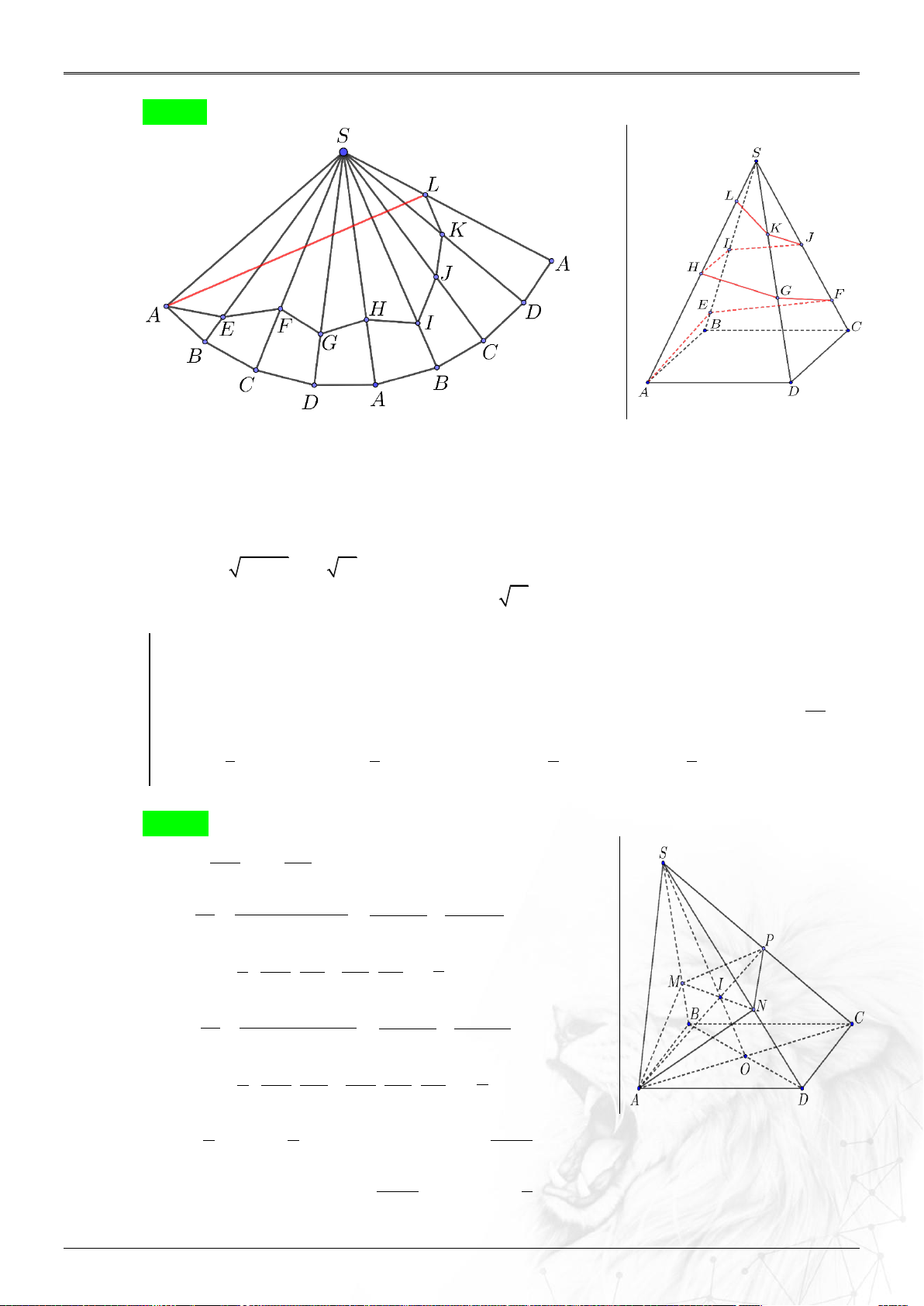
Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều . S ABCD cạnh bên
bằng 200m, góc ASB 15 bằng đường gấp khúc dây đèn led vòng quanh kim
tự tháp AEFGHIJKLS . Trong đó điểm L cố định và LS 40m (tham khảo hình
vẽ). Hỏi khi đó cần dung ít nhất bao nhiêu mét dây đèn led để trang trí?
A. 40 67 40 mét.
B. 20 111 40 mét.
C. 40 31 40 mét.
D. 40 111 40 mét.
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 26
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Lời giải Chọn C
Ta sử dụng phương pháp trải đa diện
Cắt hình chóp theo cạnh bên SA rồi trải ra mặt phẳng hai lần, ta có hình vẽ sau
Từ đó suy ra chiều dài dây đèn led ngắn nhất là bằng AL LS.
Từ giả thiết về hình chóp đều .
S ABCD ta có ASL 120 . Ta có 2 2 2 2 2
AL SA SL 2S . A S .
L cos ASL 200 40 2 2 . 00 4 . 0.co 1 s 20 49600 .
Nên AL 49600 40 31 .
Vậy, chiều dài dây đèn led cần ít nhất là 40 31 40 mét. Ví dụ 2.5.5 Cho hình chóp .
S ABCD có đáy là hình bình hành và có thể tích là V . Điểm P là
trung điểm của SC . Một mặt phẳng qua AP cắt hai cạnh SB và SD lần lượt tại V
M và N . Gọi V là thể tích của khối chóp .
S AMPN . Tìm giá trị nhỏ nhất của 1 1 V 1 1 2 3 A. B. C. D. 3 8 3 8 Lời giải Chọn A SM Đặt x SN , y
, 0 x, y 1 . SB SD V V V V V Ta có 1 S.AMP S.ANP S.AMP S.ANP V V 2V 2V S.ABC S.ADC 1 SM SP SN SP 1 . .
x y (1) 2 SB SC SD SC 4 V V V V V Lại có 1 S.AMN S.PMN S.AMN S.PMN V V 2V 2V S.ABD S.CBD 1 SM SN SM SN SP 3 . . . xy (2). 2 SB SD SB SD SC 4 1 3 x
Suy ra x y xy x y 3xy y . 4 4 3x 1 x 1
Từ điều kiện 0 y 1, ta có 1, hay x . 3x 1 2
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 27
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 2 V 3 x
Thay vào (2) ta được tỉ số thể tích 1 . . V 4 3x 1 x 0 ( ) L x 2 3 3x 2x Đặt f x 2 3 1 . , x ;
1 , ta có f x .
, f x 0 2 . 4 3x 1 2 4 3x 2 1 x (N) 3 1 2 1 V f f 3 1 , f , do đó 1 min 2 1
min f x f . 2 8 3 3 1 V 3 3 x 1 ; 2 Ví dụ 2.5.6
Cho hình hộp chữ nhật ABC . D A B C D
có AB a, AD a 2, AA a 3 . Gọi G là
trung điểm của BD , mặt phẳng P đi qua G và cắt các tia AD,CD,D B tương
ứng tại ba điểm phân biệt H, I,K . Tìm giá trị nhỏ nhất của biểu thức 1 1 1 T 2 2 2 D' H D' K D' I 1 4 4 1 A. T B. T C. T D. T 2 3a 2 a 2 3a 2 12a Lời giải Chọn C D H D I D K Đặt x, y, z . D A D C D B 1 1 1 1 ta có D G D B D A D C D D 2 2 2 2 Ta có D H xD A xD D 1 D A D H D D D A x D I yD C yD D 1 D C
D I D D D C y D K zD A zD A 1 D C D K D A D C z 1 1 1 D G D H D I D K 4x 4y 4z 1 1 1
Do DG, DH, DI, DK không đồng phẳng nên 1. 4x 4y 4z D A D C D B 4 D H D I D K 2 D A D C D B 1 1 1 2 4 2 2 2 D A D C D B 2 2 2 D H D I D K D H D I D K 16 16 4 T 2 2 2 2 2 D A D C D B 12a 3a
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 28
Tổng Hợp Lý Thuyết
Năm học: 2023-2024 Ví dụ 2.5.7 Cho hình chóp .
S ABCD . Một mặt phẳng song song mặt đáy cắt các cạnh S ; A S ;
B SC;SD lần lượt tại M, N , P,Q . Gọi M ', N ', P ',Q' lần lượt là hình chiếu của SM
M, N , P,Q lên mặt đáy. Tìm tỉ số
để thể tích khối đa điện M . NPQ M N P Q SA lớn nhất. SM 3 SM SM SM A. 2 B. 1 C. 1 D. SA 4 SA 3 SA 2 SA 3 Lời giải Chọn B SM Đặt SN SP SQ x . Suy ra x . SA SB SC SD
Gọi h, h' là chiều cao . S ABCD và M . NPQ M N P Q . SM MN MN
Do MN / / AB nên x
MN xAB . SA AB AB
Tương tự ta có BC . x NP Ta có 2 2 S x .S S x S ( MNP ABC MNPQ ABCD ΔMNP ~ ΔABC ) AM h' SA SM h' h' Mặt khác 1 x
h' 1 xh AS h SA h h Ta có V h'.S x . h x .S x x . . h S
MNPQ.M'N'P'Q' MNPQ 2 ABCD 2 1 1 ABCD Do h,S
không thay đổi nên V ABCD 1 x x MNPQ.M N P Q 2 . max max 3 x x 1 x x x 2 2 4 Ta có 1 x 2
x 4.1 x 4. 2 2 27 27 x Dấu 2
xảy ra khi và chỉ khi 1 x x . 2 3 ----------Hết----------
Biên soạn: Gv Lê Minh Tâm - 093.337.6281 Trang 29




