




















































Preview text:
TỔNG ÔN
CỰC TRỊ SỐ PHỨC
Sưu tầm và biên soạn: Phạm Minh Tuấn Wednesday, 21 April
Luôn yêu để Sống, luôn sống để học Toán, luôn học toán để Yêu Contents
CHUYÊN ĐỀ CỰC TRỊ SỐ PHỨC ........................................................................................................ 1 1.
MỘT SỐ VÍ DỤ MÌNH HỌA ......................................................................................................... 1 2.
ĐỀ TỰ LUYỆN ................................................................................................................................... 4
ĐỀ SỐ 1 ................................................................................................................................................... 4
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 1 ................................................................................................... 7
ĐỀ SỐ 2 ................................................................................................................................................. 14
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 2 ................................................................................................. 16
ĐỀ SỐ 3 ................................................................................................................................................. 22
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 3 ................................................................................................. 25
ĐỀ SỐ 4 ................................................................................................................................................. 33
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 4 ................................................................................................. 35
ĐỀ SỐ 5 ................................................................................................................................................. 44
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 5 ................................................................................................. 48
CHUYÊN ĐỀ CỰC TRỊ SỐ PHỨC
1. MỘT SỐ VÍ DỤ MÌNH HỌA
Ví dụ 1: [THPT Nguyễn Khuyến] Xét số phức z thỏa mãn 2 z 1 3 z i 2 2. Mệnh đề nào
dưới đây đúng? 1 3 3
A. z 2 .
B. z 1 . C.
z . D.
z 2 . 2 2 2 2 HƯỚNG DẪN GIẢI
Cách 1. Chọn z i . Cách 2.
2 2 2 z 1 3 z i 2 z 1 z i z i 2 z 1 z i z i
2 i 1 z i 2 2 z i 2 2 .
Dấu " " xảy ra khi z i 0 hay z i z i 1. . 1 PMT
Ví dụ 2: [THPT Kim Liên-HN - 2017] Cho số phức z thỏa mãn z 2 3i 1 . Tìm giá trị lớn nhất
của z 1 i .
A. 6 .
B. 13 1 . C. 13 2 .
D. 4 . HƯỚNG DẪN GIẢI
Đặt w z 1 i .
Ta có z 2 3i 1 z 2 3i 1 z 2 3i 1 z 1 i 3 2i 1 .
w 3 2i 1.
Ta có: 1 w 3 2i w 3 2i w 1 13 .
Max z 1 i 1 13 .
Ví dụ 3: [THPT Hùng Vương-PT ] Cho số phức z thỏa mãn điều kiện z 1 1 i z . Đặt
m z , tìm giá trị lớn nhất của m . A. 1.
B. 2 .
C. 2 1.
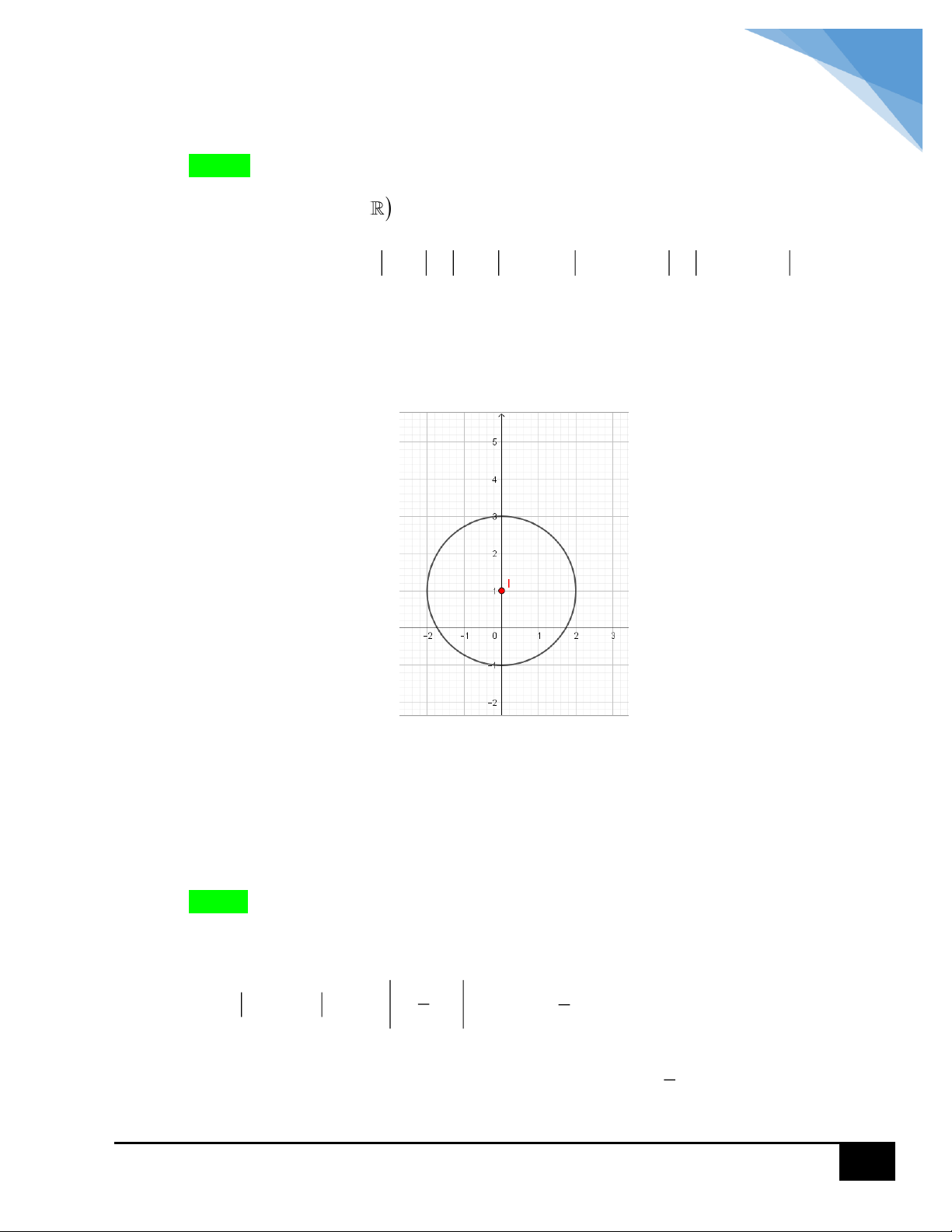
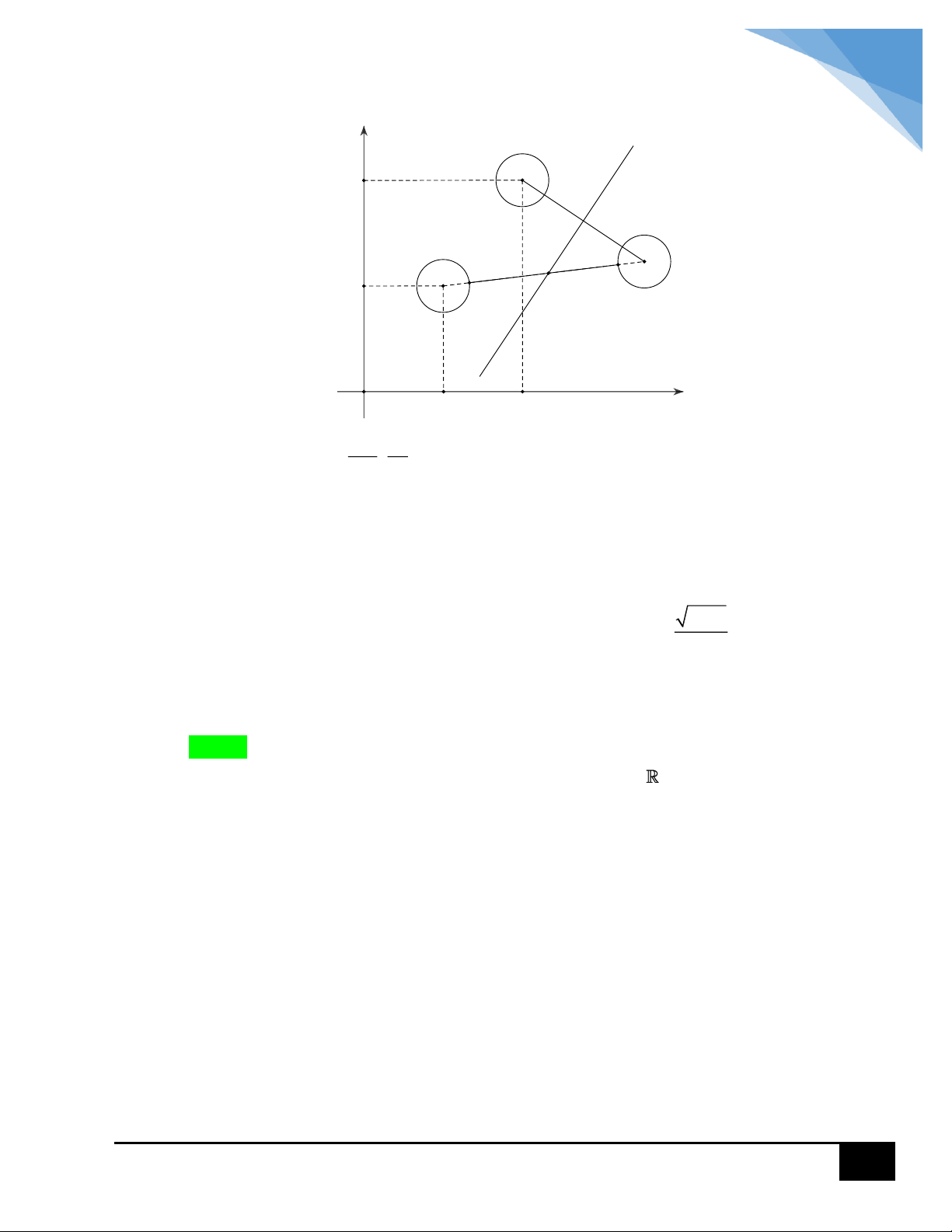
D. 2 1 . HƯỚNG DẪN GIẢI y x I M 2 1 O x .
Đặt z x iy với x, y .
Ta có z 1 1 i z z 1 1 i . z . x 2 2 y 2 x 2 1 2 y 2 x 2
y 2x 1 0 .
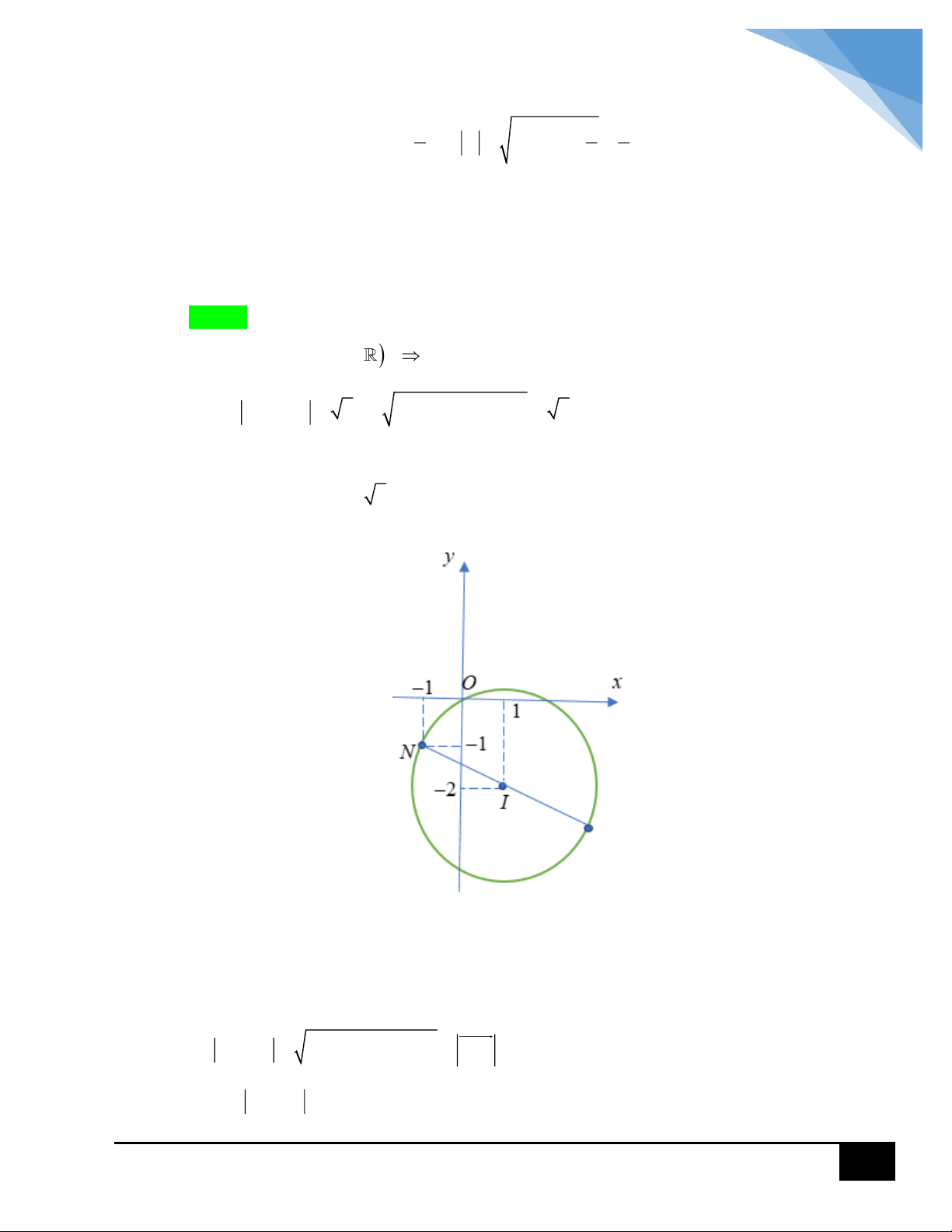
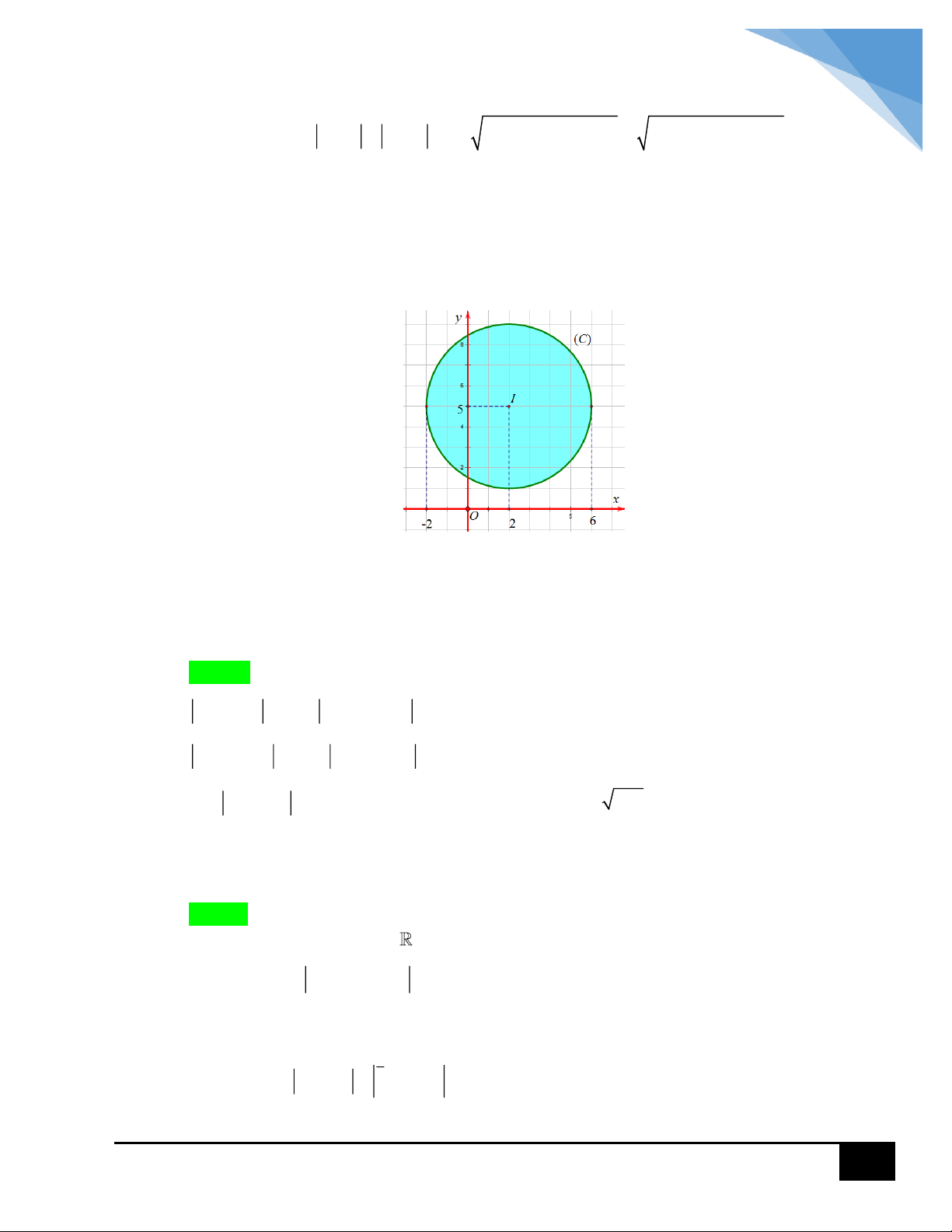
tập các điểm biểu diễn z là đường tròn tâm I 1;0 và bán kính R 2 . 2 PMT
Max z OM OI R 1 2 . 2
Ví dụ 4: [THPT chuyên Phan Bội Châu] Cho số phức z thỏa mãn z 2 3i 1 . Giá trị lớn nhất
của z 1 i là.
A. 4 .
B. 13 1 . C. 13 2 .
D. 6 . HƯỚNG DẪN GIẢI M2 M1 I H .
Gọi z x yi ta có z 2 3i x yi 2 3i x 2 y 3i . 2 2
Theo giả thiết x 2 y 3 1 nên điểm M biểu diễn cho số phức z nằm trên đường
tròn tâm I 2; 3 bán kính R 1 . 2 2
Ta có z 1 i x yi 1 i x 1 1 yi x 1 y 1 . 2 2
Gọi M x; y và H 1;1 thì HM x 1 y 1 .
Do M chạy trên đường tròn, H cố định nên MH lớn nhất khi M là giao của HI với đường tròn.
x 2 3t
Phương trình HI :
, giao của HI và đường tròn ứng với t thỏa mãn: y 3 2t 3 2 3 2 2 t 2
t t 1 9 4 1 nên M 2 ; 3 , M 2 ; 3 . 13 13 13 13 13
Tính độ dài MH ta lấy kết quả HM 13 1. z
Ví dụ 5: [TT Hiếu Học Minh Châu] Cho số phức z thỏa mãn z không phải số thực và w 2 2 z
là số thực. Giá trị lớn nhất của biểu thức P z 1 i là. 3 PMT
A. 2 2 .
B. 2 2 .
C. 8 .
D. 2 . HƯỚNG DẪN GIẢI 1 2
Cách 1. Xét z 0 suy ra
z . Gọi z a bi,b 0 . w z 1 2 2a 2 Suy ra z a b 1 i . 2 2 2 2 w z a b a b 1 2 b 0 Vì nên b 1 0 . 2 2 w a b a b 2 2 2
Suy ra tập hợp điểm biểu diễn số phức z trên mặt phẳng Oxy là đường tròn C 2 x 2 : y 2 .
Xét điểm A 1;1 là điểm biểu diễn số phức z 1 i suy ra 0
P MA max P OA r 2 2 .
Với r là bán kính đường tròn C 2 x 2 : y 2 . z 1
Cách 2. w w 2 z z z
z 2 0 * . * là phương trình bậc hai với hệ 2
2 2 2 z w 1 số thực
. Vì z thỏa * nên z là nghiệm phương trình * . Gọi z ,z là hai nghiệm w 1 2
của * suy ra z .z 2 z .z 2 z z 2 z 2 . Suy ra 1 2 1 2 1 2
P z 1 i z 1 i 2 2 2 2 . Dấu bằng xảy ra khi z 1 i . 2. ĐỀ TỰ LUYỆN ĐỀ SỐ 1
THỜI GIAN LÀM BÀI: 60 PHÚT Câu 1:
(Sở GD Cần Thơ-Đề 324-2018) Cho số phức z thoả mãn đồng thời hai điều kiện 2 2
z 3 4i 5 và biểu thức M z 2 z i đạt giá trị lớn nhất. Môđun của số
phức z 2 i bằng A. 5 . B. 9 . C. 25 . D. 5 . 4 PMT Câu 2:
Cho số phức z , z thỏa mãn z 3 , z 2 được biểu diễn trong mặt phẳng phức 1 2 1 2 z z
lần lượt là các điểm M, N . Biết OM,ON
, tính giá trị của biểu thức 1 2 . 6 z z 1 2 7 3 1 A. 13 . B. 1 . C. . D. . 2 13 Câu 3:
(THTT - Số 484 - Tháng 10 - 2017 - BTN) Cho số phức z a bi a,b . Biết tập
hợp các điểm A biểu diễn hình học số phức z là đường tròn C có tâm I 4; 3 và
bán kính R 3 . Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F 4a 3b 1 .
Tính giá trị M m .
A. M m 63 .
B. M m 48 .
C. M m 50 . D. M m 41 1 Câu 4:
(THPT Chuyên Lê Quý Đôn - Q Trị - HKII) Cho số phức z thỏa mãn z 4 . Tính z
giá trị lớn nhất của z . A. 2 3 . B. 4 5 . C. 4 3 . D. 2 5 . Câu 5:
(THPT Chuyên Lê Quý Đôn - Q Trị - HKII) Gọi M và m là giá trị lớn nhất, nhỏ nhất
của môđun số phức z thỏa mãn z 1 2 . Tính M m . A. 3 . B. 2 . C. 4 . D. 5 . Câu 6:
[THPT Hà Huy Tập - 2017] Cho số phức z thỏa mãn z 1 z i . Tìm mô đun nhỏ
nhất của số phức w 2z 2 i . 3 2 3 3 A. . B. . C. 3 2 . D. . 2 2 2 2 Câu 7:
[THPT TH Cao Nguyên - 2017] Cho các số phức z 3i , z 1 3i , z m 2i . 1 2 3
Tập giá trị tham số m để số phức z có môđun nhỏ nhất trong 3 số phức đã cho là. 3 A. 5; 5 .
B. ; 5 5; . C. 5; 5 . D. 5; 5. Câu 8:
(Chuyên Quang Trung - Bình Phước) Cho số phức z thỏa mãn z 2i z 4i và
z 3 3i 1 . Giá trị lớn nhất của biểu thức P z 2 là: 5 PMT A. 13 1 . B. 10 1 . C. 13 . D. 10 . Câu 9:
(Chuyên Quang Trung - Bình Phước) Trong tập hợp các số phức, gọi z , z là nghiệm 1 2 2017 của phương trình 2 z z
0 , với z có thành phần ảo dương. Cho số phức z 4 2
thoả mãn z z 1 . Giá trị nhỏ nhất của P z z là 1 2 2017 1 2016 1 A. 2016 1. B. . C. . D. 2017 1. 2 2
Câu 10: (THPT Chuyên Hạ Long - Quảng Ninh) Cho các số phức z 2 i , z 2 i và số 1 2 2 2
phức z thay đổi thỏa mãn z z
z z 16. Gọi M và m lần lượt là giá trị lớn 1 2
nhất và giá trị nhỏ nhất của z . Giá trị biểu thức 2 2 M m bằng A. 15 B. 7 C. 11 D. 8
Câu 11: (Chuyên KHTN - Lần 3) Cho số phức z thỏa mãn 2z 3 4i 10 . Gọi M và m lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Khi đó M m bằng. A. 5 . B. 15 . C. 10 . D. 20 .
Câu 12: (THPT Kinh Môn - Hải Dương)
Cho hai số phức z , z thỏa mãn 1 2
z 5 5, z 1 3i z 3 6i . Giá trị nhỏ nhất của z z là: 1 2 2 1 2 5 7 1 3 A. B. C. D. 2 2 2 2
Câu 13: (THPT Thăng Long - Hà Nội - Lần 2) Cho z là số phức thay đổi thỏa mãn
1iz 2i 4 và Mx;y là điểm biểu diễn cho z trong mặt phẳng phức. Tìm
giá trị lớn nhất của biểu thức T x y 3 . A. 4 2 2 . B. 8 . C. 4 . D. 4 2 .
Câu 14: (THPT Chuyên Quốc Học Huế - Lần 2) Cho số phức z x yi với x,y thỏa
mãn z 1 i 1 và z 3 3i 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị M
lớn nhất của biểu thức P x 2y . Tính tỉ số . m 9 7 5 14 A. . B. . C. . D. . 4 2 4 5 6 PMT
Câu 15: (Sở GD và ĐT Cần Thơ) Cho số phức z thỏa mãn z 1. Giá trị lớn nhất của biểu
thức P 1 z 2 1 z bằng A. 5 . B. 6 5 . C. 2 5 . D. 4 5 .
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 1 CÂU 1: Lời giải Chọn D 2 2
Đặt z x yi , x, y z 3 4i 5 x 3 y 4 5 1 . 2 2 2 2
Ta có: M z 2 z i x 2 y 2 2
x y
1 4x 2y 3 2 2
4 x 3 2 y 4 23 20 x 3 y 4 23 33 . x 3 4
x y 5 z 5 5i
Dấu " " xảy ra khi chỉ khi
kết hợp với 1 suy ra y 4 2
x 1, y 3 z 1 3i Thử lại ta có M
33 z 5 5i z 2 i 5. max CÂU 2: Lời giải Chọn B
Dựng hình bình hành OMPN trong mặt phẳng phức, khi đó biểu diễn của : 7 PMT 2 2 0 z z OP z z z
z 2 z z cos 150 1 1 2 1 2 1 2 1 2 z z MN 2 2 1 2
z z z z 2 z z cos 0 30 1 1 2 1 2 1 2 z z z z 1 2 1 2 . z 1 z z z 1 2 1 2 CÂU 3: Lời giải Chọn B. 2 2
Cách 1. Ta có phương trình đường tròn C : x 4 y 3 9 . 2 2
Do điểm A nằm trên đường tròn C nên ta có a 4 b 3 9 .
Mặt khác F 4a 3b 1 4 a 4 3b 3 24 F 24 4a 4 3b 3 .
4 a 4 3 b 3 2 2 2 2 2 Ta có
4 3 a4 b3 25.9 255 .
15 4a 4 3b 3 15 15 F 24 15 9 F 39 .
Khi đó M 39 , m 9 .
Vậy M m 48 . F b
Cách 2. Ta có F a b a 1 3 4 3 1 4 2 F b
a 42 b 32 1 3 9 4 2
b 6b 9 9 4 2
25b 2 3F 3b 2 F 225 0
F 2 2 3 3 25F 5625 2 0
16F 18F 5625 0 9 F 39. CÂU 4: Lời giải Chọn D 1 1 Ta có z z 1 4 z z 2 5 . z z z CÂU 5: Lời giải Chọn C 8 PMT
Gọi z x yi được biểu diễn bởi điểm M x; y . Khi đó OM z . 2 2
z 1 2 x 2 1
y 2 x 2 1
y 4 1 . Chứng tỏ M thuộc đường
tròn C có phương trình 1 , tâm I 1; 0 , bán kính R 2 .
Yêu cầu bài toán M C sao cho OM lớn nhất, nhỏ nhất.
Ta có OI 1 nên điểm O nằm trong đường tròn R OI OM OI R 1 OM 3 .
Do đó M 3 và m 1.
Vậy M m 4 . CÂU 6: Lời giải Chọn A
Giả sử z a bi z a bi . Khi đó z 1 z i a 1 bi a b 1i .
a 2 b a b 2 2 2 1
1 a b 0 .
Khi đó w 2z 2 i 2 a ai 2 i 2a 2 i a 1 . 3 2
a 2 a 2 w 2 2 2 1 2
8a 4a 5 . 2 CÂU 7: Lời giải Chọn A
Ta có: z 3 , z 10 , z 2 m 4 . 1 2 3
Để số phức z có môđun nhỏ nhất trong 3 số phức đã cho thì 3 2
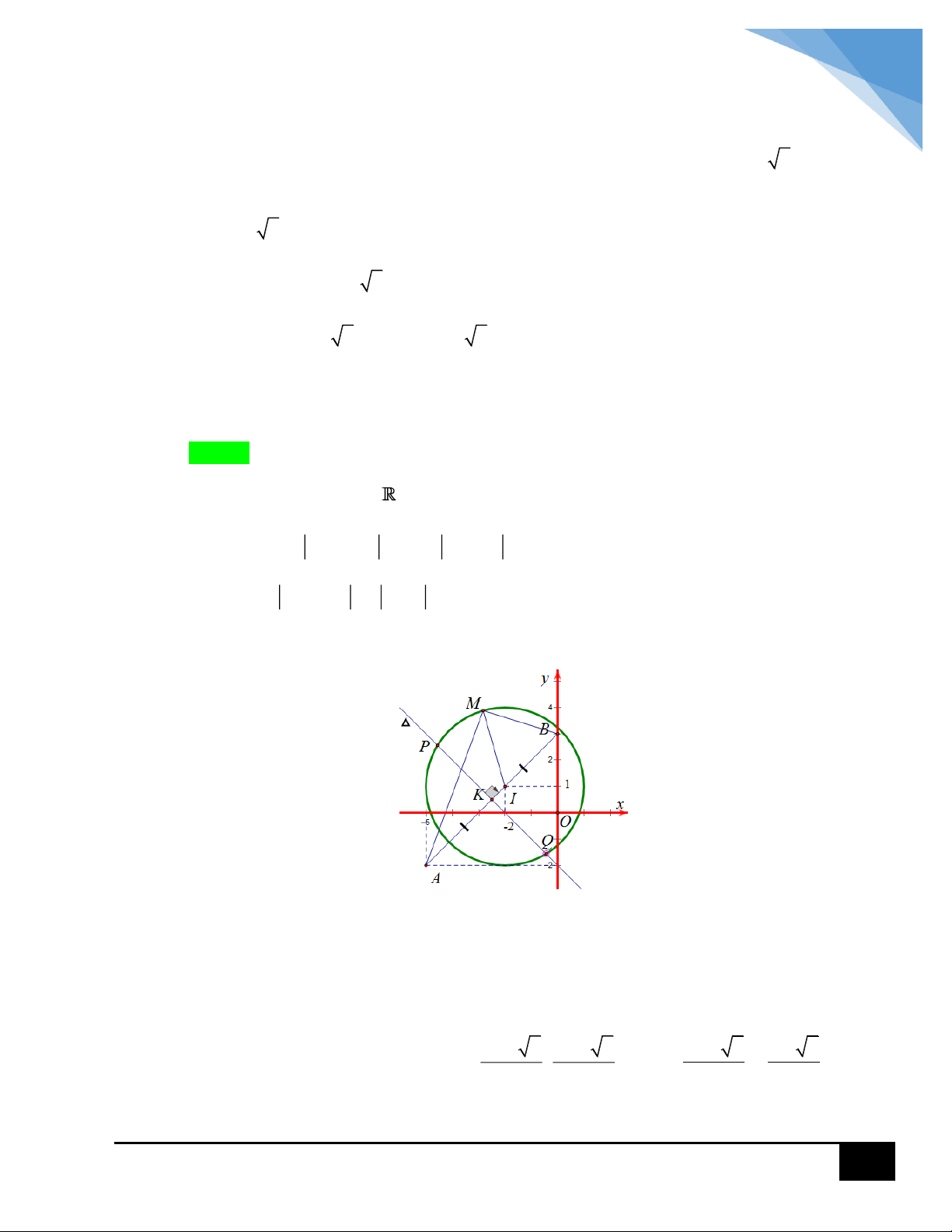
m 4 3 5 m 5 . CÂU 8: Lời giải Chọn C 9 PMT
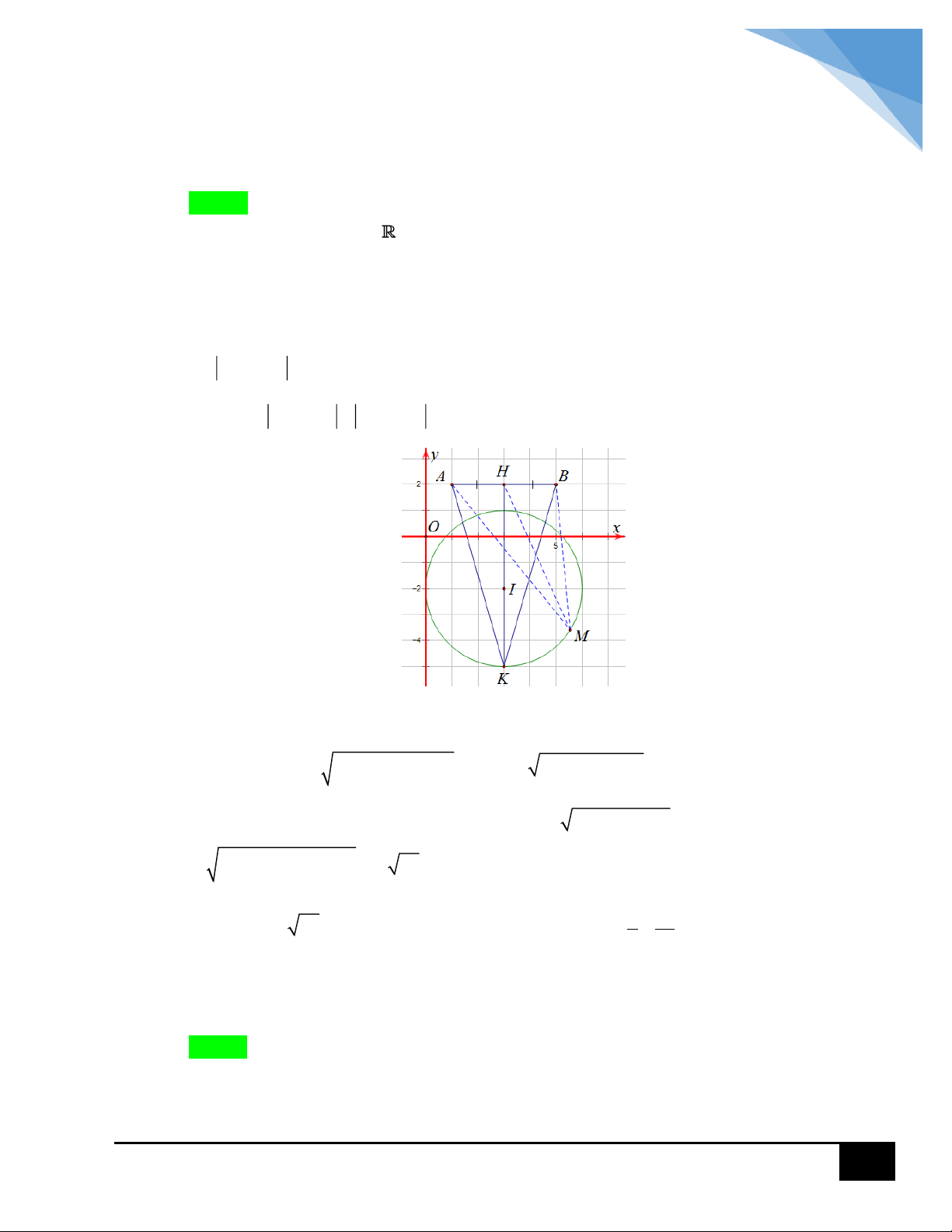
Gọi M x; y là điểm biểu diễn số phức z ta có: z 2i z 4i
x y 2 x y 2 2 2 2 4
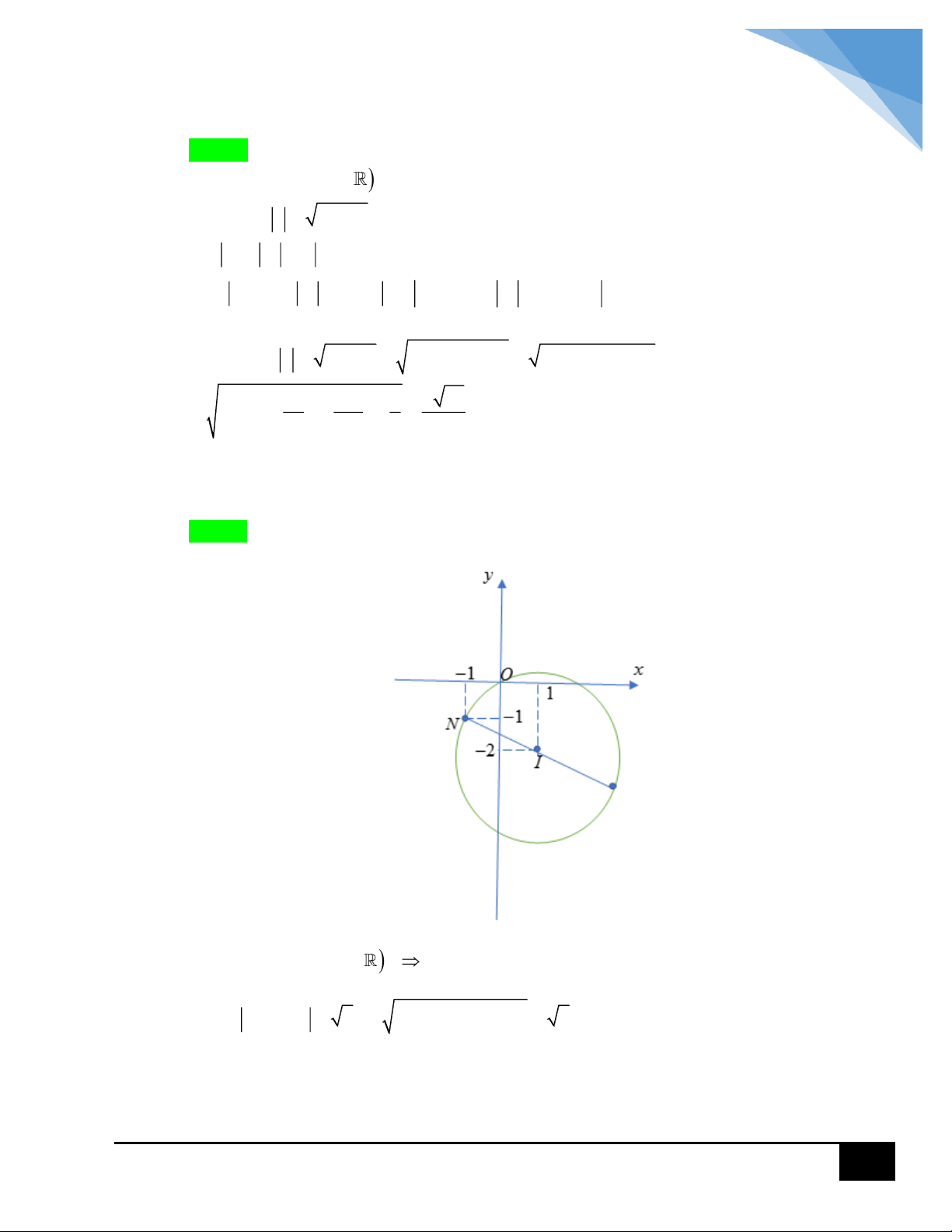
y 3; z 3 3i 1 điểm M nằm trên đường tròn tâm I 3; 3 và bán kính
bằng 1. Biểu thức P z 2 AM trong đó A 2; 0 , theo hình vẽ thì giá trị lớn nhất 2 2
của P z 2 đạt được khi M 4; 3 nên max P 4 2 3 0 13 . CÂU 9: Lời giải Chọn A 2017 Xét phương trình 2 z z 0 4
z 1 2016 i 1
Ta có: 2016 0 phương trình có hai nghiệm phức 2 2 . z 1 2016 i 2 2 2
Khi đó: z z i 2016 1 2
z z z z z z z z z z P 2016 1 . 2 1 1 2 1 2 1 Vậy P 2016 1. min CÂU 10: 10 PMT Lời giải Chọn D
Giả sử z x yi x, y . 2 2 2 2 Ta có: z z
z z 16 x yi 2 i x yi 2 i 16 1 2
x y 2 2 1 4 .
Suy ra tập hợp điểm biểu diễn của số phức z là đường tròn tâm số phức I 0;1 bán kính R 2 .
Do đó m 1, M 3 . Vậy 2 M 2 m 8. CÂU 11: Lời giải Chọn C
Đặt z x yi . 2 3 3 2
Ta có: 2z 3 4i 10 z
2i 5 x y 2 25 . 2 2 3
Tập hợp điểm biểu diễn số phức thỏa đề là đường tròn tâm I ; 2 , bán kính R 5 . 2 11 PMT
m IO R Khi đó:
M m 2R 10. M IO R CÂU 12: Lời giải Chọn A
Giả sử z a b i a ,b
, z a b i a ,b . 2 2 2 2 2 1 1 1 1 1 Ta có 2
z 5 5 a 5 b
25 . Do đó, tập hợp các điểm A biểu diễn cho số phức 1 2 1 1 2
z là đường tròn C x 2 : 5
y 25 có tâm là điểm I 5; 0 và bán kính R 5 . 1 2 2 2 2
z 1 3i z 3 6i a 1 b 3 a 3 b 6 2 2 2 2 2 2
8a 6b 35 0. Do đó tập hợp các điểm B biểu diễn cho số phức z là đường 2 2 2
thẳng : 8x 6y 35 0 .
Khi đó, ta có z z AB . 1 2 8.5 6.0 35 Suy ra z z AB
dI; R 5 5 .` 1 2 min min 2 8 2 6 2 5
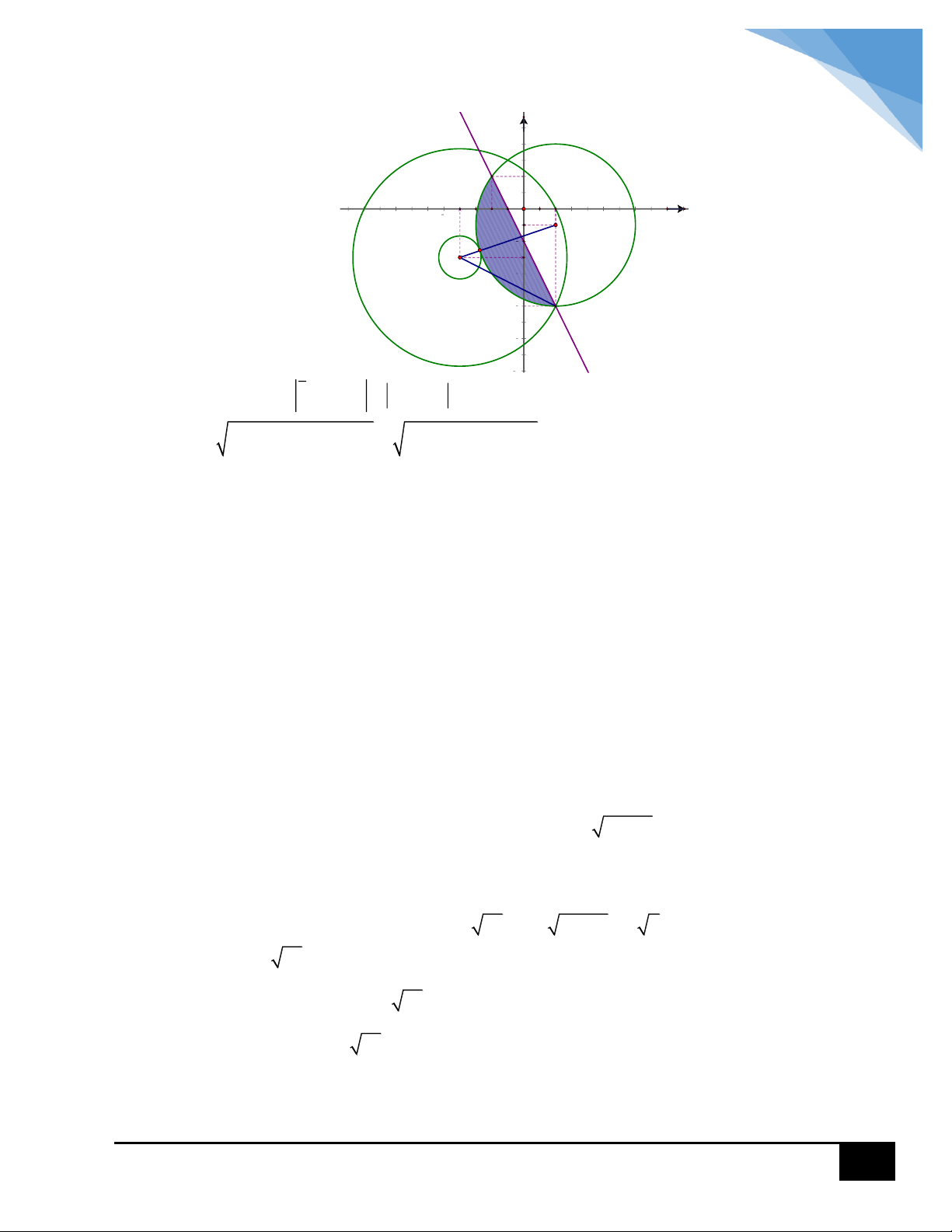
Vậy giá trị nhỏ nhất của z z là . 1 2 2 CÂU 13: Lời giải Chọn B 1 3
Ta có 1 i z 2 i 4 z i 2 2 . Vậy quỹ tích điểm biểu diễn cho số 2 2 1 3
phức z là đường tròn C tâm I
; bán kính R 2 2 (1). 2 2
x y 3 T 0
Biểu thức T x y 3 , với T 0 thì ta có (2).
x y 3 T 0 12 PMT
Khi đó điểm M là điểm thuộc đường tròn C và một trong hai đường thẳng trong (2).
Điều kiện để một trong hai đường thẳng trên cắt đường tròn C là 4 T 2 2 2 0 T 8
0 T 8 . Vậy maxT 8 . T 8 T 4 0 2 2 2 CÂU 14: y Lời giải Chọn B J 3 I 1 x O 1 3
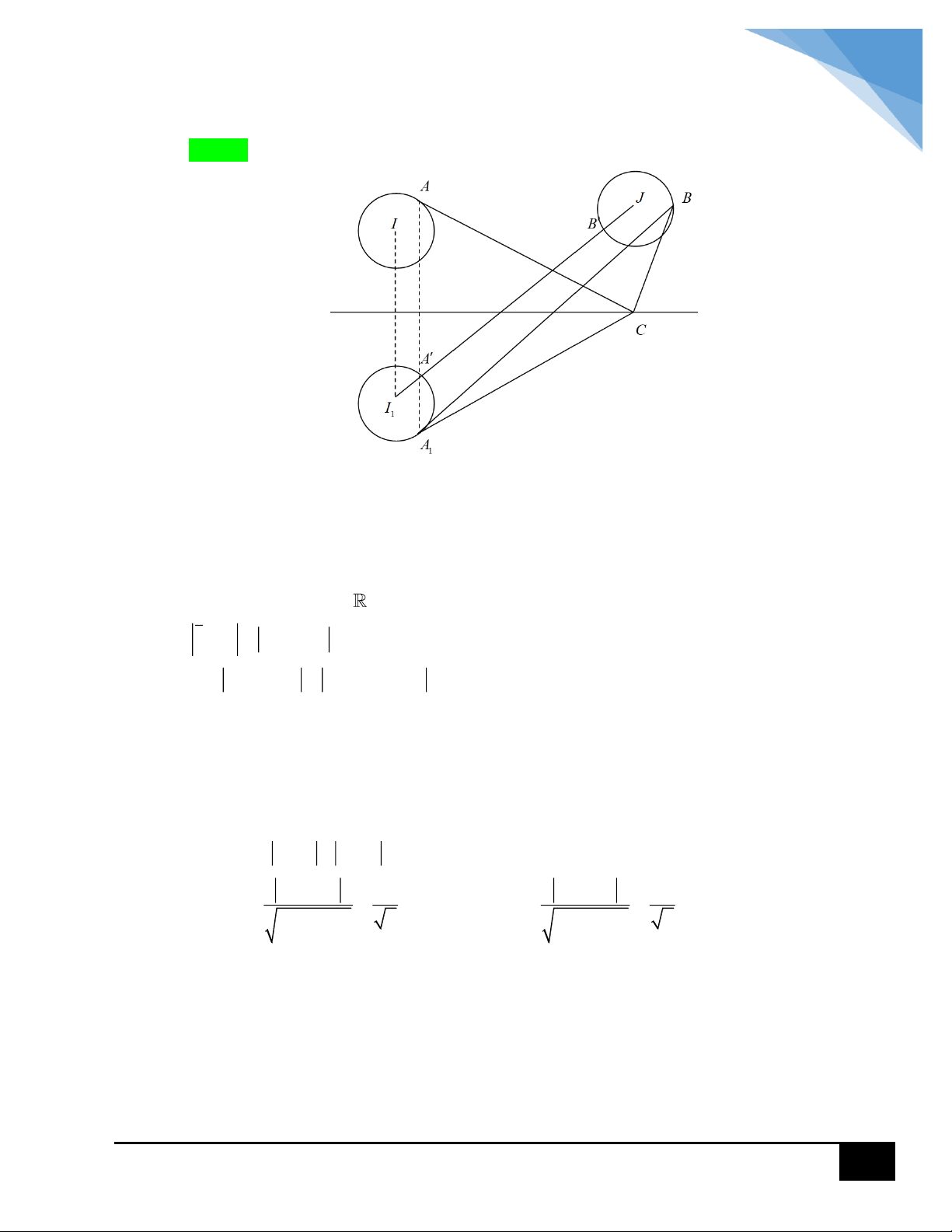
Gọi A là điểm biểu diễn của số phức z .
Từ giả thiết z 1 i 1 ta có A là các điểm nằm bên ngoài hình tròn C có tâm 1
I 1;1 bán kính R 1 . 1
Mặt khác z 3 3i 5 ta có A là các điểm nằm bên trong hình tròn C có tâm 2
J 3; 3 bán kính R 5 . 2
Ta lại có: P x 2y x 2y P 0 . Do đó để tồn tại x, y thì và phần 9 P
gạch chéo phải có điểm chung tức là d J; 5 5 5 M
9 P 5 4 P 14 . Suy ra m M 7 4; 14 . m 2 CÂU 15: 13 PMT Lời giải Chọn C
Gọi số phức z x i
y , với x, y .
Theo giả thiết, ta có z 1 2 x 2
y 1 . Suy ra 1 x 1 . 2 2
Khi đó, P 1 z 2 1 z x 2 y x 2 1 2 1
y 2x 2 2 2 2x .
Suy ra P 2 2 1
2 2x 2 2
2x hay P 2 5 , với mọi 1 x 1 . Vậy P
2 5 khi 2 2x 2 2 2x x 3 , y 4 . max 5 5
------------------------------------------------------------------------------------------------------------------------------- ĐỀ SỐ 2
THỜI GIAN LÀM BÀI: 60 PHÚT Câu 1:
(THPT Chuyên Tiền Giang - Lần 1) Biết số phức z thỏa mãn z 3 4i 5 và biểu 2 2
thức T z 2 z i đạt giá trị lớn nhất. Tính z . A. z 33 . B. z 50 . C. z 10 . D. z 5 2 . Câu 2:
(Đoàn Trí Dũng - Lần 7) Biết rằng z 1 2 . Tìm giá trị lớn nhất của module số phức
w z 2i ? A. 5 2 B. 5 2 C. 2 5 D. 2 5 z 1 1 Câu 3:
(THPT Quảng Xương 1 - Thanh Hóa) Cho số phức z thỏa mãn . Tìm giá z 3i 2
trị lớn nhất của biểu thức P z i 2 z 4 7i . A. 8 . B. 10 . C. 2 5 . D. 4 5 . Câu 4:
(Sở GD Bạc Liêu - HKII - 2018 Xét số phức z a bi a,b R,b 0 thỏa mãn z 1.
Tính P a 2 2 4b khi 3
z z 2 đạt giá trị lớn nhất . A. P 4 .
B. P 2 2 . C. P 2 .
D. P 2 2 . 14 PMT Câu 5:
(THPT Quốc Oai - Hà Nội - HKII) Trong các số phức z thỏa mãn z i z 2 3i .
Hãy tìm z có môđun nhỏ nhất. 27 6 6 27 6 27 3 6 A. z i . B. z i . C. z i . D. z i . 5 5 5 5 5 5 5 5 Câu 6:
[TRẦN HƯNG ĐẠO – NB] Trong các số phức thỏa mãn điều kiện z 3i z 2 i .
Tìm số phức có môđun nhỏ nhất? 1 2 1 2
A. z 1 2i .
B. z i . C. z i .
D. z 1 2i 5 5 5 5 . Câu 7:
[LẠNG GIANG SỐ 1] Cho số phức z thỏa mãn z 3 z 3 8 . Gọi M , m lần
lượt giá trị lớn nhất và nhỏ nhất z . Khi đó M m bằng A. 4 7. B. 4 7. C. 7. D. 4 5. 2z i Câu 8:
Cho số phức z thỏa mãn z 1 . Đặt A
. Mệnh đề nào sau đây đúng? 2 iz A. A 1 . B. A 1 . C. A 1 . D. A 1 . Câu 9:
Cho số phức z thỏa mãn z 1. Tìm giá trị lớn nhất M
và giá trị nhỏ nhất M max min
của biểu thức M 2
z z 3 1 z 1 . A. M 5; M 1 . B. M 5; M 2 . max min max min C. M 4; M 1. D. M 4; M 2 . max min max min
Câu 10: Cho số phức z thỏa z 2 . Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức z i P . z 3 2 A. . B. 1. C. 2 . D. . 4 3
Câu 11: Cho số phức z thỏa mãn z 1. Tìm giá trị lớn nhất của biểu thức P 1 z 3 1 z . A. 3 15 . B. 6 5 . C. 20 . D. 2 20 .
Câu 12: Cho số phức z thỏa mãn z 1 2i 2 . Tìm môđun lớn nhất của số phức z. 15 PMT A. 9 4 5 . B. 11 4 5 . C. 6 4 5 . D. 5 6 5 .
Câu 13: Cho số phức z thỏa mãn 1 i z 6 2i 10 . Tìm môđun lớn nhất của số phức z. A. 4 5 B. 3 5. C. 3. D. 3 5
Câu 14: Trong các số phức thỏa mãn điều kiện z 2 4i z 2i . Tìm môđun nhỏ nhất của số phức z 2 . i A. 5 B. 3 5. C. 3 2 D. 3 2
Câu 15: Cho số phức z thỏa mãn z 1 2i 3 . Tìm môđun nhỏ nhất của số phức z 1 . i A. 4. B. 2 2. C. 2. D. 2.
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 2 CÂU 1: Lời giải Chọn D 2 2
Đặt z x yi , theo giả thiết z 3 4i 5 x 3 y 4 5 . C 2 2
Ngoài ra T z 2 z i 4x 2y 3 T 0 đạt giá trị lớn nhất. 23 T
Rõ ràng C và có điểm chung do đó
5 13 T 33. 2 5
Vì T đạt giá trị lớn nhất nên T 33 suy ra 4x 2y 30 0 y 15 2x thay vào C ta được 2
5x 50x 125 0 x 5 y 5 . Vậy z 5 2 . CÂU 2: Lời giải Chọn D
Quỹ tích M z là đường tròn tâm I 1,0 bán kính R 2 . Còn w z 2i MA
với A 0, 2 . Khi đó w
IA R 2 5 . max 16 PMT CÂU 3: Lời giải Chọn B
Gọi z x yi với x, y
, gọi M là điểm trong mặt phẳng tọa độ biểu diễn số z 1 1 phức z . Ta có:
2 z 1 z 3i 2 x
1 yi x y 3i z 3i 2 2 2
x 2 y x y 2 2 2 2 1 3
x 2 y 3 20.
Như vậy, tập hợp điểm M biểu diễn số phức z là đường tròn C tâm I 2; 3 và bán kính R 2 5 .
Gọi A 0; 1, B4; 7 lần lượt là các điểm biểu diễn các số phức z i , z 4 7i . 1 2
Dễ thấy A, B thuộc đường tròn C . Vì AB 4 5 2R nên AB là đường kính của
đường tròn C 2 MA 2 MB 2 AB 20 . Từ đó:
P z i 2 z 4 7i z i 2 z 4 7i
MA MB 2 2 2 MA 2 2 1 2 MB 10 . MB 2MA MA 2 Dấu " " xảy ra khi .
MA MB 20 MB 2 2 4 Vậy max P 10 . CÂU 4: Lời giải Chọn C z 1 1 z z
Do b 0 1 a 1 1 2 2 Ta có : 3
z z 2 z z z 2
2z 2 bi a bi 2 z z bi 2 a 2 2
b 2abi AB 2 6 17 PMT = 2 b 2 2 4ab 1 2 a a 2 2 1 4 1 a 1 3 a 2 2 4 a 4a 2
Biểu thức trên đạt GTLN trên miền 1 a 1 khi a 1 b 3 (do b 0 ) 2 2
Vậy P a 2 2 4b 2 CÂU 5: Lời giải Chọn D
Giả sử z x yi x, y z x yi .
Ta có x yi i x yi 2 3i x y 1i x 2 y 3i
x y 2 x 2 y 2 2 1 2 3
12y 134x 6y 4x 12 8y x 2y 3 . 2 2 2 6 9 9 Do đó 2 2 z x y 2y 3 2 y 2
5y 12y 9 y 5 . 5 5 5 3 3 6
Dấu " " xảy ra y 6 , khi đó x
z i . 5 5 5 5 CÂU 6: Lời giải Chọn C
Phương pháp tự luận
Giả sử z x yi x, y
z i z i x y i x y i x y 2 x 2 y 2 2 3 2 3 2 1 3 2 1
6y 9 4x 4 2y 1 4x 8y 4 0 x 2y 1 0 x 2y 1 2 2 2 z x y y 2 2 2 y 2 y y y 1 5 2 1 5 4 1 5 5 5 5 5 2 1 Suy ra z khi y x min 5 5 5 1 2 Vậy z i. 5 5
Phương pháp trắc nghiệm
Giả sử z x yi x, y 18 PMT
z i z i x y i x y i x y 2 x 2 y 2 2 3 2 3 2 1 3 2 1
6y 9 4x 4 2y 1 4x 8y 4 0 x 2y 1 0
Vậy tập hợp các điểm biểu diễn số phức z thỏa điều kiện z 3i z 2 i là đường
thẳng d : x 2y 1 0.
Phương án A: z 1 2i có điểm biểu diễn 1; 2 d nên loại A. 1 2 1 2
Phương án B: z i có điểm biểu diễn ; d nên loại B. 5 5 5 5
Phương án D: z 1 2i có điểm biểu diễn 1; 2 d nên loại B. 1 2 1 2 Phương án C: z
i có điểm biểu diễn ; d 5 5 5 5 CÂU 7: Lời giải Chọn B
Gọi z x yi với ; x y .
Ta có 8 z 3 z 3 z 3 z 3 2z z 4 .
Do đó M max z 4 . Mà z z
x yi x yi x 2 y x 2 2 2 3 3 8 3 3 8 3 3 y 8 .
Áp dụng bất đẳng thức Bunhiacopxki, ta có
8 1. x 32 y 1. x 32 y
1 1 x 32 y x 32 2 2 2 2 2 2 y
2x 2y 2x 2 8 2 2 2 18 2 2 2y 18 64 2 x 2 y 2 x 2 7
y 7 z 7 .
Do đó M min z 7 .
Vậy M m 4 7 . CÂU 8: 19 PMT Lời giải Chọn A
Đặt Có a a bi a b 2 a 2 , ,
b 1 (do z 1 ) 2z i
2a 2b 1i
4a 2b 12 2 A 2 iz 2 b ai
2b2 2a
4a 2b 2 2 1 Ta chứng minh 1 . 2 b2 2 a
4a 2b 2 2 1 2 2 Thật vậy ta có 1 2 4a 2b 1 2 b a a b 1 2
2 2 2
2b 2a Dấu “=” xảy ra khi 2 a 2 b 1. Vậy A 1 . CÂU 9: Lời giải Chọn A 2 3
Ta có: M z z 1 z 1 5 , khi z 1 M 5 M 5. max 1 3 z 1 3 z 1 3 z 1 3 z 1 3 z Mặt khác: M 1 3 z 1, khi 1 z 2 2 2
z 1 M 1 M 1. min CÂU 10: Lời giải Chọn A i 1 3 i 1 1 Ta có P 1 1
. Mặt khác: 1 1 . z |z| 2 z |z| 2 1 3
Vậy, giá trị nhỏ nhất của P là
, xảy ra khi z 2i; giá trị lớn nhất của P bằng xảy 2 2 ra khi z 2 . i CÂU 11: Lời giải 20 PMT Chọn D
Gọi z x yi; x ; y . Ta có: z 2 x 2 y 2 y 2 1 1
1 x x 1; 1 2 2
Ta có: P z
z x 2 y x 2 1 3 1 1 3 1
y 2 1 x 3 21 x .
Xét hàm số f x 21 x 3 21 x; x1;
1 . Hàm số liên tục trên 1; 1 1 3 4
và với x 1;1 ta có: f x
0 x 1;1 x x 5 2 1 2 1 4
Ta có: f 1 2; f 1 6; f 2 20 P 2 20 . 5 max CÂU 12: Lời giải Chọn A 2 2
Gọi z x yi; x ; y . Ta có: z 1 2i 2 x
1 y 2 4.
Đặt x 1 2 sin t; y 2 2 cos t; t 0; 2 . Lúc đó: 2 z t2 t2 t t 2 2 1 2sin 2 2cos 9 4sin 8cos 9 4
8 sint ; 2 z 9 4 5 sin t
z 9 4 5 ; 9 4 5 5 2 5 10 4 5 z
9 4 5 đạt được khi z i . max 5 5 CÂU 13: Lời giải Chọn B
Gọi z x yi; x ; y . Ta có: iz i i 6 z 2i 1 6 2 10 1 .
10 z 2 4i 5 x 22 y 42 5. 1 i
Đặt x 2 5 sin t; y 4 5 cost; t 0; 2 . Lúc đó: 21 PMT 2 2 2
z 2 5 sint 4 5 cost 25 4 5 sint 8 5 cost 2 2
25 4 5 8 5 sint ; 2
z 25 20sint z 5; 3 5 z
3 5 đạt được khi z 3 6i . max CÂU 14: Lời giải Chọn C
Gọi z x yi; x ; y . Ta có:
z i z i x 2 y 2 x y 2 2 2 4 2 2 4 2
x y 4 0 y 4 . x 2 2 2 2
Ta có: z i 2
x y 2
x x 2 2 2 6
2x 12x 36 2x 3 18 18 z 2i
18 3 2 khi z 3 .i min CÂU 15: Lời giải Chọn C
Gọi z x yi; x ; y z 1 i x 1 y 1i . Ta có:
z i x 2 y 2 1 2 9 1 2 9 .
Đặt x 1 3 sin t; y 2 3 cos t; t 0; 2 . z 1 2
i 3sint2 1 3cost2 10 6cost 2 z 2i 4 z 1 i 2 min , khi z 1 . i
------------------------------------------------------------------------------------------------------------------------------- ĐỀ SỐ 3
THỜI GIAN LÀM BÀI: 60 PHÚT m i Câu :
Cho số phức z m
. Tìm môđun lớn nhất của z.
1 mm 2i , 22 PMT 1 A. 1. B. 0. C. . D.2. 2 Câu 2:
(Toán học tuổi trẻ tháng 1) Cho 2018 phức z thoả mãn z 3 4i 5 . Gọi M và 2 2
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P z 2 z i . Tính
môđun của 2018 phức w M mi . A. w 1258 . B. w 1258 .
C. w 2 314 . D. w 2 309 . Câu 3:
(SGD BINH THUAN) Xét các số phức z 3 4i và z 2 mi , m . Giá trị nhỏ 1 2 z
nhất của môđun số phức 2 bằng? z1 2 1 A. . B. 2 . C. 3 . D. . 5 5 Câu 4.
[SGD SOC TRANG] Cho số phức z a bi a,b thỏa z 4 z 4 10 và
z 6 lớn nhất. Tính S a b . A. S 3. B. S 5 . C. S 5 . D. S 11 . Câu 5:
(Sở GD Kiên Giang) Cho hai số phức z , z thỏa mãn z 2 3i 2 và 1 2 1
z 1 2i 1. Tìm giá trị lớn nhất của P z z . 2 1 2
A. P 3 34 .
B. P 3 10 . C. P 6 . D. P 3 . Câu 6:
(SỞ GD-ĐT PHÚ THỌ) Có bao nhiêu giá trị nguyên của m để có đúng 2 số phức z
thỏa z m 1 i 8 và z 1 i z 2 3i . A. 130 . B. 66 . C. 65 . D. 131 . Câu 7:
[NGUYỄN TRÃI] Cho số phức z thỏa mãn: z 2 2i 1 . Số phức z i có môđun nhỏ nhất là: A. 5 1. B. 5 1. C. 5 2 . D. 5 2 . Câu 8: [CHUYÊN LƯƠNG THẾ VINH] Cho số phức z thỏa mãn 2
z 2z 5 z 1 2iz 3i
1 . Tính min|w|, với w z 2 2i . 23 PMT A. w 3 min| | . B. min|w | 2 . C. min|w | 1 . D. 2 w 1 min| | . 2 Câu 9:
[CHUYÊN SƠN LA]Cho số phức z thỏa mãn điều kiện: z 1 2i 5 và
w z 1 i có môđun lớn nhất. Số phức z có môđun bằng: A. 2 5 . B. 3 2 . C. 6 . D. 5 2 .
Câu 10: [CHU VĂN AN – HN] Cho số phức z thỏa mãn điều kiện z 1 2 . Tìm giá trị lớn
nhất của T z i z 2 i .
A. maxT 8 2 . B. maxT 4 .
C. maxT 4 2 . D. maxT 8 .
Câu 11: (SGD Bà Rịa - Vũng Tàu)Cho số phức z thỏa mãn z 2 3i 5 . Gọi m , M lần 2 2
lượt là giá trị nhỏ nhất và lớn nhất của biểu thức P z i z 2 . Tính A m M . A. A 3 . B. A 2 . C. A 5 . D. A 10 .
Câu 12: (THPT Ninh Giang - Hải Dương) Cho các số phức z thỏa mãn z 3 z i . Tìm
giá trị nhỏ nhất của P z . 10 2 10 A. P . B. P 3 . C. P . D. min 5 min min 5 P 3 10 . min 5
Câu 13: [CHUYÊN SƠN LA - 2017] Cho số phức z thỏa mãn điều kiện: z 1 2i 5 và
w z 1 i có môđun lớn nhất. Số phức z có môđun bằng: A. 6 . B. 3 2 . C. 5 2 . D. 2 5 .
Câu 14: [THPT THÁI PHIÊN HP - 2017] Trong tập hợp các số phức z thỏa mãn:
z 2 i
Tìm môđun lớn nhất của số phức z i . z 2. 1 i A. 2 2 . B. 3 2 . C. 3 2 . D. 2 2 . 24 PMT
Câu 15: [THPT Lý Thường Kiệt - 2017] Trong mặt phẳng với hệ toạ độ Oxy, cho điểm
A 4; 4 và M là điểm biển diễn số phức z thoả mãn điều kiện z 1 z 2 i . Tìm
toạ độ điểm M để đoạn thẳng AM nhỏ nhất.
A. M 1; 1 .
B. M 2; 4 .
C. M 1; 5 .
D. M 2; 8 .
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 3 CÂU 1: Lời giải Chọn A Ta có: m z i m i 1 z z z i m . m m 2i 1 1 ; 0 1 2 m 2 1 m 2 1 m max 1 CÂU 2: Lời giải Chọn B
Giả sử z a bi ( a,b ) . z i
a 2 b 2 3 4 5 3 4 5 (1) . 2 2 P z 2 z i a 22 b a b 2 2 2 1
4a 2b 3 (2) . Từ (1) và (2) ta có 2 a Pa 2 20 64 8
P 22P 137 0 (*) .
Phương trình (*) có nghiệm khi 2
4P 184P 1716 0
13 P 33 w 1258 . CÂU 3: Lời giải Chọn A z 2 mi
2mi34i 64m3m8i 64m 3m8 2 i z 3 4i 3 4i 3 4i 25 25 25 1 25 PMT z
6 4m 2 3m 8 2 z 36 48m 2 16m 2 9m 48m 64 2 2 z 25 25 2 z 25 1 1 2 z 25m 2 100 z m 4 4 2 2 2 . 2 z 25 z 25 25 5 1 1 z z
Hoặc dùng công thức: 2 2 . z z 1 1 CÂU 4: Lời giải Chọn C
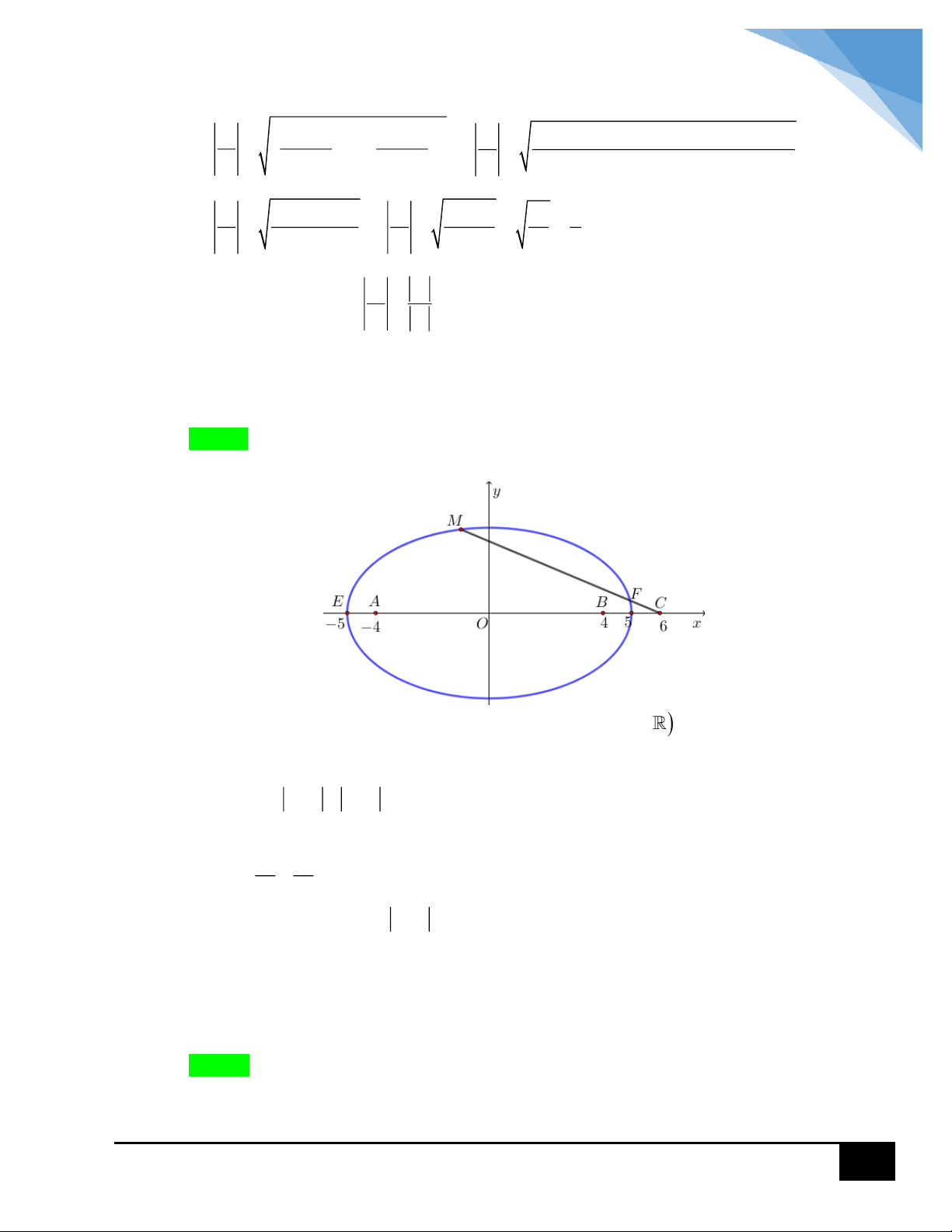
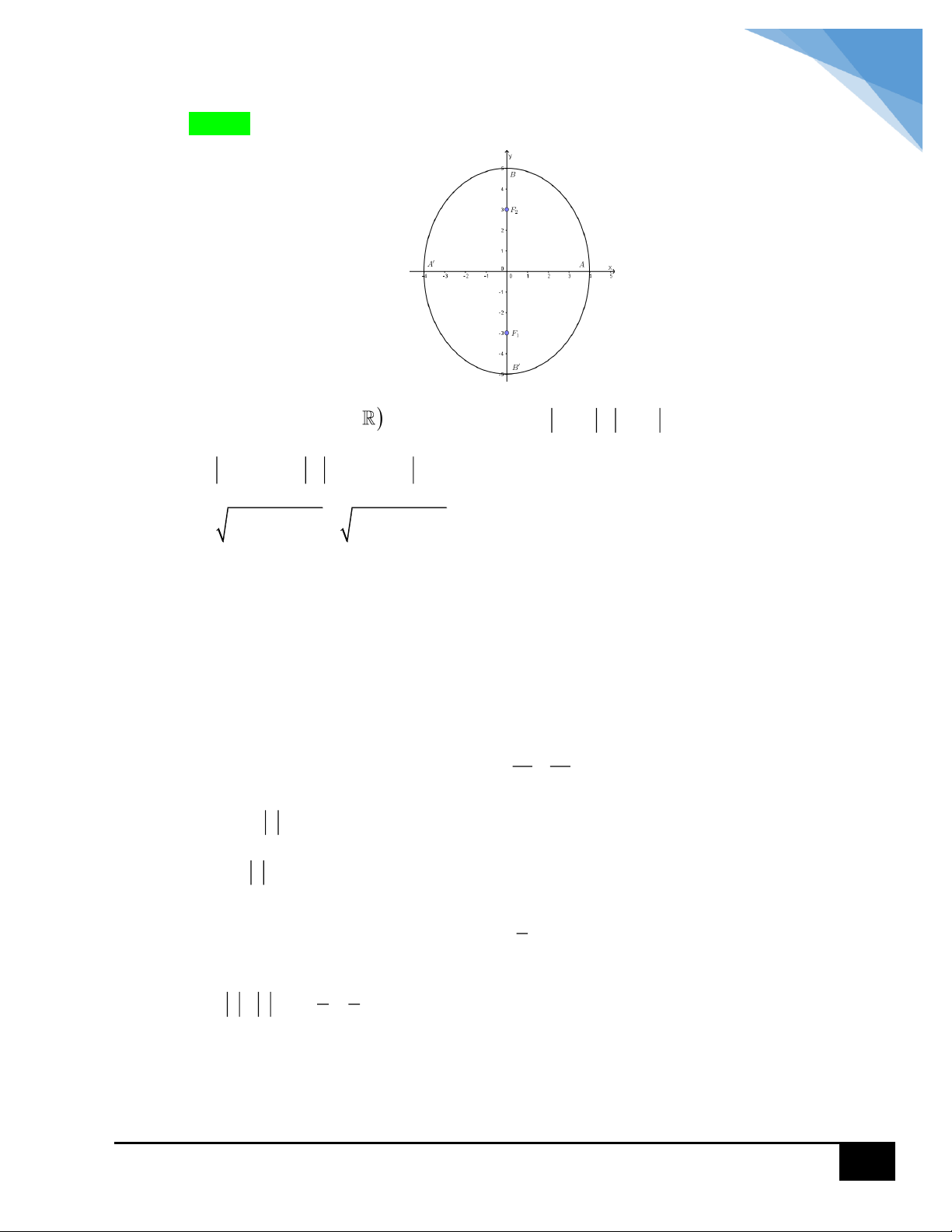
Gọi M a; b là điểm biểu diễn số phức z a bi a,b , A4; 0 , B4; 0 ,
C 6; 0 lần lượt là điểm biểu diễn số phức z 4 , z 4 , z 6 . 1 2 3
Khi đó ta có z 4 z 4 10 MA MB 10 suy ra tập hợp điểm M là E nhận
A , B là các tiêu điểm, độ dài trục lớn 2a 10 a 5, tiêu cự 2c 8 c 4 , b 3 2 2 x y E : 1. 25 9
Ta tìm giá trị lớn nhất của z 6 MC , khi đó MC
EF FC 11, khi đó M E max
với E5; 0 , F 5; 0 z 5. Vậy S a b 5 . CÂU 5: Lời giải Chọn A 26 PMT
Gọi M x ; y
là điểm biều diễn số phức z , N x ; y là điểm biểu diễn số phức z 2 2 1 1 1 2 2 2
Số phức z thỏa mãn z 2 3i 2 x 2 y 3
4 suy ra M x ; y 1 1 1 1 1 1
nằm trên đường tròn tâm I 2; 3 và bán kính R 2 . 1 2 2
Số phức z thỏa mãn z 1 2i 1 x 1 y 2
1 suy ra N x ; y 2 2 2 1 2 2
nằm trên đường tròn tâm J 1; 2 và bán kính R 1 . 2
Ta có z z MN đạt giá trị lớn nhất bằng R IJ R 2 34 1 3 34 . 1 2 1 2 CÂU 6: Lời giải Chọn B
Đặt z x iy x, y
Ta có: z m 1 i 2 tập hợp các điểm M biểu diễn số phức z là đường
tròn tâm I m 1; 1 , bán kính R 8 .
Ta có: z 1 i z 2 3i tập hợp các điểm M biểu diễn số phức z là đường
thẳng d : 2x 8y 11 0 .
Yêu cầu bài toán khoảng cách từ I đến d nhỏ hơn R 2m 21 8 68 21 m 21 4 68 4 68 2 2 Vì m
nên 22 m 43 có 66 giá trị thỏa yêu cầu bài toán. 27 PMT CÂU 7: Lời giải Chọn A y I 1 M O 1 x
Gọi z x yi , x, y .
Ta có: z i x
y i x 2 y 2 2 2 1 ( 2) ( 2) 1 ( 2) ( 2) 1 .
Tập hợp các điểm trong mặt phẳng Oxy biểu diễn của số phức z là đường tròn (C) tâm
I(2; 2) và bán kính R 1 .
z i x y 2 2 1
IM , với I 2; 2 là tâm đường tròn, M là điểm chạy trên đường
tròn. Khoảng cách này ngắn nhất khi M là giao điểm của đường thẳng nối hai điểm
N 0;1Oy, I 2; 2 với đường tròn (C). IM
IN R 5 1 min CÂU 8: Lời giải Chọn C Ta có 2
z 2z 5 z 1 2iz 3i
1 z 1 2iz 1 2i z 1 2iz 3i 1
z 1 2i 0 .
z 1 2i z 3i 1
Trường hợp 1 : z 1 2i 0 w 1 w 1 1 .
Trường hợp 2: z 1 2i z 3i 1
Gọi z a bi (với a,b ) khi đó ta được
a b i a b i b 2 b 2 b 1 1 2 1 3 2 3 . 2 28 PMT 3 2 9 3
Suy ra w z 2 2i a 2
i w a 2 2. 2 4 2
Từ 1 , 2 suy ra min|w | 1 . CÂU 9: Lời giải Chọn B
Gọi z x yi x, y z 1 2i x 1 y 2i 2 2 2 2
Ta có: z 1 2i 5 x 1 y 2 5 x 1 y 2 5
Suy ra tập hợp điểm M x; y biểu diễn số phức z thuộc đường tròn C tâm
I 1; 2 bán kính R 5 như hình vẽ:
Dễ thấy O C , N 1; 1C .
Theo đề ta có: M x; y C là điểm biểu diễn cho sốphức z thỏa mãn:
w z 1 i x yi 1 i x 1 y 1i
z i x 2 y 2 1 1 1 MN
Suy ra z 1 i đạt giá trị lớn nhất MN lớn nhất. 29 PMT
Mà M, N C nên MN lớn nhất khi MN là đường kính đường tròn C . 2
I là trung điểm MN M z i z 2 3; 3 3 3 3 3 3 2 . CÂU 10: Lời giải Chọn B
T z i z 2 i z 1 1 i z 1 1 i .
Đặt w z 1. Ta có w 1 và T w 1 i w 1 i . 2
Đặt w x .
y i . Khi đó w 2 x 2 2 y .
T x 1 y 1i x 1 y 1i
x 2 y 2 x 2 y 2 1. 1 1 1. 1 1
x 2 y 2 x 2 y 2 2 2 1 1 1 1 1 1 2x 2 2 2 2y 4 4 Vậy maxT 4 . CÂU 11: Lời giải Chọn B. Đặt
z x iy ( x , y ) thì
z 2 3i 5 x iy 2 3i 5
x 2 y 2 2 3 5 . 2 2 2 2
P z 2 z 2 i
2 x iy i x iy 2 2
x y x 2 1 2 y
4x 2y 3.
Đặt x 2 5 sint , y 3 5 cost , t .
P 42 5sint23 5cost3 4 5sint 2 5cost 1. 2 P 2
1 4 5 sint 2 5 cost 80 20.1 10 P 1 10 11 P 9
Vậy A 11 9 2 . CÂU 12: 30 PMT Lời giải Chọn C
Gọi z a bi , a,b Ta có: 2 2 P z a b
Mà z 3 z i 2 2
Hay a ib 3 a ib i a 3 ib a b 1i a 2 b 2 3
a b 1
b 4 3a 2
Lúc đó P z 2 a 2 b 2
a a 2 4 3
10a 24a 16 24 144 2 x x 8 2 10 10 10 100 5 5 CÂU 13: Lời giải Chọn B
Gọi z x yi x, y z 1 2i x 1 y 2i . 2 2 2 2
Ta có: z 1 2i 5 x 1 y 2 5 x 1 y 2 5 . 31 PMT
Suy ra tập hợp điểm M x; y biểu diễn số phức z thuộc đường tròn C tâm
I 1; 2 bán kính R 5 như hình vẽ.
Dễ thấy O C , N 1; 1C .
Theo đề ta có: M x; y C là điểm biểu diễn cho số phức z thỏa mãn:
w z 1 i x yi 1 i x 1 y 1i
z i x 2 y 2 1 1 1 MN .
Suy ra z 1 i đạt giá trị lớn nhất MN lớn nhất.
Mà M, N C nên MN lớn nhất khi MN là đường kính đường tròn C I là 2
trung điểm MN M z i z 2 3; 3 3 3 3 3 3 2 . CÂU 14: Lời giải Chọn A
Đặt z x yi , x, y . z 2 i z 2 i 2
x 2 y
1 i 2 x 1 y 1 i . z 2 1 i z 1 i
x 2 y 2
x 2 y 2 2 1 2 1 1 . 2 x 22 y 2 1 2 x 2 1 y 2 2
x y 1 1 . 2. 2 Suy ra y
1 2 y 1 2 . 2 2 Ta có: 2
x y 2 1 2
x y 1 2 4y z 2
i 2 4y 2 41 2 6 4 2 .
z 1 6 4 2 2 2 . 32 PMT
Vậy z 1 2 2 là môđun lớn nhất của số phức z i . CÂU 15: Lời giải Chọn C
Gọi z x yi,x, y R . 2 2 2
Ta có z 1 z 2 i x 2 1
y x 2 y
1 3x y 2 0 .
Tập hợp điểm M x; y biểu diễn số phức z là đường thẳng d : 3x y 2 0 .
Để đoạn AM nhỏ nhất thì M là hình chiếu của A trên d .
d qua A và vuông góc với d có phương trình x 3y 16 0 . Tọa độ M là nghiệm
x 3y 16 0 x 1 của hệ phương trình .
3x y 2 0 y 5 Vậy M 1; 5 . ĐỀ SỐ 4
THỜI GIAN LÀM BÀI: 60 PHÚT Câu 1.
[Cụm 1 HCM - 2017] Cho số phức z thỏa điều kiện 2
z 4 zz 2i . Giá trị nhỏ
nhất của z i bằng ? A. 3. B. 4. C. 1. D. 2. Câu 2.
[SỞ GD-ĐT HÀ TĨNH L2 - 2017] Gọi T là tập hợp tất cả các số phức z thõa mãn
z i 2 và z 1 4 . Gọi z , z T lần lượt là các số phức có mô đun nhỏ nhất và 1 2
lớn nhất trong T . Khi đó z z bằng: 1 2 A. 5 . B. 4 i . C. 5 i . D. 5 i . Câu 3.
[THPT Chuyên Hà Tĩnh - 2017] Cho số phức z thỏa mãn z 3i z 3i 10 . Gọi
M , M lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M 1 2
là trung điểm của M M , M a; b biểu diễn số phức w , tổng a b nhận giá trị nào 1 2 sau đây? 33 PMT 7 9 A. . B. 5 . C. 4 . D. . 2 2 Câu 4.
[Sở Hải Dương - 2017] Cho số phức z thỏa mãn .
z z 1 . Tìm giá trị nhỏ nhất của biểu thức: P 3
z 3z z z z . 15 13 3 A. . B. 3 . C. . D. . 4 4 4 Câu 5:
(Sở Quảng Bình - 2018)Cho các số phức z , w thỏa mãn z 5 ,
w 4 3i z 1 2i . Giá trị nhỏ nhất của w là : A. 3 5 B. 4 5 C. 5 5 D. 6 5 Câu 6:
(SGD VĨNH PHÚC - 2018) Gọi z , z là các nghiệm phức của phương trình 1 2 2
z 4z 13 0 , với z có phần ảo dương. Biết số phức z thỏa mãn 1
2 z z z z , phần thực nhỏ nhất của z là 1 2 A. 6 B. 2 C. 1 D. 9 Câu 7:
[THPT Chuyên Thái Bình) Cho các số phức z , w thỏa mãn z 5 3i 3 ,
iw 4 2i 2 . Tìm giá trị lớn nhất của biểu thức T 3iz 2w . A. 554 5 B. 578 13 C. 578 5 D. 554 13 Câu 8:
(THPT THÁI PHIÊN-HẢI PHÒNG) Có tất cả bao nhiêu giá trị nguyên của m để có
đúng hai số phức z thỏa mãn z m 1 i 8 và z 1 i z 2 3i . A. 131 . B. 63 . C. 66 . D. 130 . Câu 9.
(Toán Học Tuổi Trẻ - Tháng 12 - 2017) Tìm giá trị lớn nhất của P 2 z z 2 z z 1
với z là số phức thỏa mãn z 1. 13 A. 3 . B. 3 . C. . D. 5 . 4
Câu 10. (TRƯỜNG CHUYÊN ĐẠI HỌC VINH) Trong các số phức z thỏa mãn 2 z 1 2 z
gọi z và z lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Khi đó môđun 1 2
của số phức w z z là 1 2 A. w 2 2 . B. w 2 . C. w 2 . D. w 1 2 . 34 PMT
Câu 11. (THPT Lê Hồng Phong - Nam Định) Cho số phức z và w thỏa mãn z w 3 4i
và z w 9 . Tìm giá trị lớn nhất của biểu thức T z w .
A. maxT 176 .
B. maxT 14 . C. maxT 4 . D. maxT 106 .
Câu 12: (Chuyên Thái Bình) Cho số phức z thỏa mãn 1 i z 2 1 i z 2 4 2 . Gọi 2018
m max z , n min z và số phức w m ni . Tính w A. 1009 4 . B. 1009 5 . C. 1009 6 . D. 1009 2 .
Câu 13: (THPT Đặng Thúc Hứa - Nghệ An) Cho số phức z thỏa mãn
5 z i z 1 3i 3 z 1 i . Tìm giá trị lớn nhất M của z 2 3i ? A. M 10 B. M 1 13 C. M 4 5 D. M 9 3
Câu 14: (THPT Chuyên Hà Tĩnh) Cho số phức z thỏa mãn z 1 i 1 , số phức w thỏa mãn
w 2 3i 2 . Tìm giá trị nhỏ nhất của z w . A. 13 3 B. 17 3 C. 17 3 D. 13 3
Câu 15: [THPT Lê Hồng Phong-HCM] Cho số phức z thỏa z 1. Gọi m , M lần lượt là giá
trị nhỏ nhất, giá trị lớn nhất của biểu thức P 5 z 3 z z 4 6
2 z 1 . Tính M m .
A. m 4 , n 3 .
B. m 4 , n 3
C. m 4 , n 4 . D. m 4 , n 4 .
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 4 CÂU 1: Lời giải Chọn C
Giả sử z x yi x, y . z
zz i z i2 2 2 4 2 2
zz 2i z 2iz 2i zz 2i
z 2i 0 1 . z 2i z 2 35 PMT
1 z 2i . Suy ra z i 2i i i 1. 2
2 x yi i x yi 2
x y 2 x 2 y 2 x 2
y y 2 x 2 2 2 4 4 y y 1. 2
Suy ra z i x yi i 2
x y 2 1
x 4 2 , x .
Vậy giá trị nhỏ nhất của z i bằng 1 . CÂU 2: Lời giải Chọn C .
Đặt z x yi khi đó ta có: z i 2
x y 1i 2
x y 12 2 4 . z 1 4 x 1 2 yi 4 x 1 2 y 16
Vậy T là phần mặt phẳng giữa hai đường tròn C
tâm I 0; 1 bán kính r 2 và 1 1 1
đường tròn C tâm I 1; 0 bán kính r 4 . 2 2 2
Dựa vào hình vẽ ta thấy z 0 i, z 5 là hai số phức có điểm biểu diễn lần lượt là 1 2
M 0; 1 , M 5; 0 có mô-đun nhỏ nhất và lớn nhất. Do đó z z i 5 5 i . 1 2 1 CÂU 3: Lời giải 36 PMT Chọn D .
Gọi z x yi , x, y . Theo giả thiết, ta có z 3i z 3i 10 .
x y 3i x y 3i 10 .
x y 2 x y 2 2 2 3 3 10 .
Gọi Ex; y , F 0; 3 và F 0; 3 . 2 1
Khi đó MF MF 10 F F 6 nên tập hợp các điểm E là đường elip E 1 2 1 2
có hai tiêu điểm F và F . Và độ dài trục lớn bằng 10 . 1 2
Ta có c 3 ; 2b 10 b 5 và 2 a 2 b 2 c 16 . 2 2 x y
Do đó, phương trình chính tắc của E là 1 . 16 25
Vậy max z OB
OB 5 khi z 5i có điểm biểu diễn là M 0; 5 . 1
và min z OA
OA 4 khi z 4 có điểm biểu diễn là M 4; 0 . 2 5
Tọa độ trung điểm của M M là M 2; . 1 2 2 5 9
Vậy a b 2 . 2 2 CÂU 4: Lời giải 37 PMT Chọn D
Gọi z a bi , với a,b . 2
Ta có: z z 2a ; .
z z 1 z 1 z 1. z Khi đó P 3
z z z z z 2 3 z z 3 z z . z 2 2 z P z . z 3
z z 2 z 2zz 2
z 1 z z . 2 z 2 P z z2 1
z z 2 a a 2
a a 2 a 3 3 1 4 1 2 4 1 2 . 2 4 4 3 Vậy P . min 4 CÂU 5: Lời giải Chọn B w 1 2i
Theo giả thiết ta có w 4 3i
z 1 2i z . 4 3i w 1 2i Mặt khác z 5
5 w 1 2i 5 5 . 4 3i
Vậy tập hợp điểm biễu diễn số phức w là đường tròn tâm I 1; 2 và bán kính 5 5 .
Do đó min w R OI 4 5 . CÂU 6: Lời giải Chọn B Ta có 2
z 4z 13 0 z 2 3i hoặc z 2 3i . 1 2
Gọi z x i
y , với x, y . 38 PMT 2 2 2 2
Theo giả thiết, 2 z z z z 2 x 2 y 3 x 2 y 3 1 2 2 2
x 22 y 32
x 22 y 32 4
x 2 y 5 16.
Suy ra tập hợp các điểm biểu diễn số phức z là miền trong của hình tròn C có tâm
I 2; 5 , bán kính R 4 , kể cả hình tròn đó.
Do đó, phần thực nhỏ nhất của z là x 2 . min CÂU 7: Lời giải Chọn D
z 5 3i 3 3iz 15i 9 9 là đường tròn có tâm I 9;15 và R 9 .
iw 4 2i 2 2w 8i 4 4 là đường tròn có tâm J 4; 8 và R 4 .
T 3iz 2w đạt giá trị lớn nhất khi T IJ R R 554 13 . CÂU 8: Lời giải Chọn C
- Đặt z x yi , với x , y . 2 2
- Từ giả thiết z m 1 i 8 x m
1 y 1 64 , do đó tập hợp các
điểm M biểu diễn số phức z là đường tròn T có tâm I m 1; 1 , bán kính R 8 . 2 2 2 2
- Từ giả thiết z 1 i z 2 3i x 1 y
1 x 2 y 3 39 PMT
2x 8y 11 0 hay M nằm trên đường thẳng : 2x 8y 11 0.
- Yêu cầu bài toán cắt T tại 2 điểm phân biệt 2m 1 8 11
dI; R
8 2m 21 16 17 2 17 21 16 17 21 m
16 17 , do m nên m22;21;...;42; 43 . 2 2
Vậy có tất cả 66 giá trị của m thỏa mãn yêu cầu bài toán. CÂU 9: Lời giải Chọn C
Đặt z a bi a,b . Do z 1 nên 2 a 2 b 1. 2 Sử dụng công thức: .
u v u v ta có: 2
z z z z z a 2 1 1 1
b 2 2a .
z z a bi2 a bi a b a ab bi a b a 2 ab b2 2 2 2 2 2 1 1 1 2 1 2 a a
b a 2 2 2 2 (2 1) 2 1 2a 1 (vì 2 a 2 b 1).
Vậy P 2a 1 2 2a . TH1: a 1 . 2
Suy ra P 2a 1 2 2a 2 2a 2 2a 3 4 2 3 3 (vì 0 2 2a 2 ). TH2: a 1 . 2 2 1 1 13 Suy ra P 2a 1 2 2a 2 2a
2 2a 3 2 2a 3 . 2 4 4 Xảy ra khi a 7 . 16 CÂU 10: Lời giải Chọn A 40 PMT 2
Đặt z a bi a,b thì 2
z 1 2 z a bi 1 2 a bi 2 2 a 2
b 1 2abi 2 a bi 2 a 2 b 2 2 a b 2 a 2 1 4 4 b 2 4 a 4 b 2 a 2 b 2 2 1 2 6 2a b 0 2 a 2 b 2 1 4b 0 2 a 2
b b 2 a 2 1 2
b 1 2b 0 2 a 2
b 1 2b 0 2 a 2
b 1 2b 0 2 TH1: 2 a 2
b 1 2b 0 2
a b 1 2 .
Khi đó tập hợp điểm M a; b biểu diễn số phức z là đường tròn có tâm I 0;1 , bán 1
kính R 2 , giao điểm của OI (trục tung) với đường tròn là M 0; 2 1 và 1 M 0;1 2 2 w 2
1 i 1 2i w 2i w 2 2 TH2: 2 a 2
b 1 2b 0 2
a b 1 2 .
Khi đó tập hợp điểm M a; b biểu diễn số phức z là đường tròn có tâm I 0; 1 , 2
bán kính R 2 , giao điểm của OI (trục tung) với đường tròn là M 0; 2 1 và 3 M 0; 2 1 4 w 2
1 i 1 2i w 2i w 2 . CÂU 11: Lời giải Chọn D
Đặt z x yi x, y . Do z w 3 4i nên w 3 x 4 yi . 41 PMT
Mặt khác z w 9 nên
z w x 2 y 2 2 x 2 2 3 2 4 4
4y 12x 16y 25 9 2 2 2 x 2 2
2y 6x 8y 28 1 . Suy ra T z w 2 x 2
y 3 x 4 y .
Áp dụng bất đẳng thức Bunyakovsky ta có 2 T 2 x 2 2 2
2y 6x 8y 25 2 . 2 2
Dấu " " xảy ra khi 2 x 2
y 3 x 4 y .
Từ 1 và 2 ta có 2
T 2.28 25 106 T 106 . Vậy MaxT 106 . CÂU 12: Lời giải Chọn C
Ta có 1 i z 2 1 i z 2 4 2 z 1 i z 1 i 4 .
Gọi M là điểm biểu diễn của số phức z , F 1;1 là điểm biểu diễn của số phức 1
z 1 i và F 1; 1 là điểm biểu diễn của số phức z 1 i . Khi đó ta có 2 1 2
MF MF 4 . Vậy tập hợp điểm M biểu diễn số phức z là Elip nhận F và F làm 1 2 1 2 hai tiêu điểm.
Ta có F F 2c 2c 2 2 c 2 . 1 2
Mặt khác 2a 4 a 2 suy ra b 2 a 2 c 4 2 2 .
Do đó Elip có độ dài trục lớn là A A 2a 4 , độ dài trục bé là B B 2b 2 2 . 1 2 1 2
Mặt khác O là trung điểm của AB nên m max z maxOM OA a 2 và 1
n min z minOM OB b 2 . 1 2018
Do đó w 2 2i suy ra w 6 w 1009 6 . CÂU 13: Lời giải
Gọi A 0;1 , B1; 3 ,C 1; 1 . Ta thấy A là trung điểm của BC 42 PMT 2 MB 2 2 2 2 MC BC BC MA 2 MB 2 MC 2 MA 2 2 2MA 10 . 2 4 2
Ta lại có : 5 z i z 1 3i 3 z 1 i
MA MB MC 2 MB 2 5 3 10. MC 2 MA 2 25
10 2MA 10 MC 2 5
Mà z 2 3i z i 2 4i z i 2 4i z i 2 5 4 5 . z i 2 5
Dấu " " xảy ra khi a b
, với z a bi ; a, b . 1 2 4
z 2 3i loai . z 2 5i CÂU 14: Lời giải Chọn B
Gọi M x; y biểu diễn số phức z x iy thì M thuộc đường tròn C có tâm 1
I 1;1 , bán kính R 1 . 1 1
N x; y biểu diễn số phức w x i
y thì N thuộc đường tròn C có tâm 2
I 2; 3 , bán kính R 2 . Giá trị nhỏ nhất của z w chính là giá trị nhỏ nhất của 2 2 đoạn MN .
Ta có I I 1; 4 I I 17 R R C và C ở ngoài nhau. 2 1 1 2 1 2 1 2 MN
I I R R 17 3 min 1 2 1 2 CÂU 15: Lời giải Chọn A Vì z 1 và 2 . z z z nên ta có 1 z . z 43 PMT Từ đó, P 5 z 3 z z 4 6 2 z 1 4 z z 4 z 4 6 2 z 1 4 z 4 z 4 6 2 z 1 . Đặt 4
z x iy , với x, y . Do z 1 nên 4 z 2 x 2
y 1 và 1 x, y 1. 2
Khi đó P x iy x iy 6 2 x iy 1 x x 2 2 6 2 1 y 2
2x 6 2 2x 2 2x 2 1 3.
Do đó P 3 . Lại có 1 x 1 0 2x 2 2 1 2x 2 1 1 P 4 . Vậy M 4 khi 4
z 1 và m 3 4 1 3 khi z
i . Suy ra M m 1. 2 2 ĐỀ SỐ 5
THỜI GIAN LÀM BÀI: 90 PHÚT Câu 1:
(THPT Hậu Lộc 2 - Thanh Hóa) Cho hai số phức z , z thỏa mãn z 1 i 2 và 1 2 1
z iz . Tìm giá trị nhỏ nhất m của biểu thức z z ? 2 1 1 2
A. m 2 1 . B. m 2 2 . C. m 2 . D. m 2 2 2 Câu 2:
(SGD Hà Nam - Năm) Xét các số phức z a bi , a,b thỏa mãn 1
z z i iz z 2 4 15
1 . Tính F a 4b khi z 3i đạt giá trị nhỏ nhất 2 A. F 7 . B. F 6 . C. F 5 . D. F 4 . Câu 3.
(SỞ GD VÀ ĐT HƯNG YÊN NĂM 2018) Xét số phức z và số phức liên hợp của nó
có điểm biểu diễn là M , M . Số phức z 4 3i và số phức liên hợp của nó có điểm biểu
diễn lần lượt là N , N . Biết rằng M , M , N , N là bốn đỉnh của hình chữ nhật. Tìm
giá trị nhỏ nhất của z 4i 5 . 1 4 5 2 A. . B. . C. . D. . 2 13 34 5 Câu 4:
CHUYÊN VINH LẦN 3-2018) Cho các số phức w , z thỏa mãn 3 5 w i và 5
5w 2 iz 4 . Giá trị lớn nhất của biểu thức P z 1 2i z 5 2i bằng 44 PMT A. 6 7 . B. 4 2 13 . C. 2 53 . D. 4 13 . Câu 5:
(THPT Chuyên Quốc Học Huế) Cho z x yi với x , y là số phức thỏa mãn
điều kiện z 2 3i z i 2 5 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức P 2 x 2
y 8x 6y . Tính M m . 156 156 A. 20 10 . B. 60 20 10 . C. 20 10 .
D. 60 2 10 . 5 5 Câu 6:
(THPT HAU LOC 2_THANH HOA) Cho các số phức z , z , z thỏa mãn 1 2
z 4 5i z 1 và z 4i z 8 4i . Tính M z z khi P z z z z 1 2 1 2 1 2
đạt giá trị nhỏ nhất. A. 41 . B. 6 . C. 2 5 . D. 8 . Câu 7:
[SGD NINH BINH] Xét các số phức z a bi ( a , b
) có môđun bằng 2 và phần 2018
ảo dương. Tính giá trị biểu thức S 5a b 2 khi biểu thức
P 2 z 3 2 z đạt giá trị lớn nhất. A. S 1 . B. S 2018 2 . C. S 1009 2 . D. S 0 . Câu 8:
(Sở GD Thanh Hoá) Cho số phức z thỏa mãn z 2i 1 z 2i 1 10 . Gọi M
, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Tính tổng S M m . A. S 9 . B. S 8 . C. S 2 21 . D. S 2 21 1. Câu 9.
(SỞ GD-ĐT HẬU GIANG) Cho hai số phức z, z thỏa mãn z 5 5 và
z 1 3i z 3 6i . Tìm giá trị nhỏ nhất của z z . 5 5 A. . B. . C. 10 . D. 3 10 . 2 4
Câu 10. (Chuyên Thái Nguyên) Tìm số phức z thỏa mãn z 1 i 5 và biểu thức
T z 7 9i 2 z 8i đạt giá trị nhỏ nhất.
A. z 5 2i .
B. z 1 6i .
C. z 1 6i và z 5 2i .
D. z 4 5i . 45 PMT
Câu 11: [Đề thi thử-Liên trường Nghệ An] Biết rằng hai số phức z , z thỏa mãn 1 2 1
z 3 4i 1 và z 3 4i
. Số phức z có phần thực là a và phần ảo là b thỏa 1 2 2
mãn 3a 2b 12 . Giá trị nhỏ nhất của P z z z 2z 2 bằng: 1 2 9945 9945 A. P . B. P 5 2 3 . C. P . D. min 11 min min 13 P 5 2 5 . min
Câu 12: (THPT Chuyên Võ Nguyên) Cho số phức z , z thỏa mãn z 12 và z 3 4i 5 1 2 1 2
. Giá trị nhỏ nhất của z z là: 1 2 A. 0 . B. 2 C. 7 D. 17
Câu 13: (THPT Ninh Giang - Hải Dương) Cho các số phức z thỏa mãn z 4 3i 2 . Giả
sử biểu thức P z đạt giá trị lớn nhất, giá trị nhỏ nhất khi z lần lượt bằng
z a b i a ,b
và z a b i a ,b
. Tính S a a 2 2 1 1 1 1 1 2 2 2 1 2 A. S 4 . B. S 6 . C. S 8 . D. S 10 .
Câu 14: (THPT Ninh Giang - Hải Dương) Cho các số phức z thỏa mãn 2
z 4 z 2iz 1 2i . Tìm giá trị nhỏ nhất của P z 3 2i . 7 A. P 4 . B. P 2 . C. P . D. P 3 . min min min 2 min
Câu 15: (THPT Ninh Giang - Hải Dương) Cho các số phức z thỏa mãn
z 1 i z 8 3i 53 . Tìm giá trị lớn nhất của P z 1 2i . 185 A. P 53. B. P . C. P 106 . D. max max 2 max P 53 max
Câu 16: (SGD - Quảng Nam - Lần 1) Cho số phức z thỏa mãn z 2 . Giá trị nhỏ nhất của
biểu thức P 2 z 1 2 z 1 z z 4i bằng: A. 4 2 3 . B. 2 3 . C. 14 4 . D. 7 2 . 15 15 46 PMT
Câu 17: (PTNK Cơ Sở 2 - TPHCM) Nếu z là số phức thỏa z z 2i thì giá trị nhỏ nhất của
z i z 4 là A. 2 . B. 3 . C. 4 . D. 5 .
Câu 18: (THPT Vũng Tàu - BRVT) Cho số phức z thỏa mãn z 1 i z 3i và số phức 1 w
. Tìm giá trị lớn nhất của w . z 4 5 2 5 9 5 A. w . B. w . C. w . D. max 7 max 7 max 10 w 7 5 . max 10
Câu 19. [THPT Hoàng Văn Thụ] Cho z , z
là hai nghiệm của phương trình 1 2 8
6 3i iz 2z 6 9i , thỏa mãn z z
. Giá trị lớn nhất của z z bằng. 1 2 5 1 2 31 56 A. . B. 4 2 . C. 5. D. . 5 5
Câu 20: (THPT-Chuyên Ngữ Hà Nội) Cho hai số phức z , z thỏa mãn z 3i 5 2 và 1 2 1
iz 1 2i 4 . Tìm giá trị lớn nhất của biểu thức T 2iz 3z . 2 1 2 A. 313 16 . B. 313 . C. 313 8 . D. 313 2 5 .
Câu 21: (Chuyên Vinh - Lần 1 - 2018) Giả sử z , z là hai trong số các số phức z thỏa mãn 1 2
iz 2 i 1 và z z 2 . Giá trị lớn nhất của z z bằng 1 2 1 2 A. 4 . B. 2 3 . C. 3 2 . D. 3 .
Câu 22: (SGD VĨNH PHÚC) Cho hai số phức u , v thỏa mãn 3 u 6i 3 u 1 3i 5 10 ,
v 1 2i v i . Giá trị nhỏ nhất của u v là: 10 2 10 5 10 A. B. C. 10 D. 3 3 3 Câu 23:
(THPT Kim Liên-Hà Nội)
Xét các số phức zV a bi ( a,b ) thỏa mãn ũ
z 3 2i 2 . Tính a b khi z 1 2i 2 z 2 5i đạt giá trị nhỏ nhất. V ă A. 4 3 . B. 2 3 . C. 3 . D. 4 3 . n B ắ c 47 PMT
Câu 24: (THPT Sơn Tây - Hà Nội) Gọi n là số các số phức z đồng thời thỏa mãn
iz 1 2i 3 và biểu thức T 2 z 5 2i 3 z 3i đạt giá trị lớn nhất. Gọi M là
giá trị lớn nhất của T . Giá trị tích của . M n là A. 10 21 B. 6 13 C. 5 21 D. 2 13
ĐÁP ÁN CHI TIẾT ĐỀ SỐ 5 CÂU 1: Lời giải Chọn D
Đặt z a bi; a,b
z b ai 1 2
z z a b b a i . 1 2 2 2 Nên z z a b b a 2. z 1 2 1
Ta lại có 2 z 1 i z 1 i z 2 1 1 1
z 2 2 . Suy ra z z 2. z 2 2 2 . 1 1 2 1 a b Dấu " " xảy ra khi 0 . 1 1
Vậy m min z z 2 2 2 . 1 2 CÂU 2: Lời giải Chọn A Ta có 2
z z i iz z 2 4 15
1 4a bi a bi 15i i a bi a bi 1 b a 2 8 15 2 1 suy ra b 15 . 8
z 1 3i 1 2a 12 2b 62 1 8b 15 2
4b 24b 36 1 2
4b 32b 21 2 2 2 2 48 PMT
Xét hàm số f x 2
4x 32x 21 với x 15 8 15
f x x x 15 8 32 0,
suy ra f x là hàm số đồng biến trên ; nên 8 8 f x 15 f 4353 . 8 16 1 1 4353 15 1 Do đó z
3i đạt giá trị nhỏ nhất bằng khi b ; a . 2 2 16 8 2
Khi đó F a 4b 7 . CÂU 3: Lời giải Chọn A
Gọi z a bi M a; b , Ma; b .
Ta có: z 4 3i a bi4 3i 4a 3b 3a 4bi
N 4a 3b;3a 4b,N4a 3b;3a 4b.
Vì MM và NN cùng vuông góc với trục Ox nên M , M , N , N là bốn đỉnh của
b2 a b2 2 6 8
MM NN hình chữ nhật khi
3a 3b.0 3a 3b.2b 0 MN MM
b 0,3a4b 0 a b 0 .
b 0, 3a 4b 0 2 2 2 2
Khi đó: z 4i 5 a 5 b 4i a 5 b 4 a 5 4 a 9 2 2 1 1
2a 18a 41 2 a . 2 2 2 1 9 9
Vậy giá trị nhỏ nhất của z 4i 5 là khi a b . 2 2 2 49 PMT CÂU 4: Lời giải Chọn C
Gọi z x i
y , với x, y . Khi đó M x; y là điểm biểu diễn cho số phức z .
Theo giả thiết, 5w 2 iz 4 5w i 2 iz 4 5i
2 iw i z 3 2i 2 2
z 3 2i 3 . Suy ra M x; y thuộc đường tròn C : x 3 y 2 9 .
Ta có P z 1 2i z 5 2i MA MB , với A 1; 2 và B5; 2 .
Gọi H là trung điểm của AB , ta có H 3; 2 và khi đó:
P MA MB 2 2 2 MA MB hay P 2 MH 2 4 AB .
Mặt khác, MH KH với mọi M C nên P 2 KH 2 4 AB 2 2 4 IH R AB 2 53 . M K 3 11 Vậy P 2 53 khi
hay z 3 5i và w i . max MA MB 5 5 CÂU 5: Lời giải Chọn B 50 PMT 6 y 4 2 B x 2 x 15 10 5 -1 5 10 15 -1 I 2 K J 4 6 A 8 10
- Theo bài ra: z 2 3i z i 2 5
x 2 y 2 x 2 y 2 2 3 2 1 5
2x y 2 0
x22 y 21 25
tập hợp điểm biểu diễn số phức z là miền mặt phẳng T thỏa mãn
2x y 2 0
x22 y 2 1 25
- Gọi A 2; 6 , B2; 2 là các giao điểm của đường thẳng 2x y 2 0 và đường 2 2
tròn C : x 2 y 1 25 . 2 2 - Ta có: P 2 x 2
y 8x 6y x 4 y 3 P 25 .
Gọi C là đường tròn tâm J 4; 3 , bán kính R P 25 .
- Đường tròn C cắt miền T khi và chỉ khi
JK R JA IJ IK R IA 2 10 5 25 P 3 5
40 20 10 P 20
M 20 và m 40 20 10 .
Vậy M m 60 20 10 . CÂU 6: 51 PMT Lời giải Chọn C
Gọi I 4; 5 , J 1; 0 .
Gọi A, B lần lượt là các điểm biểu diễn số phức z , z . 1 2
Khi đó A nằm trên đường tròn tâm I bán kính R 1 , B nằm trên đường tròn tâm J bán kính R 1 .
Đặt z x yi , x, y . Ta có:
z 4i z 8 4i
x yi 4i x yi 8 4i
x y2 x 2 y 2 2 4 8 4
16x 16y 64 0
: x y 4 0
Gọi C là điểm biểu diễn số phức z thì C .
Ta có: P z z z z CA CB . 1 2 1 0 4 3 dI 4 5 4 5 ,
1 R , dJ, 1 R . 2 2 2 2 1 1 2 2 1 1
x y 4x y 4 454104 0 hai đường tròn không cắt và I I J J nằm cùng phía với .
Gọi A là điểm đối xứng với A qua , suy ra A nằm trên đường tròn tâm I bán 1 1 1
kính R 1 (với I là điểm đối xứng với I qua ). Ta có I 9; 0 . 1 1 52 PMT A A
Khi đó: P CA CB CA CB A B nên P A B 1 . 1 1 min 1 min B B 1 7 Khi đó: I A
I J A8; 0 ; I B I J B 2; 0 . 1 1 8 1 1 8 A4;4 Như vậy: P khi A đối xứng A qua và B B . Vậy min B2;0
M z z AB 20 2 5 . 1 2 CÂU 7: Lời giải Chọn D
z a bi ; z 2 2 a 2 b 2 2 a 2 b 4. 2 2
P 2 z 3 2 z a 2 b a 2 2 3 2
b 4a 8 3 8 4a .
4a 8 3 8 4a 2 2 1
3 8 4a 8 4a 4 10 . 4a 8 a
Dấu đẳng thức xẩy ra khi
8 4 94a 8 8 4a a 8 . 1 3 5
Với a 8 b 6 (do b 0 ). 5 5 2018 8 6 8 6
Vậy min P 4 10 z i . Khi đó S 5 2 0 . 5 5 5 5 CÂU 8: Lời giải Chọn C
Giả sử z a bi , a,b z a bi .
Chia hai vế cho i ta được: z 2 i z 2 i 10 .
Đặt M a ; b , N a ; b , A2 ;1 , B2 ; 1 , C 2 ;1 NB MC . 53 PMT 2 2 X Y
Ta có: MA MC 10 M E : 1. 25 21
Elip này có phương trình chính tắc với hệ trục tọa độ IXY , I 0 ;1 là trung điểm AC . X x x y 2 2 1
Áp dụng công thức đổi trục . Y y 1 1 25 21 a 5sin t 2 Đặt , t 0 ; 2 2 2 2 z OM a b b 1 21 cos t 2 2
25 sin t 1 21 cost 2 26
4cos t 2 21 cost . a 0 z
1 21 cost 1 . max b 1 21 a 0 z
1 21 cost 1 . min b 1 21
M m 2 21 . CÂU 9: Hướng dẫn giải Chọn A 54 PMT
Gọi M x; y là điểm biểu diễn của số phức z x yi , N x; y là điểm biểu diễn
của số phức z x y i . 2 Ta có z
x yi x 2 y 2 5 5 5 5 5 5 . 2
Vậy M thuộc đường tròn C x 2 y 2 : 5 5
z 1 3i z 3 6i
x 1 y 3i
x 3 y 6i x 2 y 2 x 2 y 2 1 3 3 6 8 x 6 y 35
Vậy N thuộc đường thẳng : 8x 6y 35
Dễ thấy đường thẳng không cắt C và z z MN
Áp dụng bất đẳng thức tam giác, cho bộ ba điểm I, M, N ta có. 8. 5 6.0 5 5
MN IN IM IN R IN R d I, R 5 0 2 2 2 8 6
Dấu bằng đạt tại M M ; N N . 0 0 CÂU 10: Lời giải Chọn B 55 PMT M I K A M0 B
Từ giả thiết z 1 i 5 suy ra tập hợp các điểm M biểu diễn số phức z là đường tròn (C)
tâm I 1;1 , bán kính R 5 .
Xét các điểm A 7; 9 và B0; 8 . Ta thấy IA 10 2.IM . 5
Gọi K là điểm trên tia IA sao cho IK 1 IA K ; 3 4 2 IM IK Do
1 , góc MIK chung IKM ∽ IMA c.g.c IA IM 2
MK IK 1 MA 2.MK . MA IM 2
Lại có: T z 7 9i 2 z 8i MA 2.MB 2 MK MB 2.BK 5 5
T 5 5 M BK C , M nằm giữa B và K x 5 0 . min M 2
Ta có: phương trình đường thẳng BK là: 2x+y-8=0 x 1
2x y 8 0 y 6
Tọa độ điểm M là nghiệm của hệ: M 1;6 . x 2 1 y 2 1 25 x 5 y 2
Vậy z 1 6i là số phức cần tìm. CÂU 11:
Hướng dẫn giải Chọn C
Gọi M , M , M lần lượt là điểm biểu diễn cho số phức z , 2z , z trên hệ trục tọa 1 2 1 2
độ Oxy . Khi đó quỹ tích của điểm M là đường tròn C
tâm I 3; 4 , bán kính 1 1 R 1 ;
quỹ tích của điểm M là đường C
tròn tâm I 6; 8 , bán kính R 1 ; 2 2
quỹ tích của điểm M là đường thẳng d : 3x 2y 12 0 .
Bài toán trở thành tìm giá trị nhỏ nhất của MM MM 2 . 1 2 56 PMT y I2 8 I3 B I A 1 M 4 O 3 6 x 138 64 Gọi C có tâm I ;
, R 1 là đường tròn đối xứng với C qua d . Khi 2 3 3 13 13
đó min MM MM 2 min MM MM 2 với M C . 3 3 1 2 1 3
Gọi A , B lần lượt là giao điểm của đoạn thẳng I I với C , C . Khi đó với mọi 3 1 1 3
điểm M C , M C
, M d ta có MM MM 2 AB 2 , dấu "=" xảy ra 3 3 1 1 1 3 9945
khi M A, M B. Do đó P
AB 2 I I 2 2 I I . 1 3 min 1 3 1 3 13 CÂU 12: Lời giải Chọn B
Gọi z x y i và z x y i , trong đó x , y , x , y
; đồng thời M x ; y 1 1 1 1 1 1 2 2 2 1 1 2 2 và M x ; y
lần lượt là điểm biểu diễn các số phức z , z . 2 2 2 1 2 2 x 2 y 144 1 1
Theo giả thiết, ta có: . 2 2 x 3 y 4 25 2 2
Do đó M thuộc đường tròn C
có tâm O 0; 0 và bán kính R 12 , M thuộc 1 1 1 2 đường tròn C
có tâm I 3; 4 và bán kính R 5 . 2 2
OC2 Mặt khác, ta có nên C chứa trong C . 1 2
OI 5 7 R R 1 2 57 PMT M1 M (C 2 2) I O (C1)
Khi đó z z M M . Suy ra z z M M
M M R 2R 2 . 1 2 1 2 1 2 1 2 min min 1 2 1 2 CÂU 13: Lời giải Chọn C
Gọi z a bi , a,b
z 4 3i 2 a ib 4 3i 2 a 4 b 3i 2
a 2 b 2 4 3 4
Khi đó tập hợp các điểm M a; b biểu diễn số phức z a bi thuộc vào đường tròn
C có tâm I4;3, R 2. Ta có OI 2 2 3 4 5 . Suy ra z
OI R 5 2 7 , z
OI R 5 2 3. max min
Gọi là đường thẳng qua hai điểm OI ta có
phương trình của : 3x 4y 0 . Gọi M và N lần lượt là hai giao điểm của và C
sao cho OM 3 và ON 7 khi đó 3 12 9
OM OI M ; z 28 21 i 5 5 5 1 28 12 5 5 S 8 . 7 28 21 12 9 5 5
ON OI N ; z i 5 5 5 2 5 5 CÂU 14: Lời giải Chọn D 58 PMT Ta có 2
z 4 z 2iz 1 2i z 2i z 2i z 1 2i 0
z 2i 0 .
z 2i z 1 2i
Do đó tập hợp các điểm N biểu diễn số phức z trên mặt phẳng tọa độ Oxy là điểm
A 0; 2 và đường trung trực của đoạn thẳng BC với B0; 2 , C 1; 2 . 1
Ta có BC 1; 0 , M ; 0 là trung điểm BC nên phương trình đường trung trực 2
của BC là : 2x 1 0 .
Đặt D 3; 2 , DA 3 , dD 7 , . 2
Khi đó P z 3 2i DN , với N là điểm biểu diễn cho z .
Suy ra min P minDA,dD, 3 . CÂU 15: Lời giải Chọn C
Xét A 1;1 , B8; 3 ta có AB 53
các điểm biểu diễn z là đoạn thẳng AB
P z 1 2i MM với M là điểm biểu diễn số phức z , M là điểm biểu diễn số phức
z 1 2i
Phương trình đường thẳng AB : 2x 7y 5 0 87 13
Hình chiếu vuông góc của M lên AB là M ; 1 53 53
Ta có A nằm giữa M và B nên P MM lớn nhất MM lớn nhất 1 1
M B z 8 3i P 106 . max CÂU 16: Lời giải Chọn A
Gọi z x yi, x, y . Theo giả thiết, ta có z 2 x 2 2 y 4 .
Suy ra 2 x, y 2 . 59 PMT 2 2 2 2
Khi đó, P 2 z 1 2 z 1 z z 4i 2
x 1 y x 1 y y 2 P 2 x 12 y 1 x2 2 2 y y 2 2
2 2 1 y 2 y .
Dấu “ ” xảy ra khi x 0 .
Xét hàm số f y 2
2 1 y 2 y trên đoạn 2; 2 , ta có: 2y 1 2 2y y f y 1
; f y y 1 0 . 1 2 y 1 2 y 3 1 Ta có f
2 3 ; f 2 4 2 5 ; f 2 2 5 . 3
Suy ra min f y 2 3 khi y 1 . 2; 2 3
Do đó P 22 3 4 2 3 . Vậy P 4 2 3 khi z 1 i . min 3 CÂU 17: Lời giải Chọn D
Đặt z x yi với x , y
theo giả thiết z z 2i y 1. d
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng d .
Gọi A 0;1 , B4; 0 suy ra z i z 4 P là tổng khoảng cách từ điểm M x; 1
đến hai điểm A , B .
Thấy ngay A 0;1 và B4; 0 nằm cùng phía với d . Lấy điểm đối xứng với A 0;1
qua đường thẳng d ta được điểm A0; 3 .
Do đó khoảng cách ngắn nhất là A B 2 2 3 4 5 . CÂU 18: Lời giải Chọn B. 60 PMT
Đặt z a bi a,b .
z i z i a 2 b 2 a b 2 2 1 3 1 1
3 a b 7 2 . 2 2 7 2 7 49 49 2 2 z a b 2b 2 b 2 5b 14b 5 b 7 2 4 5 20 2 5 1 w
1 2 5 . Đẳng thức xảy ra khi b 7 và a 63 . z z 7 5 10 2 5 Vậy w . max 7 min|w | 1 . CÂU 19: Lời giải Chọn D
Đặt z a bi , a, b . Ta có
i iz z i 2 a 2 6 3 2 6 9
b 6a 8b 24 0 . z 3 4i 1 2 2 1
a 3 b 4 1 z 3 4i 1 . z 3 4i 1 2 2 2 hbh 2 2
Ta lại có: 2 z 3 4i z 3 4i z z z z 6 8i . 1 2
1 2 1 2
64 z z 6 2 1 1 6 8i z z 6 8i . 1 2 2 1 2 2 25 5 6 56
Ta có: z z z z 6 8i 6 8i z z 6 8i 6 8i 10 . 1 2 1 2 1 2 5 5 CÂU 20: Lời giải Chọn A 61 PMT
Ta có z 3i 5 2 2iz 6 10i 4 1 ; iz 1 2i 4 3z 6 3i 12 2 2 1 1 2.
Gọi A là điểm biểu diễn số phức 2iz , B là điểm biểu diễn số phức 3z . Từ 1 và 1 2
2 suy ra điểm A nằm trên đường tròn tâm I 6;10 và bán kính R 4; điểm 1 1
B nằm trên đường tròn tâm I 6; 3 và bán kính R 12 . 2 2 B A I I 2 1
Ta có T 2iz 3z AB I I R R 2 12 2
13 4 12 313 16 . 1 2 1 2 1 2
Vậy maxT 313 16 . CÂU 21: Lời giải Chọn A
Ta có iz 2 i 1 z 1 i 2 1. Gọi z 1 i 2 có điểm biểu diễn là 0 I 1; 2.
Gọi A , B lần lượt là các điểm biểu diễn của z , z . Vì z z 2 nên I là trung 1 2 1 2 điểm của AB .
Ta có z z OA OB 2 OA OB 4OI AB 16 4 . 1 2 2 2 2 2
Dấu bằng khi OA OB . CÂU 22: Lời giải Chọn B 62 PMT
Ta có: 3 u 6i 3 u 1 3i 5 10 u i u i 5 10 6 1 3 S 3
MF MF 5 10 . 1 2 3
u có điểm biểu diễn M thuộc elip với hai tiêu điểm F 0;6 , F 1; 3 , tâm 1 2 1 9
I ; và độ dài trục lớn là a 5 10 2
a 5 10 . 2 2 3 6
F F 1; 3 F F : 3x y 6 0 . 1 2 1 2
Ta có: v 1 2i v i v i NA NB
v có điểm biểu diễn N thuộc đường thẳng d là trung trực của đoạn AB với
A 1; 2 , B0;1 . 1 1
AB 1; 3 , K ;
là trung điểm của AB d : x 3y 2 0 . 2 2 1 27 2
d I d 2 2 3 10 , 2 2 2 1 3
Dễ thấy F F d u v
MN dI d a 2 10 min min , . 1 2 3 CÂU 23: Lời giải Chọn D Cách 1:
Đặt z 3 2i w với w x yi x, y . Theo bài ra ta có w 2 x 2 2 y 4 . Ta có
P z i z i w
w i x 2 y x 2 y 2 2 1 2 2 2 5 4 2 1 3 4 2 1 3 x
x 2 y 2 x
x 2 y 2 20 8 2 1 3 2 5 2 2 1 3 2 x y 2x 1
x 12 y 32 2 x 12 y
x 12 y 32 2 2 2 63 PMT
2 y y 3 2 y 3 y 6. x 1 x 1 P 6 y 3 y 0 . y 3 x y 2 2 4
Vậy GTNN của P là bằng 6 đạt được khi z 2 2 3i . Cách 2:
z 3 2i 2 MI 2 M I; 2 với I 3; 2 .
P z 1 2i 2 z 2 5i MA 2MB với A 1; 2 , B 2; 5 .
Ta có IM 2 ; IA 4 . Chọn K 2; 2 thì IK 1. Do đó ta có IA IK 2 . IM IA IM IM IK AM IM
IAM và IMK đồng dạng với nhau
2 AM 2MK . MK IK
Từ đó P MA 2MB 2 MK MB 2BK .
Dấu bằng xảy ra khi và chỉ khi M , K , B thẳng hàng và M thuộc đoạn thẳng BK .
Từ đó tìm được M 2;2 3. Cách 3: 64 PMT
Gọi M a; b là điểm biểu diễn số phức z a b .i Đặt I 3; 2 , A1; 2 và B2; 5 .
Ta xét bài toán: Tìm điểm M thuộc đường tròn C có tâm I , bán kính R 2 sao cho
biểu thức P MA 2MB đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K x; y sao cho MA 2MK M C . 2 2
Ta có MA MK 2 MA 2 2
4MK MI IA 4MI IK 2 MI 2
IA MI IA 2 MI 2
IK MI IK MI IA IK 2 R 2 IK 2 2 . 4 2 . 2 4 3 4 IA *. IA 4IK 0
* luôn đúng M C .
3R 4IK IA 2 2 2 0
4x 3 4 x
IA IK 2 4 0 . 4y 2 0 y 2
Thử trực tiếp ta thấy K 2; 2 thỏa mãn 2 R 2 IK 2 3 4 IA 0 . Vì 2 BI 2 2 2 1 3
10 R 4 nên B nằm ngoài C . Vì 2 KI 2
1 R 4 nên K nằm trong C .
Ta có MA 2MB 2MK 2MB 2 MK MB 2KB .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK .
Do đó MA 2MB nhỏ nhất khi và chỉ khi M là giao điểm của C và đoạn thẳng . BK
Phương trình đường thẳng BK : x 2 . 2 2
Phương trình đường tròn C : x 3 y 2 4 . 65 PMT x 2 x 2
Tọa độ điểm M là nghiệm của hệ 2 2 hoặc
x 3 y 2 4 y 2 3 x 2 . y 2 3
Thử lại thấy M 2;2 3 thuộc đoạn BK .
Vậy a 2 , b 2 3 a b 4 3 . CÂU 23: Lời giải Chọn A
Gọi z x i
y , với x, y . Khi đó M x; y là điểm biểu diễn cho số phức z . 2 2
Theo giả thiết, iz 1 2i 3 z 2 i 3 x 2 y 1 9 .
Ta có T 2 z 5 2i 3 z 3i 2MA 3MB , với A 5; 2 và B0; 3 .
Nhận xét rằng A , B , I thẳng hàng và 2IA 3IB . Cách 1:
Gọi là đường trung trực của AB , ta có : x y 5 0 .
T 2MA 3MB PA PB . Dấu “ ” xảy ra khi M P hoặc M Q .
x y 5 0 8 2 2 2 8 2 2 2 Giải hệ P ; và Q ; .
x 22 y 2 1 9 2 2 2 2 66 PMT
Khi đó M maxT 5 21 .
Vậy M.n 10 21 . Cách 2:
Ta có A , B , I thẳng hàng và 2IA 3IB nên 2IA 3IB 0 . 2 2 2 MA 2 2
3MB 2 MI IA 3MI IB 2 MI 2 IA 2 5 2 3IB 105 . 2 Do đó 2
T 2. 2MA 3. 3MB 2 MA 2 5 2
3MB 525 hay T 5 21 .
Khi đó M maxT 5 21 . Dấu “ ” xảy ra khi M P hoặc M Q .
Vậy M.n 10 21 . 67 PMT




