Tổng ôn tập TN THPT 2020 môn Toán: Đường tiệm cận của đồ thị hàm số

Tài liệu gồm 38 trang, được tổng hợp và biên soạn bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm chuyên đề đường tiệm cận của đồ thị hàm số, có đáp án và lời giải chi tiết, giúp học sinh tổng ôn kiến thức để chuẩn bị cho kỳ thi tốt nghiệp THPT 2020 môn Toán.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

38 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Tiệm cận ngang: Cho hàm số
( )y f x
xác định trên một khoảng vô hạn (là khoảng dạng
( ; ),a 
( ; )b
hoặc
( ; )). 
Đường thẳng
y
là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số
( )y f x
nếu ít
nhất một trong các điều kiện sau được thỏa mãn:
lim ( ) , lim ( ) .
x x
f x f x
 
Nhận xét:
Để tìm tiệm cận ngang của đồ thị hàm số ta cần tính giới hạn của hàm số tại vô cực.
Tìm giới hạn ở vô cực của hàm
( )
;
( )
P x
y
Q x
với
( ), ( )P x Q x
là các đa thức không căn:
Bậc của
( )P x
nhỏ hơn bậc của
( )Q x
lim 0
x
y

Tiệm cận ngang
: 0.Ox y
Bậc của
( )P x
bằng bậc của
( )Q x
lim
x
y

HÖ sè bËc cao cña ( )
HÖ sè bËc cao cña ( )
x P x
x Q x
.
Suy ra tiệm cận ngang
.y
Bậc của
( )P x
lớn hơn bậc của
( )Q x
lim
x
y


Không có tiệm cận ngang.
Kỹ năng sử dụng máy tính (tham khảo):
Tính
lim ( )
x
f x

thì nhập
( )f x
và CALC
10
10 .x
Tính
lim ( )
x
f x

thì nhập
( )f x
và CALC
10
10 .x
Tiệm cận ngang: Đường thẳng
x x
được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của
đồ thị hàm số
( )y f x
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim ( ) ,
x x
f x
lim ( ) ,
x x
f x
lim ( ) ,
x x
f x
lim ( ) .
x x
f x
Nhận xét:
Để tìm tiệm cận đứng của đồ thị hàm số, ta cần tính giới hạn một bên của
,x
với
x
thường là điều
kiện biên của hàm số (hay tại
x
thì hàm số không xác định).
Kỹ năng sử dụng máy tính (tham khảo):
Tính
lim ( )
x x
f x
thì nhập
( )f x
và CALC
9
10 .x x
Tính
lim ( )
x x
f x
thì nhập
( )f x
và CALC
9
10 .x x
Một số lưu ý cần nhớ
Hàm số nhất biến
( 0, 0)
ax b
y c ad bc
cx d
có
:
: 0
a
TCN y
c
TCD cx d
Kiểm tra xem hàm số đã cho đã “Chuẩn thức hay chưa”, nếu chưa chuẩn thức (còn tồn tại nghiệm mẫu
và tử trùng nhau) ta nên chuẩn thức. Nếu gặp đa thức sẽ phân tích thành tích số, gặp căn thức sẽ
nhân lượng liên hợp.
Tìm tiệm cận đứng (tại vị trí hàm số không xác định), kết quả giới hạn phải ra

hoặc
.
Tìm tiệm cận ngang (tại vị trí
),
kết quả sẽ ra một số cụ thể.
Hãy nhớ điều này để giải quyết những bài toán cho dạng bảng biến thiên, mà câu hỏi hỏi đúng, sai?
TIỆM CẬN ĐỒ THỊ HÀM SỐ
Vấn đề 5
Tiệ
m
cận
đứn
g
Tiệm cận ngang
2
2
x
y
O
2 1
2
x
y
x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua bảng biến thiên – đồ thị)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Cho hàm số
y f x
có bảng biến thiên như sau
Đồ thị hàm số có tổng số đường tiệm cận đứng là
a
và tổng số đường tiệm cận ngang là
b
. Khi đó
2a b
bằng
A.
4
. B.
6
. C.
3
. D.
2
.
Câu 2. Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 3. Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 4. Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 5. Cho hàm số
3
2
ax
y f x
x b
có bảng biến thiên như sau
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Giá trị
2a b
bằng?
A.
8
B.
6
C.
0
D.
10
Câu 6. Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 7. Cho hàmsố
( )f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 8. Cho hàm số
( )f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 9. Cho hàm số
( )y f x
xác định trên
\ 4R
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau
Tổng số tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 10. Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 11. Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 12. Cho hàm số
( )y f x
có bảng biến thiên
Số tiệm cận ngang của đồ thị hàm số
( )y f x
là
A.
3
. B.
1
. C.
2
. D.
0
Câu 13. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ
Khẳng định nào sao đây sai?
A. Đồ thị hàm có tiệm cận ngang
3y
B. Đồ thị hàm số có một tiệm cận đứng
2x
.
C. Đồ thị hàm số có một tiệm cận ngang
3y
và một tiệm cận đứng
2x
.
D. Đồ thị hàm số có hai tiệm cận ngang
3y
và
4y
Câu 14. Cho hàm số
( )y f x
xác định trên
\ 1, 1D
, có bảng biến thiên như hình vẽ bên dưới.
Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 15. Cho hàm số
( )y f x
xác định trên
\ 1D
, liên tục trên mỗi khoảng xác định và có bảng
biến thiên như hình vẽ bên dưới. Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có một đường tiệm cận đứng là đường thẳng
1x
và một trong các đường tiệm
cận ngang là đường thẳng
3y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
B. Đồ thị hàm số không có đường tiệm cận đứng và có hai tiệm cận ngang là đường thẳng
3y
và
5y
.
C. Đồ thị hàm số chỉ có một đường tiệm cận đứng, không có tiệm cận ngang
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng
1x
và hai tiệm cận đứng là đường thẳng
3y
và
5y
.
Câu 16. Cho hàm số
( )y f x
xác định trên
\ 0D
, liên tục trên mỗi khoảng xác định và có bảng
biến thiên như hình vẽ bên dưới.
Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có hai tiệm cận đứng là đường thẳng
0x
và
2x
tiệm cận ngang là đường
thẳng
2y
.
B. Đồ thị hàm số không có đường tiệm cận đứng và có một tiệm cận ngang.
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng
0x
và tiệm cận ngang là đường thẳng
2y
.
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng
0x
và hai tiệm cận đứng là đường thẳng
2y
và
3y
.
Câu 17. Cho hàm số
y f x
liên tục trên
\ 2;2
và có bảng biến thiên như hình vẽ:
Chọn khẳng định đúng trong các khẳng định sau đây.
A. Đồ thị hàm số có đúng
4
tiệm cận. B. Đồ thị hàm số có đúng
2
tiệm cận.
C. Đồ thị hàm số có đúng
1
tiệm cận. D. Đồ thị hàm số có đúng
3
tiệm cận.
Câu 18. Cho hàm số
f x
có bảng biến thiên như hình sau:
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 19. Cho hàm số
y f x
có bảng biến thiên như sau:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tổng số tiệm cận đứng của đồ thị hàm số
y
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 20. Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến thiên như sau:
Đồ thị hàm số
1
2 5
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
4
. C.
2
. D.
1
.
Câu 21. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 22. Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến thiên như sau:
Đồ thị hàm số
1
2 3
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
1
. B.
2
. C.
0
. D.
2
.
Câu 23. Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến thiên như sau:
Đồ thị hàm số
1
2 5
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
1
. C.
2
. D.
4
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 24. Cho hàm số
y f x
có bảng biến thiên nhưsau:
Đồ thị hàm số có tổng số đường tiệm cận đứng là
a
và tổng số đường tiệm cận ngang là
b
. Khi
đó giá trị của biểu thức
2 3
2 2
2a b
a b
thuộc khoảng nào sau đây?
A.
0;4
. B.
6; 4
. C.
2;0
. D.
4; 2
.
Câu 25. Cho hàm số
y f x
có đạo hàm liên tục trên
và có bảng biến thiên như sau:
Hỏi đồ thị hàm số
2
2
1
4
x
g x
f x f x
có bao nhiêu đường tiệm cận đứng?
A.
4
. B.
3
. C.
2
. D.
1
.
B. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua hàm số)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
là
A.
2y
. B.
1y
. C.
1x
. D.
2x
.
Câu 2. Tiệm cận ngang của đồ thị hàm số
2020
2019
x
y
x
là
A.
2019y
. B.
1y
. C.
2019x
. D.
2020x
.
Câu 3. Tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
là
A.
2y
. B.
1y
. C.
1x
. D.
2x
.
Câu 4. Tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số
2
1
x
y
x
là
A.
1;1I
. B.
1;1I
. C.
1; 1I
. D.
1; 1I
.
Câu 5. Số đường tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
là
A.
0
. B.
1
. C.
2
. D. 3.
Câu 6. Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A.
2
3 2
1
x x
y
x
B.
2
2
1
x
y
x
C.
2
1 y x
D.
1
x
y
x
Câu 7. Tìm số tiệm cận của đồ thị hàm số
2
2
5 4
1
x x
y
x
.
A.
2
B.
3
C.
0
D.
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 8. Tìm số tiệm cận đứng của đồ thị hàm số:
2
2
3 4
16
x x
y
x
A.
2
B.
3
C.
1
D.
0
Câu 9. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
5 4 1
1
x x
y
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 10. Cho hàm số
2
2
2
4
ax bx
y f x
x
. Biết rằng đồ thị hàm số có đúng một đường tiệm cận ngang
là
1y
và một đường tiệm cận đứng là
2
x
. Khi đó giá trị của biểu thức
b a
bằng?
A.
2
B.
4
C.
2
D.
4
Câu 11. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
4
x x
y
x
là
A.
1
B.
2
C.
3
D.
4
Câu 12. Đồ thị hàm số
2
1
1
x
f x
x
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 13. Số tiệm cận đứng của đồ thị hàm số
2
25 5
x
y
x x
là
A.
3
B.
2
C.
0
D.
1
Câu 14. Số tiệm cận đứng của đồ thị hàm số
2
16 4
x
y
x x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 15. Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
2 1 3
5 6
x x x
y
x x
.
A.
3
x
và
2
x
. B.
3
x
. C.
3
x
và
2
x
. D.
3
x
.
Câu 16. Số tiệm cận đứng của đồ thị hàm số
2
4 2
x
y
x x
là
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 17. Tìm số đường tiệm cận của đồ thị hàm số
1
4 3 1 3 5
x
y
x x
.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 18. Cho hàm số
2
4 2
2 3
3 2
x x
y
x x
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 19. Đồ thị hàm số
2
5 8
3
x
y
x x
có bao nhiêu đường tiệm cận?
A. 2. B. 4. C. 1. D. 3.
Câu 20. Đồ thị hàm số
2
4 2 1
1
x x x
y
x
có bao nhiêu đường tiệm cận?
A.
1
. B.
0
. C.
2
. D.
3
.
C. ĐỊNH m ĐỂ ĐỒ THỊ HÀM SỐ CÓ ĐƯỜNG TIỆM CẬN THỎA MÃN ĐIỀU KIỆN CHO
TRƯỚC
Đường tiệm cận ngang
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Cho hàm số
y f x
có TXD:
D
Điều kiện cần:
D
phải chứa

hoặc

Điều kiện đủ:
Dạng 1.
( )
( )
( )
P x
y f x
Q x
.
Nếu
:degP x degQ x
thì không có tiệm cận ngan
Nếu
:degP x degQ x
TCN
0
y
Nếu
:degP x degQ x
y k
(k là tỉ số hệ số bậc cao nhất của tử và mẫu)
Dạng 2:
( )
y f x u v
(hoặc
u v
): Nhân liên hợp
2
( )
u v
y f x
u v
(hoặc
u v
u v
)
Đường tiệm cận đứng
Cho hàm số
P x
y
Q x
có TXD:
D
Đkiện cần: giải
0
0
Q x x x
là TCĐ khi thỏa mãn đk đủ
Đkiện đủ:
Đkiện 1:
0
x
làm cho
( )P x
và
( )Q x
xác định.
Đkiện 2: -
0
x
không phải nghiêm
0
( )
P x x x
là TCĐ
-
0
x
là nghiêm
0
( )
P x x x
là TCĐ nếu
0
lim ( )
x x
f x
Câu 1. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
2
1
1
x
y
mx
có hai tiệm cận
ngang
A.
0
m
B.
0
m
C.
0
m
D. Không có giá trị thực nào của
m
thỏa mãn yêu cầu đề bài
Câu 2. Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
2
2
3 2
x m
y
x x
có đúng hai đường
tiệm cận.
A.
1
m
B.
{1;4}
m
C.
4
m
D.
{ 1; 4}
m
Câu 3. Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
có đúng
một đường tiệm cận?
A.
0
. B.
2
. C.
1
. D. Vô số.
Câu 4. Tìm tất cả các giá trị của tham số
m
sao cho đồ thị hàm số
2
5 3
2 1
x
y
x mx
không có tiệm cận
đứng.
A.
1
1
m
m
B.
1 1
m
C.
1
m
D.
1
m
Câu 5. Cho hàm số
2
1
2 4
x
x
y f
m
x
x
. Tìm tất cả các giá trị của tham số
m
để đồ thị có ba đường
tiệm cận
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
m
B.
2
5
2
m
m
C.
2
2
5
2
m
m
m
D.
2
2
m
m
Câu 6. Biết rằng đồ thị của hàm số
3 2017
3
n x n
y
x m
(
,m n
là các số thực) nhận trục hoành làm
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng
m n
.
A.
0
B.
3
C.
3
D.
6
Câu 7. Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
8 2
x
y
mx x
có đúng bốn
đường tiệm cận?
A.
8
B.
6
C.
7
D. Vô số
Câu 8. Với giá trị nào của hàm số
m
để đồ thị hàm số
2
3 7
y x mx x
có tiệm cạn ngang.
A.
1
m
B.
1
m
C.
1
m
D. Không có
m
Câu 9. Cho hàm số
1
2
mx
y
x m
với tham số
0
m
. Giao điểm của hai đường tiệm cận của đồ thị hàm số
thuộc đường thẳng có phương trình nào dưới đây?
A.
2y x
. B.
2 0
x y
. C.
2 0
x y
. D.
2 0
x y
.
Câu 10. Tìm tất cả các giá trị của m để đồ thị hàm số
2
2
4
mx
y
x
có đúng 2 tiệm cận?
A.
1
m
. B.
1
m
. C.
1
m
. D.
0
m
Câu 11. Tìm tham số
m
để đồ thị hàm số
1 5
2
m x m
y
x m
có tiệm cận ngang là đường thẳng
1y
A.
1
m
. B.
1
2
m
. C.
2
m
. D.
1
m
.
Câu 12. Có bao nhiêu giá trị nguyên
10;10
m
sao cho đồ thị hàm số
2
1
2 6 3
x
y
x x m
có hai
đường tiệm cận đứng?
A.
19
. B.
15
. C.
17
. D.
18
.
Câu 13. Có bao nhiêu giá trị nguyên của
m
để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
3 4
2
mx mx
y
x
bằng 3?
A.
4
. B.
2
. C. Vô số. D.
3
.
Câu 14. Tổng các giá trị của tham số
m
để đồ thị của hàm số
2 2
1
2 1 2
x
y
x m x m
có đúng một
tiệm cận đứng.
A.
1
2
. B.
2
. C.
3
. D.
3
2
.
Câu 15. Tìm tất cả các giá trị của
m
để đồ thị hàm số
2
2
2
2
x x
y
x x m
có 3 đường tiệm cận.
A.
1
8
m
m
. B.
1
8
m
m
. C.
1
.
8
m
m
D.
8
m
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 16. Cho
hàm số
3
2 2
3
3
2 1
x
y
x mx m x m
.
Có bao nhiêu giá trị nguyên thuộc đoạn
6
;6
của
tham số
m
để
đồ thị hàm số có bốn đường tiệm cận?
A.
1
2
. B.
9
. C.
8
. D.
11
.
Câu 17. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
2
2
3
x
x m
y
x
m
không
có tiệm
cận đứng.
A.
1
m
. B.
1
m
. C.
1
m
và
0
m
. D.
0
m
.
Câu 18. Có
bao nhiêu giá trị nguyên của tham số thực
m
thuộc
đoạn
2
017;2017
để
đồ thị hàm số
2
2
4
x
y
x
x m
có hai
tiệm cận đứng.
A.
2
019
. B.
2
021
. C.
2
018
. D.
2
020
.
-------------------- HẾT --------------------
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Tiệm cận ngang: Cho hàm số
( )y f x
xác định trên một khoảng vô hạn (là khoảng dạng
( ; ),
a 
( ; )b
hoặc
( ; )). 
Đường thẳng
y
là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số
( )y f x
nếu ít
nhất một trong các điều kiện sau được thỏa mãn:
lim ( ) , lim ( ) .
x x
f x f x
 
Nhận xét:
Để tìm tiệm cận ngang của đồ thị hàm số ta cần tính giới hạn của hàm số tại vô cực.
Tìm giới hạn ở vô cực của hàm
( )
;
( )
P x
y
Q x
với
( ), ( )P x Q x
là các đa thức không căn:
Bậc của
( )P x
nhỏ hơn bậc của
( )Q x
lim 0
x
y

Tiệm cận ngang
: 0.Ox y
Bậc của
( )P x
bằng bậc của
( )Q x
lim
x
y

HÖ sè bËc cao cña ( )
HÖ sè bËc cao cña ( )
x P x
x Q x
.
Suy ra tiệm cận ngang
.y
Bậc của
( )P x
lớn hơn bậc của
( )Q x
lim
x
y


Không có tiệm cận ngang.
Kỹ năng sử dụng máy tính (tham khảo):
Tính
lim ( )
x
f x

thì nhập
( )f x
và CALC
10
10 .x
Tính
lim ( )
x
f x

thì nhập
( )f x
và CALC
10
10 .x
Tiệm cận ngang: Đường thẳng
x x
được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ
thị hàm số
( )y f x
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim ( ) ,
x x
f x
lim ( ) ,
x x
f x
lim ( ) ,
x x
f x
lim ( ) .
x x
f x
Nhận xét:
Để tìm tiệm cận đứng của đồ thị hàm số, ta cần tính giới hạn một bên của
,x
với
x
thường là điều kiện
biên của hàm số (hay tại
x
thì hàm số không xác định).
Kỹ năng sử dụng máy tính (tham khảo):
Tính
lim ( )
x x
f x
thì nhập
( )f x
và CALC
9
10 .x x
Tính
lim ( )
x x
f x
thì nhập
( )f x
và CALC
9
10 .x x
Một số lưu ý cần nhớ
Hàm số nhất biến
( 0, 0)
ax b
y c ad bc
cx d
có
:
: 0
a
TCN y
c
TCD cx d
Kiểm tra xem hàm số đã cho đã “Chuẩn thức hay chưa”, nếu chưa chuẩn thức (còn tồn tại nghiệm mẫu và
tử trùng nhau) ta nên chuẩn thức. Nếu gặp đa thức sẽ phân tích thành tích số, gặp căn thức sẽ nhân
lượng liên hợp.
Tìm tiệm cận đứng (tại vị trí hàm số không xác định), kết quả giới hạn phải ra

hoặc
.
Tìm tiệm cận ngang (tại vị trí
),
kết quả sẽ ra một số cụ thể.
Hãy nhớ điều này để giải quyết những bài toán cho dạng bảng biến thiên, mà câu hỏi hỏi đúng, sai?
TIỆM CẬN ĐỒ THỊ HÀM SỐ
Vấn đề 5
Tiệ
m
cận
đứn
g
Tiệm cận ngang
2
2
x
y
O
2 1
2
x
y
x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua bảng biến thiên – đồ thị)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Cho hàm số
y f x
có bảng biến thiên như sau
Đồ thị hàm số có tổng số đường tiệm cận đứng là
a
và tổng số đường tiệm cận ngang là
b
. Khi đó
2a b
bằng
A.
4
. B.
6
. C.
3
. D.
2
.
Lời giải
Chọn B
Dựa vào bảng biến thiên suy ra đồ thị có hai tiệm cận đứng là
1x
,
1x
và hai tiệm cận ngang là
3y
,
3y
. Suy ra
2a
và
2b
.
Vậy
2 6a b
.
Câu 2. Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận của đồ thị hàm số đã cho là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta có
lim 1
x
y

1y
là đường tiệm cận ngang.
1
lim
x
y
;
1
lim
x
y
1x
là đường tiệm cận đứng.
1
lim
x
y

;
1
lim
x
y

1x
là đường tiệm cận đứng.
Vậy số đường tiệm cận của đồ thị hàm số đã cho là 3.
Câu 3. Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Từ bảng biến thiên ta có
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
lim 0
x
y

0y
là tiệm cận ngang của đồ thị hàm số.
lim 6
x
y

6y
là tiệm cận ngang của đồ thị hàm số.
1
lim
x
y

1x
là tiệm cận đứng của đồ thị hàm số.
1
lim
x
y

;
1
lim
x
y

1x
là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có
4
tiệm cận.
Câu 4. Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
Từ bảng biến thiên ta có
lim 2
x
y

;
lim 1
x
y

do đó đồ thị hàm số có hai đường tiệm cận ngang là
2y
;
1y
.
2
lim
x
y

do đó đồ thị hàm số có một đường tiệm cận đứng là
2x
.
Vậy tổng số có
3
đường tiệm cận.
Câu 5. Cho hàm số
3
2
ax
y f x
x b
có bảng biến thiên như sau
Giá trị
2a b
bằng?
A.
8
B.
6
C.
0
D.
10
Lời giải
Chọn C
Đk:
. 6 0 . 6a b a b
Từ BBT ta dễ dàng nhận thấy ĐTHS có TCN là:
2y
và tiệm cận đứng là:
1x
Suy ra
2 4
2
a
a
và
1 2
2
b
b
(TMĐK)
Vậy
2 4 2.2 0a b
.
Câu 6. Cho hàm số
( )y f x
có bảng biến thiên như sau
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D
Dựa vào bảng biến thiên của hàm số ta có:
lim ( ) 2 2
x
f x y

là một tiệm cận ngang
1
lim ( ) 1
x
f x x

là một tiệm cận đứng
Vậy đồ thị hàm số có tổng số đường tiệm cận là
2
.
Câu 7. Cho hàmsố
( )f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn C
Dựa vào bảng biến thiên của hàm số ta có:
lim ( ) 0 0
x
f x y

là một tiệm cận ngang
lim ( ) 5 5
x
f x y

là một tiệm cận ngang
1
lim ( ) 1
x
f x x

là một tiệm cận đứng
Vậy đồ thị hàm số có tổng số đường tiệm cận là 3.
Câu 8. Cho hàm số
( )f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
1
lim ( ) 1
x
f x x

là một tiệm cận đứng
lim ( )
x
f x


nên đồ thị hàm số không có tiệm cận ngang
Vậy đồ thị hàm số có tổng số đường tiệm cận là 1.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 9. Cho hàm số
( )y f x
xác định trên
\ 4R
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau
Tổng số tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lờigiải
Chọn B
Dựa vào bảng biến thiên của hàm số ta có:
lim ( ) 9 9
x
f x y

là một tiệm cận ngang
4
lim ( ) 4
x
f x x

là một tiệm cận đứng
Vậy đồ thị hàm số có tổng số đường tiệm là
2
.
Câu 10. Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn A
lim 0
x
y

nên đường thẳng
0y
là tiệm cận ngang của đồ thị hàm số.
lim 1
x
y

nên đường thẳng
1y
là tiệm cận ngang của đồ thị hàm số.
2
lim
x
y

nên đường thẳng
2x
là tiệm cận đứng của đồ thị hàm số.
2
lim
x
y

nên đường thẳng
2x
là tiệm cận đứng của đồ thị hàm số.
Vậy hàm số đã cho có tổng số tiệm cận đứng và tiệm cận ngang là 4. Chọn đáp án A.
Câu 11. Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
lim
x
y


và
lim 1
x
y

nên đường thẳng
1y
là tiệm cận ngang của đồ thị hàm số.
1
lim 3
x
y
và
1
lim 10
x
y
nên đường thẳng
1x
không là tiệm cận đứng của đồ thị hàm số.
Vậy hàm số đã cho có tổng số tiệm cận đứng và tiệm cận ngang là 1. Chọn đáp án B.
Câu 12. Cho hàm số
( )y f x
có bảng biến thiên
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số tiệm cận ngang của đồ thị hàm số
( )y f x
là
A.
3
. B.
1
. C.
2
. D.
0
Lời giải
Chọn C
Quan sát bảng biến thiên ta có
lim 8
x
f x

và
lim 10
x
f x

nên đồ thị hàm số có hai tiệm cận
ngang
8y
,
10y
.
Câu 13. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ
Khẳng định nào sao đây sai?
A. Đồ thị hàm có tiệm cận ngang
3y
B. Đồ thị hàm số có một tiệm cận đứng
2x
.
C. Đồ thị hàm số có một tiệm cận ngang
3y
và một tiệm cận đứng
2x
.
D. Đồ thị hàm số có hai tiệm cận ngang
3y
và
4y
Lời giải
Chọn D
Quan sát bảng biến thiên ta có
lim 3
x
f x

và
lim
x
f x


nên đồ thị hàm số có một tiệm cận
ngang
3y
;
0
lim 4
x
f x
và
0
lim
x
f x

nên đồ thị hàm số có một tiệm cận đứng
2x
.
Câu 14. Cho hàm số
( )y f x
xác định trên
\ 1, 1D
, có bảng biến thiên như hình vẽ bên dưới. Hỏi
đồ thị hàm số có bao nhiêu đường tiệm cận?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Quan sát bảng biến thiên ta có
lim
x
f x

và
lim 3
x
f x
nên đồ thị hàm số có một tiệm cận
ngang
3y
;
1
lim
x
f x
và
1 1
lim ; lim
x x
f x f x
nên đồ thị hàm số hai tiệm cận
đứng
1x
. Vậy đồ thị hàm số có tổng cộng ba đường tiệm cận.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 15. Cho hàm số
( )y f x
xác định trên
\ 1D
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình vẽ bên dưới. Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có một đường tiệm cận đứng là đường thẳng
1x
và một trong các đường tiệm cận
ngang là đường thẳng
3y
.
B. Đồ thị hàm số không có đường tiệm cận đứng và có hai tiệm cận ngang là đường thẳng
3y
và
5y
.
C. Đồ thị hàm số chỉ có một đường tiệm cận đứng, không có tiệm cận ngang
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng
1x
và hai tiệm cận đứng là đường thẳng
3
y
và
5y
.
Lời giải
Chọn A
Quan sát bảng biến thiên ta có
lim 5
x
f x

và
lim 3
x
f x

nên đồ thị hàm số có hai tiệm cận
ngang
3y
và
5y
;
1
lim
x
f x

và
1
lim
x
f x

nên đồ thị hàm số một tiệm cận đứng
1x
.
Câu 16. Cho hàm số
( )y f x
xác định trên
\ 0D
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình vẽ bên dưới.
Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có hai tiệm cận đứng là đường thẳng
0x
và
2x
tiệm cận ngang là đường thẳng
2y
.
B. Đồ thị hàm số không có đường tiệm cận đứng và có một tiệm cận ngang.
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng
0x
và tiệm cận ngang là đường thẳng
2y
.
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng
0x
và hai tiệm cận đứng là đường thẳng
2
y
và
3y
.
Lời giải
Chọn C
Quan sát bảng biến thiên ta có
lim
x
f x


và
lim 2
x
f x

nên đồ thị hàm số có một tiệm cận
ngang
2y
;
0
lim 3
x
f x
và
0
lim
x
f x

nên đồ thị hàm số một tiệm cận đứng
0x
.
Câu 17. Cho hàm số
y f x
liên tục trên
\ 2;2
và có bảng biến thiên như hình vẽ:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn khẳng định đúng trong các khẳng định sau đây.
A. Đồ thị hàm số có đúng
4
tiệm cận. B. Đồ thị hàm số có đúng
2
tiệm cận.
C. Đồ thị hàm số có đúng
1
tiệm cận. D. Đồ thị hàm số có đúng
3
tiệm cận.
Lời giải
Chọn D
Dựa vào bảng biến thiên của hàm số ta có:
+
2
lim
x
f x

,
2
lim
x
f x

nên đồ thị hàm số có một tiệm cận đứng là
2x
.
+
2
lim
x
f x

,
2
lim
x
f x

nên đồ thị hàm số có một tiệm cận đứng là
2x
.
+
lim 0
x
f x

nên đồ thị hàm số có một tiệm cận ngang là
0y
.
+
lim
x
f x


nên đồ thị hàm số không có một tiệm cận ngang.
Vậy đồ thị hàm số có
3
đường tiệm cận.
Câu 18. Cho hàm số
f x
có bảng biến thiên như hình sau:
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn B
Từ bảng biến thiên ta suy ra:
+
2
lim
x
f x


nên có đường thẳng
2x
là một tiệm cận đứng của đồ thị hàm số.
+
0
lim
x
f x

nên có đường thẳng
0x
là một tiệm cận đứng của đồ thị hàm số.
+
lim 0
x
f x

nên có đường thẳng
0y
là tiệm cận ngang của đồ thị hàm số.
Do đó, đồ thị hàm số
y f x
có ba tiệm cận.
Câu 19. Cho hàm số
y f x
có bảng biến thiên như sau:
Tổng số tiệm cận đứng của đồ thị hàm số
2020
y
f x
là
A.
1
. B.
2
. C.
3
. D.
4
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Lời giải
Chọn C
Số tiệm cận đứng của đồ thị hàm số
2018
y
f x
là số nghiệm phương trình
0f x
bằng số giao
điểm của đồ thị hàm số
f x
và trục hoành. Nhìn bảng biến thiên ta có số giao điểm bằng 3 nên đồ
thị hàm số
2020
y
f x
có 3 tiệm cận đứng.
Câu 20. Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến thiên như sau:
Đồ thị hàm số
1
2 5
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
4
. C.
2
. D.
1
.
Lời giải
Ta có:
5
2 5 0 1
2
f x f x
. Phương trình
1
có
4
nghiệm phân biệt
1 2 3 4
, , , 1x x x x
và
giới hạn của hàm số
1
2 5
y
f x
tại các điểm
1 2 3 4
, , ,x x x x
đều bằng .
Mặt khác
1
1
lim 0
2 5
x
f x
nên
1x
không phải tiệm cận đứng.
Vậy đồ thị hàm số
1
2 5
y
f x
có
4
đường tiệm cận đứng.
Câu 21. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Số tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
đúng bằng số nghiệm thực của phương trình
1
2 1 0
2
f x f x
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mà số nghiệm thực của phương trình
1
2
f x
bằng số giao điểm của đồ thị hàm số
y f x
với
đường thẳng
1
2
y
.
Dựa vào bảng biến thiên ta thấy đường thẳng
1
2
y
cắt đồ thị hàm số
( )y f x
tại 2 điểm phân biệt.
Vậy đồ thị hàm số
1
2 1
y
f x
có 2 tiệm cận đứng.
Lại có
1
lim 1
2 1
x
f x

đồ thị hàm số có một tiệm cận ngang là
1y
.
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là
3
.
Câu 22. Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến thiên như sau:
Đồ thị hàm số
1
2 3
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
1
. B.
2
. C.
0
. D.
2
.
Lời giải
Từ bảng biến thiên ta suy ra phương trình
3
2
f x
có hai nghiệm phân biệt
a
và
b
(với
0a
và
0 1b
.
Nên, tập xác định của hàm số
1
2 3
y
f x
là
\ 1; ;a b
.
Ta có
1
lim
2 3
x a
f x

;
1
lim
2 3
x b
f x

;
1
1
lim 0
2 3
x
f x
;
1
1
lim 0
2 3
x
f x
.
Do đó, đồ thị hàm số
1
2 3
y
f x
có
2
đường tiệm cận đứng.
Câu 23. Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến thiên như sau:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Đồ thị hàm số
1
2 5
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn D
Ta có
5
2 5 0
2
f x f x
1
.
Dựa vào BBT ta suy ra phương trình
1
có
4
nghiệm phân biệt
1
x ,
2
x ,
3
x ,
4
x (với
1 2 3 4
2 1 2x x x x ).
Mặt khác hàm số
1
2 5
y g x
f x
có tử thức là hằng số nên ta suy ra đồ thị hàm số
y g x
có
4
tiệm cận đứng.
Câu 24. Cho hàm số
y f x
có bảng biến thiên nhưsau:
Đồ thị hàm số có tổng số đường tiệm cận đứng là
a
và tổng số đường tiệm cận ngang là
b
. Khi đó
giá trị của biểu thức
2 3
2 2
2a b
a b
thuộc khoảng nào sau đây?
A.
0;4
. B.
6; 4
. C.
2;0
. D.
4; 2
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta có:
lim 1
x
f x

suy ra đồ thị hàm số có đường tiệm cận ngang
1y
.
lim 3
x
f x

suy ra đồ thị hàm số có đường tiệm cận ngang
3y
.
Suy ra tổng số đường tiệm cận ngang của đồ thị hàm số là
2 2b
.
2
lim
x
f x

suy ra đồ thị hàm số có đường tiệm cận đứng
2x
.
Suy ra tổng số đường tiệm cận đứng của đồ thị hàm số là
1 1.a
Vậy ta có:
2 3 2 3
2 2 2 2
2 2.1 2 10
3.333
1 2 3
a b
a b
.
Câu 25. Cho hàm số
y f x
có đạo hàm liên tục trên
và có bảng biến thiên như sau:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hỏi đồ thị hàm số
2
2
1
4
x
g x
f x f x
có bao nhiêu đường tiệm cận đứng?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn A
Ta có:
2
0
4 0
4
f x
f x f x
f x
.
Dựa vào bảng biến thiên ta thấy:
+ Xét trường hợp
0f x
có 2 nghiệm
1
1x
và
2
1x
là nghiệm bội hai (do đồ thị tiếp
xúc với trục hoành tại
1x
). Trường hợp này đồ thị hàm số có 2 tiệm cận đứng.
+ Xét trường hợp
4f x
có 2 nghiệm
3
1x
và
4
1x
là nghiệm bội hai (do đồ thị tiếp
xúc với đường thẳng
4y
tại
1x
). Trường hợp này đồ thị hàm số có 2 tiệm cận đứng.
Vậy đồ thị có 4 tiệm cận đứng.
B. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua hàm số)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
là
A.
2y
. B.
1y
. C.
1x
. D.
2x
.
Lời giải
Chọn B
Ta có
2
lim 1
1
x
x
x

và
2
lim 1
1
x
x
x

Suy ra
1y
là tiệm cận ngang của đồ thị hàm số.
Câu 2. Tiệm cận ngang của đồ thị hàm số
2020
2019
x
y
x
là
A.
2019y
. B.
1y
. C.
2019x
. D.
2020x
.
Lời giải
Chọn B
Ta có
2020
lim 1
2019
x
x
x

và
2020
lim 1
2019
x
x
x

Suy ra
1y
là tiệm cận ngang của đồ thị hàm số.
Câu 3. Tiệm cận đứng của đồ thị hàm số
2
1
x
y
x
là
A.
2y
. B.
1y
. C.
1x
. D.
2x
.
Lời giải
Chọn C
Ta có
1
2
lim
1
x
x
x

và
1
2
lim
1
x
x
x

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Suy ra
1x
là tiệm cận đứng của đồ thị hàm số.
Câu 4. Tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số
2
1
x
y
x
là
A.
1;1
I
. B.
1;1
I
. C.
1; 1
I
. D.
1; 1
I
.
Lời giải
Chọn B
Ta có
2
lim 1
1
x
x
x

và
2
lim 1
1
x
x
x

Suy ra
1y
là tiệm cận ngang của đồ thị hàm số.
Ta có
1
2
lim
1
x
x
x

và
1
2
lim
1
x
x
x

Suy ra
1x
là tiệm cận đứng của đồ thị hàm số.
Vậy tọa độ giao điểm hai đường tiệm cận là
1;1
I
.
Câu 5. Số đường tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
là
A.
0
. B.
1
. C.
2
. D. 3.
Lời giải
Chọn B
Ta có
2
lim 1
1
x
x
x

và
2
lim 1
1
x
x
x

Suy ra
1y
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có 1 đường tiệm cận ngang.
Câu 6. Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A.
2
3 2
1
x x
y
x
B.
2
2
y
C.
2
1
y x
D.
1
x
y
x
Lời giải
Chọn D
Ta có
1 1
lim , lim
1 1

x x
x x
x x
nên đường thẳng
1
x
là tiệm cận đứng của đồ thị hàm số.
Câu 7. Tìm số tiệm cận của đồ thị hàm số
2
2
5 4
1
x x
y
x
.
A.
2
B.
3
C.
0
D.
1
Lời giải
Chọn A
Tập xác định:
\ 1
D
Ta có:
2
2
2
2
5 4
1
5 4
lim lim lim 1
1
1
1
x x x
x x
x x
y
x
x
  
1y
là đường tiệm cận ngang.
Mặc khác:
2
2
1 1
1 1
1 4 4
5 4 3
lim lim lim lim
1 1 1 1 2
x x
x x
x x x
x x
y
x x x x
1x
không là đường tiệm cận đứng.
2
2
1
1 1 1
1 4 4
5 4
lim lim lim lim
1 1 1 1
x
x x x
x x x
x x
y
x x x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
1 1 1 1
1 4 4
5 4
lim lim lim lim
1 1 1 1
x x x x
x x x
x x
y
x x x x

1
x
là đường tiệm cận đứng.
Vậy đồ thị hàm số có 2 đường tiệm cận
Câu 8. Tìm số tiệm cận đứng của đồ thị hàm số:
2
2
3 4
16
x x
y
x
A.
2
B.
3
C.
1
D.
0
Lời giải
Chọn C
Ta có
2
2
3 4 1
4
16
x x x
y
x
x
(với điều kiện xác định), do đó đồ thị hàm có 1 tiệm cận đứng.
Câu 9. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
5 4 1
1
x x
y
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C
Tiệm cận ngang:
Ta có:
2
2
2
2
2
2
2
2
4 1
4 1
5
5
5 4 1
lim lim lim lim 5
1
1
1
1
1
x x x x
x
x x
x
x
x
x
y
x
x
x
x
   
nên đồ thị hàm số
có một tiệm cận ngang
5
y
.
Tiệm cận đứng:
Cho
2
1
1
1
x
x
x
Ta có:
2
2
1 1 1 1
5 1 1
5 4 1 5 1 6
lim lim lim lim 3
1 1 1 2
1
x x x x
x x
x x x
y
x x x
x
nên
1x
không là tiệm cận
đứng.
2 2 2
2
1 1 1 1
5 4 1 5 4 1 1 5 4 1
lim lim lim lim .
1 1 1 1
1
x x x x
x x x x x x
y
x x x x
x

vì
1
2
1
1
lim
1
5 4 1
lim 4 0
1
x
x
x
x x
x

.
Khi đó, đồ thị hàm số có một tiệm cận đứng
1
x
.
Tổng cộng đồ thị hàm số có 2 tiệm cận.
Câu 10. Cho hàm số
2
2
2
4
ax bx
y f x
x
. Biết rằng đồ thị hàm số có đúng một đường tiệm cận ngang là
1y
và một đường tiệm cận đứng là
2
x
. Khi đó giá trị của biểu thức
b a
bằng?
A.
2
B.
4
C.
2
D.
4
Lời giải
Chọn A
ĐTHS có TCN là:
1y
. Suy ra
1 1
1
a
a
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Phương trình
2
2
4 0
2
x
x
x
ĐTHS có TCĐ là:
2
x
. Suy ra phương trình
2
2 0
x bx
phải có hai nghiệm phân biệt trong đó
một nghiệm là
2
x
và nghiệm còn lại phải khác 2.
Ta có hệ điều kiện:
2
2
0
( 2) 2 2 0 3
(2) 2 2 0
b b
b
3 1 2
b a
Câu 11. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
4
x x
y
x
là
A.
1
B.
2
C.
3
D.
4
Lời giải
Chọn B
ĐKXĐ:
2
2
2 0
2;
; 2 2;
4 0
x
x
x
x
x

2
2
2
lim 2
4
x
x x
x
x

là tiệm cận đứng của đồ thị hàm số.
2
2
lim 1 1
4
x
x x
y
x

là tiệm cận ngang của đồ thị hàm số.
Tổng cộng có 2 tiệm cận.
Câu 12. Đồ thị hàm số
2
1
1
x
f x
x
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
A.
4
. B.
3
. C.
1
. D.
2
.
Lờigiải
Chọn B
Tập xác định của hàm số
; 1 1;D
 
TH1:
1 1 0
x x
. Khi đó
2
2
1
1 1
1
1 1
1
x
x x
f x
x
x x
x
.
Suy ra đồ thị hàm số có TCN
1
y
, không có TCĐ.
TH2:
1 1 0
x x
. Khi đó
2
2
1
1 1
1
1 1
1
x
x x
f x
x
x x
x
.
Suy ra đồ thị hàm số có TCN
1y
, TCĐ
1
x
.
Vậy đồ thị hàm số có 2 TCN và 1 TCĐ.
Câu 13. Số tiệm cận đứng của đồ thị hàm số
2
25 5
x
y
x x
là
A.
3
B.
2
C.
0
D.
1
Lời giải
Chọn D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tập xác định
25; \ 1;0
D 
. Biến đổi
1
( ) .
1 25 5
f x
x x
Vì
1 1
1
lim lim
1 25 5
x x
y
x x

nên đồ thị hàm số đã cho có 1 tiệm cận đứng
1
x
.
Câu 14. Số tiệm cận đứng của đồ thị hàm số
2
16 4
x
y
x x
là
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C
Tập xác định hàm số
16; \ 1;0
D 
.
Ta có
0 0 0 0
16 4 1 1
lim lim lim lim
1 8
1 16 4 1 16 4
x x x x
x x
y
x x
x x x x x
.
1 1 1
16 4 1
lim lim lim
1
1 16 4
x x x
x
y
x x
x x

.
vì
1
lim 16 4 15 4 0
x
x
,
1
lim 1 0
x
x
và
1
x
thì
1 1 0
x x
.
Tương tự
1 1
1
lim lim
1 16 4
x x
y
x x

.
Vậy đồ thị hàm số đã cho có tiệm cận đứng là
1
x
.
Câu 15. Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
2 1 3
5 6
x x x
y
x x
.
A.
3
x
và
2
x
. B.
3
x
.
C.
3
x
và
2
x
. D.
3
x
.
Lời giải
Chọn B
Tập xác định
2;3
\
D
2 2
2 2
2
2
2 2 2
2 2 2 2
2 1 3 2 1 3
2 1 3
lim lim lim
5 6
5 6 2 1 3 5 6 2 1 3
x x x
x x x x x x
x x x
x x
x x x x x x x x x x
2 2
(3 1) 7
lim
6
3 2 1 3
x
x
x x x x
Tương tự
2
2
2
2 1 3 7
lim
5 6 6
x
x x x
x x
. Suy ra đường thẳng
2
x
không là tiệm cận đứng của đồ
thị hàm số đã cho.
2 2
2 2
3 3
2 1 3 2 1 3
lim ; lim
5 6 5 6
 
x x
x x x x x x
x x x x
. Suy ra đường thẳng
3
x
là tiệm cận
đứng của đồ thị hàm số đã cho.
Câu 16. Số tiệm cận đứng của đồ thị hàm số
2
4 2
x
y
x x
là
A.
3
. B.
0
. C.
1
. D.
2
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Lời giải
Chọn C
Tập xác định
4; \ 1;0
D 
.
Ta có:
2
1 1
4 2
lim lim
x x
x
y
x x

Nên đường thẳng
1
x
là một đường tiệm cận đứng của đồ thị hàm số đã cho.
2
0 0 0 0
4 2 4 2
4 2 1 1
lim lim lim lim
4
1 4 2 1 4 2
x x x x
x x
x
y
x x
x x x x x
Nên đường thẳng
0
x
không là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có một tiệm cận đứng
1
x
.
Câu 17. Tìm số đường tiệm cận của đồ thị hàm số
1
4 3 1 3 5
x
y
x x
.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn A
Tập xác định:
1
; \ 1
3
D

+ Ta có:
2
1 1 1
1 4 3 1 3 5
1 4 3 1 3 5
lim lim lim
9 1
4 3 1 3 5
9 1
x x x
x x x
x x x
x
x x
x

do đó đường thẳng
1x
là đường tiệm cận đứng của đồ thị hàm số.
+
2
1
1
1 1
lim lim
3
4 3 1 3 5 3 1 5
4 3
x x
x
x
x x
x x x
 
do đó đường thẳng
1
3
y
là đường
tiệm cận ngang của đồ thị hàm số. Vậy đồ thị hàm số có 2 đường tiệm cận.
Câu 18. Cho hàm số
2
4 2
2 3
3 2
x x
y
x x
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Lời giải
Chọn B
□ Tập xác định
; 2 1;1 2;D
 
.
□
1 1
2 2
lim lim lim lim
x x
x x
y y y y

.
Các đường tiệm cận đứng của đồ thị là
2
x
,
1
x
.
□
lim lim 1
x x
y y
 
đồ thị có một tiệm cận ngang
1y
.
Câu 19. Đồ thị hàm số
2
5 8
3
x
y
x x
có bao nhiêu đường tiệm cận?
A. 2. B. 4. C. 1. D. 3.
Lời giải
Chọn B
Tập xác định
;0 3;D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
8
5
5 8 5 8
lim lim lim lim 5
3 3
3
1 1
x x x x
x x
x
y
x x
x
x x
   
Đường thẳng
5
y
là tiệm cận ngang của đồ thị hàm số.
2
8
5
5 8 5 8
lim lim lim lim 5
3 3
3
1 1
x x x x
x x
x
y
x x
x
x x
   
Đường thẳng
5
y
là tiệm cận ngang của đồ thị hàm số.
2
0 0
5 8
lim lim
3
x x
x
y
x x
( vì
2 2
0 0
lim(5 8) 8 0; lim 3 0; 3 0 0 )
x x
x x x x x x
Suy ra: đường thẳng
0
x
là tiệm cận đứng của đồ thị hàm số.
2
3 3
5 8
lim lim
3
x x
x
y
x x
( vì
2 2
3 3
lim(5 8) 7 0; lim 3 0; 3 0 3 )
x x
x x x x x x
Suy ra: đường thẳng
3
x
là tiệm cận đứng của đồ thị hàm số.
Câu 20. Đồ thị hàm số
2
4 2 1
1
x x x
y
x
có bao nhiêu đường tiệm cận?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn C
Hàm số
2
4 2 1
1
x x x
y
x
xác định
2
1 5
4
4 2 1 0
1 5
1 0
4
1
x
x x
x
x
x
.
Tập xác định của hàm số đã cho là
1 5 1 5
; 1 1; ;
4 4
D
 
.
2
2
2 1
4
4 2 1
lim lim lim
1 1
x x x
x x
x x x
x x
y
x x
  
2 2
2 1 2 1
4 4 1
lim lim 1
1
1
1
x x
x x
x x x x
x
x
 
.
1
y
là đường tiệm cận ngang của đồ thị hàm số khi
x
.
2
2
2 1
4
4 2 1
lim lim lim
1 1
x x x
x x
x x x
x x
y
x x
  
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
2 2
2 1 2 1
4 4 1
lim lim 3
1
1
1
x x
x x
x x x x
x
x
 
.
3
y
là đường tiệm cận ngang của đồ thị hàm số khi
x 
.
2 2 2
1 1 1 1
2 2
1 3 1
4 2 1 4 2 1
lim lim lim lim 2.
1
1 4 2 1 1 4 2 1
x x x x
x x
x x x x x x
y
x
x x x x x x x x
   
Vậy đồ thị hàm số
2
4 2 1
1
x x x
y
x
có
2
đường tiệm cận.
C. ĐỊNH m ĐỂ ĐỒ THỊ HÀM SỐ CÓ ĐƯỜNG TIỆM CẬN THỎA MÃN ĐIỀU KIỆN CHO
TRƯỚC
Đường tiệm cận ngang
Cho hàm số
y f x
có TXD:
D
Điều kiện cần:
D
phải chứa

hoặc

Điều kiện đủ:
Dạng 1.
( )
( )
( )
P x
y f x
Q x
.
Nếu
:degP x degQ x
thì không có tiệm cận ngan
Nếu
:degP x degQ x
TCN
0
y
Nếu
:degP x degQ x
y k
(k là tỉ số hệ số bậc cao nhất của tử và mẫu)
Dạng 2:
( )
y f x u v
(hoặc
u v
): Nhân liên hợp
2
( )
u v
y f x
u v
(hoặc
u v
u v
)
Đường tiệm cận đứng
Cho hàm số
P x
y
Q x
có TXD:
D
Đkiện cần: giải
0
0
Q x x x
là TCĐ khi thỏa mãn đk đủ
Đkiện đủ:
Đkiện 1:
0
x
làm cho
( )P x
và
( )Q x
xác định.
Đkiện 2: -
0
x
không phải nghiêm
0
( )
P x x x
là TCĐ
-
0
x
là nghiêm
0
( )
P x x x
là TCĐ nếu
0
lim ( )
x x
f x
Câu 1. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
2
1
1
x
y
mx
có hai tiệm cận
ngang
A.
0
m
B.
0
m
C.
0
m
D. Không có giá trị thực nào của
m
thỏa mãn yêu cầu đề bài
Lời giải
Chọn C
Xét các trường hơp sau:
Với
0
m
: hàm số trở thành
1y x
nên không có tiệm cận ngang.
Với
0
m
:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
hàm số
2 2
1 1
1 1
x x
y
mx m x
có tập xác định là
1 1
;D
m m
suy ra không tồn tại giới
hạn
lim
x
y

hay hàm số không có tiệm cận ngang.
Với
0
m
:
Ta có:
2
2 2 2
1
1
1 1 1 1
lim lim lim lim lim .
1 1 1
1
x x x x x
x x x
x
y
m
mx
x m x m m
x x x
    
và
2
2 2 2
1
1
1 1 1 1
lim lim lim lim lim .
1 1 1
1
x x x x x
x x x
x
y
m
mx
x m x m m
x x x
    
Vậy hàm số có hai tiệm cận ngang là :
1 1
;y y
m m
khi
0
m
.
Câu 2. Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
2
2
3 2
x m
y
x x
có đúng hai đường tiệm
cận.
A.
1
m
B.
{1;4}
m
C.
4
m
D.
{ 1; 4}
m
Lời giải
2 2
2
3 2 1 2
x m x m
y
x x x x
.
lim 1
x
y

1y
là đường tiệm cận ngang.
Đồ thị hàm số
2
2
3 2
x m
y
x x
có đúng hai đường tiệm cận
đồ thị hàm số có đúng một tiệm cận
đứng
pt
2
0
x m
nhận nghiệm
1x
hoặc
2
x
.
Khi đó:
1
4
m
m
.
Với
1
m
có một tiệm cận đứng
2
x
.
Với
4
m
có một tiệm cận đứng
1x
.
Vậy
{ 1; 4}
m
.
Câu 3. Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm số
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
có đúng một
đường tiệm cận?
A.
0
. B.
2
. C.
1
. D. Vô số.
Lời giải
Kí hiệu
C
là đồ thị hàm số
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
.
* Trường hợp 1:
0
m
.
Khi đó
2
6 3
6 3 9 1
x
y
x x
. Đồ thị hàm số có đúng một đường tiệm cận ngang
0
y
.
Do đó chọn
0
m
.
* Trường hợp 2:
0
m
.
Xét phương trình
2 2
6 3 9 6 1 0 1
mx x x mx
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Nhận thấy:
C
luôn có một đường tiệm cận ngang
0
y
và phương trình
1
không thể có duy nhất
một nghiệm đơn với mọi
m
.
Do đó
C
có đúng một đường tiệm cận khi và chỉ khi
C
không có tiệm cận đứng
1
vô
nghiệm
2
9 3 0
9 9 0
m
m
3
1 1
m
m
, ( không tồn tại
m
).
Kết hợp các trường hợp ta được
0
m
.
Câu 4. Tìm tất cả các giá trị của tham số
m
sao cho đồ thị hàm số
2
5 3
2 1
x
y
x mx
không có tiệm cận đứng.
A.
1
1
m
m
B.
1 1
m
C.
1
m
D.
1
m
lời giải
Chọn B
để hàm số không có tiệm cận đứng thì
2
2 1 0
x mx
vô nghiệm
suy ra
2
1 0 1 1
m m
Câu 5. Cho hàm số
2
1
2 4
x
x
y f
m
x
x
. Tìm tất cả các giá trị của tham số
m
để đồ thị có ba đường
tiệm cận
A.
2
m
B.
2
5
2
m
m
C.
2
2
5
2
m
m
m
D.
2
2
m
m
Lời giải
Chọn C
Để đồ thị có ba đường tiệm cận thì
2
2 4 0
x mx
có hai nghiệm phân biệt
1
2
2
0
2
1 2 1 4 0
5
2
m
m
m
m
Câu 6. Biết rằng đồ thị của hàm số
3 2017
3
n x n
y
x m
(
,m n
là các số thực) nhận trục hoành làm tiệm
cận ngang và trục tung là tiệm cận đứng. Tính tổng
m n
.
A.
0
B.
3
C.
3
D.
6
Lờigiải
Chọn A
Theo công thức tìm nhanh tiệm cận của đồ thị hàm số
ax b
y
cx d
ta có
Đồ thị hàm số nhận
3 0
d
x m
c
làm TCĐ
3
m
Đồ thị hàm số nhận
3 0
a
y n
c
làm TCN
3
n
.
Vậy
0
m n
.
Câu 7. Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
8 2
x
y
mx x
có đúng bốn đường
tiệm cận?
A.
8
B.
6
C.
7
D. Vô số
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
TH1:
0
m
suy ra tập xác định của hàm số là
1 2
;
D x x
, (
1 2
;x x
là nghiệm của phương trình
2
8 2 0
mx x
). Do đó
0
m
không thỏa yêu cầu của bài toán.
TH2:
1
0
8 2

x
m y
x
suy ra tập xác định của hàm số là
;4
D
.
4
lim ; lim

 
x
x
y y
. Khi đó ta có
4
x
là đường tiệm cận đứng của đồ thị hàm số.
Do đó
0
m
không thỏa yêu cầu của bài toán
TH3:
0
m
suy ra tập xác định của hàm số là
1 2
; ;
 
D x x
(
1 2
;x x
là nghiệm của phương
trình
2
8 2 0
mx x
). Do đó đồ thị hàm số có bốn đường tiệm cận khi phương trình
2
8 2 0
mx x
có hai nghiệm phân biệt khác
16 2 0 8
1 0; 0; 1;2;3;4;5;7
8 2 0 6
m m
m m m m m
m m
. Suy ra có tất cả
6
giá trị nguyên của tham
số
m
thỏa mãn yêu cầu của bài toán.
Câu 8. Với giá trị nào của hàm số
m
để đồ thị hàm số
2
3 7
y x mx x
có tiệm cạn ngang.
A.
1
m
B.
1
m
C.
1
m
D. Không có
m
Lời giải
Chọn A
Đồ thị hàm số có tiệm cận ngang
Hàm số xác định trên một trong các miền
; , ; , ,
  
a a a
hoặc
;

a
0
m
TH1:
0 3 7, lim


x
m y x x y
đồ thị không có tiệm cận ngang
TH2:
2
0, 3 7
m y x mx x
Khi
2
3 7 3
lim lim
2


x
x
y x x m
x x
đồ thị hàm số có tiệm cận ngang khi và chỉ khi
1
m
.
Vậy
1
m
Cách trắc nghiệm:
Thay
1
m
2 2
3
3 7 lim 3 7
2

x
y x x x x x x
đồ thị hàm số có tiệm cận ngang
2
lim 3 7
x
x x x
không có tiệm cận ngang.
Thay
1
m
2 2
3 7 lim 3 7

x
y x x x x x x
không xác định.
2
lim 3 7

x
x x x
không xác định.
Vậy
1
m
Câu 9. Cho hàm số
1
2
mx
y
x m
với tham số
0
m
. Giao điểm của hai đường tiệm cận của đồ thị hàm số
thuộc đường thẳng có phương trình nào dưới đây?
A.
2y x
. B.
2 0
x y
. C.
2 0
x y
. D.
2 0
x y
.
Lời giải
Chọn C
Khi đồ thị hàm số có hai đường tiệm cận thì:
Đường tiệm cận ngang có phương trình:
y m
Đường tiệm cận đứng có phương trình:
2x m
. Vậy giao điểm hai tiệm cận là
(2 ; )I m m
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Khử
m
từ hệ
2
y m
x m
ta được
2 0
x y
.
Vậy giao điểm của hai tiệm cận thuộc đường thẳng có phương trình
2 0
x y
.
Câu 10. Tìm tất cả các giá trị của m để đồ thị hàm số
2
2
4
mx
y
x
có đúng 2 tiệm cận?
A.
1
m
. B.
1
m
. C.
1
m
. D.
0
m
Lời giải
Chọn B
Cách 1: Trắc nghiệm
Thế
1
m
vào
2
2
4
mx
y
x
ta được
2
2
4
x
y
x
đồ thị có 2 tiệm cận:
2; 0
x y
.
Thế
1
m
vào
2
2
4
mx
y
x
ta được
2
2
4
x
y
x
đồ thị có 2 tiệm cận:
2; 0
x y
.
Cách 2: Tự luận
; 2 2;D

.
2
2
lim 0 ( )
4
x
mx
m
x

Hàm số có 1 TCN.
Để hàm số có đúng 2 tiệm cận thì hàm số cần có thêm 1 TCĐ.
+ Xét
2
x
không là TCĐ khi
2
x
là nghiệm của
2 2 2 0 1
mx m m
.
Thử lại: với
1
m
thì
2
2 2
2 1
lim lim
4 2
x x
x
x x

2
x
là TCĐ.
+ Xét
2
x
không là TCĐ khi
2
x
là nghiệm của
2 2 2 0 1
mx m m
.
Thử lại: với
1
m
thì
2
x
là TCĐ.
Câu 11. Tìm tham số
m
để đồ thị hàm số
1 5
2
m x m
y
x m
có tiệm cận ngang là đường thẳng
1y
A.
1
m
. B.
1
2
m
. C.
2
m
. D.
1
m
.
Lời giải
Chọn D
TXĐ:
\
2
m
D
Ta có
1 5
1
lim lim
2 2
x x
m x m
m
y
x m
 
.
1 5
1
lim lim
2 2
x x
m x m
m
y
x m
 
.
1
2
m
y
là TCN của đồ thị hàm số.
ycbt
1
1 1
2
m
m
.
Câu 12. Có bao nhiêu giá trị nguyên
10;10
m
sao cho đồ thị hàm số
2
1
2 6 3
x
y
x x m
có hai đường
tiệm cận đứng?
A.
19
. B.
15
. C.
17
. D.
18
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có đồ thị hàm số
2
1
2 6 3
x
y
x x m
có hai đường tiệm cận đứng khi phương trình
2
2 6 3 0
x x m
có hai nghiệm phân biệt khác
1
2
2
3 2 3 0
2.1 6.1 3 0
m
m
15
2
5
m
m
Từ đó ta suy ra tập các giá trị nguyên của
m
thỏa mãn là
7, 6, 5, 4, 3, 2, 1,0,1,2,3,4,6,7,8,9,10
. Vậy có
17
giá trị nguyên của
m
thỏa mãn.
Câu 13. Có bao nhiêu giá trị nguyên của
m
để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
3 4
2
mx mx
y
x
bằng 3?
A.
4
. B.
2
. C. Vô số. D.
3
.
Lời giải
Chọn B
Đồ thị hàm số
2
3 4
2
mx mx
y
x
có nhiều nhất một tiệm cận đứng và hai tiệm cận ngang.
Điều kiện để đồ thị hàm số
2
3 4
2
mx mx
y
x
có 3 tiệm cận là nó có đúng 1 tiệm cận đứng và 2
tiệm cận ngang.
* Xét điều kiện tồn tại
lim
x
y

và
lim
x
y
Trường hợp 1:
2
3 4 0
g x mx mx
với
x
2
0
16
0
0
9
9 16 0
m
m
m
m m
Trường hợp 2:
2
3 4 0
g x mx mx
với
1 2
; ;x x x
 
với
1
x
;
2
x
là nghiệm của
g x
2
0
16
9
9 16 0
m
m
m m
Vậy
0
m
thì tồn tại
lim
x
y
và
lim
x
y
Khi đó:
2
2
3 4
3 4
lim lim lim
2
2
1
x x x
m
m
mx mx
x x
y m
x
x
  
2
2
3 4
3 4
lim lim lim
2
2
1
x x x
m
m
mx mx
x x
y m
x
x
  
Vậy điều kiện để đồ thị hàm số có hai đường tiệm cận ngang là
0
m
* Xét trường hợp
2
x
là nghiệm của tử số
2
x
là nghiệm của
2
3 4
g x mx mx
2 0 2
g m
Khi đó
2
2 6 4
2
x x
y
x
2 2
2 1 2
2 1
lim lim
2 2
x x
x x
x
y
x x
Đồ thị hàm số có một tiệm cận đứng
2
x
.
2
m
thỏa mãn
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
* Xét trường hợp
2
x
không là nghiệm của tử số, để
2
x
là tiệm cận đứng của đồ thị hàm số
thì
2 0
2 0 4 2 0 2
2 0
g
g m m
g
đồ thị hàm số có một đường tiệm cận đứng
2
x
với
0;2
m
Vậy điều kiện để đồ thị hàm số
2
3 4
2
mx mx
y
x
có 3 tiệm cận là
0;2
m
Vậy có hai giá trị nguyên của
m
thỏa mãn đề bài là
1
m
;
2
m
.
Câu 14. Tổng các giá trị của tham số
m
để đồ thị của hàm số
2 2
1
2 1 2
x
y
x m x m
có đúng một tiệm
cận đứng.
A.
1
2
. B.
2
. C.
3
. D.
3
2
.
Lời giải
Chọn A
Đặt
2 2
2 1 2
x m mf x x
Đồ thị hàm số có đúng một tiệm cận đứng khi và chỉ khi
0
f x
có 2 nghiệm phân biệt trong đó có
1 nghiệm
1x
hoặc
0
f x
có nghiệm kép
2
2
2
3
1 2 0
0
1
2
1 2 1 2 0
1 0 3
1; 3
3
3
3
0
2
2
2
m m
m
m
m m
f m
m m
m
m
m
.
Vậy tổng các giá trị
m
thỏa mãn là:
1
2
.
Câu 15. Tìm tất cả các giá trị của
m
để đồ thị hàm số
2
2
2
2
x x
y
x x m
có 3 đường tiệm cận.
A.
1
8
m
m
. B.
1
8
m
m
. C.
1
.
8
m
m
D.
8
m
.
Lời giải
Chọn A
Ta có:
2
2
2
lim lim 1
2
x x
x x
y
x x m
 
, suy ra đồ thị hàm số luôn có một đường tiệm cận ngang là
1.
y
Do đó, đồ thị hàm số
2
2
2
2
x x
y
x x m
có 3 đường tiệm cận khi và chỉ khi đồ thị hàm số có thêm hai
đường tiệm cận đứng. Khi đó, phương trình
2
2 0
x x m
có 2 ngiệm phân biệt không trùng với
các nghiệm của phương trình
2
2 0
x x
, hay
2
2
1 0
1
1
1 2.1 0 1 .
8
8
2 2. 2 0
m
m
m
m m
m
m
m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 16. Cho hàm số
3 2 2
3
3 2 1
x
y
x mx m x m
. Có bao nhiêu giá trị nguyên thuộc đoạn
6;6
của
tham số
m
để đồ thị hàm số có bốn đường tiệm cận?
A.
12
. B.
9
. C.
8
. D.
11
.
Lời giải
Chọn B
lim lim 0
x x
y y
 
nên đồ thị hàm số có tiệm cận ngang là đường thẳng
0
y
.
Do đó, đồ thị hàm số có bốn đường tiệm cận khi phương trình
3 2 2
3 2 1 0
x mx m x m
có 3
nghiệm phân biệt
3
x
.
Xét phương trình
3 2 2
3 2 1 0
x mx m x m
(*) ta có
3 2 2
3 2 1 0
x mx m x m
2
2 1 0
x m x mx
2
2 1 0
x m
x mx
.
Phương trình (*) có ba nghiệm phân biệt
3
x
khi và chỉ khi
3
m
và phương trình
2
2 1 0
x mx
có hai nghiệm phân biệt
3
x
2
2
3
3
1
1 0
1
3 2.3. 1 0
5
3
m
m
m
m
m
m
m
.
Do
m
nguyên và
6;6
m
nên
6; 5; 4; 3; 2;2;4;5;6
m
.
Vậy có
9
giá trị nguyên của
m
thỏa mãn đề bài.
Câu 17. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
2
2 3
x x m
y
x m
không có tiệm cận
đứng.
A.
1
m
. B.
1
m
. C.
1
m
và
0
m
. D.
0
m
.
Lời giải
Chọn C
TXĐ
\
m
.
Có
2 2
2 3 2 2
lim lim 2 2 3
x m x m
x x m m m
x m
x m x m
.
Để đồ thị hàm số không có tiệm cận đứng thì phải tồn tại
2
2 3
lim
x m
x x m
x m
,
2
0
2 2 0
1
m
m m
m
Vậy đáp án C.
Câu 18. Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để đồ thị hàm số
2
2
4
x
y
x x m
có hai tiệm cận đứng.
A.
2019
. B.
2021
. C.
2018
. D.
2020
.
Lời giải
Chọn D
Để đồ thị hàm số
2
2
4
x
y
x x m
có hai tiệm cận đứng thì phương trình
2
4 0
x x m
có hai
nghiệm phân biệt khác
2
TÀI L
IỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
2017
4
4 0
12 20
17; 2016;..;3 \ 12
12 0
m
m
m m
m
m
.
Do đó số giá trị nguyên của tham số m thỏa đề bài là: 3 - (-2017) + 1 - 1 = 2020 giá trị.
--------------- HẾT ---------------
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 5
TIỆM CẬN ĐỒ THỊ HÀM SỐ
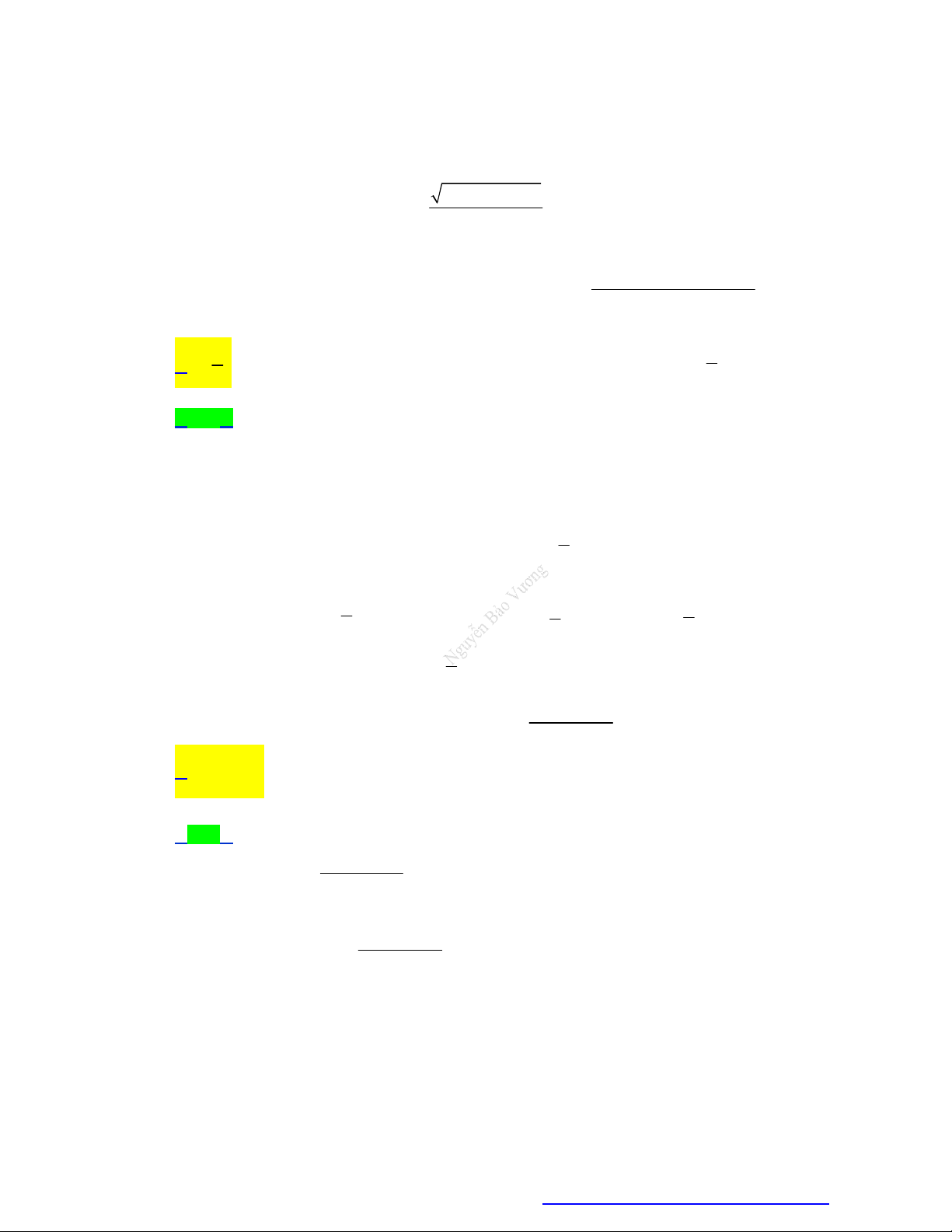
Tiệm cận ngang: Cho hàm số y  f (x) xác định trên một khoảng vô hạn (là khoảng dạng (a; ),  (  ;  b) hoặc ( ;  )). 
Đường thẳng y  là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y f (x) nếu ít
nhất một trong các điều kiện sau được thỏa mãn: lim f (x)  ,
lim f (x)  . x  x Nhận xét:
Để tìm tiệm cận ngang của đồ thị hàm số ta cần tính giới hạn của hàm số tại vô cực. P(x)
Tìm giới hạn ở vô cực của hàm y
; với P(x), Q(x) là các đa thức không căn: ( Q x)
Bậc của P(x) nhỏ hơn bậc của Q(x)  lim y  0  Tiệm cận ngang Ox : y  0. x 
HÖ sè x bËc cao cña P(x)
Bậc của P(x) bằng bậc của Q(x)  lim y  . x 
HÖ sè x bËc cao cña Q(x)
Suy ra tiệm cận ngang y  .
Bậc của P(x) lớn hơn bậc của Q(x)  lim y    Không có tiệm cận ngang. x 
Kỹ năng sử dụng máy tính (tham khảo):
Tính lim f (x) thì nhập f (x) và CALC 10 x  10 . x
Tính lim f(x) thì nhập f (x) và CALC 10 x  1  0 . x
Tiệm cận ngang: Đường thẳng x  x được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của
đồ thị hàm số y f (x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f (x)   ,
 lim f (x)   ,
 lim f (x)   ,
 lim f (x)   .  x x   x x   x x   x x       Nhận xét:
Để tìm tiệm cận đứng của đồ thị hàm số, ta cần tính giới hạn một bên của x , với x thường là điều   y
kiện biên của hàm số (hay tại x thì hàm số không xác định). Tiệ
Kỹ năng sử dụng máy tính (tham khảo): m cận  2x  1
Tính lim f (x ) thì nhập f (x) và CALC 9
x x  10 . đứn y   x x   g x  2  2
Tính lim f (x) thì nhập f (x) và CALC 9
x x  10 .
Tiệm cận ngang x x   x  2 O
Một số lưu ý cần nhớ  a ax b TCN  : y  
Hàm số nhất biếny
(c  0, ad bc  0) có c cx d TCD  : cx d  0 
Kiểm tra xem hàm số đã cho đã “Chuẩn thức hay chưa”, nếu chưa chuẩn thức (còn tồn tại nghiệm mẫu
và tử trùng nhau) ta nên chuẩn thức. Nếu gặp đa thức sẽ phân tích thành tích số, gặp căn thức sẽ
nhân lượng liên hợp.
Tìm tiệm cận đứng (tại vị trí hàm số không xác định), kết quả giới hạn phải ra  hoặc  . 
Tìm tiệm cận ngang (tại vị trí  )
 , kết quả sẽ ra một số cụ thể.
Hãy nhớ điều này để giải quyết những bài toán cho dạng bảng biến thiên, mà câu hỏi hỏi đúng, sai?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
A. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua bảng biến thiên – đồ thị)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
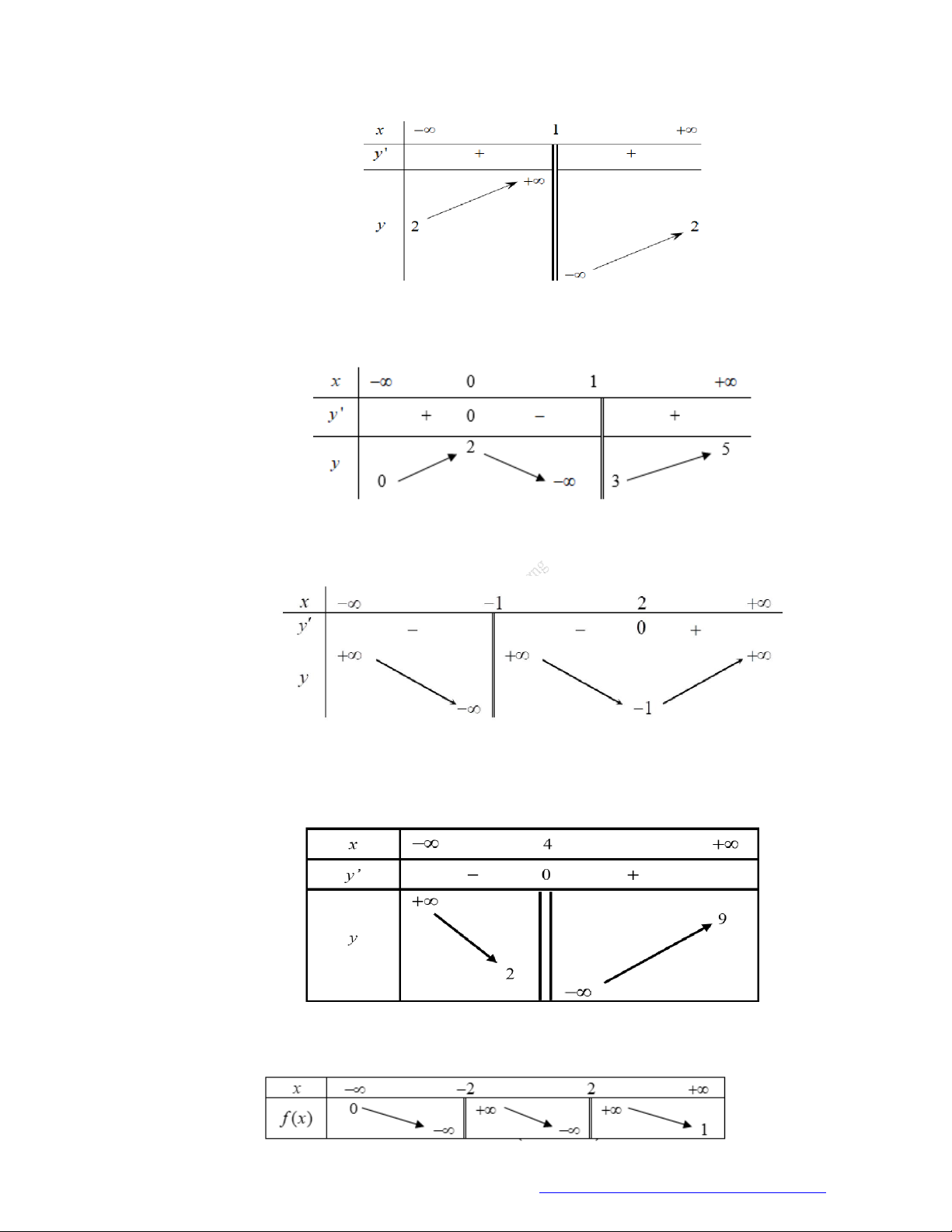
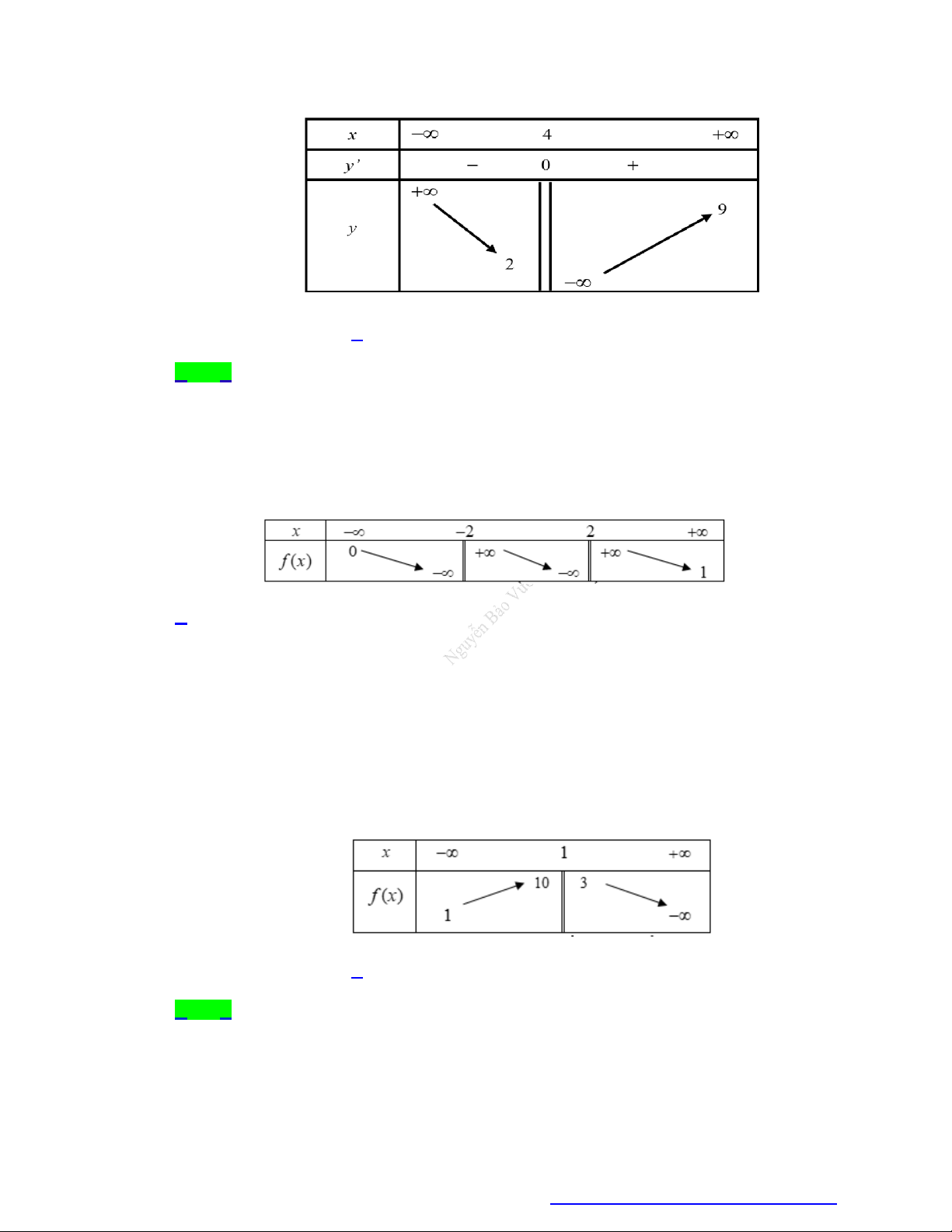
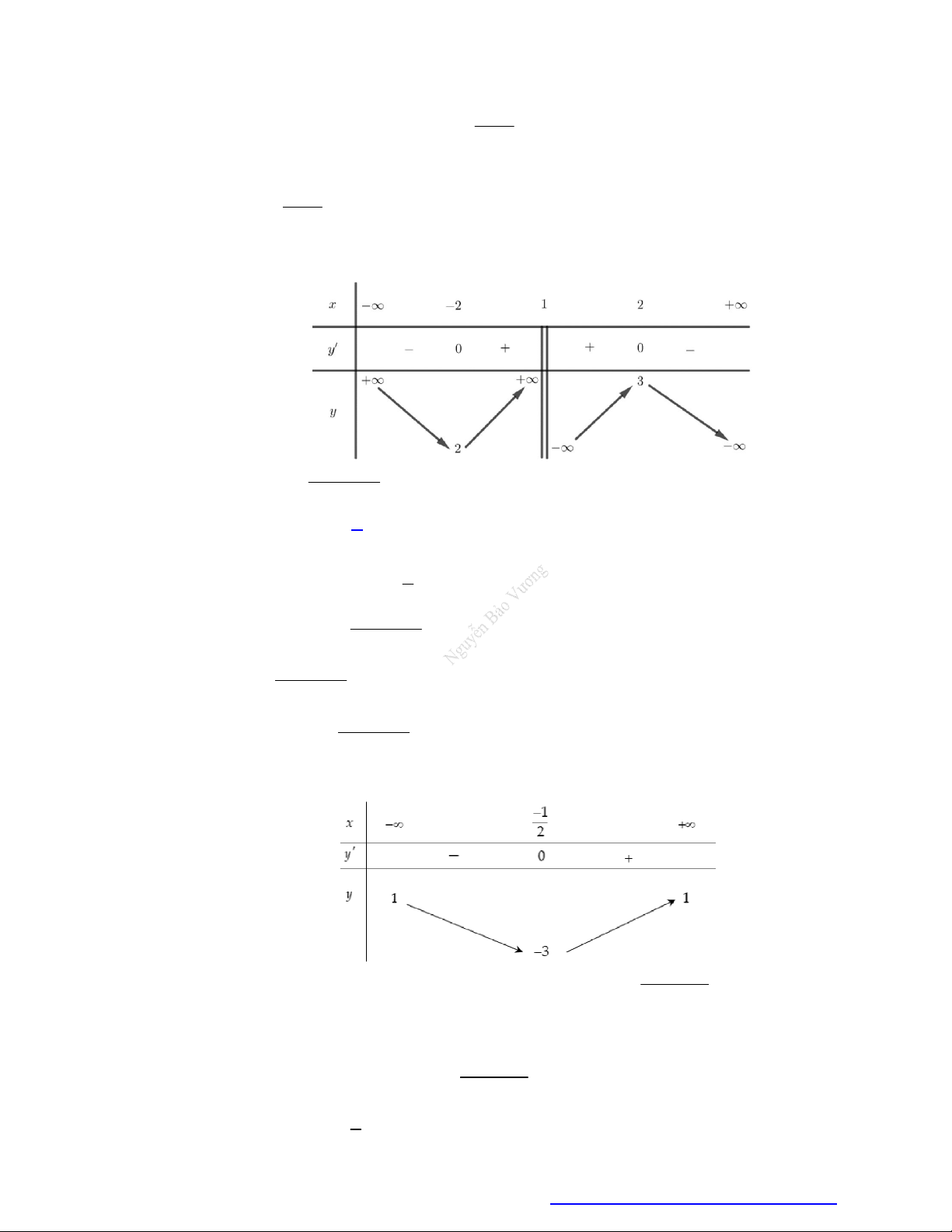
Cho hàm số y f x có bảng biến thiên như sau
Đồ thị hàm số có tổng số đường tiệm cận đứng là a và tổng số đường tiệm cận ngang là b . Khi đó
2a b bằng A. 4 . B. 6 . C. 3. D. 2 . Câu 2.
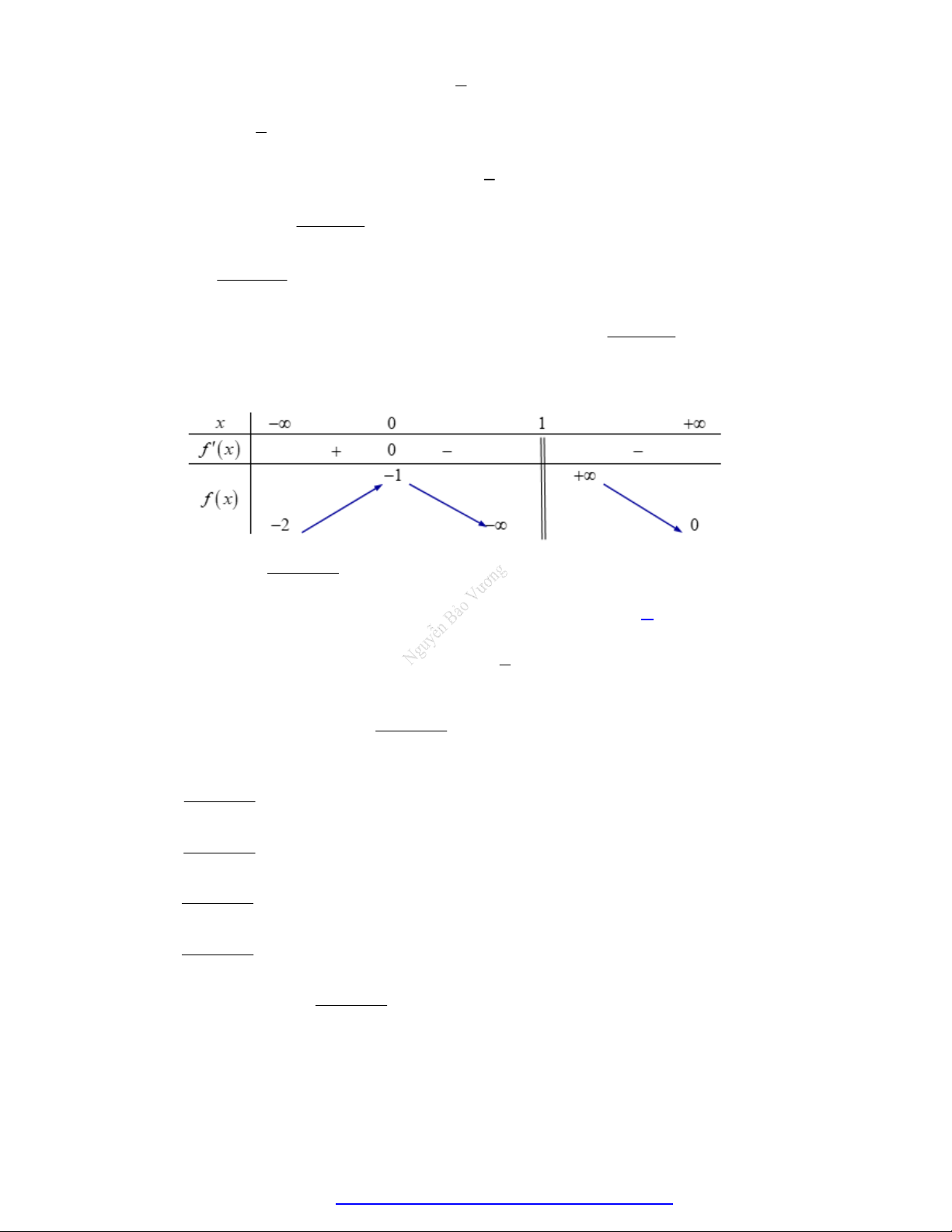
Cho hàm số y f x có bảng biến thiên như sau
Tổng số đường tiệm cận của đồ thị hàm số đã cho là A. 3. B. 1. C. 4. D. 2. Câu 3.
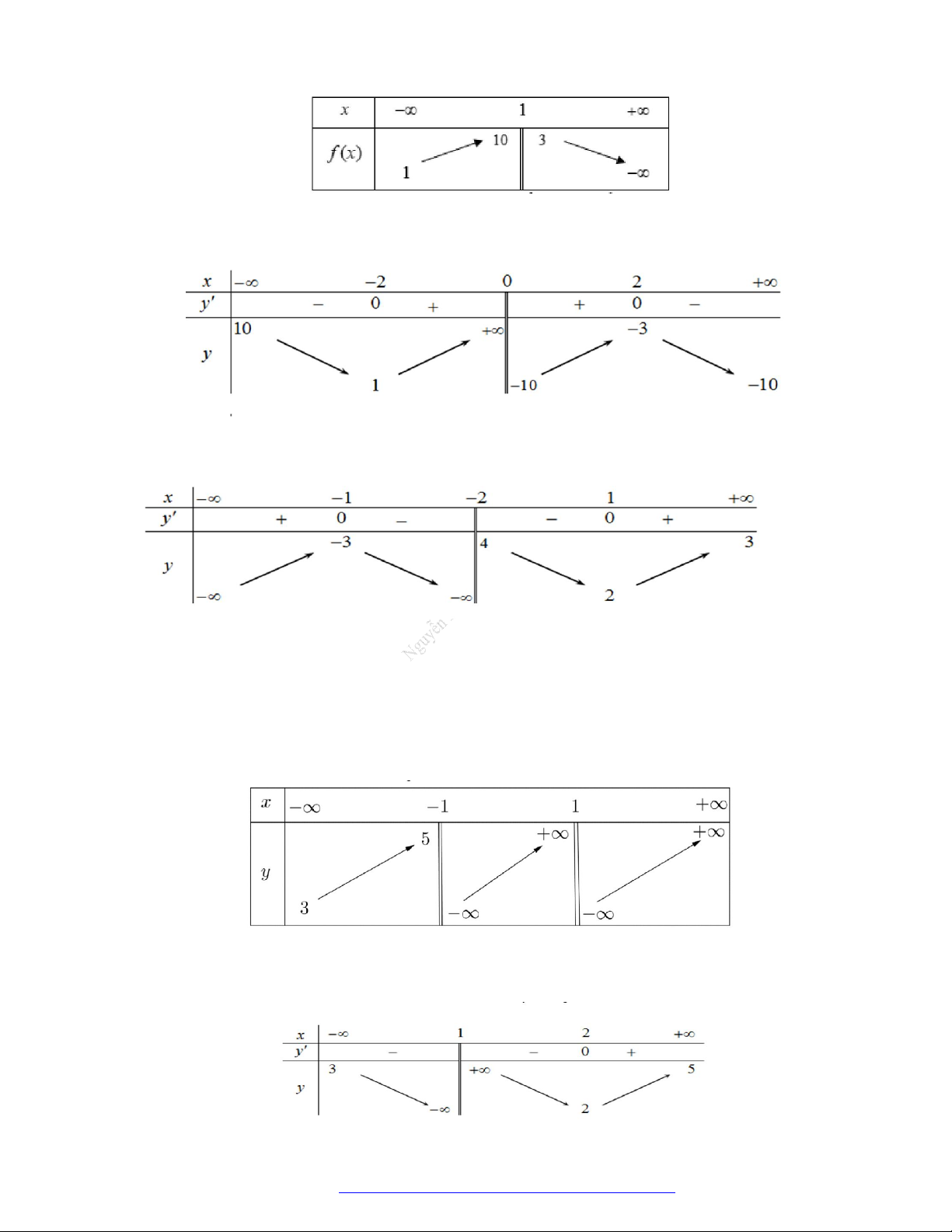
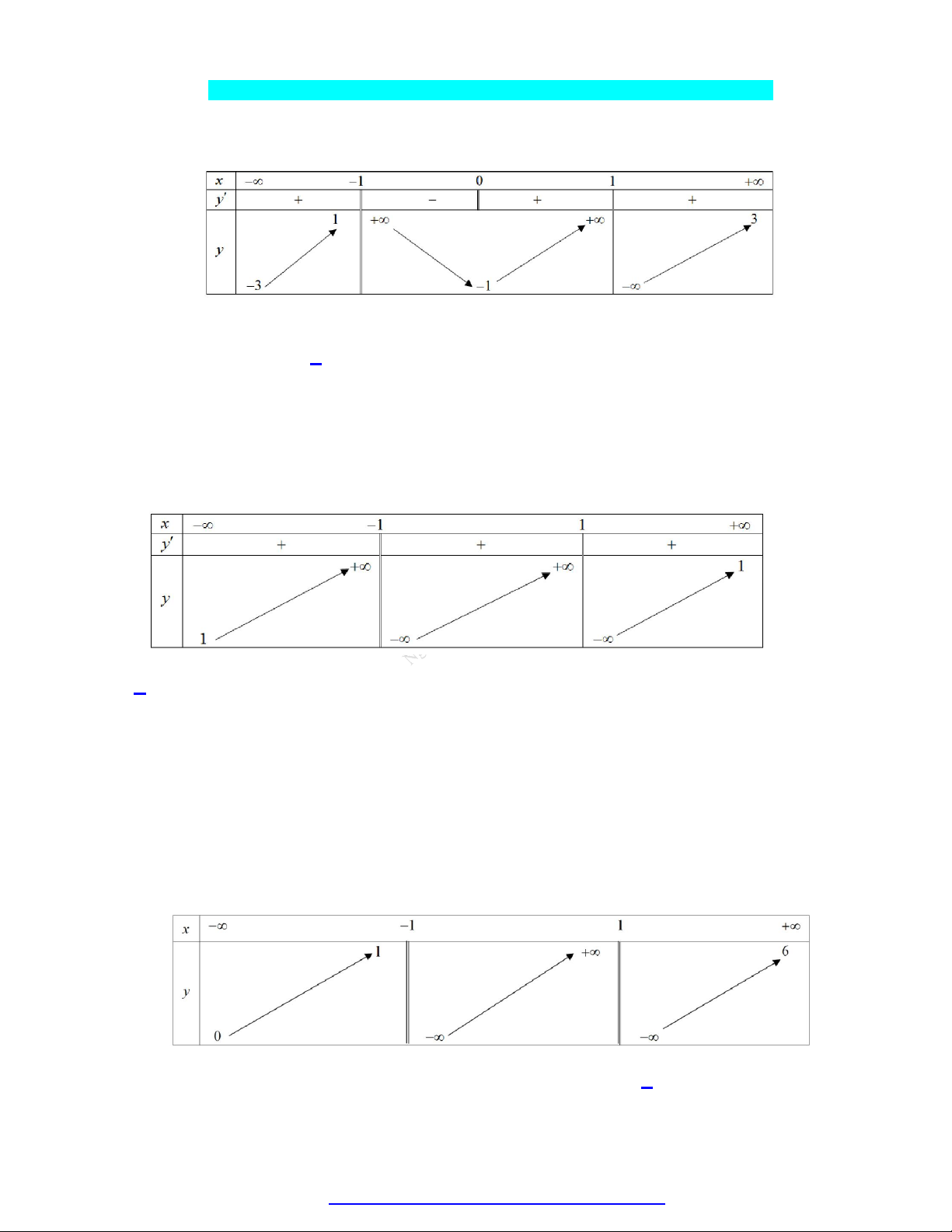
Cho hàm số y f x có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 1. B. 2 . C. 3. D. 4 . Câu 4.
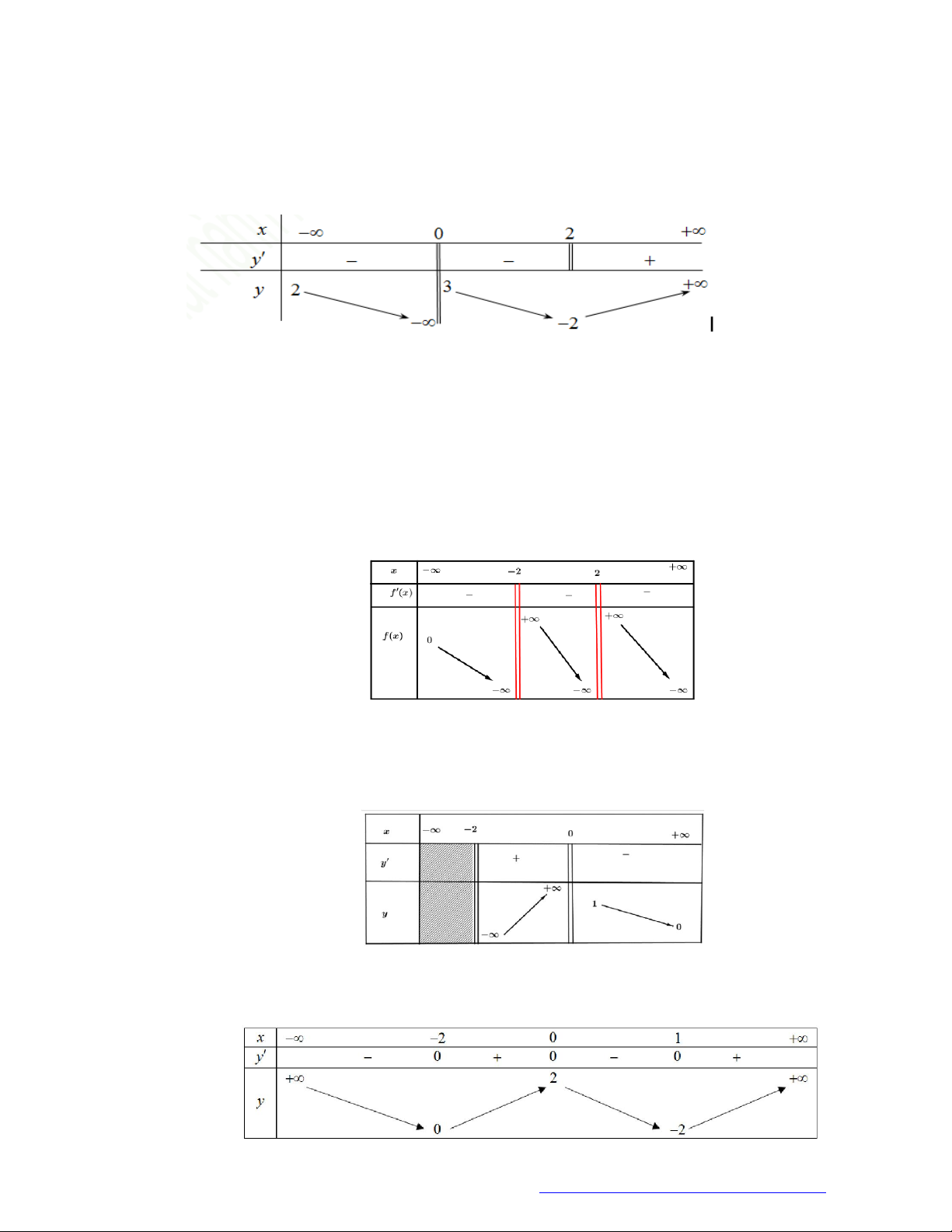
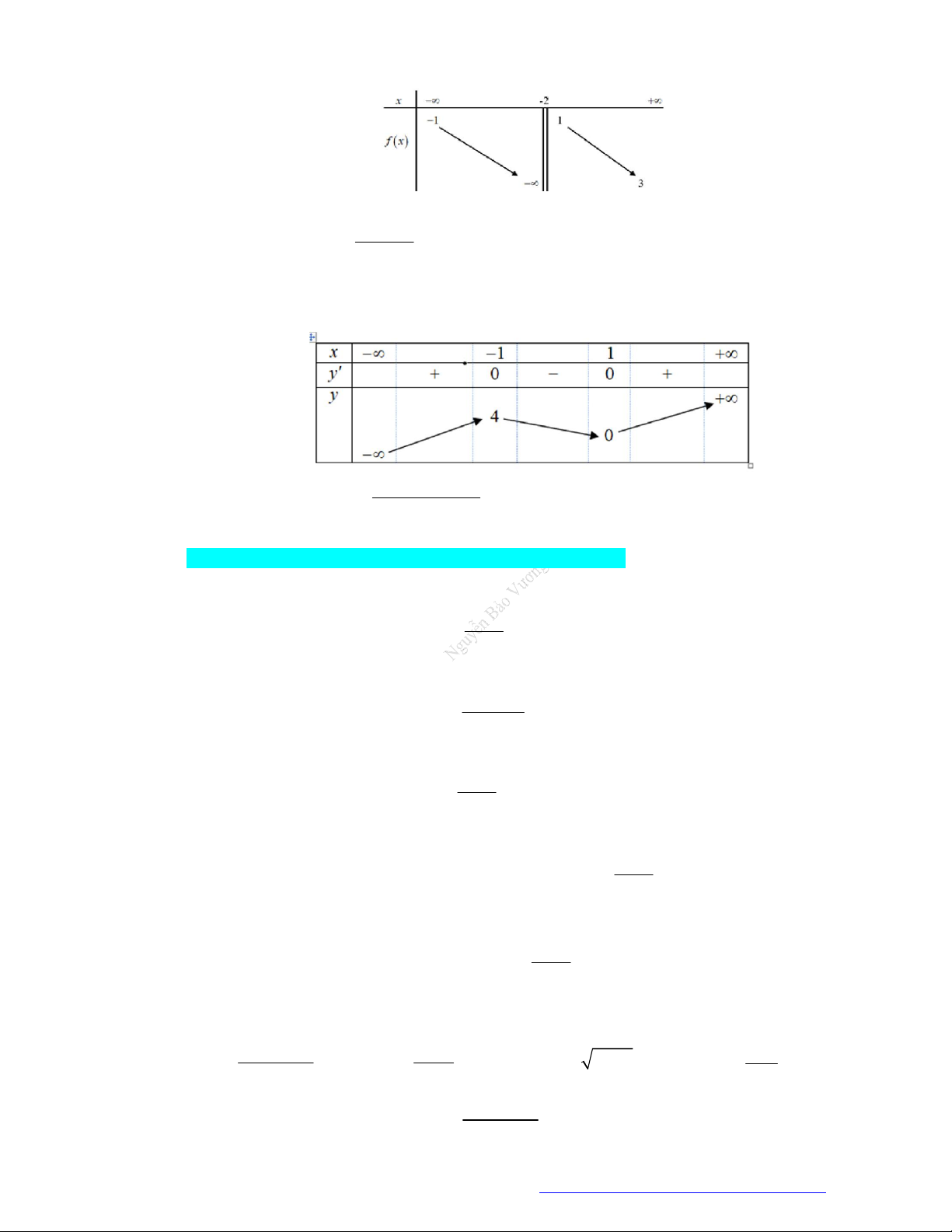
Cho hàm số y f x có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 1. B. 4 . C. 2 . D. 3 . ax  3 Câu 5.
Cho hàm số y f x 
có bảng biến thiên như sau 2x b
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Giá trị a  2b bằng? A. 8 B. 6  C. 0 D. 10 Câu 6.
Cho hàm số y f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Câu 7.
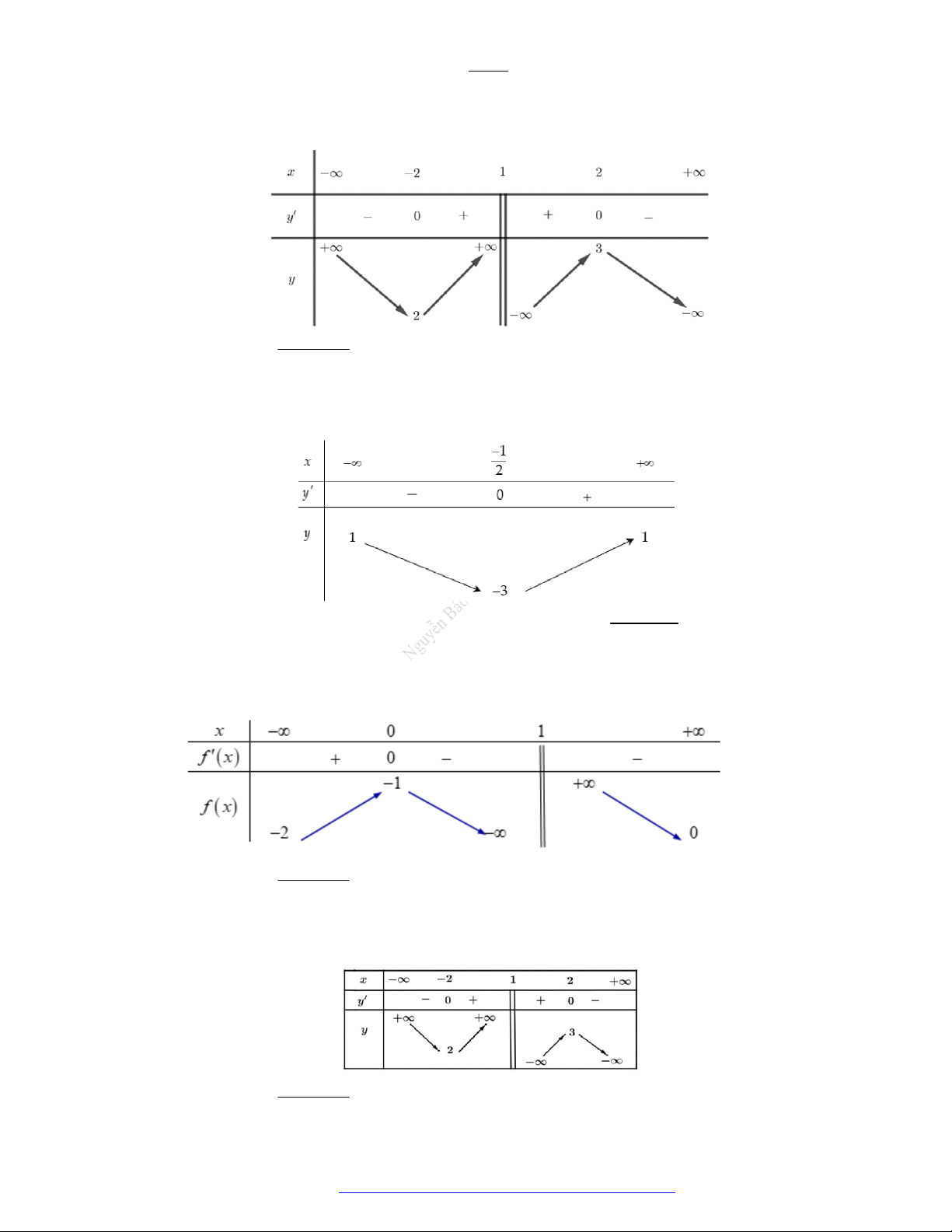
Cho hàmsố f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Câu 8.
Cho hàm số f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Câu 9.
Cho hàm số y f (x) xác định trên R \  
4 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
Tổng số tiệm cận ngang của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 .
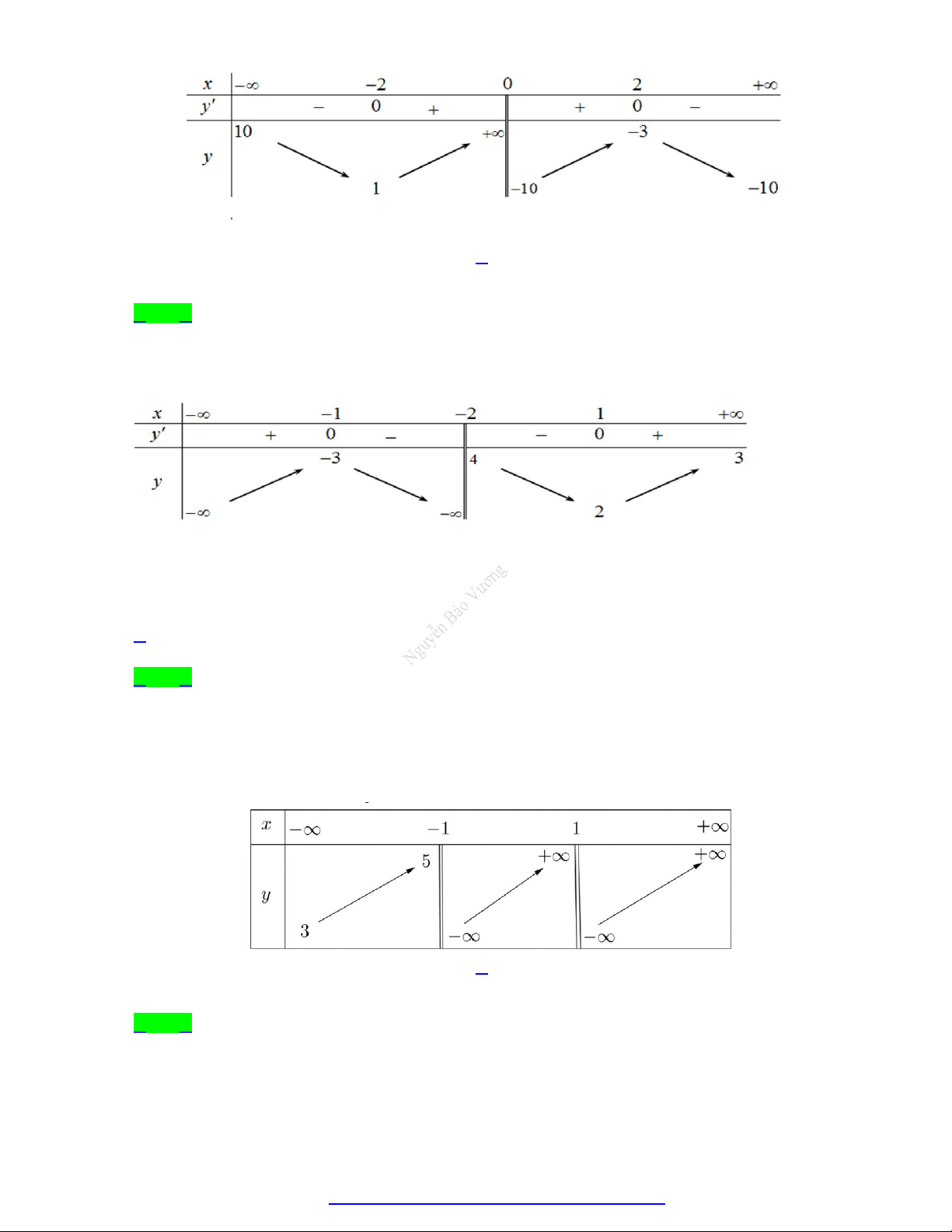
Câu 10. Cho hàm số y f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 A. 4 . B. 1. C. 3 . D. 2 .
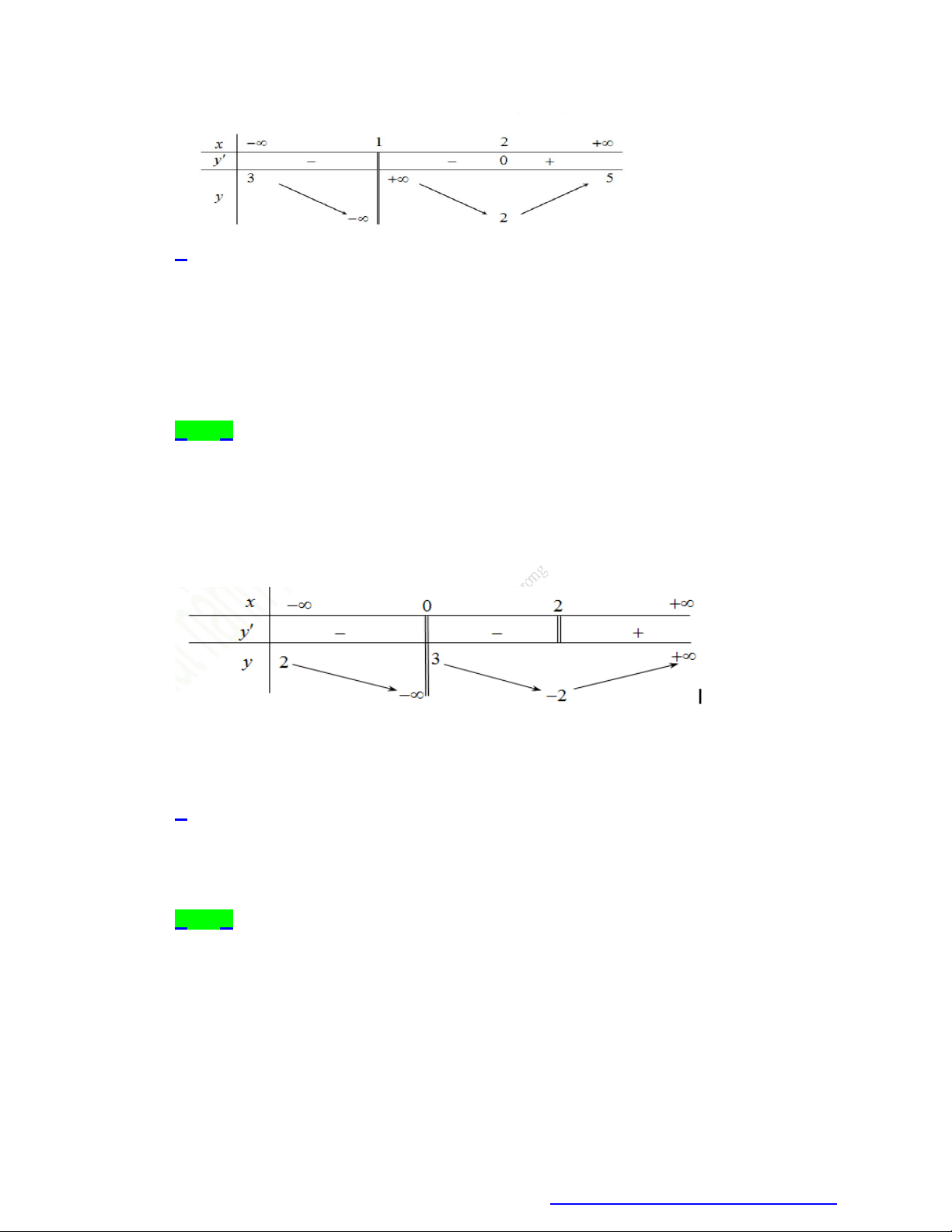
Câu 11. Cho hàm số y f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 .
Câu 12. Cho hàm số y f (x) có bảng biến thiên
Số tiệm cận ngang của đồ thị hàm số y f (x) là A. 3 . B. 1. C. 2 . D. 0
Câu 13. Cho hàm số y f (x) có bảng biến thiên như hình vẽ
Khẳng định nào sao đây sai?
A. Đồ thị hàm có tiệm cận ngang y  3
B. Đồ thị hàm số có một tiệm cận đứng x  2 .
C. Đồ thị hàm số có một tiệm cận ngang y  3 và một tiệm cận đứng x  2 .
D. Đồ thị hàm số có hai tiệm cận ngang y  3 và y  4
Câu 14. Cho hàm số y f (x) xác định trên D   \  1  , 
1 , có bảng biến thiên như hình vẽ bên dưới.
Hỏi đồ thị hàm số có bao nhiêu đường tiệm cận? A. 1 . B. 2 . C. 3 . D. 4 .
Câu 15. Cho hàm số y f (x) xác định trên D   \  
1 , liên tục trên mỗi khoảng xác định và có bảng
biến thiên như hình vẽ bên dưới. Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có một đường tiệm cận đứng là đường thẳng x  1 và một trong các đường tiệm
cận ngang là đường thẳng y  3 .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
B. Đồ thị hàm số không có đường tiệm cận đứng và có hai tiệm cận ngang là đường thẳng
y  3 và y  5 .
C. Đồ thị hàm số chỉ có một đường tiệm cận đứng, không có tiệm cận ngang
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng x  1 và hai tiệm cận đứng là đường thẳng
y  3 và y  5 .
Câu 16. Cho hàm số y f (x) xác định trên D   \  
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ bên dưới.
Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có hai tiệm cận đứng là đường thẳng x  0 và x  2 tiệm cận ngang là đường thẳng y  2 .
B. Đồ thị hàm số không có đường tiệm cận đứng và có một tiệm cận ngang.
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng x  0 và tiệm cận ngang là đường thẳng y  2 .
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng x  0 và hai tiệm cận đứng là đường thẳng
y  2 và y  3 .
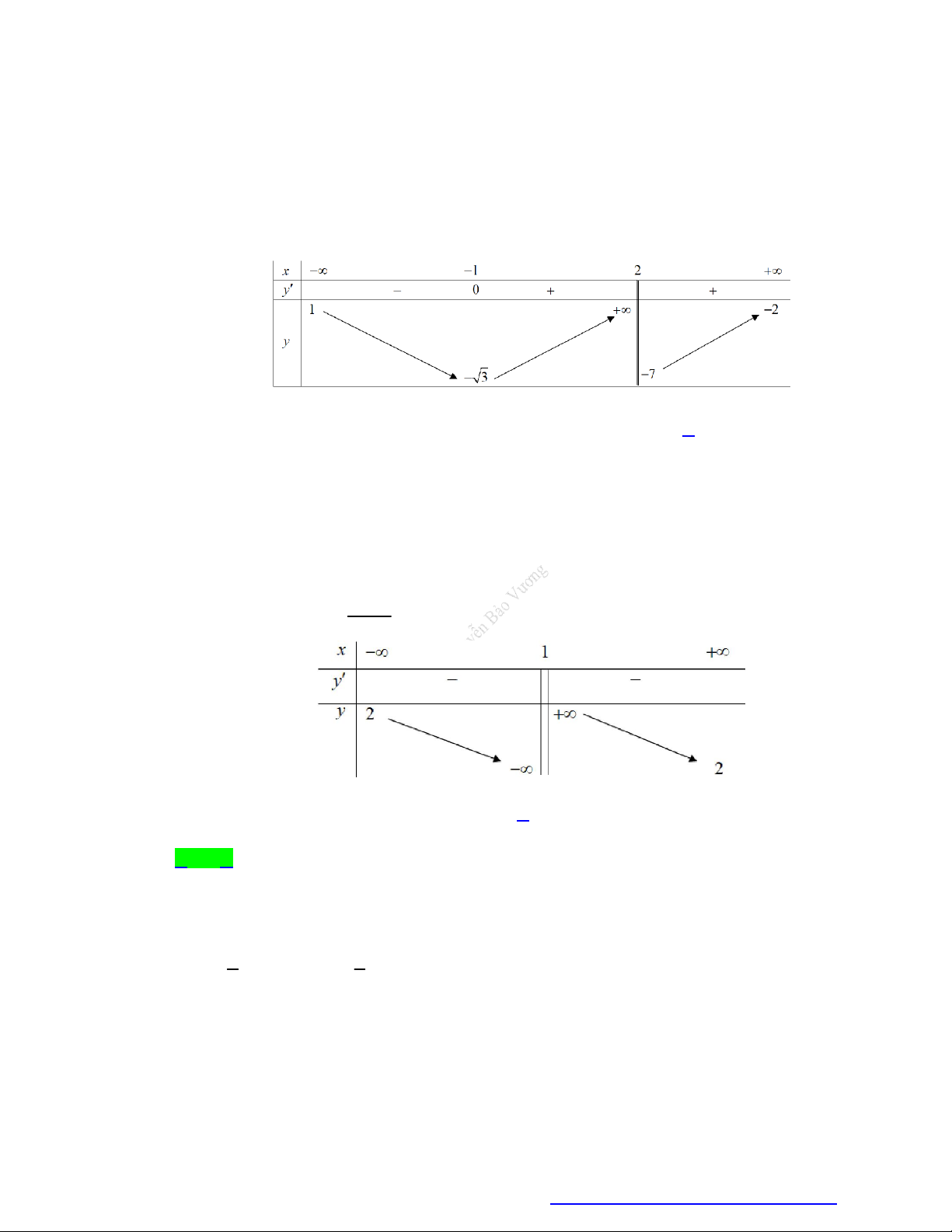
Câu 17. Cho hàm số y f x liên tục trên  \ 2; 
2 và có bảng biến thiên như hình vẽ:
Chọn khẳng định đúng trong các khẳng định sau đây.
A. Đồ thị hàm số có đúng 4 tiệm cận.
B. Đồ thị hàm số có đúng 2 tiệm cận.
C. Đồ thị hàm số có đúng 1 tiệm cận.
D. Đồ thị hàm số có đúng 3 tiệm cận.
Câu 18. Cho hàm số f x có bảng biến thiên như hình sau:
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? A. 1. B. 3 . C. 2 . D. 4 .
Câu 19. Cho hàm số y f x có bảng biến thiên như sau:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 2020
Tổng số tiệm cận đứng của đồ thị hàm số y  là f xA. 1. B. 2 . C. 3. D. 4 .
Câu 20. Cho hàm số y f x liên tục trên  \  
1 và có bảng biến thiên như sau: 1
Đồ thị hàm số y
có bao nhiêu đường tiệm cận đứng?
2 f x  5 A. 0 . B. 4 . C. 2 . D. 1.
Câu 21. Cho hàm số y f x có bảng biến thiên như hình dưới đây. 1
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y  là
2 f x 1 A. 0. B. 1. C. 2. D. 3.
Câu 22. Cho hàm số y f x liên tục trên  \  
1 và có bảng biến thiên như sau: 1
Đồ thị hàm số y
có bao nhiêu đường tiệm cận đứng?
2 f x  3 A. 1. B. 2 . C. 0 . D. 2 .
Câu 23. Cho hàm số y f x liên tục trên  \ 
1 và có bảng biến thiên như sau: 1
Đồ thị hàm số y
có bao nhiêu đường tiệm cận đứng?
2 f x  5 A. 0 . B. 1. C. 2 . D. 4 .
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
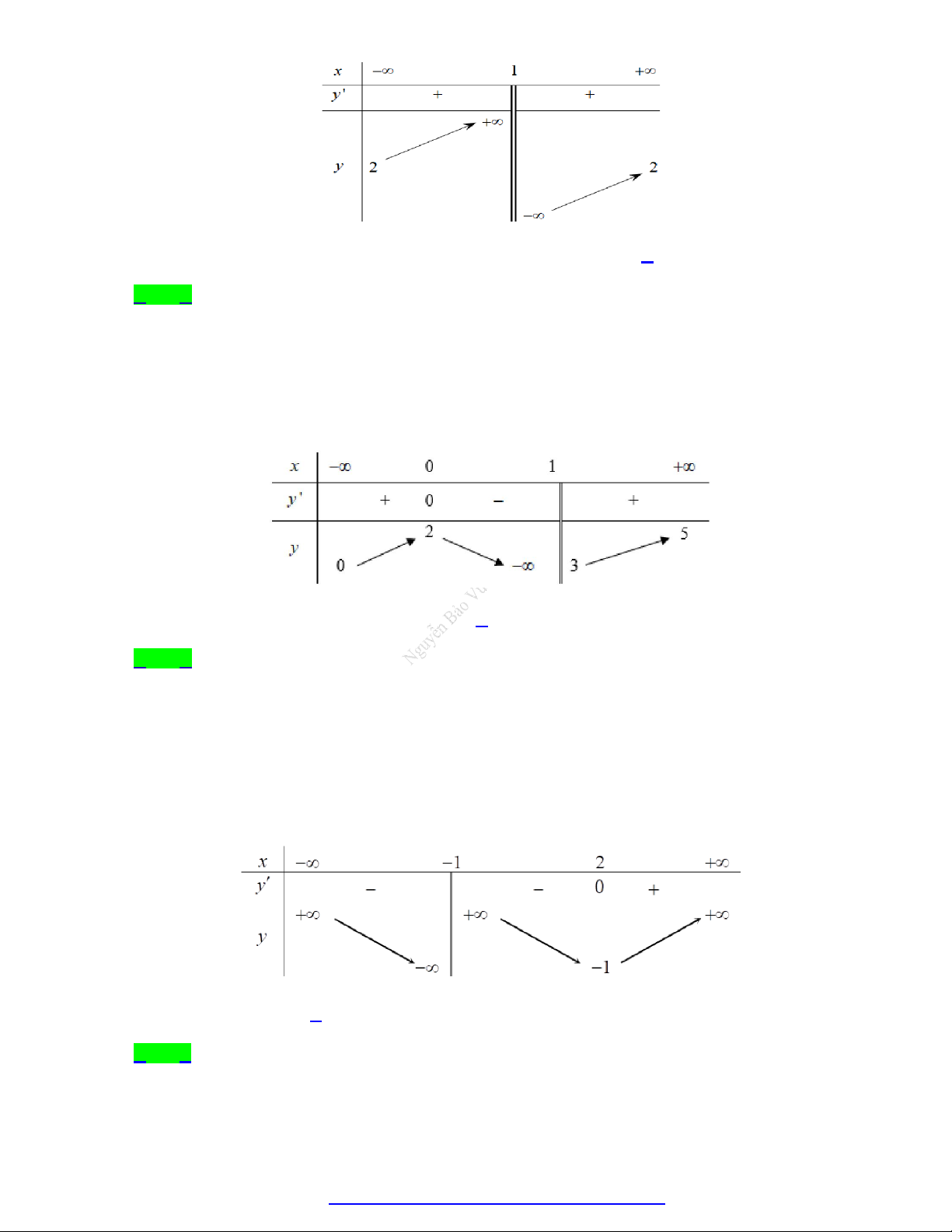
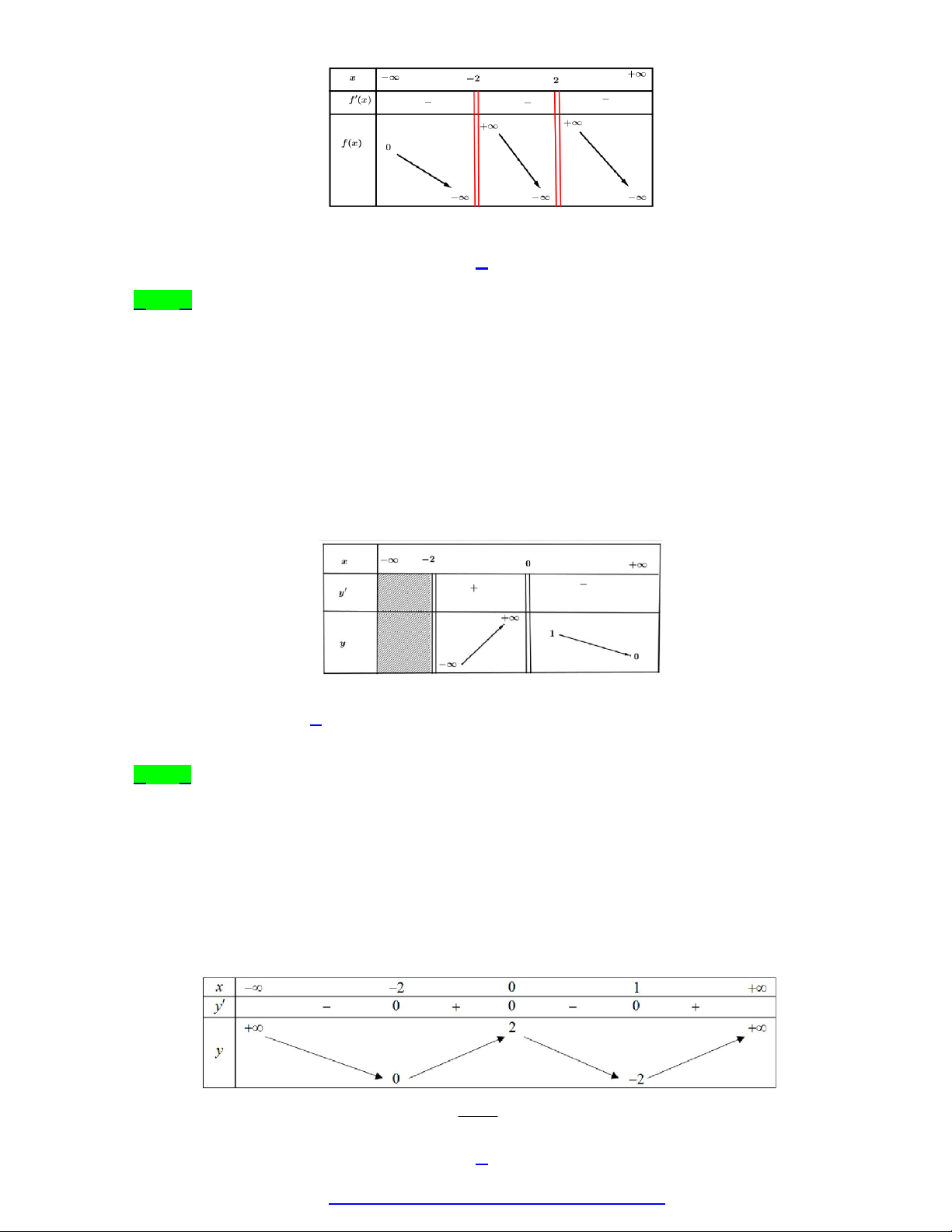
Câu 24. Cho hàm số y f x có bảng biến thiên nhưsau:
Đồ thị hàm số có tổng số đường tiệm cận đứng là a và tổng số đường tiệm cận ngang là b . Khi 2 3 2a b
đó giá trị của biểu thức
thuộc khoảng nào sau đây? 2 2 a b A. 0; 4 . B.  6  ;  4 . C. 2;0 . D.  4  ;  2 .
Câu 25. Cho hàm số y f x có đạo hàm liên tục trên  và có bảng biến thiên như sau: 2 x 1
Hỏi đồ thị hàm số g x 
có bao nhiêu đường tiệm cận đứng? 2
f x  4 f xA. 4 . B. 3 . C. 2 . D. 1.
B. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua hàm số)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA x  2 Câu 1.
Tiệm cận ngang của đồ thị hàm số y  là x 1 A. y  2  .
B. y  1. C. x  1  .
D. x  2 . x  2020 Câu 2.
Tiệm cận ngang của đồ thị hàm số y  là x  2019 A. y  2  019 .
B. y  1. C. x  2  019 .
D. x  2020 . x  2 Câu 3.
Tiệm cận đứng của đồ thị hàm số y  là x  1
A. y  2 .
B. y  1. C. x  1  .
D. x  2 . x  2 Câu 4.
Tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số y  là x 1 A. I 1;  1 . B. I  1  ;  1 .
C. I 1;   1 . D. I  1  ;   1 . x  2 Câu 5.
Số đường tiệm cận ngang của đồ thị hàm số y  là x  1 A. 0 . B. 1. C. 2 . D. 3. Câu 6.
Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 x  3x  2 2 x x A. y B. y C. 2 y x 1 D. y x 1 2 x 1 x  1 2 x  5x  4 Câu 7.
Tìm số tiệm cận của đồ thị hàm số y  . 2 x 1 A. 2 B. 3 C. 0 D. 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 2 x  3x  4 Câu 8.
Tìm số tiệm cận đứng của đồ thị hàm số: y 2 x  16 A. 2 B. 3 C. 1 D. 0 2 5x  4x 1 Câu 9.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x 1 A. 0. B. 1. C. 2. D. 3. 2 ax bx  2
Câu 10. Cho hàm số y f x 
. Biết rằng đồ thị hàm số có đúng một đường tiệm cận ngang 2 x  4
là y  1 và một đường tiệm cận đứng là x  2 . Khi đó giá trị của biểu thức b a bằng? A. 2 B. 4 C. 2 D. 4 x x  2
Câu 11. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x  4 A. 1 B. 2 C. 3 D. 4 x  1
Câu 12. Đồ thị hàm số f x 
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang? 2 x  1 A. 4 . B. 3 . C. 1. D. 2 . x  25  5
Câu 13. Số tiệm cận đứng của đồ thị hàm số y  là 2 x x A. 3 B. 2 C. 0 D. 1 x 16  4
Câu 14. Số tiệm cận đứng của đồ thị hàm số y  là 2 x x A. 3 . B. 2 . C. 1. D. 0 . 2
2x 1 x x  3
Câu 15. Tìm tất cả các tiệm cận đứng của đồ thị hàm số y  . 2 x  5x  6
A. x 3 và x  2.
B. x  3. C. x  3  và x  2  . D. x  3  . x  4  2
Câu 16. Số tiệm cận đứng của đồ thị hàm số y  là 2 x x A. 3 . B. 0 . C. 1. D. 2 . x 1
Câu 17. Tìm số đường tiệm cận của đồ thị hàm số y  .
4 3x 1  3x  5 A. 2 . B. 3 . C. 1. D. 0 . 2 x  2x  3
Câu 18. Cho hàm số y
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x  3x  2 A. 4 . B. 5 . C. 3 . D. 6 . 5x 8
Câu 19. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 x 3x A. 2. B. 4. C. 1. D. 3. 2
4x  2x 1  x
Câu 20. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? x 1 A. 1. B. 0 . C. 2 . D. 3 .
C. ĐỊNH m ĐỂ ĐỒ THỊ HÀM SỐ CÓ ĐƯỜNG TIỆM CẬN THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC
Đường tiệm cận ngang
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Cho hàm số y f x có TXD: D
Điều kiện cần: D phải chứa  hoặc  Điều kiện đủ: P(x)
Dạng 1. y f (x)  . Q(x)
Nếu degP x  degQ x : thì không có tiệm cận ngan
Nếu degP x  degQx :TCN y  0
Nếu degP x  degQ x : y k (k là tỉ số hệ số bậc cao nhất của tử và mẫu) 2 u v u v
Dạng 2: y f (x)  u v (hoặc u v ): Nhân liên hợp  y f (x)  (hoặc ) u v u v
Đường tiệm cận đứng P x Cho hàm số y  có TXD: D Q x
Đkiện cần: giải Q x  0  x x là TCĐ khi thỏa mãn đk đủ 0 Đkiện đủ:
Đkiện 1: x làm cho P(x) và Q(x) xác định. 0
Đkiện 2: - x không phải nghiêm P(x)  x x là TCĐ 0 0
- x là nghiêm P(x)  x x là TCĐ nếu lim f (x)   0 0 xx0 x 1 Câu 1.
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y  có hai tiệm cận 2 mx 1 ngang A. m  0 B. m  0 C. m  0
D. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài 2 x m Câu 2.
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y  có đúng hai đường 2 x  3x  2 tiệm cận. A. m  1 B. m {1; 4} C. m  4
D. m { 1; 4  } 6x  3 Câu 3.
Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y  có đúng  2
mx  6x  3 2
9x  6mx   1 một đường tiệm cận? A. 0 . B. 2 . C. 1. D. Vô số. 5x  3 Câu 4.
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y  không có tiệm cận 2 x  2mx 1 đứng. m  1 A. B. 1   m  1 C. m  1  D. m  1 m  1  x 1 Câu 5.
Cho hàm số y f x 
. Tìm tất cả các giá trị của tham số m để đồ thị có ba đường 2 x  2mx  4 tiệm cận
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489  m  2  m  2     m  2 m  2 A. m  2 B.   5 C. D. m     5 m  2   2 m     2
n  3 x n  2017 Câu 6.
Biết rằng đồ thị của hàm số y
( m, n là các số thực) nhận trục hoành làm x m  3
tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng m n . A. 0 B. 3  C. 3 D. 6 x 1 Câu 7.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y  có đúng bốn 2 mx  8x  2 đường tiệm cận? A. 8 B. 6 C. 7 D. Vô số Câu 8.
Với giá trị nào của hàm số m để đồ thị hàm số 2
y x mx  3x  7 có tiệm cạn ngang. A. m 1 B. m  1  C. m  1 
D. Không có m mx 1 Câu 9. Cho hàm số y
với tham số m  0 . Giao điểm của hai đường tiệm cận của đồ thị hàm số x  2m
thuộc đường thẳng có phương trình nào dưới đây?
A. y  2x .
B. 2x y  0 .
C. x  2 y  0 .
D. x  2 y  0 . mx  2
Câu 10. Tìm tất cả các giá trị của m để đồ thị hàm số y
có đúng 2 tiệm cận? 2 x  4 A. m  1. B. m  1. C. m  1. D. m  0 m   1 x  5m
Câu 11. Tìm tham số m để đồ thị hàm số y
có tiệm cận ngang là đường thẳng y  1 2x m 1 A. m  1. B. m  . C. m  2 . D. m  1. 2 x 1
Câu 12. Có bao nhiêu giá trị nguyên m  1
 0;10 sao cho đồ thị hàm số y  có hai 2
2x  6x m  3
đường tiệm cận đứng? A. 19 . B. 15 . C. 17 . D. 18.
Câu 13. Có bao nhiêu giá trị nguyên của m để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 2 mx  3mx  4 y  bằng 3? x  2 A. 4 . B. 2 . C. Vô số. D. 3 . x 1
Câu 14. Tổng các giá trị của tham số m để đồ thị của hàm số y  có đúng một 2
x  2m   2 1 x m  2 tiệm cận đứng. 1 3 A.  . B. 2 . C. 3  . D. . 2 2 2 x x  2
Câu 15. Tìm tất cả các giá trị của m để đồ thị hàm số y  2
x  2x m có 3 đường tiệm cận. m  1 m  1 m  1 A.  . B.  . C.  . D. m  8 . m  8  m  8  m  8 
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 x 3
Câu 16. Cho hàm số y
. Có bao nhiêu giá trị nguyên thuộc đoạn  6  ;6 của 3 2 x  3mx  2 2m   1 x m
tham số m để đồ thị hàm số có bốn đường tiệm cận? A. 12 . B. 9 . C. 8 . D. 11. 2
2x  3x m
Câu 17. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y  không có tiệm x m cận đứng. A. m  1. B. m  1.
C. m  1và m  0 . D. m  0 .
Câu 18. Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn   2017; 2017 để đồ thị hàm số x  2 y
có hai tiệm cận đứng. 2
x  4x m A. 2019 . B. 2021. C. 2018 . D. 2020 .
-------------------- HẾT --------------------
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 5
TIỆM CẬN ĐỒ THỊ HÀM SỐ
Tiệm cận ngang: Cho hàm số y  f (x) xác định trên một khoảng vô hạn (là khoảng dạng (a; ),  (  ;  b) hoặc ( ;  )). 
Đường thẳng y  là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y f (x) nếu ít
nhất một trong các điều kiện sau được thỏa mãn: lim f (x)  ,
lim f (x)  . x  x Nhận xét:
Để tìm tiệm cận ngang của đồ thị hàm số ta cần tính giới hạn của hàm số tại vô cực. P(x)
Tìm giới hạn ở vô cực của hàm y
; với P(x), Q(x) là các đa thức không căn: ( Q x)
Bậc của P(x) nhỏ hơn bậc của Q(x)  lim y  0  Tiệm cận ngang Ox : y  0. x 
HÖ sè x bËc cao cña P(x)
Bậc của P(x) bằng bậc của Q(x)  lim y  . x
HÖ sè x bËc cao cña Q(x)
Suy ra tiệm cận ngang y  .
Bậc của P(x) lớn hơn bậc của Q(x)  lim y    Không có tiệm cận ngang. x 
Kỹ năng sử dụng máy tính (tham khảo):
Tính lim f (x) thì nhập f (x) và CALC 10 x  10 . x 
Tính lim f(x) thì nhập f (x) và CALC 10 x  1  0 . x 
Tiệm cận ngang: Đường thẳng x  x được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ
thị hàm số y f (x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f (x)   ,
 lim f (x)   ,
 lim f (x)   ,
 lim f (x)   .  x x   x x   x x   x x       Nhận xét:
Để tìm tiệm cận đứng của đồ thị hàm số, ta cần tính giới hạn một bên của x , với x thường là điều kiện   y
biên của hàm số (hay tại x thì hàm số không xác định). Tiệ
Kỹ năng sử dụng máy tính (tham khảo): m cận  2x  1
Tính lim f (x ) thì nhập f (x) và CALC 9
x x  10 . đứn y   x x   g x  2  2
Tính lim f (x) thì nhập f (x) và CALC 9
x x  10 .
Tiệm cận ngang x x   x  2 O
Một số lưu ý cần nhớ  a ax b TCN  : y  
Hàm số nhất biếny
(c  0, ad bc  0) có c cx d TCD  : cx d  0 
Kiểm tra xem hàm số đã cho đã “Chuẩn thức hay chưa”, nếu chưa chuẩn thức (còn tồn tại nghiệm mẫu và
tử trùng nhau) ta nên chuẩn thức. Nếu gặp đa thức sẽ phân tích thành tích số, gặp căn thức sẽ nhân lượng liên hợp.
Tìm tiệm cận đứng (tại vị trí hàm số không xác định), kết quả giới hạn phải ra  hoặc  . 
Tìm tiệm cận ngang (tại vị trí  )
 , kết quả sẽ ra một số cụ thể.
Hãy nhớ điều này để giải quyết những bài toán cho dạng bảng biến thiên, mà câu hỏi hỏi đúng, sai?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
A. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua bảng biến thiên – đồ thị)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
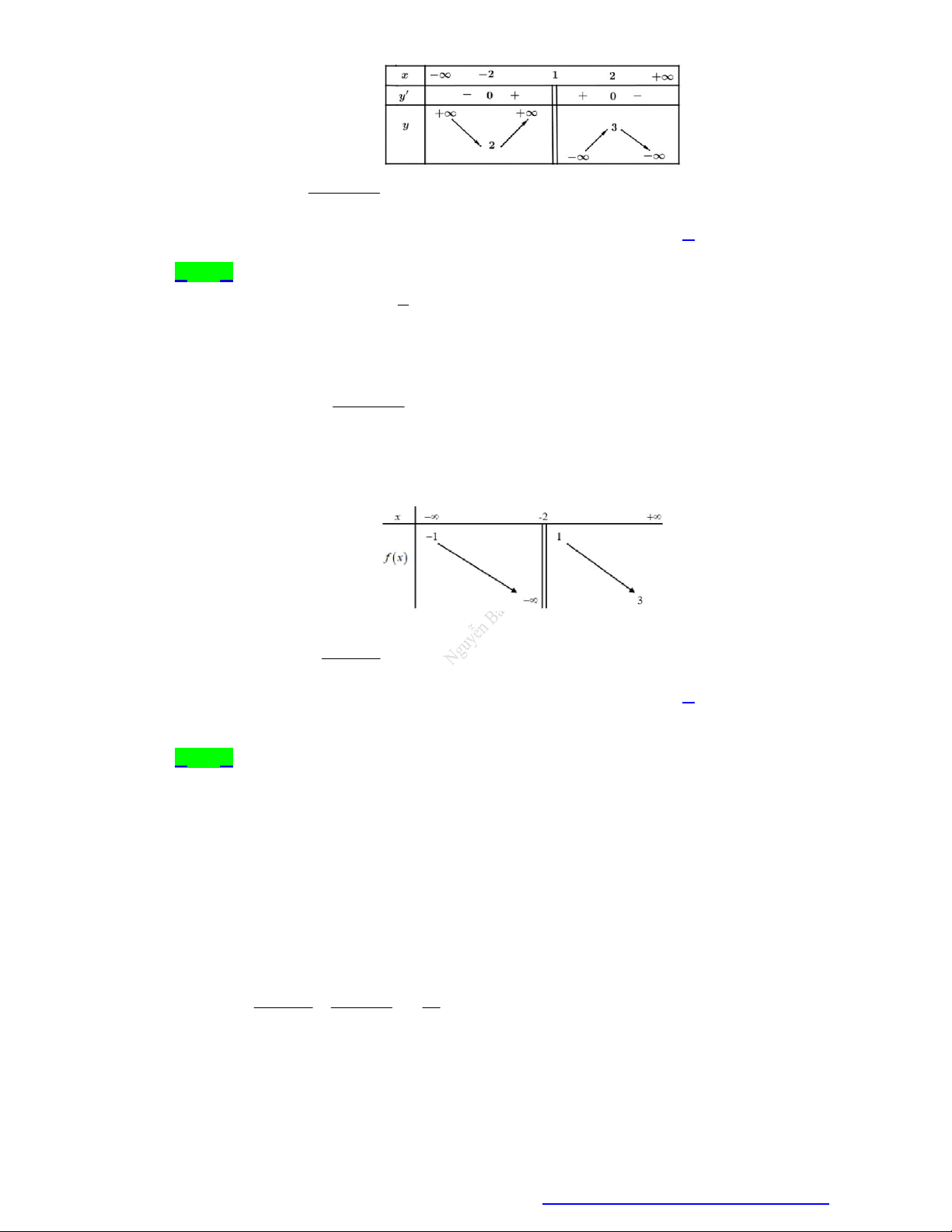
Cho hàm số y f x có bảng biến thiên như sau
Đồ thị hàm số có tổng số đường tiệm cận đứng là a và tổng số đường tiệm cận ngang là b . Khi đó
2a b bằng A. 4 . B. 6 . C. 3. D. 2 . Lời giải Chọn B
Dựa vào bảng biến thiên suy ra đồ thị có hai tiệm cận đứng là x  1 , x  1
 và hai tiệm cận ngang là
y  3 , y  3 . Suy ra a  2 và b  2 .
Vậy 2a b  6 . Câu 2.
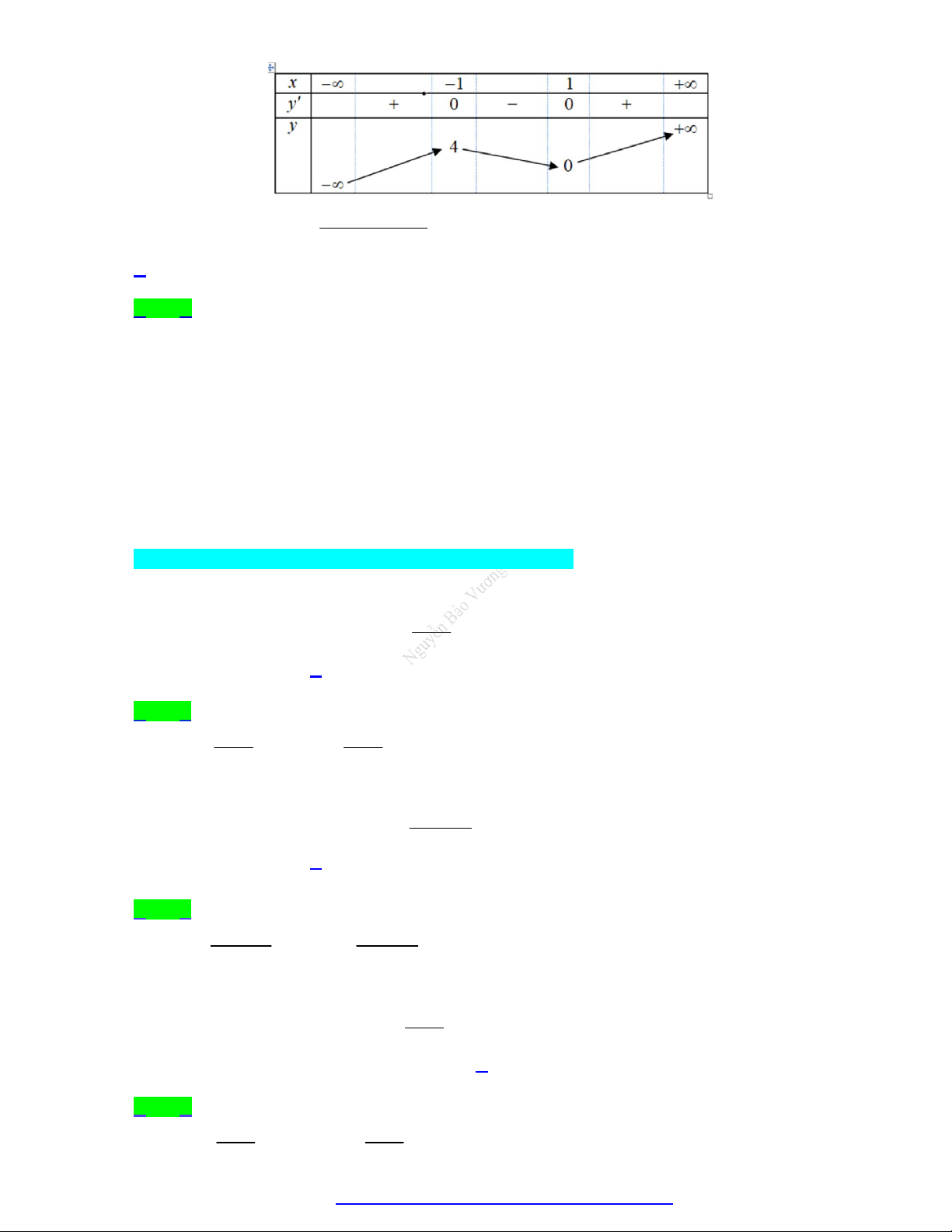
Cho hàm số y f x có bảng biến thiên như sau
Tổng số đường tiệm cận của đồ thị hàm số đã cho là A. 3. B. 1. C. 4. D. 2. Lời giải Chọn A
Dựa vào bảng biến thiên ta có
lim y  1  y  1 là đường tiệm cận ngang. x
lim y   ; lim y    x  1
 là đường tiệm cận đứng.   x     1 x     1
lim y   ; lim y    x  1 là đường tiệm cận đứng. x 1  x 1 
Vậy số đường tiệm cận của đồ thị hàm số đã cho là 3. Câu 3.
Cho hàm số y f x có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn D
Từ bảng biến thiên ta có
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
lim y  0  y  0 là tiệm cận ngang của đồ thị hàm số. x
lim y  6  y  6 là tiệm cận ngang của đồ thị hàm số. x
lim y    x  1
 là tiệm cận đứng của đồ thị hàm số. x 1 
lim y   ; lim y    x  1 là tiệm cận đứng của đồ thị hàm số. x 1  x 1 
Vậy đồ thị hàm số có 4 tiệm cận. Câu 4.
Cho hàm số y f x có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 1. B. 4 . C. 2 . D. 3 . Lời giải Chọn D
Từ bảng biến thiên ta có lim y  2
 ; lim y  1 do đó đồ thị hàm số có hai đường tiệm cận ngang là y  2  ; y  1. x x
lim y   do đó đồ thị hàm số có một đường tiệm cận đứng là x  2 . x 2 
Vậy tổng số có 3 đường tiệm cận. ax  3 Câu 5.
Cho hàm số y f x 
có bảng biến thiên như sau 2x b
Giá trị a  2b bằng? A. 8 B. 6  C. 0 D. 10 Lời giải Chọn C Đk:  . a b  6  0  . a b  6 
Từ BBT ta dễ dàng nhận thấy ĐTHS có TCN là: y  2
và tiệm cận đứng là: x  1 a b Suy ra  2  a  4 và
 1  b  2 (TMĐK) 2 2
Vậy a  2b  4  2.2  0 . Câu 6.
Cho hàm số y f (x) có bảng biến thiên như sau
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn D
Dựa vào bảng biến thiên của hàm số ta có:
lim f (x)  2  y  2 là một tiệm cận ngang x
lim f (x)    x  1 là một tiệm cận đứng x 1 
Vậy đồ thị hàm số có tổng số đường tiệm cận là 2 . Câu 7.
Cho hàmsố f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn C
Dựa vào bảng biến thiên của hàm số ta có:
lim f (x)  0  y  0 là một tiệm cận ngang x
lim f (x)  5  y  5 là một tiệm cận ngang x
lim f (x)    x  1 là một tiệm cận đứng x 1 
Vậy đồ thị hàm số có tổng số đường tiệm cận là 3. Câu 8.
Cho hàm số f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn B
lim f (x)    x  1là một tiệm cận đứng x 1 
lim f (x)   nên đồ thị hàm số không có tiệm cận ngang x
Vậy đồ thị hàm số có tổng số đường tiệm cận là 1.
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Câu 9.
Cho hàm số y f (x) xác định trên R \  
4 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
Tổng số tiệm cận ngang của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Lờigiải Chọn B
Dựa vào bảng biến thiên của hàm số ta có:
lim f (x)  9  y  9 là một tiệm cận ngang x
lim f (x)    x  4 là một tiệm cận đứng x 4 
Vậy đồ thị hàm số có tổng số đường tiệm là 2 .
Câu 10. Cho hàm số y f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn A
lim y  0 nên đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số. x
lim y  1nên đường thẳng y  1 là tiệm cận ngang của đồ thị hàm số. x
lim y   nên đường thẳng x  2 là tiệm cận đứng của đồ thị hàm số. x 2 
lim y   nên đường thẳng x  2 là tiệm cận đứng của đồ thị hàm số. x 2 
Vậy hàm số đã cho có tổng số tiệm cận đứng và tiệm cận ngang là 4. Chọn đáp án A.
Câu 11. Cho hàm số y f (x) có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn B
lim y   và lim y  1 nên đường thẳng y  1 là tiệm cận ngang của đồ thị hàm số. x x
lim y  3 và lim y  10 nên đường thẳng x 1 không là tiệm cận đứng của đồ thị hàm số. x 1  x 1 
Vậy hàm số đã cho có tổng số tiệm cận đứng và tiệm cận ngang là 1. Chọn đáp án B.
Câu 12. Cho hàm số y f (x) có bảng biến thiên
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Số tiệm cận ngang của đồ thị hàm số y f (x) là A. 3 . B. 1. C. 2 . D. 0 Lời giải Chọn C
Quan sát bảng biến thiên ta có lim f x  8 và lim f x  10 nên đồ thị hàm số có hai tiệm cận x  x 
ngang y  8 , y  10 .
Câu 13. Cho hàm số y f (x) có bảng biến thiên như hình vẽ
Khẳng định nào sao đây sai?
A. Đồ thị hàm có tiệm cận ngang y  3
B. Đồ thị hàm số có một tiệm cận đứng x  2 .
C. Đồ thị hàm số có một tiệm cận ngang y  3 và một tiệm cận đứng x  2 .
D. Đồ thị hàm số có hai tiệm cận ngang y  3 và y  4 Lời giải Chọn D
Quan sát bảng biến thiên ta có lim f x  3 và lim f x   nên đồ thị hàm số có một tiệm cận x x
ngang y  3 ; lim f x  4 và lim f x   nên đồ thị hàm số có một tiệm cận đứng x  2 . x 0  x 0 
Câu 14. Cho hàm số y f (x) xác định trên D   \  1  , 
1 , có bảng biến thiên như hình vẽ bên dưới. Hỏi
đồ thị hàm số có bao nhiêu đường tiệm cận? A. 1 . B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Quan sát bảng biến thiên ta có lim f x   và lim f x  3 nên đồ thị hàm số có một tiệm cận x  x
ngang y  3 ; lim f x   và lim f x  ; lim f x   nên đồ thị hàm số hai tiệm cận x 1   x 1 x 1   đứng x  1
 . Vậy đồ thị hàm số có tổng cộng ba đường tiệm cận.
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 15. Cho hàm số y f (x) xác định trên D   \  
1 , liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình vẽ bên dưới. Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có một đường tiệm cận đứng là đường thẳng x  1 và một trong các đường tiệm cận
ngang là đường thẳng y  3 .
B. Đồ thị hàm số không có đường tiệm cận đứng và có hai tiệm cận ngang là đường thẳng y  3 và y  5 .
C. Đồ thị hàm số chỉ có một đường tiệm cận đứng, không có tiệm cận ngang
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng x  1 và hai tiệm cận đứng là đường thẳng y  3 và y  5 . Lời giải Chọn A
Quan sát bảng biến thiên ta có lim f x  5 và lim f x  3 nên đồ thị hàm số có hai tiệm cận x x
ngang y  3 và y  5 ; lim f x   và lim f x   nên đồ thị hàm số một tiệm cận đứng x 1  x 1  x  1 .
Câu 16. Cho hàm số y f (x) xác định trên D   \  
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ bên dưới.
Phát biểu nào sao đây đúng?
A. Đồ thị hàm số có hai tiệm cận đứng là đường thẳng x  0 và x  2 tiệm cận ngang là đường thẳng y  2 .
B. Đồ thị hàm số không có đường tiệm cận đứng và có một tiệm cận ngang.
C. Đồ thị hàm số có tiệm cận đứng là đường thẳng x  0 và tiệm cận ngang là đường thẳng y  2 .
D. Đồ thị hàm số có tiệm cận ngang là đường thẳng x  0 và hai tiệm cận đứng là đường thẳng y  2 và y  3 . Lời giải Chọn C
Quan sát bảng biến thiên ta có lim f x   và lim f x  2 nên đồ thị hàm số có một tiệm cận x x
ngang y  2 ; lim f x  3 và lim f x   nên đồ thị hàm số một tiệm cận đứng x  0 . x 0  x 0 
Câu 17. Cho hàm số y f x liên tục trên  \ 2; 
2 và có bảng biến thiên như hình vẽ:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Chọn khẳng định đúng trong các khẳng định sau đây.
A. Đồ thị hàm số có đúng 4 tiệm cận.
B. Đồ thị hàm số có đúng 2 tiệm cận.
C. Đồ thị hàm số có đúng 1 tiệm cận.
D. Đồ thị hàm số có đúng 3 tiệm cận. Lời giải Chọn D
Dựa vào bảng biến thiên của hàm số ta có:
+ lim f x   , lim f x   nên đồ thị hàm số có một tiệm cận đứng là x  2  .   x   2   x   2  
+ lim f x   , lim f x   nên đồ thị hàm số có một tiệm cận đứng là x  2 . x 2  x 2 
+ lim f x  0 nên đồ thị hàm số có một tiệm cận ngang là y  0. x
+ lim f x   nên đồ thị hàm số không có một tiệm cận ngang. x
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 18. Cho hàm số f x có bảng biến thiên như hình sau:
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? A. 1. B. 3 . C. 2 . D. 4 . Lời giải Chọn B
Từ bảng biến thiên ta suy ra:
+ lim f x   nên có đường thẳng x  2
 là một tiệm cận đứng của đồ thị hàm số. x 2 
+ lim f x   nên có đường thẳng x  0 là một tiệm cận đứng của đồ thị hàm số. x 0 
+ lim f x  0 nên có đường thẳng y  0 là tiệm cận ngang của đồ thị hàm số. x
Do đó, đồ thị hàm số y f x có ba tiệm cận.
Câu 19. Cho hàm số y f x có bảng biến thiên như sau: 2020
Tổng số tiệm cận đứng của đồ thị hàm số y  là f xA. 1. B. 2 . C. 3. D. 4 .
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Lời giải Chọn C 2018
Số tiệm cận đứng của đồ thị hàm số y
là số nghiệm phương trình f x  0 bằng số giao f x
điểm của đồ thị hàm số f x và trục hoành. Nhìn bảng biến thiên ta có số giao điểm bằng 3 nên đồ 2020 thị hàm số y  có 3 tiệm cận đứng. f x
Câu 20. Cho hàm số y f x liên tục trên  \  
1 và có bảng biến thiên như sau: 1
Đồ thị hàm số y
có bao nhiêu đường tiệm cận đứng?
2 f x  5 A. 0 . B. 4 . C. 2 . D. 1. Lời giải 5
Ta có: 2 f x  5  0  f x    1 . Phương trình  
1 có 4 nghiệm phân biệt x , x , x , x  1 và 2 1 2 3 4 1
giới hạn của hàm số y
tại các điểm x , x , x , x đều bằng  .
2 f x  5 1 2 3 4 1 Mặt khác lim
 0 nên x  1 không phải tiệm cận đứng. x 1 
2 f x  5 1
Vậy đồ thị hàm số y
có 4 đường tiệm cận đứng.
2 f x  5
Câu 21. Cho hàm số y f x có bảng biến thiên như hình dưới đây. 1
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y  là
2 f x 1 A. 0. B. 1. C. 2. D. 3. Lời giải 1
Số tiệm cận đứng của đồ thị hàm số y
đúng bằng số nghiệm thực của phương trình
2 f x 1 1
2 f x 1  0  f x  . 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 1
Mà số nghiệm thực của phương trình f x 
bằng số giao điểm của đồ thị hàm số y f x với 2 1 đường thẳng y  . 2 1
Dựa vào bảng biến thiên ta thấy đường thẳng y
cắt đồ thị hàm số y f (x) tại 2 điểm phân biệt. 2 1
Vậy đồ thị hàm số y  có 2 tiệm cận đứng.
2 f x 1 1 Lại có lim
1 đồ thị hàm số có một tiệm cận ngang là y  1.
x 2 f x 1 1
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y  là 3 .
2 f x 1
Câu 22. Cho hàm số y f x liên tục trên  \  
1 và có bảng biến thiên như sau: 1
Đồ thị hàm số y
có bao nhiêu đường tiệm cận đứng?
2 f x  3 A. 1. B. 2 . C. 0 . D. 2 . Lời giải 3
Từ bảng biến thiên ta suy ra phương trình f x   có hai nghiệm phân biệt a và b (với a  0 và 2 0  b  1 . 1
Nên, tập xác định của hàm số y  là  \ 1; a;  b .
2 f x  3 Ta có 1 lim   ; x a 
2 f x  3 1 lim   ; x b 
2 f x  3 1 lim  0 ; x 1 
2 f x  3 1 lim  0 . x 1 
2 f x  3 1
Do đó, đồ thị hàm số y
có 2 đường tiệm cận đứng.
2 f x  3
Câu 23. Cho hàm số y f x liên tục trên  \ 
1 và có bảng biến thiên như sau:
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1
Đồ thị hàm số y
có bao nhiêu đường tiệm cận đứng?
2 f x  5 A. 0 . B. 1. C. 2 . D. 4 . Lời giải Chọn D 5
Ta có 2 f x  5  0  f x    1 . 2
Dựa vào BBT ta suy ra phương trình  
1 có 4 nghiệm phân biệt x , x , x , x (với 1 2 3 4
x  2  x  1  x  2  x ). 1 2 3 4 1
Mặt khác hàm số y
g x có tử thức là hằng số nên ta suy ra đồ thị hàm số y g x
2 f x  5 có 4 tiệm cận đứng.
Câu 24. Cho hàm số y f x có bảng biến thiên nhưsau:
Đồ thị hàm số có tổng số đường tiệm cận đứng là a và tổng số đường tiệm cận ngang là b . Khi đó 2 3 2a b
giá trị của biểu thức
thuộc khoảng nào sau đây? 2 2 a b A. 0; 4 . B.  6  ;  4 . C. 2;0 . D.  4  ;  2 . Lời giải Chọn D
Dựa vào bảng biến thiên ta có:
lim f x  1
 suy ra đồ thị hàm số có đường tiệm cận ngang y  1. x
lim f x  3 suy ra đồ thị hàm số có đường tiệm cận ngang y  3 . x
Suy ra tổng số đường tiệm cận ngang của đồ thị hàm số là 2  b  2 .
lim f x   suy ra đồ thị hàm số có đường tiệm cận đứng x  2  .  x   2  
Suy ra tổng số đường tiệm cận đứng của đồ thị hàm số là 1 a  1. 2 3 2 3 2a b 2.1  2 10 Vậy ta có:     3  .333 . 2 2 2 2 a b 1  2 3
Câu 25. Cho hàm số y f x có đạo hàm liên tục trên  và có bảng biến thiên như sau:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 2 x 1
Hỏi đồ thị hàm số g x 
có bao nhiêu đường tiệm cận đứng? 2
f x  4 f xA. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn A
f x  0 Ta có: 2
f x  4 f x  0   .
f x  4 
Dựa vào bảng biến thiên ta thấy:
+ Xét trường hợp f x  0 có 2 nghiệm x  1
 và x  1 là nghiệm bội hai (do đồ thị tiếp 1 2
xúc với trục hoành tại x  1 ). Trường hợp này đồ thị hàm số có 2 tiệm cận đứng.
+ Xét trường hợp f x  4 có 2 nghiệm x 1 và x  1
 là nghiệm bội hai (do đồ thị tiếp 3 4
xúc với đường thẳng y  4 tại x  1 ). Trường hợp này đồ thị hàm số có 2 tiệm cận đứng.
Vậy đồ thị có 4 tiệm cận đứng.
B. TÌM TIỆM CẬN ĐỒ THỊ HÀM SỐ (thông qua hàm số)
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA x  2 Câu 1.
Tiệm cận ngang của đồ thị hàm số y  là x 1 A. y  2  .
B. y  1. C. x  1  .
D. x  2 . Lời giải Chọn B x  2 x  2 Ta có lim  1 và lim  1
x x  1
x x  1
Suy ra y  1 là tiệm cận ngang của đồ thị hàm số. x  2020 Câu 2.
Tiệm cận ngang của đồ thị hàm số y  là x  2019 A. y  2  019 .
B. y  1. C. x  2  019 .
D. x  2020 . Lời giải Chọn B x  2020 x  2020 Ta có lim  1 và lim  1
x x  2019
x x  2019
Suy ra y  1 là tiệm cận ngang của đồ thị hàm số. x  2 Câu 3.
Tiệm cận đứng của đồ thị hàm số y  là x  1
A. y  2 .
B. y  1. C. x  1  .
D. x  2 . Lời giải Chọn C x  2 x  2 Ta có lim   và lim   x 1  x 1 x 1  x 1
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Suy ra x  1
 là tiệm cận đứng của đồ thị hàm số. x  2 Câu 4.
Tọa độ giao điểm hai đường tiệm cận của đồ thị hàm số y  là x  1 A. I 1  ;1 . B. I  1  ;  1 .
C. I 1;   1 . D. I  1  ;   1 . Lời giải Chọn B x  2 x  2 Ta có lim  1 và lim  1
x x  1
x x  1
Suy ra y  1 là tiệm cận ngang của đồ thị hàm số. x  2 x  2 Ta có lim   và lim   x 1  x  1 x 1  x 1 Suy ra x  1
 là tiệm cận đứng của đồ thị hàm số.
Vậy tọa độ giao điểm hai đường tiệm cận là I  1  ;  1 . x  2 Câu 5.
Số đường tiệm cận ngang của đồ thị hàm số y  là x  1 A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn B x  2 x  2 Ta có lim  1 và lim  1
x x  1
x x  1
Suy ra y  1 là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có 1 đường tiệm cận ngang. Câu 6.
Đồ thị của hàm số nào dưới đây có tiệm cận đứng? 2 x  3x  2 2 x x A. y B. y C. 2 y x 1 D. y x 1 2 x 1 x  1 Lời giải Chọn D x x Ta có lim  , lim
  nên đường thẳng x  1 là tiệm cận đứng của đồ thị hàm số. x 1 x 1 x  1    x 1 2 x  5x  4 Câu 7.
Tìm số tiệm cận của đồ thị hàm số y  . 2 x 1 A. 2 B. 3 C. 0 D. 1 Lời giải Chọn A
Tập xác định: D   \   1 5 4 2 1  2 x  5x  4 Ta có: lim  lim  lim x x y
 1  y  1 là đường tiệm cận ngang. 2 x x x 1 x 1 1 2 x Mặc khác: 2 x  5x  4  x   1  x  4  x  4 3 lim y  lim  lim  lim   2 x 1  x 1  x 1 x 1   x   1  x   x 1 1   x   1 2
x  1 không là đường tiệm cận đứng. 2 x  5x  4  x   1  x  4  x  4 lim y  lim  lim  lim     2   x  1 x  1 x 1 x 1   x   1  x   1 x  1  x   1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 2 x  5x  4  x   1  x  4  x  4 lim y  lim  lim  lim     2   x  1 x  1 x 1 x  1  x   1  x   1 x  1  x   1  x  1
 là đường tiệm cận đứng.
Vậy đồ thị hàm số có 2 đường tiệm cận 2 x  3x  4 Câu 8.
Tìm số tiệm cận đứng của đồ thị hàm số: y 2 x  16 A. 2 B. 3 C. 1 D. 0 Lời giải Chọn C 2 x  3x  4 x  1 Ta có y  
(với điều kiện xác định), do đó đồ thị hàm có 1 tiệm cận đứng. 2 x  16 x  4 2 5x  4x 1 Câu 9.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x 1 A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C Tiệm cận ngang: 2  4 1  4 1 2 x 5     5   2 2 5x  4x 1  x x x Ta có: lim  lim  lim  lim x y
 5 nên đồ thị hàm số 2 x x x 1 x 2  1  x 1 x 1 1  2  2  x x
có một tiệm cận ngang y  5 . Tiệm cận đứng: x  Cho 2 1 x  1   x  1   2 5x  4x 1 5x   1  x   1 5x 1 6 Ta có: lim y  lim  lim  lim 
 3 nên x  1 không là tiệm cận 2 x 1  x 1  x 1 x 1   x   1  x   1 x 1  x 1 2 đứng. 2 2 2 5x  4x 1 5x  4x 1  1
5x  4x 1 lim y  lim  lim  lim  .          x     x     2 1 1 x 1 x     1  x   1  x   1 x     1 x 1 x 1    1 lim     x      1 x 1 vì  . 2 5x  4x 1  lim  4   0  x     1 x 1 
Khi đó, đồ thị hàm số có một tiệm cận đứng x  1  .
Tổng cộng đồ thị hàm số có 2 tiệm cận. 2 ax bx  2
Câu 10. Cho hàm số y f x 
. Biết rằng đồ thị hàm số có đúng một đường tiệm cận ngang là 2 x  4
y  1 và một đường tiệm cận đứng là x  2 . Khi đó giá trị của biểu thức b a bằng? A. 2 B. 4 C. 2 D. 4 Lời giải Chọn A a
ĐTHS có TCN là: y  1. Suy ra  1  a  1 1
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020x  2 Phương trình 2 x  4  0   x  2  
ĐTHS có TCĐ là: x  2 . Suy ra phương trình 2
x bx  2  0 phải có hai nghiệm phân biệt trong đó
một nghiệm là x  2
 và nghiệm còn lại phải khác 2. Ta có hệ điều kiện:   0  2 ( 2) 
 2b  2  0  b  3  2 (2)  2b  2  0 
b a  3 1  2 x x  2
Câu 11. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  là 2 x  4 A. 1 B. 2 C. 3 D. 4 Lời giải Chọn B x  2  0 x  2  ĐKXĐ:   
x  2;  2 x  4  0 x     ;
 2  2;   x x  2 lim
   x  2 là tiệm cận đứng của đồ thị hàm số.  2 x2 x  4 x x  2 lim
 1  y  1 là tiệm cận ngang của đồ thị hàm số. x 2 x  4
Tổng cộng có 2 tiệm cận. x  1
Câu 12. Đồ thị hàm số f x 
có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang? 2 x  1 A. 4 . B. 3 . C. 1. D. 2 . Lờigiải Chọn B
Tập xác định của hàm số D   ;    1  1;  x  1   x  2 1 x  1 TH1: x  1
  x  1  0 . Khi đó f x     . 2 x  1  x   1  x   1 x  1
Suy ra đồ thị hàm số có TCN y  1  , không có TCĐ. x  1  x  2 1 x  1
TH2: x  1  x  1  0 . Khi đó f x    . 2 x  1  x   1  x   1 x  1
Suy ra đồ thị hàm số có TCN y  1, TCĐ x  1 .
Vậy đồ thị hàm số có 2 TCN và 1 TCĐ. x  25  5
Câu 13. Số tiệm cận đứng của đồ thị hàm số y  là 2 x x A. 3 B. 2 C. 0 D. 1 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 1
Tập xác định D   2  5;  \ 1  ; 
0 . Biến đổi f (x)  .  x   1  x  25  5 1 Vì lim y  lim
  nên đồ thị hàm số đã cho có 1 tiệm cận đứng x  1  .   x  1 x  1  x   1  x  25  5 x 16  4
Câu 14. Số tiệm cận đứng của đồ thị hàm số y  là 2 x x A. 3 . B. 2 . C. 1. D. 0 . Lời giải Chọn C
Tập xác định hàm số D   1  6;  \ 1  ;  0 . Ta có x 16  4 x 1 1 lim y  lim  lim  lim  . x0 x0  x   x0 1 x x x  
1  x 16  4 x0  x  
1  x 16  4 8 x 16  4 1 lim y  lim  lim   .    x  1 x     1  x   1 x x  1  x   1  x 16  4  vì lim      , lim  x  
1  0 và x    1 thì x  1   x 1  0 .   x 16 4 15 4 0  x  1 x     1 1
Tương tự lim y  lim   .   x  1 x  1  x   1  x 16  4
Vậy đồ thị hàm số đã cho có tiệm cận đứng là x  1  . 2
2x 1 x x  3
Câu 15. Tìm tất cả các tiệm cận đứng của đồ thị hàm số y  . 2 x  5x  6
A. x 3 và x  2.
B. x 3. C. x  3  và x  2  . D. x  3  . Lời giải Chọn B
Tập xác định D  \2;  3 x   x x  2x  2 1
  x x  3 2x  2 2 1   2 2 x x  3 2 1 3  lim  lim  lim  2 x 2 x 2 x  5x  6   2   
x  5x  6 2 2 x  1 
x x  3  x2  2
x  5x  6 2 2 x  1 
x x  3  (3x  1) 7  lim   x 2   x   2 x   x x   6 3 2 1 3 2
2x 1 x x  3 7 Tương tự lim  
. Suy ra đường thẳng x  2 không là tiệm cận đứng của đồ  2 x2 x  5x  6 6 thị hàm số đã cho. 2 2
2x 1 x x  3
2x 1 x x  3 lim   ;  lim
  . Suy ra đường thẳng x 3 là tiệm cận  2  2 x 3  x 3 x  5x  6  x  5x  6
đứng của đồ thị hàm số đã cho. x  4  2
Câu 16. Số tiệm cận đứng của đồ thị hàm số y  là 2 x x A. 3 . B. 0 . C. 1. D. 2 .
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Lời giải Chọn C
Tập xác định D   4  ;  \  1  ;  0 . x  4  2 Ta có: lim y  lim     2 x     1 x     1 x x
Nên đường thẳng x  1
 là một đường tiệm cận đứng của đồ thị hàm số đã cho. x  
x  4  2 x  4  2 4 2  1 1 lim y  lim  lim  lim  2 x0 x0 x0 x x x x   1  x  4  2
x0  x  
1  x  4  2 4
Nên đường thẳng x  0 không là tiệm cận đứng của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có một tiệm cận đứng x  1  . x 1
Câu 17. Tìm số đường tiệm cận của đồ thị hàm số y  .
4 3x 1  3x  5 A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn A  1 
Tập xác định: D   ;  \     1  3   x   1 x
4 3x 13x 5 1 
4 3x 1  3x  5 + Ta có: lim  lim  lim   x
 4 3x 1  3x  5 x  9  x  2 1 1 x 1 1     9  x   1
do đó đường thẳng x  1 là đường tiệm cận đứng của đồ thị hàm số. 1 1 x 1 1 1 + lim  lim x
  do đó đường thẳng y   là đường
x 4 3x 1  3x  5 x 3 1 5 3 3 4   3  2 x x x
tiệm cận ngang của đồ thị hàm số. Vậy đồ thị hàm số có 2 đường tiệm cận. 2 x  2x  3
Câu 18. Cho hàm số y
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? 4 2 x  3x  2 A. 4 . B. 5 . C. 3 . D. 6 . Lời giải Chọn B
□ Tập xác định D   ;   2    1   ;1   2; . □ lim
y  lim y  lim y  lim y   .       x     1 x x x       1 2 2
 Các đường tiệm cận đứng của đồ thị là x   2 , x  1 .
□ lim y  lim y  1  đồ thị có một tiệm cận ngang y  1. x x 5x 8
Câu 19. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 x 3x A. 2. B. 4. C. 1. D. 3. Lời giải Chọn B
Tập xác định D   ;  0 3;
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 8 5  5x  8 5x  8 lim  lim  lim  lim x y  5 x x 2 x  3 x x  3 x 3 x 1 1 x x
 Đường thẳng y  5 là tiệm cận ngang của đồ thị hàm số. 8 5  5x  8 5x  8 lim  lim  lim  lim x y  5  x x 2 x  3 x x  3 x 3 x 1  1 x x
Đường thẳng y  5 là tiệm cận ngang của đồ thị hàm số. 5x 8 lim y  lim   x 0 x 0   2 x  3x 2 2 
( vì lim(5x 8)  8
  0; lim x 3x  0; x 3x  0 x   0 ) x 0  x 0 
Suy ra: đường thẳng x  0 là tiệm cận đứng của đồ thị hàm số. 5x 8 lim y  lim   x 3 x 3   2 x  3x 2 2 
( vì lim(5x 8)  7  0; lim x 3x  0; x  3x  0 x  3 ) x 3  x 3 
Suy ra: đường thẳng x  3 là tiệm cận đứng của đồ thị hàm số. 2
4x  2x 1  x
Câu 20. Đồ thị hàm số y
có bao nhiêu đường tiệm cận? x 1 A. 1. B. 0 . C. 2 . D. 3 . Lời giải Chọn C  1   5  x   4 2 2
4x  2x 1  x
4x  2x 1  0   Hàm số y  xác định     1   5 . x 1 x 1  0  x   4  x  1    1   5   1 5 
Tập xác định của hàm số đã cho là D   ;    1   1  ;  ;     .  4 4      2 1 2 x 4    x 2
4x  2x 1  x x x lim y  lim  lim x x x 1 x x 1 2 1 2 1 x 4    x  4   1 2 2 x x x x  lim  lim  1. x x 1 x 1 1 x
y  1 là đường tiệm cận ngang của đồ thị hàm số khi x   . 2 1 2 x 4    x 2
4x  2x 1  x x x lim y  lim  lim x x x 1 x x 1
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 1 2 1 x 4    x 4   1 2 2 x x x x  lim  lim  3 . x x 1 x 1 1 x
y  3 là đường tiệm cận ngang của đồ thị hàm số khi x   . 2 2 2
4x  2x 1  x
4x  2x 1 xx   1 3x   1 lim y  lim  lim  lim  2  . x 1  x 1  x 1 x 1   x   1  2
4x  2x 1  xx 1x   1  2
4x  2x 1  x 2
4x  2x 1  x
Vậy đồ thị hàm số y  có 2 đường tiệm cận. x 1
C. ĐỊNH m ĐỂ ĐỒ THỊ HÀM SỐ CÓ ĐƯỜNG TIỆM CẬN THỎA MÃN ĐIỀU KIỆN CHO TRƯỚC
Đường tiệm cận ngang
Cho hàm số y f x có TXD: D
Điều kiện cần: D phải chứa  hoặc  Điều kiện đủ: P(x)
Dạng 1. y f (x)  . Q(x)
Nếu degP x  degQ x : thì không có tiệm cận ngan
Nếu degP x  degQx :TCN y  0
Nếu degP x  degQ x : y k (k là tỉ số hệ số bậc cao nhất của tử và mẫu) 2 u v u v
Dạng 2: y f (x)  u v (hoặc u v ): Nhân liên hợp  y f (x)  (hoặc ) u v u v
Đường tiệm cận đứng P x Cho hàm số y  có TXD: D Q x
Đkiện cần: giải Q x  0  x x là TCĐ khi thỏa mãn đk đủ 0 Đkiện đủ:
Đkiện 1: x làm cho P(x) và Q(x) xác định. 0
Đkiện 2: - x không phải nghiêm P(x)  x x là TCĐ 0 0
- x là nghiêm P(x)  x x là TCĐ nếu lim f (x)   0 0 x 0 x x 1 Câu 1.
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y  có hai tiệm cận 2 mx 1 ngang A. m  0 B. m  0 C. m  0
D. Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài Lời giải Chọn C
Xét các trường hơp sau:
Với m  0 : hàm số trở thành y x 1 nên không có tiệm cận ngang. Với m  0 :
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 x 1 x 1  1 1  hàm số y  
có tập xác định là D    ;
 suy ra không tồn tại giới 2 2 mx 1 1 m xm m   
hạn lim y hay hàm số không có tiệm cận ngang. x Với m  0 :  1   1   x 1 x 1 x 1  x  1 Ta có: lim y  lim  lim  lim  lim   . x x 2 mx 1 x 1 x 1 x 1 m x m  x m m  2 2 2 x x x  1  1   x 1 x 1 x 1  x  1 và lim y  lim  lim  lim  lim  . x x 2 mx 1 x 1 x 1 x 1 m x m x m m  2 2 2 x x x 1 1
Vậy hàm số có hai tiệm cận ngang là : y  ; y   khi m  0 . m m 2 x m Câu 2.
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y
có đúng hai đường tiệm 2 x  3x  2 cận. A. m  1 B. m {1; 4} C. m  4
D. m { 1; 4  } Lời giải 2 2 x m x m y   . 2 x  3x  2  x   1  x  2
lim y  1  y  1 là đường tiệm cận ngang. x 2 x m
Đồ thị hàm số y
có đúng hai đường tiệm cận  đồ thị hàm số có đúng một tiệm cận 2 x  3x  2 đứng  pt 2
x m  0 nhận nghiệm x  1 hoặc x  2 . m  1  Khi đó:  . m  4  
Với m  1 có một tiệm cận đứng x  2 . Với m  4
 có một tiệm cận đứng x  1 . Vậy m { 1; 4  } . 6x  3 Câu 3.
Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y  có đúng một  2
mx  6x  3 2
9x  6mx   1 đường tiệm cận? A. 0 . B. 2 . C. 1. D. Vô số. Lời giải 6x  3
Kí hiệu C  là đồ thị hàm số y  .  2
mx  6x  3 2
9x  6mx   1
* Trường hợp 1: m  0 . 6x  3 Khi đó y
. Đồ thị hàm số có đúng một đường tiệm cận ngang y  0 . 6x  3 2 9x   1
Do đó chọn m  0 .
* Trường hợp 2: m  0 . Xét phương trình  2
mx x   2 6
3 9x  6mx   1  0   1
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Nhận thấy: C  luôn có một đường tiệm cận ngang y  0 và phương trình   1 không thể có duy nhất
một nghiệm đơn với mọi m .
Do đó C  có đúng một đường tiệm cận khi và chỉ khi C  không có tiệm cận đứng    1 vô 9   3m  0 m  3 nghiệm    
, ( không tồn tại m ). 2 9m  9  0  1   m  1 
Kết hợp các trường hợp ta được m  0 . 5x  3 Câu 4.
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y
không có tiệm cận đứng. 2 x  2mx 1 m  1 A. B. 1   m  1 C. m  1  D. m  1 m  1  lời giải Chọn B
để hàm số không có tiệm cận đứng thì 2
x  2mx 1  0 vô nghiệm suy ra 2
m 1  0  1  m  1 x 1 Câu 5.
Cho hàm số y f x 
. Tìm tất cả các giá trị của tham số m để đồ thị có ba đường 2 x  2mx  4 tiệm cận  m  2  m  2     m  2 m  2 A. m  2 B.   5 C. D. m     5 m  2   2 m     2 Lời giải Chọn C
Để đồ thị có ba đường tiệm cận thì 2
x  2mx  4  0 có hai nghiệm phân biệt  1    m  2    0     m  2        2 1  2m   1  4  0   5 m      2
n  3 x n  2017 Câu 6.
Biết rằng đồ thị của hàm số y
( m, n là các số thực) nhận trục hoành làm tiệm x m  3
cận ngang và trục tung là tiệm cận đứng. Tính tổng m n . A. 0 B. 3  C. 3 D. 6 Lờigiải Chọn A ax b
Theo công thức tìm nhanh tiệm cận của đồ thị hàm số y  ta có cx d d
Đồ thị hàm số nhận x  
 m  3  0 làm TCĐ  m  3  c a
Đồ thị hàm số nhận y
n  3  0 làm TCN  n  3. c
Vậy m n  0 . x 1 Câu 7.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y  có đúng bốn đường 2 mx  8x  2 tiệm cận? A. 8 B. 6 C. 7 D. Vô số
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải
TH1: m  0 suy ra tập xác định của hàm số là D   x ; x , ( x ; x là nghiệm của phương trình 1 2  1 2 2
mx  8x  2  0 ). Do đó m  0 không thỏa yêu cầu của bài toán. x 1
TH2: m  0  y
suy ra tập xác định của hàm số là D   ;  4 . 8  x  2
lim y  ; lim y   . Khi đó ta có x  4
 là đường tiệm cận đứng của đồ thị hàm số. x x 4  
Do đó m  0 không thỏa yêu cầu của bài toán
TH3: m  0 suy ra tập xác định của hàm số là D   ;
x x ;  ( x ; x là nghiệm của phương 1   2  1 2 trình 2
mx  8x  2  0 ). Do đó đồ thị hàm số có bốn đường tiệm cận khi phương trình 2
mx  8x  2  0 có hai nghiệm phân biệt khác 16   2m  0 m  8  
1  m  0;m    m  0; m    m  1;2;3; 4;5; 
7 . Suy ra có tất cả 6 giá trị nguyên của tham m 8 2 0     m  6  
số m thỏa mãn yêu cầu của bài toán. Câu 8.
Với giá trị nào của hàm số m để đồ thị hàm số 2
y x mx  3x  7 có tiệm cạn ngang. A. m 1 B. m  1  C. m  1 
D. Không có m Lời giải Chọn A
Đồ thị hàm số có tiệm cận ngang
 Hàm số xác định trên một trong các miền  ;  a, ;
a,a,  hoặc  ; a  m  0
TH1: m  0  y x  3
x  7, lim y   đồ thị không có tiệm cận ngang x TH2: 2
m  0, y x mx  3x  7  3 7  3
Khi lim y  lim  x x m    
đồ thị hàm số có tiệm cận ngang khi và chỉ khi m 1. 2 x   x x x 2   Vậy m 1
Cách trắc nghiệm: 3 Thay m 1 2  y x
x  3x  7  lim x x x  
đồ thị hàm số có tiệm cận ngang x  2 3 7  2   2 lim x
x  3x  7   không có tiệm cận ngang. x  Thay m  1  2
y x   x x   x x x không xác định. x  2 3 7 lim    3  7    x x x không xác định. x  2 lim    3  7   Vậy m 1 mx  1 Câu 9. Cho hàm số y
với tham số m  0 . Giao điểm của hai đường tiệm cận của đồ thị hàm số x  2m
thuộc đường thẳng có phương trình nào dưới đây?
A. y  2x .
B. 2x y  0 .
C. x  2 y  0 .
D. x  2 y  0 . Lời giải Chọn C
Khi đồ thị hàm số có hai đường tiệm cận thì:
Đường tiệm cận ngang có phương trình: y m
Đường tiệm cận đứng có phương trình: x  2m . Vậy giao điểm hai tiệm cận là I (2m ; m)
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020y m Khử m từ hệ 
ta được x  2 y  0 . x  2  m
Vậy giao điểm của hai tiệm cận thuộc đường thẳng có phương trình x  2 y  0 . mx  2
Câu 10. Tìm tất cả các giá trị của m để đồ thị hàm số y
có đúng 2 tiệm cận? 2 x  4 A. m  1. B. m  1. C. m  1. D. m  0 Lời giải Chọn B Cách 1: Trắc nghiệm mx  2 x  2
Thế m  1vào y  ta được y
 đồ thị có 2 tiệm cận: x  2; y  0 . 2 x  4 2 x  4 mx  2 x  2
Thế m  1 vào y  ta được y
 đồ thị có 2 tiệm cận: x  2; y  0 . 2 x  4 2 x  4 Cách 2: Tự luận D   ;  2    2;  . mx  2 lim  0 ( m
  )  Hàm số có 1 TCN. 2
x x  4
Để hàm số có đúng 2 tiệm cận thì hàm số cần có thêm 1 TCĐ.
+ Xét x  2 không là TCĐ khi x  2 là nghiệm của mx  2  2m  2  0  m  1. x  2 1
Thử lại: với m  1thì lim  lim    x  2  là TCĐ.  2 x 2 x 2 x  4    x  2
+ Xét x  2 không là TCĐ khi x  2 là nghiệm của mx  2  2
m  2  0  m  1  .
Thử lại: với m  1
 thì x  2 là TCĐ. m   1 x  5m
Câu 11. Tìm tham số m để đồ thị hàm số y
có tiệm cận ngang là đường thẳng y  1 2x m 1 A. m  1. B. m  . C. m  2 . D. m  1. 2 Lời giải Chọn D m
TXĐ: D   \    2  m   1 x  5m m 1 Ta có lim y  lim  . x x 2x m 2 m   1 x  5m m 1 lim y  lim  . x x 2x m 2 m 1  y
là TCN của đồ thị hàm số. 2 m 1 ycbt   1  m  1. 2 x 1
Câu 12. Có bao nhiêu giá trị nguyên m  1
 0;10 sao cho đồ thị hàm số y  có hai đường 2
2x  6x m  3 tiệm cận đứng? A. 19 . B. 15 . C. 17 . D. 18. Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489 x 1
Ta có đồ thị hàm số y
có hai đường tiệm cận đứng khi phương trình 2
2x  6x m  3 2  15 3   2  m  3  0 m   2
2x  6x m  3  0 có hai nghiệm phân biệt khác 1     2 2
2.1  6.1 m  3  0  m  5 
Từ đó ta suy ra tập các giá trị nguyên của m thỏa mãn là  7  , 6  , 5  , 4  , 3  , 2  , 1
 , 0,1, 2,3, 4, 6, 7,8,9,1 
0 . Vậy có 17 giá trị nguyên của m thỏa mãn.
Câu 13. Có bao nhiêu giá trị nguyên của m để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 2 mx  3mx  4 y  bằng 3? x  2 A. 4 . B. 2 . C. Vô số. D. 3 . Lời giải Chọn B 2 mx  3mx  4
Đồ thị hàm số y
có nhiều nhất một tiệm cận đứng và hai tiệm cận ngang. x  2 2 mx  3mx  4
Điều kiện để đồ thị hàm số y
có 3 tiệm cận là nó có đúng 1 tiệm cận đứng và 2 x  2 tiệm cận ngang.
* Xét điều kiện tồn tại lim y và lim y x   x  m  0  16
Trường hợp 1: g x 2
mx  3mx  4  0 với x  m  0  0  m    9 2
   9m 16m  0 
Trường hợp 2: g x 2
mx  3mx  4  0 với x    ;
x x ;  với x ; x là nghiệm của 1   2  1 2 m  0 16
g x    m  2
  9m 16m  0 9 
Vậy m  0 thì tồn tại lim y và lim y x   x   Khi đó: 3m 4 2 m   2 mx  3mx  4 x x lim y  lim  lim  m x   x   x  2 x  2 1  x 3m 4 2  m   2 mx  3mx  4 x x lim y  lim  lim   m x  x   x  2 x  2 1  x
Vậy điều kiện để đồ thị hàm số có hai đường tiệm cận ngang là m  0
* Xét trường hợp x  2 là nghiệm của tử số  x  2 là nghiệm của g x 2
mx  3mx  4  g  2
   0  m  2 2 2 x  6x  4
2  x  1 x  2  2  x  1  Khi đó y   lim y   lim     x  2 x 2 x 2 x  2      x  2    
 Đồ thị hàm số có một tiệm cận đứng x  2 .
m  2 thỏa mãn
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
* Xét trường hợp x  2 không là nghiệm của tử số, để x  2 là tiệm cận đứng của đồ thị hàm số g  2  0 thì 
g 2  0  4  2m  0  m  2 g  2  0 
 đồ thị hàm số có một đường tiệm cận đứng x  2 với m  0;  2 2 mx  3mx  4
Vậy điều kiện để đồ thị hàm số y
có 3 tiệm cận là m  0;  2 x  2
Vậy có hai giá trị nguyên của m thỏa mãn đề bài là m  1; m  2 . x 1
Câu 14. Tổng các giá trị của tham số m để đồ thị của hàm số y  có đúng một tiệm 2
x  2m   2 1 x m  2 cận đứng. 1 3 A.  . B. 2 . C. 3  . D. . 2 2 Lời giải Chọn A
Đặt f x 2
x  m   2 2 1 x m  2
Đồ thị hàm số có đúng một tiệm cận đứng khi và chỉ khi f x  0 có 2 nghiệm phân biệt trong đó có
1 nghiệm x  1 hoặc f x  0 có nghiệm kép     m   2   2 m    3 1 2  0    0 m      m  1   2 2     f    1   2m   1  m  2  0 1 0      
m  1; m  3  m  3       .   3    0 3  3  m    m  m   2  2  2 1
Vậy tổng các giá trị m thỏa mãn là:  . 2 2 x x  2
Câu 15. Tìm tất cả các giá trị của m để đồ thị hàm số y  2
x  2x m có 3 đường tiệm cận. m  1 m  1 m  1 A.  . B.  . C.  . D. m  8 . m  8  m  8  m  8  Lời giải Chọn A 2 x x  2 Ta có: lim y  lim
 1 , suy ra đồ thị hàm số luôn có một đường tiệm cận ngang là 2 x
x x  2x m y  1. 2 x x  2
Do đó, đồ thị hàm số y  2
x  2x m có 3 đường tiệm cận khi và chỉ khi đồ thị hàm số có thêm hai
đường tiệm cận đứng. Khi đó, phương trình 2
x  2x m  0 có 2 ngiệm phân biệt không trùng với
  1 m  0 m  1    m  1
các nghiệm của phương trình 2
x x  2  0, hay 2 1   2.1 m  0  m  1    . m  8      2    m  8 2 2. 2  m  0  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489 x  3
Câu 16. Cho hàm số y
. Có bao nhiêu giá trị nguyên thuộc đoạn  6  ;6 của 3 2 x  3mx  2 2m   1 x m
tham số m để đồ thị hàm số có bốn đường tiệm cận? A. 12 . B. 9 . C. 8 . D. 11. Lời giải Chọn B
lim y  lim y  0 nên đồ thị hàm số có tiệm cận ngang là đường thẳng y  0 . x x
Do đó, đồ thị hàm số có bốn đường tiệm cận khi phương trình 3 2 x mx  2 3 2m  
1 x m  0 có 3
nghiệm phân biệt x  3 . Xét phương trình 3 2 x mx  2 3 2m  
1 x m  0 (*) ta có x m 3 2 x mx  2 3 2m  
1 x m  0  x m 2
x  2mx   1  0   . 2
x  2mx 1 0 
Phương trình (*) có ba nghiệm phân biệt x  3 khi và chỉ khi m  3 và phương trình m3 m  3     m 1   2
x  2mx 1  0 có hai nghiệm phân biệt x  3 2  m 1   0      . m  1   2 3  2.3.m 1 0    5 m   3
Do m nguyên và m  6
 ;6 nên m  6  ; 5  ; 4  ; 3  ; 2  ;2;4;5;  6 .
Vậy có 9 giá trị nguyên của m thỏa mãn đề bài. 2
2x  3x m
Câu 17. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y  không có tiệm cận x m đứng. A. m  1. B. m  1.
C. m  1và m  0 . D. m  0 . Lời giải Chọn C TXĐ \    m . 2 2
2 x  3x m  2m  2m  Có lim
 lim 2 x  2m  3    . x m xx m m x   m  2
2x  3x m
Để đồ thị hàm số không có tiệm cận đứng thì phải tồn tại lim , xm x mm  0 2
 2m  2m  0   m  1  Vậy đáp án C.
Câu 18. Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn   2017; 2017 để đồ thị hàm số x  2 y
có hai tiệm cận đứng. 2
x  4x m A. 2019 . B. 2021. C. 2018 . D. 2020 . Lời giải Chọn D x  2
Để đồ thị hàm số y
có hai tiệm cận đứng thì phương trình 2
x  4x m  0 có hai 2
x  4x m
nghiệm phân biệt khác 2
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  20  17  m  4 4  m  0       m  12
m  2017;2016;..;  3 \   12 . 12   m  0   m  
Do đó số giá trị nguyên của tham số m thỏa đề bài là: 3 - (-2017) + 1 - 1 = 2020 giá trị.
--------------- HẾT ---------------
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Document Outline

  • 5. Tiệm cận - câu hỏi.pdf
  • 5. Tiệm cận - đáp án.pdf