Tổng ôn tập TN THPT 2020 môn Toán: Góc và khoảng cách trong không gian Toán 12

Tài liệu gồm 47 trang, được tổng hợp và biên soạn bởi thầy giáo Nguyễn Bảo Vương, tuyển chọn các câu hỏi và bài tập trắc nghiệm chuyên đề góc và khoảng cách trong không gian, có đáp án và lời giải chi tiết, giúp học sinh tổng ôn kiến thức để chuẩn bị cho kỳ thi tốt nghiệp THPT 2020 môn Toán.Mời bạn đọc đón xem.

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

47 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
A. GÓC TRONG KHÔNG GIAN
Góc giữa đường thẳng
a
và đường thẳng
b
Phương pháp 1. Sử dụng song song, tức dựng đường thẳng
c b
và
c
cắt
.a
Khi đó
( ; ) ( ; )a b a c
như hình vẽ.
Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số sin, côsin để tìm góc
.
Phương pháp 2. Sử dụng tích vô hướng, nghĩa là
.
cos( ; ) cos( ; ) cos .
.
a b
a b a b
a b
Khi đó, ta cần chèn điểm phù hợp để tính tích vô hướng.
Phương pháp 3. Ghép vào hệ trục tọa độ
.Oxyz
Lưu ý: Góc giữa hai đường thẳng là góc nhọn, còn góc giữa hai véctơ là góc nhọn hoặc góc tù. Nghĩa là
nếu tính
( ; ) 90a b
thì góc giữa
, a b
là
,
còn nếu tính
( ; ) 90a b
thì góc giữa hai
đường thẳng
( ; ) 180 .a b
Góc giữa đường thẳng
AB
và mặt phẳng
( )P
Cần nhớ: “Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó lên mặt phẳng”.
Phương pháp 1. Sử dụng hình học 11.
B. 1. Tìm
( ) { }AB P A
(1)
B. 2. Tìm hình chiếu của
B
lên mặt phẳng
( ).P
Đặt câu hỏi và trả lời: “Đường nào qua
B
và vuông góc với
( )P
? “(có sẵn hoặc dựng thêm)
Trả lời:
( )BH P
tại
H
(2)
Từ
(1),(2),
suy ra
AH
là hình chiếu của
AB
lên mặt phẳng
( ).P
Do đó góc giữa đường thẳng
AB
và mp
( )P
là góc giữa
AB
và
,AH
chính là góc
.BAH
B. 3. Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số côsin hoặc định lí hàm sin trong tam
giác thường để suy ra góc
.BAH
Phương pháp 2. Ghép vào hệ trục tọa độ
.Oxyz
Góc giữa mặt phẳng
( )P
và mặt phẳng
( ).Q
Phương pháp 1. Dựa vào định nghĩa
Ta có:
1 1 2
2
( ) ( )
( ) (( ),( )) ( , ) .
( )
P Q u
u d P P Q d d
u d Q
Phhương pháp 2. Tìm hai đường thẳng
1
d
và
2
d
lần lượt vuông góc với mặt phẳng
( )P
và mặt phẳng
( ).Q
Góc giữa hai mặt phẳng là góc giữa
1
d
và
2
.d
Phương pháp 3. Sử dụng công thức hình chiếu
.cos .S S
Phương pháp 4. Trong trường hợp quá khó, nên sử dụng công thức
,( )
( , )
sin
A Q
A u
d
d
Trong đó
(( ),( )), ( )P Q A P
và
( ) ( )P Q u
là giao tuyến của
( )P
và
( ).Q
Phương pháp 5. Ghép vào hệ trục tọa độ
.Oxyz
GÓC - KHOẢNG CÁCH
Vấn đề 7
α
(Q)
(P)
u
d
2
d
1
a
b
c
B
A
H
P
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Chohìnhchóp
.S ABCD
cóđáylàhìnhvuôngcạnh
3a
,
SA
vuônggócvớimặtphẳngđáyvà
2SA a
.Gócgiữa
SC
vàmặtphẳng
( )ABCD
bằng
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Câu 2. Chohìnhchóp
.S ABC
có
SA
vuônggócvớimặtphẳng
,ABC
2,SA a
tamgiác
ABC
vuông
cântại
B
và
2AC a
(minhhọanhứhìnhbên).Gócgiữađườngthẳng
SB
vàmặtphẳng
ABC
bằng
A.
30 .
B.
45 .
C.
60 .
D.
90 .
Câu 3. Cho hình chóp
.S ABC
có
SB
vuông góc với mặt phẳng
ABC
, 3SB a , tam giác
ABC
vuôngtại
A
,
AB a
và
2AC a
.Gócgiữađườngthẳng
SC
vàmặtphẳng
SAB
bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Câu 4. Chohìnhchópđều
.S ABCD
có
2AB a
,
2SB a
.Gócgiữađườngthẳng
SA
vàmặtphẳng
SBD
bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Câu 5. Cho hìnhchóp
.S ABC
có
SA
vuônggóc với mặt phẳng
ABC
, 6SB a , tamgiác
ABC
vuôngcântại
C
,
2AB a
.Gócgiữađườngthẳng
SC
vàmặtphẳng
SAB
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 6. Cho hình chóp
.S ABCD
có
SA
vuông góc với mặt phẳng
ABCD
,
ABCD
là hình chữ nhật,
2, 2AB a BC a
,
3SA a
.Gọi
M
làtrungđiểmcủa
BC
.Tínhgócgiữađườngthẳng
SM
và
mặtphẳng
ABCD
.
A.
30
. B.
60
. C.
45
. D.
120
.
S
C
B
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 7. Chotứdiệnđều
ABCD
cócạnhbằng
2a
.Gọi
làgócgiữađườngthẳng
AB
vàmặtphẳng
BCD
.Tính
cos
.
A.
3
cos
6
. B.
6
cos
3
. C.
3
cos
3
. D.
2
cos
3
.
Câu 8. Chohìnhchóp
.S ABC
có
SA
vuônggócvớimặtphẳng
,ABC
tamgiác
ABC
vuôngcântại
B
và
2AC a
(minhhọanhưhìnhbên).Gócgiữađườngthẳng
SB
vàmặtphẳng
ABC
bằng
60 .
Tính
độdàicạnhbên
SA
.
A.
6
.
3
a
B.
6.a
C.
3.a
D.
2 3.a
Câu 9. Chohìnhchóp
.S ABCD
cóđáylàhìnhchữnhậtvới
2 , 2AB a AD a
,
SA
vuônggócvớimặt
phẳngđáyvà
2SA a
.Gócgiữađườngthẳng
SC
vàmặtphẳng
ABCD
bằng
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Câu 10. Chochópđều
.S ABCD
cócạnhđáybằng
2a
,cạnhbênbằng
3a
(minhhọanhưhìnhbên).Gọi
làgócgiữagiữacạnhbênvàmặtđáy.Mệnhđềnàosauđâyđúng?
A.
14
tan .
7
B.
3
tan .
2
C.
0
45 .
D.
14
tan .
2
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. Cholăngtrụđứng
. ' ' 'ABC A B C
có đáylà
ABC
vuôngcântại
B
,
2 2AC a
(minhhọanhư
hìnhbên).Gócgiữađườngthẳng
'A B
vàmặtphẳng
ABC
bằng
60 .
Tínhđộdàicạnhbêncủa
hìnhlăngtrụ.
A.
2 3
.
3
a
B.
2 3.a
C.
2 6.a
D.
2 .a
Câu 12. Chohìnhchóp
.S ABCD
cóđáylàhìnhthoicạnhbằng
a
,
0
60ABC
,
SA
vuônggócvớimặt
phẳng đáy và
3SA a
. Gọi
là góc giữa đường thẳng
SC
và mặt phẳng
ABCD
. Tính
tan
A.
3
. B. 1. C.
6
2
. D.
1
3
.
Câu 13. Chochóp
.S ABCD
cóđáylàhìnhvuôngtâm
O
cạnhbằng
2a
,cạnhbên
SA
vuônggócvớimặt
phẳng
,ABCD
3.SA a
Gọi
gócgiữađườngthẳng
SO
vàmặtphẳng
ABCD
.Mệnhđềnào
sauđâyđúng?
A.
tan 6.
B.
45 .
C.
60 .
D.
90 .
Câu 14. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
. Gọi M là trung điểm của AB,
SM ABCD
và
5SM a
. Gọi
làgóc giữa đường thẳng
SC
và mặt phẳng
ABCD
.
Tính
tan
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
30
3
. B.
2
. C.
22
4
. D.
5
2
.
Câu 15. Chohìnhchóp
.S ABC
có
SA
vuônggócvớimặtphẳng
,ABC
3,SA a
tamgiác
ABC
đều(minh
họanhưhìnhbên).Gócgiữađườngthẳng
SC
vàmặtphẳng
ABC
bằng
30 .
Tínhthểtíchkhối
chóp
.S ABC
.
A.
3
9
.
4
a
B.
3
27
.
4
a
C.
3
.
4
a
D.
3
81
.
4
a
Câu 16. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làhìnhvuôngtâm
O
cạnh
2a
.Cạnhbên
SA
vuônggóc
vớiđáyvà
2SA a
.Gócgiữađườngthẳng
SB
vàmặtphẳng
SAC
bằng:
A.
45 .
B.
30 .
C.
60 .
D.
90 .
Câu 17. Chohìnhhộpchữnhật
.ABCD A B C D
cóđáy
ABCD
làhìnhvuông,
2AC a
.Gọi
P
là
mặtphẳngqua
AC
cắt
,BB DD
lầnlượttại
,M N
saochotamgiác
AMN
cântại
A
có
MN a
.Tính
cos
với
,P ABCD
.
A.
2
2
. B.
1
2
. C.
1
3
. D.
3
3
.
Câu 18. Chohìnhhộpchữnhật
.ABCD A B C D
cócáccạnh
2, 3; 4AB AD AA
.Gócgiữahaimặt
phẳng
AB D
và
A C D
là
.Tínhgiátrịgầnđúngcủagóc
?
A.
45,2
. B.
38,1
. C.
53,4
. D.
61,6
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. Chohìnhhộpchữnhật
.ABCD A B C D
cócáccạnh
2, 3; 4AB AD AA
.Gócgiữahai
mặtphẳng
'BC D
và
A C D
là
.Tínhgiátrịgầnđúngcủagóc
?
A.
45,2
. B.
38,1
. C.
53,4
. D.
61,6
.
Câu 20. Chotứdiện
ABCD
có
2BD
.Haitamgiác
ABD
và
BCD
códiệntíchlầnlượtlà
6
và
10
.
Biếtthểtíchkhốitứdiện
ABCD
bằng
16
.Tínhsốđogócgiữahaimặtphẳng
ABD
và
.BCD
A.
4
arccos
15
. B.
4
arcsin
5
. C.
4
arccos
5
. D.
4
arcsin
15
.
Câu 21. Chohìnhchóp
.S ABCD
đáy
ABCD
làhìnhthoi,
SA SC
.Gócgiữahaimặtphẳng
SBD
và
ABCD
bằng?
A.
90
. B.
30
. C.
60
. D.
45
.
Câu 22. Chohìnhchóp
.S ABCD
đáy
ABCD
làhìnhchữnhật,tamgiác
SAB
làtam giácđềuvànằm
trongmặtphẳngvuônggócvớiđáy.Gócgiữahaimặtphẳng
SAB
và
SAD
bằng?
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 23. Chohìnhvuông
ABCD
.Gọi
S
làđiểmtrongkhônggiansaocho
SAB
làtamgiácđềuvànằm
trongmặtphẳngvuônggócvớiđáy.Gọi
H
và
I
lầnlượtlàtrungđiểmcủa
AB
và
BC
.Góc
giữahaimặtphẳng
SHC
và
SDI
bằng.
A.
30
. B.
60
. C.
90
. D.
45
.
Câu 24. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làhìnhvuôngtâm
O
,cạnh
a
.Đườngthẳng
SO
vuông
góc với mặt phẳng đáy
ABCD
và
3
2
a
SO
. Tính góc giữa hai mặt phẳng
SBC
và
ABCD
.
A.
30
. B.
45
. C.
60
. D.
90
.
B. KHOẢNG CÁCH TRONG KHÔNG GIAN
Tính khoảng cách từ chân đường cao của hình chóp đến mặt bên của hình chóp.
Tínhkhoảngcáchtừ
A
đếnmặtbên
( )SBC
củahìnhchóp
.S ABC
có
( )SA ABC
B1.Xácđịnhgiaotuyếncủamặtbênvàmặtphẳngđáy
( ) ( ) .SBC ABC BC
B2.Dựnghình ( ).
AH BC
AI SBC
AI SH
Suyra
( ;( )) .d A SBC AI
B3.Tính
.AI
Cácphươngphápquyvềbàitoánchânđườngcao:
―Kẻsongsongđểdờiđiểmvềchânđườngvuônggóc.
―Dùngtỉsốkhoảngcáchđểdờivềchânđườngvuônggóc.
―Tạochânđườngcaogiả(
đườngcao,khimặtchứachân).
Tính khoảng cách giữa cạnh bên và cạnh thuộc mặt đáy.
Chohìnhchóp
.S ABCD
có
( ).SA ABCD
Hãytínhkhoảng
cáchgiữacạnhbên
SB
vàcạnhthuộcmặtđáy
.AC
B1.Xácđịnhgiaođiểmcủacạnhbên
SB
vàmặtphẳngđáy
( ) .SB ABCD B
B2.Quagiaođiểm
,B
dựngđườngthẳng
d
songsongvới
.AC
Khiđó:
( , ) ( ,( , )) ( ,( , )).d AC SB d AC SB d d A SB d
Đâylàbàitoántìmkhoảngcáchtừchânđếnmặtbên.Cụthể:
( , ) ( ,( , )) ( ,( , )) .d AC SB d AC SB d d A SB d AK
K
H
D
B
A
C
S
d
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Chohìnhchóp
.S ABC
cóđáylàtamgiácvuôngtại
A
,
2AB a
,
4AC a
,
SA
vuônggócvới
mặtphẳngđáyvà
SA a
(hìnhminhhọa).Gọi
M
làtrungđiểmcủa
AB
.Khoảngcáchgiữahai
đườngthẳng
SM
và
BC
bằng
A.
2
3
a
. B.
6
3
a
. C.
3
3
a
. D.
2
a
.
Câu 2. Chohìnhchóp
.S ABCD
cóđáylàhìnhthang,
2AB a
,
AD DC CB a
,
SA
vuônggócvới
mặtphẳngđáyvà
3SA a
(minhhọanhưhìnhbên).Gọi
M
làtrungđiểmcủa
AB
.Khoảngcách
giữahaiđườngthẳng
SB
và
DM
bằng
A.
3
4
a
. B.
3
2
a
. C.
3 13
13
a
. D.
6 13
13
a
.
Câu 3. Chohìnhlăngtrụđứng
.ABC A B C
cóđáy
ABC
làtamgiácđềucạnh
a
vàcạnhbêncóđộdài
bằng
a
.Tínhkhoảngcáchtừ
C
đếnmặtphẳng
A BC
.
A.
2
4
a
. B.
3
7
a
. C.
21
7
a
. D.
2
16
a
.
Câu 4. Chohìnhhộp
.ABCD A B C D
cóđáy
ABCD
làhìnhvuôngcạnh
a
,tâm
O
.Hìnhchiếuvuông
góccủa
A
lênmặtphẳng
ABCD
trùngvới
O
.Biếttamgiác
AAC
vuôngcântại
A
.Tính
khoảngcách
h
từđiểm
D
đếnmặtphẳng
ABB A
.
A.
6
6
a
h
. B.
2
3
a
h
. C.
2
6
a
h
. D.
6
3
a
h
.
Câu 5. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làhìnhthangvuôngtại
A
và
D
với
2AD a
,
DC a
,
2AB a
.Gọi
I
làtrungđiểmcạnh
AD
,haimặtphẳng
SIB
,
SIC
cùngvuônggócvớimặt
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
phẳ
ngđáyvàmặtphẳng
SB
C
tạ
ovớiđáymộtgóc
60
.
Tínhkhoảngcách
h
từ
I
đến
mặt
phẳng
SB
C
.
A.
1
5
15
a
h
. B.
1
5
5
a
h
. C.
3
15
10
a
h
. D.
3
5
5
a
h
.
C
âu 6. Chohìnhchóp
.S
ABCD
cóđáy
lànửalụcgiác đều
A
BCD
nội
tiếptrongđườngtròn đườngkính
2A
D a
vàcócạn
h
S
A
v
uônggócvớimặtphẳngđáy
A
BCD
với
6S
A a .Tínhkhoảngcáchtừ
B
đến
mặtphẳng
S
CD
.
A.
2a
. B. 3a . C.
2
2
a
. D.
3
2
a
.
Câu 7. Cho
hình chóp
.S ABC
có
đáy
ABC
là
tam giác vuông tại
A
,
(
)SAC ABC
,
3AB a
,
5BC
a
.
Biếtrằng
2
3SA a
và
0
3
0SAC
.
Khoảngcáchtừđiểm
A
đến
mặtphẳng
(
)SBC
bằng:
A.
3
17
4
a
. B.
6
7
7
a
. C.
3
7
14
a
. D.
1
2
5
a
.
Câu 8. Cho
tứdiệnđều
ABCD
cócạnhbằng
a
.Gọi M làtrungđiểm
CD
.Khoảngcáchgiữa
AC
và
BM là
A.
1
54
28
a
. B.
2
a
. C.
22
11
a
. D.
2
3
a
.
Câu 9. Cho
hìnhchóp
.S ABC
,cóđáylàtamgiácđềucạnh
2a
,
2SA a
,
SA
vuônggócvớimặtphẳng
đáy(minhhọanhưhìnhvẽ).Gọi
,M N
lầnlượtlàtrungđiểmcủa
,AB AC
.Khoảngcáchgiữa
haiđườngthẳng
M
N
và
S
C
bằng.
A.
2
1
7
a
. B.
2
1
14
a
. C.
2
57
19
a
. D.
5
7
19
a
.
Câu 10. Cho
hìnhchóp
.S
ABCD
c
óđáylàhìnhchữnhật
A
BCD
có
2
, 4 , ( ) AB a AD a SA ABCD
,
2
15SA a .Gọi
M
làtrungđiểmcủa ,BC N làđiểmnằmtrêncạnh
A
D
sa
ocho
4A
D DN
.
K
hoảngcáchgiữa
MN và SB
là
A.
4 285
19
a
B.
2 285
15
a
C.
285
19
a
D.
2 285
19
a
Câu 11. Cho
hìnhchóp
.S
ABCD
có
đáylàhìnhvuôngcạnh
2a
,
S
A
vuôn
ggócvớimặtphẳngđáyvà
SA a
.Gọi
M
l
àtrungđiểm
.AB
Khoả
ngcáchgiữahaiđườngthẳng
SB
và
DM
bằ
ng
A.
2
21
21
a
B.
21
8
a
C.
4
21
21
a
D.
a
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu
12. Chohìnhchópđáylàhìnhvuôngcạnh
1
7
,
2
a
a SD
,
hìnhchiếuvuônggóccủa
S
l
ênmặtphẳng
A
BCD
t
rungđiểm H củađoạn
A
B
.
Gọi K làtrungđiểmcủađoạn
A
D
.
Tínhkhoảngcách
giữahaiđườngthẳng HK và
SD
theo
a
.
A.
3
5
a
B.
28
6
26
a
C.
5
3
3
a
D.
39
3
a
Câu
13. Chohìnhchóp
.S ABCD
có
đáylàhìnhvuôngcạnh
3a
,
SA
vuôn
ggócvớimặtphẳngđáyvà
S
A a
.
Gọi
M
là
điểmthàomãn
2 0MB MC
 
.
Khoảngcáchgiữahaiđườngthẳng
S
C
và
DM
bằng
A.
154
77
a
. B.
3 154
154
a
. C.
6 154
77
a
. D.
2 154
77
a
.
Câu
14. Chohìnhchóp
.S
ABCD
có
đáy
A
BCD
là
hìnhvuôngcạnh
a
.
Gọi M và
N
lầ
nlượtlàtrung
điểmcủacáccạnh
A
B
và
AD
; H làgiaođiểmcủa
C
N
với DM .Biết
SH
vuônggócvớimặt
phẳng
A
BCD
và
3S
H a
.Tí
nhkhoảngcáchgiữahaiđườngthẳng DM và
S
C
the
o
a
.
A.
2
3
19
a
. B.
21
7
a
. C.
57
6
a
. D.
3
3
19
a
.
Câu 15. Chohìnhchóp
.S
ABCD
cóđáy
AB
CD
làhìnhvuôngcạnh
2a
,cạnhbên
5S
A a
,mặtbên
S
AB
làtamgiáccânđỉnh
S
vàthuộcmặtphẳngvuônggócvớimặtphẳngđáy.Khoảngcáchgữa
haiđườngthẳng
AD
và
S
C
bằng:
A.
2
5
5
a
. B.
4
5
5
a
. C.
15
5
a
. D.
2
15
5
a
.
Câu 16. Cho lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông tại
A
,
A
B a
,
2B
C a
. Gọi
M
,
N
,
P
lầl
ượtlàtrungđiểmcủa
A
C
,
C
C
,
A
B
và
H
l
àhìnhchiếucủa
A
lên
B
C
.
Tính
khoảngcáchgiữa
MP
và
N
H
.
A.
3
4
a
. B.
3
8
a
. C.
3
2
a
. D.
2
a
.
Câu
17. Cho hình chóp
.S ABC
đều.
Gọi
G
là
trọng tâm của tam giác
ABC
s
ao cho
SG AB a
.
Khoả
ngcáchgiữahaiđườngthẳng
SA
và
CG
bằng
A.
2
a
. B.
a
. C.
5
5
a
. D.
3
3
a
.
Câu
18. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làvuôngcạnh
a
,
2SA a
vàvuônggócvới
A
BCD
.
Gọi
M
làtrungđiểmcủa
S
D
.Tínhkhoảng
cách
d
giữa
haiđườngthẳng
S
B
và
C
M
.
A.
2
3
3
a
d
. B.
3
2
a
d
. C.
2
3
a
d
. D.
3
a
d
.
Câu
19. Chohìnhchóp
.S ABCD
c
óđáylàhìnhchữnhật.Tamgiác
SAB
vuôn
gcântại
A
và
nằmtrong
mặtphẳngvuônggócvớiđáyvà
4
2SB
.
Gọi
M
là
trungđiểmcủacạnh
SD
.T
ínhkhoảng
C
B
A
D
S
NGUYỄN BẢO VƯƠNG - 0946798489
cách
l
từđiểm
M
đếnmặtphẳ
ng
SBC
A.
2l
. B.
2 2
l
. C.
2
l
. D.
2
2
l
.
Câu 20. Chohình
chóp
.
S AB
CD
cóđá
ylàhìnhthoicạnh
a
,
60
BAD
,
SB a
vàmặ
tphẳng
SBA
và
mặ
tphẳng
SBC
cùngvuônggóc
vớimặtphẳngđáy.Khoảngcáchtừ
B
đếnmặ
tphẳng
SCD
bằng
A.
21
7
a
. B.
5
7
a
. C.
21
3
a
. D.
15
3
a
.
Câu 21. Chohìnhchóp
.
S ABCD
cóđáy
ABCD
làhìnhthoicạnhbằng
2 3a
,góc
BAD
bằng
120
.
Haimặtphẳng
SAB
và
SAD
cùngvuônggóc
vớiđáy.Gócgữamặtphẳng
SBC
và
ABC
D
bằng
45
.
Khoảngc
ách
h
từ
A
đếnmặ
tphẳng
SBC
là
A.
2 2.
h a
B.
2 2
.
3
a
h
C.
3 2
.
2
a
h
D.
3.
h a
Câu 22. Cho
hìnhchóp
.
S ABCD
cóđá
ylàhìnhbìnhhành,
30
ADC
,
AB a
,
2AD a
,
SA a
và
SA
vuônggócvớimặtphẳngđá
y.Khoảngcáchtừ
B
đếnmặt
phẳng
SCD
bằng
A.
3
2
a
. B.
2
3
a
. C.
2
2
a
. D.
2
a
.
Câu 23. Chohình
chóp
.
S ABCD
cóđáylàhìnhbìnhhành,
AB a
,
3AD a
,
2AC a
,
2SA a
và
SA
vuônggócvớimặtphẳngđáy.Khoảngcáchtừ
B
đếnmặt
phẳng
SCD
bằng
A.
3a
. B.
2a
. C.
84
7
a
. D.
2
2
a
.
Câu 24. Hìnhc
hóp
.
S ABCD
cóđáy
làhìnhthoitâm
O
cạnh
2a
,
60
ABC
,hìnhc
hiếuvuônggóccủa
S
lên
ABC
D
trùngvớit
rungđiểm
I
của
BO
,
3SI a
.Khoả
ngcáchtừ
B
đếnm
ặtphẳng
SCD
bằng
A.
3 3
5
a
. B.
2 3
5
a
. C.
3
5
a
. D.
4 3
5
a
.
Câu 25. Chohình
chóp
.
S ABCD
cóđá
ylàhìnhthangcânđáy
AD
có
2 2 2AD
AB BC a
,
SA a
và
SA
vuônggócvới
mặtphẳngđáy.Khoảngcáchtừ
B
đếnmặt
phẳng
SCD
bằng
A
.
3
2
a
. B.
3
3
a
. C.
3
4
a
. D.
2a
.
-------------------- HẾT --------------------
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
A. GÓC TRONG KHÔNG GIAN
Góc giữa đường thẳng
a
và đường thẳng
b
Phương pháp 1. Sử dụng song song, tức dựng đường thẳng
c b
và
c
cắt
.a
Khi đó
( ; ) ( ; )a b a c
như hình vẽ.
Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số sin, côsin để tìm góc
.
Phương pháp 2. Sử dụng tích vô hướng, nghĩa là
.
cos( ; ) cos( ; ) cos .
.
a b
a b a b
a b
Khi đó, ta cần chèn điểm phù hợp để tính tích vô hướng.
Phương pháp 3. Ghép vào hệ trục tọa độ
.Oxyz
Lưu ý: Góc giữa hai đường thẳng là góc nhọn, còn góc giữa hai véctơ là góc nhọn hoặc góc tù. Nghĩa là
nếu tính
( ; ) 90a b
thì góc giữa
, a b
là
,
còn nếu tính
( ; ) 90a b
thì góc giữa hai
đường thẳng
( ; ) 180 .a b
Góc giữa đường thẳng
AB
và mặt phẳng
( )P
Cần nhớ: “Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó lên mặt phẳng”.
Phương pháp 1. Sử dụng hình học 11.
B.1. Tìm
( ) { }AB P A
(1)
B.2. Tìm hình chiếu của
B
lên mặt phẳng
( ).P
Đặt câu hỏi và trả lời: “Đường nào qua
B
và vuông góc với
( )P
? “(có sẵn hoặc dựng thêm)
Trả lời:
( )BH P
tại
H
(2)
Từ
(1),(2),
suy ra
AH
là hình chiếu của
AB
lên mặt phẳng
( ).P
Do đó góc giữa đường thẳng
AB
và mp
( )P
là góc giữa
AB
và
,AH
chính là góc
.BAH
B.3. Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số côsin hoặc định lí hàm sin trong
tam giác thường để suy ra góc
.BAH
Phương pháp 2. Ghép vào hệ trục tọa độ
.Oxyz
Góc giữa mặt phẳng
( )P
và mặt phẳng
( ).Q
Phương pháp 1. Dựa vào định nghĩa
Ta có:
1 1 2
2
( ) ( )
( ) (( ),( )) ( , ) .
( )
P Q u
u d P P Q d d
u d Q
Phhương pháp 2. Tìm hai đường thẳng
1
d
và
2
d
lần lượt vuông góc với mặt phẳng
( )P
và mặt phẳng
( ).Q
Góc giữa hai mặt phẳng là góc giữa
1
d
và
2
.d
Phương pháp 3. Sử dụng công thức hình chiếu
.cos .S S
GÓC - KHOẢNG CÁCH
Vấn đề 7
α
(Q)
(P)
u
d
2
d
1
a
b
c
B
A
H
P
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương pháp 4. Trong trường hợp quá khó, nên sử dụng công thức
,( )
( , )
sin
A Q
A u
d
d
Trong đó
(( ),( )), ( )P Q A P
và
( ) ( )P Q u
là giao tuyến của
( )P
và
( ).Q
Phương pháp 5. Ghép vào hệ trục tọa độ
.Oxyz
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Chohìnhchóp
.S ABCD
cóđáylàhìnhvuôngcạnh
3a
,
SA
vuônggócvớimặtphẳngđáy
và
2SA a
.Gócgiữa
SC
vàmặtphẳng
( )ABCD
bằng
A.
0
45
. B.
0
60
. C.
0
30
. D.
0
90
.
Lời giải
Chọn C
Tacó
( )SA ABCD
nêntacó
( ,( ))SC ABCD SCA
0
2 1
tan 30
3 . 2 3
SA a
SCA SCA
AC
a
Câu 2. Chohình chóp
.S ABC
có
SA
vuônggóc với mặt phẳng
,ABC
2,SA a
tam giác
ABC
vuôngcântại
B
và
2AC a
(minhhọanhứhìnhbên).Gócgiữađườngthẳng
SB
vàmặtphẳng
ABC
bằng
A.
30 .
B.
45 .
C.
60 .
D.
90 .
Lời giải
S
C
B
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Chọn B
Tacó
SB ABC B
AB
SA ABC
làhìnhchiếucủa
SB
trênmặtphẳng
ABC
,SB ABC SBA
Dotamgiác
ABC
vuôngcântại
2
2 2 2 2 2 2
2 2 2 2.4B AB AB a ABBC AC a AB a
Xéttamgiácvuông
SAB
vuôngtại
,A
có
2SA AB a SAB
vuôngcântại
A
45 .SBA
Câu 3. Cho hình chóp
.S ABC
có
SB
vuông góc với mặt phẳng
ABC
,
3SB a
, tam giác
ABC
vuông tại
A
,
AB a
và
2AC a
. Góc giữa đường thẳng
SC
và mặt phẳng
SAB
bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Lời giải
Chọn A
Tacó
CA AB
CA SAB
CA SB
.
Dođógócgiữađườngthẳng
SC
vàmặtphẳng
SAB
là
CSA .
Tacó
2 2 2 2
3 2SA SB AB a a a
;
2
tan 1 45
2
AC a
CSA CSA
SA a
.
Câu 4. Cho hình chóp đều
.S ABCD
có
2AB a
,
2SB a
. Góc giữa đường thẳng
SA
và mặt
phẳng
SBD
bằng
A.
45
. B.
60
. C.
30
. D.
90
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
O AC BD
.Vì
.S ABCD
làhìnhchópđềunên
SO ABCD
.
Dođó
AO SBD
gócgiữađườngthẳng
SA
vàmặtphẳng
SBD
là
ASO .
Tacó
2 ; 2SA a AC a AO a
;
1
sin 30
2 2
AO a
ASO ASO
SA a
.
Câu 5. Chohìnhchóp
.S ABC
có
SA
vuônggócvớimặtphẳng
ABC
, 6SB a ,tamgiác
ABC
vuôngcântại
C
,
2AB a
.Gócgiữađườngthẳng
SC
vàmặtphẳng
SAB
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Lời giải
Chọn A
Gọi
H
làtrungđiểmcủa
AB
.Vì
ABC
cântại
C CH AB
CH SAB
.
Dođóhìnhchiếuvuônggóccủa
C
lênmặtphẳng
SAB
là
H
.
gócgiữa
SC
vàmặtphẳng
SAB
bằnggóc
CSH
.
Tacó
ABC
vuôngcântại
, 2 2; C AB a CA CB a CH a
;
2 2 2 2
6 4 2SA SB AB a a a
;
2 2 2 2
2 2 2SC SA AC a a a
.
Xét
SHC
vuôngtại
H
có
2 30SC CH CSH .
Câu 6. Chohìnhchóp
.S ABCD
có
SA
vuônggócvớimặtphẳng
ABCD
,
ABCD
làhìnhchữnhật,
2, 2AB a BC a
,
3SA a
.Gọi
M
làtrungđiểmcủa
BC
.Tínhgócgiữađườngthẳng
SM
và
mặtphẳng
ABCD
.
A.
30
. B.
60
. C.
45
. D.
120
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Vì
SA ABCD
nêngócgiữađườngthẳng
SM
vàmặtphẳng
ABCD
làgóc
SMA.
Tacó
2 2 2 2
; 2 3
2
BC
BM a AM AB BM a a a
;
3
tan 3 60 .
3
SA a
SMA SMA
AM
a
Câu 7. Chotứdiệnđều
ABCD
cócạnhbằng
2a
.Gọi
làgócgiữađườngthẳng
AB
vàmặtphẳng
BCD
.Tính
cos
.
A.
3
cos
6
. B.
6
cos
3
. C.
3
cos
3
. D.
2
cos
3
.
Lời giải
Chọn C
Gọi
O
làtrọngtâmtamgiác
BCD
.Vì
ABCD
làtứdiệnđềunên
AO BCD
.
Dođógócgiữađườngthẳng
AB
vàmặtphẳng
ABC
bằng
ABO
.
Tacó
3 2 2 3
. 3
2 3 3
a
BM BC a BO BM
;
2 3
3
3
cos cos
2 3
a
BO
ABO
AB a
.
Câu 8. Chohìnhchóp
.S ABC
có
SA
vuônggócvớimặtphẳng
,ABC
tamgiác
ABC
vuôngcântại
B
và
2AC a
(minh họa như hình bên). Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
60 .
Tínhđộdàicạnhbên
SA
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
6
.
3
a
B.
6.a
C.
3.a
D.
2 3.a
Lời giải
Chọn B
Tacó
SB ABC B
SA ABC
AB
làhìnhchiếucủa
SB
trên
,ABC
0
, , 60 SB ABC SB AB SBA
Màtamgiác
ABC
vuôngcântại
B
và
2 2 AC a AB a
Khiđóxéttrongtamgiácvuông
SAB
suyra
0
tan60 6 SA AB a
Câu 9. Chohìnhchóp
.S ABCD
cóđáylàhìnhchữnhậtvới
2 , 2AB a AD a
,
SA
vuônggócvới
mặtphẳngđáyvà
2SA a
.Gócgiữađườngthẳng
SC
vàmặtphẳng
ABCD
bằng
A.
0
45
. B.
0
30
. C.
0
60
. D.
0
90
.
Lời giải
Chọn B
Vì
SA ABCD
nên
AC
làhìnhchiếucủa
SC
trênmặtphẳng
ABCD
Dođógócgiữa
SC
vàmặtphẳng
ABCD
là
SCA
Đáy
ABCD
làhìnhchữnhậtcó
2 , 2AB a BC AD a
nên
2 2 2 2
4 2 6AC AB BC a a a
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Trongtamgiácvuông
:SAC
2 3
tan
3
6
SA a
SCA
AC
a
30SCA
.
Vậygócgiữađườngthẳng
SC
vàmặtphẳng
( )ABCD
bằng
30
.
Câu 10. Chochópđều
.S ABCD
cócạnhđáybằng
2a
,cạnhbênbằng
3a
(minhhọanhưhìnhbên).Gọi
làgócgiữagiữacạnhbênvàmặtđáy.Mệnhđềnàosauđâyđúng?
A.
14
tan .
7
B.
3
tan .
2
C.
0
45 .
D.
14
tan .
2
Lời giải
Chọn D
Gọi
O AC BD SO ABCD AO
làhìnhchiếucủa
SA
trênmp
ABCD
, , SA ABCD SA AO SAO
Xéttrongtamgiácvuông
SAO
tacó
1 1 14
3 , 2 . 2 2 7 tan .
2 2 2
SO
SA a AO AC a a SO a
AO
Câu 11. Cholăngtrụđứng
. ' ' 'ABC A B C
cóđáylà
ABC
vuôngcântại
B
,
2 2AC a
(minhhọanhư
hìnhbên).Gócgiữađườngthẳng
'A B
vàmặtphẳng
ABC
bằng
60 .
Tínhđộdàicạnhbêncủa
hìnhlăngtrụ.
A.
2 3
.
3
a
B. 2 3.a C. 2 6.a D.
2 .a
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó
'
'
A B ABC B
A A ABC
AB
làhìnhchiếucủa
'A B
trên
.ABC
0
' , ' , ' 60 A B ABC A B AB A BA
Khiđóxéttrongtamgiácvuông
'A BA
tacó:
0
'
2 , tan ' ' tan 60 2 3.
2
AC A A
AB a A BA A A AB a
AB
Câu 12. Chohìnhchóp
.S ABCD
cóđáylàhìnhthoicạnhbằng
a
,
0
60ABC
,
SA
vuônggócvớimặt
phẳngđáyvà
3SA a
.Gọi
làgócgiữađườngthẳng
SC
vàmặtphẳng
ABCD
.Tính
tan
A.
3
. B. 1. C.
6
2
. D.
1
3
.
Lời giải
Chọn A
Vì
SA ABCD
nên
AC
làhìnhchiếucủa
SC
trênmặtphẳng
ABCD
Dođógócgiữa
SC
vàmặtphẳng
ABCD
là
SCA
Đáy
ABCD
làhìnhthoicó
0
60ABC
nên
ABC
đều
AC AB BC a
Xét
SAC
vuôngtạiA:
3
tan 3
SA a
AC a
Câu 13. Chochóp
.S ABCD
cóđáylàhìnhvuôngtâm
O
cạnhbằng
2a
,cạnhbên
SA
vuônggócvới
mặtphẳng
,ABCD
3.SA a
Gọi
gócgiữađườngthẳng
SO
vàmặtphẳng
ABCD
.Mệnh
đềnàosauđâyđúng?
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A.
tan 6.
B.
45 .
C.
60 .
D.
90 .
Lời giải
Chọn C
Tacó
SO ABCD O
SA ABCD
AO
làhìnhchiếucủa
SO
trên
ABCD
.
, , SO ABCD SO AO SOA
.
Khiđóxéttrongtamgiácvuông
SOA
tacó:
0
1 1
2 . 2 ; 3 tan 3 60
2 2
SA
AO AC a a SA a SOA SOA
AO
.
Câu 14. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
2a
. Gọi M là trung điểm của AB,
SM ABCD
và
5SM a
.Gọi
làgócgiữađườngthẳng
SC
vàmặtphẳng
ABCD
.
Tính
tan
A.
30
3
. B.
2
. C.
22
4
. D.
5
2
.
Lời giải
Chọn B
Vì
SM ABCD
nên
MC
làhìnhchiếucủa
SC
trênmặtphẳng
ABCD
Dođógócgiữa
SC
vàmặtphẳng
ABCD
là
SCM
Đáy
ABCD
làhìnhvuôngcạnh
2a
nên
2
2 2
AB a
BM
2 2
10
2
a
MC BC BM
Xét
SMC
vuôngtạiM:
5
tan 2
10
2
SM a
MC
a
.
Câu 15. Chohìnhchóp
.S ABC
có
SA
vuônggócvớimặtphẳng
,ABC
3,SA a
tamgiác
ABC
đều
(minhhọanhưhìnhbên).Gócgiữađườngthẳng
SC
vàmặtphẳng
ABC
bằng
30 .
Tínhthểtích
khốichóp
.S ABC
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
9
.
4
a
B.
3
27
.
4
a
C.
3
.
4
a
D.
3
81
.
4
a
Lời giải
Chọn A
Tacó
SC ABC C
SA ABC
AB
làhìnhchiếucủa
SC
trên
,ABC
0
, , 30 SC ABC SC AB SCA
.
Khiđóxéttrongtamgiácvuông
SAC
tacó
0
tan 30 3
SA
AC a
AC
.
Tamgiác
ABC
đềunên
2
2 2 3
3 3
9 3 1 9 3 9
3.
4 4 3 4 4
ABC SABC
a
a a a
S V a
.
Câu 16. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làhìnhvuôngtâm
O
cạnh
2a
.Cạnhbên
SA
vuông
gócvớiđáyvà
2SA a
.Gócgiữađườngthẳng
SB
vàmặtphẳng
SAC
bằng:
A.
45 .
B.
30 .
C.
60 .
D.
90 .
Lời giải
Chọn B
Tacó
SB SAC S
BO SAC
SO
làhìnhchiếucủa
SB
trên
,ABCD
, ,SB SAC SB SO BSO
.
Khiđóxéttrongtamgiácvuông
SBO
tacó:
1 1
2 . 2 2; 2 6
2 2
BO BD a a SA a SO a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
0
1
tan 30
3
BO
BSO BSO
SO
Câu 17. Chohìnhhộpchữnhật
.ABCD A B C D
cóđáy
ABCD
làhìnhvuông,
2AC a
.Gọi
P
là
mặtphẳngqua
AC
cắt
,BB DD
lầnlượttại
,M N
saochotamgiác
AMN
cântại
A
có
MN a
.Tính
cos
với
,P ABCD
.
A.
2
2
. B.
1
2
. C.
1
3
. D.
3
3
.
Lời giải
Chọn A
Tacó
AMC N
làhìnhbìnhhành,màtamgiác
AMN
cântại
A
nên
MN AC
.
Tacó
' '
BDD B
cắtbamặtphẳng
ABCD
,
' ' ' '
A B C D
,
'
AMC N
lầnlượttheobagiao
tuyến
' '
/ / / /BD B D MN
.
Haimặtphẳng
P
và
ABCD
cóđiểmchung
A
vàlầnlượtchứahaiđườngthẳngsongsong
MN
,
BD
nêngiaotuyếncủachúnglàđườngthẳng
d
điqua
A
vàsongsongvới
,MN BD
.
Trênhaimặtphẳng
P
và
ABCD
lầnlượtcóhaiđườngthẳng
AC
và
AC
cùngvuônggóc
với
d
nêngócgiữahaimặtphẳng
P
và
ABCD
chínhlàgócgiữa
AC
và
AC
,bằnggóc
CAC
.Xéttamgiác
'
C CA
vuôngtại
C
có:
2
cos
2
2
AC BD MN a
AC AC AC
a
Cách 2:
Theochứngminhởtrênthì
//MN BD
và
MN BD a
.
Đagiác
AMC N
nằmtrênmặtphẳng
P
cóhìnhchiếutrênmặt
ABCD
làhìnhvuông
ABCD
nên:
2
2
2
2
cos
1 1
2
. .
2 2
ABCD
AMC N
BD
S
AB
S
AC MN AC MN
.
Câu 18. Chohìnhhộpchữnhật
.ABCD A B C D
cócáccạnh
2, 3; 4AB AD AA
.Gócgiữahai
mặtphẳng
AB D
và
A C D
là
.Tínhgiátrịgầnđúngcủagóc
?
A.
45,2
. B.
38,1
. C.
53,4
. D.
61,6
.
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Cách 1: Haimặtphẳng
AB D
và
A C D
cógiaotuyếnlà
EF
nhưhìnhvẽ.
Do
//EF AB
mà
A D A ABB
nên
AD AB
' '
/ /EF A D
Từ
A
kẻvuônggóclêngiaotuyến
EF
tại
H
thì
'
A H EF
EF ADH
EF D H
.Khiđó,gócgiữahaimặtphẳngcầntìmchínhlàgócgiữahai
đườngthẳng
AH
và
D H
.
Tamgiác
'
D EF
lầnlượtcó
13
2 2
D B
D E
,
5
2 2
D A
D F
,
5
2
B A
EF
.
TheoHê-rôngtacó:
'
61
4
DEF
S
.Suyra
2 305
10
DEF
S
D H
EF
.
Dễthấy
' '
A EF D EF
' '
A H D H
.
Tamgiác
DA H
có:
2 2 2
29
cos
2 . 61
HA HD A D
A HD
HA HD
.
Dođó
118,4A HD
hay
, 180 118,4 61,6A H D H
.
Cách 2:Gắnhìnhhộpchữnhật
.ABCD A B C D
vàohệtrụctọađộnhưhìnhvẽ.Khiđó
0;0;0 ,A
2;0;0 ,B
0;3;0 ,D
2;3;0 ,C
0;0;4 ,A
2;0;4 ,B
0;3;4 ,D
2;3;4C
.
Gọi
1
n
làvéctơpháptuyếncủa
AB D
.Có
1
; 12; 8; 6n AB AD
 
.
Gọi
2
n
làvéctơpháptuyếncủa
A C D
.Có
2
; 12;8;6n A C A D
 
.
Gọi
làgócgiữahaimặtphẳng
AB D
và
A C D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
1 2
1 2
29
cos
61
n n
n n
.Vậygiátrịgầnđúngcủagóc
là
61, 6
.
Cách 3.
Dohaimặtphẳng
AB D
và
A C D
chứahaiđường
AB
và
CD
songsongvớinhaunên
giaotuyếncủachúngsongsonghaiđườngđó.
Kẻ
A H AB
,
H AB
,dựnghìnhbìnhhành
AHKD
cótâm
I
nhưhìnhvẽ.
Do
A D A ABB
nên
AD AB
suyra
AB A HKD
gócgiữahaimặtphẳng
AB D
và
A C D
làgócgiữa
AK
và
D H
.
Trongtamgiácvuông
AAB
có
AH
làđườngcaonên
2 2 2
1 1 1 1 1 5
4 16 16A H A B AA
.
Vậy
4
5
AH
.
Xéttamgiác
AIH
có
cos cosI A H
29
cos cos sin sin
61
A H A H
.
Vậygócgiữahaimặtphẳng
AB D
và
A C D
gầnđúngbằng
61, 6
.
Câu 19. Chohìnhhộpchữnhật
.ABCD A B C D
cócáccạnh
2, 3; 4AB AD AA
.Gócgiữahai
mặtphẳng
'BC D
và
A C D
là
.Tínhgiátrịgầnđúngcủagóc
?
A.
45,2
. B.
38,1
. C.
53,4
. D.
61,6
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
Dựnghệtọađộ
Oxyz
nhưhìnhvẽ,tacó
0;0;0 , 2;0;0 , 0;3;0A B D
và
0;0;4 , 2;3;4A C
.
0;3;4 , 2;3;0 , 2;3;0 , 0;3; 4BC BD A C A D
Véctơpháptuyếncủa
BC D
là:
1
, 12; 8;6n BC BD

Véctơpháptuyếncủa
A C D
là:
2
, 12;8;6n A C A D
.
Tacó:
1 2
29
cos cos , 61,6
61
n n
Câu 20. Chotứdiện
ABCD
có
2BD
.Haitamgiác
ABD
và
BCD
códiệntíchlầnlượtlà
6
và
10
.
Biết thể tích khối tứ diện
ABCD
bằng
16
. Tính số đo góc giữa hai mặt phẳng
ABD
và
.BCD
A.
4
arccos
15
. B.
4
arcsin
5
. C.
4
arccos
5
. D.
4
arcsin
15
.
Lời giải
Chọn B
Gọi
H
làhìnhchiếucủa
A
xuống
BCD
.Tacó
1
.
3
ABCD BCD
V AH S
3 24
5
BCD
V
AH
S
.
4
3
2
z
y
x
D'
C'
D
B'
A'
C
B
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Gọi
K
làhìnhchiếucủa
A
xuống
BD
,dễthấy
HK BD
.Vậy
,ABD BCD AKH
Mặtkhác
1
.
2
ABD
S AK BD
2
6
ABD
S
AK
BD
.
Dođó
4
, arcsin arcsin
5
AH
ABD BCD AKH
AK
.
Cách khác
Gọi
H
làhìnhchiếucủa
A
xuống
BCD
.Tacó
1
.
3
ABCD BCD
V AH S
3 24
5
BCD
V
AH
S
.
Tacó: 6
ABD
S
.
Gọi
K
làhìnhchiếucủa
A
xuống
BD
.Do
2BD
nên
2
6
ABD
S
SK
BD
.
Có
2 2
18
5
KH SK AH
1 18
.
2 5
HBD
S HK BD
.
Gọi
làgócgiữamặtphẳng
ABD
và
BCD
.
Vì
HBD
làhìnhchiếucủa
ABD
trên
BCD
nên
3
cos
5
HBD
ABD
S
S
.
Vậy
4
sin
5
4
arcsin
5
.
Câu 21. Chohìnhchóp
.S ABCD
đáy
ABCD
làhìnhthoi,
SA SC
.Gócgiữahaimặtphẳng
SBD
và
ABCD
bằng?
A.
90
. B.
30
. C.
60
. D.
45
.
Lời giải
Chọn A
Gọi
O
làtâmcủahìnhthoi
ABCD
.
Tacó
AC BD
AC SO
AC SBD
ABCD SBD
.
Vậygócgiữahaimặtphẳng
SBD
và
ABCD
bằng
90
.
Câu 22. Chohìnhchóp
.S ABCD
đáy
ABCD
làhìnhchữnhật,tamgiác
SAB
làtamgiácđềuvànằm
trongmặtphẳngvuônggócvớiđáy.Gócgiữahaimặtphẳng
SAB
và
SAD
bằng?
A.
30
. B.
90
. C.
60
. D.
45
.
Lời giải
Chọn B
O
C
B
A
D
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
H
làtrungđiểmcủa
AB
SH ABCD
.
Tacó
AD AB
AD AH
AD SAB
SAD SAB
.
Vậygócgiữahaimặtphẳng
SAB
và
SAD
bằng
90
.
Câu 23. Chohìnhvuông
ABCD
.Gọi
S
làđiểmtrongkhônggiansaocho
SAB
làtamgiácđềuvànằm
trongmặtphẳngvuônggócvớiđáy.Gọi
H
và
I
lầnlượtlàtrungđiểmcủa
AB
và
BC
.Góc
giữahaimặtphẳng
SHC
và
SDI
bằng.
A.
30
. B.
60
. C.
90
. D.
45
.
Lời giải
Chọn C
Do
H
làtrungđiểmcủa
AB
SH ABCD
DI SH
.
Talạicó:
. .BCH CDI c g c
1 1
C D ,mà
1 1
90D I
1 1
90C I
DI HC
Khiđó
DI SHC
SDI SHC
Vậygócgiữahaimặtphẳng
SHC
và
SDI
bằng
90
.
Câu 24. Cho hình chóp
.S ABCD
có đáy
ABCD
là hìnhvuông tâm
O
, cạnh
a
. Đường thẳng
SO
vuônggócvớimặtphẳngđáy
ABCD
và
3
2
a
SO
.Tínhgócgiữahaimặtphẳng
SBC
và
ABCD
.
A.
30
. B.
45
. C.
60
. D.
90
.
Lời giải
Chọn C
H
B
S
C
D
A
1
11
I
H
A
B
C
D
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Gọi
Q
làtrungđiểm
BC
,suyra
OQ BC
.
Tacó
BC OQ
BC SOQ
BC SO
Dođó
, , .SBC ABCD SQ OQ SQO
Tamgiácvuông
SOQ
,có
tan 3.
SO
SQO
OQ
Vậymặtphẳng
SBC
hợpvớimặtđáy
ABCD
mộtgóc
60
.
B. KHOẢNG CÁCH TRONG KHÔNG GIAN
Tính khoảng cách từ chân đường cao của hình chóp đến mặt bên của hình chóp.
Tínhkhoảngcáchtừ
A
đếnmặtbên
( )SBC
củahìnhchóp
.S ABC
có
( )SA ABC
B1.Xácđịnhgiaotuyếncủamặtbênvàmặtphẳngđáy
( ) ( ) .SBC ABC BC
B2.Dựnghình ( ).
AH BC
AI SBC
AI SH
Suyra
( ;( )) .d A SBC AI
B3.Tính
.AI
Cácphươngphápquyvềbàitoánchânđườngcao:
―Kẻsongsongđểdờiđiểmvềchânđườngvuônggóc.
―Dùngtỉsốkhoảngcáchđểdờivềchânđườngvuônggóc.
―Tạochânđườngcaogiả(
đườngcao,khimặtchứachân).
Tính khoảng cách giữa cạnh bên và cạnh thuộc mặt đáy.
Chohìnhchóp
.S ABCD
có
( ).SA ABCD
Hãytínhkhoảng
cáchgiữacạnhbên
SB
vàcạnhthuộcmặtđáy
.AC
B1.Xácđịnhgiaođiểmcủacạnhbên
SB
vàmặtphẳngđáy
( ) .SB ABCD B
B2.Quagiaođiểm
,B
dựngđườngthẳng
d
songsongvới
.AC
Khiđó:
( , ) ( ,( , )) ( ,( , )).d AC SB d AC SB d d A SB d
Đâylàbàitoántìmkhoảngcáchtừchânđếnmặtbên.Cụthể:
( , ) ( ,( , )) ( ,( , )) .d AC SB d AC SB d d A SB d AK
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Chohìnhchóp
.S ABC
cóđáylàtamgiácvuôngtại
A
,
2AB a
,
4AC a
,
SA
vuônggócvới
mặtphẳngđáyvà
SA a
(hìnhminhhọa).Gọi
M
làtrungđiểmcủa
AB
.Khoảngcáchgiữa
haiđườngthẳng
SM
và
BC
bằng
QO
S
D
C
B
A
K
H
D
B
A
C
S
d
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
3
a
. B.
6
3
a
. C.
3
3
a
. D.
2
a
.
Lời giải
Chọn A
Gọi
N
làtrungđiểmcủa
AC
,tacó:
//BCMN
nêntađược
//BC SMN
.
Dođó
, , , ,d BC SM d BC SMN d B SMN d A SMN h
.
Tứdiện
.A SMN
vuôngtại
A
nêntacó:
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 9 2
4 4 3
a
h
h AS AM AN a a a a
.
Vậy
2
,
3
a
d BC SM
.
Câu 2. Chohìnhchóp
.S ABCD
cóđáylàhìnhthang,
2AB a
,
AD DC CB a
,
SA
vuônggóc
với mặt phẳng đáy và
3SA a
(minh họa như hình bên). Gọi
M
là trung điểm của
AB
.
Khoảngcáchgiữahaiđườngthẳng
SB
và
DM
bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
A.
3
4
a
. B.
3
2
a
. C.
3 13
13
a
. D.
6 13
13
a
.
Lời giải
Chọn A
Tacó
M
làtrungđiểmcủa
AB
.
Theogiảthiếtsuyra
ABCD
lànửalụcgiácđềunộitiếpđườngtrònđườngkính
AB
90 ; 60
3
ACB ABC
AC a
Vì
// //DM BC DM SBC
Dođó
1
, , , ,
2
d DM SB d DM SBC d M SBC d A SBC
(vì
1
2
MB AB
)
Kẻ
AH SC
.
Talạicó
BC AC
BC SAC
BC SA
AH BC
.
Khiđó
,
AH SC
AH SBC d A SBC AH
AH BC
.
Xéttamgiác
SAC
vuôngtại
A
,tacó
2
2
2 2 2
2
2
2 2
2
3 . 3
. 9
4
3 3
a a
AC SA a
AH
AC SA
a a
3
2
AH a
.
Vậy
1 1 3
, ,
2 2 4
a
d DM SB d A SBC AH
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. Chohìnhlăngtrụđứng
.ABC A B C
cóđáy
ABC
làtamgiácđềucạnh
a
vàcạnhbêncóđộ
dàibằng
a
.Tínhkhoảngcáchtừ
C
đếnmặtphẳng
A BC
.
A.
2
4
a
. B.
3
7
a
. C.
21
7
a
. D.
2
16
a
.
Lời giải
Chọn C
Ởđâynếutínhtrựctiếprấtdàivàkhónêntasẽvậndụngphươngphápthểtích.
.
1
. ;
3
C A BC A BC
V S d C A BC
.
Cách 1. [Không dùng công thức nhanh về tỉ số thể tích]
Gọi
H
làtrungđiểmcủa
B C
.Dễchứngminh
A H
làđườngcaocủahìnhchóp
.A BCC B
.
3
2
'.
1 1 3 3
.
3 3 2 6
A BCC B BCC B
a a
V S A H a
.
Suyra
3
. . .
1 3
2 12
A BCC A BCC B C A BC
a
V V V
.
Mặtkhác
2BC BA a
và
A C a
,dùngHê-rôngtađược
2
7
4
A BC
a
S
.
Vậykhoảngcách
.
3
21
;
7
C A BC
A BC
V
a
d C A BC
S
.
Cách 2. [Dùng công thức nhanh về tỉ số thể tích]
Tacóthểtíchkhốilăngtrụđãcholà
3
3
.
4
ABC
a
V S AA
.
Thểtíchkhốitứdiệncó4đỉnhlà4đỉnhcủalăngtrụ,cóthểtíchlà
3
.
1 3
3 12
C A BC
a
V V
.
Mặtkhác
2BC BA a
và
A C a
,dùngHê-rôngtađược
2
7
4
A BC
a
S
.
Vậykhoảngcách
.
3
21
;
7
C A BC
A BC
V
a
d C A BC
S
.
Câu 4. Cho hình hộp
.ABCD A B C D
có đáy
ABCD
là hình vuông cạnh
a
, tâm
O
. Hình chiếu
vuônggóccủa
A
lênmặtphẳng
ABCD
trùngvới
O
.Biếttamgiác
AAC
vuôngcântại
A
.
Tínhkhoảngcách
h
từđiểm
D
đếnmặtphẳng
ABB A
.
C
B
A'
B'
C'
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
A.
6
6
a
h
. B.
2
3
a
h
. C.
2
6
a
h
. D.
6
3
a
h
.
Lời giải
Chọn D
Tacó
// //CD AB CD ABB A
.
; ;d D ABB A d C ABB A
(1)
Do
CO
cắt
ABB A
tại
A
;
2
;
d C ABBA
AC
AO
d O ABB A
(2)
Gọi
M
làtrungđiểm
AB
và
H
làhìnhchiếucủa
O
lên
SM
.
Khiđó
;d O ABB A OH
(3)
AA C
vuôngcântại
A
có
2
2
2
a
AC a A O
.
OM
làđườngtrungbìnhcủa
ABC
2 2
BC a
OM
2 2
. 6
6
A O OM a
OH
A O OM
.
(1)(2)(3)
6
; 2
3
a
d D ABB A OH
.
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
với
2AD a
,
DC a
,
2AB a
.Gọi
I
làtrungđiểmcạnh
AD
,haimặtphẳng
SIB
,
SIC
cùngvuông
gócvớimặtphẳngđáyvàmặtphẳng
SBC
tạovớiđáymộtgóc
60
.Tínhkhoảngcách
h
từ
I
đếnmặtphẳng
SBC
.
A.
15
15
a
h
. B.
15
5
a
h
. C.
3 15
10
a
h
. D.
3 5
5
a
h
.
Lời giải
Chọn C
M
B'
C'
D'
O
C
A
D
B
A'
H
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Theogiảthiết,tacó:
SIB ABCD
SIC ABCD SI ABCD
SIB SIC SI
.
Gọi
E
làhìnhchiếucủa
I
trên
BC
,
H
làhìnhchiếucủa
I
trên
SE
,
F
làtrungđiểm
AB
.
BC IE
BC SIE
BC SI
; 60
SBC ABCD BC
IE BC SBC ABCD SEI
SE BC BC SIE
.
,
;
SIE SBC BC SIE
SIE SBC SE d I SBC IH
IH SE
.
2 2
5BC CF FB a
1 1 1
. . .
2 2 2
IBC ABCD IAB ICD IBC
S S S S S AD AB CD IA AB ID DC
2 2 2
2 2
3 1 3
3 .
2 2 2 2
IBC
a a a
S a a IE BC
2
3 3
5 5
a a
IE
a
.
Tamgiác
HIE
vuôngtại
H
:
3 3 3 15
.sin 60
10
2 5
a a
IH IE
.
Câu 6. Chohìnhchóp
.S ABCD
cóđáylànửalụcgiácđều
ABCD
nộitiếptrongđườngtrònđườngkính
2AD a
vàcócạnh
SA
vuônggócvớimặtphẳngđáy
ABCD
với 6SA a .Tínhkhoảngcách
từ
B
đếnmặtphẳng
SCD
.
A.
2a
. B. 3a . C.
2
2
a
. D.
3
2
a
.
Lời giải
Chọn C
H
E
I
B
C
D
A
S
F
E
I
D
C
B
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Từgiảthiếtsuyra:
2
AD
AB BC CD a
, 3AC a .
Gọi
E AB CD
,suyratamgiác
ADE
đều.
Khiđó
C
làtrungđiểmcủa
ED
và
AC ED
.
Dựng
AH SC
thì
AH SCD
,suyra
, d A SCD AH
.
Xéttamgiác
SAC
vuôngtại
A
,có
AH
làđườngcao
Suyra:
2 2 2
1 1 1
2AH a
AH SA AC
.
Mà
1 1 2
, ,
2 2 2
a
d B SCD d A SCD AH
.
Câu 7. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
( )SAC ABC
,
3AB a
,
5BC a
.Biếtrằng
2 3SA a
và
0
30SAC
.Khoảngcáchtừđiểm
A
đếnmặtphẳng
( )SBC
bằng:
A.
3 17
4
a
. B.
6 7
7
a
. C.
3 7
14
a
. D.
12
5
a
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
H
làhìnhchiếucủa
S
lên
AC
.Tacó
SAC ABC
SH ABC
SH AC
.
Xéttamgiác
SAH
,tacó
sin30 3SH SA a
và
2 2
3AH SA SH a
.
Xéttamgiác
ABC
,tacó
2 2
4AC BC AB a
và
HC AC HA a
.
Gọi
E
làhìnhchiếuvuônggóccủa
H
lên
BC
và
F
làhìnhchiếuvuônggóccủa
H
lên
SE
.
Tacó
BC HE
BC SH SH ABC BC
suyra
BC SHE HF
.
Dođó
HF BC
HF SBC
HF SE
suyra
,d H SBC HF
.
Gọi
K
làhìnhchiếuvuônggóccủa
A
lên
BC
.Tacó
//AK HE
,dođó
2 2
1 1 1 12 3
4 4 4 5 5
HE CH AB AC
HE a a
AK CA
AB AC
.
Suyra
2 2
3 7
,
14
HS HE
d H SBC HF a
HS HE
.
Tacó
,
6 7
4 , 4
7
H,
d A SBC
CA
d A SBC HF a
CH
d SBC
.
Câu 8. Chotứdiệnđều
ABCD
cócạnhbằng
a
.Gọi M làtrungđiểm
CD
.Khoảngcáchgiữa
AC
và
BM là
A.
154
28
a
. B.
2
a
. C.
22
11
a
. D.
2
3
a
.
Lời giải
Chọn C
Gọi
G
làtâmtamgiácđều
BCD
AG BCD
.
Trongmặtphẳng
BCD
,dựnghìnhhìnhbìnhhành
BMCN
mà
BM CM
nên
BMCN
là
hìnhchữnhật.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Tacó
//BM ACN
, , , d BM AC d BM ACN d G ACN
.
Kẻ
GK NC
K NC
và
GH AK
H AK
, d G ACN GH
.
Tacó
2
2 2 2
2 3 6
.
3 2 3
a a
AG AB BG a
2
a
GK CM
.
Vậy
2 2
. 22
cm
11
AG GK a
GH
AG GK
.
Câu 9. Cho hình chóp
.S ABC
,có đáy là tamgiácđềucạnh
2a
,
2SA a
,
SA
vuông góc với mặt
phẳngđáy(minhhọanhưhìnhvẽ).Gọi
,M N
lầnlượtlàtrungđiểmcủa
,AB AC
.Khoảng
cáchgiữahaiđườngthẳng
MN
và
SC
bằng.
A.
21
7
a
. B.
21
14
a
. C.
2 57
19
a
. D.
57
19
a
.
Lời giải
Chọn A
Tacó:
1
// // , , , ,
2
MN BC MN SBC d MN SC d MN SBC d N SBC d A SBC
Gọi
I
làtrungđiểmcủa
BC
.Tacó:
BC AI
BC SAI SBC SAI
BC SA
,
1SBC SAI SI
Trong
SAI
kẻ
AH SI
(2).
Từ(1)và(2)tasuyra
2 2
.
,
SA AI
AH SBC d A SBC AH
SA AI
Tacó:
2 2
3 2 . 3 2 21
2 ; 2 . 3
2 7
4 3
a a a
SA a AI a a AH
a a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
1 1 21
, , , ,
2 2 7
a
d MN SC d MN SBC d N SBC d A SBC AH
.
Câu 10. Chohìnhchóp
.S ABCD
cóđáylàhìnhchữnhật
ABCD
có
2 , 4 , ( ) AB a AD a SA ABCD
,
2 15SA a . Gọi M là trung điểm của ,BC N là điểm nằm trên cạnh
AD
sao cho
4AD DN
.Khoảngcáchgiữa
MN và SB
là
A.
4 285
19
a
B.
2 285
15
a
C.
285
19
a
D.
2 285
19
a
Lời giải
Chọn D
2 2
4 16 2 5 . AC a a a
Gọi E làđiểmthuộccạnh
AD
saocho
4AD AE
.
EBMN
làhìnhbìnhhành
// // EB MN MN SEB
, , d MN SB d MN SEB
, 2 , 2 d N SEB d A SEB d
Talạicó
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 76 285 2 285
,
60 4 60 19 19
d a d MN SB a
d SA AB AE a a a a
Câu 11. Chohìnhchóp
.S ABCD
cóđáylàhìnhvuôngcạnh
2a
,
SA
vuônggócvớimặtphẳngđáyvà
SA a
.Gọi
M
làtrungđiểm
.AB
Khoảngcáchgiữahaiđườngthẳng
SB
và
DM
bằng
2a
4a
E
N
M
C
B
A
D
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
A.
2 21
21
a
B.
21
8
a
C.
4 21
21
a
D.
a
Lời Giải
Chọn A
Gọi
N
làtrungđiểmcủa
CD
;Lấy
,I H
lầnlượtlàhìnhchiếucủa
A
lên
,BN SI
.
Tacó
1 1
/ / , , ,
2 2
DM SNB d DM SB d DM SNB d A SNB AH
.
Tamgiáccódiệntích:
2
2
4
2. 2
5
ANB
ANB ABCD ADN
S
a
S S S a AI
BN
.
Tamgiácvuôngcó
2 2 2 2 2
2
1 1 1 1 1 21 4 21
16
16 21
5
AH a
AH AI SA a a
a
.
2 21
,
21
d DM SB a
.
Câu 12. Chohìnhchópđáylàhìnhvuôngcạnh
17
,
2
a
a SD
,hìnhchiếuvuônggóccủa
S
lênmặt
phẳng
ABCD
trung điểm
H
của đoạn
AB
. Gọi
K
là trung điểm của đoạn
AD
. Tính
khoảngcáchgiữahaiđườngthẳng
HK
và
SD
theo
a
.
A.
3
5
a
B.
286
26
a
C.
5 3
3
a
D.
39
3
a
Lời giải
Chọn A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó
2 2 2 2 2 2 2
3 3 SH SD HD SD AH AD a SH a .
Do
// , , , HK SBD d HK SD d HK SBD d H SBO h
, với
O
là tâm hình
vuông
ABCD
.
Tacó
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 25 3
3 3 5
a
h
h SH BH OH a a a a
.
Vậy
3
,
5
a
d HK SD
.
Câu 13. Chohìnhchóp
.S ABCD
cóđáylàhìnhvuôngcạnh
3a
,
SA
vuônggócvớimặtphẳngđáyvà
SA a
.Gọi
M
làđiểmthàomãn
2 0MB MC
 
.Khoảngcáchgiữahaiđườngthẳng
SC
và
DM
bằng
A.
154
77
a
. B.
3 154
154
a
. C.
6 154
77
a
. D.
2 154
77
a
.
Lời giải
Chọn B
Gọi
N
làđỉnhthứtưcủahìnhbìnhhành
DMCN
;Lấy
,E H
lầnlượtlàhìnhchiếucủa
A
lên
,CN SE
.
Tacó
1 1
/ / , , , ,
4 4
DM SCN d DM SC d DM SNB d O SCN d A SCN AH
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Tamgiác
ANC
códiệntích:
2 2
2
2
1 9 3 6 10
6
2 2 2 5
ANB
ACN ABCD DNC
S
a a a
S S S a AE
CN
Tamgiácvuông
SAE
có
2 2 2 2 2
2
1 1 1 1 1 77 6 154
72
72 77
5
AH a
AH AE SA a a
a
.
6 154 3 154
4
( ,
54
)
.77 1
ad SC DM a
.
Câu 14. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làhìnhvuôngcạnh
a
.Gọi
M
và
N
lầnlượtlàtrung
điểmcủacáccạnh
AB
và
AD
; H làgiaođiểmcủa
CN
với DM .Biết
SH
vuônggócvới
mặtphẳng
ABCD
và
3SH a
.Tínhkhoảngcáchgiữahaiđườngthẳng
DM
và
SC
theo
a
.
A.
2 3
19
a
. B.
21
7
a
. C.
57
6
a
. D.
3 3
19
a
.
Lờigiải
ChọnA
Gọi K làhìnhchiếucủa H trên
SC
.
Do
ABCD
làhìnhvuôngnên
DM CN
.
Có
SH ABCD SH DM
.
Suyra
DM SHC
DM HK
.
Vậy HK làđoạnvuônggócchungcủa DM và
SC
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có DH làđườngcaocủatamgiácvuông
CDN
nên
2
. CH CN DC
2
2
5
DC a
CH
CN
.
Lạicó HK làđườngcaotrongtamgiácvuông
SHC
nên
2 2 2 2 2 2
1 1 1 1 5 19
3 4 12
HK SH HC a a a
2 3
19
a
HK .
Câu 15. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làhìnhvuôngcạnh
2a
,cạnhbên
5SA a
,mặtbên
SAB
làtamgiáccânđỉnh
S
vàthuộcmặtphẳngvuônggócvớimặtphẳngđáy.Khoảngcách
gữahaiđườngthẳng
AD
và
SC
bằng:
A.
2 5
5
a
. B.
4 5
5
a
. C.
15
5
a
. D.
2 15
5
a
.
Lời giải
Chọn B
Gọi
H
làtrungđiểmcủacạnh
AB
.
Dotamgiác
SAB
cântại
S
vànằmtrongmặtphẳngvuônggócvớimặtphẳngđáynên
SH ABCD
.
Theogiảthiếttacó
2AB a AH a
.
Màtalạicó
5SA a
nên
2 2
2SH SA AH a
Tacó
// //AD BC AD SBC
, ,d AD SC d AD SBC
, 2 ,d A SBC d H SBC
.
Domặtphẳng
SBC SAB
nêntừ
H
kẻ
HK SB
thì
,HK d H SBC
.
C
B
A
D
S
H
C
B
A
D
S
K
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Tacó
. 2 . 2 5
5
5
SH HB a a a
HK
SB
a
4 5
, 2
5
a
d AD SC HK
.
Câu 16. Cho lăng trụ đứng
.
ABC A B C
có đáy là tam giác vuông tại
A
,
AB a
,
2BC a
. Gọi
M
,
N
,
P
lầlượtlàtrungđiểmcủa
AC
,
CC
,
A B
và
H
làhìnhchiếucủa
A
lên
BC
.Tính
khoảngcáchgiữa
MP
và
NH
.
A.
3
4
a
. B.
3
8
a
. C.
3
2
a
. D.
2
a
.
Lời giải
ChọnA
Vì
A B BA
làhìnhbìnhhànhnên
P
cũnglàtrungđiểmcủa
AB
.Dođó
//
MP B C
.Mặtphẳng
BCC B
chứa
NH
vàsongsongvới
MP
nên
d ,MP NH
d ,
MP BCC B
d ,
M BCC B
1
d ,
2
A BCC B
1
2
AH
.
Tamgiác
ABC
vuôngtại
A
,
AB a
,
2BC a
suyra
3AC a
.
AC AB
AH
BC
. 3
2
a a
a
3
2
a
.
Vậy
3
d ,
4
a
MP NH
.
Câu 17. Cho hìnhchóp
.S ABC
đều.Gọi
G
làtrọngtâmcủatam giác
ABC
sao cho
SG AB a
.
Khoảngcáchgiữahaiđườngthẳng
SA
và
CG
bằng
A.
2
a
. B.
a
. C.
5
5
a
. D.
3
3
a
.
Lời giải
Chọn C
P
N
M
C'
B
'
A
B
C
A
'
H
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
M
làtrungđiểmcủa
AB
.Từ
A
kẻ
// ( )//Ax CM SAx CM
.Khiđó
( , ) ( , ) ( , )d SA GC d GC SAx d G SAx
Kẻ
;GI Ax GH SI
.Tacó
( )
SG Ax
SGI Ax GH Ax
IG Ax
Mà
SI GH
.Nên
( ) ,( )GH SAx d G SAx GH
Tacó
//
//
AM GI
AI GM AIGM
GM AM
làhìnhchữnhật
2
a
AM GI
.
Xéttamgiác
SGI
vuôngtại
G
có:
5 5
( , )
5 5
a a
GH SI GH d SA GC
.
Câu 18. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làvuôngcạnh
a
,
2SA a
vàvuônggócvới
ABCD
.
Gọi M làtrungđiểmcủa
SD
.Tínhkhoảngcách
d
giữahaiđườngthẳng
SB
và
CM
.
A.
2 3
3
a
d
. B.
3
2
a
d
. C.
2
3
a
d
. D.
3
a
d
.
Lờigiải
ChọnC
A
C
B
S
x
M
G
I
H
a
2a
H
K
I
O
D
S
C
B
A
M
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Gọi
O AC BD
; I và K lầnlượtlàtrungđiểmcủa
AD
và
OA
; H làhìnhchiếuvuông
góccủa
I
lên
MK
,tacó
//SB MO
// SB MAC
.
Dođó
;d SB CM
; d SB MAC
; d B MAC
; d D MAC
2 ; d I MAC
.
Mặtkhác,tacó
AC MI
AC KI
AC MKI
.Suyra
IH MAC
hay
; d I MAC IH
.
Vậy
;d SB CM
2 IH
2 2
.
2.
MI IK
MI IK
2 2
.
2.
MI IK
MI IK
2
3
a
.
Câu 19. Cho hìnhchóp
.S ABCD
cóđáylà hìnhchữnhật.Tamgiác
SAB
vuôngcântại
A
vànằm
trong
mặtphẳngvuônggócvớiđáyvà
4 2SB
.Gọi
M
làtrungđiểmcủacạnh
SD
.Tínhkhoảng
cách
l
từđiểm
M
đếnmặtphẳng
SBC
A.
2l
. B.
2 2l
. C.
2l
. D.
2
2
l
.
Lời giải
Chọn C
Theogiảthiết,tacó
,SAB ABCD SAB ABCD AB
SA AB
SA ABCD
.
Gọi
, ,N H K
lầnlượtlàtrungđiểmcáccạnh
,SA SB
vàđoạn
SH
.
Tacó
BC SA
BC SAB BC AH
BC AB
.
Mà
AH SB
(
ABC
cântạiA có
AH
làtrungtuyến).
Suyra
AH SBC
,dođó
KN SBC
(vì
||KN AH
,do
KN
đườngtrungbìnhcủa
SAH
).
Mặtkhác
|| ||MN BC MN SBC
.
Nên
1
, , 2
2
l d M SBC d N SBC NK AH
.
Câu 20. Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
a
,
60BAD ,
SB a
và mặt phẳng
SBA
vàmặtphẳng
SBC
cùngvuônggócvớimặtphẳngđáy.Khoảngcáchtừ
B
đếnmặt
phẳng
SCD
bằng
4 2
M
K
N
H
A
B
C
D
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
21
7
a
. B.
5
7
a
. C.
21
3
a
. D.
15
3
a
.
Lời giải
Chọn A
Gọi
M
làtrungđiểmcủa
CD
.Dotamgiác
BCD
đềucạnh
a
nên
BM DC
và
3
2
a
BM
Suyra
DC SBM
.Trongtamgiác
SBM
kẻ
BH SM
tại
H CD BH
D ; D
BH SM
BH SC d B SC BH
BH DC
Trongtamgiácvuông
SBM
tacó
2 2 2 2
1 1 1 7 21
21 7
a
BH
BH SB BM a
.
Câu 21. Chohìnhchóp
.S ABCD
cóđáy
ABCD
làhìnhthoicạnhbằng
2 3a
,góc
BAD
bằng
120
.
Haimặtphẳng
SAB
và
SAD
cùngvuônggócvớiđáy.Gócgữamặtphẳng
SBC
và
ABCD
bằng
45
.
Khoảngcách
h
từ
A
đếnmặtphẳng
SBC
là
A.
2 2.h a
B.
2 2
.
3
a
h
C.
3 2
.
2
a
h
D. 3.h a
Lời giải
Chọn C
Từgiảthiếtsuyra
ABC
đều.Gọi
H
làtrungđiểmcủa
CB AH BC
và
2 3. 3
3
2
a
AH a
Tacó
BC AH
BC SH
BC SA
A
S
D
C
B
H
I
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Tacó
, 45
SBC ABCD BC
AH BC SBC ABCD SHA
SH BC
Trongtamgiác
SAH
vuôngtại
A
,kẻ
AI SH
tại
.I
Dođó
AI SBC
Vì
AI SH
AI CB
nên
AI
làkhoảngcáchtừ
A
đếnmặtphẳng
.SBC
Trongtamgiácvuông
AIH
tacó
3 2
sin .sin 3 .sin 45
2
AI a
H AI AH H a
AH
3 2
, .
2
a
d A SBC AI
Câu 22. Chohìnhchóp
.S ABCD
cóđáylàhìnhbìnhhành,
30ADC ,
AB a
,
2AD a
,
SA a
và
SA
vuônggócvớimặtphẳngđáy.Khoảngcáchtừ
B
đếnmặtphẳng
SCD
bằng
A.
3
2
a
. B.
2
3
a
. C.
2
2
a
. D.
2
a
.
Lời giải
Chọn C
Tacó
// //AB CD AB SCD
,suyra
, ,d B dS D DAC SC
.
Trongmặt phẳng
ABCD
,kẻ
AK CD
tại
K
khi đótamgiác
AKD
vuôngtại
K
và có
30ADK
AK a
.
Trongmặtphẳng
SAK
,kẻ
AH SK
tại
H
,AH SCD d A SCD AH
.
Do
SA AK a
nêntamgiác
SAK
vuôngcântại
A
suyra
1 2
2 2
a
AH SK
.
Vậy
2
,
2
SCD
a
d B
.
Câu 23. Chohìnhchóp
.S ABCD
cóđáylàhìnhbìnhhành,
AB a
,
3AD a
,
2AC a
,
2SA a
và
SA
vuônggócvớimặtphẳngđáy.Khoảngcáchtừ
B
đếnmặtphẳng
SCD
bằng
A.
3a
. B.
2a
. C.
84
7
a
. D.
2
2
a
.
A
B
C
D
S
K
H
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Tacó
// //AB CD AB SCD
,suyra
, ,d B dS D DAC SC
.
Xét tam giác
ADC
ta có
2 2 2 2
4AC AD DC a
nên
AC CD
mà
SA CD
CD SAC
SCD SAC
lạicó
SCD SAC SC
nêntừ
A
dựng
AH SC
tại
H
thì
AH SCD
,AH d A SCD
Tacó
2 2 2 2 2 2
1 1 1 1 1 1
2
4 4 2
AH a
AH AC AS a a a
Vậy
, 2SCd DB a .
Câu 24. Hìnhchóp
.S ABCD
cóđáylàhìnhthoitâm
O
cạnh
2a
,
60ABC
,hìnhchiếuvuônggóc
của
S
lên
ABCD
trùngvớitrungđiểm
I
của
BO
,
3SI a
.Khoảngcáchtừ
B
đếnmặt
phẳng
SCD
bằng
A.
3 3
5
a
. B.
2 3
5
a
. C.
3
5
a
. D.
4 3
5
a
.
Lời giải
Chọn D
Tacó
BI SCD D
,suyra
4
, ,
3
d B dCD DIS SC
.
Trongmặtphẳng
ABCD
,kẻ
IK CD
tại
K
.
A
B
C
D
S
H
O
H
I
K
D
C
B
A
S
I
K
D
C
B
A
O
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Trong
mặtphẳng
SIK
,kẻ
I
H SK
tại
H
,IH SCD d I SCD IH
.
Xé
ttamgiác
I
DK
vuôngtại
K
tacó
3
0BDC
1 1 3 3
. . 3
2 2 2 4
IK ID BO a
(dotamgiác
A
BC
đềucạnh
2a
nên
3B
O a
).
Tacó
2
2 2 2 2 2
1
1 1 16 1 25 3 3
27 3 27 5
a
IH
IH IK IS a a a
Vậ
y
4
3 3 4 3
, .
3 5 5
B D
a
Cd S
a
.
Câu
25. Chohìnhchóp
.S
ABCD
có
đáylàhìnhthangcânđáy
A
D
c
ó
2
2 2AD AB BC a
,
S
A a
và
S
A
vuôn
ggócvớimặtphẳngđáy.Khoảngcáchtừ
B
đế
nmặtphẳng
S
CD
bằ
ng
A.
3
2
a
. B.
3
3
a
. C.
3
4
a
. D.
2a
.
Lời
giải
Chọn C
Gọi
O
l
àtrungđiểmcủa
AD
khiđó
tứgiác
ABCO
là
hìnhthoinên
1
2
CO
a CO AD
ACD
vuôngtại
C
AC CD
mà
S
A CD
C
D SAC
S
CD SAC
Tacó
S
CD SAC SC
nêntừ
A
dựng
AH
SC
tại
H
thì
A
H SCD
,A
H d A SCD
.
ACD
vuôn
gtạiC
2
2
3A
C AD DC a
.
Ta
có
2
2 2 2 2 2
1
1 1 1 1 4 3
3 3 2
a
AH
AH AC AS a a a
.
Trong
mặtphẳng
ABCD
gọi
I
l
àgiaođiểmcủa
A
B
và
C
D
khiđó
B
C
l
àđườngtrungbình
củatamgiác
I
AD
1
3
, ,
2 4
a
d B dSCD SCDA
.
--------------------- HẾT --------------------
I
O
H
C
B
D
A
S
| 1/47
| | Tải xuống

Có thể bạn quan tâm:

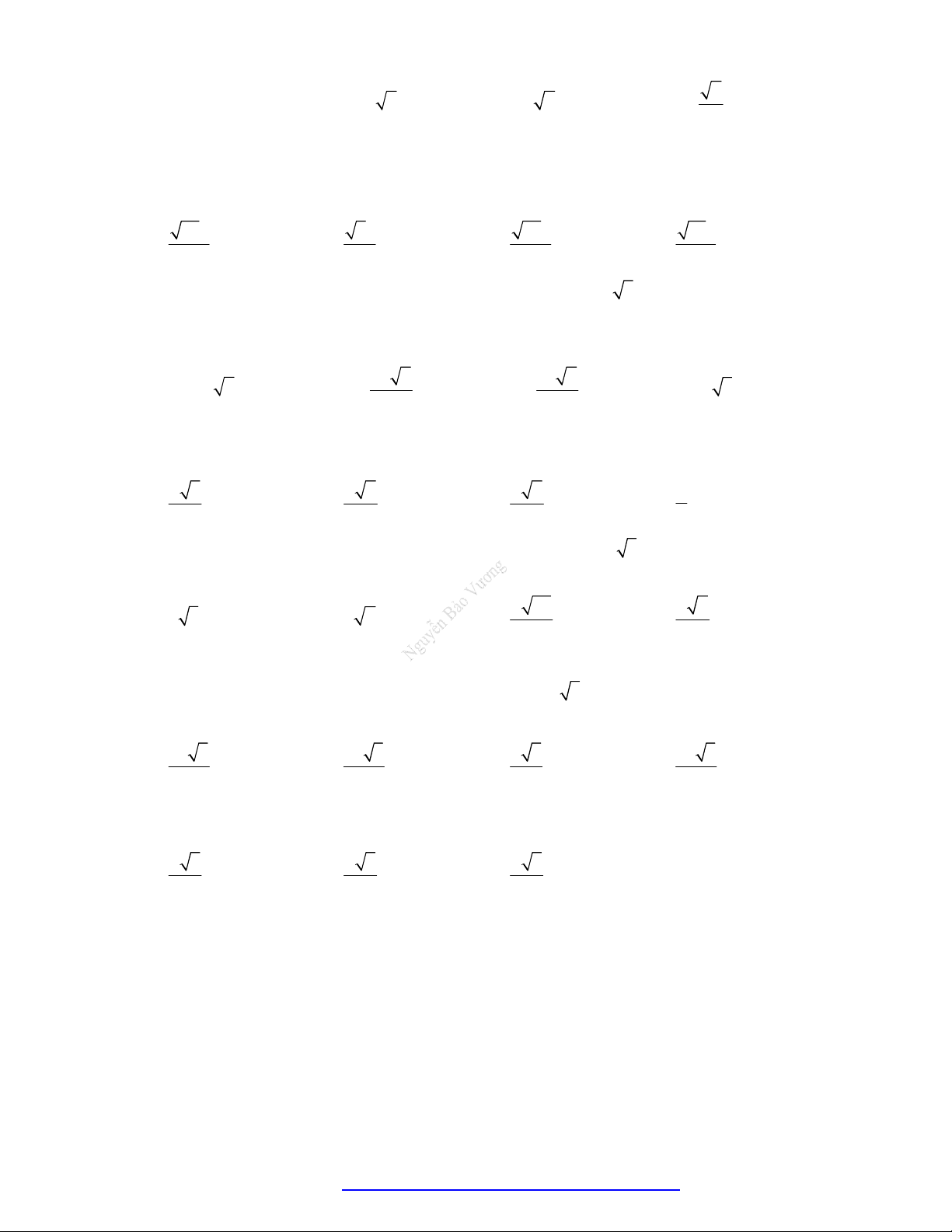
Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 7 GÓC - KHOẢNG CÁCH
A. GÓC TRONG KHÔNG GIAN
Góc giữa đường thẳng a và đường thẳng b
Phương pháp 1. Sử dụng song song, tức dựng đường thẳng c  b và c cắt . a a  
Khi đó (a;b)  (a;c)   như hình vẽ. c
Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số sin, côsin để tìm góc . b     a.b
Phương pháp 2. Sử dụng tích vô hướng, nghĩa là cos(a;b)  cos(a;b )    cos . a . b
Khi đó, ta cần chèn điểm phù hợp để tính tích vô hướng.
Phương pháp 3. Ghép vào hệ trục tọa độ Oxyz.
Lưu ý: Góc giữa hai đường thẳng là góc nhọn, còn góc giữa hai véctơ là góc nhọn hoặc góc tù. Nghĩa là  
nếu tính (a;b)   90 thì góc giữa a, b là ,
 còn nếu tính (a;b)   90 thì góc giữa hai
đường thẳng (a;b)  180  .
Góc giữa đường thẳng AB và mặt phẳng (P )
Cần nhớ: “Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó lên mặt phẳng”. B
Phương pháp 1. Sử dụng hình học 11.
B. 1. Tìm AB  (P )  { } A (1) A
B. 2. Tìm hình chiếu của B lên mặt phẳng (P ). P H
Đặt câu hỏi và trả lời: “Đường nào qua B và vuông góc với (P) ? “(có sẵn hoặc dựng thêm)
Trả lời: BH  (P ) tại H (2)
Từ (1),(2), suy ra AH là hình chiếu của AB lên mặt phẳng (P ).
Do đó góc giữa đường thẳng AB và mp(P) là góc giữa AB và AH, chính là góc BAH .
B. 3. Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số côsin hoặc định lí hàm sin trong tam
giác thường để suy ra góc BAH .
Phương pháp 2. Ghép vào hệ trục tọa độ Oxyz.
Góc giữa mặt phẳng (P) và mặt phẳng (Q). (P) d1
Phương pháp 1. Dựa vào định nghĩa α u (
 P)  (Q)  u    Ta có: u
  d  (P)  ((P),(Q))  (d ,d )  . 1 1 2  d2 u
  d  (Q) (Q)  2 
Phhương pháp 2. Tìm hai đường thẳng d và d lần lượt vuông góc với mặt phẳng (P) và mặt phẳng (Q). 1 2
Góc giữa hai mặt phẳng là góc giữa d và d . 1 2
Phương pháp 3. Sử dụng công thức hình chiếu S   S. cos . d ,( )
Phương pháp 4. Trong trường hợp quá khó, nên sử dụng công thức sin A Q     d( ,Au) 
Trong đó   ((P),(Q)), A  (P) và (P)  (Q)  u là giao tuyến của (P) và (Q).
Phương pháp 5. Ghép vào hệ trục tọa độ Oxyz.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
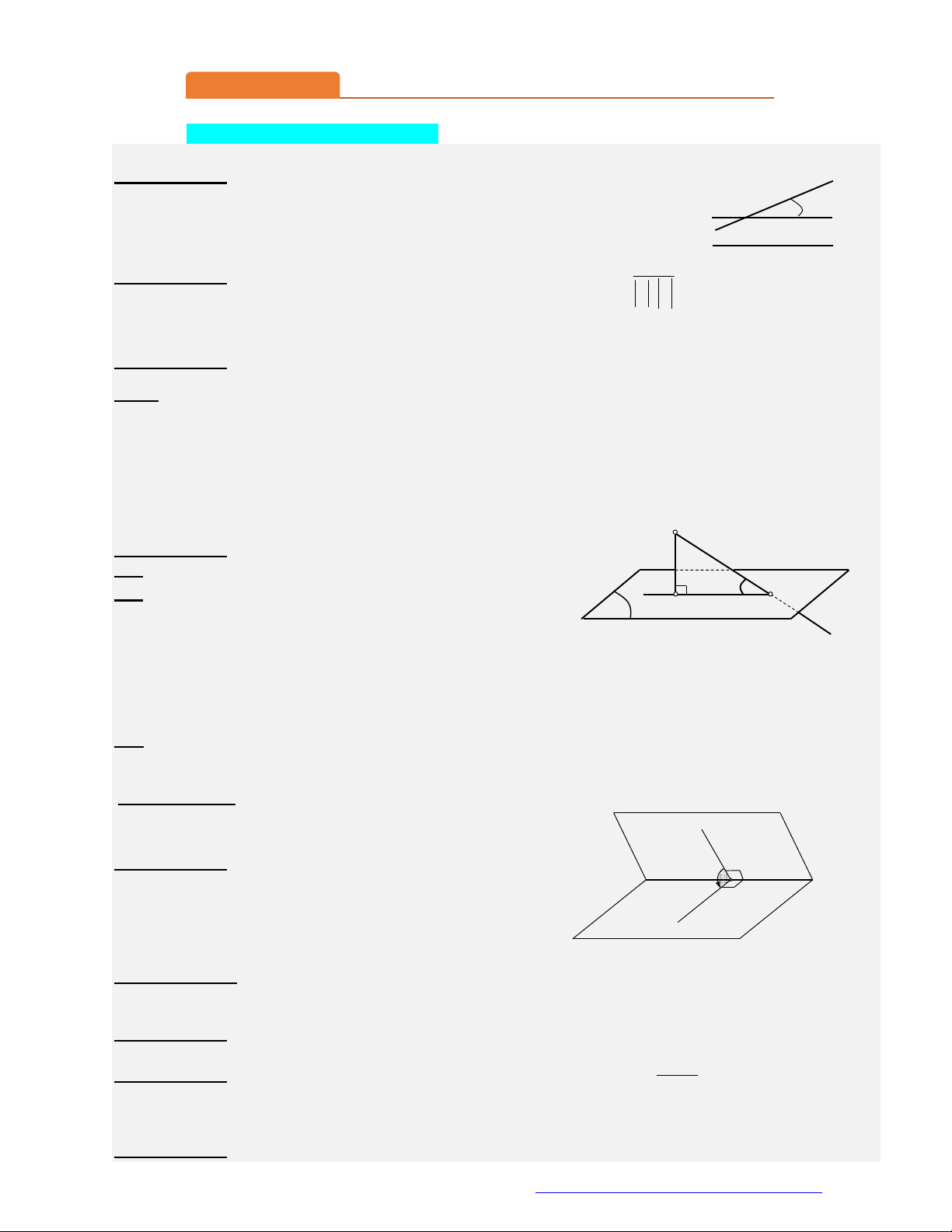
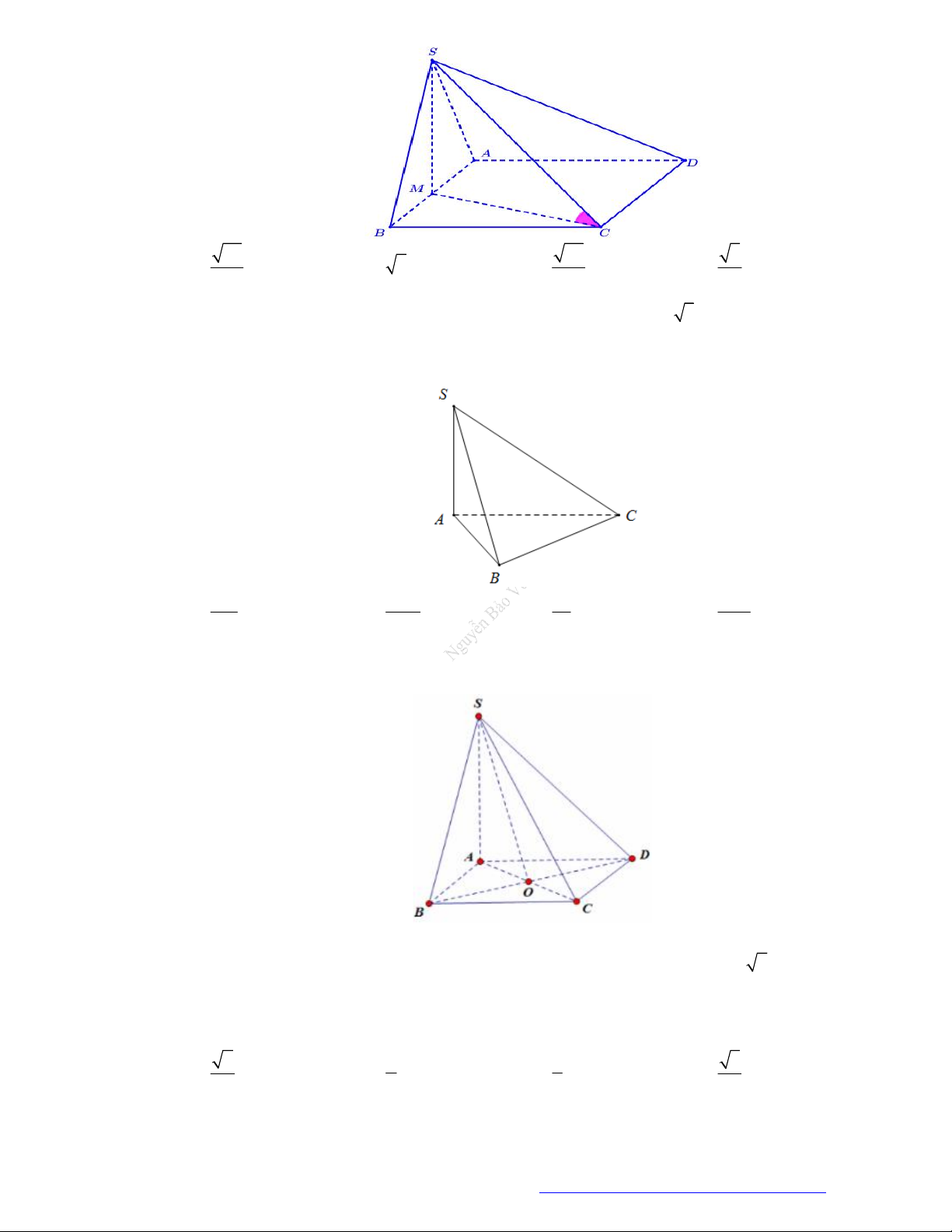
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và
SA  2a . Góc giữa SC và mặt phẳng (ABCD) bằng S A D B C A. 0 45 . B. 0 60 . C. 0 30 . D. 0 90 . Câu 2.
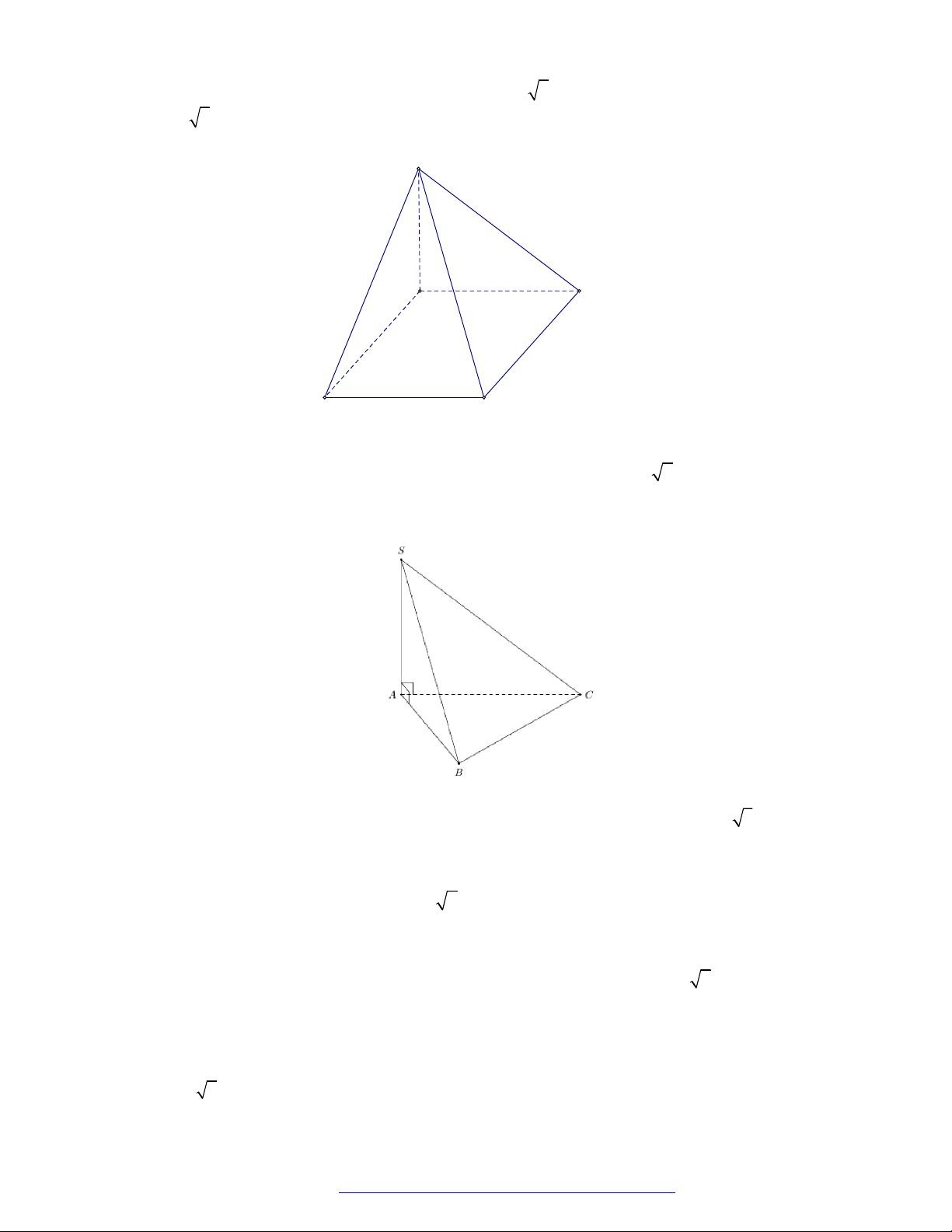
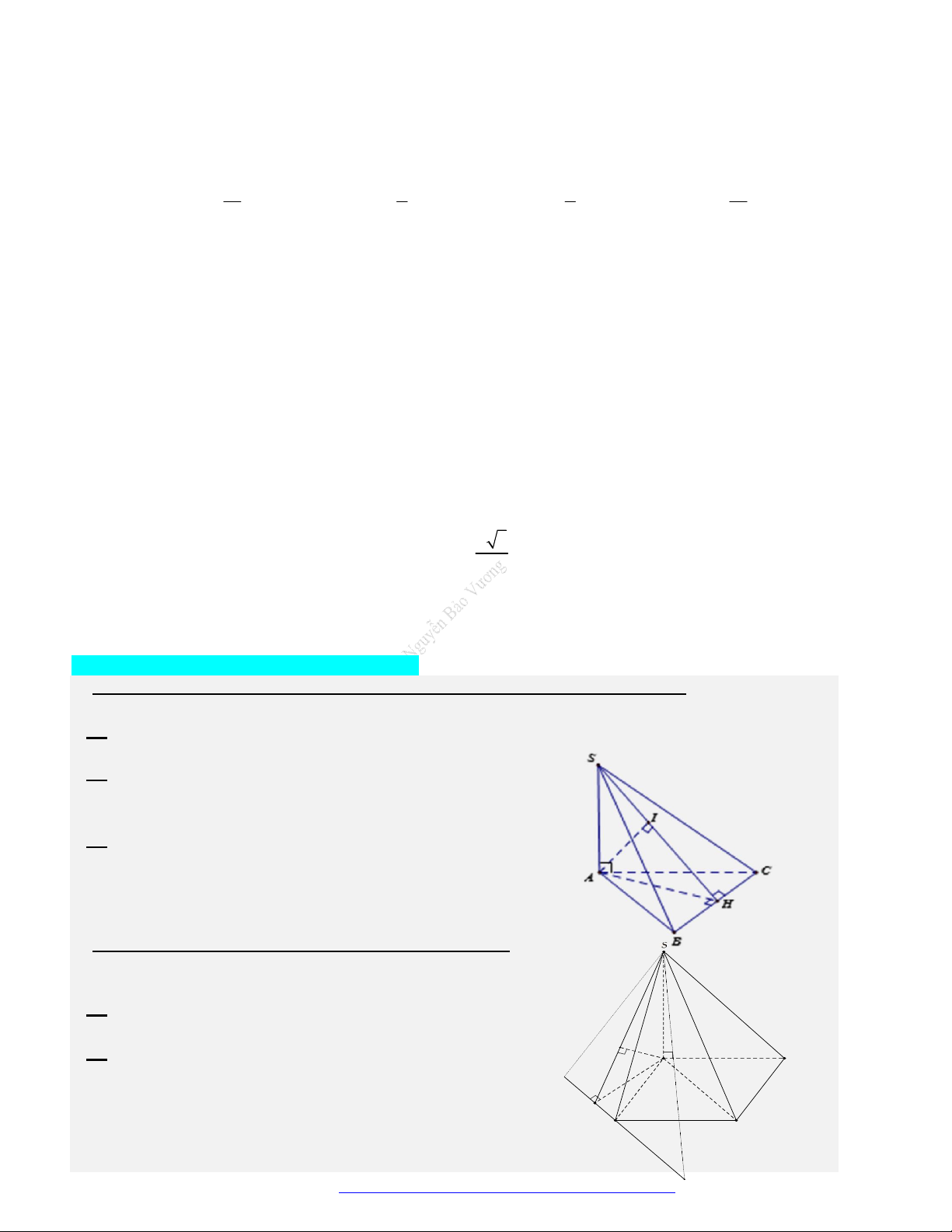
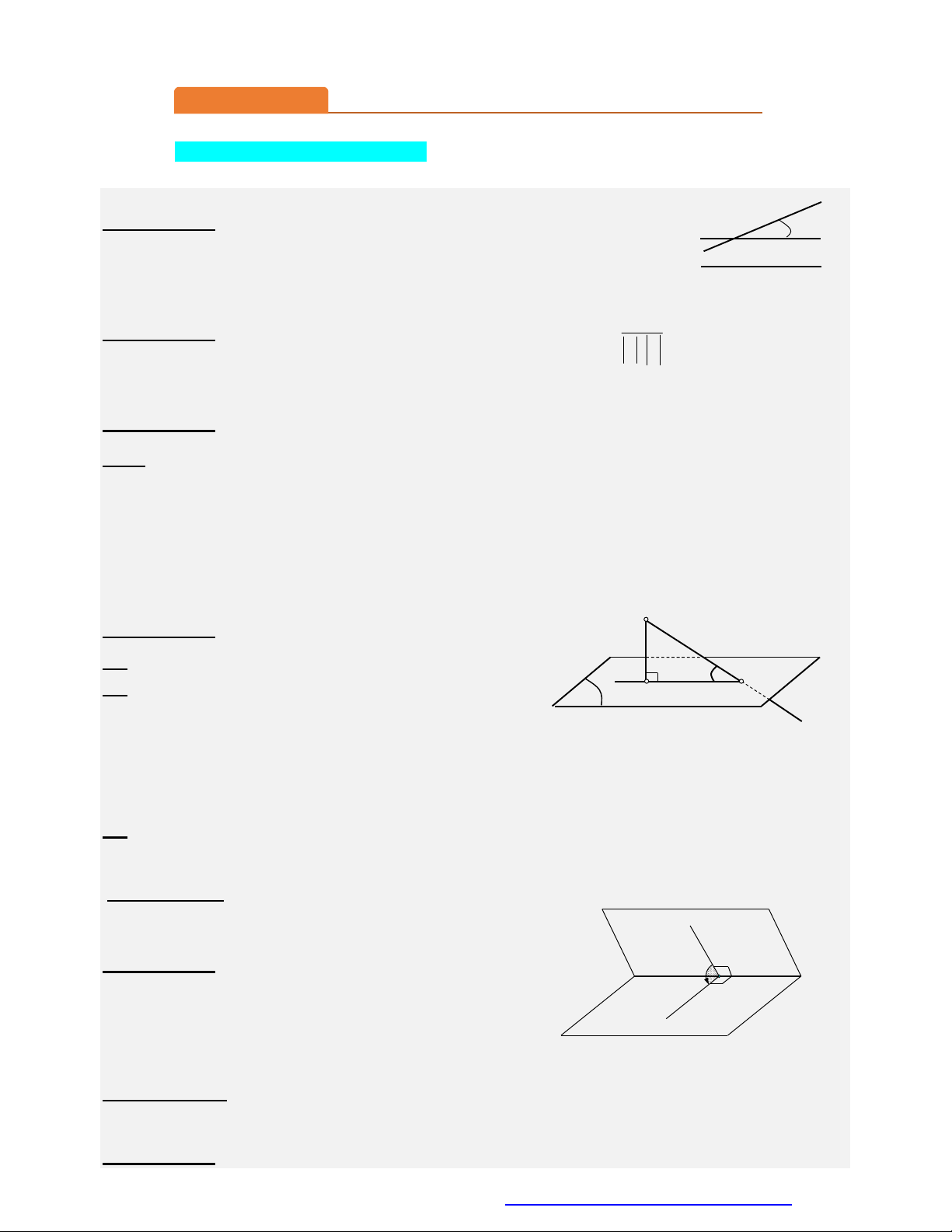
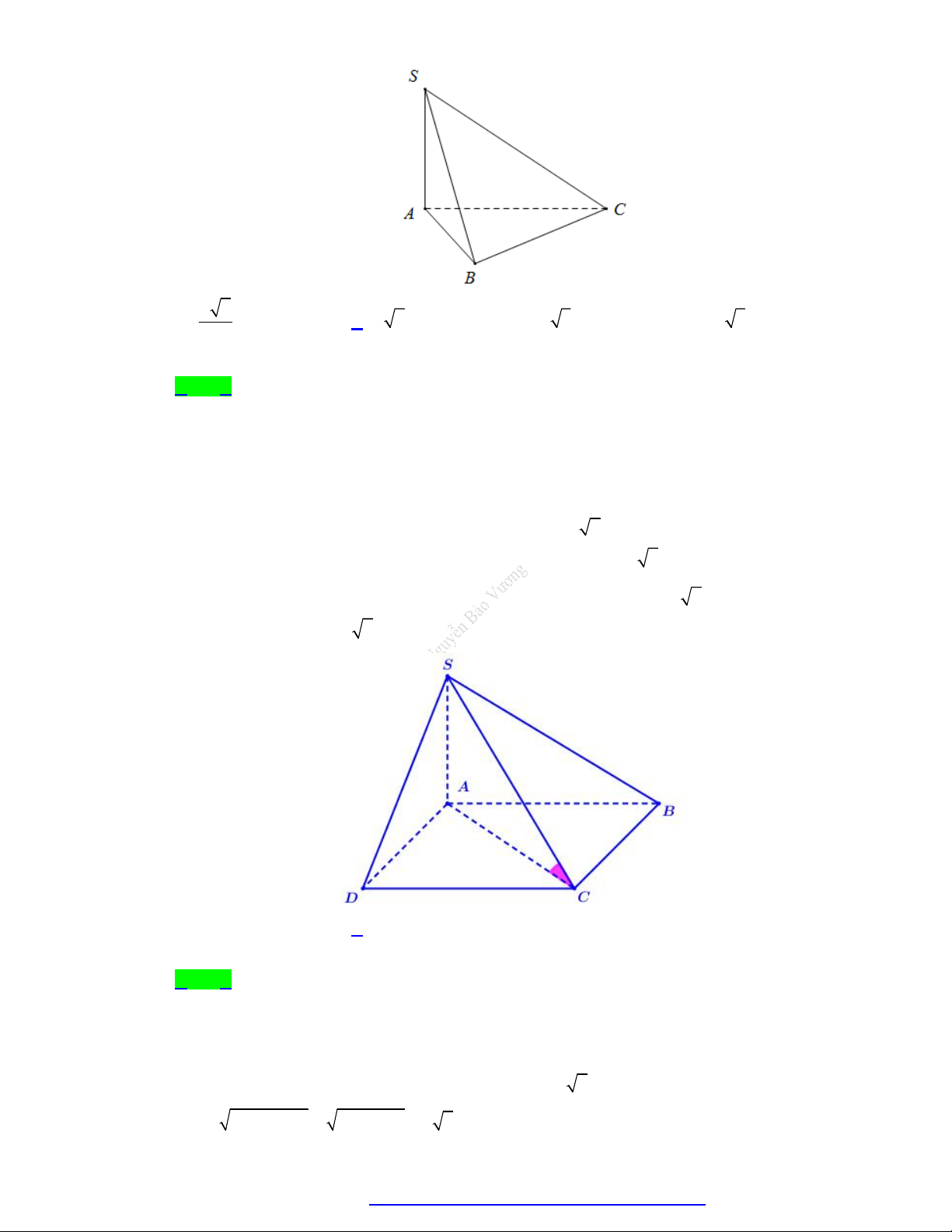
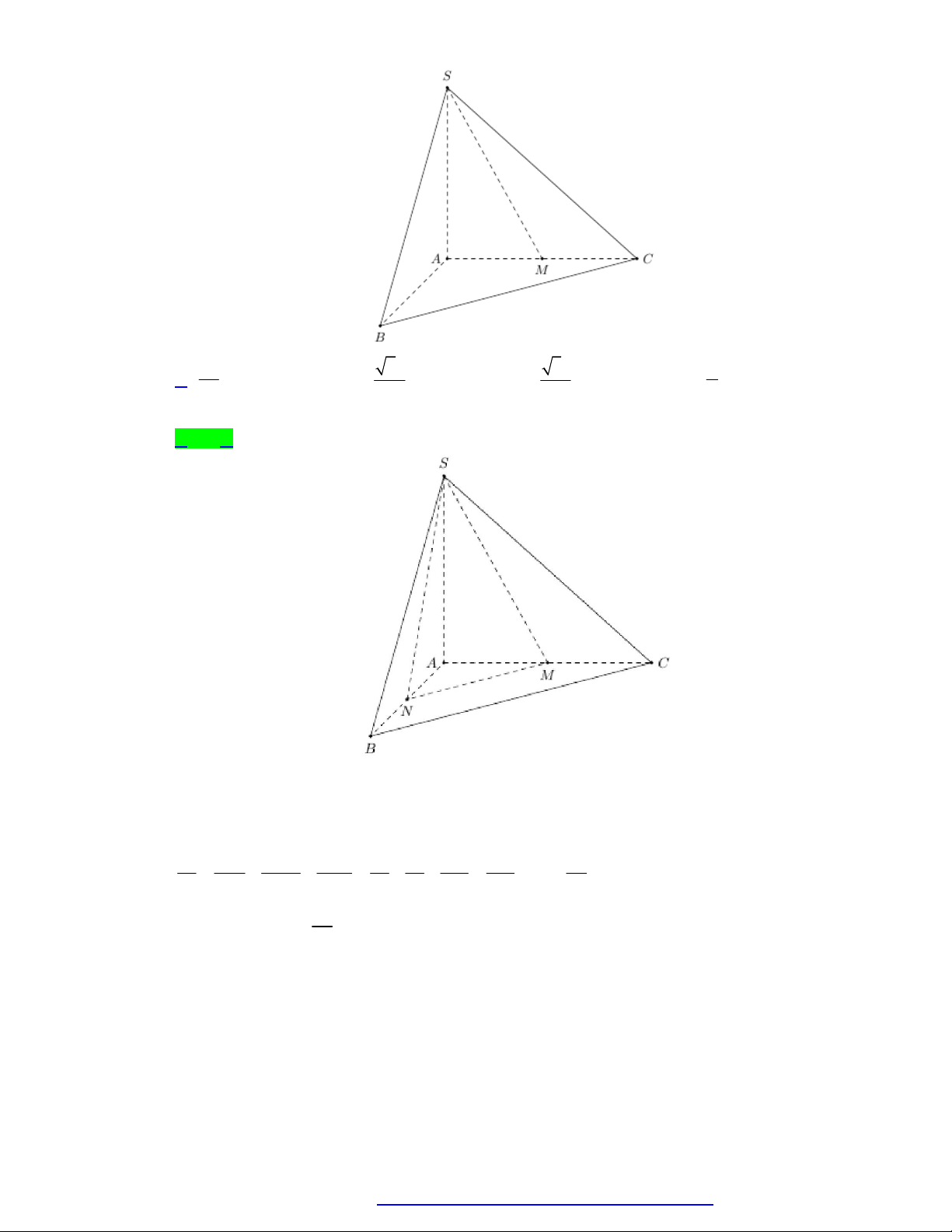
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, SA a 2, tam giác ABC vuông
cân tại B và AC  2a (minh họa nhứ hình bên). Góc giữa đường thẳng SB và mặt phẳng  ABC bằng A. 30. B. 45. C. 60. D. 90. Câu 3.
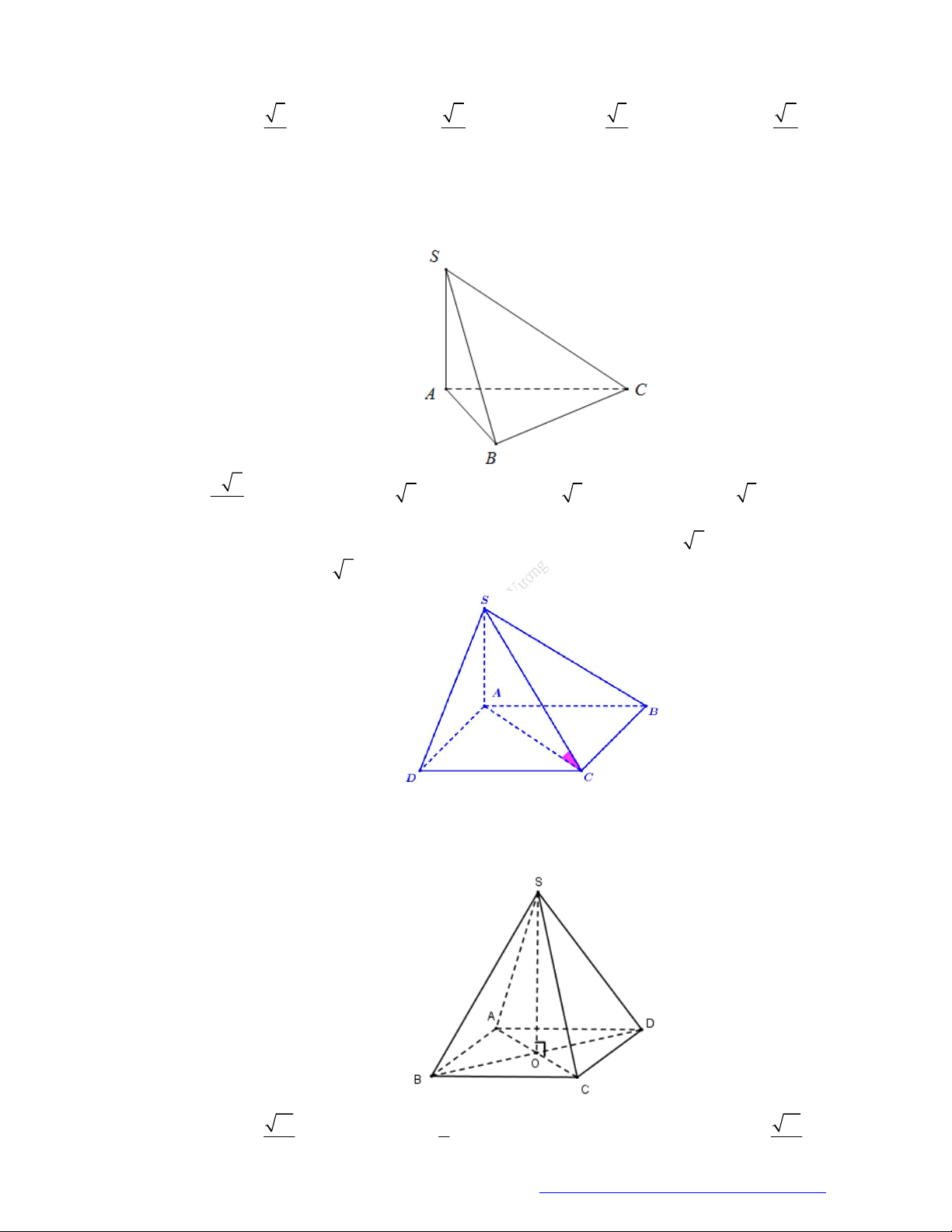
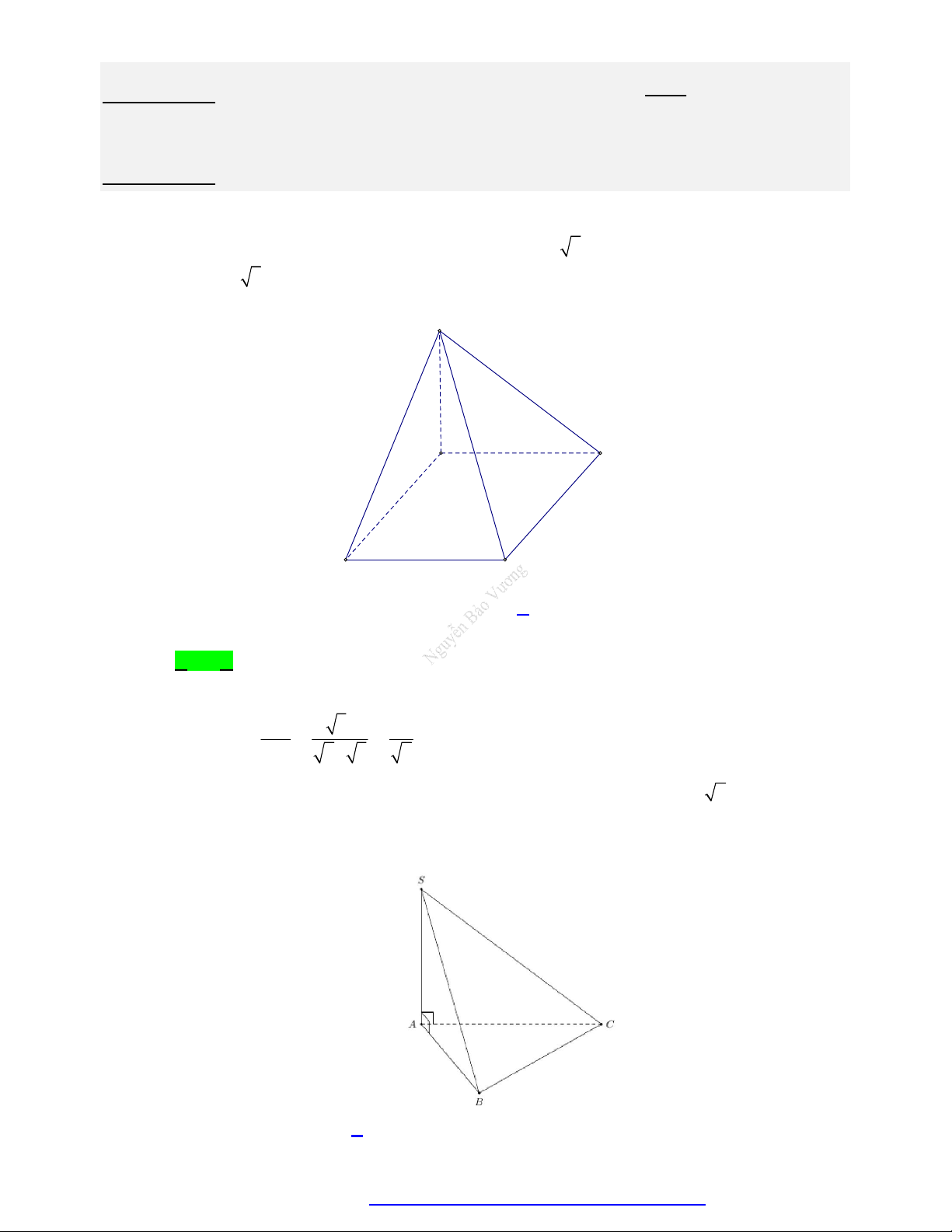
Cho hình chóp S.ABC có SB vuông góc với mặt phẳng  ABC , SB a 3 , tam giác
ABC vuông tại A, AB a và AC  2a . Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 45 . B. 60 . C. 30 . D. 90 . Câu 4.
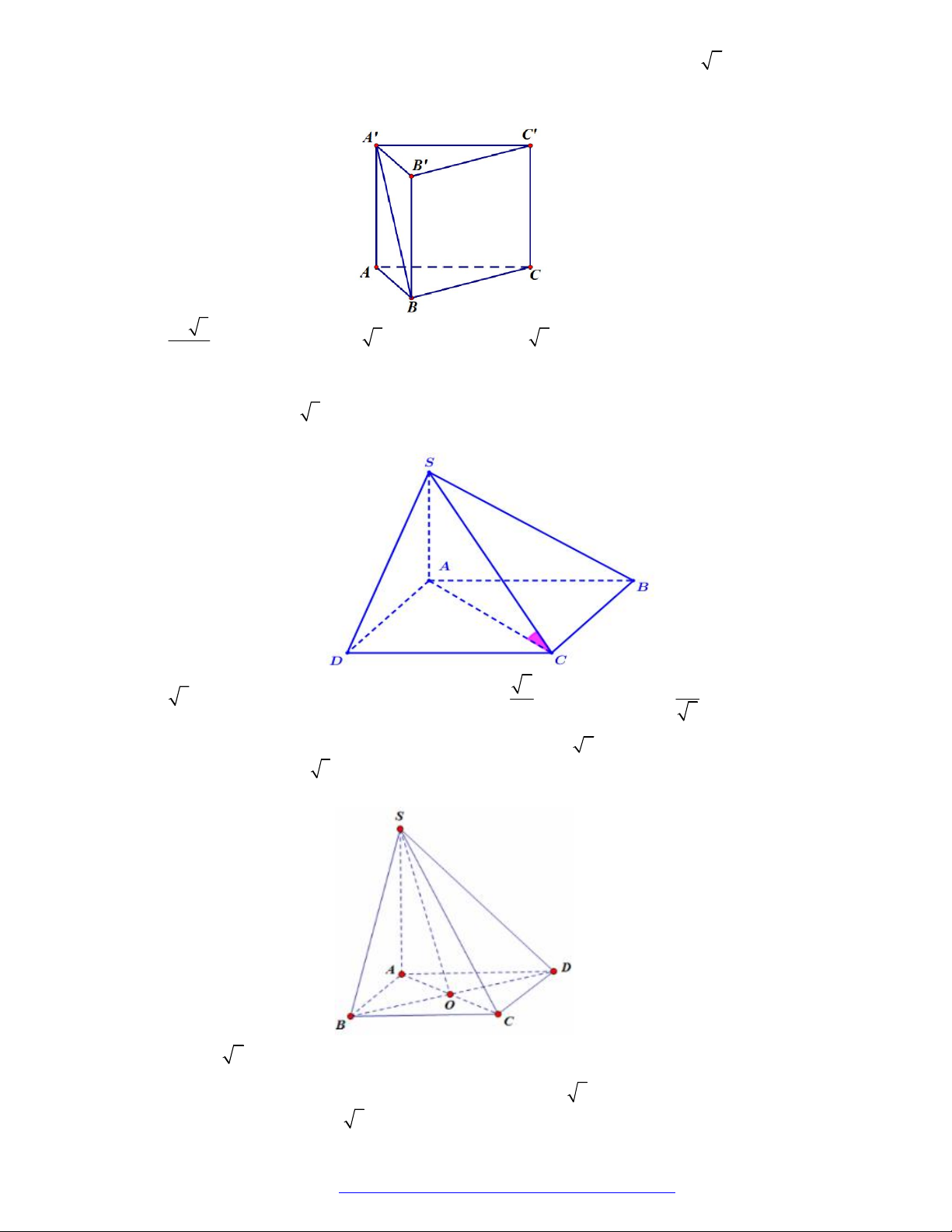
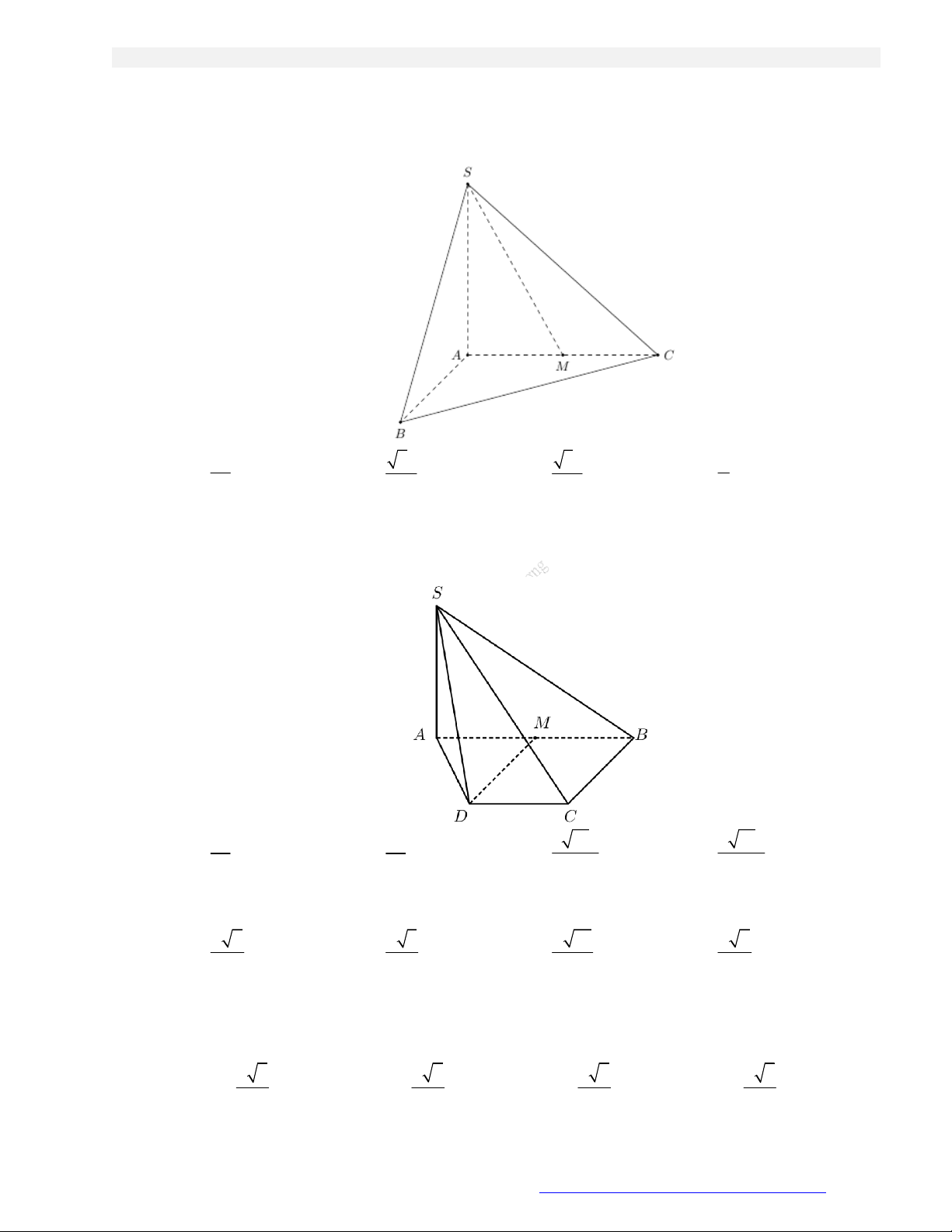
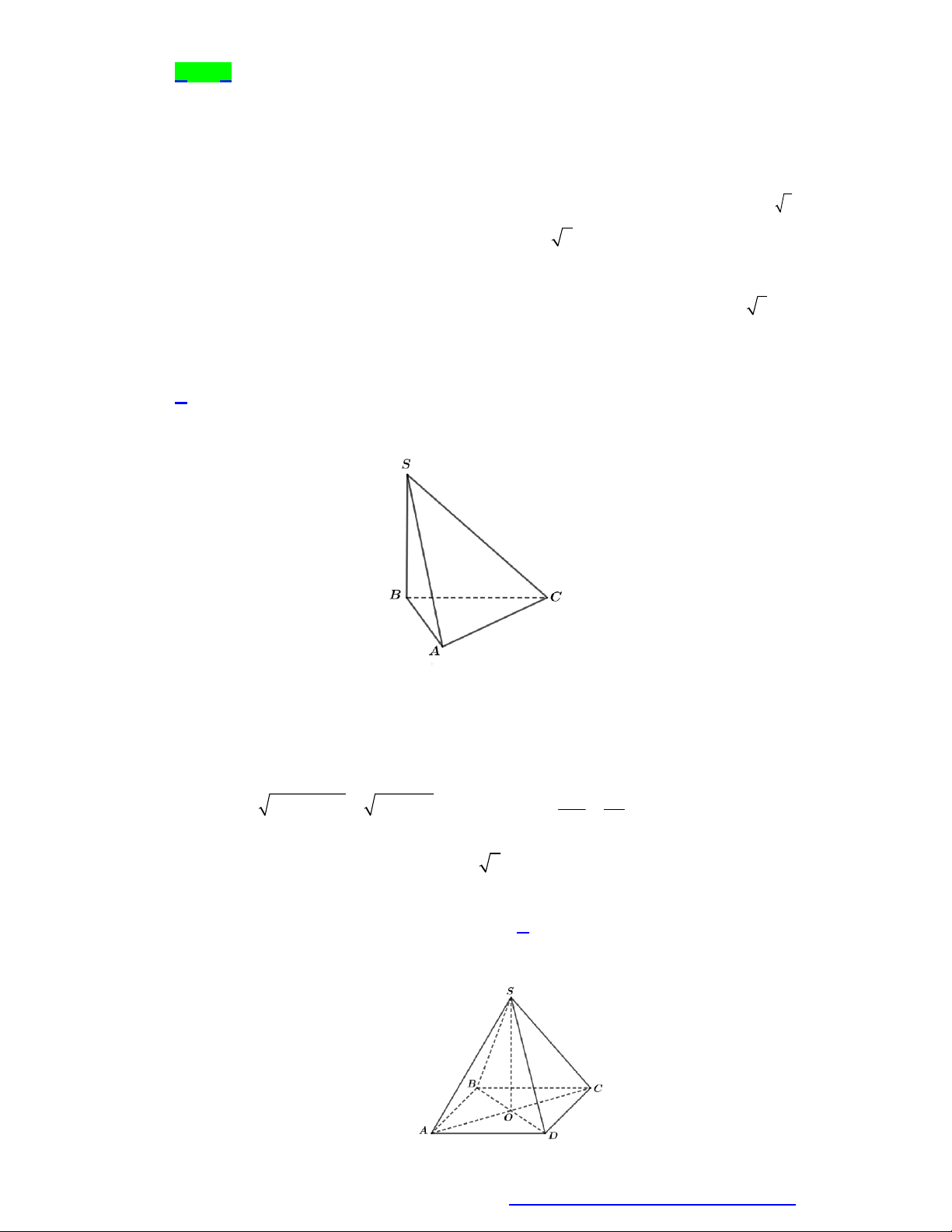
Cho hình chóp đều S.ABCD có AB a 2 , SB  2a . Góc giữa đường thẳng SA và mặt phẳng SBD bằng A. 45 . B. 60 . C. 30 . D. 90 . Câu 5.
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC , SB a 6 , tam giác ABC
vuông cân tại C , AB  2a . Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 . B. 60 . C. 45 . D. 90 . Câu 6.
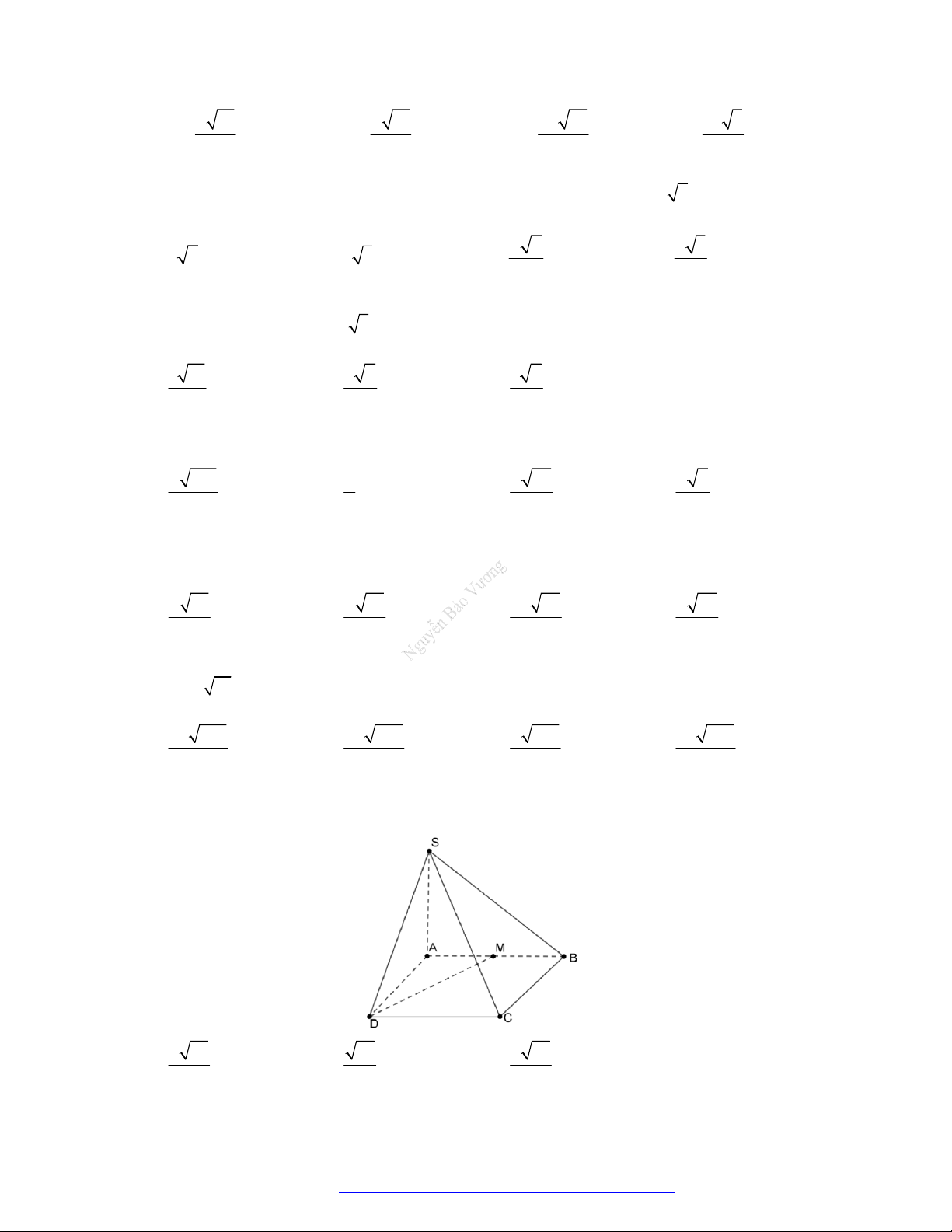
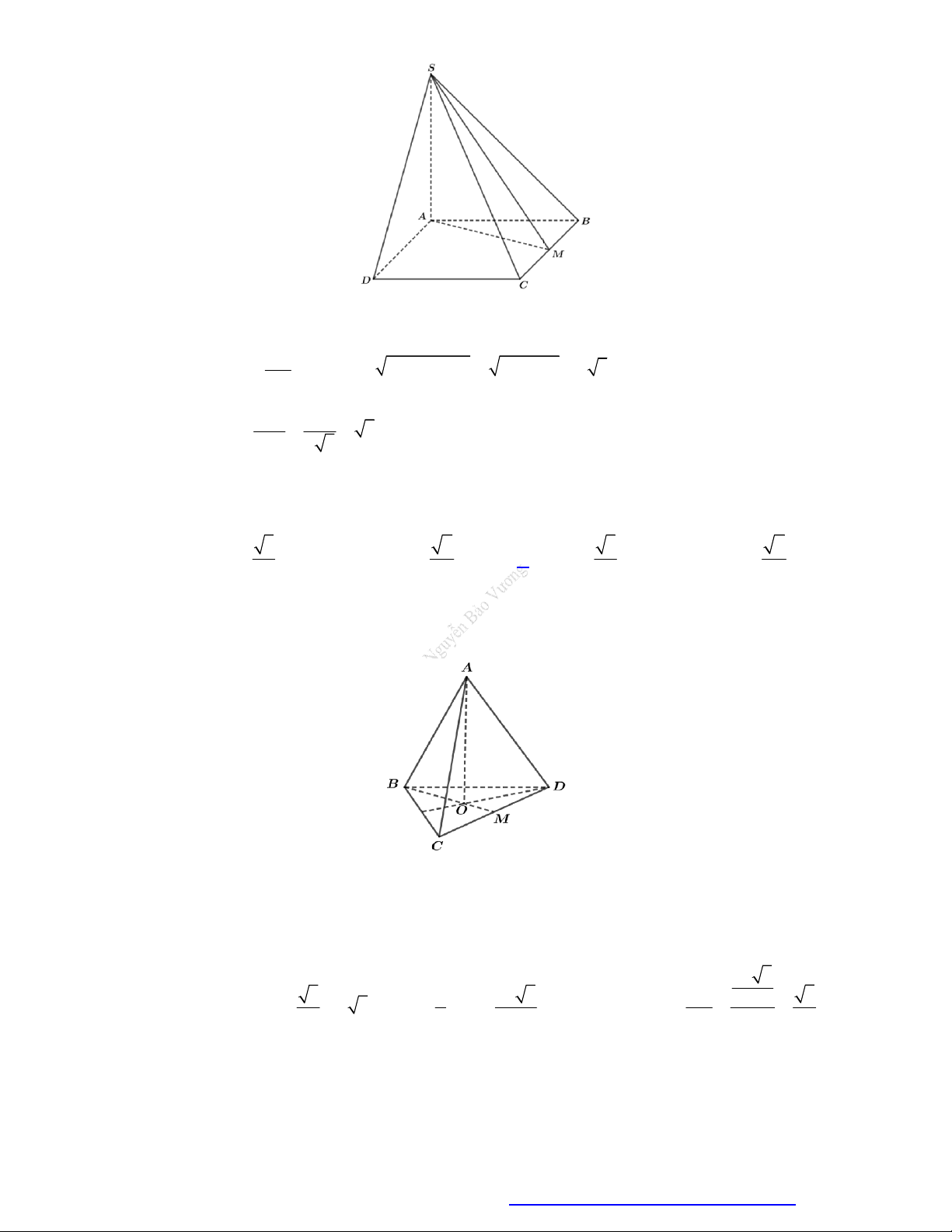
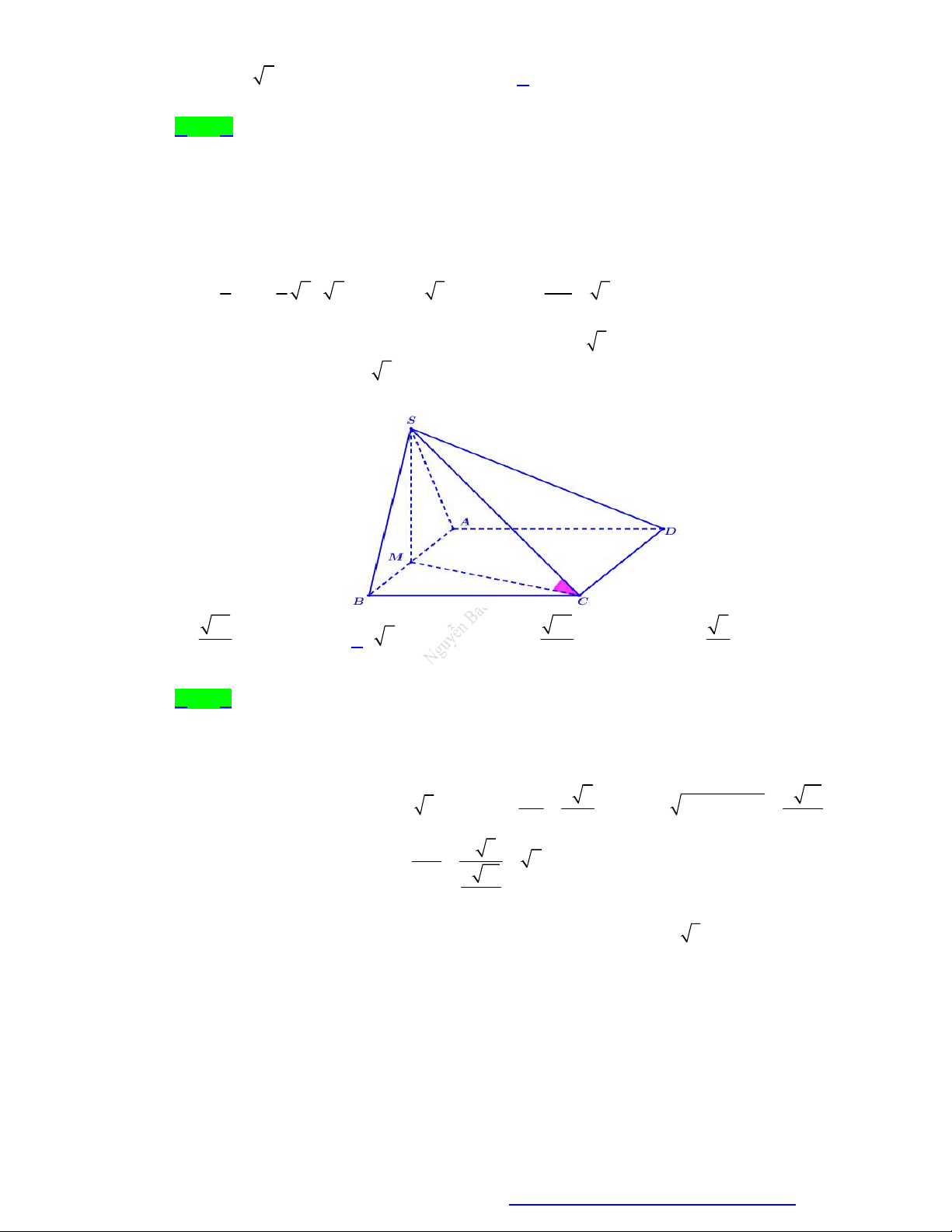
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng  ABCD , ABCD là hình chữ nhật,
AB a 2, BC  2a , SA  3a . Gọi M là trung điểm của BC . Tính góc giữa đường thẳng SM và
mặt phẳng  ABCD . A. 30 . B. 60 . C. 45 . D. 120 .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Câu 7.
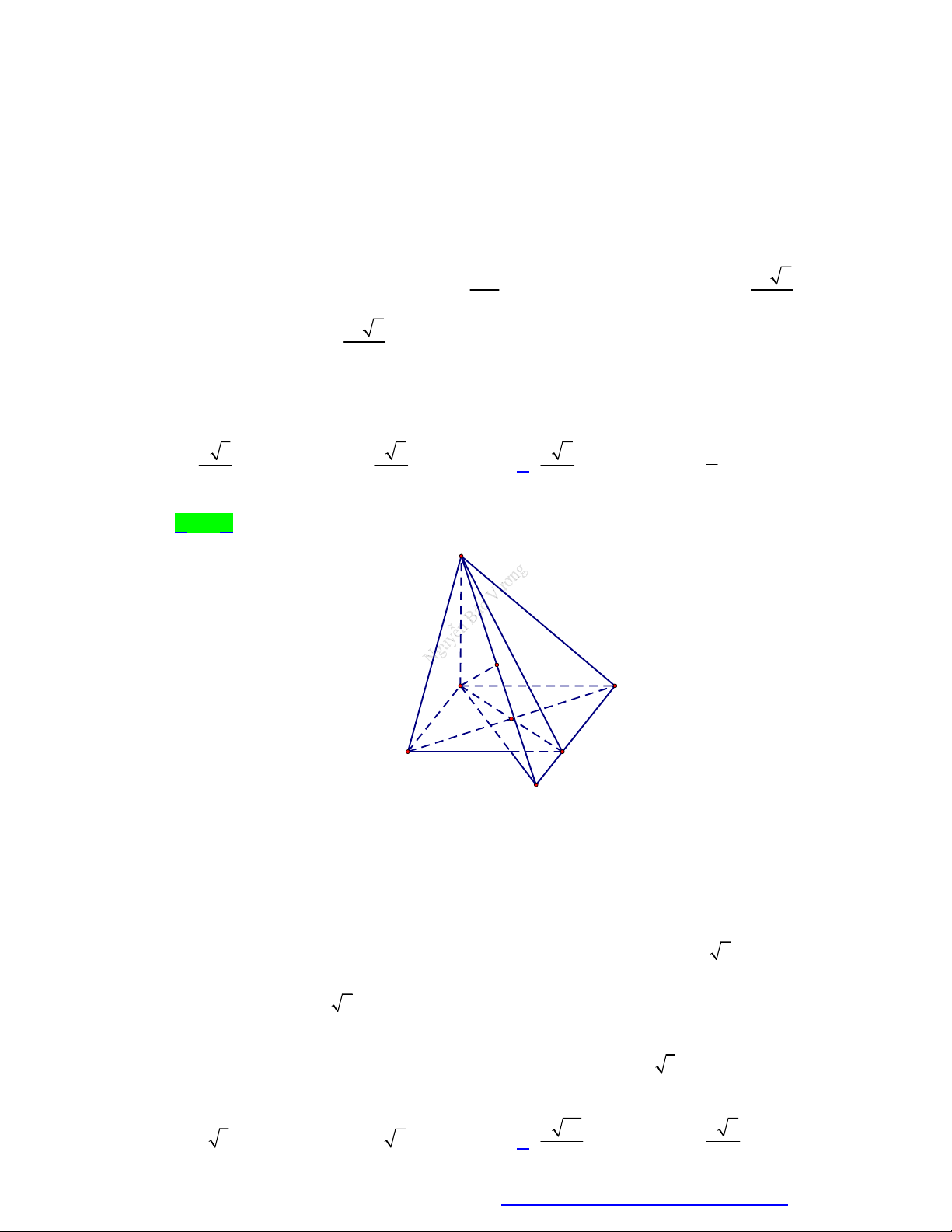
Cho tứ diện đều ABCD có cạnh bằng 2a . Gọi  là góc giữa đường thẳng AB và mặt phẳng
BCD . Tính cos . 3 6 3 2 A. cos  . B. cos  . C. cos  . D. cos  . 6 3 3 3 Câu 8.
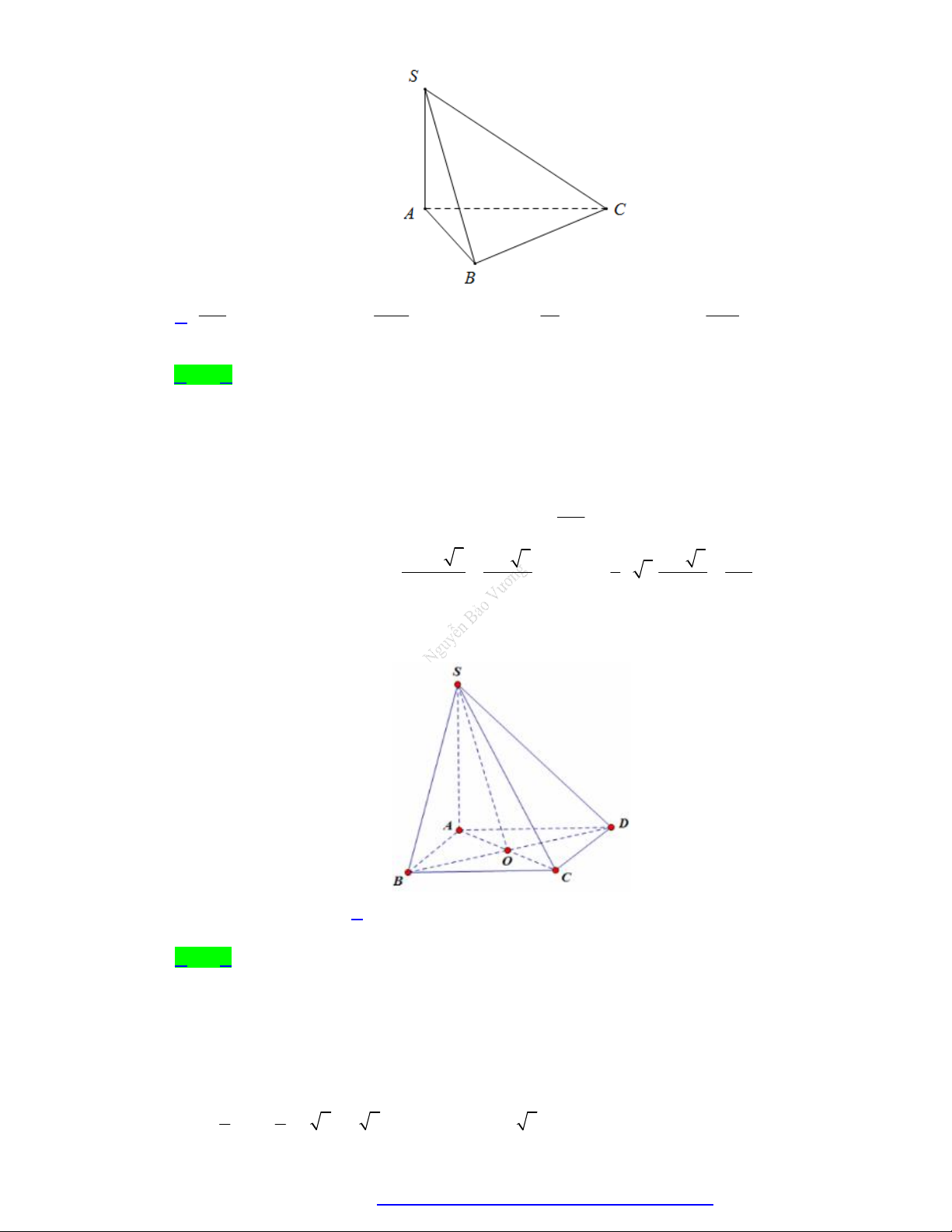
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, tam giác ABC vuông cân tại B và
AC  2a (minh họa như hình bên). Góc giữa đường thẳng SB và mặt phẳng  ABC bằng 60 .  Tính
độ dài cạnh bên SA . a 6 A. . B. a 6. C. a 3. D. 2a 3. 3 Câu 9.
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  2a , AD a 2 , SA vuông góc với mặt
phẳng đáy và SA a 2 . Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 .
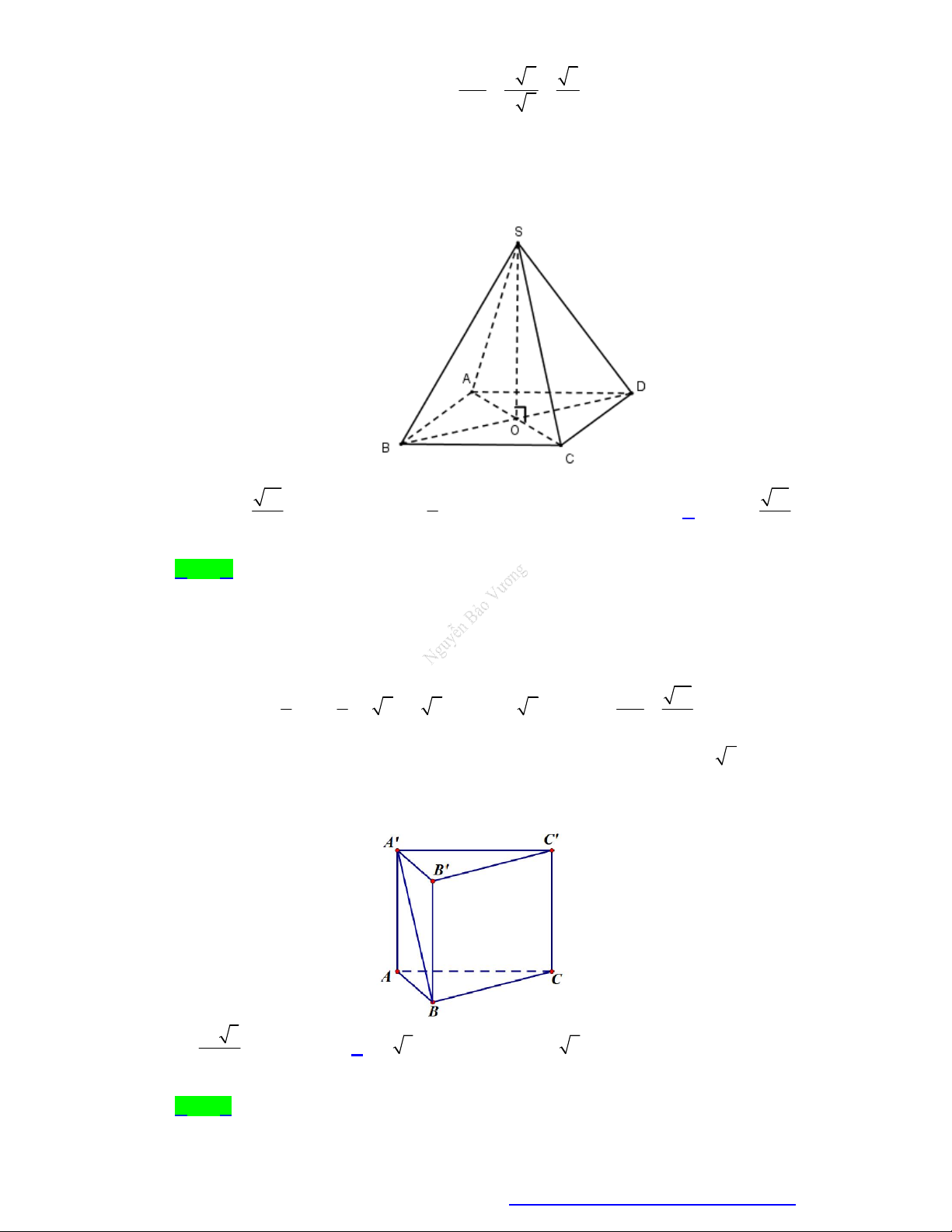
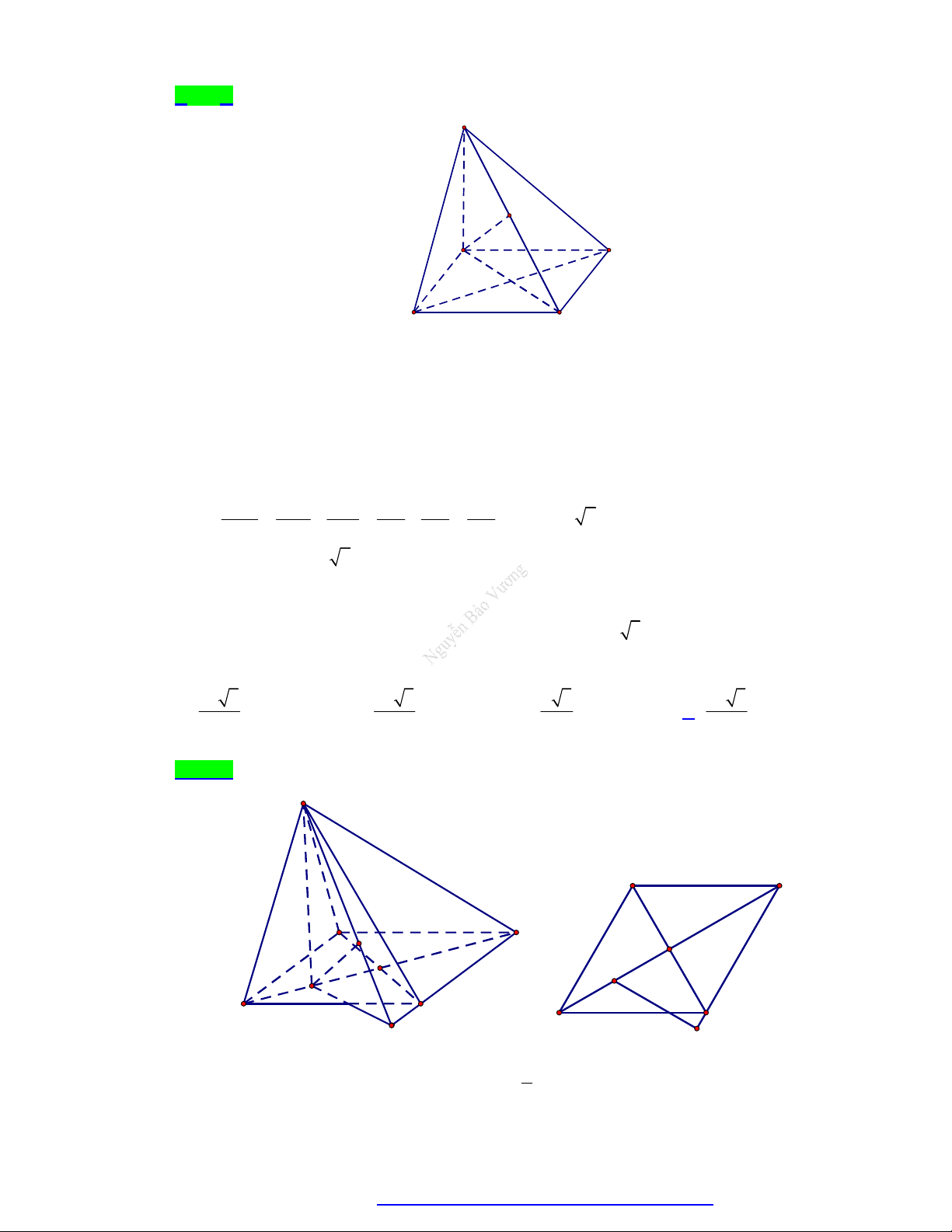
Câu 10. Cho chóp đều S.ABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a (minh họa như hình bên). Gọi 
là góc giữa giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng? 14 3 14 A. tan   . B. tan   . C. 0   45 . tan   . 7 2 D. 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
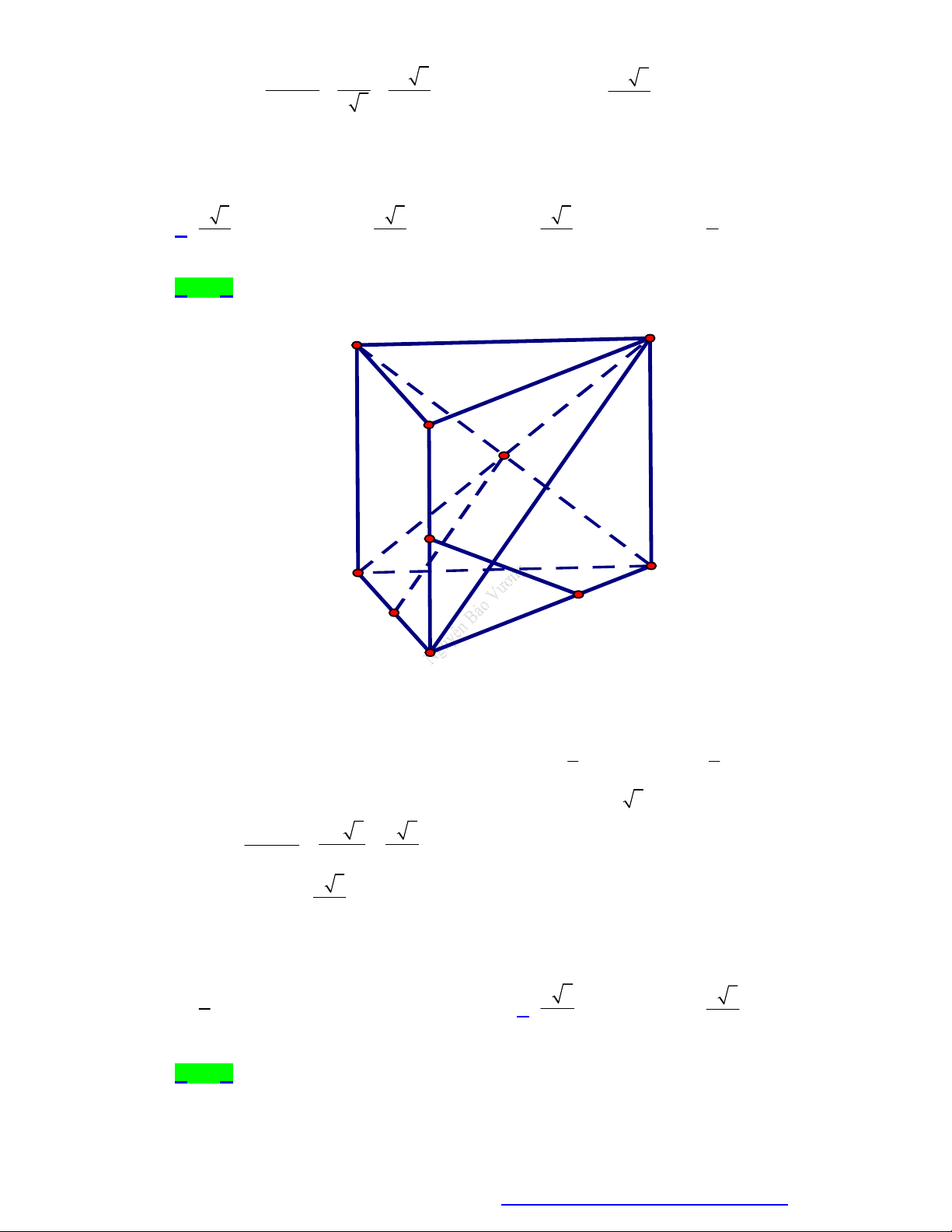
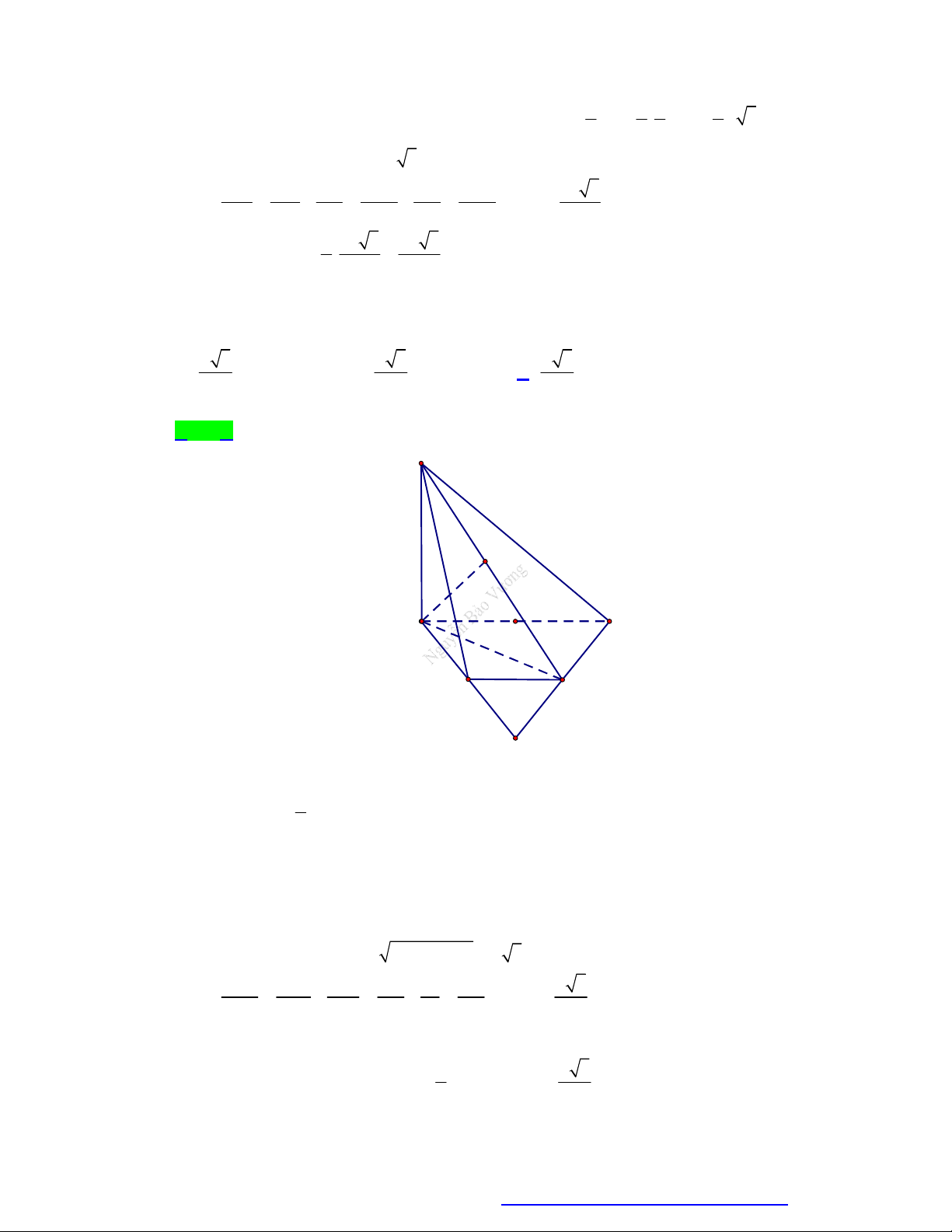
Câu 11. Cho lăng trụ đứng ABC.A' B'C ' có đáy là A
BC vuông cân tại B , AC  2 2a (minh họa như
hình bên). Góc giữa đường thẳng A ' B và mặt phẳng  ABC  bằng 60. Tính độ dài cạnh bên của hình lăng trụ. 2a 3 A. .
B. 2a 3. C. 2a 6. D. 2 . a 3 
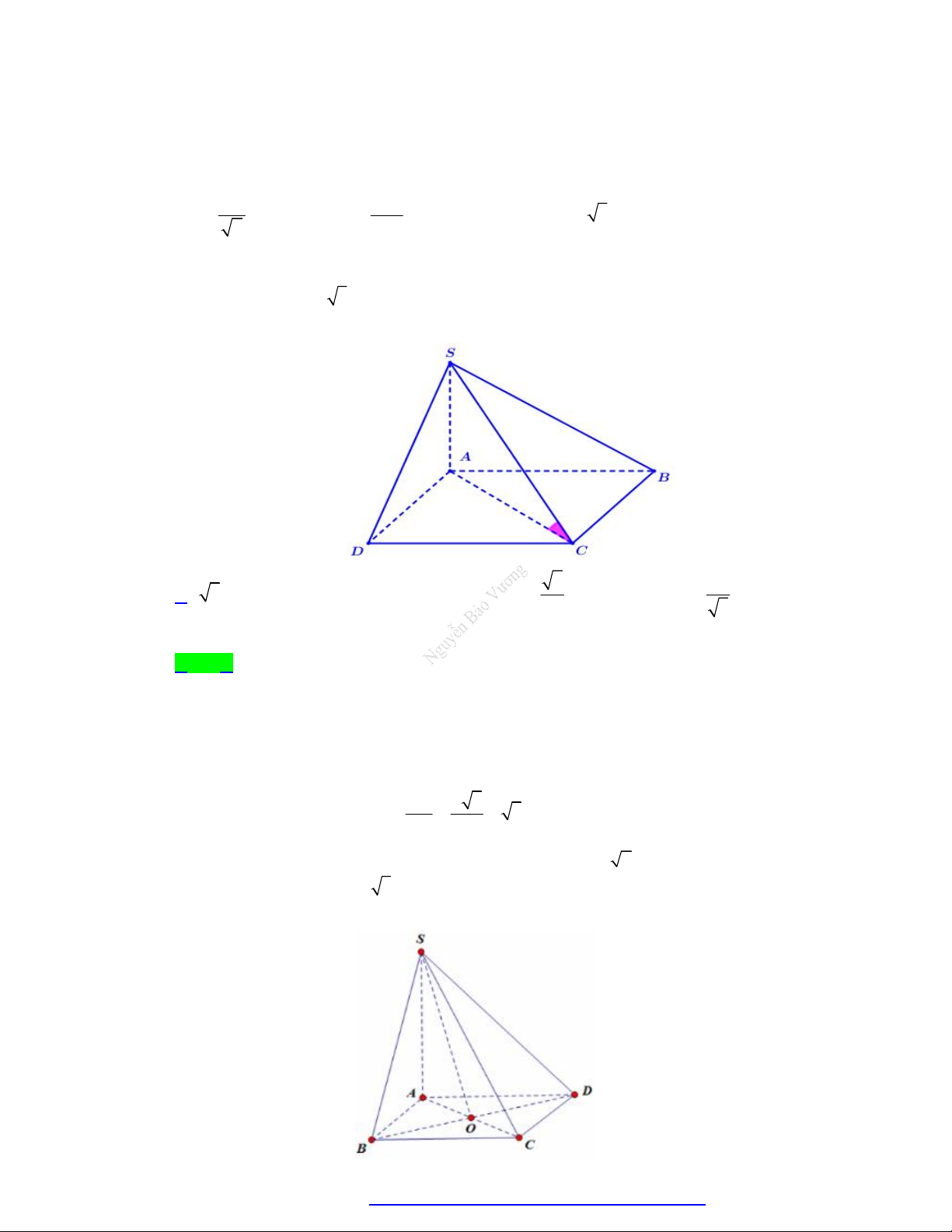
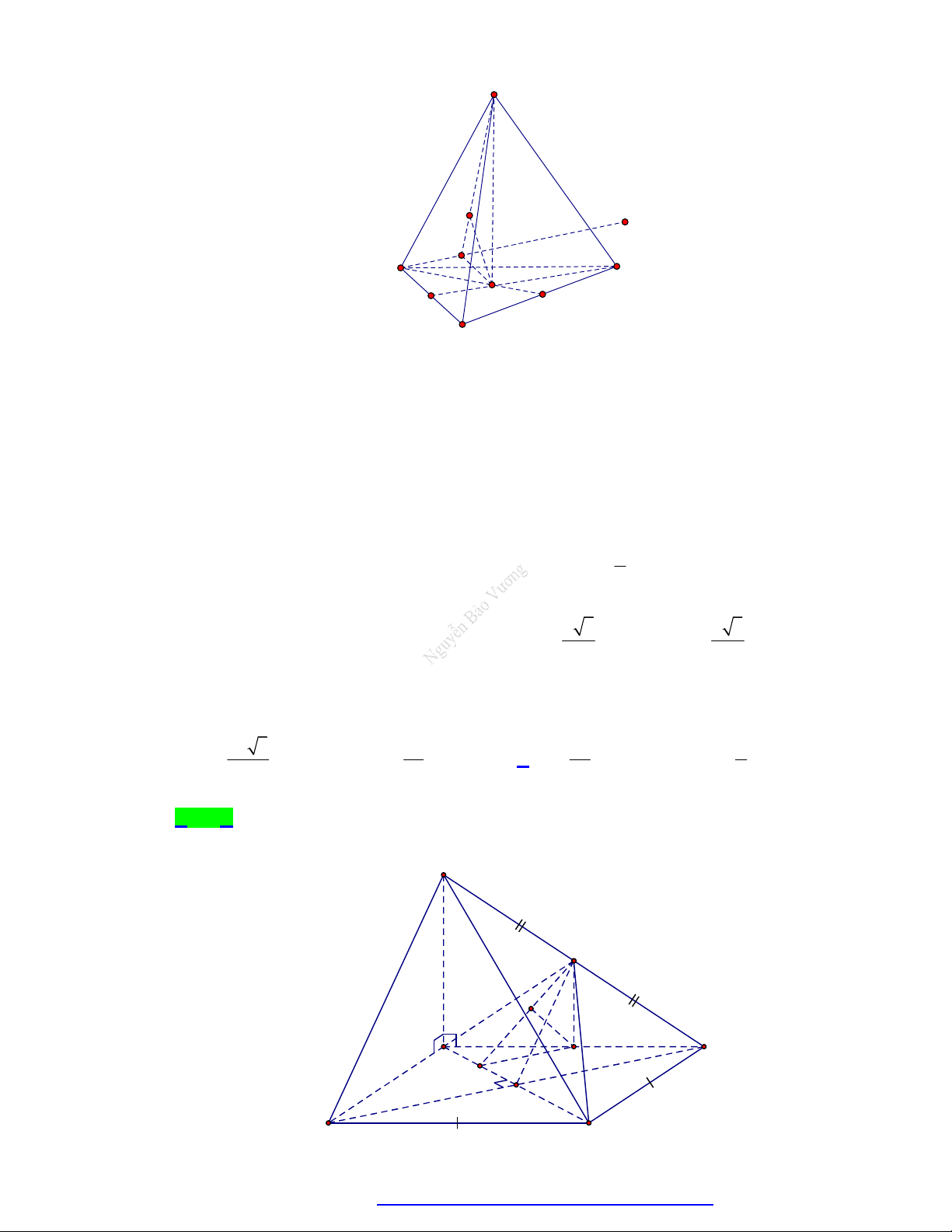
Câu 12. Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a , 0
ABC  60 , SA vuông góc với mặt
phẳng đáy và SA a 3 . Gọi  là góc giữa đường thẳng SC và mặt phẳng  ABCD . Tính tan  6 1 A. 3 . B. 1. C. . D. . 2 3
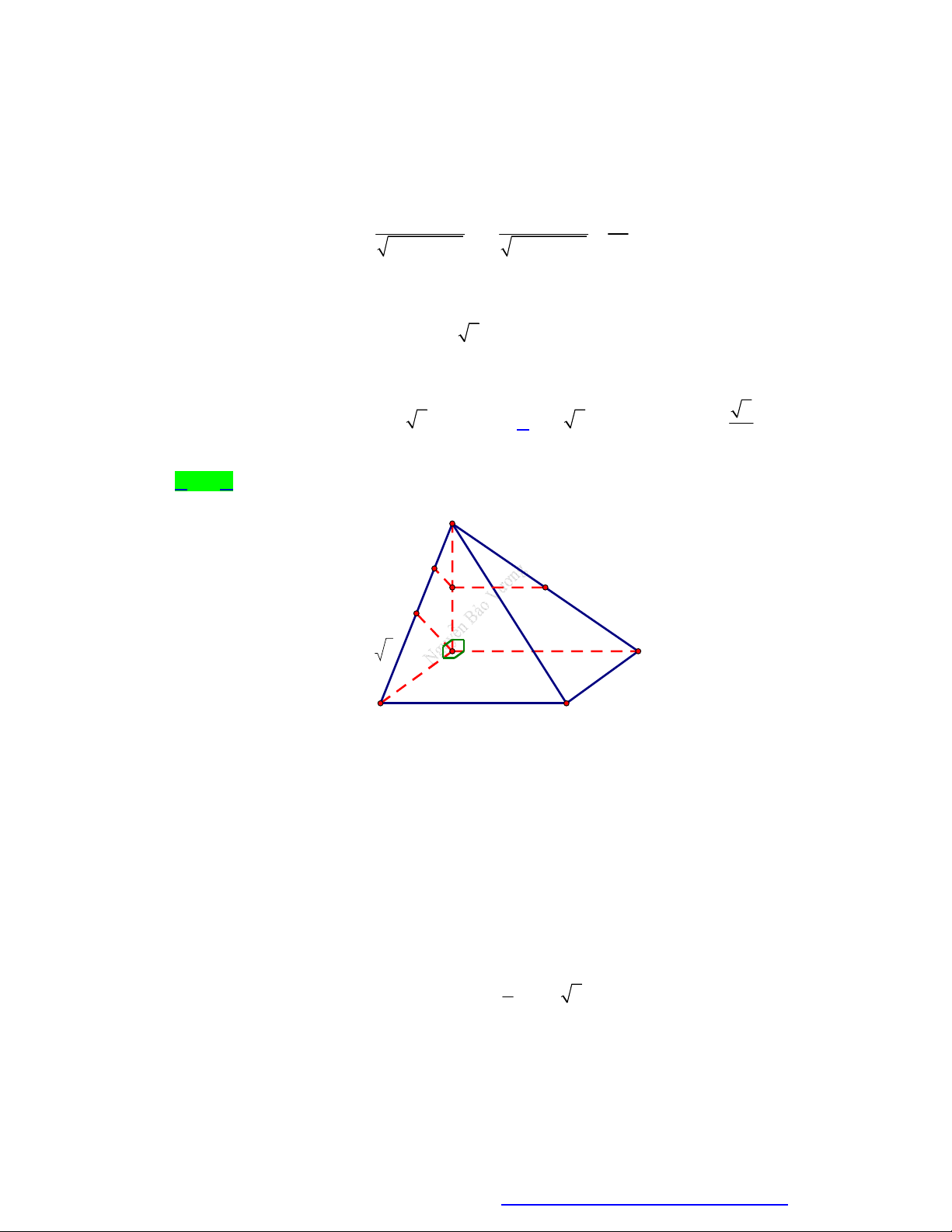
Câu 13. Cho chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng 2a , cạnh bên SA vuông góc với mặt
phẳng  ABCD, SA a 3. Gọi  góc giữa đường thẳng SO và mặt phẳng  ABCD . Mệnh đề nào sau đây đúng? A. tan   6. B.   45 .  C.   60 .  D.   90 . 
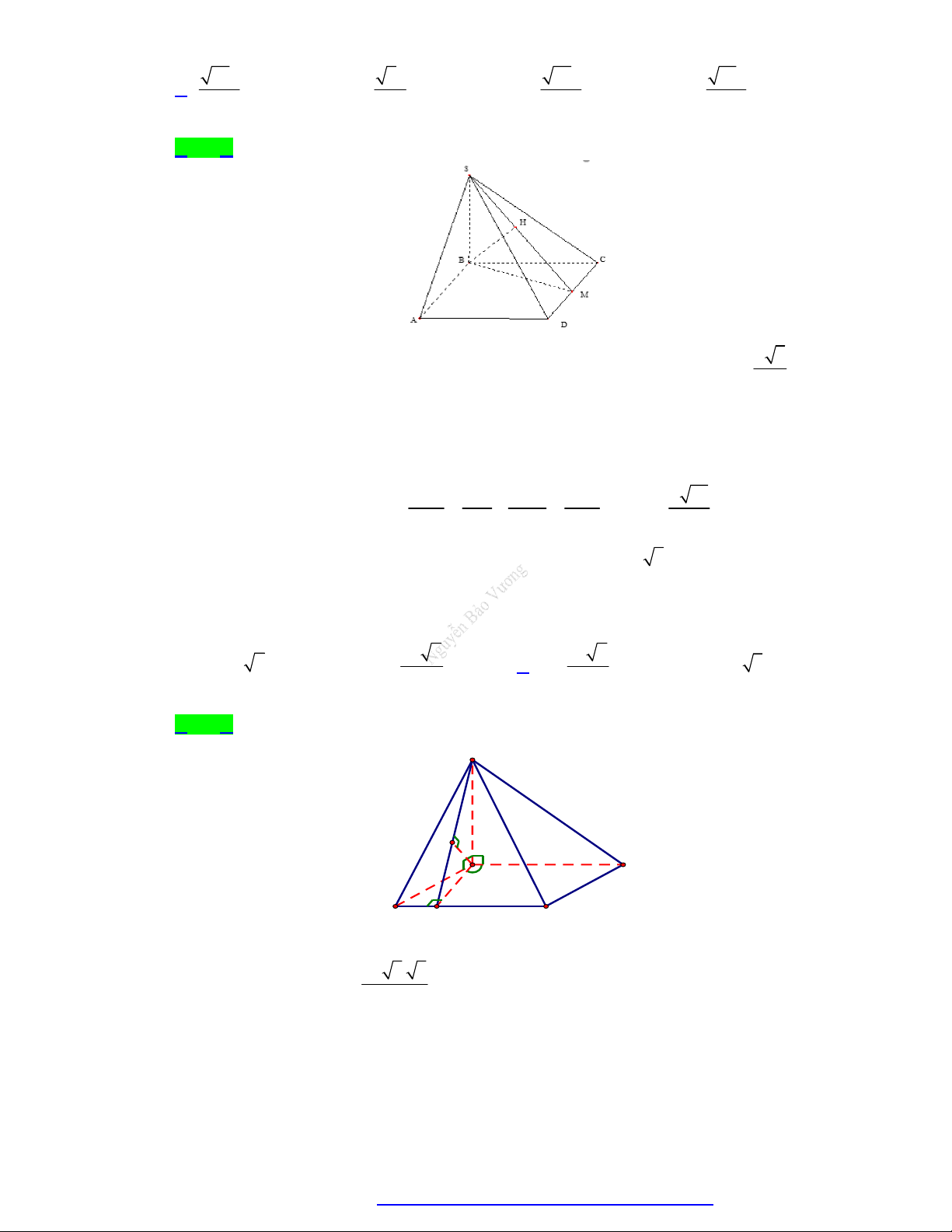
Câu 14. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 2 . Gọi M là trung điểm của AB,
SM   ABCD và SM a 5 . Gọi  là góc giữa đường thẳng SC và mặt phẳng  ABCD . Tính tan 
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 30 22 5 A. . B. 2 . C. . D. . 3 4 2
Câu 15. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, SA a 3, tam giác ABC đều (minh
họa như hình bên). Góc giữa đường thẳng SC và mặt phẳng  ABC bằng 30 .  Tính thể tích khối chóp S.ABC . 3 9a 3 27a 3 a 3 81a A. . B. . C. . D. . 4 4 4 4
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Cạnh bên SA vuông góc
với đáy và SA  2a .Góc giữa đường thẳng SB và mặt phẳng SAC  bằng: A. 45 .  B. 30 .  C. 60. D. 90 . 
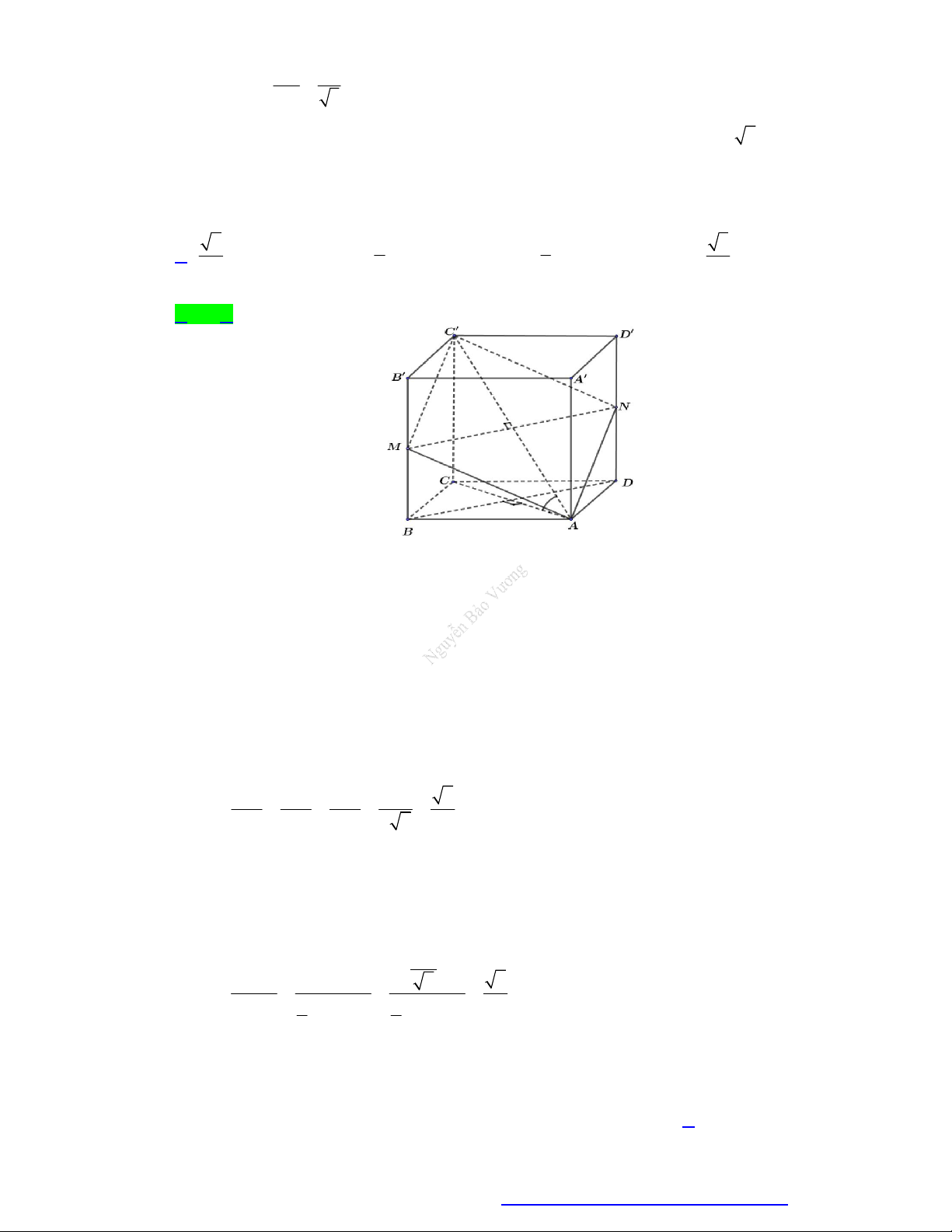
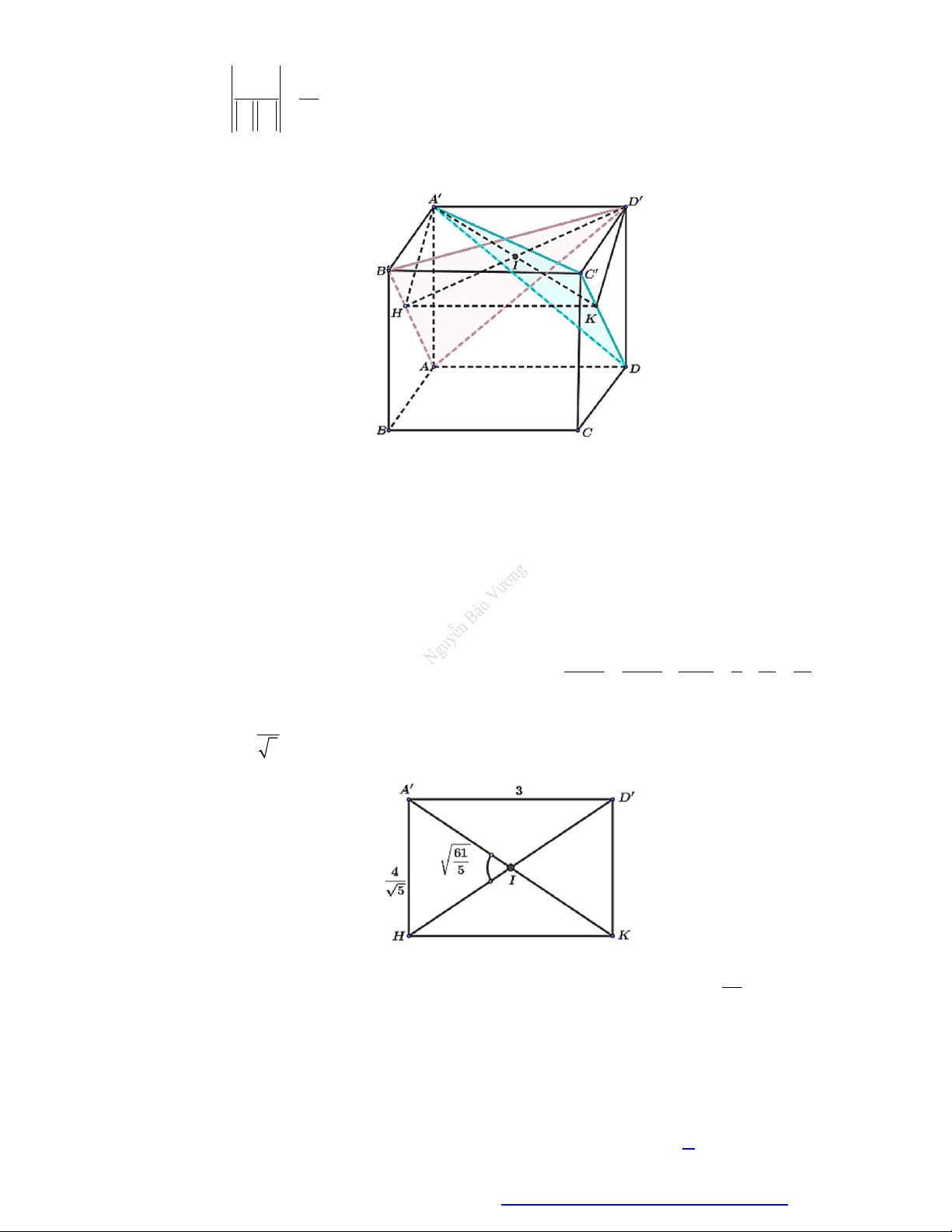
Câu 17. Cho hình hộp chữ nhật ABC . D AB CD
  có đáy ABCD là hình vuông, AC  a 2 . Gọi  P là
mặt phẳng qua AC cắt BB ,
DD lần lượt tại M , N sao cho tam giác AMN cân tại A có
MN a . Tính cos với    P, ABCD   . 2 1 1 3 A. . B. . C. . D. . 2 2 3 3
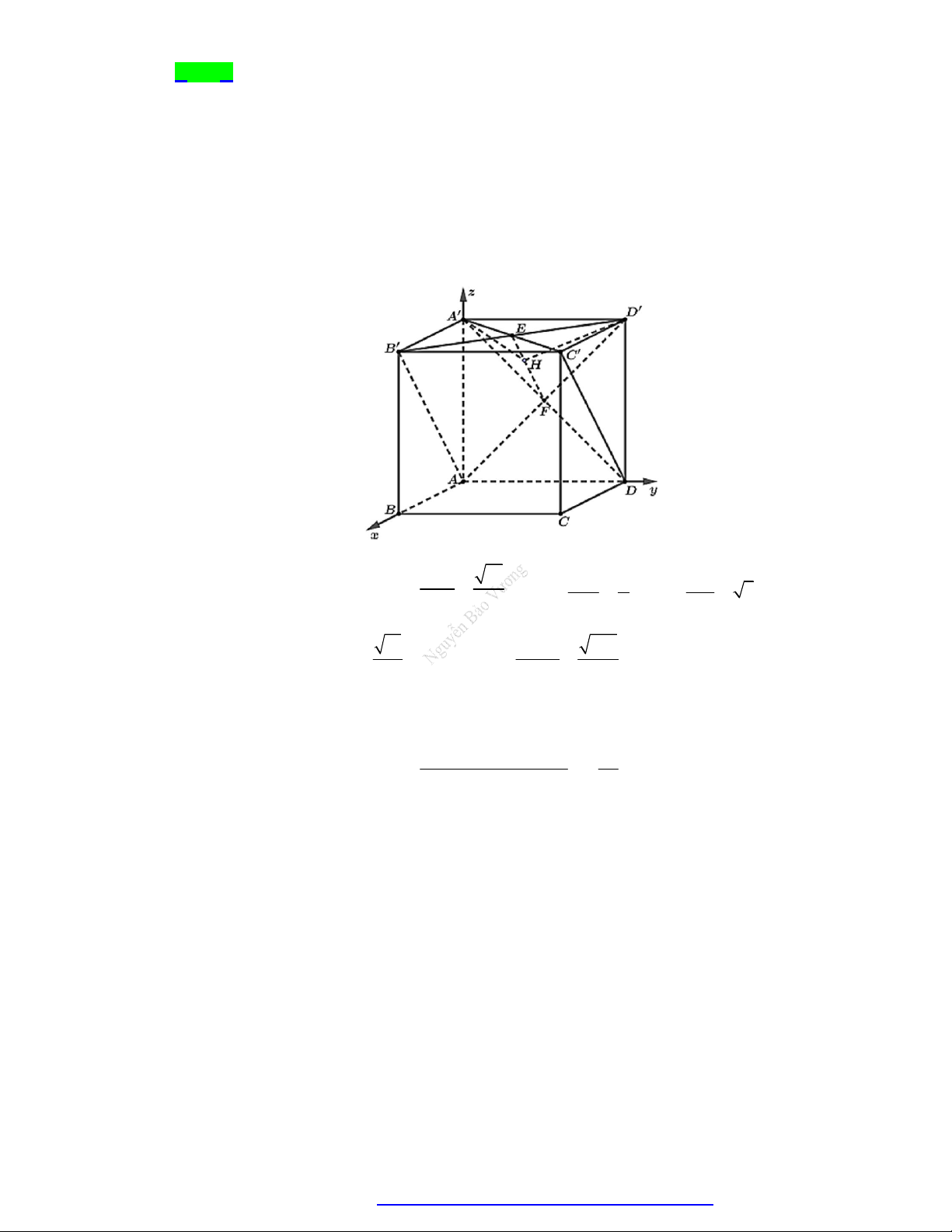
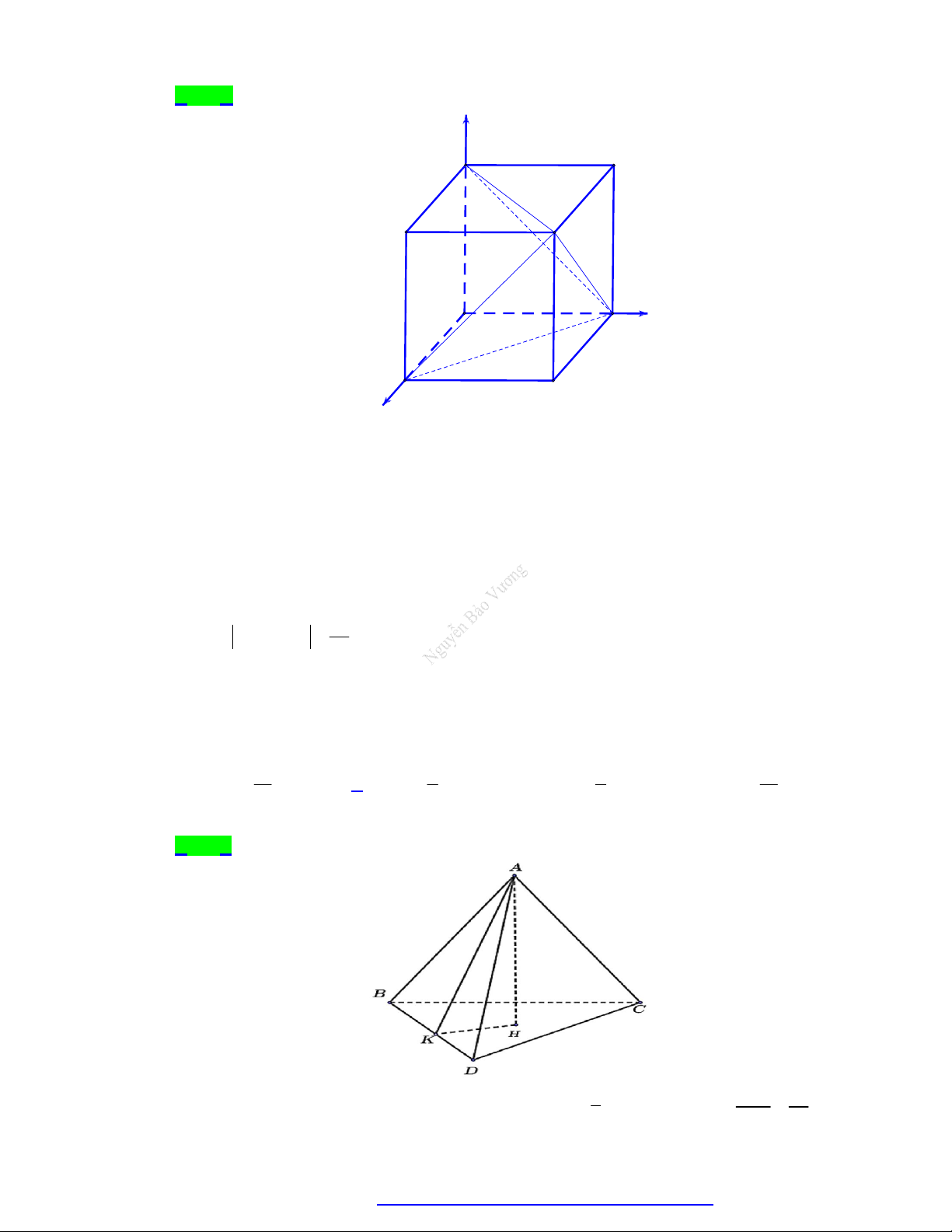
Câu 18. Cho hình hộp chữ nhật ABC . D AB CD
  có các cạnh AB  2, AD  3; AA  4 . Góc giữa hai mặt phẳng  AB D   và  A CD
  là  . Tính giá trị gần đúng của góc  ? A. 45, 2 . B. 38,1 . C. 53, 4 . D. 61, 6 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 19. Cho hình hộp chữ nhật ABC . D AB CD
  có các cạnh AB  2, AD  3; AA  4 . Góc giữa hai
mặt phẳng  BC ' D và  AC D
  là  . Tính giá trị gần đúng của góc  ? A. 45, 2 . B. 38,1 . C. 53, 4 . D. 61,6.
Câu 20. Cho tứ diện ABCD có BD  2 . Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10 .
Biết thể tích khối tứ diện ABCD bằng 16 . Tính số đo góc giữa hai mặt phẳng  ABD vàBCD.  4   4   4   4  A. arccos   .
B. arcsin   .
C. arccos   . D. arcsin   .  15   5   5   15 
Câu 21. Cho hình chóp S.ABCD đáy ABCD là hình thoi, SA SC . Góc giữa hai mặt phẳng SBD và
ABCD bằng? A. 90 . B. 30 . C. 60 . D. 45 .
Câu 22. Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, tam giác SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng  SAB và SAD bằng? A. 30 . B. 90 . C. 60 . D. 45 .
Câu 23. Cho hình vuông ABCD . Gọi S là điểm trong không gian sao cho SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi H và I lần lượt là trung điểm của AB và BC . Góc
giữa hai mặt phẳng SHC  và  SDI  bằng. A. 30 . B. 60 . C. 90 . D. 45 .
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a . Đường thẳng SO vuông a 3
góc với mặt phẳng đáy  ABCD và SO
. Tính góc giữa hai mặt phẳng  SBC  và 2  ABCD . A. 30 . B. 45 . C. 60 . D. 90 .
B. KHOẢNG CÁCH TRONG KHÔNG GIAN
Tính khoảng cách từ chân đường cao của hình chóp đến mặt bên của hình chóp.
Tính khoảng cách từ A đến mặt bên (SBC ) của hình chóp S.ABC có SA  (ABC )
B1. Xác định giao tuyến của mặt bên và mặt phẳng đáy (SBC )  (ABC )  BC. A  H BC
B2. Dựng hình 
AI  (SBC ). AI SH  Suy ra d( ;
A (SBC))  AI.
B3. Tính AI .
Các phương pháp quy về bài toán chân đường cao:
― Kẻ song song để dời điểm về chân đường vuông góc.
― Dùng tỉ số khoảng cách để dời về chân đường vuông góc.
― Tạo chân đường cao giả ( đường cao, khi mặt chứa chân).
Tính khoảng cách giữa cạnh bên và cạnh thuộc mặt đáy. S
Cho hình chóp S.ABCD có SA  (ABCD). Hãy tính khoảng
cách giữa cạnh bên SB và cạnh thuộc mặt đáy AC .
B1. Xác định giao điểm của cạnh bên SB và mặt phẳng đáy
SB  (ABCD)  . B
B2. Qua giao điểm B, dựng đường thẳng d song song với K D AC . A
Khi đó: d(AC,SB)  d(AC,(S , B d))  d( , A (S , B d)).
Đây là bài toán tìm khoảng cách từ chân đến mặt bên. Cụ thể:
d(AC,SB)  d(AC,(S , B d))  d( , A (S , B d))  AK. H B C d
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  2a , AC  4a , SA vuông góc với
mặt phẳng đáy và SA a (hình minh họa). Gọi M là trung điểm của AB . Khoảng cách giữa hai
đường thẳng SM và BC bằng 2a 6a 3a a A. . B. . C. . D. . 3 3 3 2 Câu 2.
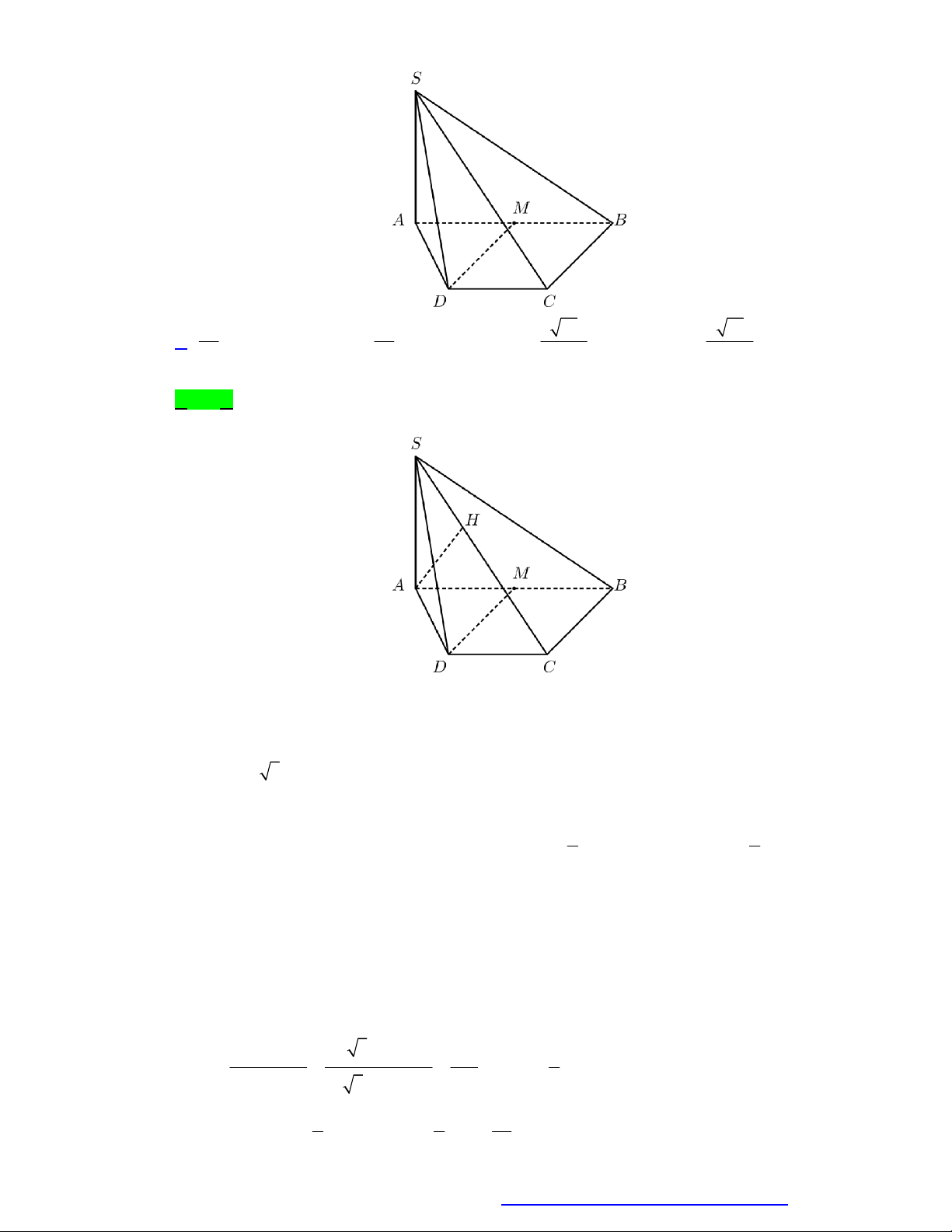
Cho hình chóp S.ABCD có đáy là hình thang, AB  2a , AD DC CB a , SA vuông góc với
mặt phẳng đáy và SA  3a (minh họa như hình bên). Gọi M là trung điểm của AB . Khoảng cách
giữa hai đường thẳng SB và DM bằng 3a 3a 3 13a 6 13a A. . B. . C. . D. . 4 2 13 13 Câu 3.
Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác đều cạnh a và cạnh bên có độ dài
bằng a . Tính khoảng cách từ C đến mặt phẳng  A BC   . a 2 a 3 a 21 a 2 A. . B. . C. . D. . 4 7 7 16 Câu 4. Cho hình hộp ABC . D A BCD
  có đáy ABCD là hình vuông cạnh a , tâm O . Hình chiếu vuông
góc của A lên mặt phẳng  ABC
D trùng với O . Biết tam giác AA C
 vuông cân tại A. Tính
khoảng cách h từ điểm D đến mặt phẳng  ABB A   . a 6 a 2 a 2 a 6 A. h  . B. h  . C. h  . D. h  . 6 3 6 3 Câu 5.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AD  2a , DC a ,
AB  2a . Gọi I là trung điểm cạnh AD , hai mặt phẳng  SIB , SIC  cùng vuông góc với mặt
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
phẳng đáy và mặt phẳng  SBC  tạo với đáy một góc 60 . Tính khoảng cách h từ I đến mặt phẳng SBC  . a 15 a 15 3a 15 3a 5 A. h  . B. h  . C. h  . D. h  . 15 5 10 5 Câu 6.
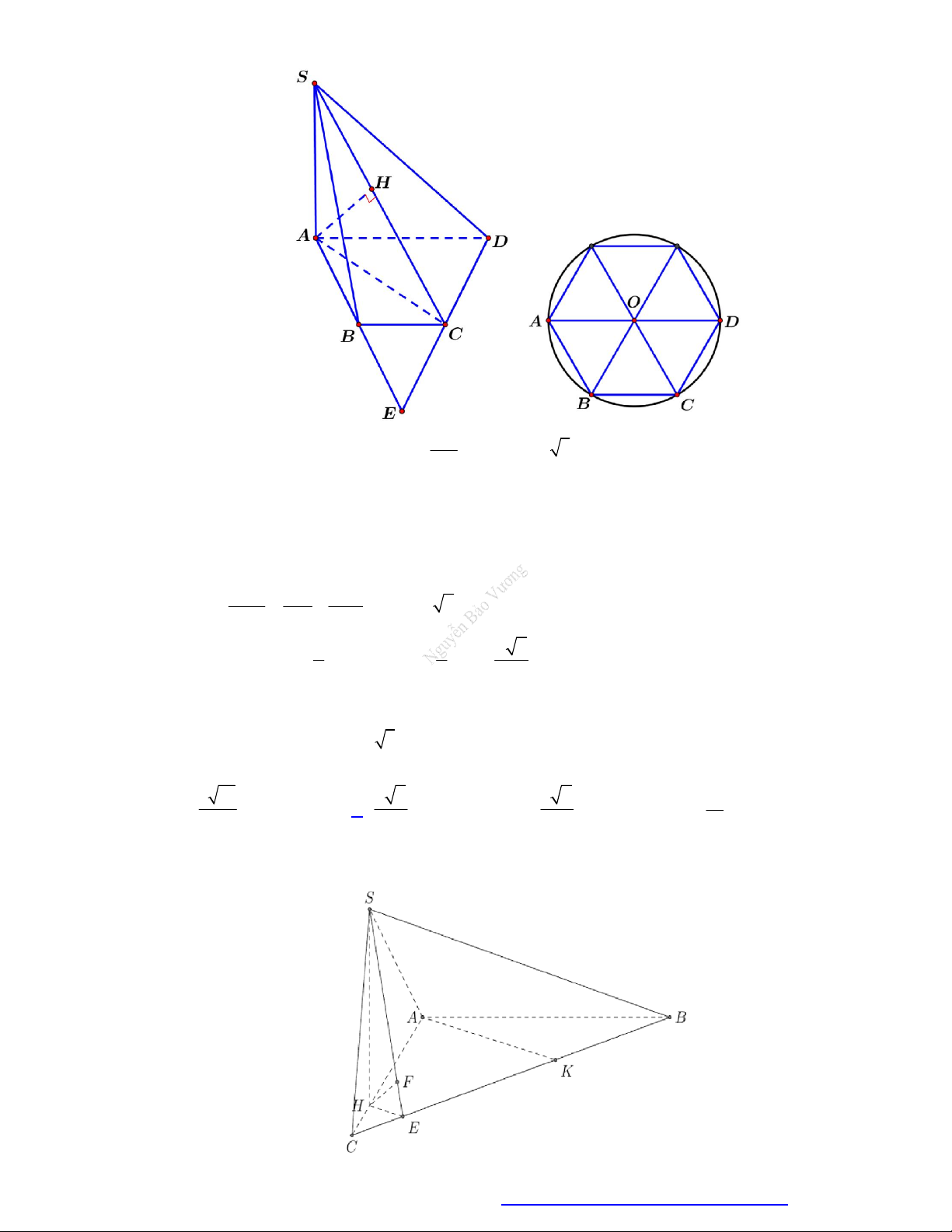
Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính
AD  2a và có cạnh SA vuông góc với mặt phẳng đáy  ABCD với SA a 6 . Tính khoảng cách từ
B đến mặt phẳng  SCD . a 2 a 3 A. a 2 . B. a 3 . C. . D. . 2 2 Câu 7.
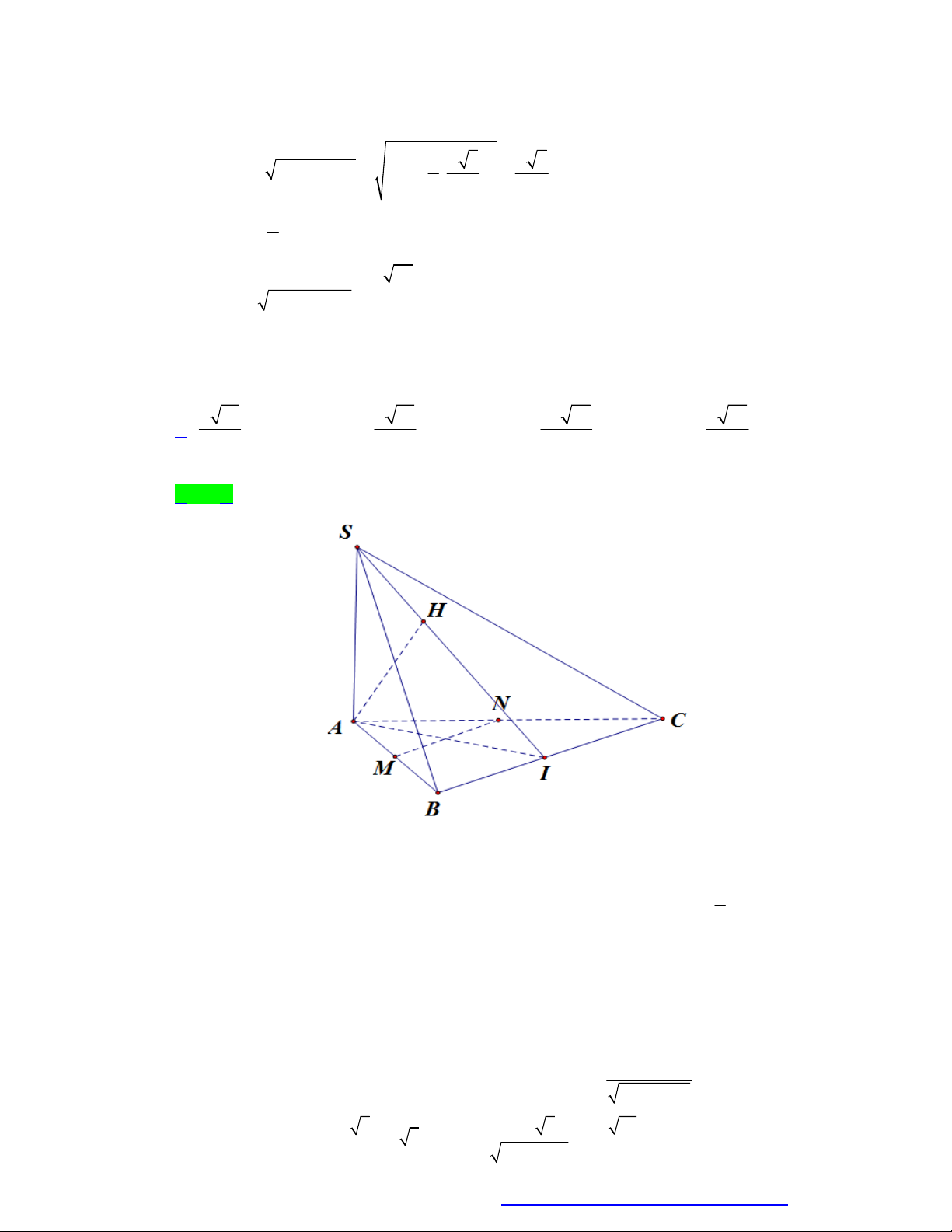
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , (SAC)   ABC  , AB  3a , 
BC  5a . Biết rằng SA  2a 3 và 0
SAC  30 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng : 3 17 6 7 3 7 12 A. a . B. a . C. a . D. a . 4 7 14 5 Câu 8.
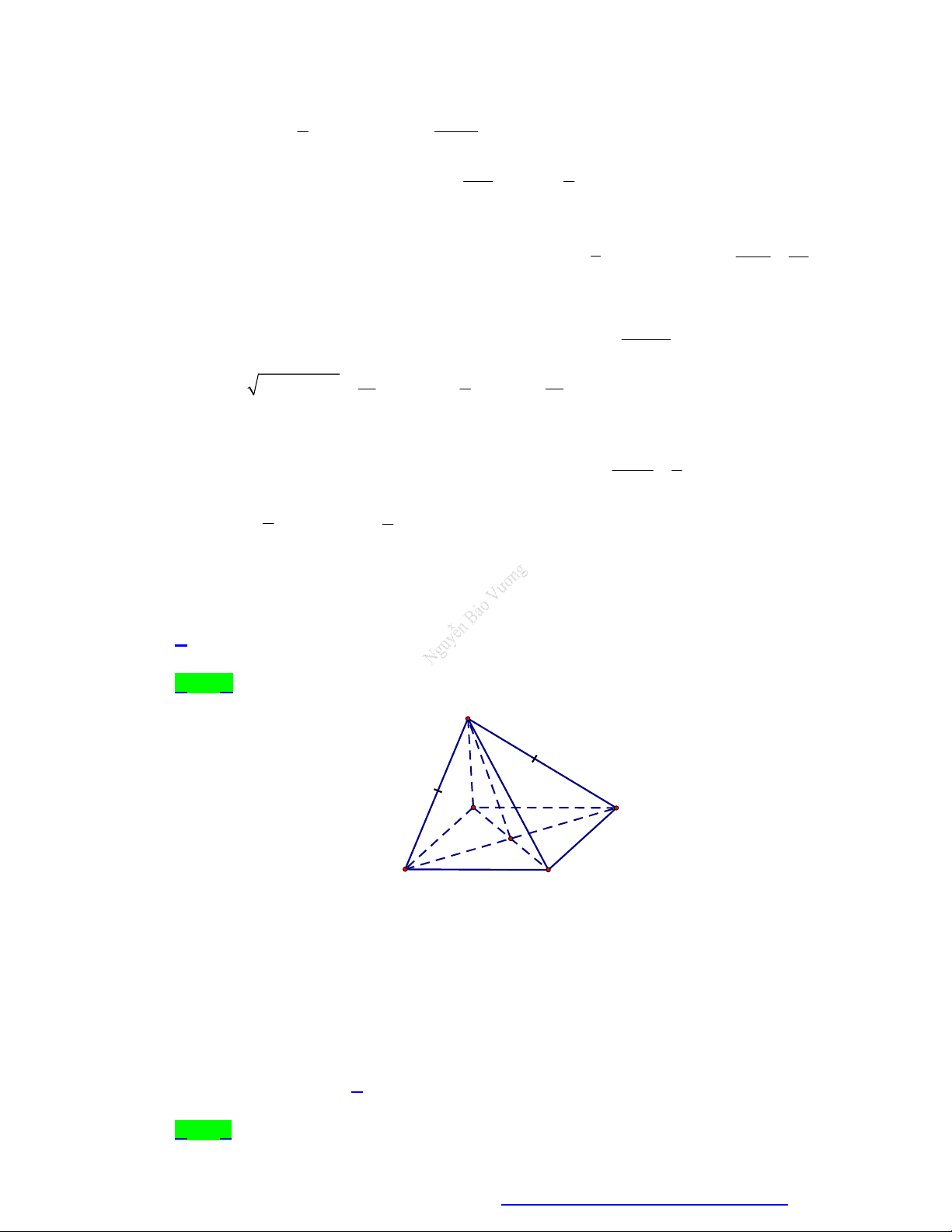
Cho tứ diện đều ABCD có cạnh bằng a . Gọi M là trung điểm CD . Khoảng cách giữa AC và BM là a 154 a a 22 a 2 A. . B. . C. . D. . 28 2 11 3 Câu 9.
Cho hình chóp S.ABC , có đáy là tam giác đều cạnh 2a , SA  2a , SA vuông góc với mặt phẳng
đáy ( minh họa như hình vẽ ). Gọi M , N lần lượt là trung điểm của AB, AC . Khoảng cách giữa
hai đường thẳng MN và SC bằng. a 21 a 21 2a 57 a 57 A. . B. . C. . D. . 7 14 19 19
Câu 10. Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB  2a, AD  4a, SA  ( ABCD) ,
SA  2a 15 . Gọi M là trung điểm của BC, N là điểm nằm trên cạnh AD sao cho AD  4DN .
Khoảng cách giữa MN và SB là 4a 285 2a 285 a 285 2a 285 A. B. C. D. 19 15 19 19
Câu 11. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a , SA vuông góc với mặt phẳng đáy và
SA a . Gọi M là trung điểm AB. Khoảng cách giữa hai đường thẳng SB và DM bằng 2 21 21 4 21 A. a B. a C. a D. a 21 8 21
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
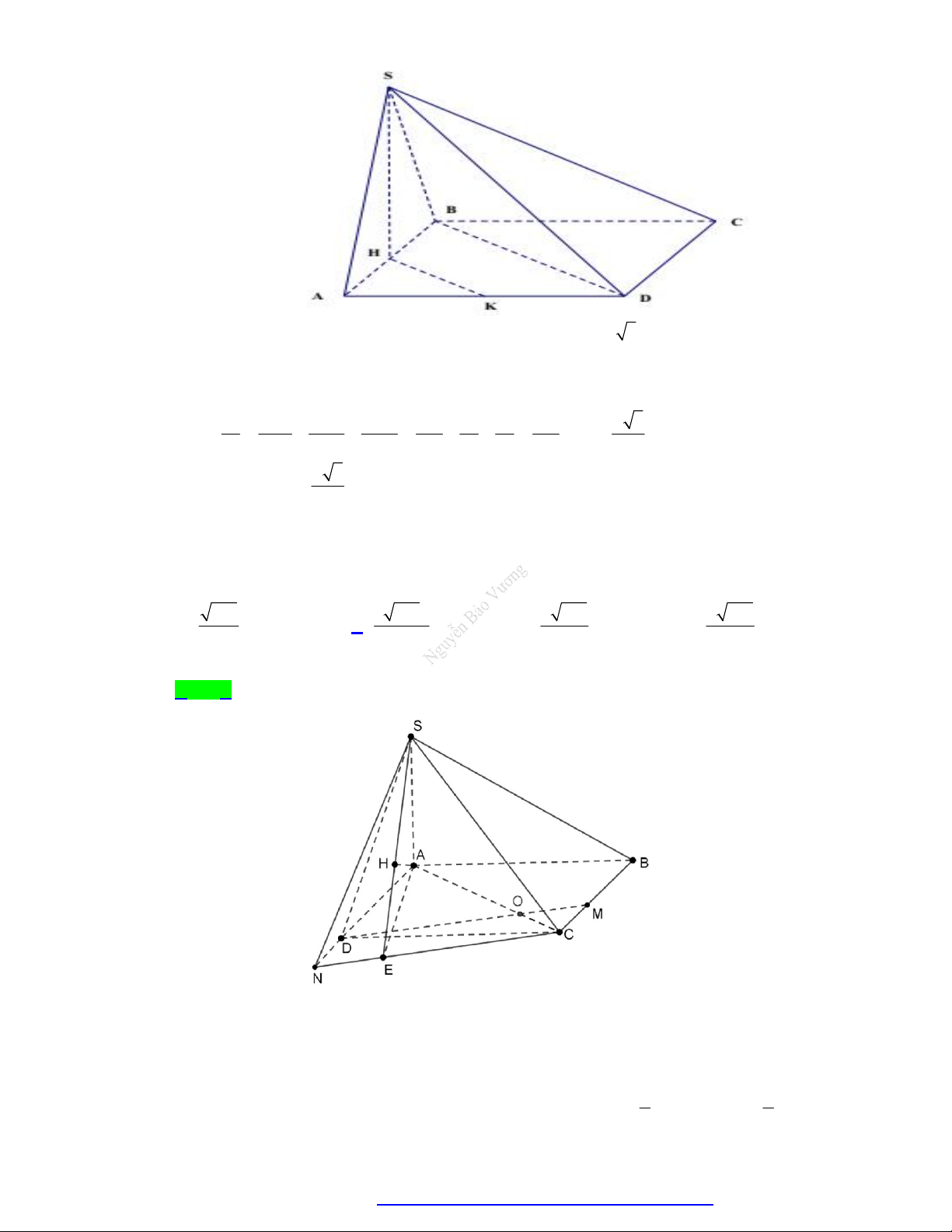
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 a 17
Câu 12. Cho hình chóp đáy là hình vuông cạnh a, SD
, hình chiếu vuông góc của S lên mặt phẳng 2
ABCD trung điểm H của đoạn AB . Gọi K là trung điểm của đoạn AD . Tính khoảng cách
giữa hai đường thẳng HK và SD theo a . a 3 a 286 5a 3 a 39 A. B. C. D. 5 26 3 3
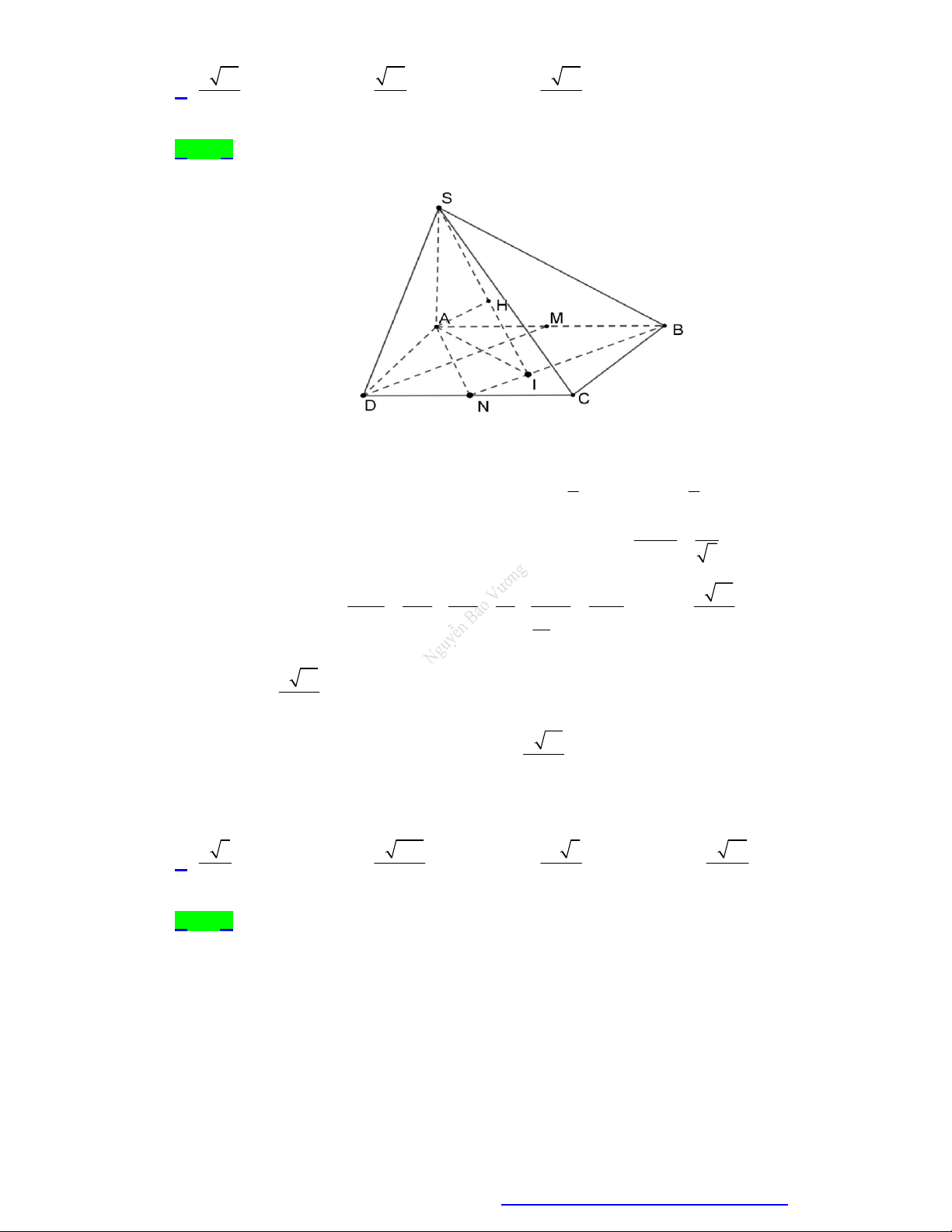
Câu 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và   
SA a . Gọi M là điểm thào mãn MB  2MC  0 . Khoảng cách giữa hai đường thẳng SC và DM bằng 154 3 154a 6 154 2 154 A. a . B. . C. a . D. a . 77 154 77 77
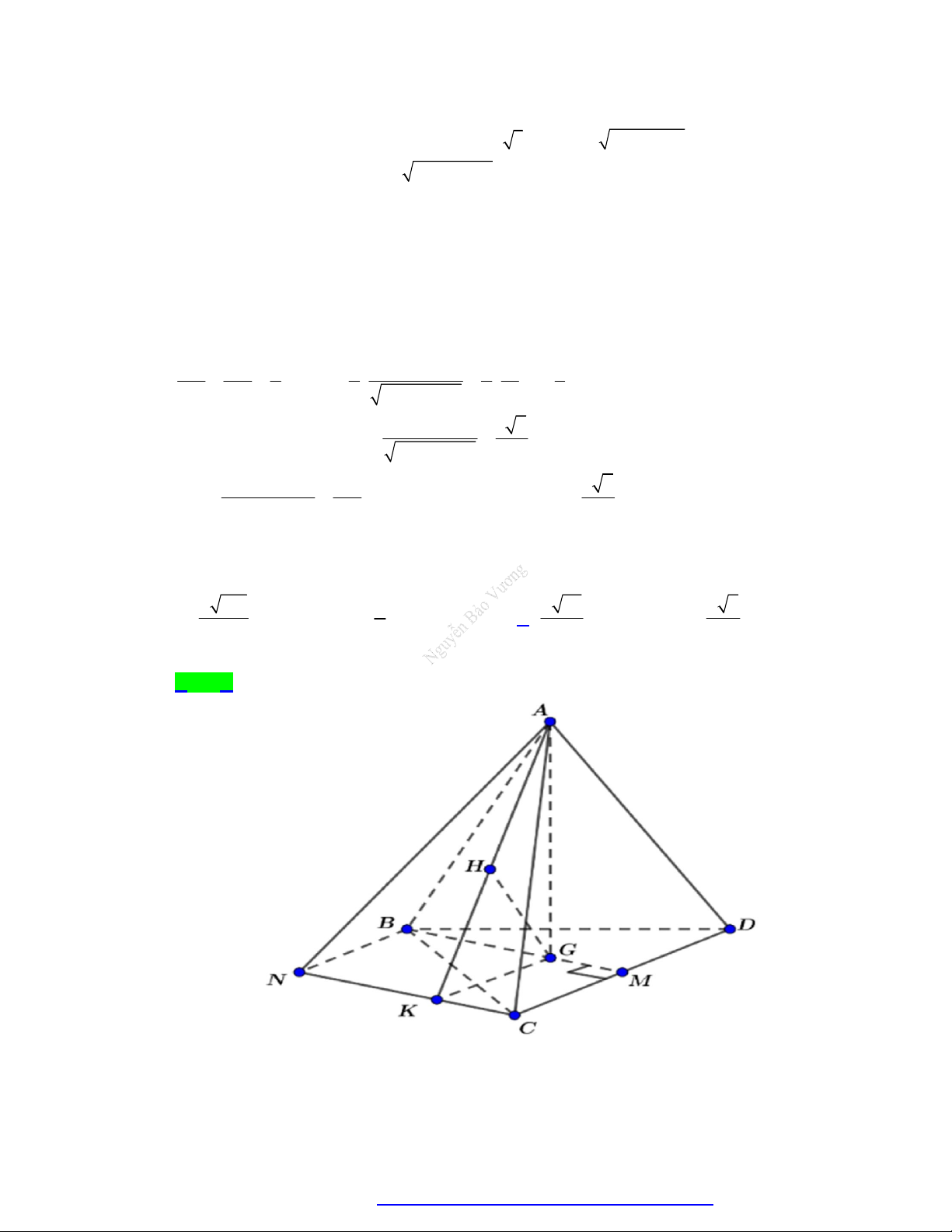
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung
điểm của các cạnh AB và AD ; H là giao điểm của CN với DM . Biết SH vuông góc với mặt
phẳng  ABCD và SH a 3 .Tính khoảng cách giữa hai đường thẳng DM và SC theo a. 2 3a 21a a 57 3 3a A. . B. . C. . D. . 19 7 6 19
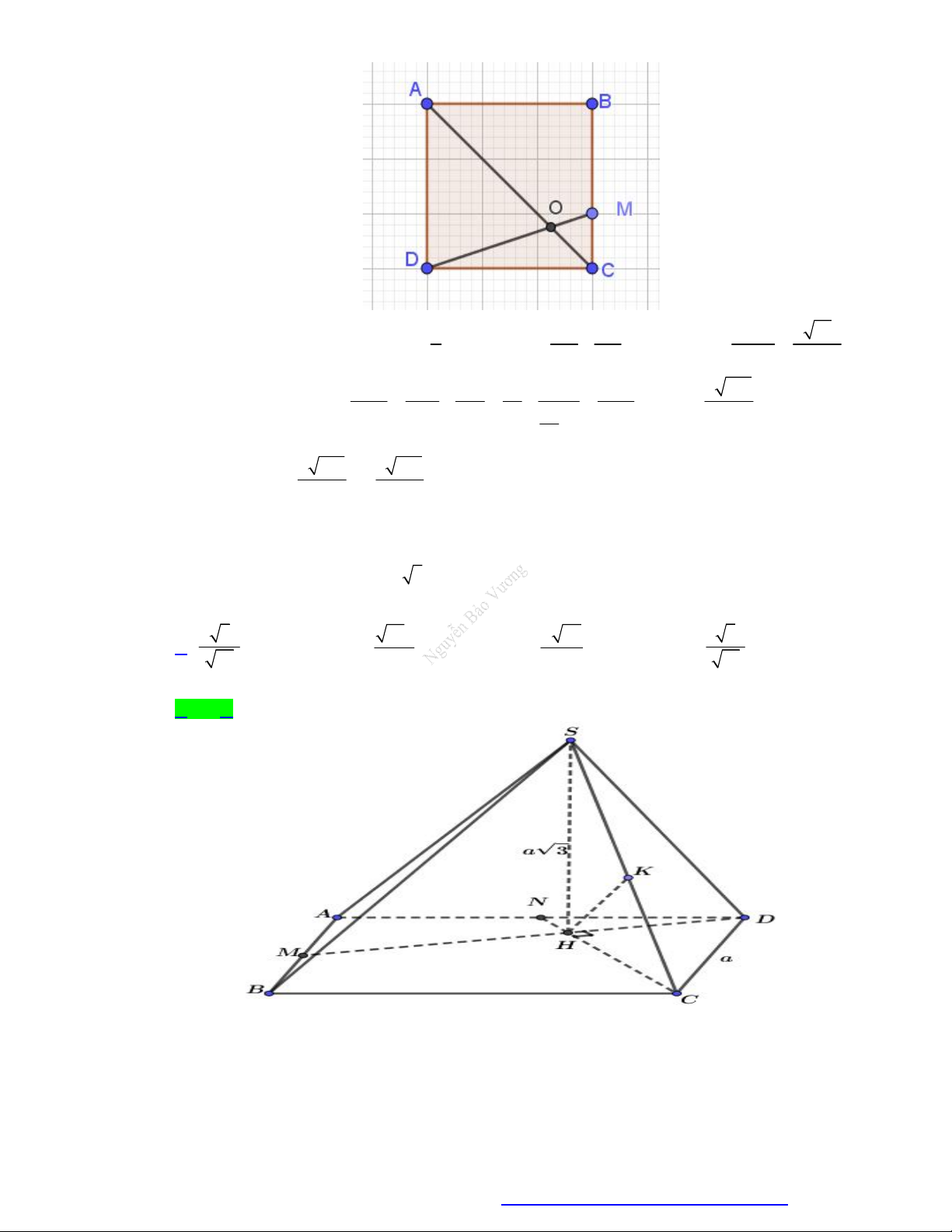
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh bên SA a 5 , mặt bên
SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách gữa
hai đường thẳng AD và SC bằng: S D A B C 2a 5 4a 5 a 15 2a 15 A. . B. . C. . D. . 5 5 5 5
Câu 16. Cho lăng trụ đứng AB . C A
B C có đáy là tam giác vuông tại A , AB a , BC  2a . Gọi
M , N , P lầ lượt là trung điểm của AC , CC , 
A B và H là hình chiếu của A lên BC . Tính
khoảng cách giữa MP và NH . a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 2 2
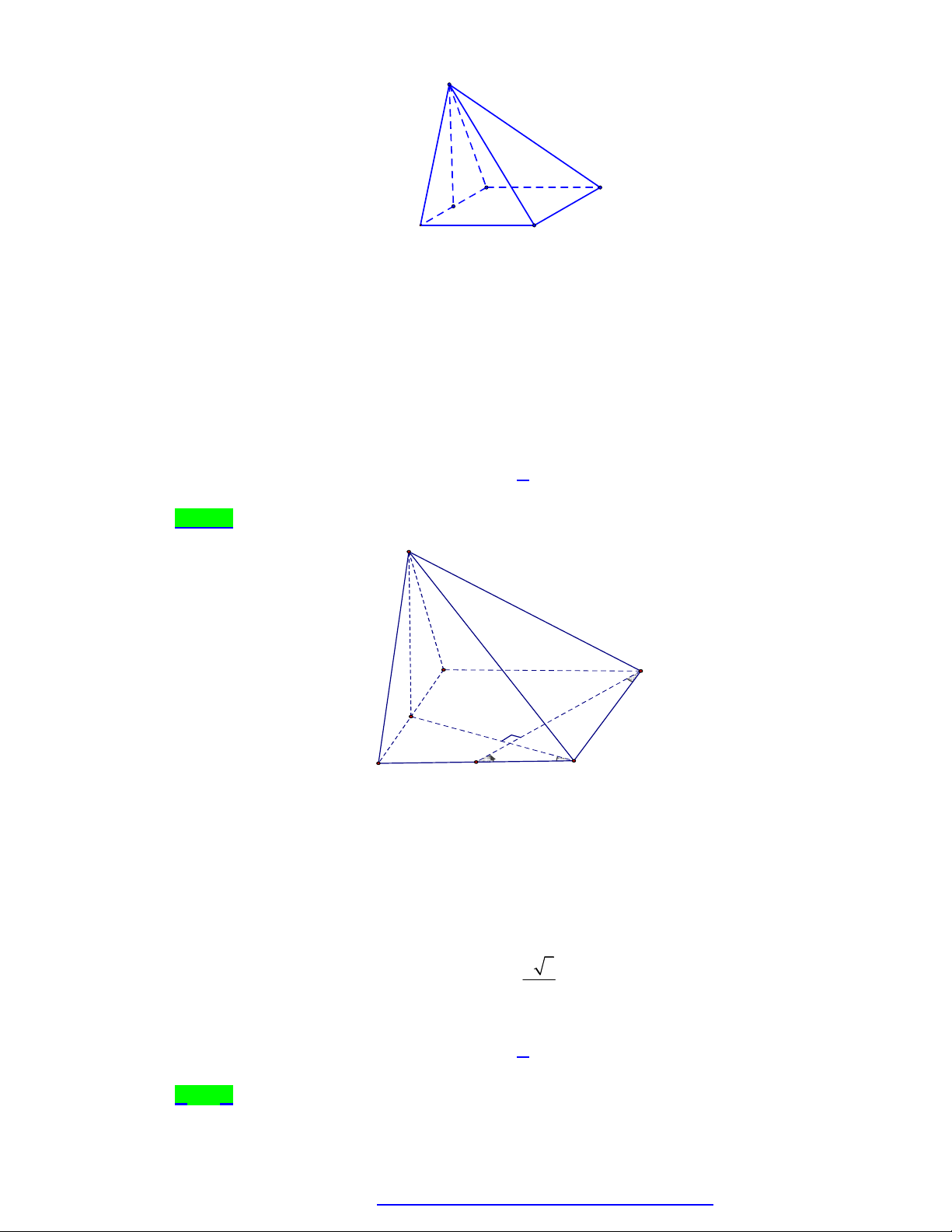
Câu 17. Cho hình chóp S.ABC đều. Gọi G là trọng tâm của tam giác ABC sao cho SG AB a .
Khoảng cách giữa hai đường thẳng SA và CG bằng a a 5 a 3 A. . B. a . C. . D. . 2 5 3
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là vuông cạnh a , SA  2a và vuông góc với  ABCD .
Gọi M là trung điểm của SD . Tính khoảng cách d giữa hai đường thẳng SB và CM . 2a 3 3a 2a a A. d  . B. d  . C. d  . D. d  . 3 2 3 3
Câu 19. Cho hình chóp S.ABCD có đáy là hình chữ nhật. Tam giác SAB vuông cân tại A và nằm trong
mặt phẳng vuông góc với đáy và SB  4 2 . Gọi M là trung điểm của cạnh SD . Tính khoảng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
cách l từ điểm M đến mặt phẳng SBC 2 A. l  2 . B. l  2 2 . C. l  2 . D. l  . 2
Câu 20. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a ,
BAD  60 , SB a và mặt phẳng SBA và
mặt phẳng  SBC  cùng vuông góc với mặt phẳng đáy. Khoảng cách từ B SCD đến mặt phẳng   bằng 21a 5a 21a 15a A. . B. . C. . D. . 7 7 3 3 
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 2a 3 , góc BAD bằng 120 .
Hai mặt phẳng SAB và  SAD cùng vuông góc với đáy. Góc gữa mặt phẳng  SBC  và
ABCD bằng 45 . Khoảng cách h từ A đến mặt phẳng SBC là 2a 2 3a 2
A. h  2a 2. B. h  . C. h  .
D. h a 3. 3 2 
Câu 22. Cho hình chóp S.ABCD có đáy là hình bình hành, ADC  30 , AB a , AD  2a , SA a và SA
vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng  SCD bằng a 3 a 2 a 2 a A. . B. . C. . D. . 2 3 2 2
Câu 23. Cho hình chóp S.ABCD có đáy là hình bình hành, AB a , AD a 3 , AC  2a , SA  2a và SA
vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng  SCD bằng a 84 a 2 A. a 3 . B. a 2 . C. . D. . 7 2 
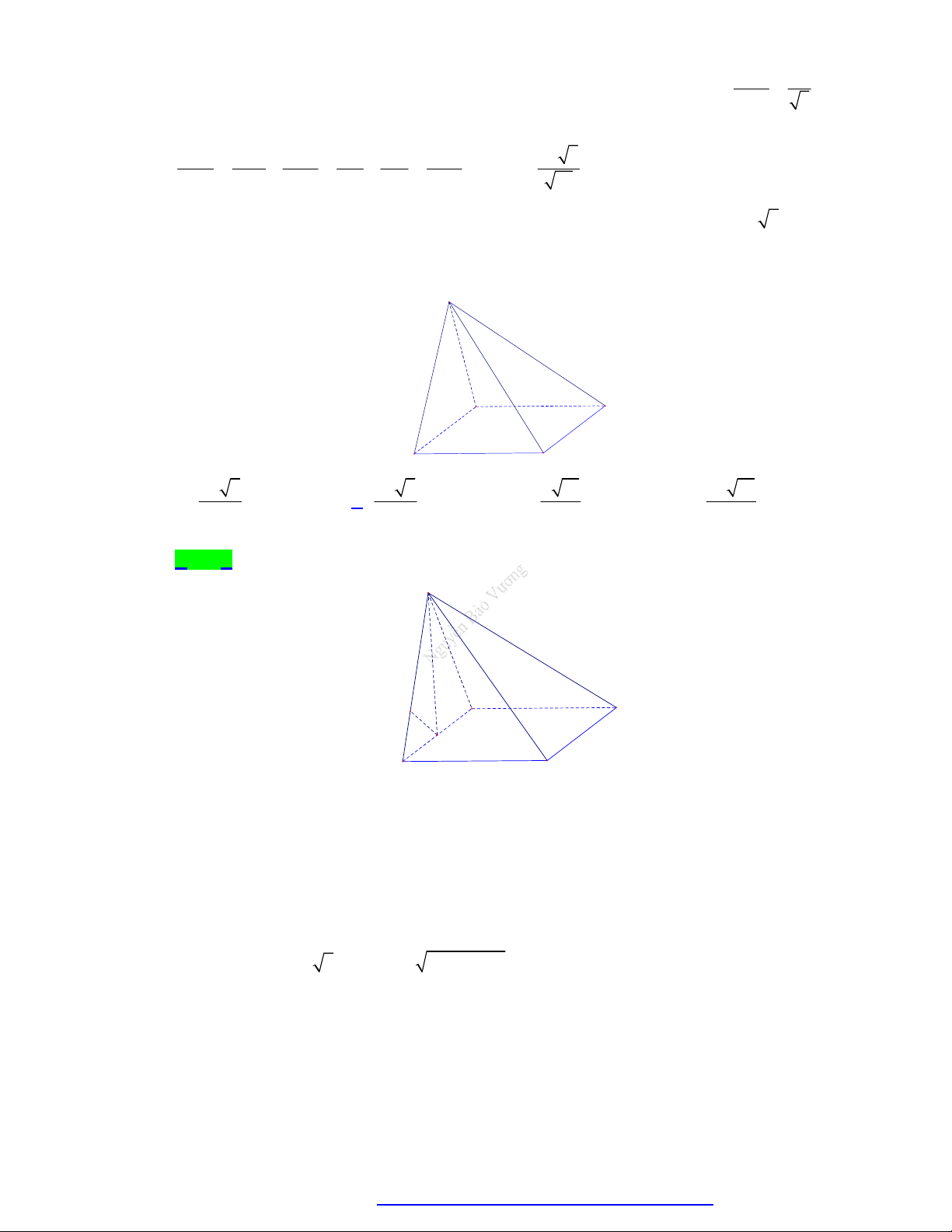
Câu 24. Hình chóp S.ABCD có đáy là hình thoi tâm O cạnh 2a , ABC  60 , hình chiếu vuông góc của
S lên  ABCD trùng với trung điểm I của BO , SI a 3 . Khoảng cách từ B đến mặt phẳng SCD bằng 3a 3 2a 3 a 3 4a 3 A. . B. . C. . D. . 5 5 5 5
Câu 25. Cho hình chóp S.ABCD có đáy là hình thang cân đáy AD có AD  2 AB  2BC  2a , SA a và
SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng  SCD bằng a 3 a 3 a 3 A. . B. . C. . D. 2a . 2 3 4
-------------------- HẾT --------------------
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 7 GÓC - KHOẢNG CÁCH A. GÓC TRONG KHÔNG GIAN a
Góc giữa đường thẳng a và đường thẳng b
Phương pháp 1. Sử dụng song song, tức dựng đường thẳng c b và c cắt . a c  
Khi đó (a;b)  (a;c)   như hình vẽ. b
Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số sin, côsin để tìm góc .     a.b
Phương pháp 2. Sử dụng tích vô hướng, nghĩa là cos(a;b)  cos(a;b )    cos . a . b
Khi đó, ta cần chèn điểm phù hợp để tính tích vô hướng.
Phương pháp 3. Ghép vào hệ trục tọa độ Oxyz.
Lưu ý: Góc giữa hai đường thẳng là góc nhọn, còn góc giữa hai véctơ là góc nhọn hoặc góc tù. Nghĩa là  
nếu tính (a;b)   90 thì góc giữa a, b là ,
 còn nếu tính (a;b)   90 thì góc giữa hai
đường thẳng (a;b)  180  .
Góc giữa đường thẳng AB và mặt phẳng (P )
Cần nhớ: “Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó lên mặt phẳng”. B
Phương pháp 1. Sử dụng hình học 11.
B.1. Tìm AB  (P )  { } A (1) A
B.2. Tìm hình chiếu của B lên mặt phẳng (P). P H
Đặt câu hỏi và trả lời: “Đường nào qua B và vuông góc với (P) ? “(có sẵn hoặc dựng thêm)
Trả lời: BH  (P ) tại H (2)
Từ (1),(2), suy ra AH là hình chiếu của AB lên mặt phẳng (P ).
Do đó góc giữa đường thẳng AB và mp(P) là góc giữa AB và AH, chính là góc BAH .
B.3. Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số côsin hoặc định lí hàm sin trong
tam giác thường để suy ra góc BAH .
Phương pháp 2. Ghép vào hệ trục tọa độ Oxyz. (P)
Góc giữa mặt phẳng (P) và mặt phẳng (Q). d1
Phương pháp 1. Dựa vào định nghĩa α u (
 P)  (Q)  u    d Ta có: u
  d  (P)  ((P),(Q))  (d ,d )  . (Q) 2 1 1 2
u  d (Q)  2 
Phhương pháp 2. Tìm hai đường thẳng d và d lần lượt vuông góc với mặt phẳng (P) và mặt phẳng 1 2
(Q). Góc giữa hai mặt phẳng là góc giữa d và d . 1 2
Phương pháp 3. Sử dụng công thức hình chiếu S   S. cos .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 d ,( )
Phương pháp 4. Trong trường hợp quá khó, nên sử dụng công thức sin A Q     d( ,Au) 
Trong đó   ((P),(Q)), A  (P) và (P)  (Q)  u là giao tuyến của (P) và (Q).
Phương pháp 5. Ghép vào hệ trục tọa độ Oxyz.
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và SA
2a . Góc giữa SC và mặt phẳng (ABCD) bằng S A D B C A. 0 45 . B. 0 60 . C. 0 30 . D. 0 90 . Lời giải Chọn C  
Ta có SA  (ABCD) nên ta có (SC,(ABCD))  SCA SA 2a 1  0 tan SCA     SCA  30 AC 3a. 2 3 Câu 2.
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, SA a 2, tam giác ABC
vuông cân tại B và AC  2a (minh họa nhứ hình bên). Góc giữa đường thẳng SB và mặt phẳng  ABC bằng A. 30. B. 45. C. 60. D. 90. Lời giải
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Chọn B
SB   ABC   B Ta có
  AB là hình chiếu của SB trên mặt phẳng  ABC
SA   ABC   
 SB ABC   ,  SBA
Do tam giác ABC vuông cân tại BAB BC AC AB  2 2 2 2 2 2 2 2 2a 2
AB 4a ABa 2.
Xét tam giác vuông SAB vuông tại ,
A có SA AB a 2  SAB vuông cân tại 
A SBA  45. Câu 3.
Cho hình chóp S.ABC có SB vuông góc với mặt phẳng  ABC , SB a 3 , tam giác
ABC vuông tại A, AB a và AC  2a . Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 45 . B. 60 . C. 30 . D. 90 . Lời giải Chọn A CA AB Ta có
  CA   SAB . CA SB
Do đó góc giữa đường thẳng SC và mặt phẳng  SAB là  CSA .  AC 2a  Ta có 2 2 2 2
SA SB AB  3a a  2a ; tan CSA  
 1  CSA  45 . SA 2a Câu 4.
Cho hình chóp đều S.ABCD có AB a 2 , SB  2a . Góc giữa đường thẳng SA và mặt
phẳng SBD bằng A. 45 . B. 60 . C. 30 . D. 90 . Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Gọi O AC BD . Vì S.ABCD là hình chóp đều nên SO   ABCD .
Do đó AO  SBD  góc giữa đường thẳng SA và mặt phẳng SBD là  ASO .  AO a 1  Ta có SA  2 ;
a AC  2a AO a ; sin ASO     ASO  30 . SA 2a 2 Câu 5.
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC , SB a 6 , tam giác ABC
vuông cân tại C , AB  2a . Góc giữa đường thẳng SC và mặt phẳng SAB bằng A. 30 . B. 60 . C. 45 . D. 90 . Lời giải Chọn A
Gọi H là trung điểm của AB . Vì A
BC cân tại C CH AB CH  SAB .
Do đó hình chiếu vuông góc của C lên mặt phẳng SAB là H .
 góc giữa SC và mặt phẳng SAB bằng góc  CSH . Ta có A
BC vuông cân tại C , AB  2a CA CB a 2 ; CH a ; 2 2 2 2 SA SB AB
6a  4a a 2 ; 2 2 2 2 SC SA AC
2a  2a  2a . Xét SH
C vuông tại H có 
SC  2CH CSH  30 . Câu 6.
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng  ABCD , ABCD là hình chữ nhật,
AB a 2, BC  2a , SA  3a . Gọi M là trung điểm của BC . Tính góc giữa đường thẳng SM và
mặt phẳng  ABCD . A. 30 . B. 60 . C. 45 . D. 120 . Lời giải Chọn B
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Vì SA   ABCD nên góc giữa đường thẳng SM và mặt phẳng  ABCD là góc  SMA . BC Ta có 2 2 2 2 BM   a; AM AB BM
2a a a 3 ; 2  SA 3a  tan SMA    3  SMA  60. AM a 3 Câu 7.
Cho tứ diện đều ABCD có cạnh bằng 2a . Gọi  là góc giữa đường thẳng AB và mặt phẳng
BCD . Tính cos . 3 6 3 2 A. cos  . B. cos  . C. cos  . D. cos  . 6 3 3 3 Lời giải Chọn C
Gọi O là trọng tâm tam giác BCD . Vì ABCD là tứ diện đều nên AO   BCD .
Do đó góc giữa đường thẳng AB và mặt phẳng  ABC bằng  ABO   . 2a 3 3 2 2a 3 BO 3
Ta có BM BC.
a 3  BO BM  ;  3 cos  cos ABO    . 2 3 3 AB 2a 3 Câu 8.
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, tam giác ABC vuông cân tại B và
AC  2a (minh họa như hình bên). Góc giữa đường thẳng SB và mặt phẳng  ABC  bằng
60. Tính độ dài cạnh bên SA .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 a 6 A. . B. a 6. C. a 3. D. 2a 3. 3 Lời giải Chọn B
SB   ABC   B Ta có
  AB là hình chiếu của SB trên  ABC ,
SA   ABC   
SB ABC       SB AB  0 , ,  SBA  60
Mà tam giác ABC vuông cân tại B và AC  2a AB a 2
Khi đó xét trong tam giác vuông SAB suy ra 0
SA AB tan 60  a 6 Câu 9.
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  2a , AD a 2 , SA vuông góc với
mặt phẳng đáy và SA a 2 . Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 0 45 . B. 0 30 . C. 0 60 . D. 0 90 . Lời giải Chọn B
Vì SA   ABCD nên AC là hình chiếu của SC trên mặt phẳng  ABCD 
Do đó góc giữa SC và mặt phẳng  ABCD là SCA
Đáy ABCD là hình chữ nhật có AB  2a , BC AD a 2 nên 2 2 2 2
AC AB BC  4a  2a a 6
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020SA a 2 3 
Trong tam giác vuông SAC : tan SCA     SCA  30 . AC a 6 3
Vậy góc giữa đường thẳng SC và mặt phẳng ( ABCD) bằng 30 .
Câu 10. Cho chóp đều S.ABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a (minh họa như hình bên). Gọi
 là góc giữa giữa cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng? 14 3 14 A. tan   . B. tan   . C. 0   45 . tan   . 7 2 D. 2 Lời giải Chọn D
Gọi O AC BD SO   ABCD  AO là hình chiếu của SA trên mp ABCD
SA ABCD      SA AO  , ,  SAO  
Xét trong tam giác vuông SAO ta có 1 1 SO 14
SA  3a, AO AC  2 .
a 2  a 2  SO a 7  tan    . 2 2 AO 2
Câu 11. Cho lăng trụ đứng AB .
C A' B'C ' có đáy là A
BC vuông cân tại B , AC  2 2a (minh họa như
hình bên). Góc giữa đường thẳng A ' B và mặt phẳng  ABC  bằng 60. Tính độ dài cạnh bên của hình lăng trụ. 2a 3 A. .
B. 2a 3.
C. 2a 6. D. 2 . a 3 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
A ' B   ABC   B Ta có
  AB là hình chiếu của A ' B trên  ABC .
A ' A   ABC   
A B ABC        A B AB  0 ' , ' ,
A ' BA  60
Khi đó xét trong tam giác vuông A ' BA ta có: ACA ' A 0 AB
 2a, tan A' BA
A' A AB tan 60  2a 3. 2 AB
Câu 12. Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng a , 0
ABC  60 , SA vuông góc với mặt
phẳng đáy và SA a 3 . Gọi  là góc giữa đường thẳng SC và mặt phẳng  ABCD . Tính tan  6 1 A. 3 . B. 1. C. . D. . 2 3 Lời giải Chọn A
Vì SA   ABCD nên AC là hình chiếu của SC trên mặt phẳng  ABCD 
Do đó góc giữa SC và mặt phẳng  ABCD là SCA   
Đáy ABCD là hình thoi có 0
ABC  60 nên ABC đều  AC AB BC a SA a 3
Xét SAC vuông tại A: tan     3 AC a
Câu 13. Cho chóp S.ABCD có đáy là hình vuông tâm O cạnh bằng
2a , cạnh bên SA vuông góc với
mặt phẳng  ABCD, SA a 3. Gọi  góc giữa đường thẳng SO và mặt phẳng  ABCD . Mệnh đề nào sau đây đúng?
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. tan   6. B.   45 .  C.   60 .  D.   90 .  Lời giải Chọn C
SO   ABCD   O Ta có
  AO là hình chiếu của SO trên  ABCD .
SA   ABCD  
SO ABCD      SO AO  , ,  SOA .
Khi đó xét trong tam giác vuông SOA ta có: 1 1  SA  0 AO AC  2 .
a 2  a; SA a 3  tan SOA   3  SOA  60 . 2 2 AO
Câu 14. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 2 . Gọi M là trung điểm của AB,
SM   ABCD và SM a 5 . Gọi  là góc giữa đường thẳng SC và mặt phẳng  ABCD . Tính tan  30 22 5 A. . B. 2 . C. . D. . 3 4 2 Lời giải Chọn B
Vì SM   ABCD nên MC là hình chiếu của SC trên mặt phẳng  ABCD 
Do đó góc giữa SC và mặt phẳng  ABCD là SCM   AB a 2 a 10
Đáy ABCD là hình vuông cạnh a 2 nên BM   2 2
MC BC BM  2 2 2 SM a 5
Xét SMC vuông tại M: tan     2 . MC a 10 2
Câu 15. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC, SA a 3, tam giác ABC đều
(minh họa như hình bên). Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng 30 .  Tính thể tích
khối chóp S.ABC .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 3 9a 3 27a 3 a 3 81a A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn A
SC   ABC   C  Ta có
  AB là hình chiếu của SC trên  ABC ,
SA   ABC   
SC ABC       SC AB  0 , ,  SCA  30 . SA
Khi đó xét trong tam giác vuông SAC ta có 0 tan 30   AC  3a . ACa2 2 2 3 3 3 9a 3 1 9a 3 9a
Tam giác ABC đều nên S    Va 3.  . ABC 4 4 SABC 3 4 4
Câu 16. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Cạnh bên SA vuông
góc với đáy và SA  2a .Góc giữa đường thẳng SB và mặt phẳng SAC bằng: A. 45 .  B. 30 .  C. 60. D. 90 .  Lời giải Chọn B
SB  SAC   S  Ta có
  SO là hình chiếu của S B trên  ABCD,
BO   SAC   
SB SAC       SB SO  , ,  BSO .
Khi đó xét trong tam giác vuông SBO ta có: 1 1 BO BD  2 .
a 2  a 2; SA  2a SO a 6 . 2 2
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020BO 1  0  tan BSO    BSO  30 SO 3
Câu 17. Cho hình hộp chữ nhật ABC . D AB CD
  có đáy ABCD là hình vuông, AC  a 2 . Gọi  P là
mặt phẳng qua AC cắt BB ,
DD lần lượt tại M , N sao cho tam giác AMN cân tại A có
MN a . Tính cos với    P, ABCD   . 2 1 1 3 A. . B. . C. . D. . 2 2 3 3 Lời giải Chọn A Ta có AMC N
 là hình bình hành, mà tam giác AMN cân tại A nên MN AC . Ta có  ' '
BDD B  cắt ba mặt phẳng  ABCD ,  ' ' ' ' A B C D  ,  '
AMC N  lần lượt theo ba giao tuyến ' '
BD / /B D / /MN .
Hai mặt phẳng  P và  ABCD có điểm chung A và lần lượt chứa hai đường thẳng song song
MN , BD nên giao tuyến của chúng là đường thẳng d đi qua A và song song với MN, BD .
Trên hai mặt phẳng  P và  ABCD lần lượt có hai đường thẳng AC và AC cùng vuông góc
với d nên góc giữa hai mặt phẳng  P và  ABCD chính là góc giữa AC và AC , bằng góc 
CAC . Xét tam giác '
C CA vuông tại C có: AC BD MN a 2 cos      ACACACa 2 2 Cách 2:
Theo chứng minh ở trên thì MN //BD và MN BD a . Đa giác AMC N
 nằm trên mặt phẳng P có hình chiếu trên mặt  ABCD là hình vuông ABCD nên: 2  BD  2 S   AB ABCD  2  2 cos     . S 1 1 2 AMC NAC .MN AC .MN 2 2
Câu 18. Cho hình hộp chữ nhật ABC . D AB CD
  có các cạnh AB  2, AD  3; AA  4 . Góc giữa hai mặt phẳng  AB D
  và  AC D
  là  . Tính giá trị gần đúng của góc  ? A. 45, 2 . B. 38,1 . C. 53, 4 . D. 61, 6 . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn D
Cách 1: Hai mặt phẳng  AB D   và  A CD
  có giao tuyến là EF như hình vẽ.
Do EF //AB mà A D     A A
BB nên A D    AB ' '  EF / / A D
Từ A kẻ vuông góc lên giao tuyến EF tại H thì ' A H EF EF   A DH
   EF D H
. Khi đó, góc giữa hai mặt phẳng cần tìm chính là góc giữa hai đường thẳng AH  và D H  . D B   13 D A  5 B A  Tam giác '
D EF lần lượt có D E    , D F    , EF   5 . 2 2 2 2 2 61 2S 305
Theo Hê-rông ta có: S  . Suy ra DEF D H    . ' D EF 4 EF 10 Dễ thấy ' '
A EF  D EF ' '
A H D H .  2 2 2
HA  HD  A D   29 Tam giác D AH  có: cos A HD    . 2HA .HD 61   Do đó A H
D 118, 4 hay  A H  , D H
  180118,4  61,6.
Cách 2: Gắn hình hộp chữ nhật ABC . D A BCD
  vào hệ trục tọa độ như hình vẽ. Khi đó  A 0;0;  0 , B2;0;  0 , D0;3;  0 , C2;3; 
0 , A0;0;4, B2;0;4, D0;3;4, C2;3;4 .    
Gọi n là véc tơ pháp tuyến của  AB D   . Có     . 1 n AB ; AD  12;  8; 6 1      
 
Gọi n là véc tơ pháp tuyến của  A CD   . Có       . 2 n
A C ; A D  12; 8; 6 2    
Gọi  là góc giữa hai mặt phẳng  AB D   và  A CD  
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  n n 29 1 2
cos    
. Vậy giá trị gần đúng của góc  là 61, 6 . n n 61 1 2 Cách 3.
Do hai mặt phẳng  AB D   và  A CD
  chứa hai đường AB và C D  song song với nhau nên
giao tuyến của chúng song song hai đường đó. Kẻ A H
AB , H AB, dựng hình bình hành A H
KD có tâm I như hình vẽ. Do A D     A A
BB nên A D
   AB suy ra AB   A H
KD góc giữa hai mặt phẳng  AB D   và  A CD
  là góc giữa AK  và D H  . 1 1 1 1 1 5
Trong tam giác vuông AAB   có AH  là đường cao nên      . 2 2 2 AH ABAA 4 16 16 4 Vậy A H   . 5 29 Xét tam giác A I
H có cos I  cos A  H    cos A cos H  sin Asin H  . 61
Vậy góc giữa hai mặt phẳng  AB D   và  A CD
  gần đúng bằng 61, 6 .
Câu 19. Cho hình hộp chữ nhật ABC . D AB CD
  có các cạnh AB  2, AD  3; AA  4 . Góc giữa hai
mặt phẳng  BC ' D và  AC D
  là  . Tính giá trị gần đúng của góc  ? A. 45, 2 . B. 38,1 . C. 53, 4 . D. 61, 6.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn D z A' D' 4 B' C' 3 A D y B x 2 C
Dựng hệ tọa độ Oxyz như hình vẽ, ta có A0;0;0, B 2;0;0, D 0;3;0 và
A0;0;4,C2;3; 4 .    
BC  0;3; 4, BD  2;3;0, AC  2;3;0, A D   0;3;  4   
Véc tơ pháp tuyến của  BC D
  là: n  BC , BD  12; 8;6 1    
  
Véc tơ pháp tuyến của  A CD
  là: n   A C  ,  AD  12  ;8; 6 . 2     Ta có:   29
cos  cos n , n     61, 6 1 2  61
Câu 20. Cho tứ diện ABCD có BD  2 . Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10 .
Biết thể tích khối tứ diện ABCD bằng 16 . Tính số đo góc giữa hai mặt phẳng  ABD vàBCD.  4   4   4   4  A. arccos   .
B. arcsin   .
C. arccos   . D. arcsin   .  15   5   5   15  Lời giải Chọn B 1 3V 24
Gọi H là hình chiếu của A xuống  BCD . Ta có VAH.SAH   . ABCD 3 BCD S 5 BCD
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi K là hình chiếu của A xuống BD , dễ thấy HK BD . Vậy  ABD  BCD     ,  AKH 1 2S Mặt khác SAK.BD ABDAK   6 . ABD 2 BD AH  
Do đó  ABD  BCD     4 ,  AKH  arcsin  arcsin   . AK  5  Cách khác 1 3V 24
Gọi H là hình chiếu của A xuống  BCD . Ta có VAH.SAH   . ABCD 3 BCD S 5 BCD Ta có: S  6 . ABD  2S
Gọi K là hình chiếu của A xuống BD . Do BD  2 nên ABD SK   6 . BD 18 1 18 Có 2 2
KH SK AH   SHK.BD  . 5 HBD 2 5
Gọi  là góc giữa mặt phẳng  ABD và  BCD . S 3 Vì H
BD là hình chiếu của A
BD trên  BCD nên cos HBD     . S 5 ABD 4  4  Vậy sin     arcsin   . 5  5 
Câu 21. Cho hình chóp S.ABCD đáy ABCD là hình thoi, SA SC . Góc giữa hai mặt phẳng SBD và
ABCD bằng? A. 90 . B. 30 . C. 60 . D. 45 . Lời giải Chọn A S D C O A B
Gọi O là tâm của hình thoi ABCD .  AC BD Ta có 
AC   SBD   ABCD   SBD . AC SO
Vậy góc giữa hai mặt phẳng  SBD và  ABCD bằng 90 .
Câu 22. Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, tam giác SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng  SAB và  SAD bằng? A. 30 . B. 90 . C. 60 . D. 45 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 S D A H B C
Gọi H là trung điểm của AB SH   ABCD .  AD AB Ta có 
AD   SAB   SAD   SAB . AD AH
Vậy góc giữa hai mặt phẳng  SAB và SAD bằng 90 .
Câu 23. Cho hình vuông ABCD . Gọi S là điểm trong không gian sao cho SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi H và I lần lượt là trung điểm của AB và BC . Góc
giữa hai mặt phẳng SHC và SDI  bằng. A. 30 . B. 60 . C. 90 . D. 45 . Lời giải Chọn C S A D 1 H 1 1 B I C
Do H là trung điểm của AB SH   ABCD  DI SH .       Ta lại có: BCH CDI  .
c g.c  C D , mà D I  90  C I  90  DI HC 1 1 1 1 1 1
Khi đó DI   SHC   SDI   SHC
Vậy góc giữa hai mặt phẳng SHC và  SDI  bằng 90 .
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a . Đường thẳng SO a 3
vuông góc với mặt phẳng đáy  ABCD và SO
. Tính góc giữa hai mặt phẳng  SBC  và 2  ABCD . A. 30 . B. 45 . C. 60 . D. 90 . Lời giải Chọn C
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 S B A O Q D C
Gọi Q là trung điểm BC , suy ra OQ BC . BC OQ Ta có 
BC   SOQBC SO
Do đó SBC   ABCD    SQ OQ  , ,  . SQO SO
Tam giác vuông SOQ , có  tan SQO   3. OQ
Vậy mặt phẳng  SBC  hợp với mặt đáy  ABCD một góc 60 .
B. KHOẢNG CÁCH TRONG KHÔNG GIAN
Tính khoảng cách từ chân đường cao của hình chóp đến mặt bên của hình chóp.
Tính khoảng cách từ A đến mặt bên (SBC ) của hình chóp S.ABC có SA  (ABC )
B1. Xác định giao tuyến của mặt bên và mặt phẳng đáy (SBC )  (ABC )  BC. AH   BC
B2. Dựng hình 
AI  (SBC ). AI   SH  Suy ra d( ;
A (SBC ))  AI.
B3. Tính AI .
Các phương pháp quy về bài toán chân đường cao:
― Kẻ song song để dời điểm về chân đường vuông góc.
― Dùng tỉ số khoảng cách để dời về chân đường vuông góc.
― Tạo chân đường cao giả ( đường cao, khi mặt chứa chân). S
Tính khoảng cách giữa cạnh bên và cạnh thuộc mặt đáy.
Cho hình chóp S.ABCD có SA  (ABCD). Hãy tính khoảng
cách giữa cạnh bên SB và cạnh thuộc mặt đáy AC .
B1. Xác định giao điểm của cạnh bên SB và mặt phẳng đáy K
SB  (ABCD)  . B D A
B2. Qua giao điểm B, dựng đường thẳng d song song với
AC . Khi đó: d(AC,SB)  d(AC,(S , B d))  d( , A (S , B d)). H B C
Đây là bài toán tìm khoảng cách từ chân đến mặt bên. Cụ thể:
d(AC,SB)  d(AC,(S , B d))  d( , A (S , B d))  AK. d
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  2a , AC  4a , SA vuông góc với
mặt phẳng đáy và SA a (hình minh họa). Gọi M là trung điểm của AB . Khoảng cách giữa
hai đường thẳng SM và BC bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 2a 6a 3a a A. . B. . C. . D. . 3 3 3 2 Lời giải Chọn A
Gọi N là trung điểm của AC , ta có: MN //BC nên ta được BC // SMN  .
Do đó d BC, SM   d BC,SMN   d B,SMN   d  ,
A SMN   h . Tứ diện .
A SMN vuông tại A nên ta có: 1 1 1 1 1 1 1 9 2a         h  . 2 2 2 2 2 2 2 2 h AS AM AN a a 4a 4a 3 2a
Vậy d BC, SM   . 3 Câu 2.
Cho hình chóp S.ABCD có đáy là hình thang, AB  2a , AD DC CB a , SA vuông góc
với mặt phẳng đáy và SA  3a (minh họa như hình bên). Gọi M là trung điểm của AB .
Khoảng cách giữa hai đường thẳng SB và DM bằng
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 3a 3a 3 13a 6 13a A. . B. . C. . D. . 4 2 13 13 Lời giải Chọn A
Ta có M là trung điểm của AB .
Theo giả thiết suy ra ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB    ACB  90 ;  ABC  60    AC a 3 
Vì DM //BC DM // SBC  1 1
Do đó d DM , SB  d DM ,SBC   d M ,SBC   d  ,
A SBC  (vì MB AB ) 2 2
Kẻ AH SC . BC AC Ta lại có 
BC  SAC   AH BC . BC   SAAH SC Khi đó 
AH  SBC   d  ,
A SBC   AH . AH   BC
Xét tam giác SAC vuông tại A , ta có a 32 .3 . a AC SA 2 2 2 2 9a 2 3 AH     AH a . 2 2 AC SA
a 2  a2 4 3 3 2 1 1 3a
Vậy d DM , SB  d  ,
A SBC   AH  . 2 2 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 3.
Cho hình lăng trụ đứng AB . C AB C
  có đáy ABC là tam giác đều cạnh a và cạnh bên có độ
dài bằng a . Tính khoảng cách từ C đến mặt phẳng  ABC . a 2 a 3 a 21 a 2 A. . B. . C. . D. . 4 7 7 16 Lời giải Chọn C A' B' C' A B C
Ở đây nếu tính trực tiếp rất dài và khó nên ta sẽ vận dụng phương pháp thể tích. 1 VS
.d C; A BC    C. A BCABC   3   .
Cách 1. [Không dùng công thức nhanh về tỉ số thể tích]
Gọi H là trung điểm của B C
  . Dễ chứng minh AH là đường cao của hình chóp A .BCC B   . 3 1 1 a a VS . AH a  . A BCC B   BCC B    3 3 2 '.  3 3 2 6 3 1 a 3 Suy ra VV   V . A .  BCCA.BCC B   C.   2 12 A BC 2 a 7
Mặt khác BC  BA  a 2 và A C
   a , dùng Hê-rông ta được S  . A BC   4 3V a 21
Vậy khoảng cách d C; A BC
C. ABC      . S 7 A BC
Cách 2. [Dùng công thức nhanh về tỉ số thể tích] 3 a 3
Ta có thể tích khối lăng trụ đã cho là V S . AA  . ABC 4 3 1 a 3
Thể tích khối tứ diện có 4 đỉnh là 4 đỉnh của lăng trụ, có thể tích là VV  .
C. ABC 3 12 2 a 7
Mặt khác BC  BA  a 2 và A C
   a , dùng Hê-rông ta được S  . A BC   4 3V a 21
Vậy khoảng cách d C; A BC
C. ABC      . S 7 A BCCâu 4. Cho hình hộp ABC . D A BCD
  có đáy ABCD là hình vuông cạnh a , tâm O . Hình chiếu
vuông góc của A lên mặt phẳng  ABC
D trùng với O . Biết tam giác AA C
 vuông cân tại A.
Tính khoảng cách h từ điểm D đến mặt phẳng  ABB A   .
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 a 6 a 2 a 2 a 6 A. h  . B. h  . C. h  . D. h  . 6 3 6 3 Lời giải Chọn D A' D' B' C' H A D M O B C
Ta có CD // AB CD //  ABB A   .
d D; ABB A
   d C; ABB A       (1)
Do CO cắt  ABB A   tại A d  ; C ABB A     AC    2 (2) d  ; O ABB A   AO  
Gọi M là trung điểm AB và H là hình chiếu của O lên SM . Khi đó d  ; O ABB A    OH   (3) a 2 AA C
 vuông cân tại A có AC a 2  A O   . 2 AO.OM a 6 OM BC a
là đường trung bình của ABC   OM   OH   . 2 2 2 2  6 A O OM a 6 (1) (2) (3)  d  ; D ABB A
   2OH    . 3 Câu 5.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AD  2a ,
DC a , AB  2a . Gọi I là trung điểm cạnh AD , hai mặt phẳng SIB , SIC  cùng vuông
góc với mặt phẳng đáy và mặt phẳng SBC  tạo với đáy một góc 60 . Tính khoảng cách h từ
I đến mặt phẳng  SBC  . a 15 a 15 3a 15 3a 5 A. h  . B. h  . C. h  . D. h  . 15 5 10 5 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489 S F A B H I A B E I E D C D C
SIB   ABCD 
Theo giả thiết, ta có: 
SIC    ABCD  SI   ABCD . 
SIBSIC  SI
Gọi E là hình chiếu của I trên BC , H là hình chiếu của I trên SE , F là trung điểm AB . BC IE
BC   SIE BC SI  
SBC  ABCD  BC  IE BC
 SBC  ABCD  ;  SEI  60 .
SE BCBC SIE 
SIE   SBC , BC  SIE   
 SIE    SBC   SE
d I;SBC   IH . IH SE   2 2
BC CF FB a 5 1 1 1 SSSSS  . AD AB CD IA AB ID DC IBC ABCD IAB ICD IBC   . . 2 2 2 2 2 2 a 3a 1 3a 2 3a 3a 2 2  S  3a a    IE.BC   IE   . IBC 2 2 2 2 a 5 5 3a 3 3a 15
Tam giác HIE vuông tại H : IH IE.sin 60   . 2 5 10 Câu 6.
Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính
AD  2a và có cạnh SA vuông góc với mặt phẳng đáy  ABCD với SA a 6 . Tính khoảng cách
từ B đến mặt phẳng  SCD . a 2 a 3 A. a 2 . B. a 3 . C. . D. . 2 2 Lời giải Chọn C
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 AD
Từ giả thiết suy ra: AB BC CD
a , AC a 3 . 2
Gọi E AB CD , suy ra tam giác ADE đều.
Khi đó C là trung điểm của ED và AC ED .
Dựng AH SC thì AH   SCD , suy ra d , A SCD    AH .
Xét tam giác SAC vuông tại A , có AH là đường cao 1 1 1 Suy ra:    AH  2a . 2 2 2 AH SA AC 1 1 a 2
Mà d B, SCD    d , A SCD     AH  . 2 2 2 Câu 7.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , (SAC)   ABC  , AB  3a , 
BC  5a . Biết rằng SA  2a 3 và 0
SAC  30 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng : 3 17 6 7 3 7 12 A. a . B. a . C. a . D. a . 4 7 14 5 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489  
SAC    ABC
Gọi H là hình chiếu của S lên AC . Ta có 
SH   ABC . SH AC
Xét tam giác SAH , ta có SH SA sin 30  a 3 và 2 2 AH
SA SH  3a .
Xét tam giác ABC , ta có 2 2 AC
BC AB  4a và HC AC HA a .
Gọi E là hình chiếu vuông góc của H lên BC và F là hình chiếu vuông góc của H lên SE . BC HE  Ta có 
suy ra BC  SHE   HF . BC SH
SH   ABC  BC  HF BC Do đó 
HF  SBC  suy ra d H ,SBC   HF . HF SE
Gọi K là hình chiếu vuông góc của A lên BC . Ta có AK // HE , do đó HE CH 1 1 AB AC 1 12 3    HE      a a . 2 2 AK CA 4 4 4 5 5 AB AC HS HE 3 7
Suy ra d H ,SBC   HF   a . 2 2 14 HS HE d  , A SBC CA 6 7 Ta có   4  d  ,
A SBC  4 HF a .
d H,SBC CH 7 Câu 8.
Cho tứ diện đều ABCD có cạnh bằng a . Gọi M là trung điểm CD . Khoảng cách giữa AC và BM là a 154 a a 22 a 2 A. . B. . C. . D. . 28 2 11 3 Lời giải Chọn C
Gọi G là tâm tam giác đều BCD AG   BCD .
Trong mặt phẳng BCD , dựng hình hình bình hành BMCN mà BM CM nên BMCN là hình chữ nhật.
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Ta có BM //  ACN   d BM , AC   d BM , ACN   d G, ACN  .
Kẻ GK NC K NC và GH AK H AK   d G, ACN   GH . 2  2 a 3  a 6 Ta có 2 2 2 AG AB BG a  .    3 2 3   a GK CM  . 2 AG.GK a 22 Vậy GH   cm . 2 2 11 AG GK Câu 9.
Cho hình chóp S.ABC , có đáy là tam giác đều cạnh 2a , SA  2a , SA vuông góc với mặt
phẳng đáy ( minh họa như hình vẽ ). Gọi M , N lần lượt là trung điểm của A , B AC . Khoảng
cách giữa hai đường thẳng MN và SC bằng. a 21 a 21 2a 57 a 57 A. . B. . C. . D. . 7 14 19 19 Lời giải Chọn A Ta có: 1
MN // BC MN// SBC  d MN,SC  d MN,SBC  d N,SBC  d  , A SBC 2
Gọi I là trung điểm của BC . Ta có: BC AI
BC   SAI    SBC   SAI  , SBC SAI   SI   1 BC SA
Trong SAI  kẻ AH SI ( 2 ). . SA AI
Từ (1) và (2) ta suy ra AH  SBC   d  ,
A SBC   AH  2 2 SA AI 3 2 . a a 3 2a 21
Ta có: SA  2a; AI  2 . a
a 3  AH   2 2 2 7 4a  3a
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 a 21
Vậy d MN, SC  d MN,SBC  d N,SBC  d  ,
A SBC  AH  . 2 2 7
Câu 10. Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB  2a, AD  4a, SA  ( ABCD) ,
SA  2a 15 . Gọi M là trung điểm của BC, N là điểm nằm trên cạnh AD sao cho
AD  4DN . Khoảng cách giữa MN và SB là 4a 285 2a 285 a 285 2a 285 A. B. C. D. 19 15 19 19 Lời giải Chọn D S A 4a D 2a E N B M C 2 2
AC  4a  16a  2 5 . a
Gọi E là điểm thuộc cạnh AD sao cho AD  4 AE .
EBMN là hình bình hành
EB // MN MN // SEB  d MN , SB  d MN ,SEB
d N ,SEB  2d  ,
A SEB  2d Ta lại có 1 1 1 1 1 1 1 76 285 2 285         d
a d MN , SB  a 2 2 2 2 2 2 2 2 d SA AB AE 60a 4a a 60a 19 19
Câu 11. Cho hình chóp S .ABCD có đáy là hình vuông cạnh 2a , SA vuông góc với mặt phẳng đáy và
SA a . Gọi M là trung điểm AB. Khoảng cách giữa hai đường thẳng SB và DM bằng
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 21 21 4 21 A. a B. a C. a D. a 21 8 21 Lời Giải Chọn A
Gọi N là trung điểm của CD ; Lấy I , H lần lượt là hình chiếu của A lên BN, SI . 1 1
Ta có DM / / SNB  d DM , SB  d DM ,SNB  d  ,
A SNB  AH . 2 2 2S 4a Tam giác có diện tích: 2 SS  2.S  2 ANB a AI   . ANB ABCD ADN BN 5 1 1 1 1 1 21 4 21 Tam giác vuông có       AH a . 2 2 2 2 2 AH AI SA a 16 2 16a 21 a 5 2 21
d DM , SB  a . 21 a 17
Câu 12. Cho hình chóp đáy là hình vuông cạnh a, SD
, hình chiếu vuông góc của S lên mặt 2
phẳng  ABCD trung điểm H của đoạn AB . Gọi K là trung điểm của đoạn AD . Tính
khoảng cách giữa hai đường thẳng HK và SD theo a . a 3 a 286 5a 3 a 39 A. B. C. D. 5 26 3 3 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489 Ta có 2 2 2 2 2 2 2
SH SD HD SD AH AD  3a SH a 3 .
Do HK // SBD  d HK, SD  d HK,SBD  d H ,SBO  h , với O là tâm hình vuông ABCD . 1 1 1 1 1 1 1 25 a 3 Ta có         h  . 2 2 2 2 2 2 2 2 h SH BH OH 3a a a 3a 5 a 3
Vậy d HK, SD  . 5
Câu 13. Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và   
SA a . Gọi M là điểm thào mãn MB  2MC  0 . Khoảng cách giữa hai đường thẳng SC và DM bằng 154 3 154a 6 154 2 154 A. a . B. . C. a . D. a . 77 154 77 77 Lời giải Chọn B
Gọi N là đỉnh thứ tư của hình bình hành DMCN ; Lấy E, H lần lượt là hình chiếu của A
lên CN , SE . Ta có 1 1
DM / /  SCN   d DM , SC   d DM ,SNB  d O,SCN   d  ,
A SCN   AH 4 4
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2 2 1 9a 3a 2S 6 10a
Tam giác ANC có diện tích: 2 SSS    6 ANB a AE   ACN 2 ABCD DNC 2 2 CN 5 1 1 1 1 1 77 6 154
Tam giác vuông SAE có       AH a . 2 2 2 2 2 AH AE SA a 72 2 72a 77 a 5 6 154 3 154
d (SC, DM )  a a . 4.77 154
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung
điểm của các cạnh AB và AD ; H là giao điểm của CN với DM . Biết SH vuông góc với
mặt phẳng  ABCD và SH a 3 .Tính khoảng cách giữa hai đường thẳng DM và SC theo a . 2 3a 21a a 57 3 3a A. . B. . C. . D. . 19 7 6 19 Lời giải Chọn A
Gọi K là hình chiếu của H trên SC .
Do ABCD là hình vuông nên DM CN .
Có SH   ABCD  SH DM .
Suy ra DM  SHC  DM HK .
Vậy HK là đoạn vuông góc chung của DM và SC .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489 2 DC 2a
Có DH là đường cao của tam giác vuông CDN nên 2
CH .CN DC CH   . CN 5
Lại có HK là đường cao trong tam giác vuông SHC nên 1 1 1 1 5 19 2a 3       HK  . 2 2 2 2 2 2 HK SH HC 3a 4a 12a 19
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , cạnh bên SA a 5 , mặt bên
SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách
gữa hai đường thẳng AD và SC bằng: S D A B C 2a 5 4a 5 a 15 2a 15 A. . B. . C. . D. . 5 5 5 5 Lời giải Chọn B S K D A H B C
Gọi H là trung điểm của cạnh AB .
Do tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy nên
SH   ABCD .
Theo giả thiết ta có AB  2a AH a .
Mà ta lại có SA a 5 nên 2 2 SH
SA AH  2a
Ta có AD // BC AD //  SBC   d A ,
D SC   d A ,
D SBC  d  ,
A SBC  2d H,SBC .
Do mặt phẳng SBC  SAB nên từ H kẻ HK SB thì HK d H ,SBC .
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 SH.HB 2 . a a 2a 5 4a 5 Ta có HK   
d AD, SC   2HK  . SB a 5 5 5
Câu 16. Cho lăng trụ đứng AB . C A
B C có đáy là tam giác vuông tại A , AB a , BC  2a . Gọi
M , N , P lầ lượt là trung điểm của AC , CC , 
A B và H là hình chiếu của A lên BC . Tính
khoảng cách giữa MP và NH . a 3 a 3 a 3 a A. . B. . C. . D. . 4 8 2 2 Lời giải Chọn A B' A' C' P N A B H M C Vì 
A BBA là hình bình hành nên P cũng là trung điểm của A
B . Do đó MP//  B C . Mặt phẳng BC C
B chứa NH và song song với MP nên 1 1
d  MP, NH   d MP,BCCB  d M ,BCCB  d  ,
A BCCB  AH . 2 2
Tam giác ABC vuông tại A , AB a , BC  2a suy ra AC a 3 AC.AB a.a 3 a 3  AH    . BC 2a 2 a 3
Vậy d  MP, NH   . 4
Câu 17. Cho hình chóp S.ABC đều. Gọi G là trọng tâm của tam giác ABC sao cho SG AB a .
Khoảng cách giữa hai đường thẳng SA và CG bằng a a 5 a 3 A. . B. a . C. . D. . 2 5 3 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
NGUYỄN BẢO VƯƠNG - 0946798489 S H x A I C M G B
Gọi M là trung điểm của AB . Từ A kẻ Ax//CM  (SAx)//CM . Khi đó d(S ,
A GC)  d(GC,SAx)  d( , G SAx) SG Ax
Kẻ GI Ax; GH SI . Ta có 
 (SGI )  Ax GH Ax IG Ax
Mà SI GH . Nên GH  (SAx)  d  ,
G (SAx)  GH AM //GIa
Ta có  AI //GM
AIGM là hình chữ nhật  AM GI  .  2 GM AMa 5 a 5
Xét tam giác SGI vuông tại G có: GH SI GH   d ( , SA GC)  . 5 5
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là vuông cạnh a , SA  2a và vuông góc với  ABCD .
Gọi M là trung điểm của SD . Tính khoảng cách d giữa hai đường thẳng SB và CM . 2a 3 3a 2a a A. d  . B. d  . C. d  . D. d  . 3 2 3 3 Lời giải Chọn C S M 2a H A D I K O a B C
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi O AC BD ; I và K lần lượt là trung điểm của AD và OA ; H là hình chiếu vuông
góc của I lên MK , ta có SB // MO SB // MAC .
Do đó d S ;
B CM   d SB;MAC  d B;MAC   d D;MAC  2d I;MAC  .  AC MI Mặt khác, ta có 
AC   MKI  . Suy ra IH   MAC hay d I; MAC   IH . AC   KI MI.IK MI.IK 2a Vậy d S ;
B CM   2IH  2.  2.  . 2 2 MI IK 2 2 MI IK 3
Câu 19. Cho hình chóp S.ABCD có đáy là hình chữ nhật. Tam giác SAB vuông cân tại A và nằm trong
mặt phẳng vuông góc với đáy và SB  4 2 . Gọi M là trung điểm của cạnh SD . Tính khoảng
cách l từ điểm M đến mặt phẳng SBC 2
A. l  2 .
B. l  2 2 . C. l  2 . D. l  . 2 Lời giải Chọn C S K M N H 4 2 D A B C  
SAB   ABCD ,  SAB   ABCD   AB Theo giả thiết, ta có 
SA   ABCD . SA AB
Gọi N , H , K lần lượt là trung điểm các cạnh S ,
A SB và đoạn SH . BC SA Ta có 
BC   SAB  BC AH . BC AB
Mà AH SB (ABC cân tại A có AH là trung tuyến).
Suy ra AH  SBC  , do đó KN  SBC (vì KN || AH ,do KN đường trung bình của SAH ).
Mặt khác MN || BC MN ||  SBC .
Nên l d M SBC  d N SBC 1 , ,  NK AH  2 . 2
Câu 20. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a ,
BAD  60 , SB a và mặt phẳng
SBA và mặt phẳng SBC cùng vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt
phẳng  SCD bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
NGUYỄN BẢO VƯƠNG - 0946798489 21a 5a 21a 15a A. . B. . C. . D. . 7 7 3 3 Lời giải Chọn A a 3
Gọi M làtrungđiểmcủa CD . Do tam giác BCD đềucạnh a nên BM DC và BM 2
Suyra  DC   SBM  . Trong tam giác SBM kẻ BH SM tại H CD BH BH SM   BH   D
SC   d  ;
B SCD  BH BH DC  1 1 1 7 a 21
Trong tam giácvuông SBM ta có     BH  . 2 2 2 2 BH SB BM 21a 7 
Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 2a 3 , góc BAD bằng 120 .
Hai mặt phẳng SAB và  SAD cùng vuông góc với đáy. Góc gữa mặt phẳng  SBC  và
ABCD bằng 45 . Khoảng cách h từ A đến mặt phẳngSBC là 2a 2 3a 2
A. h  2a 2. B. h  . C. h  .
D. h a 3. 3 2 Lời giải Chọn C S I D A B H C
Từ giả thiết suy ra ABC
đều. Gọi H là trung điểm của 2a 3. 3
CB AH BC và AH   3a 2 BC AH Ta có   BC SH BC SA
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
SBC    ABCD  BC   AH BC
 SBC , ABCD  SHA  45 Ta có SH BC
Trong tam giác SAH vuông tại A , kẻ AI SH tại I. Do đó AI  SBC   AI SH Vì 
nên AI là khoảng cách từ A đến mặt phẳng SBC . AI CBAI 3a 2
Trong tam giác vuông AIH ta có sin H
AI AH .sin H  3 . a sin 45  AH 2   a
d A SBC  3 2 ,  AI  . 2 
Câu 22. Cho hình chóp S.ABCD có đáy là hình bình hành, ADC  30 , AB a , AD  2a , SA a và
SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SCD bằng a 3 a 2 a 2 a A. . B. . C. . D. . 2 3 2 2 Lời giải Chọn C S H A D B C K
Ta có AB // CD AB // SCD , suy ra d B,S D
C   d  , A S D C  .
Trong mặt phẳng  ABCD , kẻ AK CD tại K khi đó tam giác AKDvuông tại K và có 
ADK  30  AK a .
Trong mặt phẳng SAK  , kẻ AH SK tại H AH   SCD  d  ,
A SCD  AH . 1 a 2
Do SA AK a nên tam giác SAK vuông cân tại A suy ra AH SK  . 2 2 a
Vậy d B SCD 2 ,  . 2
Câu 23. Cho hình chóp S.ABCD có đáy là hình bình hành, AB a , AD a 3 , AC  2a , SA  2a và
SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SCD bằng a 84 a 2 A. a 3 . B. a 2 . C. . D. . 7 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn C S H A D B C
Ta có AB // CD AB // SCD , suy ra d B,S D
C   d  , A S D C  . Xét tam giác ADC ta có 2 2 2 2
AC AD DC  4a nên AC CD mà
SA CD CD  SAC
 SCD  SAC lại có SCD  SAC  SC nên từ A dựng AH SC tại H thì
AH   SCD  AH d  , A SCD 1 1 1 1 1 1 Ta có       AH a 2 2 2 2 2 2 2 AH AC AS 4a 4a 2a
Vậy d B,SCD  a 2 .
Câu 24. Hình chóp S.ABCD có đáy là hình thoi tâm O cạnh 2a , ABC  60 , hình chiếu vuông góc
của S lên  ABCD trùng với trung điểm I của BO , SI a 3 . Khoảng cách từ B đến mặt
phẳng  SCD bằng 3a 3 2a 3 a 3 4a 3 A. . B. . C. . D. . 5 5 5 5 Lời giải Chọn D S A D A D H O O I I B C C B K K 4
Ta có BI   SCD   
D , suy ra d  , B C
S D  d I,S D C  . 3
Trong mặt phẳng  ABCD , kẻ IK CD tại K .
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Trong mặt phẳng  SIK  , kẻ IH SK tại H IH   SCD  d I,SCD  IH .  1 1 3 3
Xét tam giác IDK vuông tại K ta có BDC  30  IK ID  . .BO a 3 (do tam giác 2 2 2 4
ABC đều cạnh 2a nên BO a 3 ). 1 1 1 16 1 25 3a 3 Ta có       IH  2 2 2 2 2 2 IH IK IS 27a 3a 27a 5 a a
Vậy d B SCD 4 3 3 4 3 ,  .  . 3 5 5
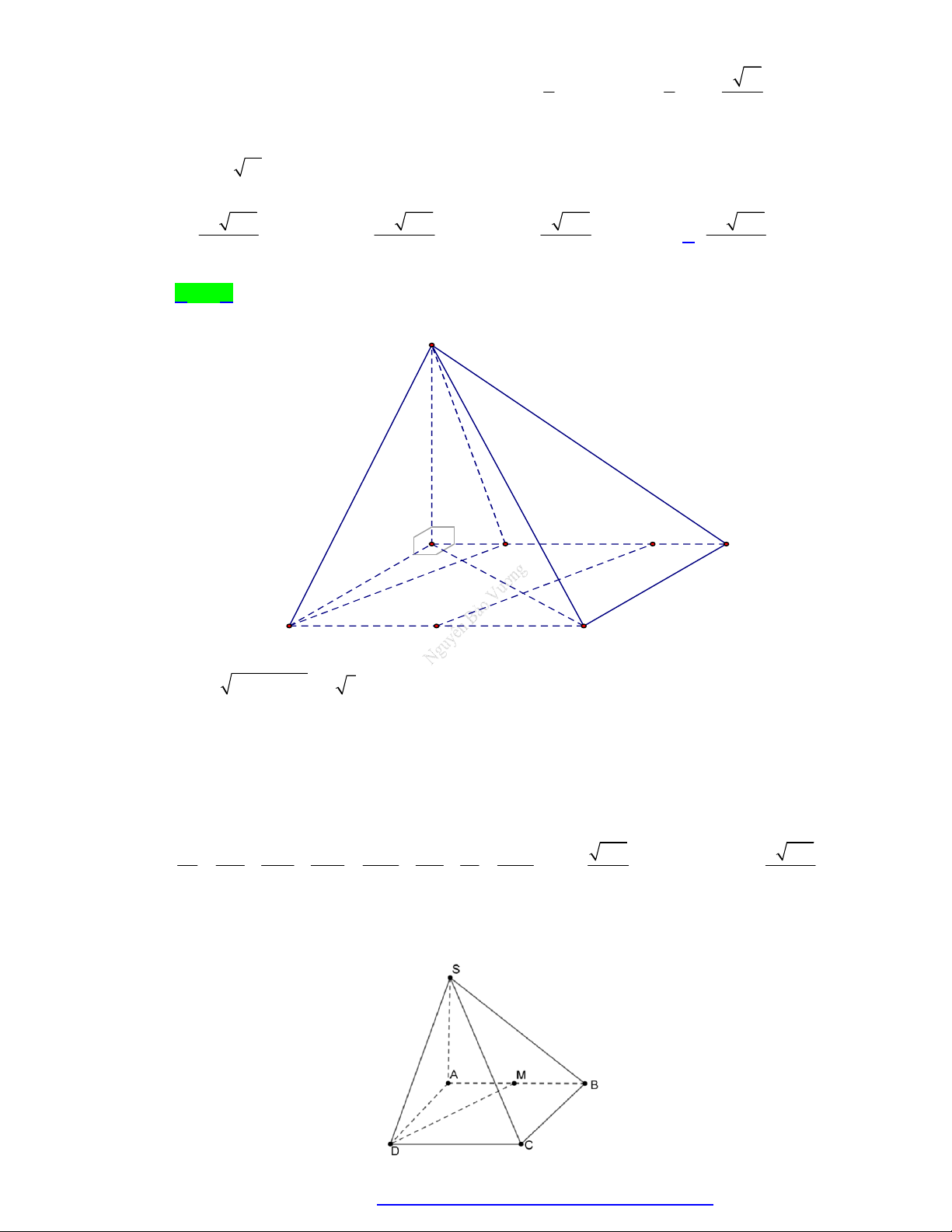
Câu 25. Cho hình chóp S.ABCD có đáy là hình thang cân đáy AD có AD  2 AB  2BC  2a , SA a
và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SCD bằng a 3 a 3 a 3 A. . B. . C. . D. 2a . 2 3 4 Lời giải Chọn C S H O D A B C I
Gọi O là trung điểm của AD khi đó tứ giác ABCO là hình thoi nên 1
CO a CO
AD  ACD vuông tại C 2
AC CD mà SA CD CD  SAC   SCD   SAC
Ta có SCD  SAC   SC nên từ A dựng AH SC tại H thì
AH  SCD  AH d  , A SCD . ACD vuông tại C 2 2  AC
AD DC a 3 . 1 1 1 1 1 4 a 3 Ta có       AH  . 2 2 2 2 2 2 AH AC AS 3a a 3a 2
Trong mặt phẳng  ABCD gọi I là giao điểm của AB và CD khi đó BC là đường trung bình 1 a 3
của tam giác IAD d B,SCD  d  ,
A SCD  . 2 4
--------------------- HẾT --------------------
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Document Outline

  • 7. Góc - khoảng cách - câu hỏi
  • 7. Góc - khoảng cách - đáp án