Tổng ôn tập TN THPT 2020 môn Toán: Số phức

Tổng ôn tập TN THPT 2020 môn Toán: Số phức được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

35 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. KHÁI NIỆM SỐ PHỨC & CÁC PHÉP TOÁN TRÊN SỐ PHỨC
Số phức
z a bi
có phần thực là
,a
phần ảo là
.b
Số phức l
iên hợp
z a
bi
và c
ần nhớ
2
1.i
Số phức
z a
bi
có điể
m biểu diễn là
( ; ).M a b
Số phức li
ên hợp
z a bi
có đi
ểm biểu diễn
( ;
).N a b
Hai điểm
M
và
N
đối xứng nhau qua trục hoành
.Ox
;z z
;z z
z z
;z z
z z
. .
;z z z z
;
z z
z z
2 2
. z
z a b
Hai số phức bằng
nhau khi thực bằng thực và ảo bằng ảo.
Mô đ
un của số phức
z
là:
2 2
z a b
.
z z z z
z
z
z z
z z z z z z
z z z z z z
Ph
ép cộng hai số phức Cho số phức
1
. z
a b i
và
2
. z
c d i
. Khi đó
1 2
. . .
.
z z
a b i c d i a c b d i
Phép trừ hai s
ố phức
1 2
. . .
. z z a b i c d i a c b d i
Ph
ép nhân hai số phức
1 2
. . . . . . z z a b i c d i ac bd ad bc i
k.
z k.(a bi) ka kbi
Ph
ép chia hai số phức
1 1
2 1 2
2
2 2 2 2 2 2 2 2
2 2 2
2
. . .
. .
.
.
a b i c d i ac bd bc ad i
z z z z z
ac
bd bc ad
i
z z z c d c d c d c d
z
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 1. Môđun của số phức
1 2i
bằn
g
A.
5
. B.
3
. C.
5
. D.
3
.
Câu 2. Số phức liên hợp của số phức
2z i
là
A.
2z i
. B.
2z i
. C.
2z i
. D.
2z i
.
Câu 3.
Trên mặt phẳng tọa độ, điểm biểu diễn số phức
1 2z i
là
điểm nào dưới đây?
A.
1;
2Q
. B.
1;
2P
. C.
1;
2N
. D.
1;
2M
.
Câu 4. Số phức liên hợp của số phức
1 2i
là
:
A.
1 2i
. B.
1 2i
. C.
2 i
. D.
1 2i
.
Câu 5. Số phức liên hợp của số phức
5 3i
là
A.
5 3i
. B.
3 5i
. C.
5 3i
. D.
5 3i
.
Câu 6. Số phức liên hợp của số phức
3 2z
i
là.
A.
3 2i
. B.
3 2i
. C.
3 2i
. D.
2 3i
.
Câu 7.
Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức
1 2
z i
?
SỐ PH
ỨC
Vấn
đề 16
x
y
O
b
b
a
( ;
)M a b
z a
bi
z a bi
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
N
. B.
P
. C.
M
. D.
Q
.
Câu 8. Số phức
5 6i
có phần thực bằng
A.
5
. B.
5
C.
6
. D.
6
.
Câu 9. T
ìm tất cả các số thực
,x y
sa
o cho
2
1
1 2x yi i
.
A.
2 , 2x y B. 2 , 2x y C.
0, 2x y
D. 2 , 2x y
Câu 10. Số phức có phần thực bằng
1
và
phần ảo bằng
3
l
à
A.
1
3i
. B.
1
3i
. C.
1
3i
. D.
1
3i
.
Câu 11. Số phức
3
7i
c
ó phần ảo bằng
A.
3
. B.
7
. C.
3
. D.
7
.
Câu 12. Số phức
nào dưới đây là số thuần ảo.
A.
2 3z i
B.
3z
i
C.
3z i
D.
2z
Câu 13. Cho số phức
3
1z
i i
. Tìm phần thực
a
và phần ảo
b
của
z
.
A.
1, 2a b
B.
2, 1a b
C.
1, 0a b
D.
0, 1a b
Câu 14. Cho số phức
2 3z i
. Tìm phần thực
a
của
z
?
A.
2a
B.
3a
C.
2a
D.
3a
Câu 15. K
í hiệu
,a
b
lần lượt là
phần thực và phần ảo của số phức
3
2 2i
. Tìm
a
,
b
.
A.
3
; 2a b
B.
3; 2 2a b
C.
3; 2a b
D.
3; 2 2a b
Câu 16. Cho
số phức
3
2z i
. Tìm phần thực
và phần ảo của số phức
z :
A. P
hần thực bằng
3
và Phần ảo bằng
2i
B. Phần thực bằng
3
và Phần ảo bằng
2
C. P
hần thực bằng
3
và P
hần ảo bằng
2i
D. P
hần thực bằng
3
và P
hần ảo bằng
2
Câu 17. Đ
iểm
M
tr
ong hình vẽ bên là điểm biểu diễn số phức
A.
2z
i
B.
1
2z i
C.
2z
i
D.
1
2z i
Câu 18. Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Tìm phần thực và phần ảo của số phức
z
.
A. P
hần thực là
2
và
phần ảo là
i
. B. Phần
thực là
1
và
phần ảo là
2
.
C. P
hần thực là
1
và
phần ảo là
2i
. D. P
hần thực là
2
và
phần ảo là
1
.
O
x
y
2
2
1
2
P
M
N
Q
1
1
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu
19. Số phức liên hợp của số phức
2z
i
là
A.
2z
i
. B.
2z
i
. C.
2z
i
. D.
2z
i
.
Câu 20. Môđun của số phức
5 2z i
bằng
A.
2
9 . B.
3
. C.
7
. D.
29
.
Câu
21. Nếu điểm
;M x y
l
à điểm biểu diễn của số phức
z
tr
ong mặt phẳng tọa độ
O
xy
thỏa
mãn
4O
M
thì
A.
1
2
z
. B.
4z
. C.
16z
. D.
2z
.
Câu
22. Nghịch đảo
1
z
của
số phức
1
3z i
bằ
ng
A.
1
3
.
10 10
i B.
1
3
.
10 10
i C.
1
3
.
10 10
i
D.
1
3
.
10 10
i
Câu
23. Môdun của số phức
4
3z i
bằng
A.
7
. B.
25
. C.
5
. D.
1
.
Câu
24. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của số phức
2
3z i
?
A.
M
. B.
P
. C.
N
. D.
Q
.
Câu
25. Modun cỉa số phức
4
3z i
là
A.
1
. B.
1
. C.
5
. D.
25
.
Câu
26. Cho hai số phức
1
3z i và
2
1 .z i Phần ảo của số phức
1 2
z
z
bằng
A.
2
.
B.
2
.i
C.
2.
D.
2
.i
Câu
27. Cho hai số phức
1
2z
i
và
2
1
3z i
. Phầ
n thực của số phức
1
2
z
z
bằng
A.
1
. B.
3
. C.
4
. D.
2
.
Câu
28. Cho hai số phức
1
3z i
và
2
1z i
.
Phần ảo của số phức
1
2
z z
bằ
ng
A.
4
. B.
4i
. C.
1
. D.
i
.
Câu 29. Cho 2 số phức
1
5 7z i
và
2
2 3z i
. T
ìm số phức
1
2
z z z
.
A.
7 4z i
B.
2 5z i
C.
3 10z i
D.
1
4
Câu 30. Cho hai số phức
1
4
3z i
và
2
7
3z i
. Tìm số phức
1 2
z
z z
.
A.
3 6z i
B.
11z
C.
1 10z i
D.
3 6z i
Câu 31. Cho số phức
2
5 .z i
Tìm số phức
w iz z
A.
7
3w i
. B.
3
3w i
. C.
3
7 .w i
. D.
7
7w i
Câu
32. Cho hai số phức
1
2
z i
và
2
1
z i
.
Trên mặt phẳng tọa độ
Oxy
,
điểm biểu diễn của số phức
1
2
2 z
z
có
tọa độ là
A.
5
; 1
. B.
1
; 5
. C.
5
; 0
. D.
0
; 5
.
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 33. Cho hai số phức
1
1z i và
2
2z i . Trên mặt phẳng tọa độ
O
xy
, điểm biểu diễn số phức
1
2
2z z có tọa độ là
A.
(
2;5)
. B.
(
3;5)
. C.
(
5;2)
. D.
(5
;3)
.
Câu 34. Cho
hai số phức
1
1z
i
và
2
2
3z i
. Tính môđun của số phức
1
2
z
z
.
A.
1
2
1z
z
. B.
1
2
5z
z . C.
1
2
13z
z . D.
1
2
5z
z
.
Câu 35. Cho
số phức
1
2 , 2z i w i
. Điểm nà
o trong hình bên biểu diễn số phức z w ?
A.
N
. B.
P
. C.
Q
. D.
M
.
Câu 36. T
ìm phần ảo của số phức
z
biế
t
2 13 1 z i i
.
A.
5 i
. B.
5i
. C.
5
. D.
5
.
Câu 37. Cho số phức
z
t
hỏa mãn:
2
(3
2 ) (2 ) 4i z i i
.
Hiệu phần thực và phần ảo của số phức
z
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 38. Phần
thực và phần ảo của số phức
(
1 2 )z i i
.
A.
1
và
2
. B.
2
và
1
. C.
1
và
2
. D.
2
và
1
.
Câu 39. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức
1
2z i i
?
A.
Q
. B.
M
. C.
P
. D.
N
.
Câu 40. T
rong hình vẽ bên dưới, điểm
P
biể
u diễn số phức
1
z ,
điểm
Q
biể
u diễn số phức
2
z .
Tìm số
phức
1 2
z
z z .
A.
1
3i
. B.
3 i
. C.
1
2i
. D.
2 i
.
x
y
M
N
P
Q
O
y
x
1
2
2
-
1
Q
P
O
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 41. Cho
số phức
,
, .z a bi a b R
Khi
đó số
1
2
z z
l
à số nào trong các số sau đây?
A. Số
2
.
B. Số
.i
C. Một
số thực. D. Một số thuần ảo.
Câu 42. Cho hai số phức
1
1
3z i
và
2
2
5z i
. Tì
m phần ảo
b
của
số phức
1 2
z
z z
.
A.
2b
B.
3b
C.
3b
D.
2b
Câu 43. Tìm
số phức
z
thỏa
mãn
2
3 3 2z i i
.
A.
1
5z i
. B.
1z
i
. C.
5
5z i
. D.
1z
i
.
Câu 44. Tìm
số phức liên hợp của số phức
3
1
z
i i
.
A.
3
z i
. B.
3
z i
. C.
3
z i
. D.
3
z i
.
Câu 45. Tính môđun của số phức
z
biết
4
3 1
z
i i
.
A.
2
5 2
z
B.
7
2
z
C.
5
2
z
D.
2
z
Câu 46. Tính m
ôđun của số phức
z
thỏa m
ãn
2
13 1z i i
.
A.
3
4
z
B.
3
4
z
C.
5
34
3
z
D.
34
3
z
Câu 47. Cho
hai số phức
1
1z
i
và
2
2
3z i
. Tính môđun của số phức
1
2
.z
z
A.
1
2
13
z
z
. B.
1
2
5
z
z
. C.
1
2
1
z
z
. D.
1
2
5
z
z
.
Câu 48. Cho
hai số phức
1
2z i
và
2
1 .z i
T
rên mặt phẳng tọa độ
,O
xy
điểm
biểu diễn số phức
1
2
2
z z
c
ó tọa độ là
A.
3
; 3
. B.
2
; 3
. C.
3
;3
. D.
3
;2
.
Câu 49. Cho
hai số phức
1
1
2z i
và
2
3
4z i
. Số phức
1
2 1 2
2
3
z
z z z
l
à số phức nào sau đây?
A.
10i
. B.
10i
. C.
11 8i
. D.
11 10i
.
Câu 50. Cho
số phức
, z a bi a b
thoả m
ãn
2
z
i z
.
Tính
4S a b
.
A.
4S
B.
2S
C.
2S
D.
4S
Câu 51. Cho số phức z thỏa mãn
|
| 5
z
và
|
3| | 3 10 |z z i
. Tìm số phức
4 3 .w z i
A.
3
8 .w i
B.
1
3 .w i
C.
1
7 .w i
D.
4
8 .w i
Câu 52. Cho số phức
,
,z a bi a b
thỏa mãn
1 3 0z i z i
.Tính
3S a b
.
A.
5S
B.
7
3
S
C.
5S
D.
7
3
S
Câu 53. Tìm ha
i số thực
x
và
y
thỏ
a mãn
2 3 1 3 6x yi i x i
với
i
là đơn
vị ảo.
A.
1
x
;
3
y
. B.
1
x
;
1
y
. C.
1x
;
1
y
. D.
1x
;
3
y
.
Câu 54. Tìm các số thực
a
và
b
thỏ
a mãn
2
1 2 a b i i i
với
i
là
đơn vị ảo.
A.
0, 2
a b
. B.
1
, 1
2
a b
. C.
0, 1 a b
. D.
1, 2
a b
.
Câu 55. Phần ảo của số phức
z
thoả mãn
2 1 4 2z i i i
là
A.
3
. B.
3i
. C.
3i
. D.
3
.
Câu 56. Cho
số phức
,z
a bi a b
thỏa
mãn
1
2 3 2 .i z z i
Tí
nh
P
a b
.
A.
1
2
P
B.
1P
C.
1P
D.
1
2
P
Câu 57. Tìm
hai số thực
x
và
y
thỏa m
ãn
2
3 3 5 4x yi i x i
với
i
là
đơn vị ảo.
A.
1
; 1
x
y
. B.
1
; 1x y
. C.
1
; 1
x
y
. D.
1
; 1x y
.
Câu 58. Tìm hai số thực
x
và
y
thỏa mãn
3
2 2 2 3x yi i x i
với
i
là đơ
n vị ảo.
A.
2
; 2
x
y
. B.
2
; 1
x
y
. C.
2
; 2
x
y
. D.
2
; 1
x
y
.
Câu 59. Cho
số
z
thỏa
mãn
2
4 8 19i z z i i
. Môđun của
z
bằ
ng
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
3
. B.
5
. C.
1
3
. D.
5
.
Câu 60. Cho
số phức
z
thoả
mãn
3
2 3 7 16 .z i i z i Môđun của
z
bằ
ng
A.
5.
B.
5
.
C.
3
.
D.
3
.
Câu 61. Cho
số phức
z
thỏa
mãn
2
3 16 2i z i z i . Môđun của
z
bằng
A.
5
. B.
1
3
. C.
1
3
. D.
5
.
Câu 62. Tìm hai số thực
x
và
y
thỏa mãn
3
4 2 5 2x yi i x i
với
i
là đơn vị ảo.
A.
2x
;
4y
B.
2x
;
4y
C.
2x
;
0y
D.
2x
;
0y
Câu 63. Cho
số phức
z
t
hỏa mãn
2
1
3 3 4i z i
. Môđun
của
z
bằng
A.
5
4
. B.
5
2
. C.
2
5
. D.
4
5
.
Câu 64. Cho số phức
2 3z i
. Môđun của
số phức
2
1w z i z
bằng
A.
4
. B.
2
. C.
1
0
. D.
2 2
.
Câu 65. Cho
hai số thực
x
,
y
thỏa mãn
3
2 1 4 1 24x i y i i
. Giá trị của
x y
bằng:
A. -3. B. 4. C. 2. D. 3.
Câu 66. Cho số phức . Môđun của số phức bằng:
A. . B. . C. . D. .
Câu 67. Cho số phức
z
a bi
,a
b R
,
thỏa mãn
3
1z z
và
2z
z i
l
à số thực.
Tính
a b
.
A.
0
. B.
4
. C.
2
. D.
2
.
Câu 68. Gọi
1 2
z ,z lần lượt có điểm biểu diễn là
M
và
N
trên mặt phẳng phức ở hình dưới đây.
Tính
1
2
z
z
.
A.
2
29 . B.
2
5 . C.
2
0
. D.
1
16
.
Câu 69. Cho
số phức
(
, )z a bi a b
t
hoả mãn
(
1 ) 2 3 2i z z i
.
Tính
P a b
A.
1P
. B.
1
2
P
. C.
1
2
P
. D.
1P
Câu 70. Cho
2
z
z
là số thực,
3
2z z . Tính
z
A. 3
2z . B.
6z . C. 2
3z . D.
3z .
Câu 71. T
ìm cac số thực
x
và
y
thỏa mã
n
3 2 2 1 1 5 ,x y i x y i
với
i
l
à đơn vị ảo.
A.
3
,
2
2
x y
. B.
3
4
,
2 3
x y
. C.
4
1
,
3
x y
. D.
3
4
,
2 3
x y
.
2
3z i
2
w z z
3
10
206
1
34
3
2
x
y
N
M
3
2
-
4
O
1
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 72. Cho
số phức
z
thỏa m
ãn điều kiện
2
1
2 4 20
i
z z i
. T
ìm
z
.
A.
25
z
. B.
7
z
. C.
4
z
. D.
5
z
.
Câu 73. Tổng p
hần thực và phần ảo của số phức
z
thoả mãn
1 2iz i z i
bằng
A.
6
. B.
2
. C.
2
. D.
6
.
Câu 74. Cho
,a b
và t
hỏa mãn
2
1 3a bi i a i
, với
i
là đơn vị ảo.
Giá trị
a
b
bằng
A.
4
. B.
10
. C.
4
. D.
10
.
Câu 75. Tìm hai số thực
x
,
y
thỏa mãn
3
2 3 4 3x yi i x i
với
i
là đơn vị ảo.
A.
3; 1
x y
. B.
2
; 1
3
x y
. C.
3; 3
x y
. D.
3; 1
x y
.
Câu 76. Cho
các số phức
1
2
,z
z
thỏa
mãn
1
2
3
z
z
và
1
2
2
z
z
.
Môđun
1
2
z
z
bằng
A.
2
. B.
3
. C.
2
. D.
2
2
.
Câu 77. Cho số phức
z
thỏa
mãn
2
3
1 2z z i
. P
hần ảo của
z
là
A.
2
. B.
2
. C.
3
4
. D.
3
4
.
B. P
HƯƠNG TRÌNH SỐ PHỨC
Phư
ơng trình
2
0a
z bz c
với
0a
có
biệt số
2
4b
ac
thì
có hai nghiệm thực hoặc phức là
1
2
b
z
a
hoặc
2
2
b
z
a
CÂU HỎI CÙN
G MỨC ĐỘ ĐỀ MINH HỌA
Câu 78. Gọi
0
z
là
nghiệm phức có phần ảo âm của phương trình
2
2
5 0
z
z
.
Môđun của số phức
0
z
i
bằ
ng
A.
2
. B.
2
. C.
10
. D.
1
0
.
Câu 79. Kí
hiệu
0
z
l
à nghiệm phức có phần ảo dương của phương trình
2
4
16 17 0
z
z
.
Trên mặt
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
0
w
iz
?
A.
1
1
;
2
2
M
. B.
2
1
;
2
2
M
. C.
3
1
;1
4
M
. D.
4
1
;1
4
M
.
Câu 80. Kí hiệu
1 2
,z
z
l
à hai nghiệm phức của phương trình
2
3
1 0z z
.
Tính
1
2
P z z
.
A.
14
3
P
B.
2
3
P
C.
3
3
P
D.
2
3
3
P
Câu 81. Kí
hiệu
1
2
,z z
l
à hai nghiệm phức của phương trình
2
6 0z z
.
Tính
1
2
1 1
P
z z
.
A.
1
12
B.
1
6
C.
1
6
D.
6
Câu 82. Kí
hiệu
1 2
;z z
là ha
i nghiệm của phương trình
2
1 0
z z
. Tí
nh
2
2
1 2 1 2
P
z z z z
.
A.
1P
B.
2P
C.
1P
D.
0
P
Câu 83. Kí
hiệu
1
2 3
,
,z z z
và
4
z
là
bốn nghiệm phức của phương trình
4
2
12 0
z z
.
Tính
tổng
1
2 3 4
T
z z z z
A.
4T
B.
2
3
T
C.
4
2 3
T
D.
2
2 3
T
Câu 84. Phương trình nào dưới đây nhận hai số phức
1 2i
và
1 2i
là nghiệm.
A.
2
2
3 0z z
B.
2
2
3 0z z
C.
2
2
3 0z z
D.
2
2
3 0z z
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
85. Kí hiệu
1
z
,
2
z
là
hai nghiệm của phương trình
2
4
0
z
.
Gọi
M
,
N
lần
lượt là điểm biểu diễn
của
1
z
,
2
z
t
rên mặt phẳng tọa độ. Tính
T
OM ON
với
O
là
gốc tọa độ.
A.
2
T
B.
2T
C.
8
T
D.
4
Câu
86. Kí hiệu
1
2
,
z z
l
à hai nghiệm phức của phương trình
2
3
z 5 0
z
. G
iá trị của
1
2
z
z
bằng
A.
2
5
. B.
5
. C.
3
. D.
10
.
Câu
87. Gọi
1
z
và
2
z
là
hai nghiệm phức của phương trình
2
4
4 3 0
z
z
.
Giá trị của biểu thức
1
2
z z
bằng:
A.
3 2
B.
2
3
C.
3
D.
3
Câu
88. Gọi
1 2
,z z
là
2 nghiệm phức của phương trình
2
4
z 5 0
z
. Giá trị
của
2
2
1 2
z z
bằng
A. 6. B. 8. C. 16. D. 26.
Câu
89. Gọi
1
2
,z
z
là hai
nghiệm phức của phương trình
2
4
7 0.
z
z
G
iá trị của
2
2
1 2
z
z
bằng
A. 10. B. 8. C. 16. D. 2.
Câu
90. Gọi
1
2
,z
z
l
à hai nghiệm phức của phương trình
2
6
10 0
z
z
. Giá trị của
2
2
1 2
z
z
bằng:
A.
16.
B.
56
. C.
20.
D.
26
.
Câu
91. Gọi
1
2
,z
z
là các nghiệm phức của phương trình
2
4
7 0
z
z
. Số phức
1 2 1 2
z
z z z
bằng
A.
2
. B.
1
0
. C.
2i
. D.
1
0i
.
Câu
92. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4 5 0
z z
;
M
,
N
lần lượt là các điểm
biểu diễn của
1
z
,
2
z
trên mặt phẳng phức. Độ dài đoạn thẳng
M
N
là
A.
2
5
. B.
4
. C.
2
. D.
2
.
Câu
93. Gọi
1
z
,
2
z
là
hai nghiệm phức của phương trình
2
3
2 0
z
z
.
Tính
2
2
1 2
zT
z
.
A.
2
3
T
. B.
8
3
T
. C.
4
3
T
. D.
1
1
9
T
.
Câu
94. Gọi
1 2
,
z z
là hai
nghiệm phức của phương trình
2
z 2z 10 0
.
Giá trị của
2
2
1 2
z
z
bằng
A.
10
. B.
2
0
. C.
2 10
. D.
10
.
Câu 95. Gọi
1 2
,z z
là
hai nghiệm phức của phương trình
2
4
29 0
z
z
.
Tính giá trị của biểu thức
4 4
1 2
z z
.
A.
8
41
. B.
5
8
. C.
1
682
. D.
2
019
.
Câu
96. Kí hiệu
1
z
và
2
z
là
2 nghiệm phức của phương trình
2
2 4 9 0
z z
.
Tính
1
2
1
1
P
z z
A.
4
9
P
. B.
4
9
P
. C.
9
4
P
. D.
9
4
P
.
Câu
97. Gọi
1
z
,
2
z
là
hai nghiệm phức của phương trình
2
5
7 0
z
z
. G
iá trị của biểu thức
1
2
z z
l
à
A.
3i
. B.
3i
. C.
3
. D.
3
2
.
Câu
98. Kí hiệu
1
2
, z z
l
à hai nghiệm phức của phương trình
2
2
z 10 0
z
. G
iá trị của
1
2
.z
z
bằng
A.
5
. B.
5
2
. C.
1
0
. D.
20
.
Câu
99. Gọi
1 2
,z z
l
à hai nghiệm phức của phương trình
2
2z 2 0
z
. T
ính giá trị của biểu thức
1
2 1 2
2
P
z z z z
.
A.
6
P
. B.
3
P
. C.
2
2 2
P
. D.
2
4
P
.
Câu 100. Kí hiệu
1
2
;z
z
l
à hai nghiệm phức của phương trình
2
3
1 0
z
z
. Tí
nh
1
2
P z z
A.
1
4
3
P
. B.
2
3
P
. C.
3
3
P
. D.
2
3
3
P
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
C. BIỂU
DIỄN ĐIỂM SỐ PHỨC
Đ
iểm biểu diễn số phức:
Số phức
z
a bi
,
,a
b
được biểu diễn bởi điểm
;M
a b
.
BÀI TOÁN: Tì
m tập hợp điểm biểu diễn của số phức thỏa mãn tính chất cho trước
Bướ
c 1. Gọi
(
; )M x y
là điể
m biểu diễn số phức
( , ).z x yi x y
Bướ
c 2. Biến đổi điều kiện
K
để
tìm mối liên hệ giữa
,
x y
v
à kết luận.
Mối
liên hệ giữa
x
v
à
y
Kết luận tập hợp
điểm
(
; )M x y
0
.Ax By C
L
à đường thẳng
:
0.d Ax By C
2
2 2
2 2
(
) ( )
2
2 0
x
a y b R
x y ax by c
L
à đường tròn
(
)C
có tâm
(
; )I a b
v
à bán kính
2
2
.R
a b c
2
2 2
2 2
( ) ( )
2
2 0
x a y b R
x y ax by c
L
à hình tròn
( )C
c
ó tâm
( ; )I a b
và
bán kính
2
2
R
a b c
(đường
tròn kể cả bên
trong)
2
2 2 2
1 2
(
) ( ) .R x a y b R
L
à những điểm thuộc miền có hình vành khăn
tạo bởi hai đường tròn đồng tâm
(
; )I a b
và
bán kính lần lượt
1
R
v
à
2
R
.
2
,
( 0).y ax bx c a
L
à một parabol
(
)P
c
ó đỉnh
;
2 4
b
I
a
a
2
2
2 2
1
x
y
a
b
với
1 2
1 2
2
2 2
MF MF a
F F c a
L
à một elíp có trục lớn
2
,a
trục
bé
2b
và
tiêu
cự là
2
2
2
2 , ( 0).c a b a b
.MA MB
 
L
à đường trung trực của đoạn thẳng
.A
B
CÂU HỎI CÙN
G MỨC ĐỘ ĐỀ MINH HỌA
Câu 101. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2
1
2z i
là điể
m nào dưới đây?
A.
3
;4
P
. B.
5
;4
Q
. C.
4
; 3
N
. D.
4
;5
M
.
Câu 102. Cho
số phước
1 2 .z i
Điểm
nào dưới đây là điểm biểu diễn số phức
w iz
trên
mặt phẳng
tọa độ
A.
2
; 1
N
B.
2
;1
P
C.
1
; 2
M
D.
1
; 2
Q
Câu 103. Cho số phức
1z
i
. Biể
u diễn số phức
2
z
là điểm
A.
2
;0
M
. B.
1
;2
P
. C.
2
;0
E
. D.
0
; 2
N
.
Câu 104. Xé
t các số phức
z
t
hỏa mãn
2
2
z
i z
là
số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức
z
l
à một đường tròn có bán kính bằng
A.
2
B.
2
2
C.
4
D.
2
Câu 105. Xé
t các số phức
z
t
hỏa mãn
2
2
z
i z
l
à số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức
z
là một
đường tròn có bán kính bằng?
A.
2
2
. B.
2
. C.
2
. D.
4
.
Câu 106. Xé
t các số phức
z
thỏa
mãn
3
i 3
z
z
là
số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức
z
l
à một đường tròn có bán kính bằng:
A.
9
2
. B.
3
2
. C.
3
. D.
3
2
2
.
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 107. Tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa mãn
2 4
z i
là đường tròn có tâm
I
và bán kính
R
lần l
ượt là
A.
2;
1
I
;
2R
. B.
2;
1
I
;
4R
. C.
2;
1
I
;
2R
. D.
2;
1
I
;
4R
.
Câu 108. T
ập hợp các điểm biểu diễn các số phức
z
thỏa
mãn
1 2
z i
là
đường tròn có tâm và bán
kính lần lượt là
A.
1;
1 , 4
I R
. B.
1;1
, 2
I R
. C.
1;
1 , 2
I R
. D.
1;
1 , 4
I R
.
Câu 109. T
ập hợp các điểm biểu diễn các số phức
z
thỏa mãn
2
z z i
là một đường thẳng có
phương trình
A.
4 2
3 0
x y
. B.
2 4
13 0
x y
. C.
4 2
3 0
x y
. D.
2 4
13 0
x y
.
Câu 110. T
ập hợp điểm biểu diễn số phức
z
biết:
(3
4 ) 2
z i
là
A. Đường tr
òn tâm
(3; 4), 2I R
. B. Đường tròn tâm
( 3;4), 2I R
.
B. Đường tròn tâm
(3
; 4), 4I R
. D. Đường
tròn tâm
( 3
;4), 4I R
.
Lời gi
ải
Chọn A
Gọi
;z x
yi x y
. T
a có:
2 2
(3
4 ) 2 ( 3) ( 4) 4
z i
x y
Vậy tập hợp
điểm biểu diễn số phức
z
là đ
ường tròn tâm
(3
; 4), 2I R
.
Chú ý
:
( ;
)
( )
I a
b
z a
bi R
R
Câu 111.
Tập hợp các điểm biểu diễn số phức
z
thỏa
mãn
1
z i
i z
là
một đường tròn,
tâm của đường tròn đó có tọa độ là
A.
1;1
. B.
0; 1
. C.
0;1
. D.
1;0
.
Câu 112. Cho số phức
z
thay
đổi thỏa mãn
1 2
.
z
Biết
rằng tập hợp điểm biểu diễn các số phức
1 3
2
w i
z là đường tròn có bán kính bằng
.R
Tính
.R
A.
8
R
. B.
2R
. C.
16
R
. D.
4R
.
Câu 113. Có bao nhiêu số phức
z
có phần th
ực bằng
2
và
1 2 3
z i
?
A.
3.
B.
0.
C.
2.
D.
1
Câu 114. Tập hợp các điểm biểu diễn các số phức
z
thỏa mãn
2 2z
i z z i
là
A. Một điểm. B. Một đường tròn. C. Một đường thẳng. D. Một Parabol.
Câu 115. Trong mặt phẳng tọa độ
Oxy
, tìm t
ập hợp điểm biểu diễn số phức
z
thỏa mãn
2 3
2
z i
.
A. Một đường th
ẳng. B. Một hình tròn. C. Một đường tròn. D. Một đường elip.
Câu 116. Có bao nhiêu số phức
z
thỏa
mãn điều kiện
1 2z
i z i
và
1
z
A.
0
. B.
2
. C.
1
. D.
4
.
Câu 117. T
ập hợp tất cả các điểm biểu diễn các số phức
z
thỏa
mãn
2 4
z i
là
đường tròn có tâm
I
và bán kính
R
lần lượt là
A.
2; 1
I
;
4R
. B.
2; 1
I
;
2R
. C.
2; 1
I
;
4R
. D.
2; 1
I
;
2R
.
-------------------------------- HẾT --------------------------------
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
A. KHÁI NIỆM SỐ PHỨC & CÁC PHÉP TOÁN TRÊN SỐ PHỨC
Số phức
z
a bi
c
ó phần thực là
,a
phần ảo
là
.b
Số phức liên hợp
z
a bi
và cần nhớ
2
1
.i
Số phức
z
a bi
c
ó điểm biểu diễn là
(
; ).M a b
Số phức
liên hợp
z
a bi
có
điểm biểu diễn
(
; ).N a b
Hai điể
m
M
và
N
đối x
ứng nhau qua trục hoành
.O
x
;z z
;z z z z
;z z z z
.
. ;z z z z
;
z z
z z
2
2
.
z z a b
Hai số phức
bằng nhau khi thực bằng thực và ảo bằng ảo.
Mô đ
un của số phức
z
l
à
:
2
2
z
a b
.
z z z z
z
z
z z
z z z z z z
z z z z z z
Phép cộng hai số phức Cho số phức
1
.
z a b i
và
2
.
z c d i
. Khi đó
1
2
.
. . . z z a b i c d i a c b d i
Phép trừ hai
số phức
1 2
.
. . . z z a b i c d i a c b d i
P
hép nhân hai số phức
1
2
. . . . . .
z z a b i c d i ac bd ad bc i
k
.z k.(a bi) ka kbi
P
hép chia hai số phức
1
1 2 1 2
2
2 2 2 2 2 2 2 2
2 2 2
2
.
. .
. .
.
.
a b i c d i ac bd bc ad i
z z z z z ac bd bc ad
i
z z z c d c d c d c d
z
Câu
1. Môđun của số phức
1
2i
bằ
ng
A.
5
. B.
3
. C.
5
. D.
3
.
Lời
giải
Chọn C
Ta
có
2
2
1
2 1 2 5
i
.
Câu
2. Số phức liên hợp của số phức
2z
i
là
A.
2z
i
. B.
2z
i
. C.
2z
i
. D.
2z
i
.
Lời
giải
Chọn C
Số
phức liên hợp của số phức
2z
i
là
2z
i
.
Câu
3. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
1
2z i
l
à điểm nào dưới đây?
A.
1
;2Q
. B.
1
;2P
. C.
1
; 2N
. D.
1
; 2M
.
Lời giải
SỐ
PHỨC
V
ấn đề 16
x
y
O
b
b
a
(
; )M a b
z
a bi
z
a bi
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Điể
m biểu diễn số phức
1
2z i
l
à điểm
1
;2
P
.
C
âu 4. Số phức liên hợp của số phức
1
2i
là:
A
.
1 2i
. B.
1 2i
. C.
2 i
. D.
1
2i
.
Lờ
i giải
Chọn
B
Theo
định nghĩa số phức liên hợp của số phức
,
,z a bi a b
l
à số phức
,
,z a bi a b
.
C
âu 5. Số phức liên hợp của số phức
5
3i
là
A
.
5
3i
. B.
3
5i
. C.
5
3i
. D.
5
3i
.
Lời
giải
Chọn
D
Số phức
liên hợp của số phức
5 3i
là
5 3i
C
âu 6. Số phức liên hợp của số phức
3
2z i
là.
A
.
3
2i
. B.
3
2i
. C.
3
2i
. D.
2
3i
.
Lờ
i giải
Chọn
B
Số phức
liên hợp của số phức
z
a bi
là số
phức
z
a bi
từ
đó suy ra chọn đáp án B.
Câu 7. Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức
1
2 z i
?
A.
N
. B.
P
. C.
M
. D.
Q
.
Lời giải
Chọn D.
Số phức
1
2 z i
c
ó điểm biểu diễn là điểm
1
;2
Q
.
C
âu 8. Số phức
5
6i
c
ó phần thực bằng
A
.
5
. B.
5
C.
6
. D.
6
.
Lời giải
Chọn B
Số phức
5
6i
c
ó phần thực bằng 5, phần ảo bằng
6
.
C
âu 9. Tìm tất cả các số thực
,x
y
sao c
ho
2
1
1 2x yi i
.
A.
2 , 2
x
y
B.
2 , 2
x
y
C.
0, 2x y
D.
2 , 2
x
y
Lời
giải
Chọn
C
Từ
2
1
1 2x yi i
2
0
1
1
2
2
x
x
y
y
Câu 10. Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A
.
1
3i
. B.
1
3i
. C.
1
3i
. D.
1
3i
.
Lời
giải
Chọn
1
3i
C
âu 11. Số phức
3 7i
có phầ
n ảo bằng
O
x
y
2
2
1
2
P
M
N
Q
1
1
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
3
. B.
7
. C.
3
. D.
7
.
Lời
giải
Chọn
7
Câu
12. Số phức nào dưới đây là số thuần ảo.
A.
2 3z i
B.
3z
i
C.
3z i
D.
2z
Lời giải
Chọn B
Số phức
z
được gọi là số thuần ảo nếu phần thực của nó bằng
0
.
Câu 13. Cho số phức
3
1z
i i
.
Tìm phần thực
a
và
phần ảo
b
của
z
.
A.
1, 2a b
B.
2, 1a b
C.
1, 0a b
D.
0, 1a b
Lời giải
Chọn A
Ta
có:
3
2
1
1 . 1 1 2z i i i i i i i i
(v
ì
2
1i
)
S
uy ra phần thực của
z
là
1a
,
phần ảo của
z
l
à
2b
.
Câu
14. Cho số phức
2 3z i
. Tìm phần thực
a
của
z
?
A.
2a
B.
3a
C.
2a
D.
3a
Lời
giải
Chọn A
Số phức
2 3z i
có
phần thực
2a
.
Câu
15. Kí hiệu
,a b
lần
lượt là phần thực và phần ảo của số phức
3
2 2i
.
Tìm
a
,
b
.
A.
3
; 2a b
B.
3; 2 2a b
C.
3; 2a b
D.
3; 2 2a b
Lời
giải
Chọn D
Số phức
3 2 2i
có
phần thực là
3a
và
phần ảo là
2 2b
.
Câu
16. Cho số phức
3
2z i
. Tìm
phần thực và phần ảo của số phức
z :
A. P
hần thực bằng
3
và P
hần ảo bằng
2i
B. P
hần thực bằng
3
và P
hần ảo bằng
2
C. P
hần thực bằng
3
và P
hần ảo bằng
2i
D. Phần
thực bằng
3
và P
hần ảo bằng
2
Lời giải
Chọn
D
3
2 3 2z i z i
. Vậy phần thực
bằng
3
và P
hần ảo bằng
2
Câu
17. Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
2z
i
B.
1
2z i
C.
2z
i
D.
1
2z i
Lời
giải
Chọn A
The
o hình vẽ
2
;1 2M z i
Câu
18. Điểm
M
tr
ong hình vẽ bên là điểm biểu diễn số phức
z
.
Tìm phần thực và phần ảo của số
phức
z
.
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. Phần thực là
2
và phần ảo là
i
. B. Phần thực là
1
và phần ảo là
2
.
C. P
hần thực là
1
và
phần ảo là
2i
. D. Phần
thực là
2
và
phần ảo là
1
.
Lời
giải
Chọn B
Điểm
M
có tọa độ
1
; 2M
nên
1 2z i
. Vậy phần thực là
1
và phần ảo là
2
.
Câu 19. Số phức liên hợp của số phức
2z
i
là
A.
2z
i
. B.
2z
i
. C.
2z
i
. D.
2z
i
.
Lời
giải
Chọn A
Số
phức liên hợp của số phức
2z
i
là
2z
i
.
Câu
20. Môđun của số phức
5
2z i
bằng
A.
2
9 . B.
3
. C.
7
. D.
2
9
.
Lời
giải
Chọn
A
Ta
có
2
2
5 2 29z
.
Câu
21. Nếu điểm
;M x y
l
à điểm biểu diễn của số phức
z
tr
ong mặt phẳng tọa độ
O
xy
t
hỏa mãn
4O
M
thì
A.
1
2
z
. B.
4z
. C.
16z
. D.
2z
.
Lời
giải
Chọn B
The
o định nghĩa môđun của số phức ta có:
4z
OM B
đúng
.
Câu 22. Nghịch đảo
1
z
của
số phức
1
3z i
bằ
ng
A.
1
3
.
10 10
i
B.
1
3
.
10 10
i
C.
1
3
.
10 10
i
D
.
1
3
.
10 10
i
Lời
giải
Chọn D
Số
phức nghịch đảo của số phức
z
l
à:
1
1 1 3 1 3
.
1 3 1 3 1 3 10 10
i
i
z i i i
Câu
23. Môdun của số phức
4
3z i
bằng
A.
7
. B.
25
. C.
5
. D.
1
.
Lời
giải
Chọn C
Môdun
của số phức
4 3z i
là
:
2
2
4
3 5z
.
Câu
24. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của số phức
2
3z i
?
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
M
. B.
P
. C.
N
. D.
Q
.
Lời
giải
Chọn C
Điểm
biểu diễn số phức liên hợp của số phức
2 3z i
là
điểm
2
;3N
.
Câu
25. Modun cỉa số phức
4
3z i
là
A.
1
. B.
1
. C.
5
. D.
2
5
.
Lời giải
Chọn C
Ta
có
2
2
4
3 5z
.
Câu
26. Cho hai số phức
1
3z
i
và
2
1
.z i
Phần ảo của số phức
1
2
z z
bằng
A.
2
.
B.
2
.i
C.
2.
D.
2
.i
Lời
giải
Chọn C
T
a có:
2
1z
i
. Do
đó
1
2
(
3 ) (1 ) 2 2 .z z i i i
Vậ
y phần ảo của số phức
1
2
z
z
bằng
2.
Câu
27. Cho hai số phức
1
2z
i
và
2
1
3z i
.
Phần thực của số phức
1
2
z
z
bằng
A.
1
. B.
3
. C.
4
. D.
2
.
Lời
giải
Chọn B
Ta
có
1
2
3 4z z i
.
P
hần thực của số phức
1
2
z z
bằ
ng
3
.
Câu
28. Cho hai số phức
1
3z
i
và
2
1z
i
.
Phần ảo của số phức
1
2
z
z
bằ
ng
A.
4
. B.
4i
. C.
1
. D.
i
.
Lời
giải
Chọn A
Ta có:

1
2
3
1 2 4z z i i i
.
Suy ra phần ảo của
1
2
z
z
bằ
ng
4
.
Câu
29. Cho 2 số phức
1
5
7z i
và
2
2
3z i
. T
ìm số phức
1
2
z
z z
.
A.
7 4z i
B.
2 5z i
C.
3 10z i
D.
1
4
Lời
giải
Chọn A
5 7 2 3 7 4z i i i
.
Câu
30. Cho hai số phức
1
4
3z i
và
2
7
3z i
. Tìm số phức
1
2
z
z z
.
A.
3 6z i
B.
11z
C.
1 10z i
D.
3 6z i
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
Ta có
1
2
z
z z
4 3 7 3i i
3 6i
.
Câu 31. Cho số phức
2
5 .z i
T
ìm số phức
w
iz z
A.
7
3w i
. B.
3
3w i
. C.
3
7 .w i
. D.
7
7w i
Lời
giải
Chọn
B
Ta
có
(
2 5 ) (2 5 ) 2 5 2 5 3 3w iz z i i i i i i
Câu 32. Cho hai số phức
1
2
z i
và
2
1
z i
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn của số
phức
1
2
2 z z
có tọa độ là
A.
5
; 1
. B.
1
; 5
. C.
5
; 0
. D.
0
; 5
.
Lời giải
Chọn A
Ta
có
1
2
2
5 z z i
.
Nên ta chọn A.
Câu 33. Cho hai số phức
1
1z
i và
2
2z
i . Trên mặt phẳng tọa độ
O
xy
,
điểm biểu diễn số phức
1
2
2z
z có tọa độ là
A.
(
2;5)
. B.
(3
;5)
. C.
(
5;2)
. D.
(
5;3)
.
Lời
giải
Chọn D
Ta
có
1
2
2
(1 ) 2(2 ) 5 3z z i i i .
Do đó điểm biểu diễn số phức
1 2
2z
z có tọa độ là
(5;3)
.
Câu
34. Cho hai số phức
1
1z
i và
2
2
3z i . Tính môđun của số phức
1
2
z
z .
A.
1
2
1z
z
. B.
1
2
5z
z . C.
1
2
13z
z . D.
1
2
5z
z
.
Lời
giải
Chọn C
Ta
có
1 2 1 2
1
2 3 3 2 3 2 13z z i i i z z i
.
Câu 35. Cho số phức
1
2 , 2z i w i
. Điểm nào trong hình bên biểu diễn số phức z w ?
A.
N
. B.
P
. C.
Q
. D.
M
.
Lời
giải
Chọn B
1z w i
.
Do
đó điểm biểu diễn của số phức z w là
1;1P
.
Câu
36. Tìm phần ảo của số phức
z
biết
2
13 1 z i i
.
A.
5 i
. B.
5i
. C.
5
. D.
5
.
Lời
giải
Chọn C
x
y
M
N
P
Q
O
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
T
a có:
1
13
2 13 1 3 5
2
i
z i i z i
i
.
Vậ
y phần ảo của số phức
z
là
5
.
Câu
37. Cho số phức
z
thỏa mãn:
2
(
3 2 ) (2 ) 4i z i i
. Hiệu phần thực và phần ảo của số phức
z
l
à
A.
2
. B.
3
. C.
1
. D.
0.
Lời giải
Chọn D
Ta có:
2
(
3 2 ) (2 ) 4 (3 2 ) 4 4 1 4i z i i i z i i
(3
2 ) 1 5
1 5 13 13
1
3 2 13
i z i
i i
z i
i
Phần thực là
1a
,
phần ảo là
1b
. Vậy
0a b
Câu
38. Phần thực và phần ảo của số phức
(1 2 )z i i
.
A.
1
và
2
. B.
2
và
1
. C.
1
và
2
. D.
2
và
1
.
Lời
giải
Chọn
B
Ta
có
(
1 2 )z i i
2 i
.
Vậ
y phần thực của số phức
z
l
à
2
và
phần ảo là
1
.
Câu
39. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức
1
2z i i
?
A.
Q
. B.
M
. C.
P
. D.
N
.
Lời
giải
Chọn A
Ta có
1 2 3z i i i
Vậy điểm
Q
tr
ong hình vẽ là điểm biểu diễn của số phức
1
2z i i
.
Câu
40. Trong hình vẽ bên dưới, điểm
P
biể
u diễn số phức
1
z ,
điểm
Q
biể
u diễn số phức
2
z .
Tìm số
phức
1
2
z
z z .
A.
1 3i
. B.
3 i
. C.
1 2i
. D.
2 i
.
y
x
1
2
2
-1
Q
P
O
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn
A
Từ hình vẽ suy ra
1
;2
P
và
2
;1
Q
. Từ đó
1
1 2z i
;
2
2z i
.
Vậy
z
1
2 2
i
i
1
3i
.
C
âu 41. Cho số phức
,
, .z a bi a b R
Khi đó số
1
2
z
z
l
à số nào trong các số sau đây?
A
. Số
2
.
B. Số
.i
C. Một
số thực. D
. Một số thuầ
n ảo.
Lờ
i giải
Chọn
C
Ta
có
z a bi
nê
n
1
1 1
.2
2
2 2
z z a bi a bi a a
.
Vậ
y
1
2
z
z
l
à số một số thực.
Câu 42. Cho hai số phức
1
1
3z i
và
2
2
5z i
. Tì
m phần ảo
b
của
số phức
1
2
z
z z
.
A.
2b
B.
3b
C.
3b
D.
2b
Lời
giải
Chọn D
Ta
có
1
2
3
2 2
z
z z i b
C
âu 43. Tìm số phức
z
thỏa
mãn
2
3 3 2z i i
.
A.
1 5z i
. B.
1z i
. C.
5 5z i
. D.
1z i
.
Lời
giải
Chọn B
2
3 3 2z i i
3
2 2 3 1z i i i
.
C
âu 44. Tìm số phức liên hợp của số phức
3 1
z i i
.
A.
3
z i
. B.
3
z i
. C.
3
z i
. D.
3
z i
.
Lời
giải
Chọn D
3
1 3z i i i
nê
n suy ra
3z
i
.
C
âu 45. Tính môđun của số phức
z
biết
4
3 1
z
i i
.
A.
2
5 2
z
B.
7
2
z
C.
5
2
z
D.
2
z
Lời giải
Chọn
C
4
3 1
z
i i
7 i
7z i
z
Câu 46. Tính môđun của số phức
z
thỏa mãn
2 13 1z i i
.
A.
3
4
z
B.
3
4
z
C.
5
34
3
z
D.
3
4
3
z
Lời
giải
Chọn
A
2
13 1z i i
1
13 2
1 13
3
5
2 2 2
i i
i
z
z z i
i i i
.
2
2
3
5 34.
z
C
âu 47. Cho hai số phức
1
1z
i
và
2
2
3z i
. Tính môđun của số phức
1
2
.z
z
A.
1
2
13
z
z
. B.
1
2
5
z
z
. C.
1
2
1
z
z
. D.
1
2
5
z
z
.
Lờ
i giải
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Chọn A
1
2
1
2 3 3 2z z i i i
nên ta có:
2
2
1 2
3
2 3 2 13
z
z i
.
C
âu 48. Cho hai số phức
1
2z i
và
2
1 .z i
Trên
mặt phẳng tọa độ
,Oxy
điểm
biểu diễn số phức
1
2
2
z
z
c
ó tọa độ là
A
.
3; 3
. B.
2; 3
. C.
3;3
. D.
3;2
.
Lời giải
Chọn
C
Ta
có:
1
2
2 4 2 1 3 3 .z z i i i
Vậy đ
iểm biểu diễn số phức
1 2
2
z
z
c
ó tọa độ là
3
;3
.
C
âu 49. Cho hai số phức
1
1
2z i
và
2
3
4z i
. Số phức
1
2 1 2
2
3
z
z z z
l
à số phức nào sau đây?
A
.
1
0i
. B.
1
0i
. C.
11
8i
. D.
1
1 10i
.
Lờ
i giải
Chọn
B
Ta
có:
1 2 1 2
2 3 2 1 2 3 3 4 1 2 3 4 10z z z z i i i i i
.
C
âu 50. Cho số phức
, z a bi a b
thoả m
ãn
2
z i z
. Tính
4S a b
.
A.
4S
B.
2S
C.
2S
D.
4S
Lời
giải
Chọn
D
Ta
có
2
2
2 2
2
, 2
2
2 1
1 0
a a b a
z i z a b i a b
b
2
2
3
1
4
4
4
2
1
1
b
a
S a b
a a
b
.
C
âu 51. Cho số phức z thỏa mãn
| | 5
z
và
| 3| | 3 10 |z z i
. Tìm số phức
4
3 .w z i
A.
3
8 .w i
B.
1
3 .w i
C.
1
7 .w i
D.
4
8 .w i
Lời
giải
Chọn
D
,
( , )
z
x yi x y
. T
heo đề bài ta có
2
2
25
x y
và
2
2 2 2
( 3) ( 3) ( 10)
x y x y
.
Giải
hệ phương trình trên ta được
0; 5
x y
. Vậy
5z
i
. Từ đó ta
có
4
8w i
.
C
âu 52. Cho số phức
, ,z a bi a b
thỏa mãn
1 3 0z i z i
.
Tính
3S a b
.
A.
5S
B.
7
3
S
C.
5S
D.
7
3
S
Lờ
i giải
Chọn
C
Ta
có:
2
2
2 2
1
1
0
1 3 0 1 3 0
4
3 0
3
a
a
z
i z i a bi i a b i
b
b a b
3 5S a b
.
C
âu 53. Tìm hai số thực
x
và
y
thỏ
a mãn
2 3 1 3 6x yi i x i
với
i
là đơn
vị ảo.
A.
1
x
;
3
y
. B.
1
x
;
1
y
. C.
1x
;
1
y
. D.
1x
;
3
y
.
Lờ
i giải
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
3 1 3 6x yi i x i
1
3 9 0x y i
1
0
3 9 0
x
y
1
3
x
y
.
Câu 54. Tìm các số thực
a
và
b
thỏ
a mãn
2 1 2 a b i i i
với
i
là
đơn vị ảo.
A.
0
, 2 a b
. B.
1
,
1
2
a b
. C.
0
, 1 a b
. D.
1
, 2 a b
.
Lời
giải
Chọn D.
Ta
có
2
1 2 a b i i i
2
1 1 2 a bi i
1
2
a
b
.
Câu
55. Phần ảo của số phức
z
thoả mãn
2
1 4 2z i i i là
A.
3
. B.
3i
. C.
3i
. D.
3
.
Lời
giải
Chọn
A
Cách 1:
2 1 4 2 4 2 2 1 1 3 1 3z i i i z i i i z i z i
Vậy phần ảo của
z
bằng
3
.
Cách 2: Đặt
,
;z x yi x y z x yi .
Kho đó
2
1 4 2 2 1 4 2 3 4 2z i i i x yi i i i x yi i i
3
4 1
3 1 4 2 1 3
1 2 3
x x
x y i i z i
y y
.
Vậy phần ảo của
z
bằng
3
.
Câu 56. Cho số phức
,z a bi a b
thỏa
mãn
1 2 3 2 .i z z i
T
ính
P
a b
.
A.
1
2
P
B.
1P
C.
1P
D.
1
2
P
Lời
giải
Chọn C
1
2 3 2 . 1 i z z i
.
Ta có:
z a bi
.
z a bi
Tha
y vào
1
ta
được
1
2 3 2 i a bi a bi i
3
3 2 a b i a b i
3
3 2 a b i a b i
1
2
2
1.
3 3 3
2
a
a b
P
a b
b
Câu 57. Tìm hai số thực
x
và
y
t
hỏa mãn
2
3 3 5 4x yi i x i
với
i
là
đơn vị ảo.
A.
1; 1x y
. B.
1; 1x y
. C.
1; 1x y
. D.
1; 1x y
.
Lời
giải
2
3 5 1
2 3 3 5 4 2 3 3 1 5 4
3 1 4 1
x x x
x yi i x i x y i x i
y y
Câu 58. Tìm hai số thực
x
và
y
t
hỏa mãn
3
2 2 2 3x yi i x i
với
i
là đơ
n vị ảo.
A.
2
; 2x y
. B.
2
; 1x y
. C.
2
; 2x y
. D.
2
; 1x y
.
Lời giải
2
1 1
2
a
b
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Ta
có:
3
2 2 2 3x yi i x i
3
2 2 1 2 3x y x i
3 2 2 2
2 1 3 2
x x x
y y
.
Câu 59. Cho số
z
thỏa
mãn
2
4 8 19i z z i i
. Môđun của
z
bằ
ng
A.
1
3
. B.
5
. C.
13
. D.
5
.
Lời giải
Chọn
A
Gọi
;
, .
z
a bi z a bi a b
Ta
có:
2
4 8 19
2
4 8 19
2
6 4 8 19
2 8 3
6 4 19 2
i z z i i
i
a bi a bi i i
a
b a b i
a b a
a b b
Vậ
y
3
2 13.
z
i z
C
âu 60. Cho số phức
z
thoả mãn
3
2 3 7 16 .z i i z i
Môđun của
z
bằ
ng
A
.
5.
B.
5
.
C.
3
.
D.
3
.
Lờ
i giải
Chọn
A
Đặ
t
;z
a bi a b
.
Theo
đề ta có

3
2 3 7 16a bi i i a bi i
3
3 3 2 2 3 3 7 16a bi i a bi ai b i
3
3 5 3 7 16a b a b i
3
7 3 7 1
3 5 3 16 3 5 13 2
a
b a b a
a b a b b
.
Vậ
y
2
2
1 2 5
z
.
C
âu 61. Cho số phức
z
thỏa mãn
2
3 16 2
i
z i z i
.
Môđun của
z
bằ
ng
A.
5
. B.
1
3
. C.
1
3
. D.
5
.
Lời giải
Chọn
C
Gọi
z
x yi
.
2
3 16 2
i
z i z i
2
3 16 2
i
x yi i x yi i
2
2 3 16 2 2 2x yi xi y i x yi i
2
3 2
2
16 2 2
x
y x
y x y
3
0
4
14
y
x
y
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
3
x
y
Suy ra
2
3z i
.
Vậy
13z .
Câu
62. Tìm hai số thực
x
và
y
thỏa mãn
3
4 2 5 2x yi i x i
với
i
là đơn vị ảo.
A.
2x
;
4y
B.
2x
;
4y
C.
2x
;
0y
D.
2x
;
0y
Lời giải
Chọn B
3 4 2 5 2x yi i x i
2 4 4 0x y i
2 4 0
4 0
x
y
2
4
x
y
.
Câu 63. Cho số phức
z
thỏa m
ãn
2
1 3 3 4i z i
.
Môđun của
z
bằng
A.
5
4
. B.
5
2
. C.
2
5
. D.
4
5
.
Lời giải
Chọn A
Ta
có
2
3
4 3 4 3 4 3 3
8 8
1 3
i
z i
i
.
S
uy ra
2
2
3
4 3 4 3 3 3 4 3 4 3 3 5
8 8 8 8 4
z i
.
Câu
64. Cho số phức
2
3z i
. Môđun
của số phức
2
1w z i z
bằng
A.
4
. B.
2
. C.
10 . D.
2 2
.
Lời
giải
Chọn C
Ta
có
2 2 3 1 2 3 3w i i i i
.
S
uy ra
1
0w
.
Câu 65. Cho hai số thực
x
,
y
thỏa
mãn
3
2 1 4 1 24x i y i i
.
Giá trị của
x
y
bằng:
A.
-3. B. 4. C. 2. D. 3.
Lời
giải
Chọn A
Ta
có:
3
2 1 4 1 24 3 (2 4 ) 1 24x i y i i x y x y i i
.
S
uy ra:
3
1 2
2 4 24 5
x y x
x y y
.
Do
đó:
3x
y
.
Câu
66. Cho số phức . Môđun của số phức bằng:
A. . B. . C. . D. .
Lời
giải
Chọn
A
2
2
2
3 2 3 3 9w z z i i i
2
2
3
9 3 10w
.
Câu 67. Cho số phức
z a bi
,a b R
, t
hỏa mãn
3 1z z
và
2z
z i
là
số thực.
Tính
a
b
.
2
3z i
2
w
z z
3
10
206
1
34
3
2
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A.
0
. B.
4
. C.
2
. D.
2
.
Lời
giải
Chọn
A
Ta có:
3
1z z
2 2
2 2
3
1a b a b
2a
Do đó:
2z z i
2
4
2 8 2 4bi bi i b b b i
là
số thực khi
2
4 0b
2b
. Do đó
0a
b
.
Câu 68. Gọi
1
2
z
,z lần lượt có điểm biểu diễn là
M
và
N
t
rên mặt phẳng phức ở hình dưới đây.
Tính
1 2
z
z
.
A. 2
29 . B.
2
5 . C.
2
0
. D.
1
16
.
Lời giải
Chọn B
Ta
có
3
2 1 4M ; ,N ;
lầ
n lượt là điểm biểu diễn hình học của số phức
1
2
z
,z suy ra
1
2
3
2 1 4z i,z i
.
Do đó
1
2 1 2
3
2 1 4 4 2 4 2 2 5z z i i i z z i .
Câu 69. Cho số phức
( , )z a bi a b
thoả mãn
(
1 ) 2 3 2i z z i
. Tính
P a b
A.
1P
. B.
1
2
P
. C.
1
2
P
. D.
1P
Lời
giải
Chọn D
(
1 ) 2 3 2 (1 )( ) 2( ) 3 2 (3 ) ( ) 3 2i z z i i a bi a bi i a b a b i i
1
3 3
2
2 3
2
a
a b
a b
b
. Suy ra:
1P a b
.
Câu 70. Cho
2
z
z
là số thực, 3 2z z . Tính
z
A.
3
2z
. B.
6z
. C.
2
3z
. D.
3z
.
Lời giải
Chọn B
Đặ
t z x yi với
,x
y
.
2
9
3 2 2 3 2
2
z z yi y
1
.
T
a có:
2
2
2
2
.z
z z
z
z
. Nên để
2
z
z
l
à số thực thì
2
.z
z
là
số thực hay:
3
x
yi
x
y
N
M
3
2
-
4
O
1
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suy ra
2
3 2 2
3
0 3 0
x
y y y x y
.
2
.
Kế
t hợp
1
và
2
ta
có:
2
2
3
9
,
2
2
x
y
. Vậ
y
2 2
6
z
x y
.
C
âu 71. Tìm cac số thực
x
và
y
thỏa mãn
3
2 2 1 1 5 ,x y i x y i
với
i
là đơn vị ảo.
A.
3
,
2
2
x
y
. B.
3 4
,
2
3
x
y
. C.
4
1
,
3
x
y
. D.
3 4
,
2
3
x
y
.
Lờ
i giải
Chọn
D
Vì
3
3
2 1
2
3
2 2 1 1 5 .
4
2
1 ( 5)
3
x
x
x
x y i x y i
y y
y
C
âu 72. Cho số phức
z
thỏa mãn điều kiện
2
1
2 4 20
i
z z i
. T
ìm
z
.
A.
2
5
z
. B.
7
z
. C.
4
z
. D.
5
z
.
Lời giải
Chọn
D
Gọi
z
a bi
,
a
,
b
. Suy ra
z
a bi
.
Từ giả thiết suy ra
:
2
1
2 4 20
i
a bi a bi i
3
4 20 4i a bi a bi i
2 4 4 4 20 4a b a b i i
2
4 20
4
4 4
a b
a b
4
3
a
b
.
S
uy ra
4
3z i
. Vậ
y
z
2
2
4 3
5
.
C
âu 73. Tổng phần thực và phần ảo của số phức
z
thoả mãn
1
2iz i z i
bằng
A
.
6
. B.
2
. C.
2
. D.
6
.
Lờ
i giải
Chọn
A
Giả
sử số phức
z
có dạ
ng:
, ,z x yi x y
.
Ta
có:
1
2iz i z i
1
2i x yi i x yi i
2 2x y yi i
.
2 0 4
2 2
x y x
y y
6
x
y
.
Tổng
phần thực và phần ảo của số phức
z
bằ
ng
6
.
C
âu 74. Cho
,a b
và thỏa m
ãn
2
1 3a bi i a i
, với
i
là đơn vị ảo.
Giá trị
a b
bằng
A
.
4
. B.
1
0
. C.
4
. D.
1
0
.
Lờ
i giải
Chọn
D
Ta
có
2
1 3
2
1 3 2 1 3
3
7
b
a a
a bi i a i b a ai i
a b
Vậy
10
a
b
.
C
âu 75. Tìm hai số thực
x
,
y
t
hỏa mãn
3 2 3 4 3x yi i x i
với
i
là đơn
vị ảo.
A.
3
; 1
x
y
. B.
2
;
1
3
x
y
. C.
3
; 3
x
y
. D.
3
; 1
x
y
.
Lờ
i giải
Chọn A
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
3
3 4 3
3 2 3 4 3 3 3 2 1 4 3
2
1 3 1
x
x x
x yi i x i x y i x i
y y
.
Câu 76. Cho các số phức
1
2
,z z
thỏa mãn
1 2
3
z
z
và
1
2
2
z
z
. Môđun
1
2
z
z
bằng
A
.
2
. B.
3
. C.
2
. D.
2
2
.
Lờ
i giải
Chọn
D
Đặt
1
1 1
1 2 2 2
2 2 2
, , ,
z a b i
a a b b
z a b i
.
Theo
giả thiết ta có
2
2 2 2
1 1 2 2
1 2 1 2
3
2
2
a
b a b
a a b b
.
S
uy ra
2 2
2
1 2 1 2 1 2
8
z
z a a b b
.
Vậy
1
2
2
2
z
z
.
C
âu 77. Cho số phức
z
thỏa mãn
2
3 1 2z z i
. Phần ảo của
z
là
A.
2
. B.
2
. C.
3
4
. D.
3
4
.
Lời giải
Chọn B
Ta
có:
2
2
3
1 2 3 1 2 3 3 4 (1).
z
z i z z i z z i
Đặt
( , )
z
x yi x y
z x yi
.
P
hương trình
(1)
t
hành
3( ) 3 4 4 2 3 4x yi x yi i x yi i
3
4
3
4
2
4
2
x
x
y
y
.
Vậy p
hần ảo của số phức
z
l
à
2
.
B. P
HƯƠNG TRÌNH SỐ PHỨC
Phư
ơng trình
2
0a
z bz c
với
0a
có
biệt số
2
4b
ac
thì
có hai nghiệm thực hoặc phức là
1
2
b
z
a
hoặc
2
2
b
z
a
C
âu 78. Gọi
0
z
là
nghiệm phức có phần ảo âm của phương trình
2
2
5 0
z
z
.
Môđun của số phức
0
z i
bằng
A.
2
. B.
2
. C.
1
0
. D.
1
0
.
Lờ
i giải
Chọn B
Ta
có:
2
2
5 0
z
z
2
2
1 4
z
z
2
2
1
4z i
1
2 1 2
1 2 1 2
z i z i
z z i
.
Vì
0
z
l
à nghiệm phức có phần ảo âm nên
0
1
2z i
0
1
2 1z i i i i
.
S
uy ra:
2
2
0
1
1 1 2
z
i i
.
C
âu 79. Kí hiệu
0
z
là nghiệm phức có phần ảo dương của phương trình
2
4
16 17 0
z
z
. Trên mặt
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
0
w iz
?
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
1
;
2
2
M
. B.
2
1
;
2
2
M
. C.
3
1
;1
4
M
. D.
4
1
;1
4
M
.
Lời
giải
Chọn
B
Xé
t phương trình
2
4
16 17 0
z
z
c
ó
2
6
4 4.17 4 2i
.
P
hương trình có hai nghiệm
1
2
8
2 1 8 2 1
2
, 2
4
2 4 2
i
i
z
i z i
.
Do
0
z
l
à nghiệm phức có phần ảo dương nên
0
1
2
2
z i
.
Ta
có
0
1
2
2
w iz i
.
Vậy điểm biểu diễn
0
w
iz
là
2
1
;
2
2
M
.
C
âu 80. Kí hiệu
1
2
,z
z
là hai nghiệm phức của phương trình
2
3
1 0z z
. Tính
1
2
P z z
.
A.
14
3
P
B.
2
3
P
C.
3
3
P
D.
2
3
3
P
Lời
giải
Chọn
D
Xé
t phương trình
2
3
1 0z z
c
ó
2
1 4.3.1 11 0
.
Căn bậc hai của
là
11i
.
P
hương trình đã cho có 2 nghiệm phức phân biệt
1
1 11 1 11
;
6
6 6
i
z
i
2
1 11 1 11
6 6 6
i
z
i
Từ đó
suy ra:
1
2
P z z
1
11 1 11
6 6 6 6
i i
2 2
2
2
1
11 1 11
6
6 6 6
3
3
3 3
2
3
3
C
âu 81. Kí hiệu
1
2
,z z
l
à hai nghiệm phức của phương trình
2
6
0z z
.
Tính
1
2
1
1
P
z
z
.
A.
1
12
B.
1
6
C.
1
6
D.
6
Lời
giải
Chọn
B
Theo
định lí Vi-et, ta có
1
2
1 2
1
6
z
z
z z
nê
n
1 2
1 2 1 2
1 1 1
. 6
z
z
P
z z z z
C
âu 82. Kí hiệu
1
2
;z z
là
hai nghiệm của phương trình
2
1
0
z
z
. Tí
nh
2
2
1
2 1 2
P
z z z z
.
A.
1P
B.
2P
C.
1P
D.
0
P
Lời giải
Chọn D
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
2
1
3
2 2
1 0
1 3
2 2
z i
z z
z
i
2 2
2 2
1 2 1 2
1
3 1 3 1 3 1 3
2 2 2 2 2 2 2
0
2
i
i iP z z z z i
C
âu 83. Kí hiệu
1
2 3
,
,z z z
và
4
z
là bốn nghiệm phức của phương trình
4
2
12 0
z z
. Tính
tổng
1
2 3 4
T
z z z z
A.
4T
B.
2
3
T
C.
4
2 3
T
D.
2
2 3
T
Lờ
i giải
Chọn C
2
4
2
2
3
3
1
2 0
2
4
z
z
i
z
z
z
z
1
2 3 4
3
3 2 2 2 3 4
T
z z z z i i
C
âu 84. Phương trình nào dưới đây nhận hai số phức
1 2i
và
1 2i
là nghiệm.
A.
2
2
3 0z z
B.
2
2
3 0z z
C.
2
2
3 0z z
D.
2
2
3 0z z
Lời giải
Chọn C
Theo
định lý Viet ta có
1 2
1 2
2
.
3
z
z
z z
, do đó
1
2
,z
z
là hai
nghiệm của phương trình
2
2 3 0z z
C
âu 85. Kí hiệu
1
z
,
2
z
l
à hai nghiệm của phương trình
2
4
0
z
.
Gọi
M
,
N
lần
lượt là điểm biểu
diễn của
1
z
,
2
z
trên
mặt phẳng tọa độ. Tính
T
OM ON
với
O
là
gốc tọa độ.
A.
2
T
B.
2T
C.
8
T
D.
4
Lời giải
Chọn D
Ta có:
1
2
2
2
4
0
2
z
i
z
i
z
S
uy ra
0
; 2
M
;
0
;2
N
nê
n
2
2
2
2 4
T
OM ON
.
C
âu 86. Kí hiệu
1
2
,
z z
là
hai nghiệm phức của phương trình
2
3
z 5 0
z
.
Giá trị của
1
2
z
z
bằ
ng
A.
2
5
. B.
5
. C.
3
. D.
10
.
Lờ
i giải
Chọn A.
Ta có :
1
2
2
3
11
2
3
5 0
3
11
2
i
z
z
z
i
z
. Suy ra
1
2 1 2
5
2 5
z z z z
.
Câu 87. Gọi
1
z
và
2
z
là
hai nghiệm phức của phương trình
2
4
4 3 0
z
z
.
Giá trị của biểu thức
1
2
z z
bằng:
A.
3
2
B.
2
3
C.
3
D.
3
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
Xét phương trình
2
4
4 3 0
z
z
ta có hai nghiệm là:
1
2
1
2
2 2
1 2
2 2
z i
z i
1
2
3
2
z
z
1
2
3
z z
C
âu 88. Gọi
1
2
,z
z
l
à 2 nghiệm phức của phương trình
2
4
z 5 0
z
. G
iá trị của
2
2
1 2
z z
bằ
ng
A
. 6. B. 8. C. 16. D. 26.
Lờ
i giải
Chọn
A
2
'
b' 4 5 1
a
c
P
hương trình có 2 nghiệm phức
1
2
2
, 2z i z i
nê
n
2 2
2 2 2 2 2
1 2
2
2 4 4 4 4 8 2 8 2 6
z
z i i i i i i i
Câu 89. Gọi
1
2
,z z
là
hai nghiệm phức của phương trình
2
4
7 0.
z
z
Giá trị
của
2
2
1 2
z
z
bằ
ng
A
. 10. B. 8. C. 16. D. 2.
Lờ
i giải
Chọn D
Ta
có
2
4
7 3 3 .
i
Do đó phư
ơng trình có hai nghiệm phức là
1
2
2
3 , 2 3 .
z
i z i
S
uy ra
2
2
2 2
1 2
2
3 2 3 4 4 3 3 4 4 3 3 2.
z
z i i i i
C
âu 90. Gọi
1 2
,z
z
là
hai nghiệm phức của phương trình
2
6
10 0
z
z
. Giá
trị của
2
2
1 2
z
z
bằng:
A
.
16
.
B.
56
. C.
2
0.
D.
2
6
.
Lời
giải
Chọn
A
Áp dụng định
lý Viet áp dụng cho phương trình trên ta được:
1
2
1 2
6
10
z z
z z
.
Khi
đó ta có
2
2
2
1 2 1 2 1 2
2
36 20 16
z
z z z z z
.
C
âu 91. Gọi
1
2
,z
z
là các
nghiệm phức của phương trình
2
4
7 0
z
z
. Số phức
1 2 1 2
z
z z z
bằng
A
.
2
. B.
10
. C.
2i
. D.
10i
.
Lờ
i giải
Chọn A
2
2
3
4
7 0
2
3
z i
z
z
z
i
Không mất tính tổng quát giả sử
1
2
2 3 , 2 3 .z i z i
1
2 1 2
2 3 2 3 2 3 2 3 2
z z z z i i i i
.
Vậy
1
2 1 2
2
.
z
z z z
C
âu 92. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4
5 0
z
z
;
M
,
N
lần lượt là các điểm
biểu diễn của
1
z
,
2
z
trên mặt phẳng phức. Độ dài đoạn thẳng
M
N
là
A.
2 5
. B.
4
. C.
2
. D.
2
.
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Lời giải
Chọn
D
Xé
t phương trình:
2
4
5 0
z
z
, ta
có
2
2
1.5
1
2
i
.
S
uy ra phương trình có hai nghiệm phức là
1
2z
i
;
2
2z
i
.
Suy ra
2;1
M
;
2; 1
N
.
Ta
có
M
N
2 2
2
2 1 1
2
.
Vậy
2
M
N
.
C
âu 93. Gọi
1
z
,
2
z
là hai
nghiệm phức của phương trình
2
3
2 0
z
z
.
Tính
2
2
1 2
zT
z
.
A.
2
3
T
. B.
8
3
T
. C.
4
3
T
. D.
11
9
T
.
Lờ
i giải
Chọn C
2
3 2 0
z z
1
2
1
23
6
1
23
6
i
z
i
z
2
2
2
1
2
2
2
2
1
23 2
6 6 3
1 23 2
6 6 3
z
z
.
Vậ
y
2
2
1 2
2
2 4
3 3 3
T z
z
.
C
âu 94. Gọi
1
2
,
z z
là
hai nghiệm phức của phương trình
2
z
2z 10 0
.
Giá trị của
2
2
1 2
z
z
bằng
A
.
10
. B.
2
0
. C.
2
10
. D.
10
.
Lờ
i giải
Chọn
B
Ta
có
2
2
2
z 2z 10 0 1 9 3 1 3z i z i
.
Do đó
2
2
1 2
z
z
=20.
C
âu 95. Gọi
1 2
,z
z
là
hai nghiệm phức của phương trình
2
4 29 0
z z
.
Tính giá trị của biểu thức
4
4
1 2
z
z
.
A
.
8
41
. B.
5
8
. C.
1
682
. D.
2
019
.
Lờ
i giải
Chọn
C
Ta
có
2 2 2
2
4
29 0 2 25 2 5 2 5z z z z i z i
.
4
4
4 4 2 2 2
2
1 2
2
5 2 5 1628
z
z
.
C
âu 96. Kí hiệu
1
z
và
2
z
là 2 nghiệm phức của phương trình
2
2
4 9 0
z
z
. Tính
1
2
1
1
P
z
z
A.
4
9
P
. B.
4
9
P
. C.
9
4
P
. D.
9
4
P
.
Lờ
i giải
Chọn
B
Theo
định lí Vi ét:
1 2
1 2 1 2
1
1 4
. 9
z z
P
z z z z
C
âu 97. Gọi
1
z
,
2
z
là
hai nghiệm phức của phương trình
2
5 7 0
z z
.
Giá trị của biểu thức
1
2
z z
là
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3i
. B.
3i
. C.
3
. D.
3
2
.
Lờ
i giải
Chọn
C
Ta
có
2
5
7 0
z
z
1
2
5
3
2
5
3
2
i
z
i
z
1
2
3
3
z
z i
Câu 98. Kí hiệu
1
2
, z z
là hai
nghiệm phức của phương trình
2
2
z 10 0
z
. Gi
á trị của
1
2
.z
z
bằng
A
.
5
. B.
5
2
. C.
10
. D.
20
.
Lờ
i giải
Chọn C
P
hương trình
2
2
z 10 0
z
có
9
nê
n phương trình có 2 nghiệm phức:
1
2
1
3 , 1 3z i z i
.
Khi
đó:
2 2 2
2
1 2
. 1 3 . 1 3 10.
z z
Câu 99. Gọi
1
2
,z
z
là
hai nghiệm phức của phương trình
2
2
z 2 0
z
.
Tính giá trị của biểu thức
1 2 1 2
2
P
z z z z
.
A
.
6
P
. B.
3
P
. C.
2
2 2
P
. D.
2
4
P
.
Lờ
i giải
Chọn A
Ta
có
1
2
2
1
2
z 2 0
1
z
i
z
z
i
.
S
uy ra
2
1 1 1 1 2 2 2 4 2 6
P
i i i i i
.
Câu 100. Kí hiệu
1
2
;z
z
là hai
nghiệm phức của phương trình
2
3
1 0
z
z
. T
ính
1
2
P
z z
A.
1
4
3
P
. B.
2
3
P
. C.
3
3
P
. D.
2
3
3
P
.
Lờ
i giải
Chọn
D
Ta
có
1
2
2
1 11
6 6
3 1 0
1
11
6 6
z i
z z
z
i
2
2
2 2
1 2
1
11 1 11 2 3
6 6 6 6 3
P
z z
.
C. BIỂU DIỄN ĐIỂM SỐ PHỨC
Đ
iểm biểu diễn số phức:
Số phứ
c
z
a bi
,
,a
b
được biể
u diễn bởi điểm
;M
a b
.
BÀI TOÁN: Tìm tập hợp
điểm biểu diễn của số phức thỏa mãn tính chất cho trước
Bướ
c 1. Gọi
( ; )M x y
là điể
m biểu diễn số phức
( , ).z x yi x y
Bướ
c 2. Biến đổi điều kiện
K
để
tìm mối liên hệ giữa
,
x y
và kế
t luận.
Mối liên
hệ giữa
x
và
y
Kết luận tập hợp điểm
(
; )M x y
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
0.Ax By C
L
à đường thẳng
: 0.d Ax By C
2
2 2
2 2
(
) ( )
2
2 0
x
a y b R
x y ax by c
Là đường tròn
( )C
có tâm
( ; )I a b
và bán kính
2
2
.R
a b c
2
2 2
2 2
(
) ( )
2 2 0
x
a y b R
x y ax by c
L
à hình tròn
(
)C
có
tâm
(
; )I a b
và
bán kính
2
2
R a b c
(đường
tròn kể cả bên
t
rong)
2
2 2 2
1 2
(
) ( ) .R x a y b R
Là những điểm thuộc miền có hình vành khăn
tạo
bởi hai đường tròn đồng tâm
(
; )I a b
v
à
bán kính lần
lượt
1
R
v
à
2
R
.
2
,
( 0).y ax bx c a
Là một parabol
(
)P
có đỉnh
;
2
4
b
I
a
a
2
2
2 2
1
x y
a b
với
1
2
1 2
2
2
2
MF
MF a
F
F c a
L
à một elíp có trục lớn
2
,a
trục
bé
2b
v
à tiêu
cự là
2
2
2
2 , ( 0).c a b a b
.MA MB
 
Là đường trung trực của đoạn thẳng
.AB
C
âu 101. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2
1
2z i
là điể
m nào dưới đây?
A
.
3
;4
P
. B.
5
;4
Q
. C.
4
; 3
N
. D.
4
;5
M
.
Lờ
i giải
Chọn
A
Ta
có
2
1
2z i
2
2
1
2.1.2 2i i
3
4i
.
Vậy trê
n mặt phẳng tọa độ, điểm biểu diễn số phức
2
1
2z i
là
điểm
3
;4
P
.
C
âu 102. Cho số phước
1 2 .z i
Đ
iểm nào dưới đây là điểm biểu diễn số phức
w
iz
trê
n mặt phẳng
tọa độ
A.
2
; 1
N
B.
2
;1
P
C.
1
; 2
M
D.
1
; 2
Q
Lời
giải
Chọn A
1 2 2w iz i i i
C
âu 103. Cho số phức
1z
i
. Biể
u diễn số phức
2
z
là điểm
A
.
2
;0
M
. B.
1
;2
P
. C.
2
;0
E
. D.
0
; 2
N
.
Lờ
i giải
Chọn
D
Ta có
1z i
. Nên
2
2
1
2z i i
. Vậy điểm biểu diễn số phức
2
z
là điểm
0
; 2
N
.
Câu 104. Xét các số phức
z
thỏa
mãn
2
2
z
i z
là
số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức
z
l
à một đường tròn có bán kính bằng
A
.
2
B.
2
2
C.
4
D.
2
Lời giải
Chọn D
Giả sử
z
x yi
với
,x
y
.
Vì
2
2 2 2
z
i z x y i x yi
2 2 2 2
x x y y xy x y i
là
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
số thuần ảo
nên có phần thực bằng không do đó
2 2 0
x x y y
2
2
1
1 2
x
y
.
Suy ra tập hợp các điểm biểu diễn các số phức
z
l
à một đường tròn có
bán kính bằng
2
.
C
âu 105. Xét các số phức
z
t
hỏa mãn
2
2
z
i z
là
số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức
z
là một đường tròn có bán kính bằng?
A
.
2 2
. B.
2
. C.
2
. D.
4
.
Lời giải
Gọi
z
a bi
,
,a b
Ta
có:
2
2
2
2 2 2 2 2 2 2z i z a bi i a bi a a b b a b i
Vì
2
2
z
i z
là số t
huần ảo nên ta có
2
2
2 2
2 2 0 1 1 2
a a b b a b
.
Tr
ên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức
z
là
một đường tròn có
bán kính bằng
2
.
Câu 106. Xét các số phức
z
t
hỏa mãn
3
i 3
z
z
l
à số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức
z
l
à một đường tròn có bán kính bằng:
A.
9
2
. B.
3 2
. C.
3
. D.
3
2
2
.
Lời
giải
Gọi
iz
x y
, với
,x
y
.
Theo giả thiết, ta có
3
i 3
z
z
2
3
3i 9i
z
z z
là
số thuần ảo khi
2
2
3
3 0
x
y x y
. Đây là phương trình đường tròn tâm
3
3
;
2 2
I
, bán kính
3
2
2
R
.
Câu 107. Tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa
mãn
2
4
z
i
l
à đường tròn có
tâm
I
và bán kí
nh
R
lần lượt
là
A
.
2
; 1
I
;
2R
. B.
2
; 1
I
;
4R
. C.
2
; 1
I
;
2R
. D.
2
; 1
I
;
4R
.
Lờ
i giải
Chọn B
Gọi
z x yi
,
z
được biể
u diễn bởi
;M x y
.
Theo
giả thiết
2 4
z i
nê
n ta có
2
4
x
yi i
2 2
2
1 4
x
y
2 2
2
2
1 4
x
y
. Vậy tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
2
; 1
I
và bán kí
nh
4R
.
C
âu 108. Tập hợp các điểm biểu diễn các số phức
z
t
hỏa mãn
1 2
z i
là
đường tròn có tâm và bán
kính lần lượt là
A
.
1
;1 , 4
I
R
. B.
1
;1 , 2
I
R
. C.
1
; 1 , 2
I
R
. D.
1
; 1 , 4
I
R
.
Lờ
i giải
Chọn
C
Gọi
;M x y
là điểm biểu diễn cho các số phức
z
x yi
2
,
, 1
x
y i
.
2
2 2 2
1 2 1 1 2 1 1 2 1 1 4
z i x y i x y x y
.
Vậ
y tập hợp các điểm biểu diễn các số phức
z
thỏa
mãn
1
2
z
i
là
đường tròn có tâm
1; 1
I
, bán kính
2R
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Câu 109. Tập hợp các điểm biểu diễn các số phức
z
thỏa mãn
2
z z i
là một đường thẳng có
phương trình
A.
4 2 3 0
x y
. B.
2 4 13 0
x y
. C.
4 2 3 0
x y
. D.
2 4 13 0
x y
.
Lời giải
Chọn A
Gọi
;M x y
là điểm biểu diễn số phức
z
.
Ta có
2 2
2 2
2 2 1 4 4 2 1 4 2 3 0
z z i x y x y x y x y
Do đó ta chọn đáp án A.
Câu 110. Tập hợp điểm biểu diễn số phức
z
biết:
(3 4 ) 2
z i
là
A. Đường tròn tâm
(3; 4), 2I R
. B. Đường tròn tâm
( 3; 4), 2I R
.
B. Đường tròn tâm
(3; 4), 4I R
. D. Đường tròn tâm
( 3; 4), 4I R
.
Lời giải
Chọn A
Gọi
;z x yi x y
. Ta có:
2 2
(3 4 ) 2 ( 3) ( 4) 4
z i x y
Vậy tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
(3; 4), 2I R
.
Chú ý:
( ; )
( )
I a b
z a bi R
R
Câu 111. Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
1
z i i z
là một đường tròn, tâm của
đường tròn đó có tọa độ là
A.
1;1
. B.
0; 1
. C.
0;1
. D.
1;0
.
Lời giải
Chọn B
Gọi
;M x y
là điểm biểu diễn số phức
,( , )
z x yi x y
.
Theo bài ra ta có:
1
z i i z x yi i z iz
2 2 2
2
1 1
x y i x y x y i x y x y x y
2
2 2 2
2 1 0 1 2.
x y y x y
Vậy tập hợp các điểm biểu diễn số phức
z
thỏa mãn yêu cầu bài toán là đường tròn tâm
0; 1
I
, bán kính
2
R
.
Câu 112. Cho số phức
z
thay đổi thỏa mãn
1 2.
z
Biết rằng tập hợp điểm biểu diễn các số phức
1 3 2
w i z là đường tròn có bán kính bằng
.R
Tính
.R
A.
8
R
. B.
2R
. C.
16
R
. D.
4R
.
Lời giải
Chọn D
Gọi
, ,
w x yi x y
.
1 3 2
w i z
1 3 2 1 3 1 1 3 2 x yi i z x yi i z i
3 3 1 3 1
x y i i z
3 3 1 3 1
x y i i z
2
2
3 3 1 3 1 x y i z
N
GUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
3 3 4
x y
2
2
3
3 16.
x y
Vậy tập hợp điểm biểu diễn các số phức
1 3 2
w i z
là đường tròn tâm
3; 3
I
, bán
kính bằ
ng
4.
R
C
âu 113. Có bao nhiêu số phức
z
c
ó phần thực bằng
2
và
1
2 3
z
i
?
A
.
3
.
B.
0
.
C.
2
.
D.
1
Lời giải
Chọn
D
Gọi số phức
z
có dạng:
2
z bi b
Ta có:
1
2 3
z
i
2
1 2 3 3 2 3
b
i i b i
2 2
9
2 3 2 0 2
b
b b
.
Vậy có một số phức
z
thỏa mãn yêu cầu bài
toán:
2 2 .z i
C
âu 114. Tập hợp các điểm biểu diễn các số phức
z
thỏa
mãn
2
2z i z z i
là
A
. Một
điểm. B
. Một
đường tròn. C. Một đường thẳng. D. Một Parabol.
Lờ
i giải
Chọn
D
Đặt
,z x yi x y
z
x yi
.
Khi đó
2 2z i z z i
2
1 2 2x y i y i
2
2
2
4
1 2 2
x
y y
2
2 2
4
4 8 4 4 8 4
x
y y y y
2
4
x
y
là một
Parabol.
Câu 115. Trong mặt phẳng tọa độ
Oxy
,
tìm tập hợp điểm biểu diễn số phức
z
thỏa
mãn
2
3 2
z
i
.
A. Một
đường thẳng. B. Một hình tròn. C. Một đường tròn. D. Một đường elip.
Lờ
i giải
Chọn
B
Gọi
; ,z x yi x y
. Từ giả t
hiết
2
3 2 (2 3 ) 2
z
i x yi i
.
2
2
( 2) ( 3) 2 2 3 4
x y i x y
.
Vậy tập hợp
điểm biểu diễn số phức
z
là một
hình tròn.
Câu 116. Có bao nhiêu số phức
z
thỏa mãn điều kiện
1
2z i z i
và
1
z
A.
0
. B.
2
. C.
1
. D.
4
.
Lờ
i giải
Chọn
B
Đặt
; ,z x yi x y
và
;M
z M x y
2
2 2
2
2
2
1 2
1
1 2
1
1
z
i z i
x y x y
z
x y
2
2
1
0
1
x
y
x y
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
S
uy ra tọa độ điểm
M
nằm
trên đường thẳng
1
0: x y
và
đường tròn
2
2
1
x y
c
ó
tâm
0
0 1
;
,O R
Ta
có
2
2
0
0 1
1
1
2
1 1
,
d
O R
S
uy ra đường thẳng cắt đường tròn tại hai điểm hay có hai số phức
z
thỏa m
ãn.
Đáp án B
Câu 117. Tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa
mãn
2
4
z
i
l
à đường tròn có tâm
I
và
bán kính
R
lần lượt
là
A
.
2
; 1
I
;
4R
. B.
2
; 1
I
;
2R
. C.
2
; 1
I
;
4R
. D.
2
; 1
I
;
2R
.
Lờ
i giải
Chọn
A
Gọi
z
x yi
(
x
;
y
;
2
1
i
).
Theo bài ra
2
4
z
i
ha
y
2 4
x yi i
.
2
2
2 1 16
x y
.
Tập hợp các điểm biểu diễn các số phức
z
là đường tròn có tâm
2
; 1
I
,
bán kính
4R
.
-------------------------------- HẾT --------------------------------
| 1/35
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 16 SỐ PHỨC
A. KHÁI NIỆM SỐ PHỨC & CÁC PHÉP TOÁN TRÊN SỐ PHỨC
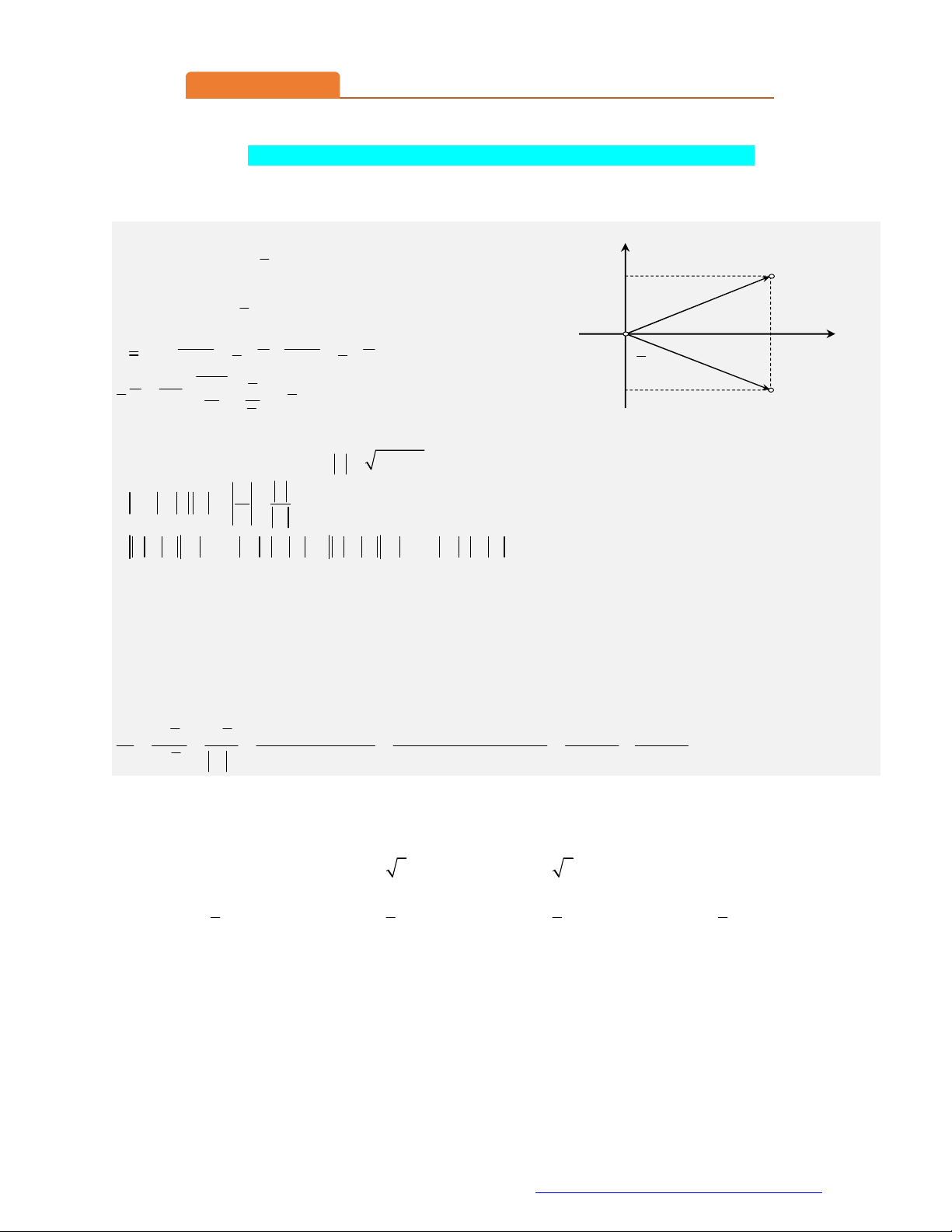
Số phức z a bi có phần thực là a, phần ảo là b. y  2
Số phức liên hợp z a bi và cần nhớ i  1  . b M(a;b)
Số phức z a bi có điểm biểu diễn là ( M ; a ) b .
z a bi
Số phức liên hợp z a bi có điểm biểu diễn N( ; a ) b  . a x
Hai điểm M và N đối xứng nhau qua trục hoành Ox. O
z z; z z  z z ; z z  z z ;
z a bi bN(a; b  )  z z z.z  . z z ;  2 2  ;   .
z z a bz  z
Hai số phức bằng nhau khi thực bằng thực và ảo bằng ảo.
Mô đun của số phức z là: 2 2 z a b z z  .
z z  z z   zz
z z  z z  z z  z z  z z  z z
Phép cộng hai số phức Cho số phức z a  .
b i và z c d.i . Khi đó 1 2
z z a  .
b i c d.i a c b d . .
i Phép trừ hai số phức 1 2        
z z a  .
b i c d.i a c b d . . i 1 2        
Phép nhân hai số phức z .z a  .
b i . c d.i ac bd ad bc . . i 1 2        
k.z  k.(a  bi)  ka  kbi
Phép chia hai số phức z z .z z .za  .
b i.c d.i
ac bd   bc ad i ac bd bc ad 1 1 2 1 2       . i 2 2 2 2 2 2 2 2 2 z z .z z c d c d c d c d 2 2 2 2
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA Câu 1.
Môđun của số phức 1 2i bằng A. 5 . B. 3 . C. 5 . D. 3 . Câu 2.
Số phức liên hợp của số phức z  2  i là
A. z  2  i .
B. z  2  i .
C. z  2  i .
D. z  2  i . Câu 3.
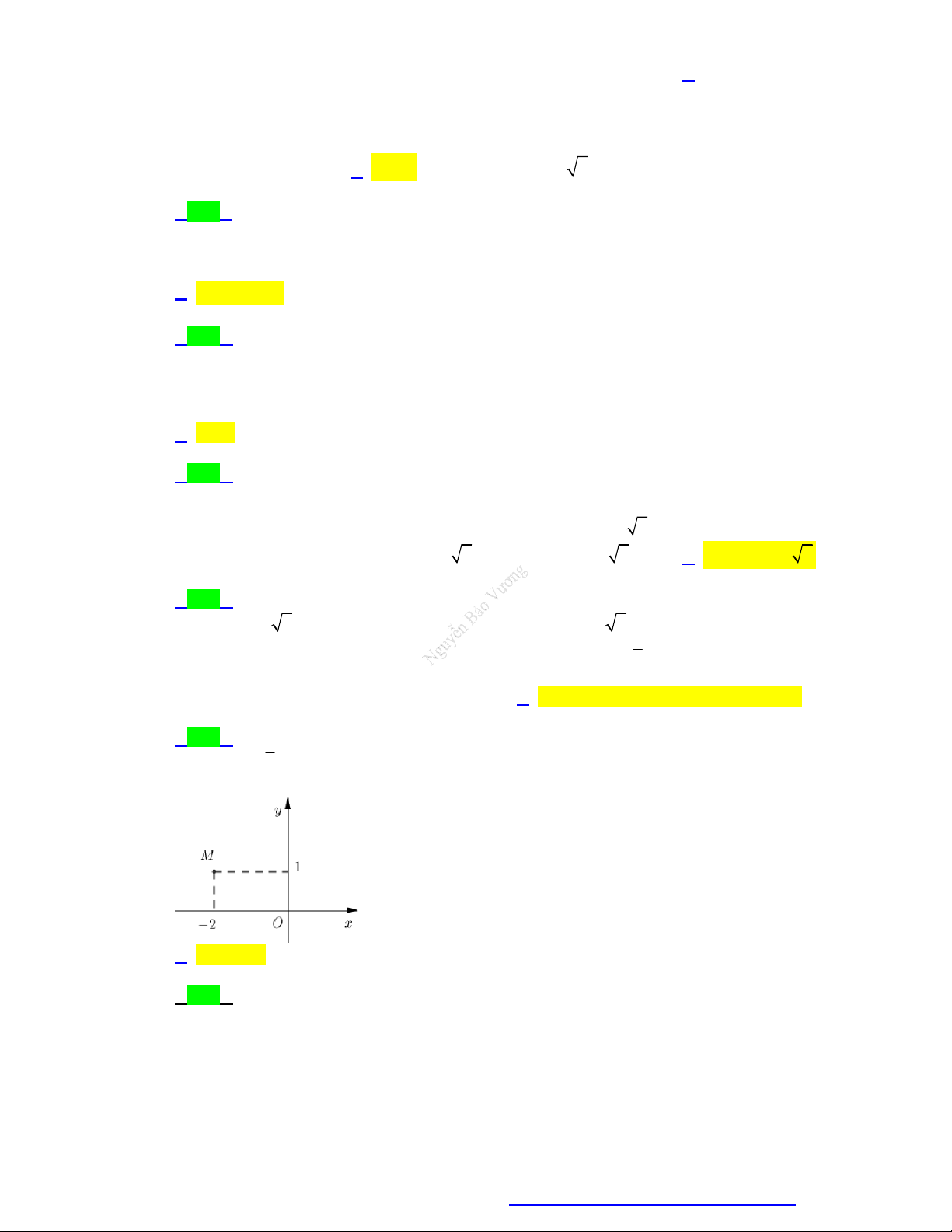
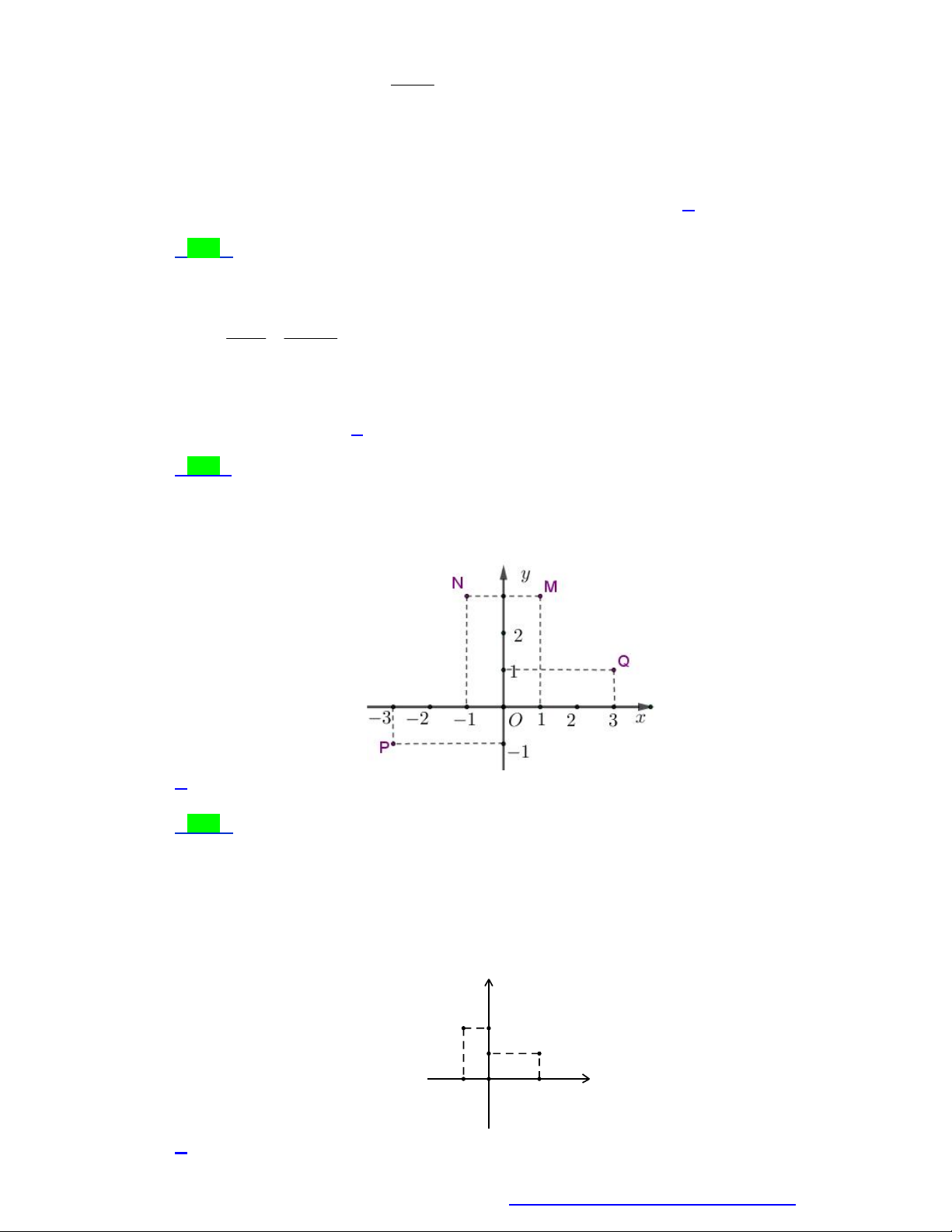
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  1 2i là điểm nào dưới đây? A. Q 1;2 . B. P  1  ; 2 . C. N 1; 2   . D. M  1  ; 2   . Câu 4.
Số phức liên hợp của số phức 1 2i là: A. 1  2i. B. 1 2i . C. 2  i . D. 1   2i . Câu 5.
Số phức liên hợp của số phức 5  3i là A. 5   3i . B. 3   5i . C. 5   3i . D. 5  3i . Câu 6.
Số phức liên hợp của số phức z  3  2i là. A. 3   2i . B. 3  2i . C. 3   2i . D. 2   3i . Câu 7.
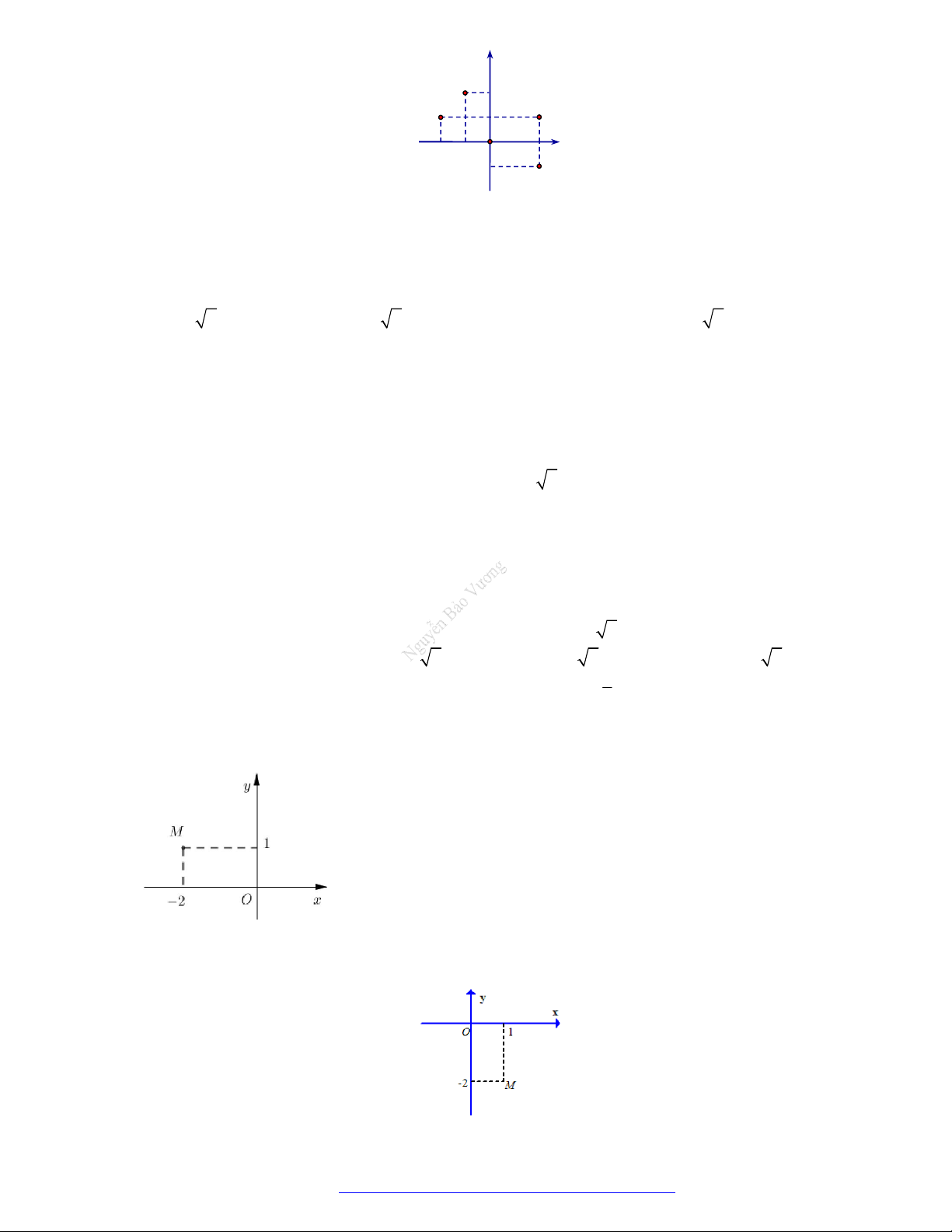
Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức z  1   2i ?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 y Q 2 P 1 N 2  1 O 2 x 1  M A. N . B. P . C. M . D. Q . Câu 8.
Số phức 5  6i có phần thực bằng A. 5  . B. 5 C. 6  . D. 6. Câu 9.
Tìm tất cả các số thực x, y sao cho 2
x  1  yi  1  2i .
A. x  2 , y  2
B. x   2 , y  2
C. x  0, y  2
D. x  2 , y  2
Câu 10. Số phức có phần thực bằng 1 và phần ảo bằng 3 là A. 1   3i . B. 1 3i . C. 1   3i . D. 1 3i .
Câu 11. Số phức 3  7i có phần ảo bằng A. 3 . B. 7 . C. 3 . D. 7 .
Câu 12. Số phức nào dưới đây là số thuần ảo.
A. z  2  3i
B. z  3i
C. z  3  i D. z  2
Câu 13. Cho số phức z   i  3 1
i . Tìm phần thực a và phần ảo b của z .
A. a  1,b  2
B. a  2,b  1
C. a  1,b  0
D. a  0,b  1
Câu 14. Cho số phức z  2  3i . Tìm phần thực a của z ? A. a  2 B. a  3 C. a  2 D. a  3
Câu 15. Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức 3  2 2i . Tìm a , b .
A. a  3;b  2
B. a  3;b  2 2
C. a  3;b  2
D. a  3;b  2  2
Câu 16. Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z :
A. Phần thực bằng 3  và Phần ảo bằng 2  i
B. Phần thực bằng 3  và Phần ảo bằng 2 
C. Phần thực bằng 3 và Phần ảo bằng 2i
D. Phần thực bằng 3 và Phần ảo bằng 2
Câu 17. Điểm M trong hình vẽ bên là điểm biểu diễn số phức A. z  2   i
B. z  1 2i
C. z  2  i
D. z  1 2i
Câu 18. Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm phần thực và phần ảo của số phức z . A. Phần thực là 2
 và phần ảo là i .
B. Phần thực là 1 và phần ảo là 2  .
C. Phần thực là 1 và phần ảo là 2  i . D. Phần thực là 2  và phần ảo là 1.
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 19. Số phức liên hợp của số phức z  2  i là
A. z  2  i . B. z  2   i . C. z  2   i .
D. z  2  i .
Câu 20. Môđun của số phức z  5  2i bằng A. 29 . B. 3 . C. 7 . D. 29 .
Câu 21. Nếu điểm M x; y là điểm biểu diễn của số phức z trong mặt phẳng tọa độ Oxy thỏa mãn OM  4 thì 1 A. z  . B. z  4 . C. z  16 . D. z  2 . 2 1 Câu 22. Nghịch đảo
của số phức z  1 3i bằng z 1 3 1 3 1 3 1 3 A.  . i B.  . i C.  . i D.  . i 10 10 10 10 10 10 10 10
Câu 23. Môdun của số phức z  4  3i bằng A. 7 . B. 25 . C. 5 . D. 1.
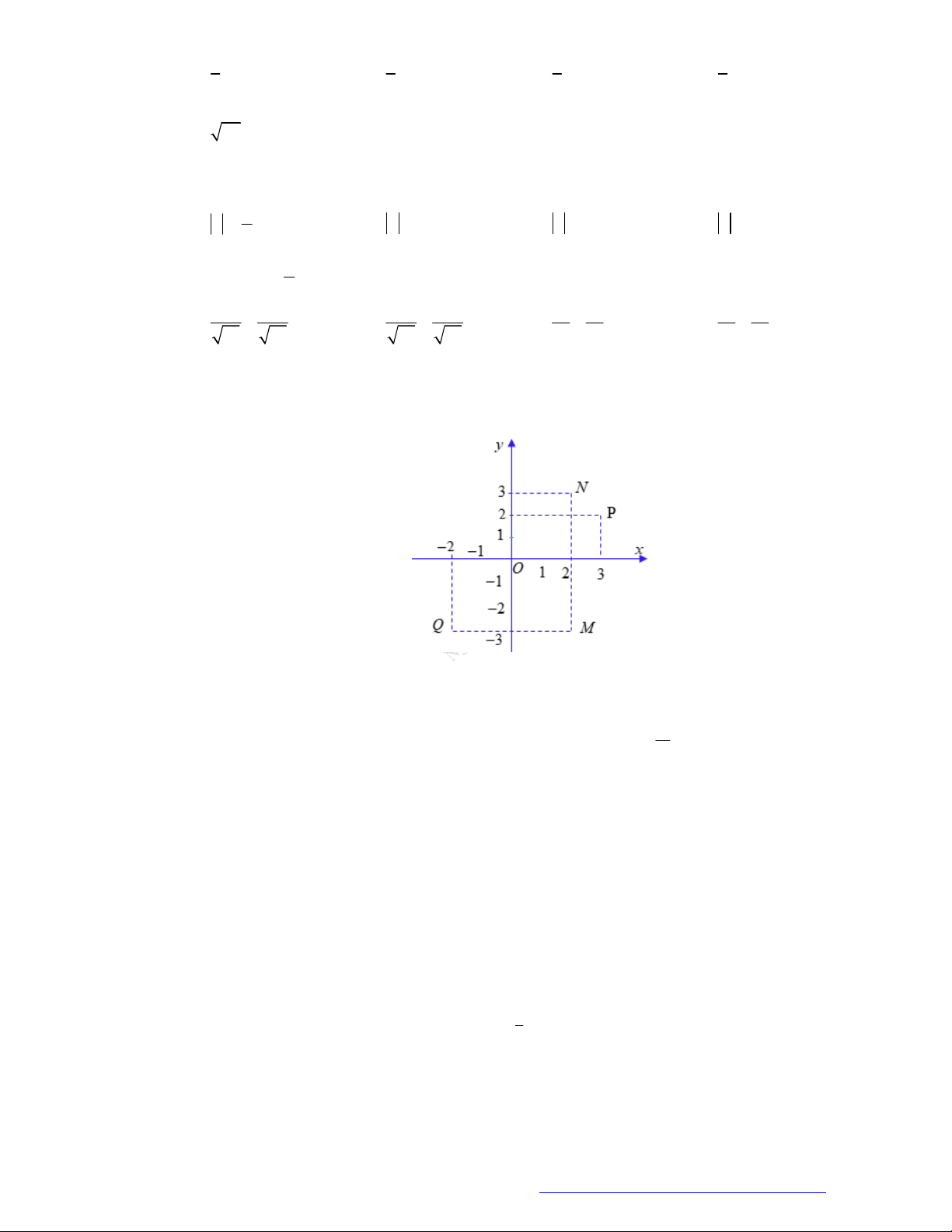
Câu 24. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của số phức z  2  3i ? A. M . B. P . C. N . D. Q .
Câu 25. Modun cỉa số phức z  4   3i là A. 1. B. 1. C. 5 . D. 25 .
Câu 26. Cho hai số phức z  3  i và z  1 .
i Phần ảo của số phức z z bằng 1 2 1 2 A. 2  . B. 2 . i C. 2. D. 2 . i
Câu 27. Cho hai số phức z  2  i và z  1 3i . Phần thực của số phức z z bằng 1 2 1 2 A. 1. B. 3 . C. 4 . D. 2 .
Câu 28. Cho hai số phức z  3 i và z  1 i . Phần ảo của số phức z z bằng 1 2 1 2 A. 4 . B. 4i . C. 1  . D. i  .
Câu 29. Cho 2 số phức z  5  7i và z  2  3i . Tìm số phức z z z . 1 2 1 2
A. z  7  4i
B. z  2  5i
C. z  3 10i D. 14
Câu 30. Cho hai số phức z  4  3i và z  7  3i . Tìm số phức z z z . 1 2 1 2
A. z  3  6i B. z  11
C. z  1  10i
D. z  3  6i
Câu 31. Cho số phức z  2  5 .
i Tìm số phức w iz z
A. w  7  3i . B. w  3   3i .
C. w  3  7 . i . D. w  7   7i
Câu 32. Cho hai số phức z  2  i và z  1 i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn của số phức 1 2
2z z có tọa độ là 1 2 A. 5;  1  . B.  1  ; 5 . C. 5; 0 . D. 0; 5 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 33. Cho hai số phức z  1 i và z  2  i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 1 2
z  2z có tọa độ là 1 2 A. (2; 5) . B. (3; 5) . C. (5; 2) . D. (5; 3) .
Câu 34. Cho hai số phức z  1 i và z  2  3i . Tính môđun của số phức z z . 1 2 1 2
A. z z  1.
B. z z  5 .
C. z z  13 .
D. z z  5 . 1 2 1 2 1 2 1 2
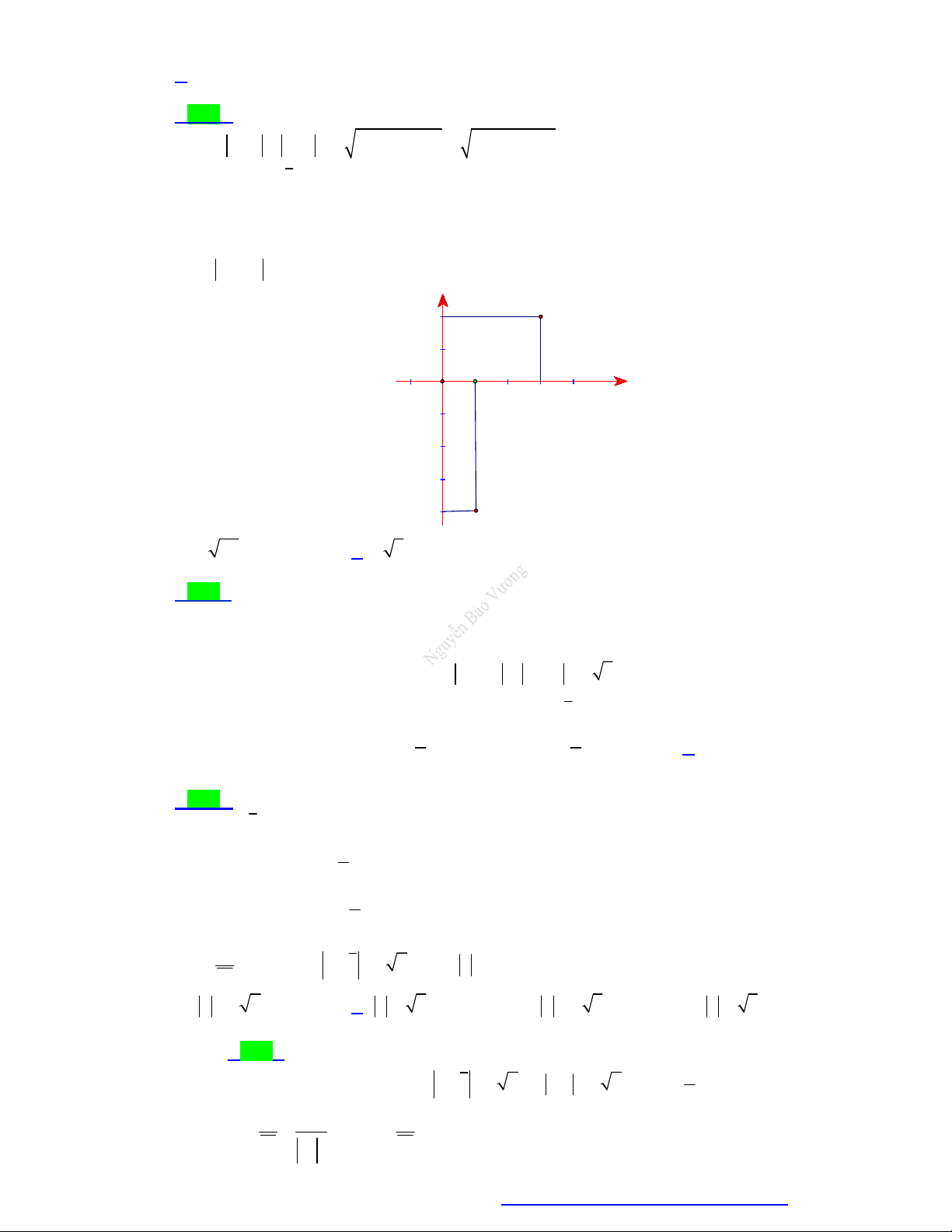
Câu 35. Cho số phức z  1 2i , w  2  i . Điểm nào trong hình bên biểu diễn số phức z w ? y N P O x M Q A. N . B. P . C. Q . D. M .
Câu 36. Tìm phần ảo của số phức z biết z 2  i 13i  1. A. 5  i . B. 5i . C. 5  . D. 5 .
Câu 37. Cho số phức z thỏa mãn: 2
(3  2i)z  (2  i)  4  i . Hiệu phần thực và phần ảo của số phức z là A. 2 . B. 3 . C. 1. D. 0.
Câu 38. Phần thực và phần ảo của số phức z  (1  2i)i . A. 1 và 2 . B. 2  và 1. C. 1 và 2  . D. 2 và 1.
Câu 39. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z  1 i2  i ? A. Q . B. M . C. P . D. N .
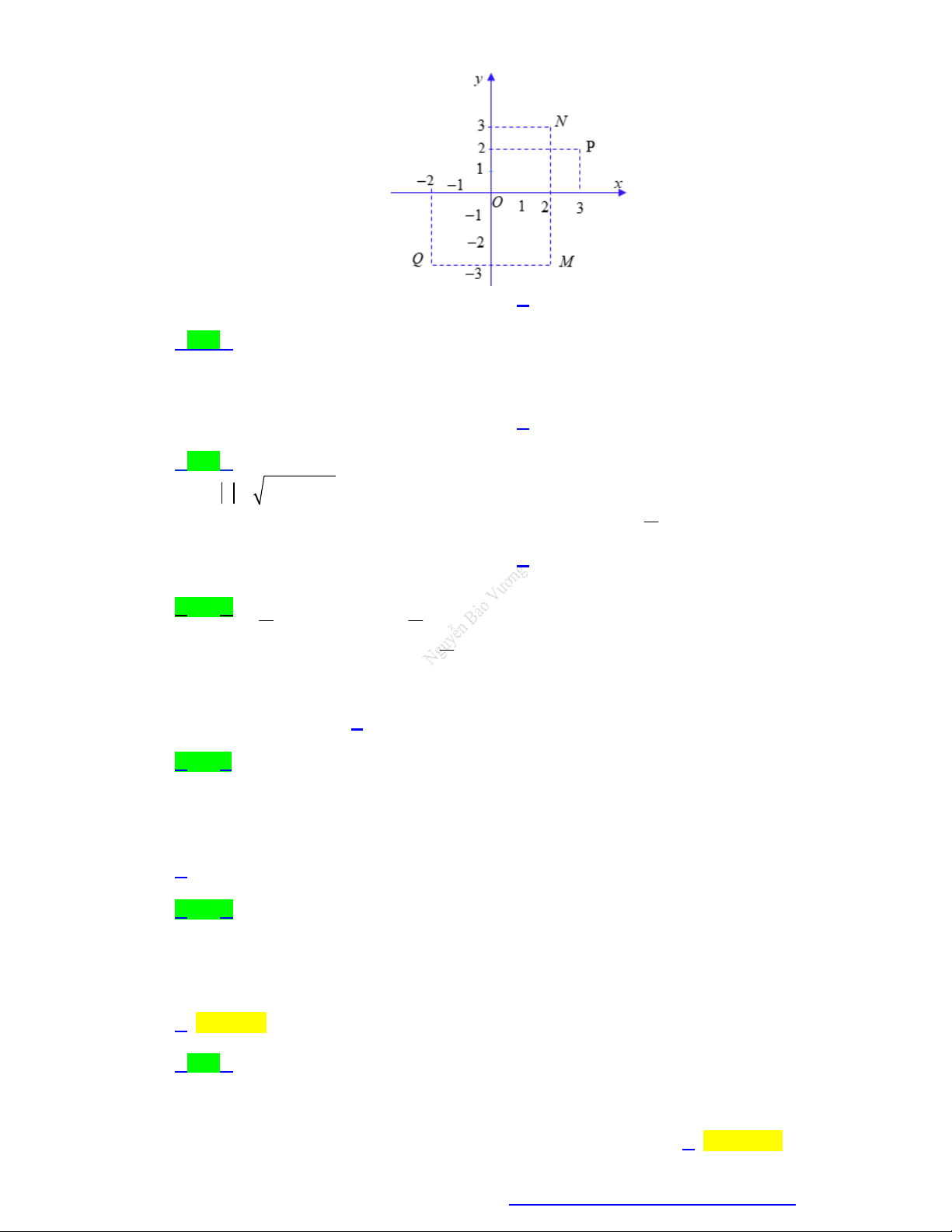
Câu 40. Trong hình vẽ bên dưới, điểm P biểu diễn số phức z , điểm Q biểu diễn số phức z . Tìm số 1 2
phức z z z . 1 2 y P 2 Q 1 -1 O 2 x A. 1 3i . B. 3   i . C. 1   2i . D. 2  i .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 Câu 41.
Cho số phức z a bi,a,b R. Khi đó số  z z là số nào trong các số sau đây? 2 A. Số 2. B. Số i. C. Một số thực.
D. Một số thuần ảo.
Câu 42. Cho hai số phức z  1  3i và z  2  5i . Tìm phần ảo b của số phức z z z . 1 2 1 2 A. b  2 B. b  3 C. b  3 D. b  2
Câu 43. Tìm số phức z thỏa mãn z  2  3i  3  2i .
A. z  1 5i .
B. z  1 i .
C. z  5  5i .
D. z  1 i .
Câu 44. Tìm số phức liên hợp của số phức z i 3i   1 .
A. z  3  i . B. z  3   i .
C. z  3  i . D. z  3   i .
Câu 45. Tính môđun của số phức z biết z  4  3i1 i . A. z  25 2 B. z  7 2 C. z  5 2 D. z  2
Câu 46. Tính môđun của số phức z thỏa mãn z 2  i 13i  1. 5 34 34 A. z  34 B. z  34 C. z D. z  3 3
Câu 47. Cho hai số phức z  1 i và z  2  3i . Tính môđun của số phức z z . 1 2 1 2
A. z z  13 .
B. z z  5 .
C. z z  1.
D. z z  5 . 1 2 1 2 1 2 1 2
Câu 48. Cho hai số phức z  2
  i và z  1 .
i Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 1 2
2z z có tọa độ là 1 2 A. 3; 3   . B. 2; 3   . C.  3  ;3 . D.  3  ; 2 .
Câu 49. Cho hai số phức z  1 2i và z  3  4i . Số phức 2z  3z z z là số phức nào sau đây? 1 2 1 2 1 2 A. 10i . B. 1  0i . C. 11 8i . D. 1110i . Câu 50.
Cho số phức z a bia, b    thoả mãn z  2  i z . Tính S  4a b . A. S  4 B. S  2 C. S  2 D. S  4
Câu 51. Cho số phức z thỏa mãn | z | 5 và | z  3 | |
z  3 10i | . Tìm số phức w z  4  3 . i A. w  3   8 . i
B. w  1 3 . i C. w  1   7 . i D. w  4   8 . i Câu 52.
Cho số phức z a bi,a,b   thỏa mãn z  1  3i z i  0 .Tính S a  3b . 7 7 A. S  5 B. S C. S  5 D. S   3 3
Câu 53. Tìm hai số thực x và y thỏa mãn 2x  3yi  1 3i  x  6i với i là đơn vị ảo. A. x  1  ; y  3  . B. x  1  ; y  1  .
C. x  1 ; y  1  .
D. x  1 ; y  3  .
Câu 54. Tìm các số thực a và b thỏa mãn 2a  b ii  1 2i với i là đơn vị ảo. 1
A. a  0, b  2 . B. a  , b  1.
C. a  0, b  1.
D. a  1, b  2 . 2
Câu 55. Phần ảo của số phức z thoả mãn z  2  i1 i  4  2i là A. 3 . B. 3i . C. 3  i . D. 3  .
Câu 56. Cho số phức z a bi a,b   thỏa mãn 1 iz  2z  3  2 .
i Tính P a b . 1 1 A. P B. P  1 C. P  1  D. P   2 2
Câu 57. Tìm hai số thực x và y thỏa mãn 2x  3yi  3  i  5x  4i với i là đơn vị ảo.
A. x  1; y  1.
B. x  1; y  1 .
C. x  1; y  1 .
D. x  1; y  1 .
Câu 58. Tìm hai số thực x và y thỏa mãn 3x  2yi  2  i  2x  3i với i là đơn vị ảo.
A. x  2; y  2 .
B. x  2; y  1.
C. x  2; y  2 .
D. x  2; y  1 . Câu 59.
Cho số z thỏa mãn 2  iz  4 z i  8
 19i . Môđun của z bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 A. 13 . B. 5 . C. 13 . D. 5 . Câu 60.
Cho số phức z thoả mãn 3z i2  3iz  7 16  .
i Môđun của z bằng A. 5. B. 5. C. 3. D. 3. Câu 61.
Cho số phức z thỏa mãn 2  iz  3 16i  2 z i . Môđun của z bằng A. 5 . B. 13. C. 13 . D. 5 . Câu 62.
Tìm hai số thực x và y thỏa mãn 3x yi  4  2i  5x  2i với i là đơn vị ảo.
A. x  2 ; y  4
B. x  2 ; y  4
C. x  2 ; y  0
D. x  2 ; y  0 Câu 63.
Cho số phức z thỏa mãn   i2 1 3
z  3 4i . Môđun của z bằng 5 5 2 4 A. . B. . C. . D. . 4 2 5 5
Câu 64. Cho số phức z  2  3i . Môđun của số phức w  2z  1 iz bằng A. 4 . B. 2 . C. 10 . D. 2 2 .
Câu 65. Cho hai số thực x , y thỏa mãn x 3  2i  y 1 4i  1 24i . Giá trị của x y bằng: A. -3. B. 4. C. 2. D. 3.
Câu 66. Cho số phức z  2  3i . Môđun của số phức 2
w z z bằng: A. 3 10 . B. 206 . C. 134 . D. 3 2 .
Câu 67. Cho số phức z a bi  ,
a bR , thỏa mãn z  3  z 1 và  z  2 z i là số thực.
Tính a b . A. 0 . B. 4 . C. 2  . D. 2 .
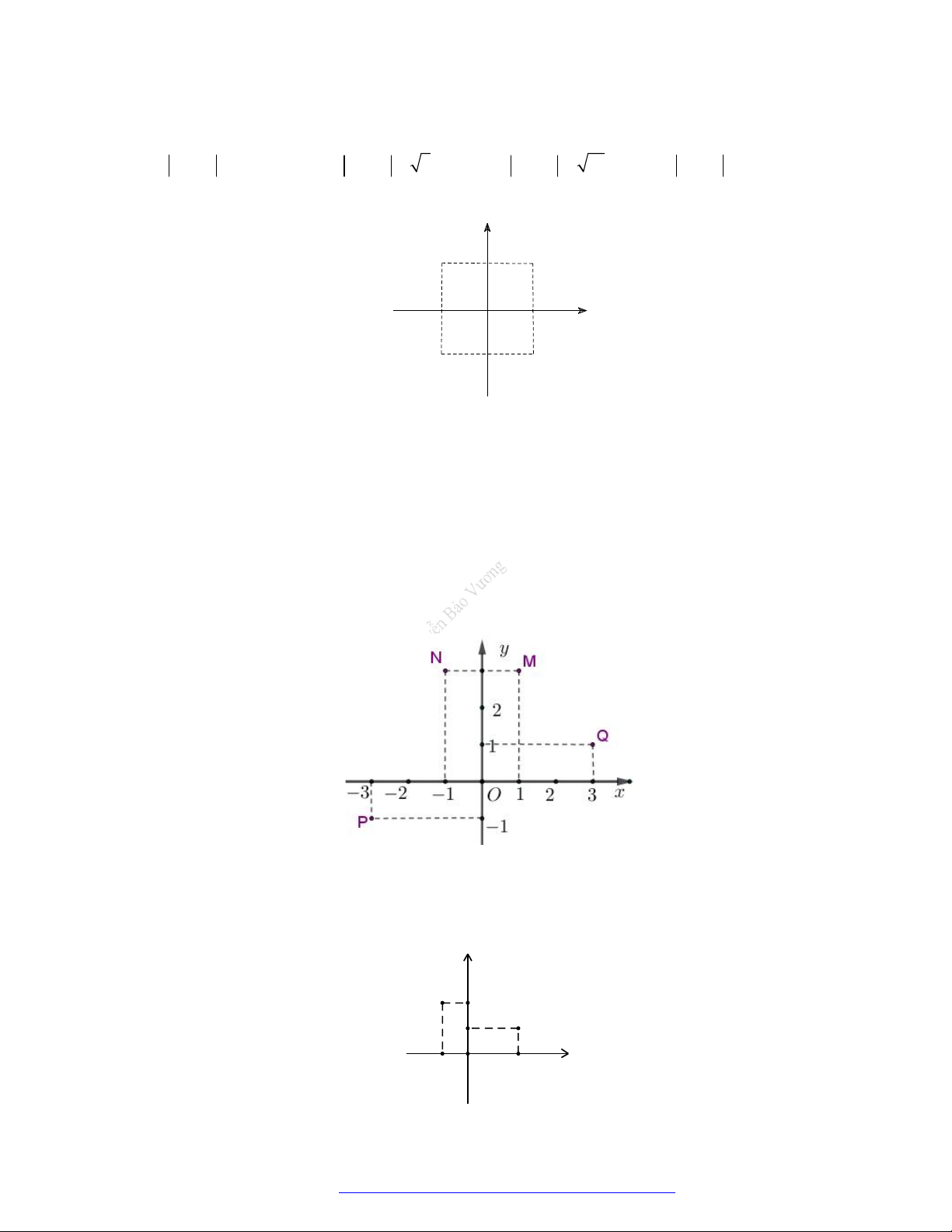
Câu 68. Gọi z , z lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình dưới đây. 1 2 Tính z z . 1 2 y M 2 x O 1 3 -4 N A. 2 29 . B. 2 5 . C. 20 . D. 116 .
Câu 69. Cho số phức z a bi (a, b  ) thoả mãn (1 i)z  2z  3  2i . Tính P a b 1 1 A. P  1 . B. P   . C. P  . D. P  1 2 2 z Câu 70. Cho
là số thực, z z  3 2 . Tính z 2 z A. z  3 2 . B. z  6 . C. z  2 3 . D. z  3 .
Câu 71. Tìm cac số thực x và y thỏa mãn 3x  2  2 y  
1 i   x  
1   y  5i, với i là đơn vị ảo. 3 3 4 4 3 4 A. x  , y  2  .
B. x   , y   .
C. x  1, y  . D. x  , y  . 2 2 3 3 2 3
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 72. Cho số phức z thỏa mãn điều kiện   i2 1 2
z z  4i  20 . Tìm z . A. z  25 . B. z  7 . C. z  4 . D. z  5 .
Câu 73. Tổng phần thực và phần ảo của số phức z thoả mãn iz  1 iz  2  i bằng A. 6 . B. 2  . C. 2 . D. 6  .
Câu 74. Cho a, b   và thỏa mãn a bii  2a  1 3i , với i là đơn vị ảo. Giá trị a b bằng A. 4 . B. 10  . C. 4  . D. 10 .
Câu 75. Tìm hai số thực x , y thỏa mãn 3x  2 yi  3  i  4x  3i với i là đơn vị ảo. 2
A. x  3; y  1. B. x  ; y  1 .
C. x  3; y  3 .
D. x  3; y  1. 3
Câu 76. Cho các số phức z , z thỏa mãn z z  3 và z z  2 . Môđun z z bằng 1 2 1 2 1 2 1 2 A. 2 . B. 3 . C. 2 . D. 2 2 .
Câu 77. Cho số phức z thỏa mãn z z    i2 3 1 2
. Phần ảo của z là 3  3 A. 2 . B. 2 . C. . D. . 4 4
B. PHƯƠNG TRÌNH SỐ PHỨC 2
Phương trình az bz c  0 với a  0 có biệt số 2
  b  4ac thì có hai nghiệm thực hoặc phức là b    b    z hoặc z   1 2a 2 2a
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 78. Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z 2z 5  0 . Môđun của số phức 0
z i bằng 0 A. 2 . B. 2 . C. 10 . D. 10.
Câu 79. Kí hiệu z là nghiệm phức có phần ảo dương của phương trình 2
4z 16z  17  0 . Trên mặt 0
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0  1   1   1   1  A. M ; 2 . B. M  ; 2 . C. M  ;1 . D. M ;1 . 1   2   3   4    2   2   4   4 
Câu 80. Kí hiệu z , z là hai nghiệm phức của phương trình 2
3z z  1  0 . Tính P z z . 1 2 1 2 14 2 3 2 3 A. P B. P C. P D. P  3 3 3 3 1 1
Câu 81. Kí hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 . Tính P   . 1 2 z z 1 2 1 1 1 A. B. C. D. 6 12 6 6
Câu 82. Kí hiệu z ; z là hai nghiệm của phương trình 2
z z 1  0 . Tính 2 2
P z z z z . 1 2 1 2 1 2 A. P  1 B. P  2 C. P  1  D. P  0
Câu 83. Kí hiệu z , z , z và z là bốn nghiệm phức của phương trình 4 2
z z 12  0 . Tính 1 2 3 4
tổng T z z z z 1 2 3 4 A. T  4 B. T  2 3
C. T  4  2 3
D. T  2  2 3
Câu 84. Phương trình nào dưới đây nhận hai số phức 1 2i và 1 2i là nghiệm. A. 2
z  2z  3  0 B. 2
z  2z  3  0 C. 2
z  2z  3  0 D. 2
z  2z  3  0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 85. Kí hiệu z , z là hai nghiệm của phương trình 2
z  4  0 . Gọi M , N lần lượt là điểm biểu diễn 1 2
của z , z trên mặt phẳng tọa độ. Tính T OM ON với O là gốc tọa độ. 1 2 A. T  2 B. T  2 C. T  8 D. 4
Câu 86. Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  3z  5  0 . Giá trị của z z bằng 1 2 1 2 A. 2 5 . B. 5 . C. 3 . D. 10 .
Câu 87. Gọi z và z là hai nghiệm phức của phương trình 2
4z  4z  3  0 . Giá trị của biểu thức z z 1 2 1 2 bằng: A. 3 2 B. 2 3 C. 3 D. 3
Câu 88. Gọi z , z là 2 nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 2 2
z z bằng 1 2 1 2 A. 6. B. 8. C. 16. D. 26.
Câu 89. Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  7  0. Giá trị của 2 2 z z bằng 1 2 1 2 A. 10. B. 8. C. 16. D. 2.
Câu 90. Gọi z , z là hai nghiệm phức của phương trình 2
z  6z  10  0 . Giá trị của 2 2
z z bằng: 1 2 1 2 A. 16. B. 56 . C. 20. D. 26 .
Câu 91. Gọi z , z là các nghiệm phức của phương trình 2
z  4z  7  0 . Số phức z z z z bằng 1 2 1 2 1 2 A. 2 . B. 10 . C. 2i . D. 10i .
Câu 92. Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  5  0 ; M , N lần lượt là các điểm 1 2
biểu diễn của z , z trên mặt phẳng phức. Độ dài đoạn thẳng MN là 1 2 A. 2 5 . B. 4 . C. 2 . D. 2 . 2 2
Câu 93. Gọi z , z là hai nghiệm phức của phương trình 2
3z z  2  0 . Tính T zz . 1 2 1 2 2 8 4 11 A. T  . B. T  . C. T  . D. T   . 3 3 3 9 2 2
Câu 94. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Giá trị của zz bằng 1 2 1 2 A. 10 . B. 20 . C. 2 10 . D. 10 .
Câu 95. Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  29  0 . Tính giá trị của biểu thức 1 2 4 4 zz . 1 2 A. 841. B. 58 . C. 1682 . D. 2019 . 1 1
Câu 96. Kí hiệu z và z là 2 nghiệm phức của phương trình 2
2z  4z  9  0 . Tính P   1 2 z z 1 2 4 4 9 9 A. P  . B. P  . C. P  . D. P  . 9 9 4 4
Câu 97. Gọi z , z là hai nghiệm phức của phương trình 2
z  5z  7  0 . Giá trị của biểu thức z z là 1 2 1 2 3 A. 3i . B.  3i . C. 3 . D. . 2
Câu 98. Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  2z  10  0 . Giá trị của z . z bằng 1 2 1 2 5 A. 5 . B. . C. 10 . D. 20 . 2
Câu 99. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  2  0 . Tính giá trị của biểu thức 1 2
P  2 z z z z . 1 2 1 2 A. P  6 . B. P  3 .
C. P  2 2  2 . D. P  2  4 .
Câu 100. Kí hiệu z ; z là hai nghiệm phức của phương trình 2
3z z  1  0 . Tính P z z 1 2 1 2 14 2 3 2 3 A. P  . B. P  . C. P  . D. P  . 3 3 3 3
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
C. BIỂU DIỄN ĐIỂM SỐ PHỨC
Điểm biểu diễn số phức:
Số phức z a bi , a ,b   được biểu diễn bởi điểm M a ;b .
BÀI TOÁN: Tìm tập hợp điểm biểu diễn của số phức thỏa mãn tính chất cho trước
Bước 1. Gọi M(x;y) là điểm biểu diễn số phức z x yi (x, y  ). 
Bước 2. Biến đổi điều kiện K để tìm mối liên hệ giữa x, y và kết luận.
Mối liên hệ giữa x và y
Kết luận tập hợp điểm M (x;y)
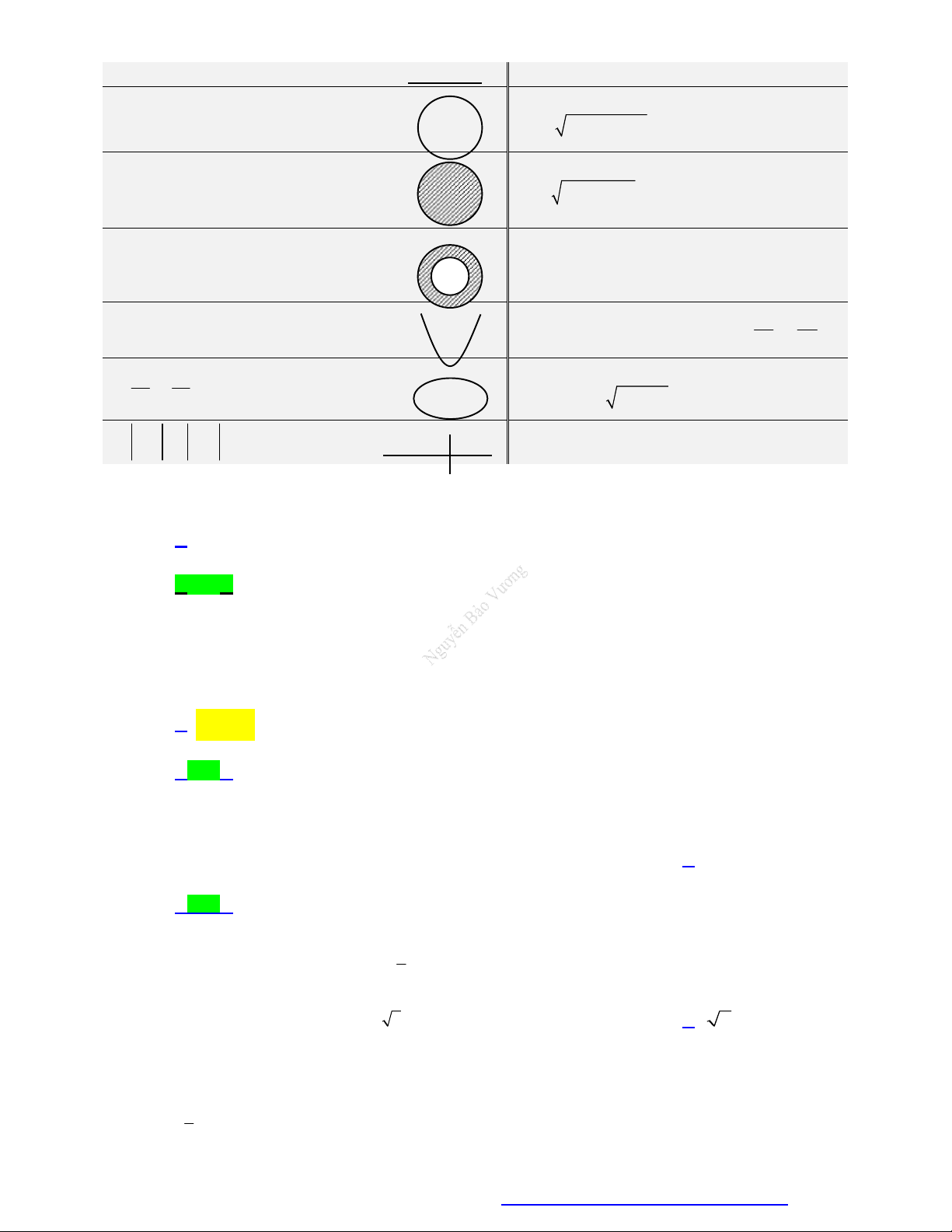
Ax By C  0.
Là đường thẳng d : Ax By C  0.  2 2 2
(x a)  (y b)  R
Là đường tròn (C ) có tâm I(a;b) và bán kính     2 2
x y  2ax  2by c  0 2 2 
R a b c.   2 2 2
(x a)  (y b)  R
Là hình tròn (C ) có tâm I( ;
a b) và bán kính     2 2
x y  2ax  2by c  0 2 2 
R a b c
(đường tròn kể cả bên trong) 2 2 2 2
R  (x a)  (y b)  R .
Là những điểm thuộc miền có hình vành khăn 1 2
tạo bởi hai đường tròn đồng tâm I(a;b) và
bán kính lần lượt R và R . 1 2  2
y ax bx  , c (a  0).  b    
Là một parabol (P) có đỉnh I   ;    2a 4a  2 2 x y MF   MF  2a
Là một elíp có trục lớn 2 ,
a trục bé 2b và tiêu    1  với 1 2   2 2 a b F
F  2c  2ac a b a b  1 2  cự là 2 2 2 2 , ( 0).   ABMA MB .
Là đường trung trực của đoạn thẳng .
CÂU HỎI CÙNG MỨC ĐỘ ĐỀ MINH HỌA
Câu 101. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z    i2 1 2
là điểm nào dưới đây?
A. P 3; 4 .
B. Q 5; 4 .
C. N 4;  3 . D. M 4;5 .
Câu 102. Cho số phước z  1  2i. Điểm nào dưới đây là điểm biểu diễn số phức w iz trên mặt phẳng tọa độ A. N 2;1
B. P 2;1
C. M 1; 2 D. Q 1; 2
Câu 103. Cho số phức z  1 i . Biểu diễn số phức 2 z là điểm A. M  2  ;0 . B. P 1;2 . C. E 2;0 .
D. N 0; 2 .
Câu 104. Xét các số phức z thỏa mãn  z  2i  z  2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 2 B. 2 2 C. 4 D. 2
Câu 105. Xét các số phức z thỏa mãn  z  2i z  2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng? A. 2 2 . B. 2 . C. 2 . D. 4 .
Câu 106. Xét các số phức z thỏa mãn  z  3i z  3 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng: 9 3 2 A. . B. 3 2 . C. 3 . D. . 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 107. Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn z  2  i  4 là đường tròn có tâm I
và bán kính R lần lượt là A. I 2;   1 ; R  2 .
B. I 2;   1 ; R  4 .
C. I 2;  
1 ; R  2 . D. I 2;   1 ; R  4 .
Câu 108. Tập hợp các điểm biểu diễn các số phức z thỏa mãn z 1 i  2 là đường tròn có tâm và bán kính lần lượt là A. I 1;  1 , R  4 . B. I 1  ;1 , R  2 .
C. I 1;   1 , R  2 .
D. I 1;   1 , R  4 .
Câu 109. Tập hợp các điểm biểu diễn các số phức z thỏa mãn z  2  z i là một đường thẳng có phương trình
A. 4x  2 y  3  0 .
B. 2x  4 y 13  0 .
C. 4x  2 y  3  0 .
D. 2x  4 y 13  0 .
Câu 110. Tập hợp điểm biểu diễn số phức z biết: z  (3  4i)  2 là
A. Đường tròn tâm I (3;4), R  2 .
B. Đường tròn tâm I (3; 4), R  2 .
B. Đường tròn tâm I (3;4), R  4 .
D. Đường tròn tâm I (3; 4), R  4 . Lời giải Chọn A
Gọi z x yi x;y  . Ta có: 2 2
z (3  4i)  2  (x  3)  (y  4)  4
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tâm I (3;4), R  2 . I  (a;b) 
Chú ý: z  (a bi)  R  R  Câu 111.
Tập hợp các điểm biểu diễn số phức z thỏa mãn z i  1 iz là một đường tròn,
tâm của đường tròn đó có tọa độ là A. 1;  1 . B. 0;   1 . C. 0;  1 . D. 1;0 .
Câu 112. Cho số phức z thay đổi thỏa mãn z 1  2. Biết rằng tập hợp điểm biểu diễn các số phức
w  1 3 iz  2 là đường tròn có bán kính bằng . R Tính . R A. R  8 . B. R  2 . C. R  16 . D. R  4 .
Câu 113. Có bao nhiêu số phức z có phần thực bằng 2 và z 1 2i  3 ? A. 3. B. 0. C. 2. D. 1
Câu 114. Tập hợp các điểm biểu diễn các số phức z thỏa mãn 2 z i z z  2i là A. Một điểm.
B. Một đường tròn.
C. Một đường thẳng. D. Một Parabol.
Câu 115. Trong mặt phẳng tọa độ Oxy , tìm tập hợp điểm biểu diễn số phức z thỏa mãn z  2  3i  2 .
A. Một đường thẳng. B. Một hình tròn.
C. Một đường tròn.
D. Một đường elip.
Câu 116. Có bao nhiêu số phức z thỏa mãn điều kiện z i  1  z  2i và z  1 A. 0 . B. 2 . C. 1. D. 4 .
Câu 117. Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn z  2  i  4 là đường tròn có tâm I
và bán kính R lần lượt là A. I  2  ;   1 ; R  4 .
B. I 2;   1 ; R  2 .
C. I 2;   1 ; R  4 . D. I  2  ;   1 ; R  2 .
-------------------------------- HẾT --------------------------------
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 16 SỐ PHỨC
A. KHÁI NIỆM SỐ PHỨC & CÁC PHÉP TOÁN TRÊN SỐ PHỨC
Số phức z a bi có phần thực là a, phần ảo là b. y  2
Số phức liên hợp z a bi và cần nhớ i  1  . b M(a;b)
Số phức z a bi có điểm biểu diễn là ( M ; a ) b .
z a bi
Số phức liên hợp z a bi có điểm biểu diễn N( ; a ) b  . a x
Hai điểm M và N đối xứng nhau qua trục hoành Ox. O
z z; z z  z z ; z z  z z ;
z a bi bN(a; b  )  z z z .z  . z z ;  2 2  ;   .
z z a bz  z
Hai số phức bằng nhau khi thực bằng thực và ảo bằng ảo.
Mô đun của số phức z là: 2 2 z a b z z  .
z z  z z   zz
z z  z z  z z  z z  z z  z z
Phép cộng hai số phức Cho số phức z a  .
b i và z c d.i . Khi đó 1 2
z z a  .
b i c d.i a c b d . .
i Phép trừ hai số phức 1 2        
z z a  .
b i c d.i a c b d . . i 1 2        
Phép nhân hai số phức z .z a  .
b i . c d.i ac bd ad bc . . i 1 2        
k.z  k.(a  bi)  ka  kbi
Phép chia hai số phức z z .z z .za  .
b i .c d.i
ac bd   bc ad i ac bd bc ad 1 1 2 1 2       . i 2 2 2 2 2 2 2 2 2 z z .z z c d c d c d c d 2 2 2 2 Câu 1.
Môđun của số phức 1 2i bằng A. 5 . B. 3 . C. 5 . D. 3 . Lời giải Chọn C Ta có 2 2
1 2i  1  2  5 . Câu 2.
Số phức liên hợp của số phức z  2  i là
A. z  2  i .
B. z  2  i .
C. z  2  i .
D. z  2  i . Lời giải Chọn C
Số phức liên hợp của số phức z  2  i là z  2  i . Câu 3.
Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  1 2i là điểm nào dưới đây? A. Q 1;2 . B. P  1  ; 2 . C. N 1; 2   . D. M  1  ; 2   . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn B
Điểm biểu diễn số phức z  1 2i là điểm P  1  ; 2 . Câu 4.
Số phức liên hợp của số phức 1 2i là: A. 1  2i . B. 1 2i . C. 2  i . D. 1 2i . Lời giải Chọn B
Theo định nghĩa số phức liên hợp của số phức z a bi, a, b   là số phức
z a bi, a, b   . Câu 5.
Số phức liên hợp của số phức 5  3i là A. 5   3i . B. 3   5i . C. 5   3i . D. 5  3i . Lời giải Chọn D
Số phức liên hợp của số phức 5  3i là 5  3i Câu 6.
Số phức liên hợp của số phức z  3  2i là. A. 3   2i . B. 3  2i . C. 3   2i . D. 2   3i . Lời giải Chọn B
Số phức liên hợp của số phức z a bi là số phức z a bi từ đó suy ra chọn đáp án B. Câu 7.
Điểm nào trong hình vẽ bên dưới là điểm biểu diễn số phức z  1 2i ? y Q 2 P 1 N 2  1  O 2 x 1 M A. N . B. P . C. M . D. Q . Lời giải Chọn D.
Số phức z  1 2i có điểm biểu diễn là điểm Q  1  ; 2 . Câu 8.
Số phức 5  6i có phần thực bằng A. 5  . B. 5 C. 6  . D. 6. Lời giải Chọn B
Số phức 5  6i có phần thực bằng 5, phần ảo bằng 6. Câu 9.
Tìm tất cả các số thực x, y sao cho 2
x  1 yi  1 2i .
A. x  2 , y  2
B. x   2 , y  2
C. x  0, y  2
D. x  2 , y  2 Lời giải Chọn C   2 x  1  1 x  0 Từ 2
x  1 yi  1 2i     y  2 y    2
Câu 10. Số phức có phần thực bằng 1 và phần ảo bằng 3 là A. 1   3i . B. 1 3i . C. 1   3i . D. 1 3i . Lời giải
Chọn 1 3i
Câu 11. Số phức 3  7i có phần ảo bằng
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. 3 . B. 7 . C. 3 . D. 7 . Lời giải Chọn 7
Câu 12. Số phức nào dưới đây là số thuần ảo.
A. z  2  3i
B. z  3i
C. z  3  i D. z  2 Lời giải Chọn B
Số phức z được gọi là số thuần ảo nếu phần thực của nó bằng 0 .
Câu 13. Cho số phức z   i  3 1
i . Tìm phần thực a và phần ảo b của z .
A. a  1,b  2
B. a  2,b  1
C. a  1,b  0
D. a  0,b  1 Lời giải Chọn A
Ta có: z   i  3
i   i  2 1 1
i .i  1 i i  1 2i (vì 2 i  1 )
Suy ra phần thực của z là a  1 , phần ảo của z là b  2 .
Câu 14. Cho số phức z  2  3i . Tìm phần thực a của z ? A. a  2 B. a  3 C. a  2 D. a  3 Lời giải Chọn A
Số phức z  2  3i có phần thực a  2 .
Câu 15. Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức 3  2 2i . Tìm a , b .
A. a  3;b  2
B. a  3;b  2 2
C. a  3;b  2
D. a  3;b  2  2 Lời giải Chọn D
Số phức 3  2 2i có phần thực là a  3 và phần ảo là b  2  2 .
Câu 16. Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z :
A. Phần thực bằng 3  và Phần ảo bằng 2  i
B. Phần thực bằng 3  và Phần ảo bằng 2 
C. Phần thực bằng 3 và Phần ảo bằng 2i
D. Phần thực bằng 3 và Phần ảo bằng 2 Lời giải Chọn D
z  3  2i z  3  2i . Vậy phần thực bằng 3 và Phần ảo bằng 2
Câu 17. Điểm M trong hình vẽ bên là điểm biểu diễn số phức A. z  2   i
B. z  1  2i
C. z  2  i
D. z  1 2i Lời giải Chọn A
Theo hình vẽ M  2  ;  1  z  2   i
Câu 18. Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm phần thực và phần ảo của số phức z .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 A. Phần thực là 2
 và phần ảo là i .
B. Phần thực là 1 và phần ảo là 2  .
C. Phần thực là 1 và phần ảo là 2  i . D. Phần thực là 2  và phần ảo là 1. Lời giải Chọn B
Điểm M có tọa độ M 1; 2 nên z 1 2i . Vậy phần thực là 1 và phần ảo là 2  .
Câu 19. Số phức liên hợp của số phức z  2  i là
A. z  2  i . B. z  2   i . C. z  2   i .
D. z  2  i . Lời giải Chọn A
Số phức liên hợp của số phức z  2  i là z  2  i .
Câu 20. Môđun của số phức z  5  2i bằng A. 29 . B. 3 . C. 7 . D. 29 . Lời giải Chọn A Ta có z    2 2 5 2  29 .
Câu 21. Nếu điểm M x; y là điểm biểu diễn của số phức z trong mặt phẳng tọa độ Oxy thỏa mãn OM  4 thì 1 A. z  . B. z  4 . C. z  16 . D. z  2 . 2 Lời giải Chọn B
Theo định nghĩa môđun của số phức ta có: z OM  4  B đúng. 1
Câu 22. Nghịch đảo
của số phức z  1 3i bằng z 1 3 1 3 1 3 1 3 A.  . i B.  . i C.  . i D.  . i 10 10 10 10 10 10 10 10 Lời giải Chọn D 1 1 1 3i 1 3
Số phức nghịch đảo của số phức z là:     . i z 1 3i
1 3i1 3i 10 10
Câu 23. Môdun của số phức z  4  3i bằng A. 7 . B. 25 . C. 5 . D. 1. Lời giải Chọn C
Môdun của số phức z  4  3i là: z    2 2 4 3  5 .
Câu 24. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của số phức z  2  3i ?
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. M . B. P . C. N . D. Q . Lời giải Chọn C
Điểm biểu diễn số phức liên hợp của số phức z  2  3i là điểm N 2;  3 .
Câu 25. Modun cỉa số phức z  4   3i là A. 1. B. 1. C. 5 . D. 25 . Lời giải Chọn C
Ta có z   2 2 4  3  5 .
Câu 26. Cho hai số phức z  3  i và z  1 .
i Phần ảo của số phức z z bằng 1 2 1 2 A. 2  . B. 2 . i C. 2. D. 2 . i Lời giải Chọn C
Ta có: z  1 i . Do đó z z  ( 3
  i)  (1 i)  2   2 . i 2 1 2
Vậy phần ảo của số phức z z bằng 2. 1 2
Câu 27. Cho hai số phức z  2  i và z  1 3i . Phần thực của số phức z z bằng 1 2 1 2 A. 1. B. 3 . C. 4 . D. 2 . Lời giải Chọn B
Ta có z z  3  4i . 1 2
Phần thực của số phức z z bằng 3 . 1 2
Câu 28. Cho hai số phức z  3 i và z  1 i . Phần ảo của số phức z z bằng 1 2 1 2 A. 4 . B. 4i . C. 1  . D. i  . Lời giải Chọn A
Ta có: z z  3i 1  i 2   4i . 1 2
Suy ra phần ảo của z z bằng 4 . 1 2
Câu 29. Cho 2 số phức z  5  7i và z  2  3i . Tìm số phức z z z . 1 2 1 2
A. z  7  4i
B. z  2  5i
C. z  3 10i D. 14 Lời giải Chọn A
z  5  7i  2  3i  7  4i .
Câu 30. Cho hai số phức z  4  3i và z  7  3i . Tìm số phức z z z . 1 2 1 2
A. z  3  6i B. z  11
C. z  1  10i
D. z  3  6i
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn D
Ta có z z z  4  3i  7  3i  3  6i . 1 2
Câu 31. Cho số phức z  2  5 .
i Tìm số phức w iz z
A. w  7  3i . B. w  3   3i .
C. w  3  7 . i . D. w  7   7i Lời giải Chọn B
Ta có w iz z i(2  5i)  (2  5i)  2i  5  2  5i  3  3i
Câu 32. Cho hai số phức z  2  i và z  1 i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn của số 1 2
phức 2z z có tọa độ là 1 2 A. 5;  1  . B.  1  ; 5 . C. 5; 0 . D. 0; 5 . Lời giải Chọn A
Ta có 2z z  5  i . Nên ta chọn A. 1 2
Câu 33. Cho hai số phức z  1 i và z  2  i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 1 2
z  2z có tọa độ là 1 2 A. (2; 5) . B. (3; 5) . C. (5; 2) . D. (5; 3) . Lời giải Chọn D
Ta có z  2z  (1 i)  2(2  i)  5  3i . 1 2
Do đó điểm biểu diễn số phức z  2z có tọa độ là (5; 3) . 1 2
Câu 34. Cho hai số phức z  1 i và z  2  3i . Tính môđun của số phức z z . 1 2 1 2
A. z z  1.
B. z z  5 .
C. z z  13 .
D. z z  5 . 1 2 1 2 1 2 1 2 Lời giải Chọn C
Ta có z z  1 i  2  3i  3  2i z z  3  2i  13 . 1 2 1 2
Câu 35. Cho số phức z  1 2i , w  2  i . Điểm nào trong hình bên biểu diễn số phức z w ? y N P O x M Q A. N . B. P . C. Q . D. M . Lời giải Chọn B
z w  1 i .
Do đó điểm biểu diễn của số phức z w là P   1;1 .
Câu 36. Tìm phần ảo của số phức z biết z 2  i 13i  1. A. 5  i . B. 5i . C. 5  . D. 5 . Lời giải Chọn C
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 13i
Ta có: z 2  i 13i  1  z   3  5i . 2  i
Vậy phần ảo của số phức z là 5  .
Câu 37. Cho số phức z thỏa mãn: 2
(3  2i)z  (2  i)  4  i . Hiệu phần thực và phần ảo của số phức z là A. 2 . B. 3 . C. 1. D. 0. Lời giải Chọn D Ta có: 2
(3  2i) z  (2  i)  4  i  (3  2i) z  4  4i 1  4  i
 (3  2i)z  1 5i 1 5i 13 13iz    1 i 3  2i 13
Phần thực là a  1, phần ảo là b  1. Vậy a b  0
Câu 38. Phần thực và phần ảo của số phức z  (1 2i)i . A. 1 và 2 . B. 2  và 1. C. 1 và 2  . D. 2 và 1. Lời giải Chọn B
Ta có z  (1  2i)i  2   i .
Vậy phần thực của số phức z là 2 và phần ảo là 1.
Câu 39. Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức z  1 i2  i ? A. Q . B. M . C. P . D. N . Lời giải Chọn A
Ta có z  1 i2  i  3  i
Vậy điểm Q trong hình vẽ là điểm biểu diễn của số phức z  1 i2  i .
Câu 40. Trong hình vẽ bên dưới, điểm P biểu diễn số phức z , điểm Q biểu diễn số phức z . Tìm số 1 2
phức z z z . 1 2 y 2 P Q 1 -1 O 2 x A. 1 3i . B. 3   i . C. 1   2i . D. 2  i .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn A
Từ hình vẽ suy ra P  1
 ; 2 và Q2;  1 . Từ đó z  1
  2i ; z  2  i . 1 2 Vậy z   1
  2i  2  i 1 3i . 1
Câu 41. Cho số phức z a bi,a,b R. Khi đó số  z z là số nào trong các số sau đây? 2 A. Số 2. B. Số i. C. Một số thực.
D. Một số thuần ảo. Lời giải Chọn C 1 1 1
Ta có z a bi nên  z z  a bi a bi  .2a a . 2 2 2 1 Vậy
z z là số một số thực. 2
Câu 42. Cho hai số phức z  1  3i và z  2  5i . Tìm phần ảo b của số phức z z z . 1 2 1 2 A. b  2 B. b  3 C. b  3 D. b  2 Lời giải Chọn D
Ta có z z z  3  2i b  2 1 2
Câu 43. Tìm số phức z thỏa mãn z  2  3i  3  2i .
A. z  1 5i .
B. z  1 i .
C. z  5  5i .
D. z  1 i . Lời giải Chọn B
z  2  3i  3  2i z  3  2i  2  3i  1 i .
Câu 44. Tìm số phức liên hợp của số phức z i 3i   1 .
A. z  3  i . B. z  3   i .
C. z  3  i . D. z  3   i . Lời giải Chọn D
z i 3i   1  3
  i nên suy ra z  3   i .
Câu 45. Tính môđun của số phức z biết z  4  3i1 i . A. z  25 2 B. z  7 2 C. z  5 2 D. z  2 Lời giải Chọn C
z  4  3i1 i  7  i z  7  i z  5 2
Câu 46. Tính môđun của số phức z thỏa mãn z 2  i 13i  1. 5 34 34 A. z  34 B. z  34 C. z D. z  3 3 Lời giải Chọn A 1 13i
113i2  i
z 2  i 13i  1  z   z
z  3  5i . z    2 2 3 5  34. 2  i
2  i2  i
Câu 47. Cho hai số phức z  1 i và z  2  3i . Tính môđun của số phức z z . 1 2 1 2
A. z z  13 .
B. z z  5 .
C. z z  1.
D. z z  5 . 1 2 1 2 1 2 1 2 Lời giải
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Chọn A
z z  1 i  2  3i  3  2i nên ta có: 2 2
z z  3  2i  3  2  13 . 1 2   1 2
Câu 48. Cho hai số phức z  2
  i và z  1 .
i Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 1 2
2z z có tọa độ là 1 2 A. 3; 3   . B. 2; 3   . C.  3  ;3 . D.  3  ; 2 . Lời giải Chọn C
Ta có: 2z z  4
  2i 1 i  3   3 . i 1 2
Vậy điểm biểu diễn số phức 2z z có tọa độ là  3  ;3 . 1 2
Câu 49. Cho hai số phức z  1 2i và z  3  4i . Số phức 2z  3z z z là số phức nào sau đây? 1 2 1 2 1 2 A. 10i . B. 1  0i . C. 11 8i . D. 1110i . Lời giải Chọn B
Ta có: 2z  3z z z  2 1  2i  3 3  4i  1  2i 3  4i  10i . 1 2 1 2       
Câu 50. Cho số phức z a bia, b    thoả mãn z  2  i z . Tính S  4a b . A. S  4 B. S  2 C. S  2 D. S  4 Lời giải Chọn D  a   2 a  2 2 2 2 b , a  2
Ta có z  2  i z  a  2  b  1i a b   b  1   0  b   3  1 a      4 S 4a b 4 . 2       a  2  2 a    1 b    1
Câu 51. Cho số phức z thỏa mãn | z | 5 và | z  3 | |
z  3 10i | . Tìm số phức w z  4  3 . i A. w  3   8 . i
B. w  1 3 . i C. w  1   7 . i D. w  4   8 . i Lời giải Chọn D
z x yi, (x, y  ) . Theo đề bài ta có 2 2
x y  25 và 2 2 2 2
(x  3)  y  (x  3)  ( y 10) .
Giải hệ phương trình trên ta được x  0; y  5 . Vậy z  5i . Từ đó ta có w  4   8i .
Câu 52. Cho số phức z a bi,a,b    thỏa mãn z  1  3i z i  0 .Tính S a  3b . 7 7 A. S  5 B. S C. S  5 D. S   3 3 Lời giải Chọn C a   a   1 1 0 2 2  
Ta có: z  1  3i z i  0  a bi  1  3i a b i  0     4 2 2
b  3  a b  0 b      3
S a  3b  5.
Câu 53. Tìm hai số thực x và y thỏa mãn 2x  3yi  1 3i  x  6i với i là đơn vị ảo. A. x  1  ; y  3  . B. x  1  ; y  1  .
C. x  1 ; y  1  .
D. x  1 ; y  3  . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489x 1  0 x  1 
Ta có: 2x  3yi  1 3i  x  6i x 1 3y  9i  0     . 3y  9  0  y  3  
Câu 54. Tìm các số thực a và b thỏa mãn 2a  b ii  1 2i với i là đơn vị ảo. 1
A. a  0, b  2 . B. a  , b  1.
C. a  0, b  1.
D. a  1, b  2 . 2 Lời giải Chọn D. 2a 1  1 a  1
Ta có 2a  b ii  1 2i  2a  
1  bi  1 2i     . b  2 b  2  
Câu 55. Phần ảo của số phức z thoả mãn z  2  i1 i  4  2i là A. 3 . B. 3i . C. 3  i . D. 3  . Lời giải Chọn A
Cách 1: z  2  i1 i  4  2i z  4  2i  2  i1 i  z  1 3i z  1 3i
Vậy phần ảo của z bằng 3 .
Cách 2: Đặt z x y ,
i x; y    z x yi .
Kho đó z  2  i1 i  4  2i x yi  2  i1 i  4  2i x yi  3  i  4  2i x  3  4 x  1
x  3   y  
1 i  4  2i    
z  1  3i . y 1  2 y  3  
Vậy phần ảo của z bằng 3 .
Câu 56. Cho số phức z a bi a,b   thỏa mãn 1 iz  2z  3  2 .
i Tính P a b . 1 1 A. P B. P  1 C. P  1  D. P   2 2 Lời giải Chọn C
1 iz  2z  3 2 .i 
1 . Ta có: z a bi z a b . i Thay vào  
1 ta được 1 ia bi  2a bi  3  2i
 a bi  3a b  3  2i  a bi  3a b  3 2i  1 a  a b  2   2      P  1.  3a b  3 3  b      2
Câu 57. Tìm hai số thực x và y thỏa mãn 2x  3yi  3  i  5x  4i với i là đơn vị ảo.
A. x  1; y  1.
B. x  1; y  1 .
C. x  1; y  1 .
D. x  1; y  1 . Lời giải
2x  3  5xx  1
2x  3yi  3  i  5x  4i  2x  3  3y  
1 i  5x  4i     3y 1  4 y  1  
Câu 58. Tìm hai số thực x và y thỏa mãn 3x  2yi  2  i  2x  3i với i là đơn vị ảo.
A. x  2; y  2 .
B. x  2; y  1.
C. x  2; y  2 .
D. x  2; y  1 . Lời giải
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Ta có: 3x  2yi  2  i  2x  3i
 3x  2  2y   1  2x  3i 3
x  2  2xx  2      . 2 y 1  3  y  2   
Câu 59. Cho số z thỏa mãn 2  iz  4 z i  8
 19i . Môđun của z bằng A. 13 . B. 5 . C. 13 . D. 5 . Lời giải Chọn A
Gọi z a bi ; z a bi a,b  . Ta có:
2  iz  4z i  8  19i
 2  ia bi  4a bi i  8  19i  2
a b  a  6b  4  8  19i  2
a b  8  a  3    
a  6b  4  19 b  2  
Vậy z  3  2i z  13 .
Câu 60. Cho số phức z thoả mãn 3z i2  3iz  7 16  .
i Môđun của z bằng A. 5. B. 5. C. 3. D. 3. Lời giải Chọn A
Đặt z a bi  ; a b   . Theo đề ta có
3a bi i2 3ia bi  7 1
 6i  3a 3bi3i 2a2bi 3ai 3b  7 1  6i           a b a b a   
a 3b 3
a5b  3  7 1  3 7 3 7 1 6i        . 3
a 5b3  16   3
a 5b  13  b   2    Vậy 2 2 z  1  2  5 .
Câu 61. Cho số phức z thỏa mãn 2  iz  3 16i  2 z i . Môđun của z bằng A. 5 . B. 13 . C. 13 . D. 5 . Lời giải Chọn C
Gọi z x yi .
2  iz  316i  2z i
 2 i x yi  316i  2 x yi i
 2x  2 yi xi y  3 16i  2x  2 yi  2i
2x y  3  2x
 2y x 16  2  y  2   y  3  0
 x  4y  14  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489x  2   y  3  
Suy ra z  2  3i . Vậy z  13 .
Câu 62. Tìm hai số thực x và y thỏa mãn 3x yi  4  2i  5x  2i với i là đơn vị ảo.
A. x  2 ; y  4
B. x  2 ; y  4
C. x  2 ; y  0
D. x  2 ; y  0 Lời giải Chọn B 2x  4  0 x  2
3x yi 4 2i  5x  2i 2x  44 yi  0   . 4  y  0  y  4 
Câu 63. Cho số phức z thỏa mãn   i2 1 3
z  3 4i . Môđun của z bằng 5 5 2 4 A. . B. . C. . D. . 4 2 5 5 Lời giải Chọn A 3  4i 3  4 3 4  3 3 Ta có z    i .   i2 8 8 1 3 2 2 3  4 3 4  3 3  3  4 3   4  3 3  5 Suy ra z   i        . 8 8  8   8  4    
Câu 64. Cho số phức z  2  3i . Môđun của số phức w  2z  1 iz bằng A. 4 . B. 2 . C. 10 . D. 2 2 . Lời giải Chọn C
Ta có w  2 2  3i  1 i2  3i  3  i .
Suy ra w  10 .
Câu 65. Cho hai số thực x , y thỏa mãn x 3  2i  y 1 4i  1 24i . Giá trị của x y bằng: A. -3. B. 4. C. 2. D. 3. Lời giải Chọn A
Ta có: x 3  2i  y 1 4i  1 24i  3x y  (2x  4 y)i  1 24i . 3
x y  1 x  2 Suy ra:    .
2x  4 y  24 y  5   
Do đó: x y  3  .
Câu 66. Cho số phức z  2  3i . Môđun của số phức 2
w z z bằng: A. 3 10 . B. 206 . C. 134 . D. 3 2 . Lời giải Chọn A 2 2
w z z   i    i2 2 2 3 2 3  3
  9i w   3     9    3 10 .
Câu 67. Cho số phức z a bi  ,
a bR , thỏa mãn z  3  z 1 và  z  2z i là số thực.
Tính a b .
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. 0 . B. 4 . C. 2  . D. 2 . Lời giải Chọn A 2 2
Ta có: z  3  z 1  a   2
b  a   2 3
1  b a  2
Do đó:  z  2 z i    bi  bi i   2 4 2
b b  8  2b  4i là số thực khi 2b  4  0  b  2
 . Do đó a b  0 .
Câu 68. Gọi z , z lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình dưới đây. 1 2 Tính z z . 1 2 y M 2 x O 1 3 -4 N A. 2 29 . B. 2 5 . C. 20 . D. 116 . Lời giải Chọn B
Ta có M 3;2 ,N 1; 4
  lần lượt là điểm biểu diễn hình học của số phức z ,z suy ra 1 2
z  3  2i, z  1 4i . 1 2
Do đó z z  3  2i 1 4i  4  2i z z  4  2i  2 5 . 1 2 1 2
Câu 69. Cho số phức z a bi (a, b  ) thoả mãn (1  i)z  2z  3  2i . Tính P a b 1 1
A. P  1 . B. P   . C. P  . D. P  1 2 2 Lời giải Chọn D
(1  i)z  2z  3  2i  (1  i)(a bi)  2(a bi)  3  2i  (3a b)  (a b)i  3  2i  1 a  3
a b  3   2    
. Suy ra: P a b  1  . a b  2 3  b      2 z Câu 70. Cho
là số thực, z z  3 2 . Tính z 2 z A. z  3 2 . B. z  6 . C. z  2 3 . D. z  3 . Lời giải Chọn B 9
Đặt z x yi với x, y   . 2
z z  3 2  2 yi  3 2  y    1 . 2 2 z z.z z Ta có:  . Nên để là số thực thì 2
z.z là số thực hay:   3 x yi   2 2 2 z z 2 z
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 Suy ra 2 3 x y y   y  2 2 3 0
3x y   0 . 2 . 3 9 Kết hợp   1 và 2 ta có: 2 2 x  , y  . Vậy 2 2 z x y  6 . 2 2
Câu 71. Tìm cac số thực x và y thỏa mãn 3x  2  2 y  
1 i   x  
1   y  5i, với i là đơn vị ảo. 3 3 4 4 3 4 A. x  , y  2  .
B. x   , y   .
C. x  1, y  . D. x  , y  . 2 2 3 3 2 3 Lời giải Chọn D  3   3  2       1 x x x    2
Vì 3x  2  2 y  
1 i   x  
1   y  5i     . 2y    1  ( y  5) 4   y    3
Câu 72. Cho số phức z thỏa mãn điều kiện   i2 1 2
z z  4i  20 . Tìm z . A. z  25 . B. z  7 .
C. z  4 . D. z  5 . Lời giải Chọn D
Gọi z a bi , a , b   . Suy ra z a bi . 2
Từ giả thiết suy ra: 1 2i a bi  a bi  4i  20   3
  4ia bi  a bi  2  0  4i  2
a  4b  20 a  4  2
a  4b  4a  4bi  2  0  4i     . 4a  4b  4  b  3 
Suy ra z  4  3i . Vậy z 2 2  4  3  5 .
Câu 73. Tổng phần thực và phần ảo của số phức z thoả mãn iz  1 iz  2  i bằng A. 6 . B. 2  . C. 2 . D. 6  . Lời giải Chọn A
Giả sử số phức z có dạng: z x yi , x , y   .
Ta có: iz  1 iz  2
i i x yi  1 i x yi  2
i x  2 y yi  2i .
x  2 y  0 x  4    
x y  6 .  y  2  y  2  
Tổng phần thực và phần ảo của số phức z bằng 6 .
Câu 74. Cho a, b   và thỏa mãn a bii  2a  1 3i , với i là đơn vị ảo. Giá trị a b bằng A. 4 . B. 1  0 . C. 4  . D. 10 . Lời giải Chọn D b   2a  1 a  3
Ta có a bii  2a  1 3i b
  2a ai  1 3i     a  3 b  7  
Vậy a b  10 .
Câu 75. Tìm hai số thực x , y thỏa mãn 3x  2 yi  3  i  4x  3i với i là đơn vị ảo. 2
A. x  3; y  1. B. x  ; y  1.
C. x  3; y  3 .
D. x  3; y  1. 3 Lời giải Chọn A
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 3
x  3  4xx  3
3x  2yi  3  i  4x  3i  3x  3  2y  
1 i  4x  3i     . 2 y 1  3  y  1   
Câu 76. Cho các số phức z , z thỏa mãn z z  3 và z z  2 . Môđun z z bằng 1 2 1 2 1 2 1 2 A. 2 . B. 3 . C. 2 . D. 2 2 . Lời giải Chọn D
z a b i Đặt 1 1 1 
a , a , b , b   . 1 2 2 2 
z a b i  2 2 2 2 2 2 2
a b a b  3  Theo giả thiết ta có 1 1 2 2  . 2
 a a b b  2  1 2 1 2  2 2 2 Suy ra z za ab b  8 . 1 2  1 2   1 2 
Vậy z z  2 2 . 1 2
Câu 77. Cho số phức z thỏa mãn z z    i2 3 1 2
. Phần ảo của z là 3  3 A. 2 . B. 2 . C. . D. . 4 4 Lời giải Chọn B 2 2
Ta có: z  3z  1 2i  z  3z  1 2i  z  3z  3   4i (1).
Đặt z x yi ( ,
x y  )  z x yi .
Phương trình (1) thành x yi  3(x yi)  3
  4i  4x  2 yi  3   4i  3 4x  3  x       4 . 2  y  4   y  2  
Vậy phần ảo của số phức z là 2 .
B. PHƯƠNG TRÌNH SỐ PHỨC Phương trình 2
az bz c  0 với a  0 có biệt số 2
  b  4ac thì có hai nghiệm thực hoặc phức là b    b    z hoặc z   1 2a 2 2a
Câu 78. Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z 2z 5  0 . Môđun của số phức 0
z i bằng 0 A. 2 . B. 2 . C. 10 . D. 10 . Lời giải Chọn B
z 1  2i
z  1 2i Ta có: 2
z  2z  5  0 2
z  2z 1  4    z  2 2 1  4i     . z 1  2 z  1 2i  
Vì z là nghiệm phức có phần ảo âm nên z  1 2i z i  1  2i i  1 i . 0 0 0
Suy ra: z i  1 i  1   2 2 1  2 . 0
Câu 79. Kí hiệu z là nghiệm phức có phần ảo dương của phương trình 2
4z 16z 17  0 . Trên mặt 0
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489  1   1   1   1  A. M ; 2 . B. M  ; 2 . C. M  ;1 . D. M ;1 . 1   2   3   4    2   2   4   4  Lời giải Chọn B Xét phương trình 2
4z 16z  17  0 có        2 64 4.17 4 2i . 8  2i 1 8  2i 1
Phương trình có hai nghiệm z
 2  i, z   2  i . 1 2 4 2 4 2 1
Do z là nghiệm phức có phần ảo dương nên z  2  i . 0 0 2 1
Ta có w iz    2i . 0 2  1 
Vậy điểm biểu diễn w iz là M  ; 2 . 0 2    2 
Câu 80. Kí hiệu z , z là hai nghiệm phức của phương trình 2
3z z  1  0 . Tính P z z . 1 2 1 2 14 2 3 2 3 A. P B. P C. P D. P  3 3 3 3 Lời giải Chọn D 2 Xét phương trình 2
3z z  1  0 có   1  4.3.1  11  0 . Căn bậc hai của  là i 11 .
Phương trình đã cho có 2 nghiệm phức phân biệt 1  i 11 1 11 1  i 11 1 11 z    i; z    i 1 6 6 6 2 6 6 6 Từ đó suy ra: 2 2 2 2 1 11 1 11      1  11  1  11 3 3
P z z   i   i            1 2     6 6 6 6      6  6  6     6  3 3 2 3  3 1 1
Câu 81. Kí hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 . Tính P   . 1 2 z z 1 2 1 1 1 A. B. C. D. 6 12 6 6 Lời giải Chọn B z z  1 1 1 z z 1
Theo định lí Vi-et, ta có 1 2  nên P    1 2  z z   6 z z z .z 6 1 2 1 2 1 2
Câu 82. Kí hiệu z ; z là hai nghiệm của phương trình 2
z z 1  0 . Tính 2 2
P z z z z . 1 2 1 2 1 2 A. P  1 B. P  2 C. P  1  D. P  0 Lời giải Chọn D
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020  1 3 z    i  2 2 2
z z 1  0   1 3 z    i  2 2 2 2  1 3   1 3   1 3   1 3  2 2
P z z z z     i      i      i    i   0 1 2 1 2  2 2   2 2   2 2   2 2         
Câu 83. Kí hiệu z , z , z và z
là bốn nghiệm phức của phương trình 4 2
z z 12  0 . Tính 1 2 3 4
tổng T z z z z 1 2 3 4 A. T  4 B. T  2 3
C. T  4  2 3
D. T  2  2 3 Lời giải Chọn C 2 z  3  z  i 3 4 2
z z 12  0     2 z  4 z  2   
T z z z z i 3  i 3  2  2  2 3  4 1 2 3 4
Câu 84. Phương trình nào dưới đây nhận hai số phức 1 2i và 1 2i là nghiệm. A. 2
z  2z  3  0 B. 2
z  2z  3  0 C. 2
z  2z  3  0 D. 2
z  2z  3  0 Lời giải Chọn C z z  2 Theo định lý Viet ta có 1 2 
, do đó z , z là hai nghiệm của phương trình z .z  1 2  3 1 2 2
z  2z  3  0
Câu 85. Kí hiệu z , z là hai nghiệm của phương trình 2
z  4  0 . Gọi M , N lần lượt là điểm biểu 1 2
diễn của z , z trên mặt phẳng tọa độ. Tính T OM ON với O là gốc tọa độ. 1 2 A. T  2 B. T  2 C. T  8 D. 4 Lời giải Chọn D z  2i Ta có: 2 1
z  4  0  z  2i  2 Suy ra M 0; 2
  ; N 0;2 nên T OM ON   2 2 2  2  4 .
Câu 86. Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  3z  5  0 . Giá trị của z z bằng 1 2 1 2 A. 2 5 . B. 5 . C. 3 . D. 10 . Lời giải Chọn A.  3  11iz  1 2 Ta có : 2
z  3z  5  0  
. Suy ra z z  5  z z  2 5 . 1 2 1 2  3  11iz  2  2
Câu 87. Gọi z và z là hai nghiệm phức của phương trình 2
4z  4z  3  0 . Giá trị của biểu thức 1 2
z z bằng: 1 2 A. 3 2 B. 2 3 C. 3 D. 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn D  1 2 z   i 1 2 2 Xét phương trình 2
4z  4z  3  0 ta có hai nghiệm là:  1 2 z   i 2  2 2 3  z z
z z  3 1 2 2 1 2
Câu 88. Gọi z , z là 2 nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 2 2
z z bằng 1 2 1 2 A. 6. B. 8. C. 16. D. 26. Lời giải Chọn A 2
'  b'  ac  4  5  1
Phương trình có 2 nghiệm phức z  2  i, z  2   i 1 2 2 2 nên 2 2
z z  2  i  2  i 2 2 2
 4  4i i  4  4i i  8  2i  8  2  6 1 2
Câu 89. Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  7  0. Giá trị của 2 2 z z bằng 1 2 1 2 A. 10. B. 8. C. 16. D. 2. Lời giải Chọn D
Ta có        i2 4 7 3 3 .
Do đó phương trình có hai nghiệm phức là z  2  3i, z  2  3 . i 1 2 2 2 Suy ra 2 2
z z  2  3i  2  3i
 4  4 3i  3  4  4 3i  3  2. 1 2    
Câu 90. Gọi z , z là hai nghiệm phức của phương trình 2
z  6z 10  0 . Giá trị của 2 2
z z bằng: 1 2 1 2 A. 16. B. 56 . C. 20. D. 26 . Lời giải Chọn A z z  6
Áp dụng định lý Viet áp dụng cho phương trình trên ta được: 1 2  . z z  10  1 2
Khi đó ta có z z   z z 2 2 2
 2z z  36  20  16 . 1 2 1 2 1 2
Câu 91. Gọi z , z là các nghiệm phức của phương trình 2
z  4z  7  0 . Số phức z z z z bằng 1 2 1 2 1 2 A. 2 . B. 10 . C. 2i . D. 10i . Lời giải Chọn Az  2   3i 2
z  4z  7  0  
z  2  3i
Không mất tính tổng quát giả sử z  2
  3i, z  2   3 . i 1 2
z z z z  2  3i 2   3i  2   3i 2   3i  2 . 1 2 1 2      
Vậy z z z z  2. 1 2 1 2
Câu 92. Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  5  0 ; M , N lần lượt là các điểm 1 2
biểu diễn của z , z trên mặt phẳng phức. Độ dài đoạn thẳng MN là 1 2 A. 2 5 . B. 4 . C. 2 . D. 2 .
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Lời giải Chọn D Xét phương trình: 2
z  4z  5  0 , ta có    2 2 1.5  1 2  i .
Suy ra phương trình có hai nghiệm phức là z  2  i ; z  2  i . Suy ra M 2  ;1 ; N 2;  1 . 1 2 2 2
Ta có MN  2  2   1    1  2 . Vậy MN  2 . 2 2
Câu 93. Gọi z , z là hai nghiệm phức của phương trình 2
3z z  2  0 . Tính T zz . 1 2 1 2 2 8 4 11 A. T  . B. T  . C. T  . D. T   . 3 3 3 9 Lời giải Chọn C 2 2      1  23 2 1 23i 2  z z         1   1   6  6 3 2 6  
3z z  2  0     .  2 1 23i 2  1  23    2  z  2 2  z          6 2 6  6     3    2 2 2 2 4 Vậy T zz    . 1 2 3 3 3 2 2
Câu 94. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Giá trị của zz bằng 1 2 1 2 A. 10 . B. 20 . C. 2 10 . D. 10 . Lời giải Chọn B 2 2 Ta có 2
z  2z 10  0   z   1  9
  3i  z  1   3i . 2 2 Do đó zz =20. 1 2
Câu 95. Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  29  0 . Tính giá trị của biểu thức 1 2 4 4 zz . 1 2 A. 841. B. 58 . C. 1682 . D. 2019 . Lời giải Chọn C 2 2 2 Ta có 2
z  4z  29  0   z  2  25   z  2  5i  z  2  5i . 4 4 4 4 zz  22   5    2    2    2 2  5  1628 . 1 2  1 1
Câu 96. Kí hiệu z và z là 2 nghiệm phức của phương trình 2
2z  4z  9  0 . Tính P   1 2 z z 1 2 4 4 9 9 A. P  . B. P  . C. P  . D. P  . 9 9 4 4 Lời giải Chọn B 1 1 z z 4 Theo định lí Vi ét: 1 2 P     z z z .z 9 1 2 1 2
Câu 97. Gọi z , z là hai nghiệm phức của phương trình 2
z  5z  7  0 . Giá trị của biểu thức z z 1 2 1 2 là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 3 A. 3i . B.  3i . C. 3 . D. . 2 Lời giải Chọn C  5  i 3 z   1 2 Ta có 2
z  5z  7  0  
z z i 3  3 1 2  5  i 3 z  2  2
Câu 98. Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  2z 10  0 . Giá trị của z . z bằng 1 2 1 2 5 A. 5 . B. . C. 10 . D. 20 . 2 Lời giải Chọn C Phương trình 2
z  2z  10  0 có   9
 nên phương trình có 2 nghiệm phức: z  1
  3i, z  1   3i . 1 2 2 2 2
Khi đó: z . z    2 1  3 . 1   3   10. 1 2    
Câu 99. Gọi z , z là hai nghiệm phức của phương trình 2
z  2z  2  0 . Tính giá trị của biểu thức 1 2
P  2 z z z z . 1 2 1 2 A. P  6 . B. P  3 .
C. P  2 2  2 . D. P  2  4 . Lời giải Chọn A z  1 i Ta có 2 1
z  2z  2  0   . z  1 i  2
Suy ra P  2 1 i 1 i  1  i  1 i  2 2  2i  4  2  6 .
Câu 100. Kí hiệu z ; z là hai nghiệm phức của phương trình 2
3z z  1  0 . Tính P z z 1 2 1 2 14 2 3 2 3 A. P  . B. P  . C. P  . D. P  . 3 3 3 3 Lời giải Chọn D Ta có  1 11 z   i  1 2 6 6
3z z 1  0   1 11  z   i 2  6 6 2 2 2 2 1  11  1  11      2 3
P z z               . 1 2 6  6  6  6      3    
C. BIỂU DIỄN ĐIỂM SỐ PHỨC
Điểm biểu diễn số phức:
Số phức z a bi , a ,b   được biểu diễn bởi điểm M a ;b .
BÀI TOÁN: Tìm tập hợp điểm biểu diễn của số phức thỏa mãn tính chất cho trước
Bước 1. Gọi M(x;y) là điểm biểu diễn số phức z x yi (x, y  ). 
Bước 2. Biến đổi điều kiện K để tìm mối liên hệ giữa x, y và kết luận.
Mối liên hệ giữa x và y
Kết luận tập hợp điểm M (x;y)
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Ax By C  0.
Là đường thẳng d : Ax By C  0.  2 2 2
(x a)  (y b)  R
Là đường tròn (C ) có tâm I(a;b) và bán kính     2 2
x y  2ax  2by c  0 2 2 
R a b c.   2 2 2
(x a)  (y b)  R
Là hình tròn (C ) có tâm I(a;b) và bán kính     2 2
x y  2ax  2by c  0 2 2 
R a b c
(đường tròn kể cả bên trong) 2 2 2 2
R  (x a)  (y b)  R .
Là những điểm thuộc miền có hình vành khăn 1 2
tạo bởi hai đường tròn đồng tâm I(a;b) và
bán kính lần lượt R và R . 1 2  2
y ax bx  , c (a  0).  b    
Là một parabol (P) có đỉnh I   ;    2a 4a  2 2 x y MF   MF  2a
Là một elíp có trục lớn 2 ,
a trục bé 2b và tiêu     1 với 1 2   2 2 a b F
F  2c  2ac a b a b  1 2  cự là 2 2 2 2 , ( 0).   AB
Là đường trung trực của đoạn thẳng .
MA MB .
Câu 101. Trên mặt phẳng tọa độ, điểm biểu diễn số phức z    i2 1 2
là điểm nào dưới đây?
A. P 3; 4 .
B. Q 5; 4 .
C. N 4;  3 . D. M 4;5 . Lời giải Chọn A
Ta có z    i2 1 2   i   i2 2 1 2.1.2 2  3   4i .
Vậy trên mặt phẳng tọa độ, điểm biểu diễn số phức z    i2 1 2
là điểm P 3; 4 .
Câu 102. Cho số phước z  1  2i. Điểm nào dưới đây là điểm biểu diễn số phức w iz trên mặt phẳng tọa độ A. N 2;1
B. P 2;1
C. M 1; 2 D. Q 1; 2 Lời giải Chọn A
w iz i 1  2i  2  i
Câu 103. Cho số phức z  1 i . Biểu diễn số phức 2 z là điểm A. M  2  ;0 . B. P 1;2 . C. E 2;0 .
D. N 0; 2 . Lời giải Chọn D
Ta có z  1 i . Nên z    i2 2 1
 2i . Vậy điểm biểu diễn số phức 2
z là điểm N 0;  2 .
Câu 104. Xét các số phức z thỏa mãn  z  2i  z  2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 2 B. 2 2 C. 4 D. 2 Lời giải Chọn D
Giả sử z x yi với x, y   . Vì
z  2i z  2  x  2  yi  x  2  yi     
x x  2  y 2  y  xy   x  22  y i     là
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489
số thuần ảo nên có phần thực bằng không do đó
xx  2  y2 y  0
  x  2   y  2 1
1  2 . Suy ra tập hợp các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng 2 .
Câu 105. Xét các số phức z thỏa mãn  z  2i z  2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng? A. 2 2 . B. 2 . C. 2 . D. 4 . Lời giải
Gọi z a bi , a, b  
Ta có:  z i z    a bi ia bi   2 2 2 2 2
2  a  2a b  2b  2 a b  2i 2 2
Vì  z  2i z  2 là số thuần ảo nên ta có 2 2
a  2a b  2b  0  a   1  b   1  2 .
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng 2 .
Câu 106. Xét các số phức z thỏa mãn  z  3i z  3 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất
cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng: 9 3 2 A. . B. 3 2 . C. 3 . D. . 2 2 Lời giải
Gọi z x yi , với x, y . 2
Theo giả thiết, ta có  z  3i z  3  z  3z  3iz  9i là số thuần ảo khi  3 3 3 2 2 2 
x y  3x  3y  0 . Đây là phương trình đường tròn tâm I ;   , bán kính R  .  2 2  2
Câu 107. Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn z  2  i  4 là đường tròn có
tâm I và bán kính R lần lượt là A. I 2;   1 ; R  2 . B. I  2  ;  
1 ; R  4 . C. I  2  ;  
1 ; R  2 . D. I 2;   1 ; R  4 . Lời giải Chọn B
Gọi z x yi , z được biểu diễn bởi M x; y . 2 2
Theo giả thiết z  2  i  4 nên ta có x yi  2  i  4   x  2   y   1  4
  x  2   y  2 2 2 1
 4 . Vậy tập hợp điểm biểu diễn số phức z là đường tròn tâm I 2;  
1 và bán kính R  4 .
Câu 108. Tập hợp các điểm biểu diễn các số phức z thỏa mãn z 1 i  2 là đường tròn có tâm và bán kính lần lượt là A. I 1  ;1 , R  4 . B. I 1  ;1 , R  2 .
C. I 1;   1 , R  2 .
D. I 1;   1 , R  4 . Lời giải Chọn C Gọi M  ;
x y  là điểm biểu diễn cho các số phức z x yi  2 ,
x y  ,i    1 . z   i
x    y  i    x  2   y  2    x  2   y  2 1 2 1 1 2 1 1 2 1 1  4 .
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn z 1 i  2 là đường tròn có tâm I 1;  
1 , bán kính R  2 .
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 109. Tập hợp các điểm biểu diễn các số phức z thỏa mãn z  2  z i là một đường thẳng có phương trình
A. 4x  2 y  3  0 .
B. 2x  4 y 13  0 .
C. 4x  2 y  3  0 .
D. 2x  4 y 13  0 . Lời giải Chọn A Gọi M  ;
x y là điểm biểu diễn số phức z . 2 2 Ta có z
z i   x   2 2 2 2
y x   y   1
 4x  4  2 y 1  4x  2 y  3  0 Do đó ta chọn đáp án A.
Câu 110. Tập hợp điểm biểu diễn số phức z biết: z  (3  4i)  2 là
A. Đường tròn tâm I (3;4), R  2 .
B. Đường tròn tâm I (3; 4), R  2 .
B. Đường tròn tâm I (3;4), R  4 .
D. Đường tròn tâm I (3; 4), R  4 . Lời giải Chọn A
Gọi z x yi x;y  . Ta có: 2 2
z (3  4i)  2  (x  3)  (y  4)  4
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tâm I (3;4), R  2 . I  (a;b) 
Chú ý: z  (a bi)  R   R 
Câu 111. Tập hợp các điểm biểu diễn số phức z thỏa mãn z i  1 iz là một đường tròn, tâm của
đường tròn đó có tọa độ là A. 1;  1 . B. 0;   1 . C. 0;  1 .
D. 1; 0 . Lời giải Chọn B
Gọi M x; y là điểm biểu diễn số phức z x yi, (x, y  ) .
Theo bài ra ta có: z i  1 iz x yi i z iz
x   y  i x y   x yi x   y  2   x y2   x y2 2 1 1
x y y  
x   y  2 2 2 2 2 1 0 1  2.
Vậy tập hợp các điểm biểu diễn số phức z thỏa mãn yêu cầu bài toán là đường tròn tâm I 0;   1 , bán kính R  2 .
Câu 112. Cho số phức z thay đổi thỏa mãn z 1  2. Biết rằng tập hợp điểm biểu diễn các số phức
w  1 3 iz  2 là đường tròn có bán kính bằng . R Tính . R
A. R  8 .
B. R  2 .
C. R  16 .
D. R  4 . Lời giải Chọn D
Gọi w x yi, , x y   .
w  1 3 iz  2
x yi  1 3 iz  2  x yi  1 3 i z   1 1 3 i  2
x  3   y  3i  1 3 i z   1
x  3   y  3i  1 3 i z   1
  x     y  2 2 3 3  1 3 i z 1
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489
  x     y  2 2 3 3  4
  x     y  2 2 3 3  16.
Vậy tập hợp điểm biểu diễn các số phức w  1 3 iz  2 là đường tròn tâm I 3; 3 , bán
kính bằng R  4.
Câu 113. Có bao nhiêu số phức z có phần thực bằng 2 và z 1 2i  3 ? A. 3. B. 0. C. 2. D. 1 Lời giải Chọn D
Gọi số phức z có dạng: z  2  bib  
Ta có: z 1 2i  3  2  bi 1 2i  3  3  b  2i  3 
 b  2   b  2 9 2 3 2  0  b  2 .
Vậy có một số phức z thỏa mãn yêu cầu bài toán: z  2  2 . i
Câu 114. Tập hợp các điểm biểu diễn các số phức z thỏa mãn 2 z i z z  2i là A. Một điểm.
B. Một đường tròn.
C. Một đường thẳng. D. Một Parabol. Lời giải Chọn D
Đặt z x yi x, y    z x yi .
Khi đó 2 z i z z  2i  2 x   y  
1 i  2 y  2ixy 2       y  2 2 4 1 2 2   2 2 2
 4x  4y  8y  4  4 y  8y  4 2 xy  là một Parabol. 4
Câu 115. Trong mặt phẳng tọa độ Oxy , tìm tập hợp điểm biểu diễn số phức z thỏa mãn
z  2  3i  2 .
A. Một đường thẳng. B. Một hình tròn.
C. Một đường tròn.
D. Một đường elip. Lời giải Chọn B
Gọi z x y ; i ,
x y  . Từ giả thiết z  2  3i  2  x yi  (2  3i)  2 .  x
y i    x  2   y  2 ( 2) ( 3) 2 2 3  4 .
Vậy tập hợp điểm biểu diễn số phức z là một hình tròn.
Câu 116. Có bao nhiêu số phức z thỏa mãn điều kiện z i  1  z  2i và z  1 A. 0 . B. 2 . C. 1. D. 4 . Lời giải Chọn B
Đặt z x  ; yi ,
x y   và M z  M  ; x y
z i 1  z  2i     x  2 1   y  2 1
x   y  22 2
x y  1  0      2 2 2 2  z  1 x y  1 x y  1   
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Suy ra tọa độ điểm M nằm trên đường thẳng  : x y  1  0 và đường tròn 2 2
x y  1 có
tâm O0;0, R  1 0  0  1 1 Ta có d  , O     1  R  2 2 2 1  1
Suy ra đường thẳng cắt đường tròn tại hai điểm hay có hai số phức z thỏa mãn. Đáp án B
Câu 117. Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn z  2  i  4 là đường tròn có tâm
I và bán kính R lần lượt là A. I  2  ;   1 ; R  4 .
B. I 2;   1 ; R  2 .
C. I 2;   1 ; R  4 . D. I  2  ;   1 ; R  2 . Lời giải Chọn A
Gọi z x yi ( x ; y ; 2 i  1 ).
Theo bài ra z  2  i  4 hay x yi  2  i  4 .
  x  2   y  2 2 1  16 .
Tập hợp các điểm biểu diễn các số phức z là đường tròn có tâm I  2  ;  
1 , bán kính R  4 .
-------------------------------- HẾT --------------------------------
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25