Tổng ôn tập TN THPT 2020 môn Toán: Thể tích khối đa diện Toán 12

Tuyển chọn các câu hỏi và bài tập trắc nghiệm chuyên đề thể tích khối đa diện, có đáp án và lời giải chi tiết, giúp học sinh tổng ôn kiến thức để chuẩn bị cho kỳ thi tốt nghiệp THPT 2020 môn Toán.Mời bạn đọc đón xem.

13 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

50 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
THỂ TÍCH KHỐI ĐA DIỆN
Thể tích khối chóp
đchãp ¸y
1
. chiÒu cao .
3
V S
Thể tích khối lăng trụ
đl¨ng trô ¸y
. chiÒu cao .V S
Thể tích khối lập phương
3
V a
với
a
là cạnh.
Thể tích khối hộp chữ nhật
V abc
với
, , a b c
lần lượt là chiều dài, chiều rộng và chiều cao.
Xác định diện tích đáy:
1 1
sin ( )( )( ) ,
2
ABC a
S ah ab C p p a p b b c
a
với
2
a b c
p
tam gi¸c vu«ng
1
(tÝch hai c¹nh gãc vu«ng)
2
S
2
tam gi¸c ®Òu
(c¹nh) 3
4
S
2
tam gi¸c vu«ng c©n
(c¹nh huyÒn)
4
S
H×nh thang
(®¸y lín ®¸y bÐ) chiÒu cao
2
S
H×nh ch÷ nhËt
dµi réng .S
2
H×nh vu«n
(c¹nh) .
g
S
Xác định chiều cao:
Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam giác
chứa trong mặt bên vuông góc với đáy.
Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai mặt bên
cùng vuông góc với mặt phẳng đáy.
Hình chóp có các cạnh bên bằng nhau: Chân đường cao của hình chóp là tâm đường tròn ngoại tiếp đa
giác đáy.
Cần nhớ: Tỉ số thể tích khối chóp có đáy là tam giác
Cho khối chóp
. ,S ABC
trên các đoạn thẳng
, , SA SB SC
lần lượt
lấy các điểm
, , A B C
khác
.S
Khi đó ta luôn có tỉ số thể tích:
.
.
S A B C
S ABC
V
SA SB SC
V SA SB SC
Chỉ có tỉ số thể tích khối chóp đáy tam giác, không có tỉ số khối chóp
đáy tứ giác. Khi tính tỉ số khối tứ giác, ta cần chia ra những hình
chóp có đáy là tam giác.
CÂU HỎI CÙNG MỨC ĐỘ VỚI ĐỀ MINH HỌA
DẠNG CÂU HỎI NHẬN BIẾT
Câu 1. Thể tích khối lăng trụ có diện tích đáy bằng
B
, chiều cao bằng
h
là
A.
1
3
V Bh
. B.
2
3
V Bh
. C.
V Bh
. D.
3V Bh
.
Câu 2. Cho khối lập phương có cạnh bằng
6
. Thể tích của khối lập phương đã cho bằng
A.
216
. B.
18
. C.
36
. D.
72
.
Câu 3. Thể tích khối lập phương cạnh
2
bằng
THỂ TÍCH KHỐI ĐA DIỆN
Vấn đề 8
b
A
a
S
c
B
C
C
A
B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
6
. B.
8
. C.
4
. D.
2
.
Câu 4. Cho khối chóp có diện tích đáy
B
và chiều cao
4
h
. Thể tích của khối chóp đã cho bằng
A.
6
. B.
12
. C.
36
. D.
4
.
Câu 5. Thể tích khối chóp có diện tích đáy bằng
2
2a
, chiều cao bằng
3a
là
A.
3
2 3
9
a
V
. B.
3
2 3
3
a
V
. C.
3
2 3
V a . D.
3
3
3
a
V
.
Câu 6. Thể tích khối chóp có diện tích đáy bằng
2
a
, chiều cao bằng
2a
là
A.
3
6V a
. B.
3
3
a
V
. C.
3
2V a
. D.
3
2
3
a
V
.
Câu 7. Thể tích khối lăng trụ có diện tích đáy bằng
2
3a
, chiều cao bằng
a
là
A.
3
3V a
. B.
3
3
a
V
. C.
3
V a
. D.
3
2
3
a
V
.
Câu 8. Thể tích khối hộp chữ nhật có ba kích thước lần lượt là
3,4,5
bằng
A.
120
V
. B.
20
V
. C.
30
V
. D.
60
V
.
Câu 9. Cho khối chóp có diện tích đáy
6
B
và chiều cao
3
h
. Thể tích của khối chóp đã cho bằng
A.
6
. B.
18
. C.
9
. D.
36
.
Câu 10. Thể tích khối lập phương cạnh
5
bằng
A.
15
. B.
25
. C.
125
. D.
75
.
Câu 11. Cho khối lập phương có độ dài đường chéo bằng
6 3
. Thể tích của khối lập phương đó bằng
A.
81 3
. B.
216
. C.
24 3
. D.
162 6
.
Câu 12. Thể tích khối lập phương
.
ABCD A B C D
có
3AC a
bằng
A.
3
a
. B.
2
a
. C.
2a
. D.
3a
.
Câu 13. Cho khối lập phương có tổng diện tích các mặt bằng
294
. Thể tích của khối lập phương đó bằng
A.
147 147
2 2
. B.
49
. C.
343
. D.
147
2
.
Câu 14. Thể tích khối lập phương
.
ABCD A B C D
có
6AC a
bằng
A.
3
8a
. B.
3
6 6
a
. C.
3
2 2
a
. D.
3
3 3
a
.
Câu 15. Khối chóp
.
S ABC
có thể tích
2 2
3
V
và diện tích đáy
3
B
. Chiều cao của khối chóp
.
S ABC
bằng
A.
2 6
9
. B.
2 6
3
. C.
2 2
3
. D.
2 6
27
.
Câu 16. Cho khối hộp chữ nhật có ba kích thước là
3;5;7
. Thể tích của khối hộp đó bằng
A.
35
. B.
105
2
. C.
105
. D.
15
.
Câu 17. Thể tích khối lập phương
.
ABCD A B C D
có
2
AB
bằng
A.
2 2
. B.
2
. C.
1
. D.
3
.
Câu 18. Cho khối chóp
.
S ABCD
có thể tích bằng
3
a
, đáy
ABCD
là hình vuông. Biết chiều cao của khối
chóp là
3h a
. Cạnh hình vuông
ABCD
bằng
A.
a
. B.
3
a
. C.
2a
. D.
3a
.
Câu 19. Cho khối lập phương
.
ABCD A B C D
biết
6 2
AC
. Thể tích của khối lập phương đó bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
432 2
. B.
108
. C.
216
. D. 48 6 .
Câu 20. Thể tích khối lập phương
.ABCD A B C D
có
2AB
bằng
A.
8
. B.
2 2
. C.
16 2
. D.
6
.
Câu 21. Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
3, 4, 5AC AB BC
và
3SA
. Tính thể
tích
V
của khối chóp
.S ABC
.
A.
18V
. B.
6V
. C.
12V
. D.
20V
.
Câu 22. Thể tích khối lập phương
.ABCD A B C D
có
2AB a
bằng:
A.
3
a
. B.
3
2a
. C.
3
4a
. D.
3
6a
.
Câu 23. Thể tích khối lập phương có cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
2 2a
. D.
3
6a
.
Câu 24. Thể tích khối hộp chữ nhật có độ dài các cạnh lần lượt là
,2 ,3a a a
bằng:
A.
3
2a
. B.
3
6a
. C.
3
2
3
a
. D.
3
3a
.
Câu 25. Thể tích khối tứ diện đều có cạnh
2a
bằng
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
2 2
3
a
. D.
3
2 3
3
a
.
Câu 26. Thể tích khối lăng trụ có diện tích đáy
2
3a
và chiều cao
a
là
A.
3
3V a
. B.
3
V a
. C.
3
9V a
. D.
3
6V a
.
DẠNG CÂU HỎI THÔNG HIỂU
Câu 27. Cho khối lăng trụ đứng .ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
a
. Biết
60BAD
,
AA a
. Thể tích của khối lăng trụ đã cho bằng
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
3
a
.
Câu 28. Cho khối lăng trụ đứng .ABC A B C
. Biết
3AB
cm,
4AC
cm,
60BAC
,
2AA
cm. Thể
tích của khối lăng trụ đã cho bằng
A.
6 3
(cm
2
). B.
2 3
(cm
3
). C.
6 3
(cm
3
). D.
6
(cm
3
).
Câu 29. Cho khối lăng trụ đứng
.ABCD A B C D
có đáy là hình thoi cạnh
a
,
3BD a
và
4AA a
(minh họa như hình bên). Thể tích của khối lăng trụ đã cho bằng
A.
3
2 3a
. B.
3
4 3a
. C.
3
2 3
3
a
. D.
3
4 3
3
a
.
Câu 30. Cho khối lăng trụ đứng .ABCD A B C D
có đáy
ABCD
là hình chữ nhật có
AB a
,
3AD a
,
2AA a
. (minh họa như hình vẽ bên).
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thể tích của khối lăng trụ đã cho bằng
A.
3
2 3a . B.
3
3a . C.
3
3
3
a
. D.
3
2 3
3
a
.
Câu 31. Cho khối lăng trụ đứng .ABCD A B C D
có đáy
ABCD
là hình vuông cạnh
2a
. Biết góc giữa
A B
với mặt phẳng
ABCD
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
A.
3
6
3
a
. B.
3
2 6
3
a
. C.
3
2 3
3
a
. D.
3
2 6a
.
Câu 32. Cho khối lăng trụ đứng .ABC A B C
có đáy là tam giác vuông tại
A
. Biết
2 2AB AA a
,
ABC
(minh họa như hình vẽ bên).
Thể tích của khối lăng trụ đã cho bằng
A.
3
sina
. B.
3
.tan
3
a
. C.
3
tana
. D.
3
tan
2
a
.
Câu 33. Tính thể tích khối lăng trụ đứng
. ' ' ' 'ABCD A B C D
biết
ABCD
là hình thoi có
10 , 8AC cm BD cm
và diện tích hình chữ nhật
' 'ACC A
bằng
2
50cm
.
A.
3
400cm
. B.
3
2000cm
. C.
3
4000cm
. D.
3
200cm
.
Câu 34. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều có cạnh bằng
a
,
SA
vuông góc với đáy và
2SA a
. Tính thể tích của khối chóp
.S ABC
.
A.
3
3
2
a
. B.
3
3
3
a
. C.
3
2
6
a
. D.
3
3
6
a
.
Câu 35. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
ABC
là tam giác vuông cân tại
A
có
2BC a
và
' 5AC a
.
A.
3
2a
. B.
3
2a
. C.
3
2
3
a
. D.
3
a
.
Câu 36. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
ABC
là tam giác đều cạnh
a
và ' 5AC a .
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
3
6
a
. D.
3
a
.
Câu 37. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
5 , 12 , 13AB cm AC cm BC cm
và
' 7CC cm
.
A.
3
210cm
. B.
3
70cm
. C.
3
105cm
. D.
3
35cm
.
C'
D'
B'
C
B
A
D
A'
α
B'
C'
A
C
B
A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 38. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
13 , 14 , 15AB cm AC cm BC cm
và
' 10CC cm
.
A.
3
420
cm
. B.
3
840
cm
. C.
3
420
cm
. D.
3
140
cm
.
Câu 39. Cho khối chóp tam giác đều có tất cả các cạnh bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
8
3
a
. B.
3
4 2
3
a
. C.
3
8 2
3
a
. D.
3
2 2
3
a
.
Câu 40. Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, các cạnh bên bằng
2a
. Thể tích của khối chóp
đã cho bằng
A.
3
14
3
a
. B.
3
4
3
a
. C.
3
14
6
a
. D.
3
2 2
3
a
.
Câu 41. Cho khối chóp tam giác đều có cạnh đáy bằng
a
, các cạnh bên bằng
2a
. Thể tích của khối
chóp đã cho bằng
A.
3
33
12
a
. B.
3
11
12
a
. C.
3
8 2
3
a
. D.
3
11
6
a
.
Câu 42. Cho khối chóp
.
S ABCD
có đáy là hình vuông cạnh a. Cạnh bên
SA
vuông góc với đáy.
2SB a
;
Thể tích của khối chóp
.
S ABCD
bằng:
A.
3
4 2
3
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
3
3
a
.
Câu 43. Cho khối chóp tam giác đều có tất cả các cạnh đều bằng
2a
. Thể tích của khối chóp đó bằng:
A.
3
2 2
3
a
. B.
3
2
3
a
. C.
3
2
12
a
. D.
3
2 6
9
a
.
Câu 44. Cho khối chóp tam giác đều có cạnh đáy bằng
a
, cạnh bên bằng
3a
. Thể tích của khối chóp đó
bằng
A.
3
2 2
3
a
. B.
3
2
3
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Câu 45. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác vuông tại
, , 60
o
A AC a ACB
. Đường
chéo
'BC
của mặt bên
' 'BCC B
tạo với mặt phẳng
' 'ACC A
một góc bằng
30
o
Tính thể tích
của khối lăng trụ theo a.
A.
3
3
a . B.
3
6
a . C.
3
3
3
a
. D.
3
6
3
a
.
Câu 46. Cho hình lăng trụ tam giác đều
. ' ' 'ABC A B C
có
AB a
, góc giữa hai mặt phẳng
'ABC
và
ABC
bằng
0
60
. Tính thể tích khối lăng trụ đã cho.
A.
3
3 3
4
a
. B.
3
3
4
a
. C.
3
3 3
8
a
. D.
3
3
8
a
.
Câu 47. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
AB a
, đường thẳng
AB
tạo với mặt phẳng
BCC B
một góc
30
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
6
4
a
V
. B.
3
6
12
a
V
. C.
3
3
.
4
a
V
D.
3
.
4
a
V
Câu 48. Một hình hộp đứng có đáy là hình thoi cạnh
a
, góc nhọn
60
và đường chéo lớn của đáy bằng
đường chéo nhỏ của hình hộp. Thể tích của khối hộp đó là
A.
3
.a
B.
3
3 .a
C.
3
3
.
2
a
D.
3
6
.
2
a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 49. Cho một tấm nhôm hình chữ nhật
ABCD
có
60AD cm
,
40AB cm
. Ta gập tấm nhôm theo hai
cạnh
MN
và
PQ
vào phía trong cho đến khi
AB
và
DC
trùng nhau như hình vẽ bên để dược
một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể tích lớn nhất bằng
A.
4000 3
3
cm
B.
2000 3
3
cm
C.
400 3
3
cm
D.
4000 2
3
cm
Câu 50. Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác đều cạnh
a
và
AB
vuông góc với
BC
. Thể
tích của lăng trụ đã cho là.
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
6
8
a
. D.
3
6
24
a
.
Câu 51. Cho hình lăng trụ tam giác đều
.ABC A B C
. Biết khoảng cách từ điểm
C
đến mặt phẳng
ABC
bằng
a
, góc giữa hai mặt phẳng
ABC
và
BCC B
bằng
với
1
cos
3
(tham
khảo hình dưới đây). Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
9 15
20
a
. B.
3
3 15
20
a
. C.
3
9 15
10
a
. D.
3
3 15
10
a
.
DẠNG CÂU HỎI VẬN DỤNG – VẬN DỤNG CAO
Câu 52. Cho khối lập phương
. ' ' ' 'AB CD A B C D
cạnh
a
. Các điểm
,E F
lần lượt là trung điểm
của
' 'C B
và
' 'C D
. Mặt phẳng
AEF
cắt khối lập phương đã cho thành 2 phần, gọi
1
V là thể
tích khối chứa điểm
'A
và
2
V
là thể tích khối chứa điểm
'C
. Khi đó
1
2
V
V
là:
A.
25
47
. B.
1
. C.
8
17
. D.
17
25
.
Câu 53. Cho khối lăng trụ
.ABC A B C
. Gọi
E
,
F
lần lượt là trung điểm của các đoạn thẳng
CC
và
BB
. Đường thẳng
'A E
cắt đường thẳng
AC
tại
K
, đường thẳng
'A F
cắt đường thẳng
AB
tại
H
. Tính tỉ số thể tích khối đa diện lồi
BFHCEK
và khối chóp
'A ABC
.
A.
1
.
3
B.
1
.
2
C.
2
. D.
1.
60cm
x
x
A
N
P
D
B
M
Q
C
M
Q
N
P
,A D
,B C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 54. Cho hình hộp
.
ABCD A B C D
có
,M
,N
P
lần lượt là trung điểm ba cạnh
,A B
BB
và
.D D
Mặt phẳng
MNP
cắt đường thẳng
A A
tại
.I
Biết thể tích khối tứ diện
IANP
là
.V
Thể tích
khối hộp đã cho
.
ABCD A B C D
bằng
A.
2 .V
B.
4 .V
C.
6 .V
D.
12 .V
Câu 55. Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
AB a
,
0
90
SBA SCA
, góc
giữa hai mặt phẳng
SAB
và
SAC
bằng
0
60
. Thể tích của khối đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Câu 56. Cho hình hộp
.
ABCD A B C D
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
, ,M N P
và
Q
lần lượt là tâm của các mặt bên
, ,
ABB A BCC B CDD C
và
DAA D
. Thể tích của khối đa diện
lồi có các đỉnh là các điểm
, , , , , ,A B C D M N P
và
Q
bằng
A.
27
. B.
30
. C.
18
. D.
36
.
Câu 57. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng
AC và
B C
. Gọi (P) là mặt phẳng qua M và song song với mặt phẳng
( )A NC
. Mặt phẳng (P) chia
khối lăng trụ
.
ABC A B C
thành hai khối đa diện, gọi (H) là khối đa diện chứa đỉnh
A
. Thể tích của
khối đa diện (H) bằng
A.
3
.
5
B.
1
.
3
C.
2
.
5
D.
1
.
2
Câu 58. Cho hình hộp đứng
.
ABCD A B C D
có
AB AD a
,
3
'
2
a
AA
,
60
BAD
. Gọi
M
,
N
lần
lượt là trung điểm
A D
,
A B
. Tính thể tích của khối đa diện
ABDMN
.
A.
3
3
16
a
. B.
3
3 3
8
a
. C.
3
9
16
a
. D.
3
3
8
a
.
Câu 59. Cho hình hộp
.
ABCD A B C D
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
, , , ,M N P Q R
và
S
lần lượt là tâm của các mặt
, , , ,
ABB A BCC B CDD C DAA D ABCD
và
A B C D
. Thể tích
của khối đa diện lồi có các đỉnh là các điểm
, , , ,M N P Q R
và
S
bằng
A.
3
. B.
24
. C.
9
. D.
1
3
.
Câu 60. Cho hình chóp
.
S ABC
có
SA ABC
, đáy là tam giác vuông cân tại
A
,
G
là trọng tâm
,ABC
khoảng cách từ
G
đến mặt phẳng
SBC
bằng
3
a
. Gọi
là góc giữa mặt phẳng
SBC
và
ABC
. Khi thể tích khối chóp
.
S ABC
nhỏ nhất thì
cos
bằng
A.
3
3
. B.
2
2
. C.
2
3
.
D.
3
2
.
Câu 61. Cho lăng trụ
.
ABC A B C
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
,M N
là hai điểm
thỏa mãn
. 1 , . 0
BM k BB k CN l CC l
. Thể tích của tứ diện
AA MN
bằng
A.
1
72
l k
. B.
24
. C.
72
. D.
1
210
l k
.
Câu 62. Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
với
6 , 3 , 3
AB BC SC
và
mặt phẳng
SAC
vuông góc với mặt đáy
ABC
. Biết hai mặt phẳng
SAB
và
SAC
tạo với
nhau góc
thỏa mãn
3
tan .
4
Thể tích khối chóp
.
S ABC
bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
8.V
B.
4
.
3
V
C.
8
.
3
V
D.
4.V
Câu 63. Cho lăng trụ
.
ABC A B C
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
,M N
lần lượt là
trung điểm của
,
AA BC
.
D
là điểm thỏa mãn
2
AD AN
. Mặt phẳng
P
qua
,M D
và song
song với
BC
cắt
,
BB CC
lần lượt tại
,E F
. Thể tích của khối đa diện lồi có các đỉnh là các
điểm
, , , ,A B C M E
và
F
bằng
A.
36
. B.
24
. C.
48
. D.
39
.
Câu 64. Cho tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
,M N
lần lượt là trung điểm của các cạnh
,AB BC
và
E
là điểm đối xứng với
B
qua
D
. Mặt phẳng
MNE
chia khối tứ diện
ABCD
thành hai
khối đa diện, trong đó khối chứa điểm
A
có thể tích
V
. Thể tích
V
bằng
A.
3
11 2
.
216
a
V
B.
3
7 2
.
216
a
V
C.
3
2
.
8
a
V
D.
3
13 2
.
216
a
V
Câu 65. Cho hình chóp
SABC
có diện tích đáy bằng
10
, chiều cao bằng
9
. Gọi
, ,M N P
lần lượt là trọng
tâm của tam giác
, ,SAB SBC SCA
. Thể tích của khối đa diện
ABCMNP
.
A.
60
B.
175
3
. C.
560
9
. D.
160
9
.
Câu 66. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Biết
,
AB SB AC SC
, góc giữa
hai mặt phẳng
SAB
và
SAC
bằng
0
60
. Thể tích khối chóp
.
S ABC
bằng
A.
3
2
24
a
. B.
3
3
36
a
. C.
3
3
6
a
. D.
3
2
36
a
.
Câu 67. Cho khối tứ diện
ABCD
có thể tích
V
. Gọi
1
G
,
2
G
,
3
G
,
4
G
là trọng tâm của bốn mặt của tứ diện
ABCD
. Thể tích khối tứ diện
1 2 3 4
GG G G
là:
A.
27
V
. B.
18
V
. C.
108
V
. D.
81
V
.
Câu 68. Cho khối chóp
.
S ABCD
có đáy là hình thang cân
AD BC
, khoảng cách giữa
AD
và
BC
bằng
a
,
BC a
,
SA ABCD
,
2SA a
. Trên cạnh
BC
lấy điểm
M
sao cho
0
MC x x a
. Thể tích khối chóp
.
S CDM
lớn nhất khi độ dài
MC
bằng
A.
2
.
2
a
B.
.
2
a
C.
.a
D.
3
.
2
a
Câu 69. Cho tứ diện
ABCD
có thể tích là
V
. Điểm
M
thay đổi trong tam giác
BCD
. Các đường thẳng
qua
M
và song song với
AB
,
AC
,
AD
lần lượt cắt các mặt phẳng
ACD
,
ABD
,
ABC
tại
N
,
P
,
Q
. Giá trị lớn nhất của khối
MNPQ
là
A.
27
V
. B.
18
V
. C.
81
V
. D.
2
27
V
.
Câu 70. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
2
. Gọi
M
là trung điểm của đoạn thẳng
AA
và
N
là điểm nằm trên cạnh
'BB
sao cho
2 'BN B N
. Đường thẳng
CM
cắt đường thẳng
C A
tại
P
, đường thẳng
CN
cắt đường thẳng
C B
tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ
bằng
A.
7
9
. B.
5
9
. C.
2
3
. D.
13
9
.
Câu 71. Cho khối lăng trụ
.
ABC A B C
. Gọi
,M N
lần lượt là trung điểm của đoạn thẳng
AA
và
'BB
.
Tính tỉ số thể tích của khối tứ diện
'CMNC
với khối lăng trụ đã cho.
A.
1
3
. B.
1
2
. C.
2
3
. D.
3
4
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 72. Cho khối lập phương
. '
ABCD A B C D
cạnh
a
. Gọi
,M N
lần lượt là trung điểm của đoạn thẳng
và
' 'C D
. Mặt phẳng
BMN
chia khối lập phương thành hai phần, gọi
V
là thể
tích phần chứa đỉnh
'B
. Tính
?V
A.
3
25
72
a
. B.
3
7
24
a
. C.
3
25
24
a
. D.
3
7
72
a
.
Câu 73. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng 6. Gọi điểm
I
là trung điểm
AA
và điểm
N
thuộc cạnh
BB
sao cho
' 2
B N BN
.Đường thẳng
'C I
cắt đường thẳng
CA
tại
P
, đường thẳng
C N
cắt đường thẳng
CB
tại
Q
. Tính thể tích khối đa diện lồi
AIPBNQ
A.
7
.
9
B.
11
.
18
C.
11
.
9
D.
7
.
3
Câu 74. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
V
. Gọi điểm
M
là trung điểm
AA
và điểm
N
thuộc cạnh
BB
sao cho
1
'
3
BN BB
.Đường thẳng
C M
cắt đường thẳng
CA
tại
D
, đường
thẳng
C N
cắt đường thẳng
CB
tại
E
. Tỉ số thể tích khối đa diện lồi
AMDBNE
và khối lăng trụ
.
ABC A B C
là
A.
13
.
18
B.
7
.
18
C.
7
.
12
D.
8
.
15
Câu 75. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
1
. Điểm
M
là thuộc cạnh
' 'A B
sao cho
1
3
A M A B
. Mặt phẳng
BCM
cắt đường thẳng
AA
tại
F
, và cắt đường thẳng
A C
tại
G
.
Thể tích khối chóp
FA MG
bằng
A.
5
24
. B.
1
6
. C.
5
36
. D.
1
54
.
Câu 76. Cho lăng trụ tam giác
.
ABC A B C
có đáy là tam giác đều cạnh
a
, điểm
A
cách đều ba điểm
A
,
B
,
C
và diện tích tam giác
ABA
bằng
2
3
6
a
. Thể tích khối đa diện
A B C BC
bằng
A.
3
3
6
a
. B.
3
3
24
a
. C.
3
3
8
a
. D.
3
3
12
a
.
Câu 77. Cho lăng trụ đều
.
ABC EFH
có tất cả các cạnh bằng
1
. Gọi
S
là điểm đối xứng của
A
qua
.BH
Thể tích khối đa diện
.
ABC SFH
bằng
A.
1
.
2
B.
3
.
3
C.
3
.
6
D.
1
.
6
Câu 78. Cho khối lăng trụ
1 1 1
.
ABC A B C
có thể tích bằng
30.
Gọi
O
là tâm của hình bình hành
1 1
ABB A
M
và
G
là trọng tâm tam giác
1 1 1
AB C
. Tính thể tích khối tứ diện
1
.COGB
A.
7
3
. B.
16
81
k
. C.
5
2
. D.
10
3
.
Câu 79. Cho khối chóp
.
S ABCD
có thể tích bằng
V
. Gọi
M
,
N
,
P
,
Q
lần lượt là trọng tâm các mặt
bên
SAB
,
SBC
,
SCD
,
SDA
. Gọi
k
là tỉ số thể tích của khối chóp
.
S MNPQ
và phần còn
lại là. Khi đó:
A.
16
81
k V
. B.
15
.
4
k V
C.
4
23
k V
. D.
4
23
k V
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
THỂ TÍCH KHỐI ĐA DIỆN
Thể tích khối chóp
đchãp ¸y
1
. chiÒu cao .
3
V S
Thể tích khối lăng trụ
đl¨ng trô ¸y
. chiÒu cao .V S
Thể tích khối lập phương
3
V a
với
a
là cạnh.
Thể tích khối hộp chữ nhật
V abc
với
, , a b c
lần lượt là chiều dài, chiều rộng và chiều cao.
Xác định diện tích đáy:
1 1
sin ( )( )( ) ,
2
ABC a
S ah ab C p p a p b b c
a
với
2
a b c
p
tam gi¸c vu«ng
1
(tÝch hai c¹nh gãc vu«ng)
2
S
2
tam gi¸c ®Òu
(c¹nh) 3
4
S
2
tam gi¸c vu«ng c©n
(c¹nh huyÒn)
4
S
H×nh thang
(®¸y lín ®¸y bÐ) chiÒu cao
2
S
H×nh ch÷ nhËt
dµi réng .S
2
H×nh vu«n
(c¹nh) .
g
S
Xác định chiều cao:
Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam giác
chứa trong mặt bên vuông góc với đáy.
Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai mặt
bên cùng vuông góc với mặt phẳng đáy.
Hình chóp có các cạnh bên bằng nhau: Chân đường cao của hình chóp là tâm đường tròn ngoại tiếp
đa giác đáy.
Cần nhớ: Tỉ số thể tích khối chóp có đáy là tam giác
Cho khối chóp
. ,S ABC
trên các đoạn thẳng
, , SA SB SC
lần lượt
lấy các điểm
, , A B C
khác
.S
Khi đó ta luôn có tỉ số thể tích:
.
.
S A B C
S ABC
V
SA SB SC
V SA SB SC
Chỉ có tỉ số thể tích khối chóp đáy tam giác, không có tỉ số khối chóp
đáy tứ giác. Khi tính tỉ số khối tứ giác, ta cần chia ra những hình
chóp có đáy là tam giác.
CÂU HỎI CÙNG MỨC ĐỘ VỚI ĐỀ MINH HỌA
DẠNG CÂU HỎI NHẬN BIẾT
Câu 1. Thể tích khối lăng trụ có diện tích đáy bằng
B
, chiều cao bằng
h
là
A.
1
3
V Bh
. B.
2
3
V Bh
. C.
V Bh
. D.
3V Bh
.
Lời giải
Chọn C
THỂ TÍCH KHỐI ĐA DIỆN
Vấn đề 8
A
S
B
C
C
A
B
b
a
c
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thể tích khối lăng trụ có diện tích đáy bằng
B
, chiều cao bằng
h
là
V Bh
.
Câu 2. Cho khối lập phương có cạnh bằng
6
. Thể tích của khối lập phương đã cho bằng
A.
216
. B.
18
. C.
36
. D.
72
.
Lời giải
Chọn A
Thể tích khối lập phương có cạnh bằng
6
là
3
6 216
V
.
Câu 3. Thể tích khối lập phương cạnh
2
bằng
A.
6
. B.
8
. C.
4
. D.
2
.
Lời giải
Chọn B
Thể tích khối lập phương cạnh
a
là
3
V a
.
Vậy thể tích khối lập phương cạnh
2
là:
3
2 8
V
.
Câu 4. Cho khối chóp có diện tích đáy
3
B
và chiều cao
4
h
. Thể tích của khối chóp đã cho bằng
A.
6
. B.
12
. C.
36
. D.
4
.
Lời giải
Chọn D
Ta có công thức thể tích khối chóp
1 1
. . .3.4 4
3 3
V B h
.
Câu 5. Thể tích khối chóp có diện tích đáy bằng
2
2a
, chiều cao bằng
3a
là
A.
3
2 3
9
a
V
. B.
3
2 3
3
a
V
. C.
3
2 3
V a . D.
3
3
3
a
V
.
Lời giải
Chọn B
Thể tích khối chóp có diện tích đáy bằng
2
2
B a
, chiều cao bằng
3
h a
là
3
2
1 1 2 3
.2 . 3
3 3 3
a
V Bh a a
.
Câu 6. Thể tích khối chóp có diện tích đáy bằng
2
a
, chiều cao bằng
2a
là
A.
3
6V a
. B.
3
3
a
V
. C.
3
2V a
. D.
3
2
3
a
V
.
Lời giải
Chọn D
Thể tích khối chóp có diện tích đáy bằng
2
a
, chiều cao bằng
2a
là
3
2
1 1 2
. .2
3 3 3
a
V Bh a a
.
Câu 7. Thể tích khối lăng trụ có diện tích đáy bằng
2
3a
, chiều cao bằng
a
là
A.
3
3V a
. B.
3
3
a
V
. C.
3
V a
. D.
3
2
3
a
V
.
Lời giải
Chọn A
Thể tích khối lăng trụ có diện tích đáy bằng
2
3a
, chiều cao bằng
a
là
2 3
3 . 3V a a a
.
Câu 8. Thể tích khối hộp chữ nhật có ba kích thước lần lượt là
3,4,5
bằng
A.
120
V
. B.
20
V
. C.
30
V
. D.
60
V
.
Lời giải
Chọn D
Thể tích khối hộp chữ nhật có ba kích thước lần lượt bằng
3,4,5
là
3.4.5 60
V
.
Câu 9. Cho khối chóp có diện tích đáy
6
B
và chiều cao
3
h
. Thể tích của khối chóp đã cho bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
6
. B.
18
. C.
9
. D.
36
.
Lời giải
Chọn A
Ta có công thức thể tích khối chóp
1 1
. . .3.6 6
3 3
V B h
nên chọn đáp án A.
Câu 10. Thể tích khối lập phương cạnh
5
bằng
A.
15
. B.
25
. C.
125
. D.
75
.
Lời giải
Chọn C
Thể tích khối lập phương cạnh
a
là
3
V a
.
Vậy thể tích khối lập phương cạnh
5
là:
3
5 125V
.
Câu 11. Cho khối lập phương có độ dài đường chéo bằng
6 3
. Thể tích của khối lập phương đó bằng
A.
81 3
. B.
216
. C.
24 3
. D.
162 6
.
Lời giải
Chọn B
Gọi
d
là đường chéo của khối lập phương và
a
là cạnh của nó, ta có
2 2
3
3
d
d a a .
Suy ra cạnh bằng
6 3
6
3
a
. Do đó
3
216 V a
.
Câu 12. Thể tích khối lập phương
.ABCD A B C D
có 3AC a
bằng
A.
3
a
. B.
2
a
. C.
2a
. D.
3a
.
Lời giải
Chọn A
.ABCD A B C D
có 3AC a
cạnh hình lập phương bằng
a
.
Vậy thể tích khối lập phương cạnh
a
là
3
V a
.
Câu 13. Cho khối lập phương có tổng diện tích các mặt bằng
294
. Thể tích của khối lập phương đó
bằng
A.
147 147
2 2
. B.
49
. C.
343
. D.
147
2
.
Lời giải
Chọn C
Hình lập phương có
6
mặt là
6
hình vuông bằng nhau. Gọi
a
là cạnh của khối lập phương
B'
C'
B
D
A
C
D'
A'
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có diện tích một mặt là
2
294
49 7 7
6
S a
. Do đó
3
343 V a
.
Câu 14. Thể tích khối lập phương
.ABCD A B C D
có
6AC a
bằng
A.
3
8a
. B.
3
6 6a
. C.
3
2 2a
. D.
3
3 3a
.
Lời giải
Chọn C
.ABCD A B C D
có
6AC a
cạnh hình lập phương bằng
2a
.
Thể tích khối lập phương cạnh
a
là
3
V a
.
Vậy thể tích khối lập phương cạnh
2a
là:
3
3
2 2 2V a a
.
Câu 15. Khối chóp
.S ABC
có thể tích
2 2
3
V
và diện tích đáy
3B
. Chiều cao của khối chóp
.S ABC
bằng
A.
2 6
9
. B.
2 6
3
. C.
2 2
3
. D.
2 6
27
.
Lời giải
Chọn B
Chiều cao của khối chóp
3 2 2 2 6
3
3
V
h
B
nên chọn đáp án B.
Câu 16. Cho khối hộp chữ nhật có ba kích thước là
3;5;7
. Thể tích của khối hộp đó bằng
A.
35
. B.
105
2
. C.
105
. D.
15
.
Lời giải
Chọn C
Công thức tính thể tích khối hộp chữ nhật có ba kích thước
, ,a b c
là
V abc
.
Do đó
. . 3.5.7 105 V a b c
.
Câu 17. Thể tích khối lập phương
.ABCD A B C D
có
2AB
bằng
A.
2 2
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
B'
C'
B
D
A
C
D'
A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
.ABCD A B C D
có
2AB
cạnh hình lập phương bằng
1
.
Thể tích khối lập phương cạnh
a
là
3
V a
.
Vậy thể tích khối lập phương cạnh
1
là:
3
1 1V
.
Câu 18. Cho khối chóp
.S ABCD
có thể tích bằng
3
a
, đáy
ABCD
là hình vuông. Biết chiều cao của
khối chóp là
3h a
. Cạnh hình vuông
ABCD
bằng
A.
a
. B.
3
a
. C.
2a
. D. 3a .
Lời giải
Chọn D
Gọi cạnh hình vuông là
x
. Ta có
2 3
1
.3
3
x a a
x a
nên chọn đáp án A.
Câu 19. Cho khối lập phương
.
ABCD A B C D
biết
6 2AC
. Thể tích của khối lập phương đó bằng
A.
432 2
. B.
108
. C.
216
. D. 48 6 .
Lời giải
Chọn C
Ta có
6 2 6 AC AB
3
6 216 V
.
Câu 20. Thể tích khối lập phương
.ABCD A B C D
có
2AB
bằng
A.
8
. B.
2 2
. C.
16 2
. D.
6
.
Lời giải
Chọn B
B'
C'
B
D
A
C
D'
A'
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
.ABCD A B C D
có
2AB
cạnh hình lập phương bằng
2
.
Thể tích khối lập phương cạnh
a
là
3
V a
.
Vậy thể tích khối lập phương cạnh
2
là:
3
2 2 2V
.
Câu 21. Cho khối chóp
.S ABC
có
SA
vuông góc với đáy,
3, 4, 5AC AB BC
và
3SA
. Tính
thể tích
V
của khối chóp
.S ABC
.
A.
18V
. B.
6V
. C.
12V
. D.
20V
.
Lời giải
Chọn B
Tam giác
ABC
vuông tại
A
.
1 1 1
. 3.4 6 6.3 6
2 2 3
B AB AC V
nên chọn đáp án
B.
Câu 22. Thể tích khối lập phương
.ABCD A B C D
có
2AB a
bằng:
A.
3
a
. B.
3
2a
. C.
3
4a
. D.
3
6a
.
Lời giải
Chọn A
ABB
vuông cân tại
B
nên:
2 2
2 .AB AB AB a
Thể tích khối lập phương là
3
.a
Câu 23. Thể tích khối lập phương có cạnh
2a
bằng
A.
3
8a
. B.
3
2a
. C.
3
2 2a
. D.
3
6a
.
Lời giải
Chọn C
Thể tích khối lập phương có cạnh
2a
bằng
3 3
( 2 ) 2 2a a
.
Câu 24. Thể tích khối hộp chữ nhật có độ dài các cạnh lần lượt là
,2 ,3a a a
bằng:
A.
3
2a
. B.
3
6a
. C.
3
2
3
a
. D.
3
3a
.
Lời giải
Chọn B
Thể tích hộp chữ nhật:
3
.2 .3 6 .a a a a
Câu 25. Thể tích khối tứ diện đều có cạnh
2a
bằng
A.
3
3
4
a
. B.
3
3
12
a
. C.
3
2 2
3
a
. D.
3
2 3
3
a
.
Lời giải
Chọn C
Thể tích khối tứ diện đều bằng:
3
3
2 2 2
2
12 3
a
V a
.
B'
C'
B
D
A
C
D'
A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 26. Thể tích khối lăng trụ có diện tích đáy
2
3a
và chiều cao
a
là
A.
3
3V a
. B.
3
V a
. C.
3
9V a
. D.
3
6V a
.
Lời giải
Chọn A
Thể tích khối chóp
2 3
3 . 3V Bh a a a
.
DẠNG CÂU HỎI THÔNG HIỂU
Câu 27. Cho khối lăng trụ đứng .ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
a
. Biết
60BAD
,
AA a
. Thể tích của khối lăng trụ đã cho bằng
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
3
a
.
Lời giải
Chọn A
ABCD
là hình thoi cạnh
a
có
60BAD
nên
BAD
là tam giác đều cạnh
a
2 2
3 3
2 2.
4 2
ABCD ABD
a a
S S
.
Do khối lăng trụ .ABCD A B C D
là lăng trụ đứng nên đường cao của lăng trụ là
AA a
.
Thể tích khối lăng trụ là
2 3
3 3
. .
2 2
ABCD
a a
V AA S a
.
Câu 28. Cho khối lăng trụ đứng .ABC A B C
. Biết
3AB
cm,
4AC
cm,
60BAC
,
2AA
cm.
Thể tích của khối lăng trụ đã cho bằng
A. 6 3 (cm
2
). B. 2 3 (cm
3
). C. 6 3 (cm
3
). D.
6
(cm
3
).
Lời giải
Chọn C
1 1
. .sin 3.4.sin 60 3 3
2 2
ABC
S AB AC BAC
(cm
2
).
Do khối lăng trụ .ABC A B C
là lăng trụ đứng nên đường cao của lăng trụ là
2AA
cm.
Thể tích khối lăng trụ là
. 2.3 3 6 3
ABC
V AA S
(cm
3
).
60°
A'
C'
B
C
A
B'
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 29. Cho khối lăng trụ đứng
.ABCD A B C D
có đáy là hình thoi cạnh
a
, 3BD a và
4AA a
(minh họa như hình bên). Thể tích của khối lăng trụ đã cho bằng
A.
3
2 3a
. B.
3
4 3a
. C.
3
2 3
3
a
. D.
3
4 3
3
a
.
Lời giải
Chọn A
Gọi
I AC BD
. Ta có:
3
,
2 2
BD a
AC BD BI
. Xét tam giác vuông
BAI
vuông tại
I
:
2
2 2
2 2 2 2 2
3 3
.
2 4 4 2
a a a a
AI BA BI a a AI AC a
Diện tích hình bình hành
ABCD
:
2
1 1 3 3
2S 2. . 2. .
2 2 2 2
ABCD ABC
a a
S BI AC a
.
Vậy:
2
3
.
3
. .4 2 3 .
2
ABCD A B C D ABCD
a
V S AA a a
Câu 30. Cho khối lăng trụ đứng .ABCD A B C D
có đáy
ABCD
là hình chữ nhật có
AB a
,
3AD a ,
2AA a
. (minh họa như hình vẽ bên).
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Thể tích của khối lăng trụ đã cho bằng
A.
3
2 3a . B.
3
3a . C.
3
3
3
a
. D.
3
2 3
3
a
.
Lời giải
Chọn A
2
. . 3 3
ABCD
S AB AD a a a
.
Do khối lăng trụ .ABC A B C
là lăng trụ đứng nên đường cao của lăng trụ là
2AA a
.
Thể tích khối lăng trụ là
2 3
. 2 . 3 2 3
ABCD
V AA S a a a
.
Câu 31. Cho khối lăng trụ đứng .ABCD A B C D
có đáy
ABCD
là hình vuông cạnh
2a
. Biết góc giữa
A B
với mặt phẳng
ABCD
bằng
30
. Thể tích của khối lăng trụ đã cho bằng
A.
3
6
3
a
. B.
3
2 6
3
a
. C.
3
2 3
3
a
. D.
3
2 6a
.
Lời giải
Chọn B
2
2
2 2
ABCD
S a a
.
A A ABCD
góc giữa
A B
với mặt phẳng
ABCD
là
30A BA
.
Tam giác
A AB
vuông tại
A
6
.tan
3
a
A A AB A BA
.
C'
D'
B'
C
B
A
D
A'
C'
D'
B'
C
B
A
D
A'
60°
C'
D'
B'
C
B
A
D
A'
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thể tích khối lăng trụ là
3
2 6
.
3
ABCD
a
V AA S
.
Câu 32. Cho khối lăng trụ đứng .ABC A B C
có đáy là tam giác vuông tại
A
. Biết
2 2AB AA a
,
ABC
(minh họa như hình vẽ bên).
Thể tích của khối lăng trụ đã cho bằng
A.
3
sina
. B.
3
.tan
3
a
. C.
3
tana
. D.
3
tan
2
a
.
Lời giải
Chọn C
Tam giác
ABC
vuông tại
A
có
AB a
,
ABC
nên
.tan .tanAC AB a
.
2
1 1
. . .tan .tan
2 2 2
ABC
a
S AB AC a a
.
Do khối lăng trụ .ABC A B C
là lăng trụ đứng nên đường cao của lăng trụ là
2AA a
Thể tích khối lăng trụ là
2
3
. 2 . .tan .tan
2
ABC
a
V AA S a a
.
Câu 33. Tính thể tích khối lăng trụ đứng
. ' ' ' 'ABCD A B C D
biết
ABCD
là hình thoi có
10 , 8AC cm BD cm
và diện tích hình chữ nhật
' 'ACC A
bằng
2
50cm
.
A.
3
400cm
. B.
3
2000cm
. C.
3
4000cm
. D.
3
200cm
.
Lời giải
Chọn D
Diện tích mặt đáy
2
1 1
. .10.8 40
2 2
B AC BC cm
Diện tích hình chữ nhật
' '
' '
50
. ' ' 5
10
ACC A
ACC A
S
S AC CC CC cm
AC
Vậy thể tích khối lăng trụ là
3
. 40.5 200V B h cm
Câu 34. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều có cạnh bằng
a
,
SA
vuông góc với đáy và
2SA a
. Tính thể tích của khối chóp
.S ABC
.
A.
3
3
2
a
. B.
3
3
3
a
. C.
3
2
6
a
. D.
3
3
6
a
.
Lời giải
α
B'
C'
A
C
B
A'
α
B'
C'
A
C
B
A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Chọn D
Công thức thể tích khối chóp có diện tích đáy
B
và chiều cao
h
là:
1
. .
3
V B h
.
SA
vuông góc với đáy nên
2h SA a
.
Do đáy của hình chóp là tam giác
ABC
đều nên diện tích đáy của hình chóp là:
2
3
4
a
B
.
Vậy thể tích khối chóp
.
S ABC
là:
2 3
1 1 3 3
. . . .2
3 3 4 6
a a
V B h a
nên chọn đáp án D.
Câu 35. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
ABC
là tam giác vuông cân tại
A
có
2BC a
và
' 5AC a
.
A.
3
2a
. B.
3
2a
. C.
3
2
3
a
. D.
3
a
.
Lời giải
Chọn D
Ta có
2 2 2 2 2 2 2 2 2
2 2 2
AB AC BC AB BC AB a AB a AB a
Diện tích mặt đáy
2
1 1 1
. . .
2 2 2
B AB AC a a a
2 2 2 2
' ' 5 2CC AC AC a a a
Vậy thể tích khối lăng trụ là
2 3
1
. .2
2
V B h a a a
.
Câu 36. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
ABC
là tam giác đều cạnh
a
và
' 5AC a
.
A.
3
3
4
a
. B.
3
3
2
a
. C.
3
3
6
a
. D.
3
a
.
Lời giải
Chọn B
Diện tích mặt đáy
2
0
1 1 3
. sin . . sin 60
2 2 4
a
B AB AC A a a
2 2 2 2
' ' 5 2CC AC AC a a a
Vậy thể tích khối lăng trụ là
2 3
3 3
. .2
4 2
a a
V B h a
.
Câu 37. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
5 , 12 , 13AB cm AC cm BC cm
và
' 7CC cm
.
A.
3
210
cm
. B.
3
70
cm
. C.
3
105
cm
. D.
3
35
cm
.
Lời giải
Chọn A
Ta có Nửa chu vi của tam giác là:
5 12 13
15
2
p
Diện tích của tam giác là:
5 12 13 15 15 5 15 12 15 13 30
S p p p p
.
Vậy thể tích khối lăng trụ là
3
. 30.7 210
V B h cm
.
Câu 38. Tính thể tích khối lăng trụ đứng
. ' ' 'ABC A B C
biết
13 , 14 , 15AB cm AC cm BC cm
và
' 10CC cm
.
A.
3
420
cm
. B.
3
840
cm
. C.
3
420
cm
. D.
3
140
cm
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn B
Nữa chu vi:
13 14 15
21.
2
p
.
Diện tích:
( 13)( 14)( 15) 84.S p p p p
.
Vậy thể tích khối lăng trụ là
3
. 84.10 840V B h cm
.
Câu 39. Cho khối chóp tam giác đều có tất cả các cạnh bằng
2a
. Thể tích của khối chóp đã cho bằng
A.
3
8
3
a
. B.
3
4 2
3
a
. C.
3
8 2
3
a
. D.
3
2 2
3
a
.
Lời giải
Chọn D
Ta có
SO ABC
và
2
2
2 3
3
4
ABC
a
S a ;
2 2 2 3 2 3
.
3 3 2 3
a a
AO AM
,
2
2
2 2
2 3 2 6
2
3 3
a a
SO SA AO a
.
Vậy thể tích khối chóp là
2 3
.
1 1 2 6 2 2
. . . 3.
3 3 3 3
S ABCD ABC
a
V S SO a a
.
Câu 40. Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, các cạnh bên bằng
2a
. Thể tích của khối chóp
đã cho bằng
A.
3
14
3
a
. B.
3
4
3
a
. C.
3
14
6
a
. D.
3
2 2
3
a
.
Lời giải
Chọn C
Ta có
SO ABCD
và
2
ABCD
S a
;
2
2 2
AC a
AO
,
O
D
C
B
A
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
2
2
2 2
2 14
2
2 2
a a
SO SA AO a
.
Vậy thể tích khối chóp là
2 3
.
1 1 14 14
. . . .
3 3 2 6
S ABCD ABCD
a
V S SO a a
.
Câu 41. Cho khối chóp tam giác đều có cạnh đáy bằng
a
, các cạnh bên bằng
2a
. Thể tích của khối
chóp đã cho bằng
A.
3
33
12
a
. B.
3
11
12
a
. C.
3
8 2
3
a
. D.
3
11
6
a
.
Lời giải
Chọn B
Ta có
SO ABC
và
2
3
4
ABC
a
S
;
2 2 3 3
.
3 3 2 3
a a
AO AM
,
2
2
2 2
3 33
2
3 3
a a
SO SA AO a
.
Vậy thể tích khối chóp là
2
3
.
1 1 3 33 11
. . . .
3 3 4 3 12
S ABC ABC
a a
V S SO a
.
Câu 42. Cho khối chóp
.S ABCD
có đáy là hình vuông cạnh a. Cạnh bên
SA
vuông góc với đáy.
2SB a
; Thể tích của khối chóp
.S ABCD
bằng:
A.
3
4 2
3
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
3
3
a
.
Lời giải
Chọn D
A
C
S
a
2a
D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Theo giả thiết ta có
2
SA ABCD
AB a
SB a
.
Do đó:
2
ABCD
S a
.
2
2 2 2
2 3SA SB AB a a a
.
Vậy
3
2
1 1 3
. 3.
3 3 3
SABCD ABCD
a
V SA S a a
.
Câu 43. Cho khối chóp tam giác đều có tất cả các cạnh đều bằng
2a
. Thể tích của khối chóp đó bằng:
A.
3
2 2
3
a
. B.
3
2
3
a
. C.
3
2
12
a
. D.
3
2 6
9
a
.
Lời giải
Chọn A
Gọi khối chóp đều là
.
S ABC
,
H
là trọng tâm của
ABC
. Khi đó
2
( )
AB a
SH ABC
Ta có
2
2
(2 ) 3
3
4
ABC
a
S a
2 2 3 2 3
.
3 2 3
a a
HC
2 2 2 2
2 3 2 2
(2 ) ( )
3
3
a a
SH SC HC a
3
2
1 1 2 2 2 2
. . . 3
3 3 3
3
SABC ABC
a a
V SH S a .
Câu 44. Cho khối chóp tam giác đều có cạnh đáy bằng
a
, cạnh bên bằng
3a
. Thể tích của khối chóp
đó bằng
A.
3
2 2
3
a
. B.
3
2
3
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Lời giải
Chọn C
H
A
C
S
2a
B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Gọi khối chóp đều là
SABC
.
H
là trọng tâm
ABC
suy ra
( )
AB a
SH ABC
.
Khi đó
2
3
4
ABC
a
S
;
2 3 3
.
3 2 3
a a
AH
.
2 2 2 2
2 2
( 3) ( )
3 3
a
SH SA AH a a
.
Vậy
2
1 1 2 2 3
. . .
3 3 4
3
SABC ABC
V SH S a a
3
2
6
a
.
Câu 45. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy là tam giác vuông tại
, , 60
o
A AC a ACB
.
Đường chéo
'BC
của mặt bên
' 'BCC B
tạo với mặt phẳng
' 'ACC A
một góc bằng
30
o
Tính thể tích của khối lăng trụ theo a.
A.
3
3a . B.
3
6a . C.
3
3
3
a
. D.
3
6
3
a
.
Lờigiải
Chọn B
Đường chéo
'BC
của mặt bên
' 'BCC B
tạo với mặt phẳng
' 'ACC A
một góc bằng
30
o
Nên
0
', ' ' ', ' ' 30 .BC ACC A BC AC BC A
2 2
0
0
' ' 2 ; 3
cos60
' : sin30 2 3 ' 2 2
AC
B C a AB BC AC a
C B AB a BB a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3
1
'. 2 2. 3. 6
2
ABC
V BB S a a a a
.
Câu 46. Cho hình lăng trụ tam giác đều
. ' ' 'ABC A B C
có
AB a
, góc giữa hai mặt phẳng
'ABC
và
ABC
bằng
0
60 . Tính thể tích khối lăng trụ đã cho.
A.
3
3 3
4
a
. B.
3
3
4
a
. C.
3
3 3
8
a
. D.
3
3
8
a
.
Lời giải
Chọn C
Gọi
H
là trung điểm của
AB
. Ta có:
3
2
a
CH
0
' , ', ' 60 .ABC ABC HC HC CHC
Xét tam giác
'CHC
vuông tại
C
ta có:
0 0
' 3 3
tan 60 ' .tan 60 . 3
2 2
CC a a
CC CH
CH
Vậy
2 3
3 3 3 3
'. .
2 4 8
ABC
a a a
V CC S
Câu 47. Cho hình lăng trụ tam giác đều
.ABC A B C
có
AB a
, đường thẳng
AB
tạo với mặt phẳng
BCC B
một góc
30
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
6
4
a
V
. B.
3
6
12
a
V
. C.
3
3
.
4
a
V
D.
3
.
4
a
V
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Gọi
M
là trung điểm
BC
, do tam giác
ABC
đều nên
AM BC
, mà
AM BB
nên
AM BCC B
. Suy ra hình chiếu vuông góc của
AB
trên
BCC B
là
B M
.
Vậy góc giữa đường thẳng
AB
và mặt phẳng
BCC B
là góc
AB M
và
30AB M
.
3
3
2
a
AM AB a
2 2
2AA AB A B a
3
6
4
a
V
.
Câu 48. Một hình hộp đứng có đáy là hình thoi cạnh
a
, góc nhọn
60
và đường chéo lớn của đáy bằng
đường chéo nhỏ của hình hộp. Thể tích của khối hộp đó là
A.
3
.a
B.
3
3 .a
C.
3
3
.
2
a
D.
3
6
.
2
a
Lời giải
Chọn D
Ta có 3AC BD a
;
2 2
2BB BD BD a
Vậy thể tích khối hộp đứng bằng
3
1 6
. . 3. 2
2 2
a
V B h a a a
.
Câu 49. Cho một tấm nhôm hình chữ nhật
ABCD
có
60AD cm
,
40AB cm
. Ta gập tấm nhôm theo
hai cạnh
MN
và
PQ
vào phía trong cho đến khi
AB
và
DC
trùng nhau như hình vẽ bên để
dược một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể tích lớn
nhất bằng
A
C
B
B'
A'
C'
M
A
B
C
D
A
B
C
D
a
a
60
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4000 3
3
cm
B.
2000 3
3
cm
C.
400 3
3
cm
D.
4000 2
3
cm
Lời giải
Chọn A
Đáy của lăng trụ là tam giác cân có cạnh bên bằng
x
, cạnh đáy bằng
60 2x
Đường cao tam giác đó là
2
2
60 2
60 900
2
x
AH x x
, với
H
là trung điểm
NP
Diện tích đáy là
1 1
. 60 900. 30 60 900 900 30 900 30
2 30
ANP
S S AH NP x x x x x
3
2
1 900
100 3
30 3
S cm
Diện tích đáy lớn nhất là
2
100 3cm
nên thể tích lớn nhất là
3
40.100 3 4000 3V cm
.
Câu 50. Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác đều cạnh
a
và
AB
vuông góc với
BC
.
Thể tích của lăng trụ đã cho là.
A.
3
6
12
a
. B.
3
6
4
a
. C.
3
6
8
a
. D.
3
6
24
a
.
Lời giải
Chọn C
Gọi
I
là trung điểm
BC
. Vì
. ' ' 'ABC A B C
là lăng trụ tam giác đều nên.
' ' 'AI BB C C AI BC

.
Lại có giả thiết
' 'AB BC
nên suy ra
' ' ' 'BC AIB BC B I 
.
Gọi
' 'H B I BC
.
A
C
B
B'
A'
C'
I
H
60cm
x
x
A
N
P
D
B
M
Q
C
M
Q
N
P
,A D
,B C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Ta có
BHI
đồng dạng
' 'C HB
1
' 2 ' 3
' ' ' 2
HI BI
B H HI B I HI
B H B C
.
Xét tam giác vuông
'B BI
có
2 2
2 2
3
. ' 3
3 12 2
BI a a
BI HI B I HI HI .
Suy ra
2
2
2 2
3 2
' '
2 2 2
a a a
BB B I BI
.
Vậy
3
2
3 2 6
.BB' a .
4 2 8
ABC
a a
V S
.
Câu 51. Cho hình lăng trụ tam giác đều
.ABC A B C
. Biết khoảng cách từ điểm
C
đến mặt phẳng
ABC
bằng
a
, góc giữa hai mặt phẳng
ABC
và
BCC B
bằng
với
1
cos
3
(tham
khảo hình dưới đây). Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
9 15
20
a
. B.
3
3 15
20
a
. C.
3
9 15
10
a
. D.
3
3 15
10
a
.
Lời giải
Chọn A
Gọi
M
là trung điểm của
AB
,
G
là trọng tâm tam giác
ABC
.
Ta có:
CC AB
CM AB
AB CC M
CC M ABC
. Mà
CC M ABC C M
nên nếu gọi
H
là hình chiếu vuông góc của
C
trên
C M
thì
H
là hình chiếu của
C
trên mặt
phẳng
ABC
;d C ABC
CH a
.
Dựng đường thẳng đi qua
G
và song song với
CH
, cắt
C M
tại điểm
K
.
G
M
C
B
A
C'
B'
A'
H
N
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
GN ABC
AG BCC B
nên góc giữa hai mặt phẳng
ABC
và
BCC B
là góc
AGN
.
1
3 3
a
GN CH
;
cos
GN
AG
a
3 3AB AG a ;
2 2 2
1 1 1
CC CH CM
2
5
9a
3 5
5
a
CC
;
2
3
3 .
4
ABC
S a
2
3 3
4
a
.
Vậy thể tích khối lăng trụ bằng .
ABC
V CC S
3
9 15
20
a
.
DẠNG CÂU HỎI VẬN DỤNG – VẬN DỤNG CAO
Câu 52. Cho khối lập phương
. ' ' ' 'AB CD A B C D
cạnh
a
. Các điểm
,E F
lần lượt là trung điểm
của
' 'C B
và
' 'C D
. Mặt phẳng
AEF
cắt khối lập phương đã cho thành 2 phần, gọi
1
V là thể
tích khối chứa điểm
'A
và
2
V là thể tích khối chứa điểm
'C
. Khi đó
1
2
V
V
là:
A.
25
47
. B.
1
. C.
8
17
. D.
17
25
.
Lời giải
Chọn A
Dựng thiết diện :
PQ
qua A và song song với
BD
(vì
/ / ' '/ /EF B D BD
)
PE
cắt các cạnh
', 'BB CC
tại M và I. Tương tự ta tìm được giao điểm N. Thiết diện là
AMEFN
.
Dựa vào đường trung bình
BD
và định lí Ta – lét cho các tam giác
, , 'IAC DNQ D NF
ta tính
được:
2
' ,
3 3
a a
IC ND
. Tương tự ta tính được:
2
3
a
MB
. Và ta có:
QD PB a
Ta có:
3
'
1 1
. . . .
3 3 2 2 2 72
IEFC
a a a a
V
. Dùng tỉ lệ thể tích ta có:
3 3
3
'
8
4 . 64.
72 9
IPQC IEFC
a a
V V
3
1 2 1
. . . .
3 3 2 9
NADQ MPAB
a a
V a a V ⇒
3 3 3 3
2
8 47
2.
9 72 9 72
a a a a
V
Thể tích khối lập phương
. ' ' ' 'AB CD A B C D
là
3
a
nên
3 3
3
1
47 25
72 72
a a
V a
1
2
25
47
V
V
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 53. Cho khối lăng trụ
.ABC A B C
. Gọi
E
,
F
lần lượt là trung điểm của các đoạn thẳng
CC
và
BB
. Đường thẳng
'A E
cắt đường thẳng
AC
tại
K
, đường thẳng
'A F
cắt đường thẳng
AB
tại
H
. Tính tỉ số thể tích khối đa diện lồi
BFHCEK
và khối chóp
'A ABC
.
A.
1
.
3
B.
1
.
2
C.
2
. D.
1.
Lời giải
Chọn C
Ta có:
'. '. ' ' . ' ' 'A ABC A BB C C ABC A B C
V V V và
'. . ' ' ' '. ' ' . ' ' '
1 2
3 3
A ABC ABC A B C A BB C C ABC A B C
V V V V
Do đó
'. '. ' ' . ' ' '
1
3
A BFEC A FB C E ACB A B C
V V V
(vì
' 'BFEC FB C E
S S )
'. '.A ABC A BFEC
V V .
Ta có:
'. . '
. ' . '
' 1
. . .
' 4
A ABC A A BC
A A HK A A HK
V V
AA AB AC
V V AA AH AK
'. '. . ' . '
1 1
.
4 2
A ABC A BFEC A A HK BFHCEK A A HK
V V V V V
Do đó
'.
2
BFHCEK
A ABC
V
V
.
Câu 54. Cho hình hộp
.ABCD A B C D
có
,M
,N
P
lần lượt là trung điểm ba cạnh
,A B
BB
và
.D D
Mặt phẳng
MNP
cắt đường thẳng
A A
tại
.I
Biết thể tích khối tứ diện
IANP
là
.V
Thể tích khối hộp đã cho
.ABCD A B C D
bằng
A.
2 .V
B.
4 .V
C.
6 .V
D.
12 .V
Lời giải
Chọn B
Gọi
.Q MNP A D
Theo tính chất của giao tuyến suy ra
MQ NP
nên
Q
là trung điểm
của
.A D
Suy ra
,M
Q
lần lượt là trung điểm
,IN
.IP
Ta có:
.
.
1 1 1 1
. . . . .
3 2 2 12 12
I A MQ
I A MQ
IANP
V
IA IM IQ V
V
V IA IN IP
Mặt khác
.
1
, .
3
I A MQ A MQ
V d I A B C D S
.
1 1 1 1
. , . .
3 2 8 48
A B C D ABCD A B C D
d A ABCD S V
Từ đó suy ra
.
4 .
ABCD A B C D
V V
H
K
E
F
A
C
A'
B'
C'
B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 55. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
AB a
,
0
90SBA SCA ,
góc giữa hai mặt phẳng
SAB
và
SAC
bằng
0
60
. Thể tích của khối đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Lời giải
Chọn D
Hai tam giác vuông
SAB
và
SAC
bằng nhau chung cạnh huyền
SA
.
Kẻ
BI
vuông góc với
SA
suy ra
CI
cũng vuông góc với
SA
và
IB IC
.
,SA IC SA IB SA IBC
tại
I
.
. . .
1 1 1 1
3 3 3 3
S ABC A IBC S IBC IBC IBC IBC IBC
V V V S AI S SI S AI SI S SA
.
0 0
, , , 60 60SAB SAC IB IC IB IC BIC
hoặc
0
120BIC .
Ta có
IC IB AB a
mà
2BC a
nên tam giác
IBC
không thể đều suy ra
0
120BIC .
Trong tam giác
IBC
đặt
0IB IC x x
có:
2
2
2 2 2
0
2
2 2
1 6 6
cos120
2 . 2 3 3
2
x a
IB IC BC a a
x IB IC
IB IC
x
.
Trong tam giác
ABI
vuông tại
I
có:
2
2 2 2
6 3
3 3
a a
AI AB IB a
.
Trong tam giác
SAB
vuông tại
B
đường cao
BI
có:
2 2
2
. 3
3
3
AB a
AB IA SA SA a
IA
a
.
Vậy
2
3
0
.
1 1 1 1 6
. . sin a 3sin120
3 3 2 6 3 6
S ABC IBC
a a
V S SA IB IC SA BIC

.
Câu 56. Cho hình hộp
.ABCD A B C D
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
, ,M N P
và
Q
lần lượt là tâm của các mặt bên
, ,ABB A BCC B CDD C
và
DAA D
. Thể tích của khối đa
diện lồi có các đỉnh là các điểm
, , , , , ,A B C D M N P
và
Q
bằng
A.
27
. B.
30
. C.
18
. D.
36
.
Lời giải
Chọn B
a
a 2
A
B
C
S
I
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Ta có
.
9.8 72
ABCD A B C D
V
.
Gọi
, , ,I J K L
lần lượt là trung điểm các cạnh
, , ,AA BB CC DD
suy ra
.
36
ABCD IJKL
V
.
Do hình chóp
.A MIQ
đồng dạng với hình chóp
.A B A D
theo tỉ số
1
2
nên
. .
1 1 1 9 3
. .8.
8 8 3 2 2
A MQI A B A D
V V
.
. . .
3
4 36 4. 30
2
ABCD MNPQ ABCD IJKL A MIQ
V V V
.
Câu 57. Cho khối lăng trụ
.ABC A B C
có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn
thẳng AC và
B C
. Gọi (P) là mặt phẳng qua M và song song với mặt phẳng
( )A NC
. Mặt phẳng (P)
chia khối lăng trụ
.ABC A B C
thành hai khối đa diện, gọi (H) là khối đa diện chứa đỉnh
A
. Thể tích
của khối đa diện (H) bằng
A.
3
.
5
B.
1
.
3
C.
2
.
5
D.
1
.
2
Lời giải
Chọn D
Gọi khối lăng trụ
.ABC A B C
có thể tích bằng
V
- Mặt phẳng (P)qua M và song song với mặt phẳng
( )A NC
nên mặt phẳng (P)cắt các mặt phẳng
( ),( ' ' ')ABC A B C
lần lượt theo các giao tuyến
,ME GF
(
( , ' ', ' ')E BC G A B F B C
cùng
song song
AN
I
A
B
C
A'
B'
C'
N
M
E
F
G
K
J
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
- Mặt phẳng (P)cắt các mặt phẳng
( ' ' ), ( ' ' )AA C C BB C C
lần lượt theo các giao tuyến
MI
( ')I AA
song song
'A C
, EF
song song
.CN
Ba đường thẳng
, , ' 'MI FG A C
đồng quy tại
,K
ba đường thẳng
, , 'MI EF CC
đồng quy tại
.J
- Mặt phẳng (P) chia khối lăng trụ
.ABC A B C
thành hai khối đa diện, gọi (T) là khối đa diện không
chứa đỉnh.
Thể tích của khối đa diện (T) bằng
1 . ' . . ' ' '
1 1 1
. ' . . '
3 3 3
9 1 1 1 1
16 48 24 2 2
J C FK J CEM I A GK C FK CEM A GK
V V V V S JC S JC S IA
V V V V
.
Câu 58. Cho hình hộp đứng
.ABCD A B C D
có
AB AD a
,
3
'
2
a
AA
,
60BAD . Gọi
M
,
N
lần lượt là trung điểm
A D
,
A B
. Tính thể tích của khối đa diện
ABDMN
.
A.
3
3
16
a
. B.
3
3 3
8
a
. C.
3
9
16
a
. D.
3
3
8
a
.
Lời giải
Chọn A
Gọi
S BN AA
. Ta có:
1
2
SM A M
SD AD
. Suy ra
M
là trung điểm của
SD
.
Mà
1
.
4
SMN
SBD
S
SM SN
S SD SB
3
4
MNBD SBD
S S
.
Tam giác
ABD
có
AB AD a
,
60BAD nên tam giác
ABD
là tam giác đều.
.
1
, .
3
A BDMN BDMN
V d A BDMN S
.
1 3 3
, .
3 4 4
SBD S ABD
d A SBD S V
.
2 3
3 1 1 3 3
. 3.
4 3 4 4 16
ABD
a a
SA S a
.
Câu 59. Cho hình hộp
.ABCD A B C D
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
, , , ,M N P Q R
và
S
lần lượt là tâm của các mặt
, , , ,ABB A BCC B CDD C DAA D ABCD
và
A B C D
. Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , ,M N P Q R
và
S
bằng
A.
3
. B.
24
. C.
9
. D.
1
3
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Gọi
, , ,I J K L
lần lượt là trung điểm các cạnh
, , ,AA BB CC DD
.
Do tam giác
MIQ
đồng dạng với tam giác
B A D
theo tỉ số
1
2
nên
1 1 9
4 8 8
MIQ B A D A B C D
S S S
. Suy ra
9 9
4 9 4.
8 2
MNPQ IJKL MIQ
S S S
.
Gọi
1 2
,h h
lần lượt là chiều cao của hai hình chóp
1 2
. , . 8R MNPQ S MNPQ h h
.
Thể tích của khối đa diện lồi có các đỉnh là các điểm
, , , ,M N P Q R
và
S
bằng
1 2
1 1 9
.8. 3
3 3 8
MNPQ
V h h S
.
Câu 60. Cho hình chóp
.S ABC
có
SA ABC
, đáy là tam giác vuông cân tại
A
,
G
là trọng tâm
,ABC
khoảng cách từ
G
đến mặt phẳng
SBC
bằng
3
a
. Gọi
là góc giữa mặt phẳng
SBC
và
ABC
. Khi thể tích khối chóp
.S ABC
nhỏ nhất thì
cos
bằng
A.
3
3
. B.
2
2
. C.
2
3
.
D.
3
2
.
Lời giải
Chọn A
Gọi là trung điểm . Ta có:
( )
BM AM
BC SAM BC AM
BC SA
Góc giữa mặt phẳng
SBC
và
ABC
là:
SMA
M
BC
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
( ) ( )BC SAM SBC SAM
;
.SBC SAM SM
Kẻ
( )GH SM GH SBC
.
, .
3
a
d G SBC GH
Xét tam giác vuông
GHM
:
3 .
sin 3sin sin
GH a a
GM AM GM
Do tam giác
ABC
vuông cân:
2
2
sin
a
BC AM
.
Xét tam giác vuông
SAM
:
.tan
cos
a
SA AM
Suy ra:
3
.
2
1
. .
3 3sin .cos
S ABC ABC
a
V SA S
Thể tích khối chóp
.S ABC
nhỏ nhất khi lớn nhất.
Đặt
cosx
.
Do
0
2
nên
0;1x
.
Xét hàm số
2
(1 )f x x x
ta có:
2
3
1 3 ; ( ) 0
3
f x x f x x
Bảng biến thiên:
Từ bảng biến thiên ta có: Thể tích khối chóp
.S ABC
nhỏ nhất khi lớn nhất khi
3
cos
3
.
Câu 61. Cho lăng trụ
.ABC A B C
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
,M N
là hai điểm
thỏa mãn
. 1 , . 0BM k BB k CN l CC l
. Thể tích của tứ diện
AA MN
bằng
A.
1
72
l k
. B.
24
. C.
72
. D.
1
210
l k
.
Lời giải
Chọn B
2
sin .cos
2
sin .cos
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Theo giả thiết
. 1 , . 0BM k BB k CN l CC l
suy ra
,M BB N CC
(như hình vẽ)
Do
|| , ,BM ACC A d M ANA d B ANA
.
Ta có
ANA ACA
S S
Có
1 1 1
, . , . , .
3 3 3
AA MN ANA ACA ACA
V d M ANA S d B ANA S d B ACA S
.A ABC
V
1
.9.8 24
3
.
Câu 62. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
với 6 , 3 , 3AB BC SC
và mặt phẳng
SAC
vuông góc với mặt đáy
ABC
. Biết hai mặt phẳng
SAB
và
SAC
tạo với nhau góc
thỏa mãn
3
tan .
4
Thể tích khối chóp
.S ABC
bằng
A.
8.V
B.
4
.
3
V
C.
8
.
3
V
D.
4.V
Lời giải
Chọn B
Dựng ,BE AC EF SA .
Vì
SAC
ABC
và
SAC ABC AC
nên
BE SA
Khi đó
SA BEF
,SAB SAC BFE
3 4 4 . 4 2
tan
4 3 3 3
BE AB BC
BFE EF BE
EF AC
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2
4
2 sin
3 2
AB EF
AE FAE
AC AE
, .sin 2 2d C SA AC SAC
và
2 .cos 2.SA AC SAC
Suy ra
. .
1 1 1 4
. 2 2.2 2
3 3 2 3
S ABC B SAC SAC
V V BES
.
Câu 63. Cho lăng trụ
.ABC A B C
có chiều cao bằng
8
và diện tích đáy bằng
9
. Gọi
,M N
lần lượt là
trung điểm của
,AA BC
.
D
là điểm thỏa mãn
2AD AN
. Mặt phẳng
P
qua
,M D
và
song song với
BC
cắt
,BB CC
lần lượt tại
,E F
. Thể tích của khối đa diện lồi có các đỉnh là
các điểm
, , , ,A B C M E
và
F
bằng
A.
36
. B.
24
. C.
48
. D.
39
.
Lời giải
Chọn C
D
là điểm thỏa mãn
2AD AN
suy ra
N
là trung điểm
AD
. Gọi
I
là trung điểm
MD
suy
ra
I BCC B
. Mặt phẳng
P
qua
,M D
và song song với
BC
nên
|| , ,P BCC B Ix BC Ix BB E Ix CC F
.
Ta có
1 1 1
2 4 4
IN AM AA EB FC AA
.
.
.
.
1 1 3 3
9.8. 48
3 2 43 4
1
A B C MEF
A B C MEF
ABC A B C
V
A M B E C F
V
V AA BB CC
.
Phương án nhiễu A: Học sinh không xác định được thiết diện, có yếu tố
M
là trung điểm
AA
nên nghĩ mặt phẳng
P
sẽ chia đôi lăng trụ.
Phương án nhiễu B: áp dụng sai công
thức
.
.
.
1 1 1 1 1
24
3 3 2 4 4
A B C MNP
A B C MNP
ABC A B C
V
AM BE CF
V
V AA BB CC
.
Phương án nhiễu D: Học sinh tính được
.
1
.4.9 12
3
M A B C
V
. Cho rằng
EFC B
đồng dạng với
BCC B
theo tỉ số
. .
3 9 9 9 2
. .8.9 27
4 16 16 16 3
EFC B BCC B M EFC B M BCC B
S S V V
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Câu 64. Cho tứ diện đều
ABCD
có cạnh bằng
a
. Gọi
,M N
lần lượt là trung điểm của các cạnh
,AB BC
và
E
là điểm đối xứng với
B
qua
D
. Mặt phẳng
MNE
chia khối tứ diện
ABCD
thành hai khối đa diện, trong đó khối chứa điểm
A
có thể tích
V
. Thể tích
V
bằng
A.
3
11 2
.
216
a
V
B.
3
7 2
.
216
a
V
C.
3
2
.
8
a
V
D.
3
13 2
.
216
a
V
Lời giải
Chọn A
Gọi
,Q ME AD P NE CD mp MNE
chia khối tứ diện
ABCD
thành hai khối đa
diện gồm
PQDBMN
và khối đa diện chứa đỉnh
A
có thể tích
V
.
Dễ thấy
,P Q
lần lượt là trọng tâm của
BCE
và
.ABE
Gọi
S
là diện tích
1 1
.
3 3 3
PDE CDE BNE
S
BCD S S S
Gọi
h
là chiều cao của tứ diện
ABCD
,
2
.
,
3
h
d M BCD
h
d Q BCD
Khi đó
.
1 . .
. , . ; .
3 6 27
M BNE BNE QPDE
S h S h
V d M BCD S V
Mà
3
2
.
12
ABCD
V a
Suy ra
3
. . .
7 . 7 11 11 2
. .
18 3 18 18 216
PQD MNB M BNE Q PDE ABCD ABCD
S h
V V V V V V a
Câu 65. Cho hình chóp
SABC
có diện tích đáy bằng
10
, chiều cao bằng
9
. Gọi
, ,M N P
lần lượt là
trọng tâm của tam giác
, ,SAB SBC SCA
. Thể tích của khối đa diện
ABCMNP
.
A.
60
B.
175
3
. C.
560
9
. D.
160
9
.
Lời giải
Chọn D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
3
2 8
.
3 27
SIJK SABC SABC
V V V
19 19 1 190
. 9.10
27 27 3 9
IJKABC SABC
V V
. . . .
( )
ABC MNP ABCIJK B MNJ A MIP C NPK
V V V V V
mà
. . .B MNJ A MIP C NPK
V V V
. .
3
ABC MNP ABCIJK B MNJ
V V V
Có
1
. .
3
BMNJ MNJ b
V S h
;
,
b
h d B IJK
4 4 40
.10
9 9 9
IJK ABC
S S
Mà
1 10
.
4 9
MNJ IJK
S S
;
1
3
3
b
h h
1 10 10
. .3
3 9 9
BMNJ
V
Vậy
190 10 160
3.
9 9 9
ABCMNP
V
Câu 66. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Biết
,AB SB AC SC
, góc
giữa hai mặt phẳng
SAB
và
SAC
bằng
0
60
. Thể tích khối chóp
.S ABC
bằng
A.
3
2
24
a
. B.
3
3
36
a
. C.
3
3
6
a
. D.
3
2
36
a
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Từ giả thiết suy ra
SAB SAC
1
.
Gọi
H
là hình chiếu của
B
trên
SA
. Theo
1
ta có
CH SA
và
BH CH
.
Đặt
, 0BH x x a
.
Theo giả thiết ta có góc
BHC bằng hoặc bù với
0
60
.
BHC không thể bằng
0
60
vì khi đó
x a
nên
0
120BHC . Khi đó
3
3
3
a
BC x a x
.
Dễ thấy
.
.
S ABC
H ABC
V
SA
V HA
.
Ta có
6
3
a
HA
,
2
2
a
SB SC
,
6
6
a
SH
3
2
SA
HA
.
3
2 0
.
1 1 2
. .sin120
3 2 36
H ABC
a
V HA x
3
.
2
24
S ABC
a
V
Câu 67. Cho khối tứ diện
ABCD
có thể tích
V
. Gọi
1
G
,
2
G
,
3
G
,
4
G
là trọng tâm của bốn mặt của tứ
diện
ABCD
. Thể tích khối tứ diện
1 2 3 4
GG G G
là:
A.
27
V
. B.
18
V
. C.
108
V
. D.
81
V
.
Lời giải
Chọn A
Gọi
, ,I J K
lần lượt là trung điểm của
BC
,
BD
và
DC
.
Gọi
h
là khoảng cách từ
A
đến
BCD
,
1
h
là khoảng cách từ
4
G
đến
1 2 3
G G G
.
x
a
x
a
S
B
A
C
H
H
2
H
1
G
3
G
2
G
1
G
4
K
J
I
B
C
D
A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
1 2 3
/ /G G G BCD
nên
4 1 2 3 1 1 2
, ,d G G G G d G BCD G H h
,
1
h AH
.
1 1
1
3
h KG
h KA
1
3
h
h
.
Gọi
S
,
S
,
1
S
lần lượt là diện tích các tam giác
BCD
,
IJK
và
1 2 3
GG G
.
Vì
, ,I J K
lần lượt là trung điểm của
BC
,
BD
và
DC
nên:
1 1 1 1 1 1
. , . . , . . . ,
2 2 2 2 4 2 4
BC
S JK d I JK d D BC BC d D BC S
1
.
Tam giác
1 2 3
GG G
đồng dạng với tam giác
KIJ
với tỉ số đồng dạng là:
1 2 1
2
3
G G AG
Ik Ak
.
2
1
2 4
3 9
S
S
1
4
9
S S
2
(Vì tỉ số diện tích bằng bình phương tỉ số đồng dạng).
Từ
1
và
2
1
9
S
S
.
Thể tích khối từ diện
1 2 3 4
GG G G
là:
1 1 1
1 1 1 1
. . . . . .
3 3 9 3 27 3 27
S h V
V S h S h
.
Câu 68. Cho khối chóp
.S ABCD
có đáy là hình thang cân
AD BC
, khoảng cách giữa
AD
và
BC
bằng
a
,
BC a
,
SA ABCD
,
2SA a
. Trên cạnh
BC
lấy điểm
M
sao cho
0MC x x a
. Thể tích khối chóp
.S CDM
lớn nhất khi độ dài
MC
bằng
A.
2
.
2
a
B.
.
2
a
C.
.a
D.
3
.
2
a
Lời giải
Chọn C
.
1
. .
3
S CDM CDM
V SA S
Ta có:
2SA a
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Và
1
. . .sin
2
CDM
S CM CD MCD
1
. .sin
2
x CD MCD
.
.
1
. . . .sin
3
S CDM
V a x CD MCD
Vì
.S CDM
V chỉ thay đổi khi
x
thay đổi, dễ thấy thể tích cần tìm lớn nhất khi
x
lớn nhất
x a M B MC a
.
Câu 69. Cho tứ diện
ABCD
có thể tích là
V
. Điểm
M
thay đổi trong tam giác
BCD
. Các đường thẳng
qua
M
và song song với
AB
,
AC
,
AD
lần lượt cắt các mặt phẳng
ACD
,
ABD
,
ABC
tại
N
,
P
,
Q
. Giá trị lớn nhất của khối
MNPQ
là
A.
27
V
. B.
18
V
. C.
81
V
. D.
2
27
V
.
Lời giải
Chọn A
Gọi
N BM CD
,
P CM BD
,
Q MD BC
.
 Tam giác
ABN
có
//MN AB
MN N M
AB N B
.
 Tam giác
ACP
có
//MP AC
MP P M
AC P C
.
 Tam giác
ADQ
có
//QM AD
MQ Q M
AD Q D
.
Khi đó:
MN MP MQ N M P M Q M
AB AC AD N B P C Q D
Mà
1
MCD MBCMBD
BCD BCD BCD
S S
SN M P M Q M
N B P C Q D S S S
nên
1
MN MP MQ
AB AC AD
Lại có
3
3
3
3
1 3 . .
MN MP MQ MN MP MQ
AB AC AD AB AC AD
(Cauchy)
1
. . . .
27
MN MP MQ AB AC AD
. .MN MP MQ
lớn nhất khi
MN MP MQ
AB AC AD
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
M
là trọng tâm tam giác
BCD
1
3
MN MP MQ
AB AC AD
//NPQ BCD
,
2
2
3
NPQ
N P Q
S
S
, Mà
1
4
N P Q BCD
S S
nên
1
9
NPQ BCD
S S
và
1
, ,
3
d M NPQ d A BCD
Vậy giá trị lớn nhất của khối tứ diện
MNPQ
là
1
. ,
3
MNPQ NPQ
V S d M NPQ
1 1 1
. . ,
3 9 3 27
MNPQ BCD
V
V S d A BCD
, với
1
. ,
3
ABCD BCD
V S d A BCD V
Câu 70. Cho khối lăng trụ
.
ABC A B C
có thể tích bằng
2
. Gọi
M
là trung điểm của đoạn thẳng
AA
và
N
là điểm nằm trên cạnh
'BB
sao cho
2 'BN B N
. Đường thẳng
CM
cắt đường thẳng
C A
tại
P
, đường thẳng
CN
cắt đường thẳng
C B
tại
Q
. Thể tích của khối đa diện lồi
A MPB NQ
bằng
A.
7
9
. B.
5
9
. C.
2
3
. D.
13
9
.
Lời giải
Chọn A
Ta có:
. '
. '
. ' ' '
1 ' 13 13
3 ' ' ' 18 9
ABC MNC
ABC MNC
ABC A B C
V
AM BN CC
V
V AA BB CC
.
Lại có:
.
.
. ' ' '
1 7 7
3 ' ' ' 18 9
ABC MNC
ABC MNC
ABC A B C
V
AM BN CC
V
V AA BB CC
.
Suy ra:
. ' . ' .
2
3
C MNC ABC MNC ABC MNC
V V V
.
Mà:
. '
. '
'
. . *
'
C MNC
C PQC
V
CM CN CC
V CP CQ CC
Ta có:
1
1
'
2'
2
'
2
' 3
CM
CM AM
CMA PMA
CPPM A M
CN BN
CN
CNB QNB
QN B N CQ
.
Thay vào
*
ta có:
. '
. ' . '
. '
1 2 1
. .1 3 2
2 3 3
C MNC
C PQC C MNC
C PQC
V
V V
V
.
Có:
' ' '. .
11
9
A B C MNC LT ABC MNC
V V V
.
' ' . ' ' ' '.
7
9
A MPB NQ C PQC A B C MNC
V V V
.
Câu 71. Cho khối lăng trụ
.
ABC A B C
. Gọi
,M N
lần lượt là trung điểm của đoạn thẳng
AA
và
'BB
.
Tính tỉ số thể tích của khối tứ diện
'CMNC
với khối lăng trụ đã cho.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
A.
1
3
. B.
1
2
. C.
2
3
. D.
3
4
.
Lời giải
Chọn A
Ta có:
.
. . ' ' '
. ' ' '
1 1 1
3 ' ' ' 3 3
ABC MNC
ABC MNC ABC A B C
ABC A B C
V
AM BN CC
V V
V AA BB CC
.
Tương tự ta có:
' ' '. '
' ' '. ' ' ' '.
' ' '.
1 ' ' ' ' 1 1
3 ' ' ' 3 3
A B C MNC
A B C MNC A B C ABC
A B C ABC
V
A M B N C C
V V
V A A B B C C
.
'
' . ' ' '
. ' ' '
1 1
3 3
CMNC
CMNC ABC A B C
ABC A B C
V
V V
V
.
Câu 72. Cho khối lập phương
. '
ABCD A B C D
cạnh
a
. Gọi
,M N
lần lượt là trung điểm của đoạn
thẳng
' 'A D
và
' 'C D
. Mặt phẳng
BMN
chia khối lập phương thành hai phần, gọi
V
là thể
tích phần chứa đỉnh
'B
. Tính
?V
A.
3
25
72
a
. B.
3
7
24
a
. C.
3
25
24
a
. D.
3
7
72
a
.
Lời giải
Chọn A
Ta có thể tích cần tính là
' ' 'BB EA MNC F
V .
Mà
' ' ' . ' . ' ' ' . '
BB EA MNC F B EA M B B A MNC B FC N
V V V V .
Ta có:
' ' ' '
' ' ' '
PA M ND M PA ND
QC N MD N QC MD
.
Lại có:
' ' ' ' ' '
2
a
MD ND PA ND MD QC
.
Mà:
' ' 1
'
2
' '
' ' 1
'
3
2
A E PA
PA E BAE
a
AE BA
A E QC
C F QC
QC F BCF
CF BC
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy ta có:
3
. ' '
1 1 1
. . ' . '
3 3 2 36
B EA M EA M
a
V BA S BA A M A E .
Dễ thấy:
3
. ' . '
36
B FC N B EA M
a
V V
.
Có:
3
. ' ' ' ' ' ' ' ' ' ' '
1 1 7
. '. '
3 3 24
B B A MNC B A MNC A B C D MD N
a
V BB S BB S S .
Vậy:
3
' ' '
25
72
BB EA MNC F
a
V
.
Câu 73. Cho khối lăng trụ
.ABC A B C
có thể tích bằng 6. Gọi điểm
I
là trung điểm
AA
và điểm
N
thuộc cạnh
BB
sao cho
' 2B N BN
.Đường thẳng
'C I
cắt đường thẳng
CA
tại
P
, đường
thẳng
C N
cắt đường thẳng
CB
tại
Q
. Tính thể tích khối đa diện lồi
AIPBNQ
A.
7
.
9
B.
11
.
18
C.
11
.
9
D.
7
.
3
Lời giải
Chọn D
. '
.
1 1 1 1 11
1
3 3 2 3 18
A
ABC INC
BABC C
V
V A
AI BN CC
CA B CB
. '
11 11
18 3
ABC INC
V V
3
. 2. 3
2
CPQ
CAB
S
CP CQ
S CA CB
3
CPQ CAB
S S
' .
1
3 3. 6
3
C CPQ C ABC A B CABC
V V V
'
7
3
C PQ AAIPBN BCINCQ
V V V
.
Câu 74. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
V
. Gọi điểm
M
là trung điểm
AA
và điểm
N
thuộc cạnh
BB
sao cho
1
'
3
BN BB
.Đường thẳng
C M
cắt đường thẳng
CA
tại
D
, đường
thẳng
C N
cắt đường thẳng
CB
tại
E
. Tỉ số thể tích khối đa diện lồi
AMDBNE
và khối lăng
trụ
.ABC A B C
là
A.
13
.
18
B.
7
.
18
C.
7
.
12
D.
8
.
15
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Gọi
1
V
là thể tích khối đa diện lồi
AMDBNE
,
2
V
là thể tích khối lăng trụ
.ABC A B C
. '
. '
.
1 1 1 1 11 11
1
3 3 2 3 18 18
ABC MNC
ABC M
A B C
NC
ABC
AM BN CC
CC
V
V V
V AA BB
1 2 1
. .
2 3 3
CAB
CDF
S
CA CB
S CD CE
3
CDE CAB
S S
' ..
1
3 3.
3
C CDE C ABC A B CABC
V V V V
. '
7
18
AMDBNE C CDE ABC C MN
V V V
V V
.
Câu 75. Cho khối lăng trụ
.ABC A B C
có thể tích bằng
1
. Điểm
M
là thuộc cạnh
' 'A B
sao cho
1
3
A M A B
. Mặt phẳng
BCM
cắt đường thẳng
AA
tại
F
, và cắt đường thẳng
A C
tại
G
. Thể tích khối chóp
FA MG
bằng
A.
5
24
. B.
1
6
. C.
5
36
. D.
1
54
.
Lời giải
Chọn D
Đường thẳng
AA
cắt
BM
tại
F
'AA BCM F
,
Đường thẳng
FC
cắt
' 'A C
tại
G
' 'A C BCM G
' ' 1
' // ;
3
FA FM A M
A M AB
FA FB AB
' 1
' // ;
3
FG FA
AG AC
FC FA
'
'
1 1 1 1 1
. .
3 3 3 27 27
FA MG
FA MG FABC
FABC
V
V V
V
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1 1 3 1
, . ',
3 3 2 2
FABC ABC ABC
V S d F ABC S d A ABC
Nên
'
1 1 1
.
27 2 54
FA MG
V
.
Câu 76. Cho lăng trụ tam giác
.ABC A B C
có đáy là tam giác đều cạnh
a
, điểm
A
cách đều ba điểm
A
,
B
,
C
và diện tích tam giác
ABA
bằng
2
3
6
a
. Thể tích khối đa diện
A B C BC
bằng
A.
3
3
6
a
. B.
3
3
24
a
. C.
3
3
8
a
. D.
3
3
12
a
.
Lời giải
Chọn D
Do điểm
A
cách đều ba điểm
, ,A B C
nên chân đường cao hạ từ
A
là trọng tâm
I
của tam
giác đều
ABC
. Gọi
M
là trung điểm của
AB
A M AB
.
Có
1 3
3 6
a
MI CM
Ta có:
1
.
2
ABA
S AB A M
2
2
3
3
ABA
S
a
A M
AB
.
Xét tam giác
'A IM
có
2 2
2
a
A I A M IM
.
Vậy
2 3
'.
1 3 3
3 4 2 24
A ABC
a a a
V
và
2 3
. ' ' '
3 3
4 2 8
ABC A B C
a a a
V
.
Do đó
3 3 3
' ' '
3 3 3
8 24 12
A B C BC
a a a
V
.
Câu 77. Cho lăng trụ đều
.ABC EFH
có tất cả các cạnh bằng
1
. Gọi
S
là điểm đối xứng của
A
qua
.BH
Thể tích khối đa diện
.ABC SFH
bằng
A.
1
.
2
B.
3
.
3
C.
3
.
6
D.
1
.
6
Lời giải
Chọn B
C'
B'
I
M
A
C
B
A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Ta có
. . .ABC SFH A BCHF S BCHF
V V V .
. .
2 2 3 3
.1.
3 3 4 6
A BCHF ABC EFH
V V
.
Vì
S
là điểm đối xứng của
A
qua
BH
nên
AS BH
tại trung điểm
N
của
AS
.
Mà
BH BCHF
suy ra khoảng cách từ
A
đến
BCHF
bằng khoảng cách từ
S
đến
BCHF
. .
3
6
A BCHF S BCHF
V V
.
Vậy
. . .
3 3 3
6 6 3
ABC SFH A BCHF S BCHF
V V V
.
Câu 78. Cho khối lăng trụ
1 1 1
.ABC A B C có thể tích bằng
30.
Gọi
O
là tâm của hình bình hành
1 1
ABB A
M
và
G
là trọng tâm tam giác
1 1 1
ABC . Tính thể tích khối tứ diện
1
.COGB
A.
7
3
. B.
16
81
k
. C.
5
2
. D.
10
3
.
Lời giải
Chọn D
Gọi
,M N
lần lượt là trung điểm của
1 1
AB và A B
Ta có
1 1 1 1 1
. .
1
15
2
BCN B C M ABC A B C
V V
1 1 1 1
. .
2
10
3
B CNMC BCN B C M
V V
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mặt khác ta lại có:
1
. 1
1
. ( ,( )).
3
B CGO CGO
V S d B CGO
Mà
1 1 1 1 1 1 1
1 1 1 1
4 12 3 3
CGO CNMC CNO CGC OMG CNMC CNMC CNMC CNMC CNMC
S S S S S S S S S S
1 1 1 1
. 1 1 .
1 1 1 1 10
. ( ,( )) ( ,( )) .
3 3 3 3 3
B CGO CGO CNMC B CNMC
V S d B CGO S d B CGO V
Câu 79. Cho khối chóp
.S ABCD
có thể tích bằng
V
. Gọi
M
,
N
,
P
,
Q
lần lượt là trọng tâm các mặt
bên
SAB
,
SBC
,
SCD
,
SDA
. Gọi
k
là tỉ số thể tích của khối chóp
.S MNPQ
và phần
còn lại là. Khi đó:
A.
16
81
k V
. B.
15
.
4
. C.
4
23
k
. D.
4
23
k V
.
Lờigiải
Chọn C
Gọi trung điểm các đoạn thẳng
, , ,AB BC CD DA
lần lượt là
, , ,I J K L
.
Ta có:
/ / ACMN
;
/ /QP AC
;
/ /MQ BD
;
/ /NP BD
Vậy
MNPQ
là hình bình hành.
1
4
AIL ABD
S S
;
IJ
1
4
B BAC
S S
;
1
4
CJK CBD
S S
;
1
4
DKL DCA
S S
IJ
1 1 1
4 4 4
1 1 1
4 4 4
AIL CJK ABD CBD ABCD
B DKL BAC DCA ABCD
S S S S S
S S S S S
Do đó:
IJ
1
2
KL ABCD
S S
.
Mặt khác
2
SMNPQ SMNP
V V
mà
IJ
2 2 2 8
. . . .
3 3 3 27
SMNP
S K
V
SM SN SP
V SI SJ SK
IJ
1 1 1 1 1 1 1 1 1 1
. . . . . .V
3 3 2 3 2 2 4 3 4 4
SIJK IJK KL ABCD ABCD SABCD
V h S h S h S h S V
P
Q
N
M
L
K
J
I
S
A
B
C
D
TÀI
LIỆU TỔNG ÔN TẬP TNTHPT 2020
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
S
uy ra
8
1 4
2. . .
27
4 27
SMN
PQ
V V V
.
Khi
đó, thể tích phần còn lại:
.
4
23
'
2
7 27
S
MNPQ
V
V V V V V
.
Vậ
y, tỉ số cần tìm
.
4
'
23
S
MNPQ
V
k
V
.
-------------------- HẾT --------------------
| 1/50
| | Tải xuống

Có thể bạn quan tâm:

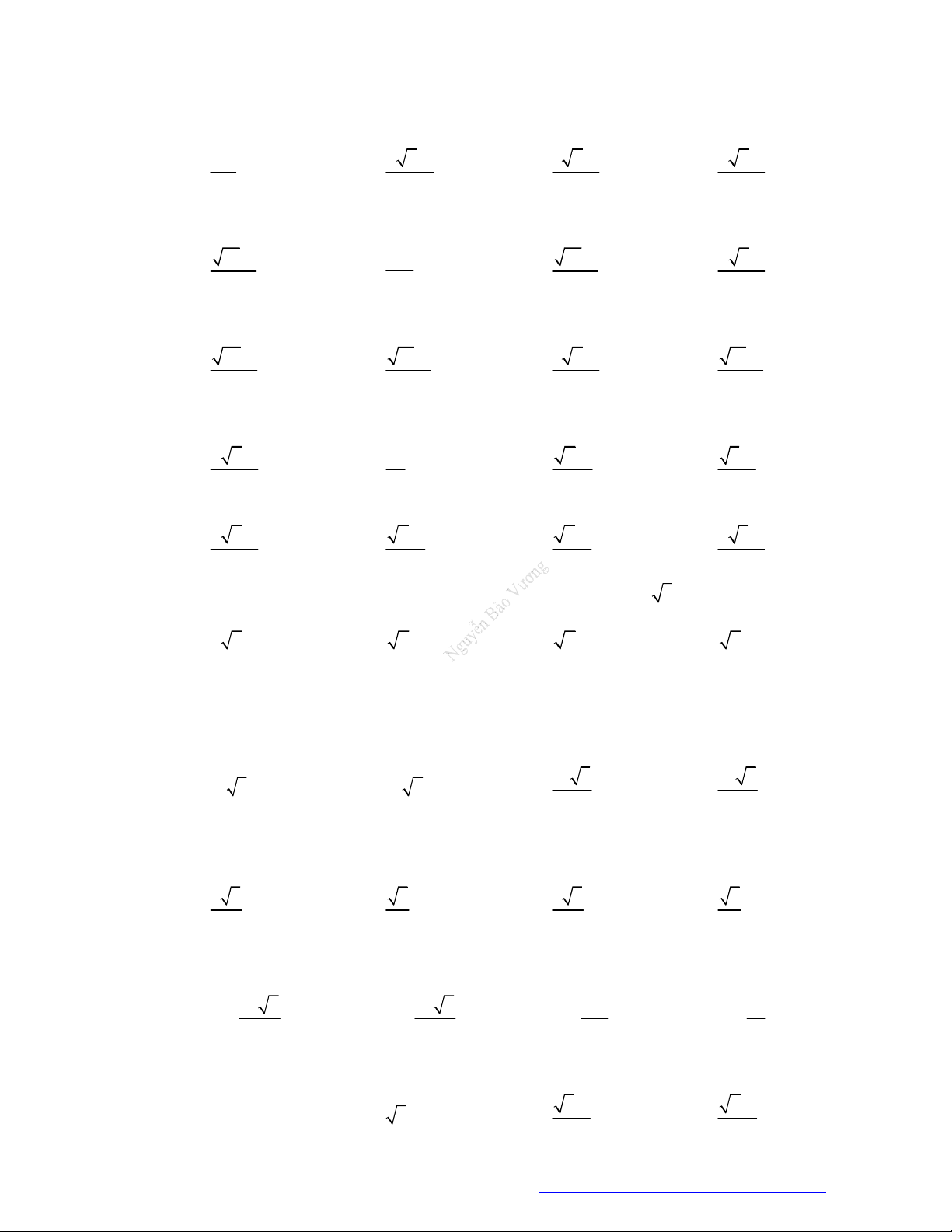
Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 8 THỂ TÍCH KHỐI ĐA DIỆN
THỂ TÍCH KHỐI ĐA DIỆN 1
Thể tích khối chóp V
  S . chiÒu cao . chãp đ¸ y 3
Thể tích khối lăng trụ V
S . chiÒu cao . c l¨ng trô đ¸ y b a
Thể tích khối lập phương 3
V a với a là cạnh.
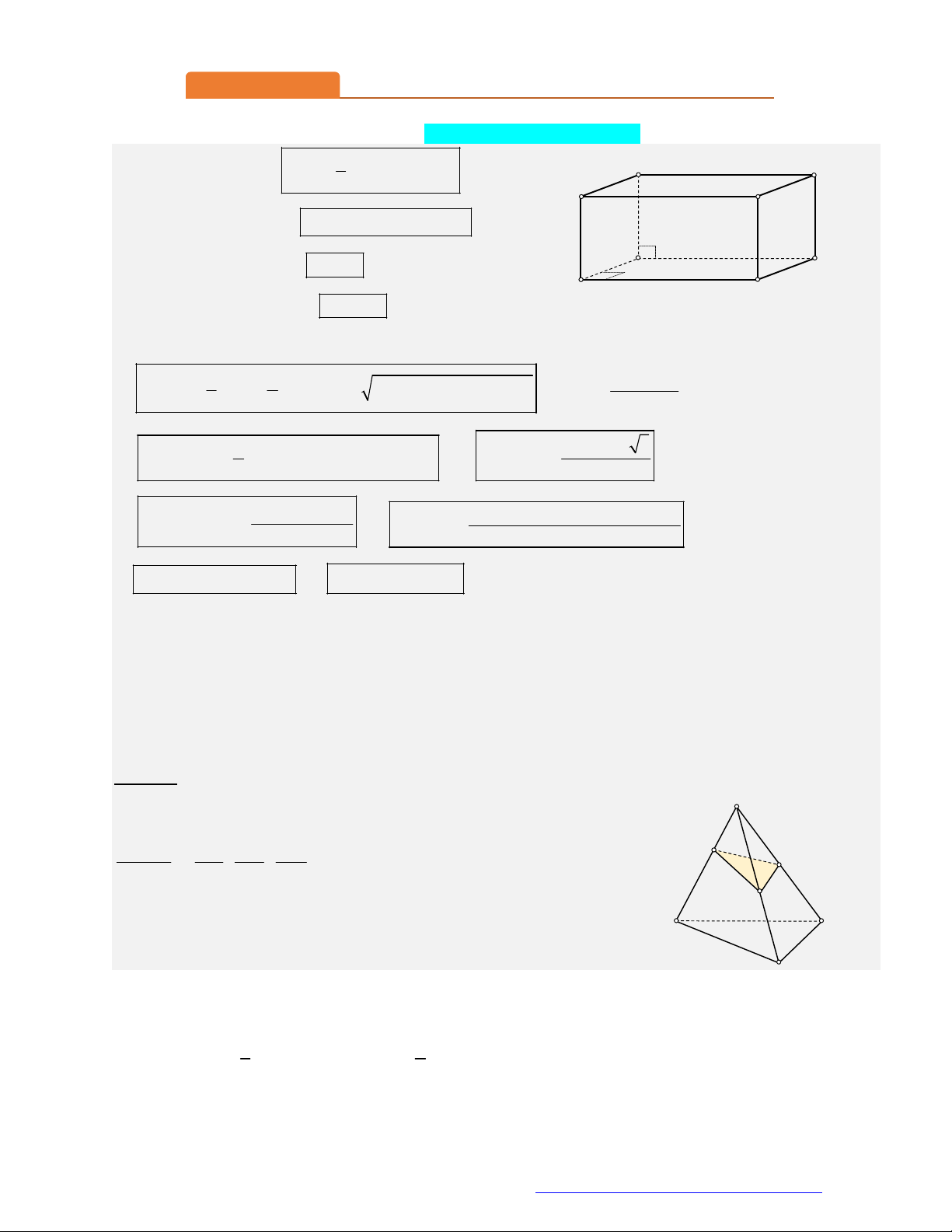
Thể tích khối hộp chữ nhật V abc với a, ,
b c lần lượt là chiều dài, chiều rộng và chiều cao.
Xác định diện tích đáy: 1 1
a b cS
ah ab sinC  (
p p a)(p b)(b c) , với p   ABC 2 a a 2 2 (c¹nh)   3 S  1
(tÝch hai c¹nh gãc vu«ng)   S   tam gi¸c vu«ng 2 tam gi¸c ®Òu 4 2 
(®¸y lín  ®¸y bÐ)chiÒu cao S  (c¹nh huyÒn)   S   tam gi¸c vu«ng c©n 4 H×nh thang 2  S
 dµiréng .  S  2 (c¹nh) . H×nh ch÷ nhËt H×nh vu«ng
Xác định chiều cao:
Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam giác
chứa trong mặt bên vuông góc với đáy.
Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai mặt bên
cùng vuông góc với mặt phẳng đáy.
Hình chóp có các cạnh bên bằng nhau: Chân đường cao của hình chóp là tâm đường tròn ngoại tiếp đa giác đáy.
Cần nhớ: Tỉ số thể tích khối chóp có đáy là tam giác
Cho khối chóp S.ABC , trên các đoạn thẳng S ,
A SB, SC lần lượt S lấy các điểm A ,
B , C khác S. Khi đó ta luôn có tỉ số thể tích: V    A    SA SB SC S .A B C     C V SA SB SC S .ABC B
Chỉ có tỉ số thể tích khối chóp đáy tam giác, không có tỉ số khối chóp
đáy tứ giác. Khi tính tỉ số khối tứ giác, ta cần chia ra những hình C A
chóp có đáy là tam giác. B
CÂU HỎI CÙNG MỨC ĐỘ VỚI ĐỀ MINH HỌA
DẠNG CÂU HỎI NHẬN BIẾT Câu 1.
Thể tích khối lăng trụ có diện tích đáy bằng B , chiều cao bằng h là 1 2 A. V Bh . B. V Bh .
C. V Bh .
D. V  3Bh . 3 3 Câu 2.
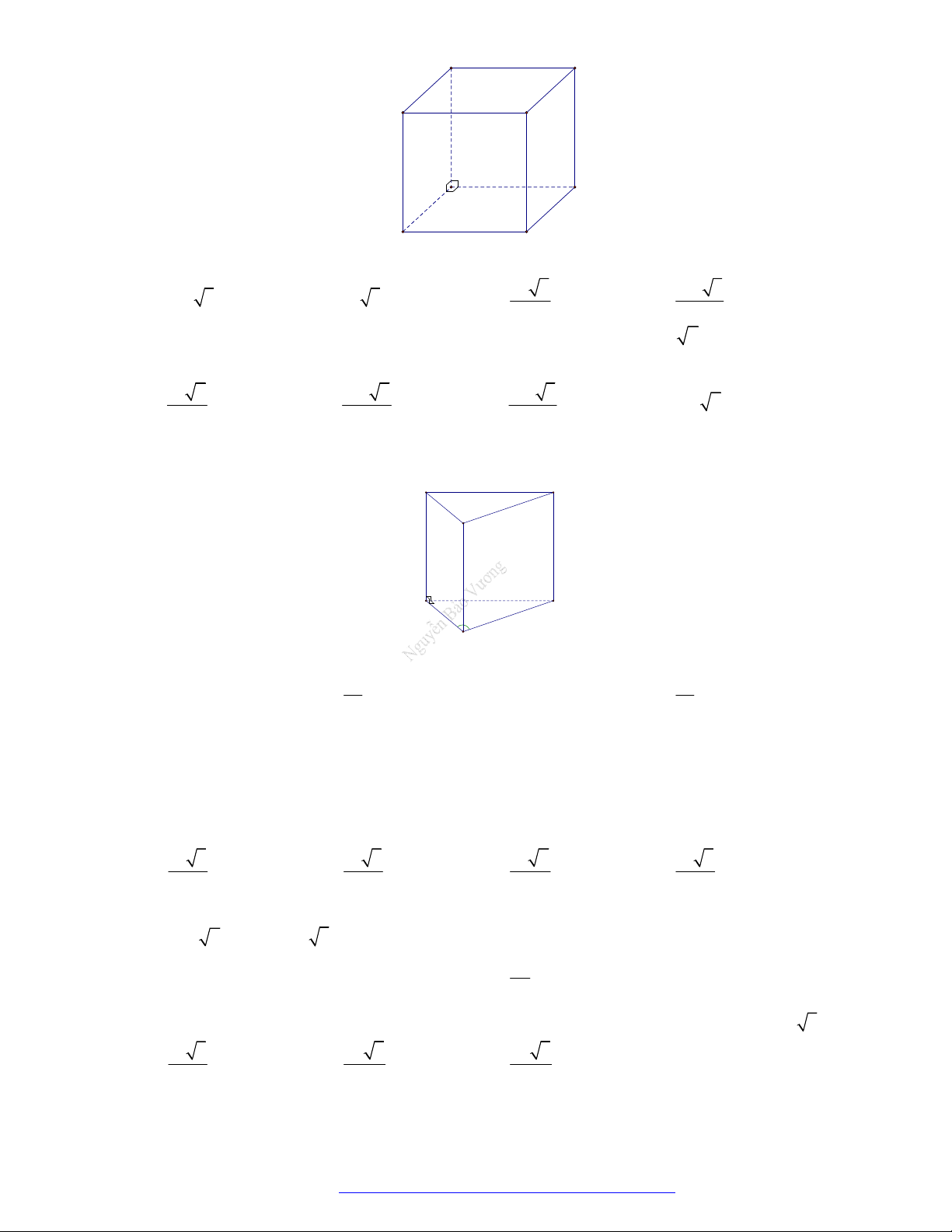
Cho khối lập phương có cạnh bằng 6 . Thể tích của khối lập phương đã cho bằng A. 216 . B. 18 . C. 36 . D. 72 . Câu 3.
Thể tích khối lập phương cạnh 2 bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 A. 6 . B. 8 . C. 4 . D. 2 . Câu 4.
Cho khối chóp có diện tích đáy B  3 và chiều cao h  4 . Thể tích của khối chóp đã cho bằng A. 6 . B. 12 . C. 36 . D. 4 . Câu 5.
Thể tích khối chóp có diện tích đáy bằng 2
2a , chiều cao bằng a 3 là 3 2a 3 3 2a 3 3 a 3 A. V  . B. V  . C. 3 V  2a 3 . D. V  . 9 3 3 Câu 6.
Thể tích khối chóp có diện tích đáy bằng 2
a , chiều cao bằng 2a là 3 a 3 2a A. 3 V  6a . B. V  . C. 3 V  2a . D. V  . 3 3 Câu 7.
Thể tích khối lăng trụ có diện tích đáy bằng 2
3a , chiều cao bằng a là 3 a 3 2a A. 3 V  3a . B. V  . C. 3 V a . D. V  . 3 3 Câu 8.
Thể tích khối hộp chữ nhật có ba kích thước lần lượt là 3, 4,5 bằng A. V  120 . B. V  20 . C. V  30 . D. V  60 . Câu 9.
Cho khối chóp có diện tích đáy B  6 và chiều cao h  3 . Thể tích của khối chóp đã cho bằng A. 6 . B. 18 . C. 9 . D. 36 .
Câu 10. Thể tích khối lập phương cạnh 5 bằng A. 15 . B. 25 . C. 125 . D. 75 .
Câu 11. Cho khối lập phương có độ dài đường chéo bằng 6 3 . Thể tích của khối lập phương đó bằng A. 81 3 . B. 216 . C. 24 3 . D. 162 6 .
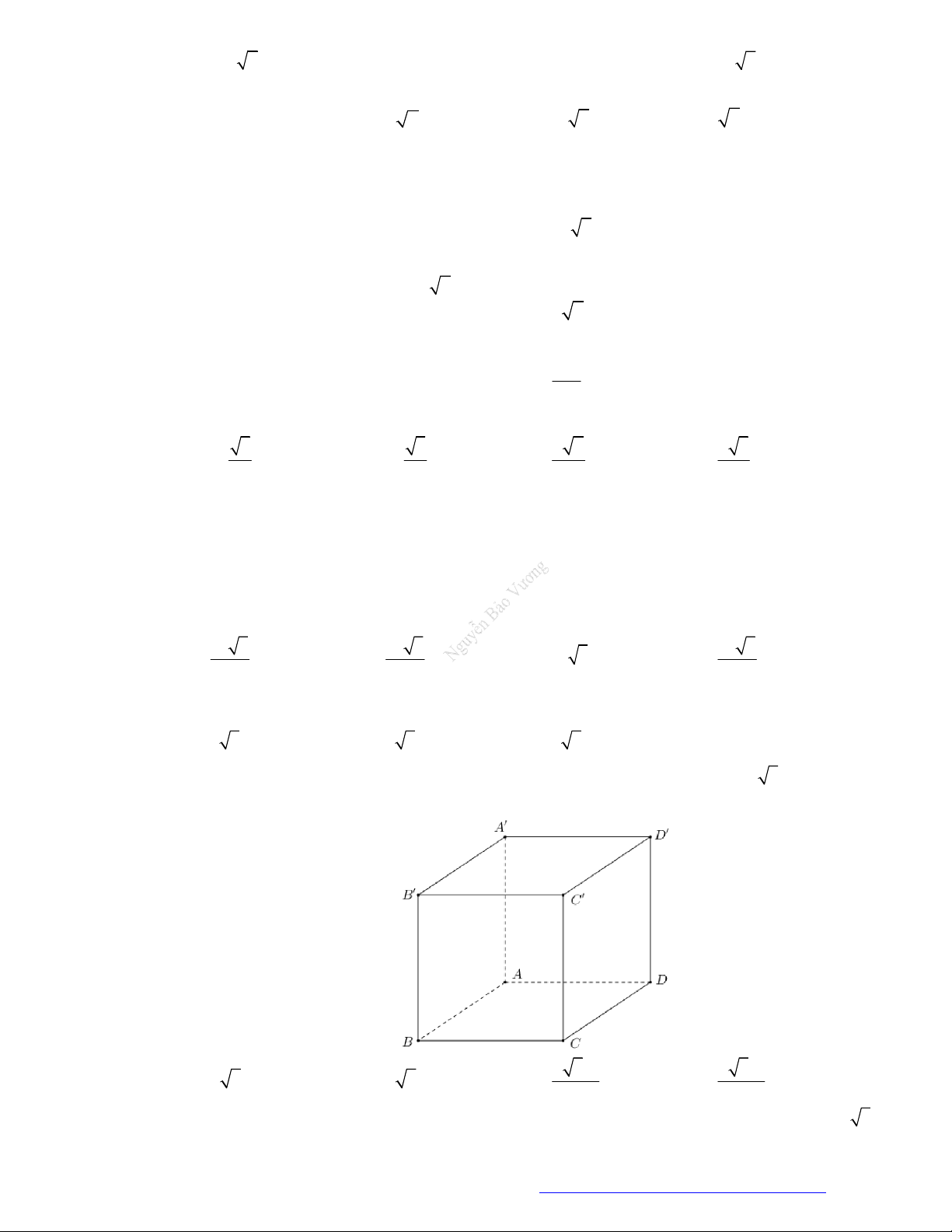
Câu 12. Thể tích khối lập phương ABC . D A BCD
  có AC  a 3 bằng A. 3 a . B. 2 a . C. 2a . D. 3a .
Câu 13. Cho khối lập phương có tổng diện tích các mặt bằng 294 . Thể tích của khối lập phương đó bằng 147 147 147 A. . B. 49 . C. 343 . D. . 2 2 2
Câu 14. Thể tích khối lập phương ABC . D A BCD
  có AC  a 6 bằng A. 3 8a . B. 3 6a 6 . C. 3 2a 2 . D. 3 3a 3 . 2 2
Câu 15. Khối chóp S.ABC có thể tích V
và diện tích đáy B  3 . Chiều cao của khối chóp 3 S.ABC bằng 2 6 2 6 2 2 2 6 A. . B. . C. . D. . 9 3 3 27
Câu 16. Cho khối hộp chữ nhật có ba kích thước là 3;5; 7 . Thể tích của khối hộp đó bằng 105 A. 35. B. . C. 105 . D. 15 . 2
Câu 17. Thể tích khối lập phương ABC . D A BCD
  có AB  2 bằng A. 2 2 . B. 2 . C. 1. D. 3 .
Câu 18. Cho khối chóp S.ABCD có thể tích bằng 3
a , đáy ABCD là hình vuông. Biết chiều cao của khối
chóp là h  3a . Cạnh hình vuông ABCD bằng a A. a . B. . C. a 2 . D. a 3 . 3
Câu 19. Cho khối lập phương ABC . D A B C 
D biết AC  6 2 . Thể tích của khối lập phương đó bằng
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. 432 2 . B. 108 . C. 216 . D. 48 6 .
Câu 20. Thể tích khối lập phương ABC . D AB CD
  có AB  2 bằng A. 8 . B. 2 2 . C. 16 2 . D. 6 .
Câu 21. Cho khối chóp S.ABC có SA vuông góc với đáy, AC  3, AB  4, BC  5 và SA  3 . Tính thể
tích V của khối chóp S.ABC .
A. V  18 .
B. V  6 .
C. V  12 .
D. V  20 .
Câu 22. Thể tích khối lập phương ABC . D AB CD
  có AB  a 2 bằng: A. 3 a . B. 3 2a . C. 3 4a . D. 3 6a .
Câu 23. Thể tích khối lập phương có cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 2 2a . D. 3 6a .
Câu 24. Thể tích khối hộp chữ nhật có độ dài các cạnh lần lượt là a, 2a, 3a bằng: 3 2a A. 3 2a . B. 3 6a . C. . D. 3 3a . 3
Câu 25. Thể tích khối tứ diện đều có cạnh 2a bằng 3 3 2 2 2 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 12 3 3
Câu 26. Thể tích khối lăng trụ có diện tích đáy 2
3a và chiều cao a là A. 3
V  3a . B. 3
V a . C. 3
V  9a . D. 3 V  6a .
DẠNG CÂU HỎI THÔNG HIỂU
Câu 27. Cho khối lăng trụ đứng ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a . Biết BAD  60,
AA  a . Thể tích của khối lăng trụ đã cho bằng 3 a 3 3 a 3 3 a 3 A. . B. . C. 3 a 3 . D. . 2 6 3
Câu 28. Cho khối lăng trụ đứng ABC.AB C
  . Biết AB  3 cm, AC  4 cm,  BAC 60 
, AA  2 cm. Thể
tích của khối lăng trụ đã cho bằng A. 6 3 (cm2). B. 2 3 (cm3). C. 6 3 (cm3). D. 6 (cm3).
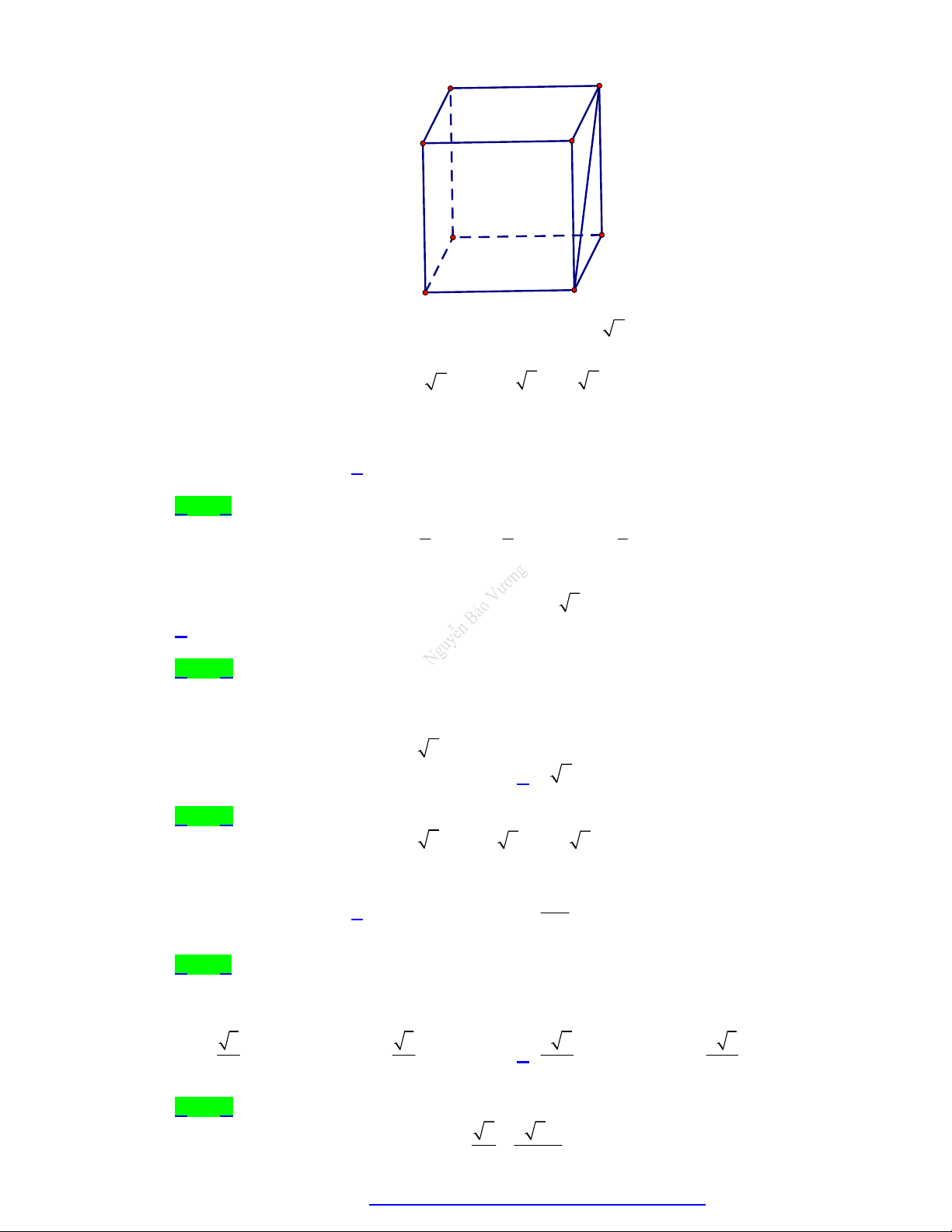
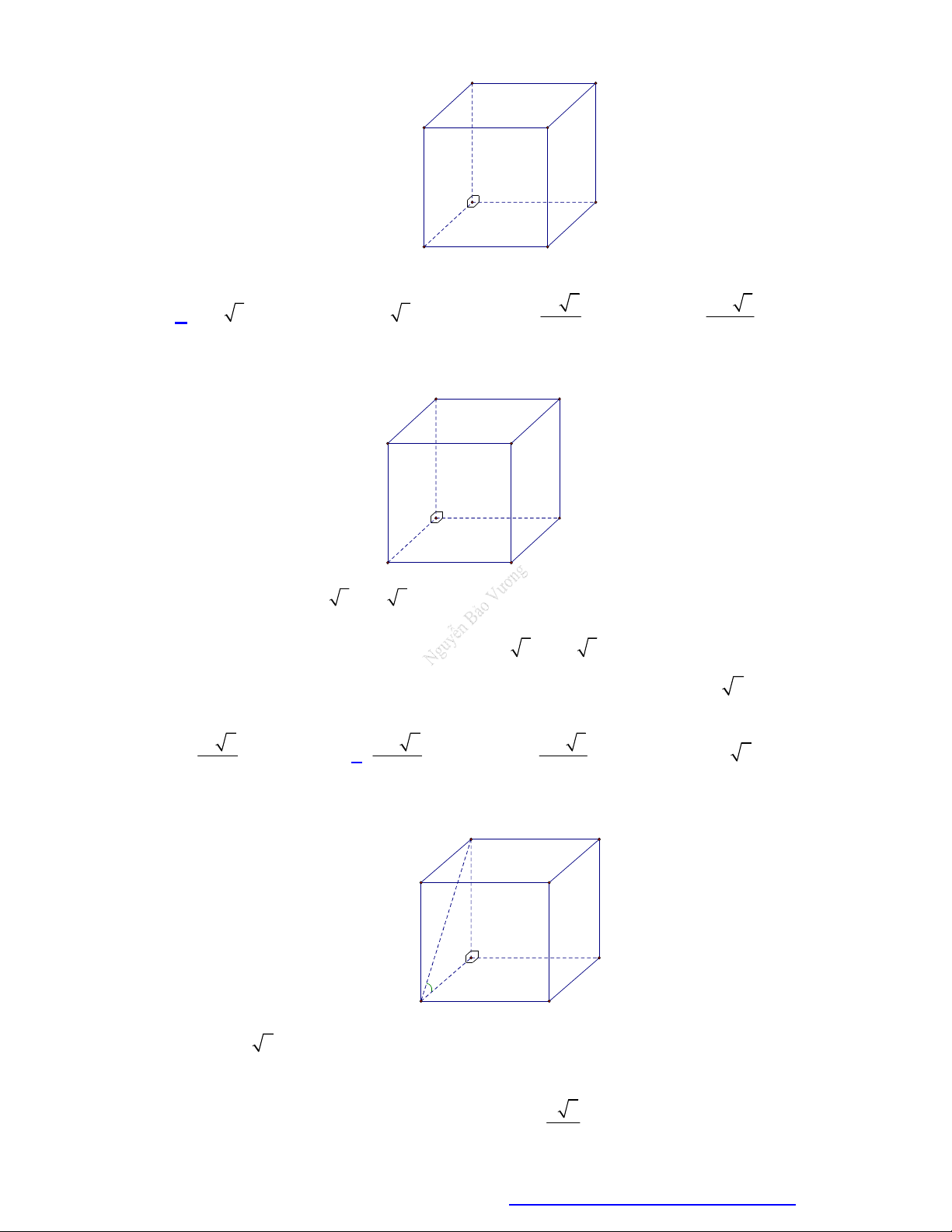
Câu 29. Cho khối lăng trụ đứng ABC . D AB CD
  có đáy là hình thoi cạnh a , BD a 3 và AA  4a
(minh họa như hình bên). Thể tích của khối lăng trụ đã cho bằng 3 2 3a 3 4 3a A. 3 2 3a . B. 3 4 3a . C. . D. . 3 3
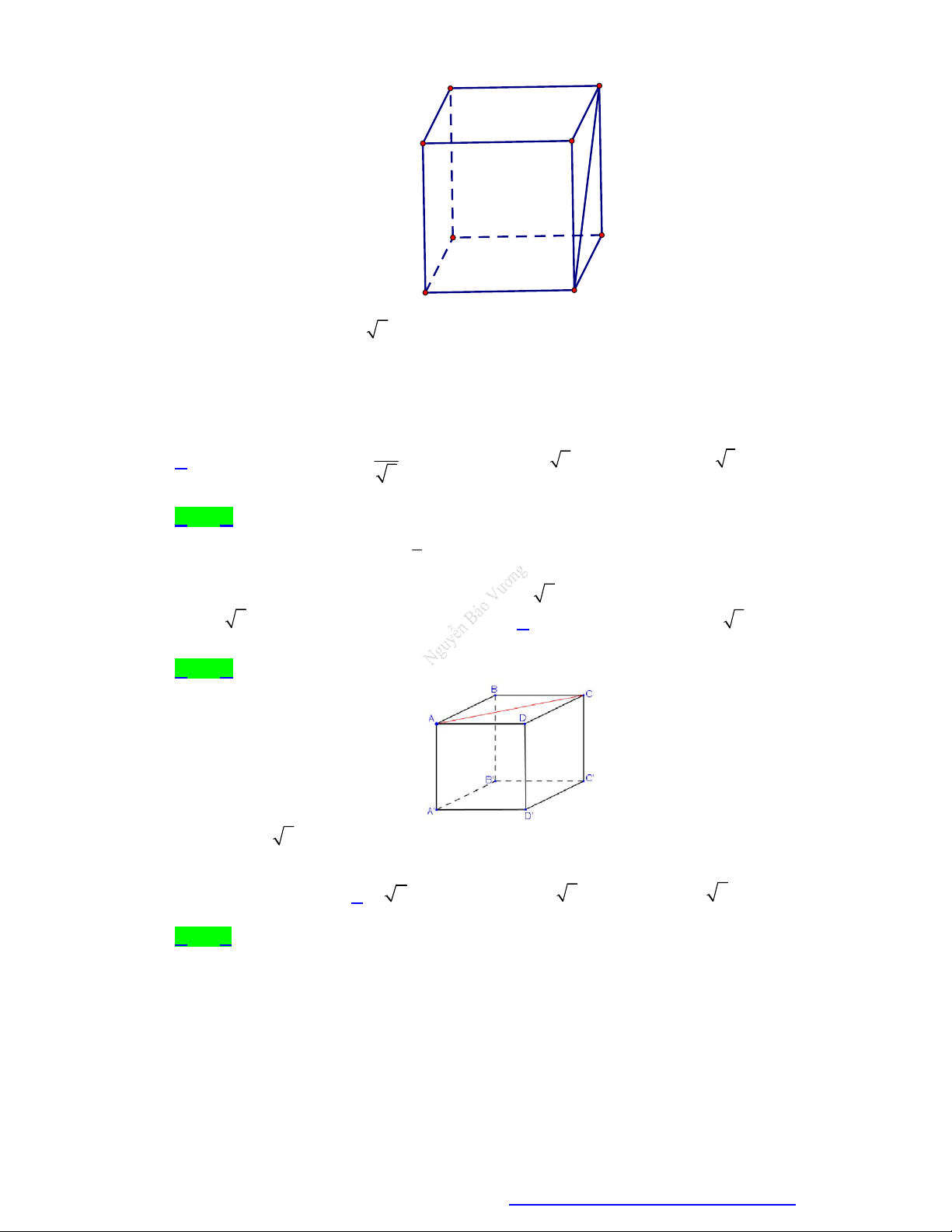
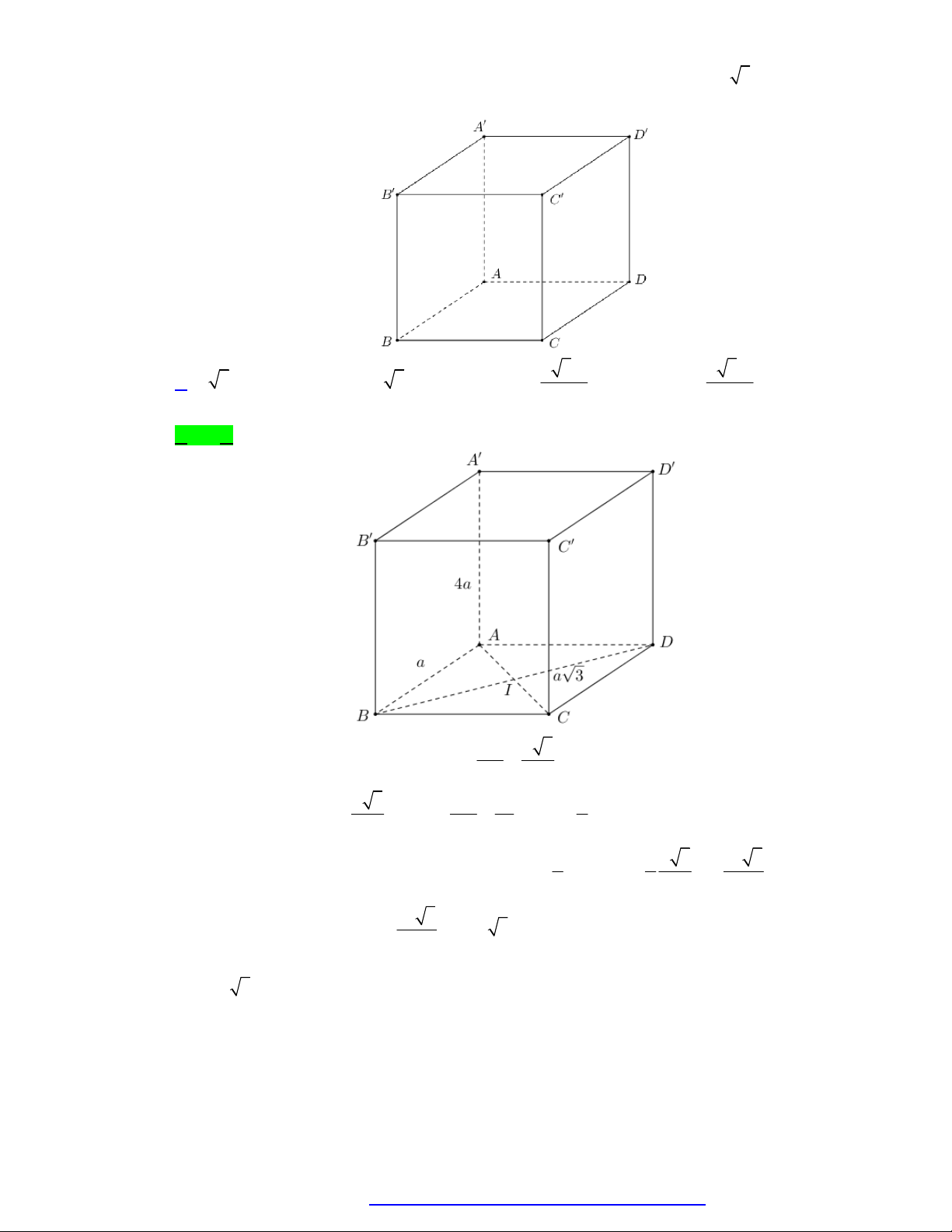
Câu 30. Cho khối lăng trụ đứng ABC . D AB CD
  có đáy ABCD là hình chữ nhật có AB a , AD a 3 ,
AA  2a . (minh họa như hình vẽ bên).
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 A' D' B' C' A D B C
Thể tích của khối lăng trụ đã cho bằng 3 a 3 3 2a 3 A. 3 2a 3 . B. 3 a 3 . C. . D. . 3 3
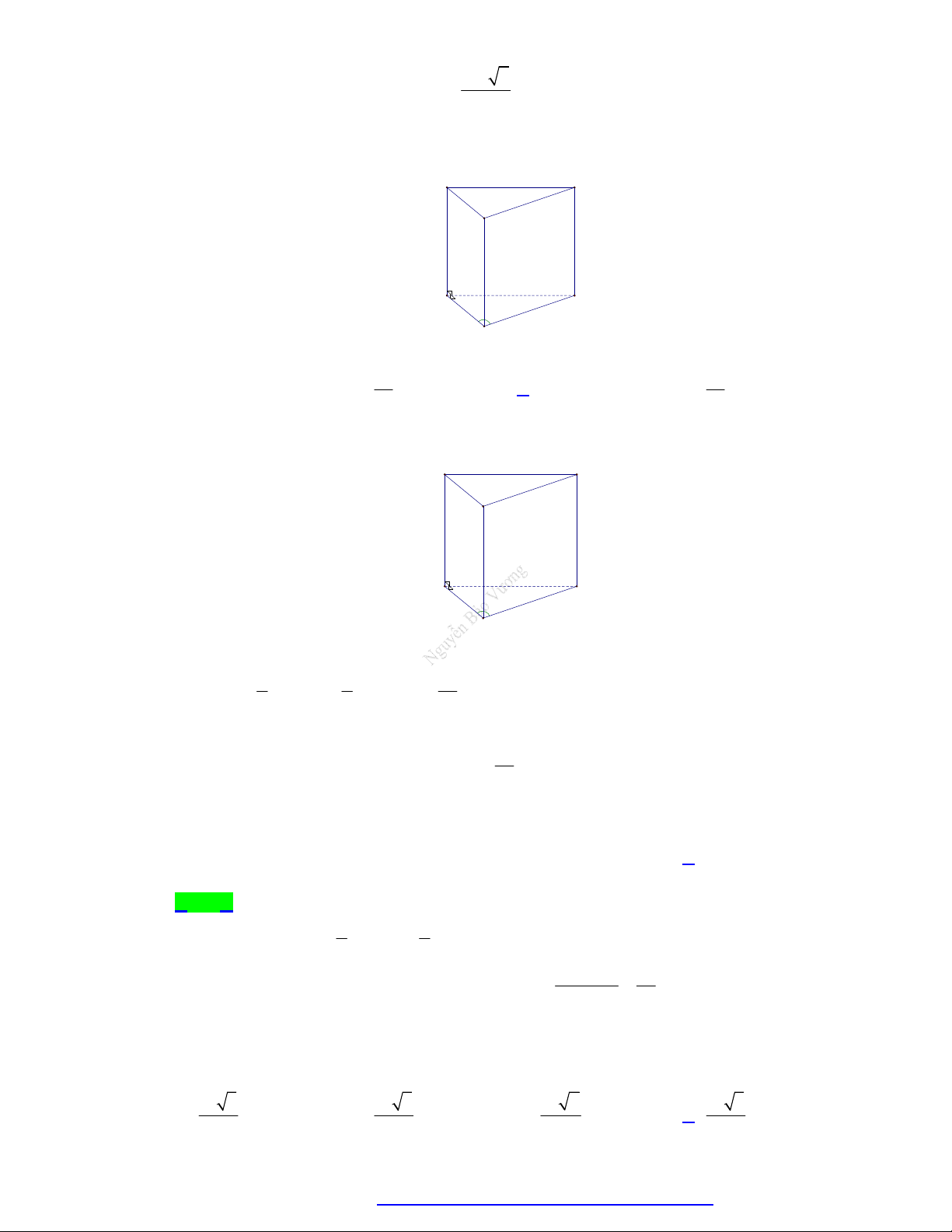
Câu 31. Cho khối lăng trụ đứng . ABCD AB CD
  có đáy ABCD là hình vuông cạnh a 2 . Biết góc giữa AB
với mặt phẳng  ABCD bằng 30 . Thể tích của khối lăng trụ đã cho bằng 3 a 6 3 2a 6 3 2a 3 A. . B. . C. . D. 3 2a 6 . 3 3 3
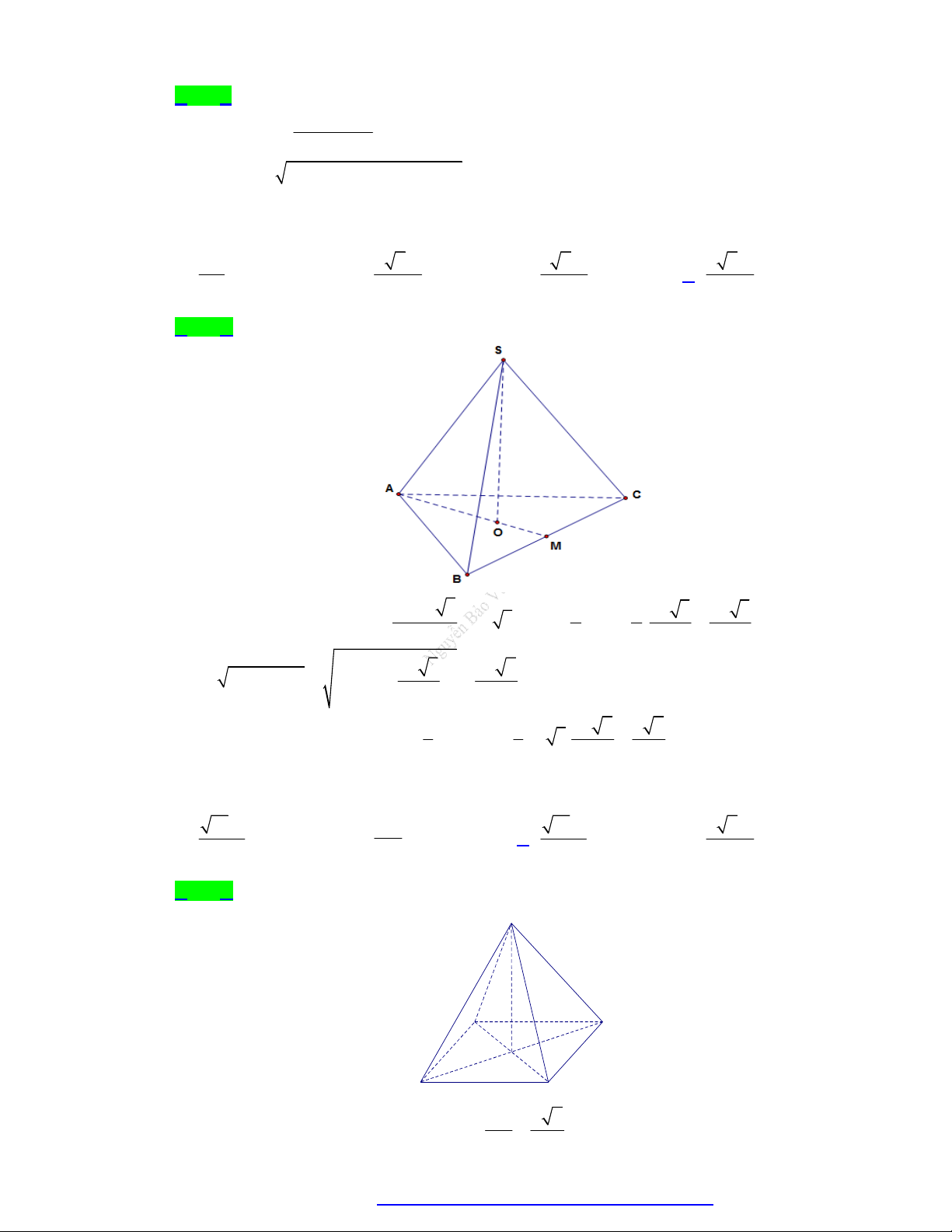
Câu 32. Cho khối lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông tại A. Biết 2AB AA  2a , 
ABC   (minh họa như hình vẽ bên). C' A' B' A C α B
Thể tích của khối lăng trụ đã cho bằng 3 a 3 a A. 3 a sin . B. . tan  . C. 3 a tan . D. tan  . 3 2
Câu 33. Tính thể tích khối lăng trụ đứng ABC .
D A' B 'C ' D ' biết ABCD là hình thoi có
AC  10cm, BD  8cm và diện tích hình chữ nhật ACC ' A' bằng 2 50cm . A. 3 400cm . B. 3 2000cm . C. 3 4000cm . D. 3 200cm .
Câu 34. Cho khối chóp S.ABC có đáy ABC là tam giác đều có cạnh bằng a , SA vuông góc với đáy và
SA  2a . Tính thể tích của khối chóp S.ABC . 3 a 3 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 2 3 6 6
Câu 35. Tính thể tích khối lăng trụ đứng AB .
C A' B 'C ' biết ABC là tam giác vuông cân tại A có
BC a 2 và AC '  a 5 . 3 2a A. 3 2a . B. 3 2a . C. . D. 3 a . 3
Câu 36. Tính thể tích khối lăng trụ đứng AB .
C A' B 'C ' biết ABC là tam giác đều cạnh a và AC '  a 5 . 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a . 4 2 6
Câu 37. Tính thể tích khối lăng trụ đứng ABC.A' B 'C ' biết AB  5cm, AC  12cm, BC  13cm và
CC '  7cm . A. 3 210cm . B. 3 70cm . C. 3 105cm . D. 3 35cm .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 38. Tính thể tích khối lăng trụ đứng ABC.A' B 'C ' biết AB  13cm, AC  14cm, BC  15cm và
CC '  10cm . A. 3 420cm . B. 3 840cm . C. 3 420cm . D. 3 140cm .
Câu 39. Cho khối chóp tam giác đều có tất cả các cạnh bằng 2a . Thể tích của khối chóp đã cho bằng 3 8a 3 4 2a 3 8 2a 3 2 2a A. . B. . C. . D. . 3 3 3 3
Câu 40. Cho khối chóp tứ giác đều có cạnh đáy bằng a , các cạnh bên bằng 2a . Thể tích của khối chóp đã cho bằng 3 14a 3 4a 3 14a 3 2 2a A. . B. . C. . D. . 3 3 6 3
Câu 41. Cho khối chóp tam giác đều có cạnh đáy bằng a , các cạnh bên bằng 2a . Thể tích của khối chóp đã cho bằng 3 33a 3 11a 3 8 2a 3 11a A. . B. . C. . D. . 12 12 3 6
Câu 42. Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy. SB  2a ;
Thể tích của khối chóp S.ABCD bằng: 3 4 2a 3 a 3 2a 3 3a A. . B. . C. . D. . 3 3 3 3
Câu 43. Cho khối chóp tam giác đều có tất cả các cạnh đều bằng 2a . Thể tích của khối chóp đó bằng: 3 2 2a 3 2a 3 2a 3 2 6a A. . B. . C. . D. . 3 3 12 9
Câu 44. Cho khối chóp tam giác đều có cạnh đáy bằng a , cạnh bên bằng 3a . Thể tích của khối chóp đó bằng 3 2 2a 3 2a 3 2a 3 2a A. . B. . C. . D. . 3 3 6 12
Câu 45. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác vuông tại  ,  ,  60o A AC a ACB . Đường
chéo BC ' của mặt bên BCC ' B
' tạo với mặt phẳng  ACC ' A
' một góc bằng 30o Tính thể tích
của khối lăng trụ theo a. 3 a 3 3 a 6 A. 3 a 3 . B. 3 a 6 . C. . D. . 3 3
Câu 46. Cho hình lăng trụ tam giác đều ABC.A' B 'C ' có AB a , góc giữa hai mặt phẳng  ABC ' và  ABC bằng 0
60 . Tính thể tích khối lăng trụ đã cho. 3 3 3 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 4 8 8
Câu 47. Cho hình lăng trụ tam giác đều ABC.AB C
  có AB a , đường thẳng AB tạo với mặt phẳng  BCC B
  một góc 30 . Tính thể tích V của khối lăng trụ đã cho. 3 a 6 3 a 6 3 3a 3 a A. V  . B. V  . C. V  . D. V  . 4 12 4 4
Câu 48. Một hình hộp đứng có đáy là hình thoi cạnh a , góc nhọn 60 và đường chéo lớn của đáy bằng
đường chéo nhỏ của hình hộp. Thể tích của khối hộp đó là 3 3a 3 6a A. 3 a . B. 3 3a . C. . D. . 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 49. Cho một tấm nhôm hình chữ nhật ABCD có AD  60cm , AB  40cm . Ta gập tấm nhôm theo hai
cạnh MN và PQ vào phía trong cho đến khi AB và DC trùng nhau như hình vẽ bên để dược
một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể tích lớn nhất bằng B M Q C M Q B, C A x N P x D N P 60cm , A D A. 4000 3  3 cm B. 2000 3  3 cm C. 400 3  3 cm D. 4000 2  3 cm
Câu 50. Cho lăng trụ đứng ABC.AB C
  có đáy là tam giác đều cạnh a và AB vuông góc với BC . Thể
tích của lăng trụ đã cho là. 3 a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 12 4 8 24
Câu 51. Cho hình lăng trụ tam giác đều ABC.A BC
  . Biết khoảng cách từ điểm C đến mặt phẳng 1
ABC bằng a , góc giữa hai mặt phẳng  ABC và BCC B
  bằng  với cos  (tham 3
khảo hình dưới đây). Thể tích khối lăng trụ ABC.A BC   bằng 3 9a 15 3 3a 15 3 9a 15 3 3a 15 A. . B. . C. . D. . 20 20 10 10
DẠNG CÂU HỎI VẬN DỤNG – VẬN DỤNG CAO
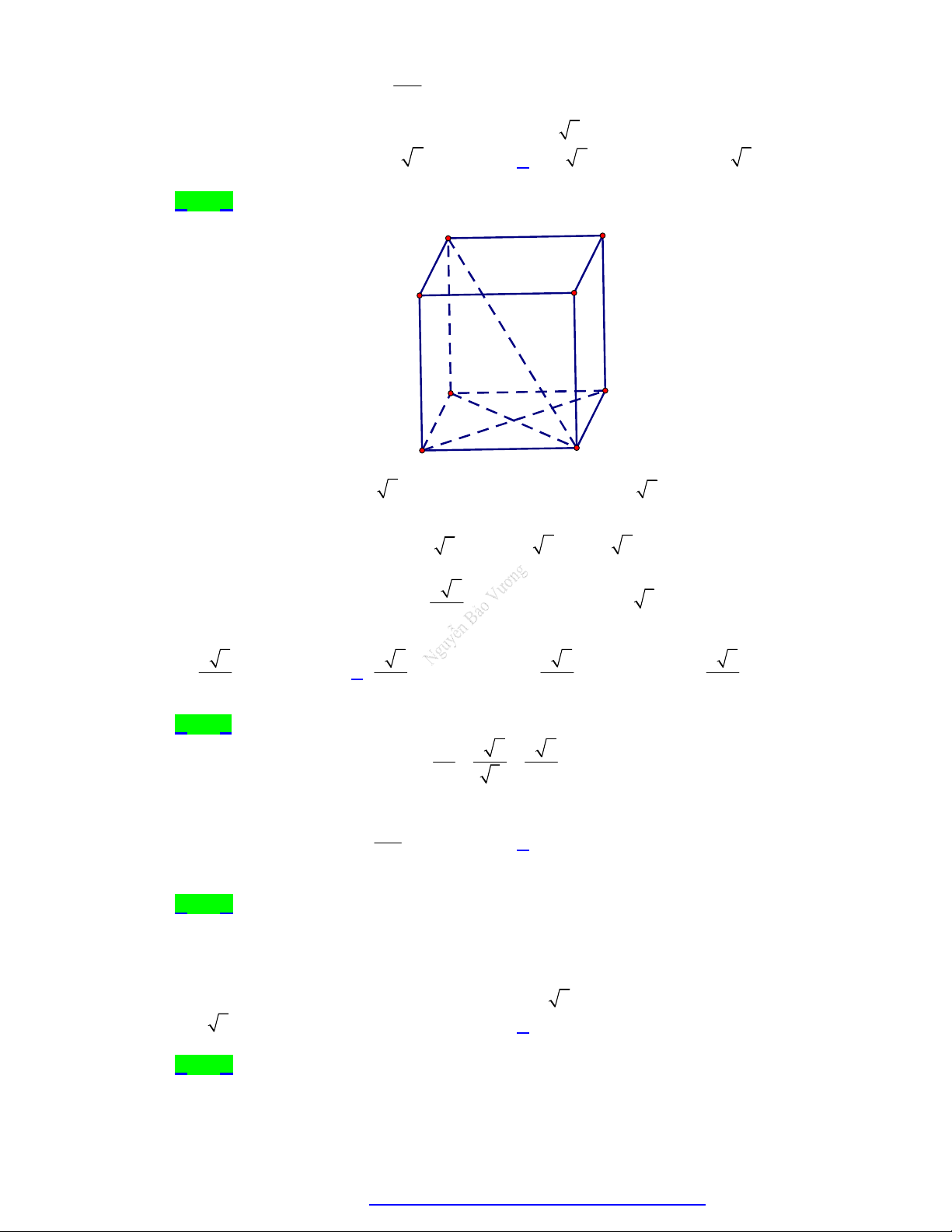
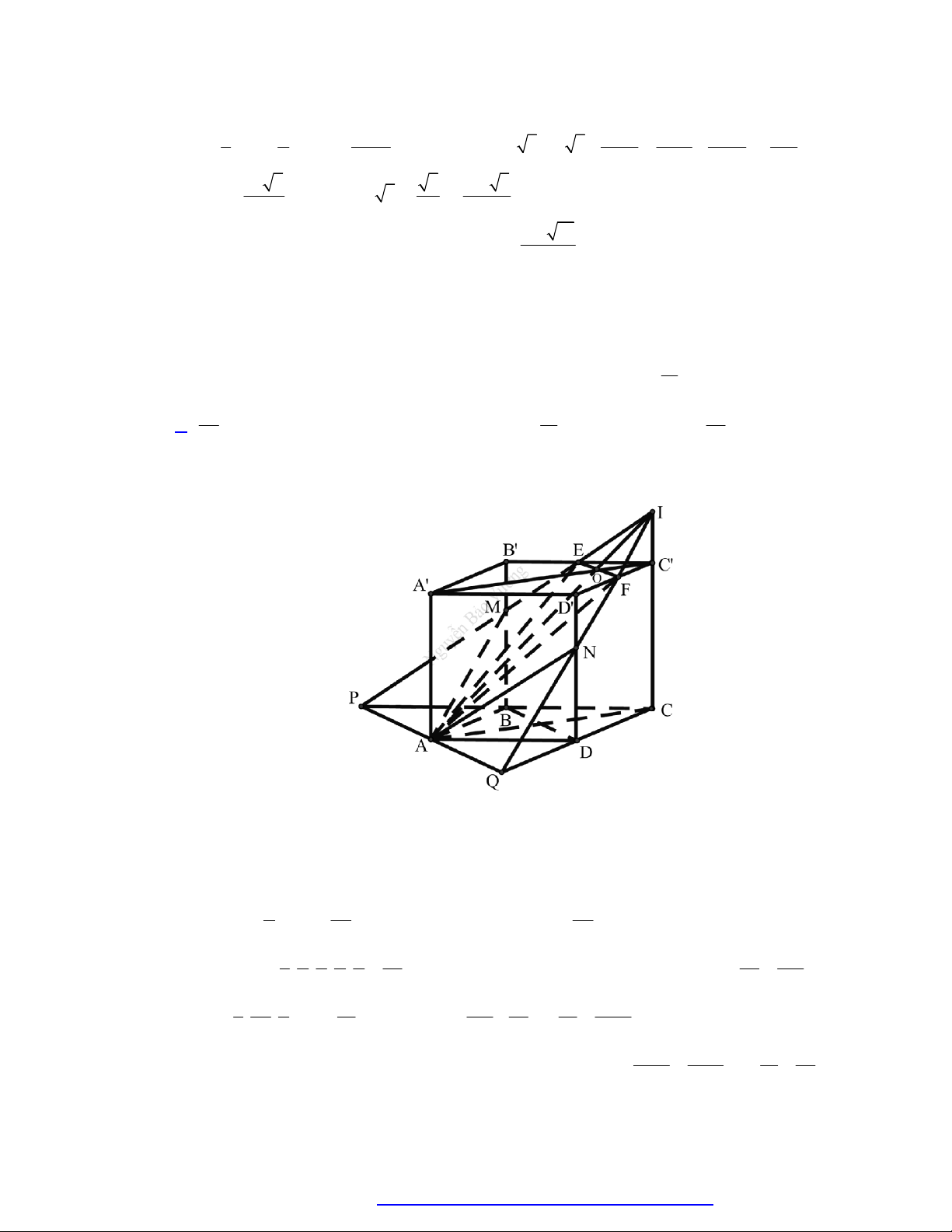
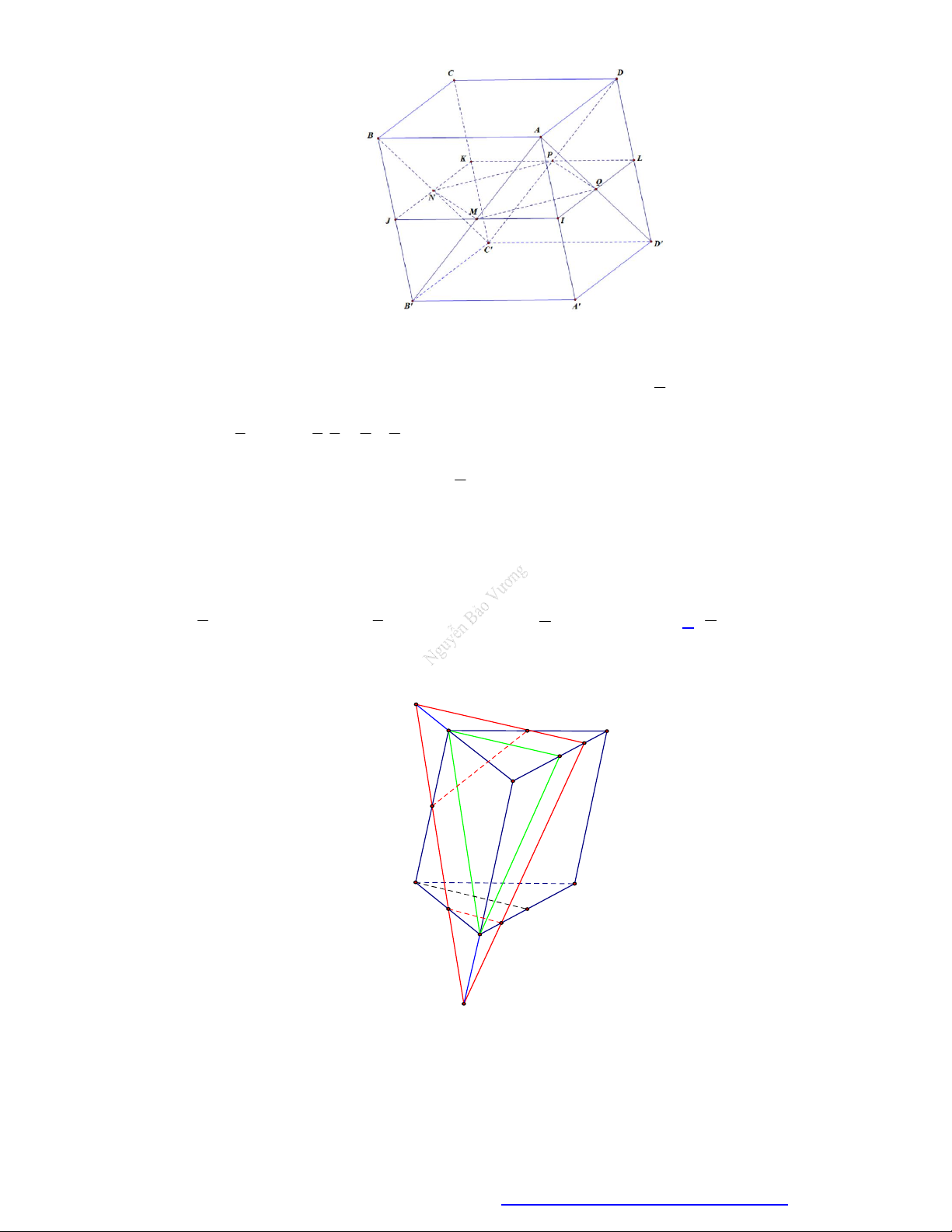
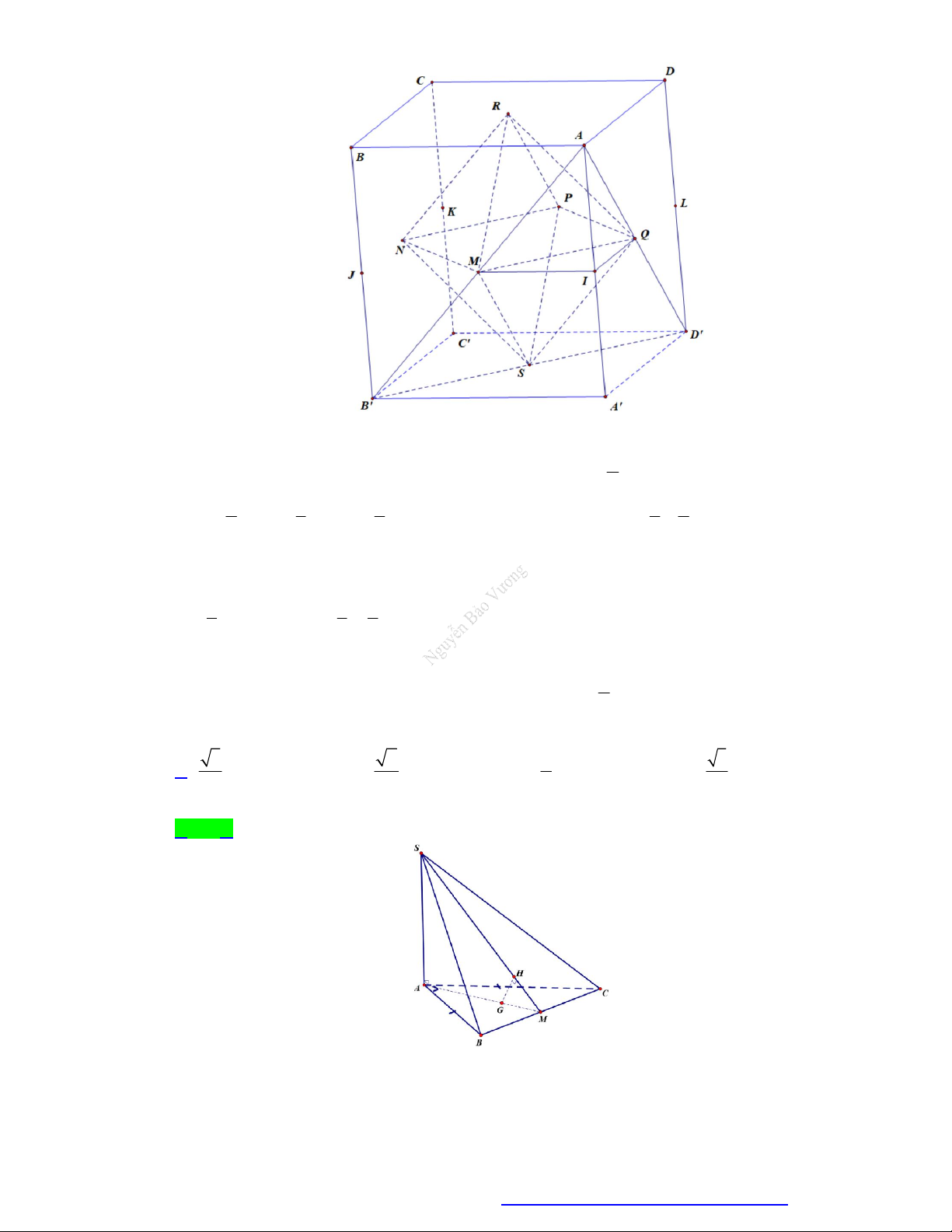
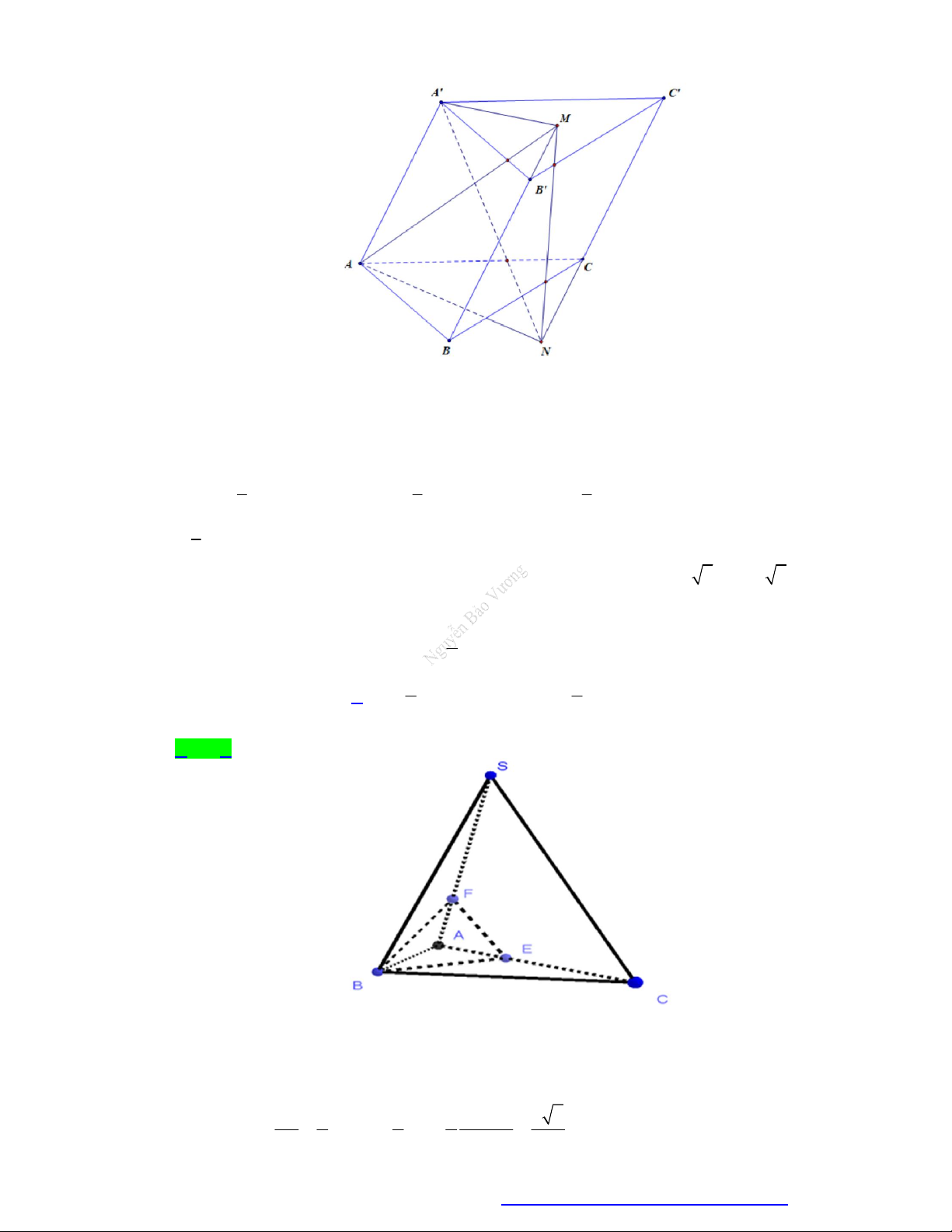
Câu 52. Cho khối lập phương AB CD. A ' B 'C ' D ' cạnh a . Các điểm E, F lần lượt là trung điểm
của C ' B ' và C ' D ' . Mặt phẳng  AEF  cắt khối lập phương đã cho thành 2 phần, gọi V là thể 1 V
tích khối chứa điểm A ' và V là thể tích khối chứa điểm C ' . Khi đó 1 là: 2 V2 25 8 17 A. . B. 1. C. . D. . 47 17 25
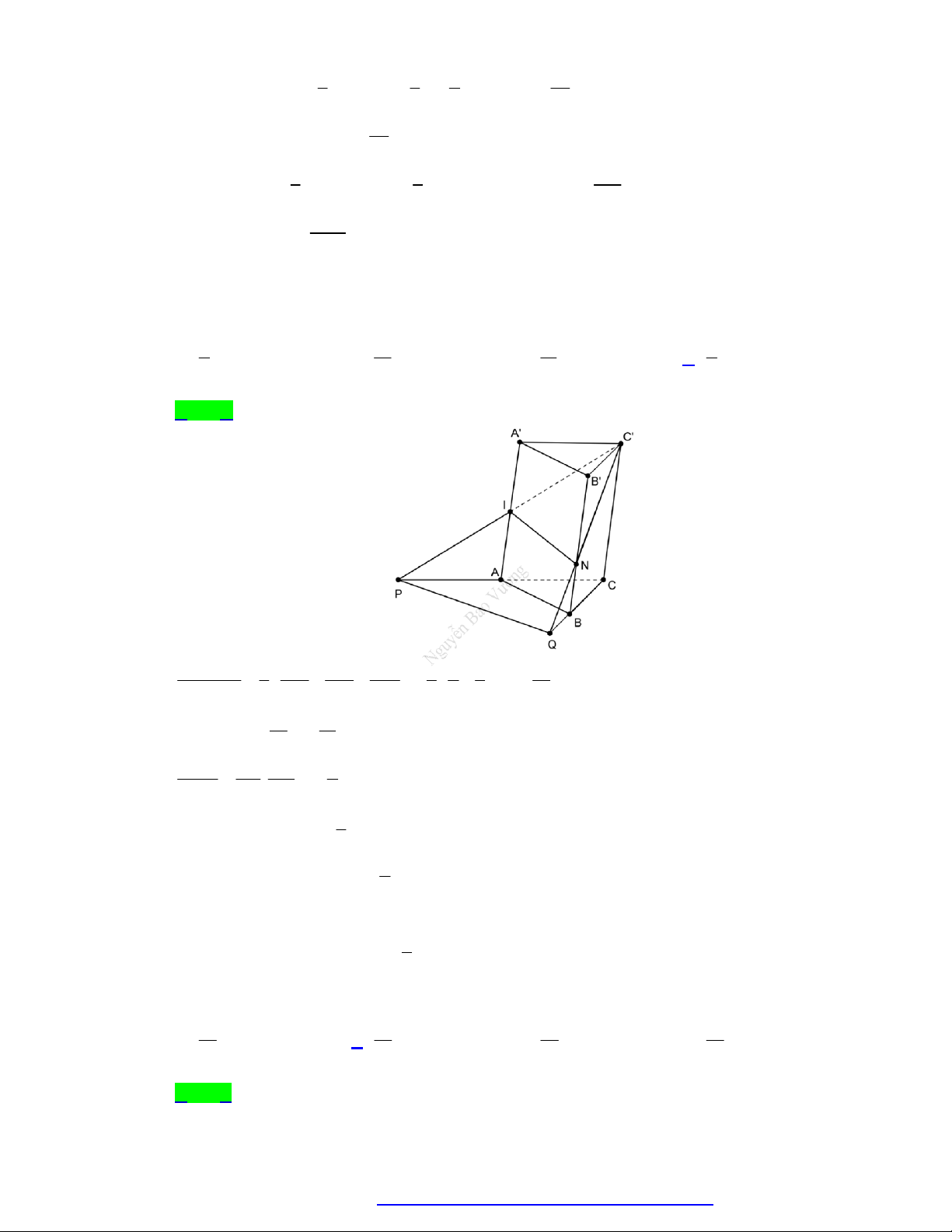
Câu 53. Cho khối lăng trụ ABC.AB C
  . Gọi E , F lần lượt là trung điểm của các đoạn thẳng CC và
BB . Đường thẳng A 'E cắt đường thẳng AC tại K , đường thẳng A 'F cắt đường thẳng AB tại
H . Tính tỉ số thể tích khối đa diện lồi BFHCEK và khối chóp A 'ABC . 1 1 A. . B. . C. 2 . D. 1. 3 2
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
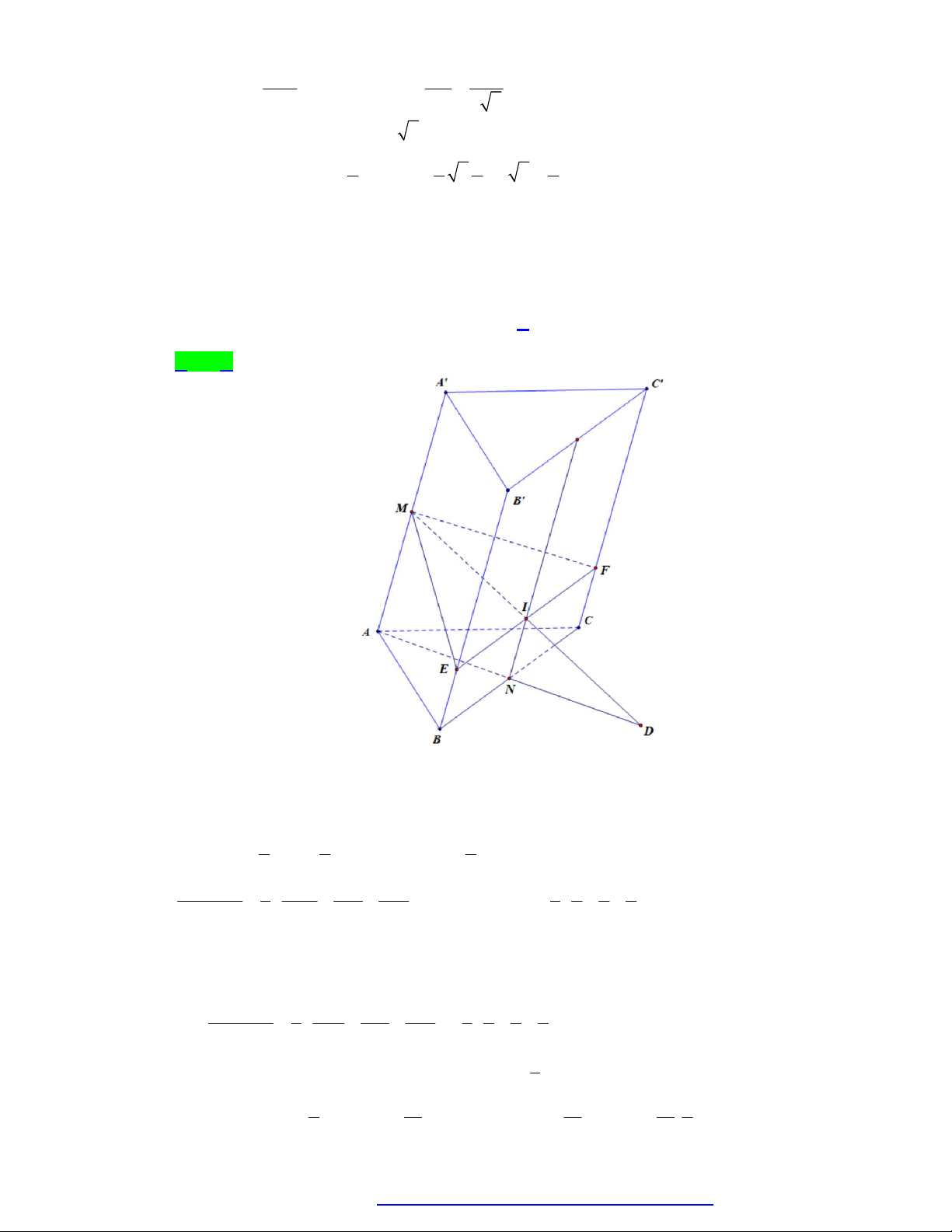
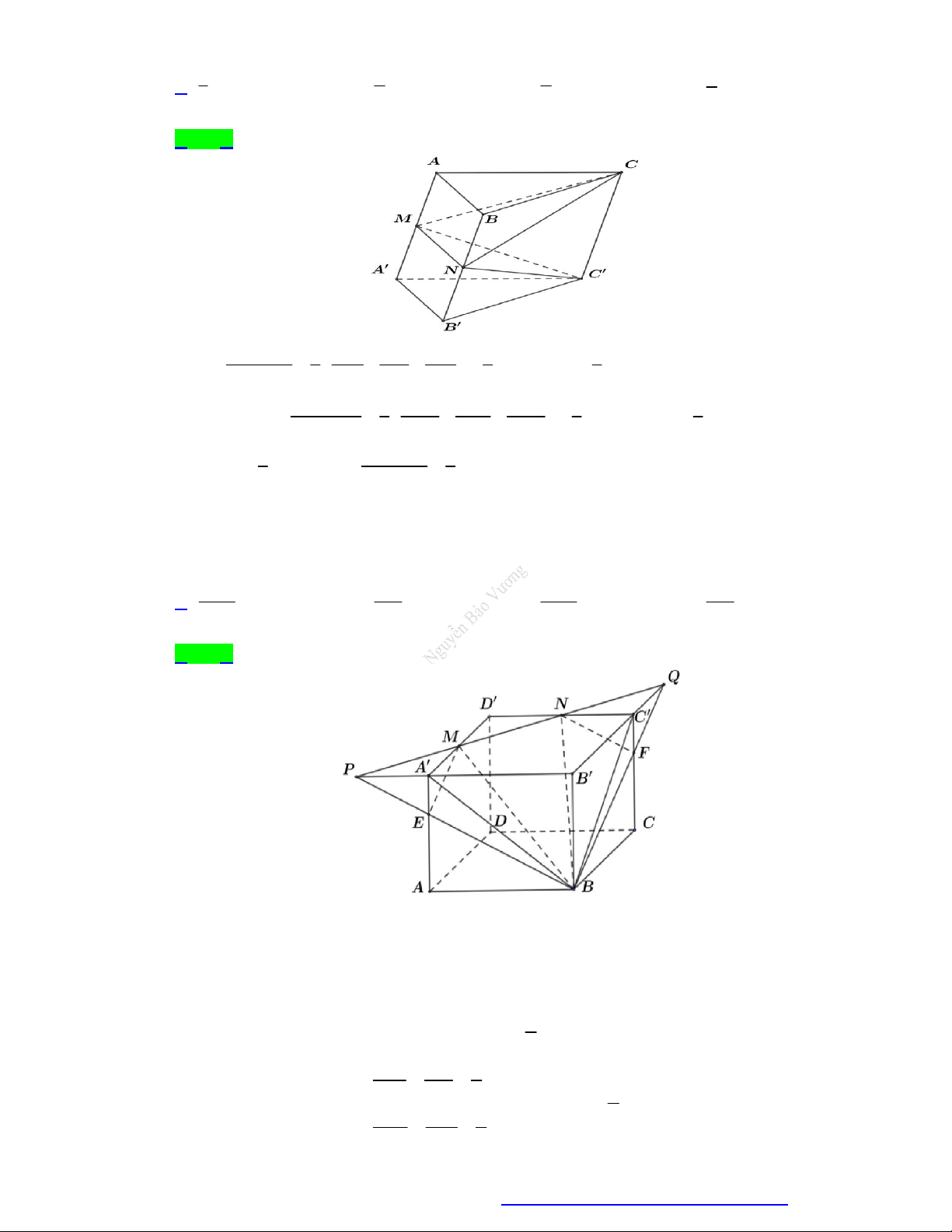
Câu 54. Cho hình hộp ABC . D A BCD
  có M , N, P lần lượt là trung điểm ba cạnh AB , BB và D . D
Mặt phẳng  MNP cắt đường thẳng AA tại I. Biết thể tích khối tứ diện IANP là V. Thể tích
khối hộp đã cho ABC . D AB CD   bằng A. 2V . B. 4V . C. 6V . D. 12V.
Câu 55. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB a ,   0
SBA SCA  90 , góc 0
giữa hai mặt phẳng  SAB và SAC  bằng 60 . Thể tích của khối đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6
Câu 56. Cho hình hộp ABC . D A BCD
  có chiều cao bằng 8 và diện tích đáy bằng 9 . Gọi M, N, P và Q
lần lượt là tâm của các mặt bên ABB A  , BCC B  , CDD C
  và DAAD . Thể tích của khối đa diện
lồi có các đỉnh là các điểm , A , B C, ,
D M , N, P và Q bằng A. 27 . B. 30 . C. 18 . D. 36 .
Câu 57. Cho khối lăng trụ AB . C A BC
  có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AC và B C
 . Gọi (P) là mặt phẳng qua M và song song với mặt phẳng (A NC
) . Mặt phẳng (P) chia
khối lăng trụ ABC.A BC
  thành hai khối đa diện, gọi (H) là khối đa diện chứa đỉnh A . Thể tích của
khối đa diện (H) bằng 3 1 2 1 A. . B. . C. . D. . 5 3 5 2 a 3 
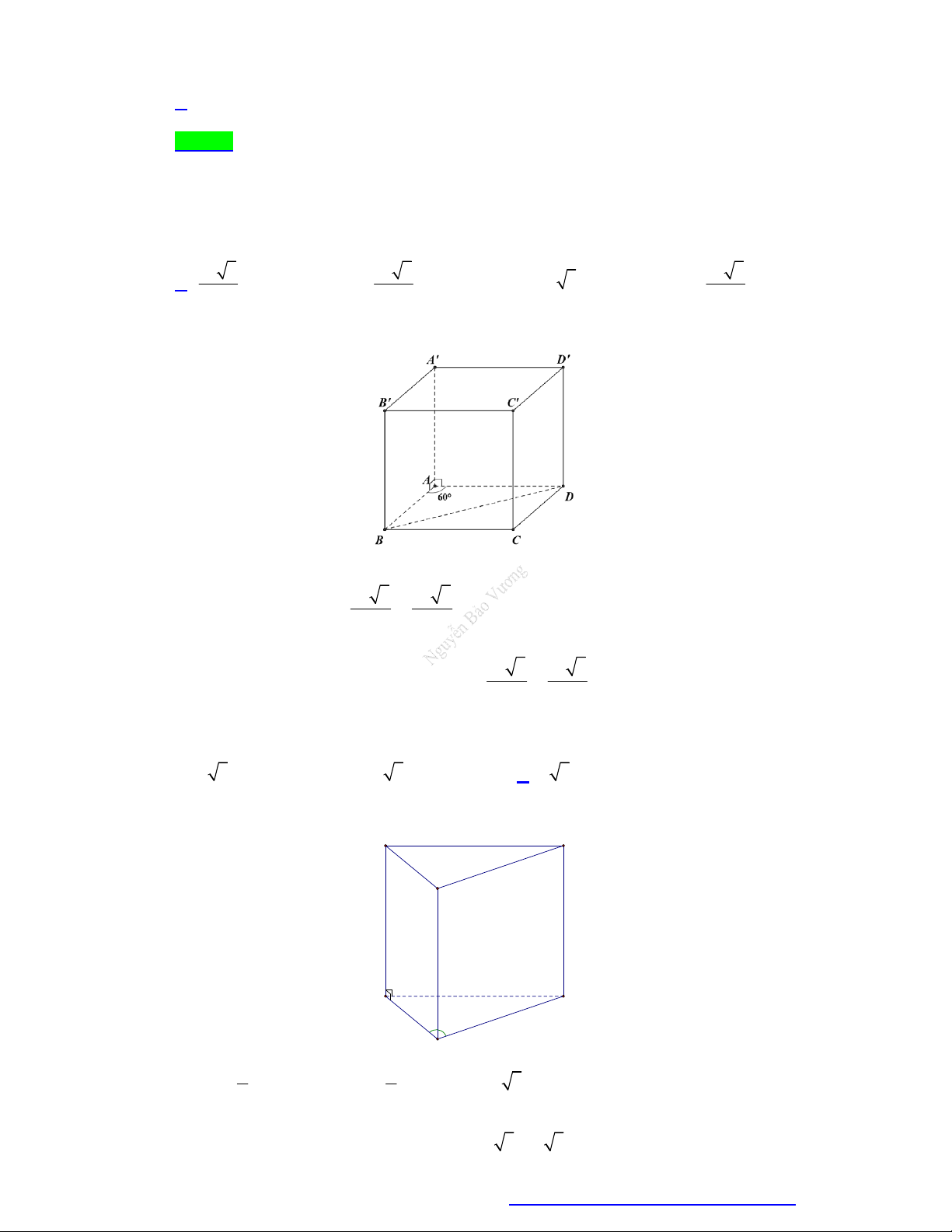
Câu 58. Cho hình hộp đứng ABC . D AB CD
  có AB AD a , AA' 
, BAD  60 . Gọi M , N lần 2
lượt là trung điểm AD , AB . Tính thể tích của khối đa diện ABDMN . 3 3a 3 3 3a 3 9a 3 3a A. . B. . C. . D. . 16 8 16 8
Câu 59. Cho hình hộp ABC . D A BCD
  có chiều cao bằng 8 và diện tích đáy bằng 9. Gọi M , N, P,Q, R và
S lần lượt là tâm của các mặt ABB A  , BCC B  , CDD C  ,
DAAD , ABCD và A BCD   . Thể tích
của khối đa diện lồi có các đỉnh là các điểm M , N , P, Q, R và S bằng 1 A. 3 . B. 24 . C. 9 . D. . 3
Câu 60. Cho hình chóp S.ABC có SA   ABC  , đáy là tam giác vuông cân tại A , G là trọng tâm ABC, a
khoảng cách từ G đến mặt phẳng SBC bằng
. Gọi  là góc giữa mặt phẳng SBC và 3
ABC . Khi thể tích khối chóp S.ABC nhỏ nhất thì cos bằng 3 2 2 3 A. . B. . C. . D. . 3 2 3 2
Câu 61. Cho lăng trụ ABC.AB C
  có chiều cao bằng 8 và diện tích đáy bằng 9 . Gọi M , N là hai điểm    
thỏa mãn BM k.BBk  
1 , CN l.CC l  0 . Thể tích của tứ diện AAMN bằng l k 1 l k 1 A. . B. 24 . C. 72 . D. . 72 210
Câu 62. Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B với AB  6 , BC  3 , SC  3 và
mặt phẳng SAC  vuông góc với mặt đáy  ABC  . Biết hai mặt phẳng SAB và SAC  tạo với 3
nhau góc  thỏa mãn tan 
. Thể tích khối chóp S.ABC bằng 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 4 8 A. V  8. B. V  . C. V  . D. V  4. 3 3
Câu 63. Cho lăng trụ ABC.AB C
  có chiều cao bằng 8 và diện tích đáy bằng 9 . Gọi M , N lần lượt là  
trung điểm của AA ,
BC . D là điểm thỏa mãn AD  2AN . Mặt phẳng  P qua M , D và song
song với BC cắt BB ,
CC lần lượt tại E, F . Thể tích của khối đa diện lồi có các đỉnh là các
điểm A , B , C ,
M , E và F bằng A. 36 . B. 24 . C. 48 . D. 39 .
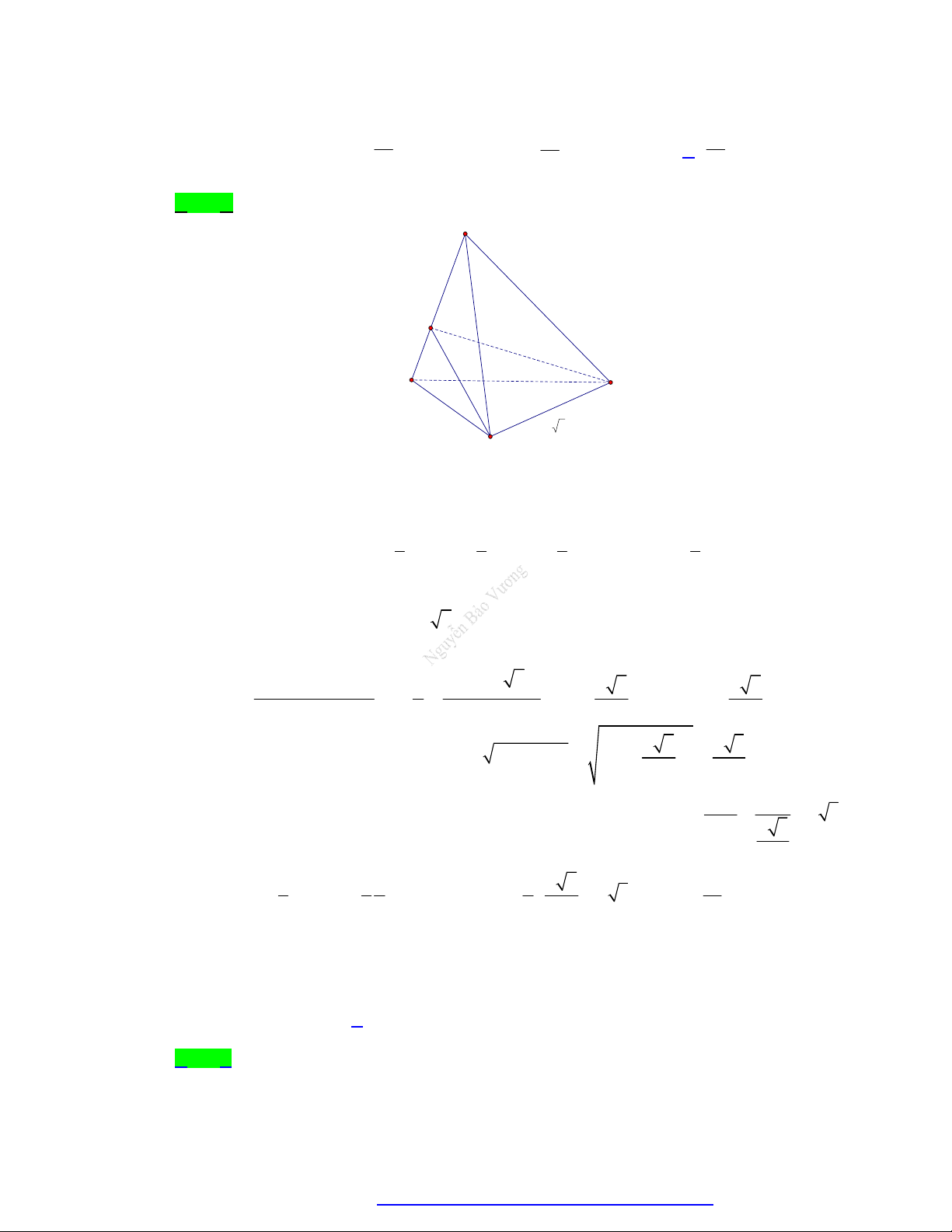
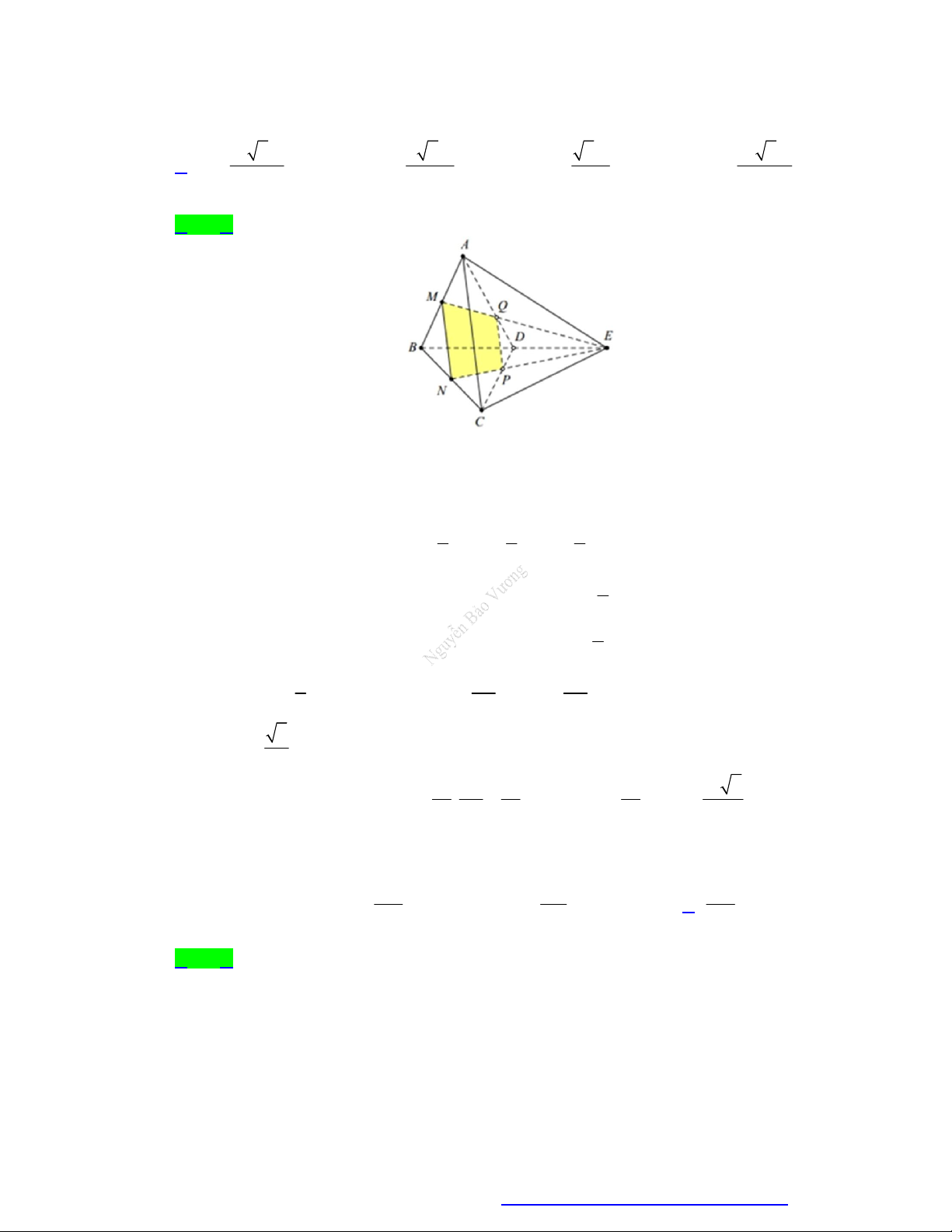
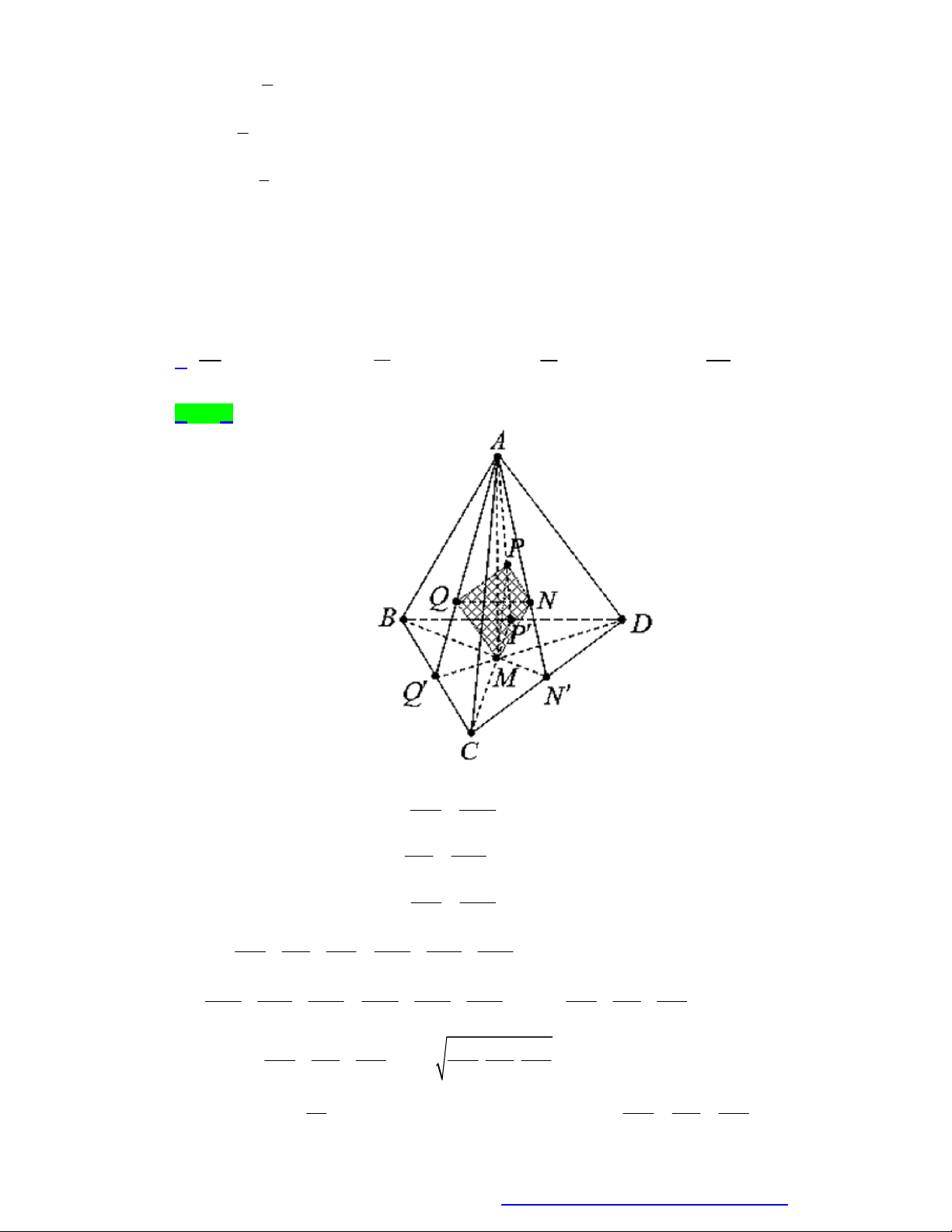
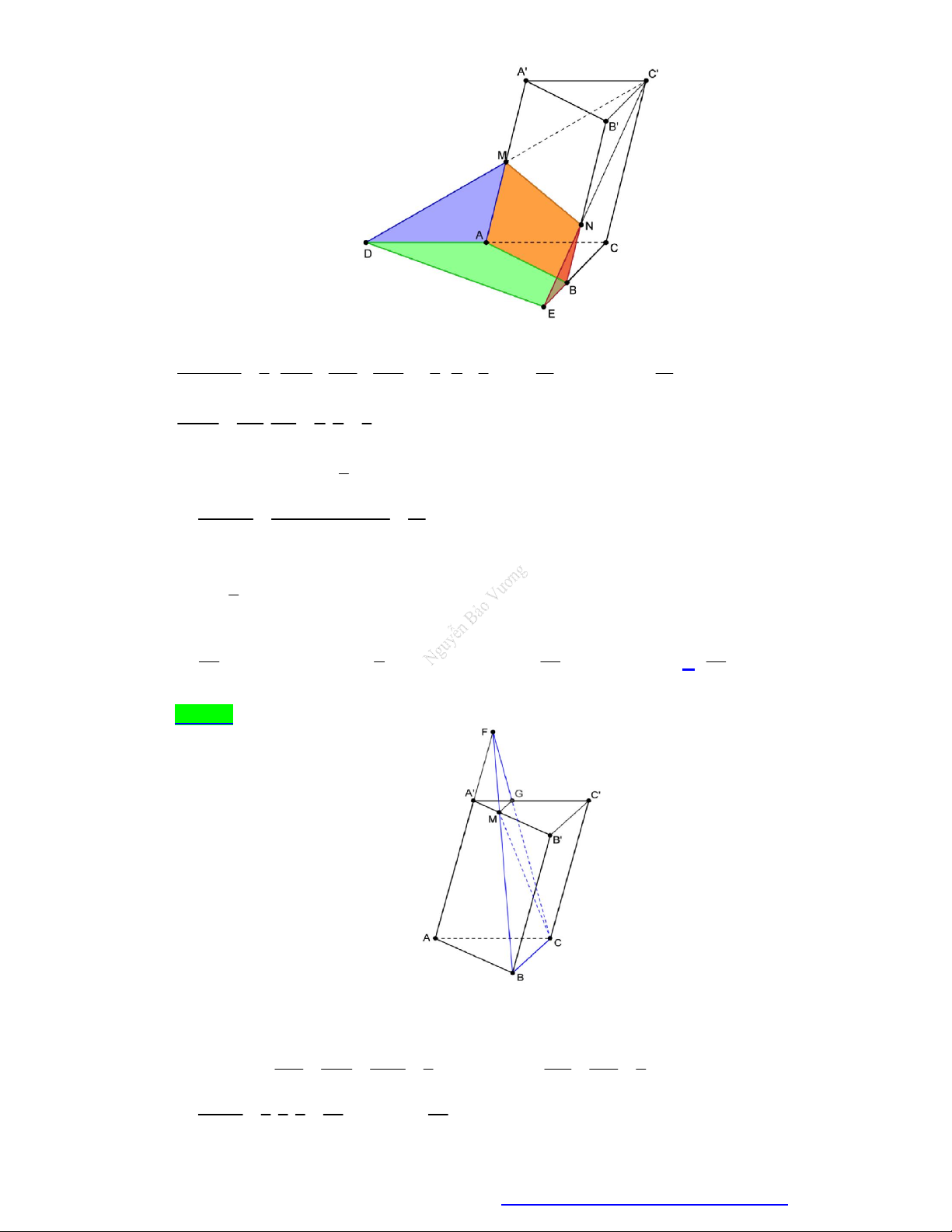
Câu 64. Cho tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm của các cạnh A , B BC
và E là điểm đối xứng với B qua D . Mặt phẳng  MNE chia khối tứ diện ABCD thành hai
khối đa diện, trong đó khối chứa điểm A có thể tích V . Thể tích V bằng 3 11 2a 3 7 2a 3 2a 3 13 2a A. V  . B. V  . C. V  . D. V  . 216 216 8 216
Câu 65. Cho hình chóp SABC có diện tích đáy bằng 10 , chiều cao bằng 9 . Gọi M , N , P lần lượt là trọng
tâm của tam giác SAB, SBC , SCA . Thể tích của khối đa diện ABCMNP . 175 560 160 A. 60 B. . C. . D. . 3 9 9
Câu 66. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Biết AB SB, AC SC , góc giữa
hai mặt phẳng SAB và SAC bằng 0
60 . Thể tích khối chóp S.ABC bằng 3 a 2 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 24 36 6 36
Câu 67. Cho khối tứ diện ABCD có thể tích V . Gọi G , G , G , G là trọng tâm của bốn mặt của tứ diện 1 2 3 4
ABCD . Thể tích khối tứ diện G G G G là: 1 2 3 4 V V V V A. . B. . C. . D. . 27 18 108 81
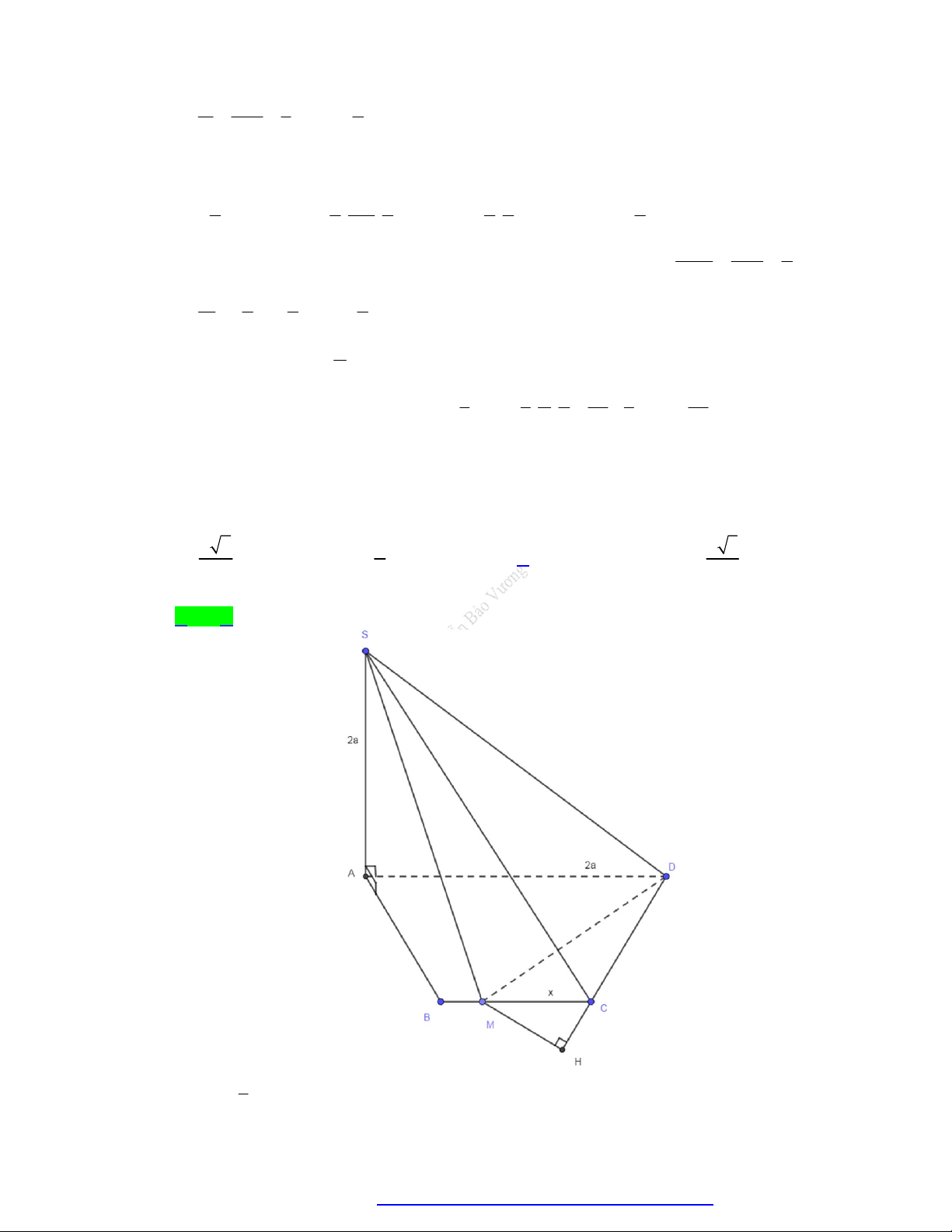
Câu 68. Cho khối chóp S.ABCD có đáy là hình thang cân  AD BC , khoảng cách giữa AD và BC bằng
a , BC a ,
SA   ABCD , SA  2a . Trên cạnh BC lấy điểm M sao cho
MC x 0  x a . Thể tích khối chóp S.CDM lớn nhất khi độ dài MC bằng a 2 a a 3 A. . B. . C. . a D. . 2 2 2
Câu 69. Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường thẳng
qua M và song song với AB , AC , AD lần lượt cắt các mặt phẳng  ACD ,  ABD ,  ABC tại
N , P , Q . Giá trị lớn nhất của khối MNPQ là V V V 2V A. . B. . C. . D. . 27 18 81 27
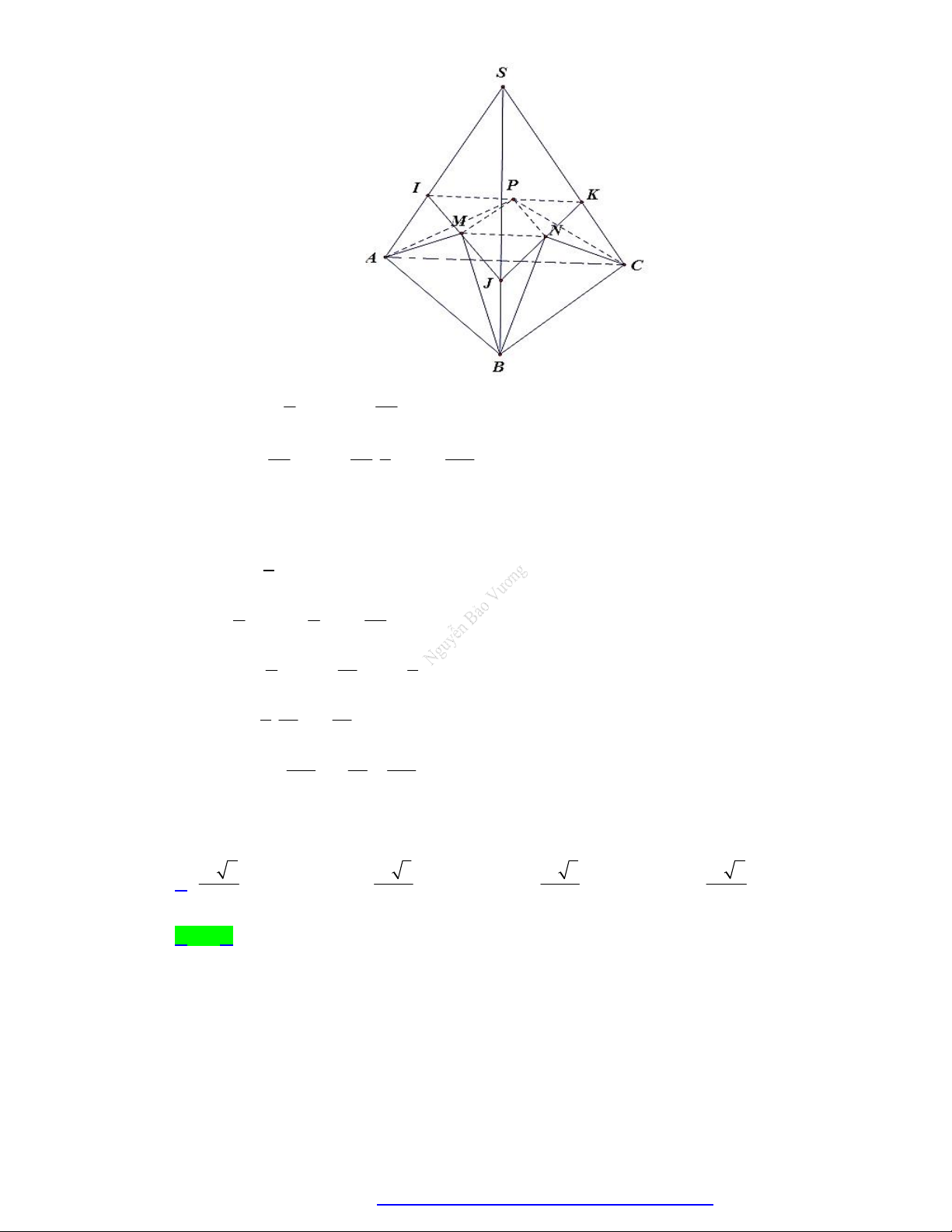
Câu 70. Cho khối lăng trụ AB . C A
B C có thể tích bằng 2 . Gọi M là trung điểm của đoạn thẳng  AA và
N là điểm nằm trên cạnh BB ' sao cho BN  2B ' N . Đường thẳng CM cắt đường thẳng C  A tại
P , đường thẳng CN cắt đường thẳng C 
B tại Q . Thể tích của khối đa diện lồi 
A MPBNQ bằng 7 5 2 13 A. . B. . C. . D. . 9 9 3 9
Câu 71. Cho khối lăng trụ AB . C A
B C. Gọi M , N lần lượt là trung điểm của đoạn thẳng A A và BB ' .
Tính tỉ số thể tích của khối tứ diện CMNC ' với khối lăng trụ đã cho. 1 1 2 3 A. . B. . C. . D. . 3 2 3 4
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
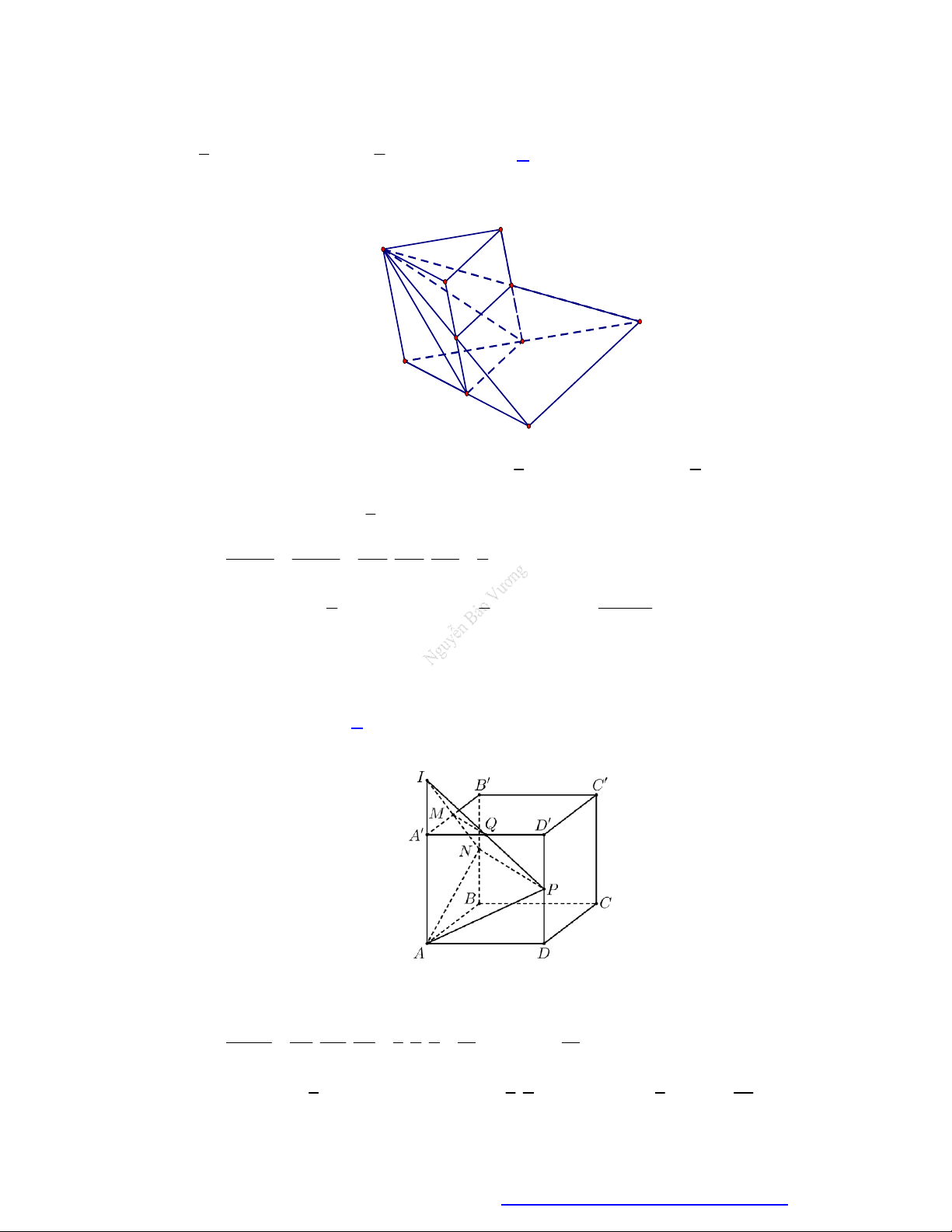
Câu 72. Cho khối lập phương ABC . D A
B CD ' cạnh a . Gọi M , N lần lượt là trung điểm của đoạn thẳng
A ' D ' và C ' D ' . Mặt phẳng  BMN  chia khối lập phương thành hai phần, gọi V là thể
tích phần chứa đỉnh B ' . Tính V ? 3 25a 3 7a 3 25a 3 7a A. . B. . C. . D. . 72 24 24 72
Câu 73. Cho khối lăng trụ ABC.AB C
  có thể tích bằng 6. Gọi điểm I là trung điểm AA và điểm N
thuộc cạnh BB sao cho B 'N  2BN .Đường thẳng C ' I cắt đường thẳng CA tại P , đường thẳng C N
 cắt đường thẳng CB tại Q . Tính thể tích khối đa diện lồi AIPBNQ 7 11 11 7 A. . B. . C. . D. . 9 18 9 3
Câu 74. Cho khối lăng trụ ABC.AB C
  có thể tích bằng V . Gọi điểm M là trung điểm AA và điểm N 1
thuộc cạnh BB sao cho BN BB ' .Đường thẳng C M
cắt đường thẳng CA tại D , đường 3 thẳng C N
 cắt đường thẳng CB tại E . Tỉ số thể tích khối đa diện lồi AMDBNE và khối lăng trụ
ABC.AB C   là 13 7 7 8 A. . B. . C. . D. . 18 18 12 15
Câu 75. Cho khối lăng trụ ABC.AB C
  có thể tích bằng 1. Điểm M là thuộc cạnh A' B ' sao cho 1 AM A B
  . Mặt phẳng  BCM  cắt đường thẳng AA tại F , và cắt đường thẳng AC tại G . 3
Thể tích khối chóp FAMG bằng 5 1 5 1 A. . B. . C. . D. . 24 6 36 54
Câu 76. Cho lăng trụ tam giác AB . C A BC
  có đáy là tam giác đều cạnh a , điểm A cách đều ba điểm A , 2 a 3
B , C và diện tích tam giác ABA bằng
. Thể tích khối đa diện A BCBC bằng 6 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 24 8 12
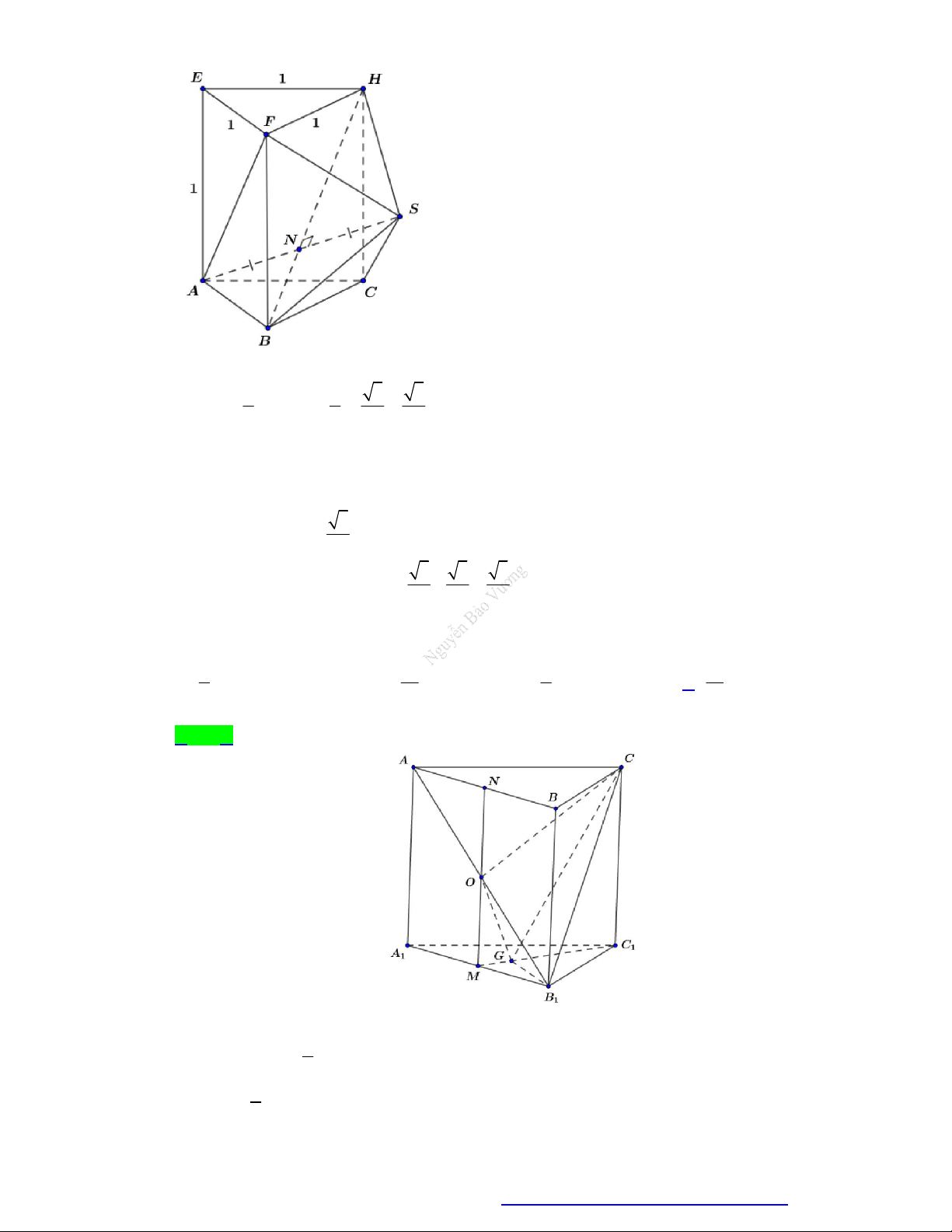
Câu 77. Cho lăng trụ đều AB .
C EFH có tất cả các cạnh bằng 1. Gọi S là điểm đối xứng của A qua BH.
Thể tích khối đa diện AB . C SFH bằng 1 3 3 1 A. . B. . C. . D. . 2 3 6 6
Câu 78. Cho khối lăng trụ ABC.A B C có thể tích bằng 30. Gọi O là tâm của hình bình hành ABB A M 1 1 1 1 1
và G là trọng tâm tam giác A B C . Tính thể tích khối tứ diện COGB . 1 1 1 1 7 16 5 10 A. . B. k  . C. . D. . 3 81 2 3
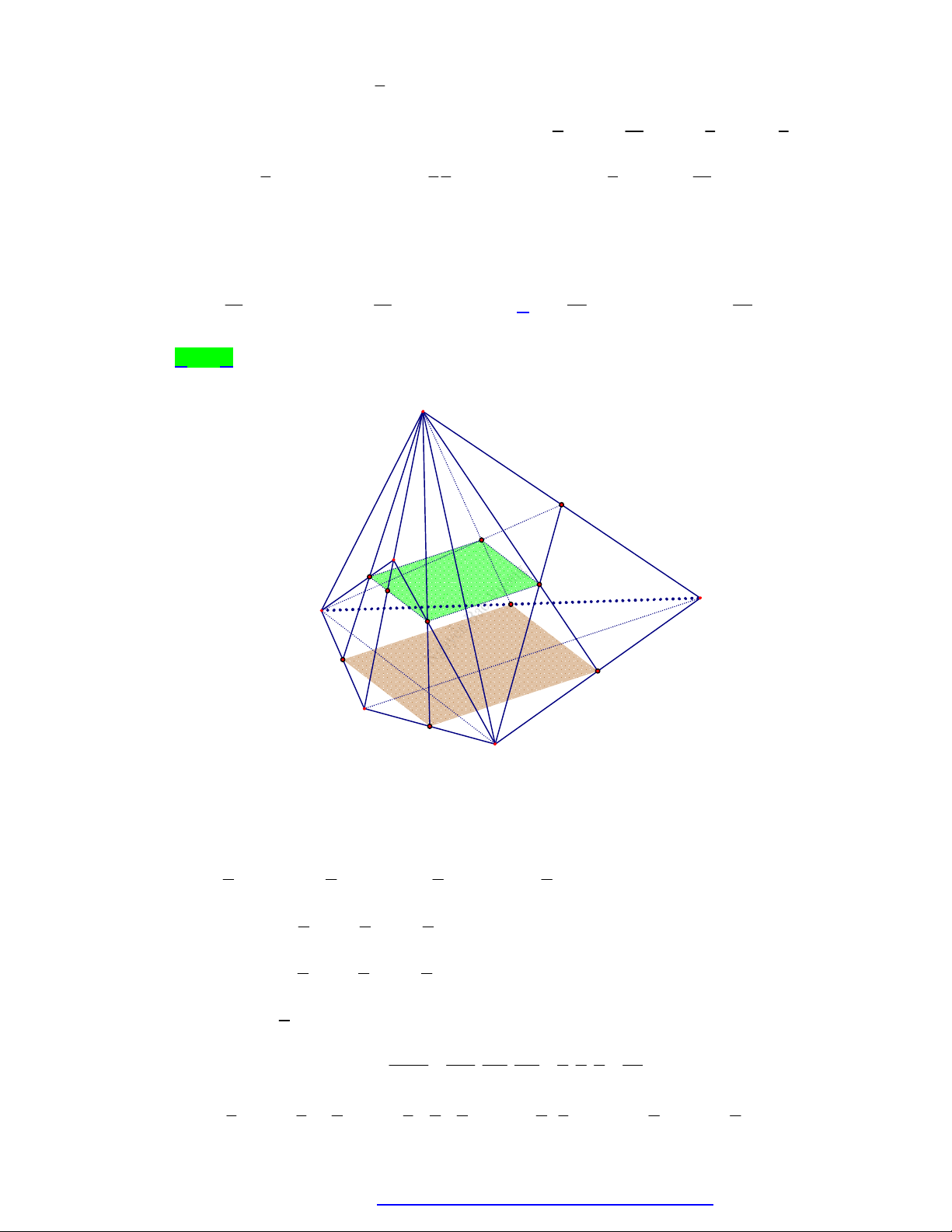
Câu 79. Cho khối chóp S.ABCD có thể tích bằng V . Gọi M , N , P , Q lần lượt là trọng tâm các mặt
bên SAB , SBC  ,  SCD , SDA . Gọi k là tỉ số thể tích của khối chóp S.MNPQ và phần còn lại là. Khi đó: 16 15 4 4 A. k V . B. k V . C. k V . D. k V . 81 4 23 23
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Vấn đề 8 THỂ TÍCH KHỐI ĐA DIỆN
THỂ TÍCH KHỐI ĐA DIỆN 1
Thể tích khối chóp V
  S . chiÒu cao . chãp đ¸ y 3 c
Thể tích khối lăng trụ V
S . chiÒu cao . l¨ng trô đ¸ y b a
Thể tích khối lập phương 3
V a với a là cạnh.
Thể tích khối hộp chữ nhật V abc với , a ,
b c lần lượt là chiều dài, chiều rộng và chiều cao.
Xác định diện tích đáy: 1 1
a b cS
ah ab sinC  (
p p a)(p b)(b c) , với p   ABC 2 a a 2 2 (c¹nh)   3 S  1
(tÝch hai c¹nh gãc vu«ng)   S   tam gi¸c vu«ng 2 tam gi¸c ®Òu 4 2 
(®¸y lín  ®¸y bÐ)chiÒu cao S  (c¹nh huyÒn)   S   tam gi¸c vu«ng c©n 4 H×nh thang 2  S
 dµiréng .  S  2 (c¹nh) . H×nh ch÷ nhËt H×nh vu«ng
Xác định chiều cao:
Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam giác
chứa trong mặt bên vuông góc với đáy.
Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai mặt
bên cùng vuông góc với mặt phẳng đáy.
Hình chóp có các cạnh bên bằng nhau: Chân đường cao của hình chóp là tâm đường tròn ngoại tiếp đa giác đáy.
Cần nhớ: Tỉ số thể tích khối chóp có đáy là tam giác S
Cho khối chóp S.ABC , trên các đoạn thẳng S ,
A SB, SC lần lượt lấy các điểm A ,
B , C khác S. Khi đó ta luôn có tỉ số thể tích: AV       SA SB SC S.A B C     C V SA SB SC S.ABC B
Chỉ có tỉ số thể tích khối chóp đáy tam giác, không có tỉ số khối chóp C
đáy tứ giác. Khi tính tỉ số khối tứ giác, ta cần chia ra những hình A
chóp có đáy là tam giác. B
CÂU HỎI CÙNG MỨC ĐỘ VỚI ĐỀ MINH HỌA
DẠNG CÂU HỎI NHẬN BIẾT Câu 1.
Thể tích khối lăng trụ có diện tích đáy bằng B , chiều cao bằng h là 1 2 A. V Bh . B. V Bh .
C. V Bh .
D. V  3Bh . 3 3 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
Thể tích khối lăng trụ có diện tích đáy bằng B , chiều cao bằng h là V Bh . Câu 2.
Cho khối lập phương có cạnh bằng 6 . Thể tích của khối lập phương đã cho bằng A. 216 . B. 18 . C. 36 . D. 72 . Lời giải Chọn A
Thể tích khối lập phương có cạnh bằng 6 là 3 V  6  216 . Câu 3.
Thể tích khối lập phương cạnh 2 bằng A. 6 . B. 8 . C. 4 . D. 2 . Lời giải Chọn B
Thể tích khối lập phương cạnh a là 3 V a .
Vậy thể tích khối lập phương cạnh 2 là: 3 V  2  8 . Câu 4.
Cho khối chóp có diện tích đáy B  3 và chiều cao h  4 . Thể tích của khối chóp đã cho bằng A. 6 . B. 12 . C. 36 . D. 4 . Lời giải Chọn D 1 1
Ta có công thức thể tích khối chóp V  . . B h  .3.4  4 . 3 3 Câu 5.
Thể tích khối chóp có diện tích đáy bằng 2
2a , chiều cao bằng a 3 là 3 2a 3 3 2a 3 3 a 3 A. V  . B. V  . C. 3 V  2a 3 . D. V  . 9 3 3 Lời giải Chọn B
Thể tích khối chóp có diện tích đáy bằng 2
B  2a , chiều cao bằng h a 3 là 3 1 1 2a 3 2 V
Bh  .2a .a 3  . 3 3 3 Câu 6.
Thể tích khối chóp có diện tích đáy bằng 2
a , chiều cao bằng 2a là 3 a 3 2a A. 3 V  6a . B. V  . C. 3 V  2a . D. V  . 3 3 Lời giải Chọn D 3 1 1 2a
Thể tích khối chóp có diện tích đáy bằng 2
a , chiều cao bằng 2a là 2 V
Bh  .a .2a  . 3 3 3 Câu 7.
Thể tích khối lăng trụ có diện tích đáy bằng 2
3a , chiều cao bằng a là 3 a 3 2a A. 3 V  3a . B. V  . C. 3 V a . D. V  . 3 3 Lời giải Chọn A
Thể tích khối lăng trụ có diện tích đáy bằng 2
3a , chiều cao bằng a là 2 3
V  3a .a  3a . Câu 8.
Thể tích khối hộp chữ nhật có ba kích thước lần lượt là 3, 4,5 bằng A. V  120 . B. V  20 . C. V  30 . D. V  60 . Lời giải Chọn D
Thể tích khối hộp chữ nhật có ba kích thước lần lượt bằng 3, 4,5 là V  3.4.5  60 . Câu 9.
Cho khối chóp có diện tích đáy B  6 và chiều cao h  3 . Thể tích của khối chóp đã cho bằng
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A. 6 . B. 18 . C. 9 . D. 36 . Lời giải Chọn A 1 1
Ta có công thức thể tích khối chóp V  . . B h
.3.6  6 nên chọn đáp án A. 3 3
Câu 10. Thể tích khối lập phương cạnh 5 bằng A. 15 . B. 25 . C. 125 . D. 75 . Lời giải Chọn C
Thể tích khối lập phương cạnh a là 3 V a .
Vậy thể tích khối lập phương cạnh 5 là: 3 V  5 125.
Câu 11. Cho khối lập phương có độ dài đường chéo bằng 6 3 . Thể tích của khối lập phương đó bằng A. 81 3 . B. 216 . C. 24 3 . D. 162 6 . Lời giải Chọn B d
Gọi d là đường chéo của khối lập phương và a là cạnh của nó, ta có 2 2
d  3a a . 3 6 3
Suy ra cạnh bằng a   6 . Do đó 3
V a  216 . 3
Câu 12. Thể tích khối lập phương ABC . D A BCD
  có AC  a 3 bằng A. 3 a . B. 2 a . C. 2a . D. 3a . Lời giải Chọn A C' B' D' A' C B D A ABC . D A BCD
  có AC  a 3  cạnh hình lập phương bằng a .
Vậy thể tích khối lập phương cạnh a là 3 V a .
Câu 13. Cho khối lập phương có tổng diện tích các mặt bằng 294 . Thể tích của khối lập phương đó bằng 147 147 147 A. . B. 49 . C. 343 . D. . 2 2 2 Lời giải Chọn C
Hình lập phương có 6 mặt là 6 hình vuông bằng nhau. Gọi a là cạnh của khối lập phương
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 294
Ta có diện tích một mặt là 2 S
 49  7  a  7 . Do đó 3
V a  343 . 6
Câu 14. Thể tích khối lập phương ABC . D A BCD
  có AC  a 6 bằng A. 3 8a . B. 3 6a 6 . C. 3 2a 2 . D. 3 3a 3 . Lời giải Chọn C C' B' D' A' C B D A ABC . D A BCD
  có AC  a 6  cạnh hình lập phương bằng a 2 .
Thể tích khối lập phương cạnh a là 3 V a .
Vậy thể tích khối lập phương cạnh a 2 là: V  a 3 3 2  2a 2 . 2 2
Câu 15. Khối chóp S.ABC có thể tích V
và diện tích đáy B  3 . Chiều cao của khối chóp 3 S.ABC bằng 2 6 2 6 2 2 2 6 A. . B. . C. . D. . 9 3 3 27 Lời giải Chọn B 3V 2 2 2 6
Chiều cao của khối chóp h   
nên chọn đáp án B. B 3 3
Câu 16. Cho khối hộp chữ nhật có ba kích thước là 3;5; 7 . Thể tích của khối hộp đó bằng 105 A. 35 . B. . C. 105 . D. 15 . 2 Lời giải Chọn C
Công thức tính thể tích khối hộp chữ nhật có ba kích thước a, b, c là V abc . Do đó V  . a .
b c  3.5.7  105 .
Câu 17. Thể tích khối lập phương ABC . D A BCD
  có AB  2 bằng A. 2 2 . B. 2 . C. 1. D. 3 . Lời giải Chọn C
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 C' B' D' A' C B D A ABC . D A BCD
  có AB  2  cạnh hình lập phương bằng 1.
Thể tích khối lập phương cạnh a là 3 V a .
Vậy thể tích khối lập phương cạnh 1 là: 3 V  1  1 .
Câu 18. Cho khối chóp S.ABCD có thể tích bằng 3
a , đáy ABCD là hình vuông. Biết chiều cao của
khối chóp là h  3a . Cạnh hình vuông ABCD bằng a A. a. B. . C. a 2 . D. a 3 . 3 Lời giải Chọn D 1
Gọi cạnh hình vuông là x . Ta có 2 3
x .3a a x a nên chọn đáp án A. 3
Câu 19. Cho khối lập phương ABC . D A B C 
D biết AC  6 2 . Thể tích của khối lập phương đó bằng A. 432 2 . B. 108 . C. 216 . D. 48 6 . Lời giải Chọn C
Ta có AC  6 2  AB  6 3  V  6  216 .
Câu 20. Thể tích khối lập phương ABC . D A BCD
  có AB  2 bằng A. 8 . B. 2 2 . C. 16 2 . D. 6 . Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 C' B' D' A' C B D A ABC . D A BCD
  có AB  2  cạnh hình lập phương bằng 2 .
Thể tích khối lập phương cạnh a là 3 V a .
Vậy thể tích khối lập phương cạnh 2 là: V   3 2  2 2 .
Câu 21. Cho khối chóp S.ABC có SA vuông góc với đáy, AC  3, AB  4, BC  5 và SA  3 . Tính
thể tích V của khối chóp S.ABC .
A. V  18 .
B. V  6 .
C. V  12 .
D. V  20 . Lời giải Chọn B 1 1 1
Tam giác ABC vuông tại A . B  . AB AC  3.4  6  V
6.3  6 nên chọn đáp án 2 2 3 B.
Câu 22. Thể tích khối lập phương ABC . D AB CD
  có AB  a 2 bằng: A. 3 a . B. 3 2a . C. 3 4a . D. 3 6a . Lời giải Chọn A
ABB vuông cân tại B nên: 2 2
2AB AB  AB  . a
Thể tích khối lập phương là 3 a .
Câu 23. Thể tích khối lập phương có cạnh 2a bằng A. 3 8a . B. 3 2a . C. 3 2 2a . D. 3 6a . Lời giải Chọn C
Thể tích khối lập phương có cạnh 2a bằng 3 3
( 2a)  2 2a .
Câu 24. Thể tích khối hộp chữ nhật có độ dài các cạnh lần lượt là a, 2a, 3a bằng: 3 2a A. 3 2a . B. 3 6a . C. . D. 3 3a . 3 Lời giải Chọn B
Thể tích hộp chữ nhật: 3
a.2a.3a  6a .
Câu 25. Thể tích khối tứ diện đều có cạnh 2a bằng 3 3 2 2 2 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 12 3 3 Lời giải Chọn C 3 3 2 2 2a
Thể tích khối tứ diện đều bằng: V  2a  . 12 3
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 26. Thể tích khối lăng trụ có diện tích đáy 2
3a và chiều cao a là A. 3
V  3a . B. 3
V a . C. 3
V  9a . D. 3
V  6a . Lời giải Chọn A Thể tích khối chóp 2 3
V Bh  3a .a  3a .
DẠNG CÂU HỎI THÔNG HIỂU
Câu 27. Cho khối lăng trụ đứng ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a . Biết BAD  60,
AA  a . Thể tích của khối lăng trụ đã cho bằng 3 a 3 3 a 3 3 a 3 A. . B. . C. 3 a 3 . D. . 2 6 3 Lời giải Chọn A
ABCD là hình thoi cạnh a có BAD  60 nên BAD là tam giác đều cạnh 2 2 a 3 a 3 a S  2S  2.  . ABCD ABD 4 2
Do khối lăng trụ ABC . D AB CD
  là lăng trụ đứng nên đường cao của lăng trụ là AA  a . 2 3 a 3 a 3
Thể tích khối lăng trụ là V AA .  S  . a  . ABCD 2 2
Câu 28. Cho khối lăng trụ đứng ABC.AB C
  . Biết AB  3cm, AC  4 cm,  BAC 60  , AA  2 cm.
Thể tích của khối lăng trụ đã cho bằng A. 6 3 (cm2). B. 2 3 (cm3). C. 6 3 (cm3). D. 6 (cm3). Lời giải Chọn C C' B' A' B C 60° A 1  1 S  .
AB AC.sin BAC  3.4.sin 60  3 3 (cm2). ABC 2 2
Do khối lăng trụ ABC.AB C
  là lăng trụ đứng nên đường cao của lăng trụ là AA  2 cm.
Thể tích khối lăng trụ là V AA .  S  2.3 3  6 3 (cm3). ABC
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 29. Cho khối lăng trụ đứng AB . CD A BCD
  có đáy là hình thoi cạnh a , BD a 3 và AA  4a
(minh họa như hình bên). Thể tích của khối lăng trụ đã cho bằng 3 2 3a 3 4 3a A. 3 2 3a . B. 3 4 3a . C. . D. . 3 3 Lời giải Chọn A BD a 3
Gọi I AC BD . Ta có: AC BD, BI  
. Xét tam giác vuông BAI vuông tại I : 2 2 2 2 2  a 3  3a a a 2 2 2 2 2
AI BA BI a     a    AI   AC  . a  2  4 4 2   2 1 1 a 3 a 3
Diện tích hình bình hành ABCD : S  2S
 2. BI.AC  2. .a  . ABCD ABC 2 2 2 2 2 a 3 Vậy: 3 VS .AA  .4a  2 3a .
ABCD. AB CD   ABCD 2
Câu 30. Cho khối lăng trụ đứng ABC . D AB CD
  có đáy ABCD là hình chữ nhật có AB a ,
AD a 3 , AA  2a . (minh họa như hình vẽ bên).
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A' D' B' C' A D B C
Thể tích của khối lăng trụ đã cho bằng 3 a 3 3 2a 3 A. 3 2a 3 . B. 3 a 3 . C. . D. . 3 3 Lời giải Chọn A A' D' B' C' A D B C 2 S
AB.AD a.a 3  a 3 . ABCD
Do khối lăng trụ ABC.AB C
  là lăng trụ đứng nên đường cao của lăng trụ là AA  2a .
Thể tích khối lăng trụ là 2 3 V AA .  S  2 . a a 3  2a 3 . ABCD
Câu 31. Cho khối lăng trụ đứng ABC . D AB CD
  có đáy ABCD là hình vuông cạnh a 2 . Biết góc giữa
AB với mặt phẳng  ABCD bằng 30 . Thể tích của khối lăng trụ đã cho bằng 3 a 6 3 2a 6 3 2a 3 A. . B. . C. . D. 3 2a 6 . 3 3 3 Lời giải Chọn B A' D' B' C' A D 60° B C S  a 2 2 2  2a . ABCD
AA   ABCD  góc giữa AB với mặt phẳng  ABCD là  A BA  30 . a
Tam giác AAB vuông tại A  6   A A  . AB tan  A BA  . 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 3 2a 6
Thể tích khối lăng trụ là V AA .  S  . ABCD 3
Câu 32. Cho khối lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông tại A. Biết 2AB AA  2a , 
ABC   (minh họa như hình vẽ bên). C' A' B' A C α B
Thể tích của khối lăng trụ đã cho bằng 3 a 3 a A. 3 a sin . B. . tan  . C. 3 a tan . D. tan  . 3 2 Lời giải Chọn C C' A' B' A C α B
Tam giác ABC vuông tại A có AB a , 
ABC   nên AC AB. tan   a. tan  . 2 1 1 aSAB.AC a.a. tan   . tan  . ABC 2 2 2
Do khối lăng trụ ABC.AB C
  là lăng trụ đứng nên đường cao của lăng trụ là AA  2a 2 a
Thể tích khối lăng trụ là 3 V AA .  S  2 . a
.tan  a .tan . ABC 2
Câu 33. Tính thể tích khối lăng trụ đứng ABC .
D A' B 'C ' D ' biết ABCD là hình thoi có
AC  10cm, BD  8cm và diện tích hình chữ nhật ACC ' A' bằng 2 50cm . A. 3 400cm . B. 3 2000cm . C. 3 4000cm . D. 3 200cm . Lời giải Chọn D 1 1 Diện tích mặt đáy 2 B AC.BC  .10.8  40cm 2 2 S 50
Diện tích hình chữ nhật ACC ' A'
S ACC ' A'  AC.CC '  CC '    5cm AC 10
Vậy thể tích khối lăng trụ là 3 V  .
B h  40.5  200cm
Câu 34. Cho khối chóp S.ABC có đáy ABC là tam giác đều có cạnh bằng a , SA vuông góc với đáy và
SA  2a . Tính thể tích của khối chóp S.ABC . 3 a 3 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 2 3 6 6 Lời giải
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Chọn D 1
Công thức thể tích khối chóp có diện tích đáy B và chiều cao h là: V  . . B h . 3
SA vuông góc với đáy nên h SA  2a . 2 a 3
Do đáy của hình chóp là tam giác ABC đều nên diện tích đáy của hình chóp là: B  . 4 2 3 1 1 a 3 a 3
Vậy thể tích khối chóp S.ABC là: V  . . B h  . .2a  nên chọn đáp án D. 3 3 4 6
Câu 35. Tính thể tích khối lăng trụ đứng ABC.A' B 'C ' biết ABC là tam giác vuông cân tại A có
BC a 2 và AC '  a 5 . 3 2a A. 3 2a . B. 3 2a . C. . D. 3 a . 3 Lời giải Chọn D Ta có 2 2 2 2 2 2 2 2 2
AB AC BC  2AB BC  2AB  2a AB a AB a 1 1 1 Diện tích mặt đáy 2 B A . B AC  . . a a a 2 2 2 2 2 2 2 CC '  AC '  AC
 5a a  2a 1
Vậy thể tích khối lăng trụ là 2 3
V B.h
a .2a a . 2
Câu 36. Tính thể tích khối lăng trụ đứng AB .
C A' B 'C ' biết ABC là tam giác đều cạnh a và
AC '  a 5 . 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a . 4 2 6 Lời giải Chọn B 2 1 1 a 3 Diện tích mặt đáy 0 B  . AB AC sin A  . . a a sin 60  2 2 4 2 2 2 2 CC '  AC '  AC
5a a  2a 2 3 a 3 a 3
Vậy thể tích khối lăng trụ là V  . B h  .2a  . 4 2
Câu 37. Tính thể tích khối lăng trụ đứng ABC.A' B 'C ' biết AB  5cm, AC  12cm, BC  13cm và
CC '  7cm . A. 3 210cm . B. 3 70cm . C. 3 105cm . D. 3 35cm . Lời giải Chọn A 5 12 13
Ta có Nửa chu vi của tam giác là: p   15 2
Diện tích của tam giác là: S
p p  5 p 12 p 13  1515  515 1215 13  30 .
Vậy thể tích khối lăng trụ là 3
V B.h  30.7  210cm .
Câu 38. Tính thể tích khối lăng trụ đứng ABC.A' B 'C ' biết AB  13cm, AC  14cm, BC  15cm và
CC '  10cm . A. 3 420cm . B. 3 840cm . C. 3 420cm . D. 3 140cm .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn B 13 14 15 Nữa chu vi: p   21. . 2 Diện tích: S
p( p 13)( p 14)( p 15)  84..
Vậy thể tích khối lăng trụ là 3 V  .
B h  84.10  840cm .
Câu 39. Cho khối chóp tam giác đều có tất cả các cạnh bằng 2a . Thể tích của khối chóp đã cho bằng 3 8a 3 4 2a 3 8 2a 3 2 2a A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D 2a2 3 2 2 2a 3 2a 3
Ta có SO   ABC  và 2 S   a 3 ; AO AM  .  , ABC 4 3 3 2 3 2  2a 3  2a 6 SO
SA AO  2a2 2 2     .  3  3   1 1 2a 6 2 2
Vậy thể tích khối chóp là 2 3 V  .S .SO  .a 3.  a . S .ABCD 3 ABC 3 3 3
Câu 40. Cho khối chóp tứ giác đều có cạnh đáy bằng a , các cạnh bên bằng 2a . Thể tích của khối chóp đã cho bằng 3 14a 3 4a 3 14a 3 2 2a A. . B. . C. . D. . 3 3 6 3 Lời giải Chọn C S A D O B C AC a 2
Ta có SO   ABCD và 2 Sa ; AO   , ABCD 2 2
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 2  a 2  a 14 SO
SA AO  2a2 2 2     .  2  2   1 1 a 14 14
Vậy thể tích khối chóp là 2 3 V  .S .SO  .a .  a . S . ABCD 3 ABCD 3 2 6
Câu 41. Cho khối chóp tam giác đều có cạnh đáy bằng a , các cạnh bên bằng 2a . Thể tích của khối chóp đã cho bằng 3 33a 3 11a 3 8 2a 3 11a A. . B. . C. . D. . 12 12 3 6 Lời giải Chọn B 2 a 3 2 2 a 3 a 3
Ta có SO   ABC  và S  ; AO AM  .  , ABC 4 3 3 2 3 2  a 3  a 33
SO SA AO  2a2 2 2      . 3  3   2 1 1 a 3 a 33 11
Vậy thể tích khối chóp là 3 V  .S .SO  . .  a . S . ABC 3 ABC 3 4 3 12
Câu 42. Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy.
SB  2a ; Thể tích của khối chóp S.ABCD bằng: 3 4 2a 3 a 3 2a 3 3a A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D S 2a A D a C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
SA   ABCD 
Theo giả thiết ta có  AB a . SB  2a  Do đó: 2 Sa . ABCD
SA SB AB   a2 2 2 2 2  a a 3 . 3 1 1 3a Vậy 2 V  . SA Sa 3.a  . SABCD 3 ABCD 3 3
Câu 43. Cho khối chóp tam giác đều có tất cả các cạnh đều bằng 2a . Thể tích của khối chóp đó bằng: 3 2 2a 3 2a 3 2a 3 2 6a A. . B. . C. . D. . 3 3 12 9 Lời giải Chọn A S A C H 2a B AB  2a
Gọi khối chóp đều là S.ABC , H là trọng tâm của ABC . Khi đó  SH  ( ABC)  2 (2a) 3 Ta có 2 S   a 3 ABC 4 2 2a 3 2a 3 HC  .  3 2 3 2a 3 2 2a 3 1 1 2 2a 2 2a 2 2 2 2 SH
SC HC  (2a)  ( )  2 VSH .S  . .a 3  . 3 SABC ABC 3 3 3 3 3
Câu 44. Cho khối chóp tam giác đều có cạnh đáy bằng a , cạnh bên bằng 3a . Thể tích của khối chóp đó bằng 3 2 2a 3 2a 3 2a 3 2a A. . B. . C. . D. . 3 3 6 12 Lời giải Chọn C
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020AB a
Gọi khối chóp đều là SABC . H là trọng tâm ABC suy ra  . SH  ( ABC)  2 a 3 2 a 3 a 3 Khi đó S  ; AH  .  . ABC 4 3 2 3 a 2 2 2 2 2 2 SH
SA AH  (a 3)  ( )  a . 3 3 1 1 2 2 3 3 2a Vậy 2 VSH.S  . a . a  . SABC 3 ABC 3 3 4 6
Câu 45. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy là tam giác vuông tại  ,  ,  60o A AC a ACB .
Đường chéo BC ' của mặt bên BCC ' B
' tạo với mặt phẳng  ACC ' A
' một góc bằng 30o
Tính thể tích của khối lăng trụ theo a. 3 a 3 3 a 6 A. 3 a 3 . B. 3 a 6 . C. . D. . 3 3 Lờigiải Chọn B
Đường chéo BC ' của mặt bên BCC ' B
' tạo với mặt phẳng  ACC ' A
' một góc bằng 30o
Nên BC ACC A   BC AC    0 ', ' ' ',
'  BC ' A  30 . AC 2 2 B 'C ' 
 2a; AB BC AC a 3 0 cos 60 0
C ' B AB : sin 30  2a 3  BB '  2a 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 1 3
V BB '.S
 2a 2. a 3.a a 6 . ABC 2
Câu 46. Cho hình lăng trụ tam giác đều AB .
C A' B 'C ' có AB a , góc giữa hai mặt phẳng  ABC ' và  ABC bằng 0
60 . Tính thể tích khối lăng trụ đã cho. 3 3 3 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 4 4 8 8 Lời giải Chọn C a 3
Gọi H là trung điểm của AB . Ta có: CH  2 
ABC  ABC  HC HC   0 ' , ',  CHC '  60 . CC ' a 3 3a
Xét tam giác CHC ' vuông tại C ta có: 0 0 tan 60 
CC '  CH . tan 60  . 3  CH 2 2 2 3 3a a 3 3a 3
Vậy V CC '.S  .  ABC 2 4 8
Câu 47. Cho hình lăng trụ tam giác đều ABC.AB C
  có AB a , đường thẳng AB tạo với mặt phẳng BCC B
  một góc 30 . Tính thể tích V của khối lăng trụ đã cho. 3 a 6 3 a 6 3 3a 3 a A. V  . B. V  . C. V  . D. V  . 4 12 4 4 Lời giải Chọn A
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 A' C' B' A C M B
Gọi M là trung điểm BC , do tam giác ABC đều nên AM BC , mà AM BB nên AM   BCC B
  . Suy ra hình chiếu vuông góc của AB trên  BCC B   là B M  . 
Vậy góc giữa đường thẳng AB và mặt phẳng  BCC B
  là góc AB M  và  AB M   30 . a 3 AM
AB  a 3 2 2 2  AA 
AB  AB  a 2 3 a 6 V  . 4
Câu 48. Một hình hộp đứng có đáy là hình thoi cạnh a , góc nhọn 60 và đường chéo lớn của đáy bằng
đường chéo nhỏ của hình hộp. Thể tích của khối hộp đó là 3 3a 3 6a A. 3 a . B. 3 3a . C. . D. . 2 2 Lời giải Chọn D B a C a 60 A D BCAD
Ta có AC BD  a 3 ; 2 2 BB 
BD  BD a 2
Vậy thể tích khối hộp đứng bằng 3 1 a 6 V  . B h  . a a 3.a 2  . 2 2
Câu 49. Cho một tấm nhôm hình chữ nhật ABCD có AD  60cm , AB  40cm . Ta gập tấm nhôm theo
hai cạnh MN và PQ vào phía trong cho đến khi AB và DC trùng nhau như hình vẽ bên để
dược một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể tích lớn nhất bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 B M Q C M Q B, C A x N P x D N P 60cm , A D A. 4000 3  3 cm B. 2000 3  3 cm C. 400 3  3 cm D. 4000 2  3 cm Lời giải Chọn A
Đáy của lăng trụ là tam giác cân có cạnh bên bằng x , cạnh đáy bằng 60  2x 2  60  2x
Đường cao tam giác đó là 2 AH x   60x  900  
, với H là trung điểm NP  2  Diện tích đáy là 1 1 S S
AH.NP  60x  900.  x x   xx ANP 30  60
900900 30 900 30  2 30 3 1  900   S   100 3    2 cm  30  3 
Diện tích đáy lớn nhất là 2
100 3cm nên thể tích lớn nhất là V    3 40.100 3 4000 3 cm  .
Câu 50. Cho lăng trụ đứng ABC.A BC
  có đáy là tam giác đều cạnh a và AB vuông góc với BC .
Thể tích của lăng trụ đã cho là. 3 a 6 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. . 12 4 8 24 Lời giải Chọn C A' C' B' H A C I B
Gọi I là trung điểm BC . Vì ABC.A' B 'C ' là lăng trụ tam giác đều nên.
AI   BB 'C 'C   AI BC ' .
Lại có giả thiết AB '  BC ' nên suy ra BC '   AIB '  BC '  B ' I .
Gọi H B ' I BC ' .
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 HI BI 1
Ta có BHI đồng dạng C  ' HB '   
B ' H  2HI B ' I  3HI . B ' H B 'C ' 2 2 2 BI a a 3
Xét tam giác vuông B ' BI có 2 2
BI HI.B ' I  3HI HI    . 3 12 2 2 2  a 3   a a 2 Suy ra 2 2 BB ' 
B ' I BI        .  2   2  2   3 3 a 2 a 6 Vậy 2 V S .BB'  a .  . ABC 4 2 8
Câu 51. Cho hình lăng trụ tam giác đều AB . C A BC
  . Biết khoảng cách từ điểm C đến mặt phẳng 1
ABC bằng a , góc giữa hai mặt phẳng  ABC và  BCC B
  bằng  với cos  (tham 3
khảo hình dưới đây). Thể tích khối lăng trụ AB . C AB C   bằng 3 9a 15 3 3a 15 3 9a 15 3 3a 15 A. . B. . C. . D. . 20 20 10 10 Lời giải Chọn A A' C' B' H N A C G M B
Gọi M là trung điểm của AB , G là trọng tâm tam giác ABC . CC  AB Ta có: 
AB  CC M    CC M
   ABC . Mà CC M
   ABC  C MCM AB
nên nếu gọi H là hình chiếu vuông góc của C trên C M
thì H là hình chiếu của C trên mặt
phẳng  ABC  d C; ABC  CH a .
Dựng đường thẳng đi qua G và song song với CH , cắt C M  tại điểm K .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489GN    ABC  Ta có 
nên góc giữa hai mặt phẳng  ABC và  BCC B
  là góc AGN   . AG   BCC B    1 a GN 1 1 1 5 GN CH  ; AG
a AB AG 3  a 3 ;    3 3 cos 2 2 2 CCCH CM 2 9a 3a 5 2 3a 3  CC  ; Sa  . ABC  2 3 3 . 5 4 4 3 9a 15
Vậy thể tích khối lăng trụ bằng V CC .S  . ABC 20
DẠNG CÂU HỎI VẬN DỤNG – VẬN DỤNG CAO
Câu 52. Cho khối lập phương AB CD. A ' B 'C ' D ' cạnh a . Các điểm E, F lần lượt là trung điểm
của C ' B ' và C ' D ' . Mặt phẳng  AEF  cắt khối lập phương đã cho thành 2 phần, gọi V là thể 1 V
tích khối chứa điểm A ' và V là thể tích khối chứa điểm C ' . Khi đó 1 là: 2 V2 25 8 17 A. . B. 1. C. . D. . 47 17 25 Lời giải Chọn A
Dựng thiết diện : PQ qua A và song song với BD (vì EF / /B ' D '/ /BD )
PE cắt các cạnh BB ', CC ' tại M và I. Tương tự ta tìm được giao điểm N. Thiết diện là AMEFN .
Dựa vào đường trung bình BD và định lí Ta – lét cho các tam giác IAC, DNQ, D ' NF ta tính a 2a 2a được: IC '  , ND
. Tương tự ta tính được: MB
. Và ta có: QD PB a 3 3 3 3 1 a 1 a a a 3 3 a 8a Ta có: V  . . . . 
. Dùng tỉ lệ thể tích ta có: 3 V  4 .V  64.  IEFC ' 3 3 2 2 2 72 IPQC IEFC ' 72 9 3 1 2a 1 a 3 3 3 3 8a a a 47a V  . . . . a a   V ⇒ V    2.  NADQ 3 3 2 9 MPAB 2 9 72 9 72 3 3 47a 25a V 25
Thể tích khối lập phương AB CD. A ' B 'C ' D ' là 3 a nên 3 V a    1  . 1 72 72 V 47 2
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 53. Cho khối lăng trụ ABC.AB C
  . Gọi E , F lần lượt là trung điểm của các đoạn thẳng CC và
BB . Đường thẳng A 'E cắt đường thẳng AC tại K , đường thẳng A 'F cắt đường thẳng AB
tại H . Tính tỉ số thể tích khối đa diện lồi BFHCEK và khối chóp A 'ABC . 1 1 A. . B. . C. 2 . D. 1. 3 2 Lời giải Chọn C C' A' B' E K F C A B H 1 2 Ta có: VVV và VVVV A'.ABC
A'.BB 'C 'C
ABC. A' B 'C ' A'. ABC
ABC . A' B 'C '
A'.BB 'C 'C
ABC . A' B 'C ' 3 3 1 Do đó VVV (vì SS )  VV . A'.BFEC
A'.FB 'C ' E
ACB. A' B 'C ' 3 BFEC FB 'C ' E A'.ABC A'.BFEC V V AA ' AB AC 1 Ta có: A'.ABC A. A' BC   . .  . V V AA ' AH AK 4 A. A' HK A.A' HK 1 1 VVVVVV
. Do đó BFHCEK  2 . A'.ABC A'.BFEC A. A' HK BFHCEK A. A' 4 2 HK VA'.ABC
Câu 54. Cho hình hộp ABC . D A BCD
  có M , N, P lần lượt là trung điểm ba cạnh AB , BB và D . D
Mặt phẳng MNP cắt đường thẳng AA tại I. Biết thể tích khối tứ diện IANP là V .
Thể tích khối hộp đã cho ABC . D A BCD   bằng A. 2V . B. 4V . C. 6V . D. 12V. Lời giải Chọn B
Gọi Q  MNP  AD . Theo tính chất của giao tuyến suy ra MQ NP nên Q là trung điểm của A D
 . Suy ra M , Q lần lượt là trung điểm IN , IP. VI AMQ IA IM IQ 1 1 1 1 V Ta có: .  . .  . .   V  . I .  V IA IN IP 3 2 2 12 A MQ 12 IANP 1 1 1 1 1 Mặt khác V
d I , AB CD    .S  . d A ,  ABCD  . SV .
I . AMQ                 3 A MQ   A B C D ABCD. 3 2 8 48 A B C D Từ đó suy ra V  4V . ABCD. A BCD  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 55. Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại A , AB a ,   0
SBA SCA  90 , 0
góc giữa hai mặt phẳng SAB và  SAC  bằng 60 . Thể tích của khối đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6 Lời giải Chọn D S I A C a a 2 B
Hai tam giác vuông SAB và SAC bằng nhau chung cạnh huyền SA .
Kẻ BI vuông góc với SA suy ra CI cũng vuông góc với SA và IB IC .
SA IC, SA IB SA   IBC  tại I . 1 1 1 1 VVVS AI S SI S AI SI S SA . S .ABC A.IBC S .IBCIBCIBCIBC   3 3 3 3 IBC
SAB SAC  IB IC  IB IC 0  0 , , ,
 60  BIC  60 hoặc  0 BIC  120 .
Ta có IC IB AB a mà BC a 2 nên tam giác IBC không thể đều suy ra  0 BIC  120 .
Trong tam giác IBC đặt IB IC x x  0 có: 2x IB IC BC    a 2 1 2 2 2 2 2 a 6 a 6 0 cos120      x
IB IC  . 2 2I . B IC 2 2x 3 3 2  a 6  a 3
Trong tam giác ABI vuông tại I có: 2 2 2 AI AB IB a     .  3  3   2 2 AB a
Trong tam giác SAB vuông tại B đường cao BI có: 2 AB I . A SA SA    a 3 . IA a 3 3 2 3 1 1 1 1  a 6  a Vậy  0 V  S SA  .
IB IC.SAsin BIC    a 3 sin120  . S . ABC 3 IBC  3 2 6  3  6  
Câu 56. Cho hình hộp ABC . D A BCD
  có chiều cao bằng 8 và diện tích đáy bằng 9 . Gọi M , N, P và
Q lần lượt là tâm của các mặt bên ABB A  , BCC B  , CDD C
  và DAAD . Thể tích của khối đa
diện lồi có các đỉnh là các điểm , A , B C, ,
D M , N, P và Q bằng A. 27 . B. 30 . C. 18 . D. 36 . Lời giải Chọn B
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Ta có V  9.8  72 .
ABCD. AB CD  
Gọi I, J, K, L lần lượt là trung điểm các cạnh AA ,
BB , CC , DD suy ra V  36 . ABCD.IJKL 1 Do hình chóp .
A MIQ đồng dạng với hình chóp . A B AD   theo tỉ số nên 2 1 1 1 9 3 VV  . .8.  . . A MQI .    8 A B A D 8 3 2 2 3 VV  4V  36  4.  30 . ABCD.MNPQ ABCD.IJKL . A MIQ 2
Câu 57. Cho khối lăng trụ AB . C AB C
  có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn
thẳng AC và B C
 . Gọi (P) là mặt phẳng qua M và song song với mặt phẳng ( ANC) . Mặt phẳng (P)
chia khối lăng trụ AB . C A BC
  thành hai khối đa diện, gọi (H) là khối đa diện chứa đỉnh A . Thể tích
của khối đa diện (H) bằng 3 1 2 1 A. . B. . C. . D. . 5 3 5 2 Lời giải Chọn D K A' G B' F N C' I A B M E C J
Gọi khối lăng trụ ABC.AB C
  có thể tích bằng V
- Mặt phẳng (P)qua M và song song với mặt phẳng ( ANC ) nên mặt phẳng (P)cắt các mặt phẳng
( ABC), ( A ' B 'C ') lần lượt theo các giao tuyến ME, GF ( (E BC, G A ' B ', F B 'C ') cùng song song A N
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489
- Mặt phẳng (P)cắt các mặt phẳng ( AA 'C 'C ), (BB 'C 'C ) lần lượt theo các giao tuyến
MI ( I AA ') song song '
A C , EF song song CN. Ba đường thẳng M I , FG , A 'C ' đồng quy tại
K, ba đường thẳng M I , EF , CC ' đồng quy tại J .
- Mặt phẳng (P) chia khối lăng trụ ABC.AB C
  thành hai khối đa diện, gọi (T) là khối đa diện không chứa đỉnh.
Thể tích của khối đa diện (T) bằng 1 1 1 V VVVS .JC ' S .JC S .IA ' 1 J .C ' FK J .CEM I . A 'GKC ' FKCEMA ' 3 3 3 GK . 9 1 1 1 1  V V V V  16 48 24 2 2 a 3
Câu 58. Cho hình hộp đứng ABC . D AB CD
  có AB AD a , AA'  , 
BAD  60 . Gọi M , N 2
lần lượt là trung điểm AD , AB . Tính thể tích của khối đa diện ABDMN . 3 3a 3 3 3a 3 9a 3 3a A. . B. . C. . D. . 16 8 16 8 Lời giải Chọn A SM AM 1
Gọi S BN AA . Ta có:  
. Suy ra M là trung điểm của SD . SD AD 2 S SM SN 1 3 Mà SMN  .   SS . S SD SB 4 MNBD 4 SBD SBD
Tam giác ABD có AB AD a , BAD  60 nên tam giác ABD là tam giác đều. 1 1 3 3 Vd  , A BDMN  .Sd  , A SBD  . SV A.BDMN   3     BDMN   . SBD S . 3 4 4 ABD 2 3 3 1 1 a 3 3a  . SA Sa 3.  . 4 3 ABD  4 4 16
Câu 59. Cho hình hộp ABC . D AB CD
  có chiều cao bằng 8 và diện tích đáy bằng 9. Gọi
M , N , P, Q, R và S lần lượt là tâm của các mặt ABB A  , BCC B  , CDD C  ,
DAAD , ABCD và A BCD
  . Thể tích của khối đa diện lồi có các đỉnh là các điểm M , N, P,Q, R và S bằng 1 A. 3 . B. 24 . C. 9 . D. . 3 Lời giải Chọn A
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi I , J , K , L lần lượt là trung điểm các cạnh AA ,
BB , CC , DD . 1
Do tam giác MIQ đồng dạng với tam giác B A
 D theo tỉ số nên 2 1 1 9 9 9 SSS  . Suy ra SS  4S  9  4.  . MIQ        4 B A D 8 A B C D 8 MNPQ IJKL MIQ 8 2
Gọi h , h lần lượt là chiều cao của hai hình chóp . R MNP ,
Q S.MNPQ h h  8 . 1 2 1 2
Thể tích của khối đa diện lồi có các đỉnh là các điểm M , N , P, Q, R và S bằng 1 1 9 V  h h S  .8.  3 . 1 2  3 MNPQ 3 8
Câu 60. Cho hình chóp S.ABC có SA   ABC  , đáy là tam giác vuông cân tại A , G là trọng tâm a A
BC, khoảng cách từ G đến mặt phẳng SBC bằng
. Gọi  là góc giữa mặt phẳng 3
SBC và  ABC . Khi thể tích khối chóp S.ABC nhỏ nhất thì cos bằng 3 2 2 3 A. . B. . C. . D. . 3 2 3 2 Lời giải Chọn A
Gọi M là trung điểm BC . Ta có: BM AM
BC  (SAM )  BC AM BC SA  
Góc giữa mặt phẳng SBC  và  ABC là:   SMA
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489
BC  (SAM )   SBC  (SAM ) ; SBC  SAM   SM.
Kẻ GH SM GH  (SBC) .  a
d G, SBC   GH  . 3 GH a a
Xét tam giác vuông GHM : GM  
AM  3GM  . sin  3sin  sin  2a
Do tam giác ABC vuông cân: BC  2 AM  . sin  a
Xét tam giác vuông SAM : SA AM . tan   cos 3 1 a Suy ra: V  . SA S  . S . ABC ABC 2 3 3sin .cos
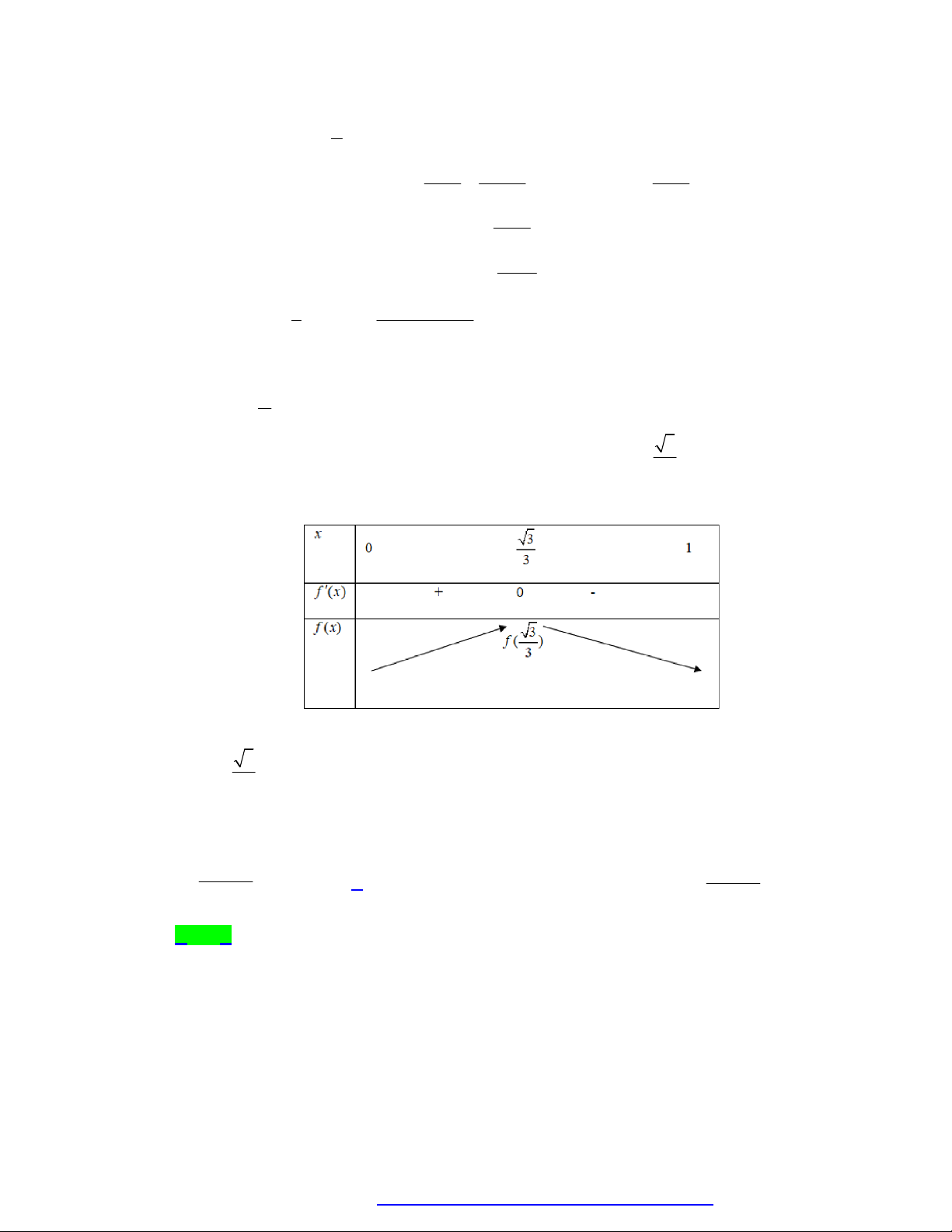
Thể tích khối chóp S.ABC nhỏ nhất khi 2
sin  .cos  lớn nhất. Đặt x  cos .  Do 0    nên x 0;  1 . 2 3
Xét hàm số f x 2
x(1 x ) ta có: f  x 2
 1 3x ; f (
x)  0  x  3 Bảng biến thiên:
Từ bảng biến thiên ta có: Thể tích khối chóp S.ABC nhỏ nhất khi 2
sin  .cos  lớn nhất khi 3 cos  . 3
Câu 61. Cho lăng trụ ABC.AB C
  có chiều cao bằng 8 và diện tích đáy bằng 9 . Gọi M , N là hai điểm    
thỏa mãn BM k.BBk  
1 , CN l.CC l  0 . Thể tích của tứ diện AAMN bằng l k 1 l k 1 A. . B. 24 . C. 72 . D. . 72 210 Lời giải Chọn B
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020    
Theo giả thiết BM k.BBk  
1 , CN l.CC l  0 suy ra M BB , N CC (như hình vẽ)
Do BM ||  ACC A
   d M , ANA  d B, ANA. Ta có SS ANAACA   Có 1 Vd M ANASd B ANASd B ACASV AA MN   1 1 ,  . ANA  , . ACA  , .    3 3 3 ACA A . ABC 1  .9.8  24 . 3
Câu 62. Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B với AB  6 , BC  3 , SC  3
và mặt phẳng SAC  vuông góc với mặt đáy  ABC  . Biết hai mặt phẳng SAB và SAC  3
tạo với nhau góc  thỏa mãn tan 
. Thể tích khối chóp S.ABC bằng 4 4 8 A. V  8. B. V  . C. V  . D. V  4. 3 3 Lời giải Chọn B
Dựng BE AC, EF SA .
Vì SAC    ABC  và SAC    ABC  AC nên BE SA
Khi đó SA  BEF  SAB ,SAC    BFE BE 3 4 4 A . B BC 4 2  tan BFE    EF BE   EF 4 3 3 AC 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489 2 ABEF 4 Ta có AE   2  sin FAE   AC AE 3 2 
d C,SA  
AC.sinSAC  2 2 và SA  2AC.cosSAC  2. 1 1 1 4 Suy ra VVB . E S  2 2.2 2  . S.ABC B.SAC 3 SAC 3 2 3
Câu 63. Cho lăng trụ ABC.A BC
  có chiều cao bằng 8 và diện tích đáy bằng 9 . Gọi M , N lần lượt là  
trung điểm của AA ,
BC . D là điểm thỏa mãn AD  2AN . Mặt phẳng  P qua M , D và
song song với BC cắt BB , CC lần lượt tại E, F . Thể tích của khối đa diện lồi có các đỉnh là
các điểm A , B , C ,
M , E và F bằng A. 36 . B. 24 . C. 48 . D. 39 . Lời giải Chọn C  
D là điểm thỏa mãn AD  2AN suy ra N là trung điểm AD . Gọi I là trung điểm MD suy
ra I  BCC B
  . Mặt phẳng  P qua M , D và song song với BC nên
P BCC B
   Ix || BC, Ix BB  E, Ix CC  F . 1 1 1 Ta có IN AM
AA  EB FC AA . 2 4 4 V 1  A MB EC F   1  1 3 3  A BC  .  MEF     V  9.8.    48   . AB C  .   V 3 MEFAABBCC  3  2 4 4 ABC.A BC   
Phương án nhiễu A: Học sinh không xác định được thiết diện, có yếu tố M là trung điểm AA
nên nghĩ mặt phẳng  P sẽ chia đôi lăng trụ.
Phương án nhiễu B: áp dụng sai công V 1  AM BE CF  1  1 1 1  thức AB C  .  MNP        V  24     . AB C  . V 3  AABBCC  3  2 4 4 MNP ABC. A BC    1
Phương án nhiễu D: Học sinh tính được V
 .4.9  12 . Cho rằng EFC B   đồng dạng với
M . AB C   3 3 9 9 9 2 BCC B
  theo tỉ số  SSVV  . .8.9  27 . EFC B   BCC B   M .EFC B   M . 4 16 16 BCC B   16 3
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Câu 64. Cho tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là trung điểm của các cạnh A ,
B BC và E là điểm đối xứng với B qua D . Mặt phẳng  MNE chia khối tứ diện ABCD
thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V . Thể tích V bằng 3 11 2a 3 7 2a 3 2a 3 13 2a A. V  . B. V  . C. V  . D. V  . 216 216 8 216 Lời giải Chọn A
Gọi Q ME AD, P NE CD mp MNE chia khối tứ diện ABCD thành hai khối đa
diện gồm PQDBMN và khối đa diện chứa đỉnh A có thể tích V . Dễ thấy ,
P Q lần lượt là trọng tâm của BCE và AB . E 1 1 S
Gọi S là diện tích BCD SSS  . PDECDE  3 3 BNE 3   h
d M,BCD   
Gọi h là chiều cao của tứ diện ABCD  2  .   h
d Q,BCD    3 1 . S h . S h Khi đó V  .d M BCD S V M BNE  , .  ;  . .  3 BNE 6 QPDE 27 2 Mà V  3 a . ABCD 12 7 . S h 7 11 11 2 Suy ra VVV  .  VV V  3 a . PQD.MNB M.BNE Q.PDE 18 3 18 ABCD 18 ABCD 216
Câu 65. Cho hình chóp SABC có diện tích đáy bằng 10 , chiều cao bằng 9 . Gọi M , N , P lần lượt là
trọng tâm của tam giác SAB, SBC , SCA . Thể tích của khối đa diện ABCMNP . 175 560 160 A. 60 B. . C. . D. . 3 9 9 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489 3  2  8 Ta có V  .VV SIJK    3 SABC  27 SABC 19 19 1 190  VV  . 9.10  IJKABC 27 SABC 27 3 9 VV  (VVV ) mà VVV ABC.MNP ABCI JK B.MNJ . A MIP C.NPK B.MNJ . A MIP C.NPKVV  3V ABC.MNP ABCIJK B.MNJ 1 Có V  .S
.h ; h d B, IJK b   BMNJ 3 MNJ b 4 4 40 SS  .10  IJK  9 ABC 9 9 1 10 1 Mà S  .S  ; h h  3 MNJ 4 IJK 9 b 3 1 10 10  V  . .3  BMNJ 3 9 9 190 10 160 Vậy V   3.  ABCMNP 9 9 9
Câu 66. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Biết AB SB, AC SC , góc
giữa hai mặt phẳng SAB và  SAC  bằng 0
60 . Thể tích khối chóp S.ABC bằng 3 a 2 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 24 36 6 36 Lời giải Chọn A
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 S H x x B C a a A
Từ giả thiết suy ra SAB  SAC   1 .
Gọi H là hình chiếu của B trên SA . Theo  
1 ta có CH SA và BH CH . Đặt BH  ,
x 0  x a .
Theo giả thiết ta có góc 
BHC bằng hoặc bù với 0 60 . 
BHC không thể bằng 0
60 vì khi đó x a nên  0 BHC  120 . Khi đó a 3
BC x 3  a x  . 3 V SA
Dễ thấy S.ABC  . V HA H . ABC a 6 a 2 a 6 SA 3 Ta có HA  , SB SC  , SH    . 3 2 6 HA 2 3 1 1 a 2 3 a 2 2 0 V  . HA x .sin120   VH . ABC 3 2 36 S . ABC 24
Câu 67. Cho khối tứ diện ABCD có thể tích V . Gọi G , G , G , G là trọng tâm của bốn mặt của tứ 1 2 3 4
diện ABCD . Thể tích khối tứ diện G G G G là: 1 2 3 4 V V V V A. . B. . C. . D. . 27 18 108 81 Lời giải Chọn A A G2 G3 G1 I C B G4 H1 H2 K J D
Gọi I , J , K lần lượt là trung điểm của BC , BD và DC .
Gọi h là khoảng cách từ A đến  BCD , h là khoảng cách từ G đến G G G . 1 2 3  1 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
NGUYỄN BẢO VƯƠNG - 0946798489
Vì G G G / / BCD nên d G , G G Gd G , BCD
G H h , h AH . 4  1 2 3    1   1 2 3    1 2 1 h KG 1 h 1 1     h  . h KA 3 1 3
Gọi S , S  , S lần lượt là diện tích các tam giác BCD, IJK và G G G . 1 1 2 3
Vì I , J , K lần lượt là trung điểm của BC , BD và DC nên: 1 1 BC 1 1 1 1 S 
JK.d I, JK   .
. d D, BC   . .BC.d D, BC   S   1 . 2 2 2 2 4 2 4 G G AG 2
Tam giác G G G đồng dạng với tam giác KIJ với tỉ số đồng dạng là: 1 2 1   . 1 2 3 Ik Ak 3 2 S  2  4 4 1       S
S 2 (Vì tỉ số diện tích bằng bình phương tỉ số đồng dạng). S 1  3  9 9 S Từ   1 và 2  S  . 1 9 1 1 S h 1  1  V
Thể tích khối từ diện G G G G là: V S .h  . .  . .S.h  . 1 2 3 4 1 1 1   3 3 9 3 27  3  27
Câu 68. Cho khối chóp S.ABCD có đáy là hình thang cân  AD BC , khoảng cách giữa AD và BC
bằng a , BC a , SA   ABCD , SA  2a . Trên cạnh BC lấy điểm M sao cho
MC x 0  x a . Thể tích khối chóp S.CDM lớn nhất khi độ dài MC bằng a 2 a a 3 A. . B. . C. . a D. . 2 2 2 Lời giải Chọn C 1 V  . . SA S S .CDM 3 CDM
Ta có: SA  2a .
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 Và  S  .CM .C . D sin MCD CDM 2 1   . x C . D sin MCD . 2 1   V  . . a . x C . D sin MCD S .CDM 3 Vì V
chỉ thay đổi khi x thay đổi, dễ thấy thể tích cần tìm lớn nhất khi x lớn nhất S.CDM
x a M B MC a .
Câu 69. Cho tứ diện ABCD có thể tích là V . Điểm M thay đổi trong tam giác BCD . Các đường thẳng
qua M và song song với AB , AC , AD lần lượt cắt các mặt phẳng  ACD ,  ABD ,  ABC
tại N , P , Q . Giá trị lớn nhất của khối MNPQ là V V V 2V A. . B. . C. . D. . 27 18 81 27 Lời giải Chọn A
Gọi N  BM CD , P  CM BD , Q  MD BC . MN N M
Tam giác ABN có MN // AB   . AB N BMP P M
Tam giác ACP có MP // AC   . AC P CMQ Q M
Tam giác ADQ có QM // AD   . AD Q DMN MP MQ N MP MQ M  Khi đó:      AB AC AD N BP CQ DN MP MQ MS S S MN MP MQ Mà MCD MBD MBC       1 nên    1 N BP CQ DS S S AB AC AD BCD BCD BCD 3 3 MN MP MQMN MP MQ    Lại có 3 3 1        3 . .  (Cauchy) AB AC ADAB AC AD      1 MN MP MQMN.M . P MQ A . B A .
C AD MN .MP.MQ lớn nhất khi   27 AB AC AD
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
NGUYỄN BẢO VƯƠNG - 0946798489 MN MP MQ 1
M là trọng tâm tam giác BCD    
  NPQ //  BCD , AB AC AD 3 2 S 1 1 1 NPQ  2     , Mà SS nên SS
và d M , NPQ  d  , A BCD    S N P Q BCD NPQ BCD  3 4 9 3 N PQ    1
Vậy giá trị lớn nhất của khối tứ diện MNPQ là VS .d M NPQ MNPQ NPQ  ,  3 1 1 1 V 1  V  . S . d A BCD  , với VS .d A BCDV ABCD BCD  ,  MNPQ BCD  ,  3 9 3 27 3
Câu 70. Cho khối lăng trụ AB . C A
B C có thể tích bằng 2 . Gọi M là trung điểm của đoạn thẳng  AA và
N là điểm nằm trên cạnh BB ' sao cho BN  2B ' N . Đường thẳng CM cắt đường thẳng C 
A tại P , đường thẳng CN cắt đường thẳng C 
B tại Q . Thể tích của khối đa diện lồi 
A MPBNQ bằng 7 5 2 13 A. . B. . C. . D. . 9 9 3 9 Lời giải Chọn A V 1 AM BN CC ABC MNC  '  13 13 Ta có: . '      V    . ABC.MNC ' V 3 AA BB CC ABC A B C  ' ' '  18 9 . ' ' ' V 1 AM BN CC ABC MNC   7 7 Lại có: .      V    . ABC. V 3 MNC AA BB CC ABC A B C  ' ' '  18 9 . ' ' ' 2 Suy ra: VVV  . C.MNC ' ABC.MNC ' ABC.MNC 3 V CM CN CC ' Mà: C.MNC'  . . * V CP CQ CC ' C.PQC ' CM AMCM 1   1   CMA PMA'     PM A'  MCP 2 Ta có:      .
CNB  QNB ' CN BN CN 2     2   QN B ' NCQ 3   V 1 2 1
Thay vào * ta có: C.MNC'  . .1   V  3V  2 . C.PQC ' C.MNC ' V 2 3 3 C.PQC ' 11 Có: VVV  .
A'B 'C '.MNC LT ABC.MNC 9 7  VVV  . A'MPB' NQ C.PQC '
A' B'C '.MNC 9
Câu 71. Cho khối lăng trụ AB . C A
B C . Gọi M , N lần lượt là trung điểm của đoạn thẳng A A và BB ' .
Tính tỉ số thể tích của khối tứ diện CMNC ' với khối lăng trụ đã cho.
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 1 1 2 3 A. . B. . C. . D. . 3 2 3 4 Lời giải Chọn A V 1 AM BN CC ABC MNC   1 1 Ta có: .      V    V . ABC.MNC
ABC. A' B 'C ' V 3 AA BB CC ABC A B C  ' ' '  3 3 . ' ' ' V 1 A M B N C C A B C MNC  ' ' ' '  1 1 Tương tự ta có: ' ' '. '      V    V .
A' B 'C '.MNC '
A' B 'C '. V 3 ABC A A B B C C A B C ABC  ' ' '  3 3 ' ' '. 1 V 1 CMNC '  VV   . CMNC '
ABC. A' B 'C ' 3 V 3
ABC. A' B 'C '
Câu 72. Cho khối lập phương ABC . D
A BCD ' cạnh a . Gọi M , N lần lượt là trung điểm của đoạn
thẳng A ' D ' và C ' D ' . Mặt phẳng  BMN  chia khối lập phương thành hai phần, gọi V là thể
tích phần chứa đỉnh B ' . Tính V ? 3 25a 3 7a 3 25a 3 7a A. . B. . C. . D. . 72 24 24 72 Lời giải Chọn A
Ta có thể tích cần tính là V .
BB ' EA'MNC ' F Mà VVVV .
BB ' EA' MNC ' F B.EA' M
B.B ' A' MNC ' B.FC ' N
PA' M  ND ' MPA '  ND ' Ta có:    .
QC ' N  MD ' N QC '  MD '   a
Lại có: MD '  ND '  PA'  ND '  MD '  QC '  . 2  A' E PA ' 1  
PA' E  BAE   AE BA 2 a Mà:   
A' E QC '  .
QC ' F  BCF C ' F QC ' 1 3       CF BC 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
NGUYỄN BẢO VƯƠNG - 0946798489 3 1 1 1 a Vậy ta có: V  . BA SB . A
A' M .A' E  . B.EA'M EA' 3 M 3 2 36 3 a Dễ thấy: VV  . B.FC ' N B.EA'M 36 3 1 1 7a Có: V  .BB '.SBB ' SS  .
B.B ' A'MNC '
B ' A'MNC '
A'B'C'D' MD ' N  3 3 24 3 25a Vậy: V  .
BB ' EA' MNC ' F 72
Câu 73. Cho khối lăng trụ ABC.AB C
  có thể tích bằng 6. Gọi điểm I là trung điểm AA và điểm N
thuộc cạnh BB sao cho B 'N  2BN .Đường thẳng C ' I cắt đường thẳng CA tại P , đường thẳng C N
 cắt đường thẳng CB tại Q . Tính thể tích khối đa diện lồi AIPBNQ 7 11 11 7 A. . B. . C. . D. . 9 18 9 3 Lời giải Chọn D V 1  AI BN CC  1  1 1  11 ABC.INC '      1      V 3  AAB B CC  3  2 3  18 ABC. A BC   11 11  VV ABC.INC ' 18 3 S CPQ CP CQ 3  .  2.  3  S  3S S CA CB 2 CPQCAB CAB 1  V  3V  3. V  6 C CPQ C ' ABC ABC.    3 A B C 7  VVV  . AIPBNQ C PQ ABCINC ' 3
Câu 74. Cho khối lăng trụ ABC.A BC
  có thể tích bằng V . Gọi điểm M là trung điểm AA và điểm N 1
thuộc cạnh BB sao cho BN BB ' .Đường thẳng C M
cắt đường thẳng CA tại D , đường 3 thẳng C N
 cắt đường thẳng CB tại E . Tỉ số thể tích khối đa diện lồi AMDBNE và khối lăng
trụ ABC.AB C   là 13 7 7 8 A. . B. . C. . D. . 18 18 12 15 Lời giải Chọn B
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020
Gọi V là thể tích khối đa diện lồi AMDBNE , V là thể tích khối lăng trụ ABC.A BC   1 2 V 1  AM BN CC  1  1 1  11 11 ABC.MNC '      1   VV     ABC.MNC ' V 3  AABBCC  3  2 3  18 18
ABC. AB C   S CA CB 1 2 1 CAB  .  .   S  3S S CD CE 2 3 3 CDE CAB CDF  1  V  3V  3. VV C CDE C '. ABC ABC. 3 A BC   V VV 7 AMDBNE C CDE
ABC.C ' MN    . V V 18
Câu 75. Cho khối lăng trụ ABC.AB C
  có thể tích bằng 1. Điểm M là thuộc cạnh A' B ' sao cho 1 A M   A B
  . Mặt phẳng  BCM  cắt đường thẳng AA tại F , và cắt đường thẳng AC tại 3
G . Thể tích khối chóp FAMG bằng 5 1 5 1 A. . B. . C. . D. . 24 6 36 54 Lời giải Chọn D
Đường thẳng AA cắt BM tại F AA'  BCM   F ,
Đường thẳng FC cắt A 'C ' tại G A'C '  BCM     G FA' FM A'M 1 FG FA' 1
A'M // AB   
 ; A'G // AC    ; FA FB AB 3 FC FA 3 V 1 1 1 1 1 FA'MG   . .   VV FA' V 3 3 3 27 MG 27 FABC FABC
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 3 1 VS
d F, ABC   S d A ABC   FABC ABC   . ',   ABC   3 3 2   2 1 1 1 Nên V  .  . FA'MG 27 2 54
Câu 76. Cho lăng trụ tam giác AB . C A BC
  có đáy là tam giác đều cạnh a , điểm A cách đều ba điểm 2 a 3
A , B , C và diện tích tam giác ABA bằng
. Thể tích khối đa diện A BCBC bằng 6 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 24 8 12 Lời giải Chọn D A' C' B' A C I M B
Do điểm A cách đều ba điểm , A ,
B C nên chân đường cao hạ từ A là trọng tâm I của tam
giác đều ABC . Gọi M là trung điểm của AB A M   AB . 1 a 3 Có MI CM  3 6 1 2 2S a 3 Ta có: SA . B A MABAA M      . ABA 2 AB 3 a
Xét tam giác A ' IM có 2 2 AI
AM IM  . 2 2 3 1 a 3 a a 3 2 3 a 3 a a 3 Vậy V   và V   . A '. ABC 3 4 2 24
ABC . A' B 'C ' 4 2 8 3 3 3 a 3 a 3 a 3 Do đó V    .
A' B 'C ' BC 8 24 12
Câu 77. Cho lăng trụ đều ABC.EFH có tất cả các cạnh bằng 1. Gọi S là điểm đối xứng của A qua
BH. Thể tích khối đa diện AB . C SFH bằng 1 3 3 1 A. . B. . C. . D. . 2 3 6 6 Lời giải Chọn B
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 Ta có VVV . ABC.SFH . A BCHF S .BCHF 2 2 3 3 VV  .1.  . . A BCHF ABC. 3 EFH 3 4 6
Vì S là điểm đối xứng của A qua BH nên AS BH tại trung điểm N của AS .
Mà BH   BCHF  suy ra khoảng cách từ A đến  BCHF  bằng khoảng cách từ S đến BCHF  3  VV  . . A BCHF S.BCHF 6 3 3 3 Vậy VVV    . ABC.SFH . A BCHF S.BCHF 6 6 3
Câu 78. Cho khối lăng trụ ABC.A B C có thể tích bằng 30. Gọi O là tâm của hình bình hành 1 1 1
ABB A M và G là trọng tâm tam giác A B C . Tính thể tích khối tứ diện COGB . 1 1 1 1 1 1 7 16 5 10 A. . B. k  . C. . D. . 3 81 2 3 Lời giải Chọn D
Gọi M , N lần lượt là trung điểm của AB và A B 1 1 1 Ta có VV  15 BCN . 1 B 1 C M ABC. 1 A 1 B 1 2 C 2 VV  10 1 B .CNM 1 C BCN . 1 B 1 3 C M
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
NGUYỄN BẢO VƯƠNG - 0946798489 1
Mặt khác ta lại có: VS
.d (B , (CGO)). 1 B .CGO CGO 1 3 1 1 1 1 Mà SSSSSSSSSS CGO CNM 1 CCNO C  1 GC OMG CNM 1 C CNM 1 C CNM 1 C CNM 1 C CNM 1 4 12 3 3 C 1 1 1 1 10  VS
.d (B ,(CGO))  S
d (B , (CGO))  V  . 1 B .CGOCGO 1 CNM 1 C 1 1 B .CN 1 3 3 3 3 MC 3
Câu 79. Cho khối chóp S.ABCD có thể tích bằng V . Gọi M , N , P , Q lần lượt là trọng tâm các mặt
bên SAB , SBC ,  SCD , SDA . Gọi k là tỉ số thể tích của khối chóp S.MNPQ và phần còn lại là. Khi đó: 16 15 4 4 A. k V . B. . . C. k  . D. k V . 81 4 23 23 Lờigiải Chọn C S Q M P D A N L I K B J C
Gọi trung điểm các đoạn thẳng AB, BC, CD, DA lần lượt là I , J , K , L .
Ta có: MN / / AC ; QP / / AC ; MQ / / BD ; NP / /BD
Vậy MNPQ là hình bình hành. 1 1 1 1 SS ; SS ; SS ; SS AIL 4 ABD BIJ 4 BAC CJK 4 CBD DKL 4 DCA  1 1 1 SSSSS AIL CJK   4 ABD 4 CBD 4 ABCD   1 1 1 S SSSS I B J DKL   4 BAC 4 DCA 4 ABCD 1 Do đó: SS . IJKL 2 ABCD V SM SN SP 2 2 2 8 Mặt khác V  2V mà SMNP  . .  . .  SMNPQ SMNP V SI SJ SK 3 3 3 27 SIJK 1 1  1  1 1  1  1  1  1 1 V  . h S  . h S  . h . S  . h S  .V  V SIJK IJK  IJ      3 3  2
KL  3 2  2 ABCD  4  3
ABCD  4 SABCD 4
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2020 8 1 4 Suy ra V  2. . .V V . SMNPQ 27 4 27 4 23
Khi đó, thể tích phần còn lại: V '  V VV V V . S .MNPQ 27 27 V Vậy, tỉ số cần tìm S .MNPQ 4 k   . V ' 23
-------------------- HẾT --------------------
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Document Outline

  • 8. Thể tích khối đa diện - câu hỏi
  • 8. Thể tích khối đa diện - đáp án