Tổng ôn tập TN THPT 2021 môn Toán: Góc và khoảng cách

Tài liệu gồm 64 trang, được tổng hợp bởi thầy giáo Nguyễn Bảo Vương, tuyển tập câu hỏi và bài tập trắc nghiệm chuyên đề góc và khoảng cách, có đáp án và lời giải chi tiết.Mời bạn đọc đón xem.

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

64 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ NHẬN BIẾT
Câu 1. (THPT Lê Lợi - Thanh Hóa - 2021) Cho tứ diện
ABCD
có tam giác
BCD
là tam giác đều cạnh
a
,
AB BCD
và
2AB a
. Góc giữa
AC
và mặt phẳng
BCD
là
A.
BCD
. B.
ACB . C.
ACD . D.
ADB
.
Câu 2. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
SA a
, tam giác
ABC
vuông tại
B
,
2AB a
và
BC a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng?
A.
45
. B.
30
. C.
90
. D.
60
.
Câu 3. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình
vuông cạnh
a
. Đường thẳng
SA
vuông góc với mặt phẳng đáy,
SA a
. Gọi
M
là trung điểm của
CD
. Khoảng cách từ
M
đến mặt phẳng
( )SAB
bằng
A.
2a
. B.
a
. C.
2a
. D.
2
2
a
.
Câu 4. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lập phương
. ' ' ' 'ABCD A B C D
. Góc giữa đường
thẳng
AB
và
' 'B D
bằng
A.
30
o
. B.
135
o
. C.
45
o
. D.
90
o
.
Câu 5. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
và
SA
vuông góc với mặt phẳng đáy. Góc giữa
SD
và mặt phẳng
ABCD
là
A.
BSD
. B.
SDA
. C.
ASD
. D.
SAD
.
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
Chủ đề 8
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
BẢ
NG ĐÁP ÁN
1.B 2.B 3.B 4.C 5.B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ NHẬN BIẾT
Câu 1. (THPT Lê Lợi - Thanh Hóa - 2021) Cho tứ diện
ABCD
có tam giác
BCD
là tam giác đều cạnh
a
,
AB BCD
và
2AB a
. Góc giữa
AC
và mặt phẳng
BCD
là
A.
BCD
. B.
ACB . C.
ACD . D.
ADB
.
Lời giải
Chọn B
Do
AB BCD
nên Góc giữa
AC
và mặt phẳng
BCD
bằng
ACB
.
Câu 2. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
SA a
, tam giác
ABC
vuông tại
B
,
2AB a
và
BC a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng?
A.
45
. B.
30
. C.
90
. D.
60
.
Lời giải
Chọn D
Góc giữa
SC
và mặt phẳng
ABC
là góc
SCA .
Xét
SAC
vuông tại
A
:
2 2
1
tan
3
2a
SA a
SCA
AC
a
30SCA .
Câu 3. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình
vuông cạnh
a
. Đường thẳng
SA
vuông góc với mặt phẳng đáy,
SA a
. Gọi
M
là trung điểm của
CD
. Khoảng cách từ
M
đến mặt phẳng
( )SAB
bằng
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
Chủ đề 8
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2a
. B.
a
. C.
2a
. D.
2
2
a
.
Lời giải
Chọn B
Gọi
N
là trung điểm của
AB
. Ta có:
;M SAB
MN AB
MN SAB d MN a
MN SA
.
Câu 4. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lập phương
. ' ' ' 'ABCD A B C D
. Góc giữa đường
thẳng
AB
và
' 'B D
bằng
A.
30
o
. B.
135
o
. C.
45
o
. D.
90
o
.
Lời giải
Chọn C
Ta có:
. ' ' ' 'ABCD A B C D
là hình lập phương
' 'ABB A
là hình vuông
/ / ' 'AB A B
Do đó góc giữa hai đường thẳng
AB
và
' 'B D
bằng góc giữa hai đường thẳng
' 'A B
và
' 'B D
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Mặ
t khác, do
.
' ' ' 'ABCD A B C D
l
à hình lập phương nên
'
' ' 'A B C D
là
hình vuông nên
'
' ' 45
o
A
B D
do đó
góc giữa 2 đường thẳng
'
'A B
và
'
'B D
bằ
ng
4
5
o
Nên góc giữa đường thẳng
A
B
và
'
'B D
bằng
45
o
.
Câu 5. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp
.S
ABCD
có
đáy
A
BCD
là
hình chữ nhật
và
S
A
vuôn
g góc với mặt phẳng đáy. Góc giữa
S
D
và
mặt phẳng
A
BCD
là
A.
B
SD
. B.
S
DA
. C.
A
SD
. D.
S
AD
.
Lờ
i giải
Chọn
B
Ta
có hình chiếu
SD
tr
ên mặt phẳng
A
BCD
là
AD
Vậy
,
,SD ABCD SD AD SDA
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ THÔNG HIỂU
Câu 1. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình chóp
.S ABC
có
SA
vuông góc với
mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông tại
A
và
1
,sin
3
AC a B (minh họ như
hình bên). Góc giữa đường thẳng
SB
với mặt phẳng
ABC
bằng
A.
0
90 .
B.
0
30 .
C.
0
45 .
D.
0
60 .
Câu 2. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương
1 1 1 1
.ABCD A B C D có cạnh
a
. Gọi
I
là trung điểm
.BD
Góc giữa hai đường thẳng
1
A D và
1
B I bằng
A.
120
B.
30 .
C.
45
. D.
60
.
Câu 3. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình chóp
.S ABC
có
( ), 3SA ABC SA a
, tam
giác
ABC
vuông tại
B
có
2AC a
,
BC a
. Góc giữa đường thẳng
SB
và mặt phằng
( )ABC
bằng
A.
60
. B.
90
. C.
30
. D.
45
.
Câu 4. (Sở Lào Cai - 2021) Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc và
2OA OB a
,
2OC a
. Khoảng cách từ điểm
O
đến mặt phẳng
ABC
bằng
A.
2a
.
B.
a
.
C.
2
a
.
D.
3
4
a
.
Câu 5. (Sở Lào Cai - 2021) Cho hình lập phương
.ABCD A B C D
. Gọi
M
,
N
lần lượt là trung điểm
AC
và
B C
,
là góc giữa đường thẳng
MN
và mặt phẳng
A B C D
. Tính giá trị
.
A.
2
sin
2
. B.
2 5
sin
5
. C.
1
sin
2
. D.
5
sin
5
.
Câu 6. (Sở Tuyên Quang - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, đường
thẳng
SA
vuông góc với mặt phẳng đáy và
2SA a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
là
. Khi đó
tan
bằng
A.
2 2
. B.
2
. C.
2
. D.
2
3
.
Câu 7. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
, 2AB a AC a
. Biết thể
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
Chủ đề 8
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
tích khối chóp
.
S ABC
bằng
3
2
a
. Khoảng cách
S
từ đến mặt phẳng
ABC
bằng
A.
2
2
a
. B.
2
6
a
. C.
3 2
4
a
. D.
3 2
2
a
.
Câu 8. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.
S ABC
có đáy
là tam giác vuông tại
B
,
SA
vuông góc với mặt phẳng
ABC
,
AH
là đường cao trong tam giác
SAB
. Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
SA BC
. B.
AH AC
. C.
AH SC
. D.
AH BC
.
Câu 9. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp
.
S ABC
có đáy
là tam giác
vuông tại
B
,
SA
vuông góc với mặt đáy. Góc giữa hai mặt phẳng
SBC
và
ABC
là
A.
. B.
SBA
. C.
SAB
. D.
SCA
.
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp
.
S ABCD
có đáy là hình vuông
ABCD
cạnh bằng
3a
,
SA
vuông góc với mặt đáy
ABCD
,
5SB a
. Tính
sin
của góc giữa cạnh
SC
và mặt đáy
ABCD
.
A.
3 2
4
. B.
2 34
17
. C.
4
5
. D.
2 2
3
.
Câu 11. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp
.
S ABC
có đáy
là tam giác
đều cạnh
a
, cạnh
SA
vuông góc với mặt phẳng đáy và
2SA a
, gọi
M
là trung điểm của
SC
.
Tính cosin của góc
là góc giữa đường thẳng
BM
và
ABC
.
A.
7
cos
14
. B.
2 7
cos
7
. C.
21
cos
7
. D.
5
cos
7
.
Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông
tâm
O
cạnh
a
,
SO
vuông góc với mặt phẳng
ABCD
và
SO a
. Khoảng cách giữa
SC
và
AB
bằng:
A.
2 3
15
a
. B.
2 5
5
a
. C.
5
5
a
. D.
3
15
a
.
Câu 13. (Chuyên KHTN - 2021) Cho hình lăng trụ tam giác đều
.
ABC A B C
có cạnh đáy bằng
a
và
cạnh bên bằng
3
2
a
. Góc giữa hai mặt phẳng
A BC
và
ABC
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 14. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp
.
S ABCD
có đáy là hình vuông
cạnh
a
,
, 2SA ABC SA a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
60
. B.
90
. C.
45
. D.
30
.
Câu 15. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương
.
ABCD A B C D
có
lần lượt là tâm
của các hình vuông
ABCD
và
A B C D
. Góc giữa hai mặt phẳng
A BD
và
ABCD
bằng
A.
A AD
. B.
A OC
. C.
A OA
. D.
OA A
.
Câu 16. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
,a
O
là tâm của mặt đáy. Khoảng cách giữa hai đường thẳng
SO
và
CD
bằng
A.
2
a
. B.
a
. C.
2
2
a
. D.
2a
.
Câu 17. (Sở Yên Bái - 2021) Cho hình chóp
.
S ABCD
có đáy là hình vuông canh
,a
SA
vuông góc với
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
mặt phẳng đáy và
6SA a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
60 .
o
B.
45 .
o
C.
90 .
o
D.
30 .
o
Câu 18. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
bằng
2a
cạnh bên bằng 5a . Góc giữa mặt bên và mặt phẳng đáy bằng
A.
60
. B.
30
. C.
70
. D.
45
.
Câu 19. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình chóp
.S ABC
có
, ,SA SB SC
đôi một vuông góc
với nhau và
SA SB SC
. Gọi
I
là trung điểm của
AB
. Góc giữa
SI
và
BC
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 20. (THPT Lương Thế Vinh - 2021) Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2,a SA
vuông góc với mặt phẳng đáy và
3 2
2
a
SA
. Góc giữa đường thẳng
SO
và
mặt phẳng
ABCD
bằng
A.
45
. B.
90
. C.
30
. D.
60
.
Câu 21. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho khối chóp đều
.S ABC
có cạnh đáy bằng
a
.
Gọi
M
là trung điểm của
SA
. Biết thể tích của khối chóp đó bằng
3
2
a
, khoảng cách từ điểm
M
đến mặt phẳng
ABC
bằng
A.
3a
. B.
3a
. C.
3
3
a
. D. 2 3a .
Câu 22. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho khối lăng trụ đứng
.ABC A B C
có
6AA a
,
đáy
ABC
là tam giác vuông cân tại
B
và
BA BC a
. Góc giữa đường thẳng
A C
và mặt
phẳng đáy bằng
A.
45
. B.
90
. C.
60
. D.
30
.
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho lăng trụ đứng
.ABC A B C
có tất cả các cạnh
đều bằng
a
. Gọi
M
là trung điểm của
CC
(tham khảo hình bên). Khoảng cách từ
M
đến mặt
phẳng
A BC
bằng
A.
21
7
a
. B.
2
4
a
. C.
21
14
a
. D.
2
2
a
.
Câu 24. (THPT Chu Văn An - Thái Nguyên - 2021) Cho chóp
.S ABC
có đáy là tam giác vuông tại
B
.
3 , 3AB a BC a
.
SA
vuông góc với đáy và
2SA a
. Góc giữa
SC
và đáy là
A.
90
. B.
45
C.
60
D.
30
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với mặt phẳng đáy và
3 2
2
a
SA
. Góc giữa đường
thẳng
SO
và mặt phẳng
ABCD
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 26. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình
vuông cạnh
a
, cạnh bên
SA
vuông góc với đáy và
3SA a
. Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
A.
2 5
5
a
. B.
3a
. C.
2
a
. D.
3
2
a
.
Câu 27. (Trung Tâm Thanh Tường - 2021) Cho hình chóp
.S ABC
có
SA ABC
, 3SA a , tam
giác
ABC
vuông tại
B
có
2 , 3AC a BC a
. Góc giữa
S B
và mặt phẳng
ABC
bằng
A.
90
. B.
45
. C.
30
. D.
60
.
Câu 28. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
bằng
2a
, cạnh bên
SA
vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng
SA
và
BD
bằng
A.
2a
. B.
2a
. C.
a
. D. 3a .
Câu 29. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh 3a ,
I
là
trung điểm
'CD
(tham khảo hình vẽ). khoảng cách từ
I
đến mặt phẳng
' 'BDD B
bằng
A.
2
4
a
. B.
4
a
. C.
6
4
a
. D.
3
4
a
.
Câu 30. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình
vuông tâm
I
, cạnh
a
. Biết
SA
vuông góc với mặt đáy
ABCD
và 3SA a (tham khảo hình
vẽ bên). Khi đó tang của góc giữa đường thẳng
SI
và mặt phẳng
ABCD
là:
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
6 . B.
6
6
. C.
3 . D.
3
3
.
BẢNG Đ
ÁP ÁN
1.C
2.B
3.D
4.B
5.B
6.C
7.D
8.B
9.B
10.B
11.C
12.B
13.B
14.C
15.C
16.A
17.A
18.A
19.B
20.D
21.A
22.
C
23.C
24.D
25.
C
26.D
27.
D
28.
A
29.
C
30.
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ THÔNG HIỂU
Câu 1. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình chóp
.S ABC
có
SA
vuông góc với
mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông tại
A
và
1
,sin
3
AC a B (minh họ như
hình bên). Góc giữa đường thẳng
SB
với mặt phẳng
ABC
bằng
A.
0
90 .
B.
0
30 .
C.
0
45 .
D.
0
60 .
Lời giải
Chọn C
Ta có
,SA ABC SB ABC SBA
1 2
sin cos
3 3
B B ;
1
tan 2
2
AC
B AB a
AB
Vậy tam giác
SAB
vuông cân tại
A
Suy ra
0
, 45SB ABC SBA
Câu 2. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương
1 1 1 1
.ABCD A B C D có cạnh
a
. Gọi
I
là trung điểm
.BD
Góc giữa hai đường thẳng
1
A D và
1
B I bằng
A.
120
B.
30 .
C.
45
. D.
60
.
Lời giải
Chọn B
Ta có
1 1
/ /B C A D
1 1 1 1
, ,A D B I B C B I
.
Vì
1 1 1 1
.ABCD A B C D là hình lập phương cạnh a nên
1 1
2 6
2; ;
2 2
a a
B C a IC B I
.
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
Chủ đề 8
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét
1
B IC có:
2 2 2
1 1
1
1 1
3
cos
2 . 2
B I B C IC
IB C
B I B C
.
1
30 .IB C
Do đó
1 1 1 1 1
, , 30 .A D B I B C B I IB C
Câu 3. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình chóp
.S ABC
có
( ), 3SA ABC SA a
, tam
giác
ABC
vuông tại
B
có
2AC a
,
BC a
. Góc giữa đường thẳng
SB
và mặt phằng
( )ABC
bằng
A.
60
. B.
90
. C.
30
. D.
45
.
Lời giải
Chọn D
AB
là hình chiếu vuông góc của
SB
lên
( )ABC
nên
, ,SB ABC SB AB SBA
.
Tam giác
ABC
vuông tại
B
nên:
2 2
(2 ) 3AB a a a
SAB
vuông cân tại
A
45SBA
.
Vậy
, 45SB ABC
.
Câu 4. (Sở Lào Cai - 2021) Cho tứ diện
OABC
có
OA
,
OB
,
OC
đôi một vuông góc và
2OA OB a
,
2OC a
. Khoảng cách từ điểm
O
đến mặt phẳng
ABC
bằng
A.
2a
.
B.
a
.
C.
2
a
.
D.
3
4
a
.
Lời giải
Chọn B
A
C
B
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Xét hệ trục tọa độ
Oxyz
như sau điểm
O
là gốc tọa độ
OA Oz
;
OB Ox
và
OC Oy
. Khi đó
ta có
0;0;0O
;
0;0;2A a
;
2 ;0;0B a
và
0; 2;0C a .
Phương trình mặt phẳng
ABC
là 1
2 2
2
x y z
a a
a
2 2 0x y z a
.
Khoảng cách từ điểm
O
đến mặt phẳng
ABC
là
0 2.0 0 2
,
1 2 1
a
d O ABC a
.
Câu 5. (Sở Lào Cai - 2021) Cho hình lập phương
.ABCD A B C D
. Gọi
M
,
N
lần lượt là trung điểm
AC
và
B C
,
là góc giữa đường thẳng
MN
và mặt phẳng
A B C D
. Tính giá trị
.
A.
2
sin
2
. B.
2 5
sin
5
. C.
1
sin
2
. D.
5
sin
5
.
Lời giải
Chọn B
Giả sử cạnh hình lập phương là
a
.
Gọi
O
là tâm của hình vuông
A B C D
. Suy ra
O N
là hình chiếu của
MN
lên
A B C D
. Do
đó góc giữa
MN
và
A B C D
là góc giữa
MN
và
O N
.
Tam giác
O MN
vuông tại
O
có
1
2
O N a
,
O M a
nên
2 2 2
2
2 5
sin
5
4
O M O M a
O NM
MN
O N O M a
a
.
Câu 6. (Sở Tuyên Quang - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, đường
thẳng
SA
vuông góc với mặt phẳng đáy và
2SA a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
là
. Khi đó
tan
bằng
A.
2 2
. B.
2
. C.
2
. D.
2
3
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
;SC ABCD SCA
.
Xét tam giác
SAC
vuông tại
A
có:
tan
SA
SCA
AC
2
2
a
a
2
tan 2
.
Câu 7. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
, 2AB a AC a
. Biết thể
tích khối chóp
.S ABC
bằng
3
2
a
. Khoảng cách
S
từ đến mặt phẳng
ABC
bằng
A.
2
2
a
. B.
2
6
a
. C.
3 2
4
a
. D.
3 2
2
a
.
Lời giải
Chọn D
Ta có
3
2
.
2
3.
3
1 2 3 2
2
. ,
2 2 2
2
2
S ABC
ABC
ABC
a
V
a a
S AB AC d S ABC
S
a
.
Câu 8. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
SA
vuông góc với mặt phẳng
ABC
,
AH
là đường cao trong tam giác
SAB
. Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
SA BC
. B.
AH AC
. C.
AH SC
. D.
AH BC
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Ta có
SA ABC SA BC
Tam giác
ABC
vuông tại
B
nên
AB BC
Có:
SA BC
BC SAB
AB BC
Mà
AH
nằm trong mặt phẳng
SAB
nên
BC AH
Mặt khác:
BC AH cmt
AH SBC AH SC
AH SB
.
Vậy khẳng định sai là
AH AC
.
Câu 9. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông tại
B
,
SA
vuông góc với mặt đáy. Góc giữa hai mặt phẳng
SBC
và
ABC
là
A.
BAC . B.
SBA. C.
SAB . D.
SCA.
Lời giải
Chọn B
Ta có
SA ABC SA BC
BC SAB
AB BC
.
Mà
SBC ABC BC
. Suy ra
+
SBC SAB
theo giao tuyến
SB
.
+
ABC SAB
theo giao tuyến
AB
.
; ;SBC ABC SB AB SBA (do
0
90SBA )
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông
ABCD
cạnh bằng
3a
,
SA
vuông góc với mặt đáy
ABCD
,
5SB a
. Tính
sin
của góc giữa cạnh
SC
và mặt đáy
ABCD
.
A.
3 2
4
. B.
2 34
17
. C.
4
5
. D.
2 2
3
.
Lời giải
Chọn B
A
S
C
B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do
SA ABCD
nên
AC
là hình chiếu của
SC
lên mặt phẳng
ABCD
. Do đó góc giữa cạnh
SC
và mặt đáy
ABCD
là
SCA .
Xét tam giác
ABC
có
2 2
3 2AC AB BC a
.
Xét tam giác
SAB
có
2 2
4SA SB AB a
.
Xét tam giác
SAC
có
2 2
34SC SA AC a
.
Xét tam giác
SAC
có
4 2 34
sin
17
34
SA a
SCA
SC
a
.
Vậy
sin
của góc giữa cạnh
SC
và mặt đáy
ABCD
bằng
2 34
17
.
Câu 11. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
đều cạnh
a
, cạnh
SA
vuông góc với mặt phẳng đáy và
2SA a
, gọi
M
là trung điểm của
SC
.
Tính cosin của góc
là góc giữa đường thẳng
BM
và
ABC
.
A.
7
cos
14
. B.
2 7
cos
7
. C.
21
cos
7
. D.
5
cos
7
.
Lời giải
Chọn C
Trong mặt phẳng
SAC
, dựng
MH AC
tại
H
.
Do
//SA ABC SA AC ABC SA MH
.
Khi đó:
MH ABC
.
Suy ra:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
2
2
3
21
2
cos cos , cos , cos
7
3 2
2 2
a
BH
BM ABC BM BH MBH
BM
a a
Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông
tâm
O
cạnh
a
,
SO
vuông góc với mặt phẳng
ABCD
và
SO a
. Khoảng cách giữa
SC
và
AB
bằng:
A.
2 3
15
a
. B.
2 5
5
a
. C.
5
5
a
. D.
3
15
a
.
Lời giải
Chọn B
/ /AB CD
⇒
d ; d ; d ; 2.d ;AB SC AB SCD A SCD O SCD
(*)
Hình chóp
.O SCD
là tam diện vuông tại
O
:
2 2
2 2 2 2 2
2
1 1 1 1 1 1 1 5
d ;
2 2
2 2
OS OC OD a a
O SCD
a a
⇔
5
d ;
5
a
O SCD
(*) ⇔
2 5
d ; 2.d ;
5
a
AB SC O SCD
.
Câu 13. (Chuyên KHTN - 2021) Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
a
và
cạnh bên bằng
3
2
a
. Góc giữa hai mặt phẳng
A BC
và
ABC
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Lời giải
Chọn B
Gọi
M
là trung điểm của
BC
AM BC
(vì tam giác
ABC
đều)
A'
C'
B'
B
C
A
M
S
a
C
D
A
B
O
a
a
a
a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2 2
3
4 2
a a
AM AB BM a
,A BC ABC AMA
Lại có:
3
2
tan 3
3
2
a
AA
AMA
AM
a
60 , 60AMA A BC ABC
Câu 14. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông
cạnh
a
,
, 2SA ABC SA a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
60
. B.
90
. C.
45
. D.
30
.
Lời giải
Chọn C
Ta có
2AC a
suy ra
SAC
vuông cân tại
A
Góc giữa
SC
và mp
ABCD
chính là góc
45SCA
Câu 15. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương
.ABCD A B C D
có
,O O
lần lượt là tâm
của các hình vuông
ABCD
và
A B C D
. Góc giữa hai mặt phẳng
A BD
và
ABCD
bằng
A.
A AD
. B.
A OC
. C.
A OA
. D.
OA A
.
Lời giải
Chọn C
Ta có
ABCD
là hình vuông nên
AO BD
, đồng thời
BD A A
BD A AO
BD A O
Ta có
A BD ABCD BD
AO BD
A O BD
; ;A BD ABCD A O AO A OA
O
O'
D
CB
A
D'
C'
B'
A'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 16. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
,a
O
là tâm của mặt đáy. Khoảng cách giữa hai đường thẳng
SO
và
CD
bằng
A.
2
a
. B.
a
. C.
2
2
a
. D.
2a
.
Lời giải
Chọn A
Vì
.S ABCD
là hình chóp tứ giác đều nên
ABCD
là hình vuông và
.SO ABCD
Gọi
M
là trung điểm của
.CD
Khi đó
OM SO
(do
SO ABCD
và
OM ABCD
).
Mà
OM CD
(do
OCD
là tam giác cân tại
O
).
Suy ra
, .
2 2
AD a
d SO CD OM
Câu 17. (Sở Yên Bái - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông canh
,a
SA
vuông góc với
mặt phẳng đáy và
6SA a
. Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
A.
60 .
o
B.
45 .
o
C.
90 .
o
D.
30 .
o
Lời giải
Chọn A.
Ta có
AC
là hình chiếu của
SC
lên mặt đáy
.ABCD
0
, , tan 3 , 60 .
SA
SC ABCD SC AC SCA SCA SC ABCD
AC
Câu 18. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
bằng
2a
cạnh bên bằng
5a
. Góc giữa mặt bên và mặt phẳng đáy bằng
A.
60
. B.
30
. C.
70
. D.
45
.
Lời giải
Chọn A
Gọi
O
là tâm hình vuông
ABCD
. Khi đó
SO ABCD
.
Gọi
H
là trung điểm cạnh
CD
. Ta có:
OH CD
và
2
CD
HD OH a
.
Do
SCD
cân tại
S
nên
SH CD
.
Vậy góc giữa mặt bên
SCD
và mặt phẳng
ABCD
là góc
SHO .
Trong
SHD
vuông tại
H
ta có
2 2 2 2
5 2SH SD HD a a a
.
Khi đó
1
cos 60
2 2
OH a
SHO SHO
SH a
.
Câu 19. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình chóp
.S ABC
có
, ,SA SB SC
đôi một vuông góc
với nhau và
SA SB SC
. Gọi
I
là trung điểm của
AB
. Góc giữa
SI
và
BC
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Lời giải
Chọn B
Ta có:
2
1
.
. . .
2
cos ;
.
.
2
SA SB BC
SI BC SA BC SB BC
SI BC
BC
SI BC BC
BC
2
.SB BC
BC
2
. .cos135SB BC
BC
2
. 2.cos135
2
SB SB
SB
2.cos135 1
2 2
.
Suy ra:
; 120SI BC
; 60SI BC
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 20. (THPT Lương Thế Vinh - 2021) Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2,a SA
vuông góc với mặt phẳng đáy và
3 2
2
a
SA
. Góc giữa đường thẳng
SO
và
mặt phẳng
ABCD
bằng
A.
45
. B.
90
. C.
30
. D.
60
.
Lời giải
Chọn D
Ta có:
ABCD
là hình thoi có tâm là
O
O
là trung điểm của
BD
.
Mà
ABD
đều nên
AO BD
Lại có
,SA ABCD SO ABCD SOA
Xét
ABO
có:
2
2
2 2
2 6
2
2 2
a a
AO AB BO a
Ta có:
3 2
2
tan 3 60
6
2
a
SA
SAO SOA
AO
a
Câu 21. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho khối chóp đều
.S ABC
có cạnh đáy bằng
a
.
Gọi
M
là trung điểm của
SA
. Biết thể tích của khối chóp đó bằng
3
2
a
, khoảng cách từ điểm
M
đến mặt phẳng
ABC
bằng
A.
3a
. B.
3a
. C.
3
3
a
. D.
2 3a
.
Lời giải
Chọn B
Ta có
2
1 3
. .sin
2 4
ABC
a
S AB AC BAC
.
Mà
.
.
3
1
. , , 2 3
3
S ABC
S ABC ABC
ABC
V
V S d S ABC d S ABC a
S
.
O
B
A
D
C
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
1
, , 3
2
d M ABC d S ABC a
.
Câu 22. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho khối lăng trụ đứng
.ABC A B C
có
6AA a
,
đáy
ABC
là tam giác vuông cân tại
B
và
BA BC a
. Góc giữa đường thẳng
A C
và mặt
phẳng đáy bằng
A.
45
. B.
90
. C.
60
. D.
30
.
Lời giải
Chọn C
Ta có:
AA ABC AC
là hình chiếu của
A C
lên mặt phẳng
ABC
.
Khi đó
, ,A C ABC A C AC A CA
.
Ta có:
2 2AC AB a
.
6
tan 3 60
2
AA a
A CA A CA
AC
a
.
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho lăng trụ đứng
.ABC A B C
có tất cả các cạnh
đều bằng
a
. Gọi
M
là trung điểm của
CC
(tham khảo hình bên). Khoảng cách từ
M
đến mặt
phẳng
A BC
bằng
A.
21
7
a
. B.
2
4
a
. C.
21
14
a
. D.
2
2
a
.
Lời giải
Chọn C
Gọi
,H K
lần lượt là hình chiếu của
A
lên
BC
và
A H
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Ta có
1 1 1
, , ,
2 2 2
d M A BC d C A BC d A A BC AK
.
Mà
3
2
a
AH
;
AA a
nên
2 2
. 21
7
AH AA a
AK
AH AA
.
Vậy
21
;
14
a
d M A BC
.
Câu 24. (THPT Chu Văn An - Thái Nguyên - 2021) Cho chóp
.S ABC
có đáy là tam giác vuông tại
B
.
3 , 3AB a BC a
.
SA
vuông góc với đáy và
2SA a
. Góc giữa
SC
và đáy là
A.
90
. B.
45
C.
60
D.
30
Lời giải
Chọn D
12AC a
0
2 1
tan
12 3
30
a
SCA
a
SCA
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với mặt phẳng đáy và
3 2
2
a
SA
. Góc giữa đường
thẳng
SO
và mặt phẳng
ABCD
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Lời giải
Chọn C
Tam giác
ABD
đều cạnh
2a
, suy ra
2 3
6
2 2
a
a
AO
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
SA ABCD
, suy ra
OA
là hình chiếu của
OS
lên mặt phẳng
ABCD
, suy ra:
;SO ABCD SOA
.
Ta có:
3 2 2
tan . 3 60
2
6
SA a
SOA SOA
AO
a
.
Vậy
; 60SO ABCD
.
Câu 26. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình
vuông cạnh
a
, cạnh bên
SA
vuông góc với đáy và 3SA a . Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
A.
2 5
5
a
. B. 3a . C.
2
a
. D.
3
2
a
.
Lời giải
Chọn D
Kẻ
AH SB
*
Ta có
BC AB
( Do
ABCD
là hình vuông )
BC SA
( Do
SA ABCD
)
Suy ra
BC SAB
Suy ra
BC AH
**
Từ
* , **
suy ra
AH SBC
. Suy ra
,d A SBC AH
2 2 2 2 2 2
1 1 1 1 1 4
3 3AH AB SA a a a
Suy ra
3
2
a
AH
Câu 27. (Trung Tâm Thanh Tường - 2021) Cho hình chóp
.S ABC
có
SA ABC
, 3SA a , tam
giác
ABC
vuông tại
B
có
2 , 3AC a BC a
. Góc giữa
SB
và mặt phẳng
ABC
bằng
A.
90
. B.
45
. C.
30
. D.
60
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Ta có
2
2
2 2
2 3AB AC BC a a a .
Dễ thấy
; ;SB ABC SB AB SBA . Khi đó
3
tan 3 60
SA a
SBA SBA
AB a
.
Vậy
; 60SB ABC
.
Câu 28. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
bằng
2a
, cạnh bên
SA
vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng
SA
và
BD
bằng
A.
2a
. B.
2a
. C.
a
. D. 3a .
Lời giải
Chọn A
Gọi
O
là tâm của hình vuông
ABCD
, ta có
AO BD
.
Mặt khác
SA ABCD SA AO
.
Vậy
AO
là đoạn vuông góc chung của hai đường thẳng
SA
và
BD
nên
1
; 2
2
d SA BD AO AC a
.
Câu 29. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình lập phương
. ' ' ' 'ABCD A B C D
cạnh
3a
,
I
là
trung điểm
'CD
(tham khảo hình vẽ). khoảng cách từ
I
đến mặt phẳng
' 'BDD B
bằng
a 3
2a
a 3
C
B
A
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
4
a
. B.
4
a
. C.
6
4
a
. D.
3
4
a
.
Lời giải
Chọn C
Do
' ' 'CI BDD B D
nên ta có
, ' '
' 1
' 2
, ' '
d I BDD B
ID
CD
d C BDD B
.
Gọi
M BD AC
. Khi đó
6
2 2
AC a
CM
.
Vậy
1 6
, ' ' , ' ' .
2 2 4
CM a
d I BDD B d C BDD B
Câu 30. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình
vuông tâm
I
, cạnh
a
. Biết
SA
vuông góc với mặt đáy
ABCD
và
3SA a
(tham khảo hình
vẽ bên). Khi đó
tang
của góc giữa đường thẳng
SI
và mặt phẳng
ABCD
là:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
6
. B.
6
6
. C.
3
. D.
3
3
.
Lờ
i giải
Chọn
A
Ta
có:
1 2
2 2
a
AI AC
Mà
S
A ABCD
nê
n
A
I
là hình c
hiếu của
S
I
trê
n mặt phẳng
A
BCD
;
;
SI
ABCD SI AI SIA
(do tam giác
S
AI
vuông
tại
A
)
Vậy
ta
n ; tan 6
SA
SI
ABCD SIA
AI
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG
Câu 1. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
SAB
vuông cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách
d
giữa
SB
và
.AC
A.
6
.
6
a
d
B.
2
.
3
a
d
C.
21
.
7
a
d
D.
30
.
5
a
d
Câu 2. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho tứ diện
OABC
có
, ,OA OB OC
đôi một
vuông góc với nhau,
OA a
và
2OB OC a
. Gọi
P
là trung điểm của
BC
(minh họa như
hình bên dưới). Khoảng cách giữa hai đường thẳng
OP
và
AB
bằng
A.
2
2
a
. B.
6
3
a
. C.
a
. D.
2 5
5
a
.
Câu 3. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông tại
A
,
M
là trung điểm
BC
, hình chiếu vuông góc của
S
lên mặt phẳng
ABC
trùng
với trung điểm của
AM
. Cho biết
, 3AB a AC a
và mặt phẳng
SAB
tạo với mặt phẳng
ABC
một góc
0
60
. Tính khoảng cách giữa hai đường thẳng
SA
và
BC
.
A.
3
2
a
. B.
3
4
a
. C.
3
2
a
. D.
4
3
a
.
Câu 4. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có
ABCD
là hình vuông
cạnh
a
,
2SA a
và vuông góc
ABCD
. Gọi
M
là trung điểm của
SD
. Tính khoảng cách
d
giữa
hai đường thẳng
SB
và
CM
.
A.
2
.
3
a
d
B.
.
3
a
d
C.
.
6
a
d
D.
2
.
2
a
d
Câu 5. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp
. DS ABC
có đáy
ABCD
là hình
chữ nhật,
2 , AD .AB a a
SA
vuông góc với mặt phẳng đáy,
3SA a
. Cosin của góc giữa
SC
và mặt đáy bằng
A.
7
4
. B.
10
4
. C.
6
4
. D.
5
4
.
Câu 6. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác
vuông,
2BA BC a
, cạnh bên
4AA a
,
M
là trung điểm
BC
(minh họa như hình dưới).
Khoảng cách giữa hai đường thẳng
B C
và
AM
bằng
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
Chủ đề 8
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2 7
7
a
. B.
6
6
a
. C.
a
. D.
6
3
a
.
Câu 7. (THPT Đồng Quan - Hà Nội - 2021) Cho lăng trụ tứ giác
.ABCD A B C D
có đáy
ABCD
là
hình thoi cạnh
a
, góc
60BAC . Biết
AA A B A D
và cạnh bên
AA
hợp với mặt phẳng
đáy góc
60
. Tính khoảng cách giữa hai đường thẳng
CC
và
BD
.
A.
3
4
a
. B.
3
2
a
. C.
6
8
a
. D.
3
4
a
.
Câu 8. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi tâm
; 2 ; 3 ,I AB a BD AC
mặt bên
SAB
là tam giác cân đỉnh
A
, hình chiếu vuông góc của đỉnh
S
trên mặt phẳng đáy trùng với trung
điểm
H
của
.AI
Khoảng cách giữa hai đường thẳng
SB
và
CD
bằng.
A.
2 7
7
a
B.
2 35
7
a
. C.
2 35
35
a
. D.
35
7
a
.
Câu 9. (Sở Vĩnh Phúc - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh bằng
a
,
0
120BAD
. Mặt bên
SAB
là tam giác đều và
SAB ABCD
(tham khảo hình vẽ).
Tính khoảng cách từ
A
đến
SBC
A.
2
a
. B.
7
7
a
. C.
3
4
a
. D.
15
5
a
.
Câu 10. (Sở Hà Tĩnh - 2021) Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
B
,
AD a
,
2AB a
,
3BC a
, mặt bên
SAB
là tam giác đều và vuông góc với mặt phẳng đáy
ABCD
.
Tính khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
3 30
10
a
. B.
3 30
5
a
. C.
30
2
a
. D.
3 2
2
a
.
Câu 11. (Sở Tuyên Quang - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 3AB a AD a
. Cạnh bên
SA
vuông góc với đáy, biết tam giác
SAD
có diện tích
2
3S a
.
Tính khoảng cách từ
C
đến
SBD
bằng
M
A
C
B'
B
A'
C'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
39
13
a
d
. B.
2 51
17
a
d
. C.
39
5
a
d
. D.
2 39
13
a
d
.
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc
với đáy. Tính khoảng cách giữa hai đường thẳng
AB
và
.SD
A.
21
7
a
. B.
3
7
a
. C.
21
3
a
. D.
7
3
a
.
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình hộp chữ nhật
1 1 1 1
.
ABCD A B C D
có ba kích
thước
AB a
,
2AD a
,
1
3AA a
. Khoảng cách từ A đến mặt phẳng
1
A BD
bằng bao nhiêu?
A.
a
. B.
7
6
a
. C.
6
7
a
. D.
5
7
a
.
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ đứng
.
ABC A B C
có đáy
là tam giác đều cạnh
a
,
2a
AA
. Gọi
M
là điểm trên cạnh
A B
,
3
a
A M
. Khoảng cách từ
M
đến mặt phẳng
AB C
bằng?
A.
4 57
57
a
. B.
2 57
57
a
. C.
57
19
a
. D.
57
57
a
.
Câu 15. (Chuyên Lê Hồng Phong - TPHCM - 2021) Hình hộp
.
ABCD A B C D
có
AB AA AD a
và
60
A AB A AD BAD
. Tính
c sin«
của góc giữa đường thẳng
CD
và mặt phẳng
A AD
:
A.
3
3
. B.
3
2
. C.
3
4
. D.
2 3
3
.
Câu 16. (Chuyên KHTN - 2021) Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
3a
,
SA ABCD
và
2SA a
. Tính góc giữa
SC
và
ABCD
.
A.
90
. B.
45
. C.
60
. D.
30
.
Câu 17. (Chuyên KHTN - 2021) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
. Cạnh
bên
SA
vuông góc với đáy. Góc giữa
SC
và mặt đáy bằng
45
. Gọi
E
là trung điểm của
BC
.
Tính khoảng cách giữa hai đường thẳng
DE
và
SC
.
A.
2 19
19
a
. B.
10
19
a
. C.
10
5
a
. D.
2 19
5
a
.
Câu 18. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương
.
ABCD A B C D
. Số đo của góc giữa hai
mặt phẳng
BA C
và
DA C
bằng
A.
60
. B.
30
. C.
45
. D.
90
.
Câu 19. (Chuyên Quốc Học Huế - 2021) Cho hình lăng trụ tam giác
. ' ' 'ABC A B C
có mặt bên
' 'ABB A
là hình thoi cạnh a,
120
A AB
và
10
' 3,
2
A C BC a AC a
. Tính khoảng cách giữa hai
đường thẳng
A B
và
AC
A.
10
20
a
B.
10
10
a
C.
3 10
20
a
D.
3 10
10
a
Câu 20. (Chuyên Quang Trung - Bình Phước - 2021) Cho hình chóp
.
S ABCD
đáy
ABCD
là hình thoi
cạnh
a
, góc
60
BAD
,
SA ABCD
,
, 45
SC ABCD
. Gọi
I
là trung điểm
SC
. Tính
khoảng cách từ
I
đến mặt phẳng
SBD
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
15
10
a
. B.
15
5
a
. C.
2 15
5
a
. D.
15
15
a
.
Câu 21. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình chóp có đáy là hình chữ
nhật
, 2 ; AB a AD a
SA
vuông góc với đáy , hợp với đáy một góc và
. Tính khoảng cách từ điểm B đến mặt phẳng
A. B. C. D.
Câu 22. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
,
3SD a
. Mặt bên
SAB
là tam giác cân và nằm trong mặt phẳng vuông góc với đáy. Gọi
H
là trung điểm của
AB
,
K
là trung điểm của
AD
. Khoảng cách giữa hai đường thẳng
SD
và
HK
bằng
A.
105
5
a
. B.
105
20
a
. C.
105
30
a
. D.
105
10
a
.
Câu 23. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp
.S ABC
có
12 , 5 , 9 , 13 , 15 SA cm AB cm AC cm SB cm SC cm
và
10BC cm
. Tan của góc giữa hai
mặt phẳng
( )SBC
và
( )ABC
bằng
A.
14
10
. B.
10 14
14
. C.
4
3
. D.
12
5
.
Câu 24. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông
cân,
2AB BC a
. Tam giác
SAC
cân tại
S
và nằm trong mặt phẳng vuông góc với
ABC
,
3SA a . Góc giữa hai mặt phẳng
SAB
và
SAC
bằng
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
90
.
Câu 25. (Sở Yên Bái - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, hình chiếu
vuông góc của
S
lên mặt phẳng
( )ABCD
là trung điểm của
,AD
góc giữa đường thẳng
SB
và
mặt đáy bằng
60
o
. Gọi
M
là trung điểm của
DC
. Khoảng cách giữa hai đường thẳng
SA
và
BM
là
A.
285
9
a
. B.
285
19
a
. C.
3 285
19
a
. D.
2 285
19
a
.
Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy là tam giác đều, tam
giác
SAB
vuông cân tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết
6.SA a
Khoảng cách từ điểm
A
đến mặt phẳng
( )SBC
bằng
A.
3 7
7
a
. B. 7a . C.
6 7
7
a
. D.
7
2
a
.
Câu 27. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chóp
.S ABC
có
, ,SA SB SC
đôi một vuông
góc nhau và
;SA a 2 ;SB a
3 .SC a
Gọi
, ,M N P
lần lượt là trung điểm của
, ,AB BC CA
.
Khoảng cách từ điểm
M
đến mặt phẳng
SNP
bằng
A.
5
7
a
. B.
6
7
a
. C.
15
2
a
. D.
13
2
a
.
Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông cân tại
A
,
2BC a
và
SB a
. Hình chiếu vuông góc của
S
lên mặt phẳng
ABC
trùng với trung điểm
M
của
BC
. Góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
.
S ABCD
ABCD
ABCD
SC
10
tan
5
.SCD
a
3
2a
3
a 3
3
2a 3
3
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
0
30
. B.
0
60
. C.
0
45
. D.
0
75
.
Câu 29. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình hộp
. ' ' ' 'ABCD A B C D
có tất cả các cạnh
đều bằng
a
và
0
' ' 60BAA DAA BAD . Gọi
G
là trọng tâm của tam giác
'AB C
. Khoảng
cách từ
G
đến mặt phẳng
' 'DA C
bằng
A.
22
66
a
. B.
4 11
11
a
. C.
2 11
11
a
. D.
22
11
a
.
Câu 30. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
có đáy là
hình vuông cạnh
a
, mặt bên
SAD
là tam giác đều và
SAD ABCD
. Gọi
M
là trung điểm
cạnh đáy
AB
. Khoảng cách giữa các đường thẳng
SA
và
CM
là.
A.
3
3
a
. B.
2
3
a
. C.
5
4
a
. D.
3
4
a
.
Câu 31. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
hình chữ nhật
, 3AB a AD
. Cạnh bên
SA
vuông góc với đáy và
2SA a
. Tính khoảng cách
d
từ điểm
C
đến mặt phẳng
SBD
:
A.
2 57
.
19
a
d
B.
2
.
5
a
d C.
5
.
2
a
d
D.
57
.
19
a
d
Câu 32. (THPT Quốc Oai - Hà Nội - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
là góc tạo bởi đường thẳng
BD
với mặt phẳng
SAD
. Khi đó
sin
bằng
A.
3
2
. B.
1
2
. C.
6
4
. D.
10
4
.
Câu 33. (THPT Quốc Oai - Hà Nội - 2021) Cho hình lăng trụ tam giác đều
. ' ' 'ABC A B C
có tất cả các
cạnh có độ dài bằng
2
(tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng
'AC
và
'A B
bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
.
2
B.
3
.
5
C.
2
.
5
D.
3
.
2
Câu 34. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác
ABC
vuông tại
A
có
2BC a
,
3AB a
. Khoảng cách giữa hai đường thẳng
AA
và
BC
là
A.
21
7
a
. B.
3
2
a
. C.
5
2
a
. D.
7
3
a
.
Câu 35. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho khối chóp
.S ABCD
có đáy là hình bình hành,
3, 4, 120 .
o
AB AD BAD
Cạnh bên 2 3SA
vuông góc với đáy. Gọi
, ,M N P
lần lượt là
trung điểm các cạnh
,SA AD
và
.BC
Gọi
là góc giữa hai mặt phẳng
( )SAC
và
( ).MNP
Chọn
khẳng định đúng trong các khẳng định sau đây.
A.
3
sin ;1
2
. B.
1
sin 0;
2
. C.
1 2
sin ;
2 2
. D.
2 3
sin ;
2 2
.
Câu 36. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho tứ diện
ABCD
có
3
,
2
a
AB CD a IJ
(
,I J
lần lượt là trung điểm của
BC
và
AD
). Số đo góc giữa hai đường thẳng
AB
và
CD
là
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
120
.
Câu 37. (Trung Tâm Thanh Tường -2021) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
4a
, cạnh
bên bằng 2 5a , gọi
O
là tâm của hình vuông
ABCD
. Khoảng cách từ
O
đến mặt phẳng
SCD
bằng
A. 3a . B.
a
. C.
2
a
. D.
2a
.
Câu 38. (Trung Tâm Thanh Tường - 2021) Cho hình chóp
SABCD
có đáy
ABCD
là hình vuông cạnh
bằng
2a
. Tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
,E F
lần lượt là
trung điểm của
,SA CD
. Khoảng cách giữa hai đường thẳng
SD
và
EF
bằng
TÀ
I LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
5
1
0
a
. B.
2
3
7
a
. C.
5
5
a
. D.
2
a
.
Câu 39. (Trung Tâm Thanh Tường -2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
bằng
2a
, SA vuông góc với đáy,
6SA
a
. Tính khoảng cách giữa hai đường thẳng SD và AC.
A.
2 10
5
a
. B.
2a
. C.
6
2
a
. D.
2a
.
Câu 40. (Trung Tâm Thanh Tường -2021) Cho hình tứ diện đều
A
BCD
.
Giá trị
t
an
của
góc giữa mặt
bên và đáy bằng
A.
2
6
3
. B.
2
. C.
2 2
. D.
2
.
Câu
41. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp
.S
ABCD
có
đáy
A
BCD
là
hình vuông
cạnh
a
;
2SA
a
và
S
A
vuôn
g góc với mặt đáy
A
BCD
.
Gọi
M
;
N
lần
lượt là hình chiếu
vuông góc của đỉnh
A
lê
n các cạnh
S
B
và
S
D
.
Khi đó góc giữa đường thẳng
S
B
và
mặt phẳng
A
MN
bằng:
A.
45
. B.
30
. C.
60
. D.
90
.
BẢNG Đ
ÁP ÁN
1.
C
2.B
3.D
4.
A
5.B
6.
D
7.D
8.
B
9.
D
10.
A
11.B
12.A
13.C
14.A
15.
A
16.D
17.
A
18.
A
19.
C
20.
A
21.D
22.
C
23.B
24.A
25.
B
26.C
27.
B
28.C
29.D
30.
D
31.A 32.C 33.C 34.B 35.A 36.A 37.C
38.
A
39.C 40.C 41.C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG
Câu 1. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
, tam giác
SAB
vuông cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách
d
giữa
SB
và
.AC
A.
6
.
6
a
d
B.
2
.
3
a
d
C.
21
.
7
a
d
D.
30
.
5
a
d
Lời giải
Chọn C
Kẻ đường thẳng
đi qua
B
và
/ /AC
.
Kẻ
HD
tại
D
.
Khi đó
/ / / /AC BD AC SDB
; ; ; 2 ;d AC SB d AC SBD d A SDB d H SDB
.
Kẻ
HK SD
tại K.
Vì
,BD DH BD SH BD SDH BD HK
.
Mà
HK SD HK SDB
;d H SDB HK
.
Ta có
SAB
vuông cân ở S nên
.
2
a
SH HB HA
Vì
/ / 60AC BD DBH BAC
.
HDB
vuông ở
D
nên
3
.sin .sin 60
2 4
a a
HD HB HBD
.
SHD
vuông ở
H
có:
2 2 2
1 1 1 21
;
14
a
HK d H SBD
SH DH HK
.
21
; 2 ; .
7
a
d SB AC d H SBD
Câu 2. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho tứ diện
OABC
có
, ,OA OB OC
đôi một
vuông góc với nhau,
OA a
và
2OB OC a
. Gọi
P
là trung điểm của
BC
(minh họa như
hình bên dưới). Khoảng cách giữa hai đường thẳng
OP
và
AB
bằng
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
Chủ đề 8
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
2
a
. B.
6
3
a
. C.
a
. D.
2 5
5
a
.
Lời giải
Chọn B
Chọn hệ trục tọa độ
Oxyz
như hình vẽ, khi đó
0;0;0 , 2 ;0;0 , 0;2 ;0 , 0;0;O B a C a A a
.
Vì
P
là trung điểm của
BC
nên
; ;0P a a
.
Ta có
; ;0 , 2 ;0; , 0;0;OP a a AB a a OA a
.
Suy ra
3
2 2 2
4 4 4
, .
2
6
, ; ; 2 ,
3
4
,
OP AB OA
a
a
OP AB a a a d OP AB
a a a
OP AB
.
Câu 3. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông tại
A
,
M
là trung điểm
BC
, hình chiếu vuông góc của
S
lên mặt phẳng
ABC
trùng
với trung điểm của
AM
. Cho biết
, 3AB a AC a
và mặt phẳng
SAB
tạo với mặt phẳng
ABC
một góc
0
60
. Tính khoảng cách giữa hai đường thẳng
SA
và
BC
.
A.
3
2
a
. B.
3
4
a
. C.
3
2
a
. D.
4
3
a
.
Lời giải
Chọn D
Dựng hình bình hành
ABCD
.
Khi đó
, , , 2 ,d SA BC d BC SAD d M SAD d H SAD
với
H
là trung điểm của
AM
.
Theo đề bài, ta suy ra
SH ABCD SH AD
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Kẻ
HJ AD
,
,HK SI HK SAD d H SAD HK
Kẻ
HI AB SI AB
, suy ra
0
, , 60SAB ABC SI HI SIH
Dễ thấy
ABC
đồng dạng với
IAH
suy ra
4
4 4
4
AB BC BC AB a
AI
BC
IA AH
Tam giác
HIA
vuông tại
I
nên
2 2
2 2
3
2 4 4
a a a
IH AH IA
Tam giác
SHI
vuông tại
H
có
0 0
3
60 tan 60
4
a
SIH SH IH
Ta có
AJH
đồng dạng
DCA
suy ra
1 3
2
2 4 4 4
a
JH AH CA a
JH
CA DA a
Tam giác
SHJ
vuông tại
H
có đường cao
HK
2 2 2 2
1 1 1 64 3
9 8
a
HK
HK SH HJ a
Vậy
3
, 2
4
a
d SA BC HK
.
Câu 4. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có
ABCD
là hình vuông
cạnh
a
,
2SA a
và vuông góc
ABCD
. Gọi
M
là trung điểm của
SD
. Tính khoảng cách
d
giữa
hai đường thẳng
SB
và
CM
.
A.
2
.
3
a
d
B.
.
3
a
d
C.
.
6
a
d
D.
2
.
2
a
d
Lời giải
Chọn A
Chọn hệ trục tọa độ như hình vẽ
Khi đó
(0;0;2 )S a
,
( ;0;0)B a
,
( ; ;0)C a a
,
0; ;
2
a
M a
( ;0; 2 )SB a a
,
; ;
2
a
CM a a

,
(0; ;0)BC a

, .
2
( , )
3
,
SB CM BC
a
d SB CM
SB CM
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp
. DS ABC
có đáy
ABCD
là hình
chữ nhật,
2 , AD .AB a a
SA
vuông góc với mặt phẳng đáy,
3SA a
. Cosin của góc giữa
SC
và mặt đáy bằng
A.
7
4
. B.
10
4
. C.
6
4
. D.
5
4
.
Lời giải
Chọn B
AC
là hình chiếu của
SC
lên mặt phẳng
ABCD
nên góc giữa
SC
và mặt phẳng
ABCD
là
góc giữa
SC
và
AC
và bằng góc
SCA
Tam giác
ADC
vuông tại D nên
2 2
5AC AD CD a
Tam giác
SAC
vuông tại
A
( do
SA ABCD
)
nên
2 2 2 2
5 5 10
cos =
4
8
3 5
AC AC a
SCA
SC
SA AC
a a
Câu 6. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình lăng trụ đứng
.ABC A B C
có đáy là tam giác
vuông,
2BA BC a
, cạnh bên
4AA a
,
M
là trung điểm
BC
(minh họa như hình dưới).
Khoảng cách giữa hai đường thẳng
B C
và
AM
bằng
A.
2 7
7
a
. B.
6
6
a
. C.
a
. D.
6
3
a
.
Lời giải
Chọn D
M
A
C
B'
B
A'
C'
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Gọi
N
là trung điểm
BB
, ta có
//MN B C
,
//AMN B C
.
Dựng
;AM B B ABC B B AM B BI AM B BI AMNBI
.
Dựng
BH B I BH AMN
. Do
AMN B B
tại
N
là trung điểm
BB
, nên ta có:
; ; ; ;d B C AM d B C AMN d B AMN d B AMN BH
.
Ta có tam giác
ABC
là tam giác vuông, sử dụng công thức đường cao của tứ diện
.B AMN
ta có:
2 2
2 2 2 2 2
1 1 1 1 1 1 1 6
3
2 2
a
BH
BH BA BM BN a
a a
.
Câu 7. (THPT Đồng Quan - Hà Nội - 2021) Cho lăng trụ tứ giác
.ABCD A B C D
có đáy
ABCD
là
hình thoi cạnh
a
, góc
60BAC . Biết
AA A B A D
và cạnh bên
AA
hợp với mặt phẳng
đáy góc
60
. Tính khoảng cách giữa hai đường thẳng
CC
và
BD
.
A.
3
4
a
. B.
3
2
a
. C.
6
8
a
. D.
3
4
a
.
Lời giải
Chọn D
Gọi
G
là trọng tâm của tam giác
ABD
, vì
AA A B A D
nên
G
là hình chiếu của
A
trên
mặt phẳng
ABCD
. Khi đó
60A AG
.
Ta có:
BD CA
BD ACC A
BD A G
và
BD ACC A O
.
; ; ; ;d CC BD d CC BDD B d C BDD B d A BDD B
; ;d AA BDD B d AA BD
.
N
M
A
C
B'
B
A'
C'
I
H
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
BD ACC A BD AA
3
; ; ;
2
d BD AA d O AA d G AA
.
Từ
G
kẻ đường thẳng vuông góc với
AA
tại
H
, suy ra:
;d G AA GH
.
Tam giác
ABC
đều nên
AC a
.Mà
G
là trọng tâm tam giác
ABD
, suy ra:
2. 2
.
3 3 2 3
AO a a
AG
3 3
sin60 .
3 2 6
a a
GH AG
.
Vậy
3 3 3 3
; ; .
2 2 6 4
a a
d BD AA d G AA
.
Câu 8. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi tâm
; 2 ; 3 ,I AB a BD AC
mặt bên
SAB
là tam giác cân đỉnh
A
, hình chiếu vuông góc của đỉnh
S
trên mặt phẳng đáy trùng với trung
điểm
H
của
.AI
Khoảng cách giữa hai đường thẳng
SB
và
CD
bằng.
A.
2 7
7
a
B.
2 35
7
a
. C.
2 35
35
a
. D.
35
7
a
.
Lời giải
Chọn B
Vì
/ /DC SAB
nên
; ; ;d DC SB d DC SAB d D SAB
Mà
I
là trung điểm
BD
;
H
là trung điểm
AI
; 2 ; 2. 2. ; 4 ;d D SAB d I SAB d H SAB d H SAB
.
Kẻ
HM BA
tại
M
, kẻ
HK SM
tại
.K
Vì
,AB SH AB HM AB SHM
.
AB HK
Mà
HK SM HK SAB
,d H SAB HK
.
Vì
ABCD
là hình thoi,
3
3
AB BC
BD AC ABC
BI AI
đều
2 .
2
a
AC AB a AH
Vì
SAB
cân ở A nên
2 .SA AB a
Xét
SAH
vuông ở
H
có:
2 2
15
2
a
SH SA AH
.
Xét
AHM
vuông ở
M
có:
3
.sin .sin 60
4
a
HM AH A AH
.
Xét
SHM
vuông ở
H
có:
2 2 2
1 1 1 35
14
a
HK
HK SH HM
,d H SAB
.
2 35
; 4 ;
7
a
d D SAB d H SAB
.
Vậy
2 35
,
7
a
d SB CD
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 9. (Sở Vĩnh Phúc - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh bằng
a
,
0
120BAD . Mặt bên
SAB
là tam giác đều và
SAB ABCD
(tham khảo hình vẽ).
Tính khoảng cách từ
A
đến
SBC
A.
2
a
. B.
7
7
a
. C.
3
4
a
. D.
15
5
a
.
Lời giải
Chọn D
Gọi
H
là trung điểm của
AB
, khi đó
SH ABCD
và
3
2
a
SH
.
Do
, 2 ,AH SBC B d A SBC d H SBC
.
Gọi
,K I
là hình chiếu của
H
lên
BC
và
SK
.
Khi đó
,BC HK BC SH BC SHK BC HI
.
Vậy
,HI BC HI SK HI SBC
hay
,d H SBC HI
.
Gọi
E
là trung điểm của
3
2
a
BC AE
, khi đó
3
4
a
HK
.
Trong tam giác vuông
SHK
ta có
2 2 2 2 2 2
1 1 1 4 16 20 15
3 3 3 10
a
HI
HI SH HK a a a
.
Vậy
15
,
5
a
d A SBC
.
Câu 10. (Sở Hà Tĩnh - 2021) Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
B
,
AD a
,
2AB a
,
3BC a
, mặt bên
SAB
là tam giác đều và vuông góc với mặt phẳng đáy
ABCD
.
Tính khoảng cách từ điểm
B
đến mặt phẳng
SCD
.
A.
3 30
10
a
. B.
3 30
5
a
. C.
30
2
a
. D.
3 2
2
a
.
Lời giải
Chọn A
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
H
là trung điểm cạnh
AB SH AB SH ABCD
và 3SH a .
Kẻ
MD BC
với
M BC
. Suy ra ta có
2MD AB a
;
2MC a
.
Suy ra
2 2 2 2
4 4 8CD MD MC a a a
.
Mặt khác ta có:
2
AB
AH a
;
2 2 2 2
2HD AH AD a a a
;
2 2 2 2
3 2 5SD SH HD a a a
;
2 2 2 2
9 10CH BH BC a a a
.
Khi đó
2 2 2 2 2 2
2 8 10a a a HD CD CH HD DC
.
Gọi
AB CD O
;
N
là trung điểm cạnh
CD
. Khi đó
2
2
AD BC
HN a
.
Ta có:
d ;
3 3
2 2
d ;
B SCD
OB BC a
OH HN a
H SCD
3
d ; d ;
2
B SCD H SCD
.
Trong
SHD
kẻ
1HK SD
với
K SD
.
Do
2
DC HD
DC SHD DC HK
DC SH
.
Từ (1) và (2) suy ra
d ;HK SCD H SCD HK
.
Trong
SHD
vuông tại
H
; đường cao
HK
ta có:
2
2 2 2
2 2 2 2
1 1 1 . 3. 2 6 30
5
5
3 2
SH HD a a a a
HK
HK SH HD
a
SH HD a a
.
Vậy
3 3 3 30
d ; d ; .
2 2 10
a
B SCD H SCD HK
.
Câu 11. (Sở Tuyên Quang - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 3AB a AD a
. Cạnh bên
SA
vuông góc với đáy, biết tam giác
SAD
có diện tích
2
3S a
.
Tính khoảng cách từ
C
đến
SBD
bằng
A.
39
13
a
d
. B.
2 51
17
a
d
. C.
39
5
a
d
. D.
2 39
13
a
d
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Do
2
2
1 6
3 . . 3
2
2 3
SAD
a
S a SA AD SA a
a
. Mặt khác ta có
, ,d C SBD d A SBD
.
Kẻ
, ,AH BD AK SH d A SBD AK
.
2 2
. .2 3 2 39
13
13
13
AB AD a a a
BD AB AD a AH
BD
a
.
2 2 2
2
2 39
3.
. 2 51
13
17
2 39
3
13
a
a
SA AH a
AK
SA AH
a
a
.
Vậy
2 51
, ,
17
a
d C SBD d A SBD
.
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc
với đáy. Tính khoảng cách giữa hai đường thẳng
AB
và
.SD
A.
21
7
a
. B.
3
7
a
. C.
21
3
a
. D.
7
3
a
.
Lời giải
Chọn A
Ta có hình chiếu
H
của
S
lên mp
ABCD
là trung điểm của cạnh
.AB
//AB SCD
nên
( ; ) , ,d AB SC d AB SCD d H SCD
Từ
H
kẻ
HM CD
CD SHM SCD SHM
Kẻ
HK SM
, .d H SCD HK
Trong tam giác vuông
SHM
có:
2 2 2
1 1 1
.
HK SH HM
a 3
2a 3
a
D
A
B
C
S
H
K
M
H
C
B
A
D
S
K
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
SH
là đường cao trong tam giác đều cạnh
a
, nên
3
;
2
a
SH
M
là trung điểm của
CD
nên
21
.
7
a
HM a HK
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình hộp chữ nhật
1 1 1 1
.ABCD A B C D có ba kích
thước
AB a
,
2AD a
,
1
3AA a . Khoảng cách từ A đến mặt phẳng
1
A BD
bằng bao nhiêu?
A.
a
. B.
7
6
a
. C.
6
7
a
. D.
5
7
a
.
Lời giải
Chọn C
Kẻ
AH BD
tại H. Ta có:
1
1 1
( )
( ( ))
BD AH
BD AA H
BD AA do AA ABCD
Kẻ
1
AK A H
tại K. Ta có:
1
1
1
( )
( ( ))
AK A H
AK A BD
AK BD do BD AA H
Do đó:
1
,( )d A A BD AK
Ta có:
2 2 2
1
1 1 1
AK AH AA
mà
2 2 2
1 1 1
AH AB AD
2 2 2 2 2 2 2 2
1
1 1 1 1 1 1 1 49
4 9 36AK AB AD AA a a a a
Vậy
6
7
AK a
hay
1
6
,( )
7
d A A BD a
.
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
,
2aAA
. Gọi
M
là điểm trên cạnh
A B
,
3
a
A M
. Khoảng cách từ
M
đến mặt phẳng
AB C
bằng?
A.
4 57
57
a
. B.
2 57
57
a
. C.
57
19
a
. D.
57
57
a
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Ta có:
;
;
2
3
M B AC
B B AC
d
IM B M
d IB BA
(
B IM
đồng dạng
AIB
)
Kẻ
BN AC
và
BH B N
.
BN AC
AC B BN AC BH
BB AC
BH AC
BH B AC
BH B N
;B B AC
d BH
.
Xét
B BN
vuông tại
B
có:
2
2 2 2 2 2
1 1 1 1 1 19
3a
4a 12a
4
BH B B BN
2 57
19
a
BH
.
Vậy
;
4 57
57
M B AC
a
d
.
Câu 15. (Chuyên Lê Hồng Phong - TPHCM - 2021) Hình hộp
.ABCD A B C D
có
AB AA AD a
và
60A AB A AD BAD
. Tính
c sin«
của góc giữa đường thẳng
CD
và mặt phẳng
A AD
:
A.
3
3
. B.
3
2
. C.
3
4
. D.
2 3
3
.
Lời giải
Chọn A
Gọi
I
là trung điểm
DD
;
G
là trọng tâm tam giác
A D D
;
H
đối xứng với
G
qua
I
Từ gt
Các tam giác
A D D
và
CD D
là các tam giác đều
A I DD
;
CI DD
DD CIA
DD CH
Mà
4 4 1
. . . . .
3 3 2
CH AD CA A H AD CA A I AD CA A D A D AD
   
2
1 1 1 1
. . .
3 3 3 3
AB AD AA AD AB AD AD AA AD
 
2 2 2
1 1
cos60 cos60 0
3 3
a a a
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
AD CH
Do đó
CH A AD
D H
là hình chiếu của
CD
trên
A AD
; ;CD A AD CD HD
Lại có:
CD a
;
3
3
a
D H D G
; tam giác
CD H
vuông tại
H
3
cos ; cos
3
HD
CD A AD CD H
CD
.
Câu 16. (Chuyên KHTN - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
3a
,
SA ABCD
và
2SA a
. Tính góc giữa
SC
và
ABCD
.
A.
90
. B.
45
. C.
60
. D.
30
.
Lời giải
Chọn D
Ta có AC là hình chiếu của
SC
trên mặt phẳng
ABCD
nên góc giữa
SC
và mặt phẳng
ABCD
là
;SC AC SCA
ABCD
là hình vuông cạnh 3a nên 6AC a .
Xét
SAC
vuông tại
A
, ta có:
2 1
tan
6 3
SA a
SAC
AC
a
Suy ra
30SAC
Vậy góc giữa
SC
và mặt phẳng
ABCD
bằng
30
.
Câu 17. (Chuyên KHTN - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
. Cạnh
bên
SA
vuông góc với đáy. Góc giữa
SC
và mặt đáy bằng
45
. Gọi
E
là trung điểm của
BC
.
Tính khoảng cách giữa hai đường thẳng
DE
và
SC
.
A.
2 19
19
a
. B.
10
19
a
. C.
10
5
a
. D.
2 19
5
a
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Ta có
ABCD
là hình vuông cạnh
2a
nên
2AC a
. Góc giữa
SC
và đáy là
45 2SCA SA AC a .
Gọi
I AC DE
, có
2
IA DA
IC CE
, gọi
K
là điểm trên
SA
sao cho
2 4
//
3 3
KA IA a
IK SC AK
SA CA
và
//SC DKI
.
Do đó
1
, , ,
2
d AC DE d C DKI d A DKI
( do
1
2
IC IA
).
Gọi
F DE AB
, do
//BE AD
và
1
2
BE AD
nên
B
là trung điểm của
AF
.
Đặt
,h d A DKF
, do
ADKF
là tam diện vuông tại
A
nên
2
2 2 2 2 2 2 2
1 1 1 1 1 1 1 19
2 8 16
4
3
h AK AD AF a a a
a
4 19
19
a
h
.
Vậy
2 19
,
19
a
d SC DE
.
Câu 18. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương
.ABCD A B C D
. Số đo của góc giữa hai
mặt phẳng
BA C
và
DA C
bằng
A.
60
. B.
30
. C.
45
. D.
90
.
Lời giải
Chọn A
Do
.ABCD A B C D
là hình lập phương nên
A D CDD C
;
CD ADD A
CD A D
;
A D CD
F
K
I
E
C
A
B
D
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
I
là trung điểm của
A D
D I A D
Mà
CD ADD A CD D I
Suy ra
D I A DC
Khi đó hình chiếu của tam giác
A D C
trên mặt phẳng
DA C
là tam giác
A IC
.cos
A IC A D C
S S
(
là góc giữa hai mặt phẳng
BA C
và
DA C
)
1 2
. .
1
2 2
cos
1
2
. 2
. .
2
A IC
A D C
a
A I CD a
S
S
a a
A D D C
.
60
.
Câu 19. (Chuyên Quốc Học Huế - 2021) Cho hình lăng trụ tam giác
. ' ' 'ABC A B C
có mặt bên
' 'ABB A
là hình thoi cạnh a,
120A AB
và
10
' 3,
2
A C BC a AC a
. Tính khoảng cách giữa hai
đường thẳng
A B
và
AC
A.
10
20
a
B.
10
10
a
C.
3 10
20
a
D.
3 10
10
a
Lời giải
Chọn C
Ta có: ' 3 'A C BC a A BC cân tại
C
và ' 2 ' 2 ' sin 60 3A B A I A A a
Suy ra
'A BC
đều, mặt khác ta lại thấy
2 2 2
AC AI IC nên suy ra
AI IC
, mà
'AI A B
nên
suy ra
' ' ' 'AI A CB A BC ABB A
và
' 'A B AIC A B AC
Khi ta kẻ
,IE AC E AC
thì đoạn
IE
chính là đoạn vuông góc chung của hai đường thẳng
A B
và
AC
Ta có:
2 2
2 2
' 3 3 '
3 ; ;
4 4 2 2 2
A B a a AB a
CI BC a AI
Suy ra
. 3 3 10
' ;
20
2 10
CI IA a
d A B AC IE a
AC
Câu 20. (Chuyên Quang Trung - Bình Phước - 2021) Cho hình chóp
.S ABCD
đáy
ABCD
là hình thoi
cạnh
a
, góc
60BAD ,
SA ABCD
,
, 45SC ABCD . Gọi
I
là trung điểm
SC
. Tính
khoảng cách từ
I
đến mặt phẳng
SBD
.
A.
15
10
a
. B.
15
5
a
. C.
2 15
5
a
. D.
15
15
a
.
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Gọi
O
là giáo điểm của
AC
và
BD
.
Ta có :
BAD
đều cạnh
3a AC a
.
Vì
SA ABCD AC
là hình chiếu của
SC
lên
ABCD
, , 45SC ABCD SC A C SCA SAC vuông cân tại
A
3SA AC a
.
Ta có:
ABCD
là hình thoi nên
AC BD
(1).
Vì
SA ABCD SA BD
(2).
Từ (1) và (2) suy ra:
BD SAC
mà
BD SBD
nên
SBD SAC
.
Trong tam giác
SAC
kẻ
CH SO CH SBD
.
Ta có:
2
2 2 2 2 2
2
1 1
. . . 3
2
15
2 2
5
3
3
2
SOC SAC
SA AC a
S S
a
CH
SO
SA OA SA OA
a
a
.
Vậy
1 15
; ;
2 10
a
d I SBD d C SBD
.
Câu 21. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình chóp có đáy là hình chữ
nhật
, 2 ; AB a AD a
SA
vuông góc với đáy , hợp với đáy một góc và
. Tính khoảng cách từ điểm B đến mặt phẳng
A. B. C. D.
Lời giải
Chọn D
.
S ABCD
ABCD
ABCD
SC
10
tan
5
.SCD
a
3
2a
3
a 3
3
2a 3
3
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Theo bài ra ta có:
2 2
(2 ) 5 AC a a a
;
10 10
tan 2
5 5
SA
SA AC a
AC
Vì
// //AB CD AB SCD
do đó
, ,d B SCD d A SCD
Từ
A
hạ đường vuông góc xuống
SD
Vì :
AH SD
AH SCD
AH DC
nên
,AH d A SCD
Ta có:
2 2 2 2 2 2
1 1 1 1 1 3
2 4 4
AH SA AD a a a
Suy ra
2 3
3
a
AH
.
Câu 22. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
, 3SD a . Mặt bên
SAB
là tam giác cân và nằm trong mặt phẳng vuông góc với đáy. Gọi
H
là trung điểm của
AB
,
K
là trung điểm của
AD
. Khoảng cách giữa hai đường thẳng
SD
và
HK
bằng
A.
105
5
a
. B.
105
20
a
. C.
105
30
a
. D.
105
10
a
.
Lời giải
Chọn C
( ) ( )
( ) ( ) ( ).
( ),
SAB ABCD
AB SAB ABCD SH ABCD
SH SAB SH AB
/ /
/ /( ) ( , ) ( ,( )) ( ,( )).
( )
HK BD
HK SBD d HK SD d HK SBD d H SBD
BD SBD
Trong
( )ABCD
, gọi I là trung điểm của
BO
.
Ta có: ( ) ( ) ( )
BO HI
BO SHI SBD SHI
BO SH
Trong
( )SHI
, dựng
HJ SI
J SI
. Từ đó suy ra
( ) ( ,( ))HJ SBD HJ d H SBD
2
2 2
2 2 2 2 2 2 2
7
( ) , .
4 2 8
a AO a
SH SD HD SD HA AD HI
2 2 2
1 1 1 105
( , ).
30
a
HJ d HK SD
SH HI HJ
Câu 23. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp
.S ABC
có
12 , 5 , 9 , 13 , 15 SA cm AB cm AC cm SB cm SC cm
và
10BC cm
. Tan của góc giữa hai
mặt phẳng
( )SBC
và
( )ABC
bằng
O
K
H
A
B
C
D
S
I
J
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
14
10
. B.
10 14
14
. C.
4
3
. D.
12
5
.
Lời giải
Chọn B
Do
2 2 2
12 5 13
nên
SA AB
và
2 2 2
12 9 15
nên
SA AC
.
Suy ra
( )SA ABC
.
Từ
A
kẻ
AH BC
. Suy ra
SH BC
và góc giữa hai mặt phẳng
( )SBC
và
( )ABC
là
SHA
Xét tam giác
,ABC
có
1
(5 9 10) 12
2
p
và
12(12 5)(12 9)(12 10) 6 14
ABC
S
;
2 12 14
10
ABC
S
AH
BC
và
6 14 10 14
tan 12: .
5 14
SA
SHA
AH
Câu 24. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông
cân,
2AB BC a
. Tam giác
SAC
cân tại
S
và nằm trong mặt phẳng vuông góc với
ABC
,
3SA a
. Góc giữa hai mặt phẳng
SAB
và
SAC
bằng
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
90
.
Lời giải
Chọn A
Gọi
H
là trung điểm của
AC
. Vì tam giác
ABC
vuông cân, có
2AB BC a
nên
ABC
là tam
giác vuông cân tại
B
. Suy ra
BH AC
.
Vì tam giác
SAC
cân tại
S
và nằm trong mặt phẳng vuông góc với
ABC
. Suy ra
SH ABC
SH BH
.
Suy ra
BH SAC
. Suy ra tam giác
SAH
là hình chiếu của tam giác
SAB
trên mặt phẳng
SAC
.
Gọi
là góc giữa hai mặt phẳng
SAB
và
SAC
.
B
S
C
A
H
H
C
B
A
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2 2AC a
;
1
2
2
BH AH AC a
;
2 2
SH SA HA a
2 2
3SB SH BH a
2
1 2
.
2 2
SAH
a
S SH HA
;
Gọi
p
là nửa chu vi của tam giác
ABC
, ta có
1
3
2
p SA AB SB a a
.
Suy ra
2
2
SAB
S p p SA p SB p AB a
.
Ta có:
2
2
2
1
2
cos
2
2
SAH
SAB
a
S
S
a
. Suy ra
0
60
.
Câu 25. (Sở Yên Bái - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, hình chiếu
vuông góc của
S
lên mặt phẳng
( )ABCD
là trung điểm của
,AD
góc giữa đường thẳng
SB
và
mặt đáy bằng
60
o
. Gọi
M
là trung điểm của
DC
. Khoảng cách giữa hai đường thẳng
SA
và
BM
là
A.
285
9
a
. B.
285
19
a
. C.
3 285
19
a
. D.
2 285
19
a
.
Lời giải
Chọn B
Vẽ hình bình hành
ABMN
.
Ta có
/ /
/ /
; ; ; 2 ; 4 ; .
MB AN
MB SAN
d MB SA d MB SAN d M SAN d D SAN d H SAN
Gọi
I
là hình chiếu vuông góc của
H
lên
,AN
J
là hình chiếu vuông góc của
H
lên
SI
.
Khi đó
;HJ d H SAN
.
Vì
H
là hình chiếu vuông góc của
S
lên
ABCD
nên
; 60 .
o
SB ABCD SBH
Xét tam giác
SHB
vuông tại
H
:
2 2
15
.tan 60 tan 60 .
2
o o
a
SH HB AH AB
Vì
AIH
và
ADN
đồng dạng nên
2
.
. 5
2 2
.
10
4
a
a a
IH AH DN AH a
IH
DN AN AN
a
a
Xét tam giác
SHI
vuông tại H:
2 2 2
1 1 1 285
76
a
HJ
HJ IH SH
M
H
A
D
C
B
S
N
I
J
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
285
; .
19
a
d MB SA
Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp
.S ABC
có đáy là tam giác đều, tam
giác
SAB
vuông cân tại
S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết
6.SA a
Khoảng cách từ điểm
A
đến mặt phẳng
( )SBC
bằng
A.
3 7
7
a
. B.
7a
. C.
6 7
7
a
. D.
7
2
a
.
Lời giải
Chọn C
Kẻ
SH AB
(
H
là trung điềm
AB
). Suy ra
( )SH ABC
.
Có
2 2 2 2
2 2 12 2 3.AB SA SB SA AB SA a a
Và
( ,( )) 2 ( ,( ))d A SBC d H SBC
Từ
H
kẻ
HN BC
(
/ /HN AM
với
M
là trung điểm
BC
) và kẻ
HK SN
.
Ta có
HN BC
và
SH BC
nên
BC SHN
, suy ra
HK BC
.
Mặt khác
HK BC
và
HK SN
nên
HK SBC
, suy ra
( ,( )) 2 ( ,( )) 2d A SBC d H SBC HK
.
Có
1
3
2
SH AB a
;
1 1 3 3
.
2 2 2 2
AB a
HN AM
và
2 2 2 2 2 2
1 1 1 1 4 7 3
3 9 9
7
a
HK
HK SH HN a a a
. Do đó
6 6 7
( ,( )) .
7
7
a a
d A SBC
Câu 27. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chóp
.S ABC
có
, ,SA SB SC
đôi một vuông
góc nhau và
;SA a 2 ;SB a
3 .SC a
Gọi
, ,M N P
lần lượt là trung điểm của
, ,AB BC CA
.
Khoảng cách từ điểm
M
đến mặt phẳng
SNP
bằng
A.
5
7
a
. B.
6
7
a
. C.
15
2
a
. D.
13
2
a
.
Lời giải
Chọn B
N
M
H
B
C
A
S
K
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
1
4
MNP ABC
S S
nên
2
. .
1 1 1
. . . .
4 4 6 4
S MNP S ABC
a
V V SA SB SC .
Mặt khác:
1 13
2 2
a
SN BC
;
1 10
2 2
a
SP AC
và
1 5
2 2
a
NP AB
. Do đó
7
8
MNP
a
S p p a p b p c
.
Từ đó
2
3
1 7 6
. . , , 3. :
3 4 8 7
SMNP
SMNP MNP
MNP
V
a a a
V S d M SNP d M SNP
S
.
Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác
vuông cân tại
A
,
2BC a
và
SB a
. Hình chiếu vuông góc của
S
lên mặt phẳng
ABC
trùng với trung điểm
M
của
BC
. Góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
A.
0
30
. B.
0
60
. C.
0
45
. D.
0
75
.
Lời giải
Chọn C
Ta có:
ABC
vuông cân tại
A
nên
AB AC a
và
2
2 2
BC a
AM
.
Xét
SBM
có
2
2 2 2
2 2
2 2
a a
SM SB BM a
.
Góc giữa đường thẳng
SA
và mặt phẳng
ABC
là góc
SAM .
Xét
SAM
có
0
2
2
tan 1 45
2
2
a
SM
SAM SAM
AM
a
.
Vậy góc giữa đường thẳng
SA
và mặt phẳng
ABC
là
0
45
.
N
M
P
S
C
B
A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 29. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình hộp
. ' ' ' 'ABCD A B C D
có tất cả các cạnh
đều bằng
a
và
0
' ' 60BAA DAA BAD . Gọi
G
là trọng tâm của tam giác
'AB C
. Khoảng
cách từ
G
đến mặt phẳng
' 'DA C
bằng
A.
22
66
a
. B.
4 11
11
a
. C.
2 11
11
a
. D.
22
11
a
.
Lời giải
Chọn D
Do
'AB AA AD a
và
0
' ' 60BAA DAA BAD
nên
'ABDA
là tứ diện đều cạnh
a
Suy ra
3
'
2
.
12
ABDA
a
V
Gọi
,E F
lần lượt là trung điểm của
AC
và
'AB
.
Ta có
3
'
1 2
.
4 48
ABEF ABDA
a
V V
Mặt khác do
' / / ' 'AB C DA C
nên
; ' ' '; ' ; ' ;d G DA C d A AB C d B AB C d B AEF
.
Xét tam giác
AEF
có
2
3 11
;
2 2 16
AEF
a a a
AE AF EF S
.
Mà
3
2
2
3.
3
1 22
48
. . ; ; .
3 11
11
16
ABEF
ABEF AEF
AEF
a
V
a
V S d B AEF d B AEF
S
a
Câu 30. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
có đáy là
hình vuông cạnh
a
, mặt bên
SAD
là tam giác đều và
SAD ABCD
. Gọi
M
là trung điểm
cạnh đáy
AB
. Khoảng cách giữa các đường thẳng
SA
và
CM
là.
A.
3
3
a
. B.
2
3
a
. C.
5
4
a
. D.
3
4
a
.
Lời giải
Chọn D
F
E
A
D
B
C
B'
C'
A'
D'
G
I
K
I
H
M
N
D
C
B
A
N
M
H
D
C
B
A
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mặt phẳng
SAD
là tam giác đều và vuông góc với đáy, gọi
H
là trung điểm
AD
SH AD
SH ABCD
. Ta có
3
2
a
SH
(đường cao tam giác đều
SAD
)
Gọi
N
là trung điểm
CD
//AN CM
//CM SAN
;
; ;
CM SA
CM SAN M SAN
d d d
Gọi
I
là hình chiếu của
H
lên
AN
;
K
là hình chiếu của
H
lên
SI
.
Ta có
HI AN
AN SHI
SH AN
AN HK
.
Ta có
HK SI
HK SAN
HK AN
;H SAN
d HK
Gọi
E
là hình chiếu của
D
lên
AN
ta có
2
2 2 2 2 2
1 1 1 1 1 5
2
DE DA DN a a
a
5
5
a
DE
1 5
2 10
a
HI DE
Tam giác
SHI
vuông tại
H
có
HK SI
, ta có
2 2
2 2 2
1 1 1 1 1
5 3
10 2
HK HI SH
a
3
8
a
HK
Dễ thấy trong hình vuông
ABCD
ta có
;AN ; ;
2.
H D AN M AN
d d d
Vậy
; ;
3
2. 2
4
M SAN H SAN
a
d d HK
Câu 31. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
hình chữ nhật
, 3AB a AD
. Cạnh bên
SA
vuông góc với đáy và
2SA a
. Tính khoảng cách
d
từ điểm
C
đến mặt phẳng
SBD
:
A.
2 57
.
19
a
d
B.
2
.
5
a
d
C.
5
.
2
a
d
D.
57
.
19
a
d
Lời giải
Chọn A
Gọi
I
,
H
lần lượt là hình chiếu của
A
lên
BD
và
SI
.
Ta có:
AH SBD
nên
,d A SBD AH
.
Vì đáy
ABCD
là hình chữ nhật nên
, ,d C SBD d A SBD AH
.
I
H
C
D
B
A
S
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Xét tam giác vuông
ABD
ta có:
2 2 2 2 2 2
1 1 1 1 1 4 3
.
3 3 2
a
AI
AI AB AD a a a
Xét tam giác vuông
SAI
ta có:
2 2 2 2 2 2
1 1 1 4 1 19 2 57
.
3 4 12 19
a
AH
AH SA AI a a a
Câu 32. (THPT Quốc Oai - Hà Nội - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SAB
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
là góc tạo bởi đường thẳng
BD
với mặt phẳng
SAD
. Khi đó
sin
bằng
A.
3
2
. B.
1
2
. C.
6
4
. D.
10
4
.
Lời giải
Chọn C
Gọi
O
là trung điểm của
AB
. Khi đó, ta có:
SO AB
và
3
2
a
SO
.
Ta lại có:
SAB ABCD
SAB ABCD AB SO ABCD
SO AB
.
Chọn hệ trục tọa độ như hình vẽ, xem
a
là
1
đơn vị, khi đó ta có:
0;0;0O
,
1
;0;0
2
B
,
1
;0;0
2
A
,
1
;1;0
2
D
,
3
0;0;
2
S
.
Ta có:
1 3
;0;
2 2
SA
,
1 3
;1;
2 2
SD
. Suy ra vectơ pháp tuyến của
SAD
là
3 1
, ;0;
2 2
n SA SD
.
Ta có:
1;1;0BD
.
Do đó, ta có:
.
sin
.
n BD
n BD
3
0 0
2
3 1
0 . 1 1 0
4 4
6
4
.
Câu 33. (THPT Quốc Oai - Hà Nội - 2021) Cho hình lăng trụ tam giác đều
. ' ' 'ABC A B C
có tất cả các
cạnh có độ dài bằng
2
(tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng
'AC
và
'A B
bằng
A
z
y
x
O
D
B
C
S
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
.
2
B.
3
.
5
C.
2
.
5
D.
3
.
2
Lời giải
Chọn C.
Gọi
H
là trung điểm
' ' .
'
BH AC
AC BH ACC A
BH AA
Dựng hình bình hành
' 'AC DA
và kẻ
' .EH A D
Gọi
, ' 'I EH AC O AC A C
và kẻ
.HK BE
2 2
', ' ', ' , ' , ' .
3 3
d AC BA d AC BDA d I BDA d H BDA HK
Ta có:
2 2
2 3 3 3 2 2 . 2
3, ' ', ' .
2 4 2 3
5
BH HE
BH HE A C d AC BA
BH HE
Vậy khoảng cách giữa hai đường thẳng
'AC
và
'A B
bằng
2
.
5
Câu 34. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho lăng trụ đứng
.ABC A B C
có đáy là tam giác
ABC
vuông tại
A
có
2BC a
,
3AB a
. Khoảng cách giữa hai đường thẳng
AA
và
BC
là
A.
21
7
a
. B.
3
2
a
. C.
5
2
a
. D.
7
3
a
.
Lời giải
Chọn B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Dựng
,AH BC H BC
.
AA ABC
AA AH
AH ABC
.
,d AA BC AH
.
Do
ABC
vuông tại
A
có
AH BC
nên
2 2
AB BC AB a
,
. 3. 3
2 2
AC AB a a a
AH
BC a
.
Vậy
3
,
2
a
d AA BC
.
Câu 35. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho khối chóp
.S ABCD
có đáy là hình bình hành,
3, 4, 120 .
o
AB AD BAD
Cạnh bên 2 3SA
vuông góc với đáy. Gọi
, ,M N P
lần lượt là
trung điểm các cạnh
,SA AD
và
.BC
Gọi
là góc giữa hai mặt phẳng
( )SAC
và
( ).MNP
Chọn
khẳng định đúng trong các khẳng định sau đây.
A.
3
sin ;1
2
. B.
1
sin 0;
2
. C.
1 2
sin ;
2 2
. D.
2 3
sin ;
2 2
.
Lời giải
Chọn A
Ta có
( )MNP SCD
nên góc giữa
( ),( )SAC MNP
bằng góc giữa
( ),( ) .SAC SCD
,( )
sin .
,
d A SCD
d A SC
*
,( ) .d A SCD
Kẻ
.AH CD
Tính được
3 3 2 3.
ACD
S AH
C'
B'
A'
A
B
C
H
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2 2
1 1 1 1
.
6
,( )
d A SCD SA AH
,( ) 6. d A SCD
* Tính được
13 .AC
2 2 2
1 1 1 25 2 39
, .
156 5
,
d A OM
d A SC SA AC
Vậy
5 26
sin .
26
Câu 36. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho tứ diện
ABCD
có
3
,
2
a
AB CD a IJ
(
,I J
lần lượt là trung điểm của
BC
và
AD
). Số đo góc giữa hai đường thẳng
AB
và
CD
là
A.
0
60
. B.
0
30
. C.
0
45
. D.
0
120
.
Lời giải
Chọn A
Gọi
K
là trung điểm của
BD
. Khi đó
IK
song song với
CD
và
JK
song song với
AB
.
Khi đó
0
, ,
180
IKJ
AB CD KI KJ
IKJ
.
Ta có
2 2 2
2 2 2
3
1
4 4 4
cos
2 2 . 2
2. .
2 2
a a a
a KI KJ IJ
KI KJ IKJ
a a
KI KJ
.
Vậy
0 0
120 , 60IKJ AB CD
.
Câu 37. (Trung Tâm Thanh Tường - 2021) Cho hình chóp
SABCD
có đáy
ABCD
là hình vuông cạnh bằng
2a
. Tam
giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy.
Gọi
,E F
lần lượt là trung điểm của
,SA CD
. Khoảng cách
giữa hai đường thẳng
SD
và
EF
bằng
A.
5
10
a
. B.
2 3
7
a
. C.
5
5
a
. D.
2
a
.
Lời giải
Chọn C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Vì
SAB ABCD
và tam giác
SAB
đều nên gọi
H
là trung điểm của
AB
.
Từ đó suy ra
SH
là đường cao của hình chóp
.S ABCD
.
Ghép hệ trục tọa độ
Oxyz
sao cho gốc tọa độ trùng với chân đường cao
H
.
Chiều dương Ox,Oy,Oz lần lược cùng chiều véc-tơ
, ,HA HF HS
. Và chọn
1a
.
Từ đó ta suy ra toại độ của các điểm:
1 3
0;0;0 , 1;0;0 , 1;2;0 , 0;2;0 , 0;0; 3 , ;0;
2 2
H A D F S E
Vậy ta có:
1 3
1;0;0 , 1;2; 3 , ;2;
2 2
FD SD EF

, 3; 3;3SD EF

Khoảng cách giữa
SD
và
EF
là:
. ,
5
,
5
,
FD SD EF
a
d SD EF
SD EF
Câu 38. (Trung Tâm Thanh Tường -2021) Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy
4a
, cạnh
bên bằng 2 5a , gọi
O
là tâm của hình vuông
ABCD
. Khoảng cách từ
O
đến mặt phẳng
SCD
bằng
A. 3a . B.
a
. C.
2
a
. D.
2a
.
Lời giải
Chọn A
Vì
.S ABCD
là hình chóp đều nên
( ).SO ABCD
Ta có:
2 2 2 2
(4 ) (4 ) 4 2 2 2 2 3 .AC a a a AO a SO SA AO a
Vẽ
OE
vuông góc
CD
, vẽ
OH
vuông góc với
SE
.
Ta có
OH SE
OH SCD
OH CD CD SOE
.
Tam giác vuông cân tại
O
, có
2 2
.
2 ; 3
SO OE
OE a d O SCD OH a
SO OE
.
Câu 39. (Trung Tâm Thanh Tường -2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
bằng
2a
, SA vuông góc với đáy, 6SA a . Tính khoảng cách giữa hai đường thẳng SD và AC.
E
F
H
C
A
B
D
S
SOE
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2 10
5
a
. B.
2a
. C.
6
2
a
. D.
2a
.
Lời giải
Chọn C
Gọi O là tâm hình vuông ABCD; M là trung điểm SB; trong mặt phẳng (SAB) kẻ
/ /MH SA
( )H AB
; trong mặt phẳng (ABCD) kẻ
HK AC
( )K AC
; trong mặt phẳng (MHK) kẻ
HP MK
( )P MK
; gọi
I DH AC
.
Khi đó ta có:
( )MH ABCD
;
( )HP MAC
.
Ta có:
/ /( )
; ;( ) ;( )
( )
SD MAC
d SD AC d SD MAC d D MAC
AC MAC
.
;( )
2 ;( ) 2 ;( ) 2
;( )
d D MAC
DI
d D MAC d H MAC HP
d H MAC HI
Xét tam giác MHK vuông tại H có:
2 2
2 2 2 2
1 1 1 1 1 8 6
3 4
6 2
2 2
a
HP
HP HM HK a
a a
.
Suy ra
6
; 2
2
a
d SD AC HP
.
Câu 40. (Trung Tâm Thanh Tường -2021) Cho hình tứ diện đều
ABCD
. Giá trị
tan
của góc giữa mặt
bên và đáy bằng
A.
2 6
3
. B.
2
. C.
2 2
. D.
2
.
Lời giải
Chọn C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Ta có:
ACD BCD CD
.
BCD
đều có
M
là trung điểm của
CD BM CD
(1).
AH BCD
AH CD
CD BCD
(2).
Từ (1) và (2) suy ra:
CD ABM CD AM
.
Khi đó:
, ,
CD BM BCD
ACD BCD AM BM AMH
CD AM ACD
(do
AMH
vuông tại
H
).
Giả sử tứ diện đều
ABCD
có cạnh bằng
a
.
Ta có:
1 3 3
.
3 2 6
a a
HM
;
3
2
a
AM
;
2 2
2 2
3 3 6
4 36 3
a a a
AH AM HM
.
Vậy
6
3
tan 2 2
3
6
a
AH
AMH
HM
a
.
Câu 41. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông
cạnh
a
;
2SA a
và
SA
vuông góc với mặt đáy
ABCD
. Gọi
M
;
N
lần lượt là hình chiếu
vuông góc của đỉnh
A
lên các cạnh
SB
và
SD
. Khi đó góc giữa đường thẳng
SB
và mặt phẳng
AMN
bằng:
A.
45
. B.
30
. C.
60
. D.
90
.
Lời giải
Chọn C
Gọi
P SC AMN
;
O AC BD
MN
;
AP
;
SO
đồng quy tại
I
Ta có:
SA BC
AB BC
BC SAB
BC AM
Mà
AM SB
nên
AM SBC
AM SC
SA CD
AD CD
CD SAD
CD AN
Mà
AN SD
nên
AN SCD
AN SC
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do
đó
S
C AMN
A
P SC
và
PM
là
hình chiếu của
S
M
trê
n mặt phẳng
A
MN
ha
y
P
M
là
hình chiếu của
S
B
trê
n mặt phẳng
AMN
;
;
SB
AMN SB PM SMP
(do tam giác
vuông tại
P
)
Từ gt
Tam giác
S
AC
vuông cân tại
A
P
là trung điểm
S
C
I
là
trọng tâm tam giác
SAC
Lại có:
S
AB SAD
S
A SB
và
A
M AN
S
AM SAN
S
M SN
SB SD
/
/MN BD
2
3
SM
SI
SB
SO
2
2
2 2 2 3
3 3 3
a
SM SB SA AB
Mặt
khác
2 2
1
1
2
2
SP SC SA AC a
Do đó
3
s
in
2
S
P
SMP
S
M
; 60
SB AMN SMP
.
| 1/64
| | Tải xuống

Có thể bạn quan tâm:

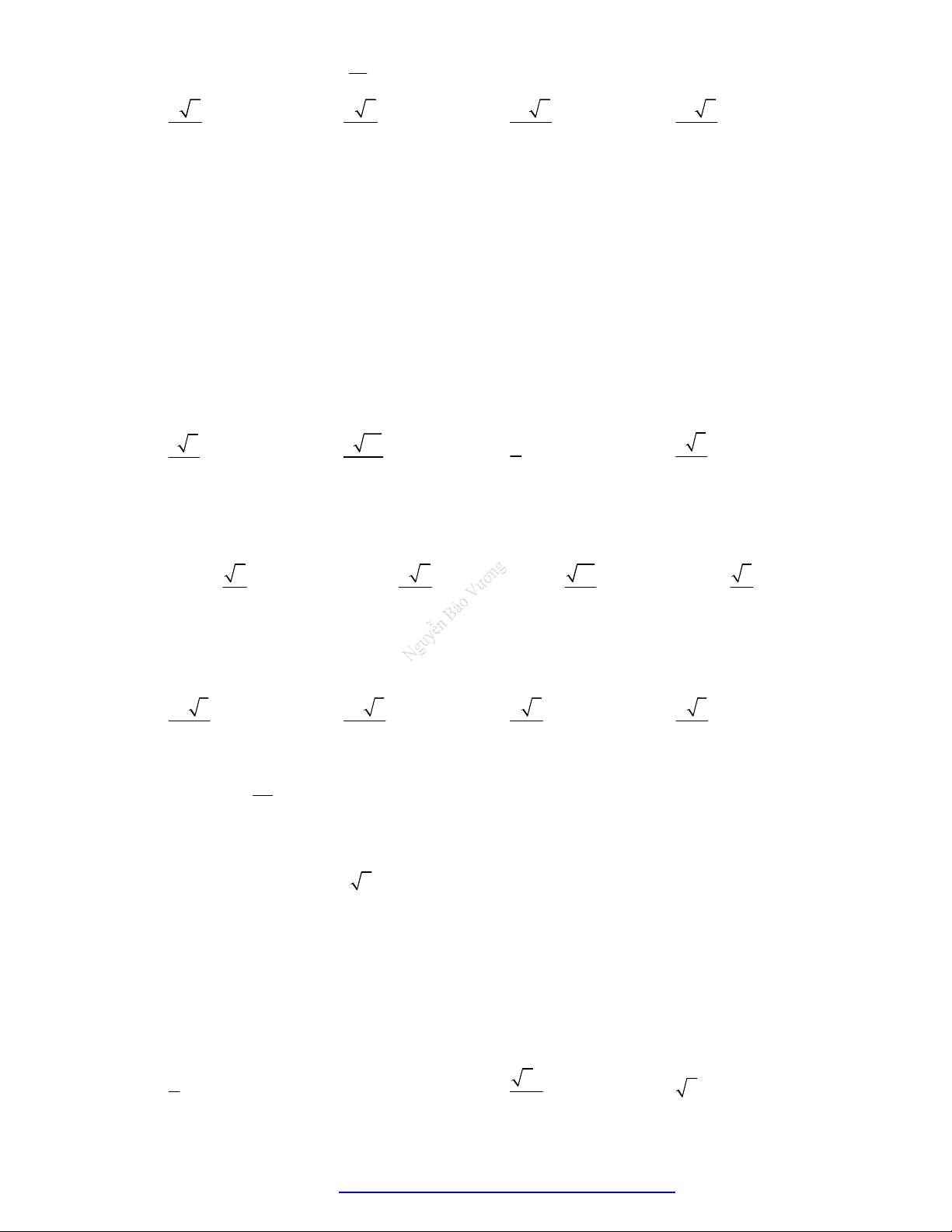
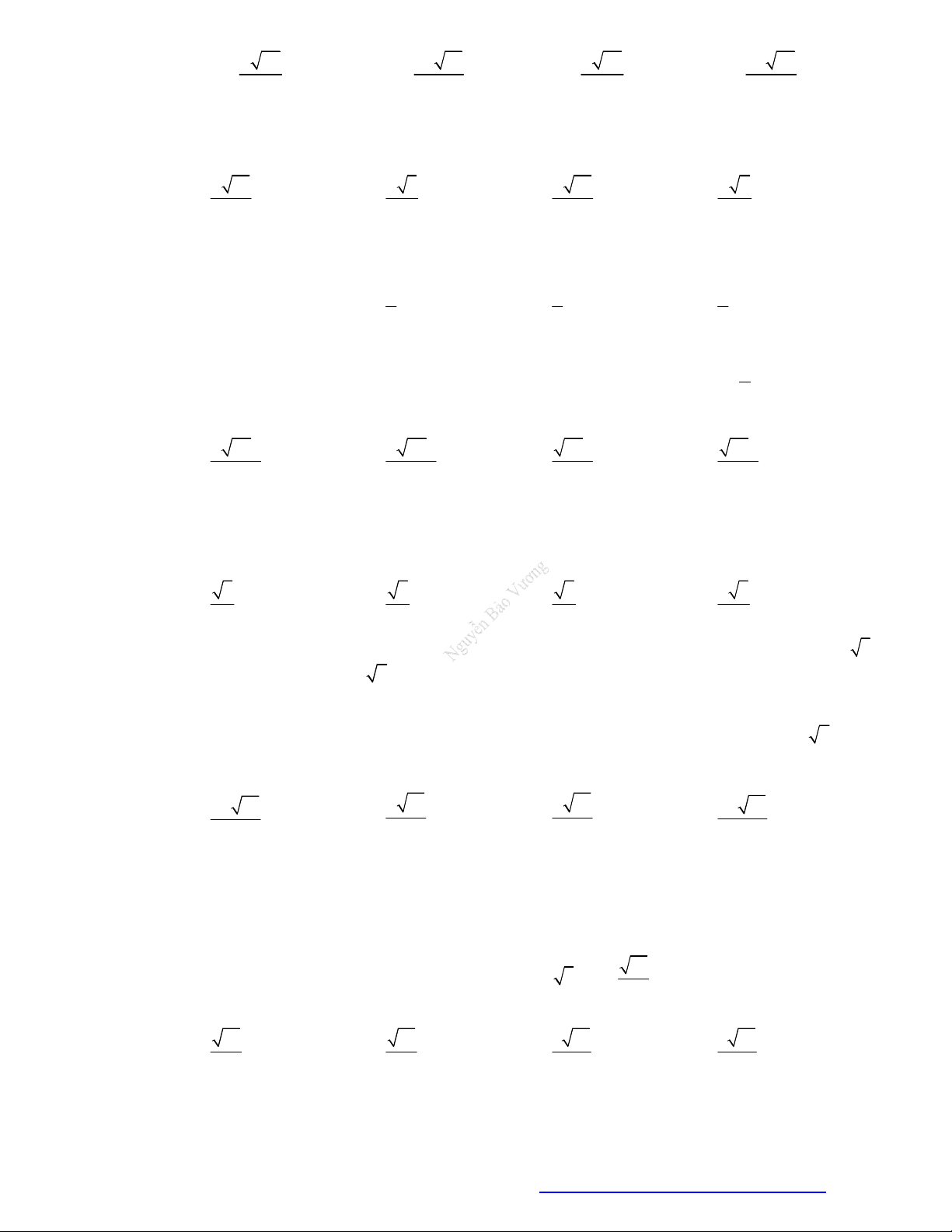
Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 8
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
MỨC ĐỘ NHẬN BIẾT Câu 1.
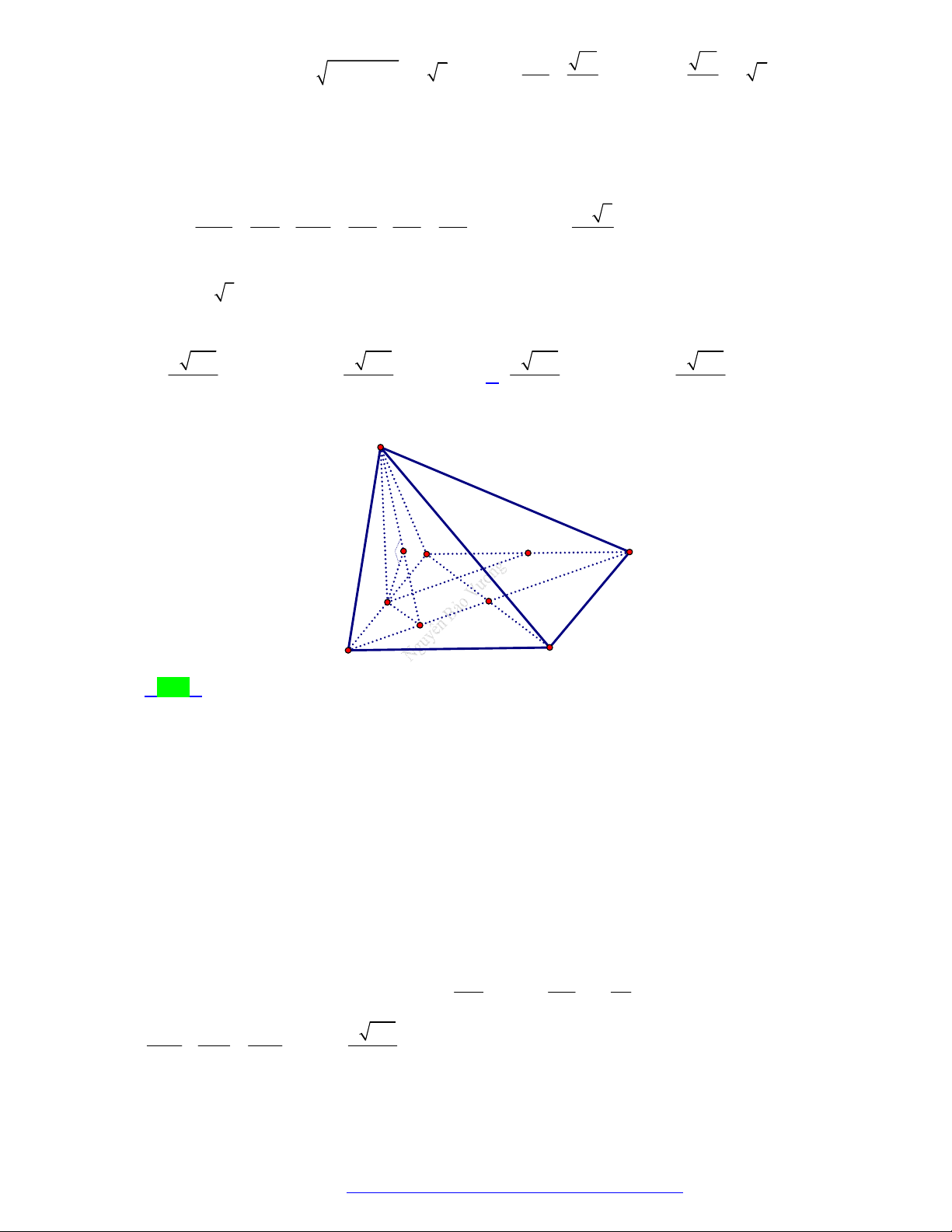
(THPT Lê Lợi - Thanh Hóa - 2021) Cho tứ diện ABCD có tam giác BCD là tam giác đều cạnh
a , AB   BCD và AB  2a . Góc giữa AC và mặt phẳng  BCD là     A. BCD . B. ACB . C. ACD . D. ADB . Câu 2.
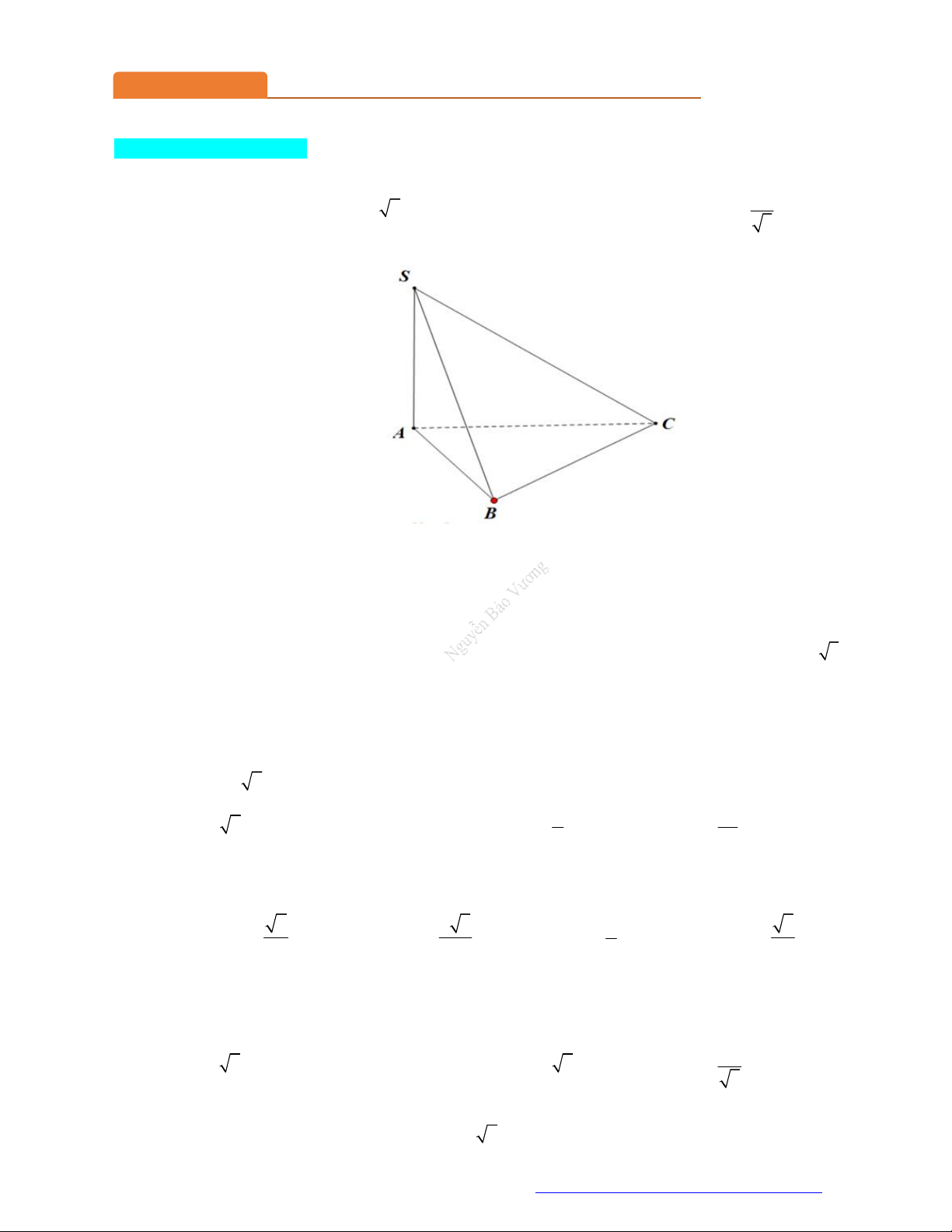
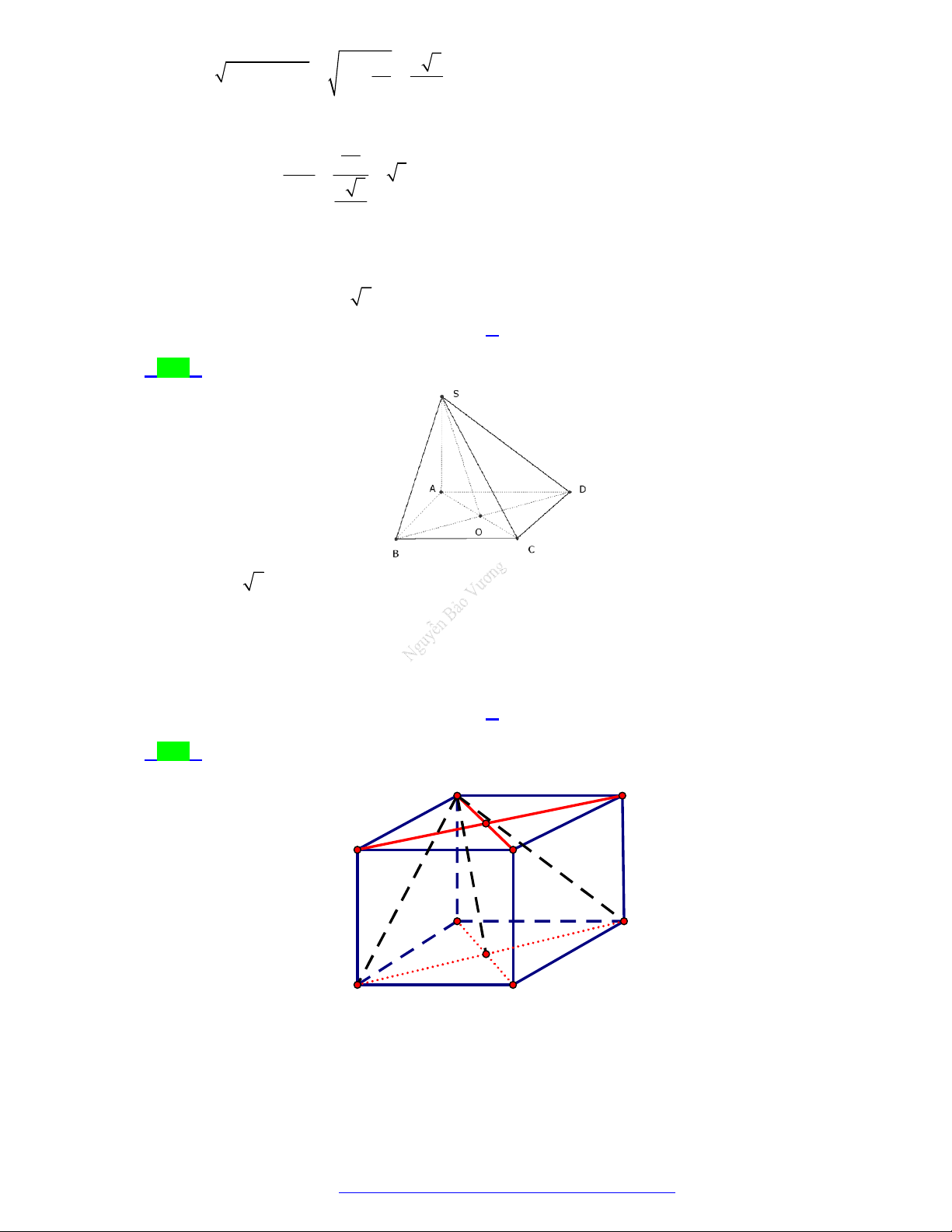
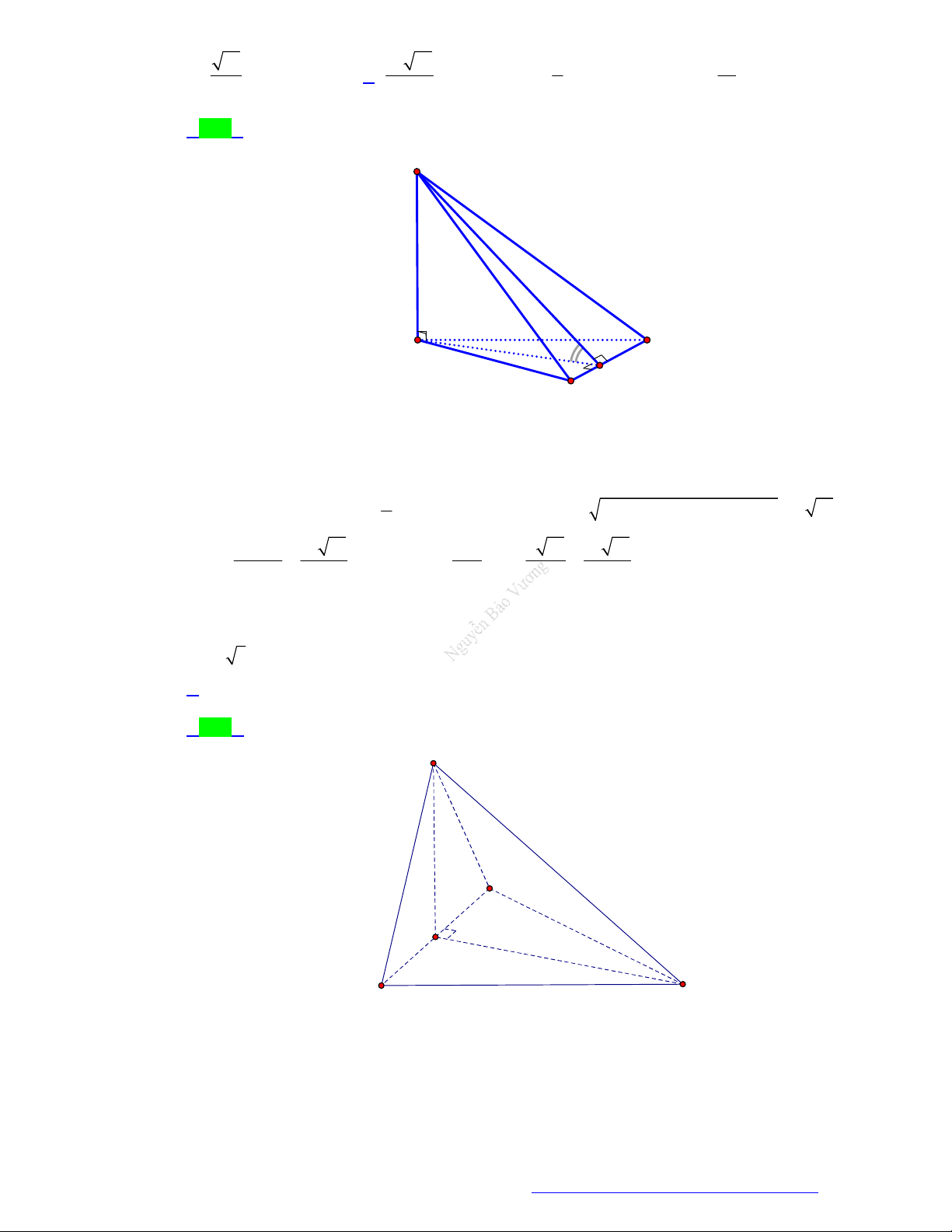
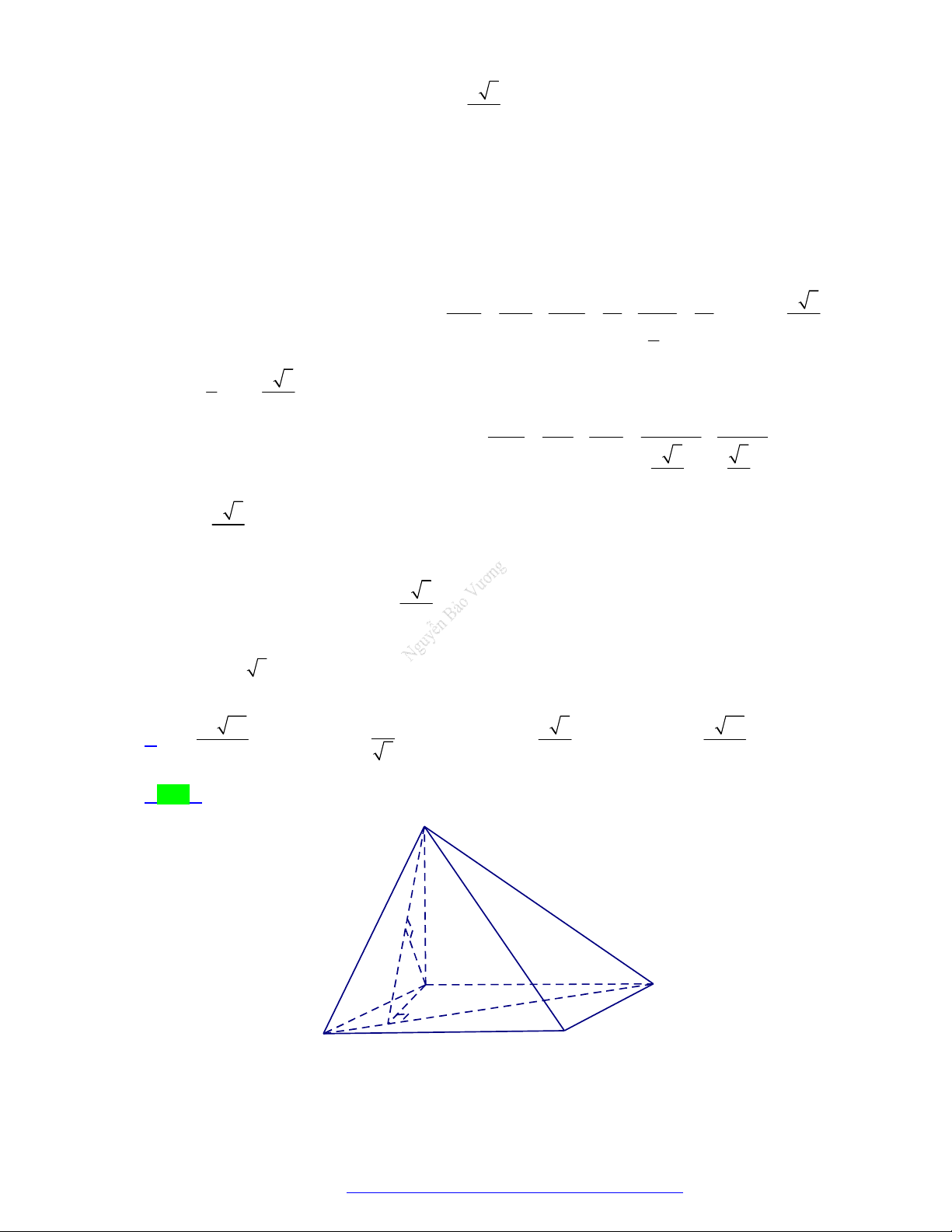
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABC có SA vuông góc với mặt phẳng
ABC , SA a , tam giác ABC vuông tại B , AB a 2 và BC a . Góc giữa đường thẳng SC
và mặt phẳng  ABC  bằng? A. 45 . B. 30 . C. 90 . D. 60 . Câu 3.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh a . Đường thẳng SA vuông góc với mặt phẳng đáy, SA a . Gọi M là trung điểm của
CD . Khoảng cách từ M đến mặt phẳng (SAB) bằng a 2 A. 2a . B. a . C. a 2 . D. . 2 Câu 4.
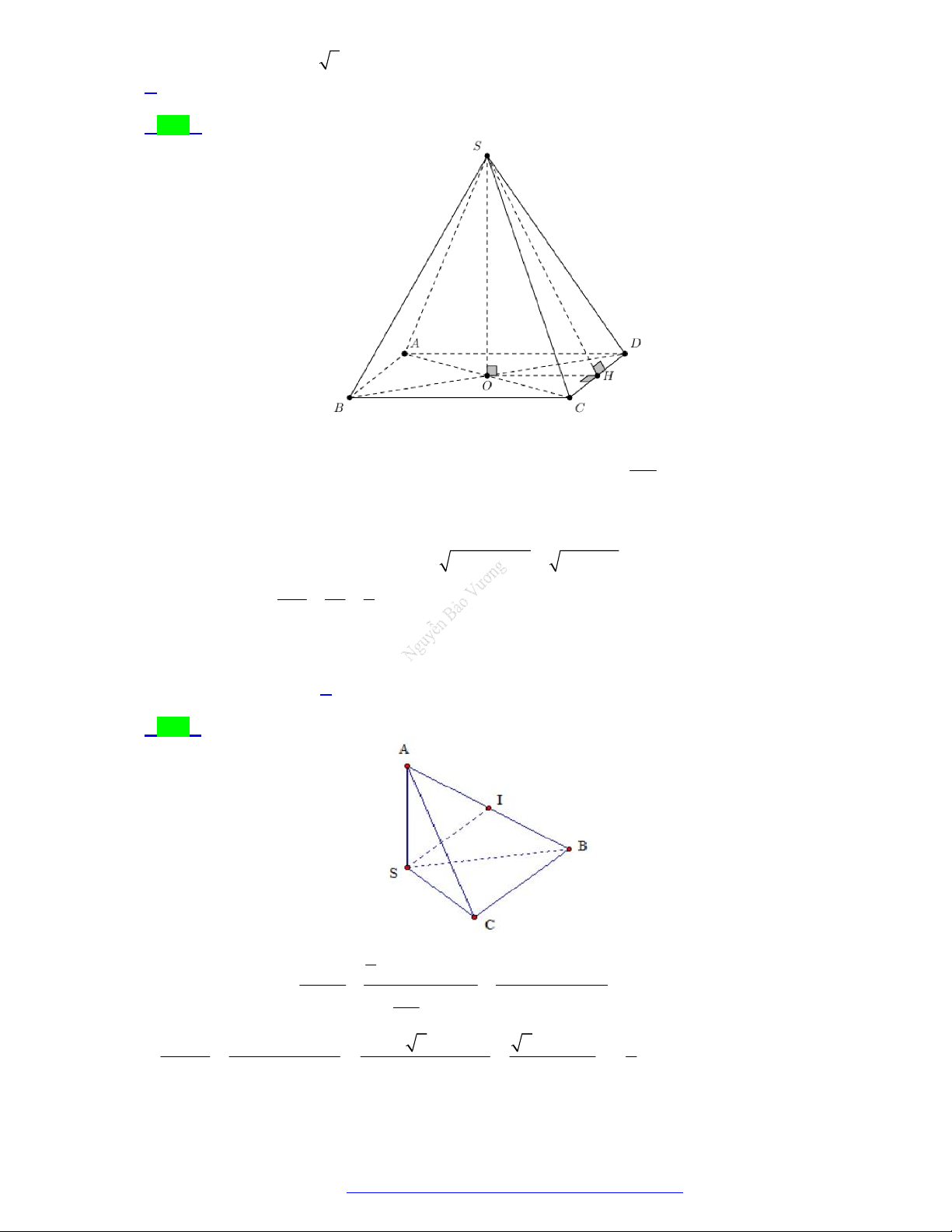
(Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lập phương ABC .
D A ' B 'C ' D ' . Góc giữa đường
thẳng AB và B ' D ' bằng A. 30o . B. 135o . C. 45o . D. 90o . Câu 5.
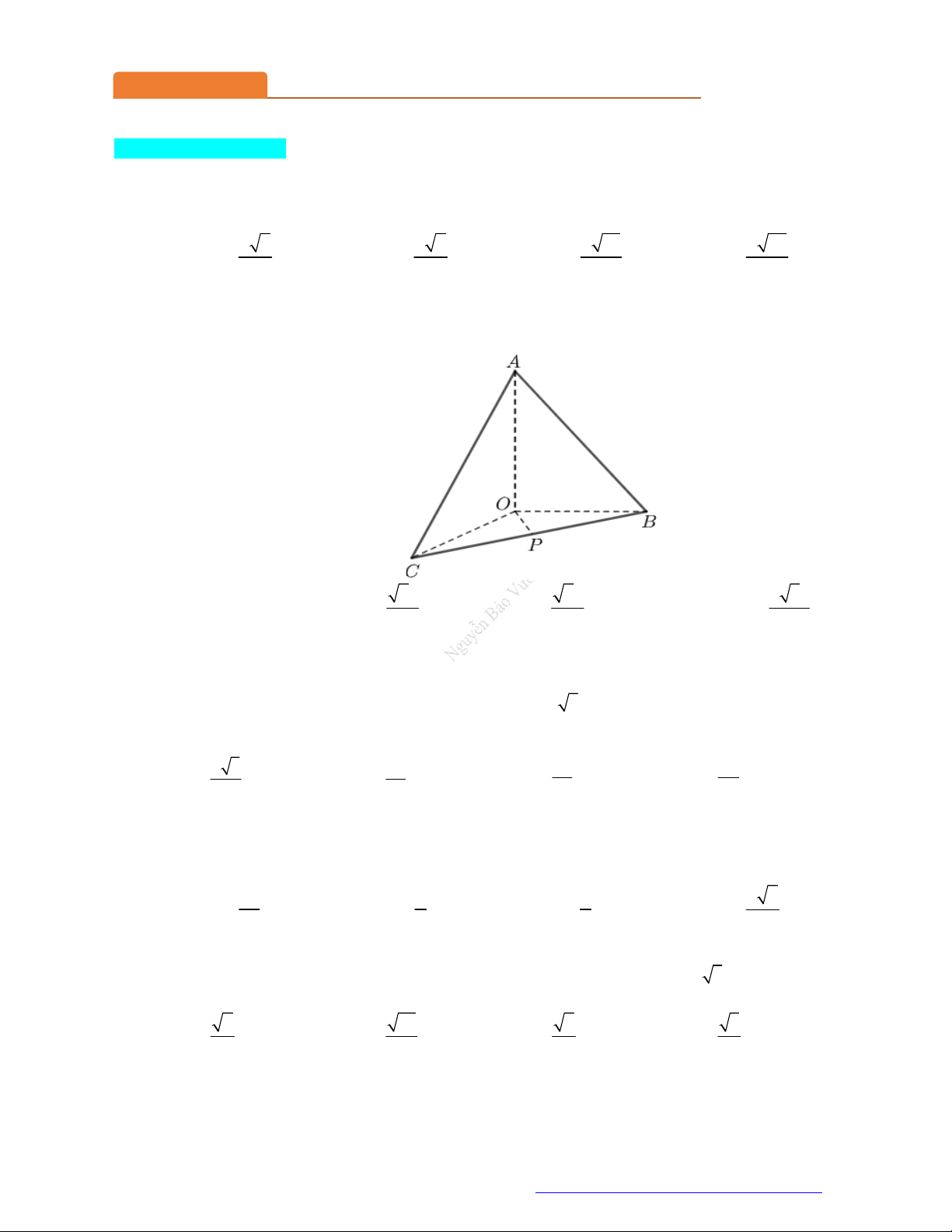
(THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật
và SA vuông góc với mặt phẳng đáy. Góc giữa SD và mặt phẳng  ABCD là A. BSD . B. SDA. C. ASD . D. SAD .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 BẢNG ĐÁP ÁN 1.B 2.B 3.B 4.C 5.B
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 8
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
MỨC ĐỘ NHẬN BIẾT Câu 1.
(THPT Lê Lợi - Thanh Hóa - 2021) Cho tứ diện ABCD có tam giác BCD là tam giác đều cạnh
a , AB   BCD và AB  2a . Góc giữa AC và mặt phẳng  BCD là     A. BCD . B. ACB . C. ACD . D. ADB . Lời giải Chọn B
Do AB   BCD nên Góc giữa AC và mặt phẳng  BCD bằng  ACB . Câu 2.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABC có SA vuông góc với mặt phẳng
ABC , SA a , tam giác ABC vuông tại B , AB a 2 và BC a . Góc giữa đường thẳng SC
và mặt phẳng  ABC  bằng? A. 45 . B. 30 . C. 90 . D. 60 . Lời giải Chọn D
Góc giữa SC và mặt phẳng  ABC là góc  SCA . SA a 1 Xét S
AC vuông tại A :  tan SCA    
SCA  30 . 2 2 AC 2a  a 3 Câu 3.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh a . Đường thẳng SA vuông góc với mặt phẳng đáy, SA a . Gọi M là trung điểm của
CD . Khoảng cách từ M đến mặt phẳng (SAB) bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 a 2 A. 2a . B. a . C. a 2 . D. . 2 Lời giải Chọn B
Gọi N là trung điểm của AB . Ta có: MN AB
MN  SAB  dMN a .
M ;SAB MN SACâu 4.
(Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình lập phương ABC .
D A ' B 'C ' D ' . Góc giữa đường
thẳng AB và B ' D ' bằng A. 30o . B. 135o . C. 45o . D. 90o . Lời giải Chọn C Ta có: ABC .
D A ' B 'C ' D ' là hình lập phương  ABB ' A ' là hình vuông  AB / / A ' B '
Do đó góc giữa hai đường thẳng AB và B ' D ' bằng góc giữa hai đường thẳng A ' B ' và B ' D '
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Mặt khác, do ABC .
D A ' B 'C ' D ' là hình lập phương nên A' B 'C ' D ' là hình vuông nên  ' ' ' 45o A B D
do đó góc giữa 2 đường thẳng A ' B ' và B ' D ' bằng 45o
Nên góc giữa đường thẳng AB và B ' D ' bằng 45o . Câu 5.
(THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật
và SA vuông góc với mặt phẳng đáy. Góc giữa SD và mặt phẳng  ABCD là A. BSD . B. SDA. C. ASD . D. SAD . Lời giải Chọn B
Ta có hình chiếu SD trên mặt phẳng  ABCD là AD Vậy S ,
D ABCD  S , D AD  SDA .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 8
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
MỨC ĐỘ THÔNG HIỂU Câu 1.
(THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình chóp S.ABC có SA vuông góc với 1
mặt phẳng  ABC  , SA a 2 , tam giác ABC vuông tại A và AC a,sin B  (minh họ như 3
hình bên). Góc giữa đường thẳng SB với mặt phẳng  ABC  bằng A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 . Câu 2.
(THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương .
ABCD A B C D có cạnh 1 1 1 1
a . Gọi I là trung điểm B .
D Góc giữa hai đường thẳng A D và B I bằng 1 1 A. 120 B. 30 .  C. 45 . D. 60 . Câu 3.
(THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình chóp S.ABC có SA  ( ABC) , SA a 3 , tam
giác ABC vuông tại B có AC  2a ,
BC a . Góc giữa đường thẳng SB và mặt phằng ( ABC) bằng A. 60 . B. 90 . C. 30 . D. 45 . Câu 4.
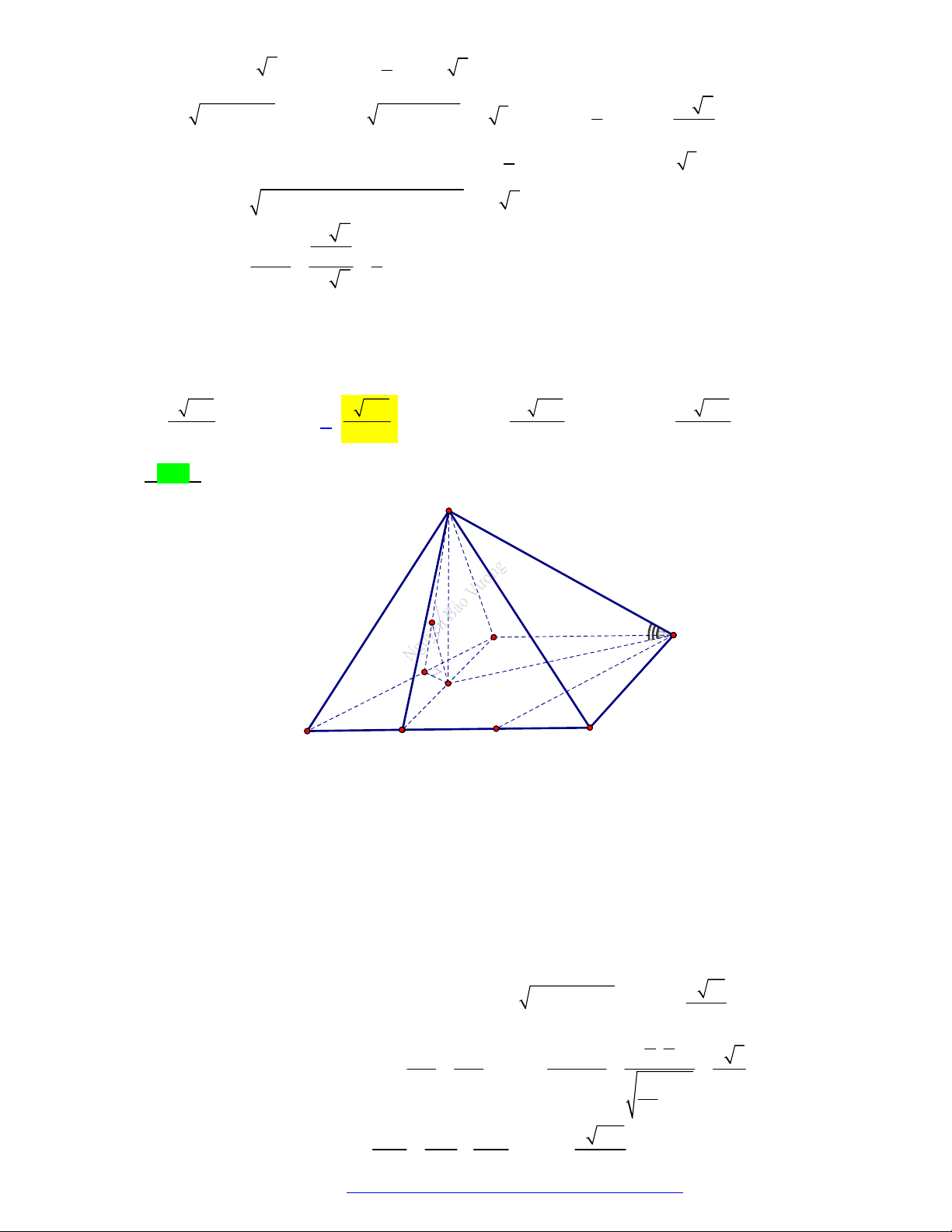
(Sở Lào Cai - 2021) Cho tứ diện OABC có OA , OB , OC đôi một vuông góc và OA OB  2a ,
OC a 2 . Khoảng cách từ điểm O đến mặt phẳng  ABC bằng a 3a A. a 2 . B. a . C. . D. . 2 4 Câu 5.
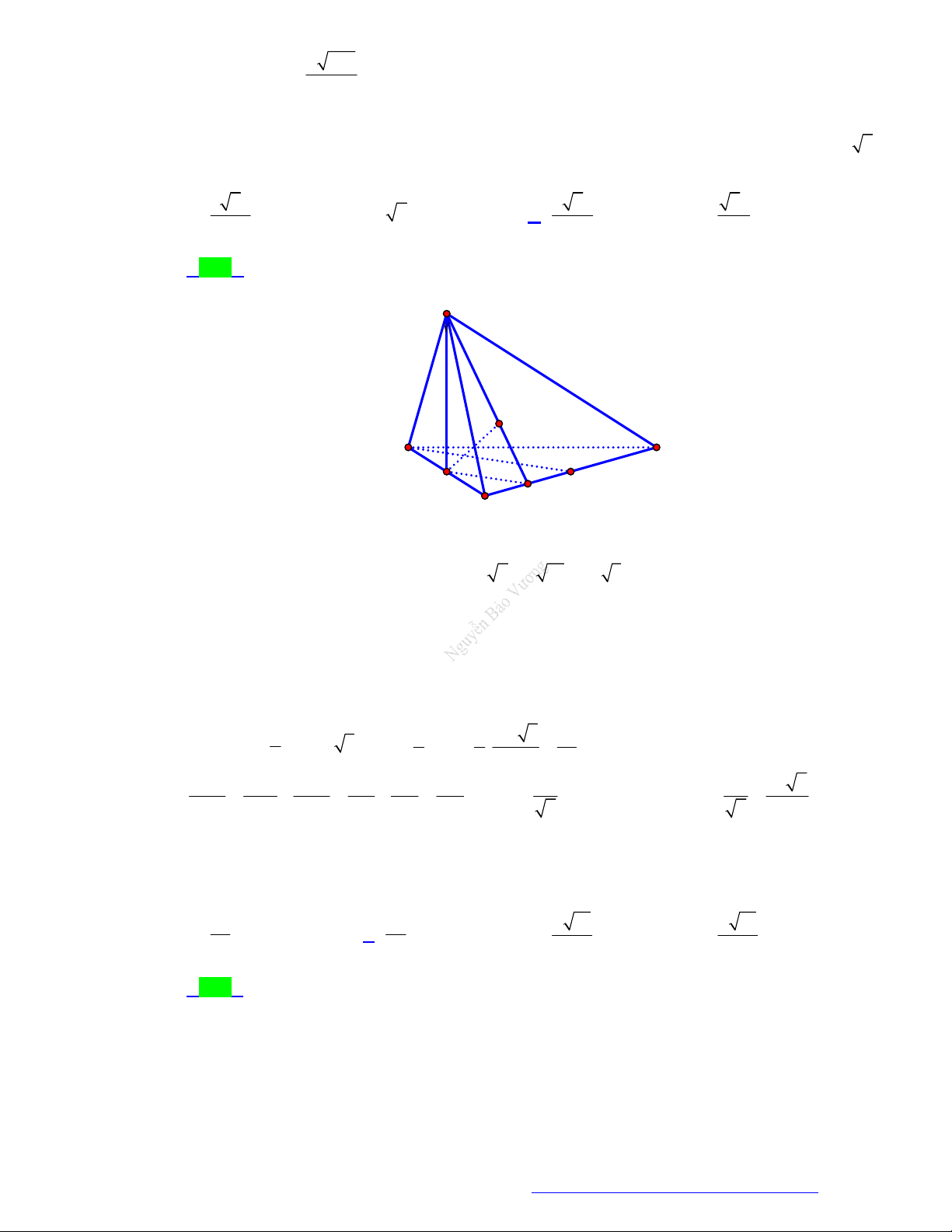
(Sở Lào Cai - 2021) Cho hình lập phương ABC . D A BCD
  . Gọi M , N lần lượt là trung điểm AC và B C
  ,  là góc giữa đường thẳng MN và mặt phẳng  AB CD
  . Tính giá trị  . 2 2 5 1 5 A. sin   . B. sin  . C. sin   . D. sin   . 2 5 2 5 Câu 6.
(Sở Tuyên Quang - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , đường
thẳng SA vuông góc với mặt phẳng đáy và SA  2a . Góc giữa đường thẳng SC và mặt phẳng
ABCD là . Khi đó tan bằng 2 A. 2 2 . B. 2 . C. 2 . D. . 3 Câu 7.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC
là tam giác vuông tại A , AB a, AC a 2 . Biết thể
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 3 a
tích khối chóp S.ABC bằng
. Khoảng cách S từ đến mặt phẳng  ABC bằng 2 a 2 a 2 3a 2 3a 2 A. . B. . C. . D. . 2 6 4 2 Câu 8.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC
là tam giác vuông tại B , SA vuông góc với mặt phẳng  ABC  , AH là đường cao trong tam giác
SAB . Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A. SA BC .
B. AH AC .
C. AH SC .
D. AH BC . Câu 9.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
vuông tại B , SA vuông góc với mặt đáy. Góc giữa hai mặt phẳng SBC và  ABC là     A. BAC . B. SBA . C. SAB . D. SCA .
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp S.ABCD có đáy là hình vuông
ABCD cạnh bằng 3a , SA SB a
vuông góc với mặt đáy  ABCD ,
5 . Tính sin của góc giữa cạnh
SC và mặt đáy  ABCD . 3 2 2 34 4 2 2 A. . B. . C. . D. . 4 17 5 3
Câu 11. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
đều cạnh a , cạnh SA vuông góc với mặt phẳng đáy và SA  2a , gọi M là trung điểm của SC .
Tính cosin của góc  là góc giữa đường thẳng BM và  ABC  . 7 2 7 21 5 A. cos  . B. cos  . C. cos  . D. cos  . 14 7 7 7
Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông
tâm O cạnh a , SO vuông góc với mặt phẳng  ABCD và SO a . Khoảng cách giữa SC và AB bằng: 2a 3 2a 5 a 5 a 3 A. . B. . C. . D. . 15 5 5 15
Câu 13. (Chuyên KHTN - 2021) Cho hình lăng trụ tam giác đều ABC.AB C
  có cạnh đáy bằng a và 3a cạnh bên bằng
. Góc giữa hai mặt phẳng  A B
C và  ABC bằng 2 A. 30 . B. 60 . C. 45 . D. 90 .
Câu 14. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp S.ABCD có đáy là hình vuông
cạnh a , SA   ABC , SA a 2 . Góc giữa đường thẳng SC và mặt phẳng  ABCD  bằng A. 60 . B. 90 . C. 45 . D. 30 .
Câu 15. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương ABC . D A BCD   có ,
O O lần lượt là tâm
của các hình vuông ABCD và AB CD
  . Góc giữa hai mặt phẳng  ABD và  ABCD bằng    
A. AAD . B. A OC  . C. A OA  .
D. OAA .
Câu 16. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a,
O là tâm của mặt đáy. Khoảng cách giữa hai đường thẳng SO và CD bằng a 2a A. . B. a . C. . D. 2a . 2 2
Câu 17. (Sở Yên Bái - 2021) Cho hình chóp S.ABCD có đáy là hình vuông canh a, SA vuông góc với
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
mặt phẳng đáy và SA a 6 . Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 60o. B. 45o. C. 90o. D. 30o.
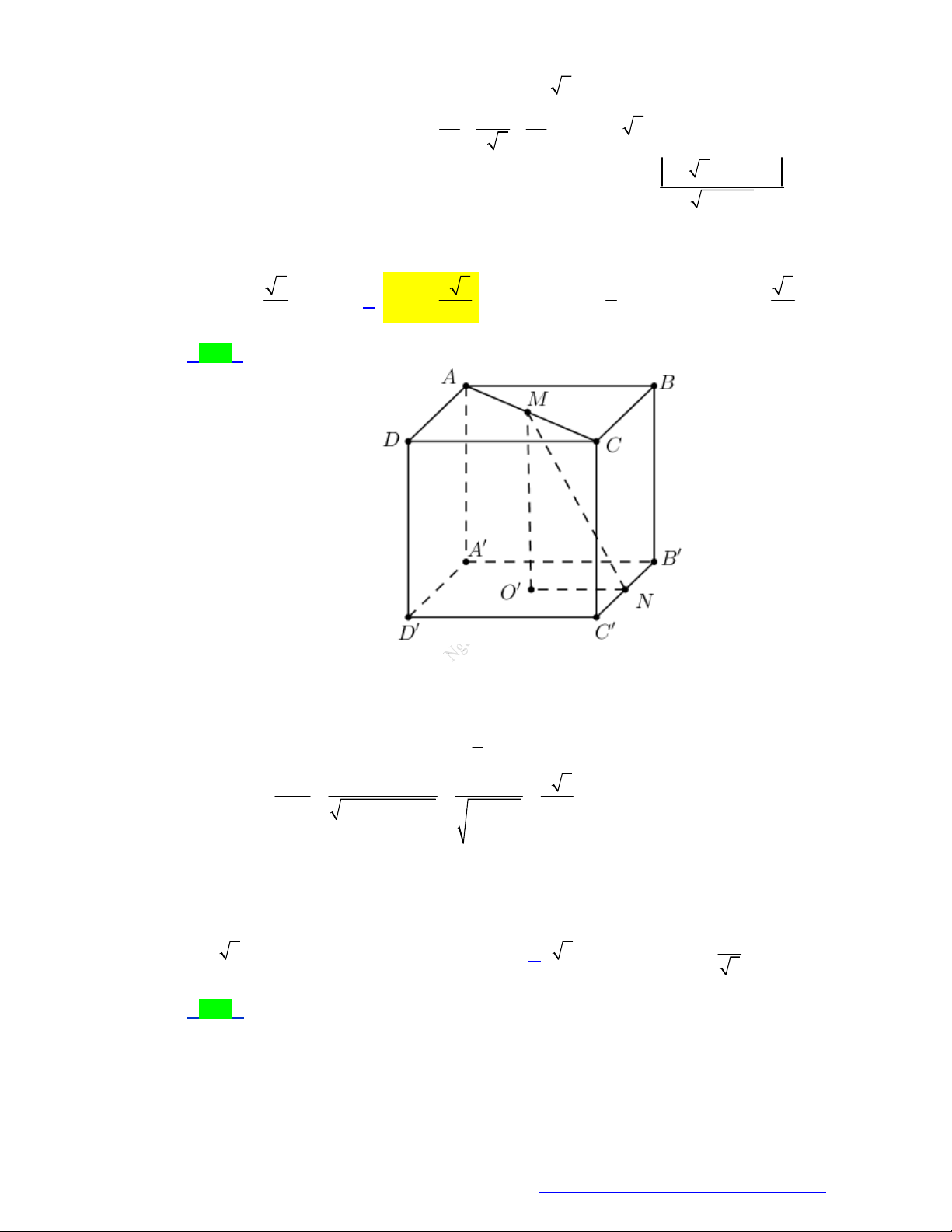
Câu 18. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy
bằng 2a cạnh bên bằng 5a . Góc giữa mặt bên và mặt phẳng đáy bằng A. 60 . B. 30 . C. 70 . D. 45 .
Câu 19. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình chóp S.ABC có S ,
A SB, SC đôi một vuông góc
với nhau và SA SB SC . Gọi I là trung điểm của AB . Góc giữa SI và BC bằng A. 30 . B. 60 . C. 45 . D. 90 .
Câu 20. (THPT Lương Thế Vinh - 2021) Cho hình chóp S.ABCD có đáy là hình thoi tâm O , ABD 3a 2
đều cạnh a 2, SA vuông góc với mặt phẳng đáy và SA
. Góc giữa đường thẳng SO và 2
mặt phẳng  ABCD bằng A. 45 . B. 90 . C. 30 . D. 60 .
Câu 21. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho khối chóp đều S.ABC có cạnh đáy bằng a . 3 a
Gọi M là trung điểm của SA . Biết thể tích của khối chóp đó bằng
, khoảng cách từ điểm M 2
đến mặt phẳng  ABC  bằng a 3 A. a 3 . B. 3a . C. . D. 2a 3 . 3
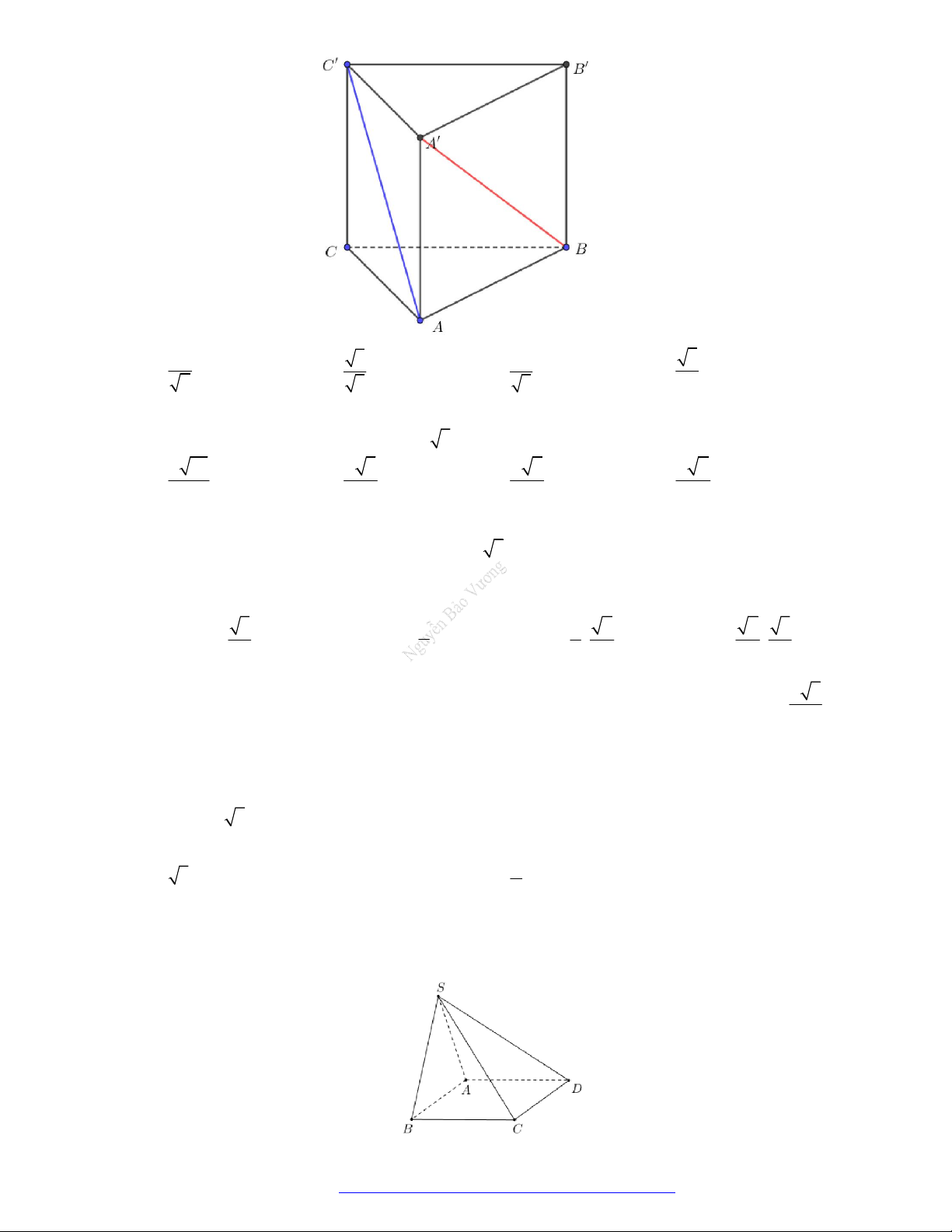
Câu 22. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho khối lăng trụ đứng ABC.AB C
  có AA  a 6 ,
đáy ABC là tam giác vuông cân tại B và BA BC a . Góc giữa đường thẳng AC và mặt phẳng đáy bằng A. 45 . B. 90 . C. 60 . D. 30 .
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho lăng trụ đứng ABC.A BC
  có tất cả các cạnh
đều bằng a . Gọi M là trung điểm của CC (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng  A BC  bằng 21a 2a 21a 2a A. . B. . C. . D. . 7 4 14 2
Câu 24. (THPT Chu Văn An - Thái Nguyên - 2021) Cho chóp S.ABC có đáy là tam giác vuông tại B .
AB  3a, BC
3a . SA vuông góc với đáy và SA  2a . Góc giữa SC và đáy là A. 90 . B. 45 C. 60 D. 30
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy là hình thoi tâm 3a 2
O , ABD đều cạnh a 2 , SA vuông góc với mặt phẳng đáy và SA  . Góc giữa đường 2
thẳng SO và mặt phẳng  ABCD bằng A. 45 . B. 30 . C. 60 . D. 90 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 26. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh a , cạnh bên SA vuông góc với đáy và SA a 3 . Khoảng cách từ A đến mặt phẳng SBC  bằng 2a 5 a a 3 A. . B. a 3 . C. . D. . 5 2 2
Câu 27. (Trung Tâm Thanh Tường - 2021) Cho hình chóp S.ABC có SA   ABC , SA a 3 , tam
giác ABC vuông tại B có AC  2 ,
a BC a 3 . Góc giữa SB và mặt phẳng  ABC bằng A. 90 . B. 45 . C. 30 . D. 60 .
Câu 28. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy là hình vuông cạnh
bằng 2a , cạnh bên SA vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BD bằng A. a 2 . B. 2a . C. a . D. a 3 .
Câu 29. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a 3 , I là
trung điểm CD ' (tham khảo hình vẽ). khoảng cách từ I đến mặt phẳng  BDD ' B ' bằng a 2 a a 6 a 3 A. . B. . C. . D. . 4 4 4 4
Câu 30. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình
vuông tâm I , cạnh a . Biết SA vuông góc với mặt đáy  ABCD và SA a 3 (tham khảo hình
vẽ bên). Khi đó tang của góc giữa đường thẳng SI và mặt phẳng  ABCD là:
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 6 3 A. 6 . B. . C. 3 . D. . 6 3 BẢNG ĐÁP ÁN 1.C 2.B 3.D 4.B 5.B 6.C 7.D 8.B 9.B 10.B 11.C 12.B 13.B 14.C 15.C 16.A 17.A 18.A 19.B 20.D 21.A 22.C 23.C 24.D 25.C 26.D 27.D 28.A 29.C 30.A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 8
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
MỨC ĐỘ THÔNG HIỂU Câu 1.
(THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình chóp S.ABC có SA vuông góc với 1
mặt phẳng  ABC  , SA a 2 , tam giác ABC vuông tại A và AC a,sin B  (minh họ như 3
hình bên). Góc giữa đường thẳng SB với mặt phẳng  ABC  bằng A. 0 90 . B. 0 30 . C. 0 45 . D. 0 60 . Lời giải Chọn C
Ta có SA   ABC   SB ABC   ,  SBA 1 2 AC 1 sin B   cos B  ; tan B  
AB a 2 Vậy tam giác SAB vuông cân tại A 3 3 AB 2
Suy ra SB ABC   0 ,  SBA  45 Câu 2.
(THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương .
ABCD A B C D có cạnh 1 1 1 1
a . Gọi I là trung điểm B .
D Góc giữa hai đường thẳng A D và B I bằng 1 1 A. 120 B. 30 .  C. 45 . D. 60 . Lời giải Chọn B
Ta có B C / / A D   A D, B I B C, B I . 1 1   1 1  1 1 a 2 a 6 Vì ABC .
D A B C D là hình lập phương cạnh a nên B C a 2; IC  ; B I  . 1 1 1 1 1 1 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489  2 2 2
B I B C IC 3 Xét BIC có: 1 1 cos IB C   . 1 1 2B I.B C 2 1 1   IB C  30 .  1
Do đó  A D, B I    B C, B I    IB C  30 .  1 1 1 1 1 Câu 3.
(THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình chóp S.ABC có SA  ( ABC) , SA a 3 , tam
giác ABC vuông tại B có AC  2a ,
BC a . Góc giữa đường thẳng SB và mặt phằng ( ABC) bằng A. 60 . B. 90 . C. 30 . D. 45 . Lời giải Chọn D S C A B
AB là hình chiếu vuông góc của SB lên ( ABC) nên SB ABC   SB AB  , ,  SBA .
Tam giác ABC vuông tại B nên: 2 2 AB
(2a)  a a 3  SA
B vuông cân tại A   SBA  45 .
Vậy SB , ABC   45 . Câu 4.
(Sở Lào Cai - 2021) Cho tứ diện OABC có OA , OB , OC đôi một vuông góc và OA OB  2a ,
OC a 2 . Khoảng cách từ điểm O đến mặt phẳng  ABC bằng a 3a A. a 2 . B. a . C. . D. . 2 4 Lời giải Chọn B
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Xét hệ trục tọa độ Oxyz như sau điểm O là gốc tọa độ OA Oz ; OB Ox và OC Oy . Khi đó
ta có O0;0;0 ; A0;0;2a ; B2 ;
a 0;0 và C 0;a 2;0 . x y z
Phương trình mặt phẳng  ABC  là  
 1  x  2y z  2a  0 . 2a a 2 2a 0  2.0  0  2a
Khoảng cách từ điểm O đến mặt phẳng  ABC là d O, ABC    a . 1 2 1 Câu 5.
(Sở Lào Cai - 2021) Cho hình lập phương ABC . D A BCD
  . Gọi M , N lần lượt là trung điểm AC và B C
  ,  là góc giữa đường thẳng MN và mặt phẳng  AB CD
  . Tính giá trị  . 2 2 5 1 5 A. sin   . B. sin  . C. sin   . D. sin   . 2 5 2 5 Lời giải Chọn B
Giả sử cạnh hình lập phương là a .
Gọi O là tâm của hình vuông AB CD   . Suy ra O N
 là hình chiếu của MN lên  AB CD   . Do
đó góc giữa MN và  A BCD
  là góc giữa MN và O N  . 1 Tam giác O M
N vuông tại O có O N   a , O M   a nên 2  O MO Ma 2 5 sin O NM      . 2 2 2 MN    5 O N O M a 2  a 4 Câu 6.
(Sở Tuyên Quang - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , đường
thẳng SA vuông góc với mặt phẳng đáy và SA  2a . Góc giữa đường thẳng SC và mặt phẳng
ABCD là . Khi đó tan bằng 2 A. 2 2 . B. 2 . C. 2 . D. . 3 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Ta có: SC ABCD   ;
SCA .  SA a
Xét tam giác SAC vuông tại A có: tan SCA  2   2 AC a 2  tan  2 . Câu 7.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC
là tam giác vuông tại A , AB a, AC a 2 . Biết thể 3 a
tích khối chóp S.ABC bằng
. Khoảng cách S từ đến mặt phẳng  ABC bằng 2 a 2 a 2 3a 2 3a 2 A. . B. . C. . D. . 2 6 4 2 Lời giải Chọn D 3 a 2 3. 1 a 2 3V 3a 2  Ta có SAB AC   d S ABC    . ABC    S . ABC 2 . , 2 2 2 Sa ABC 2 2 2 Câu 8.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC
là tam giác vuông tại B , SA vuông góc với mặt phẳng  ABC , AH là đường cao trong tam giác
SAB . Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A. SA BC .
B. AH AC .
C. AH SC .
D. AH BC . Lời giải Chọn B
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Ta có SA   ABC  SA BC
Tam giác ABC vuông tại B nên AB BC SA BC  Có:
  BC   SABAB BC
Mà AH nằm trong mặt phẳng  SAB nên BC AH
BC AH cmt  Mặt khác:
  AH   SBC   AH SC . AH SB  
Vậy khẳng định sai là AH AC . Câu 9.
(Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
vuông tại B , SA vuông góc với mặt đáy. Góc giữa hai mặt phẳng SBC và  ABC  là     A. BAC . B. SBA . C. SAB . D. SCA . Lời giải Chọn B S A C B
SA   ABC   SA BC Ta có 
BC  SAB .  AB BC
Mà  SBC    ABC   BC . Suy ra
+ SBC  SAB theo giao tuyến SB .
+  ABC   SAB theo giao tuyến AB .
 SBC   ABC    SB AB   ; ;  SBA (do  0 SBA  90 )
Câu 10. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình chóp S.ABCD có đáy là hình vuông
ABCD cạnh bằng 3a , SA SB a
vuông góc với mặt đáy  ABCD ,
5 . Tính sin của góc giữa cạnh
SC và mặt đáy  ABCD . 3 2 2 34 4 2 2 A. . B. . C. . D. . 4 17 5 3 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Do SA   ABCD nên AC là hình chiếu của SC lên mặt phẳng  ABCD  . Do đó góc giữa cạnh
SC và mặt đáy  ABCD  là  SCA .
Xét tam giác ABC có 2 2 AC
AB BC  3a 2 .
Xét tam giác SAB có 2 2 SA
SB AB  4a .
Xét tam giác SAC có 2 2 SC
SA AC a 34 . SA a
Xét tam giác SAC có  4 2 34 sin SCA    . SC a 34 17 2 34
Vậy sin của góc giữa cạnh SC và mặt đáy  ABCD  bằng . 17
Câu 11. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
đều cạnh a , cạnh SA vuông góc với mặt phẳng đáy và SA  2a , gọi M là trung điểm của SC .
Tính cosin của góc  là góc giữa đường thẳng BM và  ABC  . 7 2 7 21 5 A. cos  . B. cos  . C. cos  . D. cos  . 14 7 7 7 Lời giải Chọn C
Trong mặt phẳng SAC , dựng MH AC tại H .
Do SA   ABC   SA AC   ABC  SA//MH .
Khi đó: MH   ABC  . Suy ra:
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 a 3 BH 21   BM ABC       BM BH   2 cos cos , cos ,  cos MBH    2 BM 2 7  a 3   2a       2  2   
Câu 12. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông
tâm O cạnh a , SO vuông góc với mặt phẳng  ABCD và SO a . Khoảng cách giữa SC và AB bằng: 2a 3 2a 5 a 5 a 3 A. . B. . C. . D. . 15 5 5 15 Lời giải Chọn B S a B a C a O a A a D
AB / /CD ⇒ d  A ;
B SC   d A ;
B SCD  d  ;
A SCD  2.d  ;
O SCD (*)  Hình chóp .
O SCD là tam diện vuông tại O : 1 1 1 1 1 1 1 5 a       
⇔ O SCD 5 d ;  2 d  ; O SCD 2 2 2 2 2 2 2 OS OC OD aa 2   a 2 a  5     2 2     a
(*) ⇔  AB SC  
O SCD 2 5 d ; 2.d ;  . 5
Câu 13. (Chuyên KHTN - 2021) Cho hình lăng trụ tam giác đều ABC.AB C
  có cạnh đáy bằng a và 3a cạnh bên bằng
. Góc giữa hai mặt phẳng  A B
C và  ABC bằng 2 A. 30 . B. 60 . C. 45 . D. 90 . Lời giải Chọn B A' C' B' A C M B
 Gọi M là trung điểm của BC AM BC (vì tam giác ABC đều)
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 2 a a 3 2 2 2  AM
AB BM a   4 2
  ABC   ABC   ,  AMA 3aAA Lại có: 2 tan AMA    3 AM a 3 2 
AMA  60   ABC , ABC   60
Câu 14. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hình chóp S.ABCD có đáy là hình vuông
cạnh a , SA   ABC , SA a 2 . Góc giữa đường thẳng SC và mặt phẳng  ABCD  bằng A. 60 . B. 90 . C. 45 . D. 30 . Lời giải Chọn C
Ta có AC a 2 suy ra S
AC vuông cân tại A
Góc giữa SC và mp  ABCD chính là góc SCA  45
Câu 15. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương ABC . D A BCD   có ,
O O lần lượt là tâm
của các hình vuông ABCD và A BCD
  . Góc giữa hai mặt phẳng  ABD và  ABCD bằng    A. AAD . B. A OC .
C. AOA . D. OA A  . Lời giải Chọn C A' D' O' B' C' D A O B C
Ta có ABCD là hình vuông nên AO BD , đồng thời BD A A
  BD   AAO  BD A O    A B
D  ABCD  BD
Ta có AO BD
  ABD  ABCD    
  AO AO  ; ;  AOA
AO BD
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 16. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a,
O là tâm của mặt đáy. Khoảng cách giữa hai đường thẳng SO và CD bằng a 2a A. . B. a . C. . D. 2a . 2 2 Lời giải Chọn A
Vì S.ABCD là hình chóp tứ giác đều nên ABCD là hình vuông và SO   ABCD.
Gọi M là trung điểm của C . D
Khi đó OM SO (do SO   ABCD và OM   ABCD ).
Mà OM CD (do O
CD là tam giác cân tại O ). AD a
Suy ra d SO,CD  OM   . 2 2
Câu 17. (Sở Yên Bái - 2021) Cho hình chóp S.ABCD có đáy là hình vuông canh a, SA vuông góc với
mặt phẳng đáy và SA a 6 . Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng A. 60o. B. 45o. C. 90o. D. 30o. Lời giải Chọn A.
Ta có AC là hình chiếu của SC lên mặt đáy  ABCD.   SA
SC ABCD   SC AC     SCA SCA  
 SC ABCD  0 , , tan 3 ,  60 . AC
Câu 18. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
bằng 2a cạnh bên bằng 5a . Góc giữa mặt bên và mặt phẳng đáy bằng A. 60 . B. 30 . C. 70 . D. 45 . Lời giải Chọn A
 Gọi O là tâm hình vuông ABCD . Khi đó SO   ABCD . CD
 Gọi H là trung điểm cạnh CD . Ta có: OH CD và HD OH   a . 2  Do S
CD cân tại S nên SH CD .
 Vậy góc giữa mặt bên SCD và mặt phẳng  ABCD là góc  SHO .  Trong S
HD vuông tại H ta có 2 2 2 2
SH SD HD  5a a  2a .  OH a 1  Khi đó cos SHO     SHO  60 . SH 2a 2
Câu 19. (THPT Nguyễn Huệ - Phú Yên - 2021) Hình chóp S.ABC có S ,
A SB, SC đôi một vuông góc
với nhau và SA SB SC . Gọi I là trung điểm của AB . Góc giữa SI và BC bằng A. 30 . B. 60 . C. 45 . D. 90 . Lời giải Chọn B 1     
       BCSA SB.BC SI. S . A BC S . B BC Ta có: SI BC 2 cos ;    2 SI.BC BC BC .BC 2   . SB BC . SB BC.cos135 . SB SB 2.cos135 2.cos135 1       . 2 BC 2 BC 2 2SB 2 2  
Suy ra: SI; BC  120  SI; BC  60 .
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 20. (THPT Lương Thế Vinh - 2021) Cho hình chóp S.ABCD có đáy là hình thoi tâm O , ABD 3a 2
đều cạnh a 2, SA vuông góc với mặt phẳng đáy và SA
. Góc giữa đường thẳng SO và 2
mặt phẳng  ABCD bằng A. 45 . B. 90 . C. 30 . D. 60 . Lời giải Chọn D S D A O B C
Ta có: ABCD là hình thoi có tâm là O O là trung điểm của BD . Mà A
BD đều nên AO BD
Lại có SA   ABCD  SO ABCD   ,  SOA 2 2  a 2  a 6 Xét ABO có: 2 2 AO
AB BO  a 2      2  2   3a 2  SA 2  Ta có: tan SAO  
 3  SOA  60 AO a 6 2
Câu 21. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho khối chóp đều S.ABC có cạnh đáy bằng a . 3 a
Gọi M là trung điểm của SA . Biết thể tích của khối chóp đó bằng
, khoảng cách từ điểm M 2
đến mặt phẳng  ABC  bằng a 3 A. a 3 . B. 3a . C. . D. 2a 3 . 3 Lời giải Chọn B a Ta có  2 1 3 S  .
AB AC.sin BAC  . ABC 2 4 1 3V Mà VS .d S ABCd S ABC   a . S ABC ABC  ,   ,  S . ABC 2 3 . 3 SABC
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 1
Khi đó d M , ABC   d S, ABC   a 3 . 2
Câu 22. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho khối lăng trụ đứng ABC.AB C
  có AA  a 6 ,
đáy ABC là tam giác vuông cân tại B và BA BC a . Góc giữa đường thẳng A C  và mặt phẳng đáy bằng A. 45 . B. 90 . C. 60 . D. 30 . Lời giải Chọn C
Ta có: AA   ABC   AC là hình chiếu của A C
 lên mặt phẳng  ABC .
Khi đó  AC ABC    A CAC    , ,  ACA .
Ta có: AC AB 2  a 2 .  AAa 6  tan ACA  
 3  ACA  60 . AC a 2
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho lăng trụ đứng ABC.AB C
  có tất cả các cạnh
đều bằng a . Gọi M là trung điểm của CC (tham khảo hình bên). Khoảng cách từ M đến mặt
phẳng  ABC  bằng 21a 2a 21a 2a A. . B. . C. . D. . 7 4 14 2 Lời giải Chọn C
Gọi H , K lần lượt là hình chiếu của A lên BC và A H  .
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 1 1
Ta có d M , A B
C   d C , ABC  d  ,
A ABC   AK . 2 2 2 a 3 AH.AAa 21 Mà AH
; AA  a nên AK   . 2 2 2   7 AH AA a
Vậy d M ABC  21 ;  . 14
Câu 24. (THPT Chu Văn An - Thái Nguyên - 2021) Cho chóp S.ABC có đáy là tam giác vuông tại B .
AB  3a, BC
3a . SA vuông góc với đáy và SA  2a . Góc giữa SC và đáy là A. 90 . B. 45 C. 60 D. 30 Lời giải Chọn D AC  12a  2a 1 tan SCA   12a 3  0  SCA  30
Câu 25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy là hình thoi tâm 3a 2
O , ABD đều cạnh a 2 , SA vuông góc với mặt phẳng đáy và SA  . Góc giữa đường 2
thẳng SO và mặt phẳng  ABCD bằng A. 45 . B. 30 . C. 60 . D. 90 . Lời giải Chọn C a 2 3 a 6
Tam giác ABD đều cạnh a 2 , suy ra AO   . 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Vì SA   ABCD , suy ra OA là hình chiếu của OS lên mặt phẳng  ABCD  , suy ra:
SO ABCD  ;  SOA .  SA 3a 2 2  Ta có: tan SOA   .
 3  SOA  60 . AO 2 a 6
Vậy SO; ABCD   60 .
Câu 26. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình
vuông cạnh a , cạnh bên SA vuông góc với đáy và SA a 3 . Khoảng cách từ A đến mặt phẳng SBC  bằng 2a 5 a a 3 A. . B. a 3 . C. . D. . 5 2 2 Lời giải Chọn D
Kẻ AH SB *
Ta có BC AB ( Do ABCD là hình vuông )
BC SA ( Do SA   ABCD )
Suy ra BC  SAB
Suy ra BC AH **
Từ *,** suy ra AH  SBC  . Suy ra d A, SBC   AH 1 1 1 1 1 4      2 2 2 2 2 2 AH AB SA a 3a 3a a 3 Suy ra AH  2
Câu 27. (Trung Tâm Thanh Tường - 2021) Cho hình chóp S.ABC có SA   ABC , SA a 3 , tam
giác ABC vuông tại B có AC  2 ,
a BC a 3 . Góc giữa SB và mặt phẳng  ABC bằng A. 90 . B. 45 . C. 30 . D. 60 . Lời giải Chọn D
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 S a 3 2a A C a 3 B Ta có AB
AC BC   a  a 2 2 2 2 2 3  a . SA a 3
Dễ thấy SB ABC    SB AB   ; ;  SBA . Khi đó   tan SBA  
 3  SBA  60 . AB a
Vậy SB ABC   ;  60 .
Câu 28. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy là hình vuông cạnh
bằng 2a , cạnh bên SA vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BD bằng A. a 2 . B. 2a . C. a . D. a 3 . Lời giải Chọn A
Gọi O là tâm của hình vuông ABCD , ta có AO BD .
Mặt khác SA   ABCD  SA AO .
Vậy AO là đoạn vuông góc chung của hai đường thẳng SA và BD nên 1 d  ;
SA BD  AO AC a 2 . 2
Câu 29. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh a 3 , I là
trung điểm CD ' (tham khảo hình vẽ). khoảng cách từ I đến mặt phẳng  BDD ' B ' bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 a 2 a a 6 a 3 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn C
d I, BDD ' B ' ID ' 1
Do CI   BDD ' B '  D ' nên ta có   .
d C,BDD ' B ' CD ' 2 AC 6a
Gọi M  BD AC . Khi đó CM   . 2 2 1 CM 6a
Vậy d I, BDD ' B '   d C, BDD ' B '   . 2 2 4
Câu 30. (THPT Trần Phú - Đà Nẵng - 2021) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình
vuông tâm I , cạnh a . Biết SA vuông góc với mặt đáy  ABCD và SA a 3 (tham khảo hình
vẽ bên). Khi đó tang của góc giữa đường thẳng SI và mặt phẳng  ABCD là:
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 6 3 A. 6 . B. . C. 3 . D. . 6 3 Lời giải Chọn A 1 a 2 Ta có: AI AC  2 2
Mà SA   ABCD nên AI là hình chiếu của SI trên mặt phẳng  ABCD
 SI ABCD   SI AI   ; ;
SIA (do tam giác SAI vuông tại A ) SA Vậy
SI ABCD   tan ;  tan SIA   6 . AI
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 8
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH)
MỨC ĐỘ VẬN DỤNG Câu 1.
(THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho chóp S.ABC có đáy ABC là tam giác đều cạnh
a , tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách
d giữa SB và AC. a 6 a 2 a 21 a 30 A. d  . B. d  . C. d  . D. d  . 6 3 7 5 Câu 2.
(THPT Phan Đình Phùng - Quảng Bình - 2021) Cho tứ diện OABC có O ,
A OB , OC đôi một
vuông góc với nhau, OA a và OB OC  2a . Gọi P là trung điểm của BC (minh họa như
hình bên dưới). Khoảng cách giữa hai đường thẳng OP và AB bằng 2a 6a 2 5a A. . B. .
C. a . D. . 2 3 5 Câu 3.
(THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
vuông tại A , M là trung điểm BC , hình chiếu vuông góc của S lên mặt phẳng  ABC  trùng
với trung điểm của AM . Cho biết AB a, AC a 3 và mặt phẳng SAB tạo với mặt phẳng
ABC  một góc 0
60 . Tính khoảng cách giữa hai đường thẳng SA và BC . a 3 3a 3a 4a A. . B. . C. . D. . 2 4 2 3 Câu 4.
(THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có ABCD là hình vuông
cạnh a , SA  2a và vuông góc  ABCD . Gọi M là trung điểm của SD . Tính khoảng cách d giữa
hai đường thẳng SB và CM . 2a a a a 2 A. d  . B. d  . C. d  . D. d  . 3 3 6 2 Câu 5.
(THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp S. ABCD có đáy ABCD là hình
chữ nhật, AB  2a, AD  .
a SA vuông góc với mặt phẳng đáy, SA a 3 . Cosin của góc giữa
SC và mặt đáy bằng 7 10 6 5 A. . B. . C. . D. . 4 4 4 4 Câu 6.
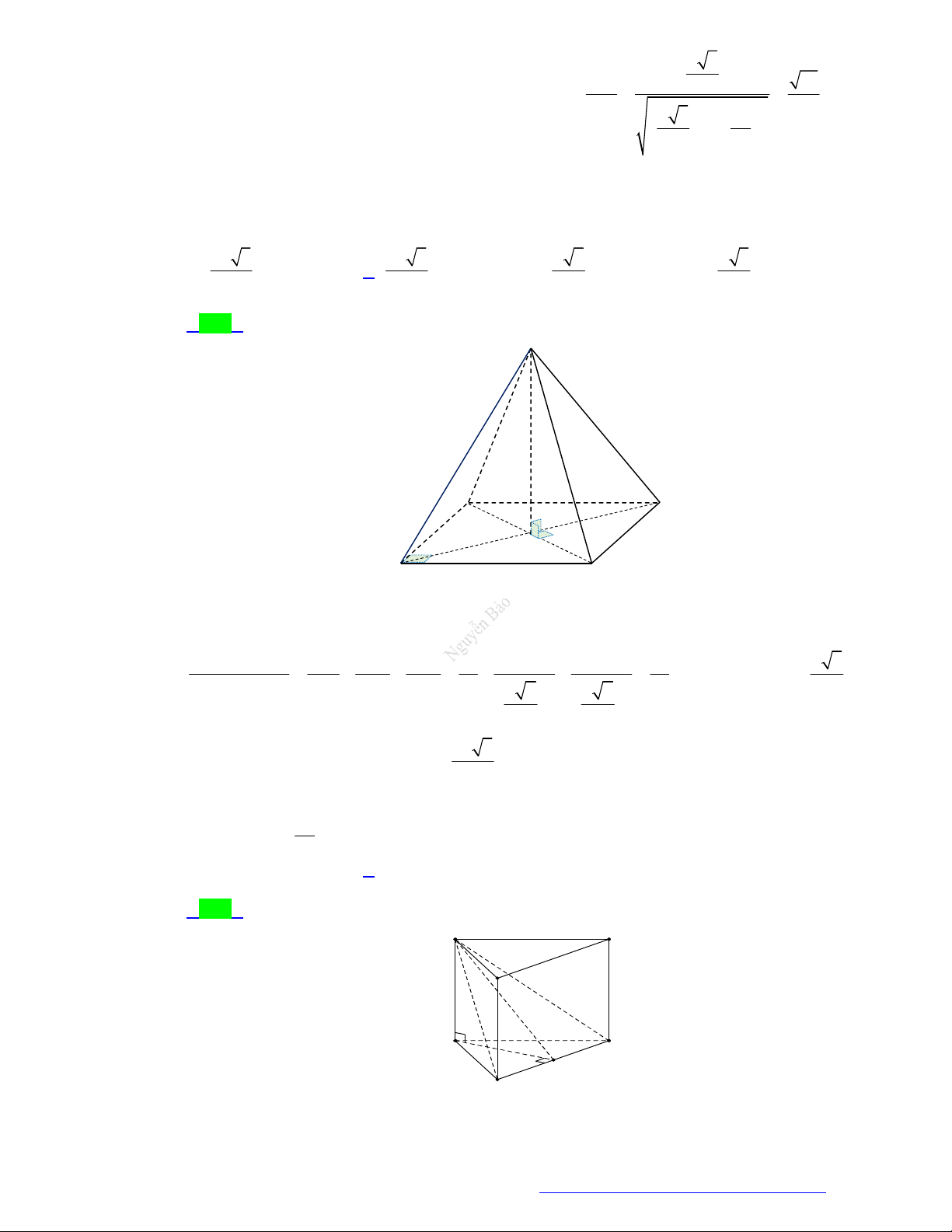
(THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình lăng trụ đứng AB . C A BC
  có đáy là tam giác
vuông, BA BC  2a , cạnh bên AA  4a , M là trung điểm BC (minh họa như hình dưới).
Khoảng cách giữa hai đường thẳng B C  và AM bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 B' C' A' M B C A 2a 7 a 6 a 6 A. . B. . C. a . D. . 7 6 3 Câu 7.
(THPT Đồng Quan - Hà Nội - 2021) Cho lăng trụ tứ giác ABC . D AB CD
  có đáy ABCD là
hình thoi cạnh a , góc 
BAC  60 . Biết AA  A B   A D
 và cạnh bên AA hợp với mặt phẳng
đáy góc 60 . Tính khoảng cách giữa hai đường thẳng CC và BD . 3a a 3 a 6 a 3 A. . B. . C. . D. . 4 2 8 4 Câu 8.
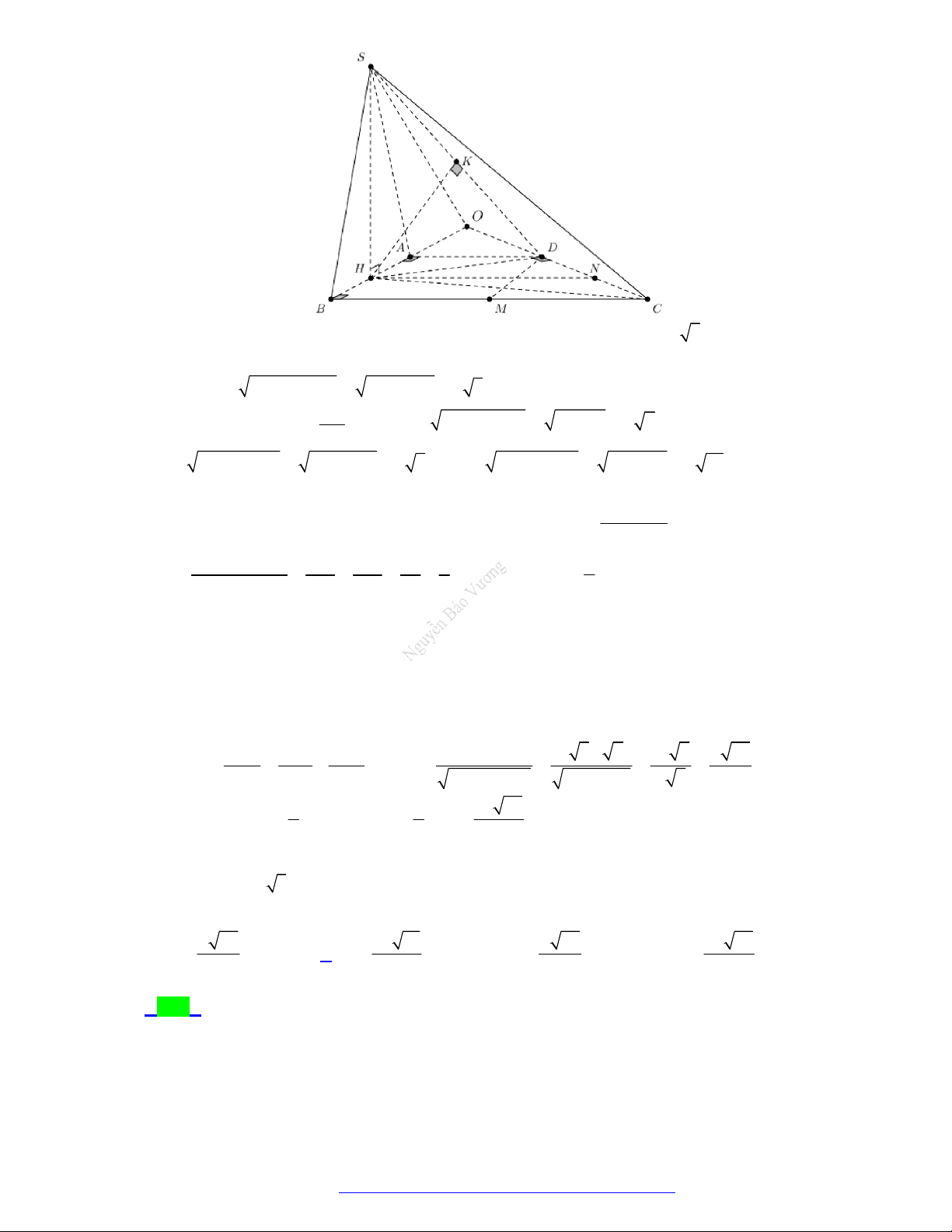
(THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I; AB  2 ;
a BD  3AC, mặt bên SAB
là tam giác cân đỉnh A , hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy trùng với trung
điểm H của AI. Khoảng cách giữa hai đường thẳng SB và CD bằng. 2a 7 2a 35 2a 35 a 35 A. B. . C. . D. . 7 7 35 7 Câu 9.
(Sở Vĩnh Phúc - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng a ,  0
BAD  120 . Mặt bên SAB là tam giác đều và  SAB   ABCD (tham khảo hình vẽ).
Tính khoảng cách từ A đến SBC a a 7 3a a 15 A. . B. . C. . D. . 2 7 4 5
Câu 10. (Sở Hà Tĩnh - 2021) Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AD a ,
AB  2a , BC  3a , mặt bên SAB là tam giác đều và vuông góc với mặt phẳng đáy  ABCD .
Tính khoảng cách từ điểm B đến mặt phẳng SCD . 3a 30 3a 30 a 30 3a 2 A. . B. . C. . D. . 10 5 2 2
Câu 11. (Sở Tuyên Quang - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB a , AD  2a 3 . Cạnh bên SA vuông góc với đáy, biết tam giác SAD có diện tích 2 S  3a .
Tính khoảng cách từ C đến SBD bằng
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 a 39 2a 51 a 39 2a 39 A. d  . B. d  . C. d  . D. d  . 13 17 5 13
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABCD có đáy
ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc
với đáy. Tính khoảng cách giữa hai đường thẳng AB và S . D a 21 a 3 a 21 a 7 A. . B. . C. . D. . 7 7 3 3
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình hộp chữ nhật AB .
CD A B C D có ba kích 1 1 1 1
thước AB a , AD  2a , AA  3a . Khoảng cách từ A đến mặt phẳng  A BD bằng bao nhiêu? 1  1 7 6 5 A. a . B. a . C. a . D. a . 6 7 7
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ đứng ABC.AB C   có đáy ABC a
là tam giác đều cạnh a , AA  2a . Gọi M là điểm trên cạnh A B   , A M   . Khoảng cách từ 3
M đến mặt phẳng  AB C   bằng? 4 57a 2 57a 57a 57a A. . B. . C. . D. . 57 57 19 57
Câu 15. (Chuyên Lê Hồng Phong - TPHCM - 2021) Hình hộp ABC . D A BCD
  có AB AA  AD a   
và AAB AAD BAD  60 . Tính c s
« in của góc giữa đường thẳng CD và mặt phẳng  AAD : 3 3 3 2 3 A. . B. . C. . D. . 3 2 4 3
Câu 16. (Chuyên KHTN - 2021) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 3 ,
SA   ABCD và SA a 2 . Tính góc giữa SC và  ABCD . A. 90 . B. 45. C. 60. D. 30 .
Câu 17. (Chuyên KHTN - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a 2 . Cạnh
bên SA vuông góc với đáy. Góc giữa SC và mặt đáy bằng 45 . Gọi E là trung điểm của BC .
Tính khoảng cách giữa hai đường thẳng DE và SC . 2a 19 a 10 a 10 2a 19 A. . B. . C. . D. . 19 19 5 5
Câu 18. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương ABC . D A BCD
  . Số đo của góc giữa hai mặt phẳng  BA C   và  DA C   bằng A. 60 . B. 30 . C. 45 . D. 90 .
Câu 19. (Chuyên Quốc Học Huế - 2021) Cho hình lăng trụ tam giác AB .
C A' B 'C ' có mặt bên ABB ' A'  10
là hình thoi cạnh a, AAB  120 và A 'C BC a 3, AC
a . Tính khoảng cách giữa hai 2 đường thẳng A B  và AC 10 10 3 10 3 10 A. a B. a C. a D. a 20 10 20 10
Câu 20. (Chuyên Quang Trung - Bình Phước - 2021) Cho hình chóp S.ABCD đáy ABCD là hình thoi cạnh a , góc 
BAD  60 , SA   ABCD , SC ABCD  ,
 45 . Gọi I là trung điểm SC . Tính
khoảng cách từ I đến mặt phẳng SBD .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 a 15 a 15 2a 15 a 15 A. . B. . C. . D. . 10 5 5 15
Câu 21. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình chữ
nhật AB a, AD  2 ;
a SA vuông góc với đáy ABCD , SC hợp với đáy một góc  và 10 tan  
. Tính khoảng cách từ điểm B đến mặt phẳng  SCD. 5 a 2a a 3 2a 3 A. B. C. D. 3 3 3 3
Câu 22. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp S.ABCD có đáy là hình vuông cạnh
a , SD a 3 . Mặt bên SAB là tam giác cân và nằm trong mặt phẳng vuông góc với đáy. Gọi
H là trung điểm của AB , K là trung điểm của AD . Khoảng cách giữa hai đường thẳng SD và HK bằng a 105 a 105 a 105 a 105 A. . B. . C. . D. . 5 20 30 10 Câu 23. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp S.ABC có
SA  12cm, AB  5 , cm AC  9 , cm SB  13 ,
cm SC  15cm và BC  10cm . Tan của góc giữa hai
mặt phẳng (SBC) và ( ABC) bằng 14 10 14 4 12 A. . B. . C. . D. . 10 14 3 5
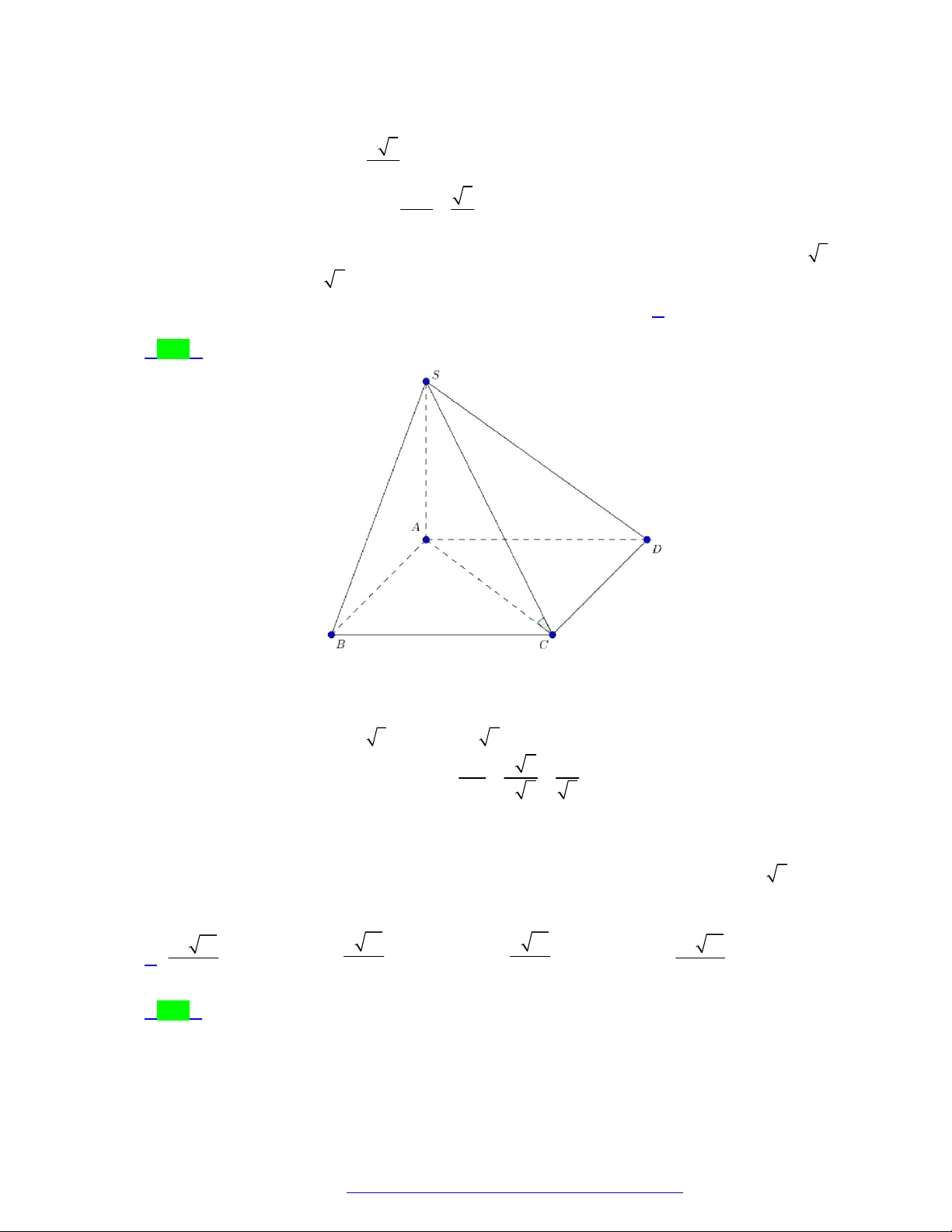
Câu 24. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác vuông
cân, AB BC  2a . Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với  ABC ,
SA  3a . Góc giữa hai mặt phẳng  SAB và  SAC  bằng A. 0 60 . B. 0 30 . C. 0 45 . D. 0 90 .
Câu 25. (Sở Yên Bái - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hình chiếu
vuông góc của S lên mặt phẳng ( ABCD) là trung điểm của AD, góc giữa đường thẳng SB và
mặt đáy bằng 60o . Gọi M là trung điểm của DC . Khoảng cách giữa hai đường thẳng SA và BM là a 285 a 285 3a 285 2a 285 A. . B. . C. . D. . 9 19 19 19
Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp S.ABC có đáy là tam giác đều, tam giác SAB SA a
vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết 6.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng 3 7a 6 7a 7a A. . B. 7a . C. . D. . 7 7 2
Câu 27. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chóp S.ABC có ,
SA SB, SC đôi một vuông góc nhau và SA  ; a SB  2 ; a SC  3 .
a Gọi M , N, P lần lượt là trung điểm của AB, BC, CA .
Khoảng cách từ điểm M đến mặt phẳng SNP bằng 5a 6a a 15 a 13 A. . B. . C. . D. . 7 7 2 2
Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
vuông cân tại A , BC a 2 và SB a . Hình chiếu vuông góc của S lên mặt phẳng  ABC
trùng với trung điểm M của BC . Góc giữa đường thẳng SA và mặt phẳng  ABC  bằng
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 0 30 . B. 0 60 . C. 0 45 . D. 0 75 .
Câu 29. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình hộp ABC .
D A' B 'C ' D ' có tất cả các cạnh    đều bằng a và 0
BAA'  DAA'  BAD  60 . Gọi G là trọng tâm của tam giác AB 'C . Khoảng
cách từ G đến mặt phẳng  DA'C ' bằng a 22 4a 11 2a 11 a 22 A. . B. . C. . D. . 66 11 11 11
Câu 30. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp S.ABCD có đáy ABCD có đáy là
hình vuông cạnh a , mặt bên SAD là tam giác đều và SAD   ABCD . Gọi M là trung điểm
cạnh đáy AB . Khoảng cách giữa các đường thẳng SA và CM là. a 3 a 2 a 5 a 3 A. . B. . C. . D. . 3 3 4 4
Câu 31. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật
AB a, AD
3 . Cạnh bên SA vuông góc với đáy và SA  2a . Tính khoảng cách d từ điểm C
đến mặt phẳng SBD : 2a 57 2a a 5 a 57 A. d  . B. d  . C. d  . D. d  . 19 5 2 19
Câu 32. (THPT Quốc Oai - Hà Nội - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S
AB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi  là góc tạo bởi đường thẳng
BD với mặt phẳng SAD . Khi đó sin bằng 3 1 6 10 A. . B. . C. . D. . 2 2 4 4
Câu 33. (THPT Quốc Oai - Hà Nội - 2021) Cho hình lăng trụ tam giác đều ABC.A ' B 'C ' có tất cả các
cạnh có độ dài bằng 2 (tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng AC ' và A' B bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 1 3 2 3 A. . B. . C. . D. . 2 5 5 2
Câu 34. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho lăng trụ đứng ABC.AB C
  có đáy là tam giác
ABC vuông tại A có BC  2a , AB a 3 . Khoảng cách giữa hai đường thẳng AA và BC là a 21 a 3 a 5 a 7 A. . B. . C. . D. . 7 2 2 3
Câu 35. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho khối chóp S.ABCD có đáy là hình bình hành,   3,  4,  120o AB AD BAD
. Cạnh bên SA  2 3 vuông góc với đáy. Gọi M , N , P lần lượt là
trung điểm các cạnh S , A AD BC và
. Gọi  là góc giữa hai mặt phẳng (SAC) và (MNP). Chọn
khẳng định đúng trong các khẳng định sau đây.  3   1   1 2   2 3  A. sin    ;1 . B. sin   0; . C. sin    ; . D. sin    ; .      2         2  2 2   2 2   a 3
Câu 36. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho tứ diện ABCD có AB CD a, IJ  ( 2
I , J lần lượt là trung điểm của BC và AD ). Số đo góc giữa hai đường thẳng AB và CD là A. 0 60 . B. 0 30 . C. 0 45 . D. 0 120 .
Câu 37. (Trung Tâm Thanh Tường -2021) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy 4a , cạnh
bên bằng 2 5a , gọi O là tâm của hình vuông ABCD . Khoảng cách từ O đến mặt phẳng SCD bằng a A. 3a . B. a . C. . D. 2a . 2
Câu 38. (Trung Tâm Thanh Tường - 2021) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh
bằng 2a . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E, F lần lượt là trung điểm của S ,
A CD . Khoảng cách giữa hai đường thẳng SD và EF bằng
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 a 5 2a 3 a 5 a A. . B. . C. . D. . 10 7 5 2
Câu 39. (Trung Tâm Thanh Tường -2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
bằng 2a , SA vuông góc với đáy, SA a 6 . Tính khoảng cách giữa hai đường thẳng SD và AC. 2 10a 6a A. . B. 2a . C. . D. 2a . 5 2
Câu 40. (Trung Tâm Thanh Tường -2021) Cho hình tứ diện đều ABCD . Giá trị tan của góc giữa mặt bên và đáy bằng 2 6 A. . B. 2 . C. 2 2 . D. 2 . 3
Câu 41. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông
cạnh a ; SA a 2 và SA vuông góc với mặt đáy  ABCD . Gọi M ; N lần lượt là hình chiếu
vuông góc của đỉnh A lên các cạnh SB và SD . Khi đó góc giữa đường thẳng SB và mặt phẳng  AMN  bằng: A. 45 . B. 30 . C. 60 . D. 90 . BẢNG ĐÁP ÁN 1.C 2.B 3.D 4.A 5.B 6.D 7.D 8.B 9.D 10.A 11.B 12.A 13.C 14.A 15.A 16.D 17.A 18.A 19.C 20.A 21.D 22.C 23.B 24.A 25.B 26.C 27.B 28.C 29.D 30.D 31.A 32.C 33.C 34.B 35.A 36.A 37.C 39.C 40.C 41.C 38.A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 8
HÌNH HỌC KHÔNG GIAN (GÓC VÀ KHOẢNG CÁCH) MỨC ĐỘ VẬN DỤNG Câu 1.
(THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho chóp S.ABC có đáy ABC là tam giác đều cạnh
a , tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách
d giữa SB và AC. a 6 a 2 a 21 a 30 A. d  . B. d  . C. d  . D. d  . 6 3 7 5 Lời giải Chọn C
Kẻ đường thẳng  đi qua B và  / / AC .
Kẻ HD   tại D .
Khi đó AC / / BD AC / / SDB
d AC; SB  d AC;SBD  d  ;
A SDB  2d H ;SDB .
Kẻ HK SD tại K.
Vì BD DH , BD SH BD   SDH   BD HK .
Mà HK SD HK  SDB
d H ;SDB  HK . a
Ta có SAB vuông cân ở S nên SH HB HA  . 2 Vì  
AC / / BD DBH BAC  60 . a a HDB  3
vuông ở D nên HD H . B sin HBD  .sin 60  . 2 4 1 1 1 a 21
SHD vuông ở H có:    HK   d H ; SBD . 2 2 2    SH DH HK 14 a
d SB AC   d H SBD 21 ; 2 ;  . 7 Câu 2.
(THPT Phan Đình Phùng - Quảng Bình - 2021) Cho tứ diện OABC có O ,
A OB , OC đôi một
vuông góc với nhau, OA a và OB OC  2a . Gọi P là trung điểm của BC (minh họa như
hình bên dưới). Khoảng cách giữa hai đường thẳng OP và AB bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 2a 6a 2 5a A. . B. .
C. a . D. . 2 3 5 Lời giải Chọn B
Chọn hệ trục tọa độ Oxyz như hình vẽ, khi đó O 0;0;0, B 2a ;0;0,C 0; 2a ;0, A0;0; a .
Vì P là trung điểm của BC nên P a; a;0 .   
Ta có OP  a ; a ;0, AB  2a ;0; a,OA  0;0; a .    3   O , P AB .OA 2  a   6a
Suy ra OP, AB   2 2 2 a ; a ; 2
a   d OP , AB        . 4 4 4   3 OP, AB
a a  4a   Câu 3.
(THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
vuông tại A , M là trung điểm BC , hình chiếu vuông góc của S lên mặt phẳng  ABC  trùng
với trung điểm của AM . Cho biết AB a, AC a 3 và mặt phẳng SAB tạo với mặt phẳng
ABC  một góc 0
60 . Tính khoảng cách giữa hai đường thẳng SA và BC . a 3 3a 3a 4a A. . B. . C. . D. . 2 4 2 3 Lời giải Chọn D
Dựng hình bình hành ABCD . Khi đó d  ,
SA BC   d BC,SAD  d M ,SAD  2d H ,SAD với H là trung điểm của AM .
Theo đề bài, ta suy ra SH   ABCD  SH AD
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Kẻ HJ AD , HK SI HK   SAD  d H ,SAD  HK
Kẻ HI AB SI AB , suy ra SAB  ABC   SI HI   0 , ,  SIH  60 AB BC BC AB a
Dễ thấy ABC đồng dạng với IAH suy ra    4  AI   IA AH BC 4 4 4 2 2  a   a a 3
Tam giác HIA vuông tại I nên 2 2 IH AH IA         2   4  4  3a
Tam giác SHI vuông tại H có 0 0
SIH  60  SH IH tan 60  4 a JH AH 1 CA a 3
Ta có AJH đồng dạng DCA suy ra 2     JH   CA DA 2a 4 4 4
Tam giác SHJ vuông tại H có đường cao HK 1 1 1 64 3a      HK  2 2 2 2 HK SH HJ 9a 8 3a Vậy d  ,
SA BC   2HK  . 4 Câu 4.
(THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có ABCD là hình vuông
cạnh a , SA  2a và vuông góc  ABCD . Gọi M là trung điểm của SD . Tính khoảng cách d giữa
hai đường thẳng SB và CM . 2a a a a 2 A. d  . B. d  . C. d  . D. d  . 3 3 6 2 Lời giải Chọn A
Chọn hệ trục tọa độ như hình vẽ  a
Khi đó S (0; 0; 2a) , B(a; 0; 0) , C(a; a; 0) , M 0; ; a    2     a  
SB  (a; 0; 2a) , CM  a;  ; a   , BC  (0; ; a 0)  2 
  
SB,CM .BC   2a
d (SB, CM )       3 SB,CM  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 Câu 5.
(THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hình chóp S. ABCD có đáy ABCD là hình
chữ nhật, AB  2a, AD  .
a SA vuông góc với mặt phẳng đáy, SA a 3 . Cosin của góc giữa
SC và mặt đáy bằng 7 10 6 5 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn B
AC là hình chiếu của SC lên mặt phẳng  ABCD  nên góc giữa SC và mặt phẳng  ABCD  là
góc giữa SC và AC và bằng góc  SCA
Tam giác ADC vuông tại D nên 2 2 AC
AD CD a 5
Tam giác SAC vuông tại A ( do SA   ABCD  )  AC AC a 5 5 10 nên cosSC = A     SC 2 2 SA AC
a 32  a 52 8 4 Câu 6.
(THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hình lăng trụ đứng AB . C A BC
  có đáy là tam giác
vuông, BA BC  2a , cạnh bên AA  4a , M là trung điểm BC (minh họa như hình dưới).
Khoảng cách giữa hai đường thẳng B C  và AM bằng B' C' A' M B C A 2a 7 a 6 a 6 A. . B. . C. a . D. . 7 6 3 Lời giải Chọn D
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 B' C' A' N H M B C I A
Gọi N là trung điểm BB , ta có MN // B C
,  AMN  // B C  .
Dựng BI AM; B B
   ABC  B B
  AM   B B
I   AM   B B
I    AMN  .
Dựng BH B I
  BH   AMN  . Do  AMN   B B
 tại N là trung điểm BB , nên ta có: d B C
 ; AM   d B C
 ;  AMN   d B ;  AMN   d B;  AMN   BH .
Ta có tam giác ABC là tam giác vuông, sử dụng công thức đường cao của tứ diện . B AMN ta có: 1 1 1 1 1 1 1 a 6        BH  . 2 2 2 2 BH BA BM BN 2a2 2 a 2a2 3 Câu 7.
(THPT Đồng Quan - Hà Nội - 2021) Cho lăng trụ tứ giác ABC . D AB CD
  có đáy ABCD là
hình thoi cạnh a , góc 
BAC  60 . Biết AA  A B   A D
 và cạnh bên AA hợp với mặt phẳng
đáy góc 60 . Tính khoảng cách giữa hai đường thẳng CC và BD . 3a a 3 a 6 a 3 A. . B. . C. . D. . 4 2 8 4 Lời giải Chọn D
Gọi G là trọng tâm của tam giác ABD , vì AA  A B   A D
 nên G là hình chiếu của A trên 
mặt phẳng  ABCD . Khi đó A AG   60 . BD CA Ta có: 
BD   ACC A
  và BD   ACC A    O .
BD AG
d CC ; BD  d CC ; BDD B
   d C;BDD B
   d  ; A BDD B  
d AA ;BDD B
   d AA ; BD .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 3
Vì BD   ACC A
   BD AA  d B ;
D AA  d  ;
O AA  d  ; G AA . 2
Từ G kẻ đường thẳng vuông góc với AA tại H , suy ra: d G; AA  GH .
Tam giác ABC đều nên AC a .Mà G là trọng tâm tam giác ABD , suy ra: 2.AO 2 a a a 3 a 3 AG   . 
GH AG sin 60  .  . 3 3 2 3 3 2 6 3 3 a 3 a 3
Vậy  d B ;
D AA  d  ; G AA  .  . 2 2 6 4 Câu 8.
(THPT Lê Lợi - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I; AB  2 ;
a BD  3AC, mặt bên SAB
là tam giác cân đỉnh A , hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy trùng với trung
điểm H của AI. Khoảng cách giữa hai đường thẳng SB và CD bằng. 2a 7 2a 35 2a 35 a 35 A. B. . C. . D. . 7 7 35 7 Lời giải Chọn B
Vì DC / / SAB nên d DC; SB  d DC;SAB  d D;SAB
Mà I là trung điểm BD ; H là trung điểm AI d  ;
D SAB  2d I;SAB  2.2.d H;SAB  4d H;SAB   .
Kẻ HM BA tại M , kẻ HK SM tại K.
Vì AB SH , AB HM AB  SHM  .  AB HK
Mà HK SM HK  SAB  d H ,SAB  HK .  AB BC
Vì ABCD là hình thoi, BD  3AC    ABC đều BI  3AIa
AC AB  2a AH  . 2
Vì SAB cân ở A nên SA AB  2 . a a 15
Xét SAH vuông ở H có: 2 2 SH SA AH  . 2 a 3 Xét A
HM vuông ở M có: HM AH.sin A AH.sin 60  . 4 1 1 1 a 35
Xét SHM vuông ở H có:    HK
d H ,SAB . 2 2 2 HK SH HM 14   a
d D SAB  d H SAB 2 35 ; 4 ;  . 7 2a 35 Vậy d  , SB CD  . 7
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Câu 9.
(Sở Vĩnh Phúc - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng a ,  0
BAD  120 . Mặt bên SAB là tam giác đều và SAB   ABCD (tham khảo hình vẽ).
Tính khoảng cách từ A đến  SBC a a 7 3a a 15 A. . B. . C. . D. . 2 7 4 5 Lời giải Chọn D a 3
Gọi H là trung điểm của AB , khi đó SH   ABCD và SH  . 2
Do AH   SBC   B d  ,
A SBC   2d H ,SBC  .
Gọi K , I là hình chiếu của H lên BC và SK .
Khi đó BC HK , BC SH BC   SHK   BC HI .
Vậy HI BC, HI SK HI   SBC  hay d H ,SBC   HI . a 3 a 3
Gọi E là trung điểm của BC AE  , khi đó HK  . 2 4 1 1 1 4 16 20 a 15
Trong tam giác vuông SHK ta có       HI  . 2 2 2 2 2 2 HI SH HK 3a 3a 3a 10 a
Vậy d A SBC  15 ,  . 5
Câu 10. (Sở Hà Tĩnh - 2021) Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AD a ,
AB  2a , BC  3a , mặt bên SAB là tam giác đều và vuông góc với mặt phẳng đáy  ABCD .
Tính khoảng cách từ điểm B đến mặt phẳng  SCD . 3a 30 3a 30 a 30 3a 2 A. . B. . C. . D. . 10 5 2 2 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
 Gọi H là trung điểm cạnh AB SH AB SH   ABCD và SH a 3 .
 Kẻ MD BC với M BC . Suy ra ta có MD AB  2a ; MC  2a . Suy ra 2 2 2 2
CD MD MC  4a  4a a 8 . AB
 Mặt khác ta có: AH   a ; 2 2 2 2 HD
AH AD a a a 2 ; 2 2 2 2 2
SD SH HD  3a  2a a 5 ; 2 2 2 2 CH
BH BC a  9a a 10 .  Khi đó 2 2 2 2 2 2
2a  8a  10a HD CD CH HD DC . AD BC
 Gọi AB CD O ; N là trung điểm cạnh CD . Khi đó HN   2a . 2
d B;SCD OB BC 3a 3 3 Ta có:      d  ;
B SCD  d H;SCD .
d  H;SCD OH HN 2a 2 2
 Trong SHD kẻ HK SD  
1 với K SD . DC HD Do
  DC   SHD  DC HK 2 . DC SH
Từ (1) và (2) suy ra HK   SCD  d  H;SCD  HK . Trong S
HD vuông tại H ; đường cao HK ta có: 2 1 1 1 SH.HD a 3.a 2 a 6 a 30    HK     . 2 2 2 2 2 2 2 HK SH HD SH HD 3a  2a a 5 5 3 3 3a 30
Vậy d B;SCD  d  H;SCD  .HK  . 2 2 10
Câu 11. (Sở Tuyên Quang - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
AB a , AD  2a 3 . Cạnh bên SA vuông góc với đáy, biết tam giác SAD có diện tích 2 S  3a .
Tính khoảng cách từ C đến SBD bằng a 39 2a 51 a 39 2a 39 A. d  . B. d  . C. d  . D. d  . 13 17 5 13 Lời giải Chọn B
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 S a 3 K 2a 3 A D a H B C 2 1 6a Do 2 S  3a  . . SA AD SA
a 3 . Mặt khác ta có d C,SBD  d  ,
A SBD . SAD 2 2a 3
Kẻ AH BD , AK SH d  ,
A SBD  AK . A . B AD .2 a a 3 2a 39 2 2 BD
AB AD a 13  AH    . BD a 13 13 2a 39 a 3. . SA AH 2a 51 13  AK    . 2 2 2 17 SA AH    a 2 2a 39 3    13   a
Vậy d C SBD  d A SBD 2 51 , ,  . 17
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hình chóp S.ABCD có đáy
ABCD là hình vuông cạnh a . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc
với đáy. Tính khoảng cách giữa hai đường thẳng AB và S . D a 21 a 3 a 21 a 7 A. . B. . C. . D. . 7 7 3 3 Lời giải Chọn A S K B C H M A D
Ta có hình chiếu H của S lên mp  ABCD là trung điểm của cạnh A . B
AB // SCD nên d(A ;
B SC)  d A ,
B SCD  d H,SCD
Từ H kẻ HM CD CD  SHM   SCD  SHM
Kẻ HK SM d H,SCD  HK. 1 1 1
Trong tam giác vuông SHM có:   . 2 2 2 HK SH HM
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 a 3
SH là đường cao trong tam giác đều cạnh a , nên SH
; M là trung điểm của CD nên 2 a 21
HM a HK  . 7
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hình hộp chữ nhật ABC .
D A B C D có ba kích 1 1 1 1
thước AB a , AD  2a , AA  3a . Khoảng cách từ A đến mặt phẳng  A BD bằng bao nhiêu? 1  1 7 6 5 A. a . B. a . C. a . D. a . 6 7 7 Lời giải Chọn C BD AH
Kẻ AH BD tại H. Ta có: 
BD  ( AA H ) 1
BD AA (do AA  ( ABCD))  1 1  AK A H
Kẻ AK A H tại K. Ta có: 1 
AK  ( A BD) 1 1
AK BD (do BD  ( AA H ))  1 Do đó: d  ,
A ( A BD)  AK 1  1 1 1 1 1 1 Ta có:   mà   2 2 2 AK AH AA 2 2 2 AH AB AD 1 1 1 1 1 1 1 1 49         2 2 2 2 2 2 2 2 AK AB AD AA a 4a 9a 36a 1 6 6 Vậy AK a hay d  , A ( A BD)  a . 1  7 7
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hình lăng trụ đứng ABC.AB C   có đáy ABC a
là tam giác đều cạnh a , AA  2a . Gọi M là điểm trên cạnh A B
  , AM  . Khoảng cách từ 3
M đến mặt phẳng  AB C   bằng? 4 57a 2 57a 57a 57a A. . B. . C. . D. . 57 57 19 57 Lời giải Chọn A
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
dM;B AC   IM B M  2 Ta có:    ( BI
M đồng dạng AIB ) d IB BA 3 B ;B AC  
Kẻ BN AC và BH B N  . BN AC
AC   B BN
  AC BH BB  AC  BH AC
BH   B AC    dBH . BH B N  B ;B AC   1 1 1 1 1 19 2 57a Xét BB
N vuông tại B có:       BH  . 2 2 2 2 2 2 BH B BBN 4a 3a 12a 19 4 4 57a Vậy d  . M ;B AC   57
Câu 15. (Chuyên Lê Hồng Phong - TPHCM - 2021) Hình hộp ABC . D A BCD
  có AB AA  AD a    và A AB
AAD BAD  60 . Tính c s
« in của góc giữa đường thẳng CD và mặt phẳng  A AD : 3 3 3 2 3 A. . B. . C. . D. . 3 2 4 3 Lời giải Chọn A
Gọi I là trung điểm DD ; G là trọng tâm tam giác A DD
 ; H đối xứng với G qua I
Từ gt  Các tam giác AD D  và CD D
 là các tam giác đều  A I
  DD ; CI DD
DD  CIA  DD  CH  
      
    4   4 1 
Mà CH .AD  CA  AH .AD CA  AI .AD CA  .   
AD AD .AD 3 3 2                1 1  1 2 1   AB AD
AA .AD   . AB AD AD AA .AD    3 3  3 3 1 1 2 2 2
 a cos 60  a a cos 60  0 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489AD CH
Do đó CH   AAD  D H
là hình chiếu của CD trên  AAD
 CD  AAD
  CDHD  ; ; a 3
Lại có: CD  a ; D H   D G   ; tam giác CD H  vuông tại H 3 HD 
CD  AAD   3 cos ;  cos CD H    . CD 3
Câu 16. (Chuyên KHTN - 2021) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 3 ,
SA   ABCD và SA a 2 . Tính góc giữa SC và  ABCD . A. 90 . B. 45. C. 60. D. 30 . Lời giải Chọn D
 Ta có AC là hình chiếu của SC trên mặt phẳng  ABCD nên góc giữa SC và mặt phẳng
ABCD là SC AC  ;  SCA
ABCD là hình vuông cạnh a 3 nên AC a 6 . SA a 2 1  Xét S
AC vuông tại A , ta có: tan SAC    AC a 6 3
 Suy ra SAC  30
 Vậy góc giữa SC và mặt phẳng  ABCD bằng 30.
Câu 17. (Chuyên KHTN - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a 2 . Cạnh
bên SA vuông góc với đáy. Góc giữa SC và mặt đáy bằng 45 . Gọi E là trung điểm của BC .
Tính khoảng cách giữa hai đường thẳng DE và SC . 2a 19 a 10 a 10 2a 19 A. . B. . C. . D. . 19 19 5 5 Lời giải Chọn A
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 S K B A F E I D C
 Ta có ABCD là hình vuông cạnh a 2 nên AC  2a . Góc giữa SC và đáy là 
SCA  45  SA AC  2a . IA DA
 Gọi I AC DE , có 
 2 , gọi K là điểm trên SA sao cho IC CE KA IA 2 4a IK //SC     AK
và SC//  DKI  . SA CA 3 3 1 1
Do đó d AC, DE  d C, DKI   d  ,
A DKI  ( do IC IA ). 2 2 1
 Gọi F DE AB , do BE//AD và BE
AD nên B là trung điểm của AF . 2
Đặt h d  ,
A DKF  , do ADKF là tam diện vuông tại A nên 1 1 1 1 1 1 1 19 4 19a         h  . 2 2 2 2 2 2 2 2 h AK AD AF  4a 2a 8a 16a  19    3  2 19a
Vậy d SC, DE   . 19
Câu 18. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương ABC . D AB CD
  . Số đo của góc giữa hai
mặt phẳng  BAC  và  DA C   bằng A. 60 . B. 30 . C. 45 . D. 90 . Lời giải Chọn A Do ABC . D AB CD
  là hình lập phương nên AD  CDD C
  ; CD   ADD A    CD A D  ; A D    CD
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489
Gọi I là trung điểm của AD D I   A D
Mà CD   ADD A
   CD D I Suy ra D I    A DC
Khi đó hình chiếu của tam giác A DC
 trên mặt phẳng  DA C
  là tam giác A IC SS
.cos ( là góc giữa hai mặt phẳng  BAC và  DA C   ) A ICA  D C  1 a 2 AI.CD .a S 1 AIC 2 2  cos      . S 1    a a A D C . 2 2 .A D  .D C  2    60 .
Câu 19. (Chuyên Quốc Học Huế - 2021) Cho hình lăng trụ tam giác ABC.A' B 'C ' có mặt bên ABB ' A'  10
là hình thoi cạnh a, AAB  120 và A 'C BC a 3, AC
a . Tính khoảng cách giữa hai 2 đường thẳng A B  và AC 10 10 3 10 3 10 A. a B. a C. a D. a 20 10 20 10 Lời giải Chọn C
Ta có: A'C BC a 3  A
 ' BC cân tại C và A' B  2 A' I  2A' Asin 60  a 3 Suy ra A
 ' BC đều, mặt khác ta lại thấy 2 2 2
AC AI IC nên suy ra AIIC , mà AI A ' B nên
suy ra AI  A'CB   A' BC    ABB ' A' và A' B   AIC   A' BAC
Khi ta kẻ IEAC, E AC thì đoạn IE chính là đoạn vuông góc chung của hai đường thẳng A B  và AC 2 2 A' B 3a 3a AB ' a Ta có: 2 2 CI BC   3a   ; AI   ; 4 4 2 2 2 . CI IA 3a 3 10
Suy ra d A' ;
B AC   IE    a AC 2 10 20
Câu 20. (Chuyên Quang Trung - Bình Phước - 2021) Cho hình chóp S.ABCD đáy ABCD là hình thoi cạnh a , góc 
BAD  60 , SA   ABCD , SC ABCD  ,
 45 . Gọi I là trung điểm SC . Tính
khoảng cách từ I đến mặt phẳng SBD . a 15 a 15 2a 15 a 15 A. . B. . C. . D. . 10 5 5 15 Lời giải Chọn A
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
 Gọi O là giáo điểm của AC và BD .  Ta có : B
AD đều cạnh a AC a 3 .
 Vì SA   ABCD  AC là hình chiếu của SC lên
ABCD  SC ABCD   SC A C   , ,
SCA  45  SAC vuông cân tại
A S A AC a 3 .
 Ta có: ABCD là hình thoi nên AC BD (1).
 Vì SA   ABCD  SA BD (2).
 Từ (1) và (2) suy ra: BD  SAC mà BD  SBD nên SBD  SAC .
 Trong tam giác SAC kẻ CH SO CH  SBD . 1 1 . . SA AC . S Sa 3 2 2 a 15  Ta có: SOC SAC  2 2 CH      . 2 2 2 2 2 SO 5 SA OA SA OAa  2 3 3a    2   1 a 15
 Vậy d I;SBD  d C;SBD  . 2 10
Câu 21. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình chữ
nhật AB a, AD  2 ;
a SA vuông góc với đáy ABCD , SC hợp với đáy một góc  và 10 tan  
. Tính khoảng cách từ điểm B đến mặt phẳng  SCD. 5 a 2a a 3 2a 3 A. B. C. D. 3 3 3 3 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 SA 10 10 Theo bài ra ta có: 2 2
AC a  (2a)  a 5 ; tan    SA ACa 2 AC 5 5
Vì AB//CD AB// SCD do đó d B,SCD  d  ,
A SCD
Từ A hạ đường vuông góc xuống SD AH SD Vì : 
AH   SCD nên AH d  , A SCD AH   DC 1 1 1 1 1 3 2a 3 Ta có:      Suy ra AH  . 2 2 2 2 2 2 AH SA AD 2a 4a 4a 3
Câu 22. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hình chóp S.ABCD có đáy là hình vuông cạnh
a , SD a 3 . Mặt bên SAB là tam giác cân và nằm trong mặt phẳng vuông góc với đáy. Gọi
H là trung điểm của AB , K là trung điểm của AD . Khoảng cách giữa hai đường thẳng SD và HK bằng a 105 a 105 a 105 a 105 A. . B. . C. . D. . 5 20 30 10 Lời giải S J A K D O H I B C Chọn C
(SAB)  ( ABCD) 
AB  (SAB)  ( ABCD)  SH  ( ABCD).
SH  (SAB), SH AB  HK / / BD
HK / /(SBD)  d (HK , SD)  d (HK , (SBD))  d (H , (SBD)). BD  (SBD) 
Trong ( ABCD) , gọi I là trung điểm của BO . BO HI Ta có: 
BO  (SHI )  (SBD)  (SHI ) BO SH  HJ SI
Trong (SHI ) , dựng 
. Từ đó suy ra HJ  (SBD)  HJ d (H , (SBD)) J SI  2 2 2 2 2 2 2 2 2 7a 2  AO a
SH SD HD SD  (HA AD )  , HI   .   4  2  8 1 1 1 a 105    HJ
d (HK, SD). 2 2 2 SH HI HJ 30 Câu 23. (Chuyên ĐHSP Hà Nội - 2021) Cho hình chóp S.ABC có
SA  12cm, AB  5 , cm AC  9 , cm SB  13 ,
cm SC  15cm và BC  10cm . Tan của góc giữa hai
mặt phẳng (SBC) và ( ABC) bằng
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 14 10 14 4 12 A. . B. . C. . D. . 10 14 3 5 Lời giải Chọn B S C A H B Do 2 2 2
12  5  13 nên SA AB và 2 2 2
12  9  15 nên SA AC Suy ra SA  ( ABC) . .
Từ A kẻ AH BC . Suy ra SH BC và góc giữa hai mặt phẳng (SBC) và ( ABC) là SHA 1
Xét tam giác ABC, có p  (5  9 10)  12 và S
 12(12  5)(12  9)(12 10)  6 14 ; 2 ABC 2S 12 14 SA 6 14 10 14  AH ABC  và tan SHA   12 :  . BC 10 AH 5 14
Câu 24. (Chuyên ĐH Vinh - Nghệ An - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác vuông
cân, AB BC  2a . Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với  ABC ,
SA  3a . Góc giữa hai mặt phẳng SAB và  SAC  bằng A. 0 60 . B. 0 30 . C. 0 45 . D. 0 90 . Lời giải Chọn A S A H C B
Gọi H là trung điểm của AC . Vì tam giác ABC vuông cân, có AB BC  2a nên ABC là tam
giác vuông cân tại B . Suy ra BH AC .
Vì tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với  ABC . Suy ra SH   ABC   SH BH .
Suy ra BH  SAC  . Suy ra tam giác SAH là hình chiếu của tam giác SAB trên mặt phẳng SAC .
Gọi  là góc giữa hai mặt phẳng SAB và SAC  .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 1
Ta có: AC  2a 2 ; BH AH AC a 2 ; 2 2 2 2 1 a 2
SH SA HA a 2 2
SB SH BH a 3  SSH .HA  ; SAH 2 2 1
Gọi p là nửa chu vi của tam giác ABC , ta có p
SA AB SB  a a 3 . 2 Suy ra Sp     . 
p SA p SB p AB 2 a 2 SAB 2 a 2 S 1 Ta có: SAH 2 cos     . Suy ra 0   60 . 2 Sa SAB 2 2
Câu 25. (Sở Yên Bái - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , hình chiếu
vuông góc của S lên mặt phẳng ( ABCD) là trung điểm của AD, góc giữa đường thẳng SB và
mặt đáy bằng 60o . Gọi M là trung điểm của DC . Khoảng cách giữa hai đường thẳng SA và BM là a 285 a 285 3a 285 2a 285 A. . B. . C. . D. . 9 19 19 19 Lời giải Chọn B S J A B I H N D M C
Vẽ hình bình hành ABMN . Ta có MB / / AN
MB / / SAN   d M ;
B SA  d M ;
B SAN   d M ;SAN   2d  ;
D SAN   4d H;SAN .
Gọi I là hình chiếu vuông góc của H lên AN , J là hình chiếu vuông góc của H lên SI .
Khi đó HJ d H;SAN  .
Vì H là hình chiếu vuông góc của S lên  ABCD nên      ;   60 . o SB ABCD SBH
Xét tam giác SHB vuông tại H : o 2 2 o a 15 SH  . HB tan 60 
AH AB tan 60  . 2 a a . IH AH DN.AH a 5
Vì AIH và A
DN đồng dạng nên 2 2   IH    . DN AN AN 2 10 a aa 4 1 1 1 a 285
Xét tam giác SHI vuông tại H:    HJ  2 2 2 HJ IH SH 76
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 a 285
d MB; SA  . 19
Câu 26. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp S.ABC có đáy là tam giác đều, tam giác SAB SA a
vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy, biết 6.
Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng 3 7a 6 7a 7a A. . B. 7a . C. . D. . 7 7 2 Lời giải Chọn C S K C A H M N B
 Kẻ SH AB SH ABC
( H là trung điềm AB ). Suy ra ( ) .  Có 2 2 2 2
AB SA SB  2SA AB SA 2  a 12  2a 3.  Và d( ,
A (SBC))  2d (H , (SBC))
 Từ H kẻ HN BC ( HN / /AM với M là trung điểm BC ) và kẻ HK SN .
 Ta có HN BC và SH BC nên BC  SHN  , suy ra HK BC .
 Mặt khác HK BC và HK SN nên HK  SBC , suy ra d ( ,
A (SBC))  2d (H , (SBC))  2HK . 1 1 1 AB 3 3a  Có SH
AB a 3 ; HN AM  .  và 2 2 2 2 2 1 1 1 1 4 7 3a 6a 6a 7       HK  . Do đó d ( , A (SBC))   . 2 2 2 2 2 2 HK SH HN 3a 9a 9a 7 7 7
Câu 27. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hình chóp S.ABC có S ,
A SB, SC đôi một vuông
góc nhau và SA a; SB  2 ; a SC  3 .
a Gọi M , N, P lần lượt là trung điểm của AB, BC,CA .
Khoảng cách từ điểm M đến mặt phẳng SNP bằng 5a 6a a 15 a 13 A. . B. . C. . D. . 7 7 2 2 Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
NGUYỄN BẢO VƯƠNG - 0946798489 A P M S C N B 1 2 1 1 1 a Vì SS nên VV  . . . SA S . B SC  . MNP 4 ABC S.MNP S . 4 ABC 4 6 4 1 a 13 1 a 10 1 a 5 Mặt khác: SN BC  ; SP AC  và NP AB  . Do đó 2 2 2 2 2 2 7a Sp p a p b p c  . MNP     8 2 1 3V a 7a 6a Từ đó V  .S .d M SNPd M SNP    . SMNP MNP  ,   ,  SMNP 3. : 3 S 4 8 7 MNP
Câu 28. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình chóp S.ABC có đáy ABC là tam giác
vuông cân tại A , BC a 2 và SB a . Hình chiếu vuông góc của S lên mặt phẳng  ABC
trùng với trung điểm M của BC . Góc giữa đường thẳng SA và mặt phẳng  ABC  bằng A. 0 30 . B. 0 60 . C. 0 45 . D. 0 75 . Lời giải Chọn C BC a 2 Ta có: AB
C vuông cân tại A nên AB AC a và AM   . 2 2 2  a 2  a 2 2 2 2 Xét SBM có SM
SB BM a      . 2  2  
Góc giữa đường thẳng SA và mặt phẳng  ABC  là góc  SAM . a 2 SM Xét SAM có  2  0 tan SAM    1  SAM  45 . AM a 2 2
Vậy góc giữa đường thẳng SA và mặt phẳng  ABC  là 0 45 .
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 29. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hình hộp ABC .
D A' B 'C ' D ' có tất cả các cạnh
đều bằng a và    0
BAA'  DAA'  BAD  60 . Gọi G là trọng tâm của tam giác AB 'C . Khoảng
cách từ G đến mặt phẳng  DA'C ' bằng a 22 4a 11 2a 11 a 22 A. . B. . C. . D. . 66 11 11 11 Lời giải Chọn D A D E B C F G D' A' B' C'
Do AB AA '  AD a và    0
BAA '  DAA '  BAD  60 nên ABDA' là tứ diện đều cạnh a 3 a 2 Suy ra V  . Gọi E, F AB . ABDA'
lần lượt là trung điểm của AC và ' 12 3 1 a 2 Ta có VV  .
AB 'C / / DA'C ' nên ABEF ABDA' Mặt khác do     4 48 d  ;
G DA'C '  d A'; AB 'C  d  ;
B AB 'C  d  ;
B AEF  . 2 a 3 a a 11
Xét tam giác AEF có AE AF  ; EF   S  . 2 2 AEF 16 3 a 2 3. 1 3V a 22 Mà VS d B AEFd B AEF    ABEF AEF       ABEF 48 . . ; ; . 2 3 S a AEF 11 11 16
Câu 30. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hình chóp S.ABCD có đáy ABCD có đáy là
hình vuông cạnh a , mặt bên SAD là tam giác đều và SAD   ABCD . Gọi M là trung điểm
cạnh đáy AB . Khoảng cách giữa các đường thẳng SA và CM là. a 3 a 2 a 5 a 3 A. . B. . C. . D. . 3 3 4 4 Lời giải Chọn D S A H D I M N K B C H D A I M N B C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
NGUYỄN BẢO VƯƠNG - 0946798489
 Mặt phẳng SAD là tam giác đều và vuông góc với đáy, gọi H là trung điểm AD a 3
SH AD SH   ABCD . Ta có SH
(đường cao tam giác đều SAD ) 2
Gọi N là trung điểm CD AN //CM CM //  SAN   dddCM ;SA
CM ;SAN 
M ;SAN 
Gọi I là hình chiếu của H lên AN ; K là hình chiếu của H lên SI . HI AN Ta có 
AN  SHI   AN HK . SH AN  HK SI Ta có 
HK   SAN   dHK HK AN
H ;SAN   1 1 1 1 1 5 a 5
Gọi E là hình chiếu của D lên AN ta có       DE  2 2 2 2 2 2 DE DA DN aa a  5    2  1 a 5  HI DE  2 10 1 1 1 1 1
Tam giác SHI vuông tại H có HK SI , ta có     2 2 2 2 2 HK HI SHa 5   3      10 2     a 3  HK  8
Dễ thấy trong hình vuông ABCD ta có 2.dddH ;AN  D;AN  M ;AN a 3 Vậy d  2.d  2HK
M ;SAN 
H ;SAN  4
Câu 31. (THPT Ba Đình - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD hình chữ nhật
AB a, AD
3 . Cạnh bên SA vuông góc với đáy và SA  2a . Tính khoảng cách d từ điểm C
đến mặt phẳng SBD : 2a 57 2a a 5 a 57 A. d  . B. d  . C. d  . D. d  . 19 5 2 19 Lời giải Chọn A S H A D I B C
Gọi I , H lần lượt là hình chiếu của A lên BD và SI .
Ta có: AH  SBD nên d A,SBD  AH .
Vì đáy ABCD là hình chữ nhật nên d C ,SBD  d A,SBD  AH .
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 1 1 1 1 4 a 3 Xét tam giác vuông ABD ta có:       AI  . 2 2 2 2 2 2 AI AB AD a 3a 3a 2 1 1 1 4 1 19 2a 57 Xét tam giác vuông SAI ta có:       AH  . 2 2 2 2 2 2 AH SA AI 3a 4a 12a 19
Câu 32. (THPT Quốc Oai - Hà Nội - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S
AB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi  là góc tạo bởi đường thẳng
BD với mặt phẳng SAD . Khi đó sin bằng 3 1 6 10 A. . B. . C. . D. . 2 2 4 4 Lời giải Chọn C z S A D O y B C x a 3
Gọi O là trung điểm của AB . Khi đó, ta có: SO AB và SO  . 2 
SAB   ABCD  Ta lại có: 
SAB   ABCD  AB SO   ABCD . SO AB
Chọn hệ trục tọa độ như hình vẽ, xem a là 1 đơn vị, khi đó ta có:  1   1   1   3 
O 0;0;0 , B ; 0; 0   , A  ; 0; 0   , D  ;1; 0   , S  0; 0;  .  2   2   2   2      1 3    1 3 
Ta có: SA    ;0; 
 , SD    ;1; 
. Suy ra vectơ pháp tuyến của SAD   2 2      2 2       3 1  là n   , SA SD   ; 0;   .    2 2    
Ta có: BD  1;1; 0 .   3   0  0 . n BD 2 6
Do đó, ta có: sin      . n . BD 3 1 4  0  . 11 0 4 4
Câu 33. (THPT Quốc Oai - Hà Nội - 2021) Cho hình lăng trụ tam giác đều ABC.A ' B 'C ' có tất cả các
cạnh có độ dài bằng 2 (tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng AC ' và A' B bằng
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
NGUYỄN BẢO VƯƠNG - 0946798489 1 3 2 3 A. . B. . C. . D. . 2 5 5 2 Lời giải Chọn C. BH AC
Gọi H là trung điểm AC  
BH   ACC ' A'. BH AA ' 
Dựng hình bình hành AC ' DA' và kẻ EH A ' . D
Gọi I EH AC,O AC ' A'C và kẻ HK BE. 2 2
d AC ', BA'  d AC ', BDA'  d I, BDA'  d H, BDA'  HK. 3 3 2 3 3 3 2 2 BH.HE 2 Ta có: BH   3, HE A'C
d AC ', BA'   . 2 2 2 4 2 3 BH HE 5 2
Vậy khoảng cách giữa hai đường thẳng AC ' và A' B bằng . 5
Câu 34. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho lăng trụ đứng ABC.AB C
  có đáy là tam giác
ABC vuông tại A có BC  2a , AB a 3 . Khoảng cách giữa hai đường thẳng AA và BC là a 21 a 3 a 5 a 7 A. . B. . C. . D. . 7 2 2 3 Lời giải Chọn B
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A' C' B' A C H B
Dựng AH BC, H BC .
AA   ABC   AA  AH .
AH   ABC 
d AA , BC   AH . Do ABC vuông tại A có AH BC nên 2 2 AB
BC AB a , AC.AB a 3.a a 3 AH    . BC 2a 2 a 3
Vậy d AA , BC   . 2
Câu 35. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho khối chóp S.ABCD có đáy là hình bình hành,   3,  4,  120o AB AD BAD
. Cạnh bên SA  2 3 vuông góc với đáy. Gọi M , N , P lần lượt là
trung điểm các cạnh S , A AD BC và
. Gọi  là góc giữa hai mặt phẳng (SAC) và (MNP). Chọn
khẳng định đúng trong các khẳng định sau đây.  3   1   1 2   2 3  A. sin    ;1 . B. sin  0; . C. sin    ; . D. sin    ; .      2         2  2 2   2 2   Lời giải Chọn A
Ta có MNP  (SCD) nên góc giữa (SAC),(MNP) bằng góc giữa (SAC), (SCD). d  , A (SCD) sin   . d  , A SC  * d  ,
A (SCD). Kẻ AH C . D Tính được S 3 3 AH 2 3.     ACD
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
NGUYỄN BẢO VƯƠNG - 0946798489 1 1 1 1    . 2 d  , A (SCD) 2 2 SA AH 6  d  ,
A (SCD)  6.
* Tính được AC  13 . 1 1 1 25 2 39     d  , A OM   . 2 d  , A SC  2 2 SA AC 156 5 5 26 Vậy sin   . 26 a 3
Câu 36. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho tứ diện ABCD có AB CD a, IJ  ( 2
I , J lần lượt là trung điểm của BC và AD ). Số đo góc giữa hai đường thẳng AB và CD là A. 0 60 . B. 0 30 . C. 0 45 . D. 0 120 . Lời giải Chọn A
Gọi K là trung điểm của BD . Khi đó IK song song với CD và JK song song với AB .  IKJ
Khi đó  AB,CD
  KI,KJ     . 0  1  80  IKJ  2 2 2 a a 3a   a  2 2 2
KI KJ IJ 1 Ta có 4 4 4 KI KJ   cos IKJ     . 2 2KI.KJ a a 2 2. . 2 2 Vậy  0 IKJ    AB CD  0 120 ,  60 .
Câu 37. (Trung Tâm Thanh Tường - 2021) Cho hình chóp
SABCD có đáy ABCD là hình vuông cạnh bằng 2a . Tam
giác SAB đều và nằm trong mặt phẳng vuông góc với đáy.
Gọi E, F lần lượt là trung điểm của S , A CD . Khoảng cách
giữa hai đường thẳng SD và EF bằng a 5 2a 3 a 5 a A. . B. . C. . D. . 10 7 5 2 Lời giải Chọn C
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 S E A D F H B C
Vì SAB   ABCD và tam giác SAB đều nên gọi H là trung điểm của AB .
Từ đó suy ra SH là đường cao của hình chóp S.ABCD .
Ghép hệ trục tọa độ Oxyz sao cho gốc tọa độ trùng với chân đường cao H .
  
Chiều dương Ox,Oy,Oz lần lược cùng chiều véc-tơ H ,
A HF, HS . Và chọn a  1.
Từ đó ta suy ra toại độ của các điểm:   H   A  D  F   S   1 3 0; 0; 0 , 1; 0; 0 , 1; 2; 0 , 0; 2; 0 , 0; 0; 3 , E  ;0;   2 2           Vậy ta có: FD   SD   1 3 1; 0; 0 , 1; 2; 3 , EF   ; 2; 
 SD, EF      3; 3;3  2 2   
   .
FD SD, EF    5a
Khoảng cách giữa SD và EF là: d SD, EF        5 SD, EF  
Câu 38. (Trung Tâm Thanh Tường -2021) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy 4a , cạnh
bên bằng 2 5a , gọi O là tâm của hình vuông ABCD . Khoảng cách từ O đến mặt phẳng SCD bằng a A. 3a . B. a . C. . D. 2a . 2 Lời giải Chọn A
Vì S.ABCD là hình chóp đều nên SO  (ABCD). Ta có: 2 2 2 2
AC  (4a)  (4a)  4 2a AO  2 2a SO SA AO  2 3 . a
Vẽ OE vuông góc CD , vẽ OH vuông góc với SE . OH SE  Ta có 
OH  SCD .
OH CD CD   SOE  . SO OE Tam giác SOE
vuông cân tại O , có OE  2a d  ;
O SCD  OH   a 3 . 2 2 SO OE
Câu 39. (Trung Tâm Thanh Tường -2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
bằng 2a , SA vuông góc với đáy, SA a 6 . Tính khoảng cách giữa hai đường thẳng SD và AC.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
NGUYỄN BẢO VƯƠNG - 0946798489 2 10a 6a A. . B. 2a . C. . D. 2a . 5 2 Lời giải Chọn C
 Gọi O là tâm hình vuông ABCD; M là trung điểm SB; trong mặt phẳng (SAB) kẻ MH / /SA
(H AB) ; trong mặt phẳng (ABCD) kẻ HK AC (K AC) ; trong mặt phẳng (MHK) kẻ
HP MK (P MK ) ; gọi I DH AC .
 Khi đó ta có: MH  (ABCD) ; HP  (MAC) . SD / /(MAC)  Ta có:   d  ;
SD AC   d  ;
SD (MAC)  d  ; D (MAC) . AC  (MAC)  d  ; D (MAC) DI   2  d  ;
D (MAC)  2d H;(MAC)  2HP
d H;(MAC) HI
 Xét tam giác MHK vuông tại H có: 1 1 1 1 1 8 a 6       HP  . 2 2 2 2 2 2 HP HM HK 3a 4  a 6   a 2      2 2     a 6  Suy ra d  ;
SD AC   2HP  . 2
Câu 40. (Trung Tâm Thanh Tường -2021) Cho hình tứ diện đều ABCD . Giá trị tan của góc giữa mặt bên và đáy bằng 2 6 A. . B. 2 . C. 2 2 . D. 2 . 3 Lời giải Chọn C
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
 Ta có:  ACD BCD  CD .  B
CD đều có M là trung điểm của CD BM CD (1). AH   BCD  
AH CD (2). CD   BCD 
 Từ (1) và (2) suy ra: CD   ABM   CD AM . CD BM   BCD  Khi đó: 
  ACD BCD   AM BM   , ,  AMH (do AMH vuông tại CD AM    ACD  H ).
 Giả sử tứ diện đều ABCD có cạnh bằng a . 1 a 3 a 3 a 3 2 2 3a 3a a 6  Ta có: HM  .  ; AM  ; 2 2 AH AM HM    . 3 2 6 2 4 36 3 a 6  AH 3  Vậy tan AMH    2 2 . HM a 3 6
Câu 41. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hình chóp S.ABCD có đáy ABCD là hình vuông
cạnh a ; SA a 2 và SA vuông góc với mặt đáy  ABCD . Gọi M ; N lần lượt là hình chiếu
vuông góc của đỉnh A lên các cạnh SB và SD . Khi đó góc giữa đường thẳng SB và mặt phẳng  AMN  bằng: A. 45 . B. 30 . C. 60 . D. 90 . Lời giải Chọn C
Gọi P SC   AMN  ; O AC BD MN ; AP ; SO đồng quy tại I SA BC Ta có: 
BC  SAB  BC AM AB BC
Mà AM SB nên AM  SBC   AM SC SA CD
CD  SAD  CD AN AD CD
Mà AN SD nên AN  SCD  AN SC
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
NGUYỄN BẢO VƯƠNG - 0946798489
Do đó SC   AMN   AP SC và PM là hình chiếu của SM trên mặt phẳng  AMN  hay
PM là hình chiếu của SB trên mặt phẳng  AMN
 SB AMN    SB PM    ; ;
SMP (do tam giác SMP vuông tại P )
Từ gt Tam giác SAC vuông cân tại A P là trung điểm SC
I là trọng tâm tam giác SAC Lại có: SAB S
AD SA SB và AM AN SAM SAN SM SN SM SI 2 2 2 2a 3    MN / /BD     2 2 SM SB SA AB SB SD SB SO 3 3 3 3 1 1 Mặt khác 2 2 SP SC
SA AC a 2 2 SP Do đó  3 sin SMP  
 SB AMN    ;  SMP  60 . SM 2
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • [NBV]-Chủ đề 8-HHKG-Mức độ nhận biết-câu hỏi
  • [NBV]-Chủ đề 8-HHKG-Mức độ nhận biết-đáp án
  • [NBV]-Chủ đề 8-HHKG-Mức độ thông hiểu-câu hỏi
  • [NBV]-Chủ đề 8-HHKG-Mức độ thông hiểu-đáp án
  • [NBV]-Chủ đề 8-HHKG-Mức độ vận dụng-câu hỏi
  • [NBV]-Chủ đề 8-HHKG-Mức độ vận dụng-đáp án