Tổng ôn tập TN THPT 2021 môn Toán: Số phức

Tổng ôn tập TN THPT 2021 môn Toán: Số phức được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

84 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ NHẬN BIẾT
Câu 1. (Sở Vĩnh Phúc - 2021) Tìm phần thực của số phức
2 3z i
A.
2
. B.
3
. C.
2
. D.
3
.
Câu 2. (Sở Lào Cai - 2021) Cho hai số phức
1
2z i và
2
1 2z i . Khi đó phần ảo của số phức
1 2
.z z
bằng:
A.
2
. B.
3i
. C.
3
. D.
2i
.
Câu 3. (Sở Lào Cai - 2021) Mô đun của số phức
2 3z i
bằng
A.
5
. B.
13
. C.
5
. D.
13
.
Câu 4. (Sở Hà Tĩnh - 2021) Cho hai số phức
1
3 2z i và
2
2z i . Số phức
1 2
z z bằng
A.
5 i
. B.
5 i
. C.
5 i
. D.
5 i
.
Câu 5. (Sở Hà Tĩnh - 2021) Số phức liên hợp của số phức
2 6z i
là
A.
2 6z i
. B.
2 6z i
. C.
2 6z i
. D.
2 6z i
.
Câu 6. (Sở Hà Tĩnh - 2021) Trên mặt phẳng, điểm
1;3M
là điểm biểu diễn số phức
z
. Phần thực
của
z
bằng
A.
1
. B.
3
. C.
3
. D.
1
.
Câu 7. (Sở Yên Bái - 2021) Phần ảo của số phức
12 18z i
là
A.
18
. B.
18
. C.
18i
. D.
12
.
Câu 8. (Sở Tuyên Quang - 2021) Tìm phần thực và phần ảo của số phức
3 2z i
.
A. Phần thực bằng
3
và phần ảo bằng
2i
.
B. Phần thực bằng
3
và phần ảo bằng
2
.
C. Phần thực bằng
3
và phần ảo bằng
2i
.
D. Phần thực bằng
3
và phần ảo bằng
2
.
Câu 9. (Sở Tuyên Quang - 2021) Điểm
M
trong hình vẽ dưới đây biểu thị cho số phức:
A.
2 3i
. B.
3 2i
. C.
2 3i
. D.
3 2i
.
Câu 10. (Sở Tuyên Quang - 2021) Tính môđun của số phức
4 3z i
.
A.
5z
. B.
7z
. C.
25z
. D.
7z
.
Câu 11. (Sở Tuyên Quang - 2021) Cho số phức
1 2 . z i
Tìm phần ảo của số phức
1
P
z
A.
2
. B.
2
3
. C.
2
. D.
2
3
.
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hai số phức
1 2
2 3 , 3 2z i z i . Tích
1 2
z z bằng
SỐ PHỨC
Chủ đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
5i
. B.
5i
. C.
6 6i
. D.
12 5i
Câu 13. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng
Oxy
điểm
1; 2M
biểu diễn cho số phức nào sau đây.
A.
1 2z i
. B.
1 2z i
C.
2z i
. D.
1 2z i
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức có điểm biểu diễn là
M
như hình vẽ.
Phần ảo của số phức
z
là
A.
3
. B.
3
. C.
2
. D.
2
.
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Môđun của số phức
2 i
là
A. 5 . B. 3 . C.
3
. D.
5
.
Câu 16. (Chuyên KHTN - 2021) Mô đun của số phức
3 2z i
bằng
A.
13
. B.
13
. C.
5
. D.
5
.
Câu 17. (Chuyên KHTN - 2021) Cho hai số phức
1
2 3z i và
2
2z i . Số phức
1 2 2
w z z z
có phần
thực bằng
A.
7.
B.
9.
C.
4.
D.
3.
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức có phần thực bằng
2
và phần ảo bằng
1
là
A.
2 .i
B.
1 2 .i
C.
2 .i
D.
1 2 .i
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai số phức
1
4 3z i và
2
7 5z i . Số
phức
2 1
z z z là
A.
11 8i
. B.
11 8i
. C.
11 8i
. D.
11 8i
.
Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Nghiệm phức có phần ảo dương của phương trình
2
2 5 0z z
là
A.
1 2i
. B.
1 2i
. C.
1 2i
. D.
1 2i
.
Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức
1 2 z i
. Điểm biểu diễn số phức
liên hợp của
z
trong mặt phẳng tọa độ
Oxy
là điểm
A. Q. B. N. C. P. D. M.
Câu 22. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức
z
thỏa mãn
1 0i z i
là
A.
1 1
2 2
z i
. B.
1 1
2 2
z i
. C.
1 1
2 2
z i
. D.
1 1
2 2
z i
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 23. (Chuyên Quốc Học Huế - 2021) Số phức liên hợp của số phức
3 5z i
là
A.
3 5z i
. B.
3 5z i
. C.
5 3z i
. D.
3 5z i
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Cho số phức
,z a bi a b
. Chọn phương
án đúng.
A. Phần ảo của số phức
z
là
b
. B. Phần ảo của số phức
z
là
bi
.
C. Phần thực của số phức
là
b
. D. Mô đun của số phức
z
là
2 2
a b
.
Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Gọi
1 2
,z z
là nghiệm của phương trình
2
2 2 0
z z
. Biết số phức
1
z
có phần ảo âm. Phần ảo của số phức
2
z
.
A.
1
. B.
1
. C.
i
. D.
1 i
.
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021)
7 3 9
i i
bằng
A.
16 2i
. B.
16 2i
. C.
2 4i
. D.
16 2i
.
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hai số phức
1 2
2 ; 3 2z i z i
. Trên mặt phẳng
tọa độ
Oxy
, điểm biểu diễn số phức
1 2
2
z z
có tọa độ là
A.
7;1
. B.
0;7
. C.
5;1
. D.
7;0
.
Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức
4 3z i
. Tìm phần thực và phần ảo của
số phức liên hợp của số phức
z
A. Phần thực bằng 4 và phần ảo bằng 3 B. Phần thực bằng
4
và phần ảo bằng
3i
C. Phần thực bằng
4
và phần ảo bằng
3i
D. Phần thực bằng 4 và phần ảo bằng
3
Câu 29. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Số phức liên hợp của số phức
4 5i
là
A.
4 5i
. B.
5 4i
. C.
4 5i
. D.
4 5i
.
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số thực
,x y
thỏa mãn
2 5 ,yi x i
trong đó
i
là đơn
vị ảo. Giá trị của
x
và
y
là
A.
2, 5.
x y
B.
2, 5 .x y i
C.
5, 2.
x y
D.
5 , 2.
x i y
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Số phức liên hợp của số phức
3 4z i
là
A.
3 4z i
. B.
3 4z i
. C.
3 4z i
. D.
3 4z i
.
Câu 32. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hai số phức
1
1z i
,
2
2 3z i
. Số phức
liên hợp của
1 2
z z z
là
A. . B. . C. . D. .
Câu 33. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hai số phức
1 2
2 2 ; 3 3z i z i
. Khi đó số
phức
1 2
z z
là
A.
1 i
B.
5 5i
C.
5i
D.
5 5i
Câu 34. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức
2 4z i
, mô đun của số phức
w 1z
bằng
A.
5
. B.
2 5 1
. C.
2 5
. D.
7
.
Câu 35. (THPT Nguyễn Huệ - Phú Yên - 2021) Số phức
z
thỏa mãn
3 1 4i z i
là
A.
7 11
10 10
i
. B.
7 11
10 10
i
. C.
7 11
10 10
i
. D.
7 11
10 10
i
.
Câu 36. (THPT Lương Thế Vinh - 2021) Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
2z 5 0
z
.
Giá trị của
2 2
1 2
z z
bằng
A. 10. B. 50. C. 5. D. 18.
Câu 37. (THPT Lương Thế Vinh - 2021) Số phức
2 4i i
bằng số phức nào dưới đây?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4 2i
. B.
4 2i
. C.
4 2i
. D.
4 2i
.
Câu 38. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Điểm nào trong hình vẽ bên dưới là điểm biểu diễn
số phức
3 4z i
,
A. Điểm
A
. B. Điểm
D
. C. Điểm
C
. D. Điểm
B
.
Câu 39. (THPT Đào Duy Từ - Hà Nội - 2021) Số phức liên hợp của
4 3i
là
A.
3 4i
. B.
4 3i
. C.
3 4i
. D.
4 3i
.
Câu 40. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
3 4z i
. Tìm phần thực
a
và phần ảo
b
của số phức
z
:
A.
3, 4a b
. B.
4, 3a b
. C.
4, 3a b
. D.
3, 4a b
.
Câu 41. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Phần ảo của số phức
3 2z i
là
A. 2. B.
2i
. C.
2i
. D.
2
.
Câu 42. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức
2z i
. Trong mặt phẳng tọa độ
Oxy
điểm biểu diễn hình học số phức liên hợp
z
có tọa độ là
A.
2;1
. B.
2; 1
. C.
1;2
. D.
1; 2
.
Câu 43. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hai số phức
1 2
1 3 ; 3 2z i z i . Số phức
1 2
2z z bằng
A.
4 i
B.
7 i
C.
5 4i
D.
10 2i
Câu 44. (THPT Chu Văn An - Thái Nguyên - 2021) Trong mặt phẳng phức
Oxy
, số phức
2 3z i
được biểu diễn bởii điểm nào sau đây?
A.
(3;2)Q
. B.
(2; 3)M
. C.
(2;3)N
. D.
( 3;2).P
Câu 45. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hai số phức
1
3z i và
2
1 2z i . Phần thực
của số phức
1 2
z z bằng
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 46. (THPT Ba Đình - Thanh Hóa - 2021) Cho số phức
5 8z i
, phần ảo của
z
là
A. 8. B.
8i
. C.
5
. D.
8
.
Câu 47. (THPT Ba Đình - Thanh Hóa - 2021) Tính môdun của số phức
3 4z i
.
A. 5. B. 3. C. 7. D. 7 .
Câu 48. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho số phức
4 3z i
. Tìm phần thực và phần ảo của số
phức liên hợp của số phức
z
A. Phần thực bằng 4 và phần ảo bằng 3 B. Phần thực bằng
4
và phần ảo bằng
3i
C. Phần thực bằng
4
và phần ảo bằng
3i
D. Phần thực bằng 4 và phần ảo bằng
3
Câu 49. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức
3 4z i
. Khẳng định nào sau đây là khẳng
định sai?
A. Số phức liên hợp của
z
là
3 4i
B. Điểm biểu diễn cuả
z
là
4;3M
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
C. Môđun của số phức
z
là
5
D. Số phức liên hợp của
z
là
3 4i
Câu 50. (THPT Quốc Oai - Hà Nội - 2021) Số nào trong các số phức sau là số thuần ảo?
A.
10 10 2i i
. B.
5 7 5 7
i i
.
C.
3 3
i i
. D.
7 7
i i
.
Câu 51. (THPT Quảng Xương 1-Thanh Hóa - 2021) Số phức liên hợp của số phức
3 12z i
là
A.
3 12z i
. B.
3 12z i
. C.
3 12z i
. D.
3 12z i
.
Câu 52. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức
1
2z i
và
2
1 3z i
. Phần thực
của số phức
1 2
z z
bằng
A.
1
. B.
3
. C.
4
. D.
2
.
Câu 53. (THPT Quảng Xương 1-Thanh Hóa - 2021) Trong mặt phẳng tọa độ, điểm
3; 1
A
biểu diễn
số phức nào dưới đây?
A.
1 3z i
. B.
1 3z i
. C.
3z i
. D.
3z i
.
Câu 54. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức
1
2 3z i
,
2
4 5z i
. Tính
1 2
z z z
A.
2 2z i
. B.
2 2z i
. C.
2 2z i
. D.
2 2z i
.
Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Số phức liên hợp của số phức
4 7z i
là
A.
4 7z i
. B.
4 7z i
. C.
4 7z i
. D.
4 7z i
.
Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức
12 5z i
. Mô đun của số phức
là:
A.
17
. B.
13
. C.
13
. D.
5
.
Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Số phức liên hợp
z
của số phức
1 2021z i
là
A.
1 2021z i
. B.
1 2021z i
. C.
2021z i
. D.
1 20211z i
.
Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tính môđun của số phức
3 4z i
A.
3
. B.
7
. C.
7
. D.
5
.
Câu 59. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức
1 2
2 3 , 4 5z i z i
. Số phức
1 1
z z z
là
A.
2 2z i
. B.
2 2z i
. C.
2 2z i
. D.
2 2z i
.
Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Số phức liên hợp của số phức
2 3z i
là.
A.
3 2z i
. B.
3 2z i
. C.
2 3z i
. D.
2 3z i
.
Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hai số phức
1
5 6z i
và
2
2 3z i
. Số phức
1 2
3 4z z
là.
A.
14 33i
. B.
236i
. C.
26 5i
. D.
7 30i
.
Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Cho số phức
z
được biểu diễn bởi điểm
1;3
M
trên mặt
phẳng tọa độ. Môđun của số phức
z
bằng
A.
10
. B.
2 2
. C.
10
. D.
8
.
Câu 63. (THPT Đồng Quan - Hà Nội - 2021) Số phức liên hợp của số phức
2 3z i
là:
A.
3 2z i
. B.
2 3z i
. C.
2 3z i
. D.
3 2z i
.
Câu 64. (THPT Lê Lợi - Thanh Hóa - 2021) Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng 3 và phần ảo bằng 4. B. Phần thực bằng 3 và phần ảo bằng
4i
.
C. Phần thực bằng 4 và phần ảo bằng
3i
. D. Phần thực bằng 4 và phần ảo bằng 3.
Câu 65. (THPT Lê Lợi - Thanh Hóa - 2021) Số phức liên hợp của số phức
3 2z i
?
A.
3 2z i
. B.
3 2z i
. C.
2 3z i
. D.
3 2z i
.
Câu 66. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hai số phức
1
5 7z i  và
2
2 3z i  . Tìm số phức
1 2
z z z 
A.
7 4z i
. B.
2 5z i
. C.
2 5z i
. D.
3 10z i
.
Câu 67. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Phần thực của số phức
3 1 4z i i
là
A.
13.
B.
1.
C.
13.
D.
1.
Câu 68. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìm số phức liên hợp của số phức
3 1z i i
A.
3z i
. B.
3z i
. C.
3z i
. D.
3z i
.
Câu 69. (Trung Tâm Thanh Tường - 2021) Cho hai số phức
1 2
1 2 , 2z i z i . Phần ảo của số phức
1 2
z z bằng
A. 3. B. 1. C.
i
. D.
3i
.
Câu 70. (Trung Tâm Thanh Tường - 2021) Cho số phức
1 2
2 3 , 1z i z i . Điểm nào sau đây là điểm
biểu diễn của số phức
1 2
?w z z
A. Điểm
1; 4Q
. B. Điểm
1; 4P
. C. Điểm
3; 2M
. D. Điểm
2; 3Q
.
Câu 71. (Trung Tâm Thanh Tường - 2021) Cho biết số phức liên hợp của số phức
z
là
1 3z i
. Số
phức
z
là
A.
3z i
. B.
1 3z i
. C.
3z i
. D.
1
1 3
z
i
.
Câu 72. (Trung Tâm Thanh Tường - 2021) Cho số phức
1 3z i
. Tìm phần thực của số phức
3w i z z
.
A.
0
. B. 3. C. 9. D. 6.
Câu 73. (Trung Tâm Thanh Tường -2021) Số phức liên hợp của số phức
2
2z i
là
A.
3 4z i
. B.
3 4z i
. C.
3 4z i
. D.
3 4z i
.
Câu 74. (Trung Tâm Thanh Tường -2021) Trong mặt phẳng tọa độ
Oxy
, cho điểm
M
như hình vẽ bên
là điểm biểu diễn số phức
z
Kết quả
2
1 z
bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
2
1
2 2z i
. B.
2
1
2z i
. C.
2
1
1z i
. D.
2
1
2z i
.
Câu 75. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho số phức
2
3z i
, khi
đó phần ảo của số phức
z
là
A
.
2
. B.
3
. C.
3
. D.
2
.
Câu 76. (THPT
Triệu Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức
1
2z i
c
ó tọa độ là:
A
.
1
;2
. B.
2
; 1
. C.
1
; 2
. D.
1
;2
.
Câu 77. (THPT
Triệu Sơn - Thanh Hóa - 2021) Gọi
1
2
,z
z
l
à hai nghiệm phức của phương trình
2
2
9 0
z
z
, khi
đó
1
2
z
z
bằ
ng
A.
18
. B.
3
. C.
9
. D.
6
.
Câu 78. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức
3
4z i
và
2
3w i
.
Số phức
2z
w
bằng
A.
1 7i
. B.
1 10i
. C.
7 2i
. D.
1 10i
.
Câu 79. (THPT
Trần Phú - Đà Nẵng - 2021) Tính môđun của số phức
z
biết
3
2 1 5z i i
A.
5
z
. B.
13
z
. C.
53
z
. D.
6
5
z
.
Câu 80. (THPT
Trần Phú - Đà Nẵng - 2021) Trên mặt phẳng tọa độ điểm biểu diễn số phức
1
4i
c
ó
tọa độ là
A
.
4
; 1
. B.
4
; 1
. C.
1
; 4
. D.
1
;4
.
Câu 81. (THPT
Trần Phú - Đà Nẵng - 2021) Cho hai số phức
1
1z
i
và
2
1
3z i
.
Phần thực của số
phức
1 2
.z
z
bằng
A
.
2
. B.
2
. C.
4
. D.
4
.
BẢNG ĐÁP ÁN
1.C
2.
C
3.
B
4.D
5.A
6.
D
7.
A
8.
D
9.C
10.A
11.D
12.D
13.D
14.B
15.A
16.
A
17.
D
18.
A
19.
C
20.D
21.C
22.C
23.D
24.A
25.A
26.B
27.
D
28.
A
29.
C
30.A
31.B
32.B
33.D
34.A
35.A
36.A
37.B
38.B
39.D
40.A
41.A
42.B
43.C
44.B
45.
B
46.
D
47.
A
48.
A
49.
B
50.
B
51.B
52.B
53.D
54.D
55.
B
56.C
57.
D
58.
D
59.
D
60.
C
61.D
62.C
63.B
64.A
65.D
66.A
67.B
68.C
69.B
70.C
71.B
72.A
73.B
74.B
75.
B
76.
D
77.
D
78.
D
79.
B
80.D
81.C
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ NHẬN BIẾT
Câu 1. (Sở Vĩnh Phúc - 2021) Tìm phần thực của số phức
2 3z i
A.
2
. B.
3
. C.
2
. D.
3
.
Lời giải
Chọn C
Câu 2. (Sở Lào Cai - 2021) Cho hai số phức
1
2z i và
2
1 2z i . Khi đó phần ảo của số phức
1 2
.z z
bằng:
A.
2
. B.
3i
. C.
3
. D.
2i
.
Lời giải
Chọn C
1 2
.z z
2 1 2i i
2
2 4 2 4 3i i i i
.
Khi đó phần ảo của số phức
1 2
.z z bằng
3.
Câu 3. (Sở Lào Cai - 2021) Mô đun của số phức
2 3z i
bằng
A.
5
. B. 13 . C. 5 . D.
13
.
Lời giải
Chọn B.
Ta có
2
2
2 3 13z
.
Câu 4. (Sở Hà Tĩnh - 2021) Cho hai số phức
1
3 2z i
và
2
2z i
. Số phức
1 2
z z
bằng
A.
5 i
. B.
5 i
. C.
5 i
. D.
5 i
.
Lời giải
Chọn D
Ta có :
1 2
5z z i .
Câu 5. (Sở Hà Tĩnh - 2021) Số phức liên hợp của số phức
2 6z i
là
A.
2 6z i
. B.
2 6z i
. C.
2 6z i
. D.
2 6z i
.
Lời giải
Chọn A
Số phức liên hợp của số phức
2 6z i
là
2 6z i
.
Câu 6. (Sở Hà Tĩnh - 2021) Trên mặt phẳng, điểm
1;3M
là điểm biểu diễn số phức
z
. Phần thực
của
z
bằng
A.
1
. B.
3
. C.
3
. D.
1
.
Lời giải
Chọn D
1;3M
là điểm biểu diễn số phức
1 3z i
. Phần thực của
z
bằng
1
.
Câu 7. (Sở Yên Bái - 2021) Phần ảo của số phức
12 18z i
là
A.
18
. B.
18
. C.
18i
. D.
12
.
Lời giải
Chọn A
Phần ảo của số phức
12 18z i
là
18
.
Câu 8. (Sở Tuyên Quang - 2021) Tìm phần thực và phần ảo của số phức
3 2z i
.
A. Phần thực bằng
3
và phần ảo bằng
2i
.
B. Phần thực bằng
3
và phần ảo bằng
2
.
SỐ PHỨC
Chủ đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C. Phần thực bằng
3
và phần ảo bằng
2i
.
D. Phần thực bằng
3
và phần ảo bằng
2
.
Lời giải
Chọn D
Ta có số phức
3 2z i
có phần thực
3a
và phần ảo
2b
.
Câu 9. (Sở Tuyên Quang - 2021) Điểm
M
trong hình vẽ dưới đây biểu thị cho số phức:
A.
2 3i
. B.
3 2i
. C.
2 3i
. D.
3 2i
.
Lời giải
Chọn C
Điểm
M
trong hình vẽ dưới đây biểu thị cho số phức
2 3z i
.
Câu 10. (Sở Tuyên Quang - 2021) Tính môđun của số phức
4 3z i
.
A.
5z
. B. 7z . C.
25z
. D.
7z
.
Lời giải
Chọn A
Ta có
2
2
4 3 5z
.
Câu 11. (Sở Tuyên Quang - 2021) Cho số phức
1 2 . z i
Tìm phần ảo của số phức
1
P
z
A.
2
. B.
2
3
. C.
2
. D.
2
3
.
Lời giải
Chọn D
Ta có
1 1 1 2
3 3
1 2
P i
z
i
. Nên phần ảo của số phức
1
P
z
là
2
3
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hai số phức
1 2
2 3 , 3 2z i z i . Tích
1 2
z z bằng
A.
5i
. B.
5i
. C.
6 6i
. D.
12 5i
Lời giải
Chọn D
1 2
2
2 3 3 2 6 4 9 6 12 5i i i iz iz i
.
Câu 13. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng
Oxy
điểm
1; 2M
biểu diễn cho số phức nào sau đây.
A.
1 2z i
. B.
1 2z i
C.
2z i
. D.
1 2z i
Lời giải
Chọn D
Trong mặt phẳng
Oxy
điểm
1; 2M
biểu diễn cho số phức
1 2z i
.
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức có điểm biểu diễn là
M
như hình vẽ.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Phần ảo của số phức
z
là
A.
3
. B.
3
. C.
2
. D.
2
.
Lời giải
Chọn B
2;3 2 3i 2 3iM z z .
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Môđun của số phức
2 i
là
A.
5
. B.
3
. C.
3
. D.
5
.
Lời giải
Chọn A
Ta có mô đun của số phức
z z bi
là
2 2
z a b
Do đó
2 2
2 2 1 5i
.
Câu 16. (Chuyên KHTN - 2021) Mô đun của số phức
3 2z i
bằng
A.
13
. B.
13
. C.
5
. D.
5
.
Lời giải
Chọn A
Ta có:
2 2
3 2 3 2 13z i
.
Câu 17. (Chuyên KHTN - 2021) Cho hai số phức
1
2 3z i và
2
2z i . Số phức
1 2 2
w z z z
có phần
thực bằng
A.
7.
B.
9.
C.
4.
D.
3.
Lời giải
Chọn D
Ta có
1 2 2
2 3 2 2 3 7w z z z i i i i
Suy ra
w
có phần thực bằng
3.
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức có phần thực bằng
2
và phần ảo bằng
1
là
A.
2 .i
B.
1 2 .i
C.
2 .i
D.
1 2 .i
Lời giải
Chọn A
Số phức có phần thực bằng
2
và phần ảo bằng
1
là
2z i
.
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai số phức
1
4 3z i
và
2
7 5z i
. Số
phức
2 1
z z z
là
A.
11 8i
. B.
11 8i
. C.
11 8i
. D.
11 8i
.
Lời giải
Chọn C
Ta có:
2 1
7 5 4 3 11 8z z z i i i
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Nghiệm phức có phần ảo dương của phương trình
2
2 5 0z z
là
A.
1 2i
. B.
1 2i
. C.
1 2i
. D.
1 2i
.
Lời giải
Chọn D
Ta có:
2
1 2
2 5 0
1 2
z i
z z
z i
Theo yêu cầu bài toán suy ra nghiệm phức cần tìm là
1 2z i
.
Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức
1 2 z i
. Điểm biểu diễn số phức
liên hợp của
z
trong mặt phẳng tọa độ
Oxy
là điểm
A. Q. B. N. C. P. D. M.
Lời giải
Chọn C
Ta có: số phức liên hợp của số phức
1 2z i
là số phức
1 2z i
.
Do đó, điểm biểu diễn của
z
là
1; 2P .
Câu 22. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức
z
thỏa mãn
1 0i z i
là
A.
1 1
2 2
z i
. B.
1 1
2 2
z i
. C.
1 1
2 2
z i
. D.
1 1
2 2
z i
.
Lời giải
Chọn C
Số phức
1 0i z i
1 1
1 2 2
i
z i
i
.
Câu 23. (Chuyên Quốc Học Huế - 2021) Số phức liên hợp của số phức
3 5z i
là
A.
3 5z i
. B.
3 5z i
. C.
5 3z i
. D.
3 5z i
Lời giải
Chọn D
Ta có
3 5 3 5z i z i
.
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Cho số phức
,z a bi a b
. Chọn phương
án đúng.
A. Phần ảo của số phức
z
là
b
. B. Phần ảo của số phức
z
là
bi
.
C. Phần thực của số phức
z
là
b
. D. Mô đun của số phức
z
là
2 2
a b
.
Lời giải
Chọn A
Cho số phức
( , )z a bi a b
, ta có:
Phần thực của số phức
z
bằng
a
.
Phần ảo của số phức
z
bằng
b
.
Mô đun của số phức
z
bằng
2 2
z a b
.
Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Gọi
1 2
,z z là nghiệm của phương trình
2
2 2 0z z
. Biết số phức
1
z có phần ảo âm. Phần ảo của số phức
2
z .
A.
1
. B.
1
. C.
i
. D.
1 i
.
Lời giải
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Chọn A
Ta có :
2
1
2 2 0
1
z i
z z
z i
Vì số phức
1
z
có phần ảo âm nên
1
1z i
và
2
1z i
.
Phần ảo của số phức
2
z
bằng
1
.
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021)
7 3 9
i i
bằng
A.
16 2i
. B.
16 2i
. C.
2 4i
. D.
16 2i
.
Lời giải
Chọn B
Ta có
7 3 9 7 3 9 16 2i i i i i
.
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hai số phức
1 2
2 ; 3 2z i z i
. Trên mặt phẳng
tọa độ
Oxy
, điểm biểu diễn số phức
1 2
2
z z
có tọa độ là
A.
7;1
. B.
0;7
. C.
5;1
. D.
7;0
.
Lời giải
Chọn D
Số phức
1 2
2 2 2 3 2 4 2 3 2 7z z i i i i
.
Như vậy điểm biểu diễn số phức
1 2
2
z z
là
7;0
.
Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức
4 3z i
. Tìm phần thực và phần ảo của
số phức liên hợp của số phức
z
A. Phần thực bằng 4 và phần ảo bằng 3 B. Phần thực bằng
4
và phần ảo bằng
3i
C. Phần thực bằng
4
và phần ảo bằng
3i
D. Phần thực bằng 4 và phần ảo bằng
3
Lời giải
Chọn A
Số phức liên hợp của số phức
4 3z i
là
4 3z i
Phần thực bằng 4 và phần ảo bằng 3
Câu 29. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Số phức liên hợp của số phức
4 5i
là
A.
4 5i
. B.
5 4i
. C.
4 5i
. D.
4 5i
.
Lời giải
Chọn C
Số phức liên hợp của số phức
4 5i
là
4 5i
.
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số thực
,x y
thỏa mãn
2 5 ,yi x i
trong đó
i
là đơn
vị ảo. Giá trị của
x
và
y
là
A.
2, 5.
x y
B.
2, 5 .x y i
C.
5, 2.
x y
D.
5 , 2.
x i y
Lời giải
Chọn A
Giá trị của
x
và
y
là
2, 5.
x y
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Số phức liên hợp của số phức
3 4z i
là
A.
3 4z i
. B.
3 4z i
. C.
3 4z i
. D.
3 4z i
.
Lời giải
Chọn B
Ta có số phức liên hợp của số phức
3 4z i
là
3 4z i
.
Câu 32. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hai số phức , . Số phức
liên hợp của là
A. . B. . C. . D. .
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Ta có: .
Vậy số phức liên hợp của là .
Câu 33. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hai số phức
1 2
2 2 ; 3 3z i z i
. Khi đó số
phức
1 2
z z
là
A.
1 i
B.
5 5i
C.
5i
D.
5 5i
Lời giải
Chọn D
1 2 1 2
2 2 ; 3 3 2 2 3 3 5 5z i z i z z i i i
.
Câu 34. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức
2 4z i
, mô đun của số phức
w 1z
bằng
A.
5
. B.
2 5 1
. C.
2 5
. D.
7
.
Lời giải
Chọn A
Ta có
w 1 3 4z i
.
Nên
3 4 5
i
.
Câu 35. (THPT Nguyễn Huệ - Phú Yên - 2021) Số phức
thỏa mãn
3 1 4i z i
là
A.
7 11
10 10
i
. B.
7 11
10 10
i
. C.
7 11
10 10
i
. D.
7 11
10 10
i
.
Lời giải
Chọn A
Ta có
1 4 7 11 7 11
3 1 4
3 10 10 10 10
i
i z i z i z i
i
.
Câu 36. (THPT Lương Thế Vinh - 2021) Gọi
1 2
,z z
là hai nghiệm phức của phương trình
2
2z 5 0
z
.
Giá trị của
2 2
1 2
z z
bằng
A. 10. B. 50. C. 5. D. 18.
Lời giải
Chọn A
Ta có
2 2
2
1 2 1 2
2z 5 0 1 2 ; 1 2 5 5 10
z z i z i z z
.
Câu 37. (THPT Lương Thế Vinh - 2021) Số phức
2 4i i
bằng số phức nào dưới đây?
A.
4 2i
. B.
4 2i
. C.
4 2i
. D.
4 2i
.
Lời giải
Chọn B
Ta có :
2
2 4 2 4 2 4 4 2i i i i i i
.
Câu 38. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Điểm nào trong hình vẽ bên dưới là điểm biểu diễn
số phức
3 4z i
,
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A. Điểm
A
. B. Điểm
D
. C. Điểm
C
. D. Điểm
B
.
Lời giải
Chọn B
Điểm biểu diễn số phức
3 4z i
là
3; 4D
Câu 39. (THPT Đào Duy Từ - Hà Nội - 2021) Số phức liên hợp của
4 3i
là
A.
3 4i
. B.
4 3i
. C.
3 4i
. D.
4 3i
.
Lời giải
Chọn D
Câu 40. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
3 4z i
. Tìm phần thực
a
và phần ảo
b
của số phức
z
:
A.
3, 4a b
. B.
4, 3a b
. C.
4, 3a b
. D.
3, 4a b
.
Lời giải
Chọn A
Câu 41. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Phần ảo của số phức
3 2z i
là
A. 2. B.
2i
. C.
2i
. D.
2
.
Lời giải
Chọn A
Phần ảo của số phức
3 2z i
là 2.
Câu 42. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức
2z i
. Trong mặt phẳng tọa độ
Oxy
điểm biểu diễn hình học số phức liên hợp
z
có tọa độ là
A.
2;1
. B.
2; 1
. C.
1;2
. D.
1; 2
.
Lời giải
Chọn B
Số phức
2z i
2z i
. Do đó số phức
z
được biểu diễn bởi điểm
2; 1M
.
Câu 43. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hai số phức
1 2
1 3 ; 3 2z i z i
. Số phức
1 2
2z z
bằng
A.
4 i
B.
7 i
C.
5 4i
D.
10 2i
Lời giải
Chọn C
Ta có
1 2
2z 2(1 3 ) 3 2 5 4z i i i .
Câu 44. (THPT Chu Văn An - Thái Nguyên - 2021) Trong mặt phẳng phức
Oxy
, số phức
2 3z i
được biểu diễn bởii điểm nào sau đây?
A.
(3;2)Q
. B.
(2; 3)M
. C.
(2;3)N
. D.
( 3;2).P
Lời giải
Chọn B
Theo lý thuyết,
z a bi
thì sẽ được biểu diễn bởi điểm có tọa độ
( , )a b
.Vậy chọn B.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 45. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hai số phức
1
3z i
và
2
1 2z i
. Phần thực
của số phức
1 2
z z
bằng
A.
4
. B.
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có
1 2
3 1 2 2 3z z i i i
.
Phần thực của số phức
1 2
z z
bằng
2
.
Câu 46. (THPT Ba Đình - Thanh Hóa - 2021) Cho số phức
5 8z i
, phần ảo của
z
là
A. 8. B.
8i
. C.
5
. D.
8
.
Lời giải
Chọn D
Phần ảo của số phức
z
là
8
Câu 47. (THPT Ba Đình - Thanh Hóa - 2021) Tính môdun của số phức
3 4z i
.
A. 5. B. 3. C. 7. D.
7
.
Lời giải
Chọn A
Ta có
2 2
3 ( 4) 5
z
.
Câu 48. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho số phức
4 3z i
. Tìm phần thực và phần ảo của số
phức liên hợp của số phức
z
A. Phần thực bằng 4 và phần ảo bằng 3 B. Phần thực bằng
4
và phần ảo bằng
3i
C. Phần thực bằng
4
và phần ảo bằng
3i
D. Phần thực bằng 4 và phần ảo bằng
3
Lời giải
Chọn A
Số phức liên hợp của số phức
4 3z i
là
4 3z i
Phần thực bằng 4 và phần ảo bằng 3
Câu 49. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức
3 4z i
. Khẳng định nào sau đây là khẳng
định sai?
A. Số phức liên hợp của
z
là
3 4i
B. Điểm biểu diễn cuả
z
là
4;3
M
C. Môđun của số phức
z
là
5
D. Số phức liên hợp của
z
là
3 4i
Lời giải
Chọn B
Lý thuyết
(Điểm biểu diễn của
z
là
3;4
M
)
Câu 50. (THPT Quốc Oai - Hà Nội - 2021) Số nào trong các số phức sau là số thuần ảo?
A.
10 10 2i i
. B.
5 7 5 7
i i
.
C.
3 3
i i
. D.
7 7
i i
.
Lời giải
Chọn B
Ta có
5 7 5 7 2 7i i i
.
Câu 51. (THPT Quảng Xương 1-Thanh Hóa - 2021) Số phức liên hợp của số phức
3 12z i
là
A.
3 12z i
. B.
3 12z i
. C.
3 12z i
. D.
3 12z i
.
Lời giải
Chọn B
Ta có:
3 12z i
3 12z i
.
Câu 52. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức
1
2z i
và
2
1 3z i
. Phần thực
của số phức
1 2
z z
bằng
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn B
1 2
2 1 3 3 4z z i i i
phần thực của số phức
1 2
z z
bằng
3
Câu 53. (THPT Quảng Xương 1-Thanh Hóa - 2021) Trong mặt phẳng tọa độ, điểm
3; 1
A
biểu diễn
số phức nào dưới đây?
A.
1 3z i
. B.
1 3z i
. C.
3z i
. D.
3z i
.
Lời giải
Chọn D
Ta có điểm
3; 1
A
biểu diễn số phức
3z i
.
Câu 54. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức
1
2 3z i
,
2
4 5z i
. Tính
1 2
z z z
A.
2 2z i
. B.
2 2z i
. C.
2 2z i
. D.
2 2z i
.
Lời giải
Chọn D
Ta có
1 2
2 3 4 5 2 2z z z i i i
.
Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Số phức liên hợp của số phức
4 7z i
là
A.
4 7z i
. B.
4 7z i
. C.
4 7z i
. D.
4 7z i
.
Lời giải
Chọn B
Ta có
4 7z i
.
Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức
12 5z i
. Mô đun của số phức
là:
A.
17
. B.
13
. C.
13
. D.
5
.
Lời giải
Chọn C
Ta có
2 2
12 5 13
z
.
Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Số phức liên hợp
z
của số phức
1 2021z i
là
A.
1 2021z i
. B.
1 2021z i
. C.
2021z i
. D.
1 20211z i
.
Lời giải
Chọn D
Ta có
1 2021 1 2021 .z i z i
Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tính môđun của số phức
3 4z i
A.
3
. B.
7
. C.
7
. D.
5
.
Lời giải
Chọn D.
Ta có:
2 2
3 4 5
z
.
Câu 59. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức
1 2
2 3 , 4 5z i z i
. Số phức
1 1
z z z
là
A.
2 2z i
. B.
2 2z i
. C.
2 2z i
. D.
2 2z i
.
Lời giải
Chọn D
1 2
2 3 4 5 2 2 .z z z i i i
Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Số phức liên hợp của số phức
2 3z i
là.
A.
3 2z i
. B.
3 2z i
. C.
2 3z i
. D.
2 3z i
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Ta có Số phức liên hợp của số phức
2 3z i
là
2 3z i
.
Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hai số phức
1
5 6z i và
2
2 3z i . Số phức
1 2
3 4z z là.
A.
14 33i
. B.
236i
. C.
26 5i
. D.
7 30i
.
Lời giải
Chọn D
Ta có
1 2
3 4 7 30z z i
Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Cho số phức
z
được biểu diễn bởi điểm
1;3M
trên mặt
phẳng tọa độ. Môđun của số phức
z
bằng
A.
10
. B.
2 2
. C.
10
. D.
8
.
Lời giải
Chọn C
Số phức được biểu diễn bởi điểm
1;3M
trên mặt phẳng tọa độ nên
1 3 z i
. Do đó
2
2
1 3 10 z .
Câu 63. (THPT Đồng Quan - Hà Nội - 2021) Số phức liên hợp của số phức
2 3z i
là:
A.
3 2z i
. B.
2 3z i
. C.
2 3z i
. D.
3 2z i
.
Lời giải
Chọn B
Câu 64. (THPT Lê Lợi - Thanh Hóa - 2021) Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
.
Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng 3 và phần ảo bằng 4. B. Phần thực bằng 3 và phần ảo bằng
4i
.
C. Phần thực bằng 4 và phần ảo bằng
3i
. D. Phần thực bằng 4 và phần ảo bằng 3.
Lời giải
Chọn A
Từ hình vẽ ta có
3;4M
nên
3 4z i
. Vậy phần thực bằng
3
và phần ảo bằng
4
.
Câu 65. (THPT Lê Lợi - Thanh Hóa - 2021) Số phức liên hợp của số phức
3 2z i
?
A.
3 2z i
. B.
3 2z i
. C.
2 3z i
. D.
3 2z i
.
Lời giải
Chọn D
Câu 66. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hai số phức
1
5 7z i
và
2
2 3z i
. Tìm số phức
1 2
z z z
A.
7 4z i
. B.
2 5z i
. C.
2 5z i
. D.
3 10z i
.
Lời giải
Chọn A
Ta có
1 2
5 2 7 3 7 4z z z i i
.
Câu 67. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Phần thực của số phức
3 1 4z i i
là
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
13.
B.
1.
C.
13.
D.
1.
Lời giải
Chọn B
Ta có
3 1 4 1 13z i i i
. Vậy phần thực của số phức
là
1
.
Câu 68. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìm số phức liên hợp của số phức
3 1
z i i
A.
3z i
. B.
3z i
. C.
3z i
. D.
3z i
.
Lời giải
Chọn C
3 1 3 3z i i i z i
.
Câu 69. (Trung Tâm Thanh Tường - 2021) Cho hai số phức
1 2
1 2 , 2z i z i
. Phần ảo của số phức
1 2
z z
bằng
A. 3. B. 1. C.
i
. D.
3i
.
Lời giải
Chọn B
1 2
1 2 2 3z z i i i
Phần ảo của
1 2
z z
bằng 1.
Câu 70. (Trung Tâm Thanh Tường - 2021) Cho số phức
1 2
2 3 , 1z i z i
. Điểm nào sau đây là điểm
biểu diễn của số phức
1 2
?w z z
A. Điểm
1;4
Q
. B. Điểm
1; 4
P
. C. Điểm
3; 2
M
. D. Điểm
2; 3
Q
.
Lời giải
Chọn C.
Ta có:
1 2
2 3 1 3 2 .w z z i i i
Vậy điểm biểu diễn
1 2
w z z
là
3; 2
M
.
Câu 71. (Trung Tâm Thanh Tường - 2021) Cho biết số phức liên hợp của số phức
z
là
1 3z i
. Số
phức
z
là
A.
3z i
. B.
1 3z i
. C.
3z i
. D.
1
1 3
z
i
.
Lời giải
Chọn B.
Ta có
1 3z i
suy ra
1 3z i
.
Câu 72. (Trung Tâm Thanh Tường - 2021) Cho số phức
1 3z i
. Tìm phần thực của số phức
3w i z z
.
A.
0
. B. 3. C. 9. D. 6.
Lời giải
Chọn A
Ta có:
3 1 3 3 1 3 3 3 9 8w i z z i i i i i i
.
Câu 73. (Trung Tâm Thanh Tường -2021) Số phức liên hợp của số phức
2
2
z i
là
A.
3 4z i
. B.
3 4z i
. C.
3 4z i
. D.
3 4z i
.
Lời giải
Chọn B
Ta có
2
2
2 4 4 3 4 3 4z i i i i z i
.
Câu 74. (Trung Tâm Thanh Tường -2021) Trong mặt phẳng tọa độ
Oxy
, cho điểm
M
như hình vẽ bên
là điểm biểu diễn số phức
z
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Kết quả
2
1 z
bằng
A.
2
1 2 2z i
. B.
2
1 2z i
. C.
2
1 1z i
. D.
2
1 2z i
.
Lời giải
Chọn B
Số phức biểu diễn điểm
M
là
2 2
2
2 1 1 2 1 2 2z i z i i i i
.
Câu 75. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho số phức
2 3z i
, khi đó phần ảo của số phức
z
là
A.
2
. B.
3
. C.
3
. D.
2
.
Lời giải
Chọn B
Số phức
z
có phần ảo
là:
3
.
Câu 76. (THPT Triệu Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức
1 2z i
có tọa độ là:
A.
1;2
. B.
2; 1
. C.
1; 2
. D.
1;2
.
Lời giải
Chọn D
Câu 77. (THPT Triệu Sơn - Thanh Hóa - 2021) Gọi
1 2
,z z là hai nghiệm phức của phương trình
2
2 9 0z z
, khi đó
1 2
z z
bằng
A.
18
. B.
3
. C.
9
. D.
6
.
Lời giải
Chọn D
Ta có:
1
2
2
1 2 2
2 9 0
1 2 2
z i
z z
z i
Khi đó
1 2
1 2 2 1 2 2 6z z i i .
Câu 78. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức
3 4z i
và
2 3w i
. Số phức
2z w
bằng
A.
1 7i
. B.
1 10i
. C.
7 2i
. D.
1 10i
.
Lời giải
Chọn D
2 3 4 2 2 3 3 4 4 6 1 10z w i i i i i
Câu 79. (THPT Trần Phú - Đà Nẵng - 2021) Tính môđun của số phức
z
biết
3 2 1 5z i i
A.
5z
. B. 13z . C. 53z . D. 65z .
Lời giải
Chọn B
2 2
3 2 1 5 2 3 2 3 13z i i z i z
.
Câu 80. (THPT Trần Phú - Đà Nẵng - 2021) Trên mặt phẳng tọa độ điểm biểu diễn số phức
1 4i
có
tọa độ là
A.
4; 1
. B.
4; 1
. C.
1; 4
. D.
1;4
.
Lời giải
Chọn D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Tr
ong mặt phẳng tọa độ
Oxy
,
điểm biểu diễn số phức
1
4z i
c
ó tọa độ là
1
;4
.
Câu 81. (THPT
Trần Phú - Đà Nẵng - 2021) Cho hai số phức
1
1z
i
và
2
1
3z i
.
Phần thực của số
phức
1
2
.z
z
bằng
A.
2
. B.
2
. C.
4
. D.
4
.
Lờ
i giải
Chọn
C
Số phức
1
2
.
1 1 3 4 2z z i i i
có phần thực là
4
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ THÔNG HIỂU
Câu 1. (Sở Vĩnh Phúc - 2021) Cho số phức
z
thỏa mãn
z z
. Trong mặt phẳng tọa độ
Oxy
, tập hợp tất
cả các điểm biểu diễn cho số phức
z
là đường thẳng nào trong các đường thẳng sau đây?
A. Đường thẳng
0y
. B. Đường thẳng
0x
.
C. Đường thẳng
y x
. D. Đường thẳng
y x
.
Câu 2. (Sở Lào Cai - 2021) Cho số phức
2 1z i
. Điểm nào sau đây là điểm biểu diễn của số phức
z
trên mặt phẳng tọa
độ?
A.
1;2H
. B.
2; 1T
. C.
1; 2G
. D.
2;1K
.
Câu 3. (Sở Lào Cai - 2021) Cho hai số phức
1 2
2 , 2 4z i z i . Tính
1 1 2
.z z z
.
A.
5
5
. B.
1
. C. 5 5 . D. 5 .
Câu 4. (Sở Hà Tĩnh - 2021) Cho số phức
z
thỏa mãn
2 3 2 11 16z i i z i . Môđun của số
phức
z
bằng.
A. 5 . B.
5
. C. 13 . D.
3
.
Câu 5. (Sở Yên Bái - 2021) Kí hiệu
1 2
,z z
là hai nghiệm phức của phương trình
2
6z 18 0z
. Tính giá
trị của biểu thức
2
1 2
P z z
bằng
A.
6
. B.
36
. C.
18
. D.
24
.
Câu 6. (Sở Yên Bái - 2021) Tính môđun của số phức
z
thỏa mãn
(2 ) 13 1i z i
.
A.
5 34
3
z
. B. 34z . C.
34z
. D.
34
3
z
.
Câu 7. (Sở Tuyên Quang - 2021) Cho hai số phức
1
2 4z i
và
2
1 3z i
. Phần ảo của số phức
1 2
z iz
bằng
A.
5
. B.
3
. C.
3i
. D.
5i
.
Câu 8. (Sở Tuyên Quang - 2021) Tìm số phức liên hợp của số phức
2
4 1 1 3z i i
A.
9 2z i
. B.
9 2z i
. C.
9 2z i
. D.
9 2z i
.
Câu 9. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho các số phức
1 2 , w 2z i i
.
Số phức
.wu z
có
A. Phần thực là
0
và phần ảo là
3
. B. Phần thực là
4
và phần ảo là
3
.
C. Phần thực là
0
và phần ảo là
3i
. D. Phần thực là
4
và phần ảo là
3i
.
Câu 10. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho số phức
1 2z i
. Tìm phần
ảo của số phức
1
P
z
.
A.
2
. B.
2
3
. C.
2
. D.
2
3
.
SỐ PHỨC
Chủ đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng
Oxy
, tập hợp điểm
M
biểu diễn số phức cho số phức
z
thỏa mãn
1 2 1z i
là một đường tròn
C
, tâm
I
của
đường tròn đó là
A.
1; 2
I
. B.
2 ; 1
I
C.
2 ; 1
I
. D.
2 ;1
I
Câu 12. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Phương trình
2
2 5 0
z z
có hai
nghiệm phức
1 2
,z z
. Khi đó
2 2
1 2
z z
bằng
A.
10
. B.
10
. C.
5
. D.
2 5
.
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho số phức
5 4z i
. Số phức đối của
z
có tọa
độ điểm biểu diễn là
A.
5; 4
. B.
5;4
. C.
5;4
. D.
5; 4
.
Câu 14. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Kí hiệu
1
z
,
2
z
là hai nghiệm của phương trình
2
4 0
z
. Gọi
M
,
N
lần lượt là điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ. Tính
T OM ON
với
O
là gốc tọa độ.
A.
2T
. B.
2
T
. C.
8
T
. D.
4T
.
Câu 15. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hai số phức
1
4 3z i
và
2
7 3z i
. Tìm số
phức
1 2
z z z
.
A.
3 6z i
. B.
1 10z i
. C.
11z
. D.
3 6z i
.
Câu 16. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức
z
thỏa mãn:
2 5 ( 2 )iz i i z i
.
Tính môđun của số phức
1w z i
.
A.
4 3
5 5
i
. B.
1
. C.
9
5
. D.
1
5
.
Câu 17. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hai số phức
1
2 3z m n m i
và
2
3
z n m ni
với
,m n
. Biết rằng
1 2
z z
, khẳng định nào sau đây đúng?
A.
0
m n
. B.
5
m n
. C.
3
m n
. D.
3
m n
.
Câu 18. (Chuyên Lam Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn của số phức
2
2
z i
là điểm nào dưới đây?
A.
3;4
P
. B.
5;4
M
. C.
4;5
N
. D.
4;3
Q
.
Câu 19. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức
1
1z i
và
2
3 2z i
. Phần ảo của số
phức
1 2
2
z z
bằng
A.
0
. B.
2
. C.
4
. D.
4
.
Câu 20. (Chuyên KHTN - 2021) Trên mặt phẳng phức, biết rằng tập hợp các điểm biểu diễn các số phức
z
thỏa mãn
2 1z i
là một đường tròn. Đường tròn đó có tâm là
A.
2
1; 2
I
. B.
1
2; 1
I
. C.
3
2;1
I
. D.
4
1; 2
I
.
Câu 21. (Chuyên KHTN - 2021) Cho số phức
z
thỏa mãn
2 1 9 2i z i i
. Môđun của số phức
z
bằng
A.
13
. B.
13
. C.
5
. D.
5
.
Câu 22. (Chuyên KHTN - 2021) Phương trình
4
16
z
có bao nhiêu nghiệm phức?
A.
0
. B.
. C.
. D.
1
.
Câu 23. (Chuyên KHTN - 2021) Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
1 3 1z i z i
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
2 0
x y
. B.
2 2 0
x y
. C.
2 0
x y
. D.
2 0
x y
.
Câu 24. (Chuyên KHTN - 2021) Cho số phức
z
thỏa mãn
3 8 0
z i z
.Tổng phần thực và phần ảo
của
z
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 25. (Chuyên Quốc Học Huế - 2021) Gọi
C
là đường cong trong mặt phẳng
Oxy
biểu diễn các số
phức
z
thỏa mãn
2
. 1
z z z z
và
H
là hình phẳng giới hạn bởi
C
. Diện tích của hình phẳng
H
bằng
A.
2
.
5
B.
5.
C.
2 5.
D.
.
5
Câu 26. (Chuyên Quang Trung - Bình Phước - 2021) Cho
z
thỏa
2 12
z z
. Phần ảo của
z
là
A. 0 B. 4 C.
12
D.
2
Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức
4 3z i
. Chọn khẳng định đúng trong các
khẳng định sau
A. Số phức liên hợp của
z
là
4 3z i
.
B. Điểm biểu diễn của số phức
z
là
3;4
M
.
C. Môđun của số phức
z
bằng
2
2
4 3i
.
D. Số phức nghịch đảo của
z
là
1 4 3
25 25
i
z
.
Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số phức
z
thỏa mãn
1 2 8 14z i z i
.
A.
3 4 .z i
B.
3 .z i
C.
1 2 .z i
D.
2z i
Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm các số thực
x
,
y
thỏa mãn
2x 1 2y i i i
A.
1x
và
2
y
. B.
1x
và
2
y
. C.
1
x
và
2
y
. D.
1
x
và
2
y
.
Câu 30. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Gọi
1 2
,z z
là nghiệm phức của phương trình
2
5 8 0
z z
. Giá trị
2 2
1 2
z z
bằng
A.
41
. B.
9
. C.
16
. D.
17
.
Câu 31. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức
1
3 4z i
và
2
2z i
. Số phức
1 2
z iz
bằng
A.
5 3i
B.
5 3i
C.
2 2i
D.
2 2i
Câu 32. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi
0
z
là nghiệm phức có phần ảo dương của phương
trình
2
4 8 0
z z
. Trên mặt phẳng tọa độ
Oxy
, điểm nào dưới đây là điểm biểu diễn của số
phức
0
?iz
A.
2;2
Q
. B.
2;2
M
. C.
2; 2
P
. D.
2; 2
N
.
Câu 33. (Chuyên Hạ Long - Quảng Ninh - 2021) Trong mặt phẳng với hệ tọa độ
Oxy
, biết điểm
3; 5
M
là điểm biểu diễn số phức
z
. Phần ảo của số phức
2z i
bằng
A.
5
. B.
2
. C.
3
. D.
5
.
Câu 34. (Chuyên Hạ Long - Quảng Ninh - 2021) Số phức liên hiệp của
4 3 1z i
là:
A.
4 3 1z i
. B.
4 1 3z i
. C.
4 1 3z i
. D.
4 3 1z i
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 35. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi
1
z
;
2
z
là các nghiệm của phương trình
2
3 5 0
z z
. Mô đun của số phức
1 2
2 3 2 3
z z
bằng
A.
7
. B.
11
. C.
29
. D.
1
.
Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức
1
1 2z i
và
2
3z i
. Môđun của số
phức
1 2 1 2
z z z z
bằng
A.
5 34
. B.
4 35
. C.
5 43
. D.
5 10
.
Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Trên mặt phẳng toạ độ
Oxy
, biết điểm
2;1
M
là điểm biểu
diễn số phức
z
. Phần thực của số phức
3 2i z
bằng
A.
8
. B.
7
. C.
1
. D.
4
.
Câu 38. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số phức
4 3z i
và
1w i
. Mô đun của số phức
.z w
bằng
A.
5 2.
B.
4 2.
C.
5.
D.
3 2.
Câu 39. (Chuyên ĐH Vinh - Nghệ An - 2021) Gọi
1
z
;
2
z
là các nghiệm của phương trình
2
3 5 0
z z
.
Mô đun của số phức
1 2
2 3 2 3
z z
bằng
A.
7
. B.
11
. C.
29
. D.
1
.
Câu 40. (THPT Thanh Chương 1- Nghệ An - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức
là điểm nào dưới đây?
A. . B. . C. . D. .
Câu 41. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Phần ảo
của số phức bằng
A. . B. . C. . D. .
Câu 42. (THPT Thanh Chương 1- Nghệ An - 2021) Gọi , là hai nghiệm của phương trình
. Giá trị biểu thức bằng
A. . B. . C. . D. .
Câu 43. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hai số phức
1
1 5z i
và
2
3z i
. Số phức
1 2
z z
là
A.
2 6i
. B.
2 6i
. C.
2 6i
. D.
2 6i
Câu 44. (THPT Nguyễn Huệ - Phú Yên - 2021) Trên tập số phức, phương trình
2
3 5 0
z z
có hai
nghiệm
1 2
,z z
. Giá trị
1 2
4
z z
bằng
A.
2 5
. B.
4 5
. C.
3 5
. D.
3 5
.
Câu 45. (THPT Lương Thế Vinh - 2021) Cho
,a b
thoả mãn
3 2
1
a bi
i
i
. Giá trị của tích
ab
bằng
A. 5. B.
5
. C.
1
. D.
1
.
Câu 46. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho số phức
4 3z i
. Có bao nhiêu số thực
a
để
số phức
z az
có mô đun bằng
5
.
A.
1
. B.
. C.
3
. D.
0
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hai số phức
1
3z i
và
2
1z i
.
Phần ảo
của số phức
1
2
z
z
z
là
A.
2i
. B.
i
. C.
2
. D.
1
.
Câu 48. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
1 0
z z
. Khi đó
2 2 2
1 2 1 2 1 1
z z z z z z
bằng
A.
1
. B.
1
2
. C.
1
. D.
2
.
Câu 49. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
z a bi
và
1
w
2
z z
. Mệnh đề nào
dưới đây ĐÚNG?
A.
w 2
. B.
w
là một số thực.
C.
w i
. D.
w
là số thuần ảo.
Câu 50. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
1 2
1
i
z
i
. Trong mặt phẳng tọa độ, điểm
biểu diễn số phức
là điểm nào dưới đây?
A.
1 3
;
2 2
. B.
1 3
;
2 2
. C.
1 3
;
2 2
. D.
1 3
;
2 2
.
Câu 51. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Gọi
1
z
,
2
z
là các ngiệm phức của phương trình
2
2 5 0
z z
. Giá trị của biểu thức
2
1 2
z z
bằng:
A.
16
. B.
4
. C.
4
. D.
16
.
Câu 52. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức
thỏa mãn
2 4 3i z i
. Môđun
của số phức
bằng
A.
2
. B.
1
. C.
5
. D.
5
.
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hai số phức
1
5 2z i
và
2
2 3z i
. Điểm biểu diễn
cho số phức
1 2
z z
là
A.
3; 5
M
. B.
3;5
M
. C.
3;5
M
. D.
3; 5
M
.
Câu 54. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho
số thực
a
và
thỏa mãn
2 18 2 19a b i i a i
với
i
là đơn vị ảo. Tính giá trị biểu thức
P a b
?
A.
19
. B.
17
. C.
39
. D.
37
.
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Kí hiệu
1 2
,z z
là hai nghiệm phức của phương trình
2
2 4 0
z z
. Giá trị của
1 2
1 1
z z
bằng
A.
2
. B.
1
2
. C.
1
. D.
1
2
.
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức
2
3 2 1
z i i
. Môđun của
w
iz z
là
A.
2 2
. B.
1
. C.
2
. D.
2
.
Câu 57. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức
1
3z i
và
2
1z i
. Phần ảo
của số phức
1 2
z z
bằng
A.
4
B.
4i
C.
1
D.
i
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Gọi
0
z là nghiệm phức có phần ảo âm của phương
trình
2
2 5 0z z
. Môđun của số phức
0
z i bằng
A. 2. B.
2
. C. 10 . D.
10
.
Câu 59. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tính mô-đun của số phức
2
2 1 1z i i
.
A. 17z . B.
17z
. C. 15z . D.
3z
.
Câu 60. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức
z
thỏa mãn phương trình
(2 3 )(4 )z i i
là
z a bi
. Khi đó
a b
bằng
A.
21
. B.
1
. C.
21
. D.
1
.
Câu 61. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức
z
thỏa mãn phương trình
2 1 3i z i
. Phần thực của số phức
z
bằng
A.
2
. B.
1
. C.
2
. D.
1
.
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn
của số phức
1 2
z z z ( với
1
5 3z i và
2
6 4z i ) là điểm nào dưới đây?
A.
1; 1M
. B.
11;7Q
. C.
1; 1P
. D.
11; 7
.
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Điểm biểu diễn số phức
7z bi
với
b
nằm trên đường thẳng có phương trình là
A.
7.x
B.
7.y
C.
7.y
D.
7.x
Câu 64. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho số phức
z
thỏa mãn
1 3 1 4 2i z i i
.
Tính mô-đun của
z
.
A.
2 2z
. B.
5 2z
. C.
5z
. D.
2z
.
Câu 65. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức
z
thỏa mãn
2 8z z i
. Tìm số
phức liên hợp của
z
A.
15 8i
. B.
15 2i
. C.
15 7i
. D.
15 8i
.
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Phần gạch chéo trong hình vẽ trên là tập hợp các
điểm biểu diễn số phức
z
thỏa mãn điều kiện nào?
A.
1z
. B.
3z
. C. 1 3z . D.
1 3z
.
Câu 67. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Phương trình
2
3 9 0zz
có hai nghiệm phức
1 2
,z z . Tính
1 2 1 2
S=z z z +z .
A.
12S
. B.
6S
. C.
6S
. D.
12S
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số thực
,x y
thỏa mãn phương trình
2 3 4x i yi
. Khi đó, giá trị của
x
và
y
là :
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
1
3
;
2
x
y
. B.
1
3
;
2
x
y
.
C
.
1
3
;
2
x
i y
. D.
3
; 2
x
y
.
Câu 69. (THPT
Mai Anh Tuấn - Thanh Hóa - 2021) Trong mặt phẳng phức, gọi
,
, ,A B C D
lần lượt là
các điểm biểu diễn số phức
1
1z
i
,
2 3 4
1
2 , 2 , 3z i z i z i
. Gọi
S
là diện tích tứ giác
A
BCD
. Tính
S
?
A.
2
1
2
S
. B.
1
9
2
S
. C.
23
2
S
. D.
1
7
2
S
.
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho số phức
z
t
hỏa mãn
3
i
z i z
.
Tổng phần thực
và phần ảo của số phức
3
w
z z
bằng
A.
8.
B.
5.
C.
5.
D.
8.
Câu 71. (THPT
Hậu Lộc 4 - Thanh Hóa - 2021) Gọi
0
z
là
nghiệm phức có phần ảo dương của phư
ơng
trình
2
2
10 0
z
z
. M
ôđun của số phức
0
z
i
bằng
A
.
3
. B.
5
. C.
1
. D.
3
.
Câu 72. (THPT Đồng Quan - Hà Nội - 2021) Cho hai số phức
1
1z
i
và
2
1z
i
.
Giá trị
1
2
z
iz
bằng
A.
2
2i
. B.
2i
. C.
2
. D.
2
2i
.
Câu 73. (THPT
Lê Lợi - Thanh Hóa - 2021) Cho số phức
z
t
hỏa mã
n
1
2 5
z
i
và
;M
x y
là
điể
m
biểu diễn số phức
z
. Tập hợp các điểm
M
thuộc đường tròn nào sau đây?
A
.
2
2
1 2 5
x y
. B.
2
2
1 2 25
x y
.
C
.
2
2
1
2 5
x
y
. D.
2
2
1
2 25
x
y
.
Câu 74. (Tr
ung Tâm Thanh Tường -2021) Gọi
,
A B
lần lượt là điểm biểu diễn cho hai số phức
1
1z i
và
2
1 3z i
. Gọi
M
là trung điểm của đoạn thẳng
AB
. Khi đó
M
là điểm biểu diễn
cho số phức nào dưới đây?
A
.
i
. B.
1 i
. C.
2
2i
. D.
1 i
.
Câu 75. (THPT
Trần Phú - Đà Nẵng - 2021) Cho số phức
2
020 2021 2022
2 5 3
z i i i
.
Phần thực của
z
bằng
A.
3
. B.
2
. C.
4
. D.
5
.
BẢNG ĐÁP
ÁN
1.A
2.
C
3.
C
4.
B
5.B
6.
B
7.B
8.
A
9.B
10.D
11.A
12.B
13.C
14.D
15.A
16.B
17.B
18.
A
19.
D
20.
B
21.A
22.C
23.C
24.D
25.D
26.
A
27.
D
28.
A
29.
A
30.
B
31.C
32.B
33.C
34.B
35.B
36.A
37.D
38.A
39.B
40.A
41.C
42.C
43.C
44.D
45.
B
46.B
47.
D
48.
D
49.
B
50.D
51.A
52.C
53.A
54.C
55.
C
56.
A
57.
A
58.B
59.
A
60.
C
61.B
62.B
63.A
64.C
65.D
66.
D
67.C
68.
A
69.
D
70.D
71.B
72.C
73.D
74.B
75.D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ THÔNG HIỂU
Câu 1. (Sở Vĩnh Phúc - 2021) Cho số phức
z
thỏa mãn
z z
. Trong mặt phẳng tọa độ
Oxy
, tập hợp tất
cả các điểm biểu diễn cho số phức
z
là đường thẳng nào trong các đường thẳng sau đây?
A. Đường thẳng
0y
. B. Đường thẳng
0x
.
C. Đường thẳng
y x
. D. Đường thẳng
y x
.
Lời giải
Chọn A
Đặt
,z x yi x y
.
Ta có:
0z z x yi x yi y
.
Vậy tập hợp tất cả các điểm biểu diễn cho số phức
z
là đường thẳng
0y
.
Câu 2. (Sở Lào Cai - 2021) Cho số phức
2 1z i
. Điểm nào sau đây là điểm biểu diễn của số phức
z
trên mặt phẳng tọa
độ?
A.
1;2H
. B.
2; 1T
. C.
1; 2G
. D.
2;1K
.
Lời giải
Chọn C
Ta có
2 1 1 2 1; 2z i z i G
Câu 3. (Sở Lào Cai - 2021) Cho hai số phức
1 2
2 , 2 4z i z i . Tính
1 1 2
.z z z
.
A.
5
5
. B.
1
. C. 5 5 . D. 5 .
Lời giải
Chọn C
Ta có:
1 2
. 2 2 4 10z z i i i
,
1 1 2
. 2 10 2 11z z z i i i
.
Vậy
2
2
1 1 2
. 2 11 2 11 5 5z z z i
.
Câu 4. (Sở Hà Tĩnh - 2021) Cho số phức
z
thỏa mãn
2 3 2 11 16z i i z i . Môđun của số
phức
z
bằng.
A.
5
. B.
5
. C.
13
. D.
3
.
Lời giải
Chọn B
Gọi
z x yi
. Ta có:
2 3 2 11 16z i i z i
2 3 2 11 16x yi i i x yi i
2 2 2 3 3 2 2 11 16x yi i x yi xi y i
2 2 5 2 11 16x y y x i i
2 11
2 5 2 16
x y
y x
2 11
2 5 14
x y
x y
3
4
x
y
Vậy
3 4 5z i z
.
Câu 5. (Sở Yên Bái - 2021) Kí hiệu
1 2
,z z
là hai nghiệm phức của phương trình
2
6z 18 0z
. Tính giá
trị của biểu thức
2
1 2
P z z
bằng
SỐ PHỨC
Chủ đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
6
. B.
36
. C.
18
. D.
24
.
Lời giải
Chọn B
Ta có :
2 2
2 2
1 2
3 3
6z 18 0 3 3 3 3 6 36.
3 3
z i
z z z i i
z i
Câu 6. (Sở Yên Bái - 2021) Tính môđun của số phức
z
thỏa mãn
(2 ) 13 1i z i
.
A.
5 34
3
z
. B.
34
z
. C.
34
z
. D.
34
3
z
.
Lời giải
Chọn A
Ta có
1 13
(2 ) 13 1 3 5
2
i
i z i z z i
i
.
Suy ra
2 2
3 ( 5) 34
z
.
Câu 7. (Sở Tuyên Quang - 2021) Cho hai số phức
1
2 4z i
và
2
1 3z i
. Phần ảo của số phức
1 2
z iz
bằng
A.
5
. B.
3
. C.
3i
. D.
5i
.
Lời giải
Chọn B
Ta có:
1 2
2 4 (1 3 ) 2 4 3 5 3z iz i i i i i i
Phần ảo của số phức
1 2
z iz
bằng
3
Câu 8. (Sở Tuyên Quang - 2021) Tìm số phức liên hợp của số phức
2
4 1 1 3z i i
A.
9 2z i
. B.
9 2z i
. C.
9 2z i
. D.
9 2z i
.
Lời giải
Chọn A
Ta có
2
4 1 1 3 4 1 6 8 9 2z i i i i i
. Do đó số phức liên hợp của
z
là
9 2z i
.
Câu 9. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho các số phức
1 2 , w 2z i i
.
Số phức
.wu z
có
A. Phần thực là
0
và phần ảo là
3
. B. Phần thực là
và phần ảo là
3
.
C. Phần thực là
0
và phần ảo là
3i
. D. Phần thực là
4
và phần ảo là
3i
.
Lời giải
Chọn B
Ta có
.w 1 2 2 4 3u z i i i
.
Vậy số phức
.wu z
có phần thực là
4
và phần ảo là
3
.
Câu 10. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho số phức
1 2z i
. Tìm phần
ảo của số phức
1
P
z
.
A.
2
. B.
2
3
. C.
2
. D.
2
3
.
Lời giải
Chọn D
Ta có
1 1 1 2 1 2
3 3 3
1 2
i
P i
z
i
. Do đó phần ảo của số phức
P
là
2
3
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 11. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng
Oxy
, tập hợp điểm
M
biểu diễn số phức cho số phức
z
thỏa mãn
1 2 1z i
là một đường tròn
C
, tâm
của
đường tròn đó là
A.
1; 2
I
. B.
2 ; 1
I
C.
2 ; 1
I
. D.
2 ;1
I
Lời giải
Chọn A
Gọi
,z x yi z x yi x y
.
Ta có
2 2
1 2 1 1 2 1 1 2 1
z i x yi i x y
.
Vậy tập hợp điểm
M
biểu diễn số phức cho số phức
z
thỏa mãn
1 2 1z i
là một đường tròn
C
có tâm
1; 2
I
.
Câu 12. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Phương trình
2
2 5 0
z z
có hai
nghiệm phức
1 2
,z z
. Khi đó
2 2
1 2
z z
bằng
A.
10
. B.
10
. C.
5
. D.
2 5
.
Lời giải
Chọn B
Ta có:
1
2
2
1 2
2 5 0
1 2
z i
z z
z i
2
2
2 2 2
2
1 2
1 2 1 2 5 5 10
z z
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho số phức
5 4z i
. Số phức đối của
z
có tọa
độ điểm biểu diễn là
A.
5; 4
. B.
5;4
. C.
5;4
. D.
5; 4
.
Lời giải
Chọn C
Gọi
w
là số phức đối của
0 5 4z w z w i
.
Như vậy điểm biểu diễn
w
có tọa độ là
5;4
.
Câu 14. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Kí hiệu
1
z
,
2
z
là hai nghiệm của phương trình
2
4 0
z
. Gọi
M
,
N
lần lượt là điểm biểu diễn của
1
z
,
2
z
trên mặt phẳng tọa độ. Tính
T OM ON
với
O
là gốc tọa độ.
A.
2T
. B.
2
T
. C.
8
T
. D.
4T
.
Lời giải
Chọn D
1
2
2
2
4 0
2
z i
z
z i
.
Khi đó:
0;2
M
,
0; 2
N
.
Vậy
2 2 4
T OM ON
.
Câu 15. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hai số phức
1
4 3z i
và
2
7 3z i
. Tìm số
phức
1 2
z z z
.
A.
3 6z i
. B.
1 10z i
. C.
11z
. D.
3 6z i
.
Lời giải
Chọn A
Ta có
1 2
(4 3 ) (7 3 ) 3 6z z z i i i
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 16. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức
z
thỏa mãn:
2 5 ( 2 )iz i i z i
.
Tính môđun của số phức
1w z i
.
A.
4 3
5 5
i
. B.
1
. C.
9
5
. D.
1
5
.
Lời giải
Chọn B
Gọi
,
z a bi a b R
.
2 5 2 2 5 2iz i i z i i a bi i i a bi i
2 5 2 1 3
b a i a b i
9
2 5 2 5
5
2 1 3 2 2 8
5
a
b a a b
a b a b
b
9 8 4 3
1 1.
5 5 5 5
w i i i w
Câu 17. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hai số phức
1
2 3z m n m i
và
2
3
z n m ni
với
,m n
. Biết rằng
1 2
z z
, khẳng định nào sau đây đúng?
A.
0
m n
. B.
5
m n
. C.
3
m n
. D.
3
m n
.
Lời giải
Chọn B
Ta có:
1 2
2 3
3
m n n m
z z
m n
4 0 1
3 4
m n m
m n n
5
m n
.
Câu 18. (Chuyên Lam Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn của số phức
2
2
z i
là điểm nào dưới đây?
A.
3;4
P
. B.
5;4
M
. C.
4;5
N
. D.
4;3
Q
.
Lời giải
Chọn A
Ta có
2
2
2 4 4 3 4 3;4
z i i i i P
là điểm biểu diễn của
2
2
z i
.
Câu 19. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức
1
1z i
và
2
3 2z i
. Phần ảo của số
phức
1 2
2
z z
bằng
A.
0
. B.
2
. C.
4
. D.
4
.
Lời giải
Chọn D
Ta có
1 2
2 2 1 3 2 5 4z z i i i
.
Vậy phần ảo của số phức
1 2
2
z z
bằng
4
.
Câu 20. (Chuyên KHTN - 2021) Trên mặt phẳng phức, biết rằng tập hợp các điểm biểu diễn các số phức
z
thỏa mãn
2 1z i
là một đường tròn. Đường tròn đó có tâm là
A.
2
1; 2
I
. B.
1
2; 1
I
. C.
3
2;1
I
. D.
4
1; 2
I
.
Lời giải
Chọn B
Gọi
;M x y
là tập hợp các điểm biểu diễn số phức
z x yi
(
,x y
).
Ta có
2 1z i
2 1x yi i
2 1 1x y i
2 2
2 1 1 1
x y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Khi đó, tập hợp các điểm
;M x y
biểu diễn các số phức
z
thỏa mãn
2 1z i
là một đường
tròn
C
có phương trình (1). Và đường tròn
C
đó có tâm là
1
2; 1
I
.
Câu 21. (Chuyên KHTN - 2021) Cho số phức
z
thỏa mãn
2 1 9 2i z i i
. Môđun của số phức
bằng
A.
13
. B.
13
. C.
5
. D.
5
.
Lời giải
Chọn A
Ta có:
8 6 17
2 1 9 2 2 8
2 5 5
i
i z i i i z i z z i
i
Suy ra:
2 2
6 17
13
5 5
z
.
Câu 22. (Chuyên KHTN - 2021) Phương trình
4
16
z
có bao nhiêu nghiệm phức?
A.
0
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn C
Ta có:
2
4
2 2
4 2
16
2
4 4
z z
z
z i
z i
.
Vậy phương trình có hai nghiệm phức là
2i
.
Câu 23. (Chuyên KHTN - 2021) Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
1 3 1z i z i
.
A.
2 0
x y
. B.
2 2 0
x y
. C.
2 0
x y
. D.
2 0
x y
.
Lời giải
Chọn C
,z x yi x y
thì
1 3 1z i z i
1 3 1x yi i x yi i
2 2 2 2
1 3 1 1
x y x y
4 4 8 0
x y
2 0
x y
.
Câu 24. (Chuyên KHTN - 2021) Cho số phức
z
thỏa mãn
3 8 0
z i z
.Tổng phần thực và phần ảo
của
z
bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Lời giải
Chọn D
Gọi số phức
2
; , , 1.
z a bi a b i
3 8 0 3 8 0
z i z a bi i a bi
3 0 1
3 3 8 0
3 8 0 3
a b a
a b a b i
a b b
Vậy
2
a b
Câu 25. (Chuyên Quốc Học Huế - 2021) Gọi
C
là đường cong trong mặt phẳng
Oxy
biểu diễn các số
phức
z
thỏa mãn
2
. 1
z z z z
và
H
là hình phẳng giới hạn bởi
C
. Diện tích của hình phẳng
H
bằng
A.
2
.
5
B.
5.
C.
2 5.
D.
.
5
Lời giải
Chọn D
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
; ,z x yi x y
.
Ta có
2
2
. 1 ( ) 1
z z z z x yi x yi x yi x yi
2 2
2 2 2 2 2
4 1 5 1 1
1
1
5
x y
x y y x y
Do đó tập hợp điểm biểu diễn số phức
z
là elip có
1
a
;
1
5
b
.
Suy ra diện tích hình phẳng
H
là
5
S ab
.
Câu 26. (Chuyên Quang Trung - Bình Phước - 2021) Cho
z
thỏa
2 12
z z
. Phần ảo của
là
A. 0 B. 4 C.
12
D.
2
Lời giải
Chọn A
Gọi
z a bi
2 2
2 2
2 12
2 12
2 12
0
z z
a bi a b
a a b
b
Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức
4 3z i
. Chọn khẳng định đúng trong các
khẳng định sau
A. Số phức liên hợp của
z
là
4 3z i
.
B. Điểm biểu diễn của số phức
z
là
3;4
M
.
C. Môđun của số phức
z
bằng
2
2
4 3i
.
D. Số phức nghịch đảo của
z
là
1 4 3
25 25
i
z
.
Lời giải
Chọn D
Số phức nghịch đảo của
z
là
1 1 4 3 4 3 4 3
4 3 4 3 4 3 25 25 25
i i
i
z i i i
.
Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số phức
thỏa mãn
1 2 8 14z i z i
.
A.
3 4 .z i
B.
3 .z i
C.
1 2 .z i
D.
2z i
Lời giải
Chọn A
Gọi số phức
z a bi
,
,
a b R
.
Khi đó
1 2 8 14z i z i
1 2 8 14a bi i a bi i
2 8
2 2 2 8 14
2 2 14
b
b a b i i
a b
3
4
a
b
.
Vậy số phức cần tìm là
3 4 .z i
Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm các số thực
x
,
y
thỏa mãn
2x 1 2y i i i
A.
1x
và
2
y
. B.
1x
và
2
y
. C.
1
x
và
2
y
. D.
1
x
và
2
y
.
Lời giải
Chọn A
2x 1 2 2 2 2y i i i x yi i
2 2 0 1
2 2
x x
y y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 30. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Gọi
1 2
,z z
là nghiệm phức của phương trình
2
5 8 0
z z
. Giá trị
2 2
1 2
z z
bằng
A.
41
. B.
9
. C.
16
. D.
17
.
Lời giải
Chọn B
Vì
1 2
,z z
là nghiệm phức của phương trình
2
5 8 0
z z
nên
1 2
1 2
5
. 8
z z
z z
.
Suy ra
2
2 2 2
1 2 1 2 1 2
2 . 5 2.8 9
z z z z z z
.
Câu 31. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức
1
3 4z i
và
2
2z i
. Số phức
1 2
z iz
bằng
A.
5 3i
B.
5 3i
C.
2 2i
D.
2 2i
Lời giải.
CHỌN C
Ta có:
1 2
(3 4 ) (2 ) 2 2z iz i i i i
Câu 32. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi
0
z
là nghiệm phức có phần ảo dương của phương
trình
2
4 8 0
z z
. Trên mặt phẳng tọa độ
Oxy
, điểm nào dưới đây là điểm biểu diễn của số
phức
0
?iz
A.
2;2
Q
. B.
2;2
M
. C.
2; 2
P
. D.
2; 2
N
.
Lời giải
Chọn B
Ta có
2
2 2
4 8 0
2 2
z i
z z
z i
Vì
0
z
là nghiệm phức có phần ảo dương
0 0
2 2 2 2 2 2z i iz i i i
.
Vậy điểm biểu diễn số phức
0
iz
là
2;2
M
.
Câu 33. (Chuyên Hạ Long - Quảng Ninh - 2021) Trong mặt phẳng với hệ tọa độ
Oxy
, biết điểm
3; 5
M
là điểm biểu diễn số phức
z
. Phần ảo của số phức
2z i
bằng
A.
5
. B.
2
. C.
3
. D.
5
.
Lời giải
Chọn C
Ta có
3 5 2 3 5 2 3 3z i z i i i i
.
Phần ảo của số phức
2z i
bằng
3
.
Câu 34. (Chuyên Hạ Long - Quảng Ninh - 2021) Số phức liên hiệp của
4 3 1z i
là:
A.
4 3 1z i
. B.
4 1 3z i
. C.
4 1 3z i
. D.
4 3 1z i
.
Lời giải
Chọn B
4 3 1 4 3 1 4 1 3z i z i i
.
Câu 35. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi
1
z
;
2
z
là các nghiệm của phương trình
2
3 5 0
z z
. Mô đun của số phức
1 2
2 3 2 3
z z
bằng
A.
7
. B.
11
. C.
29
. D.
1
.
Lời giải
Chọn B
Phương trình
2
3 5 0
z z
có nghiệm là
3 11
2 2
z i
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Không mất tính tổng quát, giả sử:
1
3 11
2 2
z i
và
2
3 11
2 2
z i
Ta có:
2
1 2
2 3 2 3 3 11 3 3 11 3 11 11 11 11
z z i i i i i
Vậy mô đun của số phức
1 2
2 3 2 3
z z
bằng
11
.
Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức
1
1 2z i
và
2
3z i
. Môđun của số
phức
1 2 1 2
z z z z
bằng
A.
5 34
. B.
4 35
. C.
5 43
. D.
5 10
.
Lời giải
Chọn A
Ta có
1 2 1 2
25 15z z z z i
. Số phức này có môđun bằng
2 2
25 15 5 34
.
Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Trên mặt phẳng toạ độ
Oxy
, biết điểm
2;1
M
là điểm biểu
diễn số phức
z
. Phần thực của số phức
3 2i z
bằng
A.
8
. B.
7
. C.
1
. D.
4
.
Lời giải
Chọn D
Ta có
2z i
nên
3 2 2 3 2 6 4 3 2 4 7i z i i i i i
.
Vậy phần thực của số phức
3 2i z
là
4
.
Câu 38. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số phức
4 3z i
và
1w i
. Mô đun của số phức
.z w
bằng
A.
5 2.
B.
4 2.
C.
5.
D.
3 2.
Lời giải
Chọn A
Ta có
. 4 3 1 5 2
z w i i
.
Câu 39. (Chuyên ĐH Vinh - Nghệ An - 2021) Gọi
1
z
;
2
z
là các nghiệm của phương trình
2
3 5 0
z z
.
Mô đun của số phức
1 2
2 3 2 3
z z
bằng
A.
7
. B.
11
. C.
29
. D.
1
.
Lời giải
Chọn B
Phương trình
2
3 5 0
z z
có nghiệm là
3 11
2 2
z i
Không mất tính tổng quát, giả sử:
1
3 11
2 2
z i
và
2
3 11
2 2
z i
Ta có:
2
1 2
2 3 2 3 3 11 3 3 11 3 11 11 11 11
z z i i i i i
Vậy mô đun của số phức
1 2
2 3 2 3
z z
bằng
11
.
Câu 40. (THPT Thanh Chương 1- Nghệ An - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức
là điểm nào dưới đây?
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Vậy điểm biểu diễn số phức là điểm .
Câu 41. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Phần ảo
của số phức bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Vậy phần ảo của số phức bằng .
Câu 42. (THPT Thanh Chương 1- Nghệ An - 2021) Gọi , là hai nghiệm của phương trình
. Giá trị biểu thức bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có:
Vậy .
Câu 43. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hai số phức
1
1 5z i
và
2
3z i
. Số phức
1 2
z z
là
A.
2 6i
. B.
2 6i
. C.
2 6i
. D.
2 6i
Lời giải
Chọn C
1 2
1 3 5 1 2 6z z i i
.
Câu 44. (THPT Nguyễn Huệ - Phú Yên - 2021) Trên tập số phức, phương trình
2
3 5 0
z z
có hai
nghiệm
1 2
,z z
. Giá trị
1 2
4
z z
bằng
A.
2 5
. B.
4 5
. C.
3 5
. D.
3 5
.
Lời giải
Chọn D
Ta có
1
2
2
3 11
2 2
3 5 0
3 11
2 2
z i
z z
z i
.
Vậy
1 2
4 3 5
z z
.
Câu 45. (THPT Lương Thế Vinh - 2021) Cho
,a b
thoả mãn
3 2
1
a bi
i
i
. Giá trị của tích
ab
bằng
A. 5. B.
5
. C.
1
. D.
1
.
Lời giải
Chọn B
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
3 2 1 3 2 5
1
a bi
i a bi i i a bi i
i
5
5
1
a
ab
b
Câu 46. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho số phức
4 3z i
. Có bao nhiêu số thực
a
để
số phức
z az
có mô đun bằng
5
.
A.
1
. B.
. C.
3
. D.
0
.
Lời giải
Chọn B
Ta có:
4 3 4 3z i z i
.
Do đó:
4 3 4 3z az a i a ai
;
2 2
2
4 3 25z a a a
.
Theo bài ra:
2
5 25 5
z a
2 2
25 25 1 1
a a a
.
Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hai số phức
1
3z i
và
2
1z i
.
Phần ảo
của số phức
1
2
z
z
z
là
A.
2i
. B.
i
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có:
2
1
2 2
2
3 1
3 3 3
2
1 1 2
i i
z i i i i
z i
z i i
Phần ảo của số phức
z
là
1
.
Câu 48. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
1 0
z z
. Khi đó
2 2 2
1 2 1 2 1 1
z z z z z z
bằng
A.
1
. B.
1
2
. C.
1
. D.
2
.
Lời giải
Chọn D
Theo định lý Viet ta có :
1 2
1 2
1
. 1
z z
z z
.
Mặt khác
1
z
là nghiệm của phương trình nên
2 2
1 1 1 1
1 0 1
z z z z
,
Do đó:
2 2 2 2
1 2 1 2 1 1 1 2 1 2 1 1
1. 1 1 2
z z z z z z z z z z z z
.
Câu 49. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
z a bi
và
1
w
2
z z
. Mệnh đề nào
dưới đây ĐÚNG?
A.
w 2
. B.
w
là một số thực.
C.
w i
. D.
w
là số thuần ảo.
Lời giải
Chọn B
Ta có
1 1
w .2
2 2
z a bi z z a a
.
Câu 50. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
1 2
1
i
z
i
. Trong mặt phẳng tọa độ, điểm
biểu diễn số phức
z
là điểm nào dưới đây?
A.
1 3
;
2 2
. B.
1 3
;
2 2
. C.
1 3
;
2 2
. D.
1 3
;
2 2
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Lời giải
Chọn D
Ta có
1 2 1
1 2 1 3
1 1 1 2 2
i i
i
z i
i i i
.
Vậy điểm biểu diễn số phức
là
1 3
;
2 2
Câu 51. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Gọi
1
z
,
2
z
là các ngiệm phức của phương trình
2
2 5 0
z z
. Giá trị của biểu thức
2
1 2
z z
bằng:
A.
16
. B.
4
. C.
4
. D.
16
.
Lời giải
Chọn A
2 2
2
1 2 1 2 1 2
4 2 4.5 16
z z z z z z
.
Câu 52. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức
thỏa mãn
2 4 3i z i
. Môđun
của số phức
bằng
A.
2
. B.
1
. C.
5
. D.
5
.
Lời giải
Chọn C
Ta có :
4 3 2
4 3
2 4 3 1 2 5
2 2 2
i i
i
i z i z i z
i i i
.
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hai số phức
1
5 2z i
và
2
2 3z i
. Điểm biểu diễn
cho số phức
1 2
z z
là
A.
3; 5
M
. B.
3;5
M
. C.
3;5
M
. D.
3; 5
M
.
Lời giải
Chọn A
Gọi
;M x y
là điểm biểu diễn số phức
1 2
z z
.
Ta có:
1 2
5 2 2 3 3 5z z i i
.
Vậy
3; 5
M
.
Câu 54. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho
số thực
a
và
thỏa mãn
2 18 2 19a b i i a i
với
i
là đơn vị ảo. Tính giá trị biểu thức
P a b
?
A.
19
. B.
17
. C.
39
. D.
37
.
Lời giải
Chọn C
Ta có:
2 18 2 19 2 18 2 19a b i i a i a bi a i
2 18 2 20
19 19
a a a
b b
.
Vậy
20 19 39
P a b
.
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Kí hiệu
1 2
,z z
là hai nghiệm phức của phương trình
2
2 4 0
z z
. Giá trị của
1 2
1 1
z z
bằng
A.
2
. B.
1
2
. C.
1
. D.
1
2
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2
1 2
1 4 3 3 1 3; 1 3.i z i z i
1 2
1 2
1 1 1 1
1 3 2 1
2 2
z z
z z
.
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức
2
3 2 1
z i i
. Môđun của
w
iz z
là
A.
2 2
. B.
1
. C.
2
. D.
2
.
Lời giải
Chọn A
Ta có
2
3 2 1 2 3 2 4 6z i i i i i
.
Khi đó
w 4 6 4 6 2 2 w 2 2
iz z i i i i
.
Câu 57. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức
1
3z i
và
2
1z i
. Phần ảo
của số phức
1 2
z z
bằng
A.
4
B.
4i
C.
1
D.
i
Lời giải
Chọn A
Ta có
2
1 2
3 1 3 3 2 4 .z z i i i i i i
Vậy phần ảo của số phức
1 2
z z
là
4
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Gọi
0
z
là nghiệm phức có phần ảo âm của phương
trình
2
2 5 0
z z
. Môđun của số phức
0
z i
bằng
A. 2. B.
2
. C.
10
. D.
10
.
Lời giải
Chọn B
2
0 0 0
1 2
2 5 0 1 2 1 2
1 2
z i
z z z i z i i z
z i
.
Câu 59. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tính mô-đun của số phức
2
2 1 1
z i i
.
A.
17
z
. B.
17
z
. C.
15
z
. D.
3
z
.
Lời giải
Chọn A
Ta có
2 2
2
2 1 1 1 4 1 4 17
z i i i z
.
Câu 60. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức
thỏa mãn phương trình
(2 3 )(4 )z i i
là
z a bi
. Khi đó
a b
bằng
A.
21
. B.
1
. C.
21
. D.
1
.
Lời giải
Chọn C
Ta có
2
(2 -3 )(4 ) 8 2 -12 -3 11 10 .z i i i i i i
11 10
z i a bi
. Do đó
11, 10 11 10 21
a b a b
.
Câu 61. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức
thỏa mãn phương trình
2 1 3i z i
. Phần thực của số phức
z
bằng
A.
2
. B.
1
. C.
2
. D.
1
.
Lời giải
Chọn B
Ta có
2
1 3 2
1 3 2 6 3 5 5
2 1 3 1
2 2 2 5 5
i i
i i i i i
i z i z i
i i i
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Vậy phần thực của số phức
z
đã cho là
1
.
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn
của số phức
1 2
z z z
( với
1
5 3z i
và
2
6 4z i
) là điểm nào dưới đây?
A.
1; 1
M
. B.
11;7
Q
. C.
1; 1
P
. D.
11; 7
.
Lời giải
Chọn B
Ta có
1 2
5 3 6 4 11 7z z z i i i
.
Vậy điểm biểu diễn của số phức
1 2
z z z
là điểm
11;7
Q
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Điểm biểu diễn số phức
7
z bi
với
b
nằm trên đường thẳng có phương trình là
A.
7.
x
B.
7.
y
C.
7.
y
D.
7.
x
Lời giải
Chọn A
Điểm biểu diễn số phức
7
z bi
với
b
kí hiệu là
7; ,M b b
Khi đó
7; ,M b b
nằm trên đường thẳng
7
x
với
b
.
Câu 64. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho số phức
z
thỏa mãn
1 3 1 4 2i z i i
.
Tính mô-đun của
z
.
A.
2 2
z
. B.
5 2
z
. C.
5
z
. D.
2
z
.
Lời giải
Chọn C
Ta có
1 3 1 4 2 1 5 5i z i i i z i
.
2 2
5 5 1 5 2
5 5
5
1 1 1 1 1
i i i
i
z z z i
i i i
.
Vậy
2
2
5 0 5 5
z i
.
Câu 65. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức
z
thỏa mãn
2 8z z i
. Tìm số
phức liên hợp của
z
A.
15 8i
. B.
15 2i
. C.
15 7i
. D.
15 8i
.
Lời giải
Chọn D
Đặt
, .
z a bi a b
Khi đó
2 2
2 2
2
2 8 2 8
8
a a b
z z i a bi a b i
b
2
15
64 2
.
8
8
a
a a
b
b
Suy ra
15 8 .z i
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Phần gạch chéo trong hình vẽ trên là tập hợp các
điểm biểu diễn số phức
z
thỏa mãn điều kiện nào?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1z
. B.
3z
. C. 1 3z . D.
1 3z
.
Lời giải
Chọn D
Phần gạch chéo trong hình vẽ nằm giữa hai đường tròn
2 2
1x y
và
2 2
9x y
2
1 9z
1 3z
.
Vậy phần gạch chéo trong hình vẽ trên là tập hợp các điểm biểu diễn số phức
z
thỏa mãn điều
kiện
1 3z
.
Câu 67. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Phương trình
2
3 9 0zz
có hai nghiệm phức
1 2
,z z . Tính
1 2 1 2
S=z z z +z .
A.
12S
. B.
6S
. C.
6S
. D.
12S
Lời giải
Chọn C
Ta có :
2
1,2 1 2 1 2
3 3
3 9 0 9 3 6.
2 2
z S=z z z +zz z i
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số thực
,x y
thỏa mãn phương trình
2 3 4x i yi
. Khi đó, giá trị của
x
và
y
là :
A.
1
3;
2
x y
. B.
1
3;
2
x y
.
C.
1
3 ;
2
x i y
. D.
3; 2x y
.
Lời giải
Chọn A
Ta có:
2 3 4x i yi
3
4 2
3
1
2
x
y
x
y
Do đó chọn phương án A.
Câu 69. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Trong mặt phẳng phức, gọi
, , ,A B C D
lần lượt là
các điểm biểu diễn số phức
1
1z i ,
2 3 4
1 2 , 2 , 3z i z i z i . Gọi
S
là diện tích tứ giác
ABCD
. Tính
S
?
A.
21
2
S
. B.
19
2
S
. C.
23
2
S
. D.
17
2
S
.
Lời giải
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Chọn D
Trong mặt phẳng phức ta xác định các điểm
, , ,A B C D
như hình vẽ.
IJLK LAB JBC ILCD KAD
S S S S S S
1 1 1 1 17
3.5 1.2 1.3 2.2 1.4
2 2 2 2 2
S
.
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho số phức
z
thỏa mãn
3iz i z
. Tổng phần thực
và phần ảo của số phức
3w z z
bằng
A.
8.
B.
5.
C.
5.
D.
8.
Lời giải
Chọn D
Ta có:
3
3 1 3 1 2 .
1
i
iz i z i z i z i
i
Suy ra
3 3 1 2 1 2 4 4 .w z z i i i
Do đó tổng phần thực và phần ảo của
w
bằng 8.
Vậy ta chọn phương án D.
Câu 71. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Gọi
0
z là nghiệm phức có phần ảo dương của phương
trình
2
2 10 0z z
. Môđun của số phức
0
z i
bằng
A.
3
. B.
5
. C.
1
. D.
3
.
Lời giải
Chọn B
2
1 3
2 10 0
1 3
z i
z z
z i
.
Do
0
z là nghiệm phức có phần ảo dương của phương trình đã cho nên
0
1 3z i .
0
1 3 1 2z i i i i .
Suy ra
2
2
0
1 2 1 2 5z i i
.
Câu 72. (THPT Đồng Quan - Hà Nội - 2021) Cho hai số phức
1
1z i
và
2
1z i
. Giá trị
1 2
z iz
bằng
A.
2 2i
. B.
2i
. C.
2
. D.
2 2i
.
Lời giải
Chọn C
Ta có
1 2
1 1 1 1 2z iz i i i i i .
Câu 73. (THPT Lê Lợi - Thanh Hóa - 2021) Cho số phức
z
thỏa mãn
1 2 5z i
và
;M x y
là điểm
biểu diễn số phức
z
. Tập hợp các điểm
M
thuộc đường tròn nào sau đây?
A.
2 2
1 2 5x y
. B.
2 2
1 2 25x y
.
C.
2 2
1 2 5x y
. D.
2 2
1 2 25x y
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời
giải
Chọn D
T
a có
1
2 5 1 2 5
z
i z i
*
.
Gọi
1
;2
A
là
điểm biểu diễn số phức
1
1
2z i
thì
*
1
5
z
z
5
MA
.
Vậy tập
hợp các điểm
M
là
đường tròn tâm
1;2
A
, bán kính
5
R
.
Câu
74. (Trung Tâm Thanh Tường -2021) Gọi
,
A B
lần
lượt là điểm biểu diễn cho hai số phức
1
1z
i
và
2
1
3z i
.
Gọi
M
là t
rung điểm của đoạn thẳng
AB
.
Khi đó
M
là điểm
biểu diễn
cho số phức nào dưới đây?
A.
i
. B.
1 i
. C.
2
2i
. D
.
1 i
.
Lời giải
Chọn B
Do
, A B
lần lượt
là điểm biểu diễn cho hai số phức
1
1z
i
và
2
1
3
z
i
1
;1 , 1; 3
A
B
.
M
là t
rung điểm của đoạn thẳng
1
; 1
A
B M
. Vậy số phứ
c biểu diễn điểm
M
l
à
1 i
.
Câu
75. (THPT Trần Phú - Đà Nẵng - 2021) Cho số phức
2
020 2021 2022
2 5 3
z i i i
.
Phần thực của
z
bằng
A.
3
. B.
. C.
. D.
5
.
Lời
giải
Chọn D
T
a có
2020 2021 2022
1
, , 1
i
i i i
2
.1 5. 3 1 5 5z i i
.
Do
đó phần thực của
bằ
ng 5.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG
Câu 1. (Sở Lào Cai - 2021) Cho
1 2
,z z là 2 số phức liên hợp của nhau và thỏa mãn
1
2
2
z
z
và
1 2
2 3z z . Tính mô đun của số phức
1
z
A.
1
2z
. B.
1
5z . C.
1
3z
. D.
1
5
2
z
.
Câu 2. (Sở Hà Tĩnh - 2021) Cho số phức
z
thỏa mãn
1 2 3.z i
Tính giá trị nhỏ nhất của biểu thức
4 6 .P z i
A.
3
min
2
P
. B.
min 2P
. C.
min 1P
. D.
min 8P
.
Câu 3. (Sở Hà Tĩnh - 2021) Biết số phức
3
w
2
iz
z
có biểu diễn hình học trong mặt phẳng tọa độ
Oxy
là một đường thẳng. Khi đó môđun của
z
bằng?
A.
2
. B.
3
2
. C.
2
2
. B.
2
.
Câu 4. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Có bao nhiêu số phức
z
thoả mãn
2 2 2z i
và
2
1z
là số ảo?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho số phức
,z a bi a b
thỏa
mãn
3 0z i z i
. Tổng
2S a b ab
bằng
A.
23
. B.
24
. C.
23
. D.
24
.
Câu 6. (Chuyên Lê Hồng Phong - TPHCM - 2021) Gọi
1
z ,
2
z là hai nghiệm phức của phương trình
2
15 3 19 0z z
. Tính giá trị của biểu thức:
2 2
1 2 1 2
K z z z z
.
A.
22
15
K
. B.
41
15
K
. C.
11
50
K
. D.
7
3
K
.
Câu 7. (Chuyên KHTN - 2021) Cho số phức
z a bi
thỏa mãn
1 2 3 4z i z i
và
2z i z
là số
thực. Tổng
a b
bằng:
A.
1
. B.
1
. C.
3
. D.
3
.
Câu 8. (Chuyên Quốc Học Huế - 2021) Có bao nhiêu số phức
z
có mô đun bằng
2
và thỏa mãn
3 4 3z i
?
A.
0
. B.
1
. C.
4
. D.
2
.
Câu 9. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức
z
thỏa mãn
3 4 1i z
. Tìm giá trị nhỏ nhất
của
z
.
A.
6
. B.
3 2
. C.
4
. D.
5
.
Câu 10. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức
z
thỏa mãn
3( ) (2 ). 3 10z i i z i
.
Mô đun của
z
bằng
A. 3 . B.
3
. C.
5
. D. 5 .
SỐ PHỨC
Chủ đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức
z
thỏa mãn điều kiện
1 2z i z i
là đường nào sau đây?
A. Elip B. Đường thẳng C. Đường tròn D. Parabol
Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số phức
z
đôi một khác nhau thoả mãn
2
z i
và
4
( 2)
z
là số thực?
A.
4
. B.
5
. C.
. D.
7
.
Câu 13. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số nguyên
a
để phương trình
2 2
3 0
z a z a a
có 2 nghiệm phức
1 2
,z z
thỏa mãn
1 2 1 2
z z z z
?
A. 4. B. 2. C. 1. D. 3.
Câu 14. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Trên mặt phẳng tọa
độ , tập hợp điểm biểu diễn các số phức là một đường tròn có bán kính bằng
A. B. C. D.
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức
thỏa mãn
2 3
1 2
3 2
i
z
i
. Mô đun
lớn nhất của số phức
z
bằng
A.
13
. B.
2
. C.
1 2
. D.
26
.
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hai số phức
1
z
;
2
z
thỏa mãn
1
2
z
;
2
1
z
và
1 2
2 3 4
z z
. Tính giá trị của biểu thức
1 2
2P z z
.
A.
10
P . B.
11
P
. C.
15
P . D.
2 5
P .
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho các số phức
thoả mãn
1 1 2
iz i
.
Biết rằng tập hợp các điểm biểu diễn các số phức
là đường tròn
C
. Tìm tâm
I
và bán kính
R
của đường tròn
C
.
A.
0; 1 , 3
I R
. B.
0; 1 , 3
I R
. C.
0;1 , 3
I R
. D.
0;1 , 3
I R
.
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
z
thỏa mãn
2 4 8 19i z z i i
.
Môđun của
z
bằng
A. 5. B. 18. C.
5
. D.
13
Câu 19. (THPT Đào Duy Từ - Hà Nội - 2021) Xét các số phức
z
thoả mãn
3 2 4
iz i
. Trên mặt
phẳng toạ độ
Oxy
, tập hợp điểm biểu diễn số phức
2 5 6w iz i
là một đường tròn có tâm
;I a b
, bán kính
R
. Tính
T a b R
A.
21
. B.
17
. C.
5
. D.
1
.
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Xét các số phức
z
thỏa mãn
4
z
, biết rằng tập
hợp các điểm biểu diễn của số phức
3 4 5w i z i
một đường tròn. Bán kính
r
của đường
tròn đó là:
A.
10
r
. B.
20
r
. C.
18
r
. D.
25
r
.
Câu 21. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức
,z a bi a b
thỏa mãn
1 3 0.
z i z i
Tính
2 3S a b
A.
5.
S
B.
6.
S
C.
6
S
D.
5
S
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 22. (THPT Chu Văn An - Thái Nguyên - 2021) Xét các số phức
z
thỏa mãn điều kiện
2 1
z i z i
là số thực. Biết rằng tập hợp các điểm biểu diễn hình học của
z
là một đường
thằng có phương trình
y ax b
. Mệnh đề nào sau đây sai?
A.
2
a b
. B.
2
a b
. C.
2
3 4
a b
. D.
2
5 6
b a
.
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức
z
thỏa mãn
1 2 15z i iz i
. Tìm
mô đun của số phức
z
.
A.
2 5
z
. B.
4
z
. C.
2 3
z
. D.
5
z
.
Câu 24. (THPT Ba Đình - Thanh Hóa - 2021) Có bao nhiêu số phức
z
thỏa mãn
1 2 13 2i z i z i
?
A. 2. B. 1. C. 4. D. 3.
Câu 25. (THPT Quế Võ 1 - Bắc Ninh - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức
z
thỏa mãn điều kiện
1 2z i z i
là đường nào sau đây?
A. Elip B. Đường thẳng C. Đường tròn D. Parabol
Câu 26. (THPT Quốc Oai - Hà Nội - 2021) Số phức
z
thoả mãn hệ thức
2 10
z i
và
. 25
z z
là
A.
3 4 , 5
z i z
. B.
3 4 , 5
z i z
. C.
3 4 , 5
z i z
. D.
3 4 , 5
z i z
.
Câu 27. (THPT Quốc Oai - Hà Nội - 2021) Số thực
,x y
để hai số phức
2 7
1
9 4 10z y xi
và
2 11
2
8 20z y i
là liên hợp của nhau.
A.
2; 2
x y
. B.
2; 2
x y
. C.
2; 2
x y
. D.
2; 2
x y
.
Câu 28. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức
,z a bi a b
thỏa mãn
2 3 3z iz i
. Tính giá trị biểu thức
2019 2018
P a b
A.
4036 2019
2019
3 3
5
P
. B.
4036 2019
2019
3 3
5
P
.
C.
2P
. D.
0
P
.
Câu 29. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức
z
thỏa mãn
2.
z
Biết rằng tập
hợp các điểm biểu diễn số phức
w 3 2 2
i i z
là một đường tròn. Bán kính
R
của đường
tròn đó bằng
A.
2.
B.
5.
C.
2 5.
D.
5.
Câu 30. (THPT Lê Lợi - Thanh Hóa - 2021) Cho số phức
z
thỏa mãn
1 2 5
z i
. Khi đó
1w z i
có modul lớn nhất bằng bao nhiêu?
A.
5
. B.
5 2
. C.
20
. D.
2 5
.
Câu 31. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức
1
z
,
2
z
thỏa mãn
1 2
39
z z
và
1 2
2 3
z z
. Khi đó
1 2
z z
bằng
A.
8
. B.
2 39
. C.
12
. D.
2 3
.
Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Cho số phức
z x yi
có phần ảo âm, biết
z
thỏa mãn
2 3
z i i
và
3
z i
z
là số thực. Giá trị của
2x y
bằng
A.
3
. B.
5
. C.
4
. D.
11
3
.
Câu 33. Có bao nhiêu số phức
z
thỏa mãn
4
z i z i
và
z i z
là số thực?
A.
1
. B.
2
. C.
0
. D.
4
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
34. Có bao nhiêu số phức
z
t
hỏa mãn
1
z
z z
?
A.
0
. B.
1
. C.
. D.
3
.
Câu
35. Có bao nhiêu số phức
z
t
hỏa mãn
1
3
1
z
z i
z i z i
?
A
.
3
. B.
. C.
. D.
1
.
Câu
36. Có tất cả bao nhiêu số phức
z
mà
phần thực và phần ảo của nó trái dấu đồng thời thỏa mãn
4
z
z z z
và
2
2 3 2.
z
i
A.
1
. B.
3
. C.
. D.
0
.
Câu
37. Có bao nhiêu số phức
z
thỏa
2
3z i z i
và
2
3 2
z
i
?
A
. Vô số B.
. C.
. D.
1
.
Câu 38. Có bao nhiêu số phức
z
thỏa mãn
5
z
và
3
2
z
i z
là số thực?
A
.
1
.
B.
0.
C.
3
.
D.
2
.
Câu
39. Có bao nhiêu số phức
z
thỏa
mãn
4z
z
và
3
2 3 2
z
i z
là số t
huần ảo?
A
.
1
.
B.
0.
C.
3
.
D.
2
.
Câu
40. Cho hai số phức
,z
w
t
hỏa mãn
2
z
i
và
1
2
z i
w
z i
. Tì
m giá trị nhỏ nhất của
w
.
A.
4
. B.
7
3
a
. C.
5
2
0
. D.
7
2
a
.
Câu
41. Xét các số phức
z
thỏa mãn
2
2
z
z i
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số
phức
luôn thuộc
một đường tròn cố định. Bán kính của đường tròn đó bằng
A
.
1
. B.
2
. C.
2 2
. D.
2
.
Câu
42. Có bao nhiêu số phức
z
t
hỏa mãn
13
z
và
2
4z i z i
là số thuần ảo?
A
.
1
. B.
. C.
. D.
4
.
BẢ
NG ĐÁP ÁN
1.A
2.B
3.
A
.
4.
D
5.
C
6.B
7.A
8.
B
9.
C
10.D
11.
B
12.B
13.A
14.D
15.C
16.B
17.B
18.D
19.C
20.B
21.
C
22.
A
23.
B
24.B
25.B
26.A
27.B
28.C
29.C
30.D
31.
C
32.C
33.
B
34.C
35.
D
36.C
37.A
38.D
39.D
40.C
41.
B
42.B
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG
Câu 1. (Sở Lào Cai - 2021) Cho
1 2
,z z là 2 số phức liên hợp của nhau và thỏa mãn
1
2
2
z
z
và
1 2
2 3z z . Tính mô đun
của số phức
1
z
A.
1
2z
. B.
1
5z . C.
1
3z
. D.
1
5
2
z
.
Lời giải
Chọn A
Giả sử
1
,z a bi a b
thì
2
z a bi .
1 2
2 3 2 2 3 3 1z z bi b
2 2 2 2 2 2 2 2
1
2 2 2
2
2
2 2 2 2 2 2
2
2 2 2
2
a bi a b abi a a b ab b a b a b
z
i
z
a b ab a b a b
1
2
2
z
z
thì
2 2 2 2 3
2 2
0 2
2 0 3 0
3 3
b
b a b a b a b b
b a
Do
3b
nên
0b
loại.
Thay
1
vào
3
ta có
2
1 4a
.
Từ
1
vào
2 2
1
4 1 3 2z a b
.
Câu 2. (Sở Hà Tĩnh - 2021) Cho số phức
z
thỏa mãn
1 2 3.z i
Tính giá trị nhỏ nhất của biểu thức
4 6 .P z i
A.
3
min
2
P
. B.
min 2P
. C.
min 1P
. D.
min 8P
.
Lời giải
Chọn B
Ta có:
1 2 3z i
nên
z
biểu diễn bởi
M
nằm trên đường tròn
C
, tâm
1;2I
, bán kính 3.
Ta có:
4 6 4 6P z i z i MA
(với là khoảng cách từ
M C
và
4;6 .A
Khi đó
min 5 3 2P IA R
.
Câu 3. (Sở Hà Tĩnh - 2021) Biết số phức
3
w
2
iz
z
có biểu diễn hình học trong mặt phẳng tọa độ
Oxy
là một
đường thẳng. Khi đó môđun của
z
bằng?
A.
2
. B.
3
2
. C.
2
2
. B.
2
.
Lời giải
Chọn A
Ta có
3 3
w w 2 3 w 2 w
2 2
iz
z iz z i
z
,
suy ra
3 3
w 2 w w w
2 2 2
z
z i i
.
SỐ PHỨC
Chủ đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ giả thiết
3
w
2
iz
z
có biểu diễn hình học trong mặt phẳng tọa độ
Oxy
là một đường thẳng
nên suy ra
1 2
2
z
z
.
Câu 4. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Có bao nhiêu số phức
z
thoả mãn
2 2 2z i
và
2
1z
là số ảo?
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
Gọi
z x yi
thoả mãn
;x y
. Điểm biểu diễn của
z
là
;M x y
Ta có
2 2 2z i
2 1 2 2x y i
2 2
2 1 2 2x y
2 2
2 1 8x y
Vậy
M
thuộc đường tròn tâm
2;1I
, bán kính
2 2
2
2
1 2 1z z z
2
2 1x yi x yi
2 2
2 2 1x xyi y x yi
2 2
2 1 2 2x x y xyi yi
2
1z
là số ảo nên
2 2
2 1 0x x y
2
2
1x y
1
1
y x
y x
Trên cùng một hệ trục toạ độ, ta vẽ đường tròn tâm
2;1I
, bán kính
2 2
và hai đồ thị hàm số
1y x
;
1y x
.
Ta thấy hai đường thẳng cắt đường tròn tại ba điểm phân biệt, vậy có 3 điểm
M
thoả mãn, vậy có
ba số phức
z
thoả mãn.
Câu 5. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho số phức
,z a bi a b
thỏa
mãn
3 0z i z i
. Tổng
2S a b ab
bằng
A.
23
. B.
24
. C.
23
. D.
24
.
Lời giải
Chọn C
Ta có:
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
2 2 2 2
2
2 2
3 0 3 0 3 1 0
3
3 0
1 9 0 1
1 0
z i z i a bi i a b i a b a b i
a
a
b b
b a b
Xét
1
2
2
2
1 0
1
9 1
4
9 1
b
b
b b
b
b b
Vậy
3 4 2. 3 .4 23
S
Câu 6. (Chuyên Lê Hồng Phong - TPHCM - 2021) Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
15 3 19 0
z z
. Tính giá trị của biểu thức:
2 2
1 2 1 2
K z z z z
.
A.
22
15
K
. B.
41
15
K
. C.
11
50
K
. D.
7
3
K
.
Lời giải
Chọn B
1
2
2
3 1131
30
15 3 19 0
3 1131
30
i
z
z z
i
z
.
Khi đó:
2 2
1 2 1 2
K z z z z
2 2
3 1131 3 1131 3 1131 3 1131
30 30 30 30
i i i i
19 19 1 41
15 15 5 15
.
Câu 7. (Chuyên KHTN - 2021) Cho số phức
z a bi
thỏa mãn
1 2 3 4z i z i
và
2z iz
là số
thực. Tổng
a b
bằng:
A.
1
. B.
1
. C.
3
. D.
3
.
Lời giải
Chọn A
Ta có:
2 2 2 2
1 2 3 4 1 2 3 4
1 2 3 4
3 5 (1)
z i z i a b i a b i
a b a b
a b
Mặt khác:
2 2 ( ) 2 2
z i z a bi i a bi a b a b i
là số thực nên
2 0 (2)
a b
Từ (1) và (2) ta có
3 5 1
2 0 2
a b a
a b b
Tổng
1a b
.
Câu 8. (Chuyên Quốc Học Huế - 2021) Có bao nhiêu số phức
z
có mô đun bằng
2
và thỏa mãn
3 4 3
z i
?
A.
0
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn B
Gọi
, ,z a bi a b
; ta có
2 2
z a b
và
2 2
3 4 3 4
z i a b
.
Theo bài ra ta có hệ
2 2
2 2
2 2
2 2
3 4 3
3 4 9
4
2
a b
a b
a b
a b
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
2 2
2 2
3 4 10 0
6 8 16 0
4
4
a b
a b a b
a b
a b
2 2
4 10
3
4
b
a
a b
2
2
4 10
3
4 10
4
3
b
a
b
b
2
4 10
3
25 80 64 0
b
a
b b
6
5
8
5
a
b
.
Vậy
6 8
5 5
z i
.
Câu 9. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức
z
thỏa mãn
3 4 1
i z
. Tìm giá trị nhỏ nhất
của
z
.
A.
6
. B.
3 2
. C.
. D.
5
.
Lời giải
Chọn C
Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối:
A B A B A B
ta được:
3 4 3 4 5 1 4
i z i z z z
.
Vậy giá trị nhỏ nhất của
z
là
.
Câu 10. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức
z
thỏa mãn
3( ) (2 ). 3 10z i i z i
.
Mô đun của
z
bằng
A.
3
. B.
3
. C.
5
. D.
5
.
Lời giải
Chọn D
Đặt
,z a bi a b
3( ) (2 ). 3 10
3 2 3 10
3 3 3 2 2 3 10
5 3 3 10
3 2
5 3 10 1
z i i z i
a bi i i a bi i
a b i a b a b i i
a b a b i i
a b a
a b b
Vậy:
2 5
z i z
Câu 11. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức
z
thỏa mãn điều kiện
1 2z i z i
là đường nào sau đây?
A. Elip B. Đường thẳng C. Đường tròn D. Parabol
Lời giải
Chọn B
Gọi số phức
, ,z a bi a b
Khi đó
1 2z i z i
2 2 2
2
1 2
1 1 2
3 1 0
a bi i a bi i
a b a b
a b
Vậy tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện trên là đường thẳng.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số phức
z
đôi một khác nhau thoả mãn
2
z i
và
4
( 2)
z
là số thực?
A.
4
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn B
Xét số phức
; ,z a bi a b
. Ta có
2 2
2 ( 1) 2 ( 1) 4 (1)
z i a b i a b
.
4 2 4 3 2 2 3 4
4 2 2 4 3 3
( 2) [( 2) ] ( 2) 4( 2) . 6( 2) ( ) 4( 2)( ) ( )
( 2) 6( 2) [4( 2) . 4( 2) ] .
z a bi a a bi a bi a bi bi
a a b b a b a b i
4
( 2)
z
là số thực khi
3 3 2 2
2 0
0
4( 2) . 4( 2) 0 ( 2) [( 2) ] 0
2
2
a
b
a b a b a b a b
b a
b a
+
2 0 2
a a
thay vào
(1)
tìm được
1
b
2z i
.
+
0
b
thay vào
(1)
tìm được
3 3
a z
+
2
b a
thay vào
(1)
tìm được
1 7 1 7 3 7 1 7 3 7
; .
2 2 2 2 2
a z i z i
+
2
b a
thay vào
(1)
ta có:
2 2 2
(3 ) 4 2 6 5 0 :
a a a a PTVN
Vậy có
5
số phức thoả mãn yêu cầu bài toán.
Câu 13. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số nguyên
a
để phương trình
2 2
3 0
z a z a a
có 2 nghiệm phức
1 2
,z z
thỏa mãn
1 2 1 2
z z z z
?
A. 4. B. 2. C. 1. D. 3.
Lời giải
Chọn A
Ta có
2
3 10 9
a a
.
+ TH1:
0
, phương trình có 2 nghiệm
1,2
3
2
a
z
, khi đó
2
2
1 2 1 2
0
3 3 4 4 0
1
a
z z z z a a a a
a
. Thỏa mãn điều kiện
0
.
+ TH2:
0
, phương trình có 2 nghiệm
1,2
3
2
a i
z
, khi đó
2
2
1 2 1 2
1
3 3 2 16 18 0
9
a
z z z z a i a a a
a

. Thỏa mãn
điều kiện
0
.
Vậy có 4 giá trị của
a
thỏa mãn yêu cầu bài toán.
Câu 14. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Trên mặt phẳng tọa
độ , tập hợp điểm biểu diễn các số phức là một đường tròn có bán kính bằng
A. B. C. D.
Lời giải
Chọn D
Theo bài ra
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
Tập hợp điểm biểu diễn là đường tròn bán kính .
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức
thỏa mãn
2 3
1 2
3 2
i
z
i
. Mô đun
lớn nhất của số phức
z
bằng
A.
13
. B.
2
. C.
1 2
. D.
26
.
Lời giải
Chọn C
Đặt
;z x yi x y
.
Ta có:
2
2
2 3
1 2 1 2 1 2
3 2
i
z iz x y
i
.
Vậy tập hợp điểm
M
biểu diễn số phức
z
nằm trên đường tròn tâm
0; 1
I
bán kính
2
R
Ta có
z OM
.
Do đó mô đun của số phức
z
lớn nhất khi
OM
lớn nhất nghĩa là
, ,O M I
thẳng hàng suy ra Mô
đun lớn nhất của số phức
z
bằng
1 2
.
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hai số phức
1
z
;
2
z
thỏa mãn
1
2
z
;
2
1
z
và
1 2
2 3 4
z z
. Tính giá trị của biểu thức
1 2
2P z z
.
A.
10
P
. B.
11
P
. C.
15
P
. D.
2 5
P
.
Lời giải
Chọn B
Đặt
1
z a bi
;
2
z c di
; ; ;a b c d
.
Theo bài ra:
2 2
1
2 2 4
z a bi a b
.
1
2 2
2
1 1 1
z c di c d
.
2
1 2
2 3 4 2 3 4
z z a bi c di
2 2
2 3 2 3 16
a c b d
.
2 2 2 2
4 12 9 4 12 9 16
a ac c b bd d
.
2 2 2 2
4 9 12 16
a b c d ac bd
.
3
Thay
1
,
2
vào
3
ta được:
3
4.4 9.1 12 16
4
ac bd ac bd
.
4
Khi đó,
2 2
1 2
2 2 2 2
P z z a bi c di a c b d
2 2 2 2
3
4 4 4 4 4. 11
4
a b c d ac bd
.
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho các số phức
thoả mãn
1 1 2
iz i
.
Biết rằng tập hợp các điểm biểu diễn các số phức
là đường tròn
C
. Tìm tâm
I
và bán kính
R
của đường tròn
C
.
A.
0; 1 , 3
I R
. B.
0; 1 , 3
I R
. C.
0;1 , 3
I R
. D.
0;1 , 3
I R
.
Lời giải
Chọn B
Ta có
, ,
z x yi x y
, thì ta có
1 1 2 1 3 1 3
iz i i x yi y xi
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
2
2 2
2 2
1 3 1 3
y x x y
. Vậy tập hợp các điểm biểu diễn các số phức
z
là
đường tròn
C
có tâm và bán kính là
0; 1 , 3
I R
.
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức
z
thỏa mãn
2 4 8 19i z z i i
.
Môđun của
z
bằng
A. 5. B. 18. C.
5
. D.
13
Lời giải
Chọn D
Đặt
,
z a bi a b R
Khi đó :
2 8 3
2 4 8 19 2 8 6 15 0
6 15 2
a b a
i z z i i a b a b i
a b b
3 2 13
z i z
.
Câu 19. (THPT Đào Duy Từ - Hà Nội - 2021) Xét các số phức
z
thoả mãn
3 2 4
iz i
. Trên mặt
phẳng toạ độ
Oxy
, tập hợp điểm biểu diễn số phức
2 5 6w iz i
là một đường tròn có tâm
;I a b
, bán kính
R
. Tính
T a b R
A.
21
. B.
17
. C.
5
. D.
1
.
Lời giải
Chọn C
Ta có
3 2 4
iz i
2 3 2 8
iz i
2 6 4 8
iz i
2 5 6 1 2 8
iz i i
2 5 6 1 2 8
iz i i
1 2 8
w i
.
Giả sử
, ,w x yi x y
.
Suy ra
2 2 2 2
1 2 8 1 2 8 1 2 64
w i x y x y
.
Do đó tập hợp điểm
M
biểu diễn số phức
2 5 6w iz i
là một đường tròn có tâm
1; 2
I
,
bán kính
8
R
.
Vậy
1 2 8 5
T a b R
.
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Xét các số phức
z
thỏa mãn
4
z
, biết rằng tập
hợp các điểm biểu diễn của số phức
3 4 5w i z i
một đường tròn. Bán kính
r
của đường
tròn đó là:
A.
10
r
. B.
20
r
. C.
18
r
. D.
25
r
.
Lời giải
Chọn B
Gọi
;w x yi x y
.
Ta có
(3 4 ) 5w i z i
5
3 4
w
z
i
.
Mà
4
z
5
4
3 4
w
i
5 20
w
2
2
5 400
x y
.
Vậy tập hợp điểm biểu diễn số phức
3 4 5w i z i
là đường tròn có bán kính
20
r
.
Câu 21. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức
,z a bi a b
thỏa mãn
1 3 0.
z i z i
Tính
2 3S a b
A.
5.
S
B.
6.
S
C.
6
S
D.
5
S
.
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
Từ giả thiết suy ra
2 2
2 2 2
1 1
1 3 0
3 0 3 1
a a
a b a b i
b a b b b
1
4
3
a
b
Vậy
4
2 3 2( 1) 3. 6
3
S a b
Câu 22. (THPT Chu Văn An - Thái Nguyên - 2021) Xét các số phức
z
thỏa mãn điều kiện
2 1
z i z i
là số thực. Biết rằng tập hợp các điểm biểu diễn hình học của
z
là một đường
thằng có phương trình
y ax b
. Mệnh đề nào sau đây sai?
A.
2
a b
. B.
2
a b
. C.
2
3 4
a b
. D.
2
5 6
b a
.
Lời giải
Chọn A
Đặt
z x yi
2 2
2 2
2 2
2 1 2 1
2 2 2
3 2
3 2 ( 1)
z i z i x yi i x yi i
x xyi xi xyi y y xi y x yi i
x y xi yi y x i
x y x y x y i
Ta có:
2 1
z i z i
là số thực
1 0 1x y y x
.
Vậy
1
1
a
b
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức
z
thỏa mãn
1 2 15z i iz i
. Tìm
mô đun của số phức
z
.
A.
2 5
z
. B.
4
z
. C.
2 3
z
. D.
5
z
.
Lời giải
Chọn B
Giả sử
,z x yi x y
.z x yi
Phương trình
(1 2 ) 15
z i iz i
trở thành
( )(1 2 ) 15x yi i i x yi i
2 2 15x y xi yi xi y i
3 15x y x y i i
3 15 3
1 4
x y x
x y y
.
Vậy
2 2
3 4 5
z
.
Câu 24. (THPT Ba Đình - Thanh Hóa - 2021) Có bao nhiêu số phức
z
thỏa mãn
1 2 13 2i z i z i
?
A. 2. B. 1. C. 4. D. 3.
Lời giải
Chọn B
Đặt
z a bi
với
,a b
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
1 2 13 2 1 2 13 2i z i z i i a bi i a bi i
3 2 13 2a b bi i
3 2 13 3
2 2
a b a
b b
.
Vậy:
3 2z i
nên có 1 số phức
z
thỏa yêu cầu đề bài.
Câu 25. (THPT Quế Võ 1 - Bắc Ninh - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức
z
thỏa mãn điều kiện
1 2z i z i
là đường nào sau đây?
A. Elip B. Đường thẳng C. Đường tròn D. Parabol
Lời giải
Chọn B
Gọi số phức
, ,z a bi a b
Khi đó
1 2z i z i
2 2 2
2
1 2
1 1 2
3 1 0
a bi i a bi i
a b a b
a b
Vậy tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện trên là đường thẳng
Câu 26. (THPT Quốc Oai - Hà Nội - 2021) Số phức
z
thoả mãn hệ thức
2 10
z i
và
. 25
z z
là
A.
3 4 , 5
z i z
. B.
3 4 , 5
z i z
. C.
3 4 , 5
z i z
. D.
3 4 , 5
z i z
.
Lời giải
Chọn A
Giả sử
;z a bi a b
z a bi
Ta có:
2 2
. 25 25 25 1
z z a bi a bi a b
2 2
2 2
2 10 2 10 2 1 10 2 1 10
4 2 5 0 2
z i a bi i a b i a b
a b a b
Từ
1
và
2
ta có hệ phương trình:
2 2
2 2
25
4 2 5 0
a b
a b a b
2 2
25
4 2 20 0
a b
a b
2
2
10 2 25
10 2
a a
b a
2
5 40 75 0
10 2
a a
b a
3
4
5
0
a
b
a
b
Vậy có
2
số phức
z
thỏa mãn yêu cầu bài toán là
3 4 , 5
z i z
.
Câu 27. (THPT Quốc Oai - Hà Nội - 2021) Số thực
,x y
để hai số phức
2 7
1
9 4 10z y xi
và
2 11
2
8 20z y i
là liên hợp của nhau.
A.
2; 2
x y
. B.
2; 2
x y
. C.
2; 2
x y
. D.
2; 2
x y
.
Lời giải
Chọn B.
Ta có
2 7 2
1
9 4 10 9 4 10z y xi y xi
và
2 11 2
2
8 20 8 20z y i y i
.
Ta có
2 2 2
2 2
1 2
2
9 4 8 4
9 4 10 8 20
2
10 20 2
x
y y y
z z y xi y i
y
x x
.
Vậy
2; 2
x y
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức
,z a bi a b
thỏa mãn
2 3 3z iz i
. Tính giá trị biểu thức
2019 2018
P a b
A.
4036 2019
2019
3 3
5
P
. B.
4036 2019
2019
3 3
5
P
.
C.
2P
. D.
0
P
.
Lời giải
Chọn C
Ta có:
z a bi
.
2 3 3 2 3 3z iz i a bi i a bi i
2 2 3 3a b a b i i
2 3 1
2 3 1
a b a
a b b
.
Suy ra
2019 2018 2019 2018
1 1 2
P a b
.
Câu 29. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức
z
thỏa mãn
2.
z
Biết rằng tập
hợp các điểm biểu diễn số phức
w 3 2 2
i i z
là một đường tròn. Bán kính
R
của đường tròn đó bằng
A.
2.
B.
5.
C.
2 5.
D.
5.
Lời giải
Chọn C
Cách 1: Gọi số phức w cần tìm có dạng:
2 2
w , 0
a bi a b
Khi đó ta có
3 2 2
a bi i i z
3 2 2
3 2
2 2
a b i i
a bi i
z
i i
2 3 6 4 2 2
5
a ai i b i bi i
z
2 8 2 1
5 5
a b a b
z i
Mà
2
z
, nên
2 2
2 8 2 1
4
5 5
a b a b
2 2
3 2 20
a b
20 2 5.
R
Cách 2: Ta có
3 2
w 3 2
w 3 2 2 5
2
5
w i
i
z z i
i
.
Câu 30. (THPT Lê Lợi - Thanh Hóa - 2021) Cho số phức
z
thỏa mãn
1 2 5
z i
. Khi đó
1w z i
có modul lớn nhất bằng bao nhiêu?
A.
5
. B.
5 2
. C.
20
. D.
2 5
.
Lời giải
Chọn D
Gọi số phức
z x yi
,
,x y
.
1 2 5
z i
2 2
1 2 5
x y
.
Tập hợp điểm
M
biểu diễn số phức
z
là đường tròn tâm
1; 2
I
, bán kính
5
R
.
Gọi
1; 1
N
là điểm biểu diễn số phức
1
1z i
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
1
w z i MN
.
Để modul số phức
w
lớn nhất khi và chỉ khi
MN
lớn nhất
MN IN R
5 5 2 5
.
Câu 31. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức
1
z
,
2
z
thỏa mãn
1 2
39
z z
và
1 2
2 3
z z
. Khi đó
1 2
z z
bằng
A.
8
. B.
2 39
. C.
12
. D.
2 3
.
Lời giải
Chọn C
Gọi
A
và
B
lần lượt là điểm biểu diễn của
1
z
và
2
z
trên mặt phẳng tọa độ. Khi đó:
39
OA OB và
2 3
AB .
Nhận xét:
OAB
cân tại
O
. Khi đó:
2
2
1 2
2 2 2 39 3 12
2
AB
z z OC OA
với
C
là
trung điểm cạnh
AB
.
Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Cho số phức
z x yi
có phần ảo âm, biết
z
thỏa mãn
2 3
z i i
và
3
z i
z
là số thực. Giá trị của
2x y
bằng
A.
3
. B.
5
. C.
4
. D.
11
3
.
Lời giải
Chọn C
Ta có
2 2
2 3 2 1 4
z i i x y
1
.
Ta có
2
2
1
1
1 3
3 3
3
x y i
z i
x y i x yi
z x yi
x y
2
2
1
3 1 3 3
3
x x y y x y i
x y
là số thực nên
3 3 0
x y
3 3x y
2 .
Thay
2
vào
1
, ta được:
2 2
2
3 1 1 4 10 8 2 0
y y y y
1
1 18
1
5 5
5
y l
y x
y tm
.
Vậy
2 4
x y
.
Câu 33. Có bao nhiêu số phức
z
thỏa mãn
4
z i z i
và
z i z
là số thực?
A.
1
. B.
2
. C.
0
. D.
4
.
Lời giải
Chọn B
Gọi
z x yi
với
,x y
.
Ta có
2 2
. 0
z i z z z iz x y y xi x
.
Mà
2 2
2 2
4 1 1 4
z i z i x y x y
1 1 4 (2)
y y
(do
0
x
).
TH 1: Nếu
1y
thì
2 2 4 2 2y y z i
.
TH 2: Nếu
1 1y
thì
2 1 1 4
y y
vô nghiệm.
TH 3: Nếu
1
y
thì
2 1 1 4 2 2y y y z i
Vậy có 2 số phức thoả yêu cầu bài toán.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 34. Có bao nhiêu số phức
z
thỏa mãn
1
z z z
?
A.
0
. B.
1
. C.
. D.
3
.
Lời giải
Chọn C
Ta có Giả sử
z x yi
,
x y
2 z x yi z z x
.
Bài ra ta có
2 2
2 2
1
1
1
1
1
2 1
2
x y
z
x y
z z
x
x
Với
2
1 1 3
1
2 4 2
x y y
.
Do đó có 4 số phức thỏa mãn là
1
1 3
2 2
z i
,
2
1 3
2 2
z i
,
3
1 3
2 2
z i
,
4
1 3
2 2
z i
.
Câu 35. Có bao nhiêu số phức
z
thỏa mãn
1 3
1
z z i
z i z i
?
A.
3
. B.
. C.
. D.
1
.
Lời giải
Chọn D
Ta có: Gọi
z a bi
,a b
.
Ta có:
1
3
z z i
z i z i
2 2
2 2
2 2
2 2
1 1
3 1
a b a b
a b a b
2 1 2 1
6 9 2 1
a b
b b
1
1
a
b
.
Vậy có một số phức thỏa mãn là
1z i
.
Câu 36. Có tất cả bao nhiêu số phức
z
mà phần thực và phần ảo của nó trái dấu đồng thời thỏa mãn
4
z z z z
và
2 2 3 2.
z i
A.
1
. B.
3
. C.
. D.
0
.
Lời giải
Chọn C
Gọi điểm
;M x y
là điểm trên mp tọa độ
Oxy
biểu diễn số phức
( , )
z x yi x y z x yi
4 2 2 2 2
z z z z x yi x y
. Khi đó tập hợp điểm
;M x y
biểu diễn số phức
z
là hai cạnh đối
,AD BC
của hình vuông
ABCD
độ dài cạnh bằng
2 2
và tâm là gốc tọa độ
O
2 2
2 2 3 2 2 2 18
z i x y
. Tập hợp điểm
;M x y
biểu diễn số phức
z
là đường
tròn tâm
2;2 , 3 2
I R
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Vậy có 2 điểm biểu diễn
,M P
thỏa yêu cầu bài toán.
Câu 37. Có bao nhiêu số phức
z
thỏa
2 3z i z i
và
2 3 2z i
?
A. Vô số B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A
Gọi điểm
;M x y
là điểm trên mp tọa độ
Oxy
biểu diễn số phức
( , )z x yi x y
2 3z i z i
: Tập hợp
;M x y
là trung trực của đoạn thẳng
AB
với
2;1 , 0;3A B
2 3 2z i
: Tập hợp
;M x y
là hình tròn (kể cả biên) có bán kính
2r
và tâm
2;3I
Do đó có vô số só phức thỏa yêu cầu bài toán.
Câu 38. Có bao nhiêu số phức
z
thỏa mãn 5z và
3 2 z i z
là số thực?
A.
1.
B. 0. C.
3.
D.
2.
Lời giải
Chọn D
Gọi
z a bi
Ta có
2 2
3 2 3 2 2 3 2 3 6 z i z a bi i a bi a a b b b a i
Theo đề ta có hệ phương trình
2 2
5
2 3 6 0
a b
b a
Giải hệ này tìm được 2 nghiệm, suy ra có 2 số phức thỏa yêu cầu bài toán.
Câu 39. Có bao nhiêu số phức
z
thỏa mãn
4zz
và
3 2 3 2 z i z
là số thuần ảo?
A.
1.
B.
0.
C.
3.
D.
2.
Lời giải
Chọn D
Gọi
z a bi
Ta có
2 2
3 2 3 2 3 2 3 2 2 2 9 9 2 4 3 4 6 z i z a b i a bi a a b b a b i
Theo đề ta có hệ phương trình
2 2
2 2
4
2 9 9 2 4 0
a b
a a b b
Giải hệ này tìm được 2 nghiệm, suy ra có 2 số phức thỏa yêu cầu bài toán.
Câu 40. Cho hai số phức
,z w
thỏa mãn
2 z i
và
1
2
z i
w
z i
. Tìm giá trị nhỏ nhất của
w
.
6
4
2
2
4
5 5
P
M
I
B
A
D
C
N
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4
. B.
7
3
a
. C.
5
20
. D.
7
2
a
.
Lời giải
Chọn C
Ta có:
1
2 1 1 2 1
2
z i
w wz w wi z i z w w wi i
z i
2 1 2 1 2 1 2
1 1 1
w wi i w wi i w i
z z i i z i
w w w
2 1 2
2 1 2 1 2 1
1
w i
z i w w i
w
Đặt
2
, , 1
w x yi x y i
, ta có:
2 2 2
2
1 2 1 2 2 1 2 2 1 2 1 2 2
x yi x yi i x y x y
2 2 2 2
4 8 4 4 4 4 1 4 8 4 4 8 1 0
x x y x x y y x y
.
Suy ra tập hợp điểm biểu diễn số phức
w
là đường thẳng
d
có phương trình
4 8 1 0
x y
.
Vậy
min
2 2
1 5
,
20
4 8
w d O d
.
Câu 41. Xét các số phức
z
thỏa mãn
2
2
z
z i
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số
phức
luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng
A.
1
. B.
2
. C.
2 2
. D.
2
.
Chọn B
Lời giải
Đặt
, ,z a bi a b
. Gọi
;M a b
là điểm biểu diễn cho số phức
z
.
Có
2 2
w
2 2
z a bi
z i a b i
2
2
2 2
2
a bi a b i
a b
2
2
2 2 2 2
2
a a b b a b ab i
a b
w
là số thuần ảo
2
2
2 2 0 1
2 0
a a b b
a b
Có
2 2
1 2 2 0
a b a b
.
Suy ra
M
thuộc đường tròn tâm
1;1
I
, bán kính
2
R
.
Câu 42. Có bao nhiêu số phức
z
thỏa mãn
13
z
và
2 4z i z i
là số thuần ảo?
A.
1
. B.
. C.
. D.
4
.
Lời giải
Chọn B
Gọi
z x yi
với
,x y
.
Ta có
2 2
13 13 (1)
z x y
.
Mà
2 2
2 4 2 4 2 8 ( 6 ).z i z i x yi i x yi i x y y x i
là số thuần ảo khi
2 2
5
2 8 0 13 2 8 0
2
x y y y y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Từ
5
2
y
thay vào (1) ta được
3 3
2
3 3
2
x
x
.
Vậy có 2 số phức thoả yêu cầu bài toán.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG CAO
Câu 1. (Sở Lào Cai - 2021) Cho hai số phức
1 2
;z z
thỏa mãn
1 2
1 1; 2 2z i z i
. Số phức
z
thỏa mãn
1 1
1z z i z và
2 2
2z z i z là các số thuần ảo. Tìm giá trị nhỏ nhất của
3 2z i
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 2. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho các số phức
z
thỏa mãn điều kiện số phức
(1 ) (2 )w z i i
là một số thuần ảo. Trong các số phức
z
đó hãy tìm giá trị nhỏ nhất của
7 5T z i
A.
2 2
. B.
2
. C.
74
. D.
38
5
.
Câu 3. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức
1 2 3
, ,z z z , là các số phức cùng thoả
mãn điều kiện
2
4. 33z z z . Biết rằng giá trị lớn nhất có thể đạt được của
1 2 2 3 3 1
z z z z z z
là số thực
M
. Giá trị
M
thuộc tập hợp nào trong các tập hợp dưới
đây?
A.
0;2 11 157
. B.
2 11 157 ;2 7 274
.
C.
2 7 274 ;51, 2
. D.
51, 2;
.
Câu 4. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức
1 2
;z z là hai nghiệm của phương trình
2 1 2z iz
, biết
1 2
1z z
. Giá trị của biểu thức
1 2
P z z
bằng
A.
2
. B.
2
2
. C.
3
. D.
3
2
.
Câu 5. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức
;z a bi a b
thỏa mãn
2
4 15 1z z i i z z
và môđun của số phức
1
3
2
z i
đạt giá trị nhỏ nhất. Khi đó giá trị
của
4
a
b
bằng::
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 6. (Chuyên Quốc Học Huế - 2021) Cho số phức
( , )z x yi x y
thỏa mãn
2x y
và
2 3.x y
Tìm giá trị nhỏ nhất của
2020 2021 .P x y
A.
5389
. B.
2693
. C.
3214
. D.
2102
.
Câu 7. (Chuyên Quang Trung - Bình Phước - 2021) Cho
z
thỏa mãn
1 2 1
1 2 2
z i
z i
. Giá trị
min maxS z z
bằng:
A. 3 5 1 B. 5 2 C. 2 5 1 D. 2 5 1
Câu 8. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức , biết các số phức
z
thỏa mãn
Tìm giá trị lớn nhất của
SỐ PHỨC
Chủ đề 4
4
1
iz
w
z
2.
z
w
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. B. . C. D.
Câu 9. (THPT Nguyễn Huệ - Phú Yên - 2021) Xét các số phức thỏa mãn
2 3 4 5 10z i z i
.
Gọi
m
,
M
lần lượt là giá trị nhỏ nhất, lớn nhất của
3 1z i
. Tính
P m M
.
A. 135 365 . B. 2 135 365 . C. 2 365 . D. 2 135 .
Câu 10. (THPT Lương Thế Vinh - 2021) Xét các số phức
z
thỏa mãn
3 4 2z i
. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
. Tổng
2 2
M m
bằng
A.
58
. B.
52
. C.
65
. D.
45
.
Câu 11. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Xét các số phức
z
thỏa mãn
2 6z z z z
.
Gọi
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
3 2P z i
. Khi đó
M m
bằng
A.
2 53 3 2
2
. B.
6 2
. C.
2 53 2
2
. D. 53 5 .
Câu 12. (THPT Chu Văn An - Thái Nguyên - 2021) Xét số phức
z a bi
,a b
thỏa mãn
4 3 5z i
. Tính
P a b
khi
1 3 1z i z i
đạt giá trị lớn nhất?
A.
8P
. B.
4P
. C.
6P
. D.
10P
.
Câu 13. (THPT Quốc Oai - Hà Nội - 2021) Trong mặt phẳng phức
Oxy
, trong các số phức
z
thỏa mãn
1 1z i
. Nếu số phức
z
có môđun lớn nhất thì số phức
z
có phần thực bằng bao nhiêu?
A.
2 2
2
. B.
2 2
2
. C.
2 2
2
. D.
2 2
2
.
Câu 14. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức
z
thỏa mãn
3 8 7z i
và số phức
4 3w i
. Gọi
M
là giá trị lớn nhất của biểu thức
P z w
. Chọn khẳng định đúng trong các
khẳng định sau
A.
18;19M
. B.
21;22M
. C.
19;20M
. D.
20;21M
.
Câu 15. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức
1 2
,z z thỏa mãn đồng thời hai điều
kiện sau:
| 1| 34z
,
| 1 | | 2 |z mi z m i
( trong đó
m
là số thực ) và sao cho
1 2
z z
lớn
nhất. Khi đó giá trị của
1 2
z z
bằng
A. 2. B. 10. C. 130 . D.
2
.
Câu 16. (Trung Tâm Thanh Tường - 2021) Cho số phức z thỏa mãn hệ thức
2 3 .z i z i
Giá trị
nhỏ nhất của biểu thức
2 1 2P z i i
bằng
A.
7 2
.
3
B.
7 2
.
2
C.
7
2
. D.
7 3
3
.
Câu 17. (THPT Trần Phú - Đà Nẵng - 2021) Xét hai số phức
1 2
,z z thỏa mãn
1 1 1
2 3z i i z z
và
2 2
3 1 2z i z i
. Giá trị nhỏ nhất của
1 2
z z
bằng:
A. 4 6 . B. 2 6 . C.
34
5
. D.
28
15
.
Câu 18. Xét hai số phức
1 2
,z z thỏa mãn
1 2
2, 1 6z i z
và
1 2
5z z . Giá trị lớn nhất
1 2
2 2021z z
bằng
20
20 34
34
34 20
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
2044
. B.
23 2021
. C.
23 2021
. D.
2 23 2021
.
Câu 19. Xét hai số phức
1 2
;z z
thỏa mãn
1 2
1; 4
z z
và
1 2
5
z z
. Giá trị lớn nhất của
1 2
z 2 7z i
bằng
A.
7 89
. B.
7 89
. C.
7 2 89
. D.
7 2 89
.
Câu 20. Cho hai số phức
,u v
thỏa mãn
10
u v
và
3 4 50
u v
. Tìm Giá trị lớn nhất của biểu thức
4 3 10u v i
.
A.
30
. B.
40
. C.
60
. D.
50
.
Câu 21. Cho hai số phức
,u v
thỏa mãn
10
u v
và
3 4 50
u v
. Tìm Giá trị lớn nhất của biểu thức
4 3 10u v i
.
A.
30
. B.
40
. C.
60
. D.
50
.
Câu 22. Cho các số phức
1
z
và
2
z
thỏa mãn
1
1 1z i
và
2
2 3 2
z i
. Tìm giá trị nhỏ nhất của biểu
thức
1 2
.P z z
A.
2
. B.
3
2
. C.
5
2
. D.
3
.
Câu 23. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hai số phức
1
z
có điểm biểu diễn
M
, số phức
2
z
có
điểm biểu diễn là
N
thỏa mãn
1
1
z
,
2
3
z
và
120
MON
. Giá trị lớn nhất của
1 2
3z 2 3z i
là
0
M
, giá trị nhỏ nhất của
1 2
3z 2 1 2z i
là
0
m
. Biết
0 0
7 5 3
M m a b c d
, với
, , ,a b c d
. Tính
a b c d
?
A.
9
. B.
8
. C.
7
. D.
6
.
Câu 24. Xét hai số phức
1 2
;z z
thỏa mãn
1 2
2; 5
z z
và
1 2
3
z z
. Giá trị lớn nhất của
1 2
z 2 3z i
bằng
A.
3 2 3
. B.
3 3 2
. C.
3 26
. D.
26 3
.
Câu 25. Cho hai số phức
1 2
,z z
thỏa mãn
1 2
3 4z z i
và
1 2
5
z z
. Tính giá trị lớn nhất của biểu thức
1 2
P z z
A.
10
. B.
5 2
. C.
5
. D.
10 2
.
Câu 26. Xét các số phức
1
z
,
2
z
thỏa mãn
1
4 1
z
và
2
2 1
iz
. Giá trị lớn nhất của
1 2
2 6z z i
bằng
A.
2 2 2
. B.
4 2
. C.
4 2 9
. D.
4 2 3
.
Câu 27. Cho các số phức
1 2 3
, ,z z z
thỏa mãn
1 2
1 4 2, 4 6 1z i z i
và
3 3
1 2z z i
. Tìm giá
trị nhỏ nhất của biểu thức
3 1 3 2
P z z z z
.
A.
14
2
2
. B.
29 3
. C.
14
2 2
2
. D.
85 3
.
Câu 28. (THPT Đoàn Thượng - Hải Dương - 2021) Biết số phức
z
thoả mãn
| 3 4 | 5
z i
và biểu
thức
2 2
| 2 | | |T z z i
đạt giá trị lớn nhất. Tính
| |z
.
A.
| | 33
z
. B.
| | 5 2
z
. C.
| | 50
z
. D.
| | 10
z
.
Câu 29. (THPT Ngô Quyền - Quảng Ninh - 2021) Cho Xét các số phức
1 2
,z z
thỏa mãn
2 2
1 1
1 2 1
z z i
;
2
3 5.
z i
Giá trị nhỏ nhất của
1 2
P z z
bằng
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
5
. B.
3
5
5
. C.
2
5
. D.
2
5
5
.
BẢ
NG ĐÁP ÁN
1.A
2.A
3.D
4.C
5.D
6.A
7.A
8.
B
9.
C
10.A
11.A
12.D
13.D
14.D
15.A
16.B
17.D
18.C
19.B
20.C
21.
C
22.
A
23.
B
24.B
25.B
26.C
27.D
28.B
29.D
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
MỨC ĐỘ VẬN DỤNG CAO
Câu 1. (Sở Lào Cai - 2021) Cho hai số phức
1 2
;z z
thỏa mãn
1 2
1 1; 2 2z i z i
. Số phức
z
thỏa mãn
1 1
1z z i z và
2 2
2z z i z là các số thuần ảo. Tìm giá trị nhỏ nhất của
3 2z i
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn A
Gọi
1 1 1 2 2 2
; ; .a b i z a b i z m ni z
Khi đó điểm biểu diễn hình học của các số phức
1 2
, ,z z z lần lượt là
1 1 2 2
; , ; , ;A a b B a b M m n
Do
1
1 1z i
nên điểm
A
thuộc đường tròn
2 2
1
: 1 1 1.C x y
Do
2
2 2z i
nên điểm B thuộc đường tròn
2 2
2
: 2 1 4.C x y
Ta có:
1 1
1z z i z là số thuần ảo nên
1 1 1 1
1 1 0m a a n b b
.
2 2
2z z i z là số thuần ảo nên
2 2 2 2
2 1 0m a a n b b
Suy ra điểm M là giao điểm của hai đường thẳng lần lượt là tiếp tuyến của
1 2
,C C
tại , .A B
2 2
3 2 3 2z i m n
là khoảng cách giữa M và
3;2I
Dựa vào hình vẽ ta thấy
min
0IM .
Câu 2. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho các số phức
z
thỏa mãn điều kiện số phức
(1 ) (2 )w z i i
là một số thuần ảo. Trong các số phức
z
đó hãy tìm giá trị nhỏ nhất của
7 5T z i
A.
2 2
. B.
2
. C. 74 . D.
38
5
.
Lời giải
SỐ PHỨC
Chủ đề 4
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn A
Giả sử
,( , ).z x yi x y R
Khi đó
z
có điểm biểu diễn là
( ; ).M x y
Có
w ( )(1 ) (2 ) ( 2) ( 1)x yi i i x y x y i
là số thuần ảo nên
2 0x y
Suy ra tập hợp các điểm
M
là đường thẳng
: 2 0d x y
Có
7 5 (7 5 )T z i z i MA
với
(7;5)A
Có
T
nhỏ nhất khi
MA
ngắn nhất, tức là
2 2
7 5 2
4
min ( , ) 2 2
2
1 ( 1)
T d A
Câu 3. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức
1 2 3
, ,z z z , là các số phức cùng thoả
mãn điều kiện
2
4. 33z z z . Biết rằng giá trị lớn nhất có thể đạt được của
1 2 2 3 3 1
z z z z z z
là số thực
M
. Giá trị
M
thuộc tập hợp nào trong các tập hợp dưới
đây?
A.
0;2 11 157
. B.
2 11 157 ;2 7 274
.
C.
2 7 274 ;51,2
. D.
51,2;
.
Lời giải
Chọn D
Đặt
2
2 2
4 33 8 33z a bi z z z a b a
2
2
2 2 2
8 16 49 4 7a a b a b
1 1 1
1 2 3
2 1 1
: 4;0 , 7 0
, ,
: 4;0 , 7 0
C I R khi x
z z z
C I R khi x
Ta có
1 2 2 3 3 1
P z z z z z z AB BC CA
* TH1:
, ,A B C
cùng thuộc một trong hai đường tròn
1 2
,C C
Khi đó:
2 sin sin sinP AB BC CA R A B C
Mà
sin sin sin sin sin sinA B C A B A B
sin sin sin .cos cos .sinA B A B A B
2 3 3 sin sin
sin sin 3 .cos cos .
2 2
3 3 3
A B
A B B A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
2 2
2 2 2 2
1 3 3 sin sin
sin sin .2 s s
4 2 3 3
3
3 3 3
3
2 2
A B
A B co A co B
Nên
1,2
3 3
2 . 3 3 21 3
2
7
P R R
R R
* TH2: Đặc biệt hoá như sau (*)
11;0 , ,
A d A BC AH
Ta có:
2 2 2
2
49
2 49
OH x
BH OB OH x
BC x
2
2
2
2 2
11 11 49
256
2 11 49 2 49 51,2
5
AH AO OH x AB AC x x
M f x x x x
Câu 4. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức
1 2
;z z
là hai nghiệm của phương trình
2 1 2
z iz
, biết
1 2
1
z z
. Giá trị của biểu thức
1 2
P z z
bằng
A.
2
. B.
2
2
. C.
3
. D.
3
2
.
Lời giải
Chọn C
Gọi
;z a bi a b
.
Ta có:
2 2
2 2 2 2
2 1 2 2 1 4 2 1
z iz a b b a a b
.
Do đó:
1 2
1
z z
.
Gọi
1 1 1 2 2 2
;
z a b i z a b i
2 2 2 2
1 1 2 2 1 1 2 2
; ; ; ; 1; 1
a b a b a b a b
.
Khi đó:
2 2
1 2 1 2 1 2 1 2 1 2
1 1 2 2 1
z z a a b b a a b b
.
Vậy
2 2
1 2 1 2 1 2
P z z a a b b
2 2 2 2
1 1 2 2 1 2 1 2
2 2 3
a b a b a a b b
.
Câu 5. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức
;z a bi a b
thỏa mãn
2
4 15 1
z z i i z z
và môđun của số phức
1
3
2
z i
đạt giá trị nhỏ nhất. Khi đó giá trị
của
4
a
b
bằng::
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn D
Ta có:
z a bi
Do đó
2
4 15 1
z z i i z z
2
8 15 2 1
bi i i a
2
8 15 2 1
b i i a
2
8 15 2 1
b a
2
1 15
2
2 4
a b
15
8
b
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
2
2 2
1 1 1 15
3 3 3 2 3
2 2 2 4
z i a b i a b b b
2
2
21 15 15 21 39
8 8
4 8 8 4 8
b b
Dấu bằng xảy ra
1
2
15
8
a
b
Do đó
2
4
a
b
.
Câu 6. (Chuyên Quốc Học Huế - 2021) Cho số phức
( , )z x yi x y
thỏa mãn
2x y
và
2 3.x y
Tìm giá trị nhỏ nhất của
2020 2021 .P x y
A.
5389
. B.
2693
. C.
3214
. D.
2102
.
Lời giải
Chọn A
Ta có
2
2 2
3 2 3
2 3
x y
x y
x y
x y
Biểu diễn miền nghiệm của hệ phương trình
Miền nghiệm của hệ là miền tứ giác
ABCD
với
1 7 5 1 1 7 5 1
; , ; , ; , ;
3 3 3 3 3 3 3 3
A B C D
Ta biết
2020 2021P x y
đạt GTNN tại 1 trong các đỉnh của tứ giác
ABCD
. Thay tọa độ các
điểm
, , ,A B C D
vào ta được:
1 7 5 1
; 5389, ; 2693
3 3 3 3
1 7 5 1
; 5389, ; 2693
3 3 3 3
P P
P P
Vậy GTNN của
2020 2021P x y
bằng
5389
.
Câu 7. (Chuyên Quang Trung - Bình Phước - 2021) Cho
z
thỏa mãn
1 2 1
1 2 2
z i
z i
. Giá trị
min maxS z z
bằng:
A.
3 5 1
B.
5 2
C.
2 5 1
D.
2 5 1
Lời giải
Chọn A
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Gọi
M
là điểm biểu diễn số phức z x yi (với
;x y
) trên mặt phẳng phức.
Ta có:
1 2 1
1 2 2
z i
z i
2 2
2 2
1 2 1
2 4 4
x y
x y
Do đó
M
thuộc phần chung của hai hình tròn
1
;1I
và
2
;2I
, với
1
1;2I
và
2
2;4I
.
Phương trình đường thẳng
1 2
I I là
2y x
.
Dựa vào hình vẽ ta thấy
z
lớn nhất khi
M Q
và
z
nhỏ nhất khi
M P
, trong đó
P
;
Q
lần
lượt là giao điểm của đường thẳng
2y x
với các đường tròn
2
;2I
và
1
;1I
sao cho
P
;
Q
nằm giữa
1
I và
2
I .
Dễ thấy
2 5 4 5
2 ;4
5 5
P
;
5 2 5
1 ;2
5 5
Q
Vậy min max 3 5 1S z z OP OQ .
Câu 8. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức , biết các số phức
z
thỏa mãn
Tìm giá trị lớn nhất của
A. B. . C. D.
Lời giải
Chọn B
Đặt w x yi .Theo bài ra ta có:
2 2
2 2
2 2
4 4
w
1 1
1 4
1 4
1 4
2 1 4
8 4 14 0
iz iz
x yi
z z
x yi z iz
z x y i x yi
z x y i x yi
x y x y
x y x y
Vậy tập hợp số phức
w
là một đường tròn tâm
4;2I
, bán kính 34R
4
1
iz
w
z
2.
z
w
20
20 34
34
34 20
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó giá trị lớn nhất của
w
là : w 34 20 R IO
Câu 9. (THPT Nguyễn Huệ - Phú Yên - 2021) Xét các số phức thỏa mãn
2 3 4 5 10z i z i
.
Gọi
m
,
M
lần lượt là giá trị nhỏ nhất, lớn nhất của
3 1z i
. Tính
P m M
.
A. 135 365 . B. 2 135 365 . C. 2 365 . D. 2 135 .
Lời giải
Chọn C
+ Ta có:
2 3 4 5 10z i z i
3 6 9 3 12 15 30
z i z i
3 6 9 3 12 15 30z i z i
*
.
+ Đặt
3w z
, gọi
C
,
A
,
B
lần lượt là điểm biểu diễn của các số phức
w
,
6 9i
và
12 15i
.
Khi đó
*
trở thành:
30AC BC
.
+ Mặt khác:
2 2
18 24 30AB
.
Suy ra:
AC BC AB
điểm
C
chạy trên đoạn
AB
.
+ Lại có
3 1 1z i w i
CD
với
D
là điểm biểu diễn số phức
1 i
.
+ Ta có:
:12 9 9 0AB x y
.
; 2d D AB
; 5 5AD ; 365BD .
+ Suy ra
max
365CD M
,
min
2CD m .
+ Vậy: 2 365P m M .
Câu 10. (THPT Lương Thế Vinh - 2021) Xét các số phức
z
thỏa mãn
3 4 2z i
. Gọi
M
và
m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
. Tổng
2 2
M m
bằng
A.
58
. B.
52
. C.
65
. D.
45
.
Lời giải
Chọn A
Gọi
z x yi
với
,x y
.
Khi đó
3 4 2 3 4 2 3 4 2z i x yi i x y i
2 2 2 2
3 4 2 3 4 4x y x y
.
Tập hợp các số phức
z
thỏa mãn
3 4 2z i
là đường tròn
2 2
: 3 4 4C x y
có tâm
3; 4I
, bán kính
2R
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Gọi điểm biểu diễn của số phức z x yi là
;M x y
.
Khi đó
2 2
z x y OM
với
O
là gốc tọa độ.
max
max
z OM
, khi đó
2
2
3 4 2 7OM OI R M
min
min
z OM
, khi đó
2
2
3 4 2 3OM OI R m
.
Vậy
2 2 2 2
7 3 58M m
.
Câu 11. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Xét các số phức
z
thỏa mãn
2 6z z z z
.
Gọi
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
3 2P z i
. Khi đó
M m
bằng
A.
2 53 3 2
2
. B.
6 2
. C.
2 53 2
2
. D. 53 5 .
Lời giải
Chọn A
Giả sử
, ,z x yi x y
khi đó ta có
2z z x
và
2z z y
do đó từ giả thiết bài toán ta
được
2 6 2 2 2 6 1 3z z z z x y x y
.
Từ đây ta có bốn trường hợp sau
1, 0
:
2
x y
I
x y
1, 0
:
4
x y
II
x y
1, 0
:
2
x y
III
x y
và
1, 0
:
4
x y
IV
x y
. Hình biểu diễn của
I
là đoạn
AB
, của
II
là đoạn
CD
, của
III
là
đoạn
BC
và của
IV
là đoạn
AD
. Với
ABCD
là hình vuông như hình vẽ.
Đặt
(3;2)M
khi đó
3 2P z i MN
với
N
là điểm thuộc cạnh của hình vuông
ABCD
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựng đường thẳng đi qua
M
và vuông góc với
AB
cắt
AB
tại
E
và cắt
CD
tại
F
. Từ hình
vẽ ta có
3
max min ( , ) 53
2
P P ME MD d M AB MD
.
Hay
2 53 3 2
2
M m
.
Câu 12. (THPT Chu Văn An - Thái Nguyên - 2021) Xét số phức
z a bi
,a b
thỏa mãn
4 3 5
z i
. Tính
P a b
khi
1 3 1z i z i
đạt giá trị lớn nhất?
A.
8
P
. B.
4P
. C.
6
P
. D.
10
P
.
Lời giải
Chọn D
4 3 5
z i
⇔
4 3 5
a y i
⇔
2 2
4 3 5
a y
Do đó tập hợp các điểm
M
biểu diễn số phức
là đường tròn
C
tâm
4;3
I
, bán kính:
5
r
Gọi
1;3
A
;
1; 1
B
;
0;1
E
là trung điểm của
AB
Nhận xét:
2; 4
AB
;
4; 2
IE
;
. 8 8 0
AB IE
⇒
IE AB
1 3 1
T z i z i MA MB
Xét:
2
2 2 2 2 2 2
2 4
2
4
0
T MA MB MA MB ME AB ME
⇒ Giá trị của
maxT
đạt được khi
max
ME
Khi đó điểm
M
thỏa mãn hệ điều kiện đẳng thức xảy ra:
*
MA MB
M M
Ta có:
5 1
3
5 2 5
MI r
r IE
ME
⇒
1
3
6;4
1
1
3
OI ME
OM
Vậy
maxT
đạt được khi
6 4z i
. Khi đó:
6 4 10
P a b
.
Câu 13. (THPT Quốc Oai - Hà Nội - 2021) Trong mặt phẳng phức
Oxy
, trong các số phức
z
thỏa mãn
1 1z i
. Nếu số phức
z
có môđun lớn nhất thì số phức
z
có phần thực bằng bao nhiêu?
A.
2 2
2
. B.
2 2
2
. C.
2 2
2
. D.
2 2
2
.
Lời giải
Chọn D
Ta có:
1 1
z i
.
Vậy trong mặt phẳng phức
Oxy
, các số phức
z
thỏa mãn
1 1z i
là hình tròn tâm
1;1
I
,
bán kính
1R
.
Vậy số phức có mô đun lớn nhất:
max
1 2
z OI R
.
B
A
M
I
E
M*
(C)
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Nếu gọi
;M x y
là điểm biểu diễn số phức đó thì
.
OM
OM OI
OI
1 2
.
2
OM OI

1 2
2
1 2
2
x
y
.
Vậy số phức có phần thực
1 2 2 2
2
2
x
.
Câu 14. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức
z
thỏa mãn
3 8 7z i
và số phức
4 3w i
. Gọi
M
là giá trị lớn nhất của biểu thức
P z w
. Chọn khẳng định đúng trong các
khẳng định sau
A.
18;19M
. B.
21;22M
. C.
19;20M
. D.
20;21M
.
Lời giải
Chọn D
Giả sử
A z
. Theo giả thiết
3 8 7z i A
đường tròn
C
tâm
3; 8 , 7I R
.
Giả sử
4;3 7;11 170 49 7B w B IB IB R
. Suy ra
B
nằm ngoài
đường tròn
C
.
Khi đó:
P z w AB
. Suy ra:
max max
M P AB
.Xảy ra khi và chỉ khi
A
là giao điểm (nằm
ngoài đoạn
IB
) của đường thẳng
IB
với đường tròn
C
.
170 7 20,04 20;21 .
max max
M P AB IB R
Câu 15. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức
1 2
,z z thỏa mãn đồng thời hai điều
kiện sau:
| 1| 34z
,
| 1 | | 2 |z mi z m i
( trong đó
m
là số thực ) và sao cho
1 2
z z
lớn
nhất. Khi đó giá trị của
1 2
z z
bằng
A. 2. B. 10. C. 130 . D.
2
.
Lời giải
Chọn A
Đặt
( , )z x yi x y
.
Từ giả thiết ta có hệ phương trình:
2 2
2 2
2 2 2 2
( 1) 34
( 1) 34( )
(2 2 ) (2 4) 3 0( )
( 1) ( ) ( ) ( 2)
x y
x y C
m x m y
x y m x m y
Hai số phức
1 2
,z z là hai nghiệm của hệ phương trình trên. Gọi
,M N
lần lượt là các điểm biểu
diễn cho
1 2
,z z
khi đó
1 2
z z MN
.
Ta có
1 2
z z
lớn nhất khi đường thẳng
( )
cắt đường tròn
( )C
theo dây cung
MN
có độ dài
lớn nhất, tức là
( )
đi qua tâm
(1;0)I
của
( )C
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thay tọa độ
I
vào
( )C
ta có:
1
2
m
Với
1
2
m
giải hệ
2 2
( 1) 34
( ; ) {( 4; 3);(6;3)}
3 5 3 0
x y
x y
x y
Giả sử
1 2 1 2
4 3 , 6 3 2
z i z i z z
.
Câu 16. (Trung Tâm Thanh Tường - 2021) Cho số phức z thỏa mãn hệ thức
2 3 .z i z i
Giá trị
nhỏ nhất của biểu thức
2 1 2P z i i
bằng
A.
7 2
.
3
B.
7 2
.
2
C.
7
2
. D.
7 3
3
.
Lời giải
Chọn B
Gọi
2
, , 1
z x yi x y i
và
;M x y
là điểm biểu diễn của số phức z.
2 2 2
2
2 3 2 3 1 3 0.
z i z i x y x y x y
Vậy tập hợp điểm biểu diễn của số phức z là
: 3 0.
x y
1
2 1 2 1
2 2
P
P z i i z i
Gọi
1
1; 2 .
2
A P MA
Do
min min
2P MA
M là hình chiếu của A lên đường thẳng
.
min
7 2
2 ; .
2
P d A
Câu 17. (THPT Trần Phú - Đà Nẵng - 2021) Xét hai số phức
1 2
,z z
thỏa mãn
1 1 1
2 3
z i i z z
và
2 2
3 1 2z i z i
. Giá trị nhỏ nhất của
1 2
z z
bằng:
A.
4 6
. B.
2 6
. C.
34
5
. D.
28
15
.
Lời giải
Chọn D
+ Gọi
1 2
,
z x yi z x y i
+ Ta có :
1 1 1 1 1 1
2 2
2 2
2 3 2 2
1 5
2 1 2 ( )
2 2
z i i z z z i z z
x y y y x x P
và
2 2
3 1 2 8 6 5 0( )z i z i x y d
.
Do đó, tập hợp các điểm biểu diễn của
1
z
là
2
1 5
( ) : 2
2 2
P y x x
; tập hợp các điểm biểu diễn
của
2
z
là
( ) :8 6 5 0
d x y
+ Gọi
( )
là đường thẳng tiếp xúc với
( )P
và song song với
( )d
thì
( )
có phương trình là:
41
8 6 0
3
x y
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Vậy
1 2
2 2
41
5
28
3
min ( , )
15
8 6
z z d d
Câu 18. Xét hai số phức
1 2
,z z
thỏa mãn
1 2
2, 1 6z i z
và
1 2
5z z . Giá trị lớn nhất
1 2
2 2021z z
bằng
A.
2044
. B.
23 2021
. C.
23 2021
. D.
2 23 2021
.
Lời giải
Chọn C
Đặt
1 2
,z a bi z c di với
, , , .a b c d
Theo giả thiết thì
1
1
z
2 2
4a b
2 2
6
1 6 3
1
i z z
i
2 2
3c d
1 2
5z z
2 2
5a c b d
Do đó
2 2 2 2
2 2 5 1a ac c b bd d ac bd
Ta có
1 2
2 2 2
z z a c b d i
nên
2 2 2
2 2 2 2
1 2
2 2 2 4 4 23z z a c b d a b c d ac bd
Áp dụng bất đẳng thức
z z z z
, ta có
1 2 1 2
2 2021 2 2021 23 2021.z z z z
Câu 19. Xét hai số phức
1 2
;z z
thỏa mãn
1 2
1; 4z z
và
1 2
5z z . Giá trị lớn nhất của
1 2
z 2 7z i
bằng
A.
7 89
. B.
7 89
. C.
7 2 89
. D.
7 2 89
.
Lời giải
Chọn B
Đặt
1 2
,z a bi z c di với
, , , .a b c d
Theo giả thiết thì
2 2 2 2 2 2
1, 16, ( ) ( ) 5.a b c d a c b d
Do đó
2 2 2 2
2 2 5 6.a ac c b bd d ac bd
Ta có
1 2
2 ( 2 ) ( 2 )z z a c b d i nên
2 2 2 2 2 2
1 2
2 ( 2 ) ( 2 ) 4( ) 4( ) 89.
z z a c b d a b c d ac bd
Áp dụng bất đẳng thức
z z z z
, ta có ngay
1 2 1 2
2 7 2 7 7 89z z i z z i
Câu 20. Cho hai số phức
,u v
thỏa mãn
10u v
và
3 4 50u v
. Tìm Giá trị lớn nhất của biểu thức
4 3 10u v i
.
A.
30
. B.
40
. C.
60
. D.
50
.
Lời giải
(d)
(
P
)
x
( )
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
Ta có
2
.z z z
. Đặt
3 4T u v
,
4 3M u v
.
Khi đó
2
3 4 3 4T u v u v
2 2
9 16 12
u v uv vu
.
Tương tự ta có
2
4 3 4 3M u v u v
2 2
16 9 12
u v uv vu
.
Do đó
2 2
2 2
25 5000
M T u v
.
Suy ra
2 2
5000
M T
2
5000 50 2500
hay
50
M
.
Áp dụng
z z z z
ta có
4 3 10 4 3 10 50 10 60
u v i u v i
.
Suy ra
max 4 3 10 60
u v i
.
Câu 21. Cho hai số phức
,u v
thỏa mãn
10
u v
và
3 4 50
u v
. Tìm Giá trị lớn nhất của biểu thức
4 3 10u v i
.
A.
30
. B.
40
. C.
60
. D.
50
.
Lời giải
Chọn C
Ta có
2
.z z z
. Đặt
3 4T u v
,
4 3M u v
.
Khi đó
2
3 4 3 4T u v u v
2 2
9 16 12
u v uv vu
.
Tương tự ta có
2
4 3 4 3M u v u v
2 2
16 9 12
u v uv vu
.
Do đó
2 2
2 2
25 5000
M T u v
.
Suy ra
2 2
5000
M T
2
5000 50 2500
hay
50
M
.
Áp dụng
z z z z
ta có
4 3 10 4 3 10 50 10 60
u v i u v i
.
Suy ra
max 4 3 10 60
u v i
.
Câu 22. Cho các số phức
1
z
và
2
z
thỏa mãn
1
1 1z i
và
2
2 3 2
z i
. Tìm giá trị nhỏ nhất của biểu
thức
1 2
.P z z
A.
2
. B.
3
2
. C.
5
2
. D.
3
.
Lời giải
Chọn A
Giả sử M, N lần lượt là điểm biểu diễn của số phức
1
z
và
2
z
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
1
1 1 ;1 , 1; 1z i M I I
2
2 3 2 ;2 , 2;3z i N J J
1 2
P z z MN
Ta thấy hai đường tròn (I) và (J) nằm ngoài nhau. Do đó
'' '' ' 'M N MN M N
.
1 2
P z z MN
đạt giá trị nhỏ nhất khi và chỉ khi
'', ''M M N N
.
min
2, 8
max
P IJ R r P I R r .
Câu 23. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hai số phức
1
z có điểm biểu diễn
M
, số phức
2
z có
điểm biểu diễn là
N
thỏa mãn
1
1z
,
2
3z
và
120MON . Giá trị lớn nhất của
1 2
3z 2 3z i
là
0
M
, giá trị nhỏ nhất của
1 2
3z 2 1 2z i
là
0
m
. Biết
0 0
7 5 3M m a b c d
, với
, , ,a b c d
. Tính
a b c d
?
A.
9
. B.
8
. C.
7
. D.
6
.
Lời giải
Chọn B
Gọi
1
M là điểm biểu diễn của số phức
1
3z , suy ra
1
3OM .
Gọi
1
N là điểm biểu diễn của số phức
2
2z , suy ra
1
6ON . Gọi
P
là điểm sao cho
1 1
OM ON OP
. Suy ra tứ giác
1 1
OM PN là hình bình hành.
Do từ giả thiết
120MON , suy ra
1 1
120M ON .
Dùng định lí cosin trong tam giác
1 1
OM N ta tính được
1 1
1
9 36 2.3.6. 3 7
2
M N
;
5
4
3
2
1
1
2
y
2 2 4
x
M'
M''
N''
O
I
J
N'
M
N
120
x
y
P
N
1
N
M
1
O
1
M
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
và định lí cosin trong tam giác
1
OM P ta có
1
9 36 2.3.6. 3 3
2
OP
.
Ta có
1 1 1 2
3 2 3 7M N z z ;
1 2
3 2 3 3OP z z .
 Tìm giá trị lớn nhất của
1 2
3z 2 3z i
.
Đặt
1 2 1 1
3 2 3 3z z w w , suy ra điểm biểu diễn
1
w là
A
thuộc đường tròn
1
C
tâm
0;0O
bán kính
1
3 3R
. Gọi điểm
1
Q là biểu diễn số phức
3i
.
Khi đó
1 2 1
3z 2 3z i AQ
, bài toán trở thành tìm
1
max
AQ
biết điểm
A
trên đường tròn
1
C
.
Dễ thấy
1 1 1
3 3 3
max
AQ OQ R .
 Tìm giá trị nhỏ nhất của
1 2 1 2
3z 2 1 2 3z 2 1 2z i z i
.
Đặt
1 2 2 2
3 2 3 7z z w w , suy ra điểm biểu diễn
2
w là
B
thuộc đường tròn
2
C
tâm
0;0O
bán kính
1
3 7R
. Gọi điểm
2
Q là biểu diễn số phức
1 2i
.
Khi đó
1 2 2
3z 2 1 2z i BQ
, bài toán trở thành tìm
2
min
BQ
biết điểm
B
trên đường tròn
2
C
. Dễ thấy điểm
2
Q nằm trong đường tròn
2
C
nên
2 2 2
min
3 7 5BQ R OQ .
Vậy
0 0
3 7 3 3 5 3M m
.
Câu 24. Xét hai số phức
1 2
;z z
thỏa mãn
1 2
2; 5z z và
1 2
3z z
. Giá trị lớn nhất của
1 2
z 2 3z i
bằng
A.
3 2 3
. B.
3 3 2
. C.
3 26
. D. 26 3 .
Lời giải
Chọn B
Cách 1:
Đặt
1 2
,z a bi z c di
(với
, , ,a b c d
)
Theo bài ra ta có:
2 2 2 2
1 2
2 2; 5 5z a b z c d
2 2
2 2 2 2
1 2
3 9 2 9z z a c b d a b c d ac bd
1ac bd
2 2
2 2 2 2
1 2
2 2 2 4 4 18 3 2z z a c b d a b c d ac bd
Theo tính chất
' 'z z z z
ta có:
1 2 1 2
z 2 3 z 2 3 3 2 3z i z i
Cách 2:
x
y
Q
N
3
R
O
P
M
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Gọi M là điểm biểu diễn cho số phức
1
z
, M thuộc đường tròn tâm O bán kính
2 2
OM
Gọi N là điểm biểu diễn cho số phức
2
z
, N thuộc đường tròn tâm O bán kính
5 5
ON
Suy ra
NM OM ON
là điểm biểu diễn cho
1 2 1 2
3
z z MN z z
Gọi P là điểm biểu diễn cho số phức
2
2z
, P thuộc đường tròn tâm O bán kính
2 5 2 5
OP
Gọi Q là điểm biểu diễn cho số phức
3i
,
0;3 3
Q OQ
Dựng hình bình hành
OMRP
ta có
OR OM OP
R là điểm biểu diễn cho số phức
1 2
2z z
Ta có:
2 2 2
2 5 9 1
cos
2. .
2. 2. 5 10
OM ON MN
MON
OM ON
2 2 2 2 2
2. . .cos 2. . .cos
OR OP PR OP PR OPR OP OM OPOM MON
1
20 2 2.2 5. 2. 3 2
10
OR
1 2
z 2 3
T z i OR OQ QR QR

T đạt giá trị lớn nhất khi QR lớn nhất
0
180 3 3 2
QOR QR OQ OR
Vậy T đạt giá trị lớn nhất bằng
3 3 2
.
Câu 25. Cho hai số phức
1 2
,z z
thỏa mãn
1 2
3 4z z i
và
1 2
5
z z
. Tính giá trị lớn nhất của biểu thức
1 2
P z z
A.
10
. B.
5 2
. C.
5
. D.
10 2
.
Lời giải
Chọn B
Đặt
1
2
, , , .
z a bi
a b c d
z c di
Theo giả thiết ta có:
1 2
1 2
2 2
3
3 4
4 .
5
5
a c
z z i
b d
z z
a c b d
Xét
2 2 2 2 2 2 2 2
1 2
1 1 . .P z z a b c d a b c d
Mà
2 2 2 2
2 2 2
2 2 2 2
3 4 5
25.
2 2
a c b d a c b d
a b c d
Nên
5 2.
P
Câu 26. Xét các số phức
1
z
,
2
z
thỏa mãn
1
4 1
z
và
2
2 1
iz
. Giá trị lớn nhất của
1 2
2 6z z i
bằng
A.
2 2 2
. B.
4 2
. C.
4 2 9
. D.
4 2 3
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
3 2
2 ,z z suy ra
1 2 1 2 1 3
2 6 ( 2 ) 6i 6 .P z z i z z z z i
Và
2 3
1
2
z z
thế vào
2 3 3
1 1
2 1 2 1 2 . 2 1. 2
2 2
iz iz iz i i
3
4 2.z i
Gọi
, A B
là hai điểm biểu diễn cho hai số phức
3 1
, .z z
3
4 2 z i A
thuộc đường tròn tâm
3
(0;4), 2.I R
1
4 1 z B
thuộc đường tròn tâm
1
(4;0), 1.J R
1 3 1 3 1 3
6 6 6 6 4 2 1 2 6 4 2 9.P z z i z z i AB IJ R R
Vậy
max
4 2 9
P
.
Câu 27. Cho các số phức
1 2 3
, ,z z z
thỏa mãn
1 2
1 4 2, 4 6 1z i z i
và
3 3
1 2z z i
. Tìm giá
trị nhỏ nhất của biểu thức
3 1 3 2
P z z z z
.
A.
14
2
2
. B.
29 3
. C.
14
2 2
2
. D.
85 3
.
Lời giải
Chọn D
Đặt
1 1 1
z x y i
1 1
,x y
.
2 2
1 1 1
1 4 2 1 4 4z i x y
.
Vậy tập hợp điểm
M
biểu diễn số phức
1
z
là đường tròn
2 2
1
: 1 4 4C x y
có tâm
1
1;4I
, bán kính
1
2R
.
Đặt
2 2 2
z x y i
2 2
,x y
.
2 2
2 2 2
4 6 1 4 6 1z i x y
.
Vậy tập hợp điểm
N
biểu diễn số phức
2
z
là đường tròn
2 2
2
: 4 6 1C x y
có tâm
2
4;6I
, bán kính
2
1R
.
Đặt
3 3 3
z x y i
3 3
,x y
.
3 3 3 3
1 2 2 0z z i x y
.
Vậy tập hợp điểm
A
biểu diễn số phức
3
z
là đường thẳng
: 2 0d x y
.
Khi đó:
3 1 3 2
P z z z z AM AN
Mặt khác,
1 1 2 2
14
, ; , 2 2
2
d I d R d I d R
và
1 2
,I I
nằm cùng phía đối với
d
.
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Gọi
2
C
là đường tròn đối xứng với với
2
C
qua
d
, suy ra
2 2
2
: 8 2 1C x y
và gọi
N
là điểm đối xứng với
N
qua
d
.
2
C
có tâm
2
8;2I
, bán kính
2
1R
.
Ta có:
1 1 1 1 1
2AM MI AI AM AI MI AI
.
2 2 2 2 2 2
1AN NI AN N I AI AN AI N I AI
.
Suy ra
1 2 1 2
3 3 85 3P AM AN AM AN AI AI I I
. Đẳng thức xảy ra khi và
chỉ khi 3 điểm
1 2
, ,I A I
thẳng hàng.
Vậy
min 85 3P
.
Câu 28. (THPT Đoàn Thượng - Hải Dương - 2021) Biết số phức
z
thoả mãn
| 3 4 | 5z i
và biểu
thức
2 2
| 2 | | |T z z i
đạt giá trị lớn nhất. Tính
| |z
.
A.
| | 33z
. B.
| | 5 2z
. C.
| | 50z
. D.
| | 10z
.
Lời giải
Chọn B
Gọi số phức
( ; )z x yi x y
Ta có
2 2
| 3 4 | 5 | 3 4 | 5 3 4 5z i x yi i x y
Suy ra tập hợp điểm biểu diễn số phức
z
là đường tròn
C
tâm
3;4I
, bán kính
5R
(1)
Mà
2 2
2 2 2 2 2 2
| 2 | | | | 2 | | | 2 1
T z z i x yi x yi i x y x y
4 2 3 4 2 3 0T x y x y T
Suy ra tập hợp điểm biểu diễn số phức
z
là đường thẳng
:4 2 3 0d x y T
(2)
Do tập hợp điểm biểu diễn số phức
z
thoả mãn hai điều kiện (1) và (2) nên
C
và
d
có điểm
chung
2 2
| 4.3 2.4 3 |
( , ) 5 | 23 | 10 13 33
4 2
T
d I d R T T
2 2
5
3 4 5
33 5 5 | | 5 2
5
4 2 30 0
x
x y
MaxT z i z
y
x y
.
Câu 29. (THPT Ngô Quyền - Quảng Ninh - 2021) Cho Xét các số phức
1 2
,z z thỏa mãn
2 2
1 1
1 2 1z z i
;
2
3 5.z i
Giá trị nhỏ nhất của
1 2
P z z
bằng
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A
.
5 . B.
3 5
5
. C
.
2
5 . D.
2 5
5
.
Lời giải
Chọn D
Gọi
1
1 1 1 1
, ,z x iy x y
,
2
2 2 2 2
, ,z x iy x y
khi
đó
1
1
;M x y
,
2
2
;N x y
là
điểm biểu
diễn của số phức
1
z ,
2
z tr
ong mặt phẳng
Oxy
.
T
a có
2
2
1 1
1 2 1z z i
2
2
1
1 1 1
1
2 1x iy x i y
1
1
2
2 0x y . Suy ra
M
thuộc
đường thẳng
:
2 2 0x y
.
Mặt
khác
2
3
5z i Suy ra
N
thuộc
đường tròn tâm
3
;1I
,
bán kính
5R .
T
a có
7
5
,
5
d I
khôn
g cắt đường tròn.
Khi đó
1
2
P
z z MN AH
min
7 5 2 5
, 5
5 5
MN AH IH IA d I R
.
| 1/84
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ NHẬN BIẾT Câu 1.
(Sở Vĩnh Phúc - 2021) Tìm phần thực của số phức z  2  3i A. 2  . B. 3 . C. 2 . D. 3  . Câu 2.
(Sở Lào Cai - 2021) Cho hai số phức z  2  i và z  1 2i . Khi đó phần ảo của số phức z .z 1 2 1 2 bằng: A. 2 . B. 3i . C. 3 . D. 2  i . Câu 3.
(Sở Lào Cai - 2021) Mô đun của số phức z  2 3i bằng A. 5 . B. 13 . C. 5 . D. 13 . Câu 4.
(Sở Hà Tĩnh - 2021) Cho hai số phức z  3  2i và z  2  i . Số phức z z bằng 1 2 1 2 A. 5   i . B. 5  i . C. 5   i . D. 5  i . Câu 5.
(Sở Hà Tĩnh - 2021) Số phức liên hợp của số phức z  2   6i là A. z  2   6i . B. z  2   6i .
C. z  2  6i .
D. z  2  6i . Câu 6.
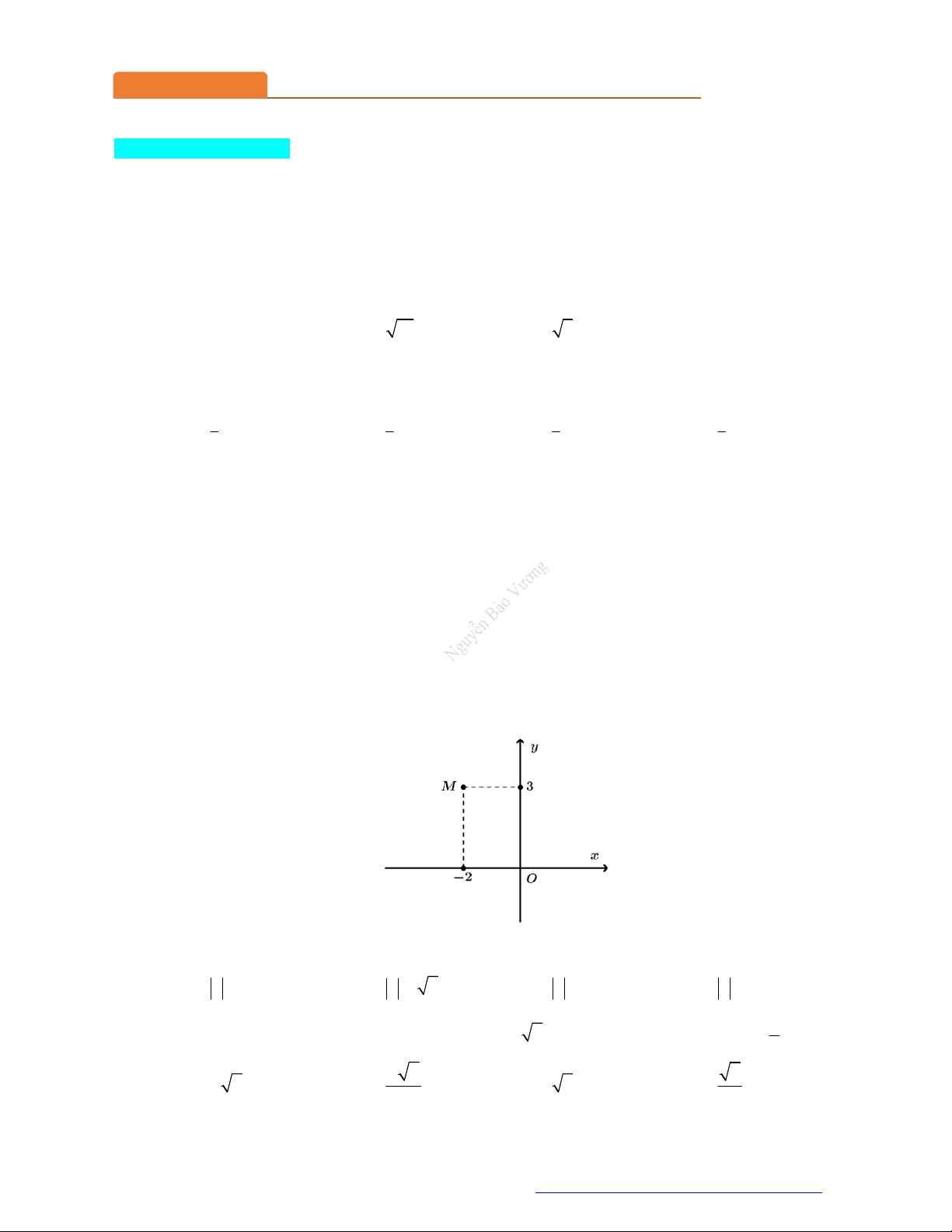
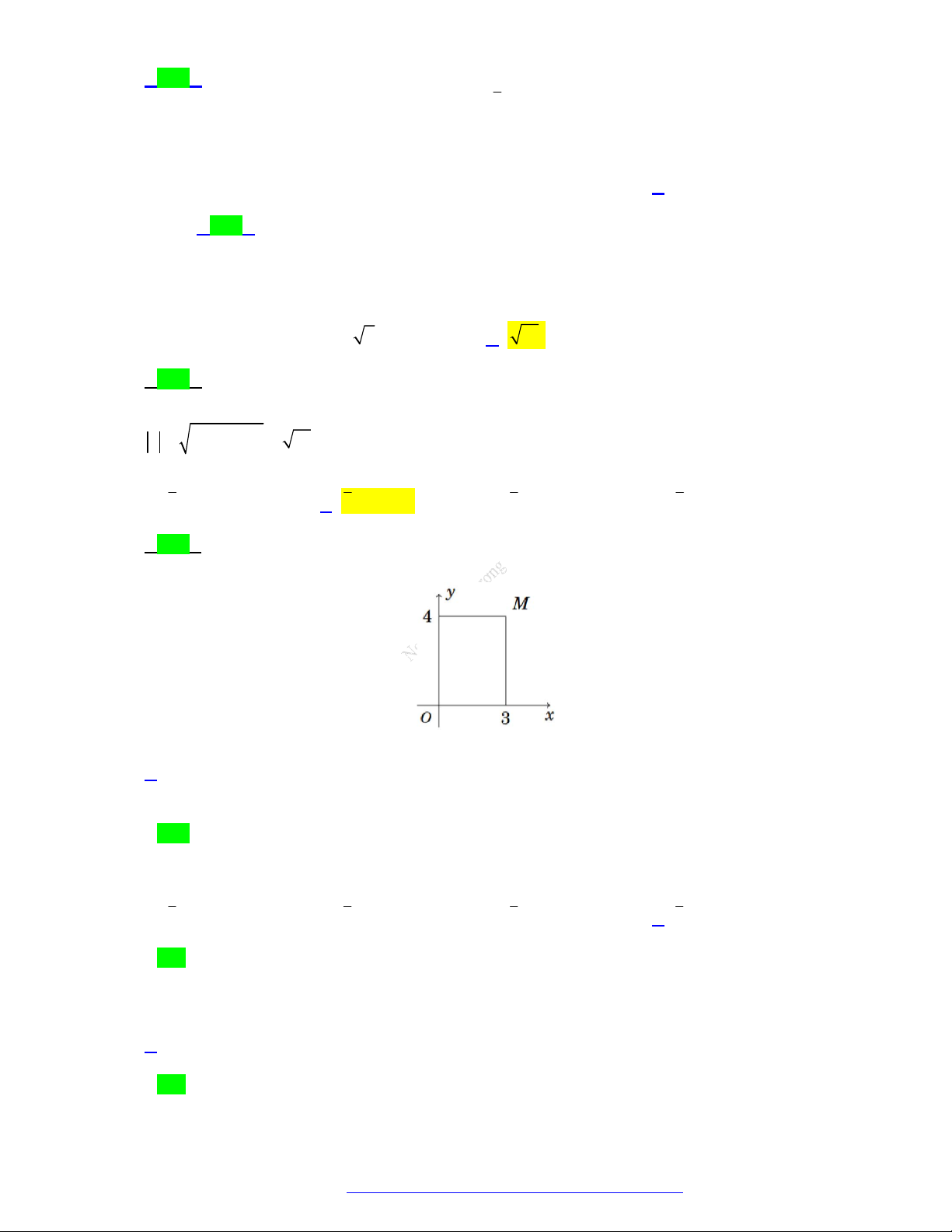
(Sở Hà Tĩnh - 2021) Trên mặt phẳng, điểm M  1
 ;3 là điểm biểu diễn số phức z . Phần thực của z bằng A. 1. B. 3 . C. 3  . D. 1  . Câu 7.
(Sở Yên Bái - 2021) Phần ảo của số phức z  12 18i là A. 18 . B. 18 . C. 1  8i . D. 12. Câu 8.
(Sở Tuyên Quang - 2021) Tìm phần thực và phần ảo của số phức z  3  2i .
A. Phần thực bằng 3
 và phần ảo bằng 2i .
B. Phần thực bằng 3
 và phần ảo bằng 2 .
C. Phần thực bằng 3 và phần ảo bằng 2i .
D. Phần thực bằng 3 và phần ảo bằng 2 . Câu 9.
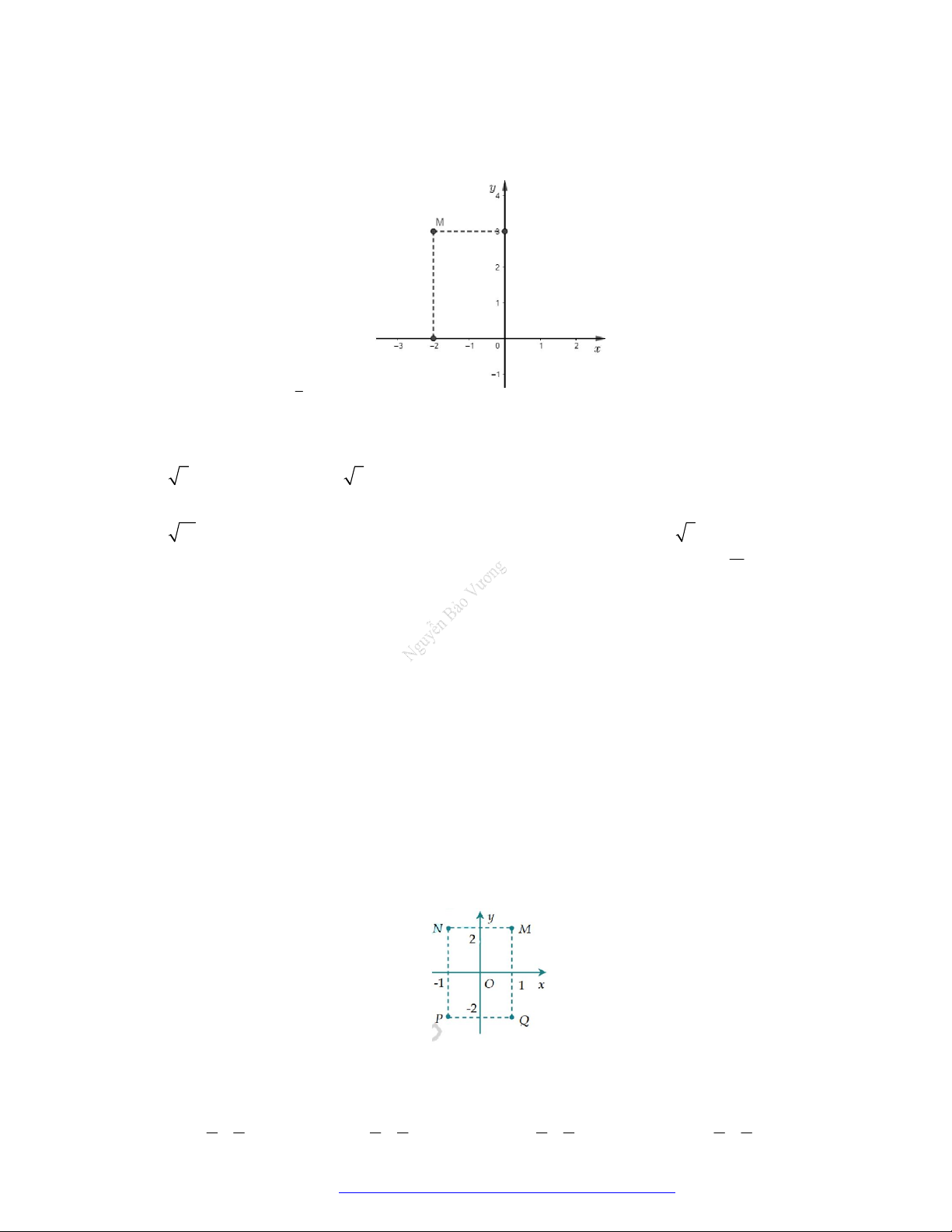
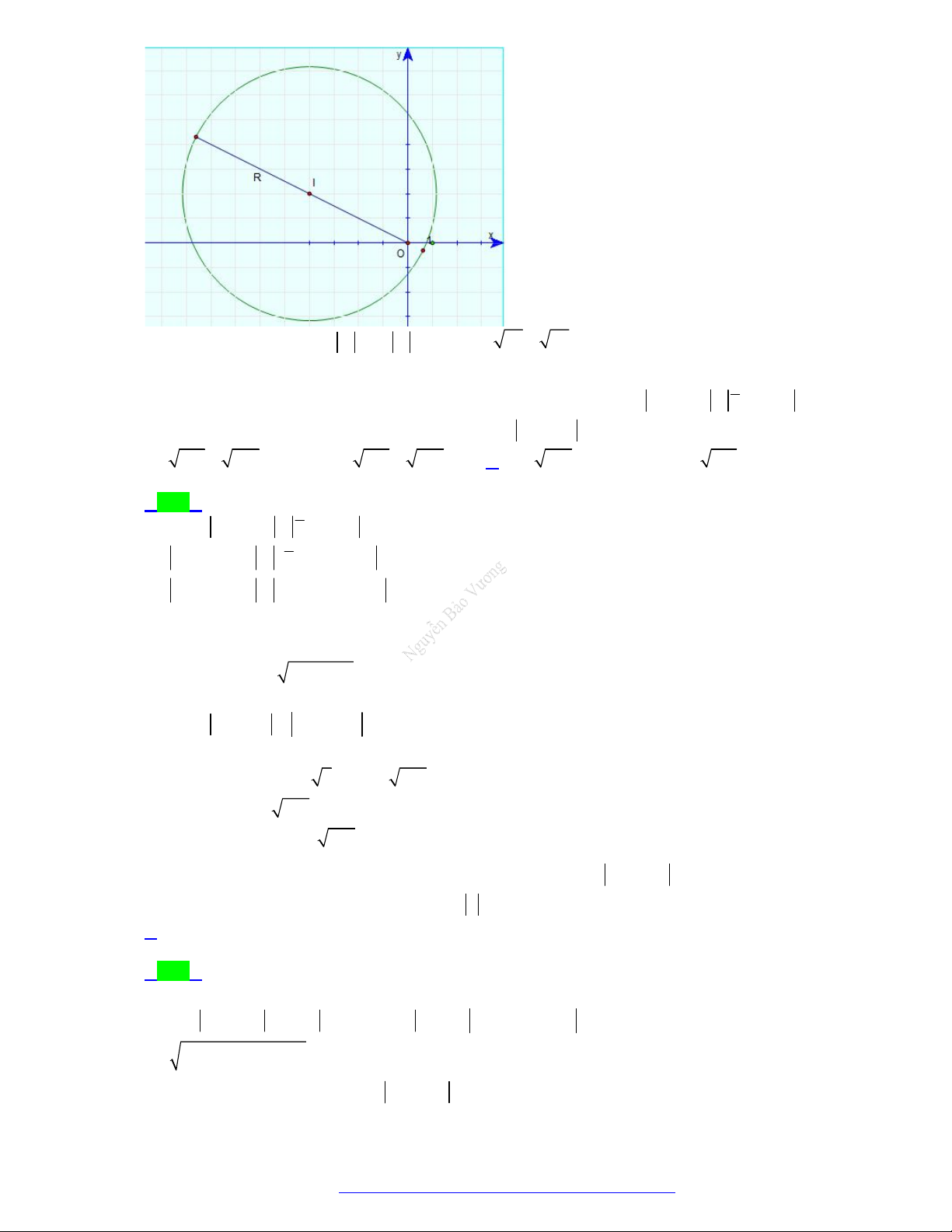
(Sở Tuyên Quang - 2021) Điểm M trong hình vẽ dưới đây biểu thị cho số phức: A. 2  3i . B. 3  2i . C. 2   3i . D. 3  2i .
Câu 10. (Sở Tuyên Quang - 2021) Tính môđun của số phức z  4  3i . A. z  5 . B. z  7 . C. z  25 . D. z  7 . 1
Câu 11. (Sở Tuyên Quang - 2021) Cho số phức z  1 2 .
i Tìm phần ảo của số phức P z  2 2 A.  2 . B. . C. 2 . D. . 3 3
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hai số phức
z  2  3i, z  3  2i . Tích z z bằng 1 2 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 A. 5  i . B. 5i . C. 6  6i . D. 12  5i
Câu 13. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng Oxy điểm
M 1;  2  biểu diễn cho số phức nào sau đây.
A. z  1 2i . B. z  1   2i C. z  2   i .
D. z  1 2i
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức có điểm biểu diễn là M như hình vẽ.
Phần ảo của số phức z là A. 3 . B. 3  . C. 2 . D. 2  .
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Môđun của số phức 2  i là A. 5 . B. 3 . C. 3 . D. 5 .
Câu 16. (Chuyên KHTN - 2021) Mô đun của số phức z  3  2i bằng A. 13 . B. 13 . C. 5 . D. 5 .
Câu 17. (Chuyên KHTN - 2021) Cho hai số phức z  2  3i và z  2  i . Số phức w z z z có phần 1 2 1 2 2 thực bằng A. 7. B. 9. C. 4. D. 3.
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức có phần thực bằng 2 và phần ảo bằng 1 là A. 2  . i B. 1  2 . i C. 2  . i D. 1 2 . i
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai số phức z  4  3i và z  7  5i . Số 1 2
phức z z z là 2 1 A. 1  1 8i . B. 11 8i . C. 1  1 8i . D. 11 8i .
Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Nghiệm phức có phần ảo dương của phương trình 2
z  2z  5  0 là A. 1   2i . B. 1 2i . C. 1 2i . D. 1   2i .
Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức z  1
  2i . Điểm biểu diễn số phức
liên hợp của z trong mặt phẳng tọa độ Oxy là điểm A. Q. B. N. C. P. D. M.
Câu 22. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức z thỏa mãn 1 iz i  0 là 1 1 1 1 1 1 1 1 A. z    i . B. z   i . C. z   i . D. z    i . 2 2 2 2 2 2 2 2
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 23. (Chuyên Quốc Học Huế - 2021) Số phức liên hợp của số phức z  3  5i là
A. z  3  5i .
B. z  3  5i .
C. z  5  3i .
D. z  3  5i
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Cho số phức z a bi  ,
a b   . Chọn phương án đúng.
A. Phần ảo của số phức z là b .
B. Phần ảo của số phức z là bi .
C. Phần thực của số phức z là b .
D. Mô đun của số phức z là 2 2 a b .
Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Gọi z , z là nghiệm của phương trình 1 2 2
z  2z  2  0 . Biết số phức z có phần ảo âm. Phần ảo của số phức z . 1 2 A. 1. B. 1  . C. i . D. 1 i .
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) 7  3i   9   i bằng A. 1  6  2i . B. 16  2i . C. 2   4i . D. 16  2i .
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hai số phức z  2  ;
i z  3  2i . Trên mặt phẳng 1 2
tọa độ Oxy , điểm biểu diễn số phức 2z z có tọa độ là 1 2 A. 7  ;1 . B. 0;7 . C. 5;  1 . D. 7;0 .
Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức z  4  3i . Tìm phần thực và phần ảo của
số phức liên hợp của số phức z
A. Phần thực bằng 4 và phần ảo bằng 3
B. Phần thực bằng 4
 và phần ảo bằng 3i
C. Phần thực bằng 4 và phần ảo bằng 3i
D. Phần thực bằng 4 và phần ảo bằng 3
Câu 29. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Số phức liên hợp của số phức 4  5i là A. 4  5i . B. 5  4i .
C. 4  5i . D. 4  5i .
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số thực x, y thỏa mãn 2  yi x  5i, trong đó i là đơn
vị ảo. Giá trị của x và y là
A. x  2, y  5  .
B. x  2, y  5  . i C. x  5  , y  2. D. x  5  i, y  2.
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Số phức liên hợp của số phức z  3  4i là
A. z  3  4i .
B. z  3  4i .
C. z  3  4i .
D. z  3  4i .
Câu 32. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hai số phức z  1
  i , z  2  3i . Số phức 1 2
liên hợp của z z z là 1 2 A. . B. . C. . D. .
Câu 33. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hai số phức z  2  2 ; i z  3
  3i . Khi đó số 1 2
phức z z là 1 2 A. 1   i B. 5   5i C. 5  i D. 5  5i
Câu 34. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức z  2  4i , mô đun của số phức w  z 1 bằng A. 5 . B. 2 5 1. C. 2 5 . D. 7 .
Câu 35. (THPT Nguyễn Huệ - Phú Yên - 2021) Số phức z thỏa mãn 3  iz 1  4i là 7 11 7 11 7 11 7 11 A.   i . B. i . C.   i . D. i . 10 10 10 10 10 10 10 10
Câu 36. (THPT Lương Thế Vinh - 2021) Gọi z , z là hai nghiệm phức của phương trình 2 z  2z  5  0 . 1 2 2 2 Giá trị của zz bằng 1 2 A. 10. B. 50. C. 5. D. 18.
Câu 37. (THPT Lương Thế Vinh - 2021) Số phức 2  4ii bằng số phức nào dưới đây?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 A. 4   2i . B. 4   2i . C. 4  2i . D. 4  2i .
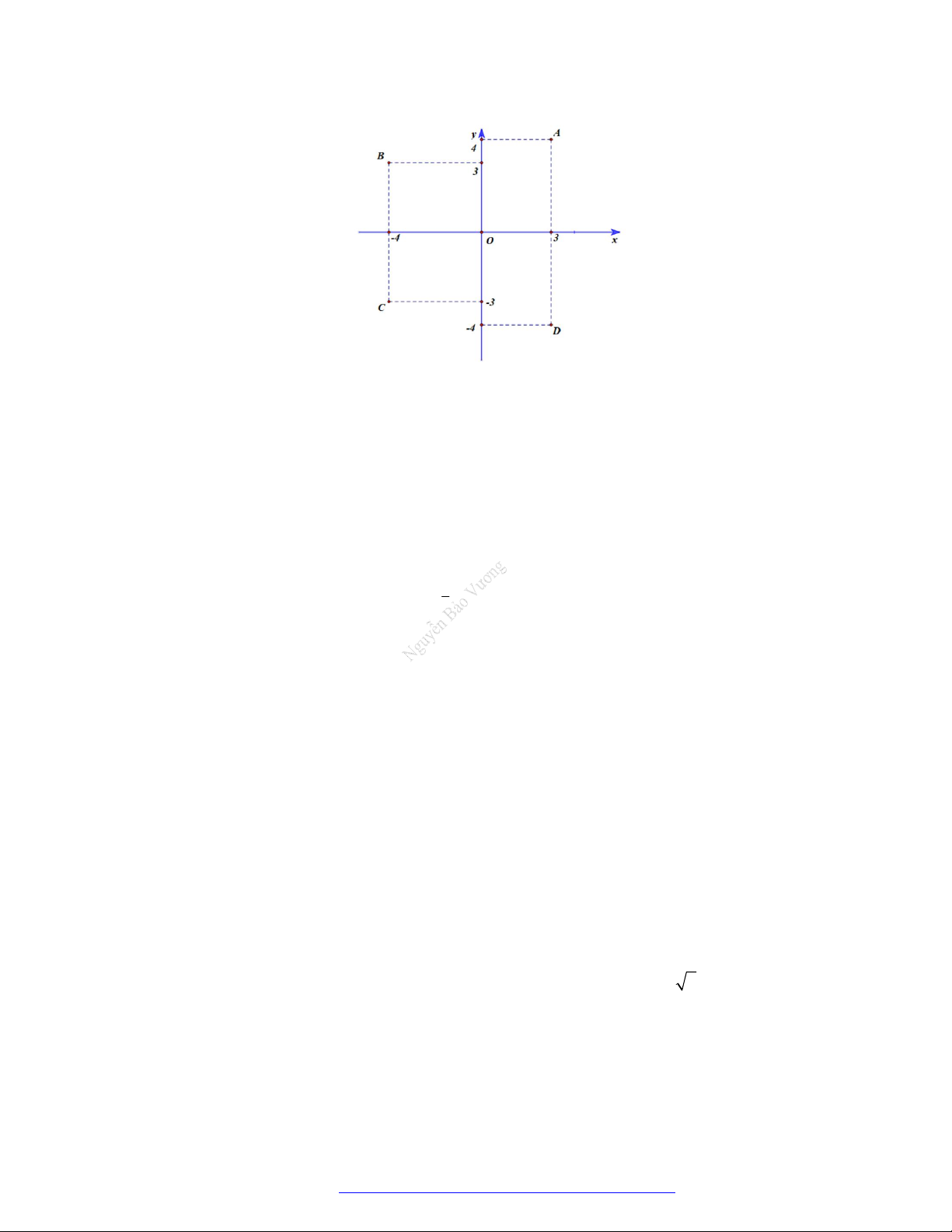
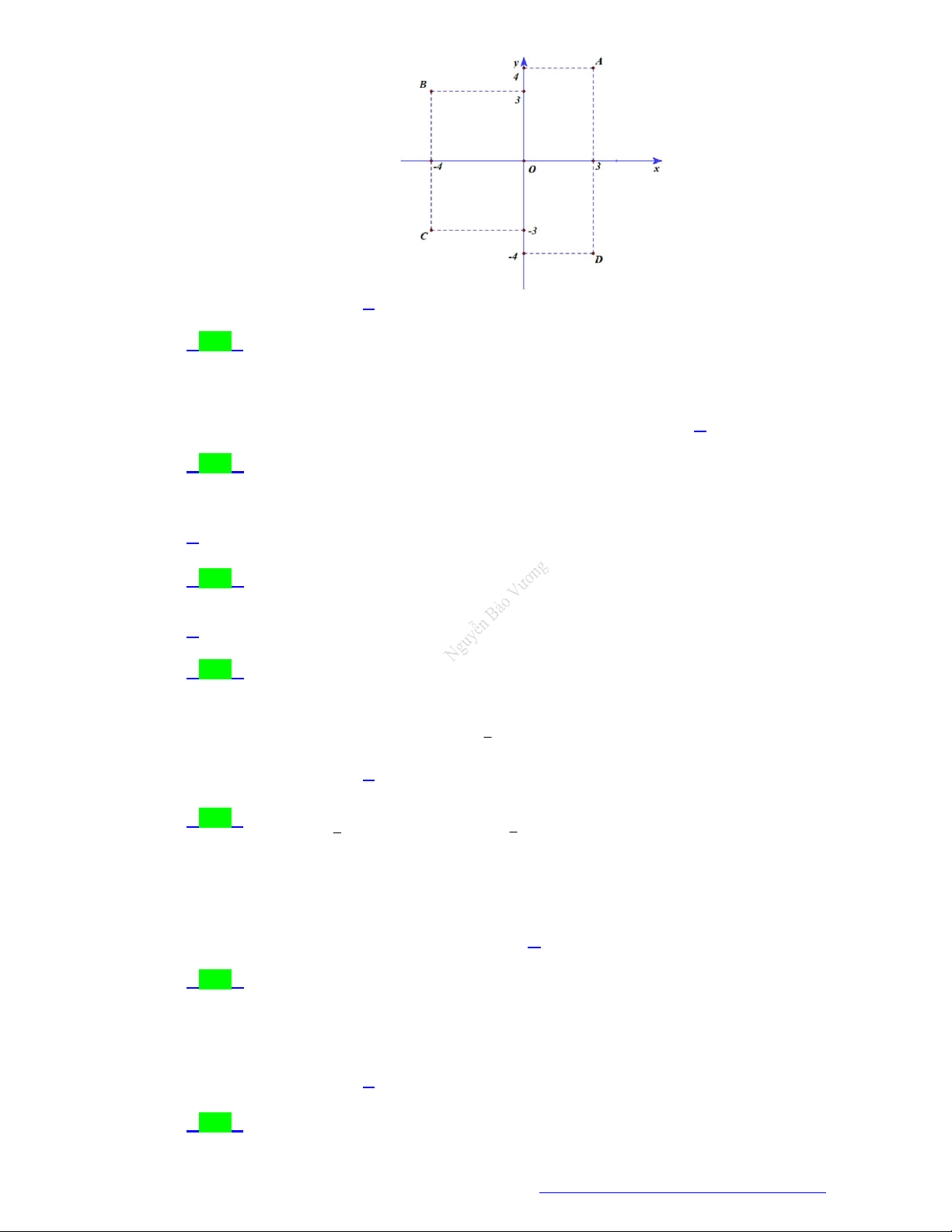
Câu 38. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Điểm nào trong hình vẽ bên dưới là điểm biểu diễn
số phức z  3  4i ,
A. Điểm A .
B. Điểm D .
C. Điểm C . D. Điểm B .
Câu 39. (THPT Đào Duy Từ - Hà Nội - 2021) Số phức liên hợp của 4  3i là A. 3  4i . B. 4   3i . C. 3  4i . D. 4  3i .
Câu 40. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z  3  4i . Tìm phần thực a và phần ảo b của số phức z :
A. a  3,b  4 .
B. a  4,b  3.
C. a  4,b  3  .
D. a  3,b  4  .
Câu 41. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Phần ảo của số phức z  3  2i là A. 2. B. 2i . C. 2  i . D. 2  .
Câu 42. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức z  2  i . Trong mặt phẳng tọa độ Oxy
điểm biểu diễn hình học số phức liên hợp z có tọa độ là A.  2  ;  1 . B. 2;  1  . C. 1; 2 . D. 1; 2   .
Câu 43. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hai số phức z  1 3 ;
i z  3  2i . Số phức 1 2 2z  z bằng 1 2 A. 4  i B. 7  i C. 5  4i D. 10  2i
Câu 44. (THPT Chu Văn An - Thái Nguyên - 2021) Trong mặt phẳng phức Oxy , số phức z  2  3i
được biểu diễn bởii điểm nào sau đây? A. Q(3; 2) . B. M (2; 3  ) . C. N (2;3) . D. P( 3  ; 2).
Câu 45. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hai số phức z  3  i và z  1 2i . Phần thực 1 2
của số phức z z bằng 1 2 A. 4 . B. 2 . C. 1  . D. 3 .
Câu 46. (THPT Ba Đình - Thanh Hóa - 2021) Cho số phức z  5  8i , phần ảo của z là A. 8. B. 8  i . C. 5 . D. 8  .
Câu 47. (THPT Ba Đình - Thanh Hóa - 2021) Tính môdun của số phức z  3  4i . A. 5. B. 3. C. 7. D. 7 .
Câu 48. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho số phức z  4  3i . Tìm phần thực và phần ảo của số
phức liên hợp của số phức z
A. Phần thực bằng 4 và phần ảo bằng 3
B. Phần thực bằng 4
 và phần ảo bằng 3i
C. Phần thực bằng 4 và phần ảo bằng 3i
D. Phần thực bằng 4 và phần ảo bằng 3
Câu 49. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức z  3  4i . Khẳng định nào sau đây là khẳng định sai?
A. Số phức liên hợp của z là 3  4i
B. Điểm biểu diễn cuả z là M 4;3
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
C. Môđun của số phức z là 5
D. Số phức liên hợp của z là 3   4i
Câu 50. (THPT Quốc Oai - Hà Nội - 2021) Số nào trong các số phức sau là số thuần ảo?
A. 10  i  10  2i .
B. 5  i 7   5  i 7  .
C. 3  i   3   i .
D.  7  i   7  i .
Câu 51. (THPT Quảng Xương 1-Thanh Hóa - 2021) Số phức liên hợp của số phức z  312i là
A. z  312i .
B. z  3 12i .
C. z  3 12i .
D. z  312i .
Câu 52. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức z  2  i và z  1 3i . Phần thực 1 2
của số phức z z bằng 1 2 A. 1. B. 3 . C. 4 . D. 2  .
Câu 53. (THPT Quảng Xương 1-Thanh Hóa - 2021) Trong mặt phẳng tọa độ, điểm A 3  ;   1 biểu diễn
số phức nào dưới đây?
A. z  1 3i .
B. z  1  3i . C. z  3   i .
D. z  3  i .
Câu 54. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức z  2  3i , z  4
  5i . Tính z z z 1 2 1 2 A. z  2   2i .
B. z  2  2i .
C. z  2  2i . D. z  2   2i .
Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Số phức liên hợp của số phức z  4  7i là A. z  4   7i .
B. z  4  7i .
C. z  4i  7 . D. z  4   7i .
Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức z  12  5i . Mô đun của số phức z là: A. 17 . B. 13  . C. 13 . D. 5 .
Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Số phức liên hợp z của số phức z  1 2021i là
A. z  1 2021i .
B. z  1 2021i .
C. z  2021 i .
D. z  1 20211i .
Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tính môđun của số phức z  3  4i A. 3 . B. 7 . C. 7 . D. 5 .
z  2  3i, z  4  5i
Câu 59. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức 1 2 . Số phức
z z z 1 1 là
A. z  2  2i .
B. z  2  2i .
C. z  2  2i . D. z  2   2i .
Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Số phức liên hợp của số phức z  2  3i là.
A. z  3  2i .
B. z  3  2i .
C. z  2  3i . D. z  2   3i .
Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hai số phức z  5  6i và z  2  3i . Số phức 1 2 3z  4z là. 1 2 A. 14  33i . B. 236i . C. 26  5i . D. 7  30i .
Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Cho số phức z được biểu diễn bởi điểm M  1  ;3 trên mặt
phẳng tọa độ. Môđun của số phức z bằng A. 10 . B. 2 2 . C. 10 . D. 8 .
Câu 63. (THPT Đồng Quan - Hà Nội - 2021) Số phức liên hợp của số phức z  2  3i là:
A. z  3  2i .
B. z  2  3i . C. z  2   3i .
D. z  3  2i .
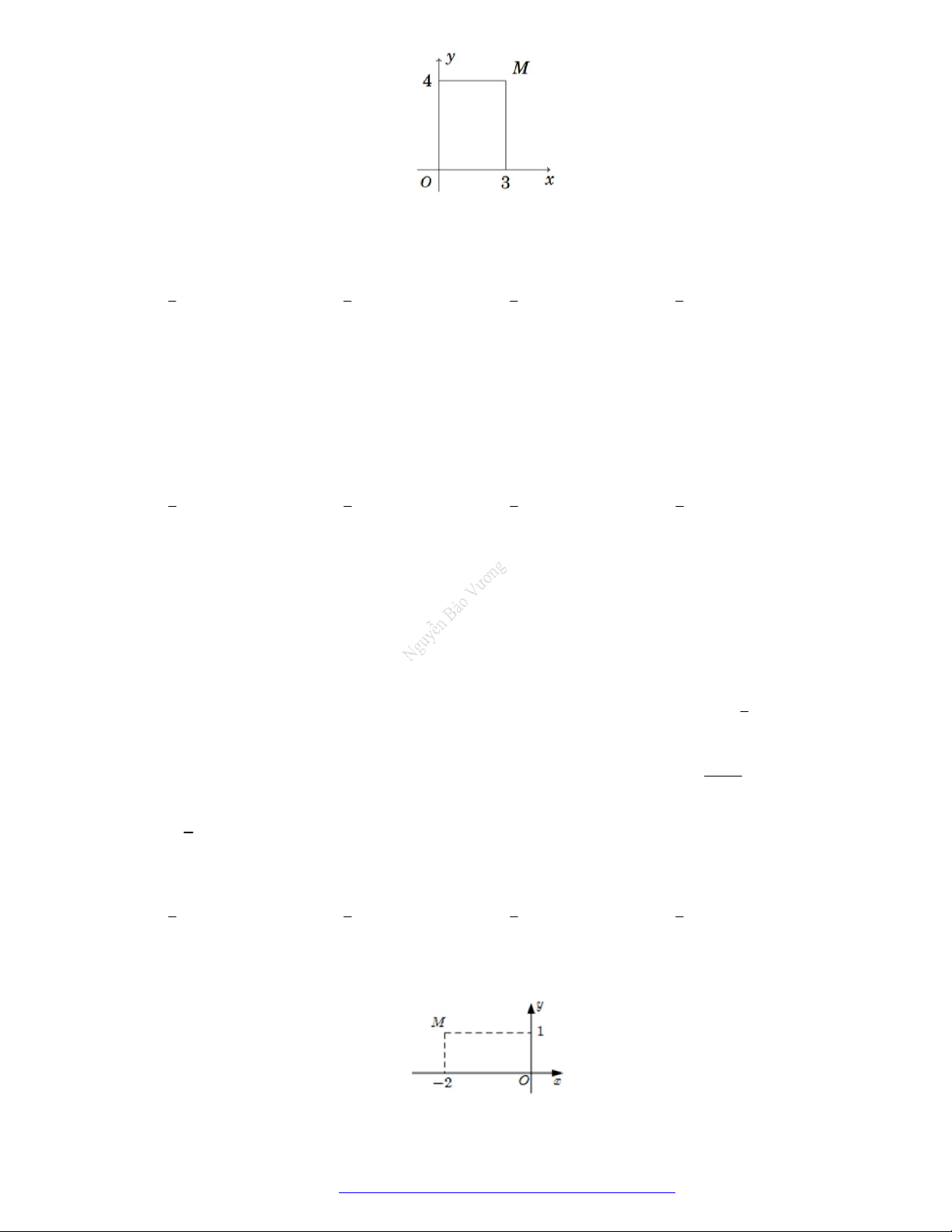
Câu 64. (THPT Lê Lợi - Thanh Hóa - 2021) Điểm M trong hình vẽ bên là điểm biểu diễn số phức z .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 4.
B. Phần thực bằng 3 và phần ảo bằng 4i .
C. Phần thực bằng 4 và phần ảo bằng 3i .
D. Phần thực bằng 4 và phần ảo bằng 3.
Câu 65. (THPT Lê Lợi - Thanh Hóa - 2021) Số phức liên hợp của số phức z  3  2i ? A. z  3   2i . B. z  3   2i . C. z  2   3i .
D. z  3  2i .
Câu 66. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hai số phức z  5 7i và z  2 3i . Tìm số phức 1 2
z z z 1 2
A. z  7 4i .
B. z  2  5i . C. z  2  5i . D. z  3 1  0i .
Câu 67. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Phần thực của số phức z  3  i 1 4i là A. 1  3. B. 1  . C. 13. D. 1.
Câu 68. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìm số phức liên hợp của số phức z i 3i   1 A. z  3   i .
B. z  3  i . C. z  3   i .
D. z  3  i .
Câu 69. (Trung Tâm Thanh Tường - 2021) Cho hai số phức z  1  2i, z  2  i . Phần ảo của số phức 1 2 z z bằng 1 2 A. 3. B. 1. C. i . D. 3i .
Câu 70. (Trung Tâm Thanh Tường - 2021) Cho số phức z  2  3i, z  1  i . Điểm nào sau đây là điểm 1 2
biểu diễn của số phức w z z ? 1 2
A. Điểm Q 1; 4 .
B. Điểm P 1; 4 .
C. Điểm M 3; 2 . D. Điểm Q 2; 3 .
Câu 71. (Trung Tâm Thanh Tường - 2021) Cho biết số phức liên hợp của số phức z là z 13i . Số phức z là 1
A. z  3  i .
B. z  1 3i .
C. z  3i . D. z  . 13i
Câu 72. (Trung Tâm Thanh Tường - 2021) Cho số phức z  1 3i . Tìm phần thực của số phức
w i z  3z . A. 0 . B. 3. C. 9. D. 6.
Câu 73. (Trung Tâm Thanh Tường -2021) Số phức liên hợp của số phức z    i2 2 là
A. z  3  4i .
B. z  3  4i . C. z  3   4i . D. z  3   4i .
Câu 74. (Trung Tâm Thanh Tường -2021) Trong mặt phẳng tọa độ Oxy , cho điểm M như hình vẽ bên
là điểm biểu diễn số phức z Kết quả   2 1 z bằng
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A.   z2 1  2  2i . B.   z2 1  2  i . C.   z2 1  1   i .
D.   z 2 1  2i .
Câu 75. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho số phức z  2  3i , khi đó phần ảo của số phức z là A. 2 . B. 3  . C. 3 . D. 2 .
Câu 76. (THPT Triệu Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  1
  2i có tọa độ là: A. 1; 2 . B. 2;  1  . C.  1  ; 2   . D.  1  ; 2 .
Câu 77. (THPT Triệu Sơn - Thanh Hóa - 2021) Gọi z , z là hai nghiệm phức của phương trình 1 2 2
z  2z  9  0 , khi đó z z bằng 1 2 A. 18 . B. 3 . C. 9 . D. 6 .
Câu 78. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức z  3  4i và w  2  3i . Số phức
z  2w bằng A. 1   7i . B. 110i . C. 7  2i . D. 1  10i .
Câu 79. (THPT Trần Phú - Đà Nẵng - 2021) Tính môđun của số phức z biết z  3  2i  1 5i
A. z  5 .
B. z  13 .
C. z  53 . D. z  65 .
Câu 80. (THPT Trần Phú - Đà Nẵng - 2021) Trên mặt phẳng tọa độ điểm biểu diễn số phức 1   4i có tọa độ là A.  4  ;   1 . B. 4;  1  . C.  1  ; 4   . D.  1  ; 4 .
Câu 81. (THPT Trần Phú - Đà Nẵng - 2021) Cho hai số phức z  1 i và z  1 3i . Phần thực của số 1 2
phức z .z bằng 1 2 A. 2 . B. 2 . C. 4 . D. 4 . BẢNG ĐÁP ÁN 1.C 2.C 3.B 4.D 5.A 6.D 7.A 8.D 9.C 10.A 11.D 12.D 13.D 14.B 15.A 16.A 17.D 18.A 19.C 20.D 21.C 22.C 23.D 24.A 25.A 26.B 27.D 28.A 29.C 30.A 31.B 32.B 33.D 34.A 35.A 36.A 37.B 38.B 39.D 40.A 41.A 42.B 43.C 44.B 45.B 46.D 47.A 48.A 49.B 50.B 51.B 52.B 53.D 54.D 55.B 56.C 57.D 58.D 59.D 60.C 61.D 62.C 63.B 64.A 65.D 66.A 67.B 68.C 69.B 70.C 71.B 72.A 73.B 74.B 75.B 76.D 77.D 78.D 79.B 80.D 81.C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ NHẬN BIẾT Câu 1.
(Sở Vĩnh Phúc - 2021) Tìm phần thực của số phức z  2  3i A. 2  . B. 3 . C. 2 . D. 3  . Lời giải Chọn C Câu 2.
(Sở Lào Cai - 2021) Cho hai số phức z  2  i và z  1 2i . Khi đó phần ảo của số phức z .z 1 2 1 2 bằng: A. 2 . B. 3i . C. 3 . D. 2  i . Lời giải Chọn C
z .z  2  i1 2i 2
 2  4i i  2i  4  3i . 1 2
Khi đó phần ảo của số phức z .z bằng 3. 1 2 Câu 3.
(Sở Lào Cai - 2021) Mô đun của số phức z  2 3i bằng A. 5 . B. 13 . C. 5 . D. 13 . Lời giải Chọn B. Ta có z   2 2 2 3  13 . z  3  2i z  2  i z z Câu 4.
(Sở Hà Tĩnh - 2021) Cho hai số phức 1 và 2 . Số phức 1 2 bằng A. 5   i . B. 5  i . C. 5   i . D. 5  i . Lời giải Chọn D
Ta có : z z  5  i . 1 2 Câu 5.
(Sở Hà Tĩnh - 2021) Số phức liên hợp của số phức z  2   6i là A. z  2   6i . B. z  2   6i .
C. z  2  6i .
D. z  2  6i . Lời giải Chọn A
Số phức liên hợp của số phức z  2
  6i là z  2   6i . Câu 6.
(Sở Hà Tĩnh - 2021) Trên mặt phẳng, điểm M  1
 ;3 là điểm biểu diễn số phức z . Phần thực của z bằng A. 1. B. 3 . C. 3  . D. 1  . Lời giải Chọn D M  1
 ;3 là điểm biểu diễn số phức z  1
  3i . Phần thực của z bằng 1  . Câu 7.
(Sở Yên Bái - 2021) Phần ảo của số phức z  12 18i là A. 18 . B. 18 . C. 1  8i . D. 12. Lời giải Chọn A
Phần ảo của số phức z  12 18i là 18 . Câu 8.
(Sở Tuyên Quang - 2021) Tìm phần thực và phần ảo của số phức z  3  2i .
A. Phần thực bằng 3
 và phần ảo bằng 2i .
B. Phần thực bằng 3
 và phần ảo bằng 2 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
C. Phần thực bằng 3 và phần ảo bằng 2i .
D. Phần thực bằng 3 và phần ảo bằng 2 . Lời giải Chọn D
Ta có số phức z  3  2i có phần thực a  3 và phần ảo b  2 . Câu 9.
(Sở Tuyên Quang - 2021) Điểm M trong hình vẽ dưới đây biểu thị cho số phức: A. 2  3i . B. 3  2i . C. 2   3i . D. 3  2i . Lời giải Chọn C
Điểm M trong hình vẽ dưới đây biểu thị cho số phức z  2   3i .
Câu 10. (Sở Tuyên Quang - 2021) Tính môđun của số phức z  4  3i . A. z  5 . B. z  7 . C. z  25 . D. z  7 . Lời giải Chọn A Ta có z    2 2 4 3  5 . 1
Câu 11. (Sở Tuyên Quang - 2021) Cho số phức z  1 2 .
i Tìm phần ảo của số phức P z  2 2 A.  2 . B. . C. 2 . D. . 3 3 Lời giải Chọn D 1 1 1 2 1 2 Ta có P    
i . Nên phần ảo của số phức P  là z 1 2i 3 3 z 3
Câu 12. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hai số phức
z  2  3i, z  3  2i . Tích z z bằng 1 2 1 2 A. 5  i . B. 5i . C. 6  6i . D. 12  5i Lời giải Chọn D 2
z z  2  3i 3  2i  6  4i  9i  6i  12  5i . 1 2   
Câu 13. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng Oxy điểm
M 1;  2  biểu diễn cho số phức nào sau đây.
A. z  1 2i . B. z  1   2i C. z  2   i .
D. z  1 2i Lời giải Chọn D
 Trong mặt phẳng Oxy điểm M 1;  2  biểu diễn cho số phức z 1 2i .
Câu 14. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức có điểm biểu diễn là M như hình vẽ.
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Phần ảo của số phức z là A. 3 . B. 3  . C. 2 . D. 2  . Lời giải Chọn B M  2  ;3  z  2
  3i  z  2  3i .
Câu 15. (Chuyên Lam Sơn - Thanh Hóa - 2021) Môđun của số phức 2  i là A. 5 . B. 3 . C. 3 . D. 5 . Lời giải Chọn A
Ta có mô đun của số phức z z bi là 2 2 z a b Do đó 2 2 2  i  2 1  5 .
Câu 16. (Chuyên KHTN - 2021) Mô đun của số phức z  3  2i bằng A. 13 . B. 13 . C. 5 . D. 5 . Lời giải Chọn A  Ta có: 2 2
z  3  2i  3  2  13 .
Câu 17. (Chuyên KHTN - 2021) Cho hai số phức z  2  3i và z  2  i . Số phức w z z z có phần 1 2 1 2 2 thực bằng A. 7. B. 9. C. 4. D. 3. Lời giải Chọn D
Ta có w z z z  2  3i
2  i  2  i  3  7i 1 2 2     
Suy ra w có phần thực bằng 3.
Câu 18. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức có phần thực bằng 2 và phần ảo bằng 1 là A. 2  . i B. 1  2 . i C. 2  . i D. 1 2 . i Lời giải Chọn A
Số phức có phần thực bằng 2 và phần ảo bằng 1 là z  2  i . z  4  3i z  7   5i
Câu 19. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho hai số phức 1 và 2 . Số
z z z phức 2 1 là A. 1  1 8i . B. 11 8i . C. 1  1 8i . D. 11 8i . Lời giải Chọn C
 Ta có: z z z  7
  5i  4  3i  11   8i . 2 1    
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 20. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Nghiệm phức có phần ảo dương của phương trình 2
z  2z  5  0 là A. 1   2i . B. 1 2i . C. 1 2i . D. 1   2i . Lời giải Chọn D z  1   2i Ta có: 2
z  2z  5  0   z  1   2  i
Theo yêu cầu bài toán suy ra nghiệm phức cần tìm là z  1   2i .
Câu 21. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức z  1
  2i . Điểm biểu diễn số phức
liên hợp của z trong mặt phẳng tọa độ Oxy là điểm A. Q. B. N. C. P. D. M. Lời giải Chọn C
Ta có: số phức liên hợp của số phức z  1
  2i là số phức z  1   2i .
Do đó, điểm biểu diễn của z là P  1  ; 2   .
Câu 22. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Số phức z thỏa mãn 1 iz i  0 là 1 1 1 1 1 1 1 1 A. z    i . B. z   i . C. z   i . D. z    i . 2 2 2 2 2 2 2 2 Lời giải Chọn C i  1 1
Số phức 1 iz i  0  z    i . 1 i 2 2
Câu 23. (Chuyên Quốc Học Huế - 2021) Số phức liên hợp của số phức z  3  5i là
A. z  3  5i .
B. z  3  5i .
C. z  5  3i .
D. z  3  5i Lời giải Chọn D
Ta có z  3  5i z  3  5i .
Câu 24. (Chuyên Quang Trung - Bình Phước - 2021) Cho số phức z a bi a,b   . Chọn phương án đúng.
A. Phần ảo của số phức z là b .
B. Phần ảo của số phức z là bi .
C. Phần thực của số phức z là b .
D. Mô đun của số phức z là 2 2 a b . Lời giải Chọn A
 Cho số phức z a bi (a,b  ) , ta có:
Phần thực của số phức z bằng a .
Phần ảo của số phức z bằng b .
Mô đun của số phức z bằng 2 2 z a b .
Câu 25. (Chuyên Quang Trung - Bình Phước - 2021) Gọi z , z là nghiệm của phương trình 1 2 2
z  2z  2  0 . Biết số phức z có phần ảo âm. Phần ảo của số phức z . 1 2 A. 1. B. 1  . C. i . D. 1 i . Lời giải
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn A z  1 i  Ta có : 2
z  2z  2  0   z  1 i
 Vì số phức z có phần ảo âm nên z  1 i và z  1 i . 1 1 2
 Phần ảo của số phức z bằng 1. 2
7  3i   9   i
Câu 26. (Chuyên Ngoại Ngữ Hà Nội- 2021) bằng A. 1  6  2i . B. 16  2i . C. 2   4i . D. 16  2i . Lời giải Chọn B
Ta có 7  3i   9
  i  7  3i  9  i  16  2i .
Câu 27. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho hai số phức z  2  ;
i z  3  2i . Trên mặt phẳng 1 2
tọa độ Oxy , điểm biểu diễn số phức 2z z có tọa độ là 1 2 A. 7  ;1 . B. 0;7 . C. 5;  1 . D. 7;0 . Lời giải Chọn D
Số phức 2z z  2 2  i  3  2i  4  2i  3  2i  7 . 1 2    
Như vậy điểm biểu diễn số phức 2z z là 7;0 . 1 2
Câu 28. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức z  4  3i . Tìm phần thực và phần ảo của
số phức liên hợp của số phức z
A. Phần thực bằng 4 và phần ảo bằng 3
B. Phần thực bằng 4
 và phần ảo bằng 3i
C. Phần thực bằng 4 và phần ảo bằng 3i
D. Phần thực bằng 4 và phần ảo bằng 3 Lời giải Chọn A
Số phức liên hợp của số phức z  4  3i là z  4  3i
 Phần thực bằng 4 và phần ảo bằng 3
Câu 29. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Số phức liên hợp của số phức 4  5i là A. 4  5i . B. 5  4i .
C. 4  5i . D. 4  5i . Lời giải Chọn C
Số phức liên hợp của số phức 4  5i là 4  5i .
Câu 30. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số thực x, y thỏa mãn 2  yi x  5i, trong đó i là đơn
vị ảo. Giá trị của x và y là
A. x  2, y  5  .
B. x  2, y  5  . i C. x  5  , y  2. D. x  5  i, y  2. Lời giải Chọn A
Giá trị của x và y là x  2, y  5  .
Câu 31. (Chuyên ĐHSP Hà Nội - 2021) Số phức liên hợp của số phức z  3  4i là
A. z  3  4i .
B. z  3  4i .
C. z  3  4i .
D. z  3  4i . Lời giải Chọn B
Ta có số phức liên hợp của số phức z  3  4i là z  3  4i .
Câu 32. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hai số phức , . Số phức liên hợp của là A. . B. . C. . D. . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn B  Ta có: .
 Vậy số phức liên hợp của là .
Câu 33. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Cho hai số phức z  2  2 ; i z  3
  3i . Khi đó số 1 2
phức z z là 1 2 A. 1   i B. 5   5i C. 5  i D. 5  5i Lời giải Chọn D z  2  2 ; i z  3
  3i z z  2  2i  3  3i  5  5i . 1 2 1 2
Câu 34. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức z  2  4i , mô đun của số phức w  z 1 bằng A. 5 . B. 2 5 1 . C. 2 5 . D. 7 . Lời giải Chọn A
Ta có w  z 1  3  4i . Nên 3  4i  5 .
Câu 35. (THPT Nguyễn Huệ - Phú Yên - 2021) Số phức z thỏa mãn 3  iz 1  4i là 7 11 7 11 7 11 7 11 A.   i . B. i . C.   i . D. i . 10 10 10 10 10 10 10 10 Lời giải Chọn A 1 4i 7 11 7 11
Ta có 3  iz 1  4i z     i z    i . 3  i 10 10 10 10
Câu 36. (THPT Lương Thế Vinh - 2021) Gọi z , z là hai nghiệm phức của phương trình 2 z  2z  5  0 . 1 2 2 2 Giá trị của zz bằng 1 2 A. 10. B. 50. C. 5. D. 18. Lời giải Chọn A 2 2 Ta có 2
z  2z  5  0  z  1
  2i; z  1   2i zz  5  5  10 . 1 2 1 2
Câu 37. (THPT Lương Thế Vinh - 2021) Số phức 2  4ii bằng số phức nào dưới đây? A. 4   2i . B. 4   2i . C. 4  2i . D. 4  2i . Lời giải Chọn B
Ta có :   i 2
2 4 i  2i  4i  2i  4  4   2i .
Câu 38. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Điểm nào trong hình vẽ bên dưới là điểm biểu diễn
số phức z  3  4i ,
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
A. Điểm A .
B. Điểm D .
C. Điểm C . D. Điểm B . Lời giải Chọn B
Điểm biểu diễn số phức z  3  4i là D 3; 4  
Câu 39. (THPT Đào Duy Từ - Hà Nội - 2021) Số phức liên hợp của 4  3i là A. 3  4i . B. 4   3i . C. 3  4i . D. 4  3i . Lời giải Chọn D
Câu 40. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z  3  4i . Tìm phần thực a và phần ảo b của số phức z :
A. a  3,b  4 .
B. a  4,b  3.
C. a  4,b  3  .
D. a  3,b  4  . Lời giải Chọn A
Câu 41. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Phần ảo của số phức z  3  2i là A. 2. B. 2i . C. 2  i . D. 2  . Lời giải Chọn A
Phần ảo của số phức z  3  2i là 2.
Câu 42. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức z  2  i . Trong mặt phẳng tọa độ Oxy
điểm biểu diễn hình học số phức liên hợp z có tọa độ là A.  2  ;  1 . B. 2;  1  . C. 1; 2 . D. 1; 2   . Lời giải Chọn B
Số phức z  2  i z  2  i . Do đó số phức z được biểu diễn bởi điểm M 2;   1 .
z  1 3i; z  3  2i
Câu 43. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho hai số phức 1 2 . Số phức 2z  z 1 2 bằng A. 4  i B. 7  i C. 5  4i D. 10  2i Lời giải Chọn C
 Ta có 2z  z  2(1 3i)  3  2i  5  4i . 1 2
Câu 44. (THPT Chu Văn An - Thái Nguyên - 2021) Trong mặt phẳng phức Oxy , số phức z  2  3i
được biểu diễn bởii điểm nào sau đây? A. Q(3; 2) . B. M (2; 3  ) . C. N (2;3) . D. P( 3  ; 2). Lời giải Chọn B
Theo lý thuyết, z a bi thì sẽ được biểu diễn bởi điểm có tọa độ ( ,
a b) .Vậy chọn B.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 45. (THPT Chu Văn An - Thái Nguyên - 2021) Cho hai số phức z  3  i và z  1 2i . Phần thực 1 2
của số phức z z bằng 1 2 A. 4 . B. 2 . C. 1  . D. 3 . Lời giải Chọn B
 Ta có z z  3  i  1 2i  2  3i . 1 2  
 Phần thực của số phức z z bằng 2 . 1 2
Câu 46. (THPT Ba Đình - Thanh Hóa - 2021) Cho số phức z  5  8i , phần ảo của z là A. 8. B. 8  i . C. 5 . D. 8  . Lời giải Chọn D
Phần ảo của số phức z là 8 
Câu 47. (THPT Ba Đình - Thanh Hóa - 2021) Tính môdun của số phức z  3  4i . A. 5. B. 3. C. 7. D. 7 . Lời giải Chọn A Ta có 2 2
z  3  (4)  5 .
Câu 48. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho số phức z  4  3i . Tìm phần thực và phần ảo của số
phức liên hợp của số phức z
A. Phần thực bằng 4 và phần ảo bằng 3
B. Phần thực bằng 4 và phần ảo bằng 3i
C. Phần thực bằng 4 và phần ảo bằng 3i
D. Phần thực bằng 4 và phần ảo bằng 3 Lời giải Chọn A
Số phức liên hợp của số phức z  4  3i là z  4  3i
 Phần thực bằng 4 và phần ảo bằng 3
Câu 49. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức z  3  4i . Khẳng định nào sau đây là khẳng định sai?
A. Số phức liên hợp của z là 3  4i
B. Điểm biểu diễn cuả z là M 4;3
C. Môđun của số phức z là 5
D. Số phức liên hợp của z là 3   4i Lời giải Chọn B Lý thuyết
(Điểm biểu diễn của z là M 3;4 )
Câu 50. (THPT Quốc Oai - Hà Nội - 2021) Số nào trong các số phức sau là số thuần ảo?
A. 10  i  10  2i . B. 5  i 7   5  i 7  .
C. 3  i   3   i .
D.  7  i   7  i . Lời giải Chọn B
Ta có 5  i 7   5  i 7   2 7i .
Câu 51. (THPT Quảng Xương 1-Thanh Hóa - 2021) Số phức liên hợp của số phức z  312i là
A. z  312i .
B. z  3 12i .
C. z  3 12i .
D. z  312i . Lời giải Chọn B
Ta có: z  312i z  3 12i .
Câu 52. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức z  2  i và z  1 3i . Phần thực 1 2
của số phức z z bằng 1 2
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 1. B. 3. C. 4 . D. 2  . Lời giải Chọn B
z z  2  i  1 3i  3  4i  phần thực của số phức z z bằng 3 1 2     1 2
Câu 53. (THPT Quảng Xương 1-Thanh Hóa - 2021) Trong mặt phẳng tọa độ, điểm A 3  ;   1 biểu diễn
số phức nào dưới đây?
A. z  1 3i .
B. z  1  3i . C. z  3   i .
D. z  3  i . Lời giải Chọn D
Ta có điểm A 3  ;  
1 biểu diễn số phức z  3   i .
Câu 54. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức z  2  3i , z  4
  5i . Tính z z z 1 2 1 2 A. z  2   2i .
B. z  2  2i .
C. z  2  2i . D. z  2   2i . Lời giải Chọn D
Ta có z z z  2  3i  4   5i  2   2i . 1 2  
Câu 55. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Số phức liên hợp của số phức z  4  7i là A. z  4   7i .
B. z  4  7i .
C. z  4i  7 . D. z  4   7i . Lời giải Chọn B
Ta có z  4  7i .
Câu 56. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức z  12  5i . Mô đun của số phức z là: A. 17 . B. 13  . C. 13 . D. 5 . Lời giải Chọn C 2 2 Ta có z   12     5    13 .
Câu 57. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Số phức liên hợp z của số phức z  1 2021i là
A. z  1 2021i .
B. z  1 2021i .
C. z  2021 i .
D. z  1 20211i . Lời giải Chọn D Ta có z  1
  2021i z  1   2021 . i
Câu 58. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Tính môđun của số phức z  3  4i A. 3 . B. 7 . C. 7 . D. 5 . Lời giải Chọn D. Ta có: 2 2 z  3  4  5 .
z  2  3i, z  4  5i
Câu 59. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức 1 2 . Số phức
z z z 1 1 là
A. z  2  2i .
B. z  2  2i .
C. z  2  2i . D. z  2   2i . Lời giải Chọn D
z z z  2  3i  4  5i  2  2 . i 1 2
Câu 60. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Số phức liên hợp của số phức z  2  3i là.
A. z  3  2i .
B. z  3  2i .
C. z  2  3i . D. z  2   3i .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn C
Ta có Số phức liên hợp của số phức z  2  3i là z  2  3i .
Câu 61. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hai số phức z  5  6i và z  2  3i . Số phức 1 2 3z  4z là. 1 2 A. 14  33i . B. 236i . C. 26  5i . D. 7  30i . Lời giải Chọn D
Ta có 3z  4z  7  30i 1 2
Câu 62. (THPT Đồng Quan - Hà Nội - 2021) Cho số phức z được biểu diễn bởi điểm M  1  ;3 trên mặt
phẳng tọa độ. Môđun của số phức z bằng A. 10 . B. 2 2 . C. 10 . D. 8 . Lời giải Chọn C
Số phức được biểu diễn bởi điểm M  1
 ;3 trên mặt phẳng tọa độ nên z  1   3i . Do đó z   2 2 1  3  10 .
Câu 63. (THPT Đồng Quan - Hà Nội - 2021) Số phức liên hợp của số phức z  2  3i là:
A. z  3  2i .
B. z  2  3i . C. z  2   3i .
D. z  3  2i . Lời giải Chọn B
Câu 64. (THPT Lê Lợi - Thanh Hóa - 2021) Điểm M trong hình vẽ bên là điểm biểu diễn số phức z .
Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3 và phần ảo bằng 4.
B. Phần thực bằng 3 và phần ảo bằng 4i .
C. Phần thực bằng 4 và phần ảo bằng 3i .
D. Phần thực bằng 4 và phần ảo bằng 3. Lời giải Chọn A
Từ hình vẽ ta có M 3; 4 nên z  3  4i . Vậy phần thực bằng 3 và phần ảo bằng 4 .
Câu 65. (THPT Lê Lợi - Thanh Hóa - 2021) Số phức liên hợp của số phức z  3  2i ? A. z  3   2i . B. z  3   2i . C. z  2   3i .
D. z  3  2i . Lời giải Chọn D z  5 7i z  2  3i
Câu 66. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hai số phức 1 và 2 . Tìm số phức
z z z 1 2
A. z  7 4i .
B. z  2  5i . C. z  2  5i . D. z  3 1  0i . Lời giải Chọn A
Ta có z z z  5   2  7   
3 i  7  4i . 1 2
Câu 67. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Phần thực của số phức z  3  i 1 4i là
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 1  3. B. 1  . C. 13. D. 1. Lời giải Chọn B
Ta có z  3  i1 4i  1
 13i . Vậy phần thực của số phức z là 1  .
Câu 68. (THPT Nguyễn Công Trứ - Hà Tĩnh - 2021) Tìm số phức liên hợp của số phức z i 3i   1 A. z  3   i .
B. z  3  i . C. z  3   i .
D. z  3  i . Lời giải Chọn C
z i 3i  
1  3  i z  3  i .
Câu 69. (Trung Tâm Thanh Tường - 2021) Cho hai số phức z  1 2i, z  2  i . Phần ảo của số phức 1 2 z z bằng 1 2 A. 3. B. 1. C. i . D. 3i . Lời giải Chọn B
z z  1 2i  2  i  3  i 1 2
Phần ảo của z z bằng 1. 1 2
Câu 70. (Trung Tâm Thanh Tường - 2021) Cho số phức z  2  3i, z  1 i . Điểm nào sau đây là điểm 1 2
biểu diễn của số phức w z z ? 1 2 Q 1; 4 P 1; 4 M 3; 2 Q 2; 3 A. Điểm . B. Điểm . C. Điểm . D. Điểm . Lời giải Chọn C.
Ta có: w z z  2  3i 1 i  3  2 .
i Vậy điểm biểu diễn w z z là M 3; 2 . 1 2 1 2
Câu 71. (Trung Tâm Thanh Tường - 2021) Cho biết số phức liên hợp của số phức z là z 13i . Số phức z là 1
A. z  3  i .
B. z  1 3i .
C. z  3 i . D. z  . 13i Lời giải Chọn B.
Ta có z 13i suy ra z  1 3i .
Câu 72. (Trung Tâm Thanh Tường - 2021) Cho số phức z  1 3i . Tìm phần thực của số phức
w i z  3z . A. 0 . B. 3. C. 9. D. 6. Lời giải Chọn A
Ta có: w i z  3z i 1 3i  31 3i  i  3  3  9i  8  i .
Câu 73. (Trung Tâm Thanh Tường -2021) Số phức liên hợp của số phức z    i2 2 là
A. z  3  4i .
B. z  3  4i . C. z  3   4i . D. z  3   4i . Lời giải Chọn B
Ta có z    i2 2 2
 4  4i i  3  4i z  3  4i .
Câu 74. (Trung Tâm Thanh Tường -2021) Trong mặt phẳng tọa độ Oxy , cho điểm M như hình vẽ bên
là điểm biểu diễn số phức z
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Kết quả   2 1 z bằng
A.   z 2 1  2  2i . B.   z2 1  2  i .
C.   z 2 1  1   i . D.   z2 1  2i . Lời giải Chọn B 2 2
Số phức biểu diễn điểm M là z    i    z     i 2 2 1 1 2
 1 2i i  2  i .
Câu 75. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho số phức z  2  3i , khi đó phần ảo của số phức z là A. 2 . B. 3  . C. 3 . D. 2  . Lời giải Chọn B
 Số phức z có phần ảo là: 3  .
Câu 76. (THPT Triệu Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức z  1
  2i có tọa độ là: A. 1; 2 . B. 2;  1  . C.  1  ; 2   . D.  1  ; 2 . Lời giải Chọn D
Câu 77. (THPT Triệu Sơn - Thanh Hóa - 2021) Gọi z , z là hai nghiệm phức của phương trình 1 2 2
z  2z  9  0 , khi đó z z bằng 1 2 A. 18 . B. 3 . C. 9 . D. 6 . Lời giải Chọn D
z  1 2 2i Ta có: 2 1
z  2z  9  0  
z  1 2 2i  2
Khi đó z z  1 2 2i  1 2 2i  6 . 1 2
Câu 78. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức z  3  4i và w  2  3i . Số phức
z  2w bằng A. 1   7i . B. 110i . C. 7  2i . D. 1  10i . Lời giải Chọn D
z  2w  3  4i  22  3i  3  4i  4  6i  1  10i
Câu 79. (THPT Trần Phú - Đà Nẵng - 2021) Tính môđun của số phức z biết z  3  2i  1 5i
A. z  5 .
B. z  13 .
C. z  53 . D. z  65 . Lời giải Chọn B
z   i   i z    i z   2   2 3 2 1 5 2 3 2 3  13 .
Câu 80. (THPT Trần Phú - Đà Nẵng - 2021) Trên mặt phẳng tọa độ điểm biểu diễn số phức 1   4i có tọa độ là A.  4  ;   1 . B. 4;  1  . C.  1  ; 4   . D.  1  ; 4 . Lời giải Chọn D
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Trong mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z  1
  4i có tọa độ là  1  ; 4 .
Câu 81. (THPT Trần Phú - Đà Nẵng - 2021) Cho hai số phức z  1 i và z  1 3i . Phần thực của số 1 2
phức z .z bằng 1 2 A. 2 . B. 2 . C. 4 . D. 4 . Lời giải Chọn C
Số phức z .z  1 i 1 3i  4
  2i có phần thực là 4 . 1 2   
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ THÔNG HIỂU Câu 1.
(Sở Vĩnh Phúc - 2021) Cho số phức z thỏa mãn z z . Trong mặt phẳng tọa độ Oxy , tập hợp tất
cả các điểm biểu diễn cho số phức z là đường thẳng nào trong các đường thẳng sau đây?
A. Đường thẳng y  0 . B. Đường thẳng x  0 .
C. Đường thẳng y x . D. Đường thẳng y  x . Câu 2.
(Sở Lào Cai - 2021) Cho số phức z  2i 1 . Điểm nào sau đây là điểm biểu diễn của số phức z trên mặt phẳng tọa độ?
A. H 1; 2 .
B. T 2;   1 . C. G 1; 2   . D. K 2  ;1 . Câu 3.
(Sở Lào Cai - 2021) Cho hai số phức z  2  i, z  2  4i . Tính z z .z . 1 2 1 1 2 5 A. . B. 1. C. 5 5 . D. 5 . 5 Câu 4.
(Sở Hà Tĩnh - 2021) Cho số phức z thỏa mãn 2  z i  3  2iz  11 
16i . Môđun của số phức z bằng. A. 5 . B. 5 . C. 13 . D. 3 . Câu 5.
(Sở Yên Bái - 2021) Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  6z 18  0 . Tính giá 1 2
trị của biểu thức P   z z 2 bằng 1 2 A. 6 . B. 36 . C. 18 . D. 24 . Câu 6.
(Sở Yên Bái - 2021) Tính môđun của số phức z thỏa mãn (2  i)z 13i  1. 5 34 34 A. z  .
B. z  34 .
C. z  34 . D. z  . 3 3 Câu 7.
(Sở Tuyên Quang - 2021) Cho hai số phức z  2  4i và z  1 3i . Phần ảo của số phức z iz 1 2 1 2 bằng A. 5  . B. 3  . C. 3i . D. 5  i . Câu 8.
(Sở Tuyên Quang - 2021) Tìm số phức liên hợp của số phức z i     i2 4 1 1 3
A. z  9  2i . B. z  9   2i .
C. z  9  2i . D. z  9   2i . Câu 9.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho các số phức z  1 2i, w  2  i .
Số phức u z.w có
A. Phần thực là 0 và phần ảo là 3.
B. Phần thực là 4 và phần ảo là 3.
C. Phần thực là 0 và phần ảo là 3i .
D. Phần thực là 4 và phần ảo là 3i .
Câu 10. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho số phức z  1 2i . Tìm phần 1
ảo của số phức P  . z 2 2 A.  2 . B.  . C. 2 . D. . 3 3
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 11. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng Oxy , tập hợp điểm
M biểu diễn số phức cho số phức z thỏa mãn z 1 2i  1 là một đường tròn C  , tâm I của đường tròn đó là
A. I 1; 2  .
B. I 2 ; 1  C. I  2  ; 1  .
D. I 2 ;1 
Câu 12. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Phương trình 2
z  2z  5  0 có hai 2 2
nghiệm phức z , z . Khi đó zz bằng 1 2 1 2 A. 10 . B. 10 . C. 5 . D. 2 5 .
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho số phức z  5  4i . Số phức đối của z có tọa
độ điểm biểu diễn là A. 5; 4   . B. 5;4 . C.  5  ;4 . D.  5  ; 4   .
Câu 14. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Kí hiệu z , z là hai nghiệm của phương trình 1 2 2
z  4  0 . Gọi M , N lần lượt là điểm biểu diễn của z , z trên mặt phẳng tọa độ. Tính 1 2
T OM ON với O là gốc tọa độ. A. T  2 . B. T  2 . C. T  8 . D. T  4 . z  4  3i z  7  3i
Câu 15. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hai số phức 1 và 2 . Tìm số
z z z phức 1 2 . A. z  3   6i . B. z  1  10i . C. z  11.
D. z  3  6i .
Câu 16. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức z thỏa mãn: 2iz  5  i i  (z  2i) .
Tính môđun của số phức w z 1 i . 4 3 9 1 A. i . B. 1. C. . D. . 5 5 5 5
Câu 17. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hai số phức z m  2n m  3 i và 1    
z n  3m ni với ,
m n   . Biết rằng z z , khẳng định nào sau đây đúng? 2   1 2
A. m n  0 .
B. m n  5 .
C. m n  3.
D. m n  3  .
Câu 18. (Chuyên Lam Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn của số phức
z    i2 2
là điểm nào dưới đây?
A. P 3; 4 .
B. M 5; 4 .
C. N 4;5 .
D. Q 4;3 .
Câu 19. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức z  1 i và z  3  2i . Phần ảo của số 1 2
phức 2z z bằng 1 2 A. 0 . B. 2 . C. 4 . D. 4 .
Câu 20. (Chuyên KHTN - 2021) Trên mặt phẳng phức, biết rằng tập hợp các điểm biểu diễn các số phức
z thỏa mãn z  2  i  1 là một đường tròn. Đường tròn đó có tâm là A. I 1; 2 . B. I 2;  1 . C. I 2;1 . D. I 1;  2 . 4   3   1   2  
Câu 21. (Chuyên KHTN - 2021) Cho số phức z thỏa mãn 2  iz  1  i  9  2i . Môđun của số phức z bằng A. 13 . B. 13 . C. 5 . D. 5 .
Câu 22. (Chuyên KHTN - 2021) Phương trình 4
z  16 có bao nhiêu nghiệm phức? A. 0 . B. 4 . C. 2 . D. 1.
Câu 23. (Chuyên KHTN - 2021) Tập hợp các điểm biểu diễn số phức z thỏa mãn z 1
  3i z 1i .
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
A. x y  2  0 .
B. x  2 y  2  0 .
C. x y  2  0 .
D. x y  2  0 .
Câu 24. (Chuyên KHTN - 2021) Cho số phức z thỏa mãn 3z i z  8  0 .Tổng phần thực và phần ảo của z bằng A. 1. B. 1  . C. 2 . D. 2  .
Câu 25. (Chuyên Quốc Học Huế - 2021) Gọi C  là đường cong trong mặt phẳng Oxy biểu diễn các số 2 phức z thỏa mãn .
z z z z  1 và H là hình phẳng giới hạn bởi C  . Diện tích của hình phẳng H bằng 2  A. . B.  5. C. 2 5. D. . 5 5
Câu 26. (Chuyên Quang Trung - Bình Phước - 2021) Cho z   thỏa z  2 z  12 . Phần ảo của z là A. 0 B. 4 C. 12  D. 2
Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức z  4  3i . Chọn khẳng định đúng trong các khẳng định sau
A. Số phức liên hợp của z là z  4   3i .
B. Điểm biểu diễn của số phức z là M  3  ; 4 .
C. Môđun của số phức z bằng   2 2 4 3i . 1 4 3
D. Số phức nghịch đảo của z là   i . z 25 25
Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số phức z thỏa mãn z  1 2iz  8 14i .
A. z  3  4 . i B. z  3  . i
C. z  1 2 . i
D. z  2  i
Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm các số thực x , y thỏa mãn 2x  
1   y ii  2i
A. x  1 và y  2 .
B. x  1 và y  2 .
C. x  1 và y  2 . D. x  1 và y  2 .
Câu 30. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Gọi z , z là nghiệm phức của phương trình 1 2 2
z  5z  8  0 . Giá trị 2 2 z z bằng 1 2 A. 41 . B. 9 . C. 16 . D. 17 . z  3  4i z  2  i
Câu 31. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức 1 và 2 . Số phức z iz 1 2 bằng A. 5  3i B. 5  3i C. 2  2i D. 2  2i
Câu 32. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi z là nghiệm phức có phần ảo dương của phương 0 trình 2
z  4z  8  0 . Trên mặt phẳng tọa độ Oxy , điểm nào dưới đây là điểm biểu diễn của số phức iz ? 0
A. Q 2; 2 .
B. M 2; 2 . C. P  2  ; 2   . D. N 2; 2   .
Câu 33. (Chuyên Hạ Long - Quảng Ninh - 2021) Trong mặt phẳng với hệ tọa độ Oxy , biết điểm M 3; 5
  là điểm biểu diễn số phức z . Phần ảo của số phức z  2i bằng A. 5  . B. 2 . C. 3  . D. 5 .
Câu 34. (Chuyên Hạ Long - Quảng Ninh - 2021) Số phức liên hiệp của z  4   3   1 i là:
A. z  4   3   1 i .
B. z  4  1 3i . C. z  4  1 3i . D. z  4   3   1 i .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 35. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi z ; z là các nghiệm của phương trình 1 2 2
z  3z  5  0 . Mô đun của số phức 2z  3 2z  3 bằng 1  2  A. 7 . B. 11. C. 29 . D. 1. z  1  2i z  3  i
Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức 1 và 2 . Môđun của số
phức  z z z z bằng 1 2  1 2 A. 5 34 . B. 4 35 . C. 5 43 . D. 5 10 .
Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Trên mặt phẳng toạ độ Oxy , biết điểm M  2   ;1 là điểm biểu
diễn số phức z . Phần thực của số phức 3  2iz bằng A. 8  . B. 7 . C. 1  . D. 4  .
Câu 38. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số phức z  4  3i và w  1 i . Mô đun của số phức z.w bằng A. 5 2. B. 4 2. C. 5. D. 3 2.
Câu 39. (Chuyên ĐH Vinh - Nghệ An - 2021) Gọi z ; z là các nghiệm của phương trình 2
z  3z  5  0 . 1 2
Mô đun của số phức 2z  3 2z  3 bằng 1  2  A. 7 . B. 11. C. 29 . D. 1.
Câu 40. (THPT Thanh Chương 1- Nghệ An - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức
là điểm nào dưới đây? A. . B. . C. . D. .
Câu 41. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Phần ảo của số phức bằng A. . B. . C. . D. .
Câu 42. (THPT Thanh Chương 1- Nghệ An - 2021) Gọi ,
là hai nghiệm của phương trình . Giá trị biểu thức bằng A. . B. . C. . D. . z  1 5i z  3  i z z
Câu 43. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hai số phức 1 và 2 . Số phức 1 2 là A. 2   6i . B. 2  6i . C. 2   6i . D. 2  6i
Câu 44. (THPT Nguyễn Huệ - Phú Yên - 2021) Trên tập số phức, phương trình 2
z  3z  5  0 có hai
nghiệm z , z . Giá trị 4z z bằng 1 2 1 2 A. 2 5 . B. 4 5 . C. 3 5 . D. 3 5 . a bi
Câu 45. (THPT Lương Thế Vinh - 2021) Cho a, b   thoả mãn
 3  2i . Giá trị của tích ab 1 i bằng A. 5. B. 5  . C. 1  . D. 1.
Câu 46. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho số phức z  4  3i . Có bao nhiêu số thực a để
số phức z  az có mô đun bằng 5 . A. 1. B. 2 . C. 3 . D. 0 .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hai số phức z  3  i và z  1 i 1 2 . Phần ảo z của số phức 1 z  là z 2 A. 2i . B. i  . C. 2 . D. 1  .
Câu 48. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Gọi z và z là hai nghiệm phức của phương trình 1 2 2
z z 1  0 . Khi đó 2 2 2
z z z z z z bằng 1 2 1 2 1 1 1 A. 1. B.  . C. 1  . D. 2  . 2 1
Câu 49. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z a bi và w 
z z. Mệnh đề nào 2 dưới đây ĐÚNG? A. w  2 .
B. w là một số thực. C. w  i .
D. w là số thuần ảo. 1  2i
Câu 50. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z
. Trong mặt phẳng tọa độ, điểm 1  i
biểu diễn số phức z là điểm nào dưới đây?  1 3   1 3   1 3   1 3  A. ;   . B.  ;    . C. ;   . D.  ;   .  2 2   2 2   2 2   2 2 
Câu 51. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Gọi z , z là các ngiệm phức của phương trình 1 2 2
z  2z  5  0 . Giá trị của biểu thức  z z 2 bằng: 1 2 A. 16  . B. 4 . C. 4 . D. 16 .
Câu 52. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức z thỏa mãn 2  iz  4  3i . Môđun
của số phức z bằng A. 2 . B. 1. C. 5 . D. 5 .
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hai số phức z  5  2i và z  2  3i . Điểm biểu diễn 1 2
cho số phức z z là 1 2 A. M 3; 5   . B. M  3  ;5 .
C. M 3;5 . D. M  3  ; 5   .
Câu 54. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho 2 số thực a và b thỏa mãn
2a  b 18ii a  2 19i với i là đơn vị ảo. Tính giá trị biểu thức P a b ? A. 19 . B. 17 . C. 39 . D. 37 .
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Kí hiệu z , z là hai nghiệm phức của phương trình 1 2 1 1 2
z  2z  4  0 . Giá trị của  bằng z z 1 2 1 1 A. 2 . B. . C. 1. D. . 2 2
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức z    i  i2 3 2 1
. Môđun của w  iz z là A. 2 2 . B. 1. C. 2 . D. 2 .
Câu 57. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức z  3  i và z  1  i . Phần ảo 1 2
của số phức z z bằng 1 2 A. 4 B. 4i C. 1 D. i
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Gọi z là nghiệm phức có phần ảo âm của phương 0 trình 2
z  2z  5  0 . Môđun của số phức z i bằng 0 A. 2. B. 2 . C. 10 . D. 10 .
Câu 59. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tính mô-đun của số phức z    i  i2 2 1 1 .
A. z  17 .
B. z  17 .
C. z  15 . D. z  3 .
Câu 60. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức z thỏa mãn phương trình
z  (2  3i)(4  i) là z a bi . Khi đó a b bằng A. 2  1. B. 1. C. 21 . D. 1  .
Câu 61. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức z thỏa mãn phương trình
2  iz 1  3i . Phần thực của số phức z bằng A. 2  . B. 1  . C. 2 . D. 1.
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Trên mặt phẳng tọa độ Oxy , điểm biểu diễn
của số phức z z z ( với z  5  3i và z  6  4i ) là điểm nào dưới đây? 1 2 1 2
A. M 1;  1 .
B. Q 11;7 . C. P  1  ;   1 . D.  1  1;  7 .
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Điểm biểu diễn số phức z  7  bi với b  
nằm trên đường thẳng có phương trình là A. x  7. B. y  7. C. y  7  . D. x  7  .
Câu 64. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho số phức z thỏa mãn 1 iz  3i 1  4  2i .
Tính mô-đun của z . A. z  2 2 . B. z  5 2 . C. z  5 . D. z  2 .
Câu 65. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức z thỏa mãn z z  2  8i . Tìm số
phức liên hợp của z A. 1  5  8i . B. 1  5  2i . C. 1  5  7i . D. 1  5  8i .
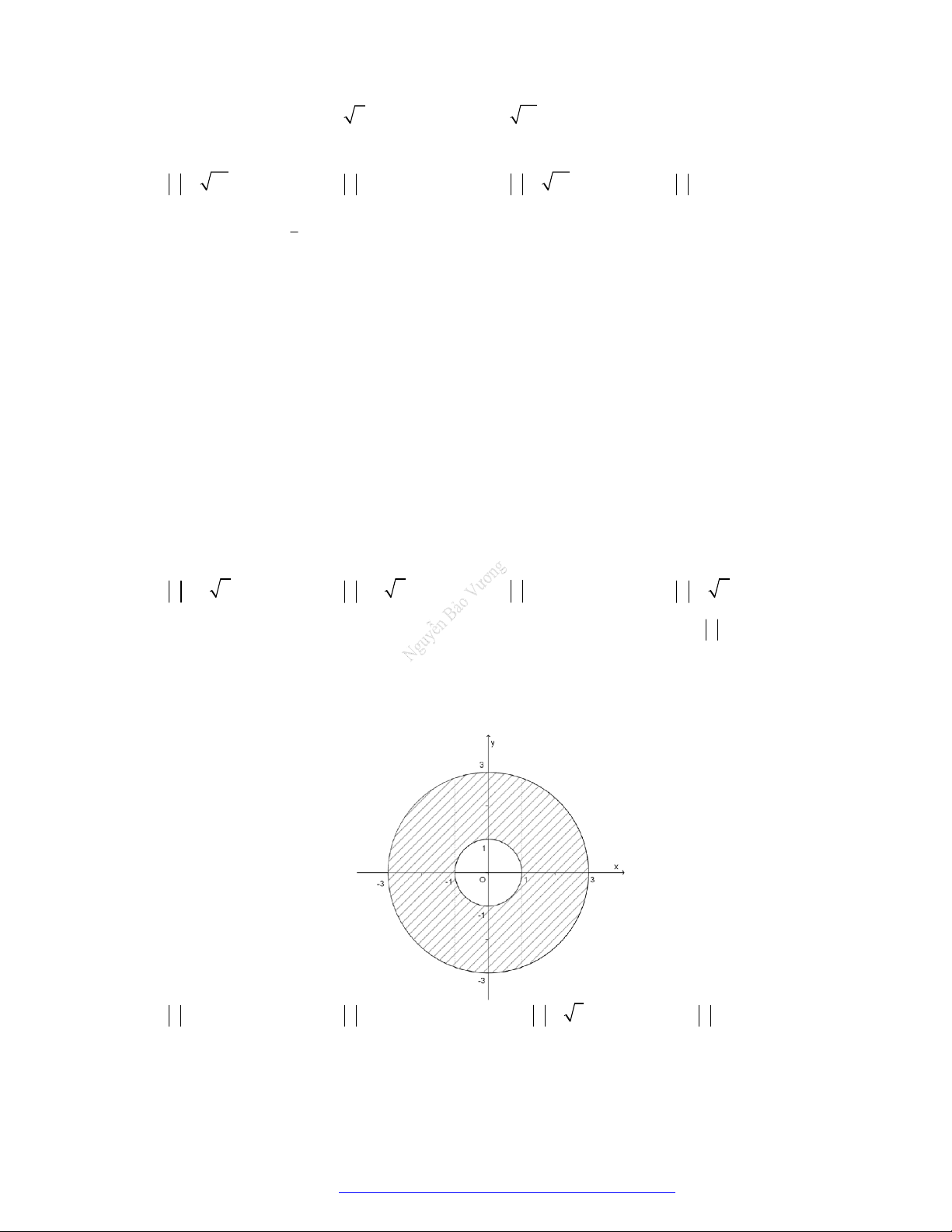
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Phần gạch chéo trong hình vẽ trên là tập hợp các
điểm biểu diễn số phức z thỏa mãn điều kiện nào? A. z  1. B. z  3.
C. 1  z  3 .
D. 1  z  3 .
Câu 67. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Phương trình 2
z  3z  9  0 có hai nghiệm phức
z , z . Tính S=z z  z +z . 1 2 1 2 1 2
A. S  12 . B. S  6 . C. S  6 . D. S  12
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số thực ,
x y thỏa mãn phương trình
x  2i  3  4 yi . Khi đó, giá trị của x và y là :
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 1 1
A. x  3; y  .
B. x  3; y   . 2 2 1
C. x  3i; y  .
D. x  3; y  2 . 2
Câu 69. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Trong mặt phẳng phức, gọi ,
A B,C, D lần lượt là
các điểm biểu diễn số phức z  1
  i , z  1 2i, z  2  i, z  3
i . Gọi S là diện tích tứ giác 1 2 3 4
ABCD . Tính S ? 21 19 23 17 A. S  . B. S  . C. S  . D. S  . 2 2 2 2
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho số phức z thỏa mãn iz  3  i z . Tổng phần thực
và phần ảo của số phức w  3z z bằng A. 8  . B. 5. C. 5. D. 8.
Câu 71. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Gọi z là nghiệm phức có phần ảo dương của phương 0 trình 2
z  2z 10  0 . Môđun của số phức z i bằng 0 A. 3 . B. 5 . C. 1. D. 3 . z  1 i z  1 i z iz
Câu 72. (THPT Đồng Quan - Hà Nội - 2021) Cho hai số phức 1 và 2 . Giá trị 1 2 bằng A. 2  2i . B. 2i . C. 2 . D. 2  2i .
Câu 73. (THPT Lê Lợi - Thanh Hóa - 2021) Cho số phức z thỏa mãn z 1 2i  5 và M  ; x y  là điểm
biểu diễn số phức z . Tập hợp các điểm M thuộc đường tròn nào sau đây? 2 2 2 2 A. x  
1   y  2  5. B. x   1
  y  2  25 . 2 2 2 2 C. x   1
  y  2  5. D. x   1
  y  2  25.
Câu 74. (Trung Tâm Thanh Tường -2021) Gọi ,
A B lần lượt là điểm biểu diễn cho hai số phức
z  1 i và z  1 3i . Gọi M là trung điểm của đoạn thẳng AB . Khi đó M là điểm biểu diễn 1 2
cho số phức nào dưới đây? A. i . B. 1 i . C. 2  2i . D. 1 i .
Câu 75. (THPT Trần Phú - Đà Nẵng - 2021) Cho số phức 2020 2021 2022 z  2i  5i  3i . Phần thực của z bằng A. 3 . B. 2 . C. 4 . D. 5 . BẢNG ĐÁP ÁN 1.A 2.C 3.C 4.B 5.B 6.B 7.B 8.A 9.B 10.D 11.A 12.B 13.C 14.D 15.A 16.B 17.B 18.A 19.D 20.B 21.A 22.C 23.C 24.D 25.D 26.A 27.D 28.A 29.A 30.B 31.C 32.B 33.C 34.B 35.B 36.A 37.D 38.A 39.B 40.A 41.C 42.C 43.C 44.D 45.B 46.B 47.D 48.D 49.B 50.D 51.A 52.C 53.A 54.C 55.C 56.A 57.A 58.B 59.A 60.C 61.B 62.B 63.A 64.C 65.D 66.D 67.C 68.A 69.D 70.D 71.B 72.C 73.D 74.B 75.D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ THÔNG HIỂU Câu 1.
(Sở Vĩnh Phúc - 2021) Cho số phức z thỏa mãn z z . Trong mặt phẳng tọa độ Oxy , tập hợp tất
cả các điểm biểu diễn cho số phức z là đường thẳng nào trong các đường thẳng sau đây?
A. Đường thẳng y  0 . B. Đường thẳng x  0 .
C. Đường thẳng y x . D. Đường thẳng y  x . Lời giải Chọn A
Đặt z x yi x, y   .
Ta có: z z x yi x yi y  0 .
Vậy tập hợp tất cả các điểm biểu diễn cho số phức z là đường thẳng y  0 . Câu 2.
(Sở Lào Cai - 2021) Cho số phức z  2i 1 . Điểm nào sau đây là điểm biểu diễn của số phức z trên mặt phẳng tọa độ?
A. H 1; 2 .
B. T 2;   1 . C. G 1; 2   . D. K 2  ;1 . Lời giải Chọn C
Ta có z  2i 1  z  1 2i G 1; 2 Câu 3.
(Sở Lào Cai - 2021) Cho hai số phức z  2  i, z  2  4i . Tính z z .z . 1 2 1 1 2 5 A. . B. 1. C. 5 5 . D. 5 . 5 Lời giải Chọn C
Ta có: z .z  2  i 2  4i  1
 0i , z z .z  2  i  1
 0i  2 11i . 1 1 2   1 2   
Vậy z z .z  2 11i  2   1  2 2 1  5 5 . 1 1 2 Câu 4.
(Sở Hà Tĩnh - 2021) Cho số phức z thỏa mãn 2  z i  3  2iz  11 
16i . Môđun của số phức z bằng. A. 5 . B. 5 . C. 13 . D. 3 . Lời giải Chọn B
Gọi z x yi . Ta có:
2  z i  3 2iz  11 
16i  2 x yi i  3  2i x yi  1  116i
 2x  2 yi  2i  3x  3yi  2xi  2 y  1  116i
 x  2 y  2  5y  2xi  1  116i
x  2 y  11 
x  2 y  11 x  3      
2  5 y  2x  16 
2x  5 y  14   y  4  
Vậy z  3  4i z  5 . Câu 5.
(Sở Yên Bái - 2021) Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  6z 18  0 . Tính giá 1 2
trị của biểu thức P   z z 2 bằng 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 A. 6 . B. 36 . C. 18 . D. 24 . Lời giải Chọn B
z  3  3i 2 2 Ta có : 2
z  6z 18  0   
z z   3  3i  3 3i 2  6  36. 1 2 z  3  3iCâu 6.
(Sở Yên Bái - 2021) Tính môđun của số phức z thỏa mãn (2  i)z 13i  1. 5 34 34 A. z  .
B. z  34 .
C. z  34 . D. z  . 3 3 Lời giải Chọn A 113i
Ta có (2  i)z 13i  1  z
z  3  5i . 2  i Suy ra 2 2
z  3  (5)  34 . Câu 7.
(Sở Tuyên Quang - 2021) Cho hai số phức z  2  4i và z  1 3i . Phần ảo của số phức z iz 1 2 1 2 bằng A. 5  . B. 3  . C. 3i . D. 5  i . Lời giải Chọn B
Ta có: z iz  2  4i i(1 3i)  2  4i  3  i  5  3i 1 2
Phần ảo của số phức z iz bằng 3 1 2 Câu 8.
(Sở Tuyên Quang - 2021) Tìm số phức liên hợp của số phức z i     i2 4 1 1 3
A. z  9  2i . B. z  9   2i .
C. z  9  2i . D. z  9   2i . Lời giải Chọn A 2
Ta có z  4i 1 1 3i  4i 1 6i 8  9  2i . Do đó số phức liên hợp của z là z  9  2i . Câu 9.
(Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho các số phức z  1 2i, w  2  i . Số phức u  . z w có
A. Phần thực là 0 và phần ảo là 3.
B. Phần thực là 4 và phần ảo là 3.
C. Phần thực là 0 và phần ảo là 3i .
D. Phần thực là 4 và phần ảo là 3i . Lời giải Chọn B
 Ta có u z.w  1 2i2  i  4  3i .
 Vậy số phức u z.w có phần thực là 4 và phần ảo là 3.
Câu 10. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho số phức z  1  2i . Tìm phần 1
ảo của số phức P  . z 2 2 A.  2 . B.  . C. 2 . D. . 3 3 Lời giải Chọn D 1 1 1 2i 1 2 2 Ta có P     
i . Do đó phần ảo của số phức P là . z 1 2i 3 3 3 3
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 11. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Trong mặt phẳng Oxy , tập hợp điểm
M biểu diễn số phức cho số phức z thỏa mãn z 1 2i  1là một đường tròn C , tâm I của đường tròn đó là
A. I 1; 2  .
B. I 2 ; 1  C. I  2  ; 1  .
D. I 2 ;1  Lời giải Chọn A
 Gọi z x yi z x yi x, y   .  2 2
Ta có z 1 2i  1  x yi 1 2i  1   x  
1   y  2  1.
Vậy tập hợp điểm M biểu diễn số phức cho số phức z thỏa mãn z 1 2i  1 là một đường tròn
C có tâm I 1; 2  .
Câu 12. (Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Phương trình 2
z  2z  5  0 có hai 2 2
nghiệm phức z , z . Khi đó zz bằng 1 2 1 2 A. 10 . B. 10 . C. 5 . D. 2 5 . Lời giải Chọn B z  1 2i  Ta có: 2 1
z  2z  5  0   z  1 2i  2  zz
  1 2   1 2  2 2 2 2 2 2  5  5  10 1 2
Câu 13. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho số phức z  5  4i . Số phức đối của z có tọa
độ điểm biểu diễn là A. 5; 4   . B. 5;4 . C.  5  ;4 . D.  5  ; 4   . Lời giải Chọn C
Gọi w là số phức đối của z w z  0  w  5   4i .
Như vậy điểm biểu diễn w có tọa độ là  5  ;4 .
Câu 14. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Kí hiệu z , z là hai nghiệm của phương trình 1 2 2
z  4  0 . Gọi M , N lần lượt là điểm biểu diễn của z , z trên mặt phẳng tọa độ. Tính 1 2
T OM ON với O là gốc tọa độ. A. T  2 . B. T  2 . C. T  8 . D. T  4 . Lời giải Chọn D z  2i 2 1 z  4  0   . z  2  i  2
Khi đó: M 0;2 , N 0; 2   .
Vậy T OM ON  2  2  4 . z  4  3i z  7  3i
Câu 15. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hai số phức 1 và 2 . Tìm số
z z z phức 1 2 . A. z  3   6i . B. z  1  10i . C. z  11.
D. z  3  6i . Lời giải Chọn A
 Ta có z z z  (4  3i)  (7  3i)  3  6i . 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 16. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức z thỏa mãn: 2iz  5  i i  (z  2i) .
Tính môđun của số phức w z 1 i . 4 3 9 1 A. i . B. 1. C. . D. . 5 5 5 5 Lời giải Chọn B
Gọi z a bia,b R .
2iz  5  i i   z  2i  2i a bi  5  i i  a bi  2i
  2b  5  2a  
1 i  a  3  bi  9 a
2b  5  a
a  2b  5   5      
2a 1  3  b 2a b  2 8   b      5 9 8 4 3  w
i 1 i
i w  1. 5 5 5 5
Câu 17. (Chuyên Lê Hồng Phong - TPHCM - 2021) Cho hai số phức z m  2n m  3 i và 1    
z n  3m ni với ,
m n   . Biết rằng z z , khẳng định nào sau đây đúng? 2   1 2
A. m n  0 .
B. m n  5 .
C. m n  3.
D. m n  3  . Lời giải Chọn B
m  2n n  3m
4m n  0 m  1
Ta có: z z    
m n  5 . 1 2   m  3  nm n  3  n  4   
Câu 18. (Chuyên Lam Sơn - Thanh Hóa - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn của số phức
z    i2 2
là điểm nào dưới đây?
A. P 3; 4 .
B. M 5; 4 .
C. N 4;5 .
D. Q 4;3 . Lời giải Chọn A 2
Ta có z    i 2 2
 4  4i i  3  4i P 3;4 là điểm biểu diễn của z    i2 2 .
Câu 19. (Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức z  1 i và z  3  2i . Phần ảo của số 1 2
phức 2z z bằng 1 2 A. 0 . B. 2 . C. 4 . D. 4 . Lời giải Chọn D
 Ta có 2z z  2 1 i  3  2i  5  4i . 1 2  
 Vậy phần ảo của số phức 2z z bằng 1 2 4 .
Câu 20. (Chuyên KHTN - 2021) Trên mặt phẳng phức, biết rằng tập hợp các điểm biểu diễn các số phức
z thỏa mãn z  2  i  1 là một đường tròn. Đường tròn đó có tâm là A. I 1; 2 . B. I 2;  1 . C. I 2;1 . D. I 1;  2 . 4   3   1   2   Lời giải Chọn B Gọi M  ;
x y là tập hợp các điểm biểu diễn số phức z x yi ( , x y   ). 2 2
Ta có z  2  i  1  x yi  2  i  1  x  2   y  
1 i  1   x  2   y   1  1  1 .
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Khi đó, tập hợp các điểm M  ;
x y biểu diễn các số phức z thỏa mãn z  2  i  1 là một đường
tròn C  có phương trình (1). Và đường tròn C  đó có tâm là I 2; 1 . 1  
Câu 21. (Chuyên KHTN - 2021) Cho số phức z thỏa mãn 2  iz  1  i  9  2i . Môđun của số phức z bằng A. 13 . B. 13 . C. 5 . D. 5 . Lời giải Chọn A 8  i 6 17
Ta có: 2  iz  1  i  9  2i  2  i z  8  i z   z   i 2  i 5 5 2 2  6   17  Suy ra: z    13     .  5   5 
Câu 22. (Chuyên KHTN - 2021) Phương trình 4
z  16 có bao nhiêu nghiệm phức? A. 0 . B. 4 . C. 2 . D. 1. Lời giải Chọn C 2 z  4  z  2 Ta có: 4 z  16    . 2 2  z  4   4i z  2i  
Vậy phương trình có hai nghiệm phức là 2  i .
Câu 23. (Chuyên KHTN - 2021) Tập hợp các điểm biểu diễn số phức z thỏa mãn z 1
 3i z 1i .
A. x y  2  0 .
B. x  2 y  2  0 .
C. x y  2  0 .
D. x y  2  0 . Lời giải Chọn C
z x yix, y   thì z 1
  3i z 1i  2 2 2 2 x yi 1
 3i xyi 1i  x  1  y   3  x   1 y   1
 4x  4 y  8  0  x y  2  0 .
Câu 24. (Chuyên KHTN - 2021) Cho số phức z thỏa mãn 3z i z  8  0 .Tổng phần thực và phần ảo của z bằng A. 1. B. 1  . C. 2 . D. 2  . Lời giải Chọn D  Gọi số phức 2
z a bi; , a b  ,  i  1  .
 3z i z  8  0  3a bi  i a bi  8  0 3
a b  0 a  1
 3a b  a  3b  8i  0    
a  3b  8  0 b  3  
 Vậy a b  2
Câu 25. (Chuyên Quốc Học Huế - 2021) Gọi C  là đường cong trong mặt phẳng Oxy biểu diễn các số 2 phức z thỏa mãn .
z z z z  1 và H là hình phẳng giới hạn bởi C  . Diện tích của hình phẳng H bằng 2  A. . B.  5. C. 2 5. D. . 5 5 Lời giải Chọn D
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Đặt z x y ;
i x, y   . 2 2 Ta có .
z z z z  1   x yi x yi  x yi  (x yi)  1 2 2 x y 2 2 2 2 2
x y  4 y  1  x  5y  1    1 1 1 5 1
Do đó tập hợp điểm biểu diễn số phức z là elip có a  1; b  . 5 
Suy ra diện tích hình phẳng H là S   ab  . 5
Câu 26. (Chuyên Quang Trung - Bình Phước - 2021) Cho z   thỏa z  2 z  12 . Phần ảo của z là A. 0 B. 4 C. 12  D. 2 Lời giải Chọn A
Gọi z a bi z  2 z  12 2 2
a bi  2 a b  12 2 2 
a  2 a b  12  b   0 
Câu 27. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức z  4  3i . Chọn khẳng định đúng trong các khẳng định sau
A. Số phức liên hợp của z là z  4   3i .
B. Điểm biểu diễn của số phức z là M  3  ; 4 .
C. Môđun của số phức z bằng   2 2 4 3i . 1 4 3
D. Số phức nghịch đảo của z là   i . z 25 25 Lời giải Chọn D 1 1 4  3i 4  3i 4 3
Số phức nghịch đảo của z là      i . z 4  3i
4  3i4  3i 25 25 25
Câu 28. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm số phức z thỏa mãn z  1 2iz  8 14i .
A. z  3  4 . i B. z  3  . i
C. z  1 2 . i D. z  2   i Lời giải Chọn A
Gọi số phức z a bi , a, b R .
Khi đó z  1 2iz  8 14i a bi  1 2ia bi  8 14i 2b  8 a  3
 2b  2a  2bi  8 14i     . 2a  2b  14  b  4 
Vậy số phức cần tìm là z  3  4 . i
Câu 29. (Chuyên Ngoại Ngữ Hà Nội- 2021) Tìm các số thực x , y thỏa mãn 2x  
1   y ii  2i
A. x  1 và y  2 .
B. x  1 và y  2 .
C. x  1 và y  2 . D. x  1 và y  2 . Lời giải Chọn A 2x  2  0 x  1 2x  
1   y ii  2i  2x  2  yi  2i     . y  2 y  2  
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 30. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Gọi z , z là nghiệm phức của phương trình 1 2 2
z  5z  8  0 . Giá trị 2 2 z z bằng 1 2 A. 41 . B. 9 . C. 16 . D. 17 . Lời giải Chọn B z z  5
Vì z , z là nghiệm phức của phương trình 2
z  5z  8  0 nên 1 2 . 1 2 z .z  8  1 2
Suy ra z z   z z 2 2 2 2
 2z .z  5  2.8  9 . 1 2 1 2 1 2 z  3  4i z  2  i
Câu 31. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức 1 và 2 . Số phức z iz 1 2 bằng A. 5  3i B. 5  3i C. 2  2i D. 2  2i Lời giải. CHỌN C
Ta có: z iz  (3  4i)  i(2  i)  2  2i 1 2
Câu 32. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi z là nghiệm phức có phần ảo dương của phương 0 trình 2
z  4z  8  0 . Trên mặt phẳng tọa độ Oxy , điểm nào dưới đây là điểm biểu diễn của số phức iz ? 0
A. Q 2; 2 .
B. M 2; 2 . C. P  2  ; 2   . D. N 2; 2   . Lời giải Chọn B
z  2  2i Ta có 2
z  4z  8  0   z  2  2i
Vì z là nghiệm phức có phần ảo dương  z  2  2i iz i 2  2i  2   2i . 0 0   0
Vậy điểm biểu diễn số phức iz là M  2  ; 2 . 0
Câu 33. (Chuyên Hạ Long - Quảng Ninh - 2021) Trong mặt phẳng với hệ tọa độ Oxy , biết điểm M 3; 5
  là điểm biểu diễn số phức z . Phần ảo của số phức z  2i bằng A. 5 . B. 2 . C. 3 . D. 5 . Lời giải Chọn C
Ta có z  3  5i z  2i  3  5i  2i  3  3i .
Phần ảo của số phức z  2i bằng 3  .
Câu 34. (Chuyên Hạ Long - Quảng Ninh - 2021) Số phức liên hiệp của z  4   3   1 i là:
A. z  4   3   1 i .
B. z  4  1 3i . C. z  4  1 3i . D. z  4   3   1 i . Lời giải Chọn B
z  4   3  
1 i z  4   3  
1 i  4  1 3i .
Câu 35. (Chuyên Hạ Long - Quảng Ninh - 2021) Gọi z ; z là các nghiệm của phương trình 1 2 2
z  3z  5  0 . Mô đun của số phức 2z  3 2z  3 bằng 1  2  A. 7 . B. 11. C. 29 . D. 1. Lời giải Chọn B 3 11 Phương trình 2
z  3z  5  0 có nghiệm là z   i 2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 3 11 3 11
Không mất tính tổng quát, giả sử: z   i và z   i 1 2 2 2 2 2
Ta có: 2z  32z  3  3 i 11  33 i 11  3   i  11 2
i 11  11i  11 1 2
Vậy mô đun của số phức 2z  3 2z  3 bằng 11. 1  2  z  1  2i z  3  i
Câu 36. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho hai số phức 1 và 2 . Môđun của số
phức  z z z z bằng 1 2  1 2 A. 5 34 . B. 4 35 . C. 5 43 . D. 5 10 . Lời giải Chọn A
Ta có  z z z z  25 15i . Số phức này có môđun bằng 2 2 25 15  5 34 . 1 2  1 2
Câu 37. (Chuyên ĐHSP Hà Nội - 2021) Trên mặt phẳng toạ độ Oxy , biết điểm M  2   ;1 là điểm biểu
diễn số phức z . Phần thực của số phức 3  2iz bằng A. 8  . B. 7 . C. 1  . D. 4  . Lời giải Chọn D Ta có z  2
  i nên 3  2iz   2
  i3  2i  6
  4i  3i  2  4   7i .
Vậy phần thực của số phức 3  2iz là 4  .
Câu 38. (Chuyên ĐHSP Hà Nội - 2021) Cho hai số phức z  4  3i và w  1 i . Mô đun của số phức z.w bằng A. 5 2. B. 4 2. C. 5. D. 3 2. Lời giải Chọn A Ta có .
z w  4  3i1 i  5 2 .
Câu 39. (Chuyên ĐH Vinh - Nghệ An - 2021) Gọi z ; z là các nghiệm của phương trình 2
z  3z  5  0 . 1 2
Mô đun của số phức 2z  3 2z  3 bằng 1  2  A. 7 . B. 11. C. 29 . D. 1. Lời giải Chọn B 3 11 Phương trình 2
z  3z  5  0 có nghiệm là z   i 2 2 3 11 3 11
Không mất tính tổng quát, giả sử: z   i và z   i 1 2 2 2 2 2
Ta có: 2z  32z  3  3 i 11  33 i 11  3   i  11 2 i 11  11  i  11 1 2
Vậy mô đun của số phức 2z  3 2z  3 bằng 11. 1  2 
Câu 40. (THPT Thanh Chương 1- Nghệ An - 2021) Trên mặt phẳng tọa độ, điểm biểu diễn số phức
là điểm nào dưới đây? A. . B. . C. . D. . Lời giải Chọn A  Ta có:
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
 Vậy điểm biểu diễn số phức là điểm .
Câu 41. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Phần ảo của số phức bằng A. . B. . C. . D. . Lời giải Chọn C
Vậy phần ảo của số phức bằng .
Câu 42. (THPT Thanh Chương 1- Nghệ An - 2021) Gọi ,
là hai nghiệm của phương trình . Giá trị biểu thức bằng A. . B. . C. . D. . Lời giải Chọn C Ta có: Vậy . z  1 5i z  3  i z z
Câu 43. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hai số phức 1 và 2 . Số phức 1 2 là A. 2   6i . B. 2  6i . C. 2   6i . D. 2  6i Lời giải Chọn C
z z  1 3  5 1 i  2   6i . 1 2    
Câu 44. (THPT Nguyễn Huệ - Phú Yên - 2021) Trên tập số phức, phương trình 2
z  3z  5  0 có hai
nghiệm z , z . Giá trị 4z z bằng 1 2 1 2 A. 2 5 . B. 4 5 . C. 3 5 . D. 3 5 . Lời giải Chọn D  3 11 z   i 1  2 2 Ta có 2
z  3z  5  0   .  3 11 z   i 2  2 2
 Vậy 4z z  3 5 . 1 2 a bi
Câu 45. (THPT Lương Thế Vinh - 2021) Cho a,b   thoả mãn
 3  2i . Giá trị của tích ab 1 i bằng A. 5. B. 5  . C. 1  . D. 1. Lời giải Chọn B
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 a bi Ta có:
 3  2i a bi  1 i3  2i  a bi  5  i 1 ia  5    ab  5  b  1  
Câu 46. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho số phức z  4  3i . Có bao nhiêu số thực a để
số phức z  az có mô đun bằng 5 . A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn B
 Ta có: z  4  3i z  4  3i .  2 2
Do đó: z  az a 4  3i  4a  3ai ; z   a   a 2 4 3  25a . Theo bài ra: 2
z  5  25a  5 2 2
 25a  25  a  1  a  1 .
Câu 47. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hai số phức z  3  i và z  1 i 1 2 . Phần ảo z của số phức 1 z  là z 2 A. 2i . B. i  . C. 2 . D. 1  . Lời giải Chọn D z 3  i
3  i1 i 2
3  3i i i Ta có: 1 z      2  i 2 2 z 1  i 1  i 2 2
Phần ảo của số phức z là 1  .
Câu 48. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Gọi z và z là hai nghiệm phức của phương trình 1 2 2
z z 1  0 . Khi đó 2 2 2
z z z z z z bằng 1 2 1 2 1 1 1 A. 1. B.  . C. 1  . D. 2  . 2 Lời giải Chọn D z z  1 
Theo định lý Viet ta có : 1 2  . z .z  1  1 2
Mặt khác z là nghiệm của phương trình nên 2 2
z z 1  0  z z  1 , 1 1 1 1 1 Do đó: 2 2 2
z z z z z z z z z z    2 z z
 1. 1  1  2 . 1 2 1 2 1 1 1 2 1 2 1 1      1
Câu 49. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z a bi và w 
z z. Mệnh đề nào 2 dưới đây ĐÚNG? A. w  2 .
B. w là một số thực. C. w  i .
D. w là số thuần ảo. Lời giải Chọn B 1 1
Ta có z a bi  w 
z z  .2a a . 2 2 1  2i
Câu 50. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z
. Trong mặt phẳng tọa độ, điểm 1  i
biểu diễn số phức z là điểm nào dưới đây?  1 3   1 3   1 3   1 3  A. ;   . B.  ;    . C. ;   . D.  ;   .  2 2   2 2   2 2   2 2 
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Lời giải Chọn D 1  2i
1 2i1 i 1 3 Ta có z      i . 1 i
1 i1 i 2 2  1 3 
Vậy điểm biểu diễn số phức z là  ;    2 2 
Câu 51. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Gọi z , z là các ngiệm phức của phương trình 1 2 2
z  2z  5  0 . Giá trị của biểu thức  z z 2 bằng: 1 2 A. 16  . B. 4 . C. 4 . D. 16 . Lời giải Chọn A  2 2
z z    z z  2
 4z z  2  4.5  16  . 1 2 1 2 1 2
Câu 52. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho số phức z thỏa mãn 2  iz  4  3i . Môđun
của số phức z bằng A. 2 . B. 1. C. 5 . D. 5 . Lời giải Chọn C 4  3i
4  3i2  i
Ta có : 2  iz  4  3i z  
 1 2i z  5 . 2  i
2  i2  i
Câu 53. (THPT Ba Đình - Thanh Hóa - 2021) Cho hai số phức z  5  2i và z  2  3i . Điểm biểu diễn 1 2
cho số phức z z là 1 2 A. M 3; 5   . B. M  3  ;5 .
C. M 3;5 . D. M  3  ; 5   . Lời giải Chọn A Gọi M  ;
x y là điểm biểu diễn số phức z z . 1 2
Ta có: z z  5  2  2
  3 i  3  5i . 1 2     Vậy M 3; 5   .
Câu 54. (THPT Quế Võ 1 - Bắc Ninh - 2021) Cho 2 số thực a và b thỏa mãn
2a  b 18ii a  2 19i với i là đơn vị ảo. Tính giá trị biểu thức P a b ? A. 19 . B. 17 . C. 39 . D. 37 . Lời giải Chọn C
Ta có: 2a  b 18ii a  2 19i  2a 18  bi a  2 19i
2a 18  a  2 a  20     . b  19 b  19  
Vậy P a b  20 19  39 .
Câu 55. (THPT Quế Võ 1 - Bắc Ninh - 2021) Kí hiệu z , z là hai nghiệm phức của phương trình 1 2 1 1 2
z  2z  4  0 . Giá trị của  bằng z z 1 2 1 1 A. 2 . B. . C. 1. D. . 2 2 Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Ta có   1 4  3
   3i2  z 1 i 3; z 1 i 3. 1 2 1 1 1 1
z z  1 3  2      1. 1 2 z z 2 2 1 2
Câu 56. (THPT Quốc Oai - Hà Nội - 2021) Cho số phức z    i  i2 3 2 1
. Môđun của w  iz z là A. 2 2 . B. 1. C. 2 . D. 2 . Lời giải Chọn A 2
Ta có z  3  2i1 i  2i 3  2i  4  6i .
Khi đó w  iz z i 4  6i  4  6i  2  2i  w  2 2 .
Câu 57. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hai số phức z  3  i và z  1  i . Phần ảo 1 2
của số phức z z bằng 1 2 A. 4 B. 4i C. 1 D. i Lời giải Chọn A
Ta có z z  3  i1 i 2
 3  3i i i  2  4 . i 1 2
Vậy phần ảo của số phức z z là 4 1 2
Câu 58. (THPT Quảng Xương 1-Thanh Hóa - 2021) Gọi z là nghiệm phức có phần ảo âm của phương 0 trình 2
z  2z  5  0 . Môđun của số phức z i bằng 0 A. 2. B. 2 . C. 10 . D. 10 . Lời giải Chọn B z  1 2i 2
z  2z  5  0 
z  1 2i z i  1 i z  2  . 0 0 0 z  1 2i
Câu 59. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Tính mô-đun của số phức z    i  i2 2 1  1 .
A. z  17 .
B. z  17 .
C. z  15 . D. z  3 . Lời giải Chọn A 2 2
Ta có z    i   i     i z    2 2 1 1 1 4 1  4  17 .
Câu 60. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức z thỏa mãn phương trình
z  (2  3i)(4  i) là z a bi . Khi đó a b bằng A. 2  1. B. 1. C. 21 . D. 1  . Lời giải Chọn C Ta có 2
z  (2 - 3i)(4  i)  8  2i -12i - 3i  1110 . i
z  1110i a bi . Do đó a  11, b  10  a b  11 10  21 .
Câu 61. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức z thỏa mãn phương trình
2  iz 1  3i . Phần thực của số phức z bằng A. 2  . B. 1  . C. 2 . D. 1. Lời giải Chọn B 1   3i
  i  i 2 1 3 2 2
  i  6i  3i 5   5i
Ta có 2  iz 1  3i z      1   i 2  i
2  i2  i 5 5
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Vậy phần thực của số phức z đã cho là 1  .
Câu 62. (THPT Phan Đình Phùng - Quảng Bình - 2021) Trên mặt phẳng tọa độ Oxy , điểm biểu diễn
của số phức z z z ( với z  5  3i và z  6  4i ) là điểm nào dưới đây? 1 2 1 2
A. M 1;  1 .
B. Q 11;7 . C. P  1  ;   1 . D.  1  1;  7 . Lời giải Chọn B
Ta có z z z  5  3i  6  4i  11 7i . 1 2
Vậy điểm biểu diễn của số phức z z z là điểm Q 11;7 1 2
Câu 63. (THPT Phan Đình Phùng - Quảng Bình - 2021) Điểm biểu diễn số phức z  7  bi với b  
nằm trên đường thẳng có phương trình là A. x  7. B. y  7. C. y  7  . D. x  7  . Lời giải Chọn A
Điểm biểu diễn số phức z  7  bi với b   kí hiệu là M 7;b,b  
Khi đó M 7;b,b   nằm trên đường thẳng x  7 với b   .
Câu 64. (THPT Nguyễn Tất Thành - Hà Nội - 2021) Cho số phức z thỏa mãn 1 iz  3i 1  4  2i .
Tính mô-đun của z . A. z  2 2 . B. z  5 2 . C. z  5 . D. z  2 . Lời giải Chọn C
Ta có 1 iz  3i 1  4  2i  1 iz  5  5i . 5  5i
5  5i1 i 5 2i  z   z   z   5i . 1  i
1 i1 i 2 2 1 1
Vậy z   i    2 2 5 0 5  5 .
Câu 65. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho số phức z thỏa mãn z z  2  8i . Tìm số
phức liên hợp của z
A. 15  8i .
B. 15  2i .
C. 15  7i .
D. 15  8i . Lời giải Chọn D
Đặt z a bia,b  . 2 2 
a a b  Khi đó 2 2 2
z z  2  8i a bi a b  2  8i   b   8   2 
a  64  2  aa  1  5     . Suy ra z  1  5  8 . i b   8  b  8   
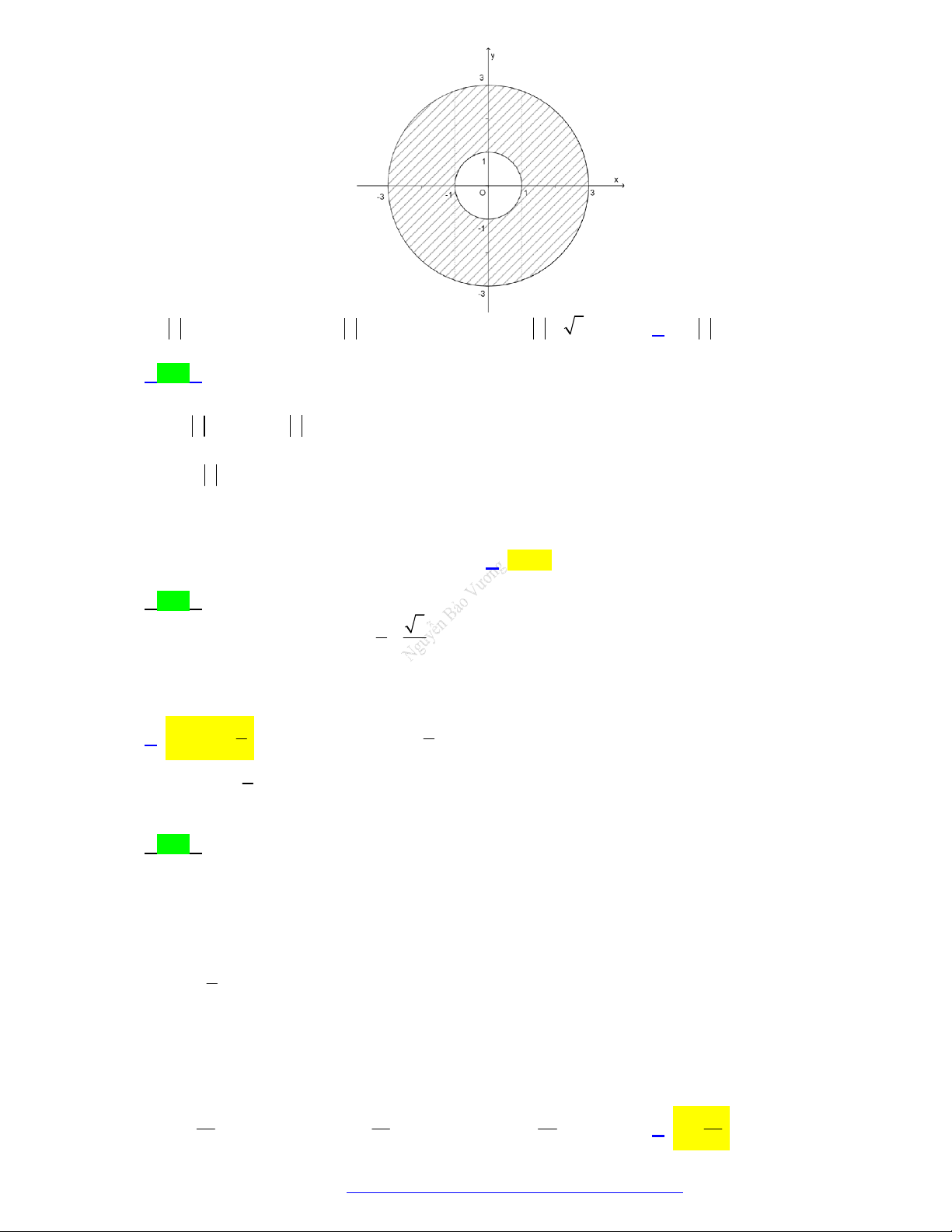
Câu 66. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Phần gạch chéo trong hình vẽ trên là tập hợp các
điểm biểu diễn số phức z thỏa mãn điều kiện nào?
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 A. z  1. B. z  3 .
C. 1  z  3 .
D. 1  z  3 . Lời giải Chọn D
Phần gạch chéo trong hình vẽ nằm giữa hai đường tròn 2 2
x y  1 và 2 2 x y  9 2
 1  z  9  1  z  3 .
Vậy phần gạch chéo trong hình vẽ trên là tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện 1  z  3 .
Câu 67. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Phương trình 2
z  3z  9  0 có hai nghiệm phức
z , z . Tính S=z z  z +z . 1 2 1 2 1 2
A. S  12 . B. S  6 . C. S  6 . D. S  12 Lời giải Chọn C 3 3 Ta có : 2
z  3z  9  0  z   
i  S=z z  z +z  9  3  6. 1,2 1 2 1 2 2 2
Câu 68. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số thực ,
x y thỏa mãn phương trình
x  2i  3  4 yi . Khi đó, giá trị của x và y là : 1 1
A. x  3; y  .
B. x  3; y   . 2 2 1
C. x  3i; y  .
D. x  3; y  2 . 2 Lời giải Chọn A
Ta có: x  2i  3  4 yi x  3  4y  2  x  3    1 y    2 Do đó chọn phương án A.
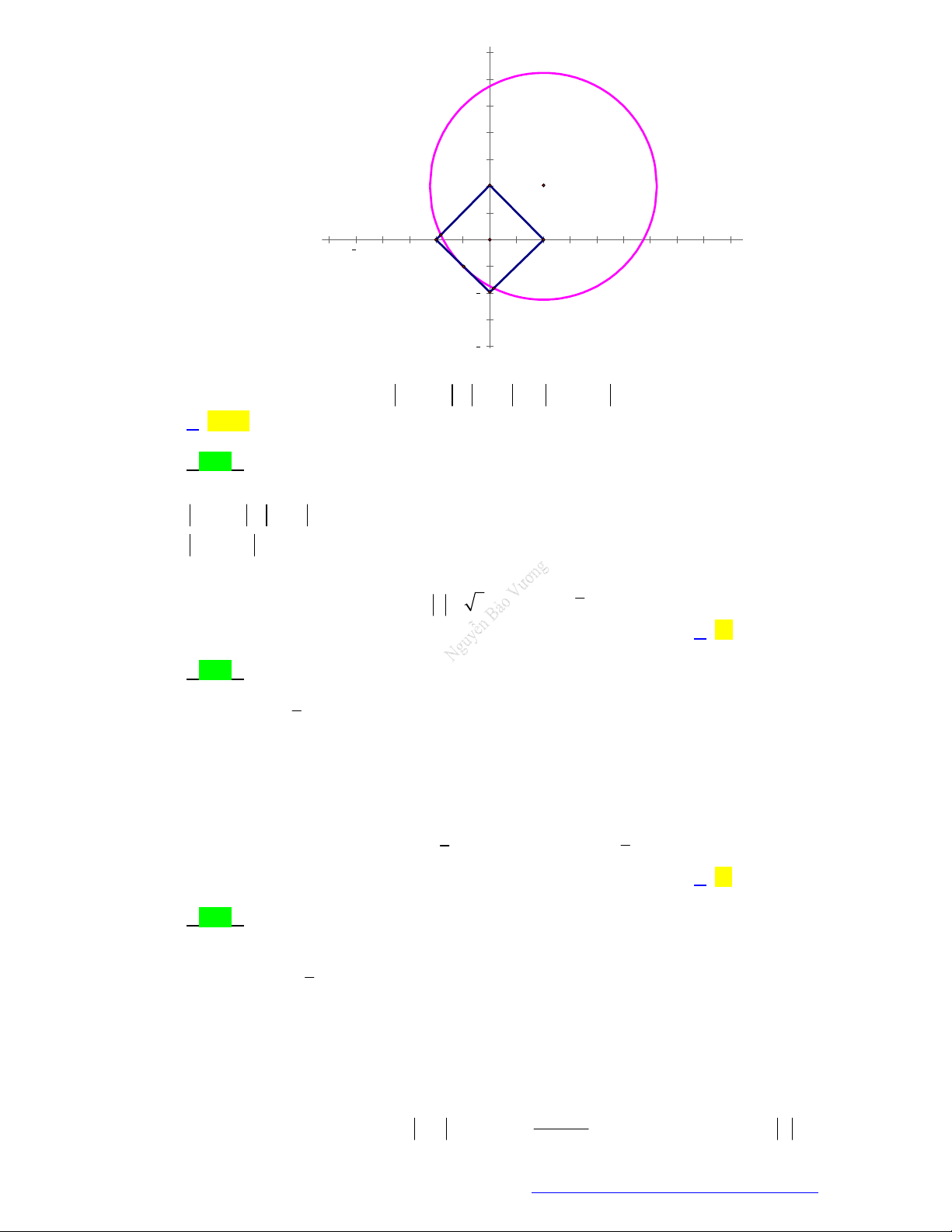
Câu 69. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Trong mặt phẳng phức, gọi ,
A B,C, D lần lượt là
các điểm biểu diễn số phức z  1 i , z  1 2i, z  2  i, z  3
i . Gọi S là diện tích tứ giác 1 2 3 4
ABCD . Tính S ? 21 19 23 17 A. S  . B. S  . C. S  . D. S  . 2 2 2 2 Lời giải
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chọn D
Trong mặt phẳng phức ta xác định các điểm ,
A B,C, D như hình vẽ. S SSSSS IJLK LAB JBC ILCD KAD 1 1 1 1 17
S  3.5  1.2  1.3  2.2  1.4  . 2 2 2 2 2
Câu 70. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho số phức z thỏa mãn iz  3  i z . Tổng phần thực
và phần ảo của số phức w  3z z bằng A. 8.  B. 5. C. 5. D. 8. Lời giải Chọn D Ta có: 3  i
iz  3  i z  1 iz  3  i z   1 2 . i 1  i
Suy ra w  3z z  31 2i  1 2i  4  4 .i
Do đó tổng phần thực và phần ảo của w bằng 8. Vậy ta chọn phương án D.
Câu 71. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Gọi z là nghiệm phức có phần ảo dương của phương 0 trình 2
z  2z 10  0 . Môđun của số phức z i bằng 0 A. 3 . B. 5 . C. 1. D. 3 . Lời giải Chọn B z  1   3i 2
z  2z 10  0   . z  1   3i
Do z là nghiệm phức có phần ảo dương của phương trình đã cho nên z  1   3i . 0 0
z i  1
  3i i  1   2i . 0
Suy ra z i  1 2i   2 2 1  2  5 . 0 z  1 i z  1 i z iz
Câu 72. (THPT Đồng Quan - Hà Nội - 2021) Cho hai số phức 1 và 2 . Giá trị 1 2 bằng A. 2  2i . B. 2i . C. 2 . D. 2  2i . Lời giải Chọn C
Ta có z iz  1 i  1 i i  1 i i 1  2 . 1 2  
Câu 73. (THPT Lê Lợi - Thanh Hóa - 2021) Cho số phức z thỏa mãn z 1 2i  5 và M  ; x y  là điểm
biểu diễn số phức z . Tập hợp các điểm M thuộc đường tròn nào sau đây? 2 2 2 2 A. x  
1   y  2  5. B. x   1
  y  2  25 . 2 2 2 2 C. x   1
  y  2  5. D. x   1
  y  2  25 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489 Lời giải Chọn D
Ta có z 1  2i  5  z  1 2i  5 * .
Gọi A 1; 2 là điểm biểu diễn số phức z  1 2i thì *  z z  5  MA  5 . 1 1
Vậy tập hợp các điểm M là đường tròn tâm A 1; 2 , bán kính R  5 .
Câu 74. (Trung Tâm Thanh Tường -2021) Gọi ,
A B lần lượt là điểm biểu diễn cho hai số phức
z  1 i và z  1 3i . Gọi M là trung điểm của đoạn thẳng AB . Khi đó M là điểm biểu diễn 1 2
cho số phức nào dưới đây? A. i  . B. 1 i . C. 2  2i . D. 1 i . Lời giải Chọn B Do ,
A B lần lượt là điểm biểu diễn cho hai số phức z  1 i và z  1 3i A1  ;1 , B 1; 3   . 1 2
M là trung điểm của đoạn thẳng AB M 1; 
1 . Vậy số phức biểu diễn điểm M là 1 i .
Câu 75. (THPT Trần Phú - Đà Nẵng - 2021) Cho số phức 2020 2021 2022 z  2i  5i  3i . Phần thực của z bằng A. 3 . B. 2 . C. 4 . D. 5 . Lời giải Chọn D  Ta có 2020 2021 2022 i  1, ii, i  1
  z  2.1 5.i  3  1  5  5i .
 Do đó phần thực của z bằng 5.
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ VẬN DỤNG z Câu 1.
(Sở Lào Cai - 2021) Cho z , z là 2 số phức liên hợp của nhau và thỏa mãn 1   và 1 2 2 z2
z z  2 3 . Tính mô đun của số phức z 1 2 1 5
A. z  2 .
B. z  5 .
C. z  3 . D. z  . 1 1 1 1 2 Câu 2.
(Sở Hà Tĩnh - 2021) Cho số phức z thỏa mãn z 1 2i  3. Tính giá trị nhỏ nhất của biểu thức
P z  4  6i . 3 A. min P  .
B. min P  2 . C. min P  1.
D. min P  8 . 2 3  iz Câu 3.
(Sở Hà Tĩnh - 2021) Biết số phức w 
có biểu diễn hình học trong mặt phẳng tọa độ Oxy 2  z
là một đường thẳng. Khi đó môđun của z bằng? 3 2 A. 2 . B. . C. . B. 2 . 2 2 Câu 4.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Có bao nhiêu số phức z thoả mãn
z  2  i  2 2 và  z  2 1 là số ảo? A. 2 . B. 1. C. 4 . D. 3 . Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho số phức z a bi a,b   thỏa
mãn z  3  i z i  0 . Tổng S a b  2ab bằng A. 23. B. 24 . C. 23  . D. 24  . Câu 6.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Gọi z , z là hai nghiệm phức của phương trình 1 2 2 2 2
15z  3z 19  0 . Tính giá trị của biểu thức: K zzz z . 1 2 1 2 22 41 11 7 A. K  . B. K  . C. K  . D. K  . 15 15 50 3 Câu 7.
(Chuyên KHTN - 2021) Cho số phức z a bi thỏa mãn z 1 2i z  3  4i và z  2i z là số
thực. Tổng a b bằng: A. 1. B. 1  . C. 3 . D. 3  . Câu 8.
(Chuyên Quốc Học Huế - 2021) Có bao nhiêu số phức z có mô đun bằng 2 và thỏa mãn
z  3  4i  3 ? A. 0 . B. 1. C. 4 . D. 2 . Câu 9.
(Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức z thỏa mãn 3  4i z  1. Tìm giá trị nhỏ nhất của z . A. 6 . B. 3 2 . C. 4 . D. 5 .
Câu 10. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức z thỏa mãn 3( z i)  (2  i).z  3  10i .
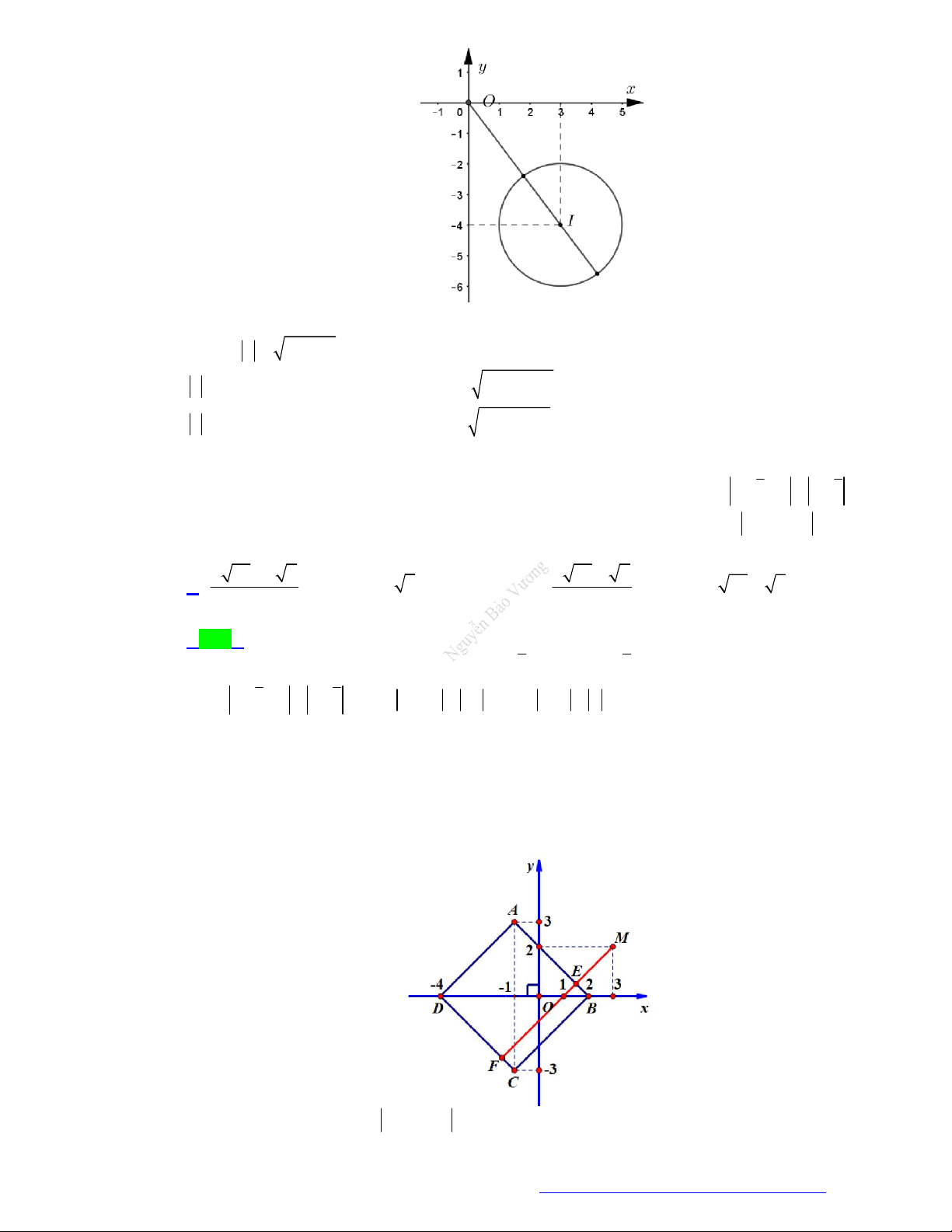
Mô đun của z bằng A. 3 . B. 3 . C. 5 . D. 5 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 11. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức z thỏa mãn điều kiện z  1 i  z  2i là đường nào sau đây? A. Elip B. Đường thẳng C. Đường tròn D. Parabol
Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số phức z đôi một khác nhau thoả mãn
z i  2 và 4
(z  2) là số thực? A. 4 . B. 5 . C. 6 . D. 7 .
Câu 13. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số nguyên a để phương trình 2
z  a   2
3 z a a  0 có 2 nghiệm phức z , z thỏa mãn z z z z ? 1 2 1 2 1 2 A. 4. B. 2. C. 1. D. 3.
Câu 14. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Trên mặt phẳng tọa độ
, tập hợp điểm biểu diễn các số phức
là một đường tròn có bán kính bằng A. B. C. D. 2  3i
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức z thỏa mãn z 1  2 . Mô đun 3  2i
lớn nhất của số phức z bằng A. 13 . B. 2 . C. 1 2 . D. 26 .
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hai số phức z ; z thỏa mãn z  2 ; z  1 và 1 2 1 2
2z  3z  4 . Tính giá trị của biểu thức P z  2z . 1 2 1 2 A. P  10 . B. P  11 . C. P  15 . D. P  2 5 .
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho các số phức z thoả mãn iz 1  1 2i .
Biết rằng tập hợp các điểm biểu diễn các số phức z là đường tròn C  . Tìm tâm I và bán kính
R của đường tròn C  .
A. I 0;   1 , R  3 .
B. I 0;   1 , R  3 . C. I 0  ;1 , R  3 . D. I 0  ;1 , R  3 .
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z thỏa mãn 2  iz  4 z i  8  19i .
Môđun của z bằng A. 5. B. 18. C. 5 . D. 13
Câu 19. (THPT Đào Duy Từ - Hà Nội - 2021) Xét các số phức z thoả mãn i z  3  2i  4 . Trên mặt
phẳng toạ độ Oxy , tập hợp điểm biểu diễn số phức w  2iz  5  6i là một đường tròn có tâm
I a;b , bán kính R . Tính T a b R A. 21 . B. 17 . C. 5 . D. 1 .
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Xét các số phức z thỏa mãn z  4 , biết rằng tập
hợp các điểm biểu diễn của số phức w  3  4iz  5i một đường tròn. Bán kính r của đường tròn đó là: A. r  10 . B. r  20 . C. r  18 . D. r  25 .
Câu 21. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức z a bi a,b   thỏa mãn
z 1 3i z i  0. Tính S  2a  3b A. S  5  . B. S  6. C. S  6  D. S  5.
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 22. (THPT Chu Văn An - Thái Nguyên - 2021) Xét các số phức z thỏa mãn điều kiện
z  2i  
1  z i là số thực. Biết rằng tập hợp các điểm biểu diễn hình học của z là một đường
thằng có phương trình y ax b . Mệnh đề nào sau đây sai?
A. a b  2  .
B. a b  2 . C. 2
a  3b  4 . D. 2
5b a  6 .
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức z thỏa mãn z 1 2i  i z  15  i . Tìm
mô đun của số phức z . A. z  2 5 . B. z  4 . C. z  2 3 . D. z  5 .
Câu 24. (THPT Ba Đình - Thanh Hóa - 2021) Có bao nhiêu số phức z thỏa mãn
1 iz  2 iz 13 2i ? A. 2. B. 1. C. 4. D. 3.
Câu 25. (THPT Quế Võ 1 - Bắc Ninh - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức z thỏa mãn điều kiện z  1 i  z  2i là đường nào sau đây? A. Elip B. Đường thẳng C. Đường tròn D. Parabol
Câu 26. (THPT Quốc Oai - Hà Nội - 2021) Số phức z thoả mãn hệ thức z  2  i  10 và . z z  25 là
A. z  3  4i, z  5 .
B. z  3  4i, z  5 .
C. z  3  4i, z  5 . D. z  3  4i, z  5 .
Câu 27. (THPT Quốc Oai - Hà Nội - 2021) Số thực ,
x y để hai số phức 2 7
z  9 y  4 10xi và 1 2 11
z  8y  20i là liên hợp của nhau. 2 A. x  2  ; y  2 .
B. x  2; y  2 .
C. x  2; y  2 .
D. x  2; y  2 .
Câu 28. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức z a bi  ,
a b   thỏa mãn
z  2iz  3  3i . Tính giá trị biểu thức 2019 2018 P ab 4036 2019 3  3 4036 2019 3  3 A. P   . B. P  . 2019 5 2019 5 C. P  2 . D. P  0 .
Câu 29. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức z thỏa mãn z  2. Biết rằng tập
hợp các điểm biểu diễn số phức w  3  2i  2  iz là một đường tròn. Bán kính R của đường tròn đó bằng A. 2. B. 5. C. 2 5. D. 5.
Câu 30. (THPT Lê Lợi - Thanh Hóa - 2021) Cho số phức z thỏa mãn z 1
  2i  5 . Khi đó
w z 1 i có modul lớn nhất bằng bao nhiêu? A. 5 . B. 5 2 . C. 20 . D. 2 5 .
Câu 31. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức z , z thỏa mãn z z  39 và 1 2 1 2
z z  2 3 . Khi đó z z bằng 1 2 1 2 A. 8 . B. 2 39 . C. 12 . D. 2 3 .
Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Cho số phức z x yi có phần ảo âm, biết z thỏa mãn z i
z  2  i  3  i và
là số thực. Giá trị của x  2 y bằng z  3 11 A. 3 . B. 5 . C. 4 . D. . 3
Câu 33. Có bao nhiêu số phức z thỏa mãn z i z i  4 và  z iz là số thực? A. 1. B. 2 . C. 0 . D. 4 .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 34. Có bao nhiêu số phức z thỏa mãn z z z  1? A. 0 . B. 1. C. 4 . D. 3 . z 1 z  3i
Câu 35. Có bao nhiêu số phức z thỏa mãn   1? z i z i A. 3 . B. 0 . C. 2 . D. 1.
Câu 36. Có tất cả bao nhiêu số phức z mà phần thực và phần ảo của nó trái dấu đồng thời thỏa mãn
z z z z  4 và z  2  2i  3 2. A. 1. B. 3 . C. 2 . D. 0 .
Câu 37. Có bao nhiêu số phức z thỏa z  2  i z  3i và z  2  3i  2 ? A. Vô số B. 0 . C. 2 . D. 1.
Câu 38. Có bao nhiêu số phức z thỏa mãn z  5 và  z  3i z  2 là số thực? A. 1. B. 0. C. 3. D. 2.
Câu 39. Có bao nhiêu số phức z thỏa mãn zz  4 và  z  3  2i3  2z  là số thuần ảo? A. 1. B. 0. C. 3. D. 2. z 1 i
Câu 40. Cho hai số phức z, w thỏa mãn z i  2 và w
. Tìm giá trị nhỏ nhất của w . z  2  i 7 5 a 7 A. 4 . B. a . C. . D. . 3 20 2 z  2
Câu 41. Xét các số phức z thỏa mãn
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số z  2i
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng A. 1. B. 2 . C. 2 2 . D. 2 .
Câu 42. Có bao nhiêu số phức z thỏa mãn z  13 và  z  2i z  4i là số thuần ảo? A. 1. B. 2 . C. 0 . D. 4 . BẢNG ĐÁP ÁN 1.A 2.B 3.A. 4.D 5.C 6.B 7.A 8.B 9.C 10.D 11.B 12.B 13.A 14.D 15.C 16.B 17.B 18.D 19.C 20.B 21.C 22.A 23.B 24.B 25.B 26.A 27.B 28.C 29.C 30.D 31.C 32.C 33.B 34.C 35.D 36.C 37.A 38.D 39.D 40.C 41.B 42.B
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ VẬN DỤNG z Câu 1.
(Sở Lào Cai - 2021) Cho z , z là 2 số phức liên hợp của nhau và thỏa mãn 1   và 1 2 2 z2
z z  2 3 . Tính mô đun 1 2
của số phức z 1 5
A. z  2 .
B. z  5 .
C. z  3 . D. z  . 1 1 1 1 2 Lời giải Chọn A
Giả sử z a bi a  ,
b  thì z a bi . z z  2 3  2bi  2 3  b  3 1 1 2   1   2
a bi 2 2
a b  2abia  2 2 a b  2  2ab b  2 2 a b  2  2a b z1    i 2 za b 2 2 2  2ab2 2 2  2 2 a b   2 2 2 a b zb  0 2 1   thì b  2 2 a b  2 2 3
 2a b  0  3a b b  0   2 z 2 2
b  3a 3 2 
Do b  3 nên b  0 loại. Thay   1 vào 3 ta có 2 a  1 4 . Từ   1 vào 4 2 2
z a b  1 3  2 . 1 Câu 2.
(Sở Hà Tĩnh - 2021) Cho số phức z thỏa mãn z 1 2i  3. Tính giá trị nhỏ nhất của biểu thức
P z  4  6i . 3 A. min P  .
B. min P  2 . C. min P  1.
D. min P  8 . 2 Lời giải Chọn B
Ta có: z 1 2i  3 nên z biểu diễn bởi M nằm trên đường tròn C , tâm I 1;2 , bán kính 3.
Ta có: P z  4  6i z  4  6i  MA (với là khoảng cách từ M C và A4;6.
Khi đó min P IA R  5  3  2 . 3  iz Câu 3.
(Sở Hà Tĩnh - 2021) Biết số phức w 
có biểu diễn hình học trong mặt phẳng tọa độ Oxy 2  z là một
đường thẳng. Khi đó môđun của z bằng? 3 2 A. 2 . B. . C. . B. 2 . 2 2 Lời giải Chọn A 3  iz  3  Ta có w 
 w 2  z   3  iz z  w  i  2  w   , 2  z  2   3  z 3
suy ra z  w  i  2  w  w  i   w   .  2  2 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 3  iz Từ giả thiết w 
có biểu diễn hình học trong mặt phẳng tọa độ Oxy là một đường thẳng 2  z z nên suy ra  1  z  2 . 2 Câu 4.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Có bao nhiêu số phức z thoả mãn
z  2  i  2 2 và  z  2 1 là số ảo? A. 2 . B. 1. C. 4 . D. 3 . Lời giải Chọn D
 Gọi z x yi thoả mãn  ; x y  
 . Điểm biểu diễn của z là M  ; x y Ta có
z  2  i  2 2 2 2 2 2
  x  2   y  
1 i  2 2   x  2   y   1
 2 2   x  2   y   1  8
Vậy M thuộc đường tròn tâm I  2   ;1 , bán kính 2 2   2 z  2 2 1
z  2z 1   x yi  2 x yi 1 2 2
x  2xyi y  2 x yi 1 2 2
x  2x y 1 2xyi  2 yi y x 1  z  2 1 là số ảo nên 2 2
x  2x y 1  0   x  2 2 1  y   y  1 x
Trên cùng một hệ trục toạ độ, ta vẽ đường tròn tâm I  2  
;1 , bán kính 2 2 và hai đồ thị hàm số
y x 1; y  1 x .
Ta thấy hai đường thẳng cắt đường tròn tại ba điểm phân biệt, vậy có 3 điểm M thoả mãn, vậy có
ba số phức z thoả mãn. Câu 5.
(Liên trường huyện Quảng Xương - Thanh Hóa - 2021) Cho số phức z a bi  , a b   thỏa
mãn z  3  i z i  0 . Tổng S a b  2ab bằng A. 23. B. 24 . C. 2  3 . D. 2  4 . Lời giải Chọn C Ta có:
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2
z  3  i z i  0  a bi  3  i a b i  0  a  3   2 2
b 1 a b i  0 a  3  0 a  3        2 2 2 b
 1 a b  0
b 1 9  b  0     1  b  1  0  b   1  Xét 1 2
 9  b b 1     9  b   b  2 2 1 b  4  
Vậy S  3  4  2.3.4  23 Câu 6.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Gọi z , z là hai nghiệm phức của phương trình 1 2 2 2 2
15z  3z 19  0 . Tính giá trị của biểu thức: K zzz z . 1 2 1 2 22 41 11 7 A. K  . B. K  . C. K  . D. K  . 15 15 50 3 Lời giải Chọn B  3   i 1131 z   1 2 30
15z  3z 19  0   .  3   i 1131 z  2  30 2 2 2 2 3   i 1131 3   i 1131 3  i 1131 3   i 1131
Khi đó: K zzz z     1 2 1 2 30 30 30 30 19 19 1 41     . 15 15 5 15 Câu 7.
(Chuyên KHTN - 2021) Cho số phức z a bi thỏa mãn z 1 2i z  3  4i và z  2i z là số
thực. Tổng a b bằng: A. 1. B. 1  . C. 3 . D. 3  . Lời giải Chọn A  Ta có:
z  1  2i z  3  4i a  1  b  2i a  3  b  4i  a  2 1
 b  22  a  32  b  42
a  3b  5 (1)
 Mặt khác: z  2i z a bi  2i(a bi)  a  2b  2a bi là số thực nên 2a b  0 (2)
a  3b  5 a  1 Từ (1) và (2) ta có    2a b  0 b  2  
Tổng a b  1. Câu 8.
(Chuyên Quốc Học Huế - 2021) Có bao nhiêu số phức z có mô đun bằng 2 và thỏa mãn
z  3  4i  3 ? A. 0 . B. 1. C. 4 . D. 2 . Lời giải Chọn B  2 2
Gọi z a bi,a,b   ; ta có 2 2 z
a b và z  3  4i  a  3  b  4 . 
 a  32  b  42  3  
a  32  b  42  9
 Theo bài ra ta có hệ    2 2 2 2    a b  4 a b 2  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489  4b 10 a  2 2  4b 10  
a b  6a  8b 16  0 3
a  4b 10  0 a    3       3   2 2 2 2 2 a b  4 a b  4    4b 10 2 2   a b  4 2    b  4    3    6  4b 10 a a     5   3   . 8 2
25b  80b  64  0   b     5 6 8  Vậy z   i . 5 5 Câu 9.
(Chuyên Ngoại Ngữ Hà Nội- 2021) Cho số phức z thỏa mãn 3  4i z  1. Tìm giá trị nhỏ nhất của z . A. 6 . B. 3 2 . C. 4 . D. 5 . Lời giải Chọn C
Áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối: A B A B A B ta được:
3  4i z  3  4i  z  5  z  1  z  4 .
Vậy giá trị nhỏ nhất của z là 4 .
Câu 10. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức z thỏa mãn 3( z i)  (2  i).z  3  10i .
Mô đun của z bằng A. 3 . B. 3 . C. 5 . D. 5 . Lời giải Chọn D
Đặt z a bi a,b  
3(z i)  (2  i).z  3  10i
 3a bi i  2  ia bi  3  10i  3a   3
b  3i  2a b  a  2bi  3  10i
 a b  a  5b  3i  3  10ia b  3 a  2    
a  5b  3  10 b  1   
Vậy: z  2  i z  5
Câu 11. (Chuyên Lê Quý Đôn - Điện Biên - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức z thỏa mãn điều kiện
z  1 i  z  2i là đường nào sau đây? A. Elip B. Đường thẳng C. Đường tròn D. Parabol Lời giải Chọn B
Gọi số phức z a bi, a,b  
Khi đó z  1 i  z  2i
a bi 1 i a bi  2i  a  2 1  b  2 1
a  b  22 2
a  3b 1  0
Vậy tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện trên là đường thẳng.
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Câu 12. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số phức z đôi một khác nhau thoả mãn
z i  2 và 4
(z  2) là số thực? A. 4 . B. 5 . C. 6 . D. 7 . Lời giải Chọn B
Xét số phức z a bi; a, b   . Ta có 2 2
z i  2  a  (b 1)i  2  a  (b 1)  4 (1) . 4 2 4 3 2 2 3 4
(z  2)  [(a  2)  bi]  (a  2)  4(a  2) .bi  6(a  2) (bi)  4(a  2)(bi)  (bi) 4 2 2 4 3 3
 (a  2)  6(a  2) b b  [4(a  2) .b  4(a  2)b ] . ia  2  0 b  0 4
(z  2) là số thực khi 3 3 2 2
4(a 2) .b 4(a 2)b 0 (a 2) [ b (a 2) b ] 0            b a  2 b  2  a
+ a  2  0  a  2 thay vào (1) tìm được b  1
  z  2  i .
+ b  0 thay vào (1) tìm được a   3  z   3 1  7 1 7 3  7 1  7 3  7
+ b a  2 thay vào (1) tìm được a   z   i; z   . i 2 2 2 2 2
+ b  2  a thay vào (1) ta có: 2 2 2
a  (3  a)  4  2a  6a  5  0 : PTVN
Vậy có 5 số phức thoả mãn yêu cầu bài toán.
Câu 13. (Chuyên ĐH Vinh - Nghệ An - 2021) Có bao nhiêu số nguyên a để phương trình 2
z  a   2
3 z a a  0 có 2 nghiệm phức z , z thỏa mãn z z z z ? 1 2 1 2 1 2 A. 4. B. 2. C. 1. D. 3. Lời giải Chọn A Ta có 2
  3a 10a  9 . a  3  
+ TH1:   0 , phương trình có 2 nghiệm z  , khi đó 1,2 2 a  0
z z z z a  3    a  32 2
   4a  4a  0  . Thỏa mãn điều kiện 1 2 1 2 a  1     0 .
a  3  i 
+ TH2:   0 , phương trình có 2 nghiệm z  , khi đó 1,2 2 a  1
z z z z a  3  i   a  32 2
   2a 16a 18  0  . Thỏa mãn 1 2 1 2 a  9   điều kiện   0 .
Vậy có 4 giá trị của a thỏa mãn yêu cầu bài toán.
Câu 14. (THPT Thanh Chương 1- Nghệ An - 2021) Cho số phức thỏa mãn . Trên mặt phẳng tọa độ
, tập hợp điểm biểu diễn các số phức
là một đường tròn có bán kính bằng A. B. C. D. Lời giải Chọn D  Theo bài ra
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489 Đặt
Tập hợp điểm biểu diễn
là đường tròn bán kính . 2  3i
Câu 15. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho số phức z thỏa mãn z 1  2 . Mô đun 3  2i
lớn nhất của số phức z bằng A. 13 . B. 2 . C. 1 2 . D. 26 . Lời giải Chọn C
Đặt z x yi  ; x y   . 2   3i Ta có: z 1  2  iz 1 
2  x   y  2 2 1  2 . 3  2i
Vậy tập hợp điểm M biểu diễn số phức z nằm trên đường tròn tâm I 0;   1 bán kính R  2
Ta có z OM .
Do đó mô đun của số phức z lớn nhất khi OM lớn nhất nghĩa là O, M , I thẳng hàng suy ra Mô
đun lớn nhất của số phức z bằng 1 2 .
Câu 16. (THPT Lương Thế Vinh - 2021) Cho hai số phức z ; z thỏa mãn z  2 ; z  1 và 1 2 1 2
2z  3z  4 . Tính giá trị của biểu thức P z  2z . 1 2 1 2 A. P  10 . B. P  11 . C. P  15 . D. P  2 5 . Lời giải Chọn B
Đặt z a bi ; z c di  ; a ; b ; c d   . 1 2 Theo bài ra: 2 2
z  2  a bi  2  a b  4 .   1 1 2 2
z  1  c di  1  c d  1. 2 2 2 2
2z  3z  4  2 a bi  3 c di  4  2a  3c  2b  3d   16 . 1 2     2 2 2 2
 4a 12ac  9c  4b 12bd  9d  16 .   2 2
a b    2 2 4
9 c d  12ac bd   16 . 3 3 Thay  
1 , 2 vào 3 ta được: 4.4  9.112ac bd   16  ac bd  . 4 4 2 2
Khi đó, P z  2z a bi  2 c di a  2cb  2d 1 2       3 2 2
a b  4  2 2
c d   4ac bd   4  4  4.  11 . 4
Câu 17. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho các số phức z thoả mãn iz 1  1 2i .
Biết rằng tập hợp các điểm biểu diễn các số phức z là đường tròn C  . Tìm tâm I và bán kính
R của đường tròn C  .
A. I 0;   1 , R  3 .
B. I 0;   1 , R  3 . C. I 0  ;1 , R  3 . D. I 0  ;1 , R  3 . Lời giải Chọn B
Ta có z x yi, x, y   , thì ta có iz 1  1 2i i x yi 1  3   y   1  xi  3
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 
y  2  x
x   y  2 2 2 1 3 1
 3 . Vậy tập hợp các điểm biểu diễn các số phức z là
đường tròn C  có tâm và bán kính là I 0;   1 , R  3 .
Câu 18. (THPT Đào Duy Từ - Hà Nội - 2021) Cho số phức z thỏa mãn 2  iz  4 z i  8  19i .
Môđun của z bằng A. 5. B. 18. C. 5 . D. 13 Lời giải Chọn D
Đặt z a bi a,b R Khi đó :
2a b  8 a  3
2  iz  4z i  8 19i   2
a b  8  a  6b 15i  0     a  6b  15 b  2  
z  3  2i z  13 .
Câu 19. (THPT Đào Duy Từ - Hà Nội - 2021) Xét các số phức z thoả mãn i z  3  2i  4 . Trên mặt
phẳng toạ độ Oxy , tập hợp điểm biểu diễn số phức w  2iz  5  6i là một đường tròn có tâm
I a;b , bán kính R . Tính T a b R A. 21 . B. 17 . C. 5 . D. 1 . Lời giải Chọn C
Ta có i z  3  2i  4  2 iz  3  2i  8  2iz  6  4i  8  2iz  5  6i 1 2i  8
 2iz  5  6i 1 2i  8  w 1 2i  8 .
Giả sử w x yi,  , x y   . 2 2 2 2
Suy ra w 1 2i  8   x  
1   y  2  8   x  
1   y  2  64 .
Do đó tập hợp điểm M biểu diễn số phức w  2iz  5  6i là một đường tròn có tâm I 1; 2 , bán kính R  8 .
Vậy T a b R  1   2  8  5 .
Câu 20. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Xét các số phức z thỏa mãn z  4 , biết rằng tập
hợp các điểm biểu diễn của số phức w  3  4iz  5i một đường tròn. Bán kính r của đường tròn đó là: A. r  10 . B. r  20 . C. r  18 . D. r  25 . Lời giải Chọn B
Gọi w x yi x; y   . w  5
Ta có w  (3  4i)z  5i z  . 3  4i w  5 Mà z  4 
 4  w  5  20   x  2 2 5  y  400 . 3  4i
Vậy tập hợp điểm biểu diễn số phức w  3  4iz  5i là đường tròn có bán kính r  20 .
Câu 21. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức z a bi a,b   thỏa mãn
z 1 3i z i  0. Tính S  2a  3b A. S  5.  B. S  6. C. S  6  D. S  5. Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn C a  1   a  1   
Từ giả thiết suy ra a 1  2 2
b  3  a b i  0     2 2 2
b  3  a b  0 b    3  b 1   a  1     4 b     3  4 
Vậy S  2a  3b  2( 1  )  3.  6     3 
Câu 22. (THPT Chu Văn An - Thái Nguyên - 2021) Xét các số phức z thỏa mãn điều kiện
z  2i  
1  z i là số thực. Biết rằng tập hợp các điểm biểu diễn hình học của z là một đường
thằng có phương trình y ax b . Mệnh đề nào sau đây sai?
A. a b  2  .
B. a b  2 . C. 2
a  3b  4 . D. 2
5b a  6 . Lời giải Chọn A
Đặt z x yi
z  2i  
1  z i   x yi  2i  
1  x yi i 2 2
x xyi xi xyi y y  2xi  2 y  2  x yi i 2 2
x y xi yi  3y  2  x i   2 2
x y x  3y  2  (x y 1)i
Ta có:  z  2i  
1  z i là số thực  x y 1  0  y  x 1. a  1 Vậy  b  1 
Câu 23. (THPT Chu Văn An - Thái Nguyên - 2021) Cho số phức z thỏa mãn z 1 2i  i z  15  i . Tìm
mô đun của số phức z . A. z  2 5 . B. z  4 . C. z  2 3 . D. z  5 . Lời giải Chọn B
 Giả sử z x yi  ,
x y    z x y .i
Phương trình z(1  2i)  i z  15  i trở thành (x yi)(1 2i)  i x yi  15  i
  x  2y  2xi yi   xi y  15  i
  x  3y  x yi  15  i
x  3y  15 x  3     . x y  1 y  4    Vậy 2 2 z  3  4  5 .
Câu 24. (THPT Ba Đình - Thanh Hóa - 2021) Có bao nhiêu số phức z thỏa mãn
1 iz  2  iz 13 2i ? A. 2. B. 1. C. 4. D. 3. Lời giải Chọn B
Đặt z a bi với a,b   .
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
1 iz  2  iz 13 2i  1 ia bi  2  ia bi 13 2i  3a  2b  bi 13 2i 3
a  2b  13  a  3     . b  2 b  2  
Vậy: z  3 2i nên có 1 số phức z thỏa yêu cầu đề bài.
Câu 25. (THPT Quế Võ 1 - Bắc Ninh - 2021) Trên mặt phẳng tọa độ. Tập hợp điểm biểu diễn các số
phức z thỏa mãn điều kiện z  1 i  z  2i là đường nào sau đây? A. Elip B. Đường thẳng C. Đường tròn D. Parabol Lời giải Chọn B
Gọi số phức z a bi, a,b  
Khi đó z  1 i  z  2i
a bi 1 i a bi  2i  a  2 1  b  2 1
a  b  22 2
a  3b 1  0
Vậy tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện trên là đường thẳng
Câu 26. (THPT Quốc Oai - Hà Nội - 2021) Số phức z thoả mãn hệ thức z  2  i  10 và . z z  25 là
A. z  3  4i, z  5 .
B. z  3  4i, z  5 .
C. z  3  4i, z  5 . D. z  3  4i, z  5 . Lời giải Chọn A
Giả sử z a bi a;b    z a bi Ta có: z z
 a bia bi 2 2 . 25
 25  a b  25  1
z  2  i  10  a bi  2  i  10  a  2  b  
1 i  10  a  22  b  2 1  10 2 2
a b  4a  2b  5  02 2 2 
a b  25 2 2
a b  25 Từ  
1 và 2 ta có hệ phương trình:    2 2
a b  4a  2b  5  0  4
a  2b  20  0  a  3   2 a    a2 2 10 2  25 5
a  40a  75  0 b  4       b    10  2ab  10  2a  a  5   b  0 
Vậy có 2 số phức z thỏa mãn yêu cầu bài toán là z  3  4i, z  5 .
Câu 27. (THPT Quốc Oai - Hà Nội - 2021) Số thực ,
x y để hai số phức 2 7
z  9 y  4 10xi và 1 2 11
z  8 y  20i là liên hợp của nhau. 2 A. x  2  ; y  2  .
B. x  2; y  2  .
C. x  2; y  2 . D. x  2  ; y  2 . Lời giải Chọn B. Ta có 2 7 2
z  9 y  4 10xi  9 y  4  10xi và 2 11 2
z  8y  20i  8y  20i . 1 2 2 2 2 9
y  4  8yy  4 x  2 Ta có 2 2
z z  9 y  4  10xi  8y  20i      . 1 2  10x  20 x  2 y  2   
Vậy x  2; y  2 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 28. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức z a bi a,b   thỏa mãn
z  2iz  3  3i . Tính giá trị biểu thức 2019 2018 P ab 4036 2019 3  3 4036 2019 3  3 A. P   . B. P  . 2019 5 2019 5 C. P  2 . D. P  0 . Lời giải Chọn C
Ta có: z a bi .
z  2i z  3  3i a bi  2i a bi  3  3i
a  2b  2a bi  3  3i
a  2b  3 a  1     . 2a b  3 b  1   Suy ra 2019 2018 2019 2018 P ab  1 1  2 .
Câu 29. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho số phức z thỏa mãn z  2. Biết rằng tập
hợp các điểm biểu diễn số phức
w  3  2i  2  iz là một đường tròn. Bán kính R của đường tròn đó bằng A. 2. B. 5. C. 2 5. D. 5. Lời giải Chọn C
Cách 1: Gọi số phức w cần tìm có dạng:
a bi  2 2 w
, a b  0
Khi đó ta có a bi  3  2i  2  iz
a bi  3  2i
a  3  2  bi 2  iz      2  i 2  i
2a ai  3i  6  4  2b  2i biiz  5 2a b  8
a  2b 1   z   i   5  5  2 2
 2a b  8 
a  2b 1  Mà z  2 , nên   4      5   5 
 a  2  b  2 3 2  20  R  20  2 5. w  3  2i
w  3  2i Cách 2: Ta có z   z
 w  3  2i  2 5 . 2  i 5
Câu 30. (THPT Lê Lợi - Thanh Hóa - 2021) Cho số phức z thỏa mãn z 1
  2i  5 . Khi đó
w z 1 i có modul lớn nhất bằng bao nhiêu? A. 5 . B. 5 2 . C. 20 . D. 2 5 . Lời giải Chọn D
Gọi số phức z x yi , x, y   . 2 2 z 1
  2i  5 x  1  y   2  5 .
Tập hợp điểm M biểu diễn số phức z là đường tròn tâm I 1; 
2 , bán kính R  5 . Gọi N  1  ; 
1 là điểm biểu diễn số phức z  1  i . 1
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
w z 1i MN .
Để modul số phức w lớn nhất khi và chỉ khi MN lớn nhất  MN IN R  5  5  2 5 .
Câu 31. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hai số phức z , z thỏa mãn z z  39 và 1 2 1 2
z z  2 3 . Khi đó z z bằng 1 2 1 2 A. 8 . B. 2 39 . C. 12 . D. 2 3 . Lời giải Chọn C
Gọi A và B lần lượt là điểm biểu diễn của z và z trên mặt phẳng tọa độ. Khi đó: 1 2
OA OB  39 và AB  2 3 . 2  AB  Nhận xét: O
AB cân tại O . Khi đó: 2
z z  2OC  2 OA
 2 39  3  12 với C là 1 2    2 
trung điểm cạnh AB .
Câu 32. (THPT Trần Phú - Đà Nẵng - 2021) Cho số phức z x yi có phần ảo âm, biết z thỏa mãn z i
z  2  i  3  i và
là số thực. Giá trị của x  2 y bằng z  3 11 A. 3 . B. 5 . C. 4 . D. . 3 Lời giải Chọn C 2 2
Ta có z  2  i
3  i   x  2   y   1  4   1 . z i
x   y   1 i 1 Ta có  
x y 1 i  x  3  yi 2     z 3 x 3 yi         x  3 2  y 1 
x x  3  y y 1  x  3y  3 i là số thực nên x  3y  3  0 2          x  3 2  y
x  3y  3 2. 2 2 Thay 2 vào  
1 , ta được:  y     y   2 3 1 1
 4  10 y  8y  2  0
y  1 l  1 18   1  y    x   .
y   tm 5 5  5
Vậy x  2 y  4  .
Câu 33. Có bao nhiêu số phức z thỏa mãn z i z i  4 và  z iz là số thực? A. 1. B. 2 . C. 0 . D. 4 . Lời giải Chọn B
Gọi z x yi với , x y   .
Ta có  z i 2 2 z  .
z z i z x y y xi    x  0 . 2 2 Mà 2
z i z i  
x   y   2 4 1
x   y   1
 4  y 1  y 1  4 (2) (do x  0 ).
TH 1: Nếu y  1 thì 2  2y  4  y  2  z  2i . TH 2: Nếu 1
  y  1 thì 2  y 11 y  4 vô nghiệm. TH 3: Nếu y  1
 thì 2   y 11 y  4  y  2   z  2  i
Vậy có 2 số phức thoả yêu cầu bài toán.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489
Câu 34. Có bao nhiêu số phức z thỏa mãn z z z  1? A. 0 . B. 1. C. 4 . D. 3 . Lời giải Chọn C
Ta có Giả sử z x yi x, y    z x yi z z  2x . 2 2  2 2 x y  1  z  1  
x y  1  Bài ra ta có      1 z z  1  2x  1 x        2 1 1 3 Với 2 x   
y  1  y   . 2 4 2 1 3 1 3 1 3 1 3
Do đó có 4 số phức thỏa mãn là z   i , z   i , z    i , z    i . 1 2 2 2 2 2 3 2 2 4 2 2 z 1 z  3i
Câu 35. Có bao nhiêu số phức z thỏa mãn   1? z i z i A. 3 . B. 0 . C. 2 . D. 1. Lời giải Chọn D
Ta có: Gọi z a bi a,b   . Ta có: 2 2
z 1  z i 2 2    a  
1  b a  b    1  2
a 1  2b 1 a  1        .
z  3i z i 2 2  2 2 
a  b  3  a  b   1 6
b  9  2b 1 b  1   
Vậy có một số phức thỏa mãn là z  1 i .
Câu 36. Có tất cả bao nhiêu số phức z mà phần thực và phần ảo của nó trái dấu đồng thời thỏa mãn
z z z z  4 và z  2  2i  3 2. A. 1. B. 3 . C. 2 . D. 0 . Lời giải Chọn C
Gọi điểm M  ;
x y  là điểm trên mp tọa độ Oxy biểu diễn số phức
z x yi ( , x y  )
  z x yi
z z z z  4  2x  2 yi  2  x y  2 . Khi đó tập hợp điểm M  ;
x y  biểu diễn số phức
z là hai cạnh đối AD, BC của hình vuông ABCD độ dài cạnh bằng 2 2 và tâm là gốc tọa độ O z   i
  x  2   y  2 2 2 3 2 2 2
 18 . Tập hợp điểm M  ;
x y  biểu diễn số phức z là đường
tròn tâm I 2;2, R  3 2 .
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 6 4 A 2 I M 5 5 D B N P 2 C 4
Vậy có 2 điểm biểu diễn M , P thỏa yêu cầu bài toán.
Câu 37. Có bao nhiêu số phức z thỏa z  2  i z  3i và z  2  3i  2 ? A. Vô số B. 0 . C. 2 . D. 1. Lời giải Chọn A
Gọi điểm M  ;
x y  là điểm trên mp tọa độ Oxy biểu diễn số phức z x yi ( , x y  ) 
z  2  i z  3i : Tập hợp M  ;
x y  là trung trực của đoạn thẳng AB với A2  ;1 , B 0;3
z  2  3i  2 : Tập hợp M  ;
x y  là hình tròn (kể cả biên) có bán kính r  2 và tâm I 2;3
Do đó có vô số só phức thỏa yêu cầu bài toán.
Câu 38. Có bao nhiêu số phức z thỏa mãn z  5 và  z  3i z  2 là số thực? A. 1. B. 0. C. 3. D. 2. Lời giải Chọn D
Gọi z a bi
Ta có  z i z    a bi ia   bi   2 2 3 2 3 2
a  2a b  3b  2b  3a  6i
Theo đề ta có hệ phương trình 2 2 a b  5 
2b  3a  6  0 
Giải hệ này tìm được 2 nghiệm, suy ra có 2 số phức thỏa yêu cầu bài toán.
Câu 39. Có bao nhiêu số phức z thỏa mãn zz  4 và  z  3  2i3  2z  là số thuần ảo? A. 1. B. 0. C. 3. D. 2. Lời giải Chọn D
Gọi z a bi Ta có
z   i  z   a   b  i  a bi   2 2 3 2 3 2 3 2 3 2 2
2a  9a  9  2b  4b   3a  4b  6i
Theo đề ta có hệ phương trình 2 2  a b  4  2 2
2a  9a  9  2b  4b  0 
Giải hệ này tìm được 2 nghiệm, suy ra có 2 số phức thỏa yêu cầu bài toán. z 1 i
Câu 40. Cho hai số phức z, w thỏa mãn z i  2 và w
. Tìm giá trị nhỏ nhất của w . z  2  i
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 7 5 a 7 A. 4 . B. a . C. . D. . 3 20 2 Lời giải Chọn C Ta có: z 1 i w
wz  2w wi z 1 i z w  
1  2w wi 1 i z  2  i
2w wi 1 i
2w wi 1 i 2w 1 2iz   z i
i z i w 1 w 1 w 1 2w 1 2iz i
 2 w 1  2w 1  2i   1 w 1
Đặt w x yi  2 , x y  ,  i    1 , ta có:
   x yi   x yi   i
x  2  y   x  2   y  2 2 1 2 1 2 2 1 2 2 1 2 1 2 2 2 2 2 2
 4x 8x  4  4y  4x  4x 1 4y 8y  4  4x  8y 1  0 .
Suy ra tập hợp điểm biểu diễn số phức w là đường thẳng d có phương trình 4x  8 y 1  0 . 1 5 Vậy wd  , O d    . min 2 2 20 4  8 z  2
Câu 41. Xét các số phức z thỏa mãn
là số thuần ảo. Biết rằng tập hợp các điểm biểu diễn các số z  2i
phức z luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng A. 1. B. 2 . C. 2 2 . D. 2 . Chọn B Lời giải
Đặt z a bi, a,b   . Gọi M  ;
a b là điểm biểu diễn cho số phức z . z  2 a  2  bi
a  2  bi a  b  2i   Có w    z  2i
a  b  2i
a  b  22 2
a a  2  bb  2  a  2b  2  abi   
a  b  22 2
a a  2  bb  2  0   1 
w là số thuần ảo   a   b  22 2  0  Có   2 2
1  a b  2a  2b  0 .
Suy ra M thuộc đường tròn tâm I  1  ; 
1 , bán kính R  2 .
Câu 42. Có bao nhiêu số phức z thỏa mãn z  13 và  z  2i z  4i là số thuần ảo? A. 1. B. 2 . C. 0 . D. 4 . Lời giải Chọn B
Gọi z x yi với x, y   . Ta có 2 2
z  13  x y  13 (1) .
Mà  z i z i   x yi i x yi i   2 2 2 4 2 4
x y  2 y  8  (6x).i là số thuần ảo khi 5 2 2
x y  2 y  8  0  13  2 y  8  0  y   . 2
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021  3 3 x  5 2 Từ y   thay vào (1) ta được  . 2  3 3 x    2
Vậy có 2 số phức thoả yêu cầu bài toán.
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ VẬN DỤNG CAO Câu 1.
(Sở Lào Cai - 2021) Cho hai số phức z ; z thỏa mãn z  1  i  1; z  2  i  2 . Số phức z 1 2 1 2
thỏa mãn z z 1 i z và z z 2  i z
là các số thuần ảo. Tìm giá trị nhỏ nhất của 2   2  1   1  z  3  2i A. 0 . B. 3 . C. 2 . D. 1. Câu 2.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho các số phức z thỏa mãn điều kiện số phức
w z(1 i)  (2  i) là một số thuần ảo. Trong các số phức z đó hãy tìm giá trị nhỏ nhất của
T z  7  5i 38 A. 2 2 . B. 2 . C. 74 . D. . 5 Câu 3.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức z , z , z , là các số phức cùng thoả 1 2 3 2 mãn điều kiện
z  4. z z  33 . Biết rằng giá trị lớn nhất có thể đạt được của
z z z z z z là số thực M . Giá trị M thuộc tập hợp nào trong các tập hợp dưới 1 2 2 3 3 1 đây?
A. 0; 2 11 157  . B. 211 157 ;27  274  .    
C. 2 7  274 ;51,2 . D. 51, 2; .   Câu 4.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức z ; z là hai nghiệm của phương trình 1 2
2z 1  2  iz , biết z z  1. Giá trị của biểu thức P z z bằng 1 2 1 2 2 3 A. 2 . B. . C. 3 . D. . 2 2 Câu 5.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức z a bi a;b thỏa mãn  1
z z   i i z z  2 4 15
1 và môđun của số phức z
 3i đạt giá trị nhỏ nhất. Khi đó giá trị 2 a của  b bằng:: 4 A. 3. B. 4 . C. 1 . D. 2 . Câu 6.
(Chuyên Quốc Học Huế - 2021) Cho số phức z x yi (x, y ) thỏa mãn x y  2 và
2x y  3.Tìm giá trị nhỏ nhất của P  2020x  2021 . y A. 5  389 . B. 2  693 . C. 3  214 . D. 2  102 .
z 1 2i  1  Câu 7.
(Chuyên Quang Trung - Bình Phước - 2021) Cho z   thỏa mãn  . Giá trị
z 1 2i  2  
S  min z  max z bằng: A. 3 5 1 B. 5  2 C. 2 5 1 D. 2  5 1 4  iz Câu 8.
(Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức w
, biết các số phức z thỏa mãn 1 z
z  2. Tìm giá trị lớn nhất của w
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 A. 20 B. 20  34 . C. 34 D. 34  20 Câu 9.
(THPT Nguyễn Huệ - Phú Yên - 2021) Xét các số phức thỏa mãn z  2  3i z  4  5i  10 .
Gọi m , M lần lượt là giá trị nhỏ nhất, lớn nhất của 3z 1 i . Tính P m M . A. 135  365 . B. 2 135  365 . C. 2  365 . D. 2  135 .
Câu 10. (THPT Lương Thế Vinh - 2021) Xét các số phức z thỏa mãn z  3  4i  2 . Gọi M và m lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Tổng 2 2 M m bằng A. 58 . B. 52 . C. 65 . D. 45 .
Câu 11. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Xét các số phức z thỏa mãn z z  2  z z  6 .
Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P z  3  2i . Khi đó M m bằng 2 53  3 2 2 53  2 A. . B. 6 2 . C. . D. 53  5 . 2 2
Câu 12. (THPT Chu Văn An - Thái Nguyên - 2021) Xét số phức z a bi  ,
a b   thỏa mãn
z  4  3i  5 . Tính P a b khi z 1 3i z 1 i đạt giá trị lớn nhất? A. P  8 . B. P  4 . C. P  6 . D. P  10 .
Câu 13. (THPT Quốc Oai - Hà Nội - 2021) Trong mặt phẳng phức Oxy , trong các số phức z thỏa mãn
z 1 i  1. Nếu số phức z có môđun lớn nhất thì số phức z có phần thực bằng bao nhiêu? 2  2 2  2 2  2 2   2 A. . B. . C. . D. . 2 2 2 2
Câu 14. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức z thỏa mãn z  3  8i  7 và số phức w  4
  3i . Gọi M là giá trị lớn nhất của biểu thức P z w . Chọn khẳng định đúng trong các khẳng định sau
A. M  18;19 .
B. M 21; 22 .
C. M 19; 20 .
D. M 20;2  1 .
Câu 15. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức z , z thỏa mãn đồng thời hai điều 1 2
kiện sau: | z 1| 34 , | z  1 mi | |
z m  2i | ( trong đó m là số thực ) và sao cho z z lớn 1 2
nhất. Khi đó giá trị của z z bằng 1 2 A. 2. B. 10. C. 130 . D. 2 .
Câu 16. (Trung Tâm Thanh Tường - 2021) Cho số phức z thỏa mãn hệ thức z  2  3i z i . Giá trị
nhỏ nhất của biểu thức P  2z i 1 2i bằng 7 2 7 2 7 7 3 A. . B. . C. . D. . 3 2 2 3 Câu 17. (THPT Trần Phú - Đà Nẵng - 2021) Xét hai số phức
z , z thỏa mãn 1 2
z  2  i
3  i z z và z  3  i z 1 2i . Giá trị nhỏ nhất của z z bằng: 1   1 1 2 2 1 2 34 28 A. 4 6 . B. 2 6 . C. . D. . 5 15
Câu 18. Xét hai số phức z , z thỏa mãn z  2, 1 i z  6 và z z  5 . Giá trị lớn nhất 1   1 2 2 1 2
2z z  2021 bằng 1 2
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 A. 2044 .
B.  23  2021. C. 23  2021.
D. 2 23  2021.
Câu 19. Xét hai số phức
z  1; z  4 và z z
. Giá trị lớn nhất của 1
z ; z thỏa mãn 2 1 2 1 2 5 1
z  2z2  7i bằng A. 7  89 . B. 7  89 . C. 7  2 89 . D. 7  2 89 .
Câu 20. Cho hai số phức u, v thỏa mãn u v 10 và 3u  4v  50 . Tìm Giá trị lớn nhất của biểu thức 4u  3v 1  0i . A. 30 . B. 40 . C. 60 . D. 50 .
Câu 21. Cho hai số phức u, v thỏa mãn u v 10 và 3u  4v  50 . Tìm Giá trị lớn nhất của biểu thức 4u  3v 1  0i . A. 30 . B. 40 . C. 60 . D. 50 .
Câu 22. Cho các số phức z và z thỏa mãn z 1 i  1 và z  2  3i  2 . Tìm giá trị nhỏ nhất của biểu 1 2 1 2
thức P z z . 1 2 3 5 A. 2 . B. . C. . D. 3 . 2 2
Câu 23. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai số phức 1
z có điểm biểu diễn M , số phức z có 2
điểm biểu diễn là N thỏa mãn 1
z  1, z2  3 và 
MON  120 . Giá trị lớn nhất của 3 m 1
z  2z2  3i là M , giá trị nhỏ nhất của
3z  2z 1 2i là . Biết 0 1 2 0
M m a 7  b 5  c 3  d , với a,b, c, d   . Tính a b c d ? 0 0 A. 9 . B. 8 . C. 7 . D. 6 .
Câu 24. Xét hai số phức 1
z ; z2 thỏa mãn z z  1 z  2; z2  5 và 1 2
3 . Giá trị lớn nhất của 1
z  2z2  3i bằng A. 3 2  3 . B. 3  3 2 . C. 3  26 . D. 26  3 .
Câu 25. Cho hai số phức z , z thỏa mãn z z  3  4i và z z  5 . Tính giá trị lớn nhất của biểu thức 1 2 1 2 1 2
P z z 1 2 A. 10 . B. 5 2 . C. 5 . D. 10 2 .
Câu 26. Xét các số phức z z
z  4  1 và iz  2  1. Giá trị lớn nhất của z  2z  6i bằng 1 , 2 thỏa mãn 1 2 1 2 A. 2 2  2 . B. 4  2 . C. 4 2  9 . D. 4 2  3 .
Câu 27. Cho các số phức
z 1 4i  2, z  4  6i  1 và z 1  z  2  i . Tìm giá 1
z , z2 , z thỏa mãn 3 1 2 3 3
trị nhỏ nhất của biểu thức P  3 z  1 z  3 z z2 . 14 14 A.  2 . B. 29  3 . C.  2 2 . D. 85  3 . 2 2
Câu 28. (THPT Đoàn Thượng - Hải Dương - 2021) Biết số phức z thoả mãn | z  3  4i | 5 và biểu thức 2 2
T | z  2 |  | z i | đạt giá trị lớn nhất. Tính | z |. A. | z | 33 .
B. | z | 5 2 .
C. | z | 50 .
D. | z | 10 .
Câu 29. (THPT Ngô Quyền - Quảng Ninh - 2021) Cho Xét các số phức z , z thỏa mãn 1 2 2 2
z 1  z  2i  1; z  3  i  5. Giá trị nhỏ nhất của P z z bằng 1 1 2 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 3 5 2 5 A. 5 . B. . C. 2 5 . D. . 5 5 BẢNG ĐÁP ÁN 1.A 2.A 3.D 4.C 5.D 6.A 7.A 8.B 9.C 10.A 11.A 12.D 13.D 14.D 15.A 16.B 17.D 18.C 19.B 20.C 21.C 22.A 23.B 24.B 25.B 26.C 27.D 28.B 29.D
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Chủ đề 4 SỐ PHỨC
MỨC ĐỘ VẬN DỤNG CAO Câu 1.
(Sở Lào Cai - 2021) Cho hai số phức z ; z thỏa mãn z  1  i  1; z  2  i  2 . Số phức z 1 2 1 2
thỏa mãn z z 1 i z và z z 2  i z
là các số thuần ảo. Tìm giá trị nhỏ nhất của 2   2  1   1  z  3  2i A. 0 . B. 3 . C. 2 . D. 1. Lời giải Chọn A Gọi 1 z  1 a  1
b i; z2  a2  2
b i; z m  . ni
Khi đó điểm biểu diễn hình học của các số phức z , z , z lần lượt là Aa ;b , B a ;b , M ; m n 1 1   2 2    1 2 2 2 Do
C : x 1  y 1  1. 1
z  1  i  1 nên điểm A thuộc đường tròn  1      2 2 Do z C : x  2  y  1  4.
2  2  i  2 nên điểm B thuộc đường tròn  2      Ta có:
z z 1 i z là số thuần ảo nên m a 1 a n b 1 b  0 . 1   1   1   1  1   1 
z z 2  i z là số thuần ảo nên m a 2  a n b 1 b  0 2   2   2   2  2   2 
Suy ra điểm M là giao điểm của hai đường thẳng lần lượt là tiếp tuyến của C , C tại , A . B 1   2 
z   i  m  2  n  2 3 2 3 2
là khoảng cách giữa M và I 3;2
Dựa vào hình vẽ ta thấy IM  0 . min Câu 2.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho các số phức z thỏa mãn điều kiện số phức
w z(1 i)  (2  i) là một số thuần ảo. Trong các số phức z đó hãy tìm giá trị nhỏ nhất của
T z  7  5i 38 A. 2 2 . B. 2 . C. 74 . D. . 5 Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn A
 Giả sử z x yi, (x, y R).Khi đó z có điểm biểu diễn là M ( ; x y).
 Có w  (x yi)(1 i)  (2  i)  (x y  2)  (x y 1)i là số thuần ảo nên
x y  2  0
 Suy ra tập hợp các điểm M là đường thẳng d : x y  2  0
 Có T z  7  5i z  (7  5i)  MA với (7 A ;5) 7  5  2 4
 Có T nhỏ nhất khi MA min T d ( , A )    2 2 ngắn nhất, tức là 2 2 1  ( 1  ) 2 Câu 3.
(Chuyên Lê Hồng Phong - TPHCM - 2021) Cho số phức z , z , z , là các số phức cùng thoả 1 2 3 2 mãn điều kiện
z  4. z z  33 . Biết rằng giá trị lớn nhất có thể đạt được của
z z z z z z là số thực M . Giá trị M thuộc tập hợp nào trong các tập hợp dưới 1 2 2 3 3 1 đây?
A. 0; 2 11 157  . B. 211 157 ;27  274  .    
C. 2 7  274 ;51,2 . D. 51,2; .   Lời giải Chọn D 2 Đặt 2 2
z a bi z  4 z z  33  a b  8 a  33 2 2  a a   b    a  2 2 2 8 16 49 4  b  7 
C : I 4; 0 , R  7 khi x  0  1  1   1
z , z , z  1 2 3
C :I 4;0 ,R  7khi x  0   2  1   1
Ta có P z z z z z z AB BC CA 1 2 2 3 3 1 * TH1: ,
A B,C cùng thuộc một trong hai đường tròn C , C 1   2 
Khi đó: P AB BC CA  2R sin A  sin B  sin C
Mà sin A  sin B  sin C  sin A  sin B  sin  A B
 sin A  sin B  sin .
A cos B  cos . A sin B 2  3 3   sin A sin B    sin A  sin B   3 .cos B  cos . A     3 2 2    3 3 
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2 1  3  3  sin A sin B  2 2 2 2 
sin A  sin B  .2  
co s A co s B     3  4  2 3 3   3 3 3  3   2 2  3 3 P  2 . R  3 3R  21 3 Nên  2
R  7  R1,2 
* TH2: Đặc biệt hoá như sau (*) A 1  1;0, d  ,
A BC   AH OH   x   Ta có: 2 2 2
BH OB OH  49  x  2
BC  2 49  x
AH AO OH  11 x AB AC  11 x2   2 49  x  256
M f x  2 11 x2   2 49  x   2  2 49  x    51, 2 5 Câu 4.
(Chuyên Lam Sơn - Thanh Hóa - 2021) Cho hai số phức z ; z là hai nghiệm của phương trình 1 2
2z 1  2  iz , biết z z  1. Giá trị của biểu thức P z z bằng 1 2 1 2 2 3 A. 2 . B. . C. 3 . D. . 2 2 Lời giải Chọn C
 Gọi z a bi  ; a b   .  2 2 Ta có: z  
iz   a   2
b    b 2 2 2 2 1 2 2 1 4 2
a a b  1.
 Do đó: z z  1. 1 2
 Gọi z a b ;
i z a b i  2 2 2 2
a ;b ; a ;b  ;
a b  1;a b  1 . 1 1 2 2 1 1 2 2  1 1 1 2 2 2  2 2
Khi đó: z z  1  a ab b
 1  2a a  2b b  1. 1 2  1 2   1 2  1 2 1 2  2 2
Vậy P z z a ab b 2 2 2 2 
a b a b  2a a  2b b  3 . 1 2  1 2   1 2  1 1 2 2 1 2 1 2 Câu 5.
(Chuyên Hoàng Văn Thụ - Hòa Bình - 2021) Cho số phức z a bi a;b thỏa mãn  1
z z   i i z z  2 4 15
1 và môđun của số phức z
 3i đạt giá trị nhỏ nhất. Khi đó giá trị 2 a của  b bằng:: 4 A. 3. B. 4 . C. 1 . D. 2 . Lời giải Chọn D
Ta có: z a bi
Do đó  z z  i i z z  2 4 15 1  bi
i i a  2 8 15 2 1   b
i i a  2 8 15 2 1 2  1  15 15  b    a  2 8 15 2 1  a   2b     b   2  4 8
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
NGUYỄN BẢO VƯƠNG - 0946798489 2 1 1  1  2 15 2 Khi đó z   3i a
 b  3i a    
b  3  2b   b  3 2 2  2  4 2 21  15   15  21 39 2  b  8b    8       4  8   8  4 8  1 a    2 Dấu bằng xảy ra   15 b     8 a Do đó  b  2 . 4 Câu 6.
(Chuyên Quốc Học Huế - 2021) Cho số phức z x yi (x, y ) thỏa mãn x y  2 và
2x y  3.Tìm giá trị nhỏ nhất của P  2020x  2021 . y A. 5  389 . B. 2  693 . C. 3  214 . D. 2  102 . Lời giải Chọn A
x y  2 
2  x y  2  Ta có    2x y  3
3  2x y  3   
Biểu diễn miền nghiệm của hệ phương trình
Miền nghiệm của hệ là miền tứ giác ABCD  1 7   5 1   1 7   5 1  với A  ; , B ; , C ;  , D  ;           3 3   3 3   3 3   3 3 
Ta biết P  2020x  2021y đạt GTNN tại 1 trong các đỉnh của tứ giác ABCD . Thay tọa độ các điểm ,
A B,C, D vào ta được:  1 7   5 1  P  ;  53  89, P ;  2693      3 3   3 3   1 7   5 1  P ;   5389, P  ;   26  93      3 3   3 3 
Vậy GTNN của P  2020x  2021y bằng 5  389 .
z 1 2i  1  Câu 7.
(Chuyên Quang Trung - Bình Phước - 2021) Cho z   thỏa mãn  . Giá trị
z 1 2i  2  
S  min z  max z bằng: A. 3 5 1 B. 5  2 C. 2 5 1 D. 2  5 1 Lời giải Chọn A
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Gọi M là điểm biểu diễn số phức z x yi (với x ; y   ) trên mặt phẳng phức. 2 2
z 1 2i  1    x   
1   y  2  1 Ta có:   
z 1 2i  2 2 2   
x  2   y  4  4 
Do đó M thuộc phần chung của hai hình tròn  I ;1 và  I ;2 , với I 1; 2 và I 2; 4 . 2   1   2  1 
Phương trình đường thẳng I I là y  2x . 1 2
Dựa vào hình vẽ ta thấy z lớn nhất khi M Q và z nhỏ nhất khi M P , trong đó P ; Q lần
lượt là giao điểm của đường thẳng y  2x với các đường tròn  I ;2 và  I ;1 sao cho P ; Q 1  2 
nằm giữa I và I . 1 2  2 5 4 5   5 2 5  Dễ thấy P  2  ; 4   ; Q 1 ; 2    5 5      5 5  
Vậy S  min z  max z OP OQ  3 5 1. 4  iz Câu 8.
(Chuyên Lê Quý Đôn - Điện Biên - 2021) Cho số phức w
, biết các số phức z thỏa mãn 1 z
z  2. Tìm giá trị lớn nhất của w A. 20 B. 20  34 . C. 34 D. 34  20 Lời giải Chọn B
Đặt w  x yi .Theo bài ra ta có: 4  iz 4  iz w   x yi  1 z 1 z
  x yi1 z  4  iz
z x   y  
1 i  4  x  yi    
z x   y  
1 i  4  x  yi
2 x   y  2 1  4  x2 2 2  y 2 2
x y  8x  4 y 14  0
Vậy tập hợp số phức w là một đường tròn tâm I 4; 2 , bán kính R  34
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
NGUYỄN BẢO VƯƠNG - 0946798489
Khi đó giá trị lớn nhất của w là : w  R IO  34  20 Câu 9.
(THPT Nguyễn Huệ - Phú Yên - 2021) Xét các số phức thỏa mãn z  2  3i z  4  5i  10 .
Gọi m , M lần lượt là giá trị nhỏ nhất, lớn nhất của 3z 1 i . Tính P m M . A. 135  365 . B. 2 135  365 . C. 2  365 . D. 2  135 . Lời giải Chọn C
+ Ta có: z  2  3i z  4  5i  10
 3z  6  9i  3z  12 15i  30
 3z  6  9i  3z   1
 2 15i  30   * .
+ Đặt w  3z , gọi C , A , B lần lượt là điểm biểu diễn của các số phức w , 6  9i và 1  2 15i . Khi đó  
* trở thành: AC BC  30 . + Mặt khác: 2 2
AB  18  24  30 .
Suy ra: AC BC AB  điểm C chạy trên đoạn AB .
+ Lại có 3z 1 i w  1 i  CD với D là điểm biểu diễn số phức 1 i .
+ Ta có: AB :12x  9 y  9  0 .
d D; AB  2 ; AD  5 5 ; BD  365 . + Suy ra CD
 365  M , CD  2  m . max min
+ Vậy: P m M  2  365 .
Câu 10. (THPT Lương Thế Vinh - 2021) Xét các số phức z thỏa mãn z  3  4i  2 . Gọi M và m lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Tổng 2 2 M m bằng A. 58 . B. 52 . C. 65 . D. 45 . Lời giải Chọn A
Gọi z x yi với x, y   .
Khi đó z  3  4i  2  x yi  3  4i  2  x  3   y  4i  2 
x  2   y  2    x  2   y  2 3 4 2 3 4  4 . 2 2
Tập hợp các số phức z thỏa mãn z  3  4i  2 là đường tròn C  :  x  3   y  4  4 có tâm I 3; 4
  , bán kính R  2 .
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Gọi điểm biểu diễn của số phức z x yi là M  ; x y . Khi đó 2 2 z
x y OM với O là gốc tọa độ. zOM
, khi đó OM OI R    2 2 3 4  2  7  M max max zOM
, khi đó OM OI R    2 2 3 4  2  3  m . min min Vậy 2 2 2 2
M m  7  3  58 .
Câu 11. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Xét các số phức z thỏa mãn z z  2  z z  6 .
Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P z  3  2i . Khi đó M m bằng 2 53  3 2 2 53  2 A. . B. 6 2 . C. . D. 53  5 . 2 2 Lời giải Chọn A
 Giả sử z x yi, x, y  khi đó ta có z z  2x và z z  2y do đó từ giả thiết bài toán ta
được z z  2  z z  6  2x  2  2 y  6  x 1  y  3 . x  1  , y  0 x  1  , y  0
x  1, y  0
 Từ đây ta có bốn trường hợp sau  I  :   II  :   III  :  và x y  2  x y  4   x y  2 
x  1, y  0 IV  : 
. Hình biểu diễn của  I  là đoạn AB , của  II  là đoạn CD , của  III  là x y  4  
đoạn BC và của  IV  là đoạn AD . Với ABCD là hình vuông như hình vẽ.
 Đặt M (3;2) khi đó P z  3  2i MN với N là điểm thuộc cạnh của hình vuông ABCD .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
NGUYỄN BẢO VƯƠNG - 0946798489
 Dựng đường thẳng đi qua M và vuông góc với AB cắt AB tại E và cắt CD tại F . Từ hình 3
vẽ ta có max P  min P ME MD d (M , AB)  MD   53 . 2 2 53  3 2 Hay M m  . 2
Câu 12. (THPT Chu Văn An - Thái Nguyên - 2021) Xét số phức z a bi  ,
a b   thỏa mãn
z  4  3i  5 . Tính P a b khi z 1 3i z 1 i đạt giá trị lớn nhất? A. P  8 . B. P  4 . C. P  6 . D. P  10 . Lời giải Chọn D M* (C) M I A E B  2 2
z  4  3i  5 ⇔ a  4   y  3i  5 ⇔ a  4   y  3  5
Do đó tập hợp các điểm M biểu diễn số phức z là đường tròn C  tâm I 4;3 , bán kính: r  5  Gọi A 1
 ;3 ; B 1;  1 ; E 0 
;1 là trung điểm của AB    
Nhận xét: AB  2; 4 ; IE   4  ; 2   ; .
AB IE  8  8  0 ⇒ IE AB
T z 1 3i z 1 i MA MB 2 Xét: 2
T   MA MB   2 2 MA MB  2 2 2 2
 4ME AB  4ME  20
⇒ Giá trị của maxT đạt được khi max ME MA MB
Khi đó điểm M thỏa mãn hệ điều kiện đẳng thức xảy ra:  M M *   1  OI ME MI r 5 1  Ta có:    ⇒ 3 OM   6;4 ME r IE 5  2 5 3 1 1 3
Vậy max T đạt được khi z  6  4i . Khi đó: P a b  6  4  10 .
Câu 13. (THPT Quốc Oai - Hà Nội - 2021) Trong mặt phẳng phức Oxy , trong các số phức z thỏa mãn
z 1 i  1. Nếu số phức z có môđun lớn nhất thì số phức z có phần thực bằng bao nhiêu? 2  2 2  2 2  2 2   2 A. . B. . C. . D. . 2 2 2 2 Lời giải Chọn D Ta có: z   1   i  1.
Vậy trong mặt phẳng phức Oxy , các số phức z thỏa mãn z 1 i  1 là hình tròn tâm I 1;  1 , bán kính R  1 .
Vậy số phức có mô đun lớn nhất: z
OI R  1 2 . max
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 Nếu gọi M  ;
x y  là điểm biểu diễn số phức đó thì  1 2  x   OM 
 1 2   2 OM  .OI OM  .OI   . OI 2  1 2 y    2 1 2 2  2
Vậy số phức có phần thực x    . 2 2
Câu 14. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho số phức z thỏa mãn z  3  8i  7 và số phức w  4
  3i . Gọi M là giá trị lớn nhất của biểu thức P z w . Chọn khẳng định đúng trong các khẳng định sau
A. M  18;19 .
B. M 21;22 .
C. M 19;20 .
D. M 20; 2  1 . Lời giải Chọn D
Giả sử Az . Theo giả thiết z  3  8i  7  Ađường tròn C  tâm I 3; 8, R  7 . 
Giả sử B w  B  4
 ;3  IB  7; 
11  IB  170  49  7  R . Suy ra B nằm ngoài
đường tròn C  .
Khi đó: P z w AB . Suy ra: M PAB
.Xảy ra khi và chỉ khi A là giao điểm (nằm max max ngoài đoạn IB ) của đường thẳng IB với đường tròn C . M PAB
IB R  170  7  20, 04  20;  21 . max max
Câu 15. (THPT Mai Anh Tuấn - Thanh Hóa - 2021) Cho hai số phức z , z thỏa mãn đồng thời hai điều 1 2
kiện sau: | z 1 | 34 , | z 1  mi | |
z m  2i | ( trong đó m là số thực ) và sao cho z z lớn 1 2
nhất. Khi đó giá trị của z z bằng 1 2 A. 2. B. 10. C. 130 . D. 2 . Lời giải Chọn A
Đặt z x yi(x, y  ) .
Từ giả thiết ta có hệ phương trình: 2 2 2 2
(x 1)  y  34 
(x 1)  y  34(C)    2 2 2 2
 (x 1)  ( y m)  (x m)  ( y  2)
(2  2m)x  (2m  4) y  3  0()  
Hai số phức z , z là hai nghiệm của hệ phương trình trên. Gọi M , N lần lượt là các điểm biểu 1 2
diễn cho z , z khi đó z z MN . 1 2 1 2
Ta có z z lớn nhất khi đường thẳng () cắt đường tròn (C ) theo dây cung MN có độ dài 1 2
lớn nhất, tức là () đi qua tâm I (1;0) của (C ) .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
NGUYỄN BẢO VƯƠNG - 0946798489 1
Thay tọa độ I vào (C ) ta có: m   2 2 2 1
(x 1)  y  34 Với m   giải hệ   ( ; x y)  {( 4  ; 3  );(6;3)} 2
3x  5y  3  0  Giả sử z  4
  3i, z  6  3i z z  2 . 1 2 1 2
Câu 16. (Trung Tâm Thanh Tường - 2021) Cho số phức z thỏa mãn hệ thức z  2  3i z i . Giá trị
nhỏ nhất của biểu thức P  2z i 1 2i bằng 7 2 7 2 7 7 3 A. . B. . C. . D. . 3 2 2 3 Lời giải Chọn B
Gọi z x yi  2 , x y  ,  i    1 và M  ;
x y  là điểm biểu diễn của số phức z.
z   i z i   x  2   y  2  x   y  2 2 2 3 2 3
1  x y  3  0.
Vậy tập hợp điểm biểu diễn của số phức z là  : x y  3  0. P 1
P  2z i 1 2i   z 1 i 2 2  1  Gọi A 1  ;   P  2M . A    2  Do P  2MA
M là hình chiếu của A lên đường thẳng . min min 7 2 P  2d ; A   . min   2 Câu 17. (THPT Trần Phú - Đà Nẵng - 2021) Xét hai số phức
z , z thỏa mãn 1 2
z  2  i
3  i z z và z  3  i z 1 2i . Giá trị nhỏ nhất của z z bằng: 1   1 1 2 2 1 2 34 28 A. 4 6 . B. 2 6 . C. . D. . 5 15 Lời giải Chọn D
+ Gọi z x yi, z x  y i  1 2 + Ta có :
z  2  i
3  i z z  2 z  2  i z z 1   1 1 1 1 1 1 5
  x  22   y  2 2 2 1  y y x  2x  (P) 2 2
và z  3  i z 1 2i  8x  6 y  5  0 (d ) . 2 2 1 5
Do đó, tập hợp các điểm biểu diễn của z là 2 (P) : y x  2x
; tập hợp các điểm biểu diễn 1 2 2
của z là (d ) : 8x  6 y  5  0 2
+ Gọi () là đường thẳng tiếp xúc với (P) và song song với (d) thì () có phương trình là: 41 8x  6 y   0 . 3
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 y ( ) (P) (d) x 1 41  5 3 28
Vậy min z z d (d , )   1 2 2 2 15 8  6
Câu 18. Xét hai số phức z , z thỏa mãn z  2, 1 i z  6 và z z  5 . Giá trị lớn nhất 1   1 2 2 1 2
2z z  2021 bằng 1 2 A. 2044 .
B.  23  2021. C. 23  2021.
D. 2 23  2021. Lời giải Chọn C
Đặt z a bi, z c di với a, , b c, d  .  Theo giả thiết thì 1 2 z  1  2 2 a b  4 1 6
1 iz  6  z   3 2 2
c d  3 2 2 1 i 2 2
z z  5  a c  b d   5 1 2 Do đó 2 2 2 2
a  2ac c b  2bd d  5  ac bd  1
Ta có 2z z  2a c  2b d i nên 1 2     2 2z z
 2a c2  2b d 2  4 2 2
a b    2 2 c d
 4 ac bd  23 1 2   
Áp dụng bất đẳng thức z z  z z , ta có
2z z  2021  2z z  2021   23  2021. 1 2 1 2
Câu 19. Xét hai số phức
z  1; z  4 và z z
. Giá trị lớn nhất của 1
z ; z thỏa mãn 2 1 2 1 2 5 1
z  2z2  7i bằng A. 7  89 . B. 7  89 . C. 7  2 89 . D. 7  2 89 . Lời giải Chọn B
Đặt z a bi, z c di với a, , b c, d  .  Theo giả thiết thì 1 2 2 2 2 2 2 2
a b  1, c d  16, (a c)  (b d )  5. Do đó 2 2 2 2
a 2ac c b 2bd d 5  ac bd  6.
Ta có z  2z  (a  2c)  (b  2d )i nên 1 2 2 2 2 2 2 2
z  2z  (a  2c)  (b  2d )  a b  4(c d )  4(ac bd )  89. 1 2
Áp dụng bất đẳng thức z z  z z , ta có ngay
z  2z 7i z  2z  7  i  7  89 1 2 1 2
Câu 20. Cho hai số phức u, v thỏa mãn u v 10 và 3u  4v  50 . Tìm Giá trị lớn nhất của biểu thức 4u  3v 1  0i . A. 30 . B. 40 . C. 60 . D. 50. Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
NGUYỄN BẢO VƯƠNG - 0946798489 Chọn C 2
Ta có z z.z . Đặt T  3u  4v , M  4u  3v . 2 2 Khi đó 2
T  3u  4v3u  4v  9 u 16 v 12uv vu . 2 2 Tương tự ta có 2
M  4u  3v4u  3v 16 u  9 v 12uv vu. 2 2 Do đó 2 2
M T  25 u v  5000 . Suy ra 2 2 M  5000 T 2
 500050  2500 hay M  50.
Áp dụng z z  z z ta có 4u 3v 1
 0i  4u 3v  1
 0i  5010  60 .
Suy ra max 4u  3v 1  0i  60 .
Câu 21. Cho hai số phức u, v thỏa mãn u v 10 và 3u  4v  50 . Tìm Giá trị lớn nhất của biểu thức 4u  3v 1  0i . A. 30 . B. 40 . C. 60 . D. 50. Lời giải Chọn C 2
Ta có z z.z . Đặt T  3u 4v , M  4u 3v . 2 2 Khi đó 2
T  3u  4v3u  4v  9 u 16 v 12uv vu . 2 2 Tương tự ta có 2
M  4u  3v4u  3v 16 u  9 v 12uv vu. 2 2 Do đó 2 2
M T  25 u v  5000 . Suy ra 2 2 M  5000 T 2
 500050  2500 hay M  50.
Áp dụng z z  z z ta có 4u 3v 1
 0i  4u 3v  1
 0i  5010  60 .
Suy ra max 4u  3v 1  0i  60 .
Câu 22. Cho các số phức z và z thỏa mãn z 1 i  1 và z  2  3i  2 . Tìm giá trị nhỏ nhất của biểu 1 2 1 2
thức P z z . 1 2 3 5 A. 2 . B. . C. . D. 3 . 2 2 Lời giải Chọn A
Giả sử M, N lần lượt là điểm biểu diễn của số phức z và z 1 2
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 y 5 N N' 4 3 J 2 1 N'' M O x 2 2 4 M'' 1 I 2 M'
z 1 i  1  M I;1 , I 1  ; 1  1    
z  2  3i  2  N J; 2 , J 2;3 2    
P z z MN 1 2
Ta thấy hai đường tròn (I) và (J) nằm ngoài nhau. Do đó
M ' N '  MN M ' N ' .
P z z MN đạt giá trị nhỏ nhất khi và chỉ khi M M ' , N N ' . 1 2 P
IJ R r  2, P
I R r  8 . min max
Câu 23. Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai số phức 1
z có điểm biểu diễn M , số phức z có 2
điểm biểu diễn là N thỏa mãn 1
z  1, z2  3 và 
MON  120 . Giá trị lớn nhất của 3 m 1
z  2z2  3i là M , giá trị nhỏ nhất của
3z  2z 1 2i là . Biết 0 1 2 0
M m a 7  b 5  c 3  d , với a, b, c, d   . Tính a b c d ? 0 0 A. 9 . B. 8 . C. 7 . D. 6 . Lời giải Chọn B y P N1 M1 N 120 M x O 1
Gọi M là điểm biểu diễn của số phức 3z , suy ra OM  3 . 1 1 1
Gọi N là điểm biểu diễn của số phức 2z , suy ra ON  6 . Gọi P là điểm sao cho 1 2 1
  
OM ON OP . Suy ra tứ giác OM PN là hình bình hành. 1 1 1 1 Do từ giả thiết 
MON  120 , suy ra  M ON  120 . 1 1  1 
Dùng định lí cosin trong tam giác OM N ta tính được M N  9  36  2.3.6.   3 7 ; 1 1 1 1    2 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
NGUYỄN BẢO VƯƠNG - 0946798489 1
và định lí cosin trong tam giác OM P ta có OP  9  36  2.3.6.  3 3 . 1 2
Ta có M N  3z  2z  3 7 ; OP  3z  2z  3 3 . 1 1 1 2 1 2
Tìm giá trị lớn nhất của 3 1
z  2z2  3i .
Đặt 3z  2z w w  3 3 , suy ra điểm biểu diễn w là A thuộc đường tròn C tâm 1  1 2 1 1 1
O 0;0 bán kính R  3 3 . Gọi điểm Q là biểu diễn số phức 3i . 1 1 Khi đó 3 1
z  2z2  3i A 1
Q , bài toán trở thành tìm  AQ
biết điểm A trên đường tròn C . 1  1 max Dễ thấy  AQ
OQ R  3  3 3 . 1  1 1 max
Tìm giá trị nhỏ nhất của 3 1
z  2z2 1 2i  3 1 z  2z2   1   2i  .
Đặt 3z  2z w w  3 7 , suy ra điểm biểu diễn w là B thuộc đường tròn C tâm 2  1 2 2 2 2
O 0;0 bán kính R  3 7 . Gọi điểm Q là biểu diễn số phức 1   2i . 1 2 Khi đó 3 1 z  2z2   1
  2i  B 2
Q , bài toán trở thành tìm  BQ
biết điểm B trên đường tròn 2 min
C . Dễ thấy điểm Q nằm trong đường tròn C nên BQ
R OQ  3 7  5 . 2  2  2  2 2 2 min
Vậy M m  3 7  3 3  5  3 . 0 0
Câu 24. Xét hai số phức 1
z ; z2 thỏa mãn 1
z  2; z2  5 và 1 z  2
z  3 . Giá trị lớn nhất của 1
z  2z2  3i bằng A. 3 2  3 . B. 3  3 2 . C. 3  26 . D. 26  3 . Lời giải Chọn B Cách 1:
Đặt z a bi, z c di (với a, , b , c d   ) 1 2 Theo bài ra ta có: 2 2 2 2
z  2  a b  2; z  5  c d  5 1 2
z z  3  a c2  b d 2 2 2 2 2
 9  a b c d  2 ac bd  9  ac bd  1  1 2  
z  2z  a  2c2  b  2d 2 2 2
a b  4  2 2 c d
 4 ac bd  18  3 2 1 2   
Theo tính chất z z '  z z ' ta có: 1
z  2z2  3i  1 z  2z2  3  i  3 2  3 Cách 2: y Q 3 O x M N P R
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021
Gọi M là điểm biểu diễn cho số phức z , M thuộc đường tròn tâm O bán kính 2  OM  2 1
Gọi N là điểm biểu diễn cho số phức z , N thuộc đường tròn tâm O bán kính 5  ON  5 2
  
Suy ra NM OM ON là điểm biểu diễn cho z z MN z z  3 1 2 1 2
Gọi P là điểm biểu diễn cho số phức 2z , P thuộc đường tròn tâm O bán kính 2 5  OP  2 5 2
Gọi Q là điểm biểu diễn cho số phức 3i , Q 0;3  OQ  3
  
Dựng hình bình hành OMRP ta có OR OM OP  R là điểm biểu diễn cho số phức z  2z 1 2  2 2 2
OM ON MN 2  5  9 1  Ta có: cos MON    2.OM .ON 2. 2. 5 10 2 2 2  2 2 
OR OP PR  2.O . P P .
R cos OPR OP OM  2.O . P OM.cos MON  1   OR  20  2  2.2 5. 2.  3 2    10     T  1
z  2z2  3i OR OQ QR QR
T đạt giá trị lớn nhất khi QR lớn nhất 0
QOR  180  QR OQ OR  3  3 2
Vậy T đạt giá trị lớn nhất bằng 3  3 2 .
Câu 25. Cho hai số phức z , z thỏa mãn z z  3  4i và z z  5 . Tính giá trị lớn nhất của biểu thức 1 2 1 2 1 2
P z z 1 2 A. 10 . B. 5 2 . C. 5 . D. 10 2 . Lời giải Chọn B
z a bi Đặt 1  a, , b , c d  .
z c di  2 a c  3
z z  3  4i   1 2  Theo giả thiết ta có:   b   d  4 . z z  5   1 2 a c
2  b d 2  5  Xét 2 2 2 2
P z z a b c d  1  1 . 2 2 2 2
a b c d . 1 2  a cb da cb d 3  4  5 2 2 2 2  2  2  2  2 2 2 2
Mà a b c d    25. 2 2 Nên P  5 2.
Câu 26. Xét các số phức z z
z  4  1 và iz  2  1. Giá trị lớn nhất của z  2z  6i bằng 1 , 2 thỏa mãn 1 2 1 2 A. 2 2  2 . B. 4  2 . C. 4 2  9 . D. 4 2  3 . Lời giải Chọn C
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
NGUYỄN BẢO VƯƠNG - 0946798489
Đặt z  2z , suy ra P z  2z  6i z  ( 2
z )  6i  z z  6i . 3 2 1 2 1 2 1 3 1 1 1 Và z  
z thế vào iz  2  1   iz  2  1   iz  2 . 2i  1. 2i z  4i  2. 2 3 2 2 3 3 2 2 3 Gọi ,
A B là hai điểm biểu diễn cho hai số phức z , z . 3 1
z  4i  2  Athuộc đường tròn tâm I (0;4), R  2. 3 3
z  4 1 B thuộc đường tròn tâm J (4;0), R  1. 1 1
P z z  6i z z  6i AB  6  IJ R R  6  4 2  1  2  6  4 2  9. 1 3 1 3 1 3 Vậy P  4 2  9 . max
Câu 27. Cho các số phức
z 1 4i  2, z  4  6i  1 và z 1  z  2  i . Tìm giá 1
z , z2 , z thỏa mãn 3 1 2 3 3
trị nhỏ nhất của biểu thức P  3 z  1 z  3 z z2 . 14 14 A.  2 . B. 29  3 . C.  2 2 . D. 85  3 . 2 2 Lời giải Chọn D Đặt x , y   . 1 z  1 x   1 1  1 y i
z 1 4i  2   x  2 1   y  42 1 1 1  4 . 2 2
Vậy tập hợp điểm M biểu diễn số phức C : x 1  y  4  4 có tâm 1
z là đường tròn  1     1 I  1;
 4 , bán kính R  2 . 1 Đặt z  2
x , y2   .
2  x2  y2i
z  4  6i  1   x  42   y  62 2 2 2  1. Vậy tập hợp điểm 2 2
N biểu diễn số phức z là đường tròn C có tâm
2  :  x  4   y  6 2  1 I R  1 2  4 ; 6 , bán kính . 2 Đặt z  3 x , 3 y    . 3  3 x y3i 3 z 1  3
z  2  i  3 x  3 y  2  0 .
Vậy tập hợp điểm A biểu diễn số phức z là đường thẳng d : x y  2  0 . 3 Khi đó: P  3 z  1 z  3
z z2  AM AN 14
Mặt khác, d I , d
R ; d I , d  2 2  R và I , I nằm cùng phía đối với d . 1  1  2  2 2 1 2
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TÀI LIỆU TỔNG ÔN TẬP TNTHPT 2021 2 2
Gọi C là đường tròn đối xứng với với C qua d , suy ra C và gọi
2  :  x  8   y  2  1 2  2 
N là điểm đối xứng với N qua d . C có tâm I R  1 2 8 ; 2 , bán kính . 2  2 Ta có: AM M . 1 I A 1
I AM A 1 I M 1 I A 1 I  2 AN NI                 . 2 AN N I2 AI2 AN AI2 N I2 AI2 1
Suy ra P AM AN AM AN        1 AI AI2 3 1
I I2  3  85  3. Đẳng thức xảy ra khi và
chỉ khi 3 điểm I , , A I  thẳng hàng. 1 2 Vậy min P  85  3 .
Câu 28. (THPT Đoàn Thượng - Hải Dương - 2021) Biết số phức z thoả mãn | z  3  4i | 5 và biểu thức 2 2
T | z  2 |  | z i | đạt giá trị lớn nhất. Tính | z |. A. | z | 33 .
B. | z | 5 2 .
C. | z | 50 .
D. | z | 10 . Lời giải Chọn B
Gọi số phức z x yi (x  ; y  ) 2 2
Ta có | z  3  4i | 5 | x yi  3  4i | 5   x  3   y  4  5
Suy ra tập hợp điểm biểu diễn số phức z là đường tròn C  tâm I 3; 4 , bán kính R  5 (1) 2 2 Mà 2 2 2 2 T z z i x yi x yi ix  2 2 | 2 | | | | 2 | | | 2 yxy  1                   
T  4x  2 y  3  4x  2 y  3  T  0
Suy ra tập hợp điểm biểu diễn số phức z là đường thẳng d :4x  2 y  3  T  0 (2)
Do tập hợp điểm biểu diễn số phức z thoả mãn hai điều kiện (1) và (2) nên C  và d có điểm
| 4.3  2.4  3  T |
chung  d (I , d )  R   5 |
 23  T |10  13 T  33 2 2 4  2  
x  32   y  42  5 x  5  MaxT  33    
z  5  5i | z | 5 2 . y  5
 4x  2 y  30  0  
Câu 29. (THPT Ngô Quyền - Quảng Ninh - 2021) Cho Xét các số phức z , z thỏa mãn 1 2 2 2
z 1  z  2i  1; z  3  i  5. Giá trị nhỏ nhất của P z z bằng 1 1 2 1 2
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
NGUYỄN BẢO VƯƠNG - 0946798489 3 5 2 5 A. 5 . B. . C. 2 5 . D. . 5 5 Lời giải Chọn D
Gọi z x iy , x , y   , z x iy , x , y   khi đó M x ; y , N x ; y là điểm biểu 2 2  1 1  2 2 2  2 2  1 1 1  1 1 
diễn của số phức z , z trong mặt phẳng Oxy . 1 2 2 2 2
Ta có z 1  z  2i  1  x 1 iy
x i y  2
 1  x  2 y  2  0 . Suy ra M 1 1 1  1  2 1 1 1 1
thuộc đường thẳng   : x  2 y  2  0 .
Mặt khác z  3  i  5 Suy ra N thuộc đường tròn tâm I 3 
;1 , bán kính R  5 . 2 7 5
Ta có d I ,  
  không cắt đường tròn. 5 7 5 2 5
Khi đó P z z MN AH MN
AH IH IA d I ,   R   5  . min   1 2 5 5
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Document Outline

  • [NBV]-Chủ đề 4-Số phức-Mức độ nhận biết-câu hỏi
  • [NBV]-Chủ đề 4-Số phức-Mức độ nhận biết-đáp án
  • [NBV]-Chủ đề 4-Số phức-Mức độ thông hiểu-câu hỏi
  • [NBV]-Chủ đề 4-Số phức-Mức độ thông hiểu-đáp án
  • [NBV]-Chủ đề 4-Số phức-Mức độ vận dụng-câu hỏi
  • [NBV]-Chủ đề 4-Số phức-Mức độ vận dụng-đáp án
  • [NBV]-Chủ đề 4-Số phức-Mức độ VDC-câu hỏi
  • [NBV]-Chủ đề 4-Số phức-Mức độ VDC-đáp án