TOP 05 đề ôn thi giữa học kì 1 môn Toán 11 Kết Nối Tri Thức Với Cuộc Sống

Tài liệu gồm 67 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tuyển tập 05 đề ôn thi giữa học kì 1 môn Toán 11 bộ sách Kết Nối Tri Thức Với Cuộc Sống (KNTTvCS); các đề được biên soạn theo cấu trúc 70% trắc nghiệm + 30% tự luận (theo thang điểm), thời gian làm bài 90 phút, có đáp án và lời giải chi tiết.

64 32 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Thông tin:

67 trang 6 tháng trước

Tác giả:

Profile H. Phượng
05 ĐỀ ÔN GIỮA KÌ 1
TOÁN 11
KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 01_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Cho góc hình học
uOv
có số đo bằng
30
(tham khảo hình vẽ).
30
o
O
u
v
Khẳng định nào sau đây đúng?
A.
s® ; 60 .Ou Ov
B.
s® ; 30 .Ou Ov 
C.
s® ; 90 .Ou Ov 
D.
s® ; 30 .Ou Ov
Câu 2: Cho dãy số
n
u
, biết
21
n
n
n
u
. Ba số hạng đầu tiên của dãy số
n
u
là
A.
1 2 3
;;
234
. B.
11
1; ;
2 16
. C.
11
1; ;
48
. D.
23
1; ;
37
.
Câu 3: Phương trình nào sau đây có nghiệm?
A.
sin 2.x
B.
cos2 2.x 
C.
2
sin3 .
3
x
D.
cos .x
Câu 4: Trong các dãy số sau, dãy số nào không phải cấp số cộng?
A.
1 3 5 7 9
;;;;
22222
. B.
1;1;1;1;1
. C.
8; 6; 4; 2;0
. D.
3;1; 1; 2; 4
.
Câu 5: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
-1
2
__
π
O
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
sin .yx
C.
cos .yx
D.
cos .yx
Câu 6: Cho tam giác đều
ABC
(tham khảo hình vẽ).
A
B
C
Khẳng định nào sau đây sai?
A.
s® ; 60 360 , .AB AC k k
B.
s® ; 300 360 , .AB AC k k
C.
s® ; 300 .AB AC
D.
s® ; 60 .AB AC 
Câu 7: Cho cấp số cộng
n
u
có
1
3u 
,
6
27u
. Tính công sai
d
.
A.
7d
. B.
5d
. C.
8d
. D.
6d
.
Câu 8:
6
x
là một nghiệm của phương trình nào dưới đây?
A.
sin 1.x
B.
3
sin .
2
x
C.
cot 3.x
D.
tan 3.x
Câu 9: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số giảm?
A.
1
2
n
n
u
. B.
4
3
1

n
u
n
. C.
2
n
un
. D.
2
n
un
.
Câu 10: Tập xác định của hàm số
1
sin
y
x
là
A.
D \ 0 .
B.
D \ 2 , .
kk
C.
D \ , .
kk
D.
D \ 0; .
Câu 11: Nghiệm âm lớn nhất của phương trình
2sin 1 0x 
là
A.
11
.
6
x
B.
.
6
x
C.
5
.
6
x
D.
7
.
6
x
Câu 12: Cho dãy số
n
u
có
2
1
n
u n n
. Số
19
là số hạng thứ mấy của dãy
n
u
?
A.
5
. B.
7
. C.
6
. D.
4
.
Câu 13: Cho
n
u
là một cấp số cộng thỏa mãn
13
8uu
và
4
10u
. Công sai của cấp số cộng đã cho
bằng
A.
3
. B.
6
. C.
2
. D.
4
.
Câu 14: Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho
60AOM
(tham
khảo hình vẽ).
x
y
60
o
O
M
A
Gọi
N
là điểm đối xứng với điểm
M
qua trục
Oy
, khẳng định nào sau đây đúng?
A.
s® ; 120 360 , .OA ON k k
B.
s® ; 120 360 , .OA ON k k
C.
s® ; 240 360 , .OA ON k k
D.
s® ; 60 360 , .OA ON k k
Câu 15: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
2
cos2 1 2cos


. B.
2
cos2 2sin 1


.
C.
2
cos2 2cos 1


. D.
2
cos2 1 2sin


.
Câu 16: Số nghiệm của phương trình
2cos 1 0x 
trên đoạn
0;2


là
A.
1.
B.
3.
C.
2.
D.
4.
Câu 17: Cho cấp số nhân
n
u
với
1
3u
và
2
6u 
. Công bội
q
của cấp số nhân đó là
A.
2
. B.
2
. C.
9
. D.
9
.
Câu 18: Cho mẫu số liệu ghép nhóm về chiều cao của
25
cây dừa giống, như sau:
Mốt của mẫu số liệu ghép nhóm này là
A.
70
3
o
M
. B.
50
3
o
M
. C.
70
2
o
M
. D.
80
3
o
M
.
Câu 19: Đổi số đo góc
115
sang rađian, ta được
A.
23
.
36
rad
B.
23
.
36
rad
C.
13
.
36
rad
D.
13
.
36
rad
Câu 20: Tập giá trị của hàm số
sin2yx
là
A.
2;2


. B. . C.
1;1


. D.
0;2


.
Câu 21: Cho biết dãy số
1;8;...; x
là một cấp số cộng. Tìm
x
sao cho
1 8 15 22 7944x
.
A.
330x
. B.
220x
. C.
351x
. D.
407x
.
Câu 22: Các cặp góc lượng giác nào dưới đây có cùng điểm biểu diễn trên đường tròn lượng giác?
A.
3
và
2
.
3
B.
3
và
2
.
3
C.
3
và
5
.
3
D.
3
và
4
.
3
Câu 23: Tổng 10 số hạng đầu cấp số nhân
()
n
u
với
1
1
2
u
và công bội
3q
là:
A.
14762
. B.
9841
2
. C.
3069
512
. D.
1640
.
Câu 24: Khẳng định nào sau đây đúng?
A. Các hàm số
sinyx
,
cosyx
,
cotyx
đều là hàm số chẵn.
B. Các hàm số
sinyx
,
cosyx
,
cotyx
đều là hàm số lẻ.
C. Các hàm số
sinyx
,
cotyx
,
tanyx
đều là hàm số chẵn.
D. Các hàm số
sinyx
,
cotyx
,
tanyx
đều là hàm số lẻ.
Câu 25: Cho góc
thỏa mãn
1
sin
3
với
.
2


Tính
sin 2 .
A.
42
.
9
B.
42
.
9
C.
22
.
9
D.
22
.
9
Câu 26: Cho cấp số nhân
n
u
có
1
6u 
và
2q 
. Tống
n
số hạng đầu tiên của cấp số nhân đã cho
bằng 2046. Tìm
.n
A.
9n
. B.
10n
. C.
11n
. D.
12n
.
Câu 27: Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu
ghép nhóm sau:
Giá trị đại diện của nhóm
60;80
là
A.
40
. B.
70
. C.
60
. D.
30
.
Câu 28: Với
,ab
là các góc bất kì. Trong các công thức sau, công thức nào đúng?
A.
cos cos .sin sin .sina b a b a b
. B.
sin sin .cos cos .sina b a b a b
.
C.
sin sin .cos cos .sina b a b a b
. D.
cos cos .cos sin .sina b a b a b
.
Câu 29: Chu kì tuần hoàn của hàm số
sin 2yx
là
A.
2
. B.
2
. C.
2k
. D.
.
Câu 30: Cho các góc
,

thỏa mãn
,
2

,
1
sin
3
,
2
cos
3

. Tính
sin

.
A.
2 2 10
9

. B.
2 10 2
9
. C.
5 4 2
9
. D.
5 4 2
9
.
Câu 31: Phương trình
sin2 3cos 0xx
tương đương với phương trình nào dưới đây?
A.
sin 0.x
B.
sin 1.x
C.
cos 0.x
D.
cos 1.x
Câu 32: Một cơ sở khoan giếng có đơn giá như sau: giá của mét khoan đầu tiên là
40000
đồng và kể
từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm
3%
so với giá của mét khoan
ngay trước đó. Số tiền mà chủ nhà phải trả cho cơ sở khoan giếng để khoan được
50 m
giếng gần nhất số nào sau đây? (đơn vị: đồng)
A.
4176336
. B.
4341626
. C.
4511875
. D.
4687231
.
Câu 33: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả:
Chiều cao
(cm)
150;152
152;154
154;156
156;158
158;160
160;162
162;168
Số học sinh
5
18
40
25
8
3
1
Mẫu số liệu trên có bao nhiêu nhóm?
A. 7. B. 6. C. 5. D. 8.
Câu 34: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả:
Chiều cao (cm)
150;152
152;154
154;156
156;158
158;160
160;162
162;168
Số học sinh
5
18
40
25
8
3
1
Số học sinh có chiều cao trong khoảng
154;156
là
A. 40. B. 18. C. 5. D. 8.
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết
quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A.
3
13Q
. B.
3
14Q
. C.
3
15Q
. D.
3
12Q
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm tập xác định của hàm số
4
2tan 2 .
3
yx




2) (0,75 điểm). Cho cấp số cộng
n
u
thỏa mãn
2 4 6
8 7 4
7
.
2
u u u
u u u

Tính
6 1 2 6
... .S u u u
Câu 2: (1,0 điểm). Giải phương trình:
1 tan 2 2 sin .
4
xx



Câu 3: (0,5 điểm). Để tích lũy cho việc học đại học của con gái, cô Hoa quyết định hằng tháng
bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi 0,5% cộng dồn hằng tháng. Cô bắt
đầu chương trình tích lũy này khi con gái cô tròn 3 tuổi. Cô ấy sẽ tích lũy được bao nhiêu tiền
vào thời điểm gửi khoản tiền thứ 180? Lúc này con gái cô Hoa bao nhiêu tuổi?
____________________HẾT____________________
Huế, 14h40’ Ngày 27 tháng 8 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 01_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Cho góc hình học
uOv
có số đo bằng
30
(tham khảo hình vẽ).
30
o
O
u
v
Khẳng định nào sau đây đúng?
A.
s® ; 60 .Ou Ov
B.
s® ; 30 .Ou Ov 
C.
s® ; 90 .Ou Ov 
D.
s® ; 30 .Ou Ov
Câu 2: Cho dãy số
n
u
, biết
21
n
n
n
u
. Ba số hạng đầu tiên của dãy số
n
u
là
A.
1 2 3
;;
234
. B.
11
1; ;
2 16
. C.
11
1; ;
48
. D.
23
1; ;
37
.
Lời giải:
1 2 3
23
1, ,
37
u u u
.
Câu 3: Phương trình nào sau đây có nghiệm?
A.
sin 2.x
B.
cos2 2.x 
C.
2
sin3 .
3
x
D.
cos .x
Lời giải:
Do
2
1;1
3



nên phương trình
2
sin3
3
x
có nghiệm.
Câu 4: Trong các dãy số sau, dãy số nào không phải cấp số cộng?
A.
1 3 5 7 9
;;;;
22222
. B.
1;1;1;1;1
. C.
8; 6; 4; 2;0
. D.
3;1; 1; 2; 4
.
Lời giải:
Cấp số cộng là một dãy số (hữu hạn hay vô hạn) mà trong đó kể từ số hạng thứ hai, mỗi số
hạng đều bằng tổng của số hạng đứng ngay trước nó và một số d không đổi.
Đáp án A: Là cấp số cộng với
1
1
;1
2
ud
.
Đáp án B: Là cấp số cộng với
1
1; 0ud
.
Đáp án C: Là cấp số cộng với
1
8; 2ud
.
Đáp án D: Không là cấp số cộng vì
2 1 4 3
2 ; 1u u u u
.
Câu 5: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
-1
2
__
π
O
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
sin .yx
C.
cos .yx
D.
cos .yx
Lời giải:
Kiểm tra các sự kiện: Đồ thị hàm số đi qua các điểm
0;0 , ; 1 .
2
OA



Câu 6: Cho tam giác đều
ABC
(tham khảo hình vẽ).
A
B
C
Khẳng định nào sau đây sai?
A.
s® ; 60 360 , .AB AC k k
B.
s® ; 300 360 , .AB AC k k
C.
s® ; 300 .AB AC
D.
s® ; 60 .AB AC 
Lời giải:
Các kết quả đúng:
s®
s®
; 60 360
,.
; 300 360
AB AC k
k
AB AC k
Câu 7: Cho cấp số cộng
n
u
có
1
3u 
,
6
27u
. Tính công sai
d
.
A.
7d
. B.
5d
. C.
8d
. D.
6d
.
Lời giải:
Ta có
61
5 27 6u u d d
.
Câu 8:
6
x
là một nghiệm của phương trình nào dưới đây?
A.
sin 1.x
B.
3
sin .
2
x
C.
cot 3.x
D.
tan 3.x
Lời giải:
Thay
6
x
vào phương trình
cot 3x
thấy thỏa mãn.
Câu 9: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số giảm?
A.
1
2
n
n
u
. B.
4
3
1

n
u
n
. C.
2
n
un
. D.
2
n
un
.
Lời giải:
Ta có
1
2
n
n
u
1
1
1
2
n
n
u

*
n
.
Câu 10: Tập xác định của hàm số
1
sin
y
x
là
A.
D \ 0 .
B.
D \ 2 , .
kk
C.
D \ , .
kk
D.
D \ 0; .
Lời giải:
Hàm số
1
sin
y
x
xác định khi và chỉ khi
sin 0x
,.x k k
Câu 11: Nghiệm âm lớn nhất của phương trình
2sin 1 0x 
là
A.
11
.
6
x
B.
.
6
x
C.
5
.
6
x
D.
7
.
6
x
Lời giải:
Ta có:
2
1
6
2sin 1 0 sin , .
5
2
2
6
xk
x x k
xk


Vậy nghiệm âm lớn nhất của phương trình đã cho là
57
2.
66
x

Câu 12: Cho dãy số
n
u
có
2
1
n
u n n
. Số
19
là số hạng thứ mấy của dãy
n
u
?
A.
5
. B.
7
. C.
6
. D.
4
.
Lời giải:
Giả sử
19
n
u 
,
*
n
.
Suy ra
2
1 19nn
2
20 0nn
5
4
n
nl

.
Vậy số
19
là số hạng thứ
5
của dãy số.
Câu 13: Cho
n
u
là một cấp số cộng thỏa mãn
13
8uu
và
4
10u
. Công sai của cấp số cộng đã cho
bằng?
A.
3
. B.
6
. C.
2
. D.
4
.
Lời giải:
Ta có
13
1 1 1
1
11
4
8
2 8 2 2 8
1
3 10 3 10
10
3
uu
u u d u d
u
u d u d
u
d



.
Vậy công sai của cấp số cộng là
3d
.
Câu 14: Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho
60AOM
(tham
khảo hình vẽ).
x
y
60
o
O
M
A
Gọi
N
là điểm đối xứng với điểm
M
qua trục
Oy
, khẳng định nào sau đây đúng?
A.
s® ; 120 360 , .OA ON k k
B.
s® ; 120 360 , .OA ON k k
C.
s® ; 240 360 , .OA ON k k
D.
s® ; 60 360 , .OA ON k k
Lời giải:
x
y
N
A
M
O
60
o
Ta có:
s®
s®
; 120 360
120 , .
; 240 360
OA ON k
AON k
OA ON k

Câu 15: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
2
cos2 1 2cos


. B.
2
cos2 2sin 1


.
C.
2
cos2 2cos 1


. D.
2
cos2 1 2sin


.
Câu 16: Số nghiệm của phương trình
2cos 1 0x 
trên đoạn
0;2


là
A.
1.
B.
3.
C.
2.
D.
4.
Lời giải:
Cách 1:
Ta có:
2
2
1
3
2cos 1 0 cos , .
2
2
2
3
xk
x x k
xk


+) Xét
2
2 , .
3
x k k
Do
0;2x


nên
2 1 2
0 2 2
2
0.
3 3 3
3
kk
kx
kk





+) Xét
2
2 , .
3
x k k
Do
0;2x


nên
2 1 4
0 2 2
4
1.
3 3 3
3
kk
kx
kk





Cách 2: Dùng đường tròn lượng giác.
x
y
O
A
Câu 17: Cho cấp số nhân
n
u
với
1
3u
và
2
6u 
. Công bội
q
của cấp số nhân đó là
A.
2
. B.
2
. C.
9
. D.
9
.
Lời giải:
Vì
n
u
là cấp số nhân nên
2
1
6
2
3
u
q
u
.
Câu 18: Cho mẫu số liệu ghép nhóm về chiều cao của
25
cây dừa giống, như sau:
Mốt của mẫu số liệu ghép nhóm này là
A.
70
3
o
M
. B.
50
3
o
M
. C.
70
2
o
M
. D.
80
3
o
M
.
Lời giải:
Tần số lớn nhất là 7 nên nhóm chứa mốt là
20;30
.
Ta có:
3j
,
3
20a
,
3
7m
,
24
6, 5mm
,
10h
.
Do đó:
7 6 70
20 .10
7 6 7 5 3
o
M
.
Câu 19: Đổi số đo góc
115
sang rađian, ta được
A.
23
.
36
rad
B.
23
.
36
rad
C.
13
.
36
rad
D.
13
.
36
rad
Lời giải:
Cách 1: Ta có:
5 23
.
180 36
11
115




rad rad
Cách 2: Sử dụng MTCT
Câu 20: Tập giá trị của hàm số
sin2yx
là
A.
2;2


. B. . C.
1;1


. D.
0;2


.
Lời giải:
Ta có
1 sin 2 1,xx
.
Vậy tập giá trị của hàm số
sin2yx
là
1;1


.
Câu 21: Cho biết dãy số
1;8;...; x
là một cấp số cộng. Tìm
x
sao cho
1 8 15 22 7944x
.
A.
330x
. B.
220x
. C.
351x
. D.
407x
.
Lời giải:
Ta có cấp số cộng với
1
1u
,
7d
,
n
ux
,
7944
n
S
.
Áp dụng công thức
1
2
2 1 2.1 1 7
7944 7 5 15888 0
22
n
u n d n n n
S n n
48
331
7

n TM
nL
.
Vậy
48
1 47.7 330xu
.
Câu 22: Các cặp góc lượng giác nào dưới đây có cùng điểm biểu diễn trên đường tròn lượng giác?
A.
3
và
2
.
3
B.
3
và
2
.
3
C.
3
và
5
.
3
D.
3
và
4
.
3
Lời giải:
Ta có:
5
2.
33





Câu 23: Tổng 10 số hạng đầu cấp số nhân
()
n
u
với
1
1
2
u
và công bội
3q
là:
A.
14762
. B.
9841
2
. C.
3069
512
. D.
1640
.
Lời giải:
Ta có:
10
10
1
. 1 3
2
14762
13
S

.
Câu 24: Khẳng định nào sau đây đúng?
A. Các hàm số
sinyx
,
cosyx
,
cotyx
đều là hàm số chẵn.
B. Các hàm số
sinyx
,
cosyx
,
cotyx
đều là hàm số lẻ.
C. Các hàm số
sinyx
,
cotyx
,
tanyx
đều là hàm số chẵn.
D. Các hàm số
sinyx
,
cotyx
,
tanyx
đều là hàm số lẻ.
Lời giải:
Ta có, các hàm số
sinyx
,
cotyx
,
tanyx
là các hàm số lẻ, hàm số
cosyx
là hàm số
chẵn.
Câu 25: Cho góc
thỏa mãn
1
sin
3
với
.
2


Tính
sin 2 .
A.
42
.
9
B.
42
.
9
C.
22
.
9
D.
22
.
9
Lời giải:
Ta có:
22
22
cos
8
3
cos 1 sin .
9
22
cos
3

Do
2


nên
cos 0

chọn
22
cos .
3
Vậy
42
sin2 2sin cos .
9

Câu 26: Cho cấp số nhân
n
u
có
1
6u 
và
2q 
. Tống
n
số hạng đầu tiên của cấp số nhân đã cho
bằng 2046. Tìm
.n
A.
9n
. B.
10n
. C.
11n
. D.
12n
.
Lời giải:
Ta có
1
1
2046
1
n
n
q
Su
q
12
6
12
n


2 2 1
n
2 1024 10
n
n
.
Câu 27: Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu
ghép nhóm sau:
Giá trị đại diện của nhóm
60;80
là
A.
40
. B.
70
. C.
60
. D.
30
.
Lời giải:
Ta có giá trị đại diện là
60 80
70
2
.
Câu 28: Với
,ab
là các góc bất kì. Trong các công thức sau, công thức nào đúng?
A.
cos cos .sin sin .sina b a b a b
. B.
sin sin .cos cos .sina b a b a b
.
C.
sin sin .cos cos .sina b a b a b
. D.
cos cos .cos sin .sina b a b a b
.
Lời giải:
Theo công thức cộng ta có:
sin sin .cos cos .sina b a b a b
.
Câu 29: Chu kì tuần hoàn của hàm số
sin 2yx
là
A.
2
. B.
2
. C.
2k
. D.
.
Lời giải:
Chu kì tuần hoàn của hàm số
sin 2yx
là
2
2
T

.
Câu 30: Cho các góc
,

thỏa mãn
,
2

,
1
sin
3
,
2
cos
3

. Tính
sin

.
A.
2 2 10
9

. B.
2 10 2
9
. C.
5 4 2
9
. D.
5 4 2
9
.
Lời giải:
Ta có:
1
1
cos 1
sin
9
3
2
4
cos
sin 1
3
9




.
Vì
,
2

nên
22
cos
3
5
sin
3

.
Và:
sin sin .cos sin .cos
.
Suy ra:
1 2 5 2 2
sin
3 3 3 3








.
Vậy
2 2 10
sin( )
9



.
Câu 31: Phương trình
sin2 3cos 0xx
tương đương với phương trình nào dưới đây?
A.
sin 0.x
B.
sin 1.x
C.
cos 0.x
D.
cos 1.x
Lời giải:
Ta có:
sin2 3cos 0 2sin cos 3cos 0 cos 2sin 3 0x x x x x x x
v« nghiÖm
cos 0
cos 0
cos 0.
3
2sin 3 0
sin
2
x
x
x
x
x

Câu 32: Một cơ sở khoan giếng có đơn giá như sau: giá của mét khoan đầu tiên là
40000
đồng và kể
từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm
3%
so với giá của mét khoan
ngay trước đó. Số tiền mà chủ nhà phải trả cho cơ sở khoan giếng để khoan được
50 m
giếng gần nhất số nào sau đây? (đơn vị: đồng)
A.
4176336
. B.
4341626
. C.
4511875
. D.
4687231
.
Lời giải:
Đặt
1
S
là giá của mét khoan đầu tiên thì
1
40000S
đồng.
Kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm
3%
so với giá của mét khoan
ngay trước đó.
Suy ra
2 1 1 1
.3% (1 0,03)S S S S
.
Tương tự
3 2 2 2
.3% (1 0,03)S S S S
.
Vậy các giá trị
1 2 50
, ,...,S S S
lập thành một cấp số nhân có số hạng đầu
1
40000S
và công bội
1 0,03q 
.
Gọi
T
là tổng số tiền mà chủ nhà phải thanh toán khi khoan
50 m
giếng, ta có:
50
1 2 50
1 0,03 1
... 40 000. 4511875
1 0,03 1
T S S S


(đồng)
Câu 33: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả:
Chiều cao
(cm)
150;152
152;154
154;156
156;158
158;160
160;162
162;168
Số học sinh
5
18
40
25
8
3
1
Mẫu số liệu trên có bao nhiêu nhóm?
A. 7. B. 6. C. 5. D. 8.
Câu 34: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả:
Chiều cao (cm)
150;152
152;154
154;156
156;158
158;160
160;162
162;168
Số học sinh
5
18
40
25
8
3
1
Số học sinh có chiều cao trong khoảng
154;156
là
A. 40. B. 18. C. 5. D. 8.
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết
quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A.
3
13Q
. B.
3
14Q
. C.
3
15Q
. D.
3
12Q
.
Lời giải:
Cỡ mẫu :
2 4 7 4 3 20n
.
Tứ phân vị thứ ba
3
Q
là
15 16
2
xx
. Do
15 16
,xx
đều thuộc nhóm
12;16
nên nhóm này chứa
3
Q
.
Do đó:
4p
,
4
12a
,
4
4m
,
1 2 3
2 4 7 13m m m
,
54
4aa
.
Ta có:
3
3.20
13
4
12 .4 14
4
Q
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm tập xác định của hàm số
4
2tan 2 .
3
yx




Lời giải:
Hàm số xác định
5
cos 2 0 2 , ,
3 3 2 12 2
k
x x k k x k



.
Vậy tập xác định của hàm số là
5
\.
12 2
k
Dk




2) (0,75 điểm). Cho cấp số cộng
n
u
thỏa mãn
2 4 6
8 7 4
7
.
2
u u u
u u u

Tính
6 1 2 6
... .S u u u
Lời giải:
Ta có:
1 1 1
2 4 6
1
1
8 7 4 1
11
3 5 7
7
7
5
.
2 2 5 0
2
7 6 2 3
l
u d u d u d
u u u
ud
u
u u u u d
d
u d u d u d

Vậy
1
6
6 2 5
0.
2
ud
S

Câu 2: (1,0 điểm). Giải phương trình:
1 tan 2 2 sin .
4
xx



Lời giải:
Điều kiện:
\.
2
x k k



Phương trình
sin
1 2 sin cos sin cos 2cos 1 0
cos
x
x x x x x
x
4
sin cos 0
2.
1
3
cos
2
2
3
xk
xx
xk
x
xk

Đối chiếu điều kiện ta có nghiệm của phương trình là
; 2 ; 2 , .
4 3 3
x k x k x k k
Câu 3: (0,5 điểm). Để tích lũy cho việc học đại học của con gái, cô Hoa quyết định hằng tháng
bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi 0,5% cộng dồn hằng tháng. Cô bắt
đầu chương trình tích lũy này khi con gái cô tròn 3 tuổi. Cô ấy sẽ tích lũy được bao nhiêu tiền
vào thời điểm gửi khoản tiền thứ 180? Lúc này con gái cô Hoa bao nhiêu tuổi?
Lời giải:
Gọi
n
u
là số triệu đồng mà cô Hoa có trong chương trình tích lũy ở lần gửi thứ
n
(vào đầu
tháng thứ
n
).
Kí hiệu:
0,5a
triệu đồng,
0,5%.r
Số tiền của cô Hoa trong chương trình ở đầu tháng 1 là
1
.ua
Số tiền của cô Hoa trong chương trình ở đầu tháng 2 là
21
1.u u r a
Số tiền của cô Hoa trong chương trình ở đầu tháng 3 là
2
32
1 1 1 .u u r a a r a r a
Tương tự cho các tháng tiếp theo, suy ra số tiền cô Hoa trong chương trình ở đầu tháng
n
là
12
1 1 1 1
1 1 1 . . .
11
nn
nn
n
rr
u a r a r a r a a a
r
r


Vào thời điểm gửi khoản tiền thứ 180, cô ấy sẽ tích lũy được
180
180
11
. 145,41
r
ua
r


triệu
đồng.
Khi đó, tuổi của con gái cô Hoa là
180
3 18
12

tuổi.
____________________HẾT____________________
Huế, 14h40’ Ngày 27 tháng 8 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Tập nghiệm của phương trình
sin 1x 
là
A.
2 , .
2
S k k


B.
2 , .
2
S k k


C.
2 , .S k k

D.
2 , .S k k

Câu 2: Cho dãy số có các số hạng đầu là: 9; 99; 999; 9999,… Số hạng tổng quát của dãy số này là
A.
.
1
n
n
u
n
B.
10 1.
n
n
u
C.
9.
n
n
u
D.
9.
n
un
Câu 3: Cho cấp số cộng
n
u
với công sai
.d
Gọi
n
S
là tổng
n
số hạng đầu tiên của
.
n
u
Đẳng thức
nào dưới đây đúng?
A.
1
*
,.
2
n
n
n u u
Sn
B.
11
*
,.
2
n
n
n u u
Sn
C.
1
*
,.
2
n
n
n u u
Sn
D.
*
1
,.
2
n
n
nu u
Sn
Câu 4: Cho góc
thỏa mãn
0
2

và
1
cos
3
. Tính
sin .
A.
22
3
. B.
22
3
. C.
2
3
. D.
2
3
.
Câu 5: Cho cấp số nhân
n
u
với công bội
.q
Đẳng thức nào dưới đây đúng?
A.
*
11
. , .
n
n
u u q n
B.
*
11
,.
n
n
u u q n
C.
1*
11
. , .
n
n
u u q n
D.
1*
11
. , .
n
n
u u q n
Câu 6: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
-1
2
__
π
O
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
sin2 .yx
C.
cos .yx
D.
cos2 .yx
Câu 7: Cho cấp số cộng
:
n
u
1,4,7,...
. Số hạng thứ 100 của cấp số cộng
n
u
là
A.
297
. B.
301
. C.
295
. D.
298
.
Câu 8: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên
một công ty như sau:
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 đến dưới 20 phút?
A.
25
. B.
14
. C.
13
. D.
6
.
Câu 9: Rút gọn biểu thức
sin sin3
2cos
xx
M
x
(với giả thiết biểu thức có nghĩa).
A.
sin 4 .Mx
B.
sin .Mx
C.
sin 2 .Mx
D.
cos2 .Mx
Câu 10: Khẳng định nào dưới đây sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương.
Câu 11: Cho hình vuông
ABCD
tâm
O
(tham khảo hình vẽ).
D
C
B
A
O
Khẳng định nào sau đây đúng?
A.
s® ; 90 .OA OB
B.
s® ; 180 .OA OB 
C.
s® ; 0 .OA OB 
D.
s® ; 270 .OA OB
Câu 12: Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Tính trung vị của mẫu số liệu ghép nhóm này.
A.
17,5.
B.
19.
C.
18,4.
D.
18,1.
Câu 13: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 1; 1; 1
. B.
1; 3; 9;10
. C.
1; 0; 0;0
. D.
32; 16; 8;4
.
Câu 14: Cho hai góc nhọn
và
phụ nhau. Hệ thức nào sau đây sai?
A.
sin cos


. B.
cos sin

. C.
cos sin

. D.
cot tan

.
Câu 15: Cho bốn cung (trên một đường tròn định hướng):
5 25 19
, , , .
6 3 3 6
Các
cung nào có điểm cuối trùng nhau?
A.
và
;
và
.
B.
và
;
và
.
C.
, , .
D.
, , .
Câu 16: Cho cấp số cộng
n
u
với
52
n
un
. Tìm công sai của cấp số cộng đã cho.
A.
3d
. B.
2d 
. C.
1d
. D.
2d
.
Câu 17: Bảng số liệu ghép nhóm sau cho biết chiều cao
(cm)
của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.
153,58
. B.
153,18
. C.
153
. D.
154,1
.
Câu 18: Biết nghiệm dương nhỏ nhất của phương trình
2cos 3 0x 
có dạng
, ; ,
aa
ab
bb
là phân
số tối giản. Tổng
ab
bằng
A.
6.
B.
8.
C.
7.
D.
9.
Câu 19: Cho dãy số
,
n
u
biết
1
1
n
u
n
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
111
; ; .
2 3 4
B.
11
1; ; .
23
C.
1 1 1
; ; .
2 4 6
D.
11
1; ; .
35
Câu 20: Tập hợp các giá trị x thỏa mãn
,2 , 3x x x
theo thứ tự lập thành một cấp số nhân là
A.
0; 1
. B.
. C.
1
. D.
0.
Câu 21: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
tan 2 2tan .

B.
2
2tan
tan2 .
1 tan
C.
2
2tan
tan2 .
1 tan
D.
2
tan
tan2 .
1 tan
Câu 22: Cho
3
sin
4
. Tính
cos2
.
A.
1
8
. B.
7
4
. C.
7
4
. D.
1
8
.
Câu 23: Biểu thức
sin
6
a



được viết lại thành
A.
1
sin
2
a
. B.
31
sin cos
22
aa
. C.
31
sin cos
22
aa
. D.
13
sin cos
22
aa
.
Câu 24: Cho hai góc lượng giác
,ab
thỏa mãn
13
tan ;tan
74
ab
. Tính
tan ab
.
A.
2
. B.
1
. C.
25
.
28
D.
11
.
3
Câu 25: Tập xác định của hàm số
2
1
cos
x
y
x
là
A.
D
. B.
\,
2
D k k



.
C.
\,D k k
. D.
\,
2
k
Dk



.
Câu 26: Số nghiệm của phương trình
2sin 2 1 0x 
trên đoạn
0;2


là
A.
1.
B.
3.
C.
2.
D.
4.
Câu 27: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
8sin 2 5yx
.
A.
max 11; min 21yy
. B.
max 8; min 8yy
.
C.
max 4; min 6yy
. D.
max 3; min 13yy
.
Câu 28: Tập xác định của hàm số
sin
2cos 1
x
y
x
là
A.
1
\.
2
D



B.
\ 2 ; 2 , , .
33
D k m k m





C.
5
\ 2 ; 2 , , .
66
D k m k m





D.
5
\ ; , , .
66
D k m k m





Câu 29: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
cot 4yx
. B.
sin 1
cos
x
y
x
. C.
2
tanyx
. D.
cotyx
.
Câu 30: Chu kỳ của hàm số
5sin 2020yx
là
A.
1010 .
B.
2.
C.
.
1010
D.
.
2020
Câu 31: Tập hợp tất cả các giá trị của tham số
m
để phương trình
sin 1xm
có nghiệm là
A.
1;1 .


B.
2; 2 .


C.
0;2 .


D.
1;2 .


Câu 32: Cho cấp số nhân
n
u
với
1
2u
và công bội
3q
. Giá trị của
2
u
bằng
A.
6
. B.
9
. C.
8
. D.
2
3
.
Câu 33: Số nghiệm của phương trình
sin2
0
cos 1
x
x
trên
0;3


là
A.
7.
B.
6.
C.
4.
D.
5.
Câu 34: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào giảm?
A.
4
.
3
n
n
u



B.
1 5 1 .
n
n
n
u
C.
3.
n
n
u 
D.
4.
n
un
Câu 35: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu
ghép nhóm sau:
Giá trị đại diện của nhóm
[20;40)
là
A. 10. B. 20. C. 30. D. 40.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất của hàm số
5 4cos2 2.yx
2) (0,75 điểm). Cho cấp số nhân
n
u
thỏa mãn
20 17
35
8
.
240
uu
uu

Tính
3
.u
Câu 2: (1,0 điểm). Giải phương trình
2
2
cos2 1
tan 3tan .
2
cos
x
xx
x



Câu 3: (0,5 điểm). Một cầu thang bằng gạch có tổng cộng 30 bậc. Bậc dưới cùng cần 100 viên
gạch. Mỗi bậc tiếp theo cần ít hơn 2 viên gạch so với bậc ngay trước nó.
a) Cần bao nhiêu viên gạch cho bậc trên cùng?
b) Cần bao nhiêu gạch để xây cầu thang?
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 02_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10
Hương
Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Tập nghiệm của phương trình
sin 1x 
là
A.
2 , .
2
S k k


B.
2 , .
2
S k k


C.
2 , .S k k

D.
2 , .S k k

Câu 2: Cho dãy số có các số hạng đầu là: 9; 99; 999; 9999,… Số hạng tổng quát của dãy số này là
A.
.
1
n
n
u
n
B.
10 1.
n
n
u
C.
9.
n
n
u
D.
9.
n
un
Lời giải:
Nhận xt:
1
1
10 1u 
;
2
2
10 1u 
;
3
3
10 1u 
;
4
4
10 1u 
.
Câu 3: Cho cấp số cộng
n
u
với công sai
.d
Gọi
n
S
là tổng
n
số hạng đầu tiên của
.
n
u
Đẳng thức
nào dưới đây đúng?
A.
1
*
,.
2
n
n
n u u
Sn
B.
11
*
,.
2
n
n
n u u
Sn
C.
1
*
,.
2
n
n
n u u
Sn
D.
*
1
,.
2
n
n
nu u
Sn
Câu 4: Cho góc
thỏa mãn
0
2

và
1
cos
3
. Tính
sin .
A.
22
3
. B.
22
3
. C.
2
3
. D.
2
3
.
Lời giải:
Ta có:
2
22
22
sin
18
3
sin 1 cos 1 .
39
22
sin
3




Do
0
2

nên chọn
22
sin .
3
Câu 5: Cho cấp số nhân
n
u
với công bội
.q
Đẳng thức nào dưới đây đúng?
A.
*
11
. , .
n
n
u u q n
B.
*
11
,.
n
n
u u q n
C.
1*
11
. , .
n
n
u u q n
D.
1*
11
. , .
n
n
u u q n
Câu 6: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
-1
2
__
π
O
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
sin2 .yx
C.
cos .yx
D.
cos2 .yx
Lời giải:
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm
; 1 .
2
A



Câu 7: Cho cấp số cộng
:
n
u
1,4,7,...
. Số hạng thứ 100 của cấp số cộng
n
u
là
A.
297
. B.
301
. C.
295
. D.
298
.
Lời giải:
Cấp số cộng
1,4,7,...
. có số hạng đầu
1
1u
và công sai
3d
.
Số hạng thứ 100 của cấp số cộng là:
100 1
99. 1 99.3 298u u d
.
Câu 8: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên
một công ty như sau:
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 đến dưới 20 phút?
A.
25
. B.
14
. C.
13
. D.
6
.
Câu 9: Rút gọn biểu thức
sin sin3
2cos
xx
M
x
(với giả thiết biểu thức có nghĩa).
A.
sin 4 .Mx
B.
sin .Mx
C.
sin 2 .Mx
D.
cos2 .Mx
Lời giải:
Ta có:
sin sin3 sin3 sin 2sin2 cos
sin2
2cos 2cos 2cos

x x x x x x
Mx
x x x
.
Câu 10: Khẳng định nào dưới đây sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương.
Lời giải:
A. Đúng vì dãy số đã cho là cấp số nhân với công bội
1q
.
B. Đúng vì dãy số đã cho là cấp số cộng với công sai
0d
.
C. Đúng vì dãy số đã cho là cấp số cộng có công sai dương nên:
1
0
nn
u u d
1nn
uu

.
D. Sai. Ví dụ dãy
5
;
2
;
1
;
3
; … là dãy số có
30d 
nhưng không phải là dãy số dương.
Câu 11: Cho hình vuông
ABCD
tâm
O
(tham khảo hình vẽ).
D
C
B
A
O
Khẳng định nào sau đây đúng?
A.
s® ; 90 .OA OB
B.
s® ; 180 .OA OB 
C.
s® ; 0 .OA OB 
D.
s® ; 270 .OA OB
Lời giải:
Các kết quả đúng:
s®
s®
; 90 360
,.
; 270 360
OA OB k
k
OA OB k
Câu 12: Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Tính trung vị của mẫu số liệu ghép nhóm này.
A.
17,5.
B.
19.
C.
18,4.
D.
18,1.
Lời giải:
Cỡ mẫu là
3 12 15 24 2 56n
.
Gọi
1 56
,,xx
là thời gian vào Internet của 56 học sinh và giả sử dãy này đã được sắp xếp theo
thứ tự tăng dần.
Khi đó, trung vị là
28 29
2
xx
. Do 2 giá trị
28 2 9
,xx
thuộc nhóm
[15,5;18,5)
nên nhóm này chứa
trung vị.
Do đó,
3 3 1 2 4 3
3; 15,5; 15; 3 12 15; 3p a m m m a a
và ta có
56
15
2
15,5 3 18,1.
15
e
M
Câu 13: Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 1; 1; 1
. B.
1; 3; 9;10
. C.
1; 0; 0;0
. D.
32; 16; 8;4
.
Lời giải:
Nếu
n
u
là cấp số nhân với công bội
q
ta có:
1
1
.
n
nn
n
u
u u q q
u
.
1; 1;1; 1
là cấp số nhân với
1q 
.
1;3;9;10
không là cấp số nhân.
1;0;0;0
là cấp số nhân với
0q
.
32;16;8;4
là cấp số nhân với
1
2
q
.
Câu 14: Cho hai góc nhọn
và
phụ nhau. Hệ thức nào sau đây sai?
A.
sin cos


. B.
cos sin

. C.
cos sin

. D.
cot tan

.
Câu 15: Cho bốn cung (trên một đường tròn định hướng):
5 25 19
, , , .
6 3 3 6
Các
cung nào có điểm cuối trùng nhau?
A.
và
;
và
.
B.
và
;
và
.
C.
, , .
D.
, , .
Lời giải:
Ta có:
4
2
cung
và
có điểm cuối trùng nhau.
8
hai cung
và
có điểm cuối trùng nhau.
Câu 16: Cho cấp số cộng
n
u
với
52
n
un
. Tìm công sai của cấp số cộng đã cho.
A.
3d
. B.
2d 
. C.
1d
. D.
2d
.
Lời giải:
Ta có
1
5 2 1 5 2 5 2 2 5 2 2 2.
nn
u u n n n n d
Câu 17: Bảng số liệu ghép nhóm sau cho biết chiều cao
(cm)
của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.
153,58
. B.
153,18
. C.
153
. D.
154,1
.
Lời giải:
Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150; 155). Ta có,
22
2, 150, 14j a m
,
13
7, 10, 5m m h
.
Do đó
0
14 7
150 5 153,18.
(14 7) (14 10)
M
Câu 18: Biết nghiệm dương nhỏ nhất của phương trình
2cos 3 0x 
có dạng
, ; ,
aa
ab
bb
là phân
số tối giản. Tổng
ab
bằng
A.
6.
B.
8.
C.
7.
D.
9.
Lời giải:
Ta có:
2
3
6
2cos 3 0 cos , .
2
2
6
xk
x x k
xk


Vậy nghiệm dương nhỏ nhất của phương trình đã cho là
1
.
6
6
a
x
b

Câu 19: Cho dãy số
,
n
u
biết
1
1
n
u
n
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào
dưới đây?
A.
111
; ; .
2 3 4
B.
11
1; ; .
23
C.
1 1 1
; ; .
2 4 6
D.
11
1; ; .
35
Lời giải:
Ta có
1 2 3
1 1 1
,,
2 3 4
u u u
.
Câu 20: Tập hợp các giá trị x thỏa mãn
,2 , 3x x x
theo thứ tự lập thành một cấp số nhân là
A.
0; 1
. B.
. C.
1
. D.
0.
Lời giải:
Gọi
q
là công bội của cấp số nhân.
Ta có:
2 . 2 . 2
3 2 . 3 2.2 1
x x q x x q q
x x q x x x

Tập hợp các giá trị x thỏa mãn
,2 , 3x x x
theo thứ tự lập thành một cấp số nhân là
1
.
Câu 21: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
tan 2 2tan .

B.
2
2tan
tan2 .
1 tan
C.
2
2tan
tan2 .
1 tan
D.
2
tan
tan2 .
1 tan
Câu 22: Cho
3
sin
4
. Tính
cos2
.
A.
1
8
. B.
7
4
. C.
7
4
. D.
1
8
.
Lời giải:
Ta có
2
cos2 1 2sin


91
12
16 8
.
Câu 23: Biểu thức
sin
6
a



được viết lại thành
A.
1
sin
2
a
. B.
31
sin cos
22
aa
. C.
31
sin cos
22
aa
. D.
13
sin cos
22
aa
.
Lời giải:
Ta có
31
sin sin cos cos sin sin cos
6 6 6 2 2
a a a a a



.
Câu 24: Cho hai góc lượng giác
,ab
thỏa mãn
13
tan ;tan
74
ab
. Tính
tan ab
.
A.
2
. B.
1
. C.
25
.
28
D.
11
.
3
Lời giải:
Ta có
13
tan tan
74
tan 1
13
1 tan .tan
1.
74
ab
ab
ab
.
Câu 25: Tập xác định của hàm số
2
1
cos
x
y
x
là
A.
D
. B.
\,
2
D k k



.
C.
\,D k k
. D.
\,
2
k
Dk



.
Lời giải:
Điều kiện:
cos 0 ,
2
x x k k
.
Vậy tập xác định của hàm số là
\,
2
D k k



.
Câu 26: Số nghiệm của phương trình
2sin 2 1 0x 
trên đoạn
0;2


là
A.
1.
B.
3.
C.
2.
D.
4.
Lời giải:
Cách 1:
Ta có:
22
1
6
12
2sin2 1 0 sin2 , .
55
2
22
6 12
xk
xk
x x k
x k x k




+) Xét
,.
12
x k k
Do
0;2x


nên
1 23
02
13
0; 1 ; .
12 12 12
12 12
kk
k k x x
kk






+) Xét
5
2 , .
12
x k k
Do
0;2x


nên
5 5 19
02
5 17
0; 1 ; .
12 12 12
12 12
kk
k k x x
kk






Cách 2: Dùng đường tròn lượng giác.
Ta có:
0;2 2 0;4 .xx


x
y
A
O
Câu 27: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
8sin 2 5yx
.
A.
max 11; min 21yy
. B.
max 8; min 8yy
.
C.
max 4; min 6yy
. D.
max 3; min 13yy
.
Lời giải:
Ta có
: 1 sin 2 1 8 8sin 2 8 13 8sin 2 5 3 x x x x
Vậy
ma x 3;min 13yy
.
Câu 28: Tập xác định của hàm số
sin
2cos 1
x
y
x
là
A.
1
\.
2
D



B.
\ 2 ; 2 , , .
33
D k m k m





C.
5
\ 2 ; 2 , , .
66
D k m k m





D.
5
\ ; , , .
66
D k m k m





Lời giải:
Hàm số xác định
2
1
3
2cos 1 0 cos , , .
2
2
3
xk
x x k m
xm


Câu 29: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
cot 4yx
. B.
sin 1
cos
x
y
x
. C.
2
tanyx
. D.
cotyx
.
Lời giải:
Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Trong các hàm số trên, chỉ có hàm số
cot 4yx
là hàm số lẻ.
Vậy, hàm số nào có đồ thị đối xứng qua gốc tọa độ là
cot 4yx
.
Câu 30: Chu kỳ của hàm số
5sin 2020yx
là
A.
1010 .
B.
2.
C.
.
1010
D.
.
2020
Lời giải:
Chu kì của hàm số đã cho
2
2020 1010
T


.
Câu 31: Tập hợp tất cả các giá trị của tham số
m
để phương trình
sin 1xm
có nghiệm là
A.
1;1 .


B.
2; 2 .


C.
0;2 .


D.
1;2 .


Lời giải:
Ta có:
: sin 0;1 .xx


Phương trình
sin 1xm
có nghiệm
0 1 1 1 2.mm
Câu 32: Cho cấp số nhân
n
u
với
1
2u
và công bội
3q
. Giá trị của
2
u
bằng
A.
6
. B.
9
. C.
8
. D.
2
3
.
Lời giải:
Ta có
21
. 2.3 6u u q
.
Câu 33: Số nghiệm của phương trình
sin2
0
cos 1
x
x
trên
0;3


là
A.
7.
B.
6.
C.
4.
D.
5.
Lời giải:
Điều kiện:
cos 1.x
Ta có:
sin2
0 sin2 0 , .
cos 1 2
xk
x x k
x
x
y
A
O
Đối chiếu điều kiện, số nghiệm của phương trình đã cho trên
0;3


là 5.
Câu 34: Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào giảm?
A.
4
.
3
n
n
u



B.
1 5 1 .
n
n
n
u
C.
3.
n
n
u 
D.
4.
n
un
Lời giải:
Với A: Ta có:
1
1
4 4 4 4 4 1 4
. . 0
3 3 3 3 3 3 3
n n n n n
nn
uu
loại A.
Với B: Dãy
n
u
với
1 5 1 .
n
n
n
u
có các số hạng đan dấu nên dãy không tăng, không
giảm
loại B.
Với C:
1
1
3 3 3.3 3 2.3 0
n n n n n
nn
uu
Chọn C.
Với D:
1
1
5 4 0
54
nn
u u n n
nn
loại D.
Câu 35: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu
ghép nhóm sau:
Giá trị đại diện của nhóm
[20;40)
là
A. 10. B. 20. C. 30. D. 40.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất của hàm số
5 4cos2 2.yx
Lời giải:
Ta có:
: 1 cos2 1 3 5 4cos2 2 5.x x x
Suy ra:
max 5y
khi
cos2 1 , .x x k k
2) (0,75 điểm). Cho cấp số nhân
n
u
thỏa mãn
20 17
35
8
.
240
uu
uu

Tính
3
.u
Lời giải:
Ta có
19 16
3
20 17
11
1
24
24
35
11
11
8
8
8 12
240
2
240
240
uu
u q u q
qu
uu
q
u q u q
u q u q






.
Vậy
2
31
48.u u q
Câu 2: (1,0 điểm). Giải phương trình
2
2
cos2 1
tan 3tan .
2
cos
x
xx
x



Lời giải:
Điều kiện:
sin 0
sin2 0 \ .
cos 0
2
x
x x k k
x


2
2 2 2
2
2 2 3
2sin
(1) cot 3tan cot 2tan 3tan
cos
1
cot tan tan tan 1 tan 1
tan
x
x x x x x
x
x x x x x
x
,.
4
x k k
Đối chiếu điều kiện, phương trình đã cho có tập nghiệm là
,.
4
S k k


Câu 3: (0,5 điểm). Một cầu thang bằng gạch có tổng cộng 30 bậc. Bậc dưới cùng cần 100 viên
gạch. Mỗi bậc tiếp theo cần ít hơn 2 viên gạch so với bậc ngay trước nó.
a) Cần bao nhiêu viên gạch cho bậc trên cùng?
b) Cần bao nhiêu gạch để xây cầu thang?
Lời giải:
Gọi số viên gạch cần xây cho bậc dưới cùng là
1
100u
Ta thấy Mỗi bậc tiếp theo cần ít hơn 2 viên gạch so với bậc ngay trước nó nên ta có
Bậc thứ 2 cần số viên gạch để xây là:
21
2uu
Bậc thứ 3 cần số viên gạch để xây là:
32
2uu
…..
Như vậy dãy các số viên gạch ở mỗi bậc tạo thành một cấp số cộng có
1
100; 2ud
a) Ta có: Bậc trên cùng là bậc 30 nên ta có áp dụng CT số hạng TQ của CSC ta có
30 1
29 2 42uu
.
Vậy bậc trên cùng cần 42 viên gạch.
b) Ta có:
1
30 1 2 30
30 2 29 2
... 2130.
2
u
S u u u

Vậy cần 2130 viên gạch để xây cầu thang.
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 03_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Cho dãy số
: 2,8,32,128,512.
n
u
n
u
là một cấp số nhân với công bội là
A.
1
4
q
. B.
6q
. C.
4q
. D.
1
2
q
.
Câu 2: Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho
60AOM
(tham
khảo hình vẽ).
x
y
60
o
O
M
A
Gọi
N
là điểm đối xứng với điểm
M
qua trục
Ox
, khẳng định nào sau đây đúng?
A.
s® ; 120 360 , .OA ON k k
B.
s® ; 120 360 , .OA ON k k
C.
s® ; 300 360 , .OA ON k k
D.
s® ; 60 360 , .OA ON k k
Câu 3:
3
x
là một nghiệm của phương trình nào dưới đây?
A.
sin 1.x
B.
1
sin .
2
x
C.
sin 0.x
D.
3
sin .
2
x
Câu 4: Cho cấp số nhân
n
u
có
4
108u 
và
5
324.u 
Khi đó, số hạng đầu
1
u
và công bội
q
là
A.
1
3, 5uq
. B.
1
3, 5uq
. C.
1
4, 3uq
. D.
1
4, 3uq
.
Câu 5: Cho cấp số cộng
n
u
có
13
8u
và
3d 
. Tìm số hạng thứ ba của cấp số cộng
n
u
.
A.
50
. B.
28
. C.
38
. D.
44
.
Câu 6: Tập xác định của hàm số
1 cos
sin
x
y
x
là
A.
\|D k k
. B.
\|
2
D k k



.
C.
\ 2 |D k k
. D.
\ 2 |
2
D k k



.
Câu 7: Đổi số đo góc
105
sang rađian, ta được
A.
5
.
12
rad
B.
7
.
12
rad
C.
9
.
12
rad
D.
5
.
8
rad
Câu 8: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
22
cos2 cos sin .

B.
22
cos2 cos sin .

C.
22
cos2 2cos sin .

D.
22
cos2 2cos sin .

Câu 9: Biết nghiệm dương bé nhất của phương trình
1
sin
2
x 
có dạng
, ; ,
aa
ab
bb
là phân số tối
giản. Tính
.ab
A.
2.
B.
10.
C.
13.
D.
8.
Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
cos3yx
. B.
cot 4yx
. C.
sin 2yx
. D.
tan5yx
.
Câu 11: Biết trên đường tròn lượng giác có 4 điểm
, , ,M N P Q
cùng là điểm biểu diễn các góc lượng
giác
,.
2
k
k
Diện tích tứ giác
MNPQ
bằng
A.
2 2.
B.
2.
C.
4.
D.
3 2.
Câu 12: Cho cấp số nhân
n
u
có
1
5u
và
2
5
.
2
u
Tổng 8 số hạng đầu tiên của cấp số nhân trên là
A.
123
23
. B.
342
67
. C.
1275
128
. D.
654
231
.
Câu 13: Cho góc
thỏa mãn
1
sin
3

, và
3
2


. Tính
sin 2
.
A.
7
9
. B.
42
9
. C.
42
9
. D.
2
3
.
Câu 14: Cho dãy số
n
u
là một cấp số cộng có
1
3u
và công sai
4d
. Biết tổng
n
số hạng đầu của
dãy số
n
u
là
253
n
S
. Tìm
n
.
A.
9
. B.
11
. C.
12
. D.
10
.
Câu 15: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
π
-
π
O
-
π
__
2
π
__
2
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
tan .yx
C.
cos .yx
D.
cot .yx
Câu 16: Hàm số nào dưới đây xác định trên
?
A.
2 sin
.
3 2sin
x
y
x
B.
2 sin
.
1 2sin
x
y
x
C.
2 sin
.
1 2sin
x
y
x
D.
2 sin
.
sin
x
y
x
Câu 17: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
2
3 2017
n
un
. B.
3 2018
n
un
. C.
3
n
n
u
. D.
1
3

n
n
u
.
Câu 18: Số
a
thỏa mãn có 25% giá trị trong mẫu số liệu nhỏ hơn
a
và 75% giá trị trong mẫu số liệu
lớn hơn
a
là
A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất. D. Tứ phân vị thứ ba.
Câu 19: Cho dãy số
n
u
với
21
n
un
, số hạng thứ
2019
của dãy là
A.
4039
. B.
4390
. C.
4930
. D.
4093
.
Câu 20: Số nghiệm của phương trình
3 tan 3 0x 
trên đoạn
0;3


là
A.
4.
B.
3.
C.
2.
D.
5.
Câu 21: Mệnh đề nào dưới đây đúng với mọi
,ab
?
A.
cos( ) sin sin cos cosa b a b a b
. B.
cos( ) cos cos sin sina b a b a b
.
C.
cos( ) cos cos sin sina b a b a b
. D.
cos( ) cos sin sin cosa b a b a b
.
Câu 22: Ông
A
gửi
120
triệu đồng tiền vào ngân hàng với lãi suất
6% /
năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho
năm tiếp theo. Hỏi sau
10
năm, tổng số tiền mà ông
A
nhận được là bao nhiêu, giả định
trong khoảng thời gian này lãi suất không thay đổi và ông
A
không rút tiền ra? (Lấy kết quả
gần đúng đến hàng phần trăm)
A.
214,90
triệu đồng. B.
224,10
triệu đồng. C.
234,90
triệu đồng. D.
215,10
triệu đồng.
Câu 23: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Số trung bình của mẫu số liệu là
A.
5,0.
B.
5,32.
C.
5,75.
D.
6,5.
Câu 24: Giá trị lớn nhất của hàm số
3sinyx
là
A.
1
. B.
2
. C.
3
. D.
3
.
Câu 25: Mệnh đề nào dưới đây đúng?
A.
cot 1 , .
4
x x k k
B.
cot 1 , .
4
x x k k
C.
cot 1 , .
4
x x k k
D.
cot 1 2 , .
4
x x k k
Câu 26: Cho dãy số có các số hạng đầu là:
;
3
1
;
3
1
;
3
1
;
3
1
;
3
1
5432
… Tìm số hạng tổng quát của dãy số này.
A.
1
11
.
33
n
n
u
. B.
1
3
1
n
n
u
. C.
n
n
u
3
1
. D.
1
3
1
n
n
u
.
Câu 27: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Nhóm chứa trung vị của mẫu số liệu là
A.
2;3,5 .
B.
3,5;5 .
C.
5;6,5 .
D.
6,5;8 .
Câu 28: Trên đường tròn bán kính
5r
, độ dài của cung đo
8

là
A.
.
8
l
B.
3
.
8
l
C.
5
.
8
l
D.
.
4
l
Câu 29: Cho
1
sin
3
với
0.
2

Tính
cos .
3



A.
6
3
6
. B.
61
62
. C.
63
. D.
1
6
2
.
Câu 30: Nhóm số liệu rời rạc
12
kk
với
1 2 1 2
,,k k k k
là nhóm các giá trị
A.
1
k
và
2
.k
B.
12
1,..., .kk
C.
12
,..., 1.kk
D.
1 1 2
, 1,..., .k k k
Câu 31: Rút gọn biểu thức
2sin 2 sin 4
2sin 2 sin 4


T
(với giả thiết biểu thức có nghĩa).
A.
2
tan
T
. B.
2
tan
T
. C.
2
tan 2
T
. D.
2
cot
T
.
Câu 32: Chu kỳ của hàm số
3sin
2
x
y
là
A.
0
. B.
2
. C.
4
. D.
.
Câu 33: Cho cấp số cộng
n
u
có
1
3u
và công sai
7d
. Kể từ số hạng nào trở đi thì các số hạng của
n
u
đều lớn hơn
2018
?
A.
287
. B.
289
. C.
288
. D.
286
.
Câu 34: Tập xác định của hàm số
tan
3tan 3
x
y
x
là
A.
\ , .
6
D k k



B.
\ ; , , .
26
D k m k m





C.
\ ; , , .
26
D k m k m





D.
\ ; 2 , , .
26
D k m k m





Câu 35: Tìm số hạng đầu
1
u
của cấp số nhân
n
u
biết rằng:
1 2 3
21u u u
và
4 5 6
567u u u
.
A.
3
. B.
21
13
. C.
9
D.
13
21
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Cho góc
thỏa mãn
1
sin
3
và
.
2


Tính
cos .
3



2) (0,75 điểm). Cho cấp số cộng
n
u
thỏa mãn
3
5
12
.
35
S
S
Tính
4
.u
Câu 2: (1,0 điểm). Giải phương trình:
sin2 2cos sin 1
0.
tan 3
x x x
x
Câu 3: (0,5 điểm). Một tấm bìa hình vuông
1
H
có cạnh bằng 100, có diện tích
1
.S
Ta kẻ một
đường tròn
1
C
nội tiếp hình vuông
1
H
, có diện tích
/
1
.S
Ta dựng một hình vuông
2
H
nội tiếp
1
C
, có diện tích
2
.S
Tiếp tục, ta kẻ một đường tròn
2
C
nội tiếp hình vuông
2
H
,
có diện tích
/
2
.S
Tiến hành thực hiện quá trình này 10 lần.
(xem hình vẽ minh họa).
Tính gần đúng tổng tất cả diện tích các hình vuông và hình tròn tạo thành theo quá trình trên.
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 03_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Cho dãy số
: 2,8,32,128,512.
n
u
n
u
là một cấp số nhân với công bội là
A.
1
4
q
. B.
6q
. C.
4q
. D.
1
2
q
.
Lời giải:
Ta có:
8 32 128 512
4
2 8 32 128
nên dãy số đã cho là một cấp số nhân với công bội
4q
.
Câu 2: Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho
60AOM
(tham
khảo hình vẽ).
x
y
60
o
O
M
A
Gọi
N
là điểm đối xứng với điểm
M
qua trục
Ox
, khẳng định nào sau đây đúng?
A.
s® ; 120 360 , .OA ON k k
B.
s® ; 120 360 , .OA ON k k
C.
s® ; 300 360 , .OA ON k k
D.
s® ; 60 360 , .OA ON k k
Lời giải:
x
y
N
A
M
O
60
o
Ta có:
s®
s®
; 60 360
60 , .
; 300 360
OA ON k
AON k
OA ON k

Câu 3:
3
x
là một nghiệm của phương trình nào dưới đây?
A.
sin 1.x
B.
1
sin .
2
x
C.
sin 0.x
D.
3
sin .
2
x
Lời giải:
Thay
3
x
vào phương trình
3
sin
2
x
thấy thỏa mãn.
Câu 4: Cho cấp số nhân
n
u
có
4
108u 
và
5
324.u 
Khi đó, số hạng đầu
1
u
và công bội
q
là
A.
1
3, 5uq
. B.
1
3, 5uq
. C.
1
4, 3uq
. D.
1
4, 3uq
.
Lời giải:
Ta có:
3
41
. u u q
và
4
51
. u u q
. Chia vế theo vế hai đẳng thức trên, ta được
3
41
4
51
.
1 108 1
3
. 324
u u q
q
u u q q q
Khi đó,
33
4 1 1 1
. 108 . 3 4.u u q u u
Vậy cấp số nhân
n
u
có số hạng đầu
1
4u 
và
3.q
Cách khác:
Ta có
5
4
324
3
108
u
q
u
. Ta có
33
4 1 1 1
. 108 . 3 4.u u q u u
Câu 5: Cho cấp số cộng
n
u
có
13
8u
và
3d 
. Tìm số hạng thứ ba của cấp số cộng
n
u
.
A.
50
. B.
28
. C.
38
. D.
44
.
Lời giải:
Ta có:
13 1
12u u d
1
8 12. 3u
1
44u
31
2 44 6 38u u d
.
Câu 6: Tập xác định của hàm số
1 cos
sin
x
y
x
là
A.
\|D k k
. B.
\|
2
D k k



.
C.
\ 2 |D k k
. D.
\ 2 |
2
D k k



.
Lời giải:
Điều kiện
sin 0 ,x x k k
.
Tập xác định
\|D k k
.
Câu 7: Đổi số đo góc
105
sang rađian, ta được
A.
5
.
12
rad
B.
7
.
12
rad
C.
9
.
12
rad
D.
5
.
8
rad
Lời giải:
Cách 1: Ta có:
.10
105 7
180 12
5




rad rad
Cách 2: Sử dụng MTCT
Câu 8: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
22
cos2 cos sin .

B.
22
cos2 cos sin .

C.
22
cos2 2cos sin .

D.
22
cos2 2cos sin .

Câu 9: Biết nghiệm dương bé nhất của phương trình
1
sin
2
x 
có dạng
, ; ,
aa
ab
bb
là phân số tối
giản. Tính
.ab
A.
2.
B.
10.
C.
13.
D.
8.
Lời giải:
Ta có:
2
1
6
sin , .
7
2
2
6
xk
xk
xk


Vậy nghiệm dương bé nhất của phương trình là
7
7
13.
3
6
a
x a b
b
 
Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
cos3yx
. B.
cot 4yx
. C.
sin 2yx
. D.
tan5yx
.
Lời giải:
Xét hàm số
cos3y f x x
có tập xác định
D
+) Với mọi
x D x D
+)
cos 3 cos3f x x x f x
Suy ra
cos3yx
là hàm số chẵn.
Câu 11: Biết trên đường tròn lượng giác có 4 điểm
, , ,M N P Q
cùng là điểm biểu diễn các góc lượng
giác
,.
2
k
k
Diện tích tứ giác
MNPQ
bằng
A.
2 2.
B.
2.
C.
4.
D.
3 2.
Lời giải:
Các điểm
, , ,M N P Q
như hình bên dưới:
x
y
Q
P
N
M
O
Tứ giác
MNPQ
là hình vuông cạnh
2
2 2 2.
MNPQ
S
Câu 12: Cho cấp số nhân
n
u
có
1
5u
và
2
5
.
2
u
Tổng 8 số hạng đầu tiên của cấp số nhân trên là
A.
123
23
. B.
342
67
. C.
1275
128
. D.
654
231
.
Lời giải:
Theo công thức số hạng tổng quát của cấp số nhân, ta có:
21
51
. 5.
22
u u q q q
.
Vậy cấp số nhân
n
u
có số hạng đầu
1
5u
và
1
.
2
q
Gọi S là tổng 8 số hạng đầu của cấp số
nhân trên.
Ta được
8
1
51
2
1275
.
1
128
1
2
S








Câu 13: Cho góc
thỏa mãn
1
sin
3

, và
3
2


. Tính
sin 2
.
A.
7
9
. B.
42
9
. C.
42
9
. D.
2
3
.
Lời giải:
Ta có:
2
1 2 2
sin cos 1 sin
33
Theo giả thiết:
3 2 2
cos
23
Vậy
1 2 2 4 2
sin2 2sin .cos 2.
3 3 9







.
Câu 14: Cho dãy số
n
u
là một cấp số cộng có
1
3u
và công sai
4d
. Biết tổng
n
số hạng đầu của
dãy số
n
u
là
253
n
S
. Tìm
n
.
A.
9
. B.
11
. C.
12
. D.
10
.
Lời giải:
Ta có
1
2 1 2.3 1 .4
253
22
n
n u n d n n
S
2
11( )
4 2 506 0
23
2

n TM
nn
nL
.
Vậy
11n
.
Câu 15: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
π
-
π
O
-
π
__
2
π
__
2
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
tan .yx
C.
cos .yx
D.
cot .yx
Lời giải:
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm
;0
2
A



và hàm số không xác định tại
.x
Câu 16: Hàm số nào dưới đây xác định trên
?
A.
2 sin
.
3 2sin
x
y
x
B.
2 sin
.
1 2sin
x
y
x
C.
2 sin
.
1 2sin
x
y
x
D.
2 sin
.
sin
x
y
x
Lời giải:
Xét hàm số
2 sin
.
3 2sin
x
y
x
Ta có:
:sin 1;1 3 2sin 1;5 .x x x
Suy ra:
2 sin
3 2sin
x
y
x
xác định trên
.
Câu 17: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
A.
2
3 2017
n
un
. B.
3 2018
n
un
. C.
3
n
n
u
. D.
1
3

n
n
u
.
Lời giải:
Ta có
11
3( 1) 2018 (3 2018) 3 3

n n n n
u u n n u u
.
Vậy dãy số trên là cấp số cộng có công sai
3d
.
Câu 18: Số
a
thỏa mãn có 25% giá trị trong mẫu số liệu nhỏ hơn
a
và 75% giá trị trong mẫu số liệu
lớn hơn
a
là
A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất. D. Tứ phân vị thứ ba.
Câu 19: Cho dãy số
n
u
với
21
n
un
, số hạng thứ
2019
của dãy là
A.
4039
. B.
4390
. C.
4930
. D.
4093
.
Lời giải:
Ta có:
2019
2.2019 1 4039u
.
Câu 20: Số nghiệm của phương trình
3 tan 3 0x 
trên đoạn
0;3


là
A.
4.
B.
3.
C.
2.
D.
5.
Lời giải:
Cách 1:
Ta có:
3 tan 3 0 tan 3 ,
3
x x x k k
Ta có:
18
,
03
0;1;2 .
3
3 3 3
0;3
x k k
kk
k
x
kk


 


Phương trình có nghiệm là
47
; ; .
3 3 3
x x x

Cách 2: Dùng đường tròn lượng giác
x
y
3
O
1
Câu 21: Mệnh đề nào dưới đây đúng với mọi
,ab
?
A.
cos( ) sin sin cos cosa b a b a b
. B.
cos( ) cos cos sin sina b a b a b
.
C.
cos( ) cos cos sin sina b a b a b
. D.
cos( ) cos sin sin cosa b a b a b
.
Lời giải:
Vì theo công thức cộng, thì
cos( ) cos cos sin sina b a b a b
.
Câu 22: Ông
A
gửi
120
triệu đồng tiền vào ngân hàng với lãi suất
6% /
năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho
năm tiếp theo. Hỏi sau
10
năm, tổng số tiền mà ông
A
nhận được là bao nhiêu, giả định
trong khoảng thời gian này lãi suất không thay đổi và ông
A
không rút tiền ra? (Lấy kết quả
gần đúng đến hàng phần trăm)
A.
214,90
triệu đồng. B.
224,10
triệu đồng. C.
234,90
triệu đồng. D.
215,10
triệu đồng.
Lời giải:
Ta có
120a
triệu đồng.
Đặt
n
T
là số tiền nhận được sau
n
năm.
Sau 1 năm số tiền có được (cả gốc và lãi ) là
1
.6% 1 0,06T a a a
.
Sau 2 năm số tiền có được là
2
2
1 0,06Ta
.
Gọi
T
là tổng tiền mà
A
nhận được
sau
10
năm.
10
10
1 0,06 120.1.06 214,90Ta
.
Câu 23: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Số trung bình của mẫu số liệu là
A.
5,0.
B.
5,32.
C.
5,75.
D.
6,5.
Câu 24: Giá trị lớn nhất của hàm số
3sinyx
là
A.
1
. B.
2
. C.
3
. D.
3
.
Lời giải:
Hàm số
sinyx
có tập giá trị là
1;1
.
Do đó
3 3sin 3x
,
x
.
Vậy giá trị lớn nhất của hàm số
3sinyx
là 3, xảy ra khi
sin 1 2 , .
2
x x k k
Câu 25: Mệnh đề nào dưới đây đúng?
A.
cot 1 , .
4
x x k k
B.
cot 1 , .
4
x x k k
C.
cot 1 , .
4
x x k k
D.
cot 1 2 , .
4
x x k k
Câu 26: Cho dãy số có các số hạng đầu là:
;
3
1
;
3
1
;
3
1
;
3
1
;
3
1
5432
… Tìm số hạng tổng quát của dãy số này.
A.
1
11
.
33
n
n
u
. B.
1
3
1
n
n
u
. C.
n
n
u
3
1
. D.
1
3
1
n
n
u
.
Lời giải:
5 số hạng đầu là
1 2 3 4 5
1 1 1 1 1
; ; ; ; ;...
3 3 3 3 3
nên
1
3
n
n
u
.
Câu 27: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Nhóm chứa trung vị của mẫu số liệu là
A.
2;3,5 .
B.
3,5;5 .
C.
5;6,5 .
D.
6,5;8 .
Câu 28: Trên đường tròn bán kính
5r
, độ dài của cung đo
8

là
A.
.
8
l
B.
3
.
8
l
C.
5
.
8
l
D.
.
4
l
Lời giải:
Độ dài cung AB :
5
..
8
lr
Câu 29: Cho
1
sin
3
với
0.
2

Tính
cos .
3



A.
6
3
6
. B.
61
62
. C.
63
. D.
1
6
2
.
Lời giải:
Vì
0
2

cos 0

.
Ta có:
2 2 2 2
2
sin os 1 os 1 sin
3
cc
6
cos
3

.
cos
3



cos .cos sin .sin
33



6 1 1 3 6 1
..
3 2 2 6 2
3
.
Câu 30: Nhóm số liệu rời rạc
12
kk
với
1 2 1 2
,,k k k k
là nhóm các giá trị
A.
1
k
và
2
.k
B.
12
1,..., .kk
C.
12
,..., 1.kk
D.
1 1 2
, 1,..., .k k k
Câu 31: Rút gọn biểu thức
2sin 2 sin 4
2sin 2 sin 4


T
(với giả thiết biểu thức có nghĩa).
A.
2
tan
T
. B.
2
tan
T
. C.
2
tan 2
T
. D.
2
cot
T
.
Lời giải:
Ta có:
2sin 2 sin 4
2sin 2 sin 4


T
2sin2 2sin2 cos2
2sin2 2sin 2 cos2
2sin 2 1 cos2
2sin 2 1 cos2


2
2
sin
cos
2
tan
Câu 32: Chu kỳ của hàm số
3sin
2
x
y
là
A.
0
. B.
2
. C.
4
. D.
.
Lời giải:
Chu kì của hàm số
2
4
1
2
T

.
Câu 33: Cho cấp số cộng
n
u
có
1
3u
và công sai
7d
. Kể từ số hạng nào trở đi thì các số hạng của
n
u
đều lớn hơn
2018
?
A.
287
. B.
289
. C.
288
. D.
286
.
Lời giải:
Ta có:
1
1
n
u u n d
3 7 1n
74n
;
2018
n
u
7 4 2018n
2022
7
n
.
Vậy
289n
.
Câu 34: Tập xác định của hàm số
tan
3tan 3
x
y
x
là
A.
\ , .
6
D k k



B.
\ ; , , .
26
D k m k m





C.
\ ; , , .
26
D k m k m





D.
\ ; 2 , , .
26
D k m k m





Lời giải:
Hàm số xác định
cos 0
2
, , .
3tan 3 0
6
xk
x
km
x
xm





Câu 35: Tìm số hạng đầu
1
u
của cấp số nhân
n
u
biết rằng:
1 2 3
21u u u
và
4 5 6
567u u u
.
A.
3
. B.
21
13
. C.
9
D.
13
21
.
Lời giải:
Ta có:
1 2 3
4 5 6
21
567
u u u
u u u
2
1 1 1
32
1 1 1
. . 21
. . 567
u u q u q
q u u q u q
2
1 1 1
32
1 1 1
. . 21
. . 567
u u q u q
q u u q u q
2
1 1 1
3
. . 21
.21 567
u u q u q
q
2
1 1 1
3
.3 .3 21
q
u u u
1
3
21
13
q
u
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Cho góc
thỏa mãn
1
sin
3
và
.
2


Tính
cos .
3



Lời giải:
Ta có:
22
22
cos
8
3
cos 1 sin .
9
22
cos
3

Do
2


nên
cos 0

chọn
22
cos .
3
Lúc đó:
2 2 1 1 3 3 2 2
cos cos cos sin sin . . .
3 3 3 3 2 3 2 6



2) (0,75 điểm). Cho cấp số cộng
n
u
thỏa mãn
3
5
12
.
35
S
S
Tính
4
.u
Lời giải:
Ta có:
3
5
12
35
S
S
1
1
1
1
1
3
2 2 12
2 2 8
1
2
.
5 2 4 14
3
2 4 35
2
ud
ud
u
ud
d
ud




Vậy
41
3 10.u u d
Câu 2: (1,0 điểm). Giải phương trình:
sin2 2cos sin 1
0.
tan 3
x x x
x
Lời giải:
Điều kiện:
cos 0
2
, , .
tan 3
3
xk
x
km
x
xm





(1) sin2 2cos sin 1 0 2cos sin 1 sin 1 0x x x x x x
lo¹i do ®k sin 1 ( cos 0 )
sin 1 2cos 1 0
1
cos
2
xx
xx
x
Ta xét:
2
1
3
cos , .
2
2
3
xk
xk
xk

Đối chiếu điều kiện, ta có nghiệm của phương trình là:
2 , .
3
x k k
Câu 3: (0,5 điểm). Một tấm bìa hình vuông
1
H
có cạnh bằng 100, có diện tích
1
.S
Ta kẻ một
đường tròn
1
C
nội tiếp hình vuông
1
H
, có diện tích
/
1
.S
Ta dựng một hình vuông
2
H
nội tiếp
1
C
, có diện tích
2
.S
Tiếp tục, ta kẻ một đường tròn
2
C
nội tiếp hình vuông
2
H
,
có diện tích
/
2
.S
Tiến hành thực hiện quá trình này 10 lần.
(xem hình vẽ minh họa).
Tính gần đúng tổng tất cả diện tích các hình vuông và hình tròn tạo thành theo quá trình trên.
Lời giải:
A
2
A
1
D
C
B
O
A
+) Hình vuông
1
H
có cạnh
1
100a 
Diện tích là
2
11
.Sa
+) Đường tròn
1
C
có bán kính
1
1
2
a
r 
Diện tích là
2
/
1
1
.
4
a
S
+) Hình vuông
2
H
có cạnh
21
1
2
2
aa
Diện tích là
2
1
2
.
2
a
S
+) Đường tròn
2
C
có bán kính
21
2
2
24
aa
r
Diện tích là
2
/
1
2
.
8
a
S
+) Hình vuông
3
H
có cạnh
1
32
1
2
22
a
aa
Diện tích là
2
1
3
.
4
a
S
+) Đường tròn
3
C
có bán kính
3
1
3
24
a
a
r
Diện tích là
2
/
1
3
.
16
a
S
Vậy tổng cần tìm là
2 2 2 2 2 2 2
/ / / / 2
1 1 1 1 1 1 1
1 2 3 10 1 2 3 10 1
9 11
... ... ... ...
2 4 4 8 16
22
a a a a a a a
T S S S S S S S S a
10 10
2 2 2 2
1 1 1 1
9 11
11
11
22
1 1 1 1 1 1 1 1
1 ... ... .1. . . 35673.
11
2 4 4 8 16 4
22
11
22
a a a a



____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 04_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Cho cấp số nhân
()
n
u
với
1
3u
và công bội
4q
. Giá trị của
2
u
bằng
A.
64
. B.
81
. C.
12
. D.
3
4
.
Câu 2: Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho
60AOM
(tham
khảo hình vẽ).
x
y
60
o
O
M
A
Gọi
N
là điểm đối xứng với điểm
M
qua gốc
O
, khẳng định nào sau đây đúng?
A.
s® ; 120 360 , .OA ON k k
B.
s® ; 120 360 , .OA ON k k
C.
s® ; 240 360 , .OA ON k k
D.
s® ; 60 360 , .OA ON k k
Câu 3: Dãy số
1 1 1 1 1
, , , ,
3 6 12 24 48

là một cấp số nhân với công bội là
A.
1
2
q
. B.
2q 
. C.
1
4
q
. D.
1
2
q
.
Câu 4: Trong các dãy số sau, dãy số nào là một cấp số cộng?
A.
1; 2; 4; 6; 8
. B.
1; 3; 6; 9; 12
. C.
1; 3; 7; 11; 15
. D.
1; 3; 5; 7; 9
.
Câu 5: Số
a
thỏa mãn có 75% giá trị trong mẫu số liệu nhỏ hơn
a
và 25% giá trị trong mẫu số liệu
lớn hơn
a
là
A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất. D. Tứ phân vị thứ ba.
Câu 6: Mệnh đề nào dưới đây đúng?
A. Hàm số
cotyx
là hàm số chẵn. B. Hàm số
sinyx
là hàm số chẵn.
C. Hàm số
tanyx
là hàm số chẵn. D. Hàm số
cosyx
là hàm số chẵn.
Câu 7: Cho cấp số nhân
n
u
có
1
3u 
và
2q
. Tống
n
số hạng đầu tiên của cấp số nhân đã cho
bằng -1533. Tìm
.n
A.
9n
. B.
10n
. C.
11n
. D.
12n
.
Câu 8: Tập xác định của hàm số
2021
1 cos
y
x
là
A.
\ , .
2
k
Dk



B.
\ 2 , .D k k
C.
\ , .
2
D k k



D.
\ , .D k k
Câu 9: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây sai?
A.
2
cos2 1 2sin .


B.
22
cos2 cos sin .

C.
cos2 cos sin .

D.
2
cos2 2cos 1.


Câu 10: Cho dãy số có các số hạng đầu là:
5;10;15;20;25;...
Số hạng tổng quát của dãy số này là
A.
5( 1)
n
un
. B.
5
n
un
. C.
5
n
un
. D.
51
n
un
.
Câu 11: Cho cấp số nhân
n
u
có
1
6u 
và
2q 
. Tống
n
số hạng đầu tiên của cấp số nhân đã cho
bằng 2046. Tìm
.n
A.
9n
. B.
10n
. C.
11n
. D.
12n
.
Câu 12: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
O
π
__
2
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
sin2 .yx
C.
cos .yx
D.
cos2 .yx
Câu 13: Cho cấp số cộng
n
u
với
1
2u
và
2
8u
. Công sai của cấp số cộng đã cho bằng
A.
10
. B.
6
. C.
4
. D.
6
.
Câu 14: Mẫu số liệu ghép nhóm với tần số các nhóm bằng nhau có số mốt là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 15: Chu kì bán rã của nguyên tố phóng xạ poloni
210
là
138
ngày (nghĩa là sau
138
ngày khối
lượng của nguyên tố đó chỉ còn một nửa). Khối lượng còn lại của
200
gam poloni
210
sau
1656
ngày gần nhất với số nào dưới đây? (đơn vị: gam)
A.
0,0244
. B.
0,0488
. C.
0,0977
. D.
0,1025
.
Câu 16: Góc có số đo
2
5
đổi sang độ là
A.
240 .
B.
135 .
C.
72 .
D.
270 .
Câu 17:
6
x
là một nghiệm của phương trình nào dưới đây?
A.
cos 1.x
B.
1
cos .
2
x
C.
sin 1.x
D.
1
sin .
2
x
Câu 18: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu là
A.
2;3,5 .
B.
3,5;5 .
C.
5;6,5 .
D.
6,5;8 .
Câu 19: Trên đường tròn bán kính
15r
, độ dài của cung có số đo
50

là
A.
750l
. B.
180
15.l
. C.
15
.
180
l
D.
25
.
6
l
Câu 20: Xác định số hàng đầu
1
u
và công sai
d
của cấp số cộng
n
u
có
92
5uu
và
13 6
25uu
A.
1
3u
và
4d
. B.
1
3u
và
5d
. C.
1
4u
và
5d
. D.
1
4u
và
3d
.
Câu 21: Cho dãy số
n
u
với
21
n
un
. Khẳng định nào dưới đây đúng?
A.
n
u
bị chặn trên bởi 1. B.
n
u
giảm.
C.
n
u
bị chặn dưới bởi 2. D.
n
u
tăng.
Câu 22: Cho góc
thỏa mãn
1
sin
3
và
0.
2

Tính
tan 2 .
A.
22
.
7
B.
22
.
7
C.
42
.
7
D.
42
.
7
Câu 23: Biết nghiệm âm lớn nhất của phương trình
tan 3x
có dạng
, ; ,
aa
ab
bb
là phân số tối
giản. Tính
.ab
A.
2.
B.
10.
C.
5.
D.
8.
Câu 24: Cho góc
thỏa mãn
0
2

và
2
cos
3
. Tính
sin .
A.
22
3
. B.
5
3
. C.
2
3
. D.
5
3
.
Câu 25: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Số mốt của mẫu số liệu ghép nhóm này là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 26: Hàm số
cosyx
nghịch biến trên khoảng nào dưới đây?
A.
;
22




. B.
;
2




. C.
0;
. D.
;0
2



.
Câu 27: Trong các công thức sau, công thức nào đúng?
A.
cos – cos .cos sin .sina b a b a b
. B.
cos cos .cos sin .sina b a b a b
.
C.
sin – sin .cos cos .sina b a b a b
. D.
sin sin .cos cos.sina b a b b
.
Câu 28: Cho
3
sin
5
và
2


. Giá trị của
tan
4



bằng
A.
1
7
. B.
1
7
. C.
7
. D.
7
.
Câu 29: Mệnh đề nào dưới đây đúng?
A.
sin 1 , .
2
x x k k
B.
sin 1 , .
2
x x k k
C.
sin 1 2 , .
2
x x k k
D.
sin 1 2 , .
2
x x k k
Câu 30: Biết
1
tan ,
3
x
tính giá trị của biểu thức
cos5 cos3
.
sin5 sin3
xx
I
xx
A.
1
3
I
. B.
1
3
I 
. C.
3I
. D.
3I 
.
Câu 31: Hàm số nào dưới đây có tập xác định khác với tập xác định các hàm số còn lại?
A.
tan .yx
B.
1
.
cos
y
x
C.
cot .yx
D.
2
1
.
1 sin
y
x
Câu 32: Tập xác định của hàm số
sin
2sin 1
x
y
x
là
A.
\ 2 ; 2 , , .
66
D k m k m





B.
5
\ 2 ; 2 , , .
66
D k m k m





C.
5
\ ; , , .
66
D k m k m





D.
2
\ 2 ; 2 , , .
33
D k m k m





Câu 33: Giá trị lớn nhất và nhỏ nhất của hàm số là
2 sinyx
lần lượt là
A.
1
và
3
. B.
4
và
4
. C.
2
và
4
. D.
3
và
1
.
Câu 34: Số nghiệm của phương trình
2
16 cos 0xx
là
A.
4.
B.
3.
C.
2.
D.
5.
Câu 35: Cho cấp số cộng
n
u
có
1
1u
và công sai
2d
. Tổng
10 1 2 3 10
.....S u u u u
bằng:
A.
10
110S
. B.
10
100S
. C.
10
21S
. D.
10
19S
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Giải phương trình
2 sin 2cos 2 sin2 .x x x
2) (0,75 điểm). Cho một cấp số nhân có bảy số hạng, số hạng thứ tư bằng 6 và số hạng thứ bảy
gấp 243 lần số hạng thứ hai. Hãy tìm số hạng thứ hai của cấp số nhân đó.
Câu 2: (1,0 điểm). Tìm
m
để hàm số
cos2 2sin 4y x x m
xác định trên
.
Câu 3: (0,5 điểm). Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với
mức lương khởi điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm,
thì sẽ mất bao nhiêu năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la?
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 04_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Cho cấp số nhân
()
n
u
với
1
3u
và công bội
4q
. Giá trị của
2
u
bằng
A.
64
. B.
81
. C.
12
. D.
3
4
.
Lời giải:
Ta có:
21
. 3.4 12u u q
.
Câu 2: Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho
60AOM
(tham
khảo hình vẽ).
x
y
60
o
O
M
A
Gọi
N
là điểm đối xứng với điểm
M
qua gốc
O
, khẳng định nào sau đây đúng?
A.
s® ; 120 360 , .OA ON k k
B.
s® ; 120 360 , .OA ON k k
C.
s® ; 240 360 , .OA ON k k
D.
s® ; 60 360 , .OA ON k k
Lời giải:
x
y
N
A
M
O
60
o
Ta có:
s®
s®
; 120 360
120 , .
; 240 360
OA ON k
AON k
OA ON k

Câu 3: Dãy số
1 1 1 1 1
, , , ,
3 6 12 24 48

là một cấp số nhân với công bội là
A.
1
2
q
. B.
2q 
. C.
1
4
q
. D.
1
2
q
.
Lời giải:
Ta có:
11
11
1
6 48
12 24
1 1 1 1
2
3 6 12 24

nên dãy số đã cho là một cấp số nhân với công bội
1
.
2
q
Câu 4: Trong các dãy số sau, dãy số nào là một cấp số cộng?
A.
1; 2; 4; 6; 8
. B.
1; 3; 6; 9; 12
. C.
1; 3; 7; 11; 15
. D.
1; 3; 5; 7; 9
.
Lời giải:
Dãy số
n
u
có tính chất
1nn
u u d

thì được gọi là một cấp số cộng.
Ta thấy dãy số:
1; 3; 7; 11; 15
là một cấp số cộng có số hạng đầu là
1
1u
và công sai
4d
.
Câu 5: Số
a
thỏa mãn có 75% giá trị trong mẫu số liệu nhỏ hơn
a
và 25% giá trị trong mẫu số liệu
lớn hơn
a
là
A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất. D. Tứ phân vị thứ ba.
Câu 6: Mệnh đề nào dưới đây đúng?
A. Hàm số
cotyx
là hàm số chẵn. B. Hàm số
sinyx
là hàm số chẵn.
C. Hàm số
tanyx
là hàm số chẵn. D. Hàm số
cosyx
là hàm số chẵn.
Lời giải:
Xét hàm số
cosyx
có tập xác định
D
.
Câu 7: Cho cấp số nhân
n
u
có
1
3u 
và
2q
. Tống
n
số hạng đầu tiên của cấp số nhân đã cho
bằng -1533. Tìm
.n
A.
9n
. B.
10n
. C.
11n
. D.
12n
.
Lời giải:
Ta có
1
1
1533
1
n
n
q
Su
q
12
3
12
n
3 2 1
n
9
2 512 2 9
n
n
.
Câu 8: Tập xác định của hàm số
2021
1 cos
y
x
là
A.
\ , .
2
k
Dk



B.
\ 2 , .D k k
C.
\ , .
2
D k k



D.
\ , .D k k
Lời giải:
Hàm số xác định khi
cos 1 2 , .x x k k
Câu 9: Với
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây sai?
A.
2
cos2 1 2sin .


B.
22
cos2 cos sin .

C.
cos2 cos sin .

D.
2
cos2 2cos 1.


Câu 10: Cho dãy số có các số hạng đầu là:
5;10;15;20;25;...
Số hạng tổng quát của dãy số này là
A.
5( 1)
n
un
. B.
5
n
un
. C.
5
n
un
. D.
51
n
un
.
Lời giải:
Ta có:
5 5.1
10 5.2
15 5.3
20 5.4
25 5.5
Suy ra số hạng tổng quát
5
n
un
(chứng minh được bằng phương pháp quy nạp toán học)
Câu 11: Cho cấp số nhân
n
u
có
1
6u 
và
2q 
. Tống
n
số hạng đầu tiên của cấp số nhân đã cho
bằng 2046. Tìm
.n
A.
9n
. B.
10n
. C.
11n
. D.
12n
.
Lời giải:
Ta có
1
1
2046
1
n
n
q
Su
q
12
6
12
n


2 2 1
n
2 1024 10
n
n
.
Câu 12: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
O
π
__
2
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
sin2 .yx
C.
cos .yx
D.
cos2 .yx
Lời giải:
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm
0;0 , ;0 .
2
OA



Câu 13: Cho cấp số cộng
n
u
với
1
2u
và
2
8u
. Công sai của cấp số cộng đã cho bằng
A.
10
. B.
6
. C.
4
. D.
6
.
Lời giải:
Vì
n
u
là cấp số cộng nên ta có
2 1 2 1
8 2 6u u d d u u
.
Câu 14: Mẫu số liệu ghép nhóm với tần số các nhóm bằng nhau có số mốt là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 15: Chu kì bán rã của nguyên tố phóng xạ poloni
210
là
138
ngày (nghĩa là sau
138
ngày khối
lượng của nguyên tố đó chỉ còn một nửa). Khối lượng còn lại của
200
gam poloni
210
sau
1656
ngày gần nhất với số nào dưới đây? (đơn vị: gam)
A.
0,0244
. B.
0,0488
. C.
0,0977
. D.
0,1025
.
Lời giải:
Kí hiệu
n
u
(gam) là khối lượng còn lại của
200
gam poloni sau
n
chu kì bán rã.
Ta có
1656
ngày gồm
1656
12
138
chu kì bán rã.
Như thế, khối lượng còn lại của
200
gam poloni
210
sau
1656
ngày (
12
chu kì) là
12
u
.
Vì cứ sau một chu kì thì khối lượng của nguyên tố phóng xạ poloni
210
chỉ còn một nửa nên
ta suy ra dãy số
()
n
u
là một cấp số nhân với số hạng đầu
1
200
100
2
u 
và công bội
1
2
q
.
Do đó
1
12
1
1
0,0488
2
100.u


(gam).
Câu 16: Góc có số đo
2
5
đổi sang độ là
A.
240 .
B.
135 .
C.
72 .
D.
270 .
Lời giải:
Cách 1: Ta có:
o
2 2.180
.2
5
7
5



Cách 2: Sử dụng MTCT
Câu 17:
6
x
là một nghiệm của phương trình nào dưới đây?
A.
cos 1.x
B.
1
cos .
2
x
C.
sin 1.x
D.
1
sin .
2
x
Lời giải:
Thay
6
x
vào phương trình
1
sin
2
x
thấy thỏa mãn.
Câu 18: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu là
A.
2;3,5 .
B.
3,5;5 .
C.
5;6,5 .
D.
6,5;8 .
Câu 19: Trên đường tròn bán kính
15r
, độ dài của cung có số đo
50

là
A.
750l
. B.
180
15.l
. C.
15
.
180
l
D.
25
.
6
l
Lời giải:
Ta có:
0
5
50
18
25
.
6
lr
Câu 20: Xác định số hàng đầu
1
u
và công sai
d
của cấp số cộng
n
u
có
92
5uu
và
13 6
25uu
A.
1
3u
và
4d
. B.
1
3u
và
5d
. C.
1
4u
và
5d
. D.
1
4u
và
3d
.
Lời giải:
Ta có:
1
1
n
u u n d
.
Theo đề bài ta có:
92
13 6
5
25

uu
uu
11
11
85
12 2 5 5
u d u d
u d u d
1
1
1
4 3 0
3
25
4
ud
u
ud
d



.
Câu 21: Cho dãy số
n
u
với
21
n
un
. Khẳng định nào dưới đây đúng?
A.
n
u
bị chặn trên bởi 1. B.
n
u
giảm.
C.
n
u
bị chặn dưới bởi 2. D.
n
u
tăng.
Lời giải:
*
n
ta có:
1
2 1 1 2 1 2 0
nn
u u n n
nên
1nn
uu
vậy dãy số
n
u
tăng.
Câu 22: Cho góc
thỏa mãn
1
sin
3
và
0.
2

Tính
tan 2 .
A.
22
.
7
B.
22
.
7
C.
42
.
7
D.
42
.
7
Lời giải:
Ta có:
22
22
cos
8
3
cos 1 sin .
9
22
cos
3

Do
0
2

nên
cos 0

chọn
22
cos .
3
Suy ra:
sin 2
tan .
cos 4

Vậy
2
2tan 4 2
tan2 .
7
1 tan

Câu 23: Biết nghiệm âm lớn nhất của phương trình
tan 3x
có dạng
, ; ,
aa
ab
bb
là phân số tối
giản. Tính
.ab
A.
2.
B.
10.
C.
5.
D.
8.
Lời giải:
Ta có:
tan 3 , .
3
x x k k
Vậy nghiệm âm lớn nhất của phương trình là
2
2
5.
3
33
a
x a b
b

 
Câu 24: Cho góc
thỏa mãn
0
2

và
2
cos
3
. Tính
sin .
A.
22
3
. B.
5
3
. C.
2
3
. D.
5
3
.
Lời giải:
Ta có:
2
22
5
sin
25
3
sin 1 cos 1 .
39
5
sin
3




Do
0
2

nên
sin 0

chọn
5
sin .
3
Câu 25: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như
sau:
Tuổi thọ
2;3,5
3,5;5
5;6,5
6,5;8
Số bóng đèn
8
22
35
15
Số mốt của mẫu số liệu ghép nhóm này là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 26: Hàm số
cosyx
nghịch biến trên khoảng nào dưới đây?
A.
;
22




. B.
;
2




. C.
0;
. D.
;0
2



.
Lời giải:
Hàm số
cosyx
nghịch biến trên
0;
.
Câu 27: Trong các công thức sau, công thức nào đúng?
A.
cos – cos .cos sin .sina b a b a b
. B.
cos cos .cos sin .sina b a b a b
.
C.
sin – sin .cos cos .sina b a b a b
. D.
sin sin .cos cos.sina b a b b
.
Câu 28: Cho
3
sin
5
và
2


. Giá trị của
tan
4



bằng
A.
1
7
. B.
1
7
. C.
7
. D.
7
.
Lời giải:
Vì
2


, nên
cos 0
.
Vậy
2
94
cos 1 sin 1
25 5

, suy ra
sin 3
tan
cos 4
.
Mặt khác
3
tan tan 1
1
44
tan
3
47
1 tan .tan 1
44





.
Câu 29: Mệnh đề nào dưới đây đúng?
A.
sin 1 , .
2
x x k k
B.
sin 1 , .
2
x x k k
C.
sin 1 2 , .
2
x x k k
D.
sin 1 2 , .
2
x x k k
Câu 30: Biết
1
tan ,
3
x
tính giá trị của biểu thức
cos5 cos3
.
sin5 sin3
xx
I
xx
A.
1
3
I
. B.
1
3
I 
. C.
3I
. D.
3I 
.
Lời giải:
Ta có
2cos4 cos 1
cot 3
2cos4 sin tan
xx
Ix
x x x
.
Câu 31: Hàm số nào dưới đây có tập xác định khác với tập xác định các hàm số còn lại?
A.
tan .yx
B.
1
.
cos
y
x
C.
cot .yx
D.
2
1
.
1 sin
y
x
Lời giải:
Các hàm số ở các phương án A, B, D có tập xác định là
\.
2
kk




Hàm số ở phương án C là
\.kk
Câu 32: Tập xác định của hàm số
sin
2sin 1
x
y
x
là
A.
\ 2 ; 2 , , .
66
D k m k m





B.
5
\ 2 ; 2 , , .
66
D k m k m





C.
5
\ ; , , .
66
D k m k m





D.
2
\ 2 ; 2 , , .
33
D k m k m





Lời giải:
Hàm số xác định
2
1
6
2sin 1 0 sin , , .
5
2
2
6
xk
x x k m
xm


Câu 33: Giá trị lớn nhất và nhỏ nhất của hàm số là
2 sinyx
lần lượt là
A.
1
và
3
. B.
4
và
4
. C.
2
và
4
. D.
3
và
1
.
Lời giải:
Ta có
: 1 sin 1 1 2 sin 3 1 3 x x x y
.
Suy ra,
max 3y
khi
sin 1 2 , .
2
x x k k
và
min 1y
khi
sin = 1 2 , .
2
x x k k
Câu 34: Số nghiệm của phương trình
2
16 cos 0xx
là
A.
4.
B.
3.
C.
2.
D.
5.
Lời giải:
Điều kiện:
2
16 0 4;4 .xx


Ta có:
2
2
16 0
16 cos 0 .
cos 0
x
xx
x

+)
2
16 0 4xx
(thỏa mãn điều kiện)
+)
44
cos 0
,
44
22
1;0 .
2
2
4;4
4;4
x
x k k
k
k
k
x
x
k
k









Vậy phương trình có tập nghiệm là
3
4;4; ; .
22
S





Câu 35: Cho cấp số cộng
n
u
có
1
1u
và công sai
2d
. Tổng
10 1 2 3 10
.....S u u u u
bằng:
A.
10
110S
. B.
10
100S
. C.
10
21S
. D.
10
19S
.
Lời giải:
Ta có:
10
10 2 10 1 .2
100
2



S
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Giải phương trình
2 sin 2cos 2 sin2 .x x x
Lời giải:
Điều kiện:
.x
Phương trình
2sin cos 2 2 cos 2 sin 2 0x x x x
(v« nghiÖm)
(nhËn)
sin 2
sin 2 2cos 2 0
2
cos
2
x
xx
x

Ta có:
3
2
2
4
cos , .
3
2
2
4
xk
xk
xk

Vậy tập nghiệm của phương trình là
33
2 ; 2 .
44
S k k k




2) (0,75 điểm). Cho một cấp số nhân có bảy số hạng, số hạng thứ tư bằng 6 và số hạng thứ bảy
gấp 243 lần số hạng thứ hai. Hãy tìm số hạng thứ hai của cấp số nhân đó.
Lời giải:
Gọi cấp số nhân cần tìm là
1 2 3 7
, , , ...,u u u u
với công bội
q
.
Theo giả thiết, ta có hệ phương trình:
3
41
6
72
11
6 6 (1)
243
243 (2)
u u q
uu
u q u q



.
Xét (2):
65
11
243 243 3u q u q q q
(Do
1
0u
và
0q
không thỏa mãn điều kiện ban đầu)
Thay
3q
vào (1), ta có:
1
6
.
27
u
Vậy số hạng thứ hai của cấp số nhân là
21
62
.3
27 3
u u q
.
Câu 2: (1,0 điểm). Tìm
m
để hàm số
cos2 2sin 4y x x m
xác định trên
.
Lời giải:
Ta có:
cos2 2sin 4 0, cos2 2sin 4,x x m x m x x x
22
1 2sin 2sin 4, 2sin 2sin 3,m x x x m x x x
(*)
Đặt
sin ; 1;1 .t x t


Xét hàm số
2
2 2 3, 1;1 .g t t t t


Bảng biến thiên:
t
1
1
2
1
gt
7
5
2
3
Dựa vào BBT, (*)
1;1
max 7.
t
m g t


Câu 3: (0,5 điểm). Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với
mức lương khởi điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm,
thì sẽ mất bao nhiêu năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la?
Lời giải:
Gọi
n
u
là lương anh Nam nhận được ở năm thứ n
Ta có: Lương khởi điểm là 35000 đô la mỗi năm nên
1
35000u
Mỗi năm và được tăng thêm 1400 đô la lương mỗi năm nên
*
1
1400, 2,
nn
u u n n N
Như vậy dãy số tiền lương của anh Nam nhận được qua các năm là
1 2 3
; ; ;,,,,,
n
u u u u
là một
cấp số cộng có
1
35000; 1400ud
.
Áp dụng công thức tính tổng
n
số hạng đầu của cấp số cộng với
1
319200; 35000; 1400.
n
S u d
Ta có:


1
2 1 1400
8( )
319200
57 ( )
2
n
n u n
n TM
S
nL
Vậy sau 8 năm làm việc thì tổng lương mà anh Nam nhận được là 319200 đô la.
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 05_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Dãy số
n
u
là dãy số giảm khi chỉ khi
A.
*
1
,.
nn
u u n
B.
*
1
,.
nn
u u n
C.
*
1
,.
nn
u u n
D.
*
1
,.
nn
u u n
Câu 2: Cho góc hình học
uOv
có số đo bằng
30
(tham khảo hình vẽ).
30
o
O
u
v
Khẳng định nào sau đây sai?
A.
s® ; 330 .Ou Ov
B.
s® ; 30 .Ou Ov 
C.
s® ; 30 360 , .Ou Ov k k
D.
s® ; 330 360 , .Ou Ov k k
Câu 3: Phương trình nào sau đây vô nghiệm?
A.
cos 1.x
B.
cos2 0,7.x 
C.
cos3 0,4.x
D.
cos4 .x
Câu 4: Dãy số nào dưới đây là cấp số cộng?
A.
1;3;4.
B.
3;5;7.
C.
5;7;6.
D.
3;5;8.
Câu 5: Tập xác định của hàm số
tanyx
là
A.
D \ 2 , .kk
B.
D \ 2 , .
2
kk



C.
D \ , .
2
kk



D.
D \ , .kk
Câu 6: Chu kỳ của hàm số
cos2yx
là
A.
2k
. B.
2
3
. C.
. D.
2
.
Câu 7:
2
3
x
là một nghiệm của phương trình nào dưới đây?
A.
sin 1.x
B.
3
sin .
2
x
C.
1
cos .
2
x
D.
3
cos .
2
x
Câu 8: Cho cấp số cộng
1
:2
n
uu
và công sai
2.d
Số hạng thứ 3 của
n
u
là
A.
3
4.u
B.
3
6.u
C.
3
8.u
D.
3
12.u
Câu 9: Góc có số đo
4
15
đổi sang độ là
A.
.48
B.
135 .
C.
72 .
D.
270 .
Câu 10: Giá trị lớn nhất của hàm số
sin 2yx
bằng
A.
2
. B.
0
. C.
1
. D.
1
.
Câu 11: Cho dãy số
: sin .
nn
u u n
Khẳng định nào sau đây đúng?
A.
n
u
bị chặn. B.
n
u
bị chặn dưới và không bị chặn trên.
C.
n
u
bị chặn trên và không bị chặn dưới. D.
n
u
tăng.
Câu 12: Hàm số
cosyx
đồng biến trên khoảng nào dưới đây?
A.
;0
. B.
;
2



. C.
0;
. D.
;
22




.
Câu 13: Cho cấp số cộng
13
: 2, 8.
n
u u u
Công sai của cấp số cộng đã cho là
A.
4.d
B.
6.d
C.
1.d
D.
3.d
Câu 14: Với
x
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
sin 2 2sin cosx x x
. B.
sin 2 sin cosx x x
. C.
sin 2 2cosxx
. D.
sin 2 2sinxx
.
Câu 15: Tập nghiệm của phương trình
tan 3x
là
A.
2 , .
3
S k k


B.
,.
3
S k k


C.
,.
6
S k k


D.
,.
6
S k k


Câu 16: Bảng số liệu ghép nhóm sau cho biết chiều cao
(cm)
của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.
153,58
. B.
153,18
. C.
153
. D.
154,1
.
Câu 17: Cho góc
thỏa mãn
2


và
1
sin
4
. Tính
cos .
A.
15
4
. B.
15
4
. C.
15
16
. D.
15
16
.
Câu 18: Sau quãng thời gian 4 giờ kim giờ sẽ quay được một góc là
A.
3
. B.
2
3
. C.
3
4
. D.
4
.
Câu 19: Khẳng định nào sau đây đúng?
A. Hàm số
sinyx
là hàm số chẵn. B. Hàm số
cosyx
là hàm số lẻ.
C. Hàm số
tanyx
là hàm số lẻ. D. Hàm số
cotyx
là hàm số chẵn.
Câu 20: Điều tra cân nặng của các học sinh lớp 11D cho trong bảng sau:
Cân nặng
(kg)
[40,5; 45,5)
[45,5; 50,5)
[50,5; 55,5)
[55,5; 60,5)
[60,5; 65,5)
[65,5; 70,5)
Số học sinh
10
7
16
4
2
3
Cân nặng trung bình của học sinh lớp 11D gần với giá trị nào dưới đây?
A.
48, 44 kg
. B.
61, 81 kg
. C.
51, 81 kg
. D.
52,84 kg
.
Câu 21: Tìm
x
sao cho
2 ;3 2;5 3x x x
là ba số hạng liên tiếp của một cấp số cộng.
A.
2.x 
B.
1
.
2
x 
C.
1.x
D.
3
.
2
x 
Câu 22: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
6cos2 7yx
trên đoạn
;
36




. Tính
.Mm
A.
14.
B.
3.
C.
11.
D.
10.
Câu 23: Cho cấp số nhân
n
u
có
1
2u 
và công bội
3q
. Số hạng
2
u
là
A.
2
6.u 
B.
2
1u
. C.
2
18.u 
D.
2
6.u
Câu 24: Cho góc
thỏa mãn
2
cos
3
với
0.
2

Tính
sin 2 .
A.
25
.
9
B.
25
.
9
C.
45
.
9
D.
45
9
Câu 25: Tập hợp tất cả các giá trị của tham số
m
để phương trình
2cos 2 1xm
có nghiệm là
A.
1;1 .


B.
1;3 .


C.
0;2 .


D.
1;3 .


Câu 26: Cấp số nhân
n
u
có công bội âm, biết
3
12u
,
7
192u
. Tìm
10
u
.
A.
10
1536u
. B.
10
1536u 
. C.
10
3072u
. D.
10
3072u 
.
Câu 27: Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất
bao lâu để đu quay quay được góc
270
?
A.
1
3
phút. B.
1
6
phút. C.
1
4
phút. D.
1,5
phút.
Câu 28: Cho
tan 2
. Tính
π
tan
4



.
A.
1
3
. B.
1
3
. C. 1. D.
2
3
.
Câu 29: Biết
53
sin ,cos
13 5
ab
với
0,
22
ab

. Tính
cos ab
.
A.
63
.
65
B.
21
.
65
C.
16
.
65
D.
56
.
65
Câu 30: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
O
π
__
2
2
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
2sin .yx
C.
cos .yx
D.
2cos .yx
Câu 31: Dãy số nào sau đây là cấp số nhân?
A.
1; 1; 1; 1
. B.
1;3;5;7.
C.
1; 2; 3;4
. D.
1;4;9;16.
Câu 32: Bảng thống kê sau cho biết tốc độ (km/h) của một số xe máy khi đi qua vị trí có cảnh sát giao
thông đang làm nhiệm vụ.
Tốc độ
20;35
35;50
50;60
60;70
70;85
85;100
Số phương tiện giao
thông
27
70
8
3
1
1
Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?
A. Số xe được đo tốc độ là 100 xe.
B. Mẫu số liệu đã cho gồm 5 nhóm có độ dài bằng nhau.
C. Tổng độ dài các nhóm là 80.
D. Số xe máy thuộc nhóm
60 70
là ít nhất.
Câu 33: Cho dãy số
: 2 1.
nn
u u n
Số hạng thứ 3 của dãy là
A.
3
7.u
B.
3
5.u
C.
3
3.u
D.
3
9.u
Câu 34: Rút gọn biểu thức
cos cos5
sin4 sin 2
aa
P
aa
(với giả thiết biểu thức có nghĩa).
A.
2cotPa
. B.
2cosPa
. C.
2tanPa
. D.
2sinPa
.
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết
quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A.
3
13Q
. B.
3
14Q
. C.
3
15Q
. D.
3
12Q
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2cos3 .yx
2) (0,75 điểm). Cho cấp số cộng
n
u
thỏa mãn:
16
23
2 26
.
3 18
uu
uu


Tính
10
.u
Câu 2: (1,0 điểm). Giải phương trình:
2sin 1 cos2 sin2 1 2cos .x x x x
Câu 3: (0,5 điểm). Do ảnh hưởng của dịch Covid
19
nên doanh thu
6
tháng đầu năm của
công ty
A
không đạt kế hoạch. Cụ thể, doanh thu
6
tháng đầu năm đạt
20
tỷ đồng, trong đó
tháng
6
đạt
6
tỷ đồng. Để đảm bảo doanh thu cuối năm đạt được kế hoạch năm, công ty
đưa ra chỉ tiêu: kể từ tháng
7
mỗi tháng phải tăng doanh thu so với tháng kề trước
10%
. Hỏi
theo chỉ tiêu đề ra thì doanh thu cả năm của công ty
A
đạt được là bao nhiêu tỷ đồng (làm
tròn đến một chữ số thập phân)?
____________________HẾT____________________
Huế, 14h40’ Ngày 14 tháng 10 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
ĐỀ ÔN TẬP SỐ 05_TrNg 2023
¤N TËP KIÓM TRA GI÷A K× 1
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Dãy số
n
u
là dãy số giảm khi chỉ khi
A.
*
1
,.
nn
u u n
B.
*
1
,.
nn
u u n
C.
*
1
,.
nn
u u n
D.
*
1
,.
nn
u u n
Câu 2: Cho góc hình học
uOv
có số đo bằng
30
(tham khảo hình vẽ).
30
o
O
u
v
Khẳng định nào sau đây sai?
A.
s® ; 330 .Ou Ov
B.
s® ; 30 .Ou Ov 
C.
s® ; 30 360 , .Ou Ov k k
D.
s® ; 330 360 , .Ou Ov k k
Lời giải:
Các kết quả đúng:
s®
s®
; 30 360 , .
,.
; 330 360 , .
Ou Ov k k
k
Ou Ov k k
Câu 3: Phương trình nào sau đây vô nghiệm?
A.
cos 1.x
B.
cos2 0,7.x 
C.
cos3 0,4.x
D.
cos4 .x
Lời giải:
Do
1;1



nên phương trình
cos4x
vô nghiệm.
Câu 4: Dãy số nào dưới đây là cấp số cộng?
A.
1;3;4.
B.
3;5;7.
C.
5;7;6.
D.
3;5;8.
Lời giải:
Dãy số hữu hạn
3;5;7
là cấp số cộng với
1
3u
và công sai
2.d
Câu 5: Tập xác định của hàm số
tanyx
là
A.
D \ 2 , .kk
B.
D \ 2 , .
2
kk



C.
D \ , .
2
kk



D.
D \ , .kk
Lời giải:
Hàm số
tanyx
xác định khi và chỉ khi
cos 0x
,.
2
x k k
Vậy TXĐ là:
D \ , .
2
kk



Câu 6: Chu kỳ của hàm số
cos2yx
là
A.
2k
. B.
2
3
. C.
. D.
2
.
Lời giải:
Chu kỳ của hàm số
cos2yx
là:
2
2
T

.
Câu 7:
2
3
x
là một nghiệm của phương trình nào dưới đây?
A.
sin 1.x
B.
3
sin .
2
x
C.
1
cos .
2
x
D.
3
cos .
2
x
Lời giải:
Thay
2
3
x
vào phương trình
3
sin
2
x
thấy thỏa mãn.
Câu 8: Cho cấp số cộng
1
:2
n
uu
và công sai
2.d
Số hạng thứ 3 của
n
u
là
A.
3
4.u
B.
3
6.u
C.
3
8.u
D.
3
12.u
Lời giải:
Ta có:
31
2 6.u u d
Câu 9: Góc có số đo
4
15
đổi sang độ là
A.
.48
B.
135 .
C.
72 .
D.
270 .
Lời giải:
Cách 1: Ta có:
o
4 4.180
.
15 15
48



Cách 2: Sử dụng MTCT
Câu 10: Giá trị lớn nhất của hàm số
sin 2yx
bằng
A.
2
. B.
0
. C.
1
. D.
1
.
Lời giải:
Ta có
: 1 sin 2 1, xx
x
.
Vậy
max 2y
khi
sin 2 1x
22
2
xk
4
xk
(
k
).
Câu 11: Cho dãy số
: sin .
nn
u u n
Khẳng định nào sau đây đúng?
A.
n
u
bị chặn. B.
n
u
bị chặn dưới và không bị chặn trên.
C.
n
u
bị chặn trên và không bị chặn dưới. D.
n
u
tăng.
Lời giải:
Ta có:
*
1 sin 1, .
n
u n n
Vậy
n
u
bị chặn.
Câu 12: Hàm số
cosyx
đồng biến trên khoảng nào dưới đây?
A.
;0
. B.
;
2



. C.
0;
. D.
;
22




.
Lời giải:
Dựa vào đồ thị của hàm số
cosyx
, ta có hàm số này đồng biến trên khoảng
;0
.
Câu 13: Cho cấp số cộng
13
: 2, 8.
n
u u u
Công sai của cấp số cộng đã cho là
A.
4.d
B.
6.d
C.
1.d
D.
3.d
Lời giải:
Ta có:
31
2 8 2 2 3.u u d d d
Câu 14: Với
x
là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A.
sin 2 2sin cosx x x
. B.
sin 2 sin cosx x x
. C.
sin 2 2cosxx
. D.
sin 2 2sinxx
.
Câu 15: Tập nghiệm của phương trình
tan 3x
là
A.
2 , .
3
S k k


B.
,.
3
S k k


C.
,.
6
S k k


D.
,.
6
S k k


Câu 16: Bảng số liệu ghép nhóm sau cho biết chiều cao
(cm)
của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.
153,58
. B.
153,18
. C.
153
. D.
154,1
.
Lời giải:
Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150; 155). Ta có,
22
2, 150, 14j a m
,
13
7, 10, 5m m h
.
Do đó
0
14 7
150 5 153,18.
(14 7) (14 10)
M
Câu 17: Cho góc
thỏa mãn
2


và
1
sin
4
. Tính
cos .
A.
15
4
. B.
15
4
. C.
15
16
. D.
15
16
.
Lời giải:
Ta có:
2
22
15
cos
1 15
4
cos 1 sin 1 .
4 16
15
cos
4




Do
2


nên chọn
15
cos .
4
Câu 18: Sau quãng thời gian 4 giờ kim giờ sẽ quay được một góc là
A.
3
. B.
2
3
. C.
3
4
. D.
4
.
Lời giải:
Sau 1 giờ kim giờ sẽ quay được một góc là
6
Sau 4 giờ kim giờ sẽ quay được một góc là
2
.4 .
63

Câu 19: Khẳng định nào sau đây đúng?
A. Hàm số
sinyx
là hàm số chẵn. B. Hàm số
cosyx
là hàm số lẻ.
C. Hàm số
tanyx
là hàm số lẻ. D. Hàm số
cotyx
là hàm số chẵn.
Câu 20: Điều tra cân nặng của các học sinh lớp 11D cho trong bảng sau:
Cân nặng
(kg)
[40,5; 45,5)
[45,5; 50,5)
[50,5; 55,5)
[55,5; 60,5)
[60,5; 65,5)
[65,5; 70,5)
Số học sinh
10
7
16
4
2
3
Cân nặng trung bình của học sinh lớp 11D gần với giá trị nào dưới đây?
A.
48, 44 kg
. B.
61, 81 kg
. C.
51, 81 kg
. D.
52,84 kg
.
Lời giải:
Tổng số học sinh là
42n
. Cân nặng trung bình của học sinh lớp 11D là
10.43 7.48 16.43 4.58 2.63 3.68
51,81
42
x kg
Câu 21: Tìm
x
sao cho
2 ;3 2;5 3x x x
là ba số hạng liên tiếp của một cấp số cộng.
A.
2.x 
B.
1
.
2
x 
C.
1.x
D.
3
.
2
x 
Lời giải:
Do
2 ;3 2;5 3x x x
là ba số hạng liên tiếp của một cấp số cộng nên
2 5 3 2 3 2 1.x x x x
Câu 22: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
6cos2 7yx
trên đoạn
;
36




. Tính
.Mm
A.
14.
B.
3.
C.
11.
D.
10.
Lời giải:
Ta có:
36
x

2
2
33
x

1
cos2 1 10 6cos2 7 1
2
xx
.
Suy ra
1, 10.Mm
Vậy
11.Mm
Câu 23: Cho cấp số nhân
n
u
có
1
2u 
và công bội
3q
. Số hạng
2
u
là
A.
2
6.u 
B.
2
1u
. C.
2
18.u 
D.
2
6.u
Lời giải:
Ta có
21
.u u q
2.3 6
.
Câu 24: Cho góc
thỏa mãn
2
cos
3
với
0.
2

Tính
sin 2 .
A.
25
.
9
B.
25
.
9
C.
45
.
9
D.
45
9
Lời giải:
Ta có:
22
5
sin
5
3
sin 1 cos .
9
5
sin
3

Do
0
2

nên
sin 0

chọn
5
sin .
3
Vậy
45
sin2 2sin cos .
9

Câu 25: Tập hợp tất cả các giá trị của tham số
m
để phương trình
2cos 2 1xm
có nghiệm là
A.
1;1 .


B.
1;3 .


C.
0;2 .


D.
1;3 .


Lời giải:
Phương trình
1
2cos2 1 cos2
2
m
x m x
có nghiệm
1
1 1 1 3.
2
m
m
Câu 26: Cấp số nhân
n
u
có công bội âm, biết
3
12u
,
7
192u
. Tìm
10
u
.
A.
10
1536u
. B.
10
1536u 
. C.
10
3072u
. D.
10
3072u 
.
Lời giải:
Gọi
q
là công bội của cấp số nhân đề bài cho
0q
.
Ta có
2
31
6
71
12
192
u u q
u u q


6
1
2
1
192
12
uq
uq

4
16q
(Do
1
,0uq
)
Mà
0q
2q
1
2
12
3u
q
.
Suy ra:
9
9
10 1
. 3. 2 1536u u q
.
Câu 27: Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất
bao lâu để đu quay quay được góc
270
?
A.
1
3
phút. B.
1
6
phút. C.
1
4
phút. D.
1,5
phút.
Lời giải:
Tính được:
270 3 3
270 .2 .
180 2 4
Vậy đu quay quay được góc
270
khi nó quay được
3
4
vòng.
Ta có: Đu quay quay được 1 vòng trong
1
3
phút.
Đu quay quay được
3
4
vòng trong
3 1 1
.
4 3 4
phút.
Câu 28: Cho
tan 2
. Tính
π
tan
4



.
A.
1
3
. B.
1
3
. C. 1. D.
2
3
.
Lời giải:
Ta có:
π
tan tan
π tan 1 1
4
tan
π
4 1 tan 3
1 tan .tan
4



.
Câu 29: Biết
53
sin ,cos
13 5
ab
với
0,
22
ab

. Tính
cos ab
.
A.
63
.
65
B.
21
.
65
C.
16
.
65
D.
56
.
65
Lời giải:
Ta có:
2
22
5 144
cos 1 sin 1 ;
13 169



aa
2
22
3 16
sin 1 cos 1
5 25



bb
Vì
0
2
a

nên suy ra
cos 0a
, ta chọn
12
cos
13
a
Vì
2
b

nên suy ra
sin 0b
, ta chọn
4
sin
5
b
.
12 3 5 4 56
cos cos .cos sin .sin . . .
13 5 13 5 65



a b a b a b
Câu 30: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D.
x
y
O
π
__
2
2
1
Hỏi hàm số đó là hàm số nào?
A.
sin .yx
B.
2sin .yx
C.
cos .yx
D.
2cos .yx
Lời giải:
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm
0;0 , ;2 .
2
OA



Câu 31: Dãy số nào sau đây là cấp số nhân?
A.
1; 1; 1; 1
. B.
1;3;5;7.
C.
1; 2; 3;4
. D.
1;4;9;16.
Lời giải:
Dãy hữu hạn
1; 1; 1; 1
là một cấp số nhân với
1
1;u
công bội
1.q
Câu 32: Bảng thống kê sau cho biết tốc độ (km/h) của một số xe máy khi đi qua vị trí có cảnh sát giao
thông đang làm nhiệm vụ.
Tốc độ
20;35
35;50
50;60
60;70
70;85
85;100
Số phương tiện giao
thông
27
70
8
3
1
1
Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?
A. Số xe được đo tốc độ là 100 xe.
B. Mẫu số liệu đã cho gồm 5 nhóm có độ dài bằng nhau.
C. Tổng độ dài các nhóm là 80.
D. Số xe máy thuộc nhóm
60 70
là ít nhất.
Câu 33: Cho dãy số
: 2 1.
nn
u u n
Số hạng thứ 3 của dãy là
A.
3
7.u
B.
3
5.u
C.
3
3.u
D.
3
9.u
Câu 34: Rút gọn biểu thức
cos cos5
sin4 sin 2
aa
P
aa
(với giả thiết biểu thức có nghĩa).
A.
2cotPa
. B.
2cosPa
. C.
2tanPa
. D.
2sinPa
.
Lời giải:
Ta có:
cos cos5 2sin3 .sin 2
sin4 sin 2 2sin3 .cos
a a a a
P
a a a a

sin 2
cos
a
a
2sin .cos
cos
aa
a
2sin a
.
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết
quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A.
3
13Q
. B.
3
14Q
. C.
3
15Q
. D.
3
12Q
.
Lời giải:
Cỡ mẫu :
2 4 7 4 3 20n
.
Tứ phân vị thứ ba
3
Q
là
15 16
2
xx
. Do
15 16
,xx
đều thuộc nhóm
12;16
nên nhóm này chứa
3
Q
.
Do đó:
4p
,
4
12a
,
4
4m
,
1 2 3
2 4 7 13m m m
,
54
4aa
.
Ta có:
3
3.20
13
4
12 .4 14
4
Q
.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2cos3 .yx
Lời giải:
Ta có:
: 1 cos3 1 2 4 2cos3 6.x x x
Vậy
2
max 6 cos3 1 , ;
33
k
y x x k

2
min 2 cos3 1 , .
3
k
y x x k
2) (0,75 điểm). Cho cấp số cộng
n
u
thỏa mãn:
16
23
2 26
.
3 18
uu
uu


Tính
10
.u
Lời giải:
Ta có:
11
16
1
1
2 3 1
11
2 5 26
2 26
3 10 26
2
.
3 18 4 5 18
2
3 2 18
u u d
uu
ud
u
u u u d
d
u d u d

Suy ra:
10 1
9 20.u u d
Câu 2: (1,0 điểm). Giải phương trình:
2sin 1 cos2 sin2 1 2cos .x x x x
Lời giải:
Điều kiện:
.x
2
(1) 2sin .2cos 2sin cos 1 2cos 0 2sin cos 2cos 1 1 2cos 0
1
2cos 1 0
cos
2cos 1 2sin cos 1 0
2
2sin cos 1 0
sin2 1
x x x x x x x x x
x
x
x x x
xx
x



+) Với
2
2
1
3
cos , .
2
2
2
3
xk
xk
xk

+) Với
sin2 1 , .
4
x x k k
Câu 3: (0,5 điểm). Do ảnh hưởng của dịch Covid
19
nên doanh thu
6
tháng đầu năm của
công ty
A
không đạt kế hoạch. Cụ thể, doanh thu
6
tháng đầu năm đạt
20
tỷ đồng, trong đó
tháng
6
đạt
6
tỷ đồng. Để đảm bảo doanh thu cuối năm đạt được kế hoạch năm, công ty
đưa ra chỉ tiêu: kể từ tháng
7
mỗi tháng phải tăng doanh thu so với tháng kề trước
10%
. Hỏi
theo chỉ tiêu đề ra thì doanh thu cả năm của công ty
A
đạt được là bao nhiêu tỷ đồng (làm
tròn đến một chữ số thập phân)?
Lời giải:
Ta có:
Doanh thu của công ty trong tháng
7
7:T 6. 1 10%
;
Doanh thu của công ty trong tháng
2
8
8:T 6. 1 10%
;
…
Doanh thu của công ty trong tháng
6
12
12:T 6. 1 10%
;
Do đó, theo chỉ tiêu đề ra thì doanh thu cả năm của công ty
A
đạt được là
6
26
1 10% 1
20 6. 1 10% 6. 1 10% .... 6. 1 10% 20 6. 1 10% . 70,9
10%
T

(tỷ).
____________________HẾT____________________
Huế, 14h40’ Ngày 14 tháng 10 năm 2023
| 1/67
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 11
KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 05 ĐỀ ÔN GIỮA KÌ 1
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 01_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Cho góc hình học uOv có số đo bằng 30 (tham khảo hình vẽ). v 30o O u
Khẳng định nào sau đây đúng? A. s® ; Ou Ov  6  0 .  B. s® ; Ou Ov  30 .  C. s® ; Ou Ov  90 .  D. s® ; Ou Ov  3  0 .  n Câu 2:
Cho dãy số u , biết u u là n n
2n  . Ba số hạng đầu tiên của dãy số  n  1 1 2 3 1 1 1 1 2 3 A. ; ; . B. 1; ; . C. 1; ; . D. 1; ; . 2 3 4 2 16 4 8 3 7 Câu 3:
Phương trình nào sau đây có nghiệm? 2
A. sin x  2. B. cos 2x  2  .
C. sin 3x  .
D. cos x  . 3 Câu 4:
Trong các dãy số sau, dãy số nào không phải cấp số cộng? 1 3 5 7 9 A. ; ; ; ; . B. 1;1;1;1;1 .
C. 8; 6; 4; 2; 0 .
D. 3;1; 1; 2; 4 . 2 2 2 2 2 Câu 5:
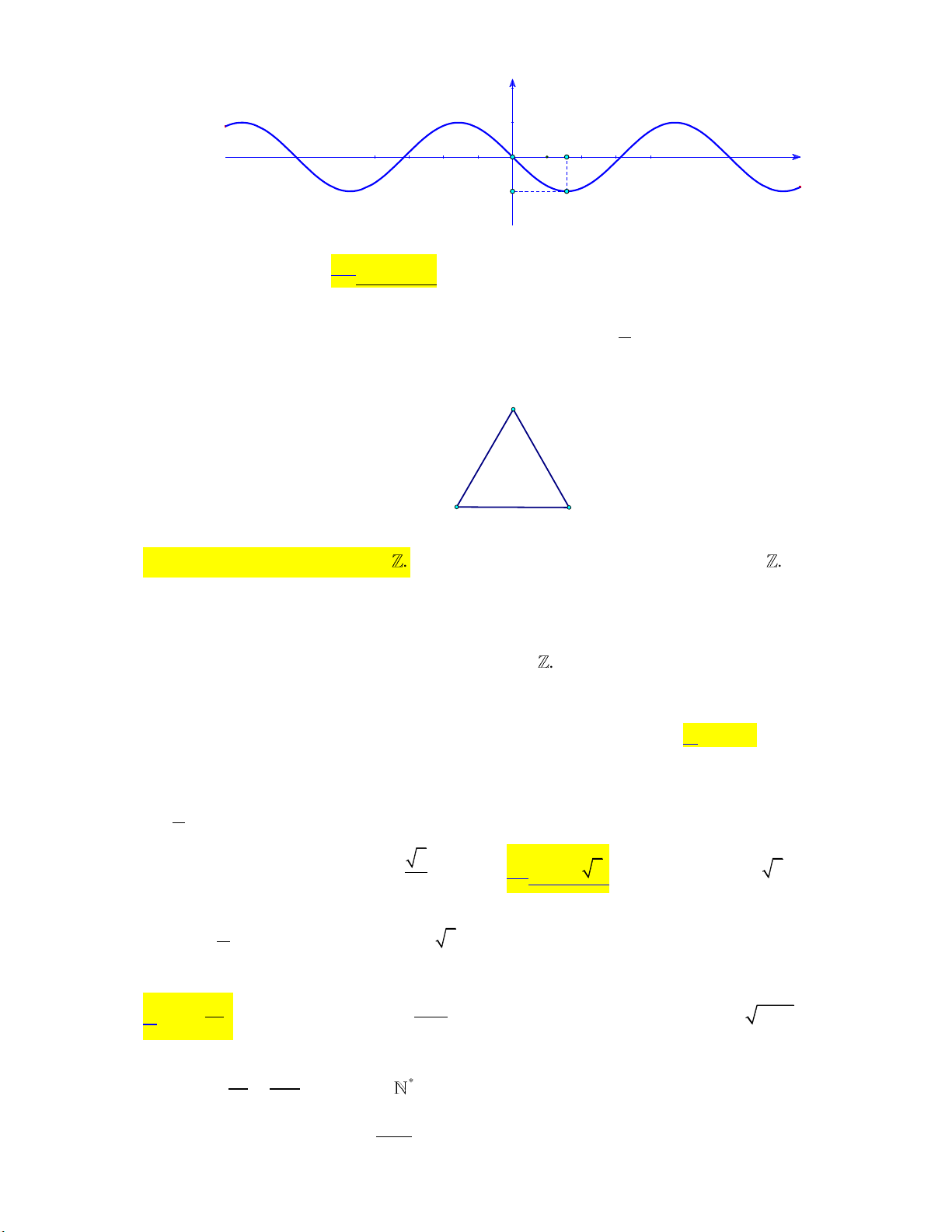
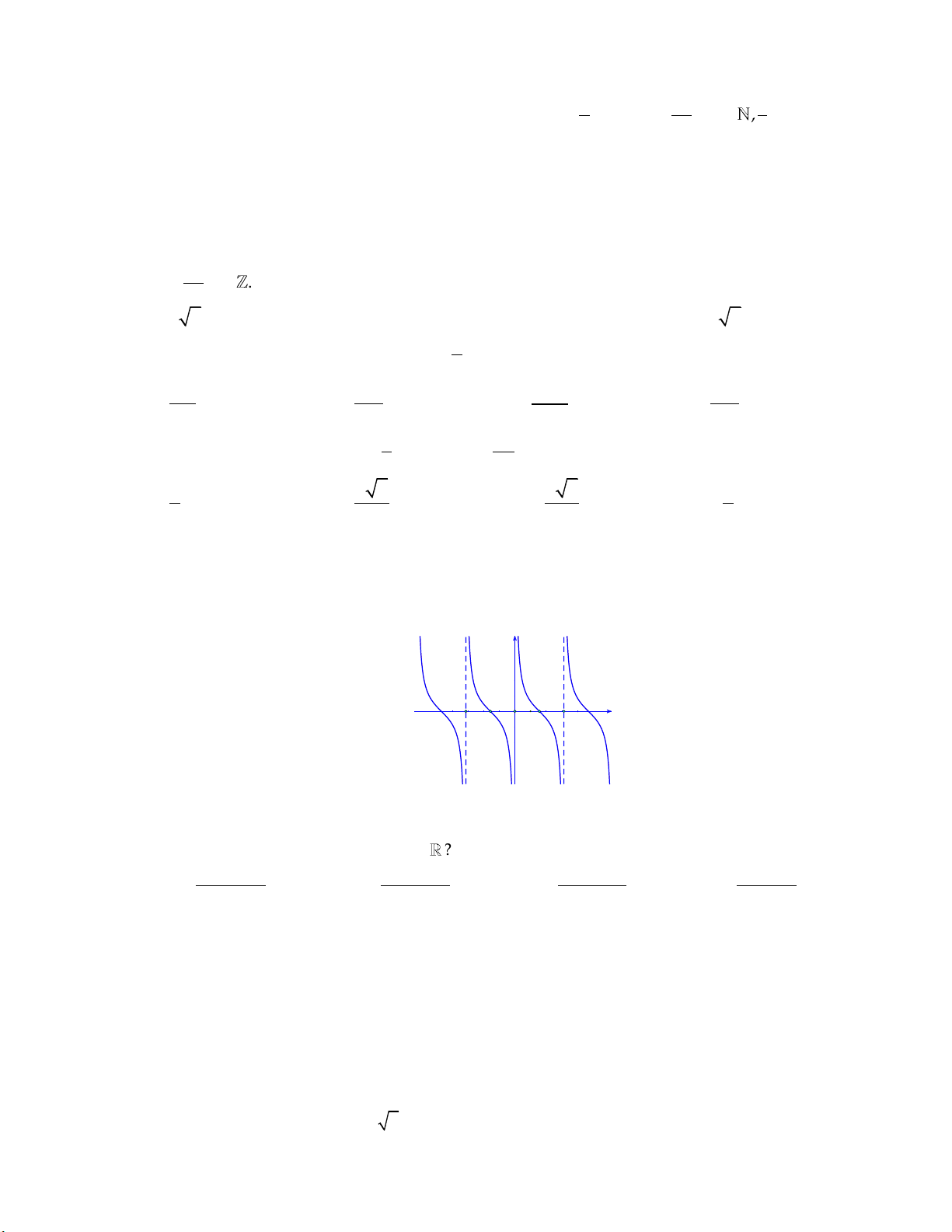
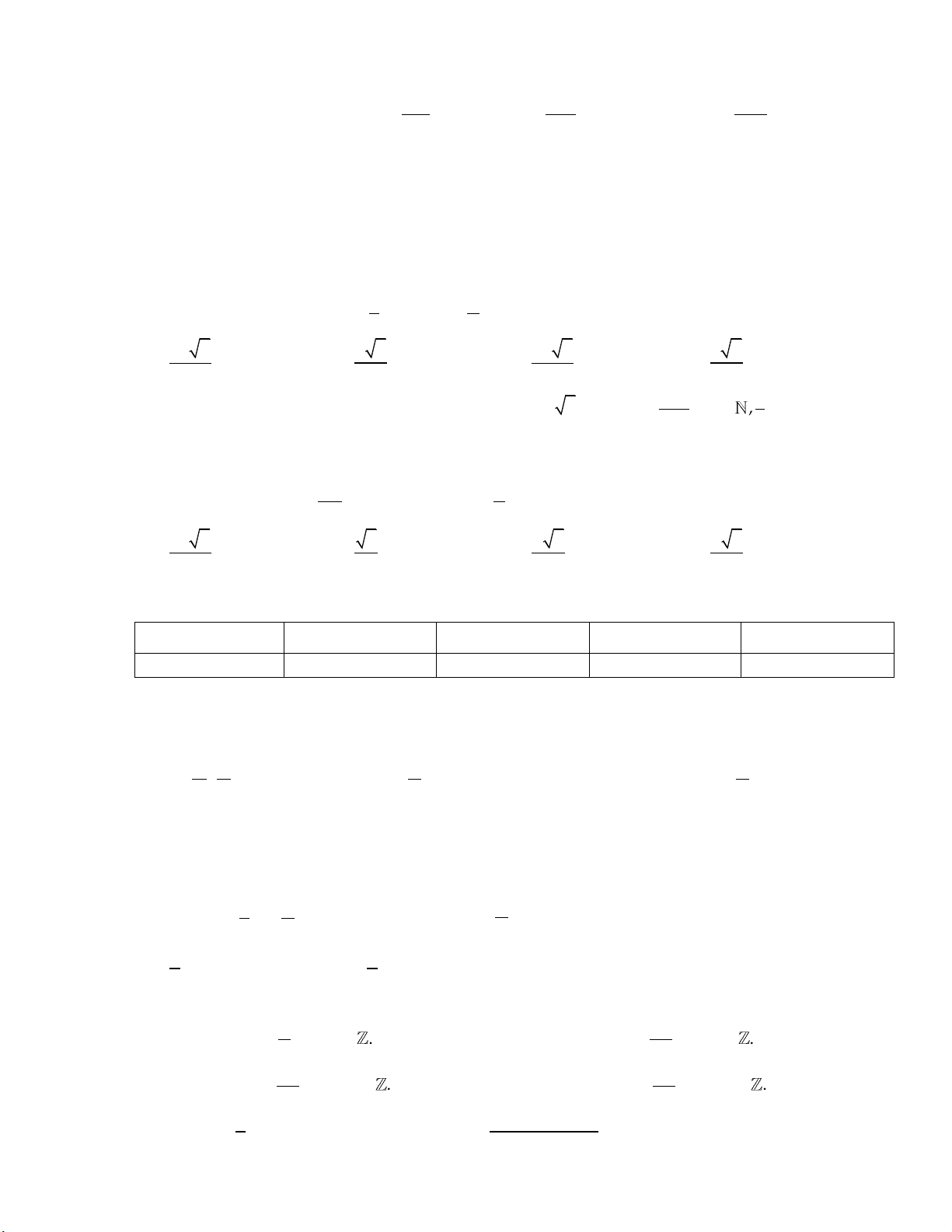
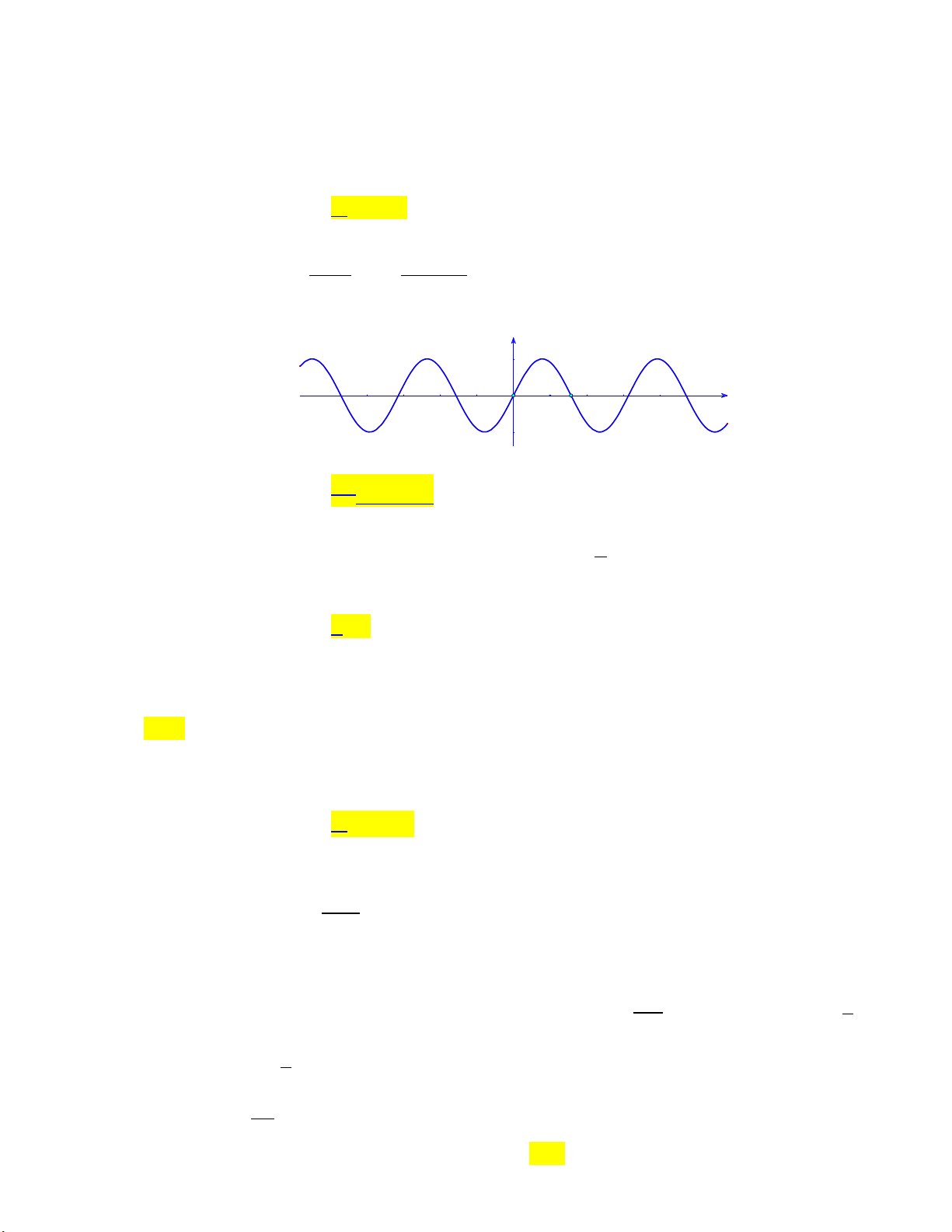
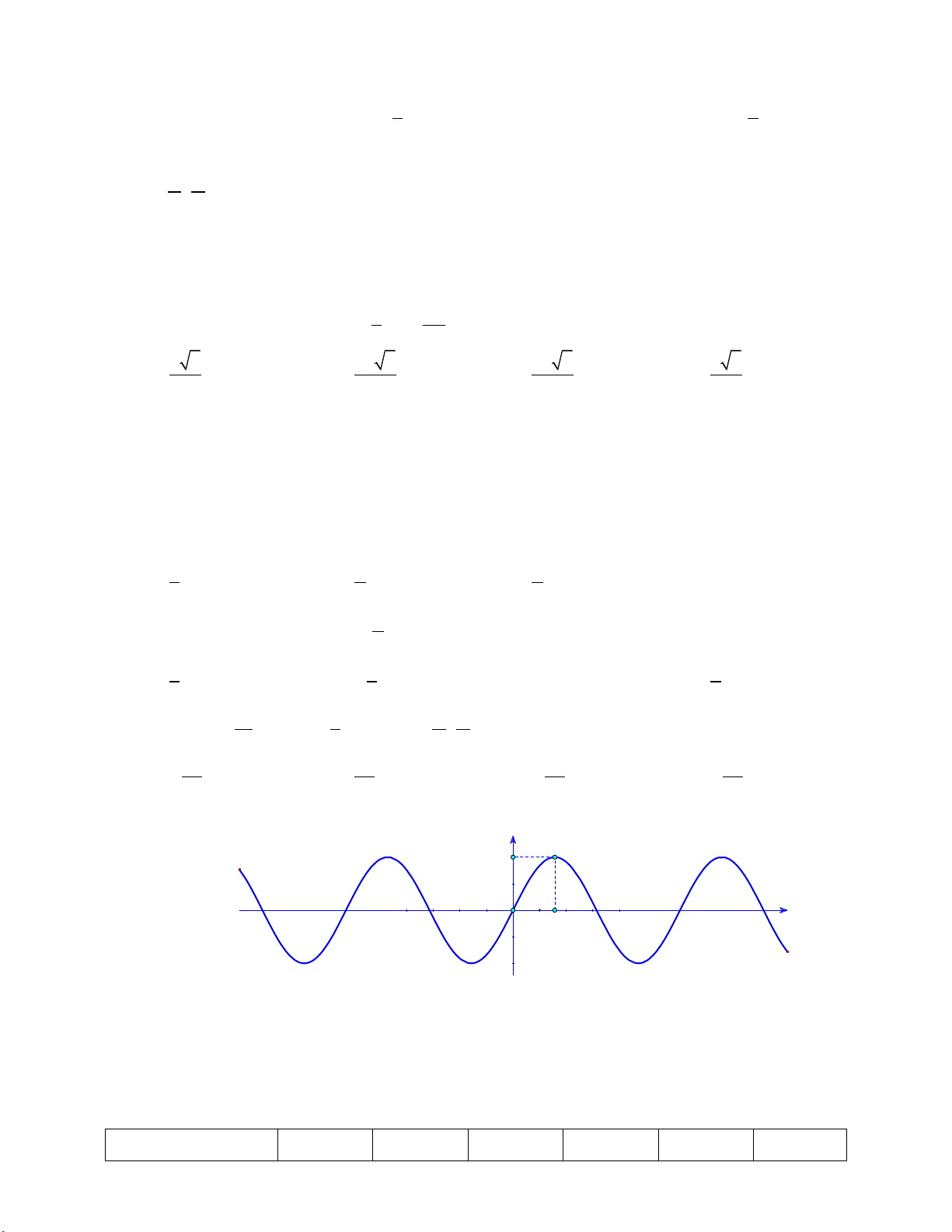
Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y __ π 1 2 x O -1
Hỏi hàm số đó là hàm số nào? A. y  sin . x
B. y  sin . x C. y  cos . x
D. y  cos . x Câu 6:
Cho tam giác đều ABC (tham khảo hình vẽ). A B C
Khẳng định nào sau đây sai? A. s® A ; B AC  6
 0  k360,k  .
B. s® A ; B AC  3
 00  k360,k  .
C. s®  A ; B AC   300  . 
D. s® A ; B AC  60 .  Câu 7:
Cho cấp số cộng u có u  3, u  27 . Tính công sai d . n  1 6
A. d  7 .
B. d  5 .
C. d  8 . D. d  6 .  Câu 8: x
là một nghiệm của phương trình nào dưới đây? 6 3
A. sin x  1. B. sin x  .
C. cot x  3.
D. tan x  3. 2 Câu 9:
Trong các dãy số u cho bởi số hạng tổng quát u sau, dãy số nào là dãy số giảm? n n 1 4 A. u  . B. u  3  . C. 2
u n .
D. u n  2 . n 2n n n 1 n n 1
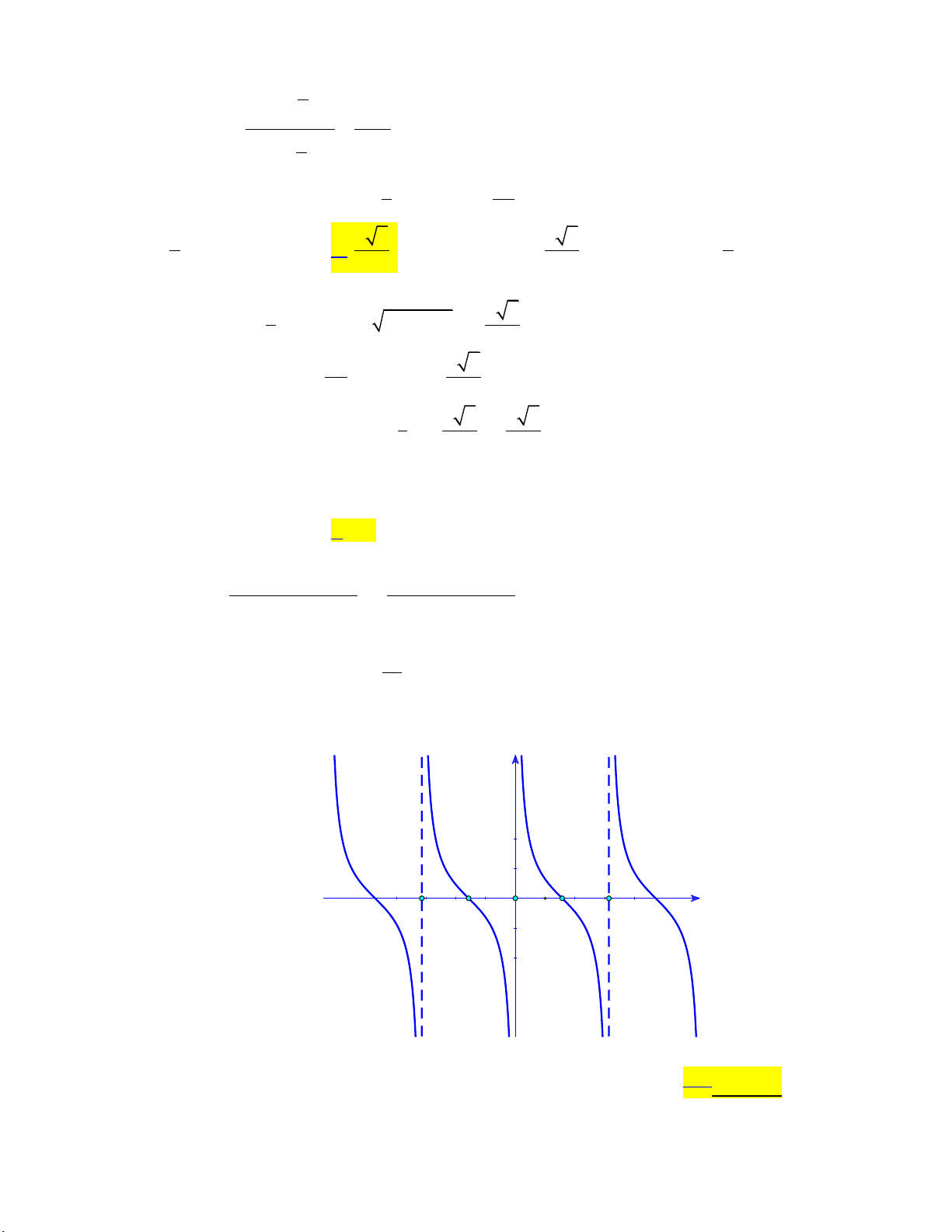
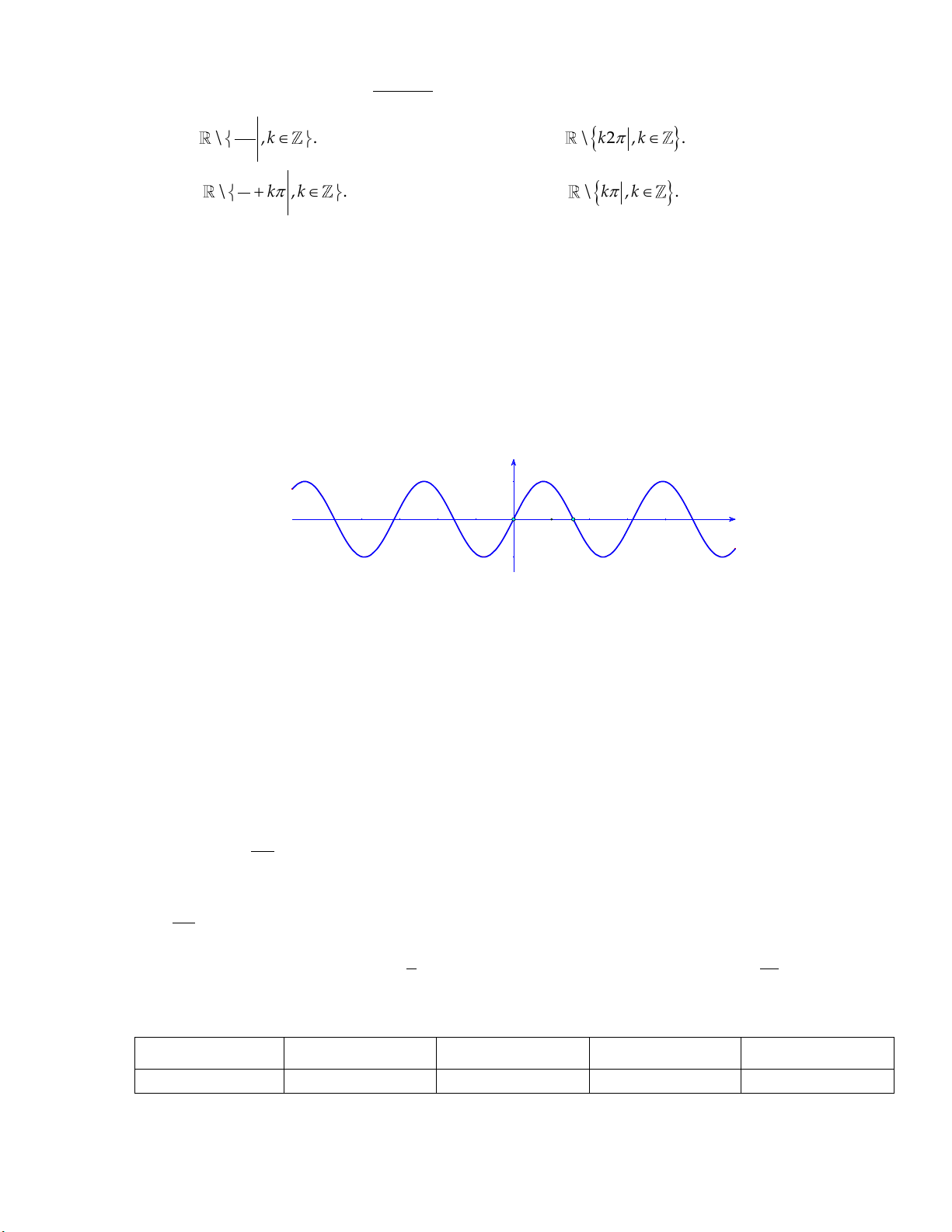
Câu 10: Tập xác định của hàm số y  là sin x A. D  \   0 . B. D 
\ k2 , k  . C. D 
\ k , k  . D. D  \ 0;.
Câu 11: Nghiệm âm lớn nhất của phương trình 2 sin x  1  0 là 11     5   7   A. x  . B. x  . C. x  . D. x  . 6 6 6 6
Câu 12: Cho dãy số u có 2
u  n n 1. Số 19 là số hạng thứ mấy của dãy u ? n n n A. 5 . B. 7 . C. 6 . D. 4 .
Câu 13: Cho u là một cấp số cộng thỏa mãn u u  8 và u  10 . Công sai của cấp số cộng đã cho n  1 3 4 bằng A. 3 . B. 6 . C. 2 . D. 4 .
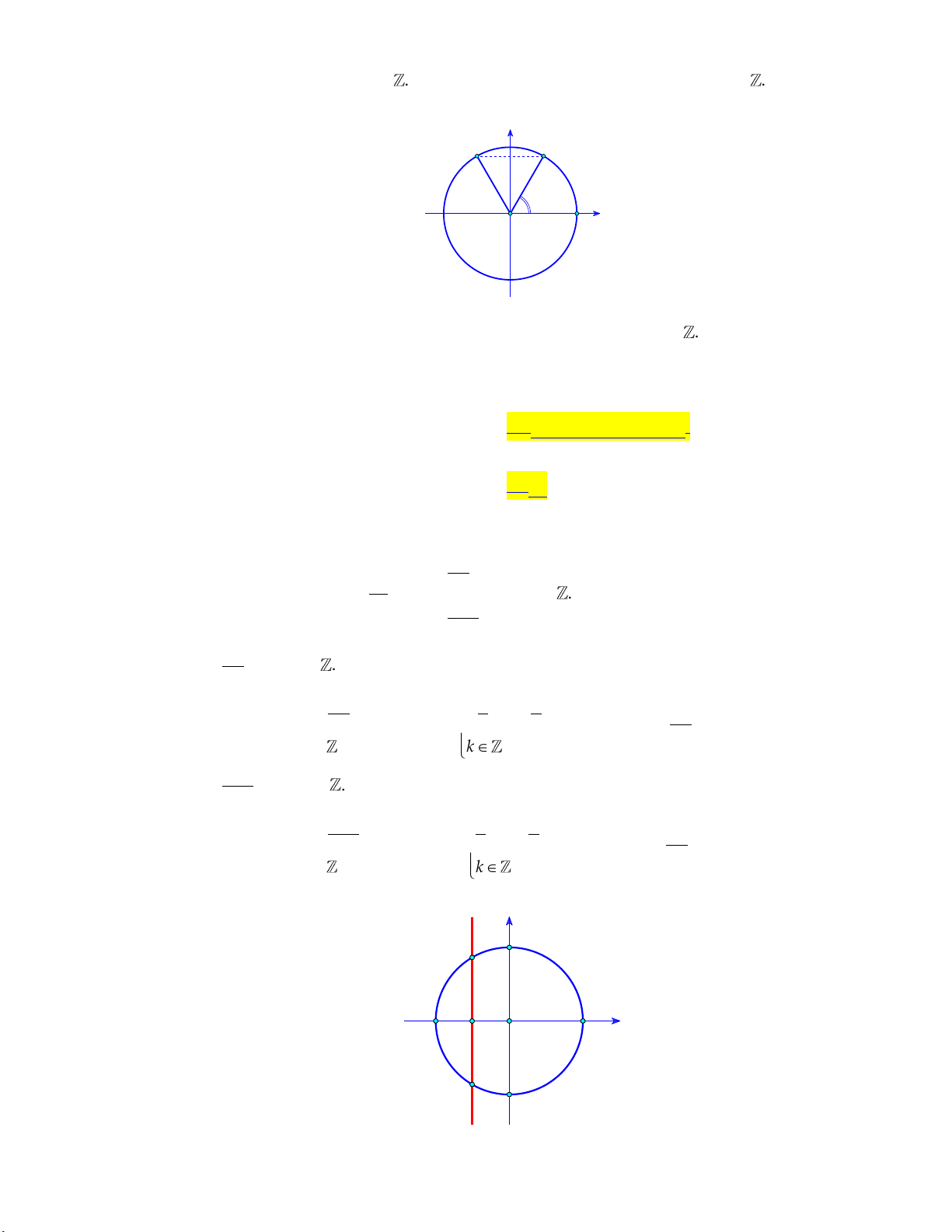
Câu 14: Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho AOM  60 (tham khảo hình vẽ). y M 60o x O A
Gọi N là điểm đối xứng với điểm M qua trục Oy , khẳng định nào sau đây đúng?
A. s®OA;ON  120  k360,k  .
B. s®OA;ON  1
 20  k360,k  .
C. s®OA;ON  240  k360,k  .
D. s®OA;ON  60  k360,k  .
Câu 15: Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng? A. 2
cos 2  1  2 cos  . B. 2 cos 2  2 sin   1. C. 2
cos 2  2 cos   1 . D. 2
cos 2  1  2 sin  .
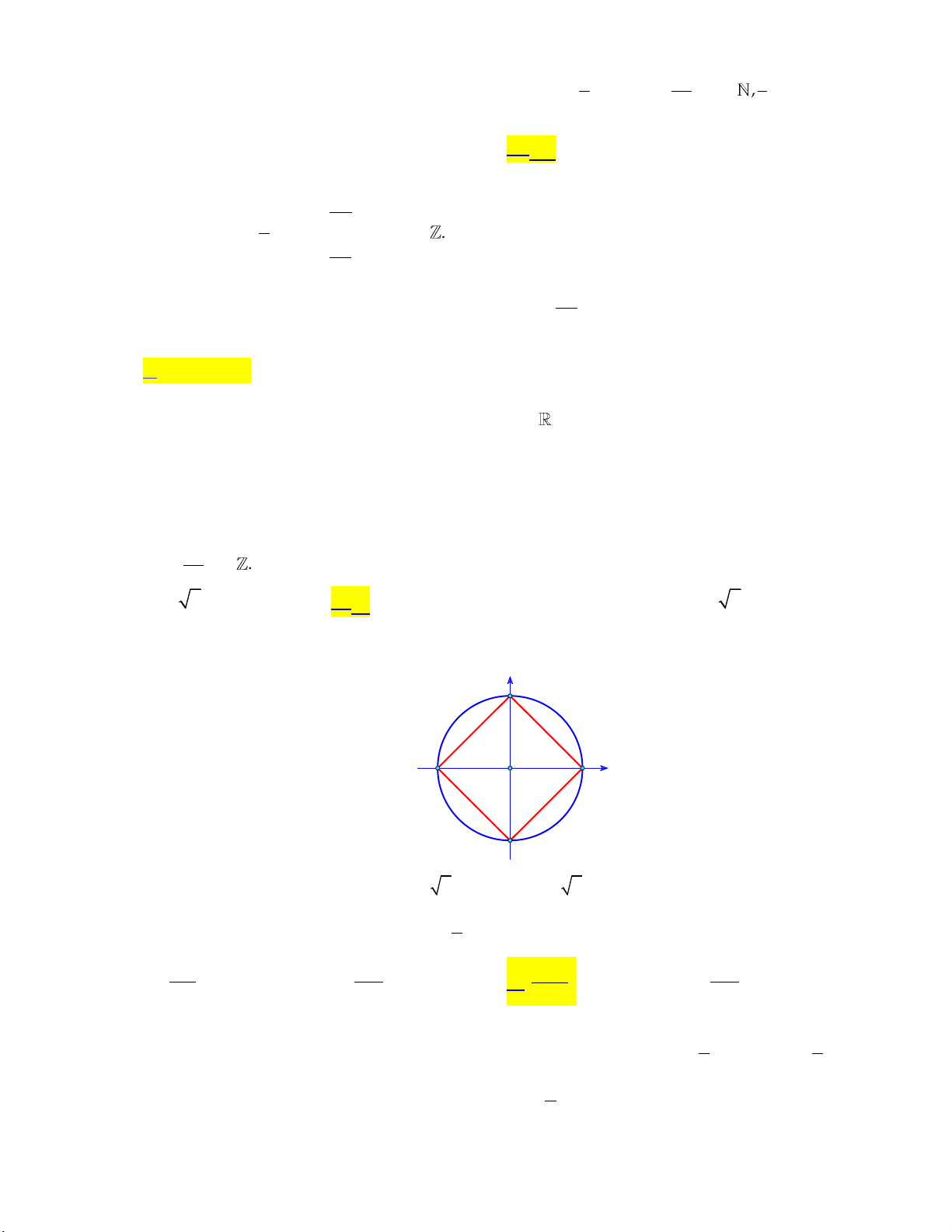
Câu 16: Số nghiệm của phương trình 2 cos x  1  0 trên đoạn 0; 2    là A. 1. B. 3. C. 2. D. 4.
Câu 17: Cho cấp số nhân u với u  3 và u  6 . Công bội q của cấp số nhân đó là n  1 2 A. 2 . B. 2 . C. 9  . D. 9 .
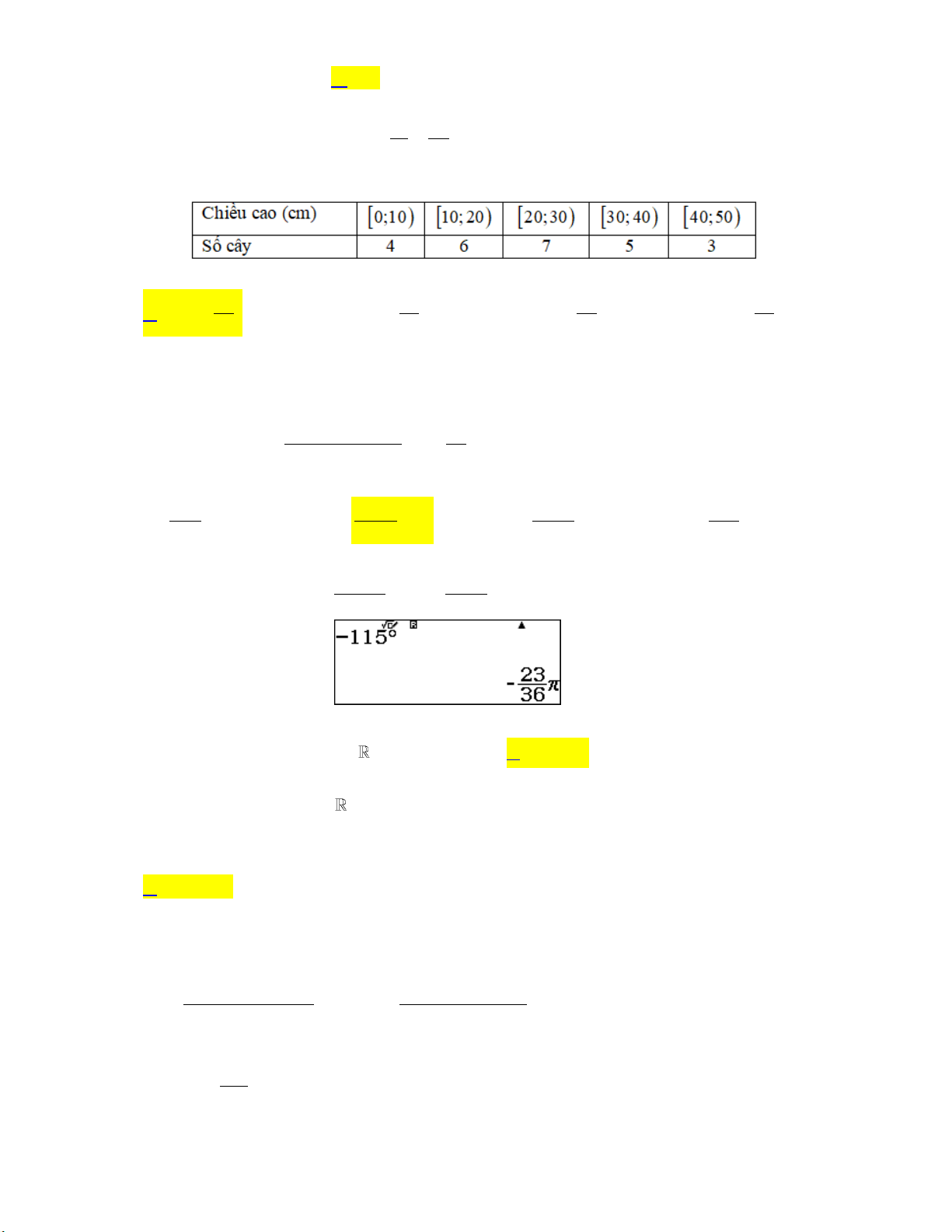
Câu 18: Cho mẫu số liệu ghép nhóm về chiều cao của 25 cây dừa giống, như sau:
Mốt của mẫu số liệu ghép nhóm này là 70 50 70 80 A. M  . B. M  . C. M  . D. M  . o 3 o 3 o 2 o 3
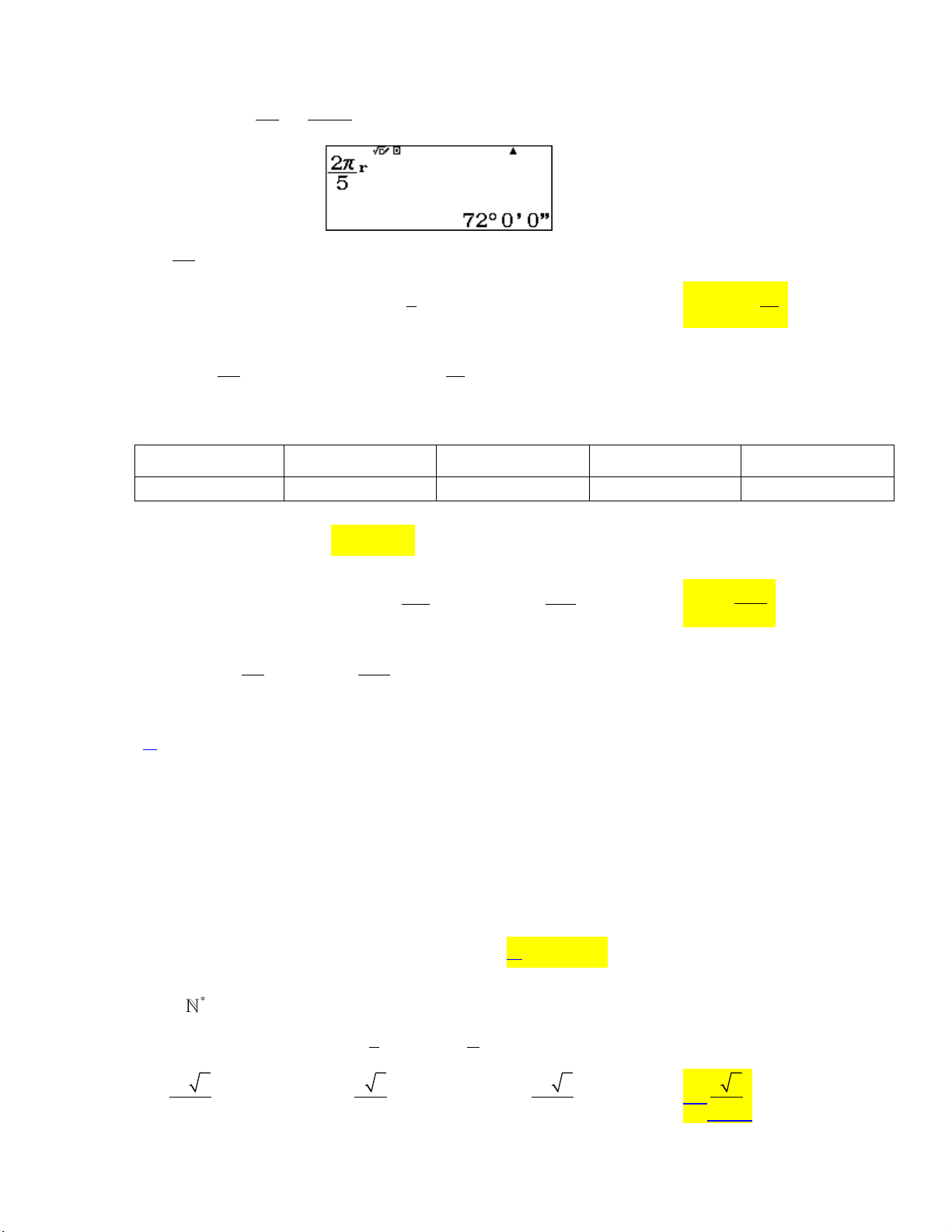
Câu 19: Đổi số đo góc 115 sang rađian, ta được 23 23   13   13 A. rad. B. rad. C. rad. D. rad. 36 36 36 36
Câu 20: Tập giá trị của hàm số y  sin 2x là A. 2; 2   . B. . C. 1;1   . D. 0; 2   .
Câu 21: Cho biết dãy số 1; 8;...; x là một cấp số cộng. Tìm x sao cho 1 8 15  22  x  7944 .
A. x  330 .
B. x  220 .
C. x  351 . D. x  407 .
Câu 22: Các cặp góc lượng giác nào dưới đây có cùng điểm biểu diễn trên đường tròn lượng giác?  2  2     5   4 A. và . B. và . C. và . D. và . 3 3 3 3 3 3 3 3 1
Câu 23: Tổng 10 số hạng đầu cấp số nhân (u ) với u
và công bội q  3 là: n 1 2 9841 3069 A. 14762 . B. . C. . D. 1640 . 2 512
Câu 24: Khẳng định nào sau đây đúng?
A. Các hàm số y  sin x , y  cos x , y  cot x đều là hàm số chẵn.
B. Các hàm số y  sin x , y  cos x , y  cot x đều là hàm số lẻ.
C. Các hàm số y  sin x , y  cot x , y  tan x đều là hàm số chẵn.
D. Các hàm số y  sin x , y  cot x , y  tan x đều là hàm số lẻ. 1 
Câu 25: Cho góc  thỏa mãn sin  với
   . Tính sin 2. 3 2 4  2 4 2 2  2 2 2 A. . B. . C. . D. . 9 9 9 9
Câu 26: Cho cấp số nhân u có u  6 và q  2 . Tống n số hạng đầu tiên của cấp số nhân đã cho n  1 bằng 2046. Tìm . n A. n  9 . B. n  10 . C. n  11 . D. n  12 .
Câu 27: Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm 60;80 là A. 40 . B. 70 . C. 60 . D. 30 .
Câu 28: Với a,b là các góc bất kì. Trong các công thức sau, công thức nào đúng?
A. cos a b  cos .
a sin b  sin . a sin b .
B. sin a b  sin .
a cos b  cos . a sin b .
C. sin a b  sin .
a cos b  cos . a sin b .
D. cos a b  cos .
a cos b  sin . a sin b .
Câu 29: Chu kì tuần hoàn của hàm số y  sin 2x là A. 2 . B. . C. k 2 . D.  . 2 1 2
Câu 30: Cho các góc  ,  thỏa mãn
 ,    , sin  , cos    . Tính sin     . 2 3 3 2 2 10 2 10  2 5  4 2 5  4 2 A. . B. . C. . D. . 9 9 9 9
Câu 31: Phương trình sin 2x  3cos x  0 tương đương với phương trình nào dưới đây?
A. sin x  0.
B. sin x  1.
C. cos x  0.
D. cos x  1.
Câu 32: Một cơ sở khoan giếng có đơn giá như sau: giá của mét khoan đầu tiên là 40000 đồng và kể
từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 3% so với giá của mét khoan
ngay trước đó. Số tiền mà chủ nhà phải trả cho cơ sở khoan giếng để khoan được 50m
giếng gần nhất số nào sau đây? (đơn vị: đồng) A. 4176336 . B. 4341626 . C. 4511875 . D. 4 687 231 .
Câu 33: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả: Chiều cao 
158;160 160;162 162;168
150;152 152;154 154;156 156;158 (cm) Số học sinh 5 18 40 25 8 3 1
Mẫu số liệu trên có bao nhiêu nhóm? A. 7. B. 6. C. 5. D. 8.
Câu 34: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả: 160;162
Chiều cao (cm) 150;152 152;154 154;156 156;158 158;160 162;168 Số học sinh 5 18 40 25 8 3 1
Số học sinh có chiều cao trong khoảng 154;156 là A. 40. B. 18. C. 5. D. 8.
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A. Q  13.
B. Q  14 .
C. Q  15 . D. Q  12 . 3 3 3 3
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).   
1) (0,75 điểm). Tìm tập xác định của hàm số 4 y  2 tan 2x   .  3  u
  u u  7 
2) (0,75 điểm). Cho cấp số cộng u thỏa mãn 2 4 6 
. Tính S u u  ...  u . n u   u  2u  6 1 2 6 8 7 4   
Câu 2: (1,0 điểm). Giải phương trình: 1  tan x  2 2 sin x   .  4 
Câu 3: (0,5 điểm). Để tích lũy cho việc học đại học của con gái, cô Hoa quyết định hằng tháng
bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi 0,5% cộng dồn hằng tháng. Cô bắt
đầu chương trình tích lũy này khi con gái cô tròn 3 tuổi. Cô ấy sẽ tích lũy được bao nhiêu tiền
vào thời điểm gửi khoản tiền thứ 180? Lúc này con gái cô Hoa bao nhiêu tuổi?
____________________HẾT____________________
Huế, 14h40’ Ngày 27 tháng 8 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 01_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Cho góc hình học uOv có số đo bằng 30 (tham khảo hình vẽ). v 30o O u
Khẳng định nào sau đây đúng? A. s® ; Ou Ov  6  0 .  B. s® ; Ou Ov  30 .  C. s® ; Ou Ov  90 .  D. s® ; Ou Ov  3  0 .  n Câu 2:
Cho dãy số u , biết u u là n n
2n  . Ba số hạng đầu tiên của dãy số  n  1 1 2 3 1 1 1 1 2 3 A. ; ; . B. 1; ; . C. 1; ; . D. 1; ; . 2 3 4 2 16 4 8 3 7 Lời giải: 2 3 u  1,u  ,u  . 1 2 3 3 7 Câu 3:
Phương trình nào sau đây có nghiệm? 2
A. sin x  2. B. cos 2x  2  .
C. sin 3x  .
D. cos x  . 3 Lời giải: 2 2 Do   1  ;1 
 nên phương trình sin 3x  có nghiệm. 3 3 Câu 4:
Trong các dãy số sau, dãy số nào không phải cấp số cộng? 1 3 5 7 9 A. ; ; ; ; . B. 1;1;1;1;1 .
C. 8; 6; 4; 2; 0 .
D. 3;1; 1; 2; 4 . 2 2 2 2 2 Lời giải:
Cấp số cộng là một dãy số (hữu hạn hay vô hạn) mà trong đó kể từ số hạng thứ hai, mỗi số
hạng đều bằng tổng của số hạng đứng ngay trước nó và một số d không đổi. 1
Đáp án A: Là cấp số cộng với u  ; d  1 . 1 2
Đáp án B: Là cấp số cộng với u  1; d  0 . 1
Đáp án C: Là cấp số cộng với u  8; d  2 . 1
Đáp án D: Không là cấp số cộng vì u u  2
 ;u u  1  . 2 1   4 3   Câu 5:
Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y __ π 1 2 x O -1
Hỏi hàm số đó là hàm số nào? A. y  sin . x
B. y  sin . x C. y  cos . x
D. y  cos . x Lời giải:   
Kiểm tra các sự kiện: Đồ thị hàm số đi qua các điểm O0;0 , A ; 1   .  2  Câu 6:
Cho tam giác đều ABC (tham khảo hình vẽ). A B C
Khẳng định nào sau đây sai? A. s® A ; B AC  6
 0  k360,k  .
B. s® A ; B AC  3
 00  k360,k  .
C. s®  A ; B AC   300  . 
D. s® A ; B AC  60 .  Lời giải: s®A ;
B AC  60  k360 Các kết quả đúng:  , k  . s®   A ; B AC  3  00  k360 Câu 7:
Cho cấp số cộng u có u  3, u  27 . Tính công sai d . n  1 6
A. d  7 .
B. d  5 .
C. d  8 . D. d  6 . Lời giải:
Ta có u u  5d  27  d  6 . 6 1  Câu 8: x
là một nghiệm của phương trình nào dưới đây? 6 3
A. sin x  1. B. sin x  .
C. cot x  3.
D. tan x  3. 2 Lời giải:  Thay x
vào phương trình cot x  3 thấy thỏa mãn. 6 Câu 9:
Trong các dãy số u cho bởi số hạng tổng quát u sau, dãy số nào là dãy số giảm? n n 1 4 A. u  . B. u  3  . C. 2
u n .
D. u n  2 . n 2n n n 1 n n Lời giải: 1 1 Ta có u    u * n   . n   2n n 1 1 2 n 1
Câu 10: Tập xác định của hàm số y  là sin x A. D  \   0 . B. D 
\ k2 , k  . C. D 
\ k , k  . D. D  \ 0;. Lời giải: 1 Hàm số y
xác định khi và chỉ khi sin x  0  x k , k  . sin x
Câu 11: Nghiệm âm lớn nhất của phương trình 2 sin x  1  0 là 11     5   7   A. x  . B. x  . C. x  . D. x  . 6 6 6 6 Lời giải:   x   k2 1  Ta có: 6
2 sin x  1  0  sin x    , k  . 2  5 x   k2  6 5 7
Vậy nghiệm âm lớn nhất của phương trình đã cho là x 2     . 6 6
Câu 12: Cho dãy số u có 2
u  n n 1. Số 19 là số hạng thứ mấy của dãy u ? n n n A. 5 . B. 7 . C. 6 . D. 4 . Lời giải:
Giả sử u  19 ,  * n  . n Suy ra 2
n n 1  19  2
 n n  20  0 n  5   . n  4   l
Vậy số 19 là số hạng thứ 5 của dãy số.
Câu 13: Cho u là một cấp số cộng thỏa mãn u u  8 và u  10 . Công sai của cấp số cộng đã cho n  1 3 4 bằng? A. 3 . B. 6 . C. 2 . D. 4 . Lời giải: u   u  8 u
  u  2d  8
2u  2d  8 u  1 Ta có 1 3 1 1 1 1        . u  10 u  3d  10 u  3d  10    d  3 4 1 1
Vậy công sai của cấp số cộng là d  3 .
Câu 14: Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho AOM  60 (tham khảo hình vẽ). y M 60o x O A
Gọi N là điểm đối xứng với điểm M qua trục Oy , khẳng định nào sau đây đúng?
A. s®OA;ON  120  k360,k  .
B. s®OA;ON  1
 20  k360,k  .
C. s®OA;ON  240  k360,k  .
D. s®OA;ON  60  k360,k  . Lời giải: y N M 60o x O A s®O ;
A ON  120  k360
Ta có: AON  120   , k  . s®  O ; A ON  2  40  k360
Câu 15: Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng? A. 2
cos 2  1  2 cos  . B. 2 cos 2  2 sin   1. C. 2
cos 2  2 cos   1 . D. 2
cos 2  1  2 sin  .
Câu 16: Số nghiệm của phương trình 2 cos x  1  0 trên đoạn 0; 2    là A. 1. B. 3. C. 2. D. 4. Lời giải: Cách 1:  2 x   k2 1   Ta có: 3
2 cos x  1  0  cos x    , k  . 2  2   x   k2  3 2 +) Xét x
k2 ,k  . 3  2  1 2 0   k2  2   k  2 Do x  0; 2    nên  3   3 3  k  0   x  . 3 k k   2   +) Xét x
k2 ,k  . 3  2   1 4 0   k2  2   k  4 Do x  0; 2    nên  3  3 3  k  1   x  . 3 k k  
Cách 2: Dùng đường tròn lượng giác. y x O A
Câu 17: Cho cấp số nhân u với u  3 và u  6 . Công bội q của cấp số nhân đó là n  1 2 A. 2 . B. 2 . C. 9  . D. 9 . Lời giải: u 6 
Vì u là cấp số nhân nên 2 q    2  . n u 3 1
Câu 18: Cho mẫu số liệu ghép nhóm về chiều cao của 25 cây dừa giống, như sau:
Mốt của mẫu số liệu ghép nhóm này là 70 50 70 80 A. M  . B. M  . C. M  . D. M  . o 3 o 3 o 2 o 3 Lời giải:
Tần số lớn nhất là 7 nên nhóm chứa mốt là 20;30 .
Ta có: j  3 , a  20 , m  7 , m  6, m  5 , h  10 . 3 3 2 4 7  6 70 Do đó: M  20   . o     .10 7 6 7 5 3
Câu 19: Đổi số đo góc 115 sang rađian, ta được 23 23   13   13 A. rad. B. rad. C. rad. D. rad. 36 36 36 36 Lời giải:   5 11   23   Cách 1: Ta có: 115    rad rad.    180  36
Cách 2: Sử dụng MTCT
Câu 20: Tập giá trị của hàm số y  sin 2x là A. 2; 2   . B. . C. 1;1   . D. 0; 2   . Lời giải:
Ta có 1  sin 2x  1, x   .
Vậy tập giá trị của hàm số y  sin 2x là 1;1   .
Câu 21: Cho biết dãy số 1; 8;...; x là một cấp số cộng. Tìm x sao cho 1 8 15  22  x  7944 .
A. x  330 .
B. x  220 .
C. x  351 . D. x  407 . Lời giải:
Ta có cấp số cộng với u  1 , d  7 , u x , S  7944 . 1 n n Áp dụng công thức
2u n 1 d n
2.1 n 1 7 n  1        2 S   7944 
 7n  5n 15888  0 n 2 2
n  48 TM    331  . n    L  7
Vậy x u  1 47.7  330 . 48
Câu 22: Các cặp góc lượng giác nào dưới đây có cùng điểm biểu diễn trên đường tròn lượng giác?  2  2     5   4 A. và . B. và . C. và . D. và . 3 3 3 3 3 3 3 3 Lời giải: 5     Ta có:     2. 3  3  1
Câu 23: Tổng 10 số hạng đầu cấp số nhân (u ) với u
và công bội q  3 là: n 1 2 9841 3069 A. 14762 . B. . C. . D. 1640 . 2 512 Lời giải: 1 . 10 1 3  Ta có: 2 S   14762 10 1 . 3
Câu 24: Khẳng định nào sau đây đúng?
A. Các hàm số y  sin x , y  cos x , y  cot x đều là hàm số chẵn.
B. Các hàm số y  sin x , y  cos x , y  cot x đều là hàm số lẻ.
C. Các hàm số y  sin x , y  cot x , y  tan x đều là hàm số chẵn.
D. Các hàm số y  sin x , y  cot x , y  tan x đều là hàm số lẻ. Lời giải:
Ta có, các hàm số y  sin x , y  cot x , y  tan x là các hàm số lẻ, hàm số y  cos x là hàm số chẵn. 1 
Câu 25: Cho góc  thỏa mãn sin  với
   . Tính sin 2. 3 2 4  2 4 2 2  2 2 2 A. . B. . C. . D. . 9 9 9 9 Lời giải:  2 2 cos  8 Ta có: 2 2      3 cos  1 sin  . 9  2  2 cos   3  2 2 Do
    nên cos  0   chọn cos   . 2 3 4 2 Vậy sin 2 2sin cos    . 9
Câu 26: Cho cấp số nhân u có u  6 và q  2 . Tống n số hạng đầu tiên của cấp số nhân đã cho n  1 bằng 2046. Tìm . n A. n  9 . B. n  10 . C. n  11 . D. n  12 . Lời giải: n 1 nq 1 2 n n
Ta có 2046  S u   6  2 2    1   2
  1024  n 10 . n 1 1 q 1 2
Câu 27: Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm 60;80 là A. 40 . B. 70 . C. 60 . D. 30 . Lời giải: 60  80
Ta có giá trị đại diện là  70. 2
Câu 28: Với a,b là các góc bất kì. Trong các công thức sau, công thức nào đúng?
A. cos a b  cos .
a sin b  sin . a sin b .
B. sin a b  sin .
a cos b  cos . a sin b .
C. sin a b  sin .
a cos b  cos . a sin b .
D. cos a b  cos .
a cos b  sin . a sin b . Lời giải:
Theo công thức cộng ta có: sin a b  sin .
a cos b  cos . a sin b .
Câu 29: Chu kì tuần hoàn của hàm số y  sin 2x là A. 2 . B. . C. k 2 . D.  . 2 Lời giải: 2
Chu kì tuần hoàn của hàm số y  sin 2x là T    . 2  1 2
Câu 30: Cho các góc  ,  thỏa mãn
 ,    , sin  , cos    . Tính sin     . 2 3 3 2 2 10 2 10  2 5  4 2 5  4 2 A. . B. . C. . D. . 9 9 9 9 Lời giải: 1   1 sin   cos   1  3  9 Ta có:    . 2   4 cos    sin    1  3  9  2 2      cos  3 Vì  ,    nên  . 2  5 sin    3
Và: sin      sin.cos   sin .cos .     Suy ra:     1 2 5 2 2 sin             . 3  3  3 3   2 2 10 Vậy sin(   )  . 9
Câu 31: Phương trình sin 2x  3cos x  0 tương đương với phương trình nào dưới đây?
A. sin x  0.
B. sin x  1.
C. cos x  0.
D. cos x  1. Lời giải:
Ta có: sin 2x  3cos x  0  2sin xcos x  3cos x  0  cos x2sin x  3  0 cos x  0 cos x  0        x    x   cos x 0. 3 2 sin 3 0 sin v« nghiÖm  2
Câu 32: Một cơ sở khoan giếng có đơn giá như sau: giá của mét khoan đầu tiên là 40000 đồng và kể
từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 3% so với giá của mét khoan
ngay trước đó. Số tiền mà chủ nhà phải trả cho cơ sở khoan giếng để khoan được 50m
giếng gần nhất số nào sau đây? (đơn vị: đồng) A. 4176336 . B. 4341626 . C. 4511875 . D. 4 687 231 . Lời giải:
Đặt S là giá của mét khoan đầu tiên thì S  40 000 đồng. 1 1
Kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 3% so với giá của mét khoan ngay trước đó.
Suy ra S S S .3%  S (1 0, 03) . 2 1 1 1
Tương tự S S S .3%  S (1 0, 03) . 3 2 2 2
Vậy các giá trị S , S ,..., S lập thành một cấp số nhân có số hạng đầu S  40000 và công bội 1 2 50 1 q  1 0, 03 .
Gọi T là tổng số tiền mà chủ nhà phải thanh toán khi khoan 50m giếng, ta có: 10,0350 1
T S S  ...  S  40 000.  4511875 1 2 50 1 0, 03  (đồng) 1
Câu 33: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả: Chiều cao 
158;160 160;162 162;168
150;152 152;154 154;156 156;158 (cm) Số học sinh 5 18 40 25 8 3 1
Mẫu số liệu trên có bao nhiêu nhóm? A. 7. B. 6. C. 5. D. 8.
Câu 34: Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả: 160;162
Chiều cao (cm) 150;152 152;154 154;156 156;158 158;160 162;168 Số học sinh 5 18 40 25 8 3 1
Số học sinh có chiều cao trong khoảng 154;156 là A. 40. B. 18. C. 5. D. 8.
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A. Q  13.
B. Q  14 .
C. Q  15 . D. Q  12 . 3 3 3 3 Lời giải:
Cỡ mẫu : n  2  4  7  4  3  20 . x x
Tứ phân vị thứ ba Q là 15
16 . Do x , x đều thuộc nhóm 12;16 nên nhóm này chứa 3 2 15 16 Q . 3
Do đó: p  4 , a  12 , m  4 , m m m  2  4  7  13 , a a  4 . 4 4 1 2 3 5 4 3.20 13 Ta có: 4 Q  12  .4  14 . 3 4
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).   
1) (0,75 điểm). Tìm tập xác định của hàm số 4 y  2 tan 2x   .  3  Lời giải:      5 k
Hàm số xác định  cos 2x
 0  2x    k ,k  x   ,k    .  3  3 2 12 2 5 k 
Vậy tập xác định của hàm số là D  \  k  .  12 2  u
  u u  7 
2) (0,75 điểm). Cho cấp số cộng u thỏa mãn 2 4 6 
. Tính S u u  ...  u . n u   u  2u  6 1 2 6 8 7 4 Lời giải: u
  u u  7 
u d u  3d u  5d  7  u   d  7  u   5  2 4 6 1   1   1  Ta có: 1 1        . u   u  2u
u  7d u  6d  2 u  3d  
2u  5d  0 d  2 8 7 4  1   1   l  1 62u  5d 1  Vậy S   0. 6 2   
Câu 2: (1,0 điểm). Giải phương trình: 1  tan x  2 2 sin x   .  4  Lời giải:  
Điều kiện: x  \  kk  .  2  sin x Phương trình  1 
 2sinx  cosx  sinx  cosx2cosx 1  0 cos x   x    k  4
sin x  cos x  0     
x   k2 . 1  cos x   3  2  
x    k2  3
Đối chiếu điều kiện ta có nghiệm của phương trình là    x  
k ; x   k2 ; x    k2 ,k . 4 3 3
Câu 3: (0,5 điểm). Để tích lũy cho việc học đại học của con gái, cô Hoa quyết định hằng tháng
bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi 0,5% cộng dồn hằng tháng. Cô bắt
đầu chương trình tích lũy này khi con gái cô tròn 3 tuổi. Cô ấy sẽ tích lũy được bao nhiêu tiền
vào thời điểm gửi khoản tiền thứ 180? Lúc này con gái cô Hoa bao nhiêu tuổi? Lời giải:
Gọi u là số triệu đồng mà cô Hoa có trong chương trình tích lũy ở lần gửi thứ n (vào đầu n tháng thứ n ).
Kí hiệu: a  0,5 triệu đồng, r  0,5%.
Số tiền của cô Hoa trong chương trình ở đầu tháng 1 là u  . a 1
Số tiền của cô Hoa trong chương trình ở đầu tháng 2 là u u 1  r  . a 2 1   2
Số tiền của cô Hoa trong chương trình ở đầu tháng 3 là u u 1  r a a 1  r a 1  r  . a 3 2      
Tương tự cho các tháng tiếp theo, suy ra số tiền cô Hoa trong chương trình ở đầu tháng n là n n    r   r u ara r
a r a aa n  n 1  n 2   1  1 1  1 1 1 1 .  r . . 1  1 r 1 r180 1
Vào thời điểm gửi khoản tiền thứ 180, cô ấy sẽ tích lũy được u  . a  145,41 triệu 180 r đồng. 180
Khi đó, tuổi của con gái cô Hoa là 3   18 tuổi. 12
____________________HẾT____________________
Huế, 14h40’ Ngày 27 tháng 8 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 02_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ. NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Tập nghiệm của phương trình sin x  1  là      
A. S    k2 ,k  . B. S  
k2 ,k  .  2   2 
C. S  k2 ,k  .
D. S    k2 ,k  .
Câu 2: Cho dãy số có các số hạng đầu là: 9; 99; 999; 9999,… Số hạng tổng quát của dãy số này là n A. u  .
B. u  10n 1.
C. u  9n. D. u  9 . n n n 1 n n n
Câu 3: Cho cấp số cộng u với công sai d. Gọi S là tổng n số hạng đầu tiên của u Đẳng thức n  . n n nào dưới đây đúng?
n u u
n u u 1 n 1   1 n A. * S  ,n  . B. * S  ,n  . n 2 n 2
n u u 1 n nu u C. * S  ,n  . D. 1 n * S  ,n  . n 2 n 2  1
Câu 4: Cho góc  thỏa mãn 0   
và cos  . Tính sin. 2 3 2  2 2 2  2 2 A. . B. . C. . D. . 3 3 3 3
Câu 5: Cho cấp số nhân u với công bội q. Đẳng thức nào dưới đây đúng? n A. n * u
u .q ,n  . B. n * u
u q ,n  . n 1  1 n 1  1 C. n 1  * u
u .q ,n  . D. n 1  * u
u .q ,n  . n 1  1 n 1  1
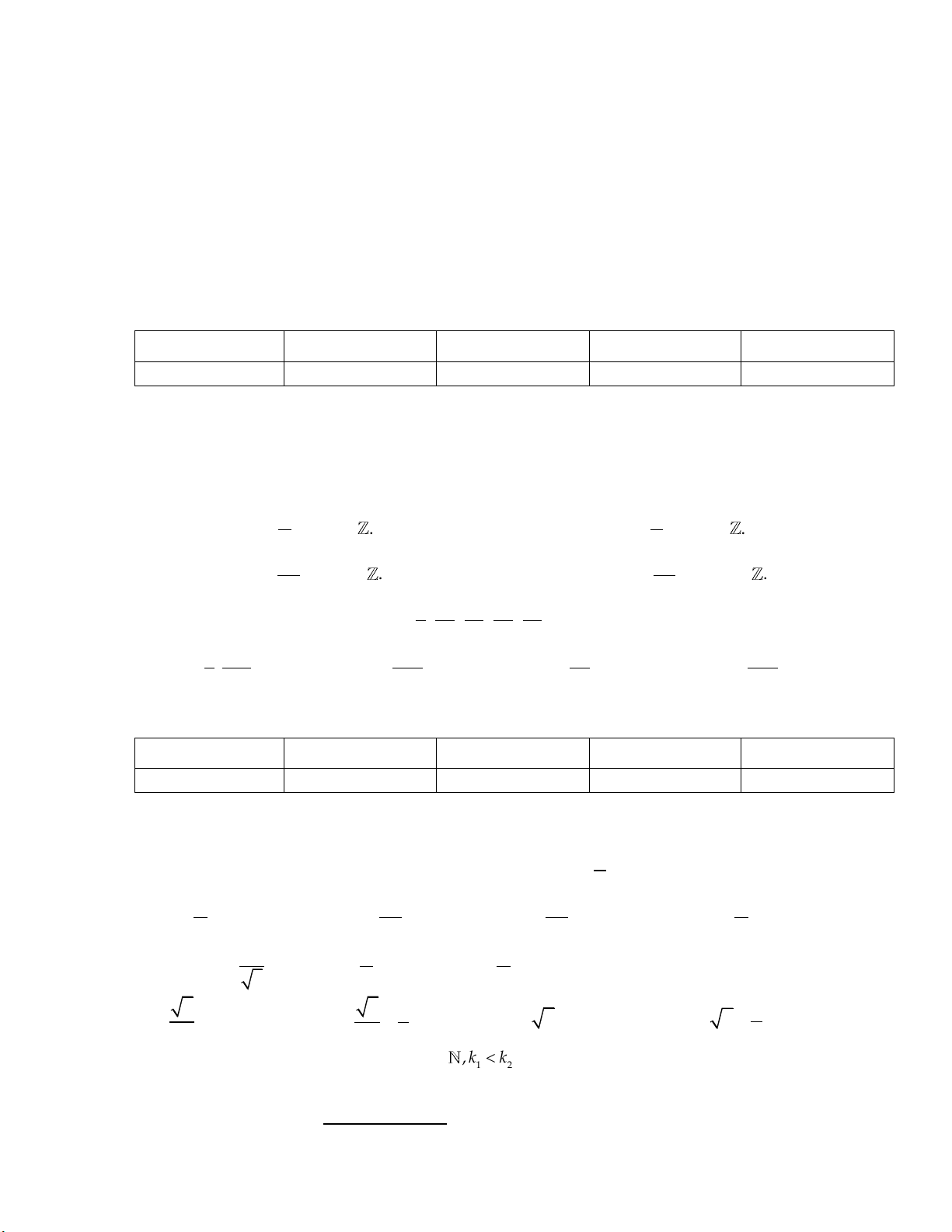
Câu 6: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y __ π 2 O 1 x -1
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  sin 2 . x C. y  cos . x D. y  cos 2 . x
Câu 7: Cho cấp số cộng u  : 1,4,7,.... Số hạng thứ 100 của cấp số cộng u là n n A. 297 . B. 301 . C. 295 . D. 298 .
Câu 8: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 đến dưới 20 phút? A. 25 . B. 14 . C. 13 . D. 6 . sin  sin 3
Câu 9: Rút gọn biểu thức  x x M
(với giả thiết biểu thức có nghĩa). 2cosx A. M  sin 4 . x B. M  sin . x C. M  sin 2 . x D. M  cos2 . x
Câu 10: Khẳng định nào dưới đây sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương.
Câu 11: Cho hình vuông ABCD tâm O (tham khảo hình vẽ). B A O C D
Khẳng định nào sau đây đúng?
A. s®OA;OB  9
 0 . B. s®OA;OB  180 . C. s®OA;OB  0 . D. s®OA;OB  270  . 
Câu 12: Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Tính trung vị của mẫu số liệu ghép nhóm này. A. 17,5. B. 19. C. 18, 4. D. 18,1.
Câu 13: Dãy số nào sau đây không phải là cấp số nhân?
A. 1; 1; 1; 1 .
B. 1;  3; 9;10 . C. 1; 0; 0; 0 . D. 32; 16; 8; 4 .
Câu 14: Cho hai góc nhọn  và  phụ nhau. Hệ thức nào sau đây sai?
A. sin   cos  .
B. cos  sin  .
C. cos   sin .
D. cot  tan  . 5  25 19
Câu 15: Cho bốn cung (trên một đường tròn định hướng):   ,   ,  ,  . Các 6 3 3 6
cung nào có điểm cuối trùng nhau?
A.  và  ;  và  . B.  và  ;  và  . C. ,  , . D.  , , .
Câu 16: Cho cấp số cộng u với u  5  2n . Tìm công sai của cấp số cộng đã cho. n n
A. d  3 .
B. d  2 .
C. d  1 . D. d  2 .
Câu 17: Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.  153, 58 . B.  153,18 . C.  153 . D.  154,1 . aa
Câu 18: Biết nghiệm dương nhỏ nhất của phương trình 2 cos x  3  0 có dạng
,a; b  , là phân b b
số tối giản. Tổng a b bằng A. 6. B. 8. C. 7. D. 9. 1
Câu 19: Cho dãy số u ,  n biết u
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào n n  1 dưới đây? 1 1 1 1 1 1 1 1 1 1 A. ; ; . B. 1; ; . C. ; ; . D. 1; ; . 2 3 4 2 3 2 4 6 3 5
Câu 20: Tập hợp các giá trị x thỏa mãn x, 2x, x  3 theo thứ tự lập thành một cấp số nhân là A. 0;  1 . B.  . C.   1 . D.   0 .
Câu 21: Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng? 2 tan
A. tan 2  2 tan. B. tan 2  . 2 1 tan  2 tan tan C. tan 2  . D. tan 2  . 2 1 tan  2 1 tan  3 Câu 22: Cho sin  . Tính cos 2 . 4 1 7 7 1 A. . B. . C.  . D.  . 8 4 4 8   
Câu 23: Biểu thức sin a  
 được viết lại thành  6  1 3 1 3 1 1 3
A. sin a  . B. sin a  cos a . C. sin a
cos a . D. sin a  cos a . 2 2 2 2 2 2 2 1 3
Câu 24: Cho hai góc lượng giác a,b thỏa mãn tan a  ; tan b
. Tính tan a b . 7 4 25 11 A. 2 . B.1. C. . D. . 28 3 2 x  1
Câu 25: Tập xác định của hàm số y  là cos x   A. D  .
B. D  \  k ,k   .  2  k  C. D  
\ k , k   . D. D  \ , k   .  2 
Câu 26: Số nghiệm của phương trình 2 sin 2x  1  0 trên đoạn 0; 2    là A. 1. B. 3. C. 2. D. 4.
Câu 27: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  8sin 2x  5 .
A. max y  11; min y  21  .
B. max y  8; min y  8  .
C. max y  4  ; min y  6  .
D. max y  3; min y  13  . sin x
Câu 28: Tập xác định của hàm số y  là 2 cos x  1 1    
A. D  \ .
B. D  \  k2 ;
m2 ,k,m . 2   3 3   5   5 
C. D  \  k2 ;
m2 ,k,m .
D. D  \  k ;
m ,k,m .  6 6   6 6 
Câu 29: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ? sin x 1
A. y  cot 4x . B. y  . C. 2
y  tan x .
D. y  cot x . cos x
Câu 30: Chu kỳ của hàm số y  5
 sin 2020x là   A. 1010 . B. 2 . C. . D. . 1010 2020
Câu 31: Tập hợp tất cả các giá trị của tham số m để phương trình sin x m  1 có nghiệm là A. 1;1.   B. 2; 2.   C. 0; 2.   D. 1  ;2.  
Câu 32: Cho cấp số nhân u với u  2 và công bội q  3 . Giá trị của u bằng n  1 2 2 A. 6 . B. 9 . C. 8 . D. . 3 sin 2x
Câu 33: Số nghiệm của phương trình  0 trên 0;3    là cos x  1 A. 7. B. 6. C. 4. D. 5.
Câu 34: Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào giảm? n n n  4  A. n u  .
B. u    1 5n
C. u  3n.
D. u n  4. n 1. n    n 3  n
Câu 35: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm [20; 40) là A. 10. B. 20. C. 30. D. 40.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất của hàm số y  5  4cos 2x  2. u   8u
2) (0,75 điểm). Cho cấp số nhân u thỏa mãn 20 17  . Tính u . n u   u  240  3 3 5    cos2x  1
Câu 2: (1,0 điểm). Giải phương trình 2 tan  x     3tan . x 2  2  cos x
Câu 3: (0,5 điểm). Một cầu thang bằng gạch có tổng cộng 30 bậc. Bậc dưới cùng cần 100 viên
gạch. Mỗi bậc tiếp theo cần ít hơn 2 viên gạch so với bậc ngay trước nó.
a) Cần bao nhiêu viên gạch cho bậc trên cùng?
b) Cần bao nhiêu gạch để xây cầu thang?
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 02_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O
Trưêng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 Hương Trà, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm)
Câu 1: Tập nghiệm của phương trình sin x  1  là      
A. S    k2 ,k  . B. S  
k2 ,k  .  2   2 
C. S  k2 ,k  .
D. S    k2 ,k  .
Câu 2: Cho dãy số có các số hạng đầu là: 9; 99; 999; 9999,… Số hạng tổng quát của dãy số này là n A. u  .
B. u  10n 1.
C. u  9n. D. u  9 . n n n 1 n n n Lời giải: Nhận xét: 1 u  10 1 ; 2 u  10 1; 3 u  10 1; 4 u  10 1. 1 2 3 4
Câu 3: Cho cấp số cộng u với công sai d. Gọi S là tổng n số hạng đầu tiên của u Đẳng thức n  . n n nào dưới đây đúng?
n u u
n u u 1 n 1   1 n A. * S  ,n  . B. * S  ,n  . n 2 n 2
n u u 1 n nu u C. * S  ,n  . D. 1 n * S  ,n  . n 2 n 2  1
Câu 4: Cho góc  thỏa mãn 0   
và cos  . Tính sin. 2 3 2  2 2 2  2 2 A. . B. . C. . D. . 3 3 3 3 Lời giải:  2 2 2 sin   1  8 Ta có: 2 2        3 sin  1 cos  1   .  3  9  2  2 sin   3  2 2 Do 0    nên chọn sin  . 2 3
Câu 5: Cho cấp số nhân u với công bội q. Đẳng thức nào dưới đây đúng? n A. n * u
u .q ,n  . B. n * u
u q ,n  . n 1  1 n 1  1 C. n 1  * u
u .q ,n  . D. n 1  * u
u .q ,n  . n 1  1 n 1  1
Câu 6: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y __ π 2 O 1 x -1
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  sin 2 . x C. y  cos . x D. y  cos 2 . x Lời giải:   
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm A ; 1   .  2 
Câu 7: Cho cấp số cộng u  : 1,4,7,.... Số hạng thứ 100 của cấp số cộng u là n n A. 297 . B. 301 . C. 295 . D. 298 . Lời giải:
Cấp số cộng 1,4,7,... . có số hạng đầu u  1 và công sai d  3 . 1
Số hạng thứ 100 của cấp số cộng là: u
u  99.d  1  99.3  298 . 100 1
Câu 8: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 đến dưới 20 phút? A. 25 . B. 14 . C. 13 . D. 6 . sin  sin 3
Câu 9: Rút gọn biểu thức  x x M
(với giả thiết biểu thức có nghĩa). 2cosx A. M  sin 4 . x B. M  sin . x C. M  sin 2 . x D. M  cos2 . x Lời giải: sin x  sin 3x sin 3x  sin x 2sin 2x cos x Ta có: M     sin 2x . 2cosx 2cosx 2cosx
Câu 10: Khẳng định nào dưới đây sai?
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
B. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
C. Một cấp số cộng có công sai dương là một dãy số tăng.
D. Một cấp số cộng có công sai dương là một dãy số dương. Lời giải:
A. Đúng vì dãy số đã cho là cấp số nhân với công bội q  1 .
B. Đúng vì dãy số đã cho là cấp số cộng với công sai d  0 .
C. Đúng vì dãy số đã cho là cấp số cộng có công sai dương nên: u
u d  0  u u . n 1  n n 1  n D. Sai. Ví dụ dãy 5  ; 2
 ; 1; 3 ; … là dãy số có d  3  0 nhưng không phải là dãy số dương.
Câu 11: Cho hình vuông ABCD tâm O (tham khảo hình vẽ). B A O C D
Khẳng định nào sau đây đúng?
A. s®OA;OB  9
 0 . B. s®OA;OB  180 . C. s®OA;OB  0 . D. s®OA;OB  270  .  Lời giải:
s®OA;OB  90  k360 Các kết quả đúng:  , k  . s®
 OA;OB  2  70  k360
Câu 12: Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Tính trung vị của mẫu số liệu ghép nhóm này. A. 17,5. B. 19. C. 18, 4. D. 18,1. Lời giải:
Cỡ mẫu là n  3 12 15  24  2  56 .
Gọi x ,, x là thời gian vào Internet của 56 học sinh và giả sử dãy này đã được sắp xếp theo 1 56 thứ tự tăng dần. x x Khi đó, trung vị là 28
29 . Do 2 giá trị x , x thuộc nhóm [15,5;18,5) nên nhóm này chứa 28 29 2 trung vị.
Do đó, p  3; a  15,5; m  15; m m  3 12  15; a a  3 3 3 1 2 4 3 56 15 và ta có 2 M  15, 5  3  18,1. e 15
Câu 13: Dãy số nào sau đây không phải là cấp số nhân?
A. 1; 1; 1; 1 .
B. 1;  3; 9;10 . C. 1; 0; 0; 0 . D. 32; 16; 8; 4 . Lời giải: u
Nếu u là cấp số nhân với công bội q ta có: 1 uu . n q q   . n n 1  n un 1; 1  ;1; 1
 là cấp số nhân với q  1. 1
 ;3;9;10 không là cấp số nhân.
1; 0; 0; 0 là cấp số nhân với q  0 . 1
32;16;8; 4 là cấp số nhân với q  . 2
Câu 14: Cho hai góc nhọn  và  phụ nhau. Hệ thức nào sau đây sai?
A. sin   cos  .
B. cos  sin  .
C. cos   sin .
D. cot  tan  . 5  25 19
Câu 15: Cho bốn cung (trên một đường tròn định hướng):   ,   ,  ,  . Các 6 3 3 6
cung nào có điểm cuối trùng nhau?
A.  và  ;  và  . B.  và  ;  và  . C. ,  , . D.  , , . Lời giải:
Ta có:    4  2 cung  và  có điểm cuối trùng nhau.
    8  hai cung  và  có điểm cuối trùng nhau.
Câu 16: Cho cấp số cộng u với u  5  2n . Tìm công sai của cấp số cộng đã cho. n n
A. d  3 .
B. d  2 .
C. d  1 . D. d  2 . Lời giải: Ta có u
u  5  2 n 1  5  2n  5  2n  2  5  2n  2   d  2. n 1  n     
Câu 17: Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.  153, 58 . B.  153,18 . C.  153 . D.  154,1 . Lời giải:
Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150; 155). Ta có, j  2, a  150, m  14 , 2 2
m  7, m  10, h  5 . 1 3 14  7 Do đó M  150  5 153,18. 0 (14  7)  (14  10) aa
Câu 18: Biết nghiệm dương nhỏ nhất của phương trình 2 cos x  3  0 có dạng
,a; b  , là phân b b
số tối giản. Tổng a b bằng A. 6. B. 8. C. 7. D. 9. Lời giải:   x   k2 3  Ta có: 6
2 cos x  3  0  cos x    , k  . 2    x   k2  6  a  1
Vậy nghiệm dương nhỏ nhất của phương trình đã cho là x    . 6 b   6 1
Câu 19: Cho dãy số u ,  n biết u
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào n n  1 dưới đây? 1 1 1 1 1 1 1 1 1 1 A. ; ; . B. 1; ; . C. ; ; . D. 1; ; . 2 3 4 2 3 2 4 6 3 5 Lời giải: 1 1 1 Ta có u  , u  , u  . 1 2 3 2 3 4
Câu 20: Tập hợp các giá trị x thỏa mãn x, 2x, x  3 theo thứ tự lập thành một cấp số nhân là A. 0;  1 . B.  . C.   1 . D.   0 . Lời giải:
Gọi q là công bội của cấp số nhân. 2x  . x q 2x  . x qq  2 Ta có:      x  3  2 . x q
x  3  2.2xx 1
Tập hợp các giá trị x thỏa mãn x, 2x, x  3 theo thứ tự lập thành một cấp số nhân là   1 .
Câu 21: Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng? 2 tan
A. tan 2  2 tan. B. tan 2  . 2 1 tan  2 tan tan C. tan 2  . D. tan 2  . 2 1 tan  2 1 tan  3 Câu 22: Cho sin  . Tính cos 2 . 4 1 7 7 1 A. . B. . C.  . D.  . 8 4 4 8 Lời giải: Ta có 2 cos 2  1 9 1 2 sin   1 2    . 16 8   
Câu 23: Biểu thức sin a  
 được viết lại thành  6  1 3 1 3 1 1 3
A. sin a  . B. sin a  cos a . C. sin a
cos a . D. sin a  cos a . 2 2 2 2 2 2 2 Lời giải:      3 1 Ta có sin a
 sin a cos  cos asin  sin a  cos a   .  6  6 6 2 2 1 3
Câu 24: Cho hai góc lượng giác a,b thỏa mãn tan a  ; tan b
. Tính tan a b . 7 4 25 11 A. 2 . B.1. C. . D. . 28 3 Lời giải: 1 3  tan a  tan b Ta có a b 7 4 tan    1. 1  tan . a tan b 1 3 1  . 7 4 2 x  1
Câu 25: Tập xác định của hàm số y  là cos x   A. D  .
B. D  \  k ,k   .  2  k  C. D  
\ k , k   . D. D  \ , k   .  2  Lời giải:
Điều kiện: cos x  0  x
k , k  . 2  
Vậy tập xác định của hàm số là D  \  k ,k   .  2 
Câu 26: Số nghiệm của phương trình 2 sin 2x  1  0 trên đoạn 0; 2    là A. 1. B. 3. C. 2. D. 4. Lời giải: Cách 1:     2x   k2 x    k 1  Ta có: 6 12
2 sin 2x  1  0  sin 2x      , k  . 2  5  5 2x   k2 x   k  6  12  +) Xét x
k ,k  . 12    1 23 0   k  2   k   13 Do x  0; 2    nên  12   12
12  k  0; k  1   x  ; x  . 12 12 k k   5 +) Xét x
k2 ,k  . 12  5  5 19 0   k  2   k  5 17 Do x  0; 2    nên  12   12
12  k  0; k  1   x  ; x  . 12 12 k k  
Cách 2: Dùng đường tròn lượng giác.
Ta có: x  0; 2   2x 0;4 .     y x O A
Câu 27: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  8sin 2x  5 .
A. max y  11; min y  21  .
B. max y  8; min y  8  .
C. max y  4  ; min y  6  .
D. max y  3; min y  13  . Lời giải: Ta có x
: 1  sin 2x  1  8
  8sin 2x  8  13
  8sin 2x  5  3
Vậy max y  3; min y  13  . sin x
Câu 28: Tập xác định của hàm số y  là 2 cos x  1 1    
A. D  \ .
B. D  \  k2 ;
m2 ,k,m . 2   3 3   5   5 
C. D  \  k2 ;
m2 ,k,m .
D. D  \  k ;
m ,k,m .  6 6   6 6  Lời giải:   x   k2 1  Hàm số xác định 3
 2cos x  1  0  cosx    ,k,m . 2   x   m2  3
Câu 29: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ? sin x 1
A. y  cot 4x . B. y  . C. 2
y  tan x .
D. y  cot x . cos x Lời giải:
Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Trong các hàm số trên, chỉ có hàm số y  cot 4x là hàm số lẻ.
Vậy, hàm số nào có đồ thị đối xứng qua gốc tọa độ là y  cot 4x .
Câu 30: Chu kỳ của hàm số y  5
 sin 2020x là   A. 1010 . B. 2 . C. . D. . 1010 2020 Lời giải: 2 
Chu kì của hàm số đã cho T   . 2020 1010
Câu 31: Tập hợp tất cả các giá trị của tham số m để phương trình sin x m  1 có nghiệm là A. 1;1.   B. 2; 2.   C. 0; 2.   D. 1  ;2.   Lời giải: Ta có: x
  : sin x  0;1.  
Phương trình sin x m  1 có nghiệm  0  m  1  1  1  m  2.
Câu 32: Cho cấp số nhân u với u  2 và công bội q  3 . Giá trị của u bằng n  1 2 2 A. 6 . B. 9 . C. 8 . D. . 3 Lời giải:
Ta có u u .q  2.3  6 . 2 1 sin 2x
Câu 33: Số nghiệm của phương trình  0 trên 0;3    là cos x  1 A. 7. B. 6. C. 4. D. 5. Lời giải:
Điều kiện: cos x  1. sin 2x k Ta có:
 0  sin2x  0  x  , k  . cos x  1 2 y x O A
Đối chiếu điều kiện, số nghiệm của phương trình đã cho trên 0; 3    là 5.
Câu 34: Trong các dãy số u
cho bởi số hạng tổng quát u sau, dãy số nào giảm? n n n  4  A. n u  .
B. u    1 5n
C. u  3n.
D. u n  4. n 1. n    n 3  n Lời giải: n 1  n n n n  4   4  4  4   4  1  4  Với A: Ta có: uu    .   .  0  loại A. n 1  n            3   3  3  3   3  3  3  n
Với B: Dãy u với u    1 5n
có các số hạng đan dấu nên dãy không tăng, không n 1. n  giảm  loại B. Với C: n 1 uu  3    3n  3
 .3n  3n  2
 .3n  0  Chọn C. n 1  n 1 Với D: u
u n  5  n  4   0  loại D. n 1  n
n  5  n  4
Câu 35: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm [20; 40) là A. 10. B. 20. C. 30. D. 40.
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất của hàm số y  5  4cos 2x  2. Lời giải: Ta có: x
  :  1  cos2x  1  3  5  4cos2x  2  5.
Suy ra: max y  5 khi cos 2x  1  x k , k  . u   8u
2) (0,75 điểm). Cho cấp số nhân u thỏa mãn 20 17  . Tính u . n u   u  240  3 3 5 Lời giải: 19 16 3 u   8u u
 q  8u q q  8 u   12 Ta có 20 17 1 1 1        . 2 4 2 4 u   u  240  u
 q u q  240 u
 q u q  240 q  2 3 5 1 1 1 1 Vậy 2
u u q  48. 3 1    cos2x  1
Câu 2: (1,0 điểm). Giải phương trình 2 tan  x     3tan . x 2  2  cos x Lời giải: sin x  0    Điều kiện: 
 sin2x  0  x \k k . cos x  0  2  2 2  sin x 2 2 2 (1)  cot x
 3tan x  cot x  2
 tan x  3tan x 2 cos x 2 1 2 3
 cot x  tan x  
 tan x  tan x  1   tan x  1  tan x
x    k ,k  . 4   
Đối chiếu điều kiện, phương trình đã cho có tập nghiệm là S    k ,k  .  4 
Câu 3: (0,5 điểm). Một cầu thang bằng gạch có tổng cộng 30 bậc. Bậc dưới cùng cần 100 viên
gạch. Mỗi bậc tiếp theo cần ít hơn 2 viên gạch so với bậc ngay trước nó.
a) Cần bao nhiêu viên gạch cho bậc trên cùng?
b) Cần bao nhiêu gạch để xây cầu thang? Lời giải:
Gọi số viên gạch cần xây cho bậc dưới cùng là u  100 1
Ta thấy Mỗi bậc tiếp theo cần ít hơn 2 viên gạch so với bậc ngay trước nó nên ta có
Bậc thứ 2 cần số viên gạch để xây là: u u  2 2 1
Bậc thứ 3 cần số viên gạch để xây là: u u  2 ….. 3 2
Như vậy dãy các số viên gạch ở mỗi bậc tạo thành một cấp số cộng có
u  100; d  2 1
a) Ta có: Bậc trên cùng là bậc 30 nên ta có áp dụng CT số hạng TQ của CSC ta có u u  29 2   42 . 30 1  
Vậy bậc trên cùng cần 42 viên gạch. 302u  29 2  1  
b) Ta có: S u u  ...  u   2130. 30 1 2 30 2
Vậy cần 2130 viên gạch để xây cầu thang.
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 03_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Cho dãy số u  : 2,8,32,128,512. u là một cấp số nhân với công bội là n n 1 1 A. q  . B. q  6 . C. q  4 . D. q  . 4 2 Câu 2:
Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho AOM  60 (tham khảo hình vẽ). y M 60o x O A
Gọi N là điểm đối xứng với điểm M qua trục Ox , khẳng định nào sau đây đúng?
A. s®OA;ON  120  k360,k  .
B. s®OA;ON  1
 20  k360,k  .
C. s®OA;ON  300  k360,k  .
D. s®OA;ON  60  k360,k  .  Câu 3: x
là một nghiệm của phương trình nào dưới đây? 3 1 3 A. sin x  1. B. sin x  . C. sin x  0. D. sin x  . 2 2 Câu 4:
Cho cấp số nhân u có u  108  và u  324. 
Khi đó, số hạng đầu u và công bội q là n  4 5 1
A. u  3, q  5  . B. u  3  , q  5.
C. u  4, q  3 .
D. u  4, q  3 . 1 1 1 1 Câu 5:
Cho cấp số cộng u có u  8 và d  3 . Tìm số hạng thứ ba của cấp số cộng u . n n  13 A. 50 . B. 28 . C. 38 . D. 44 . 1 cos x Câu 6:
Tập xác định của hàm số y  là sin x   A. D
\ k | k   . B. D
\   k | k   .  2    C. D
\ k 2 | k   . D. D
\   k2 | k   .  2  Câu 7:
Đổi số đo góc 105 sang rađian, ta được 5 7 9 5 A. rad. B. rad. C. rad. D. rad. 12 12 12 8 Câu 8:
Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng? A. 2 2
cos 2  cos   sin . B. 2 2
cos 2  cos   sin . C. 2 2
cos 2  2 cos   sin . D. 2 2
cos 2  2 cos   sin . 1 aa Câu 9:
Biết nghiệm dương bé nhất của phương trình sin x   có dạng
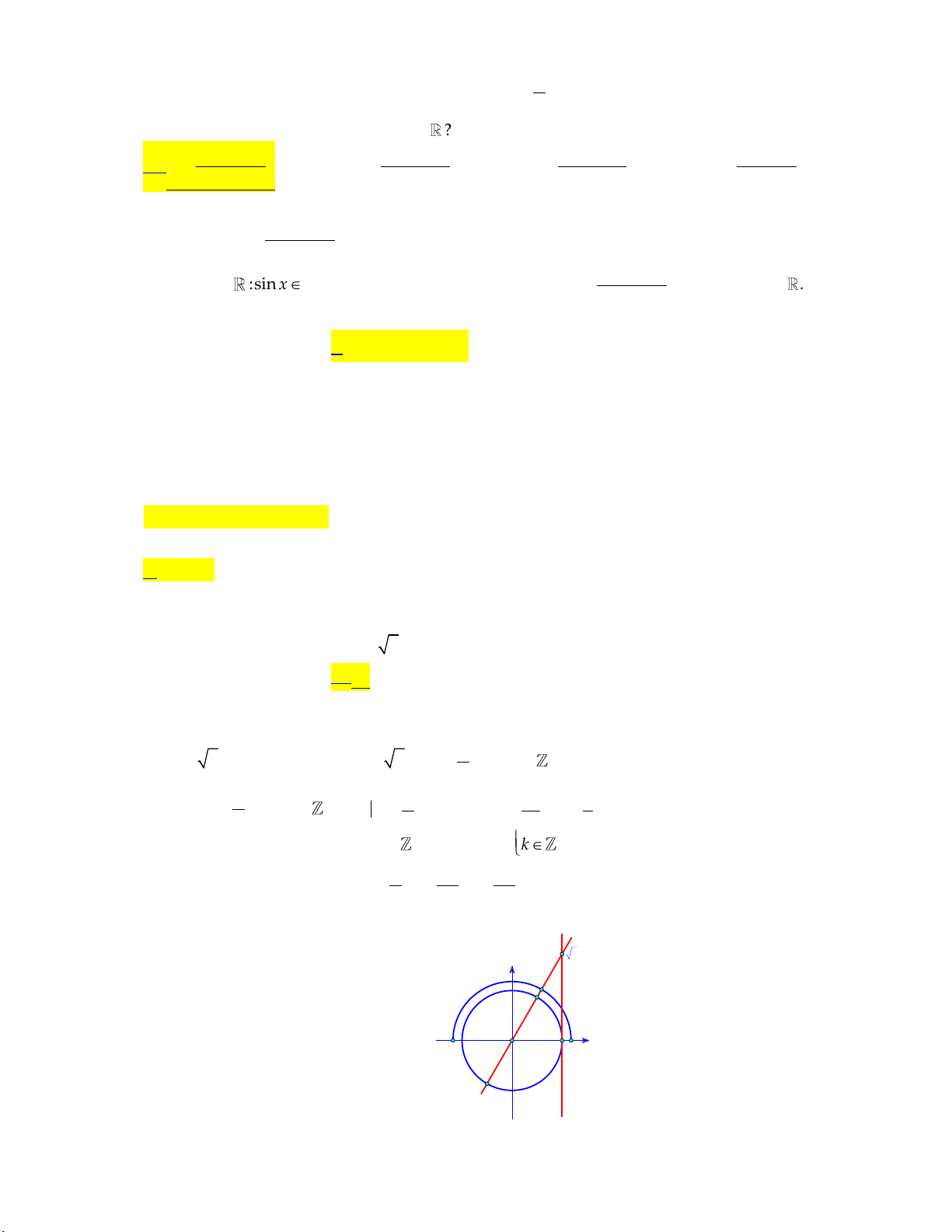
,a; b  , là phân số tối 2 b b giản. Tính a  . b A. 2. B. 10. C. 13. D. 8.
Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y  cos 3x .
B. y  cot 4x .
C. y  sin 2x .
D. y  tan 5x .
Câu 11: Biết trên đường tròn lượng giác có 4 điểm M, N, P,Q cùng là điểm biểu diễn các góc lượng k giác
, k  . Diện tích tứ giác MNPQ bằng 2 A. 2 2. B. 2. C. 4. D. 3 2. 5
Câu 12: Cho cấp số nhân u có u  5 và u  . Tổng 8 số hạng đầu tiên của cấp số nhân trên là n  1 2 2 123 342 1275 654 A. . B. . C. . D. . 23 67 128 231 1 3
Câu 13: Cho góc  thỏa mãn sin   , và     . Tính sin 2 . 3 2 7 4 2 4 2 2 A. . B. . C.  . D.  . 9 9 9 3
Câu 14: Cho dãy số u là một cấp số cộng có u  3 và công sai d  4 . Biết tổng n số hạng đầu của n  1
dãy số u là S  253 . Tìm n . n n A. 9 . B. 11. C. 12 . D. 10 .
Câu 15: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y -π O π -π __ 1 π x __ 2 2
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  tan . x C. y  cos . x D. y  cot . x
Câu 16: Hàm số nào dưới đây xác định trên ? 2  sin x 2  sin x 2  sin x 2  sin x A. y  . B. y  . C. y  . D. y  . 3  2 sin x 1  2 sin x 1  2 sin x sin x
Câu 17: Trong các dãy số sau đây, dãy số nào là cấp số cộng? nA. 2
u  3n  2017 .
B. u  3n  2018 .
C. u  3n . D. u  . n   1 3 n n n
Câu 18: Số a thỏa mãn có 25% giá trị trong mẫu số liệu nhỏ hơn a và 75% giá trị trong mẫu số liệu lớn hơn a là A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất.
D. Tứ phân vị thứ ba.
Câu 19: Cho dãy số u với u  2n 1, số hạng thứ 2019 của dãy là n n A. 4039 . B. 4390 . C. 4930 . D. 4093 .
Câu 20: Số nghiệm của phương trình 3 tan x  3  0 trên đoạn 0; 3    là A. 4. B. 3. C. 2. D. 5.
Câu 21: Mệnh đề nào dưới đây đúng với mọi a,b ?
A. cos(a b)  sin a sin b  cos a cos b .
B. cos(a b)  cos a cos b  sin a sin b .
C. cos(a b)  cos a cos b  sin a sin b .
D. cos(a b)  cos a sin b  sin a cos b .
Câu 22: Ông A gửi 120 triệu đồng tiền vào ngân hàng với lãi suất 6% / năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho
năm tiếp theo. Hỏi sau 10 năm, tổng số tiền mà ông A nhận được là bao nhiêu, giả định
trong khoảng thời gian này lãi suất không thay đổi và ông A không rút tiền ra? (Lấy kết quả
gần đúng đến hàng phần trăm)
A. 214,90 triệu đồng. B. 224,10 triệu đồng. C. 234,90 triệu đồng. D. 215,10 triệu đồng.
Câu 23: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Số trung bình của mẫu số liệu là A. 5,0. B. 5,32. C. 5,75. D. 6,5.
Câu 24: Giá trị lớn nhất của hàm số y  3sin x là A. 1. B. 2 . C. 3 . D. 3  .
Câu 25: Mệnh đề nào dưới đây đúng?  
A. cot x  1  x
k ,k  . B. cot x  1
  x   k ,k  . 4 4    
C. cot x  1  x
k ,k  . D. cot x  1   x
k2 ,k  . 4 4 1 1 1 1 1
Câu 26: Cho dãy số có các số hạng đầu là: ; ; ; ;
; … Tìm số hạng tổng quát của dãy số này. 3 32 33 34 35 1 1 1 1 1 A. u  . . B. u  . C. u  . D. u  . n n 1 3 3  n n 1 n n 3  n 3 n 1 3 
Câu 27: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Nhóm chứa trung vị của mẫu số liệu là A. 2; 3,5  . B. 3,5; 5  . C. 5; 6,5  . D. 6,5; 8  . 
Câu 28: Trên đường tròn bán kính r  5 , độ dài của cung đo   là 8  3 5  A. l  . B. l  . C. l  . D. l  . 8 8 8 4 1     Câu 29: Cho sin  với 0    . Tính cos   .   3 2  3  6 6 1 1 A.  3. B.  . C. 6  3 . D. 6  . 6 6 2 2
Câu 30: Nhóm số liệu rời rạc k k với k , k  , k k là nhóm các giá trị 1 2 1 2 1 2
A. k và k .
B. k  1,..., k .
C. k ,..., k  1.
D. k , k  1,...,k . 1 2 1 2 1 2 1 1 2 2sin 2  sin 4
Câu 31: Rút gọn biểu thức T
(với giả thiết biểu thức có nghĩa). 2sin 2  sin 4 A. 2 T  tan  . B. 2
T   tan  . C. 2
T  tan 2 . D. 2 T  cot  . x
Câu 32: Chu kỳ của hàm số y  3sin là 2 A. 0 . B. 2 . C. 4 . D.  .
Câu 33: Cho cấp số cộng u có u  3 và công sai d  7 . Kể từ số hạng nào trở đi thì các số hạng của n  1
u đều lớn hơn 2018 ? n A. 287 . B. 289 . C. 288 . D. 286 . tan x
Câu 34: Tập xác định của hàm số y  là 3 tan x  3     
A. D  \  k ,k  .
B. D  \  k ;  m ,k,m .  6   2 6        
C. D  \  k ;
m ,k,m .
D. D  \  k ;  m2 ,k,m .  2 6   2 6 
Câu 35: Tìm số hạng đầu u của cấp số nhân u biết rằng: u u u  21 và u u u  567 . n  1 1 2 3 4 5 6 21 13 A. 3 . B. . C. 9 D. . 13 21
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm). 1    
1) (0,75 điểm). Cho góc  thỏa mãn sin  và
   . Tính cos    . 3 2  3  S   12
2) (0,75 điểm). Cho cấp số cộng u thỏa mãn 3  . Tính u . n S   35  4 5
sin 2x  2cos x  sin x  1
Câu 2: (1,0 điểm). Giải phương trình:  0. tan x  3
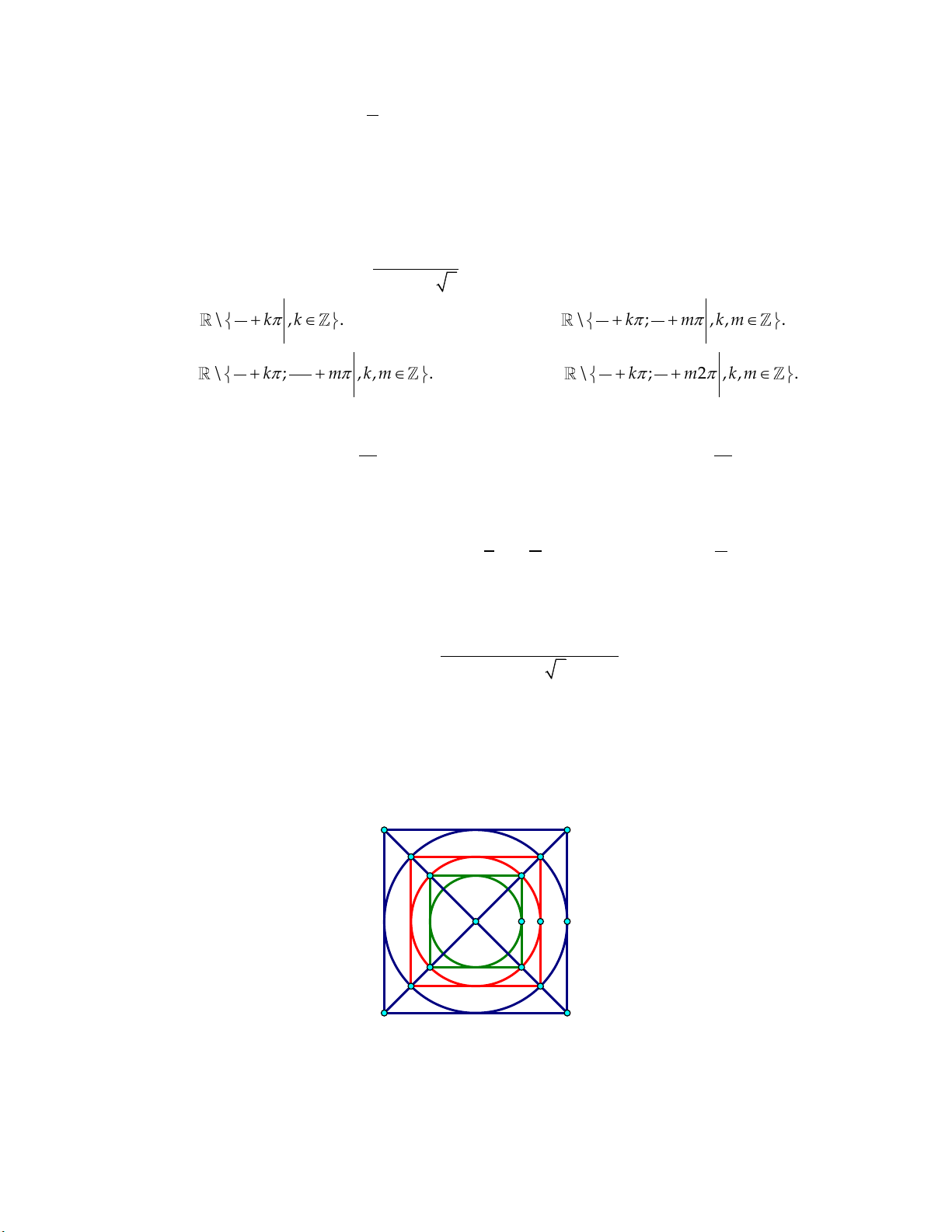
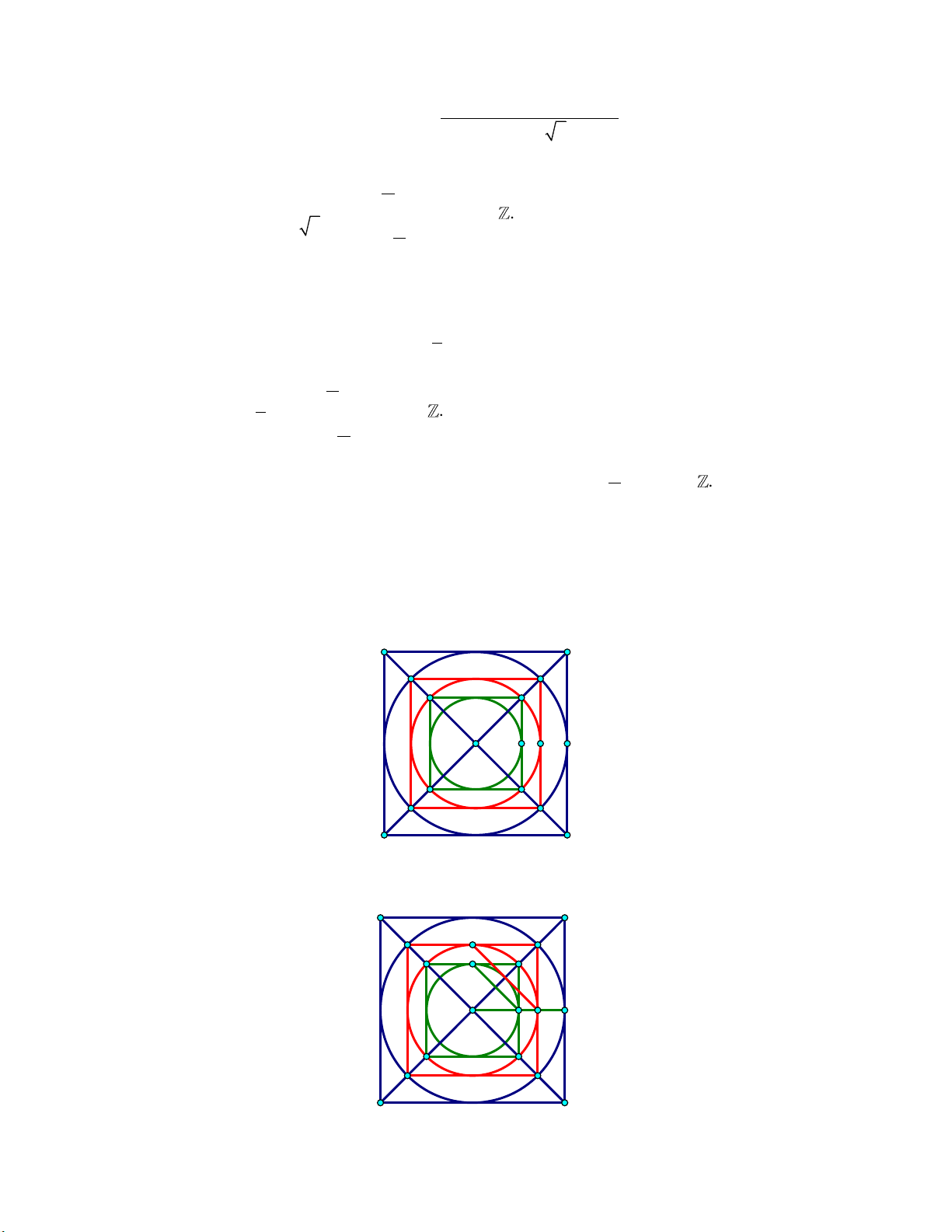
Câu 3: (0,5 điểm). Một tấm bìa hình vuông H có cạnh bằng 100, có diện tích S . Ta kẻ một 1  1
đường tròn C nội tiếp hình vuông H , có diện tích /
S . Ta dựng một hình vuông H 2  1  1  1
nội tiếp C , có diện tích S . Tiếp tục, ta kẻ một đường tròn C nội tiếp hình vuông H , 2  2  1  2 có diện tích /
S . Tiến hành thực hiện quá trình này 10 lần. 2
(xem hình vẽ minh họa).
Tính gần đúng tổng tất cả diện tích các hình vuông và hình tròn tạo thành theo quá trình trên.
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 03_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Cho dãy số u  : 2,8,32,128,512. u là một cấp số nhân với công bội là n n 1 1 A. q  . B. q  6 . C. q  4 . D. q  . 4 2 Lời giải: 8 32 128 512 Ta có:   
 4 nên dãy số đã cho là một cấp số nhân với công bội q  4 . 2 8 32 128 Câu 2:
Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho AOM  60 (tham khảo hình vẽ). y M 60o x O A
Gọi N là điểm đối xứng với điểm M qua trục Ox , khẳng định nào sau đây đúng?
A. s®OA;ON  120  k360,k  .
B. s®OA;ON  1
 20  k360,k  .
C. s®OA;ON  300  k360,k  .
D. s®OA;ON  60  k360,k  . Lời giải: y M 60o x O A N s®O ; A ON  6  0  k360
Ta có: AON  60   , k  . s®  O ;
A ON  300  k360  Câu 3: x
là một nghiệm của phương trình nào dưới đây? 3 1 3 A. sin x  1. B. sin x  . C. sin x  0. D. sin x  . 2 2 Lời giải:  3 Thay x
vào phương trình sin x  thấy thỏa mãn. 3 2 Câu 4:
Cho cấp số nhân u có u  108  và u  324. 
Khi đó, số hạng đầu u và công bội q là n  4 5 1
A. u  3, q  5  . B. u  3  , q  5.
C. u  4, q  3 .
D. u  4, q  3 . 1 1 1 1 Lời giải: Ta có: 3
u u . q và 4
u u . q . Chia vế theo vế hai đẳng thức trên, ta được 4 1 5 1 3 u u . q 1 1  08 1 4 1      q  3 4 u u . q q 3  24 q 5 1 Khi đó, 3 3
u u . q  1
 08  u . 3  u  4  . 4 1 1 1
Vậy cấp số nhân u có số hạng đầu u  4 và q  3. n  1 Cách khác: u 324  Ta có 5 q    3
u u . q  1
 08  u . 3  u  4  . u 108  . Ta có 3 3 4 1 1 1 4 Câu 5:
Cho cấp số cộng u có u  8 và d  3 . Tìm số hạng thứ ba của cấp số cộng u . n n  13 A. 50 . B. 28 . C. 38 . D. 44 . Lời giải:
Ta có: u u 12d  8  u 12. 3 
u  44  u u  2d  44  6  38. 1   13 1 1 3 1 1 cos x Câu 6:
Tập xác định của hàm số y  là sin x   A. D
\ k | k   . B. D
\   k | k   .  2    C. D
\ k 2 | k   . D. D
\   k2 | k   .  2  Lời giải:
Điều kiện sin x  0  x k , k  .
Tập xác định D
\ k | k   . Câu 7:
Đổi số đo góc 105 sang rađian, ta được 5 7 9 5 A. rad. B. rad. C. rad. D. rad. 12 12 12 8 Lời giải: 105  7
Cách 1: Ta có: 105  rad rad.    180  12
Cách 2: Sử dụng MTCT Câu 8:
Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng? A. 2 2
cos 2  cos   sin . B. 2 2
cos 2  cos   sin . C. 2 2
cos 2  2 cos   sin . D. 2 2
cos 2  2 cos   sin . 1 aa Câu 9:
Biết nghiệm dương bé nhất của phương trình sin x   có dạng
,a; b  , là phân số tối 2 b b giản. Tính a  . b A. 2. B. 10. C. 13. D. 8. Lời giải:    x   k2 1  Ta có: 6 sin x     , k  . 2  7 x   k2  6 7 a  7
Vậy nghiệm dương bé nhất của phương trình là x    
a b  13. 6 b   3
Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y  cos 3x .
B. y  cot 4x .
C. y  sin 2x .
D. y  tan 5x . Lời giải:
Xét hàm số y f x  cos3x có tập xác định D
+) Với mọi x D  x D
+) f x  cos  3
x  cos3x f x
Suy ra y  cos 3x là hàm số chẵn.
Câu 11: Biết trên đường tròn lượng giác có 4 điểm M, N, P,Q cùng là điểm biểu diễn các góc lượng k giác
, k  . Diện tích tứ giác MNPQ bằng 2 A. 2 2. B. 2. C. 4. D. 3 2. Lời giải:
Các điểm M, N, P,Q như hình bên dưới: y N M x P O Q
Tứ giác MNPQ là hình vuông cạnh  S   2 2 2  2. MNPQ 5
Câu 12: Cho cấp số nhân u có u  5 và u  . Tổng 8 số hạng đầu tiên của cấp số nhân trên là n  1 2 2 123 342 1275 654 A. . B. . C. . D. . 23 67 128 231 Lời giải: 5 1
Theo công thức số hạng tổng quát của cấp số nhân, ta có: u u . q
 5. q q  . 2 1 2 2 1
Vậy cấp số nhân u có số hạng đầu u  5 và q  . Gọi S là tổng 8 số hạng đầu của cấp số n  1 2 nhân trên. 8  1    5 1        2    1275 Ta được S   . 1 128 1 2 1 3
Câu 13: Cho góc  thỏa mãn sin   , và     . Tính sin 2 . 3 2 7 4 2 4 2 2 A. . B. . C.  . D.  . 9 9 9 3 Lời giải: 1 2 2 Ta có: 2
sin    cos   1 sin    3 3 3 2 2
Theo giả thiết:      cos   2 3  1  2 2  4 2
Vậy sin 2  2sin .cos  2.         .  3  3 9  
Câu 14: Cho dãy số u là một cấp số cộng có u  3 và công sai d  4 . Biết tổng n số hạng đầu của n  1
dãy số u là S  253 . Tìm n . n n A. 9 . B. 11. C. 12 . D. 10 . Lời giải:
n 2u n 1 d
n 2.3  n 1 .4 1        Ta có S    253 n 2 2 n  11(TM ) 2 4n 2n 506 0       23  . n   L  2
Vậy n  11 .
Câu 15: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y -π O π -π __ 1 π x __ 2 2
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  tan . x C. y  cos . x D. y  cot . x Lời giải:   
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm A ;0 và hàm số không xác định tại x .  2 
Câu 16: Hàm số nào dưới đây xác định trên ? 2  sin x 2  sin x 2  sin x 2  sin x A. y  . B. y  . C. y  . D. y  . 3  2 sin x 1  2 sin x 1  2 sin x sin x Lời giải: 2  sin x Xét hàm số y  . 3  2 sin x 2  sin x Ta có: x   :sin x  1
 ;1  3  2sin x 1  ;5.     Suy ra: y  xác định trên . 3  2 sin x
Câu 17: Trong các dãy số sau đây, dãy số nào là cấp số cộng? nA. 2
u  3n  2017 .
B. u  3n  2018 .
C. u  3n . D. u  . n   1 3 n n n Lời giải: Ta có u
u  3(n 1)  2018  (3n  2018)  3  u u  3 . n 1  n n 1  n
Vậy dãy số trên là cấp số cộng có công sai d  3 .
Câu 18: Số a thỏa mãn có 25% giá trị trong mẫu số liệu nhỏ hơn a và 75% giá trị trong mẫu số liệu lớn hơn a là A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất.
D. Tứ phân vị thứ ba.
Câu 19: Cho dãy số u với u  2n 1, số hạng thứ 2019 của dãy là n n A. 4039 . B. 4390 . C. 4930 . D. 4093 . Lời giải: Ta có: u  2.2019 1  4039 . 2019
Câu 20: Số nghiệm của phương trình 3 tan x  3  0 trên đoạn 0; 3    là A. 4. B. 3. C. 2. D. 5. Lời giải: Cách 1:
Ta có: 3 tan x  3  0  tan x  3  x   k ,k 3      1  8
x   k ,k
0   k  3   k  Ta có:  3   3   3 3  k 0;1;  2 . x0;3  k k       4 7
Phương trình có nghiệm là x  ; x  ; x  . 3 3 3
Cách 2: Dùng đường tròn lượng giác 3 y x O 1
Câu 21: Mệnh đề nào dưới đây đúng với mọi a,b ?
A. cos(a b)  sin a sin b  cos a cos b .
B. cos(a b)  cos a cos b  sin a sin b .
C. cos(a b)  cos a cos b  sin a sin b .
D. cos(a b)  cos a sin b  sin a cos b . Lời giải:
Vì theo công thức cộng, thì cos(a b)  cos a cos b  sin a sin b .
Câu 22: Ông A gửi 120 triệu đồng tiền vào ngân hàng với lãi suất 6% / năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho
năm tiếp theo. Hỏi sau 10 năm, tổng số tiền mà ông A nhận được là bao nhiêu, giả định
trong khoảng thời gian này lãi suất không thay đổi và ông A không rút tiền ra? (Lấy kết quả
gần đúng đến hàng phần trăm)
A. 214,90 triệu đồng. B. 224,10 triệu đồng. C. 234,90 triệu đồng. D. 215,10 triệu đồng. Lời giải:
Ta có a  120 triệu đồng.
Đặt T là số tiền nhận được sau n năm. n
Sau 1 năm số tiền có được (cả gốc và lãi ) là T a  .6
a %  a 1 0, 06 . 1  
Sau 2 năm số tiền có được là T a 1 0,062 . 2
Gọi T là tổng tiền mà A nhận được sau 10 năm. T a   10 10 1 0, 06 120.1.06  214,90 .
Câu 23: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Số trung bình của mẫu số liệu là A. 5,0. B. 5,32. C. 5,75. D. 6,5.
Câu 24: Giá trị lớn nhất của hàm số y  3sin x là A. 1. B. 2 . C. 3 . D. 3  . Lời giải:
Hàm số y  sin x có tập giá trị là  1  ;  1 .
Do đó 3  3sin x  3, x  . 
Vậy giá trị lớn nhất của hàm số y  3sin x là 3, xảy ra khi sin x  1  x
k2 ,k  . 2
Câu 25: Mệnh đề nào dưới đây đúng?  
A. cot x  1  x
k ,k  . B. cot x  1
  x   k ,k  . 4 4    
C. cot x  1  x
k ,k  . D. cot x  1   x
k2 ,k  . 4 4 1 1 1 1 1
Câu 26: Cho dãy số có các số hạng đầu là: ; ; ; ;
; … Tìm số hạng tổng quát của dãy số này. 3 32 33 34 35 1 1 1 1 1 A. u  . . B. u  . C. u  . D. u  . n n 1 3 3  n n 1 n n 3  n 3 n 1 3  Lời giải: 1 1 1 1 1 1 5 số hạng đầu là ; ; ; ; ;... nên u  . 1 2 3 4 5 3 3 3 3 3 n 3n
Câu 27: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Nhóm chứa trung vị của mẫu số liệu là A. 2; 3,5  . B. 3,5; 5  . C. 5; 6,5  . D. 6,5; 8  . 
Câu 28: Trên đường tròn bán kính r  5 , độ dài của cung đo   là 8  3 5  A. l  . B. l  . C. l  . D. l  . 8 8 8 4 Lời giải: 5
Độ dài cung AB : l r.  . 8 1     Câu 29: Cho sin  với 0    . Tính cos   .   3 2  3  6 6 1 1 A.  3. B.  . C. 6  3 . D. 6  . 6 6 2 2
Lời giải:  Vì 0     cos  0 . 2 2 Ta có: 2 2 2 2 sin   o c s   1  o
c s   1 sin   6  cos  . 3 3      cos      cos.cos  6 1 1 3 6 1 sin .sin  .  .   .  3  3 3 3 2 3 2 6 2
Câu 30: Nhóm số liệu rời rạc k k với k , k  , k k là nhóm các giá trị 1 2 1 2 1 2
A. k và k .
B. k  1,..., k .
C. k ,..., k  1.
D. k , k  1,...,k . 1 2 1 2 1 2 1 1 2 2sin 2  sin 4
Câu 31: Rút gọn biểu thức T
(với giả thiết biểu thức có nghĩa). 2sin 2  sin 4 A. 2 T  tan  . B. 2
T   tan  . C. 2
T  tan 2 . D. 2 T  cot  . Lời giải: 2sin 2  sin 4 2sin 2  2sin 2cos2 2sin 2 1 cos2  2 sin  Ta có: T     2  tan  2sin 2  sin 4 2sin 2  2sin 2cos2 2sin 2 1 cos2  2 cos  x
Câu 32: Chu kỳ của hàm số y  3sin là 2 A. 0 . B. 2 . C. 4 . D.  . Lời giải: 2
Chu kì của hàm số T   4 . 1 2
Câu 33: Cho cấp số cộng u có u  3 và công sai d  7 . Kể từ số hạng nào trở đi thì các số hạng của n  1
u đều lớn hơn 2018 ? n A. 287 . B. 289 . C. 288 . D. 286 . Lời giải:
Ta có: u u n 1 d  3  7 n   1  7n  4 ; n 1  
u  2018  7n  4  2022 2018  n  . n 7
Vậy n  289 . tan x
Câu 34: Tập xác định của hàm số y  là 3 tan x  3     
A. D  \  k ,k  .
B. D  \  k ;  m ,k,m .  6   2 6        
C. D  \  k ;
m ,k,m .
D. D  \  k ;  m2 ,k,m .  2 6   2 6  Lời giải:      cos   0 x k x  Hàm số xác định 2     , k,m .
3tan x  3  0 
x   m  6
Câu 35: Tìm số hạng đầu u của cấp số nhân u biết rằng: u u u  21 và u u u  567 . n  1 1 2 3 4 5 6 21 13 A. 3 . B. . C. 9 D. . 13 21 Lời giải: 2 2 u
  u u  21 u
  u .q u .q  21  u
  u .q u .q  21 1 1 1  1 1 1 Ta có: 1 2 3     
u u u  567  3 q  3 2   2
u u .q u .q  567 q
 u u .q u .q  567 1 1 1  1 1 1  4 5 6   2 q 3 u
 u .q u .q  21 q  3  1 1 1       21 . 3 q .21 567 2
u u .3  u .3  21  u  1 1 1  1  13
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm). 1    
1) (0,75 điểm). Cho góc  thỏa mãn sin  và
   . Tính cos    . 3 2  3  Lời giải:  2 2 cos  8 Ta có: 2 2      3 cos  1 sin  . 9  2  2 cos   3  2 2 Do
    nên cos  0   chọn cos   . 2 3      2  2 1 1 3  3  2 2 Lúc đó: cos  
 cos cos  sin sin  .  .    .  3  3 3 3 2 3 2 6 S   12
2) (0,75 điểm). Cho cấp số cộng u thỏa mãn 3  . Tính u . n S   35  4 5 Lời giải: 3
 2u  2d  12 1  S   12 
2u  2d  8 u   1 Ta có: 3  2 1 1       . S   35  5 
2u  4d  14 d  3 5 2u  4d 1  35 1 2
Vậy u u  3d  10. 4 1
sin 2x  2cos x  sin x  1
Câu 2: (1,0 điểm). Giải phương trình:  0. tan x  3 Lời giải:      cos   0 x k x  Điều kiện: 2    , k,m . tan x   3 
x    m  3
(1)  sin 2x  2 cos x  sin x  1  0  2 cos xsin x  1  sin x  1  0 sin x  
1 ( lo¹i do ®k cos x  0 )  
 sin x  12cosx 1  0  1  cos x   2   x   k2 1  Ta xét: 3 cos x    , k  . 2   x    k2  3 
Đối chiếu điều kiện, ta có nghiệm của phương trình là: x
k2 ,k  . 3
Câu 3: (0,5 điểm). Một tấm bìa hình vuông H có cạnh bằng 100, có diện tích S . Ta kẻ một 1  1
đường tròn C nội tiếp hình vuông H , có diện tích /
S . Ta dựng một hình vuông H 2  1  1  1
nội tiếp C , có diện tích S . Tiếp tục, ta kẻ một đường tròn C nội tiếp hình vuông H , 2  2  1  2 có diện tích /
S . Tiến hành thực hiện quá trình này 10 lần. 2
(xem hình vẽ minh họa).
Tính gần đúng tổng tất cả diện tích các hình vuông và hình tròn tạo thành theo quá trình trên. Lời giải: D A A2 A1 O B C
+) Hình vuông H có cạnh a  100  Diện tích là 2 S a . 1  1 1 1 a 2  a
+) Đường tròn C có bán kính 1 r   Diện tích là / 1 S  . 1  1 2 1 4 1 2 a
+) Hình vuông H có cạnh a a 2  Diện tích là 1 S  . 2  2 1 2 2 2 a a 2 2  a
+) Đường tròn C có bán kính 2 1 r    Diện tích là / 1 S  . 2  2 2 4 2 8 1 a 2 a
+) Hình vuông H có cạnh 1 a a 2   Diện tích là 1 S  . 3  3 2 2 2 3 4 a a 2  a
+) Đường tròn C có bán kính 3 1 r    Diện tích là / 1 S  . 3  3 2 4 3 16 Vậy tổng cần tìm là    a a a    aaaa T
S S S  ...  S   S S S  ...  S  2 2 2 2 2 2 2 / / / / 2 1 1 1 1 1 1 1  a    ...       ...  1 2 3 10 1 2 3 10 1  9   11 2 4 2 4 8 16 2      10 10  1   1  1  1       1 1 1   1 1 1 1   2  1  2  2 2 2 2
a 1   ...    a    ...  a .1.   a . .      35673. 1 9 1 11 1 1  2 4 2   4 8 16 2  1 4 1 1  1  2 2
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 04_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Cho cấp số nhân (u ) với u  3 và công bội q  4 . Giá trị của u bằng n 1 2 3 A. 64 . B. 81. C. 12 . D. . 4 Câu 2:
Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho AOM  60 (tham khảo hình vẽ). y M 60o x O A
Gọi N là điểm đối xứng với điểm M qua gốc O , khẳng định nào sau đây đúng?
A. s®OA;ON  120  k360,k  .
B. s®OA;ON  1
 20  k360,k  .
C. s®OA;ON  2
 40  k360,k  .
D. s®OA;ON  60  k360,k  . 1 1  1 1  1 Câu 3: Dãy số , , , ,
là một cấp số nhân với công bội là 3 6 12 24 48 1  1 1 A. q  . B. q  2 . C. q  . D. q  . 2 4 2 Câu 4:
Trong các dãy số sau, dãy số nào là một cấp số cộng?
A. 1; 2; 4; 6; 8 . B. 1; 3  ; 6  ; 9  ; 12  . C. 1; 3  ; 7  ; 11  ; 15
 . D. 1;3;5;7;9 . Câu 5:
Số a thỏa mãn có 75% giá trị trong mẫu số liệu nhỏ hơn a và 25% giá trị trong mẫu số liệu lớn hơn a là A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất.
D. Tứ phân vị thứ ba. Câu 6:
Mệnh đề nào dưới đây đúng?
A. Hàm số y  cot x là hàm số chẵn.
B. Hàm số y  sin x là hàm số chẵn.
C. Hàm số y  tan x là hàm số chẵn.
D. Hàm số y  cos x là hàm số chẵn. Câu 7:
Cho cấp số nhân u có u  3 và q  2 . Tống n số hạng đầu tiên của cấp số nhân đã cho n  1 bằng -1533. Tìm . n A. n  9 . B. n  10 . C. n  11 . D. n  12 . 2021 Câu 8:
Tập xác định của hàm số y là 1  cos xk  A. D  \ , k  . B. D  
\ k2 , k  .  2   
C. D  \  k ,k  . D. D  
\ k , k  .  2  Câu 9:
Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây sai? A. 2 cos 2  1 2 sin . B. 2 2
cos 2  cos   sin .
C. cos 2  cos  sin . D. 2 cos 2  2 cos  1.
Câu 10: Cho dãy số có các số hạng đầu là: 5;10;15; 20; 25;... Số hạng tổng quát của dãy số này là
A. u  5(n 1) .
B. u  5n .
C. u  5  n .
D. u  5n 1 . n n n n
Câu 11: Cho cấp số nhân u có u  6 và q  2 . Tống n số hạng đầu tiên của cấp số nhân đã cho n  1 bằng 2046. Tìm . n A. n  9 . B. n  10 . C. n  11 . D. n  12 .
Câu 12: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y π __ O 2 1 x
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  sin 2 . x C. y  cos . x D. y  cos 2 . x
Câu 13: Cho cấp số cộng u với u  2 và u  8 . Công sai của cấp số cộng đã cho bằng n  1 2 A. 10 . B. 6 . C. 4 . D. 6  .
Câu 14: Mẫu số liệu ghép nhóm với tần số các nhóm bằng nhau có số mốt là A. 0. B. 1. C. 2. D. 3.
Câu 15: Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày (nghĩa là sau 138 ngày khối
lượng của nguyên tố đó chỉ còn một nửa). Khối lượng còn lại của 200 gam poloni 210 sau
1656 ngày gần nhất với số nào dưới đây? (đơn vị: gam) A. 0, 0244 . B. 0, 0488 . C. 0, 0977 . D. 0,1025 . 2
Câu 16: Góc có số đo đổi sang độ là 5 A. 240 .  B. 135 .  C. 72 .  D. 270 .    Câu 17: x
là một nghiệm của phương trình nào dưới đây? 6 1 1  A. cos x  1. B. cos x  . C. sin x  1. D. sin x  . 2 2
Câu 18: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu là A. 2; 3,5  . B. 3,5; 5  . C. 5; 6,5  . D. 6,5; 8  .
Câu 19: Trên đường tròn bán kính r  15 , độ dài của cung có số đo   50 là 180 15 25
A. l  750 . B. l  15.  l   . C. l . D. . 180 6
Câu 20: Xác định số hàng đầu u và công sai d của cấp số cộng u có u  5u và u  2u  5 n  1 9 2 13 6
A. u  3 và d  4 .
B. u  3 và d  5 .
C. u  4 và d  5 .
D. u  4 và d  3 . 1 1 1 1
Câu 21: Cho dãy số u với u  2n 1. Khẳng định nào dưới đây đúng? n n
A. u bị chặn trên bởi 1.
B.u giảm. n n
C.u bị chặn dưới bởi 2. D.u tăng. n n  1 
Câu 22: Cho góc  thỏa mãn sin  và 0    . Tính tan 2. 3 2 2  2 2 2 4  2 4 2 A. . B. . C. . D. . 7 7 7 7 aa
Câu 23: Biết nghiệm âm lớn nhất của phương trình tan x  3 có dạng
,a; b  , là phân số tối b b giản. Tính a  . b A. 2. B. 10. C. 5. D. 8.   2
Câu 24: Cho góc  thỏa mãn
   0 và cos  . Tính sin. 2 3 2  2 5  2  5 A. . B. . C. . D. . 3 3 3 3
Câu 25: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Số mốt của mẫu số liệu ghép nhóm này là A. 0. B. 1. C. 2. D. 3.
Câu 26: Hàm số y  cos x nghịch biến trên khoảng nào dưới đây?           A.  ;   . B.   ;   .
C. 0;  . D.  ;0   .  2 2   2   2 
Câu 27: Trong các công thức sau, công thức nào đúng?
A. cos a – b  cos .
a cos b  sin . a sin b .
B. cos a b  cos .
a cos b  sin . a sin b .
C. sin a – b  sin .
a cos b  cos . a sin b .
D. sin a b  sin .
a cos b  cos.sin b . 3     Câu 28: Cho sin  và
    . Giá trị của tan     bằng 5 2  4  1 1 A. . B.  . C. 7  . D. 7 . 7 7
Câu 29: Mệnh đề nào dưới đây đúng?   
A. sin x  1  x
k ,k  . B. sin x  1   x
k ,k  . 2 2    
C. sin x  1  x
k2 ,k  . D. sin x  1   x
k2 ,k  . 2 2 1
cos 5x  cos 3x
Câu 30: Biết tan x  , tính giá trị của biểu thức I  . 3
sin 5x  sin 3x 1 1 A. I  . B. I   . C. I  3 . D. I  3 . 3 3
Câu 31: Hàm số nào dưới đây có tập xác định khác với tập xác định các hàm số còn lại? 1 1 A. y  tan . x B. y  . C. y  cot . x D. y  . cos x 2 1  sin x sin x
Câu 32: Tập xác định của hàm số y  là 2 sin x  1      5 
A. D  \  k2 ;
m2 ,k,m .
B. D  \  k2 ;
m2 ,k,m .  6 6   6 6   5   2 
C. D  \  k ;
m ,k,m .
D. D  \  k2 ;
m2 ,k,m .  6 6   3 3 
Câu 33: Giá trị lớn nhất và nhỏ nhất của hàm số là y  2  sin x lần lượt là A. 1 và 3 . B. 4 và 4  . C. 2 và 4 . D. 3 và 1.
Câu 34: Số nghiệm của phương trình 2
16  x cos x  0 là A. 4. B. 3. C. 2. D. 5.
Câu 35: Cho cấp số cộng u có u  1 và công sai d  2 . Tổng S u u u .....  u bằng: n  1 10 1 2 3 10
A. S  110 .
B. S  100 .
C. S  21. D. S  19 . 10 10 10 10
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Giải phương trình 2 sin x  2cos x  2  sin 2 . x
2) (0,75 điểm). Cho một cấp số nhân có bảy số hạng, số hạng thứ tư bằng 6 và số hạng thứ bảy
gấp 243 lần số hạng thứ hai. Hãy tìm số hạng thứ hai của cấp số nhân đó.
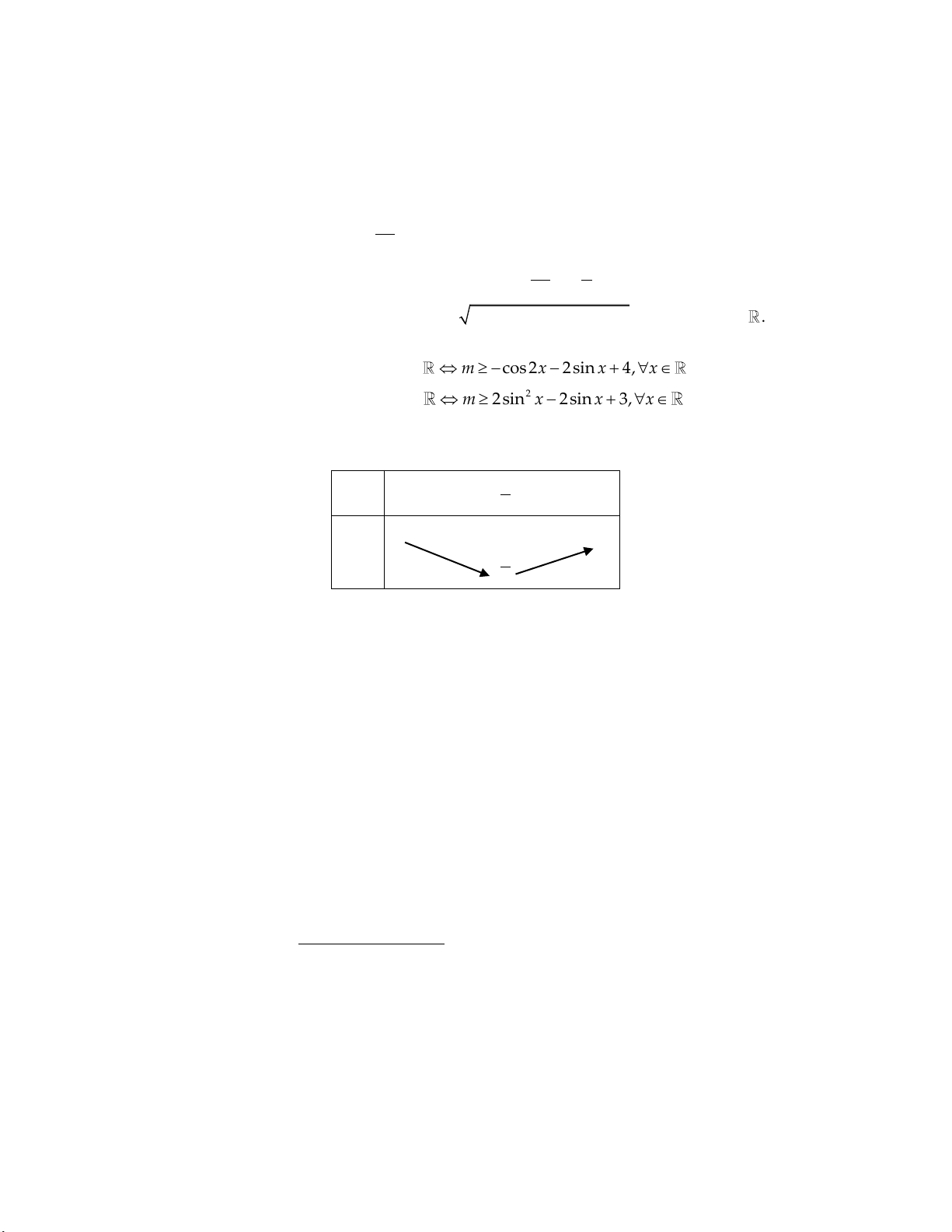
Câu 2: (1,0 điểm). Tìm m để hàm số y  cos 2x  2sin x  4  m xác định trên .
Câu 3: (0,5 điểm). Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với
mức lương khởi điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm,
thì sẽ mất bao nhiêu năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la?
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 04_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Cho cấp số nhân (u ) với u  3 và công bội q  4 . Giá trị của u bằng n 1 2 3 A. 64 . B. 81. C. 12 . D. . 4 Lời giải:
Ta có: u u .q  3.4  12 . 2 1 Câu 2:
Trên đường tròn với điểm gốc là A . Điểm M thuộc đường tròn sao cho AOM  60 (tham khảo hình vẽ). y M 60o x O A
Gọi N là điểm đối xứng với điểm M qua gốc O , khẳng định nào sau đây đúng?
A. s®OA;ON  120  k360,k  .
B. s®OA;ON  1
 20  k360,k  .
C. s®OA;ON  2
 40  k360,k  .
D. s®OA;ON  60  k360,k  . Lời giải: y M 60o x O A N s®O ; A ON  1  20  k360
Ta có: AON  120   , k  . s®  O ;
A ON  240  k360 1 1  1 1  1 Câu 3: Dãy số , , , ,
là một cấp số nhân với công bội là 3 6 12 24 48 1  1 1 A. q  . B. q  2 . C. q  . D. q  . 2 4 2 Lời giải: 1  1 1  1 1  1  Ta có: 6 12 24 48     q  . 1 1  1 1 
nên dãy số đã cho là một cấp số nhân với công bội 2 2 3 6 12 24 Câu 4:
Trong các dãy số sau, dãy số nào là một cấp số cộng?
A. 1; 2; 4; 6; 8 . B. 1; 3  ; 6  ; 9  ; 12  . C. 1; 3  ; 7  ; 11  ; 15
 . D. 1;3;5;7;9 . Lời giải:
Dãy số u có tính chất u
u d thì được gọi là một cấp số cộng. n n 1  n Ta thấy dãy số: 1; 3  ; 7  ; 11  ; 15
 là một cấp số cộng có số hạng đầu là u 1 và công sai 1 d  4 . Câu 5:
Số a thỏa mãn có 75% giá trị trong mẫu số liệu nhỏ hơn a và 25% giá trị trong mẫu số liệu lớn hơn a là A. Số trung bình. B. Số trung vị.
C. Tứ phân vị thứ nhất.
D. Tứ phân vị thứ ba. Câu 6:
Mệnh đề nào dưới đây đúng?
A. Hàm số y  cot x là hàm số chẵn.
B. Hàm số y  sin x là hàm số chẵn.
C. Hàm số y  tan x là hàm số chẵn.
D. Hàm số y  cos x là hàm số chẵn. Lời giải:
Xét hàm số y  cos x có tập xác định D  . Câu 7:
Cho cấp số nhân u có u  3 và q  2 . Tống n số hạng đầu tiên của cấp số nhân đã cho n  1 bằng -1533. Tìm . n A. n  9 . B. n  10 . C. n  11 . D. n  12 . Lời giải: 1 nq 1 2n  Ta có 1533   S u   3   32n     1 n 9
 2  512  2  n  9 . n 1 1 q 1 2 2021 Câu 8:
Tập xác định của hàm số y là 1  cos xk  A. D  \ , k  . B. D  
\ k2 , k  .  2   
C. D  \  k ,k  . D. D  
\ k , k  .  2  Lời giải:
Hàm số xác định khi cos x  1  x k2 , k  . Câu 9:
Với  là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây sai? A. 2 cos 2  1 2 sin . B. 2 2
cos 2  cos   sin .
C. cos 2  cos  sin . D. 2 cos 2  2 cos  1.
Câu 10: Cho dãy số có các số hạng đầu là: 5;10;15; 20; 25;... Số hạng tổng quát của dãy số này là
A. u  5(n 1) .
B. u  5n .
C. u  5  n .
D. u  5n 1 . n n n n Lời giải: Ta có: 5  5.1 10  5.2 15  5.3 20  5.4 25  5.5
Suy ra số hạng tổng quát u  5n (chứng minh được bằng phương pháp quy nạp toán học) n
Câu 11: Cho cấp số nhân u có u  6 và q  2 . Tống n số hạng đầu tiên của cấp số nhân đã cho n  1 bằng 2046. Tìm . n A. n  9 . B. n  10 . C. n  11 . D. n  12 . Lời giải: n 1 nq 1 2 n n
Ta có 2046  S u   6  2 2    1   2
  1024  n 10 . n 1 1 q 1 2
Câu 12: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y π __ O 2 1 x
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  sin 2 . x C. y  cos . x D. y  cos 2 . x Lời giải:   
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm O0;0 , A ;0.  2 
Câu 13: Cho cấp số cộng u với u  2 và u  8 . Công sai của cấp số cộng đã cho bằng n  1 2 A. 10 . B. 6 . C. 4 . D. 6  . Lời giải:
Vì u là cấp số cộng nên ta có u u d d u u  8  2  6 . n  2 1 2 1
Câu 14: Mẫu số liệu ghép nhóm với tần số các nhóm bằng nhau có số mốt là A. 0. B. 1. C. 2. D. 3.
Câu 15: Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày (nghĩa là sau 138 ngày khối
lượng của nguyên tố đó chỉ còn một nửa). Khối lượng còn lại của 200 gam poloni 210 sau
1656 ngày gần nhất với số nào dưới đây? (đơn vị: gam) A. 0, 0244 . B. 0, 0488 . C. 0, 0977 . D. 0,1025 . Lời giải:
Kí hiệu u (gam) là khối lượng còn lại của 200 gam poloni sau n chu kì bán rã. n 1656 Ta có 1656 ngày gồm
12 chu kì bán rã. 138
Như thế, khối lượng còn lại của 200 gam poloni 210 sau 1656 ngày (12 chu kì) là u . 12
Vì cứ sau một chu kì thì khối lượng của nguyên tố phóng xạ poloni 210 chỉ còn một nửa nên 200 1
ta suy ra dãy số (u ) là một cấp số nhân với số hạng đầu u
100 và công bội q  . n 1 2 2 11  1  Do đó u  100.  0,0488 (gam). 12    2  2
Câu 16: Góc có số đo đổi sang độ là 5 A. 240 .  B. 135 .  C. 72 .  D. 270 .  Lời giải: o 2  2.180  Cách 1: Ta có:   2 7 .    5  5 
Cách 2: Sử dụng MTCT   Câu 17: x
là một nghiệm của phương trình nào dưới đây? 6 1 1  A. cos x  1. B. cos x  . C. sin x  1. D. sin x  . 2 2 Lời giải:   1  Thay x
vào phương trình sin x  thấy thỏa mãn. 6 2
Câu 18: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu là A. 2; 3,5  . B. 3,5; 5  . C. 5; 6,5  . D. 6,5; 8  .
Câu 19: Trên đường tròn bán kính r  15 , độ dài của cung có số đo   50 là 180 15 25
A. l  750 . B. l  15.  l   . C. l . D. . 180 6 Lời giải: 5  Ta có: 0 50  25  l   r  . 18 6
Câu 20: Xác định số hàng đầu u và công sai d của cấp số cộng u có u  5u và u  2u  5 n  1 9 2 13 6
A. u  3 và d  4 .
B. u  3 và d  5 .
C. u  4 và d  5 .
D. u  4 và d  3 . 1 1 1 1 Lời giải:
Ta có: u u n 1 d . n 1   u  5u
u  8d  5 u   d      1  1  4u 3d 0 u 3 Theo đề bài ta có: 9 2    1 1     . u  2u  5 
u 12d  2 u  5d  5  u  2d  5   d  4 1  1  13 6 1
Câu 21: Cho dãy số u với u  2n 1. Khẳng định nào dưới đây đúng? n n
A. u bị chặn trên bởi 1.
B.u giảm. n n
C.u bị chặn dưới bởi 2. D.u tăng. n n Lời giải: * n   ta có: u
u  2 n 1 1 2n 1  2  0 nên u u vậy dãy số u tăng. n n 1  n     n 1  n 1 
Câu 22: Cho góc  thỏa mãn sin  và 0    . Tính tan 2. 3 2 2  2 2 2 4  2 4 2 A. . B. . C. . D. . 7 7 7 7 Lời giải:  2 2 cos  8 Ta có: 2 2      3 cos  1 sin  . 9  2  2 cos   3  2 2 Do 0    nên cos  0   chọn cos  . 2 3 sin 2 2 tan 4 2 Suy ra: tan   . Vậy tan 2   . cos 4 2 1  tan  7 aa
Câu 23: Biết nghiệm âm lớn nhất của phương trình tan x  3 có dạng
,a; b  , là phân số tối b b giản. Tính a  . b A. 2. B. 10. C. 5. D. 8. Lời giải:
Ta có: tan x  3  x
k ,k  . 3  2   a  2
Vậy nghiệm âm lớn nhất của phương trình là x      
a b  5. 3 3 b   3   2
Câu 24: Cho góc  thỏa mãn
   0 và cos  . Tính sin. 2 3 2  2 5  2  5 A. . B. . C. . D. . 3 3 3 3 Lời giải:  5 2 sin   2  5 Ta có: 2 2        3 sin  1 cos  1   .  3  9   5 sin   3   5 Do
   0 nên sin  0  chọn sin   . 2 3
Câu 25: Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau: Tuổi thọ 2;3,5   3,5;5   5;6,5   6,5;8   Số bóng đèn 8 22 35 15
Số mốt của mẫu số liệu ghép nhóm này là A. 0. B. 1. C. 2. D. 3.
Câu 26: Hàm số y  cos x nghịch biến trên khoảng nào dưới đây?           A.  ;   . B.   ;   .
C. 0;  . D.  ;0   .  2 2   2   2  Lời giải:
Hàm số y  cos x nghịch biến trên 0;  .
Câu 27: Trong các công thức sau, công thức nào đúng?
A. cos a – b  cos .
a cos b  sin . a sin b .
B. cos a b  cos .
a cos b  sin . a sin b .
C. sin a – b  sin .
a cos b  cos . a sin b .
D. sin a b  sin .
a cos b  cos.sin b . 3     Câu 28: Cho sin  và
    . Giá trị của tan     bằng 5 2  4  1 1 A. . B.  . C. 7  . D. 7 . 7 7 Lời giải:  Vì
    , nên cos  0 . 2 9 4 sin  3 Vậy 2
cos   1  sin    1    , suy ra tan    . 25 5 cos 4  3 tan  tan 1     1 Mặt khác 4 4 tan        .  4   3 7 1  tan . tan  1  4 4
Câu 29: Mệnh đề nào dưới đây đúng?   
A. sin x  1  x
k ,k  . B. sin x  1   x
k ,k  . 2 2    
C. sin x  1  x
k2 ,k  . D. sin x  1   x
k2 ,k  . 2 2 1
cos 5x  cos 3x
Câu 30: Biết tan x  , tính giá trị của biểu thức I  . 3
sin 5x  sin 3x 1 1 A. I  . B. I   . C. I  3 . D. I  3 . 3 3 Lời giải: 2 cos 4x cos x 1 Ta có I   cot x   3 . 2 cos 4x sin x tan x
Câu 31: Hàm số nào dưới đây có tập xác định khác với tập xác định các hàm số còn lại? 1 1 A. y  tan . x B. y  . C. y  cot . x D. y  . cos x 2 1  sin x Lời giải:  
Các hàm số ở các phương án A, B, D có tập xác định là \  kk  .  2 
Hàm số ở phương án C là 
\ kk  . sin x
Câu 32: Tập xác định của hàm số y  là 2 sin x  1      5 
A. D  \  k2 ;
m2 ,k,m .
B. D  \  k2 ;
m2 ,k,m .  6 6   6 6   5   2 
C. D  \  k ;
m ,k,m .
D. D  \  k2 ;
m2 ,k,m .  6 6   3 3  Lời giải:   x   k2 1  Hàm số xác định 6
 2sin x  1  0  sin x    , k,m . 2 5 x   m2  6
Câu 33: Giá trị lớn nhất và nhỏ nhất của hàm số là y  2  sin x lần lượt là A. 1 và 3 . B. 4 và 4  . C. 2 và 4 . D. 3 và 1. Lời giải: Ta có x
: 1   sin x  1  1  2  sin x  3  1  y  3 . 
Suy ra, max y  3 khi sin x  1
  x    k2 ,k  . 2 
và min y  1 khi sin x = 1  x
k2 ,k  . 2
Câu 34: Số nghiệm của phương trình 2
16  x cos x  0 là A. 4. B. 3. C. 2. D. 5. Lời giải: Điều kiện: 2
16  x  0  x   4  ;4.   2 1  6  x  0 Ta có: 2
16  x cos x  0   . cos x   0 +) 2
16  x  0  x  4 (thỏa mãn điều kiện)        4   4  cosx  0
x   k ,k   4    k  4  +) 2 2    2   2    k   k  1  ;  0 . x   4   ; 4      x 4  ;4     k   k    3 
Vậy phương trình có tập nghiệm là S   4  ;4; ; .  2 2 
Câu 35: Cho cấp số cộng u có u  1 và công sai d  2 . Tổng S u u u .....  u bằng: n  1 10 1 2 3 10
A. S  110 .
B. S  100 .
C. S  21. D. S  19 . 10 10 10 10 Lời giải: 10 2  10   1 .2   Ta có: S  100 10 . 2
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Giải phương trình 2 sin x  2cos x  2  sin 2 . x Lời giải:
Điều kiện: x  .
Phương trình  2 sin xcos x  2 2 cos x  2 sin x  2  0   x  
 sin x  2 2cosx  2 sin 2 (v« nghiÖm)  0   2 cos x   (nhËn)  2  3 x   k2 2  Ta có: 4 cos x     , k  . 2  3 x    k2  4 3 3   
Vậy tập nghiệm của phương trình là S    k2 ;
k2 k  .  4 4 
2) (0,75 điểm). Cho một cấp số nhân có bảy số hạng, số hạng thứ tư bằng 6 và số hạng thứ bảy
gấp 243 lần số hạng thứ hai. Hãy tìm số hạng thứ hai của cấp số nhân đó. Lời giải:
Gọi cấp số nhân cần tìm là u , u , u , ..., u với công bội q . 1 2 3 7 3 u   6 u  q  6 (1)
Theo giả thiết, ta có hệ phương trình: 4 1    . 6 u    243u u
 q  243u q (2) 7 2 1 1 Xét (2): 6 5
u q  243u q q  243  q  3 1 1
(Do u  0 và q  0 không thỏa mãn điều kiện ban đầu) 1 6
Thay q  3 vào (1), ta có: u  . 1 27 6 2
Vậy số hạng thứ hai của cấp số nhân là u u q  .3  . 2 1 27 3
Câu 2: (1,0 điểm). Tìm m để hàm số y  cos 2x  2sin x  4  m xác định trên . Lời giải:
Ta có: cos 2x  2sin x  4  m  0, x
   m  cos2x  2sin x  4, x    m   2  x 2 1 2 sin
 2sin x  4, x
   m  2sin x  2sin x  3, x   (*)
Đặt t  sin x;t   1  ;1. 
 Xét hàm số gt 2
 2t  2t  3,t   1  ;1.   Bảng biến thiên: t 1 1 1 2 7 g t 5 3 2
Dựa vào BBT, (*)  m  max g t  7. t 1  ;1  
Câu 3: (0,5 điểm). Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với
mức lương khởi điểm là 35000 đô la mỗi năm và được tăng thêm 1400 đô la lương mỗi năm,
thì sẽ mất bao nhiêu năm làm việc để tổng lương mà anh Nam nhận được là 319200 đô la? Lời giải:
Gọi u là lương anh Nam nhận được ở năm thứ n n
Ta có: Lương khởi điểm là 35000 đô la mỗi năm nên u  35000 1
Mỗi năm và được tăng thêm 1400 đô la lương mỗi năm nên * u u
1400,n  2,n N n n 1 
Như vậy dãy số tiền lương của anh Nam nhận được qua các năm là u ;u ;u ;,,,,,u là một 1 2 3 n
cấp số cộng có u  35000; d  1400 . 1
Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng với
S  319200;u  35000; d  1400. n 1
n2u n 1 1400 1     n8(TM)
Ta có: 319200  S   n  2 n    57 ( ) L
Vậy sau 8 năm làm việc thì tổng lương mà anh Nam nhận được là 319200 đô la.
____________________ HẾT ____________________
Huế, 17h00’ Ngày 01 tháng 9 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 05_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ. NỘI DUNG ĐỀ BÀI
Trong quá trình biên soạn, nếu tài liệu có sai sót gì thì rất mong nhận được sự góp ý của quý thầy
cô cùng các em học sinh! Xin chân thành cảm ơn!
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Dãy số u là dãy số giảm khi chỉ khi n A. * u u , n   . B. * u u , n   . n n1 n n1 C. * u u , n   . D. * u u , n   . n n1 n n1 Câu 2:
Cho góc hình học uOv có số đo bằng 30 (tham khảo hình vẽ). v 30o O u
Khẳng định nào sau đây sai? A. s®  ; Ou Ov  330  .  B. s®  ; Ou Ov  30 .  C. s®  ;
Ou Ov  30  k360,k  . D. s®  ;
Ou Ov  330  k360,k  . Câu 3:
Phương trình nào sau đây vô nghiệm?
A. cos x  1. B. cos 2x  0  ,7.
C. cos 3x  0,4.
D. cos 4x   . Câu 4:
Dãy số nào dưới đây là cấp số cộng? A. 1; 3; 4. B. 3; 5;7. C. 5;7; 6. D. 3; 5; 8. Câu 5:
Tập xác định của hàm số y  tan x là   A. D  
\ k2 , k  .
B. D  \  k2 ,k  .  2   
C. D  \  k ,k  . D. D  
\ k , k  .  2  Câu 6:
Chu kỳ của hàm số y  cos 2x là 2
A. k 2 . B. . C.  . D. 2 . 3 2 Câu 7: x
là một nghiệm của phương trình nào dưới đây? 3 3 1 3
A. sin x  1. B. sin x  .
C. cos x  . D. cos x  . 2 2 2 Câu 8:
Cho cấp số cộng u  :u  2 và công sai d  2. Số hạng thứ 3 của u là n n 1
A. u  4.
B. u  6.
C. u  8. D. u  12. 3 3 3 3 4   Câu 9: Góc có số đo đổi sang độ là 15 A. 48 .  B. 135 .  C. 72 .  D. 270 . 
Câu 10: Giá trị lớn nhất của hàm số y  sin 2x bằng A. 2 . B. 0 . C. 1. D. 1  .
Câu 11: Cho dãy số u  :u  sin .
n Khẳng định nào sau đây đúng? n n
A. u bị chặn.
B. u bị chặn dưới và không bị chặn trên. n n
C. u bị chặn trên và không bị chặn dưới. D. u tăng. n n
Câu 12: Hàm số y  cos x đồng biến trên khoảng nào dưới đây?         A.    ;0 . B. ;   .
C. 0;  . D. ;   .  2   2 2 
Câu 13: Cho cấp số cộng u  :u  2,u  8. Công sai của cấp số cộng đã cho là n 1 3
A. d  4.
B. d  6.
C. d  1. D. d  3.
Câu 14: Với x là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A. sin 2x  2sin x cos x . B. sin 2x  sin x cos x . C. sin 2x  2 cos x .
D. sin 2x  2 sin x .
Câu 15: Tập nghiệm của phương trình tan x  3 là    
A. S    k2 ,k  .
B. S    k ,k  .  3   3       
C. S    k ,k  . D. S  
k ,k  .  6   6 
Câu 16: Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.  153, 58 . B.  153,18 . C.  153 . D.  154,1 .  1
Câu 17: Cho góc  thỏa mãn
    và sin  . Tính cos. 2 4 15 15 A. . B.  15 . C. . D.  15 . 4 4 16 16
Câu 18: Sau quãng thời gian 4 giờ kim giờ sẽ quay được một góc là  2 3  A. . B. . C. . D. . 3 3 4 4
Câu 19: Khẳng định nào sau đây đúng?
A. Hàm số y  sin x là hàm số chẵn.
B. Hàm số y  cos x là hàm số lẻ.
C. Hàm số y  tan x là hàm số lẻ.
D. Hàm số y  cot x là hàm số chẵn.
Câu 20: Điều tra cân nặng của các học sinh lớp 11D cho trong bảng sau: Cân nặng [40,5; 45,5) [45,5; 50,5) [50,5; 55,5) [55,5; 60,5) [60,5; 65,5) [65,5; 70,5) (kg) Số học sinh 10 7 16 4 2 3
Cân nặng trung bình của học sinh lớp 11D gần với giá trị nào dưới đây?
A. 48, 44 kg  .
B. 61, 81 kg  .
C. 51, 81 kg  .
D. 52, 84 kg  .
Câu 21: Tìm x sao cho 2x; 3x  2; 5x  3 là ba số hạng liên tiếp của một cấp số cộng. 1 3
A. x  2.
B. x   .
C. x  1. D. x   . 2 2
Câu 22: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  6 cos 2x  7 trên đoạn      ;   . Tính M  . m  3 6  A. 14. B. 3. C. 11. D. 10.
Câu 23: Cho cấp số nhân u có u  2 và công bội q  3 . Số hạng u là n  1 2 A. u  6. B. u  1. C. u  18.
D. u  6. 2 2 2 2 2  
Câu 24: Cho góc  thỏa mãn cos  với
   0. Tính sin 2. 3 2 2 5 2  5 4  5 4 5 A. . B. . C. . D. 9 9 9 9
Câu 25: Tập hợp tất cả các giá trị của tham số m để phương trình 2 cos 2x m  1 có nghiệm là A. 1;1.   B. 1; 3.   C. 0; 2.   D. 1  ;3.  
Câu 26: Cấp số nhân u có công bội âm, biết u  12 , u  192 . Tìm u . n  3 7 10
A. u  1536 . B. u  1536  .
C. u  3072 . D. u  3072  . 10 10 10 10
Câu 27: Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất
bao lâu để đu quay quay được góc 270 ? 1 1 1 A. phút. B. phút. C. phút.
D. 1,5 phút. 3 6 4  π 
Câu 28: Cho tan  2 . Tính tan     .  4  1 1 2 A. . B.  . C. 1. D. . 3 3 3 5 3  
Câu 29: Biết sin a
, cos b   với 0  a  ,
b   . Tính cosa b . 13 5 2 2 63 21 16 56 A.  . B. . C.  . D.  . 65 65 65 65
Câu 30: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y 2 O 1 π x __ 2
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  2sin . x C. y  cos . x D. y  2cos . x
Câu 31: Dãy số nào sau đây là cấp số nhân? A. 1; 1; 1; 1. B. 1;3;5; 7. C. 1; 2; 3; 4 . D. 1; 4;9;16.
Câu 32: Bảng thống kê sau cho biết tốc độ (km/h) của một số xe máy khi đi qua vị trí có cảnh sát giao
thông đang làm nhiệm vụ. Tốc độ 20;35
35;50 50;60 60;70 70;85 85;100
Số phương tiện giao 27 70 8 3 1 1 thông
Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?
A. Số xe được đo tốc độ là 100 xe.
B. Mẫu số liệu đã cho gồm 5 nhóm có độ dài bằng nhau.
C. Tổng độ dài các nhóm là 80.
D. Số xe máy thuộc nhóm 60  70 là ít nhất.
Câu 33: Cho dãy số u  :u  2n  1. Số hạng thứ 3 của dãy là n n
A. u  7.
B. u  5.
C. u  3. D. u  9. 3 3 3 3 cos a  cos 5a
Câu 34: Rút gọn biểu thức P  sin4a
(với giả thiết biểu thức có nghĩa). sin 2a
A. P  2 cot a .
B. P  2 cos a .
C. P  2 tan a .
D. P  2sin a .
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A. Q  13.
B. Q  14 .
C. Q  15 . D. Q  12 . 3 3 3 3
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  4  2 cos 3 . x u   2u  26
2) (0,75 điểm). Cho cấp số cộng u thỏa mãn: 1 6  . Tính u . n
3u u  18  10 2 3
Câu 2: (1,0 điểm). Giải phương trình: 2sin x1  cos2x  sin 2x  1  2cos . x
Câu 3: (0,5 điểm). Do ảnh hưởng của dịch Covid 19 nên doanh thu 6 tháng đầu năm của
công ty A không đạt kế hoạch. Cụ thể, doanh thu 6 tháng đầu năm đạt 20 tỷ đồng, trong đó
tháng 6 đạt 6 tỷ đồng. Để đảm bảo doanh thu cuối năm đạt được kế hoạch năm, công ty
đưa ra chỉ tiêu: kể từ tháng 7 mỗi tháng phải tăng doanh thu so với tháng kề trước 10% . Hỏi
theo chỉ tiêu đề ra thì doanh thu cả năm của công ty A đạt được là bao nhiêu tỷ đồng (làm
tròn đến một chữ số thập phân)?
____________________HẾT____________________
Huế, 14h40’ Ngày 14 tháng 10 năm 2023
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
¤N TËP KIÓM TRA GI÷A K× 1 M«n: To¸n 11
Kết nối tri thức và cuộc sống
ĐỀ ÔN TẬP SỐ 05_TrNg 2023 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ Trung t©m KM 10 H-¬ng Trµ, HuÕ.
LỜI GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu _ 7,0 điểm) Câu 1:
Dãy số u là dãy số giảm khi chỉ khi n A. * u u , n   . B. * u u , n   . n n1 n n1 C. * u u , n   . D. * u u , n   . n n1 n n1 Câu 2:
Cho góc hình học uOv có số đo bằng 30 (tham khảo hình vẽ). v 30o O u
Khẳng định nào sau đây sai? A. s®  ; Ou Ov  330  .  B. s®  ; Ou Ov  30 .  C. s®  ;
Ou Ov  30  k360,k  . D. s®  ;
Ou Ov  330  k360,k  . Lời giải: s®O ;
u Ov  30  k360,k  . Các kết quả đúng:  , k  . s®  O ; u Ov  3
 30  k360,k  . Câu 3:
Phương trình nào sau đây vô nghiệm?
A. cos x  1. B. cos 2x  0  ,7.
C. cos 3x  0,4.
D. cos 4x   . Lời giải: Do    1  ;1 
 nên phương trình cos 4x   vô nghiệm. Câu 4:
Dãy số nào dưới đây là cấp số cộng? A. 1; 3; 4. B. 3; 5;7. C. 5;7; 6. D. 3; 5; 8. Lời giải:
Dãy số hữu hạn 3; 5;7 là cấp số cộng với u  3 và công sai d  2. 1 Câu 5:
Tập xác định của hàm số y  tan x là   A. D  
\ k2 , k  .
B. D  \  k2 ,k  .  2   
C. D  \  k ,k  . D. D  
\ k , k  .  2  Lời giải:
Hàm số y  tan x xác định khi và chỉ khi cos x  0  x
k ,k  . 2  
Vậy TXĐ là: D  \  k ,k  .  2  Câu 6:
Chu kỳ của hàm số y  cos 2x là 2
A. k 2 . B. . C.  . D. 2 . 3 Lời giải: 2
Chu kỳ của hàm số y  cos 2x là: T    . 2 2 Câu 7: x
là một nghiệm của phương trình nào dưới đây? 3 3 1 3
A. sin x  1. B. sin x  .
C. cos x  . D. cos x  . 2 2 2 Lời giải: 2 3 Thay x
vào phương trình sin x  thấy thỏa mãn. 3 2 Câu 8:
Cho cấp số cộng u  :u  2 và công sai d  2. Số hạng thứ 3 của u là n n 1
A. u  4.
B. u  6.
C. u  8. D. u  12. 3 3 3 3 Lời giải:
Ta có: u u  2d  6. 3 1 4   Câu 9: Góc có số đo đổi sang độ là 15 A. 48 .  B. 135 .  C. 72 .  D. 270 .  Lời giải: o 4    4  .180  Cách 1: Ta có:   48 .     15  15 
Cách 2: Sử dụng MTCT
Câu 10: Giá trị lớn nhất của hàm số y  sin 2x bằng A. 2 . B. 0 . C. 1. D. 1  . Lời giải: Ta có x
: 1  sin 2x  1, x  .  
Vậy max y  2 khi sin 2x  1  2x
k2  x   k ( k  ). 2 4
Câu 11: Cho dãy số u  :u  sin .
n Khẳng định nào sau đây đúng? n n
A. u bị chặn.
B. u bị chặn dưới và không bị chặn trên. n n
C. u bị chặn trên và không bị chặn dưới. D. u tăng. n n Lời giải: Ta có: * 1
  u  sinn  1, n   . n
Vậy u bị chặn. n
Câu 12: Hàm số y  cos x đồng biến trên khoảng nào dưới đây?         A.    ;0 . B. ;   .
C. 0;  . D. ;   .  2   2 2  Lời giải:
Dựa vào đồ thị của hàm số y  cos x , ta có hàm số này đồng biến trên khoảng    ;0 .
Câu 13: Cho cấp số cộng u  :u  2,u  8. Công sai của cấp số cộng đã cho là n 1 3
A. d  4.
B. d  6.
C. d  1. D. d  3. Lời giải:
Ta có: u u  2d  8  2  2d d  3. 3 1
Câu 14: Với x là góc bất kì và các biểu thức có nghĩa. Đẳng thức nào dưới đây đúng?
A. sin 2x  2sin x cos x . B. sin 2x  sin x cos x . C. sin 2x  2 cos x .
D. sin 2x  2 sin x .
Câu 15: Tập nghiệm của phương trình tan x  3 là    
A. S    k2 ,k  .
B. S    k ,k  .  3   3       
C. S    k ,k  . D. S  
k ,k  .  6   6 
Câu 16: Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A:
Tính mốt của mẫu số liệu ghép nhóm này.
A.  153, 58 . B.  153,18 . C.  153 . D.  154,1 . Lời giải:
Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150; 155). Ta có, j  2, a  150, m  14 , 2 2
m  7, m  10, h  5 . 1 3 14  7 Do đó M  150  5 153,18. 0 (14  7)  (14  10)  1
Câu 17: Cho góc  thỏa mãn
    và sin  . Tính cos. 2 4 15 15 A. . B.  15 . C. . D.  15 . 4 4 16 16 Lời giải:  15 2 cos   1  15 Ta có: 2 2        4 cos  1 sin  1   .  4  16   15 cos   4  15 Do
    nên chọn cos   . 2 4
Câu 18: Sau quãng thời gian 4 giờ kim giờ sẽ quay được một góc là  2 3  A. . B. . C. . D. . 3 3 4 4 Lời giải:
Sau 1 giờ kim giờ sẽ quay được một góc là 6  2
Sau 4 giờ kim giờ sẽ quay được một góc là .4  . 6 3
Câu 19: Khẳng định nào sau đây đúng?
A. Hàm số y  sin x là hàm số chẵn.
B. Hàm số y  cos x là hàm số lẻ.
C. Hàm số y  tan x là hàm số lẻ.
D. Hàm số y  cot x là hàm số chẵn.
Câu 20: Điều tra cân nặng của các học sinh lớp 11D cho trong bảng sau: Cân nặng [40,5; 45,5) [45,5; 50,5) [50,5; 55,5) [55,5; 60,5) [60,5; 65,5) [65,5; 70,5) (kg) Số học sinh 10 7 16 4 2 3
Cân nặng trung bình của học sinh lớp 11D gần với giá trị nào dưới đây?
A. 48, 44 kg  .
B. 61, 81 kg  .
C. 51, 81 kg  .
D. 52, 84 kg  . Lời giải:
Tổng số học sinh là n  42 . Cân nặng trung bình của học sinh lớp 11D là
10.43  7.48 16.43  4.58  2.63  3.68 x   51, 81kg 42
Câu 21: Tìm x sao cho 2x; 3x  2; 5x  3 là ba số hạng liên tiếp của một cấp số cộng. 1 3
A. x  2.
B. x   .
C. x  1. D. x   . 2 2 Lời giải:
Do 2x; 3x  2; 5x  3 là ba số hạng liên tiếp của một cấp số cộng nên
2x5x  3  23x  2  x 1.
Câu 22: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  6 cos 2x  7 trên đoạn      ;   . Tính M  . m  3 6  A. 14. B. 3. C. 11. D. 10.
Lời giải:   2  1 Ta có:   x     2x     cos 2x 1  1
 0  6cos 2x  7  1  . 3 6 3 3 2 Suy ra M  1  , m  10. 
Vậy M m  11.
Câu 23: Cho cấp số nhân u có u  2 và công bội q  3 . Số hạng u là n  1 2 A. u  6. B. u  1. C. u  18.
D. u  6. 2 2 2 2 Lời giải:
Ta có u u .q  2.3  6 . 2 1 2  
Câu 24: Cho góc  thỏa mãn cos  với
   0. Tính sin 2. 3 2 2 5 2  5 4  5 4 5 A. . B. . C. . D. 9 9 9 9 Lời giải:  5 sin  5 Ta có: 2 2      3 sin  1 cos  . 9   5 sin   3   5 Do
   0 nên sin  0   chọn sin   . 2 3 4 5 Vậy sin 2 2sin cos    . 9
Câu 25: Tập hợp tất cả các giá trị của tham số m để phương trình 2 cos 2x m  1 có nghiệm là A. 1;1.   B. 1; 3.   C. 0; 2.   D. 1  ;3.   Lời giải: m  1 m  1
Phương trình 2cos 2x m  1  cos 2x  có nghiệm  1    1  1   m  3. 2 2
Câu 26: Cấp số nhân u có công bội âm, biết u  12 , u  192 . Tìm u . n  3 7 10
A. u  1536 . B. u  1536  .
C. u  3072 . D. u  3072  . 10 10 10 10 Lời giải:
Gọi q là công bội của cấp số nhân đề bài cho q  0 . 2 u  12  u q 6 u q 192 Ta có 3 1  1   4
q 16 (Do u , q  0 ) 6 2 1 u  192  u qu q 12 7 1 1 12
Mà q  0  q  2   u   3 . 1 2 q
Suy ra: u u .q  3. 2  9 9  15  36. 10 1
Câu 27: Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất
bao lâu để đu quay quay được góc 270 ? 1 1 1 A. phút. B. phút. C. phút.
D. 1,5 phút. 3 6 4 Lời giải: 270 3 3
Tính được: 270      .2. 180 2 4 3
Vậy đu quay quay được góc 270 khi nó quay được vòng. 4 1
Ta có: Đu quay quay được 1 vòng trong phút. 3 3 3 1 1 Đu quay quay được vòng trong .  phút. 4 4 3 4  π 
Câu 28: Cho tan  2 . Tính tan     .  4  1 1 2 A. . B.  . C. 1. D. . 3 3 3 Lời giải: π tan  tan  π  tan 1 1 Ta có: 4 tan        .  4 π  1 tan  3 1 tan .tan 4 5 3  
Câu 29: Biết sin a
, cos b   với 0  a  ,
b   . Tính cosa b . 13 5 2 2 63 21 16 56 A.  . B. . C.  . D.  . 65 65 65 65 Lời giải: 2   2   Ta có: 2 2 5 144
cos a  1 sin a  1  ;   2 2 3 16
sin b  1 cos b  1     13  169  5  25  12 Vì 0  a
nên suy ra cos a  0 , ta chọn cos a  2 13  4 Vì
b   nên suy ra sin b  0 , ta chọn sin b  . 2 5 a b 12  3  5 4 56 cos  cos .
a cos b  sin . a sin b  .   .   .   13  5  13 5 65
Câu 30: Đồ thị trong hình vẽ là đồ thị của một trong các hàm số được cho ở các phương án A, B, C, D. y 2 O 1 π x __ 2
Hỏi hàm số đó là hàm số nào? A. y  sin . x B. y  2sin . x C. y  cos . x D. y  2cos . x Lời giải:   
Kiểm tra các sự kiện: Đồ thị hàm số đi qua điểm O0;0 , A ;2.  2 
Câu 31: Dãy số nào sau đây là cấp số nhân? A. 1; 1; 1; 1. B. 1;3;5; 7. C. 1; 2; 3; 4 . D. 1; 4;9;16. Lời giải:
Dãy hữu hạn 1; 1; 1; 1 là một cấp số nhân với u  1; công bội q  1. 1
Câu 32: Bảng thống kê sau cho biết tốc độ (km/h) của một số xe máy khi đi qua vị trí có cảnh sát giao
thông đang làm nhiệm vụ. Tốc độ 20;35
35;50 50;60 60;70 70;85 85;100
Số phương tiện giao 27 70 8 3 1 1 thông
Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?
A. Số xe được đo tốc độ là 100 xe.
B. Mẫu số liệu đã cho gồm 5 nhóm có độ dài bằng nhau.
C. Tổng độ dài các nhóm là 80.
D. Số xe máy thuộc nhóm 60  70 là ít nhất.
Câu 33: Cho dãy số u  :u  2n  1. Số hạng thứ 3 của dãy là n n
A. u  7.
B. u  5.
C. u  3. D. u  9. 3 3 3 3 cos a  cos 5a
Câu 34: Rút gọn biểu thức P  sin4a
(với giả thiết biểu thức có nghĩa). sin 2a
A. P  2 cot a .
B. P  2 cos a .
C. P  2 tan a .
D. P  2sin a . Lời giải: cos a  cos 5a 2sin 3 . a sin 2a sin 2a a a Ta có: P    2sin .cos   2 sin a .
sin 4a  sin 2a 2sin 3 . a cos a cos a cos a
Câu 35: Tìm hiểu thời gian hoàn thành một bài tập ( đơn vị: phút) của một số học sinh thu được kết quả sau:
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm này là
A. Q  13.
B. Q  14 .
C. Q  15 . D. Q  12 . 3 3 3 3 Lời giải:
Cỡ mẫu : n  2  4  7  4  3  20 . x x
Tứ phân vị thứ ba Q là 15
16 . Do x , x đều thuộc nhóm 12;16 nên nhóm này chứa 3 2 15 16 Q . 3
Do đó: p  4 , a  12 , m  4 , m m m  2  4  7  13 , a a  4 . 4 4 1 2 3 5 4 3.20 13 Ta có: 4 Q  12  .4  14 . 3 4
II. PHẦN TỰ LUẬN (03 câu _ 3,0 điểm)
Câu 1: (1,5 điểm).
1) (0,75 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  4  2 cos 3 . x Lời giải: Ta có: x
  : 1  cos3x  1  2  4  2cos3x  6.  k2
Vậy max y  6  cos 3x  1   x   , k  ; 3 3 k2
min y  2  cos 3x  1  x  , k  . 3 u   2u  26
2) (0,75 điểm). Cho cấp số cộng u thỏa mãn: 1 6  . Tính u . n
3u u  18  10 2 3 Lời giải: u   2u  26 u   
2 u  5d  26
3u  10d  26 u   2 1 6 1  1  Ta có: 1 1        .
3u u  18 
3 u d u  2d  18  
4u  5d  18 d  2 2 3  1   1  1
Suy ra: u u  9d  20. 10 1
Câu 2: (1,0 điểm). Giải phương trình: 2sin x1  cos2x  sin 2x  1  2cos . x Lời giải:
Điều kiện: x  . 2 (1)  2 sin .2
x cos x  2 sin xcos x  1  2cos x  0  2sin xcos x2cos x  1  1  2cos x  0  1         x   x x   2 cos x 1 0 cos x 2 cos 1 2 sin cos 1  0    2
2 sin xcos x  1   0  sin2x  1  2 x   k2 1  +) Với 3 cos x     , k  . 2  2 x    k2  3 
+) Với sin 2x  1  x
k ,k  . 4
Câu 3: (0,5 điểm). Do ảnh hưởng của dịch Covid 19 nên doanh thu 6 tháng đầu năm của
công ty A không đạt kế hoạch. Cụ thể, doanh thu 6 tháng đầu năm đạt 20 tỷ đồng, trong đó
tháng 6 đạt 6 tỷ đồng. Để đảm bảo doanh thu cuối năm đạt được kế hoạch năm, công ty
đưa ra chỉ tiêu: kể từ tháng 7 mỗi tháng phải tăng doanh thu so với tháng kề trước 10% . Hỏi
theo chỉ tiêu đề ra thì doanh thu cả năm của công ty A đạt được là bao nhiêu tỷ đồng (làm
tròn đến một chữ số thập phân)? Lời giải: Ta có:
Doanh thu của công ty trong tháng 7 : T  6. 110% ; 7  
Doanh thu của công ty trong tháng 8 : T  6.110%2 ; 8 …
Doanh thu của công ty trong tháng 12 : T  6.110%6 ; 12
Do đó, theo chỉ tiêu đề ra thì doanh thu cả năm của công ty A đạt được là   T                    6 2 6 1 10% 1 20 6. 1 10% 6. 1 10% .... 6. 1 10% 20 6. 1 10% .  70,9 (tỷ). 10%
____________________HẾT____________________
Huế, 14h40’ Ngày 14 tháng 10 năm 2023