Top 07 đề tham khảo kiểm tra giữa học kì 1 Toán 11 KNTTVCS

Tài liệu gồm 56 trang, tuyển tập 07 đề tham khảo kiểm tra giữa học kì 1 môn Toán 11 sách Kết Nối Tri Thức Với Cuộc Sống (viết tắt: KNTTVCS); các đề được biên soạn theo hình thức 70% trắc nghiệm kết hợp với 30% tự luận, trong đó phần trắc nghiệm gồm 35 câu,

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Thông tin:

56 trang 6 tháng trước

Tác giả:

Profile Kim Oanh
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1: Trên đường tròn lượng giác gốc , biết góc lượng giác có số đo bằng , điểm
nằm ở góc phần tư thứ mấy?
A. . B. . C. . D. .
Câu 2: Đường tròn lượng giác có bán kính bằng:
A.
2
. B.
1
. C.
2
π
. D.
π
.
Câu 3: Khi quy đổi
1
o
ra đơn vị radian, ta được kết quả là
A.
rad.
π
B.
180
rad.
π
C.
rad.
180
π
D.
rad.
360
π
Câu 4: Mệnh đề nào sau đây sai?
A.
sin( ) sin .
πα α
+=
B.
C. . D.
tan( ) tan .
πα α
+=
Câu 5: Cho
4
sin ,
52
π
α απ
= <<
. Tính
cos
α
.
A.
3
cos
5
α
= −
. B.
1
cos
5
α
=
. C.
3
cos
5
α
=
. D.
1
cos
5
α
=
.
Câu 6: Trong các công thức dưới đây, công thức nào đúng?
A.
cos cos 2cos cos .
22
ab ab
ab
+−
−=
B.
cos cos 2sin sin .
22
ab ab
ab
+−
−=
C.
cos cos 2cos cos .
22
ab ab
ab
+−
−=−
D.
cos cos 2sin sin .
22
ab ab
ab
+−
−=−
Câu 7: Trong các công thức dưới đây, công thức nào đúng?
A.
( )
cos sin .cos cos .sinab a b a b+= −
. B.
( )
cos sin .cos cos .sinab a b a b+= +
.
C.
( )
cos cos .cos sin .sinab a b a b+= +
. D.
( )
cos cos .cos sin .sinab a b a b+= −
.
Câu 8: Cho
1
cos =
3
α
. Tính
cos2
α
.
A.
7
cos2
9
α
=
. B.
1
cos2
3
α
=
. C.
7
cos2
9
α
= −
. D.
2
cos2
3
α
=
.
Câu 9: Rút gọn biểu thức
sin sin
33
Tx x
ππ

= +− −


ta được kết quả là
A.
3 cosTx=
. B.
sinTx=
. C.
3
2
. D.
sin 2Tx=
.
Câu 10: Tập xác định hàm số
sinyx=
là:
A.
[ 1;1].D = −
B.
.D =
A
( )
,OA OM
0
410
M
I
III
II
IV
( )
cos cos
πα α
+=−
C.
{ }
\, .D kk
π
= ∈
D.
\, .
2
D kk
π
∈

=


Câu 11: Mệnh đề nào sau đây là đúng?
A. Hàm số là hàm số chẵn. B. Hàm số
cosyx=
là hàm số chẵn.
C. Hàm số
là hàm số chẵn. D. Hàm số là hàm số chẵn.
Câu 12:
Cho hàm số
()y fx=
có đồ thị như hình bên dưới. Mệnh đề nào sau đây là
đúng
?
A.
Hàm số đồng biến trên
3
;.
22
ππ

−−


B.
Hàm số đồng biến trên
3
;.
22
ππ



C. Hàm số đồng biến trên
;.
22
ππ

−


D. Hàm số đồng biến trên
;0 .
2
π

−


Câu 13: Hàm số
sin 2
4
yx
π

= −


đồng biến trên khoảng nào trong các khoảng sau đây?
A.
3
;
88
ππ

−


. B.
3
;
44
ππ

−


. C.
;
22
ππ

−


. D.
;
44
ππ

−


.
Câu 14: Phương trình nào sau đây có nghiệm?
A.
1
sin .
2
x =
B.
sin 2.x = −
C.
2 sin 2.x =
D.
cos 2.x =
Câu 15: Phương trình
sin sinx
α
=
có tập nghiệm là:
A.
{
}
2| .S kk
πα
=+∈
B.
{
}
|.S kk
πα
=+∈
C.
{ }
2; 2 | .S k kk
ααππ
=++− ∈
D.
{ }
2; 2 | .S k kk
α παππ
=++− ∈
Câu 16: Phương trình
cos 2 1x =
có nghiệm là:
A.
,xk k
π
= ∈
. B.
2,
2
x kk
π
π
=+∈
. C.
,
2
k
xk
π
= ∈
. D.
2,
4
x kk
π
π
=+∈
.
Câu 17: Tìm tổng nghiệm dương bé nhất và nghiệm âm lớn nhất của phương trình
( )
sin cos 2xx=
.
A.
3
π
−
. B.
0
. C.
4
π
. D.
2
3
π
.
Câu 18: Cho dãy số (
n
u
) với
( 5)
n
n
u = −
. Mệnh đề nào sau đây đúng?
A.
4
625u = −
. B.
4
20u =
. C.
4
625u =
. D.
4
20u = −
.
Câu 19: Cho dãy số
()
n
u
. Mệnh đề nào sau đây đúng?
A. Nếu
*
1
,
nn
uun
+
> ∀∈
thì
()
n
u
là dãy số giảm.
B. Nếu
*
1
,
nn
uun
+
≤ ∀∈
thì
()
n
u
là dãy số giảm.
sinyx=
tanyx=
cotyx=
C. Nếu
*
1
,
nn
uun
+
< ∀∈
thì
()
n
u
là dãy số giảm.
D. Nếu
*
1
,
nn
uun
+
≥ ∀∈
thì
()
n
u
là dãy số giảm.
Câu 20: Trong các dãy số
(
)
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy số tăng?
A.
1
.
2
n
n
u =
B.
1
.
n
u
n
=
C.
5
.
31
n
n
u
n
+
=
+
D.
21
.
1
n
n
u
n
−
=
+
Câu 21: Cho cấp số cộng
(
)
n
u
có
1
3u =
và công sai
2d
=
. Số hạng tổng quát của cấp số cộng
( )
n
u
là:
A.
32
n
un
= +
. B.
32
n
un
= −
. C.
22
n
un
= −
. D.
21
n
un= +
.
Câu 22: Cấp số cộng
(
)
n
u
có số hạng đầu
1
u
và công sai
d
thì tổng
n
số hạng đầu của cấp số cộng
(
)
n
u
được xác định bởi công thức
A.
1
( 1)
2
n
nn
S nu d
+
= +
. B.
1
( 1)
2
n
nn
S nu d
+
= −
.
C.
1
( 1)
2
n
nn
S nu d
−
= −
. D.
1
( 1)
2
n
nn
S nu d
−
= +
.
Câu 23: Cho dãy số
( )
n
u
là một cấp số cộng với công sai
d
, ta có công thức truy hồi
A.
*
1
.,
nn
u udn
+
= ∈
. B.
*
1
,
nn
u u dn
+
=+∈
.
C.
*
1
,
n
n
u
un
d
+
= ∈
. D.
*
1
,
nn
u u dn
+
=−∈
.
Câu 24: Tìm
x
để ba số thực
1; ; 5x
theo thứ tự lập thành một cấp số cộng.
A.
1x =
. B.
0
x
=
. C.
2x =
. D.
3
x =
.
Câu 25: Tìm tổng
S
của
100
số nguyên dương đầu tiên và đều chia
5
dư
1
.
A.
24353
. B.
25100
. C.
50200
. D.
5001
.
Câu 26: Cho cấp số nhân
( )
n
u
có công bội
.
q
Mệnh đề nào sau đây đúng?
A.
1
1
. ( 2)
n
n
u uq n
−
= ≥
. B.
1
1
. ( 2)
n
n
u uq n
+
= ≥
. C.
1
. ( 2)
n
n
u uq n= ≥
. D.
( 2)
n
n
u qn= ≥
.
Câu 27: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A.
2; 4; 8; 16;
B.
1; 1; 1; 1; −−
C.
2222
1 ; 2 ; 3 ; 4 ;
D.
( )
357
; ; ; ; 0 .aa a a a≠
Câu 28: Cho cấp số nhân
( )
n
u
với
1
2u = −
và
5.q = −
Viết bốn số hạng đầu tiên của cấp số nhân
( )
n
u
.
A.
2; 10; 50; 250.−−
B.
2; 10; 50; 250.−−
C.
2; 10; 50; 250.−− − −
D.
2; 10; 50; 250.−
Câu 29: Cho cấp số nhân
( )
n
u
có các số hạng lần lượt là
3; 9; 27; 81; ...
. Tìm số hạng tổng quát
n
u
của
cấp số nhân
( )
n
u
.
A.
1
3.
n
n
u
−
=
B.
3.
n
n
u =
C.
1
3.
n
n
u
+
=
D.
3 3.
n
n
u = +
Câu 30: Bác Bình gửi tiết kiệm
500
triệu đồng kì hạn
1
tháng với lãi suất
6%
một năm theo hình thức
lãi suất kép. Nếu sau đúng một năm bác Bình mới đến ngân hàng rút tiền thì số tiền lãi Bác Bình
có được gần nhất với số nào sau đây.
A.
63,58
(triệu đồng). B.
60,15
triệu đồng. C.
60
triệu đồng. D.
62,58
triệu đồng.
Câu 31: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Thời gian (phút)
[
)
0; 20
[
)
20;40
[
)
40;60
[
)
60;80
[
)
80;100
Số học sinh
5
9
12
10
6
Giá trị đại diện của nhóm
[20;40)
là
A. 10. B. 20. C. 30. D. 40.
Câu 32: Tuổi thọ (năm) của 50 bình ắc quy ô tô thu được mẫu số liệu ghép nhóm sau:
Tuổi thọ (năm)
[
)
2; 2, 5
[
)
2,5; 3
[
)
3; 3, 5
[
)
3, 5; 4
[
)
4; 4, 5
[
)
4,5; 5
Tần số
4
9
14
11
7
5
Mẫu số liệu ghép nhóm này có số mốt bằng
A. 14. B. 9. C. 7. D. 5.
Câu 33: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một
công ty như sau:
Thời gian
[
)
15;20
[
)
20;25
[
)
25;30
[
)
30;35
[
)
35;40
[
)
40;45
[
)
45;50
Số nhân viên
6
14
25
37
21
13
9
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 phút đến dưới 20
phút?
A. 6. B. 9. C. 14. D. 13.
Câu 34: Cho mẫu số liệu ghép nhóm sau:
Nhóm
[
)
12
;aa
.
[
)
1
;
ii
aa
+
.
[
)
1
;
kk
aa
+
Tần số
1
m
.
i
m
.
k
m
Với
12
...
k
nm m m= + ++
là cỡ mẫu và
1
2
ii
i
aa
x
+
+
=
(
1,...ik=
) là giá trị đại diện của nhóm
[
)
1
;
ii
aa
+
. Khi đó công thức tính số trung bình cộng của mẫu số liệu ghép nhóm trên là:
A.
11 kk
x
mx
n
mx
=
+…+
. B.
( ) ( )
11 kk
mx mx
x
n
…
=
.
C.
11 kk
mx m x
x
n
−−…
=
. D.
11 kk
mx mx
x
n
+…+
=
Câu 35: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Thời gian (phút)
[
)
0; 20
[
)
20;40
[
)
40;60
[
)
60;80
[
)
80;100
Số học sinh
5
9
12
10
6
Nhóm chứa trung vị là
A.
[0;200)
. B.
[20;40)
. C.
[40;60)
. D.
[60;80)
.
II. PHẦN TỰ LUẬN
(3 điểm).
Bài 1. (1,0 điểm).
a) Tìm tập xác định của hàm số.
1
1 cos
y
x
=
+
.
b) Cho dãy số
( )
,
n
u
biết
1
1
n
u
n
=
+
. Viết ba số hạng đầu tiên của dãy số
( )
n
u
.
Bài 2. (1 điểm). Tìm m để phương trình để
2
2sin 3 sin 5 0
2
x
xm+ −=
luôn có nghiệm.
Bài 3. (1 điểm). Một đa giác có chu vi là
158cm
, độ dài các cạnh của nó lập thành một cấp số
cộng. Biết cạnh lớn nhất có độ dài là
44cm
. Tìm số cạnh của đa giác đó?
……………… HẾT ………………
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng.
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
A
B
C
A
A
D
D
C
B
B
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
B
D
A
A
D
A
A
C
C
D
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
D
D
B
D
A
A
C
B
B
A
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
C
A
A
D
C
II. PHẦN TỰ LUẬN
Câu
Nội dung
Điểm
1
a. Tìm tập xác định của hàm số
1
1 cos
y
x
=
+
.
Điều kiện xác định của hàm số là:
cos 1x ≠−
0,25
hay
2xk
ππ
≠+
(
k ∈
).
Tập xác định của hàm số
1
1 cos
y
x
=
+
là
{
}
\ 2|D kk
ππ
=+∈
0,25
b. Cho dãy số
( )
,
n
u
biết
1
1
n
u
n
=
+
. Viết ba số hạng đầu tiên của dãy số
(
)
n
u
.
1
1
2
u =
0,25
0,25
ố hạng đầu tiên của dãy số
( )
n
u
là:
111
;;.
234
2
Tìm m để phương trình để
2
2sin 3 sin 5 0
2
x
xm
+ −=
luôn có nghiệm.
2
2sin 3 sin 5 0
2
3 sin cos 5 1 0
x
xm
x xm
+ −=
⇔ − − +=
0.25
2sin 5 1 0
6
xm
π

⇔ − − +=


0.25
Hay
51
sin
62
m
x
π
−

−=


Mà
1 sin 1
6
x
π

−≤ − ≤


0.25
Nên để phương trình trên luôn có nghiệm khi
51
11
2
m −
−≤ ≤
13
55
m
⇔− ≤ ≤
0.25
3
Một đa giác có chu vi là
158cm
, độ dài các cạnh của nó lập thành một cấp số cộng. Biết cạnh lớn
nhất có độ dài là
44cm
. Tìm số cạnh của đa giác đó?
Giả sử đa giác có
n
cạnh (
,3
nn
∈≥
).
Gọi độ dài các cạnh của đa giác là
123
, , ,...,
n
uuu u
theo thứ tự lập thành cấp số cộng và cạnh
lớn nhất có độ dài là nên
123
0 ... 44
n
u u u u cm< < < << =
.
0,25
Vì đa giác có chu vi là
158cm
nên
(
)
1
123
...
2
n
nn
u un
S uuu u
+
= + + ++ =
hay
( )
1
44
158
2
un+
=
suy ra
1
316
44
n
u
=
+
0,25
Mà
n
∈
nên
1
44u +
là ước nguyên dương của
316
hay
{ }
1
44 2; 4; 79; 158; 316u +∈
0.25
1
44u +
2
4
79
158
316
1
u
1
0u <
(loại)
1
0u <
(loại)
1
35u =
1
114u =
(không thỏa
mãn vì
44
n
u cm=
)
1
272u
=
(không thỏa
mãn vì
44
n
u cm=
)
Vậy đa giác đã cho có
316
4
79
n
= =
cạnh.
0.25
Trang 1
TRƯỜNG THPT
ĐỀ CHÍNH THỨC
(Đề có 05 trang)
ĐỀ KIỂM TRA GIỮA KÌ I NĂM HỌC 2023 - 2024
MÔN: TOÁN - LỚP: 11 (SÁCH KNTT)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
ĐỀ 1
Họ và tên thí sinh: ....................................................................... Số báo danh: ...................
I. PHẦN TRẮC NGHIỆM (7,0 điểm).
Câu 1: Cung có số đo
250
°
thì có số đo theo đơn vị là radian là
A.
35
18
π
. B.
25
18
π
. C.
25
12
π
. D.
25
9
π
.
Câu 2: Cho góc
α
thỏa mãn
0
2
π
α
<<
. Khẳng định nào sau đây đúng?
A.
sin 0
α
>
. B.
cot 0
α
<
. C.
sin 0
α
<
. D.
cos 0
α
<
.
Câu 3: Khẳng định nào sau đây đúng?
A.
22
sin cos 1
αα
+=
. B.
22
sin cos 0
αα
+=
.
C.
22
sin cos 2
αα
+=
. D.
22
sin cos 1
αα
+=−
.
Câu 4:
sin 2a
bằng
A.
2sin .cosaa
. B.
sin a
. C.
cos a
. D.
cos 2a
.
Câu 5: Chu kỳ tuần hoàn của hàm số
sinyx
=
là
A.
2k
π
()k ∈
. B.
2
π
. C.
π
. D.
2
π
.
Câu 6: Tập giá trị của hàm số
cos2023yx=
là
A.
[ ]
1;1−
. B.
( 1;1)−
. C.
[ ]
2023;2023−
. D.
11
;
22

−


.
Câu 7: Nghiệm của phương trình
tan 1x
=
là
A.
,
4
x kk
π
π
=+∈
. B.
3
,
4
x kk
π
π
=+∈
.
C.
,xk k
π
= ∈
. D.
,
2
x kk
π
π
=+∈
.
Câu 8: Cho dãy số
(
)
n
u
xác định bởi
21
n
un= −
với
1n ≥
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Câu 9: Dãy số nào sau đây là dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6; 4; 2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Trang 2
Câu 10: Cho cấp số cộng
( )
n
u
với
1
3u =
và
2
5.u =
Công sai của cấp số cộng đã cho bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 11: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
2
1
n
un= +
. B.
2
1
3
n
u
n
= −
. C.
sin
n
un n= +
. D.
2
sin
n
un=
.
Câu 12: Cho
a
,
b
,
c
là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng?
A.
2
b ac=
. B.
2bac= +
. C.
2ab c+=
. D.
2bc a+=
.
Câu 13: Dãy số nào sau đây là cấp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x ≠
.
Câu 14: Cho cấp số cộng
( )
n
u
biết
6
48u =
và
11
83u =
. Tìm cặp
(
)
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
(
)
13; 7
. D.
( )
13; 7−−
.
Câu 15: Cho cấp số nhân với và công bội . Tìm giá trị của biết số hạng tổng quát
.
A. . B. . C. . D. .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau:
Nhóm
Chiều cao (cm)
Số học sinh
1
[
)
150;152
5
2
[
)
152;154
18
3
[
)
154;156
40
4
[
)
156;158
26
5
[
)
158;160
8
6
[
)
160;162
3
100N =
Giá trị đại diện của nhóm thứ tư là
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
( )
n
u
1
3u =
2= −q
n
1536= −
n
u
8=n
9n =
257n =
10n =
Trang 3
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là
A.
[40;60)
.
B.
[
20;40
)
.
C.
[
60;80
)
.
D.
[80;100)
.
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
[
)
7; 9
.
B.
[
)
9; 11
.
C.
[
)
11; 13
.
D.
[
)
13; 15
.
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8, 6
.
Câu 21: Biết
4
sin
5
α
−
=
và
3
2
π
πα
<<
. Giá trị
cos
α
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
±
D.
9
.
5
Câu 22: Giá trị của biểu thức
sin
34
A
ππ

= +


là
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Câu 23: Hàm số nào sau đây là hàm số lẻ?
A.
2cosyx= −
. B.
2
2sin 2yx=−+
. C.
2sinyx= −
. D.
2cos 2yx=−+
.
Câu 24: Tập nghiệm của phương trình
cos 1x = −
là
A.
2| .
2
S kk
π
π

=+∈


B.
2| .
2
S kk
π
π

=−+ ∈


C.
{ }
2| .Sk k
π
= ∈
D.
{ }
2| .S kk
ππ
=+∈
Trang 4
Câu 25: Cho dãy số
11 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng
quát của dãy số đã cho là
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Câu 26: Cho cấp số cộng
(
)
n
u
có
1
2; 5ud= = −
. Số hạng thứ
20
của cấp số cộng là
A.
93−
. B.
10
. C.
93
. D.
23
.
Câu 27: Cho cấp số nhân
( )
n
x
có
2
3x = −
và
4
27.x = −
Tính số hạng đầu
1
x
và công bội
q
của cấp số
nhân.
A.
1
1, 3xq=−=−
hoặc
1
1, 3.xq
= =
B.
1
1, 3xq=−=
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq=−=
D.
1
3, 1xq= =
hoặc
1
3, 1.xq
=−=−
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi
bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Doanh thu
[
)
5; 7
[
)
7;9
[
)
9;11
[
)
11;13
[
)
13;15
Số ngày
2
7
7
3
1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
[
)
7; 9
.
B.
[
)
9; 11
.
C.
[
)
11; 13
.
D.
[
)
13; 15
.
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Nhóm chứa trung vị là
A.
[
)
30;45
. B.
[
)
15;30
. C.
[
)
45;60
. D.
[
)
60;75
.
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi
hàm số
( )
5sin
5
ht t
π

=


, trong đó
( )
ht
là độ cao tính bằng cetimét trên mực nước biển trung
bình tại thời điểm
t
giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc phao lại
ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Trang 5
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
33
sin 3
42
x
π

−=


bằng
A.
.
9
π
B.
.
6
π
−
C.
.
6
π
D.
.
9
π
−
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng
1
cây, hàng
thứ hai trồng
2
cây, hàng thứ ba trồng
3
cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Câu 34: Một cấp số nhân có số hạng đầu
1
3u =
, công bội
2
q =
. Biết
765
n
S =
. Tìm
n
.
A.
8n =
. B.
9n =
. C.
6n =
. D.
7
n
=
.
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một
công ty như sau:
Thời gian
[
)
15;20
[
)
20;25
[
)
25;30
[
)
30;35
[
)
35;40
[
)
40;45
[
)
45;50
Số nhân viên
7
14
25
37
21
14
10
Tứ phân vị thứ nhất
1
Q
và tứ phân vị thứ ba
3
Q
của mẫu số liệu ghép nhóm này là
A.
13
1360 800
,
37 21
QQ= =
. B.
13
1360 3280
,
37 83
QQ= =
.
C.
13
136 3280
,
5 83
QQ
= =
. D.
13
136 800
,
5 21
QQ= =
.
II. PHẦN TỰ LUẬN (3,0 điểm).
Câu 36: (1,0 điểm)
a. Giải phương trình
cot 3
3
x
π

+=


.
b. Cho
2
sin
3
α
=
, tính giá trị của biểu thức
(1 3 cos )(1 3 cos )P
αα
=−+
.
Câu 37: (1,0 điểm)
Giải phương trình
cos3 sin 2 0xx−=
.
Câu 38: (1,0 điểm) Giải phương trình
sin cos
3
xx
π

= +


.
Câu 39: (0,5 điểm) Một công ty khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là
100000
đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm
30000
đồng so với giá của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng
sâu
20
mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia
đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
-------------- HẾT --------------
Trang 6
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM (7,0 điểm).
BẢNG ĐÁP ÁN
1.B
2.A
3.A
4.A
5.D
6.C
7.A
8.A
9.A
10.A
11.D
12.B
13.C
14.C
15.D
16.B
17.A
18.A
19.B
20.C
21.A
22.B
23.C
24.D
25.B
26.A
27.B
28.C
29.B
30.A
31.B
32.C
33.A
34.A
35.D
ĐÁP ÁN CHI TIẾT
Câu 1: Cung có số đo
250°
thì có số đo theo đơn vị là radian là
A.
35
18
π
. B.
25
18
π
. C.
25
12
π
. D.
25
9
π
.
Lời giải
Chọn B
Số đo theo đơn vị là radian là
0
0
250 . 25.
18
180
ππ
=
.
Câu 2: Cho góc
α
thỏa mãn
0
2
π
α
<<
. Khẳng định nào sau đây đúng?
A.
sin 0
α
>
. B.
cot 0
α
<
. C.
sin 0
α
<
. D.
cos 0
α
<
.
Lời giải
Chọn A
Câu 3: Khẳng định nào sau đây đúng?
A.
22
sin cos 1
αα
+=
. B.
22
sin cos 0
αα
+=
.
C.
22
sin cos 2
αα
+=
. D.
22
sin cos 1
αα
+=−
.
Lời giải
Chọn A
Câu 4:
sin 2a
bằng
A.
2sin .cosaa
. B.
sin a
. C.
cos a
. D.
cos 2a
.
Lời giải
Chọn A
Câu 5: Chu kỳ tuần hoàn của hàm số
sinyx=
là
A.
2k
π
()k ∈
. B.
2
π
. C.
π
. D.
2
π
.
Lời giải
Chọn D
Câu 6: Tập giá trị của hàm số
cos2023yx=
là
A.
[ ]
1;1−
. B.
( 1;1)−
. C.
[ ]
2023;2023−
. D.
11
;
22

−


.
Trang 7
Lời giải
Chọn C
Câu 7: Nghiệm của phương trình
tan 1
x =
là
A.
,
4
x kk
π
π
=+∈
. B.
3
,
4
x kk
π
π
=+∈
.
C.
,xk k
π
= ∈
. D.
,
2
x kk
π
π
=+∈
.
Lời giải
Chọn A
Ta có
tan 1 ,
4
x x kk
π
π
=⇔= + ∈
Câu 8: Cho dãy số
( )
n
u
xác định bởi
21
n
un= −
với
1n ≥
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Lời giải
Chọn A
Ta có:
1
2.1 1 1u = −=
Câu 9: Dãy số nào sau đây là dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6; 4; 2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Lời giải
Chọn A
Câu 10: Cho cấp số cộng
(
)
n
u
với
1
3u =
và
2
5.u =
Công sai của cấp số cộng đã cho bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Chọn A
Công sai của cấp số cộng
21
53 2
du u= − =−=
.
Câu 11: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
2
1
n
un= +
. B.
2
1
3
n
u
n
= −
. C.
sin
n
un n= +
. D.
2
sin
n
un=
.
Lời giải
Chọn D
Với mọi
*
,n
∈
ta có
2
1 sin 1 0 sin 1nn−≤ ≤⇒ ≤ ≤
nên dãy số đã cho bị chặn.
Phân tích phương án nhiễu:
A. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
B. Sai do dãy số này bị chặn trên nhưng không bị chặn dưới.
C. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
Trang 8
Câu 12: Cho
a
,
b
,
c
là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng?
A.
2
b ac=
. B.
2bac= +
. C.
2ab c+=
. D.
2bc a+=
.
Lời giải
Chọn B
Phân tích phương án nhiễu:
A: Sai vì nhớ nhầm của cấp số nhân.
B, C: Sai vì không phân biệt thứ tự của các số hạng của cấp số cộng.
Câu 13: Dãy số nào sau đây là cấp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x ≠
.
Lời giải
Chọn C
6 3.2=
,
12 6.2=
,
24 12.2=
.
Phân tích phương án nhiễu:
A. Sai do thay
21
:2uu= −
nhưng
43
:2uu=
.
B. Sai do học sinh lầm tưởng đây là cấp số nhân với công bội
11q =
.
D. Sai do dãy số trên là cấp số cộng, không phải cấp số nhân.
Câu 14: Cho cấp số cộng
( )
n
u
biết
6
48u =
và
11
83u =
. Tìm cặp
( )
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
( )
13; 7
. D.
( )
13; 7−−
.
Lời giải
Chọn C
Ta có:
6
11
48
83
u
u
=
=
1
1
5 48
10 83
ud
ud
+=
⇔
+=
1
13
7
u
d
=
⇔
=
.
Phân tích phương án nhiễu:
A. Sai vì đặt nhầm thứ tự của yêu cầu bài toán.
B. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình và đặt nhầm thứ tự
của yêu cầu bài toán.
D. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình.
Câu 15: Cho cấp số nhân với và công bội . Tìm giá trị của biết số hạng tổng quát
?
A. . B. . C. . D. .
Lời giải
Chọn D
.
( )
n
u
1
3u =
2= −q
n
1536= −
n
u
8=n
9n =
257n =
10n =
11
1
1536 . 1536 3.( 2) 1536
−−
=−⇔ =−⇔−=−
nn
n
u uq
Trang 9
.
Phân tích phương án nhiễu:
A. Sai do tính .
B. Sai do nhầm công thức số hạng tổng quát .
C. Sai do tính .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau:
Nhóm
Chiều cao (cm)
Số học sinh
1
[
)
150;152
5
2
[
)
152;154
18
3
[
)
154;156
40
4
[
)
156;158
26
5
[
)
158;160
8
6
[
)
160;162
3
100N =
Giá trị đại diện của nhóm thứ tư là
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Lời giải
Chọn B
Giá trị đại diện của nhóm thứ tư là
156 158
157
2
+
=
.
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Lời giải
Chọn A
Mốt
0
M
chứa trong nhóm
[40;60)
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
( )
9
1
( 2) 512 2 10
−
⇔− =− =− ⇔ =
n
n
( )
1
2 512
−
−=−
n
( )
( )
2
512 2 512 : ( 2) 256
2
−
⇔ =− ⇔− =− − =
−
n
n
8n⇔=
( )
1
. 1536 2 512 9
n
n
uq n=− ⇔− =− ⇔ =
( )
1
512
2 512 1 256 257
2
−
−
− =− ⇔ −= = ⇔ =
−
n
nn
Trang 10
Lời giải
Chọn A
Ta có:
42
n =
Nên trung vị của mẫu số liệu trên là
21 22
2
2
xx
Q
+
=
Mà
[
)
21 22
, 40;60
xx∈
Vậy nhóm chứa trung vị của mẫu số liệu trên là
nhóm
[40;60)
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
[
)
7; 9
.
B.
[
)
9; 11
.
C.
[
)
11; 13
.
D.
[
)
13; 15
.
Lời giải
Chọn B
Bảng tần số ghép nhóm theo giá trị đại diện là
Số trung bình:
2.6 7.8 7.10 3.12 1.14
9, 4
20
x
++ + +
= =
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8, 6
.
Lời giải
Chọn C
Gọi
1 2 20
, ,...,xx x
là doanh thu bán hàng trong 20 ngày xếp theo thứ tự không giảm.
Khi đó:
[
)
12
, 5; 7xx∈
,
[
)
39
,..., 7; 9xx∈
,,
[
)
9 16
,..., 9; 11xx∈
[
)
17 19
,..., 11; 13xx∈
,
[
)
20
13; 15x ∈
Do đó, tứ phân vị thứ nhất
của mẫu số liệu thuộc nhóm
[
)
7;9
1
20, 7, 2, 7, 9
m mm
n n Cu u
+
= = = = =
Trang 11
1
1.20
2
4
7 ()
7
89 7 7,86Q −≈= + ≈
−
Câu 21: Biết
4
sin
5
α
−
=
và
3
2
π
πα
<<
. Giá trị
cos
α
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
±
D.
9
.
5
Lời giải
Chọn A
Vì
3
π
πα
2
<<
nên
cosα0<
. Mặt khác
22
sin α cos α 1+=
ta có
2
cosα 1 sin α=−−
2
1
43
55

=− −− =−


.
Câu 22: Giá trị của biểu thức
sin
34
A
ππ

= +


là
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Lời giải
Chọn B
Ta có
3 2 21 6 2
sin sin cos sin cos . . .
34 34 432222 4
A
ππ ππ ππ
+

= += + = + =


Câu 23: Hàm số nào sau đây là hàm số lẻ?
A.
2cosyx= −
. B.
2
2sin 2yx=−+
. C.
2sinyx= −
. D.
2cos 2
yx=−+
.
Lời giải
Chọn C
Tập xác định của hàm số
( )
2siny fx x= = −
là
D =
.
Do đó, nếu
x
thuộc tập xác định
D
thì
x−
cũng thuộc tập xác định
D
.
Ta có
( )
( )
2sin( ) sinf x x x fx
−=− −= =−
. Vậy
2sinyx= −
là hàm số lẻ.
Câu 24: Tập nghiệm của phương trình
cos 1x = −
là
A.
2| .
2
S kk
π
π

=+∈


B.
2| .
2
S kk
π
π

=−+ ∈


C.
{
}
2| .Sk k
π
= ∈
D.
{ }
2| .S kk
ππ
=+∈
Lời giải
Chọn D
Ta có
cos 1 2 ,x x kk
ππ
=−⇔ = + ∈
.
Trang 12
Câu 25: Cho dãy số
11 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng
quát của dãy số đã cho là
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Lời giải
Chọn D
Câu 26: Cho cấp số cộng
(
)
n
u
có
1
2; 5ud= = −
. Số hạng thứ
20
của cấp số cộng là
A.
93
−
. B.
10
. C.
93
. D.
23
.
Lời giải
Chọn D
20 1
19 2 19( 5) 93
uu d=+ =+ −=−
.
Câu 27: Cho cấp số nhân
( )
n
x
có
2
3
x = −
và
4
27.x = −
Tính số hạng đầu
1
x
và công bội
q
của cấp số
nhân.
A.
1
1, 3
xq=−=−
hoặc
1
1, 3.
xq= =
B.
1
1, 3xq=−=
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq=−=
D.
1
3, 1xq= =
hoặc
1
3, 1.
xq=−=−
Lời giải
Chọn B
2
21
3
41 1
1
9
33 3
3
27. 27. 1.
.
q
x xq q
x xq x
x
q
=
=−=− =±


⇔ ⇔⇔

=−=− =
= −


Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi
bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
Lời giải
Chọn C
Theo bảng thống kê, giá trị lớn nhất là 60 thuộc lớp
[
)
6,5;8
nên giá trị đại diện là
6,5 8
7,25
2
+
=
.
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Trang 13
Doanh thu
[
)
5; 7
[
)
7;9
[
)
9;11
[
)
11;13
[
)
13;15
Số ngày
2
7
7
3
1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
[
)
7; 9
.
B.
[
)
9; 11
.
C.
[
)
11; 13
.
D.
[
)
13; 15
.
Lời giải
Chọn B
Số trung bình của mẫu số liệu trên là:
6.2 8.7 10.7 12.3 14.1
9, 4
20
x
++ + +
= =
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Nhóm chứa trung vị là
A.
[
)
30;45
. B.
[
)
15;30
. C.
[
)
45;60
. D.
[
)
60;75
.
Lời giải
Chọn A
Cỡ mẫu:
9 5 15 14 7 50n =++ + +=
.
Gọi
1 50
,...,xx
là thời gian khảo sát tập thể dục trong ngày của 50 học sinh khối 11 và giả sử dãy
này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là
25 26
2
xx+
. Do hai giá trị
25 26
,xx
thuộc nhóm
[
)
30;45
.
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa
bởi hàm số
( )
5sin
5
ht t
π

=


, trong đó
(
)
ht
là độ cao tính bằng cetimét trên mực nước biển
trung bình tại thời điểm
t
giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc
phao lại ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm
số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Lời giải
Chọn B
Ta có mô hình hóa chiều cao của sóng nước là hàm hàm số
( )
5sin
5
ht t
π

=


nên để chiếc phao
ở vị trí đỉnh ở hai lần liên tiếp thì cách nhau một chu kì của sóng
( )
2
10
5
Ts
π
π
= =
.
Trang 14
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
33
sin 3
42
x
π

−=


bằng:
A.
.
9
π
B.
.
6
π
−
C.
.
6
π
D.
.
9
π
−
Lời giải
Chọn C
Ta có
3
32
33 3
43
sin 3 sin 3 sin
3
42 4 3
32
43
xk
xx
xk
ππ
π
π ππ
ππ
ππ
−=+
 
−=⇔ −= ⇔
 
 
− =−+
.
( )
13 2
13
32
36 3
12
.
17 17 2
32
12 36 3
xk
xk
kZ
xkxk
ππ
π
π
π ππ
π
= +
= +
⇔⇔ ∈
=+=+
TH1. Với
min
max
13 13
00
13 2
24 36
.
13 11
36 3
01
24 36
Cho
xk k x
xk
xk k x
π
ππ
π
> ⇔ >− ⇒ = → =
= + →
< ⇔ <− ⇒ =− → =−
TH2. Với
min
max
17 17
00
17 2
24 36
.
17 7
36 3
01
24 36
Cho
xk k x
xk
xk k x
π
ππ
π
> ⇔ >− ⇒ = → =
= + →
< ⇔ <− ⇒ =− → =−
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là
7
36
x
π
= −
và nghiệm dương nhỏ nhất là
13
.
36
x
π
=
Khi đó tổng hai nghiệm bằng
13 7
.
36 36 6
π ππ
−=
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng
1
cây, hàng
thứ hai trồng
2
cây, hàng thứ ba trồng
3
cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Lời giải
Chọn A
Gọi số cây ở hàng thứ
n
là
n
u
.
Ta có:
1
1u =
,
2
2
u =
,
3
3u =
, … và
123
... 3003
n
Suu u u= + + ++ =
.
Nhận xét dãy số
( )
n
u
là cấp số cộng có
1
1u =
, công sai
1d =
.
Trang 15
Khi đó
(
)
1
21
2
nu n d
S
+−


=
3003=
(
)
2.1 1 1
3003
2
nn
+−


⇔=
( )
1 6006
nn⇔ +=
2
6006 0nn⇔ +− =
77
78
n
n
=
⇔
= −
77n
⇔=
(vì
n ∈
).
Câu 34: Một cấp số nhân có số hạng đầu
1
3u =
, công bội
2q =
. Biết
765
n
S =
. Tìm
n
?
A.
8n =
. B.
9
n
=
. C.
6
n
=
. D.
7
n
=
.
Lời giải
Chọn A
Áp dụng công thức của cấp số nhân ta có:
( ) ( )
1
1 3. 1 2
765
1 12
nn
n
uq
S
q
−−
= = =
−−
8n
⇔=
.
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một
công ty như sau:
Thời gian
[
)
15;20
[
)
20;25
[
)
25;30
[
)
30;35
[
)
35;40
[
)
40;45
[
)
45;50
Số nhân viên
7
14
25
37
21
14
10
Tứ phân vị thứ nhất
1
Q
và tứ phân vị thứ ba
3
Q
của mẫu số liệu ghép nhóm này là
A.
13
1360 800
,
37 21
QQ= =
. B.
13
1360 3280
,
37 83
QQ
= =
.
C.
13
136 3280
,
5 83
QQ
= =
. D.
13
136 800
,
5 21
QQ= =
.
Lời giải
Chọn D
Cỡ mẫu là
128n =
.
Tứ phân vị thứ nhất
1
Q
là
32 33
2
xx
+
. Do
32 33
,xx
đều thuộc nhóm
[25;30)
nên nhóm này chứa
1
Q
.
Do đó,
2
13 3 43
3; 25; 25; 21, 5pa m m am
a= = = = −=+
và ta có
1
21
136
4
25
8
5
5
12
25
Q
−
= + ⋅=
Với tứ phân vị thứ ba
3
Q
là
96 97
2
xx
+
. Do
96 97
,xx
đều thuộc nhóm
[35;40)
nên nhóm này chứa
3
Q
.
Do đó,
125 5 4 653
5; 35; 21; 7 14 25 37 83; 5
p a m mmmm aa= = = + + + =+++ = −=
và ta có
3
3.128
83
800
4
35 5
21 21
Q
−
= + ⋅=
.
Trang 16
II. PHẦN TỰ LUẬN (3,0 điểm).
Câu
Đáp án
Biểu điểm
36a
Giải phương trình
cot 3
3
x
π

+=


.
0.5
cot 3
3 36
x xk
π ππ
π

+ = ⇔+ = +


0.25
6
xk
π
π
⇔=−+
()k ∈
.
0.25
36b
Cho
2
sin
3
α
=
, tính giá trị của biểu thức
(1 3 cos )(1 3 cos )P
αα
=−+
.
0.5
( )
2
2
(1 3cos )(1 3cos ) 1 3cos 1 9cosP
αα α α
=− +=− =−
.
0.25
2
sin
3
α
=
,
22 2
5
sin cos 1 cos
9
αα α
+=⇒=
.
5
1 9. 4
9
P =−=−
.
0.25
37
Giải phương trình
cos3 sin 2 0
xx−=
.
1.0
cos3 sin 2 0 cos3 sin 2 cos3 cos 2
2
xx x x x x
π

−=⇔=⇔= −


0.25
3 22
2
x xk
π
π

⇔=±− +


0.25
52
2
2
2
xk
xk
π
π
π
π
= +
⇔
=−+
0.25
2
10 5
()
2
2
xk
k
xk
ππ
π
π
= +
⇔∈
=−+
0.25
38
Giải phương trình
sin cos
3
xx
π

= +


1.0
sin cos
3
cos cos
23
xx
xx
π
ππ

= +



⇔ −= +


0,25
( )
2
23
2
23
xx k
k
xx k
ππ
π
ππ
π
−=+ +
⇔∈
− =−− +
0,25
22
6
xk
π
π
⇔− =− +
( )
k ∈
0,25
12
xk
π
π
⇔= −
( )
k ∈
.
0,25
Trang 17
39
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu
tiên là
100000
đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm
30000
đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng
với cơ sở khoan giếng này để khoan giếng sâu
20
mét lấy nước dùng cho sinh
hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh
toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
0.5
Giá tiền mỗi mét khoan giếng lập thành một cấp số cộng với
1
100000u =
(số tiền mét khoan đầu tiên),
21
30000uu= +
(số tiền mét khoan thứ hai),
32 1
30000 2.30000
uu u
=+=+
(số tiền mét khoan thứ ba)
…
20 19 1
30000 19.30000
uu u
=+=+
(số tiền mét khoan thứ 20),
và công sai
30000d =
.
0,25
Tổng chi phí cần phải thanh toán là
20 1 2 3 20
...
S uuu u= + + ++
20(2.10000 19.30000)
2
+
=
7700000=
.
0,25
-------------- HẾT --------------
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Trong các khẳng định sau, khẳng định nào sai?
A.
(
)
sin sin
πα α
−=
. B.
( )
cos cos
πα α
−=
.
C.
(
)
sin sin
πα α
+=−
. D.
( )
cos cos
πα α
+=−
.
Câu 2. Cho góc hình học
uOv
có số đo bằng
0
60
(hình 1.4). Số đo của các góc lượng giác
( )
,Ou Ov
là
A.
( )
00
60 360=+∈, .,sñ Ou Ov k k
. B.
(
)
00
60 180=+∈, .,sñ Ou Ov k k
.
C.
(
)
00
60 180=−∈
, .,
sñ Ou Ov k k
. D.
( )
00
60 360=−+ ∈
, .,
sñ Ou Ov k k
.
Câu 3. Trong các khẳng định sau, khẳng định định nào đúng?
A.
( )
sin sin cos sin cos .ab a b b a−= −
B.
( )
sin cos cos sin sin .ab a b a b−= −
C.
( )
sin cos sin sin cos .ab a b a b−= +
D.
( )
sin sin cos cos sin .ab a a b b−= −
Câu 4. Trong các khẳng định sau, khẳng định định nào sai?
A.
sin 2 2sin cos .a aa=
B.
22
cos 2 sin cos .aaa
= −
C.
2
cos2 2cos 1.aa= −
D.
2
cos 2 1 2sin .aa= −
Câu 5. Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số được liệt kê ở bốn
phương án A, B, C, D?
A.
1 sin 2yx= +
. B.
cosyx
=
. C.
sinyx=
. D.
cosyx= −
.
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
tan .
yx=
B.
cot .yx=
C.
sin .yx=
D.
cos .yx=
Câu 7. Điều kiện có nghiệm của phương trình
cos xm=
là
A.
1
m <
. B.
1m
>
. C.
1m ≤
. D.
1m ≥
.
Câu 8. Cho dãy số
( )
n
u
, biết
2
1
n
u
n
=
+
. Số hạng thứ 10 của dãy số đã cho là
A.
2
.
11
B.
2
.
3
C.
2
.
5
D.
1.
Câu 9. Khẳng định nào sau đây là sai?
A. Một dãy số tăng thì bị chặn dưới. B.Một dãy số giảm thì bị chặn trên.
C. Một dãy số bị chặn thì phải tăng hoặc giảm. D.Một dãy số không đổi thì bị chặn.
Câu 10. Cho cấp số cộng
( )
n
u
có số hạng đầu
1
2, 3ud= = −
. Năm số hạng đầu của cấp số cộng là
A.
2;1;4;7;10.−−−−
B.
2;3;6;9;12.−−−−
C.
2; 6;18; 54;162.−−
D.
2; 2; 2; 2; 2.
Câu 11. Cho cấp số cộng
( )
n
u
, biết
1
1u =
và công sai
3
5u =
. Khẳng định nào sau đây đúng?
A.
2
3.
u =
B.
2
2.u =
C.
2
1.
u =
D.
2
3.u = −
Câu 12. Cho cấp số cộng
( )
n
u
. Gọi
n
S
là tổng của
n
số hạng đầu của cấp số cộng. Khẳng định nào sau đây
đúng?
A.
( )
1
1
2
n
nn
S nu d
−
= +
. B.
( )
1
1
2
n
nu n n
Sd
+−
=
.
C.
( )
1
1
n
S nu n n d=+−
. D.
( )
1
1
2
n
n
S nu d
−
= +
.
Câu 13. Cho cấp số nhân
( )
n
u
, biết
12
2, 10uu= =
. Công bội của cấp số nhân là
A.
5q =
. B.
8q =
. C.
5
q
= −
. D.
12q =
.
Câu 14. Cho cấp số nhân
( )
n
u
. Gọi
n
S
là tổng của
n
số hạng đầu của cấp số nhân. Khẳng định nào sau đây
đúng?
A.
( )
1
1
1
n
n
uq
S
q
−
=
−
. B.
( )
1
1
1
n
n
uq
S
q
−
=
−
.
C.
( )
1
1
n
n
q
S
q
−
=
−
. D.
( )
1
1
1
n
n
uq
S
q
−
=
−
.
Câu 15. Cho cấp số nhân
( )
n
u
, biết
2.3
n
n
u =
. Khẳng định nào sau đây đúng?
A.
4
54u =
. B.
4
18
u =
. C.
4
6u
=
. D.
4
162u
=
.
Câu 16. Điều tra về chiều cao của học sinh khối lớp 11, ta được mẫu số liệu sau:
Chiều cao (cm)
Số học sinh
[
)
150;152
5
[
)
152;154
18
[
)
154;156
40
[
)
156;158
26
[
)
158;160
8
[
)
160;162
3
Tổng
100N =
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm?
A.
5
. B.
6
. C.
7
. D.
12
.
Câu 17. Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm
[
)
;ab
được tính như thế nào?
A.
.
2
ab+
B.
.ba−
C.
.ab+
D.
..ab
Câu 18. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Mốt. B. Số trung bình.
C. Số trung vị. D. Tứ phân vị.
Câu 19. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 20. Trong các khẳng định sau, khẳng định nào là đúng
A. Số trung bình không bị ảnh hưởng bởi các giá trị quá lớn hay quá bé.
B. Số trung bình luôn là một số liệu nào đó của mẫu.
C. Số trung bình chính là số trung vị.
D. Số trung bình là
11
...
kk
mx m x
x
n
++
=
.
Câu 21. Biết
1
sin
3
α
=
và
0
2
π
α
<<
. Giá trị
cos
α
bằng
A.
22
.
3
B.
22
.
3
−
C.
2
.
3
D.
2
.
3
−
Câu 22. Biết
4
cos
5
α
= −
và
2
π
απ
<<
. Giá trị
cos
4

+


π
α
bằng
A.
2
.
10
−
B.
22
.
10
C.
7
.
10
−
D.
7
.
10
Câu 23. Tập giá trị của hàm số
2 sinyx=
là
A.
[ ]
1;1 .−
B.
0; 2 .


C.
{ }
2; 2 .−
D.
2; 2 .

−

Câu 24. Tập nghiệm của phương trình
cos 1x =
là
A.
2| .
2
S kk
π
π

=+∈


B.
{ }
|.S kk
π
= ∈
C.
{ }
2| .Sk k
π
= ∈
D.
2| .
2
S kk
π
π

=−+ ∈


Câu 25. Cho dãy số
1234
;;;;...
2345
. Số hạng tổng quát của dãy số này là
A.
1
n
n
u
n
+
=
. B.
1
n
n
u
n
=
+
. C.
1
n
n
u
n
−
=
. D.
2
1
n
nn
u
n
−
=
+
.
Câu 26. Cho cấp số cộng
( )
n
u
có
1
0,1; 0,1ud
=−=
. Số hạng thứ 7 của cấp số cộng là
A.
1, 6
. B.
6
. C.
0,5
. D.
0,6
.
Câu 27. Cho cấp số nhân
( )
n
u
có
1
2
3;
3
uq=−=
. Số hạng thứ 5 của cấp số nhân là
A.
5
27
16
u = −
. B.
5
16
27
u =
. C.
5
16
27
u = −
. D.
5
27
16
u =
.
Câu 28. Tìm hiểu thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:
Thời gian (giờ)
[0; 5)
[5; 10)
[10; 15)
[15; 20)
[20; 25)
Số học sinh
8
16
4
2
2
Giá trị đại diện của nhóm
[
)
20;25
là
A.
22,5
. B.
23
. C.
20
. D.
5
.
Câu 29. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa tứ phân vị thứ ba của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 30. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở
bảng sau (đơn vị: triệu đồng)
Câu 31. Nếu
( )
00
1
sin cos 135 180
5
aa a− = <<
thì giá trị của biểu thức
tan 2a
bằng
A.
20
.
7
−
B.
20
.
7
C.
24
.
7
D.
24
.
7
−
Câu 32. Số nghiệm của phương trình
1
cos 2
2
x = −
thuộc đoạn
[ ]
;
ππ
−
là
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 33. Cho cấp số cộng có
1
3; 2ud=−=
. Khẳng định nào sau đây đúng?
A.
5
5.S =
B.
5
10.S =
C.
5
15.S =
D.
5
20.S =
Câu 34. Cho cấp số nhân có
7 11
127; 2047SS=−=−
. Tổng
8 9 10 11
Su u u u=++ +
có kết quả là
A.
1920.S = −
B.
1920.S =
C.
2174.S = −
D.
5
2174.S =
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
[
)
7; 9
.
B.
[
)
9; 11
.
C.
[
)
11; 13
.
D.
[
)
13; 15
.
Câu 35. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Số trung vị của mẫu số liệu ghép nhóm ở bảng trên là
A.
18,1
.
B.
18, 2
.
C.
18,3
.
D.
18, 4
.
( )
n
u
( )
n
u
II. PHẦN TỰ LUẬN
(3 điểm).
Bài 1
(1 điểm).
a. Cho
3
sin
52
xx
π
π

= <<


. Tính giá trị lượng giác
cot x
.
b. Tìm tập xác định của hàm số
1
cos 2
y
x
=
.
Bài 2 (1 điểm). Giải phương trình:
3 6 sin 2 0
3
x
π

− −=


.
Bài 3 (1 điểm). Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân
theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10, bậc 2 từ số
11 đến số 20, bậc 3 từ số thứ 21 đến số thứ 30,…Bậc 1 có giá là 1500 đồng/1 số, giá của mỗi số ở bậc thứ
1n +
tăng so với giá của mỗi số ở bậc thứ n là 2,5%. Biết rằng gia đình ông An sử dụng hết 345 số trong
tháng 1, hỏi tháng 1 ông An phải đóng bao nhiêu tiền?
……………… HẾT ………………
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng.
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
B
A
A
B
C
D
C
A
C
A
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
A
A
A
A
D
B
A
A
A
D
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
A
A
D
C
B
C
C
A
C
B
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
C
B
A
A
A
II. PHẦN TỰ LUẬN
Bài
Đáp án
Biểu điểm
1
1a. Cho
3
sin
52
xx
π
π

= <<


. Tính giá trị lượng giác của
cot x
Ta có
22
sin cos 1
xx+=
2
22
3 16
cos 1 sin 1
5 25
xx

⇒ =− =−=


4
cos
5
x⇒=±
cos 0
2
xx
π
π
<<⇒ <
, chọn
4
cos
5
x = −
.
0,25
4
cos 4
5
cot
3
sin 3
5
x
x
x
−
= = = −
0,25
1b. Tìm tập xác định của hàm số
1
cos 2
y
x
=
Hàm số xác định khi và chỉ khi
cos 2 0 2 ;
2 42
k
x x kx k≠⇔ ≠+ ⇔≠+ ∈
π ππ
π
0,25
Vậy tập xác định của hàm số là
\,
42
k
Dk

=+∈



ππ
.
0,25
2
Giải phương trình:
3 6 sin 2 0
3
x
π

− −=


2
sin 2
32
x
π

⇔ −=


22
34
22
34
xk
xk
ππ
π
ππ
ππ
−=+
⇔
−=−+
0,25
0,25
(
)
7
24
13
24
xk
kZ
xk
π
π
π
π
= +
⇔∈
= +
0,5
3
Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10,
bậc 2 từ số 11 đến số 20, bậc 3 từ số thứ 21 đến số thứ 30,…Bậc 1 có giá là 1500 đồng/1 số,
giá của mỗi số ở bậc thứ
1n +
tăng so với giá của mỗi số ở bậc thứ n là 2,5%. Biết rằng gia
đình ông An sử dụng hết 345 số trong tháng 1, hỏi tháng 1 ông An phải đóng bao nhiêu tiền?
Gọi
1
u
là số tiền phải trả cho 10 số điện đầu tiên
Suy ra
1
10.1500 15000u
= =
(đồng)
2
u
là số tiền phải trả cho các số điện từ 11 đến 20
Suy ra
( )
21
1 0,025
uu= +
…
0,25
34
u
là số tiền phải trả cho các số điện từ 331 đến 340
Suy ra
(
)
33
34 1
1 0,025uu= +
Các số
1 2 34
; ;...;uu u
lập thành cấp số nhân với
1
15000
u =
; công bội
1 0,025q = +
0,25
Số tiền phải trả cho 340 số điện đầu tiên là
(
)
( )
(
)
( )
34 34
11 1
1 1 0,025 1 1 0,025
. 15000. 789193, 28
1 1 0,025 1 1 0,025
Su S
−+ −+
= ⇒= =
−+ −+
0,25
Số tiền ông An phải trả cho các số điện từ 341 đến 345 là
( )
34
2
5.1500 1 0,025 17364,92S = +=
Vậy tháng 1 gia đình ông An phải trả số tiền là:
12
806558SS S=+≈
(đồng)
0,25
Mã đề 000 Trang 1/6
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG THPT
--------------------
(Đề thi có ___ trang)
KIỂM TRA HỌC KỲ I
NĂM HỌC 2023 - 2024
MÔN: TOÁN
Thời gian làm bài: ___ phút
(không kể thời gian phát đề)
Họ và tên: .........................................................................
Số báo danh: ............
Mã đề 000
I. PHẦN TRẮC NGHIỆM
(7 điểm).
Câu 1. Cho
2
a
π
π
<<
. Kết quả đúng là
A.
sin 0a >
,
cos 0
a >
. B.
sin 0a
<
,
cos 0a <
. C.
sin 0a >
,
cos 0a
<
. D.
sin 0a <
,
cos 0a >
.
Câu 2. Chọn đẳng thức sai trong các đẳng thức sau
A.
sin cos
2
xx
π

−=


. B.
sin cos
2
xx
π

= −


. C.
tan cot
2
xx
π

−=


. D.
tan cot
2
xx
π

−=−


.
Câu 3. Trong các công thức sau, công thức nào sai?
A.
22
cos2 cos – sin .a aa=
B.
22
cos2 cos sin .a aa= +
C.
2
cos2 2cos –1.
aa=
D.
2
cos2 1– 2sin .
aa=
Câu 4. Trong các công thức sau, công thức nào sai?
A.
( ) ( )
1
cos cos cos – cos .
2
a b ab ab= + +

B.
( ) ( )
1
sin sin cos – – cos .
2
a b ab ab= +

C.
( ) ( )
.
1
sin cos sin – sin
2
a b ab ab= +

+
D.
( ) ( )
1
sin cos sin cos .
2
a b ab ab= −− +

Câu 5. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương
án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A.
tan .yx=
B.
cos .yx=
C.
sin .yx= −
D.
cotyx=
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx
=
B.
cos .yx=
C.
tan .yx
=
D.
cot .yx
=
Câu 7. Tìm tất các các giá trị thực của tham số
m
để phương trình
sin
xm=
có nghiệm.
A.
1.m ≤
B.
1.m ≥−
C.
1 1.m−≤ ≤
D.
1.m ≤−
Câu 8. Cho dãy số
( )
n
u
, biết
31
n
n
n
u =
−
. Ba số hạng đầu tiên của dãy số đó là
A.
111
;;.
248
B.
11 3
;; .
2426
C.
11 1
;; .
2 4 16
D.
123
;;.
234
Câu 9. Cho dãy số
( )
n
u
, biết
1
2
n
n
u
+
=
. Khẳng định nào sau đây đúng?
A.
5
3.u =
B.
4
32.u =
C.
5
10.u =
D.
5
8.u =
Câu 10. Cấp số cộng
( )
n
u
có số hạng đầu
1
3u =
, công sai
5d =
, số hạng thứ tư là
Mã đề 000 Trang 2/6
A.
4
23u =
. B.
4
1u =
. C.
4
2u =
. D.
4
4u =
.
Câu 11. Cho một cấp số cộng có
12
3; 3uu
=−=
. Tìm
d
?
A.
5d =
. B.
7d =
. C.
6d =
. D.
8d =
.
Câu 12. Cho cấp số cộng
( )
n
u
có
1
2019u =
, công sai
5d =
. Khẳng định nào sau đây là đúng?
A.
2019 5
n
un= +
. B.
( )
5 2019 1
n
un=+−
. C.
( )
2019 5 1
n
un= +−
. D.
5 2019
n
un= +
.
Câu 13. Cho cấp số nhân
( )
n
u
có số hạng đầu
1
3
u
= −
và công bội
2
3
q =
. Số hạng thứ năm của
( )
n
u
là
A.
27
16
. B.
16
27
. C.
27
16
−
. D.
16
27
−
.
Câu 14. Cho cấp số nhân
( )
n
u
với
17
1
; 32
2
uu=−=−
. Tìm
q
?
A.
1
2
q = ±
. B.
2
q
= ±
. C.
4q = ±
. D.
1q = ±
.
Câu 15. Tổng 10 số hạng đầu tiên của cấp số nhân
()
n
u
với
1
3; 2uq
=−=−
bằng
A. -511. B. -1025. C. 1025. D. 1023.
Câu 16. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Mốt. B. Số trung bình. C. Số trung vị. D. Độ lệch chuẩn.
Câu 17. Trong mẫu số liệu ghép nhóm, độ dài mỗi nhóm
[
)
2;5
được tính bằng
A.
3.
B.
4.
C.
5.
D.
7
.
Câu 18. Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm
[
)
2;6
được tính bằng
A.
4.
B.
5.
C.
8.
D.
3.
Câu 19. Trung vị của mẫu số liệu ghép nhóm xấp xỉ cho trung vị của mẫu số liệu gốc, nó chia mẫu số liệu thành
hai phần. Mỗi phần chứa bao nhiêu phần trăm giá trị?
A.
20
. B.
30
. C.
40
. D.
50
.
Câu 20. Điểm thi (tính thang điểm 10) của
25
học sinh trong một trường THPT ta thu được cho bảng dưới đây
Điểm thi
[
)
3;5
[
)
7;9
Số học sinh
20
5
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm?
A.
2
. B.
6
. C.
1
. D.
3
.
Câu 21. Cho
4
cos
5
α
=
với
0
2
π
α
<<
. Tính
sin
α
.
A.
1
sin
5
α
=
. B.
1
sin
5
α
= −
. C.
3
sin
5
α
=
. D.
3
sin
5
α
= ±
.
Câu 22. Cho
cos
α
với
2
π
απ
<<
, khi đó giá trị của
sin
α
bằng
A.
7
274
. B.
15
274
. C.
7
274
−
. D.
15
274
−
.
Câu 23. Tập giá trị
T
của hàm số
cotyx=
là
A.
.T =
B.
{ }
\ 0.T =
C.
{ }
\, .T kk
π
= ∈
D.
\ ,.
2
T kk
π
π

= +∈



Mã đề 000 Trang 3/6
Câu 24. Giải phương trình
cos cos
4
x
π
=
.
A.
2 , ( )
6
x kk
π
π
=±+ ∈
. B.
2 , ( )
5
x kk
π
π
=±+ ∈
.
C.
2 , ( )
3
x kk
π
π
=±+ ∈
. D.
2 , ( )
4
x kk
π
π
=±+ ∈
.
Câu 25. Cho dãy số
111 1
1; ; ; ; ;...
2 4 8 16
. Số hạng tổng quát của dãy số này là
A.
1
n
u
n
=
. B.
1
2
n
n
u =
. C.
1
2
n
n
u
−
=
. D.
( )
1
2
n
n
u =
−
.
Câu 26. Một cấp số cộng biết
1
2, 3ud= =
. Số hạng tổng quát của cấp số cộng là
A.
23
n
un= −
. B.
13
n
un= −
. C.
21
n
un= +
. D.
31
n
un= −
.
Câu 27. Cho cấp số nhân:
11
; ;
5 125
a
−−
. Giá trị của
a
bằng
A.
1
.
5
a = ±
B.
1
.
25
a
= ±
C.
1
.
5
a = ±
D.
5.a = ±
Câu 28. Độ dài của 60 lá dương xỉ trưởng thành được cho bằng bảng phân bố tần số ghép lớp như sau.
Giá trị đại diện của nhóm thứ
2
là
A.
25.
B.
35.
C.
15.
D.
45.
Câu 29. Giá trị thành phẩm quy ra tiền( nghìn đồng) trong một tuần lao động của
7
công nhân trong một công
ty là:
180;200;210;190;210;190;220.
Mốt của mẫu số liệu trên là
A.
220.
B.
210.
C.
190;210.
D.
180.
Câu 30. Tiền thưởng của
20
công nhân trong một công ty được thống kê bởi mẫu số liệu:
3;2; 4;4;5;4;3;4;5;3;5;2; 2;4;5;4;3;5;4;5
(đơn vị: triệu đồng). Tứ phân vị của mẫu số liệu là
A.
123
2; 4; 3.QQQ= = =
B.
123
3; 3; 5.QQ Q= = =
C.
123
2; 3; 4.QQQ= = =
D.
12 3
3; 4; 5.QQ Q= = =
.
Câu 31. Tìm tập xác định
D
của hàm số
1 sin
.
cos 1
x
y
x
−
=
−
A.
D.=
B.
D\ , .
2
kk
π
π

= +∈



C.
{ }
D \, .kk
π
= ∈
D.
{ }
D \ 2, .kk
π
= ∈
Câu 32. Tổng các nghiệm của phương trình
( )
0
tan 2 15 1x −=
trên khoảng
( )
00
90 ;90−
bằng
A.
0
0.
B.
0
30 .−
C.
0
30 .
D.
0
60 .−
Mã đề 000 Trang 4/6
Câu 33. Cho cấp số công
( )
15
4
6 5 28
:
14
n
uu
u
S
+=
=
. Số hạng đầu
1
u
và công sai
d
của cấp số cộng bằng
A.
1
6
2
u
d
=
=
. B.
1
2
6
u
d
=
=
. C.
1
3
8
u
d
= −
=
. D.
1
8
3
u
d
=
= −
.
Câu 34. Cho cấp số nhân
( )
n
u
có
1
1
1;
10
uq
−
=−=
. Số
103
1
10
là số hạng thứ bao nhiêu?
A. số hạng thứ 103. B. số hạng thứ 104. C. số hạng thứ 105. D. số hạng thứ 106.
Câu 35. Thời gian(phút) truy cập Internet của mỗi buổi tối của một số học sinh được cho trong bảng sau
Chiều cao
[
)
9,5;12,5
[
)
12,5;15,5
[
)
15,5;18,5
[
)
18,5;21,5
[
)
21,5;24,5
Số học sinh
3
12
15
24
2
Tính số trung vị của mẫu ghép nhóm này.
A.
18,1
. B.
18
. C.
17
. D.
12
.
II. PHẦN TỰ LUẬN
(3 điểm).
Bài 1 (1 điểm).
a)
Cho
3
sin
5
α
=
và
00
90 180
α
<<
. Tính giá trị của biểu thức
cot 2tan
tan 3cot
E
αα
αα
−
=
+
.
b)
Tìm tập xác định của hàm số
1 sin
sin 2 1
x
y
x
−
=
+
.
Bài 2 (1 điểm). Giải phương trình
2
2sin 3sin 1 0xx− +=
và tìm các nghiệm thuộc
0;
2
π



.
Bài 3 (1 điểm). Một tam giác vuông có chu vi bằng và độ dài các cạnh lập thành một cấp số cộng.
Tính độ dài các cạnh của tam giác đó.
-------------------- HẾT --------------------
3
Mã đề 000 Trang 5/6
ĐÁP ÁN
HƯỚNG DẪN PHẦN TRẮC NGHIỆM
1.A
11.A
21D
2.A
12.C
22.D
3.A
13.D
23.C
4.D
14.C
24.B
5.B
15.B
25.C
6.B
16.B
26.D
7.D
17.A
27.D
8.A
18.A
28.C
9.A
19.B
29.D
10.C
20.C
30.D
31.A
32.B
33.B
34.D
35.C
HƯỚNG DẪN GIẢI PHẦN TỰ LUẬN
Câu 1 (1 điểm).
a) Cho
3
sin
5
α
=
và
00
90 180
α
<<
. Tính giá trị của biểu thức
cot 2tan
tan 3cot
E
αα
αα
−
=
+
.
Lời giải
22
sin cos 1
αα
+=
22
9 16
cos =1 sin 1
25 25
αα
⇒ − =−=
4
cos
5
4
cos
5
α
α
=
⇔
= −
Vì
00
90 180
α
<<
4
cos
5
α
⇒=−
. Vậy
3
tan
4
α
= −
và
4
cot
3
α
= −
.
43
2.
cot 2 tan 2
34
34
tan 3cot 57
3.
43
E
αα
αα

−− −

−

= = = −
+

−+ −


.
b) Tập xác định của hàm số
1 sin
sin 1
x
y
x
−
=
+
là:
Lời giải
Hàm số xác định
sin 2 1 0x
⇔ +≠
( ) ( )
33
sin 2 1 2 2
24
x xkk xkk
ππ
ππ
⇔ ≠−⇔≠+ ∈⇔≠+ ∈
Vậy tập xác định:
( )
3
4
x kk
π
π
≠+ ∈
.
Câu 2 (1 điểm). Giải phương trình
2
2sin 3sin 1 0xx− +=
và tìm các nghiệm thuộc
0;
2
π



Lời giải
Mã đề 000 Trang 6/6
Đặt
( )
sin 1 1tx t= −≤≤
, phương trình trở thành:
2
1
2 3 10
1
2
t
tt
t
=
− += ⇔
=
Với
1t =
, ta có:
( )
sin 1 2 .
2
x x kk
π
π
=⇔= + ∈
Do
0
2
x
π
≤<
nên
02
22
k
ππ
π
≤+ <
1
0.
4
k
−
⇔ ≤<
Vì
k ∈
nên không tồn tại k.
Với
1
2
t =
, ta có:
1
sin sin
26
x
π
= =
2
6
5
2
6
xk
xk
π
π
π
π
= +
⇔
= +
.
Do
0
2
x
π
≤<
nên
.
6
x
π
=
Vậy phương trình có nghiệm
6
x
π
=
thỏa điều kiện
0
2
x
π
≤<
.
Bài 3 (1 điểm). Một tam giác vuông có chu vi bằng và độ dài các cạnh lập thành một cấp số cộng.
Tính độ dài các cạnh của tam giác đó.
Lời giải
Gọi là công sai của cấp số cộng và các cạnh có độ dài lần lượt là , ,
Vì tam giác có chu vi bằng nên .
Vì tam giác vuông nên theo định lý Pytago ta có .
Suy ra ba cạnh của tam giác có độ dài là .
------ HẾT ------
3
d
ad−
a
ad+
( )
0 da<<
3
33a =
1a⇔=
( ) ( )
22
2
1 11dd+=−+
41d⇔=
1
4
d⇔=
35
;1;
44
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Trên đường tròn lượng giác, cho góc lượng giác có số đo
2
π
thì mọi góc lượng giác có cùng tia đầu và
tia cuối với góc lượng giác trên đều có số đo dạng
A.
2
π
. B.
( )
,
22
kk
ππ
+∈
. C.
( )
2,
2
kk
π
π
+∈
. D.
(
)
,
2
kk
π
π
+∈
.
Câu 2. Trên đường tròn có bán kính
5r =
cm, độ dài của cung có số đo
8
π
là
A.
8
l
π
=
cm. B.
40
l
π
=
cm. C.
5
8
l
π
=
cm. D.
5.180
8
l
=
cm.
Câu 3. Biểu thức
sin cos cos sinx y xy−
bằng
A.
( )
cos xy−
. B.
( )
cos xy+
. C.
( )
sin xy−
. D.
( )
sin yx−
.
Câu 4. Cho góc lượng giác
.a
Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
2
cos 2 1 2sinaa= −
. B.
22
cos 2 cos sina aa= −
. C.
2
cos 2 1 2cosaa= −
. D.
2
cos 2 2cos 1aa= −
.
Câu 5. Tìm tập xác định của hàm số
tan
yx=
.
A.
\|
2
kk
π
π

+∈


.B.
{ }
\|kk
π
∈
. C.
\ 2|
2
kk
π
π

+∈


. D.
{ }
\ 2|
kk
π
∈
.
Câu 6. Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A.
tanyx
=
. B.
2
2024yx= +
. C.
sinyx=
. D.
cosyx=
.
Câu 7. Nghiệm của phương trình
sin sin
3
x
π
=
là
A.
( )
2
3
2
3
xk
k
xk
π
π
π
π
= +
∈
=−+
. B.
( )
2
3
2
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
.
C.
( )
3
x kk
π
π
=+∈
. D.
( )
3
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
.
Câu 8: Cho các dãy số sau, dãy số nào là dãy số vô hạn?
A.
0, 2,4, 6,8,10.
B.
111 1
1, , , ,..., ,...
248 2
n
C.
1, 4,9,16, 25.
D.
1,1,1,1,1.
Câu 9: Cho dãy số:
5;10;15;20;25;...
Số hạng tổng quát của dãy số này là
A.
5( 1)
n
un= −
. B.
5
n
un=
. C.
5
n
un
= +
. D.
51
n
un= +
.
Câu 10: Trong các dãy số sau, dãy số nào là một cấp số cộng?
A.
1;2;4;6;8
−−−−
. B.
1;3;6;9;12.
−−−−
C.
1;3;7;11;15.−−− −
D.
1;3;5;7;9
−−−−
.
Câu 11: Cho cấp số cộng
( )
n
u
với
52
n
un= −
. Tìm công sai của cấp số cộng.
A.
3d =
. B.
2
d = −
. C.
1d =
. D.
2d =
.
Câu 12: Cho cấp số cộng
( )
n
u
có
1
1u =
và
2
3u =
. Giá trị của
3
u
bằng
A.
6.
B.
9.
C.
4.
D.
5.
Câu 13: Cho các dãy số sau. Dãy số nào là dãy số giảm?
A.
1; 1; 1; 1; 1; 1.
B.
1 1 11
1; ; ; ; .
2 4 8 16
−−
C.
1; 3; 5; 7.
D.
11; 9; 7; 5; 3.
Câu 14: Cho dãy số
(
)
n
u
có
1
n
u
n
=
. Khẳng định nào sau đây sai?
A.
1
1u =
. B. Dãy số
(
)
n
u
là dãy số tăng.
C. Dãy số
( )
n
u
bị chặn trên bởi 1. D. Dãy số
( )
n
u
là dãy số giảm.
Câu 15: Cho dãy số
(
)
n
u
có
21
1
n
n
u
n
−
=
+
. Khi đó,
2
u
bằng
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 16. Đo chiều cao (tính bằng cm) của
500
học sinh trong một trường THPT ta thu được kết quả như sau:
Chiều cao (cm)
[
)
150;155
[
)
155;160
[
)
160;165
[
)
165;170
[
)
170;175
[
)
175;180
Số học sinh
25
50
200
165
50
10
Các em có chiều cao 170 cm được xếp vào nhóm:
A.
[
)
155;160
. B.
[
)
160;165
. C.
[
)
165;170
. D.
[
)
170;175
.
Câu 17. Trong mẫu số liệu ghép nhóm, giá trị đại diện
i
x
của nhóm
[
)
1
;
ii
aa
+
được tính bằng công thức
A.
1
2
ii
i
aa
x
+
+
=
. B.
1
2
ii
i
aa
x
+
−
=
. C.
1i ii
xaa
+
= +
. D.
1ii i
xa a
+
= −
.
Câu 18. Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành hai phần, mỗi phần
chứa
50%
giá trị?
A. số trung vị. B. số trung bình. C. mốt. D. tứ phân vị.
Câu 19. Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành bốn phần, mỗi phần
chứa
25%
giá trị?
A. số trung vị. B. số trung bình. C. mốt. D. tứ phân vị.
Câu 20. Khẳng định nào sau đây sai?
A. Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc.
B. Mốt của mẫu số liệu ghép nhóm bằng mốt của mẫu số liệu gốc.
C. Mốt là một trong các số đặc trưng để đo xu thế trung tâm của mẫu số liệu.
D. Mốt của mẫu số liệu là các giá trị xuất hiện với tần số lớn nhất.
Mức 2
Câu 21. Cho
1
cos
2
α
=
và
3
2
2
π
απ
<<
. Tính
sin
α
.
A.
3
2
−
. B.
3
2
. C.
2
2
. D.
2
2
−
.
Câu 22. Cho
tan 2
α
=
. Tính
tan
4
π
α

−


.
A.
1
3
−
. B.
1
. C.
2
3
. D.
1
3
.
Câu 23. Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
4sin cos 1y xx= +
. Tính
Mm+
.
A.
2
. B.
4
. C.
3
. D.
1−
.
Câu 24. Cung lượng giác có điểm biểu diễn là
12
,MM
như hình vẽ là nghiệm của phương trình lượng giác nào
sau đây?
A.
sin 0
3
x
π

−=


. B.
sin 0x =
. C.
cos 0
3
x
π

−=


. D.
sin 0
3
x
π

+=


.
Câu 25: Cho dãy số
n
u
xác định bởi
1
1
2
.
1
1
3
nn
u
uu

Tìm số hạng
3
.u
A.
3
5
.
9
u
B .
3
1.u
C.
3
2
.
3
u
D.
3
14
.
27
u
Câu 26: Cho cấp số cộng
( )
n
u
có số hạng đầu
1
0,1u = −
và công sai
0,1d =
. Số hạng thứ 7 của cấp số cộng này
là
A.
1, 6
. B.
6
. C.
0 , 5
. D.
0,6
.
Câu 27: Cho cấp số nhân có các số hạng lần lượt là
3; ; 27; 81;...
x
Tìm
x
.
A.
9−
. B. 9. C.
81−
. D.
81
.
Câu 28. Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:
Thời gian (giờ)
[
)
0; 4
[
)
4;8
[
)
8; 12
[
)
12;16
[
)
16;20
Số học sinh
3
15
10
8
4
Tính tổng số học sinh được khảo sát.
A. 40. B. 15. C. 20. D. 5.
Câu 29. Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:
Thời gian (giờ)
[
)
0; 4
[
)
4;8
[
)
8; 12
[
)
12;16
[
)
16;20
Số học sinh
3
15
10
8
4
Thời gian xem tivi trung bình trong tuần trước của các bạn học sinh này là
A. 9,5 giờ. B. 11,5 giờ. C. 7,5 giờ. D. 15 giờ.
Câu 30. Doanh thu bán hàng trong 30 ngày của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):
Doanh thu
;57
;79
;9 11
;11 13
;13 15
Số ngày
4
10
12
3
1
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là
A.
;79
. B.
;57
. C.
;9 11
. D.
;9 11
.
Mức 3
Câu 31. Tìm tập xác định
D
của hàm số
tan 2
4
yx
π

= −


.
A.
3
\,
82
k
Dk
ππ

= +∈



. B.
3
\,
4
D kk
π
π

= +∈



.
C.
3
\,
42
k
Dk
ππ

= +∈



. D.
\,
2
D kk
π
π

= +∈



.
Câu 32. Phương trình
2sin 3 0x +=
có tổng nghiệm dương nhỏ nhất và nghiệm âm lớn nhất bằng
A.
4
3
π
. B.
2
π
. C.
3
π
. D.
π
.
Câu 33: Cho dãy số
( )
n
u
là cấp số cộng có
1
1; 2.ud=−=
Tìm
n
biết
483.
n
S =
A.
20=n
. B.
21=n
. C.
22=n
. D.
23=
n
.
Câu 34: Cho cấp số nhân
( )
n
u
có
1
1; 2uq= = −
. Tổng của 10 số hạng đầu tiên của cấp số nhân đó bằng
A.
341−
B.
341
C.
1023
D.
1023−
Câu 35. Đo chiều cao (tính bằng cm) của
500
học sinh trong một trường THPT ta thu được kết quả như sau:
Chiều cao
[
)
150;155
[
)
155;160
[
)
160;165
[
)
165;170
[
)
170;175
[
)
175;180
Số học sinh
25 50 200 165 50 10
Tính mốt của mẫu số liệu ghép nhóm trên.
A. 160. B. 164,05. C. 162,5. D. 160,94.
II. PHẦN TỰ LUẬN
(3 điểm).
Câu 1 (1 điểm).
a) Cho
12
sin
13
α
=
với
2
π
απ
<<
. Tính
sin 2
α
.
b) Tìm tập xác định của hàm số
cos
sin 1
x
y
x
=
−
.
Câu 2 (1 điểm). Giải phương trình
5 4cos2 6sin .sin 3x xx−=
.
Câu 3 (1 điểm). Ước tính dân số năm 2022 của tỉnh Kon Tum là 579 914 người, tỷ lệ tăng dân số 1,5% so với
năm trước. Nếu lấy kết quả chính xác đến hàng nghìn thì dân số của tỉnh Kon Tum năm 2030 là bao nhiêu?
-------------------- HẾT --------------------
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
LỚP 11 − ĐỀ 1
Câu
Ý
Đáp án
Điểm
1
(1,0 điểm)
a
2
22
12 25 5
cos 1 sin 1 cos
13 169 13
αα α

=− =− =⇒=±


Vì
2
π
απ
<<
nên
cos 0
α
<
. Suy ra
5
cos
13
α
= −
0,25
12 5 120
sin 2 2sin .cos 2. .
13 13 169
α αα

= = −=−


0,25
b
Hàm số
os
sin 1
cx
y
x
=
−
xác định khi và chỉ khi
sin 1 2 ,
2
x x kk
π
≠⇔≠+π∈
0.25
Tập xác định của hàm số đã cho là
\ 2,
2
D kk
π

= + π∈



0.25
2
(1,0 điểm)
3
3cos 4 x = 6sinx.sin 3x
2
−
⇔
3
3cos4 3(cos2 cos 4 )
2
−= −x xx
0.25
⇔
3
3cos2
2
=x
0.25
⇔
1
cos 2
2
x =
0.25
x k ,k
6
π
⇔=±+π∈
0.25
3
(1,0 điểm)
Đặt P
0
= 579914 và r = 1,5% = 0,015
Gọi P
n
là dân số của tỉnh Kon Tum sau n năm nữa.
0.25
Sau 1 năm, dân số của tỉnh là:
1 00 0
P = P +P .r P (1+r)=
Sau 2 năm, dân số của tỉnh là:
2
2 11 0
P = P +P .r P (1+r)=
…
0.25
Sau n năm, dân số của tỉnh là:
n
n n-1 n-1 0
P = P +P .r P (1+r)=
Suy ra (P
n
) là một cấp số nhân với số hạng đầu P
0
và công bội q = 1+ r.
0.25
Do đó dân số của tỉnh Kon Tum năm 2030 là:
88
80
P .(1 ) 579914.(1,015) 653000Pr= += ≈
người.
0.25
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Cho
α
thuộc góc phần tư thứ hai của đường tròn lượng giác. Hãy chọn kết quả đúng
trong các kết quả sau đây.
A.
sin 0; 0.cos
αα
>>
B.
sin 0; 0.cos
αα
<<
C.
sin 0; 0.cos
αα
><
D.
sin 0; 0.cos
αα
<>
Câu 2. Một chiếc đồng hồ, có kim chỉ giờ
OG
chỉ số
9
và kim phút
OP
chỉ số
12
. Số đo của góc
lượng giác
,OG OP
là
A.
2,
2
kk

. B.
00
270 360 , .
kk
C.
00
270 360 ,
kk
.
D.
9
2,
10
kk

.
Câu 3. Trong các khẳng định sau, khẳng định định nào đúng?
A.
( )
sin sin cos cos sinab a b a b−= −
B.
( )
sin sin cos cos sinab a b a b−= +
C.
( )
sin sin cos cos sinab a b a b+= −
D.
( )
sin sin cos cos sinab a b a b+= −
Câu 4. Trong các khẳng định sau, khẳng định định nào sai?
A.
sin 2 2sin cos .
a aa=
B.
22
cos 2 cos sin .a aa= −
C.
2
cos2 2cos 1.
aa= +
D.
2
cos 2 1 2sin .aa
= −
Câu 5. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A.
tan
yx=
. B.
sin
yx=
. C.
cotyx=
. D.
cos
yx=
.
Câu 6. Hàm số nào sau đây là một hàm số lẻ ?
A.
cosyx=
B. y = 1 + cosx C. y = x + sinx D. y = cos2x
Câu 7. Tập hợp tất cả các giá trị của tham số
m
để phương trình
cosxm=
có nghiệm là
A.
( )
; 1.−∞ −
B.
[ ]
1;1 .−
C.
( )
1; .+∞
D.
.
Câu 8. Cho dãy số
( )
n
u
, biết
2
2
n
u
n
=
. Ba số hạng đầu tiên của dãy số là
A.
11
1;;.
35
B.
12
2; ; .
29
C.
12
2; ; .
39
D.
12
1; ; .
23
Câu 9. Cho dãy số
( )
n
u
, biết
3
n
n
u =
. Khẳng định nào sau đây đúng?
A.
3
27.u =
B.
4
82.u =
C.
5
240.u
=
D.
2
10.u =
Câu 10. Cho cấp số cộng
( )
n
u
, biết
12
1, 2uu=−=
. Công sai của cấp số cộng là
A.
1d =
. B.
3d =
. C.
3d = −
. D.
4d =
.
Câu 11. Cho cấp số cộng
( )
n
u
, biết
1
2
u
=
và công sai
3d = −
. Khẳng định nào sau đây đúng?
A.
2
1.u = −
B.
2
1.u =
C.
2
5.u =
D.
2
5.u = −
Câu 12. Cho cấp số cộng
( )
n
u
có
1
2u =
và
1.d =
Gọi
5
S
là tổng
5
số hạng đầu tiên của cấp số
cộng đã cho. Mệnh đề nào sau đây đúng?
A.
5
10.S =
B.
5
15.S
=
C.
5
20.S =
D.
5
5.S =
Câu 13. Cho cấp số nhân
( )
n
u
, biết
56
4, 2uu
=−=−
. Công bội của cấp số nhân là
A.
1
2
q
=
. B.
2q = −
. C.
2q
=
. D.
1
2
q = −
.
Câu 14. Cho cấp số nhân
( )
n
u
, biết
3
2u =
, công bội
4
q =
. Tìm
4
u
.
A.
3
32.
u
=
B.
3
8.u =
C.
3
12.u =
D.
3
10.u =
Câu 15. Cho cấp số nhân
( )
n
u
, khẳng định nào sau đây là đúng?
A.
2
11
.
k kk
u uu
−+
=
. B.
11
.
k kk
u uu
−+
=
.
C.
2
11
kk k
uu u
−+
= +
. D.
2
11
.
k kk
u uu
−+
=
.
Câu 16. Trong mẫu số liệu ghép nhóm, độ dài của nhóm
[
)
1; 9
được tính như thế nào?
A. 8. B. 5. C. 10 . D. 9 .
Câu 17. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. Số trung bình. B. Mốt.
C. Số trung vị. D. Tứ phân vị.
Câu 18.
Khối lượng của
30
củ khoai tây thu hoạch ở một nông trường được thống kê như bảng sau.
Tần suất ghép nhóm của lớp
[
)
100;110
là.
A.
0
0
20
. B.
0
0
40
. C.
0
0
60
. D.
0
0
80
.
Câu 19. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Khi đó trung vị của mẫu số liệu ghép nhóm này là:
A. 16,2. B. 15. C. 18,1 . D. 9 .
Câu 20. Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì
được đo như sau:
Thời gian [485; 510) [510; 535) [535; 560) [560; 585) [585; 610) [610; 635) [635; 660]
Số cầu thủ 8 2 1 2 1 1 1
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm?
A.
5
. B.
6
. C.
7
. D.
12
Câu 21. Biết
2
cos
3
α
= −
và
3
2
π
πα
<<
. Giá trị
sin
α
bằng
A.
5
3
−
B.
5
3
C.
5
2
D.
2
5
−
Câu 22. Biết
4
cos
5
α
=
và
0
2
π
α
−<<
. Giá trị
sin2
α
bằng
A.
24
.
5
−
B.
2
.
5
C.
24
.
25
−
D.
8
.
25
−
Câu 23. Tập giá trị của hàm số
2 sinyx
= +
là
A.
[ ]
1;1 .
−
B.
[ ]
0; 2 .
C.
[ ]
1; 2 .−
D.
[ ]
1; 3 .
Câu 24. Nghiệm của phương trình
cot 1x = −
là
A.
Zkkx ∈+−= ,
2
π
π
. B.
Z
kk
x ∈
+= ,
2
π
π
. C.
Z
kk
x
∈+
−
= ,
4
π
π
. D.
Zkk
x
∈+=
,
4
π
π
.
Câu 25. Cho dãy số có các số hạng đầu là:
2;0; 2; 4;6; .−
Số hạng tổng quát của dãy số này là
công thức nào dưới đây?
A.
2.
n
un= −
B.
2.
n
un= −
C.
( )
2 1.
n
un=−+
D.
2 4.
n
un
= −
Câu 26. Cho cấp số cộng
( )
n
u
có
1
0,1; 0, 2ud=−=
. Số hạng thứ 8 của cấp số cộng là
A.
2,3
. B.
3
. C.
1 , 3
. D.
0,6
.
Câu 27. Tìm
x
để các số
2; 8; ; 128x
theo thứ tự đó lập thành một cấp số nhân.
A.
14.x
B.
32.
x
C.
64.x
D.
68.x
Câu 28. Điều tra về điểm của học sinh lớp 11, ta có kết quả sau:
Nhóm
Chiều cao (cm)
Số học sinh
1
[
)
0; 2
1
2
[
)
2; 4
6
3
[
)
4;6
8
4
[
)
6;8
10
5
[
)
8;10
9
N=34
Giá trị đại diện của nhóm thứ tư là
A. 10 . B.
7
. C. 9 . D. 5 .
Câu 29. Thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả
sau:
Thời gian (giờ)
;57
;79
;9 11
;11 13
;13 15
Số học sinh
2
5
3
10
1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
[
)
7; 9
.
B.
[
)
9; 11
.
C.
[
)
11; 13
.
D.
[
)
13; 15
.
Câu 30. Khảo sát số kg giấy vụn ủng hộ của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm như sau:
Giấy vụn (kg)
;02
;24
;46
;68
;8 10
Số học sinh
7
19
10
8
5
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là
A.
[
4;6)
.
B.
[2;4)
.
C.
[6;8)
.
D.
[8;10)
.
Câu 31. Tập xác định của hàm số
1 sin
1 cos
x
y
x
+
=
−
là:
A.
\ 2,
2
R k kZ
π
π

+∈


B.
{ }
\,R kkZ
ππ
+∈
C.
{ }
\ 2,Rk kZ
π
∈
D.
\ 2,
2
R k kZ
π
π

−+ ∈


Câu 32. Phương trình
2sin 1x =
có bao nhiêu nghiệm thuộc tập
[ ]
;
ππ
−
A.
1.
B.
2.
C.
3.
D.
4.
Câu 33. Cho cấp số cộng
( )
n
u
thỏa mãn
135
16
15
.
27
uuu
uu
−+=
+=
Số hạng thứ 100 của cấp số cộng là
A. 417 B. 375 C. - 417 D. - 375
Câu 34. Cho cấp số nhân
n
u
có
1
3u
và
2
q 
. Số
192
là số hạng thứ mấy của cấp số nhân đã
cho?
A. Số hạng thứ 5. B. Số hạng thứ 6.
C. Số hạng thứ 7. D. Không là số hạng của cấp số đã cho.
Câu 35. Trong hoạt động bảo vệ môi trường, các học sinh lớp 11A1 tiến hành trồng cây. Kết quả
sau hoạt động được ghi lại ở bảng sau:
Số cây
[
)
1; 8
[
)
8;15
[
)
15;22
[
)
22;29
[
)
29;36
Số học sinh
7
15
6
10
3
Hãy tìm số trung vị của mẫu số liệu ghép nhóm trên.
A. 11,5. B. 25,5 . C. 18 . D. 26.
II. PHẦN TỰ LUẬN
(3 điểm).
Bài 1
(1 điểm).
a)
Cho
2
cos =
3
α
. Tính
tan 3cot
tan cot
A
αα
αα
+
=
+
.
b) Tìm tập xác định của hàm số
sin 3
cos 1
x
y
x
=
+
.
Bài 2 (1 điểm). Giải phương trình
sin 4 1 2cos 2 sin 2x xx
+− =
.
Bài 3 (1 điểm).
Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt
20000
đồng, mỗi lần sau tiền
đặt gấp đôi lần tiền đặt cọc trước. Người đó thua
9
lần liên tiếp và thắng ở lần thứ
10.
Hỏi du khác trên
thắng hay thua bao nhiêu?
……………… HẾT ………………
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng.
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
C
A
A
C
D
C
B
B
A
B
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
A
C
A
B
D
A
B
A
C
C
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
A
C
D
C
D
C
B
B
C
A
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
C
D
A
C
A
II. PHẦN TỰ LUẬN
Bài
Đáp án
Biểu điểm
1
a) Cho
2
cos =
3
α
. Tính
tan 3cot
tan cot
A
αα
αα
+
=
+
Ta có
2
2
2
2
2
11
tan 3 2
tan 3
tan cos
1 2cos
11
tan 1
tan
tan cos
A
α
α
αα
α
α
α
αα
++
+
= = = = +
+
+
.
0,25
Suy ra
4 17
1 2.
99
A =+=
0,25
b) Tìm tập xác định của hàm số
sin 3
cos 1
x
y
x
=
+
.
Hàm số xác định khi
cos 1 0x +≠
0,25
cos 1 2 ,x x kk
ππ
⇔ ≠− ⇔ ≠ + ∈
Vậy tập xác định của hàm số là
{ }
\ 2, .D kk
ππ
=+∈
0,25
2
Giải phương trình
sin 4 1 2cos 2 sin 2
x xx
+− =
2sin 2 .cos 2 1 2cos2 sin 2 0xx x x+− − =
0,25
( )( )
sin2x-1 2cos 2 1 0x⇔ −=
0,25
sin 2 1
1
cos2x=
2
x =
⇔
0,25
(
)
4
.
x=
6
xk
k
k
π
π
π
π
= +
⇔∈
+
0,25
3
Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt
20000
đồng, mỗi lần sau tiền đặt gấp
đôi lần tiền đặt cọc trước. Người đó thua
9
lần liên tiếp và thắng ở lần thứ
10.
Hỏi du khác
trên thắng hay thua bao nhiêu?
Số tiền du khác đặt trong mỗi lần (kể từ lần đầu) là một cấp số nhân có
1
20 000u
và công bội
2.q
0,25
Du khách thua trong 9 lần đầu tiên nên tổng số tiền thua là:
9
1
9 12 9
1
... 10220000
1
up
S uu u
p

0,25
Số tiền mà du khách thắng trong lần thứ
10
là
9
10 1
. 10240000
u up
0,25
Ta có
10 9
20 000 0uS

nên du khách thắng 20 000.
0,25
1
ĐỀ KIỂM TRA MINH HOẠ GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Giá trị nào sau đây mang dấu dương?
A.
0
cos120
B.
0
sin120
C.
0
tan120
. D.
0
cot120
.
Câu 2. Trong mặt phẳng cho ba tia
,,Ou Ov Ox
. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
( ) ( ) ( )
π
= + +∈, , , 2,sñ Ou Ov sñ Ou Ox sñ Ox Ov k k
.
B.
( )
( )
( )
π
= + +∈
, , , 2,
sñ Ou Ov sñ Ou Ov sñ Ox Ou k k
.
C.
( ) ( ) ( )
π
= + +∈, , , 2,sñ Ou Ov sñ Ov Ox sñ Ox Ou k k
.
D.
( )
( )
( )
π
= + +∈
, , , 2,
sñ Ou Ov sñ Ov Ox sñ Ou Ox k k
.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A.
( )
cos cos cos sin sin .ab a b a b
+= −
B.
( )
cos cos cos sin sin .ab a b a b+= +
C.
( )
cos cos sin sin cos .ab a b a b+= +
D.
( )
cos sin cos cos sin .ab a a b b+= +
Câu 4. Trong các khẳng định sau, khẳng định nào sai?
A.
22
sin 2 cos sina aa= −
B.
cos 2 2sinaa=
C.
2
cos2 2cos 1.
aa= −
D.
2
cos 2 1 2sin .
aa= −
Câu 5. Đồ thị dưới đây là đồ thị của hàm số nào?
A.
1 sin 2yx= +
. B.
cos
yx=
. C.
sinyx= −
. D.
cos
yx= −
.
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
tan .
yx
=
B.
cot .yx=
C.
sin .yx=
D.
cos .yx=
Câu 7. Điều kiện có nghiệm của phương trình
sin xm=
là
A.
1m <
. B.
1m >
. C.
1m ≤
. D.
1m ≥
.
Câu 8. Cho dãy số
( )
n
u
, biết
2
n
un= +
. Ba số hạng đầu tiên của dãy số lần lượt là
A.
3; 4; 5.
B.
0;1; 2.
C.
2;3; 4.
D.
1; 2; 3.
Câu 9. Trong các dãy số sau dãy số nào là dãy số hữu hạn
A.
2345
11111
, , , , ....
33333
B.
5,10,15,20,25....
C.
8,15,22,29,36.
D.
2,0, 4,6,8,...
2
Câu 10. Cho cấp số cộng
( )
n
u
, biết
12
2, 8uu= =
. Công sai của cấp số cộng là
A.
6
d =
. B.
16d =
. C.
10d =
. D.
4d =
.
Câu 11. Cho cấp số cộng
(
)
n
u
, biết
1
2u =
và công sai
3d =
. Khẳng định nào sau đây đúng?
A.
2
5.u =
B.
2
2.u =
C.
2
6.u =
D.
2
3.u
=
Câu 12. Cho cấp số cộng
( )
n
u
. Gọi
n
S
là tổng của
n
số hạng đầu của cấp số cộng. Khẳng định đúng là
A.
( )
1
1
2
n
nn
S nu d
−
= +
. B.
( )
1
1
2
n
nu n n
Sd
+−
=
.
C.
( )
1
1
n
S nu n n d=+−
. D.
( )
1
1
2
n
n
S nu d
−
= +
.
Câu 13. Dãy số nào sau đây không phải là cấp số nhân?
A.
1; 3;9; 27;54
−−
. B.
1;2;4;8;16
. C.
1; 1;1; 1;1−−
. D.
1; 2;4; 8;16−−
.
Câu 14. Cho cấp số nhân
( )
n
u
với
1
81u =
và
4
3u =
. Tìm công bội
q
?
A.
1
3
1
3
−
. B.
1
3
−
. C.
3
. D.
3−
.
Câu 15. Cho cấp số nhân
( )
n
u
với
1
2
u =
và công bội
3q =
. Giá trị của
2
u
bằng
A.
6
. B.
9
. C.
8
. D.
2
3
.
Câu 16. Trong mẫu số liệu ghép nhóm, độ dài mỗi nhóm
[
)
;ab
được tính như thế nào?
A.
.ba−
B.
.
2
ab+
C.
.ab+
D.
..ab
Câu 17. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là
A. mốt. B. số trung bình.
C. số trung vị. D. tứ phân vị.
Câu 18. Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm
[
)
;ab
được tính như thế nào?
A.
.
2
ab+
B.
.ba−
C.
.ab+
D.
..ab
Câu 19. Trong các khẳng định sau, khẳng định nào là đúng?
A. Số trung vị là
( )
( )
11
1
...
2
p
ep p p
p
n
mm
Ma a a
m
+
+
− ++
=+−
.
B. Số trung vị bị ảnh hưởng bởi các giá trị quá lớn hay quá bé.
C. Số trung vị luôn là một số liệu nào đó của mẫu.
D. Số trung vị chính là số trung bình.
Câu 20. Đo chiều cao (tính bằng
cm
) của
500
học sinh trong một trường THPT ta thu được kết quả như
sau:
Chiều cao
[
)
150;154
[
)
154;158
[
)
158;162
[
)
162;166
[
)
166;170
3
Số học sinh
25
50
200
175
50
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm?
A.
5
. B.
6
. C.
7
. D.
12
.
Câu 21. Biết
1
sin
3
α
=
và
.
2
π
απ
<<
. Giá trị
cos
α
bằng
A.
22
.
3
−
B.
23
.
3
−
C.
32
.
2
−
D.
33
.
2
−
Câu 22. Biết
1
sin
4
α
=
. Giá trị
cos 2
α
bằng
A.
7
.
8
B.
8
.
7
C.
7
.
8
−
D.
8
.
7
−
Câu 23. Tập giá trị của hàm số
2sin
yx=
là
A.
[ ]
1;1 .−
B.
[ ]
0; 2 .
C.
{ }
2; 2 .−
D.
[ ]
2; 2 .−
Câu 24. Tập nghiệm của phương trình
cos 0x
=
là
A.
2| .
2
S kk
π
π

=+∈


B.
|.
2
S kk
π
π

=+∈


C.
{ }
2| .Sk k
π
= ∈
D.
2| .
2
S kk
π
π

=−+ ∈


Câu 25. Xét tính tăng giảm của dãy số
1111
;;;.
2345
−−−−
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng không giảm D. Dãy số vừa tăng vừa giảm
Câu 26. Cho một cấp số cộng có các số hạng lần lượt là
1, 6,11, .x
Khi đó giá trị của
x
là
A. 5 . B. 18. C. 17. D. 16.
Câu 27. Cho cấp số nhân có các số hạng lần lượt là 1; 4; 16; 64. Gọi
n
S
là tổng của n số hạng đầu tiên của
cấp số nhân đó. Mệnh đề nào sau đây đúng?
A.
41
3
n
n
S
−
=
. B.
( )
1
14
2
n
n
n
S
−
+
=
. C.
1
4
n
n
S
−
=
. D.
( )
44 1
3
n
n
S
−
=
.
Câu 28. Bảng số liệu ghép nhóm sau cho biết chiều cao
( )
cm
của 45 học sinh lớp
11A
.
Mẫu số liệu ghép nhóm này có số mốt là
A.
2
. B.
1
. C.
0
. D.
3
.
4
Câu 29. Cơ cấu dân số Việt Nam năm
2020
theo độ tuổi được cho trong bảng sau:
(Theo:http://ourwoldindata.org)
Chọn
85
là giá trị đại diện cho nhóm trên
65
tuổi. Tính tuổi trung bình của người Việt Nam năm
2020
.
A.
36,17
. B.
34,82
. C.
35,6
. D.
37,12
.
Câu 30. Khảo sát chiều cao (cm) của 52 học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị là
A.
[
)
165;170
. B.
[
)
160;165
. C.
[
)
170;175
. D.
[
)
175;180
.
Câu 31. Tập xác đinh của hàm số
sin cosyxx= +
là
A.
.
B.
{ }
\| .
kk
π
∈

C.
{ }
\| .k
π
∈
D.
{ }
\ 2| .kk
π
∈
Câu 32. Phương trình
2cos 3x = −
có bao nhiêu nghiệm thuộc tập
[ ]
;3
ππ
−
A. 4. B. 3. C. 2. D. 1.
Câu 33. Cho dãy số
( )
n
u
xác định bởi
222 2
111 1
...
123
n
u
n
= + + ++
. Chọn mệnh đề đúng?
A. Dãy số
( )
n
u
bị chặn.
B. Dãy số
( )
n
u
bị chặn trên, nhưng không bị chặn dưới.
C. Dãy số
( )
n
u
bị chặn dưới, nhưng không bị chặn trên.
D. Dãy số
( )
n
u
không bị chặn.
Câu 34. Gọi
1 11 111 ... 111...1S =+ + ++
(
n
số
1
) thì
S
nhận giá trị nào sau đây?
A.
1 10 1
10
99
n
Sn


−
= −




. B.
10 1
10
81
n
S

−
=


.
C.
10 1
10
81
n
Sn

−
= −


. D.
10 1
81
n
S
−
=
.
Câu 35. Khảo sát vận tốc (dặm/h;
1
dặm
1,609km=
) của
300
xe ô tô chạy trên con đường
A
thu được
mẫu số liệu ghép nhóm như sau:
5
Nhóm chứa tứ phân vị thứ nhất là
A.
[
)
32,5 ;37,5
. B.
[
)
27,5 ;32,5
. C.
[
)
37,5 ;42,5
. D.
[
)
42,5 ;47,5
.
II. PHẦN TỰ LUẬN
(3 điểm).
Câu 36
(1 điểm).
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liệu trên?
Câu 37
(1 điểm).
a) Tìm tập xác định của hàm số sau:
22
sin
sin cos
=
−
x
y
xx
.
b) Giải phương trình
( )
sin cos 1x
π
=
.
Câu 38 (1 điểm). Người ta trồng
2145
cây theo hình một tam giác như sau: hàng thứ nhất có
1
cây, hàng
thứ hai có
2
cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
……………… HẾT ………………
6
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng.
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
B
A
A
B
B
D
C
A
C
A
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
A
A
A
A
A
A
A
A
A
A
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
A
A
D
B
B
D
A
A
A
A
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
A
A
A
A
A
II. PHẦN TỰ LUẬN
Câu
Đáp án
Biểu điểm
36
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liệu trên?
T
ần số lớn nhất là
16
nên nhóm chứa mốt là nhóm
[
)
50,5;55,5
và
3j =
0,25
Ta có
3 4 43
50,5; 55,5 5
u u hu u= = ⇒= − =
0,25
Tần số:
23 4
7; 16; 4nn n= = =
.
0,25
( ) ( )
( ) ( )
1
2
3
11
3
3
2 34
jj
oj
jj jj
n
n
M u hu h
n
n
n
n
n
n n
n
n
n
−
−+
−
−
= + ⋅= + ⋅
−+−
− +−
0
16 7
50,5 .5 52,6
(16 7) ) (16 4
M
−
=+=
−−+
0,25
37
a) Tìm tập xác định của hàm số sau:
22
sin
sin cos
=
−
x
y
xx
.
Điều kiện xác định của hàm số là
22
sin cos 0 cos 2 0 2 ;
2 42
π ππ
π
− ≠⇔− ≠⇔ ≠ + ⇔≠ + ∈
k
x x x x kx k
.
0,25
Vậy tập xác định của hàm số là
\;
42
ππ

= +∈



k
Dk
0,25
b) Giải phương trình
( )
sin cos 1x
π
=
.
7
( )
sin cos 1 cos 2 ,
2
x x kk
π
ππ π
=⇔ =+∈
1
cos 2 ,
2
x kk⇔ =+∈
0,25
Vì
1 cos 1x−≤ ≤
nên
1 31
1 21
2 44
kk− ≤ + ≤ ⇔− ≤ ≤
.
Do
0
kk∈⇒=
suy ra
1
cos 2 ,
23
x x mm
π
π
=⇔=±+ ∈
.
0,25
38
Người ta trồng
2145
cây theo hình một tam giác như sau: hàng thứ nhất có
1
cây, hàng thứ hai
có
2
cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
Gọi số hàng cây là
n
, hàng thứ
n
có
n
cây.
0,25
Ta có
1 2 3 ... 2145n+++ + =
0,25
(
)
1
2145
2
nn+
⇒=
.
0,25
65n⇒=
0,25
======
TOANMATH.com
| 1/56
| | Tải xuống

Có thể bạn quan tâm:

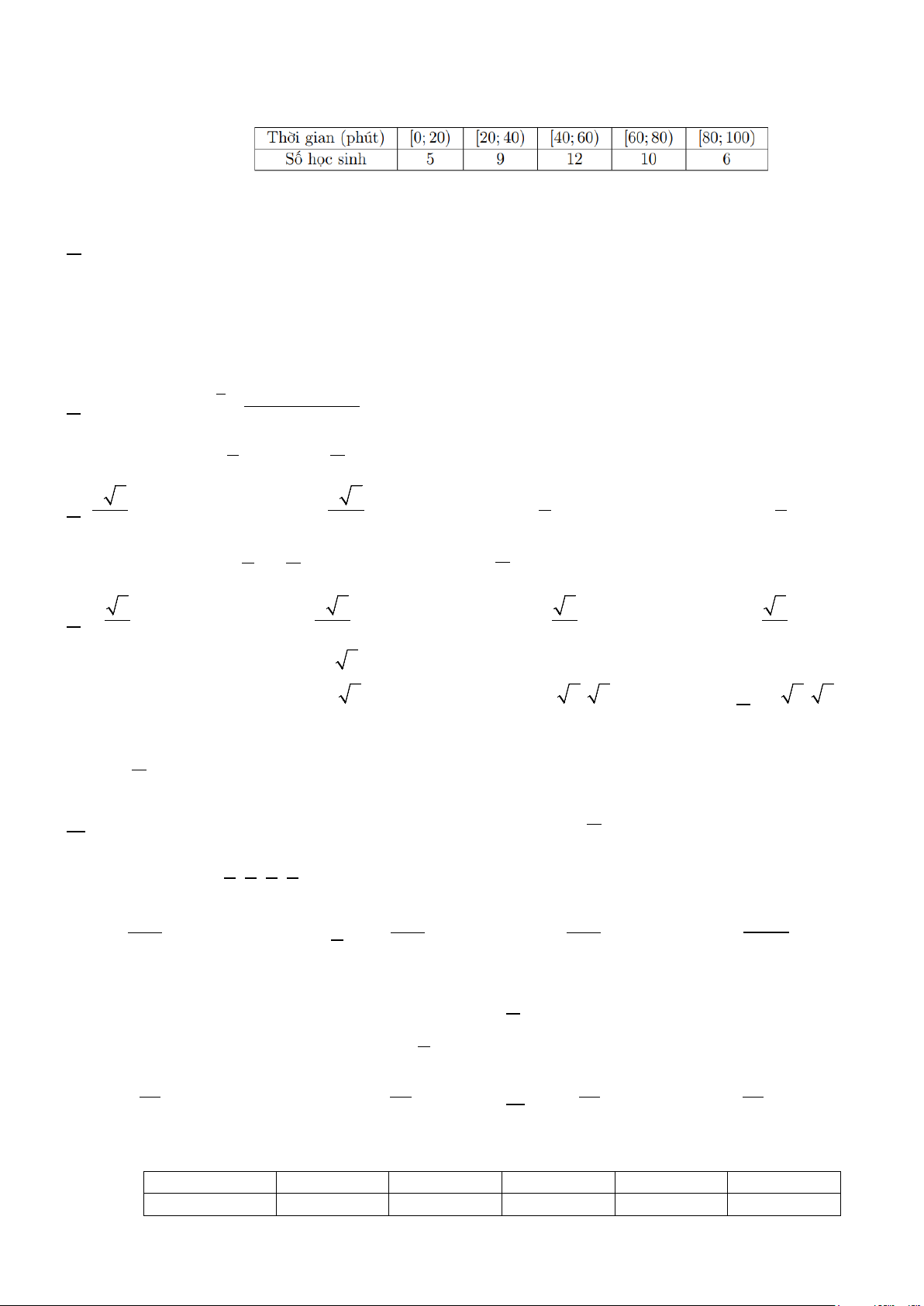
Preview text:

ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1: Trên đường tròn lượng giác gốc A , biết góc lượng giác ( ,
OA OM ) có số đo bằng 0 410 , điểm
M nằm ở góc phần tư thứ mấy? A. I . B. III . C. II . D. IV .
Câu 2: Đường tròn lượng giác có bán kính bằng: π A. 2 . B. 1. C. . D. π . 2
Câu 3: Khi quy đổi 1o ra đơn vị radian, ta được kết quả là π π A. π rad. B. 180 rad. C. rad. D. rad. π 180 360
Câu 4: Mệnh đề nào sau đây sai?
A. sin(π +α) = sinα.
B. cot(π +α) = cotα.
C. cos(π +α ) = −cosα .
D. tan(π +α) = tanα. Câu 5: π Cho 4
sinα = , < α < π . Tính cosα . 5 2 A. 3 cosα = − . B. 1 cosα = . C. 3 cosα = . D. 1 cosα = . 5 5 5 5
Câu 6: Trong các công thức dưới đây, công thức nào đúng? A. cos cos 2cos a b cos a b a b + − − = . B. cos cos 2sin a b sin a b a b + − − = . 2 2 2 2 C. cos cos 2cos a b cos a b a b + − − = − . D. cos cos 2sin a b sin a b a b + − − = − . 2 2 2 2
Câu 7: Trong các công thức dưới đây, công thức nào đúng?
A. cos(a + b) = sin . a cosb − cos .
a sin b .
B. cos(a + b) = sin . a cosb + cos . a sin b .
C. cos(a + b) = cos . a cosb + sin .
a sin b .
D. cos(a + b) = cos . a cosb − sin . a sin b . Câu 8: Cho 1 cosα = . Tính cos2α . 3 A. 7 cos2α = . B. 1 cos2α = . C. 7 cos2α = − . D. 2 cos2α = . 9 3 9 3
Câu 9: Rút gọn biểu thức  π   π T sin x sin x = + − −  ta được kết quả là 3 3     
A. T = 3 cos x .
B. T = sin x . C. 3 .
D. T = sin 2x . 2
Câu 10: Tập xác định hàm số y = sin x là:
A. D = [ −1;1]. B. D = .  C.  π
D =  \{kπ ,k ∈ }
 . D. D  \ k ,k ∈  =  .  2 
Câu 11: Mệnh đề nào sau đây là đúng?
A. Hàm số y = sin x là hàm số chẵn.
B. Hàm số y = cos x là hàm số chẵn.
C. Hàm số y = tan x là hàm số chẵn.
D. Hàm số y = cot x là hàm số chẵn.
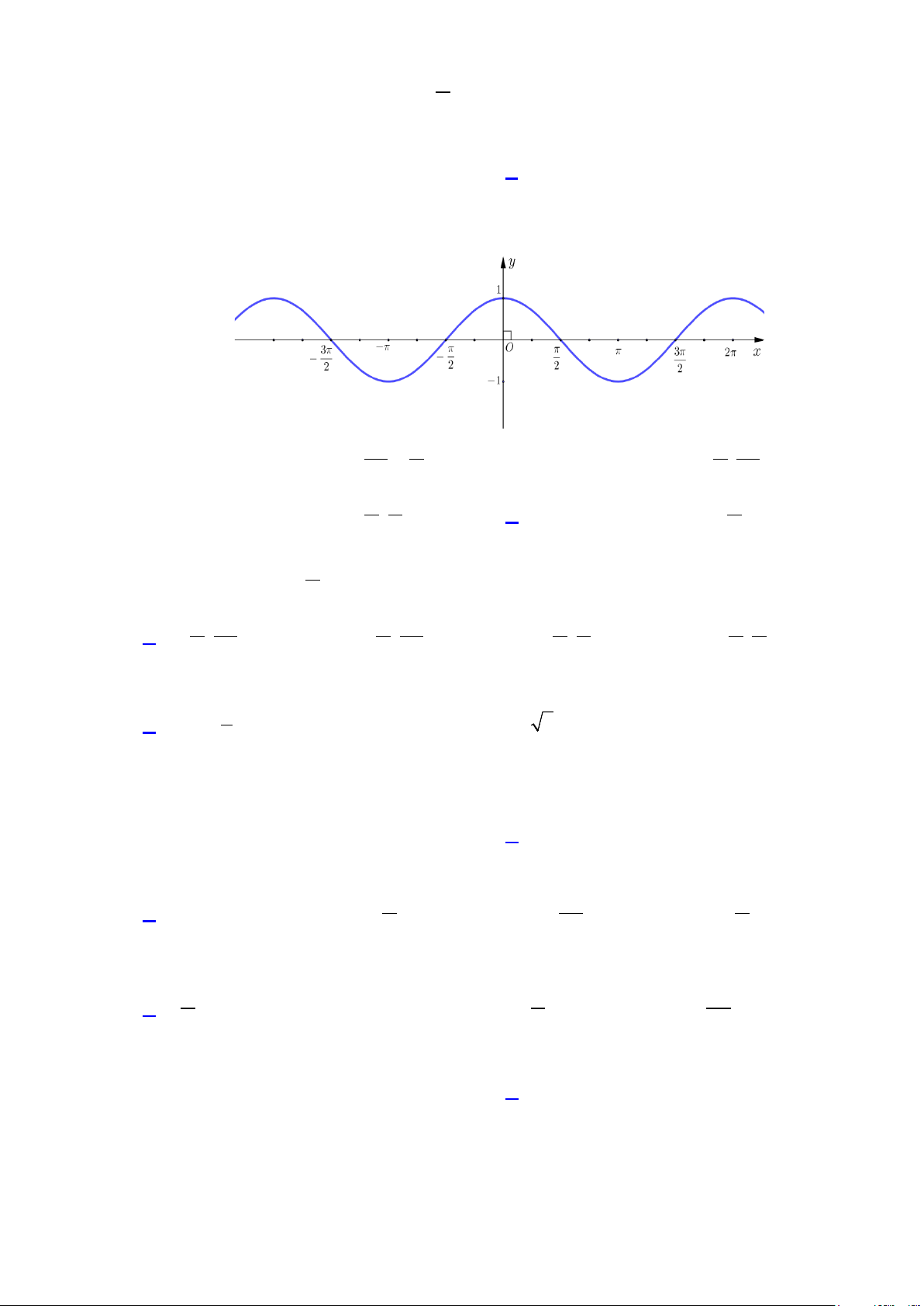
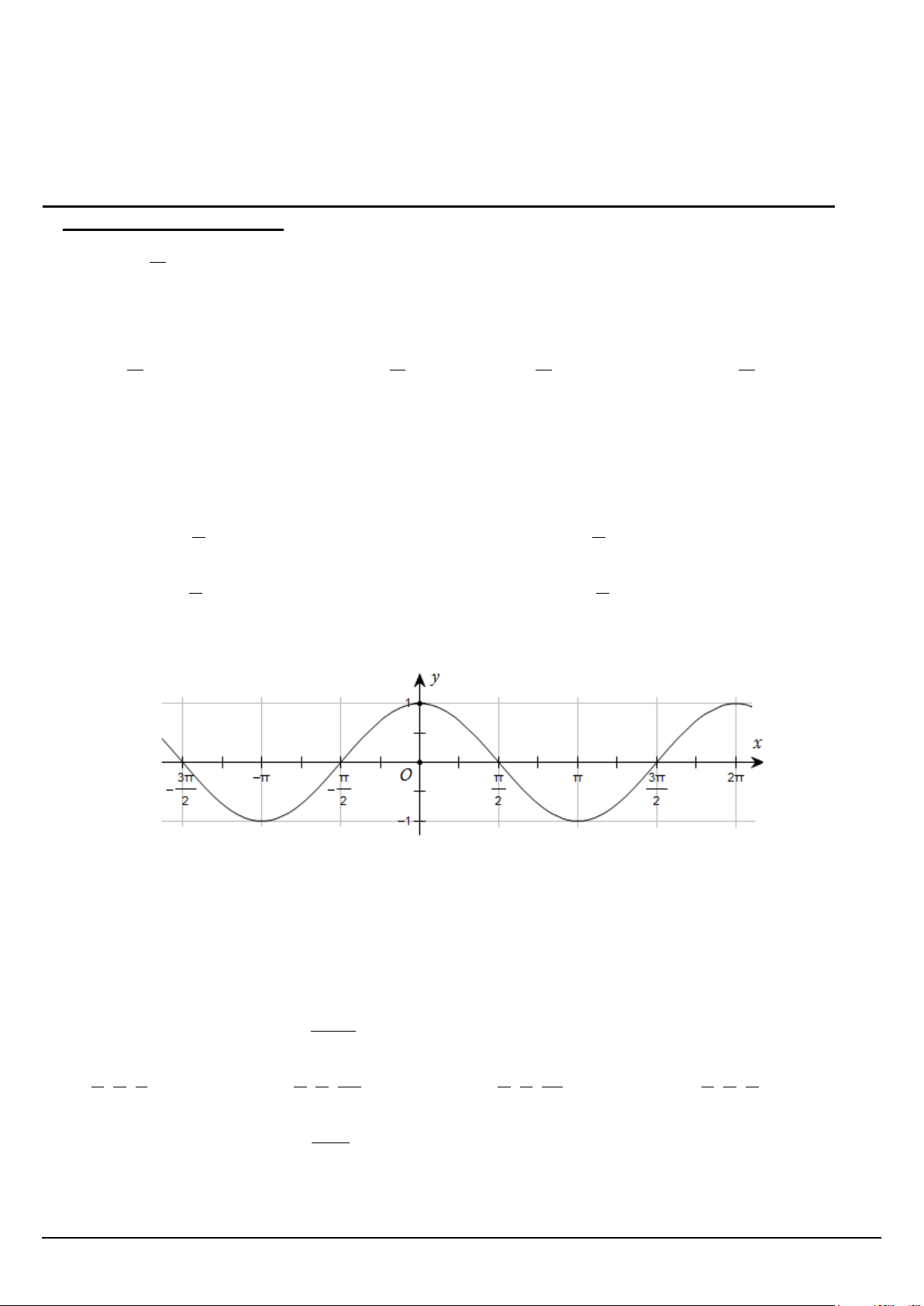
Câu 12: Cho hàm số y = f (x) có đồ thị như hình bên dưới. Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên  3π π  π π ;  − −   .
B. Hàm số đồng biến trên 3  ; .  2 2   2 2 
C. Hàm số đồng biến trên  π π  π ;  −   .
D. Hàm số đồng biến trên −  ;0.  2 2   2  Câu 13: Hàm số  π y sin 2x  = − 
đồng biến trên khoảng nào trong các khoảng sau đây? 4    A.  π 3π  π π  π π  π π ;  −     . B. 3 −  ; . C. −  ; . D. −  ; . 8 8        4 4   2 2   4 4 
Câu 14: Phương trình nào sau đây có nghiệm? A. 1 sin x = . B. sin x = 2. −
C. 2 sin x = 2. D. cos x = 2. 2
Câu 15: Phương trình sin x = sinα có tập nghiệm là:
A. S = {α + k2π | k ∈ }  .
B. S = {α + kπ | k ∈ }  .
C. S = {α + k2π; α
− + k2π | k ∈ }  .
D. S = {α + k2π;π −α + k2π | k ∈ }  .
Câu 16: Phương trình cos 2x =1 có nghiệm là: π π π
A. x = kπ , k ∈ k  .
B. x = + k2π , k ∈ . C. x = , k ∈.
D. x = + k2π , k ∈ . 2 2 4
Câu 17: Tìm tổng nghiệm dương bé nhất và nghiệm âm lớn nhất của phương trình sin x = cos(2x) . π π π A. − . B. 0 . C. . D. 2 . 3 4 3
Câu 18: Cho dãy số ( u ) với u = − . Mệnh đề nào sau đây đúng? n ( 5)n n A. u = 625 − .
B. u = 20.
C. u = 625 . D. u = 20 − . 4 4 4 4
Câu 19: Cho dãy số (u . Mệnh đề nào sau đây đúng? n ) A. Nếu * u > ∀ ∈
u là dãy số giảm. + u n n n , 1  thì ( n) B. Nếu * u ≤ ∀ ∈
u là dãy số giảm. + u n n n , 1  thì ( n) C. Nếu * u < ∀ ∈
u là dãy số giảm. + u n n n , 1  thì ( n) D. Nếu * u ≥ ∀ ∈
u là dãy số giảm. + u n n n , 1  thì ( n)
Câu 20: Trong các dãy số (u
u sau, dãy số nào là dãy số tăng?
n ) cho bởi số hạng tổng quát n A. 1 u + − = B. 1 u = C. n 5 u = D. 2n 1 u = n . n . n . n . 2n n 3n +1 n +1
Câu 21: Cho cấp số cộng (u có u = 3 và công sai d = 2 . Số hạng tổng quát của cấp số cộng (u là: n ) n ) 1
A. u = n + .
B. u = n − .
C. u = n − .
D. u = n + . n 2 1 n 2 2 n 3 2 n 3 2
Câu 22: Cấp số cộng (u có số hạng đầu u và công sai d u n ) 1
thì tổng n số hạng đầu của cấp số cộng ( n )
được xác định bởi công thức A. n(n +1) S + = nu + d . B. n(n 1) S = nu − d . n 1 2 n 1 2 C. n(n −1) S − = nu − d . D. n(n 1) S = nu + d . n 1 2 n 1 2
Câu 23: Cho dãy số (un ) là một cấp số cộng với công sai d , ta có công thức truy hồi A. * u = ∈ u = + ∈ + u d n n n , + u d n n n. , 1  . B. * 1  . C. un * u = ∈ u = − ∈ + u d n n n , + n n , 1  . D. *  . d 1
Câu 24: Tìm x để ba số thực 1; ;
x 5 theo thứ tự lập thành một cấp số cộng. A. x =1.
B. x = 0 .
C. x = 2 .
D. x = 3.
Câu 25: Tìm tổng S của 100 số nguyên dương đầu tiên và đều chia 5dư 1. A. 24353. B. 25100 . C. 50200. D. 5001.
Câu 26: Cho cấp số nhân (u có công bội .q Mệnh đề nào sau đây đúng? n ) A. n 1 u u q − = n ≥ . B. n 1 u u q + =
n ≥ . C. u = u . n q n ≥ . D. n u = q n ≥ . n ( 2) n ( 2) n . ( 2) n . ( 2) 1 1 1
Câu 27: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A. 2; 4; 8; 16;  B. 1; −1; 1; −1;  C. 2 2 2 2 1 ; 2 ; 3 ; 4 ;  D. 3 5 7 ; ; a a a ; a ;  (a ≠ 0).
Câu 28: Cho cấp số nhân (u với u = 2 − và q = 5.
− Viết bốn số hạng đầu tiên của cấp số nhân (u . n ) n ) 1 A. 2
− ; 10; 50; − 250. B. 2 − ; 10; − 50; 250. C. 2
− ; −10; −50; −250. D. 2 − ; 10; 50; 250.
Câu 29: Cho cấp số nhân (u có các số hạng lần lượt là 3; 9; 27; 81; .... Tìm số hạng tổng quát u của n ) n cấp số nhân (u . n ) A. n 1 u − = B. u = C. n 1 u + = D. u = + n 3 3 .n n 3 . n 3 .n n 3 .
Câu 30: Bác Bình gửi tiết kiệm 500 triệu đồng kì hạn 1 tháng với lãi suất 6% một năm theo hình thức
lãi suất kép. Nếu sau đúng một năm bác Bình mới đến ngân hàng rút tiền thì số tiền lãi Bác Bình
có được gần nhất với số nào sau đây.
A. 63,58 (triệu đồng). B. 60,15 triệu đồng. C. 60 triệu đồng.
D. 62,58 triệu đồng.
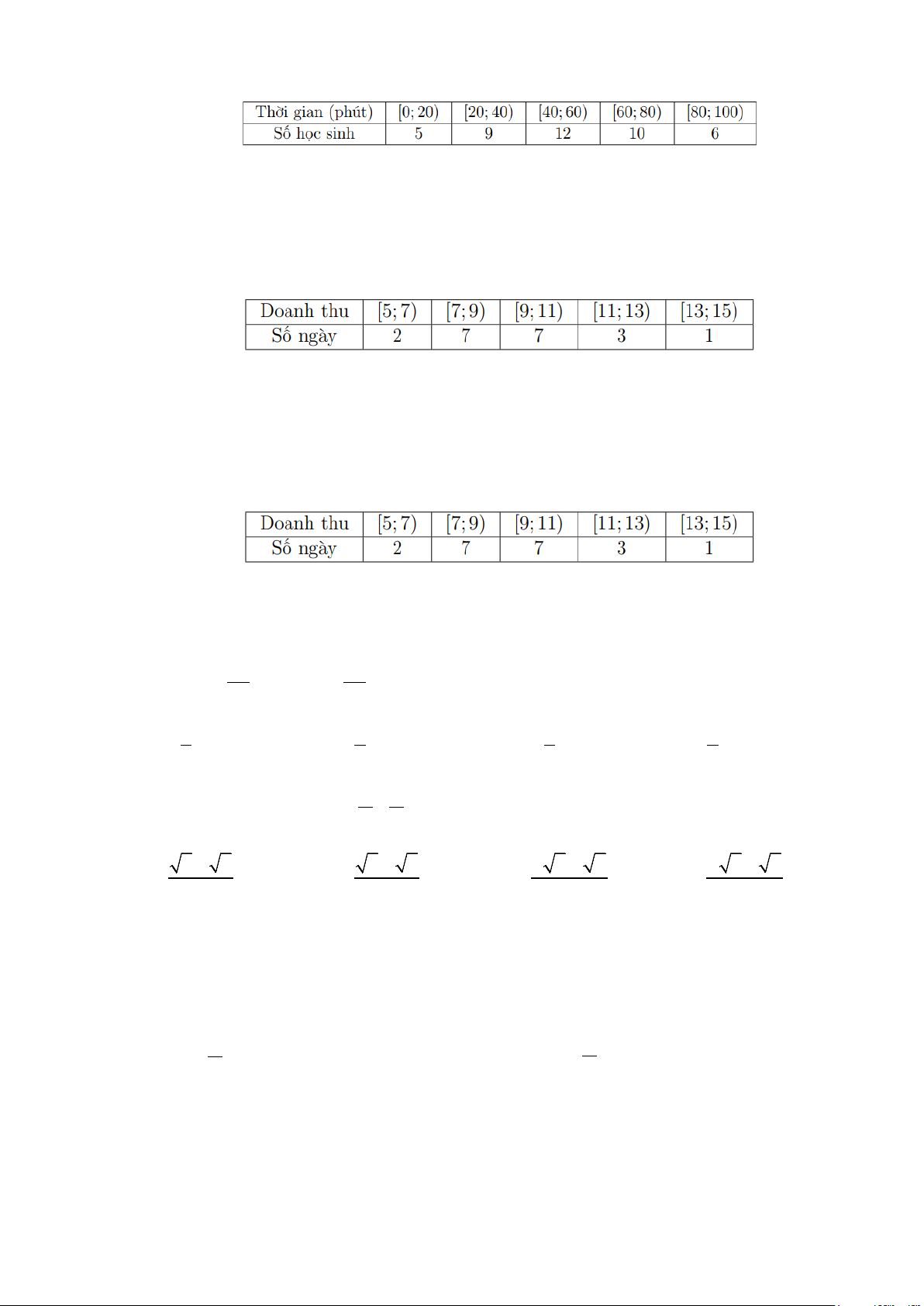
Câu 31: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
[0;20) [20;40) [40;60) [60;80) [80;100) Số học sinh 5 9 12 10 6
Giá trị đại diện của nhóm [20;40) là A. 10. B. 20. C. 30. D. 40.
Câu 32: Tuổi thọ (năm) của 50 bình ắc quy ô tô thu được mẫu số liệu ghép nhóm sau: Tuổi thọ (năm)
[2;2,5) [2,5;3) [3;3,5) [3,5;4) [4;4,5) [4,5;5) Tần số 4 9 14 11 7 5
Mẫu số liệu ghép nhóm này có số mốt bằng A. 14. B. 9. C. 7. D. 5.
Câu 33: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
[15;20) [20;25) [25;30) [30;35) [35;40) [40;45) [45;50) Số nhân viên 6 14 25 37 21 13 9
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 phút đến dưới 20 phút? A. 6. B. 9. C. 14. D. 13.
Câu 34: Cho mẫu số liệu ghép nhóm sau: Nhóm [a ;a . [a a . [a a k ; k 1 + ) i ; i 1 + ) 1 2 ) Tần số m . m . m 1 i k Với n +
= m + m +...+ m là cỡ mẫu và a a i i 1 x + =
(i =1,...k ) là giá trị đại diện của nhóm 1 2 k i 2
[a a . Khi đó công thức tính số trung bình cộng của mẫu số liệu ghép nhóm trên là: i ; i 1 + ) (m x … m x 1 1 ) ( k k ) A. x n = . B. x = . m x +…+ m x n 1 1 k k C.
m x −…− m x m x +…+ m x 1 1 k k x = . D. 1 1 k k x = n n
Câu 35: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
[0;20) [20;40) [40;60) [60;80) [80;100) Số học sinh 5 9 12 10 6 Nhóm chứa trung vị là A. [0;200). B. [20;40) . C. [40;60). D. [60;80) .
II. PHẦN TỰ LUẬN (3 điểm).
Bài 1. (1,0 điểm).
a) Tìm tập xác định của hàm số. 1 y = . 1+ cos x
b) Cho dãy số (u biết 1 u =
. Viết ba số hạng đầu tiên của dãy số (u . n ) n ) , n n +1
Bài 2. (1 điểm). Tìm m để phương trình để 2
2sin x + 3 sin x − 5m = 0luôn có nghiệm. 2
Bài 3. (1 điểm). Một đa giác có chu vi là 158cm , độ dài các cạnh của nó lập thành một cấp số
cộng. Biết cạnh lớn nhất có độ dài là 44cm . Tìm số cạnh của đa giác đó?
……………… HẾT ………………
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng. Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 A B C A A D D C B B
Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 B D A A D A A C C D
Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 D D B D A A C B B A
Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 C A A D C II. PHẦN TỰ LUẬN Câu Nội dung Điểm
a. Tìm tập xác định của hàm số 1 y = . 1+ cos x
Điều kiện xác định của hàm số là: cos x ≠ 1 − 0,25
hay x ≠ π + k2π ( k ∈ ).
Tập xác định của hàm số 1 y =
là D =  \{π + k2π | k ∈ }  0,25 1+ cos x
b. Cho dãy số (u biết 1 u =
. Viết ba số hạng đầu tiên của dãy số (u . n ) n ) , 1 n n +1 1 u = 1 2 0,25 0,25
ố hạng đầu tiên của dãy số (u là: 1 1 1 ; ; . n ) 2 3 4
Tìm m để phương trình để 2
2sin x + 3 sin x − 5m = 0luôn có nghiệm. 2 2
2sin x + 3 sin x − 5m = 0 2 0.25
⇔ 3 sin x − cos x − 5m +1 = 0  π  2 ⇔ 2sin x − − 5m +1 =   0  6  0.25 Hay  π  5m −1 sin x − =  6    2 0.25 Mà  π 1 sin x  − ≤ − ≤   1  6 
Nên để phương trình trên luôn có nghiệm khi 5m −1 1 − ≤ ≤1 2 0.25 1 3 ⇔ − ≤ m ≤ 5 5 3
Một đa giác có chu vi là 158cm , độ dài các cạnh của nó lập thành một cấp số cộng. Biết cạnh lớn
nhất có độ dài là 44cm . Tìm số cạnh của đa giác đó?
Giả sử đa giác có n cạnh ( n∈, n ≥ 3).
Gọi độ dài các cạnh của đa giác là u ,u ,u ,...,u theo thứ tự lập thành cấp số cộng và cạnh 1 2 3 n 0,25
lớn nhất có độ dài là nên 0 < u < u <u <...<u = cm . n 44 1 2 3 (u +u n 0,25 1 n )
Vì đa giác có chu vi là 158cm nên S = u + u +u + +u = n ... 1 2 3 n 2 (u + 44 n 1 ) hay 158 = suy ra 316 n = 2 u + 44 1
Mà n∈ nên u + 44 là ước nguyên dương của 316 hay u + 44∈ 2; 4; 79; 158; 316 0.25 1 { } 1 u + 44 2 4 79 158 316 0.25 1 u
u < 0 u < 0
u = 35 u =114 (không thỏa u = 272 (không thỏa 1 1 1 1 1 1 (loại) (loại)
mãn vì u = cm )
mãn vì u = cm ) n 44 n 44 Vậy đa giác đã cho có 316 n = = 4 cạnh. 79 TRƯỜNG THPT
ĐỀ KIỂM TRA GIỮA KÌ I NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC
MÔN: TOÁN - LỚP: 11 (SÁCH KNTT) (Đề có 05 trang)
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ 1
Họ và tên thí sinh: ....................................................................... Số báo danh: ...................
I. PHẦN TRẮC NGHIỆM (7,0 điểm).
Câu 1: Cung có số đo 250° thì có số đo theo đơn vị là radian là A. 35π . B. 25π . C. 25π . D. 25π . 18 18 12 9 Câu 2: Cho góc π
α thỏa mãn 0 < α < . Khẳng định nào sau đây đúng? 2 A. sinα > 0. B. cotα < 0 .
C. sinα < 0 .
D. cosα < 0 .
Câu 3: Khẳng định nào sau đây đúng? A. 2 2 sin α + cos α = 1. B. 2 2 sin α + cos α = 0 . C. 2 2 sin α + cos α = 2 . D. 2 2 sin α + cos α = 1 − .
Câu 4: sin 2a bằng A. 2sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a .
Câu 5: Chu kỳ tuần hoàn của hàm số y = sin x là A. k2π π (k ∈) . B. . C. π . D. 2π . 2
Câu 6: Tập giá trị của hàm số y = cos 2023x là A. [ 1; − ] 1 . B. ( 1; − 1) . C. [ 2023 − ; ] 2023 . D.  1 1 ;  −  . 2 2  
Câu 7: Nghiệm của phương trình tan x =1 là A. π π
x = + kπ , k ∈. B. 3 x =
+ kπ , k ∈ . 4 4 C. π
x = kπ , k ∈ .
D. x = + kπ,k ∈ . 2
Câu 8: Cho dãy số (u xác định bởi u = n − n ≥ u n 2 1 với 1. Số hạng bằng n ) 1 A. 1. B. 2 . C. 3. D. 4 .
Câu 9: Dãy số nào sau đây là dãy tăng? A. 1;3;5;7;9 . B. 10;8;6;4;2 . C. 1;5;3;7;9 . D. 1;1;1;1;1. Trang 1
Câu 10: Cho cấp số cộng (u với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 4 . C. 6 . D. 8 .
Câu 11: Trong các dãy số (u sau, dãy số nào bị chặn? n ) A. 2 u = n + . B. 2 u = − .
C. u = n + n . D. 2 u = n . n sin n sin n 1 n 1 3n
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a .
Câu 13: Dãy số nào sau đây là cấp số nhân? A. 1, 2 − , 4 , 8 , 16 − .
B. 2 , 22 , 222 , 22222 . C. 3, 6 , 12, 24 .
D. x , 2x , 3x , 4x với x ≠ 0 .
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7; − 1 − 3) . C. (13; 7). D. ( 1 − 3; 7 − ) .
Câu 15: Cho cấp số nhân (un ) với 1
u = 3 và công bội q = 2
− . Tìm giá trị của n biết số hạng tổng quát u = 1536 − n . A. n = 8. B. n = 9 . C. n = 257 . D. n =10 .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 [150;152) 5 2 [152;154) 18 3 [154;156) 40 4 [156;158) 26 5 [158;160) 8 6 [160;162) 3 N =100
Giá trị đại diện của nhóm thứ tư là A. 156,5. B. 157 . C. 157,5. D. 158.
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40;60). B. [20;40) . C. [60;80) . D. [80;100) . Trang 2
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40;60). B. [20;40) . C. [60;80) . D. [80;100) .
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7; 9) . B. [9; 1 ) 1 . C. [11; 13). D. [13; 15).
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7,6 . C. 8 . D. 8,6 . Câu 21: Biết 4 π sinα − = và 3 π < α < . Giá trị cosα bằng 5 2 A. 3 − . B. 3. C. 3 ± . D. 9 . 5 5 5 5
Câu 22: Giá trị của biểu thức  π π A sin  = +  là 3 4    A. 6 − 2 . B. 6 + 2 . C. − 6 + 2 . D. − 6 − 2 . 4 4 4 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2. C. y = 2 − sin x . D. y = 2 − cos x + 2 .
Câu 24: Tập nghiệm của phương trình cos x = 1 − là  π A. π S   k2π | k  = + ∈.
B. S = − + k2π |k ∈.  2   2 
C. S = {k2π |k ∈ }  .
D. S = {π + k2π | k ∈ }  . Trang 3
Câu 25: Cho dãy số 1 1 1 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là n n 1 − (− ) 1 n A. 1 u   = . B.  1 u  = . C. 1 u = . D. u = . n  3     n  3  n 3n n n 1 3 −
Câu 26: Cho cấp số cộng (u có u = 2; d = 5 − . Số hạng thứ n ) 1
20 của cấp số cộng là A. 93 − . B. 10. C. 93. D. 23.
Câu 27: Cho cấp số nhân (x có x = 3 − và x = 27. −
Tính số hạng đầu x và công bội n ) 2 4 1 q của cấp số nhân. A. x = 1, − q = 3
− hoặc x =1,q = 3. B. x = 1,
− q = 3 hoặc x =1,q = 3 − . 1 1 1 1
C. x = 3,q = 1
− hoặc x = 3, − q =1.
D. x = 3,q =1 hoặc x = 3, − q = 1 − . 1 1 1 1
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6,5. B. 7,5. C. 7,25 . D. 8 .
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng): Doanh thu [5;7) [7;9) [9;1 )1 [11;13) [13;15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7; 9) . B. [9; 1 ) 1 . C. [11; 13). D. [13; 15).
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. [30;45) . B. [15;30) . C. [45;60) . D. [60;75) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi hàm số  π h(t) 5sin t  = 
, trong đó h(t) là độ cao tính bằng cetimét trên mực nước biển trung 5   
bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc phao lại
ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5giây. B. 10 giây. C. 2,5giây. D. 20 giây. Trang 4  π
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3  3 sin 3x − =  bằng 4    2 π π π π A. . B. − . C. . D. − . 9 6 6 9
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78.
Câu 34: Một cấp số nhân có số hạng đầu u = 3, công bội q = 2 . Biết S = . Tìm n . n 765 1 A. n = 8. B. n = 9 . C. n = 6 . D. n = 7 .
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
[15;20) [20;25) [25;30) [30;35) [35;40) [40;45) [45;50) Số nhân viên 7 14 25 37 21 14 10
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 A. 1360 800 Q = ,Q = . B. 1360 3280 Q = ,Q = . 1 3 37 21 1 3 37 83 C. 136 3280 Q = ,Q = . D. 136 800 Q = ,Q = . 1 3 5 83 1 3 5 21
II. PHẦN TỰ LUẬN (3,0 điểm). Câu 36: (1,0 điểm) a. Giải phương trình  π cot x  + =   3 .  3  b. Cho 2
sinα = , tính giá trị của biểu thức P = (1− 3cosα)(1+ 3cosα). 3 Câu 37: (1,0 điểm)
Giải phương trình cos3x − sin 2x = 0 .
Câu 38: (1,0 điểm) Giải phương trình  π sin x cos x  = +  . 3   
Câu 39: (0,5 điểm) Một công ty khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là
100000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30000 đồng so với giá của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng
sâu 20 mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia
đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
-------------- HẾT -------------- Trang 5
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM (7,0 điểm). BẢNG ĐÁP ÁN 1.B 2.A 3.A 4.A 5.D 6.C 7.A 8.A 9.A 10.A 11.D 12.B 13.C 14.C 15.D 16.B 17.A 18.A 19.B 20.C 21.A 22.B 23.C 24.D 25.B 26.A 27.B 28.C 29.B 30.A 31.B 32.C 33.A 34.A 35.D ĐÁP ÁN CHI TIẾT
Câu 1: Cung có số đo 250° thì có số đo theo đơn vị là radian là A. 35π . B. 25π . C. 25π . D. 25π . 18 18 12 9 Lời giải Chọn B 0
Số đo theo đơn vị là radian là 250 .π 25.π = . 0 180 18 Câu 2: Cho góc π
α thỏa mãn 0 < α < . Khẳng định nào sau đây đúng? 2 A. sinα > 0. B. cotα < 0 .
C. sinα < 0 .
D. cosα < 0 . Lời giải Chọn A
Câu 3: Khẳng định nào sau đây đúng? A. 2 2 sin α + cos α = 1. B. 2 2 sin α + cos α = 0 . C. 2 2 sin α + cos α = 2 . D. 2 2 sin α + cos α = 1 − . Lời giải Chọn A
Câu 4: sin 2a bằng A. 2sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a . Lời giải Chọn A
Câu 5: Chu kỳ tuần hoàn của hàm số y = sin x là A. k2π π (k ∈) . B. . C. π . D. 2π . 2 Lời giải Chọn D
Câu 6: Tập giá trị của hàm số y = cos 2023x là A. [ 1; − ] 1 . B. ( 1; − 1) . C. [ 2023 − ; ] 2023 . D.  1 1 ;  −  . 2 2   Trang 6 Lời giải Chọn C
Câu 7: Nghiệm của phương trình tan x =1 là A. π π
x = + kπ , k ∈. B. 3 x =
+ kπ , k ∈ . 4 4 C. π
x = kπ , k ∈ .
D. x = + kπ,k ∈ . 2 Lời giải Chọn A Ta có π
tan x = 1 ⇔ x = + kπ , k ∈  4
Câu 8: Cho dãy số (u xác định bởi u = n − n ≥ u n 2 1 với 1. Số hạng bằng n ) 1 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn A
Ta có: u = 2.1−1 = 1 1
Câu 9: Dãy số nào sau đây là dãy tăng? A. 1;3;5;7;9 . B. 10;8;6;4;2 . C. 1;5;3;7;9 . D. 1;1;1;1;1. Lời giải Chọn A
Câu 10: Cho cấp số cộng (u với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 4 . C. 6 . D. 8 . Lời giải Chọn A
Công sai của cấp số cộng d = u − u = 5 − 3 = 2 2 1 .
Câu 11: Trong các dãy số (u sau, dãy số nào bị chặn? n ) A. 2 u = n + . B. 2 u = − .
C. u = n + n . D. 2 u = n . n sin n sin n 1 n 1 3n Lời giải Chọn D Với mọi * n∈ , ta có 2 1
− ≤ sin n ≤1⇒ 0 ≤ sin n ≤1 nên dãy số đã cho bị chặn.
Phân tích phương án nhiễu:
A. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
B. Sai do dãy số này bị chặn trên nhưng không bị chặn dưới.
C. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên. Trang 7
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a . Lời giải Chọn B
Phân tích phương án nhiễu:
A: Sai vì nhớ nhầm của cấp số nhân.
B, C: Sai vì không phân biệt thứ tự của các số hạng của cấp số cộng.
Câu 13: Dãy số nào sau đây là cấp số nhân? A. 1, 2 − , 4 , 8 , 16 − .
B. 2 , 22 , 222 , 22222 . C. 3, 6 , 12, 24 .
D. x , 2x , 3x , 4x với x ≠ 0 . Lời giải Chọn C
6 = 3.2 , 12 = 6.2 , 24 =12.2.
Phân tích phương án nhiễu:
A. Sai do thay u :u = 2
− nhưng u :u = 2. 2 1 4 3
B. Sai do học sinh lầm tưởng đây là cấp số nhân với công bội q =11.
D. Sai do dãy số trên là cấp số cộng, không phải cấp số nhân.
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7; − 1 − 3) . C. (13; 7). D. ( 1 − 3; 7 − ) . Lời giải Chọn C u  = 48 u  + 5d = 48 u  = 13 Ta có: 6 1 ⇔ 1 ⇔ . u  =    83 u +10d =  83 d = 7 11 1
Phân tích phương án nhiễu:
A. Sai vì đặt nhầm thứ tự của yêu cầu bài toán.
B. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình và đặt nhầm thứ tự của yêu cầu bài toán.
D. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình.
Câu 15: Cho cấp số nhân (un ) với 1
u = 3 và công bội q = 2
− . Tìm giá trị của n biết số hạng tổng quát u = 1536 − n ? A. n = 8. B. n = 9 . C. n = 257 . D. n =10 . Lời giải Chọn D n 1 − n 1 un 1536 − = − ⇔ 1 u .q = 1536 − ⇔ 3.( 2) − = 1536 − . Trang 8 n 1 ( 2) − ⇔ − = 512 − = ( 2 − )9 ⇔ n =10 .
Phân tích phương án nhiễu: ( 2 − )n
A. Sai do tính ( )n 1 2 − − = 512 − ⇔ = 512 − ⇔ ( 2 − )n = 512 − : ( 2) − = 256 ⇔ n = 8. 2 −
B. Sai do nhầm công thức số hạng tổng quát . n u q = 1536 − ⇔ 2 n − = 512 − ⇔ n = 9 1 ( ) . n −
C. Sai do tính (− ) 1 − 512 2 = 512 − ⇔ n −1 = = 256 ⇔ n = 257 . 2 −
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 [150;152) 5 2 [152;154) 18 3 [154;156) 40 4 [156;158) 26 5 [158;160) 8 6 [160;162) 3 N =100
Giá trị đại diện của nhóm thứ tư là A. 156,5. B. 157 . C. 157,5. D. 158. Lời giải Chọn B
Giá trị đại diện của nhóm thứ tư là 156 +158 =157 . 2
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40;60). B. [20;40) . C. [60;80) . D. [80;100) . Lời giải Chọn A
Mốt M chứa trong nhóm [40;60) 0
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40;60). B. [20;40) . C. [60;80) . D. [80;100) . Trang 9 Lời giải Chọn A Ta có: n = 42
Nên trung vị của mẫu số liệu trên là x + x 21 22 Q = 2 2
Mà x , x ∈ 40;60 21 22 [ )
Vậy nhóm chứa trung vị của mẫu số liệu trên là nhóm [40;60)
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7; 9) . B. [9; 1 ) 1 . C. [11; 13). D. [13; 15). Lời giải Chọn B
Bảng tần số ghép nhóm theo giá trị đại diện là Số trung bình: 2.6 7.8 7.10 3.12 1.14 x + + + + = = 9,4 20
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7,6 . C. 8 . D. 8,6 . Lời giải Chọn C
Gọi x , x ,..., x là doanh thu bán hàng trong 20 ngày xếp theo thứ tự không giảm. 1 2 20
Khi đó: x , x ∈ 5;7 , x ,..., x ∈ 7; 9 ,, x ,..., x ∈ 9; 11 x ,..., x ∈ 11; 13 , x ∈ 13; 15 20 [ ) 17 19 [ ) 9 16 [ ) 3 9 [ ) 1 2 [ )
Do đó, tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm [7;9) n = 20,n = C = u = u = m 7, 2, m 7, m+ 9 1 Trang 10 1.20 −2 4 Q = 7 + (9 − 7) ≈ 7,86 ≈ 8 1 7 Câu 21: Biết 4 π sinα − = và 3 π < α < . Giá trị cosα bằng 5 2 A. 3 − . B. 3. C. 3 ± . D. 9 . 5 5 5 5 Lời giải Chọn A Vì 3π π < α <
nên cosα < 0 . Mặt khác 2 2 sin α + cos α =1 ta có 2 cosα = − 1− sin α 2 2 1  4  = − − − =  3 −  .  5  5
Câu 22: Giá trị của biểu thức  π π A sin  = +  là 3 4    A. 6 − 2 . B. 6 + 2 . C. − 6 + 2 . D. − 6 − 2 . 4 4 4 4 Lời giải Chọn B  π π  π π π π Ta có 3 2 2 1 6 + 2 A = sin + = sin cos + sin cos = . + . =   .  3 4  3 4 4 3 2 2 2 2 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2. C. y = 2 − sin x . D. y = 2 − cos x + 2 . Lời giải Chọn C
Tập xác định của hàm số y = f (x) = 2
− sin x là D =  .
Do đó, nếu x thuộc tập xác định D thì −x cũng thuộc tập xác định D .
Ta có f (−x) = 2
− sin(−x) = sin x = − f (x). Vậy y = 2
− sin x là hàm số lẻ.
Câu 24: Tập nghiệm của phương trình cos x = 1 − là  π A. π S   k2π | k  = + ∈.
B. S = − + k2π |k ∈.  2   2 
C. S = {k2π |k ∈ }  .
D. S = {π + k2π | k ∈ }  . Lời giải Chọn D Ta có cos x = 1
− ⇔ x = π + k2π,k ∈ . Trang 11
Câu 25: Cho dãy số 1 1 1 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là n n 1 − (− ) 1 n A. 1 u   = . B.  1 u  = . C. 1 u = . D. u = . n  3     n  3  n 3n n n 1 3 − Lời giải Chọn D
Câu 26: Cho cấp số cộng (u có u = 2; d = 5 − . Số hạng thứ n ) 1
20 của cấp số cộng là A. 93 − . B. 10. C. 93. D. 23. Lời giải Chọn D
u = u +19d = 2 +19( 5 − ) = 93 − . 20 1
Câu 27: Cho cấp số nhân (x có x = 3 − và x = 27. −
Tính số hạng đầu x và công bội n ) 2 4 1 q của cấp số nhân. A. x = 1, − q = 3
− hoặc x =1,q = 3. B. x = 1,
− q = 3 hoặc x =1,q = 3 − . 1 1 1 1
C. x = 3,q = 1
− hoặc x = 3, − q =1.
D. x = 3,q =1 hoặc x = 3, − q = 1 − . 1 1 1 1 Lời giải Chọn B 2   q = 9  x = 3 −  x q = 3 −   q = 3 ± 2 1  ⇔  ⇔  ⇔ 3 3 x 27. x q 27. x = −  .  = − = −   x = 1. 4 1 1 1    q
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6,5. B. 7,5. C. 7, 25 . D. 8. Lời giải Chọn C
Theo bảng thống kê, giá trị lớn nhất là 60 thuộc lớp [6,5;8) nên giá trị đại diện là 6,5 + 8 = 7,25. 2
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng): Trang 12 Doanh thu [5;7) [7;9) [9;1 )1 [11;13) [13;15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7; 9) . B. [9; 1 ) 1 . C. [11; 13). D. [13; 15). Lời giải Chọn B 6.2 8.7 10.7 12.3 14.1
Số trung bình của mẫu số liệu trên là: x + + + + = = 9,4 20
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. [30;45) . B. [15;30) . C. [45;60) . D. [60;75) . Lời giải Chọn A
Cỡ mẫu: n = 9 + 5 +15 +14 + 7 = 50 . Gọi x ,..., x 1
50 là thời gian khảo sát tập thể dục trong ngày của 50 học sinh khối 11 và giả sử dãy x + x
này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là 25 26 x , x 2 . Do hai giá trị 25 26 thuộc nhóm [30;45) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi hàm số  π h(t) 5sin t  = 
, trong đó h(t) là độ cao tính bằng cetimét trên mực nước biển 5   
trung bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc
phao lại ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5giây. B. 10 giây. C. 2,5giây. D. 20 giây. Lời giải Chọn B
Ta có mô hình hóa chiều cao của sóng nước là hàm hàm số  π h(t) 5sin t  =  nên để chiếc phao 5   
ở vị trí đỉnh ở hai lần liên tiếp thì cách nhau một chu kì của sóng 2π T = = 10(s) π . 5 Trang 13  π
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3  3 sin 3x − =  4    2 bằng: π π π π A. . B. − . C. . D. − . 9 6 6 9 Lời giải Chọn C  3π π 3x − = + k2π  π   π  π  Ta có 3 3 3 4 3 sin 3x − = ⇔  sin 3x − =  sin ⇔  .  4  2  4  3  3π π 3x − = π − + k2π  4 3  13π  13π 2π 3x = + k2π x = + k  12  36 3 ⇔  ⇔  (k ∈Z ).  17π  17π 2π 3x = + k2π x = + k  12  36 3  13 13π
x > 0 ⇔ k > −
⇒ k = 0 → x =  min π π TH1. Với 13 2 Cho 24 36 x = + k →  . 36 3  13 11π
x < 0 ⇔ k < − ⇒ k = 1 − → x = − max  24 36  17 17π
x > 0 ⇔ k > −
⇒ k = 0 → x =  min π π TH2. Với 17 2 Cho 24 36 x = + k →  . 36 3  17 7π
x < 0 ⇔ k < − ⇒ k = 1 − → x = − max  24 36
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là 7π x = −
và nghiệm dương nhỏ nhất là 36 13π π π π x =
. Khi đó tổng hai nghiệm bằng 13 7 − = . 36 36 36 6
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78. Lời giải Chọn A
Gọi số cây ở hàng thứ n là u . n
Ta có: u =1 u = 2 u = 3
S = u + u + u +...+ u = . n 3003 1 , 2 , 3 , … và 1 2 3
Nhận xét dãy số (u là cấp số cộng có u =1, công sai . n ) 1 d =1 Trang 14
n 2u + n −1 d   n 2.1+  (n − )11 1 ( ) Khi đó S  = = 3003  ⇔ = 3003 2 2 n = 77 ⇔ n(n + ) 1 = 6006 2
⇔ n + n − 6006 = 0 ⇔ 
⇔ n = 77 (vì n ∈  ). n = 78 −
Câu 34: Một cấp số nhân có số hạng đầu u = 3, công bội q = 2 . Biết S = . Tìm n ? n 765 1 A. n = 8. B. n = 9 . C. n = 6 . D. n = 7 . Lời giải Chọn A u 1 n − q 3. 1− 2n 1 ( ) ( )
Áp dụng công thức của cấp số nhân ta có: S = = = ⇔ = . n 765 n 8 1− q 1− 2
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
[15;20) [20;25) [25;30) [30;35) [35;40) [40;45) [45;50) Số nhân viên 7 14 25 37 21 14 10
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 A. 1360 800 Q = ,Q = . B. 1360 3280 Q = ,Q = . 1 3 37 21 1 3 37 83 C. 136 3280 Q = ,Q = . D. 136 800 Q = ,Q = . 1 3 5 83 1 3 5 21 Lời giải Chọn D
Cỡ mẫu là n =128.
Tứ phân vị thứ nhất Q là x + x 32
33 . Do x , x đều thuộc nhóm [25;30) nên nhóm này chứa 1 2 32 33 Q . 1
Do đó, p = 3;a = 25;m = 25;m + m = 21,a − a = 5 và ta có 3 3 1 2 4 3 8 12 −21 4 136 Q = 25 + ⋅5 = 1 25 5
Với tứ phân vị thứ ba Q là x + x 96
97 . Do x , x đều thuộc nhóm [35;40) nên nhóm này chứa 3 2 96 97 Q . 3
Do đó, p = 5;a = 35;m = 21;m + m + m + m = 7 +14 + 25 + 37 = 83;a − a = 5 và ta có 5 5 1 2 3 4 6 5 3.128 −83 4 800 Q = 35 + ⋅5 = 3 . 21 21 Trang 15
II. PHẦN TỰ LUẬN (3,0 điểm). Câu Đáp án Biểu điểm  π 0.5
Giải phương trình cot x  + =   3 .  3  0.25 36a  π  π π cot x + = 3 ⇔ x + = +   kπ  3  3 6 π
⇔ x = − + kπ (k ∈) . 0.25 6 Cho 2
sinα = , tính giá trị của biểu thức P = (1− 3cosα)(1+ 3cosα). 0.5 3 P = − α + α = − ( α )2 2 (1 3cos )(1 3cos ) 1 3cos =1− 9cos α . 0.25 36b 2 sinα 0.25 = , 2 2 2 5
sin α + cos α =1⇒ cos α = . 3 9 5 P =1− 9. = 4 − . 9
Giải phương trình cos3x − sin 2x = 0 . 1.0  π 0.25 cos3x sin 2x 0 cos3x sin 2x cos3x cos 2x − = ⇔ = ⇔ = −  2     π 0.25 3x 2x ⇔ = ± − +   k2π  2   π 0.25 37 5x = + k2π  2 ⇔  π
x = − + k2π  2  π 2π 0.25 x = + k  10 5 ⇔  (k ∈) π
x = − + k2π  2  π 1.0
Giải phương trình sin x cos x  = +  3     π sin x cos x  = +  3    0,25  π   π cos x cos x  ⇔ − = +  2 3      38 π π
− x = x + + k2π  2 3 ⇔  (k ∈) π π 0,25
 − x = −x − + k2π  2 3 π ⇔ 2
− x = − + k2π (k ∈) 0,25 6 π ⇔ x =
− kπ (k ∈) . 0,25 12 Trang 16
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu
tiên là 100000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30000
đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng 0.5
với cơ sở khoan giếng này để khoan giếng sâu 20 mét lấy nước dùng cho sinh
hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh
toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
Giá tiền mỗi mét khoan giếng lập thành một cấp số cộng với
u =100000 (số tiền mét khoan đầu tiên), 1 39
u = u + 30000 (số tiền mét khoan thứ hai), 2 1
u = u + 30000 = u + 2.30000 (số tiền mét khoan thứ ba) 0,25 3 2 1 …
u = u + 30000 = u +19.30000 (số tiền mét khoan thứ 20), 20 19 1
và công sai d = 30000 .
Tổng chi phí cần phải thanh toán là
S = u + u + u +...+ u 20(2.10000 +19.30000) = = 7700000 . 0,25 20 1 2 3 20 2
-------------- HẾT -------------- Trang 17
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Trong các khẳng định sau, khẳng định nào sai?
A. sin (π −α ) = sinα .
B. cos(π −α ) = cosα .
C. sin (π +α ) = −sinα .
D. cos(π +α ) = −cosα .
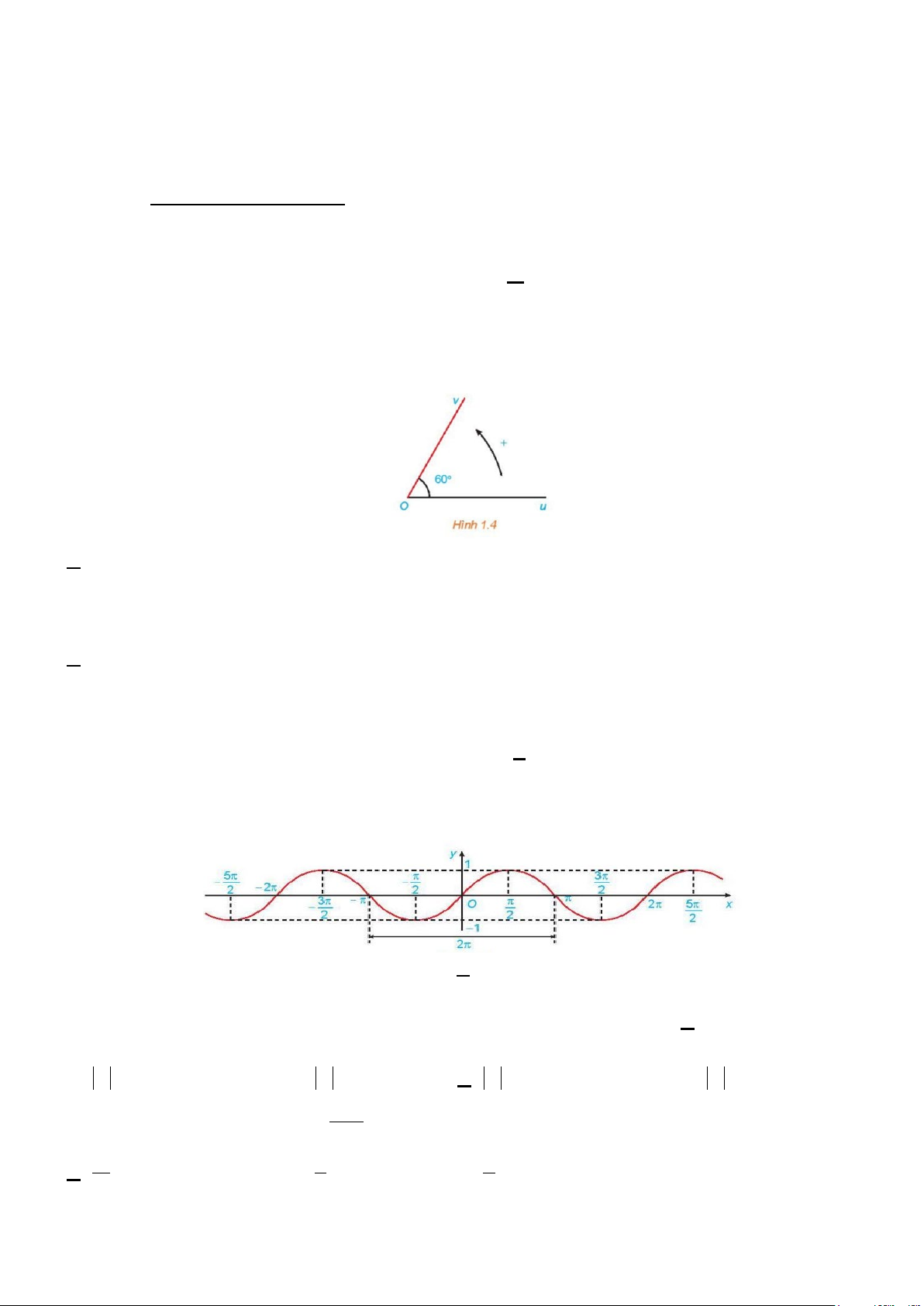
Câu 2. Cho góc hình học uOv có số đo bằng 0
60 (hình 1.4). Số đo của các góc lượng giác (Ou,Ov) là A. sñ ( , Ou Ov) 0 0
= 60 + k.360 ,k ∈. B. sñ ( , Ou Ov) 0 0
= 60 + k.180 ,k ∈. C. sñ ( , Ou Ov) 0 0
= 60 − k.180 ,k ∈. D. sñ ( , Ou Ov) 0 0 = 60 −
+ k.360 ,k ∈.
Câu 3. Trong các khẳng định sau, khẳng định định nào đúng?
A. sin (a −b) = sin a cosb −sinbcos . a
B. sin (a −b) = cos a cosb −sin asin . b
C. sin (a −b) = cos asinb + sin a cos . b
D. sin (a −b) = sin a cos a − cosbsin . b
Câu 4. Trong các khẳng định sau, khẳng định định nào sai?
A. sin 2a = 2sin a cos . a B. 2 2
cos 2a = sin a − cos . a C. 2
cos 2a = 2cos a −1. D. 2 cos 2a =1− 2sin . a
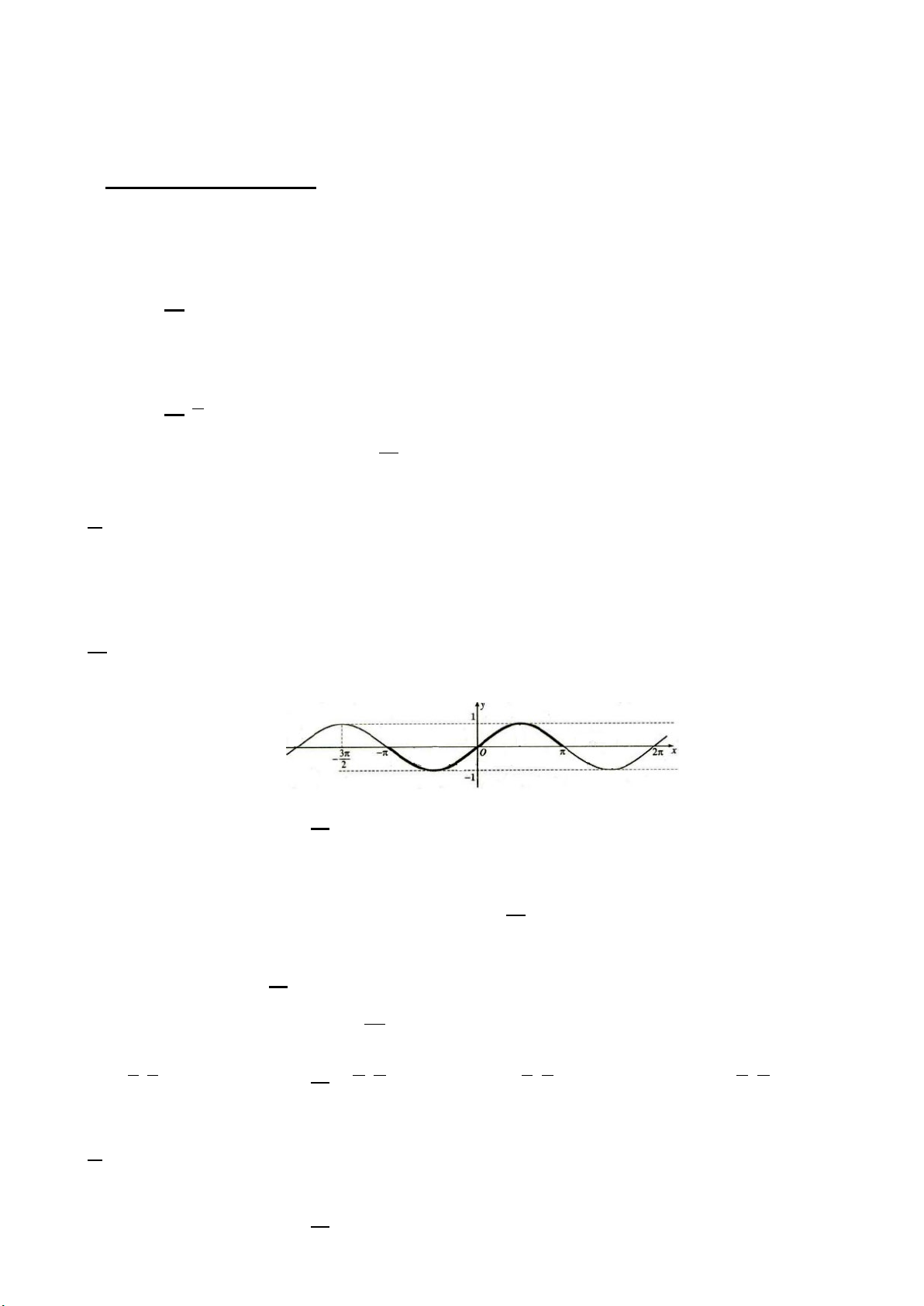
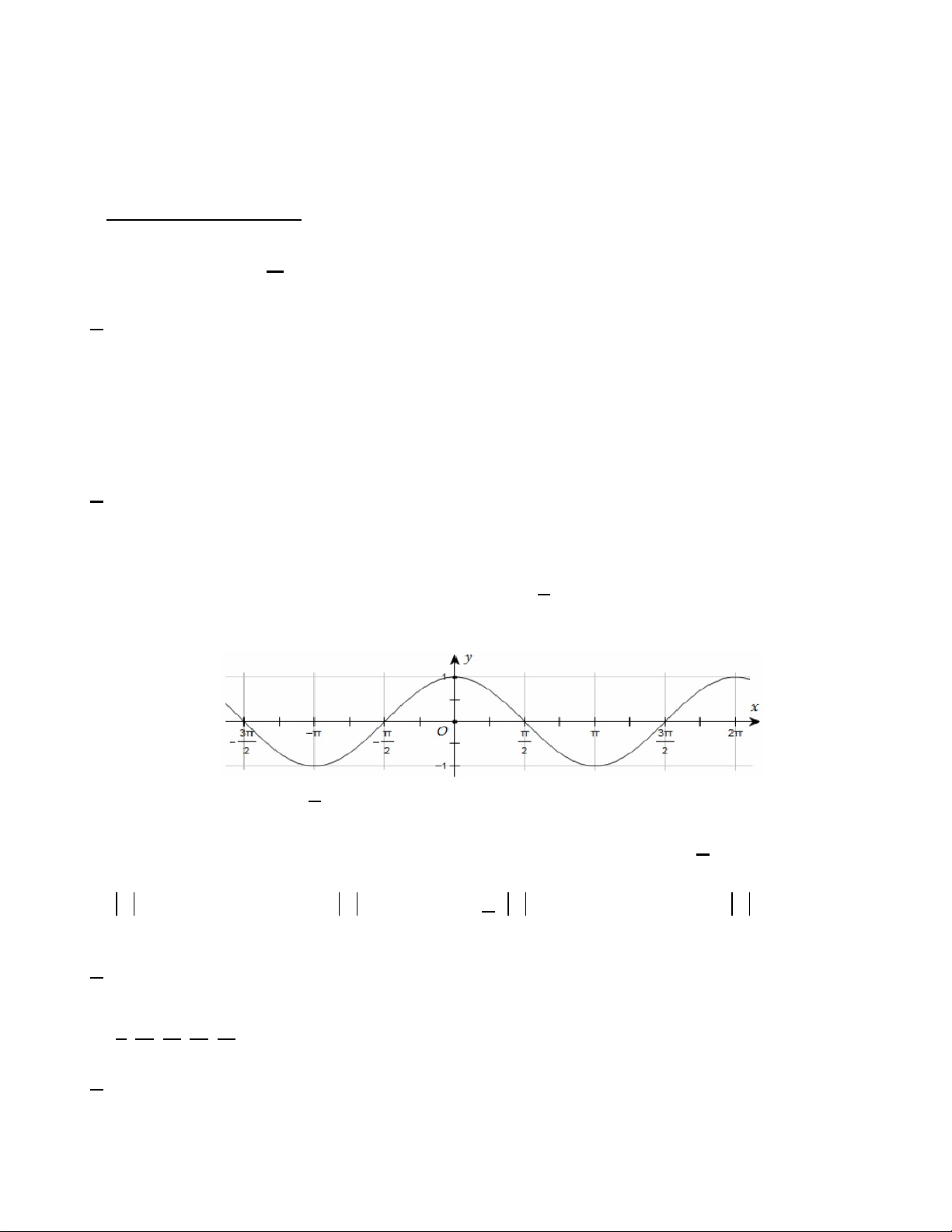
Câu 5. Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số được liệt kê ở bốn
phương án A, B, C, D?
A. y =1+ sin 2x .
B. y = cos x . C. y = sin x .
D. y = −cos x .
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = tan .x
B. y = cot .x
C. y = sin .x
D. y = cos .x
Câu 7. Điều kiện có nghiệm của phương trình cos x = m là A. m <1. B. m >1. C. m ≤1. D. m ≥1.
Câu 8. Cho dãy số (u , biết 2 u =
. Số hạng thứ 10 của dãy số đã cho là n ) n n +1 A. 2 . B. 2 . C. 2 . D. 1. 11 3 5
Câu 9. Khẳng định nào sau đây là sai?
A. Một dãy số tăng thì bị chặn dưới. B.Một dãy số giảm thì bị chặn trên.
C. Một dãy số bị chặn thì phải tăng hoặc giảm. D.Một dãy số không đổi thì bị chặn.
Câu 10. Cho cấp số cộng (u có số hạng đầu u = 2,d = 3
− . Năm số hạng đầu của cấp số cộng là n ) 1 A. 2; 1 − ; 4 − ; 7 − ; 1 − 0. B. 2; 3 − ; 6 − ; 9 − ; 1 − 2. C. 2; 6 − ;18; 54 − ;162. D. 2;2;2;2;2.
Câu 11. Cho cấp số cộng (u , biết u =1 và công sai u = 5. Khẳng định nào sau đây đúng? n ) 1 3 A. u = 3. B. u = 2. C. u =1. D. u = 3. − 2 2 2 2
Câu 12. Cho cấp số cộng (u . Gọi S là tổng của n số hạng đầu của cấp số cộng. Khẳng định nào sau đây n ) n đúng? n(n − ) 1 nu + n n −1 1 ( )
A. S = nu + d . B. S = d . n 1 2 n 2 (n − )1
C. S = nu + n n − d .
D. S = nu + d . n 1 1 ( ) n 1 2
Câu 13. Cho cấp số nhân (u , biết u = 2,u =10 . Công bội của cấp số nhân là n ) 1 2 A. q = 5 . B. q = 8. C. q = 5 − . D. q =12 .
Câu 14. Cho cấp số nhân (u . Gọi S là tổng của n số hạng đầu của cấp số nhân. Khẳng định nào sau đây n ) n đúng? u 1 n − q n 1 ( ) u 1− q 1 ( ) A. S = . B. S = . n 1− q n 1− q (1 n − q ) u 1 n − q 1 ( ) C. S = . D. S = . n 1− q n q −1
Câu 15. Cho cấp số nhân (u , biết u =
. Khẳng định nào sau đây đúng? n 2.3n n ) A. u = 54 . B. u =18 . C. u = 6 . D. u =162 . 4 4 4 4
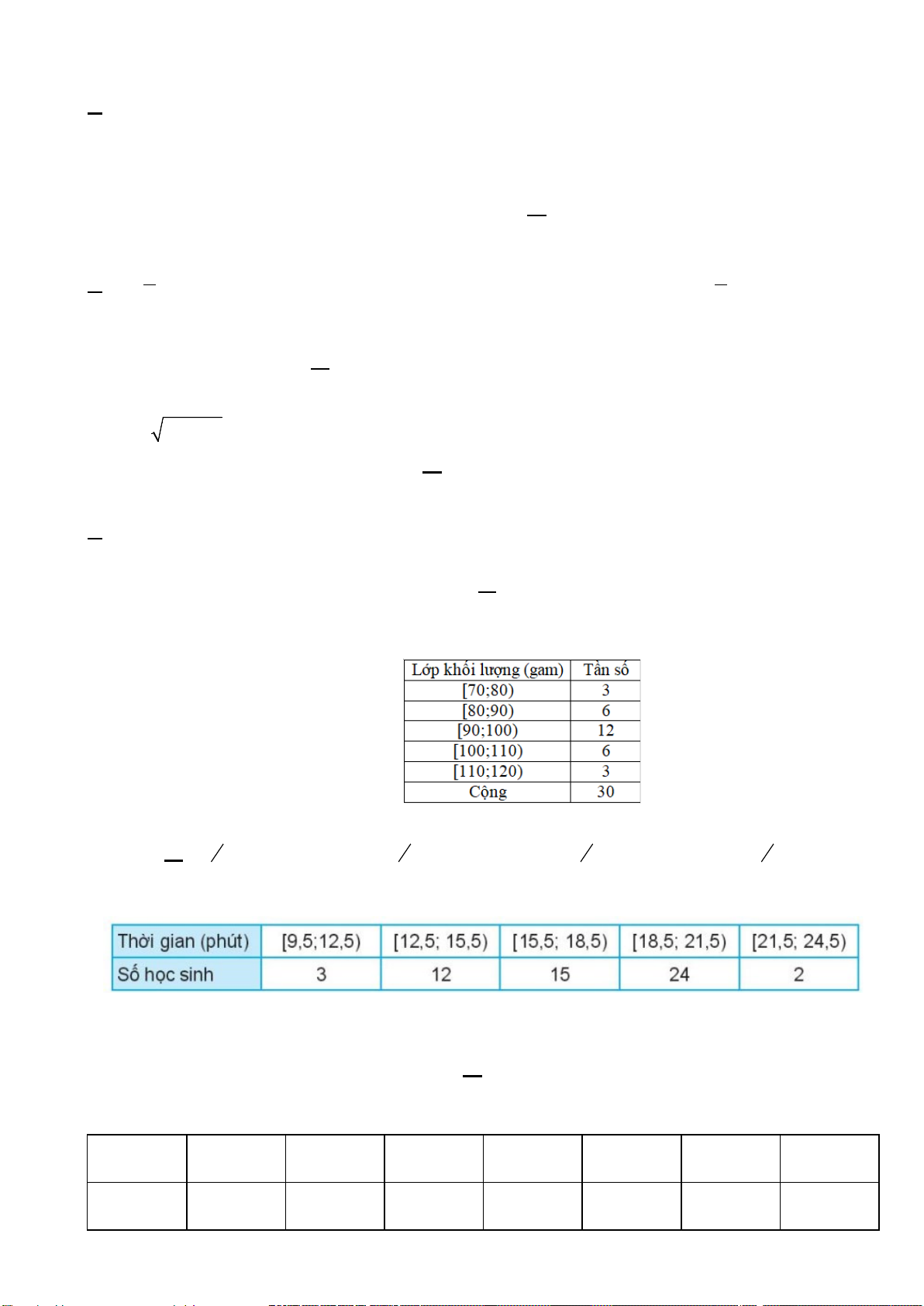
Câu 16. Điều tra về chiều cao của học sinh khối lớp 11, ta được mẫu số liệu sau: Chiều cao (cm) Số học sinh [150;152) 5 [152;154) 18 [154;156) 40 [156;158) 26 [158;160) 8 [160;162) 3 Tổng N =100
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 5. B. 6 . C. 7 . D. 12.
Câu 17. Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm [ ;
a b) được tính như thế nào?
A. a + b . B. b − . a C. a + . b D. . a . b 2
Câu 18. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. Mốt. B. Số trung bình. C. Số trung vị. D. Tứ phân vị.
Câu 19. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40;60). B. [20;40) . C. [60;80) . D. [80;100) .
Câu 20. Trong các khẳng định sau, khẳng định nào là đúng
A. Số trung bình không bị ảnh hưởng bởi các giá trị quá lớn hay quá bé.
B. Số trung bình luôn là một số liệu nào đó của mẫu.
C. Số trung bình chính là số trung vị.
D. Số trung bình là m x +...+ m x 1 1 k k x = . n Câu 21. Biết 1 π
sinα = và 0 < α < . Giá trị cosα bằng 3 2 A. 2 2 . B. 2 2 − . C. 2 . D. 2 − . 3 3 3 3 Câu 22. Biết 4 π π
cosα = − và < α < π . Giá trị cos  α + bằng 5 2  4    A. 2 − . B. 2 2 . C. 7 − . D. 7 . 10 10 10 10
Câu 23. Tập giá trị của hàm số y = 2 sin x là A. [ 1; − ] 1 . B. 0; 2. −    C. {− 2; 2}. D. 2; 2 .  
Câu 24. Tập nghiệm của phương trình cos x =1 là A. π S k2π | k  = + ∈.
B. S = {kπ |k ∈ }  .  2 
C. S = {k2π |k ∈ }  . D.  π S k2π | k  = − + ∈.  2 
Câu 25. Cho dãy số 1 2 3 4
; ; ; ;. .. Số hạng tổng quát của dãy số này là 2 3 4 5 2 A. n +1 − u − n n = . B. n u = . C. n 1 u = . D. u = . n n n n +1 n n n n +1
Câu 26. Cho cấp số cộng (u có u = 0,
− 1; d = 0,1. Số hạng thứ 7 của cấp số cộng là n ) 1 A. 1,6 . B. 6 . C. 0,5. D. 0,6 .
Câu 27. Cho cấp số nhân (u có 2 u = 3
− ; q = . Số hạng thứ 5 của cấp số nhân là n ) 1 3 A. 27 u = − . B. 16 u = . C. 16 u = − . D. 27 u = . 5 16 5 27 5 27 5 16
Câu 28. Tìm hiểu thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau: Thời gian (giờ) [0; 5) [5; 10) [10; 15) [15; 20) [20; 25) Số học sinh 8 16 4 2 2
Giá trị đại diện của nhóm [20;25)là A. 22,5. B. 23. C. 20 . D. 5.
Câu 29. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa tứ phân vị thứ ba của mẫu số liệu trên là A. [40;60). B. [20;40) . C. [60;80) . D. [80;100) .
Câu 30. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở
bảng sau (đơn vị: triệu đồng) Câu 31. Nếu 1
sin a − cos a = ( 0 0
135 < a <180 ) thì giá trị của biểu thức tan 2a bằng 5 A. 20 − . B. 20 . C. 24 . D. 24 − . 7 7 7 7
Câu 32. Số nghiệm của phương trình 1
cos 2x = − thuộc đoạn [ π − ;π ] 2 là A. 2 . B. 4 . C. 6 . D. 8 .
Câu 33. Cho cấp số cộng (un ) có u = 3
− ; d = 2 . Khẳng định nào sau đây đúng? 1 A. S = 5. B. S =10. C. S =15. D. S = 20. 5 5 5 5
Câu 34. Cho cấp số nhân (un ) có S = 127 − ; S = 2047 −
. Tổng S = u + u + u + u có kết quả là 7 11 8 9 10 11 A. S = 1920. − B. S =1920. C. S = 2174. − D. S = 2174. 5
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7; 9) . B. [9; 1 ) 1 . C. [11; 13). D. [13; 15).
Câu 35. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Số trung vị của mẫu số liệu ghép nhóm ở bảng trên là A. 18,1. B. 18,2 . C. 18,3 . D. 18,4 .
II. PHẦN TỰ LUẬN (3 điểm).
Bài 1 (1 điểm).  π a. Cho 3 sin xx π  = < <
. Tính giá trị lượng giác cot x . 5 2   
b. Tìm tập xác định của hàm số 1 y = . cos 2x Bài 2  π
(1 điểm). Giải phương trình: 3 6 sin 2x  − − =   0 .  3 
Bài 3 (1 điểm). Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân
theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10, bậc 2 từ số
11 đến số 20, bậc 3 từ số thứ 21 đến số thứ 30,…Bậc 1 có giá là 1500 đồng/1 số, giá của mỗi số ở bậc thứ
n +1 tăng so với giá của mỗi số ở bậc thứ n là 2,5%. Biết rằng gia đình ông An sử dụng hết 345 số trong
tháng 1, hỏi tháng 1 ông An phải đóng bao nhiêu tiền?
……………… HẾT ………………
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng. Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 B A A B C D C A C A
Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 A A A A D B A A A D
Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 A A D C B C C A C B
Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 C B A A A II. PHẦN TỰ LUẬN Bài Đáp án Biểu điểm 1 1a. Cho 3  π sin xx π  = < <
. Tính giá trị lượng giác của cot x 5 2    2 Ta có 2 2 sin x + cos x =1 2 2  3  16
⇒ cos x =1− sin x =1− =  4 ⇒ cos x = ± 5    25 5
π < x <π ⇒ cosx < 0, chọn 4 cos x = − . 0,25 2 5 4 cos x − 5 4 cot x = = = − 0,25 sin x 3 3 5
1b. Tìm tập xác định của hàm số 1 y = cos 2x
Hàm số xác định khi và chỉ khi π π π cos 2 ≠ 0 ⇔ 2 k x
x ≠ + kπ ⇔ x ≠ + ;k ∈ 2 4 2 0,25 π kπ  0,25
Vậy tập xác định của hàm số là D =  \  + , k ∈ .  4 2  2 Giải phương trình:  π 3 6 sin 2x  − − =   0  3   π  2 0,25 ⇔ sin 2x − =  3    2  π π 2x − = + k2π  3 4 0,25 ⇔  π π
2x − = π − + k2π  3 4  7π x = + kπ  24 0,5 ⇔  (k ∈Z )  13π x = + kπ  24 3
Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10,
bậc 2 từ số 11 đến số 20, bậc 3 từ số thứ 21 đến số thứ 30,…Bậc 1 có giá là 1500 đồng/1 số,
giá của mỗi số ở bậc thứ n +1 tăng so với giá của mỗi số ở bậc thứ n là 2,5%. Biết rằng gia
đình ông An sử dụng hết 345 số trong tháng 1, hỏi tháng 1 ông An phải đóng bao nhiêu tiền?
Gọi u là số tiền phải trả cho 10 số điện đầu tiên 1 Suy ra
u =10.1500 =15000 (đồng) 1
u là số tiền phải trả cho các số điện từ 11 đến 20 2
Suy ra u = u 1+ 0,025 2 1 ( ) 0,25 …
u là số tiền phải trả cho các số điện từ 331 đến 340 34 0,25
Suy ra u = u (1+ 0,025)33 34 1
Các số u ;u ;...;u lập thành cấp số nhân với u =15000 ; công bội 1 2 34 1 q =1+ 0,025
Số tiền phải trả cho 340 số điện đầu tiên là 1− (1+ 0,025)34 1− (1+ 0,025)34 S = u . ⇒ S =15000. = 789193,28 1 1 1− (1+ 0,025) 1 1− (1+ 0,025) 0,25
Số tiền ông An phải trả cho các số điện từ 341 đến 345 là
S = 5.1500(1+ 0,025)34 =17364,92 2
Vậy tháng 1 gia đình ông An phải trả số tiền là: S = S + S ≈ 806558 (đồng) 0,25 1 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I TRƯỜNG THPT NĂM HỌC 2023 - 2024 MÔN: TOÁN --------------------
Thời gian làm bài: ___ phút
(Đề thi có ___ trang)
(không kể thời gian phát đề)
Họ và tên: ......................................................................... Số báo danh: ............ Mã đề 000
I. PHẦN TRẮC NGHIỆM (7 điểm). π
Câu 1. Cho < a < π . Kết quả đúng là 2
A. sin a > 0 , cosa > 0 . B. sin a < 0 , cosa < 0 . C. sin a > 0 , cosa < 0 . D. sin a < 0 , cosa > 0 .
Câu 2. Chọn đẳng thức sai trong các đẳng thức sau  π  π  π  π A. sin x − =    
 cos x . B. sin x = cos −  x . C. tan − x = 
 cot x . D. tan − x = −   cot x .  2   2   2   2 
Câu 3. Trong các công thức sau, công thức nào sai? A. 2 2
cos2a = cos a – sin . a B. 2 2
cos2a = cos a + sin . a C. 2
cos2a = 2cos a –1. D. 2 cos2a =1– 2sin . a
Câu 4. Trong các công thức sau, công thức nào sai? 1 1
A. cos acosb = cos 
(a – b) + cos(a + b).
sin asinb = cos a – b – cos a + b . 2  B.  ( ) ( ) 2  1 1
C. sin acosb = sin 
(a – b) + sin(a + b).
D. sin acosb = sin 
(a −b) − cos(a + b). 2  2 
Câu 5. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào? A. y = tan . x B. y = cos . x C. y = −sin . x
D. y = cot x
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y = sin . x B. y = cos . x C. y = tan . x D. y = cot . x
Câu 7. Tìm tất các các giá trị thực của tham số m để phương trình sin x = m có nghiệm.
A. m ≤ 1. B. m ≥ 1. − C. 1 − ≤ m ≤1. D. m ≤ 1. − n
Câu 8. Cho dãy số (u , biết u =
. Ba số hạng đầu tiên của dãy số đó là n ) n 3n −1 1 1 1 1 1 3 1 1 1 1 2 3 A. ; ; . B. ; ; . C. ; ; . D. ; ; . 2 4 8 2 4 26 2 4 16 2 3 4 n 1
Câu 9. Cho dãy số (u , biết u + =
. Khẳng định nào sau đây đúng? n ) n 2 A. u = 3. u = 32. u =10. u = 8. 5 B. 4 C. 5 D. 5
Câu 10. Cấp số cộng (u có số hạng đầu u = 3 , công sai d = 5 , số hạng thứ tư là n ) 1 Mã đề 000 Trang 1/6 A. u = 23 u =1 u = 2 u = 4 4 . B. 4 . C. 4 . D. 4 .
Câu 11. Cho một cấp số cộng có u = 3 − ; u = 3 1 2 . Tìm d ?
A. d = 5 .
B. d = 7 .
C. d = 6 . D. d = 8.
Câu 12. Cho cấp số cộng (u có u = 2019 , công sai d = 5 . Khẳng định nào sau đây là đúng? n ) 1 A. u = + n u = +
n − . C. u =
+ n − . D. u = + n n 5 2019 . n 2019 5( ) 1 n 5 2019 1 n 2019 5 . B. ( ) 2
Câu 13. Cho cấp số nhân (u có số hạng đầu u = 3
− và công bội q = . Số hạng thứ năm của (u là n ) n ) 1 3 27 16 27 16 A. . B. . C. − . D. − . 16 27 16 27 1
Câu 14. Cho cấp số nhân (u với u = − ; 32
u = − . Tìm q ? n ) 1 7 2 1
A. q = ± . B. q = 2 ± . C. q = 4 ± . D. q = 1 ± . 2
Câu 15. Tổng 10 số hạng đầu tiên của cấp số nhân (u u = 3 − ;q = 2 − n ) với 1 bằng A. -511. B. -1025. C. 1025. D. 1023.
Câu 16. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. Mốt.
B. Số trung bình.
C. Số trung vị.
D. Độ lệch chuẩn.
Câu 17. Trong mẫu số liệu ghép nhóm, độ dài mỗi nhóm [2;5) được tính bằng A. 3. B. 4. C. 5. D. 7 .
Câu 18. Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm [2;6) được tính bằng A. 4. B. 5. C. 8. D. 3.
Câu 19. Trung vị của mẫu số liệu ghép nhóm xấp xỉ cho trung vị của mẫu số liệu gốc, nó chia mẫu số liệu thành
hai phần. Mỗi phần chứa bao nhiêu phần trăm giá trị? A. 20 . B. 30. C. 40 . D. 50.
Câu 20. Điểm thi (tính thang điểm 10) của 25 học sinh trong một trường THPT ta thu được cho bảng dưới đây Điểm thi [3;5) [7;9) Số học sinh 20 5
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 2 . B. 6 . C. 1. D. 3. 4 π
Câu 21. Cho cosα = với 0 < α < . Tính sinα . 5 2 1 1 3 3 A. sinα = .
B. sinα = − . C. sinα = . D. sinα = ± . 5 5 5 5 π
Câu 22. Cho cosα với < α < π , khi đó giá trị của sinα bằng 2 7 15 7 15 A. . B. . C. − . D. − . 274 274 274 274
Câu 23. Tập giá trị T của hàm số y = cot x là A. T = .  B. T =  \{ } 0 . π
C. T =  \{kπ ,k ∈ }  . D. T  \  kπ ,k  = + ∈.  2  Mã đề 000 Trang 2/6 π
Câu 24. Giải phương trình cos x = cos . 4 π π
A. x = ± + k2π , (k ∈) .
B. x = ± + k2π , (k ∈) . 6 5 π π
C. x = ± + k2π , (k ∈) .
D. x = ± + k2π , (k ∈) . 3 4 1 1 1 1
Câu 25. Cho dãy số 1; ; ; ; ;.... Số hạng tổng quát của dãy số này là 2 4 8 16 1 1 1 1
A. u = . B. u = . C. u − = . D. u = . n n n 2n n 2n n ( 2 − )n
Câu 26. Một cấp số cộng biết u = 2,d = 3 1
. Số hạng tổng quát của cấp số cộng là
A. u = n − u = − n u = n + u = n − n 2 3.
B. n 1 3 .
C. n 2 1. D. n 3 1. 1 − 1 −
Câu 27. Cho cấp số nhân: ; ; a
. Giá trị của a bằng 5 125 1 1 1 A. a = ± . B. a = ± .
C. a = ± . D. a = 5. ± 5 25 5
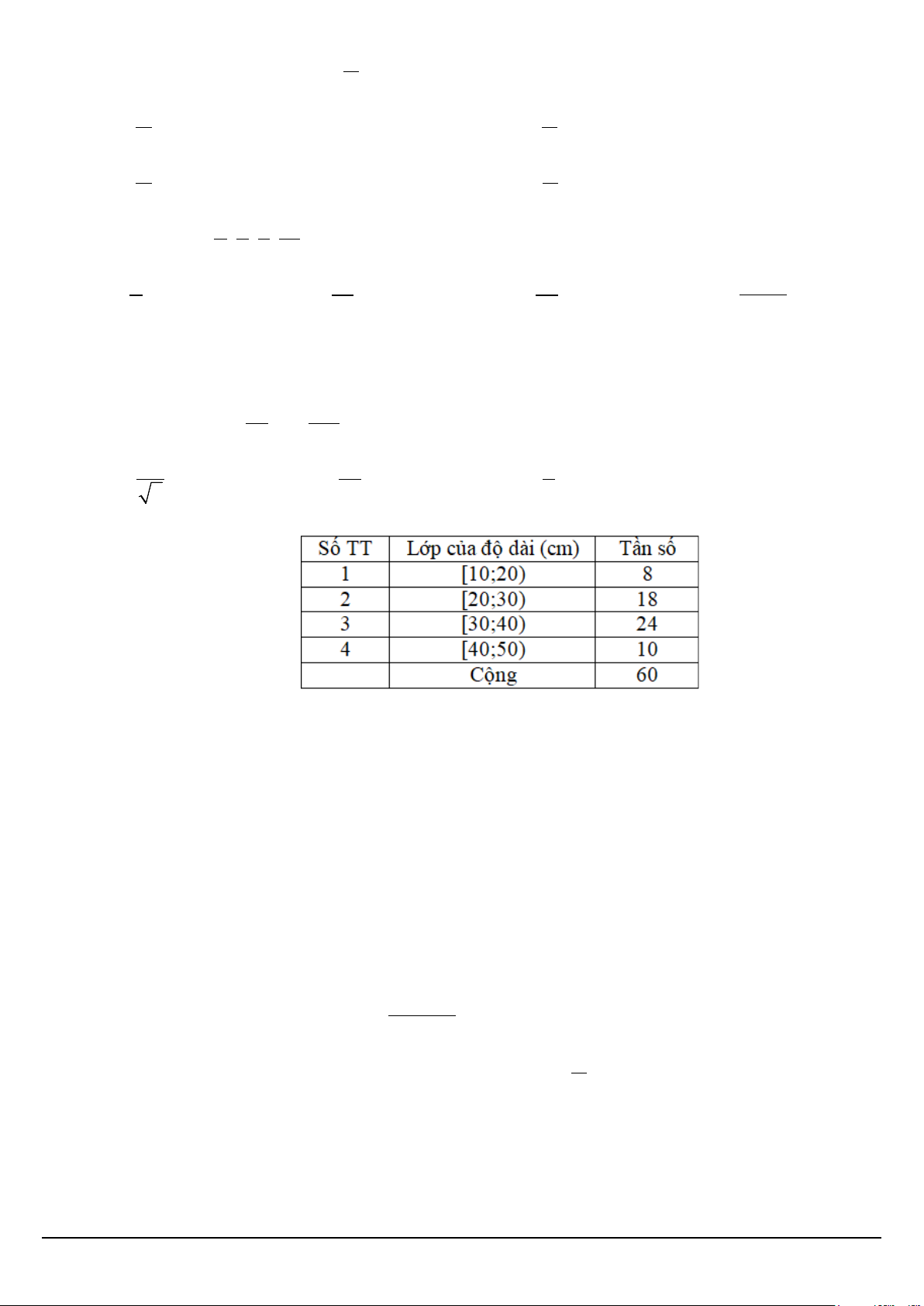
Câu 28. Độ dài của 60 lá dương xỉ trưởng thành được cho bằng bảng phân bố tần số ghép lớp như sau.
Giá trị đại diện của nhóm thứ 2 là A. 25. B. 35. C. 15. D. 45.
Câu 29. Giá trị thành phẩm quy ra tiền( nghìn đồng) trong một tuần lao động của 7 công nhân trong một công
ty là:180;200;210;190;210;190;220. Mốt của mẫu số liệu trên là A. 220. B. 210. C. 190;210. D. 180.
Câu 30. Tiền thưởng của 20 công nhân trong một công ty được thống kê bởi mẫu số liệu:
3;2;4;4;5;4;3;4;5;3;5;2;2;4;5;4;3;5;4;5 (đơn vị: triệu đồng). Tứ phân vị của mẫu số liệu là A. Q = 2; Q = 4; Q = 3. Q = 3; Q = 3; Q = 5. 1 2 3 B. 1 2 3 C. Q = 2; Q = 3; Q = 4.
Q =3; Q = 4; Q =5. 1 2 3 D. 1 2 3 . 1− sin x
Câu 31. Tìm tập xác định D của hàm số y = . cos x −1 π A. D = .  B. D  \  kπ ,k  = + ∈.  2 
C. D =  \{kπ ,k ∈ }  .
D. D =  \{k2π ,k ∈ }  .
Câu 32. Tổng các nghiệm của phương trình ( 0
tan 2x −15 ) =1 trên khoảng ( 0 0 90 − ;90 ) bằng A. 0 0 . B. 0 30 − . C. 0 30 . D. 0 60 − . Mã đề 000 Trang 3/6 6u + 5u = 28
Câu 33. Cho cấp số công (u
. Số hạng đầu u và công sai d của cấp số cộng bằng n ) 1 5 : S =  14 1 4 u  = 6 u  = 2 u  = 3 − u  = 8 A. 1  . B. 1  . C. 1  . D. 1  . d = 2 d = 6 d = 8 d = 3 − 1 1
Câu 34. Cho cấp số nhân (u có u 1;q − = − = . Số
là số hạng thứ bao nhiêu? n ) 1 10 103 10
A. số hạng thứ 103.
B. số hạng thứ 104.
C. số hạng thứ 105.
D. số hạng thứ 106.
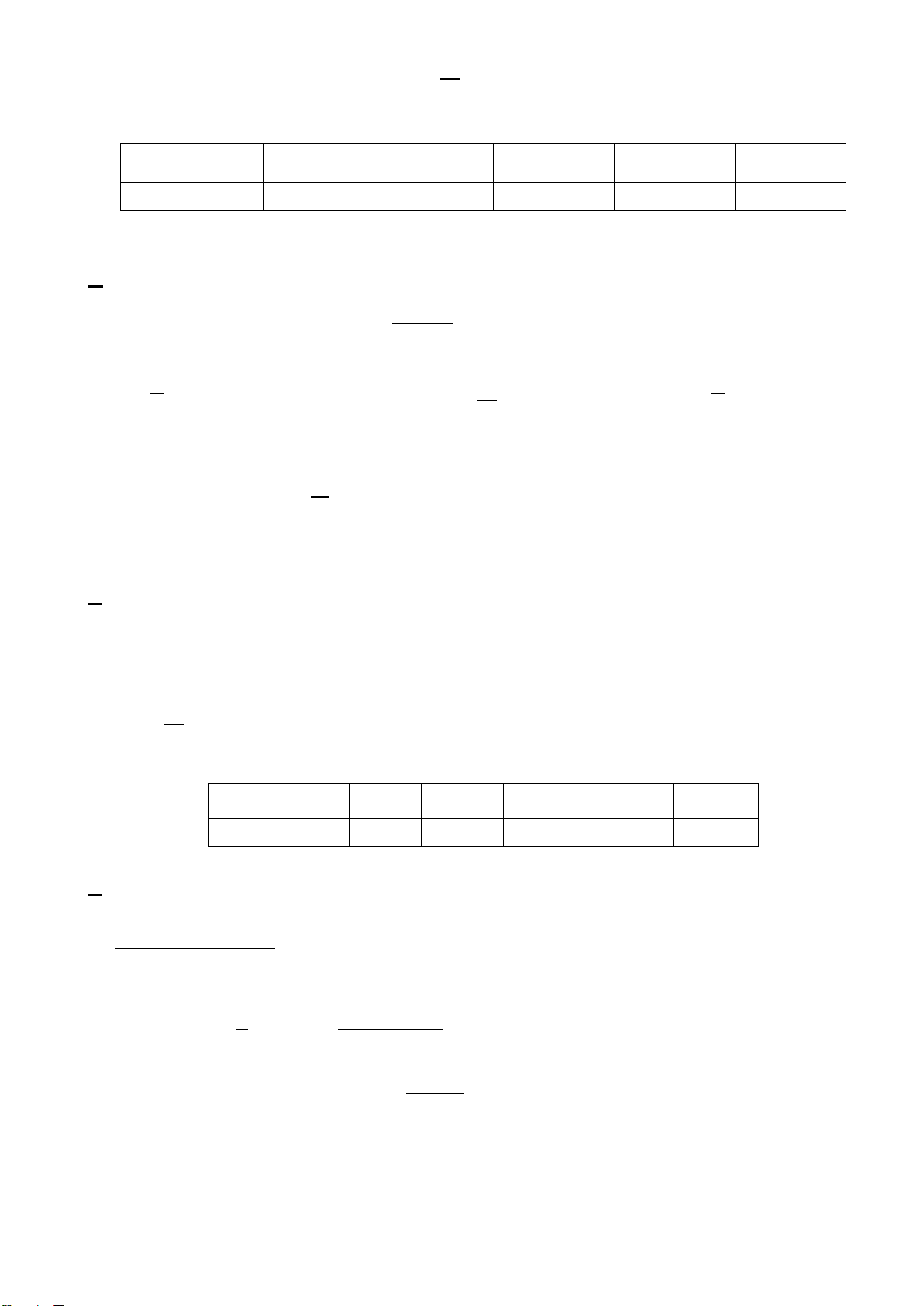
Câu 35. Thời gian(phút) truy cập Internet của mỗi buổi tối của một số học sinh được cho trong bảng sau Chiều cao
[9,5;12,5) [12,5;15,5) [15,5;18,5) [18,5;21,5) [21,5;24,5) Số học sinh 3 12 15 24 2
Tính số trung vị của mẫu ghép nhóm này. A. 18,1. B. 18. C. 17. D. 12.
II. PHẦN TỰ LUẬN (3 điểm). Bài 1 (1 điểm). a) α − α Cho 3 sinα = và 0 0
90 < α <180 . Tính giá trị của biểu thức cot 2tan E = . 5 tanα + 3cotα
b) Tìm tập xác định của hàm số 1− sin x y = . sin 2x +1
Bài 2 (1 điểm). Giải phương trình 2 2sin  π
x − 3sin x +1 = 0 và tìm các nghiệm thuộc 0;   . 2   
Bài 3 (1 điểm). Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng.
Tính độ dài các cạnh của tam giác đó.
-------------------- HẾT -------------------- Mã đề 000 Trang 4/6 ĐÁP ÁN
HƯỚNG DẪN PHẦN TRẮC NGHIỆM 1.A 11.A 21D 2.A 12.C 22.D 3.A 13.D 23.C 4.D 14.C 24.B 5.B 15.B 25.C 6.B 16.B 26.D 7.D 17.A 27.D 8.A 18.A 28.C 9.A 19.B 29.D 10.C 20.C 30.D 31.A 32.B 33.B 34.D 35.C
HƯỚNG DẪN GIẢI PHẦN TỰ LUẬN Câu 1 (1 điểm). a) Cho 3 α − α sinα = và 0 0
90 < α <180 . Tính giá trị của biểu thức cot 2tan E = . 5 tanα + 3cotα Lời giải  4 cosα =  2 2 sin α + cos α =1 2 2 9 16 ⇒ cos α =1− sin α =1− = 5 ⇔  25 25  4 cosα = −  5 Vì 0 0 90 < α <180 4 ⇒ cosα = − . Vậy 3 tanα = − và 4 cotα = − . 5 4 3 4  3 2.  − − − cotα 2tanα 3  4 −   2 E = = = − . tanα + 3cotα 3  4  57 − + 3. − 4  3  
b) Tập xác định của hàm số 1− sin x y = là: sin x +1 Lời giải
Hàm số xác định ⇔ sin 2x +1 ≠ 0 π π 3 ⇔
x ≠ − ⇔ x ≠
+ k π (k ∈) 3 sin 2 1 2 2 ⇔ x ≠
+ kπ (k ∈) 2 4 π Vậy tập xác định: 3 x ≠
+ kπ (k ∈) . 4
Câu 2 (1 điểm). Giải phương trình 2 2sin x  π
− 3sin x +1 = 0 và tìm các nghiệm thuộc 0;   2    Lời giải Mã đề 000 Trang 5/6 t = 1
Đặt t = sin x ( 1 − ≤ t ≤ )
1 , phương trình trở thành: 2 2t 3t 1 0  − + = ⇔ 1 t =  2 π
Với t =1, ta có: sin x =1 ⇔ x = + k2π (k ∈). 2 π π π Do 0 −
≤ x < nên 0 ≤ + k2π < 1 ⇔
≤ k < 0. Vì k ∈ nên không tồn tại k. 2 2 2 4  π = + π π x k2  Với 1 t = , ta có: 1 sin x = = sin 6 ⇔  . 2 2 6  5π x = + k2π  6 π π
Do 0 ≤ x < nên x = . 2 6 π π
Vậy phương trình có nghiệm x = thỏa điều kiện 0 ≤ x < . 6 2
Bài 3 (1 điểm). Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng.
Tính độ dài các cạnh của tam giác đó. Lời giải
Gọi d là công sai của cấp số cộng và các cạnh có độ dài lần lượt là a − d , a , a + d (0 < d < a)
Vì tam giác có chu vi bằng 3 nên 3a = 3 ⇔ a =1.
Vì tam giác vuông nên theo định lý Pytago ta có ( + d )2 = ( − d )2 2 1 1 +1 ⇔ 4d =1 1 ⇔ d = . 4
Suy ra ba cạnh của tam giác có độ dài là 3 5 ;1; . 4 4
------ HẾT ------ Mã đề 000 Trang 6/6
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm). Câu 1. π
Trên đường tròn lượng giác, cho góc lượng giác có số đo thì mọi góc lượng giác có cùng tia đầu và 2
tia cuối với góc lượng giác trên đều có số đo dạng π π A. π π π .
B. + k ,(k ∈) .
C. + k2π ,(k ∈) .
D. + kπ ,(k ∈). 2 2 2 2 2
Câu 2. Trên đường tròn có bán kính r π
= 5 cm, độ dài của cung có số đo là 8 π π
A. l = cm. B. 40 l = cm. C. 5 l = cm. D. 5.180 l = cm. 8 π 8 8
Câu 3. Biểu thức sin xcos y − cos xsin y bằng
A. cos(x − y) .
B. cos(x + y).
C. sin (x − y).
D. sin ( y − x).
Câu 4. Cho góc lượng giác .
a Trong các khẳng định sau, khẳng định nào là khẳng định sai? A. 2
cos2a =1− 2sin a . B. 2 2
cos2a = cos a −sin a . C. 2
cos 2a =1− 2cos a . D. 2
cos 2a = 2cos a −1.
Câu 5. Tìm tập xác định của hàm số y = tan x . π A. π   \  kπ | k  +
∈.B.  \{kπ | k ∈ } .
C.  \  + k2π | k ∈ . D.  \{k2π | k ∈ } . 2     2 
Câu 6. Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A. y = tan x . B. 2
y = x + 2024 .
C. y = sin x .
D. y = cos x . π
Câu 7. Nghiệm của phương trình sin x = sin là 3  π x = + k2π  π  x = + k2π  A. 3  (k ∈). B. 3 . π  (k ∈) x = − +k2π  2π  x = + k2π  3  3  π x = + kπ π 
C. x = + kπ (k ∈) . D. 3  (k ∈) . 3  2π x = + kπ  3
Câu 8: Cho các dãy số sau, dãy số nào là dãy số vô hạn? A. 0,2,4,6,8,10. B. 1 1 1 1 1, , , ,..., ,... C. 1,4,9,16,25. D. 1,1,1,1,1. 2 4 8 2n
Câu 9: Cho dãy số: 5;10;15;20;25;... Số hạng tổng quát của dãy số này là
A. u = n − . B. u = n .
C. u = + n .
D. u = n + . n 5 1 n 5 n 5 n 5( 1)
Câu 10: Trong các dãy số sau, dãy số nào là một cấp số cộng? A. 1; 2 − ; 4 − ; 6 − ; 8 − . B. 1; 3 − ; 6 − ; 9 − ; 1 − 2. C. 1; 3 − ; 7 − ; 1 − 1; 1 − 5. D. 1; 3 − ; 5 − ; 7 − ; 9 − .
Câu 11: Cho cấp số cộng (u với u = − n n
5 2 . Tìm công sai của cấp số cộng. n )
A. d = 3. B. d = 2 − . C. d =1. D. d = 2 .
Câu 12: Cho cấp số cộng (u có u =1 và u = 3 . Giá trị của u bằng n ) 1 2 3 A. 6. B. 9. C. 4. D. 5.
Câu 13: Cho các dãy số sau. Dãy số nào là dãy số giảm? A. 1; 1; 1; 1; 1; 1. B. 1 1 1 1 1; − ; ; − ; . C. 1; 3; 5; 7. D. 11; 9; 7; 5; 3. 2 4 8 16 1
Câu 14: Cho dãy số (u có u = . Khẳng định nào sau đây sai? n ) n n A. u = 1 1 .
B. Dãy số (u là dãy số tăng. n )
C. Dãy số (u bị chặn trên bởi 1.
D. Dãy số (u là dãy số giảm. n ) n ) 2n −1
Câu 15: Cho dãy số (u có u = . Khi đó, u bằng n ) n n +1 2 A. 1. B. 2. C. 3. D. 4.
Câu 16. Đo chiều cao (tính bằng cm) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: Chiều cao (cm) [150;155) [155;160) [160;165) [165;170) [170;175) [175;180) Số học sinh 25 50 200 165 50 10
Các em có chiều cao 170 cm được xếp vào nhóm: A. [155;160) . B. [160;165) . C. [165;170) . D. [170;175) .
Câu 17. Trong mẫu số liệu ghép nhóm, giá trị đại diện x của nhóm [a a được tính bằng công thức i ; i 1 + ) i A. + − a a a a i i 1 x + = . B. i 1 i x + = .
C. x = a + a .
D. x = a − . + a i 2 i 2 i i i 1 + i i 1 i
Câu 18. Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành hai phần, mỗi phần chứa 50% giá trị?
A. số trung vị.
B. số trung bình. C. mốt. D. tứ phân vị.
Câu 19. Trong mẫu số liệu ghép nhóm, số đặc trưng nào sau đây chia mẫu số liệu thành bốn phần, mỗi phần chứa 25% giá trị?
A. số trung vị.
B. số trung bình. C. mốt. D. tứ phân vị.
Câu 20. Khẳng định nào sau đây sai?
A. Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc.
B. Mốt của mẫu số liệu ghép nhóm bằng mốt của mẫu số liệu gốc.
C. Mốt là một trong các số đặc trưng để đo xu thế trung tâm của mẫu số liệu.
D. Mốt của mẫu số liệu là các giá trị xuất hiện với tần số lớn nhất. Mức 2 π Câu 21. Cho 1
cosα = và 3 < α < 2π . Tính sinα . 2 2 A. 3 − . B. 3 . C. 2 . D. 2 − . 2 2 2 2 Câu 22. Cho tanα  π = 2 . Tính tan α  −  . 4    A. 1 − . B. 1. C. 2 . D. 1 . 3 3 3
Câu 23. Gọi M là giá trị lớn nhất, m là giá trị nhỏ nhất của hàm số y = 4sin xcos x +1. Tính M + m . A. 2 . B. 4 . C. 3. D. 1 − .
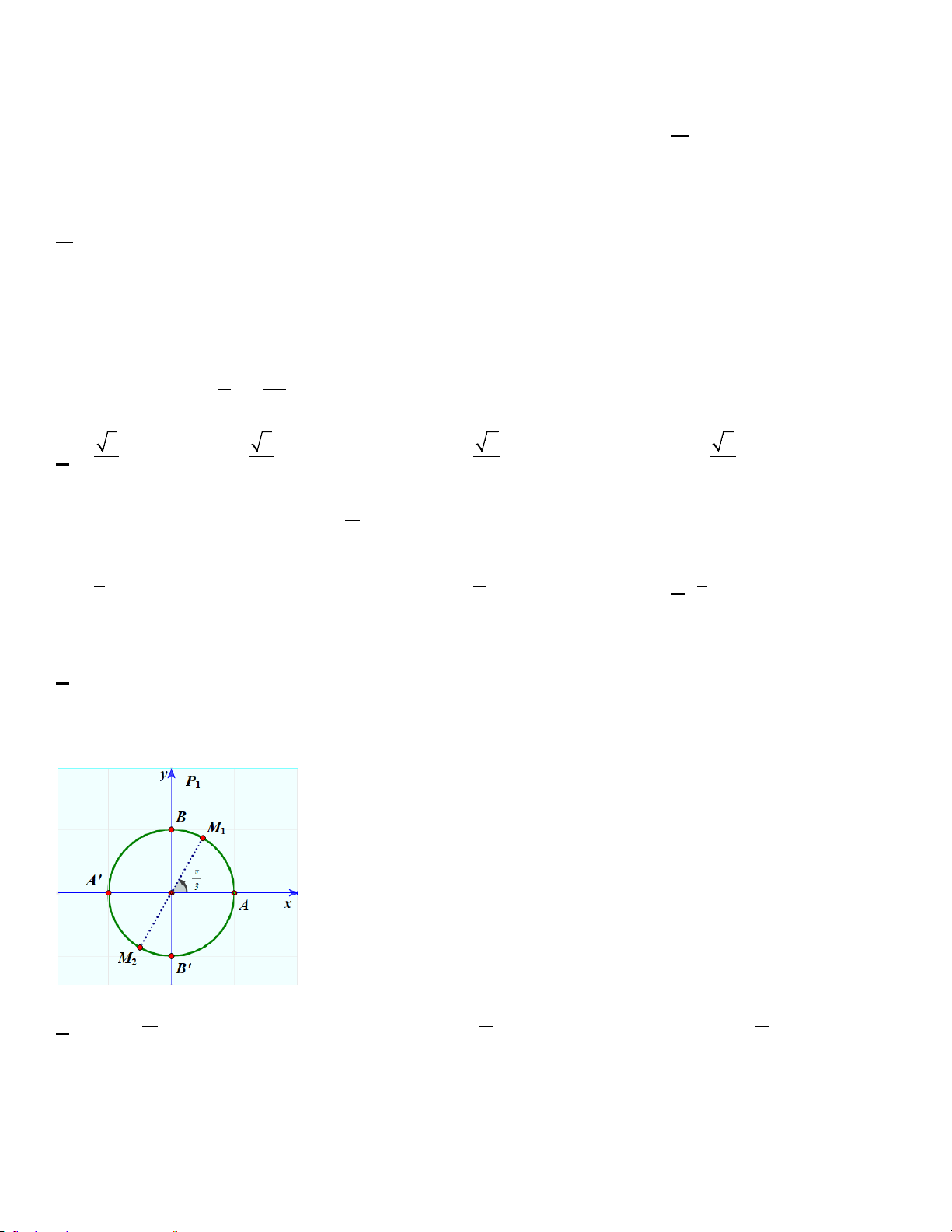
Câu 24. Cung lượng giác có điểm biểu diễn là M , M như hình vẽ là nghiệm của phương trình lượng giác nào 1 2 sau đây? A.  π  π  π sin x  − =   
 0 . B. sin x = 0. C. cos x − =   0 . D. sin x + =   0.  3   3   3  u   2 1 
Câu 25: Cho dãy số u xác định bởi  1
. Tìm số hạng u . n u    3   u n n 1 1    3 A. 5 u 2 14  .
B . u 1.
C. u  . D. u  . 3 9 3 3 3 3 27
Câu 26: Cho cấp số cộng (u có số hạng đầu u = 0,
− 1và công sai d = 0,1. Số hạng thứ 7 của cấp số cộng này n ) 1 là A. 1,6 . B. 6 . C. 0,5. D. 0,6 .
Câu 27: Cho cấp số nhân có các số hạng lần lượt là 3; ;
x 27; 81;... Tìm x . A. 9 − . B. 9. C. 81 − . D. 81.
Câu 28. Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau: Thời gian (giờ) [0; 4) [4;8) [8;12) [12;16) [16;20) Số học sinh 3 15 10 8 4
Tính tổng số học sinh được khảo sát. A. 40. B. 15. C. 20. D. 5.
Câu 29. Khảo sát về thời gian xem tivi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau: Thời gian (giờ) [0; 4) [4;8) [8;12) [12;16) [16;20) Số học sinh 3 15 10 8 4
Thời gian xem tivi trung bình trong tuần trước của các bạn học sinh này là A. 9,5 giờ. B. 11,5 giờ. C. 7,5 giờ. D. 15 giờ.
Câu 30. Doanh thu bán hàng trong 30 ngày của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng): Doanh thu  ; 5 7 7;9  ; 9  11  ; 11 13  ; 13 15 Số ngày 4 10 12 3 1
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là A.  ; 7 9. B.  ; 5 7. C.  ; 9  11 . D.  ; 9  11 . Mức 3
Câu 31. Tìm tập xác định D của hàm số  π y tan 2x  = −  . 4    A. 3π π  π  \ k D   ,k  = + ∈ . B. 3 D =  \ 
+ kπ ,k ∈ . 8 2      4  C. 3π π π  \ k D   ,k  = + ∈ .
D. D =  \  + kπ,k ∈ . 4 2      2 
Câu 32. Phương trình 2sin x + 3 = 0 có tổng nghiệm dương nhỏ nhất và nghiệm âm lớn nhất bằng π A. 4 π . B. 2π . C. . D. π . 3 3
Câu 33: Cho dãy số (u là cấp số cộng có u = 1; − d = 2.Tìm S = n ) 1 n biết n 483.
A. n = 20 . B. n = 21. C. n = 22 . D. n = 23 .
Câu 34: Cho cấp số nhân (u có u =1;q = 2
− . Tổng của 10 số hạng đầu tiên của cấp số nhân đó bằng n ) 1 A. 341 − B. 341 C. 1023 D. 1023 −
Câu 35. Đo chiều cao (tính bằng cm) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: Chiều cao [150;155) [155;160) [160;165) [165;170) [170;175) [175;180) Số học sinh 25 50 200 165 50 10
Tính mốt của mẫu số liệu ghép nhóm trên. A. 160. B. 164,05. C. 162,5. D. 160,94.
II. PHẦN TỰ LUẬN (3 điểm). Câu 1 (1 điểm). π a) Cho 12 sinα =
với < α < π . Tính sin 2α . 13 2
b) Tìm tập xác định của hàm số cos x y = . sin x −1
Câu 2 (1 điểm). Giải phương trình 5 − 4cos 2x = 6sin .xsin 3x .
Câu 3 (1 điểm). Ước tính dân số năm 2022 của tỉnh Kon Tum là 579 914 người, tỷ lệ tăng dân số 1,5% so với
năm trước. Nếu lấy kết quả chính xác đến hàng nghìn thì dân số của tỉnh Kon Tum năm 2030 là bao nhiêu?
-------------------- HẾT --------------------
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
LỚP 11 − ĐỀ 1 Câu Ý Đáp án Điểm 2 0,25 2 2 12  25 5 cos α =1− sin α =1− = ⇒   cosα = ± a 13  169 13 π
Vì < α < π nên cosα < 0 . Suy ra 5 cosα = − 2 13 12  5  120 0,25
sin 2α = 2sinα.cosα = 2. . − = −   1 13  13  169
(1,0 điểm) Hàm số os c x 0.25 y =
xác định khi và chỉ khi sin x −1 b sin x 1 x π
≠ ⇔ ≠ + k2π,k ∈ 2
Tập xác định của hàm số đã cho là D  \ π  k2 ,k  = + π ∈ 2    0.25 2 0.25
(1,0 điểm)
3 − 3cos 4 x = 6sinx.sin 3x 2
⇔ 3 − 3cos 4x = 3(cos 2x − cos 4x) 2 3 ⇔ 3cos 2x = 0.25 2 ⇔ 1 cos 2x = 0.25 2 π ⇔ x = ± + k ,k π ∈ 0.25 6 3
Đặt P0 = 579914 và r = 1,5% = 0,015 0.25
(1,0 điểm)
Gọi Pn là dân số của tỉnh Kon Tum sau n năm nữa.
Sau 1 năm, dân số của tỉnh là: P = P + P .r = P (1+ r ) 0.25 1 0 0 0
Sau 2 năm, dân số của tỉnh là: 2 P = P + P .r = P (1+ r ) 2 1 1 0 …
Sau n năm, dân số của tỉnh là: n P = P + P .r = P (1+ r ) 0.25 n n-1 n-1 0
Suy ra (Pn) là một cấp số nhân với số hạng đầu P0 và công bội q = 1+ r.
Do đó dân số của tỉnh Kon Tum năm 2030 là: 0.25 8 8
P = P .(1+ r) = 579914.(1,015) ≈ 653000 người. 8 0
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - LỚP: 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Cho α thuộc góc phần tư thứ hai của đường tròn lượng giác. Hãy chọn kết quả đúng
trong các kết quả sau đây. A. sinα > 0; 0 cosα > . B. sinα < 0; 0 cosα < . C. sinα > 0; 0 cosα < . D. sinα < 0; 0 cosα > .
Câu 2. Một chiếc đồng hồ, có kim chỉ giờ OG chỉ số 9 và kim phút OP chỉ số12. Số đo của góc
lượng giác OG,OP là
A. k2 , k   . B. 0 0
270  k360 , k  .  C. 0 0
270  k360 , k   . 2
D. 9k2 , k   . 10
Câu 3. Trong các khẳng định sau, khẳng định định nào đúng?
A. sin(a −b) = sin acosb − cosasinb
B. sin(a −b) = sin acosb + cosasinb
C. sin(a + b) = sin acosb − cosasinb
D. sin(a + b) = sin acosb − cosasinb
Câu 4. Trong các khẳng định sau, khẳng định định nào sai?
A. sin 2a = 2sin acos .a B. 2 2
cos 2a = cos a − sin . a C. 2
cos 2a = 2cos a +1. D. 2 cos 2a =1− 2sin . a
Câu 5. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A. y = tan x .
B. y = sin x .
C. y = cot x .
D. y = cos x .
Câu 6. Hàm số nào sau đây là một hàm số lẻ ?
A. y = cos x B. y = 1 + cosx C. y = x + sinx D. y = cos2x
Câu 7. Tập hợp tất cả các giá trị của tham số m để phương trình cosx = m có nghiệm là A. ( ; −∞ − ) 1 . B. [ 1; − ] 1 . C. (1;+∞). D. . 
Câu 8. Cho dãy số (u , biết 2 =
. Ba số hạng đầu tiên của dãy số là n ) un 2 n A. 1 1 1; ; . B. 1 2 2; ; . C. 1 2 2; ; . D. 1 2 1; ; . 3 5 2 9 3 9 2 3
Câu 9. Cho dãy số (u , biết
. Khẳng định nào sau đây đúng? n ) u = 3n n A. u = 27. B. u = 82. C. u = 240. D. u =10. 3 4 5 2
Câu 10. Cho cấp số cộng (u , biết u = 1,
− u = 2 . Công sai của cấp số cộng là n ) 1 2 A. d =1. B. d = 3. C. d = 3 − . D. d = 4.
Câu 11. Cho cấp số cộng (u , biết u = 2 và công sai
− . Khẳng định nào sau đây đúng? n ) 1 d = 3 A. u = 1. − B. u =1. C. u = 5. D. u = 5. − 2 2 2 2
Câu 12. Cho cấp số cộng (u có u = 2 và d =1. Gọi S là tổng 5 số hạng đầu tiên của cấp số n ) 1 5
cộng đã cho. Mệnh đề nào sau đây đúng?
A. S =10.
B. S =15.
C. S = 20.
D. S = 5. 5 5 5 5
Câu 13. Cho cấp số nhân (u , biết u = 4, − u = 2
− . Công bội của cấp số nhân là n ) 5 6 A. 1 q = . B. q = 2 − . C. q = 2. D. 1 q = − . 2 2
Câu 14. Cho cấp số nhân (u , biết u = 2 , công bội q = 4. Tìm u . n ) 3 4 A. u = 32. B. u = 8. C. u =12. D. u =10. 3 3 3 3
Câu 15. Cho cấp số nhân (u , khẳng định nào sau đây là đúng? n ) A. 2 u = u . B. u = u . − u k k . − u k k . 1 k 1 + 1 k 1 + C. 2 u = u + . D. 2 u = u . − u k k . − u k k 1 k 1 + 1 k 1 +
Câu 16. Trong mẫu số liệu ghép nhóm, độ dài của nhóm [1;9) được tính như thế nào? A. 8. B. 5. C. 10 . D. 9 .
Câu 17. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. Số trung bình. B. Mốt. C. Số trung vị. D. Tứ phân vị.
Câu 18. Khối lượng của 30 củ khoai tây thu hoạch ở một nông trường được thống kê như bảng sau.
Tần suất ghép nhóm của lớp [100;110) là. A. 0 20 0 . B. 0 40 0 . C. 0 60 0 . D. 0 80 0 .
Câu 19. Thời gian (phút) truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:
Khi đó trung vị của mẫu số liệu ghép nhóm này là: A. 16,2. B. 15. C. 18,1 . D. 9 .
Câu 20. Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được đo như sau:
Thời gian [485; 510) [510; 535) [535; 560) [560; 585) [585; 610) [610; 635) [635; 660] Số cầu thủ 8 2 1 2 1 1 1
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 5.
B. 6 . C. 7 . D. 12 Câu 21. Biết 2 π cosα = − và 3 π < α <
. Giá trị sinα bằng 3 2 A. 5 − B. 5 C. 5 D. 5 − 3 3 2 2 Câu 22. Biết 4 π
cosα = và − < α < 0 . Giá trị sin2α bằng 5 2 A. 24 − − . B. 2. C. 24 − . D. 8. 5 5 25 25
Câu 23. Tập giá trị của hàm số y = 2 + sin x là A. [ 1; − ] 1 . B. [0;2]. C. [ 1; − 2]. D. [1; ] 3 .
Câu 24. Nghiệm của phương trình cot x = 1 − là A. π π π π x −
= − + kπ ,k ∈ Z . B. x = + kπ ,k ∈ Z . C. x =
+ kπ ,k ∈ Z . D. x = + kπ ,k ∈ Z . 2 2 4 4
Câu 25. Cho dãy số có các số hạng đầu là: 2;
− 0;2;4;6;. Số hạng tổng quát của dãy số này là
công thức nào dưới đây?
A. u = − n
B. u = n −
C. u = − n +
D. u = n − n 2 4. n 2( )1. n 2. n 2 .
Câu 26. Cho cấp số cộng (u có u = 0,
− 1; d = 0,2 . Số hạng thứ 8 của cấp số cộng là n ) 1 A. 2,3. B. 3. C. 1 ,3. D. 0,6 .
Câu 27. Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành một cấp số nhân. A. x 14. B. x  32. C. x  64. D. x  68.
Câu 28. Điều tra về điểm của học sinh lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 [0;2) 1 2 [2;4) 6 3 [4;6) 8 4 [6;8) 10 5 [8;10) 9 N=34
Giá trị đại diện của nhóm thứ tư là A. 10 . B. 7 . C. 9 . D. 5 .
Câu 29. Thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau: Thời gian (giờ)  ; 5 7  ; 7 9  ; 9  11  ; 11 13  ; 13 15 Số học sinh 2 5 3 10 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. [7; 9) . B. [9; 1 )
1 . C. [11; 13). D. [13; 15).
Câu 30. Khảo sát số kg giấy vụn ủng hộ của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm như sau: Giấy vụn (kg)  ; 0 2  ; 2 4  ; 4 6  ; 6 8  ; 8 10 Số học sinh 7 19 10 8 5
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là A. [4;6). B. [2;4) . C. [6;8) . D. [8;10).
Câu 31. Tập xác định của hàm số 1+ sin x y = là: 1− cos x A. π  π R \   k2π ,k Z  + ∈
B. R \{π + kπ,k ∈Z} C. R \{k2π,k ∈Z} D. R \ − + k2π,k ∈Z 2      2 
Câu 32. Phương trình 2sin x =1 có bao nhiêu nghiệm thuộc tập [ π − ;π ] A. 1. B. 2. C. 3. D. 4. Câu 33  − + = . Cho cấp số cộng ( u u u 15 u thỏa mãn 1 3 5
Số hạng thứ 100 của cấp số cộng là n )  . u + u =  27 1 6 A. 417 B. 375 C. - 417 D. - 375
Câu 34. Cho cấp số nhân u có u  3 và q 2 . Số 192 là số hạng thứ mấy của cấp số nhân đã n  1 cho?
A. Số hạng thứ 5.
B. Số hạng thứ 6.
C. Số hạng thứ 7.
D. Không là số hạng của cấp số đã cho.
Câu 35. Trong hoạt động bảo vệ môi trường, các học sinh lớp 11A1 tiến hành trồng cây. Kết quả
sau hoạt động được ghi lại ở bảng sau: Số cây
[1;8) [8;15) [15;22) [22;29) [29;36) Số học sinh 7 15 6 10 3
Hãy tìm số trung vị của mẫu số liệu ghép nhóm trên. A. 11,5. B. 25,5 . C. 18 . D. 26.
II. PHẦN TỰ LUẬN (3 điểm).
Bài 1 (1 điểm). a) Cho 2 α + α cosα= . Tính tan 3cot A = . 3 tanα + cotα
b) Tìm tập xác định của hàm số sin 3x y = . cosx +1
Bài 2 (1 điểm). Giải phương trình sin 4x +1− 2cos2x = sin 2x .
Bài 3 (1 điểm). Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau tiền
đặt gấp đôi lần tiền đặt cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khác trên thắng hay thua bao nhiêu?
……………… HẾT ………………
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng.
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 C A A C D C B B A B
Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 A C A B D A B A C C
Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 A C D C D C B B C A
Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 C D A C A II. PHẦN TỰ LUẬN Bài Đáp án Biểu điểm 1 a) Cho 2 α + α cosα= . Tính tan 3cot A = 3 tanα + cotα 1 1 tanα + 3 0,25 2 + 2 Ta có 2 tanα tan α + 3 cos α 2 A = = = = 1+ 2cos α . 2 1 tan α +1 1 tanα + 2 tanα cos α Suy ra 4 17 A =1+ 2. = 0,25 9 9
b) Tìm tập xác định của hàm số sin 3x y = . cosx +1
Hàm số xác định khi cosx +1≠ 0 0,25 ⇔ cosx ≠ 1
− ⇔ x ≠ π + k2π ,k ∈ 0,25
Vậy tập xác định của hàm số là D =  \{π + k2π,k ∈ }  . 2
Giải phương trình sin 4x +1− 2cos2x = sin 2x
2sin 2 .xcos 2x +1− 2cos 2x − sin 2x = 0 0,25 ⇔ (sin2x- ) 1 (2cos 2x − ) 1 = 0 0,25 sin 2x =1 0,25  ⇔ 1 cos2x=  2  π 0,25 x = + kπ  4 ⇔  (k ∈). π  x= + kπ  6 3
Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau tiền đặt gấp
đôi lần tiền đặt cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khác
trên thắng hay thua bao nhiêu?
Số tiền du khác đặt trong mỗi lần (kể từ lần đầu) là một cấp số nhân có 0,25
u  20 000 và công bội q  2. 1
Du khách thua trong 9 lần đầu tiên nên tổng số tiền thua là: 0,25 u  9 1 p 1 
S u u ...u   10220000 9 1 2 9 1 p
Số tiền mà du khách thắng trong lần thứ 10 là 9
u u .p 10240000 0,25 10 1
Ta có u S  20 000 0 nên du khách thắng 20 000. 0,25 10 9
ĐỀ KIỂM TRA MINH HOẠ GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Giá trị nào sau đây mang dấu dương? A. 0 cos120 B. 0 sin120 C. 0 tan120 . D. 0 cot120 .
Câu 2. Trong mặt phẳng cho ba tia Ou,Ov,Ox . Trong các mệnh đề sau, mệnh đề nào đúng? A. sñ ( , Ou Ov) = sñ ( ,
Ou Ox) + sñ (Ox,Ov) + k π 2 ,k ∈. B. sñ ( , Ou Ov) = sñ ( ,
Ou Ov) + sñ (Ox,Ou) + k π 2 ,k ∈. C. sñ ( ,
Ou Ov) = sñ (Ov,Ox) + sñ (Ox,Ou) + k π 2 ,k ∈. D. sñ ( ,
Ou Ov) = sñ (Ov,Ox) + sñ ( , Ou Ox) + k π 2 ,k ∈.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A. cos(a + b) = cos acosb −sin asin . b
B. cos(a + b) = cos acosb + sin asin . b
C. cos(a + b) = cos asin b + sin acos . b
D. cos(a + b) = sin acos a + cosbsin . b
Câu 4. Trong các khẳng định sau, khẳng định nào sai? A. 2 2
sin 2a = cos a − sin a
B. cos 2a = 2sin a C. 2
cos 2a = 2cos a −1. D. 2 cos 2a =1− 2sin . a
Câu 5. Đồ thị dưới đây là đồ thị của hàm số nào?
A. y =1+ sin 2x . B. y = cos x . C. y = −sin x . D. y = −cos x .
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = tan .x
B. y = cot .x
C. y = sin .x
D. y = cos .x
Câu 7. Điều kiện có nghiệm của phương trình sin x = m là A. m <1. B. m >1. C. m ≤1. D. m ≥1.
Câu 8. Cho dãy số (u , biết u = n + . Ba số hạng đầu tiên của dãy số lần lượt là n 2 n ) A. 3;4;5. B. 0;1;2. C. 2;3;4. D. 1;2;3.
Câu 9. Trong các dãy số sau dãy số nào là dãy số hữu hạn A. 1 1 1 1 1
, , , , .... B. 5,10,15,20,25.... 2 3 4 5 3 3 3 3 3
C. 8,15,22,29,36. D. 2,0,4,6,8,. . 1
Câu 10. Cho cấp số cộng (u , biết u = 2,u = 8. Công sai của cấp số cộng là n ) 1 2 A. d = 6 . B. d =16 . C. d =10 . D. d = 4 .
Câu 11. Cho cấp số cộng (u , biết u = 2 và công sai d = 3. Khẳng định nào sau đây đúng? n ) 1 A. u = 5. B. u = 2. C. u = 6. D. u = 3. 2 2 2 2
Câu 12. Cho cấp số cộng (u . Gọi S là tổng của n số hạng đầu của cấp số cộng. Khẳng định đúng là n ) n n(n − ) 1 nu + n n −1 1 ( )
A. S = nu + d . B. S = d . n 1 2 n 2 (n − )1
C. S = nu + n n − d .
D. S = nu + d . n 1 1 ( ) n 1 2
Câu 13. Dãy số nào sau đây không phải là cấp số nhân?
A. 1;− 3;9;− 27;54 . B. 1;2;4;8;16 . C. 1;−1;1;−1;1. D. 1;− 2;4;−8;16 .
Câu 14. Cho cấp số nhân (un ) với 1
u = 81 và u4 = 3. Tìm công bội q ? A. 1 1 − . B. 1 − . C. 3. D. 3 − . 3 3 3
Câu 15. Cho cấp số nhân (u với
và công bội q = 3. Giá trị của n ) u = 2 u bằng 1 2 A. 6 . B. 9. C. 8 . D. 2 . 3
Câu 16. Trong mẫu số liệu ghép nhóm, độ dài mỗi nhóm [ ;
a b) được tính như thế nào? A. b − . a
B. a + b . C. a + . b D. . a . b 2
Câu 17. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. mốt. B. số trung bình. C. số trung vị. D. tứ phân vị.
Câu 18. Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm [a;b) được tính như thế nào?
A. a + b . B. b − . a C. a + . b D. . a . b 2
Câu 19. Trong các khẳng định sau, khẳng định nào là đúng?
n −(m +...+m 1 1 + ) A. Số trung vị là 2 p M = a + a − . + a e p ( p 1 p) mp
B. Số trung vị bị ảnh hưởng bởi các giá trị quá lớn hay quá bé.
C. Số trung vị luôn là một số liệu nào đó của mẫu.
D. Số trung vị chính là số trung bình.
Câu 20. Đo chiều cao (tính bằng cm ) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: Chiều cao [150;154) [154;158) [158;162) [162;166) [166;170) 2 Số học sinh 25 50 200 175 50
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 5.
B. 6 . C. 7 . D. 12. Câu 21. Biết 1 π
sinα = và < α < π. . Giá trị cosα bằng 3 2 A. 2 2 − . B. 2 3 − . C. 3 2 − . D. 3 3 − . 3 3 2 2 Câu 22. Biết 1
sinα = . Giá trị cos 2α bằng 4 A. 7 . B. 8 . C. 7 − . D. 8 − . 8 7 8 7
Câu 23. Tập giá trị của hàm số y = 2sin x là A. [ 1; − ] 1 . B. [0;2]. C. { 2; − } 2 . D. [ 2; − 2].
Câu 24. Tập nghiệm của phương trình cos x = 0 là A. π π S   k2π | k  = + ∈.
B. S =  + kπ |k ∈.  2   2 
C. S = {k2π |k ∈ }  π  . D. S k2π | k  = − + ∈.  2 
Câu 25. Xét tính tăng giảm của dãy số 1 1 1 1 − ;− ;− ;− . 2 3 4 5 A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Dãy số vừa tăng vừa giảm
Câu 26. Cho một cấp số cộng có các số hạng lần lượt là1,6,11, .x Khi đó giá trị của x là A. 5 . B. 18. C. 17. D. 16.
Câu 27. Cho cấp số nhân có các số hạng lần lượt là 1; 4; 16; 64. Gọi S là tổng của n số hạng đầu tiên của n
cấp số nhân đó. Mệnh đề nào sau đây đúng? n n( n 1 1 4 − + ) 4(4n − ) 1 A. 4 1 S − = . B. S = . C. 1 S − = . D. S = . n 4n n 3 n 2 n 3
Câu 28. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 45 học sinh lớp 11A .
Mẫu số liệu ghép nhóm này có số mốt là A. 2 . B. 1. C. 0 . D. 3. 3
Câu 29. Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau:
(Theo:http://ourwoldindata.org)
Chọn 85 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020 . A. 36,17 . B. 34,82 . C. 35,6. D. 37,12 .
Câu 30. Khảo sát chiều cao (cm) của 52 học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. [165;170) . B. [160;165) . C. [170;175) . D. [175;180) .
Câu 31. Tập xác đinh của hàm số y = sin x + cos x là A. . 
B.  \{kπ |k ∈ }  .
C.  \{π |k ∈ }  .
D.  \{k2π |k ∈ }  .
Câu 32. Phương trình 2cos x = − 3 có bao nhiêu nghiệm thuộc tập [ π − ;3π ] A. 4. B. 3. C. 2. D. 1.
Câu 33. Cho dãy số (u xác định bởi 1 1 1 1 u = + + + + . Chọn mệnh đề đúng? n ... n ) 2 2 2 2 1 2 3 n
A. Dãy số (u bị chặn. n )
B. Dãy số (u bị chặn trên, nhưng không bị chặn dưới. n )
C. Dãy số (u bị chặn dưới, nhưng không bị chặn trên. n )
D. Dãy số (u không bị chặn. n )
Câu 34. Gọi S =1+11+111+...+111...1 ( n số 1 ) thì S nhận giá trị nào sau đây? n   −   n A. 1 10 1 S  −  = 10    − n . B. 10 1 S =10 . 9     9     81  n n C. 10 −1 S =10  − n . D. 10 1 S − = .  81  81
Câu 35. Khảo sát vận tốc (dặm/h; 1 dặm =1,609km ) của 300 xe ô tô chạy trên con đường A thu được
mẫu số liệu ghép nhóm như sau: 4
Nhóm chứa tứ phân vị thứ nhất là A. [32,5 ;37,5) . B. [27,5 ;32,5). C. [37,5 ;42,5). D. [42,5 ;47,5) .
II. PHẦN TỰ LUẬN (3 điểm).
Câu 36 (1 điểm). Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liệu trên?
Câu 37 (1 điểm).
a) Tìm tập xác định của hàm số sau: sin = x y . 2 2 sin x − cos x
b) Giải phương trình sin (π cos x) =1.
Câu 38 (1 điểm). Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây, hàng
thứ hai có 2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
……………… HẾT ……………… 5
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN - LỚP: 11
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng. Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 B A A B B D C A C A
Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 A A A A A A A A A A
Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 A A D B B D A A A A
Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 A A A A A II. PHẦN TỰ LUẬN Câu Đáp án Biểu điểm 36
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liệu trên? 0,25
Tần số lớn nhất là 16 nên nhóm chứa mốt là nhóm [50,5;55,5) và j = 3
Ta có u = 50,5;u = 55,5 ⇒ h = u − u = 5 0,25 3 4 4 3
Tần số: n = 7;n =16;n = 4 2 3 4 . 0,25 n − n 0,25 j j 1 − n − n M = u + ⋅ h = u + ⋅ h o j ( 3 3 n − n + − − + − − n n n n n n j j 1 ) ( j j 1+) 2 ( 3 2) ( 3 4) 16 − 7 M = 50,5 + .5 = 52,6 0 (16 − 7) + (16 − 4) 37
a) Tìm tập xác định của hàm số sau: sin = x y . 2 2 sin x − cos x Điều kiện xác định của hàm số là 0,25 2 2 π π kπ
sin x − cos x ≠ 0 ⇔ −cos 2x ≠ 0 ⇔ 2x ≠ + kπ ⇔ x ≠ + ;k ∈ 2 4 2 . π kπ  0,25
Vậy tập xác định của hàm số là D =  \  + ;k ∈ 4 2   
b) Giải phương trình sin (π cos x) =1. 6 π
sin (π cos x) =1 ⇔ π cos x = + k2π,k ∈ 1
 ⇔ cos x = + 2k,k ∈ 0,25 2 2 Vì 1
− ≤ cos x ≤1 nên 1 3 1 1 0,25
− ≤ + 2k ≤1 ⇔ − ≤ k ≤ . 2 4 4 Do k ∈ π  ⇒ k = 0 suy ra 1
cos x = ⇔ x = ± + m2π ,m∈ . 2 3 38
Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai
có 2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
Gọi số hàng cây là n , hàng thứ n có n cây. 0,25
Ta có 1+ 2 + 3+...+ n = 2145 0,25 n(n + ) 1 0,25 ⇒ = 2145. 2 ⇒ n = 65 0,25 ====== TOANMATH.com 7
Document Outline

  • 1. GIUA KI 1 - TOAN 11 - KNTT
    • ĐỀ KIỂM TRA GIỮA HỌC KÌ I
    • MÔN: TOÁN - LỚP: 11 - KNTT
    • MÔN: TOÁN - LỚP: 11
  • 2. GIUA KI 1 - TOAN 11 - KNTT
  • 3. GIUA KI 1 - TOAN 11 - KNTT
    • ĐỀ KIỂM TRA GIỮA HỌC KÌ I
    • MÔN: TOÁN - LỚP: 11 - KNTT
    • MÔN: TOÁN - LỚP: 11
  • 4. GIUA KI 1 - TOAN 11 - KNTT
  • 5. GIUA KI 1 - TOAN 11 - KNTT
  • 6. GIUA KI 1 - TOAN 11 - KNTT
    • ĐỀ KIỂM TRA GIỮA HỌC KÌ I
    • MÔN: TOÁN - LỚP: 11 - KNTT
    • MÔN: TOÁN - LỚP: 11
  • 7. GIUA KI 1 - TOAN 11 - KNTT
    • MÔN: TOÁN - KHỐI LỚP 11 - KNTT
    • MÔN: TOÁN - LỚP: 11