TOP 102 bài toán bất đẳng thức và giá trị lớn nhất, giá trị nhỏ nhất chọn lọc

Tài liệu gồm 58 trang, được tổng hợp bởi thầy giáo Cù Minh Quảng, tuyển tập 102 bài toán bất đẳng thức và giá trị lớn nhất, giá trị nhỏ nhất chọn lọc, có đáp án và lời giải chi tiết, giúp học sinh ôn tập để chuẩn bị cho kỳ thi chọn học sinh giỏi Toán bậc THCS các cấp và ôn thi vào lớp 10 môn Toán.

89 45 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi vào 10 môn Toán

Môn: Môn Toán

Thông tin:

58 trang 7 tháng trước

Tác giả:

Profile Nguyễn Vân
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 95 GIÁO VIÊN CÙ MINH QUẢNG
BÀI TẬP VẬN DỤNG
Bài 1. Với
, ,
x y z
là các số thực dương sao cho
1
. .
6
x y z
.
Chứng minh:
3 3 3 3 3 3
1 1 1
1.
8 1 8 27 1 27 1x y y z z x
Lời giải
Có:
1
. . 6 . . 1
x y z x y z
Ta có:
3
3
2 .2 2
x y x y x y
3
3
3
3
1 1
2 1 2 2 3
2 2 3
2 1
x y xy x y z
xy x y z
x y
Chứng minh tương tự:
3 3
1 1
6 2 3
2 3 1
yz x y z
y z
3
3
1 1
3 2 3
3 1
xz x y z
z x
3 3 3 3
3 3
1 1 1 1 1 1 1
2 3 2 6 3
2 1 2 3 1 3 1
x y z xy yz zx
x y y z z x
3 3 3 3 3 3
1 1 1
1.
8 1 8 27 1 27 1x y y z z x
Bài 2. Cho
x
,
y
là các số thực dương thỏa mãn
3
x y
.
Tìm giá trị nhỏ nhất của biểu thức:
2 3
3 1
A
xy y
Lời giải
2 3 2 3
3 1 3
3 1
A
xy y xy
y
2 2
3
2 6 2 6 4 1 2
3 3 1 3 6 4 6 6 3
xy y
xy y
xy y xy y
3 1
1
2 . 1
6
y
A y x
2
2
1 1 1 2 4 1
2 . 3 1 2 . 4 2 4 4 2
6 6 6 3 3 6
y y y y y y y
4
3
A
với mọi
,
x y
.
Vậy
4
3
Min
A
khi
1; 2
x y
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 96 GIÁO VIÊN CÙ MINH QUẢNG
Bài 3. Cho các số dương
,
a b
thoả mãn
3 3 2 2
1
1
3
a b a b ab a b
.
Tìm giá trị nhỏ nhất biểu thức:
2 2
8 2
a b
M
a b
.
Lời giải
Ta có
3 3 2 2
1
1
3
a b a b ab a b
2 2 2 2
1
1 1
3
a b a b ab a b ab
Vì
2 2
1 0 a,b R
a b ab
1
1 3
3
a b a b
Khi đó ta có
2 2
8 2 8 2 4 1 4 1
a b
M a b a b
a b a b a b a b
4 1 4 1
M a b
a b a b
Áp dụng bất đẳng thức Co-si cho các cặp số dương ta có:
2
4 4
2 . 2 4 4
1 1
2 . 2 1 2
2 1
4 1 9
3
3
a a
a a
b b
b b
a b a b
GTNN của
M
là
4 2 3 9
.
Dấu “
” xảy ra khi
4
2
1
1
2
a
a
a
b
b
b
a b
Vậy
M
đạt giá trị nhỏ nhất là
9
khi
2; 1
a b
.
Bài 4. Cho
x
,
y
là các số thực dương thỏa mãn
2 2
1
x y
.
Tìm giá trị nhỏ nhất của biểu thức:
1 1
P x y
x y
.
Lời giải
x
,
0
y
:
2 2
2 2 2 2 2 2 2 2
0 2 0 2 2 2
x y x xy y x y x xy y x y x y
2 2
2
x y x y
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 97 GIÁO VIÊN CÙ MINH QUẢNG
2 2
2 2 2 2
4
0 2 0 2 4 4
x y
x y x xy y x xy y xy x y xy
xy x y
1 1 4
x y x y
.
1 1 1 1 1 1 1 1 1 1 4
2 . 2 . .
2 2 2 2 2 2
P x y x y x y
x y x y x y x y x y
=
2
2 2
x y
2 2
2
2 2
2
P
x y
2
2 2 3 2
2.1
.
Dấu
" "
xảy ra khi và chỉ khi
2
2
x y
.
Vậy giá trị nhỏ nhất của
P
là
3 2
khi
2
2
x y
.
Bài 5. Chứng minh rằng:
Với mọi
1
x
,ta luôn có
2
2
3
3
1
2
1
3 xx
x
x
Lời giải
Ta có
2
2
3
3
1
2
1
3 xx
x
x
3
2
2
3
1
3
1
2 0
x
x
x
x
2
2
1 2
3 2
0
3
2x x x
x x x
2
2
1 2
2
0
1 4
2 2 4 2x x x x
x x x x
1 2 1 2 2
2 1 2 1 2 2 1
0
x x x x x
x x x x x
1 1
0
2
2 2 1x x x
x x x
2
1
1 2
2 1
0
x
x x
x x x
Vì
1
x
nên
2
0
0
1
1
2
2 1
0
x
x
x
x
x
x
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 98 GIÁO VIÊN CÙ MINH QUẢNG
Bài 6. Cho
, ,
a b c
là các số thực dương thỏa mãn: 3
ab bc ac abc
. Tìm giá trị nhỏ nhất của
biểu thức
2 2 2
2 2 2 2 2 2
a b c
K
c c a a a b b b c
.
Lời giải
1 1 1
3 3
ab bc ac abc
a b c
(1)
Ta có
2 2 2 2
2 2 2 2 2 2 2 2
1 1 1
2
Cauchy
a a c c ac
c c a
c c a c c a c c a a c a
.
Tương tự,
2
2 2
1 1
2
b
a b
a a b
,
2
2 2
1 1
2
c
b c
b b c
.
Khi đó
1
1 1 1 1 3
2 2
K
a b c
.
Vậy
, , 0
3
1
2
a b c
Min K a b c
.
Bài 7. điểm) Cho
a
,
b
là các số khác
0
thỏa mãn điều kiện:
2
a b ab a b ab
. Tìm giá
trị lớn nhất của biểu thức
3 3
1 1
2
P
a b
.
Lời giải
Theo giả thiết:
2
a b ab a b ab
2 2 2 2
a b ab a ab b
Do
0
a
;
0
b
nên chia cả hai vế cho
2 2
a b
ta được:
2 2
1 1 1 1 1
a b a ab b
.
Đặt
1
x
a
;
1
y
b
ta được :
2 2
x y x xy y
(1)
2
3
x y x y xy
2
3 3
x y
x y
xy
Mà
2
4
x y xy
hay
2
4
x y
xy
Suy ra
2 2
3 3 4
x y x y
x y
2
4 0
x y x y
0 4
x y
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 99 GIÁO VIÊN CÙ MINH QUẢNG
Ta có:
3 3
1 1
2
P
a b
3 3
2
x y
2 2
2
x y x xy y
2
2
x y
(do 1)
Mà
0 4
x y
nên
2
2 2 18
x y
.
Vậy giá trị lớn nhất của
P
là
18
khi
2
x y
và
1
2
a b
.
Bài 8. Cho các số thực thỏa mãn
2 2
– 4
x y xy
.
Tìm GTLN và GTNN của biểu thức
2 2
P x y
.
Lời giải
+) Tìm GTLN của
P
:
Ta có
2 2
– 4
x y xy
2 2
2 2 – 2 8
x y xy
2
2 2
8
x y x y
2
8
P x y
2
8
P x y
Ta có
2
0
x y
với mọi
,
x y
Suy ra
8
P
Max 8
P
2 2
0
2
4
x y
x y
x y xy
.
Vậy
Max 8
P
khi
2
x y
.
+) Tìm GTNN của
P
:
Ta có
2 2
– 4
x y xy
2 2
2 2 – 2 8
x y xy
2
2 2
3 8
x y x y
2
3 8
P x y
Ta có
2
0
x y
với mọi
,
x y
Suy ra
8
3 8
3
P P
8
Min
3
P
2 2 2
2
0
3
4 3 4
2
3
y x
x y y x
x
x y xy x
x
2
3
2
3
2
3
2
3
x
y
x
y
Vậy
8
Min
3
P
khi
2 2
;
3 3
x y
hoặc
2 2
;
3 3
x y
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 100 GIÁO VIÊN CÙ MINH QUẢNG
Bài 9. Cho ba số dương
a
,
b
,
c
thỏa mãn
1
ab bc ca
Tìm giá trị nhỏ nhất của biểu thức:
2 2 2
a b c
A
a b b c c a
Lời giải
Áp dụng bất đẳng thức:
2
2 2 2
a b c
a b c
x y z x y z
, ta được
2
2 2 2
2
2 4
a b c a b c
a b c
A
a b b c c a a b c
2
1
4 4 2
ab bc ca
a b b c c a
Dấu
" "
xảy ra khi
1
a b c
.
Vậy giá trị nhỏ nhất của biểu thức:
2 2 2
a b c
A
a b b c c a
là
1
2
khi
1
a b c
.
Bài 10. Cho
2 2 2
3
7
x y z
. Chứng minh:
8 14 8 14 8 14 3 3 7
x y z
.
Lời giải
ĐKXĐ:
4
, ,
7
x y z
.
Áp dụng bất đẳng thức Cô –si cho hai số không âm
8 2 7
và
8 14
x
, ta có:
8 2 7 8 14
8 2 7 8 14
2
x
x
2
7 1 8 14 8 7 7
x x
8 7 7
8 14
7 1
x
x
. (1)
Chứng minh tương tự, ta có:
8 7 7
8 14
7 1
y
y
. (2)
8 7 7
8 14
7 1
z
z
(3)
Cộng theo vế các bất đẳng thức (1), (2), (3) ta được:
24 3 7 7
8 14 8 14 8 14
7 1
x y z
x y z
.
Ta có:
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 101 GIÁO VIÊN CÙ MINH QUẢNG
2
2 2 2
2 2 2
x y z x y z xy yz zx
.
Mà:
2 2 2
2 2 2 2
xy yx zx x y z
.
Suy ra:
2
2 2 2
3 9
3 3.
7 7
x y z x y z
.
Do đó:
3
7
x y z
.
Suy ra:
3
24 3 7 7.
3 8 2 7
24 6 7
7
8 14 8 14 8 14 3 3 7
7 1 7 1 7 1
x y z
.
Dấu “=” xảy ra khi và chỉ khi
1
7
x y z
.
Bài 11. Tìm cặp số (x ; y) với y là số nhỏ nhất thỏa mãn điều kiện
x
2
+ 5y
2
+ 2y – 4xy – 3 = 0
Lời giải
Phương trình có nghiệm ẩn
x
khi và chỉ khi
2 2
4 5 2 3 0
y y y
2
2 3 0
y y
2
1 4 2 1 2 3 1
y y y
Giá trị nhỏ nhất của
y
là
3
khi đó phương trình
2
12 36 0 6
x x x
Bài 12. Cho
3 5.
x
Tìm giá trị nhỏ nhất của biểu thức:
2 2 1
3 5
( 3)(5 )
A
x x
x x
Lời giải
Ta có
3 5
x
nên
3 0;5 0
x x
Áp dụng BĐT Cauchy:
2 2 4 4
2.
3 5 3 5
3 5
x x x x
x x
3
3 5
A
x x
Áp dụng BĐT Cauchy:
3 5
3 5 1
2
x x
x x
Suy ra
1
1
3 5x x
Suy ra
3.
A
Vậy GTNN
3
A
khi và chỉ khi
3 5 4.
x x x
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 102 GIÁO VIÊN CÙ MINH QUẢNG
Bài 13. Cho
,
x y
là các số thực dương thỏa mãn điều kiện
6
x y
. Tìm giá trị nhỏ nhất của
biểu thức:
6 24
P x y
x y
.
Lời giải
Ta có:
6 24 4 16 2 8
P x y x y
x y x y x y
2
1 2
9
2 4 2 16 2 4 8 2. 15
6x y
Vậy giá trị nhỏ nhất của
15
P
. Dấu bằng xảy ra khi
2; 4
x y
Bài 14. Cho
, , 0
a b c
. Chứng minh rằng
2 2 2
2 2 2 2 2 2
a b c
a ab b b bc c c ca a
b c a
.
Lời giải
Đặt
2 2 2
2 2 2 2 2 2
a b c
a ab b b bc c c ca a
b c a
(*).
Vì
, , 0
a b c
nên áp dụng bất đẳng thức Cô-si cho các số không âm
2 2 2
, , , , ,
a b c
a b c
b c a
ta được
2 2
2 . 2
a a
b b a
b b
,
2 2
2 . 2
b b
c c b
c c
,
2 2
2 . 2
c c
a a c
a a
Suy ra
2 2 2 2 2 2 2 2 2
2
a b c a b c a b c
a b c a b c
b c a b c a b c a
(1)
Ta có
2 2 2 2 2 2 2 2 2
a b c a ab b b bc c c ca a
a b c a b c
b c a b c a
. (2)
Áp dụng bất đẳng thức Cô-si cho các số không âm
2 2 2 2 2 2
, , , , ,
a ab b b bc c c ca a
b c a
b c a
ta được
2 2 2 2 2 2
2 2 2 2 2 2
2 , 2 , 2
a ab b b bc c c ca a
b a ab b c b bc c a c ca a
b c a
(3)
Từ (1), (2) và (3) suy ra
2 2 2
2 2 2 2 2 2
2 2 2 2
a b c
a ab b b bc c c ca a
b c a
hay
2 2 2
2 2 2 2 2 2
a b c
a ab b b bc c c ca a
b c a
Do đó (*) được chứng minh. Dấu bằng xảy ra khi dấu bằng tại (1) và (4) xảy ra. Tức là
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 103 GIÁO VIÊN CÙ MINH QUẢNG
2 2 2
2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
, ,
, ,
, ,
, ,
a b c
b c a
a b b c c a
b c a
a ab b b bc c c ca a a ab b b b bc c c c ca a a
b c a
b c a
2 2 2 2 2 2
, ,
( ) 0, ( ) 0, ( ) 0
a b b c c a
a a b b b c c c a
.
Vì
, , 0
a b c
nên suy ra dấu bằng xảy ra khi
.
a b c
Bài 15. Cho a, b, c là độ dài 3 cạnh của một tam giác. Tìm giá trị nhỏ nhất của biểu thức:
2 2 2 2 2 2 2 2 2
2 2 2 2 2 2
a b c
P
b c a a c b a b c
Vì
, ,
a b c
là 3 cạnh của tam giác nên
2 2 2 2 2 2 2 2 2
2 2 , 2 2 , 2 2
a c b a b c b c a
đểu là các số dương.
Áp dụng công thức Cauchy ta có:
2 2 2 2
2 2 2 2 2 2 2
3 2 2
3 2 2
2
a b c a
a b c a a b c
Ta có:
2 2
2 2 2
2 2 2
2 2 2 2
3 3
2 2
3 2 2
a a a
a b c
b c a
a b c a
2 2 2
2 2 2
2 2 2 2 2 2 2 2 2
3
3
2 2 2 2 2 2
a b c
a b c
P
a b c
b c a a c b a b c
Vậy GTNN
3
P
khi và chỉ khi
a b c
hay là tam giác đều.
2) Ta coi như hình vẽ thành bài toán đường tròn tâm
O
nội tiếp tam giác đều
ABC
vậy tâm
O
của đường tròn sẽ trùng với trọng tâm tam giác
ABC
vậy nên đường cao của tam giác
đều là
3
R
(với
R
là bán kinh đường tròn
O
)
Suy ra
2.3
2 3 .
3
R
BC R
Thể tích hình nón là:
2
2 3
1 1
. 3 .3 3
3 3
V R h R R R
Thể tích hình cầu là:
3
4
3
V R
Vậy tính thể tích theo R phần hình nón nằm bên ngoài quả cầu kem là
3 3 3
4 5
3 .
3 3
V R R R
Bài 16. Cho ba số dương
a
,
b
,
c
thoả mãn
1
ab bc ca
.
Tìm giá trị nhỏ nhất của biểu thức
2 2 2
a b c
A
a b b c c a
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 104 GIÁO VIÊN CÙ MINH QUẢNG
Lời giải
Áp dụng bất đăng thức Bu-nhi-a-cốp-xki ta có
2 2 2
2
2 ( )
a b c
a b c A a b b c c a a b c
a b b c c a
Suy ra
2
a b c
A
Áp dụng bất đẳng thức Cô-si ta có
2
a b ab
2
b c bc
2
c a ca
Suy ra
2 2.1 2
a b b c c a ab bc ca
Suy ra
2 2
a b c
, hay
1
2 2
a b c
Vậy nên
1
2 2
a b c
A
Khi
1
3
a b c
thì
1
2
A
Vậy giá trị nhỏ nhất của
A
là
1
2
.
Bài 17. Cho
, 0
a b
thỏa mãn
2 4 0.
a ab
Tính giá trị nhỏ nhất của
2 2
2
.
a b
T
ab
Lời giải
Ta có
2 4 0 2 4
a ab a b
.
Kết hơp với
0
a
ta suy ra
2
b
4
2
a
b
.
Ta có
2 7 2 7
1
8 8 8
a b a a b a
T
b a b b a b
2
7 4 7 1 9
. 1 . 1
8 2 2 2
2
2
T
b b
b b
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 105 GIÁO VIÊN CÙ MINH QUẢNG
Dấu bằng xảy ra khi và chỉ khi
4
4
2
1
2
a
a
b
b
b b
.
Vậy giá trị nhỏ nhất của
T
là
9
2
, đạt được khi
4
a
và
1
b
.
Bài 18. ) Cho các số thực
; ;
x y z
thỏa mãn
2 3;4 6;4 6
x y z
và
12
x y z
.
Tìm giá trị lớn nhất của biểu thức
P xyz
.
Lời giải
Ta có
2
1
12 12
2 4
y z
P x yz x x x x
.
3 3
1 1 24 1 3 24 243
3 12 12
12 12 3 12 3 4
x
x x x
.
Vậy
243
4
MaxP
khi
9
3;
2
x y z
.
Bài 19. Cho
x
,
y
là các số thực thỏa mãn
2 2
3
x xy y
.
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức
2 2
P x y
.
Lời giải
Ta có
2 2 2 2
3 2 6
x xy y x xy y
2 2
2 2
6 6 6
x y x y P x y
Dấu
“ ”
xảy ra
2 2 2
3
3 3
3
x y x y x y
x xy y x
x y
GTLN của
P
là
6
khi và chỉ khi
3
3
x y
x y
+) Có
2
2 2 2 2
6 2 3
x xy y x y x y
2 2 2
1
3 6 3 6 2 2
3
P x y P x y P x y
Dấu
“ ”
xảy ra
2 2 2
1
1
3 3 3
1
1
x
y
x y x y
x xy y x
x
y
Vậy GTNN của
P
là
2
khi và chỉ khi
1
1
x
y
hoặc
1
1
x
y
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 106 GIÁO VIÊN CÙ MINH QUẢNG
Bài 20. Cho biểu thức
2 2
M x y
với
,
x y
là các số thực thỏa mãn
0 4
y x
và
7
x y
.
Tìm giá trị lớn nhất của biểu thức
M
Lời giải
Ta có
2 2 2 2
M x y x xy xy y x x y y x y
Do
0 4
y x
và
7
x y
nên
4 7
M x y y
4 3
3 3.7 4
25
M x y
M x y x
M
Dấu “=” xảy ra
4; 3
x y
Vậy
25
Max M
khi và chỉ khi
4; 3
x y
Bài 21. Cho
,
x y
là các số dương thỏa mãn điều kiện
5
x y
. Chứng minh
rằng:
2 2
25 12,5
4
x y xy
.
Lời giải
Dễ dàng chứng minh được với
0, 0
a b
ta có
1 1 4
a b a b
(1). Dấu “=” xảy ra khi và chỉ
khi
a b
.
Áp dụng bất đẳng thức (1) ta có:
2
2 2
1 1 4 4
2 25
x y xy
x y
2 2
25 12,5
4
x y xy
.
Dấu “=” xảy ra khi và chỉ khi
2,5
x y
( thỏa mãn).
Bài 22. Cho
x
,
y
,
z
là các số thực thỏa mãn
7
x
,
12
x y
và
15
x y z
. Tìm giá trị
nhỏ nhất của biểu thức
2 2 2
A x y z
.
Lời giải
Ta có:
7
x
,
12
x y
và
15
x y z
2
7 0,
x x
2
14 49 0
x x
2
14 49
x x
2
5 0,
y y
2
10 25 0
y x
2
10 25
y y
2
3 0,
z z
2
6 9 0
z z
2
6 9
z x
2 2 2
A x y z
14 10 6 83
x y z
6 6 6 4 4 4 83
A x y z x y x
6 4 4 83
A x y z x y x
6.15 4.12 4.7 83
A
(vì
7
x
,
12
x y
và
15
x y z
)
83
A
.
Dấu “ = ” xảy ra khi
7
x
,
5
y
,
3
z
(thỏa mãn)
Vậy
A
đạt giá trị nhỏ nhất bằng
83
khi
7
x
,
5
y
,
3
z
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 107 GIÁO VIÊN CÙ MINH QUẢNG
Bài 23. Cho
, ,
a b c
là các số dương thay đổi thỏa mãn
1 1 1
2020
a b b c c a
. Tìm giá trị lớn
nhất của biểu thức
1 1 1
2 3 3 3 2 3 3 3 2
P
a b c a b c a b c
.
Lời giải
Áp dụng bất đẳng thức Cauchy cho các số dương
, , ,
a b c d
ta có :
4
4
a b c d abcd
4
1 1 1 1 1
4
a b c d abcd
1 1 1 1
16
a b c d
a b c d
1 1 1 1 16
a b c d a b c d
Ta có :
1 1
2 3 3 ( ) ( ) ( ) ( )
a b c a b a c b c b c
Áp dụng bất đằng thức phía trên ta có :
1 1 1 1 1 1
.
( ) ( ) ( ) ( ) 16
a b a c b c b c a b a c b c b c
1 1 1 1 2
.
2 3 3 16
a b c a b a c b c
Chứng minh tương tự ta có:
1 1 1 1 2
.
3 2 3 16
a b c a b b c a c
1 1 1 1 2
.
3 3 2 16
a b c a c b c a b
1 1 1 1
.4
16
P
a b a c b c
1
.2020 505
4
P
Dấu ‘’= “ xảy ra khi
3
4040
a b c
.
Bài 24. Cho biểu thức
2 2
M x y
với
,
x y
là các số thực thỏa mãn
0 4
y x
và
7
x y
.
Tìm giá trị lớn nhất của biểu thức
M
Lời giải
Ta có
2 2 2 2
M x y x xy xy y x x y y x y
Do
0 4
y x
và
7
x y
nên
4 7
M x y y
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 108 GIÁO VIÊN CÙ MINH QUẢNG
4 3
3 3.7 4
25
M x y
M x y x
M
Dấu “=” xảy ra
4; 3
x y
Vậy
25
Max M
khi và chỉ khi
4; 3
x y
Bài 25. Tìm giá trị nhỏ nhất của biểu thức:
2 2 1 5 4 1 16
A x y x y
.
Lời giải
2 2 1 5 4 1 16
A x y x y
2 2 4 2 2 1 10 4 1 32
A x y x y
2 2 1 2 2 1 1 4 1 2 4 1.5 25 8
A x x y y
2 2
2 2 1 1 4 1 5 8 8
A x y
(với mọi
1 3
;
2 4
x y
).
4
A
.
Min 4
A
2 1 1 0
4 1 5 0
x
y
2 1 1 0
4 1 5 0
x
y
2 1 1
4 1 25
x
y
(với mọi
1 3
;
2 4
x y
).
1
13
2
x
y
(nhận).
Vậy
Min 4
A
1
13
2
x
y
.
Bài 26. Cho
a
,
b
,
0
c
thỏa mãn
2 3 20
a b c
. Tìm GTNN của biểu thức
A
. Biết
3 9 4
2
A a b c
a b c
.
Lời giải
Ta có:
3 9 4
2
A a b c
a b c
3 3 9 4 1
2 3
4 2 2 4 4
a b c
a b c
a b c
Áp dụng BĐT Cô – si cho hai số không âm, ta được
3 3 3 3
2 . 3
4 4
a a
a a
9 9
2 . 3
2 2 2 2
b b
b b
4 4
2 . 2
4 4
c c
c c
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 109 GIÁO VIÊN CÙ MINH QUẢNG
Do đó
1
3 3 2 2 3
4
A a b c
13
.
Dấu “
” xảy ra khi
2
a
;
3
b
;
4
c
.
Vậy GTNN của biểu thức
A
bằng 13 khi
2
a
;
3
b
;
4
c
.
Bài 27. Cho hai số thực
x
,
y
thoả mãn hệ điều kiện:
3 2
2 2 2
2 4 3 0 1
2 0 2
x y y
x x y y
..
Tính giá trị của biểu thức:
2020 2020
P x y
.
Lời giải
Từ
1
ta có:
2
3
2 1 1 1 1
x y x
.
3
Từ
2
ta có:
2
2
2
1
y
x
y
2
2
2 2
2
1
1
1 1
y
y
x
y y
1 1
x
.
4
Từ
3
và
4
, suy ra
1 1
x y
.
Vậy
2
P
.
Bài 28. Cho đường thẳng
d
:
2
1 4
y m x
. Tìm
m
để khoảng cách từ gốc tọa độ đến
đường thẳng
d
lớn nhất.
Lời giải
x
y
(d)
B
A
O 1
H
Vì
2
1 0
m
với mọi
m
nên đường thẳng
d
luôn xác định.
Gọi
A
là giao điểm của đường thẳng
d
với trục
Oy
,
B
là giao điểm của đường thẳng
d
với
trục
Ox
. Khi đó tọa độ của
A
và
B
là
0;4
A
;
2
4
;0
1
B
m
.
Vẽ
OH AB
, khi đó
OH
là khoảng cách từ gốc tọa độ đến đường thẳng
d
.
Ta có
4
OA
;
2
4
1
OB
m
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 110 GIÁO VIÊN CÙ MINH QUẢNG
Xét tam giác
OAB
vuông tại
O
, vì
OH AB
nên theo hệ thức lượng trong tam giác vuông ta
có:
2 2 2
1 1 1
OH OA OB
2 2
2 2
1 1 1
1
16 16 16
m m
2
2
4
1 1
OH
m
.
Ta có
2
0
m
với mọi
m
2
2
1 1
m
với mọi
m
2 2
2 2
1 1 2 1 1 2
m m
với mọi
m
2
2
4 4
2 2
2
1 1
OH
m
.
Dấu đẳng thức xảy ra khi và chỉ khi
0
m
.
Vậy với
0
m
thì khoảng cách từ gốc tọa độ đến đường thẳng
d
đạt giá trị lớn nhất là
2 2
.
Bài 29. Một doanh nghiệp xuất khẩu gạo ước tính rằng , trong tháng 2/2020 , nếu doanh
nghiệp xuất khẩu gạo với giá là
500
USD/tấn thì họ sẽ xuất khẩu được khoảng
860
tấn gạo.
Tuy nhiên nếu hạ giá gạo và cứ mỗi lần giảm giá
25
USD/tấn thì sẽ xuất khẩu thêm được
50
tấn gạo. Hỏi doanh nghiệp cần bán gạo với giá bao nhiêu USD mỗi tấn để doanh thu xuất
khẩu gạo trong tháng 2/2020 là lớn nhất?
Lời giải
Doanh thu dự kiến xuất khẩu trong tháng 2 là
860 500 430 000
(USD)
Gọi số lần giảm giá là
x
(lần), điều kiện
*
,0 20
x x
Giá gạo sau khi giảm giá là
500 25
x
(USD/tấn)
Số gạo xuất khẩu được sau khi giảm giá là
860 50
x
(tấn)
Doanh thu sau khi giảm giá gạo là
500 25 860 50
P x x
(USD)
Để doanh thu xuất khẩu gạo trong tháng 2/2020 là lớn nhất thì
P
phải lớn
hơn
430000
2
430000 0 500 25 860 50 430000 0 1250 3500 0
P x x x x
50 70 25 0 0 2,8
x x x .
Vì
* 1;2
x x
.
Với
1 432 250
x P
.
Với
2 432000
x P
.
Vậy doanh nghiệp bán gạo với giá
475
USD/tấn để doanh thu trong tháng 2/2020
lớn nhất .
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 111 GIÁO VIÊN CÙ MINH QUẢNG
Bài 30. Cho
x
,
y
là hai số không âm thỏa mãn
2 2
4
x y
. Tìm giá trị lớn nhất của biểu thức:
2 5 2 5
A x y x y y x y x
.
Lời giải
Với mọi
a
,
b
ta có
2 2
2 2 2 2
0 2 2
a b a b a b a b a b
Áp dụng kết quả trên ta được
2 2 2 2
2 5 2 5 2 2 5 2 5
A x y x y y x y x x xy y y xy x
2
2 2
2 2 20
xy x y xy
2
2 8 20
xy xy
Mặt khác theo bất đẳng thức Cô-si với hai số không âm
x
,
y
ta có
2 2
2
x y
xy
nên
ta có
4
2
2
xy
.
Vậy nên
2
2
2 8 20 2 8.2 20.2 8 3
A xy xy .
Khi
2
x y
thì
8 3
A , do đó giá trị lớn nhất của
A
là
8 3
.
Bài 31. Giải phương trình
2
2 5 7 2 3 18 29
x x x x
Lời giải
Đặt
2 5, 7 2
a x b x
Ta có:
, 0
2
a b
a b
Phương trình có dạng:
35
3. 29 4 3 11
4
ab
a b a b ab
Bình phương hai vế phương trình ta có:
2 2 2 2
16 2 9 66 121 16 2 2 9 66 121
a b ab a b ab ab a b ab
2 2
9 66 32 89 0
a b ab ab
3
1 9 9 57 89 0
ab ab ab ab
3
1
9 9 57 89 0
ab
ab ab ab
+) Với
1 1
ab ab
thế 2
b a
vào ta có
2
2 1 2 1 0
a a a a
1 3
a x
+) Với
3
9 9 57 89 0
ab ab ab
Do
1
2
a b
ab
nên
3
9 9 57 89 9 9 0 89 71
ab ab ab
nên phương trình vô
nghiệm.
Vậy phương trình có nghiệm duy nhất
3
x
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 112 GIÁO VIÊN CÙ MINH QUẢNG
Bài 32. Cho ba số dương
, ,
x y z
thỏa mãn điều kiện
1
x y z
.
Chứng minh:
3
2
xy yz xz
xy z yz x xz y
.
Lời giải
Sử dụng giả thiết
1
x y z
và bất đẳng thức AM-GM ta có:
xy yz zx
LHS
xy z x y z yz x x y z zx y x y z
xy yz zx
z x y z x y z x y z x y
1 1 1
2 2 2
x y y z z x
z x y z x y z x y z x y
1 3
2 2
x z y z y x
z x z x y z y z x y x y
Dấu
'' ''
xảy ra khi và chỉ khi
1
3
x y z
.
Bài 33. Cho các số thực
, ,
a b c
thỏa mãn
3, 7, 7
a b c
và
2 2 2
122
a b c
. Tìm giá trị nhỏ nhất
của biểu thức
8 15 17
P a b c
.
Lời giải
Có
2 2 2 2 2
122 122 7 7 24 5
a b c a
2
3 5 3 5 0 8 15 1
a a a a a
2 2 2 2 2
122 122 3 7 64 8
b a c b
2
7 8 7 8 0 15 56 2
b b b b b
2 2 2 2 2
122 122 3 7 64 8 10
c a b c
2
7 10 7 10 0 17 70 3
c c c c c
Từ
1
,
2
,
3
suy ra
2 2 2
8 15 17 15 56 70 122 141 263
a b c a b c
Xảy ra dấu “=” khi
2 2 2
122 3
8 15 17 263 8
3 5;7 8;7 8 7
a b c a
a b c b
a b c c
GTNN
263
P
3
a
,
8
b
,
7
c
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 113 GIÁO VIÊN CÙ MINH QUẢNG
Bài 34. Một doanh nghiệp xuất khẩu gạo ước tính rằng , trong tháng 2/2020 , nếu doanh
nghiệp xuất khẩu gạo với giá là
500
USD/tấn thì họ sẽ xuất khẩu được khoảng
860
tấn gạo.
Tuy nhiên nếu hạ giá gạo và cứ mỗi lần giảm giá
25
USD/tấn thì sẽ xuất khẩu thêm được
50
tấn gạo. Hỏi doanh nghiệp cần bán gạo với giá bao nhiêu USD mỗi tấn để doanh thu xuất
khẩu gạo trong tháng 2/2020 là lớn nhất?
Lời giải
Doanh thu dự kiến xuất khẩu trong tháng 2 là
860 500 430 000
(USD)
Gọi số lần giảm giá là
x
(lần), điều kiện
*
,0 20
x x
Giá gạo sau khi giảm giá là
500 25
x
(USD/tấn)
Số gạo xuất khẩu được sau khi giảm giá là
860 50
x
(tấn)
Doanh thu sau khi giảm giá gạo là
500 25 860 50
P x x
(USD)
Để doanh thu xuất khẩu gạo trong tháng 2/2020 là lớn nhất thì
P
phải lớn
hơn
430000
2
430000 0 500 25 860 50 430000 0 1250 3500 0
P x x x x
50 70 25 0 0 2,8
x x x
.
Vì
* 1;2
x x
.
Với
1 432 250
x P
.
Với
2 432000
x P
.
Vậy doanh nghiệp bán gạo với giá
475
USD/tấn để doanh thu trong tháng 2/2020
lớn nhất .
Bài 35. Cho
,
x y
là các số thực dương thỏa mãn
3
x y
.
Tìm giá trị nhỏ nhất của biểu thức
2 3
1
A
xy y
.
Lời giải
2 3 2 6
3 3 3 3 3 1
3 1
A
y y y y y
y
2
2
2 6
2 6 4 36
3 3 3 1 6 3 6 4 18 6 6 24
y y y y y y y y y
2
2
2
2 6
64 64 4
18 6 6 24 48 3
48 6 2
y y y
y
⇒ GTNN của
4
3
A
khi
1
x
,
2
y
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 114 GIÁO VIÊN CÙ MINH QUẢNG
Bài 36 Cho ba số
a
,
b
,
c
dương.
Chứng minh rằng:
2 2 2
1 1 1
2
a b c
a bc b ac c ab abc
Lời giải
+ Vì
, , 0
a b c
nên theo BĐT Cô si ta có:
2
2
2
a b ab
b c bc a b c ab bc ca
c a ac
+ Vì
, , 0
a b c
nên ta có:
2
2
2
2
1 1
2
2
a bc a bc
a bc
a bc
abc bc
a bc
Chứng minh tương tự ta có:
2
2
2
2
abc ac
b ac
abc ab
c ab
2 2 2
1
2 2 2 2 2
abc abc abc bc ac ab a b c
bc ac ab
a bc b ac c ab
2 2 2
1 1 1
2
a b c
a bc b ac c ab abc
Bài 37. Cho a,b,c là hai số thực không âm thỏa mãn
1.
a b c
Chứng minh rằng:
6.
a b b c c a
Lời giải
Vì
2
, 0 : 0 2
x y x y x y x y
và
1
a b c
nên ta có:
2
2 2 2 2
2 6 6
a b b c c a a b c a b b c b c c a c a a b
a b c a b b c b c c a c a a b a b c
Dấu bằng xảy ra khi và chỉ khi
1
3
a b c
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 115 GIÁO VIÊN CÙ MINH QUẢNG
Bài 38.
Tìm giá trị nhỏ nhất của biểu thức
2 2
1
2 2 3 2 2 2020.
P x xy y x x
x
Lời giải:
ĐK:
2.
x
Ta có:
2 2 2
1
2 4 4 2 2 2016
P x xy y x x x x
x
2 2
1
( ) ( 2) 2 2 2016.
P x y x x x
x
Theo BĐT Cô-si và
2
x
thì
1 1 3 1 3 5
2 . .2 .
4 4 4 4 2
x x
x x
x x x
Vậy
5 4037
2016 .
2 2
P
Dấu “=” khi
2
x y
. Kết luận:
4037
min .
2
P
Bài 39.
Với
a
,
b
,
c
là các số dương thỏa mãn điều kiện
6
a b c ab bc ca abc
. Chứng
minh
2 2 2
1 1 1
3
a b c
.
Lời giải
Ta có
6
a b c ab bc ca abc
6
a b c ab bc ca
abc
1 1 1 1 1 1
6
a b c ab bc ca
.
Áp dụng bất đẳng thức Cô – si ta được :
2 2 2
1 1 1 1 1 1
1 1 1 2
a b c a b c
1
2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1 1 1 1 1
2 2
a b c a b b c c a ab bc ca
2
Cộng vế với vế
1
và
2
suy ra
2 2 2
1 1 1
3
a b c
.
Dấu “=” xảy ra khi
1
a b c
.
Bài 40. Cho ba số thực dương
, ,
a b c
thỏa mãn điều kiện
24
a b b c c a
. Tìm giá trị
nhỏ nhất của biểu thức
S a b c
Lời giải
Áp dụng bất đẳng thức Cô-si ta có:
4
4 4 .
4
a ab
a ab a b a b
4
4 4 .
4
b bc
b bc b c b c
4
4 4 .
4
c ca
c ca c a c a
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 116 GIÁO VIÊN CÙ MINH QUẢNG
Do đó:
4 4 4
24
4 4 4
a ab b bc c ca
a b b c c a
4
ab bc ca
a b c
1
Mà
2 2 2 2
1 1 1
3 0
2 2 2
a b c ab bc ca a b b c c a
, ,
a b c
2
3
a b c ab bc ca
2
3
a b c
ab bc ca
2
Từ
1
và
2
suy ra :
2
24
12
a b c
a b c
2
12 288 0
a b c a b c
12 24 0
a b c a b c
Mà
24 0
a b c
với
, , 0
a b c
12 0
a b c
12
a b c
Vậy giá trị nhỏ nhất của biểu thức
S a b c
là 12 khi
4
a b c
Bài 41. Cho các số dương
a
,
b
,
c
thỏa mãn điều kiện
2019
a b c
. Tìm giá trị nhỏ nhất
của biểu thức
2 2 2 2 2 2
2 2 2 2 2 2
P a ab b b bc c c ca a
.
Lời giải
Ta có
2
2 2
2 2 2 2
2 2
3
2 3 3
2 2
2 2 2 2
a b
a b
a ab b a b
a ab b
Mà
2
2 2
2
a b
a b
2 2
2 2
3
3
3
2 2 2 4
a b
a b a b
.
Suy ra
2 2 2
2 2
3 5
2 2
2 4 4
a b a b a b
a ab b
Suy ra
2 2
5
2 2
2
a ab b a b
.
Chứng minh tương tự ta có
2 2
5
2 2
2
b bc c b c
;
2 2
5
2 2
2
c ca a c a
.
Cộng vế theo vế ta có
5
2019 5
2
P a b b c a
.
Dấu
" "
xảy ra khi
2019
a b c
a b c
673
a b c
.
Vậy giá trị nhỏ nhất của
P
bằng
2019 5
, đạt được khi
673
a b c
.
Bài 42. a) Cho
, ,
x y z
là ba số dương. Chứng minh
1 1 1
9
x y z
x y z
.
b) Cho
, ,
a b c
là ba số dương thỏa mãn
6.
a b c
Tìm giá trị lớn nhất của biểu thức
3 2 3 2 3 2
ab bc ca
A
a b c b c a c a b
Lời giải
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 117 GIÁO VIÊN CÙ MINH QUẢNG
a) Ta có:
1 1 1
x x x y y y x y z
VT x y z
x y z x y z x y z z z z
3 3 2 2 2 9
x y x z y z
y x z x z x
, dấu bằng xảy ra khi
x y z
.
(đpcm)
b) Áp dụng bất đẳng thức ở phần a) ta có:
9 9
;
3 2 2 2
ab ab ab ab a
a b c a c b c b c a c b
Tương tự
9
;
3 2 2
bc bc bc b
b c a a c a b
9
3 2 2
ca ca ca c
c a b b a b c
Cộng theo các vế của ba bất đẳng thức trên ta được
9
2 2 2
ab ab a bc bc b ca ca c
A
c a c b a c a b b a b c
9
2
ab bc ab ca bc ca a b c
A
c a a c c b b c a b b a
3( )
9
2
a b c
A
1
A
dấu bằng xảy ra khi
2
a b c
. Suy ra GTLN của
A
bằng
1
.
Bài 43. Gọi
m
là giá trị nhỏ nhất trong ba số
2 2 2
, ,
x y y z z x
với
, ,
x y z
là ba số thực
bất kì. Chứng minh
2 2 2
1
2
m x y z
.
Lời giải
Vì
x
,
y
,
z
là ba số thực bất kì nên giải sử
x y z
.
Mà
m
là giá trị nhỏ nhất trong ba số
2 2 2
, ,
x y y z z x
.
m
là số nhỏ nhất trong ba số
x y
,
y z
,
z x
.
Ta có:
2
z x x z x y y z x y y z m
.
Do đó
2
4
z x m
.
mà
2
y z m
2
x y m
2
2 2 2
0 2 2 2 0
x y z x y z xy yz xz
2 2 2
2 2 2
3 6
x y z x y y z z x m
2 2 2
2
x y z m
hay
2 2 2
1
2
m x y z
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 118 GIÁO VIÊN CÙ MINH QUẢNG
Bài 44.
Người ta giăng lưới để nuôi riêng một loại cá
trên một góc hồ. Biết rằng lưới được
giăng theo một đường thẳng từ một vị
trí trên bờ ngang đến một vị trí trên bờ
dọc và phải đi qua một cái cọc đã cắm
sẵn ở vị trí A. Hỏi diện tích nhỏ nhất có
thể giăng là bao nhiêu, biết rằng
khoảng cách từ cọc đến bờ ngang là 5
m và khoảng cách từ cọc đến bờ dọc là
12 m.
Lời giải
Đặt tên các điểm như hình vẽ. Đặt
,( 0).
CJ x x
Vì hai tam giác AJC và BKA là hai tam giác đồng dạng nên:
12 60
.
5
CJ JA x
KB
AK KB KB x
Diện tích của khu nuôi cá là:
1 60
5 . 12 .
2
S x
x
1 300 150
( ) 60 12 60 ( ) 6 60
2
S x x S x x
x x
Áp dụng bất đẳng thức Cô si ta có:
150 150
6 2 6 . 60
x x
x x
Dấu bằng xảy ra khi
2
150
6 25 5
x x x
x
.
Nên
150
( ) 6 60 60 60 120
S x x
x
Suy ra diện tích nhỏ nhất có thể giăng là
2
120( )
m
, đạt được khi
5
x m
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 119 GIÁO VIÊN CÙ MINH QUẢNG
Bài 45. Cho
, ,
x y z
là ba số thực dương thỏa mãn điều kiện 3
xy yz xz xyz
.
Tìm giá trị lớn nhất của biểu thức:
P =
2 2 2 2 2 2
1 1 1
2 2 2
x xy y y yz z z zx x
Lời giải:
Từ giả thiết ta có:
1 1 1
3
x y z
.
Ta có
2 2
2 2
5 3 7
5 3
2
4 4
x y x y
x y
x xy y
2 2
1 4
5 3
2
x y
x xy y
Tương tự:
2 2
1 4
5 3
2
y z
y yz z
;
2 2
1 4
5 3
2
z x
z zx x
64 64 64
16
4 3 4 3 4 3
P
x x y y y z z z x
16 16 16 16 16 16
16
4 4 4 3 3 3
P
x y z x y y z z x
4 4 4 4 4 4 4 4 4
2 2 2
x y z x y y y z z z x x
1 1 1
8 24
x y z
3
2
P
.
Dấu bằng xảy ra khi
1
x y z
.
Vậy max
3
.
2
P
Bài 46. Cho hình vuông
ABCD
có cạnh là
30
cm
.
Trên cạnh
AB
lấy hai điểm
E
,
G
sao
cho
AE GB x cm
và điểm
E
nằm giữa
điểm
A
và điểm
G
. Qua
E
kẻ đường
thẳng
vuông góc với
AB
cắt
CD
tại
F
; qua
G
kẻ
đường thẳng vuông góc với
AB
cắt
CD
tại
H
. Người ta gập hình vuông theo hai
cạnh
EF
và
GH
sao cho cạnh
AD
trùng cạnh
BC
như hình vẽ để tạo thành hình
lăng trụ đứng khuyết đáy. Tìm
x
để thể tích hình lăng trụ lớn nhất.
Lời giải
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 120 GIÁO VIÊN CÙ MINH QUẢNG
K
G
E
A
Ta có
(0 15) 30 2
AE GB x x EG x
.
Kẻ đường cao
AK
của
AGE
.
Vì
AGE
cân tại
A
nên
30 2
15
2 2
EG x
KE x
(cm).
AKE
vuông tại
K
15
2
AE KE x
.
Áp dụng định lý Py-ta-go vào tam giác vuông
AKE
ta có
2 2 2
AK KE AE
2 2 2
AK AE KE
2 2
AK AE KE
2
2
15
AK x x
30 225
AK x .
Diện tích đáy
AGE
là
2
1 1
. 30 225. 30 2 30 225. 15
2 2
AGE
S AK GE x x x x cm
.
Thể tích lăng trụ là
3
30. 30 225.(15 )
V x x cm
.
30. 30 225.(15 ) 30. 15. 2 15 . 15 . 15
V x x x x x
10. 15.3. 2 15. 15 . 15
x x x
.
Áp dụng bất đẳng thức Cô-si cho ba số dương
2 15
x
,
15
x
,
15
x
ta được
3
3. 2 15 15 15 2 15 15 15
x x x x x x
3
2 15 15 15 5
x x x
3
2 15 15 15 5
x x x
3
2 15 15 15 5 5 5
x x x
10. 15.3.5 5 750 3
V V
.
Dấu
" "
xảy ra khi và chỉ khi
2 15 15 10
x x x
.
Vậy
10
x
thì thể tích lăng trụ lớn nhất.
Bài 47. Cho các số thực
x
,
y
thỏa mãn
2 2
3 3 9
x x y y
. Tìm giá trị nhỏ nhất của
biểu thức
2 2
P x xy y
.
Lời giải
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 121 GIÁO VIÊN CÙ MINH QUẢNG
2 2 2 2
2 2
3 3
3 3 9 . 9 3 3 1
3 3
x y y x y x x y
y x x y
Ta có:
2 2 2 2
2 2 2 2
3 3 3 3 9
3 3 3 3 1
xy x x y y y x
xy x x y y y x
2 2
3 3 5
xy y x
Do
2 2 2 2
2 2 2 2
6 6
3 3 3 3
2 2
x y x y
y x xy y x xy
2 2
2
2 2
2 6
5 2 4 4
2
xy x y
xy x y x y
.
Ta có:
2
2
2 2 2 2 2 2
2 2 2 4 2 6
2
x y
P x y xy x y xy x y x y
2 6 3
P P
min 7
P
đạt được khi
1
x y
.
Bài 48. Cho các số
0, 0
x y
. Tìm giá trị nhỏ nhất của biểu thức
2 2
xy
x y
A
xy x y
.
Lời giải
Ta có:
2
2 2
2
x y
x y
2
2
x y
xy
A
xy x y
2 2
3
8 8
x y x y
xy
A
xy x y xy
2 2
3
2 .
8 8
x y x y
xy
A
xy x y xy
2 3.4
.
2 8
x y xy
A
xy
xy
2
2 3 3 5
. 1
2 2 2 2
xy
A
xy
Dấu bằng xảy ra khi
x y
Vậy :
min
5
2
A x y
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 122 GIÁO VIÊN CÙ MINH QUẢNG
Bài 49. Với
a
,
b
,
c
là các số dương thỏa mãn
2
ab bc ac
. Tìm giá trị nhỏ nhất của biểu
thức:
2 2
a b c b
P
a b c b
Lời giải
Với
a
,
b
,
c
là các số dương thỏa mãn
2
2 2
ac
ab bc ac b a c ac b
a c
2 2
2 2
2 2 2 2
2 2
2 2
2 2 2 2 2 2
2 2
ac ac a ac ac ac c ac
a c
a b c b
a c a c a c a c
P
ac ac
a b c b
a ac ac ac c ac
a c
a c a c
a c a c
2 2
2 2
3 3 1 3 1 3 3
1
2 2 2 2 2
2 2
a ac c ac c a c a
P
a c a c
a c
Theo bất đẳng thức AM-GM, ta có:
2 2
c a c a
a c a c
3
1 2 4
2
P
Dấu
" "
xảy ra
2
, , 0
, , 0
2
2
2
a b c
a b c
c a
a c a b c
a c
a
ac
b
b
a
a c
Vậy giá trị nhỏ nhất của biểu thức
P
là
4
khi
a b c
Bài 50.
Cho
1
xy yz zx
. Tìm giá trị nhỏ nhất của biểu thức:
2 2 2
3
S x y z
.
Lời giải
Áp dụng BĐT Cauchy, ta có:
2 2
2 2 2 2 2
2 2
2 4
4 4 6 6 2 4 4 4
4 4
x y xy
z x xz x y z xy xz yz
z y yz
2 2 2
2 3 3 4
x y z xy xz yz
2 2 2
2 3 3 4
x y z
(do
1
xy yz zx
)
2 2 2
3 3 2
x y z
2
S
Dấu “=” xảy ra
2 2
2
2
2
x y
z
z x x y
z y
. Mà
1
xy yz zx
5 2 5
;
5 5
x y z
Vậy
min
2
S
, đạt được tại
5 2 5
;
5 5
x y z
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 123 GIÁO VIÊN CÙ MINH QUẢNG
Bài 51. Với các số thực
a
,
b
,
c
thay đổi thỏa mãn
1
a
;
1
b
;
0 1
c
và
3
a b c
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
2 2 2
a b c
P
ab bc ca
.
Lời giải
Ta có:
2
2 2 2
2
a b c ab bc ca
a b c
P
ab bc ca ab bc ca
9 2
9
2
ab bc ca
ab bc ca ab bc ca
Lại có:
2 2
2 2 2 2 2 2 2 2
2 2
2
2 2 2 2 2 2 2
2
a b ab
b c bc a b c ab bc ca a b c ab bc ca
c a ca
2
2 2 2
2 2 2 3 3 3 3
a b c ab bc ca ab bc ca a b c ab bc ca
2
3
3
a b c
ab bc ca
(do
3
a b c
)
9 9
2 2 1
3
P
ab bc ca
Dấu
" "
xảy ra
1
a b c
Mặt khác:
1
a
;
1
b
1 1 0 1 0 1
a b ab a b ab a b
1 1
ab bc ca a b bc ca ab bc ca a b c a b
Mà
3 3 3 1 3
a b c a b c ab bc ca c c c
2 2
2 3 2 2 2 2
ab bc ca c c c ab bc ca c c ab bc ca c c
Do
0 1 2 0 2 2 2 2
c c c c c ab bc ca
9 9 5
2 2
2 2
P
ab bc ca
Dấu
" "
xảy ra
1 1 0
1; 2; 0
2 0
2; 1; 0
3
1; 1;0 1
a b
a b c
c c
a b c
a b c
a b c
Vậy
1
MinP
khi
1
a b c
;
5
2
MaxP
khi
1; 2; 0
2; 1; 0
a b c
a b c
Bài 52. Cho
x
,
y
là hai số thực dương sao cho
2
3
2
y
x y
x
.
Tìm giá trị nhỏ nhất của biểu thức
2
x y
P
x y
.
Lời giải
Với
x
,
y
là hai số thực dương thỏa mãn
2
2 2
3
2 2 3
y
x y x xy y
x
2
2 2 2 2
2 4 4
x xy y y x y y
2
2
4 2
x y y x y y x y
.
Mà
0
2
x y x x y x
x y
x x x y x x y
2
2 1
2
2 2
x y x
x y x
P
x y x
x y x
.
Dấu
" "
xảy ra khi và chỉ khi
0
x y
.
Vậy
1
2
MinP
khi
0
x y
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 124 GIÁO VIÊN CÙ MINH QUẢNG
Bài 53. Với
,
a b
là các số thực
1, 1
a b
. Tìm giá trị nhỏ nhất của biểu thức
2 2
1 1
a b
P
b a
Lời Giải
Vì
1
a
Suy ra
–1 0
a
,
1
b
suy ra
–1 0
b
Áp dụng bất đẳng thức Cô si ta có:
2 2
4( 1) 2 .4. 1 4
1 1
a a
b b a
b b
2 2
4( 1) 2 .4. 1 4
1 1
b b
a a b
a a
Suy ra
4 4 4 4 4 4 8
P b a a b P
Dấu “ = “xảy ra khi và chỉ khi
2
2
4 1
1
2 2
4 1 2
2 2
1
, 1
a
b
b
a b
b
a a b TM
b a
a
a b
Vậy Giá trị nhỏ nhất của
8
P
khi và chỉ khi
2
a b
Bài 54. Cho các số không âm
x
,
y
,
z
thỏa mãn
1
x y z
. Tìm giá trị lớn nhất của biểu
thức:
2 2 2
2 1 2 1 2 1
Q x x y y z z
Lời giải
Ta có
, , 0
x y z
và
1
x y z
suy ra
0 , , 1
x y z
2 2
1 0 0
x x x x x x
.
Với
2
x x
ta có
2 2 2 2
1 1
x x x x x x x x
2
2 2 2
2 1 2 1 2 1 1
x x x x x x x
2
2 1 1
x x x
Chứng minh tương tự ta có
2
2 1 1
y y y
và
2
2 1 1
z z z
.
Từ đó suy ra
2 2 2
2 1 2 1 2 1 1 1 1 3 4
x x y y z z x y z x y z
4
Q
.
Dấu bằng xảy ra
1 0
1 0 . . 0,0,1 ; 0,1,0 ; 1,0,0
1 0
x x
y y x y z
z z
Vậy
Q
đạt giá trị lớn nhất là
4
tại
. . 0,0,1 ; 0,1,0 ; 1,0,0
x y z
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 125 GIÁO VIÊN CÙ MINH QUẢNG
Bài 55. Cho a, b, c > 0 thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức :
1 1 1
2 2 2
M
ab a bc b ca c
Lời giải
Ta chứng minh bổ đề sau :
Cho
, 0
a b
, chứng minh rằng :
1 1 4
a b a b
Thực hiện xét hiệu ta được :
1 1 4 4
a b
a b a b ab a b
2 2
4
0, , 0
a b ab a b
a b
ab a b ab a b
1 1 4
a b a b
Dấu
" "
xảy ra khi :
a b
Ta có thể viết dưới dạng :
1 1 1 1
4
a b a b
Áp dụng bất đẳng thức bổ đề ta có:
1 1 1 1 1
2 1 1 4 1 1
ab a ab a ab a
1 1 1 1
4 1 4 1 1
abc c
ab abc a c a
Tương tự ta có :
1 1 1
2 4 1 1
a
bc b a b
1 1 1
2 4 1 1
b
ca c b c
Cộng vế với vế của 3 bất đẳng thức ta có :
1 1 1 1 1 3
.3
4 1 1 1 4 4
a b c
VT
a b c
3
4
max
M
. Dấu
" "
xảy ra
1
a b c
Bài 56. Cho
; ; 0
1
a b c
a b c
Tìm Min
7 9 7 9 7 9
S a b c
Lời giải
Có:
; ; 0
1
a b c
a b c
0 1;0 1;0 1
a b c
0; 0; 0;
1 0;1 0;1 0
a b c
a b c
2 2
1 0 7 9 6 9 7 9 3
a a a a a a a a a
Tương tự
7 9 3
b b
7 9 3
c c
7 9 7 9 7 9 9 10
a b c a b c S
Vậy giá trị nhỏ nhất
10
S
Dấu bằng xảy ra khi
; ; 1;0;0
a b c
và các hoán vị.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 126 GIÁO VIÊN CÙ MINH QUẢNG
Bài 57. Cho
, , 0
x y z
và
3
xy yz xz
Tìm giá trị nhỏ nhất của biểu thức
x y z
P
y z x
Lời giải
Đặt , ,
x a y b z c
, , 0
a b c
Khi đó
3
ab bc ca
Ta có:
2
2 2 2
3 9 3
a b c ab bc ca a b c ab bc ca a b c
Ta có
2
2 2 2
3
a b c
a b c
P a b c
b c a a b c
min
3
P
, dấu “=” xảy ra
1 1
a b c x y z
Bài 58. Gọi
m
là giá trị nhỏ nhất trong ba số
2
x y
,
2
y z
,
2
z x
với
x
,
y
,
z
là ba số
thực bất kì. Chứng minh
2 2 2
1
2
m x y z
Lời giải
Vì
x
,
y
,
z
có vai trò như nhau nên giả sử
x y z
.
Vì
m
là số nhỏ nhất trong ba số
2
x y
,
2
y z
,
2
z x
.
Nên
m
là số nhỏ nhất trong ba số
x y
,
y z
,
z x
.
Ta có:
2
z x x z x y y z x y y z m
.
Nên
2
4
x z m
Mà
2
y z m
;
2
x y m
.
2 2 2
2 2 2
3 6
x y z x y y z z x m
2 2 2
1
2
m x y z
Bài 59. Cho x, y là các số thực thỏa mãn
2
x
và
3
x y
.
Tìm giá trị nhỏ nhất của biểu thức :
2 2
1 1
P x y
x x y
Lời giải
Dễ thấy điểm rơi đạt tại
2; 1
x y
Khi đó
2 2
1 1
2 1 4 2 5
P x y x y
x x y
2 2
2 2
2 2
9 4 7 17
2 1 2 6 2 4 15
2 3 2 2
7 17
2 1 15
7 17 7 17 35
15
2 3 6
P x y x y x
x y x x x y
x y x
P x y
x y x x x y
P
x x y
Vậy
35
6
P
Min
. Dấu
" "
xảy ra
2; 1
x y
(thỏa mãn điều kiện)
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 127 GIÁO VIÊN CÙ MINH QUẢNG
Bài 60. Cho các số dương x, y, z thỏa mãn x + y + z = 2020. Tìm giá trị lớn nhất của biểu thức
2020 2020 2020
x y z
P
x x yz y y zx z z xy
.
Lời giải
Bổ đề: Cho
, ,
a b c
là các số dương. Chứng minh
a b a c ab ac
(1)
BĐT (1)
2 2 2 2
2 2
a ac ab bc ab ac a bc a bc a bc
(luôn đúng)
Vậy bổ đề được chứng minh.
Áp dụng
Ta có
2
2020
x yz x x y z yz x xy xz yz x y x z
Áp dụng bổ đề (1) ta có:
x y x z xy xz
2020
2020
x x x
x x yz x x y z
x x yz x y z
x x y z
Chứng minh tương tự:
2020
y
y
y y zx x y z
;
2020
z z
z z xy x y z
Suy ra:
max
2020
1 1
3
x y z
P P x y z
x y z
Bài 60. Cho
0
,
0
b
,
0
c
thỏa mãn
2 2 2
2 b bc c 3 3 a
Tìm giá trị nhỏ nhất của biểu thức
2 2 2
T a b c
a b c
Lời giải
Ta có:
2 2 2
2 3 3
b bc c a
2 2 2
2 2 2 9 3
b bc c a
2 2 2
2 2 2 3 9
b bc c a
2 2 2 2 2 2 2
2 2 2 2 2 9
a b c ab bc ca a b ab a c ac
2 2 2
9
a b c a b a c
2
9
a b c
0 3
a b c
Ta đi chứng minh bất đẳng thức phụ:
1 1 1 9
a b c a b c
Ta có:
1 1 1 9
a b c a b c
1 1 1
9
a b c
a b c
1 1 1 9
a a b b c c
b c a c a b
6
a a b b c c
b c a c a b
Áp dụng bất đẳng thức cô-si ta có:
2
a b
b a
2
b c
c b
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 128 GIÁO VIÊN CÙ MINH QUẢNG
2
a c
c a
Cộng vế theo vế ta có:
6
a a b b c c
b c a c a b
Dấu “=” xảy ra khi
a b c
.
Áp dụng cô-si cho 2 số dương theo từng cặp:
1
a 2
a
2
1
b 2
3
1
c 2
c
4
Áp dụng bất đẳng thức phụ:
1 1 1 9
a b c a b c
5
Cộng vế với vế của các bất đăng thức
2 , 3 , 4 , 5
ta được
1 1 1 1 1 1 9
T a b c 2 2 2
a b c a b c 3
Vậy giá trị nhỏ nhất của biểu thức
T
bằng:
9
khi và chỉ khi
a b c 1
.
Bài 61. Cho hai số
0
x
,
0
y
và
1
x y
.
Tìm giá trị nhỏ nhất của biểu thức
2 2
1 1
1 1M
x y
Lời giải
1) Với hai số
0
x
,
0
y
và
1
x y
ta có:
2 2
2 2 2 2 2 2
1 1
1 1 1 1
1 1
1 1
x y
x x y y
M
x y x y x y
2 2
1 1 1
2
1
y x x y xy x y
xy xy
x y
.
Ta có:
2
2
1 1 1 2
2 4 1 8
4 4
x y xy x y xy
xy xy xy
x y
2
1 9 9
M
xy
.
Dấu bằng xảy ra khi
1
2
x y
.
Vậy giá trị nhỏ nhất của
M
bằng
9
khi
1
2
x y
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 129 GIÁO VIÊN CÙ MINH QUẢNG
Bài 62. Cho bốn số dương
, , , .
a b c d
Tìm giá trị nhỏ nhất của biểu thức :
2 2 2 2
2004
a b c d b c d a
A a b c d ab bc cd da
b c d a a b c d
Lời giải:
2 2 2 2
2004
a b c d b c d a
A a b c d ab bc cd da
b c d a a b c d
Chứng minh được
16
a b c d b c d a
b c d a a b c d
(1)
Dấu “=” xảy ra khi và chỉ khi
a b c d
Chứng minh được
2 2 2 2
0
a b c d ab bc cd da
(2)
Dấu “=” xảy ra khi và chỉ khi
a b c d
Từ (1) và (2) =>
2020
A
Dấu “=” xảy ra khi và chỉ khi
a b c d
Vậy giá trị nhỏ nhất của A là 2020 khi
0
a b c d
.
Bài 63. Cho các số thực dương a, b thay đổi luôn thỏa mãn
3 3 4.
a b
Tìm giá trị lớn
nhất của biểu thức
.
P a b
Lời giải
Ta chứng minh
2 3 3
x x
với mọi
0
x
.
Thật vậy,
2
2 3 3 2 3 3 3( 1) 0
x x x x x
.
Áp dụng :
2 3 3; 2 3 3
a a b b
2( 3 3) 6 2.4 6
P a b P
.
max
2
P
khi và chỉ khi
1
1
1
a
b
a b
Bài 64. Cho a, b, c > 0 và a + b + c = 1. Tìm giá trị lớn nhất của biểu thức
ab bc ca
A
c ab a bc b ca
Lời giải
Với
, 0
a b
ta có
2
a b ab
1 1 1 1 1
1
2 2
2
a b a b
ab a b
ab ab ab
Viết lại
2
.1
c ab c ab c a b c ab ca cb c ab c c a b c a c b c a
Tương tự
a bc a b a c
và
b ca b c b a
Xét
1 1
2
ab ab ab
c b c a
c ab
c b c a
1 1
2
bc bc
a b a c
a bc
1 1
2
ca ca
b c b a
b ca
Cộng vế với vế ta được
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 130 GIÁO VIÊN CÙ MINH QUẢNG
ab bc ca
A
c ab a bc b ca
1
2
ab ab bc bc ac ac
c b c a a b a c b c a b
1
2
a b c b a c c a b
A
b c a c a b
1 1
2 2
A a b c
1
2
A
Vậy giá trị lớn nhất của A là
1
2
khi
1
3
a b c
Bài 65. Cho ba số
a
,
b
,
c
dương. Chứng minh
2 2 2
1 1 1
2
a b c
a bc b ac c ab abc
.
Lời giải
Áp dụng bất đẳng thức Cosi ta có
2
2
a bc a bc
2
2 1 1 1 1 1 1
.
2
a bc ab ac ab ac
a bc
1
.
Tương tự có:
2
2 1 1 1
2
b ac ba bc
2
.
2
2 1 1 1
2
c ab ca cb
3
.
Cộng vế với vế của
1
2
3
ta được:
2 2 2
2 2 2 1 1 1 1 1 1 1 1 1
2 2 2
a bc b ac c ab ab ac ba bc ca cb
2 2 2
2 2 2 1 2 2 2
2
a bc b ac c ab ab bc ca
2 2 2
1 1 1 1 1 1 1
2
a bc b ac c ab ab bc ca
2 2 2
1 1 1
2
a b c
a bc b ac c ab abc
(điều phải chứng minh).
Đẳng thức xảy ra khi
a b c
Bài 66. Cho
x
,
y
,
z
là các số thực dương thỏa mãn
1
x y z
. Tìm giá trị nhỏ nhất của
biểu thức:
2 2 2
1 2020
P
x y z xy yz zx
.
Lời giải
Áp dụng bất đẳng thức
1 1 1
9
x y z
x y z
, ta có :
2 2 2
2 2 2
1 1 1
9
x y z xy yz zx xy yz zx
x y z xy yz zx xy yz zx
.
2 2 2
2 2 2
1 1 1
2 2 2 9
x y z xy yz zx
x y z xy yz zx xy yz zx
.
Hay
2 2 2
1 2
9
x y z xy yz zx
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 131 GIÁO VIÊN CÙ MINH QUẢNG
Ta có :
2 2 2
0
x y y z x z
2 2 2
x y z xy yz zx
2
2 2 2
2 3
x y z x y z xy yz zx xy yz zx
2
1
3 3
x y z
xy yz zx
Từ đó suy ra:
2 2 2
1 2 2018
9 6054 6063
P
x y z xy yz zx xy yz zx
6063
P
.
Dấu bằng xảy ra
1
3
x y z
.
Vậy GTNN của
6063
P
1
3
x y z
.
Bài 67. Cho các số thực dương
, ,
a b c
.
Chứng minh rằng:
2 2 2
2 2 2 2 2 2
5
3 8 14 3 8 14 3 8 14
a b c a b c
a b ab b c bc c a ca
Lời giải
Ta có:
2 2 2 2
3 8 14 3 12 2 8
a b ab a ab ab b
3 4 2 4
a a b b a b
4 3 2
a b a b
Áp dụng bất đẳng thức Cô-si cho hai số dương
4
a b
và
3 2
a b
ta có
4 3 2
4 3 2
2
a b a b
a b a b
4 6
2 3
2
a b
a b
2 2
2 3
4 3 2
a a
a b
a b a b
hay
2 2
2 2
2 3
3 8 14
a a
a b
a b ab
Tương tự ta cũng có :
2 2
2 2
2 3
3 8 14
b b
b c
b c bc
và
2 2
2 2
2 3
3 8 14
c c
c a
c a ca
Khi đó
2 2 2 2 2 2
2 2 2 2 2 2
2 3 2 3 2 3
3 8 14 3 8 14 3 8 14
a b c a b c
a b b c c a
a b ab b c bc c a ca
1
Áp dụng bất đẳng thức Cô-si cho hai số dương
2
2 3
a
a b
và
2 3
25
a b
ta có:
2 2
2 3 2 3 2
2 .
2 3 25 2 3 25 5
a a b a a b a
a b a b
2
2 2 3 8 3
2 3 5 25 25
a a a b a b
a b
Tương tự ta cũng có
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 132 GIÁO VIÊN CÙ MINH QUẢNG
2
8 3
2 3 25
b b c
b c
và
2
8 3
2 3 25
c c a
c a
2 2 2
8 3 8 3 8 3
2 3 2 3 2 3 25 25 25 5
a b c a b b c c a a b c
a b b c c a
2
Từ
1
và
2
suy ra
2 2 2
2 2 2 2 2 2
5
3 8 14 3 8 14 3 8 14
a b c a b c
a b ab b c bc c a ca
Dấu “=” xảy ra khi
a b c
Bài 68. Cho
, ,
a b c
là các số dương và
3
a b c .
Tìm giá trị lớn nhất của biểu thức:
22 2
1 1
1
a b
P
a b
c
c
Lời giải
Vì
, , 0
a b c
, ta có :
2
2 2 2
2 2 2
2 2 2
2
3( )
1
2.
2
1
0
2
3( )
a b c ab bc ca
a b c ab bc ca
a b c ab bc ca
a b b c c a
a b c ab bc ca
2
2 2
2
3 3( )
1
1
1
a b c ab bc ca
ab bc ca
a a ab bc ca
a a b a c
2
1 1
1
a a b a c
2
1 1
1
a b a c
a
2
. (1)
1
a a a
a b a c
a
Áp dụng bất đẳng thức Cô si cho 2 số dương:
;
a a
a b a c
2 .
a a a a
a b a c a b a c
1
. (2)
2
a a a a
a b a c a b a c
Từ (1) và (2) suy ra
2
1
(*)
2
1
a a a
a b a c
a
Chứng minh tương tự, ta có
2
1
(**)
2
1
b b b
a b b c
b
2
1
(***)
2
1
c c c
a c b c
c
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 133 GIÁO VIÊN CÙ MINH QUẢNG
Cộng vế với vế của (*), (**),(***), ta có
2 2 2
1
2
1 1 1
a b c a a b b c c
a b a c a b b c a c b c
a b c
3
2
P
Dấu bằng xảy ra:
3
3
a b c
Vậy
3 3
max
2 3
P a b c
Bài 69. Cho
0
x
, tìm giá trị nhỏ nhất
2
1
9 5 2021
9
M x x
x
.
Lời giải
2
1
9 5 2021
9
M x x
x
2
1
(9 6 1) 2020
9
x x x
x
2
1
(3 1) 2020
9
x x
x
Ta có:
2
3 1 0
x
.
Vì
0
x
nên
1
0
9
x
.
Áp dụng bất đẳng thức Cauchy cho hai số
x
và
1
9
x
ta được
1 1
2 .
9 9
x x
x x
1 2
2.
3 3
.
Do đó
M
2
0 2020
3
2
2020
3
6062
3
.
Dấu
" "
xảy ra khi và chỉ khi
3 1 0
1
9
x
x
x
1
3
x
.
Vậy giá trị nhỏ nhất
6062
3
M
khi
1
3
x
.
Bài 70. Cho
, ,
x y z
là các số dương thoả mãn
4
xy yz xz xyz
.
Chứng minh:
1 1 1
1
2 2 2
P
x y z x y z x y z
Lời giải
Ta có
1 1 1
4 4 4
xy yz xz
xy yz xz xyz
xyz x y z
Áp dụng
1 1 4 1 1 1 1
4
a b a b a b a b
Ta có
1 1 1 1 1 1 1 1 1 1 1 1 1
2 4 2 4 2 4 8 2 2
x y z x y z x y z x y z
(1)
Chứng minh tương tự có
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 134 GIÁO VIÊN CÙ MINH QUẢNG
1 1 1 1 1
2 8 2 2
x y z x y z
(2)
và
1 1 1 1 1
2 8 2 2
x y z x y z
(3)
Từ (1), (2), (3) ta có
1 1 1 1 1 1 1
1
2 2 2 4
P
x y z x y z x y z x y z
.
Chú ý:
1 1 2 1 1 1 1 1 1
1
16 4
cyc cyc
P
x y z x x y z x y z
Bài 71. Cho hai số dương
x
và
y
. Chứng minh rằng
2
. 2 8
y
x
y x
Lời giải:
Có
, 0
x y
2
. 2 8
y
x
y x
2 2
8
xy y x
y x
2 2
8
xy y x
xy
2 2 8
xy y x xy
( vì
, 0
x y
)
2 2
2 2 4 8
xy x y y x xy
2 2
2 2 4 8 0
xy x y y x xy
2 2
2 2 4 4 4 0
xy x y y x xy xy
2 2
4 4 2 4 2 0
xy xy x x y xy y
2 2
4 4 2 2 1 0
x y y y x x
2 2
2 2 1 0
x y y x
( luôn đúng với
, 0
x y
)
Vậy
2
. 2 8
y
x
y x
với
, 0
x y
. Dấu “=” xảy ra
2 0
1 0
y
x
2
1
y
x
Bài 72. Cho biểu thức :
1 1
1 1 1 1B x y
y x
.
Với
0
x
,
0
y
và
2 2
1
x y
. Tìm giá trị nhỏ nhất của
B
.
Lời giải
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 135 GIÁO VIÊN CÙ MINH QUẢNG
1 1
1 1 1 1B x y
y x
1 1
2
x y
x y
x y y x
1 1 1 1
2
2 2 2 2
x y
x y
x x y y y x
1 1 1 1 1
2
2 2 2
x y
x y
x y y x x y
.
Áp dụng bất đẳng thức Cô – si ta có:
1 1
2. . 2
2 2
x x
x x
(1)
1 1
2. . 2
2 2
y y
y y
(2)
2. . 2
x y x y
y x y x
(3)
1 1 1 1
2
.
x y
x y
Áp dụng bất đẳng thức Cô – si ta có:
2 2
1
2
xy x y
2 2
1
2
xy x y
2 2
1 2
2
xy
x y
1 1 1
2 4
2 x y
Từ (1), (2), (3), (4) ta được:
1 1 1 1 1
2 4 3 2
2 2 2
x y
x y
x y y x x y
.
Vậy
4 3 2
MinB
.
Dấu đẳng thức đồng thời xảy ra khi và chỉ khi:
2 2
1
2
1
2
1; 0, 0
x y
x
x
y
y
x y x y
2
2
x y
.
Bài 73. Cho x, y, z là các số dương thoả mãn xy + yz + xz = 4xyz.
Chứng minh:
1 1 1
1
2 2 2
P
x y z x y z x y z
Lời giải:
- Ta có
1 1 1
4 4 4
xy yz xz
xy yz xz xyz
xyz x y z
- Áp dụng
1 1 4 1 1 1 1 1 1 1 1
( ) ( )
4 4
a b a b a b a b a b a b
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 136 GIÁO VIÊN CÙ MINH QUẢNG
Ta có
1 1 1 1 1 1 1 1 1 1 1 1 1
( ) ( ) ( )
2 4 2 4 2 4 8 2 2
x y z x y z x y z x y z
(1)
- Chứng minh tương tự có:
1 1 1 1 1
( )
2 8 2 2
x y z x y z
(2)
và
1 1 1 1 1
( )
2 8 2 2
x y z x y z
(3)
Từ (1), (2), (3) ta có
1 1 1 1 1 1 1
( ) 1
2 2 2 4
P
x y z x y z x y z x y z
(đpcm)
Bài 74. Cho
x
;
y
;
z
> 0 và
1 1 1
4
x y z
. Chứng minh rằng :
1 1 1
1
2 2 2
x y z x y z x y z
Lời giải
Áp dụng BĐT
1 1 4
A B A B
(với
; 0
A B
) Có
x
;
y
;
z
> 0
2 0
0
x
y z
Có
1 1 4
2 2
x y z x y z
1 1 1 1
2 4 2
x y z x y z
Có
1 1 4
y z y z
1 1 1 1
4
y z y z
1 1 1 1 1 1 1
4 2 4 2 4 4
x y z x y z
1
2
x y z
1 1 1 1
4 2 4 4
x y z
(1)
Tương tự cm :
1
2
y x z
1 1 1 1
4 2 4 4
y x z
(2) ;
1
2
z x y
1 1 1 1
4 2 4 4
z x y
(3)
Từ (1) (2) và (3)
1 1 1
1
2 2 2
x y z x y z x y z
.
Dấu « = » xảy ra
3
4
x y z
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 137 GIÁO VIÊN CÙ MINH QUẢNG
Bài 75. Với
,
x y
là các số dương thỏa mãn điều kiện
2
x y
, tìm giá trị nhỏ nhất của biểu
thức:
2 2
x y
M
xy
.
Lời giải
Ta có :
2 2
4 3
x y x y x y y
M
xy y x y x x
.
Vì
, 0
x y
, áp dụng bất đẳng thức Cô-si cho hai số dương
4
;
x y
y x
Ta có:
4 4
2 . 4
x y x y
y x y x
.
Dấu “=” xảy ra
2 2
4
4 2
x y
x y x y
y x
.
Vì
1 3 3
2
2 2
y y
x y
x x
, dấu “=” xảy ra
2
x y
Suy ra,
3 5
4
2 2
M
, dấu “=” xảy ra
2
x y
Vậy GTNN của
M
là
5
2
khi
2
x y
.
Bài 76. Cho hai số dương
a
và
b
thỏa mãn
1 1
2
a b
. Tìm giá trị lớn nhất của biểu thức:
4 2 2 4 2 2
1 1
2 2
P
a b ab b a ba
.
Lời giải
Từ giả thiết
1 1
2
a b
=>
1
2 2 2
2
ab
a b
ab a b ab
a b
ab
Áp dụng BĐT cô si với 2 số dương ta có
4 2 4 2 4 2 2 2 2
2 2 2 2
a b a b a b ab a b ab
4 2 4 2 4 2 2 2 2
2 2 2 2
b a b a b a a b ab a b
4 2 2 4 2 2 2 2 2 2
1 1 1 1 1
2 2 2 2 2 2 2
P
a b ab b a ba a b ab ab a b
Dấu “=” xảy ra
1
2
a b
.
Vậy giá trị lớn nhất của
P
là
1
2
khi
1
2
a b
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 138 GIÁO VIÊN CÙ MINH QUẢNG
Bài 77. Cho
,
a b
là các số không âm thỏa mãn
2 2
2
a b
.
Chứng minh rằng:
3 2 3 2 6
a a a b b b b a
.
Dự đoán dấu bằng xảy ra khi
1
a b
. Khi đó
3 2 , 3 2
a a b b b a
nên ta có thể áp dụng
bất đẳng thức Cauchy trực tiếp cho biểu thức trong dấu căn.
Sử dụng bất đẳng thức Cauchy dạng
2
x y
xy
, dễ thấy
2
3 2
3 2 2
2
a a b
a a a b a a ab
,
2
3 2
3 2 2
2
b b a
b b b a b b ab
.
Cộng hai bất đẳng thức này lại vế theo vế, ta được:
2 2
3 2 3 2 2 2 4 2
M a a a b b b b a a b ab ab
.
Tiếp tục sử dụng bất đẳng thức Cauchy kết hợp với giả thiết, ta có:
2 2
4 2 4 6
ab a b
. Từ
đó ta có ngay
6
M
. Dấu bằng xảy ra
1
a b
.
Bài 78. Với
a
,
b
,
c
là các số dương thoả mãn có
2
ab bc ac
. Tính giá trị nhỏ nhất của biểu
thức
2 2
a b c b
P
a b c b
.
Lời giải
Với
a
,
b
,
c
là các số dương ta có:
2
2
ac
ab bc ac b
a c
, thay vào
P
ta được
2 2
2 2
2 2
ac ac
a c
a c a c
P
ac ac
a c
a c a c
2 2
2 2 2 2
a a c ac c a c ac
a a c ac c a c ac
3 3
2 2
a c c a
a c
3 3
1 1 2 4
2 2
a c
c a
.
Vậy giá trị nhỏ nhất của
P
là 4 khi
a b c
.
Bài 79. Cho
1
x y
. Chứng minh
4 4
1
8
x y
.
Lời giải
Ta có
2
2 2
2
x y
x y
1
với mọi
x
,
y
.
Thật vậy,
2 2 2 2
1 2 2 2
x y x xy y
2 2
2 0
x xy y
2
0
x y
luôn đúng với mọi
giá trị của
x
,
y
.
Áp dụng
1
ta có:
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 139 GIÁO VIÊN CÙ MINH QUẢNG
2
2 2
2 2
4 4 2 2
2
x y
x y x y
và
2
2 2
2
x y
x y
.
Theo giả thiết ta có
1
x y
nên
2 2
1
2
x y
.
Suy ra
2
4 4
1
1
2
2 8
x y
.
Đẳng thức xảy ra khi và chỉ khi
1
2
x y
.
Bài 80. Một công ty du lịch dự định tổ chức một tour du lịch xuyên Việt nhân kỉ niệm ngày
giải phóng hoàn toàn miền Nam
30 4
. Công ty dự định nếu giá tour là
2
triệu đồng thì sẽ có
khoảng
150
người tham gia. Để kích thích mọi người tham gia, công ty sẽ quyết định giảm
giá và cứ mỗi lần giảm giá tour
100
nghìn đồng thì sẽ có thêm
20
người tham gia. Hỏi công
ty phải giảm giá tour là bao nhiêu để doanh thu từ tour xuyên Việt là lớn nhất.
Lời giải
Gọi
x
là giá tour (triệu đồng;
0 2
x
)
Giá đã giảm so với ban đầu là 2
x
(triệu đồng)
Vì mỗi lần giảm giá tour
100
nghìn đồng thì sẽ có thêm
20
người tham gia nên số người tham
gia tăng thêm khi giảm 2
x
triệu đồng là
(2 ): 0,1.20 400 200
x x
(người)
Tổng số người tham gia là:
150 400 200 550 200
x x
( người)
Tổng doanh thu là :
550 200
L x x
( triệu đồng)
Tìm
x
để doanh thu
L
lớn nhất với
0 2
x
Sử dụng bất đẳng thức Côsi, chúng ta có:
2 2
1 1 200 550 200 1 550 3025
550 200 200 550 200
200 200 2 200 2 8
x x
L x x x x
Dấ
u
" "
xảy ra ⇔
200 550 200
x x
400 550
x
1,375
x
Vậy giá tour là 1,375000 triệu đồng.
Bài 81. Cho
0; 0
x y
thỏa mãn
1
x y
. Tìm giá trị nhỏ nhất của
2
2
1 1
M x y
x y
Lời giải
Chứng minh các bất đẳng thức phụ:
Ta có: với
, 0
a b
2
2 2 2 2 2 2
0 2 0 2 2 0
a b a b ab a b a b ab
2
2 2 2 2 2 2
2 2
2
a b
a b a b ab a b
1
Lại có: với
, 0
a b
2
2 2 2 2
0 2 0 2 4
a b a b ab a b ab ab
2 2
4 4 *
ab a b ab ab a a b b a b ab .
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 140 GIÁO VIÊN CÙ MINH QUẢNG
Vì
, 0 0; 0
a b ab a b
Do đó ta được:
4
*
a a b b a b
ab
ab a b ab a b ab a b
1 1 4
a b a b
.
2
Áp dụng bất đẳng thức
1
và
2
cho
M
ta được:
2 2
1 1 1 1 4
2 2
M x y x y
x y x y
2
1 1 3
2
M x y
x y x y
2
1 3
2
2
M
x y
(Áp dụng bđt thức Cauchy cho cặp số
1
;x y
x y
2
1 25
. 2 3
2 2
M
(Vì
1
x y
)
Dấu
" "
xảy ra khi và chỉ khi
1
2
x y
Vậy giá trị nhỏ nhất của
M
là
25
2
Bài 82. Cho hai số dương
,
x y
, có
1
x y
.
Tìm giá trị nhỏ nhất của biểu thức
2 2
1 1
1 1B
x y
Lời giải
2 2
2 2 2 2
1 1
1 1
1 1
x y
B
x y x y
2 2 2 2
1 1
( 1)( 1)( 1)( 1)
xy x y xy x y
x y x y
x y x y
2 2
1 1 1 1
xy xy
x y
2 2
2 2
2 2
1
x y xy
x y xy
2
( ) 1
4 4
x y
xy
2
8
xy
2
1 9 9
B
xy
Xảy ra dấu “=” khi
1
( )
2
x y TM
Vậy GTNN
9
B
khi
1
2
x y
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 141 GIÁO VIÊN CÙ MINH QUẢNG
Bài 83. Cho các số thực
, ,
a b c
thỏa mãn
7
a b c
và
15
ab bc ca
Chứng minh rằng:
11
3
a
Lời giải
Vì 7 7
a b c b c a
2
15 15 15 7 7 15
ab bc ca bc a b c a a a a
Áp dụng định lí Vi-ét đảo có
b
và
c
là nghiệm của phương trình:
2 2
7 7 15 0
x a x a a
(ẩn
x
)
Ta có:
2
2 2
7 4 7 15 3 14 11 3 11 1
a a a a a a a
Để tồn tại hai số
b
,
c
thì
11
0 3 11 1 0 1
3
a a a
Vậy
11
3
a
Bài 84. Cho ba số thực không âm
a
;
b
;
c
thay đổi thỏa mãn
3
a b c
.
Tìm giá trị nhỏ nhất của biểu thức :
2 2 2 2 2 2
2019 4026 2019 2019 4028 2019 2020 4030 2020
M a ab b b bc c a ac c
Lời giải
Ta có
2 2
2019 4026 2019 3
a ab b a b
.
Thật vậy:
2
2 2
2019 4026 2019 3
a ab b a b
.
2 2 2 2
2019 4026 2019 3 6 3
a ab b a ab b
2 2
2016 4032 2016 0
a ab b
2 2
2016 2 0
a ab b
2
2016 0
a b
(luôn đúng )
Ta có
2 2
2020 4028 2020 3
b bc c b c
.
Thật vậy:
2
2 2
2020 4028 2020 3
a ab b a b
.
2 2 2 2
2020 4028 2020 3 6 3
b bc c b bc c
2 2
2017 4034 2017 0
b bc c
.
2 2
2017 2 0
b bc c
2
2017 0
b c
( luôn đúng).
Ta có
2 2
2021 4030 2021 3
a ac c a c
.
Thật vậy:
2
2 2
2021 4030 2021 3
a ac c a c
.
2 2 2 2
2021 4030 2021 3 6 3
a ac c a ac c
2 2
2018 4036 2018 0
a ac c
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 142 GIÁO VIÊN CÙ MINH QUẢNG
2 2
2018 2 0
a ac c
2
2018 0
a c
(luôn đúng).
2 3
M a b c
.
Ta có
2
3
a b c
a b c
.
Thật vậy:
2
3
a b c
a b c
2 2 2 2 2 2
a b c ab bc ac
.
2 2 2
0
a b b c a c
(luôn đúng)
2
2 3 2 3
.9
3 3
M a b c
6 3
M
.
Vậy giá trị nhỏ nhất
6 3
M
dấu bằng xảy ra khi
1
a b c
.
Bài 85. Cho
,
a b
là các số thực sao cho
2 2
a ab b a b
. Tìm giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức
505 505
P a b
.
Lời giải
Tìm Min:
2
2 2 2
1 3
0
2 4
a ab b a b a b a b b
505 505 505. 0
P a b a b
0
MinP
. Dấu
" "
xảy ra
0
a b
.
Tìm Max:
2
2 2
3
a ab b a b a b ab a b
.
Do
2
4
a b
ab
2 2
2
3
4
4 4
a b a b
a b a b a b a b
(do
0
a b
)
505.4 2020
P
.
Dấu
" "
xảy ra
2
a b
.
2020
MaxP
tại
2
a b
Bài 86. Với các số thực không âm
, ,
a b c
thỏa mãn
3
a b c
. Tìm giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
1
.
2
P ab bc ca abc
Lời giải
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 143 GIÁO VIÊN CÙ MINH QUẢNG
Ta có
2 2 2
9
1 1 9 1
2 2 2 2 2
a b c
P ab bc ca abc abc Q
Với
2 2 2
Q a b c abc
. Ta tìm gtln gtnn của biểu thức
Q
.
Giả sử
min , ,
c a b c
⇒
3 3
a b c c
⇒
0 1
c
.
Ta có:
2
2 2 2 2
2 2 3 2
Q a ab b c ab abc c c ab c
.
Từ giả thiết có
2 0
ab c
và
2 2
3
0
4 4
a b c
ab
⇒
2
3 2
1
3 18 3
4
c c Q c c
Ta có:
2
3
1 1 16
3 18 1 2 16 4
4 4 4
c c c c
Dấu bằng xay ra khi
1
a b c
.
Do
0 1
c
⇒
1 0
c c
⇒
2
2 2
3 2 6 9 2 1 4 9 9
c c c c c c c
Dấu đẳng thức xảy ra tại
0, 0, 3
c ab a b c
hay
0, 3, 0
c a b
hoặc
0, 0, 3
c a b
⇒
GTNN
của
Q
là 4 khi
1.
a b c
Và
GTLN
của
Q
là 9 khi
0, 3, 0
c a b
và các hoán vị của nó.
Vậy
GTLN
của
P
là
5
2
khi
1
a b c
GTNN của
P
là 0 khi
0, 3, 0
c a b
và các hoán vị của nó.
Bài 87. Cho
1
xy yz xz
. Tìm giá trị nhỏ nhất của biểu thức:
2 2 2
3
M x y z
.
Ta có:
2 2
2
a b ab
với mọi
,a b
2 2
1
2 2
2
z x xz
1
Chứng minh tương tự, ta được
2 2
1
2 2
2
z y yz
2
2 2
2
x y xy
3
Từ
1
;
2
;
3
ta suy ra
2( ) 2
M xy yz zx
.
Dấu “ = ” xảy ra khi
1
5
2
1
5
2
1
1
5
2
5
x y
z
x y z
xy yz xz
x y
z
.
Vậy
M
đạt giá trị nhỏ nhất bằng 2.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 144 GIÁO VIÊN CÙ MINH QUẢNG
Bài 88. Cho
, ,
a b c
dương và
1
a b c
. Tìm giá trị lớn nhất của biểu thức
ab bc ca
A
c ab a bc b ca
.
Ta có
ab ab
c ab
c a b c ab
1 1 1
.
2
ab
ab
b c a c
b c a c
Tương tự
1 1 1
.
2
bc
bc
b a c a
a bc
;
1 1 1
.
2
ca
ca
c b a b
b ca
Suy ra
1 1 1 1 1 1
2 2 2
ab bc ca
A
a c b c b a c a c b c a
1
2
ab bc ab ac bc ac
a c a c b c c b a b a b
1 1
2 2
a b c
.
Dấu “=” xảy ra
1
3
a b c
.
Vậy giá trị lớn nhất của
A
bằng
1
2
khi
1
3
a b c
.
Bài 89 Cho 3 số thực dương
, ,
x y z
thỏa mãn điều kiện
3
x y z
Tìm giá trị nhỏ nhất của biểu thức
2 2 2
1 1 1
x y z
P
y z x
.
Lời giải
Ta có
2
2 2
1 1
x xy
x
y y
. Do
2 2
2
2
1 2
1 2 2
xy xy xy
y y
y y
(
, , 0
x y z
)
2
1 2
x xy
x
y
Tương tự:
2
1 2
y yz
y
z
;
2
1 2
z zx
z
x
Suy ra
2
xy yz zx
P x y z
Lại có
2
2 2 2
3
3
x y z
xy yz zx x y z xy yz zx
min
3 3 3
3
2 2 2
P P
. Dấu
" "
xảy ra
1
x y z
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 145 GIÁO VIÊN CÙ MINH QUẢNG
Bài 90. Cho
x
,
y
,
z
là ba số thực thỏa mãn điều kiện:
4
1 1 1
3
x x y y z z
.
Tìm giá trị lớn nhất của biểu thức
P
, biết rằng
P x y z
.
Lời giải
Theo bất đẳng thức Cauchy-Schwarz, ta có:
2
2 2 2 2 2 2
1. 1. 1. 1 1 1
x y z x y z
2
2 2 2
3
x y z x y z
Mà
4
1 1 1
3
x x y y z z
2 2 2
4
3
x y z x y z
2 2 2
4
3
x y z x y z
2 2 2
3 4 3
x y z x y z
2
4 3
x y z x y z
2
3 4 0
x y z x y z
1 4
P x y z
4
P
.
4
4
x y z
P
x y z
4
3
x y z
.
Vậy
Max 4
P
khi
4
3
x y z
.
Bài 91. Cho các số thực dương
x
,
y
thỏa mãn:
15
x y
. Tìm giá trị lớn nhất của biểu thức
1 2
A x y
Lời giải
Với các số thực dương
x
,
y
thì
0
A , giá trị của biểu thức
A
được xác định.
1 2 1. 1 1. 2
A x y x y
điều kiện:
1; 2
x y
Chứng minh công thức:
2
2 2 2 2
ax by a b x y
Áp dụng bất đẳng thức Bunhiacopxki ta có:
2 2 2
2 2 2
1. 1 1. 2 1 2 . 1 1
( 1 2).(1 1)
( 3).2
(15 3).2 36
A x y x y
x y
x y
Suy ra
6
A ( vì
0
A )
Dấu bằng xảy ra khi
1 2 1 2 1
x y x y x y
Mà
15
x y
Nên ta có hệ phương trình
15 (15 1) : 2 8
1 (15 1) : 2 7
x y x x
x y y y
(Thỏa mãn điều
kiện)
Vậy giá trị lớn nhất của biểu thức
A
là 6 khi
8;
x
7
y
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 146 GIÁO VIÊN CÙ MINH QUẢNG
Bài 92. Cho các số thực dương
x
,
y
là những số thực thỏa mãn:
8
x y xy . Tìm giá trị nhỏ
nhất của biểu thức
2 2
P x y
.
Lời giải
Ta có:
2 2 2
2 2 2 0
x y x y
với mọi
,
x y
2 2 2 2
4 4 4 4 2 4 2 0
x x y y x xy y
2 2 2 2
3 4 8 24 8
x y x y xy x y
Dấu bằng xảy ra khi
2
x y
Vậy
8
MinP
khi
2
x y
.
Bài 93. Cho hai số thực
x
,
y
thỏa mãn:
7
2
x y xy
.
Tìm giá trị nhỏ nhất của biểu thức
2 2
4 4
P x y xy
.
Lời giải
Do
7
2
x y xy
7
( )
2
xy x y
Thay
7
( )
2
xy x y
vào
2 2
4 4
y
P
x
x y
, ta có:
2 2
7
4 4
2
P x y x y
2 2
4 14 4 4
P x y x y
2 2
4 +4 4 4 1 9
x x y y
2 2
2 2 1 9
x y
.
Vì
2
2
2 0
2 1 0
x
y
với mọi
x
;
y
9
P
.
Dấu
" "
xảy ra khi và chỉ khi
2
2
2
2 0
2 0
1
2 1 0
2 1 0
2
x
x
x
y
y
y
.
Vậy giá trị nhỏ nhất của biểu thức
P
là
9
tại
2
x
và
1
2
y
.
Bài 94. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2
2 2 4
P x x x
.
Lời giải
+ Điều kiện:
2 2
x
+ Đặt
2 2 0
t x x
và
2
2 2
2 2 4 2 4 *
t x x x
2
2
4
4
2
t
x
2
4
2
t
P t
2
2 ( 1) 5
P t
Xét biểu thức
2 2 0
t x x
2 2
4 2 4
t x
Với mọi
x
thỏa mãn điều kiện xác định thì
2
4 0
x
2
4 2 4 4
x
2
4
t
2
2
t
t
Mà
0
t
nên
2
t
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 147 GIÁO VIÊN CÙ MINH QUẢNG
2
2 4 0 2 ( )
t x x tm
Với mọi
x
thỏa mãn điều kiện xác định thì
2 0
2 0
x
x
Áp dụng BĐT Cô – si ta có:
2 (2 )(2 ) 2 2 4
x x x x
2
4 2 4 8
x
2
8
t
2 2
t
Dấu “=” xảy ra
2 2 0
x x x
(thỏa mãn)
+Vì
2
t
nên
2
2
1 (2 1)
t
2
1 1
t
2
1 5 1 5
t
2 4
P
2
P
Suy ra
max
2 2 2
P khi t x
+ Vì
2 2
t nên
2
2
1 2 2 1
t
2
2
1 2 2 1
t
2
2
1 5 2 2 1 5 4 2 4
t
2 4 2 4
P
2 2 2
P
min
2 2 2 2 2 0
P t x
Vậy
max
2 2
P khi x
và
min
2 2 2 0
P khi x
Bài 95. Cho ba số thực dương
, ,
x y z
thỏa mãn
6
x y z
. Tìm giá trị nhỏ nhất của biểu
thức
3 3 3 3 3 3
2 2 2 2 2 2
x y y z z x
P
x y y z z x
.
Lời giải
Ta có:
2 2
3 3
2 2 2 2
.
x y x y xy
x y
x y x y
2 2
. .
2 2
xy x y xy x y
x y
x y x y
x y xy
Tương tự ta có:
3 3 3 3
2 2 2 2
;
2 2
y z y z z x z x
y z z x
Khi đó ta có:
3 3 3 3 3 3
2 2 2 2 2 2
2 2 2
x y y z z x x y y z z x
P
x y y z z x
6
P x y z
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 148 GIÁO VIÊN CÙ MINH QUẢNG
Dấu “=” xảy ra
2
6
x y
y z
x y z
z x
x y z
.
Vậy
Min 6
P
khi
2
x y z
.
Bài 96. Cho
x
,
y
,
z
là các số dương thỏa mãn
2020
x y z
.
Tìm giá trị lớn nhất của biểu thức
2020 2020 2020
xy yz zx
P
z xy x yz y zx
.
Lời giải
Thay
2020
x y z
vào biểu thức
P
ta được :
xy yz zx
P
x y z z xy x y z x yz x y z y zx
2 2 2
xy yz zx
xz yz z xy x xy xz yz xy y yz zx
Áp dụng bất đẳng thức Cô-si, ta có :
2
.
xy xy xy xy
x z y z
x z y z
xz yz z xy
1
2
xy xy
y z x z
1
2
1
.
2
yz yz yz yz yz yz
x z x y x z x y
x z x y
x xy xz yz
2
2
1
.
2
zx zx zx zx zx zx
x y y z x y y z
x y y z
xy y yz zx
3
Cộng 2 vế
1
,
2
,
3
ta được :
2 2 2
xy yz zx
xz yz z xy x xy xz yz xy y yz zx
1
2
xy xy yz yz zx zx
y z x z x z x y x y y z
1
2
xy zx xy yz yz zx
y z y z x z x z x y x y
1
2
x y z y x z z x y
y z x z x y
1
2
x y z
2020
1010
2
Dấu “=” xảy ra khi và chỉ khi
2020
x y z
x y z
2020
3
x y z
.
Vậy giá trị lớn nhất của biểu thức
1010
P
khi
2020
3
x y z .
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 149 GIÁO VIÊN CÙ MINH QUẢNG
Bài 97. Cho
0
x
,
0
y
,
0
z
và
2 3 20
x y z
Tìm giá trị nhỏ nhất của biểu thức
3 9 4
2
P x y z
x y z
Lời giải
3 3 3 9 4
4 2 4 4 2 2 4
x y z x y z
P
x y z
Ta có :
3 2 3
5
4 2 4 4
x y z x y z
Ta có :
3 3 3 3
2 . 3
4 4
x x
x x
Ta có :
9 9
2 . 3
2 2 2 2
y y
y y
Ta có :
4 4
2 . 2
4 4
z z
z z
13
P
Vậy giá trị nhỏ nhất
13
P
dấu bằng xảy ra khi
2
x
;
3
y
;
4
z
Bài 98 Với
, 0
x y
, tìm giá trị nhỏ nhất của biểu thức
2 2
16
1 1
P x y
x y
.
Lời giải
Ta có
2 16 32
1 1
2 2
1 1
x y
x y
x y
x y
2
2 2
2
x y
x y
Khi đó
2
64
2
2
P x y
x y
Lại có
2 2
4 4 12 4 2
x y x y x y x y
64 64
2 12 4 2 2 4 2 . 32
2 2
P x y x y
x y x y
min
2 20 10 10
P P P
Dấu
" "
xảy ra
1
x y
.
Bài 99. Cho ba số
, , 0
x y z
thỏa mãn
x y z xyz
.
Tìm giá trị lớn nhấ tcủa biểu thức
2 2 2
1 1 1
x y z
S
yz x xz y xy z
.
Lờigiải
2 2 2
. . .
1 1 1
x y z x y z
S
yz xyz x xz xyz y xy xyz z
yz x xz y xy z
.
Mà theo đề bài,
x y z xyz
nên ta có:
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 150 GIÁO VIÊN CÙ MINH QUẢNG
. . .
x y z
S
yz x y z x xz x y z y xy x y z z
x y z
yz xz x x y xz yz y x y xy zy z x z
x y z
z x y x x y z x y y x y y x z z x z
x y z
z x x y z y x y y z x z
1
.
Tacó
, , 0
x y z
nên suy ra
x
z x
,
x
x y
,
y
z y
,
y
x y
,
z
y z
,
z
x z
đều là số dương.
Với
, , 0
x y z
, áp dụng bất đẳng thức Côsi cho 2 số dương ta được
2 . 2.
x x x x x
z x x y z x x y
z x x y
2
.
2 . 2.
y y y y y
z y x y z y x y
z y x y
3
.
2 . 2.
z z z z z
y z x z y z x z
y z x z
4
.
Dấu
" "
của
2
,
3
,
4
đồng thời xảy ra khi và chỉ khi
0
x y z
.
Cộng vế với vế của
2
,
3
,
4
ta được
2.
x x y y z z x y z
z x x y z y x y y z x z
z x x y z y x y y z x z
2.
x z x y y z x y z
z x x y z y
z x x y z y x y y z x z
3 2.
x y z
z x x y z y x y y z x z
3
2
x y z
z x x y z y x y y z x z
5
.
Từ
1
và
5
suy ra
3
2
S
.
Dấu
" "
xảy ra khi và chỉ
khi
, , 0x y z
x y z xyz
x y z
3
, , 0
3
x y z
x x
x y z
2
, , 0
3
x y z
x
x y z
, , 0
3
x y z
x
x y z
3
x y z (thỏa mãn).
Vậy giá trị lớn nhất của
S
bằng
3
2
S
đạt được khi
3
x y z
.
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 151 GIÁO VIÊN CÙ MINH QUẢNG
Bài 100. Cho
x
,
y
là các số thực dương thỏa mãn
1
x y
.
Tìm giá trị nhỏ nhất của biểu thức
2 2
1 2
4A xy
x y xy
Lời giải
Cho các số thực dương
x
,
y
ta có:
1 1
4
x y
x y
1 1 4
x y x y
Thật vậy
2
x y xy
;
1 1 2
x y
xy
1 1
4
x y
x y
1 1
4
x y
x y
.
Ta có
2
x y xy
1 2
xy
1
4
xy
.
2 2
1 2
4A xy
x y xy
2 2
1 1 1 5
4
4 2 4
xy
xy x y xy xy
.
Ta có
1
4 2
4
xy
xy
.
2
2 2
1 1 4
4
2x y xy
x y
.
2
5 5
5
4xy
x y
.
11
A
.
Vậy giá trị nhỏ nhất
11
A
dấu bằng xẩy ra khi
1
2
x y
.
Bài 101. a) Cho
, ,
x y z
là ba số dương. Chứng minh
1 1 1
9
x y z
x y z
b) Cho
, ,
a b c
là ba số dương thỏa mãn
6.
a b c
Tìm giá trị lớn nhất của biểu thức
3 2 3 2 3 2
ab bc ca
A
a b c b c a c a b
Lời giải
a) Áp dụng bất đẳng thức
2
x y
y x
cho hai số
0; 0
x y
ta chứng minh được
1 1 1
9
x y z
x y z
Áp dụng bất đẳng thức ở phần a) ta có:
9
3 2 2
ab ab ab a
;
a b c c a c b
9
3 2 2
bc bc bc b
;
b c a a c a b
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 152 GIÁO VIÊN CÙ MINH QUẢNG
9
3 2 2
ca ca ca c
c a b b a b c
Cộng theo các vế của ba bất đẳng thức trên ta được
9
2 2 2
ab ab a bc bc b ca ca c
A
c a c b a c a b b a b c
9
2
ab bc ab ca bc ca a b c
A
c a a c c b b c a b b a
Bài 102. Cho hai số thực dương
,
a b
thỏa mãn
3 1
a b ab
.
Tìm giá trị lớn nhất của biểu thức
2 2
12ab
P a b
a b
.
Ta có:
2 2 2 2
(a ) 0 2 (a ) 4 ;
b a b ab b ab
2
2 2
(a )
2
b
a b
Từ giả thiết
3 1
a b ab
2
3
1 3 1
4
a b ab a b
2
2
3 4 4 0 2 3 2 0 .
3
a b a b a b a b a b
3 1 ( ) 1 3 1
1 1 .
2 2
ab a b
a b a b a b
2
2 2 2 2
2 2
.
2 9 9
a b
a b a b
2 2 2 2
12 3 2 16
4. 2 .
9 9
ab ab
P a b a b
a b a b
Giá trị lớn nhất của P bằng
16
9
khi
1
3 1
3
a b
a b
a b ab
.
| 1/58
| | Tải xuống

Có thể bạn quan tâm:

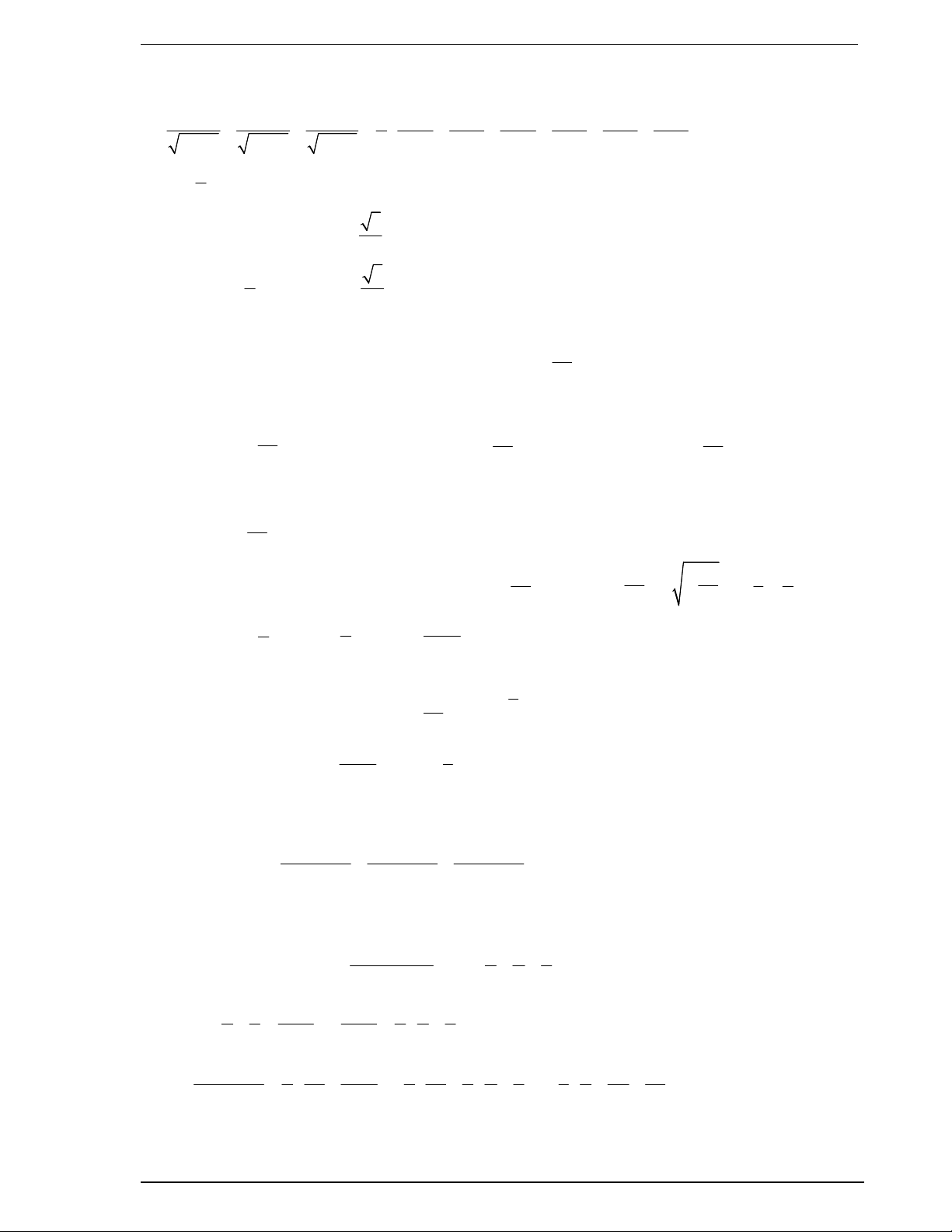
Preview text:

CHUYÊN ĐỀ BẤT ĐẲNG THỨC BÀI TẬP VẬN DỤNG 1
Bài 1. Với x, y, z là các số thực dương sao cho . x . y z  . 6 1 1 1 Chứng minh:    1. 3 3 3 3 3 3 x  8y 1 8y  27z 1  27z  x 1 Lời giải 1 Có: . x . y z   6 . x . y z  1 6 Ta có: x   y3 3 2  . x 2y x  2y  x  2y3 1 1 3
1  2xy  x  2y  3z   x  2y3 3
1 2xy  x  2y  3z Chứng minh tương tự: 1 1 
2y3  3z3 1 6yzx  2y 3z 1 1  3z3 3
 x 1 3xz  x  2y  3z 1 1 1 1  1 1 1         
x  2y3 1 2y3  3z3 1 3z3 3 3
 x 1  x  2y  3z  2xy 6yz 3zx  1 1 1    1. 3 3 3 3 3 3 x  8y 1  8y  27z 1  27z  x 1
Bài 2. Cho x , y là các số thực dương thỏa mãn x  y  3 .
Tìm giá trị nhỏ nhất của biểu thức: 2 3 A   3xy y 1 Lời giải 2 3 2 3 A     3xy y 1 3xy 3 y   1 2 6 2 xy 6 y  4 1         xy  y 2  3xy 3  y 1 3xy 6 y  4 6 6 3
   2 2  3 1  A  2  . y  x   1 6  3 y 1  1   y   y   1   y   y 1
   y  y   2 4 1 2 . 3 1 2 . 4 2 4 4     y  22 2 6 6 6 3 3 6 4  A  với mọi x, y . 3 Vậy 4 A  khi x  1; y  2 . Min 3
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 95 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC Bài 3. Cho các số dương 1 a,b thoả mãn  3 3 a  b  a  b 2 2  ab  a  b 1. 3 2 2 a  8 b  2
Tìm giá trị nhỏ nhất biểu thức: M   . a b Lời giải Ta có 1  1 3 3 a  b  a  b 2 2
 ab  a  b 1  a  b 2 2 a  b  ab   2 2 1  a  b  ab 1 3 3 Vì 2 2 a  b  ab 1  0 a  ,b R 1
 a  b 1  a  b  3 3 Khi đó ta có 2 2 a  8 b  2 8 2 4 1 4 1 M  
 a   b   a   b    a b a b a b a b  4   1   4 1   M  a   b           a   b   a b 
Áp dụng bất đẳng thức Co-si cho các cặp số dương ta có:  4 4 a   2 . a  2 4  4 a a    1 1 b    2 . b  2 1  2 b b   4 1 2 2 1 9      3 a b a  b 3
GTNN của M là 4  2  3  9 .  4 a   a   1 a  2
Dấu “ ” xảy ra khi  b    b  b 1 a  2b 
Vậy M đạt giá trị nhỏ nhất là 9khi a  2;b  1.
Bài 4. Cho x , y là các số thực dương thỏa mãn 2 2 x  y  1 .
Tìm giá trị nhỏ nhất của biểu thức: 1 1 P  x   y  . x y Lời giải  x , y  0 :
x  y2   x  xy  y   x  y   x  xy  y  x  y   x  y2 2 2 2 2 2 2 2 2 0 2 0 2 2 2  x  y   2 2 2 x  y  .
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 96 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC   2 x  y
x y  0  x  2xy  y  0  x  2xy  y  4xy   x  y2 4 2 2 2 2  4xy   xy x  y 1 1 4    . x y x  y 1 1 1 1 1  1 1  1 1 1 4 P  x   y   x   y     2 . x  2 y.  .   = 2 2 2  x y 2x 2y 2  x y  2x 2 y 2 x  y x  y 2 2 P  2 2   2 2   3 2 . 2 2 2 x  y  2.1
Dấu "  " xảy ra khi và chỉ khi 2 x  y  . 2
Vậy giá trị nhỏ nhất của P là 3 2 khi 2 x  y  . 2 Bài 5. Chứng minh rằng: Với mọi  1   1  x  1,ta luôn có 2 3 3 x   2 x   2   3   x   x  Lời giải Ta có  1   1 2 3  3 x   2 x   2   3   x   x   1   1 3 2   2 x   3 x   0  3   2   x   x   1  2 3 2   x  2x   3x   2  0   2   x  x x   1   2 1 4 2   x  2x  2  x  2    4x   2  0    2 x  x x x      1    2  1  2   2   x  x 2x  1 
2x  1  2 2x  1  0          x  x x x  x          1  1  2   x  x   2 2x  1  0      x  x  x   1    x  2 1  2   x    2x  1  0      x  x    x     1 x   0  x   x  2 1 Vì x  1 nên   0 . x   2 2x  1  0  x 
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 97 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 6. Cho a,b,c là các số thực dương thỏa mãn: ab  bc  ac  3abc . Tìm giá trị nhỏ nhất của 2 2 2 a b c biểu thức K    . c  2 2 c  a  a 2 2 a  b  b 2 2 b  c  Lời giải 1 1 1 ab  bc  ac  3abc     3 (1) a b c 2 2 2 2  1 Cauchy a a c c ac 1 1 Ta có       . c  2 2 c  a  c 2 2 c  a  c 2 2 c  a  c a 2 2 c  a  c 2a 2 b 1 1 2 c 1 1 Tương tự,   ,   . a  2 2 a  b  a 2b b 2 2 b  c  b 2c  1 1  1 1 1  3 Khi đó K       . 2  a b c  2 3
Vậy Min K   a  b  c 1. a,b,c0 2
Bài 7. điểm) Cho a , b là các số khác 0 thỏa mãn điều kiện:       2 a b ab a b  ab . Tìm giá
trị lớn nhất của biểu thức 1 1 P    2 . 3 3 a b Lời giải Theo giả thiết:       2 a b ab a b  ab 2 2 2 2
 a b  ab  a  ab  b Do 1 1 1 1 1
a  0 ; b  0 nên chia cả hai vế cho 2 2 a b ta được:     . 2 2 a b a ab b Đặt 1 x  ; 1 y  ta được : a b 2 2
x  y  x  xy  y (1)
 x  y  x  y2  3xy x  y2 x  y  xy   3 3 x  y2
Mà  x  y2  4xy hay xy  4
x  y2 x  y x  y2 Suy ra   3 3 4
  x  y2  4x  y  0  0  x  y  4
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 98 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC Ta có: 1 1 P    2 3 3
 x  y  2  x  y 2 2
x  xy  y   2   x  y2  2 (do 1) 3 3 a b
Mà 0  x  y  4 nên  x  y2 2  2  18 .
Vậy giá trị lớn nhất của P là 18 khi x  y  2 và 1 a  b  . 2
Bài 8. Cho các số thực thỏa mãn 2 2 x  y – xy  4 .
Tìm GTLN và GTNN của biểu thức 2 2 P  x  y . Lời giải +) Tìm GTLN của P : Ta có 2 2 x  y – xy  4 2 2
 2x  2y – 2xy  8  x  y  x  y2 2 2
 8  P  x  y2  8  P  x  y2 8
Ta có  x  y2  0 với mọi , x y Suy ra P  8 x  y  0 Max P  8    x  y  2  . 2 2 x  y  xy  4
Vậy Max P  8 khi x  y  2 . +) Tìm GTNN của P : Ta có 2 2 x  y – xy  4 2 2  2x  2y – 2xy  8
 x  y x  y2 2 2 3
 8  P   x  y2 3 8
Ta có  x  y2  0 với mọi , x y 8 Suy ra 3P  8  P  3  2 x   3 y  x    2  2 y    8 x  y  0 y  x  x   3 Min P         3   3 2 2 2 x  y  xy  4 3  x  4    2  2     x x      3  3   2   y    3 8 2 2 2 2 Vậy Min P  khi x  ; y   hoặc x   ; y  . 3 3 3 3 3
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 99 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 9. Cho ba số dương a , b , c thỏa mãn ab  bc  ca  1 2 2 2 a b c
Tìm giá trị nhỏ nhất của biểu thức: A    a  b b  c c  a Lời giải a b c    2 2 2 2 a b c
Áp dụng bất đẳng thức:    , ta được x y z x  y  z a b c a  b  c2 2 2 2 2a  b  c A      a  b b  c c  a 2a  b  c 4
         2 ab bc ca a b b c c a    1    4 4 2
Dấu "  " xảy ra khi a  b  c 1. 2 2 2 a b c
Vậy giá trị nhỏ nhất của biểu thức: A   
là 1 khi a  b  c 1. a  b b  c c  a 2 Bài 10. Cho 3 2 2 2
x  y  z  . Chứng minh: 814x  814y  814z 33 7 . 7 Lời giải ĐKXĐ: 4 x, y, z  . 7
Áp dụng bất đẳng thức Cô –si cho hai số không âm 82 7 và 814x, ta có:        x 8 2 7 8 14x 8 2 7 8 14  2    2
7 1 814x 8 7 7x 8  7  7x  814x  . (1) 7 1
Chứng minh tương tự, ta có: 8  7  7y 814y  . (2) 7 1 8 7  7z  814z  (3) 7 1
Cộng theo vế các bất đẳng thức (1), (2), (3) ta được:
24 3 7  7x  y  z
8 14x  814y  814z  . 7 1 Ta có:
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 100 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC x y z2 2 2 2
 x  y  z  2xy  2yz  2zx .
Mà: xy  yx  zx   2 2 2 2 2 2 2 x  y  z .
Suy ra: x  y  z2 3 3 9 2 2 2 x  y  z  3.  . 7 7 3 Do đó: x  y  z  . 7 Suy ra: 3 24 3 7  7. 3 7  82 7 24 6 7 
814x  8 14y  814z     33 7 . 7 1 7 1 7 1 1
Dấu “=” xảy ra khi và chỉ khi x  y  z  . 7
Bài 11. Tìm cặp số (x ; y) với y là số nhỏ nhất thỏa mãn điều kiện
x2 + 5y2 + 2y – 4xy – 3 = 0 Lời giải
Phương trình có nghiệm ẩn x khi và chỉ khi 2   y   2 4 5y  2 y  3  0 2   y  2y  3  0   y  2
1  4  2  y 1  2  3  y  1
Giá trị nhỏ nhất của y là 3  khi đó phương trình 2
 x 12x  36  0  x  6 Bài 12. Cho 3  x  5. 2 2 1
Tìm giá trị nhỏ nhất của biểu thức: A    x  3 5  x (x  3)(5  x) Lời giải
Ta có 3  x  5 nên x  3  0;5  x  0 2 2 4 4 Áp dụng BĐT Cauchy:   2.  x  3 5  x x 35 x x 35 x 3 A  x 35 x   
Áp dụng BĐT Cauchy:     x x 3 5 x x 3 5   1 2 1 Suy ra 1 x 35 x Suy ra A  3.
Vậy GTNN A  3 khi và chỉ khi x  3  5  x  x  4.
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 101 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 13. Cho x, y là các số thực dương thỏa mãn điều kiện x  y  6 . Tìm giá trị nhỏ nhất của 6 24
biểu thức: P  x  y   . x y Lời giải 6 24 4 16 2 8 Ta có: P  x  y    x   y    x y x y x y   2 1 2 9  2 4  2 16  2  4  8  2.  15 x  y 6
Vậy giá trị nhỏ nhất của P 15. Dấu bằng xảy ra khi x  2; y  4 Bài 14. Cho a, ,
b c  0 . Chứng minh rằng 2 2 2 a b c 2 2 2 2 2 2  
 a  ab  b  b  bc  c  c  ca  a . b c a Lời giải 2 2 2 Đặt a b c 2 2 2 2 2 2  
 a  ab  b  b  bc  c  c  ca  a (*). b c a 2 2 2 Vì a b c a, ,
b c  0 nên áp dụng bất đẳng thức Cô-si cho các số không âm a,b,c, , , ta được b c a 2 2 a a 2 2 2 2  b b c c b  2 .b  2a ,  c  2 .c  2b ,  a  2 .a  2c b b c c a a 2 2 2 2 2 2 2 2 2   Suy ra a b c a b c a b c    a  b  c  2        a  b  c (1) b c a  b c a  b c a 2 2 2 2 2 2 2 2 2       Ta có a b c a ab b b bc c c ca a    a  b  c     a  b  c . (2) b c a b c a 2 2 2 2 2 2      
Áp dụng bất đẳng thức Cô-si cho các số không âm a ab b b bc c c ca a ,b, ,c, , a b c a ta được 2 2 2 2 2 2 a  ab  b b  bc  c c  ca  a 2 2 2 2 2 2  b  2 a  ab  b ,  c  2 b  bc  c ,  a  2 c  ca  a b c a (3) 2 2 2   Từ (1), (2) và (3) suy ra a b c 2 2 2 2 2 2 2  
  2 a  ab  b  2 b  bc  c  2 c  ca  a hay  b c a  2 2 2 a b c 2 2 2 2 2 2  
 a  ab  b  b  bc  c  c  ca  a b c a
Do đó (*) được chứng minh. Dấu bằng xảy ra khi dấu bằng tại (1) và (4) xảy ra. Tức là
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 102 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 2 2 2 a b c  , b  c,  a 2 2 2 2 2 2  b c a a   b ,b  c ,c  a    2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 a  ab  b b bc  c c  ca  a 
a  ab b  b ,b bc  c  c ,c ca  a  a  , b  , c  a  b c a 2 2 2 2 2 2 a  b ,b  c ,c  a   .
a(a  b)  0,b(b  c)  0,c(c  a)  0 Vì a, ,
b c  0 nên suy ra dấu bằng xảy ra khi a  b  . c
Bài 15. Cho a, b, c là độ dài 3 cạnh của một tam giác. Tìm giá trị nhỏ nhất của biểu thức: a b c P    2 2 2 2 2 2 2 2 2 2b  2c  a 2a  2c  b 2a  2b  c
Vì a,b,c là 3 cạnh của tam giác nên 2 2 2 2 2 2 2 2 2
2a  2c  b , 2a  2b  c , 2b  2c  a đểu là các số dương. Áp dụng công thức Cauchy ta có: a  b  c  a 3a 2b  2c  a  2 2 2 2 2 2 2 2 3 2 2 2 2 2   a  b  c 2 2 2 a a 3 a 3 Ta có:   2b  2c  a 3a 2b  2c  a  2 2 2 2 2 2 2 2 2 2 a  b  c 3  2 2 2 a  b  c a b c   P      3 2 2 2 2 2 2 2 2 2 2 2 2 2b  2c  a 2a  2c  b 2a  2b  c a  b  c
Vậy GTNN P  3 khi và chỉ khi a  b  c hay là tam giác đều.
2) Ta coi như hình vẽ thành bài toán đường tròn tâm O nội tiếp tam giác đều ABC vậy tâm
O của đường tròn sẽ trùng với trọng tâm tam giác ABC vậy nên đường cao của tam giác
đều là 3R (với R là bán kinh đường tròn O ) Suy ra 2.3R BC   2 3 . R 3 Thể tích hình nón là: 1 1
V   R .h    3R2 2 3 .3R  3 R 3 3 Thể tích hình cầu là: 4 3 V   R 3
Vậy tính thể tích theo R phần hình nón nằm bên ngoài quả cầu kem là 4 5 3 3 3
V  3 R   R   R . 3 3
Bài 16. Cho ba số dương a , b , c thoả mãn ab  bc  ca  1. 2 2 2 a b c
Tìm giá trị nhỏ nhất của biểu thức A    . a  b b  c c  a
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 103 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC Lời giải
Áp dụng bất đăng thức Bu-nhi-a-cốp-xki ta có   
a  b  c A  a  b  b  c  c  a 2 2 2 a b c 2 2      (a  b  c) a  b b  c c  a   a b c Suy ra A    2
Áp dụng bất đẳng thức Cô-si ta có a  b  2 ab b  c  2 bc c  a  2 ca
Suy ra a  b  b  c  c  a  2 ab  bc  ca  2.1 2 a  b  c 1
Suy ra 2a  b  c  2, hay  2 2 a b c 1 Vậy nên A     2 2 1 1
Khi a  b  c  thì A  3 2 1
Vậy giá trị nhỏ nhất của A là . 2 2 2 a  2b
Bài 17. Cho a,b  0 thỏa mãn 2a  ab  4  0. Tính giá trị nhỏ nhất của T  . ab Lời giải
Ta có 2a  ab  4  0  a2 b  4.
Kết hơp với a  0 ta suy ra b  2 4  a  . 2  b Ta có a 2b 7a a 2b 7a T       1 b a 8b 8b a 8b 7 4 7 1 9  T  .     . 8 b2  b 1 . 1 2 2  2  b  b  2    2 
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 104 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC  4
Dấu bằng xảy ra khi và chỉ khi a     b  a 4 2 . b  1 2 b  b
Vậy giá trị nhỏ nhất của T là 9 , đạt được khi a  4 và b 1. 2
Bài 18. ) Cho các số thực x; y; z thỏa mãn 2  x  3;4  y  6;4  z  6 và x  y  z 12 .
Tìm giá trị lớn nhất của biểu thức P  xyz . Lời giải 2   Ta có  P  x  yz y z 1  x  x  
12  x12  x .  2  4 3 3      1    x  x  x 1 x 24 1 3 24 243 3 12 12          . 12 12  3  12  3  4 243 9 Vậy MaxP  khi x  3; y  z  . 4 2
Bài 19. Cho x , y là các số thực thỏa mãn 2 2 x  xy  y  3.
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức 2 2 P  x  y . Lời giải Ta có 2 2 x  xy  y    2 2 3 2 x  xy  y   6
x  y x y2   P  x y2 2 2 6 6  6  x  y  x  y  x  y  3 Dấu “ ”  xảy ra       2 2 2 x  xy  y  3 x  3 x  y   3  x  y  3
GTLN của P là 6 khi và chỉ khi  x  y   3 +) Có
 x  xy  y   x  y  x  y2 2 2 2 2 6 2 3
 P  x  y2   P   x  y2 1 3 6 3 6
 P  x  y2  2  2 3  x 1   x   y  x   y  y  1  Dấu “ ”  xảy ra      2 2 2 x  xy  y  3 3  x  3 x  1    y 1  x 1 x  1 
Vậy GTNN của P là 2 khi và chỉ khi  hoặc  y  1   y  1
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 105 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC Bài 20. Cho biểu thức 2 2 M  x  y với ,
x y là các số thực thỏa mãn 0  y  x  4 và x  y  7 .
Tìm giá trị lớn nhất của biểu thức M Lời giải Ta có 2 2 2 2
M  x  y  x  xy  xy  y  x  x  y  y  x  y
Do 0  y  x  4 và x  y  7 nên M  4x  y  7y M  4x  3y
M  3 x  y  x  3.7  4 M  25
Dấu “=” xảy ra  x  4; y  3
Vậy Max M  25 khi và chỉ khi x  4; y  3
Bài 21. Cho x, y là các số dương thỏa mãn điều kiện x  y  5 . Chứng minh 25 12,5 rằng:   4. 2 2 x  y xy Lời giải
Dễ dàng chứng minh được với a  0, b  0 ta có 1 1 4  
(1). Dấu “=” xảy ra khi và chỉ a b a  b khi a  b .
Áp dụng bất đẳng thức (1) ta có: 1 1 4 4    25 12,5    4 . 2 2 x  y 2xy x  y2 25 2 2 x  y xy
Dấu “=” xảy ra khi và chỉ khi x  y  2,5 ( thỏa mãn).
Bài 22. Cho x , y , z là các số thực thỏa mãn x  7 , x  y  12 và x  y  z  15 . Tìm giá trị
nhỏ nhất của biểu thức 2 2 2 A  x  y  z . Lời giải
Ta có: x  7 , x  y  12 và x  y  z  15 x  2 7  0,x 2  x 14x  49  0 2  x 14x  49  y  2 5  0, y  2  y 10x  25  0 2  y  10y  25 z  2 3  0,z 2  z  6z  9  0 2  z  6x  9 2 2 2
 A  x  y  z 14x 10y  6z  83
 A  6x  6y  6z  4x  4y  4x 83
 A  6x  y  z  4x  y  4x 83
 A  6.15  4.12  4.7 83 (vì x  7 , x  y  12 và x  y  z  15) A  83.
Dấu “ = ” xảy ra khi x  7 , y  5 , z  3 (thỏa mãn)
Vậy A đạt giá trị nhỏ nhất bằng 83 khi x  7 , y  5 , z  3
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 106 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 1 1 1 Bài 23. Cho a, ,
b c là các số dương thay đổi thỏa mãn  
 2020 . Tìm giá trị lớn a  b b  c c  a 1 1 1
nhất của biểu thức P   
2a  3b  3c 3a  2b  3c 3a  3b  . 2c Lời giải
Áp dụng bất đẳng thức Cauchy cho các số dương a, , b , c d ta có : 4
a  b  c  d  4 abcd 1 1 1 1 1 4     4 a b c d abcd  
 a  b  c  d  1 1 1 1     16    a b c d  1 1 1 1 16      a b c d a  b  c  d 1 1 Ta có :  2a  3b  3c
(a  b)  (a  c)  (b  c)  (b  c)
Áp dụng bất đằng thức phía trên ta có : 1 1  1 1 1 1   .     
(a  b)  (a  c)  (b  c)  (b  c) 16  a  b a  c b  c b  c  1 1  1 1 2    .    
2a  3b  3c 16  a  b a  c b  c 
Chứng minh tương tự ta có: 1 1  1 1 2   .    
3a  2b  3c 16  a  b b  c a  c  1 1  1 1 2   .    
3a  3b  2c 16  a  c b  c a  b  1  1 1 1   P  .4    
16  a  b a  c b  c  1  P  .2020  505 4 3
Dấu ‘’= “ xảy ra khi a  b  c  4040 . Bài 24. Cho biểu thức 2 2 M  x  y với ,
x y là các số thực thỏa mãn 0  y  x  4 và x  y  7 .
Tìm giá trị lớn nhất của biểu thức M Lời giải Ta có 2 2 2 2
M  x  y  x  xy  xy  y  x  x  y  y  x  y
Do 0  y  x  4 và x  y  7 nên M  4x  y  7y
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 107 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC M  4x  3y
M  3 x  y  x  3.7  4 M  25
Dấu “=” xảy ra  x  4; y  3
Vậy Max M  25 khi và chỉ khi x  4; y  3
Bài 25. Tìm giá trị nhỏ nhất của biểu thức: A  x  2y  2x 1  5 4y 1 16 . Lời giải
A  x  2y  2x 1  5 4y 1 16
 2A  2x  4y  2 2x 1 10 4y 1  32  2A  2x  
1  2 2x 1 1  4y  
1  2 4y 1.5  25  8    
 A   x   2  y   2 2 2 1 1 4 1 5  8  8 (với mọi 1 3 x  ; y  ). 2 4  A  4 .           Min A  4 2x 1 1 0  2x 1 1 0     2x 1 1 x  ; y  ). 4y 1  5  0  4y 1  5  0  4y 1  (với mọi 1 3 25 2 4 x  1   13  (nhận). y   2 x  1  Vậy Min A  4  13  . y   2
Bài 26. Cho a , b , c  0 thỏa mãn a  2b  3c  20. Tìm GTNN của biểu thức A . Biết 3 9 4 A  a  b  c    . a 2b c Lời giải Ta có: 3 9 4  3a 3   b 9   c 4  1 A  a  b  c                 a  2b 3c a 2b c  4
a   2 2b   4 c  4
Áp dụng BĐT Cô – si cho hai số không âm, ta được 3a 3 3a 3   2 .  3 4 a 4 a b 9 b 9   2 .  3 2 2b 2 2b c 4 c 4   2 .  2 4 c 4 c
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 108 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC Do đó 1
A  3  3  2  a  2b  3c 13. 4
Dấu “ ” xảy ra khi a  2; b  3; c  4.
Vậy GTNN của biểu thức A bằng 13 khi a  2; b  3; c  4. 3 2
x  2 y  4 y  3  0    1
Bài 27. Cho hai số thực x , y thoả mãn hệ điều kiện:  .. 2 2 2 x  x y  2 y  0  2
Tính giá trị của biểu thức: 2020 2020 P  x  y . Lời giải Từ  
1 ta có: x    y  2 3 2
1 1  1  x  1. 3 2 2 y  Từ  2 y y 1 2 ta có: 2 x   2 x    1  1  x  1 . 4 2 y  1 2 2 y  1 y  1
Từ 3 và 4 , suy ra x  1  y  1. Vậy P  2 .
Bài 28. Cho đường thẳng d : y   2 m  
1 x  4 . Tìm m để khoảng cách từ gốc tọa độ đến
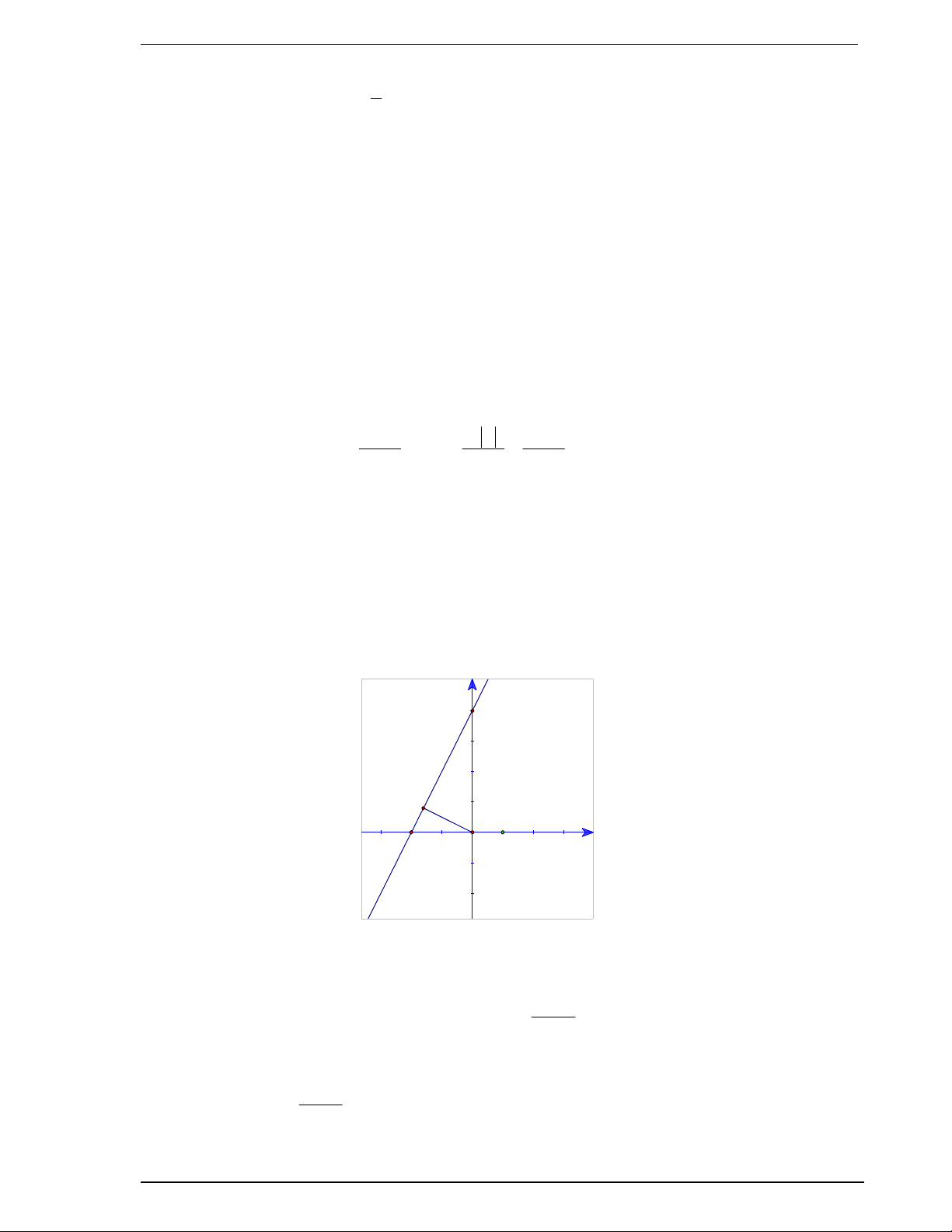
đường thẳng d lớn nhất. Lời giải y A H B O 1 x (d) Vì 2
m 1  0 với mọi m nên đường thẳng d luôn xác định.
Gọi A là giao điểm của đường thẳng d với trục Oy , B là giao điểm của đường thẳng d với   trục 4 
Ox . Khi đó tọa độ của A và B là A0;4 ; B ; 0  . 2   m 1 
Vẽ OH  AB , khi đó OH là khoảng cách từ gốc tọa độ đến đường thẳng d . Ta có 4 OA  4 ; OB  . 2 m 1
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 109 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Xét tam giác OAB vuông tại O , vì OH  AB nên theo hệ thức lượng trong tam giác vuông ta 1 m  2 m  2 2 2 1 1 1 có: 1 1 1      4  OH  . 2 2 2 OH OA OB 16 16 16 m  2 2 1 1 Ta có 2
m  0 với mọi m  m  2 2 1  1 với mọi m   4 4
m  2    m  2 2 2 1 1 2
1 1  2 với mọi m  OH    2 2 . m  2 2 2 1 1
Dấu đẳng thức xảy ra khi và chỉ khi m  0.
Vậy với m  0 thì khoảng cách từ gốc tọa độ đến đường thẳng d đạt giá trị lớn nhất là 2 2 .
Bài 29. Một doanh nghiệp xuất khẩu gạo ước tính rằng , trong tháng 2/2020 , nếu doanh
nghiệp xuất khẩu gạo với giá là 500 USD/tấn thì họ sẽ xuất khẩu được khoảng 860 tấn gạo.
Tuy nhiên nếu hạ giá gạo và cứ mỗi lần giảm giá 25 USD/tấn thì sẽ xuất khẩu thêm được 50
tấn gạo. Hỏi doanh nghiệp cần bán gạo với giá bao nhiêu USD mỗi tấn để doanh thu xuất
khẩu gạo trong tháng 2/2020 là lớn nhất? Lời giải
Doanh thu dự kiến xuất khẩu trong tháng 2 là 860 500  430000 (USD)
Gọi số lần giảm giá là x (lần), điều kiện * x   ,0  x  20
Giá gạo sau khi giảm giá là 500  25x (USD/tấn)
Số gạo xuất khẩu được sau khi giảm giá là 860  50x (tấn)
Doanh thu sau khi giảm giá gạo là P  500  25x860  50x (USD)
Để doanh thu xuất khẩu gạo trong tháng 2/2020 là lớn nhất thì P phải lớn hơn 430 000 P      x  x 2 430000 0 500 25 860 50  430000  0  1  250x  3500x  0
 50x70  25x  0  0  x  2,8 . Vì x  *   x1;  2 .
Với x  1 P  432 250 .
Với x  2  P  432000 .
Vậy doanh nghiệp bán gạo với giá 475 USD/tấn để doanh thu trong tháng 2/2020 lớn nhất .
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 110 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 30. Cho x , y là hai số không âm thỏa mãn 2 2
x  y  4 . Tìm giá trị lớn nhất của biểu thức:
A  x 2y  x  5y  y 2x y  5x . Lời giải
Với mọi a , b ta có a  b2   a  b2   2 2
a  b   a  b   2 2 0 2 2 a  b 
Áp dụng kết quả trên ta được A  x y  x  y  y x  y  x   2x  2 xy  y  2  y  2 2 5 2 5 2 2 5 2 xy  5x  
 xyx  y  xy2 2 2 2 2 20    xy xy2 2 8 20  2 2 x y
Mặt khác theo bất đẳng thức Cô-si với hai số không âm x , y ta có xy   nên 2 4 ta có xy   2. 2 Vậy nên A   xy xy2   2 2 8 20 2 8.2  20.2   8 3 .
Khi x  y  2 thì A  8 3 , do đó giá trị lớn nhất của A là 8 3 .
Bài 31. Giải phương trình 2
2x  5  7  2x  3x 18x  29 Lời giải
Đặt a  2x  5, b  7  2x  a,b  0 Ta có:  a  b  2  Phương trình có dạng: ab 35 a  b  3.  29  4
  a  b  3ab 11 4
Bình phương hai vế phương trình ta có: ab ab 2 2  a b  ab     ab 2 2 16 2 9 66 121 16 2 2  9a b  66ab 121 2 2
 9a b  66ab  32 ab  89  0  ab   ab3 1 9 9ab 57 ab 89       0    ab 1   9
  ab 3  9ab  57 ab  89  0
+) Với ab  1 ab  1 thế b  2  a vào ta có a   a 2 2
1  a  2a 1  0  a 1 x  3 +) Với  ab3 9
 9ab  57 ab  89  0  Do a b ab   1 nên  ab3 9
 9ab  57 ab 89  9  9  0  89  7
 1 nên phương trình vô 2 nghiệm.
Vậy phương trình có nghiệm duy nhất x  3.
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 111 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 32. Cho ba số dương x, y, z thỏa mãn điều kiện x  y  z  1. Chứng minh: xy yz xz 3    . xy  z yz  x xz  y 2 Lời giải
Sử dụng giả thiết x  y  z  1 và bất đẳng thức AM-GM ta có: xy yz zx LHS    xy  z  x  y  z yz  x  x  y  z zx  y  x  y  z xy yz zx     z  x y  z x  yz  x  y  zx  y 1  x y  1  y z  1  z x             
2  z  x y  z  2  x  y z  x  2  y  z x  y  1  x z   y z   y x  3              
2  z  x z  x   y  z y  z   x  y x  y  2 
Dấu '  ' xảy ra khi và chỉ khi 1 x  y  z  . 3
Bài 33. Cho các số thực a, ,
b c thỏa mãn a  3,b  7, c  7 và 2 2 2
a  b  c  122 . Tìm giá trị nhỏ nhất
của biểu thức P  8a 15b 17c . Lời giải Có 2 2 2 2 2
a  122  b  c  122  7  7  24  a  5
  a   a  a   2 3 5 3
5  0  8a  a 15  1 2 2 2 2 2
b  122  a  c  122  3  7  64  b  8
  b   b  b   2 7 8 7
8  0 15b  b  562 2 2 2 2 2
c  122  a  b  122  3  7  64  c  8  10   c   c  c   2 7 10 7
10  0 17c  c  703 Từ   1 , 2 , 3 suy ra 2 2 2
8a 15b 17c  a  b  c 15  56  70  122 141  263 2 2 2 a  b  c  122 a  3   Xảy ra dấu “=” khi 8  a 15b 17c  263  b   8 3  a 5;7 b 8;7 c 8        c  7  
GTNN P  263  a  3, b  8 , c  7 .
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 112 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 34. Một doanh nghiệp xuất khẩu gạo ước tính rằng , trong tháng 2/2020 , nếu doanh
nghiệp xuất khẩu gạo với giá là 500 USD/tấn thì họ sẽ xuất khẩu được khoảng 860 tấn gạo.
Tuy nhiên nếu hạ giá gạo và cứ mỗi lần giảm giá 25 USD/tấn thì sẽ xuất khẩu thêm được 50
tấn gạo. Hỏi doanh nghiệp cần bán gạo với giá bao nhiêu USD mỗi tấn để doanh thu xuất
khẩu gạo trong tháng 2/2020 là lớn nhất? Lời giải
Doanh thu dự kiến xuất khẩu trong tháng 2 là 860 500  430000 (USD)
Gọi số lần giảm giá là x (lần), điều kiện * x   ,0  x  20
Giá gạo sau khi giảm giá là 500  25x (USD/tấn)
Số gạo xuất khẩu được sau khi giảm giá là 860  50x (tấn)
Doanh thu sau khi giảm giá gạo là P  500  25x860  50x (USD)
Để doanh thu xuất khẩu gạo trong tháng 2/2020 là lớn nhất thì P phải lớn hơn 430000 P      x  x 2 430000 0 500 25 860 50  430000  0  1  250x  3500x  0
 50x70  25x  0  0  x  2,8 . Vì x  *   x1;  2 .
Với x  1 P  432 250 .
Với x  2  P  432000 .
Vậy doanh nghiệp bán gạo với giá 475 USD/tấn để doanh thu trong tháng 2/2020 lớn nhất .
Bài 35. Cho x , y là các số thực dương thỏa mãn x  y  3 . 2 3
Tìm giá trị nhỏ nhất của biểu thức A   xy y  . 1 Lời giải 2 3 2 6 A     3y 3 y 3 y   1 3y 3 y 3 y 1 2 6 4 36 2 62    
3y 3  y 3  y 1 6y 3 y 6 y  4 2 18y  6y  6 y  24 262 64 64 4    2 18y  6y  6y  24 48  6 y  22 48 3 4
⇒ GTNN của A  khi x  1, y  2 3
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 113 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 36 Cho ba số a , b , c dương.   Chứng minh rằng: 1 1 1 a b c    2 2 2 a  bc b  ac c  ab 2abc Lời giải
+ Vì a,b, c  0 nên theo BĐT Cô si ta có: a  b  2 ab 
b  c  2 bc   a  b  c  ab  bc  ca  c  a  2 ac 
+ Vì a,b,c  0 nên ta có: 2 a  bc  2a bc 1 1   2 a  bc 2a bc abc bc   2 a  bc 2
Chứng minh tương tự ta có: abc ac  2 b  ac 2 abc ab  2 c  ab 2 abc abc abc bc ac ab 1 a  b            c bc ac ab 2 2 2   a  bc b  ac c  ab 2 2 2 2 2 1 1 1 a  b      c 2 2 2 a  bc b  ac c  ab 2abc
Bài 37. Cho a,b,c là hai số thực không âm thỏa mãn a  b  c  1.Chứng minh rằng:
a  b  b  c  c  a  6. Lời giải Vì x  y   x  y2 , 0 :
 0  2 x y  x  y và a  b  c  1 nên ta có:
 a b  b c  c  a2  2a b c2 a b b c 2 b c c a 2 c a a b
 2a  b  c a  b  b  c  b  c  c  a  c  a  a  
b  6a  b  c  6 1
Dấu bằng xảy ra khi và chỉ khi a  b  c  . 3
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 114 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 1
Bài 38. Tìm giá trị nhỏ nhất của biểu thức 2 2
P  2x  2xy  y  3x   2 x  2  2020. x Lời giải: ĐK: 1 x  2. Ta có: 2 2 2
P  x  2xy  y  x  4x  4  x   2 x  2  2016 x 1 2 2
P  (x  y)  (x  2)  2 x  2  x   2016. x 1 x 1 3 x 1 3 5
Theo BĐT Cô-si và x  2 thì x     x  2 .  .2  . x 4 x 4 4 x 4 2 Vậy 5 4037 P  2016  
. Dấu “=” khi x  y  2 . Kết luận: 4037 min P  . 2 2 2
Bài 39. Với a , b , c là các số dương thỏa mãn điều kiện a  b  c  ab  bc  ca  6abc . Chứng 1 1 1 minh    3. 2 2 2 a b c Lời giải
Ta có a  b  c  ab  bc  ca  6abc
a  b  c  ab  bc  ca   6 abc 1 1 1 1 1 1        6 . a b c ab bc ca
Áp dụng bất đẳng thức Cô – si ta được :  1   1   1   1 1 1  1  1  1  2      1 2   2   2     a   b   c   a b c   1 1 1   1 1   1 1   1 1   1 1 1  2          2    2 2 2 2   2 2   2 2   2 2     a b c   a b   b c   c a   ab bc ca  1 1 1 Cộng vế với vế   1 và 2 suy ra    3. 2 2 2 a b c
Dấu “=” xảy ra khi a  b  c  1 .
Bài 40. Cho ba số thực dương , a ,
b c thỏa mãn điều kiện a b  b c  c a  24 . Tìm giá trị
nhỏ nhất của biểu thức S  a  b  c Lời giải
Áp dụng bất đẳng thức Cô-si ta có: 4a  ab 4a  ab  4a b  a b  . 4 4b  bc 4b  bc  4b c  b c  . 4 4c  ca 4c  ca  4c a  c a  . 4
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 115 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC Do đó: 4a  ab 4b  bc 4c  ca ab  bc  ca 24  a b  b c  c a     a  b  c  1 4 4 4 4 1 1 1
Mà a  b  c2  3ab  bc  ca  a  b2  b  c2  c  a2  0 a  ,b,c 2 2 2 a b c2
 a  b  c2  3ab  bc  ca  ab  bc  ca  2 3
Từ 1 và 2 suy ra :    a  b  c a b c2 
 24  a  b  c2 12a  b  c  288  0 12
 a  b  c 12a  b  c  24  0
Mà a  b  c  24  0   với , a , b c 0
 a b  c 12  0  a b  c 12
Vậy giá trị nhỏ nhất của biểu thức S  a  b  c là 12 khi a  b  c  4
Bài 41. Cho các số dương a , b , c thỏa mãn điều kiện a  b  c  2019 . Tìm giá trị nhỏ nhất của biểu thức 2 2 2 2 2 2
P  2a  ab  2b  2b  bc  2c  2c  ca  2a . Lời giải a  2ab  b 3a  3b a b2 3 2 2 2 2 2 2 a  b 2 2  Ta có 2a  ab  2b     2 2 2 2 a  b  2 2
3 a  b  3 a  b2 3a  b2 2 2  2 Mà a  b     . 2 2 2 2 4 a  b 3 a  b 5 a  b 2 2  2  2  2 Suy ra 2a  ab  2b    2 4 4 Suy ra 5 2 2 2a  ab  2b  a b . 2
Chứng minh tương tự ta có 5 5 2 2 2b  bc  2c  b  c ; 2 2 2c  ca  2a  c  a. 2 2 Cộng vế theo vế ta có 5 P 
a b b  c  a  2019 5 . 2 a  b  c Dấu "  " xảy ra khi   a  b  c  673. a  b  c  2019
Vậy giá trị nhỏ nhất của P bằng 2019 5 , đạt được khi a  b  c  673 .   Bài 42. a) Cho ,
x y, z là ba số dương. Chứng minh  x  y  z 1 1 1    9   .  x y z  b) Cho a, ,
b c là ba số dương thỏa mãn a  b  c  6. Tìm giá trị lớn nhất của biểu thức ab bc ca A   
a  3b  2c b  3c  2a c  3a  2b Lời giải
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 116 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC a) Ta có:
     1 1 1  x x x y y y x y z VT x y z  
          
 x y z  x y z x y z z z z
 x y   x z   y z   3       3  2  2  2  9      
, dấu bằng xảy ra khi x  y  z .
 y x   z x   z x  (đpcm)
b) Áp dụng bất đẳng thức ở phần a) ta có: 9ab 9ab ab ab a     a  b  c a  c b  c ; 3 2  2b c  a c  b 2 9bc bc bc b 9ca ca ca c Tương tự    ;    b  3c  2a
a  c a  b 2 c  3a  2b b  a b  c 2
Cộng theo các vế của ba bất đẳng thức trên ta được ab ab a bc bc b ca ca c 9A         
c  a c  b 2 a  c a  b 2 b  a b  c 2  ab bc   ab ca   bc ca  a  b  c  9A             
 c  a a  c   c  b b  c   a  b b  a  2 3(a  b  c)  9A  2
 A 1 dấu bằng xảy ra khi a  b  c  2. Suy ra GTLN của A bằng 1.
Bài 43. Gọi m là giá trị nhỏ nhất trong ba số  x  y2  y  z2  z  x2 , ,
với x, y, z là ba số thực bất kì. Chứng minh 1 m   2 2 2 x  y  z . 2 Lời giải
Vì x , y , z là ba số thực bất kì nên giải sử x  y  z .
Mà m là giá trị nhỏ nhất trong ba số  x  y2  y  z2  z  x2 , , .
 m là số nhỏ nhất trong ba số x  y , y  z , z  x . Ta có:
z  x  x  z   x  y   y  z  x  y  y  z  2 m .
Do đó z  x2  4m . mà   2 y z  m   2 x y  m x  y  z2 2 2 2
 0  x  y  z  2xy  2yz  2xz  0
 x  y  z   x  y2   y  z2 z  x2 2 2 2 3  6m 2 2 2  1
x  y  z  2m hay m   2 2 2 x  y  z . 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 117 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC Bài 44.
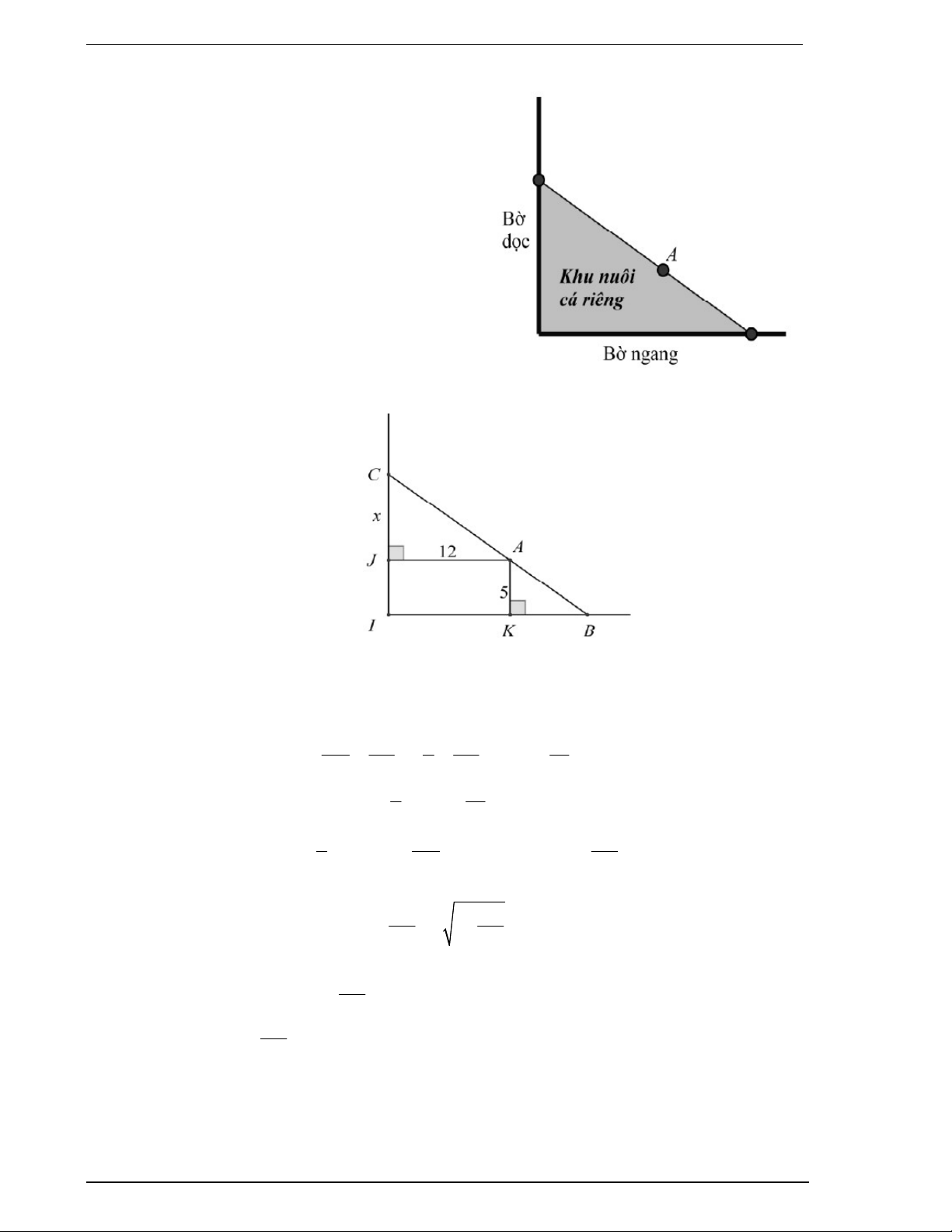
Người ta giăng lưới để nuôi riêng một loại cá
trên một góc hồ. Biết rằng lưới được
giăng theo một đường thẳng từ một vị
trí trên bờ ngang đến một vị trí trên bờ
dọc và phải đi qua một cái cọc đã cắm
sẵn ở vị trí A. Hỏi diện tích nhỏ nhất có
thể giăng là bao nhiêu, biết rằng
khoảng cách từ cọc đến bờ ngang là 5
m và khoảng cách từ cọc đến bờ dọc là 12 m. Lời giải
Đặt tên các điểm như hình vẽ. Đặt CJ  x,(x  0).
Vì hai tam giác AJC và BKA là hai tam giác đồng dạng nên: CJ JA x 12 60     KB  . AK KB 5 KB x
Diện tích của khu nuôi cá là: 1   S   x   60 5 . 12 .   2  x  1  300  150  S(x)  60 12x   60  S(x)  6x   60   2  x  x
Áp dụng bất đẳng thức Cô si ta có: 150 150 6x   2 6 . x  60 x x Dấu bằng xảy ra khi 150 2 6x   x  25  x  5 . x Nên 150 S(x)  6x   60  60  60  120 x
Suy ra diện tích nhỏ nhất có thể giăng là 2
120(m ) , đạt được khi x  5 m .
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 118 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 45. Cho x, y, z là ba số thực dương thỏa mãn điều kiện xy  yz  xz  3xyz .
Tìm giá trị lớn nhất của biểu thức: 1 1 1 P =   2 2 2 2 2 2 2x  xy  y 2y  yz  z 2z  zx  x Lời giải:
Từ giả thiết ta có: 1 1 1    3 . x y z 5x  3y  7 x  y  1 4 2 2  2  2 Ta có 5x 3y 2x  xy  y     4 4 2 2 2x  xy  y 5x  3y 1 4 1 4 Tương tự:  ;  2 2 2y  yz  z 5y  3z 2 2 2z  zx  x 5z  3x 64 64 64 16P   
4x   x  3y 4y   y  3z 4z   z  3x 16 16 16 16 16 16 16P       4x 4 y 4z x  3y y  3z z  3x  4 4 4   4 4   4 4   4 4                  
 x y z   x  y 2y   y  z 2z   z  x 2x   1 1 1   8    24    x y z  3  P  . 2
Dấu bằng xảy ra khi x  y  z 1 . 3 Vậy max P  . 2
Bài 46. Cho hình vuông ABCD có cạnh là 30cm .
Trên cạnh AB lấy hai điểm E , G sao cho
AE  GB  x cm và điểm E nằm giữa
điểm A và điểm G . Qua E kẻ đường thẳng
vuông góc với AB cắt CD tại F ; qua G kẻ
đường thẳng vuông góc với AB cắt CD tại H . Người ta gập hình vuông theo hai
cạnh EF và GH sao cho cạnh AD trùng cạnh BC như hình vẽ để tạo thành hình
lăng trụ đứng khuyết đáy. Tìm x để thể tích hình lăng trụ lớn nhất. Lời giải
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 119 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC A G K E
Ta có AE  GB  x (0  x  15)  EG  30  2x . Kẻ đường cao AK của A  GE .  Vì EG x A  GE cân tại A nên 30 2 KE    15  x (cm). 2 2  15
AKE vuông tại K  AE  KE  x  . 2
Áp dụng định lý Py-ta-go vào tam giác vuông AKE ta có 2 2 2 AK  KE  AE 2 2 2  AK  AE  KE 2 2  AK  AE  KE  AK  x    x2 2 15  AK  30x  225 . Diện tích đáy AGE là 1 1 S  AK.GE  30x  225.  x  x   x cm . AGE 30 2  30 225.15   2 2 2
Thể tích lăng trụ là V  x   x  3 30. 30 225.(15 ) cm  .
V  30. 30x  225.(15  x)  30. 15.2x 15. 15  x. 15  x
 10. 15.3. 2x 15. 15  x. 15  x .
Áp dụng bất đẳng thức Cô-si cho ba số dương 2x 15 , 15 x , 15  x ta được 3
3. 2x 1515  x15  x  2x 15  15  x  15  x 3
 2x 1515  x15  x  5
  x    x  x 3 2 15 15 15  5
  x    x  x 3 2 15 15 15  5  5 5
 V  10. 15.3.5 5  V  750 3 .
Dấu "  " xảy ra khi và chỉ khi 2x 15 15  x  x 10.
Vậy x 10 thì thể tích lăng trụ lớn nhất.
Bài 47. Cho các số thực x, y thỏa mãn  2 x   x  2 3
y  3  y   9 . Tìm giá trị nhỏ nhất của biểu thức 2 2 P x  xy y . Lời giải
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 120 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC  2 x   y  2 y   x  3 3 3 3  9  .  9   2 3  y  x 2 3  x  y  1 2 2  3  y  x 3  x  y  2 2
xy  x 3 x  y 3 y    2 3 y  2 3 x   9 Ta có:  2 2
xy  x 3 x  y 3 y   2 3 y  2 3 x  1   xy   2  y  2 3 3 x   5 2 2 2 2 6  x  y 6  x  y Do  2 3 y  2 3 x    xy   2 3 y  2 3 x   xy  2 2 2 2 2xy  6  x  y 
 5  2xy  x  y  4  x  y2 2 2  4 . 2 x  y
Ta có: P  x  y  xy  x  y  xy  x  y   x  y  2 2 2 2 2 2 2 2 2 2 2   4  2  6 2
 2P  6  P  3  min P  7 đạt được khi x  y  1.
Bài 48. Cho các số x  0, y  0 . Tìm giá trị nhỏ nhất của biểu thức 2 2 x  y xy A   . xy x  y Lời giải x  y 2 2  2 Ta có: x  y  2 x  y2 xy A  2xy x  y x  y2 xy x  y2 3 A   8xy x  y 8xy x  y2 xy x  y2 3 A 2 .  8xy x  y 8xy 2 x  y 3.4xy A .  2 xy 8xy 2 2 xy 3 3 5 A .   1  2 xy 2 2 2
Dấu bằng xảy ra khi x  y 5 Vậy : A   x  y min 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 121 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 49. Với a , b , c là các số dương thỏa mãn ab  bc  2ac . Tìm giá trị nhỏ nhất của biểu thức: a  b c  b P   2a  b 2c  b Lời giải 2ac
Với a , b , c là các số dương thỏa mãn ab  bc  2ac  ba   c  2ac  b  a  c 2 2 2ac 2ac a  ac  2ac ac  c  2ac a  c a b c b    a  c a  c a  c a  c  P       2 2 2a  b 2c  b 2ac 2ac 2a  2ac  2ac 2ac  2c  2 2  2 ac a c  a  c a  c a  c a  c 2 2 a  3ac c  3ac 1 3c 1 3a 3 c a   P        1    2 2 2a 2c 2 2a 2 2c 2 a c    c a c a 3
Theo bất đẳng thức AM-GM, ta có:   2 
 2  P  1  2  4 a c a c 2   a,b,c  0   a,b, c  0  Dấu  c a "   " xảy ra    a  c  a  b  c  a c  2   2 2 a ac  b b      2a  a  c
Vậy giá trị nhỏ nhất của biểu thức P là 4 khi a  b  c
Bài 50. Cho xy  yz  zx 1. Tìm giá trị nhỏ nhất của biểu thức: S   2 2 x  y  2 3  z . Lời giải
Áp dụng BĐT Cauchy, ta có: 2 2 2 x  y   4xy 2 2 2 2 2
z  4x  4xz   6x  6y  2z  4xy  4xz  4yz 2 2 z 4 y 4    yz    2 2 2
2 3x  3y  z   4 xy  xz  yz   2 2 2
2 3x  3y  z   4 (do xy  yz  zx 1) 2 2 2  3x  3y  z  2  S  2 2 2 x  y  z
Dấu “=” xảy ra  z  2x  x  y  . Mà 2 z  2  y 5 2 5
xy  yz  zx  1  x  y   ; z   5 5 5 2 5 Vậy S  2 x  y   ; z   min , đạt được tại 5 5
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 122 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 51. Với các số thực a , b , c thay đổi thỏa mãn a 1; b 1; 0  c 1 và a  b  c  3 2 2 2 a  b  c
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P  . ab  bc  ca Lời giải Ta có: a  b  c a  b c2 2 2 2
 2ab  bc  ca 9  2ab  bc  ca 9 P      2 ab  bc  ca ab  bc  ca ab  bc  ca ab  bc  ca 2 2 a  b  2ab  Lại có: 2 2 2 2 2 2 2 2 b
  c  2bc  2a  2b  2c  2ab  2bc  2ca  a  b  c  ab  bc  ca  2 2 c  a  2ca 
 a  b  c  ab  bc  ca  ab  bc  ca  a  b  c2 2 2 2 2 2 2 3 3 3  3ab  bc  ca a  b  c2  ab  bc  ca 
 3 (do a  b  c  3 ) 9 9  P   2   2 1 3 ab  bc  ca 3
Dấu "  " xảy ra  a  b  c 1
Mặt khác: a  1; b 1  a   1 b  
1  0  ab  a  b 1  0  ab  a  b 1
 ab  bc  ca  a  b 1 bc  ca  ab  bc  ca  a  b 1 ca  b
Mà a  b  c  3  a  b  3 c  ab  bc  ca  3  c 1 c3 c 2 2
 ab  bc  ca  2  c  3c  c  ab  bc  ca  2  2c  c  ab  bc  ca  2  c2  c
Do 0  c 1 c2  c  0  2  c2  c  2  ab  bc  ca  2 9 9 5  P   2   2  ab  bc  ca 2 2   a   1 b   1  0  c2  c  0 a  1;b  2;c  0 Dấu "  " xảy ra     a  b  c  3 a  2;b 1;c  0
a 1; b 1;0  c 1 a  1; b  2; c  0
Vậy MinP 1 khi a  b  c 1; 5 MaxP  khi 2  a  2; b  1; c  0 2 3
Bài 52. Cho x , y là hai số thực dương sao cho  2  y x y . x 2x  y
Tìm giá trị nhỏ nhất của biểu thức P  . x  y Lời giải 2 3y
Với x , y là hai số thực dương thỏa mãn 2 2 x  2 y   x  2xy  3y x
 x  xy  y  y   x  y2 2 2 2 2 2 4  4y   x  y2 2
 4 y  x  y  2y  x  y . x  y  0 x  x  y  x 2x  y  x 2x  y x 1 Mà x  y        P    . x  x  x  y 2x  x  y x  y  2x x  y 2x 2
Dấu "  " xảy ra khi và chỉ khi x  y  0 . 1
Vậy MinP  khi x  y  0 . 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 123 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 2 2 a b
Bài 53. Với a,b là các số thực a 1,b 1. Tìm giá trị nhỏ nhất của biểu thức P   b 1 a 1 Lời Giải
Vì a  1Suy ra a –1  0 , b 1suy ra b –1  0
Áp dụng bất đẳng thức Cô si ta có: 2 2 a a  4(b 1)  2 .4.b   1  4a b 1 b 1 2 2 b b  4(a 1)  2 .4.a   1  4b a 1 a 1
Suy ra P  4b  4 4a  4 4a  4b  P 8 2  a 4b  1 b 1  2  b       a   a 2b 2 4 1    a  b  2TM 
Dấu “ = “xảy ra khi và chỉ khi a 1 b    2a  2 a ,  b 1  
Vậy Giá trị nhỏ nhất của P  8khi và chỉ khi a  b  2
Bài 54. Cho các số không âm x , y , z thỏa mãn x  y  z 1. Tìm giá trị lớn nhất của biểu thức: 2 2 2
Q  2x  x 1  2y  y 1  2z  z 1 Lời giải
Ta có x, y, z  0 và x  y  z 1 suy ra 0  x, y, z 1  x  x 2 2 1
 0  x  x  0  x  x . Với 2 x  x ta có 2 2 2 2
x  x  x  x  x 1  x  x  x 1
 x  x   x  x   x  x   x  2 2 2 2 2 1 2 1 2 1 1 2  2x  x 1  x 1
Chứng minh tương tự ta có 2 2y  y 1  y 1 và 2 2z  z 1  z 1. Từ đó suy ra 2 2 2
2x  x 1  2y  y 1  2z  z 1  x 1 y 1 z 1  x  y  z  3  4  Q  4 .  x1 x  0 
Dấu bằng xảy ra  y1 y  0   . x y.z 
 0,0, 1;0,1,0;1,0,0  z  1 z  0
Vậy Q đạt giá trị lớn nhất là 4 tại  . x . y z 
 0,0, 1;0,1,0;1,0,0.
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 124 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 55. Cho a, b, c > 0 thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức : 1 1 1 M   
ab  a  2 bc  b  2 ca  c  2 Lời giải
Ta chứng minh bổ đề sau : 1 1 4
Cho a,b  0 , chứng minh rằng :   a b a b
Thực hiện xét hiệu ta được : 1 1 4 a b 4 2 2     ab 4ab ab    0,a,b  0 a b a b ab a b aba b aba b 1 1 4    a b a b
Dấu"  " xảy ra khi : a  b  
Ta có thể viết dưới dạng : 1 1 1 1     a b 4 a b
Áp dụng bất đẳng thức bổ đề ta có: 1 1 1  1 1         1 abc 1 1 c 1               ab  a  2
ab 1 a 1 4 ab 1 a 1
4 ab  abc a 1 4c 1 a 1 Tương tự ta có : 1 1  a 1     
bc b  2 4 a 1 b 1 1 1  b 1     
ca c  2 4 b 1 c 1
Cộng vế với vế của 3 bất đẳng thức ta có : 1 a 1 b 1 c 1 1 3 3 VT    
 .3  M  . Dấu""xảy ra  a b c1
4 a 1 b 1 c 1 4 4 max 4 a; ; b c  0 Bài 56. Cho 
Tìm Min S  7a  9  7b  9  7c  9 a  b  c  1 Lời giải a; ; b c  0 a  0;b  0;c  0; Có: 
 0  a 1;0  b 1;0  c 1   a  b  c  1 1
  a  0;1 b  0;1 c  0  a   a 2 2 1
 0  a  a  7a  9  a  6a  9  7a  9  a  3
Tương tự 7b  9  b  3 7c  9  c  3
 7a  9  7b  9  7c  9  a  b  c  9  S 10
Vậy giá trị nhỏ nhất S  10
Dấu bằng xảy ra khi a; ;
b c  1;0;0 và các hoán vị.
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 125 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 57. Cho x, y, z  0 và xy  yz  xz  3 x y z
Tìm giá trị nhỏ nhất của biểu thức P    y z x Lời giải Đặt x  a, y  , b z  c a, , b c  0
Khi đó ab  bc  ca  3
Ta có: a  b  c  ab  bc  ca  a  b  c2 2 2 2
 3ab  bc  ca  9  a  b  c  3 a b c a b  c2 2 2 2 Ta có P      a  b  c  3 b c a a  b  c
 P  3, dấu “=” xảy ra  a  b  c  1  x  y  z  1 min
Bài 58. Gọi m là giá trị nhỏ nhất trong ba số   2 x y ,   2 y z ,   2
z x với x , y , z là ba số
thực bất kì. Chứng minh 1 m   2 2 2 x  y  z  2 Lời giải
Vì x , y , z có vai trò như nhau nên giả sử x  y  z .
Vì m là số nhỏ nhất trong ba số   2 x y ,   2 y z ,   2 z x .
Nên m là số nhỏ nhất trong ba số x  y , y  z , z  x .
Ta có: z  x  x  z  x  y   y  z  x  y  y  z  2 m . Nên  x  z2  4m Mà   2 y z  m ;   2 x y  m .
 x  y  z   x  y2  y  z2 z  x2 2 2 2 3  6m 1  m   2 2 2 x  y  z  2
Bài 59. Cho x, y là các số thực thỏa mãn x  2 và x  y  3. 1 1
Tìm giá trị nhỏ nhất của biểu thức : 2 2 P  x  y   x x  y Lời giải
Dễ thấy điểm rơi đạt tại x  2; y  1 2 2 1 1 Khi đó P  x  2 y  1  4x  2y   5 x x  y      
 P x 2 y 2 9 4 7 17 2 1  2x   y6    2x    4     15  x  y    x  x x  y 2 2     
 P x 2 y 2 2x y  3 2x 2 7 17 2 1       15 x  y x x x y 7 17  7 17 35  P          15  x x  y   2 3  6 35 Vậy Min    x  y  P . Dấu " " xảy ra 2;
1 (thỏa mãn điều kiện) 6
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 126 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 60. Cho các số dương x, y, z thỏa mãn x + y + z = 2020. Tìm giá trị lớn nhất của biểu thức x y z P    . x  2020x  yz y  2020 y  zx z  2020z  xy Lời giải Bổ đề: Cho a, ,
b c là các số dương. Chứng minh a  ba  c  ab  ac (1) BĐT (1) 2 2 2 2
 a  ac  ab  bc  ab  ac  2 a bc  a  bc  2 a bc (luôn đúng)
Vậy bổ đề được chứng minh. Áp dụng Ta có       2 2020x yz
x x y z  yz  x  xy  xz  yz   x  yx  z
Áp dụng bổ đề (1) ta có:  x  y x  z  xy  xz x x x
x  2020x  yz  x  x  y  z     x  2020x  yz x  x  y  z  x  y  z Chứng minh tương tự: y y  z z ;  y  2020y  zx
x  y  z z  2020z  xy x  y  z x  y  z 2020 Suy ra: P 
 1 P  1  x  y  z  max x  y  z 3
Bài 60. Cho a  0 , b  0 , c  0 thỏa mãn  2 2      2 2 b bc c 3 3  a 
Tìm giá trị nhỏ nhất của biểu thức 2 2 2
T  a  b  c    a b c Lời giải Ta có:  2 2 b  bc  c    2 2 3 3  a  2 2 2
 2b  2bc  2c  9  3a 2 2 2
 2b  2bc  2c  3a  9   2 2 2
a  b  c  ab  bc  ca   2 2 a  b  ab   2 2 2 2 2 2 a  c  2ac  9
 a  b  c2  a  b2  a  c2  9  a  b  c2  9  0  a  b  c  3
Ta đi chứng minh bất đẳng thức phụ: 1 1 1 9    a b c a  b  c Ta có: 1 1 1 9       a  b  c 1 1 1    9 a a b b c c  
 1   1   1  9 a b c a  b  c  a b c  b c a c a b a a b b c c        6 b c a c a b
Áp dụng bất đẳng thức cô-si ta có: a  b  2 b a b  c  2 c b
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 127 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC a  c  2 c a Cộng vế theo vế ta có: a a b b c c       6 b c a c a b
Dấu “=” xảy ra khi a  b  c .
Áp dụng cô-si cho 2 số dương theo từng cặp: 1 a   2 2 a 1 b   2 3 b 1 c   2 4 c
Áp dụng bất đẳng thức phụ: 1 1 1 9    5 a b c a  b  c
Cộng vế với vế của các bất đăng thức 2,3,4,5 ta được 1 1 1 1 1 1 9
T  a   b   c      2  2  2  a b c a b c 3
Vậy giá trị nhỏ nhất của biểu thức T bằng: 9 khi và chỉ khi a  b  c 1.
Bài 61. Cho hai số x  0 , y  0 và x  y  1.  1  1 
Tìm giá trị nhỏ nhất của biểu thức M  1 1    2 2   x  y  Lời giải
1) Với hai số x  0 , y  0 và x  y  1 ta có:  1  1 
 2x  1  2y  1 x  1x  1y  1y  1 M  1 1        2 2 2 2 2 2  x  y  x y x y yx   1 x y   1 xy   x  y 1 2    1 . 2 2 x y xy xy Ta có: x  y  xy   x  y2 1 1 1 2 2  4xy    1   8  x  y2 4xy 4xy xy 2  1  9  M  9 . xy Dấu bằng xảy ra khi 1 x  y  . 2
Vậy giá trị nhỏ nhất của M bằng 9 khi 1 x  y  . 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 128 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 62. Cho bốn số dương a, b, c, d. Tìm giá trị nhỏ nhất của biểu thức :  a b c d  b c d a  2 2 2 2 A       
 a  b  c  d  ab  bc  cd  da  2004     b c d a  a b c d  Lời giải:  a b c d  b c d a  2 2 2 2 A       
 a  b  c  d  ab  bc  cd  da  2004     b c d a  a b c d   a b c d  b c d a  Chứng minh được       16    (1)  b c d a  a b c d 
Dấu “=” xảy ra khi và chỉ khi a  b  c  d Chứng minh được 2 2 2 2
a  b  c  d  ab  bc  cd  da  0 (2)
Dấu “=” xảy ra khi và chỉ khi a  b  c  d
Từ (1) và (2) => A  2020
Dấu “=” xảy ra khi và chỉ khi a  b  c  d
Vậy giá trị nhỏ nhất của A là 2020 khi a  b  c  d  0 .
Bài 63. Cho các số thực dương a, b thay đổi luôn thỏa mãn a  3  b  3  4. Tìm giá trị lớn
nhất của biểu thức P  a  b. Lời giải
Ta chứng minh x  2 x  3  3 với mọi x  0 . Thật vậy, 2
x  2 x  3  3  2 x  3  x  3  3( x 1)  0 .
Áp dụng : a  2 a  3  3; b  2 b  3  3  P  2( a  3  b  3)  6  P  2.4  6 .  a 1
 P  2 khi và chỉ khi   a  b 1 max  b 1
Bài 64. Cho a, b, c > 0 và a + b + c = 1. Tìm giá trị lớn nhất của biểu thức ab bc ca A    c  ab a  bc b  ca Lời giải a  b a  b   Với , a b  0 ta có a  b  1 1 1 1 1 2 ab  1        2 ab 2ab ab ab 2  a b  Viết lại
c  ab  c  ab  c a  b  c 2 .1
 ab  ca  cb  c  ab  c c  a  bc  a  c  bc  a
Tương tự a  bc  a  ba  c và b  ca  b  cb  a ab ab ab  1 1 Xét       c  ab
c bc  a 2  c b c  a  bc bc  1 1      a  bc 2  a  b a  c  ca ca  1 1      b  ca 2  b  c b  a 
Cộng vế với vế ta được
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 129 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 1  ab ab bc bc ac ac  ab bc ca A            c  ab a  bc b  ca
2  c  b c  a a  b a  c b  c a  b 
1  a b  c ba  c c a  b   A      2 b  c a  c a  b   1 1 A  a  b  c 1   A  2 2 2 1 1
Vậy giá trị lớn nhất của A là khi a  b  c  2 3 1 1 1 a  b  c
Bài 65. Cho ba số a , b , c dương. Chứng minh    . 2 2 2 a  bc b  ac c  ab 2abc Lời giải
Áp dụng bất đẳng thức Cosi ta có 2 1 1 1 1  1 1 2  a  bc  2a bc    .     1 . 2   a  bc a bc ab ac 2  ab ac  Tương tự có: 2 1  1 1    2 . 2   b  ac 2  ba bc  2 1  1 1    3 . 2   c  ab 2  ca cb 
Cộng vế với vế của  
1 2 3 ta được: 2 2 2 1  1 1  1  1 1  1  1 1          2 2 2       a  bc b  ac c  ab
2  ab ac  2  ba bc  2  ca cb  2 2 2 1  2 2 2        2 2 2   a  bc b  ac c  ab 2  ab bc ca  1 1 1 1  1 1 1        2 2 2   a  bc b  ac c  ab 2  ab bc ca  1 1 1 a  b  c    
(điều phải chứng minh). 2 2 2 a  bc b  ac c  ab 2abc
Đẳng thức xảy ra khi a  b  c
Bài 66. Cho x , y , z là các số thực dương thỏa mãn x  y  z  1. Tìm giá trị nhỏ nhất của biểu thức: 1 2020 P   . 2 2 2 x  y  z xy  yz  zx Lời giải  
Áp dụng bất đẳng thức  x  y  z 1 1 1    9   , ta có :  x y z    1 1 1  2 2 2
x  y  z   xy  yz  zx  xy  yz  zx    9   . 2 2 2   x  y  z xy  yz  zx xy  yz  zx     1 1 1  2 2 2
x  y  z  2xy  2 yz  2zx    9  . 2 2 2   x  y  z xy  yz  zx xy  yz  zx  Hay 1 2   9 . 2 2 2 x  y  z xy  yz  zx
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 130 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Ta có :  x  y2   y  z2  x  z2  0 2 2 2
 x  y  z  xy  yz  zx  x  y  z2 2 2 2
 x  y  z  2xy  yz  zx  3xy  yz  zx x  y  z2 1  xy  yz  zx   3 3 Từ đó suy ra: 1 2 2018 P     9  6054  6063 2 2 2 x  y  z xy  yz  zx xy  yz  zx  P  6063 . 1
Dấu bằng xảy ra  x  y  z  . 3 1
Vậy GTNN của P  6063  x  y  z  . 3
Bài 67. Cho các số thực dương a,b,c . 2 2 2 a b c a  b  c Chứng minh rằng:    2 2 2 2 2 2 3a  8b 14ab 3b  8c 14bc 3c  8a 14ca 5 Lời giải Ta có: 2 2 a  b  ab   2 a  ab   2 3 8 14 3 12
2ab  8b   3aa  4b  2ba  4b
 a  4b3a  2b
Áp dụng bất đẳng thức Cô-si cho hai số dương a  4b và 3a  2b ta có       a b b a  b a 4b 3a 2b a 4 3 2  4 6   2a  3b 2 2 2 2 a a 2 2   hay a a 
a  4b3a  2b 2a  3b 2 2 3a  8b 14ab 2a  3b Tương tự ta cũng có : 2 2 b b 2 2  c c và  2 2 3b  8c 14bc 2b  3c 2 2 3c  8a 14ca 2c  3a Khi đó 2 2 2 2 2 2 a b c a b c        1 2 2 2 2 2 2 3a  8b 14ab 3b  8c 14bc 3c  8a 14ca 2a  3b 2b  3c 2c  3a 2 a 
Áp dụng bất đẳng thức Cô-si cho hai số dương và 2a 3b ta có: 2a  3b 25 2 2 a 2a  3b a 2a  3b 2a   2 .  2a  3b 25 2a  3b 25 5 2 a 2a 2a  3b 8a  3b     2a  3b 5 25 25 Tương tự ta cũng có
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 131 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 2 b 8b  3c 2   c 8c 3a và  2b  3c 25 2c  3a 25 2 2 2 a b c 8a  3b 8b  3c 8c  3a a  b  c        2 2a  3b 2b  3c 2c  3a 25 25 25 5 Từ   1 và 2 suy ra 2 2 2 a b c a  b  c    2 2 2 2 2 2 3a  8b 14ab 3b  8c 14bc 3c  8a 14ca 5
Dấu “=” xảy ra khi a  b  c Bài 68. Cho , a ,
b c là các số dương và a  b  c  3 . a b c
Tìm giá trị lớn nhất của biểu thức: P    2 2 2 a 1 b 1 c 1 Lời giải Vì , a , b c  0 , ta có :
a  b c2 3(ab  bc  ca)  2 a  2 b  2 c  ab  bc  ca  1 2. 2 a  2 b  2 c  ab  bc   ca 2
 1 a  b2  b  c2  c  a2     0 2
 a  b  c2  3(ab  bc  ca)
 3  a  b  c2  3(ab  bc  ca)  1  ab  bc  ca 2 2
 a 1  a  ab  bc  ca 2
 a 1  a  ba  c 1 1    1  1 a a a   . (1) 2
a 1 a  ba  c 2 a 1 a  ba  c 2 a 1 a  b a  c a a
Áp dụng bất đẳng thức Cô si cho 2 số dương:  a  b ;a  c a a a a a a 1  a a      .     (2)
a  b a  c 2 a  b . a  c
a b ac 2 ab ac Từ (1) và (2) suy ra a 1  a a    (*) 2   a 1 2 a  b a  c 
Chứng minh tương tự, ta có b 1  b b     (**) 2   b 1 2  a  b b  c  c 1  c c     (***) 2   c 1 2  a  c b  c 
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 132 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Cộng vế với vế của (*), (**),(***), ta có a b c 1  a a b b c c           2 2 2   a 1 b 1 c 1
2 a  b a  c a  b b  c a  c b  c  3  P  2
Dấu bằng xảy ra: a  b  c  3 3 Vậy
P  3  a  b  c  3 max 2 3
Bài 69. Cho x  0 , tìm giá trị nhỏ nhất 2 1 M  9x  5x   2021. 9x Lời giải 2 1  1   1  M  9x  5x   2021 2  (9x  6x 1)  x   2020 2  (3x 1)  x   2020 9x      9x   9x  Ta có:  x  2 3 1  0 . Vì x  0 nên 1  0 . 9x 1 1
Áp dụng bất đẳng thức Cauchy cho hai số x và 1 ta được x   1 2 2 . x  2.  . 9x 9x 9x 3 3 2 Do đó M  2 0   2020   6062 2020  . 3 3 3 3  x 1  0 1 Dấu 
"  " xảy ra khi và chỉ khi  1  x  . x   3  9x 6062 1
Vậy giá trị nhỏ nhất M  khi x  . 3 3
Bài 70. Cho x, y, z là các số dương thoả mãn xy  yz  xz  4xyz . Chứng minh: 1 1 1 P     1 2x  y  z x  2y  z x  y  2z Lời giải   Ta có xy yz xz 1 1 1 xy  yz  xz  4xyz   4     4 xyz x y z Áp dụng 1 1 4 1 1  1 1         a b a  b a  b 4  a b  1 1  1 1  1  1 1  1 1  1  1 1 1  Ta có                (1) 2x  y  z 4  2x y  z  4 2x 4   y z  8   x 2y 2z  Chứng minh tương tự có
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 133 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 1 1  1 1 1       (2) x  2y  z 8  2x y 2z  1 1  1 1 1  và      (3) x  y  2z 8  2x 2y z  Từ (1), (2), (3) ta có 1 1 1 1  1 1 1  P        1   . 2x  y  z x  2y  z x  y  2z 4  x y z      Chú ý: 1 1 2 1 1 1 1 1 1 P                  cyc  x y  z x 1
16 cyc  x y z  4  x y z   2   y Bài 71. Cho hai số dương 
x và y . Chứng minh rằng x  .  2  8      y   x  Lời giải: Có x, y  0  2   y  xy  2  y  2x   x  .  2  8       8     y   x   y  x  xy  2 y  2x   8 xy
  xy  2 y  2x  8xy ( vì x, y  0 ) 2 2
 xy  2x y  2y  4x  8xy 2 2
 xy  2x y  2y  4x 8xy  0 2 2
 xy  2x y  2y  4x  4xy  4xy  0   2 xy  xy  x   2 4 4 2x y  4xy  2 y  0  x 2 y  y    y 2 4 4 2 x  2x   1  0
 x  y  2  y x  2 2 2
1  0 ( luôn đúng với x, y  0 )   y  2  0 y  2 Vậy 2  y  x  .  2  8    
với x, y  0 . Dấu “=” xảy ra      y   x  x 1  0 x 1  1   1 
Bài 72. Cho biểu thức : B  1 x 1  1 y 1     .  y   x  Với x  0 , y  0 và 2 2
x  y 1. Tìm giá trị nhỏ nhất của B . Lời giải
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 134 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC     1 1 x y B    x 1     y 1 1 1 1 1   
  2  x  y      y   x  x y y x 1 1 1 1 x y  2  x  y       2x 2x 2y 2 y y x  1   1   x y  1  1 1   2  x   y              .  2x  
2y   y x  2  x y 
Áp dụng bất đẳng thức Cô – si ta có: 1 1 x   2. . x  2 (1) 2x 2x 1 1 y   2. . y  2 (2) 2 y 2 y x y x y   2. .  2 (3) y x y x 1  1 1  1     2  x y  . x y
Áp dụng bất đẳng thức Cô – si ta có: 1 1 1 2 1  1 1  xy   2 2 x  y   xy   2 2 x  y     2    2   4 2 2 xy  2 2 x  y  2  x y 
Từ (1), (2), (3), (4) ta được:  1   1   x y  1  1 1  2  x   y       4  3 2         .  2x  
2y   y x  2  x y  Vậy MinB  4  3 2 . x  y  1 x   2x 2
Dấu đẳng thức đồng thời xảy ra khi và chỉ khi:   x  y  . 1 y  2  2y  2 2
x  y 1; x  0, y  0
Bài 73. Cho x, y, z là các số dương thoả mãn xy + yz + xz = 4xyz. Chứng minh: 1 1 1 P     1 2x  y  z x  2y  z x  y  2z Lời giải:   - Ta có xy yz xz 1 1 1 xy  yz  xz  4xyz   4     4 xyz x y z - Áp dụng 1 1 4 1 1 1 1 1 1 1 1    (  )    (  ) a b a  b a b 4 a  b a  b a b 4
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 135 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC   Ta có 1 1 1 1 1 1 1 1 1 1 1 1 1         (1) x  y z ( ) ( ) ( ) 2 4 2x y z 4  2x 4 y z       8 x 2 y 2z 1 1 1 1 1
- Chứng minh tương tự có:  (   ) (2) x  2 y  z 8 2x y 2z 1 1 1 1 1 và  (   ) (3) x  y  2z 8 2x 2 y z Từ (1), (2), (3) ta có 1 1 1 1 1 1 1 P     (   )  1 (đpcm) 2x  y  z x  2y  z x  y  2z 4 x y z
Bài 74. Cho x ; y ; z > 0 và 1 1 1
   4 . Chứng minh rằng : x y z 1 1 1    1 2x  y  z x  2 y  z x  y  2z Lời giải  2x  0 Áp dụng BĐT 1 1 4   (với  ;
A B  0 ) Có x ; y ; z > 0   A B A  B y  z  0 1 1  1 1  Có 1 1 4        2x y  z 2x  y  z 2x  y  z 4  2x y  z  1 1  1 1  1  1 1  1  1 1 1  Có 1 1 4                 y z y  z y  z 4  y z 
4  2x y  z  4  2x 4y 4z  1     1 1 1 1     (1) 2x  y  z 4  2x 4y 4z  1 1  1 1 1  1 1  1 1 1  Tương tự cm :      (2) ;      (3) 2 y  x  z 4  2y 4x 4z  2z  x  y 4  2z 4x 4y  1 1 1 Từ (1) (2) và (3)     1. 2x  y  z x  2 y  z x  y  2z Dấu « = » xảy ra  3 x  y  z  4
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 136 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 75. Với x, y là các số dương thỏa mãn điều kiện x  2 y , tìm giá trị nhỏ nhất của biểu 2 2 x  y thức: M  . xy Lời giải 2 2 x  y x y  x 4 y  3y Ta có : M         . xy y x  y x  x x 4y
Vì x, y  0 , áp dụng bất đẳng thức Cô-si cho hai số dương ; y x Ta có: x 4y x 4 y   2 .  4 . y x y x x 4y Dấu “=” xảy ra 2 2    x  4y  x  2y . y x   Vì y 1 3y 3 x  2 y    
, dấu “=” xảy ra  x  2y x 2 x 2 Suy ra, 3 5
M  4   , dấu “=” xảy ra  x  2 y 2 2
Vậy GTNN của M là 5 khi x  2 y . 2
Bài 76. Cho hai số dương a và b thỏa mãn 1 1
  2 . Tìm giá trị lớn nhất của biểu thức: a b 1 1 P   . 4 2 2 4 2 2 a b  2ab b  a  2ba Lời giải a b ab 1 Từ giả thiết 1 1   2=> 2 2ab a b 2 ab        a b ab a  b  2 
Áp dụng BĐT cô si với 2 số dương ta có 4 2 4 2 4 2 2 2 2
a b  2 a b  a b  2ab  2a b  2ab 4 2 4 2 4 2 2 2 2
b  a  2 b a  b  a  2a b  2ab  2a b 1 1 1 1 1  P      4 2 2 4 2 2 2 2 2 2 a b  2ab b a  2ba 2a b  2ab 2ab  2a b 2 Dấu “=” xảy ra 1  a  b  . 2
Vậy giá trị lớn nhất của P là 1 khi 1 a  b  . 2 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 137 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 77. Cho a,b là các số không âm thỏa mãn 2 2 a  b  2 .
Chứng minh rằng: a 3aa  2b  b 3bb  2a  6.
Dự đoán dấu bằng xảy ra khi a  b 1. Khi đó 3a  a  2b, 3b  b  2a nên ta có thể áp dụng
bất đẳng thức Cauchy trực tiếp cho biểu thức trong dấu căn. 
Sử dụng bất đẳng thức Cauchy dạng x y xy  , dễ thấy 2 a  a  b 3b  b  2a a 3a a  2b 3 2 2  a
 2a  ab , b 3bb  2a 2  b  2b  ab . 2 2
Cộng hai bất đẳng thức này lại vế theo vế, ta được: M  a
a a  b  b bb  a   2 2 3 2 3 2
2 a  b   2ab  4  2ab.
Tiếp tục sử dụng bất đẳng thức Cauchy kết hợp với giả thiết, ta có: 2 2
4  2ab  4  a  b  6 . Từ
đó ta có ngay M  6 . Dấu bằng xảy ra  a  b 1.
Bài 78. Với a , b , c là các số dương thoả mãn có ab  bc  2ac . Tính giá trị nhỏ nhất của biểu   thức a b c b P   2a  b 2c  b . Lời giải
Với a , b , c là các số dương ta có: 2ac ab  bc  2ac  b  , thay vào P ta được a  c 2ac 2ac a  c  a  c a  c P   2ac 2ac 2a  2c  a  c a  c a a  c  2ac c a  c  2ac  
2a a  c  2ac 2c a  c  2ac a  3c c  3a   2a 2c 3  a c  3 1  1 2  4   . 2  c a  2
Vậy giá trị nhỏ nhất của P là 4 khi a  b  c . 1
Bài 79. Cho x  y 1. Chứng minh 4 4 x  y  . 8 Lời giải x  y 2 2  2 Ta có x  y    1 với mọi x , y . 2 Thật vậy,   2 2 2 2
1  2x  2y  x  2xy  y 2 2
 x  2xy  y  0   x  y2  0 luôn đúng với mọi giá trị của x , y . Áp dụng   1 ta có:
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 138 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC  x  y 2 2  2
x  y  x    y  x y 2 2 2 2 2 4 4 2 2  và x  y  . 2 2 1
Theo giả thiết ta có x  y  1 nên 2 2 x  y  . 2 2  1     2  1 Suy ra 4 4 x  y   . 2 8 1
Đẳng thức xảy ra khi và chỉ khi x  y  . 2
Bài 80. Một công ty du lịch dự định tổ chức một tour du lịch xuyên Việt nhân kỉ niệm ngày
giải phóng hoàn toàn miền Nam 30  4 . Công ty dự định nếu giá tour là 2 triệu đồng thì sẽ có
khoảng 150 người tham gia. Để kích thích mọi người tham gia, công ty sẽ quyết định giảm
giá và cứ mỗi lần giảm giá tour 100 nghìn đồng thì sẽ có thêm 20 người tham gia. Hỏi công
ty phải giảm giá tour là bao nhiêu để doanh thu từ tour xuyên Việt là lớn nhất. Lời giải
Gọi x là giá tour (triệu đồng; 0  x  2 )
Giá đã giảm so với ban đầu là 2  x (triệu đồng)
Vì mỗi lần giảm giá tour 100 nghìn đồng thì sẽ có thêm 20 người tham gia nên số người tham
gia tăng thêm khi giảm 2  x triệu đồng là (2  x) : 0,1.20  400  200x (người)
Tổng số người tham gia là: 150  400  200x  550  200x ( người) Tổng doanh thu là :
L  x 550  200x ( triệu đồng)
Tìm x để doanh thu L lớn nhất với 0  x  2
Sử dụng bất đẳng thức Côsi, chúng ta có: 2 2       L  x   x 1   x    x 1 200x 550 200x 1 550 3025 550 200 200 550 200          Dấ 200 200  2  200  2  8
u "  "xảy ra ⇔ 200x  550  200x  400x  550  x  1,375
Vậy giá tour là 1,375000 triệu đồng. 2 2  1   1 
Bài 81. Cho x  0; y  0 thỏa mãn x  y  1. Tìm giá trị nhỏ nhất của M  x   y       x   y  Lời giải
Chứng minh các bất đẳng thức phụ: Ta có: với a,b  0 a b2 2 2
  a  b  ab    2 2 a  b  2 2 0 2 0 2  a  b  2ab  0    a  b  a b2 2 2 2 2 2 2 2
 a  b  2ab  a  b   1 2 Lại có: với a,b  0 a b2 2 2 2 2
 0  a  b  2ab  0  a  b  2ab  4ab 2 2
 ab  a  b  ab  4ab  aa  b  ba  b  4ab   * .
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 139 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Vì a,b  0  ab  0;a  b  0 Do đó ta được:   a a  b b a  b 4ab *   
aba  b aba  b aba  b 1 1 4    . 2 a b a  b
Áp dụng bất đẳng thức  
1 và 2 cho M ta được: 2 2 2 1  1 1  1  4      1 1 3 M  x  y    x  y       M   x  y      2  x y  2  x  y  2  x  y  x  y  2 1  3     M  2 
(Áp dụng bđt thức Cauchy cho cặp số   x  y 1 ;  2  x y     x  y  1  M    2 25 . 2 3  (Vì x  y  1) 2 2
Dấu "  " xảy ra khi và chỉ khi 1 x  y  2
Vậy giá trị nhỏ nhất của M là 25 2
Bài 82. Cho hai số dương x, y , có x  y 1 .  1  1 
Tìm giá trị nhỏ nhất của biểu thức B  1 1  2   2   x  y  Lời giải     2 x   1  2 y   1 1 1 B 1 1   2   2  2 2  x  y  x y
(x 1)(y 1)(x 1)( y 1)
xy  x  y  1xy  x  y  1   2 2 2 2 x y x y
xy 1 1xy 1  1  2 2 x y 2 2 x y  2xy 2   1 2 2 x y xy 2 (x  y) 1 xy   4 4 2   8 xy 2  1  9  B  9 xy Xảy ra dấu “=” khi 1 x  y  (TM ) 2 Vậy GTNN B  9 khi 1 x  y  2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 140 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 83. Cho các số thực a, ,
b c thỏa mãn a  b  c  7 và ab  bc  ca  15 Chứng minh rằng: 11 a  3 Lời giải
Vì a  b  c  7  b  c  7  a ab  bc  ca   bc 
 a b  c   a  a 2 15 15 15 7  a  7a 15
Áp dụng định lí Vi-ét đảo có b và c là nghiệm của phương trình: 2 x    a 2 7 x  a  7a 15  0 (ẩn x )
Ta có:     a2   2 a  a   2 7 4 7 15  3
 a 14a 11  3a 1  1 1 a
Để tồn tại hai số b , c thì     a    a 11 0 3 11 1  0  1  a  3 Vậy 11 a  3
Bài 84. Cho ba số thực không âm a ; b ; c thay đổi thỏa mãn a  b  c  3 .
Tìm giá trị nhỏ nhất của biểu thức : 2 2 2 2 2 2
M  2019a  4026ab  2019b  2019b  4028bc  2019c  2020a  4030ac  2020c Lời giải Ta có 2 2
2019a  4026ab  2019b  3 a  b . Thật vậy: a  ab  b  a  b2 2 2 2019 4026 2019 3 . 2 2 2 2
 2019a  4026ab  2019b  3a  6ab  3b 2 2
 2016a  4032ab  2016b  0   2 2
2016 a  2ab  b   0  a b2 2016  0 (luôn đúng ) Ta có 2 2
2020b  4028bc  2020c  3 b  c . Thật vậy: a  ab  b  a  b2 2 2 2020 4028 2020 3 . 2 2 2 2
 2020b  4028bc  2020c  3b  6bc  3c 2 2
 2017b  4034bc  2017c  0 .   2 2
2017 b  2bc  c   0  b c2 2017  0 ( luôn đúng). Ta có 2 2
2021a  4030ac  2021c  3 a  c . Thật vậy: a  ac  c  a  c2 2 2 2021 4030 2021 3 . 2 2 2 2
 2021a  4030ac  2021c  3a  6ac  3c 2 2
 2018a  4036ac  2018c  0 .
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 141 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC   2 2
2018 a  2ac  c   0  a c2 2018  0 (luôn đúng).
 M  2 3 a  b  c .  a  b  c2 Ta có a  b  c  . 3  a  b  c2
Thật vậy: a  b  c 
 2a  2b  2c  2 ab  2 bc  2 ac . 3
  a  b2  b  c2  a  c2  0 (luôn đúng)  M   a  b  c2 2 3 2 3  .9  M  6 3 . 3 3
Vậy giá trị nhỏ nhất M  6 3 dấu bằng xảy ra khi a  b  c 1.
Bài 85. Cho a,b là các số thực sao cho 2 2
a  ab  b  a  b . Tìm giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức P  505a  505b . Lời giải Tìm Min: 2  1  3 2 2 2
a  ab  b  a  b  a  b  a  b  b  0    2  4
 P  505a  505b  505.a  b  0  MinP  0 . Dấu "  "xảy ra  a  b  0. Tìm Max:
a  ab  b  a  b  a  b2 2 2  3ab  a  b . a b2 Do ab  4 2 2  
 a  b  a  b2 3a b a b   a  b 
 a  b  4 (do a  b  0 ) 4 4  P  505.4  2020 .
Dấu "  " xảy ra  a  b  2.
 MaxP  2020 tại a  b  2
Bài 86. Với các số thực không âm a,b, c thỏa mãn a  b  c  3. Tìm giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức 1
P  ab  bc  ca  ab . c 2 Lời giải
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 142 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 1   2 2 2 9 a  b  c  Ta có 1 9 1
P  ab  bc  ca  abc   abc   Q 2 2 2 2 2 Với 2 2 2
Q  a  b  c  abc . Ta tìm gtln gtnn của biểu thức Q . Giả sử c  min , a , b 
c ⇒ 3  a  b  c  3c ⇒ 0  c  1. Ta có:
Q  a  ab  b   c  ab  abc    c2 2 2 2 2 2 2 3  c  ab2  c . a b2  c2 3
Từ giả thiết có ab2  c  0 và 0  ab   4 4 1
⇒ c  3c 18  Q  3  c2 3 2  c 4 Ta có: 1 c 3c18 1  c  2 16 3 1 c  2 16   4 4 4   4
Dấu bằng xay ra khi a  b  c 1.
Do 0  c 1 ⇒ cc   1  0 ⇒   c2 2 2 3
 c  2c  6c  9  2cc   1  4c  9  9
Dấu đẳng thức xảy ra tại c  0, ab  0, a  b  c  3 hay c  0, a  3,b  0 hoặc c  0, a  0,b  3
⇒ GTNN của Q là 4 khi a  b  c  1.
Và GTLN của Q là 9 khi c  0, a  3, b  0 và các hoán vị của nó.
Vậy GTLN của P là 5 khi a  b  c 1 2
GTNN của P là 0 khi c  0, a  3, b  0 và các hoán vị của nó.
Bài 87. Cho xy  yz  xz  1. Tìm giá trị nhỏ nhất của biểu thức: M   2 2 x  y  2 3  z . Ta có: 1 2 2
a  b  2ab với mọi a,b   2 2  z  2x  2xz   1 2
Chứng minh tương tự, ta được 1 2 2 z  2y  2 yz 2 2 2 2 x  y  2xy 3 Từ  
1 ; 2 ; 3 ta suy ra
M  2(xy  yz  zx)  2 .  1 x  y   5   2 1 z   x  y  z  5
Dấu “ = ” xảy ra khi  2   .    1  xy  yz  xz 1  x  y   5   2  z    5
Vậy M đạt giá trị nhỏ nhất bằng 2.
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 143 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 88. Cho a,b,c dương và a  b  c 1. Tìm giá trị lớn nhất của biểu thức ab bc ca A    . c  ab a  bc b  ca ab ab ab 1  1 1 Ta có     a . b    c  ab c a  b  c  ab b  ca  c 2  b  c a  c  Tương tự bc 1  1 1   ca   b . c    ; 1 1 1  c . a    a  bc 2  b  a c  a  b  ca 2  c  b a  b  Suy ra ab  1 1  bc  1 1  ca  1 1  A            
2  a  c b  c  2  b  a c  a  2  c  b c  a  1  ab bc ab ac bc ac         
2  a  c a  c b  c c  b a  b a  b  1  a  b  c 1  . 2 2 Dấu “=” xảy ra 1  a  b  c  . 3
Vậy giá trị lớn nhất của A bằng 1 khi 1 a  b  c  . 2 3
Bài 89 Cho 3 số thực dương x, y, z thỏa mãn điều kiện x  y  z  3
Tìm giá trị nhỏ nhất của biểu thức x y z P    . 2 2 2 y 1 z 1 x 1 Lời giải 2 x xy 2 2 xy xy xy Ta có  x  . Do 2 y 1  2y    ( , x y, z  0 ) 2 2 y 1 y 1 2 y 1 2y 2 x xy   x  2 y 1 2 Tương tự: y yz  z zx y  ;  z  2 z 1 2 2 x 1 2   Suy ra xy yz zx P  x  y  z  2 x  y  z 2 2 2  2
Lại có xy  yz  zx  x  y  z  xy  yz  zx   3 3 3 3 3
 P  3    P  . Dấu "  " xảy ra  x  y  z 1. min 2 2 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 144 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 90. Cho x , y , z là ba số thực thỏa mãn điều kiện: x x    y  y    z z   4 1 1 1  . 3
Tìm giá trị lớn nhất của biểu thức P , biết rằng P  x  y  z . Lời giải
Theo bất đẳng thức Cauchy-Schwarz, ta có:
 x  y  z2   2 2 2    2 2 2 1. 1. 1. 1 1 1
x  y  z   x  y  z2   2 2 2 3 x  y  z  Mà 4
x  x    y  y    z  z   4 1 1 1    2 2 2
x  y  z   x  y  z  3 3 4 2 2 2
 x  y  z   x  y  z   2 2 2
3 x  y  z   4  3x  y  z 3
 x  y  z2  4  3 x  y  z  x  y  z2  3x  y  z  4  0
 1  P  x  y  z  4  P  4 . x  y  z  4 P  4   4  x  y  z  . x  y  z 3 Vậy MaxP  4 khi 4 x  y  z  . 3
Bài 91. Cho các số thực dương x , y thỏa mãn: x  y  15 . Tìm giá trị lớn nhất của biểu thức A  x 1  y  2 Lời giải
Với các số thực dương x , y thì A  0 , giá trị của biểu thức A được xác định.
A  x 1  y  2  1. x 1 1. y  2 điều kiện: x  1  ; y   2 Chứng minh công thức: ax by2  2 2 a b  2 2    x  y 
Áp dụng bất đẳng thức Bunhiacopxki ta có: A   x  
y  2   x  2  y  2 2   2 2 1. 1 1. 2 1 2 . 1 1 
 (x 1 y  2).(11)  (x  y  3).2  (15  3).2  36
Suy ra A  6 ( vì A  0 )
Dấu bằng xảy ra khi x 1  y  2  x 1  y  2  x  y  1 Mà x  y  15 x  y  15 x  (15 1) : 2 x  8
Nên ta có hệ phương trình      (Thỏa mãn điều x  y  1  y  (15 1) : 2 y  7 kiện)
Vậy giá trị lớn nhất của biểu thức A là 6 khi x  8; y  7
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 145 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 92. Cho các số thực dương x , y là những số thực thỏa mãn: x  y  xy  8. Tìm giá trị nhỏ nhất của biểu thức 2 2 P  x  y . Lời giải
Ta có:  x  2   y  2   x  y2 2 2 2  0 với mọi , x y 2 2 2 2
 x  4x  4  y  4y  4  2x  4xy  2y  0   2 2
x  y   x  y  xy 2 2 3 4
 8  24  x  y  8
Dấu bằng xảy ra khi x  y  2
Vậy MinP  8 khi x  y  2 . 7
Bài 93. Cho hai số thực x , y thỏa mãn: x  y  xy  . 2
Tìm giá trị nhỏ nhất của biểu thức 2 2 P  x  4y  4xy . Lời giải 7 7
Do x  y  xy   xy   (x  y) 2 2 7 Thay 7  xy   (x  y) vào 2 2 P  x  4y  4 y x , ta có: 2 2 P  x  4 y  4  x  y 2  2    2 2
P  x  4y 14  4x  4y   2 x  x  2 4 +4 4 y  4 y  
1  9   x  2   y  2 2 2 1  9 . x  2  2  0 Vì 
với mọi x ; y  P  9 . 2y   2 1  0 x   2 x  2 2  0 x  2  0 
Dấu "  " xảy ra khi và chỉ khi      .    1 2  2y 1  0 2 1 0 y y     2 1
Vậy giá trị nhỏ nhất của biểu thức P là 9 tại x  2 và y  . 2
Bài 94. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P  2  x  2  x  4  x . Lời giải + Điều kiện: 2   x  2 2
+ Đặt t  2  x  2  x  0 và 2 t    x   x  2 2 2  4  2 4  x * 2  2  2 4  4 4   t x    t P t 2  2P  (t 1)  5 2 2
Xét biểu thức t  2  x  2  x  0 2 2 t  4  2 4  x
Với mọi x thỏa mãn điều kiện xác định thì t  2 2 4  x  0 2  4  2 4  x  4 2  t  4   t  2  Mà t  0 nên t  2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 146 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 2
t  2  4  x  0  x  2 (tm) 2  x  0
Với mọi x thỏa mãn điều kiện xác định thì  2  x  0
Áp dụng BĐT Cô – si ta có:
2 (2  x)(2  x)  2  x  2  x  4 2  4  2 4  x  8 2  t  8  t  2 2
Dấu “=” xảy ra  2  x  2  x  x  0(thỏa mãn) +Vì t  2nên t  2 2 1  (2 1)  t  2 1  1  t  2 1  5  1 5  2P  4  P  2
Suy ra P  2 khi t  2  x  2  max + Vì t  2 2 nên  t      2 2 1 2 2 1  t      2 2 1 2 2 1
 t       2 2 1 5 2 2 1  5  4 2  4  2P  4 2  4  P  2 2  2
 P  2 2  2  t  2 2  x  0 min Vậy P  2 khi x  2
 và P  2 2  2 khi x  0 max min
Bài 95. Cho ba số thực dương x, y , z thỏa mãn x  y  z  6 . Tìm giá trị nhỏ nhất của biểu 3 3 3 3 3 3 x  y y  z z  x thức P    . 2 2 2 2 2 2 x  y y  z z  x Lời giải x  y x  y. 2 2 3 3 x  y  xy Ta có:  2 2 2 2 x  y x  y x . y  x  y x . y  x  y x  y  x  y   x  y   2 2 x  y 2xy 2 3 3 3 3 y  z y  z z  x z  x Tương tự ta có:  ;  2 2 2 2 y  z 2 z  x 2 3 3 3 3 3 3 x  y y  z z  x x  y y  z z  x Khi đó ta có: P       2 2 2 2 2 2 x  y y  z z  x 2 2 2  P  x  y  z  6
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 147 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC x  y   y  z Dấu “=” xảy ra    x  y  z  2 . z  x  x  y  z  6
Vậy MinP  6 khi x  y  z  2 .
Bài 96. Cho x , y , z là các số dương thỏa mãn x  y  z  2020 . xy yz zx
Tìm giá trị lớn nhất của biểu thức P    . 2020z  xy 2020x  yz 2020 y  zx Lời giải
Thay x  y  z  2020 vào biểu thức P ta được : xy yz zx P    x  y  z z  xy x  y  z x  yz x  y  z y  zx xy yz zx    2 2 2 xz  yz  z  xy x  xy  xz  yz xy  y  yz  zx
Áp dụng bất đẳng thức Cô-si, ta có : xy xy xy xy     1 xy xy .       1 2 xz  yz  z  xy x  z y  z x  z y  z 2  y  z x  z  yz yz yz yz 1  yz yz    .     2 2 x  xy  xz  yz x  zx  y x  z x  y 2  x  z x  y  zx zx zx zx 1  zx zx    .     3 2 xy  y  yz  zx x  y y  z x  y y  z 2  x  y y  z  Cộng 2 vế  
1 , 2 , 3 ta được : xy yz zx   2 2 2 xz  yz  z  xy x  xy  xz  yz xy  y  yz  zx 1  xy xy yz yz zx zx         
2  y  z x  z x  z x  y x  y y  z  1  xy zx xy yz yz zx         
2  y  z y  z x  z x  z x  y x  y 
1  x  y  z y  x  z z  x  y       2 y  z x  z x  y   1  x  y  2020 z  1010 2 2 x  y  z
Dấu “=” xảy ra khi và chỉ khi 2020   x  y  z  . x  y  z  2020 3 2020
Vậy giá trị lớn nhất của biểu thức P 1010 khi x  y  z  . 3
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 148 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 97. Cho x  0 , y  0 , z  0 và x  2y  3z  20
Tìm giá trị nhỏ nhất của biểu thức 3 9 4 P  x  y  z    x 2y z Lời giải x y 3z  3 3x   9 y   4 z  P                4 2 4  x 4   2y 2   z 4    Ta có : x y 3z x 2y 3z     5 4 2 4 4 3 3x 3 3x Ta có :   2 .  3 x 4 x 4 Ta có : 9 y 9   y 2 .  3 2 y 2 2 y 2 4 z 4 z Ta có :   2 .  2  P 13 z 4 z 4
Vậy giá trị nhỏ nhất P 13 dấu bằng xảy ra khi x  2 ; y  3 ; z  4 16
Bài 98 Với x, y  0 , tìm giá trị nhỏ nhất của biểu thức 2 2 P  x  y  . x  1 y  1 Lời giải x  y  2 16 32 Ta có x   1  y   1    2
x  1 y  1 x  y  2 x  y2 2 2 x  y  2 Khi đó P  x  y2 64 2  x  y  2
Lại có  x  y2    x  y   x  y2 4 4
12  4 x  y  2  P   x  y   64   x  y   64 2 12 4 2 2 4 2 .  32 x  y  2 x  y  2
 2P  20  P  10  P  10 min
Dấu "  " xảy ra  x  y  1.
Bài 99. Cho ba số x, y, z  0 thỏa mãn x  y  z  xyz .
Tìm giá trị lớn nhấ tcủa biểu thức x y z S    . yz  2  x  xz  2  y  xy  2 1 1 1 z  Lờigiải x y z x y z S       . yz  2 1 x  xz  2 1 y  xy  2 1 z  yz  xy . z x xz  xyz.y xy  xyz.z
Mà theo đề bài, x  y  z  xyz nên ta có:
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 149 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC x y z S    yz   x  y  z.x xz   x  y  z.y xy   x  y  z.z x y z    yz  xz  x  x  y xz  yz  y  x  y xy  zy  z  x  z x y z   
z  x  y  xx  y
z  x  y  y  x  y
y  x  z  z  x  z x y z     1 . z  xx  y z  yx  y  y  zx  z x x y y z z
Tacó x, y, z  0 nên suy ra , , , , , đều là số dương.
z  x x  y z  y x  y y  z x  z
Với x, y, z  0 , áp dụng bất đẳng thức Côsi cho 2 số dương ta được x x x x x   2 .  2. 2. z  x x  y z  x x  y z  xx  y y y y y y   2 .  2. 3. z  y x  y z  y x  y z  yx  y z z z z z   2 .  2. 4 . y  z x  z y  z x  z  y  zx  z
Dấu"  " của 2 , 3 ,4 đồng thời xảy ra khi và chỉ khi x  y  z  0.
Cộng vế với vế của 2 , 3 ,4 ta được x x y y z z  x y z        2.    z  x x  y z  y x  y y  z x  z  z  xx  y z  yx  y
 y  zx  z    x z x y y z  x y z         2.    z  x x  y z  y  z  xx  y z  yx  y
 y  zx  z     x y z   3  2.     z  xx  y z  yx  y
 y  zx  z    3 x y z     5. 2 z  xx  y z  yx  y  y  zx  z 3 Từ   1 và 5 suy ra S  . 2
Dấu"  "xảy ra khi và chỉ x , y , z  0 x, y , z  0 x, y, z  0 x, y , z  0   
khi x  y  z  xyz 3  3  x  x 2  3   x  x  3
 x  y  z  3 (thỏa mãn). x  y  z     x  y  z  x  y  z  x  y  z  3
Vậy giá trị lớn nhất của S bằng S  đạt được khi x  y  z  3 . 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 150 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC
Bài 100. Cho x , y là các số thực dương thỏa mãn x  y  1 .
Tìm giá trị nhỏ nhất của biểu thức 1 2 A  4xy   2 2 x  y xy Lời giải   Cho các số thực dương 1 1 4
x , y ta có:  x  y 1 1   4       x y  x y x  y 1 1 2    
Thật vậy x  y  2 xy ;     x  y 1 1   4     x  y 1 1   4   . x y xy  x y   x y 
Ta có x  y  2 xy 1 2 xy 1  xy  . 4 1 2 1 1 1 5 A  4xy    4xy     . 2 2 x  y xy 2 2 4xy x  y 2xy 4xy Ta có 1 4xy   2 . 4xy 1 1 4    4 . 2 2 x  y 2xy x  y2 5 5   5. 4xy x  y2  A 11.
Vậy giá trị nhỏ nhất A  11 dấu bằng xẩy ra khi 1 x  y  . 2  
Bài 101. a) Cho x, y, z là ba số dương. Chứng minh  x  y  z 1 1 1    9     x y z 
b) Cho a,b,c là ba số dương thỏa mãn a  b  c  6. Tìm giá trị lớn nhất của biểu thức ab bc ca A    
a  3b  2c b  3c  2a c  3a  2b Lời giải x y
a) Áp dụng bất đẳng thức 
 2 cho hai số x  0; y  0ta chứng minh được y x    x  y  z 1 1 1    9    x y z 
Áp dụng bất đẳng thức ở phần a) ta có: 9ab ab ab a    9bc bc bc b ;    ; a  3b  2c c  a c  b 2 b  3c  2a a  c a  b 2
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 151 GIÁO VIÊN CÙ MINH QUẢNG
CHUYÊN ĐỀ BẤT ĐẲNG THỨC 9ca ca ca c    c  3a  2b b  a b  c 2
Cộng theo các vế của ba bất đẳng thức trên ta được ab ab a bc bc b ca ca c 9A         
c  a c  b 2 a  c a  b 2 b  a b  c 2  ab bc   ab ca   bc ca  a  b  c  9A             
 c  a a  c   c  b b  c   a  b b  a  2
Bài 102. Cho hai số thực dương a,b thỏa mãn a  b  3ab  1. 12ab
Tìm giá trị lớn nhất của biểu thức 2 2 P   a b . a  b 2  Ta có: 2 2 2 2 (a )
(a b)  0  a  b  2ab  (a b)  4a ; b 2 2   b a b 2 Từ giả thiết 3
a  b  3ab  1  a  b  1 3ab  1 a  b2 4
 a  b2  a  b    a  b   a b 2 3 4 4 0 2 3
 2  0  a  b  .  3 3ab 1 (a  b) 1 3 1   1  1  . a  b a  b a  b 2 2 a b2 2 2 2 2 a  b     2 2 a  b    . 2 9 9 12ab 3ab 2 16 2 2 P   a  b  4.   2 2 a  b   2   . a  b a  b 9 9 a  b 1
Giá trị lớn nhất của P bằng 16 khi   a  b  . 9 a  b  3ab  1 3
DIỄN ĐÀN GV TOÁN THCS VIỆT NAM 152 GIÁO VIÊN CÙ MINH QUẢNG