TOP 238 bài toán biến đổi căn thức nâng cao – Lương Tuấn Đức

Được đề cập lần đầu tiền trong chương trình Đại số 7, mặc dù rất đơn giản với căn bậc hai số học, căn thức đã bước đầu gây ra sự tò mò, khám phá đối với nhiều bạn học sinh nhỏ tuổi yêu Toán.

63 32 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi vào 10 môn Toán

Môn: Môn Toán

Thông tin:

107 trang 7 tháng trước

Tác giả:

Profile Nguyễn Vân
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
1076
1077
x
P
x
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
C
C
H
H
U
U
Y
Y
Ê
Ê
N
N
Đ
Đ
Ề
Ề
C
C
Ă
Ă
N
N
T
T
H
H
Ứ
Ứ
C
C
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
T
T
R
R
U
U
N
N
G
G
Đ
Đ
O
O
À
À
N
N
N
N
H
H
Ư
Ư
N
N
G
G
U
U
Y
Y
Ệ
Ệ
T
T
–
–
Q
Q
U
U
Â
Â
N
N
Đ
Đ
O
O
À
À
N
N
T
T
U
U
Ầ
Ầ
N
N
D
D
U
U
Y
Y
Ê
Ê
N
N
C
C
H
H
Ủ
Ủ
Đ
Đ
Ạ
Ạ
O
O
:
:
B
B
I
I
Ế
Ế
N
N
Đ
Đ
Ổ
Ổ
I
I
N
N
Â
Â
N
N
G
G
C
C
A
A
O
O
C
C
Ă
Ă
N
N
T
T
H
H
Ứ
Ứ
C
C
B
B
I
I
Ế
Ế
N
N
Đ
Đ
Ổ
Ổ
I
I
Đ
Đ
Ơ
Ơ
N
N
G
G
I
I
Ả
Ả
N
N
B
B
I
I
Ể
Ể
U
U
T
T
H
H
Ứ
Ứ
C
C
C
C
H
H
Ứ
Ứ
A
A
C
C
Ă
Ă
N
N
B
B
Ậ
Ậ
C
C
H
H
A
A
I
I
.
.
R
R
Ú
Ú
T
T
G
G
Ọ
Ọ
N
N
B
B
I
I
Ể
Ể
U
U
T
T
H
H
Ứ
Ứ
C
C
C
C
H
H
Ứ
Ứ
A
A
C
C
Ă
Ă
N
N
T
T
Ổ
Ổ
N
N
G
G
H
H
Ợ
Ợ
P
P
.
.
C
C
Á
Á
C
C
C
C
Â
Â
U
U
H
H
Ỏ
Ỏ
I
I
P
P
H
H
Ụ
Ụ
Đ
Đ
Ố
Ố
I
I
V
V
Ớ
Ớ
I
I
B
B
À
À
I
I
T
T
O
O
Á
Á
N
N
T
T
Ổ
Ổ
N
N
G
G
H
H
Ợ
Ợ
P
P
.
.
B
B
À
À
I
I
T
T
O
O
Á
Á
N
N
N
N
H
H
I
I
Ề
Ề
U
U
C
C
Á
Á
C
C
H
H
G
G
I
I
Ả
Ả
I
I
.
.
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
;
;
0
0
1
1
6
6
3
3
3
3
2
2
7
7
5
5
3
3
2
2
0
0
(
(
T
T
E
E
L
L
L
L
)
)
;
;
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
M
M
Ù
Ù
A
A
T
T
H
H
U
U
2
2
0
0
1
1
6
6
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
2
“
“
N
N
o
o
n
n
s
s
ô
ô
n
n
g
g
V
V
i
i
ệ
ệ
t
t
N
N
a
a
m
m
c
c
ó
ó
t
t
r
r
ở
ở
n
n
ê
ê
n
n
t
t
ư
ư
ơ
ơ
i
i
đ
đ
ẹ
ẹ
p
p
h
h
a
a
y
y
k
k
h
h
ô
ô
n
n
g
g
,
,
d
d
â
â
n
n
t
t
ộ
ộ
c
c
V
V
i
i
ệ
ệ
t
t
N
N
a
a
m
m
c
c
ó
ó
b
b
ư
ư
ớ
ớ
c
c
t
t
ớ
ớ
i
i
đ
đ
à
à
i
i
v
v
i
i
n
n
h
h
q
q
u
u
a
a
n
n
g
g
đ
đ
ể
ể
s
s
á
á
n
n
h
h
v
v
a
a
i
i
v
v
ớ
ớ
i
i
c
c
á
á
c
c
c
c
ư
ư
ờ
ờ
n
n
g
g
q
q
u
u
ố
ố
c
c
n
n
ă
ă
m
m
c
c
h
h
â
â
u
u
đ
đ
ư
ư
ợ
ợ
c
c
h
h
a
a
y
y
k
k
h
h
ô
ô
n
n
g
g
,
,
c
c
h
h
í
í
n
n
h
h
l
l
à
à
n
n
h
h
ờ
ờ
m
m
ộ
ộ
t
t
p
p
h
h
ầ
ầ
n
n
l
l
ớ
ớ
n
n
ở
ở
c
c
ô
ô
n
n
g
g
h
h
ọ
ọ
c
c
t
t
ậ
ậ
p
p
c
c
ủ
ủ
a
a
c
c
á
á
c
c
e
e
m
m
”
”
(
(
T
T
r
r
í
í
c
c
h
h
t
t
h
h
ư
ư
C
C
h
h
ủ
ủ
t
t
ị
ị
c
c
h
h
H
H
ồ
ồ
C
C
h
h
í
í
M
M
i
i
n
n
h
h
)
)
.
.
“
“
N
N
à
à
o
o
p
p
h
h
i
i
n
n
h
h
a
a
n
n
h
h
,
,
p
p
h
h
i
i
n
n
h
h
a
a
n
n
h
h
,
,
G
G
i
i
ó
ó
r
r
e
e
o
o
t
t
r
r
ê
ê
n
n
l
l
ư
ư
n
n
g
g
đ
đ
ồ
ồ
i
i
,
,
H
H
ư
ư
ơ
ơ
n
n
g
g
l
l
ú
ú
a
a
b
b
á
á
t
t
n
n
g
g
á
á
t
t
t
t
r
r
ê
ê
n
n
đ
đ
ồ
ồ
n
n
g
g
x
x
a
a
n
n
h
h
,
,
L
L
ờ
ờ
i
i
c
c
a
a
e
e
m
m
b
b
a
a
y
y
t
t
r
r
ê
ê
n
n
t
t
r
r
ờ
ờ
i
i
m
m
â
â
y
y
,
,
N
N
ắ
ắ
n
n
g
g
q
q
u
u
ê
ê
h
h
ư
ư
ơ
ơ
n
n
g
g
b
b
ừ
ừ
n
n
g
g
s
s
a
a
y
y
,
,
B
B
ư
ư
ớ
ớ
c
c
c
c
h
h
â
â
n
n
n
n
h
h
ữ
ữ
n
n
g
g
n
n
g
g
à
à
y
y
t
t
h
h
ơ
ơ
ấ
ấ
u
u
,
,
T
T
h
h
e
e
o
o
e
e
m
m
v
v
à
à
o
o
t
t
r
r
o
o
n
n
g
g
k
k
ý
ý
ứ
ứ
c
c
,
,
L
L
ớ
ớ
n
n
l
l
ê
ê
n
n
v
v
ớ
ớ
i
i
c
c
ù
ù
n
n
g
g
t
t
h
h
ờ
ờ
i
i
g
g
i
i
a
a
n
n
,
,
N
N
à
à
o
o
p
p
h
h
i
i
n
n
h
h
a
a
n
n
h
h
n
n
h
h
a
a
n
n
h
h
l
l
ê
ê
n
n
n
n
à
à
o
o
,
,
N
N
à
à
o
o
p
p
h
h
i
i
n
n
h
h
a
a
n
n
h
h
n
n
h
h
a
a
n
n
h
h
l
l
ê
ê
n
n
n
n
à
à
o
o
,
,
H
H
â
â
y
y
h
h
â
â
y
y
…
…
H
H
â
â
y
y
h
h
â
â
y
y
…
…
”
”
(
(
L
L
ờ
ờ
i
i
b
b
à
à
i
i
h
h
á
á
t
t
t
t
r
r
o
o
n
n
g
g
p
p
h
h
i
i
m
m
H
H
o
o
a
a
c
c
ủ
ủ
a
a
t
t
r
r
ờ
ờ
i
i
–
–
G
G
i
i
ả
ả
i
i
B
B
ô
ô
n
n
g
g
s
s
e
e
n
n
B
B
ạ
ạ
c
c
;
;
L
L
i
i
ê
ê
n
n
h
h
o
o
a
a
n
n
p
p
h
h
i
i
m
m
V
V
i
i
ệ
ệ
t
t
N
N
a
a
m
m
;
;
L
L
ầ
ầ
n
n
t
t
h
h
ứ
ứ
1
1
1
1
;
;
N
N
ă
ă
m
m
1
1
9
9
9
9
6
6
Đ
Đ
ạ
ạ
o
o
d
d
i
i
ễ
ễ
n
n
Đ
Đ
ỗ
ỗ
M
M
i
i
n
n
h
h
T
T
u
u
ấ
ấ
n
n
)
)
.
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
3
C
C
H
H
U
U
Y
Y
Ê
Ê
N
N
Đ
Đ
Ề
Ề
C
C
Ă
Ă
N
N
T
T
H
H
Ứ
Ứ
C
C
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (QUYỂN 2)
T
T
R
R
U
U
N
N
G
G
Đ
Đ
O
O
À
À
N
N
N
N
H
H
Ư
Ư
N
N
G
G
U
U
Y
Y
Ệ
Ệ
T
T
–
–
Q
Q
U
U
Â
Â
N
N
Đ
Đ
O
O
À
À
N
N
T
T
U
U
Ầ
Ầ
N
N
D
D
U
U
Y
Y
Ê
Ê
N
N
--
-----------------------------------------------------------------------------------------------------------------------------------------
Được đề cập lần đầu tiền trong chương trình Đại số 7, mặc dù rất đơn giản với căn bậc hai số học, căn thức đã
bước đầu gây ra sự tò mò, khám phá đối với nhiều bạn học sinh nhỏ tuổi yêu Toán. Lên lớp 9 bậc THCS, căn thức
đã trở thành một nội dung chính thống, phổ biến và giữ vị trí quan trọng trong chương trình Đại số 9, với đầy đủ
các khái niệm, tính chất, định nghĩa căn bậc hai với một biến số, nhiều biến số, hằng đẳng thức
2
A A
,
các phép
toán khai phương một tích, khai phương một thương, liên hệ giữa phép nhân, phép chia và phép khai phương, phép
trục căn thức, cao hơn nữa là biến đổi đơn giản biểu thức chứa căn bậc hai, tính toán với căn bậc ba và căn bậc cao.
Xin lưu ý nội dung phương trình, hệ phương trình chứa căn là nội dung khó, đặc sắc, tác giả cố gắng sắp xếp nó
trong nhiều tài liệu bộ phận khác. Những bài toán biến đổi đơn giản biểu thức chứa căn bậc hai, có thể nói đây là
kiến thức hết sức cơ bản, nền tảng, xuất hiện gần như là bắt buộc trong các kỳ thi kiểm tra kiến thức thường niên,
kỳ thi chọn học sinh giỏi toán các cấp trên toàn quốc, kỳ thi tuyển sinh lớp 10 hệ THPT, lý do đó khiến nó vẫn là
một câu hỏi rất được quan tâm của các bạn học sinh, phụ huynh, các thầy cô, giới chuyên môn và đông đảo bạn đọc
yêu Toán.
Biến đổi đơn giản biểu thức chứa căn bậc hai thì có lẽ đa số bạn đọc đều biết và từng trải qua, thậm chí là xuất
hiện tâm lý “chán chường, coi thường” với khẩu hiệu “ Cho biểu thức…Tìm điều kiện xác định…Rút gọn biểu
thức…Tính giá trị của biểu thức khi…Tìm x để…Vân vân. Trước tiên là rút gọn, còn yêu cầu phía sau của dạng
toán khá đa dạng, đa chiều, mục tiêu tìm các ẩn thỏa mãn một tính chất nào đó nên để thao tác dạng toán này, các
bạn học sinh cần liên kết, phối hợp, tổng hợp các kiến thức được học về căn thức, phương trình, hệ phương trình và
bất phương trình, bất đẳng thức, đôi khi nó đòi hỏi năng lực tư duy của thí sinh rất cao, nhiều bạn học sinh trung
học cơ sở có thể làm 80%, nhưng để làm trọn vẹn thì cũng không thể nói chắc chắn như đinh đóng cột được.
Tài liệu này mang tên BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2), chủ yếu xoay quanh các bài
toán rút gọn căn thức, kèm theo nhiều câu hỏi phụ. Một khi đã rút gọn thu được căn thức nhỏ, dựa trên đặc điểm
đặc trưng căn thức đó, kết hợp kiến thức nhiều mảng trong đại số, số học, hình học, chúng ta có thể tự mình tạo ra
rất nhiều câu hỏi phụ hay, khó, thậm chí là rất khó, tầm vóc tuy nhỏ (câu hỏi phụ) nhưng mức độ có thể vượt qua
những bài toán khó riêng biệt. Trước tiên tác giả xin được giới thiệu, mở rộng và phát triển lớp bài toán cũ, tức là
các đề bài nguyên nằm trong đề thi chất lượng học kỳ I, đề thi chất lượng học kỳ II, đề thi tuyển sinh lớp 10 THPT,
tuyển sinh lớp 10 THPT Chuyên và đề thi học sinh giỏi các cấp bậc THCS trong phạm vi có thể sưu tập. Các bạn
hãy thử tưởng tượng, với 63 tỉnh thành thôi, với bề dày thi tuyển sinh hai thập niên trở lại đây, với tầm 70 trường
THPT Chuyên trên cả nước, thi tuyển sinh môn Toán gồm Toán 1 và Toán 2 (Dành cho chuyên Toán, chuyên Tin
học), giả sử đề thi nào cũng có tối thiểu một bài toán căn thức tổng hợp, chúng ta đã có thể khai thác tối thiểu bao
nhiêu bài toán. Tác giả xin làm phép thống kê sơ lược
1. Đề thi chất lượng học kỳ I và học kỳ II (Sở giáo dục và Đào tạo): 63.2 đề thi.
2. Đề thi chọn học sinh giỏi lớp 9 THCS (Sở Giáo dục và Đào tạo): 63.2 đề thi.
3. Đề thi tuyển sinh lớp 10 THPT (Đại trà): 63 đề thi.
4. Đề thi tuyển sinh lớp 10 THPT Chuyên (Toán 1 và Toán 2): 70.2 đề thi.
Như vậy, trong một năm, chúng ta sẽ có tổng cộng
6
3.2 63.2 63 70.2 455
bà
i toán cần khai thác, chỉ cần khai
thác các đề thi từ năm 1990 đến nay (2016), quãng đường 27 năm chúng ta sẽ có 12285 bài toán. Tuy nhiên, vì theo
thời gian, kéo theo phân chia địa giới hành chính, từ trung ương đến địa phương, nếu các bạn trẻ hiểu biết về các
tỉnh cũ (tỉnh ghép) Việt Nam thì số lượng đề thi thực tế không tới mức đó. Cụ thể
1. Tỉnh Hoàng Liên Sơn (Lào Cai, Yên Bái, Nghĩa Lộ). Tái lập 1991.
2. Tỉnh Bắc Thái (Bắc Cạn, Thái Nguyên). Tái lập 06.11.1996.
3. Tỉnh Cao Lạng (Cao Bằng, Lạng Sơn). Tái lập 29.12.1978.
4. Tỉnh Hà Tuyên (Hà Giang, Tuyên Quang). Tái lập 12.08.1991.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
4
5. Tỉ
nh Hà Sơn Bình (Hà Đông, Sơn Tây, Hòa Bình). Tái lập 12.08.1991.
6. Tỉnh Hà Nam Ninh (Hà Nam, Nam Định, Ninh Bình). Tái lập 26.12.1991.
7. Tỉnh Vĩnh Phú (Vĩnh Phúc, Phú Thọ). Tái lập 06.11.1996.
8. Tỉnh Hà Bắc (Bắc Giang, Bắc Ninh). Tái lập 06.11.1996.
9. Tỉnh Hải Hưng (Hải Dương, Hưng Yên). Tái lập 06.11.1996.
10. Tỉnh Nghệ Tĩnh (Nghệ An, Hà Tĩnh). Tái lập 12.08.1991.
11. Tỉnh Bình Trị Thiên (Quảng Bình, Quảng Trị, Thừa Thiên Huế). Tái lập 30.6.1989.
12. Tỉnh Quảng Nam – Đà Nẵng. Tái lập 06.11.1996.
13. Tỉnh Kon Tum – Gia Lai. Tái lập 12.08.1991.
14. Tỉnh Nghĩa Bình (Quảng Nghãi, Bình Định). Tái lập 30.06.1989.
15. Tỉnh Phú Khánh (Phú Yên, Khánh Hòa). Tái lập 30.06.1989.
16. Tỉnh Thuận Hải (Ninh Thuận, Bình Thuận, Bình Tuy). Tái lập 26.12.1991.
17. Tỉnh Sông Bé (Bình Dương, Bình Phước, Bình Long). Tái lập 01.01.1997.
18. Tỉnh Đồng Nai (Đồng Nai, Đặc khu Vũng Tàu – Côn Đảo). Tái lập 12.08.1991.
19. Tỉnh Cửu Long (Trà Vinh, Vĩnh Long). Tái lập 26.12.1991.
20. Tỉnh Hậu Giang (Cần Thơ, Sóc Trăng). Tái lập 26.12.1991.
21. Tỉnh Minh Hải (Cà Mau, Bạc Liêu). Tái lập 06.11.1996.
Theo chủ quan của tác giả, mỗi tỉnh thành trên mọi miền Tổ quốc tuy văn hóa, giáo dục mang tính thống
nhất và tươn
g đồng, nhưng đề thi vẫn có những nét đặc sắc riêng, về cấu trúc và mức độ thông hiểu, vận dụng, đánh
giá. Đề thi mang hàm lượng kiến thức, co ép thời gian và yêu cầu kỹ năng cao hơn tập trung ở những khu vực, địa
phương đông dân cư hơn, có thể kể đến đề thi các tỉnh Duyên hải Đồng bằng Bắc bộ (Khu III cũ), Bắc Trung Bộ
(Khu IV cũ), Duyên hải Nam Trung Bộ (Khu V cũ), Đông Nam Bộ. Các khu vực khác như Tây Bắc Bộ, Đông Bắc
Bộ - Việt Bắc, Tây Nguyên, Tây Nam Bộ có mật độ dân cư thấp hơn, và có cộng đồng các dân tộc thiểu số nên việc
phổ biến kiến thức còn chưa đồng bộ, khó khăn, cũng như cần có lộ trình cụ thể nếu muốn đảm bảo mặt bằng
chung. Có thể nói sự đồng bộ hóa giáo dục vẫn là bài toán mở, mang tính thời sự, tính bình đẳng nhiều thách thức
và cấp bách trong công cuộc cải cách giáo dục, văn hóa hiện nay.
Ngoài việc xử lý, tương tự hóa, rút kinh nghiệm, rèn kỹ năng phản biện, tăng cường mở rộng, đào sâu và
phát triển bài toán, trong quá trình khai thác từng bài toán trong đề thi các tỉnh thành, các bạn sẽ hiểu thêm về địa lý
đất nước, về văn phong, motip đề thi từng tỉnh, thậm chí là sự đầu tư, quan tâm giáo dục của tỉnh đó (nói chung),
các bạn chắc chắn sẽ thấy đất nước mình rất đẹp, giáo dục của mình rất phong phú, đa dạng, đa chiều. "Trăm hay
không hay bằng tay quen", các phương pháp, kỹ thuật cơ bản đã được được các thế hệ đi trước đúc kết và tận tụy
cho thế hệ tương lai, các bạn hoàn toàn đủ khả năng kế thừa, phát huy và sáng tạo không ngừng, chuẩn bị đủ hành
trang nắm bắt khoa học kỹ thuật, đưa đất nước ngày càng vững bền, phồn vinh, và hiển nhiên những bài toán trong
các kỳ thi nhất định không thể là rào cản, mà là cơ hội thử sức, cơ hội khẳng định kiến thức, minh chứng sáng ngời
cho tinh thần học tập, tinh thần ái quốc !
I
I
.
.
K
K
I
I
Ế
Ế
N
N
T
T
H
H
Ứ
Ứ
C
C
C
C
H
H
U
U
Ẩ
Ẩ
N
N
B
B
Ị
Ị
1. Kỹ thuật nhân, chia đơn thức, đa thức, hằng đẳng thức.
2. Nắm vững các phương pháp phân tích đa thức thành nhân tử.
3. Khái niệm, định nghĩa, điều kiện xác định của căn bậc hai, hằng đẳng thức
2
A
A
,
kỹ năng phân tích
bình phương biểu thức chứa căn, thuật toán khai phương một tích, khai phương một thương.
4. Liên hệ giữa phép khai phương và phép nhân, liên hệ giữa phép khai phương và phép nhân.
5. Kỹ thuật trục căn thức với căn bậc hai, căn bậc ba, trục căn liên tiếp.
6. Nắm vững các phương pháp giải, biện luận phương trình bậc nhất, bậc hai, bậc cao.
7. Sử dụng thành thạo các ký hiệu toán học, logic (ký hiệu hội, tuyển, kéo theo, tương đương).
8. Kỹ năng giải hệ phương trình cơ bản và hệ phương trình đối xứng, hệ phương trình đồng bậc, hệ phương
trình chứa căn thông thường.
9. Kỹ thuật đặt ẩn phụ, sử dụng đại lượng liên hợp, biến đổi tương đương.
10. Kiến thức nền tảng về số học, ước lượng – đánh giá, hàm số - đồ thị, bất đẳng thức – cực trị.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
5
I
I
I
I
.
.
M
M
Ộ
Ộ
T
T
S
S
Ố
Ố
B
B
À
À
I
I
T
T
Ậ
Ậ
P
P
Đ
Đ
I
I
Ể
Ể
N
N
H
H
Ì
Ì
N
N
H
H
.
.
Bài
toán 1. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2006 – 2007; Khóa thi 30.06.2006.
Cho biểu thức
2
10 2 1
6 3 2
x
x x
Q
x x x x
với
0; 9
x x
(*).
1. Rút gọn biểu thức Q.
2. Tính giá trị của biểu thức Q khi
1
6
x
.
3. Tì
m giá trị của x để
Q
.
4. Tì
m giá trị của x sao cho
1
9
Q
.
5. Tì
m giá trị lớn nhất của Q.
6. Chứng minh rằng Q không thể nhận giá trị nguyên với mọi giá trị x thỏa mãn (*).
Bài toán 2. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2013 – 2014; Khóa thi 20.06.2013.
Cho biểu thức
1
1
. 4
4
2
2
x
P x
x
x x
vớ
i
0; 4
x x
.
1. Rút gọ
n biểu thức P theo hai cách.
2. Tính giá trị của biểu thức P khi
9
x
.
3. Tính giá
trị của biểu thức P khi
1
5
14
5
2
x
.
4. Tì
m các giá trị của x để
3
P
.
5. Tì
m giá trị nhỏ nhất của biểu thức P.
6. Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên.
Bài toán 3. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2004 – 2005; Khóa thi 30.06.2004.
Cho biểu thức
2
1
4
2
8
2 2 4
a a
a a
A
a
a a a
vớ
i
0
; 4
a
a
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
9
4 5
a
.
3. Tìm giá trị của a để
3
2
A
.
4. Tì
m khoảng giá trị của a đ
ể
1
2
A
.
5. Chứng
minh rằng
3
0
2
A
, từ đó suy ra A chỉ nhận duy nhất một giá trị nguyên với
0; 4
a a
.
6. Tính giá trị của A khi a là số nguyên thỏa mãn
2
16
4.25
b
a
a b
.
Bài
toán 4. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2008 – 2009; Khóa thi 30.06.2008.
Cho biểu thức
2
3 6
1 . 1
1
1 5
P
x
x x
với
0
1x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của biểu thức P khi
6
2 5
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
6
3. Tì
m giá trị của x để
2
3
P
.
4. Tì
m tất cả các khoảng giá trị của x sao cho
2 1
x
P
x
.
5. Chứng
minh rằng biểu thức P chỉ nhận đúng một giá trị nguyên với
0 1x
.
6. Tính giá trị của P khi x là số tự nhiên thỏa mãn
3
4
3
x
x
x
.
Bài toán 5. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2015 – 2016; Khóa thi 08.06.2015.
Cho biểu thức
2
2
2 1
0
; 1
x
x x x x
P x x
x x x x x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của biểu thức P khi
3
2 2x
.
3. Tì
m giá trị của x để P nhận giá trị bằng 7.
4. So sánh P với 6.
5. Chứng minh rằng với mọi giá trị của x để biểu thức P có nghĩa thì biểu thức
7
P
chỉ
nhận một giá trị
nguyên.
6. Tính giá trị của P khi x là số nguyên lớn nhất sao cho
2
3 1
1
x
x
x
.
Bài toán 6. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2011 – 2012; Khóa thi 30.06.2011.
Cho biểu thức
3
1 3
1
1
1
x
A
x
x x
với
0
; 1x x
.
1. Rút gọn A.
2. Tính giá trị của A khi
3
2 2
x
.
3. Tì
m các khoảng giá trị của x để
1
1
5 2
A
.
4. Tì
m giá trị của x đ
ể
6
6
x
A
x
.
5. Chứng
minh rằng với
0
; 1x x
thì biểu thức A chỉ có duy nhất một giá trị nguyên.
6. Tính giá trị của A khi x là số tự nhiên nhỏ nhất sao cho
3
2
7 6n n n
ch
ia hết cho 125.
Bài toán 7. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2013 – 2014; Khóa thi 02.07.2013.
Cho biểu thức
1
2 1
:
1 1
x
x
P
x x
x
x
(với
0; 1x x
).
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi
4 2 3 3 5
x
.
3. Tì
m giá trị của x đ
ể
9
2
P
.
4. Tì
m giá trị của x để
8
,25
P
.
5. Tì
m giá trị nhỏ nhất của biểu thức P.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
7
Bài
toán 8. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2007 – 2008; Khóa thi 30.06.2007.
Cho phương trình
2
3
1
2
2
x x
A
x
x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
8
41
x
.
3. Tì
m giá trị của x để
3
A
.
4. Tì
m khoảng giá trị của x để
1A
.
5. Tì
m tất cả các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
6. Tìm giá trị của m để phương trình
A
m
có
nghiệm.
Bài toán 9. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2014 – 2015; Khóa thi 04.07.2014.
Cho biểu thức
1 1 1
:
1
2 1
x
P
x x x x x
với
0
; 1x x
.
1. Rút gọn biểu thức P.
2. Tìm x để
1P
.
3. Tính giá trị
của P khi x thỏa mãn hệ thức
1 2 1 0
x x
.
4. Tính giá trị
của P khi
9
4 5 3 5 11
x
.
5. Tìm tất cả các giá trị của x để
1
5
P
x
.
6. Tì
m giá trị nhỏ nhất của biểu thức
1
3Q
P
x
.
Bài
toán 10. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2005 – 2006.
Cho biểu thức
5
2
3
2
4
3 7 12
x
x
x
A
x x x x
.
1. Rút gọ
n biểu thức A.
2. Tìm các giá trị x để
a)
3
2
A
.
b)
A
x
.
c)
1A
.
3. Tính giá trị
của A kh
i
3
5
8
x
.
4. Tồn
tại hay không các số thực x và y thỏa mãn hệ thức
2
1
1
10 11
A
y x
.
5. Tì
m giá trị nhỏ nhất của A trong trường hợp
0
16; 9
x
x
.
Bài toán 11. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2010 – 2011; Khóa thi 20.06.2010.
Cho biểu thức
7
3 2 1
5 6 2 3
x x x
A
x
x x x
vớ
i
0
; 4; 9
x
x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
8
1. Rút gọ
n A.
2. Tính giá trị của A khi
3
2 2
x
.
3. Tìm giá trị của x để
a)
4A
.
b)
2A
.
4. Tồn
tại hay không các số thực x và y thỏa mãn đẳng thức
2
1 1
6 5
A
x y
.
5. Tì
m giá trị nhỏ nhất của biểu thức
1
6
x
B
A
x
.
Bài
toán 12. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2011 – 2012; Khóa thi 20.06.2011.
Cho biểu thức
3
2 9
2
3 6
x x x
P
x x x x
vớ
i
0
; 4
x
x
.
1. Rút gọ
n P.
2. Tìm x để
7
12
P
.
3. Tìm x để
1
2
P
.
4. Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên.
5. Tìm tất cả các giá trị hữu tỷ của x để P nhận giá trị nguyên.
Bài toán 13. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2009 – 2010.
Cho
2
4 7 1
0
; 1
3 2 3 1
x x x
A x x
x x x x
.
1. Rút gọn A.
2. Tính giá trị của A khi x thỏa mãn đẳng thức
2
5 2 0
x
x
.
3. Tì
m các giá trị của x để
1
8
x
A
.
4. Tì
m các giá trị của x để
A
.
5. Chứng minh rằng với điều kiện
0
; 1x x
th
ì A chỉ nhận duy nhất một giá trị nguyên. Tìm giá trị
nguyên đó.
Bài toán 14. Mở rộng và phát triển bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2014 – 2015; Khóa thi 02.07.2012.
Cho biểu thức
2
4
8
3
4 1 4
x
x
B
x
x x x
với
0
; 16
x
x
.
1. Rút gọ
n B.
2. Tìm giá trị của x để
1B
.
3. Tính giá trị
của B khi x thỏa mãn đẳng thức
2
1
x
x
.
4. Tì
m giá trị của x sao cho B không vượt quá
3
2
.
5. Tìm x để giá trị của B là một số nguyên.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
9
Bài
toán 15. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2016 – 2017.
Cho biểu thức
2
1 1
:
0; 1
1
1
x
x x
P x x
x
x x x x
.
1. Rút gọn biểu thức P.
2. Tìm x để
2P
.
3. Tìm x để P có giá trị nhỏ nhất.
4. Tìm khoảng giá trị của x để
12P
.
5. Tính giá trị
của P khi x thỏa mãn
1
3 7 4
x
x x
.
6. Tồn
tại hay không các số nguyên x và y thỏa mãn đẳng thức
a)
2
015 2016 2017
P
y y
.
b)
4
2
2
P
y y
.
Bài toán 16. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2012 – 2013.
Cho biểu thức
8 8 2 2 5
:
2 2 2
x x x x x
A
x x x x x x
với
0
x
.
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x thỏa mãn
1
2
x
x
.
3. Tính giá trị
của A khi x là nghiệm của phương trình
2 3
2
4 3 4x x x x
.
4. Tì
m giá trị của x đ
ể
A
.
5. Chứng
minh rằng
1A
, từ đó suy
ra A chỉ nhận duy nhất một giá trị nguyên với
0
x
.
6. Phần ngu
yên của x, ký hiệu [x], biểu thị số nguyên lớn nhất không vượt quá x.
Chứng minh rằng khi x thỏa mãn phương trình phần nguyên
4
1
2
x
x
thì A nhận hai giá trị.
Bài toán 17. Mở rộng và phát triển câu 1.b); Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2016 – 2017; Khóa thi 16.06.2016.
Cho biểu thức
3
3
.
9
3
3
x x
A
x
x x
với
0; 9
x x
.
1. Chứng minh r
ằng
1
3
A
x
.
2. Tính giá trị
của biểu thức A k
hi
1
3
2 2
1
2
x
.
3. Tính giá trị
của biểu thức A khi x thỏa mãn
5
6
x
x
.
4. Tìm tất cả các giá trị của x đ
ể
1
2
A
.
5. Tì
m x sao cho A thỏa mãn đẳng th
ức
3
5
2
3
x
A
x
.
6. Kh
i n là số tự nhiên sao cho
3
1
9
n
S
là số nguyên tố. Tìm x sao cho
1
A
S
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
10
Bài
toán 18. Mở rộng và phát triển bài 2; Đề kiểm tra chất lượng học kỳ I; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo; Quê hương Thái Bình; Năm học 2015 – 2016.
Cho biểu thức
2
2 4
4
2
2
x
x x
P
x
x x
.
1. Tì
m điều kiện xác định của biểu thức P. Rút gọn biểu thức P.
2. Tìm x để
2P
.
3. Tính giá trị của biểu thức P tại x thỏa mãn
2 2 1 0
x x
.
4. Tính giá trị
của P khi x là giá trị nhỏ nhất của biểu thức
9 2
;
0 2
2
x
S x
x x
.
5. Tì
m giá trị của x đ
ể
3
2
1
x
P
x
.
6. Tì
m tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức
2
3
1 4
A
x xy
.
Bài toán 19. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2002 – 2003.
Cho biểu thức
3
1 3 2
1
:
9
6
2 3
x
x x x
A
x
x x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A tạ
i
25
1
6
x
.
3. Với
giá trị nào của x thì biểu thức A nhận giá trị âm.
4. Tính giá trị của A khi
7
2 6 3
x
.
5. Tì
m giá trị của x sao cho
2
5
x
A
x
.
6. Tính giá trị của A khi x là giá trị lớn nhất của biểu thức
9
; 9
5
a
S a
a
.
Bài toán 20. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2014 – 2015; Khóa thi 20.06.2014.
Cho biểu thức
2 3 5 7 2 3
:
0; 4
2
2 1 2 3 2 5 10
x x
A x x
x x x x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi x thỏa mãn
2
1 7
x
x
.
3. Tì
m tất cả các giá trị của x sa
o cho
3
2
2
x
A
x
.
4. Tì
m giá trị của x sao cho
15
7
A
.
5. Tì
m x sao cho A nhận giá trị là một số nguyên.
6. Tính giá trị của A khi x là số nguyên dương thỏa mãn
2
3
3 11.49
y
x
x y
.
7. Tồn tại hay không các số thực x và y thỏa mãn
2
2
3
A
x y
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
11
Bài
toán 21. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2006 – 2007.
Cho
1
1 1 1 1
1
1 1 1 1
x x
A
x
x x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
3
4
x
.
3. Tìm giá trị của x đ
ể
2
1
3
A
x
.
4. So sánh A
và
2
2
.
5. Tính giá trị
của A khi
2
2
2
1 2015 2015
2
015 1 2015
2
2016 2016
x
.
Bài toán 22. Mở rộng và phát triển bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2010 – 2011.
Cho biểu thức
3
1 9
.
3
3
x
A
x
x x x
với
0; 9
x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
6
2 5
x
.
3. Tì
m giá trị của x sao cho
8
5
A
.
4. Tìm x sao ch
o
2
10
A
x
.
5. Tính giá trị
của A khi x là số nguyên lớn nhất sao cho
2
13
x x
là một số chính phương.
6. Tồn tại hay không các số nguyên x và y thỏa mãn
2 1A y
.
7. Tìm x sao cho
2
A
a
,
trong đó a là nghiệm lớn nhất của phương trình
2
2
4
7 7 7
a
a a a
.
Bài
toán 23. Mở rộng và phát triển bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Lê
Quý Đôn; Tỉnh Ninh Thuận; Năm học 2016 – 2017.
Cho biểu thức
2
2 1
.
1 2
2
1
x x x
P
x x
x x
vớ
i
0; 1; 2
x x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi x thỏa mãn
3
30
x x
.
3. Tì
m x để
5
2
P
x
.
4. Tì
m các giá trị nguyên của x để
2P
.
5. Tì
m các giá trị nguyên của x để P nhận giá trị nguyên.
6. Tính giá trị của P khi x là nghiệm lớn nhất trong các nghiệm
;x
y
của hệphương trình
2
2
2
1 2 ,
2 9.
x xy y x
x y
7. Chứng minh rằng không tồn tại các số thực x và y thỏa mãn
4
4
1
2 3
3
P
x xy
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
12
Bài
toán 24. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2007 – 2008; Khóa thi 19.06.2007.
Cho
2
9 3 2 1
5
6 2 3
x
x x
A
x
x x x
.
1. Rút gọ
n A.
2. Tính giá trị của A với
3
2 2
x
.
3. Tì
m giá trị của x đ
ể
6
5
x
A
.
4. Tì
m giá trị của x để
2A
.
5. Tì
m các giá trị nguyên của x để A nhận giá trị nguyên.
6. Tính giá trị của A khi x là giá trị nhỏ nhất của
4
4
1
8S
a b
a
b
, với
, 0; 1a b a b
.
Bài toán 25. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2015 – 2016.
Cho biểu thức
2
1 6 4
4
2
2
x x x x x
P
x
x x
vớ
i
0; 4
x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
9
4 5
x
.
3. Tìm giá trị của x để
2P
.
4. Tì
m giá trị của x để
3
P
x
.
5. Tì
m tất cả các giá trị của m để phương trình
P
m
có
nghiệm.
6. Tìm giá trị nhỏ nhất của biểu thức
P
.
7. Tính giá trị
của biểu thức P khi x là nghiệm phương trình
2 1 3 1x x x
.
8. Tì
m x sao cho
a
P
b
trong đ
ó a và b là hai số thực dương khác nhau thỏa mãn
10
11
a
b ab
.
Bài
toán 26. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Lê
Quý Đôn; Tỉnh Bình Định; Năm học 2016 – 2017.
Cho biểu thức
2
3
3
3
2 3 1 3
x
x x x
P
x x x x
với
0
; 9
x
x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
2
5 4 0
x x
.
3. Tính giá trị
của biểu thức P khi
7
4 3
x
.
4. Tì
m giá trị của x để
5
2
2
x
P
.
5. Tìm giá trị nhỏ nhất của biểu thức P.
6. Tìm tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Tính giá trị của P khi x là số thực nhỏ nhất thỏa mãn
2
2
2 2
;
,
a b
x a b
a
ab b
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
13
Bài
toán 27. Mở rộng và phát triển câu 1.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố
Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2003 – 2004.
Cho biểu thức
2
2
1
1
1
x x x x
M
x
x
x x x
với
0 1x
.
1. Rút gọ
n biểu thức M.
2. Tính giá trị của biểu thức M kh
i
1
4
x
.
3. Tính giá trị
của biểu thức M khi x thỏa mãn
2
9
3 1 6 1x x x
.
4. Tì
m x thỏa mãn hệ thức
1
5
9
M
x
.
Bài
toán 28. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi lớp chuyên Khoa học Tự nhiên); Đề thi chính thức; Trường THPT Chu Văn An và THPT
Chuyên Hà Nội – Amsterdam; Thủ đô Hà Nội; Năm học 2003 – 2004.
Cho biểu thức
2
2
1
2
1
1
x
x
x x x
P
x x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi x thỏa m
ãn
2 4
x x
.
3. Tính giá trị
của P khi x thỏa mãn
3
1
0
x
x
.
4. Tìm giá trị nhỏ nhất của P.
5. Tìm tất cả các giá trị x sao cho
4
5
P
x
.
6. Tìm x để biểu thức
2
x
Q
P
n
hận giá trị là số nguyên.
7. Giả sử x thỏa mãn
2
2 3 5 2 3 12 14
x x x x
. Kh
i đó giá trị của P là số hữu tỷ hay số vô tỷ ?
Bài toán 29. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi lớp chuyên Khoa học Tự nhiên); Đề thi chính thức; Trường THPT Chu Văn An và THPT
Chuyên Hà Nội – Amsterdam; Thủ đô Hà Nội; Năm học 2005 – 2006.
Cho biểu thức
1
1 1x x x x x
P
x x x x x
.
1. Rút gọ
n P.
2. Tìm x đ
ể
9
2
P
.
3. Tì
m các giá trị của x để
6
1x
P
x
.
4. Tính giá trị của P khi
3
3
2
5 2 5 3
x
.
5. Tì
m số thực a lớn nhất sao cho
P a
.
6. Tì
m tất cả các giá trị của tham số m để phương trình
P m
c
ó nghiệm.
7. Với
các số thực
1
, 2, 3
a
b c
,
phản biện bất đẳng thức
2
2 2
1
2 3 1
P
a a b b c c
.
Bài toá
n 30. Mở rộng và phát triển câu 5b (Chương trình THCS Thí điểm); Đề thi chọn học sinh giỏi lớp 9
THCS; Đề thi chính thức; Sở Giáo dục và Đào tạo Thành phố Hồ Chí Minh; Năm học 2003 – 2004.
Cho biểu thức
3
3 2 9
1 :
9
2
3 6
x
x x x x
P
x
x x x x
với
0; 4; 9
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
14
1. Thu gọn
biểu thức P.
2. Tính giá trị của P khi
7
4 3
x
.
3. Tính các giá
trị của P khi x thỏa mãn
2
2
5 3 1x x x
.
4. Tìm các giá trị của x để
1P
.
5. Tì
m các giá trị của x để
4
9
2
P
x
x
.
6. Tồn
tại hay không số thực x sao cho P là nghiệm của phương tr
ình
3
2
2
4
0
4
P
P
P
.
Bài
toán 31. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi lớp chuyên Khoa học Tự nhiên); Đề thi chính thức; Trường THPT Chu Văn An và THPT
Chuyên Hà Nội – Amsterdam; Thủ đô Hà Nội; Năm học 2004 – 2005.
Cho biểu thức
2
1
1 1
2
1
1 2
x
x x
P
x x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
16
x
.
3. Tì
m x đ
ể
5
4
x
P
.
4. Tì
m giá trị của x để
2
P
x
.
5. Tính giá trị
của P khi x là nghiệm của h
ệ
4
4 0,
4 4 0.
x
y
y x
6. Tính giá trị của P khi x là số thực nhỏ nhất thỏa mãn
5 7a a x a
.
Bài toán 32. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 1993 – 1994;
Ngày thi 08.08.1993.
Cho biểu thức
2 1 2
1 .
1
1 2 1
x x x x x x x x
A
x
x x x
.
1. Tìm điều kiện của x để A có nghĩa.
2. Rút gọn A.
3. Tính giá trị của A khi
9
x
.
4. Tì
m x bi
ết
6 6
5
A
.
5. Chứng
minh r
ằng
2
3
A
là bấ
t đẳng thức sai.
6. Tính giá trị của A khi x thỏa m
ãn
16
4
x
x
.
7. Tính giá trị
của A khi x thỏa mãn phương trình
2
2
7 3 1 3 0
x
x x x
.
Bài toán 33. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2001 – 2002.
Cho biểu thức
3 9 3 1 1 1
2
:
1
2
1 2
x x
P
x
x
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
15
1. Tì
m điều kiện của x để P có nghĩa, khi đó hãy rút gọn P.
2. Tìm các số tự nhiên x để
1
P
là số
tự nhiên.
3. Tính giá trị của P khi
4
2 3
x
.
4. Tính giá trị
của P khi
3
3
5
2 7 5 2 7
x
.
5. Tì
m x sao cho
8 16
P x x
.
6. Tì
m các giá trị của x sao cho
3
1
P
P
.
7. Phản biện
bất đẳng thức
2
2
1
3
1
y y
P
y y
.
Bài toán 34. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2003 – 2004.
Cho biểu thức
2
1 1
1 1 1
x
x
A
x x x x x
.
1. Tì
m x để A có nghĩa. Hãy rút gọn A.
2. Tính A với
33
8 2
x
.
3. Chứng minh r
ằng
1
3
A
.
4. Tì
m tất cả các giá trị x để
6
1
x
A
x
.
5. Tính giá trị của A kh
i
7
7
1
x a
a
với
1
3
a
a
.
6. Tì
m giá trị lớn nhất của A.
7. Tìm tất cả các giá trị của x để A nhận giá trị nguyên.
Bài toán 35. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2004 – 2005.
Cho biểu thức
2
1
.
1
1 2 1 2 1
x x x x x x x x
M
x
x x x x x
.
1. Hã
y tìm điều kiện của x để biểu thức M có nghĩa, sau đó rút gọn M .
2. Tìm tất cả các giá trị của x sa
o cho
6
7
P
.
3. Tính giá trị
của M khi
3
3 3
x a a
với
3
3
3
2 2 3 2 2
a
.
4. Tính giá trị của M khi x là giá trị lớn nhất của biểu thức
,
, 0
abc
S
a b c
a b b c c a
.
5. Tìm tất cả các giá trị của x sao cho
2
2
1
x
P
x
.
6. Với giá trị nào của x thì biểu thức M đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đó của M .
Bài toán 36. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2006 – 2007.
Cho biểu thức
1 2
1 : 1
1
1
1
x x
P
x
x x x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
16
1. Tì
m điều kiện của x để biểu thức P có nghĩa và rút gọn biểu thức P .
2. Tính giá trị của P khi
21
8 5
x
.
3. Tính giá trị
của P khi
3
5 3 5 10 2
x
.
4. Tính giá trị
của P khi
x
a b c
với
,
,a b c
là các
số thực thỏa mãn đồng thời các hệ thức
1
; 1
3 12 4 10 5 3
a b c a b c
.
5. Tì
m các giá trị của x sao cho
4
P
x
.
6. Tì
m các giá trị của x sao cho
4 3 1 1
4 2
x
x
P
.
7. Tì
m các giá trị nguyên của x để biểu thức
Q
P x
nhận giá trị nguyên.
Bài toán 37. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2010 – 2011;
Ngày thi 06.06.2010.
Cho biểu thức
2
1 2
:
9
3 3
x x x
P
x
x
x x x
.
1. Tìm điều kiện của x để biểu thức P có nghĩa và rút gọn P.
2. Tìm giá trị của x đ
ể
4
3
P
.
3. Tì
m tất cả các giá trị của x sa
o cho
5
1
6
x
P
x
.
4. Tì
m các giá trị của x sao cho
4
4 4
2 2 2 2 2 2
2
a
b c
P
a b b c c a
với
0
a
b c
.
5. Tính giá trị của P khi
2
4
2 2 1
x
a a
với
1 1 2
2
2
8 8
a
.
6. Chứng
minh rằng
3
S P a P b
là
một số nguyên tố, trong đó a và b là các số thực dương thỏ
a
m
ãn đẳng thức
2 2
2
1 1 1 1 1
a
b a b ab
.
Bài
toán 38. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2014 – 2015;
Ngày thi 06.06.2014.
Cho biểu thức
2 4 2 1 1 2
: 3
1
8 2 1
x x x x
A
x
x x x x
.
1. Rút gọn A.
2. Tính giá trị của A khi
9
4 5
x
.
3. Tì
m giá trị của x để
1A
.
4. Tì
m x sao cho
10
9 2
x
A
x
.
5. Tính giá trị của A khi x là số nguyên thỏa mãn
2
2
2 7 3 1 3
x x x x
.
6. Tì
m m để phương trình
A m
có nghiệm.
7. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức
8 1 2 2 3
A x y y x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
17
Bài toán
39. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1990 – 1991.
Cho
biểu thức
1
1 5 3 2
: 1
9 1
3
1 3 1 3 1
x
x x
P
x
x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
2
9 10 1 0
x x
.
3. Tính giá trị
của P khi
8 2 7
x
.
4. Tìm các giá trị của x để
P
.
5. Tìm x sao ch
o
5
3
x
P
x
.
6. Tính giá trị
của P khi
1
2 2 2 12
x
a a b b
với a
và b là các số thực thỏa mãn đồng thờ
i
4
2 2 4 8 4 4 8
4; 8
a a b b a a b b
.
Bài toán
40. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1992 – 1993.
Cho biểu thức
2 1 2
: 1
1 1 1
x x x
B
x x x x x
.
1. Rút gọn B.
2. Tính
B
khi
5
2 3
x
.
3. Tìm x để
3
1
2
1
B
x
x
.
4. Tìm giá trị của x để giá trị của B không lớn hơn giá trị biểu thức
1
2x
.
5. Với
mỗi số thực a, ký hiệu [a] là phần nguyên của a, tức là số nguyên lớn nhất không vượt quá a.
Tồn tại hay không giá trị của x để
B S
,
trong đó
1 1 1
1
...
2
3 100
S
.
6. Giả sử
,
,a b c
là độ dài ba cạnh của một tam giác. Tính giá trị của biểu thức B khi
2
a
b c b c a c a b
x max
abc
.
Bài
toán 41. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1993 – 1994.
Cho biểu thức
1 2 2
1 : 1
2
1 2 1 2 1 2 1
x x x x x x
M
x
x x x
.
1. Rút gọn M.
2. Tính giá trị của M k
hi
1
3
2 2
3
x
.
3. Tì
m tất cả các giá trị của x sao cho
4B
x
.
4. Tì
m khoảng giá trị của x sao cho
2
3
B
.
5. Tính giá trị
của M khi x là giá trị lớn nhất của biểu thức
1
8, 8
A
a a a
.
6. Với
các số thực dương
, ,a b c
,
tìm giá trị lớn nhất của biểu thức
ab
bc ca
C
B
a b c
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
18
Bài toán
42. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1994 – 1995.
Cho biểu thức
3
3
2
1 1
.
1 1
1
a a a
P
a
a
a a
a
.
1. Rút gọ
n P.
2. Tính giá trị của biểu thức P khi
11
96
a
.
3. Tì
m giá trị của a để
4
1P a a
.
4. Tì
m giá trị của a để giá trị biểu thức P không vượt quá
4
5 1a a
.
5. Xét dấ
u của biểu thức
1
P
a
.
6. Tính giá trị của biểu thức P khi a thỏa mãn hệ thức
2
5 2 2 1 0
a a b b
.
7. Tì
m tất cả các giá trị của tham số m để phương trình
2
6
P
a a m
có
nghiệm.
Bài toán 43. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1995 – 1996.
Cho biểu thức
1
1 8 3 1
:
1 1
1
1 1
a
a a a a
B
a a
a a a
.
1. Rút gọn biểu thức B.
2. Tính giá trị của B khi
3 2 2
a
.
3. Tính giá trị của B khi a là nghiệm của phương trình
2
1 3 0
a
a
.
4. Tính giá trị
của B khi
3 3
17
5 38 17 5 38
a
.
5. So sánh B
với 1.
6. Tìm tất cả các giá trị của a để B nhận giá trị là số nguyên.
7. Tìm a đ
ể
12
13
B
.
Bài toán
44. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1995 – 1996.
Cho biểu thức
1 1 1 2
:
1 2 1
a a
A
a a a a
.
1. Rút gọ
n A.
2. Tính giá trị của A với
1
6
a
.
3. Tính giá trị
của A với a thỏa mãn
3
1 10a a
.
4. Tính giá trị
của A khi
1
1 1
.
.. 5
1
2 2 3 2024 2025
a
.
5. Tì
m giá trị của a để
A
.
6. Tì
m giá trị của a để
1
6
A
a
.
7. Tì
m số thực nhỏ nhất m sao cho
A
m
.
Bài toán 45. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1996 – 1997.
Cho biểu thức
1 2 2 1 2
:
1
1
1 1
x
A
x
x x x x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
19
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi x thỏa mãn
6
20
x
x
.
3. Tính giá trị
của A khi
4
sin 60 2 sin 45 3 2 cos45
x
.
4. Tính
giá trị của A khi x là số thực nhỏ nhất thỏa mãn
2
2 , 2;2
a
a x a
.
5. Với
giá trị nào của x thì A đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
6. Tìm giá trị của x để giá trị của A không nhỏ hơn giá trị biểu thứ
c
4
x
x
.
7. Tì
m tất cả các giá trị của m sao cho tồn tại đẳng thức
A m
.
Bài toán 46. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1998 – 1999.
Cho biểu thức
3
2
1 1 4
: 1
1
1
1
x
x
P
x x x
x
.
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi
1
1
4
3
2 3 2
x
.
3. Tìm khoảng giá trị của x để giá trị của P thuộc tập giá trị của hàm số
2
2
1
;
1
y
y
f y y
y y
.
4. Tì
m giá trị nguyên của x để P nhận giá trị nguyên dương.
5. Ký hiệu [a] là phần nguyên của a, tức là số nguyên lớn nhất không vượt quá a
.
Tính gi
á trị của biểu thức P khi x là nghiệm của phương trình
4
3 5 5
5 7
x
x
.
Bài
toán 47. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1999 – 2000.
Cho biểu thức
1
1 2
:
1
1
1
x
P
x
x x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
2
3 14 5 3
1
2
x
.
3. Tìm các giá trị của x để
0
P
.
4. Tồn
tại hay không giá trị x để
3
3
847 847
6
6
2
7 27
P
.
5. Tìm các số m để có các giá trị của x thỏa mãn
P
x m x
.
6. Tì
m tất cả các giá trị x sao cho
3
3 8
P x
x
.
Bài
toán 48. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2000 – 2001.
Cho biểu thức
4
3 2
:
2
2
2
x
x x
P
x x x
x x
.
1. Rút gọn P.
2. Tính giá trị của P khi x thỏa mãn
36
x
.
3. Tính giá trị
của P biết
6
2 5
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
20
4. Tì
m x để giá trị của P không vượt quá
3
2
x
x
.
5. Tì
m x sao cho
3
2
3
P
x
.
6. Tính giá trị
của P khi x thỏa mãn hệ thức
2
2
4
4
8
4 1 1
x
y
x y
x y
.
7. Tìm các giá trị của n để có x thỏa mãn
1
P x x n
.
Bài
toán 49. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2001 – 2002.
Cho biểu thức
2 4
:
1
1
1
x x x
P x
x
x
x
.
1. Rút gọ
n P.
2. Tính giá trị của P kh
i
1
1
7
9 4 5 9 4 5
x
.
3. Tính giá trị
của P khi x thỏa mãn
3 2
6
10 6 9
x
x x x
.
4. Tì
m các giá trị x để
0
P
.
5. Tì
m các giá trị x để
5
4 3
x
P
x
.
6. Tìm giá trị nhỏ nhất của P.
7. Tìm các giá trị của m để tồn tại x sao cho
P
m
.
Bài toán 50. Mở rộng và phát triển bài 1; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức; Sở Giáo
dục và Đào tạo Thành phố Hà Nội; Năm học 2003 – 2004.
Cho biểu thức
1
1 1
:
x
x
P
x
x
x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P kh
i
2
2 3
x
.
3. Tính giá trị
của P khi
3
2x a c
với
,
,a b c
là các số thực thỏa mãn đẳng thức
2
2 2
1
2 3 3
a
b b b c a
.
4. Tì
m các giá trị của x để
1
2
P
x
.
5. Tì
m các giá trị của x thỏa mãn
6
3 4
P
x x x
.
6. Tì
m giá trị nhỏ nhất của biểu thức
3S
P x
.
Bài
toán 51. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2006 – 2007.
Cho biểu thức
3 2 1 1
:
1
1 1
2
1
a a a a
P
a
a a
a a
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
9
4 2
a
.
3. Tính giá trị
của P khi a là giá trị nhỏ nhất của
4
3
4
8 20
A
y y y
, y
là số thực.
4. So sánh P với 1.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
21
5. Tì
m a để
1 1
1
8
a
P
.
6. Chứng
minh r
ằng
2
2
2
4 5
5 ,
1
z
z
P z
z
.
Bài
toán 52. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2007 – 2008.
Cho biểu thức
3
6 4
1
1
1
x x
P
x
x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
27
10 2
x
.
3. Tìm x đ
ể
P
.
4. Tì
m x đ
ể
5
19
x
P
x
.
5. Tì
m m để phương trình
P
x m
có nghiệm thực.
6. Tính giá trị của P khi
x
max b
,
trong đó a và b là hai số thực thỏa mãn
2
2
3
a
ab
b b
.
Bài
toán 53. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2008 – 2009.
Cho biểu thức
1
:
1
x
x
P
x
x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
4
x
.
3. Tì
m giá trị của x đ
ể
13
3
P
.
4. Tính giá trị
của P khi x thỏa mãn
2
4
3 0
x
x
.
5. Tìm giá trị nhỏ nhất của biểu thức P.
6. Chứng minh rằng biểu thức
4
P
chỉ
nhận duy nhất một giá trị nguyên.
Bài toán 54. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2009 – 2010; Ngày thi 24.06.2009.
Cho biểu thức
1
1
4
2
2
x
A
x
x
x
vớ
i
0
; 4
x
x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
25
x
.
3. Tìm giá trị của x đ
ể
1
3
A
.
4. Tì
m giá trị của x đ
ể
3
2
2
x
x
A
x
.
5. Tồn
tại hay không các cặp số thực (x;y) thỏa mãn đẳng thức
3
1 2
A
x y y x
.
6. Tì
m khoảng giá trị của A khi x thỏa mãn hệ thức
3
4 1 8 6 1 5
x
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
22
Bài
toán 55. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2010 – 2011; Ngày thi 22.06.2010.
Cho biểu thức
2
3 9
9
3
3
x x x
P
x
x x
;
với
0; 9
x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
2
3 4 0
x x
.
3. Tính giá trị
của P kh
i
3
5
2
x
.
4. Tì
m giá trị của x đ
ể
P
.
5. Tì
m x để
5
8
x
A
.
6. Tính giá trị của P khi x thỏa mãn hệ thức
2
1
2 1x x x
.
7. Tìm giá trị lớn nhất của P, từ đó suy ra P chỉ nhận duy nhất một giá trị nguyên.
Bài toán 56. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2011 – 2012; Ngày thi 22.06.2011.
Cho biểu thức
1
0 5
25
5
5
x
x
A
x
x x
vớ
i
9
; 25
x
x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
9
x
.
3. Tì
m giá trị của x đ
ể
A
.
4. Tì
m giá trị nguyên của x để A nhận giá trị nguyên.
5. Tìm giá trị thực của x để A nhận giá trị nguyên.
6. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức
1 2
A x y
.
Bài toán 57. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 1999 – 2000;
Ngày thi 01.07.1999.
Cho biểu thức
2
1 1
:
x
P x
x
x x x x x
.
1. Tì
m x để biểu thức P có nghĩa. Rút gọn P.
2. Tính giá trị của P khi
4
17
2 2
x
.
3. Tìm x sao cho
4
2
4
5
5
2
x
P
x
.
4. Tì
m các số nguyên x đ
ể
2
2
1
P
x
Q
x
nhận
giá trị nguyên.
5. Với giá trị nào của x thì P có thể giữ vai trò biến b của phương trình
2
a
b ab a b
?
Bài toán 58. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2015 – 2016;
Ngày thi 06.06.2015.
Cho biểu thức
2
.
2
2
8 2
x x
x x
A
x x x x
, tro
ng đó x là biến số thực.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
23
1. Tì
m điều kiện của x để A có nghĩa và rút gọn A.
2. Tính giá trị của A khi
2
5
x
.
3. Tính giá trị
của A khi x thỏa mãn
1
2
x
x
.
4. Chứng minh với mọi giá trị thực m khác 0, phương trình
A m
luôn luô
n có nghiệm.
5. Tìm các giá trị của x sao ch
o
4
0
4
A
x
.
6. Tính giá trị
của A khi x là nghiệm của phương trình
3 3 3 3 3 3 1
x x x x x
.
7. Giả sử
ba biến số thực
, ,a b c
thỏa mãn hệ thức
5
,
8.
a
b c
ab bc ca
Tì
m khoảng giá trị của x để biểu thức A có thể giữ vai trò là một trong các biến
,
,a b c
.
Bài
toán 59. Mở rộng và phát triển câu 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2016 – 2017;
Ngày thi 04.06.2016.
Cho biểu thức
3 8 5 1 1
2 : 1
2 1 2
x x x
A x
x x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi x thỏa mãn
2
2
1 5x x
.
3. Tì
m các giá trị của x để
2
2
2
5
1 1
x
x
A
x x
.
4. Tì
m các giá trị của x để giá trị của A không vượt quá 4.
5. Tìm giá trị nguyên của x để giá trị của A là một số nguyên.
6. Tính giá trị của A khi x là nghiệm lớn nhất của phương trình
4
2
2 8 3x x x
.
7. Ký hiệu [m] là số nguyên lớn nhất không vượt quá m, tính giá trị của A khi
7
4
15
x
.
8. Tì
m khoảng giá trị của x để A có thể giữ vai trò biến a trong hệ thức
2
2 2
5
,
11
.
a
b c
a b c
Bài
toán 60. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Khối THPT Chuyên Đại học Sư phạm; Đại
học Sư phạm Hà Nội; Năm học 2007 – 2008.
Cho các biểu thức
4
2
2
1
1
:
, 7 15
x
P
Q x x
x x x x x x
.
1. Rút gọ
n biểu thức P.
2. Tìm giá trị nhỏ nhất của Q.
3. Tìm giá trị của x để
Q
x
.
4. Tính
.
P
a Q b
với
(a;b) cặp số nguyên dương có tổng lớn nhất thỏa mãn
2
2
2
a
b ab a b
.
5. Với
giá trị nào của x thì
4Q P
đạt giá trị
nhỏ nhất ?
6. Tìm khoảng giá trị của x để P có thể giữ vai trò một trong các biến thỏa mãn
2
2 2 2
5
,
7.
a
b c d
a b c d
Bài
toán 61. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1992 – 1993.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
24
Xét biểu
thức
2
3
1
1 2
1
2
1 2 1
a
P
a
a
a
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
3
a
.
3. Tính giá trị
của P khi a thỏa mãn đẳng thức
2
5
6 9 4 3 2 3
a
a a a
.
4. Tì
m giá trị nhỏ nhất của P.
5. Tìm giá trị nguyên của a để P nhận giá trị nguyên.
6. Tìm khoảng giá trị của a để tồn tại đẳng thức
2
2
2 2
0
,
x xy y
P x y
x xy y
.
Bài toán 62. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1993 – 1994.
Xét biểu thức
3
1
1
1
1 . :
1 1
a
a
a a a
P a
a
a a a
.
1. Rút gọn P.
2. Tính giá trị của P khi
2
2
2 7
2
3 2 3
a
.
3. Với điều kiện để
P
có
nghĩa, hãy so sánh
P
với P.
4. Tì
m giá trị nhỏ nhất của P trong trường hợp
0
1a
.
5. Tìm các giá trị của a để
6
6
P
a
a
.
6. Tính giá trị của P khi a là giá trị lớn nhất của hàm số
2
1 1 2 2f x x x x
.
Bài
toán 63. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1994 – 1995.
Xét biểu thức
2
2 1 1
: 1
1
1 1
x
P
x
x x x x x
.
1. Rút gọn P.
2. Tính giá trị của P khi
3
2 2
x
.
3. Tì
m x để
0
P
.
4. Tìm giá trị của x để
6 7 1
1
x x
P
x
x
.
5. Tính giá trị của P khi x thỏa mãn đẳng thức
1
2
1995 1996
2
x
y z x y z
.
6. Tìm giá trị của x để
2
2
3
18 4 5
P
max y y y y
.
7. Tìm khoảng giá trị của x để P có thể giữ vai trò là một trong các biến của hệ thức
4
,
5.
a
b c
ab bc ca
Bài
toán 64. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1995 – 1996.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
25
Cho các biểu thức
3
2
3 2 2 2
,
2
2
x x x x x
A B
x x
.
1. Rút gọn A và B.
2. Tính giá trị của B khi
11 2 10
x
.
3. Tính giá trị
của A khi x là nghiệm của phương trình
2
94 96 190 9027
x x x x
.
4. Tìm giá trị của x để
A
B
.
5. Tì
m tất cả các giá trị nguyên của x sao cho
3
1A B x x
.
6. Tìm x để
A
B a b
tro
ng đó
;a
b
là cặp
số nguyên dương có tổng lớn nhất sao c
ho
2
1
1
a
a
ab
.
Bài
toán 65. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1996 – 1997.
Xét biểu thức
3
9 3 2 1
1
2
1 2
a
a a
P
a a a a
.
1. Rút gọ
n P.
2. Tìm a đ
ể
1
P
.
3. Tính giá trị
của P khi
1
4
2
3
2 2
a
.
4. Tìm các giá trị của
a
sa
o cho
P
.
5. Tì
m a để giá trị của P lớn hơn nghiệm lớn nhất của phương trình
4
2
1 2 2 0
x x x x
.
6. Tìm các giá trị a đ
ể
1
8
x
P
x
.
7. Tì
m điều kiện của tham số m để phương trình
2
P
m
c
ó nghiệm.
Bài toán 66. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1997 – 1998.
Cho biểu thức
3 3
3
2
2 1 2
x x
x x
P
x x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
28
16 3
x
.
3. Tính giá trị của P khi
4
2
16
36
x
y y
,
trong đó
2
2 3 6 3 2 3
y
.
4. Tì
m x để
15
4
P
.
5. Giải phương trình (ẩn x
):
3
11
4
x
P
x
.
6. Chứng
minh rằng giá trị của P luôn nằm ngoài tập giá trị của biểu thức
2
2
2
4
2 4
y
y
f y
y y
.
7. Chứng
minh rằng
3
4
P
,
từ đó dẫn đến P chỉ nhận duy nhất một giá trị nguyên.
Bài toán 67. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1999 – 2000.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
26
Cho biểu thức
3
2 2
: 1
2
3 5 6 1
x x x x
P
x x x x x
.
1. Rút gọn P.
2. Tính giá trị của P khi x thỏa mãn
5
6 1 0
x
x
.
3. Tìm các giá trị nguyên của x để
0
P
.
4. Tì
m các giá trị x đ
ể
9
2
x
P
x
.
5. Với
giá trị nào của x thì biểu thức
1
P
đạt giá trị n
hỏ nhất.
6. Tìm các giá trị nguyên của x để P nhận giá trị nguyên.
7. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức
2
6
2 3 4 5P xy x
.
Bài
toán 68. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 2000 – 2001.
Cho biểu thức
2
2 1 1x x x x x
P x
x
x x x x
.
1. Rút gọn biểu thức P.
2. Tính giá trị của P với
6
2 5
x
.
3. So sánh P với 5, từ đó phản biện đẳng thức
4 2
P x y
.
4. Với
mọi giá trị của x làm P có nghĩa, chứng minh biểu thức
8
P
chỉ nhận đúng một giá trị nguyên.
5. Tính
4
2
2
7
P
y y
với y
là nghiệm của phương trình
4
2
1999
1999
y
y
.
6. Giả sử
, , ,a b c d
l
à bốn số dương, A là giá trị lớn nhất của biểu thức
ab cd
a d b c
. Tính
1
P
A
.
Bài
toán 69. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 2001 – 2002.
Cho biểu thức
2
3 2
: 2
5 6 2 3 1
x x x x
P
x
x x x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
1
81
x
.
3. Tìm giá trị của x đ
ể
2
3
P
x
.
4. Tì
m x để
1 5
2P
.
5. Giả sử A l
à giá trị lớn nhất của biểu thức
2
2
2
2 1B a b ab a b
.
Chứng tỏ
P
A
là số vô t
ỷ.
6. Tìm tất cả các giá trị thực của m để phương trình
3
P
m
có nghiệm
.
Bài toán 70. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 2002 – 2003.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
27
Cho biểu
thức
1
2 1
1
1
1
x
x x
P x
x
x
x x x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi x thỏa mãn phương trình
3
5 2 0
x
x
.
3. Tì
m giá trị lớn nhất của biểu thức
2
Q
x
P
.
4. Tính giá trị của P v
ới
1
1 1
3
1 2 2 3 3 4
x
.
5. Chứng
minh rằng
1
0
3
P
,
từ đó suy ra P chỉ nhận duy nhất một giá trị nguyên.
6. Phản biện đẳng thức
2
2
2 2
,
a ab b
P a b
a ab b
.
7. Xét
20
01 2002
2
y
y
f y
y y
với
0
Ma
x f y f y
. Chứng
minh
92
P
y
là số
hữu tỷ.
Bài toán 71. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Trường THPT Chuyên Lê Quý Đôn; Thành phố Vũng Tàu; Tỉnh Bà Rịa – Vũng Tàu; Năm
học 2011 – 2012.
Cho biểu thức
3
2
1
1
1
1
x x x
P x
x
x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
1
3 4 3
x
.
3. Tính giá trị
của P khi x là nghiệm của phương trình
5
1
5
2 4
2
2
x
x
x
x
.
4. Giải phư
ơng trình
2
1
2 3
x
P
x
.
5. Tìm giá trị nguyên của x để P nhận giá trị nguyên.
6. Chứng minh P chỉ nhận duy nhất một giá trị nguyên (khi P có nghĩa).
7. Tính
khi
1
1 1 1
...
3
2
1 1 2 3 2 2 3 2005 2004 2004 2005 2005
A
.
Bài
toán 72. Mở rộng và phát triển bài 2.3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2006 – 2007.
Cho
biểu thức
1
1 1
.
2
1
1 1
x
A
x x x
với
0
, 1x x
.
1. Rút gọn
biểu thức A.
2. Tính giá trị của A khi x thỏa mãn
2
7
10 0
x
x
.
3. Tìm x đ
ể
2
3
2
x
A
x
.
4. Tìm những giá trị nguyên của x để A nhận giá trị nguyên.
5. Tính giá trị của A khi x thỏa mãn đẳng thức
2
2 2
2
2 2 3 5 0
x
y z xy yz zx x z
.
6. Tính
giá trị của A khi x là nghiệm của phương trình
2
2 3 2 3 1 2 2 3 10 3
x x x x x x
.
7. Tồn
tại hay không các số thực x và y sao cho
1 2 1 3
A x y y x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
28
Bài
toán 73. Mở rộng và phát triển bài III; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2009 – 2010.
Cho biểu thức
1 1
1 1
x x x x
A x
x
x
với
0
, 1x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
4
2 3
x
.
3. Tìm giá trị của x để
6
1A x
.
4. Tì
m giá trị nhỏ nhất của biểu thức A.
5. Tính giá trị của A khi
3
12 1x a a
, trong
đó
3
3
4
5 1 4 5 1
a
.
6. Phản biện
bất đẳng thức
2
2
1
A
x x x
.
Bài
toán 74. Mở rộng và phát triển bài 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2011 – 2012.
Cho biểu thức
3
1
2 1
3 1
a a a
A
a a
với
0, 1a a
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
4
97
56 3
a
.
3. Tì
m a để
2
1
2 5 9
A
a a
.
4. Giải phư
ơng tr
ình
3
2
20
5
a
A
a
.
5. Tính giá trị
của A khi
1
1 1 1
...
1
5 5 9 9 13 2001 2005
a
.
6. Phản biện
bất đẳng thức
3
2
2 2
A
a a a
.
Bài
toán 75. Mở rộng và phát triển bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; chuyên Bắc Giang; Năm học 2012 – 2013.
Cho biểu thức
2
7 6 1
3 2 1 2
x
x x x
A x
x x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
1
6
x
.
3. Tính giá trị
của A khi
7
4 3
x
.
4. Giả sử
0
0
;x y
là
m cho biểu thức
2 2
20
05
S
x y xy x y
đạt giá trị
nhỏ nhất. Tính
0
6A x
.
5. Tính giá trị
biểu thức khi x thỏa mãn phương trình
2
3
1 1 2 3 4
x
x x x
.
6. Giải phư
ơng tr
ình
4
2
5
x
A
x
.
7. Tì
m tất cả các giá trị của m để phương trình
A
m
có nghiệm.
Bài toán 76. Mở rộng và phát triển câu II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2007 – 2008; Ngày thi 26.06.2007.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
29
Cho biểu
thức
2
1 1
1 1
x x x
A
x x
x
x
vớ
i với
0, 1x x
.
1. Rút gọ
n biểu thức A.
2. Tìm các giá trị nguyên của x để
6
A
n
hận giá trị nguyên.
3. Giải bất phương trình
3
1
2
x
A
.
4. Tính giá trị
của A khi x là nghiệm của phương trình
1 8 3 1x x
.
5. Tính
4
A
x
biết x thỏa mãn đẳng thức
2
2
3
1
x
xy y x y
.
6. Phần nguyên của a, ký hiệu [a], tức là số nguyên lớn nhất không vượt quá a.
Giả sử
3
3
3
3
6
0 60 60 ... 60
B
.
Chứng minh
3 4
B
và tính
A
B
.
Bài
toán 77. Mở rộng và phát triển bài II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2014 – 2015; Ngày thi 30.06.2014.
Cho biểu thức
4
2 5
1
1
1
x
B
x
x x
vớ
i
0
, 1x x
.
1. Rút gọ
n B.
2. Tính giá trị của B khi
9
4 5 9 4 5
x
.
3. Giải phương trì
nh
7
3
1
B
x
x
.
4. Tì
m các giá trị nguyên của x để B nhận giá trị nguyên.
5. Tính giá trị của B khi x là nghiệm của phương trình
3
1
3x x
.
6. Phần ngu
yên của a, ký hiệu [a], tức là số nguyên lớn nhất không vượt quá a.
Xét
3
3
3
3
2
0 20 20 ... 20 ; 24 24 24 ... 24
a
b
.
Tính
B
a b
.
Bài
toán 78. Mở rộng và phát triển câu II.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2013 – 2014; Ngày thi 30.06.2013.
Cho biểu thức
2
1
x
x x
B
x
x x
với
0, 1x x
.
1. Rút gọn biểu thức B.
2. Tính giá trị của B với
3.
27 8 : 2
x
.
3. Tính giá trị
của B khi x là nghiệm của phương trình
2
4
1 3 5 2 6
x
x x x
.
4. Giải phương trình
3
2
B
x x
.
5. Tì
m các giá trị của x sao cho
2
2
1
B
x x x
.
6. Tì
m m để phương trình
1
B
m
có
nghiệm.
7. Phản biện bất đẳng thức
2
2
2 4 3 1
B
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
30
Bài
toán 79. Mở rộng và phát triển bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; chuyên Bắc Giang; Năm học 2015 – 2016;
Ngày thi 09.06.2015.
Cho biểu thức
11
2 1
2 1 2
x x x
A
x
x x x
.
1. Tì
m điều kiện của x để A có nghĩa, khi đó rút gọn A.
2. Tính giá trị của A khi x thỏa mãn
3 8 4 0
x x
.
3. Tính giá trị của A khi
3
3
1
82 33125 182 33125
x
.
4. So sánh A và 1.
5. Tìm số chính phương x sao cho A có giá trị là số nguyên.
6. Giải phương tr
ình
3
10
4
x
A
x
.
7. Tì
m khoảng giá trị của x sao cho giá trị của A không vượt quá
3
2
.
Bài toán 80.
Mở
rộng và phát triển câu II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2015 – 2016; Ngày thi 19.07.2015.
Cho biểu thức
1 1 4 1
:
4 4
2
2
x
B
x
x
x x
với
0
; 4
x
x
.
1. Chứng
minh biểu thức B có giá trị không phụ thuộc vào biến.
2. Tìm x sao cho
2
3
9 1 2
x
x x B
.
3. Giải phư
ơng trình
10
1
x
B
x
.
4. Chứng minh rằng
2
2
2
1 4 1 , 2;2 , 0;1
x
x y y B y x
.
Bài
toán 81. Mở rộng và phát triển câu II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2016 – 2017; Ngày thi 09.06.2016.
Cho biểu thức
2
2 6
.
1
1
1 1
x x x x x x
B
x
x
x x
vớ
i
0
, 1x x
.
1. Rút gọ
n B.
2. Chứng minh biểu thức B là số tự nhiên chia hết cho 12 với mọi số tự nhiên x khác 1.
3. Tìm giá trị nhỏ nhất của B và giá trị của x tương ứng.
4. Tìm các giá trị của x sao cho giá trị của B không vượt quá 36.
5. Giải phương trình
3
6B x
.
6. Tính giá trị
của B khi x thỏa mãn đẳng thức
2
2
5
8 4 5
x
x x x
.
7. Tì
m khoảng giá trị của tham số m để phương trình
2
B
m
có
hai nghiệm phân biệt.
Bài toán 82. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 1997 – 1998; Ngày thi 27.06.1997.
Cho biểu
thức
2
2 16
4
2 2
a a
Q
a
a
a
.
1. Rút gọn
biểu thức Q.
2. Tính giá trị biểu thức Q khi
7 1
1
3
2 2 1
a
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
31
3. Tìm a để
Q
.
4. Giải phươ
ng trình
7
1Q
a
.
5. Tính
giá trị của Q khi a và b là các số không âm thỏa mãn đẳng thức
2
2
3 3 1 1
2
2
4
4 2 2
a
b b a a b
.
6. Tính
giá trị của Q khi a thỏa mãn phương trình
2
1
1 4 3a a a
.
7. Tồn tại hay không các số thực a và m thỏa mãn hệ thức
2
1 3 1
Q
a m m a
.
Bài
toán 83.
Mở
rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2001 – 2002; Ngày thi 04.07.2001.
Cho biểu thức
1
1 2
:
2
a
a a a a
A
a
a a a a
.
1. Tì
m điều kiện để biểu thức A có nghĩa.
2. Rút gọn biểu thức A.
3. Giải phương tr
ình
2
1
1
4 2
A
a
a
.
4. Tính giá trị
của A khi a là giá trị lớn nhất của biểu thức
4 3 2
2
4
9 10 7
2 2
x
x x x
f x
x
x
t
rên
.
5. Tì
m các giá trị nguyên của a để biểu thức A nhận giá trị nguyên.
6. Chứng minh rằng A có thể giữ vai trò các biến
,
,x y z
trong hệ
điề
u kiện
15
72
x
y z
xy yz xz
Bài toán 84.
Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2005 – 2006; Ngày thi 02.07.2005.
Cho biểu thức
1
1 1 1
:
1 1 1 1
A
x
x x x
.
1. Rút gọ
n A.
2. Tính giá trị của A khi
9
4 5
x
.
3. Tì
m các giá trị của x và y sao cho
2
1
1
2 3A y y
x
.
4. Tính giá trị
của A khi
4
2
si
n cos ,x max a a a
.
Bài
toán 85.
Mở
rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2003 – 2004; Ngày thi 01.07.2003.
Cho biểu thức
2
2 1
1
1
:
1
x x
x x x x
A
x
x x x x
.
1. Rút gọ
n A.
2. Tính giá trị của A khi
3
2 2
x
.
3. Tìm x đ
ể
3
2
x
A
x
.
4. Tì
m x nguyên để biểu thức A nhận giá trị nguyên.
5. Tính giá trị của A khi x thỏa mãn hệ thức
35 2 2 1 3 2 4 3
x y z x y z
.
6. Tìm khoảng giá trị của m để phương trình
2
A
m
có n
ghiệm.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
32
Bài
toán 86.
Mở
rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2000 – 2001; Ngày thi 04.07.2000.
Cho biểu thức
2
1 1 1
2
2 1 1
a a a
P
a a a
.
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi
7
4 3
a
.
3. Tì
m giá trị của a để
0
P
.
4. Giải phương trình
8
3 6
P
a
.
5. Tì
m giá trị của a sao cho
1
2 1
P a
a
.
6. Tính giá trị
của P khi
9
6 3
6 282 1
a x x x
, trong
đó
3
3
5
2 1 11
x
.
7. Chứng
minh rằng với mọi giá trị
m
,
phương trình
P
m
luô
n luôn có nghiệm x.
Bài
toán 87.
Mở rộng và phát triển câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Hà Bắc (cũ); Năm học 1995 – 1996; Ngày thi 10.08.1995.
Cho biểu thức
2
1 1 1
1 1
a a
B a
a a a
.
1. Rút gọn B.
2. Có giá trị nào của a để
0
B
kh
ông ?
3. Tìm a để
0
B
.
4. Tính giá trị
của B khi
2
3 6 2
a
.
5. Tì
m các giá trị của a sao cho
3
3
5B a
a
.
6. Tính giá trị
của B khi a là nghiệm của phương trình
7 2 7 2 3
x x x x
.
7. Phần ngu
yên của a, ký hiệu [a], tức là số nguyên lớn nhất không vượt quá a.
Xét phương trình phần nguyên
2
9
8 0
a
a
.
Tính giá trị của biểu thức B tại a.
Bài toán 88. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Hà Bắc (cũ); Năm học 1996 – 1997; Ngày thi 01.08.1996.
Cho biểu thức
4
1 2 2
1 : 1
1
4 1 4
2 1
x x x x
A
x x
x
.
1. Rút gọ
n A.
2. Tính giá trị của A với
4
2 3
x
.
3. Tì
m x để
1
2
A
.
4. Giải phương tr
ình
4
2
3
x
A
.
5. Tính giá trị
của A tại
x
max B
, trong đó
3 5 , 3;5
B a a a
.
6. Tính giá trị của A khi x là nghiệm của phương trình
1 7 4
x x
.
7. Giả sử
, ,a b c
là c
ác
số n
guyên dương sao cho
1
1 1
2
a
b c
,
trong đó a là số lớn nhất trong bộ ba số.
Tồn tại hay không giá trị x để
A
a
?
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
33
Bài
toán 89. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Hà Bắc (cũ); Năm học 1996 – 1997; Ngày thi 31.07.1996.
Cho biểu thức
1
1 1
:
1 1 1 1
x
x x
A
x
x x x
.
1. Rút gọ
n A.
2. Tính giá trị của A kh
i
1
1
2
5
3 2 2 3 2 2
x
.
3. Tì
m x để A nhận giá trị âm.
4. Giải phương tr
ình
4
2
5 1
x
A
x
x
.
5. Cho ba số
thực dương
, ,a b c
thỏ
a mãn
1
1 1
2
1
1 1a b c
.
Tính gi
á trị A khi x là số nhỏ nhất sao cho
abc x
.
6. Tính giá trị
biểu thức A khi x là số nguyên sao cho
1
7 8
S
x x x x
là số chính phươ
ng.
Bài
toán 90.
Mở
rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 1998 – 1999; Ngày thi 13.06.1998.
Cho biểu thức
1 2 4
4
2 2
x
A
x
x x
.
1. Rút gọ
n A.
2. Tính giá trị của A khi
2 4 7 2 4 7 3
x
.
3. Giải phương trình
6 4
A x x
.
4. Chứng
minh
0
A
.
5. Tì
m giá trị nguyên của x để A nhận giá trị nguyên.
6. Chứng minh
3
0
2
A
, từ đó dẫn đến A chỉ nhận duy nhất một giá trị nguyên.
7. Tính giá trị của A khi x là số thực làm cho biểu thức
2
2
2
6 5 16 2 2 2 2
P x y x y xy x y
đạt
giá
trị nhỏ nhất.
Bài
toán 91.
Mở
rộng và phát triển câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 1999 – 2000; Ngày thi 22.06.1999.
Cho biểu thức
1 1 3 2 1
: 1
4 1
2
1 2 1 2 1
a a a
P
a
a a a
.
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi
2
1
4
2 1
3 2 2
a
.
3. Tì
m giá trị a sao cho
3
3
a
P
.
4. Tính giá trị
của P khi a thỏa mãn
1
3 1 3 2
x
x x x
.
5. Tìm khoảng giá trị của m để phương trình
3
P
m
có nghiệm.
6. Giả sử p là số nguyên tố sao cho
2 2
4
1,6 1
p
p
cũ
ng là số nguyên tố. Tìm a để
P
p
.
7. Tì
m a sao ch
o
1 1 1 1
...
2
1 1 2 3 2 2 3 4 3 3 4 25 24 24 25
P
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
34
Bài
toán 92. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2000 – 2001; Ngày thi 03.07.2000.
Cho biểu thức
2
2 1
.
1
2 1
x x x
A
x
x
x x
.
1. Rút gọ
n A.
2. Tính giá trị của A kh
i
9
4
x
.
3. Giải phư
ơng trình
2
1
7 9
1 1
x
A
x
x
.
4. Tính giá trị biểu thức A khi x thỏa mãn
3
1
1
x
x
.
5. Tì
m các giá trị của biểu thức A để biểu thức A nhận giá trị nguyên.
6. Tìm giá trị của tham số m sao cho phương trình
A
m
có nghiệ
m.
7. Tính giá trị của A khi x là số thực nhỏ nhất thỏa mãn
4
5 6
a
a a x
(a là biến số thực).
Bài toán 93. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2007 – 2008.
Cho biểu thức
2
2
1
1 1 1 1
. 1
2
1 1 1 1
x x x
P
x x x x
.
1. Tì
m điều kiện của x để biểu thức P có nghĩa và rút gọn P.
2. Tìm x đ
ể
2
2
P
.
3. Tính giá trị
của P khi x thỏa mãn
2
4
2 1 4 1x x x
.
4. Tồn tại ha
y không các số thực x, y, z sao cho
2
2
2 2 4
P
x y z z
.
Bài
toán 94. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố Bắc Ninh; Tỉnh Bắc Ninh;
Năm học 2015 – 2016.
Cho biểu thức
4
1 1
:
4
2
2 2
a
a a
A
a
a a a
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị biểu thức A khi
6 4 2
a
.
3. Tì
m giá trị của a để
2
1
a
A
a
.
4. Tìm giá trị của a để
1A
.
5. Tính giá trị
của A khi a là nghiệm nguyên của phương tr
ình
2
2
5 1 3 1
a
a a
.
6. Tì
m tất cả các giá trị của m để phương trình
A m
có
nghiệm.
Bài toán 95. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Giang; Thành
phố Bắc Giang; Tỉnh Bắc Giang; Năm học 2014 – 2015.
Cho biểu thức
3
2 1 1
:
1
1 1
2
1
a a a a
P
a
a a
a a
.
1. Rút gọn P.
2. Tính giá trị của P khi
7
4 3
a
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
35
3. Chứng
minh rằng khi a là số nguyên dương thì
1
1
2
P
.
4. Tì
m a nguyên để
1
4
P
là số
nguyên.
5. Tính giá trị biểu thức P khi a thỏa mãn
2
2
1 3 2 3 2 6
a
a a a
.
6. Cho m và n là các số nguyên dương sao cho
2
2
m n
mn
. T
ìm a sao cho
2
2
m n
P
mn
.
7. Xét cá
c cặp số nguyên không âm (x;y) thỏa mãn
2
3
38 2.7
y
x
x
.
Tính P khi
2
2
a
x y
.
Bài
toán 96. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố Bắc Ninh; Tỉnh Bắc Ninh;
Năm học 2010 – 2011.
Cho biểu thức
1
:
1
a
a
P
a
a a a
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi a thỏa mãn
2
9 8 0
a a
.
3. Tì
m giá trị của a để
13
3
P
.
4. Tì
m giá trị của a để
5
2
P
.
5. Tì
m số tự nhiên a để biểu thứ
c
1
2
P
nhận
giá trị nguyên.
6. Tìm a để
P k
,
trong đó k là giá trị lớn nhất của biểu thức
5
;
2
x
S
x
x
.
7. Tồn
tại hay không số thực dương a sao cho
1
1 1 1
...
2 1 3 2 4 3 1
P
n
n
?
Bài toán 96. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố
Bắc Ninh; Tỉnh Bắc Ninh; Năm học 2008 – 2009.
Cho biểu thức
1
2 2
2
1
x x
A
x
.
1. Tì
m điều kiện của x để biểu thức A có nghĩa.
2. Rút gọn biểu thức A khi
3
x
.
3. Tính giá trị
của A khi
2
2
11,x y y y
.
4. Tì
m giá trị của x sao cho
4
2
x
x A
.
5. Tồn
tại hay không các số thực dương a, b, c, d sa
o cho
2
4
d
a b c
A
d
b c c a a b
?
Bài
toán 97. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 1997 – 1998; Ngày thi 05.08.1997.
Cho biểu thức
1
1
1
1 1
:
1
1
2
1 2 1
x x x
x x x
A
x
x
x x
.
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi
4
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
36
3. Chứng minh rằng khi
1x
t
hì
1A
.
4. Giải phương trình
2
2
1
A
x x
.
Bài toán 98. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 1997 – 1998; Ngày thi 06.08.1997.
Cho biểu thức
1 1 1
.
1
1 1
x x x x
B
x
x x x
với
0
; 1x x
.
1. Rút gọ
n biểu thức B.
2. Tính giá trị của B khi
9
x
.
3. Tìm giá trị của x để
2
21 5 0
B B
.
4. Tì
m khoảng giá trị của x để
3
7
B
.
5.
So
sánh B với 1.
6. Chứng
minh rằng với
0
; 1x x
t
hì B không thể nhận giá trị nguyên.
7. Số nguyên a chia hết cho số nguyên b thì được ký hiệu
b
a
.
Tính
giá trị của B khi x là số nguyên
lớn nhất thỏa mãn điều kiện
2 3 2
1 8 2x x x x
.
Bài
toán 99. Mở rộng và phát triển câu I.3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2016 – 2017.
Cho biểu thức
1
1 1
.
2
1
1
x
A
x
x
vớ
i
0; 1x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
4 2 3
x
.
3. Tính giá trị
của A khi
1
9
4 2
x
.
4. Tìm tất cả các giá trị của x để
2
7
A
.
5. Tìm x sao cho
2
3
x
A
.
6. Tì
m tất cả các giá trị của x để biểu thức A nhận giá trị nguyên.
7. Với
0; 1x x
, đặt
A f x
. Giả sử n là số nguyên dương lớn nhất sao cho
29
n
là một ước của
2003!
2003
! 1.2.3...2002.2003
.
Chứng minh rằng
1
,7
f
n
.
Bài toán
100. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố Bắc Ninh; Tỉnh Bắc Ninh;
Năm học 2015 – 2016.
Cho biểu thức
4
1 1
:
4
2 2 2
a
a a
A
a
a a a
với
0; 4
a a
.
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi
6
4 2
a
.
3. Tìm a để A nhận giá trị bằng 0,6.
4. Tìm a để
1
2
3 0
A
A
.
5. Tì
m a để giá trị của biểu thức A không nhỏ hơn 1.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
37
6. Tì
m tất cả các số thực b và c sao cho
1
1
4 4
A
b c a b c
?
7. Giả sử
mn
p
là ba chữ số tận cùng của số
200
4
2T
. Tính giá trị của A khi
2
a
m n p
.
Bài toán 101. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 1999 – 2000; Ngày thi 13.07.1999.
Cho biểu thức
:
a
b a b
P
a
b b a ab a b b a
với
, 0;
a b a b
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
9; 4
a b
.
3. Tính giá trị
của biểu thức P khi a và b là nghiệm của hệ phương trình
2
2
4
4 0
4 4 0
a
b
b a
4. Tính giá trị
của P khi biết a, b là hai nghiệm của phương trình ẩn x:
048
2
xx
.
5. Tính giá trị
của biểu thức P khi a và b là nghiệm của phương trình hai ẩn
2
2 2
1
2 4 4
a
a b a b
.
Bài toán 102. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Thái Bình; Năm học 2003 – 2004.
Cho biểu thức
3
2
1
2
10 3
1
1
1
x
x
x
M
x x x
x
.
1. Với
giá trị nào của x thì biểu thức có nghĩa.
2. Rút gọn biểu thức M.
3. Tính giá trị biểu thức M k
hi
9
4
x
.
4. Tính giá trị
biểu thức M khi
3
2 2
x
.
5. Tì
m x sao cho M nhận giá trị bằng
1
2
13
.
6. Tì
m khoảng giá trị của x để
2
3
M
.
7. Tìm m để phương trình
M
m
có n
ghiệm, từ đó tìm
giá
trị nhỏ nhất của biểu thức M.
8. Tồn tại hay không các số thực a và b để
1 1
M a b a b
?
Bài
toán 103. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2001 – 2002; Ngày thi 14.07.2001.
Cho biểu thức
2
2 1
.
1
2
1
a a a
A
a
a
a a
với
0; 1
a a
.
1. Chứng minh đẳng thứ
c
2
1
A
a
.
2. Tính giá trị
của A khi
4
2 3
a
.
3. Tìm a để
0
A
.
4. Giải phư
ơng tr
ình
2
3
4
1 1
a
A
a
a
.
5. Tì
m giá trị nguyên của a để biểu thức A nhận giá trị nguyên.
6. Tìm tất cả các giá trị nguyên của a đ
ể
3
5
A
nhận
giá trị nguyên.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
38
Bài
toán 104. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2003 – 2004; Ngày thi 16.07.2003.
Cho biểu thức
:
y xy
x
y x y
P x
x
y xy y xy x xy
1. Với
giá trị nào của x, y thì biểu thức P có nghĩa ?
2. Rút gọn P.
3. Tính giá trị của P khi
100
; 81
x
y
.
4. Tính giá trị
của P khi x và y là các số hữu tỷ thỏa mãn
5. Cho
3
3
5
2 7; 5 2 7
x
y
.
Chứng minh rằng
2P
.
6. Tính
giá trị của
1
P
kh
i x và y là nghiệm của hệ phương trình
3 3 3
2
8
16 ,
2 8 .
x y y
x xy y
7. Tính tỷ
số
x
y
k
hi P thỏa mãn đẳng thức
3
2 4P x y x
.
8. Tính giá trị
của P khi x và y là hai số nguyên tố thỏa mãn đẳng thức
2
2
6
1
x
y
.
Bài
toán 105. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2004 – 2005; Ngày thi 08.07.2004.
Cho biểu thức
2
2
4 3 4
:
4
2
2 2
a
a a a
M
a
a a a
.
1. Rút gọ
n biểu thức M.
2. Tìm các giá trị của a để
1M
.
3. Tì
m a sao cho
2
9 10 0
M M
.
4. Tìm các giá trị nguyên của a để biểu thức M nhận giá trị nguyên.
5. Tìm số tự nhiên a để M nhận giá trị lớn nhất.
6. Tìm tất cả các giá trị của a để phương trình
M
m
có
nghiệm.
7. Tồn tại hay không các số thực m và n để
1
9
2017
2 10
M m n
?
8. Tính giá trị
của M khi a và b là các số hữu tỷ thỏa mãn điều kiện
1
2
9
2 2
2 2a b b a
.
Bài
toán 106. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Quảng Ngãi; Năm học 2000 – 2001; Ngày thi 11.07.2000.
Cho biểu thức
2
2
1
1
x
x x x
Y
x
x x
.
1. Rút gọn Y.
2. Tính giá trị của Y khi
2
28 16 3
x
.
3. Tì
m x sao cho Y nhận giá trị không vượt quá 4.
4. Tìm x để
2
5
1
x
Y
x
.
5. Tì
m giá trị nhỏ nhất của biểu thức Y.
6. Cho
4.
x
Chứng
minh đẳng thức
0
Y
Y
.
7. Tì
m tất cả các giá trị của m để phương trình
Y
m
có nghiệm thuộc khoảng (4;9).
8. Giải phương trình
4
2 1 4
Y
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
39
Bài toán
107. Mở rộng, liên hệ và phát triển các bài toán
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Khiết; Thị xã Quảng Ngãi; Tỉnh Quảng Ngãi; Năm học 2000 –
2001.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2016 – 2017.
Cho biểu thức
2
2
1 1 1 1
1
1
1
1 1
a a
P
a
a
a
a
a a
.
1. Chứng
minh biểu thức P có giá trị độc lập với biến với
0
1a
.
2. Giải phư
ơng trình
8 3 2
P a a
vớ
i
0
1a
3. Chứng minh rằng
2
1
0
,8
a
P
a
với
0
1a
.
4. Giá trị của biểu thức P còn độc lập với biến hay không nế
u
4
3
4 3 2
1
3
2 2
b
b b
a
b
b b b
,
1
1
2
b
.
5. Kh
i
0
1a
,
hãy so sánh P và Q, trong đó
4
; ; 0
a
b a b a
Q a b b
a b
a b a b
.
Bài
toán 108. Mở rộng và phát triển bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Quảng Ngãi; Năm học 2005 – 2006; Ngày thi 15.07.2005.
Cho biểu thức
2
2 1
.
1
2 1
a a a
P
a
a a a
với
0
1
a
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị biểu thức P khi a thỏa mãn
3 1 4 3 0
a a
.
3. Tính giá trị
biểu thức P khi
2
56
24 5
a
.
4. Tì
m tất cả các giá trị của a để
2
4
a
P
.
5. Tìm a để giá trị của P không nhỏ hơn 0,45.
6. Giải phương trình
2
6
5
1 1
a
P
a a
.
7. Tìm tất cả các giá trị nguyên của a để biểu thức P nhận giá trị nguyên.
8. Tìm giá trị nguyên của a để biểu thức P đạt giá trị lớn nhất.
Bài toán 109. Mở rộng, liên hệ và phát triển các bài toán
Bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Quảng Ngãi; Năm học 2008 – 2009; Ngày thi 24.06.2008.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố Quảng Ngãi; Tỉn
h
Quảng Ngãi; Năm học 2012 – 2013.
Bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố Quảng Ngãi; Tỉnh
Quả
ng Ngãi; Năm học 2013 – 2014.
Cho biểu thức
2
4
:
a
b ab
ab
P
a
b a b b a
.
1. Xác định
a, b để biểu thức có nghĩa và hãy rút gọn P.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
40
2. Tính giá trị
của P khi
15
6 6 33 12 6; 24
a
b
.
3. Tính tỷ
số giữa a và b nếu
3
P ab
.
4. Cho số thực
x thỏa mãn
2
3 1 0
x x
. Tính giá trị biểu thức P khi
3 5
3
5
1
1
;a x b x
x
x
.
5. Chứng minh rằng nếu
0
P
t
h
ì
2
2
8
a b
a
b
ab
b
.
6. Giả sử
tồn tại x sao cho
1
15 ; 15x m n
x
.
Tìm hệ thức giữa a và b để
P
m n
.
7. Xét biểu
thức
2
4a b ab
a b b a
Q
b
a b ab
. Tì
m a và b sao cho
P
Q
.
8.
Xét
2
2
2
1
1
1
x x x x
R x
x x x x
vớ
i
0
x
. Chứ
ng minh rằng nếu
P
R
th
ì
2
2
1
b
a
.
Bài
toán 110. Mở rộng và phát triển 1.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố
Quảng Ngãi; Tỉnh Quảng Ngãi; Năm học 2014 – 2015.
Cho biểu thức
3 3
3 3 1
x x x
P
x
x x x x
.
1. Tì
m điều kiện xác định và rút gọn P.
2. Tính giá trị của P khi
7
2 3
x
.
3. Tì
m x sao cho
6
P
.
4. Tì
m giá trị nhỏ nhất của biểu thức P.
5. Tìm tất cả các giá trị của x để
2P
.
6. Giải phư
ơng trình
2
8 14 0
P x x
.
7. Xét các số hữu tỷ
, ,a b c
thỏa mãn
3
3
a
b
b c
là số hữu tỷ. Chứng minh rằng khi
3x ac
thì P có giá
trị là một số hữu tỷ.
Bài toán 111. Mở rộng và phát triển 1.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố
Quảng Ngãi; Tỉnh Quảng Ngãi; Năm học 2015 – 2016.
Cho biểu thức
2 1 2
: 1
1 1 1
x x x
A
x x x x x
.
1. Tì
m điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị của A khi
2
1
x
.
3. Tì
m x sao cho
2
17 2 0
A A
.
4. Tì
m x để A nhận giá trị lớn hơn 3.
5. Giải phương tr
ình
3
2
1
1
1
x
A
x
x
.
6. Tì
m giá trị nguyên của x để A nhận giá trị nguyên.
7. Tìm tất cả các giá trị nguyên của x để biểu th
ức
2
3
S A
nhận
giá trị nguyên.
8. Cho số thực a thỏa mãn
2
4
1 0
a
a
. Tính giá trị biểu thức P khi
7
7
1
x
a
a
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
41
Bài
toán 112. Mở rộng và phát triển đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở
Giáo dục và Đào tạo Thành phố Hồ Chí Minh; Năm học 2014 – 2015.
Cho biểu thức
1
2 6
: 1
3 3 3
x
B
x
x x x x x
.
1. Tìm điều kiện xác định và rút gọn biểu thức B.
2. Tính giá trị của biểu thức B khi
6
2 5
x
.
3. Tính giá trị của biểu thức B khi x là số lớn nhất thỏa mãn
1
1
x
y y
.
4. Tìm x để B có giá trị lớn hơn 5.
5. Tìm x sao ch
o
4
3
B
x
.
6. Tì
m giá trị nguyên của x để biểu thức
3
B
nhận giá trị nguyên.
Bài toán 113. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình
Định; Năm học 2012 – 2013; Ngày thi 14.06.2012.
Cho biểu thức
: 1
1
1 1
a b a b a b ab
D
ab
ab ab
với
0
; 0; 1a b ab
.
1. Rút gọ
n biểu thức D.
2. Tính giá trị của biểu thức D khi
2
2 3
a
.
3. Tì
m a để biểu thức D nhận giá trị bằng 0,8.
4. Tìm giá trị của a sao cho
3
2
a
D
a
.
5. Tì
m giá trị của a để D có giá trị lớn hơn 0,6.
6. Tính giá trị của biểu thức D khi a và b thỏa mãn hệ thức
3 3
4
1 4
a
b a a b
.
7. Tì
m tất cả các số nguyên a để D nhận giá trị nguyên.
Bài toán 114. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình
Định; Năm học 2009 – 2010.
Cho biểu thức
2
1 1
1
1
1
x x x
P
x
x x x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị biểu thức P khi
3
2 2
x
.
3. Tìm giá trị của x sao cho
2
13 3 0
P P
.
4. Tì
m giá trị của x sao cho
2
2
1 4P P
.
5. Giải phư
ơng trình
1
9
1
P
x
x
.
6. Chứng
minh
P
với
0
1x
.
7. Chứng
minh rằng biểu thức P chỉ nhận duy nhất một giá trị nguyên với
0 1x
.
8. Tồn
tại hay không các số thực a và b thỏa mãn đẳng th
ức
1
1
2 2
P a b a b
?
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
42
Bài toán
115. Mở rộng, liên hệ và phát triển các bài toán
Bài 1c; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Bình Định; N
ăm
họ
c 2012 – 2013; Ngày thi 30.06.2012.
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Bình Định; Năm
học 2007 – 2008.
Cho biểu thức
2
5
3 3 1 2 8
2
:
4
2 2
a a a a
A a a
a
a a
vớ
i
0
4
x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
3
2 2
a
.
3. Tính giá trị
của biểu thức A khi a thỏa mãn
4 2
5
4 0
a
a
.
4. Tìm tất cả các giá trị của a sao cho
2
2 0
A A
.
5. Tì
m giá trị của a để
4
3
A
a
.
6. Tìm khoảng giá trị của a sao cho giá trị của A lớn hơn
1
3
.
7. Tì
m tất cả các giá trị nguyên của a để A nhận giá trị nguyên.
8. Tìm giá trị của a để
2
;
0, 0,
a b b
A
a b a b
a
b
a b a b
.
Bài toán
116. Mở rộng và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình Định; Năm học 2016 –
2017; Ngày thi 06.06.2016.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình Định; Năm học 2013 –
2014; Ngày thi 14.06.2013.
Cho biểu thức
1 1
.
1 1
x x x
T x x
x x x
với
0
; 1x x
.
1. Rút gọ
n biểu thức T.
2. Tính giá trị của T khi x là nghiệm của phương trình
2
2 1 3 2 2 1
x x
.
3. Tì
m giá trị của x thỏa mãn
1
2
13
2
T
x
.
4. Tì
m giá trị nguyên của x để biểu thứ
c
1
T
x
nhận gi
á trị lớn nhất.
5. Tính giá trị của T khi x thỏa mãn dãy tỷ số bằng nhau
5
3 3 8 5 9 21
9 5 8
x
y x y
x
.
6. Cho hai số
thực a và b có tổng bình phương bằng 1. Tính giá trị của T khi
6
6 4 4 4 2 4 2
2 3 4 4x a b a b a b b a
.
7. Xét biểu
thức
1
:
1
1
x
x x
S
x
x
x x
vớ
i
0, 1
a a
.
Chứng minh rằng
.
Bài toán
117. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình
Định; Năm học 2014 – 2015.
Cho biểu thức
2
2
1
1
x
x x x
A
x
x x
với
0
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
43
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
5
5
2
x
x
.
3. Tì
m các giá trị của x để
2A
.
4. Tì
m giá trị nhỏ nhất của A.
5. Giải phương tr
ình
5
3
x
A
.
6. Tì
m giá trị của x để A nhận giá trị là một số nguyên nhỏ hơn 4.
7. Tìm tất cả các giá trị của x để
2
1
2 1
A
x x
.
8. Tì
m x sao cho
2
2
A a b
, trong đó a và b là các số thực thuộc đoạn [– 1;1] thỏa mãn
2
2
1 1 1
a b b a
.
Bài toán 118. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1997 – 1998; Ngày thi 11.06.1998.
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 2007 – 2008; Ngày thi 12.07.2007.
Cho biểu thức
2
6
1
7
18
9
3
3
x x x
A x x
x
x x
.
1. Tìm điều kiện của x để biểu thức A có nghĩa.
2. Rút gọn biểu thức A.
3. Tính giá trị biểu thức A khi
6
2 5 9 4 5
x
.
4. Giải phương trình
3
3
A
x
.
5. Tìm tất cả các giá trị x để
3
1
0A A
.
6. So sánh A
với
3
2 3 6
1
3
3 3
M
.
7. Tì
m giá trị của x sao cho
2
4
2 20 4
A
x x x
.
8. Xét biểu
thức
1
1 1
:
0; 1
1 2 1
x
B x x
x x x x x
. Tì
m giá trị nhỏ nhất của
2017
A B
.
9. Tì
m x sao cho
, vớ
i T là tổng bình phương các số nguyên
,
,a b c
thỏ
a mãn
2
2 2
3 2 4
a b c ab b c
.
Bài
toán 119. Mở rộng, liên hệ và phát triển Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo
dục và Đào tạo Tỉnh Thừa Thiên – Huế; Năm học 1992 – 1993.
Cho biểu thức
1
:
1
1
1 1 2
x
x x
P
x
x
x x
.
1. Với
giá trị nào của x thì biểu thức P được xác định.
2. Rút gọn biểu thức P.
3. Tính giá trị của biểu thức P khi
3 1
2
x
.
4. Tính giá trị biểu thức P
khi
4
7 4 7
4 7 4 7
B
.
5. Tì
m giá trị của x sao cho P nhận giá trị bằng – 2.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
44
6. Tì
m tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Tìm tất cả các giá trị của tham số m để phương trình
P
m
c
ó nghiệm.
Bài toán 120. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1994 – 1995.
Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1996 – 1997.
Cho biểu thức
:
a
b b a a b
A
a
b
b
ab ab a a b
với
0; 0;
a b a b
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị biểu thức A khi
4
2 3; 7 4 3
a
b
.
3. Chứng
minh rằng
2A
khi
3
3 13 4 3
a
b
.
4. Chứng minh bất đẳng th
ức
1
1 1
2
A
a
b
.
5. Tính giá trị
của biểu thức A khi a và b thỏa mãn hệ
2
1
5,
2 1 36.
a
b
a a b
6. Với
2
n
hoặc
2
n
,
xét biểu thứ
c
2
2
2 2
2
4 2 4
2 4 2 4
n
n n n
N
n n n n
.
So sánh giá trị biểu thức N
và biểu thức A theo n khi
2
9
a b
.
Bài toán 121. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1998 – 1999.
o Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 2000 – 2001.
o Bài 1b; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 2001 – 2002.
Cho biểu thức
3
1 1 7 7
1 1 1
x x x
P
x x x x x
.
1. Tìm điều kiện xác định cho biểu thức P có nghĩa và rút gọn biểu thức P.
2. Tính giá trị của P khi
5
2 3
x
.
3. Tính giá trị của P khi x thỏa mãn
2
7
8 2 2
x
x x
.
4. Tì
m x sao cho P nhận giá trị bằng 8.
5. Tìm giá trị của x để
2
13 48
P x x
.
6. Tì
m giá trị lớn nhất của biểu thức P.
7. Tồn tại hay không số tự nhiên x nào đó để P là một số chính phương ?
8. Xét biểu thức
1
1
:
1
1
x
x
A
x
x x
. Chứ
ng minh rằng nếu
1
2 7 1x
x
t
hì
P
A
.
9. Xét biểu
thức
b a
B
a b b a
a
ab ab b
.
Khi
b
a
,
hãy so sánh P và B theo x.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
45
Bài
toán 122. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế;
Tỉnh Thừa Thiên – Huế; Năm học 2008 – 2009.
Cho biểu thức
3
2 4 1 2
2 2 1
x
x x x
P
x x x x
1. Tì
m
x
để biểu thức
P
có
nghĩa và rút gọn
P
.
2. Kh
ông dùng máy tính bỏ túi, tính giá trị của
P
khi
4
2 3
x
.
3. Tì
m x để biểu thức P nhận giá trị bằng 0,4.
4. Tìm giá trị của x sao cho
1
5
x
P
x
.
5. Tính giá trị
của biểu thức P khi
3
9
9 70 2
x
.
6. Tính giá trị của
P khi x thỏa mãn hệ phương trìn
h
2
2
3 3
7
3
5
x
xy y
x y
7. Tì
m giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
8. Tìm m để phương trình
P
m
có nghiệm.
9. Chứng minh rằng biểu thức P chỉ nhận đúng một giá trị nguyên.
10. Giả sử tồn tại số nguyên tố p sao cho
2
2
1 ,2 1
p
p
đều là các số chính phương. Khi đó hãy so
sánh p và giá trị của biểu thức
6
P
.
Bài toán 123. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học); Đề
thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Hu
ế;
Năm học 2008 – 2009.
o Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Thừa T
hiên – Huế; Năm học 2008 – 2009.
Cho biểu thức
2
1 1
.
a
a b b b
P
a
ab b a b a b
.
1. Tì
m điều kiện đối với a và b để P có nghĩa rồi rút gọn biểu thức P.
2. Tính giá trị của biểu thức P khi a và b thỏa mãn hệ phương trình
2 2,
2 2.
a b
b a
3. Kh
i a và b là các nghiệm của phương trình bậc hai
2
3
1 0
x
x
.
Không giải phương trình này, hãy
chứng tỏ giá trị của P là một số nguyên dương.
4. Chứng minh rằng
2P
, từ đó tìm giá trị nhỏ nhất của biểu thức
1
P
P
.
5. Tìm tỷ số
a
b
để P n
hận giá trị là một số nguyên nhỏ hơn 4.
6. Khi
0
1x
,
hãy so sánh giá trị biểu thức P và giá trị biểu thức
1
1
1
x x
Q x
x x x
.
7. Tính giá trị
của biểu thức P khi a và b thỏa mãn đẳng thứ
c
2 2
2 2 4 4
4
2
25
8
a b
a b a b
ab a b
a b
.
8. Cho a và b
khác nhau thỏa mãn đẳng thức
2 2
1
1
a
b b a
.
Chứng minh
1
2P
ab
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
46
Bài toán
124. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Huế; Năm học
1998 – 1999.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán); Đề
thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Hu
ế;
Nă
m học 1999 – 2000.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán); Đề
thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Hu
ế;
Nă
m học 2003 – 2004.
Cho biểu thức
2
3
3
3 3
1
3 3 27 3
x
A
x
x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị biểu thức A khi
3 2
x
.
3. Tính giá trị
biểu thức A khi
2
28 16 3
x
.
4. Giải phư
ơng tr
ình
1
x
A
x
.
5. Tì
m tất cả các giá trị của x sa
o cho
3
2
2 5 3
x
A
x
x x
.
6. Tì
m x sao cho
2
3 2 2 6
2
2 3 2 6 2 2 3 2 6
x
x
A
x x x x
.
7. Tìm khoảng giá trị của x sao cho
2
1
1
:
x
A
x
x x x x x
.
8. Tìm giá trị nguyên của x để biểu thức
2
3
3
A
x
B
x
đạt giá trị lớn nhất.
Bài toán 124. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức;
Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam Kỳ; Tỉnh Quảng Nam; Năm họ
c
2012 – 20
13; Ngày thi 04.07.2012.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam
Kỳ; Tỉnh Quảng Nam; Năm học 2012 – 2013.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố T
am
Kỳ
; Tỉnh Quảng Nam; Năm học 2008 – 2009.
Cho biểu thức
2
3 3
4
12
3
x
x
A x
x
.
1. Tì
m điều kiện của x để biểu thức A có nghĩa.
2. Rút gọn biểu thức A.
3. Tính giá trị của A khi
4 2 3
x
.
4. Tính giá trị của A khi
3
10 20 3 6 12
1 2
5
3
x
.
5. Tính giá trị của biểu thức A khi biểu thức
2008
x x
đạt giá trị nhỏ nhất.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
47
6. Xét biể
u thức
6 1
4
2
a a
B
a
a
.
Chứng minh giá trị của biểu thức B không phụ thuộc biến
và tìm x để A và B có giá trị bằng nhau.
7. Đặt
A
f x
. Xét
2
8 16 3
3 1
x
v
à
20
12
2
2 1P x x
.
Tính
.
8. Từ
8 chữ cái Q, U, A, N, G, N, A, M ta xây dựng các cụm ký tự gồm 7 chữ cái, thí dụ QUANGNA là
một
cụm ký tự đạt yêu cầu). Giả sử xây dựng được b cụm ký tự, tìm x để
A
b
.
Bài
toán 125. Mở rộng và phát triển ài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm;
Thành phố Tam Kỳ; Tỉnh Quảng Nam; Năm học 2015 – 2016.
Cho biểu thức
1
1
1
1
x
x x
A
x
x
với
1; 0
x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A – 1 khi
20
16 2 2015
x
.
3. Tính giá trị
của A khi x thỏa mãn
2
2 2 2
6
4 7 3
0
9
11 8 12x x x x
.
4. Biểu
thức A tồn tại hay không khi x thỏa mãn hệ
2
4
4 6
8 5
x
x x y
x x y
5. Xét
1
6 2 2 3
6 4 2 3 2 2
a
. Đặt
A f x
,
hãy tính
2014
2
1f
a a
.
Bài toán
126. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố T
am
Kỳ; Tỉnh Quảng Nam; Năm học 2011 – 2012; Ngày thi 30.06.2011.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Nam; Năm học 2014 – 2015; Ngày thi 06.07.2014.
Cho biểu thức
7
1 2 3 1
5 4 4 1
x
x x
P
x x x x
vớ
i
0
x
.
1. Chứng
minh
8
3
4
x
P
x
.
2. Tính giá trị
của P khi
11
2 10
x
.
3. Tì
m giá trị của x sao cho
21
13
P
.
4. Giải phư
ơng tr
ình
2
2
1
x
P
x
.
5. Tì
m các giá trị nguyên của x để P nhận giá trị nguyên.
6. Tìm giá trị lớn nhất của P.
7. Tìm tất cả các giá trị của x để P nhận giá trị nguyên.
8. Tính giá trị của P khi x là nghiệm phương trình
2
3
1
1 1 1
x
x x x
.
9. Xét biểu thức
1
1
1 1
a a a a
B
a
a
đấy với
0; 1a a
.
Chứng minh
4P
B
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
48
Bài
toán 127. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Quảng Nam; Năm học 2006 – 2007.
Cho biểu thức
4
a
b ab a
A
a b
a
b a b
với
0; 0;
a b a b
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị biểu thức A khi
2
; 3 2 2
a
b
.
3. Cho
2A
, tìm a và b thỏa mãn
2
8 3 0
a b
.
4. Tính giá trị của A khi a và b thỏa mãn đẳng thức
3 3
3
4
8 11 25 2a b a a b
.
5. Tính giá trị
của A khi a và b là các số nguyên dương thỏa mãn
5
10 2 ,a b c d abcd c d
.
6. Chứng minh rằng nếu
2
4
5
a
b x
x
t
hì A nhận giá trị dương.
7. Chứng minh A nhận giá trị hữu tỷ khi có điều kiện
15
22 8 0
a
ab b
.
Bài toán
127. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam Kỳ; Tỉnh Quảng Nam; Năm học
2013 – 20
14.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; (Dành cho tất cả các thí sin
h
dự
thi); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam Kỳ; Tỉnh
Quảng Nam; Năm học 2015 – 2016; Ngày thi 03.06.2015.
Cho biểu thức
4 2
2 2
x x
A
x x x x
với
0
x
.
1. Rút gọ
n biểu thức A.
2. Thực hiện phép tính để tính giá trị của A khi
3
2 2
x
.
3. Tìm x để
1A
x
.
4. Giải phương trình
2
2 3
A
x x
.
5. Giải bất phương trình
2
2
2 1
A
x x x x
.
6.
Tìm giá trị nhỏ nhất của biểu thức
4
S
A
x
.
7. Tính giá trị của A khi x là nghiệm của phương trình
2
2
6
4 3 8 4
x
x x x
.
8. Xét biểu
thức
1
1 2
.
2
2
x
B
x
x x
vớ
i
0; 4
x x
.
Chứng minh
A B
.
Bài toán
128. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2006 – 2007; Ngày thi 15.06.2006.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành phố Đà Nẵng; Năm học 2007 –
2008.
Cho các biểu thức
1
1
x
P
x x x
và
1
x x
A
x
x
1. Tì
m điều kiện của x để P và A xác định.
2. Rút gọn các biểu thức P và A.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
49
3. Tính giá trị
của P và A khi
3
2 2
x
.
4. Tính giá trị
của biểu thức
P A
kh
i
1
4
10
x
x
.
5. Tì
m tất cả các số thực x sao cho
1
9
x
đồ
ng thời P nhận giá trị nguyên.
6. Tìm tất cả các giá trị của x để
8
0
A
x
.
7. Tì
m giá trị nhỏ nhất của biểu thức
2P A
.
8. Tì
m giá trị nhỏ nhất của biểu thức
2
P
A x
.
Bài toán
129. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2009 – 2010.
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2010 – 2011.
Bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2014 – 2015.
Cho biểu thức
1 1 2
:
1
1 1
a
K
a
a a a a
.
1. Rút gọn biểu thức K.
2. Tính giá trị của K khi
3
2 2
a
.
3. Tìm a sao cho
7
7K a
.
4. Tính giá trị
của K khi a thỏa mãn
2
11
16 2 3 4
a
a a
.
5. Tì
m các giá trị của a sao cho
K
.
6. Tính giá trị
của K khi
6
3 5 5 2
:
2 1 5 1 5 3
a
.
7. Giải phư
ơng trình ẩn a:
3
1
3 5
K
a
a
.
8. Xét biểu
thức
2
2 2
2
2
2
x x
P
x
x x
với
0
; 2
x
x
. Tìm a để K và P có giá trị bằng nhau.
Bài toán 130. Mở rộng và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành phố Đà Nẵng; Năm học 2008 –
2009; Ngày thi 21.06.2008.
Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành ph
ố
Đà Nẵng;
Năm học 2016 – 2017.
Cho biểu thức
3
1
1
1
x
P
x
x
với
0
; 1x x
.
1. Rút gọn biểu thức P.
2. Tìm x để
4P
.
3. Tính gi
á trị của P khi
2
6
4 2
x
.
4. Giải phư
ơng tr
ình
2
9 1
1 1
P
x
x
.
5. Tì
m giá trị nguyên của x để P đạt giá trị lớn nhất.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
50
6. Tì
m tất cả các giá trị của x để biểu thức
1
Q P x
n
hận giá trị nguyên.
7. Tính giá trị của P khi x là số nguyên dương thỏa mãn phương trình
5
4 2
1
x
x p
,
p là số nguyên tố.
Bài toán
131. Mở rộng, liên hệ và phát triển các bài toán
Bài 1 và bài 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyê
n
Toá
n, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà;
Thành phố Đà Nẵng; Năm học 2015 – 2016.
Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành ph
ố
Đà Nẵng; Năm học 2013 – 2014.
Cho biểu thức
2
49 4 2 8
3 4 4 1
x
x x x x
A
x x x x
với
0; 1x x
.
1. Rút gọn biểu thức A.
2. Tìm x để A có giá trị không vượt quá
25
6
.
3. Tì
m x sao cho
2
A
x
.
4. Tính giá trị
của A khi x thỏa mãn
2
9
38 6 4
x
x x
.
5. Tì
m giá trị nhỏ nhất của biểu thức A.
6. Chứng minh bất đẳng th
ức
2
3
25
4
x
x
A
.
7. Tính giá trị
biểu thức A khi (x;y) là nghiệm nguyên của phương trình
2
2 2 2 2 1
x
y x y
.
8. Biểu thức A nhận giá trị hữu tỷ hay giá trị vô tỷ khi x thỏa mãn phương trình
20
09 2011 2013 2010 2012 2014
6 4 2 5 3 1x x x x x x
.
9. Tính giá trị
của A khi x, y, z thỏa mãn dãy tỷ số bằng nhau
1
1 2
x y z
x
y z
y
z x z x y
.
10. Tì
m điều kiện của biến x để A nhận giá trị là một số hữu tỷ.
Bài toán 132. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Khánh Hòa; Năm học 2000 – 2001; Ngày thi 04.07.2000.
Cho biểu thức
1
3 6
0
; 4; 9
2
3 5 6
x
A x x x
x x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
1
6
25
x
.
3. Tính giá trị của A khi
4 2 3
x
.
4. Với giá trị nào của x thì A nhận giá trị bằng 3,5 ?
5. Tìm giá trị của x sao cho
5
7
x
A
x
.
6. Tì
m x thỏa mãn
9
5
A
x
.
7. Tì
m các giá trị
x
để A có giá trị nguyên.
8. Tính giá trị của A khi x, y thỏa mãn dãy tỷ số bằng nhau
5
3 4 1 5 8 1
8 5 6
x y x y
x
.
9. Tìm số chính phương x để A nhận giá trị lớn nhất.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
51
Bài toán
133. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1997 – 1998.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1996 – 1997.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1995 – 1996.
o Bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1998 – 1999.
o Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Kh
ánh Hòa; Năm học 2002 – 2003.
Với
0
; 1x x
cho hai biể
u thức
2
2
2 1 1 1
2 ;
1
2 2 2 2
x
A x B
x
x
x x
.
1. Chứng tỏ
rằng
1
x
B
x
.
2. Tìm những giá trị của x để cho
.
3A B x
.
3. Chứng minh bất đẳng thức
4A
.
4. Tính giá trị
của B khi
7 8 11
x x x
.
5. Xét biểu
thức
2
2
5
3 6 18
C
x x x x
.
Tìm x để
2
AB
C
.
6. Xét biểu
thức
2
x
x y y x y
D
xy
x y
x y
với
0; 0;
x y x y
.
Chứng minh
B D
.
7. Tính giá trị
của biểu thức B khi (x;y) thỏa mãn hệ phương trình
4
6 1 0,
9 4 1 0.
x
y
y x
Bài toán
134. Mở rộng và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2000
– 2001.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2013
–
2
014; Ngày thi 21.06.2013.
Cho biểu thức
2
2
5 3x x y y
A
x
y y
.
1. Tì
m điều kiện xác định của A.
2. Phân tích tử thức của A thành nhân tử và rút gọn biểu thức A.
3. Tính giá trị của A khi
3 13 48
x
v
à
4 2 3
y
.
4. Giải hệ
phương trìn
h
0
2
2 5
A
x
y
5. Cho biểu
thức
1
1
a
a
a
P
a
a a
với a >
0 và a ≠ 1. Chứng minh rằng nếu
2
2
x
y ay
thì P
và A có
giá trị bằng nhau.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
52
Bài toán
135. Mở rộng và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2
012
– 2013; Ngày thi 21.06.2012.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2006
–
2
007; Ngày thi 21.06.2006.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha
Trang;
Tỉnh
Khánh Hòa; Năm học 2007 – 2008; Ngày thi 22.06.2007.
Cho biểu thức
27
32 5 3 1
2 15 3 5
x
x x x
A
x x x x
.
1. Rút gọn biểu thức A.
2. Tìm x để A nhận giá trị bằng 6.
3. Tìm các giá trị của x để
1A
.
4. Tìm giá trị của x đ
ể
7
8
A
.
5. Giải phư
ơng trình
2
8
A
x
.
6. Tính giá trị
của A khi
4
15 10 6 4 15
x
.
7. Tính giá trị của A khi x là nghiệm của bất phương trình
2
2 2
5
5 1 4 4 2x y z xy yz z
.
8. Xét biểu thức
2
2
1
x x
B
x
x x
.
Tìm x sao cho
m
ax
A
B
.
9. Tì
m điều kiện cho tham số m để phương trình
A x m
có
nghiệm.
10. Tồn tại hay không các số thực a, b, c thỏa mãn
1
1 1 1
6 7 7 8 8 9 3
a
b c
A
?
Bài toán
136. Mở rộng và phát triển các bài toán
Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đ
ề
thi chí
nh thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Nă
m
họ
c 2006 – 2007; Ngày thi 22.06.2006.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2
005
– 2
006; Ngày thi 22.06.2005.
Cho biểu thức
2 2
1
2 1
x x
P
x
x x
.
1. Tì
m x để P có nghĩa.
2. Rút gọn biểu thức P.
3. Tính giá trị của P khi
9
x
.
4. Với giá trị nào của x thì
0
P
?
5. Tính giá trị của P khi x thỏa mãn
2
2
2
2 5 2 2 15 0
x x x x x
.
6. Giải phương tr
ình
5
5
1
P
x
.
7. Tính giá trị
của P khi x thỏa m
ãn
1
2
2005 2006
2
x
y z x y z
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
53
Bài toán
137. Mở rộng và phát triển các bài toán
Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đ
ề
thi
chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Nă
m
học 2014 – 2015; Ngày thi 20.06.2014.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2015
–
2
016; Ngày thi 04.06.2015.
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha
Trang;
Tỉnh
Khánh Hòa; Năm học 2015 – 2016; Ngày thi 05.06.2015.
Cho biểu thức
1
:
2
2 4 4
a a a
B
a a a a a
với
0
; 4
a
x
.
1. Rút gọn biểu thức B.
2. Tính giá trị của B khi
3
2 2
a
.
3. Tính giá trị của B khi
1
2016 2015
a
.
4. Tì
m a sao cho
2 9 12
B a a
.
5. Tì
m a để B nhận giá trị không vượt quá 3.
6. Xét biểu thức
1
x
y y y x x
M
x
y
với
điều kiện
0; 0
x y
.
S
o sánh giá trị của biểu thức M khi
2
1
3 ; 3 8
x
y
và
giá trị của biểu thức B khi
1
6
9
a
.
7. Biểu
thức B nhận giá trị hữu tỷ hay không kh
i
1
1 1
...
2
1 1 2 2 3 3 2 100 99 99 100
a
?
Bài toán
138. Mở rộng và phát triển các bài toán
Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đ
ề
thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm
họ
c 2016 – 2017; Ngày thi 02.06.2016.
Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha
Trang; Tỉnh Khánh Hòa; Năm học 2016 – 2017; Ngày thi 03.06.2016.
Cho biểu thức
2
3
3
:
x y xy
x
y
x y
A
y x
x y x y
.
1. Tì
m điều kiện xác định và rút gọn A.
2. Tính giá trị biểu thức A khi
9
; 25
x
y
.
3. Chứng minh rằng
0
A
.
4. Tính giá trị
của A khi x và y thỏa mãn
2
3
x
y xy
.
5. Tìm tỷ lệ giữa x và y sa
o cho
3
7
A
.
6. Chứng
minh rằng
0
1
A
, từ đó
tìm điều kiện giữa x và y để biểu thức A nhận giá trị là số nguyên.
7. Tồn tại hay không các số thực z, t sa
o cho
1
3
2 4
A z t z t
?
8. Giả
sử p là số nguyên tố sao cho
2
2
8
1;8 1
p
p
đều
là các số nguyên tố. Tìm tất cả các giá trị của p
và tính giá trị của biểu thức A trong trường hợp
x
py
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
54
Bài toán
139. Mở rộng và phát triển các bài toán
Bài 1 và bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành ph
ố
Tuy Hòa; Tỉnh Phú Yên; Năm học 2012 – 2013.
Bài 1 và bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đà
o
tạo Tỉnh
Phú Yên; Năm học 2010 – 2011; Ngày thi 30.06.2010.
Cho biểu thức
1
3 2
5 6 2 3
x
x
P
x x x x
.
1. Tì
m điều kiện xác định của biểu thức P.
2. Với điều kiện vừa tìm, rút gọn biểu thức P .
3. Tìm khoảng giá trị của x để
P
.
4.
Giải phươ
ng trìn
h
6
2
3
x
P
x
.
5. Tìm các số nguyên x để P có giá trị nguyên.
6. Tính giá trị của P khi x thỏa mãn
3
3 3
1005 1007 2 - 2012 0
x x x
.
7. Tì
m giá trị của m sao cho phương trình ẩn x:
P
m
có n
ghiệm.
8.
Tìm g
iá trị nhỏ nhất của biểu thức
S
Px
.
9. Giả sử
P
P x
. Xét các số thực a, b, c sao cho
0
a
b c
. Tính
3
3 3
3
P
a b c abc
.
10. Chứng minh rằng không tồn tại các số thực y, z thỏa mãn đ
ẳng thức
2
4
1
1 1
2016 2017 3
P
y z
.
11. Xét biểu thức
2 2 1
1
2
1
x x x x x x
B
x
x x x
.
Tìm x để
2
P BP
.
Bài toán
140. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy Hòa; Tỉnh Phú Yên; Năm học
2003 – 2004; Ngày thi 09.07.2003.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy
Hòa; Tỉnh Phú Yên; Năm học 2013 – 2014.
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy
Hòa; Tỉnh Phú Yên; Năm học 2011 – 2012.
Cho biểu thức
2
2
2
1 1 1 1 1
. 1
2
1 1 1 1
x x x
A
x
x
x x x
.
1. Tì
m điều kiện xác định của A.
2. Rút gọn biểu thức A.
3. Chứng minh
2
A A
.
4. Tì
m giá trị của x để
13
4
A
.
5. Cho
3
3
1
65 65 1
x
và
3
12
2009
Q
x x
. Đặt
A
f x
, tính
8039
4
f Q
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
55
6. Biểu
thức A có nghĩa hay không khi x thỏa mãn
2
2 2 1 3 2 0
x x x x
?
7. Tì
m x để A có giá trị lớn hơn 5.
8. Giả sử a, b, c là các số thực dương sao cho
a
b c ab bc ca
. Tìm
x để
a
b c
A
b
c a
.
Bài
toán 141. Mở rộng, liên hệ và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy
Hòa; Tỉnh Phú Yên; Năm học 2002 – 2003; Ngày thi 09.07.2002.
Cho biểu thức
3 5 5 2 5
1 2 2
x x x
P
x x x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi x thỏa mãn
2
2
4
5
x
x
.
3. Tính giá trị của P khi
7
2 6
x
.
4. Tì
m x để
2P
.
5. Tì
m khoảng giá trị của x để
1P
.
6. Giải phư
ơng tr
ình
5
7
x
P
x
.
7. Tì
m giá trị của m để phương trình ẩn x:
P
m
có nghiệm.
8. Tìm giá trị nguyên của x để P nhận giá trị nguyên.
9. Tồn tại hay không các số thực a, b, c sao cho
1
1 2 4
P
a b c
?
Bài toán 142. Mở rộng, liên hệ và phát triển các bài toán
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuận; Năm học 2009 – 2010.
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Ninh Thuậ
n; Năm học 2011 – 2012; Ngày thi 26.06.2011.
Cho biểu thức
4
2 1 1
:
4
2
2
x x x
P
x
x
x x x
vớ
i
0
; 4
x
x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của biểu thức P khi
3
2 2x
.
3. Tì
m x để P nhận giá trị là
2
3
.
4. Tì
m x sao cho
1,5
P
.
5. Giải phư
ơng trình
2
0
3
1
x
P
x
.
6. Tìm tất cả các giá trị m để phương trình
P m
có ng
hiệm.
7. Tính giá trị biểu thức P khi x là số lớn nhất thỏa mãn hệ thức
3
,
9.
x
y z
xy yz zx
8. Xét biểu
thức
8
3
1 ; 0
2
4
x x
Q x x
x x
.
a) Tì
m x để
P
Q
.
b) Tì
m các giá trị nguyên dương của x để biểu thức
2
1
P
Q
P
nhậ
n giá trị nguyên.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
56
Bài toán
143. Mở rộng, liên hệ và phát triển các bài toán
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Ninh Thuậ
n; Năm học 2006 – 2007.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuậ
n; Năm học 2007 – 2008.
Cho biểu thức
.
a
a b b a b
M
ab
a
b
a
b
.
1. Rút gọ
n biểu thức M và tính giá trị của M khi
9
; 4
a
b
.
2. Tính giá trị của M k
hi a và b là nghiệm của hệ
2
2
4
4 0,
6 9 0.
a
b
b a
3. Tì
m giá trị lớn nhất của biểu thức
2
3M a b
khi
4
a
b
.
4. Kh
i a và b là nghiệm của phương trình
2
27 121 0
x x
, chứng
minh
7
M
.
5. Chứng
minh bất đẳng thức
4
4
2
2 2
M
a b
.
6. Xét
biểu thức
1P
ab a b b
có
cùng điều kiện xác định với M. Tìm tất cả các giá trị nguyên
của a và b để biểu thức P có giá trị bằng 0.
Bài toán 144. Mở rộng, liên hệ và phát triển các bài toán
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuận; Năm học 2013 – 2014; Ngày thi 23.06.2013.
Bài 2 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Phan
Rang – Tháp Chàm; Tỉnh Ninh Thuận; Năm học 2012 – 2013; Ngày thi 24.06.2012.
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Phan Rang –
Tháp Chàm; Tỉnh Ninh Thuận; Năm học 2015 – 2016; Ngày thi 11.06.2015.
Bài 2 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh
Ninh Thuận; Năm học 2016 -2017; Ngày thi 14.06.2016.
Cho các biểu thức
2 1 1 1
. 1 ; 0; 1
1 1 1 1
x x x x
P x Q x x x
x x x x
.
1. Rút gọ
n các biểu thức P (x) và Q (x).
2. Tìm x để
2
2
0
x
P x
.
3. Tì
m x để Q nhận giá trị bằng 2.
4. Tìm giá trị của x để
3
4
Q
.
5. Tính giá trị
của P khi x là nghiệm của phương trình
1
1
x
x
x
x
.
6. Tính giá trị của Q khi x thỏa mãn
2
1
8 0
x
x x
.
7. Giải phư
ơng trình
5 3PQ x
.
8. Đa
thức
3
2
2 2R x x ax x a
có
ba nghiệm, trong đó một nghiệm là trung bình cộng của hai
nghiệm còn lại. Tính
4
Q
R
.
9. Xét cá
c số thực dương
, , , , ,a b c x y z
thỏa
mãn
x
y z
a b c
.
Đặt
4
a
b c x y z
t
ax by cz
,
tính
P
t
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
57
Bài toán
145. Mở rộng, liên hệ và phát triển các bài toán
Bài 1 và bài 3a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đ
ề
thi
chính thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận;
Năm học 2016 – 2017.
Bài 3b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Bình Thuậ
n; Năm học 2009 – 2010.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán); Đề
thi chính thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận;
Năm học 2015 – 2016.
Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Bình Thuận; Năm học 2016 – 2017; Ngày thi 15.07.2016.
Cho biểu thức
2
1 1 2
1
1
1
1
a a
P
a
a a
vớ
i
0; 1
a a
.
1. Rút gọ
n biểu thức P.
2. Tìm a đ
ể
11
6
P
.
3. Tì
m khoảng giá trị của a sao cho giá trị của P không nhỏ hơn – 1.
4. Tính giá trị của P khi
8 2 9 20
a a a
.
5. Cho x thỏa
mãn
2
2
4
2
4
9 0
x
x
x x
.
Tính giá trị của P khi
2
a
x
.
6. Tì
m giá trị nguyên của a để P nhận giá trị nguyên.
7. Xét biểu thức
2
1
1
1 2
a
a a a
B
a
a
. Tìm a sao cho
2
P
B B
.
8. Với các số thực dương a, b, c sao cho
3
ab
bc ca
, xét
2
2 2
6
2017
S
a b c a b c
. Tìm
khoảng giá trị của a để
min
P
S
.
9. Tì
m b theo a sao cho
1
:
a
b b a
P
ab
a b
.
Bài toán 146. Mở rộng, liên hệ và phát triển các bài toán
Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học
2014 – 2015.
Bài 3b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Bình Thuận; Năm học 2012 – 2013; Ngày thi 12.07.2012.
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học
2013 – 2014.
Cho biểu thức
1
1
1
2 3 1 3
P
x x x
.
1. Tì
m điều kiện xác định của P.
2. Rút gọn biểu thức P.
3. Tìm x để P có giá trị bằng 1.
4. Tìm x để P có giá trị dương.
5. Tính giá trị biểu thức P khi x thỏa mãn dãy tỷ số
3
1 2 6 2 2
2 3
x
y x y
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
58
6. Giải phư
ơng trình
2
3P
x
.
7. Tính giá trị
của P khi x là nghiệm của phương trình
2
4 10 1
x x x
.
8. Xét biểu
thức
2 2
2
.
8 1 4 4
2
1
Q x x x
x
với
1
0
2
x
.
Tìm x sao cho
Px
Q
.
9. Xét biểu
thức
2
2
2
2
2
3
12
2
8
x
x
A
x x
x
. Tính giá trị của P khi
5
A
.
Bài toán 147. Mở rộng, liên hệ và phát triển các bài toán
Bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận;
Năm học 2010 – 2011.
Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Bình Thuận; Năm học 2013 – 2014; Ngày thi 10.07.2013.
Cho các biểu thức
4
3
1 1
4
3
x x x x
P
x
x
v
à
1
2
1
x
B
x
x
x
với
0; 16
x x
.
1. Rút gọ
n biểu thức P.
2. Chứng minh biểu thức B không phụ thuộc giá trị biến.
3. So sánh giá trị của P và B.
4. Tìm x để P nhận giá trị bằng 9.
5. Tìm x để
2
16P B
.
6. Đặt
P
P x
. X
ét các số x, y thỏa mãn
2
2
76
; 960
xy
x y x y xy
, tính
2
2
P
x y
.
7. Giải phư
ơng trình
2
2
2 1
P
x
.
Bài toán
148. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi ch
ính
thức;
Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học
2008 – 2009.
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học
2006 – 2007.
Cho biểu thức
2
2
x y x y
x
y
N
x
y
x
y x y
với
0; 0;
x y x y
.
1. Rút gọ
n biểu thức N.
2. Tính giá trị biểu thức N khi
25; 16
x y
.
3. Tính giá trị biểu thức N khi x và y thỏa mãn hệ
4
1 2,
2 1 2.
x
y
y x
4. Tính giá trị
của N khi
3
4
x
y xy
.
5. Xét biểu
thức
2
: 1
1
1 1
x y x y
x y xy
A
xy
xy
xy
.
a) Rút gọ
n biểu thức A.
b) Tìm giá trị lớn nhất của A.
c) Tìm điều kiện của x và y sao cho
2
N
A
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
59
Bài toán
148. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2013 – 2014.
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quả
ng Trị; Năm học 2012 – 2013.
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2011 – 2012; Ngày thi 27.06.2011.
Bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Quảng Trị; Năm học 2010 – 2011; Ngày thi 24.06.2010.
Cho biểu thức
1 1
:
1
1
a a
P
a
a a a
với
0; 1
a a
.
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi
4
a
.
3. Tính giá trị của P khi
3 2 2
a
.
4. Tì
m giá trị của a để P nhận giá trị bằng 2.
5. Tìm a sao cho
1
3 8
P a
a
.
6. Xét biểu thức
1 1 1
:
1
1
1
Q
a
a
a
.
Tìm a để
P Q
.
7. Xét biểu
thức
1
1
:
4
2
2
a
R
a
a a
với
0
4
a
.
Tìm a để
2
P
R
.
8. Tì
m b theo a để
2
1
:
a b ab
P
a
b a b
.
Bài toán
149. Mở rộng, liên hệ và phát triển các bài toán
Bài 1a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2008 – 2009.
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2011 – 2012; Ngày thi 17.06.2011.
Cho biểu thức
1
1 1
:
1
1
1
x
C
x
x
x
với
0 1x
.
1. Rút gọ
n biểu thức C.
2. Tính giá trị của C khi
6
2 5
x
.
3. Tì
m x sao cho
2
13 12C C
.
4. Tì
m giá trị của x để
2
0
,8C C
.
5. Chứng
minh rằng
0
1
C
, từ đó
suy ra C chỉ nhận duy nhất một giá trị nguyên.
6. Xét biểu thức
2
1
1 1
x
D x x x x
x x
. Tìm x để
C D
.
Bài toán 150. Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Tin;Sở Giáo dục và
Đào tạo Tỉnh Quảng Trị; Năm học 2011 – 2012; Ngày thi 17.06.2011.
C
ho biểu thức
2
2 1
1
1
1
x
x x x
P x
x x x
.
1. Tì
m điều kiện của x để P có nghĩa.
2. Rút gọn P.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
60
3. Tính giá trị
của P khi x thỏa mãn
3 2 8 0
x x
.
4. Tính giá trị
của P khi
2
28
16 3
x
.
5. Tì
m x để P đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
6. Tìm x đ
ể
6
5
x x
P
x
.
7. Với
giá trị nào của x thì
0,75
P
?
8. Giải phư
ơng trình
2
1
2 3 1
P
x x
.
Bài
toán 151. Mở rộng và phát triển bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành
phố Đông Hà; Tỉnh Quảng Trị; Năm học 2013 – 2014; Ngày thi 18.06.2013.
Cho biểu thức
3 9 3 2 1
1
2
1 2
a a a
P
a a a a
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
6
2 5
a
.
3. Tìm a để P nhận giá trị bằng – 3.
4. Tìm a để giá trị của P không nhỏ hơn
5
3
.
5. Giải phư
ơng tr
ình
6
6
a
P
.
6. Tì
m a nguyên để biểu thức P nguyên.
7. Tính giá trị của P khi a thỏa mãn hệ thức
2
7
2 2 3 1 0
a
a a
.
8. Tì
m giá trị nhỏ nhất của biểu thức
P
.
Bài toán
152. Mở rộng, liên hệ và phát triển các bài toán
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2007 – 2008.
Câu 3.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Đông Hà; Tỉn
h
Quả
ng Trị; Năm học 2014 – 2015.
Cho biểu thức
1
1 1 2
:
1
2 1
a
a
A
a a a a
với a
> 0,
1
, 4
a
a
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
9
4 5 11 5 5
a
.
3. Tìm a để
0,2
A
.
4. Tìm khoảng giá trị của a sao cho giá trị của A không vượt quá 0,25.
5. Giải phương tr
ình
4
9
a
A
.
6. Tì
m giá trị nguyên của a để A nhận giá trị nguyên.
7. Tính giá trị của A khi a là nghiệm của phương trình
2
9
12 2 3 8
a
a a
.
8. Chứng
minh r
ằng
2
2 2
6
2
, , ,
9
x
y z x y z
A x y z
.
9. So sánh gi
á trị của A và giá trị của biểu thức
2
2 2
2
x
y z
B
x y z
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
61
Bài
toán 153. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành
phố Đông Hà; Tỉnh Quảng Trị; Năm học 2014 – 2015.
Cho biểu thức
2
1
1
( ) :
1
x
P x
x
x x x x
.
1. Rút gọ
n P (x).
2. Tính giá trị của P khi
7
2 6
x
.
3. Tì
m x để giá trị của P lớn hơn 5.
4. Giải phương trình ẩn x:
2
2
5 3 1
2
1
1
x x
P
x
x
.
5. Tính giá trị của P khi x là nghiệm của phương trình
2
4
1 5 1x x x
.
6. Tì
m x để P (x) nhận giá trị nguyên.
Bài toán 154. Mở rộng, liên hệ và phát triển các bài toán
Câu 9; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Quả
ng Bình; Năm học 2010 – 2011.
Bài 1 phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Quảng Bình; Năm học 2009 – 2010.
Cho biểu thức
1
1 2
4
2
2
b
P
b
b
b
vớ
i
0 4
b
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
3
2 2
b
.
3. Tì
m b đ
ể
2
3
P
.
4. Tì
m khoảng giá trị của b sao cho
2
0
,8P P
.
5. Chứng minh bất đẳng thức
P
P
.
6. Giải phương tr
ình
2
2
4 3 1
P
b
.
7. Tì
m tất cả các giá trị của b để P nhận giá trị nguyên.
8. Xét biểu thức
1
1
1 1
n n
N
n
n
vớ
i
0
; 1
n
n
.
a) Tì
m b theo n để P và N có giá trị bằng nhau.
b) Tìm tất cả các giá trị nguyên của n để biểu thức N có giá trị nguyên.
Bài toán 155. Mở rộng, liên hệ và phát triển các bài toán
Bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh
Quảng Bình; Năm học 2014 – 2015.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Bình; Năm học 2013 – 2014; Ngày thi 26.06.2013.
Cho biểu thức
1
1
4
2
2
x
A
x
x
x
vớ
i
0; 4
x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu th
ức
2
3
A
vớ
i
7
4 3
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
62
3. Tì
m giá trị nguyên của x để A nhận giá trị nguyên.
4. Tìm x để
2
2
3
A A
.
5. Tì
m x sao cho
0
,2
A
.
6. Giải phư
ơng tr
ình
8
0
4
x
A
x
.
7. Ký
hiệu
max
S
là
giá trị lớn nhất của biểu thức
2
2
2
2
a b
S
a
b b a b a a b
với a, b là các số thực
dương. Tính giá trị của A khi
m
ax
x
S
.
8. Xét biểu
thức
1 1 1
1
1
1
B
x
x x
với
0
1x
.
Tìm giá trị của x để
A
B
.
Bài toán
156. Mở rộng, liên hệ và phát triển các bài toán
Câu 1 và câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Võ Nguyên Giáp; Thành phố
Đồng Hới; Tỉnh Quảng Bình; Năm học 2016 – 2017; Ngày thi 08.06.2016.
Câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Quảng Bình; Năm học 2016 – 2017; Ngày thi 08.06.2016.
Cho biểu thức
4 3
. 2
2 2
a
P a a
a a a
với
0
; 4
a
a
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của biểu thức P khi
3 2 4 2 3
3
1
a
.
3. Tìm giá trị của a sao cho
1
7
P
a
a
.
4. Tì
m khoảng giá trị của a để
32
3
P
.
5. Tính giá trị
của P khi a là nghiệm phương trình
2
1
1
2
2017 3 2016
a
a
a
a
.
6. Xét biểu
thức
1
1 1
.
1
1
A
a
a a
với
0
1
a
.
a) Rút gọ
n A và tìm a để A có giá trị bằng 1.
b) Giải phương trình
A P
.
7. Tì
m tất cả các giá trị của m để phương trình ẩn a:
P
m
có nghiệm.
Bài toán 157. Mở rộng, liên hệ và phát triển câu 1 và câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán
(Dành cho các thí sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Võ
Nguyên Giáp; Thành phố Đồng Hới; Tỉnh Quảng Bình; Năm học 2015 – 2016.
Cho biểu thức
4
8 4 1
:
4
2
2
x x x
P
x
x x x x
vớ
i
0
; 4; 9
x
x x
.
1. Rút gọ
n biểu thức P và tìm x để
1P
.
2. Tính giá trị
của biểu thức P k
hi
1
7
5 5
5
2
x
.
3. Tính giá trị
của P khi x là nghiệm phương trình
2
4
3 1 6 0
x
x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
63
4. Giải phư
ơng tr
ình
5
4 9
x
P
x
.
5. Tì
m khoảng giá trị của x để
3
32
P
.
6. Xác định giá trị nhỏ nhất của
P
.
7. Tì
m điều kiện cần và đủ của tham số m để phương trình ẩn x:
P
m
có ngh
iệm.
8. Tìm x để bất đẳng thức sau luôn đúng:
2
2 , , 0;2
P
a a b b a b
.
Bài toán 157. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi c
hính
thức; T
rường THPT Chuyên Võ Nguyên Giáp; Thành phố Đồng Hới; Tỉnh Quảng Bình; Năm học
2010 – 2011.
Câu 12; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Quảng Bình; Năm học 2007 – 2008; Ngày thi 26.06.2007.
Cho biểu thức
2
1
1 1
2
1
1 2
x
x x
Q
x x x
với
0
; 1x x
.
1. Rút gọ
n biểu thức Q.
2. Tìm x để
2
Q
x
.
3. Tính giá trị
của Q khi
9 4 5
x
.
4. Giải phương trình
1
4
Q
x
x
.
5. Tì
m khoảng giá trị của x sao cho
Q
.
6. Tính giá trị của Q khi x là nghiệm của phương trình
2
5
2 8 3 2
x
x x
.
7. Xét biểu
thức
2
1
2
2
c
C
c
c
c
.
Tìm c theo x để
Q
C
.
Bài toán
158. Mở rộng, liên hệ và phát triển các bài toán
o Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Thanh Hóa; Năm học 2003 – 2004.
o Bài 6; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Tha
nh Hóa; Năm học 2000 – 2001.
Cho biểu thức
2
2
1 1
2
.
2
1
x x x
M x
x
.
1. Tì
m x để biểu thức M có nghĩa.
2. Tính giá trị của M khi
11
2 10
x
.
3. Giải phương trình ẩn x:
2
2
1
M
x
.
4. Tìm x sao cho
2
0
,25M M
.
5. Chứng
minh
1
4
M
.
6. Tì
m khoảng giá trị của x để M có giá trị không âm.
7. Khi x làm cho biểu thức
2
2 2
19
99 2000 2001
S
x x x
đạt giá trị nhỏ nhất thì M có
giá trị là bao nhiêu ?
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
64
Bài toán
159. Mở rộng, liên hệ và phát triển các bài toán
o Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2004 – 2005.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2005 – 2006.
o Bài 1; Đề A; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Thanh Hóa; Năm học 2006 – 2007.
Cho biểu thức
2
2 1
.
1
2
1
a a a
B
a
a
a a
.
1. Tì
m điều kiện của a để B có nghĩa.
2. Chứng minh
2
1
B
a
.
3. Tính giá trị của B khi
9
4 5
a
.
4. Giải phư
ơng trình ẩn a:
2
2 5 2
B a a
.
5. Tì
m tất cả các giá trị của a sao ch
o
5
3
3
1
5
a a a a
B
a
a
.
6. Xét biểu
thức
2
1
1
1
a a
A
a
a
a
.
a) Tìm a để
1A
.
b) Tì
m a sao cho
2
2B
AB
.
Bài toán
160. Mở rộng, liên hệ và phát triển các bài toán
o Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2012 – 2013.
o Bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Thanh Hóa; Năm học 2007 – 2008.
o Bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Thanh Hóa; Năm học 2008 – 2009.
Cho biểu thức
2
2
1 1 1
1
2
2 2 2
a
A
a
a
a
1. Tì
m điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị của a khi
3
2 2
a
.
3. Với
giá trị nào của a thì A nhận giá trị bằng
1
8
?
4. Tìm giá trị của a biế
t
A
.
5. Tì
m tất cả các giá trị nguyên của a để A nhận giá trị nguyên.
6. Chứng minh bất đẳng thức
0 1
A
.
7. Tì
m tất cả các giá trị thực của a để A nhận giá trị nguyên.
8. Tìm a sao cho giá trị của A bằng giá trị biểu thức
1 1
1 1
a a a a
B
a a
.
9. Xét biểu
thức
1 1 1
1 1 2
a a
C
a a a
.
Tìm a để
2
C
A
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
65
Bài toán
161. Mở rộng và phát triển ài 2; Đề C; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2010 – 2011.
Cho biểu thức
3
3 1 1
3
3
3
c c
C
c
c c
vớ
i
0
; 9
c
c
.
1. Rút gọ
n C.
1. Tính giá trị biểu thức C khi
3
2 2
c
.
2. Tính giá trị
biểu thức C khi
9
10c c
.
3. Tì
m c để
6
5
C
.
4. Giải phương trình
3
10
13
c
C
.
5. Tì
m c sao cho
3
16C C
.
6. Tì
m c để biểu thức C nhận giá trị nguyên.
7. Tồn tại hay không các số thực dương
t
hỏa mãn
x
y z
C
y
z x z x y
?
Bài to
án 162. Mở rộng và phát triển bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2013 – 2014.
Cho biểu thức
1
1
1
:
1
2 1
y
Q
y
y y y y
với
0
; 1y y
.
1. Rút gọn biểu thức Q.
2. Tính giá trị biểu thức Q khi
3
2 2
y
.
3. Tính giá trị
của Q khi
3 5 4 0
y y y
.
4. Tì
m y để
2
3
2Q Q
.
5. Giải phư
ơng trình
1
1
8
2
Q
y
.
6. Giải bấ
t phương trình ẩn y:
2
5
2Q Q
.
7. Chứng
minh
2, , , 0
a
b c
Q a b c
b
c a
.
8. Phản biện bất đẳng thứ
c
2 2 2
2
1
,
, , 0
2
a b c abc
Q a b c
ab bc ca
.
Bài
toán 163. Mở rộng và phát triển bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2015 – 2016; Ngày thi 21.07.2016.
Cho biểu thức
4
3 6 2
1
1
1
b
Q
b
b b
vớ
i
0
; 1b b
.
1. Rút gọ
n Q.
2. Tính giá trị của biểu thức Q khi
6 2 5
b
.
3. Tính giá trị của biểu thức Q khi b là nghiệm phương trình
2
7 7 8 7
b b b
.
4. Tì
m b sao cho
2
2
5
Q
b
.
5. Chứng
minh
0
1b
.
6. Tì
m tất cả các giá trị của b để Q nhận giá trị nguyên.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
66
Bài
toán 164. Mở rộng và phát triển bài 2.2; Đề A; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2011 – 2012.
Cho biểu thức
4
1 1
:
4
2
2 2
a
a a
A
a
a a a
vớ
i
0
; 4
a
a
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A tại
6
4 2
a
.
3. Tì
m a sao ch
o
5
6
a
A
a
.
4. Giải bấ
t phương trình
2 1 3
0
A A
A
.
5. Tính giá trị
của A khi a là nghiệm phương trình
2 2
2 3 2 3 4 2
a a a a
.
6. Tìm khoảng giá trị của m để phương trình
3
A
m
có
nghiệm.
7. Tìm m để
1
,
;4
4
A
m a
.
Bài toán 165. Mở rộng, liên hệ và phát triển các bài toán
Câu II; Đề A; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Thanh Hóa; Năm học 2016 – 2017; Ngày thi 16.06.2016.
Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Tha
nh Hóa; Năm học 2014 – 2015; Ngày thi 30.06.2014.
Cho biểu thức
2
2 1
1
1
:
1
x x
x x x x
A
x
x x x x
(vớ
i
0; 1x x
).
1. Rút gọ
n biểu thức A.
2. Tính giá trị của biểu thức A khi
8
2 7
x
.
3. Tính giá trị
của A khi x thỏa mãn
2
2
3 3 5 4
x
x x
.
4. Tì
m a sao ch
o
3
4
x
A
x
.
5. Giải bấ
t phương trình
2
2A
A
.
6. Tì
m tất cả các số nguyên x để biểu thức A có giá trị nguyên.
7. Tìm giá trị nhỏ nhất của biểu thức
A
.
8. Tì
m khoảng giá trị của m để
,
4;9
A
m x
.
9. Xét biểu
thức
2
1 1 1
.
1
x
B
x x
x x
vớ
i
0; 1x x
. Tì
m x sao cho
A
B
.
Bài
toán 165. Mở rộng và phát triển Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự chuyên Tiếng Nga, Tiếng Pháp); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố
Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2012 – 2013.
Cho biểu thức
2
3 2
: 2
5
6 2 3 1
x x x x
A
x
x x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị biểu thức A khi
6
2 5
x
.
3. Tì
m các giá trị của x sao ch
o
12
35
A
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
67
4. Tính giá trị
biểu thức A khi x là nghiệm phương trình
4
2
2
2 2 1x x x
.
5. Giải phư
ơng trình
1
9
A
x
.
6. Tìm các giá trị của x để
1
5
2A
.
7. Tì
m tất cả các giá trị của m để phương trình
A
m
có
nghiệm.
8. Tìm tất cả các giá trị
4
x
để
biểu thức A nhận giá trị nguyên.
Bài toán 166. Mở rộng, liên hệ và phát triển các bài toán
Bài 1 và bài 3.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi);
Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Nă
m
học 2011 – 2012; Ngày thi 19.06.2011.
Đề thi Olympic môn Toán; Khu vực Châu Á – Thái Bình Dương; Năm 2004 – APMO 2004.
Cho biểu thức
3
32
1
23
32
1115
x
x
x
x
xx
x
A
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi
4 2 3
x
.
3. Tính giá trị
của A khi
3
5
2 7
x
.
4. Chứng minh
2
3
A
.
5. Giải phương tr
ình
2
5
A
.
6. Tì
m khoảng giá trị của x để
2
7
2A A
.
7. Tì
m m để phương trình ẩn x:
A
m
có nghiệm
0
;3
x
.
8. Tính giá trị của biểu thức A khi x thỏa mãn
2
3
6
2
9
x
x
x
.
9. Tì
m tất cả các số thực dương
,
,a b c
thỏa m
ãn đẳng thứ
c
2 2 2
9
2
A
a b c
b
c c a a b
.
10. Phủ đị
nh hoặc khẳng định bất đẳng thức:
2 2 2
2 2 2
6
, , 0
a b c
A a b c
ab
bc ca
.
Bài toán 167. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh
Hóa; Năm học 2010 – 2011; Ngày thi 19.06.2010.
Cho biểu thức
6
1 10
: 2
4
3 6 2 2
x x
A x
x x x x x x
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi
1
3 4 3
x
.
3. Tính giá trị
biểu thức A khi
3
7 8
x x
.
4. Giải phư
ơng tr
ình
1
8
A
.
5. Tì
m x sao cho
2A
.
6. Tìm x đ
ể
6
5
x
A
x
.
7. Tì
m m để phương trình ẩn x:
A
m
có nghiệm
0
;3
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
68
Bài
toán 168. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa;
Tỉnh Thanh Hóa; Năm học 2007 – 2008.
Cho biểu thức
2
1 1
1 1 1
x x x x
P
x
x
x x x x
.
1. Tìm điều kiện của x để P có nghĩa và rút gọn P.
2. Tính giá trị của P khi
9
4 2
x
.
3. Tính giá trị
của P khi x thỏa mãn
4 2
5 4 0
a a
.
4. Tình giá trị
của P khi x là nghiệm của phương trình
2
2
7 3 1 3
x
x x x
.
5. Giải phư
ơng trình
9 15 6
P x x
.
6. Tì
m x sao cho
2
3P
P
.
7. Tì
m giá trị của x sao cho
3
4 3
x
P
x
.
Bài toán
169. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh
Hóa; Năm học 2012 – 2013; Ngày thi 17.06.2012.
Cho biểu thức
1 1 1
4
.
1 1 2
a a
P a
a
a a a
vớ
i
0; 1
a a
.
1. Chứng
minh
2
1
P
a
.
2. Tính giá trị của P khi a thỏa mãn
4
2
1
0 9 0
a
a
.
3. Tính giá trị của P khi
15
2 14
a
.
4. Tì
m a để
P a
.
5. Giải phư
ơng trình ẩn a:
2
4
5
1 1
P
a
a
.
6. Tìm a sao cho
3
3P
P
.
7. Tì
m giá trị nguyên của a để P nhận giá trị nguyên.
8. Xét trường hợp
1
; 1; 1; 4
a
b c a b c
. Tìm giá trị nhỏ nhất của biểu thức
1
1
1 1
S P
b
c
.
Bài toán 170. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức;
Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2013 –
2014; Ngày thi 24.06.2013.
Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học);
Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Nă
m
học 2009 – 2010.
Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Tha
nh Hóa; Năm học 2006 – 2007.
Cho biểu thức
2
2
:
0
2
2
x x
P x
x x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
69
1. Rút gọ
n biểu thức P.
2. Giải phương trình
3
1P x
.
3. Tính giá trị
của P khi x là nghiệm của h
ệ
2
2
2
2
1
4
4 7
x
xy
x xy y
4. Tì
m x để P có giá trị lớn hơn
1
9
6
.
5. Tính giá trị
của P khi x thỏa mãn đẳng thức
1
2
2009 2010
2
x
y z x y z
.
6. Tìm giá trị của x để
3
P
.
7. Tì
m giá trị nhỏ nhất của biểu thức P.
8. Cho ba số
k
hác 0 và thỏa mãn
1
1 1
0
x y z
.
Đặt
2
2 2
xy
yz zx
A
z x y
và đặt
P
P x
. Tính
giá
trị của
4
P
A
.
Bài toán
171. Mở rộng và phát triển bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh
Thanh Hóa; Năm học 2015 – 2016; Ngày thi 12.06.2015.
Cho biểu thức
1
:
2 2 4 4
a
a a
M
a a a a a
với
0; 4
a a
.
1. Rút gọn biểu thức M.
2. Tính giá trị biểu thức M với
16
81
a
.
3. Tính giá trị
biểu thức M khi a thỏa mãn
2
49 20 6
a
.
4. Tì
m giá trị của a sao cho M có giá trị bằng 3.
5. Giải bất phương trình
5
6M a a
.
6. Tì
m tất cả các giá trị của a để
0
M
.
7. Tính giá trị
của M khi a thỏa mãn
2
2
5 1 2 2
a a
.
8. Tì
m giá trị nhỏ nhất của biểu thức
5M a
.
9. Giải phư
ơng trình
3 8 4 3 5
M a a
.
Bài toán 172. Mở rộng và phát triển bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh
Thanh Hóa; Năm học 2016 – 2017.
Cho biểu thức
2 1 3 11
0
; 9
9
3
3
x x x
A x x
x
x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi x thỏa m
ãn
2
1 6
x
x
.
3. Tì
m x để
0
A
.
4. Tìm tất cả các giá trị của x sao cho
12A
.
5. Giải phương tr
ình
3 7
5
x
A
x
.
6. Tì
m các giá trị nguyên của x để A nhận giá trị nguyên.
7. Tính giá trị biểu thức A khi x là nghiệm phương trình
2
2
4
7 4 7
x
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
70
8. Tìm giá trị của m để phương trình
A
m
có nghiệm.
9. Tìm giá trị nhỏ nhất của biểu thức
S
A x
.
10. Tồn
tại hay không các số thực y, z sao cho
1
2 1
2
3
2
A
y y z z ?
Bài
toán 173. Mở rộng và phát triển bài 1 và bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành
cho các thí sinh dự thi chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố
Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2014 – 2015.
Cho biểu thức
3
16 7 1 3
0
; 1
2
3 3 1
x x x x
P x x
x x x x
.
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi x thỏa mãn
2
2 3
x
.
3. Tì
m x sao ch
o
3 5
3 7
x
P
x
.
4. Giải phư
ơng trình
2
4P P
.
5. Tì
m khoảng giá trị của x để
3
2
P
.
6. Tính giá trị
của P khi x là nghiệm của h
ệ
2
2
2 2
2 3 2
2 3 2
x x y
y y x
7. Tì
m các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
8. Tính giá trị của biểu thức P khi x là số nguyên thỏa mãn
3
3 2 2
5
x
y x y xy
.
9. Chứng
minh không tồn tại các số thực y, z thỏ
a mãn
1
2 2
2 3
3
3 3
P y z y z
.
Bài toán
174. Mở rộng, liên hệ và phát triển các bài toán
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học); Đề
thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm học
2009 – 2010.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học); Đề
thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm học
2005 – 2006.
Cho biểu thức
2
3
2
4 1 1
1
1
1
x
T
x
x x
;
1. Tì
m điều kiện của x để T xác định. Rút gọn T.
2. Tính giá trị của T khi
4
2 3
x
.
3. Tìm giá trị lớn nhất của T.
4. Giải phương trình
2
3 4T T
.
5. Tì
m khoảng giá trị của x sao cho
3
4T
T
.
6. Tìm giá trị nguyên của x để T nhận giá trị nguyên.
7. Tìm tất cả các giá trị thực của x để T nhận giá trị nguyên.
8. Tính giá trị của T khi x là nghiệm phương trình
2
3
3
4
3
1
x
x x
.
9. Xét biểu thức
1 2
1
1 1
x
M x
x x x
. Tì
m x để
T
M
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
71
Bài toán
175. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nghệ An; Năm học 2013 – 2014.
o Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nghệ An; Năm học 2015 – 2016.
Cho biểu thức
2
1 1
:
4
2
2
P
x
x
x
1. Tì
m điều kiện xác định và rút biểu thức P.
2. Tính giá trị của P khi x thỏa mãn
3 3 1 0
x x
.
3. Tìm
x đ
ể
3
2
P
.
4. Giải phư
ơng trình
8
15
x
P
x
.
5. So sánh P với 1, từ đó tìm tất cả các giá trị của x để giá trị của P là số nguyên.
6. Giả sử tồn tại các số hữu tỷ phân biệt
, ,a b c
sao
cho
2 2 2
1
1 1
x
a
b b c c a
.
Khi đó em hãy
chứng minh giá trị của P là một số hữu tỷ.
7. Xét biểu thức
1
4
4
2
Q
x
x
. Tì
m x để
2
3
P Q
.
8. Xét cá
c số thực
, ,a b c
bất
kỳ, phủ định hoặc khẳng định bất đẳng thức
2
2
2 2
2
2 2 3
P
a b c a b c
.
Bài toán
176. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2010 – 2011.
Cho biểu thức
2
2
1
1
1
x
A
x
x
x
.
1. Nêu điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi
9
x
.
3. Tính giá trị biểu thức A khi
4
2 3
x
.
4. Tì
m x để A nhận giá trị không vượt quá
2
3
.
5. Tì
m x sao cho
2
2
7
x
A
x
.
6. Tính giá trị của A khi x là nghiệm phương trình
3.16 2.81 5.36
x
x x
.
7. Tì
m tất cả các giá trị nguyên của x để A nhận giá trị nguyên.
8. So sánh với A với 1, từ đó tìm tất cả các giá trị của x để A nhận giá trị nguyên.
9. Khi x thỏa mãn điều kiện xác định, tìm giá trị lớn nhất của biểu thức
1
B
A x
.
10. Xét các số thực dương
, ,a b c
có tổng bằng 3. Phản biện bất đẳng thức
2
2 2
1
1 1
A
a a b b c c
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
72
Bài toán
177. Mở rộng và phát triển câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2007 – 2008.
Cho biểu thức
1
1
:
1
1
x
A
x
x x x
.
1. Nêu
điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị biểu thức A với
9
16
x
.
3. Tính giá trị của A khi
6 2 5
x
.
4. Tính giá trị
biểu thức A khi x thỏa mãn
30
36 36.5 6
x
x x
.
5. Tìm x sao cho
2
5
A
.
6. Tìm tất cả các giá trị của x sao cho
0
A
.
7. Giải phư
ơng trình
1
3
8
A
x
x
.
8. Với
giá trị nào của x thì
2
2 3A A
?
9. Tì
m tất cả các giá trị của tham số m để phương trình
A
x m x
có
nghiệm.
Bài toán 178. Mở rộng và phát triển câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2008 – 2009.
Cho biểu thức
3
1 1
:
1
1
1
P
x
x
x
.
1. Nêu
điều kiện xác định và rút gọn biểu thức P.
2. Tính giá trị của P khi
3 2 2
x
.
3. Tính giá trị của P khi x thỏa mãn
9 27 28.3
x
x
.
4. Tì
m các giá trị của x để
5
4
P
.
5. Tì
m tất cả các giá trị của x sao cho
6
3
4
x
P
x
.
6. Giải bấ
t phương trình ẩn x:
2
4 7P P
.
7. Tì
m giá trị nguyên của x để P nhận giá trị là một số nguyên.
8. Với giá trị nào của tham số m thì phương trình
P
m
có nghiệm
thực ?
9. Tìm giá trị nhỏ nhất của biểu thức
12
1
.
1
x
Q
P
x
.
10. Tồn
tại hay không các số y, z thỏa mãn
3
1 2 1 3 1 2
P
y x z x
?
Bài
toán 179. Mở rộng và phát triển câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2012 – 2013; Ngày thi 24.06.2012.
Cho biểu thức
1 1 2
.
2
2
x
A
x
x x
.
1. Tìm điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi
1
3 4 3
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
73
3. Tính giá trị
biểu thức A khi
6
3
28 27 0
x x
.
4. Tì
m tất cả giá trị của x sao cho
1
2
A
.
5. Tính giá trị
của x sao ch
o
2
7
A
.
6. Giải phư
ơng trình ẩn x:
7
1
0 40 40
A
x
x
.
7. So sánh A
với 0 và 1, từ đó tìm giá trị của x để biểu thức
7
3
B
A
nhận giá trị nguyên.
Bài toán 180. Mở rộng và phát triển câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 1999 – 2000.
Cho biểu thức
2
1
2
2
.
1
2
2
1
x
x x
P
x
x x
.
1. Tì
m điều kiện và rút gọn P.
2. Tính giá trị của P khi x thỏa m
ãn
4
1 7
x
.
3. Tính giá trị
của P khi
4 2 3
x
.
4. Tìm giá trị lớn nhất của biểu thức P.
5. Giải phương trình
5
3 8P x x
.
6. Chứng minh rằng P có giá trị hữu tỷ khi x, y thỏa mãn đẳng thức
2
2 4 3
x
y y y x y
.
7. Chứng
minh bất đẳng thức
2
6
5 0
P
P
.
8. Giải phương trình
2
1
2 1
P
x x
.
9. Tì
m khoảng giá trị của x sao cho
6
P
.
Bài toán
181. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2000 – 2001.
Đề thi Olympic; Môn Toán; Cộng hòa Hồi giáo Iran; Kỳ thi năm 1998 – Irannian MO 1998.
Cho biểu thức
1
1 1
:
1
2 1
x
P
x
x x x x
.
1. Tìm điều kiện và rút gọn P.
2. Tính P khi
0,25
x
.
3. Tính giá trị
của P khi x là nghiệm phương trình
6 36 4.3 9.2
x
x x
.
4. Tì
m giá trị của x sao cho
16
8
1
P
.
5. Tì
m khoảng giá trị của x để biểu thức
1P
.
6. So sánh P
với 1.
7. Giải phương trình ẩn x :
3 1 1
3 1
x
P
x
.
8. Tính giá trị của P khi x thỏa mãn đẳng thức
3
3
3
4
2 6 3
x
y y y x
.
9. Cho c
ác số
, , 1x y z
thỏa mãn
1
1 1
2
x y z
. Phản biện bất đẳng thức
1
1 1
2
x
y z
P
x y z
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
74
Bài toán
182. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2001 – 2002.
Câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2001 – 2002.
Cho biểu thức
2
1
a
a a
P
a
a a
.
1. Tì
m điều kiện và rút gọn P.
2. Tính giá trị của P khi
3 8
a
.
3. Giải phư
ơng trình
6 6P a a
.
4. Tìm giá trị của a sao cho
5
P a
.
5. Tì
m điều kiện của a để P nhận giá trị dương.
6. Tính giá trị của P khi x là nghiệm phương trình
3
2
2
5
2
3
y
x
x y y x
.
7. Xét biểu thức
2
1
1
x
x
Q
x
x x
.
a) Tính giá trị
của P khi
3
6
x
.
b) Tì
m x để
Q
Q
.
c) Tìm x sao cho
Q P
.
Bài
toán 183. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2009 – 2010.
Cho biểu thức
1
1
1
1
x
x x
A
x
x
.
1. Nêu
điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị biểu thức A
khi
9
4
x
.
3. Tì
m giá trị của x sao cho
4A
.
4. Tì
m tất cả các giá trị của x để
1A
.
5. Giải phư
ơng tr
ình
7
2
x
A
.
6. Tì
m giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
7. Tính giá trị của A khi x là nghiệm phương trình
3
1
,5
3
3
y
x
y x y x
.
8. Tì
m khoảng giá trị của tham số m để phương trình
A m
có
nghiệm.
Bài toán 184. Mở rộng và phát triển câu 1; phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2003 – 2004.
Cho biểu thức
1
1 3
:
3
3 3
P
x
x x
.
1. Tì
m điều kiện và rút gọn P.
2. Tính giá trị của P khi
8
1
x
.
3. Tì
m x đ
ể
1
3
P
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
75
4. Tì
m tất cả các giá trị của x đ
ể
A
.
5. Giải phư
ơng trình
1
11
x
P
x
.
6. Giải bấ
t phương trình
8
21
P
.
7. Tì
m x để biểu thức P đạt giá trị lớn nhất, tìm giá trị lớn nhất đó.
8. Tìm tất cả các giá trị của x để P nhận giá trị nguyên.
9. Tính giá trị của P khi x thỏa mãn đẳng thức
3
3
4
4 36 25x y y y x y
.
Bài toán 185. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh
Nghệ An; Năm học 2004 – 2005.
Câu 1; phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2005 – 2006.
Cho biểu thức
1
1 1
.
1
1 1
P
x x x
.
1. Tìm điều kiện và rút gọn P.
2. Tính giá trị của P kh
i
1
4
x
.
3. Tính giá trị
của P khi
1
4 2 13
x
.
4. Tì
m x sao cho
2
5
8P P
.
5. Tì
m tất cả các giá trị của x để
P
P
.
6. Tì
m giá trị của x sao cho
9
0
2
5
P
x
.
7. Xét biểu
thức
1
1
1
.
1
Q
x
x x
.
a) Tìm x đ
ể
2
.
5 2 6. 1 2005 2 3
P
x x
.
b) Giải phư
ơng trình ẩn x:
2
3Q P
.
8. Chứng minh rằng biểu thức P nhận giá trị hữu tỷ khi x thỏa mãn đẳng thức
3
3
2
3
3
y
x
y x x y
.
Bài toán 186. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Nghệ An; Năm học 2011 – 2012.
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Nghệ An; Năm học 2014 – 2015.
Đề thi Olympic; Môn Toán; Cộng hòa Hồi giáo Iran; Kỳ thi năm 2002 – Iranian MO 2002.
Cho biểu thức
2
1
1 1
:
1
1
x
A
x
x x
x
.
1. Tì
m điều kiện xác định và rút gọn biểu thức A.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
76
2. Tính giá trị
biểu thức A
khi
1
2
2
2 1
x
.
3. Tì
m giá trị của x để
A
.
4. Giải phương trình ẩn x:
7
1 1
7 1
x
A
x
.
5. Giải bấ
t phương trình ẩn x:
2
19 8A A
.
6. Chứng
minh biểu thức A nhận giá trị hữu tỷ khi x thỏa mãn đẳng thứ
c
2
3
6 1 9 8
y
y x y x y
.
7. Tì
m giá trị lớn nhất của biểu thức
9P
A x
.
8. Cho các số dương
, ,a b c
thỏ
a mãn
2
2 2
4
a b c abc
.
Khẳng định hoặc phủ định bất đẳng thức
4
a
b c A
.
Bài toán
187. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉn
h
Ng
hệ An; Năm học 2016 – 2017.
Đề thi Olympic; Môn Toán; Thủ đô Moskva; Cộng hòa Liên bang Nga; Kỳ thi năm 2000 – Moscow
Mathematical Olympiad, 2000 – Moscow MO 2000.
Cho biểu thức
1
1
.
3
9
3
x
P
x
x
x
.
1. Tì
m điều kiện xác định và rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi
17 2 2
x
.
3. Tính giá trị
của P khi x là nghiệm nguyên của phương trình
3
3
1
2 2 1x x
.
4. Tì
m các giá trị của x để
1P
.
5. Giải phương trình ẩn x:
4
0
4
15 1
P
x
.
6. Tì
m khoảng giá trị của x sao cho
3
9
P P
.
7. Chứng minh biểu thức P chỉ nhận duy nhất một giá trị nguyên.
8. Chứng minh biểu thức P nhận giá trị là số tự nhiên khi x thỏa mãn đẳng thức
2
1 4 2 0
x
y y y x y
.
9. Chứng minh rằng P nhận giá trị hữu tỷ khi x là số thực dương sao cho
2
2
2 2 4 4
2 2
1
1 1 1 1
,x a b
a b a b
a b
a b
.
10. Cho các số
thực dương
,
,a b c
có tích
bằng 1. Phản biện bất đẳng thức
2
2 2
4
3
a
b c a b c P
ab bc ca
.
Bài toán
188. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉn
h
Ng
hệ An; Năm học 2006 – 2007.
Đề thi chọn đội tuyển tham dự kỳ thi Olympic Quốc tế; Môn Toán; Kỳ thi năm 2002; Cộng hòa
Rumani – Junior TST, 2002, Rumania.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
77
Cho biểu
thức
2
1
1 1
:
1
1
x
P
x
x x
x
.
1. Nêu
điều kiện xác định và rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi
4
2 3
x
.
3. Tính giá trị biểu thức P khi x là nghiệm phương trình
4
2 2
x
x
.
4. Tì
m điều kiện của x để
0
P
.
5. Tì
m giá trị của x sao cho
2
3 1
3 1
x
P
x
.
6. Tì
m tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Cho các số thực
,
, 0;1
a
b c
.
Phản biện bất đẳng thức
1
1
1 1abc a b c P
x
.
Bài toán
189. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ
An; Năm học 2006 – 2007.
Cho biểu thức
2
1 1
1
1
1
x x x
P
x
x x x x
.
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi
9
4 5
x
.
3. Tìm giá trị của x sao cho
5
31
P
.
4. Giải phư
ơng trình ẩn x:
2
5
P
x
.
5. Tì
m khoảng giá trị của x sao cho
2
13 3P P
.
6. Tính giá trị
biểu thức P khi x thỏa mãn đẳng thức
4
2
1
2 1x x x x
.
7. Chứng minh
P
với
0; 1x x
.
8. Chứng minh rằng biểu thức P chỉ nhận duy nhất một giá trị nguyên.
9. Cho
,
,a b c
là cá
c số thực dương. Phản biện bất đẳng thứ
c
3
8
6
a
b c abc
P
a
b b c c a
abc
.
Bài toán
190. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ
An; Năm học 2007 – 2008.
Cho biểu thức
3 9 3 1 2
2 2 1
x x x x
P
x x x x
.
1. Tìm điều kiện xác định của P và rút gọn biểu thức P.
2. Tính giá trị của P khi
2
5
16
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
78
3. Tính giá trị của P khi
3
2 2
x
.
4. Tìm x sao cho P có giá trị không vượt quá 2.
5. Giải phương trình ẩn x:
6
5
14
x
P
x
.
6. Tình giá trị của P khi x thỏa mãn đẳng thức
2
6
7 3 2
x
y x x x y
.
7. Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên.
8. Tìm điều kiện của tham số m để phương trình
P
m
có nghiệm
.
9. Chứng minh rằng không tồn tại các số thực y, z sa
o cho
1 1 1
2
3 2 3
5
6 2
P
y z z y
.
Bài toán
191. Mở rộng và phát triển các bài toán
Bài 1, 3a, 3b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đ
ề
thi
chính thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ An; Năm họ
c
2005 – 20
06.
Bài 1, 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chí
nh thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ An; Năm học 200
4
– 2
005.
Cho biểu thức
4
3 2 9
3 2 5 6
a
a a
P
a a a a
.
1. Tì
m điều kiện xác định của biểu thức P.
2. Rút gọn biểu thức P.
3. Tính giá trị biểu thức P khi
4
2 3
a
.
4. Tìm a sao cho
8
5
P
.
5. Giải phương trình ẩn a:
3
P a
.
6. Tìm các số nguyên a để P nhận giá trị nguyên.
7. Tìm khoảng giá trị của a sao cho
7
5
a
P
a
.
8. Tính giá trị
của P khi a là nghiệm của phương trình
3
2
5 2 16 2 8
a a
.
9. Tính giá trị
của P khi a thỏa mãn hệ
2
1
,
2
2 1 2 .
a
b c
a
b c ab
10. Xét bố
n số thực dương
,
, ,x y z t
có tổ
ng bằng 2 và biểu thức
4
4 4 4
3 3 3 3
x
y z t
Q
x
y z t
.
T
ìm a để
m
in
P
Q
,
trong đó
m
in
Q
là k
ý hiệu giá trị nhỏ nhất của Q.
11. Xét hai số thực x, y sao cho
;
1x y xy
. So sánh giá
trị của P với giá trị nhỏ nhất của biểu thức
2
2
x y
S
x
y
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
79
Bài
toán 192. Mở rộng, liên hệ và phát triển câu 1 và câu 5; Mã đề 01; Đề thi tuyển sinh lớp 10 THPT;
Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh Hà Tĩnh; Năm học 2011 – 2012.
Cho biểu thức
1
1 2
1
2
2
A
a a a
.
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi
1
4
a
.
3. Tính giá trị biểu thức A khi
4
2 3
a
.
4. Tì
m giá trị của a để
1
2
A
.
5. Tìm giá trị của a sao cho
2
5A
A
.
6. Giải phương trình ẩn a:
6
.
1
13
a
A
a
.
7. Tì
m tất cả các giá trị của m để phương trình
A
m
có nghiệm.
8. Chứng minh rằng biểu thức A nhận giá trị nguyên khi
2
017 2017
1
a x y
, trong đó x và
y thỏa mãn
2
2
2016
2016 2016
x
x y y
.
9. Tì
m tất cả các giá trị của k để bất phương trình
A k
đ
úng với
0
;4
a
.
10. Tì
m khoảng giá trị của a sao cho
9
,
, ,
4
2
3 2 3 2 3
x y z
A x y z
y z x
.
Bài toán
193. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Mã đề 01; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và
đào tạo Tỉnh Hà Tĩnh; Năm học 2012 – 2013; Ngày thi 28.06.2012.
Câu 1b; Mã đề 01; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục v
à
đào tạo
Tỉnh Hà Tĩnh; Năm học 2015 – 2016.
Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 2007 – 2008.
Cho biểu thức
2
4
1
.
1
a a a
P
a
a a a
với
0; 1
a a
.
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi
3
2 2
a
.
3. Với những giá trị nào của a thì
3
P
?
4. Giải phương trình ẩn a:
.
2 1 5 2
P
a a
.
5. Tì
m tất cả các giá trị a sao cho
2
25 19P P
.
6. Với
giá trị nào của a thì biểu thức P đạt giá trị lớn nhất ? Tìm giá trị nhỏ nhất đó.
7. Tính giá trị của P khi
9a x y
, trong đó x và y thỏa mãn
2
2
4
4 4
x
x y y
.
8. Chứng minh biểu thức P nhận giá trị hữu tỷ khi a thỏa mãn hệ đẳng thức
1
1 1 1 9 9
3
4 4 16 16 16 16
a b b c c a
.
9. Xét biểu
thức
1
1
1 .
1
x
Q
x
x
với
0
; 1x x
. Tìm a theo x để
P
Q
.
10. Tìm tất cả các giá trị của k để phương trình
2
P
k
có
nghiệm thực.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
80
Bài toán 19
4. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉn
h
Hà Tĩnh
; Năm học 2016 – 2017; Ngày thi 14.06.2016.
Câu 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Hà Tĩnh; Năm học 2013 – 2014.
Bài 2a và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đ
ề
thi
chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 200
7
– 2008.
Cho biểu thức
1
1 3
.
1
3 3
Q
x x x
với
0; 9
x x
.
2 : (căn x +3)
1. Rút gọ
n biểu thức Q.
2. Tính giá trị biểu thức Q khi
9
25
x
.
3. Tính giá trị biểu thức Q khi
9
4 5
x
.
4. Chứng
minh
2
0
3
Q
.
5. Tì
m a sao cho
2
11
3Q Q
.
6. Giải bấ
t phương trình ẩn x:
5
7
3
x
Q
x
.
7. Chứng minh bất đẳng thức
5
2
Q
x
x
.
8. So sánh giá trị của Q với các nghiệm của phương trình
2
2 2 1 4 1x x x
.
9. Biểu
thức Q có thể nhận giá trị nguyên hay không ? Vì sao ?
10. Cho ba số dương
, ,a b c
t
hỏa mãn
1a
b c
. P
hản biện bất đẳng thức sau:
1
1
24P
ac
bc
.
11. Xét biểu
thức
1
1 3
.
3
3
x
R
x
x x
. Chứng minh
R Q
và tìm x sao cho
R Q
.
Bài toán 195. Mở rộng, liên hệ và phát triển các bài toán
Câu 1 và câu 5; Mã đề 04; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo
dục và đào tạo Tỉnh Hà Tĩnh; Năm học 2009 – 2010.
Câu 3a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà
Tĩnh; Năm học 2015 – 2016.
Câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà
Tĩnh; Năm học 2016 – 2017.
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉn
h
Hà Tĩnh
; Năm học 2014 – 2015.
Cho biểu thức
2
1
.
2
1
x x x
P
x
x x x x
với
0
x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
9 4 2 3 0
x x
.
3. Tì
m giá trị của x để
0
P
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
81
4. Giải phư
ơng trình ẩn x:
1
0 3 6
P
x x
.
5. Tì
m giá trị nhỏ nhất của P và giá trị tương ứng của x.
6. Tìm điều kiện của x sao cho
7
1 9 2 0
P
P
.
7. Tính giá trị
của P khi x là nghiệm phương trình
2
3
1 1 3 2 1x x x x
.
8. Xét cá
c số nguyên dương a, b, c phân biệt thỏa mãn
1
1 1
1
a
b c
. Tì
m x để
P
a b c
.
9. Chứng
minh rằng biểu thức P nhận giá trị nguyên khi
201
7 2017
1
x
a b
,
trong đó x và y thỏa mãn
2 2
20
17 2017 2017
a
a b b
.
10. Xét
các số thực
,
, 1;4
a
b c
sao
cho
2 3 4
a b c
.
Đặt
P
P x
và
ký hiệ
u
m
ax
S
là giá
trị lớn nhất
của biểu thức
2 2 2
2
3S a b c
. So sánh
16 4
P P
vớ
i
m
ax
S
.
11. Xét biểu
thức
1
1
.
16
4
4
Q x
x x
.
T
ìm giá trị của x để
P Q
.
Bài toán
196. Mở rộng, liên hệ và phát triển các bài toán
Câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 201
2
– 2
013.
Câu 1.1 và 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh;
Tỉnh Hà Tĩnh; Năm học 2011 – 2012.
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Hà Tĩnh; Năm học 2008 – 2009; Ngày thi 24.06.2008.
Cho biểu thức
1
2
1 2
1 1
x
x x x
M
x x
x
x
.
1. Tì
m điều kiện của x để biểu thức M có nghĩa.
2. Rút gọn biểu thức M.
3. Tính giá trị của M khi
2 3 1 0
x x
.
4. So sánh gi
á trị của M với các nghiệm của phương trình
2
2
3 2 2 3
x
x x x
.
5. Với
giá trị nào của x thì biểu thức
2
P
M
nhận giá t
rị là số nguyên ?
6. Tìm khoảng giá trị của x sao cho
5
1M x x
.
7. Tính giá trị
của M khi x là nghiệm phương trình
2
1
3 1 3 1
x
x x x
.
8. Cho
các số thực dương a, b có tổng không vượt quá 1. So sánh giá trị của M và giá trị nhỏ nhất
của
biểu
thức
1 1
2 2
P
a a b b b a
.
9. Xét
các bộ số nguyên
;
;m n p
thỏa
mãn
2
2 2 2 2
3 6 3 18 6
m n p n p m
.
Tìm tất cả các giá trị của x
sao cho
2 3 4M m n p
.
10. Xét biểu
thức
2
2 2
1
: 1
1
1
Q
x
x
x
với
1
1x
.
a) Tì
m các giá trị của x để
2
Q
Q
.
b) Tì
m x để
P Q
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
82
Bài toán
197. Mở rộng, liên hệ và phát triển các bài toán
Câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 201
3
– 2014; Ngày thi 15.06.2013.
Đề thi chọn đội tuyển dự thi Olympic Quốc tế; Môn Toán; Cộng hòa Rumani; Kỳ thi năm 2003 –
Junior TST 2003, Rumania.
Cho biểu thức
8
2 1 1
.
10
3
3 1
x x x
P x
x x x
.
1. Tì
m điều kiện của x để biểu thức P có nghĩa và rút gọn P.
2. Tìm các giá trị của x để
30
P
.
3. Tính giá trị
của P kh
i
4
1
5
2
x
.
4. Tì
m giá trị của x sao cho
16
14
P
x
.
5. Tì
m giá trị nhỏ nhất của biểu thức P.
6. Tìm khoảng giá trị của x để
2
37P P
.
7. Tính giá trị
của P khi x thỏa mãn
1
4 1 4
x
x
.
8. Chứng
minh bất đẳng thức
2
2
4 55 729
P
x x
.
9. Tính giá trị của P khi x là nghiệm của hệ
2
2
3
4
2 2 ,
;
2 8 3 0.
xy x y x y
x y
x x y
.
10. Phủ định hoặc khẳng định bất đẳng sa
u:
6 3
27
P
ab
bc ca a b c
,
trong đó
1; , , 0
abc a b c
.
Bài toán
198. Mở rộng, liên hệ và phát triển các bài toán
Bài 1 và bài 3, bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh
dự
thi);
Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm
học 2014 – 2015; Ngày thi 13.06.2014.
Đề thi Olympic Quốc gia; Môn Toán; Hợp chủng quốc Hoa Kỳ; Kỳ thi năm 2001 – United States of
American Mathematical Olympiad, 2001 – USA MO, 2001.
Cho biểu thức
2
1
: 3
9
3 3 3
x
x
P x
x x x x x
với
0; 9
x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
2
3 1 9 0
x x
.
3. Tính giá trị
biểu thức P khi
6
2 5
x
.
4. Tì
m giá trị của x đ
ể
1
4
P
.
5. Giải bấ
t phương trình ẩn x
:
0
3
1
x
P
x
.
6. Chứng
minh rằng
1
0
3
P
,
từ đó suy ra P không thể nhận bất kỳ giá trị nguyên nào.
7. Tính giá trị của P khi x là nghiệm của hệ phương trình
2
2 2
2 2 3 ,
3
1.
xy y x x
x
y y
8. Xét cá
c số thực dương
,
,a b c
sa
o cho
2 2 2
4
a b c abc
. Phủ
định hoặc khẳng định bất đẳng thức
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
83
2
ab
bc ca abc P
.
9. Giả sử tồn tại các hằng số a, b để phương trình
4
3 2
1
0
x
kx bx ax
. So sánh giá trị của biểu
thức P và giá trị nhỏ nhất của biểu thức
2
2
0
,8
S
a b
.
Bài toán 199. Mở rộng, liên hệ và phát triển câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán
(Dành cho các thí sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên
Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Năm học 2016 – 2017; Ngày thi 11.06.2016.
Cho biểu thức
2 11 15 3 1
4 3 1 3
x x x x
P
x x x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị biểu thức P khi x, y thỏa mãn
2
2
9
1
0
2
3
x y
.
3. Tính giá trị
biểu thức P khi
1
1 6 2
x
.
4. Tì
m giá trị của x để
6
P
.
5. Giải bất phương trình ẩn x:
3
P
.
6. Tì
m giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Tính giá trị của P khi x thỏa mãn đẳng thức
2
2
12
5 3 5
x
x x
.
8. Tì
m tất cả các giá trị của x sao cho
5
2
7
x
P
x
.
9. Tính giá trị của P khi x là nghiệm của hệ
2
2
2
3
2 4 2 3 ,
3 2 4 2 3 ,
3 2 4 2 3 .
x
y z x
y z x y
z x y z
10. Tìm tất cả các giá trị của m để phương trình
3
P
m
có
nghiệm thực.
11. Tính giá trị
của P khi x là số nguyên sao cho
2
3 4
1
x x x x
là số chính
phương.
Bài toán 200. Mở rộng, liên hệ và phát triển các bài toán
Câu 1, câu 3.2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chu
yên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thàn
h
phố Ninh
Bình; Tỉnh Ninh Bình; Năm học 2014 – 2015; Ngày thi 12.06.2014.
Câu 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chín
h thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Nă
m
họ
c 2014 – 2015; Ngày thi 11.06.2014.
Cho biểu thức
3
2 3 9
1 :
9
3
2 6
a
a a a a
A
a
a a a a
với
0; 4; 9
a a a
.
1. Rút gọn biểu thức A.
2. Tính giá trị của A tại
2
5
2
1
a
.
3. Tì
m a để
0
A
A
.
4. Tì
m khoảng giá trị của a sao cho
2
6 5 1 0
A A
.
5. Tìm giá trị nguyên của a để biểu thức A nhận giá trị là một số nguyên.
6. Giải phương trình ẩn a:
1
5
18
a
A
a
.
7. Tính giá trị
của A khi a thỏa mãn đẳng thức
2
2
9 3 26 177
a
a a a
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
84
8. Tính giá trị
của A khi
a
x y
,
với x, y là nghiệm của hệ
2
2
2
,
2 1 2 1.
x
y xy x y
x y y x x y
9. Xét cá
c số thực dương
có
tổng bằng 3. Tìm tập hợp D để
3
3 3 3 3 3
2 2 2
5
5 5
,
3 3 3
y x z y x z
A
a D
xy y yz z xz x
thỏa mãn
0
; 4; 9
a
a a
.
10. Xét biểu thức
1
1 3
:
4
2 2
a
N
a
a
a
. Tìm a sao cho
2
2
A N
.
11. Chứng minh rằng không tồn tại các số thực x, y sao ch
o
2
1 3 1
1
13
17
A
x y
.
Bài toán
201. Mở rộng, liên hệ và phát triển các bài toán
Câu 1, câu 3, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thàn
h
phố Ninh Bình; Tỉnh Ninh Bình; Năm học 2015 – 2016.
Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình
; Năm học 2008 – 2009.
Cho biểu thức
1
2 1
1
x
A
x
x
x x x
.
1. Tì
m điều kiện xác định (ĐKXĐ) của biểu thức A.
2. Rút gọn biểu thức A.
3. Tính giá trị của A kh
i
1 1
5 2 5 2
x
.
4. Giải phư
ơng trình ẩn x:
4
3
x
A
.
5. Tì
m khoảng giá trị của x để A có giá trị không vượt quá 5.
6. Tìm tất cả các giá trị của x sao cho
2
6
5 1 0
A
A
.
7. Tì
m giá trị của tham số m để phương trình
A
m
có
nghiệm.
8. Tính giá trị của A khi
3
3
8
5 62 7 85 62 7
x
.
9. Tì
m giá trị nguyên của x để A nhận giá trị là một số nguyên.
10. Tính giá trị của A khi x là nghiệm thực của hệ
3
3
2 2
4
16 ,
1 5 1 .
x y y x
y x
11. Xét cá
c số thực dương
, ,a b c
thỏa
mãn
1
1 1
3
a
b c
. T
ìm tập hợp D sao cho
2
2 2
1
,
1 1 1 2
a b c
ab
bc ca A x D
b c a
.
Bài toán
202. Mở rộng, liên hệ và phát triển các bài toán
Câu 2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và
Đào
tạo Tỉnh
Ninh Bình; Năm học 2016 – 2017.
Câu 1c và câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Ninh Bình; Năm học 2010 – 2011.
Câu 1c; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào t
ạo
Tỉnh
Ninh Bình; Năm học 2009 – 2010.
Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Ninh Bình; Năm học 2015 – 2016; Ngày thi 10.06.2015.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
85
Cho biểu
thức
2
3 1
1
1
1
x
x x
P
x
x
x
vớ
i
0; 1x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
3
2 2
x
.
3. Tìm giá trị của x để
2
9
P
.
4. Tính giá trị biểu thức P khi x, y là các số thực thỏa mãn
4
4 2 2
16
1 1 16
x
y x y
.
5. Giải bấ
t phương trình
2
9 4P P
.
6. Tính giá trị
biểu thức P
khi
2
2 2 2
.
2
1 2 1
x
.
7. Tì
m khoảng giá trị của x sao cho
2
3
11
x
P
x
.
8. Tì
m tất cả các giá trị của x để biểu thức P nhận giá trị là số nguyên.
9. Tính giá trị của P khi (x;y) là cặp số nguyên thỏa mãn
2
20
13 2014 2015 0
x
xy x y
.
10. Cho ba số
thực dương
, ,a b c
có tích
bằng 1.
a) So sánh giá trị của P và giá trị của biểu thức
1
1 1
1
1 1
Q
a
ab b bc c ca
.
b) Tồn
tại hay không đẳng thức
3
3 3 3 3 3
1
1 1
P
a
b abc b c abc c a abc
.
11. Xét hai
số thực dương a và b thỏa mãn hệ điều kiện
; 1a b ab
. So
sánh giá trị của biểu thức
2 2P
và giá trị
nhỏ nhất của biểu thức
2
2
a
b
M
a b
.
Bài toán
203. Mở rộng, liên hệ và phát triển các bài toán
Câu 2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và
Đào
tạo Tỉnh Ninh Bình; Năm học 2012 – 2013.
Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Ninh Bình
; Năm học 2010 – 2011.
Câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào t
ạo
Tỉnh
Ninh Bình; Năm học 2015 – 2016; Ngày thi 10.06.2015.
Cho biểu thức
1
1 1 2
:
1
1
1
Q
x
x x x x
với
0; 1x x
.
1. Rút gọn biểu thức Q.
2. Tính giá trị biểu thức Q với
7
4 3
x
.
3. Tì
m giá trị của x để Q có giá trị bằng 4.
4. Tìm x để Q có giá trị nhỏ hơn
6
5
.
5. Giải bấ
t phương trình ẩn x:
2
3
3 6 6 7 0
Q Q Q
.
6. Tính giá trị
biểu thức Q khi
3
3
26
15 3 26 15 3
x
.
7. Tì
m x để Q nhận giá trị nguyên không vượt quá 3.
8. Tính giá trị của Q khi x là nghiệm của phương trình
1
1 1 1
3
9 3 5 1 7 2
x
x x x
.
9. Tính giá trị của Q khi x, y là nghiệm nguyên của phương trình
2
2
2
x
y xy x y
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
86
10. Phản biện
bất đẳng thức
4
1
b
c c a a b a b c
P
a b c b c c a a b
,
với
, , 0
a b c
.
11. Xét biểu
thức
1
1
1
1
a a a a
Q
a a
với
0; 1a a
.
Tìm a theo x để
P Q
.
Bài toán
204. Mở rộng, liên hệ và phát triển các bài toán
Câu II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Ninh Bình; Năm học 2006 – 2007.
Câu III; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2001 – 2002.
Câu III; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2002 – 2003.
Câu IV.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2004 – 2005.
Câu 1.3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề t
hi
chín
h thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Nă
m
học 2014 – 2015; Ngày thi 11.06.2014.
Câu V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Ninh Bình
; Năm học 2005 – 2006.
Câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình;
Tỉnh Ninh Bình; Năm học 2006 – 2007.
Cho biểu thức
3
3
3 3 1
x x x
A
x
x x x x
.
1. Tì
m điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị của A khi
4
9
x
.
3. Tính giá trị
của A kh
i
61
9
2 5
x
.
4. Tì
m x sao cho A nhận giá trị bằng 2.
5. Tìm khoảng giá trị của x sao cho
9
2 6
A
.
6. Kh
i x là nghiệm phương trìn
h
2
2
5
4 13
4 1 1 3
x
x
x
x x x
t
hì A có nghĩa hay không ?
7. Tính giá trị của A khi x thỏa mãn
2
3
2 3 2 3 8
x x x
.
8. Tì
m giá trị nhỏ nhất của biểu thức A.
9. Xét biểu thức
3 2 3 2
1 :
2
3 2 5 6
a a a a
P
a a a a a
với
0
; 1; 9
a
a a
. Tìm x để
P
A
.
10. Tính giá trị của A khi (x;y) là cặp nghiệm nguyên của phương trình
2
2 2 2
4
8y x y xy
.
11. Cho hai số
dương a, b có tổng bằng 1. Tìm x sa
o cho
2
2
1
1
1
1 , ,A a b
a
b
.
12. Cho ba số
,
,a b c
có tổ
ng bằng 0. Tìm x sao cho
5 5 5 2 2 2
2
5
A
a b c abc a b c
.
Bài toán 205. Mở rộ
ng, liên hệ và phát triển các bài toán
Câu 1, câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh
Bình; Tỉnh Ninh Bình; Năm học 2009 – 2010.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
87
Câu
1, câu 5 Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi
chí
nh thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Nă
m
họ
c 2009 – 2010.
Cho biểu thức
2
1 1
1
1
1
x x x
P
x x
x
x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
5
2 2 5 5 250
x
.
3. Tì
m giá trị của x để
6 7 1P x x
.
4. Tì
m
x
sa
o cho
2
P
(
là tập
hợp các số tự nhiên).
5. Tính giá trị của P khi x thỏa mãn
4
3 2 3 2 11
x
x x
.
6. Giải phư
ơng trình
2
4 2 16 7 1
x P x x
.
7. Tính giá trị
của P khi x là nghiệm của hệ
2
2
2
2
1,
2 1,
2 1.
x
y
y z
z x
8. Xét biểu
thức
.
x x y y
A x y
x
xy y
. Tì
m hệ thức giữa x và y để
P A
.
9. Cho các số
thực dương
,a b
thỏa
mãn
4 5
23
a b
.
Tìm tập hợp D sao cho
6 7
8 18 ,
a b P x D
a b
.
Bài toán 206. Mở rộ
ng, liên hệ và phát triển các bài toán
o Câu 1, câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh
Bình; Tỉnh Ninh Bình; Năm học 2011 – 2012.
o Câu V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình; Năm học 2007 – 2008.
o Đề thi đề nghị Olympic Quốc tế; Môn Toán; Kỳ thi năm 1987 – International Mathema
tical
Ol
ympiad Shorlist, 1987.
Cho biểu thức
4 2 5
:
2
2 1 2
x x x x x
P
x x x x x x
với
, 0; 4
x x x
.
1. Rút gọn P.
2. Tính giá trị
của P khi
9
x
.
3. Tính giá trị
của P khi
4 2 3 4 2 3
x
.
4. Tìm giá trị của x thỏa mãn
4P
.
5. Tì
m tất cả các giá trị của x sa
o cho
19
5
P
.
6. Giải phư
ơng trình ẩn x:
8
3
1
x
P
x
.
7. Tì
m giá trị nhỏ nhất của P.
8. Tính giá trị biểu thức P khi
5 3 29 12 5
x
.
9. Tì
m tất cả các số chính phương x để P nhận giá trị là số nguyên.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
88
10. Tính giá trị của P khi x thỏa mãn
2
2
4
4 4 2 2 2 1
x
y xy x y x y
.
11. Tính giá trị của P khi x thỏa mãn hệ phương trìn
h
2
1,
2 1,
2 1.
x
y
y z
z x
12. Tính giá trị
của P khi
5
x
a b
với a, b
là các số nguyên thỏa mãn
1
2 3 3 3a b
.
13. Xét cá
c số thực dương
,
,a b c
có
tổng bình phương bằng 2. Khẳng định hoặc phủ định bất đẳng thức
1
2
P
x
y z xyz
.
Bài toán
207. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh
Bình; Tỉnh Ninh Bình; Năm học 2010 – 2011.
o Câu 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2014 – 2015.
o Đề thi Olympic Quốc gia; Môn Toán (Dành cho nữ sinh); Cộng hòa Nhân dân Trung Hoa; Kỳ thi
năm 2008.
Cho biểu thức
:
b ab b a a b
P
a
a
b ab a ab b ab
vớ
i
, 0;
a b a b
.
1. Rút gọ
n biểu thức P.
2. Tính P khi
4; 9
a b
.
3. Tính P biết
a
b
là hai nghiệm của phương trình
2
6
1 0
x
x
.
4. Tính giá trị của P khi a và b thỏa mãn
6 5 2 3
a b b a b
.
5. Xét ba số
thực
c
ó tổng bằng 0.
a) Tìm hệ thức giữa a và b sao cho
3 3 3
3 1P x y z xyz
.
b) Tìm điều kiện giữa a và b sao cho
2
2 2
2
2 2 2 2 2 2 2 2
x y z
P
x
y z y z x z x y
.
6. Chứng minh rằng nếu
9
9
P
b a
th
ì
0
P
.
7. Tính
giá trị của P khi
2; 5a x b y
,
trong đó x, y, z thỏa mãn đẳng thức
4
2 2 4 3 6 5
x
y z x y z
.
8. Xét
.
a
b b
B
a b b a
ab b ab a
với
0
;
a
a b
. Tì
m hệ thức giữa a và b để
P B
.
9. Xét hai số
thực x, y thỏa mãn
1
6
x
y
.
Tìm a và b để
2
2
192 , ,x xy y P x y
.
10. Xét cá
c số thực dương
, ,a b c
c
ó tổng bằng 1. Phủ định hoặc khẳng định bất đẳng thức
2
3
4
b
c
a a c P
.
Bài toán
208. Mở rộng, liên hệ và phát triển các bài toán
Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chín
h
thức; Trường THPT chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Năm học
2013 – 2014.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
89
Câu
1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2005 – 2006.
Bài V và VI; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2005 – 2006.
Cho biểu thức
2
3
2
4 1 1
1
1
1
x
A
x
x
x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
6 2 5
x
.
3. Tì
m x để
2
7
8P P
.
4. Giải bấ
t phương trình ẩn x
:
2
13
A
.
5. Tì
m giá trị lớn nhất của biểu thức A.
6. Xét biểu thức
1 1
1
1
1
B
a
a
.
a) Tì
m a theo x để
A
B
.
b) Tì
m các số nguyên tố a để giá trị biểu thức B là một số nguyên.
7. Tính giá trị của A khi (x;y) là cặp số nguyên thỏa mãn
2
3 2
4 4x x x y y
.
8. Giả
sử tồn tại các số hữu tỷ a và b để phương trình
2
0
x
ax b
nhận
2
1
x
là
nghiệm. Đặt A là
hàm số theo biến x, tức là
A
f x
. S
o sánh
,
f
a f b
.
9. Xét cá
c số thực
,
, 1;3
a
b c
có
tổng bằng 3. Tìm tập hợp D để
2
2 2
9
,
P
a b c x D
.
Bài toán
207. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đà
o
tạo Tỉnh
Nam Định; Năm học 2006 – 2007.
o Bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thái Bình; Năm học 2009 – 2010.
Cho biểu thức
1
1 2 1
:
1
1 2
x
x
A
x x x x
với
0; 1; 4
x x x
.
1. Rút gọ
n A và tính giá trị của A khi
3
2 2
x
.
2. Tí
m giá trị của x đ
ể
4
17
A
.
3. Tính giá trị
biểu thức A khi x thỏa mãn
6
1 4 0
x
x
.
4. Tì
m khoảng giá trị của x sao cho
A
.
5. Tì
m khoảng giá trị của x để
A
A
.
6. Tì
m giá trị của x đ
ể
9
7
8
x
A
.
7. Tính giá trị
của A khi x là nghiệm phương trình
1
1 1 1
3
2
3 4 3 5 6
x
x x x
.
8. So sánh giá trị của A với
1
3
.
9. Xét cá
c số thực
4, 5 , 6
a b c
s
ao cho
2
2 2
90
a b c
. Khẳng địn
h hoặc phủ định bất đẳng thức
4
8a b c A
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
90
Bài
toán 208. Mở rộng, liên hệ và phát triển bài 1 và bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề
thi chính thức; Sở Giáo dục và Đào tạo Tỉnh Nam Định; Năm học 2007 – 2008.
Cho biểu thức
5
2 4
1 .
2 3
x x
P x
x x
với
0
x
v
à
4
x
.
1. Rút gọ
n P.
2. Tính giá trị của P khi
6
2 5
x
.
3. Với
giá trị nào của x thì
2
9 2P P
?
4. Giải phương trình ẩn x:
3
3 1
x
P
x
.
5. Tìm điều kiện của x đ
ể
P
P
.
6. Tì
m tất cả các giá trị của x đ
ể
P
P
.
7. Tì
m khoảng giá trị của x để
1P
.
8. Tì
m giá trị nguyên của x để P nhận giá trị là một số nguyên.
9. Tìm tất cả các giá trị của m để phương trình
P
m
có
nghiệm.
10. Tồn tại hay không các số thực y, z sao cho
1
1
2
015 2015 2
17
19
P y z y z
?
11. Tính giá trị của P khi x là nghiệm phương trình
1
1 3 3
2 1 4 1 5 2
x
x x x
.
12. Tính giá trị của P khi x là nghiệm của phương trình
2
2
2 2 5 5 6
x y xy x y
,
trong đó
x
y
là
một
số nguyên.
Bài toán 209. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 5; phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2013 – 2014.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2005 – 2006; Ngày thi 04.07.2005.
Cho biểu thức
2
2
:
1
2
1 1
x x x
A
x
x
x x
với
0; 1x x
.
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi
6
2 5
x
.
3. Tính giá trị
của A khi
7
4 3 7 4 3
x
.
4. Tính giá trị
của A khi x thỏa mãn
2
3 4 3 0
x
x
.
5. Giải phư
ơng trình ẩn x:
2
5
1
A
x
.
6. Với
giá trị nào của x thì
2
7 4A A
?
7. Tì
m khoảng giá trị của x sao cho
A A
.
8. Tì
m khoảng giá trị của x sao cho
2
2
A
A
.
9. Tì
m tất cả các số nguyên x để biểu thức A có giá trị là số nguyên.
10. Tính giá trị của A khi x là nghiệm phương trình
2 3 2
3 6 2 1 1 2 5 4 4.
x x x x x x
11. Xét biểu
thức
4a
b ab
a b b a
B
a b ab
.
Tìm x theo a và b để
A
B
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
91
Bài toán
210. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đà
o
tạo Tỉnh
Nam Định; Năm học 2004 – 2005.
o Bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2005 – 2006; Ngày thi 04.07.2005.
o Bài 1 và bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đà
o
tạo Tỉnh
Nam Định; Năm học 2003 – 2004.
Cho biểu thức
2
2 1
1
2
1
x
x x
Q
x
x
x x
với
0; 1x x
.
1. Chứng
minh
2
1
Q
x
.
2. Tính giá trị
của Q khi
1
4 6 5 14 6 5
x
.
3. Tì
m giá trị của x để
1
0
3 1
Q
x
.
4. Tì
m khoảng giá trị của x sao cho
2
3
2Q Q
.
5. Tì
m tất cả các giá trị của x sa
o cho
3
3
Q
Q
.
6. Tì
m tất cả các giá trị của x sao cho
6 6
Q Q
.
7. Tồn
tại hay không giá trị x thỏa mãn
5
5
Q
Q
?
8. Tính Q khi x, y là nghiệm của hệ
2
5
2
,
3
1
1
,7.
x
x y
x x y
9. Tì
m số nguyên x lớn nhất để Q có giá trị là số nguyên.
10. Với giá trị nào của x thì giá trị của Q lớn hơn nghiệm lớn nhất của phương trình
2
9
16 2 2 4 4 2
x
x x
.
11. Xét biểu thức
1
1
x
B
x
x x
với
0
; 1x x
.
a) Tì
m x để giá trị của A lớn hơn giá trị của B.
b) Tính giá trị của B đ
ể
1
2
x
.
12. Tì
m tất cả các giá trị của x sa
o cho
2
2
2 6
,
2 5
y y
Q y
y y
.
Bài toán
211. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đ
ào
tạo Tỉnh
Nam Định; Năm học 2002 – 2003.
o Bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2003 – 2004.
o Bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2000 – 2001.
Cho biểu thức
2
:
y
y xy
S
x y
x
xy x xy
với
0; 0;
x y x y
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
92
1. Rút gọ
n biểu thức S và chứng minh giá trị của S không phụ thuộc biến y.
2. Tìm giá trị của x và y để
1
S
.
3. Giải phư
ơng trình
1
4
2
S
x
.
4. Tính giá trị
của S khi x là nghiệm phương trình
2
2
2
3 2 3 2 3x x x x x x
.
5. Giả sử
(a;b) là nghiệm phương trình
4
4 2 2
16
1 1 16
a
b a b
. Tìm x, y để
;S
max a b
.
6. Cho m thỏa mãn đẳng thức
2
12
1 36
m
m m
.
Tìm x sao cho
2
2
3 4 1
S
m m m
.
7. Xét biểu
thức
1
1
.
1
1
a a
P a
a
a
. Tìm a theo x và y để
.
8. Xét biểu thức
1
. 1
1
1
a a a a
Q
a a
.
a) Tì
m x theo x và y để
S Q
.
b) Tì
m a sao cho
2
Q
a
.
Bài toán
212. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1 và câu 5; phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2011 – 2012.
o Câu II và câu IV; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự
thi);
Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định;
Nă
m học 2000 – 2001.
o Câu I.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi
chí
nh thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm
học 2002 – 2003.
o Bất đẳng thức Nessbit – Shapiro.
Cho biểu thức
2
1
1
x x x x
P
x
x x
vớ
i
0; 1
x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
9
4 5
x
.
3. Tì
m x để
0
P
.
4. Tì
m x để P nhận giá trị nguyên nhỏ hơn 2.
5. Tính giá trị của P kh
i
4
4
4
4
3 5 3 5
x
.
6. Giải bấ
t phương trình ẩn x:
2
6 16 0
P P
.
7. Tì
m khoảng giá trị sao
cho
3
3
P
P
.
8. Tì
m giá trị của x sao cho
1
1 1
...
2 2 3 2 2 3 100 99 99 100
P
.
9. Tính giá trị của P khi x là nghiệm phương trình
3 2
3
2 3 2 1x x x x x x
.
10. Xét các số thực x và y thỏa mãn
2 2
5
5 5
x
x y y
.
Tì
m tất cả các cặp số (x;y) sao cho
201
5 2015
P
x y
.
11. Xét các số thực dương
, ,a b c
.
Chứng minh bất đẳng thức
1
2
a
b c
b
c c a a b
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
93
Bài toán
213. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2015 – 2016.
o Câu 1.1, câu 2.2, câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 2014 – 2015.
Cho biểu thức
3
1 1
3
.
1
1 2
x
x
A
x x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị biểu thức A khi
4
2 3
x
.
3. Tính giá trị
của A khi
4
1 3 2 0
x x
.
4. Tìm x để A nhận giá trị bằng 5.
5. Giải phương trình ẩn x:
5
14
A
x
.
6. Tì
m x đ
ể
A A
.
7. Tì
m khoảng giá trị của x sao cho
3
3
A
A
.
8. Tính giá trị
của A khi x là nghiệm phương trình
2
6
2 1 4 12 8
x
x x x
.
9. Kh
i x, y là nghiệm nguyên của phương trình
3
3
3
1x y xy
t
hì P nhận giá trị hữu tỷ hay vô tỷ ?
10. Xét các số thực dương a và b sao cho
2
2
2
5 5 10
a
b a b
.
Tìm x sao cho
4
,
,A a b a b
.
11. Xét cá
c số thực
, ,a b c
k
hác 0 sao cho
1
1 1
1a
b c
a b c
.
T
ìm tất cả các giá trị của x sao cho
1
1 1 2
A
a b c
.
Bài toán
214. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2014 – 2015.
o Câu 1.1, câu 2.2, câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 1999 – 2000.
Cho biểu thức
2 4 1 1
:
1
1
x x
A
x
x
x x x
với
0
; 1x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A kh
i
25
9
x
.
3. Tì
m x sao cho
2
5
18 0
A
A
.
4. Chứng
minh rằng A nhận giá trị nguyên khi x thỏa mãn
2
5 4 0
x x
.
5. Tính giá trị
biểu thức A khi
3 2 2 3 2 2
x
.
6. Tì
m giá trị của x để
5
8A x
.
7. Tìm khoảng giá trị của x sao cho
2
2
A
A
.
8. Tì
m giá trị nhỏ nhất của biểu thức A.
9. Tìm x để giá trị của A lớn hơn nghiệm nguyên lớn nhất của phương trình
3
2
4
25 43 3 2 22 3 2
x
x x x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
94
10. Cho ba số
thực
, ,a b c
có
tổng đôi một khác 0 sao cho
1
a
b c
b
c c a a b
.
Tì
m x để
2
2 2
a
b c
A
b
c c a a b
.
11. Xét các số thực a và b thỏa mãn điều kiện
2
2
2 2 2 2 2
2 4 6 0
a b a b a b
.
Tìm khoảng giá trị của
x sao cho
2
2
min
A
a b
,
trong đó
2
2
min
a
b
l
à ký hiệu giá trị nhỏ nhất của biểu thức
2
2
a
b
.
Bài toán
215. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2012 – 2013.
o Câu 1, câu 3, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giá
o
dụ
c và Đào tạo Tỉnh Nam Định; Năm học 2016 – 2017.
o Câu II.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh Nam Định; Năm học 2006 – 2007.
Cho biểu thức
1
2 1
:
1
1
1
x
A
x
x
x x x
với
0; 1x x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị biểu thức A khi
1
3
2 2 1
2
1
x
.
3. Tìm giá trị của x để
26
5
A
.
4. Chứng minh rằng
2
0
A
vớ
i mọi x thỏa mãn điều kiện
0; 1x x
.
5. Tì
m giá trị của x sao cho
2
2
9 10 0
A
A
.
6. Tìm tất cả các giá trị của x đ
ể
3
10 10 3A A
.
7. Giải phư
ơng trình ẩn x:
8
0
4
x
A
.
8. Tính giá trị của A khi x là nghiệm lớn nhất của phương trình
4
2
2 4 3 10 6x x x
.
9. Xét biểu
thức
1
2 4
.
1
4
2
x x
P x
x
x
x
vớ
i
0
; 4
x
x
.
Tìm x sao cho
A
P
.
10. Tì
m x sao cho
2
2
5
A
x
x
.
11. Xét số thực
m thỏa mãn
1
5
m
m
.
Tính A khi
4
4
1
x m
m
.
Bài toán
216. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2012 – 2013.
o Câu 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2012 – 2013.
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm họ
c
2004 – 20
05.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
95
Cho biểu thức
2
.
1
1 2
x
x
P
x x x x
với
0
; 1x x
.
1. Rút gọn biểu thức P.
2. Chứng minh rằng khi
3
2 2
x
thì
1
2
P
.
3. Tìm giá trị của x đ
ể
5
2
4
P
.
4. Giải phư
ơng tr
ình
5
0
1
9
P
x
.
5.
Tìm
tất cả các giá trị của x đ
ể
P
P
.
6. Tìm khoảng giá trị của x sao cho
8
3 3 8P P
.
7. Tính giá trị
của P khi x và y thỏa mãn đẳng thức
4
4
x
y y x xy
.
8. Tì
m giá trị của x để P nhận giá trị là số tự nhiên.
9. Tính giá trị của P khi x là nghiệm phương trình
2
1 2
x
x x
.
10. Xét cá
c số thực
,
,a b c
phân biệt khác 0 thỏa mãn
2
2 2
a
b c
b
c a
. Tìm x để
P
abc
.
11. Xét biểu thức
2 2
:
a b ab a b
S
a
b
a b
. Tì
m khoảng giá trị của x để có thể tồn tại đẳng thức
.
Bài toán
217. Mở rộng, liên hệ và phát triển các bài toán
Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2008 – 2009.
Câu 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2008 – 2009.
Câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2016 – 2017.
Cho biểu thức
2
1
1
:
1
1
x
x x
P
x x x x
với
0
x
.
1. Rút gọ
n biểu thức P và tìm x để P nhận giá trị âm.
2. Tính giá trị của P khi
9
4 5
x
.
3. Giải phư
ơng trình
5
4
P
.
4. Tìm giá trị của x sao cho
6
1
4
x
P
.
5. Tính giá trị
của P khi x là nghiệm của hệ
2
2
6
12 ,
3
.
xy
y
xy
x
6. Chứng
minh rằng giá trị của P không thể nhỏ hơn nghiệm phương trì
nh
3
2 3 2
2
1 3 2 5 4 1 5 3 8
x
x x x x x x
.
7. Tính giá trị của P khi x là nghiệm phương trình
4
4
3
2 2008 2008
x
x x x
.
8. Cho các số thực dương
, ,a b c
thỏ
a mãn
3
3 3
3
0
a
b c abc
.
Tì
m khoảng giá trị của x sao cho
2
7 6 2008
P
a b b c c a
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
96
Bài toán
218. Mở rộng, liên hệ và phát triển các bài toán
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm họ
c
2001 – 2002.
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm họ
c
2004 – 20
05.
o Câu 5.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2008 – 2009.
Cho biểu thức
2
1 1
1
1
1
x
x x
T
x
x
x x x
với
0
; 1x x
.
1. Rút gọn biểu thức T.
2. Tính giá trị biểu thức T khi
4
2 3
x
.
3. Tì
m tất cả các giá trị của x để
3
13
T
.
4. Giải phương trình ẩn x:
0
3
x
T
x
.
5. Tì
m tất cả các giá trị của x sa
o cho
21
4 4 21T T
.
6. Chứng
minh rằng với mọi
0; 1x x
luôn có
1
3
T
.
7. Chứng minh rằng biểu thức T chỉ nhận duy nhất một giá trị nguyên.
8. Tìm khoảng giá trị của x sao cho
2
1
4 11 2 0
T
T
.
9. So sánh T vớ
i các nghiệm của phương trình
6
2 2
x
x
.
10. Tính giá trị
của T khi x và y là các số dương thỏa mãn hệ
4
4
1,
1
8
5.
x y
x y
xy
11. Xét hai số
thực dương a và b có tổng bằng 1. Phủ định hoặc khẳng định bất đẳng thức
2
2
1
1
18T
ab
a b
.
Bài toán 219. Mở rộng, liên hệ và phát triển các bài toán
o Bài I, bài V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm
học 2006 – 2007.
o Câu I.2, câu II, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 2004 – 2005.
o Câu 4.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2013 – 2014.
Cho biểu thức
1
1 1
.
1 1
x
x
Q x
x x x
với
0; 1x x
.
1. Rút gọ
n biểu thức Q.
2. Tính giá trị của Q khi
3
2 2
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
97
3. Tì
m x để
8
Q
.
4. Chứng
minh rằng
4
Q
.
5. Tì
m các giá trị của x để
20
3
Q
.
6. Giải phư
ơng trình ẩn x:
8
0
2
x
Q
.
7. Tìm tất cả các giá trị của x sa
o cho
5
52 5 52
Q
Q
.
8. Chứng
minh rằng không tồn tại các số nguyên x để Q nhận giá trị nguyên.
9. Tính giá trị của Q khi x thỏa mãn đẳng thức
2
5
1 2 1x x x x
.
10. Tính giá trị
của Q khi x, y là các số nguyên thỏa mãn
2
3 2x y x y xy xy
.
11. Xét các số thực
,
,a b c
t
hỏa mãn
0
2;0 2;0 2
a
a c
. Tì
m x sao cho
3 3 3
,
, ,Q a b c a b c
.
12. Xét cá
c số thực dương
, ,a b c
sa
o cho
1
ab
bc ca
.
Phủ định hoặc khẳng định bất đẳng thức
2
2 2 2 2 2
2
2 2
1
1 1 1 1 1
2 1 1 1
y
z y z y z
Q
x
x x
x x x
.
13. Tính giá trị
biểu thức Q khi x là nghiệm của hệ
2
2
3 2 2
1
,
2
4 1 2 2.
x y
x x x x y xy
14. Phản biện
bất đẳng thức
1
1 1
.
.. 6,25
1
3 5 7 97 99
Q
.
Bài toán
220. Mở rộng, liên hệ và phát triển các bài toán
o Bài I, bài IV; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định;
Năm học 2007 – 2008.
o Bài I, bài V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm
học 2005 – 2006.
o Bài II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2001 – 2002.
Cho biểu thức
2
1
1
1
1 1 1
x x x x x
M
x
x x x x x
vớ
i
0
; 1x x
.
1. Rút gọ
n biểu thức M.
2. Tính giá trị của M k
hi
1
4
x
.
3. Giải bấ
t phương trình
4
6
3
M
.
4. Giải phư
ơng trình ẩn x:
6
5
3
x
M
.
5. Tìm khoảng giá trị của x sao cho
M
M
.
6. Tì
m số nguyên x để M nhận giá trị nguyên.
7. Tính giá trị của M khi x thỏa mãn
2
2
8
1 3 1
x
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
98
8. Tì
m tất cả các các nghiệm x của phương trình sau để M xác định
x
a x x b x ab
.
9. Xét biểu
thức
3
1
1
1 1
x
x
N
x x x
. Tìm x sao cho
2
M N
.
10. Tính giá trị của M khi biểu thức
2
2
1 4
P
x x x
đạt giá trị lớn nhất.
11. Xét các số thực dương
,
,a b c
c
ó tổng không vượt quá 2005. Tìm x sao cho
3
3 3 3 3 3
2 2 2
5
5 5
,
, ,
3 3 3
a
b b c c a
M
a b c
ab a bc b ac c
.
Bài toán
221. Mở rộng, liên hệ và phát triển các bài toán
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học
1999 – 20
00.
o Bài II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2001 – 2002.
o Bài II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2014 – 2015.
o Bài II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Địn
h;
Tỉnh
Nam Định; Năm học 2005 – 2006.
Cho biểu thức
a b a b
N
ab
b ab a ab
với
,a b
l
à hai số dương khác nhau.
1. Rút gọn biểu thức N.
2. Tính N khi
2
4
25
; 16
a
b
.
3. Tính giá trị
của biểu thức N khi
6
2 5; 6 2 5
a
b
.
4. Tính giá trị
của N khi
4 5
a b ab
.
5. Tính giá trị
của N khi a, b thỏa mãn đẳng thức
2
1 1
.
1 2
1
a a a a
a b b
a
a
.
6. Giả sử
(x;y) là nghiệm của h
ệ
3
2
2 2 2
3 6 4 0,
2 0.
x y y
x x y y
Tì
m hệ thức giữa a và b sao cho
5
N x y
.
7. Giả
sử
3 5 3 5 ; 3 6 3 6
n
n n n
a b
,
với n là số nguyên dương. Chứng minh rằng
biểu thức N nhận giá trị hữu tỷ.
8. Tìm mối liên hệ giữa a và b để N là nghiệm của phương trình
2
3 4 4 1 16 8 1
P P P P
.
Bài toán 222.
Mở
rộng, liên hệ và phát triển các bài toán
Câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đà
o
tạo Tỉnh
Bắc Giang; Năm học 2008 – 2009; Ngày thi 22.06.2008.
Bài 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Bắc Giang; Năm học 2012 – 2013.
Câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đà
o
tạo Tỉnh B
ắc Giang; Năm học 1997 – 1998; Ngày thi 28.06.1997.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
99
Cho biểu
thức
2
2
2
1 : 1
1
1
P
x
x
x
vớ
i
1
1x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị biểu thức P khi
2
5 5
x
.
3. Tì
m giá trị lớn nhất của biểu thức
1
P
x
.
4. Tính giá trị
của P khi x là nghiệm phương trình
2
7 5 10 3
x x x
.
5. Xét biểu
thức
1
2 3 2
. 1
2
2 2
a a
A
a a a a
vớ
i
0
, 4
a
a
.
Tìm x để
P
A
.
6. Xét biểu
thức
a
x a x a x a x
Q
a
x a x a x a x
.
Tìm a theo x để
P Q
.
Bài toán
223. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên Ngo
ại
ngữ
; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm họ
c
1998 – 19
99.
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên Ngoại
ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học
2008 – 20
09.
Cho biểu thức
2 2
2 2
1 :
xy x xy y
xy xy
A
x
y x xy y xy
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
2
1; 3 2 2
x
y
.
3. Tính giá trị biểu thức A khi x và y là nghiệm c
ủa hệ
2 2
2
1
3
3.
x y xy
x
y y
4. Tì
m giá trị lớn nhất của A khi x và y thỏa mãn đẳng thức
3
3
2
x
y
.
5. Chứng
minh rằng A nhận giá trị nguyên dương khi x và y là các số nguyên dương thỏa mãn
4
1 3
x
y
.
6. Tìm m để phương trình
A
m
có nghiệm
,x
y
thỏa
mãn
6
x
y
.
7. Xét biểu
thức
3
2
.
x
y x y x y
y
P
x
y x y
x
y y x x y y x
.
a) Chứng
minh P nhận giá trị nguyên với mọi
, 0;
x y x y
.
b) Tì
m tất cả các số nguyên dương x và y để
P
A
l
à một số nguyên.
Bài toán 224. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam;
Năm học 1998 – 1999.
Cho biểu thức
1
1
1
: 1
1
1 1 1
xy
x xy x
x x
P
xy xy xy xy
.
1. Tì
m điều kiện xác định và rút gọn P.
2. Tính giá trị của P khi
9; 4
x y
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
100
3. Cho
1
1
6
x
y
,
tìm giá trị lớn nhất của P.
4. Chứng minh P nhận giá trị vô tỷ khi (x;y) là nghiệm nguyên của phương trình
2 2
2
9
x
y x y
.
5. Tính giá trị
của P khi (x;y) là cặp số thỏa mãn các đẳng thức
3
3 3
2
8
16 ,
2 8 .
x y y
x xy y
.
Bài toán
225. Mở rộng, liên hệ và phát triển các bài toán
Câu 1 và 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên
Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà N
ội;
Nă
m học 2011 – 2012; Ngày thi 12.06.2011.
Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đào
tạo Tỉnh Bắc Giang; Năm học 1999 – 2000; Ngày thi 23.06.1999.
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên Ngo
ại
ngữ
; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm họ
c
2009 – 20
10.
Cho biểu thức
3
3
3 3
1
1 2 1 1
:
x
y x x y y
A
x
y x y x y
x y xy
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
4
2 3; 4 2 3
x
y
.
3. Tì
m x, y sao
cho
1
;
5
6
xy
A
.
4. Tính giá trị
của A khi x và y thỏa mãn
6 7
x y xy
.
5. Tính giá trị
của A khi x và y là nghiệm của hệ
2
2
4
5,
2
5 4 27.
x
y
x y xy
6. Xét biểu thức
3
3
2
:
m
p p
B
mp m p
m
p m p
. Tìm x và y sao cho
A
B
.
7. Tìm giá trị nhỏ nhất của biểu thức A khi x và y là hai số dương có tổng lập phương bằng 2.
8. Xét biểu thức
3
32 2
3
3
3 3 3
3 2
3
8 2 4
:
2 .
2 2 2
2
x x x x
C x
x x x
x
x
với
8; 8; 0
x x x
.
Chứ
ng minh rằng C có giá trị không phụ thuộc biến x và nếu
A
C
th
ì
3
x
y xy
.
Bài toán
226. Mở rộng, liên hệ và phát triển các bài toán
Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Giang; Thành phố Bắc Giang; Tỉnh
Bắc Giang; Năm học 2015 – 2016.
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Vũng Tàu;
Tỉnh Bà Rịa – Vũng Tàu; Năm học 2014 – 2015.
Cho biểu thức
2
1
1 2
2 :
1
1
1 1 1
xy xy x xy x
x
A
xy
xy xy xy xy
.
1. Tì
m điều kiện của x, y để biểu thức A có nghĩa, từ đó hãy rút gọn biểu thức A.
2. Tính giá trị của A kh
i
4
9 9
;
2
5 16
x
y
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
101
3. Cho
1
1
12
x
y
.
Chứng minh
36
A
.
4. Tì
m giá trị nhỏ nhất của biểu thức A khi x và y thỏa mãn
2 2
9
18
x
y
.
5. Cho biểu
th
ức
2
:
x x y y y
B xy x y
x y x y
vớ
i
0
; 0;
x
y x y
.
Chứ
ng minh rằng B không phụ thuộc biến, sau đó tìm hệ thức liên hệ giữa x và y sao cho
A
B
.
6. Tính giá trị
biểu thức A khi x và y thỏa mãn đẳng thức
2
2 2
2
9 9 7 3x y x x y
.
Bài toán
227. Mở rộng, liên hệ và phát triển các bài toán
o Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chu
yên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Giang; Thành phố Bắc Giang; Tỉnh
Bắc Giang; Năm học 2013 – 2014.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đào
tạo Tỉnh Hà Bắc; Năm học 1994 – 1995; Ngày thi 09.08.1994.
Cho biểu thức
2
1
1 1 1
1 1 1 1
1 1
x
x x x
A
x x x x
x x
.
1. Tì
m x để biểu thức A có nghĩa, từ đó hãy rút gọn A.
2. Tính giá trị của A tại
3
4
x
.
3. Tính giá trị của biểu thức A k
hi
3
1
2 2
x
.
4. Tì
m các giá trị của x sao ch
o
1
4
A
.
5. Giải bấ
t phương trình ẩn x:
2
3
A A
.
6. Xét biểu
thức
2
2 2 2 2 2
2
2
2 2 2
4
:
m
m n m m n m m n
B
n
m
m n m m n
.
Tìm x sao cho
A B
.
7. Tì
m khoảng giá trị của x sao cho
1
1
A
A
.
8. Tìm tất cả các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
Bài toán 228. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 1997 – 1998;
Ngày thi 03.08.1997.
Cho biểu thức
2
2
1
1
a a a a
M
a a a a
.
1. Tì
m điều kiện xác định và rút gọn biểu thức M.
2. Tính giá trị của M khi a là nghiệm phương trình
2
2
2 1 2 3 2 2 1
a
a a
.
3. Tính giá trị
của M khi
6 2 5
a
.
4. Tìm khoảng giá trị của a sao cho
3
3
M
M
.
5. Rút gọ
n biểu thức
1
1
P
M a
.
6. Giải phư
ơng trình ẩn a:
2
4
2 4 16
M
a a a
.
7. Tì
m tất cả các giá trị của a sao cho
3
2
1
a
M
a
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
102
Bài
toán 229. Mở rộng và phát triển câu 2, câu 3, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành
cho tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam
Định; Tỉnh Nam Định; Năm học 2015 – 2016.
Cho biểu thức
1
2 1
.
1
1 1
x
x x
Q
x
x
x x x
(với
0
; 1x x
).
1. Rút gọn biểu thức
Q
.
2. Tính giá trị của Q khi
3
2 2
x
.
3. Tì
m các giá trị của
x
để
1Q
.
4. Giải bất phương trình ẩn x:
2
4 0
Q
Q
.
5. Tì
m khoảng giá trị của x sao cho
5
5
Q
Q
.
6. Tì
m x để
0
0
5
Q x y
,
trong đó
0
0
;x
y
là nghiệ
m của hệ phương trình
2
2
3
3
2 5 16.
x
x y y
x x x y x
7. Chứng
minh rằng Q không thể xác định nếu x thỏa mãn đẳng thức
5
2
3
6 6 3 2 7 19 2 .x x x x x
8. Xét các số thực dương
,
,a b c
thỏa mãn
1.ab
c
Chứ
ng minh bất đẳng thức
4
4 4 4 4 4
2
a
b c
Q
b
c a a c b a b c
.
Bài
toán 230. Mở rộng và phát triển câu 2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam
Định; Tỉnh Nam Định; Năm học 2014 – 2015.
Cho biểu thức
2 1 1 2
.
1
1 1
a a a
Q
a
a a a a a
với
0; 1a a
.
1. Rút gọn biểu thức Q.
2. Tính giá trị biểu thức Q khi
9
4 5
a
.
3. Tính giá trị
của Q khi
3
3 10a a
.
4. Tì
m giá trị của a sao cho
2
2
5
Q Q
.
5. Giải phư
ơng trình ẩn a:
2
0
2
Q
a
.
6. Với khoảng giá trị nào của a thì
2
17
4Q Q
.
7. Tì
m tất cả cả các giá trị a để
3 3
13 13
Q
Q
.
8. Chứng minh rằng khi
1
a
thì giá trị củ
a biểu thức Q nhỏ hơn 1.
9. Tính giá trị của Q khi a là nghiệm phương trình
2 1 2 1 1
a a a
.
Bài toán 231. Mở rộng và phát triển các bài toán
Câu 2, câu 3.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi ban
Khoa học Tự nhiên); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam
Định;
Tỉnh Nam Định; Năm học 2016 – 2017.
Bất đẳng thức Nesbitt – Shapiro.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
103
Cho biểu thức
3
2
2
1
2 1 2
x
x
x x
P
x x x x
với
0
; 1x x
.
1. Chứng minh rằng
3
2
x
P
x
.
2. Tính giá trị của P khi
6
2 4 2 3
x
.
3. Tính giá trị
của P khi
2
5 2 0
x
x
.
4. Tì
m x sao cho
P
.
5. Tì
m tất cả các giá trị của x để P nhận giá trị không vượt quá
7
6
.
6. Chứng
minh rằng nếu
0; 1x x
thì
P
.
7. Chứng
minh rằng không tồn tại giá trị của x để P nhận giá trị nguyên.
8. Giải bất phương trình ẩn x:
5
4
9
P
P
.
9. Tìm khoảng giá trị của x sao cho
7 8 7 8
P P
.
10. Tính giá trị
của P khi x là nghiệm của h
ệ
2
2
2 0,
2 2 2 2 0.
x y xy x y
x y x
11. Phản biện
bất đẳng thứ
c
2
2 2
2
2 2 2 2 2
a
b c
P
b c a c b a
với
, ,a b c
.
Bài toán
232. Mở rộng và phát triển câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả
các thí sinh dự thi ban Khoa học Xã hội); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 2016 – 2017.
Cho biểu thức
1 1 2 1
:
3
3 3
a a
P
a
a a a a a
vớ
i
0
; 9
a
a
.
1. Rút gọ
n biểu thức P và tính giá trị của P khi
4
2 3
a
.
2. Tìm giá trị của a để
1
2
P
.
3. Tính giá trị
của P khi a thỏa mãn
4
5
a
a
.
4. Tính giá trị của P khi a và b thỏa mãn đẳng thức
2
2 2
2
4 6 4
a
b b b a
.
5. Tì
m tất cả các giá trị của a để P có giá trị không vượt quá
7
9
.
6. Chứng
minh rằng P không thể nhận bất kỳ giá trị nguyên nào.
7. Tìm khoảng giá trị của a sao cho
6
5 6 5
P
P
.
Bài toán
233. Mở rộng và phát triển các bài toán
Câu 1, câu 3, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự t
hi);
Đề
thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Địn
h;
Nă
m học 2010 – 2011.
Câu 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi
chí
nh thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm
học 2012 – 2013.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
104
Câu
2b, câu 5.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự
thi);
Đề
thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Địn
h;
Nă
m học 2011 – 2012.
Cho biểu thức
2
1 1
:
1
1 1
x
x
P
x x x x x
với
0
; 1x x
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
2 9 4 5 10
x
.
3. Tì
m giá trị của x để
1
0
P
.
4. Giải phư
ơng trình ẩn x:
3
0
2
x
P
x
.
5. Với
giá trị nào của x thì P có giá trị không lớn hơn 3 ?
6. Tìm điều kiện của x đ
ể
6
6
P
P
.
7. Tính giá trị
biểu thức P khi x là nghiệm của hệ
2
2
3
5,
1 7.
x
y xy
x y x y xy
8. Tính P khi
x là nghiệm phương trình
2
9
9 22 1
x
x x x
.
9. Xét biểu
thức
3
1
3
1
x
x
x x
A
x x x x
với
0
x
.
a) Chứng
minh rằng
4A
.
b) Tì
m x sao cho
A
P
.
10. Xét các biểu thức
3
1 1 1
:
1
1
x
Q
x
x
x x
và
3
3
3 1 3 1
3
:
4
3
x
x
M
x
x
x
/
a) Xác định
x để
P Q
.
b) Chứng
minh rằng
4M
và tìm x để
P
M
.
11. Xét hai số thực dương a và b sao cho
1a
b
. Tì
m x sao cho
4 1
,
,P a b
a b
.
Bài toán
234. Mở rộng và phát triển các bài toán
Câu 1, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận
Cầu Giấy; Thành phố Hà Nội; Năm học 2010 – 2011.
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán
,
chu
yên Tin học); Đề thi chính thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học S
ư
phạm Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học 2009 – 2010.
Cho biểu thức
3
4
2
4
2 7 6 2
4
1 4
3 1 29 78
. :
2
1 6 6 3 12 36
x
x x
x x x
A x
x x x x x x
.
1. Rút gọn A.
2. Tính giá trị của A khi
49
16
x
.
3. Tìm giá trị của x sao cho
2
3
A
.
4. Tìm tất cả các giá trị nguyên của x để A nguyên.
5. Tính giá trị của A của A khi x là nghiệm lớn nhất của phương trình
2
2
2
5
1 4 6 1
x
x x x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
105
6. Tì
m khoảng giá trị của x sao cho
7
7
A
A
.
7. Cho biểu
th
ức
3
3
2 2
3 3 3 3
2 2 2 2
.
4
2 2 2 2 2
xy xy xy xy
P
x
y xy xy xy
với
2
; 2
xy
xy
.
Tì
m x để A và P có giá trị bằng nhau.
Bài toán 235. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức;
Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2008 – 2009.
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức;
Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2014 – 2015.
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi c
hính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2013 – 2014; Ngày thi 06.06.2013.
Cho biểu thức
2
:
2
a b
a b a b b a
P
a b
a b b ab ab a
với
0; 0;
a b a b
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
200
6 2005; 2007 2006
a
b
.
3. Chứng
minh r
ằng nếu
4
2
2
3
a b c
c
t
hì
0
P
.
4. Tính giá trị
của P khi a và b thỏa mãn
2
3 5
a
b ab
.
5. Tì
m a và b sao cho
2
1
b
a
v
à
1P
.
6. Xét biểu
thức
3
3
2
3
3
a b
b b a a
a b
a
ab
Q
b
a
a
a b b
với
0; 0;
a b a b
.
Tì
m điều kiện của a và b để
P Q
.
7. Xét biểu
thức
3
2
2
3
3
a b
a a b b
ab
a
a
b
R
a
b ab a a b a
với
0
; 0;
a
b a b
.
Tì
m điều kiện của a và b để
P R
.
Bài toán
236. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2012 – 2013.
Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh
Thanh Hóa; Năm học 2012 – 2013.
Cho biểu thức
2 2
2 2 2 2
.
a
b a b a b
P
a
b a b
a b a b a b
vớ
i
0
a
b
.
1. Rút gọ
n biểu thức P.
2. Tính giá trị của P khi
2
1; 2 1
a
b
.
3. Biết
1a
b
, tìm
giá trị nhỏ nhất của P.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
106
4. Giả sử
1
a b
.
Tính giá trị của P khi biểu thức
2
2
8
4
a
b
b
a
đạ
t giá trị nhỏ nhất.
5. Chứng minh bất đẳng thức
4
1, 1
P
a a
.
6. Chứng
minh giá trị của P là một số tự nhiên khi a và b thỏa mãn đẳng thức
3
3 2
3
4
8 2 1 4
a
b b a a b
.
Bài
toán 237. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả
các thí sinh dự thi); Đề thi chính thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm
Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học 2015 – 2016.
Cho biểu thức
2
2
2
2 2
1
1
1
a
b
b
a a b
P
a b a b
b a b a
với
0; 0;
a b a b
.
1. Chứng
minh rằng
1
P
a
b
.
2. Tính giá trị của P khi
9
4 5; 5 3
a
b
.
3. Tính giá trị của P khi a và b thỏa mãn đẳng thức
3
3
3
4
8 1 4 2 a b a a b
.
4. Giả sử a,
b thay đổi sao cho
4
1 a b ab
.
Tìm giá trị nhỏ nhất của P.
5. Tính giá trị của P khi a và b là nghiệm tự nhiên của phương trình
5 2 1
a
b
.
6. Tran
g bị thêm các số thực dương
,c d
.
Phản biện bất đ
ẳng thức
1
1 1 16
P
bc cd da a c b d
.
Bài toán
238. Mở rộng, liên hệ và phát triển các bài toán
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2011 – 2012.
Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2014 – 2015.
Cho biểu thức
2 2 4 2 2
2 2 2
2 4 4 4
:
2
2
x y x y y x x y y
A
y
x y xy x x y xy x
với
2
0
; 0; 2 ; 2 2
x
y x y y x
.
1. Rút gọ
n biểu thức A.
2. Tính giá trị của A khi
2
2
2
3 4
4
2015 2016
y x y
y
.
3. Cho
1y
, tìm x để
2
5
A
.
4. Tính giá trị biểu thức A khi x và y thỏa mãn đồng thời các đẳng thức
2
3
56
21 22
4
; 4 2
4 7 2
x x
x
y y
x
x
.
BÀI
TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
_______________________________________________________________________________________________________________________________________________________________
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
107
TH
ÂN THỂ TẠI NGỤC TRUNG
TINH THẦN TẠI NGỤC NGOẠI
DỤC THÀNH ĐẠI SỰ NGHIỆP
TINH THẦN CÁNH YẾU ĐẠI
--------------------------------------------
| 1/107
| | Tải xuống

Có thể bạn quan tâm:

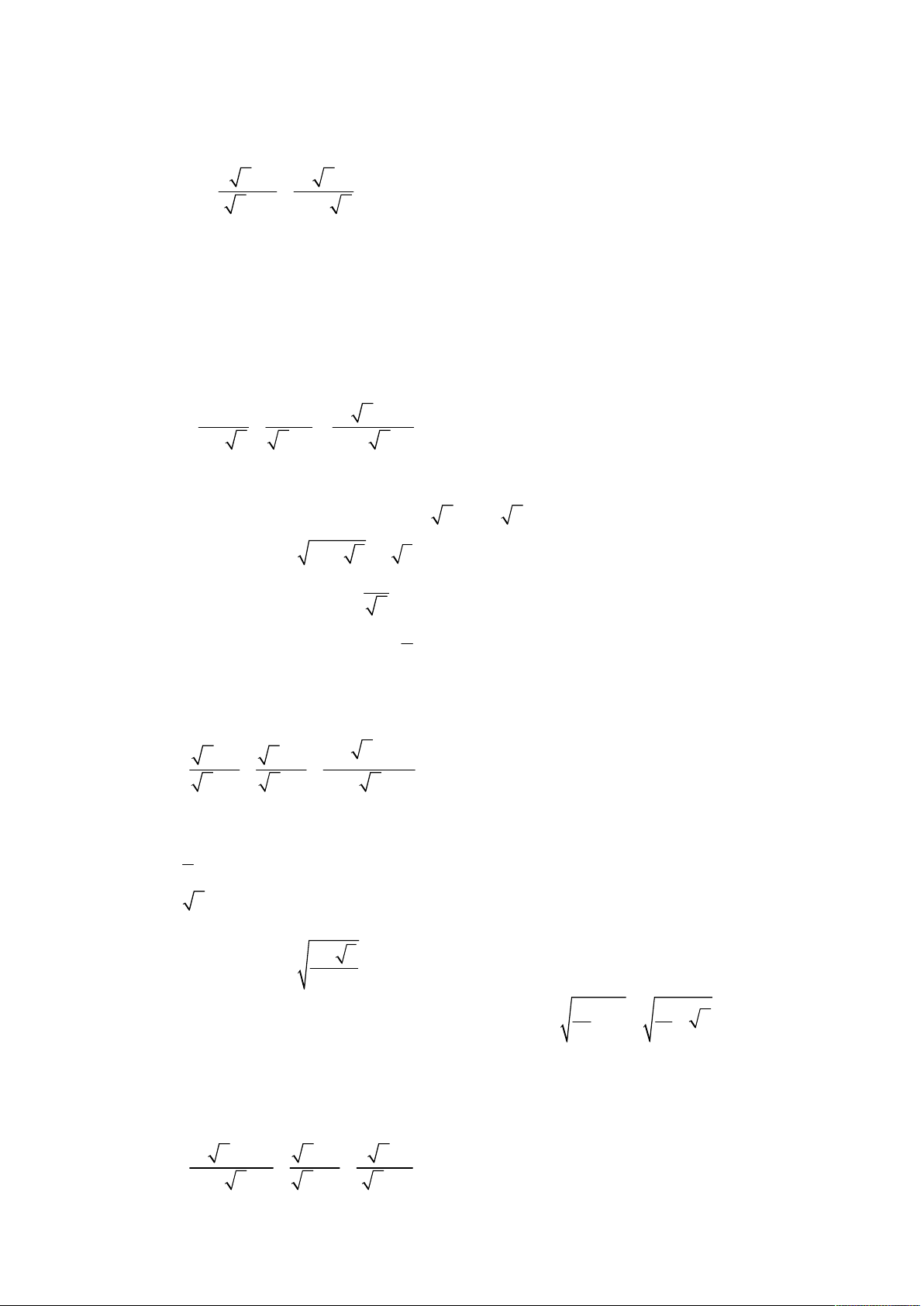
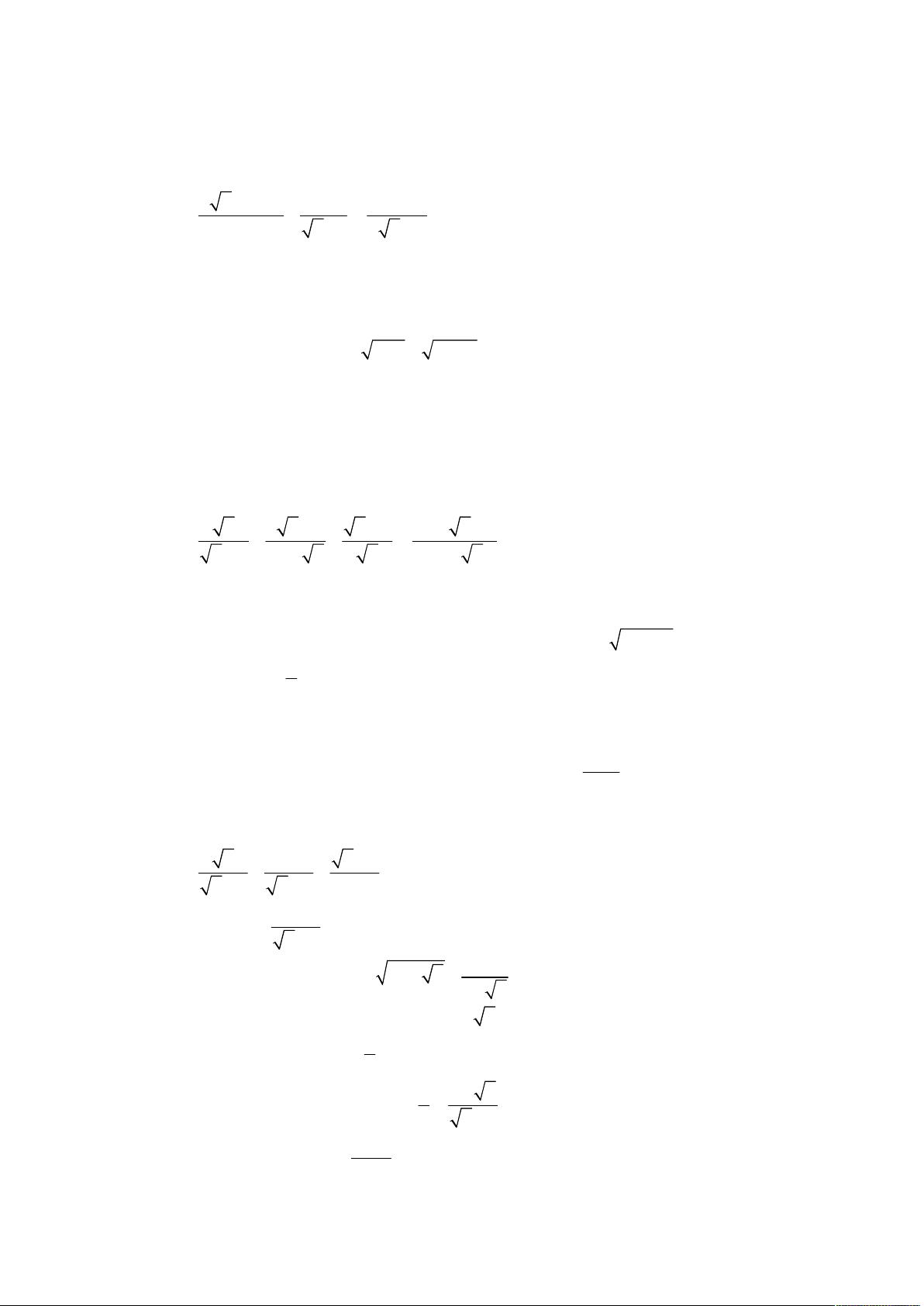
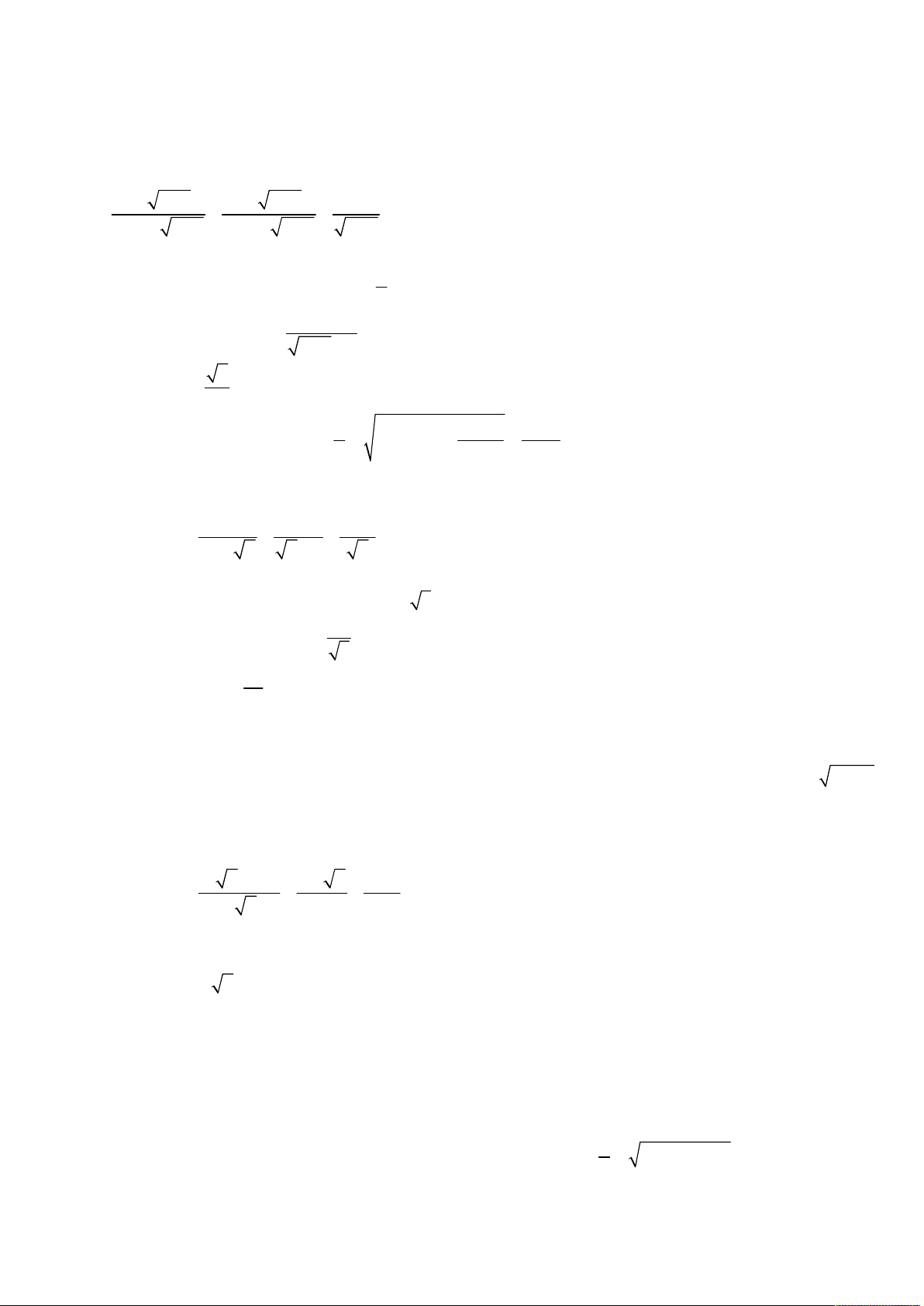
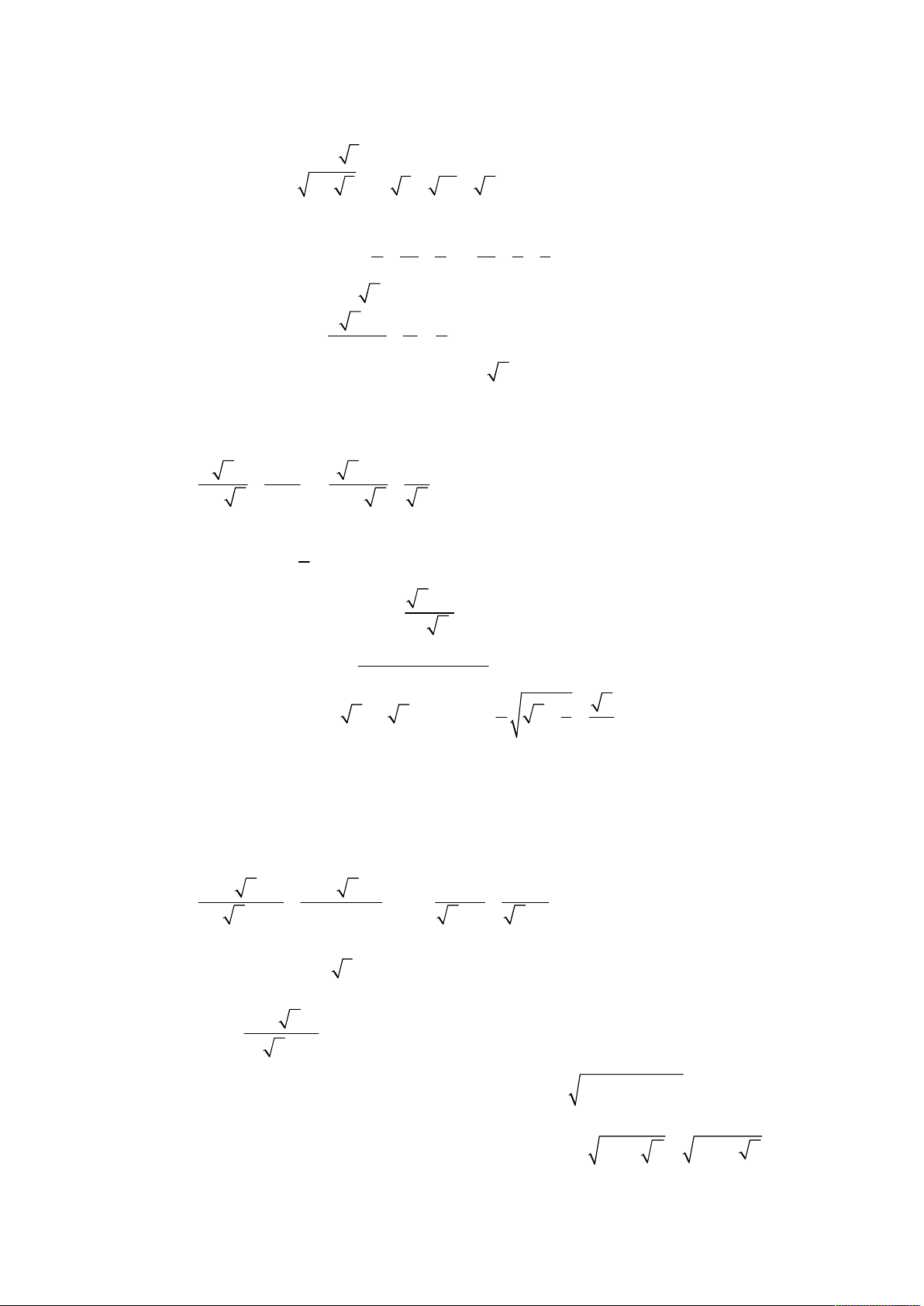
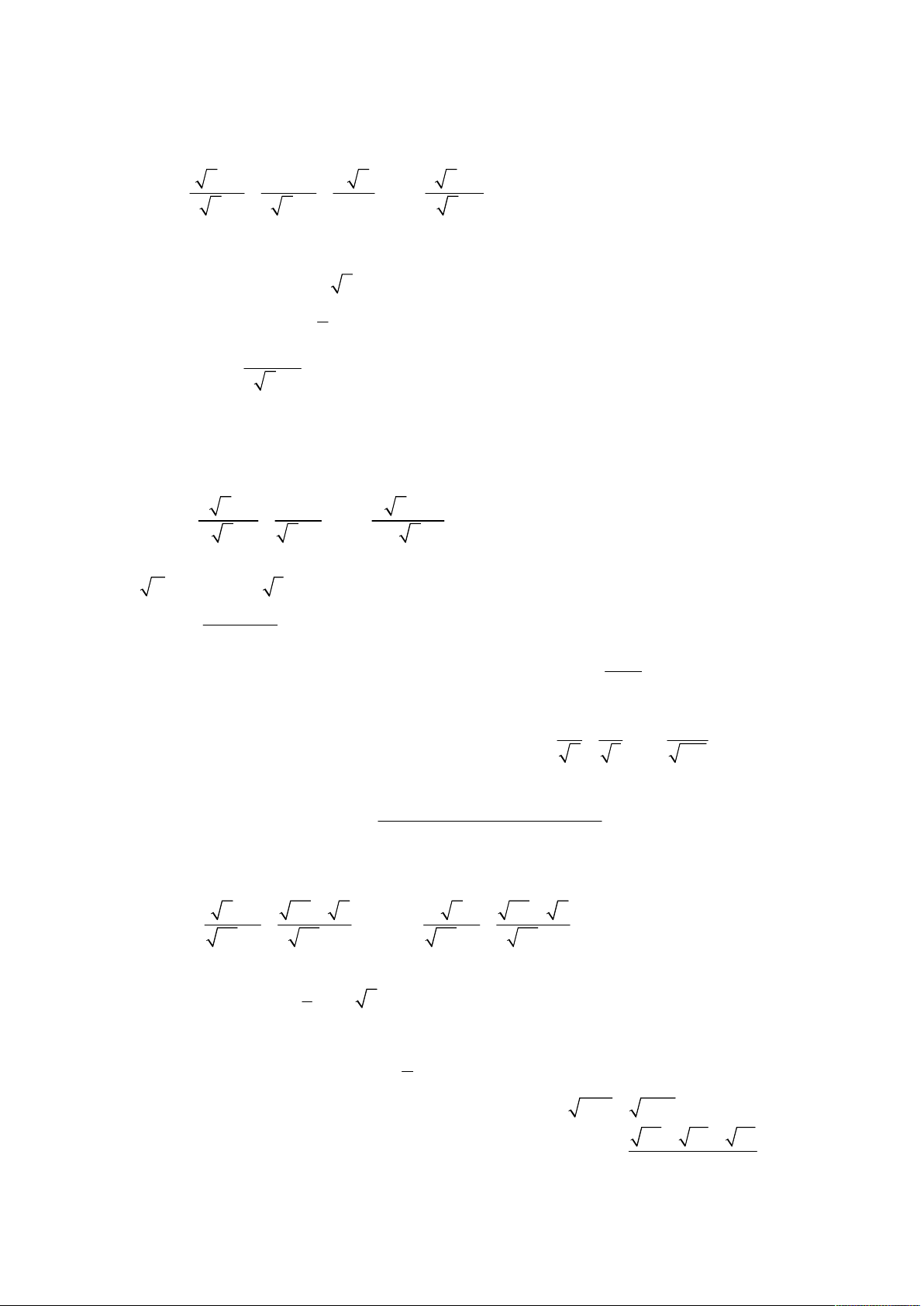
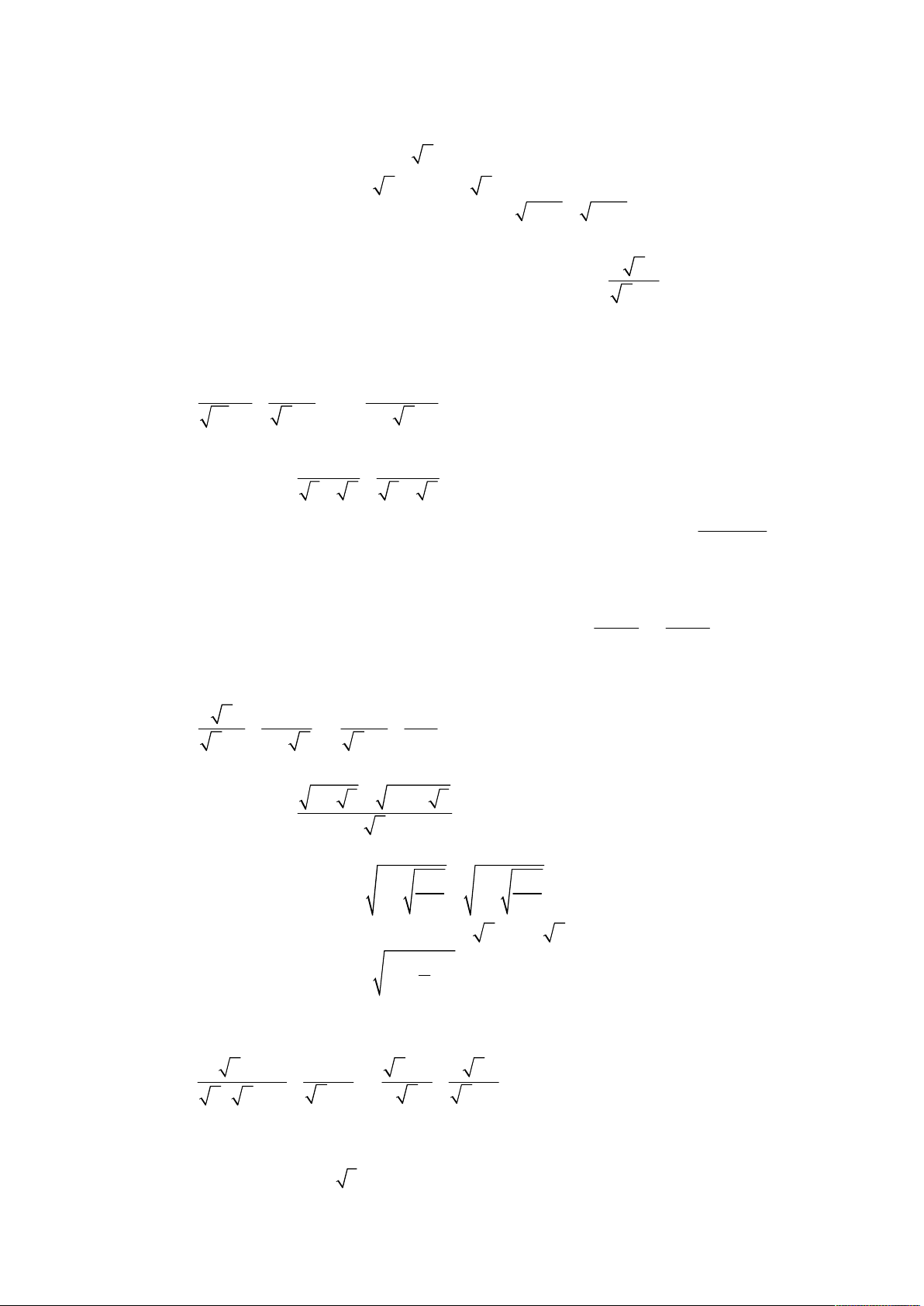
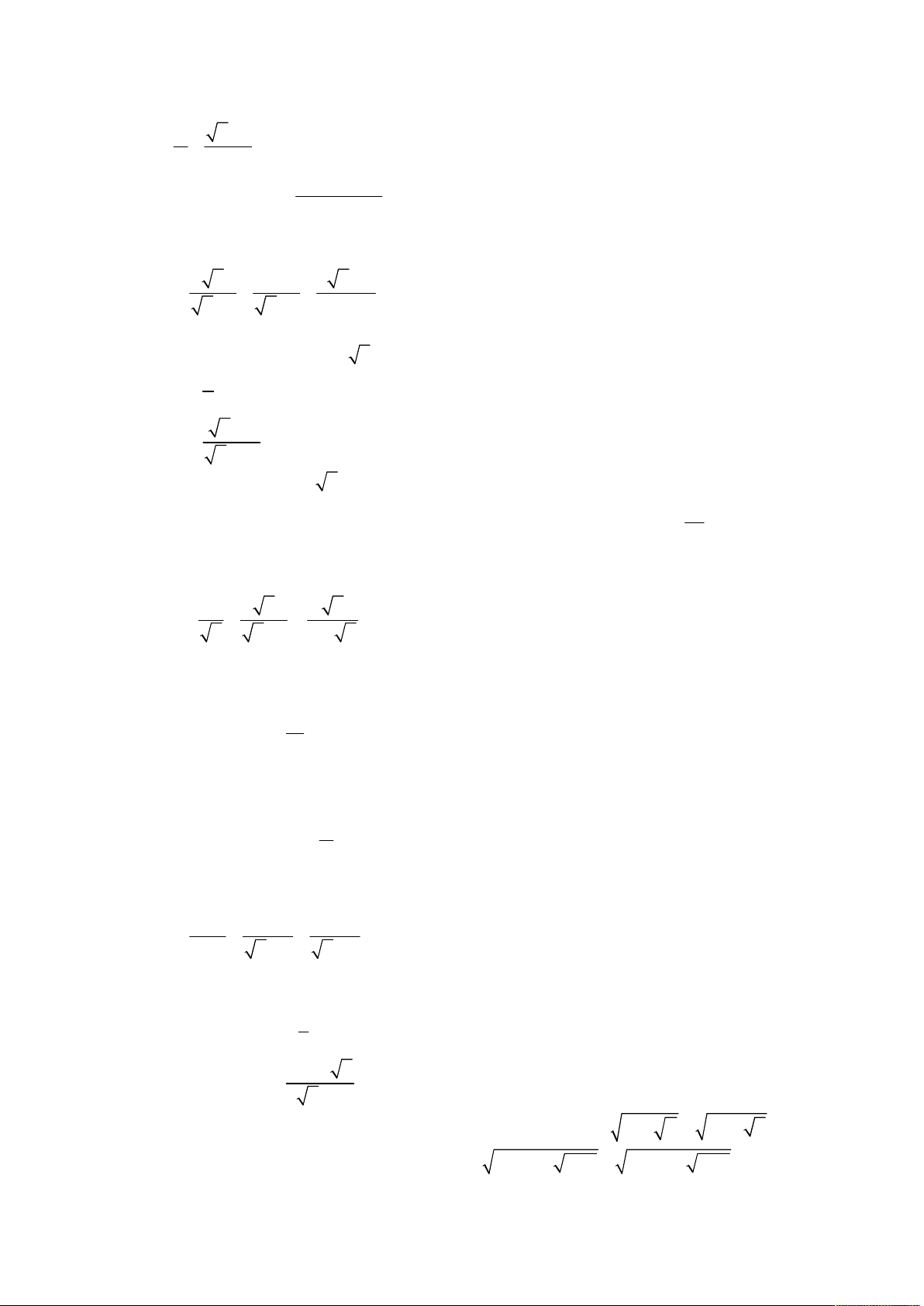
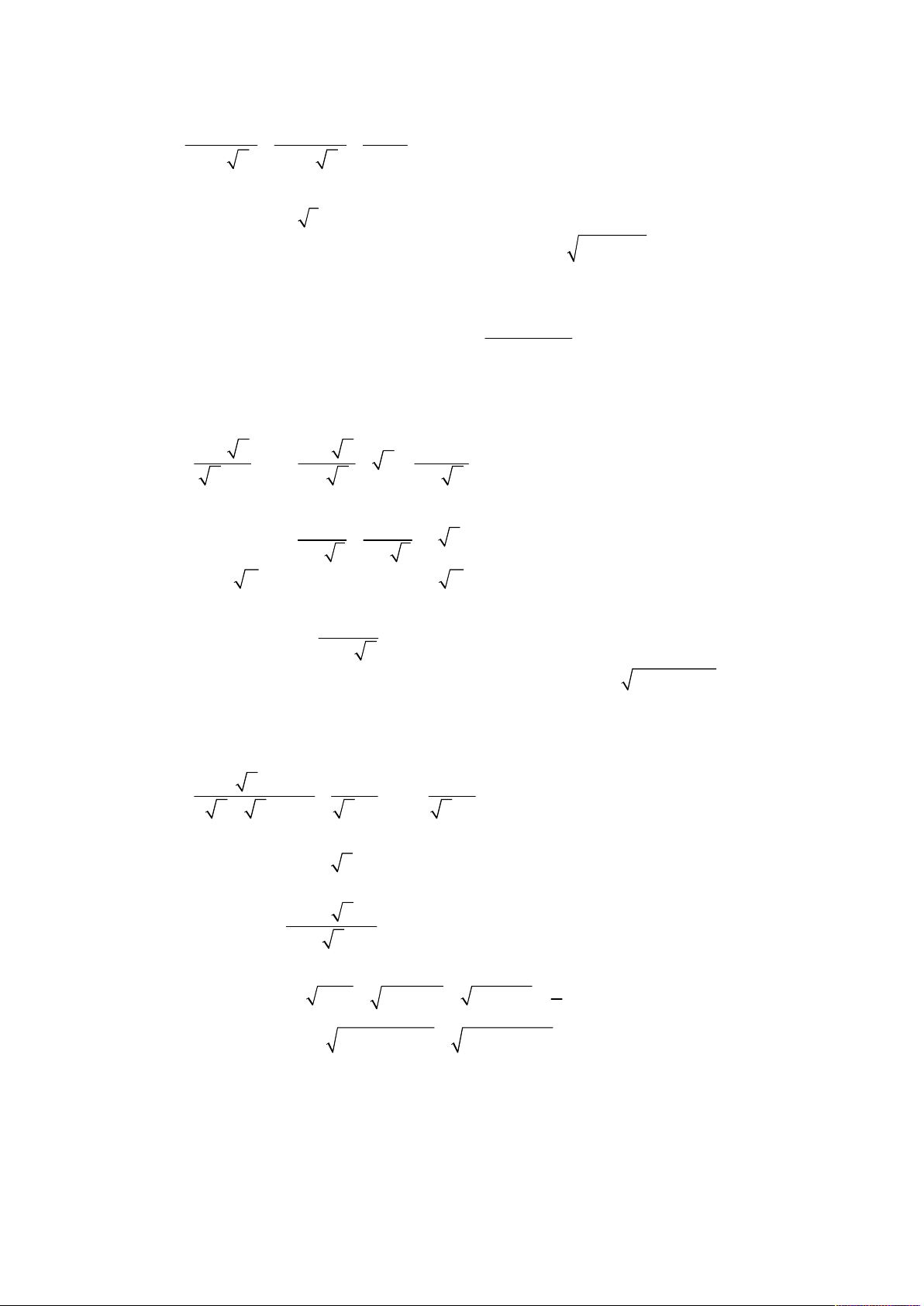
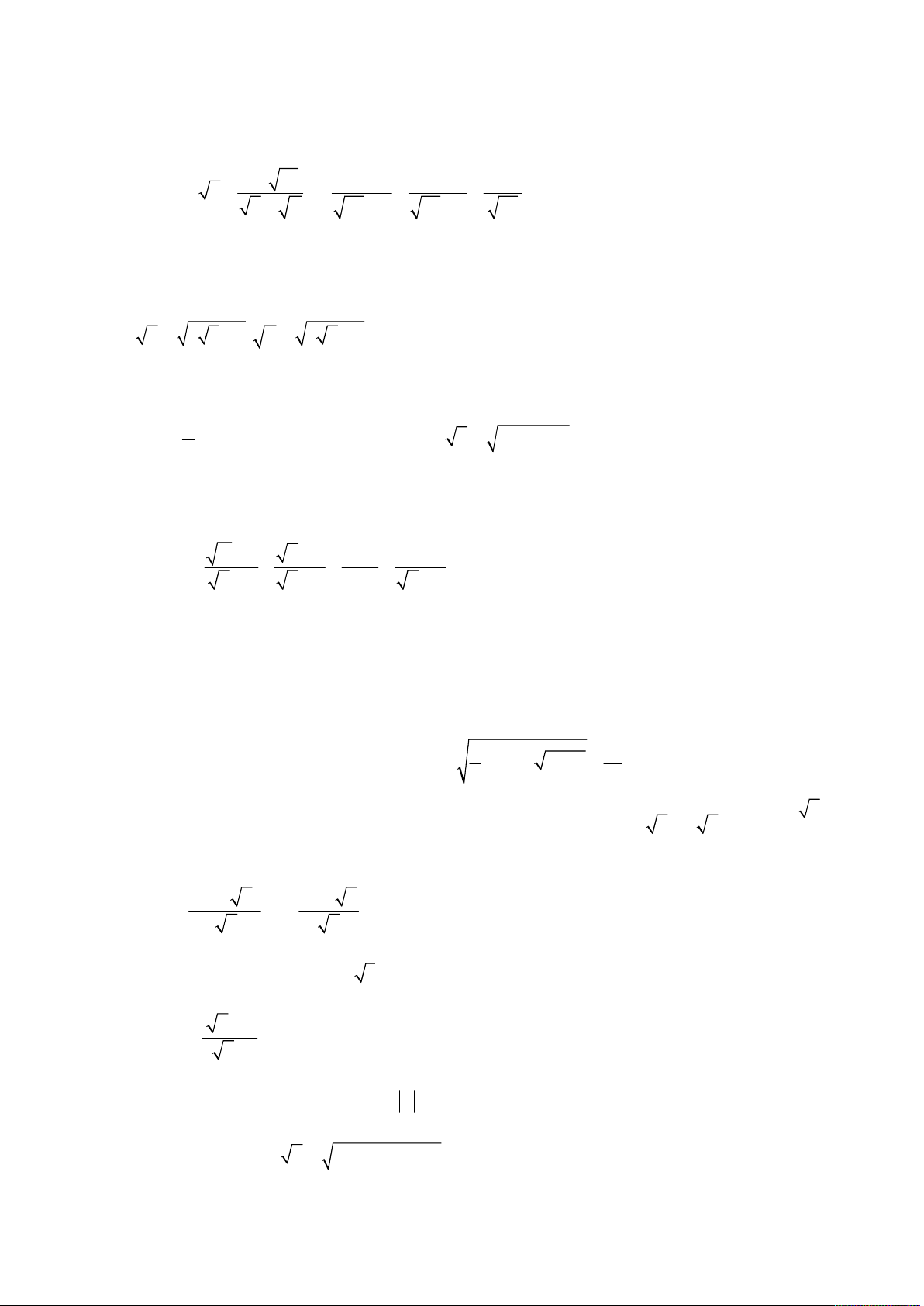
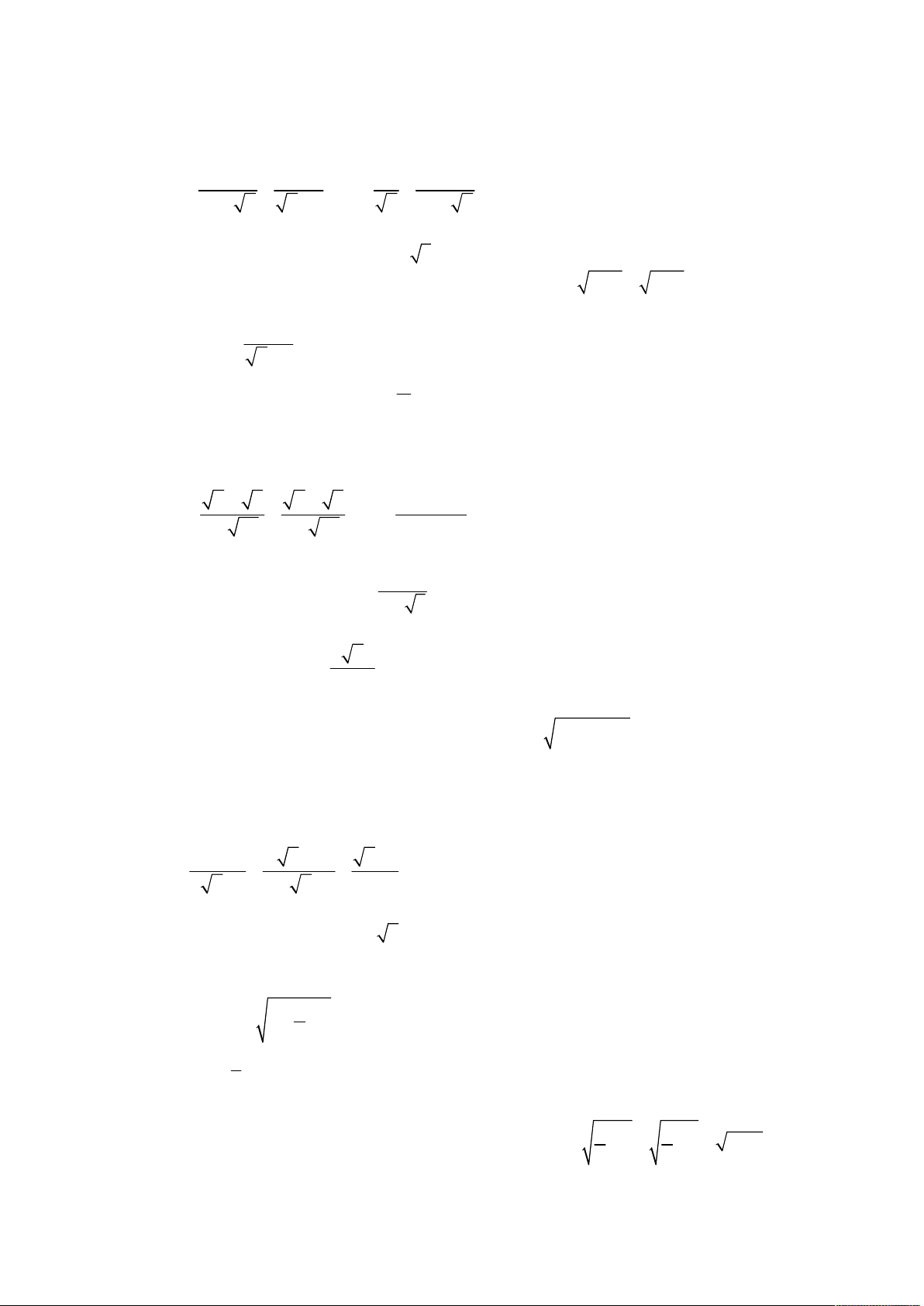
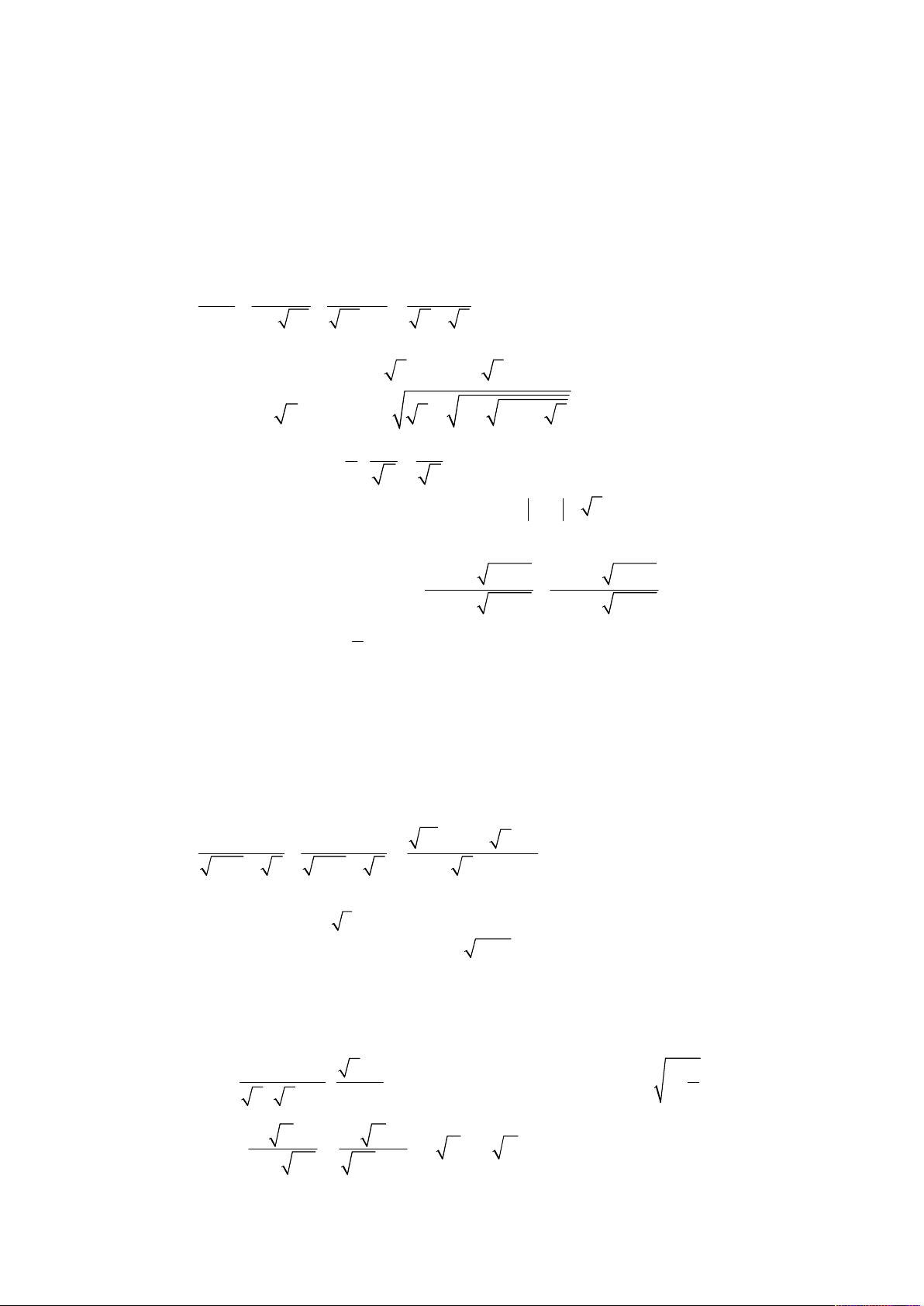
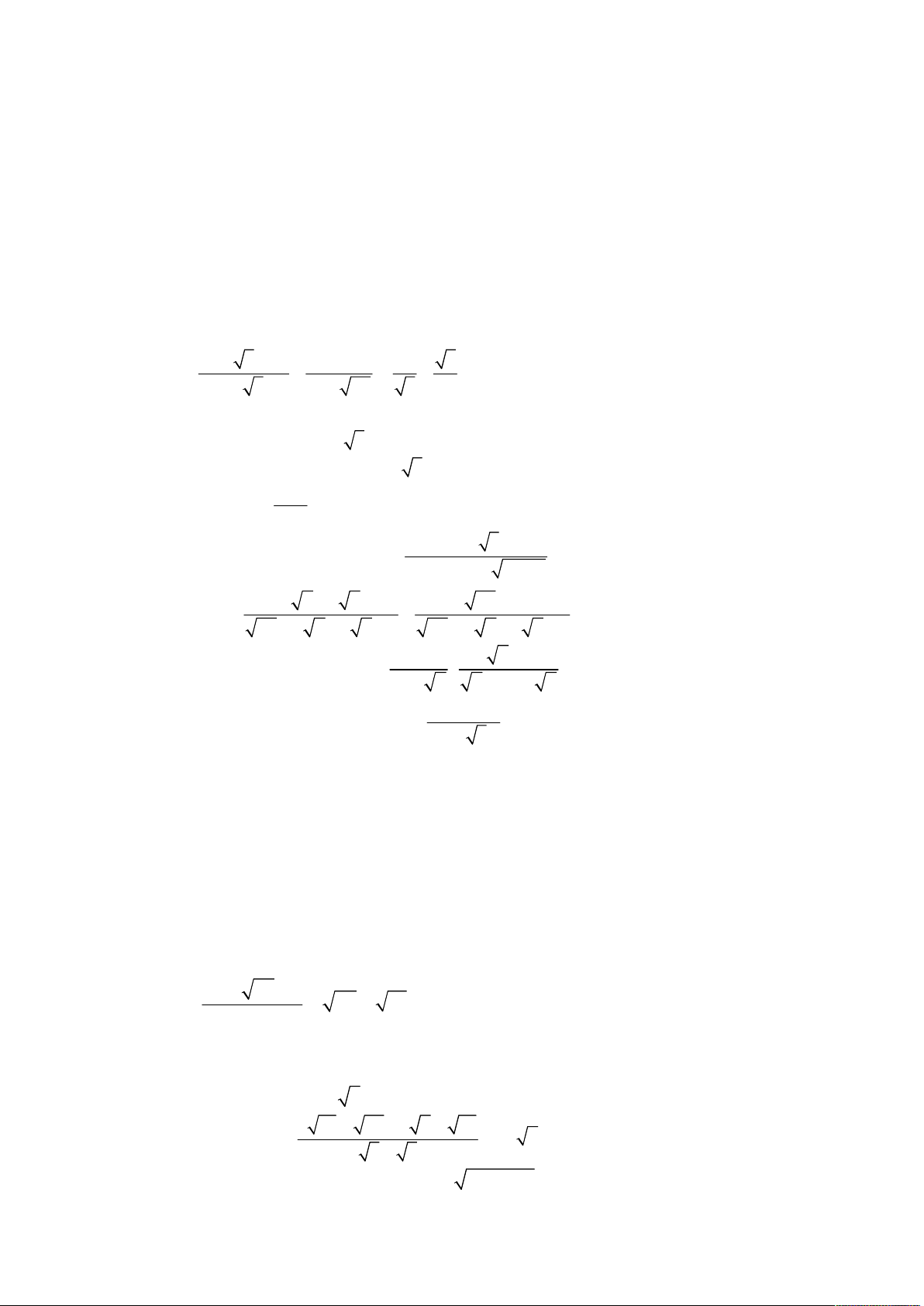
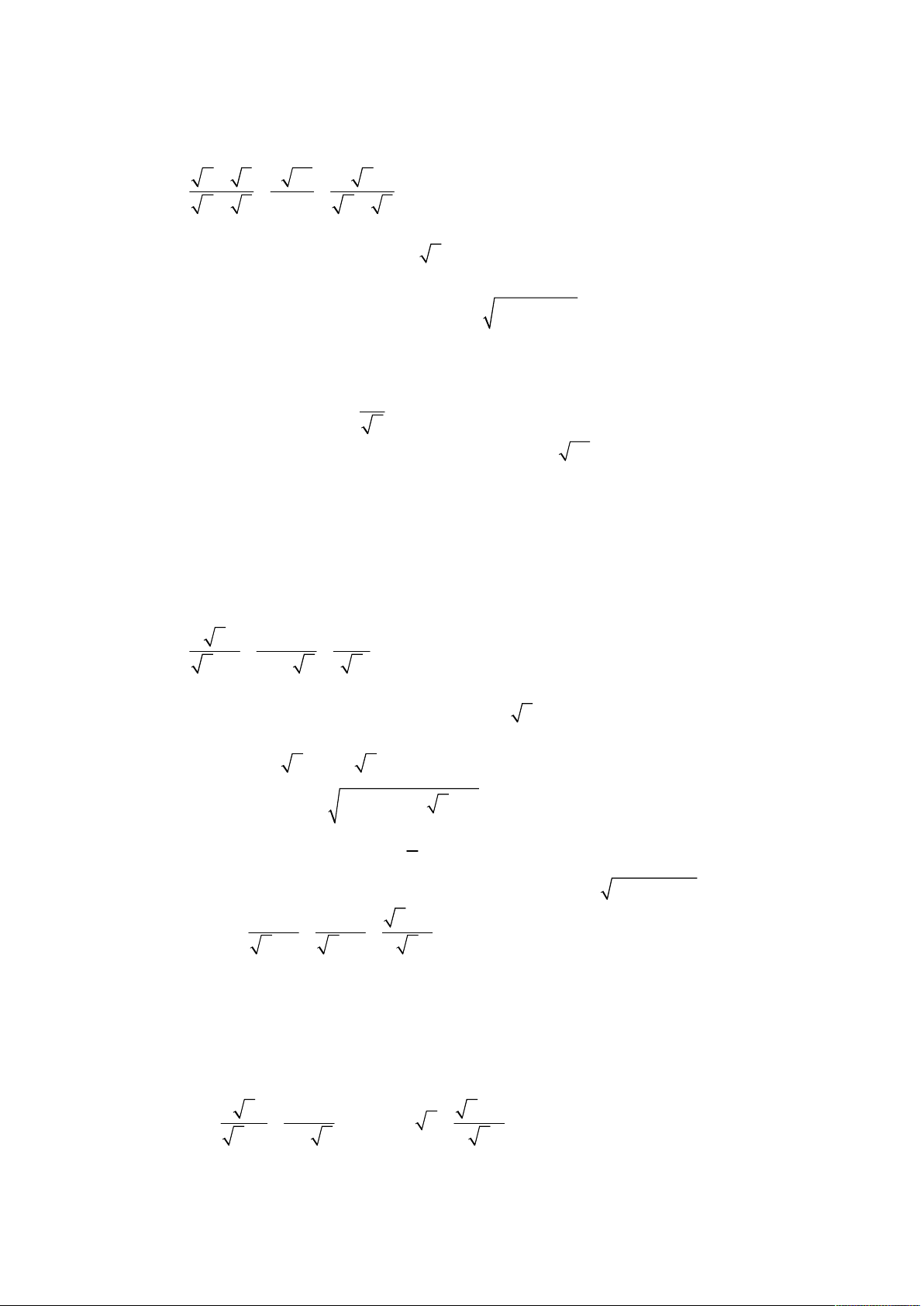
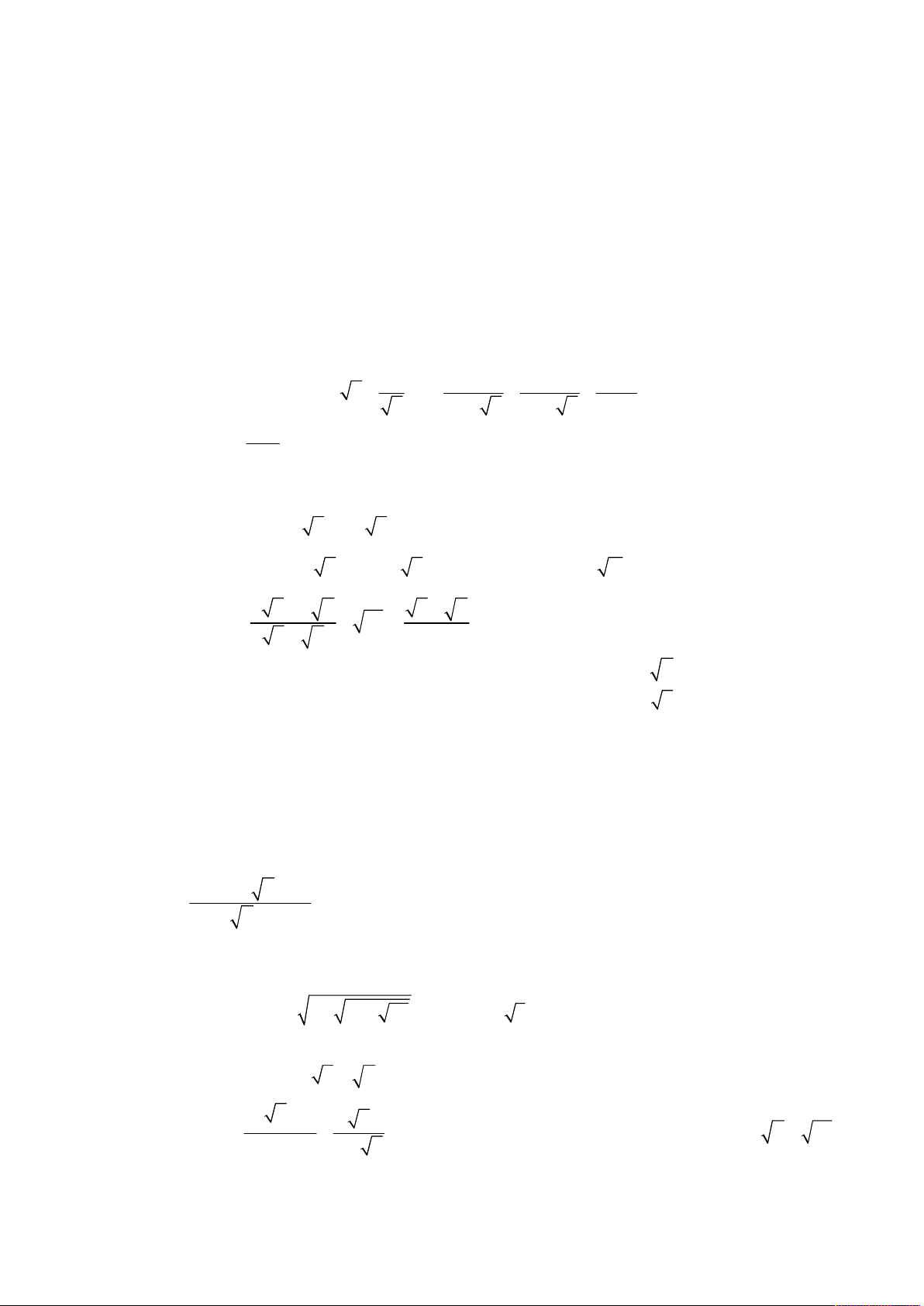
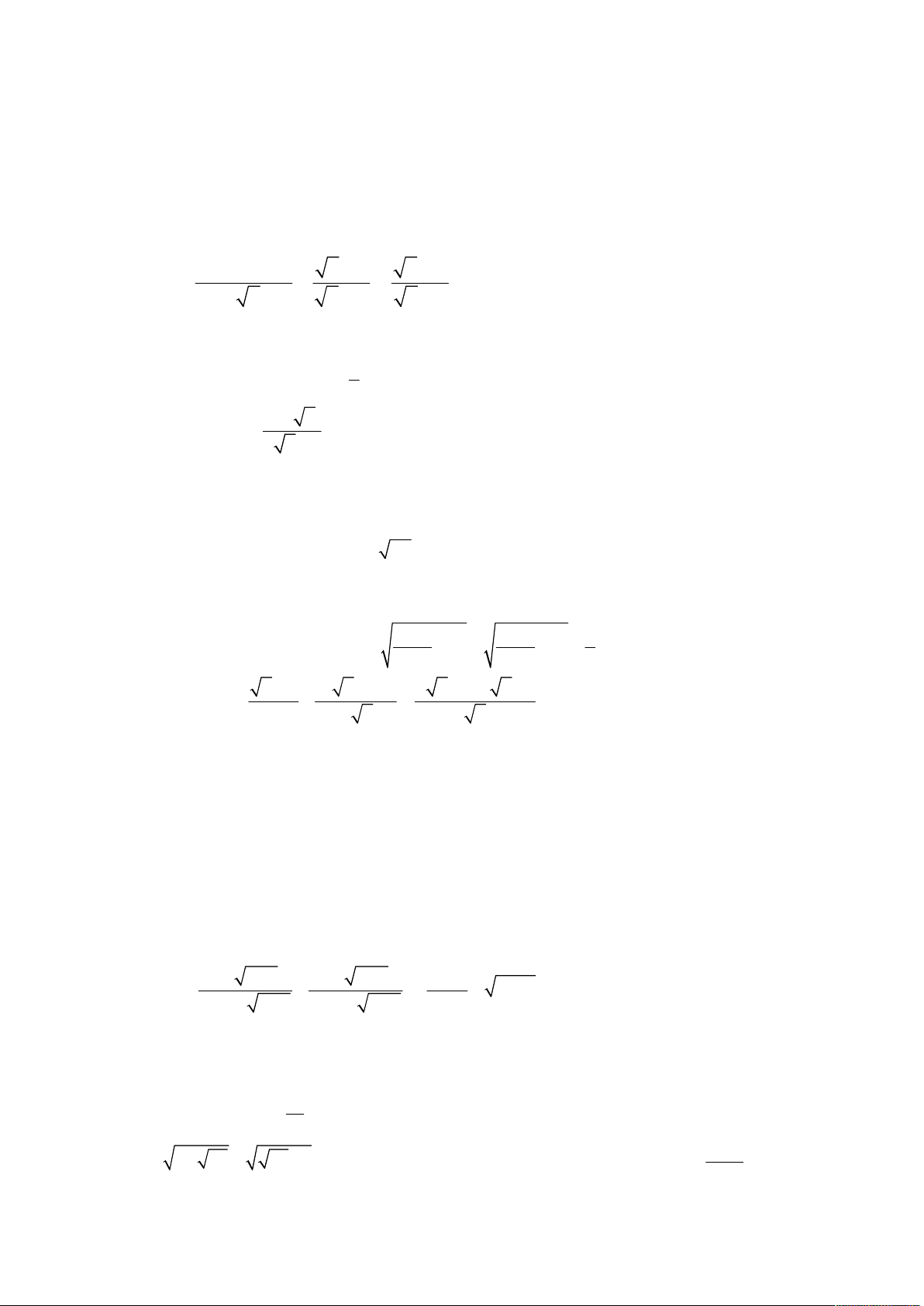
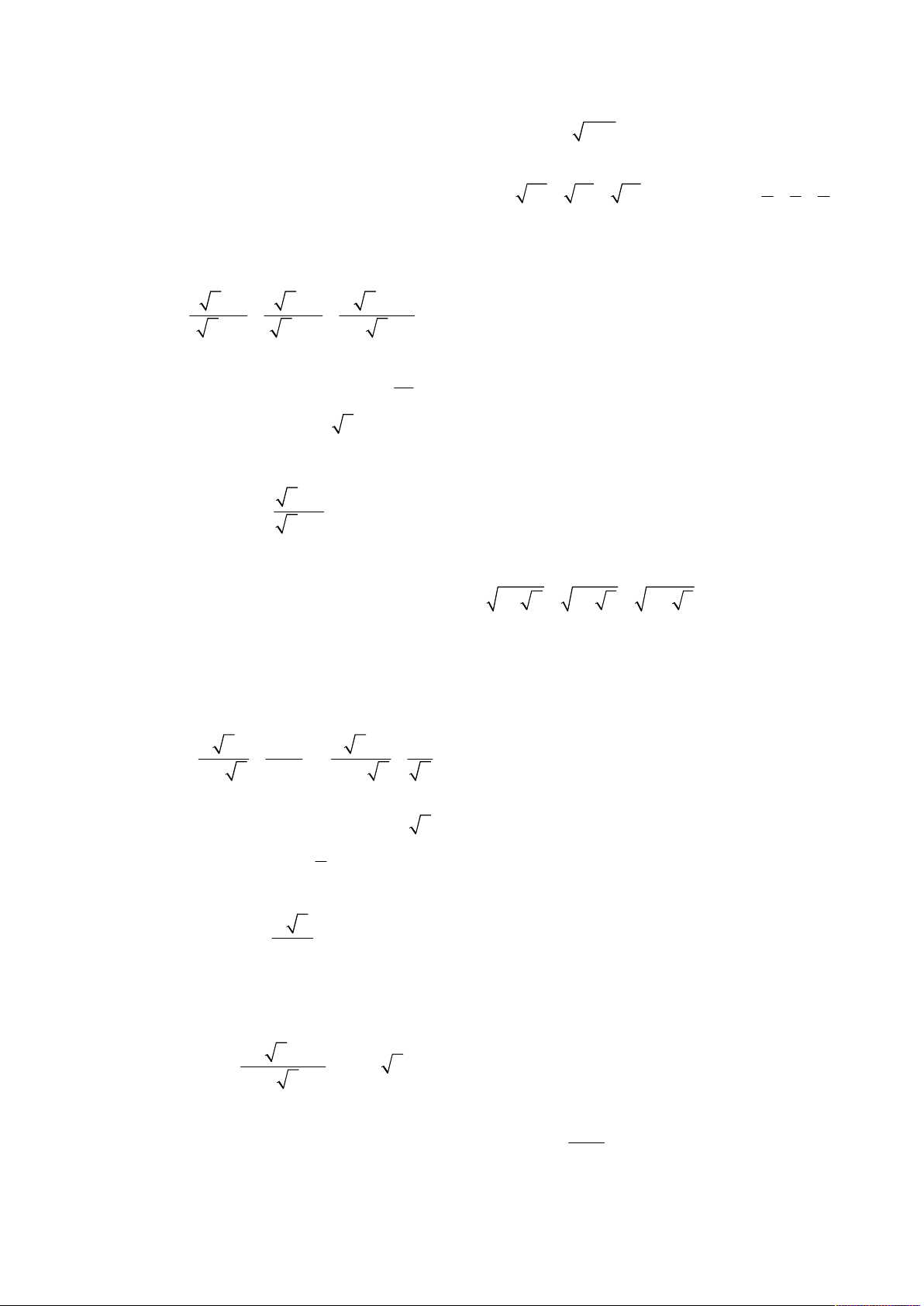
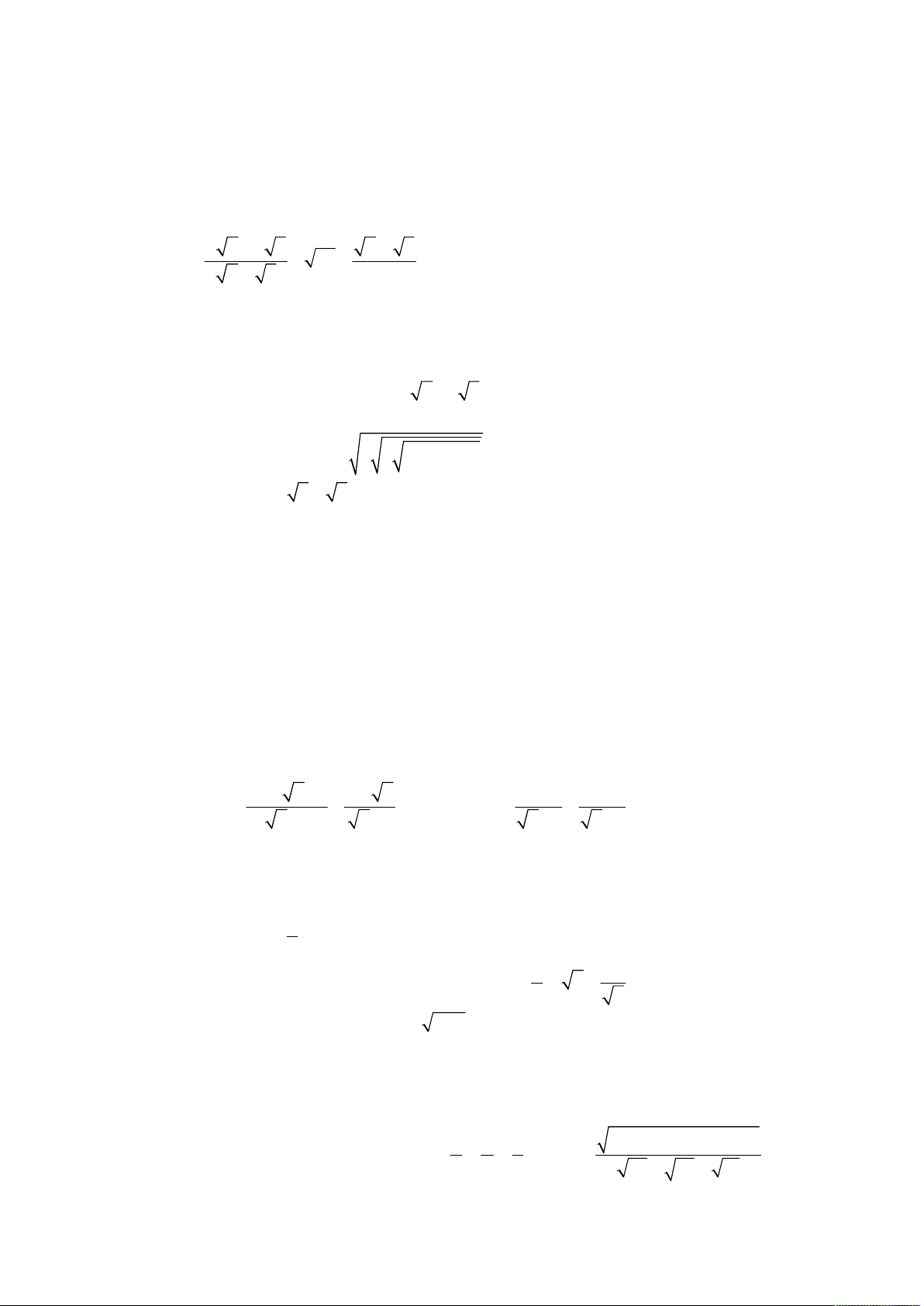
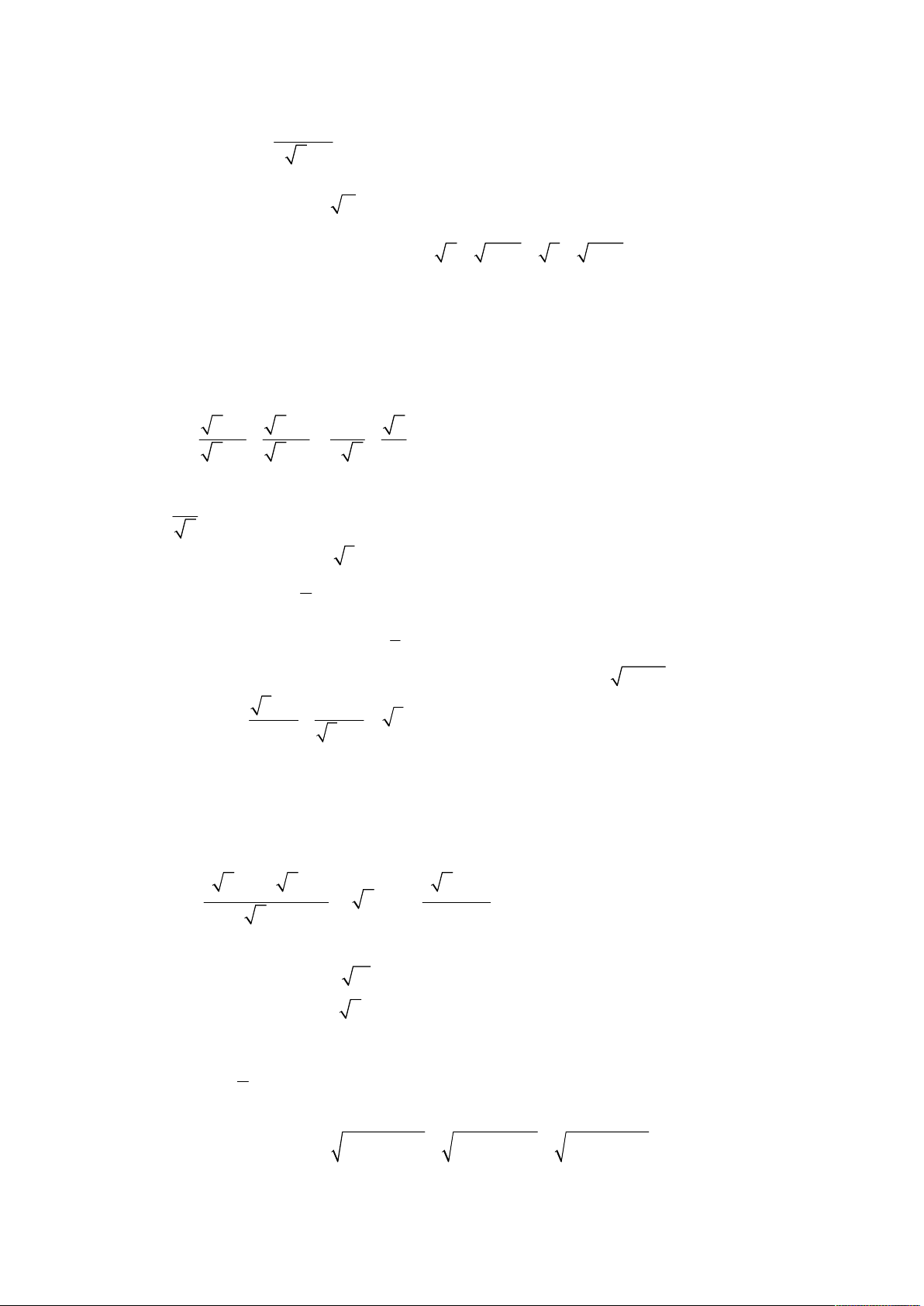
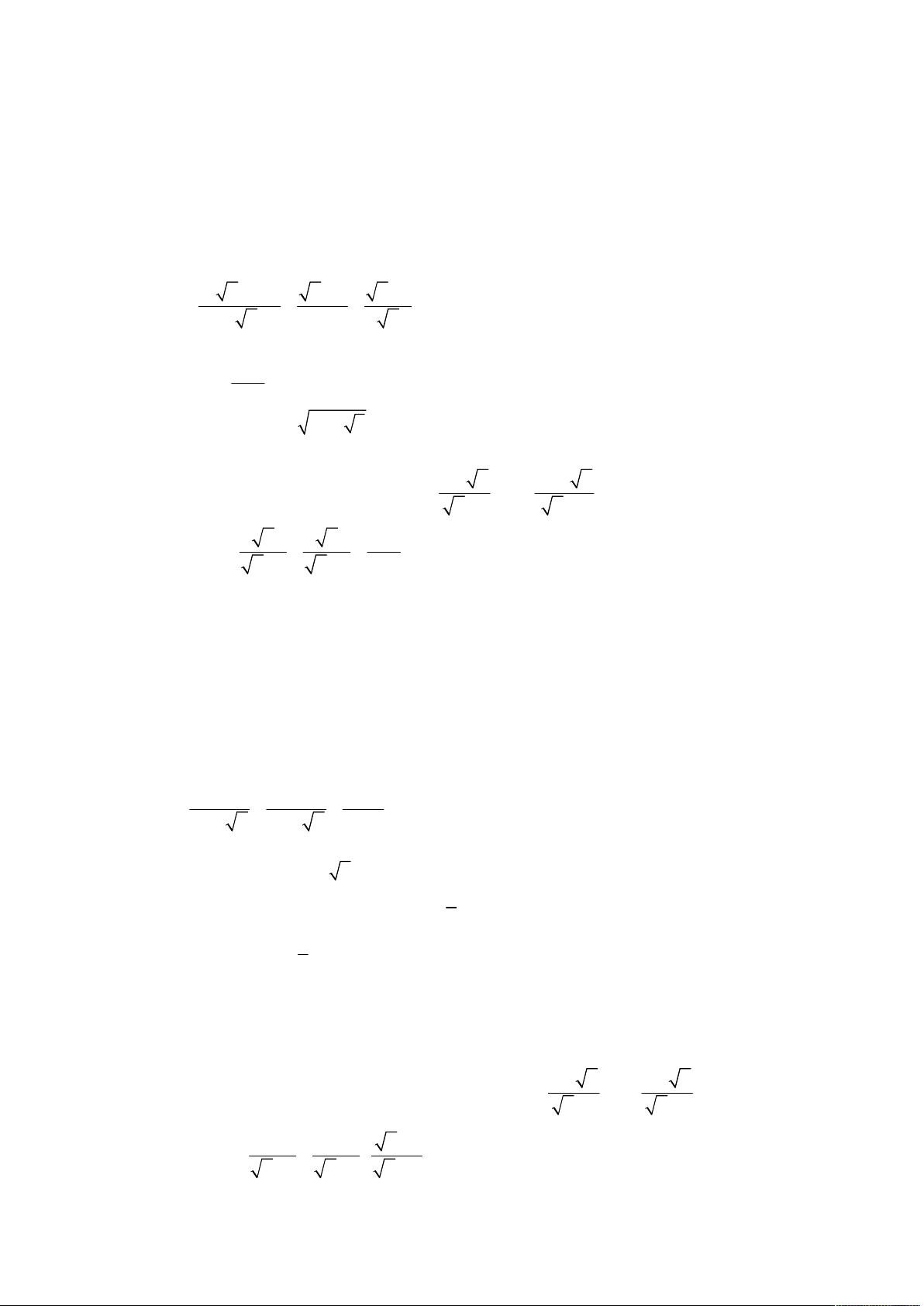
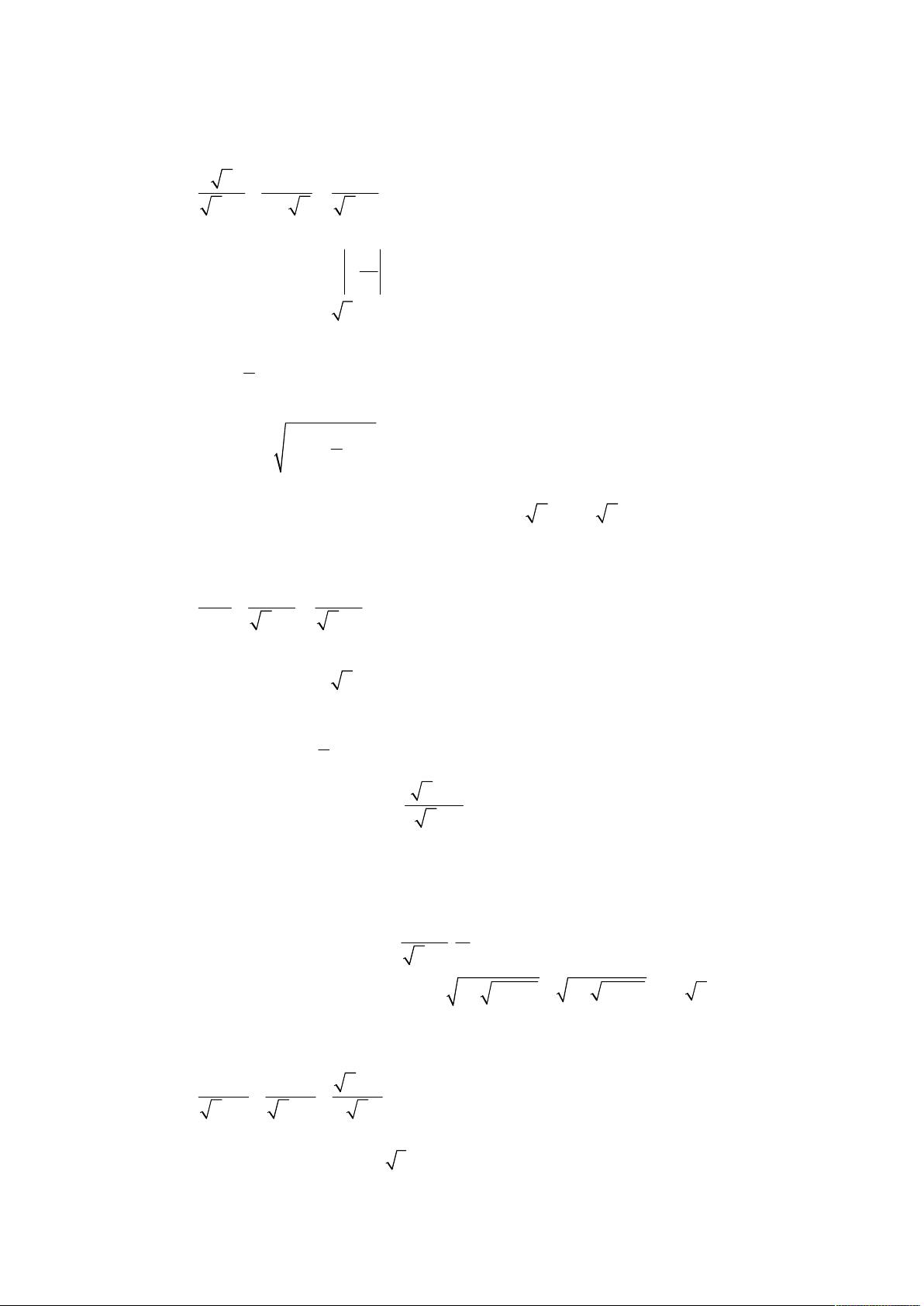
Preview text:

TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________ x 1076 P x 1077
-------------------------------------------------------------------------------------------- CHUYÊN ĐỀ CĂN THỨC
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2)
TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
CHỦ ĐẠO: BIẾN ĐỔI NÂNG CAO CĂN THỨC 
BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN BẬC HAI. 
RÚT GỌN BIỂU THỨC CHỨA CĂN TỔNG HỢP. 
CÁC CÂU HỎI PHỤ ĐỐI VỚI BÀI TOÁN TỔNG HỢP. 
BÀI TOÁN NHIỀU CÁCH GIẢI.
CREATED BY GIANG SƠN (FACEBOOK); 01633275320 (TELL); GACMA1431988@GMAIL.COM (GMAIL)
THÀNH PHỐ THÁI BÌNH – MÙA THU 2016
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 2
_______________________________________________________________________________________________________________________________________________________________
“Non sông Việt Nam có trở nên tươi đẹp hay không, dân tộc Việt Nam có bước tới đài vinh
quang để sánh vai với các cường quốc năm châu được hay không, chính là nhờ một phần lớn ở
công học tập của các em”
(Trích thư Chủ tịch Hồ Chí Minh).
“Nào phi nhanh, phi nhanh,
Gió reo trên lưng đồi,
Hương lúa bát ngát trên đồng xanh,
Lời ca em bay trên trời mây,
Nắng quê hương bừng say,
Bước chân những ngày thơ ấu, Theo em vào trong ký ức,
Lớn lên với cùng thời gian,
Nào phi nhanh nhanh lên nào,
Nào phi nhanh nhanh lên nào,
Hây hây…Hây hây…”
(Lời bài hát trong phim Hoa của trời –
Giải Bông sen Bạc; Liên hoan phim Việt Nam; Lần thứ 11; Năm 1996
Đạo diễn Đỗ Minh Tuấn).
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 3
_______________________________________________________________________________________________________________________________________________________________ CHUYÊN ĐỀ CĂN THỨC
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (QUYỂN 2)
TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
-------------------------------------------------------------------------------------------------------------------------------------------
Được đề cập lần đầu tiền trong chương trình Đại số 7, mặc dù rất đơn giản với căn bậc hai số học, căn thức đã
bước đầu gây ra sự tò mò, khám phá đối với nhiều bạn học sinh nhỏ tuổi yêu Toán. Lên lớp 9 bậc THCS, căn thức
đã trở thành một nội dung chính thống, phổ biến và giữ vị trí quan trọng trong chương trình Đại số 9, với đầy đủ
các khái niệm, tính chất, định nghĩa căn bậc hai với một biến số, nhiều biến số, hằng đẳng thức 2
A A , các phép
toán khai phương một tích, khai phương một thương, liên hệ giữa phép nhân, phép chia và phép khai phương, phép
trục căn thức, cao hơn nữa là biến đổi đơn giản biểu thức chứa căn bậc hai, tính toán với căn bậc ba và căn bậc cao.
Xin lưu ý nội dung phương trình, hệ phương trình chứa căn là nội dung khó, đặc sắc, tác giả cố gắng sắp xếp nó
trong nhiều tài liệu bộ phận khác. Những bài toán biến đổi đơn giản biểu thức chứa căn bậc hai, có thể nói đây là
kiến thức hết sức cơ bản, nền tảng, xuất hiện gần như là bắt buộc trong các kỳ thi kiểm tra kiến thức thường niên,
kỳ thi chọn học sinh giỏi toán các cấp trên toàn quốc, kỳ thi tuyển sinh lớp 10 hệ THPT, lý do đó khiến nó vẫn là
một câu hỏi rất được quan tâm của các bạn học sinh, phụ huynh, các thầy cô, giới chuyên môn và đông đảo bạn đọc yêu Toán.
Biến đổi đơn giản biểu thức chứa căn bậc hai thì có lẽ đa số bạn đọc đều biết và từng trải qua, thậm chí là xuất
hiện tâm lý “chán chường, coi thường” với khẩu hiệu “ Cho biểu thức…Tìm điều kiện xác định…Rút gọn biểu
thức…Tính giá trị của biểu thức khi…Tìm x để…Vân vân. Trước tiên là rút gọn, còn yêu cầu phía sau của dạng
toán khá đa dạng, đa chiều, mục tiêu tìm các ẩn thỏa mãn một tính chất nào đó nên để thao tác dạng toán này, các
bạn học sinh cần liên kết, phối hợp, tổng hợp các kiến thức được học về căn thức, phương trình, hệ phương trình và
bất phương trình, bất đẳng thức, đôi khi nó đòi hỏi năng lực tư duy của thí sinh rất cao, nhiều bạn học sinh trung
học cơ sở có thể làm 80%, nhưng để làm trọn vẹn thì cũng không thể nói chắc chắn như đinh đóng cột được.
Tài liệu này mang tên BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2), chủ yếu xoay quanh các bài
toán rút gọn căn thức, kèm theo nhiều câu hỏi phụ. Một khi đã rút gọn thu được căn thức nhỏ, dựa trên đặc điểm
đặc trưng căn thức đó, kết hợp kiến thức nhiều mảng trong đại số, số học, hình học, chúng ta có thể tự mình tạo ra
rất nhiều câu hỏi phụ hay, khó, thậm chí là rất khó, tầm vóc tuy nhỏ (câu hỏi phụ) nhưng mức độ có thể vượt qua
những bài toán khó riêng biệt. Trước tiên tác giả xin được giới thiệu, mở rộng và phát triển lớp bài toán cũ, tức là
các đề bài nguyên nằm trong đề thi chất lượng học kỳ I, đề thi chất lượng học kỳ II, đề thi tuyển sinh lớp 10 THPT,
tuyển sinh lớp 10 THPT Chuyên và đề thi học sinh giỏi các cấp bậc THCS trong phạm vi có thể sưu tập. Các bạn
hãy thử tưởng tượng, với 63 tỉnh thành thôi, với bề dày thi tuyển sinh hai thập niên trở lại đây, với tầm 70 trường
THPT Chuyên trên cả nước, thi tuyển sinh môn Toán gồm Toán 1 và Toán 2 (Dành cho chuyên Toán, chuyên Tin
học), giả sử đề thi nào cũng có tối thiểu một bài toán căn thức tổng hợp, chúng ta đã có thể khai thác tối thiểu bao
nhiêu bài toán. Tác giả xin làm phép thống kê sơ lược
1. Đề thi chất lượng học kỳ I và học kỳ II (Sở giáo dục và Đào tạo): 63.2 đề thi.
2. Đề thi chọn học sinh giỏi lớp 9 THCS (Sở Giáo dục và Đào tạo): 63.2 đề thi.
3. Đề thi tuyển sinh lớp 10 THPT (Đại trà): 63 đề thi.
4. Đề thi tuyển sinh lớp 10 THPT Chuyên (Toán 1 và Toán 2): 70.2 đề thi.
Như vậy, trong một năm, chúng ta sẽ có tổng cộng 63.2  63.2  63  70.2  455 bài toán cần khai thác, chỉ cần khai
thác các đề thi từ năm 1990 đến nay (2016), quãng đường 27 năm chúng ta sẽ có 12285 bài toán. Tuy nhiên, vì theo
thời gian, kéo theo phân chia địa giới hành chính, từ trung ương đến địa phương, nếu các bạn trẻ hiểu biết về các
tỉnh cũ (tỉnh ghép) Việt Nam thì số lượng đề thi thực tế không tới mức đó. Cụ thể
1. Tỉnh Hoàng Liên Sơn (Lào Cai, Yên Bái, Nghĩa Lộ). Tái lập 1991.
2. Tỉnh Bắc Thái (Bắc Cạn, Thái Nguyên). Tái lập 06.11.1996.
3. Tỉnh Cao Lạng (Cao Bằng, Lạng Sơn). Tái lập 29.12.1978.
4. Tỉnh Hà Tuyên (Hà Giang, Tuyên Quang). Tái lập 12.08.1991.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 4
_______________________________________________________________________________________________________________________________________________________________
5. Tỉnh Hà Sơn Bình (Hà Đông, Sơn Tây, Hòa Bình). Tái lập 12.08.1991.
6. Tỉnh Hà Nam Ninh (Hà Nam, Nam Định, Ninh Bình). Tái lập 26.12.1991.
7. Tỉnh Vĩnh Phú (Vĩnh Phúc, Phú Thọ). Tái lập 06.11.1996.
8. Tỉnh Hà Bắc (Bắc Giang, Bắc Ninh). Tái lập 06.11.1996.
9. Tỉnh Hải Hưng (Hải Dương, Hưng Yên). Tái lập 06.11.1996.
10. Tỉnh Nghệ Tĩnh (Nghệ An, Hà Tĩnh). Tái lập 12.08.1991.
11. Tỉnh Bình Trị Thiên (Quảng Bình, Quảng Trị, Thừa Thiên Huế). Tái lập 30.6.1989.
12. Tỉnh Quảng Nam – Đà Nẵng. Tái lập 06.11.1996.
13. Tỉnh Kon Tum – Gia Lai. Tái lập 12.08.1991.
14. Tỉnh Nghĩa Bình (Quảng Nghãi, Bình Định). Tái lập 30.06.1989.
15. Tỉnh Phú Khánh (Phú Yên, Khánh Hòa). Tái lập 30.06.1989.
16. Tỉnh Thuận Hải (Ninh Thuận, Bình Thuận, Bình Tuy). Tái lập 26.12.1991.
17. Tỉnh Sông Bé (Bình Dương, Bình Phước, Bình Long). Tái lập 01.01.1997.
18. Tỉnh Đồng Nai (Đồng Nai, Đặc khu Vũng Tàu – Côn Đảo). Tái lập 12.08.1991.
19. Tỉnh Cửu Long (Trà Vinh, Vĩnh Long). Tái lập 26.12.1991.
20. Tỉnh Hậu Giang (Cần Thơ, Sóc Trăng). Tái lập 26.12.1991.
21. Tỉnh Minh Hải (Cà Mau, Bạc Liêu). Tái lập 06.11.1996.
Theo chủ quan của tác giả, mỗi tỉnh thành trên mọi miền Tổ quốc tuy văn hóa, giáo dục mang tính thống
nhất và tương đồng, nhưng đề thi vẫn có những nét đặc sắc riêng, về cấu trúc và mức độ thông hiểu, vận dụng, đánh
giá. Đề thi mang hàm lượng kiến thức, co ép thời gian và yêu cầu kỹ năng cao hơn tập trung ở những khu vực, địa
phương đông dân cư hơn, có thể kể đến đề thi các tỉnh Duyên hải Đồng bằng Bắc bộ (Khu III cũ), Bắc Trung Bộ
(Khu IV cũ), Duyên hải Nam Trung Bộ (Khu V cũ), Đông Nam Bộ. Các khu vực khác như Tây Bắc Bộ, Đông Bắc
Bộ - Việt Bắc, Tây Nguyên, Tây Nam Bộ có mật độ dân cư thấp hơn, và có cộng đồng các dân tộc thiểu số nên việc
phổ biến kiến thức còn chưa đồng bộ, khó khăn, cũng như cần có lộ trình cụ thể nếu muốn đảm bảo mặt bằng
chung. Có thể nói sự đồng bộ hóa giáo dục vẫn là bài toán mở, mang tính thời sự, tính bình đẳng nhiều thách thức
và cấp bách trong công cuộc cải cách giáo dục, văn hóa hiện nay.
Ngoài việc xử lý, tương tự hóa, rút kinh nghiệm, rèn kỹ năng phản biện, tăng cường mở rộng, đào sâu và
phát triển bài toán, trong quá trình khai thác từng bài toán trong đề thi các tỉnh thành, các bạn sẽ hiểu thêm về địa lý
đất nước, về văn phong, motip đề thi từng tỉnh, thậm chí là sự đầu tư, quan tâm giáo dục của tỉnh đó (nói chung),
các bạn chắc chắn sẽ thấy đất nước mình rất đẹp, giáo dục của mình rất phong phú, đa dạng, đa chiều. "Trăm hay
không hay bằng tay quen", các phương pháp, kỹ thuật cơ bản đã được được các thế hệ đi trước đúc kết và tận tụy
cho thế hệ tương lai, các bạn hoàn toàn đủ khả năng kế thừa, phát huy và sáng tạo không ngừng, chuẩn bị đủ hành
trang nắm bắt khoa học kỹ thuật, đưa đất nước ngày càng vững bền, phồn vinh, và hiển nhiên những bài toán trong
các kỳ thi nhất định không thể là rào cản, mà là cơ hội thử sức, cơ hội khẳng định kiến thức, minh chứng sáng ngời
cho tinh thần học tập, tinh thần ái quốc ! I. KIẾN THỨC CHUẨN BỊ
1. Kỹ thuật nhân, chia đơn thức, đa thức, hằng đẳng thức.
2. Nắm vững các phương pháp phân tích đa thức thành nhân tử.
3. Khái niệm, định nghĩa, điều kiện xác định của căn bậc hai, hằng đẳng thức 2
A A , kỹ năng phân tích
bình phương biểu thức chứa căn, thuật toán khai phương một tích, khai phương một thương.
4. Liên hệ giữa phép khai phương và phép nhân, liên hệ giữa phép khai phương và phép nhân.
5. Kỹ thuật trục căn thức với căn bậc hai, căn bậc ba, trục căn liên tiếp.
6. Nắm vững các phương pháp giải, biện luận phương trình bậc nhất, bậc hai, bậc cao.
7. Sử dụng thành thạo các ký hiệu toán học, logic (ký hiệu hội, tuyển, kéo theo, tương đương).
8. Kỹ năng giải hệ phương trình cơ bản và hệ phương trình đối xứng, hệ phương trình đồng bậc, hệ phương
trình chứa căn thông thường.
9. Kỹ thuật đặt ẩn phụ, sử dụng đại lượng liên hợp, biến đổi tương đương.
10. Kiến thức nền tảng về số học, ước lượng – đánh giá, hàm số - đồ thị, bất đẳng thức – cực trị.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 5
_______________________________________________________________________________________________________________________________________________________________
II. MỘT SỐ BÀI TẬP ĐIỂN HÌNH.
Bài toán 1. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2006 – 2007; Khóa thi 30.06.2006. x  2 x 10 x  2 1 Cho biểu thức Q   
với x  0; x  9 (*). x x  6 x  3 x  2
1. Rút gọn biểu thức Q.
2. Tính giá trị của biểu thức Q khi x  16 . 1
3. Tìm giá trị của x để Q  . 3 1
4. Tìm giá trị của x sao cho Q  . 9
5. Tìm giá trị lớn nhất của Q.
6. Chứng minh rằng Q không thể nhận giá trị nguyên với mọi giá trị x thỏa mãn (*).
Bài toán 2. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2013 – 2014; Khóa thi 20.06.2013.  x 1 1 
Cho biểu thức P    
. x  4 với x  0; x  4 .  x  2 x  2 x 4    
1. Rút gọn biểu thức P theo hai cách.
2. Tính giá trị của biểu thức P khi x  9 . 1
3. Tính giá trị của biểu thức P khi x   5 14 . 5  2
4. Tìm các giá trị của x để P  3 .
5. Tìm giá trị nhỏ nhất của biểu thức P.
6. Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên.
Bài toán 3. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2004 – 2005; Khóa thi 30.06.2004. a 2 a   1 a  4 a  2 Cho biểu thức A   
với a  0; a  4 . 8  2 a a a  2 4  a
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi a  9  4 5 .
3. Tìm giá trị của a để 3A  2 . 1
4. Tìm khoảng giá trị của a để A  . 2 3
5. Chứng minh rằng 0  A
, từ đó suy ra A chỉ nhận duy nhất một giá trị nguyên với a  0; a  4 . 2
6. Tính giá trị của A khi a là số nguyên thỏa mãn 2  16  4.25b a ab  .
Bài toán 4. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2008 – 2009; Khóa thi 30.06.2008.  2 3   6 
Cho biểu thức P  1  . 1   
 với 0  x  1.  x 1 x 1   x  5 
1. Rút gọn biểu thức P.
2. Tính giá trị của biểu thức P khi x  6  2 5 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 6
_______________________________________________________________________________________________________________________________________________________________ 2
3. Tìm giá trị của x để P  . 3 x
4. Tìm tất cả các khoảng giá trị của x sao cho P  . 2 x 1
5. Chứng minh rằng biểu thức P chỉ nhận đúng một giá trị nguyên với 0  x  1.
x  3 x  4
6. Tính giá trị của P khi x là số tự nhiên thỏa mãn   . 3x
Bài toán 5. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2015 – 2016; Khóa thi 08.06.2015. 2 2x  2 x x 1 x x Cho biểu thức P   
x  0; x   1 . x x x x x x
1. Rút gọn biểu thức P.
2. Tính giá trị của biểu thức P khi x  3  2 2 .
3. Tìm giá trị của x để P nhận giá trị bằng 7. 4. So sánh P với 6. 7
5. Chứng minh rằng với mọi giá trị của x để biểu thức P có nghĩa thì biểu thức chỉ nhận một giá trị P nguyên. 3x 1
6. Tính giá trị của P khi x là số nguyên lớn nhất sao cho   . 2 x x 1
Bài toán 6. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2011 – 2012; Khóa thi 30.06.2011. 3 1 x  3 Cho biểu thức A   
với x  0; x  1. x 1 x 1 x 1 1. Rút gọn A.
2. Tính giá trị của A khi x  3  2 2 . 1 1
3. Tìm các khoảng giá trị của x để  A  . 5 2 x  6
4. Tìm giá trị của x để A  . 6x
5. Chứng minh rằng với x  0; x  1thì biểu thức A chỉ có duy nhất một giá trị nguyên.
6. Tính giá trị của A khi x là số tự nhiên nhỏ nhất sao cho 3 2
n  7n  6n chia hết cho 125.
Bài toán 7. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2013 – 2014; Khóa thi 02.07.2013.  x 1 x  2  1
Cho biểu thức P     :
(với x  0; x  1).  x x x 1   x 1  
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  4  2 3  3  5 . 9
3. Tìm giá trị của x để P  . 2
4. Tìm giá trị của x để P  8, 25 .
5. Tìm giá trị nhỏ nhất của biểu thức P.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 7
_______________________________________________________________________________________________________________________________________________________________
Bài toán 8. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2007 – 2008; Khóa thi 30.06.2007. 2 x  3 x
Cho phương trình A   1. x  2 x  2 x
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  841.
3. Tìm giá trị của x để A  3 .
4. Tìm khoảng giá trị của x để A  1  .
5. Tìm tất cả các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
6. Tìm giá trị của m để phương trình A m có nghiệm.
Bài toán 9. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Kỳ
thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2014 – 2015; Khóa thi 04.07.2014.  1 1  x 1 Cho biểu thức P   :  
với x  0; x  1.  x x
x 1  x  2 x 1 1. Rút gọn biểu thức P.
2. Tìm x để P  1  .
3. Tính giá trị của P khi x thỏa mãn hệ thức  x   1 2 x   1  0 .
4. Tính giá trị của P khi x  9  4 5  3 5 11. 1
5. Tìm tất cả các giá trị của x để P   5 . x 1
6. Tìm giá trị nhỏ nhất của biểu thức Q   3P . x
Bài toán 10. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình; Năm học 2005 – 2006. 5 x x   x  2 3 2  Cho biểu thức A    . x  4 x  3 x  7 x 12
1. Rút gọn biểu thức A.
2. Tìm các giá trị x để 3 a) A  . 2 b) A x . c) A  1  . 3  5
3. Tính giá trị của A khi x  . 8 1 1
4. Tồn tại hay không các số thực x và y thỏa mãn hệ thức 2 A   y   x . 10 11
5. Tìm giá trị nhỏ nhất của A trong trường hợp 0  x  16; x  9 .
Bài toán 11. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2010 – 2011; Khóa thi 20.06.2010. x  7 x  3 2 x 1 Cho biểu thức A   
với x  0; x  4; x  9 . x  5 x  6 x  2 x  3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 8
_______________________________________________________________________________________________________________________________________________________________ 1. Rút gọn A.
2. Tính giá trị của A khi x  3  2 2 .
3. Tìm giá trị của x để a) A  4 . b) A  2 . 1 1
4. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức 2 A   x y  . 6 5 1 x  6
5. Tìm giá trị nhỏ nhất của biểu thức B   . A x
Bài toán 12. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2011 – 2012; Khóa thi 20.06.2011. x  3 x  2 9  x Cho biểu thức P   
với x  0; x  4 . 2  x 3  x x x  6 1. Rút gọn P. 7
2. Tìm x để P  . 12 1
3. Tìm x để P  . 2
4. Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên.
5. Tìm tất cả các giá trị hữu tỷ của x để P nhận giá trị nguyên.
Bài toán 13. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình; Năm học 2009 – 2010. 2 x  4 x  7 x 1 Cho A   
x  0; x   1 . x  3 x  2 x  3 x 1 1. Rút gọn A.
2. Tính giá trị của A khi x thỏa mãn đẳng thức 2x  5 x  2  0 . x 1
3. Tìm các giá trị của x để A  . 8 1
4. Tìm các giá trị của x để A  . 6
5. Chứng minh rằng với điều kiện x  0; x  1thì A chỉ nhận duy nhất một giá trị nguyên. Tìm giá trị nguyên đó.
Bài toán 14. Mở rộng và phát triển bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2014 – 2015; Khóa thi 02.07.2012. 2  x  4 x 8 Cho biểu thức B   
với x  0; x  16 . x  3 x  4 x 1 x  4 1. Rút gọn B.
2. Tìm giá trị của x để B  1 .
3. Tính giá trị của B khi x thỏa mãn đẳng thức 2x 1  x . 3
4. Tìm giá trị của x sao cho B không vượt quá . 2
5. Tìm x để giá trị của B là một số nguyên.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 9
_______________________________________________________________________________________________________________________________________________________________
Bài toán 15. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình; Năm học 2016 – 2017.
x x x  2 1  1
Cho biểu thức P     :
x  0; x   1 .  x 1 x 1    x x x  
1. Rút gọn biểu thức P.
2. Tìm x để P  2 .
3. Tìm x để P có giá trị nhỏ nhất.
4. Tìm khoảng giá trị của x để P  12 .
5. Tính giá trị của P khi x thỏa mãn x 1  3x  7  x  4 .
6. Tồn tại hay không các số nguyên x và y thỏa mãn đẳng thức
a) P   y  2015 y  2016  2017 . b) 4 2
P y y  2 .
Bài toán 16. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình; Năm học 2012 – 2013.  x 8 x  8
x  2  x  2 x  5
Cho biểu thức A      : với x  0 .  x 2 x 2 x x    x  2 x  
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x thỏa mãn x x   1  2 .
3. Tính giá trị của A khi x là nghiệm của phương trình 2 3
x  2x  4  3 x  4x . 4
4. Tìm giá trị của x để A  . 5
5. Chứng minh rằng A  1, từ đó suy ra A chỉ nhận duy nhất một giá trị nguyên với x  0 .
6. Phần nguyên của x, ký hiệu [x], biểu thị số nguyên lớn nhất không vượt quá x.  x  4 
Chứng minh rằng khi x thỏa mãn phương trình phần nguyên  x 1 
thì A nhận hai giá trị. 2   
Bài toán 17. Mở rộng và phát triển câu 1.b); Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2016 – 2017; Khóa thi 16.06.2016.  x 3  x  3
Cho biểu thức A    .
với x  0; x  9 .  x  3
x  3  x  9   1
1. Chứng minh rằng A  . x  3 1
2. Tính giá trị của biểu thức A khi x  3  2 2  . 1 2
3. Tính giá trị của biểu thức A khi x thỏa mãn x  5 x  6 . 1
4. Tìm tất cả các giá trị của x để A  . 2 3 5  x
5. Tìm x sao cho A thỏa mãn đẳng thức A   . 2 x  3 3 n 1
6. Khi n là số tự nhiên sao cho S
là số nguyên tố. Tìm x sao cho A S  1. 9
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 10
_______________________________________________________________________________________________________________________________________________________________
Bài toán 18. Mở rộng và phát triển bài 2; Đề kiểm tra chất lượng học kỳ I; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo; Quê hương Thái Bình; Năm học 2015 – 2016. 2  x 2  x 4x Cho biểu thức P    . 2  x 2  x x  4
1. Tìm điều kiện xác định của biểu thức P. Rút gọn biểu thức P.
2. Tìm x để P  2 .
3. Tính giá trị của biểu thức P tại x thỏa mãn  x  22 x   1  0 . 9x 2
4. Tính giá trị của P khi x là giá trị nhỏ nhất của biểu thức S   ; 0  x  2 . 2  x x x  3
5. Tìm giá trị của x để P  . 2 x 1
6. Tìm tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức 2
A  3  1 4x xy .
Bài toán 19. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình; Năm học 2002 – 2003.  x  3 x   1 x  3 x  2 
Cho biểu thức A   1 :     .  x 9   x x 6 x 2 x 3          
1. Rút gọn biểu thức A. 25
2. Tính giá trị của A tại x  . 16
3. Với giá trị nào của x thì biểu thức A nhận giá trị âm.
4. Tính giá trị của A khi x  7  2 6  3. x
5. Tìm giá trị của x sao cho A  . 2 x  5 a  9
6. Tính giá trị của A khi x là giá trị lớn nhất của biểu thức S  ; a  9 . 5a
Bài toán 20. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2014 – 2015; Khóa thi 20.06.2014.  2 3 5 x  7  2 x  3
Cho biểu thức A      :
x  0; x  4 .  x 2 2 x 1 2x 3 x 2      5x 10 x  
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x thỏa mãn 2x 1  7  x . 3 x  2
3. Tìm tất cả các giá trị của x sao cho A  . x  2 15
4. Tìm giá trị của x sao cho A  . 7
5. Tìm x sao cho A nhận giá trị là một số nguyên.
6. Tính giá trị của A khi x là số nguyên dương thỏa mãn 2  3  3  11.49y x xy   .
7. Tồn tại hay không các số thực x và y thỏa mãn 2 2 A  3  x y .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 11
_______________________________________________________________________________________________________________________________________________________________
Bài toán 21. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình; Năm học 2006 – 2007. 1 1 x 1 1 x 1 Cho A    .
1 x  1 x
1 x  1 x 1 x
1. Rút gọn biểu thức A. 3
2. Tính giá trị của biểu thức A khi x  . 4 2
3. Tìm giá trị của x để A  . 1 x  3 2 4. So sánh A và . 2 2 1 2015 2015
5. Tính giá trị của A khi 2 x  2015  1 2015   . 2 2 2016 2016
Bài toán 22. Mở rộng và phát triển bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2010 – 2011.  3 1  x  9 Cho biểu thức A   .  
với x  0; x  9 .  x  3 x x  3  x
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi x  6  2 5 . 8
3. Tìm giá trị của x sao cho A  . 5 10
4. Tìm x sao cho A  . 2 x
5. Tính giá trị của A khi x là số nguyên lớn nhất sao cho 2
x x 13 là một số chính phương.
6. Tồn tại hay không các số nguyên x và y thỏa mãn A  2 y 1.
7. Tìm x sao cho A a  2 , trong đó a là nghiệm lớn nhất của phương trình 2
a a   a   2 4 7 7 a  7 .
Bài toán 23. Mở rộng và phát triển bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Lê
Quý Đôn; Tỉnh Ninh Thuận; Năm học 2016 – 2017.  x  2 2  x x 1
Cho biểu thức P    .
với x  0; x  1; x  2 .
x  2 x 1 x 1   x  2  
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x thỏa mãn 3 x x  30 .
3. Tìm x để P  5 x  2 .
4. Tìm các giá trị nguyên của x để P  2 .
5. Tìm các giá trị nguyên của x để P nhận giá trị nguyên.
6. Tính giá trị của P khi x là nghiệm lớn nhất trong các nghiệm  ;
x y của hệphương trình 2 
x xy 1  y  2x,  2 2
2x y  9  .  4
7. Chứng minh rằng không tồn tại các số thực x và y thỏa mãn 4 P
 1 2x  3xy . 3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 12
_______________________________________________________________________________________________________________________________________________________________
Bài toán 24. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả thí
sinh dự thi); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Thái Bình; Quê hương Thái Bình;
Năm học 2007 – 2008; Khóa thi 19.06.2007. 2 x  9 x  3 2 x 1 Cho A    . x  5 x  6 x  2 3  x 1. Rút gọn A.
2. Tính giá trị của A với x  3  2 2 . x  6
3. Tìm giá trị của x để A  . 5
4. Tìm giá trị của x để A  2 .
5. Tìm các giá trị nguyên của x để A nhận giá trị nguyên. 1
6. Tính giá trị của A khi x là giá trị nhỏ nhất của S  8 4 4 a b  
, với a,b  0; a b  1. ab
Bài toán 25. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Kỳ thi tuyển sinh lớp 10 THPT; Quê hương Thái Bình; Năm học 2015 – 2016. x x 2 x 1 x  6 x  4 Cho biểu thức P   
với x  0; x  4 . x  2 x  2 x  4
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  9  4 5 .
3. Tìm giá trị của x để P  2 .
4. Tìm giá trị của x để P x  3 .
5. Tìm tất cả các giá trị của m để phương trình P m có nghiệm.
6. Tìm giá trị nhỏ nhất của biểu thức P .
7. Tính giá trị của biểu thức P khi x là nghiệm phương trình 2x 1  3x x 1. a 8. Tìm x sao cho P
trong đó a và b là hai số thực dương khác nhau thỏa mãn a 10b  11 ab . b
Bài toán 26. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Kỳ thi tuyển sinh lớp 10 THPT Chuyên Lê
Quý Đôn; Tỉnh Bình Định; Năm học 2016 – 2017. 2 x x   x 3 3  x  3 Cho biểu thức P   
với x  0; x  9 . x  2 x  3 x 1 3  x
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi 2
x  5x  4  0 .
3. Tính giá trị của biểu thức P khi x  7  4 3 . 5 x
4. Tìm giá trị của x để P   2 . 2
5. Tìm giá trị nhỏ nhất của biểu thức P.
6. Tìm tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên. 2 2 a b
7. Tính giá trị của P khi x là số thực nhỏ nhất thỏa mãn x  ; a,b   . 2 2  
a ab b
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 13
_______________________________________________________________________________________________________________________________________________________________
Bài toán 27. Mở rộng và phát triển câu 1.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố
Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2003 – 2004. 2 2 x x x x Cho biểu thức M  
x 1 với 0  x  1. x x 1 x x 1
1. Rút gọn biểu thức M. 1
2. Tính giá trị của biểu thức M khi x  . 4
3. Tính giá trị của biểu thức M khi x thỏa mãn 2
9x  3x 1  6x 1 . 1
4. Tìm x thỏa mãn hệ thức M  5x  . 9
Bài toán 28. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi lớp chuyên Khoa học Tự nhiên); Đề thi chính thức; Trường THPT Chu Văn An và THPT
Chuyên Hà Nội – Amsterdam; Thủ đô Hà Nội; Năm học 2003 – 2004. 2 x x 2x x 2  x   1 Cho biểu thức P    . x x 1 x x 1 1. Rút gọn P.
2. Tính giá trị của P khi x thỏa mãn 2  x  4  x .
3. Tính giá trị của P khi x thỏa mãn 3 x x  10 .
4. Tìm giá trị nhỏ nhất của P.
5. Tìm tất cả các giá trị x sao cho P  4 x  5 . 2 x
6. Tìm x để biểu thức Q
nhận giá trị là số nguyên. P
7. Giả sử x thỏa mãn 2
2x  3  5  2x  3x 12x 14 . Khi đó giá trị của P là số hữu tỷ hay số vô tỷ ?
Bài toán 29. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi lớp chuyên Khoa học Tự nhiên); Đề thi chính thức; Trường THPT Chu Văn An và THPT
Chuyên Hà Nội – Amsterdam; Thủ đô Hà Nội; Năm học 2005 – 2006. x x 1 x x 1 x 1 Cho biểu thức P    . x x x x x 1. Rút gọn P. 9
2. Tìm x để P  . 2 6x 1
3. Tìm các giá trị của x để P  . x
4. Tính giá trị của P khi 3 3 x  2  5  2  5  3 .
5. Tìm số thực a lớn nhất sao cho P a .
6. Tìm tất cả các giá trị của tham số m để phương trình P m có nghiệm.
7. Với các số thực a  1, b  2, c  3 , phản biện bất đẳng thức 2 2 2
P a 1 a b 2  b c 3  c 1.
Bài toán 30. Mở rộng và phát triển câu 5b (Chương trình THCS Thí điểm); Đề thi chọn học sinh giỏi lớp 9
THCS; Đề thi chính thức; Sở Giáo dục và Đào tạo Thành phố Hồ Chí Minh; Năm học 2003 – 2004. 
x  3 x   x  3 x  2 9  x
Cho biểu thức P  1  :   
 với x  0; x  4; x  9 .  x 9   2 x 3 x x x 6          
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 14
_______________________________________________________________________________________________________________________________________________________________
1. Thu gọn biểu thức P.
2. Tính giá trị của P khi x  7  4 3 .
3. Tính các giá trị của P khi x thỏa mãn 2
2x  5  x  3x 1.
4. Tìm các giá trị của x để P  1 . 4P x
5. Tìm các giá trị của x để  . 9 x  2 3 P
6. Tồn tại hay không số thực x sao cho P là nghiệm của phương trình 2  P  4  0 . 2 4  P
Bài toán 31. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi lớp chuyên Khoa học Tự nhiên); Đề thi chính thức; Trường THPT Chu Văn An và THPT
Chuyên Hà Nội – Amsterdam; Thủ đô Hà Nội; Năm học 2004 – 2005. 2  x 1 x 1   1 x
Cho biểu thức P        .  x 1 x 1   2 x 2       
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  16 . x  5
3. Tìm x để P  . 4 P
4. Tìm giá trị của x để  2 . x
x  4 y  4  0, 
5. Tính giá trị của P khi x là nghiệm của hệ 
y  4 x  4  0. 
6. Tính giá trị của P khi x là số thực nhỏ nhất thỏa mãn a  5  7  a x a   .
Bài toán 32. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 1993 – 1994; Ngày thi 08.08.1993.
 2x x 1 2x x x x x x
Cho biểu thức A  1   . .  1 x 1 x x    2 x 1  
1. Tìm điều kiện của x để A có nghĩa. 2. Rút gọn A.
3. Tính giá trị của A khi x  9 . 6  6 4. Tìm x biết A  . 5 2
5. Chứng minh rằng A  là bất đẳng thức sai. 3 16
6. Tính giá trị của A khi x thỏa mãn x  . x  4
7. Tính giá trị của A khi x thỏa mãn phương trình 2
x  2x  7  3  x  
1  x  3  0 .
Bài toán 33. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2001 – 2002.
 3x  9x  3 1 1  1
Cho biểu thức P      2  : .
x x  2 x 1 x  2  x 1  
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 15
_______________________________________________________________________________________________________________________________________________________________
1. Tìm điều kiện của x để P có nghĩa, khi đó hãy rút gọn P. 1
2. Tìm các số tự nhiên x để là số tự nhiên. P
3. Tính giá trị của P khi x  4  2 3 .
4. Tính giá trị của P khi 3 3
x  5 2  7  5 2  7 .
5. Tìm x sao cho P  8 x  16  x . 1
6. Tìm các giá trị của x sao cho 3 P  . P 2 y y 1
7. Phản biện bất đẳng thức 3P  . 2 y y 1
Bài toán 34. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2003 – 2004. x  2 x 1 1 Cho biểu thức A    . x x 1 x x 1 x 1
1. Tìm x để A có nghĩa. Hãy rút gọn A.
2. Tính A với x  33  8 2 . 1
3. Chứng minh rằng A  . 3 x
4. Tìm tất cả các giá trị x để A  . 6 x 1 1 1
5. Tính giá trị của A khi 7 x a  với a   3 . 7 a a
6. Tìm giá trị lớn nhất của A.
7. Tìm tất cả các giá trị của x để A nhận giá trị nguyên.
Bài toán 35. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2004 – 2005.
 2x x x x x x x 1 x
Cho biểu thức M    .  .  x x 1 x 1   2x x 1 2 x 1  
1. Hãy tìm điều kiện của x để biểu thức M có nghĩa, sau đó rút gọn M . 6
2. Tìm tất cả các giá trị của x sao cho P  . 7
3. Tính giá trị của M khi 3
x a  3a  3 với 3 3
a  3  2 2  3  2 2 . abc
4. Tính giá trị của M khi x là giá trị lớn nhất của biểu thức S
a,b,c  0 .
a bb cc a 2x
5. Tìm tất cả các giá trị của x sao cho P  . 2 x 1
6. Với giá trị nào của x thì biểu thức M đạt giá trị nhỏ nhất và tìm giá trị nhỏ nhất đó của M .
Bài toán 36. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2006 – 2007.  x   1 2 x
Cho biểu thức P  1  :    1 .  x 1   x 1 x x x x 1          
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 16
_______________________________________________________________________________________________________________________________________________________________
1. Tìm điều kiện của x để biểu thức P có nghĩa và rút gọn biểu thức P .
2. Tính giá trị của P khi x  21 8 5 .
3. Tính giá trị của P khi x  3  5 3 5 10  2 .
4. Tính giá trị của P khi x a b c với a, ,
b c là các số thực thỏa mãn đồng thời các hệ thức a b c a b c    1;    1. 3 12 4 10 5 3
5. Tìm các giá trị của x sao cho P x  4 . 4 x  3 1 1
6. Tìm các giá trị của x sao cho   . x  4 P 2
7. Tìm các giá trị nguyên của x để biểu thức Q P x nhận giá trị nguyên.
Bài toán 37. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2010 – 2011; Ngày thi 06.06.2010.  x 2x   x 1 2 
Cho biểu thức P     :    .
 3 x 9 x   x  3 x x      
1. Tìm điều kiện của x để biểu thức P có nghĩa và rút gọn P. 4
2. Tìm giá trị của x để P   . 3 x  5
3. Tìm tất cả các giá trị của x sao cho P  . 16 x 4 4 4
a b c
4. Tìm các giá trị của x sao cho P
 2 với a b c  0 . 2 2 2 2 2 2
a b b c c a 1 1 2
5. Tính giá trị của P khi 2
x  4a  2a  2 1với a  2   . 2 8 8
6. Chứng minh rằng S P a  P b  3 là một số nguyên tố, trong đó a và b là các số thực dương thỏa mãn đẳng thức  2 a   2 2 1 b   1  a   1 b   1 ab   1 .
Bài toán 38. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2014 – 2015; Ngày thi 06.06.2014.
x  2 x  4
x  2 x 1   1 2 
Cho biểu thức A     : 3   .     x x  8 x 1    x  2 x 1  1. Rút gọn A.
2. Tính giá trị của A khi x  9  4 5 .
3. Tìm giá trị của x để A  1 . 10 x
4. Tìm x sao cho A  . 9  x  2
5. Tính giá trị của A khi x là số nguyên thỏa mãn 2 x x    2 2 7 3 x   1  x  3 .
6. Tìm m để phương trình A m có nghiệm.
7. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức 8A  1 2x y  2  3y x .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 17
_______________________________________________________________________________________________________________________________________________________________
Bài toán 39. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1990 – 1991.  x 1 1 5 x   3 x  2 
Cho biểu thức P      : 1  .
 3 x 1 3 x 1 9x 1  3 x 1       1. Rút gọn P.
2. Tính giá trị của P khi 2
9x 10x 1  0 .
3. Tính giá trị của P khi x  8  2 7 . 6
4. Tìm các giá trị của x để P  . 5 x
5. Tìm x sao cho P  . 5 x  3
6. Tính giá trị của P khi 12 2 2 12
x a a b b với a và b là các số thực thỏa mãn đồng thời 4 2 2 4 8 4 4 8
a a b b  4; a a b b  8 .
Bài toán 40. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1992 – 1993.  2 x x 1   x  2 
Cho biểu thức B     : 1  .  x x 1 x 1   x x 1          1. Rút gọn B.
2. Tính B khi x  5  2 3 . 1
3. Tìm x để B  . 3 2x x 1 1
4. Tìm giá trị của x để giá trị của B không lớn hơn giá trị biểu thức . x  2
5. Với mỗi số thực a, ký hiệu [a] là phần nguyên của a, tức là số nguyên lớn nhất không vượt quá a. 1 1 1
Tồn tại hay không giá trị của x để B  S  , trong đó S  1   ...  . 2 3 100 6. Giả sử a, ,
b c là độ dài ba cạnh của một tam giác. Tính giá trị của biểu thức B khi
a b cb c ac a b  x max    2 . abc  
Bài toán 41. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1993 – 1994.  x 1 2x x   x 2x x
Cho biểu thức M    1 : 1   .  2x 1 2x 1   2x 1 2x 1          1. Rút gọn M. 1
2. Tính giá trị của M khi x  3 2 2 . 3
3. Tìm tất cả các giá trị của x sao cho B x  4 . 2
4. Tìm khoảng giá trị của x sao cho B   . 3
5. Tính giá trị của M khi x là giá trị lớn nhất của biểu thức A a 1  a  8, a  8 .
ab bc ca
6. Với các số thực dương a,b, c , tìm giá trị lớn nhất của biểu thức C   B .
a b c
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 18
_______________________________________________________________________________________________________________________________________________________________
Bài toán 42. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1994 – 1995. 3  2a 1 a   1 a
Cho biểu thức P    .  a  .  3   a 1 a a 1  1 a        1. Rút gọn P.
2. Tính giá trị của biểu thức P khi a  11 96 .
3. Tìm giá trị của a để P a  4 a 1 .
4. Tìm giá trị của a để giá trị biểu thức P không vượt quá 4a  5 a 1.
5. Xét dấu của biểu thức P 1 a .
6. Tính giá trị của biểu thức P khi a thỏa mãn hệ thức a a   b 2 5 2 2  b 1  0 .
7. Tìm tất cả các giá trị của tham số m để phương trình P  2a  6 a m có nghiệm.
Bài toán 43. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1995 – 1996.  a 1 a 1
8 a   a a  3 1 
Cho biểu thức B      :    .  a 1 a 1 a 1   a 1 a 1       
1. Rút gọn biểu thức B.
2. Tính giá trị của B khi a  3  2 2 .
3. Tính giá trị của B khi a là nghiệm của phương trình 2 a  
1  a  3  0 .
4. Tính giá trị của B khi 3 3
a  17 5  38  17 5  38 . 5. So sánh B với 1.
6. Tìm tất cả các giá trị của a để B nhận giá trị là số nguyên. 12
7. Tìm a để B  . 13
Bài toán 44. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1995 – 1996.  1 1   a 1 a  2  Cho biểu thức A   :      .  a 1 a   a 2 a 1       1. Rút gọn A.
2. Tính giá trị của A với a  16 .
3. Tính giá trị của A với a thỏa mãn 31 a  10 a . 1 1 1
4. Tính giá trị của A khi a    ...   5 . 1 2 2  3 2024  2025 1
5. Tìm giá trị của a để A  . 6 1
6. Tìm giá trị của a để A  . 6  a
7. Tìm số thực nhỏ nhất m sao cho A m .
Bài toán 45. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1996 – 1997.  1 2 x  2   1 2 
Cho biểu thức A     :    .  x 1
x x x x 1     x 1 x 1 
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 19
_______________________________________________________________________________________________________________________________________________________________
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x thỏa mãn  x  6 x  20 .
3. Tính giá trị của A khi x  4sin 60  2 sin 45  3 2 cos 45 .
4. Tính giá trị của A khi x là số thực nhỏ nhất thỏa mãn 2  a  2  a x, a  2  ; 2.
5. Với giá trị nào của x thì A đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó. x
6. Tìm giá trị của x để giá trị của A không nhỏ hơn giá trị biểu thức . x  4
7. Tìm tất cả các giá trị của m sao cho tồn tại đẳng thức A m .
Bài toán 46. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1998 – 1999.  2x 1 1   x  4  Cho biểu thức P   : 1     . 3  x 1 x 1   x x 1 
1. Rút gọn biểu thức P. 1 1
2. Tính giá trị của P khi x    4 . 3  2 3  2 2 y y 1
3. Tìm khoảng giá trị của x để giá trị của P thuộc tập giá trị của hàm số f y  ; y   . 2 y y 1
4. Tìm giá trị nguyên của x để P nhận giá trị nguyên dương.
5. Ký hiệu [a] là phần nguyên của a, tức là số nguyên lớn nhất không vượt quá a.  4  3x  5x  5
Tính giá trị của biểu thức P khi x là nghiệm của phương trình   . 5    7
Bài toán 47. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 1999 – 2000.  x 1   1 2 
Cho biểu thức P     :    .  x 1 x x     x 1 x 1  1. Rút gọn P. 2  3  14  5 3
2. Tính giá trị của P khi x  1. 2
3. Tìm các giá trị của x để P  0 . 847 847
4. Tồn tại hay không giá trị x để 3 3 P  6   6  . 27 27
5. Tìm các số m để có các giá trị của x thỏa mãn P x m x . 3
6. Tìm tất cả các giá trị x sao cho P  3x   8 . x
Bài toán 48. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2000 – 2001.   x  4 3  x  2 x  Cho biểu thức P     :    .  
x x  2 x  2  x x  2     1. Rút gọn P.
2. Tính giá trị của P khi x thỏa mãn x  36 .
3. Tính giá trị của P biết x  6  2 5 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 20
_______________________________________________________________________________________________________________________________________________________________ 3
4. Tìm x để giá trị của P không vượt quá x x . 2 5. Tìm x sao cho 3
P  2  3  x . 2 2 x  4 y  4
6. Tính giá trị của P khi x thỏa mãn hệ thức 
 8  4  x 1  y 1. x y
7. Tìm các giá trị của n để có x thỏa mãn P x   1  x n .
Bài toán 49. Mở rộng và phát triển bài 1, phần B; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2001 – 2002.  x  2   x x  4  Cho biểu thức P x  :      .  x 1   x 1 1 x     1. Rút gọn P. 1 1
2. Tính giá trị của P khi x    7 . 9  4 5 9  4 5
3. Tính giá trị của P khi x thỏa mãn 3 2
x  6x 10x  6x  9 .
4. Tìm các giá trị x để P  0 . 5 x
5. Tìm các giá trị x để P  . 4  x  3
6. Tìm giá trị nhỏ nhất của P.
7. Tìm các giá trị của m để tồn tại x sao cho P m .
Bài toán 50. Mở rộng và phát triển bài 1; Đề thi tốt nghiệp THCS; Môn Toán; Đề thi chính thức; Sở Giáo
dục và Đào tạo Thành phố Hà Nội; Năm học 2003 – 2004.  1   x 1 1 x  Cho biểu thức P x  :      .  x   x x x     1. Rút gọn P. 2
2. Tính giá trị của P khi x  . 2  3
3. Tính giá trị của P khi x  3a  2c với a, ,
b c là các số thực thỏa mãn đẳng thức 2 2 2
a 1 b b 2  b c 3  a  3 . 1
4. Tìm các giá trị của x để P x  . 2
5. Tìm các giá trị của x thỏa mãn P x  6 x  3  x  4 .
6. Tìm giá trị nhỏ nhất của biểu thức S P  3 x .
Bài toán 51. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2006 – 2007.   a  3 a  2 a a  1 1  Cho biểu thức P     :  .    
a  2 a   1
a 1   a 1 a 1    1. Rút gọn P.
2. Tính giá trị của P khi a  9  4 2 .
3. Tính giá trị của P khi a là giá trị nhỏ nhất của 4 3
A y  4 y  8 y  20 , y là số thực. 4. So sánh P với 1.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 21
_______________________________________________________________________________________________________________________________________________________________ 1 a 1 5. Tìm a để   1. P 8 2 2z  4z  5
6. Chứng minh rằng P  5  , z    . 2 z 1
Bài toán 52. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2007 – 2008. x 3 6 x  4 Cho biểu thức P    . x 1 x 1 x 1 1. Rút gọn P.
2. Tính giá trị của P khi x  27 10 2 . 1
3. Tìm x để P  . 2 x  5
4. Tìm x để P  . x 19
5. Tìm m để phương trình P x m có nghiệm thực. 2 a
6. Tính giá trị của P khi x max 
b , trong đó a và b là hai số thực thỏa mãn 2
ab b b . 3
Bài toán 53. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2008 – 2009.  1 x x
Cho biểu thức P     : .  x x 1   x x   1. Rút gọn P.
2. Tính giá trị của P khi x  4 . 13
3. Tìm giá trị của x để P  . 3
4. Tính giá trị của P khi x thỏa mãn 2
x  4x  3  0 .
5. Tìm giá trị nhỏ nhất của biểu thức P. 4
6. Chứng minh rằng biểu thức
chỉ nhận duy nhất một giá trị nguyên. P
Bài toán 54. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2009 – 2010; Ngày thi 24.06.2009. x 1 1 Cho biểu thức A   
với x  0; x  4 . x  4 x  2 x  2
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi x  25 . 1
3. Tìm giá trị của x để A   . 3 3x  2 x
4. Tìm giá trị của x để A  . x  2
5. Tồn tại hay không các cặp số thực (x;y) thỏa mãn đẳng thức 3A  1 x y  2  y x .
6. Tìm khoảng giá trị của A khi x thỏa mãn hệ thức x  3  4 x 1  x  8  6 x 1  5 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 22
_______________________________________________________________________________________________________________________________________________________________
Bài toán 55. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2010 – 2011; Ngày thi 22.06.2010. x 2 x 3x  9 Cho biểu thức P   
; với x  0; x  9 . x  3 x  3 x  9 1. Rút gọn P.
2. Tính giá trị của P khi 2
x  3x  4  0 . 3  5
3. Tính giá trị của P khi x  . 2 1
4. Tìm giá trị của x để P  . 3 x  5 5. Tìm x để A  . 8
6. Tính giá trị của P khi x thỏa mãn hệ thức 2 x x 1  2x 1 .
7. Tìm giá trị lớn nhất của P, từ đó suy ra P chỉ nhận duy nhất một giá trị nguyên.
Bài toán 56. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Thành phố Hà Nội; Năm học 2011 – 2012; Ngày thi 22.06.2011. x 10 x 5 Cho biểu thức A   
với x  9; x  25 . x  5 x  25 x  5 1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  9 . 1
3. Tìm giá trị của x để A  . 3
4. Tìm giá trị nguyên của x để A nhận giá trị nguyên.
5. Tìm giá trị thực của x để A nhận giá trị nguyên.
6. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức A 1  2  x y .
Bài toán 57. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 1999 – 2000; Ngày thi 01.07.1999. 1 x 1
Cho biểu thức P x  : . 2 x x x x x x
1. Tìm x để biểu thức P có nghĩa. Rút gọn P.
2. Tính giá trị của P khi 4 x  17  2 2 . 4 x  4
3. Tìm x sao cho 5  5P  . 2 x  2 2 P  2x
4. Tìm các số nguyên x để Q  nhận giá trị nguyên. x 1
5. Với giá trị nào của x thì P có thể giữ vai trò biến b của phương trình      2 a b ab a b ?
Bài toán 58. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2015 – 2016; Ngày thi 06.06.2015.  xx
x  2  x  Cho biểu thức A     .  2 
 , trong đó x là biến số thực.  x  2
x x  8   x  2   
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 23
_______________________________________________________________________________________________________________________________________________________________
1. Tìm điều kiện của x để A có nghĩa và rút gọn A.
2. Tính giá trị của A khi x  25 .
3. Tính giá trị của A khi x thỏa mãn  x   1 x  2 .
4. Chứng minh với mọi giá trị thực m khác 0, phương trình A m luôn luôn có nghiệm. 4
5. Tìm các giá trị của x sao cho A   0 . x  4
6. Tính giá trị của A khi x là nghiệm của phương trình 3x  3  3  x x  3x  33  x 1.
a b c  5,
7. Giả sử ba biến số thực a,b, c thỏa mãn hệ thức abbc ca  8. 
Tìm khoảng giá trị của x để biểu thức A có thể giữ vai trò là một trong các biến a,b, c .
Bài toán 59. Mở rộng và phát triển câu 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2016 – 2017; Ngày thi 04.06.2016.
 3x x  8x  5 1 1 
Cho biểu thức A      2  : .    x   1 x x  2 x 1 x  2  
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x thỏa mãn  2 2 x   1  5x . 2 2x x  5
3. Tìm các giá trị của x để A   . 2 x 1 x 1
4. Tìm các giá trị của x để giá trị của A không vượt quá 4.
5. Tìm giá trị nguyên của x để giá trị của A là một số nguyên.
6. Tính giá trị của A khi x là nghiệm lớn nhất của phương trình 4 2
x  2x  8x  3 .
7. Ký hiệu [m] là số nguyên lớn nhất không vượt quá m, tính giá trị của A khi x  7 4 15    .    
a b c  5,
8. Tìm khoảng giá trị của x để A có thể giữ vai trò biến a trong hệ thức  2 2 2
a b c  11. 
Bài toán 60. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Khối THPT Chuyên Đại học Sư phạm; Đại
học Sư phạm Hà Nội; Năm học 2007 – 2008. x 1 1 Cho các biểu thức 4 2 P  : ,
Q x  7x 15 . 2 x x x x x x
1. Rút gọn biểu thức P.
2. Tìm giá trị nhỏ nhất của Q.
3. Tìm giá trị của x để Q x .
4. Tính P a.Q b với (a;b) cặp số nguyên dương có tổng lớn nhất thỏa mãn    2 2
2 a b ab a b .
5. Với giá trị nào của x thì Q  4P đạt giá trị nhỏ nhất ?
a b c d  5,
6. Tìm khoảng giá trị của x để P có thể giữ vai trò một trong các biến thỏa mãn  2 2 2 2
a b c d  7. 
Bài toán 61. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1992 – 1993.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 24
_______________________________________________________________________________________________________________________________________________________________ 2 1 1 a  2
Xét biểu thức P    .
2 1 a  21 a  3 1 a 1. Rút gọn P.
2. Tính giá trị của P khi a  3 .
3. Tính giá trị của P khi a thỏa mãn đẳng thức 2
5a  6a  9  4a 32a  3 .
4. Tìm giá trị nhỏ nhất của P.
5. Tìm giá trị nguyên của a để P nhận giá trị nguyên. 2 2
x xy y
6. Tìm khoảng giá trị của a để tồn tại đẳng thức P   0 x, y   . 2 2  
x xy y
Bài toán 62. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1993 – 1994.  1 a a   1 a a    a3 1
Xét biểu thức P   1.  a  : .  a a   1 a    1 a     1. Rút gọn P. 2 2
2. Tính giá trị của P khi a    2 7 . 2  3 2  3
3. Với điều kiện để P có nghĩa, hãy so sánh P với P.
4. Tìm giá trị nhỏ nhất của P trong trường hợp 0  a  1. 6
5. Tìm các giá trị của a để P  . a  6 a
6. Tính giá trị của P khi a là giá trị lớn nhất của hàm số f x 2
x 1 1 2x  2x .
Bài toán 63. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1994 – 1995.  2 x  2 1   1 
Xét biểu thức P     : 1   .  x x x x 1 x 1         x 1  1. Rút gọn P.
2. Tính giá trị của P khi x  3  2 2 .
3. Tìm x để P  0 . 6x  7 x 1
4. Tìm giá trị của x để P  . x x 1
5. Tính giá trị của P khi x thỏa mãn đẳng thức 1 x  2  y 1995  z 1996 
x y z . 2
6. Tìm giá trị của x để P max 2 2
y  3y 18   y  4 y  5 .
a b c  4,
7. Tìm khoảng giá trị của x để P có thể giữ vai trò là một trong các biến của hệ thức abbc ca  5. 
Bài toán 64. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1995 – 1996.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 25
_______________________________________________________________________________________________________________________________________________________________ 3 2x  3 x  2
x x  2x  2
Cho các biểu thức A  , B  . x  2 x  2
1. Rút gọn A và B.
2. Tính giá trị của B khi x  11 2 10 .
3. Tính giá trị của A khi x là nghiệm của phương trình 2
x  94  96  x x 190x  9027 .
4. Tìm giá trị của x để A B .
5. Tìm tất cả các giá trị nguyên của x sao cho A B  3  xx 1. 2 a a 1
6. Tìm x để A B a b trong đó a;b là cặp số nguyên dương có tổng lớn nhất sao cho   . ab 1
Bài toán 65. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1996 – 1997. 3a  9a  3 a  2 1
Xét biểu thức P    1. a a  2 a 1 a  2 1. Rút gọn P.
2. Tìm a để P  1. 1
3. Tính giá trị của P khi a   4 2 . 3  2 2
4. Tìm các giá trị của a   sao cho P   .
5. Tìm a để giá trị của P lớn hơn nghiệm lớn nhất của phương trình 4
x   x   2
1 x  2x  2  0 . x 1
6. Tìm các giá trị a để P  . x  8
7. Tìm điều kiện của tham số m để phương trình P m  2 có nghiệm.
Bài toán 66. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1997 – 1998.
3x x  3 x  3 x  2 Cho biểu thức P    . x x  2 x 1 x  2 1. Rút gọn P.
2. Tính giá trị của P khi x  28 16 3 .
3. Tính giá trị của P khi 4 2
x y 16 y  36 , trong đó y  2  2  3  6  3 2  3 . 15
4. Tìm x để P  . 4 3 x 11
5. Giải phương trình (ẩn x): P  . x  4 2 y  2 y  4
6. Chứng minh rằng giá trị của P luôn nằm ngoài tập giá trị của biểu thức f y  . 2 y  2 y  4
7. Chứng minh rằng 3  P  4 , từ đó dẫn đến P chỉ nhận duy nhất một giá trị nguyên.
Bài toán 67. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1999 – 2000.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 26
_______________________________________________________________________________________________________________________________________________________________  x  3 x  2 x  2   x
Cho biểu thức P      : 1  .  x 2 3 x x 5 x 6   x 1           1. Rút gọn P.
2. Tính giá trị của P khi x thỏa mãn 5x  6 x 1  0 .
3. Tìm các giá trị nguyên của x để P  0 . x  9
4. Tìm các giá trị x để P  . x  2 1
5. Với giá trị nào của x thì biểu thức
đạt giá trị nhỏ nhất. P
6. Tìm các giá trị nguyên của x để P nhận giá trị nguyên.
7. Tồn tại hay không các số thực x và y thỏa mãn đẳng thức 2 6P
2  3xy  4  5x .
Bài toán 68. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 2000 – 2001. 2x  2 x x 1 x x 1
Cho biểu thức P x    . x x x x x
1. Rút gọn biểu thức P.
2. Tính giá trị của P với x  6  2 5 .
3. So sánh P với 5, từ đó phản biện đẳng thức P  4  2  x y . 8
4. Với mọi giá trị của x làm P có nghĩa, chứng minh biểu thức
chỉ nhận đúng một giá trị nguyên. P 5. Tính P  4 2
y y  27 với y là nghiệm của phương trình 4 2 y y 1999  1999 . ab cd
6. Giả sử a,b, c, d là bốn số dương, A là giá trị lớn nhất của biểu thức
. Tính P A   1 .
a d b c
Bài toán 69. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 2001 – 2002.  x  2 x  3 x  2   x
Cho biểu thức P x      :  2   .  x 5 x 6 2 x x 3   x 1           1. Rút gọn P. 1
2. Tính giá trị của P khi x  . 81 2
3. Tìm giá trị của x để P  . x  3 1 5 4. Tìm x để   . P 2
5. Giả sử A là giá trị lớn nhất của biểu thức 2 2
B  a b ab  2a  2b 1 . Chứng tỏ P A là số vô tỷ.
6. Tìm tất cả các giá trị thực của m để phương trình P m  3có nghiệm.
Bài toán 70. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 2002 – 2003.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 27
_______________________________________________________________________________________________________________________________________________________________ x 1 x  2 x 1
Cho biểu thức P x    . x 1 x x 1 x x 1 1. Rút gọn P.
2. Tính giá trị của P khi x thỏa mãn phương trình 3x  5 x  2  0 . 2
3. Tìm giá trị lớn nhất của biểu thức Q   x . P 1 1 1
4. Tính giá trị của P với x     3 . 1  2 2  3 3  4 1
5. Chứng minh rằng   P  0 , từ đó suy ra P chỉ nhận duy nhất một giá trị nguyên. 3 2 2
a ab b
6. Phản biện đẳng thức P a, b   . 2 2  
a ab b y  2001 y  2002
7. Xét f y  
với Max f y  f y . Chứng minh P y  92 là số hữu tỷ. 0  y  2 y
Bài toán 71. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Trường THPT Chuyên Lê Quý Đôn; Thành phố Vũng Tàu; Tỉnh Bà Rịa – Vũng Tàu; Năm học 2011 – 2012. 3 2 x x x 1
Cho biểu thức P x    . x 1 x 1 x 1
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  13  4 3 . 5 1
3. Tính giá trị của P khi x là nghiệm của phương trình 5 x   2x   4 . 2 x 2x 2 x 1
4. Giải phương trình P  . 2 x  3
5. Tìm giá trị nguyên của x để P nhận giá trị nguyên.
6. Chứng minh P chỉ nhận duy nhất một giá trị nguyên (khi P có nghĩa). 1 1 1 1
7. Tính P A khi A    ...    3 . 2 1 1 2 3 2  2 3 2005 2004  2004 2005 2005
Bài toán 72. Mở rộng và phát triển bài 2.3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2006 – 2007.  1 1   x 1  Cho biểu thức A   .  2   
 với x  0, x  1.  x 1
x 1   x 1 
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x thỏa mãn 2
x  7x 10  0 . 2 x  3
3. Tìm x để A  . x  2
4. Tìm những giá trị nguyên của x để A nhận giá trị nguyên.
5. Tính giá trị của A khi x thỏa mãn đẳng thức 2 2 2
x  2 y z  2xy  2 yz zx  3x z  5  0 .
6. Tính giá trị của A khi x là nghiệm của phương trình x   x x   2 2 3 2 3
1  2 2x  3x 10x  3 .
7. Tồn tại hay không các số thực x và y sao cho A  1 2x y  1 3y x .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 28
_______________________________________________________________________________________________________________________________________________________________
Bài toán 73. Mở rộng và phát triển bài III; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2009 – 2010.  x x   x x
Cho biểu thức A   1
1  x với x  0, x  1.  x 1   x 1       
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi x  4  2 3 .
3. Tìm giá trị của x để A  6 x 1.
4. Tìm giá trị nhỏ nhất của biểu thức A.
5. Tính giá trị của A khi 3
x a 12a 1, trong đó 3 a     3 4 5 1  4  5   1 .
6. Phản biện bất đẳng thức A   2
2 x x   1  x .
Bài toán 74. Mở rộng và phát triển bài 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2011 – 2012.  a  3 a   a 1 
Cho biểu thức A    2  1 
 với a  0, a  1.  a 3      a 1 
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi 4 a  97  56 3 . 3. Tìm a để 2 A 1 
2a  5a  9 . 3 a  20
4. Giải phương trình A  . 2 a  5 1 1 1 1
5. Tính giá trị của A khi a     ...  . 1 5 5  9 9  13 2001  2005
6. Phản biện bất đẳng thức 3
A a  2a  2 a  2 .
Bài toán 75. Mở rộng và phát triển bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; chuyên Bắc Giang; Năm học 2012 – 2013. 2x  7 x  6 x x 1
Cho biểu thức Ax    . x  3 x  2 x 1 x  2
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  16 .
3. Tính giá trị của A khi x  7  4 3 .
4. Giả sử  x ; y làm cho biểu thức 2 2
S x y xy x y  2005 đạt giá trị nhỏ nhất. Tính A6x . 0  0 0 
5. Tính giá trị biểu thức khi x thỏa mãn phương trình  x   x   2 3 1 1
x  2x  3   4. x  4
6. Giải phương trình A  . 2 x  5
7. Tìm tất cả các giá trị của m để phương trình A m có nghiệm.
Bài toán 76. Mở rộng và phát triển câu II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2007 – 2008; Ngày thi 26.06.2007.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 29
_______________________________________________________________________________________________________________________________________________________________ x  2 x 1 x 1
Cho biểu thức Ax  
x với với x  0, x  1. x 1 x 1
1. Rút gọn biểu thức A. 6
2. Tìm các giá trị nguyên của x để nhận giá trị nguyên. A 3 x 1
3. Giải bất phương trình A  . 2
4. Tính giá trị của A khi x là nghiệm của phương trình x 1  8  3x 1 .
5. Tính Ax  4 biết x thỏa mãn đẳng thức 2 2
x xy y  3 x y   1 .
6. Phần nguyên của a, ký hiệu [a], tức là số nguyên lớn nhất không vượt quá a. Giả sử 3 3 3 3
B  60  60  60  ...  60 . Chứng minh 3  B  4 và tính AB .
Bài toán 77. Mở rộng và phát triển bài II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2014 – 2015; Ngày thi 30.06.2014. 4 2 x  5 Cho biểu thức B   
với x  0, x  1. x 1 1 x x 1 1. Rút gọn B.
2. Tính giá trị của B khi x  9  4 5  9  4 5 . 7 
3. Giải phương trình B  . x  3 x 1
4. Tìm các giá trị nguyên của x để B nhận giá trị nguyên.
5. Tính giá trị của B khi x là nghiệm của phương trình 3 x 1  x  3 .
6. Phần nguyên của a, ký hiệu [a], tức là số nguyên lớn nhất không vượt quá a. Xét 3 3 3 3 a
20  20  20  ...  20 ;b
24  24  24  ...  24 . Tính B a b .
Bài toán 78. Mở rộng và phát triển câu II.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2013 – 2014; Ngày thi 30.06.2013. x 2x x Cho biểu thức B  
với x  0, x  1. x 1 x x
1. Rút gọn biểu thức B.
2. Tính giá trị của B với x  3. 27  8 : 2 .
3. Tính giá trị của B khi x là nghiệm của phương trình  x   x   2 4
1  3 x  5x  2  6 .
4. Giải phương trình B x  3 x  2 .
5. Tìm các giá trị của x sao cho B x   2
2 x x   1 . 1
6. Tìm m để phương trình B  có nghiệm. m
7. Phản biện bất đẳng thức B x   2 2
2 4x  3x   1 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 30
_______________________________________________________________________________________________________________________________________________________________
Bài toán 79. Mở rộng và phát triển bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; chuyên Bắc Giang; Năm học 2015 – 2016; Ngày thi 09.06.2015. x 11 x 2 x 1 Cho biểu thức A    . x x  2 x 1 x  2
1. Tìm điều kiện của x để A có nghĩa, khi đó rút gọn A.
2. Tính giá trị của A khi x thỏa mãn 3x  8 x  4  0 .
3. Tính giá trị của A khi 3 3
x  182  33125  182  33125 . 4. So sánh A và 1.
5. Tìm số chính phương x sao cho A có giá trị là số nguyên. 3 x 10
6. Giải phương trình A  . x  4 3
7. Tìm khoảng giá trị của x sao cho giá trị của A không vượt quá . 2
Bài toán 80. Mở rộng và phát triển câu II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2015 – 2016; Ngày thi 19.07.2015.  1 1 4  x 1 Cho biểu thức B    :  
với x  0; x  4 .  x  2 x  2
x  4  x  4
1. Chứng minh biểu thức B có giá trị không phụ thuộc vào biến. 2. Tìm x sao cho 2
3x  9x 1  x  2  B . x B 3. Giải phương trình  . x 1 10 4. Chứng minh rằng 2 2
2x 1 x y 4  y 1  B, y  2; 2, x  0;  1 .
Bài toán 81. Mở rộng và phát triển câu II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2016 – 2017; Ngày thi 09.06.2016.  x  2 x  2
6x x x x
Cho biểu thức B     .
với x  0, x  1.  x 1 x 1 x 1   x 1   1. Rút gọn B.
2. Chứng minh biểu thức B là số tự nhiên chia hết cho 12 với mọi số tự nhiên x khác 1.
3. Tìm giá trị nhỏ nhất của B và giá trị của x tương ứng.
4. Tìm các giá trị của x sao cho giá trị của B không vượt quá 36.
5. Giải phương trình B  36 x .
6. Tính giá trị của B khi x thỏa mãn đẳng thức 2 2
x x  5  x  8x  4  5 .
7. Tìm khoảng giá trị của tham số m để phương trình B m  2 có hai nghiệm phân biệt.
Bài toán 82. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 1997 – 1998; Ngày thi 27.06.1997. 2  a 2  a 16 Cho biểu thức Q    . 2  a 2  a 4  a
1. Rút gọn biểu thức Q. 7 1
2. Tính giá trị biểu thức Q khi a   1. 3  2 2 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 31
_______________________________________________________________________________________________________________________________________________________________
3. Tìm a để Q  0 . 7
4. Giải phương trình Q 1  . a
5. Tính giá trị của Q khi a và b là các số không âm thỏa mãn đẳng thức  3  3   1  1 2 2  a b b a   2a  2b          .  4  4   2  2 
6. Tính giá trị của Q khi a thỏa mãn phương trình 2
a 1 1  4a  3a .
7. Tồn tại hay không các số thực a và m thỏa mãn hệ thức Q  2  a m 1  3  m a 1 .
Bài toán 83. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2001 – 2002; Ngày thi 04.07.2001.
a a 1 a a 1 a  2
Cho biểu thức A     : .  a a
a a a  2  
1. Tìm điều kiện để biểu thức A có nghĩa.
2. Rút gọn biểu thức A. 1 1
3. Giải phương trình A   . 2 a  4 a  2 4 3 2
x  4x  9x 10x  7
4. Tính giá trị của A khi a là giá trị lớn nhất của biểu thức f x  trên  . 2 x  2x  2
5. Tìm các giá trị nguyên của a để biểu thức A nhận giá trị nguyên.
x y z  15
6. Chứng minh rằng A có thể giữ vai trò các biến x, y, z trong hệ điều kiện xy yz xz  72 
Bài toán 84. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2005 – 2006; Ngày thi 02.07.2005.  1 1   1 1  Cho biểu thức A   :      .  1 x 1 x  1 x 1 x  1. Rút gọn A.
2. Tính giá trị của A khi x  9  4 5 . 1
3. Tìm các giá trị của x và y sao cho 2 A  1
y  2 y  3. x
4. Tính giá trị của A khi x max 4 2 sin a cos  a , a   .
Bài toán 85. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2003 – 2004; Ngày thi 01.07.2003.  
  2  x  2 x x x x x   1 1 1
Cho biểu thức A     : .  x x x x x 1   1. Rút gọn A.
2. Tính giá trị của A khi x  3  2 2 . x  3 3. Tìm x để A  . x  2
4. Tìm x nguyên để biểu thức A nhận giá trị nguyên.
5. Tính giá trị của A khi x thỏa mãn hệ thức x y z  35  22 x 1  3 y  2  4 z  3 .
6. Tìm khoảng giá trị của m để phương trình A m  2 có nghiệm.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 32
_______________________________________________________________________________________________________________________________________________________________
Bài toán 86. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2000 – 2001; Ngày thi 04.07.2000. 2  a 1   a 1 a 1 
Cho biểu thức P        .  2 2 a   a 1 a 1       
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a  7  4 3 .
3. Tìm giá trị của a để P  0 .
4. Giải phương trình 8P  3 a  6 .  1 
5. Tìm giá trị của a sao cho P  2 a  1   .  a
6. Tính giá trị của P khi 9 6 3
a x  6x  282x 1, trong đó 3 3 x  5  2  1 11 .
7. Chứng minh rằng với mọi giá trị m  0 , phương trình P m luôn luôn có nghiệm x.
Bài toán 87. Mở rộng và phát triển câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Hà Bắc (cũ); Năm học 1995 – 1996; Ngày thi 10.08.1995. 2  a 1 a 1   1 
Cho biểu thức B     a    .  a 1 a 1       a  1. Rút gọn B.
2. Có giá trị nào của a để B  0 không ?
3. Tìm a để B  0 .
4. Tính giá trị của B khi a  2  3  6  2 . 3
5. Tìm các giá trị của a sao cho B   3a  5 . a
6. Tính giá trị của B khi a là nghiệm của phương trình 7  x  2  x  7  x2  x  3.
7. Phần nguyên của a, ký hiệu [a], tức là số nguyên lớn nhất không vượt quá a.
Xét phương trình phần nguyên 2
a  9a  8  0 . Tính giá trị của biểu thức B tại a.
Bài toán 88. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Hà Bắc (cũ); Năm học 1996 – 1997; Ngày thi 01.08.1996.  x  4x   1 2x 2 x
Cho biểu thức A   1 :   1 .  1 4x
  1 4x 2 x 1         1. Rút gọn A.
2. Tính giá trị của A với x  4  2 3 . 1
3. Tìm x để A  . 2 x 4
4. Giải phương trình A   . 2 3
5. Tính giá trị của A tại x max B , trong đó B   a  3  5  a ,a  3  ;5.
6. Tính giá trị của A khi x là nghiệm của phương trình 1 x  7  x  4 . 1 1 1 7. Giả sử a, ,
b c là các số nguyên dương sao cho  
 2 , trong đó a là số lớn nhất trong bộ ba số. a b c
Tồn tại hay không giá trị x để A a ?
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 33
_______________________________________________________________________________________________________________________________________________________________
Bài toán 89. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Hà Bắc (cũ); Năm học 1996 – 1997; Ngày thi 31.07.1996.  x 1 x 1   1 x
Cho biểu thức A     :    .  x 1 x 1   x 1 1 x          1. Rút gọn A. 1 1
2. Tính giá trị của A khi x    2 5 . 3  2 2 3  2 2
3. Tìm x để A nhận giá trị âm. 4 x
4. Giải phương trình A  . 2x  5 x 1 1 1 1
5. Cho ba số thực dương a, , b c thỏa mãn    2 . a 1 b 1 c 1
Tính giá trị A khi x là số nhỏ nhất sao cho abc x .
6. Tính giá trị biểu thức A khi x là số nguyên sao cho S x x  
1  x  7 x  8 là số chính phương.
Bài toán 90. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 1998 – 1999; Ngày thi 13.06.1998. 1 2 4 x Cho biểu thức A    . 2  x 2  x 4  x 1. Rút gọn A.
2. Tính giá trị của A khi x  2 4  7  2 4  7  3 .
3. Giải phương trình Ax  6  x  4 .
4. Chứng minh A  0 .
5. Tìm giá trị nguyên của x để A nhận giá trị nguyên. 3
6. Chứng minh 0  A
, từ đó dẫn đến A chỉ nhận duy nhất một giá trị nguyên. 2
7. Tính giá trị của A khi x là số thực làm cho biểu thức P   x y  2 2 2 6 5 16
x y  2xy  2x  2 y  2 đạt giá trị nhỏ nhất.
Bài toán 91. Mở rộng và phát triển câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 1999 – 2000; Ngày thi 22.06.1999.  a 1 1 3a   2 a 1 
Cho biểu thức P      : 1  .
 2 a 1 2 a 1 4a 1  2 a 1      
1. Rút gọn biểu thức P. 2 1
2. Tính giá trị biểu thức P khi a    4 . 2 1 3  2 2 a  3
3. Tìm giá trị a sao cho P  . 3
4. Tính giá trị của P khi a thỏa mãn x 1  3  x   x   1 3  x  2 .
5. Tìm khoảng giá trị của m để phương trình P m  3có nghiệm.
6. Giả sử p là số nguyên tố sao cho 2 2
4 p 1, 6 p 1cũng là số nguyên tố. Tìm a để P p . 1 1 1 1
7. Tìm a sao cho P    ...  . 2 1 1 2 3 2  2 3 4 3  3 4 25 24  24 25
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 34
_______________________________________________________________________________________________________________________________________________________________
Bài toán 92. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Giang; Năm học 2000 – 2001; Ngày thi 03.07.2000.  x  2 x  2  x 1
Cho biểu thức A    . .
x  2 x 1 x 1   x   1. Rút gọn A. 9
2. Tính giá trị của A khi x  . 4 1 7x  9
3. Giải phương trình A   . 2 x 1 x 1
4. Tính giá trị biểu thức A khi x thỏa mãn 3 x 1  x  1.
5. Tìm các giá trị của biểu thức A để biểu thức A nhận giá trị nguyên.
6. Tìm giá trị của tham số m sao cho phương trình A m có nghiệm.
7. Tính giá trị của A khi x là số thực nhỏ nhất thỏa mãn a  4  a  5  a  6  x (a là biến số thực).
Bài toán 93. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 2007 – 2008. 2 2  1 1 x 1 1 xx 1
Cho biểu thức P     . 1.  1 x 1 x 1 x 1 x        2  
1. Tìm điều kiện của x để biểu thức P có nghĩa và rút gọn P. 2
2. Tìm x để P  . 2
3. Tính giá trị của P khi x thỏa mãn 2
4x  2x 1  4x 1 .
4. Tồn tại hay không các số thực x, y, z sao cho P    x   2 2 2
y z  2z  4 .
Bài toán 94. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố Bắc Ninh; Tỉnh Bắc Ninh; Năm học 2015 – 2016.  a a 4 a 1  1
Cho biểu thức A      : .  a  2 a  2 a 4   a  2  
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi a  6  4 2 . 2 a 1
3. Tìm giá trị của a để A  . a
4. Tìm giá trị của a để A  1 .
5. Tính giá trị của A khi a là nghiệm nguyên của phương trình 2
2a  5a 1  3a 1 .
6. Tìm tất cả các giá trị của m để phương trình A m có nghiệm.
Bài toán 95. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Giang; Thành
phố Bắc Giang; Tỉnh Bắc Giang; Năm học 2014 – 2015.   a  3 a  2 a a  1 1  Cho biểu thức P     :  .    
a  2 a   1
a 1   a 1 a 1    1. Rút gọn P.
2. Tính giá trị của P khi a  7  4 3 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 35
_______________________________________________________________________________________________________________________________________________________________ 1
3. Chứng minh rằng khi a là số nguyên dương thì  P  1. 2 1
4. Tìm a nguyên để P  là số nguyên. 4
5. Tính giá trị biểu thức P khi a thỏa mãn 2
2 a 1  3 a  2  a  3a  2  6 . 2 2 m n 2 2 m n
6. Cho m và n là các số nguyên dương sao cho
  . Tìm a sao cho P  . mn mn
7. Xét các cặp số nguyên không âm (x;y) thỏa mãn 2  3  38  2.7y x x . Tính P khi 2 2
a x y .
Bài toán 96. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố Bắc Ninh; Tỉnh Bắc Ninh; Năm học 2010 – 2011.  1 a a
Cho biểu thức P     : .  a a 1   a a  
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a thỏa mãn 2
a  9a  8  0 . 13
3. Tìm giá trị của a để P  . 3 5
4. Tìm giá trị của a để P  . 2 1
5. Tìm số tự nhiên a để biểu thức P  nhận giá trị nguyên. 2 x  5
6. Tìm a để P k , trong đó k là giá trị lớn nhất của biểu thức S  ; x   . x  2 1 1 1 1
7. Tồn tại hay không số thực dương a sao cho P     ...  ? 2 1 3 2 4 3 n   1 n
Bài toán 96. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố
Bắc Ninh; Tỉnh Bắc Ninh; Năm học 2008 – 2009.
x 1 2 x  2 Cho biểu thức A  . x  2 1
1. Tìm điều kiện của x để biểu thức A có nghĩa.
2. Rút gọn biểu thức A khi x  3 .
3. Tính giá trị của A khi 2 x
y  2 y 11, y   .
4. Tìm giá trị của x sao cho x  4  2x A. d a b c
5. Tồn tại hay không các số thực dương a, b, c, d sao cho A     ? 2 d  4 b c c a a b
Bài toán 97. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 1997 – 1998; Ngày thi 05.08.1997.
x  1x x  1 x 1 x 1 x 1 Cho biểu thức A  :   . x 1 2 x   1 2  x   1 x 1
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi x  4 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 36
_______________________________________________________________________________________________________________________________________________________________
3. Chứng minh rằng khi x  1 thì A  1 .
4. Giải phương trình A   2
2 x x   1 .
Bài toán 98. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 1997 – 1998; Ngày thi 06.08.1997.  x 1 x x 1  x 1
Cho biểu thức B    .
với x  0; x  1.  x 1 x 1   x x 1  
1. Rút gọn biểu thức B.
2. Tính giá trị của B khi x  9 .
3. Tìm giá trị của x để 2
21B  5B  0 . 3
4. Tìm khoảng giá trị của x để B  . 7 5. So sánh B với 1.
6. Chứng minh rằng với x  0; x  1thì B không thể nhận giá trị nguyên.
7. Số nguyên a chia hết cho số nguyên b thì được ký hiệu b a . Tính giá trị của B khi x là số nguyên
lớn nhất thỏa mãn điều kiện 2 3 2
x 1 x  8x  2x .
Bài toán 99. Mở rộng và phát triển câu I.3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2016 – 2017.  1 1  x 1 Cho biểu thức A   .  
với x  0; x  1.  x 1 x 1  2
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  4  2 3 . 1
3. Tính giá trị của A khi x  . 9  4 2 2
4. Tìm tất cả các giá trị của x để A  . 7 x  2 5. Tìm x sao cho A  . 3
6. Tìm tất cả các giá trị của x để biểu thức A nhận giá trị nguyên.
7. Với x  0; x  1, đặt A f x . Giả sử n là số nguyên dương lớn nhất sao cho 29n là một ước của
2003! 2003!  1.2.3...2002.2003 . Chứng minh rằng f n  1,7 .
Bài toán 100. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Bắc Ninh; Thành phố Bắc Ninh; Tỉnh Bắc Ninh; Năm học 2015 – 2016.  a a 4 a 1  1
Cho biểu thức A      :
với a  0; a  4 .  a  2 a  2 a 4   a  2  
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi a  6  4 2 .
3. Tìm a để A nhận giá trị bằng 0,6.  1  4. Tìm a để 2  
  A  3  0 .  A
5. Tìm a để giá trị của biểu thức A không nhỏ hơn 1.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 37
_______________________________________________________________________________________________________________________________________________________________ 1 1
6. Tìm tất cả các số thực b và c sao cho A
b c a   b c ? 4 4
7. Giả sử mnp là ba chữ số tận cùng của số 2004 T  2
. Tính giá trị của A khi a m n p  2 .
Bài toán 101. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 1999 – 2000; Ngày thi 13.07.1999.  a b   a b
Cho biểu thức P     :
 với a,b  0; a b .  ab b a ab    
  a b b a
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a  9;b  4 . 2 
a  4b  4  0
3. Tính giá trị của biểu thức P khi a và b là nghiệm của hệ phương trình  2 b   4a  4  0 
4. Tính giá trị của P khi biết a, b là hai nghiệm của phương trình ẩn x: 2
x  8x  4  0 .
5. Tính giá trị của biểu thức P khi a và b là nghiệm của phương trình hai ẩn 2 a    2 2 1
2 4a b   4a b .
Bài toán 102. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 1; Sở Giáo dục và Đào tạo Tỉnh Thái Bình; Năm học 2003 – 2004. 2 x   1 2 x 10 x  3 Cho biểu thức M    . 3 x 1 x x 1 x 1
1. Với giá trị nào của x thì biểu thức có nghĩa.
2. Rút gọn biểu thức M. 9
3. Tính giá trị biểu thức M khi x  . 4
4. Tính giá trị biểu thức M khi x  3  2 2 . 12
5. Tìm x sao cho M nhận giá trị bằng  . 13 2
6. Tìm khoảng giá trị của x để M  . 3
7. Tìm m để phương trình M m có nghiệm, từ đó tìm giá trị nhỏ nhất của biểu thức M.
8. Tồn tại hay không các số thực a và b để M  1 a  1 b a b ?
Bài toán 103. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Đợt 2; Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2001 – 2002; Ngày thi 14.07.2001.  a  2 a  2  a 1 Cho biểu thức A   .  
với a  0; a  1 . a  2 a 1 a 1 a   2
1. Chứng minh đẳng thức A  . a 1
2. Tính giá trị của A khi a  4  2 3 .
3. Tìm a để A  0 . 3a 4
4. Giải phương trình A   . 2 a 1 a 1
5. Tìm giá trị nguyên của a để biểu thức A nhận giá trị nguyên. 3
6. Tìm tất cả các giá trị nguyên của a để A  nhận giá trị nguyên. 5
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 38
_______________________________________________________________________________________________________________________________________________________________
Bài toán 104. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2003 – 2004; Ngày thi 16.07.2003.  y xy   x y x y
Cho biểu thức P   x   :      x y   xy y xy x xy        
1. Với giá trị nào của x, y thì biểu thức P có nghĩa ? 2. Rút gọn P.
3. Tính giá trị của P khi x  100; y  81.
4. Tính giá trị của P khi x và y là các số hữu tỷ thỏa mãn 5. Cho 3 3
x  5 2  7; y  5 2  7 . Chứng minh rằng P  2 . 3 3 3 1
x y  8  16 y ,  6. Tính giá trị của
khi x và y là nghiệm của hệ phương trình  P x   xy  2 2  8 y .  x 7. Tính tỷ số
khi P thỏa mãn đẳng thức P  3 x  2 y  4x . y
8. Tính giá trị của P khi x và y là hai số nguyên tố thỏa mãn đẳng thức 2 2 x  6 y  1.
Bài toán 105. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Bắc Ninh; Năm học 2004 – 2005; Ngày thi 08.07.2004.  a  2 a  2 4a  3a  4
Cho biểu thức M     : .  a  2 a  2 4 a   a  2  
1. Rút gọn biểu thức M.
2. Tìm các giá trị của a để M  1  . 3. Tìm a sao cho 2
9M 10M  0 .
4. Tìm các giá trị nguyên của a để biểu thức M nhận giá trị nguyên.
5. Tìm số tự nhiên a để M nhận giá trị lớn nhất.
6. Tìm tất cả các giá trị của a để phương trình M m có nghiệm. 1 9
7. Tồn tại hay không các số thực m và n để M
 2017 m n  ? 2 10 1 2
8. Tính giá trị của M khi a và b là các số hữu tỷ thỏa mãn điều kiện   9  2 2 . a b 2 b 2  a
Bài toán 106. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Quảng Ngãi; Năm học 2000 – 2001; Ngày thi 11.07.2000. 2 x x 2x x Cho biểu thức Y  1 . x x 1 x 1. Rút gọn Y.
2. Tính giá trị của Y khi 2 x  28 16 3 .
3. Tìm x sao cho Y nhận giá trị không vượt quá 4. x  2
4. Tìm x để Y  . 5 x 1
5. Tìm giá trị nhỏ nhất của biểu thức Y.
6. Cho x  4. Chứng minh đẳng thức Y Y  0 .
7. Tìm tất cả các giá trị của m để phương trình Y m có nghiệm thuộc khoảng (4;9).
8. Giải phương trình Y  4 x  2 x   1  x  4 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 39
_______________________________________________________________________________________________________________________________________________________________
Bài toán 107. Mở rộng, liên hệ và phát triển các bài toán 
Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Khiết; Thị xã Quảng Ngãi; Tỉnh Quảng Ngãi; Năm học 2000 – 2001. 
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2016 – 2017.  a 1 1 a   1 1 
Cho biểu thức P      1   . 2  2 1 a 1 a        1 a 1 a aa  
1. Chứng minh biểu thức P có giá trị độc lập với biến với 0  a  1.
2. Giải phương trình P a  8  3a  2 với 0  a  1 1
3. Chứng minh rằng a
P  0,8 với 0  a  1. 2 a 4 3
b b b 1 1
4. Giá trị của biểu thức P còn độc lập với biến hay không nếu a  ,   b  1. 4 3 2
b b  3b  2b  2 2 a b a b 4a
5. Khi 0  a  1, hãy so sánh P và Q, trong đó Q    ; a  ; b b  0 . a b a b a b
Bài toán 108. Mở rộng và phát triển bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Quảng Ngãi; Năm học 2005 – 2006; Ngày thi 15.07.2005.  a  2 a  2  a 1
Cho biểu thức P    . với 0  a  1 .
a  2 a 1 a 1   a  
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi a thỏa mãn 3 a  
1 4 a  3  0 .
3. Tính giá trị biểu thức P khi 2 a  56  24 5 . a
4. Tìm tất cả các giá trị của a để P   2 . 4
5. Tìm a để giá trị của P không nhỏ hơn 0,45. 6 5a
6. Giải phương trình P   . 2 a 1 a 1
7. Tìm tất cả các giá trị nguyên của a để biểu thức P nhận giá trị nguyên.
8. Tìm giá trị nguyên của a để biểu thức P đạt giá trị lớn nhất.
Bài toán 109. Mở rộng, liên hệ và phát triển các bài toán 
Bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Quảng Ngãi; Năm học 2008 – 2009; Ngày thi 24.06.2008. 
Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố Quảng Ngãi; Tỉnh
Quảng Ngãi; Năm học 2012 – 2013. 
Bài 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố Quảng Ngãi; Tỉnh
Quảng Ngãi; Năm học 2013 – 2014.
a b2  4 ab ab Cho biểu thức P  : . a b a b b a
1. Xác định a, b để biểu thức có nghĩa và hãy rút gọn P.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 40
_______________________________________________________________________________________________________________________________________________________________
2. Tính giá trị của P khi a  15  6 6  33 12 6 ;b  24 .
3. Tính tỷ số giữa a và b nếu P  3 ab . 1 1
4. Cho số thực x thỏa mãn 2
x  3x 1  0 . Tính giá trị biểu thức P khi 3 5 a x  ;b x  . 3 5 x x a ba b2
5. Chứng minh rằng nếu P  0 thì  ab  . 2 8b 1
6. Giả sử tồn tại x sao cho x  15  m  ; 
 15  n   . Tìm hệ thức giữa a và b để P m n . x
a b2  4 ab a b b a
7. Xét biểu thức Q  
b . Tìm a và b sao cho P Q . a b ab 2 2 x x x x 8. Xét 2 R  
x 1 với x  0 . Chứng minh rằng nếu P R thì 2 2 b a  1. x x 1 x x 1
Bài toán 110. Mở rộng và phát triển 1.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố
Quảng Ngãi; Tỉnh Quảng Ngãi; Năm học 2014 – 2015. 3 3 x x x Cho biểu thức P    . x  3  x x  3  x x 1
1. Tìm điều kiện xác định và rút gọn P.
2. Tính giá trị của P khi x  7  2 3 .
3. Tìm x sao cho P  6 .
4. Tìm giá trị nhỏ nhất của biểu thức P.
5. Tìm tất cả các giá trị của x để P  2 . 6. Giải phương trình 2
P x  8x 14  0 . a b 3
7. Xét các số hữu tỷ a,b, c thỏa mãn
là số hữu tỷ. Chứng minh rằng khi x ac  3thì P có giá b c 3
trị là một số hữu tỷ.
Bài toán 111. Mở rộng và phát triển 1.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Khiết; Thành phố
Quảng Ngãi; Tỉnh Quảng Ngãi; Năm học 2015 – 2016.  2 x x 1   x  2 
Cho biểu thức A     : 1  .  x x 1 x 1   x x 1         
1. Tìm điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị của A khi x  2 1. 3. Tìm x sao cho 2
17 A  2 A  0 .
4. Tìm x để A nhận giá trị lớn hơn 3. 3 1 x
5. Giải phương trình A   . 2 x 1 x 1
6. Tìm giá trị nguyên của x để A nhận giá trị nguyên. 2
7. Tìm tất cả các giá trị nguyên của x để biểu thức S A  nhận giá trị nguyên. 3 1
8. Cho số thực a thỏa mãn 2
a  4a 1  0 . Tính giá trị biểu thức P khi 7 x a  . 7 a
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 41
_______________________________________________________________________________________________________________________________________________________________
Bài toán 112. Mở rộng và phát triển đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở
Giáo dục và Đào tạo Thành phố Hồ Chí Minh; Năm học 2014 – 2015.  x 1   2 6  Cho biểu thức B   : 1      .  x  3 x x  3   x x  3 x
1. Tìm điều kiện xác định và rút gọn biểu thức B.
2. Tính giá trị của biểu thức B khi x  6  2 5 .
3. Tính giá trị của biểu thức B khi x là số lớn nhất thỏa mãn x  1 y  1 y .
4. Tìm x để B có giá trị lớn hơn 5. 4
5. Tìm x sao cho B  . x  3 3
6. Tìm giá trị nguyên của x để biểu thức nhận giá trị nguyên. B
Bài toán 113. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình
Định; Năm học 2012 – 2013; Ngày thi 14.06.2012.  a b a b  
a b ab
Cho biểu thức D     : 1 
 với a  0;b  0; ab  1.  1 ab 1 ab   1 ab   
1. Rút gọn biểu thức D. 2
2. Tính giá trị của biểu thức D khi a  . 2  3
3. Tìm a để biểu thức D nhận giá trị bằng 0,8. a
4. Tìm giá trị của a sao cho D  . 3a  2
5. Tìm giá trị của a để D có giá trị lớn hơn 0,6.
6. Tính giá trị của biểu thức D khi a và b thỏa mãn hệ thức  3 3
4 a b   a  
1 a  4  b .
7. Tìm tất cả các số nguyên a để D nhận giá trị nguyên.
Bài toán 114. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình
Định; Năm học 2009 – 2010. x  2 x 1 x 1 Cho biểu thức P    . x x 1 x x 1 x 1
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi x  3  2 2 .
3. Tìm giá trị của x sao cho 2
13P  3P  0 .
4. Tìm giá trị của x sao cho 2 21P  4P . 1
5. Giải phương trình P x   9  1. x 1 6. Chứng minh P  với 0  x  1. 3
7. Chứng minh rằng biểu thức P chỉ nhận duy nhất một giá trị nguyên với 0  x  1. 1 1
8. Tồn tại hay không các số thực a và b thỏa mãn đẳng thức P   a
b a b ? 2 2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 42
_______________________________________________________________________________________________________________________________________________________________
Bài toán 115. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1c; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Bình Định; Năm
học 2012 – 2013; Ngày thi 30.06.2012.
 Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Bình Định; Năm học 2007 – 2008. 2
 5 a  3 3 a 1 a  2 a  8 
Cho biểu thức A  a  2 a  :   
 với 0  x  4 .  a  2 a  2 a 4     1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi a  3  2 2 .
3. Tính giá trị của biểu thức A khi a thỏa mãn 4 2
a  5a  4  0 .
4. Tìm tất cả các giá trị của a sao cho 2
A  2 A  0 .
5. Tìm giá trị của a để 4A a  3. 1
6. Tìm khoảng giá trị của a sao cho giá trị của A lớn hơn . 3
7. Tìm tất cả các giá trị nguyên của a để A nhận giá trị nguyên. a b 2b
8. Tìm giá trị của a để A   
; a  0,b  0, a b . a b a b a b
Bài toán 116. Mở rộng và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình Định; Năm học 2016 – 2017; Ngày thi 06.06.2016.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình Định; Năm học 2013 – 2014; Ngày thi 14.06.2013.  x 1 x 1   x
Cho biểu thức T    . x x  
 với x  0; x  1.  x 1 x 1       x
1. Rút gọn biểu thức T.
2. Tính giá trị của T khi x là nghiệm của phương trình 2
x  2x 1  3  2 2  1. 1
3. Tìm giá trị của x thỏa mãn T  2 x 13 . 2 T
4. Tìm giá trị nguyên của x để biểu thức
nhận giá trị lớn nhất. x 1 5x  3 3y  8
5x  9 y  21
5. Tính giá trị của T khi x thỏa mãn dãy tỷ số bằng nhau   . 9 5 8x
6. Cho hai số thực a và b có tổng bình phương bằng 1. Tính giá trị của T khi x   6 6
a b    4 4 a b  4 2 4 2 2 3
a  4b b  4a .  x xx 1
7. Xét biểu thức S     :
với a  0, a  1 . Chứng minh rằng T S .  x 1 x x x 1  
Bài toán 117. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Quy Nhơn; Tỉnh Bình
Định; Năm học 2014 – 2015. 2 x x 2x x Cho biểu thức A   1 với x  0 . x x 1 x
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 43
_______________________________________________________________________________________________________________________________________________________________
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi 5
x  5 x  2 .
3. Tìm các giá trị của x để A  2 .
4. Tìm giá trị nhỏ nhất của A. x
5. Giải phương trình A   5 . 3
6. Tìm giá trị của x để A nhận giá trị là một số nguyên nhỏ hơn 4.
7. Tìm tất cả các giá trị của x để A    2 1
2 x x   1 . 8. Tìm x sao cho 2 2
A a b , trong đó a và b là các số thực thuộc đoạn [– 1;1] thỏa mãn 2 2
a 1 b b 1 a  1 .
Bài toán 118. Mở rộng, liên hệ và phát triển các bài toán 
Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1997 – 1998; Ngày thi 11.06.1998. 
Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 2007 – 2008; Ngày thi 12.07.2007.  x x 6 x 1 
Cho biểu thức A       2
x  7x 18 .  x  3 x  3 x 9    
1. Tìm điều kiện của x để biểu thức A có nghĩa.
2. Rút gọn biểu thức A.
3. Tính giá trị biểu thức A khi x  6  2 5  9  4 5 . A 4. Giải phương trình 3  x . 3
5. Tìm tất cả các giá trị x để 3 A  10 A . 3  2 3 6
6. So sánh A với M   1. 3 3  3
7. Tìm giá trị của x sao cho A x   2 4
2 x  20x  4 .  1 1  x 1
8. Xét biểu thức B   :
x  0; x    
1 . Tìm giá trị nhỏ nhất của A B  2017 .  x x
x 1  x  2 x 1
9. Tìm x sao cho A T , với T là tổng bình phương các số nguyên a, , b c thỏa mãn 2 2 2
a b c ab  3b  2c  4 .
Bài toán 119. Mở rộng, liên hệ và phát triển Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo
dục và Đào tạo Tỉnh Thừa Thiên – Huế; Năm học 1992 – 1993.  x x 1  x
Cho biểu thức P      : .  x 1 x 1 x 1   1 2 x  
1. Với giá trị nào của x thì biểu thức P được xác định.
2. Rút gọn biểu thức P. 3 1
3. Tính giá trị của biểu thức P khi x  . 2 4  7 4  7
4. Tính giá trị biểu thức P khi B   . 4  7 4  7
5. Tìm giá trị của x sao cho P nhận giá trị bằng – 2.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 44
_______________________________________________________________________________________________________________________________________________________________
6. Tìm tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Tìm tất cả các giá trị của tham số m để phương trình P m có nghiệm.
Bài toán 120. Mở rộng, liên hệ và phát triển các bài toán 
Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1994 – 1995. 
Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1996 – 1997.  a b b aa b Cho biểu thức A    :  
với a  0;b  0; a b .  a b b ab ab a a b
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi a  4  2 3;b  7  4 3 .
3. Chứng minh rằng A
2 khi a b  3  3  13  4 3 . 1  1 1 
4. Chứng minh bất đẳng thức A     . 2  a b  
a 1  b  5, 
5. Tính giá trị của biểu thức A khi a và b thỏa mãn hệ  2a 2a   1 b  36.  2 2
n  2  n  4
n  2  n  4
6. Với n  2 hoặc n  2
 , xét biểu thức N  
. So sánh giá trị biểu thức N 2 2
n  2  n  4
n  2  n  4 2
và biểu thức A theo n khi a b  . 9
Bài toán 121. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 1998 – 1999.
o Bài 1; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 2000 – 2001.
o Bài 1b; Phần B; Đề thi tốt nghiệp THCS; Môn Toán; Sở Giáo dục và Đào tạo Tỉnh Thừa Thiên –
Huế; Năm học 2001 – 2002. 3  1 1   x x 7 x 7     Cho biểu thức P       .  x 1 x x 1 x   x 1        
1. Tìm điều kiện xác định cho biểu thức P có nghĩa và rút gọn biểu thức P.
2. Tính giá trị của P khi x  5  2 3 .
3. Tính giá trị của P khi x thỏa mãn 2
x  7x  8  2 x  2 .
4. Tìm x sao cho P nhận giá trị bằng 8.
5. Tìm giá trị của x để 2
P x 13x  48 .
6. Tìm giá trị lớn nhất của biểu thức P.
7. Tồn tại hay không số tự nhiên x nào đó để P là một số chính phương ? x 1 x 1 1
8. Xét biểu thức A  :
. Chứng minh rằng nếu 27  x  1 thì P A . x x   1 x 1 xb a
9. Xét biểu thức B   
 a b b a . Khi b a , hãy so sánh P và B theo x.  a ab ab b     
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 45
_______________________________________________________________________________________________________________________________________________________________
Bài toán 122. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế;
Tỉnh Thừa Thiên – Huế; Năm học 2008 – 2009. 3x  2 x  4 x 1 x  2 Cho biểu thức P    x x  2 x  2 x 1
1. Tìm x để biểu thức P có nghĩa và rút gọn P .
2. Không dùng máy tính bỏ túi, tính giá trị của P khi x  4  2 3 .
3. Tìm x để biểu thức P nhận giá trị bằng 0,4. x 1
4. Tìm giá trị của x sao cho P  . x  5
5. Tính giá trị của biểu thức P khi 3 x  99  70 2 . 2 2
x xy y  7
6. Tính giá trị của P khi x thỏa mãn hệ phương trình  3 3 x y  35 
7. Tìm giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
8. Tìm m để phương trình P m có nghiệm.
9. Chứng minh rằng biểu thức P chỉ nhận đúng một giá trị nguyên.
10. Giả sử tồn tại số nguyên tố p sao cho  p    2 2 1 , 2 p  
1 đều là các số chính phương. Khi đó hãy so
sánh p và giá trị của biểu thức P  6 .
Bài toán 123. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học); Đề
thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Huế; Năm học 2008 – 2009.
o Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thừa Thiên – Huế; Năm học 2008 – 2009.  a a b b 2b   1 1 
Cho biểu thức P    .    .  a ab b a b        a b
1. Tìm điều kiện đối với a và b để P có nghĩa rồi rút gọn biểu thức P. 
a  2  b  2,
2. Tính giá trị của biểu thức P khi a và b thỏa mãn hệ phương trình  b  2a  2. 
3. Khi a và b là các nghiệm của phương trình bậc hai 2
x  3x 1  0 . Không giải phương trình này, hãy
chứng tỏ giá trị của P là một số nguyên dương. 1
4. Chứng minh rằng P  2 , từ đó tìm giá trị nhỏ nhất của biểu thức P  . P a 5. Tìm tỷ số
để P nhận giá trị là một số nguyên nhỏ hơn 4. b  1   x x
6. Khi 0  x  1, hãy so sánh giá trị biểu thức P và giá trị biểu thức Q x       .  x   x 1 x 1      2   2 2 2 2 a b a b  4 4 a b 25
7. Tính giá trị của biểu thức P khi a và b thỏa mãn đẳng thức    . ab a ba b4 8 1
8. Cho a và b khác nhau thỏa mãn đẳng thức 2 2
a b  1 b  1 a . Chứng minh P  2  . ab
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 46
_______________________________________________________________________________________________________________________________________________________________
Bài toán 124. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Huế; Năm học 1998 – 1999.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán); Đề
thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Huế; Năm học 1999 – 2000.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán); Đề
thi chính thức; Trường THPT Chuyên Quốc học Huế; Thành phố Huế; Tỉnh Thừa Thiên – Huế; Năm học 2003 – 2004.  3 3   x 3 
Cho biểu thức A       1 .  2 3 x x 3 3 x 27   3 x        
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi x  3  2 .
3. Tính giá trị biểu thức A khi 2 x  28 16 3 . x
4. Giải phương trình A  . x 1 x  3
5. Tìm tất cả các giá trị của x sao cho A  .
x x  2  2 5x  3 2 x  3 2 2x  6
6. Tìm x sao cho A   .
2x  2 x  3 2  6
2x  2 x  3 2  6 1 x 1
7. Tìm khoảng giá trị của x sao cho A  : . 2 x x
x x x x A2x  3
8. Tìm giá trị nguyên của x để biểu thức B
đạt giá trị lớn nhất. x  3
Bài toán 124. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam Kỳ; Tỉnh Quảng Nam; Năm học
2012 – 2013; Ngày thi 04.07.2012.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam
Kỳ; Tỉnh Quảng Nam; Năm học 2012 – 2013.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam
Kỳ; Tỉnh Quảng Nam; Năm học 2008 – 2009.
x  2 3x  3 
Cho biểu thức A  
  4x  12  . x  3  
1. Tìm điều kiện của x để biểu thức A có nghĩa.
2. Rút gọn biểu thức A.
3. Tính giá trị của A khi x  4  2 3 . 3 10  20  3 6  12
4. Tính giá trị của A khi x  1 2 . 5  3
5. Tính giá trị của biểu thức A khi biểu thức x x  2008 đạt giá trị nhỏ nhất.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 47
_______________________________________________________________________________________________________________________________________________________________ a a  6 1
6. Xét biểu thức B  
. Chứng minh giá trị của biểu thức B không phụ thuộc biến 4  a a  2
và tìm x để A và B có giá trị bằng nhau. 28 16 3
7. Đặt A f x . Xét x
và P   x x  2012 2 2 1
. Tính f P . 3 1
8. Từ 8 chữ cái Q, U, A, N, G, N, A, M ta xây dựng các cụm ký tự gồm 7 chữ cái, thí dụ QUANGNA là
một cụm ký tự đạt yêu cầu). Giả sử xây dựng được b cụm ký tự, tìm x để A b .
Bài toán 125. Mở rộng và phát triển ài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm;
Thành phố Tam Kỳ; Tỉnh Quảng Nam; Năm học 2015 – 2016. x x 1 x 1 Cho biểu thức A  
với x  1; x  0 . x 1 x 1
1. Rút gọn biểu thức A.
2. Tính giá trị của A – 1 khi x  2016  2 2015 . 6 4 7 3
3. Tính giá trị của A khi x thỏa mãn     0 . 2 2 2 2 x  9 x 11 x  8 x 12
x x  44x y  6
4. Biểu thức A tồn tại hay không khi x thỏa mãn hệ  2
x  8x y  5   1  6  2  2  3 5. Xét a
. Đặt A f x , hãy tính f a a 2014 2 1    .   6  4 2  3  2 2 
Bài toán 126. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam
Kỳ; Tỉnh Quảng Nam; Năm học 2011 – 2012; Ngày thi 30.06.2011.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Nam; Năm học 2014 – 2015; Ngày thi 06.07.2014. 7 x 1 2 x  3 x 1 Cho biểu thức P    với x  0 . x  5 x  4 x  4 x 1 8  3 x 1. Chứng minh P  . x  4
2. Tính giá trị của P khi x  11 2 10 . 21
3. Tìm giá trị của x sao cho P  . 13 x  2
4. Giải phương trình P  . 2 x 1
5. Tìm các giá trị nguyên của x để P nhận giá trị nguyên.
6. Tìm giá trị lớn nhất của P.
7. Tìm tất cả các giá trị của x để P nhận giá trị nguyên.
8. Tính giá trị của P khi x là nghiệm phương trình 2 3 x x 1  x 1  x 1 1.  a a   a a
9. Xét biểu thức B  1  1
 đấy với a  0; a  1. Chứng minh P B  4 .  a 1   a 1       
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 48
_______________________________________________________________________________________________________________________________________________________________
Bài toán 127. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Quảng Nam; Năm học 2006 – 2007. a b 4 ab a Cho biểu thức A   
với a  0;b  0; a b . a b a b a b
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi a  2;b  3  2 2 .
3. Cho A  2 , tìm a và b thỏa mãn 2
a  8b  3  0 .
4. Tính giá trị của A khi a và b thỏa mãn đẳng thức  3 3
3 4 a  8b   a a 1  1  25  2b .
5. Tính giá trị của A khi a và b là các số nguyên dương thỏa mãn
5a b c d  10 2abcdc,d         . 4 6. Chứng minh rằng nếu 2
a b x
 5 thì A nhận giá trị dương. x
7. Chứng minh A nhận giá trị hữu tỷ khi có điều kiện 15a  22 ab  8b  0 .
Bài toán 127. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam Kỳ; Tỉnh Quảng Nam; Năm học 2013 – 2014.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; (Dành cho tất cả các thí sinh
dự thi); Đề thi chính thức; Trường THPT Chuyên Nguyễn Bỉnh Khiêm; Thành phố Tam Kỳ; Tỉnh
Quảng Nam; Năm học 2015 – 2016; Ngày thi 03.06.2015. x 4 x  2 Cho biểu thức A    với x  0 . x  2 x  2 x x
1. Rút gọn biểu thức A.
2. Thực hiện phép tính để tính giá trị của A khi x  3  2 2 .
3. Tìm x để A x 1.
4. Giải phương trình A   x  22 x  3 .
5. Giải bất phương trình A x   2
2 x x  2 x   1 . 4
6. Tìm giá trị nhỏ nhất của biểu thức S A  . x
7. Tính giá trị của A khi x là nghiệm của phương trình 2 2
x  6x  4  3x  8x  4 .  1 1  x  2
8. Xét biểu thức B   .  
với x  0; x  4 . Chứng minh A B .  x  2 x  2  x
Bài toán 128. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2006 – 2007; Ngày thi 15.06.2006.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành phố Đà Nẵng; Năm học 2007 – 2008. x 1 x x
Cho các biểu thức P  
và A  1 x x 1 x x x
1. Tìm điều kiện của x để P và A xác định.
2. Rút gọn các biểu thức P và A.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 49
_______________________________________________________________________________________________________________________________________________________________
3. Tính giá trị của P và A khi x  3  2 2 . 1
4. Tính giá trị của biểu thức P A khi  4x  10 . x 1
5. Tìm tất cả các số thực x sao cho x
đồng thời P nhận giá trị nguyên. 9
6. Tìm tất cả các giá trị của x để A x  8  0 .
7. Tìm giá trị nhỏ nhất của biểu thức P  2A .
8. Tìm giá trị nhỏ nhất của biểu thức P  2 A x .
Bài toán 129. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2009 – 2010.
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2010 – 2011.
 Bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Thành phố Đà Nẵng; Năm học 2014 – 2015.  a 1   1 2 
Cho biểu thức K     :  .     a 1 a a    a 1 a 1 
1. Rút gọn biểu thức K.
2. Tính giá trị của K khi a  3  2 2 .
3. Tìm a sao cho K  7  7a .
4. Tính giá trị của K khi a thỏa mãn 2
a 11a 16  2 3a  4 .
5. Tìm các giá trị của a sao cho K  0 .  6  3 5  5  2
6. Tính giá trị của K khi a     : .  2 1 5 1    5  3   3
7. Giải phương trình ẩn a: K 1  3a   5 . a x 2 2x  2
8. Xét biểu thức P  
với x  0; x  2 . Tìm a để K và P có giá trị bằng nhau. 2 x x 2 x  2
Bài toán 130. Mở rộng và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành phố Đà Nẵng; Năm học 2008 – 2009; Ngày thi 21.06.2008.
 Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành phố
Đà Nẵng; Năm học 2016 – 2017. 3  x 1 Cho biểu thức P  
với x  0; x  1. x 1 x 1
1. Rút gọn biểu thức P.
2. Tìm x để P  4 .
3. Tính giá trị của P khi 2 x  6  4 2 . 9 1
4. Giải phương trình P   . 2 x 1 x 1
5. Tìm giá trị nguyên của x để P đạt giá trị lớn nhất.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 50
_______________________________________________________________________________________________________________________________________________________________
6. Tìm tất cả các giá trị của x để biểu thức Q P x   1 nhận giá trị nguyên.
7. Tính giá trị của P khi x là số nguyên dương thỏa mãn phương trình 5 4 2
x x 1  p , p là số nguyên tố.
Bài toán 131. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1 và bài 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà;
Thành phố Đà Nẵng; Năm học 2015 – 2016.
 Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Quận Sơn Trà; Thành phố
Đà Nẵng; Năm học 2013 – 2014.
x x  2x  49 x  4 2 x  8 Cho biểu thức A   
với x  0; x  1. x  3 x  4 x  4 x 1
1. Rút gọn biểu thức A. 25
2. Tìm x để A có giá trị không vượt quá . 6
3. Tìm x sao cho A x  2 .
4. Tính giá trị của A khi x thỏa mãn 2
x  9x  38  6 4  x .
5. Tìm giá trị nhỏ nhất của biểu thức A. 2 x  3x  25
6. Chứng minh bất đẳng thức A  . 4
7. Tính giá trị biểu thức A khi (x;y) là nghiệm nguyên của phương trình 2x  2 y  2  2 2x 1  y .
8. Biểu thức A nhận giá trị hữu tỷ hay giá trị vô tỷ khi x thỏa mãn phương trình 2009 2011 2013 2010 2012 2014      . 6  x 4  x 2  x 5  x 3  x 1 x
9. Tính giá trị của A khi x, y, z thỏa mãn dãy tỷ số bằng nhau x y z  
x y z . y z 1 x z 1 x y  2
10. Tìm điều kiện của biến x để A nhận giá trị là một số hữu tỷ.
Bài toán 132. Mở rộng và phát triển bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và Đào tạo Tỉnh Khánh Hòa; Năm học 2000 – 2001; Ngày thi 04.07.2000. 1 x  3 6 Cho biểu thức A   
x  0; x  4; x  9 . 2  x x  3 x  5 x  6
1. Rút gọn biểu thức A. 16
2. Tính giá trị của A khi x  . 25
3. Tính giá trị của A khi x  4  2 3 .
4. Với giá trị nào của x thì A nhận giá trị bằng 3,5 ? x  5
5. Tìm giá trị của x sao cho A  . x  7
6. Tìm x thỏa mãn A  9 x  5 .
7. Tìm các giá trị x   để A có giá trị nguyên. 5x  3 4 y 1 5x  8 y 1
8. Tính giá trị của A khi x, y thỏa mãn dãy tỷ số bằng nhau   . 8 5 6x
9. Tìm số chính phương x để A nhận giá trị lớn nhất.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 51
_______________________________________________________________________________________________________________________________________________________________
Bài toán 133. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1997 – 1998.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1996 – 1997.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1995 – 1996.
o Bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 1998 – 1999.
o Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Khánh Hòa; Năm học 2002 – 2003. 2 2 1 1 x 1
Với x  0; x  1cho hai biểu thức A  2 x  ; B    . 2 x 2  2 x 2  2 x 1 x x
1. Chứng tỏ rằng B  . x 1
2. Tìm những giá trị của x để cho .
A B x  3 .
3. Chứng minh bất đẳng thức A  4 .
4. Tính giá trị của B khi 7  x 8  x   x 11.
5. Xét biểu thức C x x   x  2 2 5 3
 6 x 18 . Tìm x để AB  2 C . 2  x x y y   x y
6. Xét biểu thức D    xy  
 với x  0; y  0; x y . Chứng minh B D .  x y   x y      
4x  6 y 1  0, 
7. Tính giá trị của biểu thức B khi (x;y) thỏa mãn hệ phương trình 9y4 x 1 0. 
Bài toán 134. Mở rộng và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2000 – 2001.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2013
– 2014; Ngày thi 21.06.2013. 2
2x  5x y  3y Cho biểu thức A  . x y y
1. Tìm điều kiện xác định của A.
2. Phân tích tử thức của A thành nhân tử và rút gọn biểu thức A.
3. Tính giá trị của A khi x  3  13  48 và y  4  2 3 .  A  0 
4. Giải hệ phương trình 2x 2  y 5  a a   1 a
5. Cho biểu thức P  
với a > 0 và a ≠ 1. Chứng minh rằng nếu 2x  2 y ay thì P a 1 a a
và A có giá trị bằng nhau.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 52
_______________________________________________________________________________________________________________________________________________________________
Bài toán 135. Mở rộng và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2012
– 2013; Ngày thi 21.06.2012.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2006
– 2007; Ngày thi 21.06.2006.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang;
Tỉnh Khánh Hòa; Năm học 2007 – 2008; Ngày thi 22.06.2007.
x  27 x  32 x  5 3 x 1 Cho biểu thức A    . x  2 x 15 x  3 x  5
1. Rút gọn biểu thức A.
2. Tìm x để A nhận giá trị bằng 6.
3. Tìm các giá trị của x để A  1. 7
4. Tìm giá trị của x để A   . 8
5. Giải phương trình 2A x  8 .
6. Tính giá trị của A khi x  4  15 10  6  4  15 .
7. Tính giá trị của A khi x là nghiệm của bất phương trình 2 2 2
x  5 y  5z 1  4xy  4 yz  2z . 2 x x
8. Xét biểu thức B  2 x
. Tìm x sao cho A B . max x x 1
9. Tìm điều kiện cho tham số m để phương trình A x m có nghiệm. 1 a 1 b 1 c 1
10. Tồn tại hay không các số thực a, b, c thỏa mãn A        ? 6 7 7 8 8 9 3
Bài toán 136. Mở rộng và phát triển các bài toán
 Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm
học 2006 – 2007; Ngày thi 22.06.2006.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2005
– 2006; Ngày thi 22.06.2005. x  2 x  2 Cho biểu thức P   . x 1 x  2 x 1
1. Tìm x để P có nghĩa.
2. Rút gọn biểu thức P.
3. Tính giá trị của P khi x  9 .
4. Với giá trị nào của x thì P  0 ? 2
5. Tính giá trị của P khi x thỏa mãn  2
x x     2 2 5
2 x  2x  x 15  0. 5
6. Giải phương trình P  5  . x 1 1
7. Tính giá trị của P khi x thỏa mãn x  2  y  2005  z  2006 
x y z . 2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 53
_______________________________________________________________________________________________________________________________________________________________
Bài toán 137. Mở rộng và phát triển các bài toán
 Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm
học 2014 – 2015; Ngày thi 20.06.2014.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm học 2015
– 2016; Ngày thi 04.06.2015.
 Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang;
Tỉnh Khánh Hòa; Năm học 2015 – 2016; Ngày thi 05.06.2015.  a aa 1 Cho biểu thức B   :  
với a  0; x  4 .  a  2 a
a  2  a  4 a  4
1. Rút gọn biểu thức B.
2. Tính giá trị của B khi a  3  2 2 .
3. Tính giá trị của B khi a 1  2016  2015 .
4. Tìm a sao cho B  2a  9 a 12 .
5. Tìm a để B nhận giá trị không vượt quá 3. x y y y x x
6. Xét biểu thức M
với điều kiện x  0; y  0 . 1 xy 16
So sánh giá trị của biểu thức M khi x    2 1 3
; y  3  8 và giá trị của biểu thức B khi a  . 9 1 1 1
7. Biểu thức B nhận giá trị hữu tỷ hay không khi a    ...  ? 2 1 1 2 2 3  3 2 100 99  99 100
Bài toán 138. Mở rộng và phát triển các bài toán
 Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha Trang; Tỉnh Khánh Hòa; Năm
học 2016 – 2017; Ngày thi 02.06.2016.
 Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Nha
Trang; Tỉnh Khánh Hòa; Năm học 2016 – 2017; Ngày thi 03.06.2016.  x y    x y 2 3 3  xy x y
Cho biểu thức A     : .  x y y xx y  
1. Tìm điều kiện xác định và rút gọn A.
2. Tính giá trị biểu thức A khi x  9; y  25 .
3. Chứng minh rằng A  0 .
4. Tính giá trị của A khi x và y thỏa mãn x  2 y  3 xy . 3
5. Tìm tỷ lệ giữa x và y sao cho A  . 7
6. Chứng minh rằng 0  A  1, từ đó tìm điều kiện giữa x và y để biểu thức A nhận giá trị là số nguyên. 1 3
7. Tồn tại hay không các số thực z, t sao cho A   z t   z t ? 2 4
8. Giả sử p là số nguyên tố sao cho 2 2
8 p 1;8 p 1 đều là các số nguyên tố. Tìm tất cả các giá trị của p
và tính giá trị của biểu thức A trong trường hợp x py .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 54
_______________________________________________________________________________________________________________________________________________________________
Bài toán 139. Mở rộng và phát triển các bài toán
 Bài 1 và bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố
Tuy Hòa; Tỉnh Phú Yên; Năm học 2012 – 2013.
 Bài 1 và bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Phú Yên; Năm học 2010 – 2011; Ngày thi 30.06.2010. 1 x  3 x  2 Cho biểu thức P    . x  5 x  6 x  2 x  3
1. Tìm điều kiện xác định của biểu thức P.
2. Với điều kiện vừa tìm, rút gọn biểu thức P . 1
3. Tìm khoảng giá trị của x để P  . 5 6  x
4. Giải phương trình P  . 2 x  3
5. Tìm các số nguyên x để P có giá trị nguyên.
6. Tính giá trị của P khi x thỏa mãn   x3 
x3  x 3 1005 1007 2 - 2012  0 .
7. Tìm giá trị của m sao cho phương trình ẩn x: P m có nghiệm.
8. Tìm giá trị nhỏ nhất của biểu thức S Px .
9. Giả sử P P x . Xét các số thực a, b, c sao cho a b c  0 . Tính P  3 3 3
a b c  3abc .
10. Chứng minh rằng không tồn tại các số thực y, z thỏa mãn đẳng thức 1 1 1 2 4 P   y   z  . 2016 2017 3  x  2 x  2
x x x x 1
11. Xét biểu thức B      . Tìm x để 2 P BP .  x 1 x 2 x 1     x  
Bài toán 140. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy Hòa; Tỉnh Phú Yên; Năm học
2003 – 2004; Ngày thi 09.07.2003.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy
Hòa; Tỉnh Phú Yên; Năm học 2013 – 2014.
 Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy
Hòa; Tỉnh Phú Yên; Năm học 2011 – 2012. 2 2  1 1 x 1 1 xx 1 Cho biểu thức 2 A     .  1 x .  1 x 1 x 1 x 1 x        2  
1. Tìm điều kiện xác định của A.
2. Rút gọn biểu thức A. 3. Chứng minh 2 A A . 13
4. Tìm giá trị của x để A  . 4  8039  5. Cho 3 3 x  1 65  65 1 và 3
Q x 12x  2009 . Đặt A f x , tính f Q    .  4 
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 55
_______________________________________________________________________________________________________________________________________________________________
6. Biểu thức A có nghĩa hay không khi x thỏa mãn 2
x  2 2  xx 1  3x  2  0 ?
7. Tìm x để A có giá trị lớn hơn 5. a b c
8. Giả sử a, b, c là các số thực dương sao cho a b c ab bc ca . Tìm x để A    . b c a
Bài toán 141. Mở rộng, liên hệ và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lương Văn Chánh; Thành phố Tuy
Hòa; Tỉnh Phú Yên; Năm học 2002 – 2003; Ngày thi 09.07.2002. 3 x  5 5 x  2 x  5 Cho biểu thức P    . x 1 x  2 x x  2
1. Rút gọn biểu thức P. 4
2. Tính giá trị của P khi x thỏa mãn 2 x   5 . 2 x
3. Tính giá trị của P khi x  7  2 6 .
4. Tìm x để P  2 .
5. Tìm khoảng giá trị của x để P  1  . x  5
6. Giải phương trình P  . x  7
7. Tìm giá trị của m để phương trình ẩn x: P m có nghiệm.
8. Tìm giá trị nguyên của x để P nhận giá trị nguyên.
9. Tồn tại hay không các số thực a, b, c sao cho P  1 a  1 b  2  c  4 ?
Bài toán 142. Mở rộng, liên hệ và phát triển các bài toán
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuận; Năm học 2009 – 2010.
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuận; Năm học 2011 – 2012; Ngày thi 26.06.2011.  x
x  4   2 x 1 1 
Cho biểu thức P     :  
 với x  0; x  4 .
 2  x 4 x   x  2 x x      
1. Rút gọn biểu thức P.
2. Tính giá trị của biểu thức P khi x  3  2 2 . 2
3. Tìm x để P nhận giá trị là  . 3
4. Tìm x sao cho P  1, 5 . 2 x
5. Giải phương trình P   0 . 3x 1
6. Tìm tất cả các giá trị m để phương trình P m có nghiệm.
x y z  3,
7. Tính giá trị biểu thức P khi x là số lớn nhất thỏa mãn hệ thức xy yz zx  9.   x x  8
8. Xét biểu thức Q
 31 x ; x  0 . x  2 x  4
a) Tìm x để P Q . 2P
b) Tìm các giá trị nguyên dương của x để biểu thức Q  nhận giá trị nguyên. 1 P
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 56
_______________________________________________________________________________________________________________________________________________________________
Bài toán 143. Mở rộng, liên hệ và phát triển các bài toán
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuận; Năm học 2006 – 2007.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuận; Năm học 2007 – 2008.  a a b ba b
Cho biểu thức M    ab . .  a ba b  
1. Rút gọn biểu thức M và tính giá trị của M khi a  9;b  4 . 2 
a  4b  4  0,
2. Tính giá trị của M khi a và b là nghiệm của hệ  2 b   6a  9  0. 
3. Tìm giá trị lớn nhất của biểu thức M  2 a  3 b khi a b  4 .
4. Khi a và b là nghiệm của phương trình 2
x  27x 121  0 , chứng minh M  7 .
5. Chứng minh bất đẳng thức M   4 4
2 2 2 a b  .
6. Xét biểu thức P ab a b b 1có cùng điều kiện xác định với M. Tìm tất cả các giá trị nguyên
của a và b để biểu thức P có giá trị bằng 0.
Bài toán 144. Mở rộng, liên hệ và phát triển các bài toán
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Thuận; Năm học 2013 – 2014; Ngày thi 23.06.2013.
 Bài 2 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Phan
Rang – Tháp Chàm; Tỉnh Ninh Thuận; Năm học 2012 – 2013; Ngày thi 24.06.2012.
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Phan Rang –
Tháp Chàm; Tỉnh Ninh Thuận; Năm học 2015 – 2016; Ngày thi 11.06.2015.
 Bài 2 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Ninh Thuận; Năm học 2016 -2017; Ngày thi 14.06.2016.
x  2 x 1  x x  1 1
Cho các biểu thức P x  . 1; Q x  
x  0; x   1 . x 1  x 1    x 1 x 1  
1. Rút gọn các biểu thức P (x) và Q (x). 2. Tìm x để 2
2x P x  0 .
3. Tìm x để Q nhận giá trị bằng 2. 3
4. Tìm giá trị của x để Q  . 4 1 1
5. Tính giá trị của P khi x là nghiệm của phương trình x   x  . x x
6. Tính giá trị của Q khi x thỏa mãn 2
x x x 1  8  0 .
7. Giải phương trình PQ  5x  3 .
8. Đa thức R x 3 2
x ax  2x  2a có ba nghiệm, trong đó một nghiệm là trung bình cộng của hai
nghiệm còn lại. Tính Q R4 . x y z
a b c x y z
9. Xét các số thực dương a,b, c, x, y, z thỏa mãn   . Đặt t
 4 , tính P t  . a b c
ax by cz
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 57
_______________________________________________________________________________________________________________________________________________________________
Bài toán 145. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1 và bài 3a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học 2016 – 2017.
 Bài 3b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Bình Thuận; Năm học 2009 – 2010.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán); Đề
thi chính thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học 2015 – 2016.
 Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Bình Thuận; Năm học 2016 – 2017; Ngày thi 15.07.2016. 2  a 1 a 1   2 
Cho biểu thức P     1 
 với a  0; a  1 .  a 1 a 1   a 1   
1. Rút gọn biểu thức P. 11
2. Tìm a để P  . 6
3. Tìm khoảng giá trị của a sao cho giá trị của P không nhỏ hơn – 1.
4. Tính giá trị của P khi a  8  2 a  9  a  20 . 4  2  5. Cho x thỏa mãn 2 x   4 x
 9  0 . Tính giá trị của P khi a x  2 . 2   xx
6. Tìm giá trị nguyên của a để P nhận giá trị nguyên.  a a   a  2 a
7. Xét biểu thức B  1  1  . Tìm a sao cho 2 PB B .  1 a   2 a       
8. Với các số thực dương a, b, c sao cho ab bc ca  3, xét 2 2 2
S a b c  6 a b c  2017 . Tìm
khoảng giá trị của a để P S . min a b b a 1
9. Tìm b theo a sao cho P  : . ab a b
Bài toán 146. Mở rộng, liên hệ và phát triển các bài toán
 Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học 2014 – 2015.
 Bài 3b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Bình Thuận; Năm học 2012 – 2013; Ngày thi 12.07.2012.
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học 2013 – 2014. 1 1 Cho biểu thức P   . x 1  2
x  3 x 1  3
1. Tìm điều kiện xác định của P.
2. Rút gọn biểu thức P.
3. Tìm x để P có giá trị bằng 1.
4. Tìm x để P có giá trị dương. 3x 1 y  2 6x  2 y  2
5. Tính giá trị biểu thức P khi x thỏa mãn dãy tỷ số   . 2 3 x
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 58
_______________________________________________________________________________________________________________________________________________________________ 2
6. Giải phương trình P  3  . x
7. Tính giá trị của P khi x là nghiệm của phương trình 2
x x  4  10 1 x . 2 1 8. Xét biểu thức 2 Q  . 8x  2
1 4x  4x  với 0  x  . Tìm x sao cho Px Q . 2x 1 2 x 32 2 2 12x
9. Xét biểu thức A
  x  22  8x . Tính giá trị của P khi A  5 . 2 x
Bài toán 147. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học 2010 – 2011.
 Bài 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Bình Thuận; Năm học 2013 – 2014; Ngày thi 10.07.2013. 
x  4 x   x  3 x x 1
Cho các biểu thức P  1  1  và B x  2 
với x  0; x  16 .  x 4   x 3        x 1 x
1. Rút gọn biểu thức P.
2. Chứng minh biểu thức B không phụ thuộc giá trị biến.
3. So sánh giá trị của P và B.
4. Tìm x để P nhận giá trị bằng 9. 5. Tìm x để 2 P  16B .
6. Đặt P P x . Xét các số x, y thỏa mãn 2 2
xy x y  76; x y xy  960 , tính  2 2 P x y .
7. Giải phương trình P   2 2 2 x   1 .
Bài toán 148. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học 2008 – 2009.
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Trần Hưng Đạo; Thành phố Phan Thiết; Tỉnh Bình Thuận; Năm học 2006 – 2007. x y x y x y Cho biểu thức N   
với x  0; y  0; x y .
2  x y  2 x y x y
1. Rút gọn biểu thức N.
2. Tính giá trị biểu thức N khi x  25; y  16 .
x  4  y  1 2, 
3. Tính giá trị biểu thức N khi x và y thỏa mãn hệ 
y  2  x  1 2. 
4. Tính giá trị của N khi x  3y  4 xy .  x y x y  
x y  2xy
5. Xét biểu thức A     : 1   .  1 xy 1 xy  1 xy    
a) Rút gọn biểu thức A.
b) Tìm giá trị lớn nhất của A.
c) Tìm điều kiện của x và y sao cho N A  2 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 59
_______________________________________________________________________________________________________________________________________________________________
Bài toán 148. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2013 – 2014.
 Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2012 – 2013.
 Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2011 – 2012; Ngày thi 27.06.2011.
 Bài 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Quảng Trị; Năm học 2010 – 2011; Ngày thi 24.06.2010.  a 1  a 1
Cho biểu thức P     :
với a  0; a  1 .
a 1 a a a 1  
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a  4 .
3. Tính giá trị của P khi a  3  2 2 .
4. Tìm giá trị của a để P nhận giá trị bằng 2.  1 
5. Tìm a sao cho P  3 a   8   .  a   1 1  1
6. Xét biểu thức Q   :  
. Tìm a để P Q .  a 1
a 1  a 1  1 1  a
7. Xét biểu thức R   :  
với 0  a  4 . Tìm a để 2 P R .  a  2
a  2  a  4
a b  2 ab 1
8. Tìm b theo a để P  : . a b a b
Bài toán 149. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2008 – 2009.
 Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2011 – 2012; Ngày thi 17.06.2011.  1 1  x 1 Cho biểu thức C   :   với 0  x  1.  x 1
x 1  x 1
1. Rút gọn biểu thức C.
2. Tính giá trị của C khi x  6  2 5 . 3. Tìm x sao cho 2 13C  12C .
4. Tìm giá trị của x để 2 C  0,8C .
5. Chứng minh rằng 0  C  1, từ đó suy ra C chỉ nhận duy nhất một giá trị nguyên.  x  1
6. Xét biểu thức D   x  2 x x x    
. Tìm x để C D .  x 1  x 1
Bài toán 150. Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Tin;Sở Giáo dục và
Đào tạo Tỉnh Quảng Trị; Năm học 2011 – 2012; Ngày thi 17.06.2011. 2x  2 x x x 1
Cho biểu thức P x   1. x 1 x x 1
1. Tìm điều kiện của x để P có nghĩa. 2. Rút gọn P.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 60
_______________________________________________________________________________________________________________________________________________________________
3. Tính giá trị của P khi x thỏa mãn 3 x  2 x 8  0.
4. Tính giá trị của P khi 2 x  28 16 3 .
5. Tìm x để P đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó. x x
6. Tìm x để P  . 6x  5
7. Với giá trị nào của x thì P  0, 75 ?
8. Giải phương trình P    2 1
2 x  3x   1 .
Bài toán 151. Mở rộng và phát triển bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành
phố Đông Hà; Tỉnh Quảng Trị; Năm học 2013 – 2014; Ngày thi 18.06.2013. 3a  9a  3 a  2 1 Cho biểu thức P    1. a a  2 a 1 a  2
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a  6  2 5 .
3. Tìm a để P nhận giá trị bằng – 3. 5
4. Tìm a để giá trị của P không nhỏ hơn . 3 a  6
5. Giải phương trình P  . 6
6. Tìm a nguyên để biểu thức P nguyên.
7. Tính giá trị của P khi a thỏa mãn hệ thức 2
a  7a  2  2 3a 1  0 .
8. Tìm giá trị nhỏ nhất của biểu thức P .
Bài toán 152. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Trị; Năm học 2007 – 2008.
 Câu 3.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Đông Hà; Tỉnh
Quảng Trị; Năm học 2014 – 2015.  1 1   a  1 a  2  Cho biểu thức A   :    
 với a > 0, a  1, a  4 .  a 1 a   a 2 a 1      
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi a  9  4 5 11 5 5 .
3. Tìm a để A  0  , 2 .
4. Tìm khoảng giá trị của a sao cho giá trị của A không vượt quá 0,25. a  4
5. Giải phương trình A  . 9
6. Tìm giá trị nguyên của a để A nhận giá trị nguyên.
7. Tính giá trị của A khi a là nghiệm của phương trình 2
9a 12a  2  3a  8 . 2 2 2
x y z  6  2  x y z
8. Chứng minh rằng A  , x
 , y, z   . 9 2 2 2
x y z
9. So sánh giá trị của A và giá trị của biểu thức B  .
x y z2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 61
_______________________________________________________________________________________________________________________________________________________________
Bài toán 153. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành
phố Đông Hà; Tỉnh Quảng Trị; Năm học 2014 – 2015. 1 x 1
Cho biểu thức P(x)  : . 2 x x x x   1  x
1. Rút gọn P (x).
2. Tính giá trị của P khi x  7  2 6 .
3. Tìm x để giá trị của P lớn hơn 5. 2 x  5x  3 1
4. Giải phương trình ẩn x: 2P   . 2 x 1 x 1
5. Tính giá trị của P khi x là nghiệm của phương trình 2
x  4x 1  5x 1 .
6. Tìm x để P (x) nhận giá trị nguyên.
Bài toán 154. Mở rộng, liên hệ và phát triển các bài toán
 Câu 9; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Bình; Năm học 2010 – 2011.
 Bài 1 phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Quảng Bình; Năm học 2009 – 2010. 1 1 2 b Cho biểu thức P    với 0  b  4 . b  2 b  2 b  4
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi b  3  2 2 . 2
3. Tìm b để P  . 3
4. Tìm khoảng giá trị của b sao cho 2 P  0,8P .
5. Chứng minh bất đẳng thức P P . 2
6. Giải phương trình P  . 2 4b  3 1
7. Tìm tất cả các giá trị của b để P nhận giá trị nguyên. n 1 n 1
8. Xét biểu thức N  
với n  0; n  1. n 1 n 1
a) Tìm b theo n để P và N có giá trị bằng nhau.
b) Tìm tất cả các giá trị nguyên của n để biểu thức N có giá trị nguyên.
Bài toán 155. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Quảng Bình; Năm học 2014 – 2015.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Quảng Bình; Năm học 2013 – 2014; Ngày thi 26.06.2013. 1 1 x Cho biểu thức A   
với x  0; x  4 . x  2 x  2 x  4
1. Rút gọn biểu thức A. 2
2. Tính giá trị của biểu thức A
với x  7  4 3 . 3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 62
_______________________________________________________________________________________________________________________________________________________________
3. Tìm giá trị nguyên của x để A nhận giá trị nguyên. 2 4. Tìm x để 2 A A . 3
5. Tìm x sao cho A  0, 2 . x  8
6. Giải phương trình A   0 . x  4 a b 7. Ký hiệu S
là giá trị lớn nhất của biểu thức S  
với a, b là các số thực max 2 2
a b  2b a
b a  2a b
dương. Tính giá trị của A khi x S . max  1 1   1 
8. Xét biểu thức B   1   
 với 0  x  1. Tìm giá trị của x để A B .  x 1 x 1  x
Bài toán 156. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1 và câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Võ Nguyên Giáp; Thành phố
Đồng Hới; Tỉnh Quảng Bình; Năm học 2016 – 2017; Ngày thi 08.06.2016.
 Câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Quảng Bình; Năm học 2016 – 2017; Ngày thi 08.06.2016.  a  4 3 
Cho biểu thức P    .
với a  0; a  4 . 
 a a  2 a  2 a a  2  
1. Rút gọn biểu thức P. 3 2  4 2 3
2. Tính giá trị của biểu thức P khi a  . 3 1 1
3. Tìm giá trị của a sao cho P a   7 . a 32
4. Tìm khoảng giá trị của a để P  . 3 1 1
5. Tính giá trị của P khi a là nghiệm phương trình  2a  2017   3a  2016 . 2 a a  1 1  1
6. Xét biểu thức A   .   với 0  a  1.  a 1 a 1  a
a) Rút gọn A và tìm a để A có giá trị bằng 1.
b) Giải phương trình A P .
7. Tìm tất cả các giá trị của m để phương trình ẩn a: P m có nghiệm.
Bài toán 157. Mở rộng, liên hệ và phát triển câu 1 và câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán
(Dành cho các thí sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Võ
Nguyên Giáp; Thành phố Đồng Hới; Tỉnh Quảng Bình; Năm học 2015 – 2016.  4 x 8x   x  4 1 
Cho biểu thức P     :  
 với x  0; x  4; x  9 .
 2  x 4 x   x  2 x x      
1. Rút gọn biểu thức P và tìm x để P  1  . 1
2. Tính giá trị của biểu thức P khi x   7  5 5 . 5  2
3. Tính giá trị của P khi x là nghiệm phương trình 2
x x  4 3x 1  6  0 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 63
_______________________________________________________________________________________________________________________________________________________________ 5x
4. Giải phương trình P  . 4 x  9
5. Tìm khoảng giá trị của x để 3P  32 .
6. Xác định giá trị nhỏ nhất của P .
7. Tìm điều kiện cần và đủ của tham số m để phương trình ẩn x: P m có nghiệm.
8. Tìm x để bất đẳng thức sau luôn đúng: P a  2  a b  2  b, a  ,b 0; 2 .
Bài toán 157. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Võ Nguyên Giáp; Thành phố Đồng Hới; Tỉnh Quảng Bình; Năm học 2010 – 2011.
 Câu 12; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Quảng Bình; Năm học 2007 – 2008; Ngày thi 26.06.2007. 2  x 1 x 1   1 x
Cho biểu thức Q      
 với x  0; x  1.  x 1 x 1   2 x 2       
1. Rút gọn biểu thức Q. Q 2. Tìm x để  2 . x
3. Tính giá trị của Q khi x  9  4 5 . 1
4. Giải phương trình Q x   4 . x 8
5. Tìm khoảng giá trị của x sao cho Q  . 3
6. Tính giá trị của Q khi x là nghiệm của phương trình 2
x  5x  2  8 3x  2 .  c  2 1 
7. Xét biểu thức C    
. Tìm c theo x để Q C .    c  2 c c  2  
Bài toán 158. Mở rộng, liên hệ và phát triển các bài toán
o Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2003 – 2004.
o Bài 6; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2000 – 2001.  x  x      x  2 2 1 1 Cho biểu thức M   x 2    . .  x 1  2  
1. Tìm x để biểu thức M có nghĩa.
2. Tính giá trị của M khi x  11 2 10 .
3. Giải phương trình ẩn x: M   x  2 2 1 . 4. Tìm x sao cho 2 M  0, 25M . 1 5. Chứng minh M  . 4
6. Tìm khoảng giá trị của x để M có giá trị không âm.
7. Khi x làm cho biểu thức S   x  2   x  2   x  2 1999 2000 2001
đạt giá trị nhỏ nhất thì M có giá trị là bao nhiêu ?
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 64
_______________________________________________________________________________________________________________________________________________________________
Bài toán 159. Mở rộng, liên hệ và phát triển các bài toán
o Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2004 – 2005.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2005 – 2006.
o Bài 1; Đề A; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Thanh Hóa; Năm học 2006 – 2007.  a  2 a  2  a 1
Cho biểu thức B    . .
a  2 a 1 a 1   a  
1. Tìm điều kiện của a để B có nghĩa. 2 2. Chứng minh B  . a 1
3. Tính giá trị của B khi a  9  4 5 .
4. Giải phương trình ẩn a: 2
B  2a  5a  2 .  a a   a  5 a
5. Tìm tất cả các giá trị của a sao cho B  3    3   .  a 1   a 5        a a 2
6. Xét biểu thức A    . a 1 a 1 a 1
a) Tìm a để A  1  . b) Tìm a sao cho 2 B  2 AB .
Bài toán 160. Mở rộng, liên hệ và phát triển các bài toán
o Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2012 – 2013.
o Bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Thanh Hóa; Năm học 2007 – 2008.
o Bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Thanh Hóa; Năm học 2008 – 2009. 2 1 1 a 1 Cho biểu thức A    2 2  2 a 2  2 a 1 a
1. Tìm điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị của a khi a  3  2 2 . 1
3. Với giá trị nào của a thì A nhận giá trị bằng ? 8 1
4. Tìm giá trị của a biết A  . 3
5. Tìm tất cả các giá trị nguyên của a để A nhận giá trị nguyên.
6. Chứng minh bất đẳng thức 0  A  1.
7. Tìm tất cả các giá trị thực của a để A nhận giá trị nguyên.  a a   a a
8. Tìm a sao cho giá trị của A bằng giá trị biểu thức B  1  1  .  a 1   a 1         a 1 1  a 1
9. Xét biểu thức C     . Tìm a để 2 C A .  a 1
a 1  a  2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 65
_______________________________________________________________________________________________________________________________________________________________
Bài toán 161. Mở rộng và phát triển ài 2; Đề C; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2010 – 2011.  c  3 c  3   1 1 
Cho biểu thức C      
 với c  0; c  9 .  c 3 c 3       3 c  1. Rút gọn C.
1. Tính giá trị biểu thức C khi c  3  2 2 .
2. Tính giá trị biểu thức C khi c  9  10 c . 6
3. Tìm c để C  . 5 3 c 10
4. Giải phương trình C  . 13 5. Tìm c sao cho 3 C  16C .
6. Tìm c để biểu thức C nhận giá trị nguyên. x y z
7. Tồn tại hay không các số thực dương x, y, z thỏa mãn C    ? y z x z x y
Bài toán 162. Mở rộng và phát triển bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2013 – 2014.  1 1   y 1 
Cho biểu thức Q     : 
 với y  0; y  1 .  y y y 1   y 2 y 1         
1. Rút gọn biểu thức Q.
2. Tính giá trị biểu thức Q khi y  3  2 2 .
3. Tính giá trị của Q khi  y  3 y  5 y  4  0 . 4. Tìm y để 2 3Q  2Q . 1
5. Giải phương trình Q  1 . y  8  2
6. Giải bất phương trình ẩn y: 2 5Q  2Q . a b c 7. Chứng minh Q     2, a  , , b c  0 . b c a 2 2 2
a b c  2abc 1
8. Phản biện bất đẳng thức Q  , a
 ,b, c  0 .
2ab bc ca
Bài toán 163. Mở rộng và phát triển bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính
thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2015 – 2016; Ngày thi 21.07.2016. 4 3 6 b  2 Cho biểu thức Q   
với b  0;b  1. b 1 b 1 b 1 1. Rút gọn Q.
2. Tính giá trị của biểu thức Q khi b  6  2 5 .
3. Tính giá trị của biểu thức Q khi b là nghiệm phương trình 2
b  7b  7  8b  7 . 2
4. Tìm b sao cho Q  . 2 b  5
5. Chứng minh 0  b  1 .
6. Tìm tất cả các giá trị của b để Q nhận giá trị nguyên.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 66
_______________________________________________________________________________________________________________________________________________________________
Bài toán 164. Mở rộng và phát triển bài 2.2; Đề A; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và Đào tạo Tỉnh Thanh Hóa; Năm học 2011 – 2012.  a a 4 a 1  1
Cho biểu thức A      :
với a  0; a  4 .  a  2 a  2 a 4   a  2  
1. Rút gọn biểu thức A.
2. Tính giá trị của A tại a  6  4 2 . a  5
3. Tìm a sao cho A  . 6  a 2A   1  A  3
4. Giải bất phương trình  0 . A
5. Tính giá trị của A khi a là nghiệm phương trình 2 2
2a  3a  2  3a  4a  2 .
6. Tìm khoảng giá trị của m để phương trình A m  3có nghiệm.  1 
7. Tìm m để A  , m a   ; 4   .  4 
Bài toán 165. Mở rộng, liên hệ và phát triển các bài toán
 Câu II; Đề A; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Thanh Hóa; Năm học 2016 – 2017; Ngày thi 16.06.2016.
 Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2014 – 2015; Ngày thi 30.06.2014.  
  2  x  2 x x x x x   1 1 1
Cho biểu thức A     :
(với x  0; x  1).  x x x x x 1  
1. Rút gọn biểu thức A.
2. Tính giá trị của biểu thức A khi x  8  2 7 .
3. Tính giá trị của A khi x thỏa mãn 2
x  2x  3  3 5x  4 . x  3
4. Tìm a sao cho A  . x  4
5. Giải bất phương trình 2 A  2 A .
6. Tìm tất cả các số nguyên x để biểu thức A có giá trị nguyên.
7. Tìm giá trị nhỏ nhất của biểu thức A .
8. Tìm khoảng giá trị của m để A  , m x   4;9 . x 1  1 1 
9. Xét biểu thức B  . 
với x  0; x  1. Tìm x sao cho A B . 2  
x x x x 1 
Bài toán 165. Mở rộng và phát triển Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự chuyên Tiếng Nga, Tiếng Pháp); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố
Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2012 – 2013.  x  2 x  3 x  2   x
Cho biểu thức A      :  2   .  x 5 x 6 2 x x 3   x 1          
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi x  6  2 5 . 12
3. Tìm các giá trị của x sao cho A   . 35
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 67
_______________________________________________________________________________________________________________________________________________________________
4. Tính giá trị biểu thức A khi x là nghiệm phương trình 4 2
x x  2  2 2x 1 . 1
5. Giải phương trình A  . x  9 1 5
6. Tìm các giá trị của x để   . A 2
7. Tìm tất cả các giá trị của m để phương trình A m có nghiệm.
8. Tìm tất cả các giá trị x  4 để biểu thức A nhận giá trị nguyên.
Bài toán 166. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1 và bài 3.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi);
Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm
học 2011 – 2012; Ngày thi 19.06.2011.
 Đề thi Olympic môn Toán; Khu vực Châu Á – Thái Bình Dương; Năm 2004 – APMO 2004. 15 x 11 3 x  2 2 x  3 Cho biểu thức A    x  2 x  3 1  x x  3
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  4  2 3 .
3. Tính giá trị của A khi 3 x  5 2  7 . 2 4. Chứng minh A  . 3 2
5. Giải phương trình A  . 5
6. Tìm khoảng giá trị của x để 2 7 A  2 A .
7. Tìm m để phương trình ẩn x: A m có nghiệm x 0;3 . 3x
8. Tính giá trị của biểu thức A khi x thỏa mãn x   6 2 . 2 x  9 2 2 2 9 Aa   b   c
9. Tìm tất cả các số thực dương a, ,
b c thỏa mãn đẳng thức          . 2  b c   c a   a b   2 a   2 b   2 2 2 c  2
10. Phủ định hoặc khẳng định bất đẳng thức: 6A  a, , b c  0 .
ab bc ca
Bài toán 167. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh
Hóa; Năm học 2010 – 2011; Ngày thi 19.06.2010.  x 6 1   10  x  Cho biểu thức A    : x  2       x x  4 x 3 x  6 x  2   x  2 
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi x  13  4 3 .
3. Tính giá trị biểu thức A khi 3 x  7x  8 . 1
4. Giải phương trình A   . 8
5. Tìm x sao cho A  2 . x  6 6. Tìm x để A  . 5  x
7. Tìm m để phương trình ẩn x: A m có nghiệm x 0;3 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 68
_______________________________________________________________________________________________________________________________________________________________
Bài toán 168. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí
sinh dự thi chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa;
Tỉnh Thanh Hóa; Năm học 2007 – 2008.  2x 1 x   1 x x
Cho biểu thức P       x  .  x x 1 x x 1   1 x         
1. Tìm điều kiện của x để P có nghĩa và rút gọn P.
2. Tính giá trị của P khi x  9  4 2 .
3. Tính giá trị của P khi x thỏa mãn 4 2
a  5a  4  0 .
4. Tình giá trị của P khi x là nghiệm của phương trình 2
x  2x  7  3  x   1  x  3 .
5. Giải phương trình P  9x 15 x  6 . 6. Tìm x sao cho 2 P  3P . x  3
7. Tìm giá trị của x sao cho P  . 4 x  3
Bài toán 169. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh
Hóa; Năm học 2012 – 2013; Ngày thi 17.06.2012.  a 1 a 1  1
Cho biểu thức P     4 a .
với a  0; a  1 .  a 1 a 1    2a a   2 1. Chứng minh P  . a 1
2. Tính giá trị của P khi a thỏa mãn 4 2
a 10a  9  0 .
3. Tính giá trị của P khi a  15  2 14 .
4. Tìm a để P a . 4 5
5. Giải phương trình ẩn a: P   . 2 a 1 a 1 6. Tìm a sao cho 3 P  3P .
7. Tìm giá trị nguyên của a để P nhận giá trị nguyên. 1 1
8. Xét trường hợp a  1;b  1;c  1; a b c  4 . Tìm giá trị nhỏ nhất của biểu thức S P   . b 1 c 1
Bài toán 170. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2013 – 2014; Ngày thi 24.06.2013.
 Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học);
Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2009 – 2010.
 Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2006 – 2007.  2 x  2 x
Cho biểu thức P     :  x  0 .  x x 2   x  2 x  
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 69
_______________________________________________________________________________________________________________________________________________________________
1. Rút gọn biểu thức P.
2. Giải phương trình P  3 x 1. 2 
2x xy  1
3. Tính giá trị của P khi x là nghiệm của hệ  2 2
4x  4xy y  7  19
4. Tìm x để P có giá trị lớn hơn . 6 1
5. Tính giá trị của P khi x thỏa mãn đẳng thức x  2  y  2009  z  2010 
x y z . 2
6. Tìm giá trị của x để P  3 .
7. Tìm giá trị nhỏ nhất của biểu thức P. 1 1 1 xy yz zx
8. Cho ba số x, y, z khác 0 và thỏa mãn    0 . Đặt A   
và đặt P P x . Tính giá x y z 2 2 2 z x y
trị của P A  4 .
Bài toán 171. Mở rộng và phát triển bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh
Thanh Hóa; Năm học 2015 – 2016; Ngày thi 12.06.2015.  a aa 1 Cho biểu thức M   :  
với a  0; a  4 .  a  2 a
a  2  a  4 a  4
1. Rút gọn biểu thức M. 16
2. Tính giá trị biểu thức M với a   . 81
3. Tính giá trị biểu thức M khi a thỏa mãn 2 a  49  20 6 .
4. Tìm giá trị của a sao cho M có giá trị bằng 3.
5. Giải bất phương trình M  5a  6 a .
6. Tìm tất cả các giá trị của a để M  0 .
7. Tính giá trị của M khi a thỏa mãn 2 a    2 5 1 2 a  2 .
8. Tìm giá trị nhỏ nhất của biểu thức M  5 a .
9. Giải phương trình M  3a  8  4 3a  5 .
Bài toán 172. Mở rộng và phát triển bài 1 và bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh
Thanh Hóa; Năm học 2016 – 2017. 2 x x 1 3 11 x Cho biểu thức A   
x  0; x  9 . x  3 x  3 9  x
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x thỏa mãn 2x 1  6  x .
3. Tìm x để A  0 .
4. Tìm tất cả các giá trị của x sao cho A  12 . 3 x  7
5. Giải phương trình A  . x  5
6. Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
7. Tính giá trị biểu thức A khi x là nghiệm phương trình 2
x x    x   2 4 7 4 x  7 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 70
_______________________________________________________________________________________________________________________________________________________________
8. Tìm giá trị của m để phương trình A m có nghiệm.
9. Tìm giá trị nhỏ nhất của biểu thức S A x . 1 2 1
10. Tồn tại hay không các số thực y, z sao cho A   y y   z z  ? 2 3 2
Bài toán 173. Mở rộng và phát triển bài 1 và bài 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành
cho các thí sinh dự thi chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố
Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2014 – 2015. 3x  16x  7 x 1 x  3 Cho biểu thức P   
x  0; x   1 . x  2 x  3 x  3 x 1
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi x thỏa mãn x  2 2  3 . 3 x  5
3. Tìm x sao cho P  . 3 x  7 4. Giải phương trình 2 P  4P . 3
5. Tìm khoảng giá trị của x để P  . 2 2 2 
2x  3x y  2
6. Tính giá trị của P khi x là nghiệm của hệ  2 2
2 y  3y x  2 
7. Tìm các giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
8. Tính giá trị của biểu thức P khi x là số nguyên thỏa mãn 3 3 2 2
x y x y xy  5 . 1 2 2
9. Chứng minh không tồn tại các số thực y, z thỏa mãn P   y z
 2 y  3z  . 3 3 3
Bài toán 174. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học); Đề
thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2009 – 2010.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Tin học); Đề
thi chính thức; Trường THPT Chuyên Lam Sơn; Thành phố Thanh Hóa; Tỉnh Thanh Hóa; Năm học 2005 – 2006. 2 2x  4 1 1 Cho biểu thức T    ; 3 1 x 1 x 1 x
1. Tìm điều kiện của x để T xác định. Rút gọn T.
2. Tính giá trị của T khi x  4  2 3 .
3. Tìm giá trị lớn nhất của T. 4. Giải phương trình 2 3T  4T .
5. Tìm khoảng giá trị của x sao cho 3 4T T .
6. Tìm giá trị nguyên của x để T nhận giá trị nguyên.
7. Tìm tất cả các giá trị thực của x để T nhận giá trị nguyên. 2 3
8. Tính giá trị của T khi x là nghiệm phương trình
x  3x  4x  . 3 1  1   x  2 
9. Xét biểu thức M x    1
 . Tìm x để T M .  x 1   x x 1      
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 71
_______________________________________________________________________________________________________________________________________________________________
Bài toán 175. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nghệ An; Năm học 2013 – 2014.
o Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nghệ An; Năm học 2015 – 2016.  2 1  1 Cho biểu thức P   :    x  4 x  2  x  2
1. Tìm điều kiện xác định và rút biểu thức P.
2. Tính giá trị của P khi x thỏa mãn  x  33 x   1  0 . 3
3. Tìm x để P  . 2 x  8
4. Giải phương trình P  . x 15
5. So sánh P với 1, từ đó tìm tất cả các giá trị của x để giá trị của P là số nguyên. 1 1 1
6. Giả sử tồn tại các số hữu tỷ phân biệt a, ,
b c sao cho x    . Khi đó em hãy
a b2 b c2 c a2
chứng minh giá trị của P là một số hữu tỷ. 1 4 2
7. Xét biểu thức Q  
. Tìm x để P Q  . x  2 x  4 3
8. Xét các số thực a,b, c bất kỳ, phủ định hoặc khẳng định bất đẳng thức
P  a  b  c    a b c2 2 2 2 2 2 2 3 .
Bài toán 176. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2010 – 2011. x 2 2 Cho biểu thức A    . x 1 x  1 x 1
1. Nêu điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi x  9 .
3. Tính giá trị biểu thức A khi x  4  2 3 . 2
4. Tìm x để A nhận giá trị không vượt quá . 3 2 x  2
5. Tìm x sao cho A  . x  7
6. Tính giá trị của A khi x là nghiệm phương trình 3.16x 2.81x 5.36x   .
7. Tìm tất cả các giá trị nguyên của x để A nhận giá trị nguyên.
8. So sánh với A với 1, từ đó tìm tất cả các giá trị của x để A nhận giá trị nguyên.
9. Khi x thỏa mãn điều kiện xác định, tìm giá trị lớn nhất của biểu thức B Ax   1 .
10. Xét các số thực dương a,b, c có tổng bằng 3. Phản biện bất đẳng thức A   2
a a   2
b b   2 1
1 c c   1 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 72
_______________________________________________________________________________________________________________________________________________________________
Bài toán 177. Mở rộng và phát triển câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2007 – 2008.  x 1  1
Cho biểu thức A     : .  x 1 x x    x 1  
1. Nêu điều kiện xác định và rút gọn biểu thức A. 9
2. Tính giá trị biểu thức A với x   . 16
3. Tính giá trị của A khi x  6  2 5 .
4. Tính giá trị biểu thức A khi x thỏa mãn 30x 36 36.5x 6x    . 2
5. Tìm x sao cho A  . 5
6. Tìm tất cả các giá trị của x sao cho A  0 .  1 
7. Giải phương trình A  3 x   8   .  x
8. Với giá trị nào của x thì 2 2 A  3A ?
9. Tìm tất cả các giá trị của tham số m để phương trình A x m x có nghiệm.
Bài toán 178. Mở rộng và phát triển câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2008 – 2009.  3 1  1 Cho biểu thức P   :   .  x 1 x 1  x 1
1. Nêu điều kiện xác định và rút gọn biểu thức P.
2. Tính giá trị của P khi x  3  2 2 .
3. Tính giá trị của P khi x thỏa mãn 9x 27 28.3x   . 5
4. Tìm các giá trị của x để P  . 4 x  6
5. Tìm tất cả các giá trị của x sao cho P  . 3 x  4
6. Giải bất phương trình ẩn x: 2 4P  7P .
7. Tìm giá trị nguyên của x để P nhận giá trị là một số nguyên.
8. Với giá trị nào của tham số m thì phương trình P m có nghiệm thực ? x 12 1
9. Tìm giá trị nhỏ nhất của biểu thức Q  . . x 1 P
10. Tồn tại hay không các số y, z thỏa mãn 3P  1 2 y x  1 3z x 1 2 ?
Bài toán 179. Mở rộng và phát triển câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2012 – 2013; Ngày thi 24.06.2012.  1 1  x  2 Cho biểu thức A   .   .  x  2 x  2  x
1. Tìm điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi x  13  4 3 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 73
_______________________________________________________________________________________________________________________________________________________________
3. Tính giá trị biểu thức A khi 6 3
x  28x  27  0 . 1
4. Tìm tất cả giá trị của x sao cho A  . 2 2
5. Tính giá trị của x sao cho A  . 7 7
6. Giải phương trình ẩn x: A  .
10x  40 x  40 7
7. So sánh A với 0 và 1, từ đó tìm giá trị của x để biểu thức B
A nhận giá trị nguyên. 3
Bài toán 180. Mở rộng và phát triển câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 1999 – 2000.  x  2 x  2    x2 1
Cho biểu thức P    . .  x 1 x 2 x 1     2  
1. Tìm điều kiện và rút gọn P.
2. Tính giá trị của P khi x thỏa mãn 4x 1  7 .
3. Tính giá trị của P khi x  4  2 3 .
4. Tìm giá trị lớn nhất của biểu thức P.
5. Giải phương trình P  5x  3  8 x .
6. Chứng minh rằng P có giá trị hữu tỷ khi x, y thỏa mãn đẳng thức x y  2 y y  2 x y  4  3 .
7. Chứng minh bất đẳng thức 2
P  6P  5  0 .
8. Giải phương trình P    2 1
2 x x   1 .
9. Tìm khoảng giá trị của x sao cho P  6  .
Bài toán 181. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2000 – 2001.
 Đề thi Olympic; Môn Toán; Cộng hòa Hồi giáo Iran; Kỳ thi năm 1998 – Irannian MO 1998.  1 1  x 1 Cho biểu thức P   :   .  x x
x 1  x  2 x 1
1. Tìm điều kiện và rút gọn P.
2. Tính P khi x  0, 25 .
3. Tính giá trị của P khi x là nghiệm phương trình 6x 36 4.3x 9.2x    . 16
4. Tìm giá trị của x sao cho P   . 81
5. Tìm khoảng giá trị của x để biểu thức P  1. 6. So sánh P với 1. 3x 1 1
7. Giải phương trình ẩn x :  P . 3x 1
8. Tính giá trị của P khi x thỏa mãn đẳng thức  3 3
3 4 x y   2 y  6 y  3  x . 1 1 1 x 1  y 1  z 1
9. Cho các số x, y, z  1thỏa mãn  
 2 . Phản biện bất đẳng thức  P  2 . x y z
x y z
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 74
_______________________________________________________________________________________________________________________________________________________________
Bài toán 182. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2001 – 2002.
 Câu 1; Phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2001 – 2002. a 2a a Cho biểu thức P   . a 1 a a
1. Tìm điều kiện và rút gọn P.
2. Tính giá trị của P khi a  3  8 .
3. Giải phương trình P  6a  6 a .
4. Tìm giá trị của a sao cho P  5  a .
5. Tìm điều kiện của a để P nhận giá trị dương. 3 x y 2
6. Tính giá trị của P khi x là nghiệm phương trình     2 . x y y  2 5 x  3 x 2 x 1
7. Xét biểu thức Q   . x 1 x x
a) Tính giá trị của P khi x  36 .
b) Tìm x để Q Q .
c) Tìm x sao cho Q P .
Bài toán 183. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2009 – 2010. x x 1 x 1 Cho biểu thức A   . x 1 x 1
1. Nêu điều kiện xác định và rút gọn biểu thức A. 9
2. Tính giá trị biểu thức A khi x  . 4
3. Tìm giá trị của x sao cho A  4 .
4. Tìm tất cả các giá trị của x để A  1. x  7
5. Giải phương trình A  . 2
6. Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên. x 3 y
7. Tính giá trị của A khi x là nghiệm phương trình    1, 5 . y  3 x y x  3
8. Tìm khoảng giá trị của tham số m để phương trình A m có nghiệm.
Bài toán 184. Mở rộng và phát triển câu 1; phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi
chính thức; Sở Giáo dục và đào tạo Tỉnh Nghệ An; Năm học 2003 – 2004.  1 1  3 Cho biểu thức P   :   .  x  3 x  3  x  3
1. Tìm điều kiện và rút gọn P.
2. Tính giá trị của P khi x  81. 1 3. Tìm x để P  . 3
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 75
_______________________________________________________________________________________________________________________________________________________________ 1
4. Tìm tất cả các giá trị của x để A  . 6 x 1
5. Giải phương trình P  . x 11 8
6. Giải bất phương trình P  . 21
7. Tìm x để biểu thức P đạt giá trị lớn nhất, tìm giá trị lớn nhất đó.
8. Tìm tất cả các giá trị của x để P nhận giá trị nguyên.
9. Tính giá trị của P khi x thỏa mãn đẳng thức  3 3 4 x y
y   4y  36  x  25 y .
Bài toán 185. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2004 – 2005.
 Câu 1; phần B; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào
tạo Tỉnh Nghệ An; Năm học 2005 – 2006.  1 1   1  Cho biểu thức P   . 1     .  x 1 x 1   x
1. Tìm điều kiện và rút gọn P. 1
2. Tính giá trị của P khi x  . 4
3. Tính giá trị của P khi x  14  2 13 . 4. Tìm x sao cho 2 5P  8P .
5. Tìm tất cả các giá trị của x để P P . P 9
6. Tìm giá trị của x sao cho   0 . 2 x  5  1  1
7. Xét biểu thức Q  1 .   . 
x 1  x x
a) Tìm x để P   x  2 . 5 2 6 . 1
x  2005  2  3 .
b) Giải phương trình ẩn x: 2 Q  3P .
8. Chứng minh rằng biểu thức P nhận giá trị hữu tỷ khi x thỏa mãn đẳng thức x y 3 3    . y  3 x  3 x y 2
Bài toán 186. Mở rộng, liên hệ và phát triển các bài toán 
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Nghệ An; Năm học 2011 – 2012. 
Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Nghệ An; Năm học 2014 – 2015. 
Đề thi Olympic; Môn Toán; Cộng hòa Hồi giáo Iran; Kỳ thi năm 2002 – Iranian MO 2002.  1 1  x 1 Cho biểu thức A   :   .  x x
x 1   x  2 1
1. Tìm điều kiện xác định và rút gọn biểu thức A.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 76
_______________________________________________________________________________________________________________________________________________________________ 1
2. Tính giá trị biểu thức A khi x   2  2 . 2 1 1
3. Tìm giá trị của x để A  . 3 7x 1 1
4. Giải phương trình ẩn x: A  . 7x 1
5. Giải bất phương trình ẩn x: 2 19 A  8A .
6. Chứng minh biểu thức A nhận giá trị hữu tỷ khi x thỏa mãn đẳng thức  2
3y  6 y   1
x y  9  8  x y .
7. Tìm giá trị lớn nhất của biểu thức P A  9 x .
8. Cho các số dương a,b, c thỏa mãn 2 2 2
a b c abc  4 . Khẳng định hoặc phủ định bất đẳng thức
a b c A  4 .
Bài toán 187. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Nghệ An; Năm học 2016 – 2017.
 Đề thi Olympic; Môn Toán; Thủ đô Moskva; Cộng hòa Liên bang Nga; Kỳ thi năm 2000 – Moscow
Mathematical Olympiad, 2000 – Moscow MO 2000.  x 1 1 
Cho biểu thức P    . .    x  3 x  9 x  3  
1. Tìm điều kiện xác định và rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi x  17  2 2 .
3. Tính giá trị của P khi x là nghiệm nguyên của phương trình 3 3
x  1  2 2x  1 .
4. Tìm các giá trị của x để P  1. P 4
5. Giải phương trình ẩn x:   0 . 4 15x  1
6. Tìm khoảng giá trị của x sao cho 3 9P P .
7. Chứng minh biểu thức P chỉ nhận duy nhất một giá trị nguyên.
8. Chứng minh biểu thức P nhận giá trị là số tự nhiên khi x thỏa mãn đẳng thức
2  x y  
1  y y  4 x y  2  0 .
9. Chứng minh rằng P nhận giá trị hữu tỷ khi x là số thực dương sao cho 1 1 1 1 1 x      a,b   . 2 2 2 4 4 2   a ba ba b  2 2 a b  2 2 2
a b c a b c 4P
10. Cho các số thực dương a, ,
b c có tích bằng 1. Phản biện bất đẳng thức  .
ab bc ca 3
Bài toán 188. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Nghệ An; Năm học 2006 – 2007.
 Đề thi chọn đội tuyển tham dự kỳ thi Olympic Quốc tế; Môn Toán; Kỳ thi năm 2002; Cộng hòa
Rumani – Junior TST, 2002, Rumania.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 77
_______________________________________________________________________________________________________________________________________________________________  1 1  x 1 Cho biểu thức P   :   .  x x
1 x  1 x2
1. Nêu điều kiện xác định và rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi x  4  2 3 .
3. Tính giá trị biểu thức P khi x là nghiệm phương trình x  4  x  2 2 .
4. Tìm điều kiện của x để P  0 . 2  3x 1
5. Tìm giá trị của x sao cho P  . 3x 1
6. Tìm tất cả các giá trị nguyên của x để biểu thức P nhận giá trị nguyên. 1
7. Cho các số thực a, , b c  0 
;1 . Phản biện bất đẳng thức abc  1 a1 b1 c  P  . x
Bài toán 189. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ An; Năm học 2006 – 2007. x  2 x 1 x 1 Cho biểu thức P    . x x 1 x x 1 x 1
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi x  9  4 5 . 5
3. Tìm giá trị của x sao cho P  . 31 2
4. Giải phương trình ẩn x: P  . x  5
5. Tìm khoảng giá trị của x sao cho 2 13P  3P .
6. Tính giá trị biểu thức P khi x thỏa mãn đẳng thức 4 2
x x 1  x 2x 1 . 1 7. Chứng minh P
với x  0; x  1. 3
8. Chứng minh rằng biểu thức P chỉ nhận duy nhất một giá trị nguyên.
a b c 8abc
9. Cho a,b, c là các số thực dương. Phản biện bất đẳng thức   6P . 3 abc
a bb cc a
Bài toán 190. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ An; Năm học 2007 – 2008. 3x  9x  3 x 1 x  2 Cho biểu thức P    . x x  2 x  2 x 1
1. Tìm điều kiện xác định của P và rút gọn biểu thức P. 25
2. Tính giá trị của P khi x   . 16
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 78
_______________________________________________________________________________________________________________________________________________________________
3. Tính giá trị của P khi x  3  2 2 .
4. Tìm x sao cho P có giá trị không vượt quá 2. x  6
5. Giải phương trình ẩn x: P  . 5 x 14
6. Tình giá trị của P khi x thỏa mãn đẳng thức x y   2
x  6x  7 x y  3  2 .
7. Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên.
8. Tìm điều kiện của tham số m để phương trình P m có nghiệm. 1 1 1
9. Chứng minh rằng không tồn tại các số thực y, z sao cho P
 2 y  3z
 2z  3y  . 5 6 2
Bài toán 191. Mở rộng và phát triển các bài toán
 Bài 1, 3a, 3b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ An; Năm học 2005 – 2006.
 Bài 1, 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT Chuyên Phan Bội Châu; Thành phố Vinh; Tỉnh Nghệ An; Năm học 2004 – 2005. a  4 a  3 2 a  9 Cho biểu thức P    . a  3 a  2 a  5 a  6
1. Tìm điều kiện xác định của biểu thức P.
2. Rút gọn biểu thức P.
3. Tính giá trị biểu thức P khi a  4  2 3 . 8
4. Tìm a sao cho P   . 5
5. Giải phương trình ẩn a: P a  3 .
6. Tìm các số nguyên a để P nhận giá trị nguyên. a  7
7. Tìm khoảng giá trị của a sao cho P  . a  5
8. Tính giá trị của P khi a là nghiệm của phương trình 3 a    2 5 2 16 2 a  8 .
a b c  1,
9. Tính giá trị của P khi a thỏa mãn hệ  2
2a  2b c  1 2 . ab  4 4 4 4
x y z t
10. Xét bốn số thực dương x, y, z, t có tổng bằng 2 và biểu thức Q  . 3 3 3 3
x y z t
Tìm a để P Q , trong đó Q
là ký hiệu giá trị nhỏ nhất của Q. min min
11. Xét hai số thực x, y sao cho x y; xy  1 . So sánh giá trị của P với giá trị nhỏ nhất của biểu thức 2 2 x y S  . x y
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 79
_______________________________________________________________________________________________________________________________________________________________
Bài toán 192. Mở rộng, liên hệ và phát triển câu 1 và câu 5; Mã đề 01; Đề thi tuyển sinh lớp 10 THPT;
Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh Hà Tĩnh; Năm học 2011 – 2012.  1 1   2  Cho biểu thức A   1     .  2  a 2  a  a
1. Rút gọn biểu thức A. 1
2. Tính giá trị của biểu thức A khi a  . 4
3. Tính giá trị biểu thức A khi a  4  2 3 . 1
4. Tìm giá trị của a để A  . 2
5. Tìm giá trị của a sao cho 2 A  5A . a  6
6. Giải phương trình ẩn a: . A  1. a 13
7. Tìm tất cả các giá trị của m để phương trình A m có nghiệm.
8. Chứng minh rằng biểu thức A nhận giá trị nguyên khi 2017 2017 a xy
1 , trong đó x và y thỏa mãn  2 x x   2 2016 y
y  2016   2016 .
9. Tìm tất cả các giá trị của k để bất phương trình A k đúng với a   0; 4 . x y z 9
10. Tìm khoảng giá trị của a sao cho A    , x  , y, z  . 2 y  3 2 z  3 2 x  3 4
Bài toán 193. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Mã đề 01; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và
đào tạo Tỉnh Hà Tĩnh; Năm học 2012 – 2013; Ngày thi 28.06.2012.
 Câu 1b; Mã đề 01; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và
đào tạo Tỉnh Hà Tĩnh; Năm học 2015 – 2016.
 Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 2007 – 2008.  4a aa 1
Cho biểu thức P    .
với a  0; a  1 . 2  a 1 a a    a  
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi a  3  2 2 .
3. Với những giá trị nào của a thì P  3 ?
4. Giải phương trình ẩn a: . P 2a   1  5a  2 .
5. Tìm tất cả các giá trị a sao cho 2 25P  19P .
6. Với giá trị nào của a thì biểu thức P đạt giá trị lớn nhất ? Tìm giá trị nhỏ nhất đó.
7. Tính giá trị của P khi a x y  9 , trong đó x và y thỏa mãn  2 x   x 2 4
y  4  y   4.
8. Chứng minh biểu thức P nhận giá trị hữu tỷ khi a thỏa mãn hệ đẳng thức 1 1 1 1 9 9 a   b   b   c   c   a   3 . 4 4 16 16 16 16  x 1  1
9. Xét biểu thức Q  1 .
với x  0; x  1. Tìm a theo x để P Q .  x 1   x  
10. Tìm tất cả các giá trị của k để phương trình P k  2 có nghiệm thực.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 80
_______________________________________________________________________________________________________________________________________________________________
Bài toán 194. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Hà Tĩnh; Năm học 2016 – 2017; Ngày thi 14.06.2016.
 Câu 1b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Hà Tĩnh; Năm học 2013 – 2014.
 Bài 2a và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 2007 – 2008.  1 1   3  Cho biểu thức Q   . 1   
 với x  0; x  9 . 2 : (căn x +3)  x  3 x  3   x
1. Rút gọn biểu thức Q. 9
2. Tính giá trị biểu thức Q khi x   . 25
3. Tính giá trị biểu thức Q khi x  9  4 5 . 2
4. Chứng minh 0  Q  . 3 5. Tìm a sao cho 2 11Q  3Q . 5 x
6. Giải bất phương trình ẩn x: Q  . 7 x  3 5 2
7. Chứng minh bất đẳng thức Q   . x x
8. So sánh giá trị của Q với các nghiệm của phương trình 2
2x  2x 1  4x 1 .
9. Biểu thức Q có thể nhận giá trị nguyên hay không ? Vì sao ? 1 1
10. Cho ba số dương a,b, c thỏa mãn a b c  1. Phản biện bất đẳng thức sau:   24P . ac bc  1 1  x  3
11. Xét biểu thức R   .  
. Chứng minh R Q và tìm x sao cho R Q .  x  3 x  3  x
Bài toán 195. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1 và câu 5; Mã đề 04; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo
dục và đào tạo Tỉnh Hà Tĩnh; Năm học 2009 – 2010.
 Câu 3a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà
Tĩnh; Năm học 2015 – 2016.
 Câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà
Tĩnh; Năm học 2016 – 2017.
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Hà Tĩnh; Năm học 2014 – 2015. 2  x x x   1 
Cho biểu thức P    . 2    với x  0 .  x 1 x x x       x
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi 9x  42 x  3  0 .
3. Tìm giá trị của x để P  0 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 81
_______________________________________________________________________________________________________________________________________________________________
4. Giải phương trình ẩn x: P  10x  3 x  6 .
5. Tìm giá trị nhỏ nhất của P và giá trị tương ứng của x.
6. Tìm điều kiện của x sao cho 7P  
1 9P  2  0 .
7. Tính giá trị của P khi x là nghiệm phương trình 2 3x  1 
x  1  3x  2x 1. 1 1 1
8. Xét các số nguyên dương a, b, c phân biệt thỏa mãn  
 1. Tìm x để P a b c . a b c
9. Chứng minh rằng biểu thức P nhận giá trị nguyên khi 2017 2017 x ab
1, trong đó x và y thỏa mãn  2 a a   2 2017
b b  2017   2017 .
10. Xét các số thực a, , b c  1
 ; 4 sao cho a  2b  3c  4 . Đặt P P x và ký hiệu S là giá trị lớn nhất max của biểu thức 2 2 2
S a  2b  3c . So sánh P 16  P 4 với S . max  1 1 
11. Xét biểu thức Q   . 
  x 16 . Tìm giá trị của x để P Q .  x  4 x  4 
Bài toán 196. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 2012 – 2013.
 Câu 1.1 và 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh;
Tỉnh Hà Tĩnh; Năm học 2011 – 2012.
 Bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và đào tạo Tỉnh
Hà Tĩnh; Năm học 2008 – 2009; Ngày thi 24.06.2008.  x x   1 x x
Cho biểu thức M   2 
 1 2 x x   .  x 1   1 x       
1. Tìm điều kiện của x để biểu thức M có nghĩa.
2. Rút gọn biểu thức M.
3. Tính giá trị của M khi  x  2 3 x   1  0 .
4. So sánh giá trị của M với các nghiệm của phương trình 2
x  2x  3  2 x 2x  3 . 2
5. Với giá trị nào của x thì biểu thức P
nhận giá trị là số nguyên ? M
6. Tìm khoảng giá trị của x sao cho M  5x x 1 .
7. Tính giá trị của M khi x là nghiệm phương trình 2
x 1  x  3  1 x  3 1 x .
8. Cho các số thực dương a, b có tổng không vượt quá 1. So sánh giá trị của M và giá trị nhỏ nhất của 1 1 biểu thức P   .
a a  2bb b  2a
9. Xét các bộ số nguyên  ; m ; n p thỏa mãn 2 2 2 2 2
3m  6n p  3n p 18m  6 . Tìm tất cả các giá trị của x
sao cho M  2m  3n  4 p .  2   2 
10. Xét biểu thức Q   1 x : 1     với 1   x  1. 2  1 x   1 x
a) Tìm các giá trị của x để 2 Q Q .
b) Tìm x để P Q .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 82
_______________________________________________________________________________________________________________________________________________________________
Bài toán 197. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm học 2013
– 2014; Ngày thi 15.06.2013.
 Đề thi chọn đội tuyển dự thi Olympic Quốc tế; Môn Toán; Cộng hòa Rumani; Kỳ thi năm 2003 – Junior TST 2003, Rumania.  8
2 x 1   x x 1 
Cho biểu thức P    .  x 10  .  x 3 x 3   x 1        
1. Tìm điều kiện của x để biểu thức P có nghĩa và rút gọn P.
2. Tìm các giá trị của x để P  30 . 4
3. Tính giá trị của P khi x  1. 5  2
4. Tìm giá trị của x sao cho P  16 x 14 .
5. Tìm giá trị nhỏ nhất của biểu thức P.
6. Tìm khoảng giá trị của x để 2 P  37P .
7. Tính giá trị của P khi x thỏa mãn x 1  4x 1  4 .
8. Chứng minh bất đẳng thức P   2
2 4x  55x  729 . 2 2 
4xy  2x y x  2 y,
9. Tính giá trị của P khi x là nghiệm của hệ   ; x y   . 3
2x x  8 y  3  0.  P 6 3
10. Phủ định hoặc khẳng định bất đẳng sau:  
, trong đó abc  1; a, , b c  0 . 27
ab bc ca
a b c
Bài toán 198. Mở rộng, liên hệ và phát triển các bài toán
 Bài 1 và bài 3, bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự
thi); Đề thi chính thức; Trường THPT Chuyên Hà Tĩnh; Thành phố Hà Tĩnh; Tỉnh Hà Tĩnh; Năm
học 2014 – 2015; Ngày thi 13.06.2014.
 Đề thi Olympic Quốc gia; Môn Toán; Hợp chủng quốc Hoa Kỳ; Kỳ thi năm 2001 – United States of
American Mathematical Olympiad, 2001 – USA MO, 2001.  x 2 1    x
Cho biểu thức P      : x  3  
 với x  0; x  9 .
x x  9 x  3 x  3    x  3  
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi  x   2 3 1 x  9  0 .
3. Tính giá trị biểu thức P khi x  6  2 5 . 1
4. Tìm giá trị của x để P   . 4 x
5. Giải bất phương trình ẩn x: P   0 . 3 x 1 1
6. Chứng minh rằng   P  0 , từ đó suy ra P không thể nhận bất kỳ giá trị nguyên nào. 3 2 2 2
xy  2 y  2  x  3x, 
7. Tính giá trị của P khi x là nghiệm của hệ phương trình xy 3 y1. 
8. Xét các số thực dương a,b, c sao cho 2 2 2
a b c abc  4 . Phủ định hoặc khẳng định bất đẳng thức
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 83
_______________________________________________________________________________________________________________________________________________________________
ab bc ca abc P  2 .
9. Giả sử tồn tại các hằng số a, b để phương trình 4 3 2
x kx bx ax 1  0 . So sánh giá trị của biểu
thức P và giá trị nhỏ nhất của biểu thức 2 2
S a b  0,8 .
Bài toán 199. Mở rộng, liên hệ và phát triển câu 1 và câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán
(Dành cho các thí sinh dự thi chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên
Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Năm học 2016 – 2017; Ngày thi 11.06.2016.
2x 11 x  15 3 x x  1 Cho biểu thức P    . x  4 x  3 x  1 x  3
1. Rút gọn biểu thức P.
x  2  y  2 9 1
2. Tính giá trị biểu thức P khi x, y thỏa mãn   0 . 2 3
3. Tính giá trị biểu thức P khi x  11 6 2 .
4. Tìm giá trị của x để P  6 .
5. Giải bất phương trình ẩn x: P  3 .
6. Tìm giá trị nguyên của x để biểu thức P nhận giá trị nguyên.
7. Tính giá trị của P khi x thỏa mãn đẳng thức 2 2 x  12 
x  5  3x  5 . 5 x  2
8. Tìm tất cả các giá trị của x sao cho P  . x  7 2 3
x  2 y  4  2z x  3,  
9. Tính giá trị của P khi x là nghiệm của hệ 2 3
y  2z  4  2x y  3 ,  2
3z  2x  4  2 y   z  3. 
10. Tìm tất cả các giá trị của m để phương trình P m  3có nghiệm thực.
11. Tính giá trị của P khi x là số nguyên sao cho 2 3 4
1 x x x x là số chính phương.
Bài toán 200. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1, câu 3.2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành
phố Ninh Bình; Tỉnh Ninh Bình; Năm học 2014 – 2015; Ngày thi 12.06.2014.
 Câu 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Năm
học 2014 – 2015; Ngày thi 11.06.2014. 
a  3 a   a  2 a  3 9  a
Cho biểu thức A  1  :   
 với a  0; a  4; a  9 .  a 9   a 3 2 a a a 6          
1. Rút gọn biểu thức A. 2
2. Tính giá trị của A tại a  5  . 2 1
3. Tìm a để A A  0 .
4. Tìm khoảng giá trị của a sao cho 2
6 A  5A 1  0 .
5. Tìm giá trị nguyên của a để biểu thức A nhận giá trị là một số nguyên. a 1
6. Giải phương trình ẩn a: A  . 5 a 18
7. Tính giá trị của A khi a thỏa mãn đẳng thức 2
29  a a  3  a  26a 177 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 84
_______________________________________________________________________________________________________________________________________________________________ 2 2
x  2 y xy x y, 
8. Tính giá trị của A khi a x y , với x, y là nghiệm của hệ x 2y y x1  2xy1. 
9. Xét các số thực dương x, y, z có tổng bằng 3. Tìm tập hợp D để 3 3 3 3 3 3 5 y x 5z y 5x z A    , a
  D thỏa mãn a  0; a  4; a  9 . 2 2 2 xy  3y yz  3z xz  3x  1 1  3 a
10. Xét biểu thức N   :   . Tìm a sao cho 2 2 A N .  a  2
a  2  a  4 2 1 3 1
11. Chứng minh rằng không tồn tại các số thực x, y sao cho A     1. 13 x 17 y
Bài toán 201. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1, câu 3, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành
phố Ninh Bình; Tỉnh Ninh Bình; Năm học 2015 – 2016.
 Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình; Năm học 2008 – 2009. 1 2 x 1 Cho biểu thức A    . x x x 1 x x
1. Tìm điều kiện xác định (ĐKXĐ) của biểu thức A.
2. Rút gọn biểu thức A. 1 1
3. Tính giá trị của A khi x   . 5  2 5  2 x  4
4. Giải phương trình ẩn x: A  . 3
5. Tìm khoảng giá trị của x để A có giá trị không vượt quá 5.
6. Tìm tất cả các giá trị của x sao cho 2
6 A  5A 1  0 .
7. Tìm giá trị của tham số m để phương trình A m có nghiệm.
8. Tính giá trị của A khi 3 3
x  85  62 7  85  62 7 .
9. Tìm giá trị nguyên của x để A nhận giá trị là một số nguyên. 3 3
x  4 y y 16x, 
10. Tính giá trị của A khi x là nghiệm thực của hệ  2 1 y  5   2 1 x .  1 1 1
11. Xét các số thực dương a,b, c thỏa mãn  
 3 . Tìm tập hợp D sao cho a b c a b c 1   
ab bc ca  , A x   D . 2 2 2   1 b 1 c 1 a 2
Bài toán 202. Mở rộng, liên hệ và phát triển các bài toán
 Câu 2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Ninh Bình; Năm học 2016 – 2017.
 Câu 1c và câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Ninh Bình; Năm học 2010 – 2011.
 Câu 1c; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2009 – 2010.
 Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình; Năm học 2015 – 2016; Ngày thi 10.06.2015.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 85
_______________________________________________________________________________________________________________________________________________________________ x 2 x 3x 1 Cho biểu thức P   
với x  0; x  1. x 1 x 1 x 1
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  3  2 2 . 2
3. Tìm giá trị của x để P  . 9
4. Tính giá trị biểu thức P khi x, y là các số thực thỏa mãn  4 x   4 y   2 2 16 1 1  16x y .
5. Giải bất phương trình 2 9P  4P . 2  2 2  2
6. Tính giá trị biểu thức P khi x  . . 2 1 2 1 x  2
7. Tìm khoảng giá trị của x sao cho P  . 3 x 11
8. Tìm tất cả các giá trị của x để biểu thức P nhận giá trị là số nguyên.
9. Tính giá trị của P khi (x;y) là cặp số nguyên thỏa mãn 2
x xy  2013x  2014 y  2015  0 .
10. Cho ba số thực dương a, , b c có tích bằng 1. 1 1 1
a) So sánh giá trị của P và giá trị của biểu thức Q    . a ab 1 b bc 1 c ca 1 1 1 1
b) Tồn tại hay không đẳng thức P    . 3 3 3 3 3 3
a b abc
b c abc
c a abc
11. Xét hai số thực dương a và b thỏa mãn hệ điều kiện a  ;
b ab  1. So sánh giá trị của biểu thức 2 2P 2 2 a b
và giá trị nhỏ nhất của biểu thức M  . a b
Bài toán 203. Mở rộng, liên hệ và phát triển các bài toán
 Câu 2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Ninh Bình; Năm học 2012 – 2013.
 Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình; Năm học 2010 – 2011.
 Câu 2a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2015 – 2016; Ngày thi 10.06.2015.  1 1   1 2  Cho biểu thức Q   :    
 với x  0; x  1.  x 1
x x   x 1 x 1 
1. Rút gọn biểu thức Q.
2. Tính giá trị biểu thức Q với x  7  4 3 .
3. Tìm giá trị của x để Q có giá trị bằng 4. 6
4. Tìm x để Q có giá trị nhỏ hơn . 5
5. Giải bất phương trình ẩn x:  3 3Q  6  2
6Q  7Q  0 .
6. Tính giá trị biểu thức Q khi 3 3 x  26 15 3  26 15 3 .
7. Tìm x để Q nhận giá trị nguyên không vượt quá 3. 1 1 1 1
8. Tính giá trị của Q khi x là nghiệm của phương trình    . 3x 9x  3 5x 1 7x  2
9. Tính giá trị của Q khi x, y là nghiệm nguyên của phương trình 2 2
x y xy  2  x y .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 86
_______________________________________________________________________________________________________________________________________________________________ b c c a a ba b c
10. Phản biện bất đẳng thức    P  4   1  
, với a,b, c  0 . a b cb c c a a b   a a   a a
11. Xét biểu thức Q   1
1 với a  0; a  1. Tìm a theo x để P Q .  a 1   a 1       
Bài toán 204. Mở rộng, liên hệ và phát triển các bài toán
 Câu II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình; Năm học 2006 – 2007.
 Câu III; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2001 – 2002.
 Câu III; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2002 – 2003.
 Câu IV.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2004 – 2005.
 Câu 1.3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Năm
học 2014 – 2015; Ngày thi 11.06.2014.
 Câu V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình; Năm học 2005 – 2006.
 Câu 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình;
Tỉnh Ninh Bình; Năm học 2006 – 2007. 3 3 x x x Cho biểu thức A    . x  3  x x  3  x x 1
1. Tìm điều kiện xác định và rút gọn biểu thức A.
2. Tính giá trị của A khi x  49 . 61
3. Tính giá trị của A khi x  . 9  2 5
4. Tìm x sao cho A nhận giá trị bằng 2.
5. Tìm khoảng giá trị của x sao cho A  9  2 6 . 5x 4x 13
6. Khi x là nghiệm phương trình  
thì A có nghĩa hay không ? 2 2 x  4x 1 x x 1 3
7. Tính giá trị của A khi x thỏa mãn  2 x x   3 2 3 2  3 x  8 .
8. Tìm giá trị nhỏ nhất của biểu thức A. 
a  3   a  2 a  3 a  2 
9. Xét biểu thức P  1  :   
 với a  0; a  1; a  9 . Tìm x để P A .  a 2   3 a 2 a a 5 a 6          
10. Tính giá trị của A khi (x;y) là cặp nghiệm nguyên của phương trình  2 y   2 2 x y  2 4  8xy .  1   1 
11. Cho hai số dương a, b có tổng bằng 1. Tìm x sao cho 1 1  , A a  , b  . 2   2   a  b  12. Cho ba số a, ,
b c có tổng bằng 0. Tìm x sao cho A   5 5 5
a b c   abc 2 2 2 2 5
a b c .
Bài toán 205. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1, câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh
Bình; Tỉnh Ninh Bình; Năm học 2009 – 2010.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 87
_______________________________________________________________________________________________________________________________________________________________
 Câu 1, câu 5 Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Năm học 2009 – 2010. 2  1 x x   1 x
Cho biểu thức P   x   1   x   .  1 x   1 x      
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  5 2  2 5 5  250 .
3. Tìm giá trị của x để P  6x  7 x  1. 2
4. Tìm x   sao cho
  (  là tập hợp các số tự nhiên). P
5. Tính giá trị của P khi x thỏa mãn x  4 x  3  2 3  2x  11.
6. Giải phương trình x P   2 4
2 16x  7x   1 . 2
2x y 1, 
7. Tính giá trị của P khi x là nghiệm của hệ 2
2 y z 1,  2 2z x 1.  x x y y
8. Xét biểu thức A
. x y  . Tìm hệ thức giữa x và y để P A .
x xy y 4 5 6 7
9. Cho các số thực dương a, b thỏa mãn 
 23 . Tìm tập hợp D sao cho 8a  18b   P, x   D . a b a b
Bài toán 206. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh
Bình; Tỉnh Ninh Bình; Năm học 2011 – 2012.
o Câu V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Ninh Bình; Năm học 2007 – 2008.
o Đề thi đề nghị Olympic Quốc tế; Môn Toán; Kỳ thi năm 1987 – International Mathematical Olympiad Shorlist, 1987.  x x 4   x  2
x x  5 
Cho biểu thức P     :  
 với x  , x  0; x  4 .  x x 2 x 2   x 1 x x 2            1. Rút gọn P.
2. Tính giá trị của P khi x  9 .
3. Tính giá trị của P khi x  4  2 3  4  2 3 .
4. Tìm giá trị của x thỏa mãn P  4 . 19
5. Tìm tất cả các giá trị của x sao cho P  . 5 8 x
6. Giải phương trình ẩn x: P  . 3 x 1
7. Tìm giá trị nhỏ nhất của P.
8. Tính giá trị biểu thức P khi x  5  3  29 12 5 .
9. Tìm tất cả các số chính phương x để P nhận giá trị là số nguyên.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 88
_______________________________________________________________________________________________________________________________________________________________
10. Tính giá trị của P khi x thỏa mãn 2 2
4x y  4xy  4x  2 y  2 x y  2 1 .
x  2 y 1,  
11. Tính giá trị của P khi x thỏa mãn hệ phương trình y  2 z 1,
z  2 x 1.  
12. Tính giá trị của P khi x a b  5 với a, b là các số nguyên thỏa mãn
12  3  a 3  b 3 .
13. Xét các số thực dương a,b, c có tổng bình phương bằng 2. Khẳng định hoặc phủ định bất đẳng thức P 1
x y z xyz  . 2
Bài toán 207. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên
Toán, chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lương Văn Tụy; Thành phố Ninh
Bình; Tỉnh Ninh Bình; Năm học 2010 – 2011.
o Câu 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2014 – 2015.
o Đề thi Olympic Quốc gia; Môn Toán (Dành cho nữ sinh); Cộng hòa Nhân dân Trung Hoa; Kỳ thi năm 2008.  b ab   b a a b
Cho biểu thức P    a  :   
 với a,b  0; a b .  a b      ab a ab b ab
1. Rút gọn biểu thức P.
2. Tính P khi a  4;b  9 .
3. Tính P biết a b là hai nghiệm của phương trình 2
x  6x 1  0 .
4. Tính giá trị của P khi a và b thỏa mãn a b  6 b  5  2 a b  3.
5. Xét ba số thực x, y, z có tổng bằng 0.
a) Tìm hệ thức giữa a và b sao cho 3 3 3
P x y z  3xyz 1 . 2 2 2 x y z
b) Tìm điều kiện giữa a và b sao cho P    . 2 2 2 2 2 2 2 2 2
x y z
y z x
z x y
6. Chứng minh rằng nếu P b  9  a  9 thì P  0 .
7. Tính giá trị của P khi a x  2;b y  5 , trong đó x, y, z thỏa mãn đẳng thức
x y z  4  2 x  2  4 y  3  6 z  5 .  ab b  8. Xét B    .
với a  0; a b . Tìm hệ thức giữa a và b để P B . 
  a b b a ab b ab a  
9. Xét hai số thực x, y thỏa mãn x y  16 . Tìm a và b để 2 2
x xy y  192  P, x  , y .
10. Xét các số thực dương a,b, c có tổng bằng 1. Phủ định hoặc khẳng định bất đẳng thức b c2 a
a c P  3 . 4
Bài toán 208. Mở rộng, liên hệ và phát triển các bài toán
 Câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lương Văn Tụy; Thành phố Ninh Bình; Tỉnh Ninh Bình; Năm học 2013 – 2014.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 89
_______________________________________________________________________________________________________________________________________________________________
 Câu 1.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2005 – 2006.
 Bài V và VI; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Ninh Bình; Năm học 2005 – 2006. 2 2x  4 1 1 Cho biểu thức A    . 3 1 x 1 x 1 x
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  6  2 5 . 3. Tìm x để 2 7P  8P . 2
4. Giải bất phương trình ẩn x: A  . 13
5. Tìm giá trị lớn nhất của biểu thức A. 1 1
6. Xét biểu thức B   1 . a 1 a 1
a) Tìm a theo x để A B .
b) Tìm các số nguyên tố a để giá trị biểu thức B là một số nguyên.
7. Tính giá trị của A khi (x;y) là cặp số nguyên thỏa mãn 2 3 2
x x x  4 y  4 y .
8. Giả sử tồn tại các số hữu tỷ a và b để phương trình 2
x ax b  0 nhận x  2 1là nghiệm. Đặt A là
hàm số theo biến x, tức là A f x . So sánh f a, f b .
9. Xét các số thực a, , b c  1  ; 
3 có tổng bằng 3. Tìm tập hợp D để 2 2 2
P a b c  9, x   D .
Bài toán 207. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2006 – 2007.
o Bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thái Bình; Năm học 2009 – 2010.  1 1   x  2 x 1 
Cho biểu thức A     :  
 với x  0; x  1; x  4 .  x x 1   x 1 x  2     
1. Rút gọn A và tính giá trị của A khi x  3  2 2 . 4
2. Tím giá trị của x để A  . 17
3. Tính giá trị biểu thức A khi x thỏa mãn 6 x  
1  x  4  0 . 1
4. Tìm khoảng giá trị của x sao cho A  . 5
5. Tìm khoảng giá trị của x để A A . x  9
6. Tìm giá trị của x để A  . 78 1 1  1 1 
7. Tính giá trị của A khi x là nghiệm phương trình   3    . x 2x  3  4x  3 5x  6  1
8. So sánh giá trị của A với . 3
9. Xét các số thực a  4, b  5 , c  6 sao cho 2 2 2
a b c  90 . Khẳng định hoặc phủ định bất đẳng thức
a b c  48A .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 90
_______________________________________________________________________________________________________________________________________________________________
Bài toán 208. Mở rộng, liên hệ và phát triển bài 1 và bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề
thi chính thức; Sở Giáo dục và Đào tạo Tỉnh Nam Định; Năm học 2007 – 2008.  5  
x  2 x  4 
Cho biểu thức P  1 .    x
 với x  0 và x  4 .  x 2   x 3      1. Rút gọn P.
2. Tính giá trị của P khi x  6  2 5 .
3. Với giá trị nào của x thì 2 9P  2P ? x  3
4. Giải phương trình ẩn x: P  . 31 x
5. Tìm điều kiện của x để P  P .
6. Tìm tất cả các giá trị của x để P P .
7. Tìm khoảng giá trị của x để P  1 .
8. Tìm giá trị nguyên của x để P nhận giá trị là một số nguyên.
9. Tìm tất cả các giá trị của m để phương trình P m có nghiệm. 1 1
10. Tồn tại hay không các số thực y, z sao cho P   y  2015z
 2015 y z  2 ? 17 19 1 1 3 3
11. Tính giá trị của P khi x là nghiệm phương trình    . x 2x 1 4x 1 5x  2
12. Tính giá trị của P khi x là nghiệm của phương trình 2 2
x  2 y  2xy  5x  5 y  6 , trong đó x y là một số nguyên.
Bài toán 209. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 5; phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2013 – 2014.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2005 – 2006; Ngày thi 04.07.2005.  x  2 x  2  x
Cho biểu thức A     :
với x  0; x  1.
x  2 x 1 x 1   x 1  
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  6  2 5 .
3. Tính giá trị của A khi x  7  4 3  7  4 3 .
4. Tính giá trị của A khi x thỏa mãn 2 x  34 x  3  0 . 2
5. Giải phương trình ẩn x: 5A  . x 1
6. Với giá trị nào của x thì 2 7 A  4 A ?
7. Tìm khoảng giá trị của x sao cho A A .
8. Tìm khoảng giá trị của x sao cho A  2  A  2 .
9. Tìm tất cả các số nguyên x để biểu thức A có giá trị là số nguyên.
10. Tính giá trị của A khi x là nghiệm phương trình  2 x x x    3 2 3 6 2
1 1  2x  5x  4x  4.
a b 4 ab a b b a
11. Xét biểu thức B  
. Tìm x theo a và b để A B . a b ab
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 91
_______________________________________________________________________________________________________________________________________________________________
Bài toán 210. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2004 – 2005.
o Bài 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2005 – 2006; Ngày thi 04.07.2005.
o Bài 1 và bài 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2003 – 2004.  x  2 x  2  x 1
Cho biểu thức Q     
với x  0; x  1.
x  2 x 1 x 1   x   2 1. Chứng minh Q  . x 1
2. Tính giá trị của Q khi x  14  6 5  14  6 5 . 1
3. Tìm giá trị của x để Q   0 . 3 x   1
4. Tìm khoảng giá trị của x sao cho 2 3Q  2Q .
5. Tìm tất cả các giá trị của x sao cho Q  3  Q  3.
6. Tìm tất cả các giá trị của x sao cho 6  Q Q  6 .
7. Tồn tại hay không giá trị x thỏa mãn Q  5  5  Q ?  2 5   2,   x x y
8. Tính Q khi x, y là nghiệm của hệ 3 1    1, 7.  x x y
9. Tìm số nguyên x lớn nhất để Q có giá trị là số nguyên.
10. Với giá trị nào của x thì giá trị của Q lớn hơn nghiệm lớn nhất của phương trình 2
9x 16  2 2x  4  4 2  x . 1 x
11. Xét biểu thức B  
với x  0; x  1. x 1 x x
a) Tìm x để giá trị của A lớn hơn giá trị của B. 1
b) Tính giá trị của B để x  . 2 2 y  2 y  6
12. Tìm tất cả các giá trị của x sao cho Q  , y    . 2 y  2 y  5
Bài toán 211. Mở rộng, liên hệ và phát triển các bài toán
o Bài 1 và bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2002 – 2003.
o Bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2003 – 2004.
o Bài 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Nam Định; Năm học 2000 – 2001.  y y  2 xy
Cho biểu thức S     :
với x  0; y  0; x y .
x xy x xy x y  
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 92
_______________________________________________________________________________________________________________________________________________________________
1. Rút gọn biểu thức S và chứng minh giá trị của S không phụ thuộc biến y.
2. Tìm giá trị của x và y để S  1. 1
3. Giải phương trình S  4   2 . x
4. Tính giá trị của S khi x là nghiệm phương trình 2 2
x  2x  3  x  2 
x  3x  2  x  3 .
5. Giả sử (a;b) là nghiệm phương trình  4 a   4 b   2 2 16 1
1  16a b . Tìm x, y để S max ; a b .
6. Cho m thỏa mãn đẳng thức 2
m m 12 m 1  36 . Tìm x sao cho 2
S  2m  3m  4 m 1 .  1 a a  1
7. Xét biểu thức P    a .
. Tìm a theo x và y để S P .  1 a   1 a    a a   a a
8. Xét biểu thức Q   1. 1 .  a 1   a 1       
a) Tìm x theo x và y để S Q . b) Tìm a sao cho 2 Q  a .
Bài toán 212. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1 và câu 5; phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2011 – 2012.
o Câu II và câu IV; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi);
Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2000 – 2001.
o Câu I.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2002 – 2003.
o Bất đẳng thức Nessbit – Shapiro. 2 x x x x Cho biểu thức P  
với x  0; x  1 . x x  1 x  1
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  9  4 5 .
3. Tìm x để P  0 .
4. Tìm x để P nhận giá trị nguyên nhỏ hơn 2. 4 4  4   4 
5. Tính giá trị của P khi x       .  3  5   3  5 
6. Giải bất phương trình ẩn x: 2
P  6P 16  0 .
7. Tìm khoảng giá trị sao cho P  3  3  P . 1 1 1
8. Tìm giá trị của x sao cho P    ...  . 2  2 3 2  2 3 100 99  99 100
9. Tính giá trị của P khi x là nghiệm phương trình 3 2
x 3x  2  3  2x
x x x 1 .
10. Xét các số thực x và y thỏa mãn  2 x x   2 5 y y  5   5.
Tìm tất cả các cặp số (x;y) sao cho 2015 2015 P xy . a b c 1
11. Xét các số thực dương a,b, c . Chứng minh bất đẳng thức    . b c c a a b 2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 93
_______________________________________________________________________________________________________________________________________________________________
Bài toán 213. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2015 – 2016.
o Câu 1.1, câu 2.2, câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 2014 – 2015.  3 x 1  x 1
Cho biểu thức A     3. .  x 1 x 1    x  2  
1. Rút gọn biểu thức A.
2. Tính giá trị biểu thức A khi x  4  2 3 .
3. Tính giá trị của A khi  4 x  
1 3 x  2  0 .
4. Tìm x để A nhận giá trị bằng 5.
5. Giải phương trình ẩn x: A  5 x 14 .
6. Tìm x để A A .
7. Tìm khoảng giá trị của x sao cho A  3  3  A .
8. Tính giá trị của A khi x là nghiệm phương trình  x   x   2 6 2 1
x  4x 12   8 .
9. Khi x, y là nghiệm nguyên của phương trình 3 3
x y  3xy  1thì P nhận giá trị hữu tỷ hay vô tỷ ?
10. Xét các số thực dương a và b sao cho 2 2
2a b  5a  5b  10 . Tìm x sao cho 4
A a b, a  ,b . 1 1 1
11. Xét các số thực a,b, c khác 0 sao cho  
a b c  1. a b c
Tìm tất cả các giá trị của x sao cho A  a   1 b   1 c   1  2 .
Bài toán 214. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2014 – 2015.
o Câu 1.1, câu 2.2, câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 1999 – 2000.  2 x 4x   1 1 
Cho biểu thức A     :  
 với x  0; x  1.
 1 x 1 x      x x x
1. Rút gọn biểu thức A. 25
2. Tính giá trị của A khi x   . 9 3. Tìm x sao cho 2
5A 18A  0 .
4. Chứng minh rằng A nhận giá trị nguyên khi x thỏa mãn 2
x  5x  4  0 .
5. Tính giá trị biểu thức A khi x  3  2 2  3  2 2 .
6. Tìm giá trị của x để A  5 x  8.
7. Tìm khoảng giá trị của x sao cho 2  A A  2 .
8. Tìm giá trị nhỏ nhất của biểu thức A.
9. Tìm x để giá trị của A lớn hơn nghiệm nguyên lớn nhất của phương trình 3 2
4x  25x  43x x 3x  2  22  3x  2 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 94
_______________________________________________________________________________________________________________________________________________________________ a b c
10. Cho ba số thực a, ,
b c có tổng đôi một khác 0 sao cho    1. b c c a a b 2 2 2 a b c
Tìm x để A    . b c c a a b
11. Xét các số thực a và b thỏa mãn điều kiện a b  2 2 2 2 2 2 2 2
 4a b  6a b  0 . Tìm khoảng giá trị của x sao cho 2 2
A a b , trong đó 2 2 a b
là ký hiệu giá trị nhỏ nhất của biểu thức 2 2 a b . min min
Bài toán 215. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2012 – 2013.
o Câu 1, câu 3, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo
dục và Đào tạo Tỉnh Nam Định; Năm học 2016 – 2017.
o Câu II.a; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2006 – 2007.  1 x   2 1 
Cho biểu thức A     :  
 với x  0; x  1.  x x x 1     x 1 x 1 
1. Rút gọn biểu thức A. 1
2. Tính giá trị biểu thức A khi x   3  2 2  1. 2  1 26
3. Tìm giá trị của x để A  . 5
4. Chứng minh rằng A  2  0 với mọi x thỏa mãn điều kiện x  0; x  1.
5. Tìm giá trị của x sao cho 2
2 A  9 A  10  0 .
6. Tìm tất cả các giá trị của x để 3A 10  10  3A . x  8
7. Giải phương trình ẩn x: A   0 . 4
8. Tính giá trị của A khi x là nghiệm lớn nhất của phương trình  4 x   2 2
4  3x 10x  6 .  x 1 2   x  4 
9. Xét biểu thức P    . x 1
 với x  0; x  4 . Tìm x sao cho A P .  x  2 x 4   x       2
10. Tìm x sao cho A  2x   5 . x 1 1
11. Xét số thực m thỏa mãn m   5 . Tính A khi 4 x m  . m 4 m
Bài toán 216. Mở rộng, liên hệ và phát triển các bài toán
o Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2012 – 2013.
o Câu 1.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2012 – 2013.
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2004 – 2005.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 95
_______________________________________________________________________________________________________________________________________________________________  2 x x
Cho biểu thức P    .
với x  0; x  1.  x 1 x 1    x x  2  
1. Rút gọn biểu thức P. 1
2. Chứng minh rằng khi x  3  2 2 thì P  . 2 5
3. Tìm giá trị của x để P  . 24 5
4. Giải phương trình P   0 . x 19
5. Tìm tất cả các giá trị của x để P P .
6. Tìm khoảng giá trị của x sao cho 8P  3  3  8P .
7. Tính giá trị của P khi x và y thỏa mãn đẳng thức x y  4  y x  4  xy .
8. Tìm giá trị của x để P nhận giá trị là số tự nhiên.
9. Tính giá trị của P khi x là nghiệm phương trình 2 x 1  x x  2 . 2 2 2
10. Xét các số thực a,b, c phân biệt khác 0 thỏa mãn a   b   c
. Tìm x để P abc . b c a 2 2 a b ab a b
11. Xét biểu thức S  :
. Tìm khoảng giá trị của x để có thể tồn tại đẳng thức S P . ab a b
Bài toán 217. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1, câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục
và Đào tạo Tỉnh Nam Định; Năm học 2008 – 2009.
 Câu 2.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2008 – 2009.
 Câu 5; Phần II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào
tạo Tỉnh Nam Định; Năm học 2016 – 2017. x x  2 x 1
Cho biểu thức P  1 : với x  0 . x x 1 x x 1
1. Rút gọn biểu thức P và tìm x để P nhận giá trị âm.
2. Tính giá trị của P khi x  9  4 5 . 5
3. Giải phương trình P   . 4 x  6
4. Tìm giá trị của x sao cho P  1 . 4 2 
xy  6  12  y ,
5. Tính giá trị của P khi x là nghiệm của hệ  2
xy  3  x . 
6. Chứng minh rằng giá trị của P không thể nhỏ hơn nghiệm phương trình
x   x   3 2
x x x   3 2 2 1 3 2 5 4
1  5x  3x  8 .
7. Tính giá trị của P khi x là nghiệm phương trình 4 4 x
x  3  2x  2008x  2008 .
8. Cho các số thực dương a, , b c thỏa mãn 3 3 3
a b c  3abc  0 .
Tìm khoảng giá trị của x sao cho
   27    6    2008 P a b b c c a .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 96
_______________________________________________________________________________________________________________________________________________________________
Bài toán 218. Mở rộng, liên hệ và phát triển các bài toán
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2001 – 2002.
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2004 – 2005.
o Câu 5.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2008 – 2009. x  2 x 1 x 1 Cho biểu thức T   
với x  0; x  1. x x 1 x x 1 x 1
1. Rút gọn biểu thức T.
2. Tính giá trị biểu thức T khi x  4  2 3 . 3
3. Tìm tất cả các giá trị của x để T  . 13 x
4. Giải phương trình ẩn x: T   0 . x  3
5. Tìm tất cả các giá trị của x sao cho 21T  4  4  21T . 1
6. Chứng minh rằng với mọi x  0; x  1luôn có T  . 3
7. Chứng minh rằng biểu thức T chỉ nhận duy nhất một giá trị nguyên.
8. Tìm khoảng giá trị của x sao cho 2
14T 11T  2  0 .
9. So sánh T với các nghiệm của phương trình 6  x x  2  2 .
x y  1, 
10. Tính giá trị của T khi x và y là các số dương thỏa mãn hệ 8 1 4 4 x y    5.  xy
11. Xét hai số thực dương a và b có tổng bằng 1. Phủ định hoặc khẳng định bất đẳng thức 1 1   18T . 2 2 ab a b
Bài toán 219. Mở rộng, liên hệ và phát triển các bài toán
o Bài I, bài V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2006 – 2007.
o Câu I.2, câu II, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi
chuyên Toán, chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 2004 – 2005.
o Câu 4.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2013 – 2014.  1   x 1 x 1  Cho biểu thức Q x  .    
 với x  0; x  1.  x   x 1 x 1     
1. Rút gọn biểu thức Q.
2. Tính giá trị của Q khi x  3  2 2 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 97
_______________________________________________________________________________________________________________________________________________________________
3. Tìm x để Q  8 .
4. Chứng minh rằng Q  4 . 20
5. Tìm các giá trị của x để Q  . 3 x  8
6. Giải phương trình ẩn x: Q   0 . 2
7. Tìm tất cả các giá trị của x sao cho 5Q  52  5Q  52 .
8. Chứng minh rằng không tồn tại các số nguyên x để Q nhận giá trị nguyên.
9. Tính giá trị của Q khi x thỏa mãn đẳng thức 2 5  x
x 1  x  2x 1.
10. Tính giá trị của Q khi x, y là các số nguyên thỏa mãn  x y x y xy  2  3  2xy .
11. Xét các số thực a,b, c thỏa mãn 0  a  2; 0  a  2; 0  c  2 . Tìm x sao cho 3 3 3
Q a b c , a  , , b c .
12. Xét các số thực dương a,b, c sao cho ab bc ca  1. Phủ định hoặc khẳng định bất đẳng thức  2 1 y  2 1 z   2 1 y  2 1 z   2 1 y  2 1 z Q   xxx . 2 2 2 2 1 x 1 x 1 x  1 2 2 x y  , 
13. Tính giá trị biểu thức Q khi x là nghiệm của hệ 2  4x  3 2
x x x   2
1  y  2xy  2.  1 1 1
14. Phản biện bất đẳng thức Q    ...   6, 25 . 1  3 5  7 97  99
Bài toán 220. Mở rộng, liên hệ và phát triển các bài toán
o Bài I, bài IV; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2007 – 2008.
o Bài I, bài V; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2005 – 2006.
o Bài II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2001 – 2002. 2  1 1  x x x x x
Cho biểu thức M x     
với x  0; x  1.  x 1 x 1  x x 1 x 1
1. Rút gọn biểu thức M. 1
2. Tính giá trị của M khi x   . 4 4 6
3. Giải bất phương trình M  . 3 6x  5
4. Giải phương trình ẩn x: M  . 3
5. Tìm khoảng giá trị của x sao cho M M .
6. Tìm số nguyên x để M nhận giá trị nguyên.
7. Tính giá trị của M khi x thỏa mãn x  2 x     2 8 1
3 x x   1 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 98
_______________________________________________________________________________________________________________________________________________________________
8. Tìm tất cả các các nghiệm x của phương trình sau để M xác định x a x  x b x  ab .    x x 3 1 1
9. Xét biểu thức N   . Tìm x sao cho 2 M N . 1 x 1 x x
10. Tính giá trị của M khi biểu thức 2
P  2x  1 4x x đạt giá trị lớn nhất.
11. Xét các số thực dương a,b, c có tổng không vượt quá 2005. Tìm x sao cho 3 3 3 3 3 3 5a b 5b c 5c a M    , a  , , b c . 2 2 2 ab  3a bc  3b ac  3c
Bài toán 221. Mở rộng, liên hệ và phát triển các bài toán
o Bài I; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 1999 – 2000.
o Bài II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2001 – 2002.
o Bài II; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2014 – 2015.
o Bài II.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định;
Tỉnh Nam Định; Năm học 2005 – 2006. a b a b Cho biểu thức N   
với a,b là hai số dương khác nhau. ab b ab a ab
1. Rút gọn biểu thức N. 2. Tính N khi 2 4
a  25;b  16 .
3. Tính giá trị của biểu thức N khi a  6  2 5 ;b  6  2 5 .
4. Tính giá trị của N khi a  4b  5 ab .  1 a aa a 1
5. Tính giá trị của N khi a, b thỏa mãn đẳng thức 2   a .  b b  .  1 a  1 a 2   3 2 
x  3y  6 y  4  0,
6. Giả sử (x;y) là nghiệm của hệ  2 2 2
x x y  2 y  0. 
Tìm hệ thức giữa a và b sao cho N x y  5 . n n n n
7. Giả sử a  3 5  3 5 ;b  3 6  3 6  , với n là số nguyên dương. Chứng minh rằng
biểu thức N nhận giá trị hữu tỷ.
8. Tìm mối liên hệ giữa a và b để N là nghiệm của phương trình 2
3  4P  4P 1  1
 6P  8P 1 .
Bài toán 222. Mở rộng, liên hệ và phát triển các bài toán
 Câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đào
tạo Tỉnh Bắc Giang; Năm học 2008 – 2009; Ngày thi 22.06.2008.
 Bài 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo
Tỉnh Bắc Giang; Năm học 2012 – 2013.
 Câu 4; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đào
tạo Tỉnh Bắc Giang; Năm học 1997 – 1998; Ngày thi 28.06.1997.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 99
_______________________________________________________________________________________________________________________________________________________________  2   2  Cho biểu thức P   1 x : 1     với 1   x  1. 2  1 x   1 x
1. Rút gọn biểu thức P.
2. Tính giá trị biểu thức P khi x  2 5  5 .
3. Tìm giá trị lớn nhất của biểu thức P  1 x .
4. Tính giá trị của P khi x là nghiệm phương trình 2
x  7x  5  10x  3 .  1 2
  a  3 a  2 
5. Xét biểu thức A   .   
1 với a  0, a  4 . Tìm x để P A .  a 2 a 2 a   a 2      
a x a x
a x a x
6. Xét biểu thức Q  
. Tìm a theo x để P Q .
a x a x
a x a x
Bài toán 223. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên Ngoại
ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học 1998 – 1999.
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên Ngoại
ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học 2008 – 2009.
 2xy x  2xy y   2xy 2xy
Cho biểu thức A  1   :    .  x y   x xy y xy        
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  2 1; y  3  2 2 . 2 2 
x y xy  1
3. Tính giá trị biểu thức A khi x và y là nghiệm của hệ  2 3
x y y  3. 
4. Tìm giá trị lớn nhất của A khi x và y thỏa mãn đẳng thức 3 3 x y  2 .
5. Chứng minh rằng A nhận giá trị nguyên dương khi x và y là các số nguyên dương thỏa mãn 4x 1 3y   .
6. Tìm m để phương trình A m có nghiệm x, y thỏa mãn x y  6 . 3  x y x y x y 2 y
7. Xét biểu thức P    .  .
x y y x x y y x x y x y  
a) Chứng minh P nhận giá trị nguyên với mọi x, y  0; x y . P
b) Tìm tất cả các số nguyên dương x và y để là một số nguyên. A
Bài toán 224. Mở rộng và phát triển bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các
thí sinh dự thi); Đề thi chính thức; Trường THPT Chu Văn An và THPT Chuyên Hà Nội – Amsterdam; Năm học 1998 – 1999.  x 1 xy x   xy x x 1 
Cho biểu thức P    1 : 1   .  xy 1 1 xy   xy 1 xy 1         
1. Tìm điều kiện xác định và rút gọn P.
2. Tính giá trị của P khi x  9; y  4 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 100
_______________________________________________________________________________________________________________________________________________________________ 1 1 3. Cho 
 6 , tìm giá trị lớn nhất của P. x y
4. Chứng minh P nhận giá trị vô tỷ khi (x;y) là nghiệm nguyên của phương trình 2 2
x y  2x y  9 . 3 3 3
x y  8  16 y , 
5. Tính giá trị của P khi (x;y) là cặp số thỏa mãn các đẳng thức  . x   xy  2 2  8 y . 
Bài toán 225. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1 và 2.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên
Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội;
Năm học 2011 – 2012; Ngày thi 12.06.2011.
 Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đào
tạo Tỉnh Bắc Giang; Năm học 1999 – 2000; Ngày thi 23.06.1999.
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Trường THPT Chuyên Ngoại
ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học 2009 – 2010. 3 3  1 1  2 1 1 
x y x x y y
Cho biểu thức A        : .   3 3  x y x y x y    x y xy
1. Rút gọn biểu thức A.
2. Tính giá trị của A khi x  4  2 3; y  4  2 3 . 1
3. Tìm x, y sao cho xy  ; A  5 . 6
4. Tính giá trị của A khi x và y thỏa mãn 6x y  7 xy . 2 2
x  4 y  5, 
5. Tính giá trị của A khi x và y là nghiệm của hệ x2y
5  4xy  27.  3 3  m p   2 p
6. Xét biểu thức B  
mp  : m p 
. Tìm x và y sao cho A B .  m p   m p  
7. Tìm giá trị nhỏ nhất của biểu thức A khi x và y là hai số dương có tổng lập phương bằng 2. 3 2 3 3 2 8  xx   2 x x  4 8. Xét biểu thức 3 C  :  2     x  .
với x  8; x  8; x  0 . 3 3    3  3 2 3 2  x 2  x x  2     x  2 x
Chứng minh rằng C có giá trị không phụ thuộc biến x và nếu A C thì x y xy  3 .
Bài toán 226. Mở rộng, liên hệ và phát triển các bài toán
 Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Giang; Thành phố Bắc Giang; Tỉnh
Bắc Giang; Năm học 2015 – 2016.
 Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Lê Quý Đôn; Thành phố Vũng Tàu;
Tỉnh Bà Rịa – Vũng Tàu; Năm học 2014 – 2015.  2 xy 1 1 2 x   xy x xy x
Cho biểu thức A   2     :    .  1 xy 1 xy 1 xy   xy 1 xy 1      
1. Tìm điều kiện của x, y để biểu thức A có nghĩa, từ đó hãy rút gọn biểu thức A. 49 9
2. Tính giá trị của A khi x  ; y   . 25 16
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 101
_______________________________________________________________________________________________________________________________________________________________ 1 1 3. Cho 
 12 . Chứng minh A  36 . x y
4. Tìm giá trị nhỏ nhất của biểu thức A khi x và y thỏa mãn 2 2
x  9 y  18 .  x x y y  2 y
5. Cho biểu thức B  
xy  :  x y 
với x  0; y  0; x y .  x y   x y  
Chứng minh rằng B không phụ thuộc biến, sau đó tìm hệ thức liên hệ giữa x và y sao cho A B .
6. Tính giá trị biểu thức A khi x và y thỏa mãn đẳng thức  2 2 x y  2 2 9
x  9  7x  3y .
Bài toán 227. Mở rộng, liên hệ và phát triển các bài toán
o Bài 3; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT Chuyên Bắc Giang; Thành phố Bắc Giang; Tỉnh
Bắc Giang; Năm học 2013 – 2014.
o Bài 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Đợt 2; Sở Giáo dục và Đào
tạo Tỉnh Hà Bắc; Năm học 1994 – 1995; Ngày thi 09.08.1994. 1 x 1 x
1 x  1 x Cho biểu thức A    . 2
1 x  1 x 1 x 1 x
1 x  1 x
1. Tìm x để biểu thức A có nghĩa, từ đó hãy rút gọn A. 3
2. Tính giá trị của A tại x  . 4 3 1
3. Tính giá trị của biểu thức A khi x  . 2 2 1
4. Tìm các giá trị của x sao cho A  . 4
5. Giải bất phương trình ẩn x: 2 3A A . 2 2 2 2 2 2  m m n m m n      4m m n
6. Xét biểu thức B     :
. Tìm x sao cho A B . 2  2 2 2 2  n
m m n
m m n  
7. Tìm khoảng giá trị của x sao cho A 1  1 A .
8. Tìm tất cả các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
Bài toán 228. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức;
Trường THPT Chuyên Ngoại ngữ; Đại học Ngoại ngữ; Đại học Quốc gia Hà Nội; Năm học 1997 – 1998; Ngày thi 03.08.1997. 2 2 a a a a Cho biểu thức M   . a a 1 a a 1
1. Tìm điều kiện xác định và rút gọn biểu thức M.
2. Tính giá trị của M khi a là nghiệm phương trình a  
a   a  2 2 2 1 2 3 2 2 1 .
3. Tính giá trị của M khi a  6  2 5 .
4. Tìm khoảng giá trị của a sao cho M  3  M  3 .
5. Rút gọn biểu thức P M a 1 1.
6. Giải phương trình ẩn a: M a    2 4
2 a  4a 16 . a  3
7. Tìm tất cả các giá trị của a sao cho M  . 2 a 1
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 102
_______________________________________________________________________________________________________________________________________________________________
Bài toán 229. Mở rộng và phát triển câu 2, câu 3, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành
cho tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam
Định; Tỉnh Nam Định; Năm học 2015 – 2016.  1
2   x x 1 x  Cho biểu thức Q   .    
 (với x  0; x  1 ).  x 1 x 1   x 1 x x    
1. Rút gọn biểu thức Q .
2. Tính giá trị của Q khi x  3  2 2 .
3. Tìm các giá trị của x để Q  1.
4. Giải bất phương trình ẩn x: Q  2Q  4  0 .
5. Tìm khoảng giá trị của x sao cho Q  5  Q  5 .
6. Tìm x để 5Q x y , trong đó  x ; y là nghiệm của hệ phương trình 0 0  0 0  x  2 
x y  3  y  2 x  
x  32x y  5  x 16. 
7. Chứng minh rằng Q không thể xác định nếu x thỏa mãn đẳng thức x x     x5 2 3 6 6 3 2
 7x 19 2  x.
8. Xét các số thực dương a, b, c thỏa mãn abc  1. Chứng minh bất đẳng thức a b c    Q  2 . 4 4 4 4 4 4
b c a
a c b
a b c
Bài toán 230. Mở rộng và phát triển câu 2, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho
tất cả các thí sinh dự thi); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam
Định; Tỉnh Nam Định; Năm học 2014 – 2015.
a  2 a 1  1 2 a  Cho biểu thức Q  . 
 với a  0; a  1. a 1  a 1 a a a a 1        
1. Rút gọn biểu thức Q.
2. Tính giá trị biểu thức Q khi a  9  4 5 .
3. Tính giá trị của Q khi 3a  3  10 a . 2
4. Tìm giá trị của a sao cho 2 Q Q . 5 2
5. Giải phương trình ẩn a: Q   0 . a  2
6. Với khoảng giá trị nào của a thì 2 17Q  4Q . 3 3
7. Tìm tất cả cả các giá trị a để Q   Q  . 13 13
8. Chứng minh rằng khi a  1thì giá trị của biểu thức Q nhỏ hơn 1.
9. Tính giá trị của Q khi a là nghiệm phương trình  a  2  a 1 2  a   1  1.
Bài toán 231. Mở rộng và phát triển các bài toán 
Câu 2, câu 3.2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi ban
Khoa học Tự nhiên); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam
Định; Tỉnh Nam Định; Năm học 2016 – 2017. 
Bất đẳng thức Nesbitt – Shapiro.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 103
_______________________________________________________________________________________________________________________________________________________________
3x  2 x x  2 x 1 Cho biểu thức P   
với x  0; x  1. x x  2 x 1 x  2 x  3
1. Chứng minh rằng P  . x  2
2. Tính giá trị của P khi x  6  2 4  2 3 .
3. Tính giá trị của P khi 2x  5 x  2  0 . 5 4. Tìm x sao cho P  . 3 7
5. Tìm tất cả các giá trị của x để P nhận giá trị không vượt quá . 6 3
6. Chứng minh rằng nếu x  0; x  1thì P  . 2
7. Chứng minh rằng không tồn tại giá trị của x để P nhận giá trị nguyên. 5
8. Giải bất phương trình ẩn x: 4P   9 . P
9. Tìm khoảng giá trị của x sao cho 7P  8  7P  8 . 2 2
2x y xy x y  0, 
10. Tính giá trị của P khi x là nghiệm của hệ  2xy2 22x  0.  2 2 2 a b c
11. Phản biện bất đẳng thức P   
với a,b, c   . 2 2 2 2 2 2 b c a c b a
Bài toán 232. Mở rộng và phát triển câu 2; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả
các thí sinh dự thi ban Khoa học Xã hội); Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành
phố Nam Định; Tỉnh Nam Định; Năm học 2016 – 2017.  1 1
a  2 a 1 Cho biểu thức P   :  
với a  0; a  9 .  a  3 a a  3  a a  3a
1. Rút gọn biểu thức P và tính giá trị của P khi a  4  2 3 . 1
2. Tìm giá trị của a để P  . 2 4
3. Tính giá trị của P khi a thỏa mãn a   5 . a
4. Tính giá trị của P khi a và b thỏa mãn đẳng thức  2 2 a b  2 2 4
b  6b  4  a . 7
5. Tìm tất cả các giá trị của a để P có giá trị không vượt quá . 9
6. Chứng minh rằng P không thể nhận bất kỳ giá trị nguyên nào.
7. Tìm khoảng giá trị của a sao cho 6P  5  6P  5 .
Bài toán 233. Mở rộng và phát triển các bài toán
 Câu 1, câu 3, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi);
Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2010 – 2011.
 Câu 2b; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi
chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2012 – 2013.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 104
_______________________________________________________________________________________________________________________________________________________________
 Câu 2b, câu 5.1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi);
Đề thi chính thức; Trường THPT chuyên Lê Hồng Phong; Thành phố Nam Định; Tỉnh Nam Định; Năm học 2011 – 2012.  x  2 1  x 1 Cho biểu thức P   :  
với x  0; x  1.  x x 1
x 1  x x 1
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi x  2 9  4 5 10 .
3. Tìm giá trị của x để P  10 . x  3
4. Giải phương trình ẩn x: P   0 . x  2
5. Với giá trị nào của x thì P có giá trị không lớn hơn 3 ?
6. Tìm điều kiện của x để P  6  6  P . 2 2
x y  3xy  5, 
7. Tính giá trị biểu thức P khi x là nghiệm của hệ xy
 x y   1  xy  7. 
8. Tính P khi x là nghiệm phương trình x  2
x  9 x  9  22 x   1 . 3x x x x   1 3
9. Xét biểu thức A   với x  0 . x x x x 1
a) Chứng minh rằng A  4 .
b) Tìm x sao cho A P .  3 x 1 1  1 3  3 3x 1   3x 1
10. Xét các biểu thức Q     : và M    3  : /  x 1 x 1    x x     x 3  x x  4  
a) Xác định x để P Q .
b) Chứng minh rằng M  4 và tìm x để P M . 4 1
11. Xét hai số thực dương a và b sao cho a b  1. Tìm x sao cho P   , a  , b . a b
Bài toán 234. Mở rộng và phát triển các bài toán
 Câu 1, câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề
thi chính thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận
Cầu Giấy; Thành phố Hà Nội; Năm học 2010 – 2011.
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho các thí sinh dự thi chuyên Toán,
chuyên Tin học); Đề thi chính thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư
phạm Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học 2009 – 2010. 4 3  3 
x 1  x x 4x 1  4  x  29x  78 4   2 Cho biểu thức A   x  . :   . 2  7 6  2 2 x 1
x  6x x  6 3x 12x  36     1. Rút gọn A. 49
2. Tính giá trị của A khi x   . 16 2
3. Tìm giá trị của x sao cho A  . 3
4. Tìm tất cả các giá trị nguyên của x để A nguyên.
5. Tính giá trị của A của A khi x là nghiệm lớn nhất của phương trình  x x   x     x  2 2 2 5 1 4 6 1 .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 105
_______________________________________________________________________________________________________________________________________________________________
6. Tìm khoảng giá trị của x sao cho A  7  7  A . 3 3  2 2xy xy  2  2xy xy
7. Cho biểu thức P    . 
với xy  2; xy   2 .  2 2 3 3  3 3 x y  4 2xy  2 2 xy  2 xy  2  
Tìm x để A và P có giá trị bằng nhau.
Bài toán 235. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2008 – 2009.
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2014 – 2015.
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2013 – 2014; Ngày thi 06.06.2013.      a b a b a b b a 2 Cho biểu thức P  :     
với a  0;b  0; a b .
a b a b b ab ab a  2
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a  2006  2005;b  2007  2006 . 2 3. Chứng minh rằng nếu 4
a b c   3 thì P  0 . 2 c
4. Tính giá trị của P khi a và b thỏa mãn 2a  3b  5 ab .
5. Tìm a và b sao cho b  a  2 1 và P  1  .
a b3 b b  2a aa b3 3a  3 ab
6. Xét biểu thức Q  
với a  0;b  0; a b . a a b b b a
Tìm điều kiện của a và b để P Q . 3  a b
  2a a b b    a b ab a
7. Xét biểu thức R  
với a  0;b  0; a b . 2 3a  3b ab a a b a
Tìm điều kiện của a và b để P R .
Bài toán 236. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2012 – 2013.
 Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán; Đề thi chính thức; Sở Giáo dục và Đào tạo Tỉnh
Thanh Hóa; Năm học 2012 – 2013. 2 2  a b a ba b
Cho biểu thức P    .
với a b  0 .  2 2  2 2
a b a b
a b a b a b
1. Rút gọn biểu thức P.
2. Tính giá trị của P khi a  2 1;b  2 1.
3. Biết a b  1, tìm giá trị nhỏ nhất của P.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 106
_______________________________________________________________________________________________________________________________________________________________ 2 8a b
4. Giả sử a b  1. Tính giá trị của P khi biểu thức 2
b đạt giá trị nhỏ nhất. 4a
5. Chứng minh bất đẳng thức P  4 a 1, a  1.
6. Chứng minh giá trị của P là một số tự nhiên khi a và b thỏa mãn đẳng thức  3 3
a b   b 2 3 4 8
a  2  a 1 4b .
Bài toán 237. Mở rộng và phát triển câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả
các thí sinh dự thi); Đề thi chính thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm
Hà Nội; Quận Cầu Giấy; Thành phố Hà Nội; Năm học 2015 – 2016. 2  a b   1 1   1      b a a b Cho biểu thức     P
với a  0;b  0; a b . 2 2 a ba b     2 2   b ab a  1
1. Chứng minh rằng P  . ab
2. Tính giá trị của P khi a  9  4 5 ;b  5  3 .
3. Tính giá trị của P khi a và b thỏa mãn đẳng thức  3 3
3 4 a  8b   a  
1 a  4  2b .
4. Giả sử a, b thay đổi sao cho 4a b ab  1. Tìm giá trị nhỏ nhất của P.
5. Tính giá trị của P khi a và b là nghiệm tự nhiên của phương trình 5a  2b  1. 1 1 1 16
6. Trang bị thêm các số thực dương c, d . Phản biện bất đẳng thức P     . bc cd da
a cb d
Bài toán 238. Mở rộng, liên hệ và phát triển các bài toán
 Câu 1; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2011 – 2012.
 Câu 5; Đề thi tuyển sinh lớp 10 THPT; Môn Toán (Dành cho tất cả các thí sinh dự thi); Đề thi chính
thức; Trường THPT chuyên Đại học Sư phạm Hà Nội; Đại học Sư phạm Hà Nội; Quận Cầu Giấy;
Thành phố Hà Nội; Năm học 2014 – 2015. 2 2 4 2 2  x y
x y y  2  4x  4x y y  4 Cho biểu thức A   :  với 2
x  0; y  0; x  2 y; y  2  2x . 2 2  2 2 y x
2 y xy x
x y xy    x
1. Rút gọn biểu thức A.
y x  32 2  y  42
2. Tính giá trị của A khi   y  4  . 2015 2016 2
3. Cho y  1, tìm x để A  . 5
4. Tính giá trị biểu thức A khi x và y thỏa mãn đồng thời các đẳng thức x  2
x  56 21x  22 
 4; y  4  y  2 . 3 4  7x x  2
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN
BÀI TẬP BIẾN ĐỔI TỔNG HỢP CĂN THỨC (PHẦN 2) 107
_______________________________________________________________________________________________________________________________________________________________
THÂN THỂ TẠI NGỤC TRUNG
TINH THẦN TẠI NGỤC NGOẠI
DỤC THÀNH ĐẠI SỰ NGHIỆP
TINH THẦN CÁNH YẾU ĐẠI
--------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN NHƯ NGUYỆT – QUÂN ĐOÀN TUẦN DUYÊN