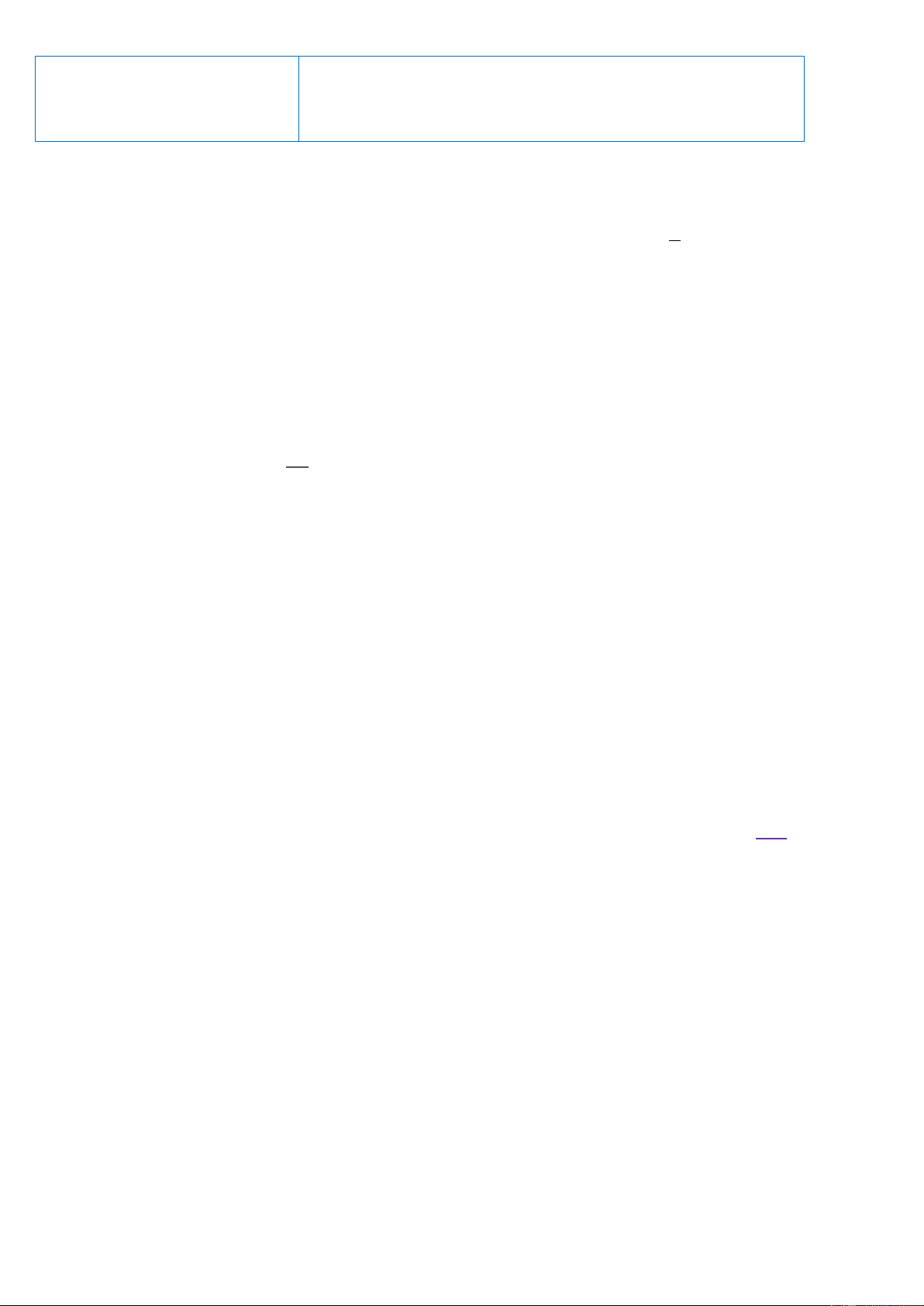





Preview text:
ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
I. PHẦN TRẮC NGHIỆM: (4,0 điểm) Khoanh tròn vào câu trả lời đúng:
Câu 1. Phương trình nào sau đây là phương trình bậc nhất hai ẩn ? 1
A. 3x2 + 2y = -1 B. x – 2y = 1 C. 3x – 2y – z = 0 D. + y = 3 x
Câu 2. Phương trình bậc nhất hai ẩn 2x + y = 4 có bao nhiêu nghiệm?
A. Hai nghiệm B. Một nghiệm duy nhất C. Vô nghiệm D. Vô số nghiệm
Câu 3. Cặp số(1;-2) là một nghiệm của phương trình nào sau đây?
A. 2x – y = 0 B. 2x + y = 1 C. x – 2y = 5 D. x – 2y = –3
Câu 4. Phương trình x - 3y = 0 có nghiệm tổng quát là:
A. (x R; y = 3x) B. (x = 3y; y R)
C. (x R; y = 3) D. (x = 0;y R)
Câu 5. Cặp số (2;-3) là nghiệm của hệ phương trình nào ? 3x 2x y 7 y 0
0x 2y 6 2x + y = 7 A. B. 2 C. D.
x 2y 4
2x 0y 1 x - y = 5
x y 1
Câu 6. Hệ phương trình : x 2y 1 có bao nhiêu nghiệm? 2x 4y 5
A. Vô nghiệm B. Vô số nghiệm C. Hai nghiệm D. Một nghiệm duy nhất
Câu 7. Hệ phương trình 2x 3y 5 vô nghiệm khi : 4x my 2
A. m = - 6 B. m = 1 C. m = -1 D. m = 6
Câu 8. Hệ phương trình 2x + y = 1 có nghiệm là: x - y = 5 A. (2;-3) B. (-2;3) C. (-4;9) D. (-4; -9)
Câu 9. Cung cả đường tròn có số đo bằng: A. Lớn hơn 0 0 0 0
360 . B. 360 . C.180 . D. Lớn hơn 180 .
Câu 10. Khi so sánh hai cung nhỏ trong một đường tròn, cách làm nào sau đây là sai ?
A. Dùng thước thẳng để đo độ dài hai cung rồi so sánh.
B. So sánh số đo của hai cung đó.
C. So sánh hai dây căng hai cung đó.
D. So sánh số đo của hai cung hoặc so sánh hai dây căng hai cung đó.
Câu 11. Trong một đường tròn, số đo của góc có đỉnh nằm bên ngoài và số đo của góc có đỉnh
nằm bên trong đường tròn cùng chắn hai cung thì:
A. Hai góc bằng nhau. B. Góc có đỉnh ở bên ngoài lớn hơn góc có đỉnh ở bên trong.
C. Góc có đỉnh ở bên trong lớn hơn góc có đỉnh ở bên ngoài. D. Không so sánh được.
Câu 12.Trong một đường tròn hai góc nội tiếp bằng nhau thì
A. Cùng chắn hai cung bằng nhau; B. Cùng chắn một cung ;
C. Cùng bằng số đo của góc ở tâm chắn cung đó, D. Có số đo bằng số đo của cung bị chắn.
Câu 13. Cho ABC có độ dài các cạnh AB = 7cm; AC = 24cm; BC = 25cm Bán kính đường
tròn ngoại tiếp ABC là: A. 10cm. B. 12cm. C. 12,5cm. D. Một số khác
Câu 14. Số đo của góc có đỉnh nằm bên trong đường tròn bằng :
A. Tổng số đo hai cung bị chắn ;
B. Nửa hiệu số đo hai cung bị chắn ; Trang 1
C. Nửa tổng số đo hai cung bị chắn ; D. Bằng số đo của góc ở tâm cùng chắn cung đó.
Câu 15. Góc nội tiếp là góc có :
A. Đỉnh nằm trên đường tròn ; B. Hai cạnh chứa hai dây của đường tròn ;
C. Đỉnh nằm trên đường tròn và hai cạnh chứa hai dây của đường tròn;
D. Đỉnh nằm trên đường tròn một cạnh là tia tiếp tuyến của đường tròn.
Câu 16. Các góc nội tiếp chắn nửa đường tròn là: A. Góc nhọn ; B. Góc tù ; C. Góc bẹt . D. Góc vuông ;
II. PHẦN TỰ LUẬN: (6,0 điểm)
Câu 17. (2đ) Giải các hệ phương trình sau: 3x y 3 x 2y 5 a/ b/ 2x y 7 3x 4y 5
Câu 18. (1đ) Một khu vườn hình chữ nhật có chu vi 46 mét, nếu tăng chiều dài 5 mét và giảm
chiều rộng 3 mét thì chiều dài gấp 4 lần chiều rộng . Hỏi kích thước khu vườn đó là bao nhiêu ?
Câu 19. (1đ) Cho hệ phương trình : (I mx y 5 2x y 2
Xác định giá trị của m để nghiệm (x
) của hệ phương trình (I) thỏa điều kiện 0; y0 : x0 + y0 = 1
Câu 20. (2đ) Cho tam giác ABC vuông tại A (AB < AC), đường cao AH, nội tiếp đường tròn
(O). M là điểm chính giữa cung AC. Tia BM cắt AC tại E cắt tiếp tuyến tại C của (O) tại F. OM cắt AC tại K.
a)Chứng minh tứ giác AHOK nội tiếp.
b)Chứng minh tam giác CEF cân
c)Chứng minh OM tiếp xúc với đường tròn ngoại tiếp tam giác AOB
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM TOÁN 9 GKII I.
Trắc nghiệm (4đ) mỗi câu đúng được 0.25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Đáp án B D C B A D A A B A C A C B C D II. Tự luận (6đ) Câu Nội dung trình bày Điểm 17
3x y 3 5x 10 x 2 x 2 1/ (2đ)
2x y 7
3x y 3 2 . 3 y 3 y 3 1.0
(Mỗi bước biến đổi tương đương được 0,5 điểm) 1.0 x 2y 5 2x 4y 10 x 5 x 5 2/ 3x 4y 5 3x 4y 5 x 2y 5 y 5
(Mỗi bước biến đổi tương đương được 0,5 điểm) 18
Gọi chiều rộng, chiều dài khu vườn hình chữ nhật lần lượt là x, y (m) 0.25 (1đ)
(ĐK: 0< x < y < 23)
Nếu tăng chiều dài 5 m thì chiều dài là: y + 5 (m) 0.25
Giảm chiều rộng 3 m thì chiều rộng là: x -3 (m) 2(x y) 46
Theo bài ra ta có hệ phượng trình. y 5 4(x 3) 0.25 x 8
Giải hệ pt ta được: thoả mãn điều kiện y 15 0.25
Vậy: chiều rộng khu vườn là 8m; chiều dài là 15m. Trang 2 19
Giả sử hệ phương trình (I) có nghiệm (x0;y0) và thỏa x0 + y0 = 1 (1đ) 3 3 x = 0
mx y 5 mx + 2x = 3 x = m + 2 Ta có : 0 0 0 0 0 m + 2 2x y 2 2x y 2 10 2m 0 0 0 0
2x y 2 y 0 0 0 0.5 2 m
Hệ đã cho có nghiệm khi m ≠ -2
Theo điều kiện bài ra ta có: 3 10 + 2m x y 1 1 m 11 0 0 2 + m 2 + m (TMĐK 0.5 Vậy: m 11 thì x0 + y0 =1 20 (2đ) F M A E K B H C O
Câu a : Tứ giác AHOK nội tiếp 0.5
-M là điểm chính giữa cung AC
=> OM AC tại K => OKA = 900
-AHOK có AHO = OKA = 900 nên nội tiếp Câu b : CEF cân 0.5
CM BM (CMB góc nội tiếp chắn nửa đường tròn)
CM là tia phân giác của ACF (do M là điểm chính giữa cung AC)
CEF có CM là đường cao cũng là phân giác nên cân tại C
Câu c: OM là tiếp tuyến của đường tròn ngoại tiếp AOB 1.0 1 ABC = ABO = sđ AC = sđ AM 2 AOM = sđ AM => ABO = AOM 1 Mà ABO =
sđ AO (vì ABO nội tiếp một đường tròn) 2 1 => AOM =
sđ AO (góc AOM có đỉnh O nằm trên đường tròn, cạnh OA 2
là dây và có số đo bằng nửa số đo của cung bị chắn) => OM là tiếp tuyến
của đường tròn ngoại tiếp ABO Trang 3 ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
Phần 1. TRẮC NGHIỆM (3,00 điểm)
Học sinh chọn một phương án đúng nhất ở mỗi câu và viết phương án chọn vào bài làm (Ví dụ: Câu 1:
A, Câu 2: B, Câu 3: D …).
Câu 1. Nghiệm của phương trình 3x y 6 là: A. 1; 3 . B. 1; 3 . C. 1; 3 . D. 1; 3 .
Câu 2. Hệ phương trình nào sau đây là hệ phương trình bậc nhất hai ẩn? x 2 2y 5
x 2y 5
x 2y 5
x 2y 5 A. B. C. D.
3x y 7 x 2 y 7 2 3x y 7
3x y 7
Câu 3. Phương trình 4x y 0 có nghiệm tổng quát là x R x R y R x R A. B. C. D. 1 y 4x x 4y y 4x y x 4
mx 2y 5 1
Câu 4. Tìm m để hệ phương trình có nghiệm ; 2
3x y 1 3 A. m 5. B. m 5 . C. m 3. D. m 3. 2 2
mx y 5
Câu 5. Tìm m để hệ phương trình vô nghiệm.
2x y 1 A. m 2.. B. m 2. C. m 5.. D. m 1.
2x y 7
Câu 6. Nghiệm của hệ phương trình là : 3
x y 8 A. 3; 1 . B. 3; 1 . C. 1; 3 . D. 1; 3 .
Câu 7. Cho đường tròn tâm O đường kính AB, C là một C
điểm thuộc đường tròn (hình bên). Biết AC = 3cm,
AB = 6cm. Số đo góc CAB bằng: A B A. 0 30 . B. 0 45 . O C. 0 60 . D. 0 90 .
Câu 8. Trong các câu sau, câu nào sai:
A.Góc nội tiếp chắn nửa đường tròn là góc vuông.
B.Góc tạo bởi tia tiếp tuyến và dây cung chắn nửa đường tròn là góc vuông.
C.Góc ở tâm chắn một phần tư đường tròn là góc vuông.
D.Góc có đỉnh ở bên ngoài đường tròn chắn nửa đường tròn là góc vuông.
Câu 9. Trong một đường tròn:
A. Các góc nội tiếp bằng nhau thì cùng chắn một cung.
B. Góc nội tiếp bằng góc ở tâm cùng chắn một cung. Trang 4
C. Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
D. Góc ở tâm bằng nửa góc nội tiếp cùng chằn một cung.
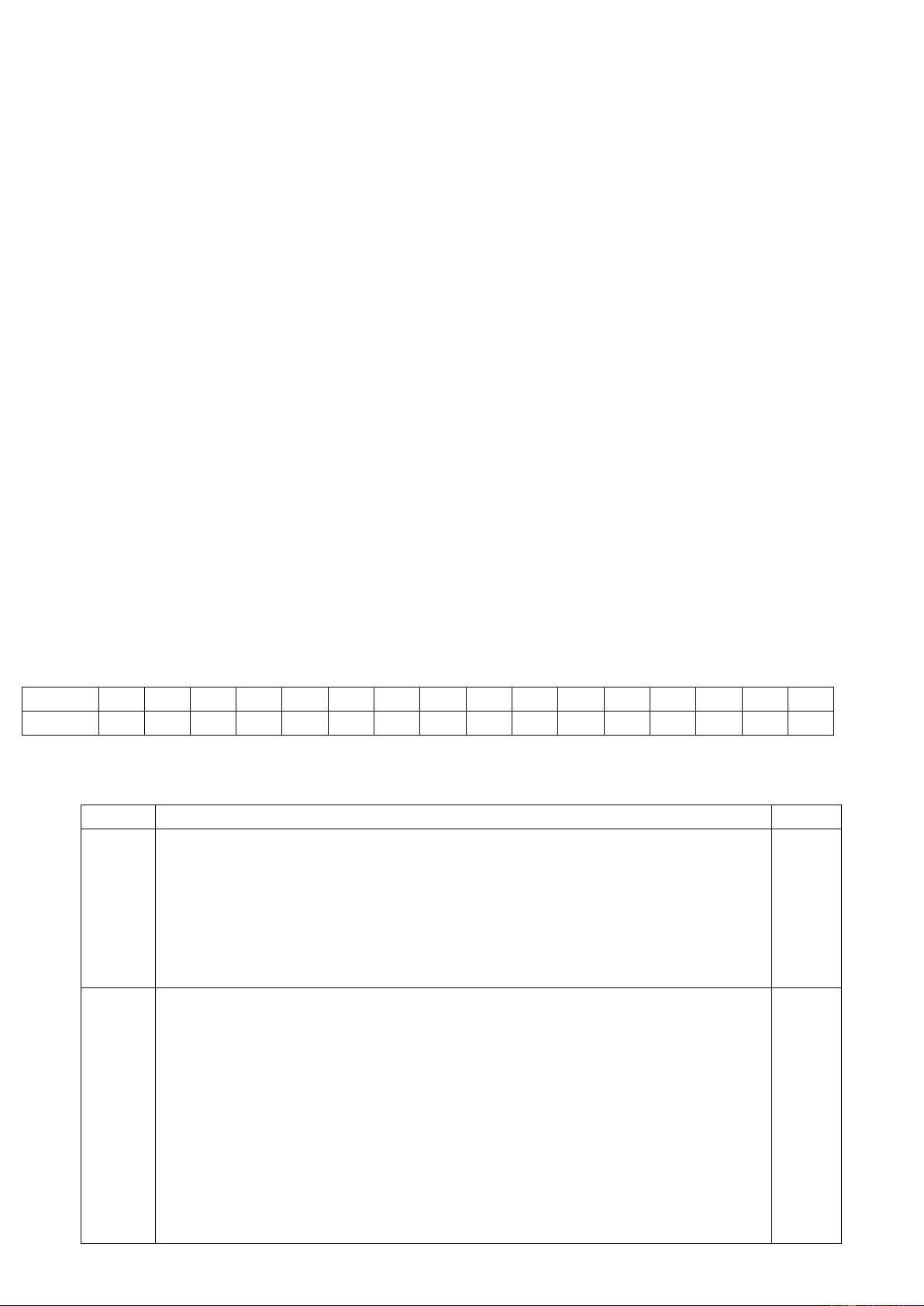
Câu 10. Cho đường tròn tâm O đường kính AB, E là một điểm
thuộc đường tròn (hình bên). Biết Số đo góc AOE bằng E 0 135 .
Số đo cung lớn EAB bằng: A 135 A. 0 135 . B. 0 45 . B O C. 0 225 . D. 0 315 .
Câu 11. Lúc 20giờ kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu độ? A. 0 60 . B. 0 90 . C. 0 120 . D. 0 240 .
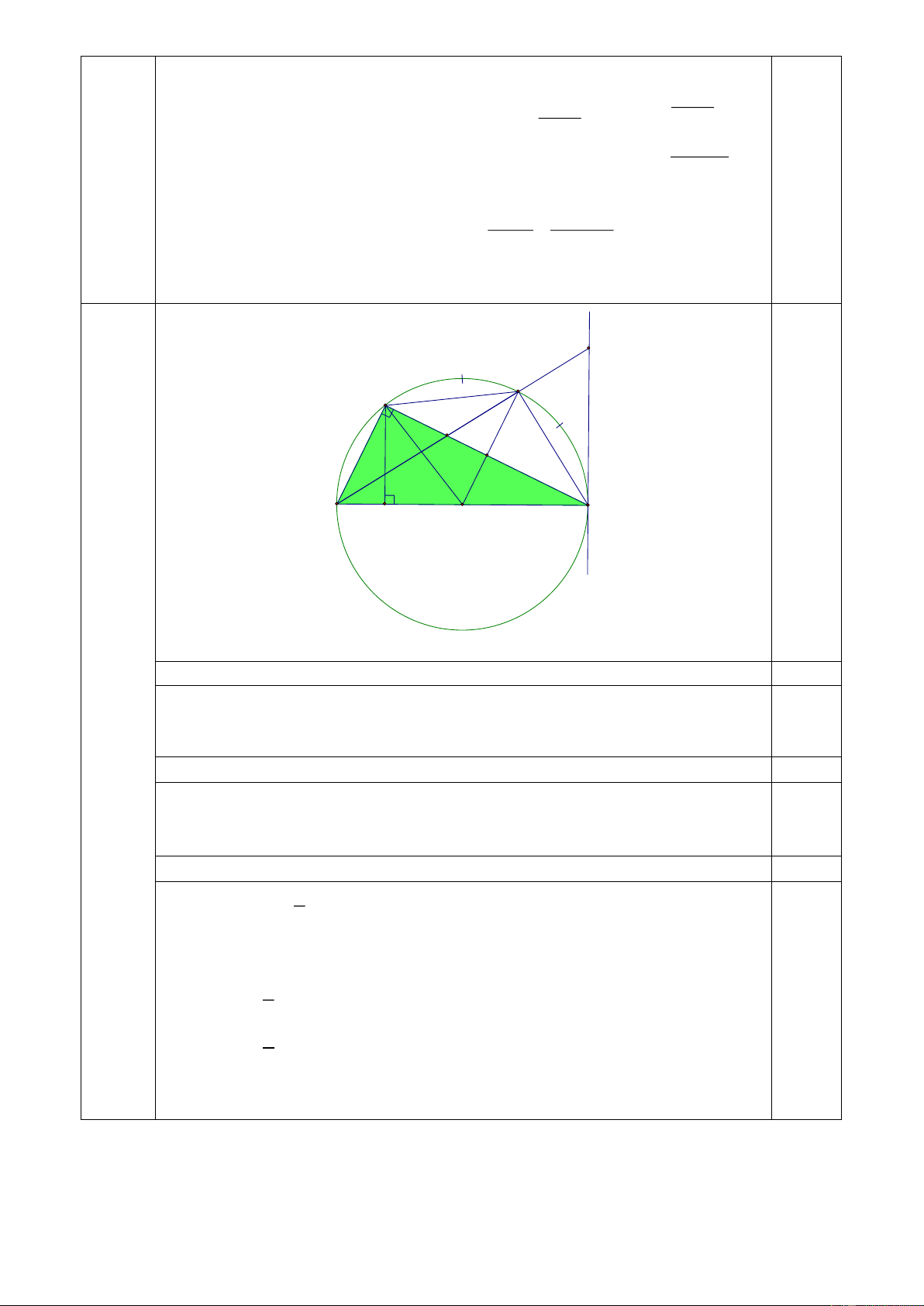
Câu 12. Cho đường tròn tâm O đường kính AB, D D
là điểm chính giữa cung AB (hình bên). Số đo cung nhỏ DB bằng: A. 0 30 . B. 0 45 . A B C. 0 60 . D. 0 90 . O
Phần 2. TỰ LUẬN (7,00 điểm)
Câu 13. (2,00 điểm) Giải hệ phương trình sau
2x 3y 0
2x 5y 16
a) x 3y 9
b) 3x 2y 5
Câu 15. (3,00 điểm) Giải bài toán bằng cách lập hệ phương trình:
Hôm qua mẹ của Lan đi chợ mua 5 trứng vịt và 10 trứng gà hết 36 000 đồng. Hôm nay mẹ Lan
mua 10 trứng vịt và 6 trứng gà chỉ hết 37 000 đồng mà giá trứng thì vẫn như cũ. Hỏi giá mỗi quả trứng mỗi loại là bao nhiêu?
Câu 16. (2,00 điểm)
Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau . Lấy một điểm M trên cung nhỏ
AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt CD tại S. Lấy điểm F thuộc cung
nhỏ BC, DF cắt OB ở E. Chứng minh: a) BD2 = DE.DF
b) MSD 2.MBA
---------------HẾT----------------
ĐÁP ÁN VÀ THANG ĐIỂM TOÁN 9
Phần 1. TRẮC NGHIỆM (3,00 điểm) Mỗi câu đúng 0,25 điểm Đề 1 Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B D C D A B C D C D C D
Phần 2. TỰ LUẬN (7,00 điểm) Câu Đáp án Biểu điểm Trang 5
Câu 13. (2,00 điểm) Giải các phương trình, hệ phương trình
2x 3y 0 3x 9 13 0,25đ
x 3y 9
x 3y 9 a) (2,00 đ) x 3 x 3 3 3y 9 y 2 0,50đ
Vậy hệ pt có nghiệm duy nhất (3;-2) 0,25đ
2x 5y 16
4x 10y 32 0,25đ 3x 2y 5
15x 10y 25 b) 19x 57 x 3
3x 2y 5 y 2 0,50đ
Vậy hệ pt có nghiệm duy nhất (3;2) 0,25đ
Gọi giá mỗi quả trứng vịt là x(đồng), mỗi quả trứng gà là 14
y(đồng); x > 0, y > 0. 0,50đ
(3,00đ) Hôm qua mẹ của Lan mua 5 trứng vịt và 10 trứng gà hết
5x + 10 y = 36 000(đồng). 0,50đ
Hôm nay mẹ Lan mua 10 trứng vịt và 6 trứng gà hết
10x + 6y = 37 000 (đồng) 0,50đ Giải hệ
5x 10y 36000 0,50đ
10x 6y 37000 x 2200 y 2500 0,50đ
Vậy giá mỗi quả trứng vịt là 2200 đồng, mỗi quả trứng gà là 0,50đ 2500 đồng. S C F 15 (2,00đ) M A B O E D
a) Chứng minh: BD2 = DE.DF b)BDE FDB 0,25đ ( vì D chung, 0
BFD ABD 45 ) 0,50đ Suy ra BD2 = DE.DF 0,25đ
b) Chứng minh: MSD 2.MBA Trang 6
sđ DAM sđ CM 0,50đ MSD đ s AM 2 0,25đ 0,25đ 2.MBA sđ M A
Vậy : MSD 2.MBA
* Ghi chú: Các cách giải khác nếu đúng đều đạt điểm tối đa. ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KÌ 2 - NĂM HỌC 2021 –2022 MÔN TOÁN 9
Bài 1: (3 điểm) Giải các phương trình và hệ pt sau. x 2y 5 a) 3x 4y 5 b) x2 – 5x + 6 = 0 c) x4 – 10x2 + 9 = 0 d) x+5 - 7 = 0 Bài 2 (2,0 điểm). Cho phương trình 2
x mx m 4 0
1 , ( x là ẩn số và m là tham số).
a) Giải phương trình 1 khi m 8 .
b) Chứng minh rằng phương trình
1 luôn có hai nghiệm phân biệt x và x với mọi m . 1 2 Bài 3 ( 1,5 điểm)
Có hai loại quặng sắt: quặng loại I và quặng loại II. Khối lượng tổng cộng của hai loại quặng là
10 tấn. Khối lượng sắt nguyên chất trong quặng loại I là 0,8 tấn, trong quặng loại II là 0,6 tấn. Biết tỉ lệ
sắt nguyên chất trong quặng loại I nhiều hơn tỉ lệ sắt nguyên chất trong quặng loại II là 10%. Tính khối
lượng của mỗi loại quặng?
Bài 4 (3,5 điểm). Cho nửa đường tròn tâm O đường kính AB = 2R. Trên nửa mật phắng chứa nửa đường
tròn tâm O có bờ là AB vẽ tia tiếp tuyến Ax. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường
tròn (C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B).
a. Chứng minh: AMDE là tứ giác nội tiếp đường tròn. b. Chứng minh: MA2 = MD.MB
c. Vẽ CH vuông góc với AB (H AB). Chứng minh rằng MB đi qua trung điểm của CH Đáp án Bài Hướng dẫn chấm Điểm 1 a. x 2y 5 2x 4y 10 x 5 x 5 1 3x 4y 5 3x 4y 5 x 2y 5 y 5 Trang 7 Bài Hướng dẫn chấm Điểm
b) x2 – 5x + 6 = 0 (a = 1; b = -5; c = 6) 0,5 đ 2
b 4ac 5 2 6 . 1 . 4 25 24 1 0 b
Suy ra phương trình có hai nghiệm phân biệt: 5 1 x 3 1 2a 2.1 0,5đ b 5 1 ; x 2 2 2a 2.1 c) c) x4 – 10x2 + 9 = 0
Đặt x2 = t sau đó tìm được t = 1; t = 9 0,5đ
Từ đó tìm được 4 nghiệm của pt : x1 =1; x2 = -1; x3=3; x4=-3 c) d) x+5 - 7 = 0 0,5 đ Tìm được x = 2 a. 2
x mx m 4 0 1 0,25đ
Thay m = 8 vào pt (1) ta có: x2 – 8x + 4 = 0 0,25đ
Vậy với m = 8 PT (1) có 2 nghiệm phân biệt: 0,5đ ; 2 Ta có: 0,75đ
Vậy PT (1) luôn có 2 nghiệm phân biệt với mọi giá trị của m. 0,25đ
Gọi khối lượng quặng loại 1 là x ( Điều kiện: 0< x < 10, tấn) ,25điểm
Thì khối lượng quặng loại 2 là : 10 – x (tấn)
Tỉ lệ sắt nguyên chất trong quặng loại 1 là: 0,8 0,25điểm x
Tỉ lệ sắt nguyên chất trong quặng loại 2 là: 0,6 10 x Do tỉ lệ sắt
nguyên chất trong quặng loại 1 nhiều hơn sắt nguyên chất trong quặng loại 2 là 10% 3
Nên ta có phương trình: 0,8 0, 6 10 0,25điểm x 10 x 100
0,8.(10 x) 0,6.x 0,1x(10 x)
8.(10 x) 6x x(10 x) 2
80 8x 6x 10x x 2
x 24x 800 , 64 0 , 0,5điểm
Do đó : x 20(l); x 4(t / ) m 1 2 Trang 8 Bài Hướng dẫn chấm Điểm
Vậy khối lượng quặng loại I là 4 tấn, khối lượng quặng loại II là: 0.25 điểm 10 – 4 = 6 (tấn). 0.5đ a) (1 đ) 0
ADB 90 (góc nội tiếp chắn nửa đường tròn) 0 ADM 90 (1) 0,25
Lại có: OA = OC = R; MA = MC (tính chất tiếp tuyến). 0,25
OM là đường trung trực của AC 0 AEM 90 (2). 0,25
Từ (1) và (2) suy ra MADE là tứ giác nội tiếp đường tròn đường kính 0,25 MA. 4 b) (1đ) Ta có 0
BAM 90 ( tính chất tiếp tuyến) ∆MAB vuông tại A 0,25 Lại có 0
ADB 90 (Góc nội tiếp chắn nửa đường tròn) AD MB 0,25
MA2 = MB.MD (hệ thức lượng trong tam giác vuông MAB) 0,5 c)(1đ)
Gọi I là giao điểm của CH và MB. Kéo dài BC cắt Ax tại N. Ta có 0
ACB 90 (góc nội tiếp chắn nửa đường tròn) 0 ACN 90 0,25 ∆ACN vuông tại C.
Lại có MC = MA nên ∆MAC cân CAM = MCA Trang 9 Bài Hướng dẫn chấm Điểm
CNM = MCN (cùng phụ với CAM ) ∆MNC cân tại M
MC = MN, do đó MA = MN (3). 0,25
Mặt khác ta có CH // NA (cùng vuông góc với AB) nên theo định lí IC IH BI Ta-lét thì (4) MN MA BM 0,25
Từ (3) và (4) suy ra IC = IH hay MB đi qua trung điểm của CH. 0,25 Trang 10




