TOP 30 Câu hỏi trắc nghiệm Toán 12 về Cực trị trong hình học không gian (có đáp án)
Trọn bộ 30 Câu hỏi trắc nghiệm về Cực trị trong hình học không gian có đáp án chi tiết giúp bạn ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!
Chủ đề: Chương 3: Phương pháp tọa độ trong không gian
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Phương pháp tọa độ trong không gian
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
CỰC TRỊ TRONG HÌNH HỌC KHÔNG GIAN
Câu 111. Cho hình chóp S.ABC có SA a , SB a 2 , SC
a 3 . Tính thể tích lớn nhất
Vmax của khối chóp đã cho. 3 a 6 3 a 6 3 a 6 A. 3 V a 6. V . V . V . max B. max C. D. 2 max 3 max 6
Câu 112. Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có độ dài đường chéo AC ' 18. Gọi S là
diện tích toàn phần của hình hộp đã cho. Tìm giá trị lớn nhất S S max của . A. S 36 3. S 18 3. S 18. S 36. max B. max C. max D. max
Câu 113. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 4 , cạnh bên SA
vuông góc với mặt phẳng đáy ABCD và SC
6 . Tính thể tích lớn nhất Vmax của khối chóp đã cho. 40 80 20 A. V . V . V . V 24. max B. C. D. 3 max 3 max 3 max
Câu 114. Cho hình chóp S.ABC có đáy ABC là tam giác đều và có SA SB SC 1. Tính
thể tích lớn nhất Vmax của khối chóp đã cho. 1 2 3 1 A. V . V . V . V . max B. C. D. 6 max 12 max 12 max 12
Câu 115. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD 4 . Các cạnh bên bằng
nhau và bằng 6 . Tìm thể tích lớn nhất Vmax của khối chóp đã cho. 130 128 125 250 A. V . V . V . V . max B. C. D. 3 max 3 max 3 max 3
Câu 116. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , cạnh bằng 1; SO vuông
góc với mặt phẳng đáy ABCD và SC
1 . Tính thể tích lớn nhất Vmax của khối chóp đã cho. 2 3 2 3 2 3 4 3 A. V . V . V . V . max B. C. D. 9 max 3 max 27 max 27
Câu 117. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với AD 4a . Các cạnh bên
của hình chóp bằng nhau và bằng a 6 . Tính thể tích lớn nhất Vmax của khối chóp đã cho. 3 8a 4 6 A. V . V a . V 8a . V 4 6 a . max B. 3 C. 3 D. 3 3 max 3 max max
Câu 118. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AB 2 . Cạnh bên
SA 1và vuông góc với mặt phẳng đáy ABC . Tính thể tích lớn nhất Vmax của khối chóp đã cho. 1 1 1 1 A. V . V . V . V . max B. C. D. 3 max 4 max 12 max 6
Câu 119. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C, cạnh bên SA vuông
góc với mặt phẳng đáy ABC . Biết SC
1, tính thể tích lớn nhất Vmax của khối chóp đã cho. 3 2 2 3 3 A. V . V . V . V . max B. C. D. 12 max 12 max 27 max 27
Câu 120. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và AB 1. Các cạnh bên SA SB SC
2. Tính thể tích lớn nhất Vmax của khối chóp đã cho. Trang 1 5 5 2 4 A. V . V . V . V . max B. C. D. 8 max 4 max 3 max 3
Câu 121. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA y y
0 và vuông góc với mặt đáy ABCD . Trên cạnh AD lấy điểm M và đặt AM x 0 x
a . Tính thể tích lớn nhất V S ABCM x y a max của khối chóp . , biết 2 2 2 . 3 a 3 3 a 3 3 a 3 3 3a 3 A. V . V . V . V . max B. C. D. 3 max 8 max 24 max 8
Câu 122. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 4, SC 6 và mặt
bên SAD là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích lớn
nhất Vmax của khối chóp đã cho. 40 80 A. V . V 40. V 80. V . max B. C. D. 3 max max max 3
Câu 123. Cho hình chóp S.ABC có SA x 0 x
3 , tất cả các cạnh còn lại đều bằng 1.
Tính thể tích lớn nhất Vmax của khối chóp đã cho. 1 1 1 1 A. V . V . V . V . max B. C. D. 4 max 8 max 12 max 16
Câu 124. (ĐỀ CHÍNH THỨC 2016 – 2017) Xét khối tứ diện ABCD có cạnh AB x và các
cạnh còn lại đều bằng 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất. A. x 3 2. B. x 6. C. x 2 3. D. x 14.
Câu 125. Trên ba tia Ox, O ,
y Oz vuông góc với nhau từng đôi, lần lượt lấy các điểm , A , B C sao cho OA , a OB , b OC
c. Giả sử A cố định còn ,
B C thay đổi nhưng luôn luôn thỏa
OA OB OC. Tính thể tích lớn nhất V OABC max của khối tứ diện . 3 a 3 a 3 a 3 a A. V . V . V . V . max B. C. D. 6 max 8 max 24 max 32
Câu 126. Cho tứ diện SABC có S , A A ,
B AC đôi một vuông góc với nhau, độ dài các cạnh BC , a SB , b SC
c . Tính thể tích lớn nhất Vmax khối tứ diện đã cho. abc 2 abc 2 abc 2 abc 2 A. V . V . V . V . max B. C. D. 4 max 8 max 12 max 24
Câu 127. Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a, cạnh bên SA a và
vuông góc với mặt đáy ABCD . Trên S ,
B SD lần lượt lấy hai điểm M, N sao cho SM SN m 0, n
0. Tính thể tích lớn nhất V
của khối chóp S.AMN biết SB SD max 2 2 2m 3n 1. 3 a 3 a 6 3 a 3 3 a A. V . V . V . V . max B. C. D. 6 max 72 max 24 max 48
Câu 128. Cho hình hộp chữ nhật ABC .
D A' B'C ' D' có đáy ABCD là một hình vuông. Biết tổng
diện tích tất cả các mặt của khối hộp bằng 32. Tính thể tích lớn nhất Vmax của khối hộp đã cho. 56 3 80 3 70 3 64 3 A. V . V . V . V . max B. C. D. 9 max 9 max 9 max 9
Câu 129. Cho hình lăng trụ đứng có thể tích V và có đáy là tam giác đều. Khi diện tích toàn phần
của hình lăng trụ nhỏ nhất thì độ dài cạnh đáy bằng bao nhiêu? A. 3 4V . B. 3 V . C. 3 2V . D. 3 6V . Trang 2
Câu 130. Cho hình chóp S.ABCD có SA x 0 x
3 , tất cả các cạnh còn lại bằng nhau và
bằng 1. Với giá trị nào của x thì thể tích khối chóp S.ABCD lớn nhất? 3 2 6 3 A. x . B. x . C. x . D. x . 3 2 2 2
Câu 131. (ĐỀ CHÍNH THỨC 2016 – 2017) Cho hình chóp S.ABC có đáy ABC là tam giác
vuông cân tại A , SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng SBC bằng 3 . Gọi
là góc giữa hai mặt phẳng SBC và ABC , tính cos
khi thể tích khối chóp S.ABC nhỏ nhất. 1 3 2 2 A. cos . B. cos . C. cos . D. cos . 3 3 2 3
Câu 132. Cho khối chóp S.ABC có đáy là tam giác vuông cân tại B. Khoảng cách từ A đến mặt
phẳng SBC bằng a 2, 0 SAB SCB
90 . Xác định độ dài cạnh AB để khối chóp S.ABC có thể tích nhỏ nhất. a 10 A. AB . B. AB a 3. C. AB 2 . a D. AB 3a 5. 2
Câu 133. Cho tam giác OAB đều cạnh a . Trên đường thẳng d qua O và vuông góc với mặt
phẳng OAB lấy điểm M sao cho OM
x . Gọi E, F lần lượt là hình chiếu vuông góc của A
trên MB và OB . Gọi N là giao điểm của EF và d . Tìm x để thể tích tứ diện ABMN có giá trị nhỏ nhất. a 2 a 6 a 3 A. x a 2. B. x . C. x . D. x . 2 12 2
Câu 134. Cho tam giác ABC vuông cân tại B , AC
2 . Trên đường thẳng qua A vuông góc
với mặt phẳng ABC lấy các điểm M, N khác phía so với mặt phẳng ABC sao cho AM.AN
1. Tính thể tích nhỏ nhất Vmin của khối tứ diện MNBC . 1 1 1 2 A. V . V . V . V . min B. C. D. 3 min 6 min 12 min 3
Câu 135. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, SA AB 2. Cạnh
bên SA vuông góc với mặt phẳng đáy ABC . Gọi H, K lần lượt là hình chiếu vuông góc của
A lên SB và SC . Tính thể tích lớn nhất V S AHK max của khối chóp . . 2 3 3 2 A. V . V . V . V . max B. C. D. 6 max 6 max 3 max 3
Câu 136. Cho hình hộp chữ nhật ABC .
D A B C D có AB x, AD
3, góc giữa đường thẳng
A C và mặt phẳng ABB A bằng 0
30 . Tìm x để thể tích khối hộp chữ nhật có thể tích lớn nhất. 3 15 3 6 3 3 3 5 A. x . B. x . C. x . D. x . 5 2 2 5
Câu 137. Cho hình hộp chữ nhật có tổng diện tích các mặt bằng 36 và độ dài đường chéo bằng
6. Tính thể tích lớn nhất Vmax của khối hộp chữ nhật đã cho. A. V 16 2. V 12. V 8 2. V 6 6. max B. max C. max D. max
Câu 138*. Cho hình hộp chữ nhật có ba kích thước là , a ,
b c . Dựng một hình lập phương có
cạnh bằng tổng ba kích thước của hình hộp chữ nhật trên. Biết rằng thể tích hình lập phương luôn
gấp 32 lần thể tích hình hộp chữ nhật. Gọi S là tỉ số giữa diện tích toàn phần hình lập phương và
diện tích toàn phần hình hộp chữ nhật. Tìm giá trị lớn nhất S S max của . Trang 3 1 16 32 48 A. S . S . S . S . max B. C. D. 10 max 5 max 5 max 5
Câu 139*. Cho hình chóp S.ABC có SA 1, SB 2, SC
3 . Gọi G là trọng tâm tam giác ABC . Mặt phẳng
đi qua trung điểm I của SG cắt các cạnh S , A S ,
B SC lần lượt tại 1 1 1
M, N, P . Tính giá trị nhỏ nhất T T min của biểu thức . 2 2 2 SM SN SP 2 3 18 A. T . T . T . T 6. min B. C. D. 7 min 7 min 7 min
Câu 140*. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, thể tích là V . Gọi M là
trung điểm của cạnh S ,
A N là điểm nằm trên cạnh SB sao cho SN 2N ; B mặt phẳng di
động qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm phân biệt K, Q . Tính
thể tích lớn nhất V S MNKQ max của khối chóp . . V V 3V 2V A. V . V . V . V . max B. C. D. 2 max 3 max 4 max 3
ĐÁP ÁN VÀ LỜI GIẢI
Vấn đề 5. CỰC TRỊ TRONG HÌNH HỌC KHÔNG GIAN
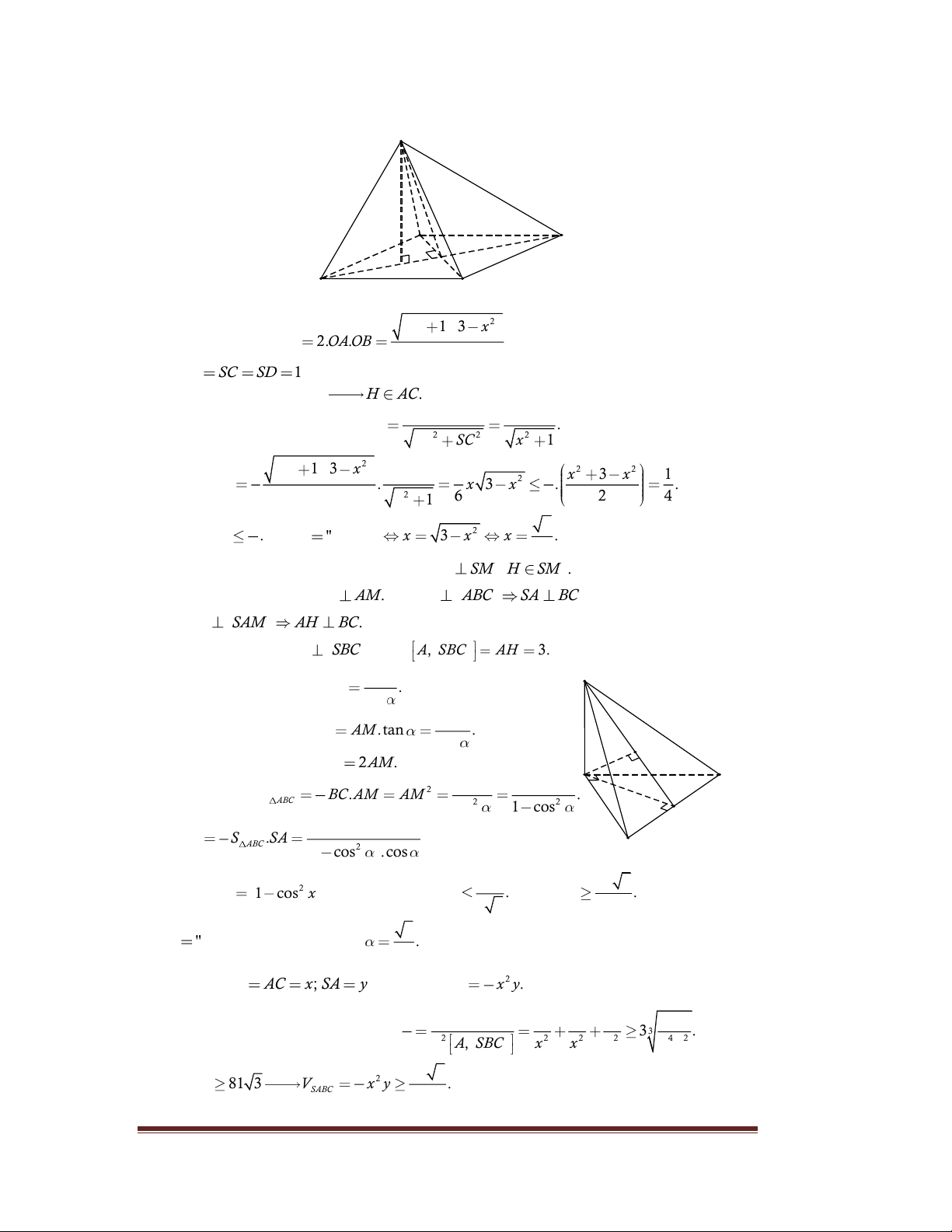
Câu 111. Gọi H là hình chiếu của A trên mặt phẳng SBC AH SBC . Ta có A AH AS . Dấu ' ' xảy ra khi AS SBC . 1 1 S
SB.SC.sin BSC . SB SC SBC . 2 2 Dấu ' ' xảy ra khi SB SC . S B 1 1 1 1 Khi đó V S .AH SB SC AS . SA . SB SC. H 3 SBC 3 2 6 Dấu ' ' xảy ra khi S , A S ,
B SC đôi một vuông góc với nhau. C 3 1 a 6
Vậy thể tích lớn nhất của khối chóp là V . SA . SB SC . max Chọn D. 6 6 Câu 112. Gọi , a ,
b c là ba kích thước của hình hộp chữ nhật. Khi đó S 2 ab bc ca . tp Theo giả thiết ta có 2 2 2 2 a b c AC ' 18. Từ bất đẳng thức 2 2 2 a b c
ab bc ca , suy ra S 2 ab bc ca 2.18 36. tp Dấu ' ' xảy ra a b c 6. Chọn D. Trang 4
Câu 113. Đặt cạnh BC x 0. S
Tam giác vuông ABC, có 2 2 AC 16 x .
Tam giác vuông SAC, có 2 2 2 SA SC AC 20 x .
Diện tích hình chữ nhật S A . B BC 4x. ABCD 6 1 4 Thể tích khối chóp 2 V S .SA x 20 x . S.ABCD 3 ABCD 3 A 4 B Áp dụng BĐT Côsi, ta có 2 2 2 x 20 x x 2 x. 20 x 10 . D C 2 4 40 Suy ra V .10 . S.ABCD 3 3 40 Dấu " " xảy ra 2 x 20 x x 10 . Vậy Vmax . Chọn A. 3 4
Cách 2. Xét hàm số 2 f x
x 20 x trên 0;2 5 . 3
Câu 114. Gọi O là tâm đường tròn ngoại tiếp tam giác đều ABC. Vì S.ABC là hình chóp đều SO ABC . 2 x 3 Đặt AB x
0. Diện tích tam giác đều S . S ABC 4 x 3 2 x 3
Gọi M là trung điểm BC AM OA AM . 2 3 3 2 x Tam giác vuông SO , A có 2 2 SO SA OA 1 . 3 A C 2 2 1 1 x 3 3 x 1 O Khi đó 2 2 V S .SO . . .x 3 x M S.ABC 3 ABC 3 4 3 12 B 1 1 Xét hàm 2 2 f x .x
3 x trên 0; 3 , ta được max f x f 2 . Chọn A. 12 0; 3 6 3 2 2 2 1 1 x x 6 2x Cách 2. Ta có 2 2 2 2 2 x 3 x
x .x . 6 2x 2. 2 2 3
Câu 115. Gọi O AC B . D Vì SA SB SC
SD suy ra hình chiếu của S trên mặt đáy
trùng với tâm đường tròn ngoại tiếp đa giác đáy SO ABCD . Đặt AB x 0.
Tam giác vuông ABC, có S 2 2 2 AC AB BC x 16. Tam giác vuông SO , A có 6 2 2 AC 128 2 2 2 x SO SA AO SA . 4 2 2 x 1 1 128 x B A Khi đó V S .SO .4x. S.ABCD 3 ABCD 3 2 O 4 1 1 128 2 2 2 . 2x 128 x . x 128 x . C D 3 3 3 128 Dấu ' ' xảy ra 2 x 128 x x 8. Suy ra V . S.ABCD Chọn B. 3 Trang 5
Câu 116. Đặt OA OC x . Tam giác vuông AO , D có S 2 2 2 OD AD OA 1 x . Suy ra 2 BD 2 1 x . 1 Diện tích hình thoi 2 S . OA BD 2x 1 x . ABCD
Tam giác vuông SOC, có B A 2 2 2 SO SC OC 1 x . x 1
Thể tích khối chóp V S .SO O 1 S.ABCD 3 ABCD C D 1 2 2 2 2
.2x 1 x . 1 x x 1 x . 3 3 1 2 Xét hàm 2 f x
x 1 x trên 0;1 , ta được max f x f . 0;1 3 3 3 4 3 Suy ra Vmax . Chọn D. 27
Cách 2. Áp dụng BDT Côsi, ta có 2 2 2 2 3 2 2 2 2x 1 x 2 2x 1 x 1 x 2 2x 1 x 1 x 4 3 . 3 3 3 3 27 Câu 117. Do SA SB SC SD
a 6 nên hình chiếu vuông góc của S trên mặt phẳng
ABCD trùng với tâm đường tròn ngoại tiếp đáy, do đó tứ giác ABCD là hình chữ nhật. Gọi H
AC BD , suy ra SH ABCD . Đặt AB x 0. Ta có S 2 2 2 2 AC AD AB x 16a . Tam giác vuông SH , A có 2 2 2 AC 8 2 a x SH SA . 4 2 A D 1 1 Khi đó V S .SH . AB . AD SH H S.ABCD 3 ABCD 3 B C 2 2 3 1 8a x a a 8 2 2 2 2 2 a .x.4 . a 2x 8a x x 8a x . Chọn A. 3 2 3 3 3
Câu 118. Đặt AC x 0. S Suy ra 2 2 2 CB AB CA 4 x . 2 1 x 4 x
Diện tích tam giác S AC.CB . ABC 2 2 1 1 Khi đó 2 V S .SA x 4 x A B S.ABC 3 ABC 6 2 2 1 x 4 x 1 . Chọn A. C 6 2 3 Trang 6
Câu 119. Giả sử CA CB x 0. S Suy ra 2 2 2 SA SC AC 1 x . 1 1 Diện tích tam giác 2 S . CA CB x . ABC 2 2 1 A B 1 1 Khi đó 2 2 V S .SA x 1 x . x x S.ABC 3 ABC 6 C 1 2 3 Xét hàm 2 2 f x x
1 x trên 0;1 , ta được max f x f . Chọn D. 6 0;1 3 27 3 2 2 2 1 1 x x 2 2x 2 3 Cách 2. Ta có 2 2 2 2 2 x 1 x
x .x . 2 2x . 2 2 3 9
Câu 120. Gọi I là trung điểm của BC. Suy ra IA IB IC
I là tâm đường tròn ngoại
tiếp tam giác ABC. Theo giả thiết, ta có SA SB
SC suy ra I là hình chiếu của S trên mặt phẳng ABC SI ABC . Đặt AC x 0. Suy ra 2 2 2 BC AB AC x 1. S 2 15 x
Tam giác vuông SBI , có 2 2 SI SB BI . 2 1 x
Diện tích tam giác vuông S AB.AC . ABC 2 2 2 B C 1 1 x 15 x Khi đó V S .SI . . S.ABC I 3 ABC 3 2 2 2 2 1 1 x 15 x 5 2 x 15 x . . Chọn A. 12 12 2 8 A Câu 121. Từ 2 2 2 2 2 x y a y a x . S BC AM a x
Diện tích mặt đáy S .AB . a ABCM 2 2 1 y
Thể tích khối chóp V S .SA S.ABCM 3 ABCM A a x B 1 a x 2 2 a 2 2 a . .a a x a x a x . M 3 2 6 D C 2 2 2 a 3 3a Xét hàm f x a x a
x trên 0;a , ta được max f x f . 0;a 2 4 3 a 3 Suy ra Vmax . Chọn B. 8
Câu 122. Gọi H là trung điểm của AD SH A . D Trang 7 Mà SAD ABCD SH ABCD . S Giả sử AD x 0 . 2 x Suy ra 2 2 HC HD CD 16. 4 2 x A
Tam giác vuông SHC, có 2 2 SH SC HC 20 . B 4 H 1 1 Khi đó V S .SH . AB . AD SH S.ABCD 3 ABCD 3 D C 2 1 x 1 1 80 2 2 2 .4.x 20 2x 80 x x 80 x . Chọn D. 3 4 3 3 3
Câu 123. Ta có tam giác ABC và SBC là những tam giác đều cạnh bằng 1 .
Gọi N là trung điểm BC . Trong tam giác SAN , kẻ SH AN . 1 Ta có 3
● SN là đường cao của tam giác đều SBC SN . 2 BC AN ● BC SAN BC SH . 2 BC SN
Từ 1 và 2 , suy ra SH ABC . S 3
Diện tích tam giác đều ABC là S . ABC x 4 1 Khi đó V S .SH S.ABC 3 ABC A C 1 1 3 3 1 S .SN . . . 3 ABC 3 4 2 8 H N Dấu ' ' xảy ra H N. Chọn B. B Câu 124. Hình vẽ. A
Cách làm tương tự như bài trên.
Tam giác BCD đều cạnh bằng 2 3 BN 3. x
VABCD lớn nhất H
N . Khi đó ANB vuông.
Trong tam giác vuông cân ANB , có B C AB BN 2 3. 2. Chọn A. H N D
Câu 125. Từ giả thiết ta có a b c. 2 3 1 1 1 b c a Do O , A O ,
B OC vuông góc từng đôi nên V abc . a bc . a . OABC 6 6 6 2 24 a Dấu ' ' xảy ra b c . Chọn C. 2 2 2 2 x y a
Câu 126. Đặt AB x, AC , y AS z. Ta có 2 2 2 x z b . S 2 2 2 y z c c z b Trang 8 y A C x a B xyz
2xy 2yz 2zx Khi đó 2 V V 6 288 2 2 2 2 2 2 2 2 2 x y y z z x a b c abc 2 V . 288 288 24 Dấu ' ' xảy ra khi x y z a b c. Chọn D. 3 a
Câu 127. Thể tích khối chóp S.ABD là V . S S.ABD 6 V SM SN Ta có S.AMN . mn M V SB SD S.ABD N 3 mna V m . nV . B S.AMN S.ABD 6 A 2 2 2. . m 3.n 2m 3n 1 Mặt khác mn . 6 2 6 2 6 D C 2m 3n 1 1 3 a 6 Dấu ' ' xảy ra m ;n . Suy ra V . Chọn B. 2 2 2m 3n 1 2 6 S.AMN 72
Câu 128. Đặt a là độ dài cạnh của hình vuông đáy, b là chiều cao của khối hộp với , a b 0. 1 16 Theo giả thiết ta có 2 2a 4ab 32 2a a 2b 32 a a 2b 16 b a . 2 a 16 Do b 0 a 0 a 4. a 1 16 1
Khi đó thể tích của khối hộp 2 3 V a . a a 8a . 2 a 2 1 4 64 3 Xét hàm 3 f a a
8a trên 0;4 , ta được max f a f . 2 0;4 3 9 Chọn D. Câu 129. Gọi h
0 là chiều cao lăng trụ; a
0 là độ dài cạnh đáy. 2 a 3 4V
Theo giả thiết ta có V S .h .h h day . 2 4 a 3 2 a 3 4V
Diện tích toàn phần của lăng trụ: S S S 3 . a tp 2 day xung quanh . 2 2 a 3 2 a 3 4 3V
Áp dụng BĐT Côsi, ta có Stoan phan 2 a 2 2 a 3 2 3V 2 3V a 2 2 3V 2 3V 3 2 3 3 . . 3 6 2V 2 a a 2 a a 2 a 3 2 3V 2 3V Dấu ' ' xảy ra khi 3 a 4V . Chọn A. 2 a a
Câu 130. Gọi O là tâm của hình thoi ABCD OA OC . 1 Theo bài ra, ta có SBD CBD OS OC. 2 1
Từ 1 và 2 , ta có OS OA OC AC
SAC vuông tại S 2 AC x 1 . 2 2 x 1 2 3 x Suy ra OA và 2 2 OB AB OA . 2 2 Trang 9 S B A H O C D 2 2 x 1 3 x
Diện tích hình thoi S 2.O . A OB . ABCD 2 Ta có SB SC SD
1, suy ra hình chiếu vuông góc H của đỉnh S trên mặt đáy là tâm đường
tròn ngoại tiếp tam giác BCD H AC. . SA SC x
Trong tam giác vuông SAC , ta có SH . 2 2 2 SA SC x 1 2 2 2 2 x 1 3 1 x x 1 1 x 3 x 1 Khi đó 2 V . x 3 x . . S.ABCD 2 3 2 x 1 6 6 2 4 1 6 Suy ra V . x 3 x x . S.ABCD Dấu ' ' xảy ra 2 Chọn C. 4 2
Câu 131. Gọi M là trung điểm của BC , kẻ AH SM H SM . 1
Tam giác ABC cân suy ra BC AM. Mà SA ABC SA BC . Suy ra BC SAM AH BC. 2
Từ 1 và 2 , suy ra AH SBC nên d , A SBC AH 3. 3 S
Tam giác vuông AMH, có AM . sin 3
Tam giác vuông SAM, có SA AM .tan . cos H
Tam giác vuông cân ABC, BC 2AM. A C 1 9 9 Diện tích tam giác 2 S BC.AM AM . ABC 2 2 2 sin 1 cos M 1 9 Khi đó V S .SA . ABC 2 3 1 cos .cos B 2 27 3 Xét hàm 2 f x
1 cos x .cos x , ta được f x . Suy ra V . 3 3 2 3
Dấu " " xảy ra khi và chỉ khi cos . Chọn B. 3 1
Cách 2. Đặt AB AC x; SA y . Khi đó 2 V x . y S.ABC 6 1 1 1 1 1 1 Vì A ,
B AC, AS đôi một vuông góc nên 33 . 2 2 2 2 4 2 9 d , A SBC x x y x y 1 27 3 Suy ra 2 2 x y 81 3 V x y . SABC 6 2 Trang 10 3
Dấu " " xảy ra khi và chỉ khi x y 3 3 cos . 3
Câu 132. Gọi D là điểm sao cho ABCD là hình vuông. AB AD Ta có AB SAD AB SD . 0 SAB 90 AB SA
Tương tự, ta cũng có BC
SD . Từ đó suy ra SD ABDC . Kẻ DH SC H SC DH SBC . S Khi đó d , A SBC d D, SBC DH . Đặt AB x 0. H
Trong tam giác vuông SDC, có 1 1 1 1 1 1 . 2 2 2 2 2 2 DH SD DC 2 SD x a D C ax 2 Suy ra SD . 2 2 x 2a A B 3 3 1 1 ax 2 a 2 x
Thể tích khối chóp V V . . . S.ABC S.ABCD 2 2 2 2 2 6 x 2a 6 x 2a 3 x Xét hàm f x trên a 2; , ta được 2 min f x f a 3 3 3a . 2 2 x 2a a 2 ; Chọn B. a
Câu 133. Do tam giác OAB đều cạnh a
F là trung điểm OB OF . 2 AF OB M Ta có AF MOB AF MB. AF MO Mặt khác, MB AE . Suy ra MB AEF MB EF. Suy ra OBM ∽ ONF nên 2 OB ON OB.OF a ON O A . OM OF OM 2x E Ta có V V V F ABMN ABOM ABON 2 2 3 1 a 3 a a 6 S OM ON x . B 3 OAB 12 2x 12 N 2 a a 2
Đẳng thức xảy ra khi x x . Chọn B. 2x 2
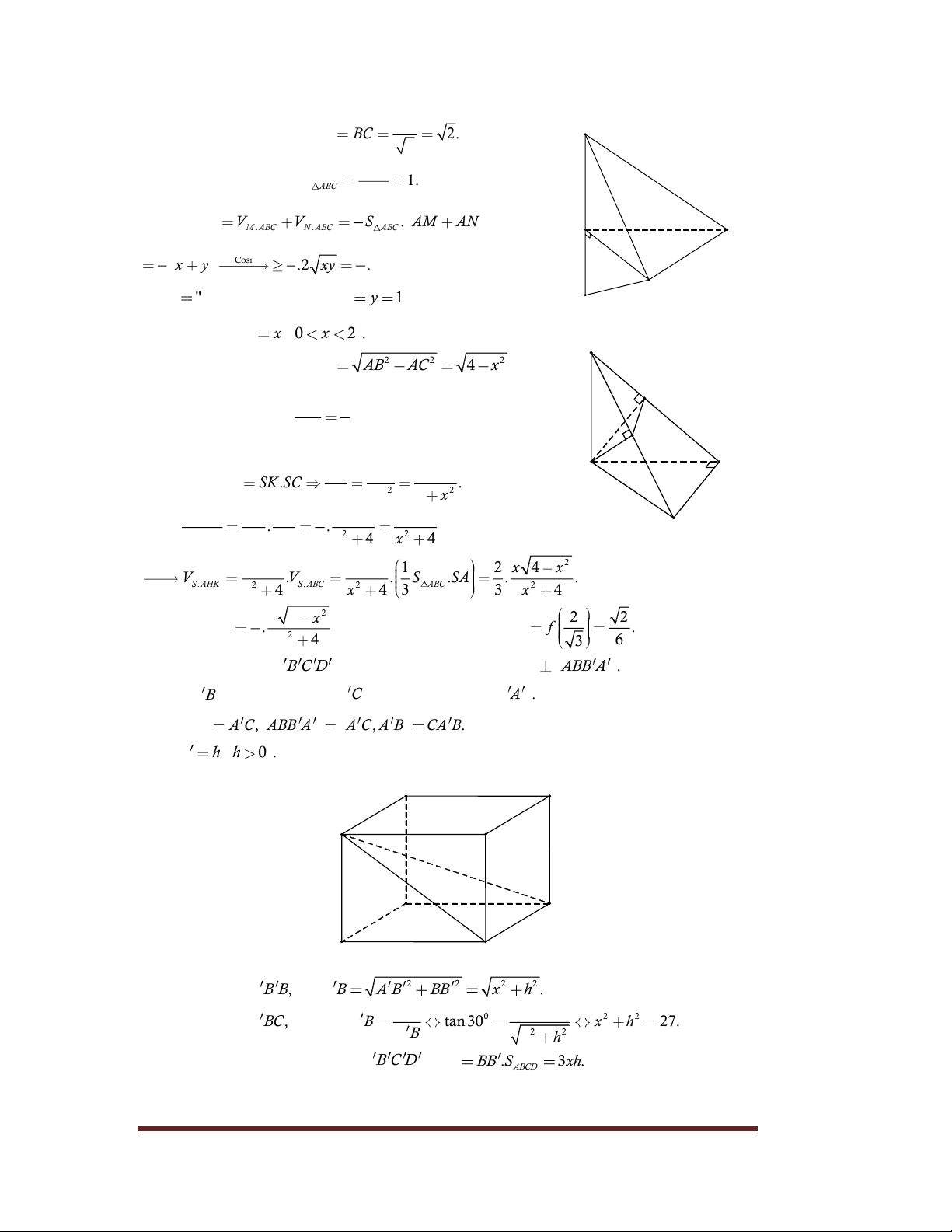
Câu 134. Đặt AM x, AN
y suy ra AM.AN x.y 1. Trang 11 AC M
Tam giác vuông ABC, có AB BC 2. 2 2 AB
Diện tích tam giác vuông S 1. ABC 2 1 Ta có V V V S . AM AN MNBC M .ABC N .ABC 3 ABC A C 1 1 2 Cosi x y .2 xy . 3 3 3 Dấu " " B
xảy ra khi và chỉ khi x y 1. Chọn D. N
Câu 135. Đặt AC x 0 x 2 . S
Tam giác vuông ABC, có 2 2 2 BC AB AC 4 x .
Tam giác SAB cân tại A , có đường cao AH suy ra H là K SH 1
trung điểm của SB nên . SB 2 H
Tam giác vuông SAC, có A C 2 SK SA 4 2 SA SK.SC . 2 2 SC SC 4 x V SH SK 1 4 2 Ta có S.AHK . . 2 2 V SB SC 2 x 4 x 4 B S.ABC 2 2 2 1 2 x 4 x V .V . S .SA . . S.AHK 2 S.ABC 2 ABC 2 x 4 x 4 3 3 x 4 2 2 x 4 x 2 2 Xét hàm f x .
trên 0;2 , ta được max f x f . Chọn A. 2 3 x 4 0;2 3 6
Câu 136. Vì ABC .
D A B C D là hình hộp chữ nhật suy ra BC ABB A .
Khi đó A B là hình chiếu của A C trên mặt phẳng ABB A . 0 Suy ra 30 A C, ABB A A C, A B CA B. Đặt BB h h 0 . D' C' A' B' h D C 3 x A B Tam giác vuông A B , B có 2 2 2 2 A B A B BB x h . BC 3
Tam giác vuông A BC, có 0 2 2 tanCA B tan 30 x h 27. 2 2 A B x h
Thể tích khối hộp chữ nhật ABC . D A B C D là V BB .S 3x . h ABCD Trang 12 2 2 x h 27 81 81
Áp dụng BĐT Côsi, ta có 3xh 3 3. V . max 2 2 2 2 x h 0 27 3 6 Dấu " " xảy ra 2 x x . Chọn B. 2 2 x h 27 2 2 Câu 137. Giả sử , a ,
b c là các kích thước của hình hộp chữ nhật.
Độ dài đường chéo của hình chữ nhật là 2 2 2 a b c
Tổng diện tích các mặt là 2 ab bc ca . 2 ab bc ca 36 ab bc ca 18 Theo giả thiết ta có . 2 2 2 2 2 2 a b c 6 a b c 36
Ta cần tìm giá trị lớn nhất của V abc. 2 Ta có 2 2 2 a b c a b c 2 ab bc ca 72 a b c 6 2. 2 2 Ta có b c 4bc 6 2 a 4 18 a 6 2 a 0 a 4 2. Khi đó 3 2 V abc a 18 a b c
a 18 a 6 2 a a 6 2a 18a Xét hàm số 3 2 f a a 6 2a 18a với a 0;4 2 , ta được max f x f 2 f 4 2 8 2. 0;4 2 Chọn C. 3 a b c
Nhận xét. Nếu sử dụng V abc 16 2 thì sai vì dấu ' ' không xảy ra. 3
Câu hỏi tương tự. Cho hình hộp chữ nhật có tổng độ dài tất cả ác cạnh bằng 32 và độ dài đường
chéo bằng 2 6. Tính thể tích lớn nhất V V 16.
max của khối hộp chữ nhật đã cho. ĐS: max
Câu 138*. Theo giả thiết ta có cạnh của hình lập phương bằng a b c .
● Hình hộp chữ nhật có: V abc và S 2 ab ac bc tp . ● Hình lập phương có: 3 V ' a b c 2 và S ' 6 a b c tp . 2 S a b c Suy ra 1 S 3. . S ab bc ca 2 3 3 3 a b c bc b c b c Ta có a b c 32abc 32 1 32 . . 3 2 a a a a a a b x 3 x y Đặt a 3 1 x y 1 32xy xy . c 32 y a 2 2 2 x y 1 x y 1 t Khi đó t x y 1 1 S 3. 3. S 96. . 3 3 x y xy x y 1 t 32t 32 x y 32 3 2 Ta có x y 1 32xy 8 x y 2 3 3 2 t 8 t 1 t 8t 16t 8 0 2 t 3 5 . 2 t 1 Xét hàm f t trên đoạn 2;3 5 , ta được max f t f 4 . 3 t 32t 32 2;3 5 10 Chọn D. Trang 13 1
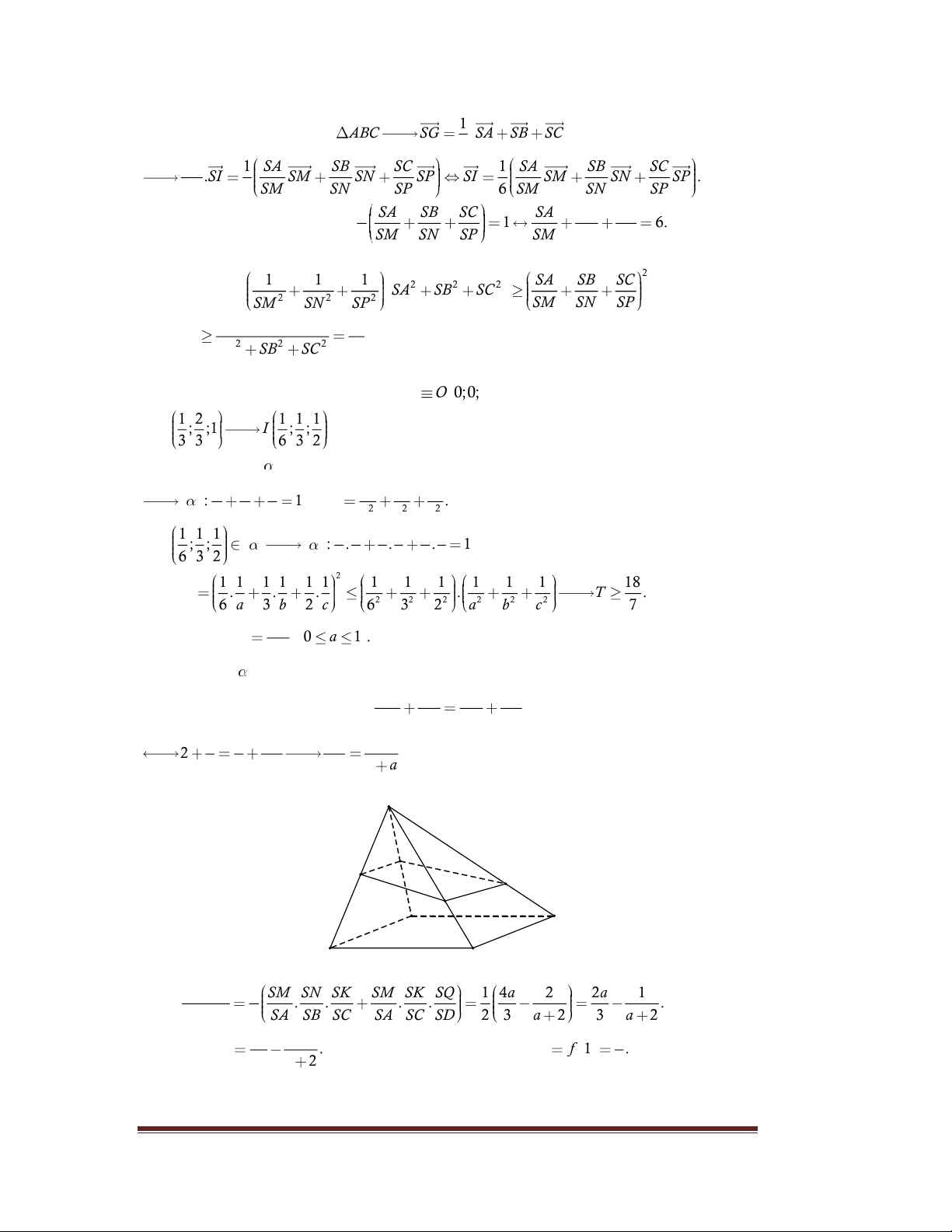
Câu 139*. Do G là trọng tâm ABC SG SA SB SC 3 SG 1 SA SB SC 1 SA SB SC .SI SM SN SP SI SM SN SP . SI 3 SM SN SP 6 SM SN SP 1 SA SB SC SA SB SC
Do I , M, N, P đồng phẳng nên 1 6. 6 SM SN SP SM SN SP
Áp dụng BĐT bunhiacopxki, ta có 2 1 1 1 2 2 2 SA SB SC SA SB SC 2 2 2 SM SN SP SM SN SP 36 18 Suy ra T . Chọn C. 2 2 2 SA SB SC 7
Cách trắc nghiệm. Do đúng với mọi hình chóp nên ta sẽ chọn trường hợp đặc biệt , SA , SB SC
đôi một vuông góc và tọa độ hóa như sau: S
O 0;0;0 , A 1;0;0 , B 0;2;0 và C 0;0;3 . Suy 1 2 1 1 1 ra G ; ;1 I ; ; . 3 3 6 3 2 Khi đó mặt phẳng cắt S , A S ,
B SC lần lượt tại M ; a 0;0 , N 0; ;
b 0 , P 0;0;c x y z 1 1 1 : 1 và T . a b c 2 2 2 a b c 1 1 1 1 1 1 1 1 1 Vì I ; ; : . . . 1. 6 3 2 6 a 3 b 2 c 2 1 1 1 1 1 1 1 1 1 1 1 1 18 Ta có 2 1 . . . . T . 2 2 2 2 2 2 6 a 3 b 2 c 6 3 2 a b c 7 SK
Câu 140*. Gọi a 0 a 1 . SC Vì mặt phẳng
di động đi qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm SA SC SB SD
phân biệt K, Q nên ta có đẳng thức SM SK SN SQ 1 3 SD SQ 2a 2 . a 2 SQ SD 2 a S M N Q P A D B C VS.MNKQ 1 SM SN SK SM SK SQ 1 4a 2 2a 1 Ta có . . . . . V 2 SA SB SC SA SC SD 2 3 a 2 3 a 2 S.ABCD 2a 1 1 Xét hàm f a
. trên đoạn 0;1 , ta được max f a f 1 . Chọn B. 3 a 2 0;1 3 Trang 14