








Preview text:
BÀI TẬP TRẮC NGHIỆM TỈ SỐ THỂ TÍCH
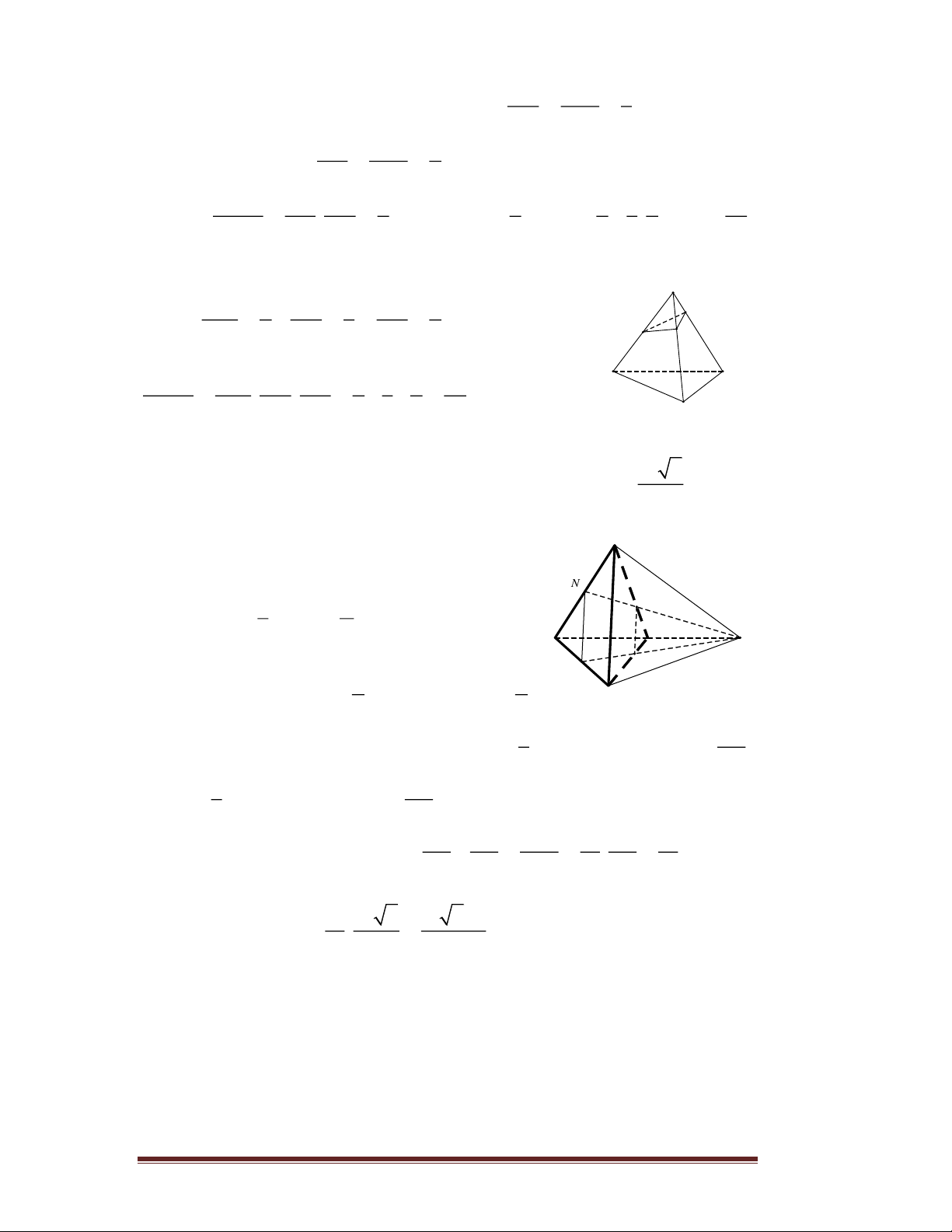
Câu 81. Cho tứ diện ABCD có các cạnh ,
AB AC và AD đôi một vuông
góc. Các điểm M, N, P lần lượt là trung điểm các đoạn thẳng BC, C , D B .
D Biết rằng AB = 4a , AC = 6a , AD = 7a . Tính thể tích V
của khối tứ diện AMNP. A. 3 V = 7a . B. 3 V = 28a . C. 3 V = 14a . D. 3 V = 21a .
Câu 82. Cho tứ diện ABCD có thể tích V . Gọi V ' là thể tích của khối tứ
diện có các đỉnh là trọng tâm của các mặt của khối tứ diện ABC . D Tính tỉ số V '. V V ' 8 V ' 23 V ' 1 V ' 4 A. = . B. = . C. = . D. = . V 27 V 27 V 27 V 27
Câu 83. Cho hình chóp S.ABC có chiều cao bằng 9 , diện tích đáy bằng 5 .
Gọi M là trung điểm của cạnh SB và N thuộc cạnh SC sao cho NS = 2N .
C Tính thể tích V của khối chóp . A BMNC . A. V = 15. B. V = 5. C. V = 30. D. V = 10.
Câu 84. Cho khối chóp S.ABC có thể tích bằng 16. Gọi M , N, P lần lượt
là trung điểm các cạnh S , A S , B S .
C Tính thể tích V của khối tứ diện AMN . P A. V = 2.
B. V = 4. C. V = 6. D. V = 8.
Câu 85. Cho tứ diện ABCD có thể tích V . Xét các điểm P thuộc đoạn
AB , điểm Q thuộc đoạn BC và điểm R thuộc đoạn BD sao cho PA = QB RB 2, = 3,
= 4 . Tính thể tích của khối tứ diện BPQR theo V. PB QC RD V V V V A. V = . B. V = . C. V = . D. V = . BPQR 5 BPQR 4 BPQR 3 BPQR 6
Câu 86. Cho tứ diện ABCD có A ,
B AC, AD đôi một vuông góc và AB = 6 , a AC = 9 ,
a AD = 3a . Gọi M , N, P lần lượt là trọng tâm của các
tam giác ABC, AC ,
D ADB . Tính thể tích V của khối tứ diện AMNP . A. 3 V = 8a . B. 3 V = 4a . C. 3 V = 6a . D. 3 V = 2a .
Câu 87. Cho hình chóp S.ABC có SA = 3, SB = 4, SC = 5 và 0
ASB = BSC = CSA = 60 . Tính thể tích V của khối chóp đã cho.
A. V = 5 2. B. V = 5 3. C. V = 10. D. V = 15.
Câu 88. (ĐỀ THAM KHẢO 2016 – 2017) Cho tứ diện có thể tích bằng V .
Gọi V là thể tích của khối đa diện có các đỉnh là các trung điểm của các V
cạnh của khối tứ diện đã cho, tính tỉ số . V Trang 1 V 1 V 1 V 2 V 5 A. = . B. = . C. = . D. = . V 2 V 4 V 3 V 8
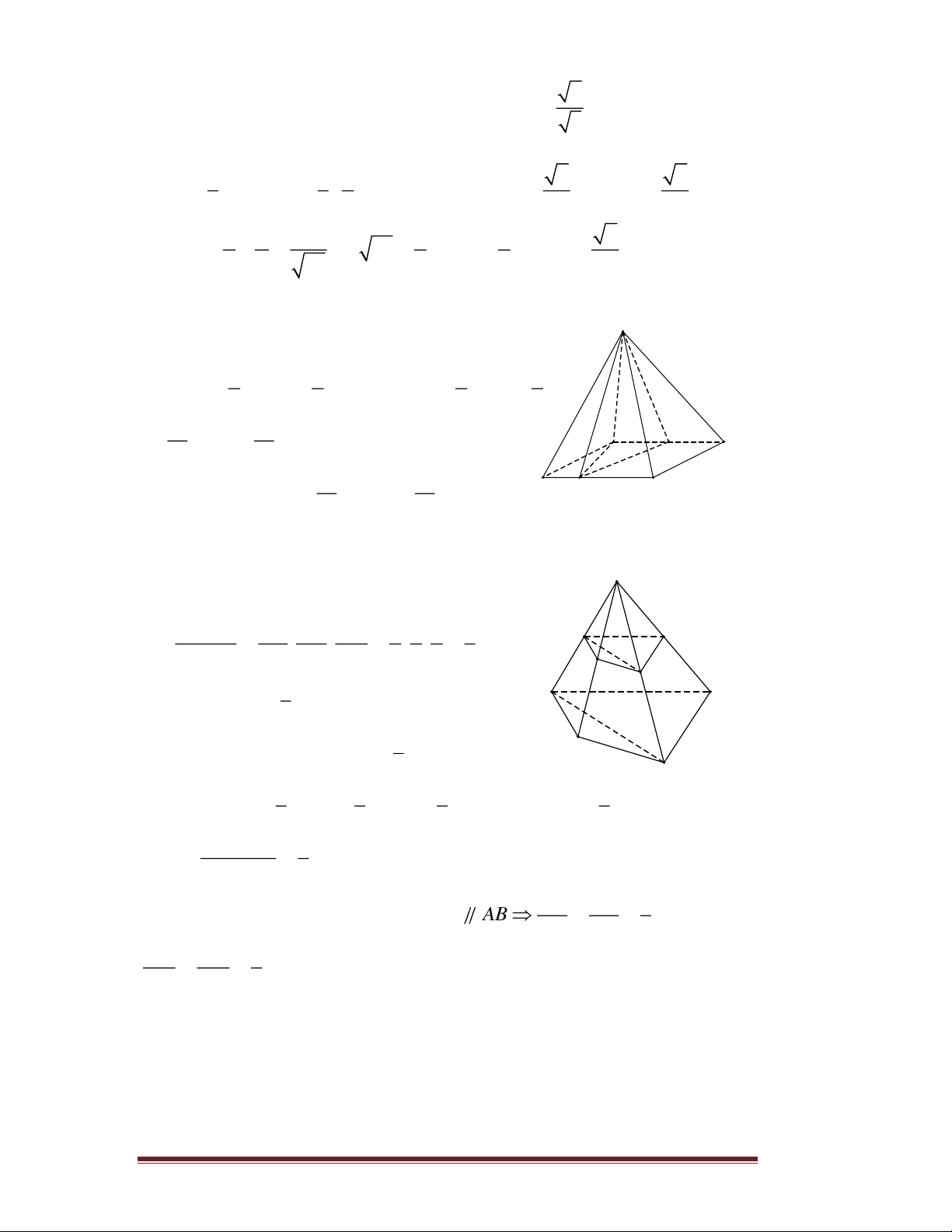
Câu 89. Cho hình chóp đều S.ABC có cạnh đáy bằng a , cạnh bên bằng
2a . Gọi M là trung điểm SB , N là điểm trên đoạn SC sao cho
NS = 2NC . Tính thể tích V của khối chóp . A BCNM. 3 11 3 11 3 11 A. = a V . B. = a V . C. = a V . 36 16 24 3 11 D. = a V . 18
Câu 90. Cho hình chóp đều S.ABC có tất cả các cạnh bằng a . Mặt phẳng
(P) song song với mặt đáy ( ABC) và cắt các cạnh bên S , A S , B SC lần
lượt tại M, N, P . Tính diện tích tam giác MNP biết mặt phẳng (P) chia
khối chóp đã cho thành hai phần có thể tích bằng nhau. 2 a 3 2 a 3 2 a 3 A. S = . S = S = B. . C. . MNP 8 MNP 16 MNP 3 4 2 2 a 3 D. S = . MNP 3 4 4
Câu 91. Cho tam giác ABC vuông cân ở A và AB = a . Trên đường thẳng qua
C và vuông góc với ( ABC ) lấy điểm D sao cho CD = a . Mặt phẳng ( )
qua C và vuông góc với BD , cắt BD tại F và cắt AD tại E . Tính thể tích V
của khối tứ diện CDEF . 3 3 3 3 A. = a V . B. = a V . C. = a V . D. = a V . 6 24 36 54
Câu 92. Cho tứ diện ABCD có thể tích V và các điểm M , N, P thỏa mãn
điều kiện AM = 2AB , AN = 3AC và AP = 4AD. Mệnh đều nào dưới đây đúng? V V A. V = . B. V = 8V. C. V
= 24V. D. V = . AMNP 24 AMNP AMNP AMNP 8
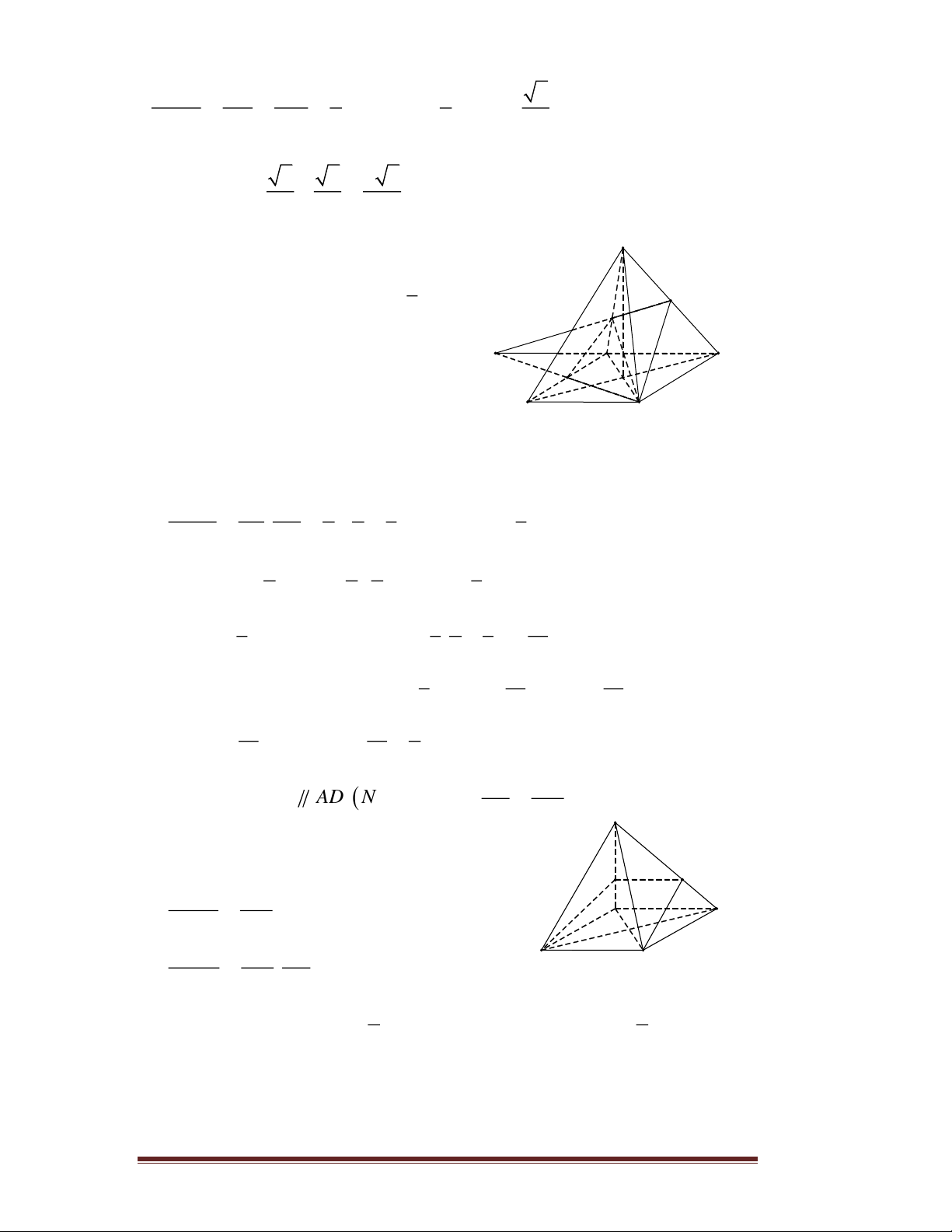
Câu 93. Cho tứ diện đều ABCD có cạnh bằng a . Gọi M , N lần lượt là
trung điểm của các cạnh A ,
B BC và E là điểm đối xứng với B qua D .
Mặt phẳng (MNE ) chia khối tứ diện ABCD thành hai khối đa diện, trong
đó khối đa diện chứa đỉnh A có thể tích V . Tính V . 3 7 2 3 11 2 3 13 2 A. = a V . B. = a V . C. = a V . 216 216 216 3 2 D. = a V . 18 Trang 2
Câu 94. Mặt phẳng đi qua trọng tâm của tứ diện, song song với một mặt
phẳng của tứ diện và chia khối tứ diện thành hai phần. Tính tỉ số thể tích
(phần bé chia phần lớn) của hai phần đó. 2 5 27 3 A. . B. . C. . D. . 3 7 37 4
Câu 95. Cho tứ diện đều SABC có cạnh bằng 1 . Mặt phẳng ( P) đi qua
điểm S và trọng tâm G của tam giác ABC cắt các cạnh A , B AC lần lượt
tại M , N . Tính thể tích nhỏ nhất V của khối tứ diện SAMN. min 2 4 2 2 A. V = . B. V = . C. V = . D. V = . min 18 min 9 min 27 min 36
Câu 96. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có
thể tích bằng 48. Gọi M , N lần lượt là điểm thuộc các cạnh A , B CD sao cho MA = M ,
B NC = 2ND . Tính thể tích V của khối chóp S.MBCN.
A. V = 8.
B. V = 20.
C. V = 28.
D. V = 40.
Câu 97. Cho hình chóp S.ABCD . Gọi A', B ', C ', D' lần lượt là trung điểm của , SA ,
SB SC, S .
D Tính tỷ số k của thể tích khối chóp
S.A' B'C ' D' chia cho thể tích khối chóp S.ABCD . 1 1 1 1 A. k = . B. k = . C. k = . D. k = . 2 4 8 16
Câu 98. Cho khối chóp S.ABCD có thể tích bằng V . Lấy điểm A' trên cạnh 1 SA sao cho SA' =
SA . Mặt phẳng ( ) qua A' và song song với đáy 3
(ABCD) cắt các cạnh S ,
B SC, SD lần lượt tại B ', C ', D' . Tính thể tích
V ' của khối chóp S.A' B'C ' D' . A. ' = V V . B. ' = V V . C. ' = V V . D. ' = V V . 3 9 27 81
Câu 99. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt phẳng ( ) đi qua ,
A B và trung điểm M của SC . Mặt phẳng ( ) chia
khối chóp đã cho thành hai phần có thể tích lần lượt là V , V với V V . 1 2 1 2 Tính tỉ số V1 . V2 V 1 V 3 V 5 V 3 A. 1 = . B. 1 = . C. 1 = . D. 1 = . V 4 V 8 V 8 V 5 2 2 2 2
Câu 100. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại
A và B , BA = BC = 1, AD = 2 . Cạnh bên SA vuông góc với đáy và SA =
2 . Gọi H là hình chiếu vuông góc của 3
V = a trên SB . Tính thể
tích V của khối đa diện SAHCD . 2 2 4 2 4 2 2 2 A. V = . B. V = . C. V = . D. V = . 3 9 3 9 Trang 3
Câu 101. Cho hình chóp đều S.ABC .
D Gọi N là trung điểm , SB M là
điểm đối xứng với B qua .
A Mặt phẳng ( MNC ) chia khối chóp S.ABCD
thành hai phần có thể tích lần lượt là V
V , V với V V . Tính tỉ số 1 . 1 2 1 2 V2 V 5 V 5 V 5 V 5 A. 1 = . B. 1 = . C. 1 = . D. 1 = . V 7 V 11 V 9 V 13 2 2 2 2
Câu 102. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,
SA = a vuông góc với mặt phẳng đáy ( ABCD). Điểm M thuộc cạnh SA SM sao cho
= k. Xác định k sao cho mặt phẳng (MBC) chia khối chóp SA
đã cho thành hai phần có thể tích bằng nhau. 1 − + 3 1 − + 5 1 − + 2 A. k = . B. k = . C. k = . 2 2 2 1+ 5 D. k = . 4
Câu 103. Gọi V là thể tích của hình lập phương ABC .
D A' B'C ' D', V là 1
thể tích tứ diện A' ABD . Hệ thức nào sau đây đúng?
A. V = 6V .
B. V = 4V .
C. V = 3V .
D. V = 2V . 1 1 1 1
Câu 104. Cho lăng trụ đứng AB .
C A' B'C ' . Gọi D là trung điểm AC . Tính
tỉ số k của thể tích khối tứ diện B'BAD và thể tích khối lăng trụ đã cho. 1 1 1 1 A. k = . B. k = . C. k = . D. k = . 4 12 3 6
Câu 105. Cho khối lăng trụ AB . C A
B C . Đường thẳng đi qua trọng tâm
của tam giác ABC và song song với BC cắt các cạnh A ,
B AC lần lượt tại
M , N. Mặt phẳng (
A MN ) chia khối lăng trụ thành hai phần. Tính tỉ số thể
tích (phần bé chia phần lớn) của chúng. 2 4 4 4 A. . B. . C. . D. . 3 23 9 27
Câu 106. Cho hình lăng trụ AB . C A
B C có đáy ABC là tam giác vuông
cân tại A, AC = 2 2 . Biết AC tạo với mặt phẳng ( ABC ) một góc 0 60 và
AC = 4 . Tính thể tích V của khối đa diện ABCC B . 16 8 3 16 3 A. V = 8 3. B. V = . C. V = . D. V = . 3 3 3
Câu 107. Cho khối hộp ABC . D A B C
D có thể tích V . Các điểm M , N, P
thỏa mãn điều kiện AM = 2AC , AN = 3A
B và AP = 4A D . Tính thể tích
của khối tứ diện AMNP theo V . A. V
= 8V. B. V = 4V. C. V = 6V. D. V = 12V. AMNP AMNP AMNP AMNP Trang 4
Câu 108. Cho hình lăng trụ AB .
C A' B'C ' có thể tích bằng V . Các điểm M , AM 1
N , P lần lượt thuộc các cạnh AA' , BB' , CC ' sao cho = , AA' 2 BN CP 2 =
= . Tính thể tích V ' của khối đa diện AB . C MN . P BB ' CC ' 3 2 9 20 11 A. V ' =
V . B. V ' = V . C. V ' = V . D. V ' = V . 3 16 27 18
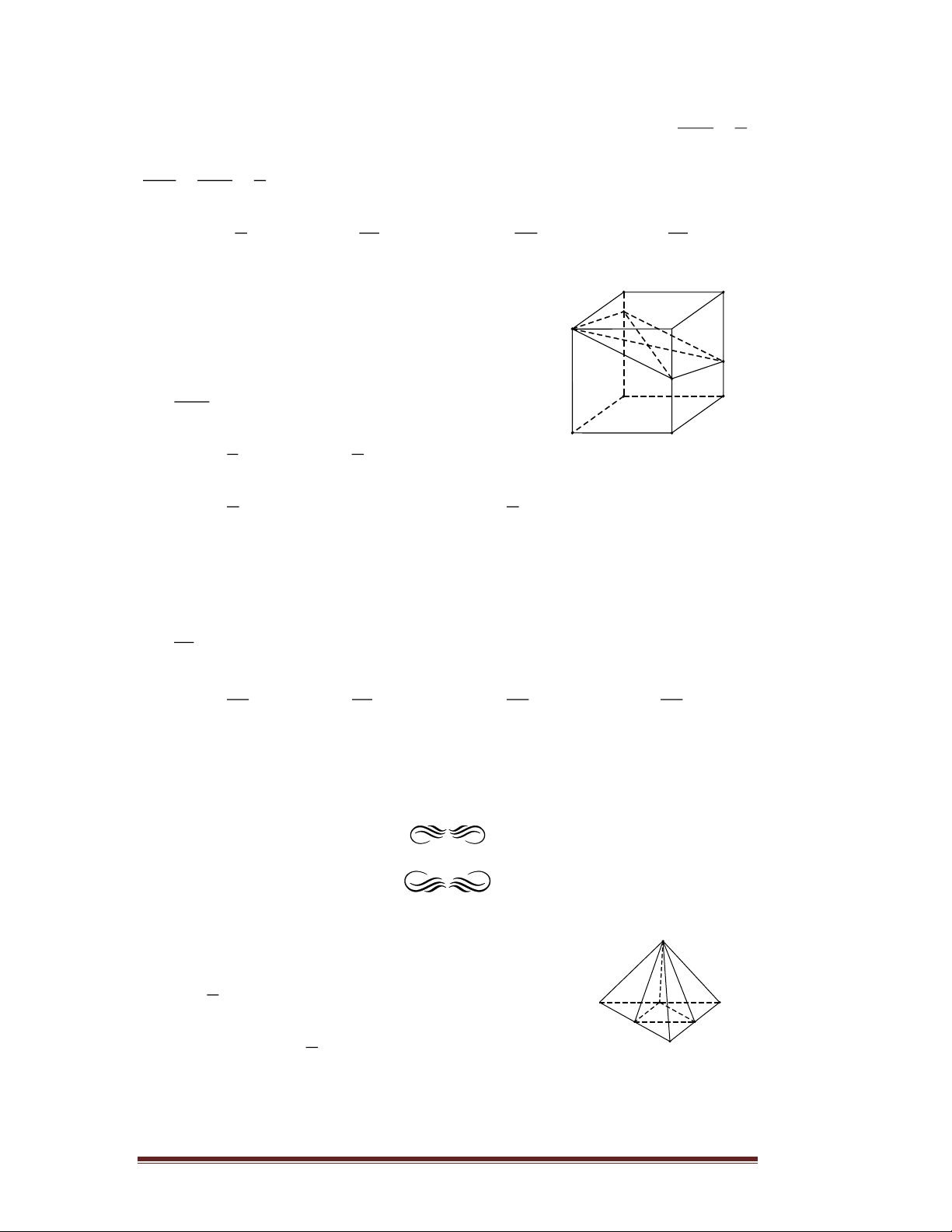
Câu 109. Người ta cần cắt một khối lập B C
phương thành hai khối đa diện bởi một mặt M
phẳng đi qua A (như hình vẽ) sao cho phần thể D A
tích của khối đa diện chứa điểm B bằng một
nửa thể tích của khối đa diện còn lại. Tính tỉ số N = CN B' P C' k . CC ' 1 2 A. k = . B. k = . A' D' 3 3 3 1 C. k = . D. k = . 4 2
Câu 110. Cho hình hộp ABC .
D A' B'C ' D'. Gọi M là điểm thuộc đoạn
CC ' thỏa mãn CC ' = 4CM . Mặt phẳng ( AB 'M ) chia khối hộp thành hai
phần có thể tích là V và V . Gọi V là phần có chứa điểm B . Tính tỉ số 1 2 1 1 = V k . V2 7 7 7 25 A. k = . B. k = . C. k = . D. k = . 32 16 25 32
ĐÁP ÁN VÀ LỜI GIẢI
Vấn đề 4. TỈ SỐ THỂ TÍCH
Câu 81. Tứ diện ABCD có các cạnh , AB AC A và AD đôi một vuông góc nên 1 3 V = A .
B AC.AD = 28a . M ABCD B C 6 1 P N Ta có S = S , suy ra MNP 4 BCD D Trang 5 1 3 V = V
= 7a . Chọn A. AMNP . 4 A BCD
Câu 82. Gọi M là trung điểm AC; E, F làn A
lượt là trọng tâm của tam giác ABC, AC . D 1 M
Trong tam giác MBD có EF = B . D E 3
Tương tự ta có các cạnh còn lại của tứ diện mới F B C
sinh ra bằng 1 cạnh của tứ diện ban đầu. 3 3 D V Do đó ' 1 1 = = . Chọn C. V 3 27 SN
Câu 83. Từ giả thiết, ta có 2 = và S SC 3 SM 1 = M . SB 2 A N B Thể tích khối chóp 1 V = .9.5 = 15. S . ABC 3 Ta có C V SM SN 1 2 S . AMN = . = V = V = 10. ABMNC S . V SB SC 3 3 ABC S . ABC Chọn D.
Câu 84. Ta có d S,(MNP) = d , A (MNP) nên V =V . AMNP SMNP V SM SN SP 1 1 Mà SMNP = . . = nên V = V = 2. Chọn A. V SA SB SC 8 AMNP S . 8 ABC SABC
Câu 85. Từ giả thiết, ta có B BP 1 BQ 3 BR 4 = , = , = . P BA 3 BC 4 BD 5 VBPQR BP BQ BR 1 3 4 1 Ta có = . . = . . = . R Q V BA BC BD 3 4 5 5 D BACD A 1 V Suy ra V = .V = . BPQR C 5 BACD 5 Chọn A. 1 Câu 86. Ta có 3 V = A .
B AC.AD = 27a . ABCD 6 Trang 6
Gọi E, F, G lần lượt là trung điểm của A BC, C , D DB . 1 27 Suy ra 3 V = V = a . AEFG 4 ABCD 4 P
Do M , N, P là trọng tâm của các tam giác M N G B D ABC, AC , D ADB nên ta có AM AN AP 2 F = = = E . AE AF AG 3 C V AM AN AP 8 Ta có . A MNP = . . = V AE AF AG 27 . A EFG 8 3 ⎯⎯ →V = V
= 2a . Chọn D. . A MNP . 27 A EFG
Câu 87. Trên các đoạn S ,
B SC lần lượt lấy S
các điểm E, F sao cho SE = SF = 3.
Khi đó S.AEF là khối tứ diện đều có cạnh a = 3. F 3 a 2 9 2 A B Suy ra V = = . S . AEF 12 4 E V SE SF 3 3 9 Ta có S.AEF = . = . = C V SB SC 4 5 20 S . ABC 20 ⎯⎯ →V = V = 5 2. Chọn A. S . ABC S . 9 AEF
Câu 88. Kí hiệu tứ diện và các điểm như hình S vẽ. Ta có A' C' V S A S B SC V S A BC 1 . = . . = V = B' S A BC . . V SA SB SC 8 8 P A C S . ABC Tương tự = = = V V V V M N A A MP B BMN C C . . . . NP 8 B Do đó V = V − V +V +V +V S . ABC
( S. ABC . A A MP B.BMN
C.CNP ) V V V V V V 1 = V − + + + = = . Chọn 8 8 8 8 2 V 2 A.
Câu 89. Gọi O là tâm của ABC , suy ra SO ⊥ ( ABC ) . Trang 7 Tam giác vuông SOA, có S 11 2 2 = − = a SO SA AO . 3 2 3 M N 1 a 3 a 11 a 11 Suy ra V = . . = . S . ABC 3 4 3 12 C A V SM SN 1 2 1 O Ta có S.AMN = . = . = . V SB SC 2 3 3 B S . ABC 3 V 2 2 a 11 Suy ra ABCNM = V = V = . ABCNM S . V 3 3 ABC 18 S . ABC Chọn D.
Câu 90. Mặt phẳng ( P)
( ABC) và cắt các cạnh S , A S ,
B SC lần lượt tại M , N, . P SM SN SP Theo Talet, ta có = = = x . S SA SB SC Do đó V SM SN SP S .MNP 3 = . . = x . V SA SB SC S . ABC M P Theo giả thiết V 1 1 1 A C S .MNP 3
= → x = → x = . N 3 V 2 2 S ABC 2 .
Suy ra tam giác MNP là tam giác đều cạnh B a . 3 2 2 2 a Vậy diện tích 3 a 3 S = . = . MNP 3 3 2 4 4 4 Chọn D. AB ⊥ AC Câu 91. Ta có
AB ⊥ ( ACD) AB ⊥ CE. ( ) 1 AB ⊥ CD D
Lại có BD ⊥ ( ) BD ⊥ CE . (2) F Từ ( )
1 và (2) , suy ra CE ⊥ ( ABD) CE ⊥ A . D E
Tam giác vuông ABC , có 2 2 BC =
AB + AC = a 2 . C B
Tam giác vuông DCB , có 2 2 BD =
BC + CD = a 3 . A Trang 8 2 DF CD 1
Tam giác vuông DCB , có 2
CD = DF.DB = = . 2 DB DB 3 2
Tương tự, ta cũng có DE CD 1 = = . 2 DA DA 2 3 V DE DF 1 1 1 a D EFC 1 1 Suy ra . 2 = . = ⎯⎯ →V = .V = . . a .a = . D.EFC D. ABC V DA DB 6 6 6 D ABC 3 2 36 . Chọn C.
Câu 92. Từ giả thiết, suy ra A AB 1 AC 1 AD 1 = D ; = ; = . AM 2 AN 3 AP 4 B C Ta có M P V AB AC AD 1 1 1 1 . A BCD = . . = = . V AM AN AP 2 3 4 24 N . A MNP Suy ra V = 24.V
= 24V. Chọn C. . A MNP . A BCD 3 a 2
Câu 93. Thể tích khối tứ diện đều ABCD cạnh a là V = . ABCD 12
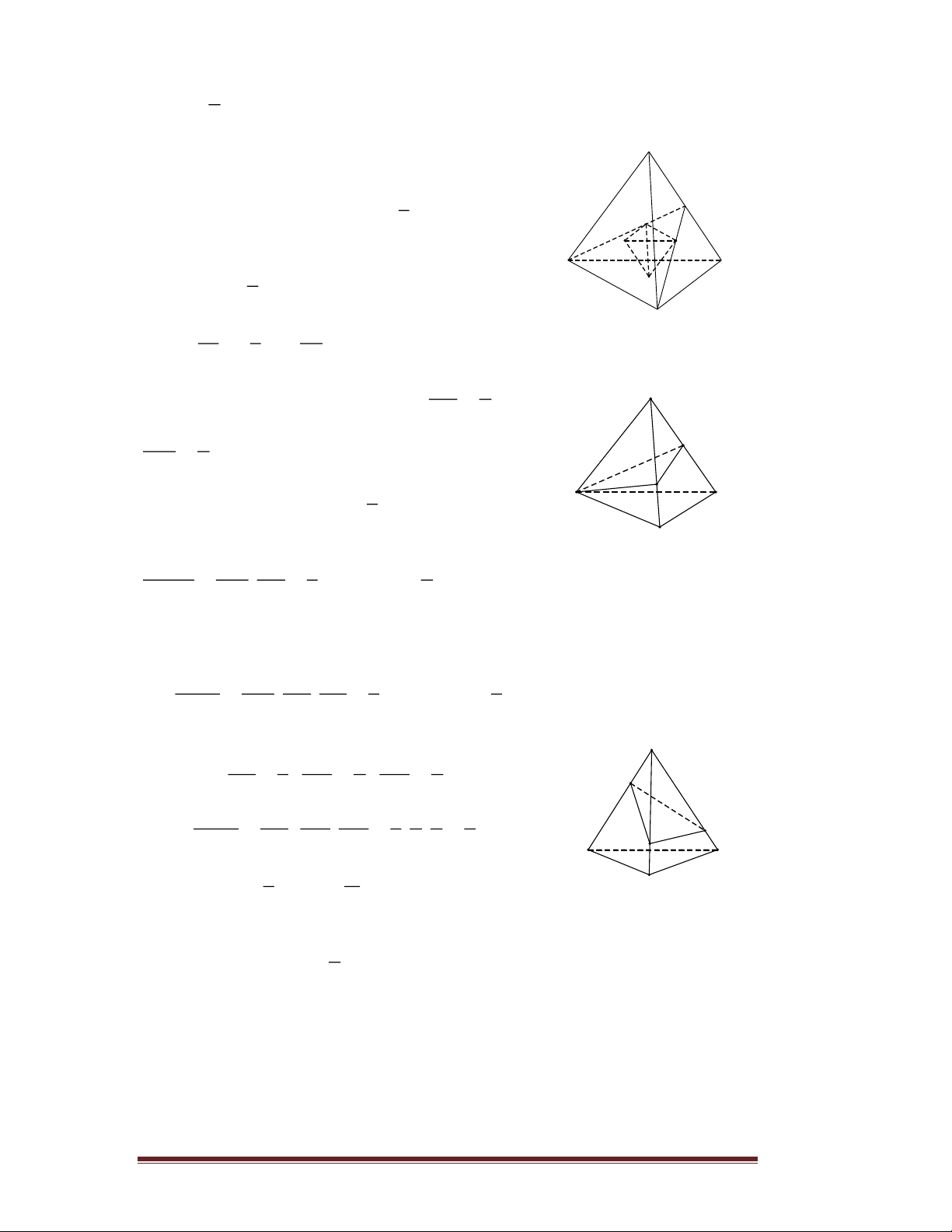
Gọi P = EN CD và Q = EM AD. A Suy ra ,
P Q lần lượt là trọng tâm của BCE và ABE .
Gọi S là diện tích tam giác BCD, suy ra S = S = S. CDE BNE M 1 S Q Ta có S = .S = . PDE 3 CDE 3 D B E
Gọi h là chiều cao của tứ diện ABCD , suy ra P h h N d M ,
(BCD) = ; d Q, (BCD) = . C 2 3 Khi đó 1 S. = h V S
.d M , BCD = ; M .BNE BNE ( ) 3 6 1 S. = h V S
.d Q, BCD = . Q.PDE PDE ( ) 3 27 S.h S.h 7S.h 7 S.h 7 Suy ra V = V −V = − = = . = .V . PQD.NMB M .BNE Q.PDE 6 27 54 18 3 18 ABCD Vậy thể tích khối đa diện chứa đỉnh A là 3 3 11 a 2 11 2 = − = a V V V . = . ABCD PQD.NMB 18 12 216 Chọn B. Trang 9
Câu 94. Gọi E, F, I lần lượt là trung điểm A
của các cạnh AC, B ,
D EF khi đó I là trọng
tâm của tứ diện ABC .
D Ta sẽ dựng mặt
phẳng qua I song song với (BCD). F
Trong mặt phẳng (EBD) dựng đường thẳng P J I
qua I song song với BD cắt F , B FD lần B M N D Q
lượt tại M , N. E
Qua M , N lần lượt kẻ các đường thẳng lần C lượt song song với BC, CD cắt A ,
B AC, AD lần lượt tại , P , Q J. AQ AP AJ AQ 3
Do Q là trung điểm của 3 EC = , suy ra = = = . AC 4 AB AD AC 4 V AP AQ AJ V A PQJ 3 3 3 27 A PQJ 27 Ta có . . = . . = . . = = . Chọn C. V AB AC AD 4 4 4 64 V 37 . A BCD PQJBCD
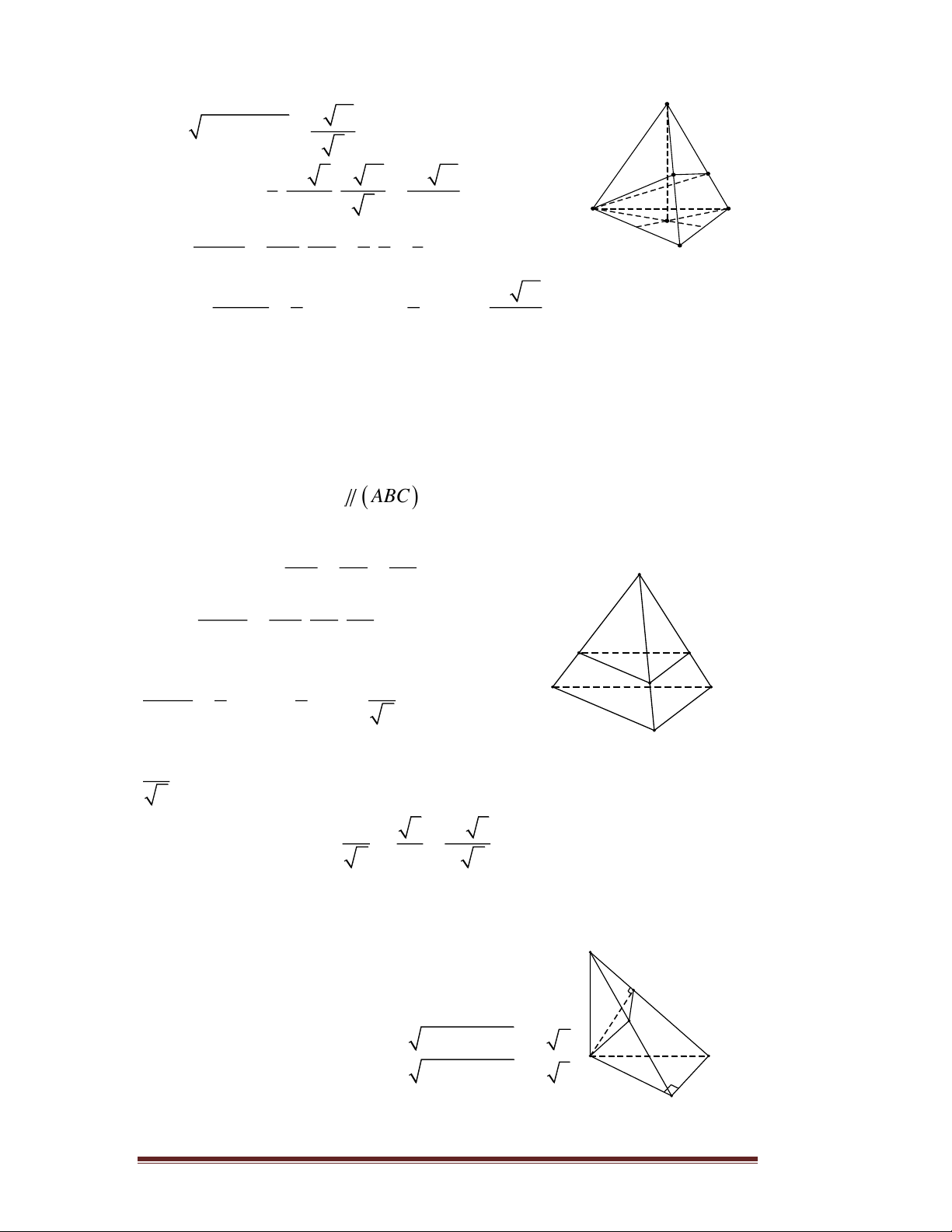
Câu 95. Gọi E là trung điểm của . BC Qua ,
B C lần lượt kẻ đường thẳng
song song với MN và cắt đường thẳng AE tại , P Q . S A N G M P A N C E C B G Q M B Theo định lí Talet, ta có AB = AP AM AG AB AC AP AQ AP + AQ + = + = . AC = AQ AM AN AG AG AG AN AG Mặt khác
BPE = CQE ⎯⎯
→ PE = QE AP + AQ = ( AE − PE) + ( AE + QE) = 2AE. Do đó AB AC 2AE 3 1 1 + = = 2. = 3 + = 3 . Đặt AM AN AG 2 AM AN AM = x 1 1 + = 3. AN = y x y Trang 10 2
Vì SABC là tứ diện đều SG ⊥ ( ABC ) và SG = . 3 Do đó 1 1 1 2 2 0 V = S .SG = AM .AN sin 60 .SG = AM .AN = x . y SAMN AMN 3 3 2 12 12 1 1 2 2 4 2 Ta có 3 = +
xy xy V = . Chọn C. min x y xy 3 9 27
Câu 96. Gọi d là khoảng cách từ đỉnh A đến cạnh . CD
Diện tích hình bình hành S = A . B d. ABCD S Ta có S = S − S − S MBCN ABCD AMN ADN 1 1 1 1 = A . B d − AM .d −
DN.d = A . B d − A . B d − A . B d 2 2 4 6 7 7 = A . B d = S . A M B 12 12 ABCD Vậy 7 7 V = V = .48 = 28. D N C S .MBCN . S . 12 ABCD 12 Chọn C.
Câu 97. Lưu ý: Tỉ số thể tích chỉ áp dụng cho khối chóp tam giác nên nếu
đáy là tứ giác ta chia đáy thành hai tam giác. S Ta có V =V +V .
S.A' B 'C ' D '
S.A' B 'C '
S.A' D 'C ' V
SA' SB ' SC ' 1 1 1 1 A' B'
Mà S.A'B'C ' = . . = . . = . V SA SB SC 2 2 2 8 S . ABC D' C' 1 A B Suy ra V = .V .
S . A ' B 'C ' S . 8 ABC Tương tự ta cũng có 1 V = .V . D
S . A ' D 'C ' S . 8 ADC C Vậy 1 1 1 1 V = V + V = V +V = V .
S . A ' B 'C ' D ' S . ABC S . ADC
( S.ABC S.ADC ) S . 8 8 8 8 ABCD V 1
Suy ra S.A'B'C 'D' = . Chọn C. V 8 S . ABCD SB SA
Câu 98. Từ giả thiết suy ra ' ' 1 A' B ' AB = = . Tương tự SB SA 3 SC ' SD ' 1 = = . SC SD 3 Trang 11 Ta có V =V +V . S
S.A' B 'C ' D '
S.A' B 'C '
S.A' D 'C ' V
SA' SB ' SC ' 1 1 1 1 A' B'
Mà S.A'B'C ' = . . = . . = . C' V SA SB SC 3 3 3 27 D' S . ABC A B 1 ⎯⎯ →V = .V .
S . A ' B 'C ' S . 27 ABC D C Tương tự ta cũng có 1 V = V .
S . A ' D 'C ' S . 27 ADC Vậy 1 1 1 1 = + = + = = V V V V V V V .
S . A ' B 'C ' D ' S . ABC S . ADC
( S.ABC S.ADC ) S . 27 27 27 27 ABCD 27 Chọn C.
Câu 99. Kẻ MN CD ( N CD) , suy ra ABMN là thiết diện của khối chóp. Ta có V =V +V . S.ABMN S.ABM S.AMN S V SM 1 1 1 S . ABM = = V = V = V . S . ABM S . ABC S . N V SC 2 2 4 ABCD M S . ABC A D V SM SN 1 1 S . AMN = . = V = V . C B S . AMN S . V SC SD 4 8 ABCD S . ACD Do đó 1 1 3 V = V + V = V . S . ABMN S . ABCD S . ABCD S . 4 8 8 ABCD 5 V 3 Suy ra V = V nên 1 = . ABMNDC S . 8 ABCD V 5 2 Chọn D.
Câu 100. Tam giác vuông SAB , có 2 2 SB = SA + AB = 3.
Gọi M là trung điểm AD ⎯⎯
→ ABCM là hình vuông nên = = = AD CM AB a 2 ⎯⎯
→ tam giác ACD vuông tại C . Ta có V =V +V . S.AHCD S.ACD S.AHC S ● 1 1 1 2 V = S .SA = A . D AB SA = S . ACD ACD 3 3 2 3 H A M D . ● B C Trang 12 2 V SH SA 2 2 2 S . AHC = = = V = V = . 2 S . AHC S . V SB SB 3 3 ABC 9 S . ABC Vậy 2 2 4 2 V = + = . Chọn B. S . AHCD 3 9 9
Câu 101. Gọi h, S lần lượt là chiều S
cao và diện tích đáy của khối chóp 1
S.ABCD . Khi đó V = S. . h N S . ABCD 3 E
Nối MN cắt SA tại E , MC cắt AD B tại M
F. Tam giác SBM có , A N lần F A
lượt là trung điểm của BM và SB
suy ra E là trọng tâm tam giác D C
SBM. Tứ giác ACDM là hình bình
hành nên F là trung điểm . MC Ta có V =V +V . BNC. AEF ABCEN E. ACF V SE SN 2 1 1 1 S.ENC = . = = ⎯⎯ →V = V S .ENC S . V SA SB 3 2 3 3 ABC S . ABC 2 2 1 1 ⎯⎯ →V = V = V = V . ABCEN S . ABC S . ABCD S . 3 3 2 3 ABCD 1 1 1 1 1 V = S
.d E, ACF = . S. h = V . E. ACF ACF ( ) S . 3 3 4 3 12 ABCD Do đó 1 1 5 V = V +V = V + V = V = V . BNC. AEF ABCEN E. ACF S . ABCD S . ABCD S . ABCD 1 3 12 12 7 V 5 Suy ra 1 V = V ⎯⎯ → = . Chọn A. 2 S . 12 ABCD V 7 2 SN SM
Câu 102. Kẻ MN
AD ( N SD) ⎯⎯ → =
= k. Khi đó mặt phẳng SD SA S
(MBC) chia khối chóp thành hai phần là S.MBCN và AMBDNC . Ta có V =V +V . S.MBCN S.MBC S.MCN M N V SM A S.MBC = = k V = k.V . D S .MBC S . ABC V SA S . ABC V SM SN S.MCN 2 2 = . = k V = k .V . B C S .MCN S . ACD V SA SD S . ACD Từ giả thiết, ta có 1 1 2 V = V k.V + k .V = V S .MBCN S . ABCD S .ABC S .ACD S . 2 2 ABCD Trang 13 V V 1 1 − + 5 S . ABCD 2 S . ABCD 2 ⎯⎯ →k. + k . = V ⎯⎯
→k + k =1→ k = . S . 2 2 2 ABCD 2 Chọn B.
Câu 103. Ta có V = S .AA' và A' D' ABCD 1 V = S .AA'. B' 1 C' 3 ABD A D 1 V Mà S = S ⎯⎯ → = 6 . ABD 2 ABCD V1 B C
Suy ra V = 6V . Chọn A. 1
Câu 104. Ta có V = S .BB' và A' B'
ABC.A' B 'C ' ABC 1 C' V = S .BB '. B ' BAD 3 BAD 1 V 1 A B Mà B ' S = S ⎯⎯ →k = BAD = . BAD 2 ABC V 6 D
ABC. A ' B 'C ' C Chọn D.
Câu 105. Gọi G là trọng tâm của tam giác A' B' ABC . C' Gọi AG 2
E là trung điểm của BC = . AE 3 M Đường thẳng A B
d đi qua G và song song BC , cắt các cạnh A , B AC G lần lượt tại M , N. E N C AM AN AG 2 = = = AB AC AE 3 2 AM = AB 3 4 S = S . ( )1 AMN 2 9 ABC AN = AC 3 1 Ta có V = S AA và V = S .AA'. (2) ABC A B C . ' . ABC A '. AMN 3 AMN Từ ( ) 4 23 1 và (2) , suy ra V = V ⎯⎯ →V = V BMNC A BC ABC A BC . A '. AMN ABC. A BC 27 . . 27 Vậy V 4 A '. AMN = . Chọn B.
VBMNC ABC 23 .
Câu 106. Gọi H là hình chiếu của A trên mặt phẳng ( A BC) .
Suy ra HC là hình chiếu của AC trên mặt phẳng ( A BC) . Trang 14 Do đó A C 0 60 = AC , (
A BC) = AC , HC = ACH. B Tam giác AHC , có
AH = AC .sin ACH = 2 3. 2 Diện tích tam giác = AC S = 4. C' ABC 2 A' H Suy ra V = S AH = ABC A BC . 8 3. . ABC B' Ta có 1 1 8 3 V = S .AH = V = A A B C A B C ABC A BC . . ' ' ' ' ' ' . 3 3 3 16 3 Suy ra V = V −V = ABCCB ABC A BC A A BC . . . 3 Chọn D.
Câu 107. Ta có V = V + V +V +V +V . AB ' D 'C
( AA'B'D' CC'B'D' D'DAC B'BAC ) V Mà V = V = V = V = D' C'
AA ' B ' D '
CC ' B ' D ' D ' DAC B ' BAC 6 A' B' . V Suy ra V = . AB ' D 'C 3 Từ giả thiết, ta có D C A B 1 AC 1 A D 1 = ; = ; = . AN 3 AM 2 AP 4 A B V A B A D AC A BD 1 Ta có . C = . . = V AN AP AM 24 . A NPM ⎯⎯ → = V V 24V = = V A NPM A BD 24. 8 . . . C 3 Chọn A.
Nhận xét: Công thức giải nhanh: Thể tích của khối tứ diện (4 đỉnh nằm trên
hai đường chéo của hai mặt đối diện) có thể tích bằng 1 của khối lăng trụ 3 tam giác. Câu 108. Công thức giải nhanh A C
m + n + p V = V với B P ABC.MNP 3 M = AM BN CP N m , n = , p = . C' A' AA' BB ' CC ' Áp dụng: 1 2 2 B' m = , n = , p = , ta dược 2 3 3 Trang 15 11 V = V . ABC.MNP 18 Chọn D. CN BM DP 0 + + V
Câu 109. Công thức giải nhanh AMNPBCD CC ' BB ' DD ' = = . V 2 2
ABCDA ' B 'C ' D ' CN 0 + Theo giả thiết, ta có V 1 1 CN 2 AMNPBCD CC ' = ⎯⎯ → = ⎯⎯ → = . V 3 2 3 CC ' 3
ABCDA ' B 'C ' D ' Chọn B.
Câu 110. Trong mặt phẳng (CDD 'C ') , kẻ MN C ' D với N CD . Suy ra 1 CN =
CD và V là khối đa điện ABB' NCM. 4 1 B' C' B' C' C' D' A' A' A' D' M M M B B C C C N N A D A A D
Ta chia khối hộp thành hai phần (như hình vẽ). Khi đó V =V +V . ABB '.NCM ABB 'CM MACN 1 0 + +1 5 1 4 V = .V = . V . ABB 'CM
ABC. A ' B 'C ' 3 12 2 1 1 1 1 1 V = . V = . V = V . MACN C '. ADC
ADC. A ' D 'C ' 4 4 16 3 96 Vậy 7 25 V 7 1 V = V +V = V ⎯⎯ →V = ⎯⎯ → = . Chọn C. 1 ABCMB ' MACN 2 32 32 V 25 2 Nhận xét. Ta có 1 1 V = . V
vì diện tích giảm 4 lần và chiều cao MACN C '. 4 4 ADC giảm 4 lần. Trang 16




