TOP 5 Đề kiểm tra giữa học kỳ I môn toán 9 (có đáp án và lời giải chi tiết)

Tổng hợp TOP 5 Đề kiểm tra giữa học kỳ I môn toán 9 (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.

42 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

18 trang 9 tháng trước

Tác giả:

Profile Minh Thư
Trang 1
ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN TOÁN 9
Thời gian: 60 phút
Phần I. Trắc nghiệm(5 điểm)
1.
Giá trị lớn nhất của biểu thức
2019 2xx
bằng:
A.
2020
B.
2019
C.
2018
D.
2019
2.
Với x, y là số đo các góc nhọn. Chọn nội dung sai trong các câu sau:
A.
sin y
tan y
cos y
B.
22
sin x cos y 1
C.
cos x
cot x
sin x
D.
3.
Cho ABC vuông tại A ,đường cao AH, ta có:
A.
2
.AC AB BC
B.
2
.AB AC HB
C.
2
.AH HB HC
D.
..AB AH AC BC
4.
Giá trị của biểu thức
2
( 11)
bằng:
A.
-11
B.
121
C.
-121
D.
11
5.
Căn bậc hai số học của 4 là
A.
2
B.
8
C.
16
D.
4
6.
Chọn khẳng định đúng:
A.
cot72
0
= cot18
0
B.
cos25
0
= sin65
0
C.
sin67
0
= sin23
0
D.
tan31
0
= cot31
0
7.
Trong một tam giác vuông. Biết cosx =
2
3
. Tính sinx.
A.
5
3
B.
5
2
C.
5
3
D.
5
2
8.
Điều kiện để
3
5x
có nghĩa là:
A.
5x
B.
5x
C.
5x
D.
x
9.
Trục căn thức ở mẫu
6
2
ta được:
A.
32
B.
22
C.
62
D.
32
2
10.
Cho tam giác DEG vuông tại E, cosG bằng:
A.
EG
ED
B.
EG
DG
C.
DE
DG
D.
ED
EG
11.
Căn bậc ba của -27 là:
A.
9
B.
3
C.
-3
D.
-9
12.
Nếu sin α =
3
5
thì cot α bằng:
A.
5
4
B.
3
4
C.
4
5
D.
4
3
13.
Cho
2
(3 1)x
bằng:
A.
3 1.x
B.
(3 1).x
C.
13x
D.
3 1.x
14.
Nếu
cos x = sin 35
0
thì x bằng:
A.
35
0
B.
45
0
C.
65
0
D.
55
0
15.
Tìm điều kiện để
23x
có nghĩa, ta có:
A.
2
3
x
B.
2
3
x
C.
2
3
x
D.
2
3
x
Trang 2
16.
Tìm điều kiện để
1
23
23
x
x

có nghĩa, ta có:
A.
3
2
x 
B.
3
2
x
C.
3
2
x 
D.
3
2
x
17.
Biểu thức liên hợp của biểu thức
1x
là:
A.
1x
B.
1.x
C.
1.x
D.
1.x
18.
Căn bậc hai của 16 là:
A.
-4 và 4
B.
16
C.
-16 và 16
D.
4
19.
Rút gọn biểu thức
3,6. 10
+ 4 bằng:
A.
10
B.
40
C.
4 36
D.
40
20.
Nếu α = 25
0
18
'
thì cot α khoảng:
A.
0,47
B.
0,43
C.
0,9
D.
2,12
21.
Cho tam giác ABC vuông ở A, BC = 25 ; AC = 20 , số đo của góc C bằng:
A.
53
0
B.
37
0
C.
36
0
D.
54
0
22.
Cho tam giác BDC vuông tại D, sinC bằng:
A.
BD
CD
B.
CD
BC
C.
BD
BC
D.
BC
BD
23.
Các tia nắng mặt trời tạo với mặt đất một góc bằng 40
0
và bóng của tháp trên mặt đất dài 20 m.
Tính chiều cao của tháp (làm tròn đến mét)
A.
24 m
B.
20 m
C.
17 m
D.
13 m
24.
Cho tam giác MNP vuông tại M, đường cao MH. Biết NH = 5 cm, HP = 9 cm. Độ dài MH
bằng:
A.
4
B.
4,5
C.
7
D.
35
25.
Giá trị của biểu thức
( 8 18 20). 2 2 10
bằng:
A.
4 10
B.
25
C.10 D.
52
Phần II. Tự luận(5 điểm)
Câu 26(2,5 điểm)
a)So sánh:
2 3 1
và
2 2 5
b) Tìm điều kiện để
23x
có nghĩa.
c)Khử căn ở mẫu
2
6
3
d)Tính giá trị biểu thức
22
22
xx
P
xx

tại
2
12x 
Câu 27(2 điểm): Cho tam giác ABC vuông tại A, AB = 3(cm), AC = 4(cm), đường
cao AH. Kẻ HK vuông góc với AC tại K, kẻ HG vuông góc với AB tại G.
a)Chứng tỏ rằng:
2
.BH AB BG
b)Tìm tanC
c)Chứng minh rằng:
AC HB
HC AK
d)Tính CK
Câu 28(0,5 điểm): Giải phương trình
2 5 3 5 2xx
ĐÁP ÁN
I. Phần trắc nghiệm
Câu
1
2
3
4
5
6
7
8
9
10
11
12
13
Trang 3
Đ.án
A
B
C
D
A
B
C
D
A
B
C
D
A
Câu
14
15
16
17
18
19
20
21
22
23
24
25
Đ.án
D
B
B
B
A
A
D
B
C
C
D
C
II. Phần tự luận
Câu
Lời giải
Điểm
26
(2,5đ)
a)So sánh:
2 3 1
và
2 2 5
Có:
2
(2 3 1) 12 4 3 1 13 4 3
2
(2 2 5) 8 4 10 5 13 4 10
Mà:
13 4 3 13 4 10
Nên:
2 3 1
<
2 2 5
Vậy:
2 3 1
<
2 2 5
0,25
0.25
b) Tìm điều kiện để
23x
có nghĩa
23x
có nghĩa khi
3
2 3 0
2
xx
Vậy:
23x
có nghĩa khi
3
2
x 
0,5
c) Khử căn ở mẫu
2
6
3
Có:
2 6 6
6 2 6
33

0,5
d) Tính giá trị biểu thức
22
22
xx
P
xx

tại
2
12x 
ĐKXĐ:
0x
Có:
33
2 2 2 ( 2)( 2 2)
2
2 2 2 2 2 2
x x x x x x
x
x x x x x x
Với
2
12x 
ta có
2
(1 2) 2 2 1 2 1P
Vậy: P = -1 khi
2
12x 
0,25
0,5
0,25
27
(2đ)
G
K
H
A
C
B
Trang 4
a) Chứng tỏ rằng:
2
.BH AB BG
Xét
0
: 90 (gt), HG AB {G}(gt)HAB AHB
2
.BH AB BG
(hệ thức về cạnh góc vuông-hình chiếu)
Vậy:
2
.BH AB BG
(đpcm)
0,25
0,25
b) Tìm tanC
Xét
0
: 90 (gt)ABC BAC
Ta có:
3
tan
4
AB
C
AC

Hoặc: Xét
0
: 90 (gt)HAC AHC
Ta có:
tan
AH
C
CH
Hoặc: Xét
0
: 90 (gt)HCK KHC
Ta có:
tan
KH
C
KC
0,5
c) Chứng minh rằng:
AC HB
HC AK
+)Xét
0
: 90 (gt), AH BC {H}(gt)ABC BAC
Có:
2
.HCAH HB
(hệ thức về đường cao-hình chiếu)
+) Xét
0
: 90 (gt), HK AC {K}(gt)HAC AHC
Có:
2
.CAH AK A
(hệ thức về cạnh góc vuông-hình chiếu)
+) Do đó:
2
. C HB.HC( )AK A AH
AC HB
HC AK

Vậy:
AC HB
HC AK
(đpcm)
0,125
0,125
0,125
0,125
d) Tính CK
+)Xét
0
: 90 (gt), AH BC {H}(gt)ABC BAC
Có:
2 2 2
CBC AB A
(Pytago)
22
25 5BC AB AC
Lại có:
2
.BCAC HC
(hệ thức về cạnh góc vuông-hình chiếu)
22
4 16
55
AC
HC
BC
(cm)
+) Xét
0
: 90 (gt), HK AC {K}(gt)HAC AHC
Có:
2
.CHC CK A
(hệ thức về cạnh góc vuông-hình chiếu)
2
2
16 64
:4 2,56
5 25
HC
CK
AC



(cm)
Vậy: CK = 12,8 (cm)
0,125
0,125
0,125
0,125
28
(0,5đ)
55352 xx
(*)
ĐKXĐ:
3
5
053
052
x
x
x
0.125
(*)
2 5 3 5 2xx
(1)
Với
5
3
x
thì 2 vế của (1) đều dương, ta bình phương 2 vế của (1)
Ta được: 2x + 5 = 3x – 5 + 4
453 x
xx 6534
(2)
0.125
Trang 5
Phương trình (2) có nghiệm khi: 6 - x ≥ 0 x ≤ 6
Khi đó: 2 vế của (2) không âm
Ta bình phương 2 vế của (2) được 16(3x – 5) = 36 - 12x + x
2
x
2
- 60x + 116 = 0
(x – 2)(x – 58) = 0
(lo¹i) 6 58
K)(TM§
x
x 2
0.125
Vậy: Tập nghiệm của phương trình là {2}
0,125
ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN TOÁN 9
Thời gian: 60 phút
Câu 1:(2 điểm) thực hiện tính:
a)
36.16
b)
36
16
:
25
9
c)
8.2
d)
3
75
Câu 2:(1 điểm) Rút gọn
a)
1212
2
b)
1252453202
Câu 3:(2 điểm) Tìm x, biết:
a) x
2
-1=3 b)
29336216 xxx
Câu 4:(2 điểm) Cho biểu thức: P=
1
1
.
1
1
1
1
xx
x
x
x
(với
0x
,
1x
)
a) Hãy rút gọn biểu thức P.
b) Tìm giá trị của x để biểu thức P=2
Câu 5:(3 điểm) Cho tam giác ABC vuông tại A có đường cao AK chia cạnh huyền BC thành hai
đoạn KB=2cm và KC=6cm.
a) Tính độ dài các đoạn thẳng: AK, AB, AC
b) Trên cạnh AC lấy điểm M ( M khác A và C) Gọi H là hình chiếu của A trên
BM. Chứng minh rằng BH.BM=BK.BC
c) Chứng minh rằng:
ABHCosSS
BMCBKH
2
.
4
1
ĐÁP ÁN
Trang 6
CÂU
ĐÁP ÁN
ĐIỂ
M
Câu 1:
(2 điểm)
a)
246.436.1636.16
b)
5
2
6
4
.
5
3
36
16
.
25
9
36
16
:
25
9
c)
4168.28.2
d)
525
3
75
3
75
0.5
0,5
0,5
0,5
Câu 2: (1,0
điểm)
a)
22121212121212
2
b)
55510595455.253.352.2
5.2525.935.421252453202
0,5
0,5
Câu 3:
a) Tìm x, biết x
2
-1=3
2
x
4
2 x
hoặc x=2
Vậy
2x
hoặc x=2
b) Tìm x, biết:
29336216 xxx
ĐKXĐ:
0x
2
23.36.24
29336216
x
xxx
xxx
x=4 (thỏa mãn ĐKXĐ)
Vậy x=4
0,25
0.5
0,25
0,25
0,25
0.25
0.25
Câu 4:
Cho biểu thức:
P=
1
1
.
1
1
1
1
xx
x
x
x
(với
0x
,
1x
)
a) Hãy rút gọn biểu thức A.
0.25
Trang 7
1
41
.
)1)(1(
4
.
1
.
)1)(1(
12
)1)(1(
12
1
.
)1)(1(
)1(
)1)(1(
)1(
1
.
)1)(1(
)1)(1(
)1)(1(
)1)(1(
1
1
.
1
1
1
1
22
xx
x
xx
x
x
x
xx
xx
xx
xx
x
x
xx
x
xx
x
x
x
xx
xx
xx
xx
xx
x
x
x
P
Vậy với
0x
,
1x
ta có:
1
4
x
P
b) Tìm giá trị của x để biểu thức P=2
với
0x
,
1x
ta có:
1
4
x
P
Giã sử P=2 hay
2
1
4
x
93624222
1
4
xxxx
x
(thỏa mãn
ĐKXĐ)
Vậy với x=9 thì P=2
0.25
0.25
0.25
0.25
0.25
0.25
0.25
Câu 5:
a/ BC=KB+KC=2+6=8 cm
ABC
vuông tại A, đường cao AK:
AB
2
=BH.BC=2.8=16
AB=4cm
●
2 2 2
BC AB AC
(định lý
aPyt go
)
2 2 2 2
8 4 4 3AC BC AB cm
● AK
2
=HB.HC=2.6=12
AK=
12
=
32
cm
b/
ABM
vuông tại A, đường cao AH
AB
2
=BH.BM
(1)
ABC
vuông tại A, đường cao AK
AB
2
=BK.BC
(2)
Từ (1)(2)
BH.BM=BK.BC
c/ Kẻ
),(; BCKIBCMEBCHI
0.25
0,25
0,25
0,25
0.25
0,25
0,25
0,25
A
B
C
K
M
H
E
I
Trang 8
ME
HI
ME
HI
BCME
BKHI
S
S
BMC
BKH
.
4
1
8
2
.
2
1
.
2
1
(3)
BM
BH
ME
HI
BMEBHI
(4)
ABM
vuông tại A có:
BM
BH
BM
BMBH
BM
AB
ABHCos
BM
AB
CosABH
22
2
2
.
(5)
Từ (3)(4)(5)
ABHCosSSABHCos
S
S
BMCBKH
BMC
BKH
22
..
4
1
.
4
1
0,25
0,25
0,25
0,25
0.25
ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN TOÁN 9
Thời gian: 60 phút
Bài 1: (1,0 đ) : Tìm điều kiện của x để các căn thức sau có nghĩa.
a)
2x
. b)
1
2x 1
Bài 2 : (2,0 đ) Tính :
a)
4.36
b)
8 3 2 . 2
c)
14 7
12
d) +
Bài 3 : (1,0 đ) Cho biểu thức A =
4 20 2 5 9 45x x x
với x
-5.
a) Rút gọn A.
b) Tìm x để A = 6
Bài 4 : (2,0 đ): Cho biểu thức M = với x > 0 , x 4
a) Rút gọn biểu thức M
b) Tính giá trị của M khi x =
3 2 2
.
c) Tìm giá trị của x để M > 0
Bài 5 (3,0 đ): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành
hai đoạn : BH = 4 cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB, AC.
b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn đến độ).
c) Kẻ AK vuông góc với BM (K thuộc BM). Chứng minh :
BK.BM = BH.BC
Bài 6 (1,0đ): Giải phương trình sau.
3000
2
1
200220012000 zyxzyx
25
2
25
2
2
44
2
xx
x
x
x
Trang 9
ĐÁP ÁN
Bài
Nội dung
Điểm
1
(1,0 đ)
1a
2x
. có nghĩa khi x – 2 ≥ 0
Û
x ≥ 2.
0.5
1b
1
2x 1
có nghĩa khi
2 1 0x
Û
x >
1
2
0,5
2
(2,0 đ)
2a
4.36
= 2.6 = 12
0,5
2b
8 3 2 . 2
=
2 2 3 2 . 2 2. 2 1
0,5
2c
0.5
2d
+ = = 4
0,5
3
(1,0 đ)
3a
4 20 2 5 9 45
2 5 5 3 5
35
A x x x
x x x x
x

( ĐK : x ≥ - 5 (
0,5
3b
6 3 5 6
54
1
Ax
x
x
0,5
4
(2,0 đ)
4a
M =
=
0,5
0,5
4b)
x =
3 2 2
(Thỏa mãn ĐK)
12x
Khi đó M =
1 2 2 2 1
3 2 2
2 1 2 1

0,5
4c)
Với ĐK x > 0 , x 4 thì M =
Do đó M > 0
>0
Vì
0x
nên
2 0 4xx
Kết hợp với ĐKXĐ ta có M > 0 khi x > 4
0,5
5
(3,0 đ)
0,25
5a
D
ABC vuông tại A : nên
AH
2
= HB.HC = 4.6 = 24
Þ
AH = (cm)
AB
2
= BC.HB = 10.4 = 40
Þ
AB = (cm)
0,5
21
714
2
21
122
25
2
25
2
2
2
25
452452
5
2
44
xx
xx
x
x 2
x
x 2
x
x 2
K
H
M
B
C
A
26
2 10
Trang 10
AC
2
= BC. HC = 10.6 = 60
Þ
AC = (cm)
0,75
5b
D
ABM vuông tại A
0
2 10 2 6
tanA
3
15
59
AB
MB
AM
AMB

0,5
0,25
5c
D
ABM vuông tại A có AK
^
BM => AB
2
= BK.BM
D
ABC vuông tại A có AH
^
BC => AB
2
= BH.BC
Þ
BK. BM = BH.BC
0,25
0,25
0,25
6
(1,0 đ)
ĐK:
2002
2001
2000
02002
02001
02000
z
y
x
z
y
x
Phương trình đã cho tương đương với
2000 2 2000 1 2001 2 2001 1
2002 2 2002 1 0
x x y y
zz
0120021200112000
222
zyx
2003
2002
2001
12002
12001
12000
12002
12001
12000
012002
012001
012000
z
y
x
z
y
x
z
y
x
z
y
x
KL: Phương trình có nghiệm:
2003;2002;2001 zyx
0,25
0,25
0,25
0,25
ĐỀ 4
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN TOÁN 9
Thời gian: 60 phút
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
a)
81 80. 0,2
b)
2
1
(2 5) 20
2

2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
a)
1x
b)
2
1
21xx
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
a)
1ab b a a
(với
0a
(
b)
41a
(với
0a
(
2. Giải phương trình:
9 9 1 20xx
2 15
Trang 11
Bài 3 (2,0 điểm).
Cho biểu thức
1 1 1 x
A = :
x 2 x x 2 x + 4 x 4



(với x > 0; x 1)
a) Rút gọn biểu thức A.
b) Tìm x để
5
A =
3
Bài 4 (3,5 điểm).
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a) Tính độ dài các đoạn thẳng AB, AC, AH.
b) Trên cạnh AC lấy điểm K (K A, K C), gọi D là hình chiếu của A trên BK.
Chứng minh rằng: BD.BK = BH.BC
c) Chứng minh rằng:
2
1
cos
4
BHD BKC
S S ABD
Bài 5 (0,5 điểm).
Cho biểu thức
33
3( ) 1993P x y x y
. Tính giá trị biểu thức P với:
33
9 4 5 9 4 5x
và
33
3 2 2 3 2 2y
.................... Hết .....................
ĐÁP ÁN
Bài 1
Ý
Nội dung
Điểm
1.a
0.5đ
2
81 80. 0,2 9 80.0,2
0.25
9 16 9 4 5
0.25
1.b
0.5đ
2
11
(2 5) 20 2 5 .2 5
22
0.25
5 2 5 2
0.25
2.a
0.5đ
Biểu thức
1x
có nghĩa
10x
0.25
1x
.
0.25
2.b
0.5đ
Biểu thức
2
1
21xx
có nghĩa
2
2
1
0 2 1 0
21
xx
xx

0.25
2
( 1) 0 1xx
0.25
Bài 2 (2,0 điểm)
Ý
Nội dung
Điểm
1.a
0.5đ
Với
0a
ta có:
1 ( 1) ( 1)ab b a a b a a a
0.25
( 1)( 1)a b a
0.25
1.b
0.5đ
Với
0a
0a
ta có:
2 2 2
4 4.( ) (2 ) 1 4 1 (2 )a a a a a
0.25
(1 2 )(1 2 )aa
0.25
2
ĐK:
1x 
0.25
Trang 12
1.0đ
9 9 1 20 9( 1) 1 20 3 1 1 20x x x x x x
0.25
4 1 20 1 5xx
1 25 24xx
(T/m ĐKXĐ)
0.25
Vậy phương trình có nghiệm duy nhất x = 24
0.25
Bài 3 (2,0 điểm).
Ý
Nội dung
Điểm
a
1.25đ
Với
0, 1xx
ta có
2
1 1 1 x
A = :
( 2) 2 ( +2)x x x x




0.25
2
1 ( x 2)
= .
( 2) ( 2) 1
x
x x x x x



0.25
2
1 ( 2)
= .
( 2) 1
xx
x x x


0.25
2
=
x
x
0.25
Vậy A
2
=
x
x
(với x > 0; x 1)
0.25
b
0.75đ
5 2 5
33
x
A
x
(ĐK: x > 0 ; x 1)
0.25
3( 2) 5xx
2 6 3 9x x x
(TMĐK)
0.25
Vậy với x = 9 thì
5
3
A
.
0.25
Bài 4 (3,5 điểm).
Ý
Nội dung
Điểm
a
1.5đ
+
ABC
vuông tại A, đường cao AH
2
. 2.8 16AB BH BC
0.25
4AB cm
(Vì AB > 0)
0.25
Ý
Nội dung
Điểm
+
2 2 2
BC AB AC
(Định lý Pitago trong tam giác vuông ABC)
0.25
2 2 2 2
8 4 48 4 3AC BC AB cm
0.25
+
Có HB + HC = BC
HC = BC – HB = 8 – 2 = 6 cm
0.25
B
A
C
H
K
D
I
E
Trang 13
2
. 2.6 12AH BH CH
12 2 3AH cm
(Vì AH > 0)
0.25
b
1.0đ
+
ABK
vuông tại A có đường cao AD
2
.AB BD BK
(1)
0.5
+ Mà
2
.AB BH BC
(Chứng minh câu a ) (2)
0.25
Từ (1) và (2)
BD.BK = BH.BC
0.25
c
1.0đ
+ Kẻ
, ( , )DI BC KE BC I K BC
1
.
2. 1
2
.
1
8. 4
.
2
BHD
BKC
BH DI
S DI DI
S KE KE
BC KE
(3)
0.25
+
DI BD
BDI BKE
KE BK
(4)
0.25
+
ABK
vuông tại A có:
2
2
22
.
cos os
AB AB BD BK BD
ABD c ABD
BK BK BK BK
(5)
0.25
Từ (3), (4), (5)
2
1
. os
4
BHD
BKC
S
c ABD
S

2
1
cos
4
BHD BKC
S S ABD
0.25
Bài 5 (0,5 điểm).
Ý
Nội dung
Điểm
0.5đ
Ta có:
33
18 3 3 18x x x x
33
6 3 3 6y y y y
0.25
33
33
3( ) 1993
( 3 ) ( 3 ) 1993 18 6 1993 2017
P x y x y
x x y y
Vậy P = 2017
với
33
9 4 5 9 4 5x
và
33
3 2 2 3 2 2y
0.25
Lưu ý:
- Trên đây là các bước giải cơ bản cho từng bài, từng ý và biểu điểm tương ứng, học
sinh phải có lời giải chặt chẽ chính xác mới công nhận cho điểm.
- Học sinh có cách giải khác đúng đến đâu cho điểm thành phần đến đó.
ĐỀ 5
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN TOÁN 9
Thời gian: 60 phút
Bài 1. (2,0 điểm). Thực hiện phép tính.
a)
3 2x 5 8 7 18xx
b)
11
3 5 3 5

Bài 2. (2,0 điểm). Giải các phương trình sau:
a)
9 9 1 20xx
b)
8 2 3. xx
Bài 3. (2,0 điểm). Cho biểu thức
1 1 1 x
A = :
x 2 x x 2 x + 4 x 4



Trang 14
a) Tìm điều kiện xác định của A?
b) Rút gọn biểu thức A.
c) Tìm x để A =
5
3
.
Bài 4. (3,0 điểm) Cho
ABC vuông tại A., đường cao AH. Biết BH = 1.8 cm; HC = 3,2 cm.
a. Tính độ dài AH ; AB; AC.
b. Tính số đo góc B và góc C.
c. Tia phân giác của góc B cắt AC tại D. Tính độ dài BD.
d. Chứng mimh rằng:
AC
tan ABD
AB BC
(số đo góc làm tròn đến độ, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ ba)
Bài 5. (1,0 điểm) Chứng minh đẳng thức sau:
2
a a b b
ab a b
ab
với
a 0; b 0
ĐÁP ÁN VÀ THANG ĐIỂM
Câu hỏi
Đáp án
Điểm
Bài 1:
(2,0 điểm)
a)
3 2x 5 8 7 18x 3 2x 10 2x 21 2x
3 10 21 . 2x 14 2x
x
1,0đ
b)
1 1 3 5 3 5 6 6 3
9 5 4 2
3 5 3 5
3 5 . 3 5


1,0đ
Bài 2:
(2,0 điểm)
a) ĐK:
1x 
9 9 1 20 9( 1) 1 20 3 1 1 20x x x x x x
4 1 20 1 5xx
1 25 24xx
(T/m ĐKXĐ)
Vậy phương trình có nghiệm duy nhất x = 24
1,0đ
b)
8 2 3 xx
80
2 3 0
8 2 3

x
x
xx
80
2 3 0
8 2 3

x
x
xx
8
3
2
5(loai)


x
x
x
Vậy không tìm được x thỏa điều kiện đề bài cho.
1,0đ
Bài 3:
(2,0 điểm)
ĐKXĐ:
0, 1xx
0,25đ
Với
0, 1xx
ta có
2
1 1 1 x
A = :
( 2) 2 ( +2)x x x x




2
1 ( x 2)
= .
( 2) ( 2) 1
x
x x x x x



0,25đ
0,25đ
Trang 15
2
1 ( 2)
= .
( 2) 1
xx
x x x


2
=
x
x
Vậy A
2
=
x
x
(với x > 0; x 1)
0,25đ
5 2 5
33
x
A
x
(ĐK: x > 0 ; x 1)
3( 2) 5xx
2 6 3 9x x x
(TMĐK)
Vậy với x = 9 thì
5
3
A
.
0,25đ
0,25đ
0,25đ
0,25đ
Bài 4:
(3,0 điểm)
0,25đ
a . Tính độ dài AH ; AB; AC.
ABC có:
o
A 90
, AH
BC (gt )
Theo hệ thức về cạnh và đường cao trong tam giác vuông ta có:
AH
2
= BH . HC = 1,8 . 3.2 = 5,76
AH =
5,76 2,4( ) cm
AHB vuông tại H theo định lí py ta go :
AB =
2 2 2 2
1,8 2,4 3( ) AH BH cm
AHC vuông tại H theo định lí py ta go:
AC =
2 2 2 2
2,4 3,2 4( ) AH CH cm
0,25đ
0,25đ
0,25đ
0,25đ
b . Tính góc B, C.
Theo định nghĩa tỉ số lượng giác của góc nhọn ta có :
tan B =
4
3
AC
AB
o
B 53
nên
o o o o
C 90 B 90 53 37
= 90
0
0,25đ
0,25đ
c. Tính BD
ABD (
o
A 90
) ,
o
o
1 53
ABD ABC 26,5
22
Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
0,25đ
0,25đ
Trang 16
0
.cos
3
3,352( )
cos26,5
cos
AB BD ABD
AB
BD cm
ABD
d.
ABD vuông tại A ta có :
tan
ABD
=
AD
AB
(1)( định nghĩa tỉ số lượng giác
Ta lại có: BD là phân giác trong của
ABC
Nên
AD AB
DC BC
(Tính chất đường phân giác)
AD DC
AB BC
=
AD DC
AB BC
=
AC
AB BC
(2)
Từ (1) và (2)
tan
ABD
=
AC
AB BC
0,25đ
0,25đ
0,25đ
Bài 5:
(1,0 điểm)
Ta có:
33
22
a b a b a ab b
a a b b
VT ab ab ab
a b a b a b
a ab b ab a 2 ab b
2
a b VP
(đpcm)
0,5đ
0,5đ
ĐỀ 6
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
MÔN TOÁN 9
Thời gian: 60 phút
Bài 1: (1 đ) : Tìm điều kiện của x để các căn thức sau có nghĩa.
a) . b)
Bài 2 : Tính : (2 đ)
a) b) c) ( d)
Bài 3 : Rút gọn biểu thức : (1.5 đ )
a)
22
(2 3) (2 3)
b) c)
5 2 2 9 4 2
Bài 4 : (1 đ) Tìm x, biết
Bài 5 : (1,5 điểm). Cho tam giác ABC vuông tại A,
0
30C
, BC = 6cm, đường cao AH.
Tính AB ; AC ; AH
2x
23x
36.4
49
16
.
81
25
2).238
21
714
333
125.26427
645952204 xxx
Trang 17
Bài 6 (2 đ): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai
đoạn : BH = 4 cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB, AC.
b) Gọi M là trung điểm của AC.
Tính số đo góc AMB (làm tròn đến độ).
Bài 7 : (1 điểm) Biết sin =
2
3
. Tính giá trị của biểu thức: A = 2sin
2
+ 5cos
2
.
2. ĐÁP ÁN VÀ THANG ĐIỂM
Bài
Nội dung
Điểm
1a
có nghĩa khi x – 2 ≥ 0
Û
x ≥ 2.
0.5
1b
có nghĩa khi 2 - 3x 0 <=>
0,5
2a
= 2.6 = 12
0,5
2b
=
0,5
2c
) =
0.5
2d
0,5
3a
22
(2 3) (2 3)
=
2 3 2 3
= 4
0,25
0,25
3b
= 3 – 4 + 2. 5 = 9
0,5
3c
5 2 2 9 4 2
=
2
5 2 2 (2 2 1)
=
5 2 3 2 2
=
2
5 2 ( 2 1)
=
3 2 2
=
21
0,1
0,1
0,1
0,1
0,1
4
( ĐK : x ≥ - 5 (
Vậy x = -1
0,25
0,25
0,25
0,25
5
Hình vẽ đúng
1/ Giải tam giác vuông ABC A
ABC vuông tại A, nên:
AB = BC sinC
0,5
2x
23x
2
3
x
36.4
49
16
.
81
25
63
20
7
4
.
9
5
2).238
2644316
21
714
2
21
122
333
125.26427
645952204 xxx
4 20 2 5 9 45 6 4( 5) 2 5 9( 5) 6
2 5 2 5 3 5 6
52
54
1
x x x x x x
x x x
x
x
x

Trang 18
= 6 sin30
0
= 3 (cm) 30
0
AC = AB cotC = AB : tanC B H C
= 3 :
3
3
=
33
(cm)
AHC vuông tại H, nên:
AH = AC sinC =
33
sin30
0
=
33
2
(cm)
0,5
0,5
6
6a
D
ABC vuông tại A : nên
AH
2
= HB.HC = 4.6 = 24
Þ
AH =
24 2 6
(cm)
AB
2
= BC.HB = 10.4 = 40
Þ
AB =
40 2 10
(cm)
AC
2
= BC. HC = 10.6 = 60
Þ
AC =
60 2 15
(cm)
0,5
0,5
0,5
6b
D
ABM vuông tại A
Þ
0,5
7
Biết sin =
2
3
. Tính giá trị của biểu thức: A = 2sin
2
+ 5cos
2
.
Ta có: sin
2
+ cos
2
= 1
Cos
2
= 1- sin
2
= 1-
2
2
3



=
5
9
Do đó: A = 2sin
2
+ 5cos
2
=
4 5 11
2. 5.
9 9 3

0,5
0,5
K
H
M
B
C
A
AB 2 10 2 6
tan g AMB
AM 3
15
o
AMB 59
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 1
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 9 Thời gian: 60 phút
Phần I. Trắc nghiệm(5 điểm)
1. Giá trị lớn nhất của biểu thức 2019  x  2 x bằng: A.2020 B.2019 C.2018 D. 2019
2. Với x, y là số đo các góc nhọn. Chọn nội dung sai trong các câu sau: sin y cos x A. tan y  B. 2 2
sin x  cos y  1 C. cot x  D. tan y.cot y  1 cos y sin x
3. Cho ABC vuông tại A ,đường cao AH, ta có: A. 2 AC  . AB BC B. 2
AB AC.HB C. 2 AH H . B HC D. A . B AH A . C BC
4. Giá trị của biểu thức 2 ( 1  1) bằng: A.-11 B.121 C.-121 D.11
5. Căn bậc hai số học của 4 là A.2 B.8 C.16 D.4
6. Chọn khẳng định đúng: A.cot720 = cot180 B.cos250 = sin650 C.sin670 = sin230 D.tan310 = cot310 2
7. Trong một tam giác vuông. Biết cosx = . Tính sinx. 3 5 5 5 5 A. B. C. D. 3 2 3 2
8. Điều kiện để 3 x  5 có nghĩa là: A. x  5 B. x  5 C. x  5 D. x  6
9. Trục căn thức ở mẫu ta được: 2 3 2 A. 3 2 B. 2 2 C. 6 2 D. 2
10. Cho tam giác DEG vuông tại E, cosG bằng: EG EG DE ED A. B. C. D. ED DG DG EG
11. Căn bậc ba của -27 là: A.9 B.3 C.-3 D.-9 3 12. Nếu sin α = thì cot α bằng: 5 5 3 4 4 A. B. C. D. 4 4 5 3 13. Cho 2 (3x 1) bằng: A. 3x 1 .
B. (3x 1). C.1 3x D. 3x 1.
14. Nếu cos x = sin 350 thì x bằng: A.350 B.450 C.650 D.550
15. Tìm điều kiện để 2  3x có nghĩa, ta có: 2 2 2 2 A. x B. x C. x D. x  3 3 3 3 Trang 1 1
16. Tìm điều kiện để 2x  3  2x  có nghĩa, ta có: 3 3 3 3 3 A. x   B. x C. x   D. x  2 2 2 2
17. Biểu thức liên hợp của biểu thức x 1 là: A. x  1 B. x 1. C. x 1. D. x 1.
18. Căn bậc hai của 16 là: A.-4 và 4 B.16 C.-16 và 16 D.4
19. Rút gọn biểu thức 3, 6. 10 + 4 bằng: A.10 B. 40 C. 4 36 D.40
20. Nếu α = 250 18' thì cot α khoảng: A.0,47 B.0,43 C.0,9 D.2,12
21. Cho tam giác ABC vuông ở A, BC = 25 ; AC = 20 , số đo của góc C bằng: A.530 B.370 C.360 D.540
22. Cho tam giác BDC vuông tại D, sinC bằng: BD CD BD BC A. B. C. D. CD BC BC BD
23. Các tia nắng mặt trời tạo với mặt đất một góc bằng 400 và bóng của tháp trên mặt đất dài 20 m.
Tính chiều cao của tháp (làm tròn đến mét) A.24 m B.20 m C.17 m D.13 m
24. Cho tam giác MNP vuông tại M, đường cao MH. Biết NH = 5 cm, HP = 9 cm. Độ dài MH bằng: A.4 B.4,5 C.7 D. 3 5
25. Giá trị của biểu thức ( 8  18  20). 2  2 10 bằng: A. 4 10 B. 2 5 C.10 D. 5 2
Phần II. Tự luận(5 điểm)
Câu 26(2,5 điểm)
a)So sánh: 2 3 1 và 2 2  5 b) Tìm điều kiện để 2x  3 có nghĩa. 2 x x  2 2 c)Khử căn ở mẫu 6
d)Tính giá trị biểu thức P  tại x    2 1 2 3 x  2x  2
Câu 27(2 điểm): Cho tam giác ABC vuông tại A, AB = 3(cm), AC = 4(cm), đường
cao AH. Kẻ HK vuông góc với AC tại K, kẻ HG vuông góc với AB tại G. a)Chứng tỏ rằng: 2 BH  . AB BG b)Tìm tanC AC HB c)Chứng minh rằng:  d)Tính CK HC AK
Câu 28(0,5 điểm): Giải phương trình 2x  5  3x  5  2 ĐÁP ÁN I. Phần trắc nghiệm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 Trang 2 Đ.án A B C D A B C D A B C D A Câu 14 15 16 17 18 19 20 21 22 23 24 25 Đ.án D B B B A A D B C C D C II. Phần tự luận Câu Lời giải Điểm
a)So sánh: 2 3 1 và 2 2  5 Có: 2
(2 3 1) 12  4 3 1 13  4 3 0,25 2
(2 2  5)  8  4 10  5 13  4 10
Mà: 13  4 3  13  4 10 0.25 Nên: 2 3 1 < 2 2  5
Vậy: 2 3 1 < 2 2  5
b) Tìm điều kiện để 2x  3 có nghĩa
2x  3 có nghĩa khi 3
2x  3  0  x   2 0,5
Vậy: 2x  3 có nghĩa khi 3 x   2 2 26 c) Khử căn ở mẫu 6 3 (2,5đ) 2 6 6 0,5 Có: 6   2 6 3 3 x x  2 2
d) Tính giá trị biểu thức P  tại x    2 1 2 x  2x  2 0,25 ĐKXĐ: x  0 3 3      Có: x x 2 2 x 2 ( x 2)(x 2x 2)    x  2 0,5 x  2x  2 x  2x  2 x  2x  2 Với x    2 1 2 ta có 2 P  (1 2)  2  2 1 2  1  0,25
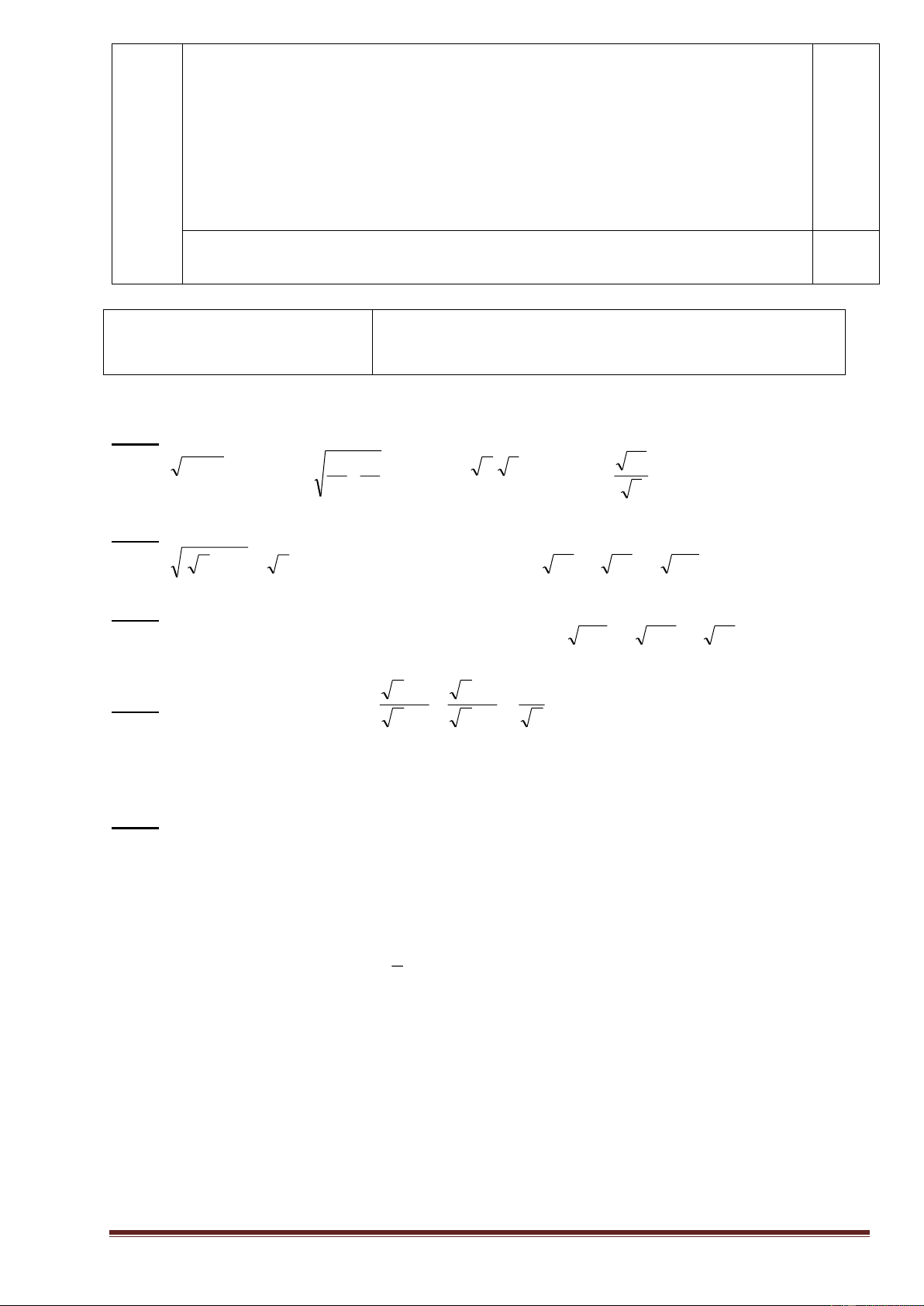
Vậy: P = -1 khi x    2 1 2 B H G 27 (2đ) A C K Trang 3 a) Chứng tỏ rằng: 2 BH  . AB BG Xét 0 H
AB : AHB  90 (gt), HG  AB  {G}(gt) 0,25 2 BH  .
AB BG (hệ thức về cạnh góc vuông-hình chiếu) Vậy: 2 BH  . AB BG (đpcm) 0,25 b) Tìm tanC AB 3 Xét 0 A
BC : BAC  90 (gt) Ta có: tan C   AC 4 0,5 AH Hoặc: Xét 0 H
AC : AHC  90 (gt) Ta có: tan C CH KH Hoặc: Xét 0 H
CK : KHC  90 (gt) Ta có: tan C KC AC HB c) Chứng minh rằng:  HC AK +)Xét 0 A
BC : BAC  90 (gt), AH  BC {H}(gt) 0,125 Có: 2 AH H .
B HC (hệ thức về đường cao-hình chiếu) +) Xét 0 H
AC : AHC  90 (gt), HK  AC  {K}(gt) 0,125 Có: 2
AH AK.A C (hệ thức về cạnh góc vuông-hình chiếu) +) Do đó: AC HB 2
AK.AC  HB.HC( AH )   0,125 HC AK AC HB Vậy:  (đpcm) 0,125 HC AK d) Tính CK +)Xét 0 A
BC : BAC  90 (gt), AH  BC {H}(gt) Có: 2 2 2 0,125
BC AB A C (Pytago) 2 2
BC AB AC  25  5 Lại có: 2
AC HC.BC (hệ thức về cạnh góc vuông-hình chiếu) 0,125 2 2 AC 4 16  HC    (cm) BC 5 5 +) Xét 0 H
AC : AHC  90 (gt), HK  AC  {K}(gt) Có: 2
HC CK.A C (hệ thức về cạnh góc vuông-hình chiếu) 0,125 2 2 HC 16  64  CK   : 4   2,56   (cm) AC  5  25 0,125 Vậy: CK = 12,8 (cm)
2x  5  3x  5  5 (*) x   ĐKXĐ: 2 5 0 5 0.125   x  3  x  5  0 3 28
(*)  2x  5  3x  5  2 (1) (0,5đ) Với 5 x
thì 2 vế của (1) đều dương, ta bình phương 2 vế của (1) 3
Ta được: 2x + 5 = 3x – 5 + 4 3x  5  4 0.125
 4 3x  5  6  x (2) Trang 4
Phương trình (2) có nghiệm khi: 6 - x ≥ 0  x ≤ 6
Khi đó: 2 vế của (2) không âm 0.125
Ta bình phương 2 vế của (2) được 16(3x – 5) = 36 - 12x + x2  x2 - 60x + 116 = 0  (x – 2)(x – 58) = 0 x  2 (TM§ K)   x   58 ( 6 lo¹i)
Vậy: Tập nghiệm của phương trình là {2} 0,125 ĐỀ 2
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 9 Thời gian: 60 phút
Câu 1:(2 điểm) thực hiện tính: 9 16 75 a) . 16 36 b) : c) 2. 8 d) 25 36 3
Câu 2:(1 điểm) Rút gọn 2 a)
 2  1  2 1 b) 2 20 3 452 125
Câu 3:(2 điểm) Tìm x, biết:
a) x2 -1=3 b) 16x  2 36x  3 9x  2  x 1 x 1  1 
Câu 4:(2 điểm) Cho biểu thức: P=   .   
1 (với x0 , x  1)  x 1 x  1  x
a) Hãy rút gọn biểu thức P.
b) Tìm giá trị của x để biểu thức P=2
Câu 5:(3 điểm) Cho tam giác ABC vuông tại A có đường cao AK chia cạnh huyền BC thành hai đoạn KB=2cm và KC=6cm.
a) Tính độ dài các đoạn thẳng: AK, AB, AC
b) Trên cạnh AC lấy điểm M ( M khác A và C) Gọi H là hình chiếu của A trên
BM. Chứng minh rằng BH.BM=BK.BC 1 SS Cos2 . ABHBKH BMC c) Chứng minh rằng: 4 ĐÁP ÁN Trang 5 CÂU ĐÁP ÁN ĐIỂ M Câu 1: a) 36 . 16  . 16 36  6 . 4  24 (2 điểm) 0.5 9 16 9 16 3 4 2 :  .  .  b) 25 36 25 36 5 6 5 0,5 c) 2. 8  8 . 2  16  4 75 75   0,5 25  5 d) 3 3 0,5 Câu 2: (1,0 0,5 điểm) 2 a)  2   1
 2 1  2 1  2 1  2 1 2 1  2 2 b) 2 20  3 45  2 125  2 5 . 4  3 5 . 9  2 5 . 25 0,5  2 . 2 5  3 . 3 5  5 . 2
5  4 5  9 5  10 5  5 5 Câu 3: a) Tìm x, biết x2 -1=3  2 x  4 0,25  0.5 x  2  hoặc x=2 0,25 Vậy x  2  hoặc x=2
b) Tìm x, biết: 16x  2 36x  3 9x  2 0,25 ĐKXĐ: x  0
16x  2 36x  3 9x  2 0,25 4 x  6 . 2 x  3 . 3 x  2 x  2 0.25 0.25 x=4 (thỏa mãn ĐKXĐ) Vậy x=4 Câu 4: Cho biểu thức:  x 1 x 1  1  P=   .    1
(với x0 , x  1)  x 1 x  1  x
a) Hãy rút gọn biểu thức A. 0.25 Trang 6  x 1 x  1   1  P   . 1      x 1 x  1  x   ( x  )( 1 x  ) 1 ( x  )( 1 x  ) 1   1  x    0.25 .      ( x  )( 1 x  ) 1 ( x  )( 1 x  ) 1   x  0.25  ( x  ) 1 2 ( x  ) 1 2  1 x    .     0.25  ( x  )( 1 x  ) 1 ( x  )( 1 x  ) 1   x
x  2 x 1 x  2 x  1  1 x    .      ( x  )( 1 x  ) 1 ( x  )( 1 x  ) 1   x   4 x  1 x  4  0.25 . .       ( x  )( 1 x  ) 1   xx  1 0.25 Vậy với 4
x0 , x  1 ta có: P  0.25 x  1
b) Tìm giá trị của x để biểu thức P=2 0.25 với 4
x0 , x  1 ta có: P x  1 Giã sử P=2 hay 4  2 x 1 4
 2  2 x  2  4  2 x  6  x  3  x  9 (thỏa mãn x 1 ĐKXĐ) Vậy với x=9 thì P=2 A 0.25 Câu 5: M H B I E C K a/ BC=KB+KC=2+6=8 cm 0,25 A
BC vuông tại A, đường cao AK: AB2=BH.BC=2.8=16  AB=4cm 0,25 ● 2 2 2
BC A B A C (định lý Pytago ) 2 2 2 2
AC BC AB  8  4  4 3cm 0,25
● AK2=HB.HC=2.6=12 AK= 12 =2 3 cm 0.25 0,25 b/ A
BM vuông tại A, đường cao AH AB2=BH.BM (1) 0,25 A
BC vuông tại A, đường cao AK  AB2=BK.BC (2) Từ (1)(2)  BH.BM=BK.BC 0,25
c/ Kẻ HI BC; ME BC(I, K BC) Trang 7 1 0,25 HI BK . S 2HI 1 HI BKH 2     . (3) S 1 8ME 4 ME 0,25 BMC ME BC . 2 HI BH BHIBME   (4) ME BM 0,25 A
BM vuông tại A có: AB AB 2 . 0,25 2 BH BM BH CosABH   Cos ABH    (5) BM BM 2 BM 2 BM Từ (3)(4)(5) S 1 1 BKH   C
. os2 ABH SS . C . os2 ABH 0.25 S BKH BMC 4 4 BMC ĐỀ 3
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 9 Thời gian: 60 phút
Bài 1: (1,0 đ) : Tìm điều kiện của x để các căn thức sau có nghĩa. a) x  2 . b) 1 2x 1
Bài 2 : (2,0 đ) Tính :  2 2 a) 4.36 b)  8 3 2. 2 c) 14 7 d) + 1 2 5  2 5  2
Bài 3 : (1,0 đ) Cho biểu thức A = 4x  20  2 x  5  9x  45 với x  -5. a) Rút gọn A. b) Tìm x để A = 6 x x
Bài 4 : (2,0 đ): Cho biểu thức M = 4 4  với x > 0 , x  4 x  2 x x  2 a) Rút gọn biểu thức M
b) Tính giá trị của M khi x = 3 2 2 .
c) Tìm giá trị của x để M > 0
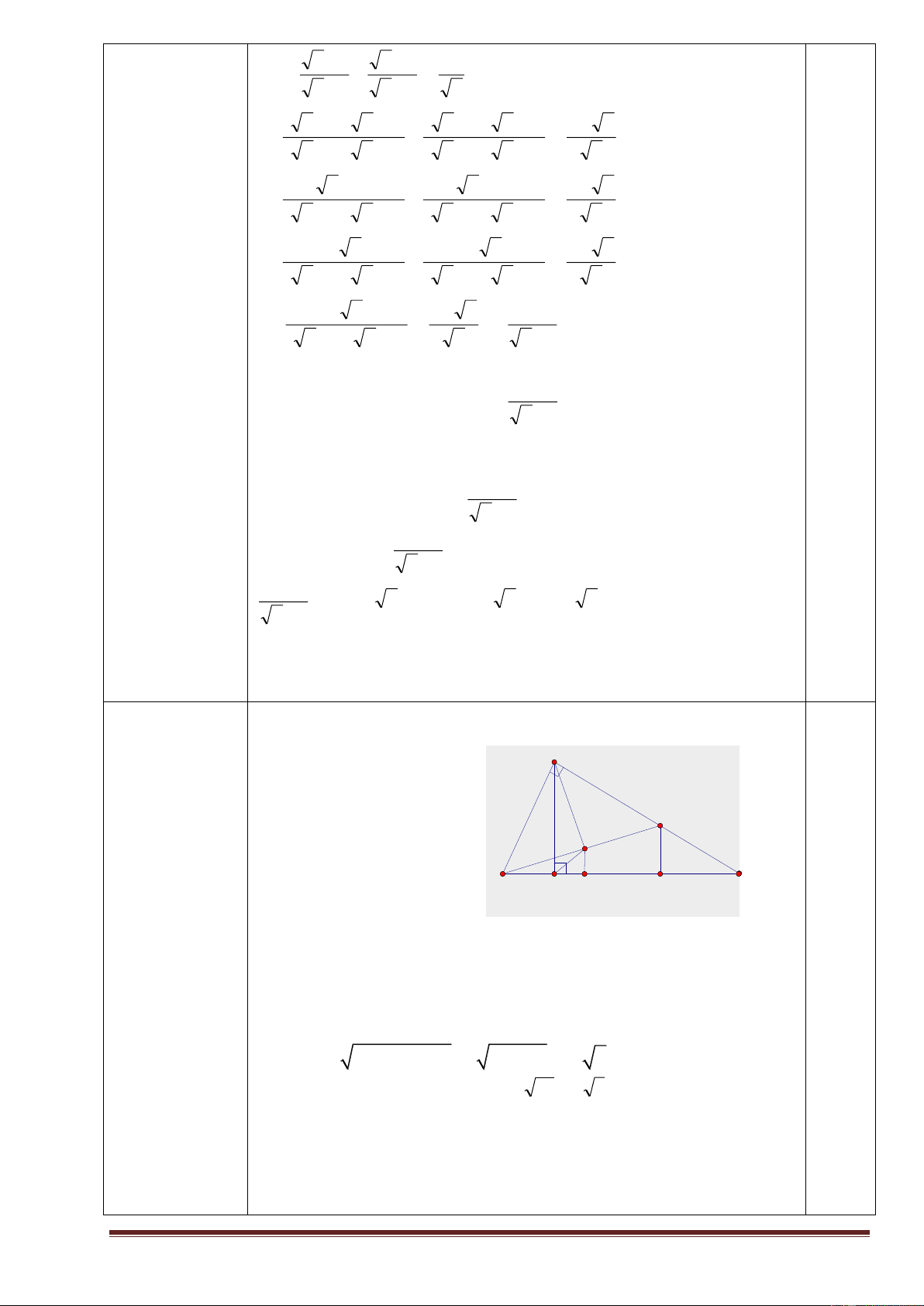
Bài 5 (3,0 đ): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành
hai đoạn : BH = 4 cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB, AC.
b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn đến độ).
c) Kẻ AK vuông góc với BM (K thuộc BM). Chứng minh : BK.BM = BH.BC
Bài 6 (1,0đ): Giải phương trình sau. 1 x  2000  y  2001 z  2002 
x y z3000 2 Trang 8 ĐÁP ÁN Bài Nội dung Điểm 1 1a
x  2 . có nghĩa khi x – 2 ≥ 0 Û x ≥ 2. 0.5 (1,0 đ) 1b 1 1 0,5
có nghĩa khi 2x 1  0 Û x > 2x 1 2 2 2a 4.36 = 2.6 = 12 0,5 (2,0 đ)
2b  8 3 2. 2 = 2 2 3 2. 2   2. 2  1  0,5 2c  2 2   1 0.5 14 7    2 1  2 1  2 2d 2 2    0,5 2 5 4 2 5 4 + = = 4 5 5  2 5  2  52 2  2 3 3a A
4x  20  2 x  5  9x  45 0,5 (1,0 đ)
 2 x  5  x x  5  3 x  5 ( ĐK : x ≥ - 5 (  3 x  5 3b
A  6  3 x  5  6 0,5  x  5  4  x  1  4 4a x x  0,5 4 4 (2,0 đ) M = x x  2 0,5 x  2 = x
4b) x = 3 2 2 (Thỏa mãn ĐK)  x 1 2    Khi đó M = 1 2 2 2 1   3  2 2 0,5 2 1 2 1 4c)  Với ĐK x > 0 , x  x 2 4 thì M = x
Do đó M > 0  x 2 >0 x 0,5
Vì x  0 nên x  2  0  x  4
Kết hợp với ĐKXĐ ta có M > 0 khi x > 4 5 A 0,25 (3,0 đ) M K B H C
5a D ABC vuông tại A : nên AH2 = HB.HC = 4.6 = 24 Þ 2 6 0,5 AH = (cm)
AB2 = BC.HB = 10.4 = 40 Þ AB = 2 10 (cm) Trang 9 2 15 0,75
AC2 = BC. HC = 10.6 = 60 Þ AC = (cm) 5b D ABM vuông tại A AB 2 10 2 6 0,5 tanAMB    0,25 AM 15 3 0  AMB  59
5c D ABM vuông tại A có AK ^ BM => AB2 = BK.BM 0,25
D ABC vuông tại A có AH ^ BC => AB2 = BH.BC 0,25 Þ BK. BM = BH.BC 0,25 6 x  2000  0 x  2000 (1,0 đ) ĐK:    0,25
y  2001 0  y  2001   z  2002  0 z  2002
Phương trình đã cho tương đương với 
x  2000  2 x  2000  
1   y  2001 2 y  2001   1 0,25
z 20022 z 2002  1  0   2 2 2 x  2000  
1   y  2001 
1   z  2002   1  0 0,25
x  2000 1  0  x  2000  1 x  2000  1 x  2001      
y  20011  0   y  2001  1  y  2001 1  y  2002    
z  2002 1  0  z  2002  1 z  2002  1 z    2003 0,25
KL: Phương trình có nghiệm: x  200 ;1 y  200 ; 2 z  2003 ĐỀ 4
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 9 Thời gian: 60 phút
Bài 1 (2,0 điểm).
1. Thực hiện phép tính. a) 81  80. 0,2 1 b) 2 (2  5)  20 2
2. Tìm điều kiện của x để các biểu thức sau có nghĩa: 1 a) x 1 b) 2 x  2x  1
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
a) ab b a
a 1 (với a  0 (
b) 4a  1 (với a  0 (
2. Giải phương trình: 9x  9  x 1  20 Trang 10
Bài 3 (2,0 điểm).  1 1  1  x Cho biểu thức A =  :   (với x > 0; x  1)  x  2 x x  2  x + 4 x  4
a) Rút gọn biểu thức A. 5 b) Tìm x để A = 3 Bài 4 (3,5 điểm).
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a) Tính độ dài các đoạn thẳng AB, AC, AH.
b) Trên cạnh AC lấy điểm K (K
A, K C), gọi D là hình chiếu của A trên BK.
Chứng minh rằng: BD.BK = BH.BC 1 c) Chứng minh rằng: 2 SS cos ABD BHD 4 BKC
Bài 5 (0,5 điểm). Cho biểu thức 3 3
P x y  3(x y) 1993 . Tính giá trị biểu thức P với: 3 3
x  9  4 5  9  4 5 và 3 3
y  3  2 2  3  2 2
.................... Hết ..................... ĐÁP ÁN Bài 1 Ý Nội dung Điểm 1.a 2
81  80. 0,2  9  80.0,2 0.25
0.5đ 9 16 94 5 0.25 1 1 1.b 2 (2  5)  20  2  5  .2 5 0.25 0.5đ 2 2  5  2  5  2  0.25 2.a    
Biểu thức x 1 có nghĩa x 1 0 0.25
0.5đ x 1. 0.25 1 1 2.b 2 Biểu thức 
 0  x  2x 1  0 0.25 2   có nghĩa 2   0.5đ x 2x 1 x 2x 1 2
 (x 1)  0  x  1 0.25
Bài 2 (2,0 điểm) Ý Nội dung Điểm 1.a       
Với a  0 ta có: ab b a a 1 b a ( a 1) ( a 1) 0.25 0.5đ
 ( a 1)(b a 1) 0.25
Với a  0  a  0 1.b 0.25 ta có: 2 2 2 4a  4
 .(a)  (2 a) 1 4a 1  (2 a) 0.5đ
 (1 2 a )(1 2 a) 0.25 2 ĐK: x  1 0.25 Trang 11 1.0đ
9x  9  x 1  20  9(x 1)  x 1  20  3 x  1  x  1  20 0.25
 4 x 1  20  x 1  5
x  1  25  x  24 (T/m ĐKXĐ) 0.25
Vậy phương trình có nghiệm duy nhất x = 24 0.25
Bài 3 (2,0 điểm). Ý Nội dung Điểm  1 1  1 x
Với x  0, x  1 ta có A =  :   0.25 2  x( x  2)
x  2  ( x +2) 2  1 x  ( x  2) =   . 0.25 x ( x  2) x ( x  2) 1  x   a 2 1  x ( x  2) 1.25đ = . 0.25 x ( x  2) 1  x x  2 = 0.25 x x  2 Vậy A = (với x > 0; x  1) 0.25 x 5 x  2 5 A    (ĐK: x > 0 ; x  1) 3 x 3 0.25 b
 3( x  2)  5 x
0.75đ  2 x  6  x  3 x  9(TMĐK) 0.25 5
Vậy với x = 9 thì A  . 0.25 3 Bài 4 (3,5 điểm). Ý Nội dung Điểm A K a 1.5đ D B C H I E + ABC
vuông tại A, đường cao AH 2
AB BH.BC  2.8 16 0.25
AB  4cm (Vì AB > 0) 0.25 Ý Nội dung Điểm + 2 2 2
BC AB AC (Định lý Pitago trong tam giác vuông ABC) 0.25 2 2 2 2
AC BC AB  8  4  48  4 3cm 0.25
+ Có HB + HC = BC  HC = BC – HB = 8 – 2 = 6 cm 0.25 Trang 12 2
AH BH.CH  2.6  12
AH  12  2 3cm (Vì AH > 0) 0.25 b
+ ABK vuông tại A có đường cao AD 2  AB B . D BK (1) 0.5 1.0đ + Mà 2
AB BH .BC (Chứng minh câu a ) (2) 0.25
Từ (1) và (2)  BD.BK = BH.BC 0.25
+ Kẻ DI BC, KE BC(I , K BC) 1 BH.DI S 2.DI 1 DI 0.25 BHD 2     . (3) S 1 8.KE 4 KE BKC BC.KE 2 c DI BD 1.0đ + BDI BKE   (4) 0.25 KE BK + ABK  vuông tại A có: 2 AB AB B . D BK BD 0.25 2 cos ABD   o c s ABD    (5) 2 2 BK BK BK BK 1 Từ (3), (4), (5) S 1 BHD 2   . os c ABD 2  SS cos ABD 0.25 S 4 BHD 4 BKC BKC
Bài 5 (0,5 điểm). Ý Nội dung Điểm Ta có: 3 3
x  18  3x x  3x  18 0.25 3 3
y  6  3y y  3y  6 3 3
P x y  3(x y) 1993 0.5đ 3 3
 (x  3x)  (y  3y) 1993 18  6 1993  2017 0.25 Vậy P = 2017 với 3 3
x  9  4 5  9  4 5 và 3 3
y  3  2 2  3  2 2 Lưu ý:
- Trên đây là các bước giải cơ bản cho từng bài, từng ý và biểu điểm tương ứng, học
sinh phải có lời giải chặt chẽ chính xác mới công nhận cho điểm.
- Học sinh có cách giải khác đúng đến đâu cho điểm thành phần đến đó. ĐỀ 5
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 9 Thời gian: 60 phút
Bài 1. (2,0 điểm). Thực hiện phép tính. 1 1
a) 3 2x  5 8x  7 18x b)  3  5 3  5
Bài 2. (2,0 điểm). Giải các phương trình sau: a) 9x  9  x 1  20 b)
x  8  2x  3.  1 1  1  x
Bài 3. (2,0 điểm). Cho biểu thức A =  :    x  2 x x  2  x + 4 x  4 Trang 13
a) Tìm điều kiện xác định của A?
b) Rút gọn biểu thức A. 5 c) Tìm x để A = . 3
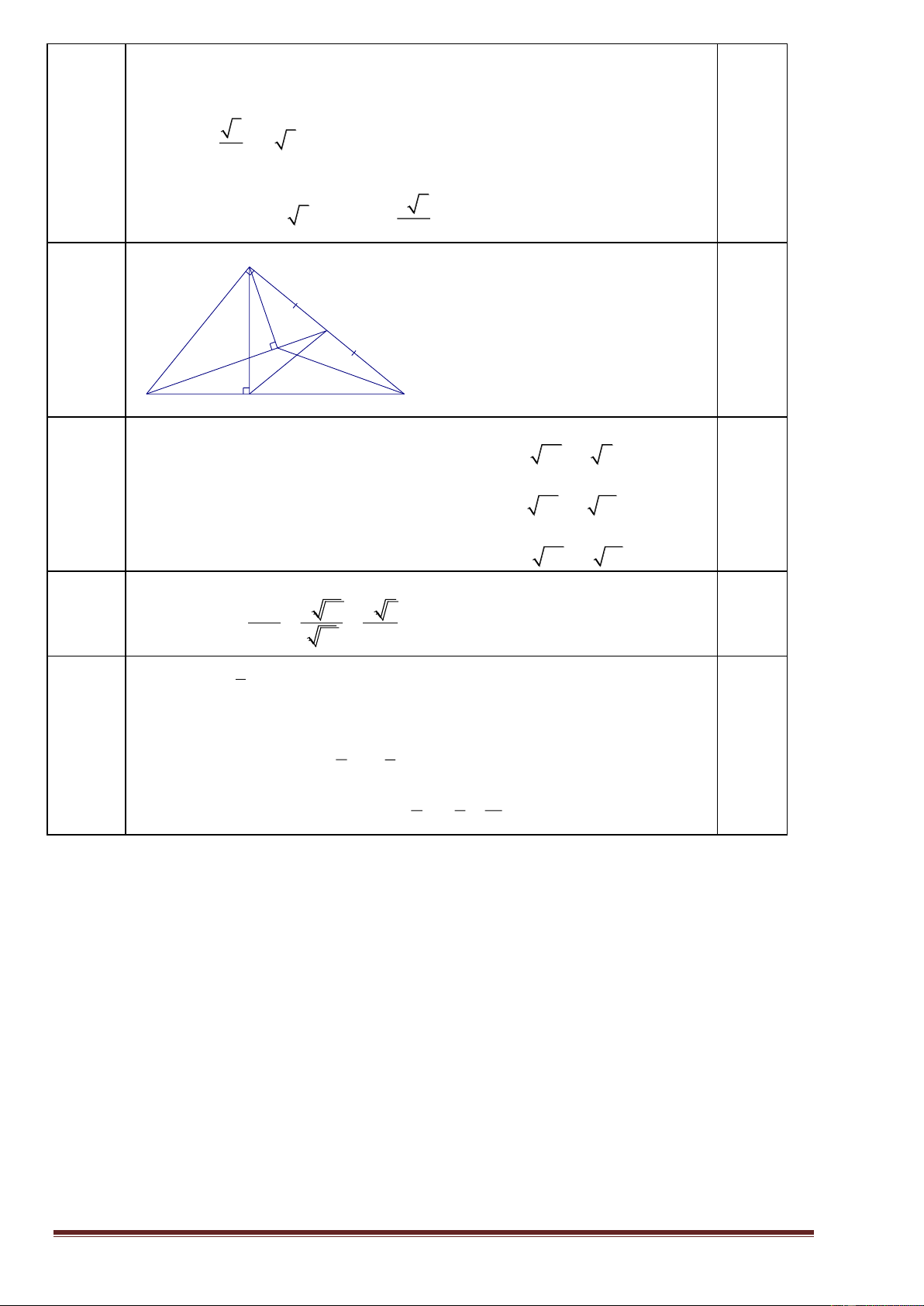
Bài 4. (3,0 điểm) Cho  ABC vuông tại A., đường cao AH. Biết BH = 1.8 cm; HC = 3,2 cm.
a. Tính độ dài AH ; AB; AC.
b. Tính số đo góc B và góc C.
c. Tia phân giác của góc B cắt AC tại D. Tính độ dài BD. AC
d. Chứng mimh rằng: tan ABD  AB  BC
(số đo góc làm tròn đến độ, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ ba)
Bài 5. (1,0 điểm) Chứng minh đẳng thức sau:      2 a a b b ab a b với a  0; b  0 a  b
ĐÁP ÁN VÀ THANG ĐIỂM Câu hỏi Đáp án Điểm
3 2x  5 8x  7 18x  3 2x 10 2x  21 2x a) 1,0đ  3 10  2   Bài 1: 1 . 2x 14 2x (2,0 điểm) 1 1 3  5  3  5 6 6 3 b)      1,0đ 3  5 3  5
3 5.3 5 95 4 2 a) ĐK: x  1 
9x  9  x 1  20  9(x 1)  x 1  20  3 x 1  x 1  20 1,0đ
 4 x 1  20  x 1  5
x 1  25  x  24 (T/m ĐKXĐ)
Vậy phương trình có nghiệm duy nhất x = 24 Bài 2: b)
x  8  2x  3 (2,0 điểm) x   8 x  8  0 x  8  0       3 2x  3  0  2x  3  0  x  1,0đ   2 
x  8  2x  3 
x  8  2x  3  x  5  (loai) 
Vậy không tìm được x thỏa điều kiện đề bài cho.
ĐKXĐ: x  0, x 1 0,25đ    Với 1 1 1 x
x  0, x  1 ta có A =  :   2  x( x  2)
x  2  ( x +2) Bài 3: 2    (2,0 điểm) 1 x ( x 2) 0,25đ =   .    x ( x 2) x ( x 2) 1 x   0,25đ Trang 14 2 1 x ( x  2) = . 0,25đ x ( x  2) 1  x x  2 = x x  2 Vậy A = (với x > 0; x  1) x 5 x  2 5 0,25đ A    (ĐK: x > 0 ; x  1) 3 x 3 0,25đ
 3( x  2)  5 x  2 x  6 
x  3  x  9 (TMĐK) 0,25đ Vậy với x = 9 thì 5 A  . 0,25đ 3 0,25đ
a . Tính độ dài AH ; AB; AC.  ABC có:  o A 90 , AH  BC (gt )
Theo hệ thức về cạnh và đường cao trong tam giác vuông ta có: 0,25đ
AH2 = BH . HC = 1,8 . 3.2 = 5,76 0,25đ  AH = 5, 76  2, 4( ) cm
 AHB vuông tại H theo định lí py ta go : 0,25đ Bài 4: AB = 2 2 2 2
AH BH  1,8  2, 4  3(c ) m (3,0 điểm)
 AHC vuông tại H theo định lí py ta go: AC = 2 2 2 2
AH CH  2, 4  3, 2  4(c ) m 0,25đ b . Tính góc B, C.
Theo định nghĩa tỉ số lượng giác của góc nhọn ta có : AC 4 tan B =    o B 53 AB 3 0,25đ nên  o   o  o  o C 90 B 90 53 37 = 900 0,25đ c. Tính BD o 1 53 o  ABD (  o A 90 ) , ABD  ABC   26,5 0,25đ 2 2
Theo hệ thức về cạnh và góc trong tam giác vuông ta có: 0,25đ Trang 15 AB  . BD cos ABD AB 3  BD   3,352(cm) 0 cos ABD cos 26, 5
d.  ABD vuông tại A ta có : AD 0,25đ tan ABD =
(1)( định nghĩa tỉ số lượng giác AB
Ta lại có: BD là phân giác trong của  ABC 0,25đ AD AB Nên 
(Tính chất đường phân giác) DC BC   AD DCAD DC AC = = (2) AB BC AB BC AB BC Từ (1) và (2)  AC tan ABD = 0,25đ AB BC Ta có:   a3  b3  a  ba ab b a a b b  VT   ab   ab   ab a  b a  b a  b 0,5đ Bài 5: 2 2
(1,0 điểm)  a  ab  b  ab   a   2 ab   b     2 a b  VP (đpcm) 0,5đ ĐỀ 6
ĐỀ KIỂM TRA GIỮA HỌC KỲ I MÔN TOÁN 9 Thời gian: 60 phút
Bài 1: (1 đ) : Tìm điều kiện của x để các căn thức sau có nghĩa. a) x  2 .  b) 2 3x
Bài 2 : Tính : (2 đ) 25 16 14  7 . 36 . 4 8 3 ). 2 2  a) b) 81 49 c) ( d) 1 2
Bài 3 : Rút gọn biểu thức : (1.5 đ ) a) 3 3 3 2 2    (2  3)  (2  3) b) 27 64 . 2 125 c) 5  2 2  9  4 2
Bài 4 : (1 đ) Tìm x, biết 4x202 x5 9x45 6
Bài 5 : (1,5 điểm). Cho tam giác ABC vuông tại A, 0
C  30 , BC = 6cm, đường cao AH. Tính AB ; AC ; AH Trang 16
Bài 6 (2 đ): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai
đoạn : BH = 4 cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB, AC.
b) Gọi M là trung điểm của AC.
Tính số đo góc AMB (làm tròn đến độ). 2
Bài 7 : (1 điểm) Biết sin  = . Tính giá trị của biểu thức: A = 2sin2  + 5cos2 . 3
2. ĐÁP ÁN VÀ THANG ĐIỂM Bài Nội dung Điểm 1a
x  2 có nghĩa khi x – 2 ≥ 0 Û 0.5 x ≥ 2. 1b 2 0,5 x
2  3x có nghĩa khi 2 - 3x  0 <=> 3 2a 0,5 36 . 4 = 2.6 = 12 2b 0,5 25 16 . 5 4 20 .  81 49 = 9 7 63 2c 0.5 ) 8 3 ). 2 2 = 163 4 46 2 2d 0,5 14  7 2 2   1    2 1  2 1  2 3a 2 2 0,25
(2  3)  (2  3) = 2  3  2  3 0,25 = 4 3b 3 3 3 27   64  . 2 = 3 125 – 4 + 2. 5 = 9 0,5 3c 0,1 5  2 2  9  4 2 = 2 5  2 2  (2 2 1) 0,1 = 5  2 3 2 2 = 0,1 2 5  2 ( 2 1) = 3  2 2 0,1 = 0,1 2 1 4
4x2 02 x5  9x4 5 6 ( ĐK : x ≥ - 5 (
4x  20  2 x  5  9x  45  6 
4(x  5)  2 x  5  9(x  5)  6 0,25
 2 x  5  2 x  5  3 x  5  6 0,25  x  5  2    0,25 x 5 4 0,25  x  1 Vậy x = -1 5 Hình vẽ đúng
1/ Giải tam giác vuông ABC A  ABC vuông tại A, nên: AB = BC sinC 0,5 Trang 17 = 6 sin300 = 3 (cm) 300
AC = AB cotC = AB : tanC B H C 0,5 3 = 3 : = 3 3 (cm) 3  AHC vuông tại H, nên: 0,5 3 3 AH = AC sinC = 3 3 sin300 = (cm) 2 6 A M K B H C 6a D ABC vuông tại A : nên
AH2 = HB.HC = 4.6 = 24 Þ AH = 24  2 6 (cm) 0,5
AB2 = BC.HB = 10.4 = 40 Þ AB = 0,5 40  2 10 (cm) 0,5
AC2 = BC. HC = 10.6 = 60 Þ AC = 60  2 15 (cm) 6b D ABM vuông tại A AB 2 10 2 6 0,5 tan g AMB    AM 15 3 Þ o AMB  59 7 Biết sin  2
= . Tính giá trị của biểu thức: A = 2sin2  + 5cos2 . 3 Ta có: sin2  + cos2  = 1 0,5 2  2  5
Cos2  = 1- sin2  = 1-   =  3  9 0,5 Do đó: 4 5 11
A = 2sin2  + 5cos2  = 2.  5.  9 9 3 Trang 18