TOP 5 Đề ôn tập giữa học kỳ 1 Toán 11 Cánh diều (có đáp án)

TOP 5 Đề ôn tập giữa học kỳ 1 Toán 11 Cánh diều có đáp án và giải chi tiết được soạn dưới dạng file PDF gồm 70 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

70 35 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

70 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 1
I. Trắc nghiệm: (7.0đ)
Câu 1: Cho cấp số nhân có số hạng đầu công bội Giá trị của bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Theo công thức số hạng tổng quát của cấp số nhân ta có: .
Câu 2: Trong các hàm số sau, hàm số nào có đồ thị nhận gốc tọa độ làm tâm đối xứng?
A. . B. . C. . D. .
Lời giải
Chọn A
Đồ thị nhận gốc tọa độ làm tâm đối xứng là đồ thị của hàm số lẻ.
A:. Hàm số :
Tập xác định: .
Ta có: và
Do đó hàm số là hàm số chẵn.
B:. Hàm số là hàm số chẵn trên .
C:. Hàm số :
Ta có: .
Lúc đó: và
Do đó, hàm số không phải là hàm số chẵn và không phải hàm số lẻ.
D:. Hàm số :
Tập xác định: .
Ta có: và
Do đó hàm số là hàm số lẻ.
Vậy đồ thị nhận gốc tọa độ làm tâm đối xứng là đồ thị của hàm số
Câu 3: Nghiệm của phương trình là
A. . B. .
C. . D. .
Lời giải
Chọn D
( )
n
u
1
1
,
2
=u
2.=q
25
u
23
2
24
2
25
2
26
2
24 24 23
25 1
1
..22
2
uuq===
sin cosyxx=
1 sinyx=-
sinyx x=
( ) sinyfx x x==
D = !
:xD xD"Î - Î
()()sin() sin ().fx x x x xfx-=- -= =
sinyx x=
!
( ) 1 sinyfx x==-
0; 2
22
ff
pp
æö æ ö
=-=
ç÷ ç ÷
èø è ø
22
ff
pp
æö æ ö
¹-
ç÷ ç ÷
èø è ø
22
ff
pp
æö æ ö
¹- -
ç÷ ç ÷
èø è ø
1 sinyx=-
( ) cos sinyfx x x==
D = !
:xD xD"Î - Î
()cos()sin() cossin ().fx x x x x fx-= - -=- =-
( ) cos sinyfx x x==
( ) cos sin .yfx x x==
1
s inx
2
=
5
;
66
xkx k
pp
pp
=+ = +
2
6
xk
p
p
=± +
5
2; 2
66
xkx k
pp
pp
=- + =- +
5
2; 2
66
xkx k
pp
pp
=+ = +
Trang 2
Câu 4: Trên đường tròn bán kính , độ dài của cung có số đo là
A. . B. . C. . D. .
Lời giải
Chọn A
Trên đường tròn bán kính , độ dài của cung có số đo là .
Câu 5: Cho cấp số nhân có số hạng đầu và công bội . Giá trị của là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có .
Câu 6: Chọn khẳng định sai trong các khẳng định sau:
A. . B. .
C. . D. .
Lời giải
Chọn B
Theo công thức nhân đôi.
Câu 7: Tập nghiệm của phương trình là
A. . B. .
C. . D. .
Lời giải
Chọn C
Ta có: .
Câu 8: Chọn mệnh đề sai trong các mệnh đề sau.
A. Hai đường thẳng phân biệt có không quá một điểm chung.
B. Hai đường thẳng cắt nhau thì không song song với nhau.
C. Hai đường thẳng không có điểm chung thì song song với nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung.
2
1
6
s inx
5
2
2
6
xk
xk
p
p
p
p
È
Í
=+
Í
=€
Í
Í
=+
Í
Í
Î
15r =
3
p
5l
p
=
7l
p
=
6l
p
=
8l
p
=
15r =
3
p
15. 5
3
l
p
p
==
( )
n
u
1
1u =
3q =
5
u
16
81
13
162
4
51
.uuq=
4
1.3=
81=
22
cos 2 cos sinaaa=-
2
cos 2 1 2cosaa=-
2
cos 2 2cos 1aa=-
2
cos 2 1 2 sinaa=-
2
cos
2
x =
5
,2
4
,2
4
kkk
pp
pp
-
Î
ìü
++
íý
îþ
!
3
2 ,
4
kk
p
p
ìü
±+
íý
îþ
Î!
2 ,
4
kk
p
p
ìü
±+
íý
îþ
Î!
3
2
4
, kk
p
p
ì
Î
ü
+
íý
îþ
!
2
cos
2
x =
cos cos
4
x
p
Û=
2
4
,xkk
p
p
Û=± + Î !
Trang 3
Lời giải
Chọn C
Hai đường thẳng không có điểm chung thì song song với nhau hoặc chéo nhau.
Câu 9: Cho cấp số cộng , biết và . Tìm công sai của cấp số cộng này.
A. . B. . C. . D. .
Lời giải
Chọn A
Câu 10: Trong các mệnh đề sau, mệnh đề nào đúng?
A. . B. .
C. . D. .
Lời giải
Chọn D
Theo công thức đổi đơn vị đo góc, ta có:
Câu 11: Cho dãy số với ( hằng số). Hỏi là số hạng nào sau đây?
A. . B. .
C. . D. .
Lời giải
Chọn C
Ta có: .
Câu 12: Biết số theo thứ tự lập thành cấp số cộng. Giá trị của bằng
A. B. C. D.
Lời giải
Chọn A
theo thứ tự lập thành cấp số cộng nên .
Câu 13: Biểu thức được viết lại thành
A. . B. .
( )
n
u
3
7u =-
4
8u =
15d =
15d =-
1d =
3d =-
43
15uudd=+Þ=
180
rad
p
p
°
æö
=
ç÷
èø
rad 1
p
°
=
rad 60
p
°
=
rad 180
p
°
=
180 .rad
p
°
=
( )
n
u
2
1
n
an
u
n
=
+
a
1n
u
+
2
1
.1
1
n
an
u
n
+
+
=
+
2
1
2
n
an
u
n
+
=
+
( )
2
1
.1
2
n
an
u
n
+
+
=
+
( )
2
1
.1
1
n
an
u
n
+
+
=
+
( )
( )
( )
22
1
.1 .1
11 2
n
an an
u
nn
+
++
==
++ +
3
5; ;15x
x
10.
20.
30.
75.
5; ;15x
5 15
10
2
x
+
==
sin
6
a
p
æö
+
ç÷
èø
13
sin sin cos
62 2
aaa
p
æö
+= -
ç÷
èø
1
sin sin
62
aa
p
æö
+= +
ç÷
èø
Trang 4
C. . D. .
Lời giải
Chọn C
Ta có .
Câu 14: Giá trị của là
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có:
Câu 15: Tập xác định của hàm số .
A. . B. .
C. . D. .
Lời giải
Chọn A
ĐK: .
TXĐ: .
Câu 16: Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là:
A. 5 mặt, 5 cạnh. B. 6 mặt, 5 cạnh. C. 6 mặt, 10 cạnh. D. 5 mặt,
10 cạnh.
Lời giải
Chọn C
31
sin sin cos
62 2
aaa
p
æö
+= +
ç÷
èø
31
sin sin cos
62 2
aaa
p
æö
+= -
ç÷
èø
31
sin sin cos cos sin sin cos
66622
aa a aa
ppp
æö
+= + = +
ç÷
èø
tan 6 0
°
0
1-
3-
3
tan 60 3 .
°
=
D
3cos
2sin 1
x
y
x
=
-
5
\2;2,
66
Dkkk
pp
pp
ìü
=++Î
íý
îþ
°¢
\2,
6
Dkk
p
p
ìü
=+Î
íý
îþ
°¢
D = °
1
\
2
D
ìü
=
íý
îþ
°
2 sin 1 0x -¹
1
sin
2
xÛ¹
sin sin
6
x
p
Û¹
2
6
,
5
2
6
xk
k
xk
p
p
p
p
ì
¹+
ï
ï
ÛÎ
í
ï
¹+
ï
î
¢
5
\2;2,
66
Dkkk
pp
pp
ìü
=++Î
íý
îþ
°¢
Trang 5
Nhìn hình dễ dàng ta có đáp án đúng là 6 mặt, 10 cạnh.
Câu 17: Cho tứ diện , là trọng tâm tam giác . Giao tuyến của hai mặt phẳng
và là
A. , với là hình chiếu của lên . B. , với là trung điểm của
.
C. , với là hình chiếu của lên . D. , với là trung điểm của
.
Lời giải
Chọn D
Mặt phẳng chính là mặt phẳng , với là trung điểm của . Vậy giao
tuyến của hai mặt phẳng và là .
Câu 18: Nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: .
Câu 19: Nghiệm của phương trình là
A
B
C
D
F
S
ABCD
G
BCD
()ACD
()GAB
AK
K
C
BD
AM
M
AB
AH
H
B
CD
AN
N
CD
B
C
D
A
N
G
( )
GAB
( )
NAB
N
CD
()ACD
()GAB
AN
sin .cos 0xx=
2
xk=
p
2xk=
p
2
6
xk=+
p
p
2
2
xk=+
p
p
( )
sin .cos 0 sin 2 0
2
k
xx x x k=Û =Û= Î!
p
3 sin cos 2xx+=
Trang 6
A. . B. .
C. . D. .
Lời giải
Chọn C
Ta có:
.
Câu 20: Hàm số nào sau đây có chu kì tuần hoàn là ?
A. . B. C. . D. .
Lời giải
Chọn D
Vì hàm số tuần hoàn với chu ki nên .
Ta có .
Vậy hàm số tuần hoàn với chu kì .
Câu 21: Tính .
A. . B. . C. . D. .
Lời giải
Chọn D
.
Câu 22: Cho dãy số có . Tìm mệnh đề đúng.
A. Dãy số tăng. B. Dãy số bị chặn.
C. Dãy số chỉ bị chặn trên. D. Dãy số chỉ bị chặn dưới.
Bài giải
Chọn B
Xét .
Với . Vậy dãy bị chặn.
Câu 23: Cho hình chóp có đáy là một tứ giác ( không song song với ).
Gọi là trung điểm của , là điểm trên cạnh sao cho , là giao
điểm của và . Gọi là giao tuyến của và . Nhận xét nào sau đây
là sai?
2,
6
xkk
p
p
=+ Î!
,
3
xkk
p
p
=+ Î!
2,
3
xkk
p
p
=+ Î!
2,
2
xkk
p
p
=+ Î!
3 sin cos 2xx+=
31
sin cos 1
22
xxÛ+=
sin 1
6
x
p
æö
Û+=
ç÷
èø
2
62
xk
pp
p
Û+ = +
2,
3
xkk
p
p
Û= + Î!
p
( )
cot 4yx=
( )
tan 3yx=
( )
sin 2yx=
p
( ) ( )
fx fxp+=
( )
( )
( ) ( )
sin 2 sin 2 2 sin 2yx x xpp=+=+=
( )
sin 2yx=
p
3
sin .sin
88
pp
35
99
12
1
22
æö
-
ç÷
ç÷
èø
12
1
22
æö
-
ç÷
ç÷
èø
2
4
31 12 2
sin .sin cos cos 0
8824 222 4
pp p p
æö
æö
=-=-=
ç÷
ç÷
ç÷
èø
èø
( )
n
u
( )
1
1
n
u
nn
=
+
( )
n
u
( )
n
u
( )
n
u
( )
n
u
1
2
n
n
u
n
un
+
=
+
1n"³
01
n
uÞ< <
( )
n
u
ABCD
AB
CD
M
SD
N
SB
2SN NB=
O
AC
BD
d
( )
SAB
( )
SCD
Trang 7
A. cắt . B. cắt . C. cắt . D. cắt .
Lời giải
Chọn B
Xét và có: chung.
Trên Gọi là điểm chung của và .
Vậy hay .
Ta có .
Mặt khác và không đồng phẳng.
Do đó cắt là mệnh đề sai.
Câu 24: Hàm số có giá trị nhỏ nhất bằng
A. B. C. D.
Lời giải
Chọn C
Ta có:
Mà:
khi
Vậy khi
Câu 25: Cho tứ diện . Gọi , lần lượt là trọng tâm các tam giác , . Đường
thẳng song song với đường thẳng
d
CD
d
MN
d
AB
d
SO
( )
SAB
( )
SCD
S
I AB CD I=ÇÞ
( )
SAB
( )
SCD
( ) ( )
SAB SCD SIÇ=
d SIº
;;dABIdCDIdSOSÇ= Ç= Ç=
d
MN
d
MN
sin cosyxx=+
1.
0.
2.-
2.
sin cos 2 sin
4
xx x
p
æö
+= +
ç÷
èø
1 sin 1 2 2 sin 2 2 2.
44
xxy
pp
æö æö
-£ + £Þ- £ + £ Þ- £ £
ç÷ ç÷
èø èø
min
2yÞ=-
( )
sin 1 2 2 .
442 2
xxkxkk
ppp p
pp
æö
+=Þ+=+ Þ=+ Î
ç÷
èø
!
min
2y =-
( )
2.
2
xkk
p
p
=+ Î!
ABCD
I
J
ABC
ABD
IJ
Trang 8
A. . B. .
C. . D. với là trung điểm cạnh .
Lời giải
Chọn C
Gọi , lần lượt là trung điểm của các cạnh và , ta có .
Vì lần lượt là trọng tâm các tam giác , nên ta có
.
Từ và suy ra .
Câu 26: Cho cấp số cộng có Khẳng định nào sau đây đúng?
A. B.
C. D.
Lời giải
Chọn B
Ta có .
Câu 27: Cho tứ diện . và theo thứ tự là trung điểm của và . là trọng tâm
tam giác . Giao tuyến của hai mặt phẳng và là đường thẳng.
A. Qua và song song với . B. Qua và song song với .
C. Qua và song song với . D. Qua và song song với .
Lời giải
Chọn D
DB
AC
CD
CM
M
BD
N
M
J
I
D
C
B
A
M
N
BD
BC
//MN CD
,IJ
ABC
ABD
2
3
AI AJ
AN AM
==
//IJ MNÞ
//IJ CD
( )
n
u
1
1
3; .
2
ud=- =
1
3 1.
2
n
un=- + -
( )
1
31.
2
n
un=- + -
( )
1
31.
4
n
un n
ʈ
˜
Á
=-+ +
˜
Á
˜
Á
˯
( )
1
31.
2
n
un=- + +
( ) ( )
1
1
131
2
nn
uu n du n=+- € =-+ -
ABCD
I
J
AD
AC
G
BCD
( )
GIJ
( )
BCD
G
BC
I
AB
J
BD
G
CD
Trang 9
Xét hai mặt phẳng và , có;
Và ( là đường trung bình của ),
Nên .
Câu 28: Cho tam giác . Mệnh đề nào sau đây đúng?
A. . B. .
C. . D. .
Lời giải
Chọn A
.
Câu 29: Rút gọn biểu thức .
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có
.
Câu 30: Cho hình chóp có lần lượt là trung điểm cạnh và điểm thỏa mãn
. Thiết diện của hình chóp khi cắt bởi mặt phẳng là hình nào
dưới đây?
A. Tam giá B. Hình bình hành.
C. Hình thang chỉ có một cặp cạnh song song D. Hình thoi.
Lời giải
( )
GIJ
( )
BCD
( ) ( )
GGIJ BCDÎÇ
//IJ CD
IJ
ACDD
( ) ( )
,IJ GJI CD BCDÌÌ
( ) ( )
GIJ BCD GyÇ=
( )
// //Gy JI CD
ABC
sin( ) sin+=AB C
cos( ) cos+=AB C
sin sin
22
+
=
AB C
cos cos
22
+
=
AB C
( ) ( )
sin sin sin
pp
++=Þ + = - =ABC AB C C
2
sin 2 sin 5 sin 3
1 cos 2sin 2
aaa
A
aa
+-
=
+-
cos a
sin a
2 cos a
2 sin a
( )
( )
2
sin 2 sin 5 sin 3
cos 1 2sin 2
aaa
A
aa
+-
=
+-
( )
2sin cos cos 4
2sin cos 2cos 4 sin
cos cos 4 cos cos 4
aa a
aa aa
aa aa
+
+
==
++
2 sin a=
.S ABC
, EF
, AB BC
G
1
2
SG SC=
!!!" !! !"
.S ABC
( )
EFG
Trang 10
Chọn B
Ta có là đường trung bình trong tam giác suy ra .
Gọi , suy ra là trung điểm và
Ta có suy ra là trung điểm của và .
Ta có là đường trung bình trong tam giác suy ra
Từ suy ra thiết diện là hình bình hành .
Câu 31: Cho hình chóp có không song song với . Gọi là một điểm thuộc
miền trong . là giao điểm của với , là giao điểm của và
. Khi đó là
A. giao điểm của với .
B. giao điểm của với .
C. giao điểm của với ( là giao tuyến của và ).
D. giao điểm của với .
Lời giải
Chọn B
EF
,ABC
( )
// 1EF AC
( ) ( ) { }
( )
( )
//
EFG SAC G
EF EFG
AC SAC
EF AC
Ç=
ü
ï
Ì
ï
Þ
ý
Ì
ï
ï
þ
( ) ( )
// //EFG SAC Gx FE ACÇ=
{ }
Gx SA HÇ=
H
SA
( )
// 2HG AC
1
,
2
SG SC=
!!!" !! !"
G
SC
( )
// 3GF SB
HE
,SAB
( )
// 4HE SB
( ) ( ) ( ) ( )
1, 2, 3, 4
FGHE
AB
CD
M
SCDD
I
BM
( )
SAC
P
SC
( )
ABM
P
SC
DI
SC
AI
SC
MK
SK
( )
SAD
( )
SBC
SC
BI
D
A
B
C
S
Trang 11
* Xác định : Gọi . Chọn .
Gọi .
Gọi .
* Xác định : Chọn .
Ta có . Gọi .
Câu 32: Cho hình chóp tứ giác có đáy là hình vuông, , . Gọi
lần lượt là trung điểm . Thiết diện tạo bởi và hình chóp là
hình gì?
A. Là tam giác cân. B. Là ngũ giác.
C. Là tam giác thường. D. Là tứ giác.
Lời giải
Chọn B
Ta được thiết diện là ngũ giác .
D
P
I
O
E
A
B
C
S
M
I
E SM C D=Ç
( )
SBE BMÉ
( ) ( )
OBE AC SO SBE SAC=ÇÞ= Ç
( )
IBMSO IBM SAC=ÇÞ=Ç
P
( )
SAC SCÉ
( ) ( )
AI SAC ABM=Ç
( )
PSC AI PSC ABM=ÇÞ=Ç
ABCD
SA AD^
,,MNP
,,SA B C CD
( )
MNP
E NP AB=Ç
F NP AD=Ç
H SB ME=Ç
I SD MF=Ç
MHNPI
Trang 12
Câu 33: Cho biết có hai cấp số nhân thỏa mãn với công bội và Giá
trị của bằng
A. B. C. D.
Lời giải
Chọn C
Ta có
Đặt , điều kiện . Ta thu được
hoặc .
Với , ta có .
Vậy
Câu 34: Tính tổng tất cả các nghiệm của phương trình trên
khoảng .
A. B. C. D.
Lời giải
Chọn A
Ta có:
Vì nên
()
n
u
123
222
123
26
364
uu u
uu u
++=
ì
í
++=
î
1
q
2
.q
12
qq+
1
.
2
7
.
3
10
.
3
5
.
2
2
2
2
2
2
2
22
22
2
2
2
2
2
1
1
1
1 26
1 676
1
13
.
7
1
1
1
1
1 364
1 364
uq
uq
q
q
q
q
q
uq
uq
q
q
q
ì
ì
æö
æö
æö
++ =
++ =
++
ï
ï
ç÷
ç÷
ç÷
ïè ø ï
èø
èø
ÞÞ=
íí
æö
æö
æö
ïï
++
++ =
++ =
ç÷
ç÷
ç÷
ïï
èø
èø
î
èø
î
1
qt
q
+=
2t ³
22 2
10
7(1 ) 13( 1) 3 7 10 0
3
tt tt t+= -Û --=Û=
1t =-
10
3
t =
3
1 10
1
3
3
q
q
q
q
=
é
ê
+= Û
ê
=
ë
12
10
.
3
qq+=
S
( )
( )
44
2cos2 5 sin cos 3 0+-+=xxx
( )
0; 2
p
4.=S
p
5.=S
p
7
.
6
=S
p
( )
( )
44
2cos2 5 sin cos 3 0xxx+-+=
( )
( )( )
2222
2 cos 2 5 sin cos sin cos 3 0xxxxx
éù
Û+ - ++=
ëû
( )( )
2cos2 5 cos2 3 0xxÛ+-+=
2
2cos 2 5cos2 3 0xxÛ- - + =
( )
1
cos 2
2
cos 2 3
x
x ptvn
é
=
ê
Û
ê
=-
ê
ë
6
,
6
xk
k
xk
p
p
p
p
é
=+
ê
ÛÎ
ê
ê
=- +
ê
ë
!
( )
0; 2x
p
Î
7511
;;;
66 6 6
x
ppp p
ìü
Î
íý
îþ
Trang 13
Vậy .
Câu 35: Biết rằng khi thì phương trình có đúng
nnghiệm thuộc khoảng . Mệnh đề nào sau đây đúng?
A. . B. . C. . D. .
Lời giải
Chọn B
Đặt . Phương trình trở thành: (1)
Yêu cầu bài toán thỏa mãn khi một trong các trường hợp sau xảy ra
TH1: Pt (1) có nghiệm: và .
+) .
Với thì (1) trở thành: không thỏa yêu cầu bài toán.
Với thì (1) trở thành: không thỏa yêu cầu bài toán.
TH2: Pt (1) có nghiệm: và .
+) .
Với thì (1) có dạng: thỏa yêu cầu bài toán.
Với thì (1) có dạng: không thỏa yêu cầu bài toán.
.
II. Tự luận: (3.0đ)
Câu 36: Giải phương trình .
Lời giải:
Điều kiện:
7511
4
66 6 6
S
ppp p
p
=+ + + =
0
mm=
( )
22
2sin 5 1 sin 2 2 0xm xmm-+ ++=
5
;3
2
p
p
æö
-
ç÷
èø
0
3m =-
0
32
;
55
m
æö
Î- -
ç÷
èø
0
1
2
m =
0
37
;
510
m
æù
Î
ç
ú
èû
( )
sin , 1txt=£
( )
22
2512 20tmtmm-+++=
2
1
1t =
2
10t-< £
2
12 3 10tmm=Þ - +=
1
1
2
m
m
=
é
ê
Û
ê
=
ë
1m =
2
2640tt-+=
1
2
m =
2
73
20
22
tt-+=
1
3
4
t
t
=
é
ê
Û
ê
=
ë
2
1
1t =-
1t =-
22
25 12 2 0 2 7 30mmm mmÞ+ ++ + =Û + +=
1
2
m =-
2
31
20
22
tt+-=
1
1
4
t
t
=-
é
ê
Û
ê
=
ë
3m =-
2
214120tt++=
1
6
t
t
=-
é
Û
ê
=-
ë
132
;
255
m
æö
=- Î - -
ç÷
èø
cos2 . tan 0xx=
( )
cos 0
2
xxkk
p
p
¹Û¹ + Î
!
Trang 14
Phương trình
So điều kiện, nhận nghiệm .
Câu 37: Cho cấp số nhân có . Số là số hạng thứ mấy của dãy
Lời giải
Ta có số hạng tổng quát của cấp số nhân là:
Câu 38: Cho tứ diện có lần lượt là trung điểm của và là một điểm
thuộc cạnh ( không trùng trung điểm cạnh) . Thiết diện của tứ diện cắt bởi
mặt phẳng là hình gì?
Lời giải
Chọn D
Trong mp kéo dài cắt nhau tại I.Trong mp kéo dài cắt
tại Ta được: Vậy thiết diện của tứ diện cắt bởi mặt phẳng
là tứ giác
( )
cos2 0
22
cos2 .tan 0
24
tan 0
x
xk xk
xx k
x
xk xk
pp
pp
pp
éé
=
=+ =+
é
êê
=Û Û Û Î
ê
êê
=
ë
==
ëë
!
( )
4
xk
k
xk
p
p
p
é
=+
ê
Î
ê
=
ë
!
()
n
u
1
1
1,
10
uq=- =-
103
1
10
11
1
1
103 103 103
104
104
11111 1
.1. .(10)
10 10 10 10 10 10
11 1 1
104
10 10 10 10
nn n
n
n
nn
uuq
n
--
-
---- -
æö æö æö
=Û=- Û =Û -=
ç÷ ç÷ ç÷
èø èø èø
---
æö æöæö
Û=Û= Û=
ç÷ ç÷ç÷
èø èøèø
ABCD
,MN
,AB CD
P
BC
P
BC
( )
MNP
Q
I
N
M
B
A
D
C
P
( )
ABC
,MP AC
( )
ACD
IN
AD
.Q
( ) ( )
( ) ( )
( ) ( )
( ) ( )
ABC MNP MP
BCD MNP PN
ACD MNP NQ
ABD MNP QM
=
=
=
=
!
!
!
!
( )
MNP
.MPNQ
Trang 15
Câu 39: Cho tứ diện có , . Cắt tứ diện bởi một mặt phẳng song song với
, để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng
Lời giải
Giả sử một mặt phẳng song song với và cắt tứ diện theo một thiết diện
là hình thoi như hình vẽ trên. Khi đó ta có: .
Cách 1: Theo định lí Ta – lét ta có:
.
Vậy hình thoi có cạnh bằng .
Cách 2: Theo định lí Ta – lét ta có:
.
------------- HẾT -------------
ABCD
6AB =
8CD =
AB
CD
K
I
N
B
D
C
A
M
AB
CD
ABCD
MNIK
// //
// //
MK AB IN
MN CD IK
MK KI
ì
ï
í
ï
=
î
MK CK
AB AC
KI AK
CD AC
ì
=
ï
ï
í
ï
=
ï
î
6
8
MK AC AK
AC
KI AK
AC
-
ì
=
ï
ï
Þ
í
ï
=
ï
î
1
6
MK AK
AC
Þ=-
1
68
MK KI
Þ=-
1
68
MK MK
Þ=-
7
1
24
MKÛ=
24
7
MKÛ=
24
7
MK CK
AB AC
KI AK
CD AC
ì
=
ï
ï
í
ï
=
ï
î
MK MK CK AK
AB CD AC AC
Þ+=+
68
MK MK AK KC
AC
+
Þ+=
7
1
24
MK AC
AC
Þ==
24
7
MKÞ=
Trang 16
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 2
I. Trắc nghiệm: (7.0đ)
Câu 1: Cho cấp số cộng với và . Công sai của cấp số cộng đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: .
Câu 2: Cho dãy số có số hạng tổng quát . Số hạng thứ của dãy số
là
A. B. C. D.
Lời giải
Chọn A
Ta có .
Câu 3: Trên đường tròn bán kính bằng , cung có số đo thì có độ dài là
A. . B. . C. . D. .
Lời giải
Chọn C
Độ dài cung là: .
Câu 4: Tập nghiệm của phương trình là:
A. . B. .
C. . D. .
Lời giải
Chọn B
Ta có: .
Câu 5: Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định bao nhiêu mặt
phẳng phân biệt từ các điểm đã cho?
( )
n
u
5
11u =
6
14u =
3
12
6
6-
65
14 11 3uud d d=+Û =+Þ=
( )
n
U
( )
*
1
,
2
n
n
UnN
n
-
=Î
+
100
100
33
.
34
U =
100
37
.
34
U =
100
39
.
34
U =
100
35
.
34
U =
100
100 1 33
100 2 34
U
-
==
+
4
8
p
3
p
16
p
2
p
4
p
4.
82
l
pp
==
2
cos
2
x =
3
2 ,
4
kk
p
p
ìü
±+
íý
îþ
Î!
2 ,
4
kk
p
p
ìü
±+
íý
îþ
Î!
3
2
4
, kk
p
p
ì
Î
ü
+
íý
îþ
!
5
,2
4
,2
4
kkk
pp
pp
-
Î
ìü
++
íý
îþ
!
2
cos
2
x =
cos cos
4
x
p
Û=
2
4
,xkk
p
p
Û=± + Î !
Trang 17
A. . B. . C. . D. .
Lời giải
Chọn D
Các mặt phẳng là .
Câu 6: Giá trị của biểu thức bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Câu 7: Mệnh đề nào trong các mệnh đề sau đây là sai?
A. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng
chung duy nhât.
B. Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì ba điểm đó thẳng
hàng.
C. Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác
nữa.
D. Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến
đó đôi một song song.
Lời giải
Chọn D
Vì nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến
đó đôi một song song hoặc đồng quy.
Câu 8: Khẳng định nào dưới đây là Sai?
A. Hàm số là hàm số lẻ. B. Hàm số là hàm số chẵn.
C. Hàm số là hàm số chẵn. D. Hàm số là hàm số lẻ.
Lời giải
Chọn B
Câu 9: Tập xác định của hàm số là:
A. . B. .
3
2
6
4
( ) ( ) ( ) ( )
,,,ABC ACD ABD BCD
sin cos sin cos
15 10 10 15
22
cos cos sin sin
5 15 15 5
pp pp
pp pp
+
-
3
1
1
2
1-
sin
sin cos sin cos sin
15 10
15 10 10 15 3
tan 3
22
2
3
cos cos sin sin cos
cos
515 155 3
15 5
pp
pp pp p
p
pp pp p
pp
æö
+
+
ç÷
èø
====
æö
-
+
ç÷
èø
2cos 1
sin 2
-
=
x
y
x
{ }
\,
p
=Î!"Dkk
\,
2
p
ìü
=Î
íý
îþ
!"
k
Dk
Trang 18
C. . D. .
Lời giải
Chọn B
Hàm số xác định . Tập xác định .
Câu 10: Cho cấp số nhân có , . Tính .
A. . B. . C. . D. .
Lời giải:
Chọn B
Ta có .
Câu 11: Biết và . Tính .
A. . B. . C. . D. .
Lời giải
Chọn A
Vì nên cùng dấu. Mà nên . Vậy .
Câu 12: Biết số theo thứ tự lập thành cấp số cộng. Giá trị của bằng
A. B. C. D.
Lời giải
Chọn C
theo thứ tự lập thành cấp số cộng nên .
Câu 13: Trong mặt phẳng , cho tứ giác có cắt tại , cắt tại , là
điểm không thuộc . Giao tuyến của và là
A. . B. . C. . D. .
Lời giải
Chọn B
\2;,
32
pp
p
ìü
=±+ Î
íý
îþ
!"
k
Dkk
\2,
3
p
p
ìü
=+Î
íý
îþ
!"Dkk
sin 2 0 ,
2
p
Û¹Û¹Î!
k
xxk
\,
2
p
ìü
=Î
íý
îþ
!"
k
Dk
1
3u =-
2
3
q =
5
u
5
16
27
u =
5
16
27
u =-
5
27
16
u =
5
27
16
u =-
4
4
51
2 16
. 3.
3 27
uuq
æö
==- =-
ç÷
èø
0
pa
-< <
cos
a
1
cos
5
a
=-
1
cos
5
a
=
2
cos
5
a
=-
2
cos
5
a
=
2
2
1
1 tan
cos
a
a
+=
2
22
111
cos
1 tan 1 2 5
a
a
Þ= ==
++
1
cos
5
a
Þ=±
sin , cos
aa
0
pa
-< <
1
cos
5
a
=-
3
5; ;15x
x
30.
75.
10.
20.
5; ;15x
5 15
10
2
x
+
==
( )
a
ABCD
AB
CD
E
AC
BD
F
S
( )
a
( )
SAB
( )
SCD
AC
SE
SF
SD
Trang 19
Hai mặt phẳng và có hai điểm chung là và nên có giao tuyến là
đường thẳng .
Câu 14: Cho cấp số nhân có , . Khi đó công bội là
A. . B. . C. . D. .
Bài giải
Chọn D
Cấp số nhân có công bội là .
Câu 15: Góc có số đo đổi ta rađian là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có (radian).
Vậy (radian). Chọn A
Câu 16: Trong các công thức sau, công thức nào sai?
A. . B. .
C. . D. .
Lời giải
Chọn D
Theo công thức nhân đôi ta có .
Vậy công thức sai là .
Câu 17: Trong các phương trình sau, phương trình nào có nghiệm?
A. . B. .
C. . D. .
Lời giải
Chọn B
Các dạng phương trình lượng giác cơ bản , có nghiệm khi và chỉ khi
.
Câu 18: Cho . Tính .
A. . B. . C. . D. .
Lời giải
Chọn A
( )
SAB
( )
SCD
S
E
SE
( )
n
U
1
1
2
U =
2
16U =
q
64
8
4
32
( )
n
U
2
1
16
32
1
2
u
q
u
===
108°
3
5
p
10
p
3
2
p
4
p
108. 3
108
180 5
pp
°= =
2
cos 2 2 cos 1aa=-
2
cos 2 1 2 sinaa=-
22
cos 2 cos sinaaa=-
22
cos 2 sin cosaaa=-
22 2 2
cos 2 cos sin 2 cos 1 1 2sinaaa a a=-= -=-
22
cos 2 sin cosaaa=-
sin 2 1
3
x
p
æö
+=
ç÷
èø
5
sin 2
2
x =
sin 2x =-
1a £
3
cos
4
a =
3
cos .cos
22
aa
7
16
23
8
23
16
7
8
Trang 20
Ta có: .
Câu 19: Giá trị bé nhất của hàm số là
A. B. C. D.
Lời giải
Chọn C
Ta có:
Câu 20: Cho hình lăng trụ . Gọi lần lượt là trung điểm của và ,
. Khẳng định nào sau đây đúng ?
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có
.
3
cos .cos
22
aa
( )
1
cos 2 cos
2
aa=+
( )
2
1
2cos 1 cos
2
aa=-+
19 3
1
28 4
æö
=-+
ç÷
èø
7
16
=
2
sin sin
3
yx x
p
æö
=++
ç÷
èø
3.
2
2.-
1.-
3.
2
-
22
2
33
sin sin 2 sin cos
322
xxxx
yx x
pp
p
æöæö
++ +-
ç÷ç÷
æö
=++=
ç÷ç÷
ç÷
èø
ç÷ç÷
èøèø
1
2sin cos 2. sin sin .
332 3 3
xxx
pp p p
æöæö æöæö
=+ = +=+
ç÷ç÷ ç÷ç÷
èøèø èøèø
1 sin 1.
3
x
p
æö
-£ + £
ç÷
èø
.
¢¢¢
ABC A B C
,MN
¢
BB
¢
CC
( ) ( )
mp mpAMN A B C
¢
Ç
¢¢
D=
// D AB
// D AC
// D BC
//
¢
D AA
( ) ( )
( )
( )
Δ
/
Δ/
//
Ç
ü
ï
Ì
ï
Þ
ý
¢¢
Ì
¢¢
¢
ï
¢
ï
¢¢
¢
=
¢
þ
C
mp AMN mp A
M
B
N
B
BC
MN
C
AMN
B
B
C
C
A
Trang 21
Câu 21: Cho phương trình . Phương trình nào sau đây tương
đương với phương trình
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có
Câu 22: Cho hình chóp có đáy là hình thang . Gọi lần lượt
là trung điểm của , và . Hãy cho biết thiết diện của hình chóp
khi
cắt bởi mặt phẳng là hình gì?
A. Hình thang. B. Hình chữ nhật.
C. Hình tam giác. D. Hình bình hành.
Lời giải
Chọn A
Trong mp , gọi .
Khi đó : và . (1)
Xét có , lần lượt là trung điểm của , .
Ta có: ; ; ;
,
qua
kẻ đường
thẳng song song với cắt tại .
Khi đó :
và . (2)
Từ (1) và (2), thiết diện của hình chóp là tứ giác .
Tứ giác có nên là hình thang.
Câu 23: Cho hình chóp tứ giác Gọi lần lượt là trọng tâm các tam giác và
Khi đó song song với đường thẳng
A. B. C. D.
Lời giải
Chọn D
cos .cos 7 cos 3 .cos 5xx xx=
( )
1
( )
1
cos 4 0x =
sin 5 0x =
sin 4 0x =
cos 3 0x =
cos .cos 7 cos 3 .cos 5xx xx=
cos8 cos 6 cos 8 cos 2xxxxÛ+=+
cos 6 cos 2 0xxÛ-=
2 sin 4 .sin 2 0xxÛ- =
sin 4 0xÛ=
ABCD
( )
//AD BC
SB
CD
AC
( )
MNP
F
E
P
A
B
D
C
S
M
N
E NP AB=Ç
( ) ( )
MNP ABCD NEÇ=
( ) ( )
MNP SAB EMÇ=
ACDD
P
N
AC
CD
Þ
// //NP AD BC
//NP BC
( )
NP MNPÌ
( )
BC SBCÌ
( ) ( )
MMNP SBCÎÇ
M
BC
SC
F
( ) ( )
MNP SBC MFÇ=
( ) ( )
MNP SCD FNÇ=
MENF
MENF
//MF EN
MENF
..S ABCD
12
,GG
SAC
.ACD
12
GG
.BC
.AC
.AD
.SD
Trang 22
Gọi là trung điểm của . Trong , ta có: , suy ra
.
Câu 24: Cho cấp số cộng có công sai và số hạng đầu . Tìm số hạng tổng quát
.
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có .
Câu 25: Cho hình tứ diện . Phát biểu nào sau đây là đúng?
A. Tồn tại một mặt phẳng chứa và . B. và song song với nhau.
C. và cắt nhau. D. và không có điểm chung.
Lời giải
Chọn D
Vì là tứ diện nên và không cùng nằm trên một mặt phẳng.
Do đó và không có điểm chung.
Câu 26: Dãy số nào trong các dãy số sau đây là dãy số bị chặn trên?
A. . B. .
E
AC
()mp SED
12
1
3
EG EG
ES ED
==
12
//GG SD
( )
n
u
4d =
1
3u =
n
u
34
n
un=+
31
n
un=+
43
n
un=+
41
n
un=-
( ) ( )
1
134141
n
uu n d n n=+- =+ -= -
ABCD
AD
BC
AB
CD
AC
BD
AC
BD
ABCD
AC
BD
AC
BD
( )
23
,
4
nn
n
uu nN
n
*
+
="Î
+
( )
,21
nn
uu n nN
*
=+"Î
Trang 23
C. . D. .
Lời giải
Chọn A
Ta có: nên dãy số bị chặn trên.
Câu 27: Giả sử được rút gọn thành khi đó bằng
A. B. C. D.
Lời giải
Chọn D
Ta có
.
Câu 28: Cho hàm số ; trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có tập xác định B. Đồ thị hàm số đi qua gốc tọa độ.
C. Hàm số là một hàm số lẻ. D. Hàm số có chu kỳ tuần hoàn .
Lời giải
Chọn B
Điều kiện: , nên hàm số có tập xác định là: ,
nên B đúng
Hàm số là hàm số lẻ nên D đúng
Hàm số là hàm số tuần hoàn chu kỳ , nên A đúng. Vậy C sai.
Câu 29: Rút gọn biểu thức ta
được
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có:
( )
2
,
nn
uu n nN
*
="Î
( )
,
nn
uu nnN
*
="Î
( )
( )
245
23 5
,22
44 4
nn
n
n
uu nN
nn n
*
+-
+
== =-<"Î
++ +
tan tan tan
33
Ax x x
pp
æöæö
=-+
ç÷ç÷
èøèø
tanA nx=
n
2
1
4
3
tan tan tan
33
Ax x x
pp
æöæö
=-+
ç÷ç÷
èøèø
3 tan 3 tan
tan . .
1 3 tan 1 3 tan
xx
x
xx
-+
=
+-
2
2
3tan
tan .
13tan
x
x
x
-
=
-
3
2
3tan tan
13tan
xx
x
-
=
-
tan 3x=
{ }
\,Dkk
p
=Î!"
T
p
=
sin 0 ,xxkk
p
¹Û¹ Î!
{ }
\,Dkk
p
=Î!"
T
p
=
( ) ( )
22
85 5
sin cos 2017 sin 33 sin
22
Ax x x x
pp
pp
æö æö
=++ ++ ++ -
ç÷ ç÷
èø èø
1A =
2A =
0A =
( ) ( )
22
85 5
sin cos 2017 sin 33 sin
22
Ax x x x
pp
pp
æö æö
=++ ++ ++ -
ç÷ ç÷
èø èø
( ) ( )
22
sin 42 cos 2016 sin 32 sin 2
22
Ax x x x
pp
pppppp
æö æö
Û= + + + +++ +++ - -
ç÷ ç÷
èø èø
( ) ( )
22
sin cos sin sin
22
Ax x x x
pp
pp
æö æö
Û= + + ++ ++ -
ç÷ ç÷
èø èø
22
cos cos sin sin
2
Axx x x
p
æö
Û= - + + -
ç÷
èø
22
sin cosAxxÛ= +
Trang 24
.
Câu 30: Phương trình có tập nghiệm là
A. . B. .
C. . D. .
Lời giải
Chọn B
PT .
Vậy tập nghiệm của phương trình là: .
Câu 31: Cho tam giác cân tại đỉnh , biết độ dài cạnh đáy , đường cao và cạnh
bên theo thứ tự lập thành cấp số nhân với công bội . Giá trị của bằng
A. . B. C. . D. .
Lời giải
Chọn A
Đặt . Theo giả thiết ta có lập cấp số nhân, suy ra
Mặt khác tam giác cân tại đỉnh nên
Do đó (vì )
Lại có nên suy ra .
Câu 32: Tính tổng T tất cả các nghiệm của phương trình trên đoạn .
A. . B. . C. . D. .
Lời giải
Chọn C
Xét phương trình:
1AÛ=
3sin2 cos2 2xx-=
2
2|
3
Skk
p
p
ìü
=+ Î
íý
îþ
!
|
3
Skk
p
p
ìü
=+ Î
íý
îþ
!
5
|
12
Skk
p
p
ìü
=+ Î
íý
îþ
!
|
32
k
Sk
pp
ìü
=+ Î
íý
îþ
!
31
sin 2 cos 2 1 sin 2 1 2 2
22 6 62 3
xx x x kxk
ppp p
pp
æö
Û-=Û-=Û-=+Û=+
ç÷
èø
|
3
Skk
p
p
ìü
=+ Î
íý
îþ
!
ABC
A
BC
AH
AB
q
2
q
21
2
+
21
2
-
22
2
+
22
2
-
;;BC a AB AC b AH h====
,,ahb
2
.h ab=
ABC
A
22 2
22
24
a
bb a
hm
+
== -
( )
22 2
22
440 222
24
bb a
ab a ab b a b
+
-=Û+ - =Û= -
,0ab>
2
bqa=
2
122221
42
22 2
b
q
a
++
== = =
-
2
2 sin 3 cos 0
44
xx
-=
0; 8
p
éù
ëû
4
p
=T
0=T
8
p
=T
16
p
=T
( )
222
2 sin 3 cos 0 2 1 cos 3 cos 0 2 cos 3 cos 2 0 1
44 4 4 44
xx x x xx
æö
-=Û- -=Û- -+=
ç÷
èø
Trang 25
Đặt: . Khi đó phương trình (1) trở thành:
Với
Xét : .
Mà
Xét : .
Mà
Vậy
Câu 33: Có bao nhiêu giá trị nguyên của tham số thuộc đoạn để phương trình
có nghiệm?
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có :
*Nếu : (vô lý) nên không thỏa phương trình.
*Nếu , chia hai vế của phương trình (*) cho ta được:
Để phương trình có nghiệm thì
Vì nguyên và nên . Vậy có tất cả giá trị
để phương trình có nghiệm.
Câu 34: Cho tứ diện . Gọi và lần lượt là trung điểm của các cạnh và ;
lần lượt là các điểm trên các đoạn và sao cho , . Gọi là
giao điểm của và ; là giao điểm của và . Khẳng định nào sau đây
sai?
A. .
B. Cá đường thẳng đồng quy.
cos ; 1;1
4
x
tt
éù
=Î-
ëû
( )
2
1
2
2320
2
t
tt
tL
é
=
ê
--+=Û
ê
=-
ê
ë
4
28
11
43 3
cos cos cos ;
242 43
4
28
43 3
x
kxk
xx
tk
x
kx k
pp
pp
p
pp
pp
éé
=+ = +
êê
=Þ =Û = Û Û Î
êê
êê
=- + =- +
êê
ëë
!
4
8
3
xk
p
p
=+
415
0; 8 0 8 8
366
xkk
p
ppp
éù
ÎÞ£+£Û-££
ëû
{ }
4
0
3
kk x
p
ìü
ÎÞÎ ÞÎ
íý
îþ
!
4
8
3
xk
p
p
=- +
417
0; 8 0 8 8
366
xkk
p
ppp
éù
ÎÞ£-+£Û££
ëû
{ }
20
1
3
kk x
p
ìü
ÎÞÎ ÞÎ
íý
îþ
!
T =
4 20
8
33
pp
p
+=
m
( )
22
11sin 2 sin 2 3cos 2xm x x+- + =
21
15
16
6
( )
22
11sin 2 sin 2 3cos 2xm x x+- + =
( ) ( )
22
11sin 2 2 sin cos 3 cos 2 *xm xx xÛ+- +=
( )
*112®=
2
cos x
( )
( )
22
11tan 2 2 tan 3 2 1 tanxm x x+- +=+
( )
2
9tan 2 2 tan 1 0xm xÛ+-+=
( ) (
] [
)
2
290 ;15;mm
¢
D= - - ³ Û Î-¥- È +¥
m
[ ]
10 ;10m Î-
{ }
10 ; 9 ;...; 1;5 ;6;...;10mÎ- - -
16
m
ABCD
I
K
AB
CD
,JE
AD
BC
3AD JD=
2EB EC=
F
IJ
BD
H
AC
IE
( )
BC IJK EÇ=
,,IE AC JK
Trang 26
C. Giao điểm của và mặt phẳng là trung điểm của .
D. .
Lời giải
Chọn C
Ta có A đúng.
.
Trong kẻ , . Ta có .
Trong tam giác có là trung điểm của đoạn .
Trong kẻ , . Ta có (1).
Lại có . (2).
Từ (1) và (2) suy ra . Do đó B đúng D
sai.
Ba mặt phẳng , và cắt nhau theo ba giao tuyến , và
nên ba đường thẳng , và đồng quy tại C đúng.
Câu 35: Cho tứ diện , và lần lượt là trung điểm và . Mặt phẳng qua
cắt tứ diện theo thiết diện là đa giá Khẳng định nào sau đây đúng?
A. là tam giá
B. là hình thang.
BC
( )
IJK
BC
( )
IJ BCD FÇ=
M
L
F
H
E
J
K
I
D
C
B
A
( ) ( )
BCD ABD BDÇ=
( )
IJ BCDÞÇ =
IJ BD FÇ=
Þ
( ) ( )
IJK BCD KFÇ=
( )
BC IJKÞÇ =
BC KF E
¢
Ç=
( )
ABD
//DL AB
LIJÎ
2
DL JD
IA JA
==
1
2
DL IAÞ=
BIF
1
2
DL BI=
!!!" !!"
DÞ
BF
( )
BCD
//DM BC
M EFÎ
1
2
DM DF
BE BF
==
¢
1
2
DM BE
¢
Þ=
1
DM KD
CE KC
==
¢
DM CE
¢
Þ=
2'BE CE
¢
=
EE
¢
º
( )
BC IJK EÞÇ =
Þ
Þ
( )
ABC
( )
ACD
( )
IJK
IE
AC
JK
IE
AC
JK
H
Þ
ABCD
M
N
AB
AC
( )
a
MN
ABCD
( )
T
( )
T
( )
T
Trang 27
C. là tam giác hoặc hình thang hoặc hình bình hành.
D. là hình chữ nhật.
Lời giải
Chọn C
TH1: Mặt phẳng cắt đoạn tại bất kỳ, .
.
Gọi trong .
Ta có: nên tứ giác là hình thang.
Nếu là trung điểm , khi đó và lần lượt là các đường trung bình trong
và , nên và . Khi đó tứ giác là hình
bình hành.
TH2: Mặt phẳng cắt đoạn tại bất kỳ, .
Dễ thấy thiết diện tạo bởi mặt phẳng và tứ diện là .
II. Tự luận: (3.0đ)
Câu 36: Tập nghiệm của phương trình là
Lời giải
( )
T
( )
T
( )
a
CD
E
,ECED¹¹
( ) ( )
( )
( )
EBCD
MN BC
MN
BC BCD
a
a
ÎÇ
ì
ï
ï
í
Ì
ï
ï
Ì
î
!
( ) ( )
// //
Ex BCD
Ex MN BC
a
=Ç
ì
Þ
í
î
F Ex BD=Ç
( )
BCD
//MN EF
MNEF
E
CD
MN
EF
ABCD
BCDD
//MN EF
1
2
MN EF BC==
MNEF
( )
a
AD
E
EA¹
( )
a
ABCD
MNED
01cos2cos =++ xx
cos 2 cos 1 0 2 0x x cosx cosx++=Û +=
Trang 28
Câu 37: Cho cấp số nhân có , công bội . Hỏi là số hạng thứ mấy của
Lời giải
Giả sử là số hạng thứ của với .Ta có
. Do đó là số hạng thứ của .
Câu 38: Cho hình chóp , là điểm nằm trong tam giác . , lần lượt là trung
điểm của và . Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng
Lời giải
Trong mặt phẳng
Trong mặt phẳng
Trong mặt phẳng
Ta có: , ,
,
Vậy Tìm thiết diện của hình chóp cắt bởi mặt phẳng là ngũ giác
( )
0
210
1
2
cosx
cosx cosx
cosx
=
é
ê
Û+=Û
ê
=-
ë
2
2
,
2
2
3
xk
k
xk
p
é
=+ p
ê
ÛÎ
ê
p
ê
=± + p
ê
ë
Z
( )
n
u
2q =-
192-
( )
?
n
u
192-
n
( )
n
u
*
n Υ
1
1
192 .
n
uq
-
-=
( ) ( )
1
192 3 . 2
n -
€- =- -
( )
1
64 2
n -
€=-
( ) ( )
61
22
n -
€- =-
61n€=-
7 n€=
192-
7
( )
n
u
G
SCD
E
F
AB
AD
( )
EFG
( )
:;ABCD EF BC I«=
EF CD J«=
( )
:;SCD GJ SC K«=
GJ SD M«=
( )
:SBC KI SB H«=
( ) ( )
GEF ABCD EF«=
( ) ( )
GEF SAD FM«=
( ) ( )
GEF SCD MK«=
( ) ( )
GEF SBC KH«=
( ) ( )
GEF SAB HE«=
( )
EFG
EFMKH
Trang 29
Câu 39: Cho hình chóp có đáy là hình thang có . là điểm di động trong
hình thang . Qua kẻ các đường thẳng song song với và lần lượt cắt
các mặt phẳng và tại và . Cho , . Tìm giá trị lớn
nhất của biểu thức .
Lời giải
Giả sử , . Khi đó .
Đặt .
Ta có:
Khi đó áp dụng bất đẳng thức Cô-si:
.
Dấu bằng xảy ra khi .
------------- HẾT -------------
//AD BC
M
ABCD
M
SA
SB
( )
SBC
( )
SBD
N
P
SA a=
SB b=
2
.TMNMP=
AM BC IÇ=
BM AD JÇ=
,NSIPSJÎÎ
;MN x MP y==
1.
MN IM
xy
SA IA
MP JM AM
ab
SB JB AI
ì
=
ï
ï
Þ+=
í
ï
==
ï
î
3
2
22 2 2
14
. . . . .4 .4
2 2 27 2 2 27
xxy x x y ab
TMNMPxy ab ab
aab a ab
æö æ ö
=== £++=
ç÷ ç ÷
èø è ø
2
3
3
a
x
b
y
ì
=
ï
ï
í
ï
=
ï
î
Trang 30
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 3
I. Trắc nghiệm: (7.0đ)
Câu 1: Ba số theo thứ tự là ba số hạng liên tiếp của một cấp số nhân. Tìm công
bội của cấp số nhân đó.
A. . B. . C. . D. .
Lời giải
Chọn A
Do là một cấp số nhân .
Vậy công bội của cấp số nhân là .
Câu 2: Hàm số nào sau đây là hàm số lẻ?
A. . B. . C. . D. .
Lời giải
Chọn B
Tập xác định .
Ta có .
Đồng thời .
Do đó hàm số là hàm số lẻ.
Câu 3: Trong các công thức sau, công thức nào đúng?
A. . B. .
C. . D. .
Lời giải
Chọn A
Ta có .
Câu 4: Cho dãy số cho bởi công thức tổng quát . Khi đó bằng
A. . B. . C. . D. .
Lời giải
Chọn D
.
Câu 5: Phương trình có nghiệm là
A. . B. . C. . D. .
Lời giải
Chọn C
3; ; 3 3x--
q
3q =±
3q =-
3q =
3q =±
3; ; 3 3x--
2
93xxÞ=Û=±
3
3
x
q ==±
-
3
1yx=+
( )
3
sin 2yx=
2
tanyx=
cos 2yx=
( )
3
sin 2yx=
D = !
xD xD"Î Þ- Î
( ) ( ) ( ) ( )
33
sin 2 sin 2yx x x yx-= - =- =-
( )
3
sin 2yx=
sin 2 2 sin cosaaa=
22
sin 2 cos sinaaa=-
sin 2 2 sinaa=
sin 2 sin cosaaa=+
sin 2 2 sin cosaaa=
( )
n
u
2*
34,
n
unn=+ Ε
5
u
97-
23
503
103
22
5
3 4 3 4.5 103
n
unu=+ Þ =+ =
sin 2 1x =
2
4
xk
p
p
=+
3
4
xk
p
p
=+
4
xk
p
p
=+
42
xk
pp
=+
Trang 31
Ta có: , .
Câu 6: Cho hai đường thẳng phân biệt và trong không gian. Có bao nhiêu vị trí tương đối
giữa và .
A. . B. . C. . D. .
Lời giải
Chọn C
Hai đường thẳng phân biệt và trong không gian có ba vị trí tương đối là: cắt nhau,
song song, chéo nhau.
Câu 7: Khẳng định nào sau đây đúng?
A. B. .
C. . D. .
Lời giải
Chọn C
Do nên .
Câu 8: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Một điểm và một đường thẳng. B. Hai đường thẳng cắt nhau.
C. Bốn điểm phân biệt. D. Ba điểm phân biệt.
Lời giải
Chọn B
A sai khi ba điểm thẳng hàng.
B sai khi điểm đó thuộc đường thẳng.
D sai khi 4 điểm thẳng hàng hoặc bốn điểm không đồng phẳng.
Câu 9: Cung có số đo đổi sang đơn vị độ bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có đổi sang đơn vị độ bằng .
Câu 10: Một đường tròn có bán kính . Tính độ dài của cung trên đường tròn đó có số
đo bằng .
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có:
.
sin 2 1 2 2
2
xxk
p
p
=Û = +
4
xk
p
p
Û= +
( )
k Î !
a
b
a
b
1
4
3
2
a
b
tan15 tan 75°= °
sin15 sin 75°= °
cos15 cos 165°=- °
sin15 sin165°=- °
15 165 180°+ °= °
( )
cos15 cos 180 15 cos165°=- °- ° =- °
5
3
rad
p
300°
5°
600°
270°
5
3
rad
p
5.180
300
3
°
=°
3Rcm=
l
0
60
2lcm
p
=
4
lcm
p
=
lcm
p
=
2
lcm
p
=
.3.
3
lR cm
p
ap
===
Trang 32
Câu 11: Phương trình có nghiệm là
A. . B. .
C. . D. .
Lời giải
Chọn A
Công thức nghiệm tổng quát của phương trình .
Câu 12: Tìm tập xác định của hàm số .
A. . B. .
C. . D. .
Lời giải
Chọn B
Hàm số xác định khi và chỉ khi , .
Câu 13: Cho hình chóp với là hình bình hành. Khi đó giao tuyến của hai mặt
phẳng và là
A. Đường thẳng . B. Đường thẳng .
C. Đường thẳng . D. Đường thẳng .
Lời giải
Chọn D
Ta thấy .
Câu 14: Giá trị biểu thức là
A. . B. . C. . D. .
Lời giải
Chọn A
.
Câu 15: Biết số theo thứ tự lập thành cấp số cộng. Giá trị của bằng
A. B. C. D.
Lời giải
cos cosx
a
=
( )
2,xkk
ap
=± + Î!
( )
,xkk
ap
=- + Î!
( )
2,xkk
ap
=+ Î!
( )
,xkk
ap
=± + Î!
cos cosx
a
=
2
2
xk
xk
ap
ap
=+
é
Û
ê
=- +
ë
( )
k Î !
{ }
\2|kk
p
Î! Z
\|
2
kk
p
p
ìü
+Î
íý
îþ
! Z
{ }
\|kk
p
Î! Z
\2|
2
kk
p
p
ìü
+Î
íý
îþ
! Z
cos 0
2
xxk
p
p
¹Û¹ +
( )
k ÎZ
ABCD
( )
SAC
( )
SAD
SA
SB
SD
SC
( ) ( )
SAC SAD SAÇ=
sin .cos sin .cos
15 10 10 15
22
cos .cos sin .sin
15 5 15 5
pp pp
pp pp
+
-
1
1-
3
2
-
3
2
sin sin
sin .cos sin .cos
15 10 6
15 10 10 15
1
22
2
cos .cos sin .sin
cos cos
15 5 15 5
15 5 3
pp p
pp pp
pp pp
pp p
æöæö
+
+
ç÷ç÷
èøèø
===
æöæö
-
+
ç÷ç÷
èøèø
3
5; ;15x
x
30.
75.
10.
20.
Trang 33
Chọn C
theo thứ tự lập thành cấp số cộng nên .
Câu 16: Cho cấp số nhân thỏa mãn Công bội của cấp số nhân bằng
A. B. C. D.
Lời giải
Chọn C
Gọi là công bội của cấp số nhân .
Với suy ra .
Vậy công bội của cấp số nhân là
Câu 17: Cho cấp số cộng có số hạng đầu và công sai . Số 100 là số hạng thứ
mấy của cấp số cộng?
A. 15. B. 20. C. 35. D. 36.
Lời giải
Chọn D
Ta có: .
Câu 18: Cho cấp số cộng thỏa mãn . Tìm của cấp số cộng đó.
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có
Suy ra .
Câu 19: Giá trị lớn nhất của hàm số là
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có .
Dấu bằng xảy ra khi .
5; ;15x
5 15
10
2
x
+
==
( )
n
u
15
3, 48.uu==
2.-
2.
2.±
16.
q
( )
n
u
15
3, 48uu==
1
1
1
4
4
1
3
3
3
2
.48
16
u
u
u
q
uq
q
=
=
=
ì
ì
ì
ÛÛ
ííí
=±
=
=
î
î
î
( )
n
u
2.q =±
( )
n
u
1
5u =-
3d =
( ) ( )
1
11005 1.310038 36
n
uu n d n n n=+- Û =-+- Û = -Û=
( )
n
u
1910
74
== u,u
10
u
29
10
=u
30
10
=u
31
10
=u
28
10
=u
4
1
1
7
1
10
310
1
19
619
3
u
ud
u
u
ud
d
=
+=
=
ì
ì
ì
ÞÞ
íí í
=
+=
=
î
î
î
10 1
928uud=+ =
3sin 2 4
2
yx
p
æö
=+-
ç÷
èø
1
7
2
1-
3sin 2 4 3 4 1
2
yx
p
æö
=+-£-=-
ç÷
èø
( )
2
sin 3 1 3 2
222 3
k
xxkxk
ppp p
p
æö
+=Û+=+ Û= Î
ç÷
èø
!
Trang 34
Câu 20: Hàm số có chu kì là
Số mệnh đề đúng là
A. . B. . C. . D. .
Lời giải
Chọn A
+ Hàm số có chu kì là . Mệnh đề 2 sai.
+ Hàm số
có chu kì . Mệnh đề 1 đúng.
+ Hàm số
có chu kì . Mệnh đề 3 sai.
Vậy có 1 mệnh đề đúng.
Câu 21: Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
. Đường thẳng nào sau đây không song song với đường thẳng ?
A. .
B.
. C. . D. .
Lời giải
Chọn D
Dễ thấy
Giả sử , vô lí.
Do đó giả sử sai. Vậy và không song song.
Câu 22: Dãy số nào trong các dãy số sau đây là dãy số bị chặn dưới?
A. . B. .
C. . D. .
Lời giải
Chọn B
2.sin 3 .cosyxx=
3
p
1
2
3
0
sin 2yx=
2
2
T
p
p
==
2 sin 2 3cos 3
36
yx x
pp
æöæö
=++-
ç÷ç÷
èøèø
22 2
;;2
23 3
T BCNN BCNN
pp p
pp
æö æö
===
ç÷ ç÷
èø èø
2.sin 3 .cos sin 4 sin 2yxxxx==+
;
42 2
T BCNN
pp p
æö
==
ç÷
èø
.S ABCD
,,,SA SB SC SD
IJ
CD
AB
EF
AD
// , // , /EF.IJ AB IJ CD IJ
IJ//AD 0 (IJ, ) ( , )
o
AD AB ADÞ= =
IJ
AD
( )
2
,
nn
uu n n
*
=- " Ε
( )
,1
nn
uu n n
*
=-"Ε
( )
,2
nn
uu nn
*
=- " Ε
( )
,
nn
uu nn
*
=- " Ε
Trang 35
Ta có: nên dãy số bị chặn dưới.
Câu 23: Rút gọn biểu thức .
A. . B. . C. . D. .
Lời giải
Chọn A
.
Câu 24: Nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có:
.
Câu 25: Tính biết .
A. . B. . C. .D. .
Lời giải
Chọn C
Cách kháC. . Ta có .
Thay vào ta được .
C2: Đặt . Với
Suy ra .
Câu 26: Tính
A. . B. . C. . D. .
( )
,10
nn
uu n n
*
=-³ "Ε
sin sin 3 sin 5
cos cos 3 cos 5
aaa
A
aaa
++
=
++
tan 3a
1 tan 3a-
sin 3a
cos 3a
sin sin 3 sin 5
cos cos 3 cos 5
aaa
A
aaa
++
=
++
sin 5 sin sin 3
cos 5 cos cos 3
aa a
aa a
++
=
++
2sin 3 .cos 2 sin 3
2cos3 .cos2 cos3
aa a
aa a
+
=
+
( )
( )
sin 3 2 cos 2 1
tan 3
cos 3 2 cos 2 1
aa
a
aa
+
==
+
sin cos cos2 0xx x=
2
k
p
4
k
p
8
k
p
k
p
sin cos cos2 0xx x=
Û
1
sin2 cos 2 0
2
xx=
Û
1
sin4 0
4
x =
Û
4xk
p
=
Û
4
k
x
p
=
( )
k Î!
15cos
32cos
B
a
a
+
=
-
tan 2
2
a
=
20
9
2
21
10
21
-
2
21
-
22
2
11
1 tan cos
225
cos
2
aa
a
+= Þ =
2
13
cos 2 cos 1 2. 1
255
a
a
=-=-=-
3
1 5.
10
5
3
21
3 2.
5
B
æö
+-
ç÷
èø
==-
æö
--
ç÷
èø
2
2
1
tan cos
21
t
t
t
a
a
-
=Þ =
+
14 3
2cos
14 5
t
a
--
=Þ = =
+
3
15
210
5
21
3
21
32
5
5
B
-
æö
+
ç÷
--
èø
===
-
æö
-
ç÷
èø
20 2 0 2 0 20 2 0
sin 5 sin 10 sin 15 ...sin 8 sin 85S =+ + + +
9
19
2
8
17
2
Trang 36
Lời giải
Chọn D
.
Câu 27: Cho tứ diện . là một điểm bất kỳ nằm trên đoạn (khác ). Mặt phẳng
qua và song song với các đường thẳng . Thiết diện của với tứ
diện đã cho là hình gì?
A. Hình thang. B. Hình vuông. C. Hình bình hành. D. Hình chữ nhật.
Lời giải
Chọn C
Trong mp , qua kẻ đường thẳng song song với , cắt tại .
Trong mp , qua kẻ đường thẳng song song với , cắt tại .
Trong mp , qua kẻ đường thẳng song song với , cắt tại .
Thiết diện của với tứ diện là tứ giác .
Mặt khác là hình bình hành.
Câu 28: Biết phương trình có nghiệm dương bé nhất là , ( với là
các số nguyên dương và phân số tối giản). Tính
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có:
20 2 0 2 0 2 0 2 0
sin 5 sin 10 sin 15 ...sin 80 sin 85S =+ + + +
( ) ( ) ( )
20 2 0 2 0 2 0 2 0 2 0 2 0
117
sin 5 sin 85 sin 10 sin 80 ... sin 15 sin 75 sin 45 8
22
=+ + + + + + =+=
ABCD
M
AC
,AC
( )
P
M
,AB CD
( )
P
( )
ABC
M
AB
BC
N
( )
ACD
M
CD
AD
Q
( )
BCD
M
CD
BD
P
Þ
( )
P
MNPQ
( )
( )
// //
// //
MQ NP CD
MN PQ AB
ì
ï
í
ï
î
MNPQÞ
3cos sin 2xx+=
a
b
p
,ab
a
b
2
.aab+
65S =
135S =
75S =
85S =
3cos sin 2xx+=
Û
31 2
cos sin
222
xx+=
Û
2
sin .cos cos .sin
332
xx
pp
+=
Û
2
sin
32
x
p
æö
+=
ç÷
èø
Û
sin sin
34
x
pp
æö
+=
ç÷
èø
Û
2
34
3
2
34
xk
xk
pp
p
pp
p
é
+=+
ê
ê
ê
+= +
ê
ë
( )
k Î!
Trang 37
.
Nghiệm dương bé nhất của phương trình là .
.
Câu 29: Cho tứ diện . Gọi và lần lượt là trọng tâm và . Chọn khẳng
định đúng.
A. cắt . B. song song với .
C. song song với . D. chéo nhau với .
Lời giải
Chọn B
Gọi là trung điểm .
Vì và lần lượt là trọng tâm tam giác và nên: .
Suy ra: .
Câu 30: Cho tứ diện có và theo thứ tự là trung điểm của và , là trọng tâm
tam giác . Giao tuyến của hai mặt phẳng và là đường thẳng
A. qua và song song với . B. qua và song song với .
C. qua và song song với . D. qua và song song với .
Lời giải
Chọn B
Û
2
12
5
2
12
xk
xk
p
p
p
p
é
=- +
ê
ê
ê
=+
ê
ë
( )
k Î!
Þ
5
12
p
Þ
5; 12ab==
Þ
2
85aab+=
ABCD
I
J
ABCD
ABDD
IJ
AB
IJ
CD
IJ
AB
IJ
CD
J
E
I
A
B
C
D
E
AB
I
J
ABC
ABD
1
3
EI EJ
EC ED
==
//IJ CD
ABCD
I
J
AD
AC
G
BCD
( )
GIJ
( )
BCD
J
BD
G
CD
G
BC
I
AB
Trang 38
+) và theo thứ tự là trung điểm của và nên là đường trung bình của tam
giác , mà . (1)
+) là trọng tâm tam giác nên là điểm chung của hai mặt phẳng
và .(2)
Từ (1) và (2) suy ra giao tuyến của hai mặt phẳng và là đường thẳng đi
qua và song song với .
Câu 31: Cho hình chóp . Gọi , lần lượt là trung điểm của và , là điểm
trên cạnh sao cho . Gọi là giao điểm của với mặt phẳng .
Tính .
A. . B. . C. . D. .
Lời giải
Chọn B
Tìm giao điểm của với mặt phẳng
Chọn mặt phẳng phụ chứa
Trong gọi
Suy ra . Khi đó là giao điểm của và .
I
J
AD
AC
IJ
ACD
// IJ CDÞ
( )
CD BCDÌ
( )
// IJ BCDÞ
G
BCD
( )
GBCDÎ
GÞ
( )
GIJ
( )
BCD
( )
GIJ
( )
BCD
G
CD
.S ABC
M
N
SA
BC
P
AB
1
3
AP
AB
=
Q
SC
( )
MNP
SQ
SC
1
6
1
3
1
2
2
3
Q
SC
( )
MNP
( )
SAC
SC
( )
ABC
H AC NP=Ç
( ) ( )
MNP SAC HMÇ=
Q
HM
SC
Trang 39
Gọi là trung điểm
Ta có (vì là trung điểm của và nên )
Mà nên
Mặt khác ta có (vì )
Mà nên .
Câu 32: Cho tứ diện đều có các cạnh đều bằng . Gọi là trọng tâm tam giác ,
là trung điểm của cạnh . Diện tích thiết diện của tứ diện khi cắt bởi mặt phẳng
(tính theo ) bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Gọi là giao điểm của và thì là trung điểm của
.
Thiết diện của tứ diện khi cắt bởi mặt phẳng là tam giác .
Ta có .
cân tại có đường cao
(đvdt).
L
AC
1
2
3
1
3
2
AB
HA AP
HL LN
AB
== =
,MN
AC
BC
1
2
LN AB=
2
3
HA HLÞ=
21
33
LC AL HL HA HL HL HL==-=- =
3
4
HL HC=
4
3
HC QC
HL ML
==
//ML SC
2ML SC=
31
23
QC SQ
SC SC
=Þ =
ABCD
a
G
ABC
M
CD
( )
AMG
a
2
11
2
a
2
11
32
a
2
11
16
a
2
11
8
a
N
AG
BC
N
BC
( )
AMG
AMN
3
2
AM AN a==
Þ
AMND
A
2
2
22
311
244
aaa
AH AM HM
æö
æö
=-= -=
ç÷
ç÷
ç÷
èø
èø
2
111111
...
224216
AMN
aaa
SAHMN== =
Trang 40
Câu 33: Cho phương trình . Tìm tập hợp tất cả các giá trị
thực của tham số để phương trình có nghiệm trên khoảng .
A. B. . C. . D. .
Lời giải
Chọn D
Ta có .
. (1)
Với , thì phương trình (1) tương đương:
.
.
Khi .
Câu 34: Số nghiệm của phương trình trên đoạn là:
A. . B. . C. . D. .
Lời giải
Chọn B
Xét phương trình:
ĐKXĐ:
Khi đó phương trình (1) trở thành:
2
(sin 1).(sin2 sin ) cosxxmxmx+-=
S
m
0;
6
p
æö
ç÷
èø
3
1;
2
S
æö
=-
ç÷
èø
( )
0;1S =
1
0;
2
S
æö
=
ç÷
èø
3
0;
2
S
æö
=
ç÷
èø
2
(sin 1).(sin2 sin ) cosxxmxmx+-=
(sin 1).(sin2 sin ) (1 sin ).(1 sin )xxmxmxxÛ+ - =- +
0; 1 sin 0
6
xx
p
æö
ÎÞ+¹
ç÷
èø
sin 2 sin (1 sin )xm x m x-=-
sin 2xmÛ=
33
0; sin 2 0; 0;
622
xxm
p
æö æö
æö
ÎÞÎ ÞÎ
ç÷ ç÷
ç÷
èø
èø èø
( ) ( )
2
1
31cot 31 0
sin
x
x
-- -+=
0;
p
éù
ëû
1
2
3
4
( ) ( )
( )
2
1
31cot 31 01
sin
x
x
-- -+=
sin 0 ;xxkk
p
¹Û¹ Î!
( ) ( )
( ) ( )
( )
( )
2
2
1cos
31. 31 0
sin
sin
1 3 1 .cos .sin 3 1 .sin 0
31 1cos2
1 .sin 2 3 1 . 0
22
31 31 1 3
.sin 2 . cos 2
22 2
62 62 62
.sin 2 .cos 2 2
44 4
x
x
x
xx x
x
x
xx
xx
-- -+=
Û- - - + =
--
Û- - + =
-+-
Û- =
-+ -
Û- =-
Trang 41
Đặt
Khi đó PT(2) trở thành:
Xét: . Vì
mà
Xét . Vì
mà , Với
Vậy phương trình đã cho có 2 nghiệm trên đoạn
Câu 35: Cho cấp số nhân thỏa mãn . Tổng số hạng đầu của cấp số nhân
là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có
.
Vậy tổng .
62
cos
4
62
sin
4
a
a
ì
-
=
ï
ï
í
+
ï
=
ï
î
( )
sin 2 . cos cos 2 .sin cos
sin 2 sin sin
22
22
2
4
;
3
22
2
4
xx
x
xk
xk
k
xk
xk
aaa
pp
aaa
p
p
aa p
ap
p
p
ap a p
p
-=-
æöæö
Û-=--=-
ç÷ç÷
èøèø
é
é
-=-+
=-+
ê
ê
ê
ÛÛÎ
ê
æö
ê
ê
-=- - +
=+
ç÷
ê
ê
ë
èø
ë
!
3
;
4
xkk
p
p
=+ Î!
331
0; 0
444
xkk
p
ppp
éù
ÎÞ£+£Û-££
ëû
3
0
4
kkx
p
ÎÞ=Þ=!
;
4
xkk
p
ap
=-+ Î!
15
0; 0
466
xkk
p
papp
éù
ÎÞ£-+£Û-££
ëû
0
4
kkx
p
a
ÎÞ=Þ= -!
62
cos
4
62
sin
4
a
a
ì
-
=
ï
ï
í
+
ï
=
ï
î
0;
p
éù
ëû
( )
n
u
123
41
13
26
uu u
uu
++=
ì
í
-=
î
8
( )
n
u
8
3280S =
8
3820S =
8
9841S =
8
1093S =
123
41
13
26
uu u
uu
++=
ì
í
-=
î
2
11 1
3
11
..13
.26
uuquq
uq u
ì
++ =
ï
Û
í
-=
ï
î
( )
( )
( )
2
1
2
1
113
.11 26
uqq
uq qq
ì
++ =
ï
Û
í
-++=
ï
î
( )
2
1
1 13
3
uqq
q
ì
++ =
ï
Û
í
=
ï
î
1
1
3
u
q
=
ì
Û
í
=
î
( )
8
1
8
1
1
uq
S
q
-
=
-
( )
8
11 3
3280
13
-
==
-
Trang 42
II. Tự luận: (3.0đ)
Câu 36: Tìm nghiệm của phương trình ?
Lời giải
+) Ta có
+)
Câu 37: Viết thêm bốn số vào giữa hai số và để được một cấp số nhân. Tổng các số hạng
của cấp số nhân đó là
Lời giải
Từ giả thiết ta có .
Suy ra tổng các số hạng của cấp số nhân đó là: .
Câu 38: Cho hình chóp tứ giác , gọi là giao điểm của hai đường chéo và .
Một mặt phẳng cắt các cạnh tương ứng tại các điểm .
CMR đồng quy
Lời giải
Trong mặt phẳng ta có .Dễ chứng minh
Do . Suy ra ba đường thẳng
đồng quy tại
Câu 39: Cho hình lập phương
có cạnh bằng . Cắt hình lập phương bằng một
mặt phẳng chứa đường chéo . Tìm giá trị nhỏ nhất của diện tích thiết diện thu
được.
Lời giải
22sin 3cos x x-=-
2
2 2 sin 3 1 2sin 2 sin 3-=-Û- -=-cos x x x x
2
sinx 1
si n si n 2 0
sinx 2 1 (VN)
xx
=
é
Û+-=Û
ê
=- <-
ë
sinx 1 2 ,
2
xkk
p
=Û = + p ÎZ
160
5
1
6
5
6
1
160
1
5
2
u
u
q
u
u
=
ì
Þ= =
í
=
î
( )
6
6
1
1
160 1
12
315
1
1
2
uq
S
q
æö
æö
-
ç÷
ç÷
ç÷
-
èø
èø
== =
-
O
AC
BD
( )
a
,,,SA SB SC SD
,,,MNPQ
,,MP NQ SO
( )
MNPQ
MP NQ RÇ=
( ) ( )
SAC SBD SOÇ=
( )
( )
( )
( )
R MP SAC R SAC
I SO
R NQ SBD R SBD
ÎÌ Î
ìì
ïï
Þ => Î
íí
ÎÌ Î
ïï
îî
,,MP NQ SO
R
.ABCD A B C D
¢¢¢¢
2
AC
¢
Trang 43
Gọi là thiết diện của hình lập phương và mặt phẳng chứa .
+ Trường hợp có một đỉnh thuộc cạnh hoặc .
Giao tuyến của và là đường thẳng , hình chiếu vuông góc của lên
là điểm . Khi đó góc giữa và là .
Vì nên , do đó , do đó
Hình chiếu vuông góc của hình lên là hình vuông , do đó
diện tich hình : .
Diện tích thiết diện nhỏ nhất khi lớn nhất, tức là . Khi đó
diện tích cần tìm là .
+ Trường hợp có một đỉnh thuộc cạnh hoặc , chọn mặt phẳng chiếu là
, chứng minh tương tự ta cũng có , .
+ Trường hợp có một đỉnh thuộc cạnh hoặc , chọn mặt phẳng chiếu là
, chứng minh tương tự ta cũng có, .
------------- HẾT -------------
A
A'
C'
H
D'
C'
B'
A'
D
C
B
A
( )
H
( )
a
AC
¢
( )
H
BB
¢
DD
¢
( )
a
( )
ABCD
¢¢¢¢
d
A
¢
d
H
( )
a
( )
ABCD
¢¢¢¢
∑
AHA
¢
AH AC
¢¢¢
£
∑
sin sin
AA AA
AC A
AH AC
a
¢¢
¢¢
=³ =
¢
∑
cos cos ACA
a
¢¢
£
( )
H
( )
ABCD
¢¢¢¢
ABCD
¢¢¢¢
( )
H
( )
.cos
ABCD
H
SS
a
¢¢¢¢
=
( )
cos
ABCD
H
S
S
a
¢¢¢¢
Þ=
cos
a
∑
2
cos cos
3
ACA
a
¢¢
==
( )
43
26
2
H
S ==
( )
H
CD
AB
¢¢
( )
BCC B
¢¢
( )
cos
BB C C
H
S
S
a
¢¢
=
( )
min 2 6
H
S =
( )
H
BC
AD
¢¢
( )
BAA B
¢¢
( )
min 2 6
H
S =
Trang 44
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 4
I. Trắc nghiệm: (7.0đ)
Câu 1: Cho cấp số nhân biết công bội Khi đó bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Câu 2: Nghiệm của phương trình là
A. . B. .
C. . D. .
Lời giải
Chọn C
Ta có .
Câu 3: Biết số theo thứ tự lập thành cấp số cộng. Giá trị của bằng
A. B. C. D.
Lời giải
Chọn A
theo thứ tự lập thành cấp số cộng nên .
Câu 4: Cho dãy số . Năm số hạng đầu của dãy số là
A.
B.
C. D.
Lời giải
Chọn A
Ta có.
; ; ; .
Câu 5: Góc có số đo bằng rađian là bao nhiêu?
A. . B. . C. . D. .
Lời giải
n
U
1
2=-U
1
.
2
q =
5
U
1
8
-
1
32
1
32
-
1
8
4
4
51
11
2.
28
UUq
æö
==- =-
ç÷
èø
2cos 3 0x -=
( )
,|
6
xkk
p
p
=± + Î!
( )
,|
3
xkk
p
p
=± + Î!
( )
2, |
6
xkk
p
p
=± + Î!
( )
2, |
3
xkk
p
p
=± + Î!
2cos 3 0x -=
3
cos
2
xÛ=
cos cos
6
x
p
Û=
( )
2,
6
xkk
p
p
Û=± + Î!
3
5; ;15x
x
10.
20.
30.
75.
5; ;15x
5 15
10
2
x
+
==
1
1
4
nn
u
uun
+
=
ì
í
=+
î
4, 5, 7,10,14.
4,16, 32, 64,128.
4, 6, 9,13 ,18.
4, 5, 6, 7,8.
21
15uu=+=
32
27uu=+=
43
310uu=+=
54
414uu=+=
0
18
p
18
p
10
p
360
p
Trang 45
Chọn C
Câu 6: Hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng đó
A. Song song. B. Chéo nhau.
C. Trùng nhau. D. Hoặc song song hoặc trùng nhau.
Lời giải
Chọn D
Câu 7: Tập xác định của hàm số là
A. . B. .
C. . D. .
Lời giải
Chọn D
Hàm số xác định (vì với mọi
Vậy tập xác định của hàm số là: .
Câu 8: Giá trị bằng bao nhiêu?
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có
Câu 9: Cho hình chóp , đáy là hình bình hành tâm . Giao tuyến của
hai mặt phẳng và là
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Câu 10: Cho cấp số nhân có và . Công bội của cấp số nhân đó bằng
A. . B. . C. . D. .
Lời giải
Chọn A
.
Vậy .
18 .18
180 10
pp
°= =
1
1cos
y
x
=
-
\2,
2
Dkk
p
p
ìü
=-+ Î
íý
îþ
!"
{ }
\2,Dkk
pp
=+Î!"
\2,
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
{ }
\2,Dkk
p
=Î!"
1 cos 0 cos 1 cos 1 2 .xxxxk
p
Û- > Û <Û ¹Û ¹
cos 1x £
).x
{ }
\2,Dkk
p
=Î!"
00
cos 45 sin 45+
2
0
3
1
00
22
cos 45 sin 45 2
22
+=+=
ABCD
ABCD
O
( )
SAC
( )
SAD
SO
SD
SA
SB
( ) ( )
SAC SAD SA«=
( )
n
u
1
2u =
2
6u =
3
1
3
6
2
1
121
..62.3
n
n
uuq uuq q q
-
=Þ=Û=Û=
3q =
Trang 46
Câu 11: Trong các công thức sau, công thức nào đúng?
A. . B.
.
C. . D. .
Lời giải
Chọn A
Ta có .
Câu 12: Cho cấp số cộng có . Tìm số hạng .
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: .
Câu 13: Nghiệm của phương trình là
A. . B. . C. . D.
.
Lờigiải
Chọn D
.
Câu 14: Cho hàm số . Tìm mệnh đề đúng?
A. Hàm số có tập giá trị là . B. Hàm số là hàm số lẻ.
C. Hàm số tuần hoàn với chu kỳ . D. Hàm số có tập xác định
Lời giải
Chọn B
Hàm số có tập xác định là , tuần hoàn với chu kỳ
, có tập giá trị là và là hàm số lẻ.
Câu 15: Cho 3 đường thẳng không cùng thuộc một mặt phẳng và cắt nhau từng đôi.
Khẳng định nào sau đây đúng
A. Các khẳng định ở A, B, C đều sai.
B. 3 đường thẳng trên trùng nhau.
C. 3 đường thẳng trên chứa 3 cạnh của một tam giác.
D. 3 đường thẳng trên đồng quy.
Lời giải
Chọn D
+) Hai đường thẳng cắt nhau sẽ xác định được một mặt phẳng.
( )
cos – cos .cos sin .sinab a b a b=+
( )
cos cos .cos sin .sinab a b a b+= +
( )
sin – sin .cos cos .sinab a b a b=+
( )
sin sin .cos cos.sinab a b b+= -
( )
cos – cos .cos sin .sinab a b a b=+
( )
n
u
1
1, 4ud==
12
u
12
45u =
12
17u =
12
31u =
12
13u =
12 1
11 45uu d=+ =
sin 1x =
,
2
kk
p
p
-+ Î!
,
2
kk
p
p
+Î!
2,
2
kk
p
p
-+ Î!
2,
2
kk
p
p
+Î!
sin 1x =
Û
2,
2
xkk
p
p
=+ Î!
[1;1]-
2T
p
=
\{ , }.Dkk
p
=Î!"
\{ , }
2
Dkk
p
p
=+Î!"
T
p
=
!
123
,,dd d
Trang 47
+) Giả sử . Khi đó 3 mặt phẳng đôi một cắt nhau bởi 3
giao tuyến phân biệt và 3 giao tuyến này hoặc song song hoặc đồng quy.
+) Theo đề bài cắt nhau.
Suy ra đồng quy.
Câu 16: Trên đường tròn bán kính , độ dài của cung có số đo là.
A. . B. . C. . D. .
Lời giải
Chọn B
Độ dài cung có số đo là .
Câu 17: Tìm khẳng định Sai:
A. . B. .
C. . D. .
Lời giải
Chọn B
Áp dụng công thức nhân đôi, ta có nên B là đáp án sai.
Câu 18: Phương trình nào sau đây vô nghiệm?
A. . B. .
C. . D. .
Lời giải
Chọn C
Ta xét phương trình có nên phương trình vô
nghiệm
Câu 19: Cho hai hình bình hành và nằm trên hai mặt phẳng phân biệt. Gọi và
lần lượt là tâm hình bình hành và . Khẳng định nào dưới đây sai?
A. đồng phẳng. B. .
C. cắt tại trung điểm đoạn . D. .
Lời giải
Chọn A
( ) ( )
( ) ( )
( ) ( )
12
13
23
,
,
,
dd P
dd Q
dd R
=
ì
ï
=
í
ï
=
î
( ) ( ) ( )
,,PQR
123
,,dd d
123
,,dd d
123
,,dd d
15r =
3
p
8l
p
=
5l
p
=
7l
p
=
16l
p
=
3
p
15.
3
l
p
=
5
p
=
2
1cos2
cos
2
x
x
+
=
22
cos sin cos
22
xx
x =-
2
1cos4 2cos2xx+=
sin 2 2 sin cosxxx=
22
cos cos sin
22
xx
x =-
3sin2 cos2 2xx-=
3sin 4 cos 5xx-=
3sin cos 3xx-=-
sin
5
x =
p
3sin cos 3xx-=-
( )
( ) ( )
2
22
313+- <-
ABCD
ABEF
O
'O
ABCD
ABEF
,AE BD
// //AB CD EF
AE
( )
BCF
AE
( )
'//OO ADF
Trang 48
+Đáp án A, đúng vì là hình bình hành nên cắt nhau tại trung điểm mỗi
đường, nên cắt tại trung điểm của .
+Đáp án B, đúng là đường trung bình của nên .
+Đáp án C, sai do và là chéo nhau.
+Đáp án D, đúng vì và là hình bình hành (giả thiết) nên và
vì vậy .
Câu 20: Gọi , lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên
đoạn . Tính giá trị biểu thức .
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có: , .
Câu 21: Cho dãy số xác định bởi với mọi . Tìm số hạng tổng quát
của dãy số.
A. . B. . C. . D. .
Lời giải
Chọn D
Dễ thấy là một cấp số cộng với số hạng đầu và công sai .
Suy ra số hạng tổng quát .
O
O'
C
A
B
D
F
E
ABEF
,AE BF
AE
( )
BCF
AE
'OO
BDFD
( )
'// '//OO DF OO BDFÞ
( )
DABEF AEÏÞ
BD
ABCD
ABEF
//AB CD
// //AB CD EF
M
m
cos 2yx=
;
36
pp
éù
-
êú
ëû
2TM m=-
5
2
T =
13T =+
3
2
T =
2T =
36
x
pp
-££
2
2
33
x
pp
Û- £ £
1
cos 2 1
2
xÞ- £ £
1
2
m =-
2TÞ=
( )
n
u
11
2; 3
nn
uuu
-
=- = +
2n ³
31
n
un=- +
35
n
un=- +
31
n
un=-
35
n
un=-
( )
n
u
1
2u =-
3d =
( ) ( )
1
123135
n
uu n d n n=+- =-+ -= -
Trang 49
Câu 22: Biến đổi thành tích biểu thức ta được
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có .
Câu 23: Cho hình chóp có đáy là hình bình hành. là một điểm thuộc đoạn
. Mặt phẳng cắt hình chóp
theo thiết diện là
A. tam giác. B. hình thang. C. hình chữ nhật. D. hình bình hành.
Lời giải
Chọn B
Do
nên mặt phẳng và
có giao tuyến là đường thẳng
song
song với
Thiết diện là hình thang .
Câu 24: Với mọi góc , biểu thức nhận giá trị
bằng
A. B. C. D.
Lời giải
Chọn B
Có số hạng, chia thành cặp.
Có
Tương tự, ; ;
;
Do đó,
Câu 25: Cho hình chóp có đáy là hình bình hành tâm . Gọi là giao tuyến
của hai mặt phẳng và . Khi đó khẳng định nào sau đây là đúng?
sin 7 sin 5
sin 7 sin 5
aa
aa
-
+
cos 2 .sin 3
aa
cot 6 . tan
aa
tan 5 . tan
aa
cos .sin
aa
sin 7 sin 5
sin 7 sin 5
aa
aa
-
+
2 cos 6 .sin
2sin 6 .cos
aa
aa
=
cot 6 . tan
aa
=
ABCD
M
SB
( )
ADM
G
A
D
C
B
S
M
//BC AD
( )
ADM
( )
SBC
MG
BC
AMGD
a
29
cos cos( ) cos( ) ... cos( )
55 5
pp p
aa a a
+++++++
1
0
10
10-
10
5
94 9 4
()cos()cos()
55 5 5
pp p p
apa a a
+=++ Þ + =- +
83
cos( ) cos( )
55
pp
aa
+=- +
72
cos( ) cos( )
55
pp
aa
+=- +
6
cos( ) cos( )
55
pp
aa
+=- +
5
cos( ) cos
5
p
aa
+=-
0P =
ABCD
O
d
( )
SAB
( )
SCD
Trang 50
A. Đường thẳng nằm trong mặt phẳng .
B. Đường thẳng đi qua và song song với và .
C. Đường thẳng trùng với đường thẳng .
D. Đường thẳng đi qua và song song với và .
Lời giải
Chọn D
Ta có:
Vì nên giao tuyến của và là đường thẳng đi qua và
song song với và .
Câu 26: Cho tứ diện . Gọi và lần lượt là trọng tâm của tam giác và .
Mệnh đề nào dưới đây đúng
A. cắt . B. và chéo nhau.
C. . D. cắt .
Lời giải
Chọn C
d
ABCD
d
S
AD
BC
d
SO
d
S
AB
CD
( )
( )
( ) ( )
S SAB
S SAB SCD
S SCD
Î
ì
ï
ÞÎ Ç
í
Î
ï
î
( )
( )
//AB DC
AB SAB
DC SCD
ì
ï
Ì
í
ï
Ì
î
( )
SAB
( )
SCD
S
AB
CD
ABCD
G
E
ABD
ABC
GE
CD
GE
CD
//GE CD
GE
AD
Trang 51
Gọi là trung điểm của . Trong tam giác có suy ra
Câu 27: Phương trình lượng giác có nghiệm là
A. . B. . C. .
D. .
Lời giải
Chọn A
.
Câu 28: Dãy số nào trong các dãy số sau đây là dãy số bị chặn?
A. . B. .
C. . D. .
Lời giải
Chọn B
Xét dãy . Ta có nên
.
Suy ra dãy số bị chặn.
Xét dãy ta có nên dãy số bị chặn dưới.
Xét dãy ta có nên dãy số bị chặn trên.
Xét dãy ta có nên dãy số bị chặn dưới.
Câu 29: Đơn giản biểu thức .
A. . B. . C. . D. .
Lời giải
Chọn B
M
AB
MCD
1
3
MG ME
MD MC
==
//GE CD
2cos 2 0x +=
3
2
4
3
2
4
xk
xk
p
p
p
p
-
é
=+
ê
ê
ê
=+
ê
ë
2
4
2
4
xk
xk
p
p
p
p
é
=+
ê
ê
-
ê
=+
ê
ë
7
2
4
7
2
4
xk
xk
p
p
p
p
é
=+
ê
ê
-
ê
=+
ê
ë
2
4
3
2
4
xk
xk
p
p
p
p
é
=+
ê
ê
ê
=+
ê
ë
( )
3
2
2
4
2cos 2 0 cos
3
2
2
4
xk
xx k
xk
p
p
p
p
-
é
=+
ê
-
+=Û = Û Î
ê
ê
=+
ê
ë
!
( )
2*
,
nn
uun n="Ε
( )
*
,
1
nn
n
uu n
n
="Î
+
•
( )
*
,1
nn
uun n=+"Ε
( )
*
,
nn
uu nn=- " Ε
( )
*
,;
1
nn
n
uu n
n
="Î
+
•
*
01;nn n<<+"Ε
*
01;
1
n
n
n
Þ< <"Î
+
•
*
01;
n
un<<"Ε
( )
n
u
( )
*
,1;
nn
uun n=+"Ε
*
12;
n
un n=+³ "Ε
( )
n
u
( )
*
,;
nn
uu nn=- " Ε
*
1;
n
un n=- £- " Ε
( )
n
u
( )
2*
,;
nn
uun n="Ε
2*
1;
n
un n=³"Ε
( )
n
u
oo
13
sin10 cos10
C =+
o
8sin 20
o
8cos20
o
4 sin 20
Trang 52
.
Câu 30: Hàm số
tuần hoàn với chu kì là
A. . B. . C. . D. .
Lời giải
Chọn C
Nhận xét: Hàm số tuần hoàn với chu kì .
Câu 31: Cho tứ diện đều có cạnh bằng . Gọi là trọng tâm tam giác . Thiết
diện tạo bởi tứ diện đều và mặt phẳng có diện tích bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi là trung điểm của , thiết diện tạo bởi tứ diện đều và mặt phẳng
là tam giác .
.
Diện tích thiết diện là .
Câu 32: Số nghiệm của phương trình thuộc là
A. . B. . C. . D. .
Lời giải
Chọn C
Đặt
oo
oo o
o
oo
oo o
13
cos10 sin10
1 3 cos10 3 sin10 4sin 40
22
8cos20
2sin10 cos 10
sin10 cos10 sin10 cos10 sin 20
4
oo
C
+
+
=+ = = = =
2 sin 2yx=
4
p
2
p
p
2
p
( )
sin , 0=+¹yaxba
2
p
a
ABCD
a
G
ABC
ABCD
()GCD
2
3
4
a
2
2
6
a
2
3
2
a
2
2
4
a
H
A
B
C
D
F
G
F
AB
ABCD
()GCD
DFC
3
2
a
DF FC==
2
2
22
3
24
2
aaa
FH DF DH
æö
Þ= - = -=
ç÷
ç÷
èø
2
12
.
24
DCF
a
SFHDC==
5
cos 2 4 cos
362
xx
pp
æö æö
++ -=
ç÷ ç÷
èø èø
[ ]
0; 2
p
4
1
2
3
Trang 53
Phương trình trở thành
Với ta có ,
Vậy trong đoạn phương trình có nghiệm .
Câu 33: Giả sử , , theo thứ tự đó là một cấp số nhân. Tính .
A. . B. . C. . D. .
Hướng dẫn giải
Chọn C
Điều kiện: .
Theo tính chất của cấp số nhân, ta có: .
.
Ta có: .
Câu 34: Tìm điều kiện của để pt có đúng 2 nghiệm
.
A. . B. . C. . D. .
Lời giải
Chọn C
.
Đặt ta được pt: (2), .
Pt (2) luôn có 2 nghiệm
Khi đó pt ban đầu có đúng 2 nghiệm thì pt (2) có đúng 1 nghiệm
22
553
cos 2 4 cos 1 2sin 4 sin 2 sin 4sin 0
22 2 2
tt tt tt
p
æö
+-=Û-+=Û-+-=
ç÷
èø
( )
3
sin
2
1
sin
2
tVN
t
é
=
ê
Û
ê
ê
=
ê
ë
1
sin
2
t =
2
2
1
36
6
sin
5
32
2
2
36
2
xk
xk
x
xk
xk
pp
p
p
p
p
pp
p
p
p
-
é
é
+=+
=+
ê
ê
æö
+=Û Û
ê
ê
ç÷
èø
ê
ê
+= +
=+
ê
ê
ë
ë
[ ]
0; 2
p
2
11
;
26
xx
pp
==
sin
6
a
cos
a
tan
a
cos 2
a
3
2
-
1
2
1
2
-
3
2
cos 0
2
k
p
aa p
¹Û ¹ +
( )
k Î!
2
sin
cos .tan
6
a
aa
=
2
2
sin
6cos
cos
a
a
a
Û=
32
6cos sin 0
aa
Û-=
32
6cos cos 1 0
aa
Û+-=
1
cos
2
a
Û=
2
2
11
cos 2 2 cos 1 2. 1
22
aa
æö
=-=-=-
ç÷
èø
m
( )
co s 2 2 1 cos 1 0xm xm-- -+=
;
22
x
pp
-
éù
Î
êú
ëû
11m-£ £
10m-£ £
01m££
( )
co s 2 2 1 cos 1 0xm xm-- -+=
( )
2
2cos 2 1 cos 0xm xmÛ---=
cos xt=
( )
2
221 0tmtm---=
[ ]
;0;1
22
xt
pp
-
éù
ÎÞÎ
êú
ëû
1
;
2
ttm
-
==
;
22
x
pp
-
éù
Î
êú
ëû
[
)
0;1t Î
Trang 54
Câu 35: Cho hình chóp . Gọi , lần lượt là trung điểm của và , là điểm
trên cạnh sao cho . Gọi là giao điểm của với mặt phẳng .
Tính .
A. . B. . C. . D. .
Lời giải
Chọn B
Tìm giao điểm của với mặt phẳng
Chọn mặt phẳng phụ chứa
Trong gọi
Suy ra . Khi đó là giao điểm của và .
Gọi là trung điểm
Ta có (vì là trung điểm của và nên )
Mà nên
Mặt khác ta có (vì )
Mà nên .
[
)
0;1mÞÎ
.S ABC
M
N
SA
BC
P
AB
1
3
AP
AB
=
Q
SC
( )
MNP
SQ
SC
1
6
1
3
1
2
2
3
Q
SC
( )
MNP
( )
SAC
SC
( )
ABC
H AC NP=Ç
( ) ( )
MNP SAC HMÇ=
Q
HM
SC
L
AC
1
2
3
1
3
2
AB
HA AP
HL LN
AB
== =
,MN
AC
BC
1
2
LN AB=
2
3
HA HLÞ=
21
33
LC AL HL HA HL HL HL==-=- =
3
4
HL HC=
4
3
HC QC
HL ML
==
//ML SC
2ML SC=
31
23
QC SQ
SC SC
=Þ =
Trang 55
II. Tự luận: (3.0đ)
Câu 36: Giải phương trình
Lời giải
Chọn C
Câu 37: Xen giữa số và số là số để được một cấp số nhân có . Khi đó là:
Lời giải
Ta có và nên .
Do đó .
Câu 38: Cho hình chóp có đáy là hình thang, đáy lớn là là trung điểm
Mặt phẳng qua song song với và cắt lần lượt tại
và Nói gì về thiết diện của mặt phẳng với khối chóp ?
Lời giải
Trong mặt phẳng , qua kẻ đường thẳng Khi đó,
Trong mặt phẳng , qua kẻ đường thẳng Khi đó,
Vậy
Xét hai mặt phẳng và có
8.cos 2 .sin 2 .cos 4 2xx x=-
8.cos 2 .sin 2 .cos 4 2 4.sin 4 .cos 4 2 2.sin 8 2
82
2
32 4
4
sin 8 ( ) ( )
2
55
82
4324
xx x x x x
xk
xk
xkk
xk xk
pp
p
p
ppp
p
=- Û =- Û =-
=- +
=- +
Û=-Û ÎÛ Î
=+ =+
é
é
ê
ê
ê
ê
ê
ê
ê
ê
ë
ë
!!
3
768
7
1
3u =
5
u
1
3u =
9
768u =
8
768 3.q=
8
256qÞ=
2qÞ=±
44
51
. 3.2 48uuq===
ABCD
.AB
M
.CD
( )
a
M
BC
.SA
( )
a
,AB SB
N
.P
( )
a
M
( )
.MN BC N BCÎ!
( )
.MN
a
Ì
( )
SAB
N
( )
.NP SA P SBÎ!
( )
.NP
a
Ì
( ) ( )
.MNP
a
º
( )
MNP
( )
SBC
Trang 56
hai mặt phẳng cắt nhau theo một giao tuyến đi qua điểm
và song song với
Trong mặt phẳng kẻ Khi đó, là giao tuyến của mặt
phẳng với mặt phẳng . Vậy mặt phẳng cắt khối chóp theo
thiết diện là tứ giác
Tứ giác có là hình bình hành. Từ đó suy ra
Trong tam giác có thuộc đoạn , thuộc đoạn và nên
Tứ giác có là hình thang có đáy lớn là
Câu 39: Cho hình chóp có đáy là hình bình hành tâm . Hai điểm lần lượt nằm
trên các đoạn sao cho . Điểm là trung
điểm của . Biết thiết diện của hình chóp cắt bởi đi qua trung điểm cạnh
. Giá trị bằng
Lời giải
Ta có nên mặt phẳng cắt mặt phẳng theo giao tuyến đi qua
và song song với , cắt tại .
Vì là trung điểm của nên là trung điểm của .
Gọi thì . Theo giả thiết thì là trung điểm .
Áp dụng định lý Menelaus cho tam giác ta có:
. Từ đó suy ra .
Vậy .
( )
( )
( ) ( )
//
,
MN MNP
BC SBC
MN BC
P MNP P SBC
Ì
ì
ï
Ì
ï
Þ
í
ï
ï
ÎÎ
î
P
.BC
( )
SBC
( )
.PQ BC Q SCÎ!
PQ
( )
a
( )
SBC
( )
a
.MNPQ
MNBC
//
//
MN BC
MNBC
MC NB
ì
Þ
í
î
.MN BC=
SBC
P
SB
Q
SC
.PQ BC<
MNPQ
//MN PQ
MNPQ
PQ MN
ì
Þ
í
<
î
.MN
.S ABCD
O
,MN
,SO SD
( )
*
,, , , 1
SM SN m
mn mn
SO SD n
== Î =•
E
BC
( )
mp MNE
SA
mn+
//MN OD
( )
MNE
( )
ABCD
E
DO
AC
K
E
BC
K
OC
G MK SA=Ç
( )
GSA MNE=Ç
G
SA
SAO
1
.. 1 ..11 3
3
MS KO GA MS MS
MO KA GS MO MO
=Þ =Þ =
3
4
m SM
n SO
==
Trang 57
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 5
I. Trắc nghiệm: (7.0đ)
Câu 1: Cung có số đo đổi sang đơn vị độ bằng
A. B. . C. . D. .
Lời giải
Chọn C
Câu 2: Chọn khẳng định sai.
A. Qua một đường thẳng và một điểm nằm ngoài đường thẳng xác định được một và
chỉ một mặt phẳng.
B. Qua ba điểm phân biệt xác định được một và chỉ một mặt phẳng.
C. Qua hai đường thẳng phân biệt cắt nhau xác định được một và chỉ một mặt phẳng.
D. Qua hai đường thẳng song song xác định được một và chỉ một mặt phẳng.
Lời giải
Chọn B
Ba điểm đó phải là ba điểm không thẳng hàng.
Câu 3: Biết số theo thứ tự lập thành cấp số cộng. Giá trị của bằng
A. B. C. D.
Lời giải
Chọn D
theo thứ tự lập thành cấp số cộng nên .
Câu 4: Mệnh đề nào sau đây sai?
A. . B. .
C. . D.
Lời giải
Chọn D
Câu 5: Trên một đường tròn có bán kính cm. Ta lấy một cung có độ đài bằng cm. Số đo
tính theo radian của cung đó là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có .
Câu 6: Hàm số nào sau đây là hàm số chẵn?
A. . B. . C. . D. .
Lời giải
5
3
π
rad
270 .°
600°
300°
5°
55.180
300 .
33
π
rad
°
==°
3
5; ;15x
x
20.
30.
75.
10.
5; ;15x
5 15
10
2
x
+
==
22
cos 2 cos sinaaa=-
2
cos 2 2 cos 1aa=-
2
cos 2 1 2 sinaa=-
cos 2 2 sin cosaaa=
30R =
8
4
30
4
15
10
3
4
9
84
30 15
l
lR
R
aa
=Þ===
cos 2yx=
tan 4yx=
sin 3yx=
Trang 58
Chọn A
Hàm số có tập xác định .
Với mọi ta có và nên hàm số là hàm số
chẵn.
Câu 7: Cho cấp số nhân với và . Công bội của cấp số nhân đã cho bằng
A. 4. B. 3. C. 9. D. .
Lời giải
Chọn A
Ta có: .
Câu 8: Cho . giá trị của bằng
A. . B. .
C. . D. .
Lời giải
Chọn D
Ta có: .
Mà .
Câu 9: Nếu một đường thẳng song song với mặt phẳng và đường thẳng chứa trong
mặt phẳng thì và sẽ
A. song song. B. cắt nhau.
C. chéo nhau. D. song song hoặc chéo nhau.
Lời giải
Chọn D
Câu 10: Với , họ nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có: .
Câu 11: Trong các công thức sau, công thức nào đúng?
cos 2yx=
D = !
xDÎ
xD-Î
( ) ( )
cos 2 cos 2xx-=
cos 2yx=
( )
n
u
1
3u =
2
12u =
1
4
2
21
1
12
.4
3
u
uuqq
u
=Þ===
3
sin
52
p
aap
æö
=<<
ç÷
èø
cos
a
2
cos
5
a
=-
4
cos
5
a
=
2
cos
5
a
=
4
cos
5
a
=-
22 2 2
916
sin cos 1 cos 1 sin 1
25 25
aa a a
+=Þ=-=-=
4
cos
25
p
ap a
<<Þ =-
d
( )
a
'd
( )
a
d
'd
k Î !
2
2
k
p
p
+
2
k
p
p
+
k
p
2k
p
cos 0 ,
2
xxkk
p
p
=Û= + Î!
Trang 59
A. . B. .
C. . D. .
Lời giải
Chọn D
Ta có .
Câu 12: Cho dãy số xác định bởi . Giá trị bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có ;
;
.
Suy ra
Câu 13: Cho bốn điểm không đồng phẳng. Gọi lần lượt là trung điểm hai đoạn
thẳng và . là giao tuyến của cặp mặt phẳng nào sau đây?
A. và . B. và .
C. và . D. và .
Lời giải
Chọn C
là điểm chung thứ nhất của hai mặt phẳng và .
là điểm chung thứ hai của hai mặt phẳng và .
Vậy .
( )
tan ta n tanab a b+= +
( )
tan tan
tan
1 tan tan
ab
ab
ab
+
-=
-
( )
tan – tan tanab a b=-
( )
tan tan
tan
1 tan tan
ab
ab
ab
+
+=
-
( )
tan tan
tan
1 tan tan
ab
ab
ab
+
+=
-
( )
n
u
*
11
3; ,
nn
uuunn
+
==+"Ε
123
uu u++
15
16
18
13
1
3u =
21
1314uu=+=+=
32
2426uu=+=+=
123
34613.uu u++=++=
,,,ABCD
,IK
AD
BC
IK
( )
IBC
( )
KBD
( )
IBC
( )
KCD
( )
IBC
( )
KAD
( )
ABI
( )
KAD
( )
( )
I AD KAD
I IBC
ÎÌ
ì
ï
í
Î
ï
î
IÞ
( )
IBC
( )
KAD
( )
( )
KBC IBC
K KAD
ÎÌ
ì
ï
í
Î
ï
î
KÞ
( )
IBC
( )
KAD
( ) ( )
IBC KAD IKÇ=
Trang 60
Câu 14: Cho cấp số nhân có và . Tìm số hạng đầu và công bội của cấp số
nhân .
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Câu 15: Cho cấp số cộng thỏa mãn Công sai của cấp số cộng bằng
A. B. C. D.
Lời giải
Chọn B
Gọi là công sai của cấp số cộng .
Ta có suy ra .
Vậy công sai của cấp số cộng là
Câu 16: Tập nghiệm của phương trình là
A. .
B. .
C. .
D. .
Lời giải
Chọn A
Ta có:
.
Câu 17: Tìm tập xác định của hàm số .
( )
n
u
4
40u =
6
160u =
( )
n
u
1
5
2
u
q
=-
ì
í
=
î
1
140
60
u
q
=-
ì
í
=
î
1
5
2
u
q
=-
ì
í
=-
î
1
2
5
u
q
=-
ì
í
=-
î
2
3
4
1
11
5
6
1
1
3
160
4
40
. 40
55
40
40
160
22
. 160
q
u
uq
uu
u
qq
uq
u
q
ì
==
ï
ì
=
=
==-
ì
ìì
ïï
ÛÛ ÛÚ
íí í íí
=
==-
=
ï
îî
î
ï
î
=
ï
î
( )
n
u
13
4, 10.uu==
6.-
3.
3.-
6.
d
( )
n
u
13
4, 10uu==
1
1
1
4
4
210
3
u
u
ud
d
=
=
ì
ì
Û
íí
+=
=
î
î
( )
n
u
3.d =
sin 2 sinxx=
2
2;
33
k
Sk k
pp
p
ìü
=+Î
íý
îþ
!
2; 2
3
Sk kk
p
pp
ìü
=-+Î
íý
îþ
!
{ }
2; 2Sk kk
pp p
=+Î!
2; 2
3
Sk kk
p
pp
ìü
=+Î
íý
îþ
!
22,
sin 2 sin
22,
xxk k
xx
xxkk
p
pp
=+ Î
é
=Û
ê
=-+ Î
ë
Z
Z
2,
2
,
33
xk k
k
xk
p
pp
=Î
é
ê
Û
ê
=+ Î
ë
Z
Z
D
1
1 sin
y
x
=
-
Trang 61
A. . B. .
C. . D. .
Lời giải
Chọn B
Điều kiện xác định của hàm số là: .
Vậy, .
Câu 18: Nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: với .
Câu 19: Cho t diện . Gọi và lần lượt là trung điểm của các cạnh và ; là
điểm thuộc đoạn sao cho . Kết luận nào sau đây đúng nhất về thiết
diện của mặt phẳng với hình chóp ?
A. Thiết diện là ngũ giác. B. Thiết diện là hình bình hành.
C. Thiết diện là hình thang. D. Thiết diện là t giác.
Lời giải
Chọn C
Gọi .
Trong mặt phẳng gọi . Khi đó thiết diện của mặt phẳng
với hình chóp là t giác .
\,
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
\2,
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
D =Æ
{ }
\,Dkk
p
=Î!"
1 sin 0x->
sin 1xÞ<
sin 1xÞ¹
2
2
xk
p
p
Þ¹ +
\2,
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
3tan3 3 0x -=
93
k
x
pp
=+
39
k
x
pp
=+
99
k
x
pp
=+
33
k
x
pp
=+
3 tan 3 3 0 tan 3 3 3
393
k
xxxkx
ppp
p
-= Û = Û = + Û = +
k Î !
ABCD
N
P
BD
AD
M
BC
2MC MB=
( )
MNP
ABCD
E
Q
P
N
M
D
C
B
A
EMNCD=Ç
Þ
( ) ( )
MNP ACD PEÇ=
( )
ACD
QPE AC=Ç
( )
MNP
ABCD
MNPQ
Trang 62
Ta có .
Do đó tứ giác là hình thang.
Câu 20: Cho tứ diện , là trọng tâm tứ diện. Gọi là giao điểm của và mp
, là giao điểm của và mp . Khẳng định nào sau đây là đúng?
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi , lần lượt là trung điểm của , . Vì là trọng tâm tứ diện nên là
giao điểm của ba đoạn thẳng nối hai trung điểm của cặp cạnh đối của tứ diện như hình
vẽ trên.
Xét : , . Trong có và là đường
trung tuyến nên là trọng tâm của tam giác do đó . Tương tự ta cũng có
suy ra .
Câu 21: Cho hình chóp , đáy là hình thang . Gọi là giao điểm
và , là giao điểm và . Trong các mệnh đề sau, mệnh đề nào sai?
A. và cắt nhau. B. với .
C. . D. .
Lời giải
Chọn A
( ) ( )
( ) ( )
//
,
MQ MNP ABC
NP AB
NP MNP AB ABC
=Ç
ì
ï
í
ï
ÌÌ
î
//MQ NPÞ
MNPQ
ABCD
G
1
G
AG
( )
BCD
2
G
BG
( )
ACD
12
//GG AB
12
//GG AC
12
//GG CD
12
//GG AD
A
B
C
D
G
1
G
2
G
M
N
M
N
DC
AC
G
G
( )
ABM
1
Ç=AG BM G
2
Ç=BG AM G
DACD
AM
DN
2
G
2
2
1
2
=
GM
GA
1
1
1
2
=
GM
GB
12
//GG AB
ABCD
( )
//AD BC
O
AC
BD
I
AB
CD
SB
AD
( ) ( )
SAD SBC SxÇ=
//Sx AD
( ) ( )
SAB SCD SIÇ=
( ) ( )
SAC SBD SOÇ=
Trang 63
Ta có: và , không cùng nằm trong một mặt phẳng
và không có điểm chung (chéo nhau).
Câu 22: Trong không gian cho tứ diện . Gọi là trung điểm của , đối xứng với
qua .
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I) Hai đường thẳng và cắt nhau.
(II) Hai đường thẳng và cắt nhau.
(III) Hai đường thẳng và cắt nhau.
(II) Hai đường thẳng và cắt nhau.
A. . B. . C. . D. .
Lời giải
Chọn B
S
A
B
C
D
O
I
( )
( )
//
//
AD BC
AD SBC
AD SBC
ì
Þ
í
Ì
î
AD
SB
ADÞ
SB
ABCD
M
AB
N
B
D
MC
BD
MN
AD
MD
BC
AB
CD
3
1
2
4
Trang 64
Trong mặt phẳng hai đường thẳng và cắt nhau tại . Các cặp đường
thẳng còn lại đều chéo nhau.
Câu 23: Cho cấp số cộng và gọi là tổng số hạng đầu tiên của nó. Biết và
. Tìm số hạng tổng quát của cấp số cộng đó
A. . B. . C. . D. .
Lời giải
Chọn C
Giả sử cấp số cộng có số hạng đầu là và công sai .
Ta có: .
Khi đó: .
Câu 24: Gọi lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số . Tính
giá trị của
A. . B. . C. . D. .
Lời giải
Chọn D
Với mọi ta có:
.
Suy ra: .
Câu 25: Giá trị của biểu thức bằng
A. . B. . C. . D. .
Lời giải:
Chọn A
K
N
M
A
B
C
D
( )
ABD
MN
AD
K
( )
n
u
n
S
n
7
77S =
n
u
45
n
un=+
54
n
un=+
32
n
un=+
23
n
un=+
1
u
d
1
7
1
1
1
12
1
7.6.
777
77
72177
5
2
12.11. 12 66 192
192
2
12 192
2
d
u
S
ud
u
dud
S
d
u
ì
+=
ï
=
+=
=
ì
ì
ì
ï
ÛÛÛ
íí í í
+=
=
=
î
î
î
ï
+=
ï
î
( ) ( )
1
152132
n
uu n d n n=+- =+ -=+
,Mm
13sin2yx=-
33
Mm+
33
9Mm+=
33
7Mm+=
33
1Mm+=-
33
7Mm+=-
x Î !
0sin2 1 3 3sin2 0 213sin2 1 2 1xx xy££Û-£- £Û-£- £Û-££
33
1
7
2
M
Mm
m
=
ì
Þ+=-
í
=-
î
22
tan cot
24 24
A
pp
=+
12 2 3
23
-
+
12 2 3
23
+
-
12 2 3
23
+
+
12 2 3
23
-
-
22
tan cot
24 24
A
pp
=+
22
11
11
cos sin
24 24
pp
=-+-
Trang 65
.
Câu 26: Chu kỳ của hàm số là
A. . B. . C. . D. .
Lời giải
Chọn C
Hàm số tuần hoàn với chu kì .
Hàm số tuần hoàn với chu kì .
Suy ra hàm số tuần hoàn với chu kì .
Câu 27: Cho , , là ba góc của một tam giác. Hệ thức nào sao đây đúng?
A. . B. .
C. . D. .
Lời giải
Chọn D
Ta có
.
Câu 28: Cho dãy số xác định bỏi , với . Khẳng định nào sau đây đúng?
A. Dãy số là dãy số giảm. B. Số hạng thứ của dãy số là .
C. Dãy số bị chặn. D. Dãy số là dãy số tăng.
Lời giải
Chọn C
Vì nên dãy bị chặn.
Câu 29: Tìm họ nghiệm của phương trình .
A. . B. .
22
1
2
cos .sin
24 24
pp
=-
2
4
2
sin
12
p
=-
8
2
1cos
6
p
=-
-
12 2 3
23
-
=
+
2
tan 3 cos 2yx x=-
3
p
2
p
p
2
p
2
1cos4 1 1
tan 3 cos 2 tan 3 tan 3 cos 4
222
x
yx xx x x
+
=- =- =- -
tan 3yx=
3
p
1
cos 4
2
yx=
2
42
pp
=
11
tan 3 cos 4
22
yx x=- -
p
A
B
C
3
sin sin
2
++
æö
=
ç÷
èø
AB C
C
( )
cos cos+=AB C
( )
sin 2 sin++ =AB C C
( )
sin 2 sin++ =-AB C C
180 2 180++= °Û++ = °+ABC AB C C
( ) ( ) ( )
sin 2 sin 180 sin 2 sinÛ++= °+Û++=-AB C C AB C C
( )
n
u
sin
3
n
n
u
p
=
1n ³
( )
n
u
2
2
1
2
u =
( )
n
u
( )
n
u
1 sin 1
3
n
p
-£ £
( )
n
u
3 sin cos 2
22
xx
-=
2
2,
3
xkk
p
p
=+ Î!
2
4,
3
xkk
p
p
=+ Î!
Trang 66
C. D. .
Lời giải
Chọn B
Ta có:
Câu 30: Giá trị của biểu thức , biết là
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Câu 31: Cho tứ diện đều ABCD cạnh a, gọi G là trọng tâm tam giác ABCắt tứ diện bởi mặt
phẳng (GCD) được thiết diện có diện tích là:
A. B. C. D.
Lời giải
Chọn B
Gọi là trung điểm của . Khi đó thiết diện cắt bởi là tam giác . Ta
có cân tại M và
Gọi N là trung điểm CD, tính được Vậy
4
2,
3
xkk
p
p
=+ Î!
4
4,
3
xkk
p
p
=+ Î!
2
3 sin cos 2 sin 1 2 4 ,
22 26 262 3
xx x x
kx kk
ppp p
pp
æö
-=Û -=Û-=+Û=+ Î
ç÷
èø
!
cos 5 cos 3
sin 5 sin 3
xx
I
xx
+
=
-
3I =
3I =-
1
3
I =
1
3
I =-
2cos4 cos 1
cot 3
2 cos 4 sin tan
xx
Ix
xx x
====
2
2
6
a
2
2
4
a
2
3
4
a
2
2
2
a
M
AB
(GCD)
CDM
CDMD
3
;
2
a
MD MC CD a== =
2
2
32
222
aaa
MN
æö
æö
=-=
ç÷
ç÷
ç÷
èø
èø
2
2.
4
CDM
a
S
D
=
Trang 67
Câu 32: Với giá trị nào của để phương trình: có đúng
nghiệm
A. B. C. D.
Lời giải
Chọn B
Với phương trình trở thành:
(vô lý)
Do đó không phải là nghiệm của phương trình
Với Chia vế cho ta được
Đặt .Yêu cầu bài toán trở thành tìm để phương trình có
nghiệm trái dấu
Câu 33: Cho hình chóp . Gọi , lần lượt là trung điểm của và , là điểm
trên cạnh sao cho . Gọi là giao điểm của với mặt phẳng .
Tính .
A. . B. . C. . D. .
Lời giải
Chọn C
Tìm giao điểm của với mặt phẳng
Chọn mặt phẳng phụ chứa
Trong gọi
m
2
sin 3sin .cos x 1 0mx x m---=
3
3
0; .
2
x
p
æö
Î
ç÷
èø
1.m ³-
1.m <-
1.m £-
1.m >-
2
x
p
=
2
sin 3sin .cos 1 0 1 0
222
mmmm
ppp
---=Û--=
10Û- =
2
x
p
=
2
x
p
¹
2
2
cos x
( ) ( )
2222
tan 3 tan . 1 ta n 1 1 tan 0 tan 3 tan 1 0mx xm x x x xm--+ -+ =Û+++=
tantx=
m
2
310ttm+++=
2
10 1mmÛ+<Û<-
.S ABC
M
N
SA
BC
P
AB
1
3
AP
AB
=
Q
SC
( )
MNP
SQ
SC
2
3
1
6
1
3
1
2
Q
SC
( )
MNP
( )
SAC
SC
( )
ABC
H AC NP=Ç
Trang 68
Suy ra . Khi đó là giao điểm của và .
Gọi là trung điểm
Ta có (vì là trung điểm của và nên )
Mà nên
Mặt khác ta có (vì )
Mà nên .
Câu 34: Phương trình có bao nhiêu nghiệm thuộc ?
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có
Trong khoảng , phương trình có các nghiệm .
Câu 35: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả
sử 1 tế bào E. Coli khối lượng khoảng g. Hỏi sau 2 ngày khối lượng do 1 tế
bào vi khuẩn sinh ra là bao nhiêu? (chọn đáp án chính xác nhất).
A. . B. . C. . D.
.
Lời giải
Chọn D
Một tế bào E. Coli
Sau 20 phút thành: tế bào.
Sau phút thành: tế bào.
Sau phút thành: tế bào.
( ) ( )
MNP SAC HMÇ=
Q
HM
SC
L
AC
1
2
3
1
3
2
AB
HA AP
HL LN
AB
== =
,MN
AC
BC
1
2
LN AB=
2
3
HA HLÞ=
21
33
LC AL HL HA HL HL HL==-=- =
3
4
HL HC=
4
3
HC QC
HL ML
==
//ML SC
2ML SC=
31
23
QC SQ
SC SC
=Þ =
22
4cos 3cos2 1 2cos
24
x
xx
p
æö
-=+-
ç÷
èø
0;
2
p
æö
ç÷
èø
2
3
0
1
22
4cos 3cos2 1 2cos
24
x
xx
p
æö
-=+-
ç÷
èø
1cos
4. 3 cos 2 1 1 cos 2
22
x
xx
p
+
æö
Û-=++-
ç÷
èø
22cos 3cos2 2sin2xxxÛ+ - =+
sin 2 3 cos 2 2 cosxxxÛ+ =
sin 2 sin cos 2 cos cos
66
xxx
pp
Û+ =
cos 2 cos
6
xx
p
æö
Û-=
ç÷
èø
( )
22 2
66
2
22
6183
xxk xk
k
xxkxxk
pp
pp
ppp
p
éé
-=+ =+
êê
ÛÛÎ
êê
êê
-=-+ = +
êê
ëë
!
0;
2
p
æö
ç÷
èø
,
618
xx
pp
==
15
15.10
-
( )
26
3, 35.10 kg
( )
29
3, 36.10 g
( )
26
2, 25.10 kg
( )
29
2, 34.10 g
1
22=
40 2.20=
2
42=
60 3.20=
3
82=
Trang 69
………………………………………………………….
Sau 2 ngày phút thành tế bào.
Vậy sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là:
.
II. Tự luận: (3.0đ)
Câu 36: Phương trình có bao nhiêu nghiệm trên khoảng ?
Lời giải
PT đã cho .
Theo đề: .
Vì nên . Vậy PT đã cho có 5 nghiệm trên khoảng .
Câu 37: Cho cấp số nhân , với công bội dương. Tính tổng số hạng đầu
tiên của cấp số nhân trên.
Lời giải
Câu 38: Cho hình lập phương có cạnh là . Gọi , lần lượt là trung điểm
của và . Tính diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng
.
Lời giải
Gọi , , , .
Từ đó suy ra thiết diện của hình lập phương khi cắt bởi mặt phẳng là ngũ giác
.
Vì , lần lượt là trung điểm của và nên suy ra ,
. Từ đó suy ra .
144
2
( ) ( )
144 15 29 26
2.15.10 3,34511178.10 3,35.10gkg
-
=»
cos 2 4 sin 5 0xx++=
( )
0;10
p
2
2sin 4sin 6 0xxÛ- + + =
( )
sin 1
sin 3 pt
x
vx n
=-
é
Û
ê
=
ë
( )
2,
2
xkkÛ=- + Î!
p
p
( )
0;10x Î
p
0210
2
kÞ<- + <
p
pp
121
44
kÛ<<
k Î !
{ }
1; 2; 3; 4; 5k Î
( )
0;10
p
( )
53
26
4
:
102
n
uu
u
uu
=
ì
í
+=
î
15
( )
53
1
26
4
:2,u3
102
n
uu
uq
uu
=
ì
Þ= =
í
+=
î
15
15 1
12
98301
12
Su
-
Þ= =
-
.ABCD A B C D
¢¢¢¢
2
M
N
BC
CD
( )
AMN
¢
H
P
Q
E
F
N
M
C'
B'
D'
C
A
D
B
A'
E MN AB=Ç
F MN AD=Ç
QAEBB
¢¢
=Ç
PAF DD
¢¢
=Ç
( )
AMN
¢
APNMQ
¢
M
N
BC
CD
1BE CN==
1DF CM==
3AE AF==
32EFÞ=
Trang 70
Ta có , tương tự . Do đó tam giác
là tam giác cân.
Gọi là trung điểm , ta có .
Diện tích tam giác là: .
Ta thấy .
Từ suy ra .
Vậy, diện tích thiết diện là .
Hay .
------------- HẾT -------------
2222
23 13AE AA AE
¢¢
=+=+=
13AF
¢
=
A EF
¢
H
EF
22
AH AE EH
¢¢
=-
2
2
32
13
2
æö
=-
ç÷
ç÷
èø
34
2
=
A EF
¢
1
.
2
SEFAH
¢
=
1 34
.3 2.
22
=
317
2
=
EQM FPND=D
1
3
EQ EM EB
EA EF EA
===
¢
11 1
..
33 9
EQM
SSS==
1
9
FPN
SSÞ=
APNMQ
¢
APNMQ EQM FPN
SSSS
¢
=- -
11
99
SSS=- -
7
9
S=
7 3 17 7 17
.
92 6
A PNMQ
S
¢
==
| 1/70
| | Tải xuống

Có thể bạn quan tâm:

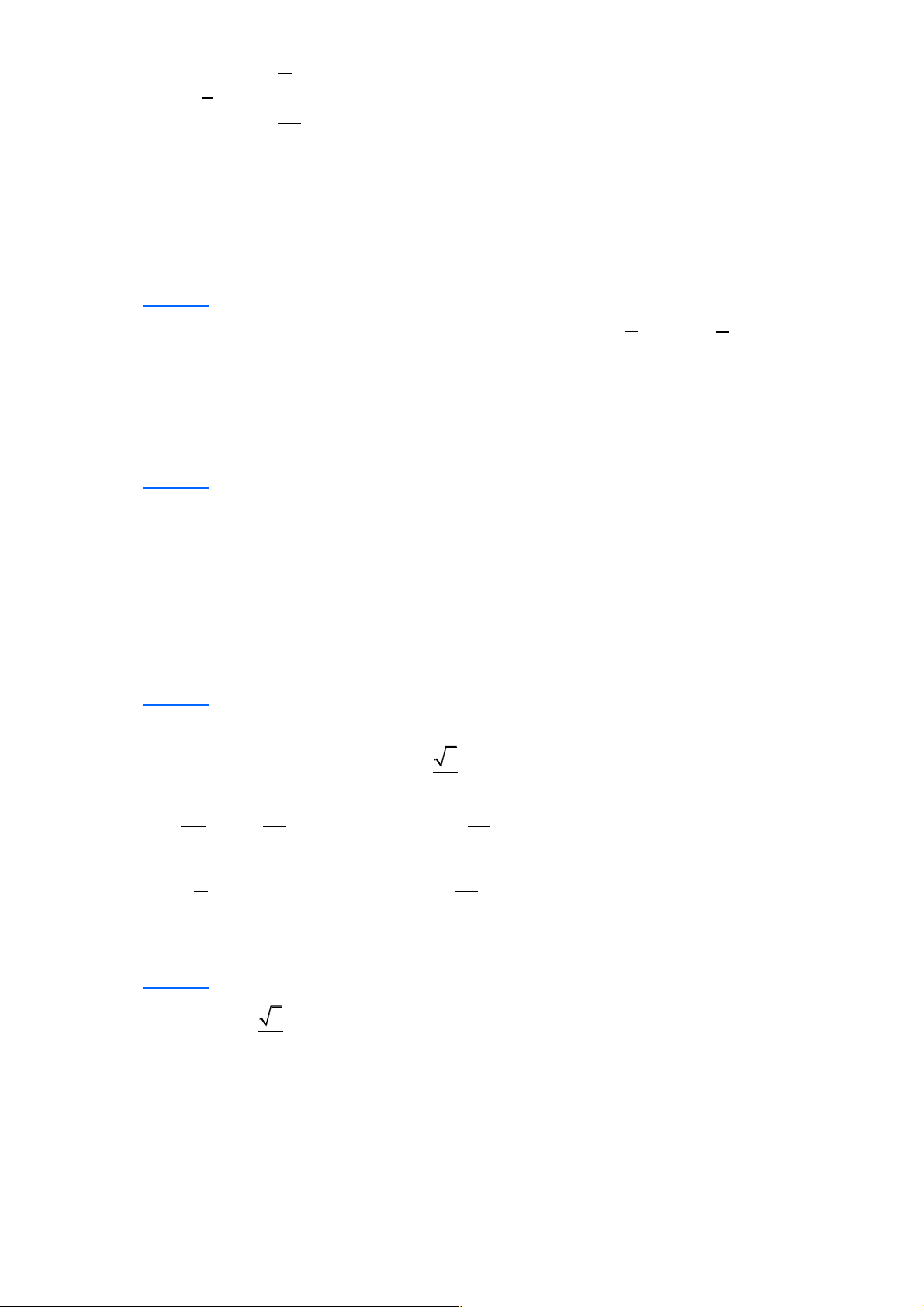
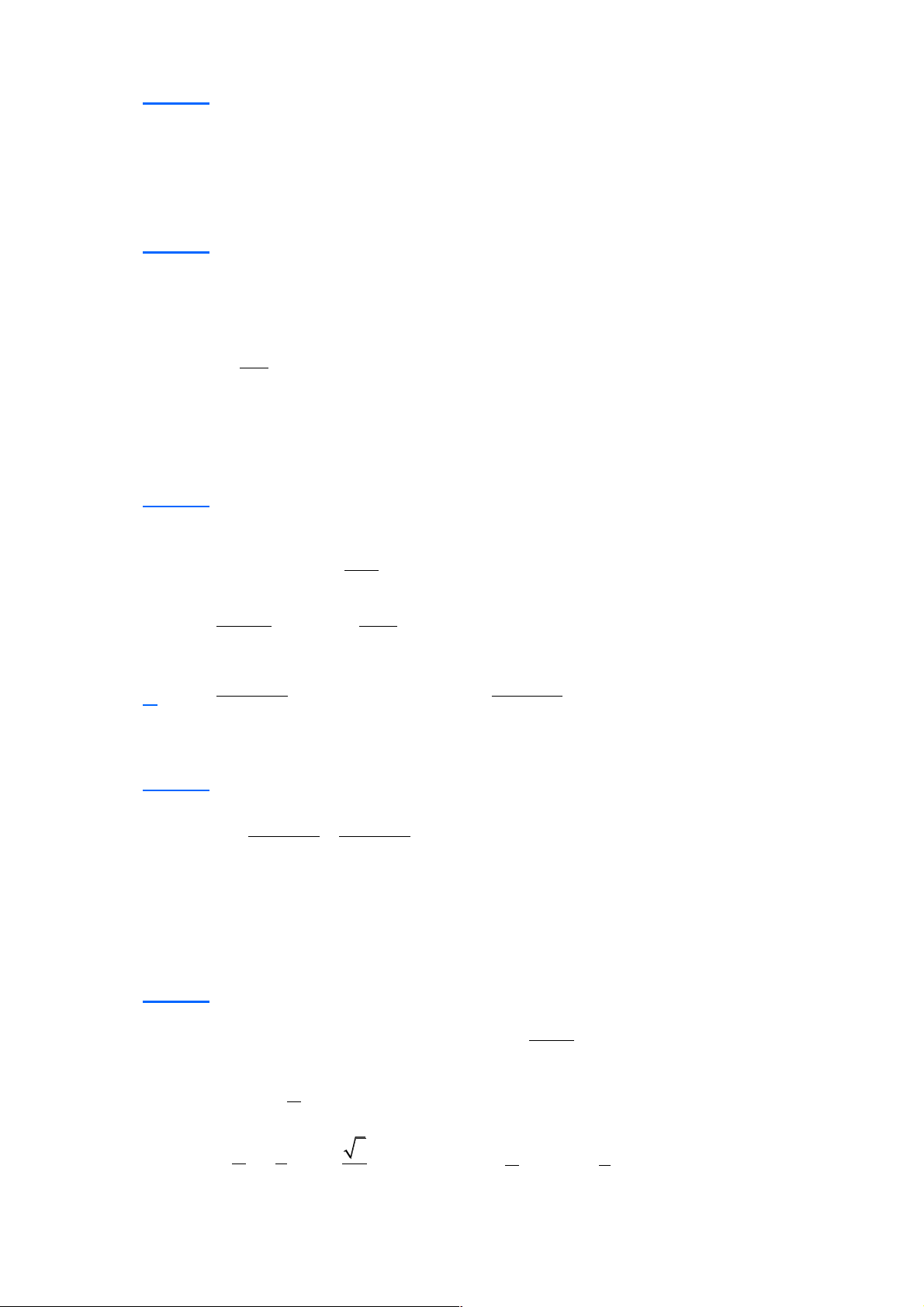
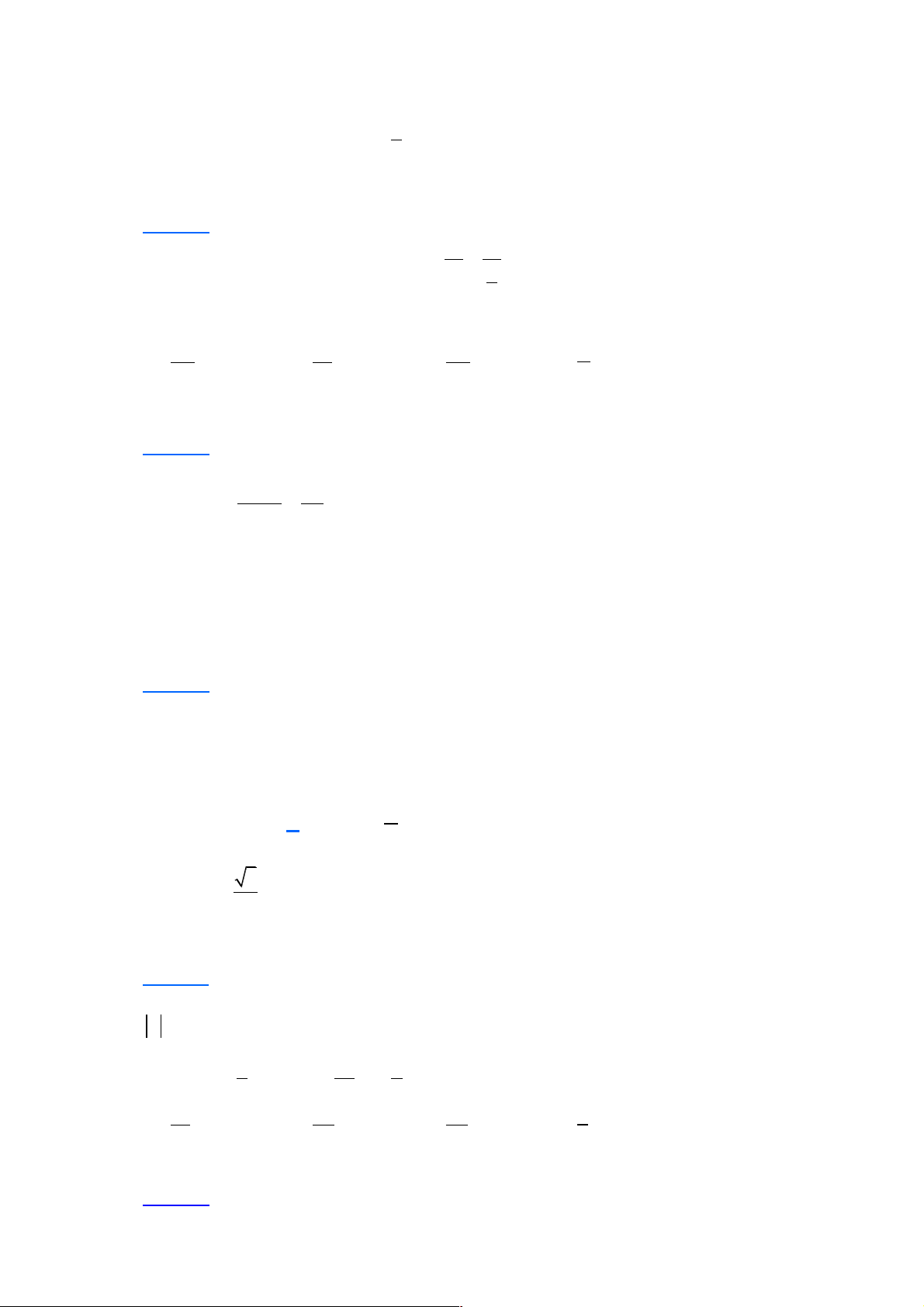
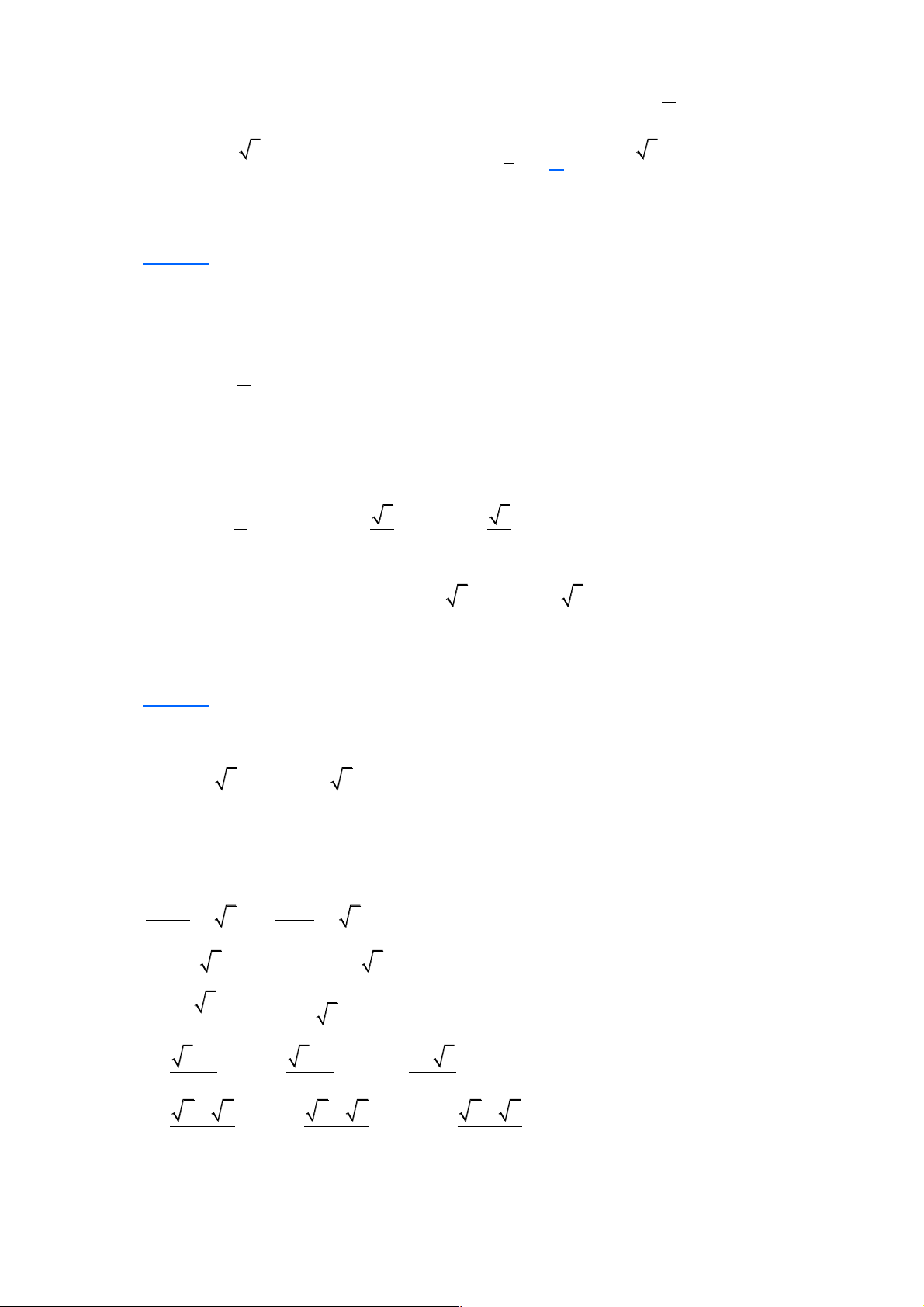
Preview text:

ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 1
I. Trắc nghiệm: (7.0đ)
Câu 1: Cho cấp số nhân ( 1 u u = , q = 2. u
n ) có số hạng đầu công bội Giá trị của bằng 1 2 25 A. 23 2 . B. 24 2 . C. 25 2 . D. 26 2 . Lời giải Chọn A
Theo công thức số hạng tổng quát của cấp số nhân ta có: 1 24 24 23
u = u .q = .2 = 2 . 25 1 2
Câu 2: Trong các hàm số sau, hàm số nào có đồ thị nhận gốc tọa độ làm tâm đối xứng?
A. y = sin x cos x . B. y = cos x .
C. y =1- sin x. D. y = xsin x. Lời giải Chọn A
Đồ thị nhận gốc tọa độ làm tâm đối xứng là đồ thị của hàm số lẻ.
A:. Hàm số y = f (x) = xsin x:
Tập xác định: D = ! . Ta có: x
" Î D : -x Î D và f (-x) = (-x)sin(-x) = xsin x = f (x).
Do đó hàm số y = xsin x là hàm số chẵn.
B:. Hàm số y = cos x là hàm số chẵn trên ! .
C:. Hàm số y = f (x) =1- sin x: æ p ö æ p Ta có: ö f = 0; f - = 2. ç ÷ ç ÷ è 2 ø è 2 ø æ p ö æ p æ p ö æ p Lúc đó: ö ö f ¹ f - và f ¹ - f - ç ÷ ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 2 ø è 2 ø
Do đó, hàm số y =1- sin x không phải là hàm số chẵn và không phải hàm số lẻ.
D:. Hàm số y = f (x) = cos xsin x :
Tập xác định: D = ! . Ta có: x
" Î D : -x Î D và f (-x) = cos(-x)sin(-x) = -cos xsin x = - f (x).
Do đó hàm số y = f (x) = cos xsin x là hàm số lẻ.
Vậy đồ thị nhận gốc tọa độ làm tâm đối xứng là đồ thị của hàm số y = f (x) = cos xsin . x 1
Câu 3: Nghiệm của phương trình sinx = là 2 p 5p p A. x = + kp; x = + kp . B. x = ± + k2p . 6 6 6 p 5p p 5p C. x = - + k2p; x = -
+ k2p . D. x = + k2p; x = + k2p . 6 6 6 6 Lời giải Chọn D Trang 1 È p x Í = + k2p 1 Í 6 sinx = € Í 2 Í 5p x Í = + k2p ÍÎ 6 p
Câu 4: Trên đường tròn bán kính r = 15 , độ dài của cung có số đo là 3
A. l = 5p .
B. l = 7p .
C. l = 6p .
D. l = 8p . Lời giải Chọn A p p
Trên đường tròn bán kính r = 15 , độ dài của cung có số đo là l =15. = 5p . 3 3
Câu 5: Cho cấp số nhân (u u =1 q = 3 u
n ) có số hạng đầu và công bội . Giá trị của là 1 5 A. 16 . B. 81. C. 13. D. 162. Lời giải Chọn B Ta có 4
u = u .q 4 = 1.3 = 81. 5 1
Câu 6: Chọn khẳng định sai trong các khẳng định sau: A. 2 2
cos 2a = cos a - sin a. B. 2
cos 2a =1- 2cos a . C. 2
cos 2a = 2cos a -1. D. 2
cos 2a =1- 2sin a . Lời giải Chọn B
Theo công thức nhân đôi.
Câu 7: Tập nghiệm của phương trình 2 cos x = là 2 ì p - 5p ì 3p A. ü ü í + k2p ,
+ k2p ,k Î!ý. B. í±
+ k2p ,k Î!ý. î 4 4 þ î 4 þ ì p ì3p C. ü
í± + k2p , k Î!ý . D. í k2p , k Î ü + !ý . î 4 þ î 4 þ Lời giải Chọn C 2 p p Ta có: cos x =
Û cos x = cos Û x = ± + k2p , k Î!. 2 4 4
Câu 8: Chọn mệnh đề sai trong các mệnh đề sau.
A. Hai đường thẳng phân biệt có không quá một điểm chung.
B. Hai đường thẳng cắt nhau thì không song song với nhau.
C. Hai đường thẳng không có điểm chung thì song song với nhau.
D. Hai đường thẳng chéo nhau thì không có điểm chung. Trang 2 Lời giải Chọn C
Hai đường thẳng không có điểm chung thì song song với nhau hoặc chéo nhau.
Câu 9: Cho cấp số cộng ( u = - u = n u ), biết và
. Tìm công sai của cấp số cộng này. 3 7 4 8
A. d = 15 .
B. d = -15 .
C. d = 1.
D. d = -3. Lời giải Chọn A
u = u + d Þ d = 4 3 15
Câu 10: Trong các mệnh đề sau, mệnh đề nào đúng? 180 ° æ ö A. p rad = ç ÷ . B. p rad 1° = . è p ø C. p rad 60° = . D. p rad 180° = . Lời giải Chọn D
Theo công thức đổi đơn vị đo góc, ta có: p rad 180 .° = 2 an
Câu 11: Cho dãy số (u u = a u n ) với ( hằng số). Hỏi
là số hạng nào sau đây? n n +1 n 1 + 2 + 2 A. . a n 1 an u = . B. u = . n 1 + n +1 n 1 + n + 2 . a (n + )2 1 . a (n + )2 1 C. u = u = + . D. + . n 1 n + 2 n 1 n +1 Lời giải Chọn C . a (n + )2 1 . a (n + )2 1 Ta có: u = = . n 1 + (n+ ) 1 +1 n + 2
Câu 12: Biết 3 số 5;x;15theo thứ tự lập thành cấp số cộng. Giá trị của x bằng A. 10. B. 20. C. 30. D. 75. Lời giải Chọn A 5 + 15
5;x;15theo thứ tự lập thành cấp số cộng nên x = = 10 . 2 æ p Câu 13: Biểu thức ö sin a +
được viết lại thành ç ÷ è 6 ø æ p ö 1 3 æ p ö 1 A. sin a + = sin a - cos a ç ÷ . B. sin a + = sin a + . è 6 ø 2 2 ç ÷ è 6 ø 2 Trang 3 æ p ö 3 1 æ p ö 3 1 C. sin a + = sin a + cos a ç ÷ . D. sin a + = sin a - cos a ç ÷ . è 6 ø 2 2 è 6 ø 2 2 Lời giải Chọn C æ p ö p p 3 1 Ta có sin a +
= sin a cos + cos asin = sin a + cos a ç ÷ . è 6 ø 6 6 2 2
Câu 14: Giá trị của tan 60° là A. 0 . B. 1 - . C. - 3 . D. 3 . Lời giải Chọn D Ta có: tan 60° = 3.
Câu 15: Tập xác định 3cos x
D của hàm số y = . 2sin x -1 ì p p ìp A. 5 ü ü D = ° \ í
+ k2p ; + k2p ,k ΢ ý.
B. D = ° \ í + k2p,k ΢ ý. î 6 6 þ î 6 þ ì1 C. ü D = ° .
D. D = ° \ í ý. î2þ Lời giải Chọn A ì p ¹ + p p x k2 ï ĐK: ï 2sin x -1 ¹ 1
0 Û sin x ¹ Û sin x ¹ sin 6 Û í , k ΢ . 2 6 5p ïx ¹ + k2p ïî 6 ì5p p TXĐ: ü D = ° \ í
+ k2p ; + k2p ,k ΢ ý. î 6 6 þ
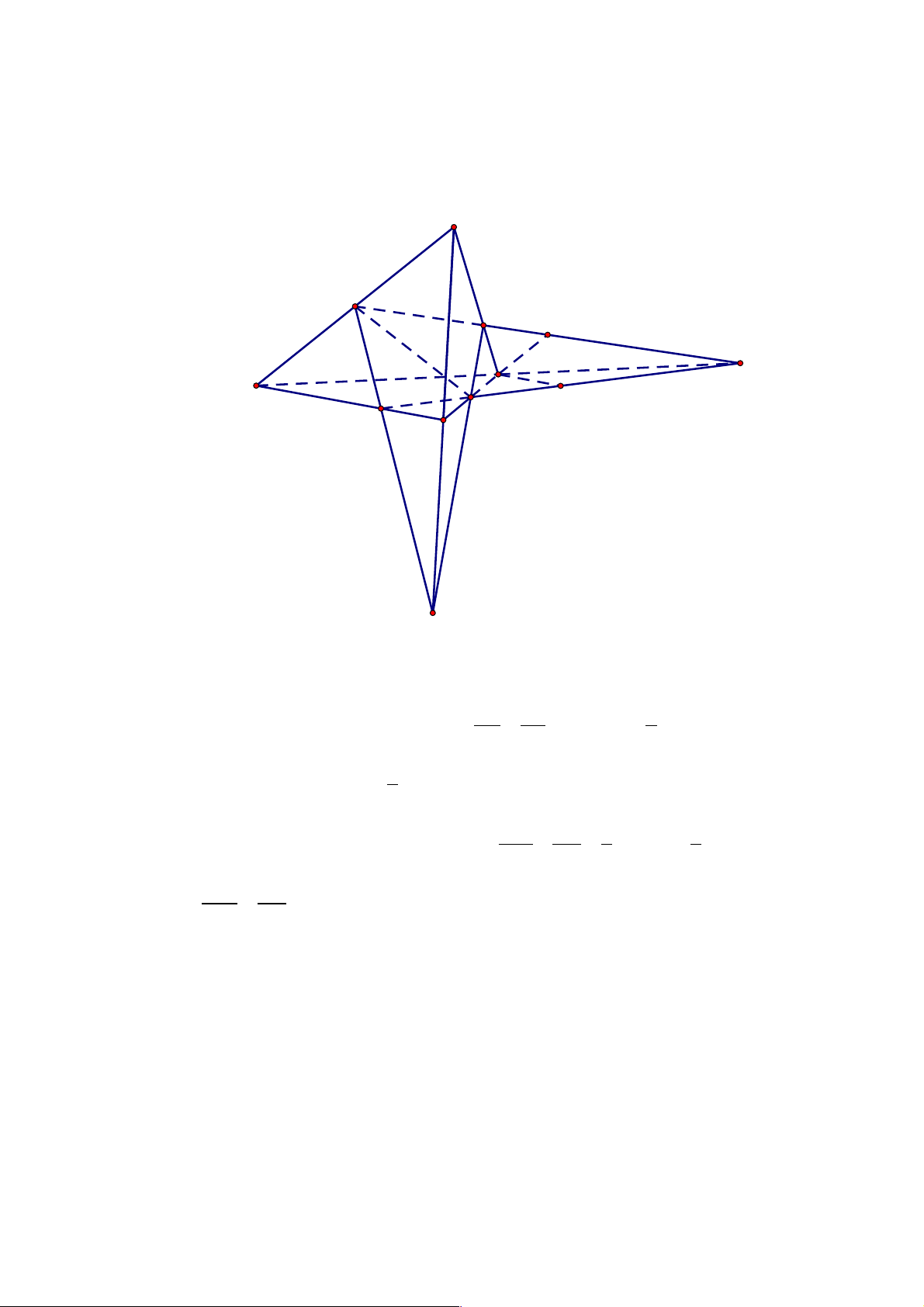
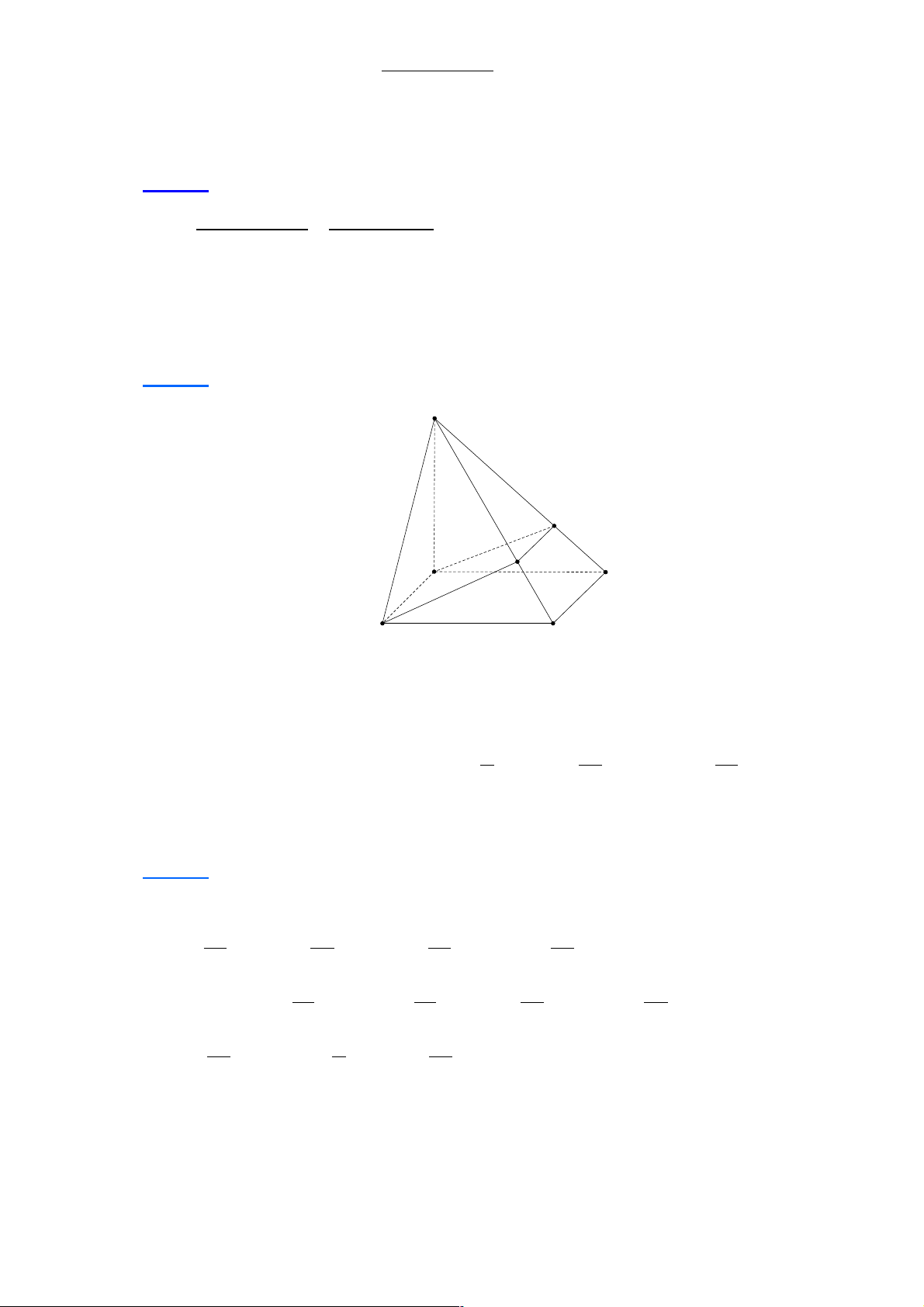
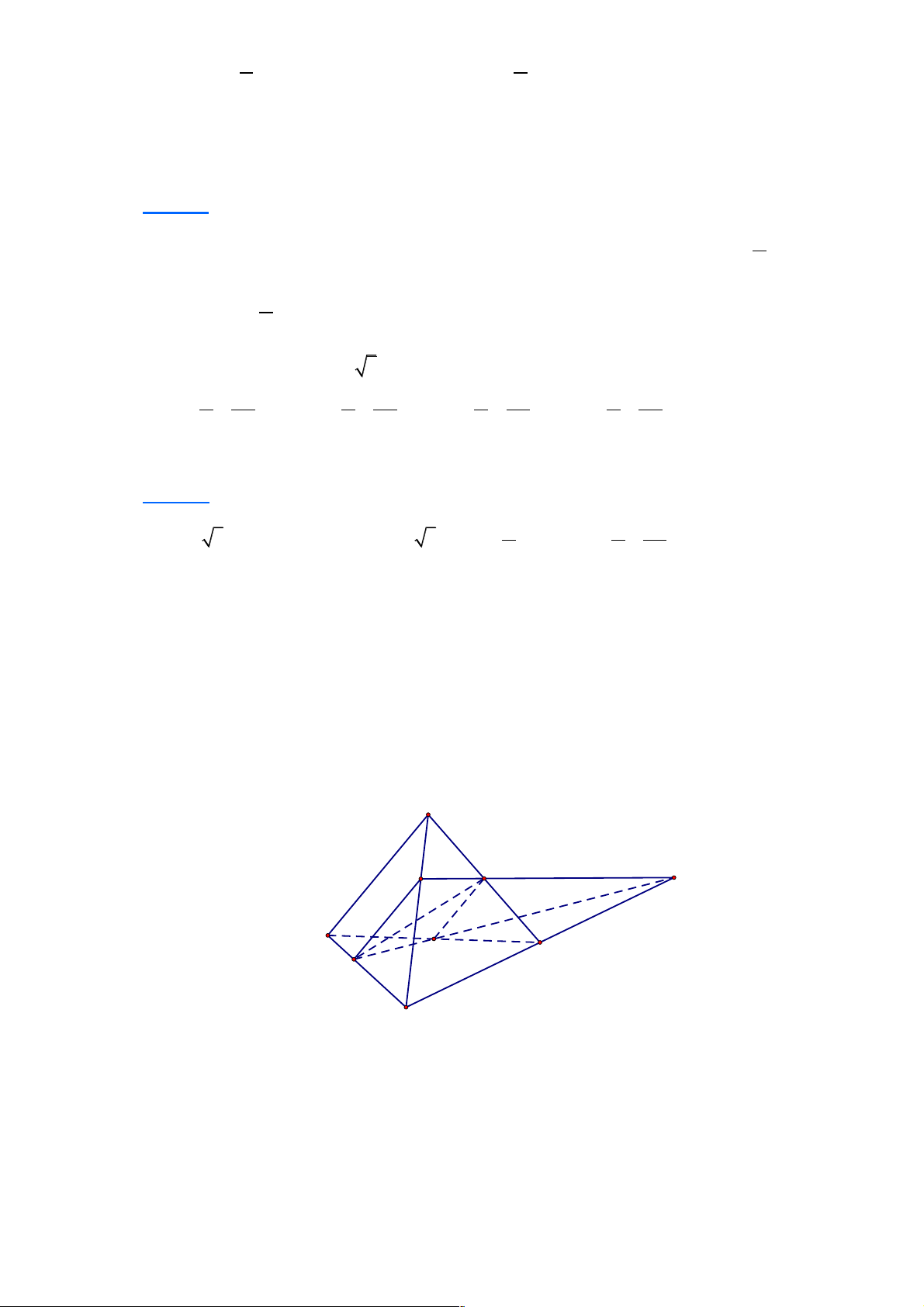
Câu 16: Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là:
A. 5 mặt, 5 cạnh. B. 6 mặt, 5 cạnh.
C. 6 mặt, 10 cạnh. D. 5 mặt, 10 cạnh. Lời giải Chọn C Trang 4 S F A D B C
Nhìn hình dễ dàng ta có đáp án đúng là 6 mặt, 10 cạnh.
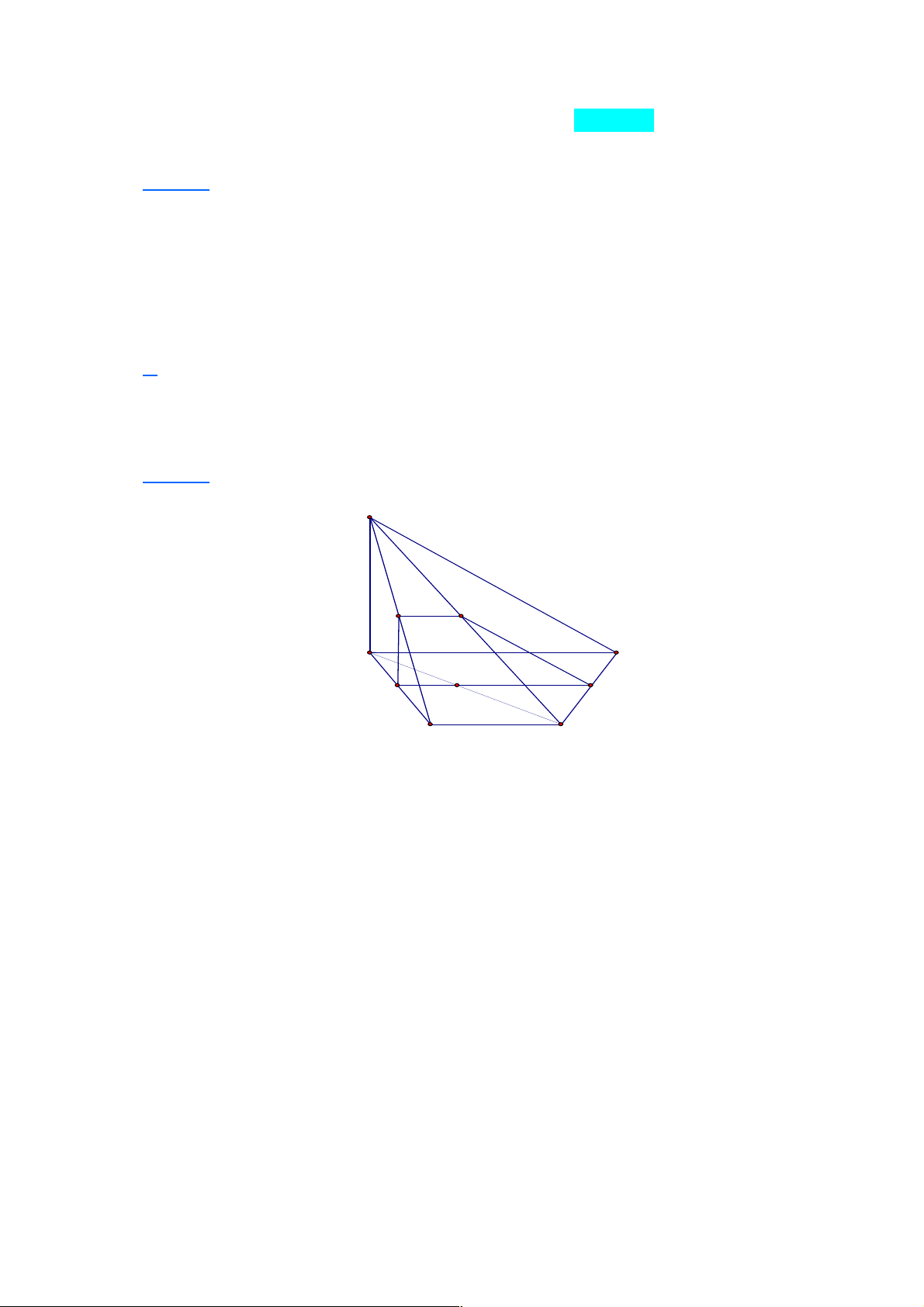
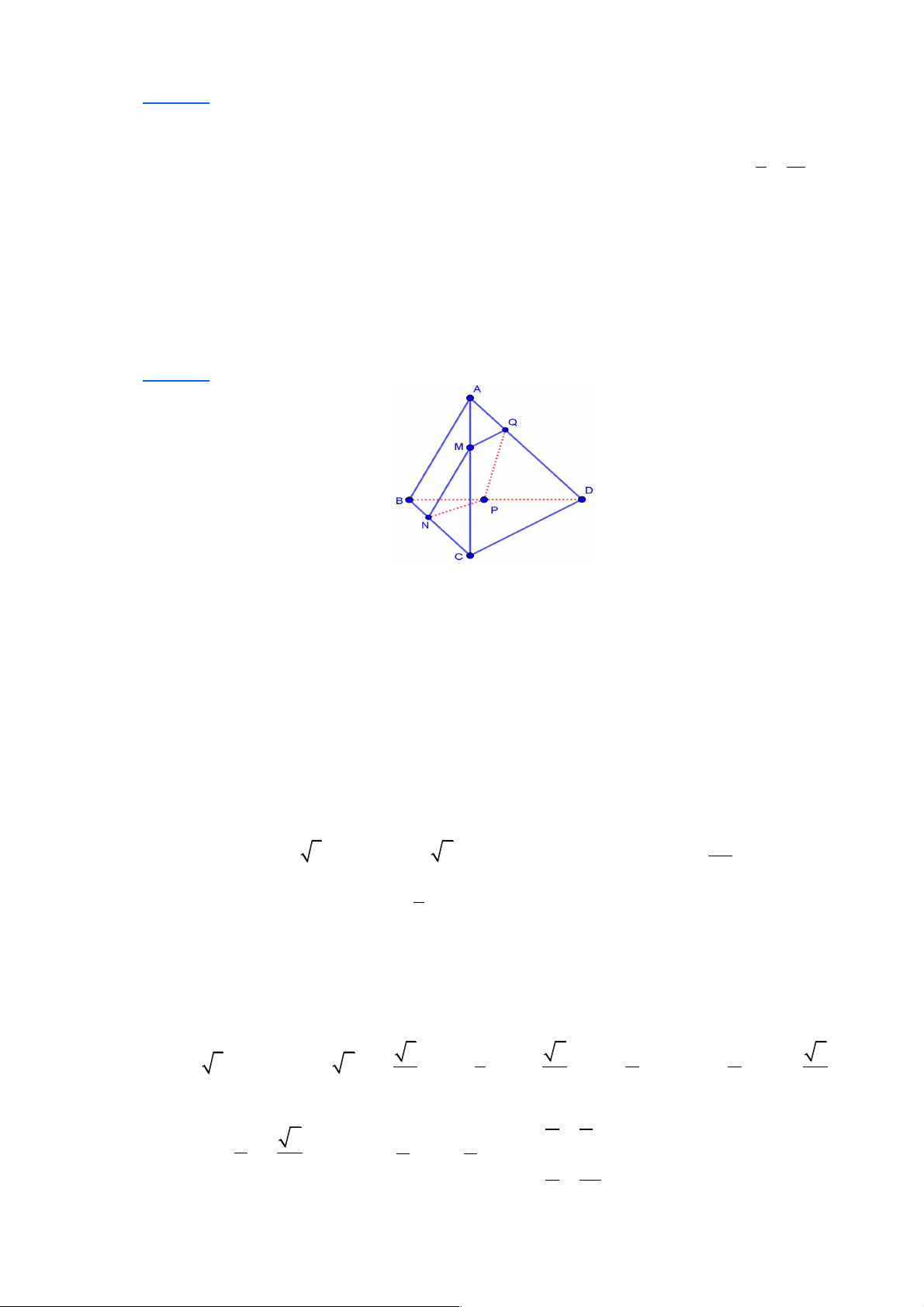
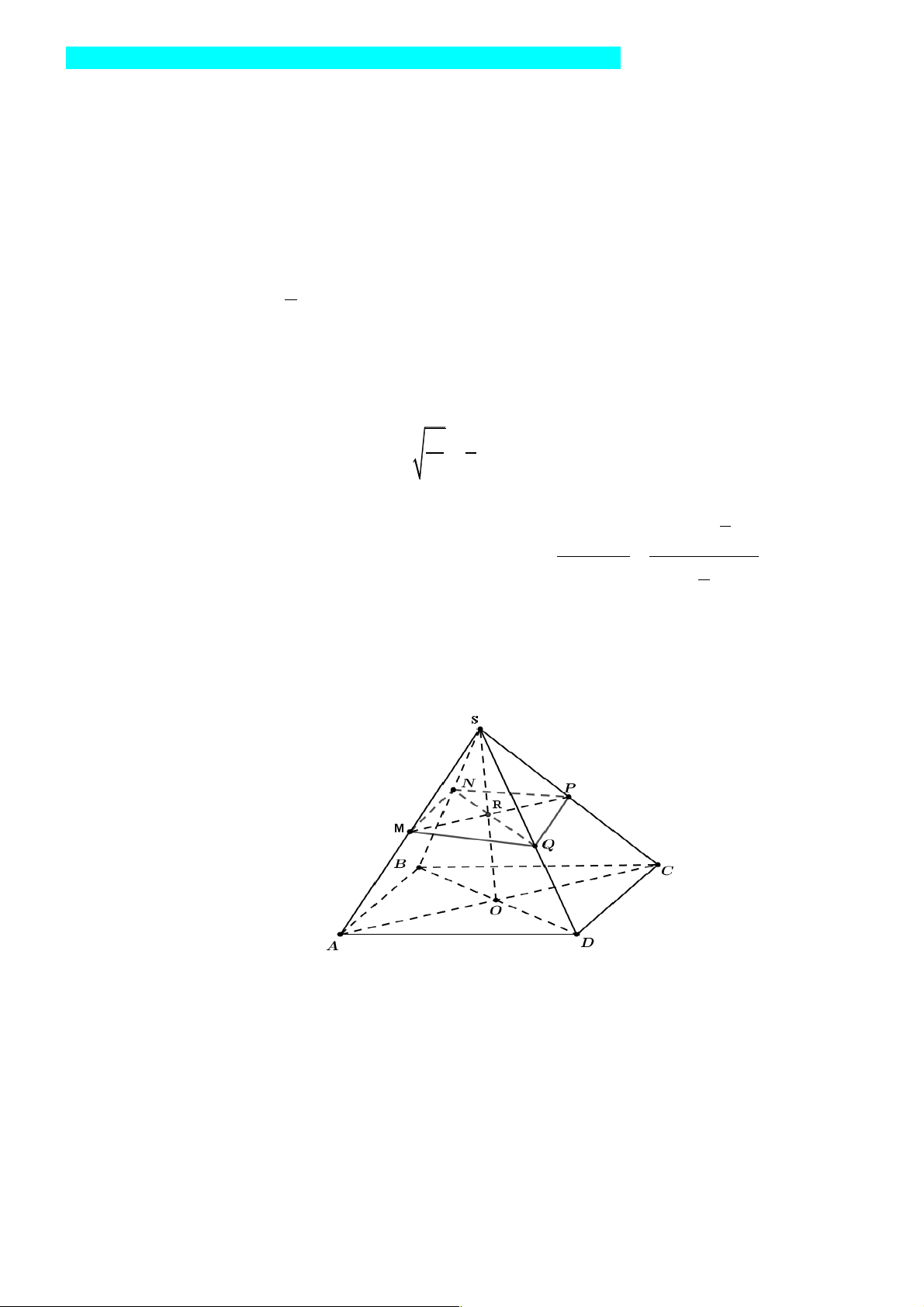
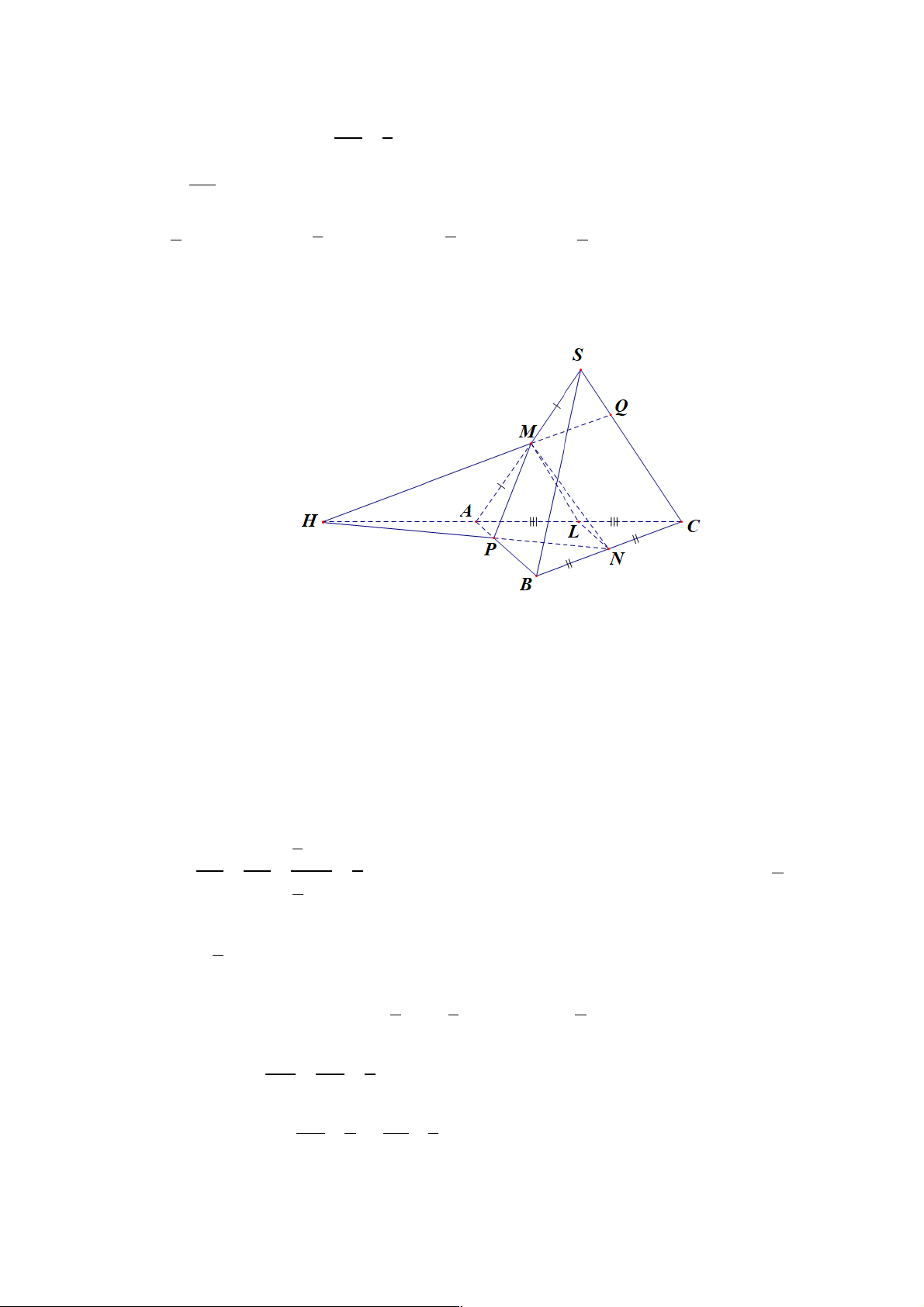
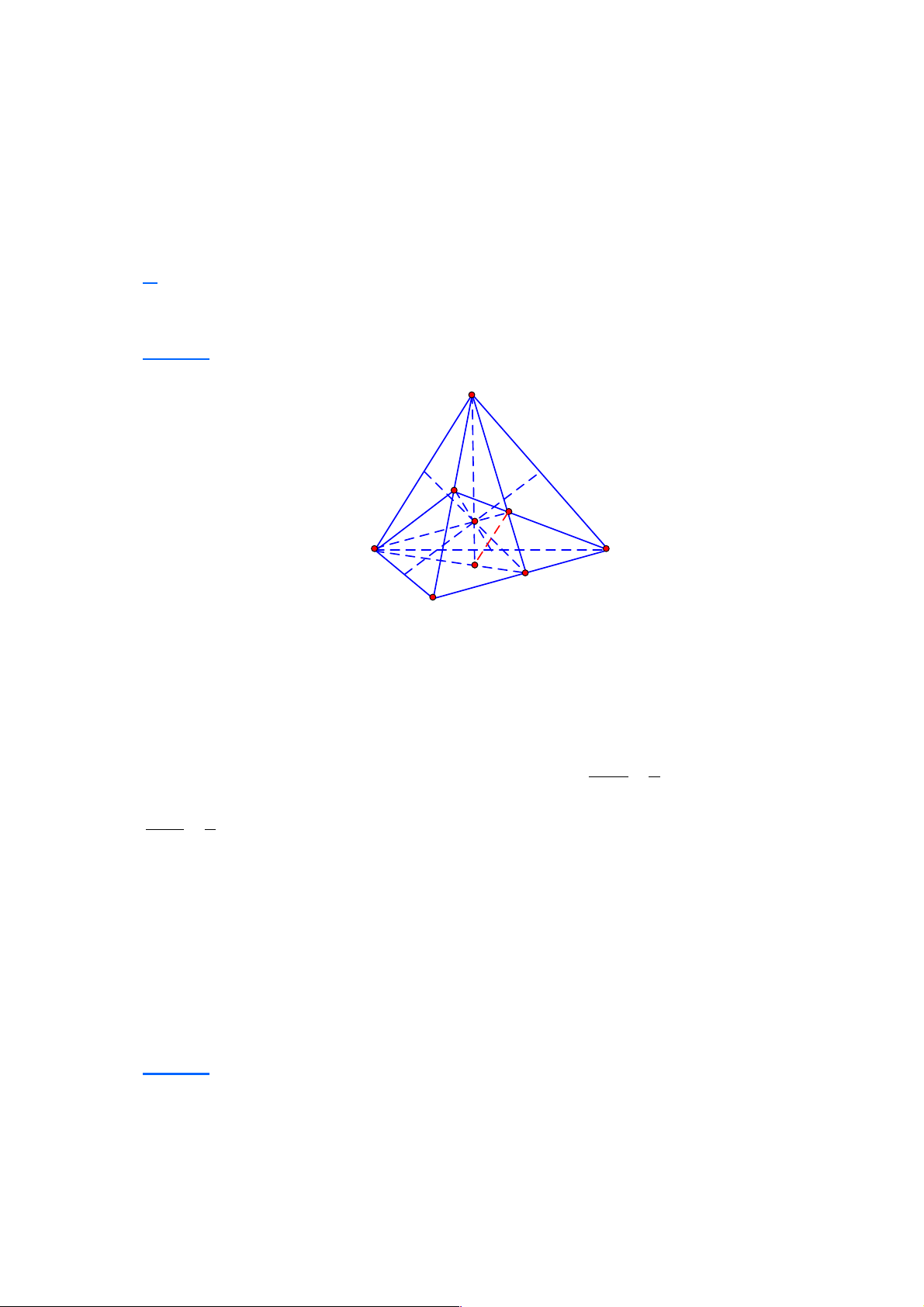
Câu 17: Cho tứ diện ABCD , G là trọng tâm tam giác BCD . Giao tuyến của hai mặt phẳng
(ACD) và (GAB)là
A. AK , với K là hình chiếu của C lên BD .
B. AM , với M là trung điểm của AB .
C. AH , với H là hình chiếu của B lên CD.
D. AN , với N là trung điểm của CD . Lời giải Chọn D A D B G N C
Mặt phẳng (GAB) chính là mặt phẳng (NAB), với N là trung điểm của CD. Vậy giao
tuyến của hai mặt phẳng (ACD) và (GAB) là AN .
Câu 18: Nghiệm của phương trình sin .
x cos x = 0 là p p p
A. x = k .
B. x = k2p .
C. x = + k2p . D. x = + k2p . 2 6 2 Lời giải Chọn A p Ta có: k sin .
x cos x = 0 Û sin 2x = 0 Û x = (k Î!). 2
Câu 19: Nghiệm của phương trình 3 sin x + cos x = 2 là Trang 5 p p
A. x = + k2p ,k Î! .
B. x = + kp , k Î!. 6 3 p p
C. x = + k2p ,k Î! .
D. x = + k2p ,k Î! . 3 2 Lời giải Chọn C
Ta có: 3 sin x + cos x = 2 3 1 æ p p p p Û ö
sin x + cos x =1 Û sin x + =1 ç ÷
Û x + = + k2p Û x = + k2p, k Î!. 2 2 è 6 ø 6 2 3
Câu 20: Hàm số nào sau đây có chu kì tuần hoàn là p ?
A. y = cot(4x .
) B. y = cos x
C. y = tan(3x .
) D. y = sin(2x . ) Lời giải Chọn D
Vì hàm số tuần hoàn với chu ki p nên f (x + p)= f (x . )
Ta có y = sin(2(x+ p))= sin(2x+ 2p)= sin(2x . )
Vậy hàm số y = sin(2x tu
) ần hoàn với chu kì p . p p Câu 21: Tính 3 sin .sin . 8 8 æ ö æ ö A. 35 . B. 1 2 1 2 2 ç1- ÷. C. ç -1÷. D. . 99 2 ç 2 ÷ ç ÷ è ø 2 2 è ø 4 Lời giải Chọn D p 3p 1 æ p p ö 1 æ 2 ö 2 sin .sin = cos - cos = ç ÷ ç - 0÷ = . 8 8 2 4 2 2 ç 2 ÷ è ø 4 è ø
Câu 22: Cho dãy số ( 1 u u = n ) có
. Tìm mệnh đề đúng. n n(n + ) 1 A. Dãy số (u (un) n ) tăng. B. Dãy số bị chặn. C. Dãy số (u (un)
n ) chỉ bị chặn trên. D. Dãy số
chỉ bị chặn dưới. Bài giải Chọn B u n Xét n 1+ = . u n + 2 n Với n
" ³ 1 Þ 0 < u <1. Vậy dãy (un ) bị chặn. n
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác ( AB không song song với CD ).
Gọi M là trung điểm của SD , N là điểm trên cạnh SB sao cho SN = 2NB , O là giao
điểm của AC và BD . Gọi d là giao tuyến của (SAB)và (SCD). Nhận xét nào sau đây là sai? Trang 6
A. d cắt CD .
B. d cắt MN . C. d cắt AB . D. d cắt SO . Lời giải Chọn B
Xét (SAB)và (SCD)có: S chung.
Trên ( ABCD)Gọi I = AB ÇCD Þ I là điểm chung của(SAB) và (SCD).
Vậy (SAB)Ç(SCD) = SI hay d º SI .
Ta có d Ç AB = I; d ÇCD = I; d Ç SO = S .
Mặt khác d và MN không đồng phẳng.
Do đó d cắt MN là mệnh đề sai.
Câu 24: Hàm số y = sin x + cos x có giá trị nhỏ nhất bằng A. 1. B. 0. C. - 2. D. 2. Lời giải Chọn C æ p Ta có: ö
sin x + cos x = 2 sin x + ç ÷ è 4 ø æ p ö æ p Mà: ö 1 - £ sin x + £1Þ - 2 £ 2 sin x + £ 2 Þ - 2 £ y £ 2. ç ÷ ç ÷ è 4 ø è 4 ø æ p ö p p p Þ y = - 2 khi sin x +
=1Þ x + = + 2kp Þ x = + 2kp (k Î ç ÷ !). min è 4 ø 4 2 2 p Vậy y
= - 2 khi x = + 2kp (k Î!). min 2
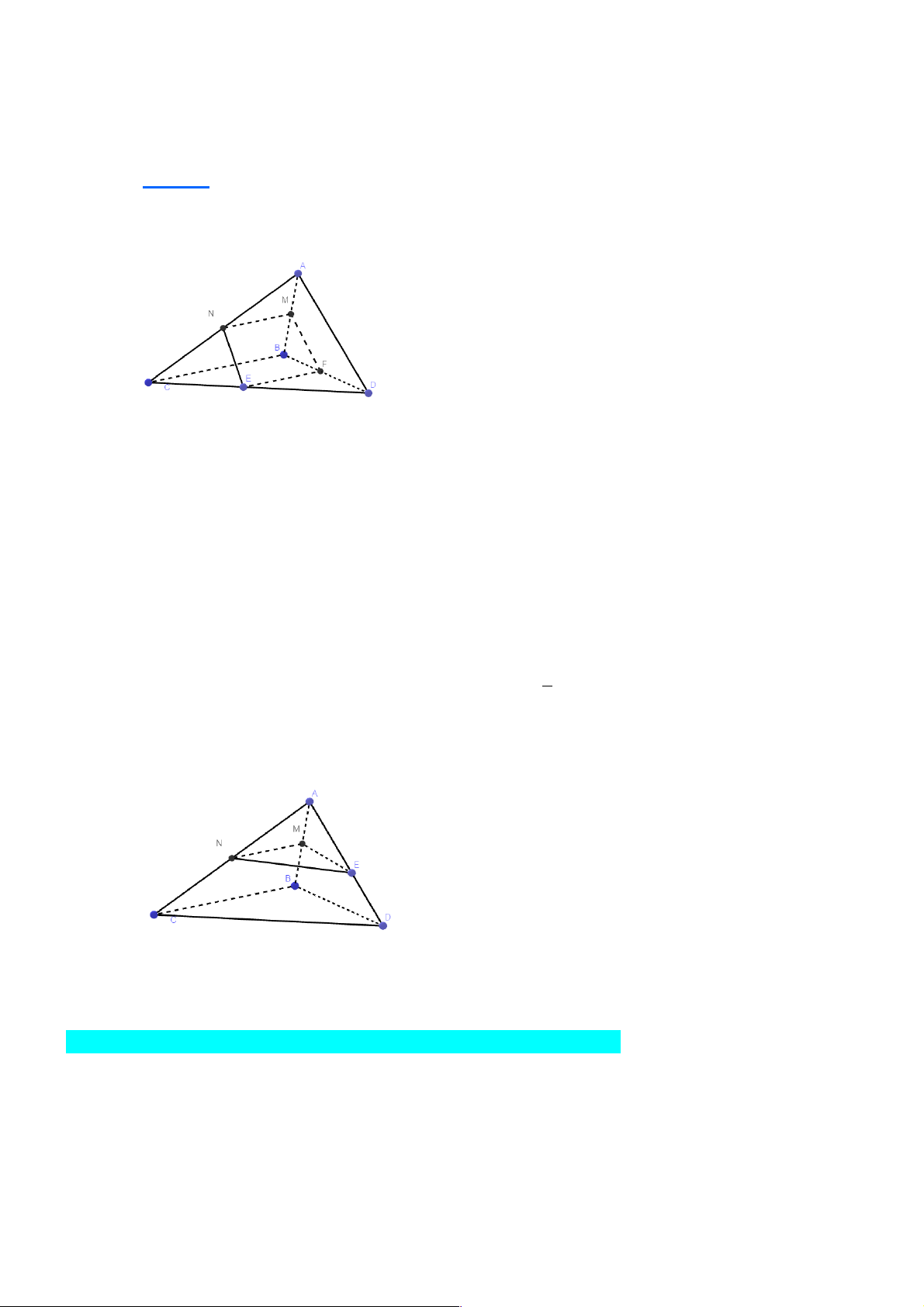
Câu 25: Cho tứ diện ABCD . Gọi I , J lần lượt là trọng tâm các tam giác ABC , ABD . Đường
thẳng IJ song song với đường thẳng Trang 7 A. DB . B. AC . C. CD .
D. CM với M là trung điểm cạnh BD . Lời giải Chọn C A J I B M D N C
Gọi M , N lần lượt là trung điểm của các cạnh BD và BC , ta có MN //CD.
Vì I, J lần lượt là trọng tâm các tam giác ABC , ABD nên ta có AI AJ 2 = = Þ IJ //MN . AN AM 3
Từ và suy ra IJ //CD .
Câu 26: Cho cấp số cộng 1
(u có u = - 3;d = . n )
Khẳng định nào sau đây đúng? 1 2 1 1
A. u = - 3 + n - 1. B. u = - 3 + n - n ( ) 1 . n 2 2 1 C. Ê 1 ˆ u = n Á- Á 3 + n ˜ + ˜ u = - 3 + n + n ( ) 1 . n ( ) 1 . D. Á Ë 4 ˜¯ 2 Lời giải Chọn B 1
Ta có u = u + n - 1 d € u = - 3 + n - 1 n 1 ( ) n ( . ) 2
Câu 27: Cho tứ diện ABCD . I và J theo thứ tự là trung điểm của AD và AC . G là trọng tâm
tam giác BCD . Giao tuyến của hai mặt phẳng (GIJ ) và (BCD) là đường thẳng.
A. Qua G và song song với BC . B. Qua I và song song với AB .
C. Qua J và song song với BD . D. Qua G và song song với CD . Lời giải Chọn D Trang 8
Xét hai mặt phẳng (GIJ ) và (BCD), có;
G Î(GIJ ) Ç(BCD)
Và IJ // CD ( IJ là đường trung bình của ACD D
), IJ Ì (GJI ),CD Ì (BCD)
Nên (GIJ )Ç(BCD) = Gy (Gy // JI //CD).
Câu 28: Cho tam giác ABC . Mệnh đề nào sau đây đúng?
A. sin(A + B) = sin C .
B. cos(A + B) = cosC . C. A + B C A + B C sin = sin . D. cos = cos . 2 2 2 2 Lời giải Chọn A
A + B + C = p Þ sin ( A+ B) = sin(p -C) = sinC .
Câu 29: Rút gọn biểu thức
sin 2a + sin 5a - sin 3a A = . 2
1+ cos a - 2sin 2a
A. cos a .
B. sin a .
C. 2cos a .
D. 2sin a . Lời giải Chọn D
sin 2a + (sin 5a - sin 3a) 2sin acos a + 2cos 4asin a 2sin a(cos a + cos 4a) Ta có A = = = cos a + ( 2 1- 2sin 2a) cos a + cos 4a cos a + cos 4a = 2sin a .
Câu 30: Cho hình chóp S.ABC có E, F lần lượt là trung điểm cạnh AB, BC và điểm G thỏa mãn !!!" 1 !!!"
SG = SC . Thiết diện của hình chóp S.ABC khi cắt bởi mặt phẳng (EFG)là hình nào 2 dưới đây? A. Tam giá B. Hình bình hành.
C. Hình thang chỉ có một cặp cạnh song song D. Hình thoi. Lời giải Trang 9 Chọn B
Ta có EF là đường trung bình trong tam giác ABC,suy ra EF / / AC ( ) 1 .
(EFG)Ç(SAC) ={ } G üï EF Ì (EFG) ï
ý Þ (EFG) Ç(SAC) = Gx / /FE / / AC AC Ì (SAC) ï EF / / AC ï þ
Gọi Gx Ç SA = {H}, suy ra H là trung điểm SA và HG / /AC (2) !!!" !!!" Ta có 1
SG = SC,suy ra G là trung điểm của SC và GF / /SB ( ) 3 . 2
Ta có HE là đường trung bình trong tam giác SAB, suy ra HE / /SB (4) Từ ( ) 1 ,(2),( )
3 ,(4)suy ra thiết diện là hình bình hành FGHE .
Câu 31: Cho hình chóp S.ABCD có AB không song song với CD . Gọi M là một điểm thuộc miền trong SC
D D . I là giao điểm của BM với (SAC), P là giao điểm của SC và
(ABM ). Khi đó P là
A. giao điểm của SC với DI .
B. giao điểm của SC với AI .
C. giao điểm của SC với MK ( SK là giao tuyến của (SAD) và (SBC)).
D. giao điểm của SC với BI . S A D B C Lời giải Chọn B Trang 10 S M A D I P E O B C
* Xác định I : Gọi E = SM ÇCD . Chọn (SBE) É BM .
Gọi O = BE Ç AC Þ SO = (SBE)Ç(SAC).
Gọi I = BM Ç SO Þ I = BM Ç(SAC).
* Xác định P : Chọn (SAC) É SC.
Ta có AI = (SAC)Ç( ABM ). Gọi P = SC Ç AI Þ P = SC Ç( ABM ).
Câu 32: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông, SA ^ AB , SA ^ AD . Gọi
M , N, P lần lượt là trung điểm ,
SA BC,CD. Thiết diện tạo bởi (MNP) và hình chóp là hình gì?
A. Là tam giác cân. B. Là ngũ giác.
C. Là tam giác thường.
D. Là tứ giác. Lời giải Chọn B
E = NP Ç AB
F = NP Ç AD
H = SB Ç ME
I = SD Ç MF
Ta được thiết diện là ngũ giác MHNPI . Trang 11
Câu 33: Cho biết có hai cấp số nhân (u ) thỏa mãn ìu + u + u = 26 1 2 3 với công bội q q . 1 và Giá n í 2 2 2 2
u + u + u = 364 î 1 2 3
trị của q + q bằng 1 2 A. 1 7 10 5 . B. . C. . D. . 2 3 3 2 Lời giải Chọn C 2 2 ì æ 1 ö ì æ 1 ö 2 æ 1 u 1 q 26 ö + + = ï ç ÷ ï + + = 2 u 1 q 676 ç ÷ +1+ q 2 q q ç q ÷ ï è ø ï è ø è ø 13 Ta có í Þ í Þ = . ï æ 1 ö ï æ ö æ 1 ö 7 1 2 2 2 2 2 u +1+ q = 364 +1+ q ç ÷ + + = 2 u 1 q 364 ç 2 ÷ 2 2 ï ï ç 2 î è q ÷ ø è q î è q ø ø 1 Đặt + q = t, điều kiện t ³ 2. Ta thu được q 2 2 2 10
7(1+ t) = 13(t -1) Û 3t - 7t -10 = 0 Û t = hoặc t = 1 - . 3 éq = 3 Với 10 1 10 t = , ta có q ê + = Û 1 . 3 q 3 êq = ë 3 Vậy 10 q + q = . 1 2 3
Câu 34: Tính tổng S tất cả các nghiệm của phương trình ( x + )( 4 4 2cos2
5 sin x - cos x)+3 = 0 trên khoảng (0;2p ). p p A. 11 S = 4p. B. S = 5p 7 . C. S = . D. S = . 6 6 Lời giải Chọn A Ta có: ( x + )( 4 4 2cos2
5 sin x - cos x)+3 = 0 Û ( x + ) éë( 2 2 x - x)( 2 2 2cos 2 5 sin cos
sin x + cos x)ù +3 = 0 û
Û (2cos2x +5)(-cos2x) +3 = 0 2 Û 2c
- os 2x -5cos 2x + 3 = 0 é 1 cos 2x = ê Û 2 ê êcos 2x = 3 - ë ( ptvn) é p x = + kp ê 6 Û ê , k Î ! p êx = - + kp êë 6 ìp 7p 5p 11p Vì ü
x Î(0;2p ) nên x Î í ; ; ; ý î 6 6 6 6 þ Trang 12 p p p p Vậy 7 5 11 S = + + + = 4p . 6 6 6 6
Câu 35: Biết rằng khi m = m thì phương trình 2 x -( m + ) 2 2sin 5
1 sin x + 2m + 2m = 0 có đúng 5 0 æ p nnghiệm thuộc khoảng ö
- ;3p . Mệnh đề nào sau đây đúng? ç ÷ è 2 ø æ 3 2 æ 3 7 A. m = 3 - . B. ö 1 ù m Î - ;- . C. m = . D. m Î ; . 0 0 ç ÷ ç è 5 5 ø 0 2 0 5 10 ú è û Lời giải Chọn B Đặt t = sin , x ( t £ )
1 . Phương trình trở thành: 2 t - ( m + ) 2 2 5
1 t + 2m + 2m = 0 (1)
Yêu cầu bài toán thỏa mãn khi một trong các trường hợp sau xảy ra
TH1: Pt (1) có 2 nghiệm: t =1 và 1 - < t £ 0. 1 2 ém = 1 +) 2
t =1Þ 2m - 3m +1 = 0 ê Û 1 . êm = ë 2 ét =1
Với m = 1 thì (1) trở thành: 2
2t - 6t + 4 = 0 Û
không thỏa yêu cầu bài toán. ê ët = 2 ét = 1 Với 1 7 3
m = thì (1) trở thành: 2 2t - t + = 0 ê Û
3 không thỏa yêu cầu bài toán. 2 2 2 êt = ë 4
TH2: Pt (1) có 2 nghiệm: t = 1 - và 0 < t <1. 1 2 é 1 m = - +) t = 1 - 2 2
Þ 2 + 5m +1+ 2m + 2m = 0 Û 2m + 7m + 3 = 0 ê 2 . ê ëm = -3 ét = -1 Với 1 3 1
m = - thì (1) có dạng: 2 2t + t - = 0 ê Û
1 thỏa yêu cầu bài toán. 2 2 2 êt = ë 4 ét = -1 Với m = 3 - thì (1) có dạng: 2
2t +14t +12 = 0 Û
không thỏa yêu cầu bài toán. ê ët = -6 1 æ 3 2 ö m = - Î - ;- . ç ÷ 2 è 5 5 ø
II. Tự luận: (3.0đ)
Câu 36: Giải phương trình cos2 .
x tan x = 0. Lời giải: p
Điều kiện: cos x ¹ 0 Û x ¹ + kp (k Î! ) 2 Trang 13 é p é p écos2x = 0 2x = + k2p x = + kp Phương trình cos2 . x tan x 0 ê 2 ê = Û Û Û 4 (k Î ê ! ) ëtan x = 0 ê ê ëx = kp ëx = kp é p x = + kp
So điều kiện, nhận nghiệm ê 4 (k Î! ). ê ëx = kp
Câu 37: Cho cấp số nhân (u ) có 1 1 u = - 1,q = - . Số
là số hạng thứ mấy của dãy n 1 10 103 10 Lời giải
Ta có số hạng tổng quát của cấp số nhân là: n 1 - n 1 1 æ 1ö æ 1 - - - - ö 1 - æ 1 n - ö - n 1 1 u = u .q Û = 1 - . Û = Û .( 1 - 0) = n 1 103 ç ÷ ç ÷ 103 ç ÷ 103 10 è 10 ø è 10 ø 10 è 10 ø 10 n n 104 æ 1 - ö 1 æ 1 - ö æ 1 - ö Û = Û = Û n = 104 ç ÷ 104 ç ÷ ç ÷ è 10 ø 10 è 10 ø è 10 ø
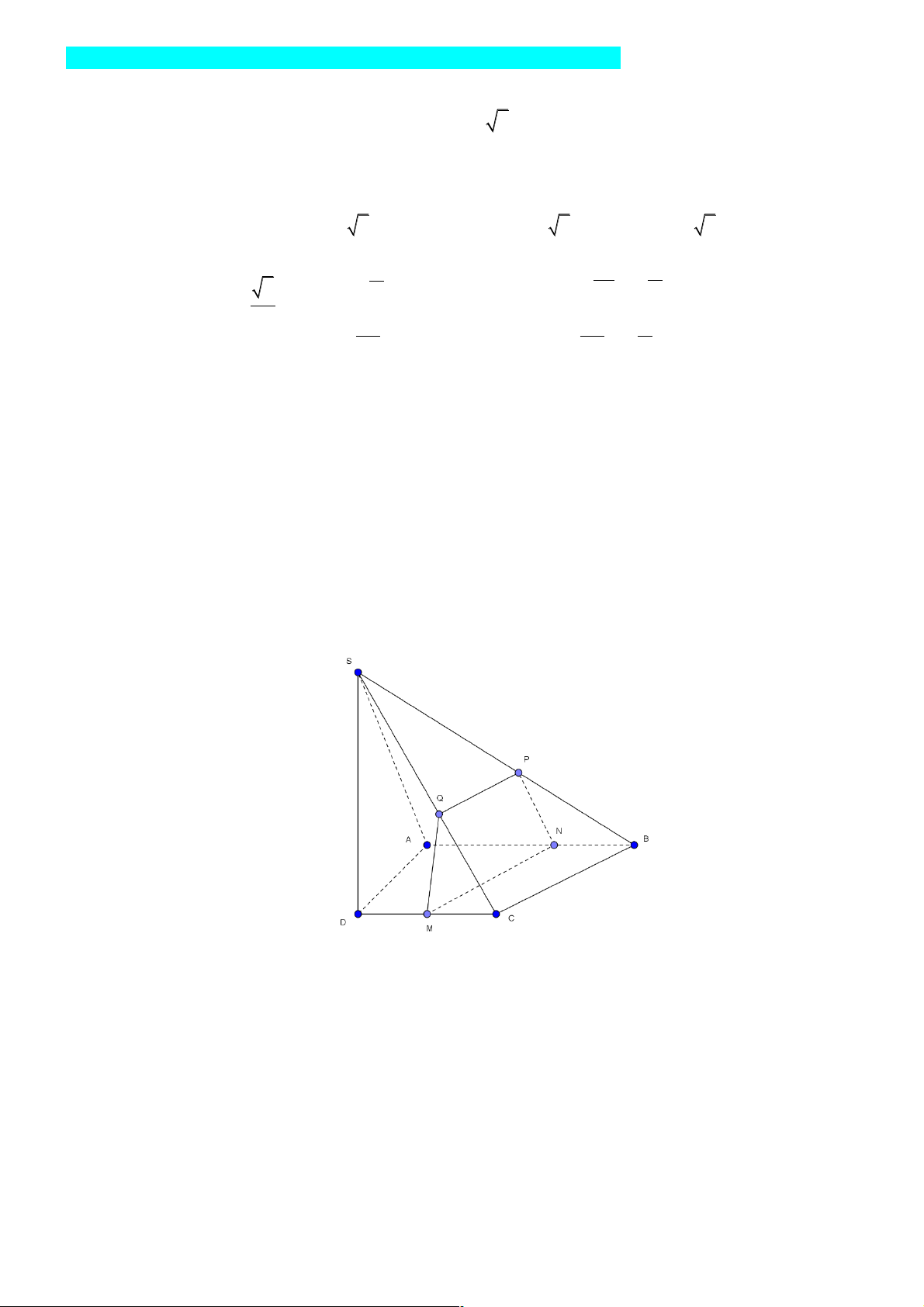
Câu 38: Cho tứ diện ABCD có M , N lần lượt là trung điểm của AB,CD và P là một điểm
thuộc cạnh BC ( P không trùng trung điểm cạnh) BC . Thiết diện của tứ diện cắt bởi
mặt phẳng (MNP) là hình gì? Lời giải Chọn D A M Q B D P N C I
Trong mp ( ABC) kéo dài MP, AC cắt nhau tại I.Trong mp( ACD)kéo dài IN cắt AD
( ABC)!(MNP) = MP
(BCD)!(MNP) = PN tại . Q Ta được:
Vậy thiết diện của tứ diện cắt bởi mặt phẳng
( ACD)!(MNP) = NQ
( ABD)!(MNP) = QM
(MNP) là tứ giác MPN . Q Trang 14
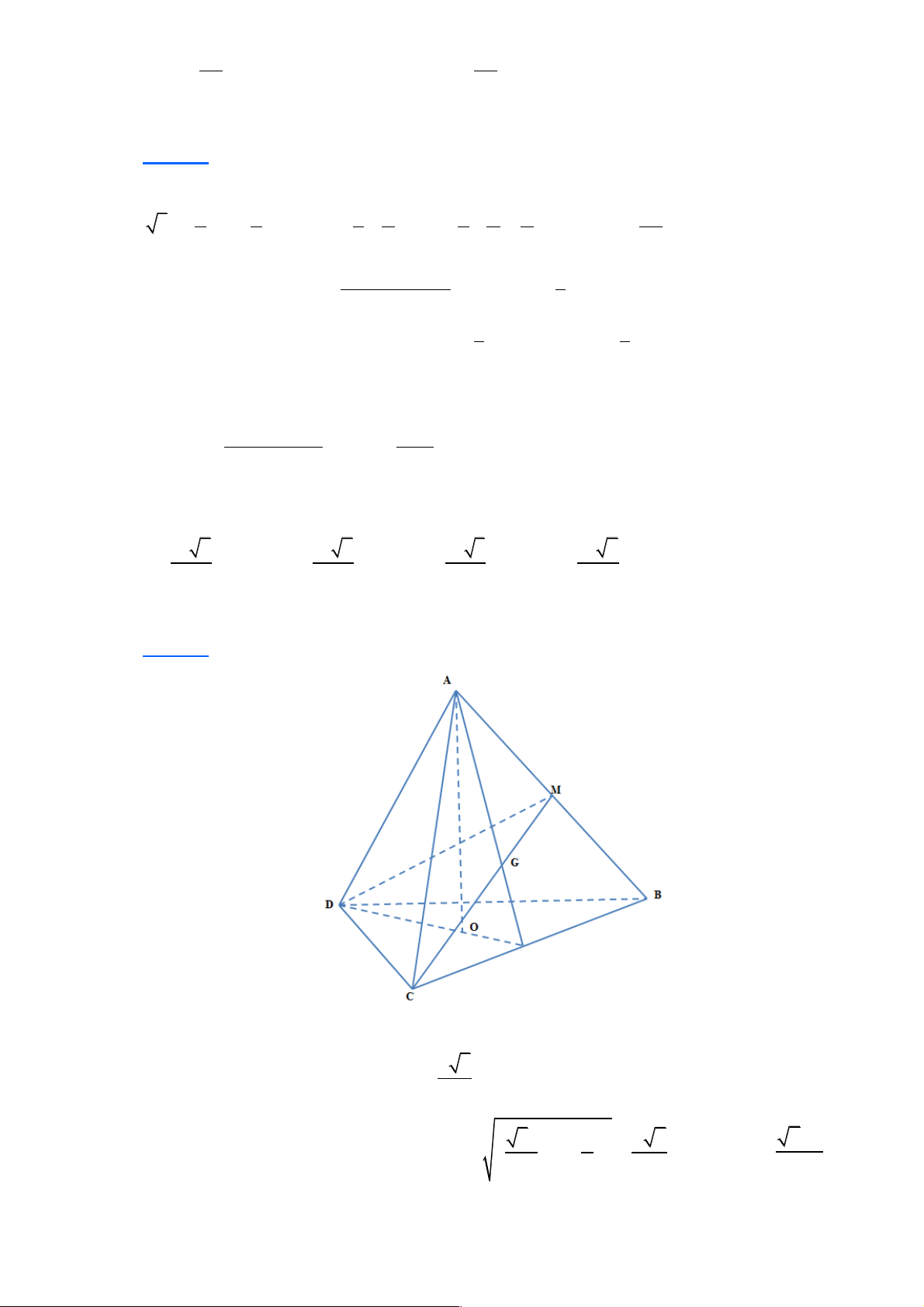
Câu 39: Cho tứ diện ABCD có AB = 6 , CD = 8 . Cắt tứ diện bởi một mặt phẳng song song với
AB , CD để thiết diện thu được là một hình thoi. Cạnh của hình thoi đó bằng Lời giải A I K B D N M C
Giả sử một mặt phẳng song song với AB và CD cắt tứ diện ABCD theo một thiết diện
ìMK // AB // IN là hình thoi ï
MNIK như hình vẽ trên. Khi đó ta có: íMN // CD // IK . ïMK = KI î ìMK CK ì - = MK AC AK ï = ï
Cách 1: Theo định lí Ta – lét ta có: ï AB AC ï 6 AC í Þ í KI AK ï = KI AK ï = ïîCD AC ïî 8 AC MK AK Þ = MK KI MK MK 1- Þ =1- Þ =1- 7 Û MK = 24 1 Û MK = . 6 AC 6 8 6 8 24 7
Vậy hình thoi có cạnh bằng 24 . 7 ìMK CK = ï
Cách 2: Theo định lí Ta – lét ta có: ï AB AC MK MK CK AK í Þ + = + KI AK ï = AB CD AC AC ïîCD AC MK MK AK + KC Þ + = 7MK AC Þ = = 24 1Þ MK = . 6 8 AC 24 AC 7
------------- HẾT ------------- Trang 15
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 2
I. Trắc nghiệm: (7.0đ)
Câu 1: Cho cấp số cộng (u u =11 u =14 n ) với và
. Công sai của cấp số cộng đã cho bằng 5 6 A. 3. B. 12 . C. 6 . D. 6 - . Lời giải Chọn A
Ta có: u = u + d Û14 =11+ d Þ d = 3. 6 5 Câu 2: Cho dãy số ( n -1 U U = , n Î N 100 n ( * )
n ) có số hạng tổng quát . Số hạng thứ của dãy số n + 2 là A. 33 37 39 35 U = . B. U = . C. U = . D. U = . 100 34 100 34 100 34 100 34 Lời giải Chọn A - Ta có 100 1 33 U = = . 100 100 + 2 34 p
Câu 3: Trên đường tròn bán kính bằng 4 , cung có số đo thì có độ dài là 8 p p p p A. . B. . C. . D. . 3 16 2 4 Lời giải Chọn C p p
Độ dài cung là: l = 4. = . 8 2
Câu 4: Tập nghiệm của phương trình 2 cos x = là: 2 ì 3p ü ì p ü A. í±
+ k2p ,k Î!ý.
B. í± + k2p ,k Î!ý . î 4 þ î 4 þ ì3p ì p - 5p ü C. í k2p , k Î ü + !ý . D. í + k2p ,
+ k2p ,k Î!ý . î 4 þ î 4 4 þ Lời giải Chọn B p p Ta có: 2 cos x =
Û cos x = cos Û x = ± + k2p , k Î!. 2 4 4
Câu 5: Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định bao nhiêu mặt
phẳng phân biệt từ các điểm đã cho? Trang 16 A. 3 . B. 2 . C. 6 . D. 4 . Lời giải Chọn D
Các mặt phẳng là (ABC ),(ACD),(ABD),(BCD .) p p p p sin cos + sin cos
Câu 6: Giá trị của biểu thức 15 10 10 15 bằng p 2p 2p p cos cos - sin sin 5 15 15 5 A. 3 . B. 1 1. C. . D. 1 - . 2 Lời giải Chọn A p p p p æ p p ö p sin cos + sin cos sin + ç ÷ sin è ø p Ta có 15 10 10 15 15 10 3 = = = tan = 3 . p 2p 2p p æ 2p p ö p 3 cos cos - sin sin cos + cos 5 15 15 5 ç ÷ è 15 5 ø 3
Câu 7: Mệnh đề nào trong các mệnh đề sau đây là sai?
A. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhât.
B. Nếu ba điểm phân biệt cùng thuộc hai mặt phẳng phân biệt thì ba điểm đó thẳng hàng.
C. Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.
D. Nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến
đó đôi một song song. Lời giải Chọn D
Vì nếu ba mặt phẳng phân biệt cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến
đó đôi một song song hoặc đồng quy.
Câu 8: Khẳng định nào dưới đây là Sai?
A. Hàm số y = tan xlà hàm số lẻ. B. Hàm số y = sin x là hàm số chẵn.
C. Hàm số y = cos x là hàm số chẵn.
D. Hàm số y = cot xlà hàm số lẻ. Lời giải Chọn B
Câu 9: Tập xác định của hàm số 2cos -1 = x y là: sin 2x ìkp A. ü D = ! \{ p k ,k Î } " . B. D = ! \ í , k Î "ý. î 2 þ Trang 17 ì p kp ìp C. ü ü
D = ! \ í± + k2p;
, k Î "ý. D. D = ! \ í + k2p ,k Î"ý. î 3 2 þ î 3 þ Lời giải Chọn B kp ìkp Hàm số xác định Û ü
sin 2x ¹ 0 Û x ¹
, k Î!. Tập xác định D = ! \ í , k Î "ý. 2 î 2 þ
Câu 10: Cho cấp số nhân có u = 3 - , 2
q = . Tính u . 1 3 5 A. 16 16 27 27 u = . B. u = - . C. u = . D. u = - . 5 27 5 27 5 16 5 16 Lời giải: Chọn B 4 æ 2ö 16 Ta có 4
u = u .q = 3. - = - ç ÷ . 5 1 è 3ø 27
Câu 11: Biết tana = 2 và p
- < a < 0 . Tính cosa . 1 A. cosa = - 1 . B. cosa = 2 . C. cosa = - 2 . D. cosa = . 5 5 5 5 Lời giải Chọn A 1 2 1+ tan a = 2 cos a 1 1 1 2 Þ cos a = = = 2 2 1+ tan a 1+ 2 5 1 Þ cosa = ± 5 1
Vì tana > 0 nên sina, cosa cùng dấu. Mà p
- < a < 0 nên cosa < 0 . Vậy cosa = - . 5
Câu 12: Biết 3 số 5;x;15theo thứ tự lập thành cấp số cộng. Giá trị của x bằng A. 30. B. 75. C. 10. D. 20. Lời giải Chọn C 5 + 15
5;x;15theo thứ tự lập thành cấp số cộng nên x = = 10 . 2
Câu 13: Trong mặt phẳng (a ), cho tứ giác ABCD có AB cắt CD tại E , AC cắt BD tại F , S là
điểm không thuộc (a ). Giao tuyến của (SAB)và (SCD)là A. AC . B. SE . C. SF . D. SD . Lời giải Chọn B Trang 18
Hai mặt phẳng (SAB)và (SCD)có hai điểm chung là S và E nên có giao tuyến là đường thẳng SE . 1
Câu 14: Cho cấp số nhân (U U = U =16 q n ) có ,
. Khi đó công bội là 1 2 2 A. 64 . B. 8 . C. 4 . D. 32 . Bài giải Chọn D Cấp số nhân ( u 16 U 2 q = = = 32
n ) có công bội là . u 1 1 2
Câu 15: Góc có số đo 108° đổi ta rađian là p p p p A. 3 . B. . C. 3 . D. . 5 10 2 4 Lời giải Chọn A
Ta có 180° = p (radian). p p Vậy 108. 3 108° = = (radian). Chọn A 180 5
Câu 16: Trong các công thức sau, công thức nào sai? A. 2
cos 2a = 2cos a - . 1 B. 2
cos 2a =1- 2sin a . C. 2 2
cos 2a = cos a - sin a. D. 2 2
cos 2a = sin a - cos a. Lời giải Chọn D
Theo công thức nhân đôi ta có 2 2 2 2
cos 2a = cos a - sin a = 2cos a -1 =1- 2sin a.
Vậy công thức sai là 2 2
cos 2a = sin a - cos a.
Câu 17: Trong các phương trình sau, phương trình nào có nghiệm? æ p A. ö cos x = 2 . B. sin 2x + = 1. ç ÷ è 3 ø 5 C. sin 2x = . D. sin x = 2 - . 2 Lời giải Chọn B
Các dạng phương trình lượng giác cơ bản sin u = a , cosu = a có nghiệm khi và chỉ khi a £ . 1 Câu 18: Cho 3 3a a cos a = . Tính cos .cos . 4 2 2 A. 7 . B. 23 . C. 23 . D. 7 . 16 8 16 8 Lời giải Chọn A Trang 19 1 æ 9 3 Ta có: 3a a 1 1 ö 7 cos .cos
= (cos2a + cos a) = ( 2
2cos a -1+ cos a) = -1+ = . ç ÷ 2 2 2 2 2 è 8 4 ø 16 æ 2p
Câu 19: Giá trị bé nhất của hàm số ö y = sin x + + sin x là ç ÷ è 3 ø 3. A. B. 2. - C. 1. - 3. D. - 2 2 Lời giải Chọn C æ 2p ö æ 2p ö + + + - æ 2 x x x x p ö ç 3 ÷ ç 3 ÷ y = sin x + + sin x = 2sin ç ÷ ç ÷cosç ÷ è 3 ø 2 2 ç ÷ ç ÷ è ø è ø æ p ö æ p ö 1 æ p ö æ p ö = 2sin x + cos = 2. sin x + = sin x + . ç ÷ ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø 2 è 3 ø è 3 ø æ p Ta có: ö 1 - £ sin x + £1. ç ÷ è 3 ø
Câu 20: Cho hình lăng trụ ABC. ¢
A B¢C¢ . Gọi M , N lần lượt là trung điểm của BB¢ và CC¢ ,
D = mp( AMN)Çmp( A B ¢ C
¢ ¢). Khẳng định nào sau đây đúng ?
A. D // AB .
B. D // AC .
C. D // BC . D. D // ¢ AA . Lời giải Chọn C Ta có
Δ = mp ( AMN ) Ç mp ( ¢ A B¢C¢)ü MN ( AMN ) ï Ì ï ý Þ Δ // C B . B¢C¢ Ì ( ¢ A B¢C¢) ï MN // ï B¢C¢ þ Trang 20
Câu 21: Cho phương trình cos .
x cos 7x = cos3 . x cos5x ( )
1 . Phương trình nào sau đây tương
đương với phương trình ( ) 1
A. cos 4x = 0.
B. sin 5x = 0 . C. sin 4x = 0 . D. cos3x = 0 . Lời giải Chọn C Ta có cos .
x cos 7x = cos3 .
x cos5x Û cos8x + cos 6x = cos8x + cos 2x Û cos 6x - cos 2x = 0 Û 2 - sin 4 .
x sin 2x = 0 Û sin 4x = 0
Câu 22: Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD / /BC). Gọi M, N, P lần lượt
là trung điểm của SB , CD và AC . Hãy cho biết thiết diện của hình chóp S.ABCD khi
cắt bởi mặt phẳng (MNP) là hình gì?
A. Hình thang. B. Hình chữ nhật.
C. Hình tam giác. D. Hình bình hành. Lời giải Chọn A S F M A D E P N B C
Trong mp ( ABCD), gọi E = NP Ç AB .
Khi đó : (MNP)Ç( ABCD) = NE và (MNP)Ç(SAB) = EM . (1) Xét ACD D
có P , N lần lượt là trung điểm của AC , CD Þ NP / / AD / / BC.
Ta có: NP//BC ; NP Ì (MNP); BC Ì (SBC); M Î(MNP)Ç(SBC), qua M kẻ đường
thẳng song song với BC cắt SC tại F .
Khi đó : (MNP)Ç(SBC) = MF
và (MNP)Ç(SCD) = FN . (2)
Từ (1) và (2), thiết diện của hình chóp là tứ giác MENF .
Tứ giác MENF có MF //EN nên MENF là hình thang.
Câu 23: Cho hình chóp tứ giác S.ABC .
D Gọi G ,G lần lượt là trọng tâm các tam giác SAC và 1 2 .
ACD Khi đó G G song song với đường thẳng 1 2 A. BC. B. AC. C. . AD D. . SD Lời giải Chọn D Trang 21 Gọi EG EG 1
E là trung điểm của AC . Trong mp(SED) , ta có: 1 2 = = , suy ra ES ED 3 G G / /SD . 1 2
Câu 24: Cho cấp số cộng (u d = 4 u = 3 n ) có công sai và số hạng đầu
. Tìm số hạng tổng quát 1 u . n
A. u = 3n + 4.
B. u = 3n +1. C. u = 4n + 3. D. u = 4n - . 1 n n n n Lời giải Chọn D
Ta có u = u + n -1 d = 3+ 4 n -1 = 4n -1 n 1 ( ) ( ) .
Câu 25: Cho hình tứ diện ABCD . Phát biểu nào sau đây là đúng?
A. Tồn tại một mặt phẳng chứa AD và BC .
B. AB và CD song song với nhau.
C. AC và BD cắt nhau.
D. AC và BD không có điểm chung. Lời giải Chọn D
Vì ABCD là tứ diện nên AC và BD không cùng nằm trên một mặt phẳng.
Do đó AC và BD không có điểm chung.
Câu 26: Dãy số nào trong các dãy số sau đây là dãy số bị chặn trên? + A. ( n u u = n " Î N* (u u n n N* = + " Î n ) , 2 1 n ) 2 3 , . B. . n n + 4 n Trang 22 C. (u u n n N* = " Î (u u n n N* = " Î n ) , n ) 2 , . D. . n n Lời giải Chọn A
2n + 3 2 n + 4 - 5 Ta có: (u u = = = - < n " Î N* n ) ( ) 5 , 2 2
nên dãy số bị chặn trên. n n + 4 n + 4 n + 4 æ p ö æ p Câu 27: Giả sử ö A = tan x tan - x tan
+ x được rút gọn thành A = tan nx khi đó n bằng ç ÷ ç ÷ è 3 ø è 3 ø A. 2 B. 1 C. 4 D. 3 Lời giải Chọn D æ p ö æ p 3 - tan x 3 + tan x 2 - Ta có ö 3 tan x A = tan x tan - x tan + x ç ÷ ç ÷ = tan . x . = tan . x è 3 ø è 3 ø
1+ 3 tan x 1- 3 tan x 2 1- 3tan x 3 3tan x - tan x = = tan 3x . 2 1- 3tan x
Câu 28: Cho hàm số y = cot x; trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có tập xác định D = ! \{kp,k Î } "
B. Đồ thị hàm số đi qua gốc tọa độ.
C. Hàm số là một hàm số lẻ.
D. Hàm số có chu kỳ tuần hoàn T = p . Lời giải Chọn B
Điều kiện: sin x ¹ 0 Û x ¹ kp ,k Î!, nên hàm số có tập xác định là: D = ! \{kp,k Î } " , nên B đúng
Hàm số là hàm số lẻ nên D đúng
Hàm số là hàm số tuần hoàn chu kỳ T = p , nên A đúng. Vậy C sai. æ 85p ö æ 5p
Câu 29: Rút gọn biểu thức ö A = sin x + + cos ç ÷ (2017p + x) 2 + sin (33p + x) 2 + sin x - ta ç ÷ è 2 ø è 2 ø được
A. A = sin x .
B. A = 1.
C. A = 2 .
D. A = 0 . Lời giải Chọn B Ta có: æ 85p ö æ p ö A = sin x + + cos ç ÷ (2017p + x) 5 2 + sin (33p + x) 2 + sin x - ç ÷ è 2 ø è 2 ø æ p ö æ p ö Û A = x + p + + ç ÷ ( p +p + x) 2 + ( p +p + x) 2 sin 42 cos 2016 sin 32 + sin x - 2p - ç ÷ è 2 ø è 2 ø æ p ö æ p ö Û A = x + + ç ÷ (p + x) 2 + (p + x) 2 sin cos sin + sin x - ç ÷ è 2 ø è 2 ø æ p 2 2 ö
Û A = cos x - cos x + sin x + sin - x ç ÷ è 2 ø 2 2
Û A = sin x + cos x Trang 23 Û A = 1.
Câu 30: Phương trình 3 sin 2x - cos 2x = 2có tập nghiệm là ì2p ìp A. ü ü S = í
+ k2p | k Î!ý.
B. S = í + kp | k Î!ý. î 3 þ î 3 þ ì5p ìp kp C. ü ü S = í
+ kp | k Î!ý. D. S = í + | k Î!ý. î12 þ î 3 2 þ Lời giải Chọn B 3 1 æ p ö p p p PT Û
sin 2x - cos 2x =1 Û sin 2x -
=1 Û 2x - = + k2p Û x = + kp ç ÷ . 2 2 è 6 ø 6 2 3 ìp
Vậy tập nghiệm của phương trình là: ü
S = í + kp | k Î!ý. î 3 þ
Câu 31: Cho tam giác ABC cân tại đỉnh A , biết độ dài cạnh đáy BC , đường cao AH và cạnh
bên AB theo thứ tự lập thành cấp số nhân với công bội q . Giá trị của 2 q bằng + - + - A. 2 1. B. 2 1 C. 2 2 . D. 2 2 . 2 2 2 2 Lời giải Chọn A Đặt BC = ; a AB = AC = ;
b AH = h. Theo giả thiết ta có a, h, b lập cấp số nhân, suy ra 2 2 2 2 h = . ab + Mặt khác tam giác b b a
ABC cân tại đỉnh A nên 2 2 h = m = - a 2 4 2 2 2 + Do đó b b a 2 2 -
= ab Û a + 4ab - 4b = 0 Û a = (2 2 -2)b (vì a, b > 0) 2 4 + + Lại có 2
b = q a nên suy ra b 1 2 2 2 2 1 2 q = = = = . a 2 2 - 2 4 2 x x
Câu 32: Tính tổng T tất cả các nghiệm của phương trình 2 2sin
- 3cos = 0 trên đoạn é0;8p ù. 4 4 ë û
A. T = 4p .
B. T = 0 .
C. T = 8p .
D. T = 16p . Lời giải Chọn C Xét phương trình: æ ö 2 x x 2 x x 2 x x 2sin - 3cos = 0 Û 2 1- cos -3cos = 0 Û 2 - cos -3cos + 2 = 0 ç ÷ (1) 4 4 è 4 ø 4 4 4 Trang 24 Đặt: x
t = cos ;t Î é 1 - ;1ù. Khi đó phương trình (1) trở thành: 4 ë û é 1 t = 2 2t 3t 2 0 ê - - + = Û 2 ê êt = 2 - ë (L) é x p é 4p = + k2p x = + k8p 1 x 1 x p ê ê Với 4 3 3
t = Þ cos = Û cos = cos Û ê Û ê ; k Î! 2 4 2 4 3 ê x p ê 4p = - + k2p x = - + k8p ê 4 3 ê ë ë 3 p p Xét 4 x = + 4 1 5
k8p : x Î é0;8p ù Þ 0 £
+ k8p £ 8p Û - £ k £ . 3 ë û 3 6 6 ì p ü
Mà k Î! Þ k Î{ } 4 0 Þ x Î í ý î 3 þ p p Xét 4 x = - + 4 1 7
k8p : x Î é0;8p ù Þ 0 £ -
+ k8p £ 8p Û £ k £ . 3 ë û 3 6 6 ì p ü
Mà k Î! Þ k Î{ } 20 1 Þ x Î í ý î 3 þ 4p 20p Vậy T = + = 8p 3 3
Câu 33: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 10 - ; ] 10 để phương trình 2 x + (m- ) 2 11sin
2 sin 2x + 3cos x = 2 có nghiệm? A. 21. B. 15 . C. 16 . D. 6 . Lời giải Chọn C Ta có : 2 x + (m- ) 2 11sin
2 sin 2x + 3cos x = 2 2 Û x + (m - ) 2 11sin 2
2 sin xcos x + 3cos x = 2 ( ) * *Nếu cos x = 0 : ( )
* ®11 = 2 (vô lý) nên cos x = 0 không thỏa phương trình.
*Nếu cos x ¹ 0 , chia hai vế của phương trình (*) cho 2 cos x ta được: 2 x + (m- ) x + = ( 2 11tan 2 2 tan 3 2 1+ tan x) 2
Û 9tan x + 2(m- 2)tan x +1= 0
Để phương trình có nghiệm thì ¢ D = (m- )2 2 -9 ³ 0 Û mÎ(- ; ¥ - ] 1 È[5;+¥)
Vì m nguyên và mÎ[ 10 - ; ] 10 nên mÎ{ 10 - ; 9 - ;...; 1 - ;5;6;...; }
10 . Vậy có tất cả 16 giá trị
m để phương trình có nghiệm.
Câu 34: Cho tứ diện ABCD . Gọi I và K lần lượt là trung điểm của các cạnh AB và CD ; J, E
lần lượt là các điểm trên các đoạn AD và BC sao cho AD = 3JD , EB = 2EC . Gọi F là
giao điểm của IJ và BD ; H là giao điểm của AC và IE . Khẳng định nào sau đây sai?
A. BC Ç(IJK ) = E .
B. Cá đường thẳng IE, AC, JK đồng quy. Trang 25
C. Giao điểm của BC và mặt phẳng (IJK ) là trung điểm của BC .
D. IJ Ç(BCD) = F . Lời giải Chọn C A I J L F D B M K E C H
Ta có (BCD)Ç( ABD) = BD Þ IJ Ç(BCD) = IJ Ç BD = F Þ A đúng.
(IJK)Ç(BCD) = KF Þ BCÇ(IJK) = BC Ç KF = E¢. Trong ( ABD) kẻ DL JD
DL//AB , L Î IJ . Ta có = = 1 2 Þ DL = IA. IA JA 2 !!!" !!" Trong tam giác 1 BIF có DL =
BI Þ D là trung điểm của đoạn BF . 2 Trong (BCD) kẻ DM DF 1 1
DM //BC , M Î EF . Ta có =
= Þ DM = BE¢ (1). BE¢ BF 2 2 Lại có DM KD =
=1 Þ DM = CE¢. (2). CE¢ KC
Từ (1) và (2) suy ra BE¢ = 2CE ' . Do đó E º E¢ Þ BC Ç(IJK) = E Þ B đúng Þ D sai.
Ba mặt phẳng ( ABC), ( ACD) và (IJK ) cắt nhau theo ba giao tuyến IE , AC và JK
nên ba đường thẳng IE , AC và JK đồng quy tại H Þ C đúng.
Câu 35: Cho tứ diện ABCD , M và N lần lượt là trung điểm AB và AC . Mặt phẳng (a )qua
MN cắt tứ diện ABCD theo thiết diện là đa giá ( T ) Khẳng định nào sau đây đúng?
A. ( T )là tam giá
B. ( T )là hình thang. Trang 26
C. ( T )là tam giác hoặc hình thang hoặc hình bình hành.
D. ( T )là hình chữ nhật. Lời giải Chọn C
TH1: Mặt phẳng (a )cắt đoạn CD tại E bất kỳ, E ¹ C, E ¹ D.
ì E Î (a ) Ç ( BCD ) ïïMN ! BC
ì Ex = (a ) Ç ( BCD ) í Þ í . MN Ì (a ) ï
î Ex//MN //BC
ïîBC Ì ( BCD )
Gọi F = Ex Ç BD trong ( BCD ).
Ta có: MN //EF nên tứ giác MNEF là hình thang.
Nếu E là trung điểm CD , khi đó MN và EF lần lượt là các đường trung bình trong 1 ABC D và BCD D
, nên MN //EF và MN = EF = BC . Khi đó tứ giác MNEF là hình 2 bình hành.
TH2: Mặt phẳng (a )cắt đoạn AD tại E bất kỳ, E ¹ A.
Dễ thấy thiết diện tạo bởi mặt phẳng (a )và tứ diện ABCD là MN D E .
II. Tự luận: (3.0đ)
Câu 36: Tập nghiệm của phương trình co 2
s x + cosx + 1 = 0 là Lời giải
cos 2x + cos x +1 = 0 Û 2cosx + cosx = 0 Trang 27 é cosx = 0 cosx (2cosx ) 1 0 ê Û + = Û 1 êcosx = - ë 2 é p x = + k2p ê 2 Û ê , k ÎZ 2p êx = ± + k2p êë 3
Câu 37: Cho cấp số nhân (u u = - 3 q = - 2 - 192 n ) có , công bội . Hỏi
là số hạng thứ mấy của 1 (un )? Lời giải
Giả sử - 192 là số hạng thứ n của (u v * n Œ• n ) ới .Ta có n- n - 6 n- 1 1 192 . n u q - - = € - = (- ) (- ) 1 192 3 . 2 € = (- ) 1 64 2 € (- ) 2 = (- ) 2 € 6 = n - 1 1
€ 7 = n . Do đó - 192 là số hạng thứ 7 của (u . n )
Câu 38: Cho hình chóp S.ABCD , G là điểm nằm trong tam giác SCD . E , F lần lượt là trung
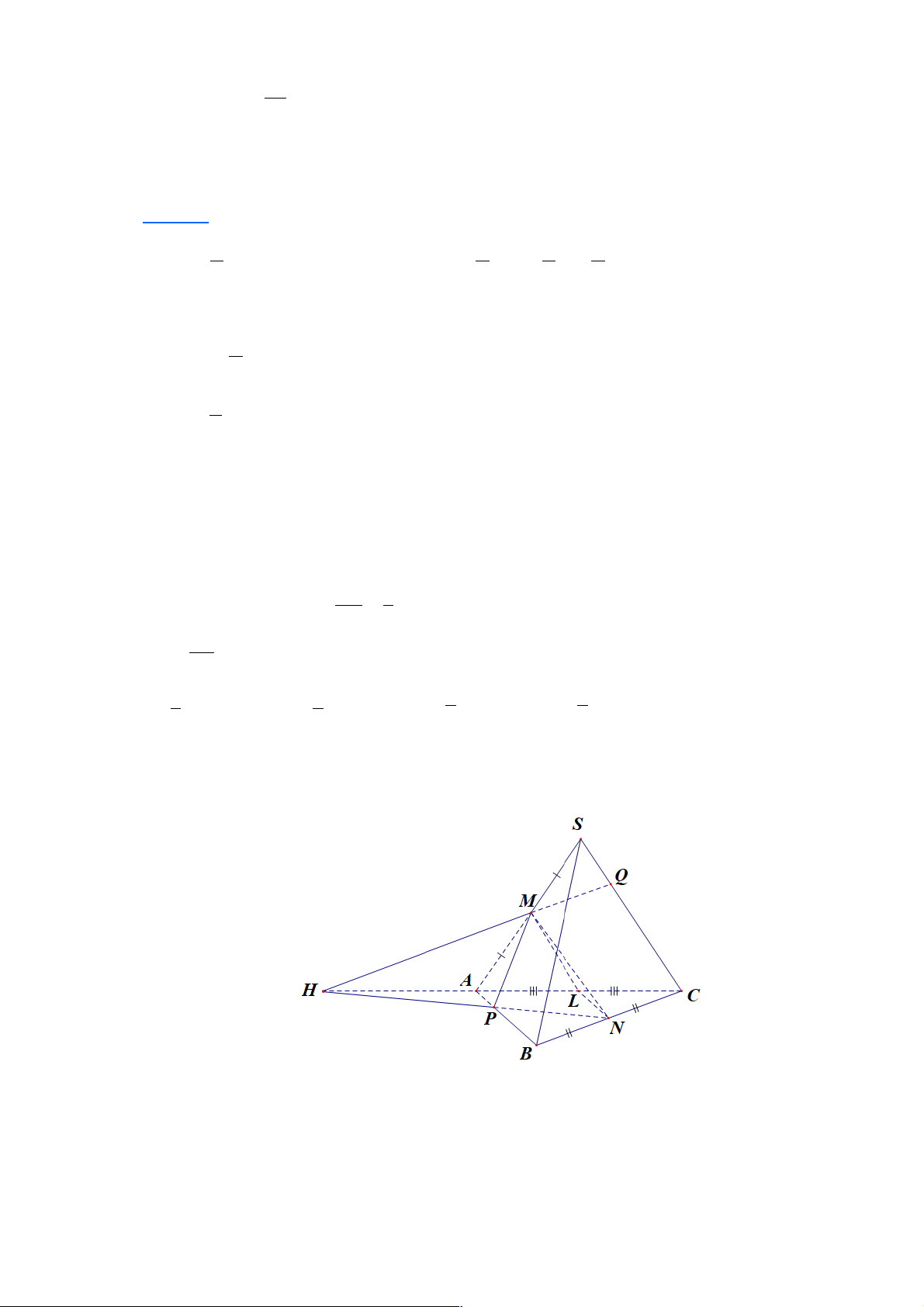
điểm của AB và AD . Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (EFG ) Lời giải
Trong mặt phẳng (ABC )
D : EF « BC = I; EF « CD = J
Trong mặt phẳng (SC )
D : GJ « SC = K; GJ « SD = M
Trong mặt phẳng (SBC): KI « SB = H
Ta có: (GEF)« (ABC )
D = EF, (GEF)« (SA )
D = FM , (GEF)« (SC ) D = MK
(GEF)« (SBC)= KH , (GEF)« (SA ) B = HE
Vậy Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (EFG ) là ngũ giác EFMKH Trang 28
Câu 39: Cho hình chóp S.ABCD có đáy là hình thang có AD / /BC . M là điểm di động trong
hình thang ABCD . Qua M kẻ các đường thẳng song song với SA và SB lần lượt cắt
các mặt phẳng (SBC) và (SBD) tại N và P . Cho SA = a , SB = b. Tìm giá trị lớn nhất của biểu thức 2
T = MN .MP . Lời giải
Giả sử AM Ç BC = I , BM Ç AD = J . Khi đó N Î SI, P Î SJ . Đặt MN = ; x MP = y. ìMN IM = ïï SA IA x y Ta có: í Þ + =1. MP JM AM a b ï = = ïî SB JB AI
Khi đó áp dụng bất đẳng thức Cô-si: 3 2 æ x x y ö 1 æ x x y ö 4a b 2 2 2 2
T = MN .MP = x .y = . . .4a b £ + + .4a b = ç ÷ ç ÷ . è 2a 2a b ø 27 è 2a 2a b ø 27 ì 2a x = ïï Dấu bằng xảy ra khi 3 í . b ïy = ïî 3
------------- HẾT ------------- Trang 29
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 3
I. Trắc nghiệm: (7.0đ)
Câu 1: Ba số - 3 ; x;- 3 3 theo thứ tự là ba số hạng liên tiếp của một cấp số nhân. Tìm công
bội q của cấp số nhân đó.
A. q = ± 3 .
B. q = - 3.
C. q = 3. D. q = 3 ± . Lời giải Chọn A
Do - 3 ; x ; - 3 3 là một cấp số nhân 2
Þ x = 9 Û x = 3 ± . x
Vậy công bội của cấp số nhân là q = = ± 3 . - 3
Câu 2: Hàm số nào sau đây là hàm số lẻ? A. 3 y = x + . 1 B. 3
y = sin (2x). C. 2
y = tan x . D. y = cos 2x. Lời giải Chọn B 3 y = sin (2x)
Tập xác định D = ! . Ta có x
" Î D Þ -x Î D .
Đồng thời y(-x) 3 = (- x) 3 sin
2 = -sin (2x) = -y(x). Do đó hàm số 3
y = sin (2x) là hàm số lẻ.
Câu 3: Trong các công thức sau, công thức nào đúng?
A. sin 2a = 2sin a cos a . B. 2 2
sin 2a = cos a - sin a .
C. sin 2a = 2sin a .
D. sin 2a = sin a + cos a . Lời giải Chọn A
Ta có sin 2a = 2sin a cos a .
Câu 4: Cho dãy số (u 2 *
u = 3 + 4n , n Î • u
n ) cho bởi công thức tổng quát . Khi đó bằng n 5 A. 97 - . B. 23. C. 503 . D. 103. Lời giải Chọn D 2 2
u = 3 + 4n Þ u = 3 + 4.5 = 103. n 5
Câu 5: Phương trình sin 2x = 1 có nghiệm là p p p p p A. x =
+ k2p . B. x =
+ k3p . C. x =
+ kp . D. x = + k . 4 4 4 4 2 Lời giải Chọn C Trang 30 p p
Ta có: sin 2x = 1 Û 2x = + k2p Û x = + kp , (k Î!). 2 4
Câu 6: Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối
giữa a và b . A. 1. B. 4 . C. 3. D. 2 . Lời giải Chọn C
Hai đường thẳng phân biệt a và b trong không gian có ba vị trí tương đối là: cắt nhau, song song, chéo nhau.
Câu 7: Khẳng định nào sau đây đúng?
A. tan15° = tan 75°
B. sin15° = sin 75° .
C. cos15° = - cos165° .
D. sin15° = -sin165° . Lời giải Chọn C
Do 15° +165° = 180° nên cos15° = -cos(180°-15°) = -cos165°.
Câu 8: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Một điểm và một đường thẳng.
B. Hai đường thẳng cắt nhau.
C. Bốn điểm phân biệt.
D. Ba điểm phân biệt. Lời giải Chọn B
A sai khi ba điểm thẳng hàng.
B sai khi điểm đó thuộc đường thẳng.
D sai khi 4 điểm thẳng hàng hoặc bốn điểm không đồng phẳng. p
Câu 9: Cung có số đo 5 rad đổi sang đơn vị độ bằng 3 A. 300° . B. 5° . C. 600°. D. 270°. Lời giải Chọn A p ° Ta có 5 5.180
rad đổi sang đơn vị độ bằng = 300°. 3 3
Câu 10: Một đường tròn có bán kính R = 3cm . Tính độ dài l của cung trên đường tròn đó có số đo bằng 0 60 . p p
A. l = 2p cm .
B. l = cm.
C. l = p cm .
D. l = cm. 4 2 Lời giải Chọn C Ta có: p l = .
R a = 3. = p cm. 3 Trang 31
Câu 11: Phương trình cos x = cosa có nghiệm là A. x = a
± + k2p ,(k Î!). B. x = a
- + kp ,(k Î!).
C. x = a + k2p ,(k Î!). D. x = a
± + kp ,(k Î!). Lời giải Chọn A éx = a + k2p
Công thức nghiệm tổng quát của phương trình cos x = cosa Û (k Î!). ê ëx = a - + k2p
Câu 12: Tìm tập xác định của hàm số y = tan x. ìp
A. ! \{k2p | k Î } Z . B. ü
! \ í + kp | k ÎZý. î 2 þ ìp C. ü ! \{kp | k Î } Z .
D. ! \ í + k2p | k ÎZý. î 2 þ Lời giải Chọn B p
Hàm số xác định khi và chỉ khi cos x ¹ 0 Û x ¹ + kp , (k ÎZ). 2
Câu 13: Cho hình chóp S.ABCD với ABCD là hình bình hành. Khi đó giao tuyến của hai mặt
phẳng (SAC) và (SAD) là
A. Đường thẳng SA .
B. Đường thẳng SB .
C. Đường thẳng SD .
D. Đường thẳng SC . Lời giải Chọn D
Ta thấy (SAC)Ç(SAD) = SA. p p p p sin .cos + sin .cos
Câu 14: Giá trị biểu thức 15 10 10 15 là 2p p 2p p cos .cos - sin .sin 15 5 15 5 A. 3 3 1. B. 1 - . C. - . D. . 2 2 Lời giải Chọn A p p p p æ p p ö æ p ö sin .cos + sin .cos sin + sin ç ÷ ç ÷ 15 10 10 15 è15 10 ø è 6 ø = = =1. 2p p 2p p æ 2p p ö æ p cos .cos sin .sin ö - cos + cos 15 5 15 5 ç ÷ ç ÷ è 15 5 ø è 3 ø
Câu 15: Biết 3 số 5;x;15theo thứ tự lập thành cấp số cộng. Giá trị của x bằng A. 30. B. 75. C. 10. D. 20. Lời giải Trang 32 Chọn C 5 + 15
5;x;15theo thứ tự lập thành cấp số cộng nên x = = 10 . 2
Câu 16: Cho cấp số nhân (u u = 3, u = 48. n ) thỏa mãn
Công bội của cấp số nhân bằng 1 5 A. 2. - B. 2. C. 2. ± D. 16. Lời giải Chọn C
Gọi q là công bội của cấp số nhân (un ). u ì = 3 u ì = 3 u ì = 3
Với u = 3, u = 48suy ra 1 1 1 í Û í Û í . 1 5 4 4 u .q = 48 î îq =16 îq = 2 ± 1
Vậy công bội của cấp số nhân (u q = 2. ± n ) là
Câu 17: Cho cấp số cộng (u u = 5 - d = 3
n ) có số hạng đầu và công sai
. Số 100 là số hạng thứ 1
mấy của cấp số cộng? A. 15. B. 20. C. 35. D. 36. Lời giải Chọn D
Ta có: u = u + n -1 d Û100 = 5
- + n -1 .3 Û100 = 3n -8 Û n = 36 n 1 ( ) ( ) .
Câu 18: Cho cấp số cộng (u u = 10 , u = 19 u n ) thỏa mãn . Tìm
của cấp số cộng đó. 4 7 10
A. u = 29 .
B. u = 30. C. u = . 31
D. u = 28 . 10 10 10 10 Lời giải Chọn D Ta có u ì =10 u ì + 3d =10 u ì =1 4 1 1 í Þ í Þ í u =19 u + 6d =19 î î îd = 3 7 1
Suy ra u = u + 9d = 28. 10 1 æ p
Câu 19: Giá trị lớn nhất của hàm số ö y = 3sin 2x + - 4 là ç ÷ è 2 ø A. 1. B. 7 . C. 2 . D. 1 - . Lời giải Chọn D æ p Ta có ö y = 3sin 2x + - 4 £ 3- 4 = 1 - . ç ÷ è 2 ø æ p ö p p k2p
Dấu bằng xảy ra khi sin 3x +
=1 Û 3x + = + k2p Û x = (k Î ç ÷ !). è 2 ø 2 2 3 Trang 33 p
Câu 20: Hàm số y = 2.sin 3x.cos x có chu kì là 3
Số mệnh đề đúng là A. 1. B. 2 . C. 3. D. 0 . Lời giải Chọn A p
+ Hàm số y = sin 2x có chu kì là 2 T = = p . Mệnh đề 2 sai. 2 æ p ö æ p + Hàm số ö y = 2sin 2x + + 3cos 3x - ç ÷ ç ÷ è 3 ø è 6 ø æ p p ö æ p có chu kì 2 2 2 ö T = BCNN ; = BCNN p ; = 2p . Mệnh đề 1 đúng. ç ÷ ç ÷ è 2 3 ø è 3 ø
+ Hàm số y = 2.sin 3x.cos x = sin 4x +sin 2x æ p p ö p
có chu kì T = BCNN ; = . Mệnh đề 3 sai. ç ÷ è 4 2 ø 2
Vậy có 1 mệnh đề đúng.
Câu 21: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm ,
SA SB, SC, SD. Đường thẳng nào sau đây không song song với đường thẳng IJ ? A. CD . AB . C. EF . D. AD . B. Lời giải Chọn D
Dễ thấy IJ //A ,
B IJ //C , D IJ /EF.
Giả sử IJ//AD Þ 0o = (IJ, AD) = ( , AB ) AD , vô lí.
Do đó giả sử sai. Vậy IJ và AD không song song.
Câu 22: Dãy số nào trong các dãy số sau đây là dãy số bị chặn dưới? A. (u u n n * = - " Ε (u u n n * = - " Ε n ) , 1 n ) 2 , . B. . n n C. (u u n n * = - " Ε (u u n n * = - " Ε n ) , n ) , 2 . D. . n n Lời giải Chọn B Trang 34 Ta có: (u u n n * = - ³ " Ε n ) , 1 0
nên dãy số bị chặn dưới. n
Câu 23: Rút gọn biểu thức
sin a + sin 3a + sin 5a A = .
cos a + cos3a + cos5a
A. tan 3a .
B. 1- tan 3a .
C. sin 3a .
D. cos3a . Lời giải Chọn A
sin a + sin 3a + sin 5a
sin 5a + sin a + sin 3a 2sin 3 .
a cos 2a + sin 3a A = = =
cos a + cos3a + cos5a
cos5a + cos a + cos3a 2cos3 .
a cos 2a + cos3a
sin 3a (2cos 2a + ) 1 = = tan 3a .
cos3a (2cos 2a + ) 1
Câu 24: Nghiệm của phương trình sinx cosxcos2x = 0là A. kp . B. kp . C. kp . D. kp . 2 4 8 Lời giải Chọn B Ta có: kp
sinx cosx cos2x = 0 Û 1 sin2x cos 2x = 0 Û 1 sin4x = 0 Û 4x = kp Û x = (k Î!). 2 4 4 + a a Câu 25: Tính 1 5cos B = biết tan = 2. 3 - 2cosa 2 A. 20 . B. 2 . C. 10 - .D. -2 . 9 21 21 21 Lời giải Chọn C a a a Cách kháC. 1 1 2 2 1 3 1+ tan = Þ cos = . Ta có 2 cosa = 2cos -1 = 2. -1 = - . 2 a 2 2 5 cos 2 5 5 2 æ 3 ö 1+ 5. - ç ÷ Thay vào ta được è 5 ø 10 B = = - . æ 3 ö 21 3 - 2. - ç ÷ è 5 ø 2 a 1 t C2: Đặt 1 4 3 tan t cosa - = Þ = . Với t 2 cosa - - = Þ = = 2 2 1+ t 1+ 4 5 æ 3 - ö 1+ 5ç ÷ è ø - - Suy ra 5 2 10 B = = = . æ 3 - ö 21 21 3 - 2ç ÷ è 5 ø 5 Câu 26: Tính 2 0 2 0 2 0 2 0 2 0
S = sin 5 + sin 10 + sin 15 +...sin 8 + sin 85 19 17 A. 9. B. . C. 8 . D. . 2 2 Trang 35 Lời giải Chọn D 2 0 2 0 2 0 2 0 2 0
S = sin 5 + sin 10 + sin 15 +...sin 80 + sin 85 = ( 1 17 2 0 2 0 sin 5 + sin 85 ) + ( 2 0 2 0 sin 10 + sin 80 ) +...( 2 0 2 0 sin 15 + sin 75 ) 2 0 + sin 45 = 8 + = . 2 2
Câu 27: Cho tứ diện ABCD . M là một điểm bất kỳ nằm trên đoạn AC (khác , A C ). Mặt phẳng
(P) qua M và song song với các đường thẳng AB,CD . Thiết diện của (P) với tứ
diện đã cho là hình gì?
A. Hình thang. B. Hình vuông. C. Hình bình hành.
D. Hình chữ nhật. Lời giải Chọn C
Trong mp ( ABC), qua M kẻ đường thẳng song song với AB , cắt BC tại N .
Trong mp ( ACD), qua M kẻ đường thẳng song song với CD, cắt AD tại Q.
Trong mp (BCD), qua M kẻ đường thẳng song song với CD, cắt BD tại P .
Þ Thiết diện của (P) với tứ diện là tứ giác MNPQ. ìMQ / /NP ï (/ / CD) Mặt khác í
Þ MNPQ là hình bình hành. ïMN / /PQ î (/ / AB) p
Câu 28: Biết phương trình 3 cos x + sin x = 2 có nghiệm dương bé nhất là a , ( với a,b là b
các số nguyên dương và phân số a tối giản). Tính 2 a + a . b b
A. S = 65 .
B. S = 135 .
C. S = 75 . D. S = 85. Lời giải Chọn D 3 1 2 p p 2
Ta có: 3 cos x + sin x = 2 Û cos x + sin x =
Û sin .cos x + cos .sin x = 2 2 2 3 3 2 é p p + = + p æ p ö x k2 2 æ p ö p ê Û sin x + = Û sin x + = sin Û 3 4 ê (k Î!) ç ÷ è 3 ø 2 ç ÷ è 3 ø 4 p 3p êx + = + k2p êë 3 4 Trang 36 é p x = - + k2p ê Û 12 ê (k Î!). 5p êx = + k2p êë 12 p
Þ Nghiệm dương bé nhất của phương trình là 5 . 12
Þ a = 5; b = 12 Þ 2 a + ab = 85.
Câu 29: Cho tứ diện ABCD . Gọi I và J lần lượt là trọng tâm ABC D và ABD D . Chọn khẳng định đúng.
A. IJ cắt AB . B. IJ song song với CD .
C. IJ song song với AB .
D. IJ chéo nhau với CD . Lời giải Chọn B A E J I B D C
Gọi E là trung điểm AB . Vì EI EJ 1
I và J lần lượt là trọng tâm tam giác ABC và ABD nên: = = . EC ED 3
Suy ra: IJ / /CD .
Câu 30: Cho tứ diện ABCD có I và J theo thứ tự là trung điểm của AD và AC , G là trọng tâm
tam giác BCD . Giao tuyến của hai mặt phẳng (GIJ )và (BCD)là đường thẳng
A. qua J và song song với BD . B. qua G và song song với CD .
C. qua G và song song với BC . D. qua I và song song với AB . Lời giải Chọn B Trang 37
+) I và J theo thứ tự là trung điểm của AD và AC nên IJ là đường trung bình của tam
giác ACD Þ IJ // CD , mà CD Ì (BCD) Þ IJ // (BCD). (1)
+) G là trọng tâm tam giác BCD nên G Î(BCD) Þ G là điểm chung của hai mặt phẳng
(GIJ )và (BCD).(2)
Từ (1) và (2) suy ra giao tuyến của hai mặt phẳng (GIJ )và (BCD)là đường thẳng đi
qua G và song song với CD .
Câu 31: Cho hình chóp S.ABC . Gọi M , N lần lượt là trung điểm của SA và BC , P là điểm trên cạnh AP 1 AB sao cho
= . Gọi Q là giao điểm của SC với mặt phẳng (MNP). AB 3 Tính SQ . SC 1 1 A. 1 . B. . C. . D. 2 . 6 3 2 3 Lời giải Chọn B
Tìm giao điểm Q của SC với mặt phẳng (MNP)
Chọn mặt phẳng phụ (SAC) chứa SC
Trong ( ABC) gọi H = AC Ç NP
Suy ra (MNP)Ç(SAC) = HM . Khi đó Q là giao điểm của HM và SC . Trang 38
Gọi L là trung điểm AC 1 AB HA AP 2 Ta có 3 = =
= (vì M , N là trung điểm của 1
AC và BC nên LN = AB ) HL LN 1 3 AB 2 2 2 Þ HA = HL 3 Mà 2 1
LC = AL = HL - HA = HL - HL = 3
HL nên HL = HC 3 3 4 Mặt khác ta có HC QC 4 =
= (vì ML / /SC ) HL ML 3 Mà QC SQ 2ML = 3 1 SC nên = Þ = . SC 2 SC 3
Câu 32: Cho tứ diện đều ABCD có các cạnh đều bằng a . Gọi G là trọng tâm tam giác ABC ,
M là trung điểm của cạnh CD . Diện tích thiết diện của tứ diện khi cắt bởi mặt phẳng
(AMG) (tính theo a) bằng 2 a 11 2 a 11 2 a 11 2 a 11 A. . B. . C. . D. . 2 32 16 8 Lời giải Chọn C
Gọi N là giao điểm của AG và BC thì N là trung điểm của BC .
Thiết diện của tứ diện khi cắt bởi mặt phẳng ( AMG) là tam giác AMN . Ta có 3
AM = AN = a . 2 2 2 æ ö Þ D AMN cân tại a 3 æ a ö a 11 A có đường cao 2 2
AH = AM - HM = ç ÷ - = ç ÷ ç ÷ 2 è ø è 4 ø 4 2 1 1 a 11 a a 11 S = AH.MN = . . = (đvdt). AMN 2 2 4 2 16 Trang 39
Câu 33: Cho phương trình 2
(sin x +1).(sin 2x - msin x) = mcos x . Tìm tập hợp S tất cả các giá trị æ p
thực của tham số m để phương trình có nghiệm trên khoảng ö 0; . ç ÷ è 6 ø æ ö æ ö A. 3 æ 1 ö 3 S = ç 1; - B. S = (0 ) ;1 . C. S = 0; . D. S = ç0; . ÷ ç ÷ ÷ 2 è ø è 2 ø 2 è ø Lời giải Chọn D Ta có 2
(sin x +1).(sin 2x - msin x) = mcos x .
Û (sin x +1).(sin2x - msin x) = m(1- sin x).(1+ sin x). (1) æ p Với ö x Î 0;
Þ 1+ sin x ¹ 0, thì phương trình (1) tương đương: ç ÷ è 6 ø
sin 2x - msin x = m(1- sin x) . Û sin 2x = m . æ p ö æ ö æ ö Khi 3 3 x Î 0; Þ sin 2x Î ç ÷ ç0; ÷ Þ mÎç0; . ÷ è 6 ø 2 2 è ø è ø
Câu 34: Số nghiệm của phương trình 1 - 3 -1 cot x - 3 +1 = 0 é0;p ù 2 ( ) ( ) trên đoạn là: sin x ë û A. 1 . B. 2 . C. 3. D. 4 . Lời giải Chọn B Xét phương trình: 1
- 3 -1 cot x - 3 +1 = 0 1 2 ( ) ( ) ( ) sin x
ĐKXĐ: sin x ¹ 0 Û x ¹ kp;k Î!
Khi đó phương trình (1) trở thành: 1 cos x - 3 -1 . - 3 +1 = 0 2 ( ) ( ) sin x sin x
Û 1- ( 3 - )1.cos x.sin x -( 3 +1) 2 .sin x = 0 3 -1 - Û -
x - ( + ) 1 cos2x 1 .sin 2 3 1 . = 0 2 2 3 -1 3 +1 1- 3 Û .sin 2x - .cos2x = 2 2 2 6 - 2 6 + 2 6 - 2 Û .sin 2x - .cos2x = - (2) 4 4 4 Trang 40 ì 6 - 2 ïcosa = ï Đặt 4 í ï 6 + 2 sina = ïî 4 Khi đó PT(2) trở thành:
sin 2x.cosa - cos2x.sina = - cosa æ p ö æ p ö Û sin (2x -a ) = -sin -a = sin a - ç ÷ ç ÷ è 2 ø è 2 ø é p 2x - = - + k2 é p a a p ê x = a - + kp 2 ê 4 Û ê Û ê ;k Î ! ê æ p ö ê 3p 2x -a = p - ê ça - + k2 ÷ p x = + kp ë è 2 ê ø ë 4 p p Xét: 3 3 3 1 x =
+ kp;k Î!. Vì x Îé0;p ù Þ 0 £
+ kp £ p Û - £ k £ 4 ë û 4 4 4 p mà 3
k Î! Þ k = 0 Þ x = 4 p p Xét 1 5
x = a - + kp;k Î!. Vì x Î é0;p ù Þ 0 £ a - + kp £ p Û - £ k £ 4 ë û 4 6 6 ì 6 - 2 p ïcosa = mà ï
k Î! Þ k = 0 Þ x = a - , Với 4 í 4 ï 6 + 2 sina = ïî 4
Vậy phương trình đã cho có 2 nghiệm trên đoạn é0;p ù ë û u ì + u + u =13
Câu 35: Cho cấp số nhân (u 1 2 3 8 n ) thỏa mãn í
. Tổng số hạng đầu của cấp số nhân u - u = 26 î 4 1 (un)là
A. S = 3280.
B. S = 3820. C. S = .
9841 D. S =1093. 8 8 8 8 Lời giải Chọn A u ì + u + u =13 2 u
ìï +u .q +u .q =13 u ìï ( 2 1+ q + q = 13 1 ) Ta có 1 2 3 í 1 1 1 Û í Û í u - u = 26 î 3 ï - = 2 4 1 u .q u 26 î u
ï . q -1 1+ q + q = 26 1 ( ) î ( ) 1 1 u ìï ( 2 1+ q + q = 13 u ì =1 1 ) Û í 1 Û í . ïîq = 3 îq = 3 u ( 8 1- q ( 8 1 1- 3 ) 1 ) Vậy tổng S = = = 3280. 8 1- q 1- 3 Trang 41
II. Tự luận: (3.0đ)
Câu 36: Tìm nghiệm của phương trình co 2 s x - 2sin x = 3 - ? Lời giải +) Ta có 2
cos2x - 2sin x = 3
- Û 1- 2sin x - 2sin x = 3 - ésinx = 1 2
Û sin x + sin x - 2 = 0 Û ê ësinx = 2 - < 1 - (VN) p +) sinx = 1Û x = + 2 k , p kÎZ 2
Câu 37: Viết thêm bốn số vào giữa hai số 160 và 5 để được một cấp số nhân. Tổng các số hạng
của cấp số nhân đó là Lời giải u ì =160 u Từ giả thiết ta có 1 1 6 í Þ q = 5 = . u = 5 u 2 î 6 1 6 æ 1 ö æ ö ç - ç ÷ ÷ u ( 160 1 6 1- q ç è 2 ÷ ø 1 )
Suy ra tổng các số hạng của cấp số nhân đó là: S è ø = = = 315 . 1- q 1 2
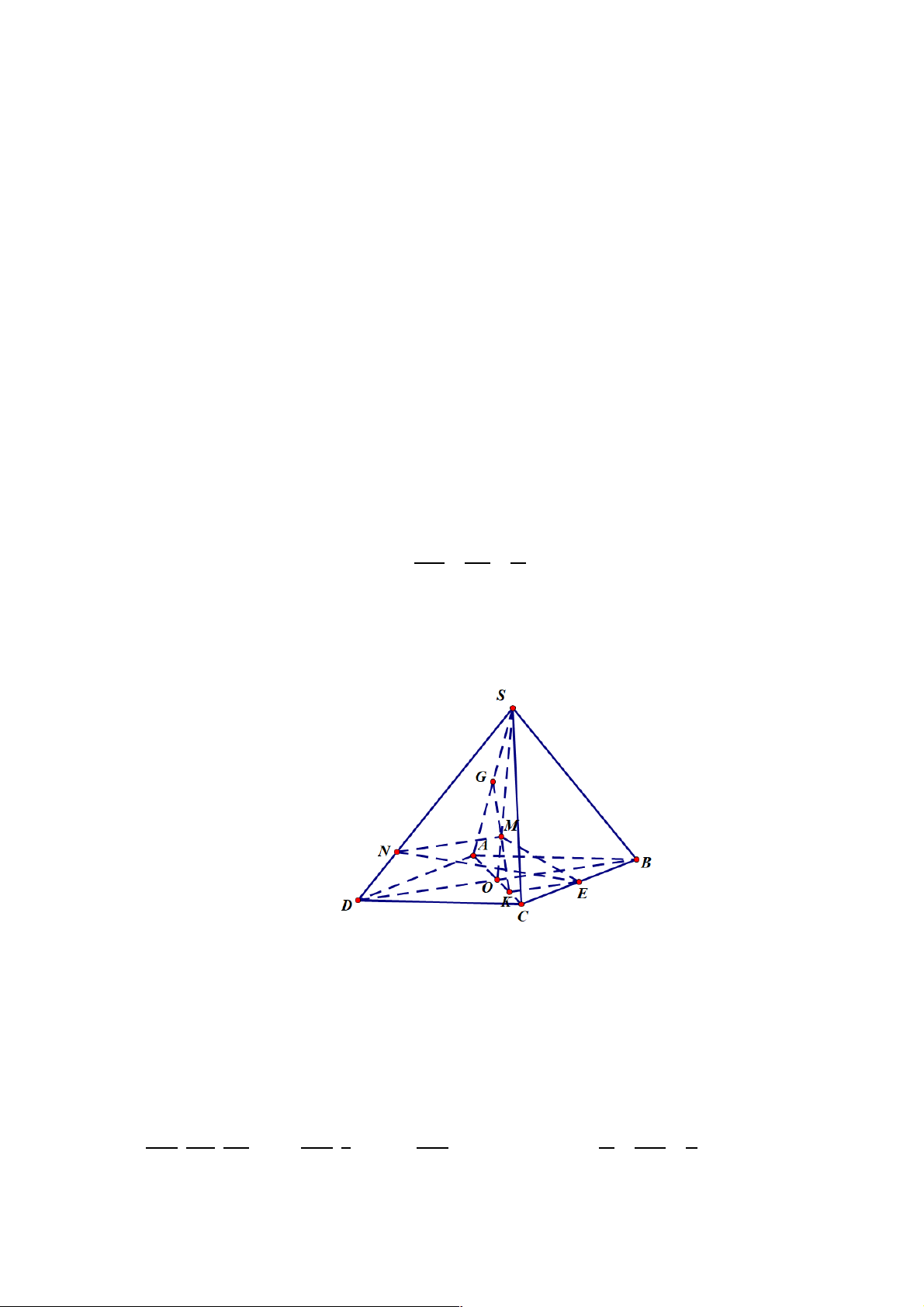
Câu 38: Cho hình chóp tứ giác S.ABCD , gọi O là giao điểm của hai đường chéo AC và BD .
Một mặt phẳng (a )cắt các cạnh ,
SA SB, SC, SD tương ứng tại các điểm M , N, , P Q.
CMR MP, NQ, SOđồng quy Lời giải
Trong mặt phẳng (MNPQ) ta có MP Ç NQ = R.Dễ chứng minh (SAC)Ç(SBD) = SO ìR Î MP Ì ï (SAC) ìRÎ ï (SAC) Do í Þ í
=> I Î SO . Suy ra ba đường thẳng MP, NQ, SO ïR Î NQ Ì î (SBD) ïRÎ î (SBD)
đồng quy tại R
Câu 39: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh bằng 2 . Cắt hình lập phương bằng một
mặt phẳng chứa đường chéo AC¢. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được. Lời giải Trang 42 B C A D A B' C' A' C' A' D' H
Gọi (H ) là thiết diện của hình lập phương và mặt phẳng (a ) chứa AC¢.
+ Trường hợp (H ) có một đỉnh thuộc cạnh BB¢ hoặc DD¢.
Giao tuyến của (a ) và ( A B ¢ C ¢ D
¢ ¢) là đường thẳng d , hình chiếu vuông góc của A¢ lên
d là điểm H . Khi đó góc giữa (a ) và ( A B ¢ C ¢ D ¢ ¢) là ∑ AHA .¢ ¢ ¢ Vì AA AA
A¢H ^ d nên A¢H £ A¢C¢ , do đó ∑ sina = ³ = sin AC A ¢ ¢, do đó AH AC¢ ∑ cosa £ cos A C ¢ A ¢
Hình chiếu vuông góc của hình (H ) lên ( A B ¢ C ¢ D
¢ ¢) là hình vuông A¢B C ¢ D ¢ ¢ , do đó diện tich hình ( S H ) : S = A¢B C ¢ D ¢ ¢ ¢ ¢ ¢ ¢ S a Þ S = . ( ).cos A B C D H (H ) cosa
Diện tích thiết diện nhỏ nhất khi cosa lớn nhất, tức là ∑ 2 cosa = cos A C ¢ A ¢ = . Khi đó 3 4 3
diện tích cần tìm là S = = 2 6 . (H ) 2
+ Trường hợp (H ) có một đỉnh thuộc cạnh CD hoặc A¢B¢ , chọn mặt phẳng chiếu là ( S BCC B
¢ ¢), chứng minh tương tự ta cũng có BB C ¢ C S ¢ = , min S = 2 6 . (H ) cosa (H)
+ Trường hợp (H ) có một đỉnh thuộc cạnh BC hoặc A¢D¢ , chọn mặt phẳng chiếu là (BAA B
¢ ¢), chứng minh tương tự ta cũng có, min S = 2 6 . (H)
------------- HẾT ------------- Trang 43
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 4
I. Trắc nghiệm: (7.0đ) 1
Câu 1: Cho cấp số nhân U U = 2 - q = . U n biết công bội Khi đó 5 bằng 1 2 1 1 A. - 1 . B. . C. - 1 . D. . 8 32 32 8 Lời giải Chọn A 4 æ 1 ö 1 Ta có 4 U = U q = 2. - = - 5 1 ç ÷ . è 2 ø 8
Câu 2: Nghiệm của phương trình 2cos x - 3 = 0 là p p
A. x = ± + kp ,(k Î!) |.
B. x = ± + kp ,(k Î!) |. 6 3 p p
C. x = ± + k2p ,(k Î!) |.
D. x = ± + k2p ,(k Î!) |. 6 3 Lời giải Chọn C p p Ta có 2cos x - 3 = 3 0 Û cos x =
Û cos x = cos Û x = ± + k2p ,(k Î!). 2 6 6
Câu 3: Biết 3 số 5;x;15theo thứ tự lập thành cấp số cộng. Giá trị của x bằng A. 10. B. 20. C. 30. D. 75. Lời giải Chọn A 5 + 15
5;x;15theo thứ tự lập thành cấp số cộng nên x = = 10 . 2 u ì = 4 Câu 4: Cho dãy số 1 í
. Năm số hạng đầu của dãy số là u = u + n î n 1+ n
A. 4,5,7,10,14. B. 4,16,32,64,128.
C. 4,6,9,13,18. D. 4,5,6,7,8. Lời giải Chọn A Ta có.
u = u +1 = 5; u = u + 2 = 7; u = u + 3 =10; u = u + 4 =14. 2 1 3 2 4 3 5 4 Câu 5: Góc 0
18 có số đo bằng rađian là bao nhiêu? p p p A. p . B. . C. . D. . 18 10 360 Lời giải Trang 44 Chọn C p p 18° = .18 = 180 10
Câu 6: Hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng đó A. Song song. B. Chéo nhau.
C. Trùng nhau. D. Hoặc song song hoặc trùng nhau. Lời giải Chọn D
Câu 7: Tập xác định của hàm số 1 y = là 1- cos x ì p A. ü
D = ! \ í- + k2p ,k Î"ý.
B. D = ! \{p + k2p,k Î } " . î 2 þ ìp C. ü
D = ! \ í + k2p ,k Î"ý.
D. D = ! \{k2p,k Î } " . î 2 þ Lời giải Chọn D
Hàm số xác định Û 1- cos x > 0 Û cos x < 1 Û cos x ¹ 1 Û x ¹ k2p. (vì cos x £ 1 với mọi x).
Vậy tập xác định của hàm số là: D = ! \{k2p,k Î } " . Câu 8: Giá trị 0 0
cos 45 + sin 45 bằng bao nhiêu? A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn A Ta có 2 2 0 0 cos 45 + sin 45 = + = 2 2 2
Câu 9: Cho hình chóp S.ABCD , đáy ABCD là hình bình hành ABCD tâm O . Giao tuyến của
hai mặt phẳng (SAC ) và (SAD ) là A. SO . B. SD . C. SA . D. SB . Lời giải Chọn C
Ta có (SAC)« (SAD)= SA.
Câu 10: Cho cấp số nhân (u u = 2 u = 6 n ) có và
. Công bội của cấp số nhân đó bằng 1 2 A. 1 3. B. . C. 6 . D. 2 . 3 Lời giải Chọn A n 1 u u .q - =
Þ u = u .q Û 6 = 2.q Û q = 3. n 1 2 1 Vậy q = 3. Trang 45
Câu 11: Trong các công thức sau, công thức nào đúng?
A. cos(a – b) = cos . a cosb + sin . a sinb.
B. cos(a +b) = cos . a cosb + sin . a sinb .
C. sin(a – b) = sin . a cosb + cos . a sin b.
D. sin(a +b) = sin .
a cosb - cos.sin b. Lời giải Chọn A
Ta có cos(a – b) = cos . a cosb + sin . a sinb.
Câu 12: Cho cấp số cộng (u u =1, d = 4 u n ) có . Tìm số hạng . 1 12
A. u = 45.
B. u = 17.
C. u = 31.
D. u =13. 12 12 12 12 Lời giải Chọn A
Ta có: u = u +11d = 45. 12 1
Câu 13: Nghiệm của phương trình sin x = 1là p p p
A. - + kp ,k Î . !
B. + kp ,k Î .
! C. - + k2p ,k Î . ! D. 2 2 2
p +k2p,k Î .! 2 Lờigiải Chọn D p sin x = 1 Û x = + k2p ,k Î!. 2
Câu 14: Cho hàm số y = tan x. Tìm mệnh đề đúng?
A. Hàm số có tập giá trị là [ -1;1].
B. Hàm số y = tan x là hàm số lẻ.
C. Hàm số tuần hoàn với chu kỳ T = 2p .
D. Hàm số có tập xác định
D = ! \{kp,k Î } " . Lời giải Chọn B p
Hàm số y = tan x có tập xác định là D = ! \{ + kp,k Î }
" , tuần hoàn với chu kỳ T = p 2
, có tập giá trị là ! và là hàm số lẻ.
Câu 15: Cho 3 đường thẳng d ,d ,d không cùng thuộc một mặt phẳng và cắt nhau từng đôi. 1 2 3
Khẳng định nào sau đây đúng
A. Các khẳng định ở A, B, C đều sai.
B. 3 đường thẳng trên trùng nhau.
C. 3 đường thẳng trên chứa 3 cạnh của một tam giác.
D. 3 đường thẳng trên đồng quy. Lời giải Chọn D
+) Hai đường thẳng cắt nhau sẽ xác định được một mặt phẳng. Trang 46 (
ì d , d = P 1 2 ) ( ) ï +) Giả sử (
í d , d = Q
(P),(Q),(R) 1 3 )
( ) . Khi đó 3 mặt phẳng
đôi một cắt nhau bởi 3 (
ï d ,d = R î 2 3 ) ( )
giao tuyến d ,d ,d phân biệt và 3 giao tuyến này hoặc song song hoặc đồng quy. 1 2 3
+) Theo đề bài d ,d ,d cắt nhau. 1 2 3
Suy ra d ,d ,d đồng quy. 1 2 3 p
Câu 16: Trên đường tròn bán kính r = 15 , độ dài của cung có số đo là. 3
A. l = 8p .
B. l = 5p .
C. l = 7p .
D. l = 16p . Lời giải Chọn B p p
Độ dài cung có số đo là l =15. = 5p . 3 3
Câu 17: Tìm khẳng định Sai: 1+ cos 2x x x A. 2 cos x = . B. 2 2 cos x = sin - cos . 2 2 2 C. 2
1+ cos 4x = 2cos 2x.
D. sin 2x = 2sin x cos x . Lời giải Chọn B x x
Áp dụng công thức nhân đôi, ta có 2 2 cos x = cos - sin
nên B là đáp án sai. 2 2
Câu 18: Phương trình nào sau đây vô nghiệm?
A. 3 sin 2x - cos 2x = 2.
B. 3sin x - 4cos x = 5. p
C. 3 sin x - cos x = 3 - .
D. sin x = . 5 Lời giải Chọn C 2
Ta xét phương trình 3 sin x - cos x = 3 - có ( ) +(- )2 < (- )2 3 1 3 nên phương trình vô nghiệm
Câu 19: Cho hai hình bình hành ABCD và ABEF nằm trên hai mặt phẳng phân biệt. Gọi O và
O ' lần lượt là tâm hình bình hành ABCD và ABEF . Khẳng định nào dưới đây sai?
A. AE, BD đồng phẳng.
B. AB // CD // EF .
C. AE cắt (BCF) tại trung điểm đoạn AE .
D. OO'// ( ADF). Lời giải Chọn A Trang 47 F E O' A B O D C
+Đáp án A, đúng vì ABEF là hình bình hành nên AE, BF cắt nhau tại trung điểm mỗi
đường, nên AE cắt (BCF) tại trung điểm của AE .
+Đáp án B, đúng OO ' là đường trung bình của BD D
F nên OO'// DF Þ OO'// (BDF).
+Đáp án C, sai do DÏ( ABEF) Þ AE và BD là chéo nhau.
+Đáp án D, đúng vì ABCD và ABEF là hình bình hành (giả thiết) nên AB // CD và
AB // EF vì vậy AB // CD // EF .
Câu 20: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = cos 2x trên é p p đoạn ù - ;
. Tính giá trị biểu thức T = M - 2m . ê 3 6 ú ë û 5 A. T = . B. T =1+ 3
3 . C. T = .
D. T = 2 . 2 2 Lời giải Chọn D p p p p Ta có: - £ x £ 2 Û - £ 2x £ 1
Þ - £ cos 2x £1 Þ M = 1
1, m = - Þ T = 2. 3 6 3 3 2 2
Câu 21: Cho dãy số (u u = 2; - u = u + 3 n ³ 2 n ) xác định bởi với mọi
. Tìm số hạng tổng quát 1 n n 1 - của dãy số. A. u = 3 - n + . 1 B. u = 3
- n + 5. C. u = 3n - .
1 D. u = 3n - 5. n n n n Lời giải Chọn D Dễ thấy (u u = 2 - d = 3
n ) là một cấp số cộng với số hạng đầu và công sai . 1
Suy ra số hạng tổng quát u = u + n -1 d = 2
- + 3 n -1 = 3n -5 n 1 ( ) ( ) . Trang 48 a - a
Câu 22: Biến đổi thành tích biểu thức sin 7 sin 5 ta được sin 7a + sin 5a
A. cos 2a.sin 3a . B. cot 6a.tana . C. tan 5a.tana . D. cosa.sina . Lời giải Chọn B a - a a a Ta có sin 7 sin 5 2cos 6 .sin = = cot 6a.tana . sin 7a + sin 5a 2sin 6a.cosa
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là một điểm thuộc đoạn
SB . Mặt phẳng ( ADM ) cắt hình chóp S.ABCD theo thiết diện là A. tam giác.
B. hình thang. C. hình chữ nhật.
D. hình bình hành. Lời giải Chọn B S M G A B D C
Do BC // AD nên mặt phẳng ( ADM )và (SBC) có giao tuyến là đường thẳng MG song song với BC
Thiết diện là hình thang AMGD .
Câu 24: Với mọi góc a , biểu thức p 2p 9 cos + cos( + ) + cos( + ) +...+ cos( p a a a a + ) nhận giá trị 5 5 5 bằng A. 1 B. 0 C. 10 D. 10 - Lời giải Chọn B
Có 10 số hạng, chia thành 5 cặp. Có 9p 4p 9p 4 + = + ( + ) Þ cos( + ) = - cos( p a p a a a + ) 5 5 5 5 Tương tự, 8p 3 cos( + ) = -cos( p a a + ) ; 7p 2 cos( + ) = -cos( p a a + ); 5 5 5 5 6 cos( p + ) = - cos( p a a + ); 5 cos( p a + ) = - cosa 5 5 5 Do đó, P = 0
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi d là giao tuyến
của hai mặt phẳng (SAB) và (SCD). Khi đó khẳng định nào sau đây là đúng? Trang 49
A. Đường thẳng d nằm trong mặt phẳng ABCD .
B. Đường thẳng d đi qua S và song song với AD và BC .
C. Đường thẳng d trùng với đường thẳng SO .
D. Đường thẳng d đi qua S và song song với AB và CD . Lời giải Chọn D ìS Î ï (SAB) Ta có: í
Þ S Î (SAB) Ç (SCD) ïS Î î (SCD) ìAB // DC ï
Vì íAB Ì (SAB) nên giao tuyến của (SAB) và (SCD) là đường thẳng đi qua S và ïDC Ì î (SCD)
song song với AB và CD .
Câu 26: Cho tứ diện ABCD . Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC .
Mệnh đề nào dưới đây đúng
A. GE cắt CD . B. GE và CD chéo nhau.
C. GE//CD .
D. GE cắt AD . Lời giải Chọn C Trang 50 Gọi MG ME 1
M là trung điểm của AB . Trong tam giác MCD có = = suy ra MD MC 3 GE//CD
Câu 27: Phương trình lượng giác 2cos x + 2 = 0có nghiệm là é 3 - p é p é 7p x = + k2p ê x = + k2p ê x = + k2p ê A. 4 ê . B. 4 ê . C. 4 ê . 3p ê p - 7 - p x = + k2p ê = + p ê = + p ê x k2 x k2 ë 4 êë 4 êë 4 é p x = + k2p ê D. 4 ê . 3p êx = + k2p êë 4 Lời giải Chọn A é 3 - p x = + k2p - 2 ê 4
2cos x + 2 = 0 Û cos x = Û ê (k Î!). 2 3p ê x = + k2p êë 4
Câu 28: Dãy số nào trong các dãy số sau đây là dãy số bị chặn? A. ( n u u = n n " Ε (u u = n " Ε n ) * , n ) 2 * , . B. . n n n +1 C. (u u = n + n " Ε (u u = n - n " Ε n ) * , n ) * , 1 . D. . n n Lời giải Chọn B Xét dãy ( n n u u = n " Î • *
0 < n < n +1; n " Ε * Þ 0 < <1; n " Î • n ) * , ; . Ta có nên n n +1 n +1 *
0 < u < 1; n " Î • . n
Suy ra dãy số (un )bị chặn. Xét dãy (u u = n + n " Ε *
u = n +1 ³ 2; n " Î • (un) n ) * , 1; ta có nên dãy số bị chặn dưới. n n Xét dãy (u u = -n n " Ε *
u = -n £ -1; n " Î • (un) n ) * , ; ta có nên dãy số bị chặn trên. n n Xét dãy (u u = n n " Ε 2 *
u = n ³ 1; n " Î • (un) n ) 2 * , ; ta có nên dãy số bị chặn dưới. n n
Câu 29: Đơn giản biểu thức 1 3 C = + . o o sin10 cos10 A. o 8sin 20 . B. o 8cos 20 . C. o 4cos 20 . D. o 4sin 20 . Lời giải Chọn B Trang 51 1 o 3 o o o cos10 + sin10 o 1 3 cos10 + 3 sin10 4sin 40 2 2 o C = + = = = = 8cos 20 . o o o o o o o sin10 cos10 sin10 cos10 2sin10 cos10 sin 20 4
Câu 30: Hàm số y = 2sin 2x tuần hoàn với chu kì là p A. 4p . B. . C. p . D. 2p . 2 Lời giải Chọn C Nhận xét: Hàm số 2p
y = sin(ax +b),a ¹ 0 tuần hoàn với chu kì . a
Câu 31: Cho tứ diện đều ABCD có cạnh bằng a . Gọi G là trọng tâm tam giác ABC . Thiết
diện tạo bởi tứ diện đều ABCD và mặt phẳng (GCD) có diện tích bằng 2 2 2 2 A. a 3 . B. a 2 . C. a 3 . D. a 2 . 4 6 2 4 Lời giải Chọn D D H A C F G B
Gọi F là trung điểm của AB , thiết diện tạo bởi tứ diện đều ABCD và mặt phẳng
(GCD) là tam giác DFC . 2 a 3 2 æ a 3 ö a a DF = FC = 2 2
Þ FH = DF - DH = ç ÷ - = . 2 ç 2 ÷ 4 2 è ø 2
Diện tích thiết diện là 1 a 2 S = FH.DC = . DCF 2 4 æ p ö æ p
Câu 32: Số nghiệm của phương trình ö 5 cos 2 x + + 4cos
- x = thuộc [0;2p ] là ç ÷ ç ÷ è 3 ø è 6 ø 2 A. 4 . B. 1. C. 2 . D. 3. Lời giải Chọn C p Đặt t = x + 3 Trang 52 Phương trình trở thành æ p ö 5 5 3 2 2 cos 2t + 4cos
- t = Û 1- 2sin t + 4sin t = Û 2
- sin t + 4sin t - = 0 ç ÷ è 2 ø 2 2 2 é 3 sin t = (VN ) ê 2 Û ê 1 êsint = êë 2 é p p é p - x + = + k2p x = + k2p æ p ê ê Với 1 ö 1 sin t = ta có 3 6 6 sin x + = Û ç ÷ ê Û ê , 2 è 3 ø 2 p 5p ê p x k2p ê + = + x = + k2p êë 3 6 êë 2 p p Vậy trong đoạn [ 11
0;2p ] phương trình có 2 nghiệm x = ; x = . 2 6 a
Câu 33: Giả sử sin , cosa , tana theo thứ tự đó là một cấp số nhân. Tính cos 2a . 6 A. 3 - . B. 1 . C. 1 3 - . D. . 2 2 2 2 Hướng dẫn giải Chọn C p
Điều kiện: cosa ¹ 0 Û a ¹ + kp (k Î!). 2 a 2 a
Theo tính chất của cấp số nhân, ta có: sin sin 2 cos a = .tana 2 Û 6cos a = . 6 cosa 3 2 Û 6cos a -sin a = 0 3 2 Û 6cos a + cos a -1 = 0 1 Û cosa = . 2 2 1 1 Ta có: 2 cos 2a 2 cos a æ ö = -1 = 2. -1 = - ç ÷ . è 2 ø 2
Câu 34: Tìm điều kiện của m để pt cos2x - (2m - )
1 cos x - m +1 = 0có đúng 2 nghiệm é p - p ù x Î ; . ê 2 2 ú ë û A. 1 - £ m £ 1. B. 1
- £ m £ 0. C. 0 £ m < 1.
D. 0 £ m £ 1 . Lời giải Chọn C cos2x - (2m - )
1 cos x - m +1 = 0 2
Û 2cos x - (2m - )
1 cos x - m = 0. é p - p Đặt ù
cos x = t ta được pt: 2 2t - (2m - )
1 t - m = 0(2), x Î ; Þ t Î[0; ] 1 . ê 2 2 ú ë û - Pt (2) luôn có 2 nghiệm 1 t = ;t = m 2 é p - p
Khi đó pt ban đầu có đúng 2 nghiệm ù x Î ;
thì pt (2) có đúng 1 nghiệm t Î[0 ) ;1 ê 2 2 ú ë û Trang 53 Þ mÎ[0 ) ;1
Câu 35: Cho hình chóp S.ABC . Gọi M , N lần lượt là trung điểm của SA và BC , P là điểm trên cạnh AP 1 AB sao cho
= . Gọi Q là giao điểm của SC với mặt phẳng (MNP). AB 3 Tính SQ . SC 1 1 A. 1 . B. . C. . D. 2 . 6 3 2 3 Lời giải Chọn B
Tìm giao điểm Q của SC với mặt phẳng (MNP)
Chọn mặt phẳng phụ (SAC) chứa SC
Trong ( ABC) gọi H = AC Ç NP
Suy ra (MNP)Ç(SAC) = HM . Khi đó Q là giao điểm của HM và SC .
Gọi L là trung điểm AC 1 AB HA AP 2 Ta có 3 = =
= (vì M , N là trung điểm của 1
AC và BC nên LN = AB ) HL LN 1 3 AB 2 2 2 Þ HA = HL 3 Mà 2 1
LC = AL = HL - HA = HL - HL = 3
HL nên HL = HC 3 3 4 Mặt khác ta có HC QC 4 =
= (vì ML / /SC ) HL ML 3 Mà QC SQ 2ML = 3 1 SC nên = Þ = . SC 2 SC 3 Trang 54
II. Tự luận: (3.0đ)
Câu 36: Giải phương trình 8.cos 2 . x sin 2 . x cos 4x = - 2 Lời giải Chọn C 8.cos 2 . x sin 2 .
x cos 4x = - 2 Û 4.sin 4 .
x cos 4x = - 2 Û 2.sin 8x = - 2 é p é p p 8x = - + k2p x = - + k ê ê 2 4 32 4 Û sin8x = - Û ê (k Î !) Û ê (k Î !) 2 5p 5p p 8 ê x = + k2p êx = + k êë 4 êë 32 4
Câu 37: Xen giữa số 3 và số 768 là 7 số để được một cấp số nhân có u = . K 3 hi đó u là: 1 5 Lời giải
Ta có u = 3 và u = 768 nên 8 768 = 3.q 8
Þ q = 256 Þ q = 2 ± . 1 9 Do đó 4 4
u = u .q = 3.2 = 48. 5 1
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là .
AB M là trung điểm .
CD Mặt phẳng (a ) qua M song song với BC và .
SA (a ) cắt AB,SB lần lượt tại N và .
P Nói gì về thiết diện của mặt phẳng (a ) với khối chóp S.ABCD ? Lời giải
Trong mặt phẳng ( ABCD), qua M kẻ đường thẳng MN ! BC(N ÎBC). Khi đó, MN Ì (a ).
Trong mặt phẳng (SAB), qua N kẻ đường thẳng NP ! SA(PÎSB). Khi đó, NP Ì (a ). Vậy (a ) º (MNP).
Xét hai mặt phẳng (MNP) và (SBC) có Trang 55 ìMN Ì (MNP) ï ïBC Ì (SBC ) í
Þhai mặt phẳng cắt nhau theo một giao tuyến đi qua điểm P MN // BC ï
ïPÎ(MNP),PÎ î (SBC)
và song song với BC.
Trong mặt phẳng (SBC) kẻ PQ ! BC(QÎSC). Khi đó, PQ là giao tuyến của mặt
phẳng (a ) với mặt phẳng (SBC). Vậy mặt phẳng (a ) cắt khối chóp S.ABCD theo
thiết diện là tứ giác MNP . Q ìMN // BC Tứ giác MNBC có í
Þ MNBC là hình bình hành. Từ đó suy ra MN = BC. îMC // NB
Trong tam giác SBC có P thuộc đoạn SB , Q thuộc đoạn SC và PQ ! BC nên PQ < BC. ìMN // PQ Tứ giác MNPQ có í
Þ MNPQ là hình thang có đáy lớn là MN. îPQ < MN
Câu 39: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Hai điểm M , N lần lượt nằm
trên các đoạn SO, SD sao cho SM SN m * = = , , m n Î • , ( ,
m n) =1. Điểm E là trung SO SD n
điểm của BC . Biết thiết diện của hình chóp cắt bởi mp(MNE) đi qua trung điểm cạnh
SA . Giá trị m + n bằng Lời giải
Ta có MN // OD nên mặt phẳng (MNE) cắt mặt phẳng ( ABCD) theo giao tuyến đi qua
E và song song với DO , cắt AC tại K .
Vì E là trung điểm của BC nên K là trung điểm của OC .
Gọi G = MK Ç SA thì G = SAÇ(MNE). Theo giả thiết thì G là trung điểm SA.
Áp dụng định lý Menelaus cho tam giác SAO ta có: MS KO GA MS 1 MS m SM . . =1Þ . .1 =1Þ = 3 3. Từ đó suy ra = = . MO KA GS MO 3 MO n SO 4
Vậy m + n = 7 . Trang 56
ĐỀ ÔN TẬP GIỮA HỌC KỲ I
MÔN TOÁN 11-CÁNH DIỀU-ĐỀ 5
I. Trắc nghiệm: (7.0đ)
Câu 1: Cung có số đo 5π rad đổi sang đơn vị độ bằng 3 A. 270 . ° B. 600°. C. 300° . D. 5° . Lời giải Chọn C 5π 5.180° rad = = 300 . ° 3 3
Câu 2: Chọn khẳng định sai.
A. Qua một đường thẳng và một điểm nằm ngoài đường thẳng xác định được một và chỉ một mặt phẳng.
B. Qua ba điểm phân biệt xác định được một và chỉ một mặt phẳng.
C. Qua hai đường thẳng phân biệt cắt nhau xác định được một và chỉ một mặt phẳng.
D. Qua hai đường thẳng song song xác định được một và chỉ một mặt phẳng. Lời giải Chọn B
Ba điểm đó phải là ba điểm không thẳng hàng.
Câu 3: Biết 3 số 5;x;15theo thứ tự lập thành cấp số cộng. Giá trị của x bằng A. 20. B. 30. C. 75. D. 10. Lời giải Chọn D 5 + 15
5;x;15theo thứ tự lập thành cấp số cộng nên x = = 10 . 2
Câu 4: Mệnh đề nào sau đây sai? A. 2 2
cos 2a = cos a - sin a. B. 2
cos 2a = 2cos a -1. C. 2
cos 2a =1- 2sin a .
D. cos 2a = 2sin a cos a Lời giải Chọn D
Câu 5: Trên một đường tròn có bán kính R = 30 cm. Ta lấy một cung có độ đài bằng 8 cm. Số đo
tính theo radian của cung đó là A. 4 . B. 4 . C. 10 . D. 4 . 30 15 3 9 Lời giải Chọn B Ta có l 8 4 l = a R Þ a = = = . R 30 15
Câu 6: Hàm số nào sau đây là hàm số chẵn?
A. y = cos 2x.
B. y = tan 4x . C. y = cot x.
D. y = sin 3x . Lời giải Trang 57 Chọn A
Hàm số y = cos 2x có tập xác định D = ! .
Với mọi x Î D ta có -x Î D và cos( 2
- x) = cos(2x) nên hàm số y = cos2x là hàm số chẵn.
Câu 7: Cho cấp số nhân (u u =3 u =12 n ) với và
. Công bội của cấp số nhân đã cho bằng 1 2 A. 4. B. 3. C. 9. D. 1 . 4 Lời giải Chọn A Ta có: u 12 2
u = u .q Þ q = = = 4. 2 1 u 3 1 3 æ p ö Câu 8: Cho sina =
< a < p . giá trị của cosa bằng ç ÷ 5 è 2 ø A. 2 4
cosa = - . B. cosa = . 5 5 C. 2 4 cosa = . D. cosa = - . 5 5 Lời giải Chọn D Ta có: 9 16 2 2 2 2
sin a + cos a = 1Þ cos a = 1- sin a =1- = . 25 25 p Mà 4 < a < p Þ cosa = - . 2 5
Câu 9: Nếu một đường thẳng d song song với mặt phẳng (a ) và đường thẳng d ' chứa trong
mặt phẳng (a ) thì d và d ' sẽ A. song song. B. cắt nhau. C. chéo nhau.
D. song song hoặc chéo nhau. Lời giải Chọn D
Câu 10: Với k Î! , họ nghiệm của phương trình cos x = 0 là p p
A. + k2p .
B. + kp . C. kp . D. k2p . 2 2 Lời giải Chọn B p
Ta có: cos x = 0 Û x = + kp , k Î!. 2
Câu 11: Trong các công thức sau, công thức nào đúng? Trang 58 + A. a b
tan(a +b) = tan a + tanb. B. (a -b) tan tan tan = . 1- tan a tan b + C. a b
tan(a – b) = tan a - tanb. D. (a +b) tan tan tan = . 1- tan a tan b Lời giải Chọn D + Ta có
(a +b) tan a tanb tan = . 1- tan a tan b *
Câu 12: Cho dãy số ( u = 3; u = u + , n " n Î • u + u + u u 1 n 1 + n 1 2 3 n ) xác định bởi . Giá trị bằng A. 15 . B. 16 . C. 18 . D. 13. Lời giải Chọn D Ta có u = 3; 1
u = u +1 = 3+1 = 4; 2 1
u = u + 2 = 4 + 2 = 6 . 3 2
Suy ra u + u + u = 3+ 4 + 6 =13. 1 2 3
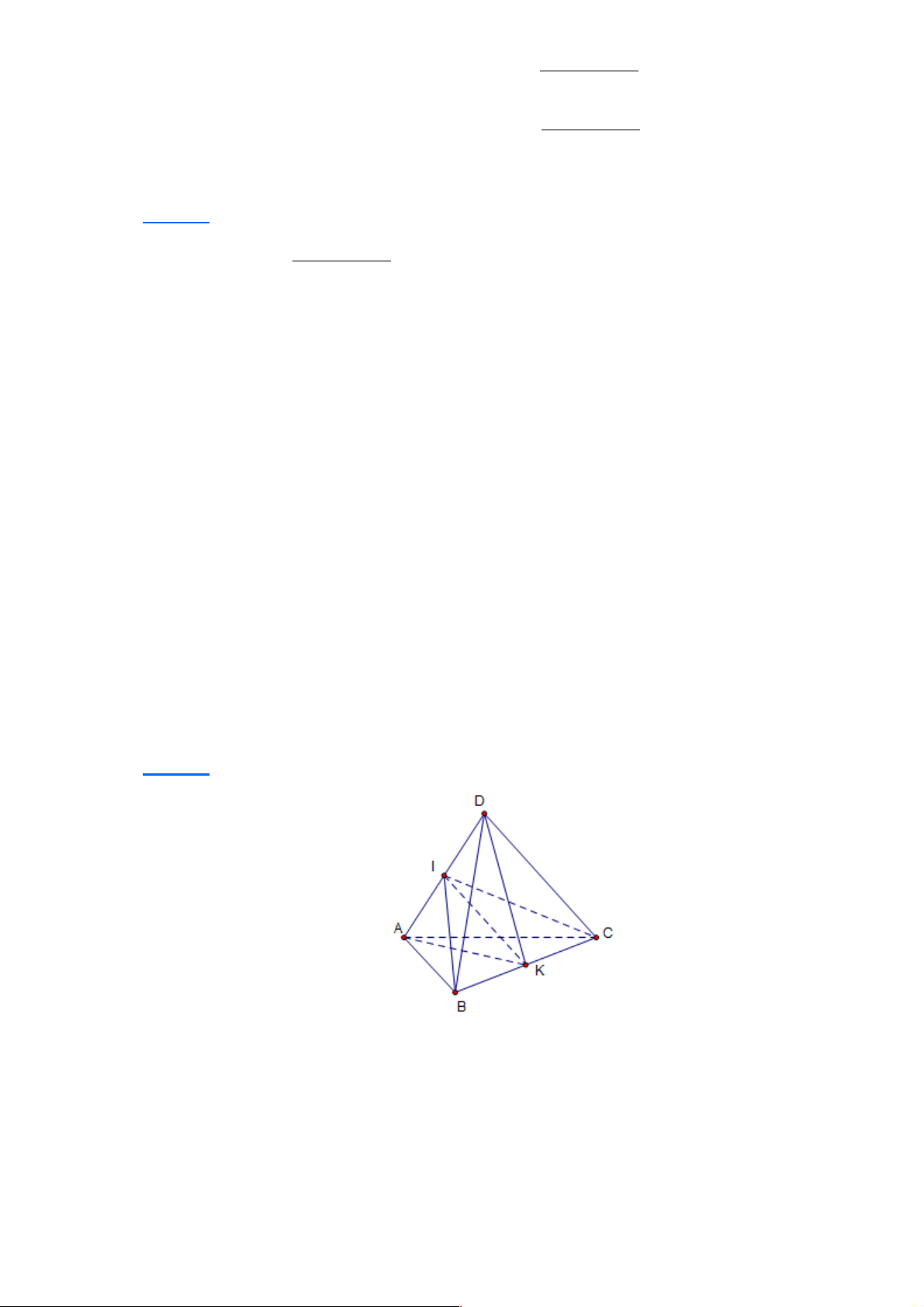
Câu 13: Cho bốn điểm ,
A B,C, D không đồng phẳng. Gọi I, K lần lượt là trung điểm hai đoạn
thẳng AD và BC . IK là giao tuyến của cặp mặt phẳng nào sau đây?
A. (IBC) và (KBD).
B. (IBC) và (KCD).
C. (IBC) và (KAD).
D. ( ABI ) và (KAD). Lời giải Chọn C ìI Î AD Ì ï (KAD) í
Þ I là điểm chung thứ nhất của hai mặt phẳng (IBC) và (KAD). ïI Î î (IBC) ìK Î BC Ì ï (IBC) í
Þ K là điểm chung thứ hai của hai mặt phẳng (IBC) và (KAD). ïK Î î (KAD)
Vậy (IBC)Ç(KAD) = IK . Trang 59
Câu 14: Cho cấp số nhân (u u = 40 u =160 n ) có và
. Tìm số hạng đầu và công bội của cấp số 4 6 nhân (un ) . u ì = 5 - u ì = 140 - u ì = 5 - u ì = 2 - A. 1 í . B. 1 í . C. 1 í . D. 1 í . îq = 2 îq = 60 îq = 2 - îq = 5 - Lời giải Chọn C ì 160 2 q = = 4 3 u ì = 40 u ìï .q = 40 ïï 40 u ì = 5 u ì = 5 - Ta có 4 1 1 1 í Û í Û í Û í Ú í . 5 u = 160 î ï = 40 u .q 160 î ï îq = 2 îq = 2 - 6 1 u = 1 3 ïî q
Câu 15: Cho cấp số cộng (u u = 4, u =10. n ) thỏa mãn
Công sai của cấp số cộng bằng 1 3 A. 6. - B. 3. C. 3. - D. 6. Lời giải Chọn B
Gọi d là công sai của cấp số cộng (un ). u ì = 4 u ì = 4
Ta có u = 4, u =10suy ra 1 1 í Û í . 1 3 u + 2d =10 î îd = 3 1
Vậy công sai của cấp số cộng (u d = 3. n ) là
Câu 16: Tập nghiệm của phương trình sin 2x = sin x là ì p k2p A. ü S = ík2p; + k Î!ý. î 3 3 þ ì p B. ü
S = ík2p;- + k2p k Î!ý. î 3 þ
C. S = {k2p;p + k2p k Î! . } ì p D. ü
S = ík2p; + k2p k Î!ý. î 3 þ Lời giải Chọn A Ta có: é é = p Î
2x = x + k2p , k ÎZ
x k2 , k Z
sin 2x = sin x Û ê Û p k2p . ê
ë2x = p - x + k2p , k ÎZ êx = + , k Î Z ë 3 3 1
Câu 17: Tìm tập xác định D của hàm số y = . 1- sin x Trang 60 ìp ìp A. ü ü
D = ! \ í + kp ,k Î"ý .
B. D = ! \ í + k2p ,k Î"ý. î 2 þ î 2 þ
C. D = Æ .
D. D = ! \{kp,k Î } " . Lời giải Chọn B p
Điều kiện xác định của hàm số là: 1- sin x > 0 Þ sin x <1 Þ sin x ¹ 1 Þ x ¹ + k2p . 2 ìp Vậy, ü
D = ! \ í + k2p ,k Î"ý. î 2 þ
Câu 18: Nghiệm của phương trình 3 tan 3x -3 = 0là p p p p p p p p A. k k k k x = + . B. x = + . C. x = + . D. x = + . 9 3 3 9 9 9 3 3 Lời giải Chọn A p p p Ta có: k
3 tan 3x - 3 = 0 Û tan 3x = 3 Û 3x = + kp Û x = + với k Î! . 3 9 3
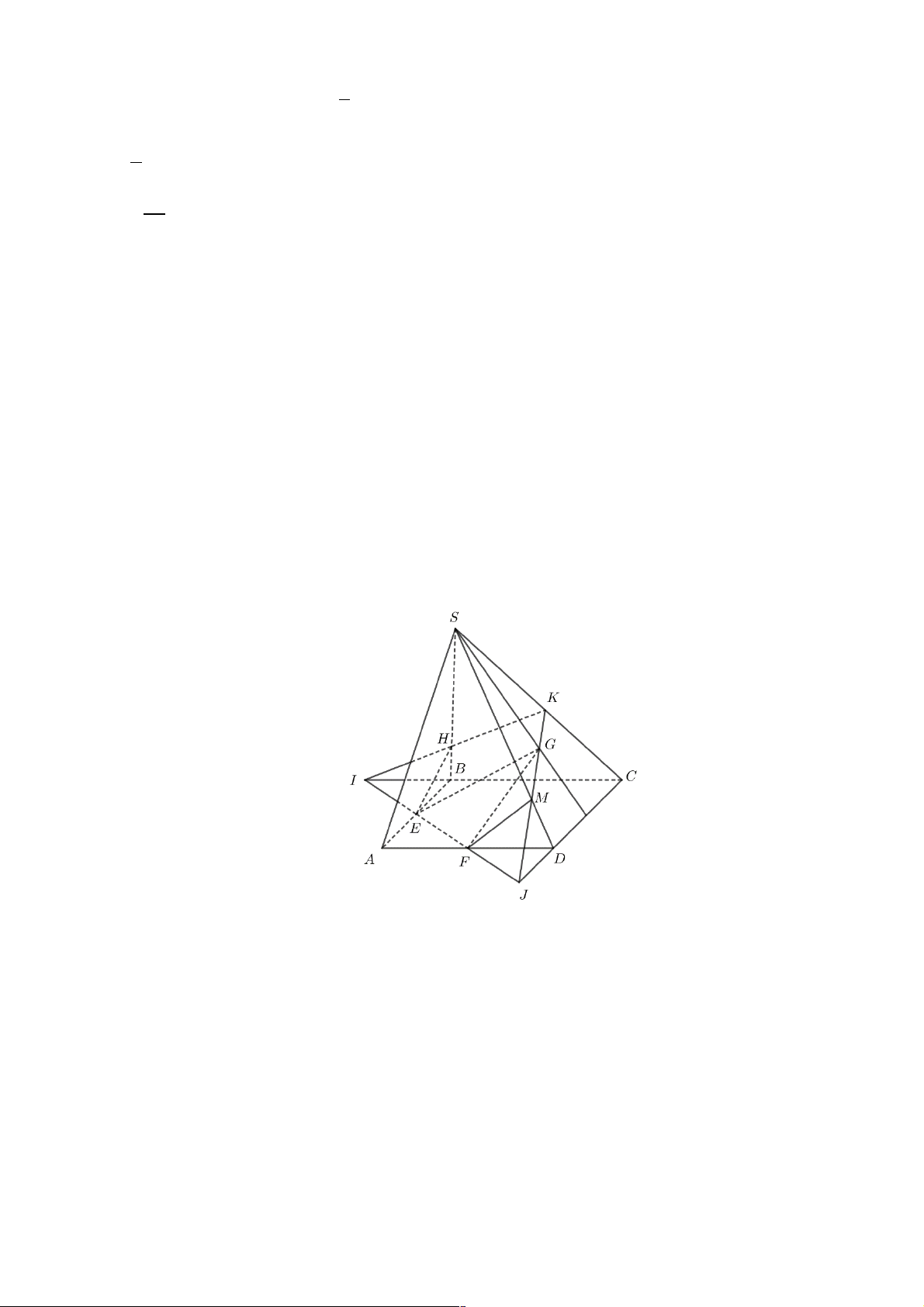
Câu 19: Cho t diện ABCD . Gọi N và P lần lượt là trung điểm của các cạnh BD và AD ; M là
điểm thuộc đoạn BC sao cho MC = 2MB . Kết luận nào sau đây đúng nhất về thiết
diện của mặt phẳng (MNP) với hình chóp ABCD ?
A. Thiết diện là ngũ giác.
B. Thiết diện là hình bình hành.
C. Thiết diện là hình thang.
D. Thiết diện là t giác. Lời giải Chọn C A E Q P B D N M C
Gọi E = MN ÇCD Þ (MNP)Ç( ACD) = PE .
Trong mặt phẳng ( ACD) gọi Q = PE Ç AC . Khi đó thiết diện của mặt phẳng (MNP)
với hình chóp ABCD là t giác MNPQ. Trang 61
ìMQ = (MNP) Ç( ABC) ï Ta có íNP//AB Þ MQ//NP .
ïNP Ì (MNP), AB Ì î (ABC)
Do đó tứ giác MNPQ là hình thang.
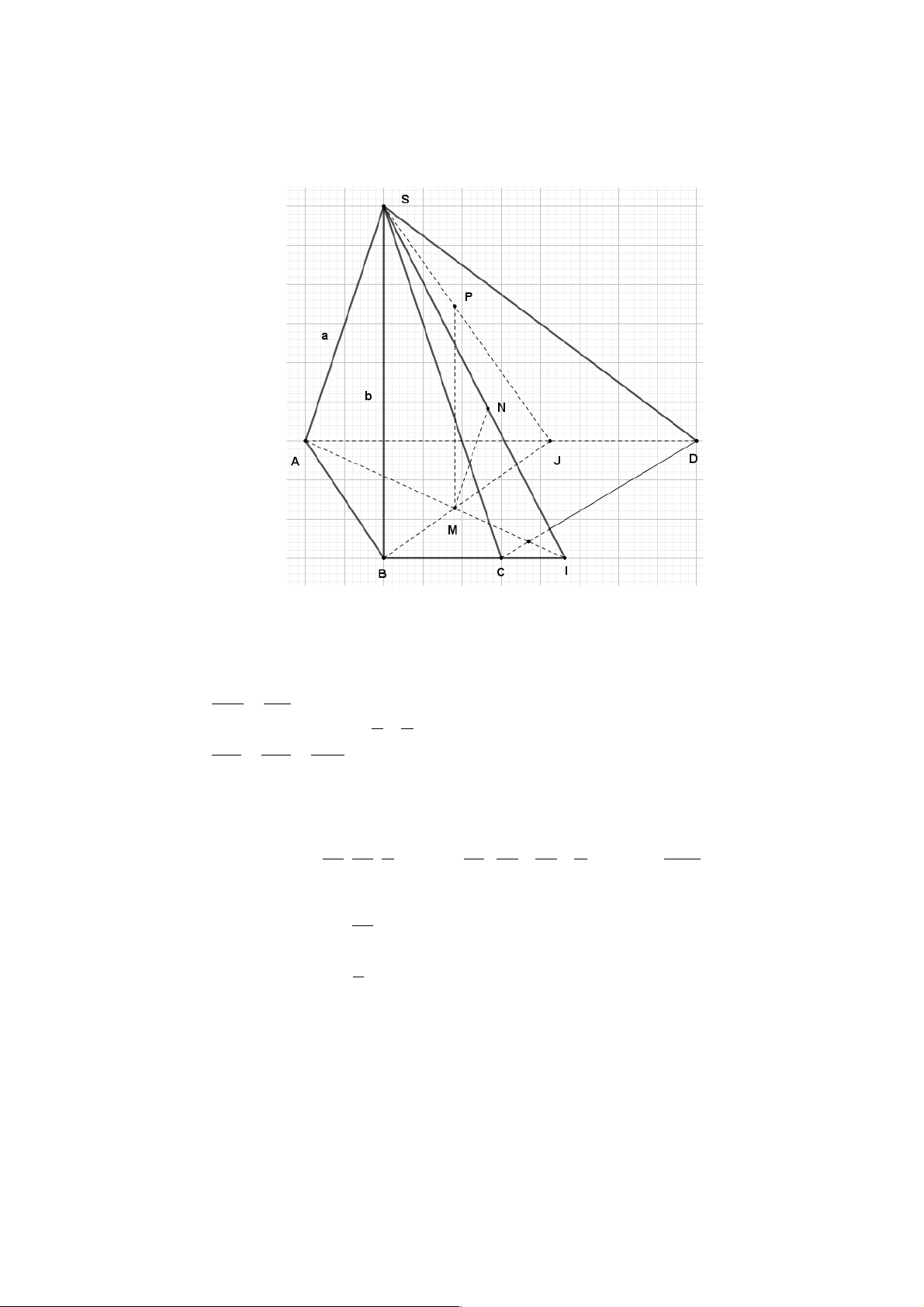
Câu 20: Cho tứ diện ABCD , G là trọng tâm tứ diện. Gọi G là giao điểm của AG và mp(BCD) 1
, G là giao điểm của BG và mp ( ACD). Khẳng định nào sau đây là đúng? 2
A. G G // AB .
B. G G // AC . C. G G // CD . D. G G // AD. 1 2 1 2 1 2 1 2 Lời giải Chọn A A N G G2 B D G1 M C
Gọi M , N lần lượt là trung điểm của DC , AC . Vì G là trọng tâm tứ diện nên G là
giao điểm của ba đoạn thẳng nối hai trung điểm của cặp cạnh đối của tứ diện như hình vẽ trên.
Xét ( ABM ): AG Ç BM = G , BG Ç AM = G . Trong DACD có AM và DN là đường 1 2 G M 1
trung tuyến nên G là trọng tâm của tam giác do đó 2 = . Tương tự ta cũng có 2 G A 2 2 G M 1 1
= suy ra G G // AB. G B 2 1 2 1
Câu 21: Cho hình chóp S.ABCD , đáy ABCD là hình thang ( AD//BC). Gọi O là giao điểm AC
và BD , I là giao điểm AB và CD . Trong các mệnh đề sau, mệnh đề nào sai?
A. SB và AD cắt nhau.
B. (SAD)Ç(SBC) = Sx với Sx//AD .
C. (SAB)Ç(SCD) = SI .
D. (SAC)Ç(SBD) = SO. Lời giải Chọn A Trang 62 S A D O B C I ì AD//BC Ta có: í
Þ AD// SBC và AD , SB không cùng nằm trong một mặt phẳng AD Ì î (SBC) ( )
Þ AD và SB không có điểm chung (chéo nhau).
Câu 22: Trong không gian cho tứ diện ABCD . Gọi M là trung điểm của AB , N đối xứng với B qua D .
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(I) Hai đường thẳng MC và BD cắt nhau.
(II) Hai đường thẳng MN và AD cắt nhau.
(III) Hai đường thẳng MD và BC cắt nhau.
(II) Hai đường thẳng AB và CD cắt nhau. A. 3 . B. 1. C. 2 . D. 4 . Lời giải Chọn B Trang 63 A M K N D B C
Trong mặt phẳng ( ABD)hai đường thẳng MN và AD cắt nhau tại K . Các cặp đường
thẳng còn lại đều chéo nhau.
Câu 23: Cho cấp số cộng (u S n S = 77 n ) và gọi
là tổng số hạng đầu tiên của nó. Biết và n 7
S =192 . Tìm số hạng tổng quát u của cấp số cộng đó 12 n
A. u = 4 + 5n.
B. u = 5 + 4n. C. u = 3+ 2n . D. u = 2 + 3n . n n n n Lời giải Chọn C
Giả sử cấp số cộng có số hạng đầu là u và công sai d . 1 ì 7.6.d 7u + = 77 ì = ï 1 S 77 ï ì7u + 21d = 77 u ì = 5 Ta có: 7 2 1 1 í Û í Û í Û í . S = 192 12.11.d 12u + 66d =192 î ï î îd = 2 12 1 12u + =192 1 ïî 2
Khi đó: u = u + n -1 d = 5+ 2 n -1 = 3+ 2n n 1 ( ) ( ) .
Câu 24: Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y =1-3 sin 2x . Tính giá trị của 3 3 M + m A. 3 3
M + m = 9. B. 3 3
M + m = 7. C. 3 3 M + m = 1 - . D. 3 3 M + m = 7 - . Lời giải Chọn D Với mọi x Î ! ta có: 0 £ sin 2x £1 Û 3 - £ 3 - sin 2x £ 0 Û 2 - £1-3 sin 2x £1Û 2 - £ y £1. ìM =1 Suy ra: 3 3 í Þ M + m = 7 - . îm = 2 - p p
Câu 25: Giá trị của biểu thức 2 2 A = tan + cot bằng 24 24 12 - 2 3 12 + 2 3 12 + 2 3 12 - 2 3 A. . B. . C. . D. . 2 + 3 2 - 3 2 + 3 2 - 3 Lời giải: Chọn A p p 1 1 2 2 A = tan + cot = -1+ -1 24 24 p p 2 2 cos sin 24 24 Trang 64 1 12 - 2 3 = - 4 2 = - 8 2 = - 2 = . p p p p 2 2 cos .sin 2 sin 1- cos 2 + 3 24 24 12 6
Câu 26: Chu kỳ của hàm số 2
y = tan 3x - cos 2x là p p A. . B. . C. p . D. 2p . 3 2 Lời giải Chọn C 1+ cos 4x 1 1 2
y = tan 3x - cos 2x = tan 3x -
= tan 3x - cos 4x - 2 2 2 p
Hàm số y = tan 3x tuần hoàn với chu kì . 3 p p Hàm số 1 y = 2
cos 4x tuần hoàn với chu kì = . 2 4 2 Suy ra hàm số 1 1
y = tan 3x - cos 4x - tuần hoàn với chu kì p . 2 2
Câu 27: Cho A , B , C là ba góc của một tam giác. Hệ thức nào sao đây đúng? æ A + B + A. 3C ö sin = sin C .
B. cos( A+ B) = cosC. ç ÷ è 2 ø
C. sin( A+ B + 2C) = sinC .
D. sin( A+ B + 2C) = -sinC. Lời giải Chọn D
Ta có A + B + C = 180° Û A + B + 2C = 180° + C
Û sin(A+ B + 2C) = sin(180°+C) Û sin(A+ B + 2C) = -sinC. p
Câu 28: Cho dãy số ( n u u = sin n ³ 1 n ) xác định bỏi , với
. Khẳng định nào sau đây đúng? n 3 A. Dãy số ( 1 u 2 u =
n ) là dãy số giảm.
B. Số hạng thứ của dãy số là . 2 2 C. Dãy số (u (un)
n ) bị chặn. D. Dãy số là dãy số tăng. Lời giải Chọn C Vì np 1 - £ sin
£1 nên dãy (un ) bị chặn. 3
Câu 29: Tìm họ nghiệm của phương trình x x 3 sin - cos = 2. 2 2 p p A. 2 2 x =
+ k2p , k Î!. B. x =
+ k4p , k Î!. 3 3 Trang 65 p p C. 4 4 x =
+ k2p , k Î! D. x =
+ k4p , k Î!. 3 3 Lời giải Chọn B Ta có: x x æ x p ö x p p 2p 3 sin - cos = 2 Û sin -
=1 Û - = + k2p Û x =
+ k4p ,k Î! ç ÷ 2 2 è 2 6 ø 2 6 2 3
Câu 30: Giá trị của biểu thức cos5x + cos3x 1 I =
, biết tan x = là sin 5x - sin 3x 3 A. 1 1 I = 3 . B. I = 3 - . C. I = . D. I = - . 3 3 Lời giải Chọn C Ta có 2cos 4x cos x 1 I = = cot x = = 3. 2cos 4xsin x tan x
Câu 31: Cho tứ diện đều ABCD cạnh a, gọi G là trọng tâm tam giác ABCắt tứ diện bởi mặt
phẳng (GCD) được thiết diện có diện tích là: 2 a 2 2 a 2 2 a 3 2 a 2 A. B. C. D. 6 4 4 2 Lời giải Chọn B
Gọi M là trung điểm của AB . Khi đó thiết diện cắt bởi (GCD) là tam giác CDM . Ta a có CD D 3
M cân tại M và MD = MC = ;CD = a 2 2 2 æ ö 2 2.a
Gọi N là trung điểm CD, tính được 3a æ a ö a 2 MN = ç ÷ - = Vậy S = ç ÷ ç ÷ 2 CD D M è ø è 2 ø 2 4 Trang 66
Câu 32: Với giá trị nào của m để phương trình: 2 msin x - 3sin .
x cos x - m -1 = 0 có đúng 3 æ 3p nghiệm ö x Î 0; . ç ÷ è 2 ø A. m ³ 1. - B. m < 1. - C. m £ 1. - D. m > 1. - Lời giải Chọn B p p p p
Với x = phương trình trở thành: 2 msin
- 3sin .cos - m -1 = 0 Û m - m -1 = 0 2 2 2 2 Û 1 - = 0 (vô lý) p
Do đó x = không phải là nghiệm của phương trình 2 p
Với x ¹ Chia 2 vế cho 2 cos x ta được 2 2 m x - x - m ( 2 + x)- ( 2 + x) 2 tan 3tan . 1 tan 1 1 tan
= 0 Û tan x +3tan x + m+1= 0
Đặt t = tan x .Yêu cầu bài toán trở thành tìm m để phương trình 2
t + 3t + m +1 = 0 có 2
nghiệm trái dấu Û m +1 < 0 Û m < 1 -
Câu 33: Cho hình chóp S.ABC . Gọi M , N lần lượt là trung điểm của SA và BC , P là điểm trên cạnh AP 1 AB sao cho
= . Gọi Q là giao điểm của SC với mặt phẳng (MNP). AB 3 Tính SQ . SC 1 1 A. 2 . B. 1 . C. . D. . 3 6 3 2 Lời giải Chọn C
Tìm giao điểm Q của SC với mặt phẳng (MNP)
Chọn mặt phẳng phụ (SAC) chứa SC
Trong ( ABC) gọi H = AC Ç NP Trang 67
Suy ra (MNP)Ç(SAC) = HM . Khi đó Q là giao điểm của HM và SC .
Gọi L là trung điểm AC 1 AB HA AP 2 Ta có 3 = =
= (vì M , N là trung điểm của 1
AC và BC nên LN = AB ) HL LN 1 3 AB 2 2 2 Þ HA = HL 3 Mà 2 1
LC = AL = HL - HA = HL - HL = 3
HL nên HL = HC 3 3 4 Mặt khác ta có HC QC 4 =
= (vì ML / /SC ) HL ML 3 Mà QC SQ 2ML = 3 1 SC nên = Þ = . SC 2 SC 3 æ p æ p
Câu 34: Phương trình x 2 2 ö ö 4cos
- 3 cos 2x =1+ 2cos x -
có bao nhiêu nghiệm thuộc 0; ? ç ÷ ç ÷ 2 è 4 ø è 2 ø A. 2 . B. 3 . C. 0 . D. 1. Lời giải Chọn A x æ p 1+ cos x æ p Ta có 2 2 ö ö 4cos
- 3 cos 2x =1+ 2cos x - ç ÷ Û 4.
- 3 cos 2x =1+1+ cos 2x - ç ÷ 2 è 4 ø 2 è 2 ø
Û 2 + 2cos x - 3 cos2x = 2 +sin 2x Û sin 2x + 3 cos2x = 2cos x p p æ p Û ö sin 2x sin
+ cos 2x cos = cos x Û cos 2x - = cos x ç ÷ 6 6 è 6 ø é p é p 2x - = x + k2p x = + k2p ê 6 ê 6 Û ê Û ê (k Î!) p p 2p ê2x x k2p ê - = - + x = x + k êë 6 êë 18 3 æ p p p Trong khoảng ö 0;
, phương trình có các nghiệm x = , x = . ç ÷ è 2 ø 6 18
Câu 35: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả
sử 1 tế bào E. Coli khối lượng khoảng 15
15.10- g. Hỏi sau 2 ngày khối lượng do 1 tế
bào vi khuẩn sinh ra là bao nhiêu? (chọn đáp án chính xác nhất). A. 26
3,35.10 (kg). B. 29 3,36.10 (g). C. 26 2,25.10 (kg). D. 29 2,34.10 (g). Lời giải Chọn D Một tế bào E. Coli Sau 20 phút thành: 1 2 = 2 tế bào. Sau 40 = 2.20 phút thành: 2 4 = 2 tế bào. Sau 60 = 3.20 phút thành: 3 8 = 2 tế bào. Trang 68
………………………………………………………….
Sau 2 ngày = 144.20 phút thành 144 2 tế bào.
Vậy sau 2 ngày khối lượng do 1 tế bào vi khuẩn sinh ra là: 144 15 - 29 = (g) 26 2 .15.10 3,34511178.10 » 3,35.10 (kg).
II. Tự luận: (3.0đ)
Câu 36: Phương trình cos 2x + 4sin x + 5 = 0 có bao nhiêu nghiệm trên khoảng (0;10p )? Lời giải ésin x = 1 - p PT đã cho 2 Û 2
- sin x + 4sin x + 6 = 0 Û
Û x = - + k2p ,(k Î!). êsin x = 3 ë ( ptvn) 2 p
Theo đề: xÎ(0;10p ) Þ 0 < - + k2p <10p 1 21 Û < k < . 2 4 4
Vì k Î! nên k Î{1;2;3;4; }
5 . Vậy PT đã cho có 5 nghiệm trên khoảng (0;10p ). u ì = 4u
Câu 37: Cho cấp số nhân (u 15 n ) 5 3 : í
, với công bội dương. Tính tổng số hạng đầu u + u = 102 î 2 6
tiên của cấp số nhân trên. Lời giải 15 ( u ì = u 1- 2 u í Þ q = = Þ S = u = 98301 n ) 4 5 3 : 2, u 3 1 u + u =102 î 15 1 1- 2 2 6
Câu 38: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ có cạnh là 2 . Gọi M , N lần lượt là trung điểm
của BC và CD . Tính diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng (A M ¢ N ). Lời giải A' D' C' B' P A F D Q N H B M C E
Gọi E = MN Ç AB , F = MN Ç AD , Q = A E
¢ Ç BB¢, P = A¢F Ç DD¢ .
Từ đó suy ra thiết diện của hình lập phương khi cắt bởi mặt phẳng ( A M ¢ N ) là ngũ giác A¢PNMQ .
Vì M , N lần lượt là trung điểm của BC và CD nên suy ra BE = CN = 1, DF = CM = 1
. Từ đó suy ra AE = AF = 3 Þ EF = 3 2 . Trang 69 Ta có 2 2 2 2 A E ¢ = A A
¢ + AE = 2 +3 = 13, tương tự A F
¢ = 13 . Do đó tam giác A¢EF là tam giác cân. 2 æ ö 34
Gọi H là trung điểm EF , ta có 2 2 2 3 2
A¢H = A¢E - EH = 13 - ç ÷ = . ç 2 ÷ è ø 2 Diện tích tam giác 1 34 A¢ 1
EF là: S = EF.A H ¢ = 3 17 .3 2. = . 2 2 2 2 Ta thấy EQ D M = FPN D . Từ EQ EM EB 1 = = = suy ra 1 1 1 S = . .S = 1 S Þ S = S . EA¢ EF EA 3 EQM 3 3 9 FPN 9
Vậy, diện tích thiết diện A¢PNMQ là S = - - 1 1 ¢ S S S = S - S - 7 S = S . A PNMQ EQM FPN 9 9 9 Hay 7 3 17 7 17 S = = ¢ . . A PNMQ 9 2 6
------------- HẾT ------------- Trang 70