Top 50 bài toán thực tế liên quan đạo hàm – tích phân có lời giải

Tài liệu gồm 54 trang, tuyển chọn 50 bài toán thực tế liên quan đạo hàm – tích phân thường gặp trong đề thi thử THPT Quốc gia môn Toán, có đáp án và lời giải chi tiết, giúp học sinh ôn thi tốt nghiệp THPT môn Toán.

76 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 9: Đạo hàm (KNTT)

Môn: Toán 11

Thông tin:

54 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
TOÁN THỰC TẾ LIÊN QUAN ĐẠO HÀM - TÍCH PHÂN
Câu 1. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
,C
cạnh bên
SA
vuông góc với
mặt phẳng đáy
( )
.ABC
Biết
1SC =
, tìm thể tích lớn nhất của khối chóp
..S ABC
A.
3
.
12
B.
C.
23
.
27
D.
3
.
27
Câu 2. Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình chóp tứ giác đều sao cho
bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp (hình vẽ).
Để thể tích khối chóp lớn nhất thì cạnh đáy
x
của hình chóp bằng:
A.
2
.
5
x =
B.
22
.
5
x =
C.
2 2.x
=
D.
2
.
5
x =
Câu 3. Tìm chiều dài
L
ngắn nhất của cái thang để có thể tựa vào tường và mặt đất, ngang qua cột đỡ
có chiều cao
33
m
2
và cách tường
0,5 m
kể từ gốc của cột đỡ.
A.
2m
. B.
4m
. C.
3m
. D.
5m
.
Câu 4. Một con kiến đậu ở đầu
B
của một thanh cứng mảnh
AB
có chiều dài
L
đang dựng cạnh một
bức tường thẳng đứng (hình vẽ).
Vào thời điểm mà đầu
B
bắt đầu chuyển động sang phải theo sàn ngang với vận tốc không đổi
v
thì con kiến bắt đầu bò dọc theo thanh với vận tốc không đổi
u
đối với thanh. Trong quá
trình bò trên thanh, con kiến đạt được độ cao cực đại
max
h
là bao nhiêu đối với sàn? Cho đầu
A
của thanh luôn tỳ lên tường thẳng đứng.
A.
2
3L
v
. B.
2
2L
v
. C.
2
3
L
v
. D.
2
2
L
v
.
Trang 2
Câu 5. Một hộp không nắp được làm từ một mảnh các tông theo mẫu. Hộp có đáy là một hình vuông
cạnh
(
)
cm
x
, chiều cao
( )
cmh
và có thể tích là
( )
3
500 cm
.
Tìm
x
sao cho diện tích mảnh các tông đó nhỏ nhất?
A.
5cm
. B.
100cm
. C.
10 cm
. D.
20 cm
.
Câu 6. Một nhà máy cần sản xuất một bể nước bằng tôn có dạng hình hộp đứng đáy là hình chữ nhật có
chiều dài gấp 2 lần chiều rộng không nắp, có thể tích
3
4
m
3
. Hãy tính độ dài chiều rộng của đáy
hình hộp sao cho tốn ít vật liệu nhất.
A. 2 m. B.
3
m. C.
2
3
m . D. 1 m.
Câu 7. Cho hai vị trí
A
,
B
cách nhau
615 m
, cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách
từ
A
và từ
B
đến bờ sông lần lượt là
118 m
và
487 m
. Một người đi từ
A
đến bờ sông để lấy
nước mang về
B
.
Đoạn đường ngắn nhất mà người đó có thể đi là
A.
596,5m
. B.
671,4 m
. C.
779,8 m
. D.
741,2 m
.
Câu 8. Trong không gian với hệ trục toạ độ
Oxyz
cho đường thẳng
∆
có phương trình tham số là:
2
1
x
yt
zt
=
= −
= +
và hai điểm
( )
1; 2; 1A −−
,
( )
4;4;5B
. Giả sử
( )
;;M abc
thuộc
∆
sao cho
MA MB+
nhỏ nhất, khi đó tích
abc
là
A.
0
. B.
2
9
. C.
1
. D.
2
.
Trang 3
Câu 9 . Một trang chữ của cuốn sách giáo khoa cần diện tích
2
384cm
. Lề trên và dưới là
3cm
, lề trái
và phải là
2 cm
. Kích thước tối ưu của trang giấy là:
A. Dài
24 cm
; rộng
16 cm
. B. Dài
24 cm
; rộng
17 cm
.
C. Dài
25cm
; rộng
15,36cm
. D. Dài
25,6cm
; rộng
15cm
.
Câu 10. Có một cơ sở in sách xác định rằng: Diện tích của toàn bộ trang sách là
2
0
)(cmS
. Do yêu cầu kỹ
thuật nên dòng đầu và dòng cuối đều phải cách mép (trên và dưới) trang sách là
(cm)
a
. Lề bên
trái và bên phải cũng phải cách mép trái và mép phải của trang sách là
(cm)b
( )
ba<
. Các kích
thước của trang sách là bao nhiêu để cho diện tích phần in các chữ có giá trị lớn nhất. Khi đó hãy
tính tỉ lệ của chiều rộng và chiều dài trang sách.
A.
ba
a
−
. B.
2
21
b
a −
. C.
b
a
. D.
ba
a
+
.
Câu 11. Một anh kỹ sư muốn tạo ra 1 cái lu hình trụ có diện tích bề mặt (không tính hai mặt đáy) là lớn
nhất. Bề mặt lu được quấn bởi mảnh tôn hình chữ nhật có chu vi 120 cm. Gọi chiều dài của hình
chữ nhật là
a
, chiều rộng của hình chữ nhật là
b
. Tính
2
3Pa b= +
.
A. 990. B. 1660. C. 2530. D. 1108.
Câu 12. Bác nông dân có
200 m
rào để ngăn đàn gà nuôi dạng hình chữ nhật. Để diện tích nuôi gà là lớn
nhất thì chiều dài hình chữ nhật là
a
(m) và chiều rộng là
b
(m). Khi đó
22
a ab b++
có giá trị
bằng
A. 7525 m. B. 7600 m. C. 7500 m. D. 7900 m.
Câu 13. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm
tổng
xy+
để diện tích hình thang
EFGH
đạt giá trị nhỏ nhất.
A.
7 cm
. B.
5cm
. C.
72
cm
2
. D.
4 2 cm
.
Câu 14. Một màn ảnh hình chữ nhật cao
1,4m
và đặt ở độ cao
1, 8 m
so với tầm mắt (tính từ đầu mép
dưới của màn hình như hình vẽ). Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn
nhất. Tính khoảng cách từ vị trí đó đến màn ảnh? Biết rằng góc
BOC
nhọn.
x
cm
y
cm
3 cm
2 cm
H
G
F
E
D
C
B
A
Trang 4
A.
2,4mAO =
. B.
2mAO =
. C.
2, 6 mAO =
. D.
3mAO =
.
Câu 15. Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính
10 cm
, biết một
cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn.
A.
2
80 cm
. B.
2
100 cm
. C.
2
160 cm
D.
2
200 cm
.
Câu 16 . Từ một khúc gỗ tròn hình trụ có đường kính bằng
40 cm
, cần xả thành một chiếc xà có tiết diện
ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng
x
của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất.
A.
( )
3 34 17 2
cm
2
x
−
=
B.
( )
3 34 19 2
cm
2
x
−
=
C.
( )
5 34 15 2
cm
2
x
−
=
D.
(
)
5 34 13 2
cm
2
x
−
=
Câu 17. Một ô tô đang chạy với vận tốc
(
)
15 m/s
thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc
( ) ( )
5 15 m/svt t=−+
trong đó
t
là khoảng thời gian tính bằng
giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển
được bao nhiêu mét ?
A.
22,5m
. B.
45m
. C.
15m
. D.
90 m
.
Câu 18. Một vật chuyển động với gia tốc
22
( ) 3 (m/s ).at t t= +
Vận tốc ban đầu của vật là
2(m/s).
Hỏi
vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó được
2s.
A.
8m/s
. B.
12 m/s
. C.
16 m/s
. D.
10 m/s
.
Câu 19. Cho mạch điện xoay chiều
RLC
mắc nối tiếp có
R
thay đổi. Biết điện trở cuộn cảm
( )
80
L
Z = Ω
, điện trở của tụ điện là
( )
200
C
Z = Ω
và hiệu điện thế hai đầu mạch là
( )
0
100cos u U tV
π
=
. Để
công suất tiêu thụ của mạch cực đại thì giá trị của
R
bằng
Trang 5
A.
( )
120 Ω
. B.
( )
50 Ω
. C.
( )
100 Ω
. D.
( )
200 Ω
.
Câu 20. Cho mạch điện xoay chiều
RLC
mắc nối tiếp có
R
thay đổi. Biết điện trở cuộn cảm
( )
100
L
Z = Ω
, điện trở của tụ điện là
( )
40
C
Z = Ω
và hiệu điện thế hai đầu mạch là
( )
120 2 cos
100 u tV
π
=
. Điện trở
R
phải có giá trị là bao nhiêu để công suất tiêu thụ của mạch
đạt cực đại và giá tri cực đại của công suất là bao nhiêu?
A.
( ) ( )
max
60 , 120 WRP=Ω=
. B.
( ) ( )
max
120 , 60 WRP=Ω=
.
C.
( ) ( )
max
40 , 180 WRP=Ω=
. D.
( ) ( )
max
120 , 180 WRP=Ω=
.
Câu 21: Thể tích
V
của
1kg
nước ở nhiệt độ
t
(
t
nằm giữa
0C°
đến
30 C
°
) được cho bởi công thức
( )
2 33
999,87 0,06426 0,0085043 0,0000679 cmV tt t=−+ −
. Nhiệt độ
t
của nước gần nhất với
giá trị nào dưới đây thì khối lượng riêng của nước là lớn nhất?
A.
0
°
. B.
4−°
. C.
30°
. D.
4°
.
Câu 22: Thể tích nước của một bể bơi sau
t
phút bơm được tính theo công thức
( )
4
3
1
30
100 4
t
Vt t

= −


( )
0 90t≤≤
. Tốc độ bơm nước tại thời điểm t được tính bởi
( ) ( )
vt V t
′
=
. Trong các khẳng định
sau, khẳng định nào đúng.
A. Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
B. Tốc độ bơm luôn giảm.
C. Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
D. Cả A, B, C đều sai.
Câu 23. Công ty XDPL muốn làm một đường ống dẫn khí từ một địa điểm
A
trên bờ biển đến một điểm
B
trên một hòn đảo. Khoảng cách ngắn nhất từ điểm
B
đến bờ biển là
6 km
. Giá để xây lắp mỗi
km đường ống trên bờ là
50.000 USD
, còn xây lắp dưới nước là
130.000 USD
.
B
′
là điểm trên
bờ biển sao cho
BB
′
vuông góc với bờ biển. Khoảng cách từ
A
đến
B
′
là
9 km
.
Hỏi vị trí điểm
M
trên bờ biển cách
A
bao xa để chi phí xây lắp đường ống từ
A
qua
M
rồi
đến
B
là ít tốn kém nhất?
A.
9 km
. B.
6 km
. C.
0 km
. D.
6.5 km
.
Câu 24. Một điểm
C
trên hòn đảo có khoảng cách ngắn nhất đến bờ biển là
60 km
,
B
là điểm trên bờ
biển sao cho
CB
vuông góc với bờ biển . Khoảng cách từ
A
trên bờ biển đến
B
là
100 km
. Để
tham dự buổi họp nhóm Strong Team Toán VD – VCD ngày 28/6/2019 , thầy Quý phải tính toán
vị trí diễn ra cuộc họp tại địa điểm
G
trên đoạn
AB
để tổng chi phí đi lại của cả hai nhóm các
thầy cô là ít nhất. Biết nhóm của thầy Quý đi từ
C
theo đường biển chi phí đi là
500
nghìn mỗi
9km
6km
đảo
bờ biển
biển
A
B
B'
Trang 6
km, nhóm cô Thêm đi từ vị trí A đi trên đất liền mỗi km chi phí là
300
nghìn. Hỏi thầy tìm được
vị trí điểm
G
cách
B
bao xa?
A.
40 km
. B.
60 km
. C.
55km
. D.
45km
.
Câu 25. Một xưởng in có
8
máy in, mỗi máy in được
4000
bản in khổ giấy
4A
trong một giờ. Chi phí
để bảo trì, vận hành một máy trong mỗi lần in là
50000
đồng. Chi phí in ấn của
n
máy chạy
trong một giờ là
( )
20 3 5n
+
nghìn đồng. Hỏi nếu in
50000
bản in khổ giấy
4A
thì phải sử dụng
bao nhiêu máy để thu được nhiều lãi nhất?
A.
4
máy. B.
7
máy. C.
6
máy. D.
5
máy.
Câu 26. Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nhiên liệu
làm vỏ lon là thấp nhất, tức là diện tích toàn phần của hình trụ nhỏ nhất. Muốn thể tích của khối
trụ đó bằng
V
và diện tích toàn phần của hình trụ nhỏ nhất thì nhà thiết kế phải thiết kế hình trụ
có bán kính bằng bao nhiêu?
A.
2
V
π
. B.
3
2
V
π
. C.
V
π
. D.
3
V
π
.
Câu 27. Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định
được số lượng vi khuẩn tăng theo thời gian bởi qui luật
( )
2
100
1000
100
t
Nt
t
= +
+
(con vi khuẩn),
trong đó
t
là thời gian (đơn vị giây). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào,
số lượng vi khuẩn tăng lên lớn nhất là bao nhiêu?
A.
0
. B.
1
. C.
10−
. D.
10
.
Câu 28. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu trên mỗi đơn vị diện tích
của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng
( )
480 20Qn n
= −
(gam).
Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được
nhiều cá nhất?
A.
12
. B.
14
. C.
10
. D.
18
.
Câu 29. Đốt cháy các hidrocacbon của dãy đồng đẳng nào dưới đây thì tỉ lệ mol
2
HO
: mol
2
CO
giảm
dần khi số cacbon tăng dần ?
A. Ankan. B. Anken. C. Ankin. D. Ankylbenzen.
Câu 30. Cho phương trình phản ứng tạo thành Nitơ (IV) Oxit từ Nitơ ddiooxxit và Oxy là
,,
22
22
o
dk t xt
NO O NO
→
+
←
. Biết rằng đây là một phản ứng thuận nghịch . Giả sử
,xy
lần lượt
là nồng độ phần trăm của khí
NO
và
2
O
tham gia phản ứng. Biết rằng tốc độ phản ứng hóa học
của phản ứng trên được xác định
2
v kx y=
, với k là hằng số của tốc độ phản ứng. Để tốc độ phản
ứng xảy ra nhanh nhất thì tỉ số giữa
x
y
là ?
A.
1
2
. B.
2
. C.
1
3
. D.
3
.
Câu 31. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức
( ) ( )
2
0,035 15Gx x x= −
, trong đó
x
là liều lượng thuốc được tiêm cho bệnh nhân (
x
được tính bằng miligam). Tính liều lượng
thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.
A.
8x =
. B.
5x =
. C.
15x =
. D.
10x =
.
Trang 7
Câu 32. Các chuyên gia Y-tế ước tính số người nhiễm virus Zika kể từ ngày xuất hiện bệnh nhân đầu tiên
đến ngày thứ
t
là
(
) (
)
23
45 , 0,1, 2,..., 25
ft t t t
=−=
. Nếu coi
( )
ft
là một hàm xác định trên đoạn
[ ]
0; 25
thì
( )
'
ft
được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm
t
. Tốc độ truyền
bệnh sẽ lớn nhất vào ngày thứ mấy?
A.
20
. B.
10
. C.
15
. D.
5
.
Câu 33. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng
70
m và chiều dài
250
m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả
hai) khi phải thực hiện lộ trình xuất phát từ
A
đến
C
và đua xe đạp tới
D
như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường
x
) thì vận động viên nên nhảy xuống để tiếp tục
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là
5
m/s;
1, 5
m/s và
10
m/s.
A.
139,52
m. B.
129,52
m. C.
109,52
m. D.
119,52
m.
Câu 34. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng
50
m và chiều dài
250
m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả
hai) khi phải thực hiện lộ trình xuất phát từ
A
đến
C
và đua xe đạp tới
D
như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường
x
) thì vận động viên nên nhảy xuống để tiếp tục
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là
5
m/s;
1, 5
m/s và
10
m/s.
A.
109,8
m. B.
105,8
m. C.
106,8
m. D.
107,8
m.
Câu 35. Cho một viên gạch men có dạng hình vuông
OABC
như hình vẽ. Sau khi tọa độ hóa, ta có
( )
0;0O
,
(
)
0;1
A
,
( )
1;1
B
,
( )
1;0
C
và hai đường cong lần lượt là đồ thị hàm số
3
yx=
và
3
yx=
. Tính diện tích của phần không được tô đậm trên viên gạch men.
A.
1
3
. B.
5
4
. C.
4
5
. D.
1
2
.
Câu 36. Người ta làm một cái lu đựng nước bằng cách cắt bỏ 2 chỏm của một khối cầu có bán kính
5 dm
bằng 2 mặt phẳng vuông góc với đường kính và cách tâm khối cầu
3 dm
. Tính thể tích của chiếc
lu.
y
x
C
A
B
O
Trang 8
A.
(
)
3
41 dm
π
. B.
( )
3
132 dm
π
. C.
( )
3
43 dm
π
. D.
( )
3
100
dm
3
π
.
Câu 37. Một cái trống trường có bán kính các đáy là
30 cm
, thiết diện vuông góc với trục và cách đều
hai đáy có diện tích là
( )
2
1600 cm
π
, chiều dài của trống là
1 m
. Biết rằng mặt phẳng chứa trục
cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu?
A.
3
425,2 dm
. B.
3
425,2 mm
. C.
3
425,2 cm
. D.
3
425,2 m
.
Câu 38. Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn
28cm
, trục nhỏ
25cm
. Biết
cứ
3
1000cm
dưa hấu sẽ làm được cốc sinh tố giá
20000
đồng. Hỏi từ quả dưa hấu trên có thể
thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
A.
180000
đồng. B.
183000
đồng. C.
185000
đồng. D.
190000
đồng.
Câu 39. Một bình hoa dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm
số
sin 2yx=−+
và trục
Ox
(tham khảo hình vẽ bên dưới). Biết đáy bình hoa là hình tròn có
bán kính bằng
2 dm
, miệng bình hoa là đường tròn bán kính bằng
1.5 dm
. Bỏ qua độ dày của
bình hoa, Thể tích của bình hoa gần với giá trị nào trong các giá trị sau đây?
A.
100
3
dm
. B.
104
3
dm
. C.
102
3
dm
. D.
103
3
dm
.
Câu 40. Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La
Mã, tòa nhà Ellipse Tower Hà Nội, sử dụng trong thiết kế logo quảng cáo, thiết bị nội thất. Xét
một Lavabo (bồn rửa) làm bằng sứ đặc hình dạng là một nửa khối elip tròn xoay có thông số kĩ
thuật mặt trên của Lavabo là: dài
×
rộng:
660 380 mm×
(tham khảo hình vẽ bên dưới), Lavabo có
độ dày đều là
20 mm
. Thể tích chứa nước của Lavabo gần với giá trị nào trong các giá trị sau:
3
dm
3
dm
5
dm
Trang 9
A.
3
18,66 dm
. B.
3
18,76 dm
. C.
3
18,86 dm
. D.
3
18,96 dm
.
Câu 41. Một vật chuyển động chậm dần đều với vận tốc
( ) 160 10 (m/s)= −vt t
. Quãng đường mà vật
chuyển động từ thời điểm
( )
0s=t
đến thời điểm mà vật dừng lại là
A.
1028 m
. B.
1280 m
. C.
1308 m
. D.
1380 m
.
Câu 42. Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức
( ) 3 2(m/s)= +vt t
. Biết tại thời điểm
( )
2s=t
thì vật đi được quãng đường là
(
)
10 m
. Hỏi tại thời
điểm
( )
30 s=t
thì vật đi được quãng đường là bao nhiêu?
A. 1140 m. B. 300 m. C. 240 m. D. 1410 m.
Câu 43. Một vật đang chuyển động với vận tốc
( )
25 m/s
v =
thì thay đổi vận tốc với gia tốc được tính
theo thời gian
t
là
( )
( )
2
2 6 m/sat t
= −
. Tính quãng đường vật đi được kể từ thời điểm thay đổi
gia tốc đến lúc vật đạt vận tốc bé nhất.
A.
107
m
5
. B.
144 m
. C.
28 m
. D.
57 m
.
Câu 44. Một mô tô chạy với vận tốc
( )
0
m/sv
thì gặp chướng ngại vật nên người lái xe đạp phanh. Từ
thời điểm đó ôtô chuyển động chậm dần với gia tốc
( )
2
8 m/sat= −
trong đó
t
là thời gian tính
bằng giây. Biết từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được
( )
12 m
. Tính
0
v
?
A.
18 m/s
. B.
3
86 m/s
. C.
3
1269 m/s
. D.
3
1296 m/s
.
Câu 45. Đầu tháng
5
năm
2019
, ông An đầu tư vào chăn nuôi tằm với số tiền vốn ban đầu là
200
(triệu
đồng). Biết rằng trong quá trình chăn nuôi gặp thuận lợi nên số tiền đầu tư của ông liên tục tăng
theo tốc độ được mô tả bằng công thức
( )
2
12000
()
5
ft
t
′
=
+
, với
t
là thời gian đầu tư tính bằng tháng
(thời điểm
0=t
ứng với đầu tháng
5
năm
2019
). Hỏi số tiền mà ông An thu về tính đến đầu
tháng
5
năm
2023
gần với số nào sau đây?
A.
2737
(triệu đồng). B.
2307
(triệu đồng).
C.
2370
(triệu đồng). D.
2703
(triệu đồng).
Câu 46. Giả sử rằng sau
t
năm, vốn đầu tư của một doanh nghiệp phát sinh lợi nhuận với tốc độ
( )
2
126
′
= +Pt t
(triệu đồng/năm). Hỏi sau
10
năm đầu tiên thì doanh nghiệp thu được lợi nhuận
là bao nhiêu (đơn vị triệu đồng).
A.
5020
. B.
1235
. C.
3257
3
. D.
4780
3
.
Trang 10
Câu 47: Một cái cổng hình parabol như hình vẽ. Chiều cao
4 m=GH
, chiều rộng
4 m
=
AB
,
0, 9 mAC BD= =
. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật
CDEF
tô đậm có
giá là
1200000
đồng/m
2
, còn các phần để trắng làm xiên hoa có giá là
900000
đồng/m
2
.
Hỏi tổng chi phí để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
A.
11445000
(đồng). B.
7368000
(đồng). C.
4077000
(đồng). D.
11370000
(đồng)
Câu 48: Để tăng thêm thu nhập, ông Bình chăn nuôi thêm 2 con bò. Do diện tích đất của nhà ông hẹp nên
ông xây chuồng bò như hình vẽ bên dưới và chia thành 2 phần bằng nhau để nhốt 2 con bò. Biết
ABCD
là hình vuông cạnh
4m
và
I
là đỉnh của một Parabol có trục đối xứng là trung trực của
BC
và parabol đi qua hai điểm
A
,
D
. Tiền xây chuồng bò hết
350000
đồng/
2
1m
. Biết
I
cách
BC
một khoảng
5m
, hãy tính số tiền chi phí ông Bình bỏ ra để xây dựng chuồng bò (làm tròn
đến hàng nghìn)?
A.
6.333.000
đồng. B.
7.533.000
đồng. C.
6.533.000
đồng. D.
7.333.000
đồng.
Câu 49. Người ta sản xuất một loại đèn trang trí ngoài trời (Trụ sở, quảng trường, công viên, sân vườn…)
gồm có hai phần: Phần bóng đèn có dạng mặt cầu bán kính
dm
R
, làm bằng thủy tinh trong suốt;
Phần đế bóng đèn làm bằng nhựa để cách điện, có dạng một phần của khối cầu bán kính
dmr
và thỏa mãn đường kính là một dây cung của hình tròn lớn bóng đèn. Một công viên muốn tạo
điểm nhấn ánh sáng, đặt loại bóng có kích thước
5 dmR =
,
3 dmr =
. Tính thể tích
V
phần
nhựa để làm đế một bóng đèn theo đơn đặt hàng (Bỏ qua ống luồn dây điện và bulông ốc trong
phần đế).
I
A
D
C
B
Trang 11
A.
3
36 dmV
π
=
. B.
3
68
dm
3
V
π
=
. C.
3
14
dm
3
V
π
=
. D.
3
40
dm
3
V
π
=
.
Câu 50. Một bồn nước Inox SONHA
®
ngang có hai đầu bồn là hình phẳng elip. Thể tích tối đa khi đóng
nắp bồn là
1
3000V =
lít. Bồn có chiều dài bằng
2, 0 ml =
và gấp
2
lần chiều cao của bồn. Để
nước bơm tự động vào bồn, người ta lắp một phao điện sao cho mực nước trong bồn cao
0, 75 mh =
so với điểm thấp nhất trong đáy bồn thì phao đóng không cho nước chảy vào bồn.
Tính thể tích nước trong bồn khi phao đóng (bỏ qua độ dày của bồn nước và kết quả làm tròn
đến phần trăm).
A.
3
2.41 m
V
=
. B.
3
2.43 mV =
. C.
3
2.40 mV =
. D.
3
2.44 mV =
.
BẢNG ĐÁP ÁN
1.D
2.B
3.B
4.D
5.C
6.D
7.C
8.A
9.A
10.C
11.A
12.C
13.C
14.A
15.B
16.C
17.A
18.B
19.A
20.A
21.D
22.A
23.D
24.D
25.D
26.B
27.D
28.A
29.A
30.B
31.D
32.C
33.D
34.D
35.D
36.B
37.A
38.B
39.D
40.B
41.A
42.D
43.D
44.D
45.C
46.D
47.A
48.C
49.D
50.A
Câu 1. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
,C
cạnh bên
SA
vuông góc với
mặt phẳng đáy
( )
.ABC
Biết
1SC
=
, tìm thể tích lớn nhất của khối chóp
..S ABC
A.
3
.
12
B.
C.
23
.
27
D.
3
.
27
Lời giải
Chọn D
Trang 12
Giả sử
( )
22 2
,0 1 1 .
CA CB x x SA SC AC x= = << ⇒ = − = −
Thể tích khối chóp:
22
.
1 11 1
. .. . 1 .
3 32 6
S ABC ABC
V S SA CA CB SA x x
∆

= = = −


Khảo sát hàm
(
)
22
1
1
6
fx x x= −
trên
( )
0;1
( )
33
2
22
1 12 3
21
66
11
x xx
fx x x
xx

−
′
= −− =

−−

.
( )
2
0
3
fx x
′
=⇔=
.
Ta được
( )
( )
0;1
23
max
3 27
fx f

= =



nên thể tích lớn nhất của khối chóp
.S ABC
là
3
27
V =
.
Câu 2. Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình chóp tứ giác đều sao cho
bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp (hình vẽ).
Để thể tích khối chóp lớn nhất thì cạnh đáy
x
của hình chóp bằng:
A.
2
.
5
x =
B.
22
.
5
x
=
C.
2 2.x =
D.
2
.
5
x =
Lời giải
Chọn B
Trang 13
Ta có
12
2 22
x
BM AB MO= −=−
.
Chiều cao của hình chóp
2
2
22
2 12
.
22 2 2
xx x
h BM MO

−

= − = −− =





Thể tích của khối chóp
45
2
1 1 21 2
3 23 2
x xx
Vx
−−
= =
.
Thể tích của khối chóp lớn nhất khi và chỉ khi
( )
45
2xx−
max trên
2
0;
2




.
Khảo sát hàm số
( )
45
2fx x x= −
trên
2
0;
2




.
( )
34
4 52fx x x
′
= −
.
( )
22
0
5
0
x
fx
x
=
′
= ⇔
=
.
Dựa vào bảng biến thiên, ta được GTLN của hàm số đạt tại
22
5
x =
.
Trang 14
Câu 3. Tìm chiều dài
L
ngắn nhất của cái thang để có thể tựa vào tường và mặt đất, ngang qua cột đỡ
có chiều cao
33
m
2
và cách tường
0,5 m
kể từ gốc của cột đỡ.
A.
2m
. B.
4m
. C.
3m
. D.
5m
.
Lời giải
Chọn B
Đặt
0;
2
ABC
π
α

= ∈


.
Dựa vào hình vẽ, ta có
AB AK KB= +
cos sin
MK KH
αα
= +
1 33
2cos 2sin
αα
= +
.
Đặt
( )
1 33
2cos 2sin
f
α
αα
= +
. Bài toán trở thành tìm
( )
0;
2
min f
π
α
α

∈


với
0;
2
π
α

∈


.
Ta có
( )
22
sin 3 3.cos
2cos 2sin
f
αα
α
αα
−
′
= +
33
22
sin 3 3.cos
2cos .sin
αα
αα
−
=
.
( )
33
0 sin 3 3.cos 0f
α αα
′
=⇔− =
3
tan 3 3
α
⇔=
tan 3
α
⇔=
0;
32
ππ
α

⇔=∈


.
Bảng biến thiên
α
0
3
π
2
π
( )
f
α
′
–
0
+
( )
f
α
4
Vậy
( )
min
0;
2
minAB f
π
α
α

∈


=
( )
4m
3
f
π

= =


.
C
B
H
Cột đỡ
Tường
A
M
K
Trang 15
Câu 4. Một con kiến đậu ở đầu
B
của một thanh cứng mảnh
AB
có chiều dài
L
đang dựng cạnh một
bức tường thẳng đứng (hình vẽ).
Vào thời điểm mà đầu
B
bắt đầu chuyển động sang phải theo sàn ngang với vận tốc không đổi
v
thì con kiến bắt đầu bò dọc theo thanh với vận tốc không đổi
u
đối với thanh. Trong quá
trình bò trên thanh, con kiến đạt được độ cao cực đại
max
h
là bao nhiêu đối với sàn? Cho đầu
A
của thanh luôn tỳ lên tường thẳng đứng.
A.
2
3
L
v
. B.
2
2L
v
. C.
2
3
L
v
. D.
2
2
L
v
.
Lời giải
Chọn D
Gọi
0
L
tt
u

<<


là thời gian con kiến đi được.
Ta có
L
t
u
=
với
L
là chiều dài thanh cứng.
Khi đầu
B
di chuyển một đoạn
.S vt=
thì con kiến đi được
.L ut=
.
Độ cao mà con kiến đạt được khi đó là
.sinhL
α
=
22
..
LS
ut
L
−
=
22 24
.
Lt v t
u
L
−
=
.
Đặt
( )
22 24
f t Lt v t= −
. Bài toán trở thành tìm
( )
max ft
.
Ta có
( )
2 23
24f t Lt v t
′
= −
,
(
)
2 23
02 4 0f t Lt v t
′
=⇔− =
0
2
t
L
t
v
=
⇔
=
.
Khi
0t
=
(không thỏa mãn), ta chọn
2
L
t
v
=
.
Bảng biến thiên
Trang 16
t
0
2
L
v
2
L
u
( )
ft
′
–
0
+
(
)
ft
2
2
L
v
Vậy
( )
2
max
2
2
LL
ft f
v
v

= =


.
Câu 5. Một hộp không nắp được làm từ một mảnh các tông theo mẫu. Hộp có đáy là một hình vuông
cạnh
( )
cmx
, chiều cao
( )
cmh
và có thể tích là
( )
3
500 cm
.
Tìm
x
sao cho diện tích mảnh các tông đó nhỏ nhất?
A.
5cm
. B.
100cm
. C.
10 cm
. D.
20 cm
.
Lời giải
Chọn C
Ta có thể tích của khối hộp là:
23
2
500
( ) 500(cm ) , 0V x xh h x
x
= = ⇒= >
.
Để chiếc hộp làm ra ít tốn bìa các tông nhất khi và chỉ khi diện tích toàn phần của hộp là nhỏ
nhất.
Diện tích của mảnh các tông dùng làm hộp là
22
2000
() 4 , 0S x x hx x x
x
=+=+ >
.
Bài toán quy về tìm
(0; )x ∈ +∞
sao cho tại đó
( )
Sx
đạt GTNN.
Ta có
3
22
2000 2( 1000)
() 2
x
Sx x
xx
−
′
=−=
.
( ) 0 10Sx x
′
=⇔=
.
Trang 17
Suy ra bảng biến thiên sau:
Dựa vào bảng biến thiên ta thấy
( )
Sx
đạt GTNN tại
10x =
. Vậy muốn tốn ít nguyên liệu nhất
ta lấy độ dài cạnh đáy của hình hộp là
10 cmx =
.
Câu 6. Một nhà máy cần sản xuất một bể nước bằng tôn có dạng hình hộp đứng đáy là hình chữ nhật có
chiều dài gấp 2 lần chiều rộng không nắp, có thể tích
3
4
m
3
. Hãy tính độ dài chiều rộng của đáy
hình hộp sao cho tốn ít vật liệu nhất.
A. 2 m. B.
3
m. C.
2
3
m . D. 1 m.
Lời giải
Chọn D
Gọi
,xh
lần lượt là chiều rộng đáy và chiều cao của khối hộp với
( )
, 0;xh∈ +∞
.
Ta có chiều dài đáy là 2x. Thể tích
2
22
2
2.. 2
23
V
V xxh x h h
xx
= = ⇔= =
.
Diện tích vật liệu làm khối hộp là
()
Sx
= S
đ
+ S
xq
=
2
4
2 . 2( 2 ). 2xx x x h x
x
++ =+
.
2
4
() 4Sx x
x
′
= −
.
2
4
() 0 4 0 1Sx x x
x
′
=⇔ − =⇔=
.
Bảng biến thiên:
Trang 18
Từ bảng biến thiên suy ra
min 6S =
khi
1x =
.
Câu 7. Cho hai vị trí
A
,
B
cách nhau
615 m
, cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách
từ
A
và từ
B
đến bờ sông lần lượt là
118 m
và
487 m
. Một người đi từ
A
đến bờ sông để lấy
nước mang về
B
.
Đoạn đường ngắn nhất mà người đó có thể đi là
A.
596,5m
. B.
671, 4 m
. C.
779,8 m
. D.
741, 2 m
.
Lời giải
Chọn C
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B.
Dễ dàng tính được
369, 492.BD EF= =
Ta đặt
,EM x=
khi đó ta được:
( )
2
22 2
492 , 118 , 492 487 .MF x MA x MB x= − = + = −+
Như vậy ta có hàm số
( )
fx
được xác định bằng tổng quãng đường
MA MB+
.
( )
( )
2
22 2
118 492 487fx x x= + + −+
với
[ ]
0; 492x ∈
.
Trang 19
Ta cần tìm giá trị nhỏ nhất của
( )
fx
để có được quãng đường ngắn nhất và từ đó xác định
được vị trí điểm
M
.
Ta có:
( )
( )
22 2
2
492
.
118
492 487
xx
fx
x
x
−
′
= −
+
−+
( )
(
)
22 2
2
492
00
118
492 487
xx
fx
x
x
−
′
=⇔− =
+
−+
(
)
22 2
2
492
118
492 487
xx
x
x
−
⇔=
+
−+
( )
( )
2
2 22
492 487 492 118x x xx⇔ −+ = − +
( ) ( )
( )
22
2 2 22
492 487 492 118
0 492
x x xx
x

−+ = − +

⇔
≤≤
( ) ( )
22
487 58056 118
0 492
xx
x
= −
⇔
≤≤
58056
605
58056
58056
605
369
0 492
x
x
x
x
=
⇔ ⇔=
= −
≤≤
.
Hàm số
( )
fx
liên tục trên đoạn
[ ]
0; 492
. So sánh các giá trị của
(0)f
,
58056
605
f



,
( )
492f
ta có giá trị nhỏ nhất là
58056
779,8 m
605
f

≈


.
Khi đó quãng đường đi ngắn nhất là xấp xỉ
779,8 m
.
Câu 8. Trong không gian với hệ trục toạ độ
Oxyz
cho đường thẳng
∆
có phương trình tham số là:
2
1
x
yt
zt
=
= −
= +
và hai điểm
( )
1; 2; 1A −−
,
( )
4;4;5B
. Giả sử
( )
;;M abc
thuộc
∆
sao cho
MA MB+
nhỏ nhất, khi đó tích
abc
là
A.
0
. B.
2
9
. C.
1
. D.
2
.
Lời giải
Chọn A
( )
2; ;1M M tt∈∆⇒ − +
.
Ta có:
2
29MA t= +
;
2
2 36
MB t= +
.
Từ đó
22
29236MA MB t t+ = ++ +
.
Đặt
( )
22
29236ft t t= ++ +
.
Trang 20
( )
22
22
29 236
tt
ft
tt
′
= +
++
.
Giải
(
)
22
22
00
29 236
tt
ft
tt
′
=⇔+ =
++
0t⇔=
. Ta có bảng biến thiên sau:
Từ bảng biến thiên suy ra
( )
min 9ft=
đạt được tại
0t =
. Vậy
( )
2;0;1M
thì
MA MB+
nhỏ
nhất.
Câu 9 . Một trang chữ của cuốn sách giáo khoa cần diện tích
2
384cm
. Lề trên và dưới là
3cm
, lề trái
và phải là
2 cm
. Kích thước tối ưu của trang giấy là:
A. Dài
24 cm
; rộng
16 cm
. B. Dài
24 cm
; rộng
17 cm
.
C. Dài
25cm
; rộng
15,36cm
. D. Dài
25,6cm
; rộng
15cm
.
Lời giải
Chọn A
Trang giấy có diện tích tối ưu khi diện tích trình bày là lớn nhất.
Gọi chiều dài trang giấy là
x
,
( 8 6)x ≥
; suy ra chiều rộng là
384
x
.
Diện tích trình bày nội dung là :
( ) ( )
384 2304
6 4 4 408fx x x
xx

=− − =−− +


.
Để diện tích là lớn nhất ta cần tìm giá trị lớn nhất của
2304
( ) 4 408
fx x
x
=−− +
với
( )
86x ≥
.
Ta có:
2
2304
'( ) 4fx
x
=−+
.
Trang 21
'( ) 0 24fx x=⇔=
.
Dựa vào bảng biến thiên ta có giá trị lớn nhất của
()fx
là 216 khi
24
x =
.
Vậy chiều dài trang giấy là
24 cm
; suy ra chiều rộng là
384
16 cm
24
=
.
Câu 10. Có một cơ sở in sách xác định rằng: Diện tích của toàn bộ trang sách là
2
0
)(cmS
. Do yêu cầu kỹ
thuật nên dòng đầu và dòng cuối đều phải cách mép (trên và dưới) trang sách là
(cm)
a
. Lề bên
trái và bên phải cũng phải cách mép trái và mép phải của trang sách là
(cm)b
(
)
ba<
. Các kích
thước của trang sách là bao nhiêu để cho diện tích phần in các chữ có giá trị lớn nhất. Khi đó hãy
tính tỉ lệ của chiều rộng và chiều dài trang sách.
A.
ba
a
−
. B.
2
21
b
a −
. C.
b
a
. D.
ba
a
+
.
Lời giải
Chọn C
Trang 22
Gọi
,xy
lần lượt là chiều rộng và chiều dài của trang sách
( )
0 xy<<
,
P
là diện tích phần in
chữ của trang sách.
Chiều rộng phần in sách là
2,
2
x
x bb

−<


.
Chiều dài phần in sách là
2,
2
y
y aa

−<


.
Diện tích phần in sách là:
( 2 )( 2 ) 2 2 4P x b y a xy by ax ab=− −=−−+
.
Mặt khác
0
0
S
S xy y
x
= ⇒=
thay vào phương trình ta được
0
0
2
42
bS
P S ab ax
x

=+− +


.
Ta nhận thấy
0
4S ab+
không đổi
0
max
2
2 min
bS
P ax
x

⇔+


.
Xét hàm số
0
2
() 2
bS
f x ax
x
= +
00
2
2
() 2 , () 0
bS bS
fx a fx x
xa
′′
⇒ = − =⇔=
.
Lại có
0
3
4
()
bS
fx
x
′′
=
. Với x dương
() 0fx
′′
⇒>
0
0
min ( ) 4
bS
f x f abS
a

⇒= =



.
Khi đó:
22
00
bS bS
bxy x b
x xx
a a a ya
= ⇒= ⇒= ⇒=
.
Câu 11. Một anh kỹ sư muốn tạo ra 1 cái lu hình trụ có diện tích bề mặt (không tính hai mặt đáy) là lớn
nhất. Bề mặt lu được quấn bởi mảnh tôn hình chữ nhật có chu vi 120 cm. Gọi chiều dài của hình
chữ nhật là
a
, chiều rộng của hình chữ nhật là
b
. Tính
2
3
Pa b= +
.
A. 990. B. 1660. C. 2530. D. 1108.
Lời giải
Chọn A
Cách 1:
60ab+=
(1).
.
lu
S ab=
.
Ta có
2
. 900
2
ab
ab
+

≤=


(B.Đ.T Cô Si) .
( )
max
900
lu
S
⇒=
. Dấu
“”=
xảy ra
30ab⇔==
.
2
3 990ab
⇒+=
.
Trang 23
Cách 2:
Ta có
60 60ab b a+= ⇔= −
.
( )
2
. 60 60
lu
S ab a a a a= = −= −
.
Xét
(
)
2
60
y fa a a= = −
với
0 60
a<<
.
60 2
ya
′
= −
.
0 30ya
′
=⇔=
.
( )
max
900
lu
S⇒=
khi
2
30 30 3 990a b ab= ⇒= ⇒ + =
.
Câu 12. Bác nông dân có
200 m
rào để ngăn đàn gà nuôi dạng hình chữ nhật. Để diện tích nuôi gà là lớn
nhất thì chiều dài hình chữ nhật là
a
(m) và chiều rộng là
b
(m). Khi đó
22
a ab b++
có giá trị
bằng
A. 7525 m. B. 7600 m. C. 7500 m. D. 7900 m.
Lời giải
Chọn C
Cách 1 : Ta có
100
ab+=
.
Diện tích
.
nuoi
S ab=
.
Ta có
2
. 2500
2
ab
ab
+

≤=


(B.Đ.T Cô Si).
( )
max
2500
nuoi
S =
. Dấu
“”=
xảy ra
50ab⇔==
.
22
. 7500a ab b⇒+ +=
.
Cách 2:
Ta có
100 100ab b a+= ⇔= −
.
( )
2
. 100 60
nuoi
S ab a a a a= = −= −
.
Xét
( )
2
100y fa a a
= = −
với
0 100a<<
.
100 2ya
′
= −
.
Trang 24
0 50ya
′
=⇔=
.
( )
max
2500
lu
S⇒=
khi
22
50 50 . 7500a b a ab b= ⇒= ⇒ + + =
.
Câu 13. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm
tổng
xy+
để diện tích hình thang
EFGH
đạt giá trị nhỏ nhất.
A.
7 cm
. B.
5cm
. C.
72
cm
2
. D.
4 2 cm
.
Lời giải
Chọn C
Ta có
EFGH
S
nhỏ nhất khi và chỉ khi
AEH CGF DGH
SS S S=++
lớn nhất.
Dễ thấy
( )( )
2 2 3 6 6 4 3 36S x y x y xy x y=++− −=−−+
(1).
Theo giả thiết, ta được
AEH CGF∆∆∽
(do có các cạnh tương ứng song song với nhau) nên
AE AH
CG CF
=
suy ra
6xy =
(2).
Từ (1) và (2) suy ra
18
2 42 4Sx
x

=−+


hay
9
21 2Sx
x

=−+


.
Theo bất đẳng thức Cô – si, ta được:
99
2 22. 218 62xx
xx
+≥ = =
nên
21 6 2S ≤−
. Từ đó
biểu thức
S
lớn nhất bằng
21 6 2−
, đạt được khi
9
2
32
cm 2 2 cm
2
0
x
xy
x
x
=
⇔= ⇒=
>
.
x
cm
y
cm
3 cm
2 cm
H
G
F
E
D
C
B
A
Trang 25
Khi đó, ta được
32 72
2 2 cm
22
xy+= + =
.
Câu 14. Một màn ảnh hình chữ nhật cao
1,4m
và đặt ở độ cao
1, 8 m
so với tầm mắt (tính từ đầu mép
dưới của màn hình như hình vẽ). Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn
nhất. Tính khoảng cách từ vị trí đó đến màn ảnh? Biết rằng góc
BOC
nhọn.
A.
2,4mAO =
. B.
2mAO =
. C.
2, 6 mAO =
. D.
3mAO =
.
Lời giải
Chọn A
Đặt độ dài cạnh
(
) (
)
m, 0
AO x x= >
. Ta được
22
3, 24 , 10, 24BO x CO x=+=+
.
Sử dụng định lí cosin trong tam giác
OBC
(
) (
)
( )
( )
22
222
22
3, 24 10, 24 1,96
cos
2.
2 3, 24 10,24
xx
OB OC BC
BOC
OB OC
xx
++ +−
+−
= =
++
( )( )
2
22
5, 76
3, 24 10, 24
x
xx
+
=
++
.
Vì góc
BOC
nhọn nên
BOC
lớn nhất khi và chỉ khi
cos BOC
nhỏ nhất. Hay bài toán trở thành tìm
x
để
( )
( )( )
2
22
5, 76
3, 24 10, 24
x
Fx
xx
+
=
++
đạt giá trị nhỏ nhất.
Đặt
( )
( )
2
3, 24 , 3, 24x tt+=>
. Suy ra
(
)
( )
( )
63
25 63
25
7 25 7
t
t
Ft
tt tt
+
+
= =
++
.
Ta đi tìm
t
để
( )
Ft
đạt giá trị nhỏ nhất.
( )
( )
( ) ( )
( )
( )
27
25 7 25 63
27
25 63 1
25 7
25 7
t
tt t
tt
t
Ft
tt
tt


+


+− +
′



+
+


′

= =

+

+




( )
( )( )
( ) ( )
( ) ( )
2
50 7 25 63 2 7
1 1 49 441
25 25
27 7 27 7
tt t t
t
tt tt tt tt

+− + +
−

= =

++ ++

.
( )
09Ft t
′
= ⇔=
Trang 26
Bảng biến thiên
t
3,24 9
+∞
(
)
Ft
′
- 0 +
( )
Ft
min
F
Thế vào biểu thức của phép đặt ta có:
( )
22
144
3,24 9 2,4m
25
xx x
+ =⇔ = ⇔=
.
Vậy để nhìn rõ nhất thì
2,4mAO =
.
Câu 15. Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính
10 cm
, biết một
cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn.
A.
2
80 cm
. B.
2
100 cm
. C.
2
160 cm
D.
2
200 cm
.
Lời giải
Chọn B
Gọi
( )
cmx
là độ dài cạnh hình chữ nhật không nằm trên đường kính của đường tròn
( )
0 10cm
x<<
.
Khi đó, độ dài cạnh hình chữ nhật nằm trên đường kính đường tròn là
( )
2
2 100 cmx−
.
Diện tích hình chữ nhật:
( )
( )
22
2 . 100 cmSx x x= −
.
( )
22
2
22
2 200 4
' 2 100
100 100
xx
Sx x
xx
−
= −− =
−−
.
( )
10 2
'0
2
Sx x=⇔=
(Do
0 10x
<<
).
Bảng biến thiên
Trang 27
Dựa vào bảng biến thiên, ta có hàm số
( )
Sx
đạt giá trị lớn nhất bằng
100
khi
10 2
2
x =
.
Vậy diện tích lớn nhất của hình chữ nhật là
2
100 cmS =
.
Câu 16 . Từ một khúc gỗ tròn hình trụ có đường kính bằng
40 cm
, cần xả thành một chiếc xà có tiết diện
ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng
x
của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất.
A.
( )
3 34 17 2
cm
2
x
−
=
B.
( )
3 34 19 2
cm
2
x
−
=
C.
( )
5 34 15 2
cm
2
x
−
=
D.
( )
5 34 13 2
cm
2
x
−
=
Lời giải
Chọn C
Gọi
x
,
y
lần lượt là chiều rộng, chiều dài của miếng phụ.
Diện tích sử dụng theo tiết diện ngang là
4
MNPQ
S S xy= +
.
Cạnh hình vuông
( )
20 2 cm
2
MP
MN = =
.
Trang 28
Suy ra
( )
(
)
2
20 2 4 800 4 1S xy xy= +=+
Ta có:
2 20 2 20 2 40 20 2x AB MN AB BD=− =− <− =−
.
0 20 10 2x
⇒<< −
.
Lại có
( )
2
222 2
2 20 2 1600AB AD BD x y+ = ⇔ + +=
.
2
800 80 2. 4y xx⇒= − −
.
Thế vào
( )
1
thì ta được
2 2 34
800 4 800 80 2. 4 800 4 800 80 2. 4S x xx x x x=+ − −=+ − −
.
Xét hàm số
( )
2 34
800 80 2. 4fx x x x=−−
với
( )
0; 20 10 2x ∈−
.
( )
23
1600 240 2. 16fx x x x
′
=−−
.
(
)
(
)
( )
0 ()
5 34 15 2
0
2
5 34 15 2
2
xl
fx x n
xl
=
−
′
=⇔=
+
=
−
.
Bảng biến thiên
Dựa vào bảng biến thiên, ta thấy hàm số
( )
fx
đạt giá trị lớn nhất khi
5 34 15 2
2
x
−
=
hay
diện tích
S
đạt giá trị lớn nhất khi
( )
5 34 15 2
cm
2
x
−
=
.
Câu 17. Một ô tô đang chạy với vận tốc
(
)
15 m/s
thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc
( ) ( )
5 15 m/svt t=−+
trong đó
t
là khoảng thời gian tính bằng
giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển
được bao nhiêu mét ?
A.
22,5m
. B.
45m
. C.
15m
. D.
90 m
.
Trang 29
Lời giải
Chọn A
Khi dừng hẳn thì
( ) 5 15 0 3vt t t=− + = ⇔=
.
Từ lúc hãm phanh đến khi dừng lại, xe di chuyển được:
3
33
2
0
00
5
( )d ( 5 15)d ( 15 ) 22,5m
2
s vt t t t t t
= = −+ =− + =
∫∫
.
Câu 18. Một vật chuyển động với gia tốc
22
( ) 3 (m/s ).
at t t= +
Vận tốc ban đầu của vật là
2(m/s).
Hỏi
vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó được
2s.
A.
8m/s
. B.
12 m/s
. C.
16 m/s
. D.
10 m/s
.
Lời giải
Chọn B
Vận tốc chuyển động
2 32
1
( ) ( )d (3 )d .
2
vt att t tt t t C= = +=++
∫∫
Chọn gốc thời gian lúc bắt đầu tăng tốc thì
32
1
(0) 2 2 ( ) 2.
2
v C vt t t=⇒=⇒ =+ +
Khi đó tại thời điểm
2s
thì
(2) 12 m/s.v =
Câu 19. Cho mạch điện xoay chiều
RLC
mắc nối tiếp có
R
thay đổi. Biết điện trở cuộn cảm
(
)
80
L
Z
= Ω
, điện trở của tụ điện là
( )
200
C
Z = Ω
và hiệu điện thế hai đầu mạch là
( )
0
100cos u U tV
π
=
. Để
công suất tiêu thụ của mạch cực đại thì giá trị của
R
bằng
A.
( )
120 Ω
. B.
( )
50
Ω
. C.
( )
100 Ω
. D.
( )
200 Ω
.
Lời giải
Chọn A
Công suất tiêu thụ của mạch:
( )
22
2
2
2
2
LC
U RU
P RI R
Z
R ZZ
= =⋅=
+−
.
( )
( )
( )
2
22
2
2
2
LC
R
LC
U ZZ R
P
R ZZ

−−

′
=

+−

.
( )
( )
0 120
LC
R
P RZ Z
′
=⇔= − = Ω
.
Ta có bảng biến thiên:
Trang 30
Suy ra công suất tiêu thụ của mạch cực đại thì
( )
120R = Ω
.
Câu 20. Cho mạch điện xoay chiều
RLC
mắc nối tiếp có
R
thay đổi. Biết điện trở cuộn cảm
( )
100
L
Z
= Ω
, điện trở của tụ điện là
( )
40
C
Z
= Ω
và hiệu điện thế hai đầu mạch là
( )
120 2 cos
100 u tV
π
=
. Điện trở
R
phải có giá trị là bao nhiêu để công suất tiêu thụ của mạch
đạt cực đại và giá tri cực đại của công suất là bao nhiêu?
A.
(
) ( )
max
60 , 120 WRP=Ω=
. B.
( ) (
)
max
120 , 60 WRP=Ω=
.
C.
( )
( )
max
40 , 180 WRP=Ω=
. D.
( )
(
)
max
120 , 180 WRP=Ω=
.
Lời giải
Chọn A
Công suất tiêu thụ của mạch:
( )
22
2
2
2
2
LC
U RU
P RI R
Z
R ZZ
= =⋅=
+−
.
(
)
( )
( )
2
22
2
2
2
LC
R
LC
U ZZ R
P
R ZZ

−−

′
=

+−

.
( )
( )
0 60
LC
R
P RZ Z
′
=⇔= − = Ω
.
Ta có bảng biến thiên:
Suy ra công suất tiêu thụ của mạch cực đại
( )
max
120 WP =
tại
( )
60R = Ω
.
Câu 21: Thể tích
V
của
1kg
nước ở nhiệt độ
t
(
t
nằm giữa
0C°
đến
30 C°
) được cho bởi công thức
( )
2 33
999,87 0,06426 0,0085043 0,0000679 cm
V tt t=−+ −
. Nhiệt độ
t
của nước gần nhất với
giá trị nào dưới đây thì khối lượng riêng của nước là lớn nhất?
A.
0°
. B.
4−°
. C.
30°
. D.
4°
.
Lời giải
Trang 31
Chọn D
Ta có:
(
)
2
0,06426 2.0,0085043 3.0,0000679
Vt t t
′
=−+ −
.
( )
( )
79,53138 0 ;30
0
3,9665
t
Vt
t
≈ ∉° °
′
= ⇔
≈
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có khối lượng riêng lớn nhất của vật khi thể tích nhỏ nhất lúc vật có
nhiệt độ xấp xỉ gần bằng
4C°
.
Nhận xét: Ta đã biết trong môn vật lý lớp 7, khối lượng riêng của nước lớn nhất khi thể tích
tương ứng của nước là nhỏ nhất.
Câu 22: Thể tích nước của một bể bơi sau
t
phút bơm được tính theo công thức
( )
4
3
1
30
100 4
t
Vt t

= −


( )
0 90t≤≤
. Tốc độ bơm nước tại thời điểm t được tính bởi
( ) ( )
vt V t
′
=
. Trong các khẳng định
sau, khẳng định nào đúng.
A. Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
B. Tốc độ bơm luôn giảm.
C. Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
D. Cả A, B, C đều sai.
Lời giải
Chọn A
Xét hàm
( )
23
91
0 90
10 100
Vt t t
′
= − ≤≤
.
2
0
93
0
60
5 100
t
V t tV
t
=
′′ ′′
=− ⇒=⇔
=
.
Bảng biến thiên:
Trang 32
Dựa vào bảng biến thiên, ta có hàm số
V
đồng biến trên
( )
0;60
, nghịch biến trên
( )
60;90
.
Câu 23. Công ty XDPL muốn làm một đường ống dẫn khí từ một địa điểm
A
trên bờ biển đến một điểm
B
trên một hòn đảo. Khoảng cách ngắn nhất từ điểm
B
đến bờ biển là
6 km
. Giá để xây lắp mỗi
km đường ống trên bờ là
50.000 USD
, còn xây lắp dưới nước là
130.000 USD
.
B
′
là điểm trên
bờ biển sao cho
BB
′
vuông góc với bờ biển. Khoảng cách từ
A
đến
B
′
là
9 km
.
Hỏi vị trí điểm
M
trên bờ biển cách
A
bao xa để chi phí xây lắp đường ống từ
A
qua
M
rồi
đến
B
là ít tốn kém nhất?
A.
9 km
. B.
6 km
. C.
0 km
. D.
6.5km
.
Lời giải
Chọn D
Đặt
kmx BM
. Khi đó
2
36, 9BM x AM x
=+=−
.
Chi phí xây dựng đường ống là
2
( ) 130000 36 50000(9 ) (USD)Sx x x
= ++ −
.
Hàm
()Sx
xác định, liên tục trên
[ ]
0;9
và
2
13
( ) 10000 5
36
x
Sx
x

′
= −

+

.
22
2
169 25( 36)
5
( ) 0 13 5 36
2
09
xx
Sx x x x
x
= +
′
=⇔ = + ⇔ ⇔=
≤≤
.
5
(0) 1.230.000; 1.170.000; (9) 1.406.165
2
SS S

= = ≈


.
Do đó chi phí thấp nhất khi
5
2
x =
. Vậy
M
cần cách
A
một khoảng
6,5 km
.
Câu 24. Một điểm
C
trên hòn đảo có khoảng cách ngắn nhất đến bờ biển là
60 km
,
B
là điểm trên bờ
biển sao cho
CB
vuông góc với bờ biển . Khoảng cách từ
A
trên bờ biển đến
B
là
100 km
. Để
-
+
0
V'
V''
90
60
0
t
9km
6km
đảo
bờ biển
biển
A
B
B'
Trang 33
tham dự buổi họp nhóm Strong Team Toán VD – VCD ngày 28/6/2019 , thầy Quý phải tính toán
vị trí diễn ra cuộc họp tại địa điểm
G
trên đoạn
AB
để tổng chi phí đi lại của cả hai nhóm các
thầy cô là ít nhất. Biết nhóm của thầy Quý đi từ
C
theo đường biển chi phí đi là
500
nghìn mỗi
km, nhóm cô Thêm đi từ vị trí A đi trên đất liền mỗi km chi phí là
300
nghìn. Hỏi thầy tìm được
vị trí điểm
G
cách
B
bao xa?
A.
40 km
. B.
60 km
. C.
55km
. D.
45km
.
Lời giải
Đặt
[ ]
(km), 0;100x BG x= ∈
.
Khi đó
2
3600, 100GC x AG x=+=−
.
Chi phí đi lại của hai nhóm người để đến vị trí
G
là
2
( ) 500 3600 300(100 )Sx x x= ++ −
( nghìn đồng).
Hàm
()
Sx
xác định, liên tục trên
[ ]
0;100
và
2
500
( ) 300
3600
x
Sx
x
′
= −
+
.
22
2
25 9(x 3600)
'( ) 0 5 3 3600 45
0 100
x
Sx x x x
x
= +
=⇔ = + ⇔ ⇔=
≤≤
.
( )
(0) 60000; S 45 54000; (100) 58310SS= = ≈
.
Do đó chi phí thấp nhất khi
45x =
. Vậy
G
cần cách
B
một khoảng
45km
.
Câu 25. Một xưởng in có
8
máy in, mỗi máy in được
4000
bản in khổ giấy
4
A
trong một giờ. Chi phí
để bảo trì, vận hành một máy trong mỗi lần in là
50000
đồng. Chi phí in ấn của
n
máy chạy
trong một giờ là
( )
20 3 5n +
nghìn đồng. Hỏi nếu in
50000
bản in khổ giấy
4A
thì phải sử dụng
bao nhiêu máy để thu được nhiều lãi nhất?
A.
4
máy. B.
7
máy. C.
6
máy. D.
5
máy.
Lời giải
Chọn D
Gọi số giờ cần in là
x
thì
n
máy in được
4000. .nx
bản in trong
x
giờ.
Ta có
25
4000. . 50000
2
n x nx
= ⇒=
.
Chi phí của
n
máy chạy trong
x
giờ là
( )
20 3 5xn+
nghìn đồng.
Chi phí để bảo trì
n
máy là
50n
nghìn đồng.
Tổng chi phí là
( ) ( )
1250
20 3 5 50 60 100 50 750 50f n x n n xn x n n
n
= ++= + +=+ +
.
Trang 34
( )
2
1250
50fn
n
′
=−+
,
( )
05fn n
′
=⇔=
.
Ta có bảng biến thiên
Để thu được tiền lãi cao nhất cần chi phí thấp nhất, vậy
5n =
thỏa mãn yêu cầu bài toán.
Câu 26. Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nhiên liệu
làm vỏ lon là thấp nhất, tức là diện tích toàn phần của hình trụ nhỏ nhất. Muốn thể tích của khối
trụ đó bằng
V
và diện tích toàn phần của hình trụ nhỏ nhất thì nhà thiết kế phải thiết kế hình trụ
có bán kính bằng bao nhiêu?
A.
2
V
π
. B.
3
2
V
π
. C.
V
π
. D.
3
V
π
.
Lời giải
Chọn B
Gọi hình trụ có chiều cao
h
, độ dài đường sinh
l
, bán kính đáy
r
.
Ta có:
( )
2
2 221
tp day xq
S S S r rl
ππ
= += +
. Mặt khác
2
22
VV
V rh h l
rr
π
ππ
= ⇒ = ⇒=
.
Thay vào công thức
(
)
1
ta được:
2
2
2
tp
V
Sr
r
π
= +
.
Xét hàm số
( )
2
2
2
V
fr r
r
π
= +
với
0
r >
. Ta có
(
) (
)
3
2
2
4;0
2
VV
fr r fr r
r
π
π
′′
= − =⇔=
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy
( )
fr
đạt giá trị nhỏ nhất khi
3
2
V
r
π
=
.
Trang 35
Hay
tp
S
đạt giá trị nhỏ nhất khi
3
2
V
r
π
=
.
Câu 27. Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định
được số lượng vi khuẩn tăng theo thời gian bởi qui luật
( )
2
100
1000
100
t
Nt
t
= +
+
(con vi khuẩn),
trong đó
t
là thời gian (đơn vị giây). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào,
số lượng vi khuẩn tăng lên lớn nhất là bao nhiêu?
A.
0
. B.
1
. C.
10−
. D.
10
.
Lời giải
Chọn D
Ta có tốc độ phát triển của đàn vi khuẩn tại thời điểm
t
là:
( )
( )
(
)
(
)
2
2
100 100 100 2
100
t tt
Nt
t
+−
′
=
+
( )
22
2
2
100 100
100
t
t
−
=
+
( )
0
t∀>
.
Xét
( )
0Nt
′
=
2
100 10 0tt⇔ = ⇔= >
.
Lập bảng biến thiên ta được:
Dựa vào bảng biến thiên, ta kết luận
( ) ( )
max 10 1005Nt N= =
.
Câu 28. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu trên mỗi đơn vị diện tích
của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng
( )
480 20Qn n= −
(gam).
Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được
nhiều cá nhất?
A.
12
. B.
14
. C.
10
. D.
18
.
Lời giải
Chọn A
Mỗi con các cân nặng trung bình sau một vụ là:
( )
480 20Qn n= −
Khi đó với
n
con cá thì cân nặng của chúng là:
( ) ( )
2
480 20P n nQ n n n= = −
( )
480 40Pn n
′
⇒=−
.
Xét
( )
0Pn
′
=
12n⇔=
. Khi đó ta có bảng biến thiên:
Trang 36
Dựa và bảng biến thiên, ta suy ra
( )
( )
max 12 2880Pn P= =
( với
0n >
).
Câu 29. Đốt cháy các hidrocacbon của dãy đồng đẳng nào dưới đây thì tỉ lệ mol
2
HO
: mol
2
CO
giảm
dần khi số cacbon tăng dần ?
A. Ankan. B. Anken. C. Ankin. D. Ankylbenzen.
Lời giải
Chọn A
Công thức tổng quát của một hidrocacbon là
2 22nn k
CH
+−
với
k
là số liên kết
π
trong phân tử .
Phương trình phản ứng cháy là:
( )
,
2 22 2 2 2
1
o
xt t
nn k
C H O nCO n k H O
+−
+ → + + −
Ta có
2
2
1
HO
CO
n
nk
nn
+−
=
. Xét hàm số
( )
*
1
,
nk
fn n N
n
+−
= ∈
.
Ta có
( )
2
1k
fn
n
−
′
=
. Theo giả thiết ta có
( )
fn
là hàm nghịch biến nên
( )
0fn
′
<
22
2
1
0 10 1 0 : :
k
nn
k
k k k CTTQ C H ankan
n
∈
+
−
⇔ <⇔−<⇔<→=⇒
.
Câu 30. Cho phương trình phản ứng tạo thành Nitơ (IV) Oxit từ Nitơ ddiooxxit và Oxy là
,,
22
22
o
dk t xt
NO O NO
→
+
←
. Biết rằng đây là một phản ứng thuận nghịch . Giả sử
,xy
lần lượt
là nồng độ phần trăm của khí
NO
và
2
O
tham gia phản ứng. Biết rằng tốc độ phản ứng hóa học
của phản ứng trên được xác định
2
v kx y=
, với k là hằng số của tốc độ phản ứng. Để tốc độ phản
ứng xảy ra nhanh nhất thì tỉ số giữa
x
y
là ?
A.
1
2
. B.
2
. C.
1
3
. D.
3
.
Lời giải
Chọn B
Ta có
( ) ( )
22
100 100% ,0 100v kx y kx x do x y x= = − += <<
.
Xét hàm số
( ) ( )
( )
2 23
100 100fxkx xk xx= −= −
.
Trang 37
Bài toán trở thành tìm
( )
( )
0;100
max ?
x
fx
∈
=
.
Ta có:
( ) ( )
( )
( )
2
0
200 3 , 0
200
0;100
3
x ktm
fx k x x fx
x
=
′′

=−=⇔

= ∈
.
Lập bảng biến thiên ta có:
Dựa vào bảng biến thiên ta suy ra
( )
( )
0;100
200
max
3
x
fx f
∈

=


.
Và do đó ta có
100
100 2
3
x
yx
y
= −= ⇒ =
.
Câu 31. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức
(
) (
)
2
0,035 15Gx x x
= −
, trong đó
x
là liều lượng thuốc được tiêm cho bệnh nhân (
x
được tính bằng miligam). Tính liều lượng
thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.
A.
8
x =
. B.
5x =
. C.
15x =
. D.
10x =
.
Lời giải
Chọn D
Điều kiện
[
]
0;15
x ∈
(vì độ giảm huyết áp không âm).
Bài toán trở thành: Tìm
[ ]
0;15x ∈
để
(
)
Gx
đạt giá trị lớn nhất.
Theo giả thiết
( )
( )
23
0,035 15Gx x x= −
( )
( )
2
0,035 30 3Gx x x
′
⇒= −
.
Cho
( )
0
0
10
x
Gx
x
=
′
= ⇔
=
. Khi đó ta có bảng biến thiên như sau
Trang 38
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là
10x =
(mg).
Câu 32. Các chuyên gia Y-tế ước tính số người nhiễm virus Zika kể từ ngày xuất hiện bệnh nhân đầu tiên
đến ngày thứ
t
là
(
) ( )
23
45 , 0,1, 2,..., 25ft t t t=−=
. Nếu coi
( )
ft
là một hàm xác định trên đoạn
[ ]
0; 25
thì
( )
'ft
được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm
t
. Tốc độ truyền
bệnh sẽ lớn nhất vào ngày thứ mấy?
A.
20
. B.
10
. C.
15
. D.
5
.
Lời giải
Chọn C
Ta có
( )
23
45ft t t= −
( )
2
' 90 3ft t t⇒=−
.
Đặt
( )
2
90 3gt t t= −
. Bài toán trở thành: Tìm
[ ]
0; 25t ∈
để
( )
gt
đạt giá trị lớn nhất.
( )
' 90 6gt t= −
. Cho
( )
' 0 15gt t=⇔=
.
Lập bảng biến thiên
Vậy tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ
15
.
Câu 33. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng
70
m và chiều dài
250
m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc
cả hai) khi phải thực hiện lộ trình xuất phát từ
A
đến
C
và đua xe đạp tới
D
như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường
x
) thì vận động viên nên nhảy xuống để tiếp tục
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là
5
m/s;
1, 5
m/s và
10
m/s.
A.
139,52
m. B.
129,52
m. C.
109,52
m. D.
119,52
m.
Lời giải
Chọn D
A
x
B
( )
250 xm−
70m
D
250m
C
Trang 39
Gọi
B
là vị trí VĐV kết thúc phần chạy điền kinh và
( )
0 250AB x x= <<
Khi đó ta đó
1
1
5
AB x
t
v
= =
là thời gian đi từ
A
đến
B
Đồng thời quãng đường bơi chính là
22
70 (250 )BC x
= +−
Suy ra
( )
2
2
2
70 250
1, 5 1, 5
x
BC
t
+−
= =
là thời gian bơi từ
B
đến
C
Thời gian đua xe đạp là
3
250
25
10 10
CD
ts= = =
Tổng thời gian của VĐV là
( )
2
2
123
70 250
25
5 1, 5
x
x
Ttt t
+−
=++=+ +
Xét hàm
( )
2
2
70 250
( ) 25
5 1, 5
x
x
fx
+−
=++
,
( )
0 250x<<
.
Bài toán trở thành tìm
(0,250)
min ( )
x
fx
∈
Ta có
( )
2
2
1 2(250 )
'( )
5
3 70 250
x
fx
x
−
= −
+−
( )
2
2
'( ) 0 3 70 250 10(250 ) 0fx x x=⇔ + − − −=
( )
2
2
3 70 250 10(250 )xx⇔ + −= −
( )
2
2
91 250 9.70x⇔ −=
0
210
250 ( )
91
210
250 ( )
91
xx
x loai
=−=
⇔
= +
Dựa vào BBT
( ) ( )
0
(0,250)
min ( ) 119,52
x
fx f x m
∈
= ≈
Câu 34. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng
50
m và chiều dài
250
m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả
hai) khi phải thực hiện lộ trình xuất phát từ
A
đến
C
và đua xe đạp tới
D
như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường
x
) thì vận động viên nên nhảy xuống để tiếp tục
Trang 40
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là
5
m/s;
1, 5
m/s và
10
m/s.
A.
109,8
m. B.
105,8
m. C.
106,8
m. D.
107,8
m.
Lời giải
Chọn D
A
x
B
( )
250 xm−
D
250m
C
Gọi
B
là vị trí VĐV kết thúc phần chạy điền kinh và
( )
0 250AB x x= <<
Khi đó ta đó
1
1
5
AB x
t
v
= =
là thời gian đi từ
A
đến
B
Đồng thời quãng đường bơi chính là
22
50 (250 )BC x= +−
Suy ra
( )
2
2
2
50 250
1, 5 1, 5
x
BC
t
+−
= =
là thời gian bơi từ
B
đến
C
Thời gian đua xe đạp là
3
250
25
10 10
CD
ts= = =
Tổng thời gian của VĐV là
( )
2
2
123
50 250
25
5 1, 5
x
x
Ttt t
+−
=++=+ +
Xét hàm
( )
2
2
50 250
( ) 25
5 1, 5
x
x
fx
+−
=++
,
( )
0 250x
<<
Bài toán trở thành tìm
(0,250)
min ( )
x
fx
∈
Ta có
(
)
2
2
1 2(250 )
'( )
5
3 50 250
x
fx
x
−
= −
+−
(
)
2
2
'( ) 0 3 50 250 10(250 ) 0fx x x=⇔ + − − −=
(
)
2
2
3 50 250 10(250 )xx⇔ + −= −
( )
2
2
91 250 9.50x⇔ −=
Trang 41
0
150
250 ( )
91
150
250 ( )
91
xx
x loai
=−=
⇔
= +
Dựa vào BBT
( ) ( )
0
(0,250)
min ( ) 107,8
x
fx f x m
∈
= ≈
Câu 35. Cho một viên gạch men có dạng hình vuông
OABC
như hình vẽ. Sau khi tọa độ hóa, ta có
( )
0;0O
,
(
)
0;1A
,
( )
1;1B
,
( )
1;0C
và hai đường cong lần lượt là đồ thị hàm số
3
yx=
và
3
yx=
. Tính diện tích của phần không được tô đậm trên viên gạch men.
A.
1
3
. B.
5
4
. C.
4
5
. D.
1
2
.
Lời giải
Chọn D
Diện tích hình vuông có cạnh bằng
1
là
2
11S = =
.
Gọi
1
S
là diện tích phần tô đậm.
Ta có
( )
11
14
4
33
3
33
1
00
1
31
dd
0
44 2
x
S xx x x x x x

=−=−= − =


∫∫
.
Vậy diện tích phần không được tô đậm trên viên gạch men bằng
1
11
1
22
SS− =−=
.
Câu 36. Người ta làm một cái lu đựng nước bằng cách cắt bỏ 2 chỏm của một khối cầu có bán kính
5 dm
bằng 2 mặt phẳng vuông góc với đường kính và cách tâm khối cầu
3 dm
. Tính thể tích của chiếc
lu.
y
x
C
A
B
O
Trang 42
A.
(
)
3
41 dm
π
. B.
( )
3
132 dm
π
. C.
( )
3
43 dm
π
. D.
( )
3
100
dm
3
π
.
Lời giải
Chọn B
Đặt hệ trục với tâm
O
là tâm của mặt cầu, đường thẳng đứng là
Ox
, đường ngang là
Oy
.
Ta có phương trình của đường tròn lớn là
22
25
xy+=
.
Thể tích cái lu là thể tích của vật tròn xoay tạo thành khi quay hình giới hạn bởi các đường cong
2
25yx= −
, trục
Ox
, đường thẳng
3, 3xx=−=
quay quanh
Ox
.
(
) ( )
3
3
23
3
3
25 d 25 132 dm
3
3
x
V xx x
ππ π
−

= −= − =

−

∫
.
Câu 37. Một cái trống trường có bán kính các đáy là
30 cm
, thiết diện vuông góc với trục và cách đều
hai đáy có diện tích là
( )
2
1600 cm
π
, chiều dài của trống là
1m
. Biết rằng mặt phẳng chứa trục
cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu?
A.
3
425,2 dm
. B.
3
425,2 mm
. C.
3
425,2 cm
. D.
3
425,2 m
.
Lời giải
Chọn A
3
dm
3
dm
5
dm
y
x
-5
5
-5
-3
3
5
O
Trang 43
Ta có chọn hệ trục như hình vẽ.
Thiết diện vuông góc với trục, cách đều hai đáy là hình tròn có bán kính
r
có diện tích là
(
)
2
1600 cm
π
, nên
2
1600 40cmrr
ππ
= ⇒=
.
Ta có: Parabol nhận
Oy
làm trục đối xứng nên phương trình Parabol có dạng:
2
y ax b= +
.
Parabol có đỉnh
(
)
0; 40I
và qua
( )
50;30
A
.
Thay tọa độ
I
và
A
vào phương trình Parabol:
2
1
40
250
50 30
40
b
a
ab
b
=
= −
⇔

+=
=
Nên Parabol có phương trình
2
1
40
250
yx=−+
Thể tích của trống là
2
50
2
50
1
40
250
V x dx
π
−

=−+


∫
3
406000
. cm
3
π
=
3
425,2dm
≈
Câu 38. Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn
28cm
, trục nhỏ
25cm
. Biết
cứ
3
1000cm
dưa hấu sẽ làm được cốc sinh tố giá
20000
đồng. Hỏi từ quả dưa hấu trên có thể
thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể.
A.
180000
đồng. B.
183000
đồng. C.
185000
đồng. D.
190000
đồng.
Lời giải
Chọn B
Oxy
Trang 44
Đường elip có trục lớn
28cm
, trục nhỏ
25cm
có phương trình
22
2
2
1
14
25
2
xy
+=



2
2
2
2
25
1
2 14
x
y


⇔= −




2
2
25
1
2 14
x
y⇔=± −
.
Do đó thể tích quả dưa là
2
14
2
2
14
25
1d
2 14
x
Vx
π
−

= −



∫
2
14
2
2
14
25
1d
2 14
x
x
π
−


= −




∫
14
2
3
2
14
25
2 3.14
x
x
π
−


= ⋅−




2
25 56
23
π

= ⋅


3
8750
cm
3
π
=
.
Do đó tiền bán nước thu được là
8750 .20000
183259
3.1000
π
≈
đồng.
Câu 39. Một bình hoa dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm
số
sin 2yx=−+
và trục
Ox
(tham khảo hình vẽ bên dưới). Biết đáy bình hoa là hình tròn có
bán kính bằng
2 dm
, miệng bình hoa là đường tròn bán kính bằng
1.5 dm
. Bỏ qua độ dày của
bình hoa, Thể tích của bình hoa gần với giá trị nào trong các giá trị sau đây?
A.
100
3
dm
. B.
104
3
dm
. C.
102
3
dm
. D.
103
3
dm
.
Lời giải
Chọn D
Giả sử thiết diện qua trục của bình hoa miêu tả như hình vẽ bên dưới. Chọn hệ trục tọa độ
Oxy
thỏa mãn gốc tọa độ
O
trùng với tâm đáy bình hoa, trục
Ox
trùng với trục của bình hoa.
Bán kính hình tròn đáy bình hoa bằng
2
A
y =
nên
sin 2 2 sin 0 0
A AA
x xx− +=⇒ =⇒ =
.
Bán kính đường tròn miệng bình hoa bằng
( )
1, 5 2 3
BB
yx
ππ
= <<
, tức là:
Trang 45
(
)
(
)
17
sin 2 1,5 sin sin 2
6 66
B B BB
x x xx
ππ π
π π ππ

− += ⇒ − = − ⇒ −=− + ⇒ =


.
Khi đó thể tích bình hoa giới hạn bởi các đường
17
sin 2; 0; 0;
6
y xyxx
π
=− +===
được xác
định theo công thức
(
)
(
)
17 17
66
2
2
00
sin 2 d 4 4sin sin d
V x x x xx
ππ
ππ
= −+ = − +
∫∫
17 17
66
00
1 cos 2 9 cos 2
4 4sin d 4sin d
2 22
xx
x x xx
ππ
ππ
−

= −+ = −−


∫∫
17
2
6
0
9 sin 2 51 32 15 3
4cos 103,07
2 4 48
x
xx
π
π
ππ
+

=+− =− ≈


( )
3
dm
.
Câu 40. Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La
Mã, tòa nhà Ellipse Tower Hà Nội, sử dụng trong thiết kế logo quảng cáo, thiết bị nội thất. Xét
một Lavabo (bồn rửa) làm bằng sứ đặc hình dạng là một nửa khối elip tròn xoay có thông số kĩ
thuật mặt trên của Lavabo là: dài
×
rộng:
660 380 mm
×
(tham khảo hình vẽ bên dưới), Lavabo có
độ dày đều là
20 mm
. Thể tích chứa nước của Lavabo gần với giá trị nào trong các giá trị sau:
A.
3
18,66 dm
. B.
3
18,76 dm
. C.
3
18,86 dm
. D.
3
18,96 dm
.
Lời giải
Chọn B
Giả sử mặt trên của Lavabo được biểu diễn như hình vẽ bên dưới. Gọi hệ trục tọa độ
Oxy
như
hình vẽ. Gọi
( )
E
là elip nhỏ bên trong.
Trang 46
Độ dài trục lớn của
( )
E
là
31
2 660 40 620mm dm
5
a = −= =
31
dm
10
a⇒=
.
Độ dài trục bé của
( )
E
là
17
2 380 40 340mm dm
5
b = −= =
17
dm
10
b⇒=
.
Vậy phương trình của
( )
E
là:
22
22
1
31 17
10 10
xy
+=
 
 
 
2
2
289 100
1
100 961
x
y

⇒= −


.
Thể tích khối tròn xoay khi quay miền giới hạn bởi
( )
E
, trục
Ox
và
31
10
x = −
,
31
10
x =
(Phần
gạch chéo trong hình) quanh trục
Ox
là:
( )
31
2
10
3
31
10
289 100 8959
1 d dm
100 961 750
x
Vx
π
π
−

= −=


∫
Vậy thể tích chứa nước của Lavabo là
3
18,76 dm
2
V
≈
.
Câu 41. Một vật chuyển động chậm dần đều với vận tốc
( ) 160 10 (m/s)= −vt t
. Quãng đường mà vật
chuyển động từ thời điểm
( )
0s=t
đến thời điểm mà vật dừng lại là
A.
1028 m
. B.
1280 m
. C.
1308 m
. D.
1380 m
.
Lời giải
Chọn A
Gọi
0
t
là thời điểm vật dừng lại, khi đó
0
() 0vt =
0
160 10 0⇔− =t
0
16⇔=t
.
Vậy quãng đường vật chuyển động đến lúc dừng lại là
16
0
(160 10 )d 1280 (m)=−=
∫
S tt
.
Trang 47
Câu 42. Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức
( ) 3 2(m/s)= +vt t
. Biết tại thời điểm
(
)
2s
=
t
thì vật đi được quãng đường là
( )
10 m
. Hỏi tại thời
điểm
( )
30 s=t
thì vật đi được quãng đường là bao nhiêu?
A. 1140 m. B. 300 m. C. 240 m. D. 1410 m.
Lời giải
Chọn D
Quãng đường của vật theo thời gian là
2
3
( ) (3 2)d 2
2
= + = ++
∫
St t t t t C
.
Vì
(2) 10 0
= ⇒=SC
. Khi đó
2
3
() 2
2
= +St t t
.
Tại thời điểm
(
)
30 s=t
thì
( )
(30) 1410 m=S
.
Câu 43. Một vật đang chuyển động với vận tốc
( )
25 m/s
v =
thì thay đổi vận tốc với gia tốc được tính
theo thời gian
t
là
( )
( )
2
2 6 m/sat t= −
. Tính quãng đường vật đi được kể từ thời điểm thay đổi
gia tốc đến lúc vật đạt vận tốc bé nhất.
A.
107
m
5
. B.
144 m
. C.
28 m
. D.
57 m
.
Lời giải
Chọn D
Vận tốc của vật khi thay đổi là
(
)
( )
2
2 6d 6vt t t t t C= − =−+
∫
.
Tại thời điểm
0t =
(khi vật bắt đầu thay đổi vận tốc) có
0
25v =
25C⇒=
.
Suy ra
( )
2
6 25vt t t=−+
.
Ta có
( ) ( )
2
3 16 16vt t=− +≥
, suy ra vận tốc của vật đạt bé nhất khi
3t
=
.
Quãng đường vật đi được trong khoảng thời gian đó là
( )
( )
33
2
00
d 6 25 d= = −+
∫∫
S vt t t t t
( )
3
32
0
1
3 25 57 m
3

= −+ =


tt t
.
Câu 44. Một mô tô chạy với vận tốc
(
)
0
m/s
v
thì gặp chướng ngại vật nên người lái xe đạp phanh. Từ
thời điểm đó ôtô chuyển động chậm dần với gia tốc
(
)
2
8 m/sat= −
trong đó
t
là thời gian tính
bằng giây. Biết từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được
( )
12 m
. Tính
0
v
?
Trang 48
A.
18 m/s
. B.
3
86 m/s
. C.
3
1269 m/s
. D.
3
1296 m/s
.
Lời giải
Chọn D
( )
22
8 / 8d 4a tm s v tt t C=− ⇒=− =− +
∫
.
Tại thời điểm
0t =
thì vận tốc của vật là
( )
0
m/s
v
nên ta có
0
vC=
.
Vậy
2
0
4v tv=−+
.
Tại thời điểm
0
t
vận tốc của vật là
0
nên ta có
22
00 0 0
04 4tv tv=− +⇔ =
.
Ta có:
( )
0
2
0
0
4 d 12
t
tvt−+ =
∫
3
0
00
4
12
3
t
vt⇔− + =
3
3
0
0
4
4 12
3
t
t⇔− + =
3
0
36
2
t⇔=
.
( )
2
3
3
0
36
4. 1296 m/s
2

⇒= =


v
.
Câu 45. Đầu tháng
5
năm
2019
, ông An đầu tư vào chăn nuôi tằm với số tiền vốn ban đầu là
200
(triệu
đồng). Biết rằng trong quá trình chăn nuôi gặp thuận lợi nên số tiền đầu tư của ông liên tục tăng
theo tốc độ được mô tả bằng công thức
( )
2
12000
()
5
ft
t
′
=
+
, với
t
là thời gian đầu tư tính bằng tháng
(thời điểm
0=t
ứng với đầu tháng
5
năm
2019
). Hỏi số tiền mà ông An thu về tính đến đầu
tháng
5
năm
2023
gần với số nào sau đây?
A.
2737
(triệu đồng). B.
2307
(triệu đồng).
C.
2370
(triệu đồng). D.
2703
(triệu đồng).
Lời giải
Chọn C
Tốc độ thay đổi vốn đầu tư của ông An vào tháng thứ
t
là
( )
2
12000
()
5
ft
t
′
=
+
nên nguyên hàm của
hàm
(t)
′
f
là hàm số
(t)f
mô tả số tiền của ôn An có được tính đến tháng thứ
t
.
Ta có
( )
2
12000 12000
() ()
5
5
dd
−
′
= = = +
+
+
∫∫
ft f t t t C
t
t
.
Số tiền của ông An tại thời điểm
0t =
là
12000
(0) 200 2600
05
f CC
−
= += ⇒=
+
.
Vậy số tiền mà ông An thu về tính đến đầu tháng 5 năm 2023 (ứng với
48t =
tháng) là
Trang 49
12000
(48) 2600 2373,585
48 5
f
−
= +=
+
(triệu đồng).
Câu 46. Giả sử rằng sau
t
năm, vốn đầu tư của một doanh nghiệp phát sinh lợi nhuận với tốc độ
(
)
2
126
′
= +
Pt t
(triệu đồng/năm). Hỏi sau
10
năm đầu tiên thì doanh nghiệp thu được lợi nhuận
là bao nhiêu (đơn vị triệu đồng).
A.
5020
. B.
1235
. C.
3257
3
. D.
4780
3
.
Lời giải
Chọn D
Sau 10 năm đầu tiên thì doanh nghiệp thu được lợi nhuận là
10
2
0
4780
(126 )d
3
= +=
∫
T tt
(triệu đồng).
Câu 49: Một cái cổng hình parabol như hình vẽ. Chiều cao
4 m=GH
, chiều rộng
4 m=AB
,
0, 9 mAC BD= =
. Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật
CDEF
tô đậm có
giá là
1200000
đồng/m
2
, còn các phần để trắng làm xiên hoa có giá là
900000
đồng/m
2
.
Hỏi tổng chi phí để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
A.
11445000
(đồng). B.
7368000
(đồng). C.
4077000
(đồng). D.
11370000
(đồng)
Lời giải
Chọn A
Gắn hệ trục tọa độ Oxy sao cho
AB
trùng
Ox
,
A
trùng
O
khi đó parabol có đỉnh
( )
2; 4G
và
đi qua gốc tọa độ.
Trang 50
Giả sử phương trình của parabol có dạng
(
)
2
0
y ax bx c a
= ++ ≠
.
Vì parabol có đỉnh là
( )
2; 4G
và đi qua điểm
( )
0; 0O
nên ta có
2
a
0
2
2
.2 .2 4
c
b
a bc
=
−
=
+ +=
1
4
0
a
b
c
= −
⇔=
=
.
Suy ra phương trình parabol là
2
() 4y fx x x= = +−
.
Diện tích của cả cổng là
4
4
3
2 22
0
0
32
( 4 )d 2 (m )
33
x
S x xx x

=−+ =− + =


∫
.
Mặt khác chiều cao
( )
0,9 2,79(m)CF DE f
= = =
;
( )
4 2.0,9 2,2 mCD
=−=
.
Diện tích hai cánh cổng là
( )
2
. 6,138 6,14 m
CDEF
S CD CF= = ≈
.
Diện tích phần xiên hoa là
2
32 6793
6,14 4,53(m )
3 1500
xh CDEF
S SS=− =−= ≈
.
Số tiền làm hai cánh cổng là
(
)
1
6,14.1200000 7368000 đT
= =
.
và tiền làm phần xiên hoa là
(
)
2
4,53.900000 4077000
đT
= =
.
Vậy tổng chi phí là
11445000
đồng.
Câu 50: Để tăng thêm thu nhập, ông Bình chăn nuôi thêm 2 con bò. Do diện tích đất của nhà ông hẹp nên
ông xây chuồng bò như hình vẽ bên dưới và chia thành 2 phần bằng nhau để nhốt 2 con bò. Biết
ABCD
là hình vuông cạnh
4m
và
I
là đỉnh của một Parabol có trục đối xứng là trung trực của
BC
và parabol đi qua hai điểm
A
,
D
. Tiền xây chuồng bò hết
350000
đồng/
2
1m
. Biết
I
cách
BC
một khoảng
5m
, hãy tính số tiền chi phí ông Bình bỏ ra để xây dựng chuồng bò (làm tròn
đến hàng nghìn)?
Trang 51
A.
6.333.000
đồng. B.
7.533.000
đồng. C.
6.533.000
đồng. D.
7.333.000
đồng.
Lời giải
Chọn C
Xét hệ trục tọa độ như hình vẽ sau
Khi đó parabol có đỉnh
( )
0; 5I −
và đi qua hai điểm
(
)
2; 2A −
,
(
)
2; 2D
−−
nên có phương trình
2
1
5
4
yx= −
.
Diện tích chuồng bò là
( )
2
22
2
1 56
5d m
43
S xx
−

=−+ =


∫
.
Vậy tổng số tiền ông Bình xây chuồng bò là
56 19600000
350000 6533000
33
⋅= ≈
đồng.
Câu 49. Người ta sản xuất một loại đèn trang trí ngoài trời (Trụ sở, quảng trường, công viên, sân vườn…)
gồm có hai phần: Phần bóng đèn có dạng mặt cầu bán kính
dmR
, làm bằng thủy tinh trong suốt;
Phần đế bóng đèn làm bằng nhựa để cách điện, có dạng một phần của khối cầu bán kính
dmr
và thỏa mãn đường kính là một dây cung của hình tròn lớn bóng đèn. Một công viên muốn tạo
điểm nhấn ánh sáng, đặt loại bóng có kích thước
5 dmR =
,
3 dmr =
. Tính thể tích
V
phần
nhựa để làm đế một bóng đèn theo đơn đặt hàng (Bỏ qua ống luồn dây điện và bulông ốc trong
phần đế).
I
A
D
C
B
y
x
-5
-2
2
I
A
D
C
B
O
Trang 52
A.
3
36 dmV
π
=
. B.
3
68
dm
3
V
π
=
. C.
3
14
dm
3
V
π
=
. D.
3
40
dm
3
V
π
=
.
Lời giải
Chọn D
Gọi
,IR
lần lượt là tâm và bán kính hình cầu phần bóng đèn và
,Kr
lần lượt là tâm và bán
kính của khối cầu để làm đế bóng đèn.
Ta có
5 dmR IA
= =
,
3 dmr KA= =
và đường kính
AB
vuông góc với đường thẳng nối hai
tâm
I
và
K
.
Chọn hệ trục tọa độ
Oxy
như hình vẽ: Gốc tọa độ
OK≡
, trục
Oy AB≡
.
Xét tam giác vuông
OIA
ta có:
2 2 22
25 9 4IK IA KA R r= − = − = −=
( )
4; 0I⇒−
và
541KD R IK= − =−=
.
Phương trình đường tròn tâm
( )
0; 0K
bán kính
3r =
là
( )
22
1
:9Cx y+=
.
Phương trình đường tròn tâm
( )
4; 0I −
bán kính
5R =
là
( ) ( )
2
2
2
: 4 25Cx y+ +=
.
Gọi
1
V
là phần thể tích khi quay hình phẳng giới hạn bởi
( )
1
C
, trục
Ox
,
0x =
và
3x =
, ta có:
( )
( )
3
3
3
23
1
0
0
9 d 9 18 dm
3
x
V xx x
ππ π

=− =−=


∫
.
Gọi
2
V
là phần thể tích khi quay hình phẳng giới hạn bởi
( )
2
C
, trục
Ox
,
0x =
và
1x =
, ta có:
Trang 53
( )
( )
( )
( )
1
3
1
2
3
2
0
0
4
14
25 4 d 25 dm
33
x
V xx x
π
ππ

+
= −+ = − =



∫
.
Do đó
12
VVV
= −
14
18
3
π
π
= −
( )
3
40
dm
3
π
=
.
Câu 50. Một bồn nước Inox SONHA
®
ngang có hai đầu bồn là hình phẳng elip. Thể tích tối đa khi đóng
nắp bồn là
1
3000V =
lít. Bồn có chiều dài bằng
2, 0 ml =
và gấp
2
lần chiều cao của bồn. Để
nước bơm tự động vào bồn, người ta lắp một phao điện sao cho mực nước trong bồn cao
0, 75 mh =
so với điểm thấp nhất trong đáy bồn thì phao đóng không cho nước chảy vào bồn.
Tính thể tích nước trong bồn khi phao đóng (bỏ qua độ dày của bồn nước và kết quả làm tròn
đến phần trăm).
A.
3
2.41 mV =
. B.
3
2.43 mV =
. C.
3
2.40 m
V =
. D.
3
2.44 mV =
.
Lời giải
Chọn A
Ta có
3
3000 lít 3 m=
.
Xét thiết diện ngang của bồn nước là hình elip
(
)
E
có độ dài trục lớn là
2a
, độ dài trục nhỏ là
2b
và chọn hệ trục tọa độ như hình vẽ
Độ dài
1mBB
′
=
là chiều cao của bồn nước, suy ra độ dài trục nhỏ của
( )
E
là
( )
1
21 m
2
bb=⇒=
.
Ta có:
1
...V abl
π
=
1
33
(m)
. . .0,5.2
V
a
bl
ππ π
⇒= = =
.
Trang 54
Vậy phương trình của Elip là:
( )
22 2
2 22 22
22
11 1
11 9 9
91 9
4 36 6
4
xy x
y xy x
ππ
ππ


+ =⇒ = − = − ⇒=± −



.
Khi phao điện đóng, mực nước trong bồn là
MN
1
0,5 0, 25 0, 25
4
OK OB BK⇒=−=− = =
.
Vì
MN
song song với trục
Ox
nên ta có phương trình
MN
là
1
4
y =
.
Hoành độ điểm
,
MN
thỏa mãn phương trình :
( )
2
22 2
2
1 1 27
9
4 36 4
xx
π
π

= − ⇔=


33 33 33
;
2 22
MN
x xx
π ππ
⇒=± ⇒ =− =
.
Phần diện tích
2
S
giới hạn bởi
( )
E
đi qua điểm
B
và đường thẳng
MN
là:
33
2
22
2
33
2
11
9d
64
S xx
π
π
π
−

= −−


∫
33
33
2
2
2
2
33
33
2
2
31
d
64
xx x
π
π
π
π
π
π
−
−

= −−


∫
33
.
64
I
π
π
= −
.
Xét:
33
2
2
2
33
2
3
dI xx
π
π
π
−

= −


∫
. Đặt
33
sin d cos d
x t x tt
ππ
= ⇒=
.
Đổi cận: Khi
33
2
x
π
= −
thì
3
sin
23
tt
π
=− ⇒=−
;
Khi
33
2
x
π
=
thì
3
sin
23
tt
π
= ⇒=
.
Khi đó:
( )
33
3
2
22
3
33
33 9 9 1
. cos d 1 cos 2 d sin 2
2 22
I tt t t x t
ππ
π
π
ππ
ππ π π
−
−−

= =+=+


∫∫
22 2
9 3 9 3 3 93
2 34 2 34 4
ππ
π π ππ

= + − −− =+



.
Vậy
2
2
3 93 33 1 33
6 4 4 28
S
π
ππ π π

= + −=−



.
Thể tích phần không gian không chứa nước khi phao đóng là:
22
33
.1
4
V Sl
π
= = −
.
Vậy thể tích nước cần tìm là:
( )
3
12
33
3 1 2.41 m
4
VVV
π

=−=−− ≈


.
| 1/54
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TOÁN THỰC TẾ LIÊN QUAN ĐẠO HÀM - TÍCH PHÂN
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C, cạnh bên SA vuông góc với
mặt phẳng đáy ( ABC). Biết SC =1, tìm thể tích lớn nhất của khối chóp S.ABC. A. 3 . B. 2 . C. 2 3 . D. 3 . 12 12 27 27
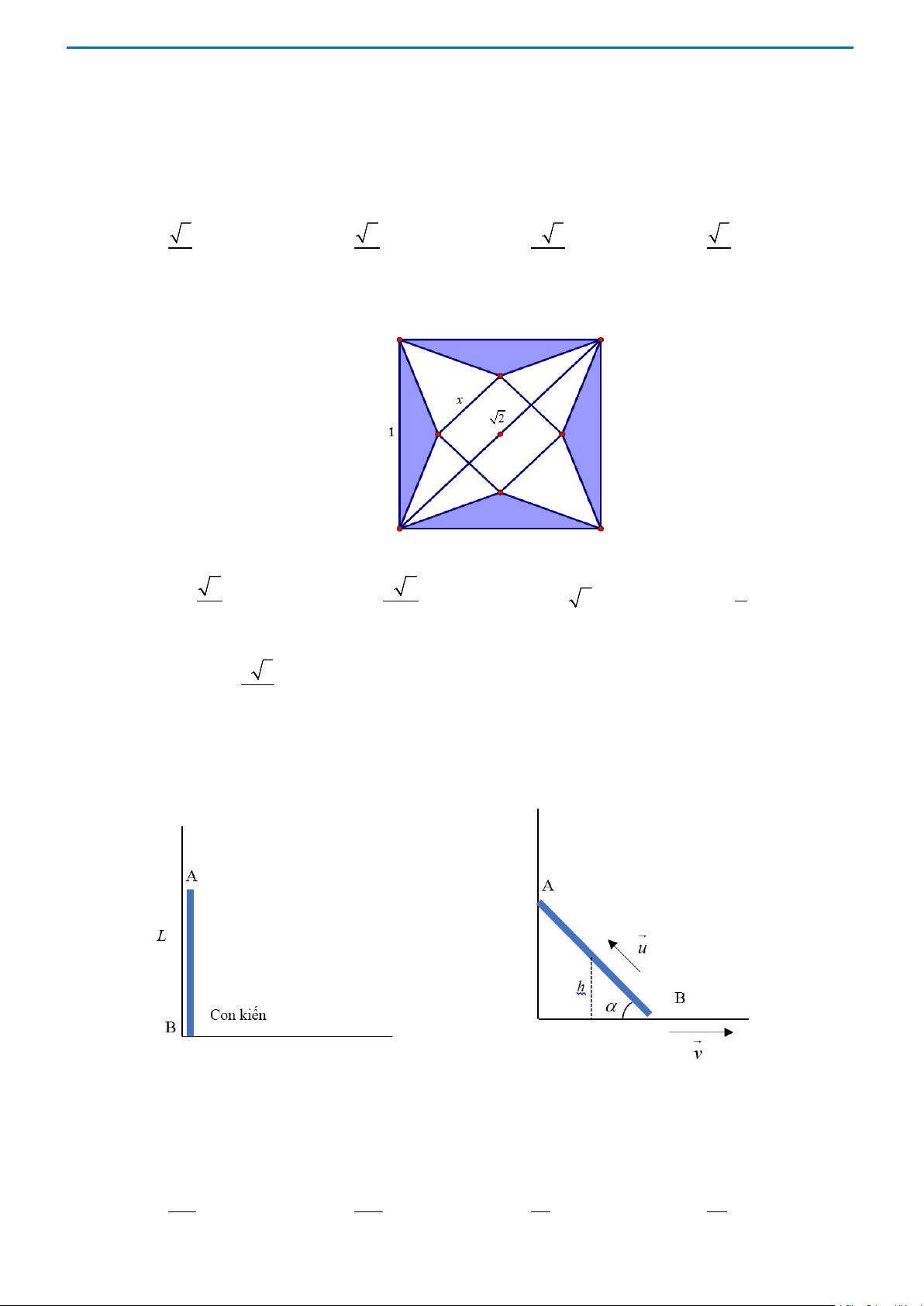
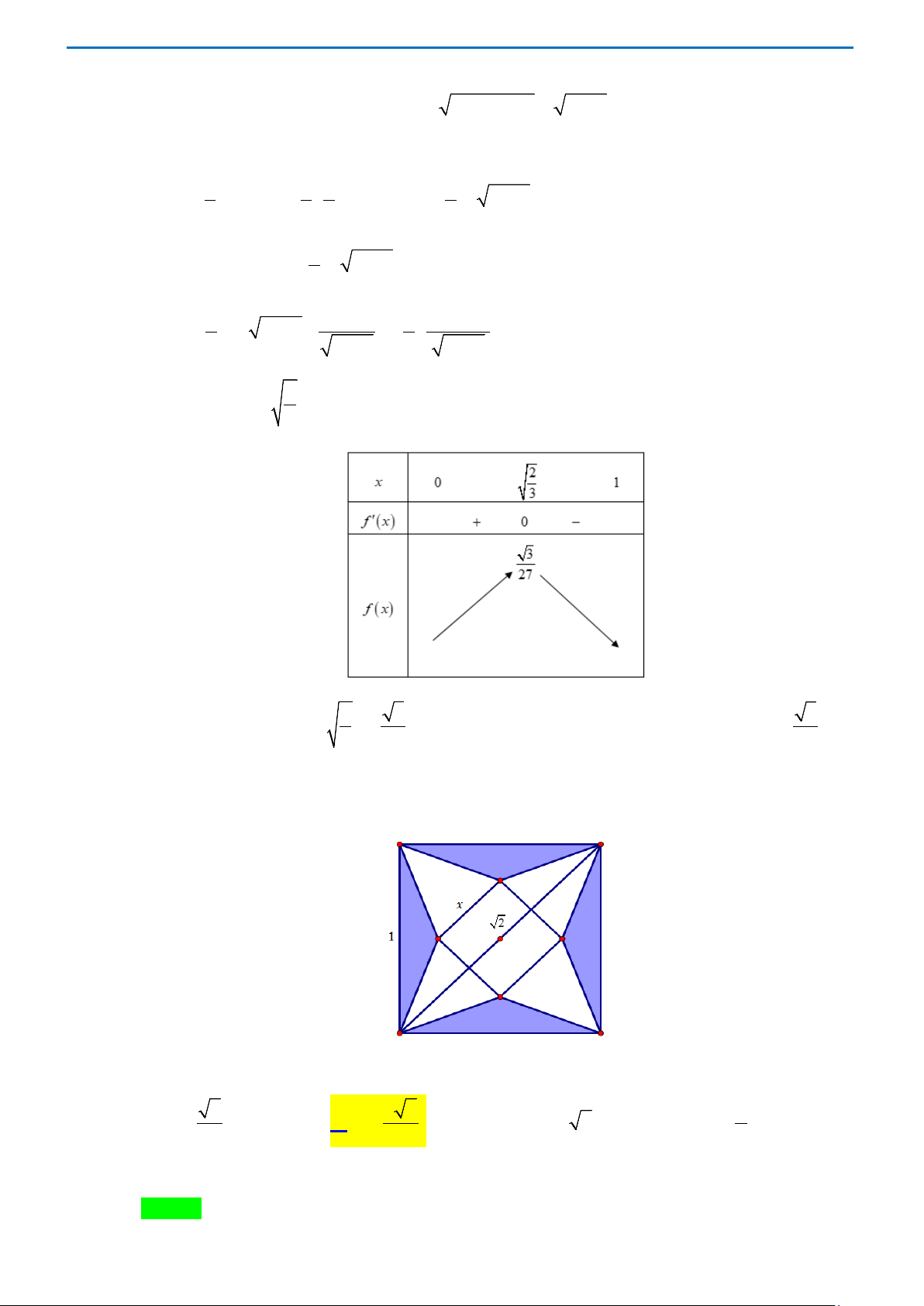
Câu 2. Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình chóp tứ giác đều sao cho
bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp (hình vẽ).
Để thể tích khối chóp lớn nhất thì cạnh đáy x của hình chóp bằng: A. 2 x = . B. 2 2 x = . C. x = 2 2. D. 2 x = . 5 5 5
Câu 3. Tìm chiều dài L ngắn nhất của cái thang để có thể tựa vào tường và mặt đất, ngang qua cột đỡ
có chiều cao 3 3 m và cách tường 0,5 m kể từ gốc của cột đỡ. 2 A. 2m . B. 4m . C. 3m . D. 5m .
Câu 4. Một con kiến đậu ở đầu B của một thanh cứng mảnh AB có chiều dài L đang dựng cạnh một
bức tường thẳng đứng (hình vẽ).
Vào thời điểm mà đầu B bắt đầu chuyển động sang phải theo sàn ngang với vận tốc không đổi
v thì con kiến bắt đầu bò dọc theo thanh với vận tốc không đổi u đối với thanh. Trong quá
trình bò trên thanh, con kiến đạt được độ cao cực đại h là bao nhiêu đối với sàn? Cho đầu A max
của thanh luôn tỳ lên tường thẳng đứng. 2 2 2 2 A. 3L . B. 2L . C. L . D. L . v v 3v 2v Trang 1
Câu 5. Một hộp không nắp được làm từ một mảnh các tông theo mẫu. Hộp có đáy là một hình vuông
cạnh x(cm) , chiều cao h(cm) và có thể tích là ( 3 500 cm ).
Tìm x sao cho diện tích mảnh các tông đó nhỏ nhất? A. 5cm . B. 100cm . C. 10cm . D. 20cm .
Câu 6. Một nhà máy cần sản xuất một bể nước bằng tôn có dạng hình hộp đứng đáy là hình chữ nhật có
chiều dài gấp 2 lần chiều rộng không nắp, có thể tích 4 3
m . Hãy tính độ dài chiều rộng của đáy 3
hình hộp sao cho tốn ít vật liệu nhất. A. 2 m. B. 3 m. C. 2 m . D. 1 m. 3
Câu 7. Cho hai vị trí A , B cách nhau 615 m , cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách
từ A và từ B đến bờ sông lần lượt là 118 m và 487 m . Một người đi từ A đến bờ sông để lấy nước mang về B .
Đoạn đường ngắn nhất mà người đó có thể đi là A. 596,5m . B. 671,4m . C. 779,8m . D. 741,2m .
Câu 8. Trong không gian với hệ trục toạ độ Oxyz cho đường thẳng ∆ có phương trình tham số là: x = 2  y = t
− và hai điểm A(1;− 2;− )
1 , B(4;4;5) . Giả sử M (a;b;c) thuộc ∆ sao cho MA+ MBz =1+  t
nhỏ nhất, khi đó tích abc là A. 0 . B. 2 . C. 1. D. 2 . 9 Trang 2
Câu 9 . Một trang chữ của cuốn sách giáo khoa cần diện tích 2
384cm . Lề trên và dưới là 3cm , lề trái
và phải là 2cm . Kích thước tối ưu của trang giấy là:
A. Dài 24cm ; rộng 16cm .
B. Dài 24cm ; rộng 17cm .
C. Dài 25cm ; rộng 15,36cm .
D. Dài 25,6cm ; rộng 15cm .
Câu 10. Có một cơ sở in sách xác định rằng: Diện tích của toàn bộ trang sách là 2
S (cm ). Do yêu cầu kỹ 0
thuật nên dòng đầu và dòng cuối đều phải cách mép (trên và dưới) trang sách là a (cm). Lề bên
trái và bên phải cũng phải cách mép trái và mép phải của trang sách là b(cm) (b < a) . Các kích
thước của trang sách là bao nhiêu để cho diện tích phần in các chữ có giá trị lớn nhất. Khi đó hãy
tính tỉ lệ của chiều rộng và chiều dài trang sách. − + A. b a . B. 2b . C. b . D. b a . a 2a −1 a a
Câu 11. Một anh kỹ sư muốn tạo ra 1 cái lu hình trụ có diện tích bề mặt (không tính hai mặt đáy) là lớn
nhất. Bề mặt lu được quấn bởi mảnh tôn hình chữ nhật có chu vi 120 cm. Gọi chiều dài của hình
chữ nhật là a , chiều rộng của hình chữ nhật là b . Tính 2
P = a + 3b . A. 990. B. 1660. C. 2530. D. 1108.
Câu 12. Bác nông dân có 200m rào để ngăn đàn gà nuôi dạng hình chữ nhật. Để diện tích nuôi gà là lớn
nhất thì chiều dài hình chữ nhật là a (m) và chiều rộng là b (m). Khi đó 2 2
a + ab + b có giá trị bằng A. 7525 m. B. 7600 m. C. 7500 m. D. 7900 m.
Câu 13. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm
tổng x + y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. A 2 cm E B x cm H 3 cm F D C G y cm A. 7cm . B. 5cm . C. 7 2 cm . D. 4 2 cm . 2
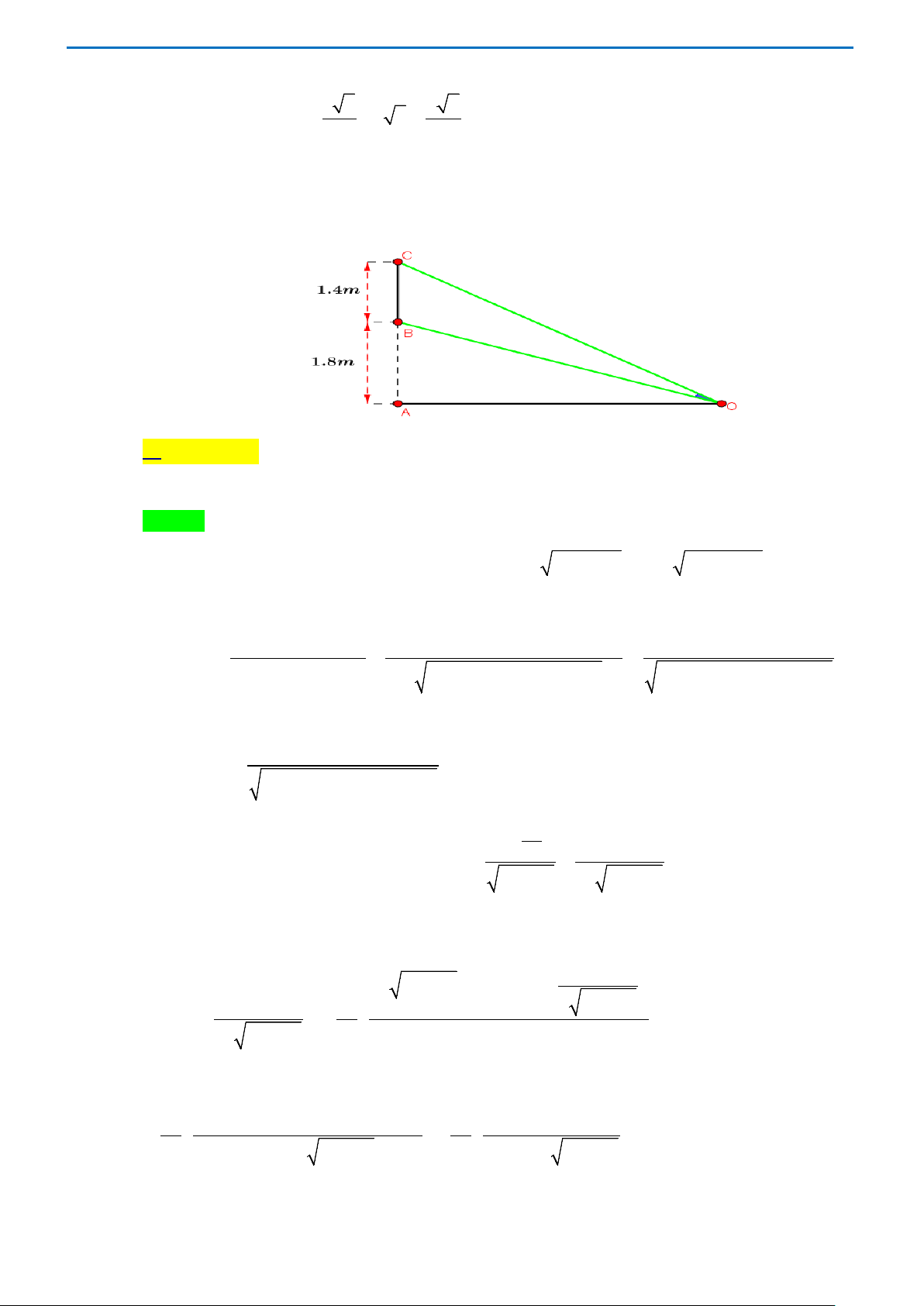
Câu 14. Một màn ảnh hình chữ nhật cao 1,4m và đặt ở độ cao 1,8m so với tầm mắt (tính từ đầu mép
dưới của màn hình như hình vẽ). Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn
nhất. Tính khoảng cách từ vị trí đó đến màn ảnh? Biết rằng góc  BOC nhọn. Trang 3 A. AO = 2,4m . B. AO = 2m . C. AO = 2,6m . D. AO = 3m .
Câu 15. Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính 10 cm , biết một
cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn. A. 2 80 cm . B. 2 100 cm . C. 2 160 cm D. 2 200 cm .
Câu 16 . Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm , cần xả thành một chiếc xà có tiết diện
ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng
x của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất. A. 3 34 17 2 x − = (cm) B. 3 34 19 2 x − = (cm) 2 2 C. 5 34 15 2 x − = (cm) D. 5 34 13 2 x − = (cm) 2 2
Câu 17. Một ô tô đang chạy với vận tốc 15(m/s) thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc v(t) = 5
− t +15(m/s) trong đó t là khoảng thời gian tính bằng
giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét ? A. 22,5m . B. 45m . C. 15m . D. 90m.
Câu 18. Một vật chuyển động với gia tốc 2 2
a(t) = 3t + t (m/s ). Vận tốc ban đầu của vật là 2(m/s). Hỏi
vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó được 2s. A. 8m/s . B. 12m/s . C. 16m/s . D. 10m/s .
Câu 19. Cho mạch điện xoay chiều RLC mắc nối tiếp có R thay đổi. Biết điện trở cuộn cảm Z = Ω L 80 ( )
, điện trở của tụ điện là Z =
Ω và hiệu điện thế hai đầu mạch là u = U cos100πt V . Để 0 ( ) C 200 ( )
công suất tiêu thụ của mạch cực đại thì giá trị của R bằng Trang 4 A. 120 (Ω). B. 50 (Ω). C. 100 (Ω). D. 200 (Ω) .
Câu 20. Cho mạch điện xoay chiều RLC mắc nối tiếp có R thay đổi. Biết điện trở cuộn cảm Z =
Ω , điện trở của tụ điện là Z =
Ω và hiệu điện thế hai đầu mạch là C 40( ) L 100 ( )
u =120 2 cos100πt (V ) . Điện trở R phải có giá trị là bao nhiêu để công suất tiêu thụ của mạch
đạt cực đại và giá tri cực đại của công suất là bao nhiêu?
A. R = 60 (Ω), P =120 W
R =120 Ω , P = 60 W max ( ). B. ( ) max ( ).
C. R = 40 (Ω), P =180 W
R =120 Ω , P =180 W max ( ). D. ( ) max ( ).
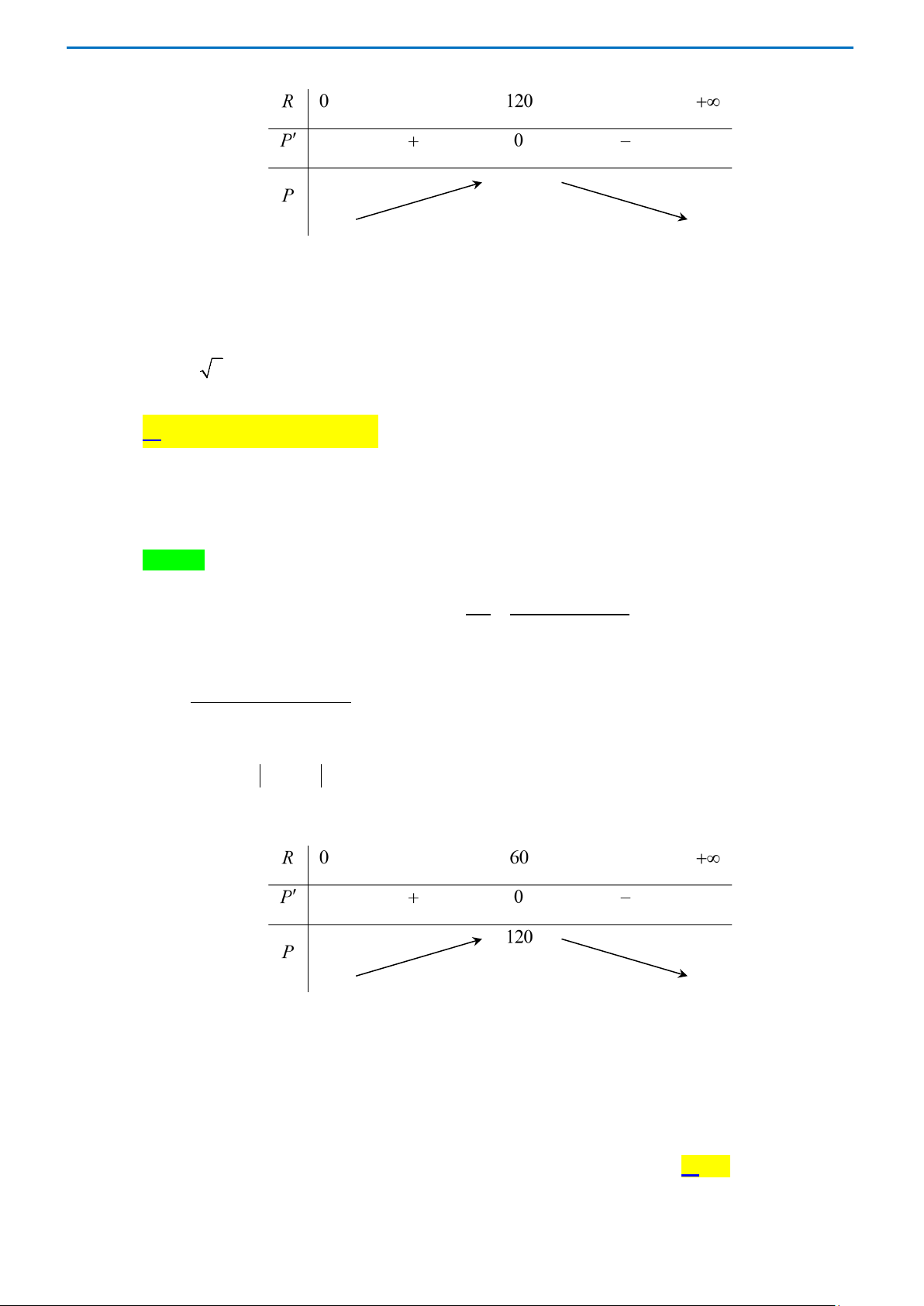
Câu 21: Thể tích V của 1kg nước ở nhiệt độ t (t nằm giữa 0°C đến 30°C) được cho bởi công thức 2 3 V = − t + t − t ( 3 999,87 0,06426 0,0085043
0,0000679 cm ) . Nhiệt độ t của nước gần nhất với
giá trị nào dưới đây thì khối lượng riêng của nước là lớn nhất? A. 0°. B. 4 − ° . C. 30° . D. 4°. 4  
Câu 22: Thể tích nước của một bể bơi sau t phút bơm được tính theo công thức ( ) 1 3 = 30 t V t t − 100 4   
(0 ≤ t ≤ 90) . Tốc độ bơm nước tại thời điểm t được tính bởi v(t) =V′(t) . Trong các khẳng định
sau, khẳng định nào đúng.
A. Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
B. Tốc độ bơm luôn giảm.
C. Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
D. Cả A, B, C đều sai.
Câu 23. Công ty XDPL muốn làm một đường ống dẫn khí từ một địa điểm A trên bờ biển đến một điểm
B trên một hòn đảo. Khoảng cách ngắn nhất từ điểm B đến bờ biển là 6km . Giá để xây lắp mỗi
km đường ống trên bờ là 50.000 USD , còn xây lắp dưới nước là 130.000 USD . B′ là điểm trên
bờ biển sao cho BB′ vuông góc với bờ biển. Khoảng cách từ A đến B′ là 9km . đảo B biển 6km B' 9km bờ biển A
Hỏi vị trí điểm M trên bờ biển cách A bao xa để chi phí xây lắp đường ống từ A qua M rồi
đến B là ít tốn kém nhất? A. 9 km . B. 6 km. C. 0 km. D. 6.5 km .
Câu 24. Một điểm C trên hòn đảo có khoảng cách ngắn nhất đến bờ biển là 60km , B là điểm trên bờ
biển sao cho CB vuông góc với bờ biển . Khoảng cách từ A trên bờ biển đến B là 100km . Để
tham dự buổi họp nhóm Strong Team Toán VD – VCD ngày 28/6/2019 , thầy Quý phải tính toán
vị trí diễn ra cuộc họp tại địa điểm G trên đoạn AB để tổng chi phí đi lại của cả hai nhóm các
thầy cô là ít nhất. Biết nhóm của thầy Quý đi từ C theo đường biển chi phí đi là 500 nghìn mỗi Trang 5
km, nhóm cô Thêm đi từ vị trí A đi trên đất liền mỗi km chi phí là 300 nghìn. Hỏi thầy tìm được
vị trí điểm G cách B bao xa? A. 40km . B. 60km . C. 55km . D. 45km .
Câu 25. Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy 4
A trong một giờ. Chi phí
để bảo trì, vận hành một máy trong mỗi lần in là 50000 đồng. Chi phí in ấn của n máy chạy
trong một giờ là 20(3n + 5) nghìn đồng. Hỏi nếu in 50000 bản in khổ giấy 4
A thì phải sử dụng
bao nhiêu máy để thu được nhiều lãi nhất? A. 4 máy. B. 7 máy. C. 6 máy. D. 5 máy.
Câu 26. Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nhiên liệu
làm vỏ lon là thấp nhất, tức là diện tích toàn phần của hình trụ nhỏ nhất. Muốn thể tích của khối
trụ đó bằng V và diện tích toàn phần của hình trụ nhỏ nhất thì nhà thiết kế phải thiết kế hình trụ
có bán kính bằng bao nhiêu? A. V . B. V V 3 . C. V . D. 3 . 2π 2π π π
Câu 27. Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định
được số lượng vi khuẩn tăng theo thời gian bởi qui luật ( ) 100 =1000 t N t + (con vi khuẩn), 2 100 + t
trong đó t là thời gian (đơn vị giây). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào,
số lượng vi khuẩn tăng lên lớn nhất là bao nhiêu? A. 0 . B. 1. C. 10 − . D. 10.
Câu 28. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu trên mỗi đơn vị diện tích
của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng Q(n) = 480 − 20n (gam).
Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất? A. 12. B. 14. C. 10. D. 18.
Câu 29. Đốt cháy các hidrocacbon của dãy đồng đẳng nào dưới đây thì tỉ lệ mol H O : mol CO giảm 2 2
dần khi số cacbon tăng dần ? A. Ankan. B. Anken. C. Ankin. D. Ankylbenzen.
Câu 30. Cho phương trình phản ứng tạo thành Nitơ (IV) Oxit từ Nitơ ddiooxxit và Oxy là , o dk t , 2 xt
NO + O →
← 2NO . Biết rằng đây là một phản ứng thuận nghịch . Giả sử x, y lần lượt 2 2
là nồng độ phần trăm của khí NO và O tham gia phản ứng. Biết rằng tốc độ phản ứng hóa học 2
của phản ứng trên được xác định 2
v = kx y , với k là hằng số của tốc độ phản ứng. Để tốc độ phản
ứng xảy ra nhanh nhất thì tỉ số giữa x là ? y A. 1 . B. 2 . C. 1 . D. 3. 2 3
Câu 31. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G (x) 2
= 0,035x (15 − x) , trong đó
x là liều lượng thuốc được tiêm cho bệnh nhân ( x được tính bằng miligam). Tính liều lượng
thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất. A. x = 8. B. x = 5. C. x =15. D. x =10 . Trang 6
Câu 32. Các chuyên gia Y-tế ước tính số người nhiễm virus Zika kể từ ngày xuất hiện bệnh nhân đầu tiên
đến ngày thứ t là f (t) 2 3
= 45t − t ,(t = 0,1,2,...,25) . Nếu coi f (t) là một hàm xác định trên đoạn
[0;25] thì f '(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t . Tốc độ truyền
bệnh sẽ lớn nhất vào ngày thứ mấy? A. 20 . B. 10. C. 15. D. 5.
Câu 33. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng 70 m và chiều dài 250 m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả
hai) khi phải thực hiện lộ trình xuất phát từ A đến C và đua xe đạp tới D như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường x ) thì vận động viên nên nhảy xuống để tiếp tục
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là 5 m/s; 1,5m/s và 10 m/s. A. 139,52m. B. 129,52m. C. 109,52m. D. 119,52m.
Câu 34. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng 50m và chiều dài 250 m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả
hai) khi phải thực hiện lộ trình xuất phát từ A đến C và đua xe đạp tới D như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường x ) thì vận động viên nên nhảy xuống để tiếp tục
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là 5 m/s; 1,5m/s và 10m/s. A. 109,8 m. B. 105,8 m. C. 106,8 m. D. 107,8 m.
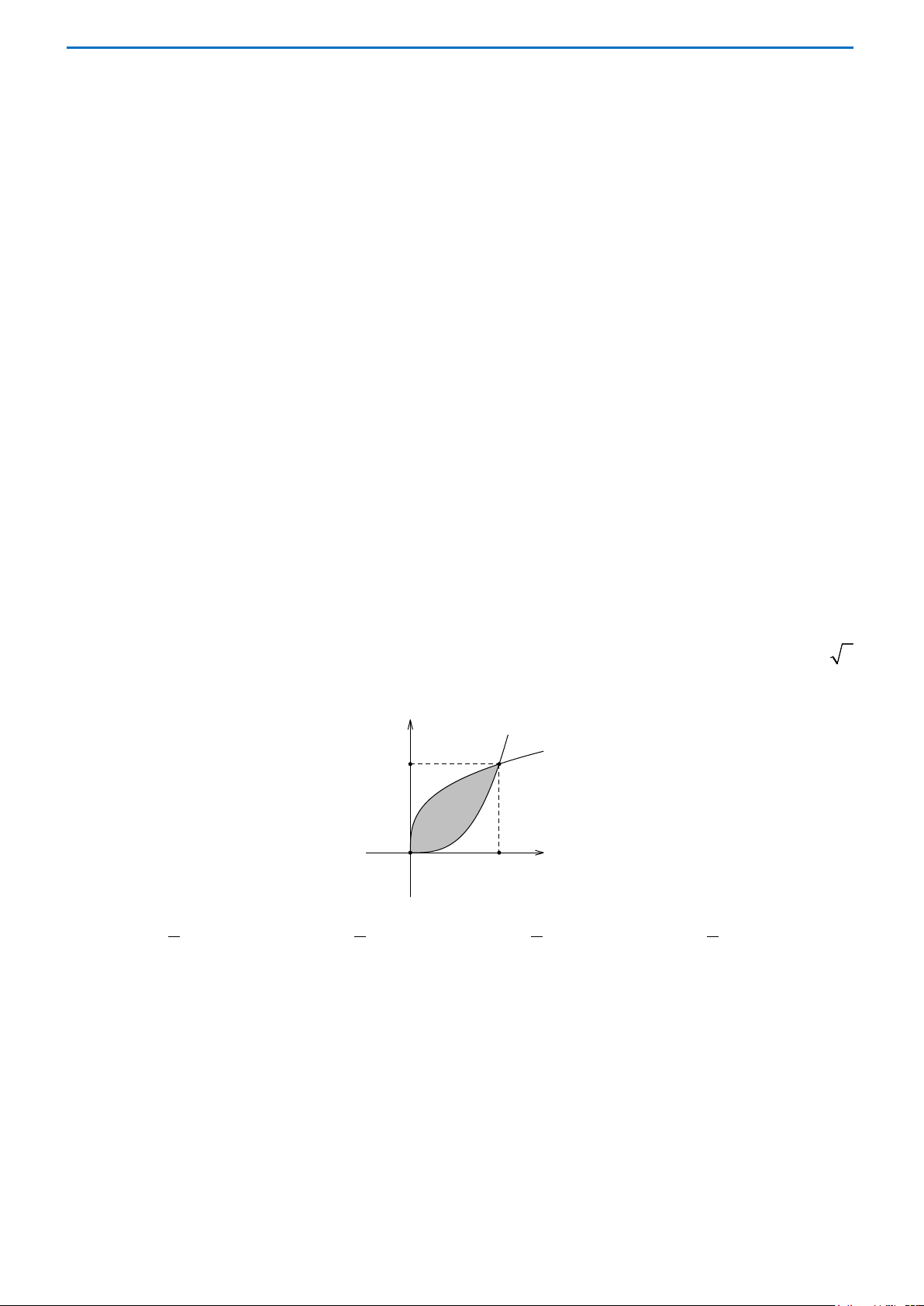
Câu 35. Cho một viên gạch men có dạng hình vuông OABC như hình vẽ. Sau khi tọa độ hóa, ta có O(0;0), A(0 ) ;1 , B(1; )
1 , C (1;0) và hai đường cong lần lượt là đồ thị hàm số 3 y = x và 3 y = x
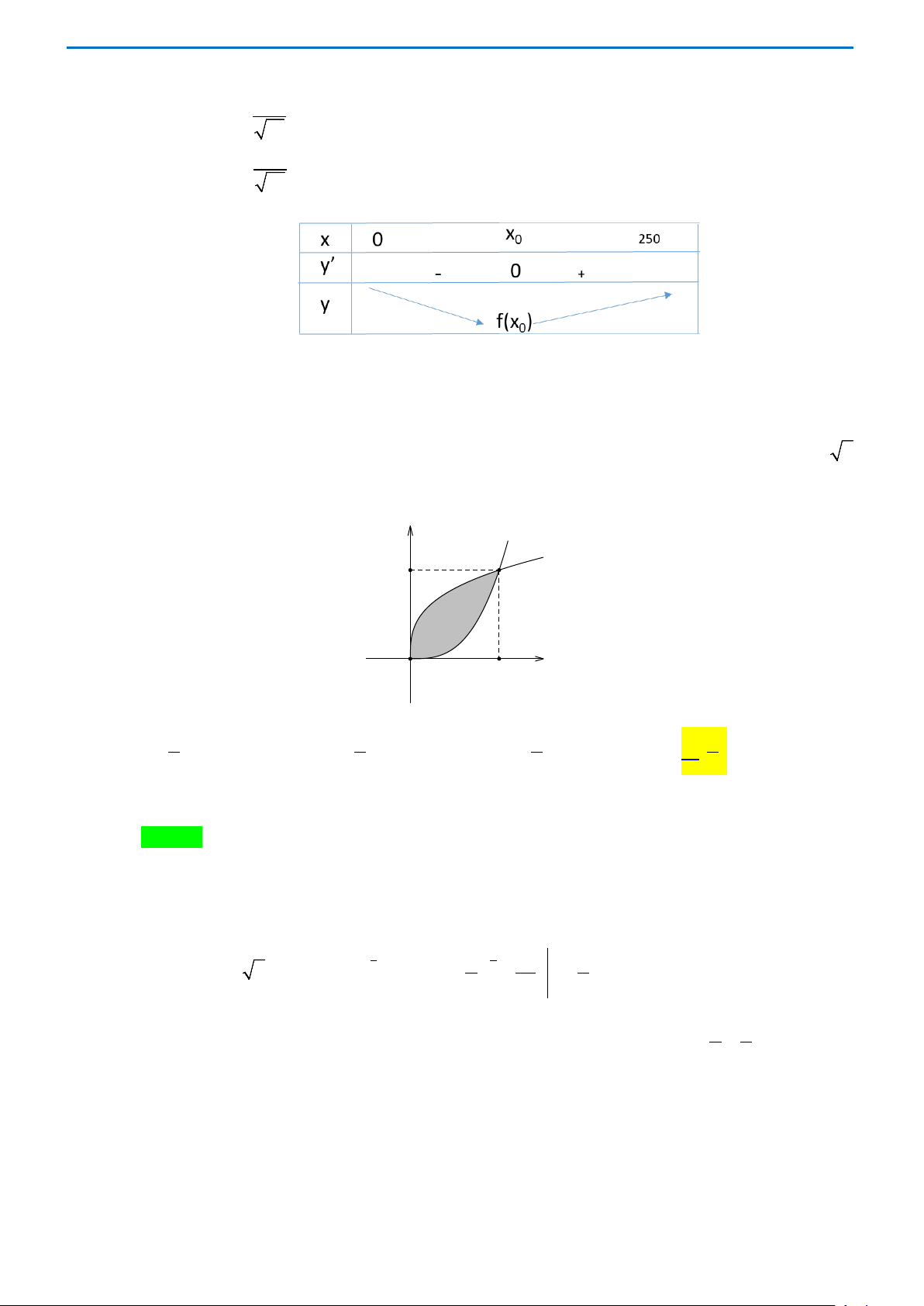
. Tính diện tích của phần không được tô đậm trên viên gạch men. y A B x O C A. 1 . B. 5 . C. 4 . D. 1 . 3 4 5 2
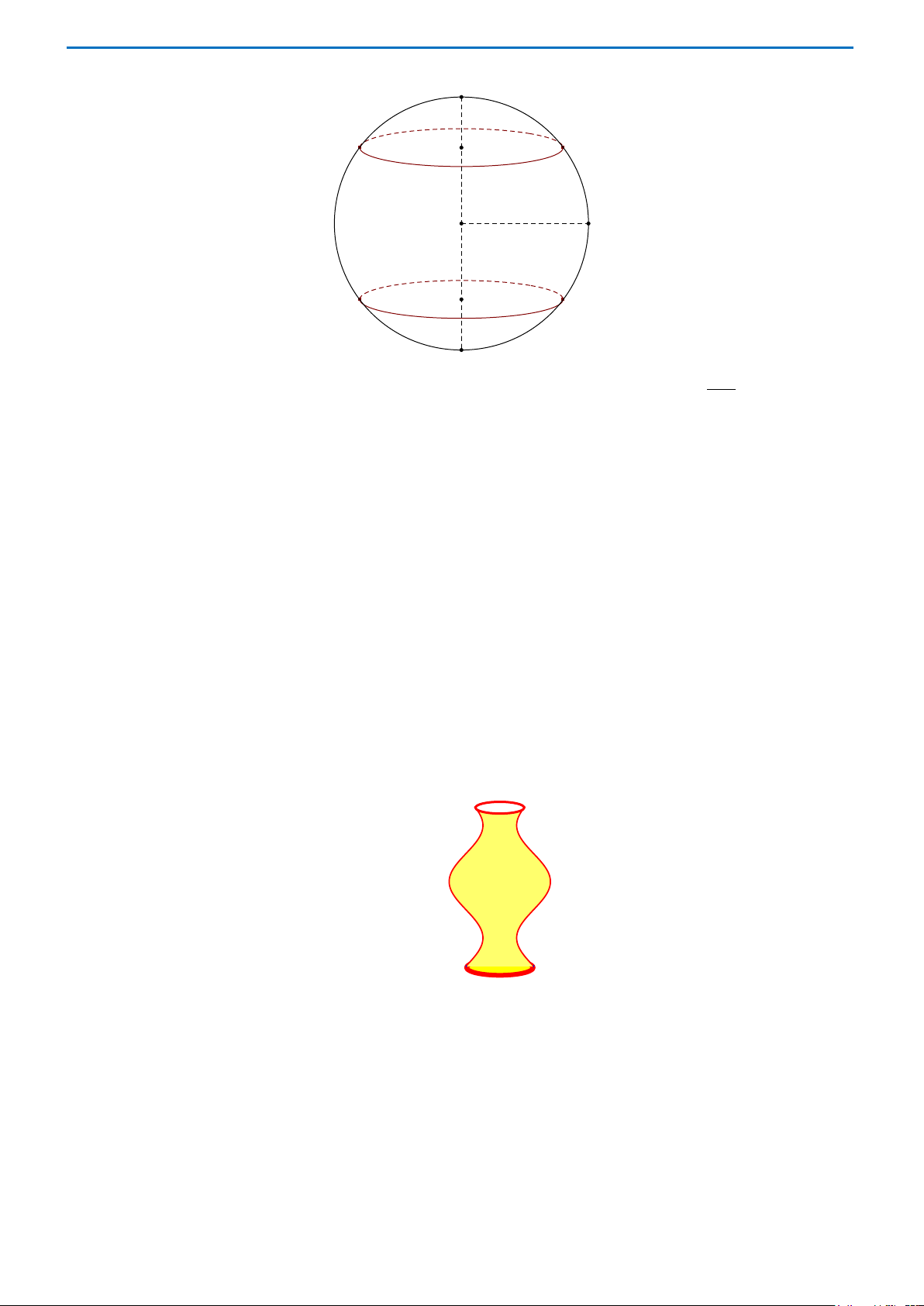
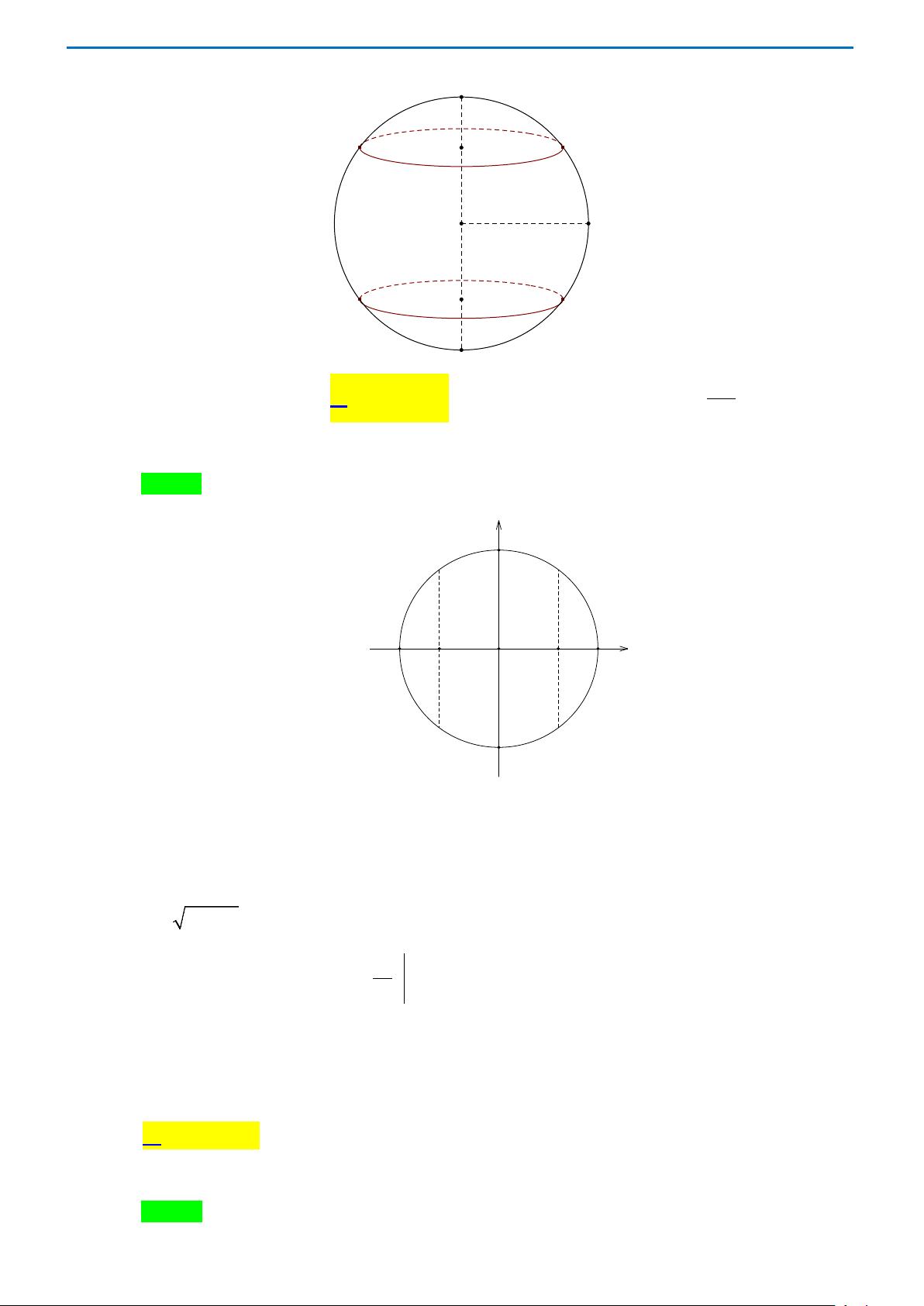
Câu 36. Người ta làm một cái lu đựng nước bằng cách cắt bỏ 2 chỏm của một khối cầu có bán kính 5 dm
bằng 2 mặt phẳng vuông góc với đường kính và cách tâm khối cầu 3 dm . Tính thể tích của chiếc lu. Trang 7 3 dm 5 dm 3 dm A. π ( 3 100 41 dm ). B. π ( 3 132 dm ) . C. π ( 3 43 dm ). D. π ( 3 dm ) . 3
Câu 37. Một cái trống trường có bán kính các đáy là 30 cm , thiết diện vuông góc với trục và cách đều
hai đáy có diện tích là π ( 2
1600 cm ) , chiều dài của trống là 1 m . Biết rằng mặt phẳng chứa trục
cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu? A. 3 425,2 dm . B. 3 425,2 mm . C. 3 425,2 cm . D. 3 425,2 m .
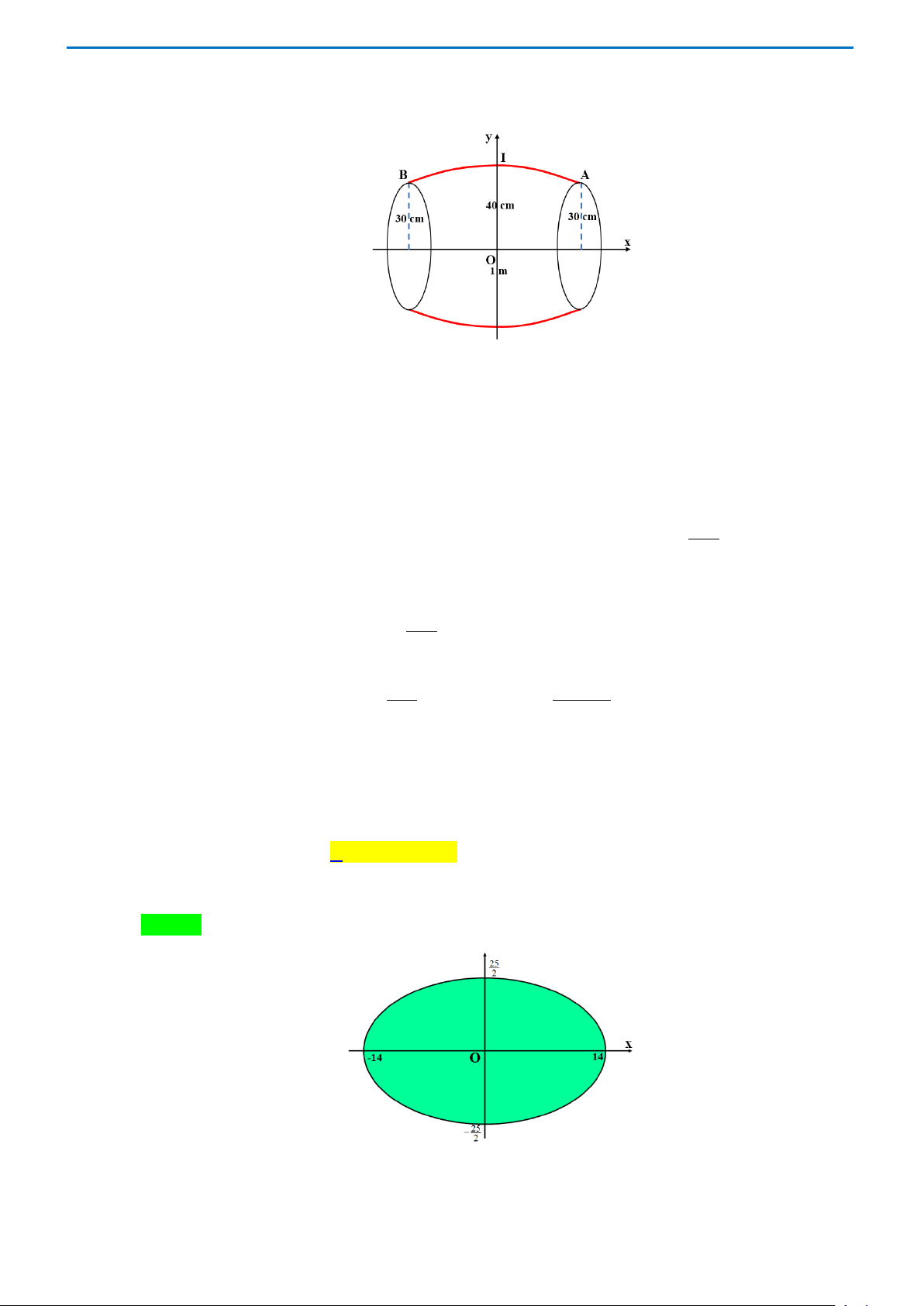
Câu 38. Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn 28cm , trục nhỏ 25cm . Biết cứ 3
1000cm dưa hấu sẽ làm được cốc sinh tố giá 20000 đồng. Hỏi từ quả dưa hấu trên có thể
thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể. A. 180000 đồng. B. 183000 đồng. C. 185000 đồng. D. 190000 đồng.
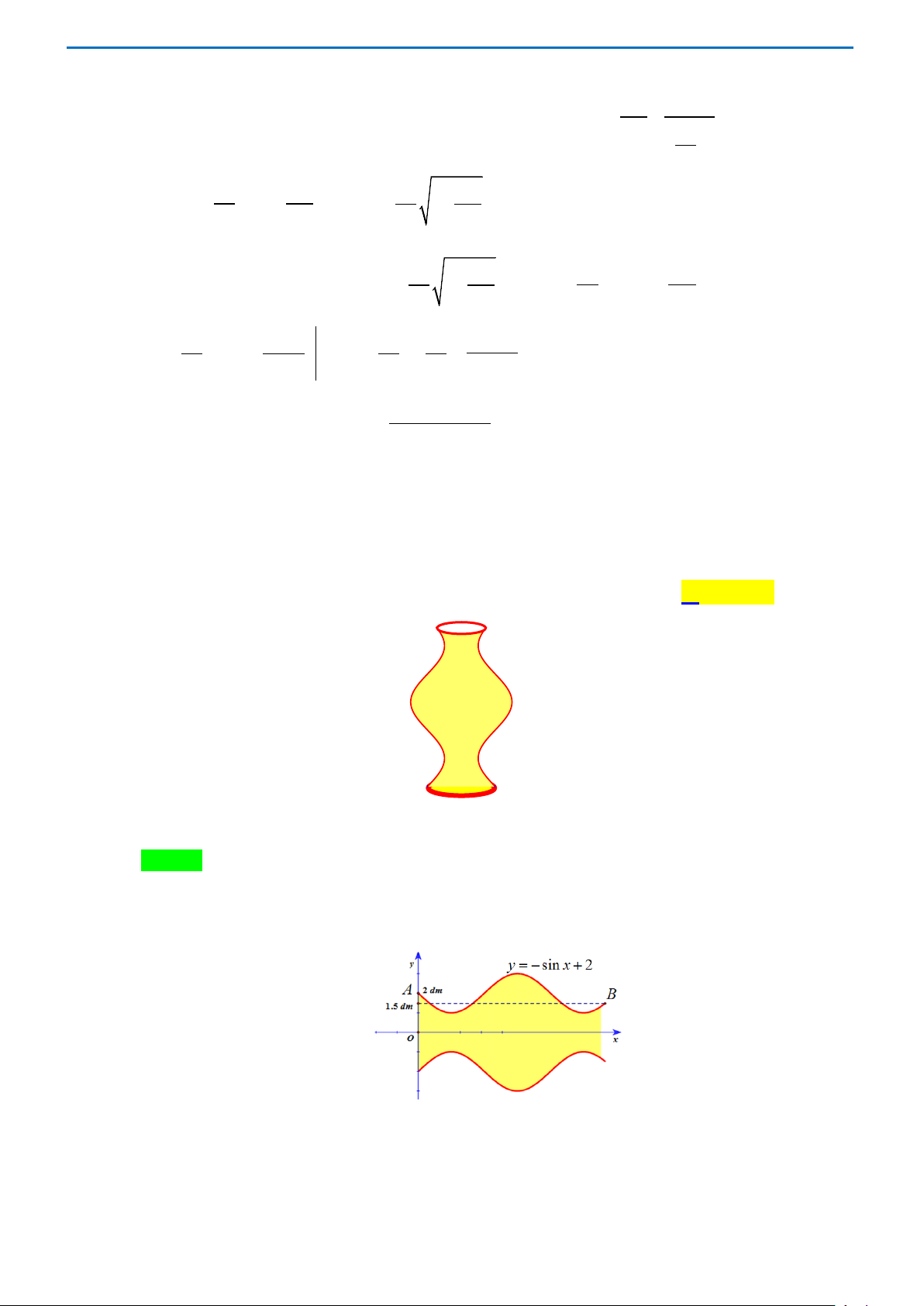
Câu 39. Một bình hoa dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm
số y = −sin x + 2 và trục Ox (tham khảo hình vẽ bên dưới). Biết đáy bình hoa là hình tròn có
bán kính bằng 2 dm , miệng bình hoa là đường tròn bán kính bằng 1.5 dm . Bỏ qua độ dày của
bình hoa, Thể tích của bình hoa gần với giá trị nào trong các giá trị sau đây? A. 100 3 dm . B. 104 3 dm . C. 102 3 dm . D. 103 3 dm .
Câu 40. Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La
Mã, tòa nhà Ellipse Tower Hà Nội, sử dụng trong thiết kế logo quảng cáo, thiết bị nội thất. Xét
một Lavabo (bồn rửa) làm bằng sứ đặc hình dạng là một nửa khối elip tròn xoay có thông số kĩ
thuật mặt trên của Lavabo là: dài×rộng: 660×380 mm (tham khảo hình vẽ bên dưới), Lavabo có
độ dày đều là 20 mm . Thể tích chứa nước của Lavabo gần với giá trị nào trong các giá trị sau: Trang 8 A. 3 18,66 dm . B. 3 18,76 dm . C. 3 18,86 dm . D. 3 18,96 dm .
Câu 41. Một vật chuyển động chậm dần đều với vận tốc v(t) = 160 −10t(m/s) . Quãng đường mà vật
chuyển động từ thời điểm t = 0(s) đến thời điểm mà vật dừng lại là A. 1028 m . B. 1280 m. C. 1308 m . D. 1380 m .
Câu 42. Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức
v(t) = 3t + 2(m/s) . Biết tại thời điểm t = 2(s) thì vật đi được quãng đường là 10(m) . Hỏi tại thời
điểm t = 30(s) thì vật đi được quãng đường là bao nhiêu? A. 1140 m. B. 300 m. C. 240 m. D. 1410 m.
Câu 43. Một vật đang chuyển động với vận tốc v = 25(m/s) thì thay đổi vận tốc với gia tốc được tính
theo thời gian t là a(t) = t − ( 2
2 6 m/s ). Tính quãng đường vật đi được kể từ thời điểm thay đổi
gia tốc đến lúc vật đạt vận tốc bé nhất. A. 107 m . B. 144 m . C. 28 m . D. 57 m . 5
Câu 44. Một mô tô chạy với vận tốc v m/s thì gặp chướng ngại vật nên người lái xe đạp phanh. Từ 0 ( )
thời điểm đó ôtô chuyển động chậm dần với gia tốc a = − t ( 2
8 m/s ) trong đó t là thời gian tính
bằng giây. Biết từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được 12 ( m) . Tính v0 ? A. 18 m/s . B. 3 86 m/s . C. 3 1269 m/s. D. 3 1296 m/s .
Câu 45. Đầu tháng 5 năm 2019 , ông An đầu tư vào chăn nuôi tằm với số tiền vốn ban đầu là 200 (triệu
đồng). Biết rằng trong quá trình chăn nuôi gặp thuận lợi nên số tiền đầu tư của ông liên tục tăng
theo tốc độ được mô tả bằng công thức 12000 f (′t) =
, với t là thời gian đầu tư tính bằng tháng (t + 5)2
(thời điểm t =0 ứng với đầu tháng 5 năm 2019 ). Hỏi số tiền mà ông An thu về tính đến đầu
tháng 5 năm 2023 gần với số nào sau đây?
A. 2737 (triệu đồng).
B. 2307 (triệu đồng).
C. 2370 (triệu đồng).
D. 2703 (triệu đồng).
Câu 46. Giả sử rằng sau t năm, vốn đầu tư của một doanh nghiệp phát sinh lợi nhuận với tốc độ P′(t) 2
= 126 + t (triệu đồng/năm). Hỏi sau 10 năm đầu tiên thì doanh nghiệp thu được lợi nhuận
là bao nhiêu (đơn vị triệu đồng). A. 5020. B. 1235. C. 3257 . D. 4780 . 3 3 Trang 9
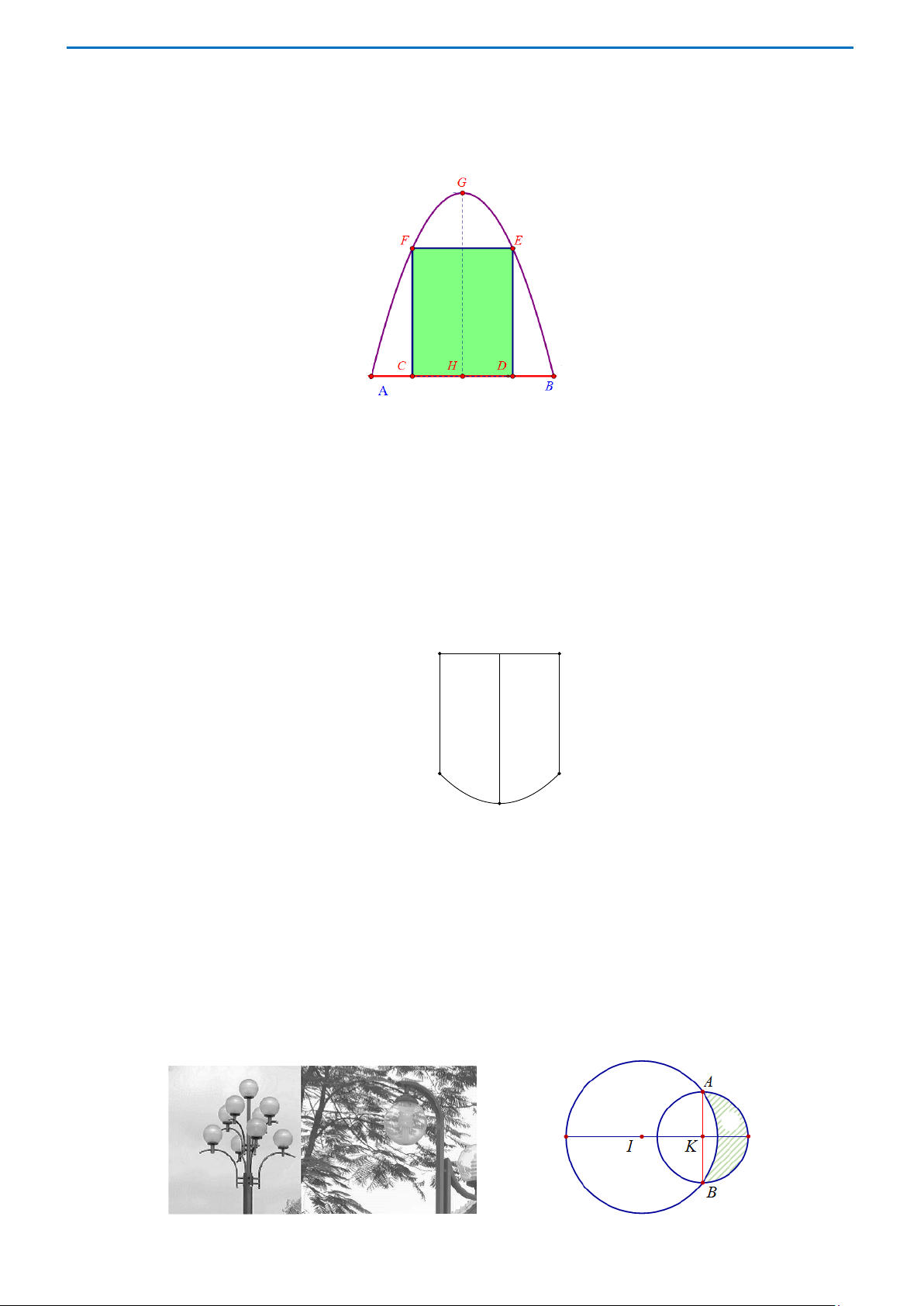
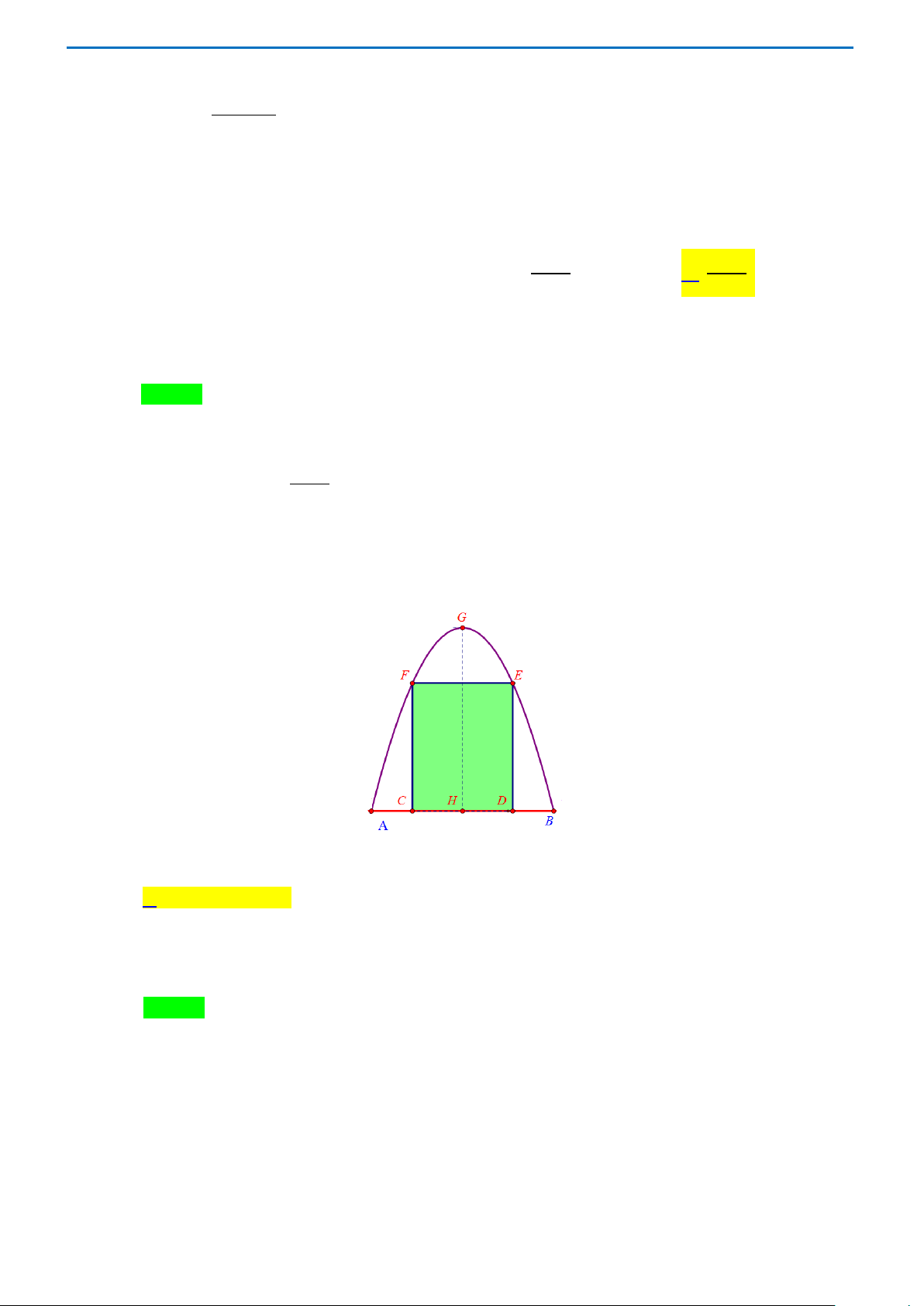
Câu 47: Một cái cổng hình parabol như hình vẽ. Chiều cao GH = 4 m , chiều rộng AB = 4 m ,
AC = BD = 0,9 m . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm có
giá là 1200000đồng/m2, còn các phần để trắng làm xiên hoa có giá là 900000đồng/m2.
Hỏi tổng chi phí để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
A. 11445000 (đồng). B. 7368000 (đồng). C. 4077000 (đồng). D. 11370000 (đồng)
Câu 48: Để tăng thêm thu nhập, ông Bình chăn nuôi thêm 2 con bò. Do diện tích đất của nhà ông hẹp nên
ông xây chuồng bò như hình vẽ bên dưới và chia thành 2 phần bằng nhau để nhốt 2 con bò. Biết
ABCD là hình vuông cạnh 4m và I là đỉnh của một Parabol có trục đối xứng là trung trực của
BC và parabol đi qua hai điểm A , D . Tiền xây chuồng bò hết 350000 đồng/ 2 1 m . Biết I cách
BC một khoảng 5m , hãy tính số tiền chi phí ông Bình bỏ ra để xây dựng chuồng bò (làm tròn đến hàng nghìn)? C B D A I
A. 6.333.000 đồng.
B. 7.533.000 đồng. C. 6.533.000 đồng. D. 7.333.000 đồng.
Câu 49. Người ta sản xuất một loại đèn trang trí ngoài trời (Trụ sở, quảng trường, công viên, sân vườn…)
gồm có hai phần: Phần bóng đèn có dạng mặt cầu bán kính R dm , làm bằng thủy tinh trong suốt;
Phần đế bóng đèn làm bằng nhựa để cách điện, có dạng một phần của khối cầu bán kính r dm
và thỏa mãn đường kính là một dây cung của hình tròn lớn bóng đèn. Một công viên muốn tạo
điểm nhấn ánh sáng, đặt loại bóng có kích thước R = 5 dm , r = 3 dm . Tính thể tích V phần
nhựa để làm đế một bóng đèn theo đơn đặt hàng (Bỏ qua ống luồn dây điện và bulông ốc trong phần đế). Trang 10 π π π A. 3 V = 36π dm . B. 68 3 V = dm . C. 14 3 V = dm . D. 40 3 V = dm . 3 3 3
Câu 50. Một bồn nước Inox SONHA® ngang có hai đầu bồn là hình phẳng elip. Thể tích tối đa khi đóng
nắp bồn là V = 3000 1
lít. Bồn có chiều dài bằng l = 2,0 m và gấp 2 lần chiều cao của bồn. Để
nước bơm tự động vào bồn, người ta lắp một phao điện sao cho mực nước trong bồn cao
h = 0,75 m so với điểm thấp nhất trong đáy bồn thì phao đóng không cho nước chảy vào bồn.
Tính thể tích nước trong bồn khi phao đóng (bỏ qua độ dày của bồn nước và kết quả làm tròn đến phần trăm). A. 3 V = 2.41 m . B. 3 V = 2.43 m . C. 3 V = 2.40 m . D. 3 V = 2.44 m . BẢNG ĐÁP ÁN 1.D 2.B 3.B 4.D 5.C 6.D 7.C 8.A 9.A 10.C 11.A 12.C 13.C 14.A 15.B 16.C 17.A 18.B 19.A 20.A 21.D 22.A 23.D 24.D 25.D 26.B 27.D 28.A 29.A 30.B 31.D 32.C 33.D 34.D 35.D 36.B 37.A 38.B 39.D 40.B 41.A 42.D 43.D 44.D 45.C 46.D 47.A 48.C 49.D 50.A
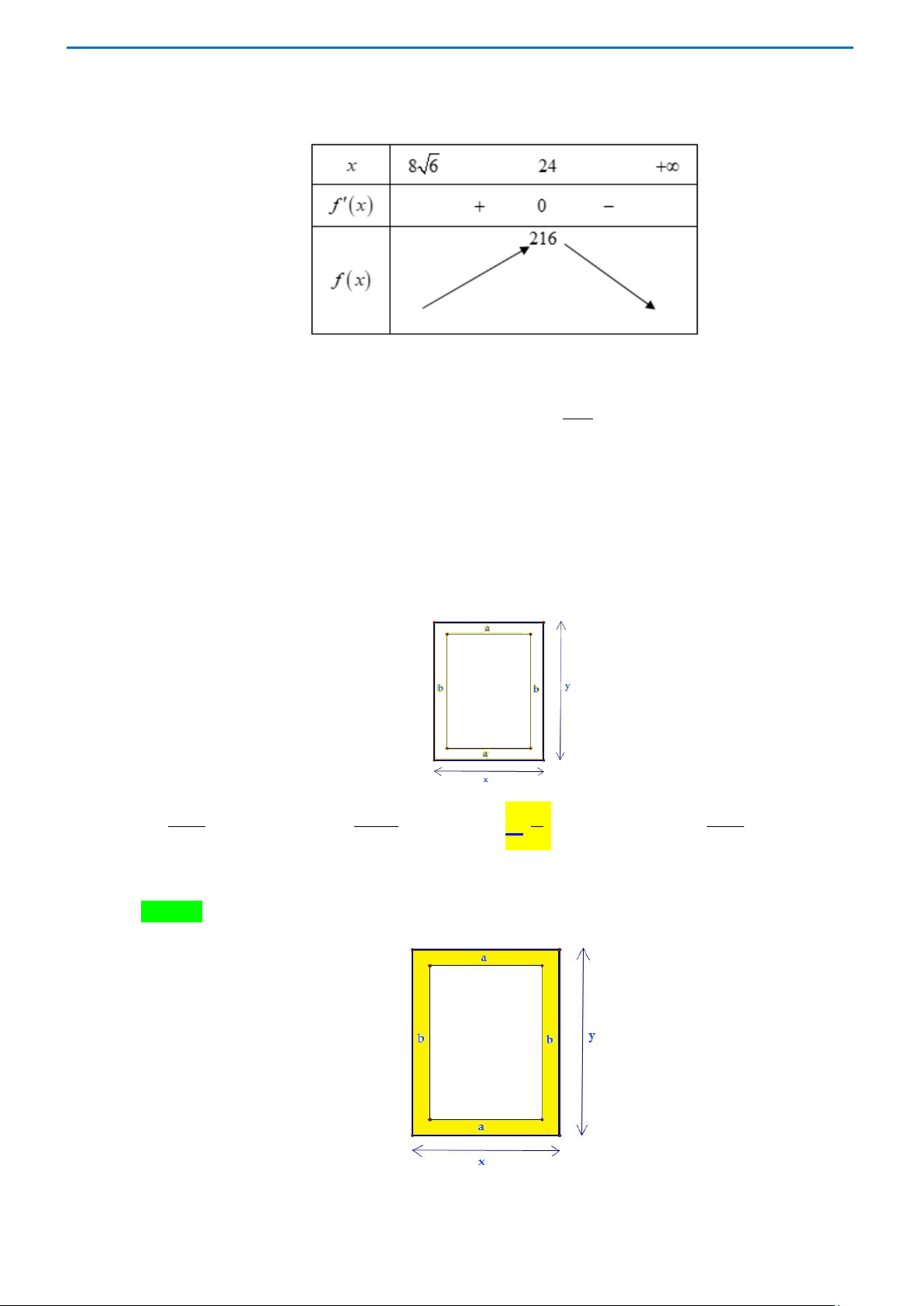
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C, cạnh bên SA vuông góc với
mặt phẳng đáy ( ABC). Biết SC =1, tìm thể tích lớn nhất của khối chóp S.ABC. A. 3 . B. 2 . C. 2 3 . D. 3 . 12 12 27 27 Lời giải Chọn D Trang 11
Giả sử CA = CB = x ( < x < ) 2 2 2 , 0
1 ⇒ SA = SC − AC = 1− x . Thể tích khối chóp: 1 1  1  1 2 2 V = S = = − ∆ SACA CB SA x x S ABC ABC . . . . 1 . . 3 3  2  6
Khảo sát hàm f (x) 1 2 2
= x 1− x trên (0; ) 1 6 3 3 ′( ) 1    −  2 x 1 2x 3 = 2 1 x f x x − x −  =   . 2 2 6 
1− x  6  1− x f ′(x) 2 = 0 ⇔ x = . 3   Ta được f (x) 2 3 max = f   =
nên thể tích lớn nhất của khối chóp S.ABC là 3 V = . (0 ) ;1  3  27   27
Câu 2. Người ta cắt một tờ giấy hình vuông cạnh bằng 1 để gấp thành một hình chóp tứ giác đều sao cho
bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp (hình vẽ).
Để thể tích khối chóp lớn nhất thì cạnh đáy x của hình chóp bằng: A. 2 x = . B. 2 2 x = . C. x = 2 2. D. 2 x = . 5 5 5 Lời giải Chọn B Trang 12 Ta có 1 2 x
BM = AB − MO = − . 2 2 2 2 2   Chiều cao của hình chóp 2 2 2 xx  1− x 2
h = BM − MO =  −  − =     . 2 2    2  2 4 5
Thể tích của khối chóp 1 2 1 x 2 1 x x 2 V x − − = = . 3 2 3 2  
Thể tích của khối chóp lớn nhất khi và chỉ khi ( 4 5
x − x 2) max trên 2 0;   . 2     
Khảo sát hàm số f (x) 4 5
= x − x 2 trên 2 0;   . 2    f ′(x) 3 4 = 4x − 5x 2 .  2 2 ′( ) = 0 x f x = ⇔ 5  . x = 0
Dựa vào bảng biến thiên, ta được GTLN của hàm số đạt tại 2 2 x = . 5 Trang 13
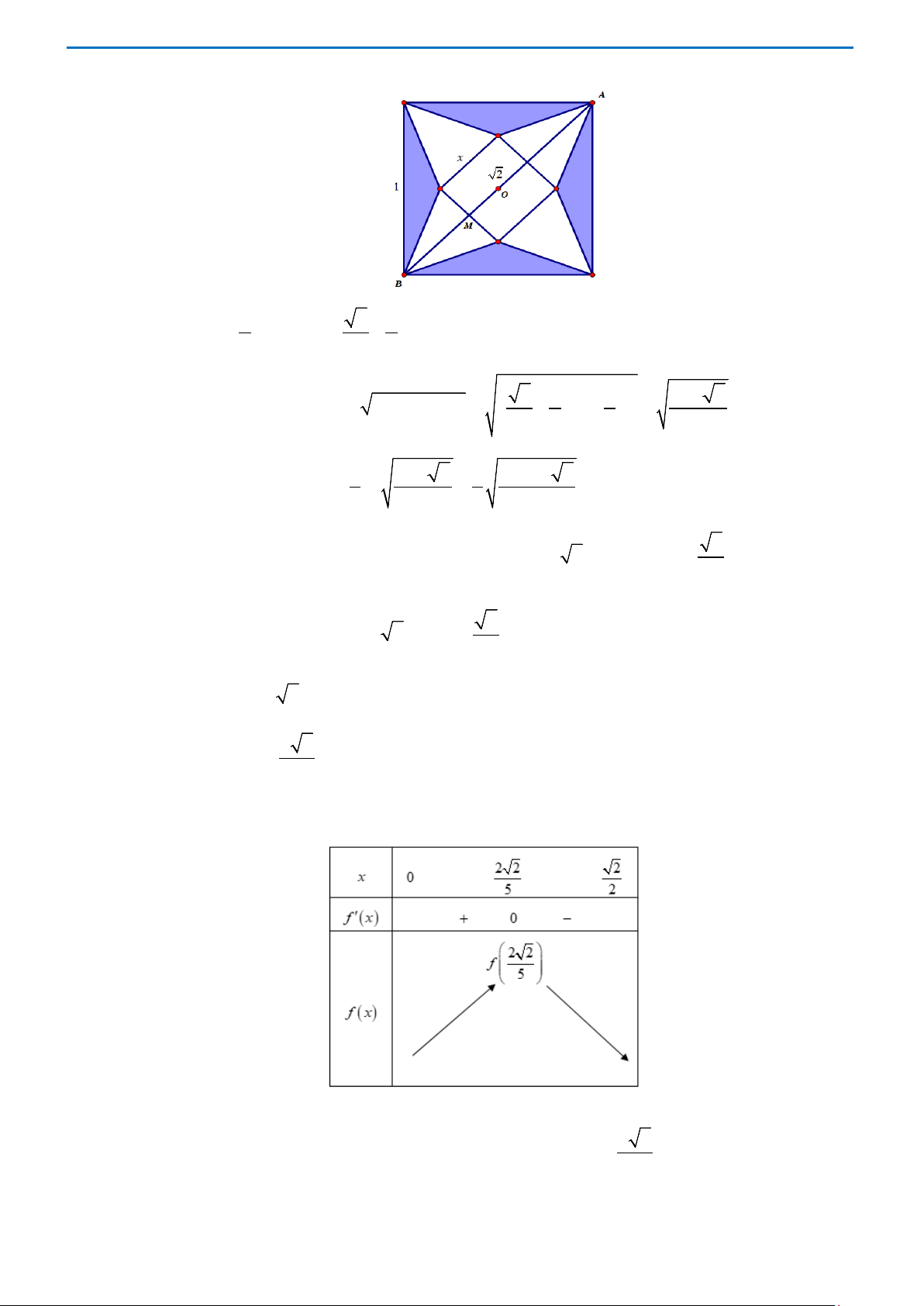
Câu 3. Tìm chiều dài L ngắn nhất của cái thang để có thể tựa vào tường và mặt đất, ngang qua cột đỡ
có chiều cao 3 3 m và cách tường 0,5 m kể từ gốc của cột đỡ. 2 A. 2m . B. 4m . C. 3m . D. 5m . Lời giải Chọn B A M K Tường Cột đỡ C B H  π Đặt α  ABC 0;  = ∈ . 2   
Dựa vào hình vẽ, ta có AB = AK + KB MK KH = + 1 3 3 = + . cosα sinα 2cosα 2sinα π Đặt f (α ) 1 3 3 = +
. Bài toán trở thành tìm min f (α ) với α 0;  ∈ . 2cosα 2sinα   π α 0;  ∈  2   2    α − α 3 3 α − α Ta có f ′(α ) sin 3 3.cos = + sin 3 3.cos = . 2 2 2cos α 2sin α 2 2 2cos α.sin α f ′(α ) 3 3 π π
= 0 ⇔ sin α − 3 3.cos α = 0 3 ⇔ tan α = 3 3 ⇔ tanα = 3 α  0;  ⇔ = ∈ . 3 2    Bảng biến thiên α π π 0 3 2 f ′(α ) – 0 + f (α ) 4  π
Vậy AB = min f α f  = =   4(m) . min ( )  π α 0;  ∈  3   2    Trang 14
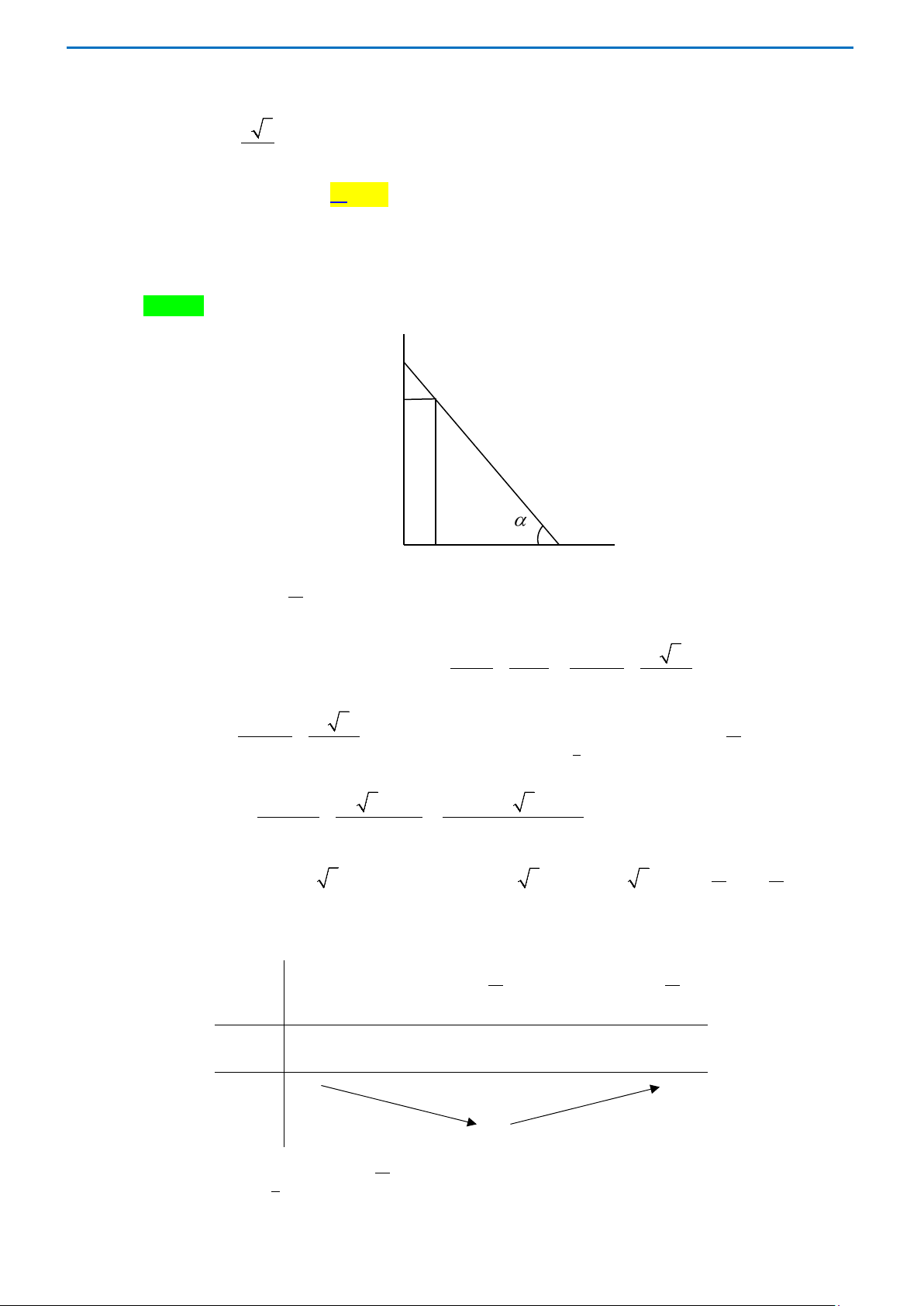
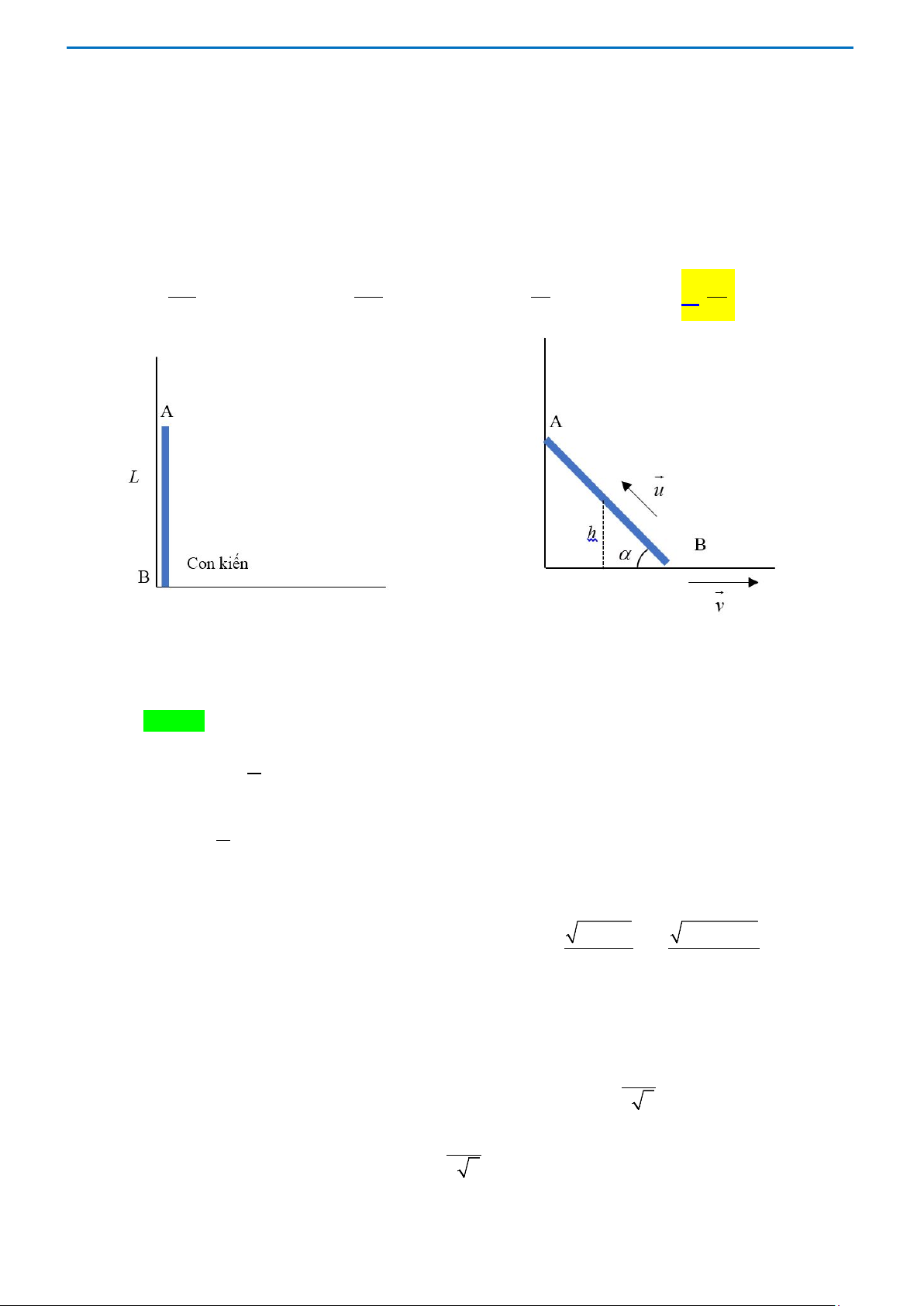
Câu 4. Một con kiến đậu ở đầu B của một thanh cứng mảnh AB có chiều dài L đang dựng cạnh một
bức tường thẳng đứng (hình vẽ).
Vào thời điểm mà đầu B bắt đầu chuyển động sang phải theo sàn ngang với vận tốc không đổi
v thì con kiến bắt đầu bò dọc theo thanh với vận tốc không đổi u đối với thanh. Trong quá
trình bò trên thanh, con kiến đạt được độ cao cực đại h là bao nhiêu đối với sàn? Cho đầu A max
của thanh luôn tỳ lên tường thẳng đứng. 2 2 2 2 A. 3L . B. 2L . C. L . D. L . v v 3v 2v Lời giải Chọn D Gọi 0 L t t  < < 
là thời gian con kiến đi được. u    Ta có L
t = với L là chiều dài thanh cứng. u
Khi đầu B di chuyển một đoạn S = .
v t thì con kiến đi được L = . u t . 2 2 − 2 2 2 4 −
Độ cao mà con kiến đạt được khi đó là h = .
L sinα = . . L S u t = . L t v t u . L L Đặt ( ) 2 2 2 4
f t = L t − v t . Bài toán trở thành tìm max f (t) . t = 0 Ta có f ′(t) 2 2 3
= 2L t − 4v t , f ′(t) 2 2 3
= 0 ⇔ 2L t − 4v t = 0  ⇔ L  . t =  v 2
Khi t = 0 (không thỏa mãn), ta chọn L t = . v 2 Bảng biến thiên Trang 15 L L t 0 v 2 2u f ′(t) – 0 + 2 L f (t) 2v 2 Vậy max ( )  L L f t = f =  . v 2    2v
Câu 5. Một hộp không nắp được làm từ một mảnh các tông theo mẫu. Hộp có đáy là một hình vuông
cạnh x(cm) , chiều cao h(cm) và có thể tích là ( 3 500 cm ).
Tìm x sao cho diện tích mảnh các tông đó nhỏ nhất? A. 5cm . B. 100cm . C. 10cm . D. 20cm . Lời giải Chọn C
Ta có thể tích của khối hộp là: 2 3 500
V (x) = x h = 500(cm ) ⇒ h = , x > 0. 2 x
Để chiếc hộp làm ra ít tốn bìa các tông nhất khi và chỉ khi diện tích toàn phần của hộp là nhỏ nhất.
Diện tích của mảnh các tông dùng làm hộp là 2 2 2000
S(x) = x + 4hx = x + , x > 0 . x
Bài toán quy về tìm x ∈(0;+∞) sao cho tại đó S (x) đạt GTNN. 3 − Ta có 2000 2( 1000) (′ ) = 2 x S x x − = . 2 2 x x
S (′x) = 0 ⇔ x = 10 . Trang 16
Suy ra bảng biến thiên sau:
Dựa vào bảng biến thiên ta thấy S (x) đạt GTNN tại x =10 . Vậy muốn tốn ít nguyên liệu nhất
ta lấy độ dài cạnh đáy của hình hộp là x =10cm .
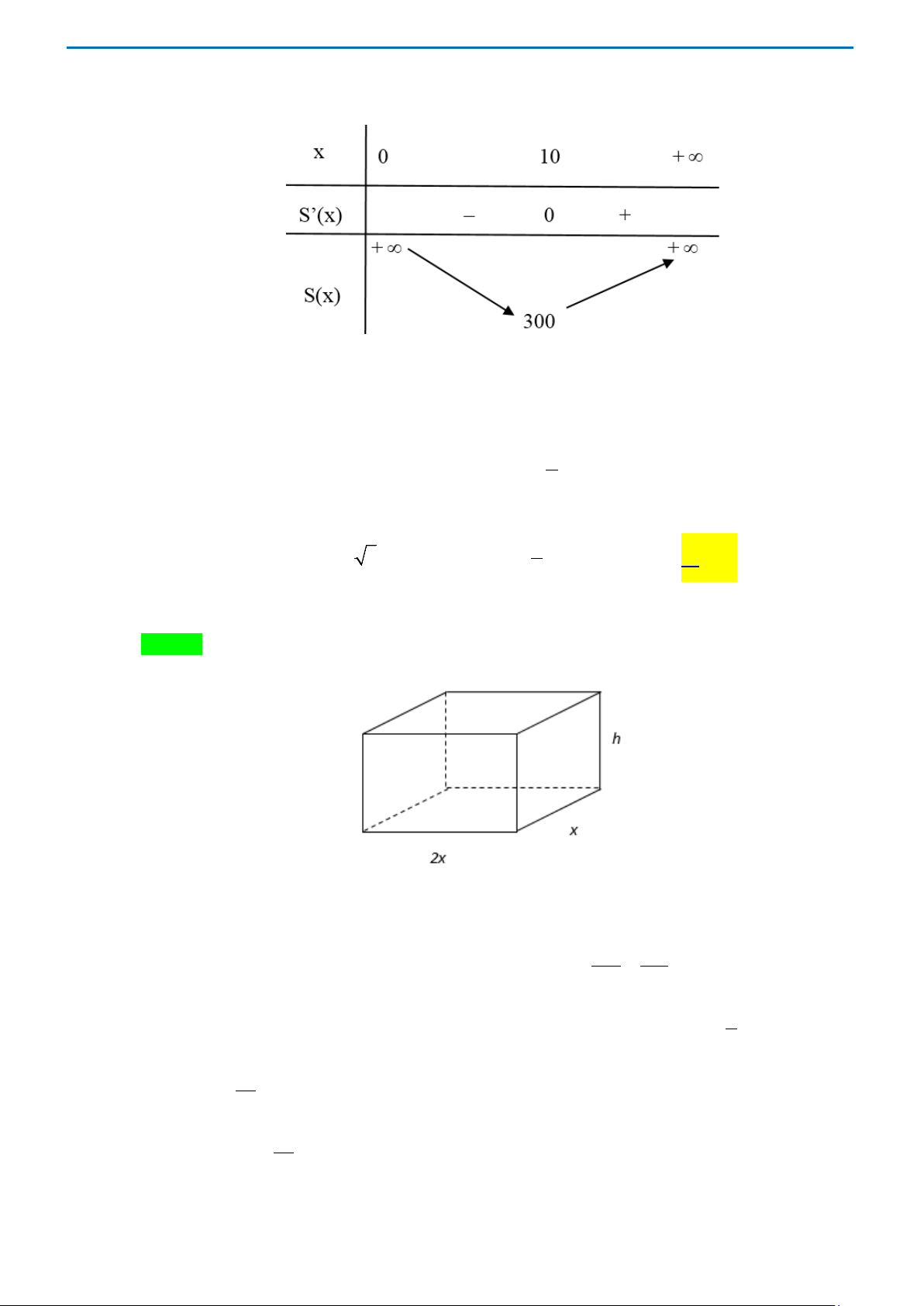
Câu 6. Một nhà máy cần sản xuất một bể nước bằng tôn có dạng hình hộp đứng đáy là hình chữ nhật có
chiều dài gấp 2 lần chiều rộng không nắp, có thể tích 4 3
m . Hãy tính độ dài chiều rộng của đáy 3
hình hộp sao cho tốn ít vật liệu nhất. A. 2 m. B. 3 m. C. 2 m . D. 1 m. 3 Lời giải Chọn D
Gọi x,h lần lượt là chiều rộng đáy và chiều cao của khối hộp với x,h∈(0;+ ∞) .
Ta có chiều dài đáy là 2x. Thể tích 2 V 2 V = 2 . x .
x h = 2x h ⇔ h = = . 2 2 2x 3x
Diện tích vật liệu làm khối hộp là S(x) = Sđ + Sxq = 2 4 2 .
x x + 2(x + 2x).h = 2x + . x 4
S (′x) = 4x − . 2 x 4
S (′x) = 0 ⇔ 4x − = 0 ⇔ x =1. 2 x Bảng biến thiên: Trang 17
Từ bảng biến thiên suy ra min S = 6 khi x =1.
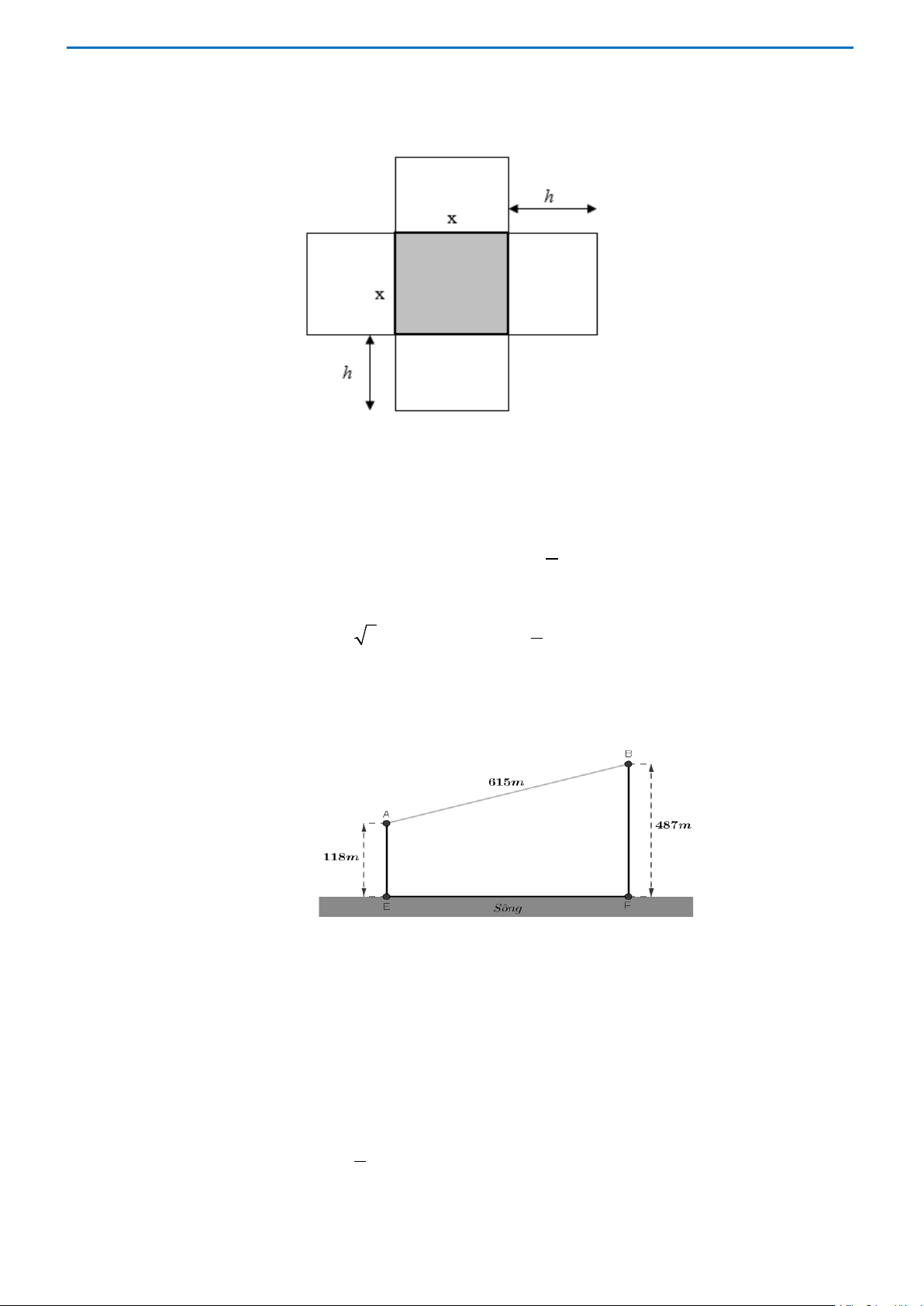
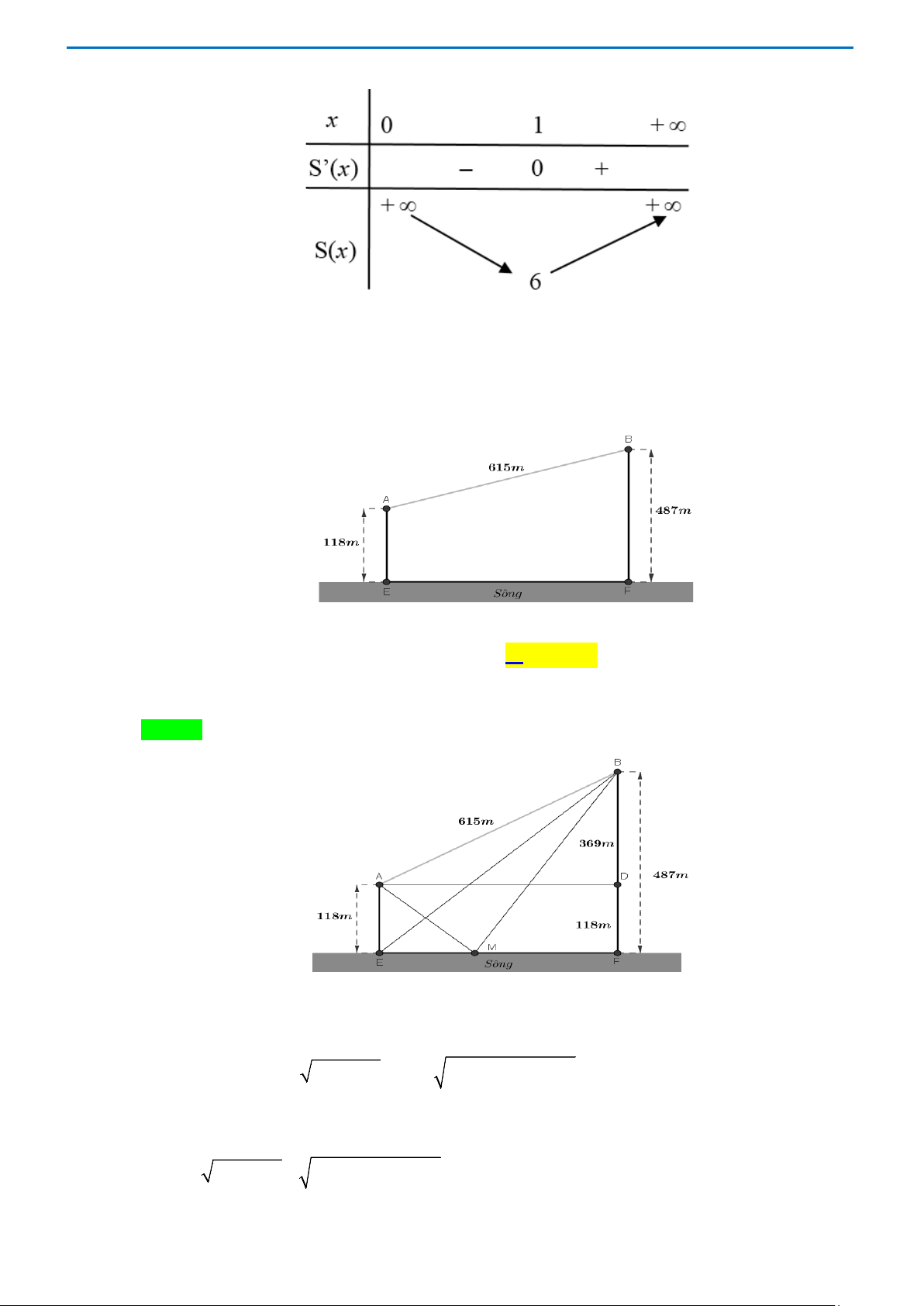
Câu 7. Cho hai vị trí A , B cách nhau 615 m , cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách
từ A và từ B đến bờ sông lần lượt là 118 m và 487 m . Một người đi từ A đến bờ sông để lấy nước mang về B .
Đoạn đường ngắn nhất mà người đó có thể đi là A. 596,5m . B. 671,4m . C. 779,8m . D. 741,2m . Lời giải Chọn C
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B.
Dễ dàng tính được BD = 369, EF = 492. Ta đặt EM = x,khi đó ta được: 2 2 MF = − x MA = x + MB = ( − x)2 2 492 , 118 , 492 + 487 .
Như vậy ta có hàm số f (x) được xác định bằng tổng quãng đường MA + MB . f (x) 2 2 = x + + ( − x)2 2 118 492
+ 487 với x ∈[0;492]. Trang 18
Ta cần tìm giá trị nhỏ nhất của f (x) để có được quãng đường ngắn nhất và từ đó xác định
được vị trí điểm M . − Ta có: ′( ) x 492 x f x = − . 2 2 x +118 (492− x)2 2 + 487 ( ) x 492 − ′ − = 0 x f x ⇔ − = 0 x 492 x ⇔ = 2 2 x +118 (492− x)2 2 + 487 2 2 x +118 (492− x)2 2 + 487 ⇔ x ( − x)2 2 + = ( − x) 2 2 492 487 492 x +118  2 x ( − x)2 2 +  = ( − x)2 ( 2 2 492 487 492 x +118 ) (  x)2 = ( − x)2 487 58056 118 ⇔    ⇔  0 ≤ x ≤ 492 0 ≤ x ≤ 492  58056 x =  605  58056 ⇔  58056 ⇔ x = x = − . 605  369  0 ≤ x ≤ 492
Hàm số f (x) liên tục trên đoạn [0;492] . So sánh các giá trị của f (0), 58056 f    , f (492) 605   
ta có giá trị nhỏ nhất là 58056 f   ≈   779,8m .  605 
Khi đó quãng đường đi ngắn nhất là xấp xỉ 779,8m .
Câu 8. Trong không gian với hệ trục toạ độ Oxyz cho đường thẳng ∆ có phương trình tham số là: x = 2  y = t
− và hai điểm A(1;− 2;− )
1 , B(4;4;5) . Giả sử M (a;b;c) thuộc ∆ sao cho MA+ MBz =1+  t
nhỏ nhất, khi đó tích abc là A. 0 . B. 2 . C. 1. D. 2 . 9 Lời giải Chọn A
M ∈∆ ⇒ M (2; t − ;1+ t). Ta có: 2 MA = 2t + 9 ; 2 MB = 2t + 36 . Từ đó 2 2
MA + MB = 2t + 9 + 2t + 36 . Đặt f (t) 2 2
= 2t + 9 + 2t + 36 . Trang 19 ′( ) 2t 2t f t = + . 2 2 2t + 9 2t + 36 Giải ′( ) 2t 2 = 0 t f t ⇔ +
= 0 ⇔ t = 0 . Ta có bảng biến thiên sau: 2 2 2t + 9 2t + 36
Từ bảng biến thiên suy ra min f (t) = 9 đạt được tại t = 0. Vậy M (2;0; )
1 thì MA + MB nhỏ nhất.
Câu 9 . Một trang chữ của cuốn sách giáo khoa cần diện tích 2
384cm . Lề trên và dưới là 3cm , lề trái
và phải là 2cm . Kích thước tối ưu của trang giấy là:
A. Dài 24cm ; rộng 16cm .
B. Dài 24cm ; rộng 17cm .
C. Dài 25cm ; rộng 15,36cm .
D. Dài 25,6cm ; rộng 15cm . Lời giải Chọn A
Trang giấy có diện tích tối ưu khi diện tích trình bày là lớn nhất.
Gọi chiều dài trang giấy là x , (x ≥ 8 6) ; suy ra chiều rộng là 384 . x
Diện tích trình bày nội dung là : f (x) = (x − ) 384  2304 6 − 4 = 4 − x − +   408 .  xx
Để diện tích là lớn nhất ta cần tìm giá trị lớn nhất của 2304 f (x) = 4 − x −
+ 408 với (x ≥ 8 6). x Ta có: 2304 f '(x) = 4 − + . 2 x Trang 20
f '(x) = 0 ⇔ x = 24 .
Dựa vào bảng biến thiên ta có giá trị lớn nhất của f (x) là 216 khi x = 24 .
Vậy chiều dài trang giấy là 24 cm ; suy ra chiều rộng là 384 = 16 cm . 24
Câu 10. Có một cơ sở in sách xác định rằng: Diện tích của toàn bộ trang sách là 2
S (cm ). Do yêu cầu kỹ 0
thuật nên dòng đầu và dòng cuối đều phải cách mép (trên và dưới) trang sách là a (cm). Lề bên
trái và bên phải cũng phải cách mép trái và mép phải của trang sách là b(cm) (b < a) . Các kích
thước của trang sách là bao nhiêu để cho diện tích phần in các chữ có giá trị lớn nhất. Khi đó hãy
tính tỉ lệ của chiều rộng và chiều dài trang sách. − + A. b a . B. 2b . C. b . D. b a . a 2a −1 a a Lời giải Chọn C Trang 21
Gọi x, y lần lượt là chiều rộng và chiều dài của trang sách (0 < x < y), P là diện tích phần in chữ của trang sách.
Chiều rộng phần in sách là 2 , x x b b  − <  . 2   
Chiều dài phần in sách là 2 , y y a a  − <  . 2   
Diện tích phần in sách là: P = (x − 2b)(y − 2a) = xy − 2by − 2ax + 4ab . S Mặt khác 0
S = xy ⇒ y =
thay vào phương trình ta được  2 0  = + − + . 0 4  2 bS P S ab ax x 0 x   
Ta nhận thấy S + 4ab không đổi  2bS0 P 2ax  ⇔ +   min . 0 max  x  Xét hàm số 2 2bS bS 0 ( ) = 2 bS f x ax + 0 0
⇒ f (′x) = 2a −
, f (′x) = 0 ⇔ x = . x 2 x a 4   Lại có bS 0 ( ′′ ) bS f x =
. Với x dương ⇒ f ( ′′ x) > 0 0
⇒ min f (x) = f   = 4 abS . 3 x 0  a    Khi đó: bS bS bxy x b 0 2 0 2 x = ⇒ x = ⇒ x = ⇒ = . a a a y a
Câu 11. Một anh kỹ sư muốn tạo ra 1 cái lu hình trụ có diện tích bề mặt (không tính hai mặt đáy) là lớn
nhất. Bề mặt lu được quấn bởi mảnh tôn hình chữ nhật có chu vi 120 cm. Gọi chiều dài của hình
chữ nhật là a , chiều rộng của hình chữ nhật là b . Tính 2
P = a + 3b . A. 990. B. 1660. C. 2530. D. 1108. Lời giải Chọn A
Cách 1: a + b = 60 (1). S = a b lu . . 2 Ta có .  a b a b +  ≤ =   900 (B.Đ.T Cô Si) .  2  ⇒ (S =
. Dấu “=” xảy ra ⇔ a = b = 30 . lu ) 900 max 2
⇒ a + 3b = 990 . Trang 22 Cách 2:
Ta có a + b = 60 ⇔ b = 60 − a .
S = a b = a
− a = a − a . lu ( ) 2 . 60 60
Xét y = f (a) 2
= 60a − a với 0 < a < 60.
y′ = 60 − 2a .
y′ = 0 ⇔ a = 30. ⇒ (S = khi 2 a = ⇒ b = ⇒ a + b = . lu ) 900 30 30 3 990 max
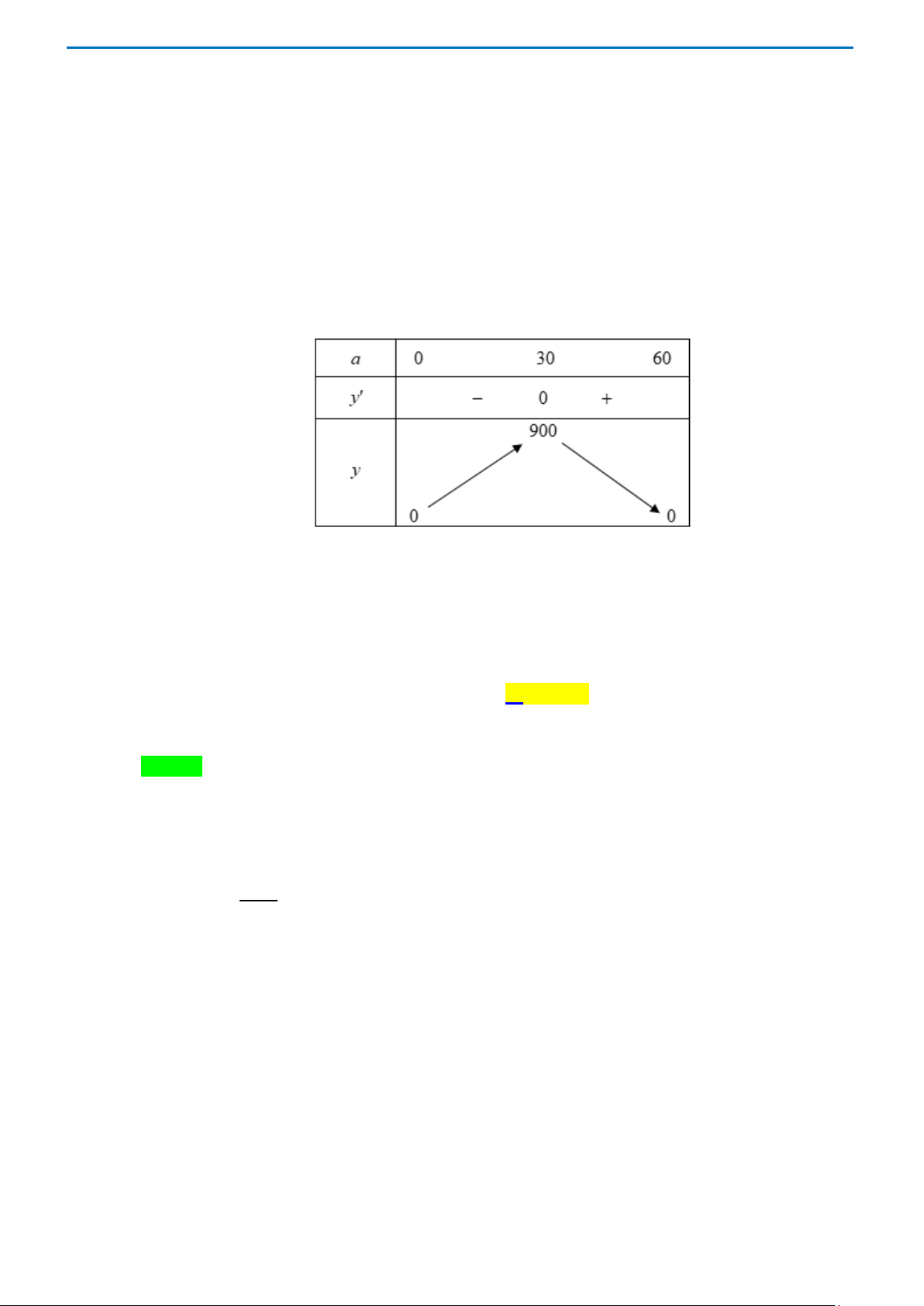
Câu 12. Bác nông dân có 200m rào để ngăn đàn gà nuôi dạng hình chữ nhật. Để diện tích nuôi gà là lớn
nhất thì chiều dài hình chữ nhật là a (m) và chiều rộng là b (m). Khi đó 2 2
a + ab + b có giá trị bằng A. 7525 m. B. 7600 m. C. 7500 m. D. 7900 m. Lời giải Chọn C
Cách 1 : Ta có a + b =100. Diện tích S = a b . nuoi . 2 Ta có .  a b a b +  ≤ =   2500 (B.Đ.T Cô Si).  2  (S =
. Dấu “=” xảy ra ⇔ a = b = 50 . nuoi ) 2500 max 2 2 ⇒ a + .
a b + b = 7500 . Cách 2:
Ta có a + b =100 ⇔ b =100 − a . S = a b = a
− a = a − a . nuoi ( ) 2 . 100 60
Xét y = f (a) 2
= 100a − a với 0 < a <100 .
y′ =100 − 2a . Trang 23
y′ = 0 ⇔ a = 50. ⇒ (S = khi 2 2 a = ⇒ b =
⇒ a + a b + b = . lu ) 2500 50 50 . 7500 max
Câu 13. Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm
tổng x + y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. A 2 cm E B x cm H 3 cm F D C G y cm A. 7cm . B. 5cm . C. 7 2 cm . D. 4 2 cm . 2 Lời giải Chọn C Ta có S
nhỏ nhất khi và chỉ khi S = S + S + S lớn nhất. EFGH AEH CGF DGH
Dễ thấy 2S = 2x + 3y + (6 − x)(6 − y) = xy − 4x − 3y + 36 (1).
Theo giả thiết, ta được A ∆ EH ∽ C
∆ GF (do có các cạnh tương ứng song song với nhau) nên AE AH = suy ra xy = 6 (2). CG CF Từ (1) và (2) suy ra  18 2S 42 4x  = − +    hay 9
S = 21− 2x + . x      x
Theo bất đẳng thức Cô – si, ta được: 9 9 2x + ≥ 2 2 .
x = 2 18 = 6 2 nên S ≤ 21− 6 2 . Từ đó x x  9 2x =
biểu thức S lớn nhất bằng 21− 6 2 , đạt được khi 3 2  x ⇔ x = cm ⇒ y = 2 2 cm . 2 x > 0 Trang 24 Khi đó, ta được 3 2 7 2 x + y = + 2 2 = cm . 2 2
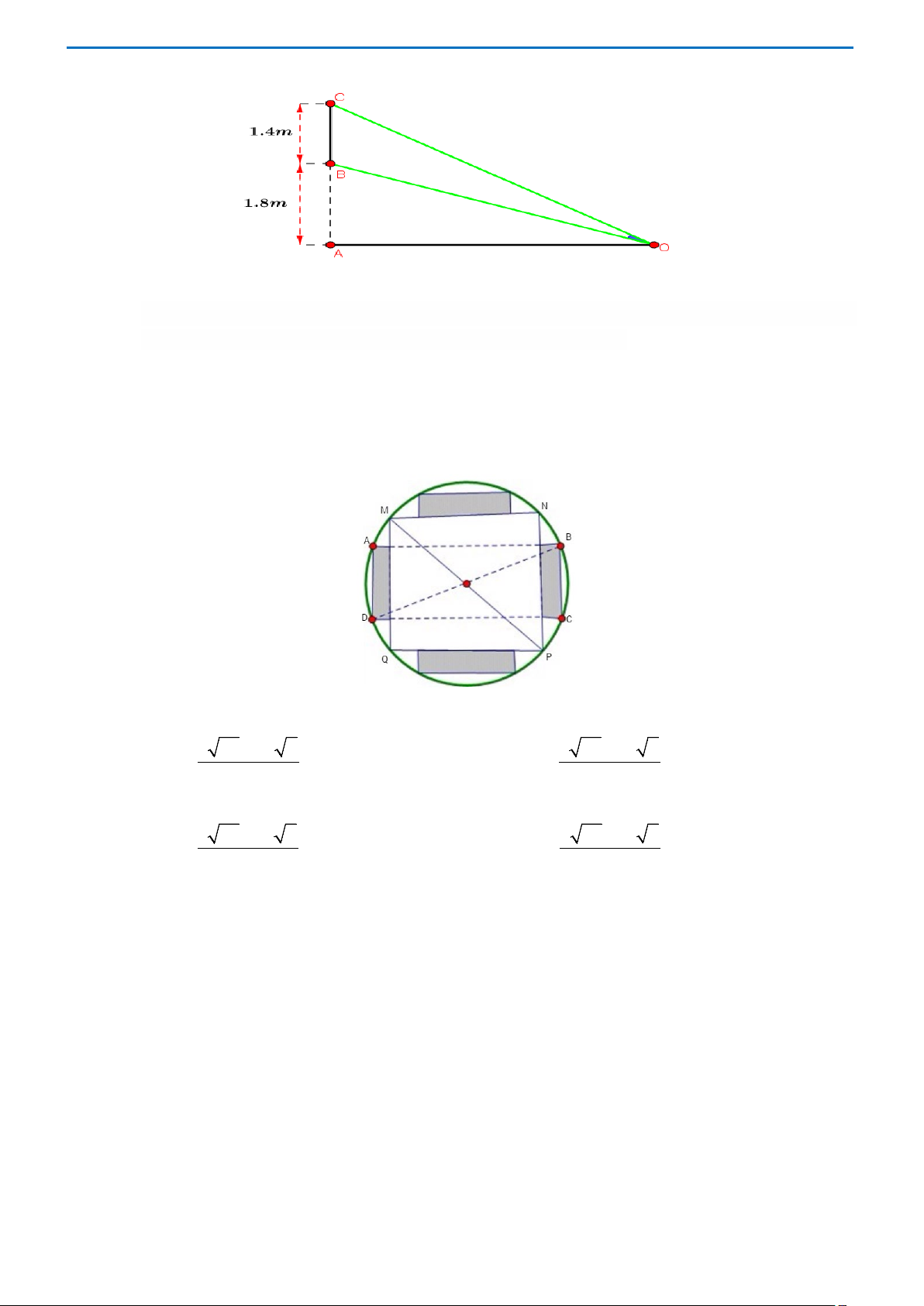
Câu 14. Một màn ảnh hình chữ nhật cao 1,4m và đặt ở độ cao 1,8m so với tầm mắt (tính từ đầu mép
dưới của màn hình như hình vẽ). Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn
nhất. Tính khoảng cách từ vị trí đó đến màn ảnh? Biết rằng góc  BOC nhọn. A. AO = 2,4m . B. AO = 2m . C. AO = 2,6m . D. AO = 3m . Lời giải Chọn A
Đặt độ dài cạnh AO = x(m),(x > 0) . Ta được 2 2
BO = 3,24 + x ,CO = 10,24 + x .
Sử dụng định lí cosin trong tam giác OBC
OB + OC − BC ( 2 3,24 + x ) + ( 2 2 2 2 10,24 + x ) 2  −1,96 5,76 + x cos BOC = = = . 2 . OB OC 2 ( 2 3,24 + x )( 2 10,24 + x ) ( 2 3,24 + x )( 2 10,24 + x ) Vì góc  BOC nhọn nên 
BOC lớn nhất khi và chỉ khi 
cos BOC nhỏ nhất. Hay bài toán trở thành tìm 2 x + để ( ) 5,76 x F x = (
đạt giá trị nhỏ nhất. 2 3,24 + x )( 2 10,24 + x ) 63 t + + Đặt ( 2
3,24 + x ) = t,(t > 3,24) . Suy ra F (t) 25 25t 63 = = .
t (t + 7) 25 t (t + 7)
Ta đi tìm t để F (t) đạt giá trị nhỏ nhất.     
t (t + ) −( t + ′ ) 2t + 7 25 7 25 63     25t + 63  1 
 2 t (t + 7)   F′(t)   =   =  
 25 t (t + 7)  25 t (t + 7)          1  ( 2
50 t + 7t) −(25t + 63)(2t + 7)  1  49t − 441  =   =   . 25 
2t (t + 7) t (t + 7)
 25  2t (t + 7) t (t + 7)     
F′(t) = 0 ⇔ t = 9 Trang 25 Bảng biến thiên t 3,24 9 +∞ F′(t) - 0 + F (t) F min
Thế vào biểu thức của phép đặt ta có: ( 2 + x ) 2 144 3,24 = 9 ⇔ x = ⇔ x = 2,4m . 25
Vậy để nhìn rõ nhất thì AO = 2,4m .
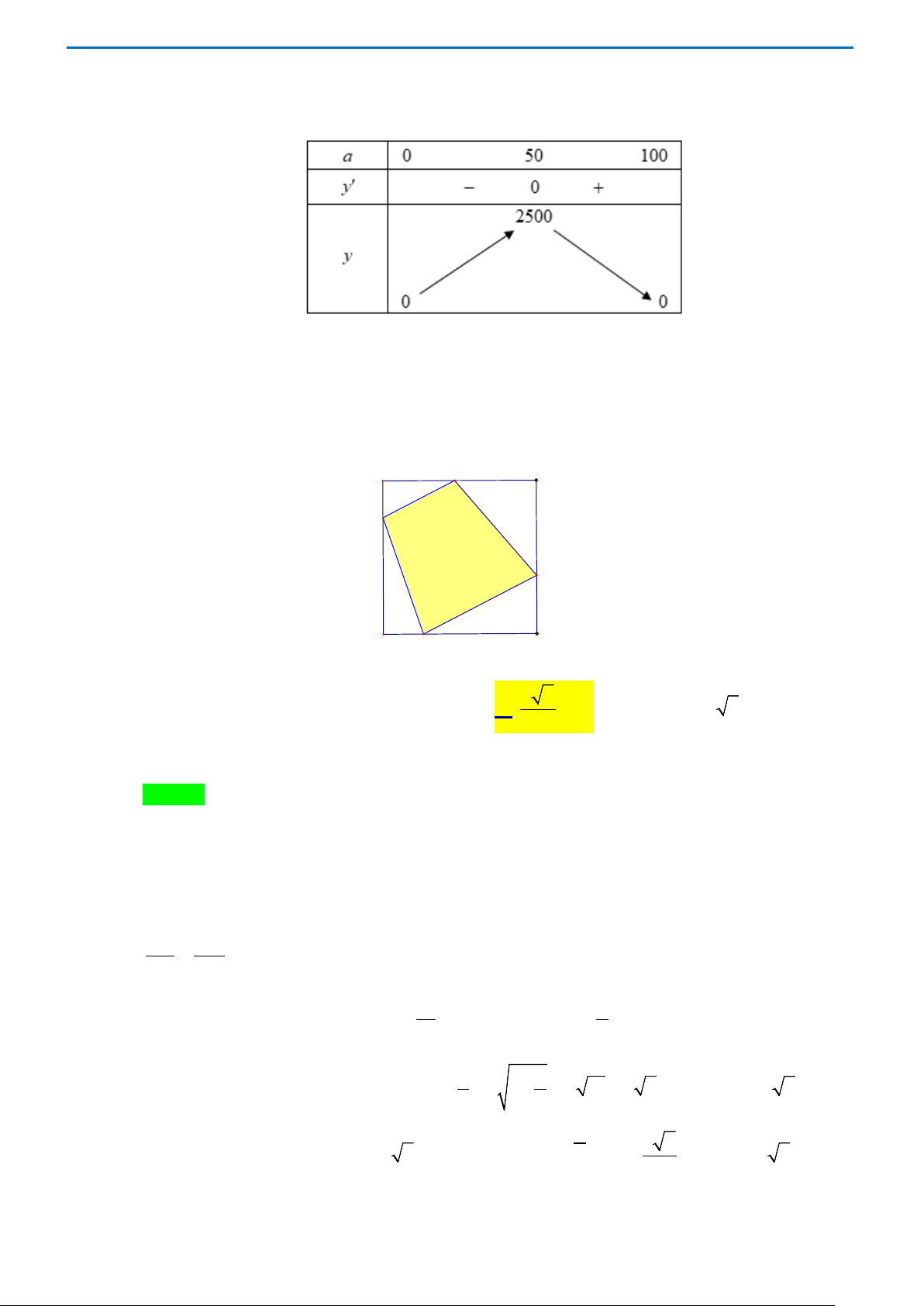
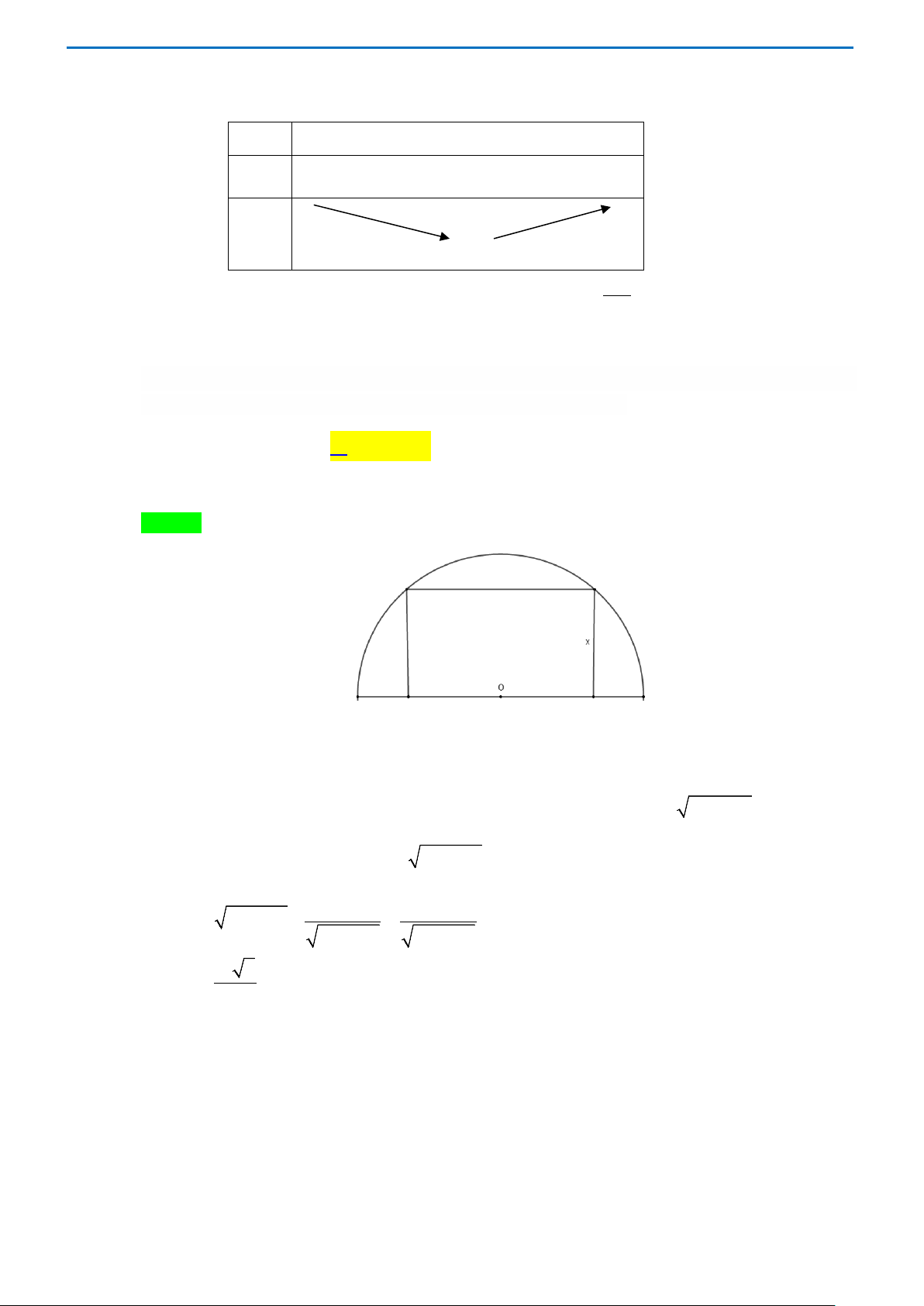
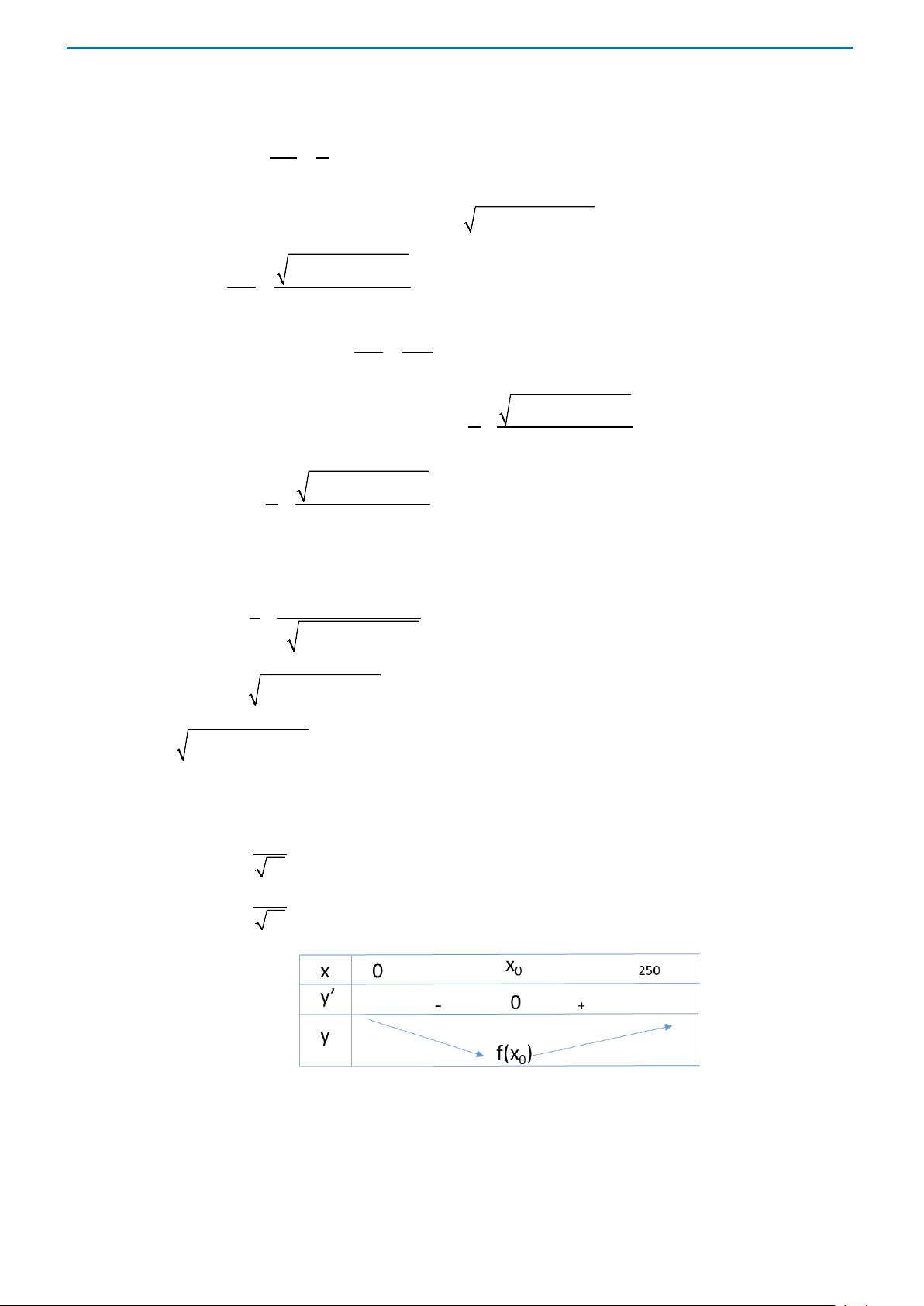
Câu 15. Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính 10 cm , biết một
cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn. A. 2 80 cm . B. 2 100 cm . C. 2 160 cm D. 2 200 cm . Lời giải Chọn B
Gọi x (cm) là độ dài cạnh hình chữ nhật không nằm trên đường kính của đường tròn (0 < x <10cm).
Khi đó, độ dài cạnh hình chữ nhật nằm trên đường kính đường tròn là 2 2 100 − x (cm) .
Diện tích hình chữ nhật: S (x) 2 = x − x ( 2 2 . 100 cm ). 2 2 2x 200 − 4x S '(x) 2 = 2 100 − x − = . 2 2 100 − x 100 − x S (x) 10 2 ' = 0 ⇔ x =
(Do 0 < x < 10 ). 2 Bảng biến thiên Trang 26
Dựa vào bảng biến thiên, ta có hàm số S (x) đạt giá trị lớn nhất bằng 100 khi 10 2 x = . 2
Vậy diện tích lớn nhất của hình chữ nhật là 2 S = 100 cm .
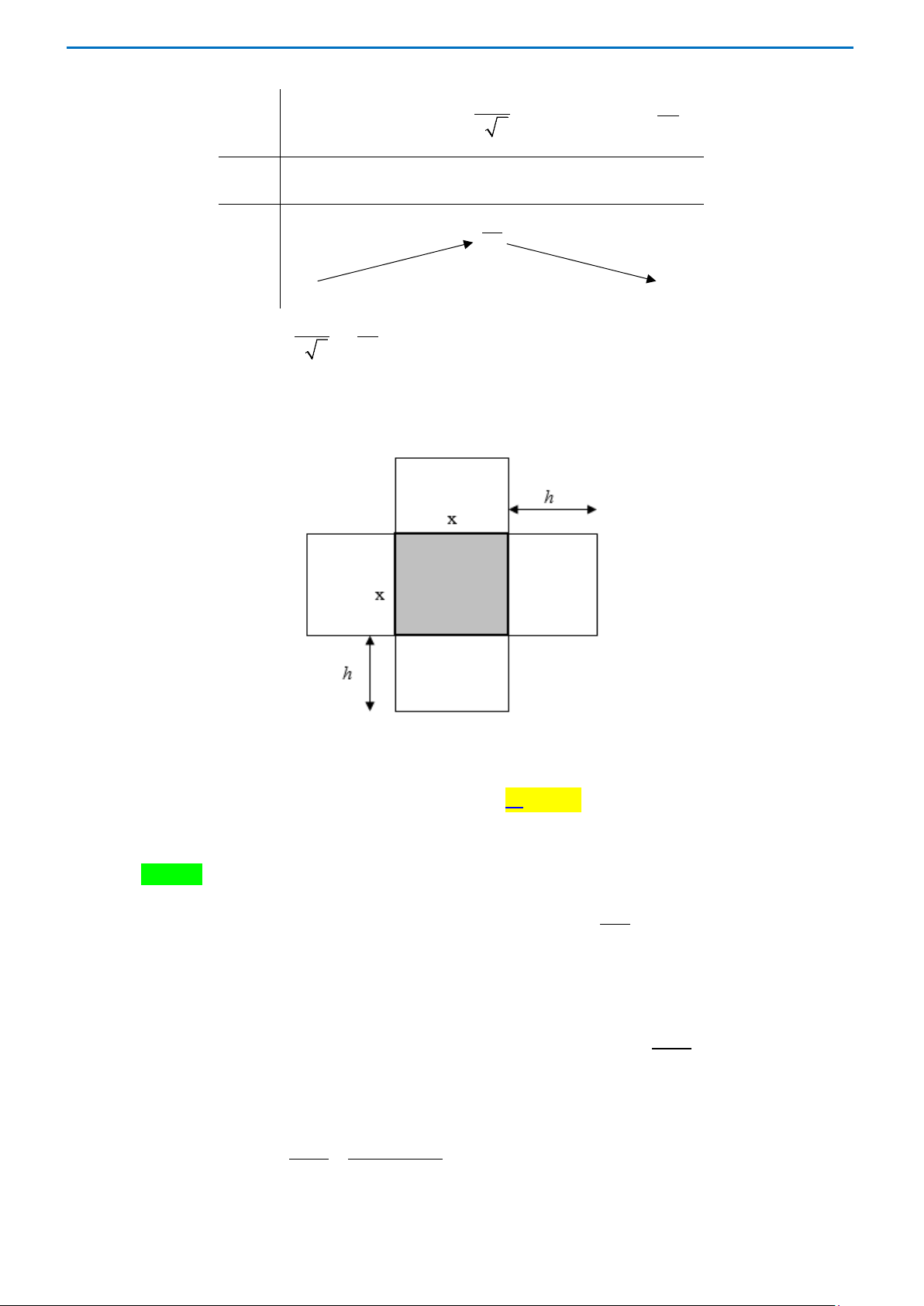
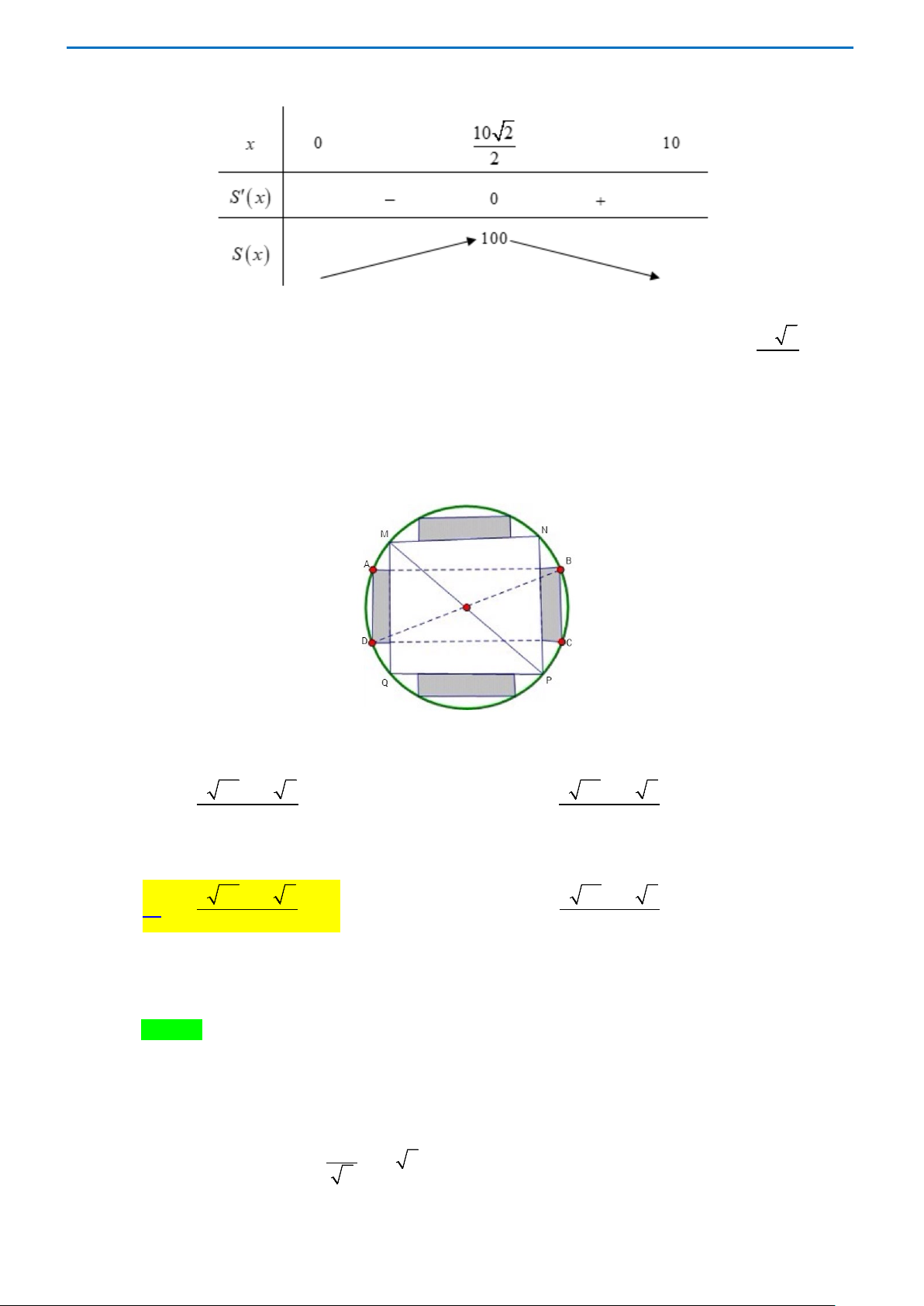
Câu 16 . Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm , cần xả thành một chiếc xà có tiết diện
ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ dưới đây. Tìm chiều rộng
x của miếng phụ để diện tích sử dụng theo tiết diện ngang là lớn nhất. A. 3 34 17 2 x − = (cm) B. 3 34 19 2 x − = (cm) 2 2 C. 5 34 15 2 x − = (cm) D. 5 34 13 2 x − = (cm) 2 2 Lời giải Chọn C
Gọi x , y lần lượt là chiều rộng, chiều dài của miếng phụ.
Diện tích sử dụng theo tiết diện ngang là S = S + xy MNPQ 4 . Cạnh hình vuông MP MN = = 20 2 (cm) . 2 Trang 27 2
Suy ra S = (20 2) + 4xy = 800+ 4xy ( ) 1
Ta có: 2x = AB − MN = AB − 20 2 < BD − 20 2 = 40 − 20 2 .
⇒ 0 < x < 20 −10 2 .
Lại có AB + AD = BD ⇔ ( x + )2 2 2 2 2 2 20 2 + y =1600 . 2
⇒ y = 800 −80 2.x − 4x . Thế vào ( ) 1 thì ta được 2 2 3 4
S = 800 + 4x 800 −80 2.x − 4x = 800 + 4 800x −80 2.x − 4x .
Xét hàm số f (x) 2 3 4
= 800x −80 2.x − 4x với x ∈(0;20 −10 2). f ′(x) 2 3
= 1600x − 240 2.x −16x .  x = 0 (l)  f ′(x)  5 34 −15 2 = 0 ⇔ x = (n)  . 2   5 34 +15 2 x = (l)  2 − Bảng biến thiên
Dựa vào bảng biến thiên, ta thấy hàm số f (x) đạt giá trị lớn nhất khi 5 34 15 2 x − = hay 2
diện tích S đạt giá trị lớn nhất khi 5 34 15 2 x − = (cm) . 2
Câu 17. Một ô tô đang chạy với vận tốc 15(m/s) thì người lái hãm phanh. Sau khi hãm phanh, ô tô chuyển
động chậm dần đều với vận tốc v(t) = 5
− t +15(m/s) trong đó t là khoảng thời gian tính bằng
giây kể từ lúc bắt đầu hãm phanh. Hỏi từ lúc hãm phanh đến khi dừng hẳn, ô tô còn di chuyển được bao nhiêu mét ? A. 22,5m . B. 45m . C. 15m . D. 90m . Trang 28 Lời giải Chọn A
Khi dừng hẳn thì v(t) = 5
− t +15 = 0 ⇔ t = 3 .
Từ lúc hãm phanh đến khi dừng lại, xe di chuyển được: 3 3 3 5 2
s = v(t)dt = ( 5
− t +15)dt = (− t +15t) = 22,5m ∫ ∫ . 2 0 0 0
Câu 18. Một vật chuyển động với gia tốc 2 2
a(t) = 3t + t (m/s ). Vận tốc ban đầu của vật là 2(m/s). Hỏi
vận tốc của vật là bao nhiêu sau khi chuyển động với gia tốc đó được 2s. A. 8m/s . B. 12m/s . C. 16m/s . D. 10m/s . Lời giải Chọn B Vận tốc chuyển động 2 3 1 2
v(t) = a(t)dt = (3t + t)dt = t + t + C. ∫ ∫ 2
Chọn gốc thời gian lúc bắt đầu tăng tốc thì 3 1 2
v(0) = 2 ⇒ C = 2 ⇒ v(t) = t + t + 2. 2
Khi đó tại thời điểm 2s thì v(2) =12m/s.
Câu 19. Cho mạch điện xoay chiều RLC mắc nối tiếp có R thay đổi. Biết điện trở cuộn cảm Z = Ω L 80 ( )
, điện trở của tụ điện là Z =
Ω và hiệu điện thế hai đầu mạch là u = U cos100πt V . Để 0 ( ) C 200 ( )
công suất tiêu thụ của mạch cực đại thì giá trị của R bằng A. 120 (Ω). B. 50 (Ω). C. 100 (Ω). D. 200 (Ω) . Lời giải Chọn A 2 2 U RU
Công suất tiêu thụ của mạch: 2
P = RI = R ⋅ = . 2 2 Z
R + (Z − Z L C )2 2
U (Z − Z − R L C )2 2   ′( P = . R) 2
R + (Z − Z L C ) 2 2  
P′ = 0 ⇔ R = Z − Z = Ω . R L C 120 ( ) ( ) Ta có bảng biến thiên: Trang 29
Suy ra công suất tiêu thụ của mạch cực đại thì R =120 (Ω).
Câu 20. Cho mạch điện xoay chiều RLC mắc nối tiếp có R thay đổi. Biết điện trở cuộn cảm Z =
Ω , điện trở của tụ điện là Z =
Ω và hiệu điện thế hai đầu mạch là C 40( ) L 100 ( )
u =120 2 cos100πt (V ) . Điện trở R phải có giá trị là bao nhiêu để công suất tiêu thụ của mạch
đạt cực đại và giá tri cực đại của công suất là bao nhiêu?
A. R = 60 (Ω), P =120 W
R =120 Ω , P = 60 W max ( ). B. ( ) max ( ).
C. R = 40 (Ω), P =180 W
R =120 Ω , P =180 W max ( ). D. ( ) max ( ). Lời giải Chọn A 2 2 U RU
Công suất tiêu thụ của mạch: 2
P = RI = R ⋅ = . 2 2 Z
R + (Z − Z L C )2 2
U (Z − Z − R L C )2 2   ′( P = . R) 2
R + (Z − Z L C ) 2 2  
P′ = 0 ⇔ R = Z − Z = Ω . R L C 60 ( ) ( ) Ta có bảng biến thiên:
Suy ra công suất tiêu thụ của mạch cực đại P =120 W tại R = 60 (Ω) . max ( )
Câu 21: Thể tích V của 1kg nước ở nhiệt độ t (t nằm giữa 0°C đến 30°C) được cho bởi công thức 2 3 V = − t + t − t ( 3 999,87 0,06426 0,0085043
0,0000679 cm ) . Nhiệt độ t của nước gần nhất với
giá trị nào dưới đây thì khối lượng riêng của nước là lớn nhất? A. 0°. B. 4 − ° . C. 30° . D. 4°. Lời giải Trang 30 Chọn D Ta có: V ′(t) 2 = 0
− ,06426 + 2.0,0085043t − 3.0,0000679t .  ≈ ∉ ° ° V ′(t) t 79,53138 (0 ;30 ) = 0 ⇔  . t ≈ 3,9665 Bảng biến thiên:
Dựa vào bảng biến thiên ta có khối lượng riêng lớn nhất của vật khi thể tích nhỏ nhất lúc vật có
nhiệt độ xấp xỉ gần bằng 4°C .
Nhận xét: Ta đã biết trong môn vật lý lớp 7, khối lượng riêng của nước lớn nhất khi thể tích
tương ứng của nước là nhỏ nhất. 4  
Câu 22: Thể tích nước của một bể bơi sau t phút bơm được tính theo công thức ( ) 1 3 = 30 t V t t − 100 4   
(0 ≤ t ≤ 90) . Tốc độ bơm nước tại thời điểm t được tính bởi v(t) =V′(t) . Trong các khẳng định
sau, khẳng định nào đúng.
A. Tốc độ bơm giảm từ phút 60 đến phút thứ 90.
B. Tốc độ bơm luôn giảm.
C. Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
D. Cả A, B, C đều sai. Lời giải Chọn A Xét hàm 9 2 1 3 V ′ = t −
t (0 ≤ t ≤ 90) . 10 100 9 3 t = 0 2 V ′′ = t −
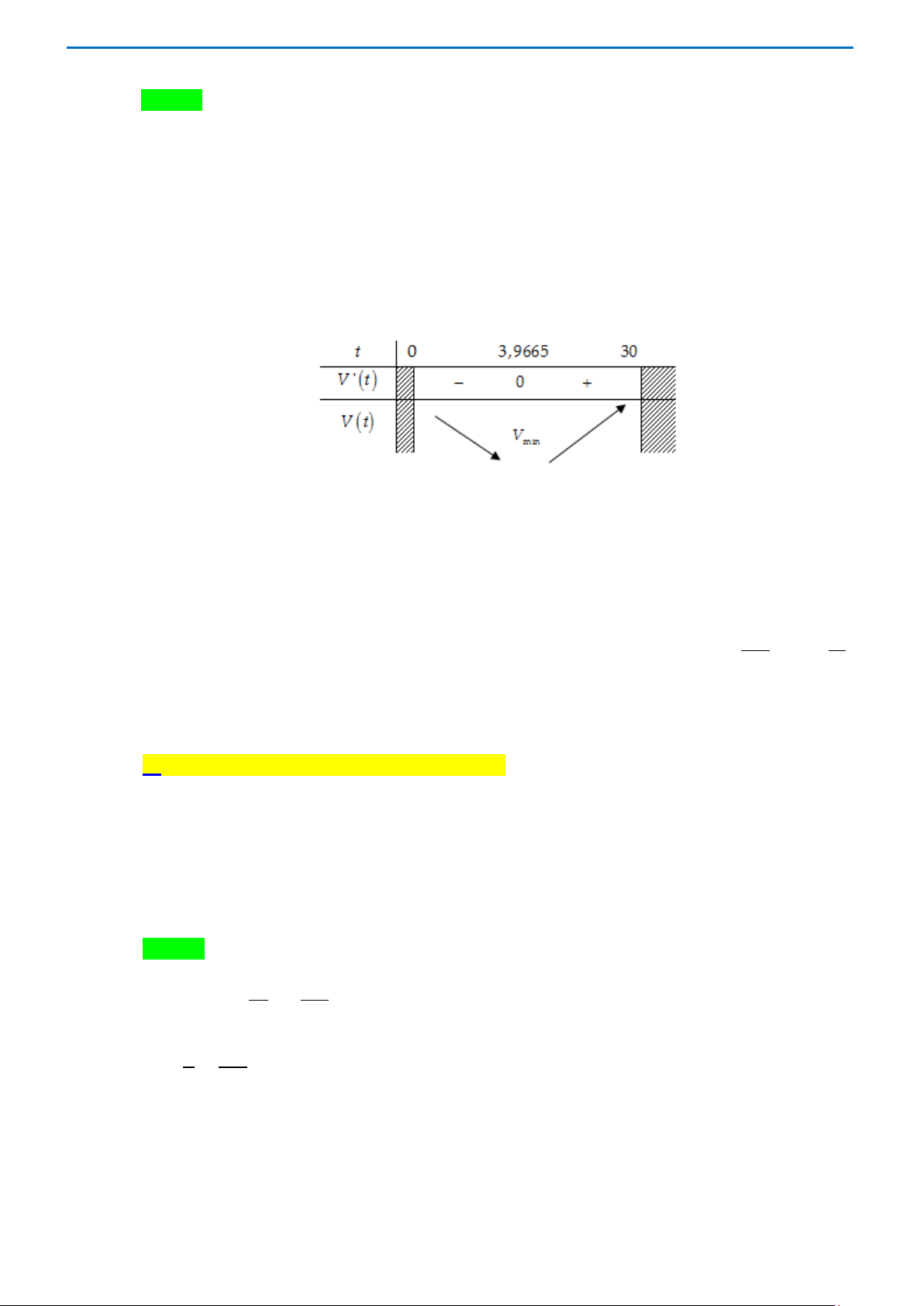
t ⇒ V ′′ = 0 ⇔ . 5 100  t = 60 Bảng biến thiên: Trang 31 t 0 60 90 V'' + 0 - V'
Dựa vào bảng biến thiên, ta có hàm số V  đồng biến trên(0;60) , nghịch biến trên(60;90) .
Câu 23. Công ty XDPL muốn làm một đường ống dẫn khí từ một địa điểm A trên bờ biển đến một điểm
B trên một hòn đảo. Khoảng cách ngắn nhất từ điểm B đến bờ biển là 6km . Giá để xây lắp mỗi
km đường ống trên bờ là 50.000 USD , còn xây lắp dưới nước là 130.000 USD . B′ là điểm trên
bờ biển sao cho BB′ vuông góc với bờ biển. Khoảng cách từ A đến B′ là 9km . đảo B biển 6km B' 9km bờ biển A
Hỏi vị trí điểm M trên bờ biển cách A bao xa để chi phí xây lắp đường ống từ A qua M rồi
đến B là ít tốn kém nhất? A. 9km . B. 6km . C. 0km . D. 6.5km . Lời giải Chọn D Đặt x B M  km. Khi đó 2
BM = x + 36, AM = 9 − x .
Chi phí xây dựng đường ống là 2
S(x) =130000 x + 36 + 50000(9 − x) (USD) .   Hàm 13x
S(x) xác định, liên tục trên [0;9] và S (′x) =10000 − 5 . 2  x + 36  2 2  = + 2 169x 25(x 36) 5
S (′x) = 0 ⇔ 13x = 5 x + 36 ⇔  ⇔ x = . 0 ≤ x ≤ 9 2  5
S(0) 1.230.000; S  = = 1.170.000;S(9) ≈   1.406.165 .  2 
Do đó chi phí thấp nhất khi 5
x = . Vậy M cần cách A một khoảng 6,5km . 2
Câu 24. Một điểm C trên hòn đảo có khoảng cách ngắn nhất đến bờ biển là 60km , B là điểm trên bờ
biển sao cho CB vuông góc với bờ biển . Khoảng cách từ A trên bờ biển đến B là 100km . Để Trang 32
tham dự buổi họp nhóm Strong Team Toán VD – VCD ngày 28/6/2019 , thầy Quý phải tính toán
vị trí diễn ra cuộc họp tại địa điểm G trên đoạn AB để tổng chi phí đi lại của cả hai nhóm các
thầy cô là ít nhất. Biết nhóm của thầy Quý đi từ C theo đường biển chi phí đi là 500 nghìn mỗi
km, nhóm cô Thêm đi từ vị trí A đi trên đất liền mỗi km chi phí là 300 nghìn. Hỏi thầy tìm được
vị trí điểm G cách B bao xa? A. 40km . B. 60km . C. 55km . D. 45km . Lời giải
Đặt x = BG (km), x ∈[0;100] . Khi đó 2
GC = x + 3600, AG =100 − x .
Chi phí đi lại của hai nhóm người để đến vị trí G là 2
S(x) = 500 x + 3600 + 300(100 − x) ( nghìn đồng). Hàm S 500x
(x) xác định, liên tục trên [0;100] và S (′x) = − 300 . 2 x + 3600 2 2  = + 2 25x 9(x 3600)
S '(x) = 0 ⇔ 5x = 3 x + 3600 ⇔  ⇔ x = 45. 0 ≤ x ≤ 100
S(0) = 60000; S(45) = 54000;S(100) ≈ 58310 .
Do đó chi phí thấp nhất khi x = 45 . Vậy G cần cách B một khoảng 45km .
Câu 25. Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy 4
A trong một giờ. Chi phí
để bảo trì, vận hành một máy trong mỗi lần in là 50000 đồng. Chi phí in ấn của n máy chạy
trong một giờ là 20(3n + 5) nghìn đồng. Hỏi nếu in 50000 bản in khổ giấy 4
A thì phải sử dụng
bao nhiêu máy để thu được nhiều lãi nhất? A. 4 máy. B. 7 máy. C. 6 máy. D. 5 máy. Lời giải Chọn D
Gọi số giờ cần in là x thì n máy in được 4000. .
n x bản in trong x giờ. Ta có 25 4000. .
n x = 50000 ⇒ nx = . 2
Chi phí của n máy chạy trong x giờ là 20x(3n + 5) nghìn đồng.
Chi phí để bảo trì n máy là 50n nghìn đồng.
Tổng chi phí là f (n) = x( n + ) 1250 20 3
5 + 50n = 60xn +100x + 50n = 750 + + 50n . n Trang 33 f ′(n) 1250 = −
+ 50 , f ′(n) = 0 ⇔ n = 5. 2 n Ta có bảng biến thiên
Để thu được tiền lãi cao nhất cần chi phí thấp nhất, vậy n = 5 thỏa mãn yêu cầu bài toán.
Câu 26. Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nhiên liệu
làm vỏ lon là thấp nhất, tức là diện tích toàn phần của hình trụ nhỏ nhất. Muốn thể tích của khối
trụ đó bằng V và diện tích toàn phần của hình trụ nhỏ nhất thì nhà thiết kế phải thiết kế hình trụ
có bán kính bằng bao nhiêu? A. V . B. V V 3 . C. V . D. 3 . 2π 2π π π Lời giải Chọn B
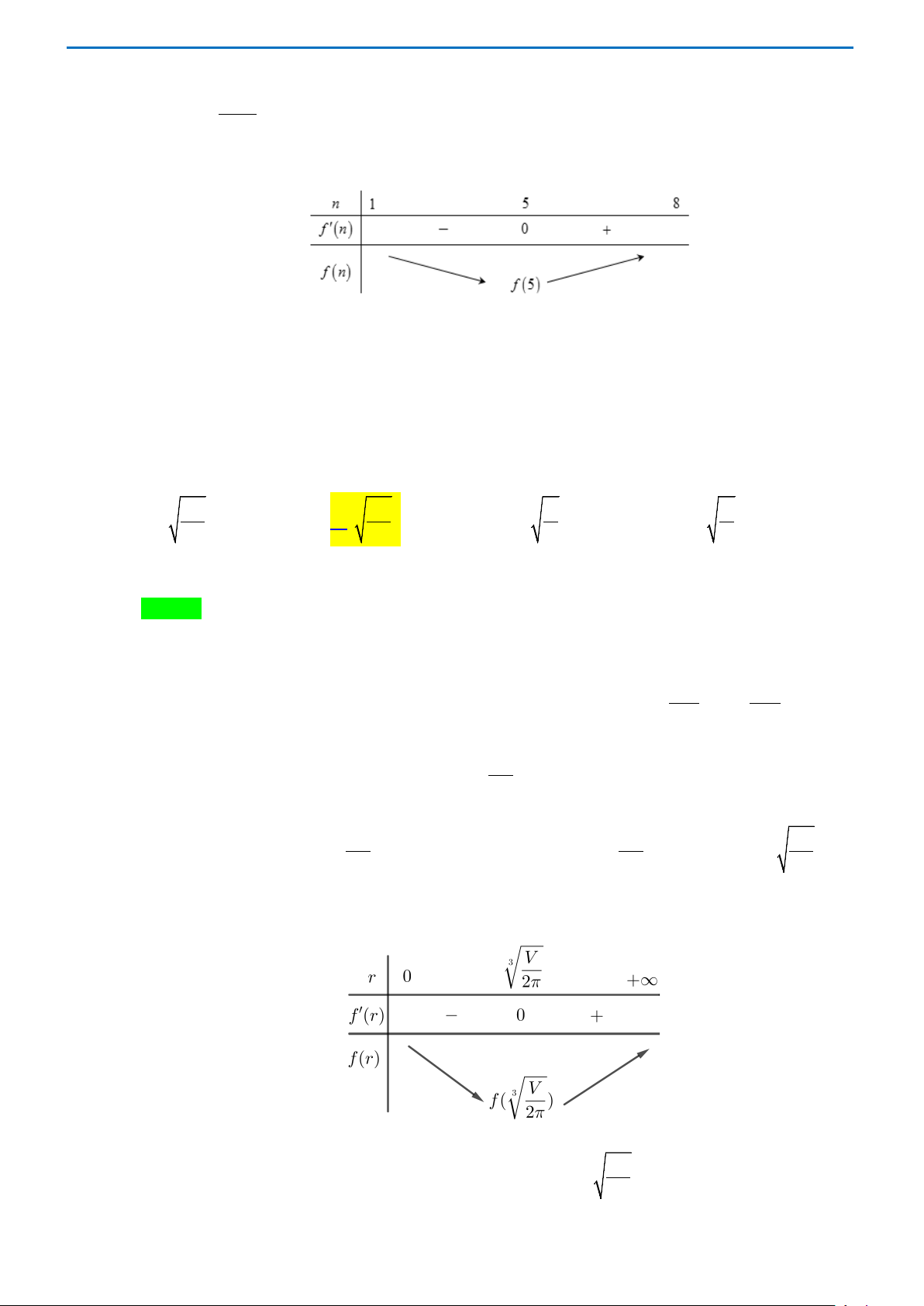
Gọi hình trụ có chiều cao h , độ dài đường sinh l , bán kính đáy r . Ta có: 2
S = S + S = π r + π rl . Mặt khác 2 V V
V = π r h ⇒ h = ⇒ l = . tp 2 day xq 2 2 ( )1 2 2 π r π r Thay vào công thức ( ) 1 ta được: 2 2V S = π r + . tp 2 r Xét hàm số ( ) 2 2 = 2 V f r π r +
với r > 0 . Ta có ′( ) 2 = 4 V π − ; ′ = 0 V f r r f r ⇔ r = . 2 ( ) 3 r r 2π Bảng biến thiên:
Từ bảng biến thiên ta thấy f (r) đạt giá trị nhỏ nhất khi V = 3 r . 2π Trang 34 Hay S V r =
tp đạt giá trị nhỏ nhất khi 3 . 2π
Câu 27. Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định
được số lượng vi khuẩn tăng theo thời gian bởi qui luật ( ) 100 =1000 t N t + (con vi khuẩn), 2 100 + t
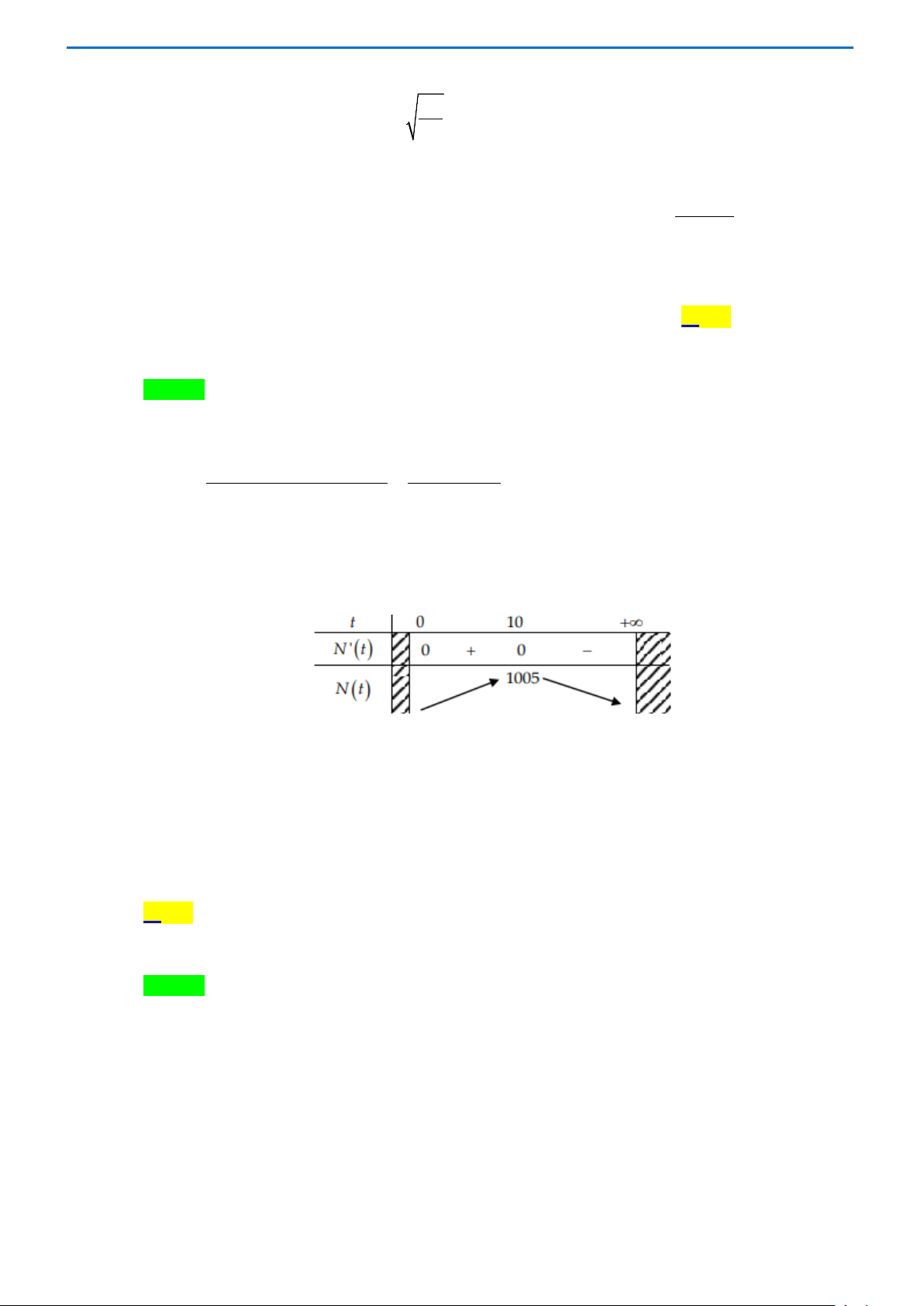
trong đó t là thời gian (đơn vị giây). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào,
số lượng vi khuẩn tăng lên lớn nhất là bao nhiêu? A. 0 . B. 1. C. 10 − . D. 10. Lời giải Chọn D
Ta có tốc độ phát triển của đàn vi khuẩn tại thời điểm t là: 100( 2
100 + t ) −100t (2t) 2 2 N′(t) − = 100 100t ( = ( t ∀ > 0) . 2 100 + t ) (100+t )2 2 Xét N′(t) = 0 2
⇔ t =100 ⇔ t =10 > 0 .
Lập bảng biến thiên ta được:
Dựa vào bảng biến thiên, ta kết luận max N (t) = N (10) =1005.
Câu 28. Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: nếu trên mỗi đơn vị diện tích
của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng Q(n) = 480 − 20n (gam).
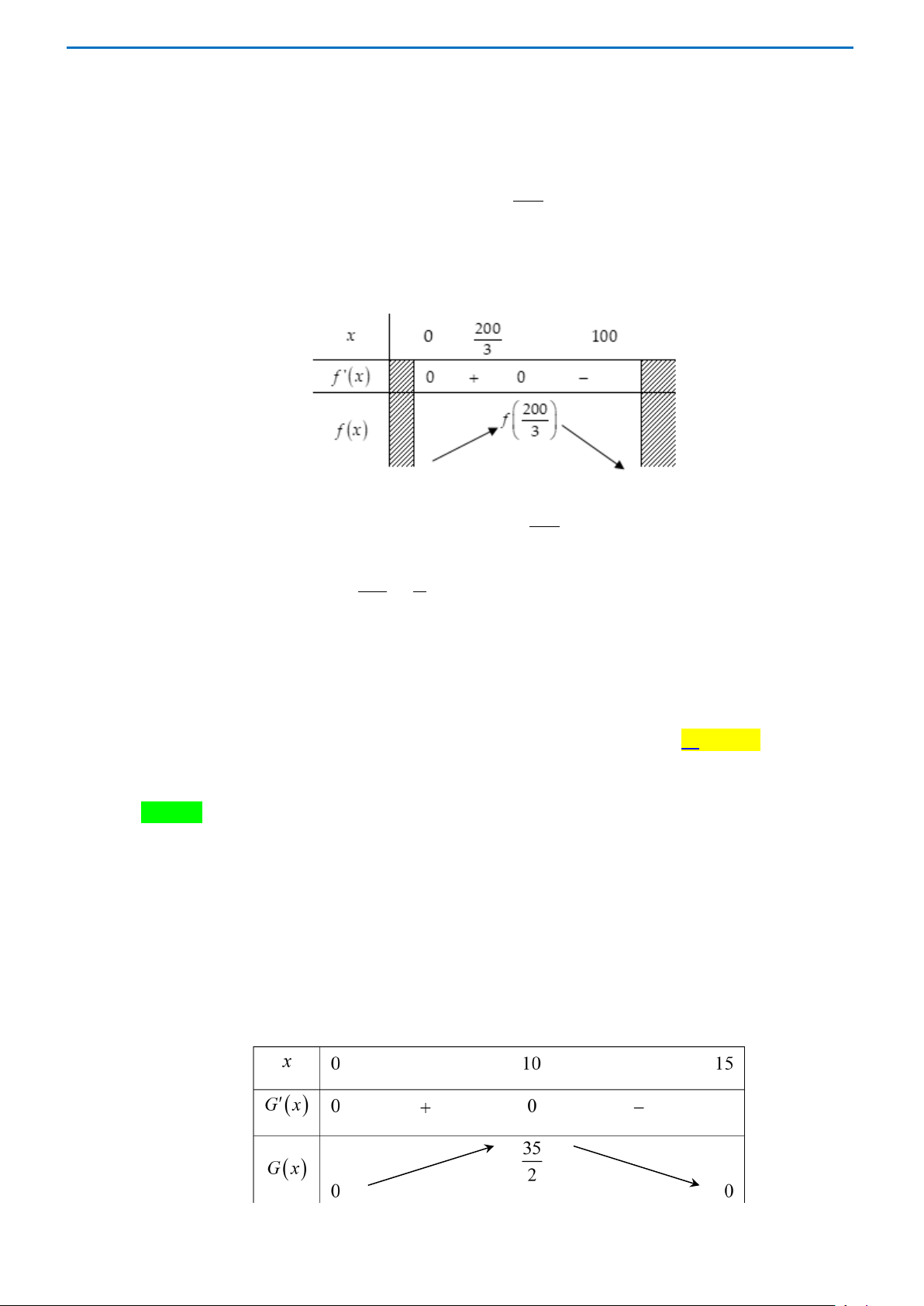
Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất? A. 12. B. 14. C. 10. D. 18. Lời giải Chọn A
Mỗi con các cân nặng trung bình sau một vụ là: Q(n) = 480 − 20n
Khi đó với n con cá thì cân nặng của chúng là:
P(n) = nQ(n) 2
= 480n − 20n ⇒ P′(n) = 480 − 40n.
Xét P′(n) = 0 ⇔ n =12 . Khi đó ta có bảng biến thiên: Trang 35
Dựa và bảng biến thiên, ta suy ra max P(n) = P(12) = 2880 ( với n > 0 ).
Câu 29. Đốt cháy các hidrocacbon của dãy đồng đẳng nào dưới đây thì tỉ lệ mol H O : mol CO giảm 2 2
dần khi số cacbon tăng dần ? A. Ankan. B. Anken. C. Ankin. D. Ankylbenzen. Lời giải Chọn A
Công thức tổng quát của một hidrocacbon là C H
với k là số liên kết π trong phân tử . n 2n+2−2k
Phương trình phản ứng cháy là: , o xt t C H +  → + + − + − O nCO n k H O n n k 1 2 2 2 2 2 ( ) 2 n + − + − Ta có H O n 1 k n 1 k 2 =
. Xét hàm số f (n) * = ,n∈ N . n n n 2 CO
Ta có f ′(n) k −1 =
. Theo giả thiết ta có f (n) là hàm nghịch biến nên f ′(n) < 0 2 n k −1 ⇔
< 0 ⇔ k −1< 0 ⇔ k <1 k∈ 
→k = 0 ⇒ CTTQ :C H . + ankan n n : 2 2 2 n
Câu 30. Cho phương trình phản ứng tạo thành Nitơ (IV) Oxit từ Nitơ ddiooxxit và Oxy là , o dk t , 2 xt
NO + O →
← 2NO . Biết rằng đây là một phản ứng thuận nghịch . Giả sử x, y lần lượt 2 2
là nồng độ phần trăm của khí NO và O tham gia phản ứng. Biết rằng tốc độ phản ứng hóa học 2
của phản ứng trên được xác định 2
v = kx y , với k là hằng số của tốc độ phản ứng. Để tốc độ phản
ứng xảy ra nhanh nhất thì tỉ số giữa x là ? y A. 1 . B. 2 . C. 1 . D. 3. 2 3 Lời giải Chọn B Ta có 2 2
v = kx y = kx (100 − x) (do x + y =100%),0 < x <100 .
Xét hàm số f (x) 2 = kx ( − x) = k ( 2 3 100 100x − x ) . Trang 36
Bài toán trở thành tìm max f (x) = ? . x ( ∈ 0;100) x = 0(ktm) Ta có: f (x) 2
= k 200x − 3x , f (x) = 0  ′ ′ ⇔    200 . x = ∈(0;100)  3
Lập bảng biến thiên ta có:
Dựa vào bảng biến thiên ta suy ra f (x)  200 max f  =   . x ( ∈ 0;100)  3  Và do đó ta có 100 =100 x y − x = ⇒ = 2. 3 y
Câu 31. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G (x) 2
= 0,035x (15 − x) , trong đó
x là liều lượng thuốc được tiêm cho bệnh nhân ( x được tính bằng miligam). Tính liều lượng
thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất. A. x = 8. B. x = 5. C. x =15. D. x =10 . Lời giải Chọn D
Điều kiện x ∈[0;15] (vì độ giảm huyết áp không âm).
Bài toán trở thành: Tìm x ∈[0;15] để G(x) đạt giá trị lớn nhất.
Theo giả thiết G (x) = ( 2 3
0,035 15x − x ) ⇒ G′(x) = ( 2
0,035 30x − 3x ) . x = Cho G′(x) 0 = 0 ⇔ 
. Khi đó ta có bảng biến thiên như sau x =10 Trang 37
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là x =10 (mg).
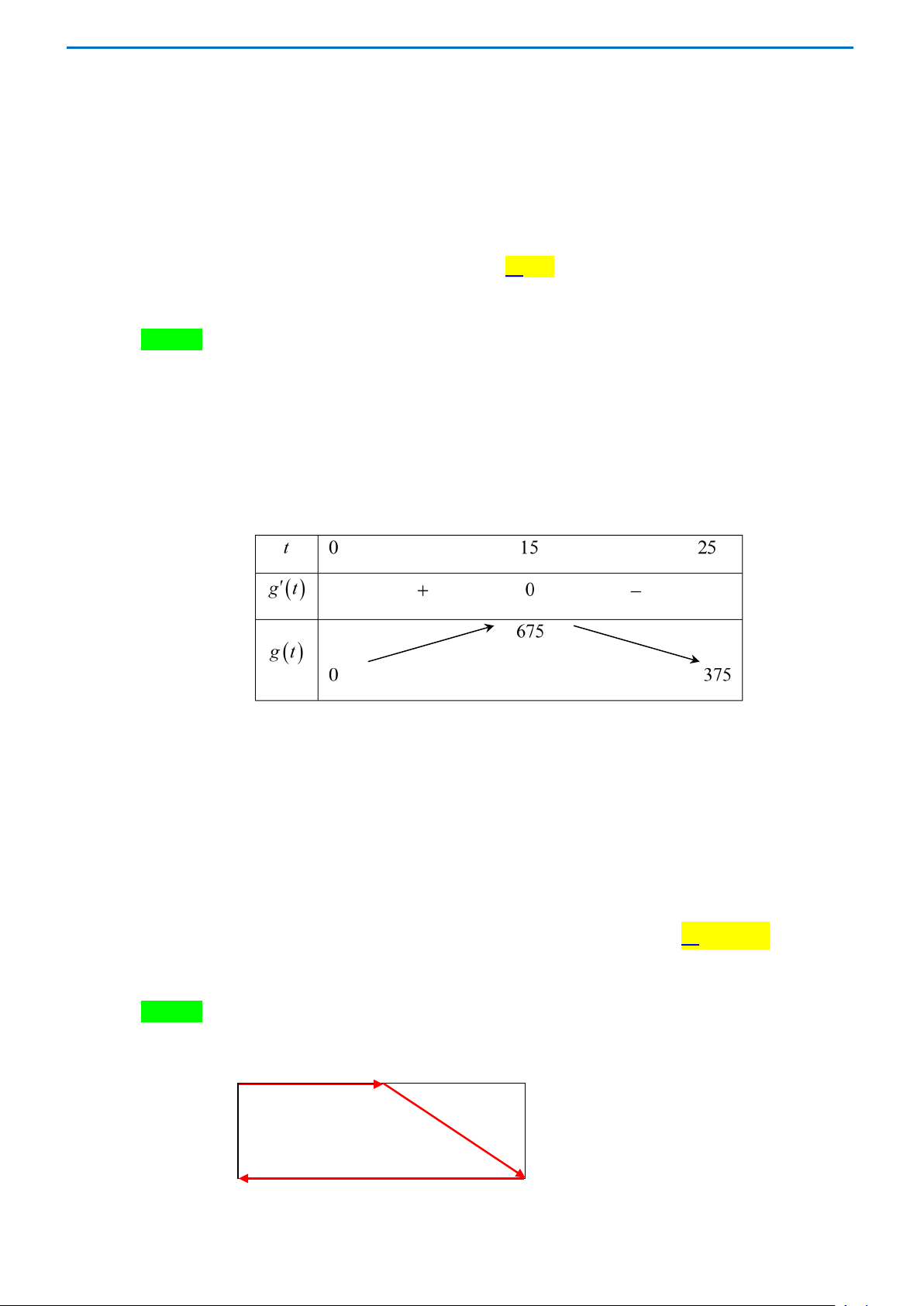
Câu 32. Các chuyên gia Y-tế ước tính số người nhiễm virus Zika kể từ ngày xuất hiện bệnh nhân đầu tiên
đến ngày thứ t là f (t) 2 3
= 45t − t ,(t = 0,1,2,...,25) . Nếu coi f (t) là một hàm xác định trên đoạn
[0;25] thì f '(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t . Tốc độ truyền
bệnh sẽ lớn nhất vào ngày thứ mấy? A. 20 . B.10. C. 15. D. 5. Lời giải Chọn C Ta có f (t) 2 3
= 45t − t ⇒ f (t) 2 ' = 90t − 3t . Đặt g (t) 2
= 90t − 3t . Bài toán trở thành: Tìm t ∈[0;25] để g (t) đạt giá trị lớn nhất.
g '(t) = 90 − 6t . Cho g '(t) = 0 ⇔ t =15. Lập bảng biến thiên
Vậy tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ 15.
Câu 33. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng 70 m và chiều dài 250 m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc
cả hai) khi phải thực hiện lộ trình xuất phát từ A đến C và đua xe đạp tới D như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường x ) thì vận động viên nên nhảy xuống để tiếp tục
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là 5 m/s; 1,5m/s và 10 m/s. A. 139,52m. B. 129,52m. C.109,52m. D.119,52m. Lời giải Chọn D
A x B (250 − x)m 70m
D 250m C Trang 38
Gọi B là vị trí VĐV kết thúc phần chạy điền kinh và AB = x(0 < x < 250) AB x Khi đó ta đó t = = 1
là thời gian đi từ A đến B v 5 1
Đồng thời quãng đường bơi chính là 2 2
BC = 70 + (250 − x) 2 BC 70 + (250 − x)2 Suy ra t = =
là thời gian bơi từ B đến C 2 1,5 1,5
Thời gian đua xe đạp là CD 250 t = = = 25s 3 10 10 2 x 70 + (250 − x)2
Tổng thời gian của VĐV là T = t + t + t = + + 25 1 2 3 5 1,5 2 x 70 + (250 − x)2
Xét hàm f (x) = +
+ 25 , (0 < x < 250) . 5 1,5
Bài toán trở thành tìm min f (x) x ( ∈ 0,250) − Ta có 1 2(250 x) f '(x) = − 5 2 3 70 + (250 − x)2 2
f '(x) = 0 ⇔ 3 70 + (250 − x)2 −10(250 − x) = 0 2
⇔ 3 70 + (250 − x)2 =10(250 − x) ⇔ ( − x)2 2 91 250 = 9.70  210 x = 250 − (= x )  0 91 ⇔   210 x = 250 + (loai)  91
Dựa vào BBT min f (x) = f (x ≈119,52 m 0 ) ( ) x ( ∈ 0,250)
Câu 34. Trong nội dung thi điền kinh, bơi lội và đua xe đạp phối hợp được diễn ra tại một hồ bơi có
chiều rộng 50m và chiều dài 250 m. Một vận động viên cần chạy phối hợp với bơi (bắt buộc cả
hai) khi phải thực hiện lộ trình xuất phát từ A đến C và đua xe đạp tới D như hình vẽ. Hỏi
rằng sau khi chạy được bao xa (quãng đường x ) thì vận động viên nên nhảy xuống để tiếp tục Trang 39
bơi về đích nhanh nhất ? Biết rằng vận tốc của vận động viên khi chạy trên bờ, khi bơi và đua
xe lần lượt là 5 m/s; 1,5m/s và 10m/s. A. 109,8 m. B. 105,8 m. C. 106,8 m. D.107,8 m. Lời giải Chọn D
A x B (250 − x)m 50m
D 250m C
Gọi B là vị trí VĐV kết thúc phần chạy điền kinh và AB = x(0 < x < 250) Khi đó ta đó AB x t =
= là thời gian đi từ A đến B 1 v 5 1
Đồng thời quãng đường bơi chính là 2 2
BC = 50 + (250 − x) 2 BC 50 + (250 − x)2 Suy ra t = =
là thời gian bơi từ B đến C 2 1,5 1,5
Thời gian đua xe đạp là CD 250 t = = = 25s 3 10 10 2 x 50 + (250 − x)2
Tổng thời gian của VĐV là T = t + t + t = + + 25 1 2 3 5 1,5 2 x 50 + (250 − x)2
Xét hàm f (x) = +
+ 25 , (0 < x < 250) 5 1,5
Bài toán trở thành tìm min f (x) x ( ∈ 0,250) − Ta có 1 2(250 x) f '(x) = − 5 2 3 50 + (250 − x)2 2
f '(x) = 0 ⇔ 3 50 + (250 − x)2 −10(250 − x) = 0 2
⇔ 3 50 + (250 − x)2 =10(250 − x) ⇔ ( − x)2 2 91 250 = 9.50 Trang 40  150 x = 250 − (= x )  0 91 ⇔   150 x = 250 + (loai)  91
Dựa vào BBT min f (x) = f (x ≈107,8 m 0 ) ( ) x ( ∈ 0,250)
Câu 35. Cho một viên gạch men có dạng hình vuông OABC như hình vẽ. Sau khi tọa độ hóa, ta có O(0;0), A(0 ) ;1 , B(1; )
1 , C (1;0) và hai đường cong lần lượt là đồ thị hàm số 3 y = x và 3 y = x
. Tính diện tích của phần không được tô đậm trên viên gạch men. y A B x O C A. 1 . B. 5 . C. 4 . D. 1 . 3 4 5 2 Lời giải Chọn D
Diện tích hình vuông có cạnh bằng 1 là 2 S =1 =1.
Gọi S là diện tích phần tô đậm. 1 1 1 1 4 4    3 x  1 Ta có S = ∫(3 3 x − x ) 1 3 3 3
dx = ∫ x − x dx =  x −  = . 1    4 4  0 2 0 0
Vậy diện tích phần không được tô đậm trên viên gạch men bằng 1 1
S − S =1− = . 1 2 2
Câu 36. Người ta làm một cái lu đựng nước bằng cách cắt bỏ 2 chỏm của một khối cầu có bán kính 5 dm
bằng 2 mặt phẳng vuông góc với đường kính và cách tâm khối cầu 3 dm . Tính thể tích của chiếc lu. Trang 41 3 dm 5 dm 3 dm A. π ( 3 100 41 dm ). B. π ( 3 132 dm ) . C. π ( 3 43 dm ). D. π ( 3 dm ) . 3 Lời giải Chọn B y 5 x -5 -3 O 3 5 -5
Đặt hệ trục với tâm O là tâm của mặt cầu, đường thẳng đứng là Ox , đường ngang là Oy .
Ta có phương trình của đường tròn lớn là 2 2 x + y = 25 .
Thể tích cái lu là thể tích của vật tròn xoay tạo thành khi quay hình giới hạn bởi các đường cong 2
y = 25 − x , trục Ox , đường thẳng x = 3,
− x = 3 quay quanh Ox . 3  
V = π ∫ (25− x ) 3 x 3
2 dx = π 25x − =   132π ( 3 dm ) . − −  3  3 3
Câu 37. Một cái trống trường có bán kính các đáy là 30 cm , thiết diện vuông góc với trục và cách đều
hai đáy có diện tích là π ( 2
1600 cm ) , chiều dài của trống là 1m . Biết rằng mặt phẳng chứa trục
cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu? A. 3 425,2 dm . B. 3 425,2 mm . C. 3 425,2 cm . D. 3 425,2m . Lời giải Chọn A Trang 42
Ta có chọn hệ trục Oxy như hình vẽ.
Thiết diện vuông góc với trục, cách đều hai đáy là hình tròn có bán kính r có diện tích là π ( 2 1600 cm ) , nên 2
π r = 1600π ⇒ r = 40cm .
Ta có: Parabol nhận Oy làm trục đối xứng nên phương trình Parabol có dạng: 2
y = ax + b .
Parabol có đỉnh I (0;40) và qua A(50;30).  1 b  = 40 a = −
Thay tọa độ I và A vào phương trình Parabol:  ⇔  250 2 50  a + b = 30 b  = 40
Nên Parabol có phương trình 1 2 y = − x + 40 250 50 2 Thể tích của trống là  1 2 V π x 40 = − + ∫ 406000   dx 3 = π. cm 3 ≈ 425,2dm 3 −  250 50 
Câu 38. Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn 28cm , trục nhỏ 25cm . Biết cứ 3
1000cm dưa hấu sẽ làm được cốc sinh tố giá 20000 đồng. Hỏi từ quả dưa hấu trên có thể
thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể. A. 180000 đồng. B. 183000 đồng. C. 185000 đồng. D. 190000 đồng. Lời giải Chọn B Trang 43 2 2
Đường elip có trục lớn 28cm , trục nhỏ 25cm có phương trình x y + = 1 2 2 14  25   2    2 2     2 2 25 ⇔ = 25 x   1 x y − ⇔ y = ± 1− . 2  2   14  2 2 14 2 14  2  2 14 2    x
Do đó thể tích quả dưa là 25 25 = π  1 x V −  dx ∫ = π   ∫ 1− dx 2   2  2  −  14 − 2 14 14   14  14 2 3  25   x  2 π = π ⋅ 25 56 8750    x − π   = ⋅ 3 = cm . 2    2   3.14   2  3 3 14 − π
Do đó tiền bán nước thu được là 8750 .20000 ≈183259 đồng. 3.1000
Câu 39. Một bình hoa dạng khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm
số y = −sin x + 2 và trục Ox (tham khảo hình vẽ bên dưới). Biết đáy bình hoa là hình tròn có
bán kính bằng 2 dm , miệng bình hoa là đường tròn bán kính bằng 1.5 dm . Bỏ qua độ dày của
bình hoa, Thể tích của bình hoa gần với giá trị nào trong các giá trị sau đây? A. 100 3 dm . B. 104 3 dm . C. 102 3 dm . D. 103 3 dm . Lời giải Chọn D
Giả sử thiết diện qua trục của bình hoa miêu tả như hình vẽ bên dưới. Chọn hệ trục tọa độ Oxy
thỏa mãn gốc tọa độ O trùng với tâm đáy bình hoa, trục Ox trùng với trục của bình hoa.
Bán kính hình tròn đáy bình hoa bằng y = nên −sin x + = ⇒ x = ⇒ x = . A 2 2 sin A 0 A 0 A 2
Bán kính đường tròn miệng bình hoa bằng y =
π < x < π , tức là: B 1,5(2 B 3 ) Trang 44 (  π  π π x −π + = ⇒ x −π = − ⇒  
x −π = − + π ⇒ x = . B ) ( B ) 17 sin 2 1,5 sin sin B 2  6  6 B 6 π
Khi đó thể tích bình hoa giới hạn bởi các đường 17
y = −sin x + 2; y = 0; x = 0; x = được xác 6 17π 17π 6 6
định theo công thức V = π ∫ (−sin x + 2)2 dx =π ∫ ( 2
4 − 4sin x + sin x)dx 0 0 17π 17π 6 6  1− cos 2x   9 cos 2 π 4 4sin d π 4sin x x x x  = − + = − − ∫   ∫  dx  2   2 2 0 0  17π 2 6   π + 9 sin 2x 51 32 15 3 = π x + 4cos x − = − π ≈   103,07 ( 3 dm ) .  2 4  4 8 0
Câu 40. Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La
Mã, tòa nhà Ellipse Tower Hà Nội, sử dụng trong thiết kế logo quảng cáo, thiết bị nội thất. Xét
một Lavabo (bồn rửa) làm bằng sứ đặc hình dạng là một nửa khối elip tròn xoay có thông số kĩ
thuật mặt trên của Lavabo là: dài×rộng: 660×380 mm (tham khảo hình vẽ bên dưới), Lavabo có
độ dày đều là 20 mm . Thể tích chứa nước của Lavabo gần với giá trị nào trong các giá trị sau: A. 3 18,66 dm . B. 3 18,76 dm . C. 3 18,86 dm . D. 3 18,96 dm . Lời giải Chọn B
Giả sử mặt trên của Lavabo được biểu diễn như hình vẽ bên dưới. Gọi hệ trục tọa độ Oxy như
hình vẽ. Gọi (E) là elip nhỏ bên trong. Trang 45
Độ dài trục lớn của (E) là 31
2a = 660 − 40 = 620mm = dm 31 ⇒ a = dm . 5 10
Độ dài trục bé của (E) là 17
2b = 380 − 40 = 340mm = dm 17 ⇒ b = dm . 5 10 2 2 2  
Vậy phương trình của (E) là: x y x + = 1 2 289 100 ⇒ y = 1− . 2 2   31 17  100  961  10 10     
Thể tích khối tròn xoay khi quay miền giới hạn bởi (E), trục Ox và 31 x = − , 31 x = (Phần 10 10
gạch chéo trong hình) quanh trục Ox là: 31 10 2 289  100x  8959π V = π ∫ 1− dx = ( 3 dm ) 31 100  961  750 −10
Vậy thể tích chứa nước của Lavabo là V 3 ≈ 18,76 dm . 2
Câu 41. Một vật chuyển động chậm dần đều với vận tốc v(t) = 160 −10t(m/s) . Quãng đường mà vật
chuyển động từ thời điểm t = 0(s) đến thời điểm mà vật dừng lại là A. 1028 m . B. 1280 m. C. 1308 m . D. 1380 m . Lời giải Chọn A Gọi t
v(t ) = 0 ⇔160 −10t = 0 ⇔ t =
0 là thời điểm vật dừng lại, khi đó 0 0 16 . 0 16
Vậy quãng đường vật chuyển động đến lúc dừng lại là S = (160 −10t)dt = 1280 (m) ∫ . 0 Trang 46
Câu 42. Một vật chuyển động với vận tốc thay đổi theo thời gian được tính bởi công thức
v(t) = 3t + 2(m/s) . Biết tại thời điểm t = 2(s) thì vật đi được quãng đường là 10(m) . Hỏi tại thời
điểm t = 30(s) thì vật đi được quãng đường là bao nhiêu? A. 1140 m. B. 300 m. C. 240 m. D. 1410 m. Lời giải Chọn D
Quãng đường của vật theo thời gian là 3 2
S(t) = (3t + 2)dt = t + 2t + ∫ C . 2 Vì 3
S(2) = 10 ⇒ C = 0 . Khi đó 2
S(t) = t + 2t . 2
Tại thời điểm t = 30(s) thì S(30) = 1410(m) .
Câu 43. Một vật đang chuyển động với vận tốc v = 25(m/s) thì thay đổi vận tốc với gia tốc được tính
theo thời gian t là a(t) = t − ( 2
2 6 m/s ). Tính quãng đường vật đi được kể từ thời điểm thay đổi
gia tốc đến lúc vật đạt vận tốc bé nhất. A. 107 m . B. 144 m . C. 28 m . D. 57 m . 5 Lời giải Chọn D
Vận tốc của vật khi thay đổi là v(t) = ∫( t − ) 2
2 6 dt = t − 6t + C .
Tại thời điểm t = 0 (khi vật bắt đầu thay đổi vận tốc) có v = 25 ⇒ C = 25 0 . Suy ra v(t) 2
= t − 6t + 25.
Ta có v(t) = (t − )2
3 +16 ≥16, suy ra vận tốc của vật đạt bé nhất khi t = 3 .
Quãng đường vật đi được trong khoảng thời gian đó là 3 3 3
S = ∫v(t)dt = ∫( 2t − 6t + 25)dt 1 3 2 t 3t 25  = − + t =   57(m) .  3  0 0 0
Câu 44. Một mô tô chạy với vận tốc v m/s thì gặp chướng ngại vật nên người lái xe đạp phanh. Từ 0 ( )
thời điểm đó ôtô chuyển động chậm dần với gia tốc a = − t ( 2
8 m/s ) trong đó t là thời gian tính
bằng giây. Biết từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được 12 ( m) . Tính v0 ? Trang 47 A. 18 m/s . B. 3 86 m/s . C. 3 1269 m/s. D. 3 1296 m/s . Lời giải Chọn D a = − t ( 2 m s ) 2 8 / ⇒ v = 8 − tdt = 4 − t + C ∫ .
Tại thời điểm t = 0 thì vận tốc của vật là v m/s nên ta có v = C . 0 ( ) 0 Vậy 2 v = 4 − t + v . 0 Tại thời điểm t = − + ⇔ =
0 vận tốc của vật là 0 nên ta có 2 2 0 4t v 4t v . 0 0 0 0 3 3 3 Ta có: t0 ∫ ( 2 4
− t + v dt =12 4t 4t 36 0 ⇔ − + = 0 3 ⇔ − + = ⇔ t = . 0 ) v t 12 4t 12 0 0 0 3 0 3 0 2 2 3  36  3 ⇒ v = 4.  = 1296 m/s . 0 ( ) 2  
Câu 45. Đầu tháng 5 năm 2019 , ông An đầu tư vào chăn nuôi tằm với số tiền vốn ban đầu là 200 (triệu
đồng). Biết rằng trong quá trình chăn nuôi gặp thuận lợi nên số tiền đầu tư của ông liên tục tăng
theo tốc độ được mô tả bằng công thức 12000 f (′t) =
, với t là thời gian đầu tư tính bằng tháng (t + 5)2
(thời điểm t =0 ứng với đầu tháng 5 năm 2019 ). Hỏi số tiền mà ông An thu về tính đến đầu
tháng 5 năm 2023 gần với số nào sau đây?
A. 2737 (triệu đồng).
B. 2307 (triệu đồng).
C. 2370 (triệu đồng).
D. 2703 (triệu đồng). Lời giải Chọn C
Tốc độ thay đổi vốn đầu tư của ông An vào tháng thứ t là 12000 f (′t) = nên nguyên hàm của (t + 5)2
hàm f (′t) là hàm số f (t) mô tả số tiền của ôn An có được tính đến tháng thứ t . − Ta có 12000 12000
f (t) = f (′t)dt = t = + ∫ ∫ C . ( d t + 5)2 t + 5
Số tiền của ông An tại thời điểm t = 0 là 12000 f − (0) =
+ C = 200 ⇒C = 2600. 0 + 5
Vậy số tiền mà ông An thu về tính đến đầu tháng 5 năm 2023 (ứng với t = 48 tháng) là Trang 48 12000 f − (48) =
+ 2600 = 2373,585 (triệu đồng). 48 + 5
Câu 46. Giả sử rằng sau t năm, vốn đầu tư của một doanh nghiệp phát sinh lợi nhuận với tốc độ P′(t) 2
= 126 + t (triệu đồng/năm). Hỏi sau 10 năm đầu tiên thì doanh nghiệp thu được lợi nhuận
là bao nhiêu (đơn vị triệu đồng). A. 5020. B. 1235. C. 3257 . D. 4780 . 3 3 Lời giải Chọn D
Sau 10 năm đầu tiên thì doanh nghiệp thu được lợi nhuận là 10 2 4780
T = (126 + t )dt = ∫ (triệu đồng). 3 0
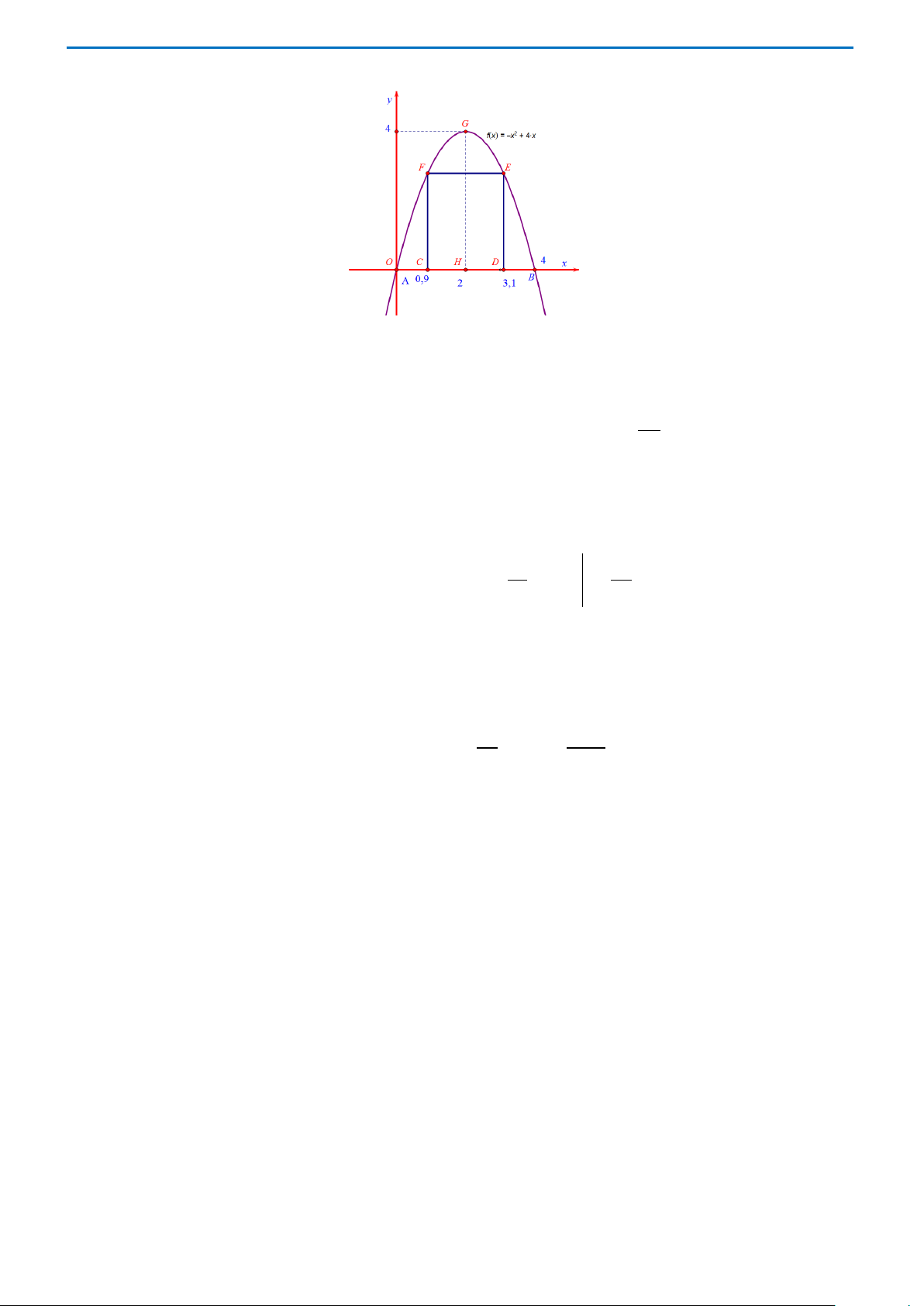
Câu 49: Một cái cổng hình parabol như hình vẽ. Chiều cao GH = 4 m , chiều rộng AB = 4 m ,
AC = BD = 0,9 m . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm có
giá là 1200000đồng/m2, còn các phần để trắng làm xiên hoa có giá là 900000đồng/m2.
Hỏi tổng chi phí để làm hai phần nói trên gần nhất với số tiền nào dưới đây? A. 11445000(đồng).
B. 7368000 (đồng). C. 4077000 (đồng). D. 11370000(đồng) Lời giải Chọn A
Gắn hệ trục tọa độ Oxy sao cho AB trùng Ox , A trùng O khi đó parabol có đỉnh G (2;4) và đi qua gốc tọa độ. Trang 49
Giả sử phương trình của parabol có dạng 2
y = ax + bx + c ( 0 a ≠ ) . c = 0  a = −1 −
Vì parabol có đỉnh là G (2;4) và đi qua điểm b O (0;0) nên ta có   = 2 ⇔ b = 4 . 2a   = 2  c 0 a.2 + .2 b + c = 4
Suy ra phương trình parabol là 2
y = f (x) = −x + 4x . 4 4 3  
Diện tích của cả cổng là 2 x 2 32 2
S = (−x + 4x)dx = − + 2x = ∫   (m ) .  3  3 0 0
Mặt khác chiều cao CF = DE = f (0,9) = 2,79(m) ; CD = 4 − 2.0,9 = 2,2(m) .
Diện tích hai cánh cổng là S = CD CF = ≈ CDEF ( 2 . 6,138 6,14 m ) .
Diện tích phần xiên hoa là 32 6793 2
S = S − S = − = ≈ . xh CDEF 6,14 4,53(m ) 3 1500
Số tiền làm hai cánh cổng là T = 6,14.1200000 = 7368000 đ . 1 ( )
và tiền làm phần xiên hoa là T = 4,53.900000 = 4077000 đ . 2 ( )
Vậy tổng chi phí là 11445000 đồng.
Câu 50: Để tăng thêm thu nhập, ông Bình chăn nuôi thêm 2 con bò. Do diện tích đất của nhà ông hẹp nên
ông xây chuồng bò như hình vẽ bên dưới và chia thành 2 phần bằng nhau để nhốt 2 con bò. Biết
ABCD là hình vuông cạnh 4m và I là đỉnh của một Parabol có trục đối xứng là trung trực của
BC và parabol đi qua hai điểm A , D . Tiền xây chuồng bò hết 350000 đồng/ 2 1 m . Biết I cách
BC một khoảng 5m , hãy tính số tiền chi phí ông Bình bỏ ra để xây dựng chuồng bò (làm tròn đến hàng nghìn)? Trang 50 C B D A I A. 6.333.000 đồng. B. 7.533.000 đồng. C. 6.533.000 đồng. D. 7.333.000 đồng. Lời giải Chọn C
Xét hệ trục tọa độ như hình vẽ sau y C B x -2 O 2 D A -5 I
Khi đó parabol có đỉnh I (0;−5) và đi qua hai điểm A(2;−2) , D (−2;−2) nên có phương trình 1 2 y = x − 5. 4 2 Diện tích chuồng bò là  1 2  56 S = − x + 5 dx = ∫   ( 2 m ).   − 4 3 2
Vậy tổng số tiền ông Bình xây chuồng bò là 56 19600000 ⋅350000 = ≈ 6533000 đồng. 3 3
Câu 49. Người ta sản xuất một loại đèn trang trí ngoài trời (Trụ sở, quảng trường, công viên, sân vườn…)
gồm có hai phần: Phần bóng đèn có dạng mặt cầu bán kính R dm , làm bằng thủy tinh trong suốt;
Phần đế bóng đèn làm bằng nhựa để cách điện, có dạng một phần của khối cầu bán kính r dm
và thỏa mãn đường kính là một dây cung của hình tròn lớn bóng đèn. Một công viên muốn tạo
điểm nhấn ánh sáng, đặt loại bóng có kích thước R = 5 dm , r = 3 dm . Tính thể tích V phần
nhựa để làm đế một bóng đèn theo đơn đặt hàng (Bỏ qua ống luồn dây điện và bulông ốc trong phần đế). Trang 51 π π π A. 3 V = 36π dm . B. 68 3 V = dm . C. 14 3 V = dm . D. 40 3 V = dm . 3 3 3 Lời giải Chọn D
Gọi I, R lần lượt là tâm và bán kính hình cầu phần bóng đèn và K, r lần lượt là tâm và bán
kính của khối cầu để làm đế bóng đèn.
Ta có R = IA = 5 dm , r = KA = 3 dm và đường kính AB vuông góc với đường thẳng nối hai tâm I và K .
Chọn hệ trục tọa độ Oxy như hình vẽ: Gốc tọa độ O ≡ K , trục Oy ≡ AB .
Xét tam giác vuông OIA ta có: 2 2 2 2
IK = IA − KA = R − r = 25 − 9 = 4 ⇒ I ( 4;
− 0) và KD = R − IK = 5 − 4 =1.
Phương trình đường tròn tâm K (0;0) bán kính r = 3 là (C ) 2 2 : x + y = 9 . 1
Phương trình đường tròn tâm I ( 4;
− 0) bán kính R = 5 là (C ) :(x + 4)2 2 + y = 25 . 2
Gọi V1 là phần thể tích khi quay hình phẳng giới hạn bởi (C , trục Ox , x = 0 và x = 3, ta có: 1 ) 3 3   = π ∫(9− ) 3 2 d = π 9 x V x x x −  = 18π ( 3 dm . 1 )  3 0  0
Gọi V2 là phần thể tích khi quay hình phẳng giới hạn bởi (C , trục Ox , x = 0 và x =1, ta có: 2 ) Trang 52 1  +  π V = π ∫( 3 1 − (x + )2 ) (x 4) 14 25
4 dx = π  25x −  = ( 3 dm . 2 )  3  3 0   0 π π
Do đó V = V −V 14 = π − 40 = ( 3 dm ) 1 2 18 . 3 3
Câu 50. Một bồn nước Inox SONHA® ngang có hai đầu bồn là hình phẳng elip. Thể tích tối đa khi đóng
nắp bồn là V = 3000 1
lít. Bồn có chiều dài bằng l = 2,0 m và gấp 2 lần chiều cao của bồn. Để
nước bơm tự động vào bồn, người ta lắp một phao điện sao cho mực nước trong bồn cao
h = 0,75 m so với điểm thấp nhất trong đáy bồn thì phao đóng không cho nước chảy vào bồn.
Tính thể tích nước trong bồn khi phao đóng (bỏ qua độ dày của bồn nước và kết quả làm tròn đến phần trăm). A. 3 V = 2.41 m . B. 3 V = 2.43 m . C. 3 V = 2.40 m . D. 3 V = 2.44 m . Lời giải Chọn A Ta có 3 3000 lít = 3 m .
Xét thiết diện ngang của bồn nước là hình elip (E) có độ dài trục lớn là 2a , độ dài trục nhỏ là
2b và chọn hệ trục tọa độ như hình vẽ
Độ dài BB′ =1 m là chiều cao của bồn nước, suy ra độ dài trục nhỏ của (E) là 1
2b =1⇒ b = (m) . 2
Ta có: V = π.a. . b l V 3 3 1 ⇒ a = = = (m) . 1 π. . b l π.0,5.2 π Trang 53
Vậy phương trình của Elip là:   2 2 2 x y   2 1 x 1 + =1⇒ y = 1−  = ( 2 2 9 − x π ) 1 2 2 ⇒ y = ± 9 − π 9 1 x . 4 9 36 6   2 2 π 4  π 
Khi phao điện đóng, mực nước trong bồn là MN 1
⇒ OK = OB − BK = 0,5 − 0,25 = 0,25 = . 4
Vì MN song song với trục Ox nên ta có phương trình MN là 1 y = . 4
Hoành độ điểm M , N thỏa mãn phương trình : 2  1  1 3 3 3 3 3 3 = ( 2 2 − x π ) 2 27 9 ⇔ x =   ⇒ x = ± ⇒ x = − x = M ; . 2  4  36 4π 2π 2 N π 2π
Phần diện tích S2 giới hạn bởi (E) đi qua điểm B và đường thẳng MN là: 3 3 3 3 3 3 2π  1 π 2 2 π 2  3  1 π π 2 2 1 S 9 x π  = − − ∫  dx 2 = − x dx − ∫ 3 3   x = .I − . 2  6 4  6  π  4 3 3 6 4π 3 3 3 3 − − − 2π 2π 2π 3 3 π 2 2 Xét:  3  2 I = −
∫   x dx. Đặt 3 3
x = sin t ⇒ dx = costdt .  π  π π 3 3 − 2π π Đổi cận: Khi 3 3 x = − thì 3 sin t = − ⇒ t = − ; 2π 2 3 π Khi 3 3 x = thì 3 sin t = ⇒ t = . 2π 2 3 Khi đó: π π π 3 3 3 3 9 I t t ∫ ∫ ( t) 3 2 9  1 . cos d 1 cos 2 dtx sin 2t  = = + = + 2 2 π π 2π 2π 2    π π π − − − 3 3 3 9  π 3  9  π 3  3 9 3 =  +  −  − −  = + . 2   2   2 2π 3 4 2π 3 4 π 4π     π  3 9 3  3 3 1 3 3 Vậy S =  +  − = − . 2  2 6 π 4π  4π 2 8π  
Thể tích phần không gian không chứa nước khi phao đóng là: 3 3
V = S .l =1− . 2 2 4π  3 3 
Vậy thể tích nước cần tìm là: V = V −V = 3 − 1−  ≈ 2.41 ( 3 m . 1 2 ) 4π   Trang 54
Document Outline

  • CĐ 22 Toán thực tế liên quan ứng dụng tích phân