TOP 69 bài toán thực tế về hình học có đáp án và lời giải

Tài liệu gồm 60 trang, tuyển tập 69 bài toán thực tế về hình học có đáp án và lời giải chi tiết; tài liệu được biên soạn bởi quý thầy, cô giáo nhóm Toán Tiểu Học – THCS – THPT Việt Nam.

106 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi vào 10 môn Toán

Môn: Môn Toán

Thông tin:

60 trang 7 tháng trước

Tác giả:

Profile Nguyễn Vân
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 1
DẠNG 1: CÁC BÀI TOÁN THỰC TẾ VỀ HÌNH HỌC
Vận dụng hệ thức lượng trong tam giác vuông – Tỉ số lượng giác của góc nhọn
Bài 1. Hằng ngày hai anh em An và Bình cùng đi bộ từ nhà ở
A
để đến trường. Trường của An ở vị
trí
B
, trường của Bình ở vị trí
C
theo hai hướng vuông góc với nhau. An đi với vận tốc
4 /km h
và đến trường sau
15
phút. Bình đi với vận tốc
3 /km h
và đến trường sau
12
phút.Tính khoảng cách
BC
giữa hai trường (làm tròn đến mét).
Bài 2. Một người
A
đang ở trên khinh khí cầu ở độ cao
150m
nhìn thấy một vật
B
trên mặt đất cách
hình chiếu của khí cầu xuống đất một khoảng
285m
. Tính góc hạ của tia
AB
. Nếu khinh khí
cầu tiếp tục bay lên thẳng đứng thì khi góc hạ của tia
AB
là
46
thì độ cao của khinh khí cầu
là bao nhiêu? (làm tròn đến mét).
Bài 3. Một người có mắt cách mặt đất
1,4m
, đứng cách tháp Eiffel
400m
nhìn thấy đỉnh tháp với góc
nâng
39
. Tính chiều cao của tháp (làm tròn đến mét).
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 2
Bài 4. Một cột đèn cao
8m
. Tính góc tạo bởi tia nắng mặt trời và mặt đất lúc nó có bóng trên mặt đất
là
5m
.
Bài 5. Một cái thang dài
4m
đang dựa vào tường, chân thang cách chân tường
2m
.Tính góc tạo bởi
thang với mặt đất và với mặt tường.
Bài 6. Tính chiều cao của một ngọn núi cho biết tại hai điểm cách nhau 1km trên mặt đất người ta
nhìn thấy đỉnh núi với góc nâng lần lượt là
40
và
32
.
Bài 7. Tính chiều cao của một cái tháp, cho biết khi các tia nắng mặt trời tạo với mặt đất một góc
42
thì bóng của tháp trên mặt đất có chiều dài 150m.
Bài 8. Để đo chiều rộng AB của một con sông mà không phải băng ngang qua sông, một người đi từ
A đến C đo được
50AC m
và từ C nhìn thấy B với góc nghiêng
62
với bờ sông. Tính bề
rộng của con sông.
1km
40°
32°
A
C
D
B
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 3
Bài 9. Một người quan sát đứng cách một tòa nhà 25m. Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà
là
36
.
1) Tính chiều cao của tòa nhà (làm tròn đến mét).
2) Nếu anh ta dịch chuyển sao cho góc nâng là
32
thì anh ta cách tòa nhà bao nhiêu mét? Khi
đó anh ta tiến lại gần hay cách ra xa tòa nhà (làm tròn đễn chữ số thập phân thứ hai).
Bài 10. Từ trên tháp quan sát của một ngọn hải đăng cao
28m
, người ta nhìn thấy một chiếc thuyền
cứu hộ với góc hạ
20
. Tính khoảng cách từ chân tháp đến thuyền.
.
Bài 11. Đài quan sát Toronto, Ontario (canada) cao
533m
. Ở một thời điểm vào ban ngày, mặt trời
chiếu tạothành bóng dài
1100 m
1100m. Hỏi lúc đó góc tạo bởi tia sát mặt trời và mặt đất là bao
nhiêu (làm tròn đến độ).
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 4
Bài 12. Hai ngư dân đứng ở một bên bờ sông cách nhau
250 m
cùng nhìn thấy một cù lao trên sông với
cácgóc nâng lần lượt là
30
và
40
.Tính khoảng cách
d
từ bờ sông đến cù lao.
Bài 13. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm
A
) đến trường (điểm
B
) phải leo lên và xuống
mộtcon dốc (như hình vẽ). Cho biết đoạn thẳng
AB
dài
762 m
, góc
A
bằng
6
, góc
B
bằng
4
.
1)Tính chiều cao
h
của con dốc.
2) Hỏi bạn An đến trường lúc mấy giờ ? Biết rằng tốc độ trung bình lên dốc là
4 km/h
và tốc độ
trung bình xuống dốc là
19 km/h
.
Bài 14. Từ đỉnh một tòa nhà cao
54 m
, người ta nhìn thấy một ô tô đang đỗ dưới một góc nghiêng
xuống là
40
. Hỏi ô tô đang đỗ cách tòa nhà đó bao nhiêu mét ?
Bài 15. Một học sinh đứng ở mặt đất cách tháp ăng ten cao
150 m
nhìn thấy đỉnh tháp theo một góc
nghiêng lên là
20
và khoảng cách từ mắt đến mặt đất là
1m
. Tính khoảng cách từ học sinh đó
đến tháp (làm tròn đến mét).
Bài 16. Một cái thang dài
4,8m
dựa vào tường làm thành một góc
58
so với mặt đất. Tính chiều cao
của thang so với mặt đất (làm tròn đến mét).
h
4°
6°
762 m
A
B
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 5
Bài 17. Một người quan sát ở đài hải đăng cao
800feet
(đơn vị đo lường Anh) so với mực nước biển
nhìn thấy một con tàu ở xa với một góc nghiêng xuống là
1 42'
. Hỏi khoảng cách từ tàu đến
chân ngọn hải đăng là bao nhiêu hải lý (1 hải lý =
5280 feet
)?
Bài 18. Một người quan sát ở đài hải đăng cao
149 m
so với mực nước biển nhìn thất một con tàu ở xa
với một góc nghiêng xuống là
27
. Hỏi tàu đang đứng cách chân hải đăng là bao nhiêu mét?
Bài 19. Một học sinh thả diều ngoài đồng, cho biết đoạn dây đã thả dài
100 m
và có góc nâng
52
.
Tính độ cao của diều so với mặt đất (làm tròn đến mét).
Bài 20. Một chiếc thuyền thả neo trên sông. Cho biết dây neo dài
30 m
và có góc nghiêng lên là
39
.
Tính độ sâu của mực nước chỗ thuyền đang đậu (làm tròn đến mét).
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 6
Bài 21. Một người đứng trên đỉnh tháp cao
325m
nhìn thấy 2 điểm
A
và
B
với hai góc hạ lần lượt là
37
và
72
.Tính khoảng cách
AB
.
Bài 22. Một người đứng cách chân tháp
14 m
nhìn thấy đỉnh tháp theo góc nghiêng
60
. Tính chiều cao
của tháp.
Bài 23. Một máy bay cất cánh theo phương có góc nâng
23
.Hỏi muốn đạt độ cao
2500 m
, máy bay
phải bay một đoạn đường là bao nhiêu mét?
Bài 24. Một cái cây có bóng trên mặt đất dài
20 m
.Cho biết tia nắng qua ngọn cây nghiêng một góc
31
so với mặt đất. Tính chiều cao của cây.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 7
Bài 25. Một cái cây cao 6m đang có bóng dài
3,2 m
. Tính góc hợp bởi tia nắng với thân cây
Bài 26. Một người đứng cách chân tháp 14 m nhìn thấy đỉnh tháp theo góc nghiêng
60
. Tính chiều
cao của tháp.
Bài 27. Ban Hùng có tầm mắt cao 1,5 m đang đứng gần một cao ốc cao 30 m thì nhìn thấy nóc tòa nhà
với góc nâng
30
. Hùng đi về phía tòa nhà cho đến khi nhìn thấy nóc tòa nhà với góc nâng
60
.
Tính quãng đường mà bạn Hùng đã đi được.
Bài 28. Một học sinh có tầm mắt cao
1,5 m
đứng trên sân thượng của một căn nhà cao
15 m
nhìn thấy
bạn mình với góc nghiêng xuống
49
. Hỏi cô bạn đang ở cách căn nhà bao nhiêu mét?
30m
60
o
30
o
1,5m
B
A
C
K
D
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 8
Bài 29. Một máy bay thể thao đang bay ngang ở độ cao
3000 m
nhìn thấy một cái cây với góc nghiêng
xuống
15
. Hỏi máy bay phải bay một đoạn đường là bao nhiêu mét thì sẽ ở ngay trên ngọn
cây?
Bài 30. Từ nóc một cao ốc cao
50 m
người ta nhìn thấy chân và đỉnh một ăng-ten với các góc hạn lần
lượt là
62
và
34
. Tính chiều cao cột ăng-ten.
Bài 31. Một cái diều đang bay ở độ cao
60 m.
Sợi dây cột diều nghiêng với mặt đất một góc
60
. Tính
chiều dài của sợi dây (làm tròn đến mét) khi nó căng thẳng (không có chỗ bị võng).
Bài 32. Tháp Capital Gate tại Abu Dhabi cao
160 m
và nghiêng
18
. Nếu không nghiêng thì tháp cao
bao nhiêu mét?
A
B
C
D
E
50m
62
0
34
0
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 9
Bài 33. Tính chiều cao của một ngọn núi, cho biết tại hai điểm cách nhau
500 m
, người ta nhìn thấy hai
đỉnh núi với góc nâng lần lượt là
34
và
38
.
Bài 34. Một cái tháp được dựng bên bờ một con sông, từ một điểm đối diện với tháp ngay bờ bên kia
người ta nhìn thấy đỉnh tháp với góc nâng
60
. Từ một điểm khác cách điểm ban đầu
20 m,
người ta cũng nhìn thấy đỉnh tháp với góc nâng
30
. Tính chiều cao của tháp.
Bài 35. Một bức tượng cao
1,6 m
được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là
60
và
45
. Tính chiều cao của cái bệ.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 10
Bài 36. Một nhà trẻ muốn thiết kế hai cái cầu tuột trong sân chơi. Đối với trẻ dưới 5 tuổi, cầu tuột cao
1,5m
và nghiêng với mặt đất một góc
30
. Đối với trẻ trên 5 tuổi cầu tuột cao 1,5 m và
nghiêng với mặt đất
một góc
45
. Tính chiều dài của mỗi máng tuột.
Bài 37. Từ chân một cái tháp cao
50 m
người ta nhìn thấy đỉnh một tòa nhà với góc nâng
30
. Trong
khi đó từchân tòa nhà lại nhìn thấy đỉnh tháp với góc nâng
60
. Tính chiều cao của tòa nhà.
Bài 38. Hai trụ điện có cùng chiều cao đặt cách nhau
80 m
. Một người đứng ở xa (thẳng hàng với hai
trụ
điện, không đứng giữa hai trụ điện) nhìn đỉnh hai trụ điện với góc nâng lần lượt là
60
và
30
. Tính chiều cao trụ điện và khoảng cách từ người đó đến chân các trụ điện. Biết mắt người
đó cách mặt đất
1, 2 m
.
Bài 39. Từ trên một ngọn hải đăng cao
75 m
, người ta quan sát hai lần thấy một chiếc thuyền đang
hướng về phía hải đăng với góc hạ lần lượt là
30
và
45
. Hỏi chiếc thuyền đi được bao nhiêu
mét giữa hai lầnquan sát?
45
30
2m
E CB
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 11
Bài 40. Một thủy thủ lái thuyền ra biển hướng về hướng đông bắc với góc nghiêng so với phương bắc
là
41
. Đi được
2,8km
anh ta phát hiện sắp hết nhiên liệu nên vội quay thuyền vào bờ, đi
được
1,8km
thì
thuyền tắt máy. Hỏi lúc đó thuyền cách bờ bao xa?
Bài 41. Từ trên đỉnh một tòa nhà cao
7m
, người ta nhìn thấy đỉnh một tháp truyền hình với góc nâng
60
và nhìn thấy chân của tháp với góc hạ
45
. Tính chiều cao của tháp truyền hình?
Bài 42. Một học sinh có khoảng cách từ mặt đến mặt đất là
1, 2m
bắt đầu quan sát một trái bóng bay
với góc nâng
60
. Một lúc sau lại nhìn thấy quả bóng bay với góc nâng
30
. Hỏi giữa hai lần
quan sát quả bóng đã bay được bao nhiêu mét? Cho biết độ cao của quả bóng luôn luôn không
đổi và bằng
88,2 m
.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 12
Bài 43. Một người đang ở trên một cái tháp có chiều cao
h =100 m
nhìn xuống một con đường chạy
thẳng đến chân tháp. Anh ta nhìn thấy một chiếc xe máy với góc hạ
30
. Sáu phút sau lại nhìn
thấy nó với góc hạ
60
. Hỏi sau bao nhiêu phút thì xe máy đến chân tháp? Cho biết vận tốc xe
máy không đổi.
Bài 44. Để đo chiều cao một cái cây
AB
. Người ta đặt gương phẳng tại vị trí
C
. Người đo đi lùi lại
(thẳng người) cho đến khi nhìn thấy bóng ngọn cây
A
(lúc này là
F
). Biết khoảng cách từ
gương đến gốc cây là
30BC
mét, khoảng cách từ gương đến chỗ đứng là
1,5CD
mét.
Khoảng cách từ mắt người đo
E
đến mặt đất là
1,6
ED
mét. Tính chiều cao của cây? (biết
BCA DCE ).
Bài 45. Quan sát hình vẽ dưới đây. Giả sử
CD h
là chiều cao của tháp trong đó
C
là chân tháp.
Chọn hai điểm
A
,
B
trên mặt đất sao cho ba điểm
A
,
B
và
C
thẳng hàng. Ta đo khoảng cách
AB
và các góc
CAD ,
CBD . Chẳng hạn ta đo được
24AB
m,
63CAD
,
48CBD
. Hãy tính chiều cao
h
của tháp.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 13
Bài 46. Một hình chữ nhật có kích thước là 20 cm và 30 cm. Người ta tăng mỗi kích thước thêm
x
cm.
Gọi
y
là chu vi của hình chữ nhật mới.
1) Hãy tính
y
theo
x
.
2) Tính giá trị của y tương ứng với
3x
cm;
5x
cm.
Bài 47. Một thửa đất hình chữ nhật có chiều dài là 32 m và chiều rộng là 24 m. Người ta định làm một
vườn cây cảnh có con đường đi xung quanh, có bề rộng x(m) (hình vẽ bên). Hỏi bề rộng của
mặt đường là bao nhiêu để diện tích phần đất còn lại là 560 m
2
.
Bài 48. Một căn phòng hình vuông được lát bằng những viên gạch men hình vuông cùng kích cỡ, vừa
hết 441 viên (không viên nào bị cắt xén). Gạch gồm 2 loại men trắng và men xanh, loại men
trắng nằm trên 2 đường chéo của nền nhà còn lại là loại men xanh. Tính số viên gạch men
xanh.
Bài 49. Bạn Nam đi xe đạp từ nhà (điểm A) đến trường (điểm B) gồm đoạn lên dốc và đoạn xuống dốc,
5A ,
4B
, đoạn lên dốc dài 325 m.
1) Tính chiều cao của dốc và chiều dài quãng đường từ nhà đến trường.
2) Biết vận tốc trung bình lên dốc là 8 km/h và vận tốc trung bình xuống dốc là 15 km/h. Tính
thời gian (phút) bạn Nam đi từ nhà đến trường. (Lưu ý kết quả của phép tính làm tròn đến chữ
số thập phân thứ nhất)
Bài 50. Một bức tượng cao 1,6 m được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là
60
và
45
. Tính chiều cao cái bệ.
Bài 51. Một cây có chiều cao 14 m mọc ở phía sau một bức tường cao 8 m và cách bức tường 12 m.
Hỏi người quan sát có chiều cao
1,8
m phải đứng cách bức tường bao nhiêu mét để có thể nhìn
thấy ngọn cây.
x
x
x
x
24 m
32 m
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 14
Bài 52. Nhà bạn An ở vị trí
A
, nhà bạn Bình ở vị trí
B
cách nhau 1200 m. Trường học ở vị trí
C
cách
nhà bạn An 500m và
AB
vuông góc với
AC
. An đi bộ đến trường với vận tốc 4 km/h, Bình đi
xe đạp đến trường với vận tốc 12 km/h. Lúc 6 giờ 30 phút, cả hai cùng xuất phát đến trường.
Hỏi bạn nào đến trường trước?
Bài 53 Bóng của tháp Bình Sơn (Vĩnh Phúc) trên mặt đất có độ dài 20 m. Cùng thời điểm đó, một cột
sắt cao
1,65
m cắm vuông góc với mặt đất có bóng dài 2 m. Tính chiều cao của tháp.
Bài 54. Một con đê được đắp chắn sóng theo hình dưới, độ dốc của con đê phía sông dài 7 m. Hỏi độ
dốc còn lại của con đê dài bao nhiêu mét?
Bài 55. Xem hình vẽ sau, người ta có thể dùng giác kế để đo được góc
43CAB và
38CBA . Hỏi
tàu đang ở vị trí điểm
H
sẽ chạy với vận tốc bao nhiêu km/h để sau 5 phút sẽ đến vị trí điểm
C
. Biết khoảng cách từ vị trí điểm
A
đến vị trí điểm
B
là 300 m và vị trí 3 điểm
A
,
H
,
B
thẳng hàng (làm tròn đến chữ số thập phân thứ hai).
Bài 56. Ba An muốn mua một cái thang dùng để lên mái nhà. Ba hỏi An phải mua cái thang dài bao
nhiều mét để đảm bảo sự an toàn và có thể leo lên được mái nhà cao
4,5
m so với mặt đất. Em
hãy giúp An tính chiều dài thang cần mua, biết góc kê thang an toàn là
75
so với phương
ngang (làm tròn đến số thập phân thứ nhất).
B
C
H
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 15
Bài 57. Một chiếc máy bay bay lên cao với vận tốc
520 /km h
. Đường bay lên tạo với phương nằm
ngang một góc
24
. Hỏi sau 90 giây máy bay lên cao được bao nhiêu km theo phương thẳng
đứng? (kết quả làm tròn đến chữ số thập phân thứ nhất)
Bài 58. Từ đài quan sát cao 10 m, Nam có thế nhìn thấy 2 chiếc thuyền dưới góc
45
và
30
so với
phương ngang. Hãy tính khoảng cách 2 chiếc thuyền, làm tròn đến chữ số thập phân thứ nhất.
(điều kiện lý tưởng: vị trí 2 chiếc thuyền và vị trí đài quan sát thẳng hàng).
Bài 59. Hình ảnh mặt cắt một quả đồi được minh họa là một
ABC
với các chi tiết như sau: cạnh đáy
là
AC
,
BH AC
,
45BAC
,
200AH
m,
210HC
m. Một nhóm học sinh đi dã ngoại
đi từ đỉnh
A
lên đỉnh
B
rồi xuống dốc trở về
C
. Hãy tính quãng đường này?
Bài 60. Hai chiếc thuyền
A
và
B
ở vị trí được minh họa như trong hình vẽ. Tính khoảng cách giữa
chúng (kết quả là tròn đến mét).
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 16
Bài 61. Lúc 6h45 phút sáng bạn Nam đi xe đạp điện từ nhà tới trường với vận tốc trung bình là
15
km/h bạn đi theo con đường từ
A B C D E G H
(như trong hình). Nếu có
1
con đường thẳng từ
A H
và đi theo con đường đó với vận tốc trung bình 15 km/h, bạn Nam
sẽ tới trường lúc mấy giờ?
Bài 62. Hai ngư dân đứng ở một bên bờ sông cách nhau
50
m cùng nhìn thấy một cù lao trên sông với
các góc nâng lần lượt là
30
và
40
. Tính khoảng cách d từ bờ sông đến cù lao.
Bài 63. Một người đi xe máy lên dốc có độ nghiêng
5
so với phương ngang với vận tốc trung bình lên
dốc là
18
km/h. Hỏi người đó mất bao lâu để lên tới đỉnh dốc? Biết đỉnh dốc cách mặt đất
18
m.
Bài 64. Từ vị trí xuất phát
A
, hai xe cùng một lúc đi thẳng theo hai hướng khác nhau, tạo một góc
70A . Xe thứ nhất đi với vận tốc 40 km/h và xe thứ hai đi với vận tốc 50 km/h. Sau 1 giờ 30
phút, hai xe cách nhau bao nhiêu km? (làm tròn đến 2 chữ số thập phân).
Bài 65. Một máy kéo nông nghiệp có bánh xe sau to hơn bánh xe trước. Bánh xe sau có đường kính
124
cm và bánh xe trước có đường kính
80
cm. Hỏi khi bánh xe sau lăn được
20
vòng thì xe
di chuyển được bao nhiêu mét (làm tròn một chữ số) và khi đó bánh xe trước lăn được mấy
vòng?
500m
400m
300m
600m
700m
1000m
Trường học
Nhà
H
G
E
D
C
B
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 17
Bài 66. Trong hình vẽ dưới đây, hai địa điểm
A
,
B
cách nhau 100 km. Một xe ô tô khởi hành từ
B
đến
A
với vận tốc 40 km/h. Cùng lúc đó, một xe đạp điện cũng khởi hành từ
A
trên đoạn đường
vuông góc với
AB
với vận tốc 20 km/h. Hỏi sau 90 phút thì hai xe cách nhau bao xa.
Bài 67. Với số liệu ghi trên hình (biết tứ giác
EFHI
là hình chữ nhật và
A
,
I
,
H
thẳng hàng). Cây
trong hình cao bao nhiêu mét? (làm tròn kết quả đến chữ số hàng đơn vị).
Bài 68. Một người quan sát đứng cách một tòa nhà khoảng 25 m (điểm
A
). Góc nâng từ chỗ anh ta
đứng đến nóc tòa nhà (điểm
C
) là
36
.
1) Tính chiều cao tòa nhà (làm tròn đến
0,5
mét)
2) Nếu anh ta đi thêm 5 m nữa, đến vị trí
D
nằm giữa
A
và
B
thì góc nâng từ
D
đến nóc nhà là
bao nhiêu? (làm tròn đến phút).
Bài 69. Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất,cọc cao 2 m và đặt xa cây 15
m. Sau khi người ấy lùi ra xa cách cọc
0,8
m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên
một đoạn đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy
là
1,6
m?
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 18
HƯỚNG DẪN GIẢI DẠNG 1: CÁC BÀI TOÁN THỰC TẾ HÌNH HỌC
Bài 1. Hằng ngày hai anh em An và Bình cùng đi bộ từ nhà ở
A
để đến trường. Trường của An ở vị
trí
B
, trường của Bình ở vị trí
C
theo hai hướng vuông góc với nhau. An đi với vận tốc
4 /km h
và đến trường sau
15
phút. Bình đi với vận tốc
3 /km h
và đến trường sau
12
phút.Tính khoảng cách
BC
giữa hai trường (làm tròn đến mét).
Lời giải
+) Quãng đường An đi từ nhà đến trường là:
15
4 1
60
AB km
.
+) Quãng đường Bình đi từ nhà đến trường là:
12 3
3
60 5
AC km
.
Áp dụng định lý Pitago trong tam giác vuông
ABC
, ta có:
2
2 2 1
3 34
1 1,166 1166
5 5
BC AB AC km m
.
Vậy khoảng cách hai trường là
1166 m
.
Bài 2. Một người
A
đang ở trên khinh khí cầu ở độ cao
150m
nhìn thấy một vật
B
trên mặt đất cách
hình chiếu của khí cầu xuống đất một khoảng
285m
. Tính góc hạ của tia
AB
. Nếu khinh khí
cầu tiếp tục bay lên thẳng đứng thì khi góc hạ của tia
AB
là
46
thì độ cao của khinh khí cầu
là bao nhiêu? (làm tròn đến mét).
Lời giải
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 19
+) Góc hạ của tia
AB
là góc
ABC
.
Trong tam giác
ABC
vuông tại
C
có:
150 10
tan
285 19
CA
ABC
CB
28ABC
.
+) Khi góc hạ là
46
, cao của kinh khí cầu là:
285 tan 46 295m
Bài 3. Một người có mắt cách mặt đất
1,4m
, đứng cách tháp Eiffel
400m
nhìn thấy đỉnh tháp với góc
nâng
39
. Tính chiều cao của tháp (làm tròn đến mét).
Lời giải
ABC
vuông tại
A
có:
tan 400 tan39AC AB ABC m
Suy ra chiều cao của tháp là:
400 tan 39 1, 4 325AC AD m
Bài 4. Một cột đèn cao
8m
. Tính góc tạo bởi tia nắng mặt trời và mặt đất lúc nó có bóng trên mặt đất
là
5m
.
Lời giải
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 20
Giả sử cột đèn có chiều cao
AB
, bóng cột đền lên mặt đất lúc đó là
BC
.
Khi đó góc tạo bởi tia nắng và mặt đất là góc
ACB
.
Trong
ABC
vuông tại
B
có:
8
tan
5
AB
ACB
BC
58ACB
.
Vậy góc tạo bởi tia nắng và mặt đất lúc đó xấp xỉ
58
.
Bài 5. Một cái thang dài
4m
đang dựa vào tường, chân thang cách chân tường
2m
.Tính góc tạo bởi
thang với mặt đất và với mặt tường.
Lời giải
Giả sử tháng có chiều dài
AC
, khoảng cách từ đầu thang tới mặt đất là
AB
(như hình vẽ).
Khi đó góc tạo bởi thang với mặt đất và với măt tường lần lượt là góc
ACB
,
CAB
.
Trong
ABC
vuông tại
B
có
4
tan 2
2
AB
ACB
BC
63 26'ACB
90 26 34'CAB ACB
.
Vậy góc tạo bởi thang với mặt đất và với măt tường lần lượt là
63 26'
,
26 36'
.
Bài 6. Tính chiều cao của một ngọn núi cho biết tại hai điểm cách nhau 1km trên mặt đất người ta
nhìn thấy đỉnh núi với góc nâng lần lượt là
40
và
32
.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 21
Lời giải:
Gỉa sử chiều cao của một ngọn núi là độ dài đoạn thẳng
CD
Hai điểm cách nhau 1 km là đoạn thẳng
1AB km
Ta có:
ACD
có
90ACD
.cotAC DC DAC
BCD
có
90BCD
.cotBC DC DBC
. cot cot
1
2,447
cot 32 cot 40
cot cot
AC BC DC DAC DBC
AC BC
DC km
DAC DBC
Vậy chiều cao của đỉnh núi là:
2,447 km
Bài 7. Tính chiều cao của một cái tháp, cho biết khi các tia nắng mặt trời tạo với mặt đất một góc
42
thì bóng của tháp trên mặt đất có chiều dài 150m.
Lời giải:
1km
40°
32°
A
C
D
B
1km
40°
32°
A
C
D
B
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 22
Giả sử
AH
là chiều cao của tháp;
42ABH
là góc bởi tia nắng mặt trời với mặt đất
Bóng của tháp trên mặt đất là
150BH m
. Khi đó
ABH
vuông tại
.tan 150.tan 42 135,061H AH BH ABH m
Vậy: chiều cao của cột tháp là:
135,061m
Bài 8. Để đo chiều rộng AB của một con sông mà không phải băng ngang qua sông, một người đi từ
A đến C đo được
50AC m
và từ C nhìn thấy B với góc nghiêng
62
với bờ sông. Tính bề
rộng của con sông.
Lời giải:
Ta có:
ABC
vuông tại
.tan 50.tan 62 94,036A AB AC ACB m
Vậy: bề rộng của con sông dài:
94,036m
Bài 9. Một người quan sát đứng cách một tòa nhà 25m. Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà
là
36
.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 23
1) Tính chiều cao của tòa nhà (làm tròn đến mét).
2) Nếu anh ta dịch chuyển sao cho góc nâng là
32
thì anh ta cách tòa nhà bao nhiêu mét? Khi
đó anh ta tiến lại gần hay cách ra xa tòa nhà (làm tròn đễn chữ số thập phân thứ hai).
Lời giải:
1) Tính chiều cao của tòa nhà (làm tròn đến mét).
Giả sử chiều cao của cột tháp là độ dài
AB
Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà là
36ACB
Khoảng cách từ vị trí người đó đứng đến tòa nhà là
25BC m
Khi đó:
ABC
vuông tại
B
.tan 25.tan 36 18AB BC ACB m
Vậy chiều cao của tòa nhà là
18m
2) Giả sử khoảng cách từ vị trí người đó đứng để tạo được góc nâng là
32
là
D
. Khi đó
khoảng cách từ vị trí người đó đứng đến tòa nhà là độ dài đoạn thẳng
BD
ABD
vuông tại
B
.cot 18cot 32 28,81BD AB ADB m
Vì
28,81 25BD BC
nên anh ta cách xa tòa nhà .
32
0
25 m
36
0
D
C
B
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 24
Bài 10. Từ trên tháp quan sát của một ngọn hải đăng cao
28m
, người ta nhìn thấy một chiếc thuyền
cứu hộ với góc hạ
20
. Tính khoảng cách từ chân tháp đến thuyền.
.
Lời giải:
Giả sử chiều cao của tháp chính là độ dài
AD
; chiếc thuyền cứu hộ với góc hạ
20
là góc
AID
; DI là khoảng cách từ thuyền đến chân tháp.
Ta có:
ADI
vuông tại
D
.cot 28.cot 20 76,929DI AD ADI m
Vậy: Khoảng cách từ chân tháp đến thuyền là 76,929
m
.
Bài 11. Đài quan sát Toronto, Ontario (canada) cao
533m
. Ở một thời điểm vào ban ngày, mặt trời
chiếu tạo thành bóng dài
1100 m
. Hỏi lúc đó góc tạo bởi tia nắng mặt trời và mặt đất là bao
nhiêu (làm tròn đến độ).
Lời giải:
20
0
28 m
I
A
D
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 25
Trên hình vẽ: Gọi
AB
là chiều cao của đài quan sát,
AC
là chiều dài bóng của nó trên mặt đất
ta có
553 (m); 1100 (m)AB AC
Khi đó góc tạo bởi tia nắng mặt trời và mặt đất là
ACB
Xét tam giác
ABC
vuông tại A có
0
553
tan 27
1100
AB
ACB ACB
AC
Vậy lúc đó góc tạo bởi tia nắng mặt trời và mặt đất là xấp xỉ
0
27
Bài 12. Hai ngư dân đứng ở một bên bờ sông cách nhau
250 m
cùng nhìn thấy một cù lao trên sông với
các góc nâng lần lượt là
30
và
40
. Tính khoảng cách
d
từ bờ sông đến cù lao.
Lời giải:
Trên hình vẽ: Giả sử hai ngư dân lần lượt đứng ở 2 vị trí
A
và
B
, cù lao ở vị trí
C
Gọi
H
là hình chiếu của
C
trên
AB
thì khoảng cách từ bờ sông đến cù lao là
d AH
Xét tam giác
AHC
vuông tại
H
có
0
.cot 30AH d
Xét tam giác
BHC
vuông tại
H
có
0
.cot 40BH d
Mà
AH BH AB
0 0
.(cot 30 cot 40 ) 250
.2,9238 250
d
d

85,5 (m)d
553m
C
B
A
1100m
40°
30°
H
C
B
A
d
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 26
Vậy khoảng cách
d
từ bờ sông đến cù lao khoảng 85,5 m
Bài 13. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm
A
) đến trường (điểm
B
) phải leo lên và xuống
một con dốc (như hình vẽ). Cho biết đoạn thẳng
AB
dài
762 m
, góc
0 0
.4 , 6 BA
1) Tính chiều cao
h
của con dốc.
2) Hỏi bạn An đến trường lúc mấy giờ ? Biết rằng tốc độ trung bình lên dốc là
4 km/h
và tốc độ
trung bình xuống dốc là
6 km/h
.
Lời giải:
1) Trên hình vẽ: Chiều cao
h
của con dốc là chiều dài đoạn thẳng
HC
Xét tam giác
AHC
vuông tại H có
0
.cot 4AH h
Xét tam giác
BHC
vuông tại H có
0
.cot 6BH h
Mà
AH BH AB
0 0
.(cot 4 cot 6 ) 762
.23,815 762
d
d

32 (m)d
Vậy c
hiều cao
h
của con dốc
là khoảng 32 m
2) Đổi
4 km/h = 4000 m/h; 6km/h=6000m/h
Gọi thời điểm An đến trường là
) (6 24x h x
Quãng đường An lên dốc là
0
32:sin 4 458,739 AC m
Thời gian An lên dốc đoạn đường
AC
hết
)4 058 ,,73 : 4000 119 5 (h
Quãng đường An xuống dốc là
0
32 :sin 6 306,137
CB m
Thời gian An xuống dốc đoạn đường
CB
hết
: 6000 0,051 ( )306,137 h
Thời gian An đi từ nhà đến trường hết
6 x h
nên ta có phương trình:
0,115 0,051 6
x=0,115 0,051 6 6,166 (h) 6h10ph
x
Vậy bạn An đến trường vào khoảng 6 giờ 10 phút.
h
4°
6°
762 m
H
A
B
C
h
4°
6°
762 m
A
B
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 27
Bài 14. Từ đỉnh một tòa nhà cao
54 m
, người ta nhìn thấy một ô tô đang đỗ dưới một góc nghiêng
xuống là
40
. Hỏi ô tô đang đỗ cách tòa nhà đó bao nhiêu mét ?
Lời giải:
Trên hình vẽ: Gọi
AB
là chiều cao của tòa nhà,
AC
là khoảng cách từ chân tường đến ô tô
Từ đỉnh tòa nhà, người ta nhìn thấy một ô tô đang đỗ dưới một góc nghiêng xuống là
40 50CBx CBA
.
Xét
ABC
vuông tại A có:
0
.tan 54.tan50 64,35 (m)AC AB ABC
Vậy ô tô đang đỗ cách tòa nhà đó khoảng 64,35 m
Bài 15. Một học sinh đứng ở mặt đất cách tháp ăng ten cao
150 m
nhìn thấy đỉnh tháp theo một góc
nghiêng lên là
20
và khoảng cách từ mắt đến mặt đất là
1m
. Tính khoảng cách từ học sinh đó
đến tháp (làm tròn đến mét).
Lời giải:
40° x
54m
C
B
A
H
D
20°
150m
C
B
A
1m
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 28
Trên hình vẽ: Gọi
BD
là chiều cao của tháp ăng ten,
C
là vị trí mắt của học sinh,
CH
là
khoảng cách từ mắt của học sinh đến mặt đất,
A
là hình chiếu của điểm
C
trên
BD
.
Ta có
ADHC
là hình chữ nhật và
150 ( ); 1 ( ) 149 ( )BD m HC m AB m
Khoảng cách từ học sinh đó đến tháp là độ dài đoạn thẳng
AC
Một học sinh đứng ở mặt đất nhìn thấy đỉnh tháp theo một góc nghiêng lên là
20ACB
Xét
ABC
vuông tại A có:
0
.cot 149.cot 20 409 (m)AC AB ACB
Vậy khoảng cách từ học sinh đó đến tháp là xấp xỉ
409m
.
Bài 16. Một cái thang dài
4,8m
dựa vào tường làm thành một góc
58
so với mặt đất. Tính chiều cao
của thang so với mặt đất (làm tròn đến mét).
Lời giải
Giả sử trong hình vẽ,
AC
là độ dài của thang thì
BC
chính là chiều cao của thang so với mặt
đất,
AB
là khoảng cách từ chân thang đến chân tường, góc tạo bởi thang với mặt đất
58CAB .
Xét
ABC
vuông tại
C
có
.sinBC AC CAB hay
4,8.sin 58 4 mBC
Vậy chiều cao của thang so với mặt đất xấp xỉ
4
mét.
Bài 17. Một người quan sát ở đài hải đăng cao
800feet
(đơn vị đo lường Anh) so với mực nước biển
nhìn thấy một con tàu ở xa với một góc nghiêng xuống là
1 42'
. Hỏi khoảng cách từ tàu đến
chân ngọn hải đăng là bao nhiêu hải lý (1 hải lý =
5280 feet
)?
Lời giải
B
4,8 m
58°
C
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 29
Giả sử trong hình vẽ
BC
là độ cao của đài hải đăng so với mực nước biển thì
AB
là khoảng
cách từ tàu đến chân ngọn hải đăng, góc nghiêng xuống
1 42ACx
1 42CAB
Xét
ABC
vuông tại
B
có
.cotanAB BC CAB
hay
800.cot1 42' 26954,8072 feet 5AB
(hải lý).
Vậy khoảng cách từ tàu đến chân ngọn hải đăng khoảng
5
hải lý.
Bài 18. Một người quan sát ở đài hải đăng cao
149 m
so với mực nước biển nhìn thất một con tàu ở xa
với một góc nghiêng xuống là
27
. Hỏi tàu đang đứng cách chân hải đăng là bao nhiêu mét?
Lời giải
Giả sử trong hình vẽ
BC
là độ cao của đài hải đăng so với mực nước biển thì
AB
là khoảng
cách từ tàu đến chân ngọn hải đăng, góc nghiêng xuống
27ACx
27CAB
Xét
ABC
vuông tại
B
có
.cotanAB BC CAB
hay
149.cotan 27 292 mAB
Vậy khoảng cách từ tàu đến chân ngọn hải đăng khoảng
292
mét.
Bài 19. Một học sinh thả diều ngoài đồng, cho biết đoạn dây đã thả dài
100 m
và có góc nâng
52
.
Tính độ cao của diều so với mặt đất (làm tròn đến mét).
1°42
'
x
B
800 feet
1°42
'
C
A
x
B
27°
149 m
27°
C
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 30
Lời giải
Giả sử trong hình vẽ,
AC
là đoạn dây diều đã thả thì
BC
là độ cao của diều so với mặt đất, góc
nâng
52CAB
Xét
ABC
vuông tại
B
có
.sinBC AC CAB
hay
100.sin 52 79 mBC
Vậy độ cao của diều so với mặt đất xấp xỉ
79
mét.
Bài 20. Một chiếc thuyền thả neo trên sông. Cho biết dây neo dài
30 m
và có góc nghiêng lên là
39
.
Tính độ sâu của mực nước chỗ thuyền đang đậu (làm tròn đến mét).
Lời giải
B
100 m
52°
C
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 31
Giả sử trong hình vẽ,
AC
là dây neo thì
BC
là độ sâu của mực nước chỗ thuyền đang đậu, góc
nghiêng lên
39CAB
Xét
ABC
vuông tại
B
có
.sinBC AC CAB
hay
30.sin 39 19 mBC
Vậy độ sâu của mực nước chỗ thuyền đang đậu xấp xỉ
19
mét.
Bài 21. Một người đứng trên đỉnh tháp cao
325m
nhìn thấy 2 điểm
A
và
B
với hai góc hạ lần lượt là
37
và
72
.Tính khoảng cách
AB
.
Lời giải:
Gọi các điểm như trên hình vẽ, ta được:
90 37 53
90 72 18
ADC
BDC
Xét
ADC
vuông tại
C
, có:
.tan 325.tan 53 431, 29( )AC DC ADC m
Xét
BDC
vuông tại
C
, có:
B
30 m
39°
C
A
325 m
37°
B
C
A
D
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 32
.tan 325.tan18 105,6BC DC BDC m
Ta có:
325,69( )AB AC BC m
Bài 22. Một người đứng cách chân tháp
14 m
nhìn thấy đỉnh tháp theo góc nghiêng
60
. Tính chiều cao
của tháp.
Lời giải
Gọi các điểm như trên hình vẽ.
Xét
ABC
vuông tại B, ta có:
.tan 14.tan 60 14 3AB BC C m
Bài 23. Một máy bay cất cánh theo phương có góc nâng
23
.Hỏi muốn đạt độ cao
2500 m
, máy bay
phải bay một đoạn đường là bao nhiêu mét?
Lời giải
14 m
60°
C
B
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 33
Đặt tên các điểm như trên hình vẽ:
Xét
ABC
vuông tại
C
sin
2500
sin 23
2500
6398,3( )
sin 23
AB
C
AC
x
x m
Vậy máy bay muốn đạt được độ cao
2500m
thì phải bay một đoạn đường khoảng
6398,3m
Bài 24. Một cái cây có bóng trên mặt đất dài
20 m
.Cho biết tia nắng qua ngọn cây nghiêng một góc
31
so với mặt đất. Tính chiều cao của cây.
Lời giải
Đặt tên các điểm như trên hình vẽ:
Xét
ABC
vuông tại
B
, ta được:
.tan 20.tan31 12,02AB BC C m
Bài 25. Một cái cây cao 6m đang có bóng dài
3, 2 m
. Tính góc hợp bởi tia nắng với thân cây
x
23°
2500 m
A
B
C
31°
20 m
A
B
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 34
Lời giải
Đặt tên các điểm như trên hình vẽ:
Xét
ABC
vuông tại C, ta được:
3,2
tan
6
28
BC
A
AC
A
Vậy góc tạo bởi tia nắng với thân cây khoảng
28
Bài 26. Một người đứng cách chân tháp 14 m nhìn thấy đỉnh tháp theo góc nghiêng
60
. Tính chiều
cao của tháp.
Lời giải
x
3,2 m
6 m
A
C
B
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 35
Gọi chiều cao của tháp là đoạn
AB
. Trong tam giác
ABC
vuông tại
A
ta có:
.tan 14.tan 60 14 3AB AC C m .
Vậy chiều cao của tháp là
14 3
m.
Bài 27. Bạn Hùng có tầm mắt cao 1,5 m đang đứng gần một cao ốc cao 30 m thì nhìn thấy nóc tòa nhà
với góc nâng
30
. Hùng đi về phía tòa nhà cho đến khi nhìn thấy nóc tòa nhà với góc nâng
60
.
Tính quãng đường mà bạn Hùng đã đi được.
Lời giải
Ta có độ dài đoạn
30 1,5 28,5AC CK AK cm
.
Trong tam giác
ABC
vuông tại
A
ta có:
.co t 28,5.cot30 28,5. 3AB AC B m .
Trong tam giác
ABD
vuông tại
A
ta có:
3
D .co t D 28,5.co t 60 28,5. 9,5 3
3
A AC m
.
Quãng đường bạn Hùng đi được là:
28,5 3 9,5 3 19BD AB AD m
Vậy bạn Hùng đi được 19 m.
Bài 28. Một học sinh có tầm mắt cao
1,5 m
đứng trên sân thượng của một căn nhà cao
15 m
nhìn thấy
bạn mình với góc nghiêng xuống
49
. Hỏi cô bạn đang ở cách căn nhà bao nhiêu mét?
60°
14 m
B
C
A
30m
60
o
30
o
1,5m
B
A
C
K
D
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 36
Lời giải
Gọi chiều cao của tòa nhà là
15AB m
, chiều cao của bạn học sinh là
1,5BC m
, ta có độ dài
15 1,5 16,5AC AB BC m
,
D 49 (hai góc so le trong), trong tam giác
DA C
vuông
tại
A
ta có:
.cot 16,5.cot 49AD AC D m
Vậy cô bạn cách căn nhà là
16,5.cot 49
m.
Bài 29. Một máy bay thể thao đang bay ngang ở độ cao
3000 m
nhìn thấy một cái cây với góc nghiêng
xuống
15
. Hỏi máy bay phải bay một đoạn đường là bao nhiêu mét thì sẽ ở ngay trên ngọn
cây?
Lời giải
Gọi đoạn đường cần bay để thấy ngọn cây là
AD x
, độ cao của máy bay là
3000CD m
.
Trong tam giác
ADC
vuông tại
D
ta có:
.cot 3000.cot15AD CD A m
.
15 m
1,5 m
49°
A
D
C
B
x
x
3000 m
15°
15°
D
B
C
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 37
Vậy quãng đường máy bay phải bay là
3000.cot15
m.
Bài 30. Từ nóc một cao ốc cao
50 m
người ta nhìn thấy chân và đỉnh một ăng-ten với các góc hạn lần
lượt là
62
và
34
. Tính chiều cao cột ăng-ten.
Lời giải
Ta có
50CD AB m
.
Trong tam giác
BDC
vuông tại
D
, ta có:
.cot 50.cot 62BD CD CBD m
.
Trong tam giác
BDE
vuông tại
D
ta có:
.tan 50.cot 62 .tan 34DE BD DBE m
.
Chiều cao của cột ăng ten là:
50 50.cot62 .tan34CE CD DE m
Vậy chiều cao của cột ăng ten là
50 50.cot 62 .tan34 67,93m
.
Bài 31. Một cái diều đang bay ở độ cao
60 m.
Sợi dây cột diều nghiêng với mặt đất một góc
60
. Tính
chiều dài của sợi dây (làm tròn đến mét) khi nó căng thẳng (không có chỗ bị võng).
Lời giải
62°
34°
50 m
D
A
C
B
E
A
B
C
D
E
50m
62
0
34
0
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 38
Phân tích bài toán ta có hình vẽ:
Xét
AHB
vuông tại
,H
áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác
vuông, ta có:
60 60
sin 69.
sin 60
3
sin
2
AH AH
ABH AB
AB
ABH
Vậy chiều dài của sợi dây khi nó căng thẳng là
69 .m
Bài 32. Tháp Capital Gate tại Abu Dhabi cao
160 m
và nghiêng
18
. Nếu không nghiêng thì tháp cao
bao nhiêu mét?
Lời giải
Phân tích bài toán ta có hình vẽ:
60m
60°
H
B
A
18°
160m
H
B
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 39
Xét
AHB
vuông tại
,H
dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác
vuông, ta có:
160
cos 168.
cos18
cos
AH AH
BAH AB
AB
BAH
Vậy nếu không nghiêng thì tháp Capital Gate tại Abu Dhabi cao
168 .m
Bài 33. Tính chiều cao của một ngọn núi, cho biết tại hai điểm cách nhau
500 m
, người ta nhìn thấy hai
đỉnh núi với góc nâng lần lượt là
34
và
38
.
Lời giải
Xét
ABC
vuông tại
,B
áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác
vuông, ta có:
tan .tan .tan38 1
AB
ACB AB BC ACB x
BC
Xét
ABD
vuông tại
,B
áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác
vuông, ta có:
tan .tan 500 .tan34 2
AB
ADB AB BD ADB x
BD
Từ
1
và
2
suy ra:
.tan38 500 .tan34x x
. tan38 tan34 500.tan34x
500.tan34
tan38 tan34
x
x
38°
34°
500m
B
A
D
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 40
Mà
.tan 38AB x
nên
500.tan34
.tan38 2468.
tan38 tan34
AB
.
Vậy ngọn núi đó cao khoảng
2468 .m
Bài 34. Một cái tháp được dựng bên bờ một con sông, từ một điểm đối diện với tháp ngay bờ bên kia
người ta nhìn thấy đỉnh tháp với góc nâng
60
. Từ một điểm khác cách điểm ban đầu
20 m,
người ta cũng nhìn thấy đỉnh tháp với góc nâng
30
. Tính chiều cao của tháp.
Lời giải
Giả sử đoạn
BC
có độ dài là
.x m
Xét
ABC
vuông tại
,B
áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác
vuông, ta có:
tan .tan .tan 60 1
AB
ACB AB BC ACB x
BC
Xét
ABD
vuông tại
,B
áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác
vuông, ta có:
tan .tan 20 .tan 30 2
AB
ADB AB BD ADB x
BD
Từ
1
và
2
suy ra:
.tan 60 20 .tan30x x
. tan 60 tan 30 20.tan30x
20.tan30
tan60 tan30
x
Mà
.tan 60AB x
nên
3
20.
20.tan30
3
.tan 60 . 3 17.
tan 60 tan30
3
3
3
AB
Vậy chiều cao của tháp xấp xỉ
17 .m
x
20 m
60°30°
B
A
D
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 41
Bài 35. Một bức tượng cao
1,6 m
được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là
60
và
45
. Tính chiều cao của cái bệ.
Lời giải
ABC
vuông tại
B
có
45
o
BAC nên
ABC
vuông cân tại
B
nên
AB BC h
.
Xét
ABD
vuông tại
,B
áp dụng định nghĩa hệ thức giữa cạnh và góc trong tam giác vuông, ta
có:
1,6
.tan 60 1, 6 . 3 3 1 1,6 2,2
3 1
BD AB h h h h h
Vậy chiều cao của cái bệ
2,2 .h m
Bài 36. Một nhà trẻ muốn thiết kế hai cái cầu tuột trong sân chơi. Đối với trẻ dưới 5 tuổi, cầu tuột cao
1,5m
và nghiêng với mặt đất một góc
30
. Đối với trẻ trên 5 tuổi cầu tuột cao 1,5 m và
nghiêng với mặt đất
một góc
45
. Tính chiều dài của mỗi máng tuột.
Lời giải
Máng tuột của cầu trượt trẻ em dưới 5 tuổi là độ dài
EA
Xét
1,5
sin sin 30 3(m)
AB
AEB AE
AE AE
Máng tượt của cầu trượt trẻ em trên 5 tuổi là độ dài
AC
Xét
1,5
sin sin 45 1,06(m)
AB
ACB AC
AC AC
Bài 37. Từ chân một cái tháp cao
50 m
người ta nhìn thấy đỉnh một tòa nhà với góc nâng
30
. Trong
khi đó từchân tòa nhà lại nhìn thấy đỉnh tháp với góc nâng
60
. Tính chiều cao của tòa nhà.
45
30
2m
E CB
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 42
Lời giải
Chiều cao tòa nhà là độ dài
AB
.
Xét
50 50 3
, 90 : tan (m)
tan 60 3
DC
DAC DCA DAC AC
AC
Xét
0 0
50 3 50
, 90 : tan .tan 30 ( )
3 3
AB
BAC CAB BCA AB m
AC
Bài 38. Hai trụ điện có cùng chiều cao đặt cách nhau
80 m
. Một người đứng ở xa (thẳng hàng với hai
trụ
điện, không đứng giữa hai trụ điện) nhìn đỉnh hai trụ điện với góc nâng lần lượt là
60
và
30
. Tính chiều cao trụ điện và khoảng cách từ người đó đến chân các trụ điện. Biết mắt người
đó cách mặt đất
1, 2 m
.
Lời giải
Chiều cao của người là độ dài
1,2mAH
.
Chiều cao cột điện là
BH BA AH
x
80m
1,2m
60
30
60
B
A
C
D
H
M
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 43
Khoảng cách 2 cột điện là
80mAC
Khoảng cách người đến cột 1 và cột 2 lần lượt là độ dài
; .AM MC
Vì 2 cây cột điện cao bằng nhau
/ / 60BD AC DBM BMA (2 góc so le trong)
180 90BMD BMA DMC
Xét
, 90 , 80(m) : cos 80.cos 60 40(m)
BM
BMD BMD DB DBM BM
BD
Xét
, 90 , 40(m) : cos 40.cos60 20(m);
AM
BMA BAM MB BMA AM
BM
.sin 60 20 3(m)AB BM
80 20 60(m)MC AC AM
20 3 1, 2 35,8(m)BH AB AH
Bài 39. Từ trên một ngọn hải đăng cao
75 m
, người ta quan sát hai lần thấy một chiếc thuyền đang
hướng về phía hải đăng với góc hạ lần lượt là
30
và
45
. Hỏi chiếc thuyền đi được bao nhiêu
mét giữa hai lầnquan sát?
Lời giải
Chiều dài quãng đường chiếc thuyền đi giữa hai lần quan sát là độ dài
CD
.
Xét
75
, 90 : tan 75(m)
tan 45
AB
BAC BAC ACB AC
AC
Xét
75
, 90 : tan 75 3(m)
tan 30
AB
DAB DAB BDA AD
AD
75 3 75 59,9(m)CD DA AC
Bài 40. Một thủy thủ lái thuyền ra biển hướng về hướng đông bắc với góc nghiêng so với phương bắc
là
41
. Đi được
2,8km
anh ta phát hiện sắp hết nhiên liệu nên vội quay thuyền vào bờ, đi
được
1,8 km
thì
thuyền tắt máy. Hỏi lúc đó thuyền cách bờ bao xa?
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 44
Lời giải
Khoảng cách từ thuyền đến bờ là độ dài
CD
góc nghiêng so với phương bắc là
xAB
0
41 49BAC
Xét
, 90 :sin 2,8.sin 49 2,11(km)
BD
DAB BDA BAD BD
AB
2,1 1,8 0,3(km)CD BD BC
Bài 41. Từ trên đỉnh một tòa nhà cao
7m
, người ta nhìn thấy đỉnh một tháp truyền hình với góc nâng
60
và nhìn thấy chân của tháp với góc hạ
45
. Tính chiều cao của tháp truyền hình?
Lời giải
Xét
ABC
vuông tại
B
có:
.cot .cot 45 7.1 7( )BC AB ACB AB m
(HTL trong tam giác vuông)
7AB BC m
Theo đề bài ta có tứ giác
ABCE
là hình chữ nhật mà
AB BC
(cmt) nên tứ giác
ABCE
là
hình vuông
7AE EC AB BC cm
.
Xét
AED
vuông tại
E
có:
.tan 7.tan 60 7 3 12,12( )DE AE DAE m
(HTL trong tam giác vuông)
Nên
7 12,12 19,12CD CE ED m
Vậy chiều cao của tháp truyền hình khoảng
19,12
m.
j
x
2,8
41
1,8
A
D
B
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 45
Bài 42. Một học sinh có khoảng cách từ mặt đến mặt đất là
1, 2m
bắt đầu quan sát một trái bóng bay
với góc nâng
60
. Một lúc sau lại nhìn thấy quả bóng bay với góc nâng
30
. Hỏi giữa hai lần
quan sát quả bóng đã bay được bao nhiêu mét? Cho biết độ cao của quả bóng luôn luôn không
đổi và bằng
88,2 m
.
Lời giải
Xét
ABP
vuông tại
B
có:
3
.cot 87.cot60 87. 50,23( )
3
AB BP BAP m
(HTL trong tam giác vuông).
Xét
ACQ
vuông tại
C
có:
.cot 87.cot30 87. 3 150,69( )AC QC BAQ m
(HTL trong tam giác vuông)
Nên
150,69 50,23 100,46PQ BC AC AB m
Vậy giữa hai lần quan sát quả bóng đã bay được khoảng
100,46
m.
Bài 43. Một người đang ở trên một cái tháp có chiều cao
h =100 m
nhìn xuống một con đường chạy
thẳng đến chân tháp. Anh ta nhìn thấy một chiếc xe máy với góc hạ
30
. Sáu phút sau lại nhìn
thấy nó với góc hạ
60
. Hỏi sau bao nhiêu phút thì xe máy đến chân tháp? Cho biết vận tốc xe
máy không đổi.
Lời giải
Gọi vận tốc xe máy là
x
(m/phút)
6 ( )CD x m
.
Xét
ABD
vuông tại
B
có:
.cot 100.cot30 173,21( )DB AB ADB m
(HTL trong tam giác vuông).
Xét
ABC
vuông tại
B
có:
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 46
3
.cot 100.cot 60 100. 57,74( )
3
CB AB ACB m
(HTL trong tam giác vuông).
173,21 57,74 115,47CD DB CB m
.
Vận tốc xe máy là:
115,47
19,25
6 6
CD
x
(m/phút) .
Thời gian xe máy đi từ
C
đến chân tháp là:
57,74 :19,25 3
(phút).
Bài 44. Để đo chiều cao một cái cây
AB
. Người ta đặt gương phẳng tại vị trí
C
. Người đo đi lùi lại
(thẳng người) cho đến khi nhìn thấy bóng ngọn cây
A
(lúc này là
F
). Biết khoảng cách từ
gương đến gốc cây là
30BC
mét, khoảng cách từ gương đến chỗ đứng là
1,5
CD
mét.
Khoảng cách từ mắt người đo
E
đến mặt đất là
1,6ED
mét. Tính chiều cao của cây? (biết
BCA DCE ).
Lời giải
Xét
ABC
và
EDC
có:
BCA DCE (gt)
90ABC EDC
Nên
ABC EDC
∽
(g.g)
30 30.1,6
32
1,6 1,5 1,5
AB BC AB
AB m
ED DC
.
Vậy chiều cao cây là
32
m.
Bài 45. Quan sát hình vẽ dưới đây. Giả sử
CD h
là chiều cao của tháp trong đó
C
là chân tháp.
Chọn hai điểm
A
,
B
trên mặt đất sao cho ba điểm
A
,
B
và
C
thẳng hàng. Ta đo khoảng cách
AB
và các góc
CAD ,
CBD . Chẳng hạn ta đo được
24AB
m,
63CAD
,
48
CBD
. Hãy tính chiều cao
h
của tháp.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 47
Lời giải
Xét
DCB
vuông tại
C
có:
.cot .cot 48 0,9. ( )CB DC CBD h h m
(HTL trong tam giác vuông).
Xét
DCA
vuông tại
C
có:
.cot .cot63 0,51. ( )CA DC CAD h h m
(HTL trong tam giác vuông).
0,9. 0,51. 0,39.AB CB CA h h h m
.
24
61,54
0,39 0,39
AB
h m .
Vậy chiều cao của tháp khoảng
61,54
m.
Bài 46. Một hình chữ nhật có kích thước là
20
cm và
30
cm. Người ta tăng mỗi kích thước thêm
x
cm.
Gọi
y
là chu vi của hình chữ nhật mới.
1) Hãy tính
y
theo
x
.
2) Tính giá trị của y tương ứng với
3x
cm;
5x
cm.
Lời giải
1) Ta có các kích thước của hình chữ nhật sau khi tăng là
20x
cm và
30x
cm.
Chu vi hình chữ nhật mới là
2. 20 30 4x 100y x x
.
Vậy
4x 100y
(cm).
2) Ta có:
4x 100y
.
Với
3 4.3 100 112x y cm
.
Với
5 4.5 100 120x y cm
.
Bài 47. Một thửa đất hình chữ nhật có chiều dài là 32 m và chiều rộng là 24 m. Người ta định làm một
vườn cây cảnh có con đường đi xung quanh, có bề rộng
x
m (hình vẽ bên). Hỏi bề rộng của
mặt đường là bao nhiêu để diện tích phần đất còn lại là 560
2
m
.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 48
Lời giải
Ta có: Chiều rộng phần đất còn lại là:
24 2x
(cm).
Chiều dài phần đất còn lại là:
32 2x
(cm).
Vì diện tích phần đất còn lại là 560
2
m
nên ta có phương trình:
24 2 32 2 560x x
2 2
768 48 64 4 560 28 52 0x x x x x
2
26
x
x
Vì
24
12 2
2
x x
.
Vậy bề rộng mặt đường là 2m.
Bài 48. Một căn phòng hình vuông được lát bằng những viên gạch men hình vuông cùng kích cỡ, vừa
hết 441 viên (không viên nào bị cắt xén). Gạch gồm 2 loại men trắng và men xanh, loại men
trắng nằm trên 2 đường chéo của nền nhà còn lại là loại men xanh. Tính số viên gạch men
xanh.
Lời giải
Gọi cạnh của mỗi viên gạch hình vuông là a (đơn vị diện tích) thì ta có diện tích nền nhà là
2
441a
, do đó cạnh của nền nhà là
2
441 21a a
. Suy ra đường chéo mỗi viên gạch dài
2a
và đường chéo của nhà là
21 2a
nên mỗi đường chéo sẽ có 21 viên gạch. Hai đường chéo lại
chung nhau một viên chính giữa nên tổng số viên gạch của hai đường chéo là 41 viên. Vậy
tổng số sẽ có 41 viên gạch trắng và 400 viên gạch xanh.
Bài 49. Bạn Nam đi xe đạp từ nhà (điểm A) đến trường (điểm B) gồm đoạn lên dốc và đoạn xuống
dốc,
5A ,
4B
, đoạn lên dốc dài 325 m.
1) Tính chiều cao của dốc và chiều dài quãng đường từ nhà đến trường.
2) Biết vận tốc trung bình lên dốc là 8 km/h và vận tốc trung bình xuống dốc là 15 km/h. Tính
thời gian (phút) bạn Nam đi từ nhà đến trường. (Lưu ý kết quả của phép tính làm tròn đến chữ
số thập phân thứ nhất).
Lời giải
1) Gọi chiều cao của dốc là
CH
.
Trong tam giác
ACH
vuông tại
H
ta có
. 325.sin5 28,3CH AC SinA m
.
x
x
x
x
24 m
32 m
325m
H
A
B
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 49
Trong tam giác
BCH
vuông tại
H
ta có
. 325.sin 5
406,1
4
CH AC SinA
BC m
SinB SinB Sin
.
Vậy chiều cao của dốc gấn bằng
28,3
m.
Chiều dài quãng đường từ nhà đến trường là
325 406,1 731,1 m
2) Đổi 8 km/h =
400
3
m/phút ; 15 km/h = 250 m/phút.
Ta có thời gian đi từ nhà đến trường là:
325 406,1
4,1
400
250
3
(phút)
Bài 50. Một bức tượng cao 1,6 m được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là
60
và
45
. Tính chiều cao cái bệ.
Lời giải
Gọi chiều cao của tượng là đoạn
BC
, Chiều cao của bệ là đoạn
AB
.
D
là điểm trên mặt đất
người ta nhìn thấy nóc tượng và nóc bệ với các góc nâng lần lượt là
60
và
45
.
Vì
45ADB nên
AB AD
.
Vì
60ADC nên
. 60 3 3AC AD Tan AD AB AB AD .
Vậy ta có
1,6
3 1,6
3 1
AC AB BC AB AB AB
.
Vậy chiều cao của cái bệ sẽ là
1,6
3 1
m.
Bài 51. Một cây có chiều cao 14 m mọc ở phía sau một bức tường cao 8 m và cách bức tường 12 m.
Hỏi người quan sát có chiều cao
1,8
m phải đứng cách bức tường bao nhiêu mét để có thể nhìn
thấy ngọn cây.
1,6m
B
C
A
D
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 50
Lời giải
Bài toán được mô tả bởi hình vẽ sau:
Độ dài cần tính là độ dài đoạn CE
Xét
0
90
ABG A
có
/ /AB DC
8
16
14 12
DC CG CG
CG m
AB AG CG
Xét
0
90
DCG C
có
/ /DC EF
1,8
3,6
8 16
EF EG EG
EG m
DC CG
Có
16 3,6 12,4
CG CE EG CE CE m
Vậy người quan sát có chiều cao
1,8
m phải đứng cách bức tường bao nhiêu 12,4 mét để có thể
nhìn thấy ngọn cây.
Bài 52. Nhà bạn An ở vị trí
A
, nhà bạn Bình ở vị trí
B
cách nhau 1200 m. Trường học ở vị trí
C
cách
nhà bạn An 500m và
AB
vuông góc với
AC
. An đi bộ đến trường với vận tốc 4 km/h, Bình đi
xe đạp đến trường với vận tốc 12 km/h. Lúc 6 giờ 30 phút, cả hai cùng xuất phát đến trường.
Hỏi bạn nào đến trường trước?
Lời giải
Bài toán được mô tả bởi hình vẽ sau :
AC
là quãng đường An đi bộ đến trường.
12m
1,8m
8m
14m
E
C
A
G
B
D
F
1200m
500m
A
B
C
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 51
BC
là quãng đường Bình đi bộ đến trường.
Xét
0
90ABC A
có:
2 2 2 2 2 2
500 1200 1300 1,3AC AB BC BC BC m km
Thời gian An đi từ nhà đến trường là :
0,5: 4 0,125 h
Thời gian Bình đi từ nhà đến trường là :
1,3:12 0,1083 h
Vậy bạn Bình là người đến trường trước.
Bài 53 Bóng của tháp Bình Sơn (Vĩnh Phúc) trên mặt đất có độ dài 20 m. Cùng thời điểm đó, một cột
sắt cao
1,65
m cắm vuông góc với mặt đất có bóng dài 2 m. Tính chiều cao của tháp.
Lời giải
Bài toán được mô tả bởi hình vẽ sau
AC
là chiều cao cột tháp ;
AB
là bóng tháp Bình Sơn
IJ
là chiều cao cột sắt ;
IK
là bóng cột sắt
Tại cùng một thời điểm, các tia sáng là các đường thẳng song song
Có
ABC IKJ
1,65
16,5
20 2
AC IJ AC
AC m
AB IK
Vậy chiều cao của tháp là
16,5m
.
Bài 54. Một con đê được đắp chắn sóng theo hình dưới, độ dốc của con đê phía sông dài 7 m. Hỏi độ
dốc còn lại của con đê dài bao nhiêu mét?
Lời giải
Ta có
BCKH
là hình chữ nhật
BH CK
Xét
0
90ABH H
có:
.sinBH AB A
0
7.sin 50BH
(m)
Có
BH CK
7.sin50CK
(m)
2m
20m
1,65m
J
A
B
C
I
K
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 52
Xét
0
90CKD K
có:
sin
CK
D
CD
0
7.sin 50
14.sin50 10,72
sin sin30
CK
CD CD m CD m
D
Vậy độ dốc còn lại của con đê gần bằng 10,72 m.
Bài 55. Xem hình vẽ sau, người ta có thể dùng giác kế để đo được góc
43CAB và
38CBA . Hỏi
tàu đang ở vị trí điểm
H
sẽ chạy với vận tốc bao nhiêu km/h để sau 5 phút sẽ đến vị trí điểm
C
. Biết khoảng cách từ vị trí điểm
A
đến vị trí điểm
B
là 300 m và vị trí 3 điểm
A
,
H
,
B
thẳng hàng (làm tròn đến chữ số thập phân thứ hai).
Lời giải
Xét
0
90AHC H
có:
0
.tanA .tan 43CH AH CH AH
Xét
0
90BHC H
có:
0
.tanB .tan38CH BH CH BH
0
.tan 43AH
=
0
.tan38BH
0
.tan 43AH
=
0
300 .tan38AH
136,76AH m
127,53 0,12753CH m km
Tàu ở vị trí H để chạy đến C sau 5 phút cần đi với vận tốc:
1
0,12753: 1,53 /
12
km h
.
Bài 56. Ba An muốn mua một cái thang dùng để lên mái nhà. Ba hỏi An phải mua cái thang dài bao
nhiều mét để đảm bảo sự an toàn và có thể leo lên được mái nhà cao
4,5
m so với mặt đất. Em
hãy giúp An tính chiều dài thang cần mua, biết góc kê thang an toàn là
75
so với phương
ngang (làm tròn đến số thập phân thứ nhất).
B
C
H
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 53
Giải
Chiều dài cái thang cần mua là:
0
4,5
4,7
sin75
m
Bài 57. Một chiếc máy bay bay lên cao với vận tốc
520 /km h
. Đường bay lên tạo với phương nằm
ngang một góc
24
. Hỏi sau 90 giây máy bay lên cao được bao nhiêu km theo phương thẳng
đứng? (kết quả làm tròn đến chữ số thập phân thứ nhất)
Giải
Giả sử
AC
là đoạn đường máy bay bay lên trong
90
giây thì
AB
là độ cao bay lên theo
phương thẳng đứng.
Vì
90
giây
0,025
giờ nên
520.0,025 13AC km
Do đó
0
13.sin 2 , 4 5 3. kmAB AC sin C
Vậy sau
90
giây máy bay lên cao được
5,3 km
.
Bài 58. Từ đài quan sát cao 10 m, Nam có thế nhìn thấy 2 chiếc thuyền dưới góc
45
và
30
so với
phương ngang. Hãy tính khoảng cách 2 chiếc thuyền, làm tròn đến chữ số thập phân thứ nhất.
(điều kiện lý tưởng: vị trí 2 chiếc thuyền và vị trí đài quan sát thẳng hàng).
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 54
Giải
Vì Nam nhìn thấy hai chiếc thuyền dưới góc
0
45
và
0
30
so với phương ngang nên ta có góc
0 0
45 ; 30BDA BCA
Xét
ABC
vuông tại
A
có:
0 0
30 60BCA CBA
Ta có:
0
.tan 10.tan 60 17,3AC AB CBA m
Xét
ABD
vuông tại
A
có:
0 0
45 45BDA DBA
0
.tan 10.tan45 10DA AB DBA m
Vậy khoảng cách giữa hai thuyền
17,3 10 7,3CD CA DA m
Bài 59. Hình ảnh mặt cắt một quả đồi được minh họa là một
ABC
với các chi tiết như sau: cạnh đáy
là
AC
,
BH AC
,
45BAC
,
200AH
m,
210HC
m. Một nhóm học sinh đi dã ngoại
đi từ đỉnh
A
lên đỉnh
B
rồi xuống dốc trở về
C
. Hãy tính quãng đường này?
Giải
0
200
282,8
cos cos 45
AH
AB m
A
Áp dụng định lí Pytago cho
ABH
vuông tại
H
và
BHC
vuông tại
H
:
2 2 2
200BH AB AH BH m
2 2 2
290BC BH HC BC m
Vậy quãng đường đi từ
A
đến đỉnh
B
rồi xuống dốc về
C
là:
282,8 290 572,8AB BC m
.
Bài 60. Hai chiếc thuyền
A
và
B
ở vị trí được minh họa như trong hình vẽ. Tính khoảng cách giữa
chúng (kết quả là tròn đến mét).
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 55
Giải
Ta có
0
.tan 50 452,9AI IK m
0
.tan 65 814,9BI IK m
Vậy khoảng cách giữa hai thuyền là
814,9 452,9 362AB BI AI m
Bài 61. Lúc 6h45 phút sáng bạn Nam đi xe đạp điện từ nhà tới trường với vận tốc trung bình là
15
km/h bạn đi theo con đường từ
A B C D E G H
(như trong hình). Nếu có
1
con đường thẳng từ
A H
và đi theo con đường đó với vận tốc trung bình 15 km/h, bạn Nam
sẽ tới trường lúc mấy giờ?
Lời giải
Gọi
O AB HG
. Ta có:
1000 600 400 2000AO
m,
500 300 700 1500HO
m.
Áp dụng định lí Pytago trong tam giác vuông
AOH
có:
2 2 2 2
2000 1500 2500AH AO HO
m
=
2,5
km
.
Thời gian đi từ nhà đến trường của bạn An là:
2,5 1
15 6
s
t
v
h
=
10
p.
Vậy thời gian bạn An đến trường lúc 6h55 phút.
Bài 62. Hai ngư dân đứng ở một bên bờ sông cách nhau
50
m cùng nhìn thấy một cù lao trên sông với
các góc nâng lần lượt là
30
và
40
. Tính khoảng cách d từ bờ sông đến cù lao.
500m
400m
300m
600m
700m
1000m
Trường học
Nhà
H
G
E
D
C
B
A
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 56
Lời giải
Đặt:
;AH x BH y
. Theo đề ta có:
tan30 3
x
y x
y
50 tan 40
tan 40 50 tan 40 50 3 tan 40 17,1
50
1 3 tan 40
x
x y x x x
y
Vậy khoảng cách d từ bờ sông đến cù lao là:
17,1
m.
Bài 63. Một người đi xe máy lên dốc có độ nghiêng
5
so với phương ngang với vận tốc trung bình lên
dốc là
18
km/h. Hỏi người đó mất bao lâu để lên tới đỉnh dốc? Biết đỉnh dốc cách mặt đất
18
m.
Lời giải
Giả sử
BC
là độ dài của dốc nghiêng
5
so với phương ngang. Khi đó độ cao của dốc là
AB
.
Trong
ABC
vuông tại
A
, ta có:
18
sin5 206,53
sin5 sin5
AB AB
BC
BC
.
Ta có:
18 /km h
=
5 /m s
.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 57
Thời gian người đó lên dốc là:
206,5
41,31
5
s
t
v
s
.
Bài 64. Từ vị trí xuất phát
A
, hai xe cùng một lúc đi thẳng theo hai hướng khác nhau, tạo một góc
70A . Xe thứ nhất đi với vận tốc 40 km/h và xe thứ hai đi với vận tốc 50 km/h. Sau 1 giờ 30
phút, hai xe cách nhau bao nhiêu km? (làm tròn đến 2 chữ số thập phân).
Lời giải
Giả sử
B
và
C
là hai vị trí của 2 xe sau 1 giờ 30 phút.
Quãng đường xe
A
đi được là . 40.1,5 60
A
AB v t km.
Quãng đường xe
B
đi được là . 50.1,5 75
B
AC v t km.
Kẻ
CH AB
. Khi đó
ACH
vuông tại
H
, ta có:
sin .sin 70 70,48
CH
A CH AC
AC
cos .cos 70 25,65
AH
A AH AC
AC
Ta có:
60 25,65 34,35AB AH HB HB HB
Áp dụng định lí Pytago trong tam giác vuông
BHC
có:
2 2
2 2
34,35 70,48 78,41BC BH CH
Vậy sau hai xe cách nhau
78, 41
km.
Bài 65. Một máy kéo nông nghiệp có bánh xe sau to hơn bánh xe trước. Bánh xe sau có đường kính
124
cm và bánh xe trước có đường kính
80
cm. Hỏi khi bánh xe sau lăn được
20
vòng thì xe
di chuyển được bao nhiêu mét (làm tròn một chữ số) và khi đó bánh xe trước lăn được mấy
vòng?
Lời giải
Chu vi bánh xe sau là:
2
2 .3,14 .3,14 124.3,14 389,36C R d .
Chu vi bánh xe trước là:
1
2 .3,14 .3,14 80.3,14 251,2C R d .
Khi bánh xe sau lăn được 20 vòng thì quãng đường xe di chuyển được là:
20.389,36 7787, 2
cm.
Số vòng bánh xe trước lăn được là:
7787, 2 : 251, 2 31
vòng.
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 58
Bài 66. Trong hình vẽ dưới đây, hai địa điểm
A
,
B
cách nhau 100 km. Một xe ô tô khởi hành từ
B
đến
A
với vận tốc 40 km/h. Cùng lúc đó, một xe đạp điện cũng khởi hành từ
A
trên đoạn đường
vuông góc với
AB
với vận tốc 20 km/h. Hỏi sau 90 phút thì hai xe cách nhau bao xa.
Lời giải
Đổi
90
phút =
1,5
giờ.
Quãng đường
BC
mà người đi từ
B
đi được trong 1,5 giờ là:
40.1,5 60
km.
Quãng đường
AD
mà người đi xe đạp điện đi được trong 1,5 giờ là:
20.1,5 30
km.
Quãng đường
AC
dài:
100 60 40BA BC
km.
Áp dụng định lý Pytato trong
ADC
vuông tại
A
ta có:
2 2 2
2 2 2
2
30 40
2500
50
DC AD AC
DC
DC
DC
Vậy sau
90
phút thì hai xe cách nhau
50
km.
Bài 67. Với số liệu ghi trên hình (biết tứ giác
EFHI
là hình chữ nhật và
A
,
I
,
H
thẳng hàng). Cây
trong hình cao bao nhiêu mét? (làm tròn kết quả đến chữ số hàng đơn vị).
Lời giải
Vì tứ giác
EFGH
là hình chữ nhật nên
EF 1,7IH
m
5,5EI FH
m
Xét
AEI
vuông tại
I
có:
.tanAI EI AIE ( Hệ thức lượng trong tam giác vuông)
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 59
0
5,5.tan 50
7
AI
AI m
7 1,7 8,7AH AI IH
m
Vậy cây trong hình cao
8,7
mét
Bài 68. Một người quan sát đứng cách một tòa nhà khoảng 25 m (điểm
A
). Góc nâng từ chỗ anh ta
đứng đến nóc tòa nhà (điểm
C
) là
36
.
1) Tính chiều cao tòa nhà (làm tròn đến
0,5
mét)
2) Nếu anh ta đi thêm 5 m nữa, đến vị trí
D
nằm giữa
A
và
B
thì góc nâng từ
D
đến nóc nhà là
bao nhiêu? (làm tròn đến phút).
Lời giải
1) Chiều cao của tòa nhà chính là độ dài đoạn thẳng
BC
Xét
ABC
vuông tại
B
có:
.tanBC AB BAC ( Hệ thức lượng trong tam giác vuông)
0
25.tan 36
18, 2
BC
BC m
Vậy chiều cao của tòa nhà là
18,2m
2)
Nếu anh ta đi thêm 5 m nữa đến vị trí
D
thì
5AD
m
25 5 20DB AB AD
m
Ta có góc nâng từ
D
đến nóc nhà là
CDB
.
Xét
DBC
vuông tại
B
có
:
36°
25m
A
B
C
D
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM
Chuyên Đề Toán Thực Tế
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 60
18,2
tan 0,91
20
BC
CDB
DB
( Hệ thức lượng trong tam giác vuông)
0 '
42 18CDB
Vậy góc nâng từ
D
đến nóc nhà là
0 '
42 18
Bài 69. Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất,cọc cao 2 m và đặt xa cây 15
m. Sau khi người ấy lùi ra xa cách cọc
0,8
m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên
một đoạn đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy
là
1,6
m?
Lời giải
Giả sử cây có độ cao
CD
, cọc ở vị trí
B
có độ dài
2FB
m, cọc cách cây một đoạn
15BC
m.
Vị trí người đứng ở
A
cách cọc một đoạn
0,8AB
m.
Khoảng cách từ chân đến mắt người đó là
1,6AE
m.
Ta có tứ giác
AEGC
là hình chữ nhật nên
1,6AE GC
m ;
0,8 15 15,8AC EG AB BC
m
Ta có tứ giác
AEHB
là hình chữ nhật nên:
1,6AE HB
m;
0,8EH AB
m
Ta có
2 1,6 0,4FH FB HB
m
Xét
EFH
vuông tại
H
có:
0,4 1
tan
0,8 2
FH
FEH
EH
( Hệ thức lượng trong tam giác vuông)
Xét
EGD
vuông tại
G
có:
.tanDG EG FEH ( Hệ thức lượng trong tam giác vuông)
1
15,8. 7,9
2
DG m
7,9 1,6 9,5DC DG GC m
Vậy cây cao
9,5m
2m
1.6m
0,8m
15m
H
A
C
E
D
F
B
G
| 1/60
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
DẠNG 1: CÁC BÀI TOÁN THỰC TẾ VỀ HÌNH HỌC
Vận dụng hệ thức lượng trong tam giác vuông – Tỉ số lượng giác của góc nhọn Bài 1.
Hằng ngày hai anh em An và Bình cùng đi bộ từ nhà ở A để đến trường. Trường của An ở vị
trí B , trường của Bình ở vị trí C theo hai hướng vuông góc với nhau. An đi với vận tốc
4km / h và đến trường sau 15 phút. Bình đi với vận tốc 3km / h và đến trường sau 12
phút.Tính khoảng cách BC giữa hai trường (làm tròn đến mét). Bài 2.
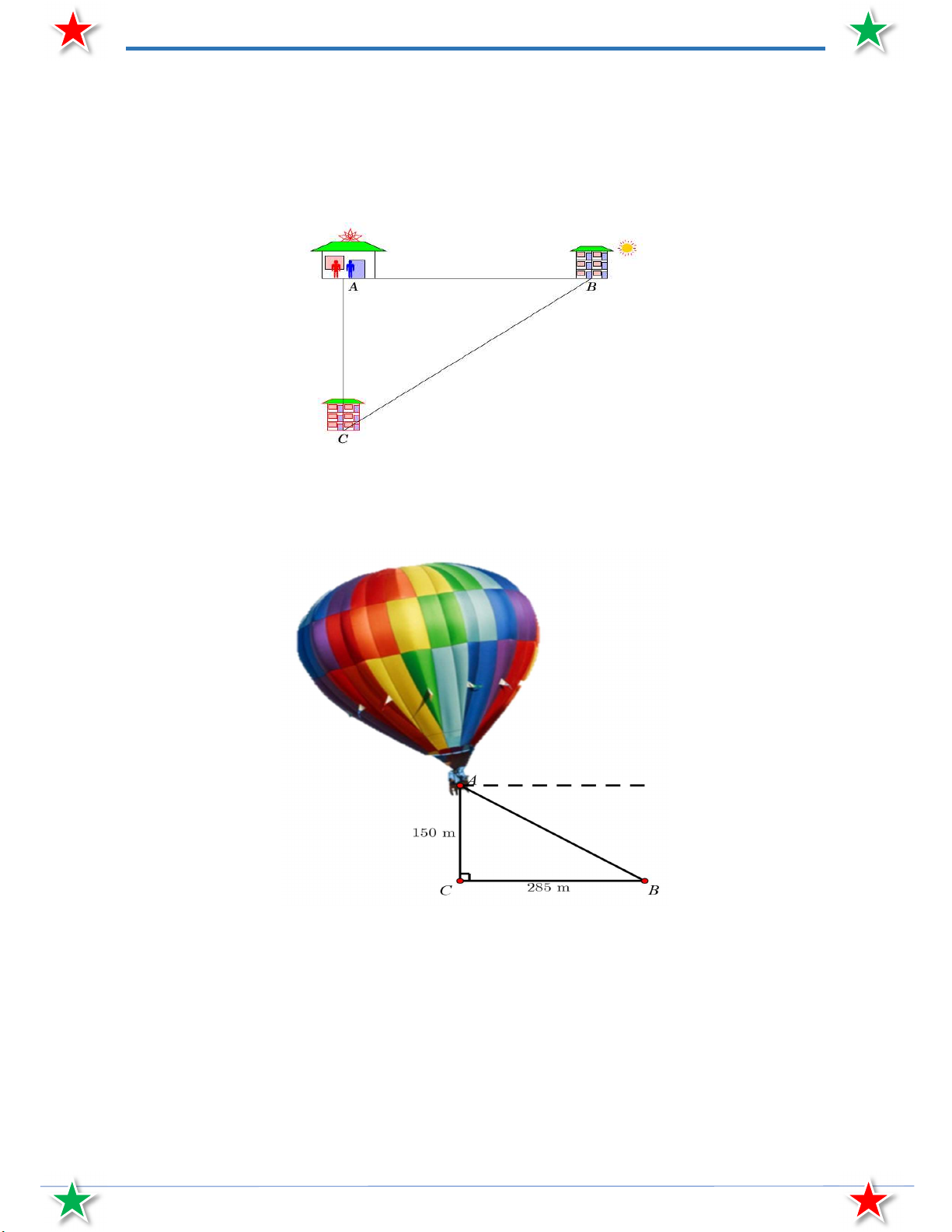
Một người A đang ở trên khinh khí cầu ở độ cao 150m nhìn thấy một vật B trên mặt đất cách
hình chiếu của khí cầu xuống đất một khoảng 285m . Tính góc hạ của tia AB . Nếu khinh khí
cầu tiếp tục bay lên thẳng đứng thì khi góc hạ của tia AB là 46 thì độ cao của khinh khí cầu
là bao nhiêu? (làm tròn đến mét). Bài 3.
Một người có mắt cách mặt đất 1, 4m , đứng cách tháp Eiffel 400m nhìn thấy đỉnh tháp với góc
nâng 39 . Tính chiều cao của tháp (làm tròn đến mét).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 1
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Bài 4.
Một cột đèn cao 8m . Tính góc tạo bởi tia nắng mặt trời và mặt đất lúc nó có bóng trên mặt đất là 5m . Bài 5.
Một cái thang dài 4m đang dựa vào tường, chân thang cách chân tường 2m .Tính góc tạo bởi
thang với mặt đất và với mặt tường. Bài 6.
Tính chiều cao của một ngọn núi cho biết tại hai điểm cách nhau 1km trên mặt đất người ta
nhìn thấy đỉnh núi với góc nâng lần lượt là 40 và 32 . D 32° 40° C A 1km B Bài 7.
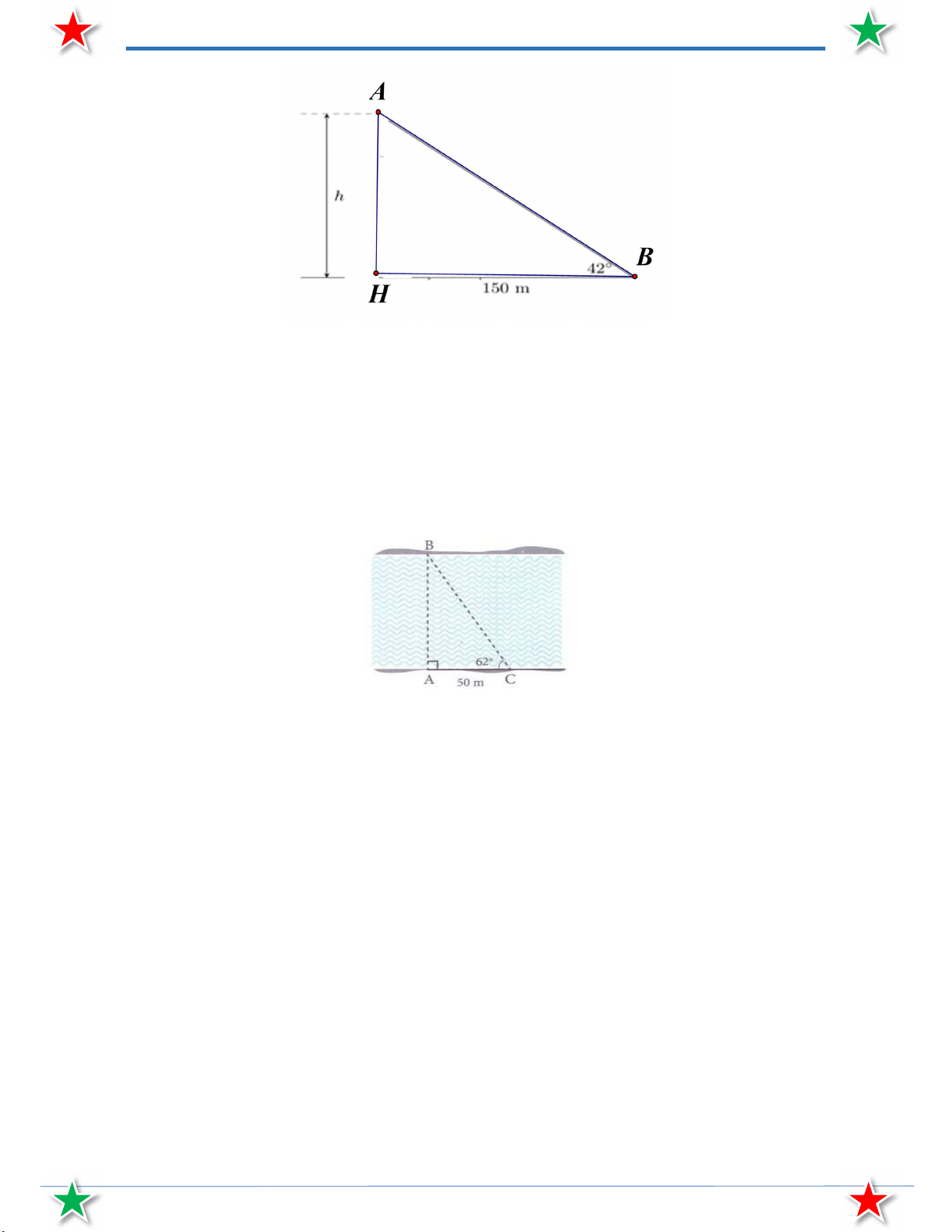
Tính chiều cao của một cái tháp, cho biết khi các tia nắng mặt trời tạo với mặt đất một góc 42
thì bóng của tháp trên mặt đất có chiều dài 150m. Bài 8.
Để đo chiều rộng AB của một con sông mà không phải băng ngang qua sông, một người đi từ
A đến C đo được AC  50m và từ C nhìn thấy B với góc nghiêng 62 với bờ sông. Tính bề rộng của con sông.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 2
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Bài 9.
Một người quan sát đứng cách một tòa nhà 25m. Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà là 36 .
1) Tính chiều cao của tòa nhà (làm tròn đến mét).
2) Nếu anh ta dịch chuyển sao cho góc nâng là 32 thì anh ta cách tòa nhà bao nhiêu mét? Khi
đó anh ta tiến lại gần hay cách ra xa tòa nhà (làm tròn đễn chữ số thập phân thứ hai).
Bài 10. Từ trên tháp quan sát của một ngọn hải đăng cao 28 m , người ta nhìn thấy một chiếc thuyền
cứu hộ với góc hạ 20 . Tính khoảng cách từ chân tháp đến thuyền. .
Bài 11. Đài quan sát Toronto, Ontario (canada) cao 533 m . Ở một thời điểm vào ban ngày, mặt trời
chiếu tạothành bóng dài 1100 m 1100m. Hỏi lúc đó góc tạo bởi tia sát mặt trời và mặt đất là bao
nhiêu (làm tròn đến độ).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 3
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
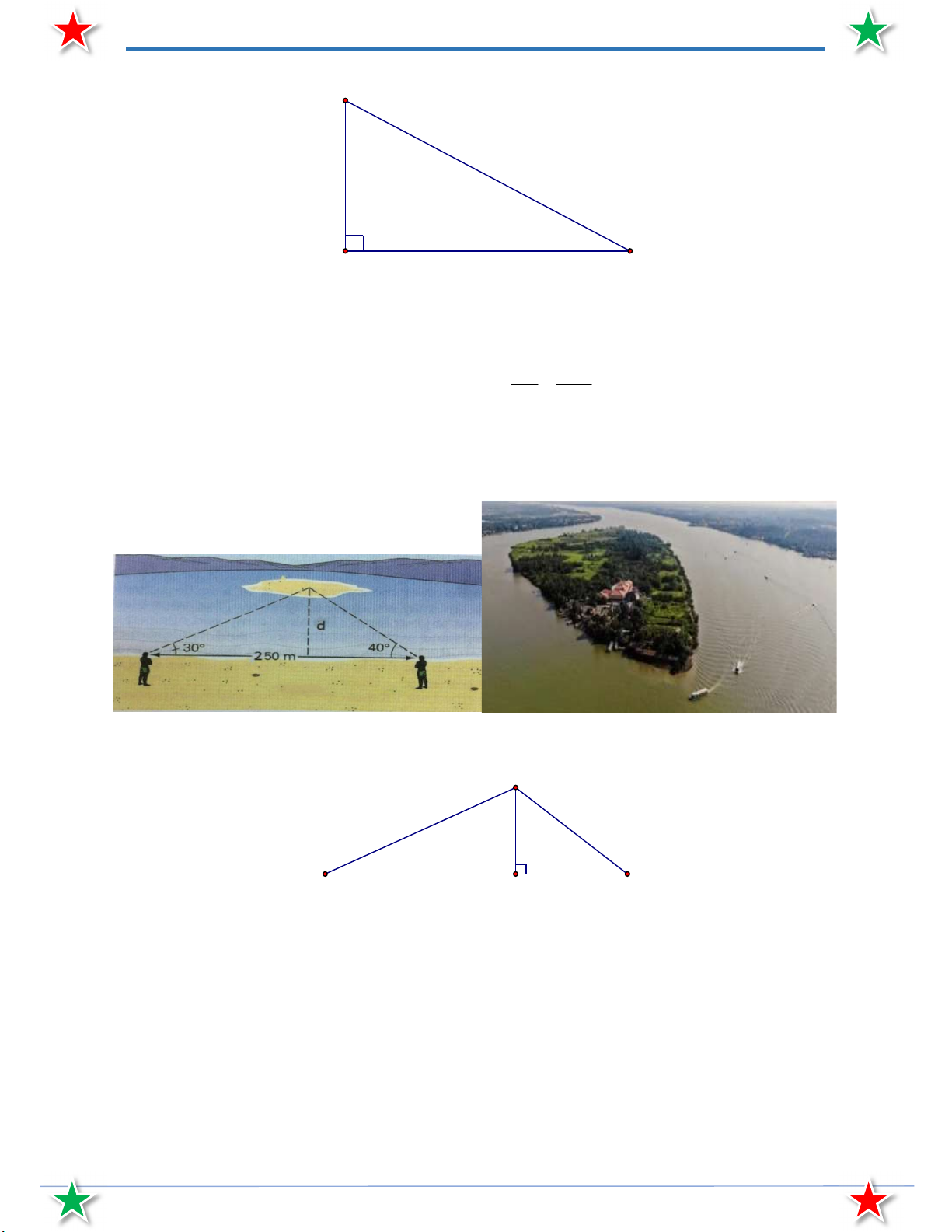
Bài 12. Hai ngư dân đứng ở một bên bờ sông cách nhau 250 m cùng nhìn thấy một cù lao trên sông với
cácgóc nâng lần lượt là 30 và 40 .Tính khoảng cách d từ bờ sông đến cù lao.
Bài 13. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống
mộtcon dốc (như hình vẽ). Cho biết đoạn thẳng AB dài 762 m , góc A bằng 6 , góc B bằng 4 . C h 4° 6° A B H 762 m
1)Tính chiều cao h của con dốc.
2) Hỏi bạn An đến trường lúc mấy giờ ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ
trung bình xuống dốc là 19 km/h .
Bài 14. Từ đỉnh một tòa nhà cao 54 m , người ta nhìn thấy một ô tô đang đỗ dưới một góc nghiêng
xuống là 40 . Hỏi ô tô đang đỗ cách tòa nhà đó bao nhiêu mét ?
Bài 15. Một học sinh đứng ở mặt đất cách tháp ăng ten cao 150 m nhìn thấy đỉnh tháp theo một góc
nghiêng lên là 20 và khoảng cách từ mắt đến mặt đất là 1m . Tính khoảng cách từ học sinh đó
đến tháp (làm tròn đến mét).
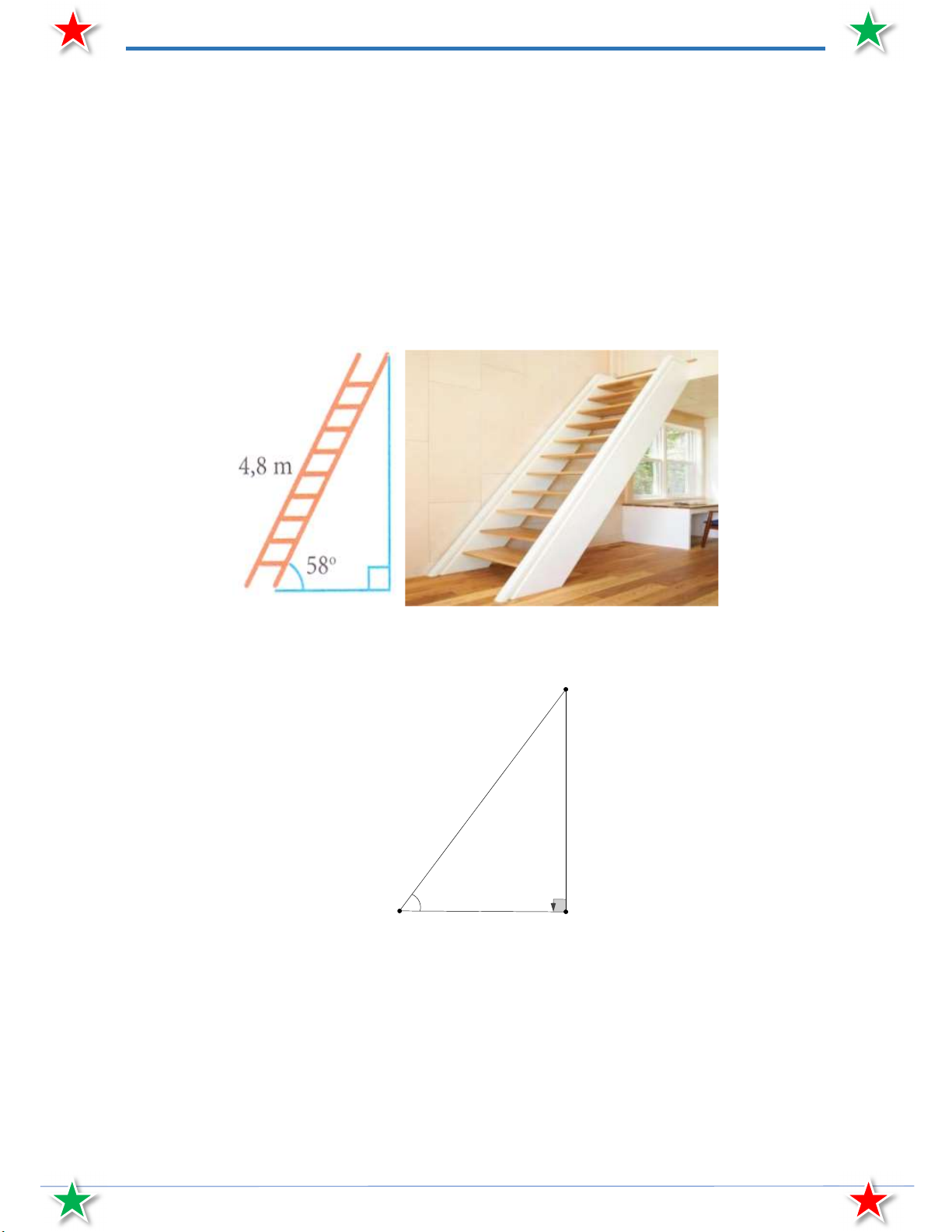
Bài 16. Một cái thang dài 4,8 m dựa vào tường làm thành một góc 58 so với mặt đất. Tính chiều cao
của thang so với mặt đất (làm tròn đến mét).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 4
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 17. Một người quan sát ở đài hải đăng cao 800 feet (đơn vị đo lường Anh) so với mực nước biển
nhìn thấy một con tàu ở xa với một góc nghiêng xuống là1 4
 2'. Hỏi khoảng cách từ tàu đến
chân ngọn hải đăng là bao nhiêu hải lý (1 hải lý = 5280 feet )?
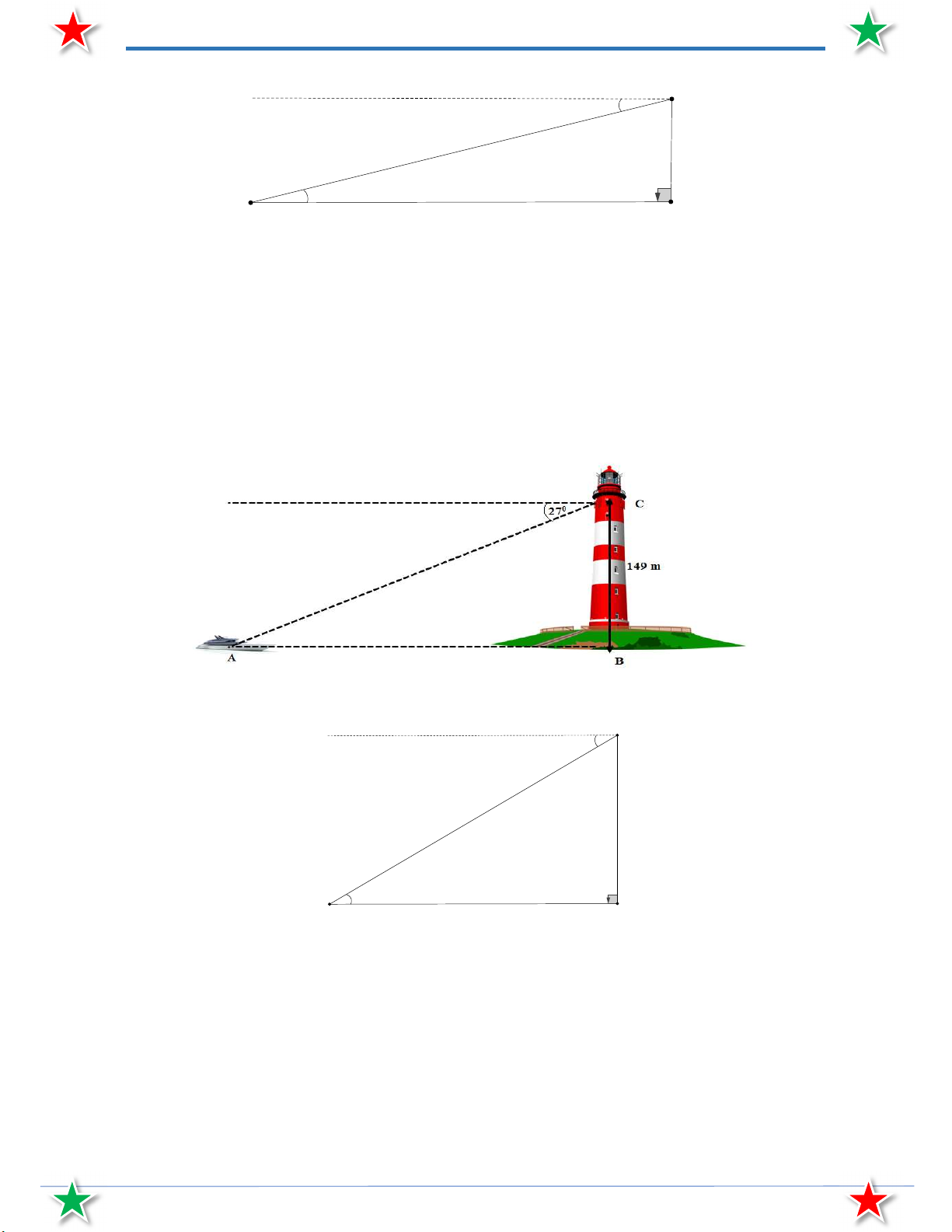
Bài 18. Một người quan sát ở đài hải đăng cao 149 m so với mực nước biển nhìn thất một con tàu ở xa
với một góc nghiêng xuống là 27 . Hỏi tàu đang đứng cách chân hải đăng là bao nhiêu mét?
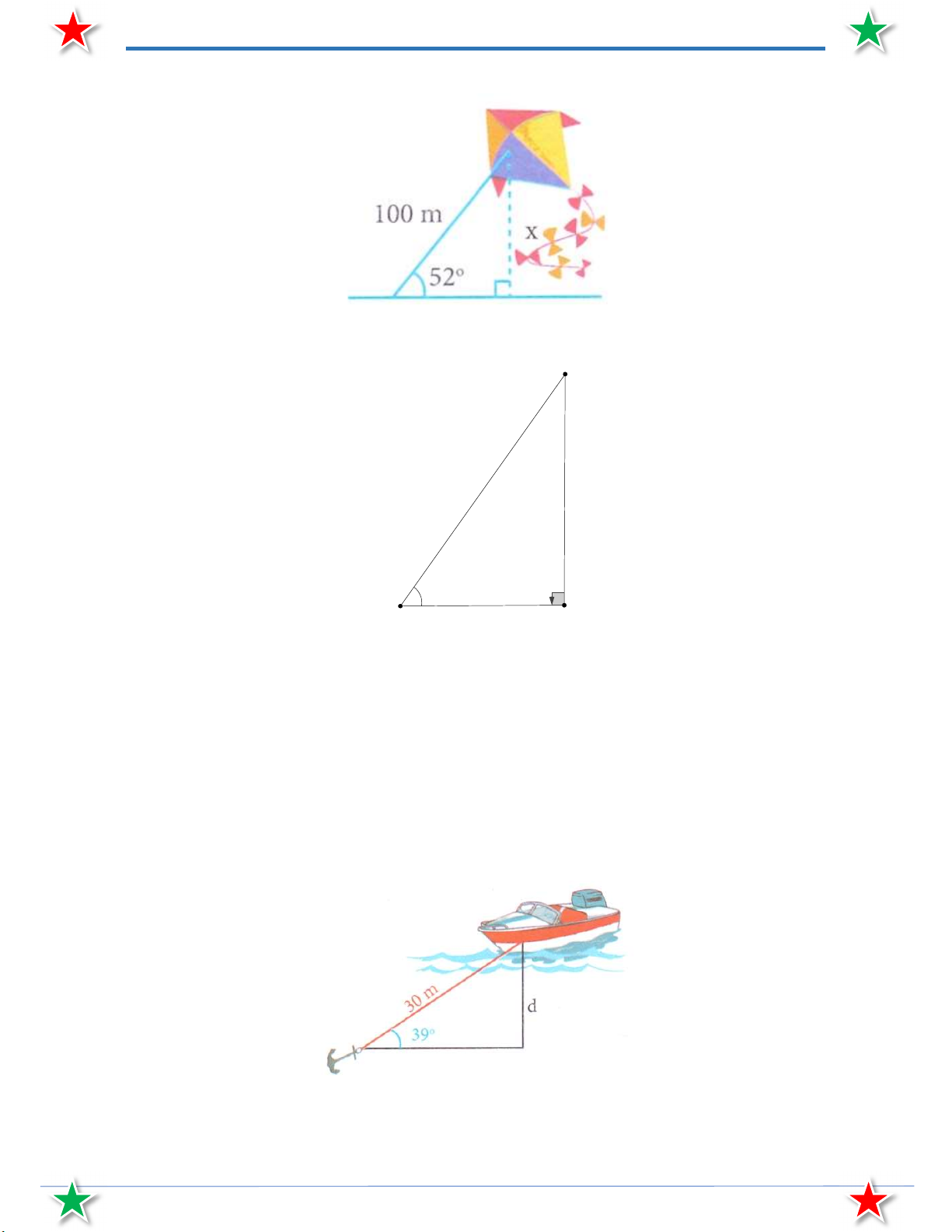
Bài 19. Một học sinh thả diều ngoài đồng, cho biết đoạn dây đã thả dài 100 m và có góc nâng 52 .
Tính độ cao của diều so với mặt đất (làm tròn đến mét).
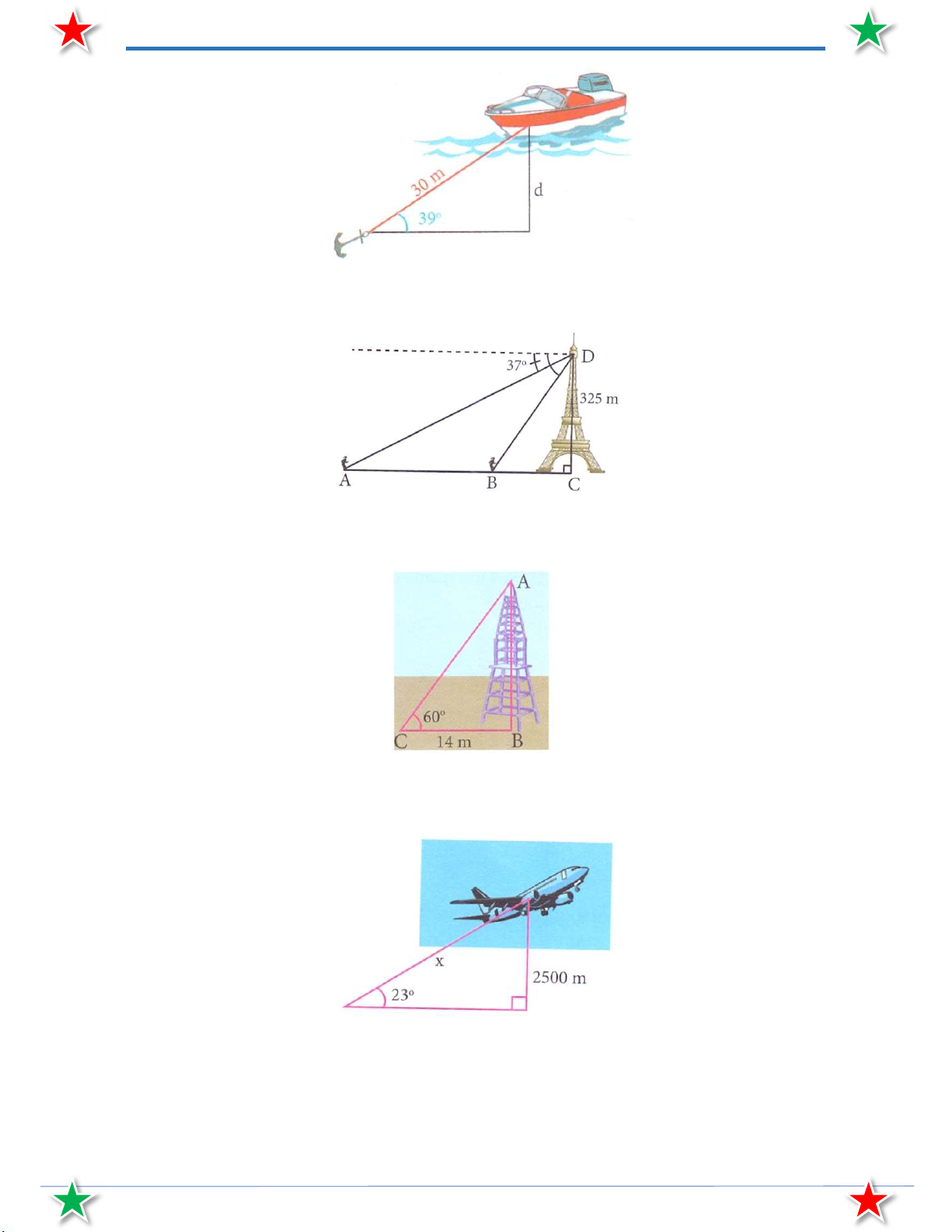
Bài 20. Một chiếc thuyền thả neo trên sông. Cho biết dây neo dài 30 m và có góc nghiêng lên là 39 .
Tính độ sâu của mực nước chỗ thuyền đang đậu (làm tròn đến mét).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 5
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
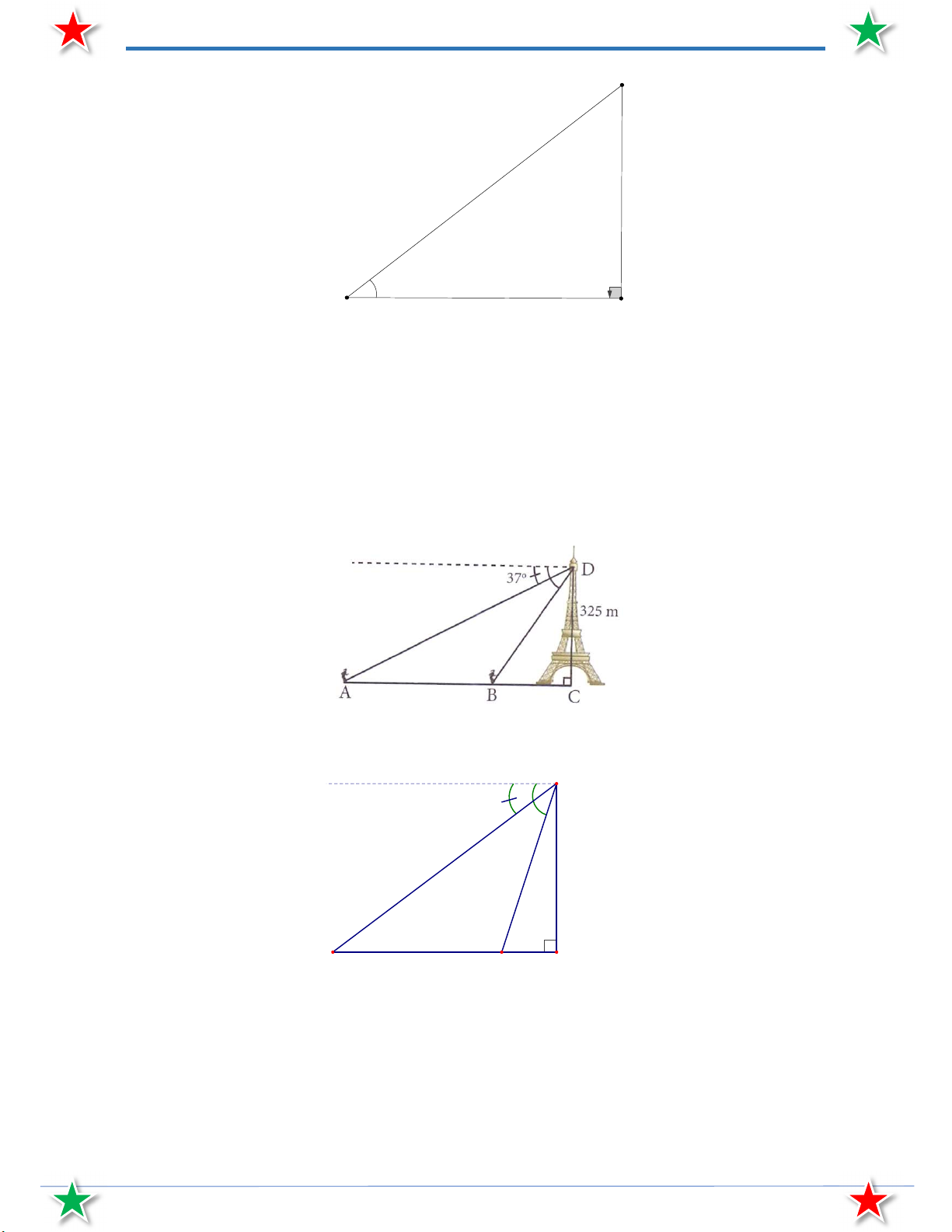
Bài 21. Một người đứng trên đỉnh tháp cao 325 m nhìn thấy 2 điểm A và B với hai góc hạ lần lượt là
37 và 72 .Tính khoảng cách AB .
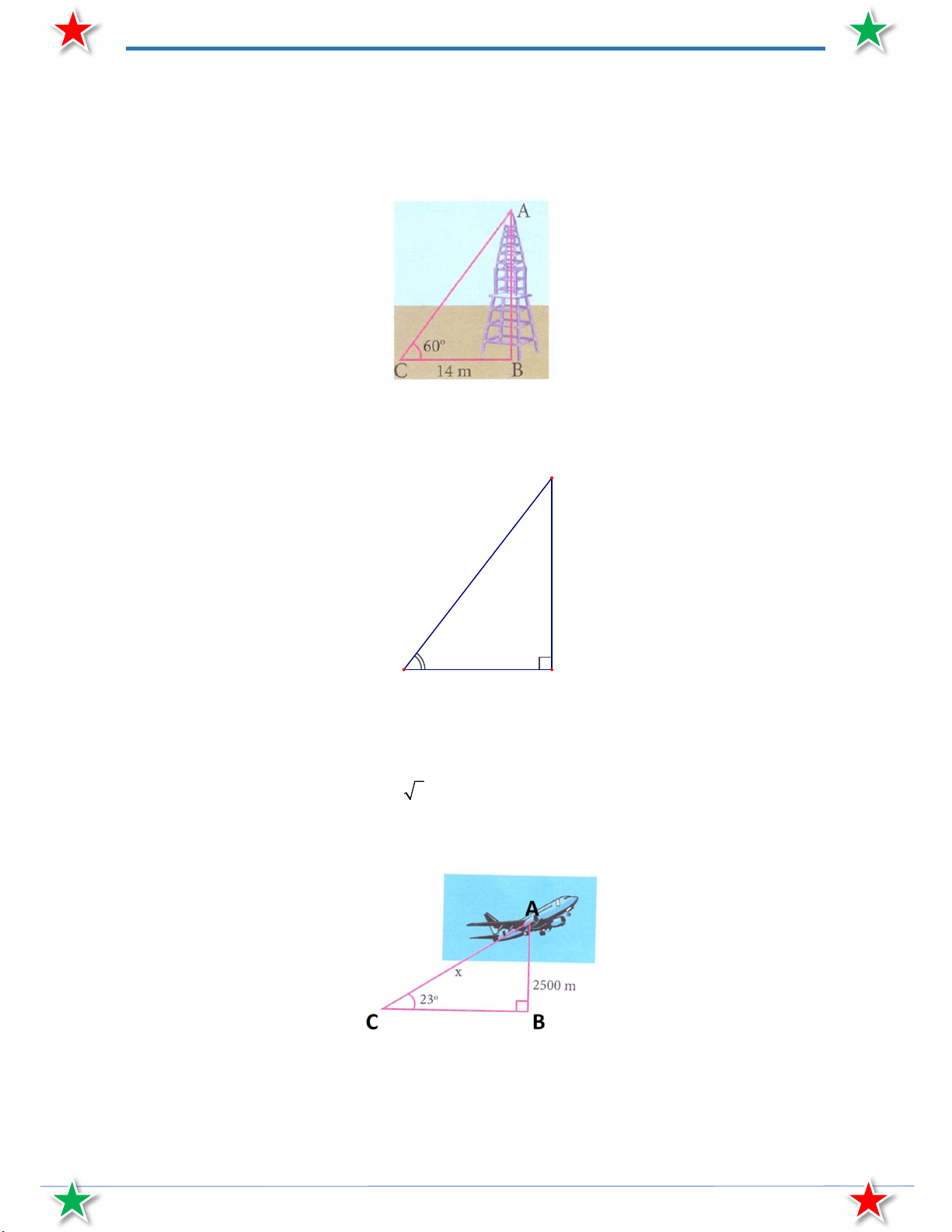
Bài 22. Một người đứng cách chân tháp 14 m nhìn thấy đỉnh tháp theo góc nghiêng 60 . Tính chiều cao của tháp.
Bài 23. Một máy bay cất cánh theo phương có góc nâng 23 .Hỏi muốn đạt độ cao 2500 m , máy bay
phải bay một đoạn đường là bao nhiêu mét?
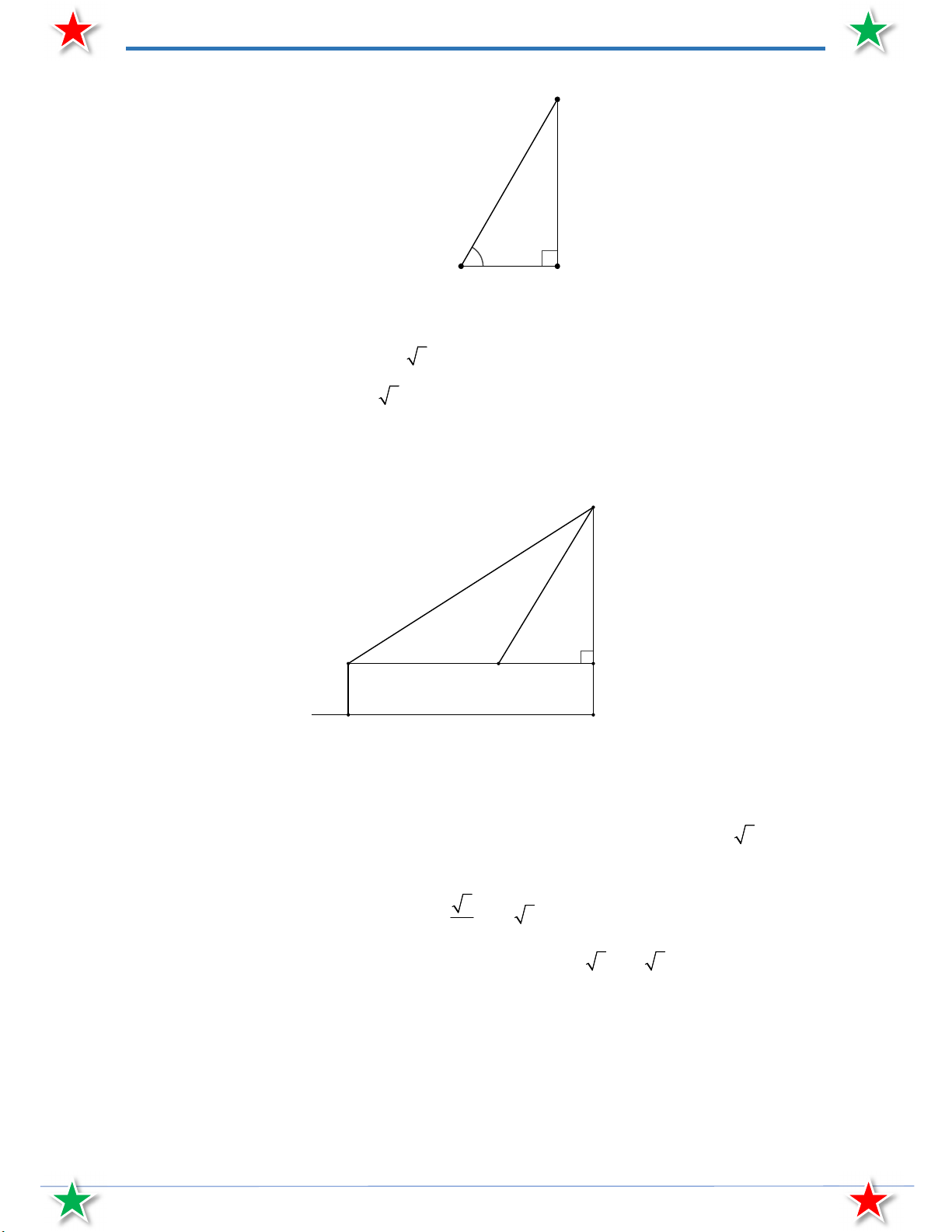
Bài 24. Một cái cây có bóng trên mặt đất dài 20 m .Cho biết tia nắng qua ngọn cây nghiêng một góc
31 so với mặt đất. Tính chiều cao của cây.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 6
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
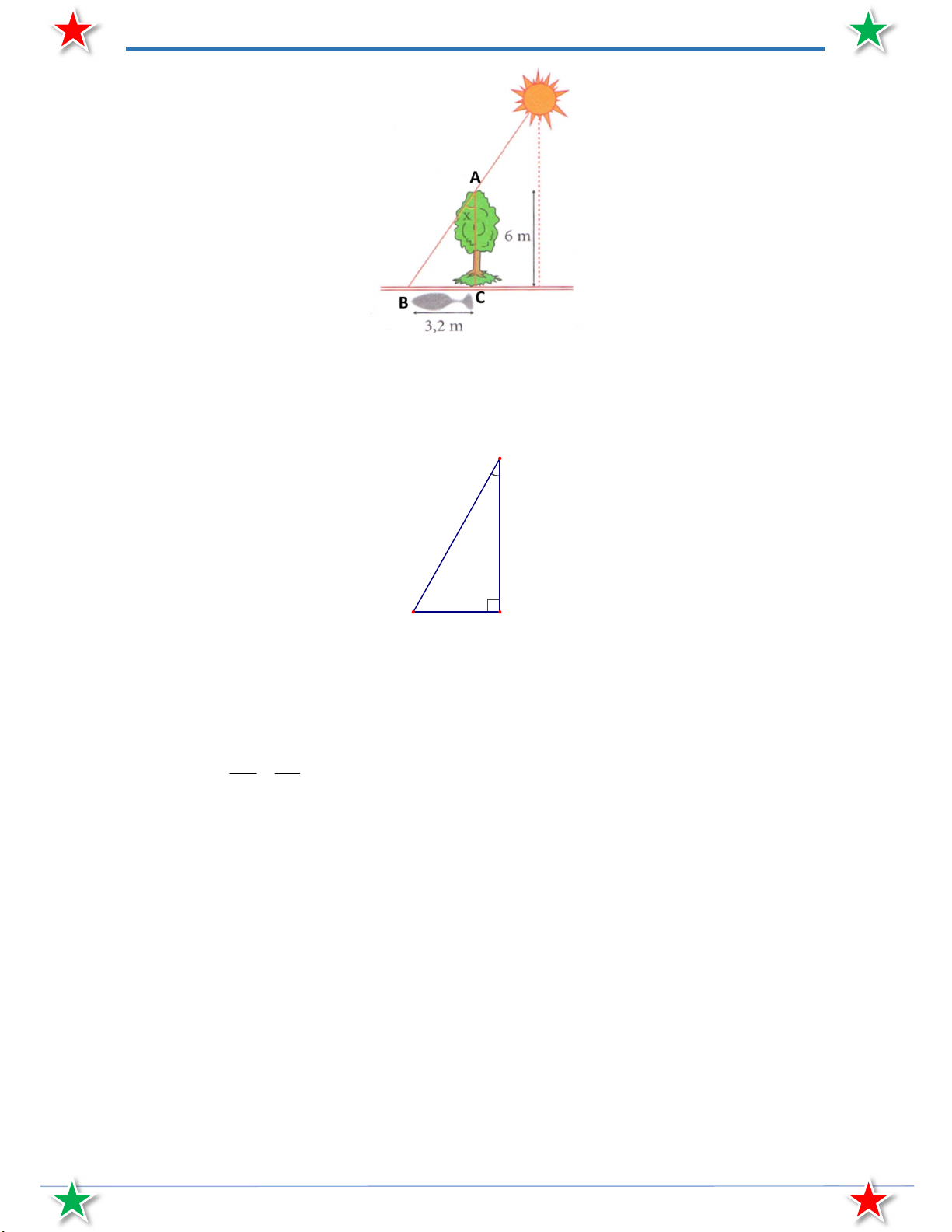
Bài 25. Một cái cây cao 6m đang có bóng dài 3, 2 m . Tính góc hợp bởi tia nắng với thân cây
Bài 26. Một người đứng cách chân tháp 14 m nhìn thấy đỉnh tháp theo góc nghiêng 60 . Tính chiều cao của tháp.
Bài 27. Ban Hùng có tầm mắt cao 1,5 m đang đứng gần một cao ốc cao 30 m thì nhìn thấy nóc tòa nhà
với góc nâng 30 . Hùng đi về phía tòa nhà cho đến khi nhìn thấy nóc tòa nhà với góc nâng 60 .
Tính quãng đường mà bạn Hùng đã đi được. C 30m 60o 30o B A D 1,5m K
Bài 28. Một học sinh có tầm mắt cao 1,5 m đứng trên sân thượng của một căn nhà cao 15 m nhìn thấy
bạn mình với góc nghiêng xuống 49 . Hỏi cô bạn đang ở cách căn nhà bao nhiêu mét?
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 7
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
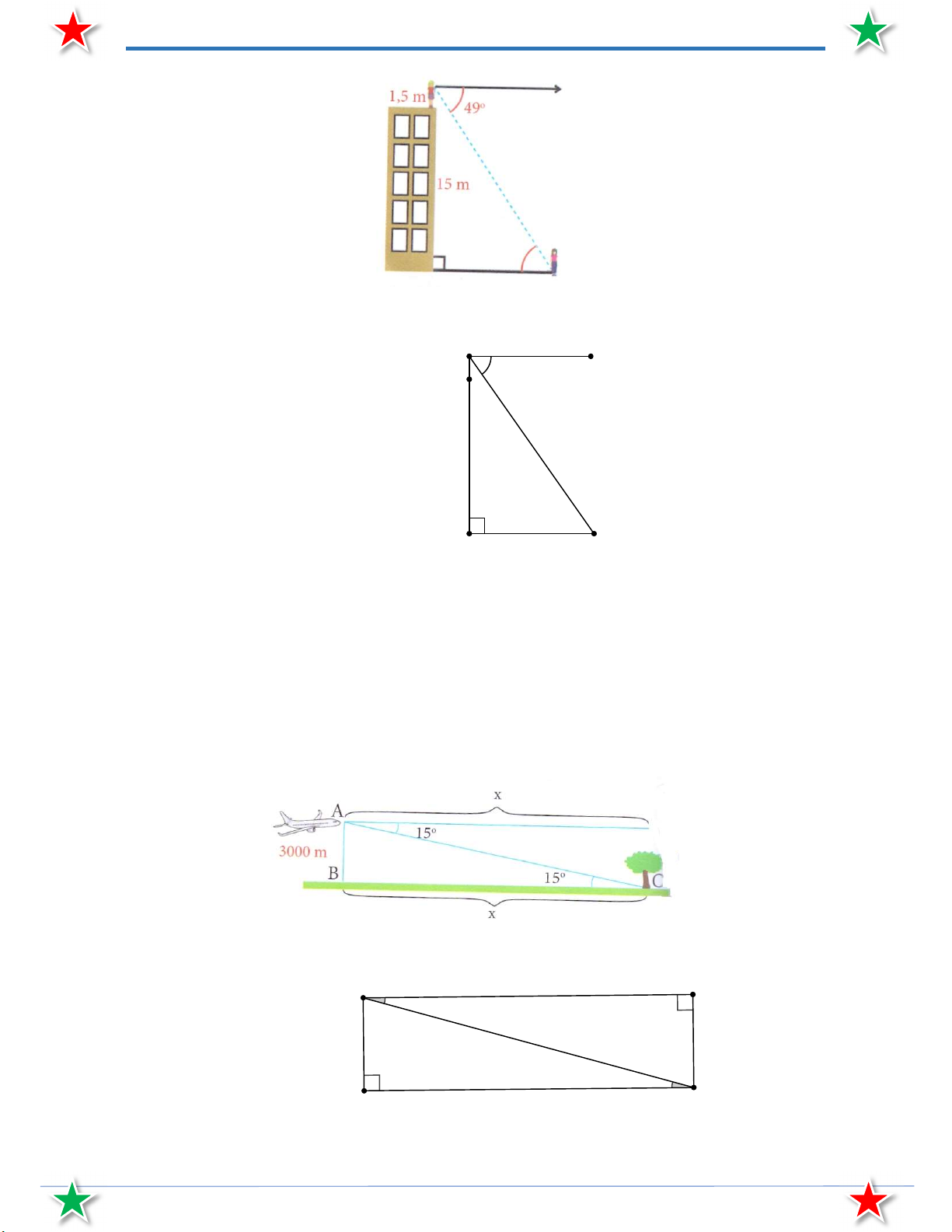
Bài 29. Một máy bay thể thao đang bay ngang ở độ cao 3000 m nhìn thấy một cái cây với góc nghiêng
xuống 15 . Hỏi máy bay phải bay một đoạn đường là bao nhiêu mét thì sẽ ở ngay trên ngọn cây?
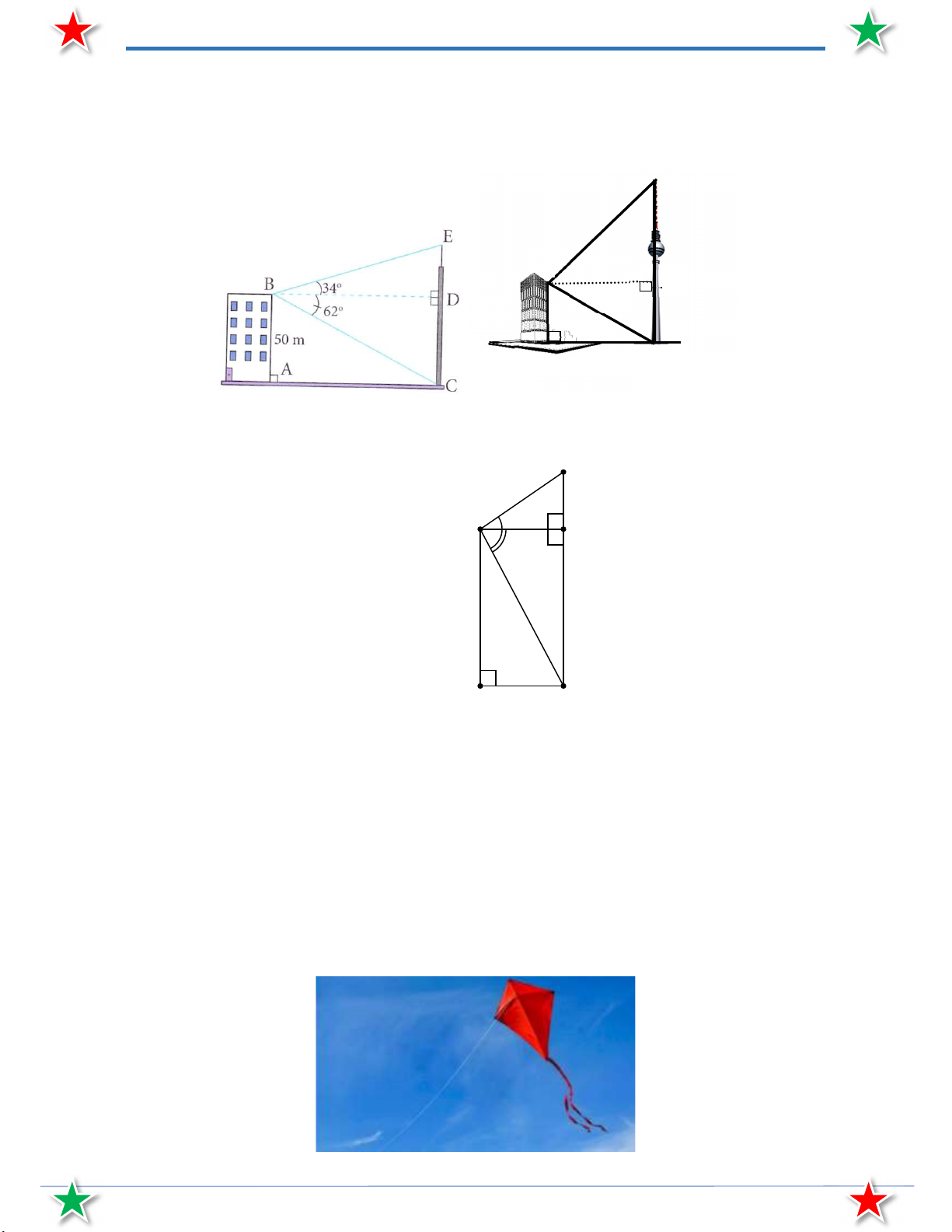
Bài 30. Từ nóc một cao ốc cao 50 m người ta nhìn thấy chân và đỉnh một ăng-ten với các góc hạn lần
lượt là 62 và 34 . Tính chiều cao cột ăng-ten. E B 340 D 620 50m A C
Bài 31. Một cái diều đang bay ở độ cao 60 m. Sợi dây cột diều nghiêng với mặt đất một góc 60 . Tính
chiều dài của sợi dây (làm tròn đến mét) khi nó căng thẳng (không có chỗ bị võng).
Bài 32. Tháp Capital Gate tại Abu Dhabi cao 160 m và nghiêng 18 . Nếu không nghiêng thì tháp cao bao nhiêu mét?
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 8
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 33. Tính chiều cao của một ngọn núi, cho biết tại hai điểm cách nhau 500 m , người ta nhìn thấy hai
đỉnh núi với góc nâng lần lượt là 34 và 38 .
Bài 34. Một cái tháp được dựng bên bờ một con sông, từ một điểm đối diện với tháp ngay bờ bên kia
người ta nhìn thấy đỉnh tháp với góc nâng 60 . Từ một điểm khác cách điểm ban đầu 20 m,
người ta cũng nhìn thấy đỉnh tháp với góc nâng 30 . Tính chiều cao của tháp.
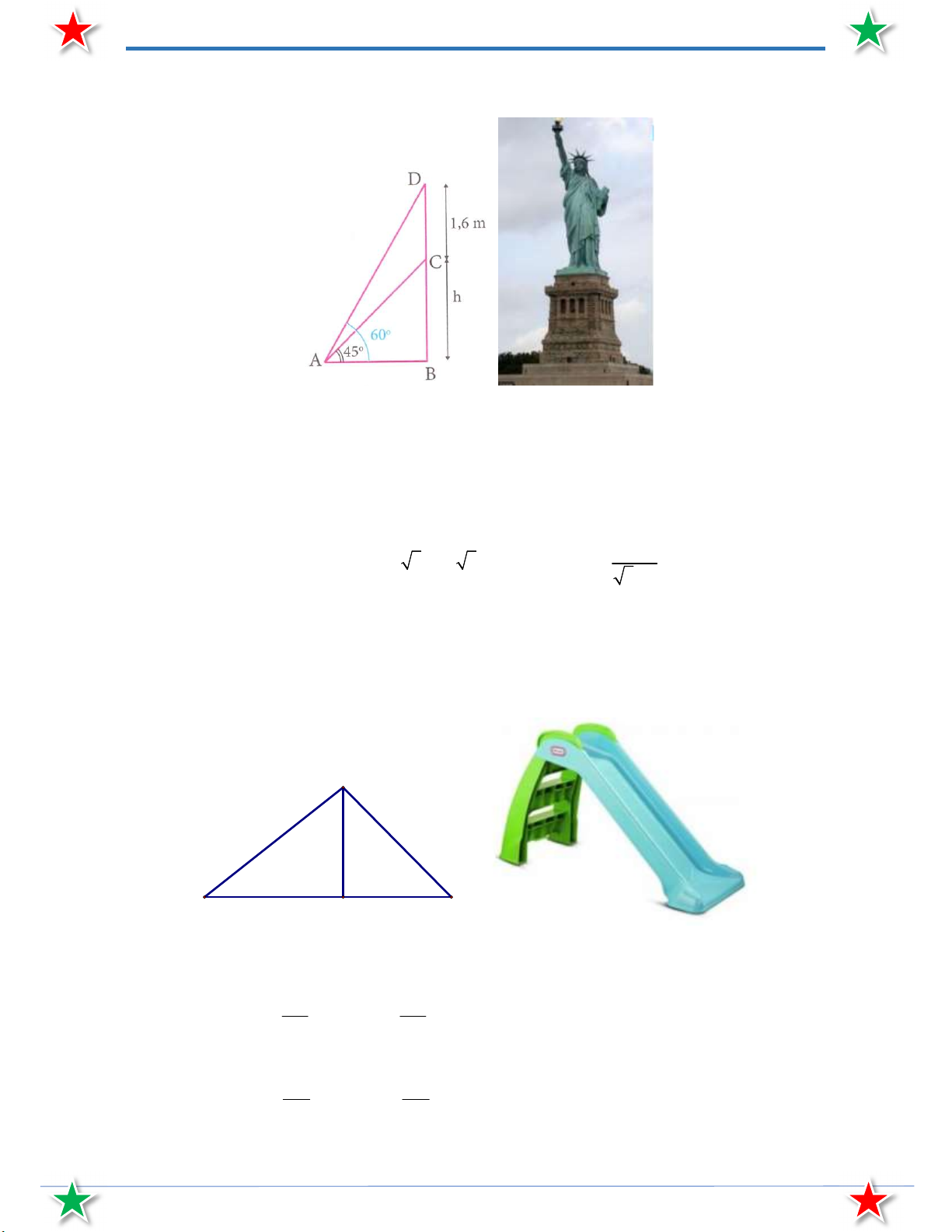
Bài 35. Một bức tượng cao 1, 6 m được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là 60 và 45 . Tính chiều cao của cái bệ.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 9
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 36. Một nhà trẻ muốn thiết kế hai cái cầu tuột trong sân chơi. Đối với trẻ dưới 5 tuổi, cầu tuột cao
1,5 m và nghiêng với mặt đất một góc 30 . Đối với trẻ trên 5 tuổi cầu tuột cao 1,5 m và
nghiêng với mặt đất một góc 45 . Tính chiều dài của mỗi máng tuột. A 2m 30 45 E B C
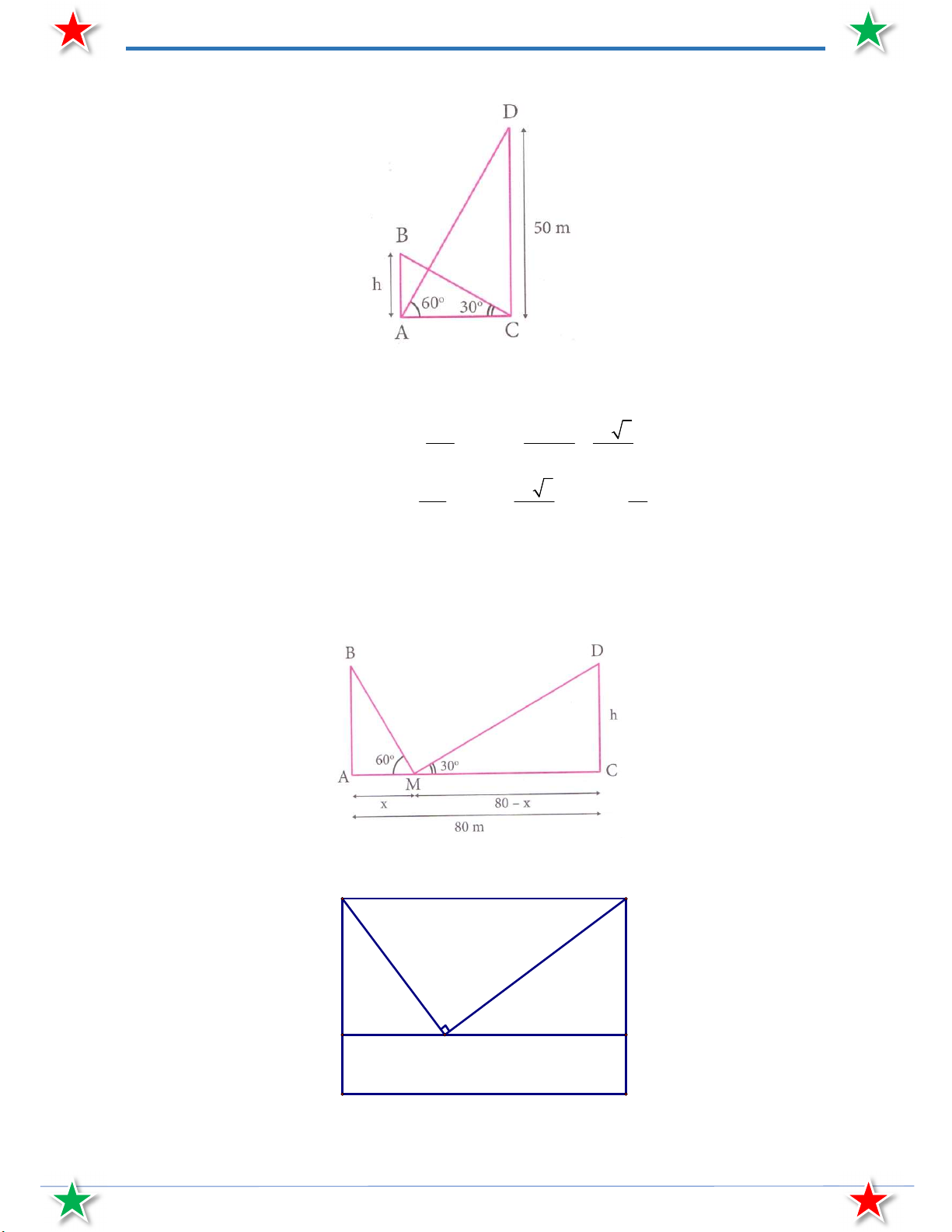
Bài 37. Từ chân một cái tháp cao 50 m người ta nhìn thấy đỉnh một tòa nhà với góc nâng 30 . Trong
khi đó từchân tòa nhà lại nhìn thấy đỉnh tháp với góc nâng 60 . Tính chiều cao của tòa nhà.
Bài 38. Hai trụ điện có cùng chiều cao đặt cách nhau 80 m . Một người đứng ở xa (thẳng hàng với hai
trụ điện, không đứng giữa hai trụ điện) nhìn đỉnh hai trụ điện với góc nâng lần lượt là 60 và
30 . Tính chiều cao trụ điện và khoảng cách từ người đó đến chân các trụ điện. Biết mắt người
đó cách mặt đất1, 2 m .
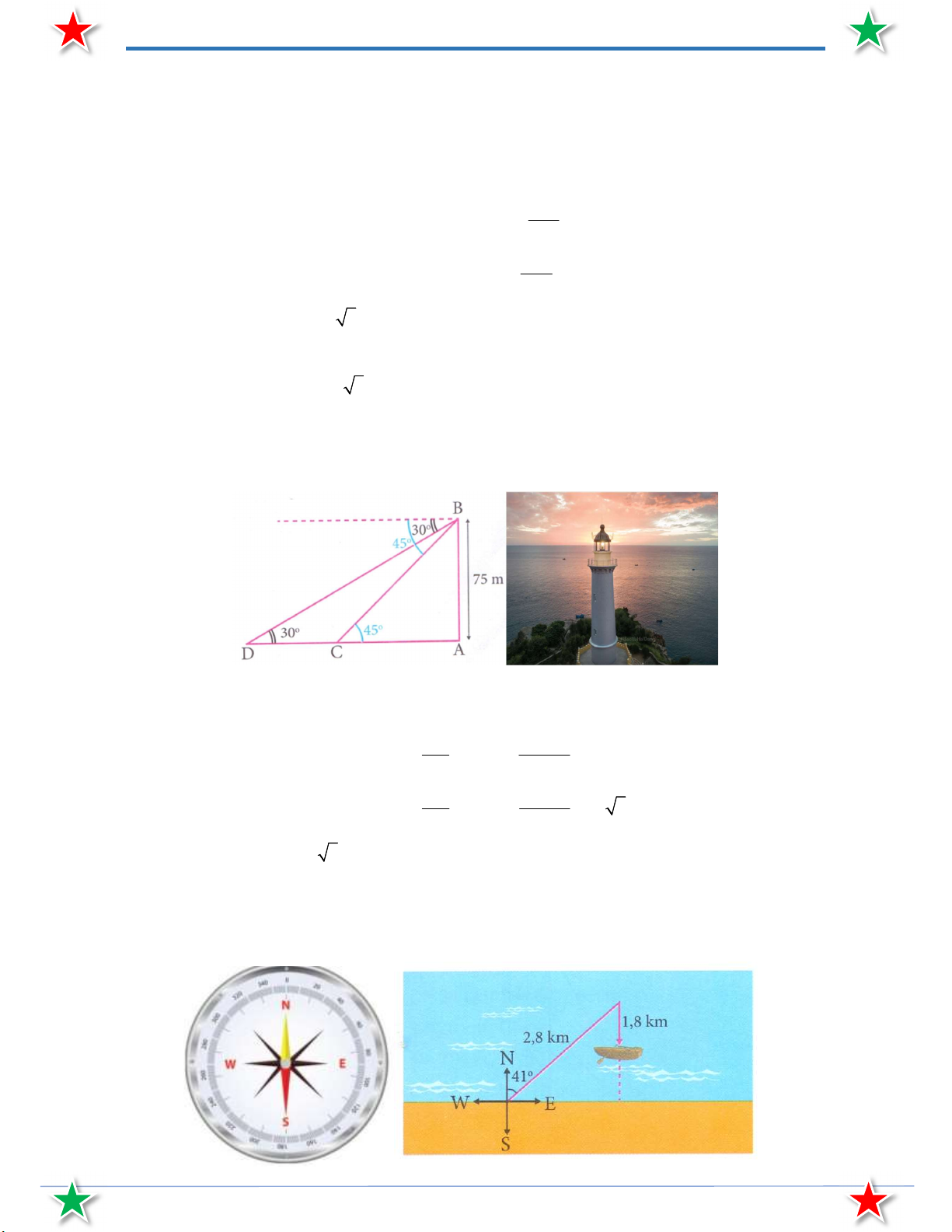
Bài 39. Từ trên một ngọn hải đăng cao 75 m , người ta quan sát hai lần thấy một chiếc thuyền đang
hướng về phía hải đăng với góc hạ lần lượt là 30 và 45 . Hỏi chiếc thuyền đi được bao nhiêu
mét giữa hai lầnquan sát?
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 10
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 40. Một thủy thủ lái thuyền ra biển hướng về hướng đông bắc với góc nghiêng so với phương bắc
là 41 . Đi được 2,8 km anh ta phát hiện sắp hết nhiên liệu nên vội quay thuyền vào bờ, đi
được 1,8 km thì thuyền tắt máy. Hỏi lúc đó thuyền cách bờ bao xa?
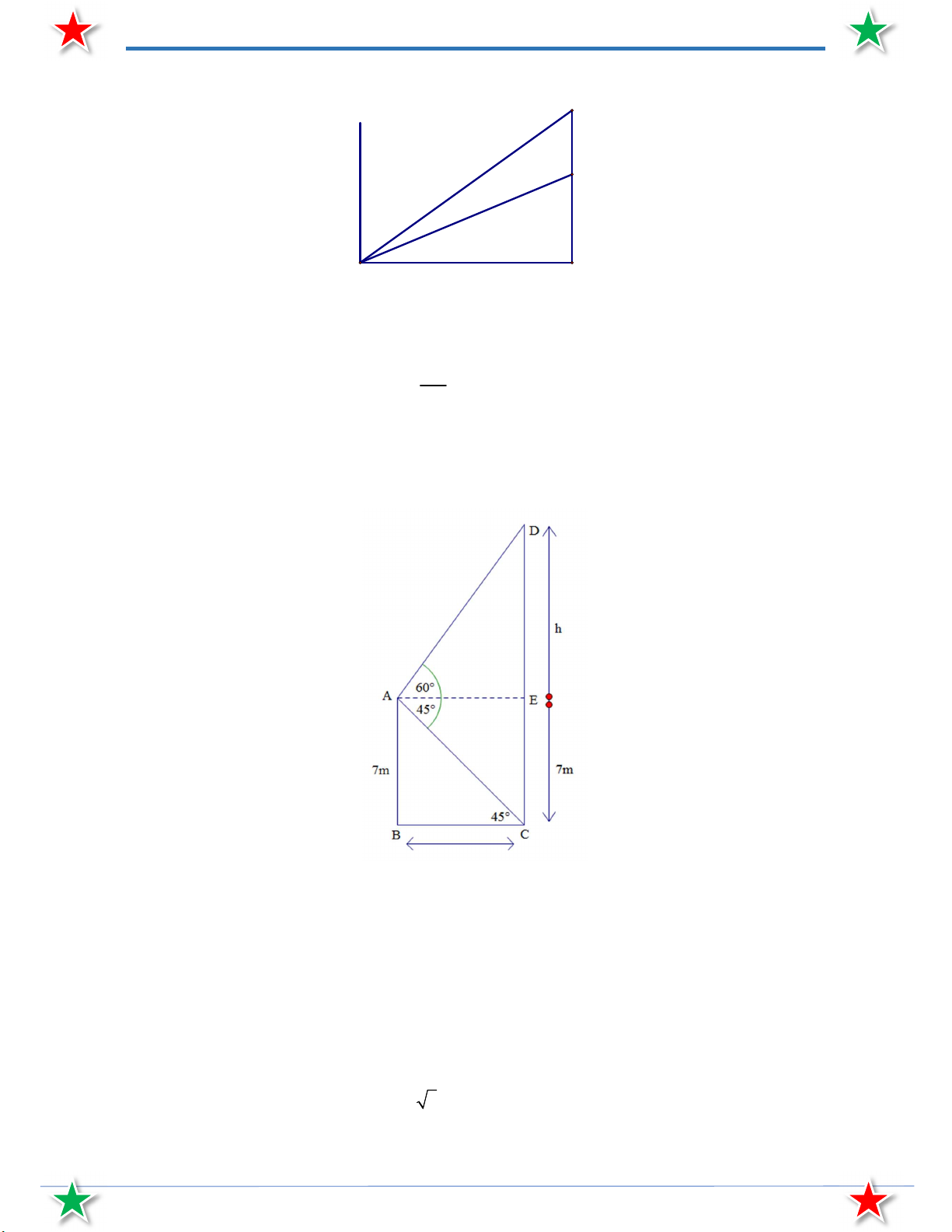
Bài 41. Từ trên đỉnh một tòa nhà cao 7m , người ta nhìn thấy đỉnh một tháp truyền hình với góc nâng
60 và nhìn thấy chân của tháp với góc hạ 45 . Tính chiều cao của tháp truyền hình?
Bài 42. Một học sinh có khoảng cách từ mặt đến mặt đất là 1, 2 m bắt đầu quan sát một trái bóng bay
với góc nâng 60 . Một lúc sau lại nhìn thấy quả bóng bay với góc nâng 30 . Hỏi giữa hai lần
quan sát quả bóng đã bay được bao nhiêu mét? Cho biết độ cao của quả bóng luôn luôn không đổi và bằng 88, 2 m .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 11
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 43. Một người đang ở trên một cái tháp có chiều cao h =100 m nhìn xuống một con đường chạy
thẳng đến chân tháp. Anh ta nhìn thấy một chiếc xe máy với góc hạ 30 . Sáu phút sau lại nhìn
thấy nó với góc hạ 60 . Hỏi sau bao nhiêu phút thì xe máy đến chân tháp? Cho biết vận tốc xe máy không đổi.
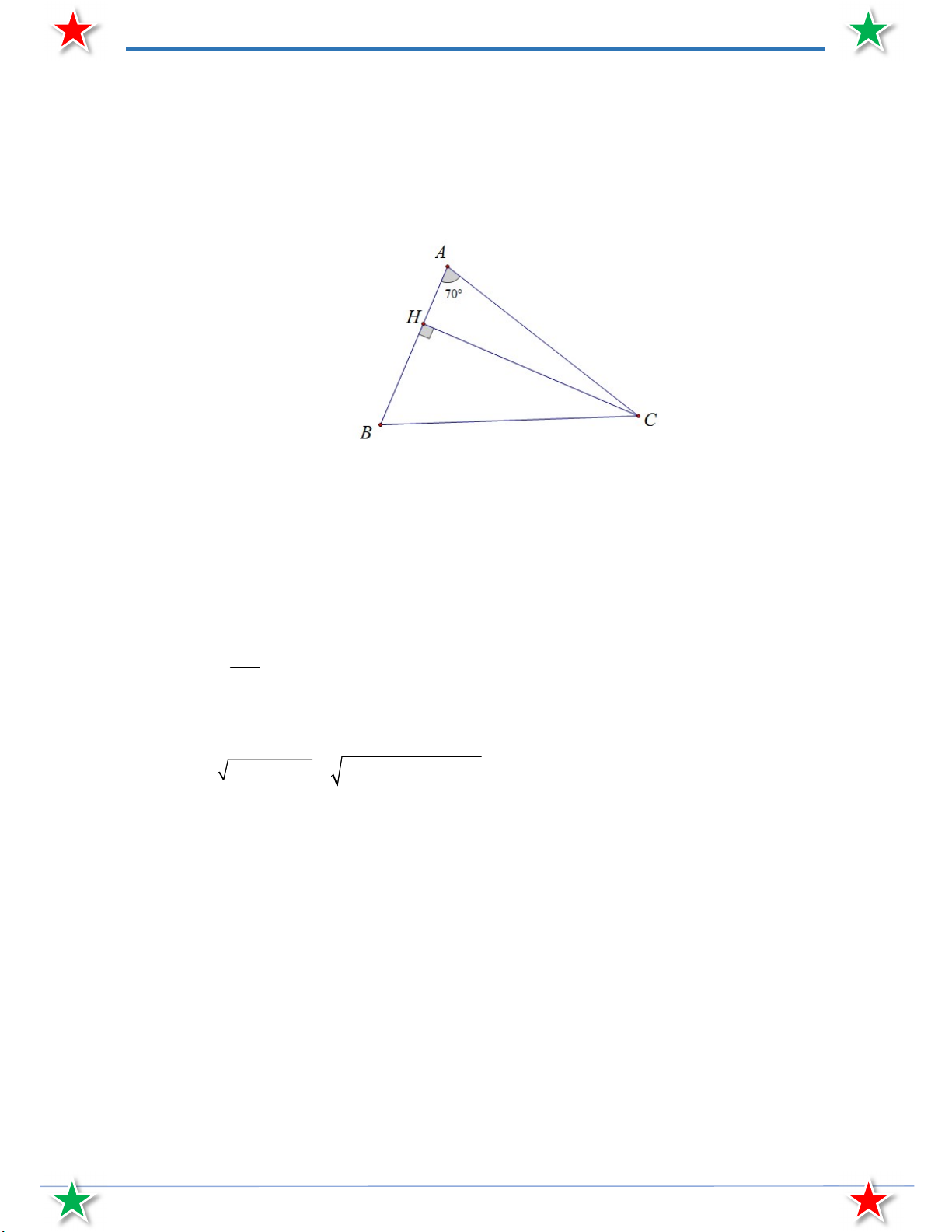
Bài 44. Để đo chiều cao một cái cây AB . Người ta đặt gương phẳng tại vị trí C . Người đo đi lùi lại
(thẳng người) cho đến khi nhìn thấy bóng ngọn cây A (lúc này là F ). Biết khoảng cách từ
gương đến gốc cây là BC  30 mét, khoảng cách từ gương đến chỗ đứng là CD  1,5 mét.
Khoảng cách từ mắt người đo E đến mặt đất là ED  1,6 mét. Tính chiều cao của cây? (biết  BCA   DCE ).
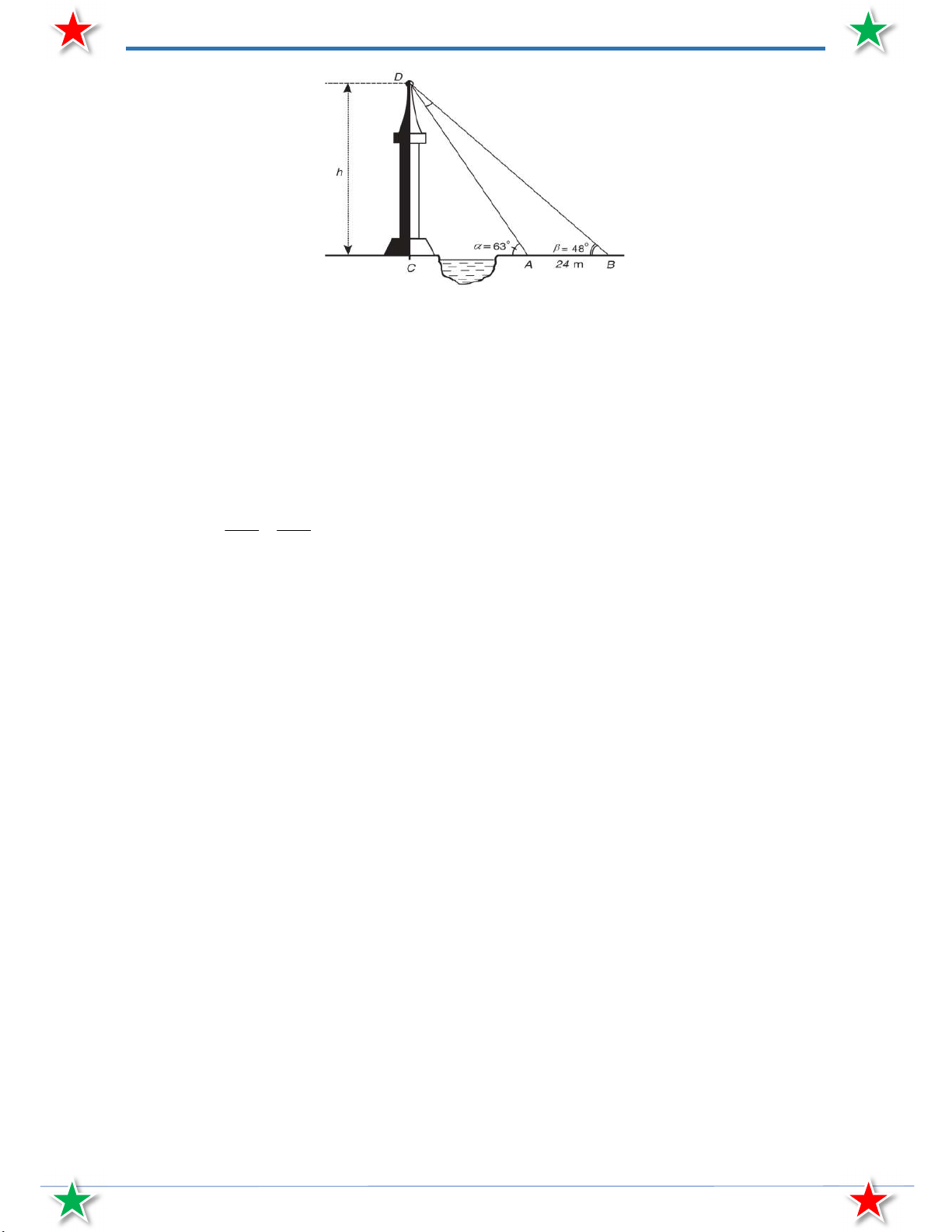
Bài 45. Quan sát hình vẽ dưới đây. Giả sử CD  h là chiều cao của tháp trong đó C là chân tháp.
Chọn hai điểm A , B trên mặt đất sao cho ba điểm A , B và C thẳng hàng. Ta đo khoảng cách AB và các góc  CAD , 
CBD . Chẳng hạn ta đo được AB  24 m,  CAD    63 , 
CBD    48 . Hãy tính chiều cao h của tháp.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 12
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 46. Một hình chữ nhật có kích thước là 20 cm và 30 cm. Người ta tăng mỗi kích thước thêm x cm.
Gọi y là chu vi của hình chữ nhật mới. 1) Hãy tính y theo x .
2) Tính giá trị của y tương ứng với x  3 cm; x  5 cm.
Bài 47. Một thửa đất hình chữ nhật có chiều dài là 32 m và chiều rộng là 24 m. Người ta định làm một
vườn cây cảnh có con đường đi xung quanh, có bề rộng x(m) (hình vẽ bên). Hỏi bề rộng của
mặt đường là bao nhiêu để diện tích phần đất còn lại là 560 m2. 32 m x x x 24 m x
Bài 48. Một căn phòng hình vuông được lát bằng những viên gạch men hình vuông cùng kích cỡ, vừa
hết 441 viên (không viên nào bị cắt xén). Gạch gồm 2 loại men trắng và men xanh, loại men
trắng nằm trên 2 đường chéo của nền nhà còn lại là loại men xanh. Tính số viên gạch men xanh.
Bài 49. Bạn Nam đi xe đạp từ nhà (điểm A) đến trường (điểm B) gồm đoạn lên dốc và đoạn xuống dốc,
A  5, B  4 , đoạn lên dốc dài 325 m.
1) Tính chiều cao của dốc và chiều dài quãng đường từ nhà đến trường.
2) Biết vận tốc trung bình lên dốc là 8 km/h và vận tốc trung bình xuống dốc là 15 km/h. Tính
thời gian (phút) bạn Nam đi từ nhà đến trường. (Lưu ý kết quả của phép tính làm tròn đến chữ
số thập phân thứ nhất)
Bài 50. Một bức tượng cao 1,6 m được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là 60 và 45. Tính chiều cao cái bệ.
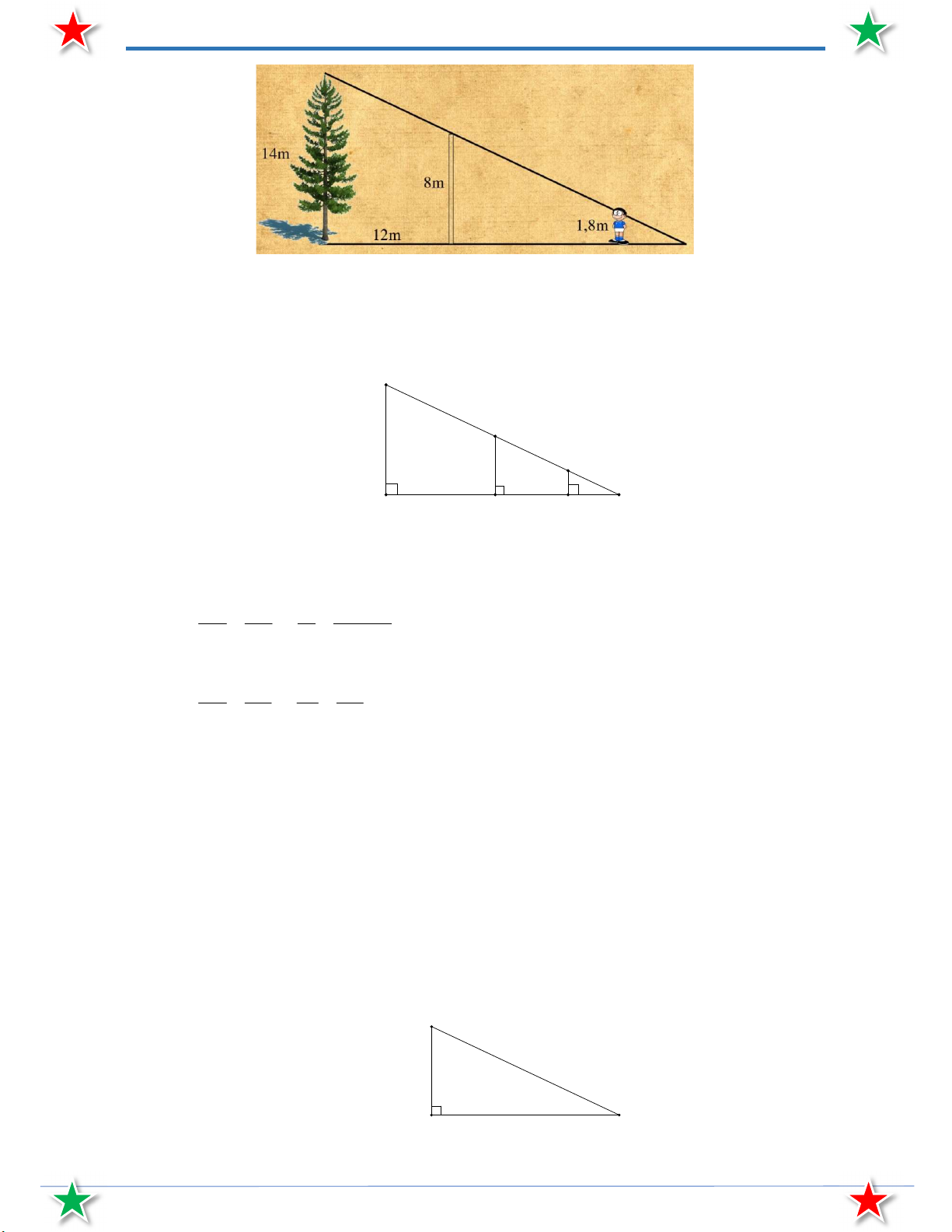
Bài 51. Một cây có chiều cao 14 m mọc ở phía sau một bức tường cao 8 m và cách bức tường 12 m.
Hỏi người quan sát có chiều cao 1,8 m phải đứng cách bức tường bao nhiêu mét để có thể nhìn thấy ngọn cây.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 13
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 52. Nhà bạn An ở vị trí A , nhà bạn Bình ở vị trí B cách nhau 1200 m. Trường học ở vị trí C cách
nhà bạn An 500m và AB vuông góc với AC . An đi bộ đến trường với vận tốc 4 km/h, Bình đi
xe đạp đến trường với vận tốc 12 km/h. Lúc 6 giờ 30 phút, cả hai cùng xuất phát đến trường.
Hỏi bạn nào đến trường trước? Bài 53
Bóng của tháp Bình Sơn (Vĩnh Phúc) trên mặt đất có độ dài 20 m. Cùng thời điểm đó, một cột
sắt cao 1, 65 m cắm vuông góc với mặt đất có bóng dài 2 m. Tính chiều cao của tháp.
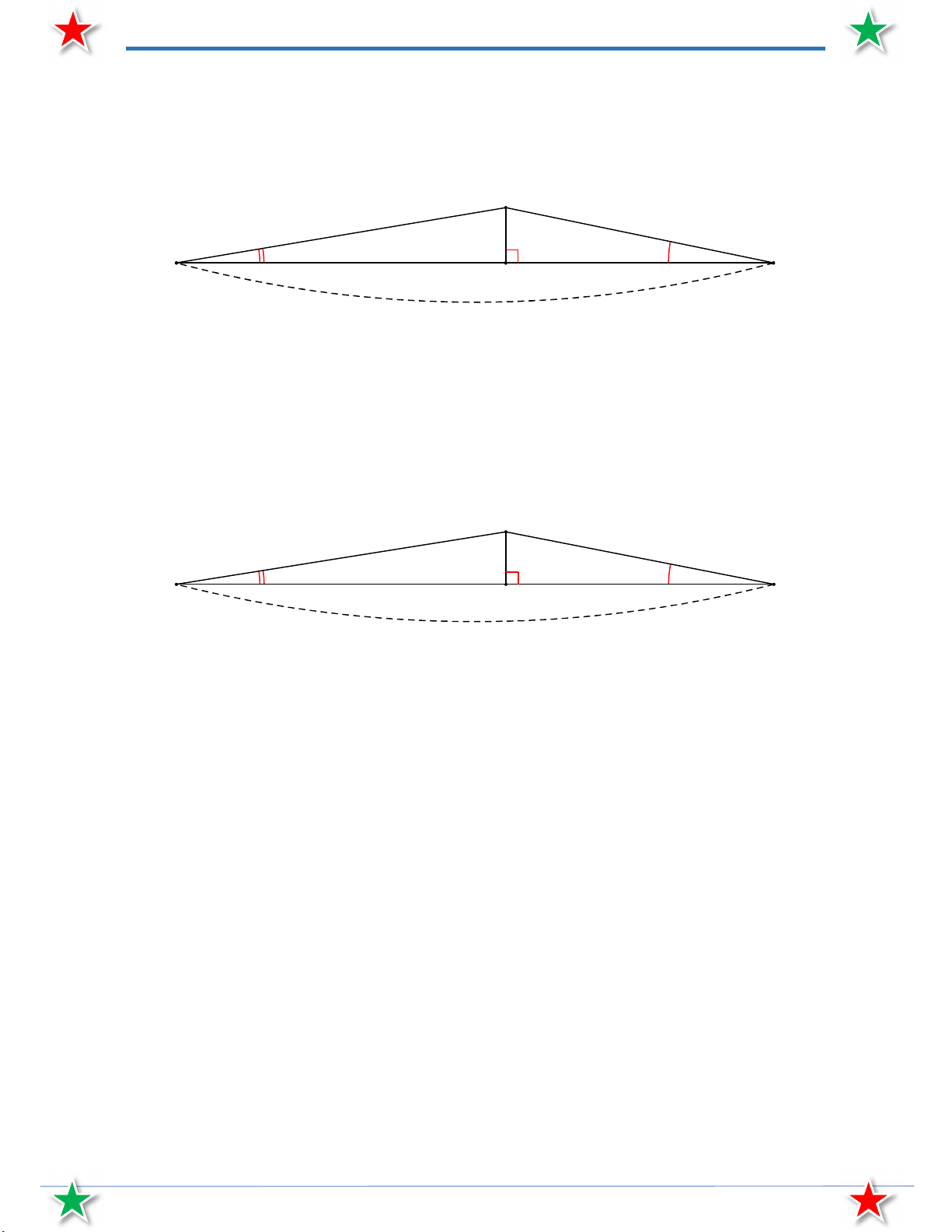
Bài 54. Một con đê được đắp chắn sóng theo hình dưới, độ dốc của con đê phía sông dài 7 m. Hỏi độ
dốc còn lại của con đê dài bao nhiêu mét?
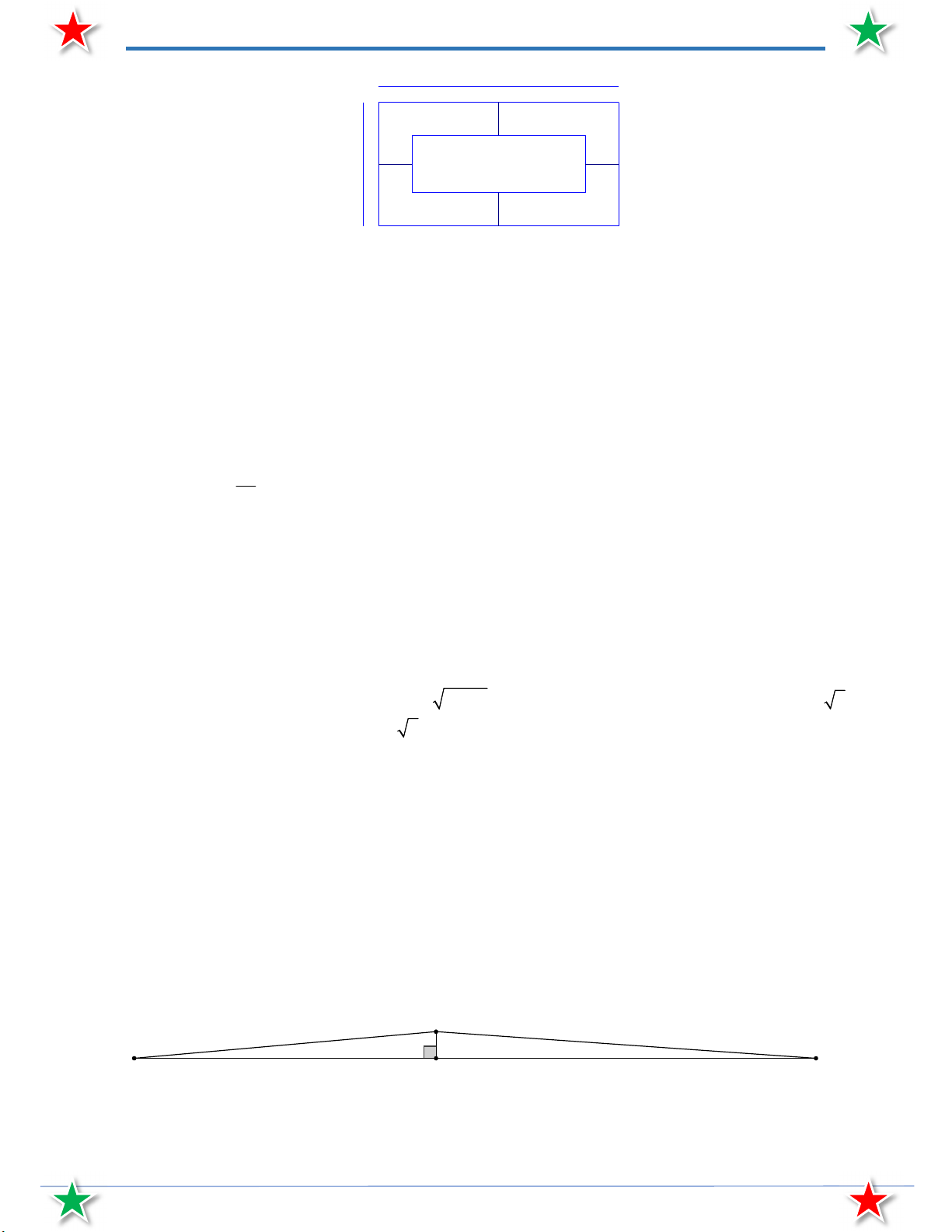
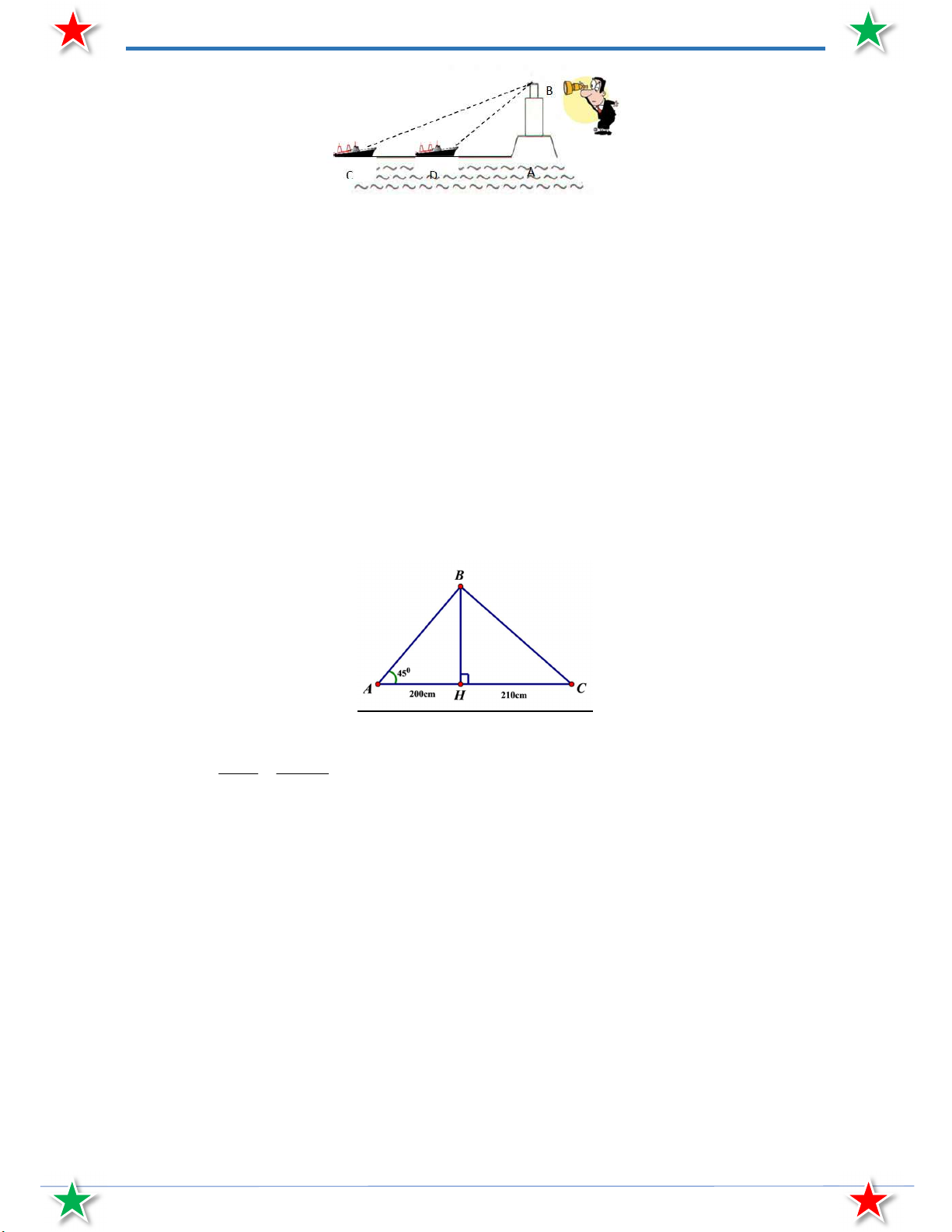
Bài 55. Xem hình vẽ sau, người ta có thể dùng giác kế để đo được góc  CAB  43 và  CBA  38 . Hỏi
tàu đang ở vị trí điểm H sẽ chạy với vận tốc bao nhiêu km/h để sau 5 phút sẽ đến vị trí điểm
C . Biết khoảng cách từ vị trí điểm A đến vị trí điểm B là 300 m và vị trí 3 điểm A , H , B
thẳng hàng (làm tròn đến chữ số thập phân thứ hai). C A H B
Bài 56. Ba An muốn mua một cái thang dùng để lên mái nhà. Ba hỏi An phải mua cái thang dài bao
nhiều mét để đảm bảo sự an toàn và có thể leo lên được mái nhà cao 4,5m so với mặt đất. Em
hãy giúp An tính chiều dài thang cần mua, biết góc kê thang an toàn là 75 so với phương
ngang (làm tròn đến số thập phân thứ nhất).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 14
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 57. Một chiếc máy bay bay lên cao với vận tốc 520 km / h . Đường bay lên tạo với phương nằm
ngang một góc 24 . Hỏi sau 90 giây máy bay lên cao được bao nhiêu km theo phương thẳng
đứng? (kết quả làm tròn đến chữ số thập phân thứ nhất)
Bài 58. Từ đài quan sát cao 10 m, Nam có thế nhìn thấy 2 chiếc thuyền dưới góc 45 và 30 so với
phương ngang. Hãy tính khoảng cách 2 chiếc thuyền, làm tròn đến chữ số thập phân thứ nhất.
(điều kiện lý tưởng: vị trí 2 chiếc thuyền và vị trí đài quan sát thẳng hàng).
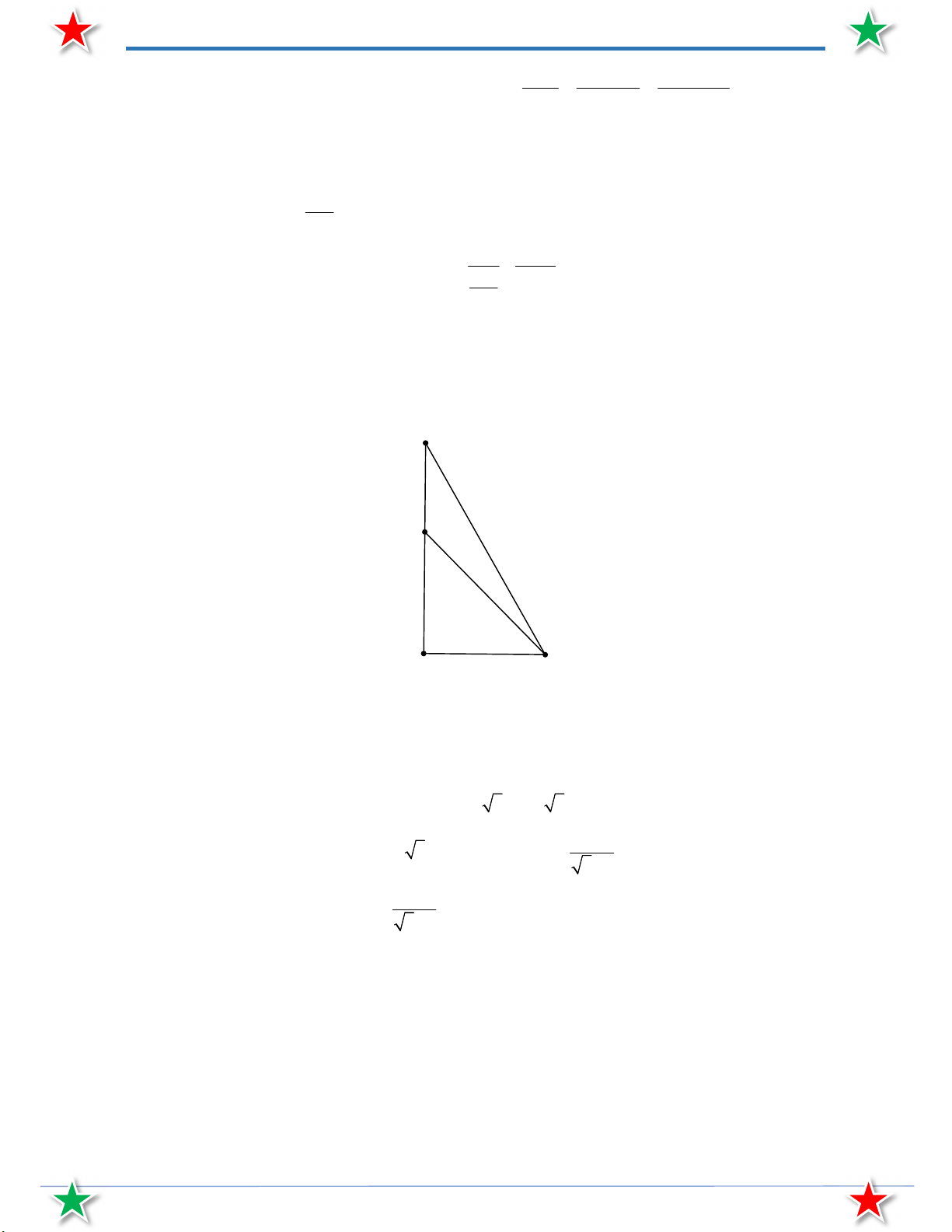
Bài 59. Hình ảnh mặt cắt một quả đồi được minh họa là một A
 BC với các chi tiết như sau: cạnh đáy là AC , BH  AC , 
BAC  45 , AH  200 m, HC  210 m. Một nhóm học sinh đi dã ngoại
đi từ đỉnh A lên đỉnh B rồi xuống dốc trở về C . Hãy tính quãng đường này?
Bài 60. Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình vẽ. Tính khoảng cách giữa
chúng (kết quả là tròn đến mét).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 15
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 61. Lúc 6h45 phút sáng bạn Nam đi xe đạp điện từ nhà tới trường với vận tốc trung bình là 15
km/h bạn đi theo con đường từ A  B  C  D  E  G  H (như trong hình). Nếu có 1
con đường thẳng từ A  H và đi theo con đường đó với vận tốc trung bình 15 km/h, bạn Nam
sẽ tới trường lúc mấy giờ? Trường học H 500m E 400m G 300m C 600m D 700m 1000m A Nhà B
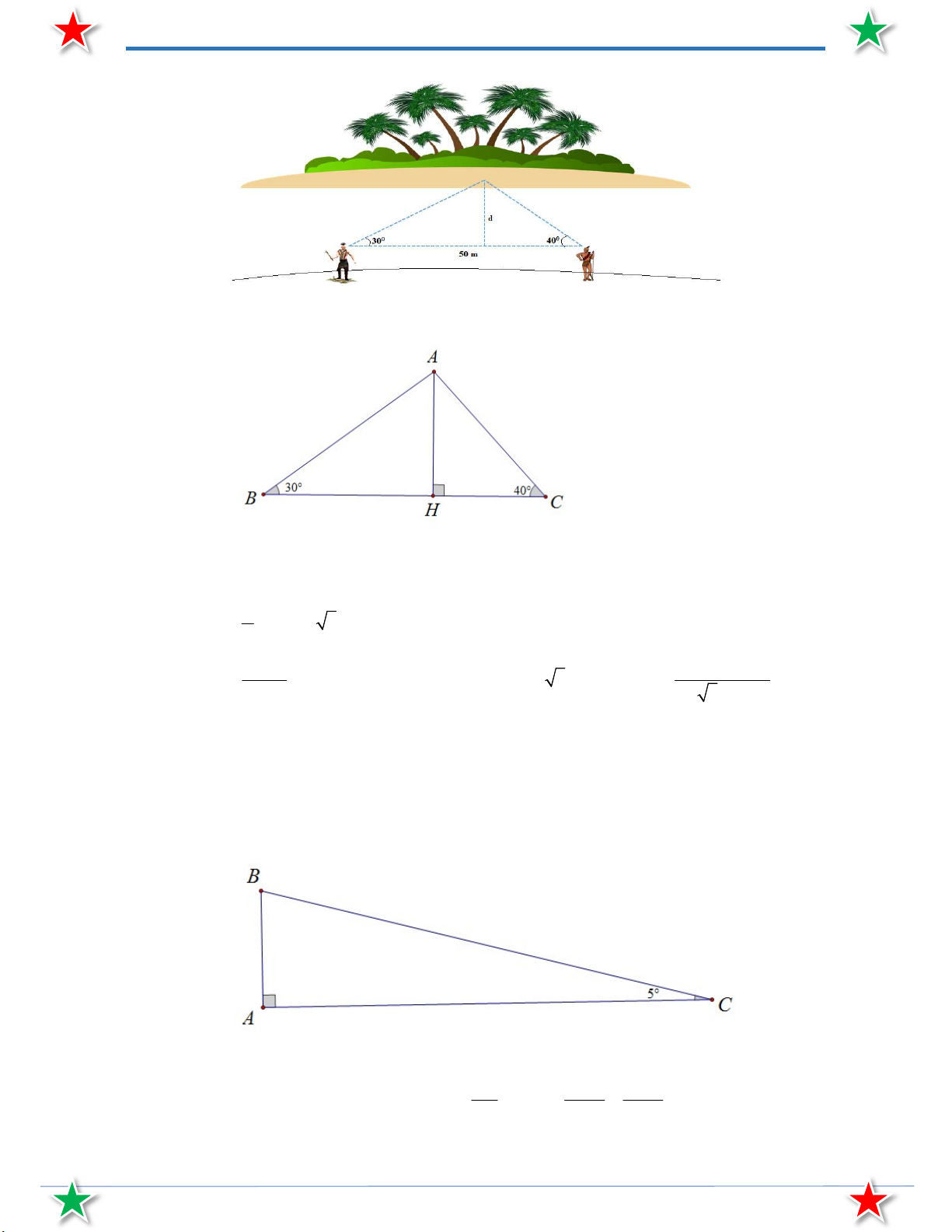
Bài 62. Hai ngư dân đứng ở một bên bờ sông cách nhau 50 m cùng nhìn thấy một cù lao trên sông với
các góc nâng lần lượt là 30 và 40. Tính khoảng cách d từ bờ sông đến cù lao.
Bài 63. Một người đi xe máy lên dốc có độ nghiêng 5 so với phương ngang với vận tốc trung bình lên
dốc là 18 km/h. Hỏi người đó mất bao lâu để lên tới đỉnh dốc? Biết đỉnh dốc cách mặt đất 18 m.
Bài 64. Từ vị trí xuất phát A , hai xe cùng một lúc đi thẳng theo hai hướng khác nhau, tạo một góc
A  70. Xe thứ nhất đi với vận tốc 40 km/h và xe thứ hai đi với vận tốc 50 km/h. Sau 1 giờ 30
phút, hai xe cách nhau bao nhiêu km? (làm tròn đến 2 chữ số thập phân).
Bài 65. Một máy kéo nông nghiệp có bánh xe sau to hơn bánh xe trước. Bánh xe sau có đường kính
124 cm và bánh xe trước có đường kính 80 cm. Hỏi khi bánh xe sau lăn được 20 vòng thì xe
di chuyển được bao nhiêu mét (làm tròn một chữ số) và khi đó bánh xe trước lăn được mấy vòng?
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 16
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 66. Trong hình vẽ dưới đây, hai địa điểm A , B cách nhau 100 km. Một xe ô tô khởi hành từ B đến
A với vận tốc 40 km/h. Cùng lúc đó, một xe đạp điện cũng khởi hành từ A trên đoạn đường
vuông góc với AB với vận tốc 20 km/h. Hỏi sau 90 phút thì hai xe cách nhau bao xa.
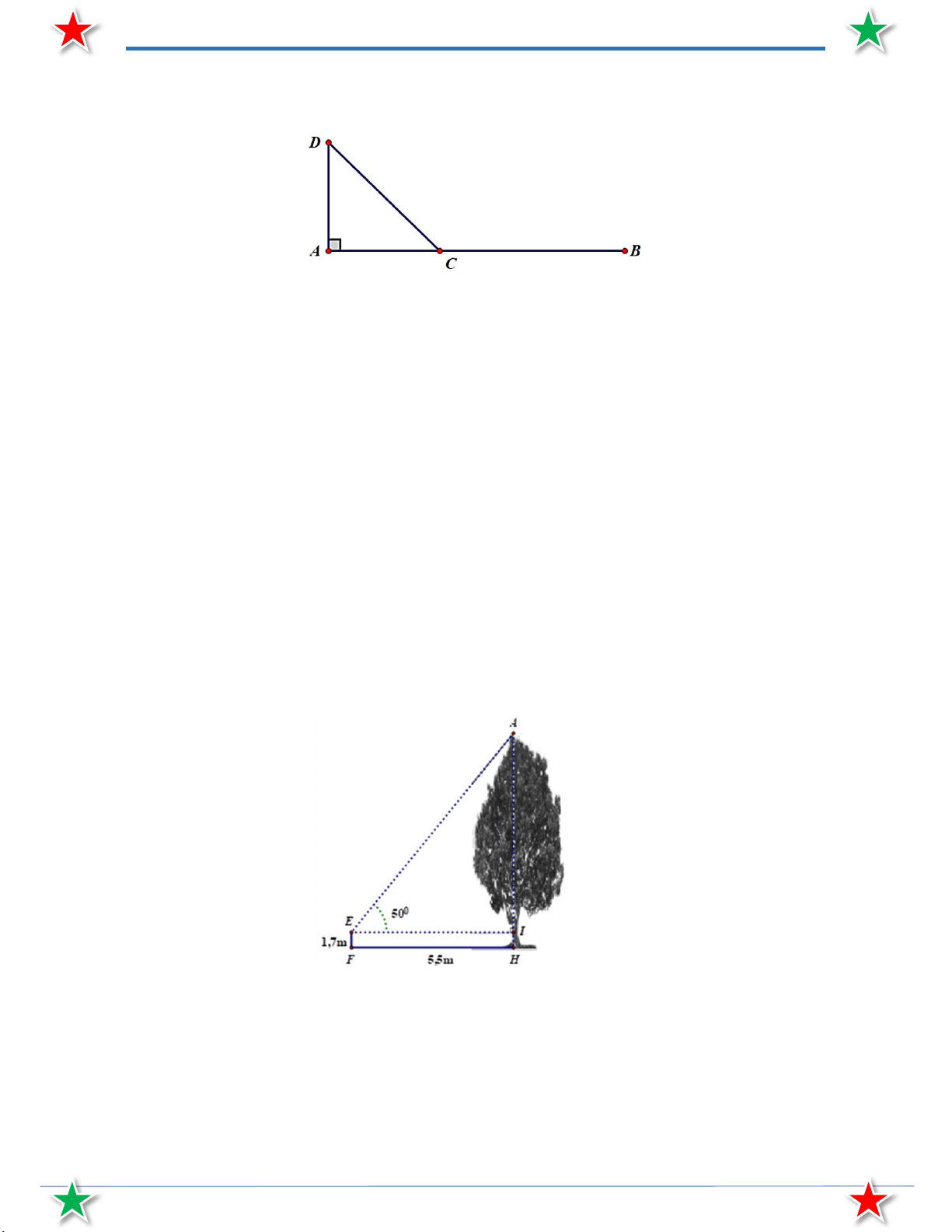
Bài 67. Với số liệu ghi trên hình (biết tứ giác EFHI là hình chữ nhật và A , I , H thẳng hàng). Cây
trong hình cao bao nhiêu mét? (làm tròn kết quả đến chữ số hàng đơn vị).
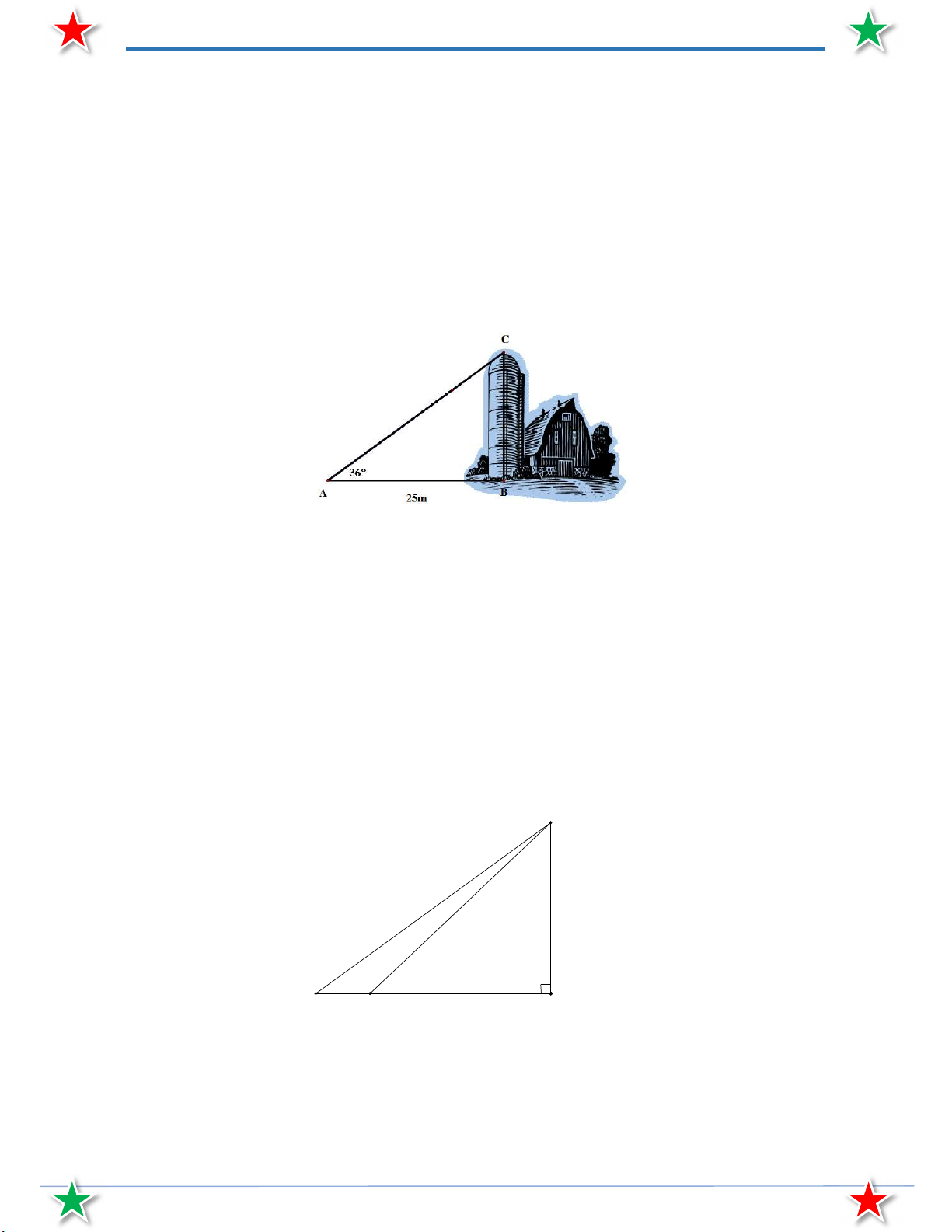
Bài 68. Một người quan sát đứng cách một tòa nhà khoảng 25 m (điểm A ). Góc nâng từ chỗ anh ta
đứng đến nóc tòa nhà (điểm C ) là 36 .
1) Tính chiều cao tòa nhà (làm tròn đến 0,5 mét)
2) Nếu anh ta đi thêm 5 m nữa, đến vị trí D nằm giữa A và B thì góc nâng từ D đến nóc nhà là
bao nhiêu? (làm tròn đến phút).
Bài 69. Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất,cọc cao 2 m và đặt xa cây 15
m. Sau khi người ấy lùi ra xa cách cọc 0,8 m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên
một đoạn đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6 m?
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 17
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
HƯỚNG DẪN GIẢI DẠNG 1: CÁC BÀI TOÁN THỰC TẾ HÌNH HỌC Bài 1.
Hằng ngày hai anh em An và Bình cùng đi bộ từ nhà ở A để đến trường. Trường của An ở vị
trí B , trường của Bình ở vị trí C theo hai hướng vuông góc với nhau. An đi với vận tốc
4km / h và đến trường sau 15 phút. Bình đi với vận tốc 3km / h và đến trường sau 12
phút.Tính khoảng cách BC giữa hai trường (làm tròn đến mét). Lời giải 15
+) Quãng đường An đi từ nhà đến trường là: AB  4   1km . 60 12 3
+) Quãng đường Bình đi từ nhà đến trường là: AC  3   km . 60 5
Áp dụng định lý Pitago trong tam giác vuông ABC , ta có: 2  3  34 2 2 1 BC  AB  AC  1    1,166km  1166 m   .  5  5
Vậy khoảng cách hai trường là 1166 m . Bài 2.
Một người A đang ở trên khinh khí cầu ở độ cao 150m nhìn thấy một vật B trên mặt đất cách
hình chiếu của khí cầu xuống đất một khoảng 285m . Tính góc hạ của tia AB . Nếu khinh khí
cầu tiếp tục bay lên thẳng đứng thì khi góc hạ của tia AB là 46 thì độ cao của khinh khí cầu
là bao nhiêu? (làm tròn đến mét). Lời giải
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 18
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
+) Góc hạ của tia AB là góc  ABC . CA
Trong tam giác ABC vuông tại C có:  150 10 tan ABC     ABC  28 . CB 285 19
+) Khi góc hạ là 46 , cao của kinh khí cầu là: 285  tan 46  295 m Bài 3.
Một người có mắt cách mặt đất 1, 4m , đứng cách tháp Eiffel 400m nhìn thấy đỉnh tháp với góc
nâng 39 . Tính chiều cao của tháp (làm tròn đến mét). Lời giải A
 BC vuông tại A có: AC  AB  tan 
ABC  400 tan 39m
Suy ra chiều cao của tháp là: AC  AD  400  tan 39  1, 4  325 m Bài 4.
Một cột đèn cao 8m . Tính góc tạo bởi tia nắng mặt trời và mặt đất lúc nó có bóng trên mặt đất là 5m . Lời giải
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 19
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Giả sử cột đèn có chiều cao AB , bóng cột đền lên mặt đất lúc đó là BC .
Khi đó góc tạo bởi tia nắng và mặt đất là góc  ACB . AB 8 Trong A
 BC vuông tại B có: tan ACB    ACB  58. BC 5
Vậy góc tạo bởi tia nắng và mặt đất lúc đó xấp xỉ 58 . Bài 5.
Một cái thang dài 4m đang dựa vào tường, chân thang cách chân tường 2m .Tính góc tạo bởi
thang với mặt đất và với mặt tường. Lời giải
Giả sử tháng có chiều dài AC , khoảng cách từ đầu thang tới mặt đất là AB (như hình vẽ).
Khi đó góc tạo bởi thang với mặt đất và với măt tường lần lượt là góc  ACB ,  CAB . AB Trong A  BC vuông tại B có  4 tan ACB    2   ACB  63 2  6' BC 2   CAB  90   ACB  26 3  4'.
Vậy góc tạo bởi thang với mặt đất và với măt tường lần lượt là 63 2  6', 26 3  6' . Bài 6.
Tính chiều cao của một ngọn núi cho biết tại hai điểm cách nhau 1km trên mặt đất người ta
nhìn thấy đỉnh núi với góc nâng lần lượt là 40 và 32 .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 20
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế D 32° 40° A 1km C B Lời giải: D 32° 40° A 1km C B
Gỉa sử chiều cao của một ngọn núi là độ dài đoạn thẳng CD
Hai điểm cách nhau 1 km là đoạn thẳng AB 1km Ta có: A  CD có 
ACD  90  AC  DC.cot  DAC B  CD có 
BCD  90  BC  DC.cot  DBC  AC  BC  DC. cot  DAC  cot   DBC  AC  BC 1  DC    km cot  DAC  cot   DBC  2, 447   cot 32  cot 40
Vậy chiều cao của đỉnh núi là: 2, 447 km Bài 7.
Tính chiều cao của một cái tháp, cho biết khi các tia nắng mặt trời tạo với mặt đất một góc 42
thì bóng của tháp trên mặt đất có chiều dài 150m. Lời giải:
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 21
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Giả sử AH là chiều cao của tháp; 
ABH  42 là góc bởi tia nắng mặt trời với mặt đất
Bóng của tháp trên mặt đất là BH  150 m . Khi đó
ABH vuông tại H  AH  BH.tan 
ABH  150.tan 42  135,061m
Vậy: chiều cao của cột tháp là: 135,061m Bài 8.
Để đo chiều rộng AB của một con sông mà không phải băng ngang qua sông, một người đi từ
A đến C đo được AC  50m và từ C nhìn thấy B với góc nghiêng 62 với bờ sông. Tính bề rộng của con sông. Lời giải: Ta có: A
 BC vuông tại A  AB  AC.tan 
ACB  50.tan 62  94,036m
Vậy: bề rộng của con sông dài: 94,036 m Bài 9.
Một người quan sát đứng cách một tòa nhà 25m. Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà là 36 .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 22
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
1) Tính chiều cao của tòa nhà (làm tròn đến mét).
2) Nếu anh ta dịch chuyển sao cho góc nâng là 32 thì anh ta cách tòa nhà bao nhiêu mét? Khi
đó anh ta tiến lại gần hay cách ra xa tòa nhà (làm tròn đễn chữ số thập phân thứ hai). Lời giải: A 360 320 B D C 25 m
1) Tính chiều cao của tòa nhà (làm tròn đến mét).
Giả sử chiều cao của cột tháp là độ dài AB
Góc nâng từ chỗ anh ta đứng đến nóc tòa nhà là  ACB  36
Khoảng cách từ vị trí người đó đứng đến tòa nhà là BC  25m Khi đó: A
 BC vuông tại B  AB  BC.tan 
ACB  25.tan 36  18m
Vậy chiều cao của tòa nhà là 18m
2) Giả sử khoảng cách từ vị trí người đó đứng để tạo được góc nâng là 32 là D . Khi đó
khoảng cách từ vị trí người đó đứng đến tòa nhà là độ dài đoạn thẳng BD
ABD vuông tại B  BD  A . B cot 
ADB  18cot 32  28,81m
Vì BD  BC 28,81 25 nên anh ta cách xa tòa nhà .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 23
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 10. Từ trên tháp quan sát của một ngọn hải đăng cao 28 m , người ta nhìn thấy một chiếc thuyền
cứu hộ với góc hạ 20 . Tính khoảng cách từ chân tháp đến thuyền. . Lời giải: A 28 m 200 I D
Giả sử chiều cao của tháp chính là độ dài AD ; chiếc thuyền cứu hộ với góc hạ 20 là góc 
AID ; DI là khoảng cách từ thuyền đến chân tháp. Ta có:
ADI vuông tại D  DI  A . D cot 
ADI  28.cot 20  76,929m
Vậy: Khoảng cách từ chân tháp đến thuyền là 76,929 m .
Bài 11. Đài quan sát Toronto, Ontario (canada) cao 533m . Ở một thời điểm vào ban ngày, mặt trời
chiếu tạo thành bóng dài 1100 m . Hỏi lúc đó góc tạo bởi tia nắng mặt trời và mặt đất là bao
nhiêu (làm tròn đến độ). Lời giải:
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 24
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế B 553m A 1100m C
Trên hình vẽ: Gọi AB là chiều cao của đài quan sát, AC là chiều dài bóng của nó trên mặt đất
ta có AB  553 (m); AC  1100 (m)
Khi đó góc tạo bởi tia nắng mặt trời và mặt đất là  ACB AB 553
Xét tam giác ABC vuông tại A có tan  ACB     0 ACB  27 AC 1100
Vậy lúc đó góc tạo bởi tia nắng mặt trời và mặt đất là xấp xỉ 0 27
Bài 12. Hai ngư dân đứng ở một bên bờ sông cách nhau 250 m cùng nhìn thấy một cù lao trên sông với
các góc nâng lần lượt là 30 và 40 . Tính khoảng cách d từ bờ sông đến cù lao. Lời giải: C d 30° 40° A H B
Trên hình vẽ: Giả sử hai ngư dân lần lượt đứng ở 2 vị trí A và B , cù lao ở vị trí C
Gọi H là hình chiếu của C trên AB thì khoảng cách từ bờ sông đến cù lao là d  AH
Xét tam giác AHC vuông tại H có 0 AH  d.cot 30 
Xét tam giác BHC vuông tại H có 0 BH  d.cot 40 Mà AH  BH  AB 0 0
 d.(cot 30  cot 40 )  250   d.2,9238  250  
     d  85,5 (m)
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 25
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Vậy khoảng cách d từ bờ sông đến cù lao khoảng 85,5 m
Bài 13. Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A ) đến trường (điểm B ) phải leo lên và xuống
một con dốc (như hình vẽ). Cho biết đoạn thẳng AB dài 762 m , góc  0 A  4 ,  0 B  6 . C h 4° 6° A B H 762 m
1) Tính chiều cao h của con dốc.
2) Hỏi bạn An đến trường lúc mấy giờ ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ
trung bình xuống dốc là 6 km/h . Lời giải: C h 4° 6° A B H 762 m
1) Trên hình vẽ: Chiều cao h của con dốc là chiều dài đoạn thẳng HC
Xét tam giác AHC vuông tại H có 0 AH  . h cot 4 
Xét tam giác BHC vuông tại H có 0 BH  . h cot 6 Mà AH  BH  AB 0 0
 d.(cot 4  cot 6 )  762   d.23,815  762  
     d  32 (m)
Vậy chiều cao h của con dốc là khoảng 32 m
2) Đổi 4 km/h = 4000 m/h; 6km/h=6000m/h
Gọi thời điểm An đến trường là x h) (6  x  24
Quãng đường An lên dốc là 0
AC  32 : sin 4  458,739 m
Thời gian An lên dốc đoạn đường AC hết 458,739 : 4000  0,115 (h)
Quãng đường An xuống dốc là 0
CB  32 : sin 6  306,137 m
Thời gian An xuống dốc đoạn đường CB hết 306,137 : 6000  0, 051 (h)
Thời gian An đi từ nhà đến trường hết x  6 h nên ta có phương trình: 0,115  0, 051  x  6
 x=0,115  0,051 6  6,166 (h)  6h10ph
Vậy bạn An đến trường vào khoảng 6 giờ 10 phút.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 26
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 14. Từ đỉnh một tòa nhà cao 54 m , người ta nhìn thấy một ô tô đang đỗ dưới một góc nghiêng
xuống là 40 . Hỏi ô tô đang đỗ cách tòa nhà đó bao nhiêu mét ? Lời giải: B 40° x 54m A C
Trên hình vẽ: Gọi AB là chiều cao của tòa nhà, AC là khoảng cách từ chân tường đến ô tô
Từ đỉnh tòa nhà, người ta nhìn thấy một ô tô đang đỗ dưới một góc nghiêng xuống là  CBx  40   CBA  50 . Xét A  BC vuông tại A có: AC  A . B tan  0
ABC  54.tan 50  64,35 (m)
Vậy ô tô đang đỗ cách tòa nhà đó khoảng 64,35 m
Bài 15. Một học sinh đứng ở mặt đất cách tháp ăng ten cao 150 m nhìn thấy đỉnh tháp theo một góc
nghiêng lên là 20 và khoảng cách từ mắt đến mặt đất là 1m . Tính khoảng cách từ học sinh đó
đến tháp (làm tròn đến mét). Lời giải: B 150m 20° A C 1m D H
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 27
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Trên hình vẽ: Gọi BD là chiều cao của tháp ăng ten, C là vị trí mắt của học sinh, CH là
khoảng cách từ mắt của học sinh đến mặt đất, A là hình chiếu của điểm C trên BD .
Ta có ADHC là hình chữ nhật và BD  150 (m); HC  1 (m)  AB  149 (m)
Khoảng cách từ học sinh đó đến tháp là độ dài đoạn thẳng AC
Một học sinh đứng ở mặt đất nhìn thấy đỉnh tháp theo một góc nghiêng lên là  ACB  20  Xét ABC vuông tại A có: AC  A . B cot  0
ACB  149.cot 20  409 (m)
Vậy khoảng cách từ học sinh đó đến tháp là xấp xỉ 409m .
Bài 16. Một cái thang dài 4,8 m dựa vào tường làm thành một góc 58 so với mặt đất. Tính chiều cao
của thang so với mặt đất (làm tròn đến mét). Lời giải C 4,8 m 58° A B
Giả sử trong hình vẽ, AC là độ dài của thang thì BC chính là chiều cao của thang so với mặt
đất, AB là khoảng cách từ chân thang đến chân tường, góc tạo bởi thang với mặt đất  CAB  58 . Xét A
 BC vuông tại C có BC  AC.sin 
CAB hay BC  4,8.sin 58  4m
Vậy chiều cao của thang so với mặt đất xấp xỉ 4 mét.
Bài 17. Một người quan sát ở đài hải đăng cao 800 feet (đơn vị đo lường Anh) so với mực nước biển
nhìn thấy một con tàu ở xa với một góc nghiêng xuống là1 4
 2'. Hỏi khoảng cách từ tàu đến
chân ngọn hải đăng là bao nhiêu hải lý (1 hải lý = 5280 feet )? Lời giải
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 28
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế x C 1°42' 800 feet 1°42' A B
Giả sử trong hình vẽ BC là độ cao của đài hải đăng so với mực nước biển thì AB là khoảng
cách từ tàu đến chân ngọn hải đăng, góc nghiêng xuống  ACx 1 4  2   CAB 1 4  2 Xét A
 BC vuông tại B có AB  BC.cotan  CAB hay AB  800.cot1 4
 2'  26954,8072feet  5(hải lý).
Vậy khoảng cách từ tàu đến chân ngọn hải đăng khoảng 5 hải lý.
Bài 18. Một người quan sát ở đài hải đăng cao 149 m so với mực nước biển nhìn thất một con tàu ở xa
với một góc nghiêng xuống là 27 . Hỏi tàu đang đứng cách chân hải đăng là bao nhiêu mét? Lời giải x C 27° 149 m 27° A B
Giả sử trong hình vẽ BC là độ cao của đài hải đăng so với mực nước biển thì AB là khoảng
cách từ tàu đến chân ngọn hải đăng, góc nghiêng xuống  ACx  27   CAB  27 Xét A
 BC vuông tại B có AB  BC.cotan  CAB
hay AB  149.cotan 27  292m
Vậy khoảng cách từ tàu đến chân ngọn hải đăng khoảng 292 mét.
Bài 19. Một học sinh thả diều ngoài đồng, cho biết đoạn dây đã thả dài 100 m và có góc nâng 52 .
Tính độ cao của diều so với mặt đất (làm tròn đến mét).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 29
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải C 100 m 52° A B
Giả sử trong hình vẽ, AC là đoạn dây diều đã thả thì BC là độ cao của diều so với mặt đất, góc nâng  CAB  52 Xét A
 BC vuông tại B có BC  AC.sin  CAB
hay BC  100.sin 52  79 m
Vậy độ cao của diều so với mặt đất xấp xỉ 79 mét.
Bài 20. Một chiếc thuyền thả neo trên sông. Cho biết dây neo dài 30 m và có góc nghiêng lên là 39 .
Tính độ sâu của mực nước chỗ thuyền đang đậu (làm tròn đến mét). Lời giải
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 30
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế C 30 m 39° B A
Giả sử trong hình vẽ, AC là dây neo thì BC là độ sâu của mực nước chỗ thuyền đang đậu, góc nghiêng lên  CAB  39 Xét A
 BC vuông tại B có BC  AC.sin  CAB
hay BC  30.sin 39  19m
Vậy độ sâu của mực nước chỗ thuyền đang đậu xấp xỉ 19 mét.
Bài 21. Một người đứng trên đỉnh tháp cao 325 m nhìn thấy 2 điểm A và B với hai góc hạ lần lượt là
37 và 72 .Tính khoảng cách AB . Lời giải: D 37° 325 m A B C
Gọi các điểm như trên hình vẽ, ta được: 
ADC  90  37  53 
BDC  90  72  18 Xét A  DC vuông tại C , có:
AC  DC.tan ADC  325.tan 53  431, 29(m) Xét B  DC vuông tại C , có:
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 31
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
BC  DC.tan BDC  325.tan18  105,6m
Ta có: AB  AC  BC  325, 69(m)
Bài 22. Một người đứng cách chân tháp 14 m nhìn thấy đỉnh tháp theo góc nghiêng 60 . Tính chiều cao của tháp. Lời giải A 60° C 14 m B
Gọi các điểm như trên hình vẽ. Xét A
 BC vuông tại B, ta có:
AB  BC.tan C  14.tan 60  14 3 m
Bài 23. Một máy bay cất cánh theo phương có góc nâng 23 .Hỏi muốn đạt độ cao 2500 m , máy bay
phải bay một đoạn đường là bao nhiêu mét? Lời giải
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 32
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế A x 2500 m 23° C B
Đặt tên các điểm như trên hình vẽ: Xét A  BC vuông tại C AB sin C  AC 2500  sin 23  x 2500  x   6398,3(m) sin 23
Vậy máy bay muốn đạt được độ cao 2500m thì phải bay một đoạn đường khoảng 6398,3m
Bài 24. Một cái cây có bóng trên mặt đất dài 20 m .Cho biết tia nắng qua ngọn cây nghiêng một góc
31 so với mặt đất. Tính chiều cao của cây. Lời giải A 31° B 20 m C
Đặt tên các điểm như trên hình vẽ: Xét A
 BC vuông tại B , ta được:
AB  BC.tan C  20.tan 31  12,02m
Bài 25. Một cái cây cao 6m đang có bóng dài 3, 2 m . Tính góc hợp bởi tia nắng với thân cây
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 33
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải A x 6 m B 3,2 m C
Đặt tên các điểm như trên hình vẽ: Xét A
 BC vuông tại C, ta được: BC 3, 2 tan A   AC 6  A  28
Vậy góc tạo bởi tia nắng với thân cây khoảng 28
Bài 26. Một người đứng cách chân tháp 14 m nhìn thấy đỉnh tháp theo góc nghiêng 60 . Tính chiều cao của tháp. Lời giải
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 34
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế B 60° C 14 m A
Gọi chiều cao của tháp là đoạn AB . Trong tam giác ABC vuông tại A ta có:
AB  AC.tan C  14.tan 60  14 3 m .
Vậy chiều cao của tháp là 14 3 m.
Bài 27. Bạn Hùng có tầm mắt cao 1,5 m đang đứng gần một cao ốc cao 30 m thì nhìn thấy nóc tòa nhà
với góc nâng 30 . Hùng đi về phía tòa nhà cho đến khi nhìn thấy nóc tòa nhà với góc nâng 60 .
Tính quãng đường mà bạn Hùng đã đi được. C 30m 60o 30o B A D 1,5m K Lời giải
Ta có độ dài đoạn AC  CK  AK  30 1,5  28,5cm .
Trong tam giác ABC vuông tại A ta có: AB  AC.co t B  28,5.cot 30  28,5. 3 m .
Trong tam giác ABD vuông tại A ta có: 3
AD  AC.co t D  28,5.co t 60  28,5.  9,5 3 m . 3
Quãng đường bạn Hùng đi được là: BD  AB  AD  28,5 3  9,5 3  19m
Vậy bạn Hùng đi được 19 m.
Bài 28. Một học sinh có tầm mắt cao 1,5 m đứng trên sân thượng của một căn nhà cao 15 m nhìn thấy
bạn mình với góc nghiêng xuống 49 . Hỏi cô bạn đang ở cách căn nhà bao nhiêu mét?
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 35
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải C 1,5 mB 49° 15 m A D
Gọi chiều cao của tòa nhà là AB  15 m , chiều cao của bạn học sinh là BC  1,5 m , ta có độ dài
AC  AB  BC  15 1,5  16,5m , 
D  49 (hai góc so le trong), trong tam giác D A C vuông
tại A ta có: AD  AC.cot D  16,5.cot 49m
Vậy cô bạn cách căn nhà là 16,5.cot 49 m.
Bài 29. Một máy bay thể thao đang bay ngang ở độ cao 3000 m nhìn thấy một cái cây với góc nghiêng
xuống 15 . Hỏi máy bay phải bay một đoạn đường là bao nhiêu mét thì sẽ ở ngay trên ngọn cây? Lời giải A x D 15° 3000 m 15° C B x
Gọi đoạn đường cần bay để thấy ngọn cây là AD  x , độ cao của máy bay là CD  3000 m .
Trong tam giác ADC vuông tại D ta có: AD  C .
D cot A  3000.cot15m .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 36
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Vậy quãng đường máy bay phải bay là 3000.cot15 m.
Bài 30. Từ nóc một cao ốc cao 50 m người ta nhìn thấy chân và đỉnh một ăng-ten với các góc hạn lần
lượt là 62 và 34 . Tính chiều cao cột ăng-ten. E B 340 D 620 50m A C Lời giải E 34° B D 62° 50 m A C Ta có CD  AB  50 m .
Trong tam giác BDC vuông tại D , ta có: BD  CD.cot  CBD  50.cot 62m .
Trong tam giác BDE vuông tại D ta có: DE  B . D tan  DBE  50.cot 62 .  tan 34m .
Chiều cao của cột ăng ten là: CE  CD  DE  50  50.cot 62 .  tan 34m
Vậy chiều cao của cột ăng ten là 50  50.cot 62 .  tan 3467,93m .
Bài 31. Một cái diều đang bay ở độ cao 60 m. Sợi dây cột diều nghiêng với mặt đất một góc 60 . Tính
chiều dài của sợi dây (làm tròn đến mét) khi nó căng thẳng (không có chỗ bị võng). Lời giải
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 37
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Phân tích bài toán ta có hình vẽ: A 60m 60° B H Xét A
 HB vuông tại H , áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:  AH AH 60 60 sin ABH   AB     AB sin  69. ABH sin 60 3 2
Vậy chiều dài của sợi dây khi nó căng thẳng là  69 m.
Bài 32. Tháp Capital Gate tại Abu Dhabi cao 160 m và nghiêng 18 . Nếu không nghiêng thì tháp cao bao nhiêu mét? Lời giải
Phân tích bài toán ta có hình vẽ: A 18° 160m H B
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 38
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Xét A
 HB vuông tại H , dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:  AH AH 160 cos BAH   AB    AB cos  168. BAH cos18
Vậy nếu không nghiêng thì tháp Capital Gate tại Abu Dhabi cao  168 m.
Bài 33. Tính chiều cao của một ngọn núi, cho biết tại hai điểm cách nhau 500 m , người ta nhìn thấy hai
đỉnh núi với góc nâng lần lượt là 34 và 38 . Lời giải A 34° x 38° D 500m C B
Xét ABC vuông tại B, áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có: AB tan  ACB   AB  BC.tan  ACB  . x tan 38   1 BC Xét A
 BD vuông tại B, áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có: AB tan  ADB   AB  B . D tan 
ADB   x  500.tan 34 2 BD Từ   1 và 2 suy ra: .
x tan 38   x  500.tan 34  .
x tan38  tan34  500.tan34 500.tan 34  x  tan 38  tan 34
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 39
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế 500.tan 34 Mà AB  . x tan 38 nên AB  .tan 38  2468. . tan 38  tan 34
Vậy ngọn núi đó cao khoảng 2468 m.
Bài 34. Một cái tháp được dựng bên bờ một con sông, từ một điểm đối diện với tháp ngay bờ bên kia
người ta nhìn thấy đỉnh tháp với góc nâng 60 . Từ một điểm khác cách điểm ban đầu 20 m,
người ta cũng nhìn thấy đỉnh tháp với góc nâng 30 . Tính chiều cao của tháp. Lời giải A 30° 60° D 20 m C x B
Giả sử đoạn BC có độ dài là x m.
Xét ABC vuông tại B, áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có: AB tan  ACB   AB  BC.tan  ACB  . x tan 60   1 BC Xét A
 BD vuông tại B, áp dụng định nghĩa tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có: AB tan  ADB   AB  B . D tan 
ADB   x  20.tan 30 2 BD Từ   1 và 2 suy ra: .
x tan 60   x  20.tan 30  .
x tan 60  tan 30  20.tan 30 20.tan 30  x  tan 60  tan 30 3 20. 20.tan 30 Mà AB  . x tan 60 nên 3 AB  .tan 60  . 3  17. tan 60  tan 30 3 3  3
Vậy chiều cao của tháp xấp xỉ 17 m.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 40
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 35. Một bức tượng cao 1, 6 m được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là 60 và 45 . Tính chiều cao của cái bệ. Lời giải A
 BC vuông tại B có  45o BAC  nên A
 BC vuông cân tại B nên AB  BC  h . Xét A
 BD vuông tại B, áp dụng định nghĩa hệ thức giữa cạnh và góc trong tam giác vuông, ta có: BD  AB   h   h     1, 6 .tan 60 1, 6 . 3 3 1 h  1, 6  h   h  2, 2 3 1
Vậy chiều cao của cái bệ h  2, 2 m.
Bài 36. Một nhà trẻ muốn thiết kế hai cái cầu tuột trong sân chơi. Đối với trẻ dưới 5 tuổi, cầu tuột cao
1,5 m và nghiêng với mặt đất một góc 30 . Đối với trẻ trên 5 tuổi cầu tuột cao 1,5 m và
nghiêng với mặt đất một góc 45 . Tính chiều dài của mỗi máng tuột. A 2m 30 45 E B C Lời giải
Máng tuột của cầu trượt trẻ em dưới 5 tuổi là độ dài EA AB Xét  1,5 sin AEB   sin 30   AE  3(m) AE AE
Máng tượt của cầu trượt trẻ em trên 5 tuổi là độ dài AC AB Xét  1,5 sin ACB   sin 45   AC  1,06(m) AC AC
Bài 37. Từ chân một cái tháp cao 50 m người ta nhìn thấy đỉnh một tòa nhà với góc nâng 30 . Trong
khi đó từchân tòa nhà lại nhìn thấy đỉnh tháp với góc nâng 60 . Tính chiều cao của tòa nhà.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 41
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải
Chiều cao tòa nhà là độ dài AB . DC Xét DAC  DCA    50 50 3 , 90 : tan DAC   AC   (m) AC tan 60 3 AB 50 3 50 Xét BAC,  0 CAB  90 : tan  0 BCA   AB  .tan 30  (m) AC 3 3
Bài 38. Hai trụ điện có cùng chiều cao đặt cách nhau 80 m . Một người đứng ở xa (thẳng hàng với hai
trụ điện, không đứng giữa hai trụ điện) nhìn đỉnh hai trụ điện với góc nâng lần lượt là 60 và
30 . Tính chiều cao trụ điện và khoảng cách từ người đó đến chân các trụ điện. Biết mắt người
đó cách mặt đất1, 2 m . Lời giải B D 60 60 30 A C x M 1,2m H 80m
Chiều cao của người là độ dài AH  1, 2m .
Chiều cao cột điện là BH  BA  AH
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 42
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Khoảng cách 2 cột điện là AC  80m
Khoảng cách người đến cột 1 và cột 2 lần lượt là độ dài AM ; MC.
Vì 2 cây cột điện cao bằng nhau  BD / / AC   DBM  
BMA  60 (2 góc so le trong)  BMD  180   BMA   DMC  90 BM Xét BMD,  BMD  90 ,  DB  80(m) : cos  DBM 
 BM  80.cos 60  40(m) BD AM Xét BM , A  BAM  90 ,  MB  40(m) : cos  BMA 
 AM  40.cos60  20(m); BM
AB  BM .sin 60  20 3(m)
 MC  AC  AM  80  20  60(m)
 BH  AB  AH  20 3 1, 2  35,8(m)
Bài 39. Từ trên một ngọn hải đăng cao 75 m , người ta quan sát hai lần thấy một chiếc thuyền đang
hướng về phía hải đăng với góc hạ lần lượt là 30 và 45 . Hỏi chiếc thuyền đi được bao nhiêu
mét giữa hai lầnquan sát? Lời giải
Chiều dài quãng đường chiếc thuyền đi giữa hai lần quan sát là độ dài CD . AB Xét BAC  BAC    75 , 90 : tan ACB   AC   75(m) AC tan 45 AB Xét DAB  DAB    75 , 90 : tan BDA   AD   75 3(m) AD tan 30
CD  DA  AC  75 3  75  59,9(m)
Bài 40. Một thủy thủ lái thuyền ra biển hướng về hướng đông bắc với góc nghiêng so với phương bắc
là 41 . Đi được 2,8 km anh ta phát hiện sắp hết nhiên liệu nên vội quay thuyền vào bờ, đi
được 1,8 km thì thuyền tắt máy. Hỏi lúc đó thuyền cách bờ bao xa?
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 43
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải B x 2,8 1,8 C j 41 A D
Khoảng cách từ thuyền đến bờ là độ dài CD
góc nghiêng so với phương bắc là  xAB     0 41 BAC  49 BD Xét DAB,  BDA  90 : sin  BAD 
 BD  2,8.sin 49  2,11(km) AB
 CD  BD  BC  2,11,8  0,3(km)
Bài 41. Từ trên đỉnh một tòa nhà cao 7m , người ta nhìn thấy đỉnh một tháp truyền hình với góc nâng
60 và nhìn thấy chân của tháp với góc hạ 45 . Tính chiều cao của tháp truyền hình? Lời giải Xét A  BC vuông tại B có: BC  A . B cot  ACB  A .
B cot 45  7.1  7(m) (HTL trong tam giác vuông)  AB  BC  7m
Theo đề bài ta có tứ giác ABCE là hình chữ nhật mà AB  BC (cmt) nên tứ giác ABCE là
hình vuông  AE  EC  AB  BC  7cm . Xét A  ED vuông tại E có: DE  AE.tan 
DAE  7.tan 60  7 3  12,12(m) (HTL trong tam giác vuông)
Nên CD  CE  ED  7 12,12 19,12m
Vậy chiều cao của tháp truyền hình khoảng 19,12 m.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 44
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 42. Một học sinh có khoảng cách từ mặt đến mặt đất là 1, 2 m bắt đầu quan sát một trái bóng bay
với góc nâng 60 . Một lúc sau lại nhìn thấy quả bóng bay với góc nâng 30 . Hỏi giữa hai lần
quan sát quả bóng đã bay được bao nhiêu mét? Cho biết độ cao của quả bóng luôn luôn không đổi và bằng 88, 2 m . Lời giải Xét A  BP vuông tại B có: AB  BP  3
.cot BAP  87.cot 60  87.  50,23( )
m (HTL trong tam giác vuông). 3 Xét A  CQvuông tại C có: AC  QC.cot 
BAQ  87.cot 30  87. 3  150,69(m) (HTL trong tam giác vuông)
Nên PQ  BC  AC  AB  150, 69  50, 23  100, 46m
Vậy giữa hai lần quan sát quả bóng đã bay được khoảng 100, 46 m.
Bài 43. Một người đang ở trên một cái tháp có chiều cao h =100 m nhìn xuống một con đường chạy
thẳng đến chân tháp. Anh ta nhìn thấy một chiếc xe máy với góc hạ 30 . Sáu phút sau lại nhìn
thấy nó với góc hạ 60 . Hỏi sau bao nhiêu phút thì xe máy đến chân tháp? Cho biết vận tốc xe máy không đổi. Lời giải
Gọi vận tốc xe máy là x (m/phút)  CD  6x(m) . Xét A  BD vuông tại B có: DB  A . B cot 
ADB 100.cot 30 173, 21(m) (HTL trong tam giác vuông). Xét A  BC vuông tại B có:
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 45
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế CB  AB  3
.cot ACB  100.cot 60  100.
 57,74(m) (HTL trong tam giác vuông). 3
 CD  DB CB 173,21 57,74 115,47m . CD 115, 47 Vận tốc xe máy là: x    19, 25 (m/phút) . 6 6
Thời gian xe máy đi từ C đến chân tháp là: 57, 74 :19, 25  3 (phút).
Bài 44. Để đo chiều cao một cái cây AB . Người ta đặt gương phẳng tại vị trí C . Người đo đi lùi lại
(thẳng người) cho đến khi nhìn thấy bóng ngọn cây A (lúc này là F ). Biết khoảng cách từ
gương đến gốc cây là BC  30 mét, khoảng cách từ gương đến chỗ đứng là CD  1,5 mét.
Khoảng cách từ mắt người đo E đến mặt đất là ED  1,6 mét. Tính chiều cao của cây? (biết  BCA   DCE ). Lời giải Xét A  BC và E  DC có:  BCA   DCE (gt)  ABC   EDC  90 Nên A  BC ∽ E  DC (g.g) AB BC AB 30 30.1,6      AB   32m . ED DC 1, 6 1,5 1,5
Vậy chiều cao cây là 32 m.
Bài 45. Quan sát hình vẽ dưới đây. Giả sử CD  h là chiều cao của tháp trong đó C là chân tháp.
Chọn hai điểm A , B trên mặt đất sao cho ba điểm A , B và C thẳng hàng. Ta đo khoảng cách AB và các góc  CAD , 
CBD . Chẳng hạn ta đo được AB  24 m,  CAD    63 , 
CBD    48 . Hãy tính chiều cao h của tháp.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 46
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải Xét D  CB vuông tại C có: CB  DC.cot  CBD  .
h cot 48  0,9.h(m) (HTL trong tam giác vuông). Xét D  CA vuông tại C có: CA  DC.cot  CAD  .
h cot 63  0,51.h(m) (HTL trong tam giác vuông).
 AB  CB  CA  0,9.h  0,51.h  0,39.hm. AB 24  h    61,54m . 0,39 0,39
Vậy chiều cao của tháp khoảng 61,54 m.
Bài 46. Một hình chữ nhật có kích thước là 20 cm và 30 cm. Người ta tăng mỗi kích thước thêm x cm.
Gọi y là chu vi của hình chữ nhật mới. 1) Hãy tính y theo x .
2) Tính giá trị của y tương ứng với x  3 cm; x  5 cm. Lời giải
1) Ta có các kích thước của hình chữ nhật sau khi tăng là x  20 cm và x  30 cm.
Chu vi hình chữ nhật mới là y  2. x  20  x  30  4x 100 . Vậy y  4x 100 (cm). 2) Ta có: y  4x 100 .
Với x  3  y  4.3 100  112cm .
Với x  5  y  4.5 100  120cm . Bài 47.
Một thửa đất hình chữ nhật có chiều dài là 32 m và chiều rộng là 24 m. Người ta định làm một
vườn cây cảnh có con đường đi xung quanh, có bề rộng x m (hình vẽ bên). Hỏi bề rộng của
mặt đường là bao nhiêu để diện tích phần đất còn lại là 560 2 m .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 47
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế 32 m x x x 24 m x Lời giải
Ta có: Chiều rộng phần đất còn lại là: 24  2x (cm).
Chiều dài phần đất còn lại là: 32  2x (cm).
Vì diện tích phần đất còn lại là 560 2
m nên ta có phương trình:
242x322x  560 2 2
 768  48x  64x  4x  560  x  28x  52  0 x  2   x  26 24 Vì x   12  x  2 . 2
Vậy bề rộng mặt đường là 2m. Bài 48.
Một căn phòng hình vuông được lát bằng những viên gạch men hình vuông cùng kích cỡ, vừa
hết 441 viên (không viên nào bị cắt xén). Gạch gồm 2 loại men trắng và men xanh, loại men
trắng nằm trên 2 đường chéo của nền nhà còn lại là loại men xanh. Tính số viên gạch men xanh. Lời giải
Gọi cạnh của mỗi viên gạch hình vuông là a (đơn vị diện tích) thì ta có diện tích nền nhà là 2
441a , do đó cạnh của nền nhà là 2
441a  21a . Suy ra đường chéo mỗi viên gạch dài a 2
và đường chéo của nhà là 21a 2 nên mỗi đường chéo sẽ có 21 viên gạch. Hai đường chéo lại
chung nhau một viên chính giữa nên tổng số viên gạch của hai đường chéo là 41 viên. Vậy
tổng số sẽ có 41 viên gạch trắng và 400 viên gạch xanh. Bài 49.
Bạn Nam đi xe đạp từ nhà (điểm A) đến trường (điểm B) gồm đoạn lên dốc và đoạn xuống
dốc, A  5 , B  4 , đoạn lên dốc dài 325 m.
1) Tính chiều cao của dốc và chiều dài quãng đường từ nhà đến trường.
2) Biết vận tốc trung bình lên dốc là 8 km/h và vận tốc trung bình xuống dốc là 15 km/h. Tính
thời gian (phút) bạn Nam đi từ nhà đến trường. (Lưu ý kết quả của phép tính làm tròn đến chữ
số thập phân thứ nhất). Lời giải C 325m A B H
1) Gọi chiều cao của dốc là CH .
Trong tam giác ACH vuông tại H ta có CH  AC.SinA  325.sin 5  28,3m .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 48
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế CH AC.SinA 325.sin 5
Trong tam giác BCH vuông tại H ta có BC     406,1m . SinB SinB Sin4
Vậy chiều cao của dốc gấn bằng 28,3 m.
Chiều dài quãng đường từ nhà đến trường là 325  406,1  731,1m 400 2) Đổi 8 km/h =
m/phút ; 15 km/h = 250 m/phút. 3 325 406,1
Ta có thời gian đi từ nhà đến trường là:   4,1 (phút) 400 250 3 Bài 50.
Một bức tượng cao 1,6 m được đặt trên một cái bệ. Tại một điểm trên mặt đất người ta nhìn
thấy nóc tượng và nóc bệ với các góc nâng lần lượt là 60 và 45. Tính chiều cao cái bệ. Lời giải C 1,6m B A D
Gọi chiều cao của tượng là đoạn BC , Chiều cao của bệ là đoạn AB . D là điểm trên mặt đất
người ta nhìn thấy nóc tượng và nóc bệ với các góc nâng lần lượt là 60 và 45. Vì 
ADB  45 nên AB  AD . Vì  ADC  60 nên AC  A .
D Tan60  AD 3  AB 3  AB  AD . 1, 6
Vậy ta có AC  AB  BC  AB 3  AB 1,6  AB  . 3 1 1,6
Vậy chiều cao của cái bệ sẽ là m. 3 1
Bài 51. Một cây có chiều cao 14 m mọc ở phía sau một bức tường cao 8 m và cách bức tường 12 m.
Hỏi người quan sát có chiều cao 1,8 m phải đứng cách bức tường bao nhiêu mét để có thể nhìn thấy ngọn cây.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 49
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải
Bài toán được mô tả bởi hình vẽ sau: B D 14m 8m F 1,8m A 12m G C E
Độ dài cần tính là độ dài đoạn CE Xét A  BG  0 A   90  có AB / /DC DC CG 8 CG      CG 16m AB AG 14 CG 12 Xét D  CG 0 C   90  có DC / /EF EF EG 1,8 EG      EG  3,6m DC CG 8 16
Có CG  CE  EG 16  CE  3,6  CE  12, 4m
Vậy người quan sát có chiều cao 1,8 m phải đứng cách bức tường bao nhiêu 12,4 mét để có thể nhìn thấy ngọn cây.
Bài 52. Nhà bạn An ở vị trí A , nhà bạn Bình ở vị trí B cách nhau 1200 m. Trường học ở vị trí C cách
nhà bạn An 500m và AB vuông góc với AC . An đi bộ đến trường với vận tốc 4 km/h, Bình đi
xe đạp đến trường với vận tốc 12 km/h. Lúc 6 giờ 30 phút, cả hai cùng xuất phát đến trường.
Hỏi bạn nào đến trường trước? Lời giải
Bài toán được mô tả bởi hình vẽ sau : C 500m A B 1200m
AC là quãng đường An đi bộ đến trường.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 50
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
BC là quãng đường Bình đi bộ đến trường. Xét A  BC  0 A   90  có: 2 2 2 2 2 2
AC  AB  BC  500 1200  BC  BC  1300m  1,3km
Thời gian An đi từ nhà đến trường là : 0,5 : 4  0,125h
Thời gian Bình đi từ nhà đến trường là : 1,3:12  0,1083h
Vậy bạn Bình là người đến trường trước. Bài 53
Bóng của tháp Bình Sơn (Vĩnh Phúc) trên mặt đất có độ dài 20 m. Cùng thời điểm đó, một cột
sắt cao 1, 65 m cắm vuông góc với mặt đất có bóng dài 2 m. Tính chiều cao của tháp. Lời giải
Bài toán được mô tả bởi hình vẽ sau C J 1,65m A B 20m I K 2m
AC là chiều cao cột tháp ; AB là bóng tháp Bình Sơn
IJ là chiều cao cột sắt ; IK là bóng cột sắt
Tại cùng một thời điểm, các tia sáng là các đường thẳng song song AC IJ AC 1,65 Có A  BC  I  KJ      AC  16,5m AB IK 20 2
Vậy chiều cao của tháp là 16,5m .
Bài 54. Một con đê được đắp chắn sóng theo hình dưới, độ dốc của con đê phía sông dài 7 m. Hỏi độ
dốc còn lại của con đê dài bao nhiêu mét? Lời giải
Ta có BCKH là hình chữ nhật  BH  CK Xét A  BH  0 H   90  có: BH  A . B sin A 0  BH  7.sin 50 (m)
Có BH  CK  CK  7.sin 50 (m)
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 51
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế CK Xét C  KD 0 K   90  có: sin D  CD CK 7.sin 50  CD   CD 
14.sin 50 m  CD 10,72 m 0     sin D sin 30
Vậy độ dốc còn lại của con đê gần bằng 10,72 m.
Bài 55. Xem hình vẽ sau, người ta có thể dùng giác kế để đo được góc  CAB  43 và  CBA  38 . Hỏi
tàu đang ở vị trí điểm H sẽ chạy với vận tốc bao nhiêu km/h để sau 5 phút sẽ đến vị trí điểm
C . Biết khoảng cách từ vị trí điểm A đến vị trí điểm B là 300 m và vị trí 3 điểm A , H , B
thẳng hàng (làm tròn đến chữ số thập phân thứ hai). C A H B Lời giải Xét A  HC  0 H   90 có: 0
CH  AH.tanA  CH  AH.tan 43 Xét B  HC  0 H   90 có: 0
CH  BH.tanB  CH  BH.tan 38  0 AH.tan 43 = 0 BH.tan 38  0 AH.tan 43 =   AH  0 300 .tan 38  AH 136,76m
 CH  127,53m  0,12753km 1
Tàu ở vị trí H để chạy đến C sau 5 phút cần đi với vận tốc: 0,12753 : 1,53km / h . 12
Bài 56. Ba An muốn mua một cái thang dùng để lên mái nhà. Ba hỏi An phải mua cái thang dài bao
nhiều mét để đảm bảo sự an toàn và có thể leo lên được mái nhà cao 4,5m so với mặt đất. Em
hãy giúp An tính chiều dài thang cần mua, biết góc kê thang an toàn là 75 so với phương
ngang (làm tròn đến số thập phân thứ nhất).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 52
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Giải 4,5
Chiều dài cái thang cần mua là:  4,7 m 0 sin 75
Bài 57. Một chiếc máy bay bay lên cao với vận tốc 520 km / h . Đường bay lên tạo với phương nằm
ngang một góc 24 . Hỏi sau 90 giây máy bay lên cao được bao nhiêu km theo phương thẳng
đứng? (kết quả làm tròn đến chữ số thập phân thứ nhất) Giải
Giả sử AC là đoạn đường máy bay bay lên trong 90 giây thì AB là độ cao bay lên theo phương thẳng đứng.
Vì 90 giây  0, 025 giờ nên AC  520.0, 025  13km Do đó 0 AB  A . C sin C 13.sin 24  , 5 3km
Vậy sau 90 giây máy bay lên cao được 5,3 km .
Bài 58. Từ đài quan sát cao 10 m, Nam có thế nhìn thấy 2 chiếc thuyền dưới góc 45 và 30 so với
phương ngang. Hãy tính khoảng cách 2 chiếc thuyền, làm tròn đến chữ số thập phân thứ nhất.
(điều kiện lý tưởng: vị trí 2 chiếc thuyền và vị trí đài quan sát thẳng hàng).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 53
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Giải
Vì Nam nhìn thấy hai chiếc thuyền dưới góc 0 45 và 0
30 so với phương ngang nên ta có góc  0 BDA   0 45 ; BCA  30
Xét ABC vuông tại A có:  0 BCA    0 30 CBA  60 Ta có: AC  AB  0
.tan CBA 10.tan 60 17,3m
Xét ABD vuông tại A có:  0 BDA    0 45 DBA  45 DA  AB  0 .tan DBA 10.tan 45 10m
Vậy khoảng cách giữa hai thuyền CD  CA  DA  17,3 10  7,3m
Bài 59. Hình ảnh mặt cắt một quả đồi được minh họa là một A
 BC với các chi tiết như sau: cạnh đáy là AC , BH  AC , 
BAC  45 , AH  200 m, HC  210 m. Một nhóm học sinh đi dã ngoại
đi từ đỉnh A lên đỉnh B rồi xuống dốc trở về C . Hãy tính quãng đường này? Giải AH 200 AB    282,8m 0 cos A cos 45
Áp dụng định lí Pytago cho A
 BH vuông tại H và BHC vuông tại H : 2 2 2
BH  AB  AH  BH  200m 2 2 2
BC  BH  HC  BC  290m
Vậy quãng đường đi từ A đến đỉnh B rồi xuống dốc về C là:
AB  BC  282,8  290  572,8m .
Bài 60. Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình vẽ. Tính khoảng cách giữa
chúng (kết quả là tròn đến mét).
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 54
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Giải Ta có 0 AI  IK.tan 50  452,9m 0 BI  IK.tan 65  814,9m
Vậy khoảng cách giữa hai thuyền là AB  BI  AI  814,9  452,9  362m
Bài 61. Lúc 6h45 phút sáng bạn Nam đi xe đạp điện từ nhà tới trường với vận tốc trung bình là 15
km/h bạn đi theo con đường từ A  B  C  D  E  G  H (như trong hình). Nếu có 1
con đường thẳng từ A  H và đi theo con đường đó với vận tốc trung bình 15 km/h, bạn Nam
sẽ tới trường lúc mấy giờ? Trường học H 500m E 400m G 300m C 600m D 700m 1000m A Nhà B Lời giải
Gọi O  AB  HG . Ta có: AO  1000  600  400  2000 m, HO  500  300  700  1500 m.
Áp dụng định lí Pytago trong tam giác vuông AOH có: 2 2 2 2
AH  AO  HO  2000 1500  2500 m = 2,5 km . s 2,5 1
Thời gian đi từ nhà đến trường của bạn An là: t    h = 10 p. v 15 6
Vậy thời gian bạn An đến trường lúc 6h55 phút.
Bài 62. Hai ngư dân đứng ở một bên bờ sông cách nhau 50 m cùng nhìn thấy một cù lao trên sông với
các góc nâng lần lượt là 30 và 40. Tính khoảng cách d từ bờ sông đến cù lao.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 55
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế Lời giải
Đặt: AH  x; BH  y . Theo đề ta có: x tan 30   y  x 3 y x     x    y   x    x  50 tan 40 tan 40 50 tan 40 50 3 tan 40  x   17,1 50  y 1 3 tan 40
Vậy khoảng cách d từ bờ sông đến cù lao là: 17,1 m.
Bài 63. Một người đi xe máy lên dốc có độ nghiêng 5 so với phương ngang với vận tốc trung bình lên
dốc là 18 km/h. Hỏi người đó mất bao lâu để lên tới đỉnh dốc? Biết đỉnh dốc cách mặt đất 18 m. Lời giải
Giả sử BC là độ dài của dốc nghiêng 5 so với phương ngang. Khi đó độ cao của dốc là AB . AB AB 18 Trong A
 BC vuông tại A , ta có: sin 5   BC    206,53. BC sin 5 sin 5 Ta có:18 km / h = 5 m / s .
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 56
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế s 206,5
Thời gian người đó lên dốc là: t    41,31 s . v 5
Bài 64. Từ vị trí xuất phát A , hai xe cùng một lúc đi thẳng theo hai hướng khác nhau, tạo một góc
A  70. Xe thứ nhất đi với vận tốc 40 km/h và xe thứ hai đi với vận tốc 50 km/h. Sau 1 giờ 30
phút, hai xe cách nhau bao nhiêu km? (làm tròn đến 2 chữ số thập phân). Lời giải
Giả sử B và C là hai vị trí của 2 xe sau 1 giờ 30 phút.
Quãng đường xe A đi được là AB  v .t  40.1,5  60 km. A
Quãng đường xe B đi được là AC  v .t  50.1,5  75 km. B Kẻ CH  AB . Khi đó A
 CH vuông tại H , ta có: CH sin A 
 CH  AC.sin 70  70,48 AC AH cos A 
 AH  AC.cos70  25,65 AC
Ta có: AB  AH  HB  60  25, 65  HB  HB  34,35
Áp dụng định lí Pytago trong tam giác vuông BHC có: BC  BH  CH   2  2 2 2 34,35 70, 48  78, 41
Vậy sau hai xe cách nhau 78, 41 km.
Bài 65. Một máy kéo nông nghiệp có bánh xe sau to hơn bánh xe trước. Bánh xe sau có đường kính
124 cm và bánh xe trước có đường kính 80 cm. Hỏi khi bánh xe sau lăn được 20 vòng thì xe
di chuyển được bao nhiêu mét (làm tròn một chữ số) và khi đó bánh xe trước lăn được mấy vòng? Lời giải
Chu vi bánh xe sau là: C  2 .
R 3,14  d.3,14  124.3,14  389,36 . 2
Chu vi bánh xe trước là: C  2 .
R 3,14  d.3,14  80.3,14  251, 2 . 1
Khi bánh xe sau lăn được 20 vòng thì quãng đường xe di chuyển được là: 20.389,36  7787, 2 cm.
Số vòng bánh xe trước lăn được là: 7787, 2 : 251, 2  31 vòng.
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 57
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế
Bài 66. Trong hình vẽ dưới đây, hai địa điểm A , B cách nhau 100 km. Một xe ô tô khởi hành từ B đến
A với vận tốc 40 km/h. Cùng lúc đó, một xe đạp điện cũng khởi hành từ A trên đoạn đường
vuông góc với AB với vận tốc 20 km/h. Hỏi sau 90 phút thì hai xe cách nhau bao xa. Lời giải Đổi 90 phút = 1,5 giờ.
Quãng đường BC mà người đi từ B đi được trong 1,5 giờ là: 40.1,5  60 km.
Quãng đường AD mà người đi xe đạp điện đi được trong 1,5 giờ là: 20.1,5  30 km.
Quãng đường AC dài: BA  BC  100  60  40 km.
Áp dụng định lý Pytato trong ADC vuông tại A ta có: 2 2 2 DC  AD  AC 2 2 2  DC  30  40 2  DC  2500  DC  50
Vậy sau 90 phút thì hai xe cách nhau 50 km.
Bài 67. Với số liệu ghi trên hình (biết tứ giác EFHI là hình chữ nhật và A , I , H thẳng hàng). Cây
trong hình cao bao nhiêu mét? (làm tròn kết quả đến chữ số hàng đơn vị). Lời giải
Vì tứ giác EFGH là hình chữ nhật nên
EF  IH  1, 7 m EI  FH  5,5 m
Xét AEI vuông tại I có: AI  EI.tan 
AIE ( Hệ thức lượng trong tam giác vuông)
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 58
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế 0  AI  5,5.tan 50  AI  7m
 AH  AI  IH  7 1,7  8,7 m
Vậy cây trong hình cao 8,7 mét
Bài 68. Một người quan sát đứng cách một tòa nhà khoảng 25 m (điểm A ). Góc nâng từ chỗ anh ta
đứng đến nóc tòa nhà (điểm C ) là 36 .
1) Tính chiều cao tòa nhà (làm tròn đến 0,5 mét)
2) Nếu anh ta đi thêm 5 m nữa, đến vị trí D nằm giữa A và B thì góc nâng từ D đến nóc nhà là
bao nhiêu? (làm tròn đến phút). Lời giải
1) Chiều cao của tòa nhà chính là độ dài đoạn thẳng BC
Xét ABC vuông tại B có: BC  A . B tan 
BAC ( Hệ thức lượng trong tam giác vuông) 0  BC  25.tan 36  BC  18, 2m
Vậy chiều cao của tòa nhà là 18, 2m 2) C 36° A B D 25m
Nếu anh ta đi thêm 5 m nữa đến vị trí D thì AD  5 m
 DB  AB  AD  25  5  20 m
Ta có góc nâng từ D đến nóc nhà là  CDB .
Xét DBC vuông tại B có :
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 59
Sản phẩm của nhóm: TOÁN TIỂU HỌC-THCS-THPT- VIỆT NAM Chuyên Đề Toán Thực Tế  BC 18,2 tan CDB    0,91 DB 20
( Hệ thức lượng trong tam giác vuông)   0 ' CDB  42 18
Vậy góc nâng từ D đến nóc nhà là 0 ' 42 18
Bài 69. Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất,cọc cao 2 m và đặt xa cây 15
m. Sau khi người ấy lùi ra xa cách cọc 0,8 m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên
một đoạn đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1, 6 m? Lời giải D F E G 2m H 1.6m A C 0,8m B 15m
Giả sử cây có độ cao CD , cọc ở vị trí B có độ dài FB  2 m, cọc cách cây một đoạn BC  15 m.
Vị trí người đứng ở A cách cọc một đoạn AB  0,8 m.
Khoảng cách từ chân đến mắt người đó là AE  1, 6 m.
Ta có tứ giác AEGC là hình chữ nhật nên
AE  GC  1, 6 m ; AC  EG  AB  BC  0,8 15  15,8 m
Ta có tứ giác AEHB là hình chữ nhật nên:
AE  HB  1,6 m; EH  AB  0,8 m
Ta có FH  FB  HB  2 1,6  0, 4 m FH Xét E  FH vuông tại H có:  0, 4 1 tan FEH  
 ( Hệ thức lượng trong tam giác vuông) EH 0,8 2
Xét EGD vuông tại G có: DG  EG.tan 
FEH ( Hệ thức lượng trong tam giác vuông) 1  DG 15,8.  7,9m 2
 DC  DG  GC  7,9 1,6  9,5m Vậy cây cao 9,5m
Sản phẩm của nhóm: TOÁN THCS VIỆT NAM Trang 60