Top 7 chuyên đề đạo hàm

Tài liệu gồm 75 trang hướng dẫn phương pháp giải 7 chuyên đề đạo hàm thường gặp trong chương trình Đại số và Giải tích 11 chương 5. 

117 59 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 9: Đạo hàm (KNTT)

Môn: Toán 11

Thông tin:

75 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
CHUYÊN ĐỀ 1
TÌM SỐ GIA
Phương pháp:
Để tính số gia của hàm số
()y f x
tại điểm
0
x
tương ứng với số gia
x
cho trước ta áp dụng
công thức tính sau:
00
y
f
x x f x
x
gọi là số gia của đối số tại điểm
0
x
và
0
x x x
.
y
gọi là số gia của hàm số tương ứng và
00
y
f
x x f x
BÀI TẬP MẪU
Bài 1. Tìm số gia của hàm số
, tương ứng với sự biến thiên của đối số từ
0
2x
đến
0
5xx
Hướng dẫn
Số gia của hàm số là
22
00
5
2 5 5 2 2 18y f x x f x f f
Bài 2. Tìm số gia của hàm số
2
– 3 4y x x
tại điểm
0
2x
ứng với số gia
x
, biết
4x
Hướng dẫn
Vì
0
0
4
6
2
x
xx
x
Khi đó
22
00
6
2 6 3.6 4 2 3.2 4y f x x f x f f
Bài 3. Tính
y
và
y
x
của hàm số
2
y x x
Hướng dẫn
Ta có:
2
2
2 2 2 2
2
2 . 2 .
2.
21
y f x x f x x x x x x x
x x x x x x x x x x x x
y x x x x
xx
xx



Bài 4. Tìm số gia của hàm số
4
f
x x
khi
0
1x
,
1x
.
Hướng dẫn
Ta có:
y
00
f
x x f x
21ff
44
2 1 15
Bài 5. Số gia của hàm số
3
f
x x x
khi
0
0x
,
1x
.
Hướng dẫn
Ta có:
y
00
f
x x f x
10ff
33
1 1 0 0
2
Bài 6. Tìm số gia của hàm số
3
3
x
fx
theo số gia
x
của đối số
x
tại
0
0x
.
Hướng dẫn
Ta có:
y
00
f
x x f x
0f
x f
33
0
33
x
3
3
x
Bài 7. Số gia của hàm số
2
f
x x x
ứng với
0
x
,
x
là
Hướng dẫn
Ta có:
y
00
f
x x f x
2
2
0 0 0 0
x x x x x x
0
21x
x x
Bài 8. Tìm số gia của hàm số
2
2f
x x
khi
0
0x
,
2x
.
Hướng dẫn
Ta có:
y
00
f
x x f x
20ff
22
2 2 0 2 4
.
Bài 9. Số gia của hàm số
3
1
1
fx
x
khi,
0
1x
,
1x
.
Lời giải
Ta có:
y
00
f
x x f x
10ff
33
1 1 7
2 1 1 1 18

.
Bài 10. Tìm số gia của hàm số
1f x x
theo số gia
x
của đối số
x
tại
0
0x
.
Hướng dẫn
Ta có:
y
00
f
x x f x
0f
x f
1x
.
BÀI TẬP TỰ GIẢI
Bài 11. Tìm số gia của hàm số
2
2 3 5y x x
, tương ứng với sự biến thiên của đối số:
a) Từ
0
1x
đến
0
2xx
b) Từ
0
2x
đến
0
0,9xx
c) Từ
0
1x
đến
1xx
d) Từ
0
2x
đến
2xx
Bài 12. Tính
y
và
y
x
của hàm số sau theo x và
x
:
a)
35yx
b)
2
37yx
c)
2
2 4 1y x x
d)
cos2yx
Bài 13. Tìm số gia của hàm số
2
–1yx
tại điểm
0
1x
ứng với số gia
x
, biết:
a)
1x
b)
–0,1x
Bài 14. Tính
y
và
y
x
của hàm số sau theo x và
x
:
a)
2
23y x x
b)
3
1y x x
c)
3
45y x x
d)
2
5
x
y
x
e)
1
23
x
y
x
f)
2
1
x
y
x
CHUYÊN ĐỀ 2
TÍNH ĐẠO HÀM
Phương pháp:
Có hai cách để tính đạo hàm:
Cách 1: Dùng định nghĩa:
0
' lim
x
f x x f x
y
x

Cách 2: Dùng bảng công thức : ( bảng này thầy đính kèm ở file đầu tiên)
BÀI TẬP MẪU
Bài 1. Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:
1)
35yx
2)
2
41y x x
3)
32
35y x x
4)
23
1
x
y
x
5)
2
y x x
6)
c
o
s 2 3yx
Hướng dẫn
Sử dụng định nghĩa:
0
' lim
x
f x x f x
y
x

.
1) Ta có:
0 0 0
3 5 3 5
3
' lim lim lim 3
x x x
f x x f x x x x
x
y
x x x
2) Ta có:
2
2
00
4 1 4 1
' lim lim
xx
x x x x x x
f x x f x
y
xx


2
00
2 . 4.
lim lim 2 4 2 4
xx
x x x x
x x x
x
3) Ta có:
32
32
00
3 5 3 5
' lim lim
xx
x x x x x x
f x x f x
y
xx


3 2 2 3 2 2 3 2
0
3 . 3 . 3 6 . 3 5 3 5
lim
x
x x x x x x x x x x x x
x

2 2 3 2
2 2 2
00
3 . 3 . 6 . 3
lim lim 3 3 . 6 3 3 6
xx
x x x x x x x x
x x x x x x x x
x
4) Ta có:
00
23
23
11
' lim lim
xx
xx
x
f x x f x x x x
y
xx


00
2 2 3 1 2 3 1
2 2 3 2 3
11
11
lim lim
xx
x x x x x x
x x x
x x x
x x x
xx


22
0
2 2 2 . 2. 3 3 2 2 . 2 3 3. 3
lim
11
x
x x x x x x x x x x x x
x x x x

2
00
5. 5 5
lim lim
1 1 1 1
1
xx
x
x x x x x x x
x
5) Ta có:
2
2
00
' lim lim
xx
x x x x x x
f x x f x
y
xx


2 2 2
0
2.
lim
x
x x x x x x x x
x

2 2 2
0
2 2 2
2.
lim
2.
x
x x x x x x x x
x x x x x x x x x

2
0
2 2 2
2.
lim
2.
x
x x x x
x x x x x x x x x

2
0
2 2 2
2 1 2 1
lim
2
2.
x
x x x
xx
x x x x x x x x


6) Ta có:
00
cos 2 3 cos 2 3
' lim lim
xx
x x x
f x x f x
y
xx




00
2sin 2 3 .sin sin
lim lim . 2sin 2 3 2sin 2 3
xx
x x x x
x x x
xx



Bài 2. Sử dụng công thức, tính đạo hàm của các hàm số sau:
1)
35yx
2)
2
41y x x
3)
32
35y x x
4)
23
1
x
y
x
5)
2
y x x
6)
c
o
s 2 3yx
Hướng dẫn
Các em tra bảng công thức để tính
1) Ta có:
3
5 ' 3 5 3 5 3 0 3y x y x x
2) Ta có:
2 2 2
4 1 4 1 4 1 2 4 0 2 4y x x y x x x x x x


3) Ta có:
3 2 3 2 2 2
3 5 3 5 3 6 0 3 6y x x y x x x x x x
.
4) (Sử dụng công thức
2
..u u v u v
vv




Ta có:
2 2 2
2 3 . 1 2 3 . 1 2. 1 2 3 .1
2 3 5
1
1 1 1
x x x x x x
x
yy
x
x x x


5) (Sử dụng công thức
2
u
u
u
)
Ta có:
2
2
22
21
'
22
xx
x
y x x y
x x x x

6) (Sử dụng công thức
c
os .sinu u u

)
c
os 2 3 2 3 .sin 2 3 2.sin 2 3y x y x x x
Bài 3. Sử dụng công thức, tính đạo hàm của các hàm số sau:
42
11y x x x
Hướng dẫn
Sử dụng công thức
.
. .u v u v u v


4 2 4 2 4 2
3 2 4 5 4 3
1 1 1 . 1 1 . 1
4 . 1 1 . 2 1 6 5 4 2 1
y x x x y x x x x x x
x x x x x x x x x

Bài 4. Tính đạo hàm các hàm số sau:
a)
32
3 2 1y x x x
d)
42
3
21
2
y x x
b)
3
31y x x
e)
21
3
x
y
x
c)
4
2
1
4
x
yx
f)
2
22
1
xx
y
x

Hướng dẫn
a) Ta có:
32
3 1 3 6 2y x x x x
b) Ta có:
32
3 1 3 3y x x x
c) Ta có:
4
23
12
4
x
y x x x



d) Ta có:
4 2 3
3
2 1 8 3
2
y x x x x



e) Ta có:
22
(2 1) ( 3) ( 3) (2 1) 7
( 3) ( 3)
x x x x
y
xx



f) Ta có:
22
2
( 2 2) ( 1) ( 2 2)( 1)
( 1)
x x x x x x
y
x

22
2
2
(2 2)( 1) ( 2 2) 2 4
( 1)
1
x x x x x x
x
x

.
Bài 5. Tìm đạo hàm của các hàm số sau :
1)

2
2 2020
3
x
y x x
với
0x
. 2)
2
1
6yx
x

với
0x
;
Hướng dẫn
1)


22
2 2020 2 2020 4 3 4
3 3 2 3 2 3
x x x x
x x x x x x x
.
2)
23
1 3 2
6 x
xx
x



.
TÍNH ĐẠO HÀM HÀM HỢP
Phương pháp:
Ta sử dụng định lý sau:
Nếu hàm số
u
g x
có đạo hàm tại
x
là
x
u
và hàm số
y
f u
có đạo hàm tại
u
là
u
y
thì
hàm hợp
y
f g x
có đạo hàm tại
x
là
.
x u x
y y u
.
Từ đó, ta có các công thức đạo hàm của hàm hợp thường gặp: với
u
u x
1
..

nn
u n u u n
2
u
u
u
2
1




u
uu
BÀI TẬP MẪU
Bài 1. Sử dụng công thức, tính đạo hàm hàm hợp của các hàm số sau:
1)
2016
2
23y x x
2)
4
5
23
y
x
3)
2
7
y
x x
4)
5
2
1
1
y
xx

Hướng dẫn
1) Sử dụng công thức:
1
..u u u

Ta có:
2016
2
23y x x
2015 2015
2 2 2
3
2016. 2 3 . 2 3 2016. 4 . 2 3
2
y x x x x x x x
x



2) Chú ý bài này các em phải chuyển đổi:
1
11
..u u u
uu





.
4
4
5
5. 2 3
23
yx
x
4 4 1
' 5. 2 3 5. 4 . 2 3 . 2 3y x x x



55
1 20
20.2. . 2 3 . 2 3
2
xx
xx

3) Sử dụng công thức
1
..u u u

2
7 7 7 6 7
2. . 2 7 1 .y x x y x x x x x x x
4) Sử dụng công thức
1
11
..u u u
uu





5
2
5
2
1
1
1
y x x
xx

66
2 2 2
5. 1 . 1 5 2 1 . 1y x x x x x x x

Bài 2. Tính đạo hàm của các hàm số sau:
a)
2
7
y
x x
. b)
5
3
1yx
. c)
3
2
5
4




yx
x
.
Hướng dẫn
a) Ta có:
7 7 7 6
2 . 2 7 1
y x x x x x x x
.
b) Ta có:
44
3332
5 1 1 15 1
y x x x x
.
c) Ta có:
22
2 2 3 2
5 5 10 5
3 4 4 3 4 4
y x x x
x x x x
.
Bài 3. Tính đạo hàm của các hàm số sau:
a)
2
12 y x x
. b)
32
32 y x x
.
Hướng dẫn
a) Ta có:
2
22
12
1
2 1 2 1 2


xx
x
y
x x x x
.
b) Ta có:


32
2
3 2 3 2
32
36
2 3 2 2 3 2
xx
xx
y
x x x x
.
Bài 4. Tính đạo hàm của các hàm số sau:
a)
2
3
25
y
x
. b)
5
2
1
1

y
xx
.
Hướng dẫn
a) Ta có:
2
4 4 3
3 2 5
12 2 5
12
2 5 2 5 2 5


x
x
y
x x x
.
b) Ta có:
5
4
2
22
2 10 6
5
22
2
1
5 1 . 1
5 2 1
11
1
xx
x x x x
x
y
x x x x
xx


.
Bài 5. Tính đạo hàm của các hàm số sau:
a)
3
21
1
x
y
x



. b)
4
5
2
5
4 1 7 3 y x x x
.
Hướng dẫn
a) Ta có:
2
22
24
9 2 1
2 1 2 1 2 1 3
33
1 1 1
11

x
x x x
y
x x x
xx
.
b) Ta có:
44
55
22
5 4 1 7 3 7 3 5 4 1





y x x x x x x
.
34
54
22
4
5 4 1 10 4 7 3 5 7 3 .7. 5 4 1
y x x x x x x x
.
3
4
22
5 4 1 7 3 4 10 4 7 3 35 5 4 1


y x x x x x x x
.
3
4
22
5
4 1 7 3 455 132 83
y x x x x x
.
Bài 6. Tính đạo hàm của các hàm số sau:
a)
22
x
y
ax
với
a
là tham số. b)
3
2yx
.
Hướng dẫn
a) Ta có:
2
22
2
22
22
3
22


x
ax
a
ax
y
ax
ax
.
b) Ta có:
3
2
33
2
32
32
2
2 2 2 2


x
x
x
y
xx
.
Bài 7. Cho hàm số
2
4
x
y
x
, tính
0y
.
Hướng dẫn
Ta có:
2
2
23
22
4
4
4
44



x
xx
x
y
xx
. Suy ra
1
0
2
y
.
Bài 8. Cho hàm số
2
32
3 2 1
2 3 2 1


xx
y
xx
, tính
0y
.
Hướng dẫn
Ta có:
2 3 2 2 3 2
2
32
3 2 1 .2 3 2 1 3 2 1 . 2 3 2 1
2 3 2 1

x x x x x x x x
y
xx
2
3 2 2
32
2
32
94
6 2 2 3 2 1 3 2 1
3 2 1
2 3 2 1


xx
x x x x x
xx
y
xx
.
3 2 2 2
2
3 2 3 2 3 2
12 4 3 2 1 9 4 3 2 1
9 8 4
4 3 2 1 3 2 1 4 3 2 1
x x x x x x x
xx
y
x x x x x x

.
Suy ra:
4
01
4
y
.
Bài 9. Cho hàm số
4
3
2
21
31

xx
y
x
, tính
1y
.
Hướng dẫn
Ta có:
34
3 2 2 3
2
2
3
4 2 1 3 2 3 1 2 1
31
31
x
x x x x x x
x
y
x
.
34
3 2 2 3
22
4 2 1 3 2 3 1 3 2 1
3 1 3 1

x x x x x x x
y
xx
.
3
3 2 2 3
22
2 1 4 3 2 3 1 3 2 1
3 1 3 1



x x x x x x x
y
xx
. Suy ra
10
y
.
BÀI TẬP TỰ GIẢI
Bài 10. Tính đạo hàm của các hàm số sau bằng định nghĩa:
1)
2
61y x x
2)
2
y x x
3)
4
4
x
y
x
4)
42
23y x x x
5)
5yx
6)
sin
2 4yx
7)
c
os 4 2018yx
8)
ta
n 5 2yx
9)
1
1
y
x
Bài 11. Tính đạo hàm của các hàm số sau:
a)
7 4 2
3 4 4 4y x x x x
b)
4
3
2 10 25y x x
x
c)
22
1 2 3 1y x x x x
d)
2
1 4 3y x x
e)
31
45
x
y
x
f)
2
2
2 3 7
23
xx
y
xx


Bài 12. Tính đạo hàm của các hàm số sau:
a)
21 23
2 3 4y x x
b)
32
4 3 2y x x
Bài 13. Tính đạo hàm của mỗi hàm số sau (
a
là hằng số):
a)
4 3 2 3
1 1 1
4 3 2
y x x x x a
b)
25
1
( 1)
y
xx

c)
52
3 (8 3 )y x x
d)
( 1)( 2)( 3)y x x x
e)
2
2
1
x
y
x
f)
2
53
1
x
y
xx

g)
1
y
xx
h)
2
1x
y
x
i)
2
25y x x
j)
2
1y x x x
k)
1
1
x
y
x
l)
22
x
y
ax
Bài 14. Tính đạo hàm của các hàm số sau:
a)
32
5
32
xx
yx
b)
2 3 4
2 4 5 6
7
y
x x x x
c)
2
3 6 7
4
xx
y
x

d)
2
31y x x
x



e)
1
1
x
y
x
f)
2
2
75
3
xx
y
xx
g)
2
1x
y
x
h)
32
2
y
x x
i)
2
22
1
xx
y
x

j)
2
53
1
x
y
xx

Bài 15. Tính đạo hàm của các hàm số sau:
a)
5
2
41y
x x
b)
2
2 3 1
23
xx
y
x

c)
2
2
61
1
xx
y
xx

d)
2
3
21
xx
y
x

e)
1
1
x
y
x
f)
2
12
x
y
x
g)
2
2
1
1
xx
y
xx


h)
2
1
x
y
x
i)
2
11y x x x
CHUYÊN ĐỀ 3
TÍNH ĐẠO HÀM CỦA HÀM SỐ TẠI Xo
Phương pháp:
Cách 1: Sử dụng định nghĩa tính đạo hàm tại là:
0
0
0
0
lim
xx
f x f x
yx
xx
Cách 2: Các em sử dụng công thức tính đạo hàm rồi thay vào.
BÀI TẬP MẪU
Bài 1. Tính đạo hàm của hàm số
2
2y x x
tại
0
5x
.
Hướng dẫn
Cách 1: Sử dụng định nghĩa:
22
55
2 5 2.5
5
5 lim lim
55
xx
xx
f x f
y
xx



2
55
57
2 35
lim lim 12
55
xx
xx
xx
xx




Cách 2: Sử dụng công thức tính đạo hàm rồi thay số:
Ta có:
22
2 2 2 2y x x y x x x
Do đó
5
2.
5 2 12y
.
Bài 2. Tính đạo hàm của hàm số
0
sin 2 30yx
tại
0
0
60x
.
Hướng dẫn
Cách 1: Sử dụng định nghĩa:
0
00
0
0
60
sin 2 30 sin90
60 lim
60
x
x
y
x

00
0 0 0
0 0 0
00
60 60
2cos 30 .sin 60 sin 60
lim lim .2cos 30 2cos 60 30 0
60 60
xx
x x x
x
xx


Cách 2: Sử dụng công thức tính đạo hàm rồi thay số:
Ta có:
0 0 0 0
sin 2 30 2 30 .cos 2 30 2.cos 2 30y x y x x x
Do đó
0 0 0
60 2cos 60 30 0y
.
Bài 3. Tính đạo hàm (bằng định nghĩa) của mỗi hàm số sau tại các điểm đã chỉ ra:
a)
2
y x x
tại
0
1x
b)
yx
tại
0
1x
c)
2
1
1
y
x
tại
0
0x
d)
1
1
y
x
tại
0
2x
e)
2
3yx
tại
0
1x
Hướng dẫn
a) Ta có:
1f
0
lim
x
y
x

00
0
lim
x
f x x f x
x

0
11
lim
x
f x f
x

2
2
0
1 1 1 1
lim
x
xx
x

0
l
im 1 1
x
x

b) Ta có:
1f
0
lim
x
y
x

00
0
lim
x
f x x f x
x

0
11
lim
x
f x f
x

0
11
lim
x
x
x

0
11
lim
11
x
x
xx

0
11
lim
2
11
x
x


c) Ta có:
0f
0
lim
x
y
x

00
0
lim
x
f x x f x
x

0
00
lim
x
f x f
x

d) Ta có:
2f
0
lim
x
y
x

00
0
lim
x
f x x f x
x

0
22
lim
x
f x f
x

0
11
2 1 2 1
lim
x
x
x

0
lim
3. 3 .
x
x
xx


0
11
lim
3. 3 9
x
x




e) Ta có:
1f
0
lim
x
y
x

00
0
lim
x
f x x f x
x

0
11
lim
x
f x f
x

2
2
0
1 3 1 3
lim
x
x
x

2
0
2 4 2
lim
x
xx
x

2
0
2
2
lim
. 2 4 2
x
xx
x x x




2
0
21
lim
2
2 4 2
x
x
xx



Bài 4. Tính đạo hàm của hàm số :
a)
2
1
x
y
x
tại
1x
. b)
2
3 ( 1)y x x
x




tại
1x
;
Hướng dẫn
a)




2
2 . 1 2 1
2
1
1
x x x x
x
x
x
2 2 2
1
. 1 2
1 2 4 1 4
2
1 2 1 2 1
xx
x x x x x
x
x x x x x
.
Vậy đạo hàm của hàm số tại
1x
là :
1
1
2
y
.
b)
2 2 2
3 1 3 . 1 3 1x x x x x x
x x x



2
1 2 1
3 . 1 3
2
xx
xx
x
Vậy đạo hàm của hàm số tại
1x
là :
5
1
2
y
.
BÀI TẬP TỰ GIẢI
Bài 5. Tính đạo hàm của hàm số
2
24y x x
tại
0
2x
Bài 6. Cho hàm số
2
21y f x x
a) Tìm đạo hàm của hàm số tại
0
2x
b) Suy ra giá trị
3 (2) 5 (2 3)ff

Bài 7. Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau tại điểm x
0
:
a)
21yx
tại
0
2x
b)
2
y x x
tại
0
1x
c)
1
1
x
y
x
tại
0
0x
d)
27yx
tại
0
1x
Bài 8. Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau (a là hằng số):
a)
3y ax
b)
2
1
2
y ax
c)
1
21
y
x
với
1
2
x
d)
3yx
với
3x
Bài 9. Tính đạo hàm của hàm số tại điểm
0
x
được chỉ ra bằng cách sử dụng công thức tính đạo
hàm rồi thay
0
x
vào :
1)
53
2 3 5y x x x
tại
0
2x
2)
2
1
1
x
y
x
tại
0
10x
3)
2
41y x x
tại
0
5x
4)
sin 2
4
yx




tại
0
6
x
5)
2
5
x
y
x
tại
0
2x 
6)
24
32y x x x
tại
0
3x 
CHUYÊN ĐỀ 4
ĐẠO HÀM CỦA HÀM LƯỢNG GIÁC
Phương pháp:
Sử dụng công thức tính đạo hàm của hàm lượng giác:
Đạo hàm
Hàm hợp
(sin )' cosxx
;
(cos )' sinxx
2
1
(tan )'
cos
x
x
;
2
1
(cot )'
sin
x
x

2
1
arcsin '
1
x
x
2
1
arccos '
1
x
x

2
1
arctan '
1
x
x
(sin )' '.cosu u u
(cos )' 'sinu u u
;
2
'
tan '
cos
u
u
u
2
'
cot '
sin
u
u
u

1
sin .sin . sin
nn
u n u u
1
cos .cos . cos
nn
u n u u
1
tan .tan . tan
nn
u n u u
1
t . t . t
nn
co u n co u co u
I. Sử dụng công thức để tính đạo hàm hàm lượng giác:
BÀI TẬP MẪU
Bài 1. Tính đạo hàm của hàm số :
1)
sin2 cos
3
x
yx
. 2)
2
sin5 1yx
3)
sin .cos4y x x
4)
22
2tan 5coty x x
Hướng dẫn
1) Ta có:
1
2.cos2 sin
33
x
yx

2) Ta có:
2 s
in5 1 sin5 1 10cos5 sin5 1y x x x x
.
3) Ta có:
sin
.cos4 sin . cos4 cos .cos4 4sin .sin4y x x x x x x x x

.
Ngoài ra các em có thể tách
1
sin .cos4 sin5 sin3
2
y x x x x
sau đó tính đạo hàm.
4) Ta có:
3 2 2
2sin 5
'
cos sin
xx
y
xx

Bài 2. Tính đạo hàm của hàm số :
1)
sin3yx
2)
5sin 3cosy x x
3)
cos 2 1yx
4)
sin( ) cos
36
y x x




5)
4cos2 5sin(2 3)y x x
6)
3sin cos 2019y x x x
7)
2
.cos3 2 sin3y x x x x
8)
22
3 sin 3 cos 2 1
4
y x x



9)
tan2yx
10)
c
ot 3 1yx
11)
1
tan
2
x
y
12)
2
cot 1yx
13)
tan
3
x
y
14)
3cos cot2y x x
15)
tan5 cot4y x x
16)
2
t
an 2 1y x x
17)
35
11
tan tan tan
35
y x x x
18)
2
tan(2 1) cosy x x x
Hướng dẫn
1) Ta có
sin3 3cos3y x y x
2) Ta có
5sin 3cos 5cos 3siny x x y x x
3) Ta có
cos 2 1yx
sin 2 1
21
x
y
x
4) Ta có
cos sin
36
y x x

.
5) Ta có
8
sin2 10cos 2 3y x x
.
6) Ta có :
3cos sin 2019y x x
7) Ta có :
22
2 cos3 3 sin3 2sin3 6 cos3 8 cos3 2 3 sin3y x x x x x x x x x x x
8) Ta có:
22
22
22
3.2sin 3 cos 3 3sin2 3
22
4 4 4
sin 2 1. sin 2 1
2 1 2 1
2 3 sin 3 2 3 sin 3
44
x x x
xx
y x x
xx
xx


.
9) Ta có:
2
2
' tan2 '
cos 2
yx
x

.
10) Ta có:
'
2
3
' cot 3 1
sin 3 1
yx
x


.
11) Ta có
'
'
22
1
11
2
' tan
11
2
cos 2cos
22
x
x
y
xx







12) Ta có:
'
2
'
2
2
2 2 2 2 2 2 2
1
1
' cot 1
sin 1 sin 1 1.sin 1
x
x
x
x
yx
x x x x
13) Ta có:
'
2
1
' tan
3
3cos
3
x
y
x




.
14) Ta có:
'
2
2
' 3cos cot2 3sin
sin 2
y x x x
x
.
15) Ta có:
'
22
54
' tan5 cot 4
cos 5 sin 4
y x x
xx
.
16) Ta có:
'
2
2
22
21
' tan 2 1
cos 2 1
xx
y x x
xx


2 2 2 2
1
2
21
cos 2 1 cos 2 1
x
xx
x
x x x x x

17) Ta có:
6
' 1 tanyx
18) Ta có:
22
22
22
' cos 2 sin cos cos sin2
cos (2 1) cos (2 1)
y x x x x x x x
xx

BÀI TẬP TỰ GIẢI
Bài 1. Tính đạo hàm của các hàm số sau:
a)
2
2
2sin sin2 sin 2sin sin
2
x
y x x x
x
b)
22
sin 2 3 1y x x
c)
2
sin 4y x x
Bài 2. Tính đạo hàm của các hàm số sau:
a)
cos
2 sin
x
y x x
x

b)
3cos
21
x
y
x
c)
2
2cos
sin
xx
y
x
d)
2cos sin
3sin cos
xx
y
xx
e)
tan
sin 2
x
y
x
f)
cot
21
x
y
x
g)
2
sin 3 2y x x
h)
cos 2 1yx
i)
2sin3 cos5y x x
j)
cos2yx
k)
2
1
tan
x
y
x
l)
2
cot 1yx
m)
3
tan cot 2y x x
n)
1 2tanyx
o)
sin
sin
xx
y
xx

p)
2
sin
1 t 2
x
y
an x
q)
tan(sin )yx
r)
2
cot 1y x x
s)
2
cos 2
4
yx

t)
sin3y x x
u)
22
tan tany x x
v)
2
2 cos 2 siny x x x x
Bài 3. Tính đạo hàm của các hàm số sau:
a)
2
sin 1yx
b)
2
sin
cos3yx
c)
2
cos 1 siny x x
d)
c
os cos cosyx


e)
2
1
cos
1
x
y
x




f)
22
sin tan
1 cot 1 tan
xx
y
xx


g)
sin cos
x
y
xx
h)
2
sin
cos
x
y
x
i)
2
1 cosyx
Bài 4. Tính đạo hàm của các hàm số sau:
a)
sin
1 cos
x
y
x
b)
2
1 cos
2
x
y 
c)
20
2
2
1 tan
1 tan
x
y
x



d)
1 cos
1 cos
x
y
x
e)
sin cosy x x x
f)
32
3tan tan3 tan tany x x x x
g)
2
cot 1y x x
h)
3
cot 2 3cot2y x x
i)
sin cos
sin cos
xx
y
xx
j)
22
22
sin 2 4cos 4
sin 2 4cos
xx
y
xx

Bài 5. Tính đạo hàm của mỗi hàm số sau:
a)
5sin 3cosy x x
b)
2
sin( 3 2)y x x
c)
cos 2 1yx
d)
sin3 .cos5y x x
e)
1 2tanyx
f)
tan3 cot3y x x
g)
4sin 3cosy x x
h)
24
4sin 3cosy x x
i)
1 cos
x
y
x
Bài 6. Tính đạo hàm của hàm số sau:
1 1 1 1 1 1
cos
2 2 2 2 2 2
yx
, với
;()0x
II. Tính đạo hàm của hàm lượng giác tại
0
x
Phương pháp:
Tính đạo hàm rồi thay
0
x
vào
BÀI TẬP MẪU
Bài 1. Tính đạo hàm của hàm số
sin 2
cos3
x
y
x
tại
4
x
.
Hướng dẫn
Ta có :
22
sin2 .cos3 sin2 . cos3
2cos2 .cos3 3sin2 .sin3
cos3 cos3
x x x x
x x x x
y
xx


Khi đó :
32
4
y



. Vậy đạo hàm của hàm số đã cho tại
4
x
là
32
.
Bài 2. Tính đạo hàm của hàm số
.cos2y x x
tại
2
x
.
Hướng dẫn
Ta có:
.
cos2 . cos2 cos2 2 .sin2y x x x x x x x

Khi đó :
'
1
2
y




. Vậy đạo hàm của hàm số đã cho tại
4
x
là
1
.
Bài 3. Tính đạo hàm của hàm số
5sin 3cosy x x
tại điểm
2
x
.
Hướng dẫn
Ta có
5
sin 3cos 5. sin 3 cos 5.cos 3siny x x x x x x
.
Suy ra
5.cos 3sin 3
2 2 2
y



.
Bài 4. Tính đạo hàm của hàm số
2sin3 cos5y x x
tại điểm
8
x
.
Hướng dẫn
Ta có
2sin3 cos5 sin8 sin2y x x x x
.
sin
8 sin 2 ' 8cos8 2cos2y x x x x
8cos 8. 2cos 2. 8 2
8 8 8
y
.
Bài 5. Tính đạo hàm của hàm số
2
1
sin
23
yx



tại điểm
3
x
.
Hướng dẫn
Ta có
2
cos
3 3 3 3 3
y








.
Bài 6. Cho hàm số
2
cos 3 sin 2
63
y x x

. Tính
3
y



.
Hướng dẫn
Ta có:
2
3sin 3 2cos 2
63
y x x

.
Vậy
2 5 7
3sin 3. 2cos 2. 3sin 2cos0
3 3 6 3 3 6 2
y
.
Bài 7. Tính đạo hàm của hàm số
2
1
cot
2
f x x
tại điểm
.
2
x
Hướng dẫn
Ta có:
2
2 2 2 2
1
2 sin sin
'fx
x
x
xx
Suy ra:
2
sin
2
2
'
2 2 2
2
f








Bài 8. Tính đạo hàm của hàm số
22
ta
n cotf x x x
tại điểm
.
4
x
Hướng dẫn
Ta có:
2 2 2 2
1 1 2tan 2cot
' 2tan . 2cot .
cos sin cos sin
xx
f x x x
x x x x



Suy ra:
22
2tan 2cot
44
'8
4
cos sin
44
f





Bài 9. Tính đạo hàm của hàm số
cot 1f x x
tại
2
x
.
Hướng dẫn
Ta có:
'
'
2
cot 1
1
' cot 1
2 cot 1 2sin . cot 1
x
f x x
x x x

2
' .cos
3
y x x




Suy ra
2
11
'
22
2sin . cot 1
22
f




Bài 10. Tính đạo hàm của hàm số
3
ta
n cot2f x x x
tại điểm
4
x
.
Hướng dẫn
Ta có:
'
32
22
12
' tan cot2 3.tan .
cos sin 2
f x x x x
xx
Suy ra
2
22
12
' 3.tan . 4
44
cos sin 2.
44
f





Bài 11. Tính đạo hàm của hàm số
tan cotf x x x
tại điểm
4
x
.
Hướng dẫn
Ta có:
22
11
(tan cot )
cos sin
()
2 tan cot 2 tan co
'
t
xx
xx
fx
x x x x


22
2 2 2
sin cos 2cos2
2sin cos tan cot sin 2 tan cot
x x x
x x x x x x x



Suy ra
2
2cos
2
'0
4
sin tan cot
2 4 4
f







BÀI TẬP TỰ GIẢI
Bài 1. Tính đạo hàm của các hàm số sau tại điểm được chỉ ra .
1)
1 sin
1 sin
x
y
x
tại
3
x
2)
cos
sin 1
x
y
x
tại
2
x
3)
2
2 coty x x x
tại
4
x
4)
1 2tanyx
tại
0x
5)
sin3 .cos4y x x
tại
3
4
x
6)
2
2cos sin2 cos
2
x
y x x
tại
5
6
x
7)
23
sin .cosy x x
tại
3
x
8)
3
tan 2
4
yx




tại
4
x
9)
22
sin cos tanyx
tại
4
x
10)
22
cot 1yx
tại
3
x
11)
32
sin 1yx
tại
0x
12)
2
sin
cos3yx
tại
3
x
Bài 2. Cho hàm số
3
yx
và
4 sin
2
x
yx

. Tính tổng
(1) (1)fg

?
III. Chứng minh biểu thức có chứa đạo hàm hàm lượng giác.
Phương pháp:
Tính đạo hàm rồi thay vào biểu thức và biến đổi.
BÀI TẬP MẪU
Bài 1. Chứng minh rằng :
'
0fx
với
6 4 2 2 4 4
( ) cos 2sin .cos 3sin .cos sinf x x x x x x x
.
Hướng dẫn
Cách 1 :
Ta có :
6 4 2 2 4 4
( ) cos 2sin .cos 3sin .cos sinf x x x x x x x
5 3 2 4
6.sin .cos 8.cos .sin .cos 4.sin .sin .cosx x x x x x x x
4 2 3 3
6.cos .sin .cos 12.sin .sin .cos 4.cos .sinx x x x x x x x
5 3 3 5 5 3 3 3
= 6.sin .cos 8sin .cos 4sin .cos 6sin .cos 12sin .cos 4.cos .sinx x x x x x x x x x x x
3 3 3 2 3 3 3 3
4sin .cos 4cos .sin . sin 1 4sin .cos 4sin .cos 0x x x x x x x x x
Cách 2 : Ta có :
4 2 4 2 2
4 2 4 2
4 4 4 2 2 4
2
2 2 2 2 2 2 2 2
sin 1 2cos cos 3sin cos
sin 1 2cos cos 1 2sin
sin cos 2sin cos 2sin cos
cos sin 2sin cos 2sin cos cos sin 1
f x x x x x x
x x x x
x x x x x x
x x x x x x x x
Khi đó :
0fx
Bài 2. Cho hàm số
siny x x
. Chứng minh:
.
2 sin 2cos 0x y y x x x y
Hướng dẫn
Ta có:
s
in .sin . sin sin cosy x x x x x x x x x


.
2
. 2 sin 2cos
.sin 2 sin cos sin 2cos sin
x y y x x x y
x x x x x x x x x x
22
sin 2 cos 2 cos sin 0x x x x x x x x
(đpcm).
Bài 3. Cho hàm số
cot 2yx
. Chứng minh:
2
2 2 0
yy
Hướng dẫn
Ta có:
22
cot2 2 1 cot 2 2 1
y x x y
2
2 2 0
yy
.
Bài 4. Cho hàm số
tanyx
. Chứng minh:
2
10yy
Hướng dẫn
Ta có:
22
tan 1 tan 1y x x y
2
10yy
.
Bài 5. Cho hàm số
sin cos
tan
x x x
y
x
.Chứng minh rằng:
3
'
2
cos
.tan
sin
x
y y x
x
Hướng dẫn
Ta tiến hành rút gọn trước khi tính đạo hàm:
'
22
2
3
2 2 2
sin cos .cos
sin cos 1
.cos sin
tan sin sin
cos cos
cos sin cos sin
sin sin
cos 1 sin
cos cos
sin sin cos
sin sin sin
x x x x
x x x
y x x x
x x x
xx
y x x x x x x
xx
xx
xx
VT x x x x x VP
x x x

Bài 6. Cho hàm số
2
cot 1yx
. Chứng minh rằng:
'4
2 . . 1 0y y x y
.
Hướng dẫn
Ta có:
'
'
2 2 2 2 2
'
2 2 2
cot 1 1 1 cot 1 . 1 1 cot 1
2 cot 1 2 cot 1 2 cot 1
x x x x x
y
x x x
22
24
2
2 2 2 2
1 cot 1
2 cot 1 . .
2 cot 1
1 cot 1 .cot 1 0
xx
VT x x x y
x
x x x x x VP

Bài 7. Cho hàm số
2
2
cos 4 1f x x
. Chứng minh rằng:
'
8,f x x
.
Hướng dẫn
Ta có:
'
'
16sin 4 1 cos 4 1 8sin 8 2
8sin 8 2 8 sin 8 2 8
f x x x x
f x x x
Dấu
""
xảy ra khi:
1
sin 8 2 1 8 2 2
2 16 4 8
1
sin 8 2 1 8 2 2
2 16 4 8
k
x x k x
k
k
x x k x
Bài 8. Cho hàm số
sin cos
.
cos sin
x x x
y
x x x
Chứng minh rằng:
2
' 2 2
sin cos 0y x x x x y
.
Hướng dẫn
Ta có:
sin cos
.
cos sin
x x x
y
x x x
''
'
2
sin cos cos sin sin cos cos sin
cos sin
x x x x x x x x x x x x
y
x x x
Tính
''
'
sin cos cos cos . cos sinx x x x x x x x x x
Tính
''
'
cos sin sin sin sin cosx x x x x x x x x x
2
'
22
sin . cos sin sin cos cos
cos sin cos sin
x x x x x x x x x x
x
y
x x x x x x

Ta có:
2
2
22
' 2 2 2
2
sin cos
sin cos . sin cos . 0
cos sin
cos sin
x x x x
VT y x x x x y x x x x VP
x x x
x x x



Bài 9. Cho hàm số
2
cot 1yx
. Chứng minh rằng:
' 2 2
. 1 . 0y x x x y
.
Hướng dẫn
Ta có:
2
cot 1yx
'
2
'
' 2 2 2 2 2 2 2
22
1
1 cot 1 . 1 1 cot 1 . 1 cot 1
2 1 1
x
x
y x x x x
xx

Ta có:
2 2 2 2 2 2 2 2 2
2
1 cot 1 . 1 .cot 1 cot 1 .cot 1 0
1
x
VT x x x x x x x x x x x
x
Bài 10. Cho hàm số
cosyx
. Chứng minh rằng:
' ' '
2 0 2
3 6 6
f x f x f f x
Hướng dẫn
Ta có:
'
'
cos sinf x x x
''
'
2 2sin sin
3 6 3 6
2
2sin .cos sin 2
3 3 3
25
sin 2 sin 2 cos 2
3 3 6
cos 2 0 cos 2 0 2
6 6 6
VT f x f x x x
x x x
x x x
x x f f x
VP


Bài 11. Cho hàm số
4 4 6 6
3 sin cos 2 sin cosy x x x x
. Chứng minh rằng:
'
0yx
.
Hướng dẫn
Ta tiến hành làm gọn biểu thức trước khi tiến hành lấy đạo hàm
Ta có:
4 4 6 6
3 sin cos 2 sin cosy x x x x
Mà:
2 2 2
4 4 2 2 2 2 2 2 2
3 3 3
6 6 2 2 2 2 2 2 2 2 2
1
sin cos sin cos sin cos 2sin cos 1 sin 2
2
3
sin cos sin cos sin cos 3sin cos sin cos 1 sin 2
4
x x x x x x x x x
x x x x x x x x x x x
22
'
13
3 1 sin 2 2 1 sin 2 1
24
0,
y x x
yx
Bài 12. Cho hàm số
3
sin
1 cos
x
y
x



. Chứng minh rằng:
'
.sin 3 0y x y
Hướng dẫn
Ta có:
3
sin
1 cos
x
y
x



2'
'
''
'
2
2
2
'
3
sin sin
3
1 cos 1 cos
sin 1 cos sin 1 cos
sin 1
1 cos 1 cos
1 cos
sin 1 3sin
3.
1 cos 1 cos
1 cos
xx
y
xx
x x x x
x
Mà
xx
x
xx
y
xx
x










Ta có:
3
2
'
3
3sin sin
.sin 3 0 .sin 3. 0
1 cos
1 cos
xx
y x y x
x
x



Bài 13. Cho hàm số
3
sin
2 1yx
. Chứng minh rằng:
'
s
in 2 1 6 .cos 2 1 0y x y x
Hướng dẫn
Ta có:
3
sin
2 1yx
'
'
' 2 2 2
3sin 2 1 sin 2 1 3sin 2 1 cos 2 1 2 1 6sin 2 1 cos 2 1y x x x x x x x
Ta có:
'
23
sin 2 1 6 cos 2 1
6sin 2 1 cos 2 1 sin 2 1 6sin 2 1 cos 2 1 0
VT y x y x
x x x x x VP
Bài 14. Cho hàm số
2
1
cos
1
x
y
x




. Chứng minh rằng:
4
'
1
. 1 2tan . 0
1
x
y x x y
x




Hướng dẫn
Ta có:
2
1
cos
1
x
y
x




'
'
'
''
'
22
'
22
1 1 1 1 1
2cos cos 2cos sin
1 1 1 1 1
1 1 1 1
11
1
11
1 1 1 1
2cos sin s
11
11
x x x x x
y
x x x x x
x x x x
x
Mà
x
x x x
xx
y
xx
x x x x













1
in 2.
1
x
x




Ta có:
4
'
4
2
2
1
. 1 2tan .
1
1
sin
.1
1
11
sin 2. 2 cos 0
11
1
1
cos
1
x
VT y x x y
x
x
xx
x
xx
VP
xx
x
xx
x












Bài 15. Cho hàm số
4 2 4 2
cos 2cos 3 sin 2sin 3y x x x x
. Chứng minh rằng
'
y
không phụ thuộc
vào x.
Hướng dẫn
Ta tiến hành làm gọn biểu thức trước khi tiến hành lấy đạo hàm
4 2 4 2
6 4 6 4
4 4 6 6
cos 2cos 3 sin 2sin 3
2cos 3cos 2sin 3sin
3 sin cos 2 sin cos 1
y x x x x
x x x x
x x x x
'
0y
. Vậy
'
y
không phụ thuộc vào x.
IV. Giải phương trình – Bất phương trình liên quan đạo hàm của hàm lượng giác
BÀI TẬP MẪU
Bài 1. Giải phương trình
'0fx
biết
3
1 sin 2cos
22
x
f x x



Hướng dẫn
Ta có:
3
1 sin 2cos
22
x
f x x



33
0 cos 2. .sin cos cos
2 2 2 2 2
x x x
f x x x

' 0 cos cos 0 cos cos cos cos
2 2 2
2
24
2
33
2
24
2
x x x
f x x x x
x
xk
k
x
x
xk
xk











Bài 2. Giải phương trình
( ) 0fx
trong cc trưng hợp sau
a)
( ) sin3 3sin 4f x x x
. b)
( ) cos2 2sin 3f x x x
. c)
( ) 3cos sin 1f x x x
.
Hướng dẫn
a)
(
) sin3 3sin 4 3cos3 3cosf x x x f x x x
0
3cos3 3cos 0 cos3 cosf x x x x x
32
42
32
2
k
x
x x k
k
x x k
xk




.
b)
(
) cos2 2sin 3 2sin2 2cosf x x x f x x x
0
2sin2 2cos 0 cos 2sin 1 0f x x x x x
22
cos 0
22
1
66
sin
2
5
22
66
x k x k
x
x k x k k
x
x k x k














c)
31
0 3sin cos 0 sin cos 0 sin 0
2 2 6
f x x x x x x



66
x
k x k k


.
Bài 3. Cho hàm số
( 1)sin cos ( 2) 1y m x m x m x
. Tìm giá trị của m để
0y
có nghiệm?
Hướng dẫn
( 1)cos sin ( 2)y m x m x m
Phương trình
0 ( 1)cos sin ( 2)y m x m x m
Điều kiện phương trình có nghiệm là
2 2 2
a b c
2 2 2 2
1
( 1) ( 2) 2 3 0
3
m
m m m m m
m

.
Bài 4. Cho hàm số
2
cos 2
3
yx




. Khi đó hãy giải phương trình
0y
.
Hướng dẫn
TXĐ :
D
Ta có:
2
2.sin 2
3
yx



Theo giả thiết
2
0 sin 2 0
3
yx



32
k
xk

.
Bài 5. Cho hàm số
sin
32
x
y




. Khi đó hãy tìm nghiệm của phương trình
'0y
.
Hướng dẫn
TXĐ :
D
Ta có:
1
cos
2 3 2
x
y



nên
0 cos 0 2
3 2 3 2 2 3
xx
y k x k k




Bài 6. Cho hàm số
tany x x
. Giải phương trình
0y
.
Hướng dẫn
TXĐ:
\,
2
D k k



Ta có:
2
2
1
1 tan
cos
yx
x
, khi đó
2
0
tan 0 tan 0y x x x k k
Bài 7. Cho hàm số
2
sin .cosy x x
, giải phương trình
2sinyx
.
Hướng dẫn
TXĐ :
D
, ta có
2 2 2 3
sin cos sin cos 2sin cos siny x x x x x x x
Vậy
2 3 2 3
2sin 2sin .cos sin 2sin 2sin 2sin .cos sin 0y x x x x x x x x x
2 3 3
2sin 1 cos sin 0 3sin 0 sin 0x x x x x x k k
.
Bài 8. Cho hàm số
2
2sin cos2y x x x
, giải phương trình
3y

.
Hướng dẫn
TXĐ :
D
Ta có:
4sin cos 2sin2 1 2sin2 2sin2 1 4sin2 1y x x x x x x
3 4sin2 1 3 sin2 1 2 2
24
y x x x k x k k


Bài 9. Cho hàm số
1
sin 1 cosy x x
, giải phương trình
2(cos sin )y x x

.
Hướng dẫn
TXĐ :
D
Ta có:
22
c
os 1 cos sin 1 sin cos sin cos siny x x x x x x x x
, nên
22
2(cos sin ) cos sin cos sin 2(cos sin )y x x x x x x x x
(cos sin )(cos sin ) (cos sin ) 0 (cos sin )(cos sin 1) 0x x x x x x x x x x
sin 0
4
4
2sin . 2 sin 1 0
2
44
1
sin
2
4
2
2
xk
x
x x k
xk
x
xk














Bài 10. Tính đạo hàm của hàm số
sin 2
2
yx




và giải phương trình
0y
.
Hướng dẫn
TXĐ :
D
Ta có
sin 2 cos2 2sin 2
2
y x x y x



. Vậy
0 sin2 0
2
y x x k k
Bài 11. Cho hàm số
2
cot
4
x
y
. Khi đó nghiệm của phương trình
'0y
Hướng dẫn
TXĐ :
\
4 ,D k k
Ta có :
2
2
1 1 1
cot . cot . 1 cot
2 4 2 4 4
sin
4
x x x
y
x








.
Nên
0 cot 0 2 4
4 4 2
xx
y k x k k
Bài 12. Cho hàm số
2
sin2 cos2f x x x
, giải phương trình
2sin2yx
.
Hướng dẫn
TXĐ :
D
Ta có :
4cos2 2sin2y x x

2sin2 4cos2 2sin2 2sin2 sin2 cos2y x x x x x x
2 1 2 cos2 0
4 8 2
tan x x k x k k do x
Bài 13. Tính đạo hàm của hàm số sau:
3
sin
2 1yx
và giải phương trình
6
cos 2 1yx

.
Hướng dẫn
TXĐ :
D
Ta có
2
6
sin 2 1 cos 2 1y x x
. Vậy
6
cos 2 1yx

22
6sin 2 1 cos 2 1 6cos 2 1 cos 2 1 1 sin 2 1 0x x x x x


3
1
cos 2 1 0 cos 2 1 0 2 1
2 2 4 2
x x x k x k k
.
Bài 14. Tính đạo hàm của hàm số sau:
3
sin cosy x x
và giải phương trình
3 3sin2yx

.
Hướng dẫn
TXĐ :
D
Ta có :
2
3 sin cos cos siny x x x x
, suy ra
2
3 3sin 2 3 sin cos cos sin 3 3sin 2y x x x x x x
.
2
22
3 sin cos cos sin 3(sin cos ) (sin cos ) cos sin 1 0x x x x x x x x x x


.
4
sin 0
sin cos 0
4
4
2
1
sin cos 1 0
2
sin
2 sin 1 0
2
4
2
4
xk
x
xk
xx
xk
xx
x
x
xk














Bài 15. Tính đạo hàm của hàm số sau:
sin2 cos2
2sin2 cos2
xx
y
xx
, giải phương trình
6y

.
Hướng dẫn
ĐK :
2sin2 cos2 0xx
.
Ta có
2
2cos2 2sin 2 2sin2 cos2 sin2 cos2 4cos2 2sin2
2sin2 cos2
x x x x x x x x
y
xx
2
6
2sin2 cos2
y
xx
2
2
6
6 6 2sin2 cos2 1
2sin2 cos2
y x x
xx
2 1 1
sin2 cos2
sin 2 sin
2sin2 cos2 1
5 5 5
2sin2 cos2 1 2 1 1
sin 2 sin
sin2 cos2
5 5 5
xx
x
xx
xx
x
xx





22
22
2
22
22
2
xk
xk
xk
xk
k
x k x k
xk
xk






với
12
sin ;cos
55


(Thỏa mãn ĐK)
Bài 16. Cho hàm số
2
sinyx
, giải phương trình
3y
.
Hướng dẫn
TXĐ :
D
Ta có :
2sin cos sin2y x x x

. Khi đó
0 sin2 0 2
2
y x x k x k k
Bài 17. Cho hàm số
cos2 5sinxyx
, giải phương trình
0y
.
Hướng dẫn
TXĐ :
D
Ta có :
2sin2 5cosy x x
.
Nên
0 2sin2 5cos 0 4sin cos 5cos 0y x x x x x
cos 5 4sin 0 cos 0 5 4sin 0
2
x x x do x x k k
.
Bài 18. Cho hàm số
3sin cos 2y x x x
, giải phương trình
0y
.
Hướng dẫn
TXĐ :
D
Ta có :
3cos sin 2y x x
,
khi đó
5
0 3cos sin 2 0 sin 1 2
36
y x x x x k k




Bài 19. Cho hàm số
22
sin 2 2cosy x x
, giải phương trình
0y
.
Hướng dẫn
TXĐ :
D
Ta có :
4sin2 cos2 2sin2y x x x

,
nên
0
2sin2 cos2 sin 2 0 sin2 2cos2 1 0y x x x x x
2
sin 2 0
2
2
1
22
cos2
3
2
3
xk
x
xk
k
xk
x
xk

.
Bài 20. Tìm m để phương trình
0y
có nghiệm biết rằng
cos 2sin 3 5y m x x x
.
Hướng dẫn
TXĐ :
D
Ta có :
sin 2cos 3y m x x
, khi đó
0
sin 2cos 3 1y m x x
Phương trình
0y
có nghiệm khi và chỉ khi (1) có nghiệm khi và chỉ khi :
22
5
4 9 5
5
m
mm
m

.
BÀI TẬP TỰ GIẢI
Bài 1. Giải phương trình
'f x g x
biết
3
sin 2 ; 4cos2 5sin4f x x g x x x
Bài 2. a) Cho
sin2 2cosy x x
. Hãy giải phương trình
0y
.
b) Cho
3sin2 4cos 12y x x x
. Hãy giải phương trình
2y
.
Bài 3. Giải phương trình
0y
trong mỗi trưng hợp sau:
a)
sin2 2cosy x x
b)
3sin2 4cos2 10y x x x
c)
2
cos siny x x
d)
tan coty x x
e)
3cos 4sin 5y x x x
f)
2
1 sin( ) 2cos
2
x
yx



g)
1
sin2 sin 3
2
y x x
h)
sin2 2cosy x x
i)
2
cos siny x x
j)
tan coty x x
k)
2 cos 3siny x x x
l)
3sin2 4cos2 10y x x x
CHUYÊN ĐỀ 5
ĐẠO HÀM HÀM KÉP – ĐIỀU KIỆN TỒN TẠI ĐẠO HÀM
I. Tính đạo hàm của hàm số
10
20
khi
khi
f x x x
fx
f x x x
Phương pháp:
Bước 1: Kiểm tra hàm số có liên tục tại
0
x
hay không:
0
0
li
m
xx
f x f x
Bước 2: Sử dụng công thức tính đạo hàm
0
0
0
0
' lim
xx
f x f x
fx
xx
BÀI TẬP MẪU
Bài 1. Tính đạo hàm của hàm số
24
khi 0
1
khi 0
4
x
x
x
fx
x

tại
0x
Hướng dẫn
Ta có:
0 0 0
2 4 1
lim lim lim 0
4
24
x x x
xx
f x f
x
xx


Suy ra hàm số liên tục tại
0x
.
Ta có:
2
2
0 0 0
2 4 1
0
1
4
' 0 lim lim lim
64
2 8 4 4
x x x
x
f x f
x
x
f
xx
x x x

Bài 2. Cho hàm số
11
khi 0
khi 0
x
x
fx
x
ax

. Tìm a để hàm số có đạo hàm tại
0x
và
tính đạo hàm tại
0x
.
Hướng dẫn
Ta có:
0 0 0
1 1 1
lim lim lim
2
11
x x x
xx
fx
x
xx

Để hàm số có đạo hàm tại
0x
thì hàm số phải liên tục tại
0x
Suy ra
0
1
lim 0
2
x
f x f a
Đạo hàm của hàm số tại
0x
là:
2
2
0 0 0
1 1 1
0
1
2
' 0 lim lim lim
08
2 2 2 1
x x x
x
f x f
x
x
f
xx
x x x

Bài 3. Tính đạo hàm của hàm số
32
11
khi 0
()
0 khi 0
xx
x
fx
x
x
tại
0x
.
Hướng dẫn
Ta có :
(0) 0f
, do đó:
32
2
32
0 0 0
( ) (0) 1 1 1 1
lim lim lim
2
11
x x x
f x f x x x
xx
xx
Vậy
1
(0) .
2
f
II. Tính đạo hàm của hàm số
10
20
khi
khi
f x x x
fx
f x x x
Phương pháp:
Bước 1: Kiểm tra hàm số có liên tục tại
0
x
hay không:
00
0
lim lim
x x x x
f x f x f x



Bước 2:
Xét
0
xx
. Sử dụng công thức tính đạo hàm
0
0
0
0
' lim
xx
f x f x
fx
xx
Xét
0
xx
. Sử dụng công thức tính đạo hàm
0
0
0
0
' lim
xx
f x f x
fx
xx
BÀI TẬP MẪU
Bài 1. Cho hàm số
2
khi 1
khi 1
xx
fx
ax b x

. Tìm
,ab
để hàm số có đạo hàm tại
1x
Hướng dẫn
Hàm số có đạo hàm tại
1x
thì hàm số phải liên tục tại
1x
.
Suy ra
11
l
im lim 1 1
xx
f x f x f a b


Hàm số có đạo hàm tại
1x
thì
'
1 ' 1ff

.
Ta có:
0
0
11
' 1 lim 2
11
' 1 lim
x
x
f x f
f
x
f x f
fa
x




Để
'
1 ' 1 2 1f f a b

Bài 2. Chứng minh rằng: Hàm số
1
x
y
x
liên tục tại
0x
nhưng không có đạo hàm tại
0x
Hướng dẫn
a) Ta có:
00
0 0 0 0
lim lim 0
1
lim lim 0 lim lim 0
1
00
xx
x x x x
x
fx
x
x
f x f x f x f
x
f



Nên hàm số liên tục tại
0x
Ta có:
00
00
0
' 0 lim lim 1
0
' 0 lim lim 1
xx
xx
f x f
f f x
x
f x f
f f x
x




Vì
'
0 ' 0ff

nên hàm số không có đạo hàm tại
0x
Bài 3. Tính đạo hàm của hàm số
32
2 3 khi 1
()
2 7 4
khi 1
1
xx
fx
x x x
x
x

tại
0
1x
.
Hướng dẫn
Ta có:
11
l
im ( ) lim 2 3 5
xx
f x x


32
2
1 1 1
2 7 4
lim ( ) lim lim 3 4 0
1
x x x
x x x
f x x x
x
Dẫn tới
11
lim ( ) lim ( )
xx
f x f x


suy ra: hàm số không liên tục tại
0
1x
nên hàm số không có đạo
hàm tại
0
1x
.
Bài 4. Chứng minh rằng hàm số
2
2 | 1|
()
1
xx
fx
x

liên tục tại
1x 
nhưng không có đạo hàm
tại điểm đó.
Hướng dẫn
Vì hàm
()fx
xác định tại
1x 
nên nó liên tục tại đó.
Ta có:
( 1) ( 1)
( ) ( 1) 2
( 1) lim lim 1
11
xx
f x f x
f
xx





( 1) ( 1)
( ) ( 1)
( 1) lim lim 2 2
1
xx
f x f
f
x




( 1) ( 1)ff


()fx
không có đạo hàm tại
1x 
.
Bài 5. Cho hàm số
2
2 1 1
11
x khi x
fx
x bx khi x

. Để hàm số này có đạo hàm tại
1x
thì giá
trị của
b
là?
Hướng dẫn
Ta có:
13f
11
l
im lim 2 1 3
xx
f x x


2
11
lim lim 1 2
xx
f x x bx b


Để hàm số
fx
có đạo hàm tại
1x
khi và chỉ khi
fx
liên tục tại
1x
11
l
im lim 1
xx
f x f x f


23b
1b
Bài 6. Tìm
,ab
để hàm số
2
1
1
x x khi x
fx
ax b khi x


có đạo hàm tại
1x
.
Hướng dẫn
Điều kiện cần để hàm số có đạo hàm tại
1x
là hàm số liên tục tại
1x
.
12f
2
11
lim lim 2
xx
f x x x


11
l
im lim
xx
f x ax b a b


Để hàm số
fx
có đạo hàm tại
1x
thì
fx
liên tục tại
1x
11
l
im lim 1
xx
f x f x f


2ab
Điều kiện đủ:
1f
1
1
lim
1
x
f x f
x
2
1
2
lim
1
x
xx
x


1
l
im 2 3
x
x

1f
1
1
lim
1
x
f x f
x
1
1
lim
1
x
f x f
x
1
lim
1
x
ax b a b
x
1
lim
1
x
ax a
a
x

Để hàm số
fx
có đạo hàm tại
1x
thì
1f
1f
31ab
Bài 7. Tìm
,ab
để hàm số
3
1
3
1
x
khi x
fx
ax b khi x

có đạo hàm tại
1x
.
Hướng dẫn
Điều kiện cần:
1
1
3
f
3
11
1
lim lim
33
xx
x
fx






11
l
im lim
xx
f x ax b a b


Để hàm số
fx
có đạo hàm tại
1x
thì
fx
liên tục tại
1x
11
l
im lim 1
xx
f x f x f


1
3
ab
Điều kiện đủ:
1f
1
1
lim
1
x
f x f
x
3
1
1
33
lim
1
x
x
x
2
1
1
lim 1
3
x
xx

1f
1
1
lim
1
x
f x f
x
1
1
lim
1
x
f x f
x
1
lim
1
x
ax b a b
x
1
lim
1
x
ax a
a
x

Để hàm số
fx
có đạo hàm tại
1x
thì
1f
1f
2
1
3
ab
BÀI TẬP TỰ GIẢI:
Bài 8. Cho hàm số
2
2
khi 1
khi 1
x a x
fx
x bx x
. Tìm
,ab
để hàm số liên tục tại
1x 
(HD:
2; 4ab
)
Bài 9. Cho
sin3 0
3 2 0
x khi x
y f x
x khi x


. Tính đạo hàm của hàm số tại
0
0x
bằng định
nghĩa.
Bài 10. Cho hàm số:
2
sin
0
()
00
x
khi x
y f x
x
khi x

a) Chứng minh rằng
fx
liên tục tại
0
0x
.
b) Tính đạo hàm (nếu có) của
fx
tại điểm
0
0x
.
Bài 11. Dùng định nghĩa, tính đạo hàm của hàm số
2
1
cos khi 0
()
0 khi 0
xx
y f x
x
x

tại
điểm
0
0x
Bài 12. Chứng minh rằng hàm số:
2
2
( 1) 0
()
0
x khi x
y f x
x khi x



không có đạo hàm
tại điểm
0
0x
nhưng có đạo hàm tại
0
2x
.
Bài 13. Tìm
, ab
để hàm số
2
21
()
11
x khi x
y f x
ax b khi x


có đạo hàm tại điểm
1x
.
Bài 14. Cho hàm số:
cos sin 0
()
10
p x q x khi x
y f x
px q khi x


Chứng minh rằng với mọi cách chọn
, pq
hàm số không thể có đạo hàm tại điểm
0x
.
Bài 15. Tìm
, ab
để hàm số
3
2
20
()
0
x khi x
y f x
x ax b khi x


có đạo hàm tại điểm
0x
.
Khi đó tính
'0f
HD:
0
; 2; ' 0 0a b f
Bài 16. Cho hàm số
2
()
21
x
y f x
x

a) Xét sự liên tục của hàm số tại
0
2x
b) Xét xem tại
0
2x
hàm số có đạo hàm không?
Bài 17. Cho
2
2
2
3
sin 0
00
x
x khi x
y f x
x
khi x

.
a) Xét sự liên tục của hàm số tại
0
0x
b) Xét xem tại
0
0x
hàm số có đạo hàm không?
Bài 18. Chứng minh rằng hàm số
2
23
31
xx
y
x

liên tục tại
3x 
nhưng không có đạo hàm tại
điểm ấy.
Bài 19. Cho hàm số:
2
sin
0
00
x
khi x
y f x
x
khi x

a) Chứng minh rằng
fx
liên tục tại
0
0x
.
b) Tính đạo hàm (nếu có) của
fx
tại điểm
0
0x
.
Bài 20. Cho hàm số:
2
1
sin 0
()
00
x khi x
y f x
x
khi x

a) Tính đạo hàm của hàm số tại mỗi
x
.
b) Chứng tỏ rằng đạo hàm
fx
không liên tục tại điểm
0
0x
.
Bài 21. Xét sự tồn tại đạo hàm của các hàm số sau trên :
a)
2
22
1
2
1
x x khi x
y
khi x
x
b)
2
1
2
1
x x khi x
y
khi x
x

Bài 22. Tìm a, b để hàm số sau có đạo hàm tại x = 1:
a)
2
1
1
x khi x
y
ax b khi x

b)
2
2
2 2 1
1
x khi x
y
x ax b khi x
Bài 23. Dùng định nghĩa, tính đạo hàm của hàm số
1
x
y
x
tại
0
0x
.
Bài 24. Chứng minh rằng hàm số
2
23
31
xx
y
x

liên tục tại
–3x
nhưng không có đạo hàm tại
điểm ấy.
Bài 25. Chứng minh rằng hàm số
3
2
yx
liên tục tại
0x
nhưng không có đạo hàm tại
0x
CHUYÊN ĐỀ 6
GIẢI PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH LIÊN QUAN ĐẾN ĐẠO HÀM
I. Sử dụng đạo hàm để tính giới hạn dạng
0
;
0
: Quy tắc LÔPITAN
Phương pháp:
Sử dụng quy tắc Lopitan:
00
lim lim
x x x x
f x f x
g x g x

BÀI TẬP MẪU
Bài 1. Tính giới hạn:
1)
2
1
1
lim
1
x
x
x
2)
2
73
lim
2
x
x
x

Hướng dẫn
1)
2
2
1 1 1
1
12
lim lim lim 2
11
1
x x x
x
xx
x
x
2)
2 2 2
1
73
7 3 1
27
lim lim lim
2 1 6
2
x x x
x
x
x
x
x


BÀI TẬP TỰ GIẢI
Bài 1. Tính các giới hạn sau theo quy tắc Lopitan:
1)
2
1
1
lim
1
x
x
x
.ĐS: 2. 2)
0
1
lim 2
x
x
x



ĐS:
1.
3)
3
2
2
8
lim
4
x
x
x
ĐS: 3 4)
2
1
3 4 1
lim
1
x
xx
x

ĐS: 2
Bài 2. Tìm các giới hạn sau theo quy tắc Lopitan:
1)
2
2
4 1 3
lim
4
x
x
x

ĐS:
1
6
2)
2
0
11
lim
x
x
x

ĐS: 0
3)
4
53
lim
4
x
x
x

ĐS:
1
6
4)
2
9
3
lim
9
x
x
xx
ĐS:
1
.
54
5)
2
7
23
lim
49
x
x
x

ĐS:
1
.
56
6)
32
1
2 7 4
lim
43
x
xx
xx

ĐS:
4
15
Bài 3. Tìm các giới hạn sau theo quy tắc Lopitan
1.
0
11
lim
x
xx
x
ĐS: 1 7.
4
35
lim
15
x
x
x


ĐS:
1
.
3
2.
1
1
lim
32
x
x
x

ĐS: 2. 8.
1
2 2 3 1
lim
1
x
xx
x
ĐS:
1
4
II. Sử dụng đạo hàm trong bài toán giải PT-BPT
Phương pháp:
Sử dụng công thức tính đạo hàm rồi thay vào bài toán để giải.
Chú ý: Cho tam thức
2
( 0),f
x ax bx c a
1. Để
,0x xf 
thì:
Trường hợp 1: Xét
0a
Trường hợp 2:
0
0
a

2) Để
( ) 0,f x x
thì:
Trường hợp 1: Xét
0a
Trường hợp 2:
0
0
a

3) Để
( ) 0,f x x
thì:
Trường hợp 1: Xét
0a
Trường hợp 2:
0
0
a

4) Để
( ) 0,f x x
thì :
Trường hợp 1: Xét
0a
Trường hợp 2:
0
0
a

BÀI TẬP MẪU
Bài 1. Cho hàm số
32
5y mx x x
. Tìm m để:
a)
y
bằng bình phương của một nhị thức bậc nhất.
b)
0y
có hai nghiệm trái dấu.
c)
0y
với mọi
x
.
Hướng dẫn
Ta có:
2
3 2 1y mx x
a) Để
y
là bình phương của một nhị thức bậc nhất thì phương trình
0y
có nghiệm kép
Suy ra
00
1
' 0 1 3 0
3
mm
m
m




. Vậy: ..
b) Để
0y
có hai nghiệm trái dấu thì
. 0 3 0 0a c m m
.
c) Để
0y
với mọi
x
thì:
3 0 0
1
' 0 1 3 0
3
mm
m
m




. Vậy………………….
Bài 2. Cho hàm số
3
1
x
fx
x
. Giải phương trình
0fx
.
Hướng dẫn
Điều kiện:
1x
.
23
32
22
31
23
11
x x x
xx
fx
xx



32
0
0 2 3 0
3
2
x
f x x x
x
. Vậy: …………….
Bài 3. Cho hàm số
2
2f x x x
. Giải bất phương trình
f
x
f x
Hướng dẫn
Ta có
2
1
2
x
fx
xx
. Khi đó
2
2
1
2
2
x
f x f x x x
xx
(1)
Đk:
;
0
2;x 
.
(1)
22
35
2
1 2 3 1 0
35
2
x
x x x x x
x
.
Kết hợp với điều kiện trên suy ra
0x
hoặc
35
2
x
.
Bài 4. Cho hàm số
2
21f x x x x
. Giải bất phương trình
0.fx
Hướng dẫn
Ta có
2
1
2 2 1 2 .
21
f x x x x x
x
2
2 2 2 1 2
21
x x x x
x
2
5 2 4
21
xx
x

.
Điều kiện
1x
.
0fx
2
5 2 4 0xx
1 21
5
1 21
5
x
x


.
Bài 5. Cho hàm số
3
2
23
3
x
f x mx m x
. Tìm các giá trị nguyên của tham số
m
để
'0fx
với mọi
x
.
Hướng dẫn
Ta có
2
22f x x mx m
0f
x
x
2
2 2 0x mx m x
10
'0
a 

2
20mm
12m
Vì
m
nguyên nên
1;
0;1;2m
.
Bài 6. Cho
2
3 2 3
2 3, 3
2
x
f x x x g x x
. Giải bất phương trình
f
x g x

.
Hướng dẫn
2
3 2 2 3 2
2 3 6 2 , 3 3
2
x
f x x x x x g x x x x




2 2 2
6 2 3 3 3 0 ;0 1;f x g x x x x x x x x

Bài 7. Cho
3
60 64
35 f x x
xx
. Giải phương trình
0fx
.
Hướng dẫn
Ta có
3 2 4
60 64 60 192
3 5 3f x x
x x x x



24
6
0 192
0 3 0 1fx
xx
. Đặt
2
1
,0tt
x
2
11
1 192 60 3 0
4 16
t t t t
Với
2
2
1 1 1
42
44
t x x
x
Với
2
2
1 1 1
16 4
16 16
t x x
x
Vậy
0fx
có 4 nghiệm
2x
,
4x
Bài 8. Cho hàm số
2
7f x x x
. Giải bất phương trình
1
2
fx
.
Hướng dẫn
Xét tam thức:
2
7xx
có
1 28 27 0
10a

2
70xx
,
x
.
Ta có
2
2
7
27
xx
fx
xx


2
21
27
x
xx

.
Do đó
1
2
fx
2
2 1 1
2
27
x
xx


2
2 1 7x x x
2
2
2 1 0
2 1 7
x
x x x

22
1
2
4 4 1 7
x
x x x x

2
1
2
3 3 6 0
x
xx

1
2
2
1
x
x
x


1x
.
Bài 9. Cho hàm số
32
1
5
32
m
xy x x m
. Tất cả các giá trị của tham số
m
để
0y
,
x
.
Hướng dẫn
32
1
5
32
y
m
x x mx 
;
2
my xx m
2
0, 0,x x mx m xy
2
4 0 0 4m m m
.
Bài 10. Cho hàm số
32
11
4 2019
34
y x x x
. Gọi
S
là tập hợp tất cả các nghiệm nguyên của bất
phương trình
0y
. Tổng tất cả các phần tử của
S
bằng bao nhiêu?
Hướng dẫn
2
1
4
2
y x x
.
0y
2
1
40
2
xx
1 65 1 65
44
x


.
1
;0;1;2S 
nên có tổng các phần tử là:
2
.
Bài 11. Cho hàm số
32
1
1010 2019 2020
3
y x x x
. Giải bất phương trình
0y
.
Hướng dẫn
Ta có
2
2020 2019y x x
.
2
0 2020 2019 0y x x
1
2019
x
x
.
Vậy tập nghiệm của bất phương trình là
;1
2019;S  
.
BÀI TẬP TỰ GIẢI
Bài 1. Giải bất phương trình
''f
x g x
biết
2
3 2 3
2 2018; 2020
3
x
f x x x g x x
Bài 2. Cho hàm số
3
2
35
3
mx
y x mx
. Xác định m để
'
0 f x x
(HD:
3m
)
Bài 3. Cho hàm số
32
1
25
3
y x x mx
. Tìm m để
'
0 0;2f x x
(HD:
0m
)
Bài 4. Cho hàm số
3 2 2
1
2 1 4
3
y x m x m x
. Tìm m để:
a)
'( ) 0fx
với mọi
0x
b)
'0fx
có hai nghiệm phân biệt cùng dấu
c) Trong trường hợp
'0fx
có hai nghiệm. Tìm hệ thức giữa hai nghiệm không phụ thuộc vào m.
Bài 5. Giải phương trình
'0fx
biết
2
2
34
1
xx
fx
xx


Bài 6. Giải bất phương trình
'f
x f x
biết
2
2f x x x
Bài 7. Cho hàm số
32
32y x x x
. Tìm
x
sao cho: a)
2y

b)
10y
Bài 8. Giải các bấy phương trình:
a)
0y
với
2
33
1
xx
y
x

b)
0y
với
2
2
1
1
xx
y
xx


Bài 9. Tìm các nghiệm của phương trình sau:
a)
0fx
với
32
1
( ) 2 6 1
3
f x x x x
. b)
–5fx
với
4 3 2
13
( ) 3
42
f x x x x
.
Bài 10. Cho hàm số
32
( ) 3 2f x x x
. Hãy giải các bất phương trình sau:
a)
( ) 0fx
b)
( ) 3fx
Bài 11. Giải bất phương trình
f
x g x

, biết rằng:
a)
3
( ) 2f x x x
và
2
( ) 3 2g x x x
b)
32
( ) 2 3f x x x
và
2
3
( ) 3
2
x
g x x
Bài 12. Cho hàm số
2
2 24y x x
. Giải bất phương trình
2 ( ) ( )f x f x
Bài 13. Cho hàm số
2
2 12y x x
. Giải bất phương trình
( ) 0fx
. (TN THPT 2010)
Bài 14. Cho hàm số:
32
( ) 2 3y f x x x mx
. Tìm
m
để:
a)
fx
là bình phương của một nhị thức bậc nhất.
b)
0,f
x x

.
c)
0,( 2) 0
; f x x
.
d)
0
, 0f x x
.
Bài 15. Cho hàm số:
32
( ) 3 2
32
mx mx
y f x m x
. Tìm
m
để:
a)
0,f
x x

.
b)
fx
có hai nghiệm phân biệt cùng dấu.
c) Chứng minh rằng trong trường hợp
fx
có hai nghiệm (hai nghiệm có thể trùng nhau) thì
các nghiệm này thỏa mãn một hệ thức độc lập với
m
.
Bài 16. Tìm
m
để:
a)
3
–y mx x
có
0,yx
.
b)
32
1
43
3
y x mx x
có
0,yx
.
c)
32
– 3 4y x mx mx
có
0,yx
.
d)
32
–
3 2 1 2 5 2y x m x m x
có
0,yx
.
e)
32
1
– 2 – 2
3
y x x mx
có
0,yx
.
f)
32
1
––
3
y x mx mx
có
0
, 0;yx
.
Bài 17. Với mỗi hàm số sau đây: ① Tìm TXĐ ② Tính
y
③ Xét dấu
y
, chỉ ra
0y
,
0y
trên khoảng, các khoảng nào:
a)
3
– 3 1y x x
b)
32
1
– 3 8 – 2
3
y x x x
c)
21
2
x
y
x
d)
2
2
1
xx
y
x

e)
2
22
1
xx
y
x
f)
1
1
2
y
x

g)
42
–4y x x
h)
42
41y x x
i)
4 1–
1
1
yx
x

j)
2
4 3 –y x x
k)
32
1
3 7 2
3
y x x x
l)
42
23y x x
m)
32
5y x x
n)
2
4yx
o)
2
2
1
xx
y
x
p)
2
2
7 12
23
xx
y
xx


q)
2
3y x x
r)
2
20y x x
s)
2
89
5
xx
y
x

t)
1
2
1
yx
x

u)
2
23y x x
III. Sử dụng đạo hàm chứng minh đẳng thức:
Phương pháp:
Sử dụng các công thức để tính đạo hàm rồi thay vào biểu thức để biến đổi
BÀI TẬP MẪU
Bài 1. Cho hàm số
2
1 y x x
. Chứng minh:
2
10
y x y
Hướng dẫn
Ta có:
2
222
1
1
111


x x x y
y
xxx
.
22
1 1 0

y x y y x y
.
Bài 2. Cho hàm số
2
1 y x x
. Chứng minh:
2
2 1 .x y y

Hướng dẫn
Ta có:
22
2
22
11
1 . 1 . 1
1
2 1 2 1
x
y x x x x
x
x x x x






22
2 2 2
2
1 1 1
.
1 2 1 2 1
21
x x x x y
x x x
xx

.
2
2 1 .x y y
.
Bài 3. Cho hàm số
3
1yx
. Chứng minh:
2
3 1 0yy

Hướng dẫn
32
3
1 1 3 1y x y x y y
2
3 1 0yy
Bài 4. Chứng minh các công thức tổng quát sau
a)
2
2
11
1 1 1 1
22
2
1 1 1
1 1 1
2
ab
a c b c
xx
ab
a c b c
ax bx c
a x b x c
a x b x c








; (
1 1 1
, , , , ,a b c a b c
là hằng số) .
b)
2
11
2
11
2
11
11
. 2 .
bc
a a x a b x
ab
ax bx c
a x b
a x b






; (
11
, , , ,a b c a b
là hằng số) .
Hướng dẫn
a)
2 2 2 2
2
1 1 1 1 1 1
22
2
1 1 1
1 1 1
..ax bx c a x b x c ax bx c a x b x c
ax bx c
a x b x c
a x b x c








=
22
1 1 1 1 1
2
2
1 1 1
2 . . 2ax b a x b x c ax bx c a x b
a x b x c

=
2
1 1 1 1 1 1
2
2
1 1 1
. . 2 . . . .a b a b x a c a c x b c b c
a x b x c

. ( đpcm)
b)
'
'
22
2
1 1 1 1
2
11
11
..ax bx c a x b ax bx c a x b
ax bx c
a x b
a x b





2
1 1 1
2
11
2 . .ax b a x b ax bx c a
a x b
.
2
1 1 1 1
2
11
. 2 . . .a a x a b x b b a c
a x b
.( đpcm)
BÀI TẬP TỰ GIẢI
Bài 1. Chứng minh rằng hàm số
ax b
y
cx d
có đạo hàm là
2
'
()
ad bc
y
cx d
Áp dụng tính đạo hàm của :
35
2
x
y
x
,
4
32
y
x
,
2
13
x
y
x
Bài 2. Chứng minh rằng hàm số
2
''
ax bx c
y
b x c

có đạo hàm là
2
2
' 2 ' ' '
'
( ' ')
ab x ac x bc b c
y
b x c
Áp dụng tính đạo hàm của :
2
27
2
xx
y
x

,
2
1
32
x
y
x
,
2
21
5
xx
y
x

Bài 3. Chứng minh hàm số
2
2
' ' '
ax bx c
y
a x b x c


có đạo hàm là:
2
22
2
' ' ' ' ' '
'
( ' ' ')
a b a c b c
xx
a b a c b c
y
a x b x c


Áp dụng tính đạo hàm của :
2
2
21
33
xx
y
xx


,
2
2
3 6 1
32
xx
y
xx


,
2
2
2 5 6
5
xx
y
x


Bài 4. Chứng minh rằng hàm số:
a)
2
2y x x
thỏa hệ thức:
3
'' 1 0yy
.
b)
3
2
1y x x
thỏa hệ thức:
2
1 '' ' 9 0x y xy y
.
c)
5
3y
x

thỏa hệ thức:
'3xy y
.
d)
3
4
x
y
x
thỏa hệ thức:
2
2( ') ( 1) ''y y y
CHUYÊN ĐỀ 7
PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ
Dạng 1. Phương trình tiếp tuyến khi biết tiếp điểm
00
;M
x y
Phương pháp:
- Bước 1: Tìm tọa độ tiếp điểm
00
;M
x y
- Bước 2: Tính
''y
f x
, rồi suy ra hệ số góc của tiếp tuyến là
0
'fx
- Bước 3: Phương trình tiếp tuyến của đồ thị
C
tại
00
;M
x y
là:
0 0 0
'.y f x x x y
BÀI TẬP MẪU
Bài 1. Viết phương trình tiếp tuyến của đồ thị
3
41y x x
tại :
a) Điểm
1; 2M
b) Tại điểm có hoành độ bằng 2.
c) Tại điểm có tung độ bằng 1.
Hướng dẫn
Ta có:
2
' 3 4yx
a) Hệ số góc của tiếp tuyến là:
2
' 1 3.1 4 1y
Phương trình tiếp tuyến là:
00
'
1 . 1 1 2 1y y x x y x x
b) Ta có:
3
0 0 0 0
2 4 1 1x y x x
Hệ số góc của tiếp tuyến là:
2
' 2 3.2 4 8y
Phương trình tiếp tuyến là:
8
2 1 8 15y x x
c) Ta có:
0
33
0 0 0 0 0 0
0
0
1 4 1 1 4 0 2
1
x
y x x x x x
x

TH1:
00
0
; 1 ' 0 4x y y
Phương trình tiếp tuyến là:
4
0 1 4 1y x x
Tương tự hai trường hợp còn lại, các em tự viết.
Bài 2. Cho hàm số
32
21y x x
có đồ thị là
C
. Viết phương trình tiếp tuyến của
C
tại
điểm
1
; 4M
Hướng dẫn
Ta có
2
34y x x

. Do đó
17y
. Phương trình tiếp tuyến tại điểm
1
; 4M
là
73yx
.
Bài 3. Viết phương trình tiếp tuyến của đồ thị hàm số
4
1
y
x
tại điểm có hoành độ
0
1x 
Hướng dẫn
Ta có
2
4
11
1
yy
x

.
Theo giả thiết ta có
0
1x 
nên
0
2y 
tiếp điểm
1
; 2M 
.
Vậy phương trình tiếp tuyến của đồ thị hàm số tại điểm
1
; 2M 
là :
1
1 2yx
3yx
.
Bài 4. Cho hàm số
3
31y x x
(C). Viết phương trình tiếp tuyến của đồ thị (C), biết tung độ
tiếp điểm bằng
3
Hướng dẫn
Ta có:
2
33yx

. Gọi
00
;M
x y
là tiếp điểm
Ta có:
3
0 0 0 0 0
3 3 2 0 2, 1y x x x x
0
1 ( 1) 0xy
. Phương trình tiếp tuyến:
3y
. Phương trình tiếp tuyến: .
Bài 5. Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của đồ thị
hàm số với trục tung
Hướng dẫn
Ta có:
2
2
2 2 1
'
21
xx
y
x

.
Giao điểm
M
của đồ thị với trục tung :
00
01xy
Hệ số góc của tiếp tuyến tại
M
là :
01k
y'
.
Phương trình tiếp tuyến tại điểm
M
là : .
Bài 6. Viết phương trình tiếp tuyến của đồ thị hàm số
23
1
x
y
x
tại giao điểm của đồ thị hàm số
với trục hoành bằng :
Lời giải
Tập xác định:
\
1 .D
0
2 (2) 9xy
9( 2) 3 9 15y x x
2
31
21
xx
y
x

1yx
Đạo hàm:
2
1
.
1
y
x
Đồ thị hàm số cắt trục hoành tại
2
; 0 .
3
A



Hệ số góc của tiếp tuyến là
2
9.
3
y



Phương trình tiếp tuyến là:
2
9 0 9 6
3
y x y x



Bài 7. Cho hàm số
24
3
x
y
x
có đồ thị là
(H)
. Phương trình tiếp tuyến tại giao điểm của
(H)
với trục hoành là:
Hướng dẫn
Giao điểm của đồ thị hàm số với trục hoành là
(2;0)A
. Ta có:
2
2
' '(2) 2
( 3)
yy
x
Phương trình tiếp tuyến cần tìm là
2( 2)yx
hay
24yx
.
Bài 8. Gọi
M
là giao điểm của đồ thị hàm số
21
2
x
y
x
với trục tung. Viết phương trình tiếp
tuyến với đồ thị hàm số trên tại điểm
M
.
Hướng dẫn
Vì
M
là giao điểm của đồ thị với trục
Oy
1
0;
2
M



2
3
( 2)
y
x
3
(0)
4
ky
Phương trình tiếp tuyến của đồ thị tại điểm
M
là:
31
42
yx
Bài 9. . Cho hàm số:
32
1 3 1 2y x m x m x m
. Tìm
m
để tiếp tuyến của đồ thị
hàm số tại điểm có hoành độ bằng
1
đi qua điểm
2
; 1A
.
Hướng dẫn
Hàm số đã cho xác định với
x
.
Ta có:
2
' 3 2 1 3 1y x m x m
Với
1
1 3 1 ' 1 6x y m y m
Phương trình tiếp tuyến tại điểm có
1x
:
6
1 3 1y m x m
Tiếp tuyến này đi qua
2
; 1A
nên có:
1 6 3 1 2mmm
Vậy,
2m 
là giá trị cần tìm.
Bài 10. Gọi (Cm) là đồ thị của hàm số
32
(2 1) ( 3) 3y x m x m x
và (d) là tiếp
tuyến của (C) tại điểm có hoành độ
2x
. Tìm m để khoảng cách từ gốc tọa độ O đến (d)
bằng
7
17
.
Hướng dẫn
Hàm số đã cho xác định với
x
.
Ta có:
2
' 3 2 2 1 3.y x m x m
Phương trình tiếp tuyến (d) :
'(2)( 2) (2)y y x y
1
1 – 7 – 2 7 – 6 11 – 7 8 – 15 (11 7 ) 8 15 0y m x m m x m m x y m
22
2
8 15
7
(0,( )) 17(8 15) 49[(11 7 ) 1]
17
(11 7 ) 1
m
d d m m
m

2
1313 3466 2153 0 1,m m m
2153
1313
m
BÀI TẬP TỰ GIẢI
Bài 1. Lập phương trình tiếp tuyến của đồ thị
1
1
x
y
x
biết hoành độ tiếp điểm là
0
0x
Bài 2. Lập phương trình tiếp tuyến của đồ thị
2yx
biết tung độ tiếp điểm là
0
2y
Bài 3. Cho hàm số
32
31y x x
có đồ thị là (C). Viết phương trình tiếp tuyến của (C) :
1. Tại điểm
M
1; 3
; 2. Tại điểm có hoành độ bằng 2 ;
3. Tại điểm có tung độ bằng 1 ;. 4. Tại giao điểm (C) với trục tung ;
ĐS:
1.
36yx
2.
24 27yx
3.
1y
,
9 28yx
4.
1y
Dạng 2. Viết phương trình tiếp tuyến khi biết hệ số góc
k
Phương pháp:
Bước 1: Tính
'fx
Bước 2: Giải phương trình
00
'f
x k x y
Bước 3: Phương trình tiếp tuyến là:
00
.y
k x x y
Chú ý:
Nếu đường thẳng song song với
y ax b
thì
ka
.
Nếu đường thẳng vuông góc với
y ax b
thì
1
k
a

.
Nếu đường thẳng tạo với trục Ox một góc
thì
tank
Nếu đường thẳng tạo với đường thẳng
d
góc
thì
tan
1.
ka
ka
. Với
a
là hệ số góc của
đường thẳng
d
Nếu đường thẳng d cắt các trục Ox, Oy lần lượt tại A, B thì
tan
OB
OAB
OA

, trong đó hệ số góc
của d được xác định bởi
'
tany x OAB
BÀI TẬP MẪU
Bài 1. Viết phương trình tiếp tuyến của đồ thị
C
:
24
6y x x
, biết tiếp tuyến vuông góc
với đường thẳng
1
1
6
yx
.
Hướng dẫn
Hàm số đã cho xác định
D
Gọi
t
là tiếp tuyến của đồ thị
C
của hàm số và
t
vuông góc với đường thẳng
1
1
6
yx
,
nên đường thẳng
t
có hệ số góc bằng
6
.
Cách 1: Gọi
00
;M
x y
là tọa độ tiếp điểm của tiếp tuyến
t
và đồ thị
C
của hàm số . Khi
đó, ta có phương trình:
3
0 0 0
' 6 4 2 6y x x x
2
0 0 0
1 2 2 3 0x x x
. Vì
2
0 0 0
2 2 3 0,x x x
nên phương trình
00
1
1 4 1;4x y y M
.
Phương trình tiếp tuyến cần tìm là:
6
1 4 6 10y x x
.
Cách 2: Phương trình
t
có dạng
6y x m
t
tiếp xúc
C
tại điểm
00
;M
x y
khi hệ phương trình sau có nghiệm
0
x
42
0 0 0
3
00
66
4 2 6
x x x m
xx
có nghiệm
0
0
1
10
x
x
m
Vậy phương trình tiếp tuyến cần tìm là:
6
1 4 6 10y x x
.
Bài 2. Cho hàm số
3
12
33
y x x
có đồ thị là (C). Tìm trên đồ thị (C) điểm mà tại đó tiếp
tuyến của đồ thị vuông góc với đường thẳng
12
33
yx
.
Hướng dẫn
Hàm số đã cho xác định
D
Ta có:
2
'1yx
Gọi
3
0 0 0 0 0
12
( ; ) ( )
33
M x y C y x x
,
Tiếp tuyến ∆ tại điểm M có hệ số góc:
2
00
'( ) 1y x x
Đường thẳng d:
12
33
yx
có hệ số góc
2
1
3
k 
22
1 2 0 0
1
. 1 ( 1) 1 4
3
d k k x x



00
00
4
2
3
20
xy
xy
Vậy, có 2 điểm
4
2;0 , 2;
3
M



là tọa độ cần tìm.
Bài 3. Cho hàm số
3
3 2 (C) y x x
. Viết phương trình tiếp tuyến của
(C)
biết hệ số góc của
tiếp tuyến bằng 9.
Hướng dẫn
Hàm số đã cho xác định và liên tục trên R.
Gọi
0
x
là hoành độ tiếp điểm M khi đó
0
x
là nghiệm của phương trình
0
22
0 0 0
0
2
'( ) 9 3 3 9 4 (2;0)
2
x
y x k x x M
x

hoặc
( 2; 4)M 
+) Với
(2;0)M
phương trình tiếp tuyến là
9 18yx
.
+) Với
( 2; 4)M 
phương trình tiếp tuyến là
9 14yx
.
Bài 4. Cho hàm số
32
31 y x x
có đồ thị
(C)
. Viết phương trình tiếp tuyến của đồ thị
(C)
song song với đường thẳng
:9 6 0 xy
.
Hướng dẫn
Đường thẳng
:9 6 0 9 6 x y y x
có hệ số góc là 9
Vì tiếp tuyến cần tìm song song với đường thẳng
suy ra tiếp tuyến có hệ số góc
9k
.
Suy ra hoành độ tiếp điểm là nghiệm của phương trình
2
3
' 3 6 9
1

x
y k x x
x
Với
1x
, phương trình tiếp tuyến là
9( 1) 3 9 6 y x y x
( loại vì trùng với đường
thẳng
).
Với
3x
, phương trình tiếp tuyến là
9( 3) 1 9 26 y x y x
( thỏa mãn ).
Vậy phương trình tiếp tuyến cần tìm là
9 6.yx
Bài 5. Viết phương trình tiếp tuyến của đồ thị hàm số
9
1
x
y
x
biết tiếp tuyến vuông góc với
đường thẳng
: 2 2 0 d x y
.
Hướng dẫn
Đường thẳng
1
: 2 2 0 1
2
d x y y x
nên đường thẳng d có hệ số góc là
1
2
d
k
.
Tiếp tuyến cần tìm có hệ số góc k vuông góc với đường thẳng
1
. 1 2
d
d k k k
k
.
Hoành độ tiếp điểm là nghiệm của phương trình:
2
1
8
'2
3
( 1)

x
yk
x
x
Với
1x
, phương trình tiếp tuyến là:
2( 1) 5 2 7. y x y x
Với
3x
, phương trình tiếp tuyến là:
2( 3) 3 2 9 y x y x
.
Vậy có hai phương trình tiếp tuyến thỏa mãn là:
1
: 2 7; 2 9 d y x y x
.
Bài 6. Cho hàm số
1
2
x
y
x
có đồ thị
(C)
và điểm
(2;1)I
. Viết phương trình tiếp tuyến d của
(C)
tại điểm M sao cho
IM d
.
Hướng dẫn
Tập xác định
\2DR
Ta có
2
1
'
( 2)

y
x
. Giả sử
0
00
0
1
( ; ) (x 2)
2
x
Mx
x
Hệ số góc của tiếp tuyến (d) tại M của đồ thị (C):
10
0
1
'( )
2

k y x
x
.
Hệ số góc của đường thẳng
0
0
2
2
00
1
1
21
:
2 ( 2)

MI
MI
x
y y x
IM k
x x x x
d
vuông góc của đường thẳng
0
4
1 2 0
22
0
00
3
11
. 1 . 1 ( 2) 1
1
( 2) ( 2)

x
IM k k x
x
xx
Với
0
3 (3;2) : 5 x M d y x
.
Với
0
1 (1;0) : 1 x M d y x
.
Vậy các tiếp tuyến thỏa mãn là
5 dx
hoặc
1 yx
.
Bài 7. Cho hàm số
22
2
x
y
x
(C)
. Viết phương trình tiếp tuyến với đồ thị
(C)
biết tiếp tuyến
tạo với đường thẳng
3yx
một góc
0
45
.
Hướng dẫn
Tập xác định
\2DR
.
Giả sử tiếp tuyến d cần tìm có hệ số góc k. Vì d tạo với đường thẳng
3yx
có hệ số góc
'k
một
góc
0
45
nên suy ra
0
2
'3
tan45 1 1
1
1 . ' 1 3
2



k
k k k
k k k
k
Gọi hoành độ tiếp điểm là nghiệm của phương trình:
2
00
0
22
0
00
2
0
2
2 (VN)
( 2) 0
2 2 1
'( )
2 1 4
( 2) ( 2) 2
( 2) 2




xx
y x k k
x
xx
x
Với
0
0x
suy ra phương trình tiếp tuyến cần tìm là:
11
( 0) 1 1.
22
y x x
Với
0
4x
suy ra phương trình tiếp tuyến là
11
( 4) 3 5
22
y x x
.
Vậy có hai tiếp tuyến thỏa mãn là
11
1; 5.
22
y x y x
Bài 8. Viết phương trình tiếp tuyến của đồ thị hàm số
2
23
x
y
x
biết rằng tiếp tuyến cắt trục
hoành và trục tung lần lượt tại
A
và
B
sao cho tam giác
OAB
cân tại
O
với
O
là gốc tọa
độ.
Hướng dẫn
Tập xác định
3
\
2



DR
.
Tam giác
OAB
vuông cân tại
O
nên suy ra hệ số góc của tiếp tuyến là
1k
hoặc
1k
.
Khi đó hoành độ tiêp điểm
0
x
là nghiệm của phương trình:
2
00
2
0
0
2
0
1
1 (VN)
(2 3) 1
1
'1
12
(2 3)
1
(2 3)

xx
yk
x
x
x
Với
00
11 xy
, phương trình tiếp tuyến là
yx
(loại vì cắt trục tung và trục hoành tại
O
nên
A B O
).
Với
00
20 xy
, phương trình tiếp tuyến là
2 yx
(thỏa mãn).
Vậy tiếp tuyến cần tìm là
2 yx
.
Bài 9. Viết phương trình tiếp tuyến của đồ thị hàm số
2
23
x
y
x
biết rằng tiếp tuyến cắt trục
hoành và trục tung lần lượt tại
A
và
B
sao cho tam giác
OAB
cân tại
O
với
O
là gốc tọa
độ.
Hướng dẫn
Tập xác định
\1DR
.
Ta có
1
tan
4

OB
OAB
OA
nên hệ số góccủa tiếp tuyến
1
4
k
hoặc
1
4
k
.
Nhưng do
2
1
' 0, 1
( 1)
yx
x
nên hệ số góc của tiếp tuyến là
1
4
k
.
Hoành độ tiếp điểm
0
x
là nghiệm phương trình
0
2
0
0
3
11
1
( 1) 4



x
x
x
.
Từ đó ta xác định được hai tiếp tuyến thỏa mãn:
1 5 1 13
;
4 4 4 4
y x y x
.
Bài 10. Cho hàm số
1
2( 1)
x
y
x
có đồ thị là
()C
. Tìm những điểm
M
trên
()C
sao cho tiếp
tuyến với
()C
tại
M
tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng
40xy
.
Hướng dẫn
Hàm số đã cho xác định
\1D
Gọi
M
(
0
0
0
1
;
2( 1)
x
x
x
)
()C
là điểm cần tìm.
Gọi
tiếp tuyến với (C) tại
M
ta có phương trình
:
'
0
00
0
1
( )( )
2( 1)
x
y f x x x
x
0
0
2
0
0
1
1
()
2( 1)
1
x
y x x
x
x
Gọi
A Ox
2
00
21
;0
2
xx
A




,
B Oy
2
00
2
0
21
0;
2( 1)
xx
B
x




.
OAB
có trọng tâm là:
G
22
0 0 0 0
2
0
2 1 2 1
;
6 6( 1)
x x x x
x



.
Do
G
thuộc đường thẳng
40xy
22
0 0 0 0
2
0
2 1 2 1
4. 0
6 6( 1)
x x x x
x
2
0
1
4
1x
(vì
2
00
2 1 0xx
)
00
00
11
1
22
13
1
22
xx
xx







Với
0
1 1 3
;
2 2 2
xM



Với
0
3 3 5
;
2 2 2
xM



.
Bài 11. Cho hàm số
32
3 9 10y x x x
có đồ thị là (C). Trong tt cả các tiếp tuyến của đồ thị
(C), hãy tìm tiếp tuyến có hệ số góc nhỏ nht.
Hướng dẫn
Hàm số đã cho xác định
D
Ta có:
2
' 3 6 9y x x
.
Gọi
00
( ; ) ( )M x y C
:
32
3 9 10y x x x
.
Tiếp tuyến tại điểm
M
có hệ số góc:
22
0 0 0 0
'( ) 3 6 9 3( 1) 12 12k y x x x x
mink 12,
đạt được khi:
00
1 y 21.x
Vậy trong tt cả các tiếp tuyến của đồ thị hàm số, tiếp tuyến tại
M
1;16
có hệ số góc nhỏ nht
và có phương trình là:
12 9yx
BÀI TẬP TỰ GIẢI
Bài 1. Cho hàm số
32
31y x x
có đồ thị là (C). Viết phương trình tiếp tuyến của (C) :
1. Có hệ số góc là
3
.
2. Vuông góc với đường thẳng (d ):
27 3 2019 0xy
.
3. Song song với đường thẳng (d’ ) :
24 2020 0xy
.
Bài 2. Viết phương trình tiếp tuyến của đồ thị
32
1
2
3
y x x
biết tiếp tuyến song song
3 2020yx
(HD:
1
3 ; 3 11
3
y x y x
)
Bài 3. Viết phương trình tiếp tuyến của đồ thị
32
21
3
33
y x x
biết tiếp tuyến vuông góc với
4 2021xy
(HD:
1 2021
4 2021
44
x y y x
. Suy ra tiếp tuyến có hệ số góc
4k 
Từ đó viết được
4
4 ; 4 1
3
y x y x
)
Bài 4. Lập phương trình tiếp tuyến của đồ thị
32
1
2 3 1
3
y x x x
biết tiếp tuyến có hệ số
góc lớn nht.
Bài 5. Lập phương trình tiếp tuyến của đồ thị
3
32y x x
biết tiếp tuyến song song trục
hoành.
Bài 6. Lập phương trình tiếp tuyến của đồ thị
2
2 3 9y x x
biết tiếp tuyến hợp với trục
hoành góc
0
45
Bài 7. Lập phương trình tiếp tuyến của đồ thị
42
6y x x
biết tiếp tuyến vuông góc với
đường thẳng
1
2019
6
yx
Dạng 3. Phương trình tiếp tuyến đi qua điểm
11
;A
x y
Phương pháp:
Cách 1:
Bước 1: Tính
'fx
Bước 2: Gọi
00
;M
x y
là tiếp điểm suy ra phương trình tiếp tuyến là:
0 0 0
'.y f x x x y
(1)
Bước 3: Vì tiếp tuyến đi qua
11
;A
x y
nên thay
11
;x x y y
vào phương trình (1) để tìm
00
xy
Bước 4: Thay
00
,xy
vào (1) để viết lại phương trình tiếp tuyến.
Cách 2:
Đường thẳng
d
đi qua điểm
11
;A
x y
có hệ số góc là
k
có dạng :
11
y
k x x y
.
Để
d
là tiếp tuyến thì hệ:
11
'
f
x k x x y
f x k
. Giải hệ trên được

00
xy
tiếp
tuyến.
BÀI TẬP MẪU
Bài 1. Viết phương trình tiếp tuyến của đồ thị
32
31y x x
biết tiếp tuyến qua
1;3A
Hướng dẫn
Ta có:
2
' 3 6y x x
.
Cách 1:
Gọi
00
;M
x y
là tiếp điểm suy ra hệ số góc của tiếp tuyến là :
2
0 0 0
' 3 6k y x x x
Phương trình tiếp tuyến là:
2 3 2
0 0 0 0 0
3 6 . 3 1y x x x x x x
(1)
(Các em chú ý
32
0 0 0
31y x x
)
Vì tiếp tuyến đi qua
1;3A
nên thay
1; 3xy
vào (1) ta được:
00
2 3 2
0 0 0 0 0
00
1 9; 3
3 3 6 . 1 3 1
2 0; 3
x k y
x x x x x
x k y



Vậy phương trình tiếp tuyến là:
9 6; 3y x y
Cách 2:
Đường thẳng
d
đi qua điểm
1;3A
có hệ số góc là
k
có dạng :
13y
k x
.
Để
d
là tiếp tuyến của đồ thị thì hệ phương trình
2
1 3 1
' 3 6 2
f x k x
k f x x x
có nghiệm.
Thay
2
vào
1
ta được:
3 2 2 3 2 3 2 2
3
3 1 3 6 1 3 3 1 3 3 6 6 3
1
2 6 4 0
2
x x x x x x x x x x x
x
xx
x

Với
1 9; 3
2 0; 3
x k y
x k y



suy ra phương trình tiếp tuyến là:
9 6; 3y x y
Bài 2. Cho đồ thị hàm số
32
:
2 3 5C y f x x x
. Lập phương trình tiếp tuyến của đồ thị
C
biết tiếp tuyến đi qua điểm
19
;4
12
A



.
Hướng dẫn
Gọi
k
hệ số góc của tiếp tuyến đi qua
19
;4
12



A
tới
C
.
Phương trình tiếp tuyến
là:
19
4
12



y k x
.
tiếp xúc với
C
32
2
19
2 3 5 4 1
12
6 6 2
x x k x
x x k




có nghiệm
Thay
k
từ
2
vào
1
ta được:
3 2 2
19
2 3 5 6 6 4
12



x x x x x
3 2 2
4 6 19 2 12 19 x x x x x x
32
8 25 19 2 0 x x x
1
2
1
8

x
x
x
.
Với
10xk
phương trình tiếp tuyến là:
4y
Với
2 12xk
phương trình tiếp tuyến là:
19
12 4 12 15
12
y x y x



Với
1 21
8 32
xk
phương trình tiếp tuyến là:
21 19 21 645
4
32 12 32 128
y x y x



Vậy từ điểm
19
;4
12



A
kẻ được
3
tiếp tuyến tới
C
Bài 3. Có hai tiếp tuyến của đồ thị hàm số
32
1
x
yC
x
đi qua điểm
9
;0A
. Tính tích hệ số
góc của hai tiếp tuyến đó?
Hướng dẫn
TXĐ:
\1
2
1
1
y
x
Đường thẳng
d
đi qua điểm
9
;0A
với hệ số góc
k
có phương trình
9y
k x
.
Đường thẳng
d
tiếp xúc với đồ thị
C
khi và chỉ khi hệ phương trình sau có nghiệm
2
32
91
1
1
2
1
x
kx
x
k
x

Thế
2
vào
1
, ta có:
2
3 2 1
. 9 3 2 1 9
1
1
x
x x x x
x
x

2
1
3 4 7 0
7
3
x
xx
x

Do đó tích hệ số góc của hai tiếp tuyến đó bằng
79
1 . .
3 64
yy





Bài 4. Tìm điểm trên đường thẳng
21yx
để từ đó kẻ được đến đồ thị
C
của hàm số
3
1
x
y
x
đúng một tiếp tuyến?
Hướng dẫn
TXĐ:
\1D
.
Gọi
;
2 1A a a
: 2 1d y x
.
Gọi
k
là hệ số góc của đường thẳng
d
đi qua
;
2 1A a a
.
Suy ra phương trình
:
2 1d y k x a a
Xét hệ phương trình:
2
3
21
1
4
1
x
k x a a
x
k
x
1
2
34
21
1
1
x
x a a
x
x

2
1
2 2 2 4 6 4 0 2
x
ax a x a
Để từ
;
2 1A a a
chỉ kẻ được một tiếp tuyến đến
C
thì
phương trình
1
có một nghiệm
phương trình
2
có một nghiệm khác
1
.
Có các trường hợp sau:
Trường hợp 1: phương trình
2
là phương trình bậc nht có nghiệm
1x
0
1
8 4 0
2
a
x
x
( T/m). Suy ra
0
;1A
thỏa mãn.
Trường hợp 2: phương trình
2
là phương trình bậc hai có nghiệm kép
1x
2
12
0
2 4 2 6 4 0
24
1
2
a
a a a
a
xx
a
2
0
8 8 16 0
a
aa
1
2
a
a

.
Suy ra có 2 điểm thỏa mãn
1; 1
2;5
A
A

Trường hợp 3: phương trình
2
là phương trình bậc hai có hai nghiệm phân biệt trong đó có
một nghiệm
1x
2
0
2 4 2 6 4 0 1
2 2 2 4 6 4 0
a
a a a a
a a a
. Suy ra
1
;3A
thỏa mãn.
Vậycó
4
điểm thỏa mãn yêu cầu đầu bài.
Bài 5. Tìm số tiếp tuyến của đồ thị hàm số
32
4 6 1 y x x
, biết tiếp tuyến đó đi qua điểm
1
; 9 .M
Hướng dẫn
TXĐ: R
Ta có:
2
12 12
y x x
.
Phương trình đường thẳngđi qua
1
; 9M 
có dạng:
:
1 9y k x
.
là tiếp tuyến của đồ thị khi và chỉ khi hệ phương trình sau có nghiệm:
32
32
2
5
4 6 1 1 9
8 6 12 10 0
4
12 12
1
x x k x
x
x x x
k x x
x


Với
1 24xk
phương trình tiếp tuyến
2
4 1 9 24 15y x y x
Với
5 15
44
xk
phương trình tiếp tuyến
15 15 21
19
4 4 4
y x y x
Có 2 tiếp tuyến thỏa mãn yêu cầu .
Bài 6. Cho hàm số
32
3y x x
có đồ thị
C
và điểm
;0Mm
sao cho từ
M
vẽ được ba tiếp
tuyến đến đồthị
C
, trong đó có hai tiếp tuyến vuông góc với nhau. Tìm giá trị của
m
?
Hướng dẫn
TXĐ: R
Ta có
2
36y x x

.
Đường thẳng
d
đi qua
;0Mm
có hệ số góc
k
có phương trình :
y
k x m
d
là tiếp tuyến của
C
khi và chỉ khi hệ phương trình sau có nghiệm:
32
2 3 2 3 2
2
3
3 6 3 2 3 1 6 0
36
k x m x x
x m x x x x x m x mx
k x x

2
0
2 3 1 6 0 1
x
x m x m
.
Khi
0x
ta có phương trình tiếp tuyến
0y
.
Đối với đồ thị hàm số không có tiếp tuyến nào vuông góc với
0y
nên yêu cầu bài toán tương
đương phương trình
1
có hai nghiệm
1
x
và
2
x
khác
0
thỏa
12
.1y
x y x


22
1 1 2 2
3 6 3 6 1x x x x
1
2 1 2 1 2
9 . . 2 4 1 0x x x x x x


9
3 3 3 1 4 1 0m m m


27 1 0m
1
27
m
.
Thay
1
27
m
vào
1
thử lại có 2 nghiệm phân biệt khác
0
.
Vậy
1
27
m
thỏa mãn yêu cầu bài toán.
Bài 7. Cho hàm số
42
22y x x
có đồ thị
C
. Lập phương trình tiếp tuyến của đồ thị
C
biết tiếp tuyến đi qua điểm
0
;2A
?
Hướng dẫn
TXĐ: R
Ta có:
3
44y x x

Đường thẳng
d
đi qua điểm
0
;2A
có hệ số góc
k
có dạng:
2y kx
Để đường thẳng
d
là tiếp tuyến của đồ thị
C
khi và khi hệ phương trình sau có nghiệm:
42
4 2 3 4 2
3
0
2 2 2
2
2 2 4 4 2 3 2 0
3
44
2
3
x
x x kx
x x x x x x x x
x x k
x


Với
00xk
phương trình tiếp tuyến là:
2y
.
Với
2 4 6
39
xk
phương trình tiếp tuyến là:
46
2
9
yx
.
Với
2 4 6
39
xk
phương trình tiếp tuyến là:
46
2
9
yx
Bài 8. Viết phương trình tiếp tuyến của đồ thị hàm số
3
31y x x
()C
biết tiếp tuyến đó đi
qua điểm
(3;19)A
Hướng dẫn
Giả sử tiếp điểm của tiếp tuyến cần tìm là điểm
00
( ; )M x y
. ta có phương trình tiếp tuyến là
23
0 0 0 0
(3 3)( ) 3 1y x x x x x
()d
d
đi qua điểm
(3;19)A
nên ta có:
23
0 0 0 0
19 (3 3)(3 ) 3 1x x x x
.
Giải phương trình trên ta được
0
3x
hoặc
0
3
2
x 
.
Với
0
3x
thì phương trình tiếp tuyến cần tìm là
24 53yx
.
Với
0
3
2
x 
thì phương trình tiếp tuyến là
15 31
44
yx
Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là
24 53yx
và
15 31
44
yx
.
Bài 9. Từ điểm
(1;3)A
có thể kẻ được bao nhiêu tiếp tuyến đến đồ thị hàm số
21
1
x
y
x
Hướng dẫn
Gọi điểm
00
( ; )M x y
là tiếp điểm của tiếp tuyến cần tìm. Phương trình tiếp tuyến của đồ thị hàm
số
21
1
x
y
x
tại
M
là:
0
00
2
00
21
3
( ) ( 1)
( 1) 1
x
y x x x
xx

.
Tiếp tuyến đi qua
(1;3)A
nên ta có
0
00
2
00
21
3
3 (1 ) ( 1)
( 1) 1
x
xx
xx

0
7x
Vậy qua điểm A kẻ được duy nht một tiếp tuyến đến đồ thị hàm số./
Bài 10. Cho hàm số
2
1
x
y
x
có đồ thị
()C
và điểm
(0; )Aa
. Tìm
a
để từ điểm
A
kẻ được
hai tiếp tuyến đến đồ thị
()C
sao cho tiếp điểm nằm về hai phía của trục hoành.
Hướng dẫn
Giả sử điểm
00
( ; )M x y
là tiếp điểm của tiếp tuyến cần tìm. Ta có phương trình tiếp tuyến tại
M
là
0
0
2
00
2
3
()
( 1) 1
x
y x x
xx

0
1x
Tiếp tuyến này đi qua điểm
A
nên ta có :
00
0
2
00
32
( 1)
( 1) 1
xx
ax
xx

2
0 0 0 0 0
2
00
( 2)( 1) ( 1) 3 0 ( 1)
(1 ) (2 4) 2 0 (*)
x x a x x x
a x a x a
Theo định lý viet ta có :
12
12
24
1
2
.
1
a
xx
a
a
xx
a

. Với
12
;xx
là hai nghiệm của (*)
Để tiếp điểm của hai tiếp tuyến nằm về hai phía đối với trục hoành thì
12
.0yy
1 2 1 2 1 2
1 2 1 2 1 2
2 2 4
2
24
2 2 2( ) 4
11
. 0 0 0
3
2 2 4
1 1 ( ) 1
1
1
11
aa
a
x x x x x x
aa
aa
x x x x x x
a
aa







Vậy với các điểm
(0; )Aa
thỏa mã
2
;1
3
aa
ta luôn kẻ được hai tiếp tuyến thỏa mãn đề bài
Bài 11. Cho hàm số
1
yx
x

có đồ thị
()C
. Tìm tập hợp các điểm mà từ đó kẻ được hai tiếp
tuyến đến đồ thị
()C
và hai tiếp tuyến y vuông góc với nhau.
Hướng dẫn
Gọi
(a;b)M
là điểm bt kì trong mặt phẳng tọa độ. Phương trình đường thẳng
d
qua M có hệ số
góc
k
là:
()y k x a b
.
d
là tiếp tuyến của đồ thị
()C
khi và chỉ khi hệ phương trình sau có nghiệm:
2
11
()
11
1 ; 1
k x a b x kx x ka b
xx
k kx x k
xx







. (1)
2 2 2
2( 2) 4 0 (2)a k ab k b
Từ
2
1
1k
x

ta thy với mỗi
1k
thì luôn có hai giá trị của x trái du, do đó hệ (1) có nghiệm
(2) có hai nghiệm
12
;1kk
.
Mặt khác, hai tiếp tuyến này vuông góc với nhau nên ta có
12
.1kk
.
Yêu cầu bài toán
(2)
có hai nghiệm phân biệt thỏa mãn :
12
12
.1
;1
kk
kk

2
22
2
0
0
4
14
(1) 0
a
a
b
ab
a
ab
f


.
Vậy tập hợp điểm
M
là đường tròn tâm
(0;0)O
, bán kính bằng 2, sau khi đã bỏ đi 4 điểm là
giao với các đường thẳng
0,x y x
.
Bài 12. Cho hàm số
2
2
1
x mx m
y
x

có đồ thị (C) . Tìm tt cả các giá trị thực của tham số
m
để từ điểm
(0;1)A
không kẻ được bt kì tiếp tuyến nào đến đồ thị
()C
.
Hướng dẫn
Phương trình tiếp tuyến của đồ thị
()C
tại điểm
00
( ; )M x y
là
22
0 0 0 0
0
2
00
2 4 2
()
( 1) 1
x x x mx m
y x x
xx

Tiếp tuyến không đi qua điểm
(0;1)A
nên phương trình
2
0 0 0
( 3) 2( 1) 1 0, ( 1) (*)m x m x m x
vô nghiệm hoặc có nghiệm
0
1x 
TH1:
3 0 3mm
ta có
0
1
2
x 
nên
3m
không thỏa mãn
TH2:
3m
.
(*)
vô nghiệm
' 0 1m
TH3:
(*)
có nghiệm
0
1x 
suy ra
20
(vô lý ).
Vậy
1m
thì không có tiếp tuyến nào của đồ thị
()C
đi qua A.
Bài 13. Viết phương trình tiếp tuyến của đồ thị hàm số
3
31y x x
biết tiếp tuyến đó đi qua
điểm
( 2; 1)A 
.
Hướng dẫn
Phương trình tiếp tuyến của đồ thị
()C
tại điểm
00
( ; )M x y
là:
23
0 0 0 0
(3 3)( ) 3 1y x x x x x
Tiếp tuyến đi qua điểm
( 2; 1)A 
nên ta có:
23
0 0 0 0
1 (3 3)( 2 ) 3 1x x x x
32
00
0
0
2 6 8 0
1
1
2 9 17
xx
x
y
x y x


Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là
1y 
và
9 17yx
Bài 14. Cho hàm số
3
4 3 2y x x
có đồ thị
()C
. Tìm trên đường thẳng
3y
các điểm mà
trên đó kẻ được ba tiếp tuyến đến đồ thị
()C
.
Hướng dẫn
Giả sử
( ;3)Am
là điểm trên đường thẳng
3y
thỏa mãn từ
A
kẻ được 3 tiếp tuyến đến đồ thị
(C).
Phương trình tiếp tuyến:
23
0 0 0
( 12 3)( ) 4 3 2y x x x x x
.
Tiếp tuyến đi qua
A
nên ta có:
23
0 0 0
3 ( 12 3)(m ) 4 3 2x x x x
Hay
32
00
2
0 0 0
8 12 3 1 0
1
(8 (4 12 ) 2 6 ) 0
2
x mx m
x x m x m



Yêu cầu bài toán
32
00
8 12 3 1 0x mx m
có 3 nghiệm phân biệt
2
00
(8 (4 12 ) 2 6 ) 0x m x m
có hai nghiệm phân biệt khác
1
2
1
'0
1
1
3
2
1
2
m
m
m
m




Vậy từ các điểm
( ;3)Am
thỏa mãn
11
( ; 1) ; \
32
m
 


kẻ được 3 tiếp tuyến đến đồ thị
(C).
Bài 15. Cho đồ thị hàm số
3
34y x x
có đồ thị
()C
. Từ điểm
(1;3)M
có thể kẻ được bao
nhiêu tiếp tuyến đến đồ thị
()C
.
Hướng dẫn
Phương trình tiếp tuyến của đồ thị
()C
tại điểm
00
( ; )M x y
là:
23
0 0 0 0
(3 12 )( ) 3 4y x x x x x
Tiếp tuyến đi qua
(1;3)M
nên ta có:
23
0 0 0 0
3 (3 12 )(1 ) 3 4x x x x
0
32
00
0
0
8 12 0
3
2
x
xx
x
Vậy qua M kẻ được hai tiếp tuyến đến đồ thị (C).
Bài 16. Cho hàm số
21
1
x
y
x
có đồ thị
(C)
và điểm
(1;2)I
. Tìm điểm
M
thuộc đồ thị
()C
có hoành độ lớn hơn 2 sao cho tiếp tuyến tại M vuông góc với đường thẳng
IM
.
Hướng dẫn
Gọi
0
0
0
21
;
1
x
Mx
x



thuộc
(C)
. Phương trình tiếp tuyến tại M là
0
0
2
00
21
1
()
( 1) 1
x
y x x
xx

Phương trình đường thẳng
2
0
1
: ( 1) 2
( 1)
MI y x
x
Tiếp tuyến tại
M
vuông góc với
MI
nên ta có:
0
22
0
00
0 ( )
11
.1
2
( 1) ( 1)
x loai
x
xx

Với
00
23xy
. Vậy điểm
(2;3)M
Bài 17. Cho hàm số
2
1
x
y
x
có đồ thị
C
và điểm
0;Aa
. Hỏi có tt cả bao nhiêu giá trị
nguyên của
a
trong đoạn
2
018;2018
để từ điểm
A
kẻ được hai tiếp tuyến đến
C
sao
cho hai tiếp điểm nằm về hai phía của trục hoành?
Hướng dẫn
TXĐ:
\1
Ta có :
2
3
1
y
x

Đường thẳng
d
đi qua điểm
0;Aa
, hệ số góc
k
có phương trình:
.
Để
d
là tiếp tuyến của
C
thì hệ phương trình
2
2
*
1
3
**
1
x
kx a
x
k
x

có nghiệm.
Thay (**) vào (*) ta được:
2
23
1
1
xx
a
x
x


2
1
2 2 2 0a x a x a
với
1x
.
1
Do từ
A
kẻ được hai tiếp tuyến đến
C
nên phương trình
1
có hai nghiệm phân biệt khác
1
.
1
2
3 2 0
1
1 2 2 2 0
a
a
a
a
a a a


.
2
Khi đó toạ độ hai tiếp điểm là
1
1
1
2
;
1
x
Mx
x



và
2
2
2
2
;
1
x
Nx
x



với
1
x
,
2
x
là nghiệm của
1
do
đó
12
22
1
a
xx
a

,
12
2
1
a
xx
a
.
Hai tiếp điểm nằm về hai phía của trục hoành khi:
12
12
22
.0
11
xx
xx


1 2 1 2
1 2 1 2
24
0
1
x x x x
x x x x

9 6 2
0
33
a
a
.
Kết hợp điều kiện
2
suy ra
2
3
1
a
a

nên trên đoạn
2
018;2018
số giá trị nguyên của
a
thỏa
yêu cầu bài toán là
2018
.
Bài 18. Gọi
S
là tập hợp các điểm thuộc đường thẳng
2y
mà qua mỗi điểm thuộc
S
đều kẻ
đượchai tiếp tuyến phân biệt tới đồ thị hàm số
2
1
x
y
x
đồng thời hai tiếp tuyến đó vuông
góc với nhau. Tính tổng hoành độ
T
của tt cả các điểm thuộc
S
.
Hướng dẫn
TXĐ:
\1
Ta có :
2
2
2
1
xx
y
x
2
1
1
11
x
yx
xx

Gọi điểm
;
2 : 2A a d y
. Đường thẳng
d
đi qua
A
có dạng
2y
k x a
Điều kiện tiếp xúc:
2
2
2
2
1
2
1
x
k x a
x
xx
k
x
2
2
1 4 4 0 *a k k
Để
2
tiếp tuyến vuông góc nhau thì phương trình ( * ) có 2 nghiệm
k
phân biệt và tích của hai
nghiệm đó bằng
1
2
4
1
1 a

3
1
a
a

Vậy tổng hai hoành độ là
2
.
BÀI TẬP TỰ GIẢI
Bài 1. Viết phương trình tiếp tuyến của đồ thị
2
yx
biết tiếp tuyến qua
0
; 1A
Bài 2. Viết phương trình tiếp tuyến của đồ thị
32
33y x x
biết tiếp tuyến qua
23
;1
9
B



Bài 3. Hãy viết phương trình tiếp tuyến của đồ thị hàm số
y
f x
, biết tiếp tuyến qua điểm
A
a)
2
4
1
xx
y
x
, với
1
; – 4A
. b)
42
2y x x
, với
0
; –1A
.
c)
3
31y x x
, với
1
; –6A
. d)
2
44
1
xx
y
x

, với
–1
; 0A
.
e)
42
69y x x
, với
0
; 9A
Bài 4. Tìm m để đường thẳng
1y mx
tiếp xúc
32
4y x x x
LỚP TOÁN THẦY THÀNH – NGÕ 58 NGUYỄN KHÁNH TOÀN – 0975.705.122
Bài 5. Tìm m để đường thẳng
7yx
tiếp xúc
2
1
xm
y
x
Bài 6. Viết phương trình tiếp tuyến với
2
:P
y x
, biết rằng tiếp tuyến đó đi qua điểm
0
; –1A
.
Bài 7. Cho hàm số
32
– 3 2y x x
. Viết phương trình tiếp tuyến của
C
, biết rằng tiếp tuyến
đó đi qua
0
; 3A
.
BÀI TẬP TỔNG HỢP:
Bài 1. Cho đường cong
3
( ):C y x
và hai điểm
1
; 1A
và
1
;1B x y
trên
()C
.
a) Tính hệ số góc của cát tuyến
AB
với
x
lần lượt là
0,1
và
0,01
b) Tìm hệ số góc của tiếp tuyến với
()C
tại
A
.
Bài 2. Cho hàm số
1
()y f x
x

. có đồ thị
()C
. Viết phương trình tiếp tuyến với
()C
, biết:
a) tiếp điểm có hoành độ bằng
2
b) Tiếp điểm có tung độ bằng
3
c) Hệ số góc của tiếp tuyến
–4k
. d) Tiếp tuyến song song với
: 9 2017d x y
e) Tiếp tuyến vuông góc với
: 4 2017d x y
. f) Tiếp tuyến qua điểm
8
; 0A
Bài 3. Cho Parabol
2
yx
và hai điểm
2
; 4A
và
2 ; 4()B x y
trên parabol đó.
a) Tính hệ số góc của cát tuyến
AB
biết
x
lần lượt bằng
1
;
0,1
và
0,001
.
b) Tính hệ số góc của tiếp tuyến của parabol đã cho tại điểm
A
.
Bài 4. Tìm hệ số góc của cát tuyến
MN
với đường cong
C
, biết:
a)
2
:2C
y x x
và hoành độ
, MN
theo thứ tự là
2, 1
MN
xx
.
b)
2
1
:
xx
Cy
x

và hoành độ
, MN
theo thứ tự là
1, 3
MN
xx
.
Bài 5. Viết phương trình tiếp tuyến của đồ thị hàm số
3
yx
, biết:
a) Tiếp điểm có hoành độ bằng
– 1
.
b) Tiếp điểm có tung độ bằng
8
.
c) Hệ số góc của tiếp tuyến bằng
3
.
Bài 6. Viết phương trình tiếp tuyến của đường hypebol
1
y
x
, biết:
a) Tại điểm
1
;2
2



.
b) Tiếp điểm có hoành độ bằng
–1
.
c) Hệ số góc của tiếp tuyến bằng
1
4
.
Bài 7. Cho đường cong
:C y x
. Viết phương trình tiếp tuyến của
C
:
a) Biết hệ số góc của tiếp tuyến bằng
1
.
b) Biết tiếp tuyến song song với
: – 4 3 0xy
.
Bài 8. Viết phương trình tiếp tuyến của đồ thị hàm số:
a)
1
1
x
y
x
, biết hoành độ tiếp điểm là
0
0x
.
b)
2yx
, biết tung độ tiếp điểm là
0
2y
.
Bài 9. Cho hai hàm số
1
2
y
x
và
2
2
x
y
. Viết phương trình tiếp tuyến với đồ thị của mội
hàm số đã cho tại giao điểm của chúng. Tính góc giữa hai tiếp tuyến kể trên.
Bài 10. Cho parabol
2
:P
y x
. Gọi
1
M
và
2
M
là hai điểm thuộc
P
lần lượt có hoành độ
1
–2x
và
2
1x
. Hãy tìm trên
P
một điểm
E
sao cho tiếp tuyến tại
E
song song với cát
tuyến
12
MM
. Viết phương trình tiếp tuyến đó.
Bài 11. Cho hàm số
32
32y x x
. Viết phương trình tiếp tuyến của đồ thị, biết rằng tiếp
tuyến vuông góc với đường thẳng
:3 –5 – 2017 0xy
.
Bài 12. Cho hàm số
42
:
– – 1
m
C y f x x mx m
. Tìm tt cả các giá trị của tham số
m
để
các tiếp tuyến của
m
C
tại
1
; 0A
và
–1
; 0B
vuông góc với nhau.
Bài 13. Cho hàm số
2
cos siny x m x
(
m
là tham số) có đồ thị
C
. Tìm
m
trong mỗi trường
hợp sau:
a) Tiếp tuyến của
C
tại điểm có
x
có hệ số góc bằng
1
.
b) Tiếp tuyến của
C
tại các điểm có các hoành độ
4
x

và
3
x
song song hoặc
trùng nhau.
Bài 14. Tìm giao điểm của hai đường cong
2
:1P
y x x
và
1
:
1
Hy
x
. Chứng minh
rằng hai đường cong đó có tiếp tuyến chung tại giao điểm của chúng.
Bài 15. Cho parabol
2
( ):P y x
. Viết phương trình tiếp tuyến với
P
, biết:
a) Tiếp tuyến song song với đường thẳng
: 4 3d y x
.
b) Tiếp tuyến đi qua điểm
0
; 1A
.
Bài 16. Viết phương trình tiếp tuyến của:
a)
1
1
x
y
x
tại điểm
2
; 3A
.
b)
32
41y x x
tại điểm có hoành độ
0
–1x
.
c)
2
44y x x
tại điểm có tung độ
0
1y
.
d)
21yx
tại điểm có hoành độ
0
4x
.
e)
2
2 15
3
xx
y
x

biết hệ số góc của tiếp tuyến bằng
3
4
.
f)
42
– 2 1y x x
biết hệ số góc của tiếp tuyến bằng
24
.
g)
32
32y x x
biết tiếp tuyến
: – 3 –15 0d D x y
.
h)
3
3y x x
tại điểm có hoành độ
0
–1x
.
i)
21
1
x
y
x
tại điểm có hoành độ
0
2x
.
Bài 17. Cho
32
:
1
x
C y f x
x

. Lập phương trình tiếp tuyến của
C
:
a) Tại điểm có hoành độ bằng
2
b) Tại điểm có tung độ bằng
5
2
c)
// : – 25d D y x
d)
: 4 – 2017d x y
.
Bài 18. Gọi
C
là đồ thị hàm số
42
21y x x
. Viết phương trình tiếp tuyến của
C
trong
mỗi trường hợp sau:
a) Biết rằng tiếp tuyến song song với đường thẳng
: –3 1d y x
.
b) Biết rằng tiếp tuyến vuông góc với đường thẳng
: – 7 2017xy
.
c) Biết rằng tiếp tuyến đi qua điểm
0
; 2A
Bài 19. Gọi
C
là đồ thị hàm số
32
52y x x
. Viết phương trình tiếp tuyến của
C
trong
mỗi trường hợp sau:
a) Biết tung độ của tiếp điểm bằng
2
.
b) Biết rằng tiếp tuyến song song với trục hoành.
c) Biết rằng tiếp tuyến vuông góc với đường thẳng
: 8 2017d x y
.
d) Biết rằng tiếp tuyến đi qua điểm
0
; – 6A
.
| 1/75
| | Tải xuống

Có thể bạn quan tâm:

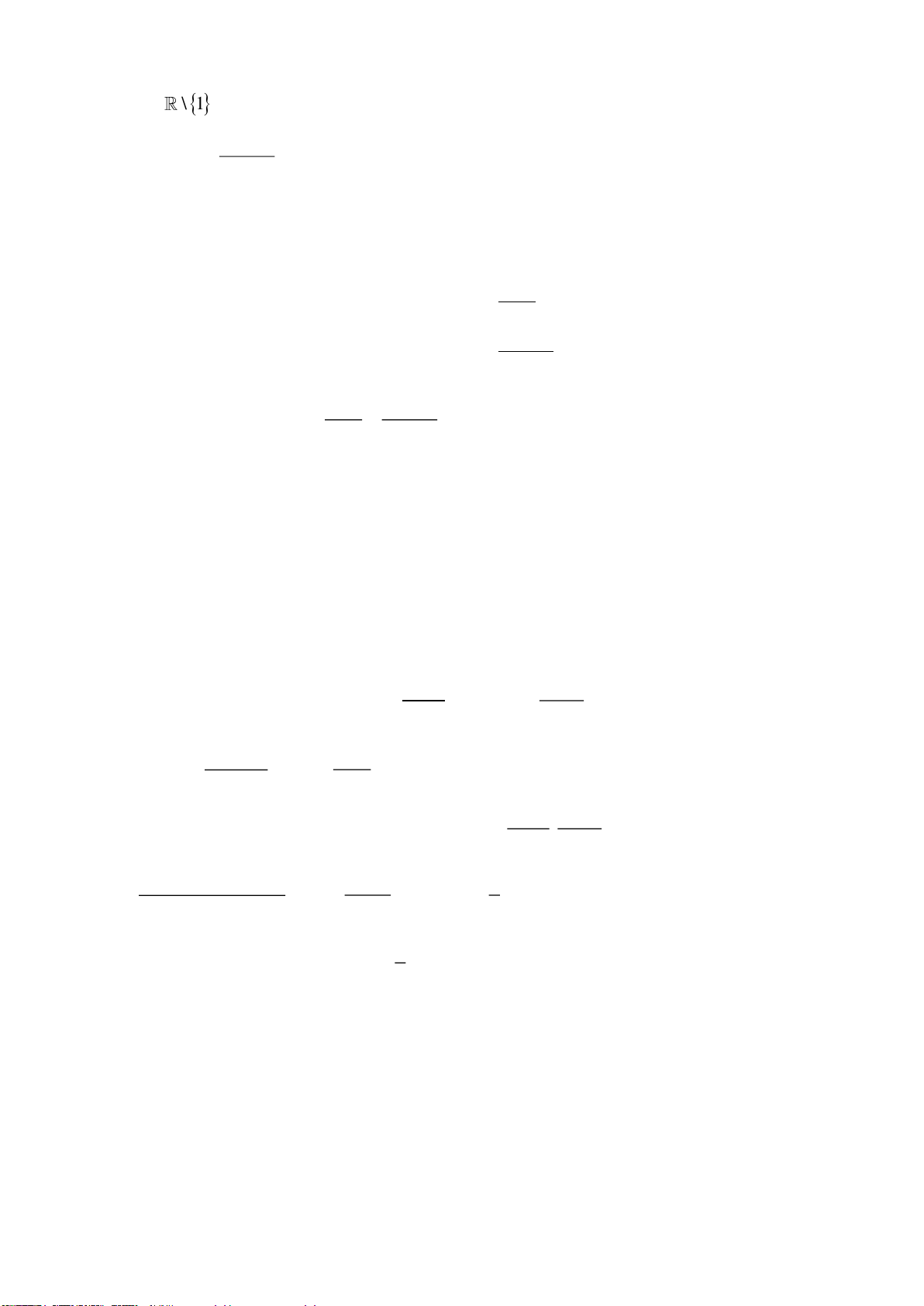
Preview text:

CHUYÊN ĐỀ 1 TÌM SỐ GIA Phương pháp:
Để tính số gia của hàm số y f (x) tại điểm x tương ứng với số gia x
 cho trước ta áp dụng 0
công thức tính sau: y
  f x x   f x 0   0 x
 gọi là số gia của đối số tại điểm x và x
  x x . 0 0 y
 gọi là số gia của hàm số tương ứng và y
  f x x   f x 0   0 BÀI TẬP MẪU
Bài 1. Tìm số gia của hàm số 2
y x x , tương ứng với sự biến thiên của đối số từ x  2 đến 0 x x   5 0 Hướng dẫn
Số gia của hàm số là y
  f x x
   f x   f  5  f  2    2 5  5    2 2  2  18 0 0 
Bài 2. Tìm số gia của hàm số 2
y x – 3x  4 tại điểm x  2 ứng với số gia x  , biết x   4 0 Hướng dẫn x   4 Vì 
x  x  6 0 x  2  0 Khi đó y
  f x x
   f x   f  6   f  2    2 6  3.6  4    2 2  3.2  4  0 0  y Bài 3. Tính y  và của hàm số 2
y x xx Hướng dẫn Ta có: y
  f x x
   f x    x x
 2   x x      2 x x      2 2 x  2 . x x   x   x x     2 x x  2  2 . x x   x   x  2 y  2 . x x   x   x     2x x   1 xx
Bài 4. Tìm số gia của hàm số   4
f x x khi x  1 , x   1 . 0 Hướng dẫn Ta có: y
  f x x
  f x f 2  f 1  4 4 2  1  15 0   0 
Bài 5. Số gia của hàm số   3
f x x x khi x  0 , x   1 . 0 Hướng dẫn Ta có: y
  f x x
  f x f 1  f 0   3    3 1 1 0  0  2 0   0  x
Bài 6. Tìm số gia của hàm số f x 3  theo số gia x
 của đối số x tại x  0 . 3 0 Hướng dẫn x  3  3 0  x  3 Ta có: y
  f x x
  f x f x
   f 0    0   0  3 3 3
Bài 7. Số gia của hàm số   2
f x x x ứng với x , x  là 0 Hướng dẫn 2 Ta có: y
  f x x
  f x  x x
  x x    2 x xx   x   2x 1 0  0 0 0 0  0   0 
Bài 8. Tìm số gia của hàm số f x 2
x  2 khi x  0 , x   2 . 0 Hướng dẫn Ta có: y
  f x x
  f x f 2  f 0  2    2 2 2 0  2  4 . 0   0  1
Bài 9. Số gia của hàm số f x 
khi, x  1 , x   1 . 3 0 x  1 Lời giải 1 1 7  Ta có: y
  f x x
  f x f 1  f 0    . 0   0  3 3 2  1 1  1 18
Bài 10. Tìm số gia của hàm số f x  x  1 theo số gia x
 của đối số x tại x  0 . 0 Hướng dẫn Ta có: y
  f x x
  f x f x
   f 0  x  1. 0   0  BÀI TẬP TỰ GIẢI
Bài 11. Tìm số gia của hàm số 2
y  2x  3x  5 , tương ứng với sự biến thiên của đối số:
a) Từ x  1 đến x x   2
b) Từ x  2 đến x x   0,9 0 0 0 0
c) Từ x  1đến x 1 x
d) Từ x  2 đến x  2  x  0 0 y Bài 12. Tính y  và
của hàm số sau theo x và x  : x
a) y  3x  5 b) 2 y  3x  7 c) 2
y  2x  4x 1 d) y  cos 2x
Bài 13. Tìm số gia của hàm số 2
y x –1 tại điểm x  1 ứng với số gia x  , biết: 0 a) x  1 b) x   –0,1 y Bài 14. Tính y  và
của hàm số sau theo x và x  : x a) 2
y  x  2x  3 b) 3
y x x  1 x  2 c) 3
y x  4x  5 d) y x  5 1  x 2 x e) y y  2x  f) 3 x  1 CHUYÊN ĐỀ 2 TÍNH ĐẠO HÀM Phương pháp:
Có hai cách để tính đạo hàm:
f x x
   f x
Cách 1: Dùng định nghĩa: y '  lim x  0  x
Cách 2: Dùng bảng công thức : ( bảng này thầy đính kèm ở file đầu tiên) BÀI TẬP MẪU
Bài 1. Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:
1) y  3x  5 2) 2
y x  4x 1 3) 3 2
y x  3x  5 2x  3 4) y  5) 2 y x x
6) y  cos 2x  3 x 1 Hướng dẫn
f x x
   f x
Sử dụng định nghĩa: y '  lim . x  0  x  1) Ta có:
f x x
   f x 3 x x
   53x  5 3 xy '  lim  lim  lim  3 x  0  x  0  x  0 xxx  2) Ta có:
f x x
   f x x x
 2  4x x   1 2 x  4x   1 y '  lim  lim x  0 x  0 xx  2 2 . x x   x   4. x   lim
 lim 2x x
  4  2x  4 x  0  x  0 x   3) Ta có:
f x x
   f x x x
 3  3x x  2 5 3 2
x  3x  5 y '  lim  lim x  0 x  0 xx  3 2 2 3 2 2 3 2
x  3x . x   3 . x x   x   3x  6 . x x   3 x
 5  x 3x  5  lim x  0  x  2 2 3 2 3x . x   3 . x x   x   6 . x x   3 x   lim  lim  2 2 3x  3 . x x   x
  6x  3 x   2  3x  6x x  0  x  0 x  4) Ta có: 2 x x    3 2x  3 
f x x
   f x x x   1 x 1 y '  lim  lim x  0 x  0 xx  2x  2 x
  3x  
1  2x  3 x x    1 2x  2 x   3 2x  3  x x    1  x       1 x x 1 x 1  lim  lim x  0 x  0 xx  2 2
2x  2x  2 . x x   2. x
  3x  3 2x  2 . x x
  2x  3x  3. x   3  lim x  0 x  x x    1  x   1 5  . x  5  5  lim    x   x  x x
  x   lim 1 1 x
   x x    1  x   1 x  2 0 0 1 5) Ta có:
f x x
   f x x x
 2  x x   2  x x y '  lim  lim x  0 x  0 xx  2 2 2 x  2 . x x   x   x x   x x  lim x  0 x   2 2 x  2 . x x   x   x x   2 x x  lim x  0 x   2 2 2 x  2 . x x   x   x x
  x x  2 2 . x x   x   x   lim x  0 x   2 2 2 x  2 . x x   x   x x
  x x  2x x  1 2x 1  lim  x  0  2 2 2 x  2 . x x   x   x x
  x x  2 2 x x 6) Ta có:
f x x
   f x cos 2   x x   3  cos  2x 3 y '  lim  lim x  0 x  0 xx  2
 sin 2x 3 x  .sin x   sin  x    lim  lim . 2  sin  2x 3 x    2  sin  2x3 x  0 x  0 xx
Bài 2. Sử dụng công thức, tính đạo hàm của các hàm số sau:
1) y  3x  5 2) 2
y x  4x 1 3) 3 2
y x  3x  5 2x  3 4) y  5) 2 y x x
6) y  cos 2x  3 x 1 Hướng dẫn
Các em tra bảng công thức để tính 1) Ta có:   
y  3x  5  y '  3x  5  3x  5  3  0  3 2) Ta có:   2  
y x x   y   2
x x     2 4 1 4 1
x   4x   
1  2x  4  0  2x  4 3) Ta có:  3 2
y x x   y   3 2 x x   2 2 3 5 3
5  3x  6x  0  3x  6x .   u
u .v u.v 4) (Sử dụng công thức    2  v v Ta có:   2x  3
2x 3 .x  
1  2x  3. x   1 2. x   1  2x  3.1 5  y   y    x 1 x  2 1 x  2 1 x  2 1  u
5) (Sử dụng công thức  u   ) 2 u Ta có:   2 x x 2x 1 2  y
x x y '   2 2 2 x x 2 x x
6) (Sử dụng công thức cos u  u  .sin u ) 
y  cos 2x  3  y  2x  3 .sin 2x  3  2  .sin 2x 3
Bài 3. Sử dụng công thức, tính đạo hàm của các hàm số sau: y   4 x   2
1 x x   1 Hướng dẫn  Sử dụng công thức  .
u v  u .v  . u v   y   4 x   1  2 x x   1  y   4 x   1 . 2 x x   1   4 x   1 . 2 x x   1 3  4x . 2 x x   1   4 x   1 .2x   5 4 3
1  6x  5x  4x  2x 1
Bài 4. Tính đạo hàm các hàm số sau: 3 a) 3 2
y x  3x  2x 1 d) 4 2 y  2  x x 1 2 2x 1 b) 3
y  x  3x 1 e) y x3 4 x 2 x  2x  2 c) 2 y   x 1 f) y  4 x 1 Hướng dẫn  a) Ta có: y   3
x x   2 3
1  3x  6x  2  b) Ta có: y   3
x x   2 3 1  3  x  3  4  x  c) Ta có: 2 3 y  
x 1  x  2x  4    3  d) Ta có: 4 2 3 y  2
x x 1  8  x  3x    2  (2x 1) (
x 3)  (x 3) (2x 1) 7  e) Ta có: y   2 2 (x  3) (x  3) 2 2
(x  2x  2) (
x 1)  (x  2x  2)(x 1) f) Ta có: y  2 (x 1) 2 2
(2x  2)(x 1)  (x  2x  2) x  2x  4   . 2 (x 1) x  2 1
Bài 5. Tìm đạo hàm của các hàm số sau : 2 2x  2020 1 1) y x x x   3 với  0 . 2) y 6 x với x  0 ; 2 x Hướng dẫn 2  2      2x  2020  2x  2020 x 4x 3 4 1)  x x    x x x x x  3            3  .     2 3 2 3    2) 1 3 2 6 x      . 2 3  x x x
TÍNH ĐẠO HÀM HÀM HỢP Phương pháp:
Ta sử dụng định lý sau:
Nếu hàm số u g x có đạo hàm tại x là u và hàm số y f u  có đạo hàm tại u là y thì x u
hàm hợp y f g x có đạo hàm tại x là y  y.u . x u x
Từ đó, ta có các công thức đạo hàm của hàm hợp thường gặp: với u u x      1  un u  n 1  .  n u .u   n      u u     2 u 2  u u BÀI TẬP MẪU
Bài 1. Sử dụng công thức, tính đạo hàm hàm hợp của các hàm số sau: 5
1) y   x x 2016 2 2 3
2) y  2 x 34 1 3)    2 7 y x x
4) y  x x 5 2 1 Hướng dẫn
1) Sử dụng công thức:    u  1
 .u .u  Ta có: y   x x 2016 2 2 3     y 
x x  x x2015 3 2016. 2 3 . 2 3  2016. 4x  . 
 2x  3 x 2015 2 2 2  2 x   1    1 
2) Chú ý bài này các em phải chuyển đổi:   1  u     .u .u      . uu  5  y   5. 2 x  3 4   4 2 x 3        y
x   4     x    x     4 1 ' 5. 2 3 5. 4 . 2 3 . 2 3        x   5   x   5 1 20 20.2. . 2 3 . 2 3 2 x x
3) Sử dụng công thức    u  1
 .u .u  
y   x x2 7  y   7 x x  7
x x   6 x    7 2. . 2 7 1 . x x  1    1  4) Sử dụng công thức   1  u     .u .u      uu  1  y   x x 1 5   5 2
 2x x 1   
y   x x   x x   6    x   x x   6 2 2 2 5. 1 . 1 5 2 1 . 1
Bài 2. Tính đạo hàm của các hàm số sau: 3  5  a) yx x2 7   .
b) y    x 5 3 1 . c) y  4x    . 2  x Hướng dẫn
a) Ta có: y   7 x x  7
x x   7 x x 6 2 . 2 7x   1 . 4 4  b) Ta có: y   3  x   3  x  2 5 1 1  1  5x  3 1 x  . 2 2   5   5   10  5 
c) Ta có: y  3 4x  4x   3 4  4x         . 2 2 3 2  x   x   x  x
Bài 3. Tính đạo hàm của các hàm số sau: a) 2
y  1 2x x . b) 3 2
y x  3x  2 . Hướng dẫn   2
1 2x x  1 x a) Ta có: y   . 2 2 2 1 2x x 1 2x x  3 2 x 3x 2   2 3x  6x b) Ta có: y   . 3 2 x  2 3x  3 2 2 x  2 3x  2
Bài 4. Tính đạo hàm của các hàm số sau: 3 1 a) y y   . b) . 2x  52
x x 5 2 1 Hướng dẫn
3 2x  52  12   2x 5 12 a) Ta có: y        . 2x  54 2x 54 2x 53   2 x x  5 1   5   2 x x  4 1 . 2 x x   1 52x   1
b) Ta có: y       .   2
x x 10 1 x x x x    6 5 2 2 2 1 1
Bài 5. Tính đạo hàm của các hàm số sau: 3  2x 1 4 5 a) y    . b) y   2
5x  4x   1 7x  3 .  x 1  Hướng dẫn 2 2 
 2x 1  2x 1  2x 1 3  92x  2 1
a) Ta có: y  3   3          .
x 1   x 1 
x 1  x  2 1 x  4 1  4  4 5 5 b) Ta có:  y   2
x x     x     x     2 5 4 1 7 3 7 3
5x  4x   1     .
y   x x  3  x   x     x  
x x 4 5 4 2 2 4 5 4 1 10 4 7 3 5 7 3 .7. 5 4 1 .
y   x x  3  x  4 2
  x   x    2 5 4 1 7 3 4 10 4 7 3 35 5x  4x   1 .
y   x x  3  x  4 2  2 5 4 1 7 3
455x 132x  83.
Bài 6. Tính đạo hàm của các hàm số sau: x a) y
với a là tham số.
b) y   x  3 2 . 2 2 a x Hướng dẫn 2 x 2 2 a x  2 2 2 a x a a) Ta có: y    . 2 2 a x  a x 3 2 2   x  23  3 x  22 3 x  2 b) Ta có: y    .  x  3 x  3 2 2 2 2 2 x
Bài 7. Cho hàm số y  , tính y0 . 2 4  x Hướng dẫn x 2 4  x x 2 4  x 4 Ta có: y    . Suy ra y  1 0  . 2 4  x 2  4x 3 2 2 2 3x  2x 1
Bài 8. Cho hàm số y  , tính y0 . 3 2 2 3x  2x 1 Hướng dẫn    2
3x  2x   3 2
1 .2 3x  2x 1   2
3x  2x   1 . 3 2
2 3x  2x 1 Ta có: y 
2 3x 2x 12 3 2  x x
6x  2 2 3x  2x 1  3x  2x   2 9 4 3 2 2 1 3 2 3x  2x 1 y   .
2 3x  2x 12 3 2 12x  4 3 2
3x  2x   1   2
9x  4x 2
3x  2x   2 1 9
x  8x  4 y   . 4 3 2
3x  2x   3 2 3 2 1 3x  2x 1 4 3x  2x 1 Suy ra: y  4 0  1. 4
x 2x 4 3 1
Bài 9. Cho hàm số y  , tính y1 . 2 3x 1 Hướng dẫn
x x 3 x   3x 4 2 1 3 2 3x 1 
x 2x 4 3 2 2 3 1 2 x  Ta có: 3 1 y  . 2 3x 1
4 x  2x  3
1 3x  23x  
1  3x x  2x  4 3 2 2 3 1 y   . 2 3x   2 1 3x 1
x 2x 3 3 1 4 2 3x  2 2 3x   1  3x  3 x  2x   1 y   . Suy ra y  1  0 . 2 3x   2 1 3x 1 BÀI TẬP TỰ GIẢI
Bài 10. Tính đạo hàm của các hàm số sau bằng định nghĩa: x  4 1) 2
y x  6x 1 2) 2
y x x 3) y x4 4) 4 2
y x  2x x  3 5) y x  5
6) y  sin 2x  4 1
7) y  cos 4x  2018
8) y  tan 5x  2 9) y x1
Bài 11. Tính đạo hàm của các hàm số sau: 3 a) 7 4 2
y x  3x  4x  4 x  4 b) 4 y  2x  10x  25 x c) y   2
x x   2 1 2
x  3x   1
d) y  2 x   1 4 x   3 3x 1 2 2x  3x  7 e) y  f) y  4x  5 2 x  2x  3
Bài 12. Tính đạo hàm của các hàm số sau: 21 23
a) y  2x  3  x  4 b) 3 2
y  4x  3x  2
Bài 13. Tính đạo hàm của mỗi hàm số sau ( a là hằng số): 1 1 1 1 a) 4 3 2 3 y x x
x x a b) y  c) 5 2
y  3x (8  3x ) 4 3 2 2 5 (x x 1) 2x 5x  3
d) y  (x 1)(x  2)(x  3) e) y  f) y  2 x 1 2 x x 1 1 2 x 1 g) y  h) y  i) 2
y  2  5x x x x x 1 x x j) 2
y x x x 1 k) y  l) y  1 x 2 2 a x
Bài 14. Tính đạo hàm của các hàm số sau: 3 2 x x 2 4 5 6 2 3x  6x  7 a) y    x 5 b) y     c) y  3 2 2 3 4 x x x 7x 4x  2  1 x 2
x  7x  5 d) y   3x x    1 e) y  f) y   x  1 x 2 x  3x 2 x 1 2 x  2x  2 g) y  h)    32 2 y x x i) y x x 1 5x  3 j) y  2 x x 1
Bài 15. Tính đạo hàm của các hàm số sau: 2 2x  3x 1 2 x  6x 1
a) y  x x  5 2 4 1 b) y  c) y  2x  3 2 x x 1 2 x x  3 1 x 2  x d) y  e) y  f) y  2x 1 1 x 1 2 x 2 1 x x x g) y  h) y
i) y   x   2 1 x x 1 2 1 x x 2 x 1 CHUYÊN ĐỀ 3
TÍNH ĐẠO HÀM CỦA HÀM SỐ TẠI Xo Phương pháp: f x f x
Cách 1: Sử dụng định nghĩa tính đạo hàm tại
là: y x  lim 0     0 xx  0 x x0
Cách 2: Các em sử dụng công thức tính đạo hàm rồi thay vào. BÀI TẬP MẪU
Bài 1. Tính đạo hàm của hàm số 2
y x  2x tại x  5 . 0 Hướng dẫn
Cách 1: Sử dụng định nghĩa: 2 2     y f x f x x 5   5 2 5 2.5  lim  lim x5 x5 x  5 x  5 2 x  2x  35
x 5x 7  lim  lim 12 x 5  x 5 x  5  x  5
Cách 2: Sử dụng công thức tính đạo hàm rồi thay số:  Ta có: 2
y x x y   2 2
x  2x  2x  2
Do đó y5  2.5  2 12 .
Bài 2. Tính đạo hàm của hàm số y   0
sin 2x  30  tại 0 x  60 . 0 Hướng dẫn
Cách 1: Sử dụng định nghĩa:  x   y 60  sin  0 2 30  0 sin 90 0  lim0 0 x60 x  60 2 cos  0 x  30 .sin  0 x  60  sin  0 x  60  0 0 0  lim  lim .2 cos x  30  2cos 60  30  0 0 0 0 0     x60  x60 x 60 x  60
Cách 2: Sử dụng công thức tính đạo hàm rồi thay số:  Ta có: y   0 x   y   0 x    0 x     0 sin 2 30 2 30 .cos 2 30 2.cos 2x  30 
Do đó y 0    0 0 60 2 cos 60  30   0 .
Bài 3. Tính đạo hàm (bằng định nghĩa) của mỗi hàm số sau tại các điểm đã chỉ ra: 1 a) 2
y x x tại x  1
b) y x tại x  1 c) y  tại x  0 0 0 2 0 x  1 1 d) y  tại x  2 e) 2 y x  3 tại x  1 0 0 x  1 Hướng dẫn y
f x x   f x f 1 x    f   1 0   0 
a) Ta có: f 1  lim  lim  lim x  0  xx  0  xx  0  x  1 x  2 1 x    2 1   1  lim  lim  x    1  1 x  0  xx  0  y
f x x   f x f 1 x    f   1 0   0 
b) Ta có: f 1  lim  lim  lim x  0  xx  0  xx  0  x  1  x  1     1 x 1 1 1 lim  lim  lim  x  0  xx  0  x   1 x    1 x  0   1 x    1 2 y
f x x   f x f 0  x    f 0 0   0 
c) Ta có: f 0  lim  lim  lim x  0  xx  0  xx  0  xy
f x x   f x f 2  x    f 2 0   0 
d) Ta có: f 2  lim  lim  lim x  0  xx  0  xx  0  x  1 1   x   2 1 2 1     x 1 1 lim  lim  lim  x  0  xx  0  3. x   3. xx  0  3. x   3 9 y
f x x   f x f 1 x    f   1 0   0 
e) Ta có: f 1  lim  lim  lim x  0  xx  0  xx  0  x   x   2 2 1  3  1  3  x  2  2 x   4  2  x  2    2 x lim  lim  lim x  0  xx  0  xx  0    x  .  x  2  2 x   4  2   x   2 1  lim  x  0   x  2 2  2 x   4  2
Bài 4. Tính đạo hàm của hàm số : x  2  2  a) y x y  
 3x( x 1) x tại  1 . b) tại x 1 ; 1  x    Hướng dẫn   x  
x 2.x 1 x 2x 1 2 a)     x 1    x  2 1
1 .x 1 x 2 2 x
x 1 2x  4 x 1 x  4 x     . x  2 1
2 x x  2 1
2 x x  2 1 1
Vậy đạo hàm của hàm số tại x  1 là : y  1  2 .  2     2   2   b)  3x
x  1  3x . 
x  1 3x x        1  x    x   x   1   2  1    3 . x 1   3x     2    x   x  2 x 5
Vậy đạo hàm của hàm số tại x  1 là : y  1  2 . BÀI TẬP TỰ GIẢI
Bài 5. Tính đạo hàm của hàm số 2
y x  2x  4 tại x  2 0
Bài 6. Cho hàm số y f x 2  2x 1
a) Tìm đạo hàm của hàm số tại x  2
b) Suy ra giá trị 3 f (  2) 5 f (2 3) 0
Bài 7. Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau tại điểm x0:
a) y  2x 1 tại x  2 b) 2
y x x tại x  1 0 0 x 1 c) y  tại x  0
d) y  2x  7 tại x  1 0 0 x 1
Bài 8. Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau (a là hằng số): 1
a) y ax  3 b) 2 y ax 2 1 1 c) y  với x
d) y  3  x với x  3 2x 1 2
Bài 9. Tính đạo hàm của hàm số tại điểm x được chỉ ra bằng cách sử dụng công thức tính đạo 0
hàm rồi thay x vào : 0 2 x 1 1) 5 3
y x  2x  3x  5 tại x  2 2) y  tại x  10 0 x 1 0     3) 2 y
x  4x 1 tại x  5
4) y  sin 2x  tại x  0    4  0 6 x  2 5) y  tại x  2  6) y   2 x x 4 3
x  2 tại x  3  0 0 x  5 CHUYÊN ĐỀ 4
ĐẠO HÀM CỦA HÀM LƯỢNG GIÁC Phương pháp:
Sử dụng công thức tính đạo hàm của hàm lượng giác: Đạo hàm Hàm hợp
(sin x) '  cos x ; (cos x) '   sin x
(sin u) '  u '.cos u 1 1 u ' (tan x) '  ; (cot x) '   (cos u) '  u
 'sinu ;  tan u '  2 cos x 2 sin x 2 cos uu ' x  1 arcsin '   cotu '   2 2 1  x sin u    nu n 1 sin  . n sin  . u sin ux  1 arccos '   2 1  xn n 1   
cos u  .ncos .ucosux  1 arctan '  2 x  1   nu n 1 tan  . n tan  . u tan u   nco u n 1 t  . n co t  .
u co t u
I. Sử dụng công thức để tính đạo hàm hàm lượng giác: BÀI TẬP MẪU
Bài 1. Tính đạo hàm của hàm số : x
1) y  sin 2x  cos . 2) y   x  2 sin 5 1 3 3) y  sin . x cos 4x 4) 2 2
y  2 tan x  5cot x Hướng dẫn 1 x
1) Ta có: y  2.cos 2x  sin 3 3 
2) Ta có: y  2sin 5x   1 sin 5x  
1  10 cos 5x sin 5x   1 .  
3) Ta có: y  sin x .cos 4x  sin .
x cos 4x  cos .
x cos 4x  4sin . x sin 4x . 1
Ngoài ra các em có thể tách y  sin . x cos 4x
sin5x sin3x sau đó tính đạo hàm. 2 2sin x 5x 4) Ta có: y '   3 2 2 cos x sin x
Bài 2. Tính đạo hàm của hàm số :
1) y  sin 3x
2) y  5sin x  3cos x
3) y  cos 2x 1    
4) y  sin(x  )  cos  x  
5) y  4cos 2x  5sin(2x  3)
6) y  3 sin x  cos x  2019x 3  6     7) 2
y x .cos 3x 2  xsin 3x 8) 2 2 y  3  sin 3x   cos 2x 1    4  x 1 9) y  tan 2x
10) y  cot 3x   1 11) y  tan 2 x 12) 2 y  cot x 1 13) y  tan
14) y  3cos x  cot 2x 3 1 1
15) y  tan 5x  cot 4x 16) y   2
tan x  2 x   1 17) 3 5
y  tan x  tan x  tan x 3 5 18) 2
y  tan(2x 1)  x cos x Hướng dẫn
1) Ta có y  sin 3x y  3cos 3x
2) Ta có y  5sin x  3cos x y  5cos x  3sin x x
3) Ta có y  cos 2x  sin 2 1 1  y   2x 1      
4) Ta có y  cos x   sin  x     .  3   6  5) Ta có y  8
 sin 2x 10cos2x 3 .
6) Ta có : y  3 cos x  sin x  2019 7) Ta có : 2 y  x x x x x x x x x   2 2 cos 3 3 sin 3 2 sin 3 6 cos 3 8 cos 3
2  3x sin 3x 8) Ta có:          3.2sin 3x  cos 3x  3sin 2 3x         4   4  2x  4  2x 2 2 y   sin 2x 1.   sin 2x 1 . 2 2         2 2x 1 2 2x 1 2 3  sin 3x  2 3  sin 3x       4   4  2
9) Ta có: y '  tan 2x'  . 2 cos 2x ' 3
10) Ta có: y '  cot  3x   1     . 2 sin 3x   1 '  x 1 '    x 1   2  1 11) Ta có y '  tan      2   x 1  x 1 2 2 cos 2 cos      2   2  x x 1 x x 12) Ta có: y   x    ' 2 ' 2 2 1 ' cot 1       2 2 2 2 2 2 2 sin x 1 sin x 1 x 1.sin x 1 '  x  1 13) Ta có: y '  tan    .  3 x  2 3cos 3 2
14) Ta có: y '  3cos x  cot 2x'  3  sin x  . 2 sin 2x 5 4
15) Ta có: y '  tan 5x  cot 4x'   . 2 2 cos 5x sin 4x ' 1 2 2x   x  2 x 1 x 2x x 1
16) Ta có: y '  tan  2
x  2 x   1      2 cos  2
x  2 x   1 2 cos  2
x  2 x   2 1 x cos  2
x  2 x   1 17) Ta có: 6
y '  1 tan x 18) Ta có: 2 y '   2 2
cos x  2x sin x cos x 2 
 cos x xsin 2x 2 2 cos (2x 1) cos (2x 1) BÀI TẬP TỰ GIẢI
Bài 1. Tính đạo hàm của các hàm số sau: x 2 a) 2
y  2sin x  sin 2x  sin x  2sin sin 2 x b) 2 y   2 sin
2x  3x   1 c) y   2 sin 4x x
Bài 2. Tính đạo hàm của các hàm số sau: cos x 3cos x 2 x  2 cos x
a) y  2 x sin x  b) y  c) y x 2x 1 sin x 2cos x  sin x tan x cot x d) y  e) y  f) y  3sin x  cos x sin x  2 2 x 1 g) y   2
sin x  3x  2
h) y  cos 2x 1
i) y  2sin 3x cos 5x x 1 j) y  cos 2x k) y  tan l) 2 y  cot x 1 2 x sin x x m) 3
y  tan x  cot 2x
n) y  1 2 tan x o) y   x sin x 2 sin x p) y
q) y  tan(sin x) r) y x  2 cot x   1 1 t an2x  s) 2 y  cos  2x
t) y x sin 3x u) 2 2
y  tan x  tan x 4 v) y   2
2  x cos x  2x sin x
Bài 3. Tính đạo hàm của các hàm số sau: a) y   2 sin 1 x  b) 2
y  sin cos 3x c) 2
y  cos x 1 sin x 1 x  2 2 sin x tan x
d) y  cos cos cos x   e) 2 y  cos     f) y   1 x   1 cot x 1 tan x x 2 sin x g) y  h) y  i) 2 y  1 cos x sin x  cos x cos x
Bài 4. Tính đạo hàm của các hàm số sau: 20 sin x x 2 1 tan x  1 cos x a) y  b) 2 y  1 cos c) y    d) y  1 cos x 2 2 1 tan x  1 cos x
e) y x sin x  cos x f) 3 2
y  3 tan x  tan 3x  tan x  tan x g) y x  2 cot x   1 sin x  cos x 2 2
sin 2x  4 cos x  4 h) 3
y  cot 2x  3cot 2x i) y  j) y  sin x  cos x 2 2
sin 2x  4 cos x
Bài 5. Tính đạo hàm của mỗi hàm số sau:
a) y  5sin x  3cos x b) 2
y  sin(x  3x  2)
c) y  cos 2x 1 d) y  sin 3 . x cos 5x
e) y  1 2 tan x
f) y  tan 3x  cot 3x x
g) y  4sin x  3cos x h) 2 4
y  4sin x  3cos x
i) y  1cos x 1 1 1 1 1 1
Bài 6. Tính đạo hàm của hàm số sau: y   
 cos x , với x( ; 0  ) 2 2 2 2 2 2
II. Tính đạo hàm của hàm lượng giác tại x0 Phương pháp:
Tính đạo hàm rồi thay x vào 0 BÀI TẬP MẪU sin 2x
Bài 1. Tính đạo hàm của hàm số y  tại x  . cos 3x 4 Hướng dẫn   
sin 2x .cos3x  sin 2 . x cos3x 2 cos 2 .
x cos 3x  3sin 2 . x sin 3x Ta có : y   cos3x2 cos3x2     Khi đó : y  3 2   x  là 3 2 .  4 
. Vậy đạo hàm của hàm số đã cho tại 4 
Bài 2. Tính đạo hàm của hàm số y  .
x cos 2x tại x  . 2 Hướng dẫn
Ta có: y  x .cos 2x  .
x cos 2x  cos 2x  2 . x sin 2x     Khi đó : ' y  1   
. Vậy đạo hàm của hàm số đã cho tại x  là 1  .  2  4 
Bài 3. Tính đạo hàm của hàm số y  5sin x  3cos x tại điểm x  . 2 Hướng dẫn   
Ta có y  5sin x  3cos x  5.sin x  3cos x  5.cos x  3sin x .      Suy ra y  5.cos  3sin  3   .  2  2 2 
Bài 4. Tính đạo hàm của hàm số y  2sin 3x cos 5x tại điểm x  . 8 Hướng dẫn
Ta có y  2sin 3x cos 5x  sin 8x  sin 2x .
y  sin8x sin 2x'  8cos8x  2cos 2x           y  8cos 8.  2cos 2.  8   2       .  8   8   8  1    
Bài 5. Tính đạo hàm của hàm số 2 y   sin  x   tại điểm x  . 2  3  3 Hướng dẫn 2     2         Ta có y '  . x cos  x y      cos       .  3  3 3  3 3  3         2    
Bài 6. Cho hàm số y  cos 3x   sin  2x   
 . Tính y  .  6   3   3  Hướng dẫn     2  Ta có: y  3  sin 3x   2cos  2x     .  6   3          2   5 7 Vậy y  3sin 3.   2cos 2.  3  sin 2cos0         .  3   3 6   3 3  6 2 1 
Bài 7. Tính đạo hàm của hàm số f x 2
 cot x tại điểm x  . 2 2 Hướng dẫn  1  2 x x
Ta có: f ' x     2 2 2 2 2 sin x sin x     2  2 Suy ra: f '          2    2 2 2   sin    2  
Bài 8. Tính đạo hàm của hàm số f x 2 2
 tan x  cot x tại điểm x  . 4 Hướng dẫn 1  1
 2 tan x 2cot x
Ta có: f ' x  2 tan . x  2cot . x      2 2 2 2 cos x
 sin x  cos x sin x   2 tan 2 cot    Suy ra: 4 4 f '    8    4    2 2 cos sin 4 4 
Bài 9. Tính đạo hàm của hàm số f x  cot x 1 tại x  . 2 Hướng dẫn cot x 1 1
Ta có: f ' x   cot x 1  ' '    2 2 cot x 1 2 sin . x cot x 1    1 1 Suy ra f '        2    2 2 2 sin . cot 1 2 2 
Bài 10. Tính đạo hàm của hàm số f x 3
 tan x  cot 2x tại điểm x  . 4 Hướng dẫn 1 2
Ta có: f ' x  tan x  cot 2x' 3 2  3.tan . x  2 2 cos x sin 2x     1 2 Suy ra 2 f '  3.tan .   4    4  4   2 2 cos sin 2. 4 4 
Bài 11. Tính đạo hàm của hàm số f x  tan x  cot x tại điểm x  . 4 Hướng dẫn 1 1   2 2
(tan x  cot x) Ta có: cos x sin ( ' ) x f x  
2 tan x  cot x
2 tan x  cot x 2 2 sin x  cos x 2  cos 2x   2 2 2
2sin x cos x tan x  cot x
sin 2x tan x  cot x  2  cos    Suy ra 2 f '   0    4       2 sin tan  cot    2  4 4 BÀI TẬP TỰ GIẢI
Bài 1. Tính đạo hàm của các hàm số sau tại điểm được chỉ ra . 1 sin x  cos x  1) y  tại x  2) y  tại x  1 sin x 3 sin x 1 2  3) 2
y  2x cot x x tại x
4) y  1 2 tan x tại x  0 4 3 x 5 5) y  sin 3 . x cos 4x tại x  6) y   x   2 2cos sin 2
cos x  tại x  4 2 6      7) 2 3 y  sin . x cos x tại x  8) 3 y  tan 2x    tại x  3  4  4   9) 2 y   2 sin
cos tan x tại x  10) 2 2 y  cot x 1 tại x  4 3  11) 3 2 y  sin
x 1 tại x  0 12) 2
y  sin cos 3x tại x  3  x Bài 2. Cho hàm số 3
y x và y  4x  sin . Tính tổng f (  1)  g (1) ? 2
III. Chứng minh biểu thức có chứa đạo hàm hàm lượng giác. Phương pháp:
Tính đạo hàm rồi thay vào biểu thức và biến đổi. BÀI TẬP MẪU
Bài 1. Chứng minh rằng : '
f x  0 với 6 4 2 2 4 4
f (x)  cos x  2sin . x cos x  3sin .
x cos x  sin x . Hướng dẫn Cách 1 : Ta có :     f x   6 x   4 2 x x   2 4 x x   4 ( ) cos 2sin .cos 3sin .cos sin x 5   x x   3 2 4 6.sin .cos 8.cos . x sin .
x cos x  4.sin . x sin . x cos x  4 2 3 x x x x x x 3 6.cos .sin .cos 12.sin .sin .cos  4.cos . x sin x 5 3 3 5 5 3 3 3 =  6.sin . x cos x  8sin . x cos x  4sin .
x cos x  6sin . x cos x 12sin .
x cos x  4.cos . x sin x 3 3 3   x x x x  2 x   3 3 3 3 4 sin .cos 4 cos .sin . sin 1  4  sin .
x cos x  4 sin . x cos x  0 Cách 2 : Ta có : f x 4  sin x 2 1 2 cos x 4  cos x 2 2
3sin x  cos x 4 sin x 2 1 2 cos x 4  cos x 2 1 2sin x 4 4 4 2 2 4
sin x  cos x  2sin x cos x  2sin xcos x
cos x  sin x2 2 2 2 2 2 2
 2sin x cos x  2sin xcos x 2 2
cos x  sin x 1
Khi đó : f  x  0
Bài 2. Cho hàm số y x sin x . Chứng minh: .
x y  2  y  sin x  x 2cos x y  0 Hướng dẫn  
Ta có: y   x sin x  x .sin x  .
x sin x  sin x x cos x . .
x y  2 y  sin x  x 2cos x y 2
x .sin x  2sin x xcos x sin x  x2cos x xsin x 2 2
x sin x  2xcos x  2xcos x x sin x  0 (đpcm).
Bài 3. Cho hàm số y  cot 2x . Chứng minh: 2
y  2 y  2  0 Hướng dẫn  Ta có: y   x    2  x    2 cot 2 2 1 cot 2 2 1 y  2
y  2y  2  0 .
Bài 4. Cho hàm số y  tan x . Chứng minh: 2
y  y 1  0 Hướng dẫn  Ta có: y   x 2 2 tan
1 tan x 1 y 2
y  y 1  0 . sin  cos 3 cos Bài 5. Cho hàm số  x x x y
.Chứng minh rằng: '  .tan   x y y x tan x 2 sin x Hướng dẫn
Ta tiến hành rút gọn trước khi tính đạo hàm:
x sin x  cos x
xsin x  cos x.cos x 1 y    . x cos x   sin x tan x sin x sin x ' cos x cos x
y  cos x xsin x
 cos x  xsin x  2 2 sin x sin x  cos x 2 1 sin cos x x  3 cos x
VT  xsin x
xsin x  cos x    VP 2 2 2 sin x sin x sin x
Bài 6. Cho hàm số y   2 cot x   1 . Chứng minh rằng: ' y y x  4 2 .
. 1 y   0 . Hướng dẫn Ta có: cot x 1 1
 1 cot x 1 . x 1
x 1 cot x 1 '    '      ' 2 2 2  2  2  y    2 cot  2 x   1 2 cot  2 x   1 2 cot  2 x   1 2 2 xx VT  2  cot  1 cot 1 2 x      4 1 .  x x y 2 cot  . 2 x   1  x 2 1 cot  2 x   1 2  x  . x cot  2 x   1  0  VP
Bài 7. Cho hàm số f x 2  2cos 4x   1 . Chứng minh rằng: '
f x  8, x   . Hướng dẫn Ta có: ' f x  1  6sin 4x   1 cos 4x   1  8  sin 8x  2 '
f x  8
 sin 8x  2  8 sin8x  2  8      x   1 k sin 8
2  1  8x  2 
k2  x     2 16 4 8
Dấu "  " xảy ra khi:  k         x   1 k sin 8 2  1
  8x  2    k2  x     2 16 4 8
sin x x cos x
Bài 8. Cho hàm số y
. Chứng minh rằng: y x x x2 ' 2 2 sin cos  x y  0 .
cos x x sin x Hướng dẫn
sin x x cos x Ta có: y  .
cos x x sin x
sin x xcos x' cos x xsin xsin x xcos xcos x xsin x' ' y
cos x xsin x2 ' ' Tính  x x x ' sin cos
 cos x x cos x  .
x cos x  x sin x ' ' Tính  x x x ' cos sin
 sin x x sin x xsin x  xcos x x sin .
x cos x x sin x  sin x x cos x 2 x cos x x '  y  
cos x xsin x2
cos x xsin x2 2 2   2 x 2 sin x x cos x  Ta có: '
VT y sin x x cos x 2 2  x y
. sin x x cos xx .  0  VP   2   2
cos x xsin x
 cos x xsin x Bài 9. Cho hàm số 2
y  cot x 1 . Chứng minh rằng: ' 2 2
y . x 1  x  . x y  0 . Hướng dẫn Ta có: 2 y  cot x 1    x  x y
1 cot  x 1 . x 1  1 cot  x 1  ' 2 ' 1 ' 2 2 2 2 2 .   2 1 cot  2 x 1 2 2  2 x 1 x 1 Ta có: x VT   2 1 cot  2 x 1 2 2
. x 1  x  . x cot  2 x 1 2
 x x cot  2x 1 2  x  . x cot  2 x 1  0 2  x 1         
Bài 10. Cho hàm số y  cos x . Chứng minh rằng: ' ' ' 2 f x f x
f 0  f 2x         3   6   6  Hướng dẫn
Ta có: f x   x' ' cos  sin x             ' '
VT  2 f x f x   2  sin x  sin  x          3   6   3   6         2   2  sin x  .cos x   sin 2x         3   3   3      2   5   sin 2  x   sin 2x   cos 2  x         3   3   6           '  cos 2x   0  cos 2x
f 0  f 2x       VP    6   6   6 
Bài 11. Cho hàm số y   4 4 x x   6 6 3 sin cos
2 sin x  cos x . Chứng minh rằng: ' y  0 x   . Hướng dẫn
Ta tiến hành làm gọn biểu thức trước khi tiến hành lấy đạo hàm Ta có: y   4 4 x x   6 6 3 sin cos
2 sin x  cos x Mà:
sin x  cos x  sin x2  cos x2  sin x  cos x2 1 4 4 2 2 2 2 2 2 2
 2sin x cos x 1 sin 2x 2
sin x  cos x  sin x3  cos x3  sin x  cos x3 3 6 6 2 2 2 2 2 2
 3sin x cos x 2 2
sin x  cos x 2 1 sin 2x 4  1   3  2 2
y  3 1 sin 2x  2 1 sin 2x 1      2   4  '  y  0, x   3  sin x
Bài 12. Cho hàm số y  
 . Chứng minh rằng: 'y.sin x  3y  0 1 cos x Hướng dẫn 3  sin x  Ta có: y    1 cos x  2 '
 sin x   sin x  ' y  3   
1 cos x  1 cos x  '  sin x
sin x' 1 cos xsin x1cos x' 1 Mà     1 cos x  1 cos x2 1 cos x 2 2  sin x  1 3sin x '  y  3 .   
1 cos x  1 cos x 1 cos x3 3 2 3sin x  sin x  Ta có: '
y .sin x  3y  0     x   1 cos x .sin 3. 0 3 1 cos x Bài 13. Cho hàm số 3
y  sin 2x   1 . Chứng minh rằng: '
y sin 2x   1  6 .
y cos 2x   1  0 Hướng dẫn Ta có: 3
y  sin 2x   1  y
x    x  ' 
x    x   x  ' ' 2 2 2 3sin 2 1 sin 2 1 3sin 2 1 cos 2 1 2
1  6sin 2x   1 cos 2x   1 Ta có: '
VT y sin 2x  
1  6 y cos 2x   1 2  6sin 2x   1 cos 2x   1 sin 2x   3
1  6sin 2x   1 cos 2x   1  0  VPx 1  x 1 Bài 14. Cho hàm số 2 y  cos   
 . Chứng minh rằng: y . x x  4 ' 1  2 tan  .y  0   x 1   x 1   Hướng dẫn x 1 Ta có: 2 y  cos     x 1   ' '  x 1   x 1  x 1
x 1 x 1 '  y  2cos  cos   2  cos sin             x 1    x 1    x 1 x 1 x 1         
x  '1 x  1 x  1 x x ' ' 1 1 1  Mà       x 1    x  2 1 x x  2 1  x 1  x 1 1  1  x 1  '  y  2  cos sin        in  2.    x 1 x 1   
x x   s 2 1 x x  2 1 x 1   Ta có:  x   VT y . x x  4 1 ' 1  2 tan  .y   x 1        x x   x 1 4 sin . 1  x 1  x 1    x 1 2                    x x  sin 2. 2 cos 0 VP 2 x 1 x 1 x 1 1   cos   x 1   Bài 15. Cho hàm số 4 y x  2 x   4  x  2 cos 2 cos 3 sin
2sin x  3 . Chứng minh rằng ' y không phụ thuộc vào x. Hướng dẫn
Ta tiến hành làm gọn biểu thức trước khi tiến hành lấy đạo hàm 4 y  cos x  2 2 cos x  3 4  sin x 2 2sin x  3 6 4 6 4
 2cos x  3cos x  2sin x 3sin x  3 4 4
sin x  cos x  2 6 6
sin x  cos x 1 '
y  0 . Vậy 'y không phụ thuộc vào x.
IV. Giải phương trình – Bất phương trình liên quan đạo hàm của hàm lượng giác BÀI TẬP MẪU x
Bài 1. Giải phương trình f ' x   0 biết f x        x  3 1 sin  2cos    2 2  Hướng dẫn x
Ta có: f x        x  3 1 sin  2cos    2 2                  x 3 x 3 x x f x 0 cos  2.  .sin   cos x  cos      2 2   2 2  2 x xx
f ' x   0  cos x  cos
 0  cos x  cos  cos x  cos    2 2  2   x x     k2  2 k 4  2 x       3 3  x  
x       k2  x  2    k4   2 
Bài 2. Giải phương trình f (
x)  0 trong các trường hợp sau
a) f (x)  sin 3x  3sin x  4 .
b) f (x)  cos 2x  2sin x  3 .
c) f (x)   3 cos x  sin x 1. Hướng dẫn
a) f (x)  sin 3x  3sin x  4  f  x  3cos 3x  3cos x
f  x  0  3cos 3x  3cos x  0  cos 3x  cos   x   kx  
3x    x k2  4 2     k  . 3x  
  x k2   x   k  2 b)
f (x)  cos 2x  2sin x  3  f  x  2
 sin 2x  2cos x
f  x  0  2
 sin 2x  2cos x  0  cos x 2  sin x   1  0     x   kx   k   2 2 cos x  0         1  x   k2
x   k2 k   sin x   6  6  2    5
x     k2 x   k2  6  6    c) f  x 3 1
 0  3 sin x  cos x  0  sin x
cos x  0  sin x   0   2 2  6   
x   k  x    k k  . 6 6
Bài 3. Cho hàm số y  (m 1)sin x m cos x  (m  2)x 1. Tìm giá trị của m để y  0 có nghiệm? Hướng dẫn
y  (m 1) cos x msin x  (m  2)
Phương trình y  0  (m 1)cos x msin x  (m  2)
Điều kiện phương trình có nghiệm là 2 2 2
a b cm  1  2 2 2 2
 (m 1)  m  (m  2)  m  2m  3  0   . m  3  2 
Bài 4. Cho hàm số y  cos  2x
 . Khi đó hãy giải phương trình y  0 .  3  Hướng dẫn TXĐ : D   2  Ta có: y  2  .sin  2x    3   2   k
Theo giả thiết y  0  sin  2x  0    x    k   .  3  3 2   x
Bài 5. Cho hàm số y  sin  
. Khi đó hãy tìm nghiệm của phương trình y '  0 .  3 2  Hướng dẫn TXĐ : D  1   x    x   x  
Ta có: y   cos  
 nên y  0  cos 
 0     k  x    k2 k     2  3 2   3 2  3 2 2 3
Bài 6. Cho hàm số y  tan x x . Giải phương trình y  0 . Hướng dẫn   TXĐ: D
\   k , k    2  1 Ta có: 2 y 
1 tan x , khi đó 2
y  0  tan x  0  tan x  0  x k k   2 cos x Bài 7. Cho hàm số 2 y  sin .
x cos x , giải phương trình y  2sin x . Hướng dẫn TXĐ : D  , ta có   y   2 x 2 x x x 2 3 sin cos sin cos
 2sin x cos x  sin x Vậy 2 3 2 3
y  2sin x  2sin .
x cos x sin x  2sin x 2sin x 2
 sin .xcos x s  in x 0   x  2  x 3 3 2 sin 1 cos
 sin x  0  3sin x  0  sin x  0  x k k   . Bài 8. Cho hàm số 2
y  2sin x  cos 2x x , giải phương trình y  3  . Hướng dẫn TXĐ : D
Ta có: y  4sin x cos x  2sin 2x 1  2sin 2x  2sin 2x 1  4sin 2x 1   y  3
  4sin 2x 1 3   sin 2x  1
  2x    k2  x    k k   2 4
Bài 9. Cho hàm số y  1 sin x1 cos x , giải phương trình y  2(cos x  sin x) . Hướng dẫn TXĐ : D  Ta có: y  x   x  x   x 2 2 cos 1 cos sin 1 sin
 cos x  sin x  cos x  sin x , nên 2 2
y  2(cos x  sin x)  cos x  sin x  cos x  sin x  2(cos x  sin x)
 (cos x sin x)(cos x  sin x)  (cos x sin x)  0  (cos x sin )
x (cos x  sin x 1)  0       x   k sin x   0     4          4   2 sin x  . 2 sin x  1  0         
x k2 k    4    4       1  sin x         4 
x   k2 2   2   
Bài 10. Tính đạo hàm của hàm số y  sin  2x
 và giải phương trình y  0 .  2  Hướng dẫn TXĐ : D      Ta có y  sin
 2x  cos 2x y  2  sin 2x  
. Vậy y  0  sin 2x  0  x kk    2  2 x Bài 11. Cho hàm số 2 y  cot
. Khi đó nghiệm của phương trình y '  0 4 Hướng dẫn
TXĐ : D  \k4 ,k     1 x  1  1 x x  Ta có : 2 y  cot .     cot . 1 cot   . 2 4 x 2 2 4  4   sin   4  x x  Nên y  0  cot
 0    k  x  2  k4 k   4 4 2
Bài 12. Cho hàm số f x  2sin 2x  cos 2x , giải phương trình y  2sin 2x . Hướng dẫn TXĐ : D
Ta có : y  4cos 2x  2sin 2x
y  2sin 2x  4 cos 2x  2sin 2x  2sin 2x  sin 2x  cos 2x   
tan2x 1 2x   k  x   k
k   do cos2x  0 4 8 2
Bài 13. Tính đạo hàm của hàm số sau: 3
y  sin 2x  
1 và giải phương trình y  6 cos 2x   1 . Hướng dẫn TXĐ : D  Ta có 2
y  6sin 2x   1 cos 2x  
1 . Vậy y  6 cos 2x 1 2 
x    x     x     x   2 6 sin 2 1 cos 2 1 6 cos 2 1 cos 2 1 1
  sin 2x   1   0    1   3 cos 2x  1 0 cos 2x  1 0 2x 1 k             x
  k k   . 2 2 4 2
Bài 14. Tính đạo hàm của hàm số sau: y   x x3 sin cos
và giải phương trình y  3  3sin 2x . Hướng dẫn TXĐ : D  2
Ta có : y  3sin x  cos x cos x  sin x , suy ra y   x   x x2 3 3sin 2 3 sin cos
cos x sin x  33sin 2x .   x x2  x x 2 2 3 sin cos cos sin
 3(sin x  cos x)  (sin x  cos x) cos x sin x1  0  .   x    k        4 sin x   0    x    k  sin x cos x 0     4  4       
x   k2 
sin x  cos x 1  0         1  2 2 sin x  1  0 sin x            4    4  2
x    k 2  
sin 2x  cos 2x
Bài 15. Tính đạo hàm của hàm số sau: y
, giải phương trình y  6  .
2sin 2x  cos 2x Hướng dẫn
ĐK : 2sin 2x  cos 2x  0 . Ta có
2cos2x 2sin 2x2sin 2x cos2xsin 2x cos2x4cos2x 2sin 2xy 
2sin 2x cos2x2 6 
y  2sin2xcos2x2 6  y  6    6
  2sin 2x  cos 2x 1 2  2
2sin2x cos2x  2 1 1 sin 2x  cos 2x  
2sin 2x  cos 2x 1 sin 5 5 5
2x   sin      
2sin 2x  cos 2x  1   2 1 1 sin    
2x   sin    sin 2x cos 2x  5 5 5
x    k
2x     k2     
x   k
2x      k2  2    1 2 k     với sin  ;cos  (Thỏa mãn ĐK) 2x      k2 x k   5 5  
2x      k2   x     k  2
Bài 16. Cho hàm số 2
y  sin x , giải phương trình y  3 . Hướng dẫn TXĐ : D  
Ta có : y  2sin x cos x  sin 2x . Khi đó y  0  sin 2x  0  2x k  x kk   2
Bài 17. Cho hàm số y  cos 2x  5sinx , giải phương trình y  0 . Hướng dẫn TXĐ : D  Ta có : y  2
 sin 2x  5cos x . Nên y  0  2
 sin 2x  5cos x  0  4
 sin xcos x  5cos x  0 
 cos x5 4sin x  0  cos x  0 do 5 4sin x  0  x   k k   . 2
Bài 18. Cho hàm số y  3 sin x  cos x  2x , giải phương trình y  0 . Hướng dẫn TXĐ : D
Ta có : y  3 cos x  sin x  2 ,     khi đó 5
y  0  3 cos x  sin x  2  0  sin x  1  x
k2 k      3  6 Bài 19. Cho hàm số 2 2
y  sin 2x  2 cos x , giải phương trình y  0 . Hướng dẫn TXĐ : D
Ta có : y  4sin 2x cos 2x  2sin 2x ,
nên y  0  2sin 2x cos 2x  sin 2x  0  sin 2x 2cos 2x   1  0   sin 2x  0 2x kx k    2  1  2   k    . cos 2x   2x    k2    2  3 x    k  3
Bài 20. Tìm m để phương trình y  0 có nghiệm biết rằng y m cos x  2sin x  3x  5 . Hướng dẫn TXĐ : D
Ta có : y  msin x  2cos x  3, khi đó y  0  m sin x  2 cos x  3   1
Phương trình y  0 có nghiệm khi và chỉ khi (1) có nghiệm khi và chỉ khi : m  5 2 2
m  4  9  m  5   . m   5 BÀI TẬP TỰ GIẢI
Bài 1. Giải phương trình f ' x   g x  biết f x  3  sin 2 ;
x g x   4cos 2x  5sin 4x
Bài 2. a) Cho y  sin 2x  2cos x . Hãy giải phương trình y  0 .
b) Cho y  3sin 2x  4cos x 12x . Hãy giải phương trình y  2 .
Bài 3. Giải phương trình y  0 trong mỗi trường hợp sau:
a) y  sin 2x  2cos x
b) y  3sin 2x  4cos 2x 10x c) 2
y  cos x  sin x
d) y  tan x  cot x  2 x
e) y  3cos x  4sin x  5x f) y  1 sin(   x)  2cos   2  1 g) y
sin 2x  sin x  3 h) y  sin 2x  2cos x i) 2
y  cos x  sin x 2
j) y  tan x  cot x
k) y  2x  cos x  3 sin x
l) y  3sin 2x  4cos 2x 10x CHUYÊN ĐỀ 5
ĐẠO HÀM HÀM KÉP – ĐIỀU KIỆN TỒN TẠI ĐẠO HÀM
f x khi x x 1  
I. Tính đạo hàm của hàm số f x  0
  f x khi x x 2   0 Phương pháp:
Bước 1: Kiểm tra hàm số có liên tục tại x hay không: f x  lim f x 0    0 x 0 xBướ f x f x
c 2: Sử dụng công thức tính đạo hàm f ' x  lim 0     0  x  0 x x x0 BÀI TẬP MẪU
 2  4  x khi x  0 
Bài 1. Tính đạo hàm của hàm số   x f x   tại x  0 1  khi x  0  4 Hướng dẫn Ta có:   f x  2 4 x x 1 lim  lim  lim   f xxx x
x  2  4  x   0  0 0 0 4
Suy ra hàm số liên tục tại x  0 . 2  4  x 1  2 f x f 0 x 1 Ta có: f       x 4 ' 0  lim  lim  lim     2 x 0 x 0 x 0 x x
2x  8  x  4 4  x  64  1  x 1  khi x  0
Bài 2. Cho hàm số f x    x
. Tìm a để hàm số có đạo hàm tại x  0 và
a khi x  0
tính đạo hàm tại x  0 . Hướng dẫn 1  x  1 x 1
Ta có: lim f x   lim  lim   x0 x0 x0 x
x  1  x  1 2
Để hàm số có đạo hàm tại x  0 thì hàm số phải liên tục tại x  0 1
Suy ra lim f x   f  0   a   x0 2
Đạo hàm của hàm số tại x  0 là: 1  x  1 1  2  f   f x f  0  x 1 x 2 ' 0  lim  lim  lim      2 x 0 x 0 x 0 x  0 x
2x x  2  2 1  x  8 3 2
x x 11  khi x  0
Bài 3. Tính đạo hàm của hàm số f (x)   x tại x  0 . 0  khi x  0 Hướng dẫn 3 2
f (x)  f (0)
x x 1 1 x 1 1
Ta có : f (0)  0 , do đó: lim  lim  lim  2 x0 x0 x0 3 2 x x    2 x x 1 1 1 Vậy f (0  )  . 2
f x khi x x 1  
II. Tính đạo hàm của hàm số f x  0
  f x khi x x 2   0 Phương pháp:
Bước 1: Kiểm tra hàm số có liên tục tại x hay không: lim f x   lim f x   f x0  0 x     0 x x 0 x Bước 2: f x f x
Xét x x . Sử dụng công thức tính đạo hàm f ' x  lim 0     0  0 x  0 x x x0 f x f x
Xét x x . Sử dụng công thức tính đạo hàm f ' x  lim 0     0  0 x  0 x x x0 BÀI TẬP MẪU 2
x khi x  1
Bài 1. Cho hàm số f x   
. Tìm a,b để hàm số có đạo hàm tại x  1
ax b khi x  1 Hướng dẫn
Hàm số có đạo hàm tại x  1 thì hàm số phải liên tục tại x  1.
Suy ra lim f x   lim f x   f 1  a b  1   x 1  x 1 
Hàm số có đạo hàm tại x  1 thì f '1  f '1   . Ta có: fx   f f '1  1  1  lim  2 x  0 xfx   f f '1  1  1  lim  a x  0 x  Để f '1  f '1 
  a  2  b  1  x
Bài 2. Chứng minh rằng: Hàm số y
x  nhưng không có đạo hàm tại
x  liên tục tại 0 1 x  0 Hướng dẫn a) Ta có: x
lim f x   lim  0   x0 x0 x 1  x
lim f x   lim
 0   lim f x   lim f x   f  0  x0 x0 x  1 x0 x0  f  0   0  
Nên hàm số liên tục tại x  0 Ta có: f x f
f ' 0   lim f x     0   lim  1  x0 x0 x f x f
f ' 0   lim f x     0   lim  1 x0 x0 x Vì f ' 0  f ' 0 
 nên hàm số không có đạo hàm tại x  0 2x  3 khi x  1 
Bài 3. Tính đạo hàm của hàm số 3 2
f (x)   x  2x  7x  4 tại x  1. 0 khi x  1  x 1 Hướng dẫn
Ta có: lim f (x)  lim 2x  3  5   x 1  x 1  3 2
x  2x  7x  4
lim f (x)  lim  lim        2 x 3x 4 0 x 1  x 1   x 1 x 1 
Dẫn tới lim f (x)  lim f (x) suy ra: hàm số không liên tục tại x  1 nên hàm số không có đạo   0 x 1  x 1  hàm tại x  1. 0 2 2x  | x 1|
Bài 4. Chứng minh rằng hàm số f (x) 
liên tục tại x  1
 nhưng không có đạo hàm x 1 tại điểm đó. Hướng dẫn
Vì hàm f (x) xác định tại x  1
 nên nó liên tục tại đó. 
f ( x )  f ( 1  ) 2x Ta có: f  (  1  )   lim  lim  1     x (  1  )  x (  1  ) x 1 x  1 
f ( x )  f ( 1  ) f  (  1  )   lim  lim 2  2     x (  1  )  x (  1  ) x 1  f (  1  )   f (  1  )      
  f (x) không có đạo hàm tại x  1  . 2x  1 khi x  1
Bài 5. Cho hàm số f x  
. Để hàm số này có đạo hàm tại x  1 thì giá 2
x bx  1 khi x  1 trị của b là? Hướng dẫn Ta có: f 1  3
lim f x  lim 2x   1  3   x 1  x 1 
lim f x  lim        2 x bx 1 b 2 x 1  x 1 
Để hàm số f x có đạo hàm tại x  1 khi và chỉ khi f x liên tục tại x  1
 lim f x  lim f x  f  
1  b  2  3  b  1   x 1  x 1  2 x x khi x  1
Bài 6. Tìm a, b để hàm số f x  
có đạo hàm tại x  1 . ax b khi x  1 Hướng dẫn
Điều kiện cần để hàm số có đạo hàm tại x  1 là hàm số liên tục tại x  1 . f 1  2
lim f x  lim  2 x x     2 x 1  x 1 
lim f x  lim ax b  a b   x 1  x 1 
Để hàm số f x có đạo hàm tại x  1 thì f x liên tục tại x  1
 lim f x  lim f x  f  
1  a b  2   x 1  x 1  Điều kiện đủ:
f x  f   1 2 x x  2 f 1    lim  lim
 lim x  2  3    x 1  x  1 x 1  x  1 x 1 
f x  f   1
f x  f   1
ax b  a bax a f 1    lim  lim  lim  lim  a     x 1  x  1 x 1  x  1 x 1  x  1 x 1  x  1 Để  
hàm số f x có đạo hàm tại x  1 thì f 1   f 1   a  3  b  1  3  xkhi x  1
Bài 7. Tìm a, b để hàm số f x   3
có đạo hàm tại x  1 . ax b khi x  1 Hướng dẫn Điều kiện cần: f   1 1  3   f x 3 x 1 lim  lim      x 1  x 1   3  3
lim f x  lim ax b  a b   x 1  x 1 
Để hàm số f x có đạo hàm tại x  1 thì f x liên tục tại x  1
 lim f x  lim f x  1 f  
1  a b    x 1  x 1  3 Điều kiện đủ: 3 x 1 
f x  f   1 2 x x  1 f 1    lim  3 3 lim  lim  1    x 1  x  1 x 1  x  1 x 1  3
f x  f   1
f x  f   1
ax b  a bax a f 1    lim  lim  lim  lim  a     x 1  x  1 x 1  x  1 x 1  x  1 x 1  x  1 Để   2
hàm số f x có đạo hàm tại x  1 thì f 1   f 1   a  1  b   3
BÀI TẬP TỰ GIẢI: 2
 x a khi x  1 
Bài 8. Cho hàm số f x   
. Tìm a,b để hàm số liên tục tại x  1  2
x bx khi x  1  (HD: a  2  ;b  4 )  x khi x
Bài 9. Cho y f x sin 3 0  
. Tính đạo hàm của hàm số tại x  0 bằng định 3
x  2 khi x  0 0 nghĩa. 2 sin xkhi x  0 Bài 10.
Cho hàm số: y f (x)   x 0 khi x  0
a) Chứng minh rằng f x liên tục tại x  0 . 0
b) Tính đạo hàm (nếu có) của f x tại điểm x  0 . 0  1 2 x cos khi x  0 Bài 11.
Dùng định nghĩa, tính đạo hàm của hàm số y f (x)   x tại 0 khi x  0 điểm x  0 0 2 (  x 1) khi x  0 Bài 12.
Chứng minh rằng hàm số: y f (x)   không có đạo hàm 2 x khi x  0
tại điểm x  0 nhưng có đạo hàm tại x  2 . 0 0 2  2  x khi x  1 Bài 13. Tìm ,
a b để hàm số y f (x)  
có đạo hàm tại điểm x 1 .
ax b 1 khi x  1
p cos x q sin x khi x  0
Bài 14. Cho hàm số: y f (x)  pxq1 khi x  0
Chứng minh rằng với mọi cách chọn p, q hàm số không thể có đạo hàm tại điểm x  0 . 3 x  2 khi x  0 Bài 15. Tìm ,
a b để hàm số y f (x)  
có đạo hàm tại điểm x  0 . 2
x ax b khi x  0
Khi đó tính f ' 0 
HD: a  0;b  2
 ; f ' 0   0 x  2
Bài 16. Cho hàm số y f (x)  2x1
a) Xét sự liên tục của hàm số tại x  2
b) Xét xem tại x  2 hàm số có đạo hàm không? 0 0 2  x  3 2 x sin khi x  0
Bài 17. Cho y f x 2   x . 0 khi x  0
a) Xét sự liên tục của hàm số tại x  0
b) Xét xem tại x  0 hàm số có đạo hàm không? 0 0 2 x  2 x  3
Bài 18. Chứng minh rằng hàm số y
liên tục tại x  3
 nhưng không có đạo hàm tại 3x 1 điểm ấy. 2 sin xkhi x  0
Bài 19. Cho hàm số: y f x   x 0 khi x  0
a) Chứng minh rằng f x liên tục tại x  0 . 0
b) Tính đạo hàm (nếu có) của f x tại điểm x  0 . 0  1 2 x sin khi x  0
Bài 20. Cho hàm số: y f (x)   x 0 khi x  0
a) Tính đạo hàm của hàm số tại mỗi x  .
b) Chứng tỏ rằng đạo hàm f  x không liên tục tại điểm x  0 . 0
Bài 21. Xét sự tồn tại đạo hàm của các hàm số sau trên : 2
x x  2 khi x  2 2     x x khi x 1  a) y   1 b) y   2 khi x  2  khi x  1   x 1  x
Bài 22. Tìm a, b để hàm số sau có đạo hàm tại x = 1: x khi x  1 2  2 x
khi  2  x  1 a) y   b) y   2
ax b khi x 1 2
x ax b khi x 1 x
Bài 23. Dùng định nghĩa, tính đạo hàm của hàm số y  tại x  0 . 1 x 0 2 x  2 x  3
Bài 24. Chứng minh rằng hàm số y
liên tục tại x  –3 nhưng không có đạo hàm tại 3x 1 điểm ấy.
Bài 25. Chứng minh rằng hàm số 3 2 y
x liên tục tại x  0 nhưng không có đạo hàm tại x  0 CHUYÊN ĐỀ 6
GIẢI PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH LIÊN QUAN ĐẾN ĐẠO HÀM 0 
I. Sử dụng đạo hàm để tính giới hạn dạng ; : Quy tắc LÔPITAN 0  Phương pháp: f xf  x
Sử dụng quy tắc Lopitan: lim  lim x   0 x g xx 0 x g xBÀI TẬP MẪU
Bài 1. Tính giới hạn: 2 x 1 x  7  3 1) lim 2) lim x 1  x 1 x2 x  2 Hướng dẫn    2 2 x x   1 1 2x 1) lim  lim  lim  2 x 1  x 1 x 1     x   x 1 1 1     x   x  1 7 3 7 3 2 x  7 1 2) lim  lim  lim  x2 x2 x  2    x   x 2 1 6 2 BÀI TẬP TỰ GIẢI
Bài 1. Tính các giới hạn sau theo quy tắc Lopitan: 2 x 1  1  1) lim .ĐS: 2. 2) lim x 2    ĐS: 1.  x 1  x 1 x0  x  3 x  8 2 3x  4x 1 3) lim ĐS: 3 4) lim ĐS: 2 2 x2 x  4 x 1  x 1
Bài 2. Tìm các giới hạn sau theo quy tắc Lopitan: 4x 1  3 2 1 x 1 1) lim 2) lim ĐS: 0 2 x2 x  ĐS: 1 4 6 x0 x x  5  3 x  3 3) lim  4) lim  x4 4  ĐS: 1 x 6 2 x9 9x  ĐS: 1 . x 54 2  x  3
2x  7  x  4 5) lim  6) lim  2 x7 x  ĐS: 1 . 49 56 3 2 x 1  x  4x  ĐS: 4 3 15
Bài 3. Tìm các giới hạn sau theo quy tắc Lopitan
1 x  1 x 3  5  x 1. lim ĐS: 1 7. lim ĐS: 1  . x0 x
x4 1 5  x 3 x 1
2x  2  3x 1 2. lim ĐS: 2. 8. lim  x 1  x  3  2 x 1  x  ĐS: 1 1 4
II. Sử dụng đạo hàm trong bài toán giải PT-BPT Phương pháp:
Sử dụng công thức tính đạo hàm rồi thay vào bài toán để giải.
Chú ý: Cho tam thức f x 2
ax bx c, (a  0)
1. Để f x   , 0 x   thì:
2) Để f (x)  0, x   thì:
Trường hợp 1: Xét a  0
Trường hợp 1: Xét a  0 a  0 a  0 Trường hợp 2:  Trường hợp 2:    0   0
3) Để f (x)  0, x   thì:
4) Để f (x)  0, x   thì :
Trường hợp 1: Xét a  0
Trường hợp 1: Xét a  0 a  0 a  0 Trường hợp 2:  Trường hợp 2:    0   0 BÀI TẬP MẪU Bài 1. Cho hàm số 3 2
y mx x x  5. Tìm m để:
a) y bằng bình phương của một nhị thức bậc nhất.
b) y  0 có hai nghiệm trái dấu.
c) y  0 với mọi x  . Hướng dẫn Ta có: 2
y  3mx  2x 1
a) Để y là bình phương của một nhị thức bậc nhất thì phương trình y  0 có nghiệm kép m  0 m  0 1 Suy ra     m  . Vậy: ..  '  0 1   3m  0 3
b) Để y  0 có hai nghiệm trái dấu thì .
a c  0  3m  0  m  0 .
c) Để y  0 với mọi x  thì: 3  m  0 m  0 1   
m  . Vậy………………….  '  0 1   3m  0 3 x
Bài 2. Cho hàm số f x 3  f x  .
x  . Giải phương trình   0 1 Hướng dẫn
Điều kiện: x 1. 2 3
  3x x   3 2 1  x 2x  3x f x   x  2 1 x  2 1 x  0 f  x 3 2
 0  2x  3x  0   3  . Vậy: ……………. x   2
Bài 3. Cho hàm số f x 2
x  2x . Giải bất phương trình f  x  f xHướng dẫn x 1 x 1
Ta có f  x 
. Khi đó f  x  f x 2   x  2x (1) 2 x  2x 2 x  2x
Đk: x ;0 2;  .  3  5 x  (1) 2 2 2
x 1 x  2x x  3x 1 0   .  3  5 x   2 3  5
Kết hợp với điều kiện trên suy ra x  0 hoặc x  . 2
Bài 4. Cho hàm số f x   2
x  2xx 1 . Giải bất phương trình f  x  0. Hướng dẫn 1
x   x   2 2 2 2 1  x  2x 2 5x  2x  4
Ta có f   x  2x   2 x 1   2 x  2x.   . 2 x 1 2 x 1 2 x 1 Điều kiện x 1.  1   21 x  5
f   x  0 2
 5x  2x  4  0   .  1   21 x   5 3 x
Bài 5. Cho hàm số f x 2 
mx  m  2 x  3. Tìm các giá trị nguyên của tham số m để 3
f ' x  0 với mọi x  . Hướng dẫn
Ta có f  x 2
x  2mx m  2
f  x  0 x   2
x  2mx m  2  0 x   a 1  0   2
m m  2  0  1   m  2  '  0
Vì m nguyên nên m  1;  0;1;  2 . x
Bài 6. Cho f x  x x g x 2 3 2 3 2 3,  x
 3 . Giải bất phương trình f  x  gx . 2 Hướng dẫn    
f  x   x x
  x x gx 2 x 3 2 2 3 2 2 3 6 2 ,
  x   3   3x x  2 
f  x  g x 2 2 2
 6x  2x  3x x  3x  3x  0  x ;01;  60 64
Bài 7. Cho f x  3x  
 5. Giải phương trình f x  0 . 3 x x Hướng dẫn   60 64  60 192
Ta có f  x  3x    5  3    3 2 4  x xx x 1 f  x 60 192  0  3   0 1 . Đặt t  , t  0 2   2 4   x x x   1 1 2
1  192t  60t  3  0  t   t  4 16 1 1 1 Với 2 t  
  x  4  x  2  2 4 x 4 1 1 1 Với 2 t   
x 16  x  4  2 16 x 16
Vậy f  x  0 có 4 nghiệm x  2  , x  4 
Bài 8. Cho hàm số f x 2
x x  7 . Giải bất phương trình f x 1  . 2 Hướng dẫn  1 28  2  7  0 Xét tam thức: 2
x x  7 có  2
x x  7  0 , x   . a 1  0   2 x x  7 2x 1
Ta có f  x   . 2 2 x x  7 2 2 x x  7  2x 1 0  Do đó 2x 1 1 f  x 1    2
 2x 1 x x  7   2 2   2 2 x x 7   2x   2 2 1
x x  7  1  1  1 x     x       x  2  2   2      x 1. x  2  2 2
4x  4x 1 x x  7 2 3
 x 3x 6  0  x 1 1 m Bài 9. Cho hàm số 3 2 y x x x m
5 . Tất cả các giá trị của tham số m để y  0 , x . 3 2 Hướng dẫn 1 m 3 2 y x
x mx  5 ; 2
y  x x m m 3 2 2 y  0, x
   x mx m  0, x   2
m  4m  0  0  m  4 . 1 1 Bài 10. Cho hàm số 3 2 y x
x  4x  2019 . Gọi S là tập hợp tất cả các nghiệm nguyên của bất 3 4
phương trình y  0 . Tổng tất cả các phần tử của S bằng bao nhiêu? Hướng dẫn 1 2 y  x x  4 . 2 1   y  0 2
x x  4  0  1 65 1 65  x  . 2 4 4 S   1  ;0;1; 
2 nên có tổng các phần tử là: 2 . 1 Bài 11. Cho hàm số 3 2 y
x 1010x  2019x  2020 . Giải bất phương trình y  0 . 3 Hướng dẫn Ta có 2
y  x  2020x  2019 . x  2
y  0  x  2020x  2019  1 0   . x  2019
Vậy tập nghiệm của bất phương trình là S    ;1 2019;  . BÀI TẬP TỰ GIẢI 2 x
Bài 1. Giải bất phương trình f ' x   g ' x  biết f x  3 2  x x g x  3 2 2018;  x   2020 3 3 mx Bài 2. Cho hàm số 2 y
 3x mx  5 . Xác định m để f ' x   0 x   (HD: m  3 ) 3 1 Bài 3. Cho hàm số 3 2 y
x  2x mx  5 . Tìm m để f ' x   0 x    0;2  3 (HD: m  0 ) 1 Bài 4. Cho hàm số 3 y
x   2m  1 2 2
x m x  4 . Tìm m để: 3
a) f '(x)  0 với mọi x  0
b) f ' x   0 có hai nghiệm phân biệt cùng dấu
c) Trong trường hợp f ' x   0 có hai nghiệm. Tìm hệ thức giữa hai nghiệm không phụ thuộc vào m. 2 x  3x  4
Bài 5. Giải phương trình f ' x   0 biết f x   2 x x  1
Bài 6. Giải bất phương trình f ' x   f x  biết f x  2  x  2x Bài 7. Cho hàm số 3 2
y x  3x x  2 . Tìm x sao cho: a) y  2  b) y  10
Bài 8. Giải các bấy phương trình: 2 x  3x  3 2 x x 1
a) y  0 với y
b) y  0 với y x 1 2 x x 1
Bài 9. Tìm các nghiệm của phương trình sau: 1 1 3
a) f  x  0 với 3 2 f (x) 
x  2x  6x 1.
b) f  x  –5 với 4 3 2 f (x)  x x x  3 . 3 4 2 Bài 10. Cho hàm số 3 2
f (x)  x  3x  2 . Hãy giải các bất phương trình sau: a) f (  x)  0 b) f (  x)  3
Bài 11. Giải bất phương trình f  x  g x , biết rằng: a) 3
f (x)  x x  2 và 2 g( )
x  3x x  2 2 x b) 3 2
f (x)  2x x  3 và 3
g(x)  x   3 2 Bài 12. Cho hàm số 2 y
x  2x  24 . Giải bất phương trình 2 f (
x)  f (x) Bài 13. Cho hàm số 2
y x  2 x 12 . Giải bất phương trình f (
x)  0 . (TN THPT 2010)
Bài 14. Cho hàm số: 3 2
y f (x)  x  2x mx  3. Tìm m để:
a) f  x là bình phương của một nhị thức bậc nhất.
b) f  x  0, x   . c) f (  x)  0, x  0; 2 .
d) f  x  0, x   0 . 3 2 mx mx
Bài 15. Cho hàm số: y f (x)  
 3 mx  2 . Tìm m để: 3 2
a) f  x  0, x   .
b) f  x có hai nghiệm phân biệt cùng dấu.
c) Chứng minh rằng trong trường hợp f  x có hai nghiệm (hai nghiệm có thể trùng nhau) thì
các nghiệm này thỏa mãn một hệ thức độc lập với m .
Bài 16. Tìm m để: a) 3
y mx – x có y  0, x   . 1 b) 3 2 y
x mx  4x  3 có y  0, x   . 3 c) 3 2
y x – 3mx  4mx có y  0, x   . d) 3 y xm   2 – 3 2
1 x  2m  5 x  2 có y  0, x   . 1 e) 3 2
y  – x  2x – mx  2 có y  0, x   . 3 1 f) 3 2 y
x – mx – mx có y  0, x  0;   . 3
Bài 17. Với mỗi hàm số sau đây: ① Tìm TXĐ ② Tính y ③ Xét dấu y , chỉ ra y  0 , y  0
trên khoảng, các khoảng nào: 1 2x 1 a) 3
y  – x  3x 1 b) 3 2 y
x – 3x  8x – 2 c) y  3 x  2 2 x x  2 2
x  2x  2 1 d) y  e) y  f) y  1 x 1 x 1 x  2 g) 4 2
y  – x  4x h) 4 2
y x  4x 1
i) y  4x 1– 1 x 1 1 j) 2
y  4  3x – x k) 3 2 y
x  3x  7x  2 l) 4 2
y x  2x  3 3 2 x  2x m) 3 2
y  x x  5 n) 2 y  4  x o) y  1 x 2 x  7x 12 p) y y x x r) 2 y x x  20 2 x  2x  q) 2 3 3 2 x  8x  9 1 s) y  t) y   2x u) 2 y x  2x  3 x  5 x 1
III. Sử dụng đạo hàm chứng minh đẳng thức: Phương pháp:
Sử dụng các công thức để tính đạo hàm rồi thay vào biểu thức để biến đổi BÀI TẬP MẪU Bài 1. Cho hàm số 2
y x x 1 . Chứng minh: 2
y 1 x y  0 Hướng dẫn 2 x x x 1 y Ta có: y  1   . 2 2 2 x 1 x 1 x 1 2 2
y 1 x y y 1 x y  0. Bài 2. Cho hàm số 2 y
x  1 x . Chứng minh: 2
2 1 x .y  y Hướng dẫn    1  1  x  Ta có: 2
y   x  1 x   . 2
x  1 x   .1  2   2 2      1 2 1 2 1  x x x x x  2 2 1 1 x x 1 x x y  .   . 2 2 2 2   1 x 2 1 x 2 1 2 1  x x x 2
 2 1 x .y  y . Bài 3. Cho hàm số 3
y  1 x . Chứng minh: 2 3y y  1  0 Hướng dẫn 3 3 2
y  1 x y  1 x  3y y  1  2  3y y  1  0
Bài 4. Chứng minh các công thức tổng quát sau a b a c b c 2 x  2 x   2
ax bx c  1 a 1 b 1 a 1 c 1 b 1 c a)     ;
( a , b , c , a , b , c là hằng số) . 2  1 1 1
a x b x c  
a x b xc 2 2 1 1 1 1 1 1 b c 2 . a a x  2 . a b x  2  1 1
ax bx c a b b) 1 1     ;
( a , b , c , 1 a , 1 b là hằng số) . a x b     a x b 2 1 1 1 1 Hướng dẫn         2
ax bx c . 2
a x b x c    2
ax bx c. 2 2   1 1 1 1 a x 1 b x 1 c ax bx c  a)     2 
a x b x c  
a x b xc 2 2 1 1 1 1 1 1
2ax b. 2
a x b x c    2    1 1 1 ax bx c.2 1 a x 1 b  =
a x b xc 2 2 1 1 1
 .ab a .b 2     1 1 x 2  . a 1 c 1
a .cx  . b 1 c 1 b .c =  . ( đpcm)
a x b x c 2 2 1 1 1             ax bx c  2 ax
bx c' .a x b   2 2 1 1 ax bx c. 1 a x 1 b ' b)     a x b     a x b 2 1 1 1 1
2ax b.a x b  2   1 1 ax bx c. 1 a   . a x b 2 1 1 2 . a    1 a x 2 . a 1 b x  . b 1 b 1 a .c  .( đpcm) a x b 2 1 1 BÀI TẬP TỰ GIẢI ax b ad bc
Bài 1. Chứng minh rằng hàm số y
có đạo hàm là y '  cx d 2 (cx d ) 3x  5 4 2x
Áp dụng tính đạo hàm của : y  , y  , y x  2 3x  2 1 3x 2
ax bx c 2
ab ' x  2ac ' x bc ' b 'c
Bài 2. Chứng minh rằng hàm số y
có đạo hàm là y ' 
b ' x c ' 2
(b ' x c ') 2 x  2x  7 2 x 1 2 2x x 1
Áp dụng tính đạo hàm của : y  , y  , y x  2 3x  2 x  5 2
ax bx c
Bài 3. Chứng minh hàm số y  có đạo hàm là: 2
a ' x b ' x c ' a b a c b c 2 x  2 x a ' b ' a ' c ' b ' c ' y '  2 2
(a ' x b ' x c ') 2 2x x 1 2 3x  6x 1 2 2x  5x  6
Áp dụng tính đạo hàm của : y  , y  , y  2 x  3x  3 2 x  3x  2 2 x  5
Bài 4. Chứng minh rằng hàm số: a) 2
y  2x x thỏa hệ thức: 3 y y ' 1  0 .
b) y  x x  3 2 1 thỏa hệ thức:  2
1 x y '  xy ' 9y  0 . 5 c) y  3 
thỏa hệ thức: xy ' y  3 . x x  3 d) y  thỏa hệ thức: 2
2( y ')  ( y 1) y ' x  4 CHUYÊN ĐỀ 7
PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ
Dạng 1. Phương trình tiếp tuyến khi biết tiếp điểm M x ; y 0 0  Phương pháp:
- Bước 1: Tìm tọa độ tiếp điểm M x ; y 0 0 
- Bước 2: Tính y '  f ' x , rồi suy ra hệ số góc của tiếp tuyến là f ' x 0 
- Bước 3: Phương trình tiếp tuyến của đồ thị  C  tại M x ; y
là: y f ' x . x xy 0   0  0 0  0 BÀI TẬP MẪU
Bài 1. Viết phương trình tiếp tuyến của đồ thị 3
y x  4x  1 tại : a) Điểm M 1; 2  
b) Tại điểm có hoành độ bằng 2.
c) Tại điểm có tung độ bằng 1. Hướng dẫn Ta có: 2 y '  3x  4
a) Hệ số góc của tiếp tuyến là: y   2 ' 1  3.1  4  1 
Phương trình tiếp tuyến là: y y '1. x x y  1
x 1  2  x 1 0  0   b) Ta có: 3
x  2  y x  4x  1  1 0 0 0 0
Hệ số góc của tiếp tuyến là: y   2 ' 2  3.2  4  8
Phương trình tiếp tuyến là: y  8 x  2   1  8x 15  x  0 0  c) Ta có: 3 3
y  1  x  4x  1  1  x  4x  0  x  2 0 0 0 0 0 0   x  1  0
TH1: x  0; y  1  y ' 0  4
  Phương trình tiếp tuyến là: 0 0   y  4
  x  0  1  4  x  1
Tương tự hai trường hợp còn lại, các em tự viết. Bài 2. Cho hàm số 3 2
y x  2x 1 có đồ thị là C  . Viết phương trình tiếp tuyến của C  tại điểm M 1; 4 Hướng dẫn Ta có 2
y  3x  4x . Do đó y 
1  7 . Phương trình tiếp tuyến tại điểm M 1; 4 là y  7x  3 . 4 y x  1 
Bài 3. Viết phương trình tiếp tuyến của đồ thị hàm số
x 1 tại điểm có hoành độ 0 Hướng dẫn 4 Ta có y    y 1   1  . 2   x   1
Theo giả thiết ta có x  1  nên y  2
  tiếp điểm M  1  ; 2   . 0 0
Vậy phương trình tiếp tuyến của đồ thị hàm số tại điểm M  1  ; 2 là : y  1  x  
1  2  y  x  3 . Bài 4. Cho hàm số 3
y x  3x 1(C). Viết phương trình tiếp tuyến của đồ thị (C), biết tung độ
tiếp điểm bằng 3 Hướng dẫn Ta có: 2
y  3x  3 . Gọi M x ; y là tiếp điểm 0 0  Ta có: 3
y  3  x  3x  2  0  x  2, x  1  0 0 0 0 0  x  1   y ( 1
 )  0 . Phương trình tiếp tuyến: y  3 0
x  2  y (2)  9 . Phương trình tiếp tuyến: y  9(x  2)  3  9x 15. 0 2 x  3x 1
Bài 5. Viết phương trình tiếp tuyến của đồ thị hàm số y
tại giao điểm của đồ thị 2x 1 hàm số với trục tung Hướng dẫn 2 2x  2x 1 Ta có: y '   . 2x  2 1
Giao điểm M của đồ thị với trục tung : x  0  y  1  0 0
Hệ số góc của tiếp tuyến tại M là : k y' 0  1 .
Phương trình tiếp tuyến tại điểm M là : y x 1 . 2  3x
Bài 6. Viết phương trình tiếp tuyến của đồ thị hàm số y
tại giao điểm của đồ thị hàm số x 1
với trục hoành bằng : Lời giải
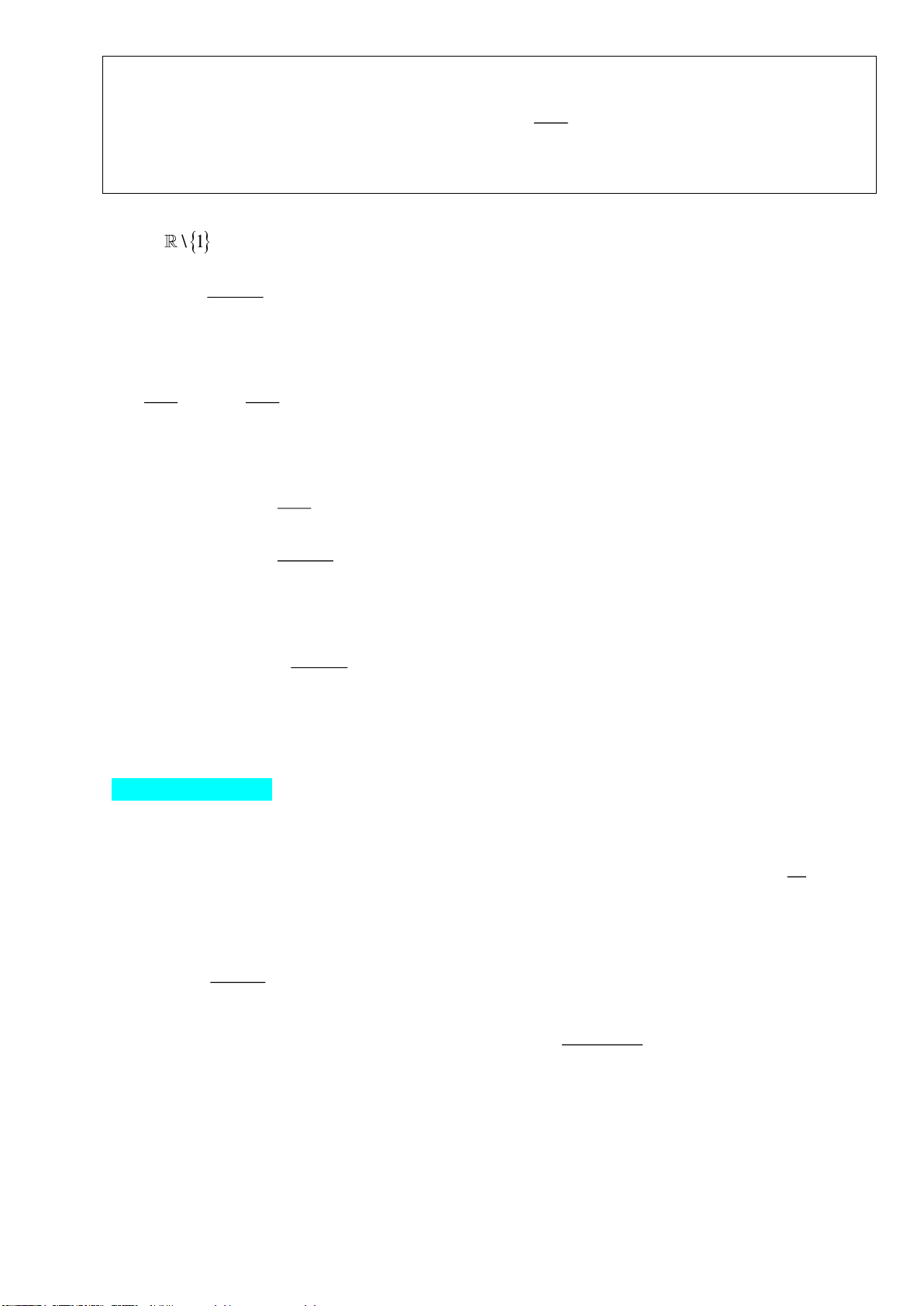
Tập xác định: D  \   1 . Đạ 1
o hàm: y  x  .2 1   Đồ 2
thị hàm số cắt trục hoành tại A ; 0 .    3   2 
Hệ số góc của tiếp tuyến là y  9.    3    Phương trình tiế 2
p tuyến là: y  9 x
 0  y  9x  6    3  2x  4
Bài 7. Cho hàm số y
có đồ thị là (H) . Phương trình tiếp tuyến tại giao điểm của (H) x  3
với trục hoành là: Hướng dẫn  Giao điể 2
m của đồ thị hàm số với trục hoành là (
A 2; 0) . Ta có: y '   y '(2)  2  2 (x  3)
Phương trình tiếp tuyến cần tìm là y  2
 (x  2) hay y  2  x  4 . x
Bài 8. Gọi M là giao điểm của đồ thị hàm số 2 1 y
với trục tung. Viết phương trình tiếp x  2
tuyến với đồ thị hàm số trên tại điểm M . Hướng dẫn   Vì 1
M là giao điểm của đồ thị với trục Oy M 0;    2  3  3 y   k y (0  )   2 (x  2) 4
Phương trình tiếp tuyến của đồ thị tại điểm M là: 3 1 y   x  4 2
Bài 9. . Cho hàm số: 3
y x   m   2
1 x   3m  1 x m  2 . Tìm m để tiếp tuyến của đồ thị
hàm số tại điểm có hoành độ bằng 1 đi qua điểm A 2; 1   . Hướng dẫn
Hàm số đã cho xác định với x   . Ta có: 2
y '  3x  2 m 1 x  3m  1
Với x  1  y 1  3m  1  y '1  m  6
Phương trình tiếp tuyến tại điểm có x  1: y   m  6  x 1  3m  1
Tiếp tuyến này đi qua A 2; 1   nên có: 1
  m  6  3m 1  m  2  Vậy, m  2
 là giá trị cần tìm. Bài 10.
Gọi (Cm) là đồ thị của hàm số 3 2
y x  (2m  1)x  (m  3)x  3 và (d) là tiếp
tuyến của (C) tại điểm có hoành độ x  2 . Tìm m để khoảng cách từ gốc tọa độ O đến (d) 7 bằng . 17 Hướng dẫn
Hàm số đã cho xác định với x   . Ta có: 2
y '  3x  2 2m  1 x m  3.
Phương trình tiếp tuyến (d) :    y y '(2)(x 2) y(2)
y  11 – 7m  x – 2   7 – 6m  11 – 7m x  8m – 15  (11  7 )
m x y  8m  15  0 8m  15 7 2 2 d (0, (d ))  
 17(8m 15)  49[(11  7 ) m  1] 2 (11  7m)  1 17 2
 1313m  3466m  2153  0  m  2153 1, m  1313 BÀI TẬP TỰ GIẢI x  1
Bài 1. Lập phương trình tiếp tuyến của đồ thị y x  0
x  biết hoành độ tiếp điểm là 1 0
Bài 2. Lập phương trình tiếp tuyến của đồ thị y
x  2 biết tung độ tiếp điểm là y  2 0 Bài 3. Cho hàm số 3 2
y x  3x  1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C) :
1. Tại điểm M  1  ; 3 ;
2. Tại điểm có hoành độ bằng 2 ;
3. Tại điểm có tung độ bằng 1 ;.
4. Tại giao điểm (C) với trục tung ; ĐS: 1. y  3  x  6
2. y  24x  27
3. y  1, y  9x  28 4. y  1
Dạng 2. Viết phương trình tiếp tuyến khi biết hệ số góc k Phương pháp:
Bước 1: Tính f ' x
Bước 2: Giải phương trình f ' x   k x y 0 0
Bước 3: Phương trình tiếp tuyến là: y k. x x y 0  0 Chú ý:
Nếu đường thẳng song song với y ax b thì k a . 1
Nếu đường thẳng vuông góc với y ax b thì k   . a
Nếu đường thẳng tạo với trục Ox một góc  thì k  tan k a
Nếu đường thẳng tạo với đường thẳng  d  góc  thì tan   1
. Với a là hệ số góc của k.a
đường thẳng  d OB
Nếu đường thẳng d cắt các trục Ox, Oy lần lượt tại A, B thì tan OAB   , trong đó hệ số góc OA
của d được xác định bởi y ' x   tan OAB BÀI TẬP MẪU
Bài 1. Viết phương trình tiếp tuyến của đồ thị  C  : 4 2
y  x x  6 , biết tiếp tuyến vuông góc 1
với đường thẳng y x  1 . 6 Hướng dẫn
Hàm số đã cho xác định D  1
Gọi  t  là tiếp tuyến của đồ thị  C  của hàm số và  t  vuông góc với đường thẳng y x  1 , 6
nên đường thẳng  t  có hệ số góc bằng 6  .
Cách 1: Gọi M x ; y
là tọa độ tiếp điểm của tiếp tuyến  t  và đồ thị  C  của hàm số . Khi 0 0 
đó, ta có phương trình: y ' x  3  6   4
x  2x  6  0 0 0   x 1 2
2x  2x  3  0  . Vì 2
2x  2x  3  0, x   0 0 0    0 0 0
nên phương trình    x  1  y y 1  4  M 1;4 . 0 0    
Phương trình tiếp tuyến cần tìm là: y  6
  x 1  4  6  x  10 .
Cách 2: Phương trình  t  có dạng y  6  x m
t  tiếp xúc  C  tại điểm M x ; y khi hệ phương trình sau có nghiệm x 0 0  0 4 2
 x x  6  6x mx  1 0 0 0  có nghiệm 0 x   3  0 4
x  2x  6 m  10 0 0
Vậy phương trình tiếp tuyến cần tìm là: y  6
  x 1  4  6  x  10 . 1 2 Bài 2. Cho hàm số 3 y x x
có đồ thị là (C). Tìm trên đồ thị (C) điểm mà tại đó tiếp 3 3
tuyến của đồ thị vuông góc với đường thẳng 1 2 y   x  . 3 3 Hướng dẫn
Hàm số đã cho xác định D  Ta có: 2 y '  x  1 1 2 Gọi 3
M (x ; y )  (C)  y x x  , 0 0 0 0 0 3 3
Tiếp tuyến ∆ tại điểm M có hệ số góc: 2
y '(x )  x  1 0 0 Đường thẳng d: 1 2 1 y   x
có hệ số góc k   3 3 2 3  4  1 
x  2  y  2 2
  d k .k  1
  (x 1)    1   x  4 0 0   1 2 0 0  3 3    x  2   y  0 0 0  
Vậy, có 2 điểm M    4 2;0 , 
2;  là tọa độ cần tìm.  3  Bài 3. Cho hàm số 3
y x  3x  2 (C) . Viết phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến bằng 9. Hướng dẫn
Hàm số đã cho xác định và liên tục trên R.
Gọi x là hoành độ tiếp điểm M khi đó x là nghiệm của phương trình 0 0 x  2 2 2 0
y '(x )  k  9  3x  3  9  x  4 
M (2;0) hoặc M ( 2  ; 4) 0 0 0 x  2   0
+) Với M (2;0) phương trình tiếp tuyến là y  9x 18 . +) Với M ( 2
 ; 4) phương trình tiếp tuyến là y  9x 14 . Bài 4. Cho hàm số 3 2
y x  3x  1 có đồ thị (C) . Viết phương trình tiếp tuyến của đồ thị (C)
song song với đường thẳng  : 9x y  6  0 . Hướng dẫn
Đường thẳng  : 9x y  6  0  y  9x  6 có hệ số góc là 9
Vì tiếp tuyến cần tìm song song với đường thẳng  suy ra tiếp tuyến có hệ số góc k  9 . x  3
Suy ra hoành độ tiếp điểm là nghiệm của phương trình 2
y '  k  3x  6x  9  x  1 
Với x  1 , phương trình tiếp tuyến là y  9(x 1)  3  y  9x  6 ( loại vì trùng với đường thẳng  ).
Với x  3, phương trình tiếp tuyến là y  9(x  3) 1  y  9x  26 ( thỏa mãn ).
Vậy phương trình tiếp tuyến cần tìm là y  9x  6. x  9
Bài 5. Viết phương trình tiếp tuyến của đồ thị hàm số y
biết tiếp tuyến vuông góc với x  1
đường thẳng d : x  2y  2  0 . Hướng dẫn Đườ 1 1
ng thẳng d : x  2y  2  0  y
x 1 nên đường thẳng d có hệ số góc là k  . 2 d 2 1
Tiếp tuyến cần tìm có hệ số góc k vuông góc với đường thẳng d k.k  1   k    2  . d k 8  x  1
Hoành độ tiếp điểm là nghiệm của phương trình: y '  k   2    2 (x  1) x  3 
Với x  1, phương trình tiếp tuyến là: y  2
 (x 1)  5  y  2  x  7. Với x  3
 , phương trình tiếp tuyến là: y  2
 (x  3)  3  y  2  x  9 .
Vậy có hai phương trình tiếp tuyến thỏa mãn là: d : y  2
x  7; y  2  x  9. 1 x 1
Bài 6. Cho hàm số y
có đồ thị (C) và điểm I (2;1) . Viết phương trình tiếp tuyến d của x  2
(C) tại điểm M sao cho IM d . Hướng dẫn
Tập xác định D R \   2 1 x 1 Ta có y '   . Giả sử 0 M (x ; ) (x  2) 2 (x  2) 0 0 x  2 0 1 
Hệ số góc của tiếp tuyến (d) tại M của đồ thị (C): k y '(x )  . 1 0 x  2 0 x 1 0 1 y y x  2 1
Hệ số góc của đường thẳng M I 0 IM : k     2 2 x x x  2 (x  2) M I 0 0
d vuông góc của đường thẳng 1  1 x  3 4 0
IM k .k  1   .  1
  (x  2)  1  1 2  2 2 0 (x  2) (x  2) x  1 0 0  0
Với x  3  M (3;2)  d : y  x  5 . 0
Với x  1  M (1;0)  d : y  x  1 . 0
Vậy các tiếp tuyến thỏa mãn là d  x  5 hoặc y  x 1 . 2x  2
Bài 7. Cho hàm số y
(C) . Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến x  2
tạo với đường thẳng y  3x một góc 0 45 . Hướng dẫn
Tập xác định D R \   2 .
Giả sử tiếp tuyến d cần tìm có hệ số góc k. Vì d tạo với đường thẳng y  3x có hệ số góc k ' một k  2  k k ' k  3 góc 0  45 nên suy ra 0  tan 45  1   1  1 1  k.k ' 1  3kk   2
Gọi hoành độ tiếp điểm là nghiệm của phương trình:  2  2  (VN)  2 2 (x  2) 2 1 x  0 0 0
y '(x )  k   k      0  2 2 (x  2)  2 1 (x  2) 2 x  4  0 0  0   2 (x  2) 2  0 1 1
Với x  0 suy ra phương trình tiếp tuyến cần tìm là: y  (x  0) 1  x  1. 0 2 2 1 1 Với x  4
 suy ra phương trình tiếp tuyến là y  (x  4)  3  x  5. 0 2 2 1 1
Vậy có hai tiếp tuyến thỏa mãn là y x 1; y x  5. 2 2 x  2
Bài 8. Viết phương trình tiếp tuyến của đồ thị hàm số y
biết rằng tiếp tuyến cắt trục 2x  3
hoành và trục tung lần lượt tại A và B sao cho tam giác OAB cân tại O với O là gốc tọa độ. Hướng dẫn 3
Tập xác định D R \   .  2 
Tam giác OAB vuông cân tại O nên suy ra hệ số góc của tiếp tuyến là k  1 hoặc k  1  .
Khi đó hoành độ tiêp điểm x là nghiệm của phương trình: 0  1   1 (VN)  2 (2x  3) 1  x  1  0 0
y '  k     1    2  1  (2x  3) x  2  0  0  1   2 (2x  3)  0 Với x  1
  y  1 , phương trình tiếp tuyến là y  x (loại vì cắt trục tung và trục hoành tại 0 0
O nên A B O ). Với x  2
  y  0 , phương trình tiếp tuyến là y  x  2 (thỏa mãn). 0 0
Vậy tiếp tuyến cần tìm là y  x  2 . x  2
Bài 9. Viết phương trình tiếp tuyến của đồ thị hàm số y
biết rằng tiếp tuyến cắt trục 2x  3
hoành và trục tung lần lượt tại A và B sao cho tam giác OAB cân tại O với O là gốc tọa độ. Hướng dẫn
Tập xác định D R \   1 . OB 1 1 1 Ta có tan OAB  
nên hệ số góccủa tiếp tuyến k  hoặc k   . OA 4 4 4  Nhưng do 1 1 y ' 
 0,x  1 nên hệ số góc của tiếp tuyến là k   . 2 (x 1) 4 1 1 x  3
Hoành độ tiếp điểm x là nghiệm phương trình 0    . 0 2 (x  1) 4 x  1  0  0 1 5 1 13
Từ đó ta xác định được hai tiếp tuyến thỏa mãn: y   x  ; y   x  . 4 4 4 4 x Bài 10. Cho hàm số 1 y
có đồ thị là (C) . Tìm những điểm M trên (C) sao cho tiếp 2(x  1)
tuyến với (C) tại M tạo với hai trục tọa độ một tam giác có trọng tâm nằm trên đường thẳng
4x y  0 . Hướng dẫn
Hàm số đã cho xác định D  \   1 x 1 Gọi M ( 0 x ;
)  (C) là điểm cần tìm. 0 2(x 1) 0
Gọi  tiếp tuyến với (C) tại M ta có phương trình  : x 1 1 x 1 ' 0
y f (x )(x x )  0  y  (x x )  0 0 2(x 1) x  2 0 1 2(x 1) 0 0 0 2
x  2x 1  2
x  2x 1
Gọi A   Ox  0 0 A 
; 0  , B   Oy  0 0 B  0;  . 2   2 2(x 1)  0  2 2        x 2x 1 x 2x 1
OAB có trọng tâm là: G 0 0 0 0   ;  . 2 6 6(x 1)  0  2 2 x  2x 1 x  2x 1
Do G thuộc đường thẳng 4x y  0  0 0 0 0 4  .   0 2 6 6(x 1) 0  1  1 x 1  x    0  0  1 2 2 4          (vì 2 x 2x 1 0 ) 0 0 x  2 1 1 3   0 x 1   x   0 0  2  2 1  1 3  Với x    M  ; 0   2  2 2  3  3 5  Với x    M  ; . 0   2  2 2 
Bài 11. Cho hàm số y  3 x  2
3x  9x  10 có đồ thị là (C). Trong tất cả các tiếp tuyến của đồ thị
(C), hãy tìm tiếp tuyến có hệ số góc nhỏ nhất. Hướng dẫn
Hàm số đã cho xác định D  Ta có: 2
y '  3x  6x  9 .
Gọi M (x ; y )(C) : 3 2
y x  3x  9x 10 . 0 0
Tiếp tuyến tại điểm M có hệ số góc: 2 2
k y '(x )  3x  6x  9  3(x 1) 12  1  2 0 0 0 0 mink  1
 2,đạt được khi: x  1   y  21. 0 0
Vậy trong tất cả các tiếp tuyến của đồ thị hàm số, tiếp tuyến tại M  1
 ;16 có hệ số góc nhỏ nhất
và có phương trình là: y  1  2x  9 BÀI TẬP TỰ GIẢI Bài 1. Cho hàm số 3 2
y x  3x  1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C) : 1. Có hệ số góc là 3  .
2. Vuông góc với đường thẳng (d ): 27x  3y  2019  0 .
3. Song song với đường thẳng (d’ ) : 24x y  2020  0 . 1
Bài 2. Viết phương trình tiếp tuyến của đồ thị 3 2
y   x x  2 biết tiếp tuyến song song 3 y  3  x  2020 1 (HD: y  3
x  ; y  3  x  11 ) 3 2 1
Bài 3. Viết phương trình tiếp tuyến của đồ thị 3 2 y x  3x
biết tiếp tuyến vuông góc với 3 3
x  4 y  2021 1 2021
(HD: x  4 y  2021  y x
. Suy ra tiếp tuyến có hệ số góc k  4  4 4 4
Từ đó viết được y  4
x  ; y  4  x  1 ) 3 1
Bài 4. Lập phương trình tiếp tuyến của đồ thị 3 2
y   x  2x  3x  1 biết tiếp tuyến có hệ số 3 góc lớn nhất.
Bài 5. Lập phương trình tiếp tuyến của đồ thị 3
y x  3x  2 biết tiếp tuyến song song trục hoành.
Bài 6. Lập phương trình tiếp tuyến của đồ thị 2
y  2x  3x  9 biết tiếp tuyến hợp với trục hoành góc 0 45
Bài 7. Lập phương trình tiếp tuyến của đồ thị 4 2
y  x x  6 biết tiếp tuyến vuông góc với đườ 1 ng thẳng y x  2019 6
Dạng 3. Phương trình tiếp tuyến đi qua điểm Ax ; y 1 1  Phương pháp: Cách 1:
Bước 1: Tính f ' x
Bước 2: Gọi M x ; y
là tiếp điểm suy ra phương trình tiếp tuyến là: 0 0 
y f ' x . x xy (1) 0   0  0
Bước 3: Vì tiếp tuyến đi qua Ax ; y nên thay x x ; y y vào phương trình (1) để tìm 1 1  1 1 x y 0 0
Bước 4: Thay x , y vào (1) để viết lại phương trình tiếp tuyến. 0 0 Cách 2:
 Đường thẳng  d  đi qua điểm Ax ; y có hệ số góc là k có dạng : y k x x y . 1  1 1  1
f x   k x x y 1   Để  1
d  là tiếp tuyến thì hệ: 
. Giải hệ trên được x y  tiếp
f ' x   k 0 0 tuyến. BÀI TẬP MẪU
Bài 1. Viết phương trình tiếp tuyến của đồ thị 3 2
y x  3x  1 biết tiếp tuyến qua A1;3  Hướng dẫn Ta có: 2
y '  3x  6x . Cách 1:
Gọi M x ; y
là tiếp điểm suy ra hệ số góc của tiếp tuyến là : k y ' x  3x  6x 0  2 0 0  0 0
Phương trình tiếp tuyến là: y   2
3x  6x . x x  3 2
x  3x 1 (1) 0 0 0 0 0 (Các em chú ý 3 2
y x  3x  1 ) 0 0 0
Vì tiếp tuyến đi qua A1;3  nên thay x  1; y  3 vào (1) ta được:  x   k y
3   3x  6x .1  x  1 9; 3 0 0 2 3 2
x  3x 1   0 0 0 0 0    x  2 
k  0; y  3 0 0
Vậy phương trình tiếp tuyến là: y  9x  6; y  3 Cách 2:
Đường thẳng  d  đi qua điểm A1;3 có hệ số góc là k có dạng : y k x 1  3 .
f x   k x  1  3 1
Để  d  là tiếp tuyến của đồ thị thì hệ phương trình  có nghiệm.
k f ' x  2
 3x  6x  2  Thay 2 vào   1 ta được: 3 2
x  3x  1   2
3x  6x  x  1 3 2 3 2 2
 3  x  3x 1  3x  3x  6x  6x  3  x  1 3
 2x  6x  4  0  x  2  x  1
k  9; y  3 Với   
suy ra phương trình tiếp tuyến là: y  9x  6; y  3  x  2 
k  0; y  3
Bài 2. Cho đồ thị hàm số C y f x 3 2 :
 2x  3x  5 . Lập phương trình tiếp tuyến của đồ thị  19 
C  biết tiếp tuyến đi qua điểm A ; 4   . 12  Hướng dẫn  
Gọi k hệ số góc của tiếp tuyến đi qua 19 A ; 4   tới C  . 12    Phương trình tiế 19
p tuyến  là: y k x   4   .  12    19  3 2 
2x  3x  5  k x   4    1
 tiếp xúc với C     12  có nghiệm  2
6x  6x k  2  19 
Thay k từ 2 vào   1 ta được: 3 2
2x  3x  5   2
6x  6xx   4    12  3 2
x x x    2 4 6 19 2
x x12x 19   x 1  3 2
 8x  25x 19x  2  0  x  2  .  1 x   8
Với x 1 k  0  phương trình tiếp tuyến là: y  4  19 
Với x  2  k 12  phương trình tiếp tuyến là: y  12 x
 4  y 12x 15    12  1 21 21  19  21 645 Với x   k  
 phương trình tiếp tuyến là: y   x   4  y   x    8 32 32  12  32 128 19  Vậy từ điểm A ; 4 
 kẻ được 3 tiếp tuyến tới C  12  3x  2
Bài 3. Có hai tiếp tuyến của đồ thị hàm số y
C đi qua điểm A9;0. Tính tích hệ số x 1
góc của hai tiếp tuyến đó? Hướng dẫn TXĐ: \  1 1 
y  x 2 1
Đường thẳng d đi qua điểm A9;0 với hệ số góc k có phương trình y k x  9 .
Đường thẳng d tiếp xúc với đồ thị C  khi và chỉ khi hệ phương trình sau có nghiệm
3x  2  kx9  1  x1  1    k 2 2   x   1 3x  2 1  Thế 2 vào   1 , ta có: 
. x  9  3x  2
x 1  9  x 2      x 1 x   1 x  1  2 
 3x  4x  7  0  7 x   3  
Do đó tích hệ số góc của hai tiếp tuyến đó bằng y  7 9 1 .y  .    3  64
Bài 4. Tìm điểm trên đường thẳng y  2x 1để từ đó kẻ được đến đồ thị C  của hàm số x  3 y  đúng một tiếp tuyến? x 1 Hướng dẫn TXĐ: D  \   1 . Gọi A ; a 2a  
1  d : y  2x 1 .
Gọi k là hệ số góc của đường thẳng d  đi qua A ; a 2a   1 .
Suy ra phương trình d : y k x a  2a 1
x  3  kxa2a1  x1 Xét hệ phương trình:   1 4   
x   k 2 1 x  3 4  x  1   
x a  2a 1   2   x 1  2 x   1 2ax  2 
2a  4 x 6a  4  0 2 Để từ A ; a 2a  
1 chỉ kẻ được một tiếp tuyến đến C  thì  phương trình   1 có một nghiệm
 phương trình 2 có một nghiệm khác 1. Có các trường hợp sau:
Trường hợp 1: phương trình 2 là phương trình bậc nhất có nghiệm x  1 a  0 1  
x  ( T/m). Suy ra A0;  1 thỏa mãn.  8  x  4  0 2
Trường hợp 2: phương trình 2 là phương trình bậc hai có nghiệm kép x  1  a  0  a  0     a 1
  2a  42  2a6a  4  0     .  2  8
a  8a 16  0 a  2 2a  4 x x   1 1 2  2aA 1  ;  1
Suy ra có 2 điểm thỏa mãn A  2;5
Trường hợp 3: phương trình 2 là phương trình bậc hai có hai nghiệm phân biệt trong đó có một nghiệm x  1 a  0 
   2a  42  2a6a  4  0  a 1. Suy ra A1;3 thỏa mãn. 2a 2 
2a  4 6a  4  0
Vậycó 4 điểm thỏa mãn yêu cầu đầu bài.
Bài 5. Tìm số tiếp tuyến của đồ thị hàm số 3 2
y  4x  6x 1, biết tiếp tuyến đó đi qua điểm M  1  ; 9  . Hướng dẫn TXĐ: R Ta có: 2
y  12x 12x .
Phương trình đường thẳngđi qua M  1  ; 9
  có dạng:  : y k x   1  9 .
 là tiếp tuyến của đồ thị khi và chỉ khi hệ phương trình sau có nghiệm:  3 2
 x x   k x   5 4 6 1 1  9 x  3 2  
 8x  6x 12x 10  0  4 2
k 12x 12x    x  1  Với x  1
  k  24  phương trình tiếp tuyến y  24x  
1  9  y  24x 15 5 15 15 15 21 Với x   k
 phương trình tiếp tuyến y
x 19  y x 4 4 4 4 4
Có 2 tiếp tuyến thỏa mãn yêu cầu . Bài 6. Cho hàm số 3 2
y x  3x có đồ thị C  và điểm M  ;
m 0 sao cho từ M vẽ được ba tiếp
tuyến đến đồthị C  , trong đó có hai tiếp tuyến vuông góc với nhau. Tìm giá trị của m ? Hướng dẫn TXĐ: R Ta có 2
y  3x  6x .
Đường thẳng d đi qua M  ;
m 0 có hệ số góc k có phương trình : y k x m
d là tiếp tuyến của C  khi và chỉ khi hệ phương trình sau có nghiệm:
k x m 3 2  x  3x
 x m 2 3x  6x 3 2 3
x  3x  2x  3m   2
1 x  6mx  0 2
k  3x  6xx  0   . 2 2x  3  m 
1 x  6m  0   1
Khi x  0 ta có phương trình tiếp tuyến y  0 .
Đối với đồ thị hàm số không có tiếp tuyến nào vuông góc với y  0 nên yêu cầu bài toán tương
đương phương trình  
1 có hai nghiệm x và x khác 0 thỏa y x .yx  1  1   2 1 2   2
3x  6x  2 3x  6x  1
  9x .x x .x  2 x x  4 1  0 1 2  1 2  1 2  1 1 2 2    9 3  m  3  m  3  m   1  4 1  0   2  7m1 1 0  m  . 27 1 Thay m  vào  
1 thử lại có 2 nghiệm phân biệt khác 0 . 27 1 Vậy m
thỏa mãn yêu cầu bài toán. 27 Bài 7. Cho hàm số 4 2
y x  2x  2 có đồ thị C  . Lập phương trình tiếp tuyến của đồ thị C
biết tiếp tuyến đi qua điểm A0; 2 ? Hướng dẫn TXĐ: R Ta có: 3
y  4x  4x
Đường thẳng d đi qua điểm A0;2 có hệ số góc k có dạng: y kx  2
Để đường thẳng d là tiếp tuyến của đồ thị C  khi và khi hệ phương trình sau có nghiệm:  x  0  4 2
x  2x  2  kx  2  2 4 2 
x  2x  2   3 4x  4x 4 2
x  2  3x  2x  0  x   3
4x  4x k 3   2 x    3
Với x  0  k  0  phương trình tiếp tuyến là: y  2 . 2 4 6 4 6 Với x   k  
 phương trình tiếp tuyến là: y   x  2 . 3 9 9 2 4 6 4 6 Với x    k
 phương trình tiếp tuyến là: y x  2 3 9 9
Bài 8. Viết phương trình tiếp tuyến của đồ thị hàm số 3
y x  3x 1 (C) biết tiếp tuyến đó đi qua điểm ( A 3;19) Hướng dẫn
Giả sử tiếp điểm của tiếp tuyến cần tìm là điểm M (x ; y ) . ta có phương trình tiếp tuyến là 0 0 2 3
y  (3x  3)(x x )  x  3x 1 (d ) 0 0 0 0 d đi qua điểm ( A 3;19) nên ta có: 2 3
19  (3x  3)(3  x )  x  3x 1. 0 0 0 0 3
Giải phương trình trên ta được x  3 hoặc x   . 0 0 2
Với x  3 thì phương trình tiếp tuyến cần tìm là y  24x  53 . 0 3 15 31 Với x  
thì phương trình tiếp tuyến là y x  0 2 4 4 15 31
Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là y  24x  53 và y x  . 4 4 2x 1 Bài 9. Từ điểm (
A 1;3) có thể kẻ được bao nhiêu tiếp tuyến đến đồ thị hàm số y x1 Hướng dẫn
Gọi điểm M (x ; y ) là tiếp điểm của tiếp tuyến cần tìm. Phương trình tiếp tuyến của đồ thị hàm 0 0 2x 1 3  2x 1 số y  tại M là: 0 y  (x x )  (x  1) . x 1 2 0 0 (x 1) x 1 0 0 3  2x 1 Tiếp tuyến đi qua ( A 1;3) nên ta có 0 3  (1 x )  (x  1) 2 0 0 (x 1) x 1 0 0  x  7 0
Vậy qua điểm A kẻ được duy nhất một tiếp tuyến đến đồ thị hàm số./ x  2
Bài 10. Cho hàm số y
có đồ thị (C) và điểm ( A 0; )
a . Tìm a để từ điểm A kẻ được x 1
hai tiếp tuyến đến đồ thị (C) sao cho tiếp điểm nằm về hai phía của trục hoành. Hướng dẫn
Giả sử điểm M (x ; y ) là tiếp điểm của tiếp tuyến cần tìm. Ta có phương trình tiếp tuyến tại M 0 0 là 3  x  2 0 y  (x x )  x 1 0  2 0 (x 1) x 1 0 0 3x x  2
Tiếp tuyến này đi qua điểm A nên ta có : 0 0 a   (x  1) 2 0 (x 1) x 1 0 0 2
 (x  2)(x 1)  a(x 1)  3x  0 (x  1) 0 0 0 0 0 2
 (1 a)x  (2a  4)x a  2  0 (*) 0 0  2a  4 x x   1 2  a 1 Theo đị  x ; x nh lý viet ta có : a  2 
. Với 1 2 là hai nghiệm của (*) x .x  1 2  a 1 Để y .y  0
tiếp điểm của hai tiếp tuyến nằm về hai phía đối với trục hoành thì 1 2 a  2 2a  4  2  4  2 x  2 x  2
x x  2(x x )  4   a   1 2 1 2 1 2 a 1 a 1  .  0   0   0   3 x 1 x 1
x x  (x x ) 1 a  2 2a  4 1 2 1 2 1 2  1 a 1 a 1 a 1 2 Vậy với các điểm ( A 0; )
a thỏa mã a   ; a  1 ta luôn kẻ được hai tiếp tuyến thỏa mãn đề bài 3 1
Bài 11. Cho hàm số y x
có đồ thị (C) . Tìm tập hợp các điểm mà từ đó kẻ được hai tiếp x
tuyến đến đồ thị (C) và hai tiếp tuyến ấy vuông góc với nhau. Hướng dẫn
Gọi M (a; b) là điểm bất kì trong mặt phẳng tọa độ. Phương trình đường thẳng d qua M có hệ số
góc k là: y k(x a)  b .
d là tiếp tuyến của đồ thị (C) khi và chỉ khi hệ phương trình sau có nghiệm:  1  1
k(x a)  b x kx x   ka b    xx    . (1) 1 1 k 1    kx x  ; k  1 2  x  x 2 2 2
a k  2(ab  2)k b  4  0 (2) 1 Từ k  1
ta thấy với mỗi k 1 thì luôn có hai giá trị của x trái dấu, do đó hệ (1) có nghiệm 2 x
 (2) có hai nghiệm k ;k 1 . 1 2
Mặt khác, hai tiếp tuyến này vuông góc với nhau nên ta có k .k  1  . 1 2 k .k  1
Yêu cầu bài toán  (2) có hai nghiệm phân biệt thỏa mãn : 1 2 k ;k 1  1 2 a  0 a  0  2 b  4  2 2    1
  a b  4 . 2 a  a bf (1)  0  
Vậy tập hợp điểm M là đường tròn tâm O(0; 0) , bán kính bằng 2, sau khi đã bỏ đi 4 điểm là
giao với các đường thẳng x  0, y x . 2
2x mx m
Bài 12. Cho hàm số y
có đồ thị (C) . Tìm tất cả các giá trị thực của tham số m x 1 để từ điểm (0
A ;1) không kẻ được bất kì tiếp tuyến nào đến đồ thị (C) . Hướng dẫn
Phương trình tiếp tuyến của đồ thị (C) tại điểm M (x ; y ) là 0 0 2 2 2x  4x
2x mx m 0 0 0 0 y  (x x )  2 0 (x 1) x 1 0 0
Tiếp tuyến không đi qua điểm (0
A ;1) nên phương trình 2
(m  3)x  2(m 1)x m 1  0, (x  1
 ) (*) vô nghiệm hoặc có nghiệm x  1  0 0 0 0 1
TH1: m  3  0  m  3 ta có x  
nên m  3 không thỏa mãn 0 2
TH2: m  3 . (*) vô nghiệm   '  0  m  1
TH3: (*) có nghiệm x  1  suy ra 2   0 (vô lý ). 0
Vậy m  1 thì không có tiếp tuyến nào của đồ thị (C) đi qua A.
Bài 13. Viết phương trình tiếp tuyến của đồ thị hàm số 3
y x  3x 1 biết tiếp tuyến đó đi qua điểm ( A 2  ; 1  ) . Hướng dẫn
Phương trình tiếp tuyến của đồ thị (C) tại điểm M (x ; y ) là: 0 0 2 3
y  (3x  3)(x x )  x  3x 1 0 0 0 0
Tiếp tuyến đi qua điểm ( A 2  ; 1  ) nên ta có: 2 3 1   (3x 3)( 2
  x )  x 3x 1 0 0 0 0 3 2  2
x  6x  8  0 0 0 x 1  y  1  0     x  2  
y  9x 17 0
Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán là y  1
 và y  9x 17 Bài 14. Cho hàm số 3 y  4
x  3x  2 có đồ thị (C) . Tìm trên đường thẳng y  3 các điểm mà
trên đó kẻ được ba tiếp tuyến đến đồ thị (C) . Hướng dẫn Giả sử ( A ;
m 3) là điểm trên đường thẳng y  3 thỏa mãn từ A kẻ được 3 tiếp tuyến đến đồ thị (C).
Phương trình tiếp tuyến: 2 3 y  ( 1
 2x  3)(x x )  4x  3x  2 . 0 0 0
Tiếp tuyến đi qua A nên ta có: 2 3 3  ( 1
 2x  3)(m x )  4x  3x  2 0 0 0 3 2
8x 12mx  3m 1  0 0 0 Hay  1  2  x  (8x  (4 12 ) m x  2  6 ) m  0  0  0 0  2  Yêu cầu bài toán 3 2
 8x 12mx  3m 1 0 có 3 nghiệm phân biệt 0 0 1 2  (8x  (4 12 ) m x  2  6 )
m  0 có hai nghiệm phân biệt khác 0 0 2 m  1    '  0 1  m    1   3 m     2 1 m   2  1  1  Vậy từ các điểm ( A ;
m 3) thỏa mãn m  ( ;  1  )  ;  \ 
   kẻ được 3 tiếp tuyến đến đồ thị  3  2 (C).
Bài 15. Cho đồ thị hàm số 3
y  3x  4x
có đồ thị (C) . Từ điểm M (1;3) có thể kẻ được bao
nhiêu tiếp tuyến đến đồ thị (C) . Hướng dẫn
Phương trình tiếp tuyến của đồ thị (C) tại điểm M (x ; y ) là: 0 0 2 3
y  (3 12x )(x x )  3x  4x 0 0 0 0
Tiếp tuyến đi qua M (1;3) nên ta có: 2 3
3  (3 12x )(1 x )  3x  4x 0 0 0 0 x  0 0 3 2 
 8x 12x  0  0 0 3 x  0  2
Vậy qua M kẻ được hai tiếp tuyến đến đồ thị (C). 2x 1
Bài 16. Cho hàm số y
có đồ thị (C) và điểm I (1; 2) . Tìm điểm M thuộc đồ thị (C) x 1
có hoành độ lớn hơn 2 sao cho tiếp tuyến tại M vuông góc với đường thẳng IM . Hướng dẫn  2x 1  Gọi 0 M x ;
 thuộc (C) . Phương trình tiếp tuyến tại M là 0 x 1  0  1  2x 1 0 y  (x x )  2 0 (x 1) x 1 0 0 Phương trình đườ 1
ng thẳng MI : y  (x 1)  2 2 (x 1) 0 1 1
x  0 (loai)
Tiếp tuyến tại M vuông góc với MI nên ta có: 0  .  1    2 2 (x 1) (x 1) x  2  0 0 0
Với x  2  y  3 . Vậy điểm M (2;3) 0 0 x  2
Bài 17. Cho hàm số y
có đồ thị C  và điểm A0;a . Hỏi có tất cả bao nhiêu giá trị x 1
nguyên của a trong đoạn  2  018;201 
8 để từ điểm A kẻ được hai tiếp tuyến đến C  sao
cho hai tiếp điểm nằm về hai phía của trục hoành? Hướng dẫn TXĐ: \  1 3
Ta có : y   x 2 1
Đường thẳng d đi qua điểm A0;a , hệ số góc k có phương trình: y kx a .
x  2  kxa  *  x1
Để d là tiếp tuyến của C  thì hệ phương trình  có nghiệm. 3    k ** 2   x   1   Thay (**) vào (*) ta đượ x 2 3x c:   a x 1 x  2 1  a   2
1 x  2 a  2 x a  2  0  1 với x  1.
Do từ A kẻ được hai tiếp tuyến đến C  nên phương trình  
1 có hai nghiệm phân biệt khác 1. a 1         a   a 2 3 2  0      a    a   a 1 1 2 2  a  2  0 . 2       Khi đó toạ x 2 x 2 độ hai tiếp điểm là 1 M x ;  và 2 N x ;
 với x , x là nghiệm của   1 do 1 x 1  2 x 1 1 2 1   2  2a  2  đó a 2 x x  , x x  . 1 2 a 1 1 2 a 1 x  2 x  2
Hai tiếp điểm nằm về hai phía của trục hoành khi: 1 2 .  0 x 1 x 1 1 2
x x  2 x x  4 9a  6 2 1 2  1 2   0   0  a   .
x x x x 1 3  3 1 2  1 2  2 a  
Kết hợp điều kiện 2 suy ra  3 nên trên đoạn  2  018;201 
8 số giá trị nguyên của a thỏa a 1
yêu cầu bài toán là 2018 .
Bài 18. Gọi S là tập hợp các điểm thuộc đường thẳng y  2 mà qua mỗi điểm thuộc S đều kẻ 2 đượ x
chai tiếp tuyến phân biệt tới đồ thị hàm số y
đồng thời hai tiếp tuyến đó vuông x 1
góc với nhau. Tính tổng hoành độ T của tất cả các điểm thuộc S . Hướng dẫn TXĐ: \  1 2 x  2x
Ta có : y  x 2 1 2 x 1 y   x 1 x 1 x 1
Gọi điểm Aa;2 d  : y  2 . Đường thẳng d đi qua A có dạng y k x a  2 2  x k
x a 2  x 1 Điề 2 u kiện tiếp xúc:     a 2 1
k  4k  4  0 * 2 x  2x   x    k 2 1
Để 2 tiếp tuyến vuông góc nhau thì phương trình ( * ) có 2 nghiệm k phân biệt và tích của hai 4  a  nghiệm đó bằng 1      3   1 a 1 2 a  1
Vậy tổng hai hoành độ là 2 . BÀI TẬP TỰ GIẢI
Bài 1. Viết phương trình tiếp tuyến của đồ thị 2 y x
biết tiếp tuyến qua A 0; 1    23 
Bài 2. Viết phương trình tiếp tuyến của đồ thị 3 2
y x  3x  3 biết tiếp tuyến qua B  ; 1    9 
Bài 3. Hãy viết phương trình tiếp tuyến của đồ thị hàm số y f x , biết tiếp tuyến qua điểm A 2 4x x a) y
, với A1; – 4 . b) 4 2
y x  2x , với A0; –  1 . x 1 2 x  4x  4 c) 3
y x  3x 1, với A1; –6 . d) y
, với A –1; 0 . x 1 e) 4 2
y x  6x  9 , với A0; 9
Bài 4. Tìm m để đường thẳng y mx  1 tiếp xúc 3 2
y x x  4x 2 x m
Bài 5. Tìm m để đường thẳng y  7  x tiếp xúc y x 1
Bài 6. Viết phương trình tiếp tuyến với  P 2
: y x , biết rằng tiếp tuyến đó đi qua điểm
A0 ; –1 . Bài 7. Cho hàm số 3 2
y x – 3x  2 . Viết phương trình tiếp tuyến của C  , biết rằng tiếp tuyến
đó đi qua A0; 3 .
BÀI TẬP TỔNG HỢP:
Bài 1. Cho đường cong 3
(C) : y x và hai điểm A1;  1 và B 1  ;1 x y   trên (C) .
a) Tính hệ số góc của cát tuyến AB với x
 lần lượt là 0,1 và 0,01
b) Tìm hệ số góc của tiếp tuyến với (C) tại A . Bài 2. Cho hàm số 1
y f (x) 
. có đồ thị (C) . Viết phương trình tiếp tuyến với (C) , biết: x
a) tiếp điểm có hoành độ bằng 2
b) Tiếp điểm có tung độ bằng 3
c) Hệ số góc của tiếp tuyến k  –4 .
d) Tiếp tuyến song song với d : x  9y  2017
e) Tiếp tuyến vuông góc với d : x  4y  2017 .
f) Tiếp tuyến qua điểm A 8  ; 0 Bài 3. Cho Parabol 2
y x và hai điểm A2; 4 và B(2   ; x 4  y  ) trên parabol đó.
a) Tính hệ số góc của cát tuyến AB biết x
 lần lượt bằng 1; 0,1 và 0,001.
b) Tính hệ số góc của tiếp tuyến của parabol đã cho tại điểm A .
Bài 4. Tìm hệ số góc của cát tuyến MN với đường cong C  , biết: a) C  2
: y x  2x và hoành độ M , N theo thứ tự là x  2, x 1. M N x x  b) C 2 1 : y
và hoành độ M , N theo thứ tự là x  1, x  3 . x M N
Bài 5. Viết phương trình tiếp tuyến của đồ thị hàm số 3
y x , biết:
a) Tiếp điểm có hoành độ bằng – 1 .
b) Tiếp điểm có tung độ bằng 8 .
c) Hệ số góc của tiếp tuyến bằng 3 . 1
Bài 6. Viết phương trình tiếp tuyến của đường hypebol y  , biết: x  1  a) Tại điểm ; 2  .  2 
b) Tiếp điểm có hoành độ bằng –1.
LỚP TOÁN THẦY THÀNH – NGÕ 58 NGUYỄN KHÁNH TOÀN – 0975.705.122 1
c) Hệ số góc của tiếp tuyến bằng  . 4
Bài 7. Cho đường cong C : y x . Viết phương trình tiếp tuyến của C  :
a) Biết hệ số góc của tiếp tuyến bằng 1.
b) Biết tiếp tuyến song song với  : x – 4 y  3  0 .
Bài 8. Viết phương trình tiếp tuyến của đồ thị hàm số: x 1 a) y
, biết hoành độ tiếp điểm là x  0 . x 1 0
b) y x  2 , biết tung độ tiếp điểm là y  2 . 0 1 2 x
Bài 9. Cho hai hàm số y  và y
. Viết phương trình tiếp tuyến với đồ thị của mội 2 x 2
hàm số đã cho tại giao điểm của chúng. Tính góc giữa hai tiếp tuyến kể trên.
Bài 10. Cho parabol  P 2
: y x . Gọi M và M là hai điểm thuộc  P lần lượt có hoành độ 1 2
x  –2 và x  1 . Hãy tìm trên  P một điểm E sao cho tiếp tuyến tại E song song với cát 1 2
tuyến M M . Viết phương trình tiếp tuyến đó. 1 2 Bài 11. Cho hàm số 3 2
y x  3x  2 . Viết phương trình tiếp tuyến của đồ thị, biết rằng tiếp
tuyến vuông góc với đường thẳng  : 3x – 5y – 2017  0 .
Bài 12. Cho hàm số C y f x 4 2 :
 –x – mx m 1. Tìm tất cả các giá trị của tham số m để m
các tiếp tuyến của C
tại A1; 0 và B  –1; 0 vuông góc với nhau. m Bài 13. Cho hàm số 2
y  cos x m sin x ( m là tham số) có đồ thị C  . Tìm m trong mỗi trường hợp sau:
a) Tiếp tuyến của C  tại điểm có x   có hệ số góc bằng 1.  
b) Tiếp tuyến của C  tại các điểm có các hoành độ x   và x  song song hoặc 4 3 trùng nhau.
Bài 14. Tìm giao điểm của hai đường cong  P 2
: y x x 1 và H  1 : y  . Chứng minh x 1
rằng hai đường cong đó có tiếp tuyến chung tại giao điểm của chúng. Bài 15. Cho parabol 2
(P) : y x . Viết phương trình tiếp tuyến với  P , biết:
a) Tiếp tuyến song song với đường thẳng d : y  4x  3 .
b) Tiếp tuyến đi qua điểm A0;   1 .
Bài 16. Viết phương trình tiếp tuyến của: x 1 a) y
tại điểm A2; 3 . x 1 b) 3 2
y x  4x 1
tại điểm có hoành độ x  –1 . 0 c) 2
y x  4x  4
tại điểm có tung độ y 1. 0 d) y  2x 1
tại điểm có hoành độ x  4 . 0 2 x  2x 15 4 e) y
biết hệ số góc của tiếp tuyến bằng . x  3 3 f) 4 2
y x – 2x 1
biết hệ số góc của tiếp tuyến bằng 24 . g) 3 2
y x  3x  2
biết tiếp tuyến d D : x – 3y –15  0 . h) 3
y x x  3
tại điểm có hoành độ x  –1 . 0 2x 1 i) y
tại điểm có hoành độ x  2 . x 1 0 x
Bài 17. Cho Cy f x 3 2 : 
. Lập phương trình tiếp tuyến của C  : x 1 5
a) Tại điểm có hoành độ bằng 2
b) Tại điểm có tung độ bằng 2
c) d //D : y  – x  25
d) d   : 4x – y  2017 .
Bài 18. Gọi C  là đồ thị hàm số 4 2
y x  2x 1. Viết phương trình tiếp tuyến của C  trong mỗi trường hợp sau:
a) Biết rằng tiếp tuyến song song với đường thẳng d : y  –3x 1 .
b) Biết rằng tiếp tuyến vuông góc với đường thẳng  : x – 7 y  2017 .
c) Biết rằng tiếp tuyến đi qua điểm A0; 2
Bài 19. Gọi C  là đồ thị hàm số 3 2
y x  5x  2 . Viết phương trình tiếp tuyến của C  trong mỗi trường hợp sau:
a) Biết tung độ của tiếp điểm bằng 2 .
b) Biết rằng tiếp tuyến song song với trục hoành.
c) Biết rằng tiếp tuyến vuông góc với đường thẳng d : x  8y  2017 .
d) Biết rằng tiếp tuyến đi qua điểm A0; – 6 .