TOP6 đề ôn tập kiểm tra giữa kỳ 2 Toán 12 có đáp án và lời giải chi tiết

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giữa học kì 2 môn Toán 12 năm học 2020 – 2021 .Mời bạn đọc đón xem.

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

70 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 1
Mã đề thi
001
Họ và tên :………………………………….Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tính tích phân
A.
2
3
−
. B.
2
3
. C.
1
3
−
. D.
1
3
.
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( )
22
2
: 1 3 5+ + + − =S x y z
. Tìm tọa độ tâm
I
và bán kính
R
của
( )
S
.
A.
( )
0; 1;3−I
và
5=R
. B.
( )
0; 1;3−I
và
5=R
.
C.
( )
0; 1;3−I
và
5=R
. D.
( )
0;1; 3−I
và
5=R
.
Câu 3. Cho
33
02
( )d , ( )d .f x x a f x x b==

Khi đó
2
0
( )df x x
bằng:
A.
ab+
. B.
ab−
. C.
ab−−
. D.
ba−
.
Câu 4. Trong không gian với hệ tọa độ
Oxy
, cho hai điểm
( )
2; 3;5M −
,
( )
6; 4; 1N −−
và đặt
L MN=
.
Mệnh đề nào sau đây là mệnh đề đúng ?
A.
( )
4; 1; 6L = − −
. B.
53L =
. C.
3 11L =
. D.
( )
4;1;6L =−
.
Câu 5. Cho tích phân
4
0
1
1 2 d .
2
I x x x=+
Đặt
1 2 ,ux=+
khi đó ta được tích phân
A.
( )
3
2
1
1
1d
4
I u u u=−
B.
( )
3
22
1
1
1d
2
I u u u=+
C.
3
53
1
1
4 5 3
uu
I

=−


D.
( )
3
22
1
1dI u u u=−
Câu 6. Trong không gian với hệ tọa độ
Oxyz
, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
( )
Oxy
?
A.
( )
1;1;1m =
. B.
( )
0;1;0j =
. C.
( )
0;0;1k =
. D.
( )
1;0;0i =
.
Câu 7. Cho hàm số
()fx
liên tục trên và F(x) là nguyên hàm của f(x), biết
( )
9
0
dx 9fx =
và F(0) = 3.
Tính F(9).
A.
( )
96F =−
. B.
( )
96F =
. C.
( )
9 12F =
. D.
( )
9 12F =−
.
Câu 8. Cho hàm số
4
2
23
()
x
fx
x
+
=
. Khẳng định nào sau đây là đúng?
A.
3
23
()
3
x
f x dx C
x
= + +
. B.
3
3
( ) 2f x dx x C
x
= − +
.
C.
3
23
()
32
x
f x dx C
x
= + +
. D.
3
23
()
3
x
f x dx C
x
= − +
.
Câu 9. Mệnh đề nào dưới đây đúng?
Trang 2/24
A.
21
2
3
3d
21
x
x
xC
x
+
=+
+
. B.
2
2
3
3d
ln3
x
x
xC=+
.
C.
2
9
3d
ln3
x
x
xC=+
. D.
2
2
3
3d
ln9
x
x
xC=+
.
Câu 10. Công thức nào sau đây sai?
A.
d
xx
e x e C=+
. B.
sin d cosx x x C= − +
C.
tan d cotx x x C= − +
. D.
cos d sinx x x C=+
.
Câu 11. Giá trị của
66
4
4
sin cos
61
x
xx
dI x
được viết dưới dạng
a
b
, trong đó
,ab
là các số nguyên dương
và
a
b
là phân số tối giản. Tính
ab
.
A.
32ab
. B.
25ab
. C.
30ab
. D.
27ab
.
Câu 12. Cho hai hàm số
( )
fx
,
( )
gx
là hàm số liên tục, có
( )
Fx
,
( )
Gx
lần lượt là nguyên hàm của
( )
fx
,
( )
gx
. Xét các mệnh đề sau:
( )
I
.
( ) ( )
F x G x+
là một nguyên hàm của
( ) ( )
f x g x+
.
( )
II
.
( )
.k F x
là một nguyên hàm của
( )
.k f x
với
k
.
( )
III
.
( ) ( )
.F x G x
là một nguyên hàm của
( ) ( )
.f x g x
.
Các mệnh đề đúng là
A.
( )
I
và
( )
III
. B.
( )
I
và
( )
II
. C.
( )
II
và
( )
III
. D. Cả
3
mệnh đề.
Câu 13. Tìm
cos
sin . d
x
x e x
.
A.
cos cos
sin . d
xx
x e x e C=+
. B.
cos cos
sin . d
xx
x e x e C= − +
.
C.
cos sin
sin . d cos .
xx
x e x x e C=+
. D.
cos sin
sin . d cos .
xx
x e x x e C= − +
.
Câu 14. Nếu
( )
2
62d
x
a
ft
tx
t
+=
, với
0x
thì hệ số
a
bằng
A.
9
. B.
19
. C.
29
. D.
5
.
Câu 15. Tính
π
0
sin dJ x x x=
.
A.
π
2
. B.
π−
. C.
π
. D.
π
4
.
Câu 16. Cho hàm số
( )
fx
thỏa mãn
( ) ( )
1
0
1 d 10x f x x
+=
và
( ) ( )
2 1 0 2ff−=
. Tính
( )
1
0
dI f x x=
.
A.
8I =
. B.
12I =−
. C.
8I =−
. D.
1I =
.
Câu 17. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
1; 3; 2A −
,
( )
3; 5; 2B −
. Phương trình mặt
phẳng trung trực của đoạn thẳng
AB
có dạng
0x ay bz c+ + + =
. Khi đó
abc++
bằng:
A.
2−
. B.
4−
. C.
3−
. D.
2
.
Câu 18. Trong không gian
Oxyz
, cho hai mặt phẳng
( )
: 2 1 0x my z
+ + − =
,
( )
: 2 3 4 5 0x y z
+ + + =
biết
( ) ( )

⊥
. Khi đó giá trị
m
là
A.
1m =
. B.
1m =−
. C.
2m =
. D.
2m =−
.
Câu 19. Biết
( )
( )
2 x
F x ax bx c e= + +
là một nguyên hàm của hàm số
( )
( )
2
55
x
f x x x e= + +
Giá trị của
23a b c++
là
A.
6
. B.
13
. C.
8
. D.
10
.
Trang 3/24
Câu 20. Họ nguyên hàm của hàm số
( ) ( )
4 1 lnf x x x=+
là :
A.
22
2 lnx x x C++
. B.
22
2 lnx x x+
.
C.
22
2 ln 3x x x C++
. D.
22
2 ln 3x x x+
.
Câu 21. Tích phân
bằng
A.
( )
200
1
199e 1
4
+
. B.
( )
200
1
199e 1
2
+
. C.
( )
200
1
199e 1
4
−
. D.
( )
200
1
199e 1
2
−
.
Câu 22. Trong không gian với hệ tọa độ
,Oxyz
cho hai vectơ
( ; 2; 1)u m m= − +
và
(3; 2 4;6).vm= − −
Tìm
tất cả các giá trị của
m
để hai vectơ
,uv
cùng phương.
A.
1m =
. B.
0m =
. C.
1m =−
. D.
2m =
.
Câu 23. Trong không gian
Oxyz
, cho hai điểm
( )
3;1; 2−A
,
( )
2; 3;5−B
. Điểm
M
thuộc đoạn
AB
sao
cho
2=MA MB
, tọa độ điểm
M
là
A.
7 5 8
;;
3 3 3

−


. B.
( )
4;5; 9−
. C.
3 17
; 5;
22

−


. D.
( )
1; 7;12−
.
Câu 24. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
22
cos 2
sin .cos
x
fx
xx
=
và
2.
4
F

=


Tính
3
F



.
A.
12 4 3
33
F
−

=


. B.
12 2 3
33
F
−

=


.
C.
12 2 3
33
F
+

=


. D.
12 4 3
33
F
+

=


.
Câu 25. Biết
( )
Fx
là một nguyên hàm của hàm
( )
sin 2f x x=
và
1
4
F

=


. Tính
6
F



.
A.
0
6
F

=


. B.
3
64
F

=


. C.
1
62
F

=


. D.
5
64
F

=


.
Câu 26. Một nguyên hàm của hàm số
( )
( )
2
2
sin 2 sin
2 sin cos
xx
fx
xx
−
=
++
là:
A.
( )
2
ln 2 sin cosF x x x= + +
. B.
( )
( )
3
2
2
2 sin cos
Fx
xx
−
=
++
.
C.
( )
2
1
2 sin cos
Fx
xx
−
=
++
. D.
( )
( )
2
1
2 2 sin cos
Fx
xx
=
++
.
Câu 27. Cho hàm số
( )
fx
thỏa mãn
( )
3 2sinf x x
=+
và
( )
03f =
. Mệnh đề nào dưới đây đúng?
A.
( )
3 2cos 5f x x x= + +
. B.
( )
3 2cos 3f x x x= + +
.
C.
( )
3 2cos 3f x x x= − +
. D.
( )
3 2cos 5f x x x= − +
.
Câu 28. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng có phương trình
1
2 3 4
x y z
+ + =
cắt 3 trục tọa
độ lần lượt tại
A
,
B
,
C
. Tính thể tích khối tứ diện
OABC
.
A.
24V =
. B.
8V =
. C.
4V =
. D.
12V =
.
Câu 29. Cho hàm số
( )
fx
liên tục trên và thỏa mãn
( )
1
5
9f x dx
−
=
. Tính tích phân
( )
2
0
1 3 9f x dx−+


A.
21
. B.
15
. C.
75
. D.
27
.
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hai điểm
( )
2; 1;3A −−
và
( )
2; 5;1B −
, điểm
M
thỏa mãn
2MA MB=
. Khi đó
M
sẽ thuộc mặt cầu nào sau đây:
Trang 4/24
A.
2 2 2
10 19 1
16
3 3 3
x y z
+ + − + + =
. B.
( ) ( )
22
2
3 2 9x y z+ + + − =
.
C.
2 2 2
10 19 1
16
3 3 3
x y z
− + + + − =
. D.
( ) ( )
22
2
3 2 9x y z+ − + + =
.
Câu 31. Tìm
ab+
biết
7 11
ln 2 ln 1
( 1)( 2)
x
dx a x b x C
xx
+
= + + + +
++
?
A.
5ab+ = −
. B.
5ab+=
. C.
11ab+=
. D.
7ab+=
.
Câu 32. Cho
( )
3
3
3f x dx =−
và
m
là số thực sao cho
( ) ( )
3
2
19m f x dx+ = −
. Tìm
m
.
A.
1.m =
B.
4m =
C.
4m =−
D.
2.m =
Câu 33. Cho
( )
4
0
16f x dx =
. Tính
( )
2
0
2f x dx
A.
16
. B.
4
. C.
32
. D.
8
.
Câu 34. Trong không gian với hệ toạ độ
,Oxyz
cho điểm
( )
2;1;0M
và mặt phẳng
( )
: 2 2 3 0.P x y z− − + =
Khoảng cách từ điểm
M
đến mặt phẳng
( )
P
bằng
A.
1
3
. B.
3
3
. C.
3
. D.
1
.
Câu 35. Cho
( ) ( ) ( )
11
00
2 d 3; d 1f x g x x f x x− = = −



. Tính
( )
1
0
dg x x
A.
2I =−
. B.
2I =
. C.
1I =
. D.
1I =−
.
PHẦN II: TỰ LUẬN
Câu 36. Tìm họ nguyên hàm của hàm số
( ) sin3 cos2 .f x x x=
Câu 37. Cho tứ diện
ABCD
có
4AB a=
,
6CD a=
, các cạnh còn lại có độ dài bằng
22a
. Tính bán kính
R
của mặt cầu ngoại tiếp tứ diện
ABCD
.
Câu 38. Cho hàm số
( )
fx
liên tục trên và các tích phân
( )
4
0
tan d 4f x x
=
và
( )
2
1
2
0
d2
1
x f x
x
x
=
+
. Tính tích
phân
( )
1
0
dI f x x=
.
Câu 39. Cho hàm số
( )
fx
liên tục, không âm trên đoạn
0;
2



, thỏa mãn
( )
03f =
và
( ) ( ) ( )
2
. ' cos . 1f x f x x f x=+
, với
0;
2
x




. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
( )
fx
trên đoạn
;
62




.
------------- HẾT -------------
Trang 5/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 2
Mã đề thi
002
Họ và tên :………………………………….Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho tam giác
ABC
biết
( )
1; 2;4A −
,
( )
0;2;5B
và
( )
5;6;3C
. Tọa độ trọng tâm
G
của
ABC
là
A.
( )
G 3;3;6
. B.
( )
G 6;3;3
. C.
( )
2;2;4G
. D.
( )
G 4;2;2
.
Câu 2. Tính tích phân
1
0
2
x
I e dx=
.
A.
22Ie=+
. B.
22Ie=−
. C.
2
2I e e=−
. D.
2Ie=
.
Câu 3. Họ nguyên hàm của hàm số
( )
2 sin 2f x x x=+
là
A.
2
2cos 2x x C−+
. B.
2
2cos 2x x C++
. C.
2
1
cos 2
2
x x C−+
. D.
2
1
cos 2
2
x x C++
.
Câu 4. Trong không gian với hệ tọa độ
Oxyz
, cho mặt cầu
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 16S x y z− + − + + =
. Tọa độ tâm
I
và bán kính
R
của
()S
là
A.
( )
1; 2;1I = − −
,
4R =
. B.
( )
1;2; 1I =−
,
4R =
.
C.
( )
1; 2;1I = − −
,
16R =
. D.
( )
1;2; 1I =−
,
16R =
.
Câu 5. Tích phân
1
0
1
d
1
Ix
x
=
+
có giá trị bằng
A.
ln 2
. B.
1 ln 2−
. C.
ln 2 1−
. D.
ln 2−
.
Câu 6. Cho tích phân
1
3
0
1dxx−
. Với cách đặt
3
1tx=−
thì tích phân đã cho bằng với tích phân nào dưới
đây?
A.
1
2
0
dtt
. B.
1
3
0
3dtt
. C.
1
0
3dtt
. D.
1
3
0
dtt
.
Câu 7. Một nguyên hàm của hàm số
( )
( )
2
3f x x=−
trên là:
A.
( )
( )
3
3
2017
3
x
Fx
−
=+
. B.
( ) ( )
3
33F x x=−
.
C.
( )
( )
3
3
3
x
F x x
−
=+
. D.
( ) ( )
23F x x=−
.
Câu 8. Tìm nguyên hàm
( )
15
2
7 dxxx+
?
A.
( )
16
2
1
7
2
xC++
B.
( )
16
2
1
7
32
xC− + +
C.
( )
16
2
1
7
16
xC++
D.
( )
16
2
1
7
32
xC++
Câu 9. Cho
( )
4
1
d9f x x =
, tính
( )
1
0
3 1 dI f x x=+
.
A.
27I =
. B.
9I =
. C.
3I =
. D.
1I =
.
Câu 10. Trong không gian với hệ tọa độ
,Oxyz
vectơ pháp tuyến của mặt phẳng
( )
Oxz
là
Trang 6/24
A.
( )
1;0;1n
. B.
( )
0;1;0n
. C.
( )
1;0;0n
. D.
( )
0;0;1n
.
Câu 11. Tính
1
0
ed
x
Ix=
.
A.
1I =
. B.
1eI =−
. C.
eI =
. D.
e1I =−
.
Câu 12. Họ nguyên hàm của hàm số
( )
2
3 sinf x x x=+
là
A.
( )
3
sinF x x x C= + +
. B.
( )
3
cosF x x x C= − +
.
C.
( )
3
3 sinF x x x C= − +
. D.
( )
3
cosF x x x C= + +
.
Câu 13. Trong không gian với hệ trục tọa độ
Oxyz
, cho 3 điểm
( ) ( ) ( )
1;0;0 , 0;2;0 , 0;0; 3A B C −
. Gọi
H
là
trực tâm của tam giác
ABC
. Tính độ dài đoạn
OH
.
A.
1
3
. B.
2
5
. C.
6
7
. D.
3
4
.
Câu 14. Cho
( )
2;0;0A
,
( )
0;2;0B
,
( )
0;0;2C
. Tập hợp các điểm
M
trên mặt phẳng
Oxy
thỏa mãn
2
.3MA MB MC+=
là
A. Một mặt cầu. B. Tập rỗng. C. Một điểm. D. Một đường tròn.
Câu 15. Tìm nguyên hàm của hàm số
( )
lnf x x x=
.
A.
( ) ( )
3
2
2
dx 3ln 1 .
9
f x x x C= − +
B.
( ) ( )
3
2
2
dx 3ln 2 .
9
f x x x C= − +
C.
( ) ( )
3
2
1
dx 3ln 2 .
9
f x x x C= − +
D.
( ) ( )
3
2
2
dx 3ln 2 .
3
f x x x C= − +
Câu 16. Tìm nguyên hàm của hàm số
( )
21f x x=−
.
A.
( ) ( )
1
2 1 2 1
3
f x dx x x C= − − +
. B.
( )
1
21
3
f x dx x C= − − +
.
C.
( )
1
21
2
f x dx x C= − +
D.
( ) ( )
2
2 1 2 1
3
f x dx x x C= − − +
.
Câu 17. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1; 1; 2A −
. Phương trình mặt phẳng
( )
Q
đi qua
các hình chiếu của điểm
A
trên các trục tọa độ là
A.
( )
:1
1 1 2
x y z
Q + + =
−−
. B.
( )
: 2 6 0Q x y z− + + =
.
C.
( )
: 2 2 2 0Q x y z− + − =
. D.
( )
:0
2
z
Q x y− + =
.
Câu 18. Tìm nguyên hàm
( )
Fx
của hàm số
( )
sin cosf x x x=+
thoả mãn
2
2
F

=


A.
( )
cos sin 1F x x x= − + −
. B.
( )
cos sin 1F x x x= − + +
.
C.
( )
cos sin 3F x x x= − +
. D.
( )
cos sin 3F x x x= − + +
.
Câu 19. Trong không gian
Oxyz
cho vec-tơ
( )
1;1;2u
và
( )
2;0;vm
. Tìm giá trị của tham số
m
biết
( )
4
cos ;
30
uv =
A.
11m =−
. B.
0m =
. C.
1m =
. D.
1; 11mm= = −
.
Câu 20. Cho
( )
Fx
là một nguyên hàm của hàm số
( ) 2
x
f x e x=+
thỏa mãn
( )
3
0
2
F =
. Tìm
( )
Fx
.
A.
( )
2
5
2
x
F x e x= + +
. B.
( )
2
3
2
x
F x e x= + +
.
Trang 7/24
C.
( )
2
1
2
x
F x e x= + +
. D.
( )
2
1
2
2
x
F x e x= + −
.
Câu 21. Gọi
( )
Fx
là một nguyên hàm của hàm số
( )
2
ln x
fx
x
=
thỏa mãn
( )
3
8Fe =
. Giá trị
(
)
3
9
Fe
bằng
A.
3
97+
. B.
3
91−
. C.
2
. D.
10
.
Câu 22. Tích phân
1000
2
2
2
1
41xx
I dx
xx
++
=
+
bằng
A.
( )
2
1000 996 1000
2 1 ln 2 1 2I

= − + +


. B.
( )
2
1000 998 1000
2 1 ln 2 1 2I

= − + +


.
C.
( )
2
1000 1998 1000
2 1 ln 2 1 2I

= − + +


. D.
( )
2
1000 996 1000
2 ln 2 1 2I

= + +


.
Câu 23. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
( )
2
3
4x=−
x
f x e x
. Hàm số
( )
2
+F x x
có bao nhiêu
điểm cực trị?
A.
3
. B.
4
. C.
6
. D.
5
.
Câu 24. Tính tích phân
π
2
0
cos 2 dI x x x=
bằng cách đặt
2
d cos 2 d
ux
v x x
=
=
. Mệnh đề nào dưới đây đúng?
A.
π
2
0
0
1
sin 2 sin 2 d
2
I x x x x x
=+
. B.
π
2
0
0
1
sin 2 2 sin 2 d
2
I x x x x x
=−
.
C.
π
2
0
0
1
sin 2 2 sin 2 d
2
I x x x x x
=+
. D.
π
2
0
0
1
sin 2 sin 2 d
2
I x x x x x
=−
.
Câu 25. Cho hàm số
)(xfy =
liên tục và có đạo hàm trên R thỏa mãn
( )
22f =−
;
2
0
( ) 1f x dx =
. Tính tích
phân
( )
=
4
0
' dxxfI
.
A.
0=I
. B.
18−=I
. C.
10−=I
. D.
5−=I
.
Câu 26. Cho hàm số
( )
2
cos
a
f x x
=+
. Tìm tất cả các giá trị của
a
để
( )
fx
có một nguyên hàm
( )
Fx
thỏa
mãn
( )
1
0
4
F =
,
44
F


=


.
A.
2
2
−
. B.
2
−
. C.
1
−
. D.
1
2
−
.
Câu 27. Với cách đổi biến
1 3lnux=+
thì tích phân
1
ln
1 3ln
e
x
dx
xx+
trở thành
A.
( )
2
2
1
2
1
9
u du−
. B.
( )
2
2
1
21u du−
. C.
2
2
1
21
9
u
du
u

−


. D.
( )
2
2
1
2
1
3
u du−
.
Câu 28. Cho
( )
2
1
1d
x
G x t t=+
. Khi đó
( )
Gx
bằng
A.
2
1
x
x+
. B.
2
1
1 x+
. C.
( )
22
11xx++
. D.
2
1 x+
.
Câu 29. Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
( )
: 3 2 5 0P x y z− + − =
. Điểm nào dưới đây
thuộc
( )
P
?
A.
( )
1;1;4M
. B.
( )
0;0; 5P −
. C.
( )
3; 2;1Q −
. D.
( )
3; 2; 5N −−
.
Trang 8/24
Câu 30. Biết rằng trên khoảng
3
;
2

+


hàm số
( )
2
20 30 7
23
xx
fx
x
−+
=
−
có một nguyên hàm
( )
( )
2
23F x ax bx c x= + + −
(
,,abc
là các số nguyên). Tổng
S a b c= + +
bằng
A.
3
. B.
5
. C.
6
. D.
4
.
Câu 31. Cho hàm số
( )
fx
liên tục trên
)
1; +
và
( )
3
0
18f x dx+=
. Tích phân
( )
2
1
.I x f x dx=
bằng:
A.
16I =
. B.
2I =
. C.
8I =
. D.
4I =
.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho các điểm
( )
1; 3; 4A −
,
( )
3; 5; 2B −−
. Tìm tọa độ trung
điểm
M
của đoạn
AB
.
A.
( )
2; 4; 3M −
. B.
( )
1; 1;1M −
. C.
( )
1;1;1M
. D.
( )
4; 8; 6M −
.
Câu 33. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
2
( ): 2x 2 y z m 3 0Pm+ + − − =
và mặt cầu
( ) ( ) ( )
2 2 2
( ): 1 1 1 9S x y z− + + + − =
. Tìm tất cả các giá trị của
m
để
()P
tiếp xúc với
()S
.
A.
2
5
m
m
=
=−
. B.
2m =
. C.
5m =−
. D.
2
5
m
m
=−
=
.
Câu 34. Biết
( )
2
2
1
3 1 d
ln
ln
3 ln
xx
b
a
x x x c
+

=+

+

với
a
,
b
,
c
là các số nguyên dương và
4c
. Tổng
abc++
bằng
A.
7
. B.
8
. C.
6
. D.
9
.
Câu 35. Khi tính nguyên hàm
3
d
1
x
x
x
−
+
, bằng cách đặt
1ux=+
ta được nguyên hàm nào?
A.
( )
2
2 4 du u u−
. B.
( )
2
4duu−
. C.
( )
2
3duu−
. D.
( )
2
2 4 duu−
.
PHẦN II: TỰ LUẬN
Câu 36. Tìm họ nguyên hàm của hàm số
2
2
( ) .
2
fx
x
=
−
Câu 37. Cho biết
2
0
sin 2 .cos
ln 2
1 cos
xx
dx a b
x
=+
+
với
,ab
là các số nguyên. Tính
23
2 3bPa= +
.
Câu 38. Cho hình chóp
.S ABCD
có
0
90 ,ABC ADC==
cạnh bên
SA
vuông góc với
( )
ABCD
, góc tạo bởi
SC
và đáy
ABCD
bằng
0
60
,
CD a=
và tam giác
ADC
có diện tích bằng
2
3
.
2
a
Tính diện tích mặt cầu
mc
S
ngoại tiếp hình chóp
.S ABCD
.
Câu 39. Cho hàm số
( )
y f x=
có đạo hàm liên tục trên
1;3
thỏa mãn
( )
3
1
8f x dx
=
và
( )
( )
3
1
2
2
fx
dx
fx
=
.
Tính
( )
3f
.
------------- HẾT -------------
Trang 9/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 3
Mã đề thi
003
Họ và tên :………………………………….Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tìm nguyên hàm của hàm số
( )
( )
e 1 e
xx
fx
−
=+
.
A.
( )
de
x
f x x x C= + +
. B.
( )
d e e
xx
f x x C
−
= + +
.
C.
( )
de
x
f x x C
−
=+
. D.
( )
de
x
f x x C=+
.
Câu 2. Tính
2
0
41x dx+
.
A.
13
3
. B.
4
3
. C.
13
. D.
4
.
Câu 3. Xét
( )
2
1
23
0
1d
xx
x e x
−+
−
, nếu đặt
2
23u x x= − +
thì
( )
2
1
23
0
1d
xx
x e x
−+
−
bằng
A.
3
2
1
d
2
u
eu
. B.
3
2
d
u
eu−
. C.
3
2
d
u
eu
. D.
3
2
1
d
2
u
eu−
.
Câu 4. Trong không gian
,Oxyz
cho điểm
(1; 2; 3).M
Hình chiếu của
M
lên trục
Oy
là
A.
(0; 2; 0).Q
. B.
(1; 0; 0).R
. C.
(0; 0; 3).S
. D.
(1; 0; 3)P
.
Câu 5. Tính tích phân
1
0
d
1
x
x +
bằng
A.
1
. B.
ln 2
. C.
ln2.−
D.
log 2
.
Câu 6. Biết
( )
2
1
x2f x d =
. Tích phân
( )
2
1
3xf x d
bằng
A.
6
. B.
1
. C.
3
. D.
5
.
Câu 7. Họ nguyên hàm của hàm số
( )
32
43f x x x=+
là:
A.
43
x x x C+ + +
. B.
43
x x C++
. C.
43
43x x C++
. D.
43
43x x x C+ + +
.
Câu 8. Trong không gian
Oxyz
, cho mặt phẳng
( )
:P
2 23 0xz+ + =
. Mặt phẳng
( )
P
có một vectơ pháp
tuyến là:
A.
( )
3
1;0;23n =
. B.
( )
4
0;2;23n =
. C.
( )
1
1;0;2n =
. D.
( )
2
1;2;3n =
.
Câu 9. Trong không gian
Oxyz
, phương trình mặt cầu tâm
( )
1; 2; 3I
và bán kính
3R =
là
A.
( ) ( ) ( )
2 2 2
1 2 3 3x y z− + − + − =
. B.
2 2 2
2 4 6 5 0x y z x y z+ + + + + + =
.
C.
( ) ( ) ( )
2 2 2
1 2 3 9x y z− + − + − =
. D.
( ) ( ) ( )
2 2 2
1 2 3 9x y z+ + + + + =
.
Câu 10. Cho hàm số
( )
fx
xác định trên
K
và
( )
Fx
là một nguyên hàm của
( )
fx
trên
K
. Khẳng định nào
dưới đây đúng?
A.
( ) ( )
F x f x=
,
xK
. B.
( ) ( )
F x f x

=
,
xK
.
C.
( ) ( )
f x F x
=
,
xK
. D.
( ) ( )
F x f x
=
,
xK
.
Câu 11. Họ nguyên hàm của hàm số
2
( ) 2 1f x x x= − +
là
A.
3
1
( ) 2
3
F x x x C= − + +
. B.
( ) 2 2F x x C= − +
.
Trang 10/24
C.
32
1
()
3
F x x x x C= − + +
. D.
32
1
( ) 2
3
F x x x x C= − + +
.
Câu 12. Cho tích phân
( )
3
0
dxf x a=
,
( )
3
2
dxf x b=
. Tính tích phân
( )
2
0
dxfx
.
A.
ab−−
. B.
ba−
. C.
ab+
. D.
ab−
.
Câu 13. Trong không gian hệ trục tọa độ
Oxyz
cho mặt cầu
( )
S
đi qua hai điểm
( ) ( )
1;1;2 ,B 3;0;1A
và có
tâm thuộc trục
Ox
. Phương trình mặt cầu
( )
S
là?
A.
( )
2
22
15x y z− + + =
. B.
( )
2
22
15x y z+ + + =
.
C.
( )
2
22
15x y z− + + =
D.
( )
2
22
15x y z+ + + =
.
Câu 14. Trong không gian
Oxyz
, cho các điểm
( )
1;2; 1A −
,
( )
2;3;4B
,
( )
3;5; 2C −
. Tìm tọa độ điểm
I
là
tâm của đường tròn ngoại tiếp tam giác
ABC
.
A.
27
;15;2
2
I

−


. B.
73
2; ;
22
I

−


. C.
5
;4;1
2
I



. D.
37
; 7;0
2
I

−


.
Câu 15. Tìm nguyên hàm
( )
Fx
của hàm số
( )
2
21
fx
x
=
−
thỏa mãn
( )
57F =
.
A.
( )
2 2 1F x x=−
. B.
( )
2 2 1 1F x x= − +
.
C.
( )
2 1 4F x x= − +
. D.
( )
2 1 10F x x= − −
.
Câu 16. Biết rằng
3
2
ln d ln 3 ln 2x x x m n p= + +
trong đó
,,m n p
. Tính
2m n p++
A.
5
4
−
. B.
5
4
. C.
9
2
. D.
0
.
Câu 17. Trong không gian với hệ trục tọa độ
Oxyz
, viết phương trình mặt phẳng
( )
P
song song với mặt phẳng
( )
: 2 2 5 0Q x y z− + + =
đồng thời khoảng cách giữa hai mặt phẳng
( )
P
và
( )
Q
bằng khoảng cách từ
( )
3; 1; 2A −
đến mặt phẳng
( )
P
.
A.
( )
: 2 2 6 0P x y z− + + =
. B.
( )
: 2 2 3 0P x y z− + − =
.
C.
( )
: 2 2 6 0P x y z− + − =
. D.
( )
: 2 2 3 0P x y z− + + =
.
Câu 18. Tính
( )
10
100 2
0
2.I x x dx= − −
A.
101
10 1060
101 3
I =+
. B.
101
10 940
101 3
I =+
. C.
101
10 1060
101 3
I =−
. D.
101
10 940
101 3
I =−
.
Câu 19. Tìm
cos 2 dx x x
.
A.
Cxxx +− 2cos
4
1
2sin.
2
1
. B.
Cxxx ++ 2cos2sin.
.
C.
11
sin 2 2
22
cosx x x C++
. D.
Cxxx ++ 2cos
4
1
2sin.
2
1
.
Câu 20. Cho hàm số
( )
y f x=
có đạo hàm liên tục trên . Đồ thị của hàm số
( )
y f x=
như hình vẽ bên.
Khi đó giá trị của biểu thức
( ) ( )
42
00
2 d 2 df x x f x x

− + +

bằng
A.
2
. B.
10
. C.
6
. D.
2−
.
Câu 21. Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( ) ( )
2;1;0 , 1;0; 2ab−−
. Tính
( )
cos ,ab
.
Trang 11/24
A.
( )
2
cos ,
5
ab =
. B.
( )
2
cos ,
25
ab =
. C.
( )
2
cos ,
25
ab =−
. D.
( )
2
cos ,
5
ab =−
.
Câu 22. Biết một nguyên hàm của hàm số
( )
2y f x=
là
( )
2
2 d sin lnf x x x x=+
. Tìm nguyên hàm
( )
df x x
.
A.
( )
2
d 2sin 2ln
2
x
f x x x C= + +
. B.
( )
2
d 2sin 2ln ln 2f x x x x C= + − +
.
C.
( )
2
d 2sin 2 2ln ln 2f x x x x C= + − +
. D.
( )
2
d sin ln
2
x
f x x x C= + +
.
Câu 23. Cho
( ) ( )
ln=+
a
F x x b
x
là một nguyên hàm của hàm số
( )
2
1 ln+
=
x
fx
x
, trong đó
, ab
. Tính
=+S a b
.
A.
1=S
. B.
2=S
. C.
0=S
. D.
2=−S
.
Câu 24. Trong không gian với hệ tọa độ
Oxyz
, gọi
,,abc
lần lượt là khoảng cách từ điểm
( )
1;3;2M
đến 3 mặt phẳng
tọa độ
( ) ( ) ( )
,,Oxy Oyz Oxz
. Tính
23
P a b c= + +
.
A.
12P =
. B.
32P =
. C.
18P =
. D.
30P =
.
Câu 25. Cho
,MN
là các số thực, xét hàm số
( )
.sin .cosf x M x N x

=+
thỏa mãn
( )
13f =
và
( )
1
2
0
1
df x x
=−
. Giá trị của
1
4
f



bằng
A.
2
2
−
. B.
52
2
. C.
52
2
−
. D.
2
2
.
Câu 26. Với
a
là một số thực khác
0
, mệnh đề nào sau đây sai?
A.
( )
( )
2
11
d cot
sin
x ax b C
ax b a
= − + +
+
. B.
( ) ( )
1
sin d cosax b x ax b C
a
+ = + +
.
C.
( )
( )
2
11
d tan
cos
x ax b C
ax b a
= + +
+
. D.
( ) ( )
1
cos d sinax b x ax b C
a
+ = + +
.
Câu 27. Một học sinh làm bài tích phân
1
2
0
d
1
x
I
x
=
+
theo các bước sau.
Bước 1: Đặt
tan , ;
22
x t t

−

=


, suy ra
2
(1 tan )ddx t t=+
.
Bước 2: Đổi cận
1 ; 0 0
4
x t x t
= = = =
.
Bước 3:
2
44
2
00
1 tan
dd
1 tan 4
t
I t t
t

+
= = =
+

.
Các bước làm ở trên, bước nào bị sai
A. Không bước nào sai. B. Bước 2.
C. Bước 3. D. Bước 1.
Câu 28. Tìm một nguyên hàm
( )
Fx
của hàm số
( )
sin 3f x x=
thỏa mãn
2
2
F

=


.
A.
( )
cos3 5
33
x
Fx= − +
. B.
( )
cos3
2
3
x
Fx= − +
.
C.
( )
cos3 2F x x= − +
. D.
( )
cos3 2F x x=+
.
Trang 12/24
Câu 29. Trong không gian với hệ trục tọa độ
Oxyz
, cho véc tơ
( )
1; 2;3=−a
. Tìm tọa độ của véc tơ
b
biết
rằng véc tơ
b
ngược hướng với véc tơ
a
và
2=ba
.
A.
( )
2; 4;6=−b
. B.
( )
2;4; 6= − −b
. C.
( )
2; 2;3= − −b
. D.
( )
2; 2;3=−b
.
Câu 30. Biết
( )
( )
1
d
2
F x x
xx
=
+
và
( )
0 ln 4F =
. Giá trị của
( )
4F
bằng
A.
2ln3
. B.
4 ln 2
. C.
2ln5
. D.
6
.
Câu 31. Cho
( )
1 ln 2
ln2
2018f x dx
+
=
. Tính
( )
1
1
ln 2
e
f x dx
x
.
A.
1009I =
. B.
4036I =
C.
1009
2
I =
. D.
2018I =
.
Câu 32. Trong không gian
Oxyz
, cho mặt phẳng
( )
P
:
3 4 1 0xz− − =
. Mặt cầu nào sau đây cắt mặt phẳng
( )
P
A.
( ) ( )
22
2
1 3 1x y z+ − + − =
. B.
( ) ( ) ( )
2 2 2
3 1 2 1x y z− + − + + =
.
C.
( )
2
22
31x y z+ − + =
. D.
( ) ( )
22
2
1 3 1x y z− + − + =
.
Câu 33. Tính tích phân
1
ln
e
I x xdx=
:
A.
1
2
I =
. B.
2
2
2
e
I
−
=
. C.
2
1
4
e
I
+
=
. D.
2
1
4
e
I
−
=
.
Câu 34. Cho hàm số
( )
y f x=
có đạo hàm liên tục trên
2;3
đồng thời
( )
22f =
,
( )
35f =
. Tích phân
( )
3
2
df x x
bằng
A.
7
. B.
10
. C.
3
. D.
3−
.
Câu 35. Cho hàm số
( )
fx
xác định trên
\2−
thỏa mãn
( ) ( ) ( )
31
, 0 1, 4 2
2
x
f x f f
x
−
= = − =
+
. Giá trị của
biểu thức
( ) ( )
23ff+−
bằng:
A.
12
. B.
10 ln 2+
. C.
3 20ln 2−
. D.
ln 2
.
PHẦN II: TỰ LUẬN
Câu 36. Tìm học nguyên hàm của
5
( ) cos .f x x=
Câu 37. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
A
,
aAB =
. Cạnh bên
SA
vuông góc với
mặt đáy. Góc giữa
SB
và mặt đáy bằng
45
. Tính thể tích của khối cầu ngoại tiếp hình chóp
.S ABC
.
Câu 38. Cho hàm số
( )
fx
liên tục trên thoả mãn
( )
4
tan cos ,f x x x=
. Tính
( )
1
0
dI f x x=
.
Câu 39. Cho
( )
fx
là hàm liên tục và nhận giá trị dương
0;1
. Biết
( ) ( )
. 1 1−=f x f x
với mọi
0;1x
Tính
( )
0
1
d
1
x
I
fx
=
+
.
------------- HẾT -------------
Trang 13/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 4
Mã đề thi
004
Họ và tên :………………………………….Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho hàm số
( )
fx
liên tục trên và
( )
4
0
d 10f x x =
,
( )
4
3
d4f x x =
. Tích phân
bằng
A.
7
. B.
3
. C.
6
. D.
4
.
Câu 2. Họ nguyên hàm của hàm số
( )
32
=+f x x x
là
A.
43
34
++
xx
C
B.
43
43
++
xx
C
. C.
43
++x x C
. D.
2
32++x x C
.
Câu 3. Cho
( )
02f x x
( )
2
2
2
21
20
22
x
fx
x
− = −
− =
−=
. Tính
2
2
3
3
0
0
x
x
x
x
=
=

=
=
.
A.
m
. B.
2
0x
. C.
( )
2
2 0, f x x
−
. D.
( )
22
2 0 2 2f x x
− −
.
Câu 4. Tìm nguyên hàm của hàm số
( )
1
52
fx
x
=
−
.
A.
1
ln 5 2
5 2 2
dx
xC
x
= − − +
−
. B.
ln 5 2
52
dx
xC
x
= − +
−
.
C.
1
ln 5 2
5 2 5
dx
xC
x
= − +
−
. D.
5ln 5 2
52
dx
xC
x
= − +
−
.
Câu 5. Mệnh đề nào sau đây sai?
A.
( ) ( ) ( ) ( )f x g x dx f x dx g x dx− = −
với mọi hàm số
( ), ( )f x g x
liên tục trên .
B.
( ) ( )f x dx f x C
=+
với mọi hàm số
()fx
có đạo hàm trên .
C.
( ) ( ) ( ) ( )f x g x dx f x dx g x dx+ = +
với mọi hàm số
( ), ( )f x g x
liên tục trên .
D.
( ) ( )kf x dx k f x dx=

với mọi hằng số
k
và với mọi hàm số
()fx
liên tục trên .
Câu 6. Cho
( )
2
1
4 2 1f x x dx−=


. Khi đó
( )
2
1
f x dx
bằng :
A.
1
. B.
3−
. C.
3
. D.
1−
.
Câu 7. Trong không gian với hệ tọa độ
Oxyz
, cho điểm
( )
1; 5;6M −
. Gọi
H
là hình chiếu vuông góc của
M
lên mặt phẳng
( )
Oxz
. Tọa độ điểm
H
là
A.
( )
1;0;6H
. B.
( )
0; 5;0H −
. C.
( )
6;0;1H
. D.
( )
1;0;0H
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, viết phương trình mặt cầu có tâm
( )
1; 4;3I −
và đi qua điểm
( )
5; 3;2A −
.
A.
( ) ( ) ( )
2 2 2
1 4 3 18x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
1 4 3 16x y z− + − + − =
.
C.
( ) ( ) ( )
2 2 2
1 4 3 16x y z− + + + − =
. D.
( ) ( ) ( )
2 2 2
1 4 3 18x y z− + + + − =
.
Trang 14/24
Câu 9. Cho hàm số
( )
fx
liên tục trên và có
( )
1
0
d2f x x =
,
( )
3
0
d6f x x =
. Tính
( )
1
1
2 1 dI f x x
−
=−
.
A.
6I =
. B.
3
2
I =
. C.
4I =
. D.
2
3
I =
.
Câu 10. Trong không gian
Oxyz
, vectơ
( )
1;2; 1n =−
là một vectơ pháp tuyến của mặt phẳng nào dưới đây ?
A.
2 1 0x y z− + + =
. B.
2 2 0x y z+ + + =
.
C.
2 2 0x y z+ − − =
. D.
2 1 0x y z+ − + =
.
Câu 11. Tìm họ nguyên hàm của hàm số
( )
51
x
fx=+
.
A.
5 ln
x
x x C++
. B.
5
x
xC++
. C.
5
ln 5
x
xC++
. D.
5
x
xC++
.
Câu 12. Xét
2
2
1
2
ln 2
d
e
x
x
x
, nếu đặt
ln2ux=
thì
2
2
1
2
ln 2
d
e
x
x
x
bằng
A.
1
2
0
duu
. B.
1
2
0
2duu
. C.
2
2
0
duu
. D.
1
2
0
1
d
2
uu
.
Câu 13. Tính tích phân
1
1
22
xx
I dx
−
−
=−
.
A.
2
ln 2
. B.
1
ln 2
. C.
ln 2
. D.
2 ln 2
.
Câu 14. Tìm nguyên hàm
( )
Fx
của hàm số
( )
2
..
x
f x x e=
A.
( )
2
11
22
x
F x e x C

= − +


. B.
( ) ( )
2
22
x
F x e x C= − +
.
C.
( )
2
1
2
2
x
F x e x C

= − +


. D.
( ) ( )
2
1
2
2
x
F x e x C= − +
.
Câu 15. Trong không gian
Oxyz
, cho các điểm
( ) ( )
3;3;0 , 3;0;3 , (0;3;3)A B C
. Tìm tọa độ
I
là tâm đường
tròn ngoại tiếp tam giác
.ABC
A.
( )
2;3;2I
B.
( )
2;2;0I
. C.
( )
2;2;2I
. D.
( )
0;2;2I
.
Câu 16. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
3; 1; 2A −
,
( )
4; 1; 1B −−
và
( )
2; 0; 2C
. Mặt
phẳng đi qua ba điểm
A
,
B
,
C
có phương trình là
A.
2 3 8 0x y z+ − + =
. B.
3 3 14 0x y z− + − =
.
C.
3 3 8 0x y z+ + − =
. D.
3 2 8 0x y z− + − =
.
Câu 17. Tìm nguyên hàm
( )
Fx
của hàm số
( )
2
e
x
fx=
, biết
( )
01F =
.
A.
( )
2
e1
22
x
Fx=+
. B.
( )
2
2e 1
x
Fx=−
. C.
( )
e
x
Fx=
. D.
( )
2
e
x
Fx=
.
Câu 18. Cho tích phân
1
0
( 2) x
x
x e d a be− = +
, với
;ab
. Tổng
+ab
bằng
A.
1−
. B.
1
. C.
−3
. D.
5
.
Câu 19. Biết
( )
2
0
2 ln 1 d .lnx x x a b+=
, với
*
,ab
,
b
là số nguyên tố. Tính
34ab+
.
A.
42
. B.
21
. C.
12
. D.
32
.
Câu 20. Trong không gian
Oxyz
, cho điểm
( )
2;1;1I
và mặt phẳng
( )
: 2 2 1 0P x y z− + + =
. Phương trình mặt
cầu
( )
S
có tâm
I
và tiếp xúc với
( )
P
là
Trang 15/24
A.
( ) ( ) ( )
2 2 2
2 1 1 2x y z+ + + + + =
. B.
( ) ( ) ( )
2 2 2
2 1 1 2x y z− + − + − =
.
C.
( ) ( ) ( )
2 2 2
2 1 1 4x y z+ + + + + =
. D.
( ) ( ) ( )
2 2 2
2 1 1 4x y z− + − + − =
.
Câu 21. Cho
()Fx
là một nguyên hàm của hàm số
( ) e 2
x
f x x=+
thỏa mãn
3
(0)
2
F =
. Tìm
()Fx
.
A.
2
1
( ) e
2
x
F x x= + +
. B.
2
1
( ) 2e
2
x
F x x= + −
.
C.
2
3
( ) e
2
x
F x x= + +
. D.
2
5
( ) e
2
x
F x x= + +
.
Câu 22. Tính tích phân
1
d
ln
Ax
xx
=
bằng cách đặt
lntx=
. Mệnh đề nào dưới đây đúng?
A.
dAt=
. B.
2
1
dAt
t
=
. C.
dA t t=
. D.
1
dAt
t
=
.
Câu 23. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
( )
P
c ó phương trình
2 2 5 0xz− − −
. Tìm tọa
độ điểm
A
nằm trên tia
Oz
sao cho khoảng cách từ
A
đến mặt phẳng
( )
P
bằng
22
.
A.
13
0;0;
2
A

−


. B.
13
0;0;
2
A



.
C.
3
0;0;
2
A



. D.
3
0;0;
2
A



hoặc
13
0;0;
2
A

−


.
Câu 24. Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
1;2;3A
trên mặt phẳng
( )
: 3 0+ + − =P x y z
là điểm
A.
( )
0;1;2M
. B.
( )
2;1;0M
. C.
( )
1;2;2−M
. D.
( )
1;1;1M
.
Câu 25. Họ nguyên hàm của hàm số
( )
2
2
x
y f x
x
==
+
là
A.
( )
2
2F x x C= + +
. B.
( )
2
1
2
2
F x x C= + +
.
C.
( )
2
22F x x C= + +
. D.
( )
2
ln 2F x x C= + +
.
Câu 26. Cho
4
0
( ) 16f x dx =
. Tính
2
0
(2 )I f x dx=
A.
32I =
. B.
8I =
. C.
16I =
. D.
4I =
Câu 27. Cho hàm số
( )
fx
có
( )
fx
liên tục trên đoạn
( )
1;3 , 1 3f− − =
và
3
1
( ) 10,f x dx
−
=
giá trị của
( )
3f
bằng
A.
7−
. B.
13
. C.
7
. D.
13−
.
Câu 28. Biết
( )
2
1
d1f x x =
. Tính
( )
4
1
1
dI f x x
x
=
.
A.
4I =
. B.
2I =
. C.
1I =
D.
1
2
I =
.
Câu 29. Biết
( )
2 2 2
d,
x x x
xe x axe be C a b= + +
. Tính
ab
.
A.
1
4
ab =
. B.
1
4
ab =−
. C.
1
8
ab =
. D.
1
8
ab =−
.
Câu 30. Tính nguyên hàm của hàm số
( )
5
2018e
e 2017
−

=−


x
x
fx
x
.
Trang 16/24
A.
( )
4
2018
d 2017e
x
f x x C
x
= − +
. B.
( )
4
2018
d 2017e
x
f x x C
x
= + +
.
C.
( )
4
504,5
d 2017e
x
f x x C
x
= + +
. D.
( )
4
504,5
d 2017e
x
f x x C
x
= − +
.
Câu 31. Trong không gian
Oxyz
, cho hai điểm
( )
1;0; 4A −
và điểm
( )
1; 2;0B −
. Phương trình mặt cầu
( )
S
có đường kính
AB
là
A.
( ) ( ) ( )
2 2 2
1 1 2 5x y z+ + − + − =
. B.
( ) ( ) ( )
2 2 2
1 1 2 5x y z− + + + + =
.
C.
( ) ( ) ( )
2 2 2
1 1 2 20x y z+ + − + − =
. D.
( ) ( ) ( )
2 2 2
1 1 2 20x y z− + + + + =
.
Câu 32. Trong không gian
Oxyz
, cho ba điểm
( )
1; 2;3A −−
,
( )
0;3;1B
,
. Côsin của góc
BAC
bằng
A.
9
35
. B.
9
2 35
. C.
9
2 35
−
. D.
9
35
−
.
Câu 33. Cho
( ) ( )
2
1
3 2 d 1f x g x x+=


,
( ) ( )
2
1
2 d 3f x g x x− = −


. Khi đó,
( )
2
1
df x x
bằng
A.
16
7
. B.
11
7
. C.
5
7
−
. D.
6
7
.
Câu 34. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
1
1
fx
x
=
−
thỏa
( )
21F =
. Tính
( )
3F
.
A.
( )
3 ln 2 1F =+
. B.
( )
3 ln 2F =
. C.
( )
3 1 ln 2F =−
. D.
( )
3 ln 2 1F =−
.
Câu 35. Cho tích phân
5
1
2
ln 2 ln 3
1
x
dx a b c
x
−
= + +
+
với a, b, c là các số nguyên. Tính P = abc.
A.
18P =
B.
0P =
C.
18P =−
D.
36P =−
PHẦN II: TỰ LUẬN
Câu 36. Tìm học nguyên hàm của
( ) .
1
x
x
e
fx
e
=
−
Câu 37. Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1; 3;2A −
,
( )
2; 1;5B −−
và
( )
3;2; 1C −
. Gọi
( )
P
là mặt phẳng qua
A
, trực tâm của tam giác
ABC
và vuông góc với mặt phẳng
( )
ABC
. Tìm phương
trình mặt phẳng
( )
P
.
Câu 38. Tính tích phân
( )
2017
2
2019
1
2
d
x
Ix
x
+
=
.
Câu 39. Cho hàm số
( )
fx
tăng, có đạo hàm liên tục trên
)
0;+
thỏa
( ) ( ) ( ) ( )
22
f x f x f x f x

=+
và
( ) ( )
0 0 1ff
==
. Tính
( )
1f
.
------------- HẾT -------------
Trang 17/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 5
Mã đề thi
005
Họ và tên :………………………………….Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Họ nguyên hàm của hàm số
( )
1
31
fx
x
=
−
là :
A.
1
ln 3 1
3
xC− − +
B.
ln 3 1xC−+
C.
3ln 3 1xC−+
D.
1
ln 3 1
3
xC−+
Câu 2. Trong không gian với hệ tọa độ
Oxyz
, phương trình nào sau đây là phương trình mặt cầu?
A.
( )
2
2
4 2 2 2018x y z x xy z− + = − + +
. B.
2 2 2
2 2 4 8 0x y z x y z+ + − + − + =
.
C.
( ) ( )
22
2
1 2 1 0x y z+ + + − =
. D.
2 2 2
2 4 1 0x y z x y+ + − + − =
.
Câu 3. Giả sử các biểu thức trong dấu nguyên hàm, tích phân đều có nghĩa, trong các khẳng định sau, khẳng
định nào sai?
A.
( ) ( ) ( ) ( ) ( ) ( )
..
b
bb
aa
a
u x v x dx u x v x u x v x dx

=−

. B.
( ) ( )
,
bb
aa
kf x dx k f x dx k=

.
C.
( ) ( )
f x dx f x C
=+
. D.
( ) ( )
,kf x dx k f x dx k=

.
Câu 4. Xét
( )
2
1
23
0
1d
xx
x e x
−+
−
, nếu đặt
2
23u x x= − +
thì
( )
2
1
23
0
1d
xx
x e x
−+
−
bằng
A.
3
2
d
u
eu−
. B.
3
2
d
u
eu
. C.
3
2
1
d
2
u
eu−
. D.
3
2
1
d
2
u
eu
.
Câu 5. Trong không gian với hệ tọa độ
,Oxyz
cho hai véctơ
(2; 3;1)a =−
và
( 1;0;4)=−b
. Tìm tọa độ véctơ
23= − +u a b
.
A.
( 7;6;10)=−u
. B.
(7;6;10)=u
. C.
( 7; 6;10)= − −u
. D.
( 7;6; 10)= − −u
.
Câu 6. Tìm họ nguyên hàm của hàm số
( ) ( )
cos 2 3f x x=+
A.
( ) ( )
.d sin 2 3f x x x C= + +
. B.
( ) ( )
.d sin 2 3f x x x C= − + +
.
C.
( ) ( )
1
.d sin 2 3
2
f x x x C= − + +
. D.
( ) ( )
1
.d sin 2 3
2
f x x x C= + +
.
Câu 7. Tính tích phân
2
1
11
e
I dx
xx

=−


A.
Ie=
B.
1
I
e
=
C.
1
1I
e
=+
D.
1I =
Câu 8. Trong không gian
Oxyz
, vectơ
( )
1;2; 1n =−
là một vectơ pháp tuyến của mặt phẳng nào dưới đây?
A.
2 2 0x y z+ − − =
. B.
2 1 0x y z+ − + =
.
C.
2 1 0x y z− + + =
. D.
2 2 0x y z+ + + =
.
Câu 9. Tính tích phân
2018
2
1
dx
I
x
=
.
A.
2018ln 2 1I =−
. B.
2018
2I =
. C.
2018.ln2I =
. D.
2018I =
.
Câu 10. Cho hai hàm số
( )
fx
,
( )
gx
liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai?
Trang 18/24
A.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x− = −


. B.
( ) ( )
ddkf x x k f x x=

( )
0;kk
.
C.
( ) ( ) ( ) ( )
d d df x g x x f x x g x x+ = +


. D.
( ) ( ) ( ) ( )
. d d . df x g x x f x x g x x=


.
Câu 11. Tìm nguyên hàm của hàm số
( )
3
x
fx=
.
A.
1
3
3 d =
1
x
x
xC
x
+
+
+
. B.
3 d =3
xx
xC+
.
C.
3
3 d =
ln 3
x
x
xC+
. D.
3 d =3 ln3
xx
xC+
.
Câu 12. Giá trị của
66
4
4
sin cos
61
x
xx
dI x
được viết dưới dạng
a
b
, trong đó
,ab
là các số nguyên dương
và
a
b
là phân số tối giản. Tính
ab
.
A.
32ab
. B.
27ab
. C.
25ab
. D.
30ab
.
Câu 13. Trong hệ trục tọa độ
Oxyz
cho
3
điểm
( )
4;2;1A
,
( )
0;0;3B
,
( )
2;0;1C
. Viết phương trình mặt phẳng
chứa
OC
và cách đều
2
điểm
,AB
.
A.
220+ + =x y z
hoặc
4 2 0x y z− − =
. B.
2 2 0+ − =x y z
hoặc
4 2 0x y z+ − =
.
C.
2 2 0+ − =x y z
hoặc
4 2 0x y z− − =
. D.
2 2 0− − =x y z
hoặc
4 2 0x y z+ − =
.
Câu 14. Cho
3
12
0
.
1
x
dx
e a e be c
x
, với
,,abc
là các số nguyên. Tính
S a b c
.
A.
0S
. B.
2S
. C.
4S
. D.
1S
.
Câu 15. Trong không gian
Oxyz
, mặt cầu
( )
S
có tâm
( )
1;2;3I
và tiếp xúc với mặt phẳng
( )
:3 4 10 0P x y− − =
. Khi đó
( )
S
là
A.
( ) ( ) ( )
2 2 2
1 2 3 25x y z− + − + − =
. B.
( ) ( ) ( )
2 2 2
1 2 3 9x y z− + − + − =
.
C.
( ) ( ) ( )
2 2 2
1 2 3 16x y z+ + + + + =
. D.
( ) ( ) ( )
2 2 2
1 2 3 4x y z+ + + + + =
.
Câu 16. Tìm nguyên hàm của hàm số
( )
3
x
fx=
.
A.
3 d 3 ln 3
xx
xC=+
. B.
1
3
3d
1
x
x
xC
x
+
=+
+
.
C.
3
3d
ln 3
x
x
xC=+
. D.
1
3 d 3
xx
xC
+
=+
.
Câu 17. Cho hàm số
( )
fx
xác định trên thỏa mãn
( )
43f x x
=+
và
( )
11f =−
. Biết rằng phương trình
( )
10fx=
có hai nghiệm thực
12
,xx
. Tính tổng
2 1 2 2
log logxx+
.
A.
3
. B.
4
. C.
8
. D.
16
.
Câu 18. Giả sử hàm số
()y f x
liên tục trên và
5
3
,( ).f x dx a a
Tích phân
2
1
21I f x dx
có giá trị là
A.
1
1.
2
a
B.
2.a
C.
1
.
2
a
D.
2 1.a +
Câu 19. Biết
( )
8
1
d2f x x =−
;
( )
4
1
d3f x x =
;
( )
4
1
d7g x x =
. Mệnh đề nào sau đây sai?
A.
( )
8
4
d1f x x =
. B.
( )
8
4
d5f x x =−
.
C.
( ) ( )
4
1
4 2 d 2f x g x x− = −


. D.
( ) ( )
4
1
d 10f x g x x+=


.
Trang 19/24
Câu 20. Họ nguyên hàm của hàm số
( )
3 cos=+y x x x
là
A.
( )
3
3 sin cos+ + +x x x x C
B.
( )
3
3 sin cos− + +x x x x C
C.
( )
3
3 sin cos+ − +x x x x C
D.
( )
3
3 sin cos− − +x x x x C
Câu 21. Biết
3
4
2
6
1 sin
32
sin
x
dx a b c
x
−
= + +
với
,,abc
. Tính
abc++
.
A.
1−
. B.
0
. C.
1
. D.
2
.
Câu 22. Trong không gian với hệ trục tọa độ
Oxyz
, cho
( )
3;4;5M
và mặt phẳng
( )
: 2 3 0P x y z− + − =
.
Hình chiếu vuông góc của
M
lên mặt phẳng
( )
P
là:
A.
( )
6;7;8H
. B.
( )
2; 3; 1H −−
. C.
( )
1;2;2H
. D.
( )
2;5;3H
.
Câu 23. Tích phân
( )
2
0
3 2 cos dx x x
+
bằng:
A.
2
3
4

+
. B.
2
1
4

+
. C.
2
1
4

−
. D.
2
3
4

−
.
Câu 24. Trong không gian
Oxyz
, cho mặt phẳng
( ) : 1 0x y z
+ + − =
. Trong các mặt phẳng sau tìm mặt
phẳng vuông góc với mặt phẳng
()
?
A.
2 1 0x y z− + + =
. B.
2 1 0x y z− − + =
.
C.
2 2 2 1 0x y z+ + − =
. D.
10x y z− − + =
.
Câu 25. Nếu
2
d
3
b
a
xx=
( )
0, 0ab
thì:
A.
1ba+=
. B.
22
1ba−=
. C.
1b b a a−=
. D.
1ba−=
.
Câu 26. Cho
( )
Fx
là một nguyên hàm của hàm số
2
4
x
y
x
=
+
thỏa
( )
21 7F =
. Tìm
( )
Fx
A.
( )
2
42F x x= + −
. B.
( )
2
42F x x= + +
.
C.
( )
2
41F x x= + +
. D.
( )
2
41F x x= + −
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
cho ba điểm
( ) ( ) ( )
1;2;0 ; 2;1;1 ; 0;3; 1A B C −
. Xét
4
khẳng định
sau:
( )
I
2BC AB=
.
( )
II
B
thuộc đoạn
.AC
( )
III
ABC
là một tam giác. (IV)
( )
IV
,,A B C
thẳng hàng.
Trong
4
khẳng định trên có bao nhiêu khẳng định đúng.
A.
1
. B.
2.
C.
3.
D.
4.
Câu 28. Với cách đổi biến
45ux=+
thì tích phân
1
1
45x x dx
−
+
trở thành
A.
( )
2
3
1
5
8
uu
du
−
. B.
( )
22
1
1
5
8
uu
du
−
−
. C.
( )
22
3
1
5
4
uu
du
−
. D.
( )
22
3
1
5
8
uu
du
−
.
Câu 29. Cho
( )
Fx
là một nguyên hàm của hàm số
( )
1
21
fx
x
=
−
; biết
( )
12F =
. Tính
( )
2F
.
A.
( )
2 ln 3 2F =+
. B.
( )
2 2ln 3 2F =−
. C.
( )
1
2 ln 3 2
2
F =+
. D.
( )
1
2 ln 3 2
2
F =−
.
Câu 30. Nguyên hàm
( )
Fx
của hàm số
( )
1
21
fx
x
=
+
, biết
e 1 3
22
F
−

=


là:
A.
( )
1
ln 2 1
2
F x x= + +
. B.
( )
1
2ln 2 1
2
F x x= + −
.
Trang 20/24
C.
( )
2ln 2 1 1F x x= + +
. D.
( )
1
ln 2 1 1
2
F x x= + +
.
Câu 31. Tính
2
1
ed
x
I x x=
.
A.
eI =
. B.
2
eI =
. C.
2
eI =−
. D.
2
3e 2eI =−
.
Câu 32. Tìm nguyên hàm
cos dI x x x=
.
A.
2
cos
2
x
I x C=+
. B.
2
sin
2
x
I x C=+
.
C.
sin cosI x x x C= + +
. D.
sin cosI x x x C= − +
.
Câu 33. Trong không gian
Oxyz
, cho
( ) ( )
2
0; 2; 3 , 0; ;1 , 3; 3;2
3
a b c

= − − = = −


. Khẳng định nào dưới đây
là sai?
A.
b
và
c
vuông góc. B.
a
và
b
vuông góc.
C.
a
và
b
cùng phương. D.
a
và
c
vuông góc.
Câu 34. Khi tính nguyên hàm
3
d
1
x
x
x
−
+
, bằng cách đặt
1ux=+
ta được nguyên hàm nào?
A.
( )
2
3duu−
. B.
( )
2
2 4 du u u−
. C.
( )
2
4duu−
. D.
( )
2
2 4 duu−
.
Câu 35. Trong không gian với hệ toạ độ
Oxyz
, cho
( )
P
là mặt phẳng đi qua hai điểm
( ) ( )
0;1;2 , 1;3;4AB−
và vuông góc với mặt phẳng
( )
: 2 4 0.Q x y z+ − + =
Khoảng cách từ gốc tọa độ đến mặt phẳng
( )
P
bằng
A.
3
2
. B.
42
3
. C.
8
33
. D.
72
10
.
PHẦN II: TỰ LUẬN
Câu 36. Tìm họ nguyên hàm của hàm số
2
( ) log .f x x=
Câu 37. Trong không gian với hệ trục tọa độ
Oxyz
cho hai đường thẳng
12
,dd
lần lượt có phương trình
1
2 2 2
:
2 1 3
x y z
d
− − −
==
,
2
1 2 1
:
2 1 4
x y z
d
− − −
==
−
, biết rằng mặt phẳng
( )
: 1 0ax by cz
+ + + =
( )
2 2 2
, , , 0a b c R a b c + +
song song và cách đều hai đường thẳng
12
,dd
. Tính
S a b c= + +
.
Câu 38. Cho hàm số
( )
fx
xác định và liên tục trên và thoả mãn đồng thời các điều kiện sau:
( )
( )
( )
( )
2
0,
.
,
1
0
f x x
f x x
f x x
x
fe
=
+
=
Tính giá trị của
( )
3f
.
Câu 39. Cho hàm số
( )
y f x=
có đạo hàm, liên tục trên và
( )
3 10f =
,
( )
1
0
2 1 d 4f x x+=
. Tính
( ) ( )
3
1
1dx f x x
−
.
------------- HẾT -------------
Trang 21/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 6
Mã đề thi
006
Họ và tên :………………………………….Lớp:………….......……..………
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Trong không gian
Oxyz
, cho mặt cầu
( )
2 2 2
: 4 2 4 7 0S x y z x y z+ + − + − − =
. Tính bán kính
R
của
mặt cầu
( )
S
.
A.
3R =
. B.
4R =
. C.
16R =
. D.
7R =
.
Câu 2. Khẳng định nào dưới đây là sai?
A. Mọi hàm số liên tục trên đoạn
;ab
đều có đạo hàm trên đoạn
;ab
.
B. Mọi hàm số có đạo hàm trên đoạn
;ab
đều có nguyên hàm trên đoạn
;ab
.
C. Mọi hàm số liên tục trên đoạn
;ab
đều có nguyên hàm trên đoạn
;ab
.
D. Mọi hàm số liên tục trên đoạn
;ab
thì đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn
;ab
.
Câu 3. Khẳng định nào đúng?
A.
22
e d e
xx
xC=+
. B.
sin d cosx x x C=+
.
C.
d
ln
x
x
a
a x C
a
=+
. D.
22
d ln
xx
a x a a C=+
.
Câu 4. Trong không gian
Oxyz
, cho
( )
3;2;1a =
,
( )
2;0;1b =−
. Độ dài
ab+
là:
A.
2
. B.
3
. C.
2
. D.
1
.
Câu 5. Khẳng định nào dưới đây đúng?
A.
2
2
1
1
1
=
x
x
dx e
e
. B.
1
2
2
1
11
=
xx
dx
ee
. C.
2
2
1
1
11
=
xx
dx
ee
. D.
2
1
2
1
1
=
x
x
dx e
e
.
Câu 6. Tích phân
8
4
1
dx
x
+
bằng
A.
4
. B.
11
81 25
−
. C.
ln9 ln5−
. D.
ln5 ln9−
.
Câu 7. Trong không gian với hệ trục tọa độ
Oxyz
, cho mặt phẳng
: 3 2 1 0P x y z
. Mặt phẳng
P
có một vectơ pháp tuyến là
A.
2;3;1n
. B.
3;2;1n
. C.
3;2; 1n
. D.
3; 2; 1n
.
Câu 8. Cho
( )
02f x x
( )
2
2
2
21
20
22
x
fx
x
− = −
− =
−=
. Tính
2
2
3
3
0
0
x
x
x
x
=
=

=
=
.
A.
m
. B.
( )
22
2 0 2 2f x x
− −
. C.
2
0x
. D.
( )
2
2 0, f x x
−
.
Câu 9. Tìm họ nguyên hàm của hàm số
( ) 2018
x
fx=
.
A.
2018
log 2018
x
C+
. B.
1
2018
1
x
C
x
+
+
+
.
C.
2018
ln 2018
x
C+
. D.
2018 .ln 2018
x
C+
.
Trang 22/24
Câu 10. Tìm nguyên hàm
( )
Fx
của hàm số
( )
6 sin 3f x x x=+
, biết
( )
2
0
3
F =
.
A.
( )
2
cos3
31
3
x
F x x= − +
. B.
( )
2
cos3
31
3
x
F x x= − −
.
C.
( )
2
cos3
31
3
x
F x x= + +
. D.
( )
2
cos3 2
3
33
x
F x x= − +
.
Câu 11. Cho tích phân
4
0
1
1 2 d .
2
I x x x=+
Đặt
1 2 ,ux=+
khi đó ta được tích phân
A.
( )
3
22
1
1dI u u u=−
B.
( )
3
2
1
1
1d
4
I u u u=−
C.
( )
3
22
1
1
1d
2
I u u u=+
D.
3
53
1
1
4 5 3
uu
I

=−


Câu 12. Cho hàm số
()fx
có đạo hàm
'( )fx
liên tục trên
;ab
,
( ) 5=fb
và
'( ) 3 5=
b
a
f x dx
. Tính giá trị
( )
fa
.
A.
( )
( ) 5 5 3=−fa
. B.
( ) 3 5=fa
.
C.
( )
( ) 5 3 5=−fa
. D.
( )
( ) 3 5 3=−fa
.
Câu 13. Cho
( )
Fx
là một nguyên hàm của hàm số
( ) ( )
51
x
f x x e=+
và
( )
03F =
. Tính
( )
1F
.
A.
( )
1 11 3Fe=−
. B.
( )
12Fe=+
. C.
( )
17Fe=+
. D.
( )
13Fe=+
.
Câu 14. Cho biết
( )
3
11
2
3
F x x x
x
= + −
là một nguyên hàm của
( )
( )
2
2
2
xa
fx
x
+
=
. Tìm nguyên hàm của
( )
cosg x x ax=
.
A.
sin cosx x x C++
. B.
11
sin 2 cos 2
24
x x x C++
.
C.
sin cosx x x C−+
. D.
11
sin 2 cos 2
24
x x x C−+
.
Câu 15. Tích phân
7
2
2
d
1
xx
x +
bằng
ln2 ln5ab−
. Giá trị của
2ab+
bằng
A.
1
. B.
3
2
. C.
2
. D.
1
2
.
Câu 16. Tính tích phân
( ) ( )
5
4
1 ln 3 dI x x x= + −
?
A.
10ln 2
. B.
19
10ln 2
4
+
. C.
19
10ln 2
4
−
. D.
19
10ln 2
4
−
.
Câu 17. Hàm số
( )
Fx
nào dưới đây là nguyên hàm của hàm số
3
1yx=+
?
A.
( ) ( )
3
3
11
4
F x x x C= + + +
. B.
( ) ( )
3
4
3
1
4
F x x C= + +
.
C.
( ) ( )
4
3
3
1
8
F x x C= + +
. D.
( ) ( )
4
3
4
1
3
F x x C= + +
.
Câu 18.
( )
Fx
là một nguyên hàm của hàm số
2sin cos3y x x=
và
( )
00F =
, khi đó
Trang 23/24
A.
( )
cos 4 cos 2 1
4 2 4
xx
Fx= − +
. B.
( )
cos 4 cos2F x x x=−
.
C.
( )
cos 2 cos 4 1
4 8 8
xx
Fx= − −
. D.
( )
cos 2 cos 4 1
2 4 4
xx
Fx= − −
.
Câu 19. Cho hàm số Biết
( )( )
3
0
d
ln 2 ln 5 ln 7
24
x
a b c
xx
= + +
++
( )
,,abc
. Giá trị của biểu thức
23a b c+−
bằng
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 20. Cho
3
1
( )d 12f x x =
. Tính tích phân
6
2
d
2
x
fx



.
A.
14
. B.
24
. C.
10
. D.
6
.
Câu 21. Tính tích phân
( )
1
0
.ln 1 dI x x x=+
.
A.
1I =
. B.
3
4
I =−
. C.
1
4
I =
. D.
2I =
.
Câu 22. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
sinf x x=
và đồ thị hàm số
( )
y F x=
đi qua điểm
( )
0;1M
. Tính
2
F



A.
0
2
F

=


. B.
1
2
F

=


. C.
2
2
F

=


. D.
1
2
F

=−


.
Câu 23. Trong không gian
Oxyz
cho ba điểm
( )
1;2; 4A −
,
( )
1; 3;1B −
,
( )
2;2;3C
. Mặt cầu
( )
S
đi qua
A
,
B
,
C
và có tâm thuộc mặt phẳng
( )
Oxy
. Khi đó bán kính của mặt cầu
( )
S
là
A.
5
. B.
26
. C.
32
. D.
2
.
Câu 24. Biết
( )
Fx
là một nguyên hàm của hàm số
( ) ( )
2
1
x
f x x e=−
và
( )
3
0
4
F =−
. Tính
( )
1F
.
A.
( )
2
1
1
4
Fe=
. B.
( )
2
1
1
4
Fe=−
. C.
( )
2
31
1
44
Fe=−
. D.
( )
2
31
1
44
Fe=+
.
Câu 25. Biết
( )
2
2
1
3 1 d
ln
ln
3 ln
xx
b
a
x x x c
+

=+

+

với
a
,
b
,
c
là các số nguyên dương và
4c
. Tổng
abc++
bằng
A.
6
. B.
9
. C.
7
. D.
8
.
Câu 26. Cho hàm số
( )
fx
liên tục trên và
( )
( )
2
2
0
3 d 10+=
f x x x
. Tính
( )
2
0
df x x
.
A.
18−
. B.
2−
. C.
18
. D.
2
.
Câu 27. Trong không gian với hệ tọa độ
Oxyz
, cho véc tơ
( ) ( )
1;1; 2 , 1;0;u v m= − =
. Tìm tất cả giá trị của
m
để góc giữa
u
,
v
bằng
45
.
A.
26m =−
. B.
26m =+
. C.
2m =
. D.
26m =
.
Câu 28. Biết
3
1
d
32
1
x
a b c
xx
= + +
+−
với
a
,
b
,
c
là các số hữu tỉ. Tính
P a b c= + +
.
A.
2
.
3
B.
5.
C.
13
.
2
D.
16
.
3
Câu 29. Trong không gian
Oxyz
, cho hai điểm
( )
4;0;1A =
và
( )
2;2;3B =−
. Phương trình nào dưới đây là
phương trình mặt phẳng trung trực của đoạn thẳng
AB
?
A.
6 2 2 1 0x y z− − − =
. B.
3 6 0x y z+ + − =
.
Trang 24/24
C.
3 1 0x y z− − + =
. D.
30x y z− − =
.
Câu 30. Trong không gian
Oxyz
, cho tam giác
ABC
với:
( )
1; 2;2AB =−
;
( )
3; 4; 6AC =−
. Độ dài đường
trung tuyến
AM
của tam giác
ABC
là:
A.
29
. B.
29
. C.
29
2
. D.
2 29
.
Câu 31. Tìm nguyên hàm
( )
Fx
của hàm số
( )
2
23
4
xx
x
x
fx

=−



.
A.
( )
12 2
ln12 3
x
xx
F x C= − +
. B.
( )
12
x
F x x x C= + +
.
C.
( )
2
23
ln 2 ln 3 4
xx
x
xx
Fx

=−



. D.
( )
2
2 3 ln 4
ln 2 ln 3 4
xx
x
xx
Fx

=−



.
Câu 32. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
( )
2;2; 2−A
và
( )
3; 1;0 .−B
Đường thẳng
AB
cắt mặt phẳng
( )
: 2 0+ − + =P x y z
tại điểm
I
. Tỉ số
IA
IB
bằng:
A.
3
. B.
4
. C.
6
. D.
2
.
Câu 33. Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 2 2 0P x y z− + − =
và điểm
( )
1;2; 1I −−
. Viết phương
trình mặt cầu
( )
S
có tâm I và cắt mặt phẳng
( )
P
theo giao tuyến là đường tròn có bán kính bằng 5.
A.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 34S x y z+ + − + + =
. B.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 16S x y z+ + − + + =
.
C.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 34S x y z− + + + − =
. D.
( ) ( ) ( ) ( )
2 2 2
: 1 2 1 25S x y z+ + − + + =
.
Câu 34. Hàm số
( )
4
1
ln
4
F x x C=+
là nguyên hàm của hàm số nào trong các hàm số dưới đây?
A.
( )
3
ln
x
fx
x
=
. B.
( )
3
ln
3
xx
fx=
. C.
( )
3
ln x
fx
x
=
. D.
( )
3
1
ln
fx
xx
=
.
Câu 35. Trong không gian với hệ trục tọa độ
Oxyz
, cho
( ) ( )
1;2;3 , 3;4;4AB
. Tìm tất cả các giá trị của tham
số
m
sao cho khoảng cách từ điểm
A
đến mặt phẳng
( )
: 2 1 0P x y mz+ + − =
bằng độ dài đoạn
AB
.
A.
2m =
B.
2m =
C.
2m =−
D.
3m =−
PHẦN II: TỰ LUẬN
Câu 36. Tìm họ nguyên hàm của hàm số
2
( ) 2 1.f x x x=−
Câu 37. Trong không gian
Oxyz
, mặt phẳng
( )
đi qua điểm
( )
4; 3;12M −
và chắn trên tia
Oz
một đoạn dài
gấp đôi các đoạn chắn trên các tia
Ox
,
Oy
. Tìm phương trình mặt phẳng
( )
.
Câu 38. Cho hàm số
( )
fx
liên tục trên và
( )
1
0
d2f x x =
;
( )
3
0
d6f x x =
. Tính
( )
1
1
2 1 dI f x x
−
=−
.
Câu 39. Cho hàm số
( )
y f x=
có đạo hàm liên tục trên đoạn
1; 4
, đồng biến trên đoạn
1; 4
và thỏa mãn
đẳng thức
( ) ( )
2
2.x x f x f x
+=


,
1;4x
. Biết rằng
( )
3
1
2
f =
, tính
( )
4
1
dI f x x=
.
------------- HẾT -------------
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên:………………………………….Lớp:………….......……..………
Mã đề thi
001
Mã đề [001]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
A
B
B
C
C
C
D
D
C
D
B
B
A
C
C
B
B
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
A
A
A
A
A
B
C
D
C
A
C
D
D
D
D
A
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn B
Ta có .
0
0
1
sin 3 d cos3
3
x x x
1 2
1 1
3 3
Câu 2.
Lời giải
Chọn A
Mặt cầu có tâm và bán kính .
2 2
2
: 1 3 5 S x y z
0; 1;3I
5R
Câu 3.
Lời giải
Chọn B
Ta có:
3 2 3
0 0 2
( )d ( )d ( )df x x f x x f x x
.
2 3 3
0 0 2
( )d ( )d ( )df x x f x x f x x a b
Câu 4.
Lời giải
Chọn B
.
2 2
2
4; 1; 6 4 1 6 53MN MN
53L
Câu 5.
Lời giải
Chọn C
Đặt
2
2
1
1 2 1 2 ; d d .
2
u
u x u x x u u x
Đổi cận:
0 1; 4 3x u x u
Suy ra
3
3
5 3
2 2
1
1
1 1
1 d .
4 4 5 3
u u
I u u u
Câu 6.
Lời giải
Chọn C
Do mặt phẳng
vuông góc với trục
nên nhận véctơ
làm một véc tơ
pháp
Oxy
Oz
0;0;1k
tuyến.
Câu 7.
Lời giải
Chọn C
Ta có: .
9
9
0
0
dx 9 9 9 0 9 9 3 9 9 12f x F x F F F F
Câu 8.
Lời giải
Chọn D
Ta có
4 3
2
2 2
2 3 3 2 3
( ) 2
3
x x
f x dx dx x dx C
x x x
Câu 9.
Lời giải
Chọn D
Vì .
2
2
9 3
3 d 9 d
ln9 ln 9
x x
x x
x x C C
Câu 10.
Lời giải
Chọn C
.
sin
tan d
cos
x
x x
x
ln cos x C
Câu 11.
Lời giải
Chọn D
Đặt
t x
=-
dx dt
Þ = -
6 6
4
4
sin ( ) cos ( )
1
1
6
t
t t
I dt
p
p
-
- + -
Þ =
+
ò
6 6
4
4
sin cos
6
6 1
t
t
t t
dt
p
p
-
+
×=
+
ò
( )
6 6
4
4
2 sin cos
I x x dx
p
p
-
Þ = +
ò
( )
2 2
4
4
1 3sin cos
x x dx
p
p
-
= -
ò
( )
4
4
1
5 3cos4
8
x dx
p
p
-
+=
ò
4
4
1 3
5 sin 4
8 4
x x
p
p
-
æ ö
÷
ç
+
÷
ç
÷
ç
è ø
=
5
16
p
=
5
32
I
p
Þ =
.
27
a b
Þ - =
Câu 12.
Lời giải
Chọn B
Theo tính chất nguyên hàm thì và là đúng, sai.
I
II
III
Câu 13.
Lời giải
Chọn B
Ta có .
cos
sin .
x
x e dx
cos
cos
x
e d x
cos x
e C
Câu 14.
Lời giải
Chọn A
Giả thiết tương đương với . Lấy đạo hàm hai vế theo ẩn , ta được:
2
2 6d
x
a
f t
t x
t
x
.
2
1
f x
x
x
f x x x
Thay vào giả thiết, ta được:
2
2 6d
x
a
t t
t x
t
2 2 6
x
a
t x
2 2 2 6x a x
a.
9a
Câu 15.
Lời giải
Chọn C
Đặt .
d sin d
u x
v x x
d d
cos
u x
v x
Ta có .
J
π
π
0
0
cos cos dx x x x
π
0
π sin x
Câu 16.
Lời giải
Chọn C
Đặt
1
d d
u x
v f x x
d d
d
u x
v f x x
Ta có
1 1
1
0
0 0
1 d 1 dx f x x x f x f x x
1
0
2 d 10f x x
.
1
0
d 2 10f x x
8
Câu 17.
Lời giải
Chọn B
Gọi là trung điểm của suy ra , .
I
AB
2;1;0I
2;8; 4 2 1;4; 2AB
Suy ra mặt phẳng phẳng trung trực của có dạng:
AB
, , .
1 2 4 1 2 0 4 2 6 0 4x y z x y z a
2b
6 4c a b c
Câu 18.
Lời giải
Chọn B
Mặt phẳng có vectơ pháp tuyến .
: 2 1 0x my z
1
1;2 ;1n m
Mặt phẳng có vectơ pháp tuyến .
:2 3 4 5 0x y z
2
2;3;4n
Ta có: .
1 2
. 0n n
1.2 2 .3 1.4 0m
1m
Câu 19.
Lời giải
Chọn B
Ta có
2
5 5 d
x
x x e x
Đặt
2
d 2 5 d
5 5
d d
x
x
u x x
u x x
v e x
v e
2 2
5 5 d 5 5 2 5 d
x x x
x x e x x x e x e x
Đặt
2 5 d 2d
d d
x x
u x u x
v e x v e
.
2 5 d 2 5 2 d 2 3
x x x x
x e x x e e x x e C
.
2 2
5 5 d 3 2
x x
x x e x x x e C
Suy ra .
1
3
2
a
b
c
2 3 13a b c
Câu 20.
Lời giải
Chọn A
Ta có
4 1 ln 4 1 lnf x x x F x x x dx
đặt
2 2 2 2 2
2
1
1 ln
2 1 ln 2 2 1 ln 2 ln
4 2
u x du
F x x x xdx x x x C x x x C
x
dv x v x
Câu 21.
Lời giải
Chọn A
Đặt
2
2
d d
1
e
d e d
2
x
x
u x
u x
v
v x
Khi đó:
.
100
100 100
2 2 2
0
0 0
1 1
.e d e e d
2 2
x x x
x x x x
100
200 2
0
1
50e e
4
x
200 200
1 1
50e e
4 4
200
1
199e 1
4
Câu 22.
Lời giải
Chọn A
Do nên cùng phương khi và chỉ khi
0v
,u v
.
: kk u v
3
: 2 2 4
1 6
m k
km k
m
k
k
1
1
3
m
k
Câu 23.
Lời giải
Chọn A
Gọi . Vì M thuộc đoạn AB nên:
M x
;y;z
7
3
3 2 2
5
2 1 2 3
3
2 2 5
8
3
x
x x
MA MB y y y
z z
z

Câu 24.
Lời giải
Chọn A
Ta có:
3 3
2 2
4 4
cos2
d d
sin .cos
x
f x x x
x x
2 2
3 3
2 2 2 2
4 4
cos sin 1 1
d d
sin .cos sin cos
x x
x x
x x x x
.
3
cot tan
4
x x
6 4 3
3
Mặt khác: .
3
4
df x x
6 4 3 12 4 3
3 4 3 3 3
F F F
Câu 25.
Lời giải
Chọn B
Vì là một nguyên hàm của hàm nên
F x
sin 2f x x
sin 2 .dF x x x
.
1
cos2
2
F x x C
Ta có
1
cos 1
4 2 2
F C
1C
1
cos2 1
2
F x x
1
cos 1
6 2 3
F
.
3
6 4
F
Câu 26.
Lời giải
Chọn C
Đặt
2
2 sin os t x c x
(sin 2 sin ) dt x x dx
Khi đó .
f x dx
2
2
1 1
2 sin os
dt
C
t t
x c x
Vậy một nguyên hàm của hàm số đã cho là .
2
1
2 sin os
F x
x c x
Câu 27.
Lời giải
Chọn D
.
df x f x x
3 2sin dx x
3 2cosx x C
.
0 3f
3.0 2cos0 3C
5C
Câu 28.
Lời giải
Chọn C
Dễ thấy mp đã cho cắt , , lần lượt tại .
Ox
Oy
Oz
2;0;0 , 0;3;0 , 0;0;4A B C
, , .
2OA
3OB
4OC
Tứ diện có đường cao là , đáy là tam giác vuông tại
OABC
OC
OAB
.O
Suy ra .
1 1
. . 4
3 2
V OC OAOB
Câu 29.
Lời giải
Chọn A
Ta có
2 2 2 2
0 0 0 0
1 3 9 1 3 9 1 3 18f x dx f x dx dx f x dx
Đặt . Đổi cận:
1 3 3t x dt dx
0 1; 2 5x t x t
Nên
2 5 1
0 1 5
1
1 3 . 3
3 3
dt
f x dx f t f t dt
Vậy .
2
0
1 3 9 3 18 21f x dx
Câu 30.
Lời giải
Gọi .
( ; ; )M x y z
Ta có
2 2
2 4MA MB MA MB
2 2 2 2 2 2
( 2) (y 1) ( 3) 4 ( 2) ( 5) ( 1)x z x y z
2 2 2
20 38 2 106
y z x y 0
3 3 3 3
x z
2 2 2
10 19 1
16.
3 3 3
x y z
Câu 31.
Lời giải
Chọn D
Ta có: .
7 11 4 3
d d
( 1)( 2) 1 2
x
x x
x x x x
4.ln 1 3ln 2x x C
. Vậy .
3
4
a
b
7a b+ =
Câu 32.
Lời giải
Chọn D
.
3
2
1 9 1 3 9 2m f x dx m m
Câu 33.
Lời giải
Chọn D
Có = = = = .
2
0
2f x dx
2
0
1
2 d 2
2
f x x
2
0
1
2
2
F x
1
4 0
2
F F
4
0
1
8
2
f x dx
Cách khác: đặt .
2 2dt = x dt = x
Ta có: .
2
0
2f x dx
4
0
1
d
2
f t t
4
0
1
d 8
2
f x x
Câu 34.
Lời giải
Chọn D
.
2 2 0 3
( ;( )) 1
1 4 4
d M P
Câu 35.
Lời giải
Chọn A
.
1 1 1 1
0 0 0 0
2 d 3 d 2 d 3 d 2f x g x x f x x g x x g x x
PHẦN II: TỰ LUẬN
Câu 36. Học sinh tự giải
Câu 37.
Lời giải
Gọi lần lượt là trung điểm các cạnh . Ta có (c-c-c) nên
,M
,N
,AB
CD
ACD BCD
do đó tam giác cân tại
AN BN
NAB
N
MN AB
Tương tự ta có
MN CD
Ta có
ABN CD
ABN BCD
mà . Trong kẻ
ABN BCD BN
ABN
AH BN AH BCD
Gọi là tâm đường tròn ngoại tiếp tam giác BCD. Dựng trục It, gọi khi đó là
I
O It MN
O
tâm mặt cầu ngoại tiếp tứ diện. Gọi là bán kính mặt cầu ngoại tiếp tứ diện.
R
Ta có
2 2 2
MN AN AM
2 2 2 2
9AD MD AM a
3 .MN a
Ta có
2 2 2 2 2
OM MA ON ND R
2 2 2 2 2
5OM ON ND MA a
2
5OM ON OM ON a
Mà
3OM ON MN a
5
3
OM ON a
Từ
7
3
3
5
2
3
3
OM ON a
OM a
OM ON a
ON a
Ta có
.
2
2
2 2
2 85
3
3 3
a
R ON NA a a
Câu 38.
Lời giải
Đặt .
tant x
2
d 1 tan dt x x
2
d
d
1
t
x
t
Đổi cận:
0 0x t
1
4
x t
Ta có: .
4
0
tan d 4f x x
1
2
0
d 4
1
f t
t
t
1
2
0
d 4
1
f x
x
x
Suy ra: .
1
0
dI f x x
2
1 1
2 2
0 0
d d
1 1
x f x f x
x x
x x
6
Câu 39.
Lời giải
Ta có:
2
. ' cos . 1f x f x x f x
2
. '
cos
1
f x f x
x
f x
2
. '
cos
1
f x f x
dx xdx
f x
2 2
1 cos 1d f x xdx f x sinx C
.
2
1 0 0 2f sin C C
trên .
2 2
2
2 1 2 1f x sinx f x sinx
0;
2
Xét trên ta có:
2
2 1f x sinx
;
6 2
Đặt
1
, ;1
2
t sinx t
2
2
2
4 3 ' 0
4 3
t
f t t t f t
t t
Giá trị nhỏ nhất:
1 21
min
2 2
f t f
Giá trị lớn nhất: .
max 1 2 2f t f
Vậy
;
.
21
2
m
2 2M
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên:………………………………….Lớp:………….......……..………
Mã đề thi
002
Mã đề [002]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C
B
C
B
A
B
A
D
C
B
D
B
C
C
B
A
C
B
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
C
C
C
B
D
D
D
A
A
D
A
A
D
B
A
A
D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn C
Ta có .
3
3
3
A B C
G
A B C
G
A B C
G
x x x
x
y y y
y
z z z
z
1 0 5
2
3
2 2 6
2
3
4 5 3
4
3
G
G
G
x
y
z
2;2;4G
Câu 2.
Lời giải
Chọn B
Ta có .
1
0
2 d
x
I e x
1
0
2
x
e
2 2e
Câu 3.
Lời giải
Chọn C
Ta có .
d 2 sin 2 df x x x x x
2
1
cos2
2
x x C
Câu 4.
Lời giải
Chọn B
Câu 5.
Lời giải
Chọn A
Cách 1: Ta có: . Chọn đáp án
1 1
1
0
0 0
1 d( 1)
d ln 1 ln 2 ln1 ln 2
1 1
x
I x x
x x
C.
Cách 2 : Sử dụng MTCT.
Câu 6.
Lời giải
Chọn B
Đặt .
3 2
3
1 1 3 d dt x t x t t x
Đổi cận: ; .
0 1x t
1 0x t
Suy ra .
1 0 1
2 3
3
0 1 0
1 d . 3 d 3 dx x t t t t t
Câu 7.
Lời giải
Chọn A
Ta có .
df x x
2
3 dx x
2
3 d 3x x
3
3
3
x
C
Chọn ta được một nguyên hàm của hàm số là .
2017C
2
3f x x
3
3
2017
3
x
F x
Câu 8.
Lời giải
Chọn D
15 15 16
2 2 2 2
1 1
7 dx 7 7 7
2 32
x x x d x x C
Câu 9.
Lời giải
Chọn C
.
1
0
3 1 dI f x x
1
0
1
3 1 d 3 1
3
f x x
4
1
1
dt 3
3
f t
Câu 10.
Lời giải
Chọn B
Do mặt phẳng vuông góc với trục nên có vectơ pháp tuyến là .
Oxz
Oy
0;1;0n
Câu 11.
Lời giải
Chọn D
Ta có .
1
1
0
0
e d e e 1
x x
I x
Câu 12.
Lời giải
Ta có .
2 3
3 sin d cosx x x x x C
Câu 13.
Lời giải
Chọn C
Phương trình mặt phẳng là .
ABC
1 6 3 2 6 0
1 2 3
x y z
x y z
.
1;2;0 ; 1;0;3AB CA
Gọi là trực tâm của tam giác .
H
ABC
Suy ra .
OH ABC
Suy ra .
6
,
7
OH d O ABC
Câu 14.
Lời giải
Chọn C
Gọi . Suy ra , , .
; ;0M x y
2 ; ;0MA x y
;2 ;0MB x y
; ;2MC x y
Ta có
2
. 3MA MB MC
2 2
2 2 2 2 1 0x x y y
2 2
1
0
2
x x y y
.
2 2
1 1
0
2 2
x y
1
2
x y
Vậy .
1 1
;
2 2
M
Câu 15.
Lời giải
Chọn B
Đặt
3
2
1
ln
2
dv dx
3
u
u x
x
x
v x
3 3
2 2
2 2 1
dx ln dx .ln . dx
3 3
f x x x x x x
x
3 3 3
2 2 2
2 2 2 2
ln 3ln 2 .
3 3 3 9
x x x C x x C
Câu 16.
Lời giải
Chọn A
Ta có:
1
2
2 1 2 1f x dx x dx x dx
.
3
2
3
2 1
1 1 2 1
. . . 2 1 . 2 1 . 2 1
2 3 2 3 3
2
x
C x C x x C
Câu 17.
Lời giải
Chọn C
Ta có: hình chiếu củađiểm trên các trục lần lượt là ,
1; 1; 2A
, ,Ox Oy Oz
1; 0; 0B
, .
0; 1; 0C
0; 0; 2D
Phương trình mặt phẳng qua là: .
Q
, ,B C D
1
1 1 2
x y z
2 2 2 0x y z
Câu 18.
Lời giải
Chọn B
Có
d sin cos d cos sinF x f x x x x x x x C
Do .
cos sin 2 1 2 1
2 2 2
F C C C
cos sin 1F x x x
Câu 19.
Lời giải
Chọn C
Ta có
2
2
4 2 2 4
cos ; 2 4 5 1
30 30
6. 4
m
u v m m
m
.
2
1
1
1
10 11 0
11
m
m
m n
m m
m l
Câu 20.
Lời giải
Chọn C
Ta có
2
2 d
x x
F x e x x e x C
Theo bài ra ta có: .
3 1
0 1
2 2
F C C
Câu 21.
Lời giải
Chọn C
Ta có .
2
ln
d
x
F x x C
x
Đặt , suy ra .
1
ln d dt x t x
x
2 3 3
2
ln ln
d d
3 3
x t x
F x x t t C C
x
Mà .
3
3
3
ln
8 8 1
3
e
F e C C
Khi đó .
3
ln
1
3
x
F x
Nên .
3
9
2F e
Câu 22.
Lời giải
Chọn B
1000
2
2
2
1
4 1x x
I dx
x x
1000
2
2
2
1
2 1x x x x
dx
x x
1000
2
2 2
1
2 1
1
x x
dx
x x x x
1000 1000 1000
2 2 2
2
1 1 1
2 1 1
1
x
dx dx dx
x x x
1000
1000
1000
2
2
2
2
2
1
1
1
ln 1
d x x
x x
x x
1000
2
1000 1000
1
2 1 ln ln 1 ln 2 1 ln 2x x
1000
2
1000 2 1000
1
2 1 ln ln 2 1 ln 2x x
1000 1000 1000 1000
2 1 ln 2 ln 2 1 ln 2 ln 2 1 ln 2
1000 1000 1000
2 1 ln 2 2ln 2 2ln 2 1
2
1000 1000 2 1000
2 1 ln 2 ln 2 ln 2 1
2
1000 998 1000
2 1 ln 2 ln 2 1
.
2
1000 998 1000
2 1 ln 2 2 1
Câu 23.
Lời giải
Ta có
F x f x
2
2
2
2 2 2 2 2
. 2x 1 4
x x
F x x f x x x x x x e x x
2
2
2 2
2x 1 1 2 2
x x
x x e x x x x
2
2
2
1
2x 1 1 2 1 2 0 2; 1; ;0;1
2
x x
x x x x x x e x
có 5 nghiệm đơn nên có 5 điểm cực trị.
2
0
F x x
2
F x x
Câu 24.
Lời giải
Chọn D
Ta có: .
2
d cos 2 d
u x
v x x
d 2 d
1
sin 2
2
u x x
v x
Khi đó: .
π
2
0
cos2 dI x x x
π
2
0
0
1
sin 2 sin 2 d
2
x x x x x
Câu 25.
Lời giải
Chọn D
Đặt . Từ đó suy ra
2
2t x x t dx tdt
4 2
0 0
x t
x t
Khi đó .
4 2 2 2
2
0
0 0 0 0
' ' 2 2 5I f x dx tf t dt tf t f t dt f f x dx
Câu 26.
Lời giải
Chọn A
.
2
1 cos 2
cos d d
2
a a x
F x x x x
1 1
sin 2
2 4
a
x x C
Do , .
1
0
4
F
4 4
F
1
1
4
4
1 1
sin
2
2 4 4 2 4
2
C
C
a
C
a
Vậy .
2
2
a
Câu 27.
Lời giải
Chọn A
Đặt .
2
1 1 2
1 3ln 1 3ln 2 3.
3
u x u x udu dx dx udu
x x
Đổi cận ; .
1 1x u
2x e u
Do đó: .
2
2 2
2
1 1 1
2 1
3 3
ln 2
1
9
1 3ln
e
u
u du
x
I dx u du
u
x x
Câu 28.
Lời giải
Chọn D
Đặt .
2
1 dF t t t
2
1F t t
2
1
1 d
x
G x t t
1F x F
1G x F x F
1F x F
2
1F x x
.
Câu 29.
Lời giải
Chọn A
Lần lượt thay tọa độ các điểm vào , ta được .
, , ,N P Q M
P
M P
Câu 30.
Lời giải
Chọn A
Ta có .
F x f x
2
2 2 3
2 3
ax bx c
F x ax b x
x
2
2 2 3
2 3
ax b x ax bx c
x
= .
2
5 3 6 3
2 3
ax b a x c b
x
2
20 30 7
2 3
x x
x
Do đó: . Vậy .
5 20
3 6 30
3 7
a
b a
c b
4
2
1
a
b
c
3S a b c
Câu 31.
Lời giải
Chọn D
Đặt .
2
1 1 2t x x t dx tdt
Đổi cận: .
0 1; 3 2x t x t
Do đó: . Vậy .
3 2 2
0 1 1
8 1 .2 2 .f x dx f t t dt t f t dt
2
1
. 4t f t dt
4I
Câu 32.
Lời giải
Chọn B
Ta có: là trung điểm của đoạn .
M
AB
1
2
1
2
1
2
A B
M
A B
M
A B
M
x x
x
y y
y
z z
z
1; 1;1M
Câu 33.
Lời giải
Chọn A
Ta có .
1; 1;1
( ) :
3
I
S
R
Để tiếp xúc với thì .
( )P
( )S
2
2
2
1 3
3 10 0 2
; 3
5
3
3 8 0
m m
m m m
d I P R
m
m m
Câu 34.
Lời giải
Chọn A
Đặt
2 2
2
1 1
3 1 d
1 1
3 d
3 ln 3 ln
x x
I x
x x x x x x
Đặt
1
3 ln d 3 dt x x t x
x
Đổi cận:
1 3x t
.
2 6 ln 2x t
Khi đó,
6 ln 2
6 ln 2
3
3
d
ln ln 6 ln 2 ln3
t
I t
t
ln 2
ln 2
3
Suy ra , , . Vậy .
2a
2b
3c
7a b c
Câu 35.
Lời giải
Chọn D
Đặt .
1u x
2
1 d 2 dx u x u u
Khi đó trở thành .
3
dx
1
x
x
2
2
4
.2 d 2 4 d
u
u u u u
u
PHẦN II: TỰ LUẬN
Câu 36.
Học sinh tự giải
Câu 37.
Lời giải
Ta có:
2 2
0
2
0
sin 2 .cos 2sin .cos
1 cos 1 cos
x x x x
I dx dx
x x
Đặt
cost x
sin .dt x dx
Đổi cận:
0 1; 0
2
x t x t
2
0 1
1
2
0
1
2 1 1
2 1 2 ln 1 2 ln 2 2ln 2 1
0
1 1 2 2
t t
I dt t dt t t
t t
Vậy .
2; 1 5a b P
Câu 38.
Lời giải
Ta có:
3
1
3
2 3 1
1
2
f x
dx f x f f
f x
Ta có:
3
1
8 3 1 3 1 3 1f x dx f f f f f f
.
3 1 4f f
3 3f
3 9f
Cách 2:
2 2
3
1
3 1 8
4
8
(3) 3 3 9
2
2
3 1 2
x f
y f
f f
x y
x y
x f f
x y
x y
f f
Câu 39.
Lời giải:
I
O
A
B
C
D
S
2
1 3
. 3
2 2
ADC
a
S AD DC AD a
Do nên tâm đường tròn ngoại tiếp tứ giác là trung điểm .
0
90ABC ADC
ABCD
AC
Gọi là trung điểm thì là tâm mặt cầu ngoại tiếp hình chóp .
I
SC
I
.S ABCD
0
tan 60 . 3IO OC a
Có
2 2 2 2
3 2R IA IO OA a a a
2
2 2
4 4 2 16
mc
S R a a
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên:………………………………….Lớp:………….......……..………
Mã đề thi
003
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
A
A
D
A
B
A
B
C
C
D
C
D
C
C
B
D
B
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
D
C
D
A
A
D
B
B
A
B
B
B
A
D
C
C
A
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn A
Ta có nên .
e 1 e
x x
f x
e 1
x
df x x
e 1 d
x
x
e
x
x C
Câu 2.
Lời giải
Chọn A
Đặt
4 1t x
2
4 1t x
2 4
2
d d d d
t
t t x x t
Đổi cận : . Do đó :
0 1, 2 3x t x t
2 3
2 3
0 1
3
1 13
4 1 . .
1
2 2 3 3
d d
t t
x x t
Cách 2: Sử dụng máy tính cầm tay.
Câu 3.
Lời giải
Đặt .
2
1
2 3 d 2 1 d 1 d d
2
u x x u x x x x u
Đổi cận: ; .
0 3x u
1 2x u
Ta có .
2
1 2 3
2 3
0 3 2
1 1
1 d d d
2 2
x x u u
x e x e u e u
Vậy chọn phương án C
Câu 4.
Lời giải
Chọn A
Hình chiếu của lên trục là điểm
(1; 2; 3).M
Oy
(0; 2; 0).Q
Câu 5.
Lời giải
Chọn B
.
1
1
0
0
d
ln 1 ln 2
1
x
x
x
Câu 6.
Lời giải
Chọn A
Ta có,
2
1
3 xf x d
2
1
3 x 6f x d
Câu 7.
Lời giải
Chọn B
Câu 8.
Lời giải
Chọn C
Mặt phẳng có một vectơ pháp tuyến là .
:P
2 23 0x z
1
1;0;2n
Câu 9.
Lời giải
Chọn C
Mặt cầu có tâm và bán kính có phương trình là
1;2;3I
3R
.
2 2 2
1 2 3 9x y z
Câu 10.
Lời giải
Chọn D
Ta có , , .
dF x f x x
x K
F x f x
x K
Câu 11.
Lời giải
Chọn C
Ta có .
2 2 3 2
1
2 1 2
3
x x dx x dx xdx dx x x x C
Câu 12.
Lời giải
Chọn D
.
3 2 3
0 0 2
dx dx dxa f x f x f x
2
0
dxf x b
2
0
dxf x a b
Câu 13.
Lời giải.
Chọn C
Ta có tâm cầu thuộc trục : .
Ox
;0;0I a
.
2
1 ;1;2 2 6IA a IA a a
2
3 ;0;1 6 10IB a IB a a
Mà mặt cầu đi qua hai điểm
S
1;1;2 ,B 3;0;1A
2 2 2 2
2 6 6 10 1 1;0;0IA IB IA IB a a a a a I
5R IA
Vậy phương trình mặt cầu là: .
S
2
2 2
1 5x y z
Câu 14.
Lời giải
Chọn C
Phương trình mặt phẳng .
:16 11 5 0ABC x y z
Gọi là tâm đường tròn ngoại tiếp .
; ;I a b c
ABC
Ta có .
5
2 2 10 23
2
4 6 2 32 4
16 11 5 1
a
I ABC
a b c
IA IB a b c b
IA IC a b c c
5
;4;1
2
I
Câu 15.
Lời giải
Chọn B
Ta có ;
d 2 1
2
d 2
2 1 2 2 1
x
x
x x
2 2 1x C
Do nên .
5 7F
6 7C
1C
Câu 16.
Lời giải
Chọn D
Đặt .
2
1
d d
ln
d d
2
u x
u x
x
v x x
x
v
.
3
3 3
2
2 2
2
1
ln d ln d
2 2
x
x x x x x x
3 3
2 2
2 2
ln
2 4
x x
x
9 5
ln3 2ln 2
2 4
Suy ra .
2 0m n p
Câu 17.
Lời giải
Chọn B
Ta có: có dạng: .
//P Q P
2 2 0 5x y z m m
Chọn điểm
0; 5; 0B Q
Ta có:
, ,d A P d Q P
, ,d A P d B P
6 1 4 5
3 3
m m
11 5
3
11 5
m m
m n
m m
Vậy: .
: 2 2 3 0P x y z
Câu 18.
Lời giải
Chọn C
.
10
10
101 3 101 3 101
100 2
0
0
10 10 10 1060
2 2 20
101 3 101 3 101 3
x x
I x x dx x
Câu 19.
Lời giải
Chọn D
Đặt: .
d d
1
d cos2 d
sin 2
2
u x
u x
v x x
v x
Khi đó: .
1 1 1 1
cos2 d sin 2 sin 2 d sin 2 cos2
2 2 2 4
x x x x x x x x x x C
Câu 20.
Lời giải
Chọn C
Xét
4
1
0
2 dI f x x
Đặt
2t x
dt dx
x
t
Đổi cận
2
0
4
2
2
1
2
dtI f t
2 2f f
2 2 4
Xét
2
2
0
2 dI f x x
Đặt
2t x
dt dx
x
t
Đổi cận
2
0
2
4
4
2
2
dt 4 2 4 2 2I f t f f
Vậy .
4 2
0 0
2 d 2 d 6f x x f x x
Câu 21.
Lời giải
Chọn D
.
. 2 0 0 2
cos ,
5
5 5
.
a b
a b
a b
Câu 22.
Lời giải
Chọn A
Đặt .
2t x
d 2dt x
Từ .
2
2 d sin lnf x x x x
2
1
dt sin ln
2 2 2
t t
f t C
, do
2
d 2sin 2ln 2ln 2 2
2
t
f t t t C
2
d 2sin 2ln 2ln 2 2
2
x
f x x x C
nên chọn đáp án B
C
Câu 23.
Lời giải.
Chọn A
.
2
1 ln
d d
x
F x f x x x
x
2 2
1 ln
d
x
x
x x
2 2
1 ln
d d
x
x x
x x
1
I C
x
Đặt: .
2
ln
1
d d
u x
v x
x
1
d d
1
u x
x
v
x
.
2
1 1
ln d
I x x
x x
1 1
ln x C
x x
Do đó: . Vậy .
2 1
ln F x x
x x
1
ln 2 x
x
1
2
a
b
1S
Câu 24.
Lời giải
Chọn D
Ta có ;
: 0Oxy z
;
: 0Oyz x
.
: 0Oxz y
Do đó .
2; 1; 3a b c
Vậy .
30P
Câu 25.
Lời giải
Chọn B
Ta có:
1 1
1
2 2
2
0 0
0
d .sin .cos d cos sin
M N M N
f x x M x N x x x x
Do đó:
1
2
0
1 1
d 1
M N
f x x M N
Mặt khác:
1 3 3 3 2f N N M
.
1 5 2
2 .cos 3 .sin
4 2
f x x x f
Câu 26.
Lời giải
Chọn B
Theo công thức nguyên hàm, đáp án D sai.
Câu 27.
Lời giải.
Chọn A
Không bước nào sai.
Câu 28.
Lời giải
Chọn B
Ta có , vì nên
cos3
sin3 d
3
x
x x C
2
2
F
2.C
Câu 29.
Lời giải
Chọn B
Ta có véc tơ ngược hướng với véc tơ và . Suy ra .
b
a
2
b a
2 2;4; 6
b a
Câu 30.
Lời giải
Chọn B
Đặt .
1
2 d d
2
t x t x
x
Suy ra .
1
d
2
F x x
x x
2
dt
t
2ln t C
2ln 2 x C
Do . Vậy .
0 ln 4F
0C
4 4ln 2F
Câu 31.
Lời giải
Chọn A
Đặt
ln 2
2
x
x t dx dt
Khi đó .
1 ln 2 1 ln 2
1 ln2 ln 2
1 1 1 2018
ln 2 1009
2 2 2
e
x
f x dx f t dt f t dt
x x
Câu 32.
Lời giải
Chọn D
Xét mặt cầu có: tâm , bán kính .
2 2
2
1 3 1x y z
1;3;0I
1R
. Vậy cắt mặt cầu.
2 2
3.1 4.0 1
2
,
5
3 4
d I P
1
P
Câu 33.
Lời giải:
Chọn C
. Đặt
1
e
I xlnxdx
2
1
du dx
u lnx
x
dv xdx
x
v
x
.
2 2 2 2 2 2 2 2
0 0
0 0
1 1 1 1
.
2 2 2 2 2 4 2 4 4 4
e e
e e
x x e e x e e e
I lnx dx xdx
x
Câu 34.
Lời giải
Chọn C
.
3
3
2
2
dI f x x f x
3 2f f
5 2 3
---Hết---
Câu 35.
Lời giải
Chọn A
Ta có .
df x x f x C
.
3 1 7
d d 3 d 3 7 ln 2
2 2
x
f x x x x x x C
x x
Do đó .
3 7 ln 2 2
3 7 ln 2 2
x x C khi x
f x
x x C khi x
Khi đó ,
0 1 7ln 2 1 1 7ln 2f C C
4 2 12 7ln 2 2 14 7ln 2.f C C
Suy ra .
3 7 ln 2 1 7ln 2 2
( )
3 7 ln 2 14 7 ln 2 2
x x khi x
f x
x x khi x
Nên .
2
2 6 7ln 2 1 7ln 2 7 7ln 2f
.
3 9 7ln1 14 7ln 2 5 7ln 2f
Vậy
2 3 12.f f
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Học sinh tự giải.
Câu 38.
Lời giải
Đặt với .
2
tan d 1 tan dx t x t t
1 ; 0 0
4
x t x t
.
4 4 4
4
2 4
2
0 0 0
0
1 1 cos2 1 1 2
tan 1 tan cos d d sin 2
cos 2 2 4 8
t
I f t t dt t t t t t
t
Câu 39.
Lời giải
Ta có:
1
. 1 1
1
f x f x f x
f x
Khi đó
1 1
0 0
1 d
d
1 1 1
f x x
x
I
f x f x
Đặt
1 d dt x t x
Đổi cận
0 1; 1 0 x t x t
Nên .
0 1
1 0
d d
1 1
f t t f x x
I
f t f x
Do đó: .
1 1
0 00
1
d
d 1
d 1
1 1 2
I
f x x
x
x I
f x f x
I
Câu 37.
Lời giải
d
S
A
C
B
I
M
E
Gọi là trung điểm khi đó là tâm đường trong ngoại tiếp tam giác .
M
BC
M
ABC
Qua dựng đường thẳng vuông góc với mp đáy.
M
d
Dựng mp trung trực của cắt tại khi đó là tâm mặt cầu ngoại tiếp hình chóp.
SA
d
I
I
.
, , 45SB ABC SB AB SBA
.
2
,
2 2
a a
SA AB a AE AM
Bán kính mặt cầu là .
2 2
2 2
3
2 4 2
a a a
IA AM EM
Thể tích của khối cầu ngoại tiếp hình chóp S.ABC là .
3
3
4 3 3
3 2 2
a a
V
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên:………………………………….Lớp:………….......……..………
Mã đề thi
004
Mã đề [004]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C
B
D
C
D
A
A
D
C
C
C
A
B
A
C
C
A
B
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
B
D
A
D
D
A
A
B
B
B
D
C
B
B
C
A
D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Theo tính chất của tích phân, ta có: .
3 4 4
0 3 0
d d df x x f x x f x x
Suy ra: .
3
0
df x x
4 4
0 3
d df x x f x x
10 4
6
Vậy .
3
0
d 6f x x
Câu 2.
Lời giải
Chọn B
.
4 3
3 2
d
4 3
x x
f x dx x x x C
Câu 3.
Lời giải
Chọn D
Đặt .
3 2
1
2 2018
3
y x mx m x
Đổi cận, thay vào ta được .
1m
Câu 4.
Lời giải
Chọn C
.
5 2
1 1
ln 5 2
5 2 5 5 2 5
d x
dx
x C
x x
Câu 5.
Lời giải
Chọn D
Do với mọi hằng số và với mọi hàm số liên tục trên nên
( ) ( )kf x dx k f x dx
0k
( )f x
A là mệnh đề sai.
Câu 6.
Lời giải
Chọn A
2
2 2 2 2
2
1 1 1 1
1
2 2
1 1
4 2 1 4 2 1 4 2. 1
2
4 4 1
x
f x x dx f x dx xdx f x dx
f x dx f x dx
Câu 7.
Lời giải
Chọn A
Câu 8.
Lời giải
Mặt cầu có tâm và đi qua điểm nên có bán kính
1; 4;3I
5; 3;2A
3 2R IA
Vậy phương trình mặt cầu cần tìm là: .
2 2 2
1 4 3 18x y z
Câu 9.
Lời giải
Chọn C
Ta có
1
1 1
2
1
1 1
2
2 1 d 2 1 d 2 1 dI f x x f x x f x x
.
0 1
3 0
1 1
d d 3 1 4
2 2
I f u u f v v
Câu 10.
Lời giải
Chọn C
Mặt phẳng có vectơ pháp tuyến .
2 2 0x y z
1;2; 1n
Câu 11.
Lời giải
ChọnA.
Ta có: .
5
5 1 d
ln5
x
x
x x C
Câu 12.
Lời giải
Đặt . Đổi cận .
d
ln 2 d
x
u x u
x
1
0; 1
2 2
e
x u x u
Vậy .
1
2
2
2
1
0
2
ln 2
d d
e
x
x u u
x
Câu 13.
Lời giải
Chọn B
ta có .
1
1
2 2
x x
I dx
2 2 0
x x
0x
1 0 1 0 1
1 1 0 1 0
2 2 2 2 2 2 2 2 2 2
x x x x x x x x x x
I dx dx dx dx dx
.
0 1
1 0
2 2 2 2 1
ln 2 ln 2 ln 2
x x x x
Có thể sử dụng máy tính.
Câu 14.
Lời giải.
Chọn A
.
2
. .
x
F x x e dx
Đặt .
2
2
1
. .
.
2
x
x
du dx
u x
v e
dv e dx
.
2 2
1 1
. . .
2 2
x x
F x x e e dx
2 2
1 1
. . .
2 4
x x
x e e C
2
1 1
.
2 2
x
e x C
Câu 15.
Lời giải
Chọn C
Ta có .
0;3; 3 , 3;3;0 , 3;0;3BA BC AC
Vì nên đều.
AB AC BC
ABC
Tâm đường tròn ngoại tiếp trùng với trọng tâm nên .
ABC
2;2;2I
Câu 16.
Lời giải
Chọn C
Ta có , nên mặt phẳng có vectơ pháp tuyến là
1; 0; 3AB
1;1; 0AC
ABC
.
, 3; 3;1AB AC
Phương trình mặt phẳng có dạng .
ABC
3 3 8 0x y z
Câu 17.
Lời giải
Chọn A
Ta có: .
2 2
1
d e d e
2
x x
F x f x x x C
Theo giả thiết: . Vậy .
1
0 1
2
F C
2
e 1
2 2
x
F x
Câu 18.
Chọn B
Đặt
1 1
1 1
0 0
0 0
2 x
( 2) x ( 2) x= 2 3 2e =
x
x x x x
x x
u x du d
x e d x e e d e e a be
dv e d v e
với
; 3, 2 1
a b a b a b
Câu 19.
Lời giải
Xét . Đặt .
2
0
2 ln 1 dI x x x
ln 1
d 2 d
u x
v x x
2
1
d d
1
1
u x
x
v x
Ta có: .
2
2
2
2
0
0
1
1 ln 1 d
1
x
I x x x
x
2
0
3ln 3 1 dx x
2
2
0
3ln 3 3ln3
2
x
x
Vậy , .
3a
3b
3 4 21a b
Câu 20.
Lời giải
Chọn D
Mặt cầu có tâm và tiếp xúc với nên bán kính .
S
I
P
, 2R d I P
Phương trình mặt cầu : .
S
2 2 2
2 1 1 4x y z
Câu 21.
Lời giải
Chọn A
Ta có:
2
( )d e 2 d e
x x
f x x x x x C
Do nên
3
(0)
2
F
0 2
3 1
e 0
2 2
C C
Vậy: .
2
1
e
2
x
F x x
Câu 22.
Lời giải
Chọn D
Đặt . Khi đó .
lnt x
1
d dt x
x
1
d
ln
A x
x x
1
dt
t
Câu 23.
Lời giải
Chọn D
Giả sử , do
0;0;A a Oz
2 5
; 2 2 2 2
8
a
d A P
.
13
13
0;0;
2 5 8
2
2
2 5 8 3
3
0;0;
2
2
A
a
a
a
a
A
Câu 24.
Lời giải
Chọn A
Đường thẳng qua và vuông góc với có phương trình . Gọi là
d
A
P
1 2 3
1 1 1
x y z
H
hình chiếu vuông góc của điểm trên , ta có .
A
P
H d
1 ;2 ;3 H t t t
Tuy nhiên nên .
H P
1 2 3 3 0 t t t
1 t
0;1;2M
Câu 25.
Lời giải
Chọn A
Đặt .
2
2x t
2 2
2t x
d dt t x x
Khi đó .
2
d
2
x
x
x
d
t
t
t
dt
t C
2
2x C
Câu 26.
Lời giải
Chọn B
Đặt . Đổi cận ;
2x =dx
2
dt
t
0 2x t
2 4x t
Khi đó ta có
2
4 4
0 0
0
1 1
(2 ) ( ) ( ) 8
2 2
I f x dx f t dt f x dx
Câu 27.
Lờigiải
Chọn B
.
3
1
( ) 10f x dx
3 1 10f f
3 3 10f
3 13f
Câu 28.
Lời giải
Chọn B
Đặt , đổi cận .
d
d
2
x
t x t
x
1 1, 4 2x t x t
.
4
1
1
dI f x x
x
4 2
1 1
1
2 d 2 d 2
2
f x x f t t
x
Câu 29.
Lời giải
Chọn D
Đặt
u x du dx
2 2
1
2
x x
dv e dx v e
.
2 2 2
1
2 2
x x x
x
xe dx e e dx
2 2
1 1
2 4
x x
xe e C
Vậy .
1 1
;
2 4
a b
1
8
ab
Câu 30.
Lời giải
Chọn C
.
5
4
504,5
d 2017e 2018 d 2017e
x x
f x x x x C
x
Câu 31.
Lời giải
Gọi là trung điểm .
I
1; 1; 2AB I
Mặt cầu có đường kính có tâm và bán kính
S
AB
1; 1; 2I
2 2 2
1 1 1 0 2 4 5R IA
.
2 2 2
: 1 1 2 5S x y z
Câu 32.
Lời giải
Chọn B
Ta có với , .
cos BAC
.
cos ,
AB AC
AB AC
AB AC
1;5; 2AB
5;4; 1AC
2 2
2 2 2 2
1.5 5.4 2 1
cos ,
1 5 2 5 4 1
AB AC
27
30 42
9
2 35
Câu 33.
Lời giải
Chọn C
Đặt , , ta có hệ phương trình
2
1
da f x x
2
1
db f x x
3 2 1
2 3
a b
a b
5
7
11
7
a
b
Vậy .
2
1
5
d
7
f x x
Câu 34.
Lời giải
Chọn A
.
1
d ln 1
1
F x x x C
x
Do . Vậy .
2 1 1F C
3 ln 2 1F
Câu 35.
Lời giải
Chọn D
Ta có
5 2 5
1 1 2
2 5
1 2
2 5
1 2
2 2 2
d d d
1 1 1
3 3
1 d 1 d
1 1
3ln 1 3ln 1
2 3ln3 1 3ln 2 5 3ln 6 2 3ln3
2 6ln 2 3ln3
x x x
x x x
x x x
x x
x x
x x x x
Vậy .
2, 6, 3 36a b c P abc
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Học sinh tự giải.
Câu 37.
Lời giải
Ta có: .
;
P ABC AH
P ABC BC P
BC AH BC ABC
Suy ra mặt phẳng đi qua và nhận làm VTPT
P
A
5;3; 6BC
Vậy: .
:5 3 6 16 0P x y z
Câu 38.
Lời giải
.
2017
2
2019
1
2
d
x
I x
x
2017
2
2
1
2 1
1 . dx
x x
Đặt .
2 2
1 1 1
d d d dt t x x t
x x x
; .
1 1x t
1
2
2
x t
Khi đó .
1
2017
1
2
1 2 .dI t t
1
2018
1
2
1 2
1
.
2 2018
t
2018 2018
3 2
4036
Câu 39.
Lời giải
Vì tăng trên .
f x
0;
0 0f x f x
1 0f x x
2 2
f x f x f x f x
2
2
1
f x f x f x
f x
1
f x
f x
Với , ta có:
0t
0 0
d d
t t
f x
x x
f x
0
t
f x
t
f x
1
f t
t
f t
1
f t
t
f t
1 1
0 0
dt 1 dt
f t
t
f t
1
2
1
0
0
1
ln
2
t
f t
3
ln 1 ln 0
2
f f
3
ln 1
2
f
.
3
2
1 .f e
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên:………………………………….Lớp:………….......……..………
Mã đề thi
005
Mã đề [005]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
D
A
D
C
A
D
B
A
C
D
C
B
C
A
B
C
A
C
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
A
B
D
A
B
C
B
B
A
C
D
B
C
B
D
D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn D
Ta có .
1 1
ln
1
dx ax b C
ax a
Câu 2.
Lời giải
Chọn A
Ta có:
2
2
4 2 2 2018x y z x xy z
2 2 2
2 4 2 2 2018x xy y z x xy z
2 2 2
4 2 2018 0x y z x z
Đây là phương trình mặt cầu có tâm , bán kính
(2;0;1)I
2 2 2
2 0 1 ( 2018)R
2023
Câu 3.
Lời giải
Chọn D
, .
kf x dx k f x dx
*
k
Câu 4.
Lời giải
Đặt .
2
1
2 3 d 2 1 d 1 d d
2
u x x u x x x x u
Đổi cận: ; .
0 3x u
1 2x u
Ta có .
2
1 2 3
2 3
0 3 2
1 1
1 d d d
2 2
x x u u
x e x e u e u
Vậy chọn phương án C
Câu 5.
Lời giải
Chọn A
Ta có và
2 4;6; 2
a
3 ( 3;0;12).
b
Suy ra .
2 3 7;6;10
u a b
Câu 6.
Lời giải
Chọn D
Ta có: .
1
cos 2 3 .d sin 2 3
2
x x x C
Câu 7.
Lời giải
Chọn B
.
2
1
1
1 1 1 1
ln
e
e
I dx x
x x x e
Câu 8.
Lời giải
Chọn A
Mặt phẳng có vectơ pháp tuyến .
2 2 0x y z
1;2; 1n
Câu 9.
Lời giải
Chọn C
Ta có .
2018
2018
2
2
1
1
ln
dx
I x
x
2018
ln 2 ln1 2018.ln 2
Câu 10.
Lời giải
Chọn D
Câu 11.
Lời giải
Chọn C
Câu 12.
Lời giải
Chọn B
Đặt
t x
=-
dx dt
Þ = -
6 6
4
4
sin ( ) cos ( )
1
1
6
t
t t
I dt
p
p
-
- + -
Þ =
+
ò
6 6
4
4
sin cos
6
6 1
t
t
t t
dt
p
p
-
+
×=
+
ò
( )
6 6
4
4
2 sin cos
I x x dx
p
p
-
Þ = +
ò
( )
2 2
4
4
1 3sin cos
x x dx
p
p
-
= -
ò
( )
4
4
1
5 3cos4
8
x dx
p
p
-
+=
ò
4
4
1 3
5 sin 4
8 4
x x
p
p
-
æ ö
÷
ç
+
÷
ç
÷
ç
è ø
=
5
16
p
=
5
32
I
p
Þ =
.
27
a b
Þ - =
Câu 13.
Lời giải
Chọn C
Gọi .
2 2 2
: 0 0Ax By Cz D A B C
nên ta có:
O
0D
1
nên ta có:
C
2 0Ax By Cz A C
2
Từ .
1 , 2 2C A
Theo đề bài: .
, ,d A d B
2 2 6A B A
2 *
2 6
2 6
4 **
B A
A B A
A B A
B A
Từ Chọn .
* :
1 2, 2A B C
: 2 2 0x y z
Từ Chọn .
** :
1 4, 2A B C
: 4 2 0x y z
Câu 14.
Lời giải
Chọn A
3
1
0
1
x
dx
I e
x
+
=
+
ò
Đặt
1t x= +
2
1t xÞ = +
2tdt dxÞ =
0 1x t= Þ =
3 2x t= Þ =
2
1
2
t
I
tdt
e
t
×=
ò
2
1
2
t
e dt=
ò
2
2
1
22 2
t
ee e= = -
2; 2; 0a b cÞ = =- =
.
2 2 0 0SÞ = - + =
Câu 15.
Lời giải
Chọn B
Khoảng cách từ đến mặt phẳng là .
1;2;3I
:3 4 10 0P x y
3 2
3 8 10
, 3
3 4
d I P
Phương trình mặt cầu tâm và tiếp xúc với mặt phẳng là
1;2;3I
:3 4 10 0P x y
.
2 2 2
1 2 3 9x y z
Câu 16.
Lời giải
Chọn C
Câu 17.
Lời giải
Ta có: .
2
4 3 2 3f x x f x x x C
Mà .
1 1 2.1 3.1 1 6f C C
Vậy
2
2 3 6f x x x
Theo bài ra ta có phương trình .
2 2
10 2 3 6 10 2 3 16 0 1f x x x x x
Phương trình có , nên có hai nghiệm thực , theo Viet ta có: .
1
137 0
1 2
,x x
1 2
. 8x x
Khi đó .
2 1 2 2 2 1 2 2
log log log . log 8 3x x x x
Câu 18.
Lời giải
Chọn C
Đặt
2 1 d 2 dt x t x x
.
1 3; 2 5x t x t
Vậy .
5
3
1
( )d
2 2
a
I f t t
Câu 19.
Lời giải
Chọn A
Ta có .
8 1 8 4 8
4 4 1 1 1
d d d d d 3 2 5f x x f x x f x x f x x f x x
Câu 20.
Lời giải
Chọn A
Ta có:
2
3 cos d 3 d 3 cos d
x x x x x x x x x
2 3
1
3 d
x x x C
2
3 cos d 3 .d sin 3 .sin 3sin d 3 .sin 3cos
x x x x x x x x x x x x C
Vậy
3
3 cos d 3 sin cos
x x x x x x x x C
Câu 21.
Lời giải
Chọn B
Lời giải đúng:
.
3
4
2
6
1 sin
d
sin
x
x
x
4
2
6
1
sin d
sin
x x
x
4
6
cot cos x x
2 3
1
2 2
Suy ra , , hay .
1
2
a
1
2
b
1 c
0a b c
Câu 22.
Lời giải
Chọn D
Gọi là đường thẳng qua và vuông góc với .
d
M
P
. Gọi là hình chiếu của trên .
3
: 4
5 2
x t
d y t
z t
H
M
P
Tọa độ của là nghiệm của hệ phương trình .
H
3
4
5 2
2 3 0
x t
y t
z t
x y z
2
5
3
1
x
y
z
t
Câu 23.
Lời giải
Chọn A
Đặt . Ta có:
2
0
3 2 cos dI x x x
.
0
1
3 2 1 cos 2 d
2
I x x x
1 2
0 0
1 1
3 2 d 3 2 cos2 d
2 2
x x x x x I I
.
1
0
3 2 dI x x
2 2
0
3 3
2 2
2 2
x x
. Dùng tích phân từng phần
2
0
3 2 cos2 dI x x x
Đặt . Khi đó
d 3d
3 2
1
d cos 2 d
sin 2
2
u x
u x
v x x
v x
.
2
0
0
1 3
3 2 sin 2 sin 2 d
2 2
I x x x x
0
3
0 cos 2 0
4
x
Vậy .
2 2
1 3 3
2
2 2 4
I
Câu 24.
Lời giải
Chọn B
Mặt phẳng có VTPT là .
1;1;1n
Mặt phẳng vuông góc với mặt phẳng khi và chỉ khi .
. 0n n
Nhận thấy mặt phẳng có VTPT thì .
: 2 1 0x y z
2; 1; 1n
. 0n n
Câu 25.
Lời giải
Chọn C
Ta có: .
2
d
3
b
a
x x
2 2
3 3
b
a
x x
1b b a a
Câu 26.
Lời giải
Chọn B
Ta có .
dF x f x x
2
4
d
x
x
x
2
2
4
1
2
4
x
x
d
2
4x C
.
21 7 2F C
Câu 27.
Lời giải
Chọn B
Ta có , , .
1; 1;1AB
1;1; 1AC
1;1; 1 ,BA
2;2; 2BC
Do đó nên đúng.
3,AB
2 3BC
I
nên nằm ngoài đoạn và thẳng hàng.
2BC BA
B
AC
, ,A B C
Suy ra sai, sai, đúng.
II
III
IV
Câu 28.
Lời giải
Chọn A
Đặt .
2
1
4 5 4 5 2 4
2
u x u x udu dx dx udu
Đổi cận: , .
1 1x u
1 3x u
Vậy tích phân trở thành .
1
1
4 5x x dx
2
3 3
2
1 1
5
5 1
.
4 2 8
u u
u
udu du
Câu 29.
Lời giải
Chọn C
Ta có ;
1
ln 2 1
2
F x x C
1 2 2F C
.
1
ln 2 1 2
2
F x x
1
2 ln 3 2
2
F
Câu 30.
Lời giải
Chọn D
Áp dụng công thức nguyên hàm mở rộng
.
1
d
2 1
F x x
x
1
ln 2 1
2
x C
Mà .
e 1 3
2 2
F
1 e 1 3
ln 2 1
2 2 2
C
1C
Câu 31.
Lời giải
Chọn B
Đặt .
d e d
x
u x
v x
d d
e
x
u x
v
Khi đó .
2
2
1
1
e e d
x x
I x x
2
2
1
2e e e
x
2 2 2
2e e e e e
Câu 32.
Lời giải
Chọn C
Đặt và .
u x
d du x
d cos dv x x
sinxv
.
cos dI x x x
sin sin xdx x x
sin cosx x x C
Câu 33.
Lời giải
. Suy ra và không vuông góc.
2 13
. 0 2 . 3 .1
3 3
a b
a
b
. Suy ra và cùng phương.
3a b
a
b
. Suy ra và vuông góc.
. 0.3 2 . 3 3 .2 0a c
a
c
. Suy ra và vuông góc.
2
. 0.3 . 3 1.2 0
3
b c
b
c
Câu 34.
Lời giải
Chọn D
Đặt , nên .
1u x
0u
2
1u x
2
d 2 d
1
x u u
x u
Khi đó .
3
d
1
x
x
x
2
1 3
.2 d
u
u u
u
2
2 4 du u
Câu 35.
Lời giải
Chọn D
Ta có: và mặt phẳng có véc tơ pháp tuyến là .
1;2;2AB
Q
2;1; 1
Q
n
Mặt phẳng nhận hai véc tơ và là cặp véc tơ chỉ phương nên có véc tơ pháp tuyến
P
AB
Q
n
là .
4;3; 5n
Do vậy đến mặt phẳng có phương trình là
hay
P
4 0 3 1 5 2 0x y z
.
4 3 5 7 0x y z
Vậy .
7 7 2
;
10
5 2
d I P
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Học sinh tự giải.
Câu 37.
Lời giải
đi qua điểm và có VTCP
1
d
2;2;2A
1
2;1;3u
đi qua điểm và có VTCP
2
d
1;2;1B
2
2; 1;4u
Do song song với hai đường thẳng nên vectơ pháp tuyến của là
1 2
,d d
suy ra phương trình .
1 2
, 7; 2; 4n u u
: 7 2 4 0x y z d
Do cách đều hai đường thẳng nên
2 2 2 2 2 2
2 3
, ,
7 2 4 7 2 4
d d
d A d B
2 3
2 3
d d
d d
1
2
d
suy ra phương trình .
1
: 7 2 4 0 14 4 8 1 0
2
x y z x y z
.
2S a b c
Câu 38.
Lời giải
2 2
.
1 1
f x x f x
x
f x
f x
x x
2
d d
1
f x
x
x x
f x
x
2
ln 1f x x C
. Vì nên .
2
1x C
f x e
0f e
0C
Vậy .
2
1 2
3
x
f x e f e
Câu 39.
Lời giải
Ta có
1
0
2 1 d 4f x x
1
0
1
2 1 d 2 1 4
2
f x x
3
1
d 8f t t
Đặt khi đó
1
d d
u x
v f x x
d du x
v f x
.
3 3 3
3
1
1 1 1
1 d 1 ( ) d 2 (3) d 2.10 8 12x f x x x f x f x x f f x x
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020
Chuyên đề:
Họ và tên:………………………………….Lớp:………….......……..………
Mã đề thi
006
Mã đề [006]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
B
A
C
B
B
C
C
B
C
A
D
A
C
A
D
D
A
D
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
A
B
C
C
B
B
C
D
A
D
D
B
A
D
A
C
B
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1.
Lời giải
Chọn B
Biến đổi phương trình mặt cầu thành .
2 2 2
2 1 2 16x y z
Vậy .
4R
Câu 2.
Lời giải
Chọn A
Câu 3.
Lời giải
Chọn C
Ta có theo bảng nguyên hàm cơ bản thì .
d
ln
x
x
a
a x C
a
Câu 4.
Lời giải
Chọn B
, .
( )
3;2;1a =
( )
2;0;1b = -
( )
1;2;2a bÞ + =
1 4 4 3a bÞ + = + + =
Câu 5.
Lời giải
Ta có .
1
2 2
2
1
2
1 1
1 1
x x
x x
dx e dx e
e e
Câu 6.
Lời giải
Chọn C
.
8
8
4
4
ln 1 ln 9 ln5
1
dx
x
x
Câu 7.
Lời giải
Chọn C
có vecto pháp tuyến là .
( )
P
( )
3;2; 1
n
= -
Câu 8.
Lời giải
Chọn B
Đặt .
3 2
1
2 2018
3
y x mx m x
Đổi cận, thay vào ta được .
1m
Câu 9.
Lời giải
Chọn C
Vì .
ln
x
x
a
a dx C
a
Câu 10.
Lời giải
Chọn A
Ta có .
2
cos3
d 6 sin 3 d 3
3
x
F x f x x x x x x C
Theo đề .
2
2 cos3.0 2
0 3.0 1
3 3 3
F C C
Vậy .
2
cos3
3 1
3
x
F x x
Câu 11.
Lời giải
Chọn D
Đặt
2
2
1
1 2 1 2 ; d d .
2
u
u x u x x u u x
Đổi cận:
0 1; 4 3x u x u
Suy ra
3
3
5 3
2 2
1
1
1 1
1 d .
4 4 5 3
u u
I u u u
Câu 12.
Lời giải.
Chọn A
Ta có : .
'( ) ( ) ( ) 3 5
b
a
f x dx f b f a
( ) 5 5 3 f a
Câu 13.
Lời giải
Chọn C
Đặt .
5 1 d
x
F x x e x
5 1 . 5 e d
x x
x e x
5 1 .e 5.e
x x
x C
5 4 e
x
x C
Vì . Khi đó: .
0 3F
4 3C
7C
5 4 7
x
F x x e
Vậy .
1 5.1 4 . 7 7F e e
Câu 14.
Lời giải
Chọn A
Ta có : .
2 2
2 2
2 2
1
d 1
x x a
F x f x x F x f x a
x x
Do đó : . Đặt :
cos dg x x x x
d d
d cos d sin
u x u x
v x x v x
.
sin sin d sin cosg x x x x x x x x C
Câu 15.
Lời giải
Chọn D
.
2
7 7
7
2
2 2
2
2 2
d 1
d 1 1 1 1
ln 1 ln 2 ln 5
1 2 1 2 2 2
x
x x
x
x x
Suy ra .
1 1 1
; 2
2 2 2
a b a b
Câu 16.
Lời giải
Chọn D
Đặt .
2
1
d d
ln 3
3
1
d 1
2
u x
u x
x
v x
v x x
2
5
2
4
1
5
1
2
ln 3 d
4
2 3
x x
I x x x x
x
5 5
2
4 4
35 1 9 9 3 3
ln 2
2 2 3 3
x x
dx dx
x x
35 1 9
ln 2 3 9ln 2 1 3ln 2
2 2 2
.
19
10ln 2
4
Câu 17.
Lời giải
Chọn A
Ta có:
3
1dI x x
Đặt:
3
1t x
3
1t x
2
3 d dt t x
2
.3 dI t t t
3
3 dt t
4
3
4
t C
4
3
3
1
4
x C
3
3
1 1
4
x x C
Vậy
3
3
1 1
4
F x x x C
Câu 18.
Lời giải
Chọn D
Ta có , vì nên .
sin 4 sin 2y x x
cos4 cos2
4 2
x x
F x C
0 0F
1
4
C
Nên .
cos2 cos 4 1
2 4 4
x x
F x
Câu 19.
Lời giải
Chọn A
3 3
0 0
d 1 1 1
d
2 4 2 2 4
x
x
x x x x
3
0
1
ln 2 ln 4
2
x x
1 1
ln5 ln 2 ln 7 ln 4 ln 2 ln5 ln 7 .
2 2
Vậy .
1 1 1
; ;
2 2 2
a b c
2 3 3a b c
Câu 20.
Lời giải
Chọn B
Đặt . Ta có .
2
x
t
1
d d d 2d
2
t x x t
6 3 3
2 1 1
d ( ).2d 2 ( )d 24
2
x
f x f t t f t t
Câu 21.
Lời giải
Cách 1.
Đặt
2
1
d d
ln( 1)
1
d d
2
u x
u x
x
v x x
x
v
Khi đó
1
0
.ln 1 dI x x x
1
1
2 2
0
0
ln 1
2 2 1
x x
x dx
x
1
1
2 2
0
0
1 1 1
ln 1 d
2 2 1 1
x x
x x
x x
1
1
2
0
0
1 1
ln 1 1 d
2 2 1
x
x x x
x
.
1
2
0
ln 2 1 1
ln 1
2 2 2 4
x
x x
Cách 2.
Đặt
2
1
d d
ln( 1)
1
d d
1
2
u x
u x
x
v x x
x
v
Khi đó
.
1
0
.ln 1 dI x x x
1
1
2
0
0
1 1
ln 1
2 2
x x
x dx
1
2
0
1
2 2
x
x
1
4
Câu 22.
Lời giải
Chọn C
Ta có .
sin d cosF x x x x C
Đồ thị hàm số đi qua điểm .
y F x
0;1M
1 cos0 2C C
cos 2F x x
.
2
2
F
Câu 23.
Lời giải.
Chọn B
Vì mặt cầu
có tâm thuộc mặt phẳng nên gọi tọa độ tâm của mặt cầu
là:
S
Oxy
S
.
; ;0I a b
Phương trình mặt cầu có dạng: .
S
2 2 2 2 2
2 2 0, 0x y z ax by d a b d
Vì mặt cầu đi qua , ,
nên: .
S
A
B
C
2 4 21 0 2 4 21 2
2 6 11 0 2 6 11 1
4 4 17 0 4 4 17 21
a b d a b d a
a b d a b d b
a b d a b d d
và bán kính mặt cầu là: .
2;1;0I
2 2 2
1 2 2 1 4 0 26R IA
Bán kính
2 2 2
4 1 21 26R a b c d
Câu 24.
Lời giải
Chọn B
Ta có: .
2 2
2 3
1
4
x x
x
f x dx x e dx e C
Do .
3
0 0
4
F C
2 2
2 3 1
1
4 4
x
x
F x e F e
Câu 25.
Lời giải
Chọn C
Đặt
2 2
2
1 1
3 1 d
1 1
3 d
3 ln 3 ln
x x
I x
x x x x x x
Đặt
1
3 ln d 3 dt x x t x
x
Đổi cận:
1 3x t
.
2 6 ln 2x t
Khi đó,
6 ln 2
6 ln 2
3
3
d
ln ln 6 ln 2 ln3
t
I t
t
ln 2
ln 2
3
Suy ra , , . Vậy .
2a
2b
3c
7a b c
Câu 26.
Lời giải
Ta có:
2
2
0
3 d 10
f x x x
2 2
2
0 0
3d d 10
f x x x x
2 2
2
0 0
1d d0 3
f x x x x
.
2
3
0
2
0
0
d 1
f x x x
2
0
10 8 2d
f x x
Câu 27.
Lời giải
+
2
, 45 cos ,
2
u v u v
. 2
2
.
u v
u v
2
1 2 1
2
6. 1
m
m
2
3 1 1 2m m
.
2 2
1 2 0
3 3 1 4 4
m
m m m
2
1
2
4 2 0
m
m m
2 6m
Câu 28.
Lời giải
Chọn D
Ta có
3 3
3 3
0 0
1 1
d 2
1 d 1 1
3
1
x
I x x x x x x x
x x
.
2 14 4
8 2 2 3 3 1 2 3 2
3 3 3
I
Do đó .
14 4 16
, 2,
3 3 3
a b c P 
Câu 29.
Lời giải
Chọn D
Gọi là mặt phẳng trung trực của đoạn thẳng .
P
AB
Véc tơ pháp tuyến của là
P
6;2;2
P
n AB
đi qua trung điểm của . Tọa độ trung điểm
P
M
AB
1;1;2M
Vậy phương trình trung trực của đoạn thẳng là: .
AB
:3 0P x y z
Câu 30.
Lời giải
Chọn B
Ta có
, , .
2
2 2 2
1 2 2 9AB
2
2 2 2
3 4 6 61AC
. 1.3 2 4 2.6 23AC AB
.
2
2
BC AC AB
2 2
2. .AC AB AC AB
61 9 2.23 24
Áp dụng công thức đường trung tuyến ta có:
.
2 2 2
2
2 4
AB AC BC
AM
9 61 24
29
2 4
Vậy .
29AM
Câu 31.
Lời giải
Chọn A
Ta có
2
2 3 12
4
x x x
x
x
f x x
Nên .
12 2
12 d
ln12 3
x
x
x x
F x x x C
Câu 32.
Lời giải
Chọn D
Phương trình đường thẳng qua có VTCP : .
AB
2;2; 2A
1; 3;2
u AB
2
2 3
2 2
x t
y t
z t
2 ;2 3 ; 2 2 I AB P I t t t
2 2 3 2 2 2 0 I P t t t
2 4; 4;2 t I
.
2
IA
IB
Cách 2. Ta có .
8
,
3
2
4
,
3
d A P
IA
IB
d B P
Câu 33.
Lời giải
Chọn A
Ta có: .
, 3d d I P
Mặt cầu có tâm I và bán kính . Do đó, chọn D
S
2 2
5 34r d
Câu 34.
Lời giải
Chọn C
.
3
1
.4.ln ln
4
F x x x
3
ln x
x
Câu 35.
Lời giải
ChọnA
Ta có:
2 2 2
2.1 2 3 1
; 3
2 1
m
d A P AB
m
2
2 2
3 3 3 5 5 1 2 m m m m m
PHẦN II: TỰ LUẬN
Câu 36.
Lời giải
Học sinh tự giải.
Câu 37.
Lời giải
Giả sử có phương trình: .
1
x y z
a b c
, , 0a b c
Theo giả thiết ta có:
2 2c a b
, .
4; 3;12M
4 3 12
1
a b c
4 3 6
1
a a a
7
1
a
7a
7b
14c
Vậy hay
: 1
7 7 14
x y z
2 2 14 0x y z
Câu 38.
Lời giải
Ta có
.
1
1
2 1 df x x
1
2
1
2 1 df x x
1
1
2
2 1 df x x
1
2
1
1 2 df x x
1
1
2
2 1 df x x
Ta có , đặt thì nên
1
2
1
1
1 2 dI f x x
1 2t x
d 2dt x
0
1
3
1
d
2
I f t t
.
3
0
1
d 3
2
f t t
Ta có , đặt thì nên .
1
1
2
2
2 1 dI f x x
2 1t x
d 2dt x
1
2
0
1
d 1
2
I f t t
Vậy .
1 2
4I I I
Câu 39.
Lời giải
Ta có:
2
2 . 1 2 .
1 2
f x
x x f x f x f x f x x x
f x
, mà
2
d d 1 2
3
1 2
f x
x x x f x x x C
f x
3 4
1
2 3
f C
.
2
2 4
1
3 3
2
x x
f x
4
1
1186
d
45
f x x
| 1/70
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 1 Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 001
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tính tích phân sin 3xdx 0 2 2 1 1 A. − . B. . C. − . D. . 3 3 3 3 2 2
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu ( S ) 2 : x + ( y + ) 1
+ ( z − 3) = 5 . Tìm tọa độ tâm
I và bán kính R của ( S ) .
A. I (0; −1;3) và R = 5 .
B. I (0; −1;3) và R = 5 .
C. I (0; −1;3) và R = 5 .
D. I (0;1; −3) và R = 5 . 3 3 2 Câu 3. Cho
f ( x)dx = a,
f ( x)dx = . b   Khi đó f ( x)dx  bằng: 0 2 0
A. a + b .
B. a − b .
C. −a − b .
D. b − a .
Câu 4. Trong không gian với hệ tọa độ Oxy , cho hai điểm M ( 2; − 3; 5) , N (6; − 4; −1) và đặt L = MN .
Mệnh đề nào sau đây là mệnh đề đúng ?
A. L = ( 4; −1; − 6) .
B. L = 53 .
C. L = 3 11 .
D. L = ( −4;1; 6) . 4 1
Câu 5. Cho tích phân I = x 1 + 2 xd . x
Đặt u = 1 + 2 x , khi đó ta được tích phân 2 0 3 1 3 1 A. 2 I = u (u −  ) 1 du B. 2 I = u ( 2 u +  )1du 4 2 1 1 5 3 3 1  u u  3 C. I = −   D. 2 I = u ( 2 u −  )1du 4 5 3   1 1
Câu 6. Trong không gian với hệ tọa độ Oxyz , vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (Oxy) ? A. m = (1;1; ) 1 .
B. j = (0;1;0) . C. k = (0;0; ) 1 .
D. i = (1; 0; 0) . 9
Câu 7. Cho hàm số f ( x ) liên tục trên
và F(x) là nguyên hàm của f(x), biết f
 (x)dx = 9 và F(0) = 3. 0 Tính F(9).
A. F (9) = −6 .
B. F (9) = 6 .
C. F (9) = 12 .
D. F (9) = −12 . 4 2x + 3
Câu 8. Cho hàm số f (x) =
. Khẳng định nào sau đây là đúng? 2 x 3 2x 3 3 A. f (x)dx = + + C  . B. 3
f ( x)dx = 2 x − + C  . 3 x x 3 2 x 3 3 2x 3 C.
f ( x)dx = + + C  . D. f (x)dx = − + C  . 3 2 x 3 x
Câu 9. Mệnh đề nào dưới đây đúng? Trang 1/24 2 x 1 + 2 x 3 x x 3 A. 2 3 dx = + C  . B. 2 3 dx = + C  . 2 x + 1 ln 3 2 x 3 x x 9x C. 2 3 dx = + C  . D. 2 3 dx = + C  . ln 3 ln 9
Câu 10. Công thức nào sau đây sai? A. x d x e x = e + C  .
B. sin xdx = − cos x + C
C. tan xdx = − cot x + C  .
D. cos xdx = sin x + C  . 6 6 sin x cos x a
Câu 11. Giá trị của 4 I
dx được viết dưới dạng
, trong đó a,b là các số nguyên dương 6x 1 b 4 a và
là phân số tối giản. Tính a b . b A. a b 32 . B. a b 25 . C. a b 30 . D. a b 27 .
Câu 12. Cho hai hàm số f ( x ) , g ( x ) là hàm số liên tục, có F ( x ) , G ( x ) lần lượt là nguyên hàm của f ( x )
, g ( x ) . Xét các mệnh đề sau:
( I ) . F ( x) + G ( x) là một nguyên hàm của f (x) + g (x).
( II ) . k.F (x) là một nguyên hàm của k. f (x) với k  .
(III ) . F ( x).G ( x) là một nguyên hàm của f (x).g (x) .
Các mệnh đề đúng là
A. ( I ) và ( III ) .
B. ( I ) và ( II ) .
C. ( II ) và ( III ) .
D. Cả 3 mệnh đề. Câu 13. Tìm cos sin . x x e dx  . A. cos x cos sin . d x x e x = e + C  . B. cos x cos sin . d x x e x = −e + C  . C. cos x sin sin . d = cos . x x e x x e + C  . D. cos x sin sin . d = − cos . x x e x x e + C  . x f (t ) Câu 14. Nếu dt + 6 = 2 x
, với x  0 thì hệ số a bằng 2 t a A. 9 . B. 19 . C. 29 . D. 5 . π
Câu 15. Tính J = x sin x dx  . 0 π π A. . B. −π . C. π . D. . 2 4 1 1
Câu 16. Cho hàm số f ( x ) thỏa mãn  ( x +1) f ( x)dx = 10 và 2 f (1) − f (0) = 2 . Tính I = f
 (x)dx . 0 0
A. I = 8 .
B. I = −12 . C. I = 8 − .
D. I = 1 .
Câu 17. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A (1; − 3; 2) , B (3; 5; − 2) . Phương trình mặt
phẳng trung trực của đoạn thẳng AB có dạng x + ay + bz + c = 0 . Khi đó a + b + c bằng: A. −2 . B. −4 . C. −3 . D. 2 .
Câu 18. Trong không gian Oxyz , cho hai mặt phẳng ( ) : x + 2my + z −1 = 0 , (  ) : 2x + 3 y + 4z + 5 = 0 biết
( ) ⊥ ( ) . Khi đó giá trị m là
A. m = 1.
B. m = −1.
C. m = 2 . D. m = 2 − . Câu 19. Biết ( ) = ( 2 + + ) x F x ax bx
c e là một nguyên hàm của hàm số ( ) = ( 2 + 5 + 5) x f x x x e Giá trị của
2a + 3b + c là A. 6 . B. 13 . C. 8 . D. 10 . Trang 2/24
Câu 20. Họ nguyên hàm của hàm số f ( x ) = 4x (1 + ln x ) là : A. 2 2
2 x ln x + x + C . B. 2 2
2 x ln x + x . C. 2 2
2x ln x + 3x + C . D. 2 2
2 x ln x + 3x . 100 Câu 21. Tích phân 2 .e x x dx  bằng 0 1 1 1 1 A. ( 200 199e +1) . B. ( 200 199e +1) . C. ( 200 199e −1) . D. ( 200 199e −1) . 4 2 4 2
Câu 22. Trong không gian với hệ tọa độ Oxyz, cho hai vectơ u = (m; −2; m + 1) và v = (3; −2m − 4; 6). Tìm
tất cả các giá trị của m để hai vectơ u, v cùng phương.
A. m = 1.
B. m = 0 .
C. m = −1.
D. m = 2 .
Câu 23. Trong không gian Oxyz , cho hai điểm A (3;1; − 2) , B (2; − 3;5) . Điểm M thuộc đoạn AB sao
cho MA = 2MB , tọa độ điểm M là  7 5 8   3 17  A. ; − ;   .
B. (4;5; − 9) . C. ; − 5 ;   . D. (1; −7 ;12) .  3 3 3   2 2  cos 2 x      
Câu 24. Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = và F = 2.  
Tính F   . 2 2 sin x.cos x  4   3     12 − 4 3    12 − 2 3 A. F =   . B. F =   .  3  3  3  3    12 + 2 3    12 + 4 3 C. F =   . D. F =   .  3  3  3  3      
Câu 25. Biết F ( x ) là một nguyên hàm của hàm f ( x ) = sin 2x và F = 1   . Tính F   .  4   6        3    1    5 A. F = 0   . B. F =   . C. F =   . D. F =   .  6   6  4  6  2  6  4
sin 2 x − sin x
Câu 26. Một nguyên hàm của hàm số f ( x) = ( là:
2 + sin x + cos x )2 2 −2 A. F ( x) 2
= ln 2 + sin x + cos x .
B. F ( x) = ( .
2 + sin x + cos x )3 2 −1 1
C. F ( x ) = .
D. F ( x) = . 2
2 + sin x + cos x 2 ( 2
2 + sin x + cos x )
Câu 27. Cho hàm số f ( x ) thỏa mãn f ( x ) = 3 + 2 sin x và f (0) = 3 . Mệnh đề nào dưới đây đúng?
A. f ( x ) = 3x + 2 cos x + 5 .
B. f ( x ) = 3x + 2 cos x + 3 .
C. f ( x ) = 3x − 2 cos x + 3 .
D. f ( x ) = 3x − 2 cos x + 5 . x y z
Câu 28. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng có phương trình + + = 1 cắt 3 trục tọa 2 3 4
độ lần lượt tại A , B , C . Tính thể tích khối tứ diện OABC .
A. V = 24 .
B. V = 8 .
C. V = 4 .
D. V = 12 . 1 2
Câu 29. Cho hàm số f ( x ) liên tục trên và thỏa mãn f
 (x)dx = 9. Tính tích phân  f
  (1−3x) + 9 dx −5 0 A. 21 . B. 15 . C. 75 . D. 27 .
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A ( −2; −1; 3) và B ( 2; −5;1) , điểm M thỏa mãn
MA = 2MB . Khi đó M sẽ thuộc mặt cầu nào sau đây: Trang 3/24 2 2 2  10   19   1  2 2 A. x + + y − + z + = 16       . B. 2
x + ( y + 3) + ( z − 2) = 9 .  3   3   3  2 2 2  10   19   1  2 2 C. x − + y + + z − = 16       . D. 2
x + ( y − 3) + ( z + 2) = 9 .  3   3   3  7 x + 11
Câu 31. Tìm a + b biết
dx = a ln x + 2 + b ln x + 1 + C  ? ( x + 1)( x + 2)
A. a + b = −5 .
B. a + b = 5 .
C. a + b = 11 .
D. a + b = 7 . 3 3 Câu 32. Cho f
 (x)dx = −3 và m là số thực sao cho (m + )1 f (x)dx = −9 . Tìm m . 3 2
A. m = 1.
B. m = 4 C. m = 4 −
D. m = 2. 4 2 Câu 33. Cho f
 (x)dx =16. Tính f (2x)dx 0 0 A. 16 . B. 4 . C. 32 . D. 8 .
Câu 34. Trong không gian với hệ toạ độ Oxyz, cho điểm M ( 2;1; 0) và mặt phẳng ( P ) : x − 2 y − 2z + 3 = 0.
Khoảng cách từ điểm M đến mặt phẳng ( P ) bằng 1 3 A. . B. . C. 3 . D. 1 . 3 3 1 1 1 Câu 35. Cho  f
  (x)− 2g (x)dx = 3; f
 (x)dx = −1. Tính g (x)dx 0 0 0
A. I = −2 .
B. I = 2 .
C. I = 1 .
D. I = −1 . PHẦN II: TỰ LUẬN
Câu 36. Tìm họ nguyên hàm của hàm số f ( x) = sin 3x cos 2 . x
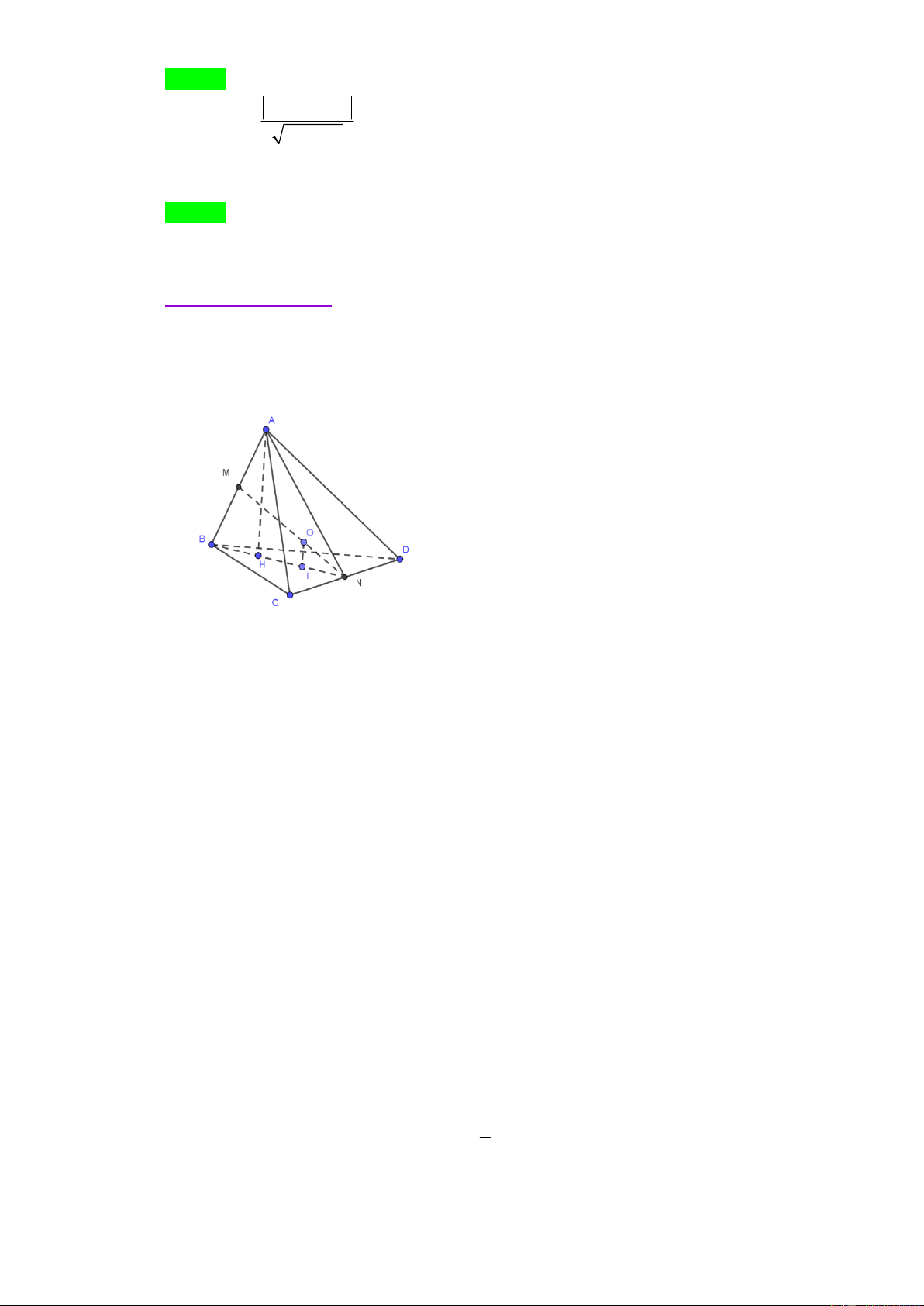
Câu 37. Cho tứ diện ABCD có AB = 4a , CD = 6a , các cạnh còn lại có độ dài bằng a 22 . Tính bán kính
R của mặt cầu ngoại tiếp tứ diện ABCD .  4 1 2 x f ( x )
Câu 38. Cho hàm số f ( x ) liên tục trên và các tích phân f
 (tan x)dx = 4 và dx = 2  . Tính tích 2 x + 1 0 0 1 phân I = f
 (x)dx . 0   
Câu 39. Cho hàm số f ( x ) liên tục, không âm trên đoạn 0; 
 , thỏa mãn f (0) = 3 và  2    
f ( x ) f ( x ) 2 . '
= cos x. 1 + f ( x) , với x  0; 
 . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số  2    
f ( x ) trên đoạn ;   .  6 2 
------------- HẾT ------------- Trang 4/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 2 Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 002
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Cho tam giác ABC biết A (1; −2; 4) , B (0; 2;5) và C (5; 6;3) . Tọa độ trọng tâm G của ABC  là A. G (3;3; 6) . B. G (6;3;3) .
C. G ( 2; 2; 4) .
D. G ( 4; 2; 2) . 1
Câu 2. Tính tích phân = 2 x I e dx  . 0
A. I = 2e + 2 .
B. I = 2e − 2 . C. 2
I = e − 2e .
D. I = 2e .
Câu 3. Họ nguyên hàm của hàm số f ( x ) = 2x + sin 2 x là 1 1 A. 2
x − 2 cos 2 x + C . B. 2
x + 2 cos 2 x + C . C. 2 x −
cos 2 x + C . D. 2 x +
cos 2 x + C . 2 2 2 2 2
Câu 4. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu ( S ) : ( x − ) 1
+ ( y − 2) + ( z + ) 1 = 16 . Tọa độ tâm
I và bán kính R của (S ) là
A. I = ( −1; −2;1) , R = 4 .
B. I = (1; 2; −1) , R = 4 .
C. I = ( −1; −2;1) , R = 16 .
D. I = (1; 2; −1) , R = 16 . 1 1
Câu 5. Tích phân I = dx  có giá trị bằng x + 1 0 A. ln 2 . B. 1 − ln 2 . C. ln 2 − 1 . D. − ln 2 . 1
Câu 6. Cho tích phân 3 1 − xdx  . Với cách đặt 3
t = 1− x thì tích phân đã cho bằng với tích phân nào dưới 0 đây? 1 1 1 1 A. 2 t dt  . B. 3 3 t dt  . C. 3 tdt  . D. 3 t dt  . 0 0 0 0
Câu 7. Một nguyên hàm của hàm số f ( x) = ( x − )2 3 trên là: x − A. F ( x) ( )3 3 = + 2017 .
B. F ( x) = ( x − )3 3 3 . 3 x − C. F ( x) ( )3 3 = + x .
D. F ( x ) = 2 ( x − 3) . 3
Câu 8. Tìm nguyên hàm x ( x +  )15 2 7 dx ? 1 1 A. (x + 7)16 2 + C B. − (x + 7)16 2 + C 2 32 1 1 C. (x + 7)16 2 + C D. (x + 7)16 2 + C 16 32 4 1 Câu 9. Cho f
 (x)dx = 9 , tính I = f
 (3x +1)dx . 1 0
A. I = 27 .
B. I = 9 .
C. I = 3 .
D. I = 1 .
Câu 10. Trong không gian với hệ tọa độ Oxyz, vectơ pháp tuyến của mặt phẳng (Oxz ) là Trang 5/24
A. n (1; 0;1) .
B. n (0;1; 0) .
C. n (1; 0; 0) .
D. n (0; 0;1) . 1 Câu 11. Tính = ex I dx  . 0
A. I = 1 .
B. I = 1− e .
C. I = e . D. I = e −1 .
Câu 12. Họ nguyên hàm của hàm số f ( x ) 2
= 3x + sin x là
A. F ( x ) 3
= x + sin x + C .
B. F ( x ) 3
= x − cos x + C .
C. F ( x ) 3
= 3x − sin x + C .
D. F ( x ) 3
= x + cos x + C .
Câu 13. Trong không gian với hệ trục tọa độ Oxyz , cho 3 điểm A (1; 0; 0) , B (0; 2; 0) , C (0; 0; −3) . Gọi H là
trực tâm của tam giác ABC . Tính độ dài đoạn OH . 1 2 6 3 A. . B. . C. . D. . 3 5 7 4
Câu 14. Cho A ( 2; 0; 0) , B (0; 2; 0) , C (0; 0; 2) . Tập hợp các điểm M trên mặt phẳng Oxy thỏa mãn 2 M .
A MB + MC = 3 là
A. Một mặt cầu.
B. Tập rỗng.
C. Một điểm.
D. Một đường tròn.
Câu 15. Tìm nguyên hàm của hàm số f ( x) = x ln x . 3 3 2 2 A. f  (x) 2 dx =
x (3 ln x −1) + C. B. f  (x) 2 dx =
x (3 ln x − 2) + C. 9 9 3 3 1 2 C. f  (x) 2 dx =
x (3 ln x − 2) + C. D. f  (x) 2 dx =
x (3 ln x − 2) + C. 9 3
Câu 16. Tìm nguyên hàm của hàm số f (x ) = 2x − 1 . 1 A. f
 (x )dx = (2x − 1) 2x − 1 +C . B. f  (x ) 1 dx = −
2x − 1 + C . 3 3 2 C. f  (x ) 1 dx =
2x − 1 + C D. f
 (x )dx = (2x − 1) 2x − 1 +C . 2 3
Câu 17. Trong không gian với hệ tọa độ Oxyz , cho điểm A (1; − 1; 2) . Phương trình mặt phẳng (Q ) đi qua
các hình chiếu của điểm A trên các trục tọa độ là x y z A. (Q ) : + + = 1.
B. (Q ) : x − y + 2z + 6 = 0 . −1 1 −2 z
C. (Q ) : 2x − 2 y + z − 2 = 0 .
D. (Q ) : x − y + = 0 . 2   
Câu 18. Tìm nguyên hàm F ( x ) của hàm số f ( x ) = sin x + cos x thoả mãn F = 2    2 
A. F ( x ) = − cos x + sin x −1.
B. F ( x ) = − cos x + sin x + 1.
C. F ( x ) = cos x − sin x + 3 .
D. F ( x ) = − cos x + sin x + 3 .
Câu 19. Trong không gian Oxyz cho vec-tơ u (1;1; 2) và v ( 2; 0; m ) . Tìm giá trị của tham số m biết (u v ) 4 cos ; = 30 A. m = 11 − .
B. m = 0 .
C. m = 1.
D. m = 1; m = −11.
Câu 20. Cho F ( x) là một nguyên hàm của hàm số ( ) x
f x = e + 2x thỏa mãn F ( ) 3 0 =
. Tìm F ( x) . 2 x 3 x 5
A. F ( x ) 2
= e + x + .
B. F ( x ) 2
= e + x + . 2 2 Trang 6/24 x 1 x 1
C. F ( x ) 2
= e + x + .
D. F ( x ) 2
= 2e + x − . 2 2 2 ln x 3
Câu 21. Gọi F ( x ) là một nguyên hàm của hàm số f ( x) = thỏa mãn F ( 3
e ) = 8 . Giá trị ( 9 F e ) bằng x A. 3 9 + 7 . B. 3 9 −1 . C. 2 . D. 10 . 1000 2 2 x + 4 x + 1
Câu 22. Tích phân I = dx  bằng 2 x + x 1 A.     I = − + ( + )2 1000 996 1000 2 1 ln 2 1 2  = − + +   . B. I ( )2 1000 998 1000 2 1 ln 2 1 2   . C.     I = − + ( + )2 1000 1998 1000 2 1 ln 2 1 2  = + +   . D. I ( )2 1000 996 1000 2 ln 2 1 2   . 2
Câu 23. Cho F ( x ) là một nguyên hàm của hàm số ( ) = x f x e
( 3x − 4x). Hàm số F ( 2x + x) có bao nhiêu điểm cực trị? A. 3 . B. 4 . C. 6 . D. 5 . π 2 u = x
Câu 24. Tính tích phân 2 I =
x cos 2 xdx  bằng cách đặt 
. Mệnh đề nào dưới đây đúng?
dv = cos 2 xdx  0  π  π 1 1 A. 2 I = x sin 2x
+ x sin 2xdx  . B. 2 I = x sin 2x
− 2 x sin 2xdx  . 2 2 0 0 0 0  π  π 1 1 C. 2 I = x sin 2x
+ 2 x sin 2xdx  . D. 2 I = x sin 2 x
− x sin 2xdx  . 2 2 0 0 0 0 2
Câu 25. Cho hàm số y = f ( x) liên tục và có đạo hàm trên R thỏa mãn f ( 2) = −2 ; f (x)dx = 1  . Tính tích 0 4
I =  f '( x ) phân dx . 0
A. I = 0 . B. I = 18 − . C. I = 10 − . D. I = 5 − . a
Câu 26. Cho hàm số f ( x ) 2 =
+ cos x . Tìm tất cả các giá trị của a để f ( x) có một nguyên hàm F ( x) thỏa      mãn F ( ) 1 0 = , F =   . 4  4  4   A. − 2 . B.  − 2 . C.  −1 . D. −1 . 2 2 e ln x
Câu 27. Với cách đổi biến u = 1+ 3ln x thì tích phân dx  trở thành x 1 + 3 ln x 1 2 2 2 2 2 2 2  u − 1  2 2 2 2 A. (u −  )1du . B. 2 (u −  )1du . C. du   . D. (u −  )1du . 9 9 u   3 1 1 1 1 x
Câu 28. Cho G ( x) 2 = 1 + t dt
. Khi đó G( x) bằng 1 x 1 A. . B. . C. ( 2 x + ) 2 1 x + 1 . D. 2 1 + x . 2 1 + x 2 1 + x
Câu 29. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng ( P ) : 3x − 2 y + z − 5 = 0 . Điểm nào dưới đây thuộc ( P ) ?
A. M (1;1; 4) .
B. P (0; 0; −5) .
C. Q (3; −2;1) .
D. N (3; −2; −5) . Trang 7/24  3  2
20 x − 30 x + 7
Câu 30. Biết rằng trên khoảng ; +  
 hàm số f ( x) = có một nguyên hàm  2  2 x − 3 F ( x) = ( 2
ax + bx + c ) 2x − 3 ( a, b, c là các số nguyên). Tổng S = a + b + c bằng A. 3 . B. 5 . C. 6 . D. 4 . 3 2
Câu 31. Cho hàm số f ( x ) liên tục trên 1; +  ) và f
 ( x +1)dx = 8 . Tích phân I = x.f
 (x)dx bằng: 0 1
A. I = 16 .
B. I = 2 .
C. I = 8 .
D. I = 4 .
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho các điểm A ( −1; 3; 4) , B (3; − 5; − 2) . Tìm tọa độ trung
điểm M của đoạn AB .
A. M ( 2 ; − 4 ; 3) .
B. M (1; −1; 1) .
C. M (1; 1; 1) .
D. M ( 4 ; − 8; 6) .
Câu 33. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng 2
(P) : 2 x+ 2 y+ z− m − 3m = 0 và mặt cầu S
(x − )2 + ( y + )2 + (z − )2 ( ) : 1 1 1
= 9 . Tìm tất cả các giá trị của m để (P) tiếp xúc với (S ) . m = 2 m = −2 A.  .
B. m = 2 . C. m = 5 − . D.  . m = −5  m = 5  2 (3x + ) 1 dx  ln b Câu 34. Biết = ln a +  
 với a , b , c là các số nguyên dương và c  4 . Tổng a + b + c bằng 2
3x + x ln xc  1 A. 7 . B. 8 . C. 6 . D. 9 . x − 3
Câu 35. Khi tính nguyên hàm dx
, bằng cách đặt u =
x + 1 ta được nguyên hàm nào? x + 1 A. u  ( 2 2
u − 4 ) d u . B.  ( 2
u − 4 ) d u . C.  ( 2
u − 3) d u . D.  ( 2
2 u − 4 ) d u . PHẦN II: TỰ LUẬN 2
Câu 36. Tìm họ nguyên hàm của hàm số f ( x) = . 2 x − 2  2 sin 2x.cos x Câu 37. Cho biết
dx = a ln 2 + b
với a, b là các số nguyên. Tính 2 3
P = 2a + 3b . 1 + cos x 0
Câu 38. Cho hình chóp S.ABCD có 0
ABC = ADC = 90 , cạnh bên SA vuông góc với ( ABCD ) , góc tạo bởi 2 a 3
SC và đáy ABCD bằng 0
60 , CD = a và tam giác ADC có diện tích bằng
. Tính diện tích mặt cầu 2 S
ngoại tiếp hình chóp S.ABCD . mc 3 3 f  ( x)
Câu 39. Cho hàm số y = f ( x ) có đạo hàm liên tục trên 1; 3 thỏa mãn f
 (x)dx = 8 và dx = 2  . 1 2 f ( x) 1 Tính f (3) .
------------- HẾT ------------- Trang 8/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 3 Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 003
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Tìm nguyên hàm của hàm số ( ) − = ex (1+ e x f x ). A.  ( ) − d = ex f x x
+ x + C .
B.  ( )d = ex + e x f x x + C . C.  ( ) − d = e x f x x + C . D.  ( )d = ex f x x + C . 2 Câu 2. Tính 4 x + 1dx  . 0 13 4 A. . B. . C. 13 . D. 4 . 3 3 1 1 Câu 3. Xét ( − + − + x −  ) 2x 2x 3 1 e dx , nếu đặt 2
u = x − 2 x + 3 thì ( x −  ) 2x 2x 3 1 e dx bằng 0 0 3 1 3 3 3 1 A. u e du  . B. u − e du  . C. u e du  . D. u − e du  . 2 2 2 2 2 2
Câu 4. Trong không gian Oxyz, cho điểm M (1; 2; 3). Hình chiếu của M lên trục Oy là
A. Q(0; 2; 0). .
B. R(1; 0; 0). .
C. S (0; 0; 3). .
D. P(1; 0; 3) . 1 dx
Câu 5. Tính tích phân  bằng x + 1 0 A. 1 . B. ln 2 . C. − ln 2. D. log 2 . 2 2
Câu 6. Biết  f ( x) dx = 2 . Tích phân  3 f ( x) dx bằng 1 1 A. 6 . B. 1 . C. 3 . D. 5 .
Câu 7. Họ nguyên hàm của hàm số f ( x ) 3 2
= 4x + 3x là: A. 4 3
x + x + x + C . B. 4 3
x + x + C . C. 4 3
4 x + 3x + C . D. 4 3
4 x + 3x + x + C .
Câu 8. Trong không gian Oxyz , cho mặt phẳng ( P ) : x + 2z + 23 = 0 . Mặt phẳng ( P ) có một vectơ pháp tuyến là:
A. n = 1; 0; 23 .
B. n = 0; 2; 23 .
C. n = 1; 0; 2 .
D. n = 1; 2;3 . 2 ( ) 1 ( ) 4 ( ) 3 ( )
Câu 9. Trong không gian Oxyz , phương trình mặt cầu tâm I (1; 2; 3) và bán kính R = 3 là 2 2 2 A. ( x − ) 1
+ ( y − 2) + ( z − 3) = 3. B. 2 2 2
x + y + z + 2x + 4 y + 6z + 5 = 0 . 2 2 2 2 2 2 C. ( x − ) 1
+ ( y − 2) + ( z − 3) = 9 . D. ( x + ) 1
+ ( y + 2) + ( z + 3) = 9 .
Câu 10. Cho hàm số f ( x ) xác định trên K và F ( x ) là một nguyên hàm của f ( x ) trên K . Khẳng định nào dưới đây đúng?
A. F ( x ) = f ( x ) , x   K .
B. F  ( x ) = f  ( x ) , x   K .
C. f  ( x ) = F ( x ) , x   K .
D. F  ( x) = f ( x ) , x   K .
Câu 11. Họ nguyên hàm của hàm số 2
f (x) = x − 2x +1 là 1 A. 3 F ( x) =
x − 2 + x + C .
B. F ( x) = 2 x − 2 + C . 3 Trang 9/24 1 1 C. 3 2 F ( x) =
x − x + x + C . D. 3 2 F ( x) =
x − 2 x + x + C . 3 3 3 3 2
Câu 12. Cho tích phân f
 (x)dx = a , f
 (x)dx = b . Tính tích phân f (x  )dx . 0 2 0
A. −a − b .
B. b − a .
C. a + b .
D. a − b .
Câu 13. Trong không gian hệ trục tọa độ Oxyz cho mặt cầu ( S ) đi qua hai điểm A (1;1; 2) , B (3; 0;1) và có
tâm thuộc trục Ox . Phương trình mặt cầu ( S ) là? A. ( x − )2 2 2 1
+ y + z = 5 . B. ( x + )2 2 2 1
+ y + z = 5 . C. ( x − )2 2 2 1
+ y + z = 5 D. ( x + )2 2 2 1
+ y + z = 5 .
Câu 14. Trong không gian Oxyz , cho các điểm A (1; 2; −1) , B ( 2; 3; 4) , C (3;5; − 2) . Tìm tọa độ điểm I là
tâm của đường tròn ngoại tiếp tam giác ABC .  27   7 3   5   37  A. I − ;15; 2   . B. I 2; ; −   . C. I ; 4;1   . D. I ; − 7; 0   .  2   2 2   2   2 
Câu 15. Tìm nguyên hàm F ( x ) của hàm số f ( x) 2 =
thỏa mãn F (5) = 7 . 2x −1
A. F ( x) = 2 2x −1 .
B. F ( x) = 2 2x −1 +1.
C. F ( x) = 2x −1 + 4 .
D. F ( x) = 2x −1 −10 . 3
Câu 16. Biết rằng x ln x dx = m ln 3 + n ln 2 + p
trong đó m, n, p
. Tính m + n + 2 p 2 5 5 9 A. − . B. . C. . D. 0 . 4 4 2
Câu 17. Trong không gian với hệ trục tọa độ Oxyz , viết phương trình mặt phẳng ( P ) song song với mặt phẳng
(Q) : 2x − y + 2z + 5 = 0 đồng thời khoảng cách giữa hai mặt phẳng (P) và (Q) bằng khoảng cách từ A(3; −1; 2)
đến mặt phẳng ( P ) .
A. ( P ) : 2x − y + 2z + 6 = 0 .
B. ( P ) : 2x − y + 2z − 3 = 0 .
C. ( P ) : 2x − y + 2z − 6 = 0 .
D. ( P ) : 2x − y + 2z + 3 = 0 . 10
Câu 18. Tính I =  ( 100 2 x
− x − 2) dx. 0 101 10 1060 101 10 940 101 10 1060 101 10 940 A. I = + . B. I = + . C. I = − . D. I = − . 101 3 101 3 101 3 101 3
Câu 19. Tìm x cos 2xdx  . 1 1 A. x.sin 2 x −
cos 2 x + C .
B. x.sin 2x + cos 2x + C . 2 4 1 1 1 1 C. x sin 2 x + co 2
s x + C . D. x.sin 2 x +
cos 2 x + C . 2 2 2 4
Câu 20. Cho hàm số y = f ( x ) có đạo hàm liên tục trên
. Đồ thị của hàm số y = f ( x) như hình vẽ bên. 4 2
Khi đó giá trị của biểu thức f
 (x − 2)dx + f
 (x + 2)dx bằng 0 0 A. 2 . B. 10 . C. 6 . D. −2 .
Câu 21. Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a (2;1;0),b (−1;0; −2) . Tính cos (a, b) . Trang 10/24 A. (a b) 2 cos , = . B. (a b) 2 cos , = . C. (a b) 2 cos , = − . D. (a b) 2 cos , = − . 5 25 25 5
Câu 22. Biết một nguyên hàm của hàm số y = f ( 2x ) là f  ( x) 2 2
dx = sin x + ln x . Tìm nguyên hàm f ( x) dx  . x A. f  (x) 2 dx = 2 sin
+ 2 ln x + C . B. f  (x) 2
dx = 2 sin x + 2 ln x − ln 2 + C . 2 x C. f  (x) 2
dx = 2 sin 2x + 2 ln x − ln 2 + C . D. f  (x) 2 dx = sin
+ ln x + C . 2 a 1 + ln
Câu 23. Cho F ( x ) =
(ln x + b) là một nguyên hàm của hàm số ( ) = x f x
, trong đó a,b  . Tính x 2 x
S = a + b .
A. S = 1.
B. S = 2 .
C. S = 0 .
D. S = −2 .
Câu 24. Trong không gian với hệ tọa độ Oxyz , gọi a, b, c lần lượt là khoảng cách từ điểm M (1; 3; 2) đến 3 mặt phẳng
tọa độ (Oxy ) , (Oyz ) , (Oxz ) . Tính 2 3
P = a + b + c .
A. P = 12 .
B. P = 32 .
C. P = 18 .
D. P = 30 .
Câu 25. Cho M , N là các số thực, xét hàm số f ( x ) = M .sin  x + N .cos  x thỏa mãn f (1) = 3 và 1 2  1  f ( x ) 1 dx = −  . Giá trị của  bằng f    4  0  2 5 2 5 2  2 A. − . B. . C. − . D. . 2 2 2 2
Câu 26. Với a là một số thực khác 0 , mệnh đề nào sau đây sai? 1 1 1 A. dx = − cot 
(ax + b) + C . B. sin
 (ax + b)dx = cos(ax + b) + C . 2 sin ( ax + b ) a a 1 1 1 C. dx = tan 
(ax + b) + C . D. cos
 (ax + b)dx = sin (ax + b) + C . 2 cos ( ax + b ) a a 1 dx
Câu 27. Một học sinh làm bài tích phân I =  theo các bước sau. 2 1 + x 0   −  
Bước 1: Đặt x = tan t, t  ;   , suy ra 2
dx = (1+ tan t)dt .  2 2  
Bước 2: Đổi cận x = 1  t =
; x = 0  t = 0 . 4   4 2 4 +  Bướ 1 tan t c 3: I = dt = dt =   . 2 1 + tan t 4 0 0
Các bước làm ở trên, bước nào bị sai
A. Không bước nào sai. B. Bước 2. C. Bước 3. D. Bước 1.   
Câu 28. Tìm một nguyên hàm F ( x ) của hàm số f ( x ) = sin 3x thỏa mãn F = 2   .  2  x x
A. F ( x ) cos 3 5 = − + .
B. F ( x ) cos 3 = − + 2 . 3 3 3
C. F ( x ) = − cos 3x + 2 .
D. F ( x ) = cos 3x + 2 . Trang 11/24
Câu 29. Trong không gian với hệ trục tọa độ Oxyz , cho véc tơ a = (1; −2;3) . Tìm tọa độ của véc tơ b biết
rằng véc tơ b ngược hướng với véc tơ a và b = 2 a .
A. b = (2; −4;6) .
B. b = (−2; 4; −6) .
C. b = (−2; −2;3) .
D. b = (2; −2;3) . 1
Câu 30. Biết F ( x) =  (
và F (0) = ln 4 . Giá trị của F ( 4) bằng + x ) dx x 2 A. 2 ln 3 . B. 4 ln 2 . C. 2 ln 5 . D. 6 . 1+ln 2 e 1 Câu 31. Cho f
 (x)dx = 2018. Tính f
(ln 2x)dx . x ln 2 1 1009
A. I = 1009 .
B. I = 4036 C. I = .
D. I = 2018 . 2
Câu 32. Trong không gian Oxyz , cho mặt phẳng ( P ) : 3x − 4z −1 = 0 . Mặt cầu nào sau đây cắt mặt phẳng (P) 2 2 2 2 2 A. 2 x + ( y − ) 1
+ ( z − 3) = 1.
B. ( x − 3) + ( y − ) 1 + ( z + 2) = 1. 2 2
C. x + ( y − )2 2 2 3 + z = 1.
D. ( x − ) + ( y − ) 2 1 3 + z = 1. e
Câu 33. Tính tích phân I = x ln xdx  : 1 1 2 e − 2 2 e + 1 2 e − 1 A. I = . B. I = . C. I = . D. I = . 2 2 4 4
Câu 34. Cho hàm số y = f ( x ) có đạo hàm liên tục trên 2; 3 đồng thời f ( 2) = 2 , f (3) = 5 . Tích phân 3 f
 (x)dx bằng 2 A. 7 . B. 10 . C. 3 . D. −3 . 3x − 1
Câu 35. Cho hàm số f ( x ) xác định trên \ − 
2 thỏa mãn f  ( x ) =
, f (0) = 1, f ( −4) = 2 . Giá trị của x + 2
biểu thức f ( 2) + f ( −3) bằng: A. 12 . B. 10 + ln 2 .
C. 3 − 20 ln 2 . D. ln 2 . PHẦN II: TỰ LUẬN
Câu 36. Tìm học nguyên hàm của 5 f (x) = cos . x
Câu 37. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A , AB = a . Cạnh bên SA vuông góc với
mặt đáy. Góc giữa SB và mặt đáy bằng 45 . Tính thể tích của khối cầu ngoại tiếp hình chóp S.ABC . 1
Câu 38. Cho hàm số f ( x ) liên tục trên thoả mãn f ( x ) 4 tan
= cos x,x  . Tính I = f
 (x)dx . 0
Câu 39. Cho f ( x ) là hàm liên tục và nhận giá trị dương0 ; 
1 . Biết f ( x ). f (1 − x ) = 1 với mọi x  0 ;  1 Tính 1 dx I =  . 1 + f x 0 ( )
------------- HẾT ------------- Trang 12/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 4 Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 004
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN 4 4 3
Câu 1. Cho hàm số f ( x ) liên tục trên và f
 (x)dx =10 , f
 (x)dx = 4 . Tích phân f (x)dx  bằng 0 3 0 A. 7 . B. 3 . C. 6 . D. 4 .
Câu 2. Họ nguyên hàm của hàm số f ( x ) 3 2
= x + x là 4 3 x x 4 3 x x A. + + C B. + + C . C. 4 3
x + x + C . D. 2
3x + 2 x + C . 3 4 4 3 2 − x = −1 2 x = 3 x =  3
Câu 3. Cho f  ( x )  0  x  2 f (2 − x ) 2 2 = 0   . Tính     . 2 2 − x = 2  2 x = 0 x = 0   A. m . B. 2  x  0 . C. f ( 2
2 − x )  0, x . D. f  ( 2 − x ) 2 2
 0  2 − x  2 .
Câu 4. Tìm nguyên hàm của hàm số f ( x ) 1 = . 5x − 2 dx 1 dx A.
= − ln 5x − 2 + C  . B.
= ln 5x − 2 + C  . 5x − 2 2 5x − 2 dx 1 dx C.
= ln 5x − 2 + C  . D.
= 5 ln 5x − 2 + C  . 5x − 2 5 5x − 2
Câu 5. Mệnh đề nào sau đây sai?
A.  f (x) − g(x)dx = f (x)dx − g(x)dx  
với mọi hàm số f ( x), g ( x) liên tục trên . B. f (
x)dx = f (x) + C
với mọi hàm số f ( x) có đạo hàm trên .
C.  f (x) + g(x)dx = f (x)dx + g(x)dx  
với mọi hàm số f ( x), g ( x) liên tục trên .
D. kf (x)dx = k f (x)dx  
với mọi hằng số k và với mọi hàm số f ( x) liên tục trên . 2 2 4 f
  (x) − 2xdx =1  f ( x )dxCâu 6. Cho 1 . Khi đó 1 bằng : A. 1 . B. −3 . C. 3 . D. −1 .
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho điểm M (1; −5; 6) . Gọi H là hình chiếu vuông góc của M
lên mặt phẳng (Oxz ) . Tọa độ điểm H là
A. H (1; 0; 6) .
B. H (0; −5; 0) .
C. H (6; 0;1) .
D. H (1; 0; 0) .
Câu 8. Trong không gian với hệ tọa độ Oxyz , viết phương trình mặt cầu có tâm I (1; − 4 ;3) và đi qua điểm
A (5; − 3; 2) . A. ( 2 2 2
x − )2 + ( y − )2 + ( z − )2 1 4 3 = 18 . B. ( x − ) 1
+ ( y − 4) + ( z − 3) = 16 . C. ( 2 2 2
x − )2 + ( y + )2 + ( z − )2 1 4 3 = 16 . D. ( x − ) 1
+ ( y + 4) + ( z − 3) = 18 . Trang 13/24 1 3 1
Câu 9. Cho hàm số f ( x ) liên tục trên và có f
 (x)dx = 2 , f
 (x)dx = 6 . Tính I = f
 ( 2x −1)dx . 0 0 −1 3 2
A. I = 6 . B. I = .
C. I = 4 . D. I = . 2 3
Câu 10. Trong không gian Oxyz , vectơ n = (1; 2; −1) là một vectơ pháp tuyến của mặt phẳng nào dưới đây ?
A. x − 2 y + z + 1 = 0 .
B. x + 2 y + z + 2 = 0 .
C. x + 2 y − z − 2 = 0 .
D. x + y − 2z + 1 = 0 .
Câu 11. Tìm họ nguyên hàm của hàm số ( ) 5x f x = +1 . 5x
A. 5x ln x + x + C .
B. 5x + x + C . C.
+ x + C .
D. 5x + x + C . ln 5 e e 2 2 ln 2x 2 2 ln 2x Câu 12. Xét dx
, nếu đặt u = ln 2x thì dx  bằng x x 1 1 2 2 1 1 2 1 1 A. 2 u du  . B. 2 2 u du  . C. 2 u du  . D. 2 u du  . 2 0 0 0 0 1
Câu 13. Tính tích phân − = 2x − 2 x I dx  . −1 2 1 A. . B. . C. ln 2 . D. 2 ln 2 . ln 2 ln 2
Câu 14. Tìm nguyên hàm F ( x ) của hàm số ( ) 2 = . x f x x e . 1   x 1 A. F ( x) 2 = e x − + C   . B. ( ) 2 = 2 x F x e
( x − 2) + C . 2  2    1 x 1 C. F ( x) 2 = 2e x − + C   . D. ( ) 2 x F x = e
( x − 2) + C .  2  2
Câu 15. Trong không gian Oxyz , cho các điểm A (3;3; 0) , B (3; 0;3) , C(0;3;3) . Tìm tọa độ I là tâm đường
tròn ngoại tiếp tam giác ABC.
A. I ( 2;3; 2)
B. I ( 2; 2; 0) .
C. I ( 2; 2; 2) .
D. I (0; 2; 2) .
Câu 16. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A (3; −1; 2) , B ( 4; −1; −1) và C ( 2; 0; 2) . Mặt
phẳng đi qua ba điểm A , B , C có phương trình là
A. 2x + 3 y − z + 8 = 0 .
B. 3x − 3 y + z −14 = 0 .
C. 3x + 3 y + z − 8 = 0 .
D. 3x − 2 y + z − 8 = 0 .
Câu 17. Tìm nguyên hàm F ( x ) của hàm số ( ) 2 e x f x =
, biết F (0) = 1 . 2 e x 1
A. F ( x) = + . B. ( ) 2 2e x F x = −1. C. ( ) ex F x = . D. ( ) 2 e x F x = . 2 2 1
Câu 18. Cho tích phân ( − 2) x x
e dx = a + be  , với ; a b
. Tổng a + b bằng 0 A. −1. B. 1. C. −3 . D. 5 . 2
Câu 19. Biết 2x ln 
(1+ x)dx = a.ln b , với * a, b
, b là số nguyên tố. Tính 3a + 4b . 0 A. 42 . B. 21 . C. 12 . D. 32 .
Câu 20. Trong không gian Oxyz , cho điểm I ( 2;1;1) và mặt phẳng ( P ) : 2x − y + 2z + 1 = 0 . Phương trình mặt
cầu ( S ) có tâm I và tiếp xúc với ( P ) là Trang 14/24 2 2 2 2 2 2
A. ( x + 2) + ( y + ) 1 + ( z + ) 1 = 2 .
B. ( x − 2) + ( y − ) 1 + ( z − ) 1 = 2 . 2 2 2 2 2 2
C. ( x + 2) + ( y + ) 1 + ( z + ) 1 = 4 .
D. ( x − 2) + ( y − ) 1 + ( z − ) 1 = 4 . 3
Câu 21. Cho F ( x) là một nguyên hàm của hàm số ( ) = ex f x
+ 2x thỏa mãn F (0) = . Tìm F (x) . 2 x 1 x 1 A. 2
F ( x) = e + x + . B. 2
F ( x) = 2e + x − . 2 2 x 5 x 3 C. 2
F ( x) = e + x + . D. 2
F ( x) = e + x + . 2 2 1
Câu 22. Tính tích phân A = dx
bằng cách đặt t = ln x . Mệnh đề nào dưới đây đúng? x ln x 1 1 A. A = dt  . B. A = dt  .
C. A = tdt  . D. A = dt  . 2 t t
Câu 23. Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng ( P ) c ó phương trình 2x − 2z − 5 − 0 . Tìm tọa
độ điểm A nằm trên tia Oz sao cho khoảng cách từ A đến mặt phẳng ( P) bằng 2 2 .  13   13  A. A 0; 0; −   . B. A 0; 0;   .  2   2   3   3   13  C. A 0; 0;   . D. A 0; 0;   hoặc A 0;0; −   .  2   2   2 
Câu 24. Trong không gian Oxyz , hình chiếu vuông góc của điểm A (1; 2;3) trên mặt phẳng
(P) : x + y + z − 3 = 0 là điểm
A. M (0;1; 2) .
B. M ( 2;1; 0) .
C. M ( −1; 2; 2) .
D. M (1;1;1) . x
Câu 25. Họ nguyên hàm của hàm số y = f ( x ) = là 2 x + 2 1
A. F ( x ) 2
= x + 2 + C .
B. F ( x ) 2 =
x + 2 + C . 2
C. F ( x ) 2
= 2 x + 2 + C .
D. F ( x ) 2
= ln x + 2 + C . 4 2 Câu 26. Cho
f ( x)dx = 16  . Tính I = f (2 x)dx 0 0
A. I =32 .
B. I =8 . C. I 16 = . D. I =4 3
Câu 27. Cho hàm số f ( x ) có f ( x ) liên tục trên đoạn−1;3, f (−1) = 3 và
f ( x)dx = 10, 
giá trị của f (3) bằng −1 A. −7 . B. 13 . C. 7 . D. −13 . 2 4 1 Câu 28. Biết f
 (x)dx =1. Tính I = f  ( x)dx. x 1 1 1
A. I = 4 .
B. I = 2 .
C. I = 1 D. I = . 2 Câu 29. Biết 2 x 2 x 2 d x xe x = axe
+ be + C (a,b   ) . Tính ab . 1 1 1 1 A. ab = . B. ab = − . C. ab = .
D. ab = − . 4 4 8 8 −  x 2018e x
Câu 30. Tính nguyên hàm của hàm số f ( x) = e 2017 −   . 5  x  Trang 15/24 2018 2018
A.  ( )d = 2017ex f x x − + C .
B.  ( )d = 2017ex f x x + + C . 4 x 4 x 504, 5 504, 5
C.  ( )d = 2017ex f x x + + C .
D.  ( )d = 2017ex f x x − + C . 4 x 4 x
Câu 31. Trong không gian Oxyz , cho hai điểm A (1; 0; −4) và điểm B (1; −2; 0) . Phương trình mặt cầu ( S )
có đường kính AB là 2 2 2 2 2 2 A. ( x + ) 1 + ( y − ) 1
+ ( z − 2) = 5 . B. ( x − ) 1 + ( y + ) 1
+ ( z + 2) = 5 . 2 2 2 2 2 2 C. ( x + ) 1 + ( y − ) 1
+ ( z − 2) = 20 . D. ( x − ) 1 + ( y + ) 1 + ( z + 2) = 20 .
Câu 32. Trong không gian Oxyz , cho ba điểm A ( −1; −2; 3) , B (0;3;1) , C ( 4; 2; 2) . Côsin của góc BAC bằng 9 9 9 9 A. . B. . C. − . D. − . 35 2 35 2 35 35 2 2 2
Câu 33. Cho 3 f
  (x)+ 2g (x)dx =1  , 2 f
  (x)− g (x)dx = −3  . Khi đó, f ( x) dx  bằng 1 1 1 16 11 5 6 A. . B. . C. − . D. . 7 7 7 7
Câu 34. Cho F ( x ) là một nguyên hàm của hàm số f ( x ) 1 =
thỏa F ( 2) = 1 . Tính F (3) . x − 1
A. F (3) = ln 2 + 1.
B. F (3) = ln 2 .
C. F (3) = 1 − ln 2 .
D. F (3) = ln 2 −1 . 5 x − 2
Câu 35. Cho tích phân
dx = a + b ln 2 + c ln 3 
với a, b, c là các số nguyên. Tính P = abc. x + 1 1
A. P = 18
B. P = 0
C. P = −18 D. P = −36 PHẦN II: TỰ LUẬN x e
Câu 36. Tìm học nguyên hàm của f (x) = . x e −1
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho ba điểm A (1; − 3; 2) , B ( −2; −1; 5) và C (3; 2; −1) . Gọi
(P) là mặt phẳng qua A , trực tâm của tam giác ABC và vuông góc với mặt phẳng ( ABC ) . Tìm phương
trình mặt phẳng ( P ) . (x + 2)2017 2
Câu 38. Tính tích phân I = dx  . 2019 x 1 2 2
Câu 39. Cho hàm số f ( x ) tăng, có đạo hàm liên tục trên 0; + ) thỏa f  ( x ) f ( x ) =  f ( x ) +  f ( x )     và
f (0) = f  (0) = 1 . Tính f (1) .
------------- HẾT ------------- Trang 16/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 5 Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 005
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Họ nguyên hàm của hàm số f ( x ) 1 = là : 3x − 1 1 1
A. − ln 3x − 1 + C
B. ln 3x − 1 + C
C. 3 ln 3x − 1 + C
D. ln 3x − 1 + C 3 3
Câu 2. Trong không gian với hệ tọa độ Oxyz , phương trình nào sau đây là phương trình mặt cầu?
A. ( x − y)2 2
+ z = 4x − 2xy + 2z + 2018 . B. 2 2 2
x + y + z − 2x + 2 y − 4z + 8 = 0 . 2 2 C. ( x + ) 2 1 + y + (2z − ) 1 = 0 . D. 2 2 2
x + 2 y + z − 4x + y −1 = 0 .
Câu 3. Giả sử các biểu thức trong dấu nguyên hàm, tích phân đều có nghĩa, trong các khẳng định sau, khẳng định nào sai? b b b b b A. u
 (x).v(x)dx u
= ( x).v ( x) − u
 (x)v(x)dx . B. kf (x)dx = kf (x)dx,k  . a a a a a
C. f ( x ) dx = f ( x ) + C .
D. kf ( x ) dx = k f ( x ) dx, k  . 1 1 Câu 4. Xét ( − + − + x −  ) 2x 2x 3 1 e dx , nếu đặt 2
u = x − 2 x + 3 thì ( x −  ) 2x 2x 3 1 e dx bằng 0 0 3 3 3 1 3 1 A. u − e du  . B. u e du  . C. u − e du  . D. u e du  . 2 2 2 2 2 2
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho hai véctơ a = (2; − 3;1) và b = (−1; 0; 4) . Tìm tọa độ véctơ u = 2
− a + 3b .
A. u = (−7; 6;10) .
B. u = (7; 6;10) .
C. u = (−7; − 6;10) .
D. u = (−7; 6; −10) .
Câu 6. Tìm họ nguyên hàm của hàm số f ( x ) = cos ( 2x + 3) A. f
 (x).dx = sin(2x + 3) + C . B. f
 (x).dx = −sin(2x +3)+C . 1 1 C. f
 (x).dx = − sin (2x + 3) + C . D. f
 (x).dx = sin (2x + 3) + C . 2 2 e  1 1 
Câu 7. Tính tích phân I = − dx   2  x x  1 1 1
A. I = e B. I = C. I = + 1 D. I = 1 e e
Câu 8. Trong không gian Oxyz , vectơ n = (1; 2; −1) là một vectơ pháp tuyến của mặt phẳng nào dưới đây?
A. x + 2 y − z − 2 = 0 .
B. x + y − 2z + 1 = 0 .
C. x − 2 y + z + 1 = 0 .
D. x + 2 y + z + 2 = 0 . 2018 2 dx
Câu 9. Tính tích phân I =  . x 1
A. I = 2018 ln 2 −1. B. 2018 I = 2 .
C. I = 2018.ln 2 .
D. I = 2018 .
Câu 10. Cho hai hàm số f ( x ) , g ( x ) liên tục trên . Trong các mệnh đề sau, mệnh đề nào sai? Trang 17/24 A. f
  (x) − g (x)dx = f
 (x)dx − g
 (x)dx . B. kf
 (x)dx = k f
 (x)dx (k  0;k  ). C. f
  (x) + g (x)dx = f
 (x)dx + g
 (x)dx . D. f
  (x).g (x)dx = f   (x)d .x g
 (x)dx .
Câu 11. Tìm nguyên hàm của hàm số ( ) 3x f x = . x 1 + x 3 A. 3 dx= + C  .
B. 3xd =3x x + C  . x + 1 x 3x C. 3 dx= + C  .
D. 3xd =3x x ln 3 + C  . ln 3 6 6 sin x cos x a
Câu 12. Giá trị của 4 I
dx được viết dưới dạng
, trong đó a,b là các số nguyên dương 6x 1 b 4 a và
là phân số tối giản. Tính a b . b A. a b 32 . B. a b 27 . C. a b 25 . D. a b 30 .
Câu 13. Trong hệ trục tọa độ Oxyz cho 3 điểm A ( 4; 2;1) , B (0; 0; 3) , C ( 2; 0;1) . Viết phương trình mặt phẳng
chứa OC và cách đều 2 điểm , A B .
A. x + 2 y + 2z = 0 hoặc x − 4 y − 2z = 0 .
B. x + 2 y − 2z = 0 hoặc x + 4 y − 2z = 0 .
C. x + 2 y − 2z = 0 hoặc x − 4 y − 2z = 0 .
D. x − 2 y − 2z = 0 hoặc x + 4 y − 2z = 0 . 3 dx Câu 14. Cho x 1 2 e a.e be
c , với a, b, c là các số nguyên. Tính S a b c . 0 x 1 A. S 0 . B. S 2 . C. S 4 . D. S 1 .
Câu 15. Trong không gian Oxyz , mặt cầu ( S ) có tâm I (1; 2; 3) và tiếp xúc với mặt phẳng
(P) :3x − 4y −10 = 0 . Khi đó (S ) là 2 2 2 2 2 2 A. ( x − ) 1
+ ( y − 2) + ( z − 3) = 25. B. ( x − ) 1
+ ( y − 2) + ( z − 3) = 9 . 2 2 2 2 2 2 C. ( x + ) 1
+ ( y + 2) + ( z + 3) = 16 . D. ( x + ) 1
+ ( y + 2) + ( z + 3) = 4 .
Câu 16. Tìm nguyên hàm của hàm số ( ) 3x f x = . x 1 + x 3
A. 3x d = 3x x ln 3 + C  . B. 3 dx = + C  . x + 1 x 3x C. 3 dx = + C  . D. x x 1 + 3 dx = 3 + C  . ln 3
Câu 17. Cho hàm số f ( x ) xác định trên
thỏa mãn f  ( x ) = 4x + 3 và f (1) = −1. Biết rằng phương trình
f ( x ) = 10 có hai nghiệm thực x , x . Tính tổng log x + log x . 1 2 2 1 2 2 A. 3 . B. 4 . C. 8 . D. 16 . 5 2
Câu 18. Giả sử hàm số y
f ( x) liên tục trên và f x dx a, (a ). Tích phân I f 2x 1 dx 3 1 có giá trị là 1 1 A. a 1. B. 2 . a C. a.
D. 2a +1. 2 2 8 4 4
Câu 19. Biết f
 (x)dx = −2 ; f
 (x)dx = 3; g
 (x)dx = 7 . Mệnh đề nào sau đây sai? 1 1 1 8 8 A. f
 (x)dx =1. B. f
 (x)dx = −5. 4 4 4 4 C. 4 f
  (x) − 2g (x)dx = −2  . D. f
  (x)+ g (x)dx =10  . 1 1 Trang 18/24
Câu 20. Họ nguyên hàm của hàm số y = 3x ( x + cos x ) là A. 3
x + 3 ( x sin x + cos x ) + C B. 3
x − 3 ( x sin x + cos x ) + C C. 3
x + 3 ( x sin x − cos x ) + C D. 3
x − 3 ( x sin x − cos x ) + C  4 3 1 − sin x Câu 21. Biết
dx = a 3 + b 2 + c
với a, b, c
. Tính a + b + c . 2 sin x  6 A. −1 . B. 0 . C. 1 . D. 2 .
Câu 22. Trong không gian với hệ trục tọa độ Oxyz , cho M (3; 4;5) và mặt phẳng ( P ) : x − y + 2z − 3 = 0 .
Hình chiếu vuông góc của M lên mặt phẳng ( P ) là:
A. H (6; 7;8) .
B. H ( 2; −3; −1) .
C. H (1; 2; 2) .
D. H ( 2; 5; 3) .
Câu 23. Tích phân  (3x + 2) 2
cos x dx bằng: 0 3 1 1 3 A. 2  +  . B. 2  +  . C. 2  −  . D. 2  −  . 4 4 4 4
Câu 24. Trong không gian Oxyz , cho mặt phẳng ( ) : x + y + z −1 = 0 . Trong các mặt phẳng sau tìm mặt
phẳng vuông góc với mặt phẳng ( ) ?
A. 2x − y + z + 1 = 0 .
B. 2x − y − z + 1 = 0 .
C. 2 x + 2 y + 2z − 1 = 0 .
D. x − y − z + 1 = 0 . b 2 Câu 25. Nếu xdx = 
( a  0, b  0) thì: 3 a
A. b + a = 1. B. 2 2
b − a = 1 .
C. b b − a a = 1 .
D. b − a = 1. x
Câu 26. Cho F ( x ) là một nguyên hàm của hàm số y =
thỏa F ( 21) = 7 . Tìm F ( x ) 2 x + 4
A. F ( x ) 2 = x + 4 − 2 .
B. F ( x ) 2 = x + 4 + 2 .
C. F ( x ) 2 = x + 4 +1.
D. F ( x ) 2 = x + 4 −1.
Câu 27. Trong không gian với hệ tọa độ Oxyz cho ba điểm A (1; 2; 0) ; B ( 2;1;1); C (0;3; −1) . Xét 4 khẳng định
sau: (I ) BC = 2AB . (II ) B thuộc đoạn AC. (III ) ABC là một tam giác. (IV) (IV ) A, B,C thẳng hàng.
Trong 4 khẳng định trên có bao nhiêu khẳng định đúng. A. 1 . B. 2. C. 3. D. 4. 1
Câu 28. Với cách đổi biến u = 4x + 5 thì tích phân x 4x + 5dx  trở thành −1 u ( 2 3 u − 5) 2 u ( 2 1 u − 5) 2 u ( 2 3 u − 5) 2 u ( 2 3 u − 5) A. du  . B. du  . C. du  . D. du  . 8 8 4 8 1 −1 1 1
Câu 29. Cho F ( x ) là một nguyên hàm của hàm số f ( x ) 1 =
; biết F (1) = 2 . Tính F ( 2) . 2 x − 1
A. F ( 2) = ln 3 + 2 .
B. F ( 2) = 2 ln 3 − 2 . C. F ( ) 1 2 = ln 3 + 2 . D. F ( ) 1 2 = ln 3 − 2 . 2 2  e −1  3
Câu 30. Nguyên hàm F ( x ) của hàm số f ( x ) 1 = , biết F =   là: 2 x + 1  2  2
A. F ( x ) 1 = ln 2x +1 + .
B. F ( x ) 1
= 2 ln 2x +1 − . 2 2 Trang 19/24
C. F ( x ) = 2 ln 2x + 1 + 1 .
D. F ( x ) 1 = ln 2x +1 +1. 2 2 Câu 31. Tính = ex I x dx  . 1
A. I = e . B. 2 I = e . C. 2 I = − e . D. 2
I = 3 e − 2 e .
Câu 32. Tìm nguyên hàm I = x cos xdx  . x x A. 2 I = x cos + C . B. 2 I = x s in + C . 2 2
C. I = x sin x + cosx + C .
D. I = x sin x − cosx + C .  2 
Câu 33. Trong không gian Oxyz , cho a = (0 ; − 2 ; − 3) , b = 0 ; ;1 , c =  
(3;− 3;2) . Khẳng định nào dưới đây  3  là sai?
A. b và c vuông góc.
B. a và b vuông góc.
C. a và b cùng phương.
D. a và c vuông góc. x − 3
Câu 34. Khi tính nguyên hàm dx
, bằng cách đặt u =
x + 1 ta được nguyên hàm nào? x + 1 A.  ( 2
u − 3)du . B. u  ( 2 2
u − 4 )du . C.  ( 2
u − 4 )du . D.  ( 2
2 u − 4 )du .
Câu 35. Trong không gian với hệ toạ độ Oxyz , cho ( P ) là mặt phẳng đi qua hai điểm A (0;1; 2) , B ( −1;3; 4)
và vuông góc với mặt phẳng (Q ) : 2x + y − z + 4 = 0. Khoảng cách từ gốc tọa độ đến mặt phẳng ( P ) bằng 3 4 2 8 7 2 A. . B. . C. . D. . 2 3 3 3 10 PHẦN II: TỰ LUẬN
Câu 36. Tìm họ nguyên hàm của hàm số f (x) = log . x 2
Câu 37. Trong không gian với hệ trục tọa độ Oxyz cho hai đường thẳng d , d lần lượt có phương trình 1 2 x − 2 y − 2 z − 2 x − 1 y − 2 z − 1 d : = = , d : = =
, biết rằng mặt phẳng ( ) : ax + by + cz + 1 = 0 1 2 2 1 3 2 −1 4 ( 2 2 2
a, b, c R, a + b + c  0) song song và cách đều hai đường thẳng d , d . Tính S = a + b + c . 1 2
Câu 38. Cho hàm số f ( x ) xác định và liên tục trên
và thoả mãn đồng thời các điều kiện sau:
f ( x)  0,x      ( ) f ( x ).x f x = , x  2  x + 1  f  (0) = e
Tính giá trị của f ( 3 ) . 1
Câu 39. Cho hàm số y = f ( x ) có đạo hàm, liên tục trên và f (3) = 10 , f
 (2x + )1dx = 4 . Tính 0 3 (x −  )
1 f  ( x) dx . 1
------------- HẾT ------------- Trang 20/24
TOÁN 185 NGUYỄN LỘ TRẠCH
ÔN TẬP KIỂM TRA GIỮA KỲ 2 – LỚP 12
Đề ôn tập: SỐ 6 Mã đề thi
Họ và tên :………………………………….Lớp:………….......……..……… 006
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN
Câu 1. Trong không gian Oxyz , cho mặt cầu ( S ) 2 2 2
: x + y + z − 4 x + 2 y − 4 z − 7 = 0 . Tính bán kính R của
mặt cầu ( S ) .
A. R = 3 .
B. R = 4 .
C. R = 16 . D. R = 7 .
Câu 2. Khẳng định nào dưới đây là sai?
A. Mọi hàm số liên tục trên đoạn a; b đều có đạo hàm trên đoạn a; b .
B. Mọi hàm số có đạo hàm trên đoạn a; b đều có nguyên hàm trên đoạn a; b .
C. Mọi hàm số liên tục trên đoạn a; b đều có nguyên hàm trên đoạn a; b .
D. Mọi hàm số liên tục trên đoạn a; b thì đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn a; b .
Câu 3. Khẳng định nào đúng? A. 2 x 2 e d = e x x + C  . B. sin d
x x = cos x + C  . x a C. x a dx = + C  . D. 2 x 2 d x a x = a ln a + C  . ln a
Câu 4. Trong không gian Oxyz , cho a = (3; 2; ) 1 , b = (−2; 0; )
1 . Độ dài a + b là: A. 2 . B. 3 . C. 2 . D. 1 .
Câu 5. Khẳng định nào dưới đây đúng? 2 2 1 2 2 2 2 1 1 1 1 1 1 1 A. dx =  x e . B. dx =  . C. dx =  . D. dx =  x e . x x x 1 e x x e e e e x 2 e 1 1 2 1 1 1 8 dx Câu 6. Tích phân  bằng + 4 x 1 1 1 A. 4 . B. − .
C. ln 9 − ln 5 .
D. ln 5 − ln 9 . 81 25
Câu 7. Trong không gian với hệ trục tọa độ Oxyz , cho mặt phẳng P : 3x 2y z 1 0 . Mặt phẳng P
có một vectơ pháp tuyến là A. n 2; 3;1 . B. n 3; 2;1 . C. n 3; 2; 1 . D. n 3; 2; 1 . 2 − x = −1 2 x = 3 x =  3
Câu 8. Cho f  ( x )  0  x  2 f (2 − x ) 2 2 = 0   . Tính     . 2 2 − x = 2  2 x = 0 x = 0   A. m . B. f ( 2 − x ) 2 2
 0  2 − x  2 . C. 2
x  0 . D. f  ( 2
2 − x )  0, x .
Câu 9. Tìm họ nguyên hàm của hàm số ( ) 2018x f x = . 2018x x 1 + 2018 A. + C . B. + C . log 2018 x + 1 2018x C. + C .
D. 2018x.ln 2018 + C . ln 2018 Trang 21/24
Câu 10. Tìm nguyên hàm F ( x ) của hàm số f ( x ) = 6x + sin 3x , biết F ( ) 2 0 = . 3 cos 3x cos 3x
A. F ( x ) 2 = 3x − +1.
B. F ( x ) 2 = 3x − −1 . 3 3 cos 3x cos 3x 2
C. F ( x ) 2 = 3x + +1.
D. F ( x ) 2 = 3x − + . 3 3 3 4 1
Câu 11. Cho tích phân I = x 1 + 2 xd . x
Đặt u = 1 + 2x , khi đó ta được tích phân 2 0 3 3 1 A. 2 I = u ( 2 u −  )1du B. 2 I = u (u −  ) 1 du 4 1 1 3 5 3 3 1 1  u u C. 2 I = u ( 2 u +  )1du D. I = −   2 4 5 3   1 1 b
Câu 12. Cho hàm số f ( x) có đạo hàm f '( x) a; b f b = f x dx = liên tục trên  , ( ) 5 và '( ) 3 5  . Tính giá trị a
f ( a ) .
A. f (a) = 5 ( 5 − 3) .
B. f (a) = 3 5 .
C. f (a) = 5 (3 − 5 ) .
D. f (a) = 3 ( 5 − 3) .
Câu 13. Cho F ( x ) là một nguyên hàm của hàm số ( ) = (5 + 1) x f x x
e và F (0) = 3 . Tính F (1) .
A. F (1) = 11e − 3 .
B. F (1) = e + 2 .
C. F (1) = e + 7 .
D. F (1) = e + 3 . 1 1 (x + a)2 2
Câu 14. Cho biết F ( x ) 3
= x + 2x − là một nguyên hàm của f ( x) = . Tìm nguyên hàm của 3 x 2 x
g ( x ) = x cos ax . 1 1
A. x sin x + cos x + C . B. x sin 2 x +
cos 2 x + C . 2 4 1 1
C. x sin x − cos x + C . D. x sin 2 x −
cos 2 x + C . 2 4 7 xdx
Câu 15. Tích phân 
bằng a ln 2 − b ln 5 . Giá trị của 2a + b bằng 2 x + 1 2 3 1 A. 1 . B. . C. 2 . D. . 2 2 5
Câu 16. Tính tích phân I =  ( x + )
1 ln ( x − 3) dx ? 4 19 19 19 A. 10 ln 2 . B. 10 ln 2 + . C. −10 ln 2 . D. 10 ln 2 − . 4 4 4
Câu 17. Hàm số F ( x) nào dưới đây là nguyên hàm của hàm số 3 y = x + 1 ? 3 3
A. F ( x ) = ( x + 1) 3 x + 1 + C .
B. F ( x ) = ( x +1)3 4 + C . 4 4 3 4
C. F ( x ) = ( x + 1)43 + C .
D. F ( x ) = ( x +1)4 3 + C . 8 3
Câu 18. F ( x ) là một nguyên hàm của hàm số y = 2 sin x cos 3x và F (0) = 0 , khi đó Trang 22/24 x x
A. F ( x ) cos 4 cos 2 1 = − + .
B. F ( x ) = cos 4x − cos 2x . 4 2 4 x x x x
C. F ( x ) cos 2 cos 4 1 = − − .
D. F ( x ) cos 2 cos 4 1 = − − . 4 8 8 2 4 4 3 dx
Câu 19. Cho hàm số Biết
= a ln 2 + b ln 5 + c ln 7 
(a,b,c  ) . Giá trị của biểu thức x + 2 x + 4 0 ( )( )
2a + 3b − c bằng A. 3 . B. 4 . C. 2 . D. 5 . 3 6  x Câu 20. Cho
f ( x)dx = 12  . Tính tích phân f dx    .  2  1 2 A. 14 . B. 24 . C. 10 . D. 6 . 1
Câu 21. Tính tích phân I = x.ln  ( x +1)dx . 0 3 1
A. I = 1 . B. I = − . C. I = . D. I = 2 . 4 4
Câu 22. Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = sinx và đồ thị hàm số y = F ( x ) đi qua điểm   
M (0;1) . Tính F    2              A. F = 0   . B. F = 1   . C. F = 2   . D. F = −1   .  2   2   2   2 
Câu 23. Trong không gian Oxyz cho ba điểm A (1; 2; − 4) , B (1; − 3;1) , C ( 2; 2;3) . Mặt cầu ( S ) đi qua A , B
, C và có tâm thuộc mặt phẳng (Oxy ) . Khi đó bán kính của mặt cầu ( S ) là A. 5 . B. 26 . C. 3 2 . D. 2 .
Câu 24. Biết F ( x ) là một nguyên hàm của hàm số ( ) = ( − ) 2 1 x f x x e và F ( ) 3 0 = − . Tính F (1) . 4 1 1 3 1 3 1 A. F (1) 2 = e . B. F (1) 2 = − e . C. F (1) 2 = − e . D. F (1) 2 = + e . 4 4 4 4 4 4 2 (3x + ) 1 dx  ln b Câu 25. Biết = ln a +  
 với a , b , c là các số nguyên dương và c  4 . Tổng a + b + c bằng 2
3x + x ln xc  1 A. 6 . B. 9 . C. 7 . D. 8 . 2 2
Câu 26. Cho hàm số f ( x ) liên tục trên
và  ( f ( x) 2
+ 3x )dx = 10 . Tính f ( x)dx  . 0 0 A. −18 . B. −2 . C. 18 . D. 2 .
Câu 27. Trong không gian với hệ tọa độ Oxyz , cho véc tơ u = (1;1; −2), v = (1;0; m) . Tìm tất cả giá trị của m để góc giữa 
u , v bằng 45 .
A. m = 2 − 6 .
B. m = 2 + 6 .
C. m = 2 .
D. m = 2  6 . 3 dx Câu 28. Biết
= a 3 + b 2 + c
với a , b , c là các số hữu tỉ. Tính P = a + b + c . x + 1 − x 1 2 13 16 A. . B. 5. C. . D. . 3 2 3
Câu 29. Trong không gian Oxyz , cho hai điểm A = ( 4; 0;1) và B = ( −2; 2; 3) . Phương trình nào dưới đây là
phương trình mặt phẳng trung trực của đoạn thẳng AB ?
A. 6x − 2 y − 2z −1 = 0 .
B. 3x + y + z − 6 = 0 . Trang 23/24
C. 3x − y − z + 1 = 0 .
D. 3x − y − z = 0 .
Câu 30. Trong không gian Oxyz , cho tam giác ABC với: AB = (1; − 2; 2) ; AC = (3; − 4; 6) . Độ dài đường
trung tuyến AM của tam giác ABC là: 29 A. 29 . B. 29 . C. . D. 2 29 . 2  x
Câu 31. Tìm nguyên hàm F ( x ) của hàm số f ( x) 2 = 2 x 3x −    . 4x   x x x
A. F ( x ) 12 2 = − + C . B. ( ) =12x F x
+ x x + C . ln12 3 2 2 x  3x x x  2 2 x  3x x x ln 4 
C. F ( x) =  −    .
D. F ( x) =  −    . ln 2 ln 3 4x   ln 2 ln 3 4x  
Câu 32. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A ( 2; 2; −2) và B (3; −1; 0). Đường thẳng AB IA
cắt mặt phẳng ( P ) : x + y − z + 2 = 0 tại điểm I . Tỉ số bằng: IB A. 3 . B. 4 . C. 6 . D. 2 .
Câu 33. Trong không gian Oxyz , cho mặt phẳng ( P ) : x − 2 y + 2z − 2 = 0 và điểm I ( −1; 2; −1) . Viết phương
trình mặt cầu ( S ) có tâm I và cắt mặt phẳng ( P ) theo giao tuyến là đường tròn có bán kính bằng 5. 2 2 2 2 2 2
A. ( S ) : ( x + ) 1
+ ( y − 2) + ( z + ) 1 = 34 .
B. ( S ) : ( x + ) 1
+ ( y − 2) + ( z + ) 1 = 16 . 2 2 2 2 2 2
C. ( S ) : ( x − ) 1
+ ( y + 2) + ( z − ) 1 = 34 .
D. ( S ) : ( x + ) 1
+ ( y − 2) + ( z + ) 1 = 25 . 1
Câu 34. Hàm số F ( x ) 4
= ln x + C là nguyên hàm của hàm số nào trong các hàm số dưới đây? 4 3 3 x x ln x ln x 1
A. f ( x ) = .
B. f ( x ) = .
C. f ( x) = .
D. f ( x ) = . 3 ln x 3 x 3 x ln x
Câu 35. Trong không gian với hệ trục tọa độ Oxyz , cho A (1; 2;3) , B (3; 4; 4) . Tìm tất cả các giá trị của tham
số m sao cho khoảng cách từ điểm A đến mặt phẳng ( P ) : 2x + y + mz −1 = 0 bằng độ dài đoạn AB . A. m = 2 
B. m = 2 C. m = 2 − D. m = 3 − PHẦN II: TỰ LUẬN
Câu 36. Tìm họ nguyên hàm của hàm số 2
f (x) = x 2x −1.
Câu 37. Trong không gian Oxyz , mặt phẳng ( ) đi qua điểm M ( 4; −3;12) và chắn trên tia Oz một đoạn dài
gấp đôi các đoạn chắn trên các tia Ox , Oy . Tìm phương trình mặt phẳng ( ) . 1 3 1
Câu 38. Cho hàm số f ( x ) liên tục trên và f
 (x)dx = 2; f
 (x)dx = 6 . Tính I = f
 ( 2x −1)dx . 0 0 −1
Câu 39. Cho hàm số y = f ( x ) có đạo hàm liên tục trên đoạn 1; 4 , đồng biến trên đoạn 1; 4 và thỏa mãn 4
đẳng thức x + x f ( x) =  f ( x) 2 2 .  
 , x  1; 4 . Biết rằng f ( ) 3 1 = , tính I = f
 (x)dx . 2 1
------------- HẾT ------------- Trang 24/24
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên:………………………………….Lớp:………….......……..……… 001 Mã đề [001] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B A B B C C C D D C D B B A C C B B 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B A A A A A B C D C A C D D D D A
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn B 1 1 2 Ta có sin 3 d x x cos 3x      1  1  .    0 3 3 3 0 Câu 2. Lời giải Chọn A
Mặt cầu S x   y  2   z  2 2 : 1
3  5 có tâm I 0; 1
 ;3 và bán kính R  5 . Câu 3. Lời giải Chọn B 3 2 3
Ta có: f (x)dx f (x)dx f (x)dx    0 0 2 2 3 3
f (x)dx f (x)dx f (x)dx a b .    0 0 2 Câu 4. Lời giải Chọn B  
MN       MN
  2   2 2 4; 1; 6 4 1 6
 53  L  53 . Câu 5. Lời giải Chọn C 2 u 1 Đặt 2
u  1 2x u  1 2x x  ;udu  d . x 2
Đổi cận: x  0  u  1; x  4  u  3 3 5 3 3 1 1  u u  Suy ra 2 I u
  2u  1du    .  4 4  5 3 1  1 Câu 6. Lời giải Chọn C
Do mặt phẳng Oxy vuông góc với trục Oz k  0;0;  1 làm một véc tơ pháp nên nhận véctơ tuyến. Câu 7. Lời giải Chọn C 9 Ta có: f
 xdx  9  F x9  9  F 9 F 0  9  F 93  9  F 9 12. 0 0 Câu 8. Lời giải Chọn D 4 3 2x  3  3  2x 3 Ta có 2
f (x)dx dx  2x dx    C    2  2  xx  3 x Câu 9. Lời giải Chọn D x 2 x Vì x x 9 3 2
3 dx  9 dx   C   C .   ln 9 ln 9 Câu 10. Lời giải Chọn C sin x tan x  dx    .   ln cos x C cos x Câu 11. Lời giải Chọn D Đặt t = x - Þdx = d - t p 6 6 sin ( t - )+cos ( t - ) p 6 6 sin t +cos t 4 Þ I = dt 4 t = × dt p ò 6 ò - 1 p - 6t +1 4 +1 4 6t p p 1 p 4 Þ 2I = 4 2 2 =
1-3sin x cos x dx 4 = 5+3cos4x dx p + ò p ò p ò ( ) - ( ) - ( 6 6
sin x cos x)dx 8 - 4 4 4 1æ 3 p ö p 4 = 5 5 ç x ç + sin4x÷÷ = 8çè 4 p ÷ø - 16 4 5 I p Þ = 32 Þ a-b = 27. Câu 12. Lời giải Chọn B
Theo tính chất nguyên hàm thì  I  và  II  là đúng, III  sai. Câu 13. Lời giải Chọn B Ta có cos sin . x x e dx cos x   e d cos x cos x  eC .     Câu 14. Lời giải Chọn A x f t
Giả thiết tương đương với
dt  2 x  6 . Lấy đạo hàm hai vế theo ẩn , ta được:  x 2 t a f x 1 
f x  x x . 2 x x x t t x
Thay vào giả thiết, ta được: dt  2 x  6 
 2 t  2 x  6  2 x  2 a  2 x  6 2 t a aa  9 a. Câu 15. Lời giải Chọn C u x du  dx Đặt    .
dv  sin x dx
v  cos x π Ta có J π
 x cos x  cos x dx  π  sin x .  π 0 0 0 Câu 16. Lời giải Chọn C u   x 1  du  dx  Đặt    dv f   xdxv f  xdx 1 1 1 Ta có x  
1 f  xdx   x  
1 f x  f  xdx 0 0 0 1  2  f
 xdx 10 0 1  f
 xdx  210  8  . 0 Câu 17. Lời giải Chọn B 
Gọi I là trung điểm của AB suy ra I 2;1;0 , AB  2;8; 4    21;4; 2   .
Suy ra mặt phẳng phẳng trung trực của AB có dạng:
1 x  2  4 y  
1  2z  0  x  4y  2z  6  0  a  4 , b  2  , c  6
  a b c  4  . Câu 18. Lời giải Chọn B 
Mặt phẳng  :x  2my z 1  0 có vectơ pháp tuyến n  1;2 ; m 1 1  . 
Mặt phẳng  :2x  3y  4z  5  0 có vectơ pháp tuyến n  2;3;4 2  .  
Ta có:     n .n  0  1.2  2 .
m 3 1.4  0  m  1  . 1 2 Câu 19. Lời giải Chọn B
Ta có  2 5 5 x x x e dx 2 u
  x  5x  5 du  2x  5dx Đặt    d x v e d x x v e
 2    x   2 5 5 d
 5  5 x  2 5 x x x e x x x e x e dx u    2x  5 du  2dx Đặt    d x v  e d x xv e
2 5 xd  2 5 x 2 xd   2 3 x x e x x e e x x e C .
 2    x   2 5 5 d  3  2 x x x e x x x e C . a 1  Suy ra b
  3  2a  3b c 13 . c  2  Câu 20. Lời giải Chọn A
Ta có f x  4x1 ln x  F x  4x1 ln xdx đặt  1 u
 1 ln x du  
x F x 2
 2x 1 ln x 2  2xdx  2x  1 ln x 2 2 2
x C  2x ln x x C 2
dv  4x v  2x Câu 21. Lời giải Chọn A du  dx u   x  Đặt    x 1 2 2 dv  e dx v  e x  2 Khi đó: 100 100 100 100 x 1 x 1 2 2 2 1 1 1 1 .e d  e  e x x x x dx 200 2 50e e x   200 200  50e  e    200 199e   1 .   2 2 4 4 4 4 0 0 0 0 Câu 22. Lời giải Chọn A    
Do v  0 nên u, v cùng phương khi và chỉ khi m  3k     m 1   k
   :u kv k    :  2   2
km  4k   1 .  k m 1  6k    3 Câu 23. Lời giải Chọn A
Gọi M x;y;z. Vì M thuộc đoạn AB nên:  7 x   3   x  2  2  x 3   MA   MB
   y     y  5 2 1 2 3  y       z        3 2 2 5 z  8 z    3 Câu 24. Lời giải Chọn A 3 3 cos2x 3 2 2 3 cos x  sin x  1 1 
Ta có: f xdx  dx    dx   dx   2 2 2 2  2 2  sin . x cos x sin . x cos x  sin x cos x  4 4 4 4    x  6 4 3 x 3 cot tan  . 3 4 3     6  4 3   12  4 3 Mặt khác: f
 xdx FF   F  .        3   4  3  3  3 4 Câu 25. Lời giải Chọn B
Vì F x là một nguyên hàm của hàm f x  sin 2x nên F x  sin 2 . x dx    F x 1  cos 2x C . 2   1      Ta có F
cos  C  1  C  1  F x 1  cos 2x  1 1  F  cos 1      4  2 2 2  6  2 3   3  F  .    6  4 Câu 26. Lời giải Chọn C Đặt 2
t  2  sin x  o
c s xdt  (sin 2x  sin x)dx dt 1 1  Khi đó f
 xdx      C .  2t t  2 2  sin x  o c s x  1 
Vậy một nguyên hàm của hàm số đã cho là F x  .  2 2  sin x  o c s xCâu 27. Lời giải Chọn D
f x  f
 xdx  3 2sin xdx  3x2cos xC .
f 0  3  3.0  2cos 0  C  3  C  5 . Câu 28. Lời giải Chọn C
Dễ thấy mp đã cho cắt Ox , Oy , Oz lần lượt tại A2;0;0, B0;3;0,C 0;0;4 .
OA  2 , OB  3 , OC  4 .
Tứ diện OABC có đường cao là OC , đáy OAB là tam giác vuông tại . O 1 1
Suy ra V OC. O . A OB  4 . 3 2 Câu 29. Lời giải Chọn A 2 2 2 2 Ta có  f
  13x9dx f
 13xdx 9dx f
 13xdx18 0 0 0 0
Đặt t  1 3x dt  3
dx . Đổi cận: x  0  t  1; x  2  t  5  2 5   dt  1 1 Nên f
 13xdx f  t.  f  
 tdt  3 0 1 5  3   3  2 Vậy  f
  13x9dx  318  21.  0 Câu 30. Lời giải Gọi M ( ; x y; z) . Ta có 2 2
MA  2MB MA  4MB 2 2 2 2 2 2
 (x  2)  (y1)  (z  3)  4 (x  2)  ( y  5)  (z 1)    20 38 2 106 2 2 2  x  y  z  x y z   0 3 3 3 3 2 2 2  10   19   1   x   y   z   16.        3   3   3  Câu 31. Lời giải Chọn D 7x 11  4 3  Ta có: dx  
dx  4.ln x 1  3ln x  2  C .   
(x 1)(x  2)
x 1 x  2  a  3  
. Vậy a +b = 7 . b   4 Câu 32. Lời giải Chọn D 3
m 1 f xdx  9   m   1  3    9   m  2 . 2 Câu 33. Lời giải Chọn D 2 2 1 1 1 4 1 Có f
 2xdx= f 2xd2x
= F 2x 2 = F 4 F 0 = f
 xdx  8. 2 0 2 2 2 0 0 0
Cách khác: đặt t = 2x dt = 2dx . 2 4 1 4 1 Ta có: f
 2xdx f
 tdt f
 xdx  8. 2 2 0 0 0 Câu 34. Lời giải Chọn D 2  2  0  3
d(M ;(P))  1. 1 4  4 Câu 35. Lời giải Chọn A 1  f
  x2gx 1  dx  3  f   x 1 dx  2 g  x 1 dx  3  g
 xdx  2  . 0 0 0 0 PHẦN II: TỰ LUẬN
Câu 36. Học sinh tự giải Câu 37. Lời giải
Gọi M , N, lần lượt là trung điểm các cạnh AB, CD . Ta có ACD BCD (c-c-c) nên
AN BN do đó tam giác NAB cân tại N MN AB
Tương tự ta có MN CD
Ta có  ABN   CD   ABN   BCD
mà  ABN    BCD  BN . Trong  ABN  kẻ AH BN AH   BCD
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD. Dựng trục It, gọi O It MN khi đó O là
tâm mặt cầu ngoại tiếp tứ diện. Gọi R là bán kính mặt cầu ngoại tiếp tứ diện. Ta có 2 2 2
MN AN AM 2 2 2 2
AD MD AM  9a MN  3 . a 2 2 2 2 2
Ta có OM MA ON ND R 2 2 2 2 2
OM ON ND MA  5a
 OM ON OM ON  2  5a
Mà OM ON MN  5
3a OM ON a 3  7 O
M ON  3a OM a    3 Từ  5  
OM ON a 2  3 ON a  3 2 2 2  2  2 a 85
Ta có R ON NA a    3a  .  3  3 Câu 38. Lời giải dt
Đặt t  tan x t   2 d
1 tan xdx   dx . 2 1 t Đổi cận:
x  0  t  0 x   t 1 4 4 1 f t 1 f x Ta có: f
 tan xdx  4  dt  4  dx  4 .   2 1 t 2 1 x 0 0 0 1 1 2 x f x 1 f x Suy ra: I f
 xdx  dx  dx  .   6 2 2 x 1 x 1 0 0 0 Câu 39. Lời giải
f x. f ' x
Ta có: f xf x 2 . '  cos .
x 1 f x   cos x 2 1 f x
f x. f ' x  dx  cos xdx   2  df  x 2 1
 cos xdx  1 f
x  sinx C 2 1 f x 2
1 f 0  sin0  C C  2 .   
f x  sinx  2   f x  sinx  2 2 2 1 2 1 trên 0; .  2     
Xét f x  sinx  2 2 1 trên ; ta có:  6 2    1  t  2
Đặt t sinx,t  ;1 2 
f t  t  4t  3  f 't   0 2    2 t  4t  3   Giá trị nhỏ nhất: f t 1 21 min  f     2  2
Giá trị lớn nhất: max f t  f   1  2 2 . 21 Vậy m  ; M  2 2 . 2
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên:………………………………….Lớp:………….......……..……… 002 Mã đề [002] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 C B C B A B A D C B D B C C B A C B 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 C C C B D D D A A D A A D B A A D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn C
x x x  1 0  5 A B C x x   2 G  3 G   3  
y y y  2   2  6 Ta có A B Cy   y
 2  G2;2;4 . G 3 G  3  
z z z  4  5  3 A B C z   z   4 G  3  G  3 Câu 2. Lời giải Chọn B 1 Ta có  2 x I
e dx  2 x e  2e  2 .  1 0 0 Câu 3. Lời giải Chọn C 1 Ta có f
 xdx  2x sin 2xdx 2
x  cos 2x C . 2 Câu 4. Lời giải Chọn B Câu 5. Lời giải Chọn A 1 1 1 d(x 1) Cách 1: Ta có: 1 I  dx
 ln x 1  ln 2  ln1  ln 2 . Chọn đáp án   0 x 1 x 1 0 0 C.
Cách 2 : Sử dụng MTCT. Câu 6. Lời giải Chọn B Đặt 3 3 2
t  1 x t  1 x  3
t dt  dx .
Đổi cận: x  0  t  1; x  1 t  0 . 1 0 1
Suy ra 3 1 xdx t.    2 3  t dt 3  3 t dt .  0 1 0 Câu 7. Lời giải Chọn A 2 x  3 3 Ta có f
 xdx  x   2
3 dx  x 3 dx 3   C . 3 x
Chọn C  2017 ta được một nguyên hàm của hàm số f x  x  2
3 là F x  3 3   2017 . 3 Câu 8. Lời giải Chọn D x  x  15 1
 x  15 d x   1 7 dx 7 7  x 716 2 2 2 2  C 2 32 Câu 9. Lời giải Chọn C 1 1 1 4 1
I f 3x    1 dx f 3x   1 d 3x    1  f  tdt  3. 3 3 0 0 1 Câu 10. Lời giải Chọn B
Do mặt phẳng Oxz vuông góc với trục Oy nên có vectơ pháp tuyến là n 0;1;0 . Câu 11. Lời giải Chọn D 1 1
Ta có  exd  ex I x  e 1. 0 0 Câu 12. Lời giải
Ta có  2x x 3 3 sin
dx x  cos x C . Câu 13. Lời giải Chọn C x y z
Phương trình mặt phẳng  ABC là  
 1  6x  3y  2z  6  0 . 1 2 3    AB   1
 ;2;0;CA  1;0;3 .
Gọi H là trực tâm của tam giác ABC .
Suy ra OH   ABC .
Suy ra OH d O ABC 6 ,  . 7 Câu 14. Lời giải Chọn C    Gọi M  ;
x y;0 . Suy ra MA  2  ;
x y;0 , MB   ;
x 2  y;0 , MC   ; x y; 2.
  2 1 Ta có M .
A MB MC  3 2 2
 2x  2x  2y  2y 1  0 2 2
x x y y   0 2 2 2  1   1   1 x   y
 0  x y  .      2   2  2  1 1  Vậy M ; .    2 2  Câu 15. Lời giải Chọn B  1    ln u u x  Đặt  x   3 dv  xdx 2 2 v x  3 3 3  f  x 2 2 1 2 2 dx  x ln d
x x  x .ln x x . dx   3 3 x 3 3 3 2 2 2 2 2 2 2
x ln x    x C x 3ln x  2  C. 3 3 3 9 Câu 16. Lời giải Chọn A Ta có:
f x dx
x dx   x     12 2 1 2 1 dx 1 2x  132 1 2   C   x  3 1 . . . 2
1 C  .2x  1. 2x  1 C . 2 3 2 3 3 2 Câu 17. Lời giải Chọn C
Ta có: hình chiếu củađiểm A1; 1; 2 trên các trục Ox, Oy , Oz lần lượt là B1; 0; 0 ,
C 0; 1; 0 , D0; 0; 2 . x y z
Phương trình mặt phẳng Q qua B, C , D là: 
  1  2x  2y z  2  0 . 1 1  2 Câu 18. Lời giải Chọn B
Có F x  f
 xdx  sin xcos xdx  cos xsin xC Do F
  cos  sin  C  2  1 C  2  C  1  F x  cos x  sin x 1.    2  2 2 Câu 19. Lời giải Chọn C   4 2  2m 4
Ta có cosu;v  2   
 2 m  4  5 1 m 2 30 6. m  4 30  m  1   m  1    
  m 1 n 2   .
m 10m 11  0 m  1  1  lCâu 20. Lời giải Chọn C
Ta có F x   x e  2xx 2
dx e x C
Theo bài ra ta có: F   3 1
0  1 C   C  . 2 2 Câu 21. Lời giải Chọn C 2 ln x
Ta có F x   dx C . x 1 2 3 3 ln x t ln x
Đặt t  ln x  dt  dx , suy ra F x 2  
dx   t dt   C   C . x x 3 3 ln e Mà F e   3 3 3  8 
C  8  C  1  . 3 3 ln x
Khi đó F x  1. 3 Nên F  39 e   2. Câu 22. Lời giải Chọn B 1000 2 2 1000 1000 x  4x 1  2 2
x x  2x   1  x 2  2x 1 xI dx   dx   1  dx  2   x x 2 x x 2 2  x x x x  1 1 1 1000 1000 1000 2 2 2 1000 2x 1 1 2 2  1000 d x x 2   1000  dx dx dx    2  x   ln x 1  2 x x x 1 1 2 1 x x 1 1 1 1 1000  2 2
1 ln x  ln x 1 1000 2 1000  ln  1000 2   1  ln 2 1000 2  2
1 ln x x  ln  1000 2   1  ln 2 1 1 1000 1000      1000      1000 2 1 ln 2 ln 2 1 ln 2 ln 2   1  ln 2 1000 1000       1000 2 1 ln 2 2 ln 2 2 ln 2   1         2 1000 1000 2 1000 2 1 ln 2 ln 2 ln 2 1       2 1000 998 1000 2 1 ln 2 ln 2 1   2 1000 998 1000 2 1 ln 2 2 1      .   Câu 23. Lời giải
Ta có F  x  f x
Fx x  f x x x x    x x x x2 2 ex x2 2 2 2 2 2 . 2x 1  4
    xx   x x2 2 e
 2x x   2 2x 1 1
2 x x  2  x x     2x  
1 x x  
1  x  2 x  
1 x x  2   2 2 1 2 e  0  x   2  ; 1  ; ;0;1  2  F  2
x x  0 có 5 nghiệm đơn nên F  2
x x có 5 điểm cực trị. Câu 24. Lời giải Chọn D du  2 d x x 2 u   x  Ta có:    1 . dv  cos 2 d x x v  sin 2x  2 π π 1 Khi đó: 2 I x cos 2 d x x 2
x sin 2x xsin 2 d x x .   2 0 0 0 Câu 25. Lời giải Chọn D
x  4  t  2 Đặt 2
t x x t dx  2tdt . Từ đó suy ra x  0t  0 4 2 2 2
Khi đó I f '
  xdx tf '
 tdt tf t 2  f
 tdt  2 f 2 f
 xdx  5  . 0 0 0 0 0 Câu 26. Lời giải Chọn A       aF xa a 1 cos 2x 2   cos x dx   dx  
x  sin 2x C .    1 1        2   2  4  1  1 C C    4    Do F   1 0  , F  4     .   4  4  4
a 1  1    sin  C     a   2   2  4 4 2 4  2 Vậy a   2 . 2 Câu 27. Lời giải Chọn A Đặt 1 1 2 2
u  1 3ln x u  1 3ln x  2udu  3. dx dx udu . x x 3
Đổi cận x  1 u  1; x e u  2 . 2 2  u 1 u du e 2   2 ln x 3  3  2 Do đó: I dx    
 2u  1du. x 1 3ln x u 9 1 1 1 Câu 28. Lời giải Chọn D Đặt F t 2 
1 t dt Ft   t .    2 1 x G x 2 
1 t dt F x F
G x  F  
  x  F   1  
  F x  F   1      1     Fx 2  1 x 1 . Câu 29. Lời giải Chọn A
Lần lượt thay tọa độ các điểm N, P,Q, M vào P , ta được M P . Câu 30. Lời giải Chọn A
Ta có F x  f x . 2
2ax b2x 3 2      ax bx c  
ax bx c F x
2ax b 2x  3   2x  3 2x  3 2
5ax  3b  6ax c  3b 2    20x 30x 7 = . 2x  3 2x  3 5  a  20 a  4   Do đó: 3
b  6a  3  0  b   2
 . Vậy S a b c  3. c 3b  7   c  1  Câu 31. Lời giải Chọn D Đặt 2
t x 1  x t 1 dx  2tdt .
Đổi cận: x  0  t  1; x  3  t  2 . 3 2 2 2 Do đó: 8  f
  x1dx f
 t.2t dt  2 t.f
 tdt t.f
 tdt  4. Vậy I  4 . 0 1 1 1 Câu 32. Lời giải Chọn B x x A B x   1  M 2   y y
Ta có: M là trung điểm của đoạn AB A By   1
  M 1; 1;  1 . M 2   z z A B z   1  M  2 Câu 33. Lời giải Chọn A I 1; 1  ;  1 Ta có (S) :  . R  3 2 2 1 m  3m
m  3m 10  0 m  2
Để (P) tiếp xúc với (S) thì d I;P  R   3    .  2 3
m  3m  8  0 m  5  Câu 34. Lời giải Chọn A 2 3x   2 1 dx 1  1  Đặt I   3  dx   2  
3x x ln x 3x  ln x x  1 1  1 
Đặt t  3x  ln x  dt  3  dx    x
Đổi cận: x  1 t  3
x  2  t  6  ln 2 . 6ln 2 dt  ln 2  Khi đó, 6ln 2 I   ln t  ln 
6 ln 2 ln3  ln 2   3 t  3  3
Suy ra a  2 , b  2 , c  3. Vậy a b c  7 . Câu 35. Lời giải Chọn D
Đặt u x 1 2
x u 1  d x  2u d u . x  3 2 u  4 Khi đó dx trở thành 2
.2u d u  2 u  4 d u .      x  1 u PHẦN II: TỰ LUẬN Câu 36. Học sinh tự giải Câu 37. Lời giải 2 2 2 sin 2 . x cos x 2sin . x cos x Ta có: I dx dx   1 cos x 1 cos x 0 0
Đặt t  cos x dt  sin . x dx
Đổi cận: x  0  t  1; x   t  0 2 0 2 1 2 2t  1   t  1  1   I  
dt  2 t 1 dt  2   
  t  ln t 1   2   ln 2  2ln 2 1   1 tt 1  2 0   2  1 0
Vậy a  2;b  1   P  5. Câu 38. Lời giải 3 f  x 3 Ta có: 2  dx  
f x  f 3 f  1 2 f x 1 1   3 Ta có: 8  f
 xdx f 3 f  1   f 3  f  1 f 3  f  1 1
f 3  f   1  4 
f 3  3  f 3  9 .
f 3  f   1  8 xf 3 2 2  x y  8 x y  4 Cách 2:     
x f (3)  3  f 3  9
f 3  f   yf   1 1 2 x y  2 x y  2  Câu 39. Lời giải: S I A D O B C 2 1 a 3 SA . D DC   AD a 3 ADC 2 2   Do 0
ABC ADC  90 nên tâm đường tròn ngoại tiếp tứ giác ABCD là trung điểm AC .
Gọi I là trung điểm SC thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD . 0
IO  tan 60 .OC a 3 Có 2 2 2 2
R IA IO OA  3a a  2a
S  R a2 2 2 4 4 2  16 a mc
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên:………………………………….Lớp:………….......……..……… 003 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 A A D A B A B C C D C D C C B D B C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 D C D A A D B B A B B B A D C C A
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn A
Ta có   ex 1 e x f x     ex  1 nên f
 xdx  ex  
1dx  ex xC . Câu 2. Lời giải Chọn A t
Đặt t  4x 1 2
t  4x 1  2tdt  4dx  dx  dt 2 2 3 2 3 t 1 t 3 13
Đổi cận : x  0  t  1, x  2  t  3. Do đó : 4x 1dx  dt  .  .   2 2 3 1 3 0 1
Cách 2: Sử dụng máy tính cầm tay. Câu 3. Lời giải 1 Đặt 2
u x  2x  3  du  2 x  
1 dx   x   1 dx  du . 2
Đổi cận: x  0  u  3 ; x  1 u  2 . 1 2 3 x xu 1 1 Ta có    2 2 3 1 d  d u x e x e u   e du .   2 2 0 3 2 Vậy chọn phương án C Câu 4. Lời giải Chọn A
Hình chiếu của M (1; 2; 3). lên trục Oy là điểm Q(0; 2; 0). Câu 5. Lời giải Chọn B 1 dx 1
 ln x 1  ln 2 .  0 x 1 0 Câu 6. Lời giải Chọn A 2 2
Ta có,  3 f x x
d  3 f x x d  6 1 1 Câu 7. Lời giải Chọn B Câu 8. Lời giải Chọn C 
Mặt phẳng P : x  2z  23  0 có một vectơ pháp tuyến là n  1;0;2 1  . Câu 9. Lời giải Chọn C
Mặt cầu có tâm I 1;2;3 và bán kính R  3 có phương trình là
x  2   y  2  z  2 1 2 3  9 . Câu 10. Lời giải Chọn D
Ta có F x  f
 xdx , x
  K  F
  x  f
x, x   K . Câu 11. Lời giải Chọn C 1 Ta có  2 x  2x   2 3 2
1 dx x dx  2 xdx dx x x x C .    3 Câu 12. Lời giải Chọn D 3 2 3 2 2 a f
 xdx  f
 xdx  f
 xdx  f
 xdx b f
 xdx  a b. 0 0 2 0 0 Câu 13. Lời giải. Chọn C
Ta có tâm cầu thuộc trục Ox : I  ; a 0;0 . 
IA    a  2 1
;1; 2  IA a  2a  6 . 
IB    a  2 3
;0;1  IB a  6a 10
Mà mặt cầu S  đi qua hai điểm A1;1;2, B3;0;  1 2 2 2 2
IA IB IA IB a  2a  6  a  6a 10  a 1 I 1;0;0  R IA  5
Vậy phương trình mặt cầu S  là: x  2 2 2
1  y z  5 . Câu 14. Lời giải Chọn C
Phương trình mặt phẳng  ABC :16x 11y z  5  0 . Gọi I  ; a ;
b c là tâm đường tròn ngoại tiếp ABC .  5     2  2 10  23 a I ABC a b c  2     5 
Ta có IA IB
 4a  6b  2c  32  b   4  I ; 4;1 .     2  IA IC 1
 6a 11b c 5       c  1     Câu 15. Lời giải Chọn B 2 d 2x   1 Ta có dx  2  x   C ;   2 2 1 2x 1 2 2x 1
Do F 5  7 nên 6  C  7  C 1. Câu 16. Lời giải Chọn D  1 du  dx u   ln x  x Đặt    . 2 dv  d x x xv   2 3 3 2 3 3 3 2 2  x 1 x x 9 5
x ln x dx  ln x x dx  ln x   ln 3  2ln 2  .   2 2 2 4 2 4 2 2 2 2 2
Suy ra m n  2 p  0 . Câu 17. Lời giải Chọn B
Ta có: P / Q  P có dạng: 2x y  2z m  0m  5 .
Chọn điểm B 0; 5; 0Q
Ta có: d A, P  d Q, P   
  d A, P  d B , P     6 1 4  m 5   m
m 11  m  5     m  3   n 3 3
m 11  5  m
Vậy: P : 2x y  2z  3  0 . Câu 18. Lời giải Chọn C 10 10    x xI xx  2 101 3 101 3 101 10 10 10 1060 100 2 dx     2x     20   .  101 3  101 3 101 3 0 0 Câu 19. Lời giải Chọn D du  dx u   x  Đặt:    1 . dv  cos 2 d x x v  sin 2x  2 1 1 1 1 Khi đó: x cos 2 d
x x x sin 2x  sin 2 d
x x x sin 2x  cos 2x C .   2 2 2 4 Câu 20. Lời giải Chọn C 4
Xét I f x  2 dx 1    0
Đặt t x  2  dt  dx x 0 4 Đổi cận t 2  2 2
I f t dt  f 2  f  2    2   2    4 1    2  2
Xét I f x  2 dx 2    0
Đặt t x  2  dt  dx x 0 2 Đổi cận t 2 4 4
I f t dt  f 4  f 2  4  2  2 2        2 4 2 Vậy f
 x 2dx f
 x  2dx  6. 0 0 Câu 21. Lời giải Chọn D        a b . a b 2 0 0 2 cos ,       . a . b 5 5 5 Câu 22. Lời giải Chọn A
Đặt t  2x  dt  2dx . 1 t t Từ f   x 2
2 dx  sin x  ln x f  t 2 dt  sin  ln  C . 2 2 2  x f  tt 2 dt  2sin
 2ln t  2ln 2  2C f  x 2 dx  2sin
 2ln x  2ln 2  2C , do 2 2
C   nên chọn đáp án B Câu 23. Lời giải. Chọn A       1 ln  1 ln  1 ln 1 d  d   d  d 
d    I C .  x F x f x x x x x   x x x 2   x 2 2  x x  2 2 x x x  1 u  ln x du  dx   Đặt: x  1   . dv  d  x 1 2  xv    x 1 1  1 1
I   ln x
dx   ln x   C .  2 x x x x 1 a  1 
Do đó: F x 2 1
   ln x   ln x  2   . Vậy S  1. x x xb  2 Câu 24. Lời giải Chọn D
Ta có Oxy : z  0 ;
Oyz: x  0 ;
Oxz: y  0.
Do đó a  2;b  1;c  3 . Vậy P  30 . Câu 25. Lời giải Chọn B 1 1 1 2 2 2  M NM N Ta có: f
 xdx  M.sin xN.cos xdx   cos x sin x      0 0 0 1 2 1 M N 1
Do đó: f xdx   
   M N  1   0 Mặt khác: f  
1  3  N  3  N  3   M  2 f x 1 5 2
 2.cos x  3.sin    x f   .    4  2 Câu 26. Lời giải Chọn B
Theo công thức nguyên hàm, đáp án D sai. Câu 27. Lời giải. Chọn A Không bước nào sai. Câu 28. Lời giải Chọn B cos3x Ta có sin 3 d x x    C , vì F  nên  2 C  2. 3    2  Câu 29. Lời giải Chọn B      
Ta có véc tơ b ngược hướng với véc tơ a và b  2 a . Suy ra b  2  a   2  ;4; 6. Câu 30. Lời giải Chọn B 1
Đặt t  2  x  dt  dx . 2 x 1
Suy ra F x  dx  
  2ln 2 xC .  2 dt  2ln t C x 2  x t
Do F 0  ln 4  C  0 . Vậy F 4  4ln 2 . Câu 31. Lời giải Chọn A x
Đặt ln 2x t dx dt 2 e 1ln 2 1ln 2 1 1 x 1 2018 Khi đó f
 ln2xdx f  tdt f
 tdt  1009 . x x 2 2 2 1 ln 2 ln 2 Câu 32. Lời giải Chọn D
Xét mặt cầu  x  2   y  2 2 1
3  z  1 có: tâm I 1;3;0 , bán kính R 1. 3.1 4.0 1
d I P 2 , 
 1. Vậy P cắt mặt cầu. 2 2 3  4 5 Câu 33. Lời giải: Chọn C  1 e   du dx u lnx I  xlnxdx  . Đặt   x  2 dv   xdx   x 1 v   x 2 e 2 2 2 2 e e e 2 2 2 x 1 x e 1 e x e e 1 e  1  I
lnx   . dx   xdx       . 2 x 2 2 2 2 4 2 4 4 4 0 0 0 0 Câu 34. Lời giải Chọn C 3 I f
 xdx f x3  f 3 f 2  52  3. 2 2 ---Hết--- Câu 35. Lời giải Chọn A Ta có f
 xdx f xC .    f   x 3x 1 7 dx  dx  3 
dx  3x  7 ln x  2  C .    x  2  x  2  3
x  7 ln x  2  C khi x  2  
Do đó f x   . 3  x  7 ln 
x  2C khi x  2 
Khi đó f 0 1 7
 ln 2  C 1  C 1 7ln 2 , f  4    2  1
 2  7ln 2  C  2  C 14  7ln 2. 3
x  7 ln x  2 1 7ln 2 khi x  2  
Suy ra f (x)   . 3  x  7 ln 
x  214 7ln 2 khi x  2  Nên f   2
2  6  7 ln 2 1 7 ln 2  7  7 ln 2 . f  3    9
  7ln114  7ln 2  5  7ln 2 .
Vậy f 2  f  3   12. PHẦN II: TỰ LUẬN Câu 36. Lời giải Học sinh tự giải. Câu 38. Lời giải Đặt x t x   2 tan d
1 tan t dt với x 1 t  ; x  0  t  0 . 4 4     t    I
f tan t 1 tan t 4 4 4 1 1 cos 2 1 1 2 2 4 dt  cos t dt  dt t  sin 2t  .   2   cos t 2  2 4  8 0 0 0 0 Câu 39. Lời giải 1
Ta có: f x. f 1 x 1  f x  f 1 x 1 1 dx
f 1 xdx Khi đó I     1 f x 1 f 1 x 0   0  
Đặt t  1 x  dt  dx
Đổi cận x  0  t  1; x  1 t  0 0 f t 1 dt
f xdx Nên I    .   1 f t 1 f x 1   0   1 1 dx f x 1 dx 1
Do đó: I I  
 dx 1  I  .    1 f x 1 f x 2 0   0   0 Câu 37. Lời giải S d E A I C M B
Gọi M là trung điểm BC khi đó M là tâm đường trong ngoại tiếp tam giác ABC .
Qua M dựng đường thẳng d vuông góc với mp đáy.
Dựng mp trung trực của SA cắt d tại I khi đó I là tâm mặt cầu ngoại tiếp hình chóp.
SB,ABC
  SB, AB    SBA  45 . a a 2
SA AB a AE  , AM  . 2 2 2 2 a a a 3 Bán kính mặt cầu là 2 2
IA AM EM    . 2 4 2 3 3 4  a 3   a 3
Thể tích của khối cầu ngoại tiếp hình chóp S.ABC là V    . 3  2  2  
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên:………………………………….Lớp:………….......……..……… 004 Mã đề [004] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 C B D C D A A D C C C A B A C C A B 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 B D A D D A A B B B D C B B C A D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải 3 4 4
Theo tính chất của tích phân, ta có: f
 xdx f
 xdx f  xdx. 0 3 0 3 4 4 Suy ra: f
 xdx f
 xdx f
 xdx 104  6. 0 0 3 3 Vậy f
 xdx  6. 0 Câu 2. Lời giải Chọn B
f xdx  x x  4 3 x x 3 2 dx    C . 4 3 Câu 3. Lời giải Chọn D 1 Đặt 3 2
y x mx  m  2 x  2018 . 3
Đổi cận, thay vào ta được m  1  . Câu 4. Lời giải Chọn C dx
1 d 5x  2 1 
 ln 5x  2  C .   5x  2 5 5x  2 5 Câu 5. Lời giải Chọn D
Do kf (x)dx k f (x)dx với mọi hằng số k  và với mọi hàm số f (x) liên tục trên  nên   0 A là mệnh đề sai. Câu 6. Lời giải Chọn A 2 2 2 2 2 2 x 4 f
 x2xdx 1 4 f
 xdx2 xdx 1 4 f
 xdx2.  1 2 1 1 1 1 1 2 2  4 f
 xdx  4  f
 xdx 1 1 1 Câu 7. Lời giải Chọn A Câu 8. Lời giải
Mặt cầu có tâm I 1; 4;3 và đi qua điểm A5; 3;2 nên có bán kính R IA  3 2
Vậy phương trình mặt cầu cần tìm là:  x  2   y  2   z  2 1 4 3  18 . Câu 9. Lời giải Chọn C 1 1 2 1 Ta có I
f  2x 1 dx f  2  x  
1 dx f 2x     1dx 1  1  1 2 0 1 1  I   f  u 1 du f
 vdv  31 4. 2 2 3 0 Câu 10. Lời giải Chọn C
Mặt phẳng x  2y z  2  0 có vectơ pháp tuyến n  1;2;  1 . Câu 11. Lời giải ChọnA. x
Ta có:  x   5 5 1 dx   x C . ln 5 Câu 12. Lời giải dx e
Đặt u  ln 2x  du  1
. Đổi cận x   u  0; x   u  1. x 2 2 e 2 2 1 ln 2x Vậy 2
dx u du .   x 1 0 2 Câu 13. Lời giải Chọn B 1  2x  2x I dx ta có xx    x  0 .  2 2 0 1  1 0 1 0
  2x  2x  2x  2x  2x  2x    
 2x 2x 1
 2x 2x I dx dx dx dxdx 1  1  0 1  0 0 1
 2x  2x
 2x  2x  1        .  ln 2   ln 2  ln 2 1  0
Có thể sử dụng máy tính. Câu 14. Lời giải. Chọn A   2  . x F x x e .dx .  du dx u   x  Đặt    x 1 . 2 2
dv e .dx v  . x e .  2   1 1 1 x  1 x 1 x 1 2 2   . . x F x x e e .dx  . .  . x x e e C 2  .e x   C .  2 2   2 2 2 4 2  2  Câu 15. Lời giải Chọn C   
Ta có BA0;3; 3  , BC  3  ;3;0, AC  3  ;0;3 .
Vì AB AC BC nên ABC đều.
Tâm đường tròn ngoại tiếp trùng với trọng tâm A
BC nên I 2;2;2 . Câu 16. Lời giải Chọn C 
Ta có AB  1; 0;  3 , AC   1
 ;1; 0 nên mặt phẳng  ABC có vectơ pháp tuyến là  
AB, AC  3;3;  1 .  
Phương trình mặt phẳng  ABC có dạng 3x  3y z 8  0. Câu 17. Lời giải Chọn A x 1
Ta có:       2 2 d  e d  e x F x f x x xC .  2 2 e x 1
Theo giả thiết: F   1
0  1 C  . Vậy F x   . 2 2 2 Câu 18. Chọn B Đặt
u x  2 du  1 1 x d 1 1     (x  2) x e x
d  (x  2) x e x e x
d =  e 2 x
e  3 2e = abe x x  0  dv e x d v  0 e 0 0 với ;
a b  a  3,b  2  ab  1 Câu 19. Lời giải  1 2 u   ln 1 x du  dx Xét I  2x ln 
1 xdx . Đặt    1 x . dv  2 d x x 0 2
v x 1 2 2 2 2 2 2 x 1  x  Ta có: I   2 x   1 ln  x   1  dx  3ln 3 
x 1 dx  3ln 3    x   3ln3.    0 x 1  2 0 0  0
Vậy a  3, b  3  3a  4b  21 . Câu 20. Lời giải Chọn D
Mặt cầu S  có tâm I và tiếp xúc với P nên bán kính R d I,P  2 .
Phương trình mặt cầu S  : x  2   y  2   z  2 2 1 1  4 . Câu 21. Lời giải Chọn A Ta có: f x x  
 x xx 2 ( )d e
2 dx  e  x C 3 3 1 Do F(0)  nên 0 2
e  0  C   C  2 2 2 x 1
Vậy: F x 2  e  x  . 2 Câu 22. Lời giải Chọn D 1
Đặt t  ln x  dt  1
dx . Khi đó A  dx  .  1dtx x ln x t Câu 23. Lời giải Chọn Da
Giả sử A0;0;aOz , do d A P 2 5 ;  2 2   2 2 8  1  3   1  3  a A 0;0;  2  a  5  8     2  2        .  2  a  5  8  3    3 a   A 0;0; 2       2  Câu 24. Lời giải Chọn A x 1 y  2 z  3
Đường thẳng d qua A và vuông góc với P có phương trình   . Gọi H là 1 1 1
hình chiếu vuông góc của điểm A trên P , ta có H d H 1 t;2  t;3  t .
Tuy nhiên H P nên 1 t  2  t  3  t  3  0  t  1   M 0;1;2 . Câu 25. Lời giải Chọn A Đặt 2 x  2  t 2 2
t x  2  tdt  d x x . x t Khi đó dx t    2
x  2  C .  d  dtt C 2 x  2 t Câu 26. Lời giải Chọn B dt Đặt t  2x 
=dx . Đổi cận x  0  t  2 ; x  2  t  4 2 2 1 4 1 4
Khi đó ta có I f (2x)dx
f (t)dt f (x)dx 8     0 0 2 2 0 Câu 27. Lờigiải Chọn B 3 f (
x)dx 10  f 3  f 1
 10  f 3 3 10  f 3 13 .      1  Câu 28. Lời giải Chọn B dx
Đặt t x  dt
, đổi cận x  1  t  1, x  4  t  2 . 2 x 4 1 4 2 1 I f   xdx  2 f
xdx  2 f tdt  2. x 2 x 1 1 1 Câu 29. Lời giải Chọn D
Đặt u x du dx x 1 2 2 x
dv e dx v e 2 x 1 x 1 x x 1 2 2 2 x xe dx e e dx x
xe e C .   2 2 2 2 2 4 1 1 1
Vậy a  ; b    ab   . 2 4 8 Câu 30. Lời giải Chọn C
f xdx   xx 504,5 5
2017e  2018x dx  2017e   C . 4 x Câu 31. Lời giải
Gọi I là trung điểm AB I 1; 1  ; 2   . Mặt cầu
S có đường kính AB có tâm I 1; 1  ; 2   và bán kính
R IA    2    2    2 1 1 1 0 2 4  5
 S  x  2   y  2  z  2 : 1 1 2  5. Câu 32. Lời giải Chọn B     AB AC   Ta có cos  BAC  AB AC . cos ,
   với AB  1;5; 2
  , AC  5;4;  1 . AB AC       27 AB AC  1.5 5.4  2  1 cos ,   9  1  5   2
 2 5  4   2 2 2 2 2 1 30 42 2 35 Câu 33. Lời giải Chọn C  5   2 2 a 3
a  2b 1  Đặt a f
 xdx, b f
 xdx , ta có hệ phương trình 7   
2a b  3  11 1 1 b    7 2 5 Vậy f
 xdx   . 7 1 Câu 34. Lời giải Chọn A F x 1 
dx  ln x 1  C .  x1
Do F 2 1 C 1. Vậy F 3  ln 2 1. Câu 35. Lời giải Chọn D Ta có 5 2 5 x  2 x  2 x  2 dx   dx  dx    x 1 x 1 x 1 1 1 2 2 5  3   3    1 dx  1 dx      x 1  x 1 1 2
 x 3ln x 1 2  x 3ln x 1 5 1 2
 2  3ln 3 1 3ln 2  5  3ln 6  2  3ln 3  2  6ln 2  3ln 3
Vậy a  2,b  6
 ,c  3  P abc  3  6 . PHẦN II: TỰ LUẬN Câu 36. Lời giải Học sinh tự giải. Câu 37. Lời giải
P  ABC  AH  Ta có: 
P   ABC
BC  P .
BC AH;BC    ABC 
Suy ra mặt phẳng P đi qua A và nhận BC  5;3; 6 làm VTPT
Vậy: P : 5x  3y  6z 16  0 . Câu 38. Lời giảix  22017 2 2 2017  2  1 I  dx  1 . dx .   2019   x 2  x x 1 1 1 1 1
Đặt t   dt   dx  dx  dt . 2 2 x x x 1
x  1  t  1; x  2  t  . 2 1 1 1 2t  1 2018 2018 2018 3  2
Khi đó I  1 2t2017 .dt  .  . 2 2018 4036 1 1 2 2 Câu 39. Lời giải
Vì f x tăng trên 0;  f x  f 0 x
  0  f x 1 x   0 .
f   xf x   f     x 2 
f x
         2      2 f x f x f x f x         1      f x 2  f   x 1    t t     t f x f  xf tf t
Với t  0 , ta có:    dx  dx    t    t   t f x f xf t 1 f t 1 0     0 0 1 f t 1 t 1  dt  t 1 dt    ln f t   1 2 1   f    f   3 ln 1 ln 0   f   3 ln 1  f t 0 2 2 2 0     0 0 3  f   2 1  e ..
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên:………………………………….Lớp:………….......……..……… 005 Mã đề [005] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 D A D C A D B A C D C B C A B C A C 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A A B D A B C B B A C D B C B D D
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn D 1 1 Ta có
dx  ln ax b C .  ax1 a Câu 2. Lời giải Chọn A
Ta có:  x y2 2
z  4x  2xy  2z  2018  2 2 2
x  2xy y z  4x  2xy  2z  2018  2 2 2
x y z  4x  2z  2018  0
Đây là phương trình mặt cầu có tâm I (2;0;1) , bán kính 2 2 2
R  2  0 1  ( 2  018)  2023 Câu 3. Lời giải Chọn D
kf xdx kf xdx , * k    . Câu 4. Lời giải 1 Đặt 2
u x  2x  3  du  2 x  
1 dx   x   1 dx  du . 2
Đổi cận: x  0  u  3 ; x  1 u  2 . 1 2 3 x xu 1 1 Ta có    2 2 3 1 d  d u x e x e u   e du .   2 2 0 3 2 Vậy chọn phương án C Câu 5. Lời giải Chọn A   Ta có 2  a   4  ;6; 2   và 3b  ( 3  ;0;12).    Suy ra u  2
a  3b   7  ;6;10 . Câu 6. Lời giải Chọn D 1 Ta có: cos
 2x 3.dx  sin2x 3C . 2 Câu 7. Lời giải Chọn B  1 1   1 e e  1 I   dx  ln x   .  2     x x   x e 1 1 Câu 8. Lời giải Chọn A
Mặt phẳng x  2y z  2  0 có vectơ pháp tuyến n  1;2;  1 . Câu 9. Lời giải Chọn C 2018 2 2018 dx Ta có 2 I   ln x    .  2018 ln 2 ln1 2018.ln 2 1 x 1 Câu 10. Lời giải Chọn D Câu 11. Lời giải Chọn C Câu 12. Lời giải Chọn B Đặt t = x - Þdx = d - t p 6 6 sin ( t - )+cos ( t - ) p 6 6 sin t +cos t 4 Þ I = dt 4 = ×6tdt p ò ò - 1 p - 6t +1 4 +1 4 6t p p 1 p 4 Þ 2I = 4 2 2 =
1-3sin x cos x dx 4 = 5+3cos4x dx p + ò p ò p ò ( ) - ( ) - ( 6 6
sin x cos x)dx 8 - 4 4 4 1æ 3 p ö p 4 = 5 5 ç x ç + sin4x÷÷ = 8çè 4 p ÷ø - 16 4 5 I p Þ = 32 Þ a-b = 27. Câu 13. Lời giải Chọn C
Gọi Ax By Cz D   2 2 2 :
0 A B C  0 .
O  nên ta có: D  0   1
C  nên ta có: Ax By Cz  2A C  0 2 Từ   1 ,2  C  2  A .
Theo đề bài: d  ,
A   d B, .
2A B  6A
B  2A *
 2A  2B  6  A    
2A B  6  AB  4  A  **
Từ * :Chọn A 1 B  2, C  2
   :x  2y  2z  0.
Từ ** :Chọn A 1 B  4  , C  2
   :x  4y  2z  0 . Câu 14. Lời giải Chọn A 3 dx x 1 I e + = ò0 x +1 Đặt t = x +1 2
Þ t = x +1 Þ 2tdt = dx x = 0 Þ t =1 x = 3 Þ t = 2 2 tdt t 2 I = e × ò 2 = 2 t e dt ò 2 t 2
= 2e = 2e -2e 1 t 1 1
Þ a = 2;b = -2;c = 0 Þ S = 2-2+0 = 0 . Câu 15. Lời giải Chọn B 3  8 10
Khoảng cách từ I 1;2;3 đến mặt phẳng P : 3x  4y 10  0 là d I,P   3. 3 2 3  4
Phương trình mặt cầu tâm I 1;2;3 và tiếp xúc với mặt phẳng P : 3x  4y 10  0 là
x  2  y  2 z  2 1 2 3  9 . Câu 16. Lời giải Chọn C Câu 17. Lời giải
Ta có: f  x  x   f x 2 4 3
 2x  3x C . Mà f   1  1
  2.1 3.1 C  1   C  6  . Vậy f x 2
 2x  3x  6
Theo bài ra ta có phương trình f x 2 2
10  2x  3x  6 10  2x  3x 16  0   1 . Phương trình  
1 có   137  0 , nên có hai nghiệm thực x , x , theo Viet ta có: x .x  8  . 1 2 1 2
Khi đó log x  log x  log x .x  log 8  3. 2 1 2 2 2 1 2 2 Câu 18. Lời giải Chọn C
Đặt t  2x 1 dt  2 d x x
x  1  t  3; x  2  t  5 . 5 1 a Vậy I
f (t)dt  .  2 2 3 Câu 19. Lời giải Chọn A 8 1 8 4 8 Ta có f
 xdx f
 xdxf
 xdx   f
 xdxf
 xdx  3   2  5  . 4 4 1 1 1 Câu 20. Lời giải Chọn A
Ta có:  xx x 2 3 cos
dx  3x dx  3x cos d   x x  2 3 3 d    x x x C1  3x cos d x x  3 .
x d sin x  3 .
x sin x  3sin d x x  3 .
x sin x  3cos x     C2 Vậy    3 3 cos d   3 sin  cos    x x x x x x x x C Câu 21. Lời giải Chọn B Lời giải đúng: 4 3 1 sin x 4  1  2 3 dx
 sin x dx   cot x  cos x   1    .     4 2  2  sin x  sin x  2 2 6 6 6 1 1
Suy ra a  , b  , c  1
 hay a b c  0 . 2 2 Câu 22. Lời giải Chọn D
Gọi d là đường thẳng qua M và vuông góc với P . x  3  t
d : y  4  t . Gọi H là hình chiếu của M trên P . z  5 2t  x  3  tx  2   y  4  ty  5
Tọa độ của H là nghiệm của hệ phương trình    . z  5  2tz  3 
x y  2z 3  0 t   1  Câu 23. Lời giải Chọn A
 Đặt I  3x  2 2
cos x dx . Ta có: 0 1 1   1
I  3x  21 cos2xdx  3x  2dx  3x  2cos2xdx  I I 1 2  . 2 2 2 0 0 0   3  3  I  3x  2 dx  2 2 x  2x 2 1   .    2  2 0 0 I
3x  2 cos 2x dx 2  
. Dùng tích phân từng phần 0 du  3dx u   3x  2  Đặt    1 . Khi đó
dv  cos 2x dx v  sin 2x  2 1 3 3 I
3x  2 sin 2x
sin 2x dx  0  cos 2x  0 2   .    2 2 4 0 0 0 1  3  3  Vậy 2 2 I
 2.   2  2  4 Câu 24. Lời giải Chọn B
Mặt phẳng  có VTPT là n 1;1; 1 .    
Mặt phẳng  vuông góc với mặt phẳng  khi và chỉ khi n .n  0 .
    
Nhận thấy mặt phẳng  : 2x y z 1  0 có VTPT n    n .n  0 2; 1; 1 thì .  
 Câu 25. Lời giải Chọn C b 2 b Ta có: x dx
x x   b b a a 1.  2 2 3 a 3 a 3 Câu 26. Lời giải Chọn B x 1 d 2 x  4
Ta có F x  f
 xdx  dx  2
x  4  C .   2 x  4 2 2 x  4
F  21  7  C  2 . Câu 27. Lời giải Chọn B     Ta có AB  1; 1  ;  1 , AC   1  ;1;  1 , BA   1  ;1;  1 , BC   2  ;2; 2   .
Do đó AB  3, BC  2 3 nên I đúng.  
BC  2BA nên B nằm ngoài đoạn AC và ,
A B,C thẳng hàng.
Suy ra II sai, III sai, IV đúng. Câu 28. Lời giải Chọn A 1 Đặt 2
u  4x  5  u  4x  5  2udu  4dx dx udu . 2 Đổi cận: x  1
  u  1, x  1 u  3 . 1 2 u  5 1 u  2 3 3 u  5
Vậy tích phân x 4x  5dx trở thành . udu du .    4 2 8 1  1 1 Câu 29. Lời giải Chọn C
Ta có F x 1
 ln 2x 1  C ; F   1  2  C  2 2  F x 1
 ln 2x 1  2  F   1 2  ln 3  2 . 2 2 Câu 30. Lời giải Chọn D
Áp dụng công thức nguyên hàm mở rộng F x 1  dx x   C .  1 ln 2 1 2x 1 2  e 1 3 1  e 1 3 Mà F   ln 2
1  C   C 1.      2  2 2  2  2 Câu 31. Lời giải Chọn B u   x du dx Đặt    .
 dv  ex dxv  ex 2 2
Khi đó  ex  ex I x dx 2e e ex    2 2 2
 2e  e e  e  e .  2 2 1 1 1 Câu 32. Lời giải Chọn C
Đặt u x  du  dx và dv  cos d
x x v  sinx . I x cos d x x x x x x x x C .  sin sin xd  sin cos Câu 33. Lời giải    
a b     2    13 . 0 2 . 3 .1  
. Suy ra a và b không vuông góc. 3 3     a  3
b . Suy ra a và b cùng phương.     . a c  0.3   2  . 3     3
 .2  0 . Suy ra a và c vuông góc.   2   . b c  0.3  . 3
  1.2  0 . Suy ra b và c vuông góc. 3 Câu 34. Lời giải Chọn D
dx  2udu
Đặt u x 1 , u  0 nên 2
u x 1   . 2 x u 1 x  3 2 u 1 3 Khi đó dx  .2udu 2
 2 u  4 du .      x 1 u Câu 35. Lời giải Chọn D  Ta có: AB   1
 ;2;2 và mặt phẳng Q có véc tơ pháp tuyến là n   Q 2;1; 1.    
Mặt phẳng P nhận hai véc tơ AB và n là cặp véc tơ chỉ phương nên có véc tơ pháp tuyến Q  là n   4  ;3; 5   .
Do vậy đến mặt phẳng P có phương trình là 4
 x  0  3 y  
1  5 z  2  0 hay
4x  3y  5z  7  0 . Vậy d I  P 7 7 2 ;    .  5 2 10 PHẦN II: TỰ LUẬN Câu 36. Lời giải Học sinh tự giải. Câu 37. Lời giải 
d đi qua điểm A2;2;2 và có VTCP u 2;1;3 1   1 
d đi qua điểm B 1;2;  1 và có VTCP u 2; 1  ;4 2   2
Do  song song với hai đường thẳng d , d nên vectơ pháp tuyến của  là 1 2   
n  u ,u   7; 2  ; 4 
:7x  2y  4z d  0 1 2   suy ra phương trình .   d  2 d  3
Do  cách đều hai đường thẳng nên d  ,
A   d B,   2 2 2 2 2 2 7  2  4 7  2  4
d  2  d  3  1   d
d  2  d  3 2
suy ra phương trình  1
: 7x  2y  4z   0  14x  4y  8z 1  0 . 2
S a b c  2 . Câu 38. Lời giải f  x
  f x.x f  xx x f x     dx  dx  
  f x 2 ln  x 1  C 2 x 1 f x 2 x 1 f x 2 x 1   2 x 1 C f x e    
. Vì f 0  e nên C  0 . Vậy f x 2 x 1 e    f   2 3  e . Câu 39. Lời giải 1 1 1 3 Ta có f
 2x 1dx  4  f
 2x 1d2x 1  4  f
 tdt  8 2 0 0 1 u   x 1  du  dx  Đặt    khi đó dv f   xdxv f  x 3 3 3 3
x 1 f xdx  x 1 f (x)  f
 xdx  2 f (3) f
 xdx  2.108 12. 1 1 1 1
TOÁN 185 NGUYỄN LỘ TRẠCH
LUYỆN THI THPT QUỐC GIA NĂM 2020 Chuyên đề: Mã đề thi
Họ và tên:………………………………….Lớp:………….......……..……… 006 Mã đề [006] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 B A C B B C C B C A D A C A D D A D 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 A B C C B B C D A D D B A D A C B
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN Câu 1. Lời giải Chọn B
Biến đổi phương trình mặt cầu thành  x  2   y  2   z  2 2 1 2  16 . Vậy R  4 . Câu 2. Lời giải Chọn A Câu 3. Lời giải Chọn C x
Ta có theo bảng nguyên hàm cơ bản thì a x a dx   C .  ln a Câu 4. Lời giải Chọn B       a =(3;2; ) 1 , b =(-2;0; )
1 Þ a +b =(1;2;2) Þ a +b = 1+ 4+ 4 = 3. Câu 5. Lời giải 2 2 1 1 2   1 Ta có
dx e dx  e  .   x x x 1 x e e 1 1 2 Câu 6. Lời giải Chọn C 8 dx 8 
 ln x 1  ln 9  ln 5 . 4 4 x  1 Câu 7. Lời giải Chọn C (P) 
có vecto pháp tuyến là n =(3;2;- ) 1 . Câu 8. Lời giải Chọn B 1 Đặt 3 2
y x mx  m  2 x  2018 . 3
Đổi cận, thay vào ta được m  1  . Câu 9. Lời giải Chọn C x a Vì x a dx   C .  ln a Câu 10. Lời giải Chọn A cos3x
Ta có F x  f
 xdx  6xsin3x 2 dx  3x   C . 3 2 cos3.0 2 Theo đề F 0 2   3.0 
C   C 1. 3 3 3 cos3x Vậy F x 2  3x  1. 3 Câu 11. Lời giải Chọn D 2 u 1 Đặt 2
u  1 2x u  1 2x x  ; d u u  d . x 2
Đổi cận: x  0  u  1; x  4  u  3 3 5 3 3 1 1  u u  Suy ra 2 I u
  2u  1du    .  4 4  5 3 1  1 Câu 12. Lời giải. Chọn A b
Ta có : f '(x)dx f (b)  f (a)  3 5  f (a)  5  5 3 . a Câu 13. Lời giải Chọn C
Đặt    5    1 x F x x
e dx  5   1 . x  5 ex x e
dx  5 1 .ex  5.ex x
C  5  4ex xC .   
Vì F 0  3  4
  C  3  C  7 . Khi đó:    5  4 x F x x e  7 . Vậy F  
1  5.1 4.e  7  e  7 . Câu 14. Lời giải Chọn Ax  2 1 x a2 2 2
Ta có : F x  f
 xdx Fx  f x    a  1. 2 2 x x u   xu x
Do đó : g x  x cos d x x . Đặt :  d d    dv  cos d x xv  sin x
g x  xsin x  sin d
x x x sin x  cos x C .  Câu 15. Lời giải Chọn D d x x 1 d  2 7 7 x   1 7 1 1 1 2 
 ln x 1  ln 2  ln 5 .   2 2 2 x 1 2 x 1 2 2 2 2 2 1 1 1
Suy ra a  ;b    2a b  . 2 2 2 Câu 16. Lời giải Chọn D  1      du  d ln 3 x u x  Đặt x  3    .
dv x 1 1 2
v x x  2 1 2 5   1  5 x x 2 2 I x x        x   2 ln 3  dx  5 5 35 1 x 9 9 x 3 3     2  4 x  3 ln 2 dx dx   4 2 2 x  3 x  3 4 4 35 1  9   ln 2   3  9ln 2    1 3ln 2 2 2  2  19 10ln 2  . 4 Câu 17. Lời giải Chọn A Ta có: 3 I x 1dx  Đặt: 3 t x 1 3  t x 1 2
 3t dt  dx 2  3 3 3
I t.3t dt
t t t C  3 3 d  4  x  4 3
1  C   x   3 1 x 1  C 4 4 4 3
Vậy F x   x   3 1 x 1  C 4 Câu 18. Lời giải Chọn D x x
Ta có y  sin 4x  sin 2x F x cos 4 cos 2   
C , vì F 0  1 0 nên C   . 4 2 4 x x
Nên F x cos 2 cos 4 1    . 2 4 4 Câu 19. Lời giải Chọn A 3 3 dx 1  1 1    1 dx    
ln x  2  ln x  4 3 x  2 x  4
2  x  2 x  4  0 2 0    0 1       1
ln 5 ln 2 ln 7 ln 4  ln 2  ln 5  ln 7. 2 2 1 1 1
Vậy a  ;b  ;c    2a  3b c  3. 2 2 2 Câu 20. Lời giải Chọn B x 6 3 3  x  Đặt t  1
. Ta có dt  dx  dx  2dt f
dx f (t).2dt  2 f (t)dt  24 .      2 2  2  2 1 1 Câu 21. Lời giải Cách 1.  1 du  dx u   ln(x 1)  x 1 Đặt    2 dv  d x x xv   2 Khi đó 1 I  . x ln  x    1 dx 0 1 2 1 2 x x  ln  x   1  dx  2 2 x 1 0 0   1 2 1 2 x      x   1 x 1 1 ln 1    dx  2
2  x 1 x 1 0 0  1 2 1 x     x   1 1 ln 1  x 1 dx   2 2  x 1 0 0 1 2 ln 2 1  x  
   x  x   1 ln 1   . 2 2  2  4 0 Cách 2.  1 du  dx u   ln(x 1)  x 1 Đặt    2 dv  d x x x 1 v   2 Khi đó 1 1 1 2 1 x 1 x 1 2 1  x  1 I  . x ln  x    1 dx  ln  x   1  dx     x  .   2 2 2  2 4 0  0 0 0 Câu 22. Lời giải Chọn C
Ta có F x  sin d
x x  cosx C . 
Đồ thị hàm số y F x đi qua điểm M 0; 
1  1  cos0  C C  2 .  F x  cosx  2    F  2 .    2  Câu 23. Lời giải. Chọn B
Vì mặt cầu S  có tâm thuộc mặt phẳng Oxy nên gọi tọa độ tâm của mặt cầu S  là: I  ; a  ; b 0 .
Phương trình mặt cầu S  có dạng: 2 2 2
x y z ax by d   2 2 2 2
0, a b d  0 .
2a  4b d  21  0
2a  4b d  2  1 a  2 Vì mặt cầu    
S  đi qua A , B , C nên: 2a  6b d 11  0  2a  6b d  1  1  b   1  .
4a 4b d 17 0 4a 4b d 17          d  2  1     I  2
 ;1;0 và bán kính mặt cầu là: R IA    2    2    2 1 2 2 1 4 0  26 . Bán kính 2 2 2
R a b c d  4 1 21  26 Câu 24. Lời giải Chọn B x x 2 3 Ta có: f
 xdx  x  2 2 1 x e dx e C . 4 2x  3 x 1 Do F   3
0    C  0 F x 2  e F   2 1   e . 4 4 4 Câu 25. Lời giải Chọn C 2 3x   2 1 dx 1  1  Đặt I   3  dx   2  
3x x ln x 3x  ln x x  1 1  1 
Đặt t  3x  ln x  dt  3  dx    x
Đổi cận: x  1 t  3
x  2  t  6  ln 2 . 6ln 2 dt  ln 2  Khi đó, 6ln 2 I   ln t  ln 
6 ln 2ln3  ln 2 3   t  3  3
Suy ra a  2 , b  2 , c  3. Vậy a b c  7 . Câu 26. Lời giải Ta có: 2 2 2 2 2  f x 2
 3x dx  10   f x 2
dx  3x dx  10 
  f x 2
dx  10  3x d  x 0 0 0 0 0 2 2
  f x 2 3 dx  0 1  x
  f xdx 10 8  2. 0 0 0 Câu 27. Lời giải      . u v 2 1 2m 1 + u v    u v 2 , 45 cos ,          2 3 m   1  1 2m 2 u . v 2 2 6. 1 m 2  1 1   2m  0 m      2  m  2  6 . 2 2 3
m  3  1 4m  4m 2
m 4m2  0 Câu 28. Lời giải Chọn D 3 3 3 3 dx 2 Ta có I   
 x1 xdx xx  x x x 1  x 3  1 1 0 0  1 1 2  I       14 4 8 2 2 3 3 1   2 3  2 . 3 3 3 14 4 16 Do đó a
, b  2, c     P  . 3 3 3 Câu 29. Lời giải Chọn D
Gọi P là mặt phẳng trung trực của đoạn thẳng AB .  
Véc tơ pháp tuyến của P là n AB   6  ;2;2 P   
P đi qua trung điểm M của AB . Tọa độ trung điểm M 1;1;2
Vậy phương trình trung trực của đoạn thẳng AB là: P : 3x y z  0 . Câu 30. Lời giải Chọn B Ta có   AB    2 2 2 2 1 2  2  9 , AC    2 2 2 2 3
4  6  61, AC.AB  1.3   2   4    2.6  23. 2      
BC   AC AB2 2 2
AC AB  2.AC.AB  61 9  2.23  24 .
Áp dụng công thức đường trung tuyến ta có: 2 2 2 AB AC BC  2 AM   9 61 24    29 . 2 4 2 4 Vậy AM  29 . Câu 31. Lời giải Chọn A x
Ta có f x 2
 2 x 3x   12x x  4x    x x x
Nên F x   x x 12 2 12 dx    C . ln12 3 Câu 32. Lời giải Chọn D   x  2  t
Phương trình đường thẳng AB qua A2;2; 2 có VTCP u AB  1; 3;2 : y  2  3t . z  2   2  t
I AB  P  I 2  t;2  3t; 2  2t
I P  2  t  2  3t   2
  2t  2  0  t  2  I 4; 4;2  IA  2 . IB 8 IA d  , A P Cách 2. Ta có 3    2 . IB
d B,P 4 3 Câu 33. Lời giải Chọn A
Ta có: d d I,P  3 .
Mặt cầu S  có tâm I và bán kính 2 2
r d  5  34 . Do đó, chọn D Câu 34. Lời giải Chọn C 3 ln x F x 1 3
.4.ln x ln x    . 4 x Câu 35. Lời giải ChọnA 2.1 2  3m 1 Ta có: d  ;
A P  AB   3 2 2 2 2 1  mm  
m   m   m  2 2 2 3 3 3 5 5 1  m  2 PHẦN II: TỰ LUẬN Câu 36. Lời giải Học sinh tự giải. Câu 37. Lời giải x y z
Giả sử  có phương trình:   1 a, , b c  0 . a b c
Theo giả thiết ta có: c  2a  2b 4 3 12 M 4; 3
 ;12     4 3 6 1     7 1 
 1  a  7  b  7 , c  14 . a b c a a a a x y z
Vậy  :  
 1 hay 2x  2y z 14  0 7 7 14 Câu 38. Lời giải Ta có 1 1 1 1 1 f
  2x1dx 2  f
  2x1dx f 2x1 dx 2  f
 12xdx f 2x1 dx 1    1    . 1  1  1  2 2 1 1 0 Ta có 2 I
f 1 2x dx t  1 2x dt  2  dx I   f t dt 1    1    , đặt thì nên 1  3 2 1 3  f
 tdt  3. 0 2 1 1 1 Ta có I
f 2x 1 dx t  2x 1 dt  2dx I f t dt  1 2    2 1    , đặt thì nên . 0 2 2
Vậy I I I  4 . 1 2 Câu 39. Lời giải 2 f x Ta có: x  2 .
x f x   f
  x  f  
x  1 2 f x   . x   x
1 2 f xf  x  x x x   f   x 2 d d 1 2
x x C , mà f   3 4 1   C
1 2 f x 3 2 3 2  2 4  x x  1   4 1186 f x  3 3     f
 xdx  . 2 45 1
Document Outline

  • 6 DE ON TAP LOP 12 GIUA KY 2 - 2021
  • BTPRO [CD] GIUA KY 2 - LOP 12 - HDG