Bài 1:
Trong các phương án sau, phương án nào KHÔNG phải là định nghĩa của kinh tế lượng? Chọn một đáp án:
a. Kiểm định thực nghiệm các quy luật kinh tế.
b. Kinh tế lượng là ngành khoa học được ra đời để chỉ ra điểm yếu của dữ liệu phi thí nghiệm.
c. Bao gồm việc áp dụng thống kê toán cho các số liệu kinh tế để củng cố về mặt thực nghiệm.
d. Một ngành khoa học xã hội kiểm định các lý thuyết kinh tế. Phản hồi
Sai. Đáp án đúng là: Kinh tế lượng là ngành khoa học được ra đời để chỉ ra điểm yếu của dữ liệu phi thí nghiệm.
Vì: Kinh tế lượng không phải là ngành khoa học ra đời để chỉ ra điểm yếu dữ liệu phi thí nghiệm.
Tham khảo: Bài 1, mục 1.1. Kinh tế lượng là gì?
The correct answer is: Kinh tế lượng là ngành khoa học được ra đời để chỉ ra điểm yếu của dữ liệu phi thí nghiệm. Câu hỏi 2 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Số liệu mảng là dạng dữ liệu Chọn một đáp án:
a. thường bao gồm nhóm kiểm soát và nhóm tác động.
b. là số liệu về nhiều đối tượng trong cùng một khoảng thời gian.
c. giống như dữ liệu chuỗi thời gian.
d. kết hợp giữa số liệu chéo và chuỗi thời gian. Phản hồi
Sai. Đáp án đúng là: kết hợp giữa số liệu chéo và chuỗi thời gian.
Vì: Dữ liệu mảng có chiều thời gian và chiều dữ liệu chéo.
Tham khảo: Bài 1, mục 1.3. Dữ liệu cho nghiên cứu kinh tế lượng.
The correct answer is: kết hợp giữa số liệu chéo và chuỗi thời gian. Câu hỏi 3 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
f(x) là hàm mật độ xác suất của biến ngẫu nhiên liên tục X thì phương án nào sau đây KHÔNG đúng? Chọn một đáp án: a. b. c. d. Phản hồi
Sai. Đáp án đúng là: Vì: , , và
đều là đặc điểm của hàm mật độ xác suất
của biến ngẫu nhiên liên tục. Phương án
là đặc điểm của biến ngẫu nhiên rời rạc.
Tham khảo: Bài 1, mục 1.4.1. Một số khái niệm cơ bản. The correct answer is: Câu hỏi 4 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Nếu Q1 có phân phối c2 với bậc tự do là k1. Q2 có phân phối c2 với bậc tự do là k2. Khi đó:
có phân phối F với bậc tự do là Chọn một đáp án: a. k1 và k2. b. k1 - k2. c. k1 + k2. d. k1 × k2. Phản hồi
Sai. Đáp án đúng là: k1 và k2.
Vì: Theo định nghĩa của phân phối F thì phương án k1 và k2 là đúng.
Tham khảo: Bài 1, mục 1.4.2. Một số hàm phân phối xác suất cơ bản.
The correct answer is: k1 và k2. Câu hỏi 5 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Đồ thị sau đây là đồ thị của phân phối nào? Chọn một đáp án: a. Khi bình phương b. Chuẩn c. F (Fisher) d. t (student) Phản hồi
Sai. Đáp án đúng là: Chuẩn
Vì: Đây là đồ thị của phân phối chuẩn. Điểm cao nhất của đồ thị nằm tại trung bình, đó cũng là trung
vị và mốt của phân phối này. Nhìn vào đồ thị này ta cũng thấy, 68% các giá trị của biến ngẫu nhiên có
phân phối chuẩn nằm trong khoảng (m - s, m + s); 95% các giá trị nằm trong khoảng (m - 2s, m + 2s);
và 99.7% các giá trị nằm trong khoảng (m - 3s, m + 3s).
Tham khảo: Bài 1, mục 1.4.2. Một số hàm phân phối xác suất cơ bản.
The correct answer is: Chuẩn Câu hỏi 6 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Số liệu lạm phát của Việt Nam từ năm 1970 đến năm 2006 là loại số liệu Chọn một đáp án: a. bảng. b. gộp. c. chéo. d. chuỗi thời gian. Phản hồi
Sai. Đáp án đúng là: chuỗi thời gian.
Vì: Đây là số liệu của một biến theo thời gian.
Tham khảo: Bài 1, mục 1.3. Dữ liệu cho nghiên cứu kinh tế lượng.
The correct answer is: chuỗi thời gian. Câu hỏi 7 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Cho phương trình sau:
, với b1 và b2 là hằng số thì var(Y) = ? Chọn một đáp án: a. b. c. d. Phản hồi
Đúng. Đáp án đúng là:
Vì: Áp dụng các tính chất sau của phương sai: var(a) = 0 với a là hằng sốvà , ta có:
Tham khảo: Bài 1, mục 1.4. Ôn tập kiến thức xác suất thống kê: Một số khái niệm cơ bản. The correct answer is: Câu hỏi 8 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Đồ thị sau là đồ thị của phân phối nào? Chọn một đáp án: a. Khi bình phương b. Chuẩn c. F (Fisher) d. t (student) Phản hồi
Sai. Đáp án đúng là: Khi bình phương
Vì: Đây là đồ thị của phân phối khi bình phương. Đồ thị của phân phối khi bình phương là đường cong
không đối xứng, với các bậc tự do k = 2, k = 5, k = 10. Ta thấy khi bậc tự do tăng lên, đồ thị của phân
phối khi bình phương gần đối xứng (dạng hình chuông).
Tham khảo: Bài 1, mục 1.4.2. Một số hàm phân phối xác suất cơ bản.
The correct answer is: Khi bình phương Câu hỏi 9 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi Nếu thì
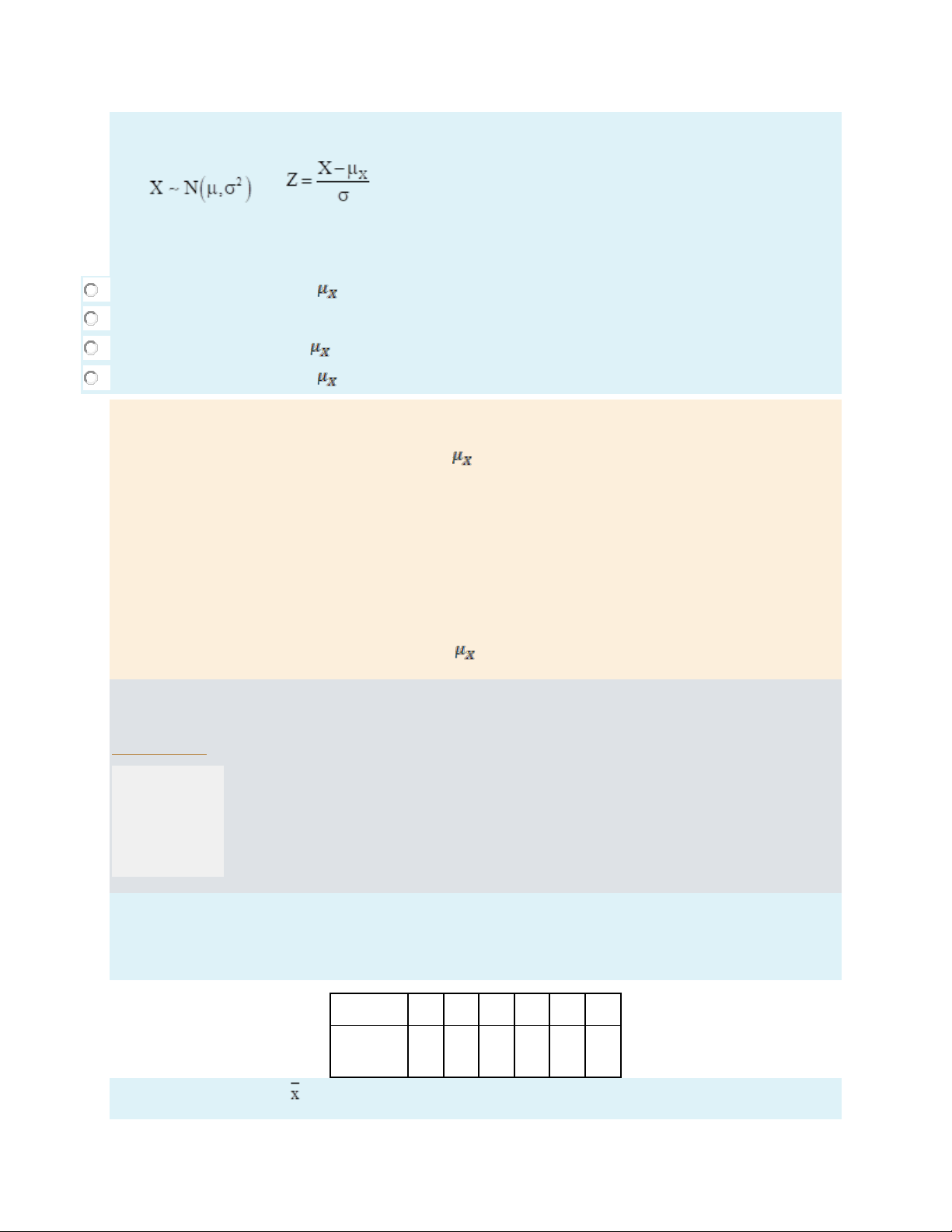
Có phân phối chuẩn hóa. Phương án nào sau đây SAI? Chọn một đáp án:
a. Nếu Z = -1 thì X thấp hơn đúng 1 độ lệch chuẩn. b. Nếu Z = 0 thì X = mX.
c. Nếu Z = 1 thì X thấp hơn đúng 1 độ lệch chuẩn.
d. Nếu Z = 2.5 thì X cao hơn đúng 2.5 độ lệch chuẩn. Phản hồi
Sai. Đáp án đúng là: Nếu Z = 1 thì X thấp hơn đúng 1 độ lệch chuẩn. Vì:
Nếu Z = 0 thì X - mX = 0, như vậy X = mX.
Nếu Z = 2.5 thì X - mX = 2.5s, hay X cao hơn m đúng 2.5 độ lệch chuẩn.
Nếu Z = -1 thì X - mX = -s hay X = mX - s, hay X thấp hơn mX đúng 1 độ lệch chuẩn.
Tham khảo: Bài 1, mục 1.4.2. Một số hàm phân phối xác suất cơ bản.
The correct answer is: Nếu Z = 1 thì X thấp hơn đúng 1 độ lệch chuẩn. Câu hỏi 10 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Ta có bảng số liệu sau đây về số xe đi qua trạm thu phí, biến X (xe/ngày), trong thời gian gần đây như sau: X 5 6 7 8 9 10 Số ngày 10 35 45 36 10 8
Giá trị trung bình mẫu bằng bao nhiêu? Chọn một đáp án: a. 8 b. 7.1736 c. 0 d. 6.1736 Phản hồi
Sai. Đáp án đúng là: 7.1736
Vì: Giá trị trung bình mẫu được tính như sau:
Tham khảo: Bài 1, mục 1.4.3. Suy diễn thống kê. The correct answer is: 7.1736 Câu hỏi 11 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Ta có bảng số liệu sau đây về số xe đi qua trạm thu phí, biến X (xe/ngày), trong thời gian gần đây như sau: X 5 6 7 8 9 10 Số ngày 10 35 45 36 10 8
Hãy ước lượng khoảng tin cậy 95% cho µ, số xe trung bình qua trạm một ngày. Biết giá trị tới hạn c = 1.96 và s = 2. Chọn một đáp án: a. (6.8469; 7.5003) b. (-6.8469; 7.5003) c. (4.8469; 7.5003) d. (5.8469; 7.5003) Phản hồi
Sai. Đáp án đúng là: (6.8469; 7.5003)
Vì: Khoảng tin cậy 95% được tính như sau: Theo đầu bài, ta có:
Như vậy ta tính khoảng tin cậy 95% cho µ như sau:
Tham khảo: Bài 1, mục 1.4.3. Suy diễn thống kê.
The correct answer is: (6.8469; 7.5003) Câu hỏi 12 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Ta gọi biến X là cân nặng của quả dưa hấu. Khi cân thử 15 quả dưa hấu ở một trang trại trồng
trọt, ta tính được
kg và s2 = 0.01. Chủ trang trại này tuyên bố trọng lượng trung bình
của quả dưa hấu là 3.5 kg, thì tuyên bố này có đáng tin với mức ý nghĩa a = 1% không? Ta biết
giả thuyết cần kiểm định là:
H0: m = 3.5 kg; H1: m ≠ 3.5 kg. Thống kê t của kiểm định này là Chọn một đáp án: a. ts = 4.6 b. ts = 18 c. ts = 0.12 d. ts = 1.2 Phản hồi
Sai. Đáp án đúng là: ts = 4.6
Vì: Công thức tính thống kê t như sau: Và theo đầu bài ta có:
; m0 = 3.5; s2 = 0.01; n = 15. Như vậy, ta tính được thống kê t cho kiểm
định của câu hỏi như sau: .
Tham khảo: Bài 1, mục 1.4.3. Suy diễn thống kê.
The correct answer is: ts = 4.6 Câu hỏi 13 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Gọi X là số xe ô tô qua trạm thu phí trong một ngày. Biến X là biến Chọn một đáp án: a. nhị phân.
b. không đủ thông tin để xác định loại biến của biến X. c. liên tục. d. rời rạc. Phản hồi
Sai. Đáp án đúng là: rời rạc.
Vì: Biến X, số xe qua trạm thu phí một ngày là biến rời rạc, biến này có tập hợp các kết quả có thể đếm
được hoặc xác định được.
Tham khảo: Bài 1, mục 1.4.1. Một số khái niệm cơ bản.
The correct answer is: rời rạc. Câu hỏi 14 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Cho a là hằng số, và X là biến số. Như vậy, var(aX) bằng Chọn một đáp án: a. var(a) + var(X). b. a2var(X). c. avar(aX). d. 0. Phản hồi
Sai. Đáp án đúng là: a2var(X).
Vì: Theo tính chất của phương sai:
var(aX) = a2var(X). Với a là hằng số và X là biến số.
Tham khảo: Bài 1, mục 1.4.1. Một số khái niệm cơ bản.
The correct answer is: a2var(X). Câu hỏi 15 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Gọi X là biến chiều cao của dân số Việt Nam. Biến X là biến Chọn một đáp án: a. rời rạc. b. liên tục. c. nhị phân.
d. không đủ thông tin để xác định loại biến của biến X. Phản hồi
Sai. Đáp án đúng là: liên tục.
Vì: Biến chiều cao của dân số Việt Nam là biến liên tục, biến này nhận giá trị một số vô hạn các kết quả.
Tham khảo: Bài 1, mục 1.4.1. Một số khái niệm cơ bản.
The correct answer is: liên tục. Câu hỏi 16 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Các biến nào sau đây là ví dụ của biến ngẫu nhiên liên tục? Chọn một đáp án:
a. Số sinh viên theo học lớp kinh tế lượng năm 2019 tại Đại học Ngoại thương.
b. Nhiệt độ tại Hà Nội ở một thời điểm nào đó.
c. Số cuộc gọi của khách hàng đến đường dây nóng.
d. Số xe qua trạm thu phí một ngày. Phản hồi
Sai. Đáp án đúng là: Nhiệt độ tại Hà Nội ở một thời điểm nào đó.
Vì: Các phương án: “Số cuộc gọi của khách hàng đến đường dây nóng, “số sinh viên theo học lớp kinh tế
lượng năm 2019 tại Đại học Ngoại thương” và “số xe qua trạm thu phí một ngày” đều là ví dụ của biến
ngẫu nhiên rời rạc vì các biến này có tập hợp các kết quả có thể đếm được hoặc xác định. Duy nhất phương
án “nhiệt độ tại Hà Nội ở một thời điểm nào đó” là biến liên tục vì biến nhận kết quả một số vô hạn.
Tham khảo: Bài 1, mục 1.4.1. Một số khái niệm cơ bản.
The correct answer is: Nhiệt độ tại Hà Nội ở một thời điểm nào đó. Câu hỏi 17 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Khi phân tích ảnh hưởng của mức lương cơ bản đến tỷ lệ thất nghiệp tại các tỉnh
thành phố tại Việt Nam từ năm 2000 đến năm 2018 ta cần số liệu Chọn một đáp án: a. chéo.
b. không đủ thông tin để đưa ra câu trả lời. c. mảng. d. thời gian. Phản hồi
Sai. Đáp án đúng là: mảng.
Vì: Dữ liệu này có chiều thời gian là từ năm 2000 đến năm 2018; và chiều dữ liệu chéo là các tỉnh/thành phố tại Việt Nam.
Tham khảo: Bài 1, mục 1.3. Dữ liệu cho nghiên cứu kinh tế lượng.
The correct answer is: mảng. Câu hỏi 18 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi Nếu
nhưng không biết s2, khi đó: Chọn một đáp án:
a. X tuân theo quy luật phân phối Poisson. b. .
c. X tuân theo quy luật phân phối F.
d. X tuân theo quy luật phân phối chuẩn hóa. Phản hồi
Sai. Đáp án đúng là: . Vì: Nếu
nhưng không biết s2, khi đó .
Tham khảo: Bài 1, mục 1.4.2. Một số hàm phân phối xác suất cơ bản. The correct answer is: . Câu hỏi 19 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Phương sai cho biết thông tin gì về biến ngẫu nhiên? Chọn một đáp án:
a. Phương sai đo mức độ biến thiên của hai biến ngẫu nhiên.
b. Phương sai cho biết mức độ tương quan tuyến tính giữa hai biến.
c. Phương sai cho biết mức độ phân tán của phân phối (các giá trị ngẫu nhiên) xung quanh giá trị kỳ vọng.
d. Phương sai cho biết giá trị trung bình của biến ngẫu nhiên. Phản hồi
Sai. Đáp án đúng là: Phương sai cho biết mức độ phân tán của phân phối (các giá trị ngẫu nhiên) xung quanh giá trị kỳ vọng.
Vì: Đây là định nghĩa của phương sai.
Tham khảo: Bài 1, mục 1.4.1. Một số khái niệm cơ bản.
The correct answer is: Phương sai cho biết mức độ phân tán của phân phối (các giá trị ngẫu nhiên)
xung quanh giá trị kỳ vọng. Câu hỏi 20 Không trả lời Đạt điểm 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Hiệp phương sai giữa biến X và biến Y Chọn một đáp án:
a. không phụ thuộc vào đơn vị của biến X và Y.
b. cho biết mức độ tương quan tuyến tính giữa hai biến.
c. là hàm mật độ xác suất của biến X và biến Y.
d. đo mức độ biến thiên cùng nhau của hai biến X và Y. Phản hồi
Sai. Đáp án đúng là: đo mức độ biến thiên cùng nhau của hai biến X và Y.
Vì: Đây là định nghĩa của hiệp phương giữa hai biến ngẫu nhiên.
Tham khảo: Bài 1, mục 1.4.1. Một số khái niệm cơ bản.
The correct answer is: đo mức độ biến thiên cùng nhau của hai biến X và Y. Bài 2:
Trong hàm hồi quy, biến độc lập là Chọn một đáp án:
a. biến số nằm ở vế phải của phương trình.
b. biến được giải thích.
c. biến số nằm ở vế trái của phương trình. d. biến phản ứng. Phản hồi
Đúng. Đáp án đúng là: biến số nằm ở vế phải của phương trình.
Vì: Trong hàm hồi quy, biến độc lập là biến số được cho là có tác động đến biến phụ thuộc, thường ký hiệu
là X và nằm ở vế phải của phương trình. Biến phụ thuộc còn được gọi là biến giải thích hay biến điều khiển.
Tham khảo: Bài 2, mục 2.2. Mô hình hồi quy tuyến tính 2 biến (Mô hình hồi quy đơn).
The correct answer is: biến số nằm ở vế phải của phương trình. Câu hỏi 2 Đúng
Đạt điểm 1,00 trên 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Đâu là dạng ngẫu nhiên của mô hình hồi quy tổng thể hai biến? Chọn một đáp án: a. E(Y|Xi) = β1 + β2Xi + u. b. Y = β1 + β2Xi. c. Y = β1 + β2Xi + u.
d. E(Y|Xi) = β1 + β2X1 + β3X2. Phản hồi
Đúng. Đáp án đúng là: Y = β1 + β2Xi + u.
Vì: Dạng ngẫu nhiên của mô hình hồi quy tổng thể 2 biến là mô hình hồi quy có 1 biến độc lập, 1 biến phụ
thuộc là giá trị thực thế của các quan sát ký hiệu là Y và yếu tố ngẫu nhiên ký hiệu là u.
Tham khảo: Bài 2, mục 2.2. Mô hình hồi quy tuyến tính 2 biến (Mô hình hồi quy đơn).
The correct answer is: Y = β1 + β2Xi + u. Câu hỏi 3 Đúng
Đạt điểm 1,00 trên 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Trong mô hình hồi quy bội
i=1,…, n. Giá trị ước lượng OLS nhận được bằng cách lấy cực tiểu hóa của Chọn một đáp án:
a. tổng bình phương các phần dư .
b. tổng bình phương các phần dư .
c. tổng bình phương các phần dư .
d. tổng giá trị tuyệt đối các phần dư . Phản hồi
Đúng. Đáp án đúng là: tổng bình phương các phần dư .
Vì: Tư tưởng của phương pháp OLS là tìm cực tiểu của tổng bình phương các phần dư Þ min; từ hàm hồi quy mẫu
suy ra được công thức tính ei.
Tham khảo: Bài 2, mục 2.6. Mở rộng cho mô hình hồi quy bội.
The correct answer is: tổng bình phương các phần dư . Câu hỏi 4 Sai
Đạt điểm 0,00 trên 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Trong hàm hồi quy tổng thể
E(Y|Xi) = β1 + β2Xi, β1 và β2 được gọi là Chọn một đáp án: a. sai số ngẫu nhiên. b. hệ số chặn. c. hệ số góc.
d. hệ số của hàm hồi quy. Phản hồi
Sai. Đáp án đúng là: hệ số của hàm hồi quy.
Vì: Trong hàm hồi quy tổng thể, β1 được gọi là hệ số chặn, β2 được gọi là hệ số góc, u được gọi là sai số ngẫu nhiên.
Tham khảo: Bài 2, mục 2.2. Mô hình hồi quy tuyến tính 2 biến (Mô hình hồi quy đơn).
The correct answer is: hệ số của hàm hồi quy. Câu hỏi 5 Đúng
Đạt điểm 1,00 trên 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Giả định mô hình hồi quy đảm bảo được các giả thiết của mô hình hồi quy tuyến
tính cổ điển, khi sử dụng phương pháp OLS để ước lượng, các ước lượng sẽ có tính chất Chọn một đáp án:
a. tuyến tính, không chệch, tốt nhất.
b. phi tuyến tính, không chệch, tốt nhất.
c. phi tuyến tính, chệch, tốt nhất.
d. tuyến tính, chệch, tốt nhất. Phản hồi
Đúng. Đáp án đúng là: tuyến tính, không chệch, tốt nhất.
Vì: Theo định lý Gauss Markov, với điều kiện các giả thiết của mô hình hồi quy tuyến tính cổ điển được đảm
bảo, khi sử dụng phương pháp OLS để ước lượng, các ước lượng sẽ có tính chất là tuyến tính, không chệch và tốt nhất.
Tham khảo: Bài 2, mục 2.3. Ước lượng mô hình hồi quy tuyến tính 2 biến bằng phương pháp bình phương
tối thiểu thông thường OLS (Ordinary Least Square).
The correct answer is: tuyến tính, không chệch, tốt nhất. Câu hỏi 6 Sai
Đạt điểm 0,00 trên 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Phân tích hồi quy nhằm mục đích gì? Chọn một đáp án:
a. Ước lượng, dự báo giá trị trung bình của các biến độc lập.
b. Ước lượng mối quan hệ tất định giữa các biến số.
c. Ước lượng, dự báo giá trị trung bình của biến phụ thuộc.
d. Dự báo mối quan hệ giữa các biến số. Phản hồi
Sai. Đáp án đúng là: Ước lượng, dự báo giá trị trung bình của biến phụ thuộc.
Vì: Phân tích hồi quy nhằm mục đích ước lượng, dự báo giá trị trung bình của biến phụ thuộc khi đã biết
giá trị của các biến độc lập.
Tham khảo: Bài 2, mục 2.1. Phân tích hồi quy.
The correct answer is: Ước lượng, dự báo giá trị trung bình của biến phụ thuộc. Câu hỏi 7 Đúng
Đạt điểm 1,00 trên 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Ưu điểm chính của việc sử dụng phân tích hồi quy bội là Chọn một đáp án:
a. Giả định rằng các phần dư được tạo ra từ phân phối chuẩn.
b. Cung cấp các ước tính định lượng về một đơn vị thay đổi của biến độc lập X ảnh hưởng thế nào tới biến phụ thuộc Y.
c. Tính toán giá trị p-value để đánh giá tính có ý nghĩa của kết quả.
d. Cung cấp một thước đo về mức độ phù hợp của mô hình. Phản hồi
Đúng. Đáp án đúng là: Cung cấp các ước tính định lượng về một đơn vị thay đổi của biến độc lập X ảnh
hưởng thế nào tới biến phụ thuộc Y.
Vì: Khác với quan hệ thống kê hay quan hệ tương quan, phân tích hồi quy cho phép đo lường/dự báo một
cách tường minh ảnh hưởng của (nhiều) biến độc lập lên biến phụ thuộc.
Tham khảo: Bài 2, mục 2.1. Phân tích hồi quy.
The correct answer is: Cung cấp các ước tính định lượng về một đơn vị thay đổi của biến độc lập X
ảnh hưởng thế nào tới biến phụ thuộc Y. Câu hỏi 8 Đúng
Đạt điểm 1,00 trên 1,00 [Góp ý - Báo lỗi] Đặt cờ Đoạn văn câu hỏi
Sai số ngẫu nhiên (ký hiệu là u) trong hàm hồi quy tổng thể là đại diện cho những nhân tố Chọn một đáp án:
a. không ảnh hưởng đến biến phụ thuộc.
b. có ảnh hưởng đến biến phụ thuộc nhưng không được đưa vào hàm hồi quy.