BÀI TẬP CÁ NHÂN - KINH TẾ LƯỢNG (HỌC PHẦN KINH TẾ LƯỢNG). Môn Kinh tế lượng | Đại học Văn Hiến.

lOMoAR cPSD| 58833082
HỌC PHẦN : KINH TẾ LƯỢNG
BÀI TẬP CÁ NHÂN – MÔN KINH TẾ LƯỢNG A. Phần bài tập : Câu 1 : βi βi
a) Ta có công thức : t = => Se (❑i¿= Se(βi) t Áp dụng vào bài toán : β0 201,97
- Se(β0¿= t = 743,27 = 0,270789 0 β1 2,33
- Se(β1¿= t = 116,5 = 0,02 1 b)
c) R2=0,9999=99.99% (rất lớn) chứng tỏ mô hình có tính gải thích rất cao. Giải thích
được 99,99% khoảng biến thiên của Y nên mô hình có ý nghãi thống kê và có mức độ
phù hợp rất cao với dữ liệu. d) Kiểm định Câu 2 :
a) Dữ liệu được cho trong bài toán là dữ liệu bảng ( dữ liệu kết hợp )
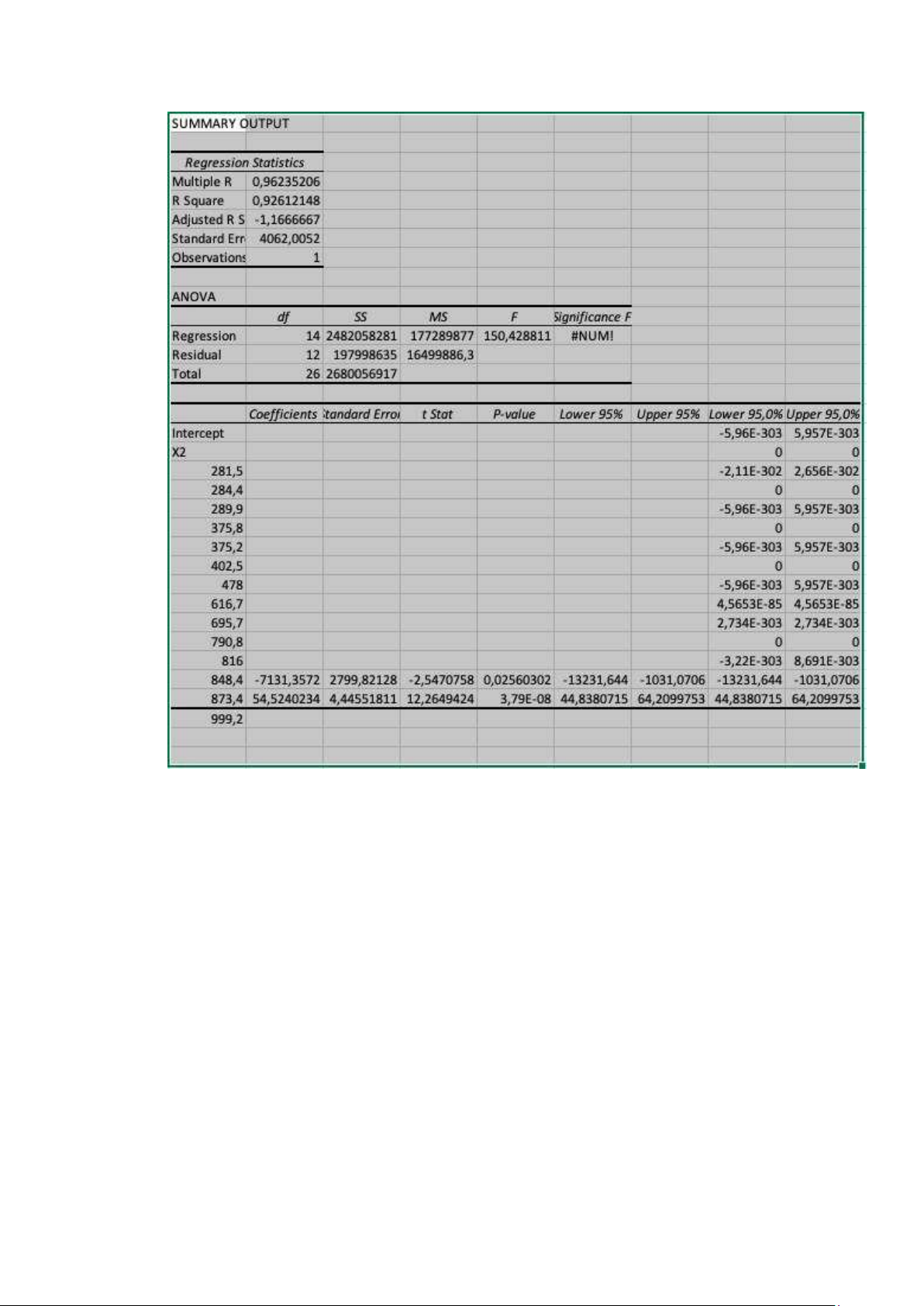
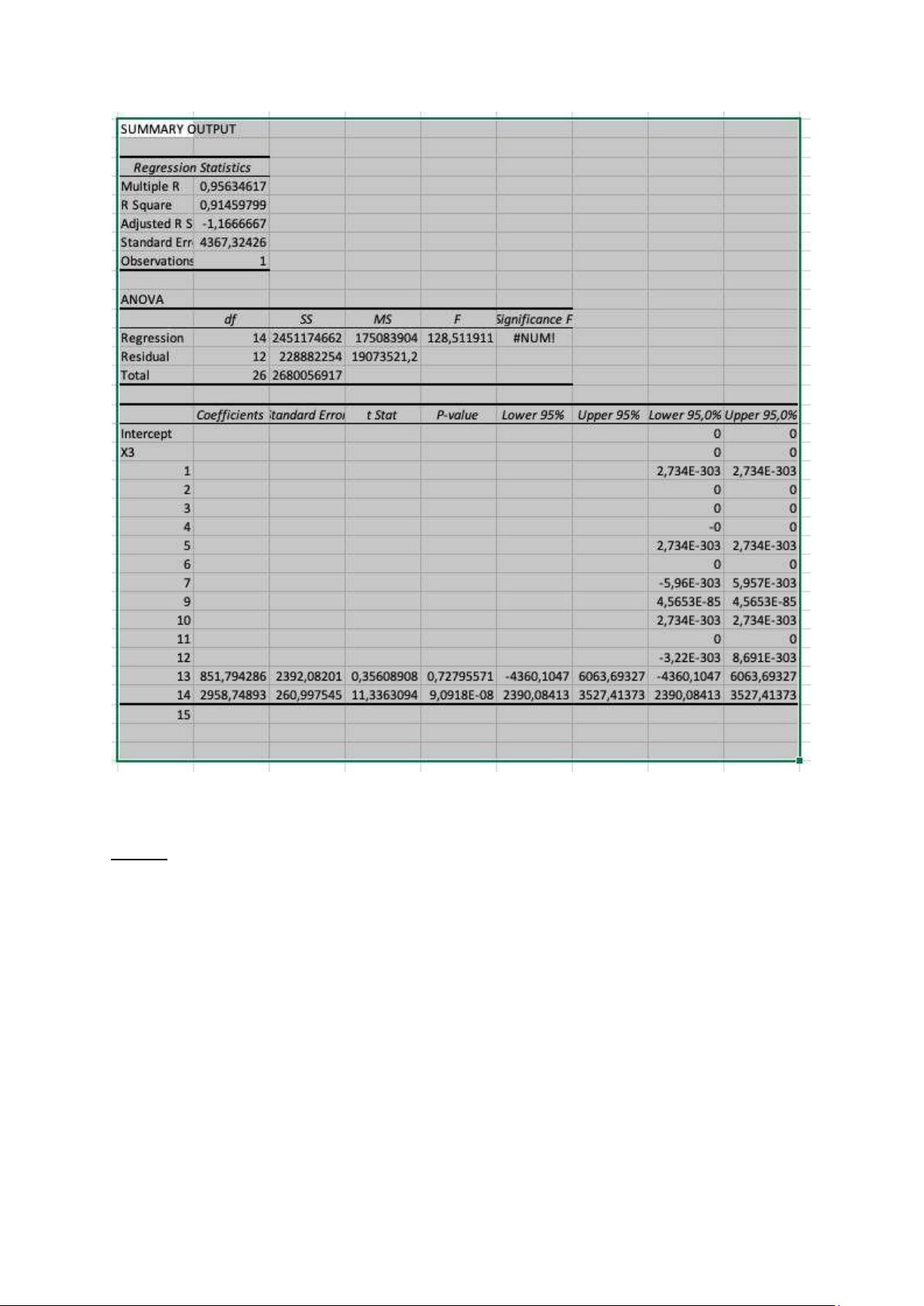
b) Các hệ số hồi quy : lOMoAR cPSD| 5883082 c) d)
e) Kết quả tìm được có ý nghãi thực tế vì trước tiên, hệ số β1, β2 đều mang dấu dương.
Điều này chứng tỏ mô hình có giá trị thực tế.
f) Y = β1+ X. β2 +e
Y = 10,2233503 + 17.1,54822335 + e
Y = 36,5431472 Câu 3 :
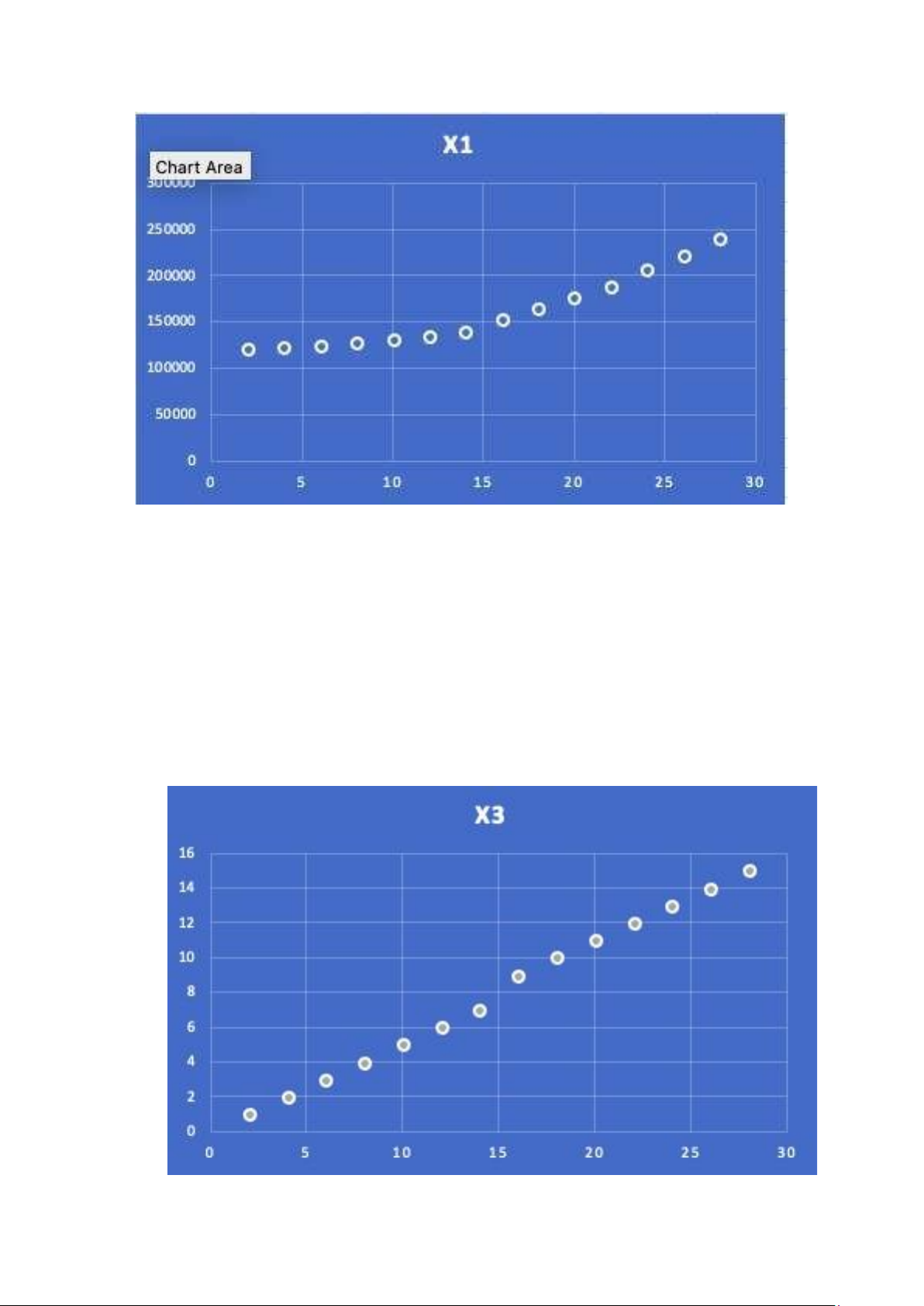
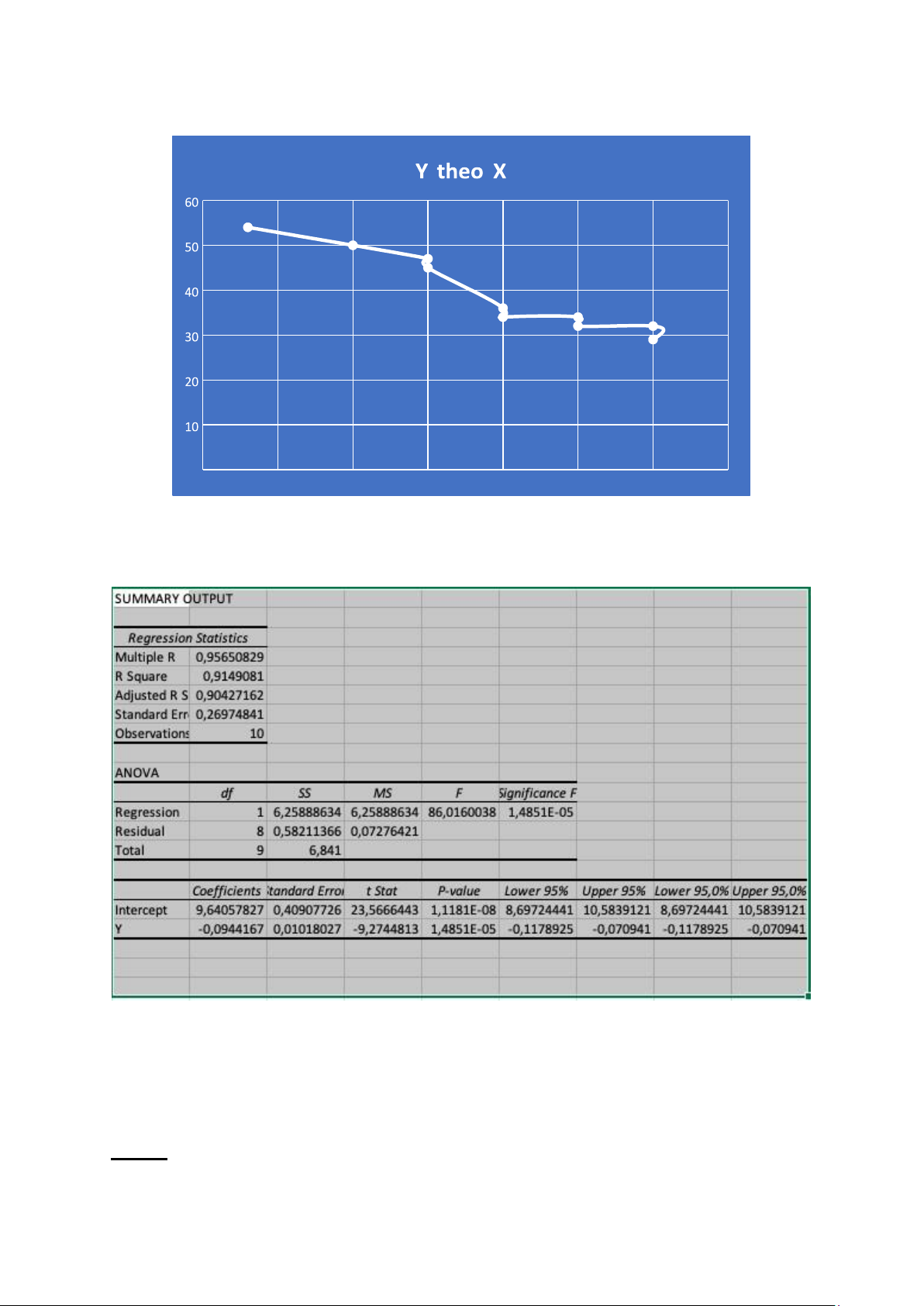
a) – Biểu đồ phân tán của : • Y theo X1 lOMoAR cPSD| 58833082 • Y theo X2 • Y theo X3 lOMoAR cPSD| 5883082 b) • Y=a+bX1+U • Y=a+bX2+U lOMoAR cPSD| 58833082 • Y=a+bX3+U lOMoAR cPSD| 5883082 Câu 4 : lOMoAR cPSD| 58833082 a) 0 4 4 . 5 5 5 . 5 6 6 . 5 7 7 . 5 b)
c) Với số liệu nói trên, ta thấy hệ số β1, β2 đều mang dấu âm. Điều này chứng tỏ mô hình
không có giá trị thực tế, nên Y không phụ thuộc vào X d) B. Phần lý thuyết : Câu 1 : lOMoAR cPSD| 5883082
Để đánh giá phương trình hồi quy tổng thể có ý nghĩa hay không cần thực hiện 2 kiểm định
quan trọng là kiểm định các hệ số hồi quy và kiểm định sự phù hợp của mô hình.
Bởi vì từ kết qủa này có thể sử dụng đồng ý hay bác bỏ một số nhận định (xét về mặt thống kê )
Trong hồi quy đơn biến, thông thường sẽ kiểm định giả thuyết thông kê của cả 2 hệ số này.
Cách thông dụng là kiểm định Student (kiểm định t) và sử dụng khoảng tin cậy
Đòi hỏi phải xác định mức độ tin cậy là bao nhiêu phần trăm (với mức ý nghĩa là , độ tin cậy
sẽ là 1- ). Xác định phương sai của hệ số hồi quy, rồi từ đó tính đến độ lệch chuẩn và trị thống kê t* Câu 2 :
Đối với hồi quy tuyến tính đơn, có thể xác định cỡ mẫu dựa vào những yếu tố : -
Độ tin cậy cần có của dữ liệu. Nghĩa là mức độ chắc chắn rằng các đặc điểm của cỡ
mẫu được chọn phải khái quát được cho đặc điểm tổng thể. -
Sai số mà nghiên cứu có thể chấp nhận được. Đó là độ chính xác chúng ta yêu cầu cho
bất kì ước lượng được thực hiện trên mẫu. -
Các loại kiểm định, phân tích sẽ thực hiện. Một số kỹ thuật thống kê yêu cầu cỡ mẫu
phải đạt một ngưỡng nhất định thì các ước lượng mới có ý nghĩa. -
Kích thước của tổng thể. Mẫu nghiên cứu sẽ cần chiếm một tỷ lệ nhất định so với kích thước của tổng thể. -
Sử dụng mức độ tin cậy, nghĩa là mức độ tin cậy cần thiết càng lớn thì cỡ mẫu càng
lớn (đưa ra yêu cầu độ chính xác không đổi). -
Sử dụng phương sai mục tiêu cho một ước tính được lấy từ mẫu cuối cùng thu được,
nghĩa là nếu cần độ chính xác cao (khoảng tin cậy hẹp) thì điều này có nghĩa là
phương sai mục tiêu thấp của công cụ ước tính. - Tham khảo chỉ số R2 -
Ước tính cỡ mẫu thông qua kiểm định F Câu 3 :
SSR : Tổng bình phương hồi qui – Tổng bình phương phương sai của mô hình n
SSR = ∑(Y^ i¿−Y )2¿ i=1 SSR = SST – SSE Câu 4 :
Dấu của hệ số Beta1 trong phương trình hồi quy tuyến tính cho biết chiều hướng của các mối liên hệ. Câu 5 :