Trắc nghiệm nâng cao hình học tọa độ Oxyz – Đặng Việt Đông Toán 12

Trắc nghiệm nâng cao hình học tọa độ Oxyz – Đặng Việt Đông Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

38 19 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay

TỌA ĐỘ CỦA ĐIỂM VÀ VÉCTƠ TRONG KHÔNG GIAN

A - LÝ THUYẾT CHUNG

1. Véc tơ trong không gian

* Định nghĩa

Trong không gian, vecto là một đoạn thẳng có định hướng tức là đoạn thẳng có quy định thứ tự của hai

đầu

 Chú ý: Các định nghĩa về hai vecto bằng nhau, đối nhau và các phép toán trên các vecto trong

không gian được xác định tương tự như trong mặt phẳng.

2. Vecto đồng phẳng

* Định nghĩa: Ba vecto

, ,

a b c

  

khác



gọi là đồng

phẳng khi giá của chúng cùng song song với một

mặt phẳng.

 Chú ý:



vecto khác



gọi là đồng phẳng khi giá

của chúng cùng song song với một mặt phẳng.

 Các giá của các vecto đồng phẳng có thể

là các đường thẳng chéo nhau.

* Điều kiện để 3 vecto khác



đồng phẳng

Định lý 1:

, ,

a b c

  

đồng phẳng ,m n

  



a mb nc

 

  

* Phân tích một vecto theo ba vecto không đồng phẳng

 Định lý 2: Cho 3 vecto

1 2 3

, ,

e e e

  

không đồng phẳng. Bất kì một vecto



nào trong không gian cũng

có thể phân tích theo ba vecto đó, nghĩa la có một bộ ba số thực





1 2 3

, ,

x x x

duy nhất

1 1 2 2 3 3

a x e x e x e

  

   

 Chú ý: Cho vecto

, ,

a b c

  

khác



, ,

a b c

  

đồng phẳng nếu có ba số thực

, ,

m n p

không đồng thời bằng 0 sao cho:

ma nb pc

  

  

, ,

a b c

  

không đồng phẳng nếu từ

0 0

ma nb pc m n p

      

  

3. Tọa độ của vecto

Trong không gian xét hệ trục

Ox ,

có trục

vuông góc với trục

tại O, và trục

vuông góc

với mặt phẳng





tại O. Các vecto đơn vị trên từng trục

Ox, ,

Oy Oz

lần lượt là













1;0;0 , 0;1;0 , 0;0;1 .

i j k  

  





1 2 3 1 2 3

; ;

a a a a a a i a j a k

    

    





, ,

M M M M M M

M x y z OM x i y j z k

   

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay

c) Cho









, , , , ,

A A A B B B

A x y z B x y z

ta có:





; ;

B A B A B A

AB x x y y z z

   



và

     

2 2 2

B A B A B A

AB x x y y z z     

d) M là trung điểm

thì

; ;

2 2 2

B A B A B A

x x y y z z

  

 

 

 

e) Cho





1 2 3

; ;

a a a a





và





1 2 3

; ;

b b b b





ta có:



1 1

2 2

3 3

a b

a b a b

a b







  









 







1 1 2 2 3 3

; ;

a b a b a b a b

    

 







1 2 3

. ; ;

k a ka ka ka











1 1 2 2 3 3

. . cos ;

a b a b a b a b a b a b

   

     



2 2 2

1 2 3

a a a a

  









1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

cos cos ;

a b a b a b

a b

a a a b b b

 

 

   

 



(với

0, 0

a b

 

   

)





và



vuông góc:

1 1 2 2 3 3

. 0 0

a b a b a b a b

     

 





và



cùng phương:

1 1

2 2

3 3

a kb

k R a kb a kb

a kb







     









 

4. Tích có hướng và ứng dụng

Tích có hướng của





1 2 3

; ;

a a a a





và





1 2 3

; ;

b b b b





là:

 

2 3 3 1 1 2

2 3 3 2 3 1 1 3 1 2 2 1

2 3 3 1 1 2

, ; ; ; ;

a a a a a a

a b a b a b a b a b a b a b

b b b b b b

 

 

    

 

 

 

 

a. Tính chất:

 , , ,

a b a a b b

   

 

   

     







, . sin ,

a b a b a b

 



 

     





và



cùng phương:

, 0

a b

 



 

  



, ,

a b c

  

đồng phẳng

, . 0

a b c

 

 

 

  

b. Các ứng dụng tích có hướng

 Diện tích tam giác:

ABC

S AB AC

 



 

 

 Thể tích tứ diện

, .

ABCD

V AB AC AD

 



 

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay

 Thể tích khối hộp:

. ' ' ' '

, .AA'

ABCD A B C D

V AB AD

 



 

  

5. Một số kiến thức khác

Nếu

chia đoạn AB theo tỉ số





k MA kMB



 

thì ta có:

; ;

1 1 1

A B A B A B

M M M

x kx y ky z kz

x y z

k k k

  

  

  

với



G là trọng tâm tam giác ; ;

3 3 3

A B C A B C A B C

G G G

x x x y y y z z z

ABC x y z

     

   

G là tr

ọng tâm tứ diện

ABCD GA GB GC GD

    

    

B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho 4 điểm

















1,2,3 ; 2,2,3 ; 1,3,3 ; 1,2,4 .

S A B C

SABC

là:

A. Tứ diện. B. Hình chóp đều.

C. Tứ diện đều. D. Hình thang vuông

Hướng dẫn giải:













1;1;0 ; 0; 1;1 ; 1;0;1

AB BC AC     

  

AB BC CA ABC

     là tam giác đều













1;0;0 ; 0;1;0 ; 0;0;1 1

SA SB SC SA SB SC

      

  

 

1 0 0

, , 0 1 0 1 0

0 0 1

D SA SB SC

  

Hay ta có thể tính

; 0

SA SB SC

 



 

   

, ,

SA SB SC



  

không đồng phẳng.

SABC



là hình chóp đều, đỉnh S.

Chọn B.

Câu 2: Cho bốn điểm

















1,2,3 ; 2,2,3 ; 1,3,3 ; 1,2,4 .

S A B C Gọi

, ,

M N P

lần lượt là trung điểm

của

BC CA

và

AB.

Khi đó

SMNP

là:

A. Hình chóp. B. Hình chóp đều. C. Tứ diện đều. D. Tam diện vuông

Hướng dẫn giải:

Tam giác:

ABC

có

AB BC CA  

MN NP PM   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay













1;0;0 ; 0;1;0 ; 0;0;1

. 0

SA SB SC

SA SB SA SB

  

   

  

 

Tương tự ,

SA SC SB SC

 

Các tam giác vuông , ,

SAB SBC SCA

vuông

tại S, có các trung tuyến:

2 2

SP SM SN MN NP PM

      

Ta có:













; ;

SP SAB SM SBC SN SCA

  

, ,

SP SM SN



  

không đồng phẳng

SMNP



là tứ diện đều.

Chọn C.

Câu 3: Cho bốn điểm

















1,2,3 ; 2,2,3 ; 1,3,3 ; 1,2,4 .

S A B C Xác định tọa độ trọng tâm G của

hình chóp

SABC





5,9,13

. B.

5 13

,3,

3 3

 

 

 

. C.

7 9

1, ,

4 4

 

 

 

. D.

5 9 13

, ,

4 4 4

 

 

 

Hướng dẫn giải:

Ta có 4

GS GA GB GC OG OA OB OC OS

       

        

 

1 5

2 1 1 1

4 4

1 9

2 3 2 2

4 4

1 13

3 3 4 3

4 4

G y



    



     





    





Chọn D.

Câu 4: Cho 3 vectơ













1,1, 2 ; 2, 1,2 ; 2,3, 2 .

a b c

      

  

Xác định vec tơ



thỏa mãn

. 4; . 5; . 7.

a d b d c d

  

     





3,6,5

. B.





3,6, 5

 

. C.

3 5

,6,

2 2

 

 

 

. D.

3,6,

 

 

 

Hướng dẫn giải:

 

. 4

2 4 1

. 5 2 2 5 2

2 3 2 7 3

. 7

a d

x y z

b d x y z

x y z

c d





  



    

 

 

   



 



 









1 2 :3 9 3

x x

   

và









2 3 : 2 12 6

y y

   

     

1 1 5 5

1 : 4 3 6 4 3;6;

2 2 2 2

z x y d

 

        

 

 



Chọn D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay

Câu 5: Trong không gian Oxyz, cho điểm













2;0; 2 , 3; 1; 4 , 2;2;0

   A B C . Điểm D trong mặt

phẳng (Oyz) có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách

từ D đến mặt phẳng (Oxy) bằng 1 có thể là:





0; 3; 1

 

D B.





0;2; 1



D C.





0;1; 1



D D.





0;3; 1



Hướng dẫn giải:









0; ;

 

D Oyz D b c

với



Theo giả thiết:

 





 

, 1 1 0; ; 1



     

 



 

 



c loai

d D Oxy c D b

Ta có













1; 1; 2 , 4;2;2 , 2; ;1

      

  

AB AC AD b

Suy ra

 

, 2;6; 2 , . 6 6

   

    

   

    

AB AC AB AC AD b

Cũng theo giả thiết, ta có:

, . 1 2





 

    



 

 



  

ABCD

V AB AC AD b

Chọn D.

Câu 6:

Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm





1;2;0

A ,





3;4;1

B ,





1;3;2

D  . Tìm

tọa độ điểm

sao cho

ABCD

là hình thang có hai cạnh đáy

và có góc

bằng

45 .







5;9;5

C . B.





1;5;3

C .





3;1;1

C  . D.





3;7;4

C .

Hướng dẫn giải:

Chọn D.

Cách 1.

(2;2;1)

AB 



Đường thẳng

có phương trình là

1 2

: 3 2

x t

CD y t

z t

  





 





 



Suy ra





1 2 ;3 2 ;2

C t t t

   

;

(4 2 ;1 2 ; 1 ),

CB t t t

    



( 2 ; 2 ; )

CD t t t

   



Ta có



2 2 2 2 2 2

(4 2 )( 2 ) (1 2 )( 2 ) ( 1 )( )

cos

(4 2 ) (1 2 ) ( 1 ) ( 2 ) ( 2 ) ( )

t t t t t t

BCD

t t t t t t

        



          

Hay

2 2 2 2 2 2

(4 2 )( 2 ) (1 2 )( 2 ) ( 1 )( ) 2

(4 2 ) (1 2 ) ( 1 ) ( 2 ) ( 2 ) ( )

t t t t t t

        



          

(1).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay

AO

Lần lượt thay

bằng

3;1; 1;2



(tham số

tương ứng với toạ độ điểm

ở các phương án A,

B, C, D), ta thấy



thoả (1).

Cách 2.

Ta có

(2;2;1), ( 2;1;2)

AB AD  

 

. Suy ra

AB CD



 

và

AB AD



. Theo giả thiết, suy

DC AB



 

. Kí hiệu

( ; ; )

C a b c

, ta có

( 1; 3; 2)

DC a b c

   



2 (4;4;2)

AB 



. Từ

đó

(3;7;4)

C .

Câu 7: Trong không gian với hệ tọa độ

Oxy

, cho hình hộp chữ nhật .

ABCD A B C D

   

có

trùng

với gốc tọa độ

, các đỉnh

( ;0;0)

B m ,

(0; ;0)

D m ,

(0;0; )

A n



với

, 0

m n



và

m n

 

. Gọi

là trung điểm của cạnh



. Khi đó thể tích tứ diện

BDA M



đạt giá trị lớn nhất bằng

245

108

. B.

. C.

. D.

Hướng dẫn giải:

Tọa độ điểm

( ; ;0), ( ; ;; ), ; ;

C m m C m m n M m m

 



 

 

   

;0; , ; ;0 , 0; ;

BA m n BD m m BM m

 



    

 

 

  





, ; ;

BA BD mn mn m

 



   

 

 

, .

6 4

BDA M

m n

V BA BD BM



 



 

 

  

Ta có

2 512 256

. .(2 )

3 27 27

m m n

m m n m n

 

 

   

 

 

BDA M



 

Chọn C.

Câu 8: Cho ba điểm













3;1;0 , 0; 1;0 , 0;0; 6

A B C

 

. Nếu tam giác

A B C

  

thỏa mãn hệ thức

A A B B C C

  

  

   

thì có tọa độ trọng tâm là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay





1;0; 2 .







2; 3;0 .

 C.





3; 2;0 .

 D.





3; 2;1 .



Hướng dẫn giải:

Chọn A

* Cách diễn đạt thứ nhất:

Gọi G, G’ theo thứ tự lần lượt là trọng tâm tam giác ABC, A’B’C’. Với mọi điểm T trong

không gian có:

 













1 : ' ' ' 0 ' ' ' 0

A A B B C C TA TA TB TB TC TC

         

          





' ' ' 2

TA TB TC TA TB TC     

     

Hệ thức (2) chứng tỏ. Nếu

T G



tức là

TA TB TC

  

   

thì ta cũng có

' ' ' 0

TA TB TC

  

   

hay

T G



hay (1) là hệ thức cần và đủ để hai tam giác ABC, A’B’C’ có cùng trọng tâm.

Ta có tọa độ của G là:

 

3 0 0 1 1 0 0 0 6

; ; 1;0; 2

3 3 3

     

 

  

 

 

Đó cũng là tọa độ trọng tâm G’ của

' ' '

A B C



* Cách diễn đạt thứ hai:

Ta có:

' ' ' 0

AA BB CC

  

   

(1)













' ' ' ' ' ' ' ' ' 0

A G G G GA B G G G GB C G G G GC

         

       

  









' ' ' ' ' ' 3 ' 0

GA GB GC A G B G C G G G

       

       

(2)

Nếu G, G’ theo thứ tự lần lượt là trọng tâm tam giác ABC, A’B’C’ nghĩa là

' ' ' ' ' '

GA GB GC A G B G C G

    

     

thì





2 ' 0 '

G G G G

   

 

Tóm lại (1) là hệ thức cần và đủ để hai tam giác ABC, A’B’C’ có cùng trọng tâm.

Ta có tọa độ của G là:

 

3 0 0 1 1 0 0 0 6

; ; 1;0; 2

3 3 3

     

 

  

 

 

. Đó cũng là tọa độ trọng

tâm G’ của

' ' '

A B C



Câu 9: Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm













3;0;0 , , ,0 , 0;0;

M N m n P p

Biết



13, 60

MN MON  , thể tích tứ diện

OMNP

bằng 3. Giá trị của biểu thức

2 2

A m n p

  

bằng

29.

27.

28.

30.

Hướng dẫn giải:









3;0;0 , ; ;0 . 3

OM ON m n OM ON m

   

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay

2 2

. 1 1

. . cos60

2 2

OM ON m

OM ON OM ON

OM ON

m n

    



 

   

 

 

3 13

MN m n   

Suy ra

2; 2 3

m n  

, . 6 3 6 3 3 3

OM ON OP p V p p

 

      

 

  

Vậy

2 2.12 3 29.

   

Câu 10: Cho hình chóp .

S ABCD

biết

















2;2;6 , 3;1;8 , 1;0;7 , 1;2;3

A B C D   . Gọi

là trung

điểm của





SH ABCD

 . Để khối chóp .

S ABCD

có thể tích bằng

(đvtt) thì có hai

điểm

1 2

S S

thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm

của

1 2

S S





0; 1; 3

 

. B.





1;0;3

I C.





0;1;3

I . D.





1;0; 3 .

 

Hướng dẫn giải:

Ta có

   

1 3 3

1; 1;2 , 1; 2;1 ,

2 2

ABC

AB AC S AB AC

 

       

 

   









2; 2;4 , 1; 1;2 2.

DC AB DC AB

       

   

ABCD



là hình thang và

9 3

ABCD ABC

S S 

Vì

. 3 3

S ABCD ABCD

V SH S SH  

Lại có

là trung điểm của





0;1;5

CD H

Gọi

       

; ; ;1 ;5 , 3;3;3 3 ;3 ;3

S a b c SH a b c SH k AB AC k k k k

 

        

 

   

Suy ra

2 2 2

3 3 9 9 9 1

k k k k

     

+) Với









1 3;3;3 3; 2;2

k SH S     



+) Với









1 3; 3; 3 3;4;8

k SH S       



Suy ra





0;1;3

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay

Câu 11: Trong không gian với hệ tọa độ

Oxyz

, cho hình vuông

ABCD

(3;0;8)

( 5; 4;0)

 

. Biết

đỉnh

thuộc mặt phẳng (

Oxy

) và có tọa độ là những số nguyên, khi đó

CA CB



 

bằng:

5 10.

6 10.

10 6.

10 5.

Hướng dẫn giải:

Ta có trung điểm

là

( 1; 2;4)

 



và điểm

thuộc mặt phẳng

( )

Oxy

nên

( ; ;0)

A a b

ABCD

là hình vuông



2 2

AB AD

AI BD









 



 



 



2 2 2 2 2

2 2 2

( 3) 8 ( 5) ( 4)

( 1) ( 2) 4 36

a b a b

a b



      







    





2 2

4 2

( 1) (6 2 ) 20

b a

a a

 







   















hoặc





















A(1; 2; 0) hoặc

17 14

; ;0

5 5



 

 

 

(loại). Với

(1;2;0)

A 

( 3; 6;8)

 

Câu 12: Trong không gian với hệ toạ độ

Oxyz

, cho 4 điểm

(2;4; 1)



(1;4; 1)



(2;4;3)

(2;2; 1)



. Biết





; ;

M x y z

, để

2 2 2 2

MA MB MC MD

  

đạt giá trị nhỏ nhất thì

x y z

 

bằng

Hướng dẫn giải:

Gọi

là trọng tâm của

ABCD

ta có:

7 14

; ;0

3 3

 

 

 

Ta có:

2 2 2 2 2 2 2 2 2

MA MB MC MD MG GA GB GC GD

       



2 2 2 2

GA GB GC GD

  

. Dấu bằng xảy ra khi



7 14

; ;0 7

3 3

G x y z

 

   

 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay

PHƯƠNG TRÌNH MẶT PHẲNG NÂNG CAO

A - LÝ THUYẾT CHUNG

1. Định nghĩa

Trong không gian

phương trình dạng

Ax By Cz D

   

với

2 2 2

A B C

  

được gọi là

phương trình tổng quát của mặt phẳng.

 Phương trình mặt phẳng





: 0

P Ax By Cz D

   

với

2 2 2

A B C

  

có vec tơ pháp tuyến là





; ; .

n A B C





 Mặt phẳng





đi qua điểm





0 0 0 0

; ;

M x y z

và nhận vecto





; ; , 0

n A B C n

 

  

làm vecto pháp tuyến

dạng

















0 0 0

: 0.

P A x x B y y C z z

     

 Nếu





có cặp vecto









1 2 3 1 2 3

; ; ; ; ;

a a a a b b b b

 

 

không cùng phương, có giá song song hoặc

nằm trên





Thì vecto pháp tuyến của





được xác định

n a b

 



 

  

2. Các trường hợp riêng của mặt phẳng

Trong không gian

cho mp





: 0,

Ax By Cz D

   



với

2 2 2

A B C

  

Khi đó:





khi và chỉ khi







đi qua gốc tọa độ.



0, 0, 0, 0

A B C D

   

khi và chỉ khi







song song trục

Ox.



0, 0, 0, 0

A B C D

   

khi và chỉ khi







song song mặt phẳng





Ox .



, , , 0.

A B C D



Đặt

, , .

D D D

a b c

A B C

     

Khi đó:

 

: 1

x y c

a b z



  

3. Vị trí tương đối của hai mặt phẳng

Trong không gian

Oxyz

cho





: 0

Ax By Cz D

   



và





' : ' ' ' ' 0

A x B y C z D

   











cắt







' '

AB A B

BC B C

CB C B







 









ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay















' '

' ' ' '

' '

AB A B

BC B C va AD A D

CB C B







  

























' '

AB A B

BC B C

CB C B

AD A D























Đặt biệt:









1 2

' . 0 . ' . ' . ' 0

n n A A B B C C

 

      

 

4. Góc giữa hai mặt phẳng

Gọi



là góc giữa hai mặt phẳng





0 0

0 90



 





: 0

P Ax By Cz D

   

và





: ' ' ' ' 0

Q A x B y C z D

   

 

2 2 2 2 2 2

. ' . ' . '

cos = cos ,

. ' ' '

P Q

n n

A A B B C C

n n

A B C A B C



 

 

   

 

B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Trong không gian với hệ tọa độ

2 2 2 0







   



x y z

Oxyz

cho điểm





1;0;0

M và





0;0; 1



N , mặt phẳng





qua điểm

M N

và tạo với mặt phẳng





: 4 0

  

Q x y một

góc bằng

. Phương trình mặt phẳng





là

2 2 2 0







   



x y z

. B.

2 2 2 0







   



x y z

2 2 2 0

   





   



x y z

. D.

2 2 2 0

  





  



x z

Hướng dẫn giải:

Gọi vectơ pháp tuyến của mp





và





lần lượt là





; ;



n a b c





2 2 2

  

a b c ,



















qua 1;0;0 : 1 0

    

P M P a x by cz





qua





0;0; 1



  

a c





hợp với





góc

 

2 2

, 45

2 2







    



 





 

P Q

a b

cos n n cos

a b

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay

Với

0 0

  

a c chọn



phương trình





: 0



P y

Với

 

a b

chọn

1 2

   

b a phương trình mặt phẳng





: 2 2 2 0

P x y z

   

Chọn A.

Câu 2: Trong không gian với hệ toạ độ

Oxyz

,cho





: 4 2 6 0

P x y z

   





: 2 4 6 0

Q x y z

   

Lập phương trình mặt phẳng







chứa giao tuyến của









P Q

và cắt các trục tọa độ tại các

điểm

, ,

A B C

sao cho hình chóp

O ABC

là hình chóp đều.

6 0

x y z

   

. B.

6 0

x y z

   

. C.

6 0

x y z

   

. D.

3 0

x y z

   

Hướng dẫn giải:

Chọn









6;0;0 , 2;2;2

M N thuộc giao tuyến của









P Q

Gọi













;0;0 , 0; ;0 , 0;0;

A a B b C c

lần lượt là giao điểm của







với các trục

, ,

Ox Oy Oz



   

: 1 , , 0

x y z

a b c

   









chứa

M N

2 2 2

a b c













  





Hình chóp

O ABC

là hình chóp đều

OA OB OC a b c

     

Vây phương trình

6 0

x y z

   

Chọn B.

Câu 3: Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng:

, và mặt cầu

Viết phương trình mặt phẳng song song với hai đường thẳng và cắt mặt cầu (S)

theo giao tuyến là đường tròn (C) có chu vi bằng .

2 1 1

1 2 3

x y z

  

  



: 2

1 2

x t

y t

z t







  





 



2 2 2

( ): 2 2 6 5 0

S x y z x y z

      

( )



1 2

 

2 365



5 3 4 0; 5 3 10 0

x y z x y z

       

5 3 10 0

x y z

   

5 3 3 511 0; 5 3 3 511 0

x y z x y z

         

5 3 4 0

x y z

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay

Chọn B.

Hướng dẫn giải:

+ qua và có vectơ chỉ phương .

qua và có vectơ chỉ phương .

+ Mặt phẳng () song song với nên có vectơ pháp tuyến:

Phương trình mặt phẳng () có dạng:

+ Mặt cầu (S) có tâm và bán kính .

Gọi r là bán kính đường tròn (C), ta có:

Khi đó:

+ Phương trình mặt phẳng .

Vì nên M

và M

không thuộc loại (1).

Vậy phương trình mặt phẳng () cần tìm là: .

Chọn B.

Câu 4: Cho tứ giác

ABCD

có

















0;1; 1 ; 1;1;2 ; 1; 1;0 ; 0;0;1 .

A B C D  Viết phương trình của

mặt phẳng





qua

A B

và chia tứ diện thành hai khối

ABCE

và

ABDE

có tỉ số thể tích

bằng 3.

15 4 5 1 0

x y z

   

. B.

15 4 5 1 0

x y z

   

15 4 5 1 0

x y z

   

. D.

15 4 5 1 0

x y z

   

Hướng dẫn giải:





cắt cạnh

tại

E E

chia đoạn

theoo tỷ số



3 1 3.0 1

4 4 4

1 3.0 1

4 4 4

0 3.1 3

4 4 4

C D

x x

y y

E y

z z

 



  





  



   









  





   

1 5 7 1

1;0;3 ; ; ; 1; 5;7

4 4 4 4

AB AE

 

    

 

 

 



(2; 1;1)

M 

(1;2; 3)

 





(0;2;1)

(1; 1;2)

u  



1 2

 

1 2

, (1; 5; 3)

u u

 

  

 

 



5 3 0

x y z D

   

I(1; 1;3)





2 365 365

5 5

r r



  

 

2 2

,( )

d I R r



  

 





  







( ): 5 3 4 0 (1) hay 5 3 10 0 (2)

x y z x y z



       

1 2

/ /( ), / /( )

 

 

( )





5 3 10 0

x y z

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay

Vecto pháp tuyến của

             

: , 15; 4; 5 : 0 15 1 4 1 5 0

15 4 5 1 0

P n AB AE P x y z

x y z

 

            

 

    

  

Chọn A.

Câu 5: Trong không gian với hệ tọa độ

2 2 2 0

x y z







   



Oxyz

cho điểm





1;0;0

M và





0;0; 1



, mặt phẳng





qua điểm

M N

và tạo với mặt phẳng





: 4 0

Q x y

  

một

góc bằng

. Phương trình mặt phẳng





là

2 2 2 0

x y z







   



. B.

2 2 2 0

x y z







   



2 2 2 0

x y z

   





   



. D.

2 2 2 0

x z

  





  



Hướng dẫn giải:

Gọi vectơ pháp tuyến của mp





và





lần lượt là





; ;

n a b c







2 2 2

a b c

  



















qua 1;0;0 : 1 0

P M P a x by cz

    





qua





0;0; 1



a c

  





hợp với





góc

 

2 2

, 45

2 2

P Q

a b

cos n n cos

a b







    



 





 

Với

0 0

a c

  

chọn



phương trình





: 0

P y



Với

a b

 

chọn

1 2

b a

   

phương trình mặt phẳng





:2 2 2 0

P x y z

   

Chọn A.

Câu 6: Cho tứ giác

ABCD

có

















0;1; 1 ; 1;1;2 ; 1; 1;0 ; 0;0;1 .

A B C D  Viết phương trình tổng

quát của mặt phẳng





song song với mặt phẳng





BCD

và chia tứ diện thành hai khối

AMNF

và

MNFBCD

có tỉ số thể tích bằng

3 3 4 0

x z

  

. B.

1 0

y z

  

4 0

y z

  

. D.

4 3 4 0

x z

  

Hướng dẫn giải:

Tỷ số thể tích hai khối

AMNF

và

MNFBCD

 



 

 

  

chia cạnh

theo tỉ số



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay

 

   

1 2.0 1

3 3

1 2.1

1 ; 2 0;1;1 ; 1;1;1

2 2 1

E y BC BD





 







      





 

 





 

Vecto pháp tuyến của









: 0;1; 1

Q n

 



        

 

: 0 1 1 0 1 0

: 1 0

M Q Q x y z

P y z

 

         

 

 

   

Chọn B.

Câu 7: Từ gốc

vẽ

vuông góc với mặt phẳng









P OH p



; gọi

, ,

  

lần lượt là các góc

tạo bởi vec tơ pháp tuyến của





với ba trục

Ox, , .

Oy Oz

Phương trình của





là:

cos cos cos 0

x y z p

  

   

. B.

sin sin sin 0

x y z p

  

   

cos cos cos 0

x y z p

  

   

. D.

sin sin sin 0

x y z p

  

   

Hướng dẫn giải:









cos , cos , cos cos , cos , cos

H p p c OH p p c

     

 



Gọi:













, , cos , cos , cos

M x y z P HM x p y p z c

  

     



     

 

cos cos cos cos cos cos

: cos cos cos 0

OH HM

x p p y p p z c p

P x y z p

     

  



     

    

 

Chọn A.

Câu 8: Viết phương trình tổng quát của mặt phẳng





cắt hai trục

y Oy

và

z Oz

tại









0, 1,0 , 0,0,1

A B và tạo với mặt phẳng





yOz

một góc

45 .

2 1 0

x y z

   

. B.

2 1 0

x y z

   

2 1 0; 2 1 0

x y z x y z

       

. D.

2 1 0; 2 1 0

x y z x y z

       

Hướng dẫn giải:

Gọi





,0,0

C a là giao điểm của





và trục

'Ox









0, 1, 1 ; ,0, 1

BA BC a

     

 

Vec tơ pháp tuyến của





là

 

, 1, ,

n BA BC a a

 

  

 

  

Vec tơ pháp tuyến của





yOz

là:





1,0,0

e 



Gọi



là góc tạo bởi





và

 

0 2

1 2 1

os45 4 2

1 2

yOz c a a

       



Vậy có hai mặt phẳng





: 2 1 2 1 0; 2 1 0

P x y z x y z x y z

            

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay

Chọn D.

Câu 9: Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình:

. Viết phương trình mặt phẳng (P) song song với giá của

véc tơ , vuông góc với mặt phẳng và tiếp xúc với (S).

2 2 3 0

2 2 21 0

   





   



x y z

. B.

2 2 3 0

2 2 21 0

   





   



x y z

2 3 0

2 1 0

   





   



x y z

. D.

2 13 0

2 1 0

   





   



x y z

Hướng dẫn giải:

Vậy: (P): hoặc (P):

(S) có tâm I(1; –3; 2) và bán kính R = 4. VTPT của là .

 VTPT của (P) là:  PT của (P) có dạng: .

Vì (P) tiếp xúc với (S) nên .

Vậy: (P): hoặc (P): .

Chọn B.

Câu 10: Cho điểm

(0;8;2)

và mặt cầu

( )

có phương trình

2 2 2

( ):( 5) ( 3) ( 7) 72

S x y z

     

và

điểm

(9; 7;23)



. Viết phương trình mặt phẳng

( )

qua

tiếp xúc với

( )

sao cho khoảng

cách từ

đến

( )

là lớn nhất. Giả sử

(1; ; )

n m n





là một vectơ pháp tuyến của

( )

. Lúc đó

. 2.

m n



. 2.

m n

 

. 4.

m n



. 4.

m n

 

Hướng dẫn giải:

Chọn D.

Mặt phẳng

( )

qua

có dạng

( 0) ( 8) ( 2) 0 8 2 0

a x b y c z ax by cz b c

           

Điều kiện tiếp xúc:

2 2 2 2 2 2

5 3 7 8 2 5 11 5

( ;( )) 6 2 6 2 6 2

a b c b c a b c

d I P

a b c a b c

     

    

   

. (*)

Mà

2 2 2 2 2 2

9 7 23 8 2 9 15 21

( ;( ))

a b c b c a b c

d B P

a b c a b c

     

 

   

2 2 2

5 11 5 4( 4 )

a b c a b c

a b c

    

 

 

2 2 2 2 2 2

2 2 2 2 2 2 2 2 2

5 11 5 4

1 ( 1) 4 .

4 6 2 4 18 2

a b c a b c

a b c

a b c a b c a b c

   

    

    

     

2 2 2

2 6 4 2 0

x y z x y z

      

(1;6;2)





( ): 4 11 0

x y z



   

2 2 3 0

x y z

   

2 2 21 0

x y z

   

( )



(1;4;1)









, (2; 1;2)

n n v  

  

2 2 0

x y z m

   

( ,( )) 4

d I P



 











2 2 3 0

x y z

   

2 2 21 0

x y z

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay

Dấu bằng xảy ra khi

1 1 4

a b c

 



. Chọn

1; 1; 4

a b c

   

thỏa mãn (*).

Khi đó

( ) : 4 0

P x y z

  

. Suy ra

1; 4

m n

  

. Suy ra:

. 4.

m n

 

Câu 11: Cho mặt phẳng





đi qua hai điểm









3,0,4 , 3,0,4

A B  và hợp với mặt phẳng





xOy

một góc

và cắt

y Oy

tại

Viết phương trình tổng quát mặt phẳng





3 4 3 0

y z

  

. B.

3 4 3 0

y z

  

3 4 3 0

y z

  

. D.

3 4 3 0

x y z

   

Hướng dẫn giải:













0, ,0 ; 3, , 4 ; 6,0,0

C c AC c AB    

 

Vec tơ pháp tuyến của

   

: , 6 0,4,

P n AC AB c

 

 

 

  

Vec tơ pháp tuyến của









: 0,0,1

xOz e 



 

       

 

0 2

cos30 48 4 3 6 0,4, 4 3

: 3 .0 0 4 4 4 3 0 3 4 3 0

c c n

P x y z y z

         



           



Chọn C.

Câu 12: Trong không gian với hệ tọa độ

Oxyz

, cho ba đường thẳng

: 0

x t

d y

















2 2

d y t

















: 0

d y

z t

















. Viết phương trình mặt phẳng đi qua điểm





3;2;1

H và cắt ba đường thẳng

lần lượt tại

sao cho

là trực tâm tam giác

ABC

2 2 11 0

x y z

   

. B.

6 0

x y z

   

2 2 9 0

x y z

   

. D.

3 2 14 0

x y z

   

Hướng dẫn giải:

Chọn A.

Gọi





A a;0;0





1; ;0

B b





1;0;

C c

















1 ; ;0 , 0; ; , 2;2;1 , 3 ;2;1

AB a b BC b c CH c AH a       

   

Yêu cầu bài toán

     

2 3

, . 0

2 2 1 1 1 0

. 0 1 9 2 0

. 0

AB BC CH

bc c a c b a

AB CH a b b b

c b

BC AH



 



     

 











       

 





 













  

 

Nếu



suy ra

A B



(loại).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay

Nếu



, tọa độ

;0;0

 

 

 

1; ;0

 

 

 





1;0;9

C . Suy ra phương trình mặt phẳng





ABC

là

2 2 11 0

x y z

   

Câu 13: Trong không gian Oxyz, cho 2 đường thẳng d: và d’:

Viết phương trình mặt phẳng () chứa (d) và tạo với mặt phẳng Oyz một góc nhỏ nhất.

A. . B. .

C. . D. .

Hướng dẫn giải:

Giả sử (β): (đk: ), (β) có vtpt là

d  (β)   

TH 1: A = 0 (không thoả đb hoặc không nhỏ nhất)

TH 2: A ≠ 0, ta có:

= = =

nhỏ nhất  lớn nhất  nhỏ nhất 

 nên . Vậy: (β):



 



  









x t

y t

z t

5 '

2 ' 3 2 5







 





  



x t

y t

z t

3 2 7 0

   

x y z

3 2 7 0

   

x y z

3 2 7 0

    

x y z

3 2 7 0

   

x y z

   

Ax By Cz D

2 2 2

  

A B C

( ; ; )





n A B C

( )

. 0

 















n a



3 2 0

2 0

  







  





A B D

A B C

2 2



  





 





D A C

B A C



cos(( ),( )) cos( , )

 



Oyz n i



2 2 2

( 2)  

A A C C



( ),( )

Oyz





cos(( ),( ))

Oyz



2 2

1 (1 2) ( )

  

C C

A A

2 2

6 12

( 3) 2. 2 ( )

3 9

  

C C

A A

6 12

( 3 )

3 9

 



( ),( )

Oyz





cos(( ),( ))

Oyz



( 3 )



3 0

 

1 (choïn)









 















 





3 2 7 0

   

x y z

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay

Chọn D.

Câu 14: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng

2 1

1 2 1

x y z

 

 



. Viết phương

trình mặt phẳng (P) chứa đường thẳng d và cắt các trục Ox, Oy lần lượt tại A và B sao cho

đường thẳng AB vuông góc với d.





: 2 5 4 0.

P x y z

   





: 2 5 5 0.

P x y z

   





: 2 4 0.

P x y z

   





:2 3 0.

P x y

  

Hướng dẫn giải:

Cách 1 (Tự luận)

Đường thẳng d qua M(2;1;0) và có VTCP





1;2; 1

 



Ta có: AB



d và AB



Oz nên AB có VTCP là:

 

, 2; 1;0

AB d

u u k

 

  

 

  

(P) chứa d và AB nên (P) đi qua M(2;1; 0), có VTPT là:

 

, 1;2;5

d AB

n u u

 

 

 

  







: 2 5 4 0

P x y z

   



Chọn A

Cách 2: Dùng phương trình mặt phẳng theo đoạn chắn.

Đường thẳng d qua 2 điểm M(2;1;0) và N(3;3;-1)

Giả sử mp(P) cắt Ox, Oy, Oz lần lượt tại A(a;0;0), B(0;b;0), C(0;0;c)



 

: 1

x y z

a b c

  



. 0 2

AB u a b

   

 

(1)





chứa d nên d cũng đi qua M, N



2 1

a b

 

(2),

3 3 1

a b c



  

(3)

Từ (1), (2), (3)



a = 4, b = 2, c =







: 2 5 4 0

P x y z

   



Chọn A

Câu 15:

Trong không gian tọa độ Oxyz cho đường thẳng và mp

. Viết phương trình mặt phẳng qua d và tạo với một góc

nhỏ nhất.

A. B.

: 1 2

x t

d y t

z t



 



  





 









: 2 2 2 0

P x y z

   









3 0

x y z

   

3 0

x y z

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay

C. D.

Hướng dẫn giải:

Đường thẳng d là giao tuyến của hai mặt phẳng: .

Do vậy mặt phẳng qua d thì thuộc chùm mặt phẳng:

Hay mp : (*). Mp có

Vậy:

Do nhỏ nhất cho nên lớn nhất khi .

Vậy thay vào (*) ta có mp .

Chọn B.

Câu 16: Cho hai đường thẳng

: 1

x t

d y t

z t

 





 









và

2 2

: 3

x t

d y

z t



 

















. Mặt phẳng cách đều hai đường

thẳng

và

có phương trình là

5 2 12 0.

x y z

   

5 2 12 0.

x y z

   

5 2 12 0.

x y z

   

5 2 12 0.

x y z

   

Hướng dẫn giải:

Chọn D.

qua





2;1;0

A và có VTCP là





1; 1;2

u  



;

qua





2;3;0

B và có VTCP là





2;0;1

u  



Có









1 2

, 1; 5; 2

u u

   

 

;





0;2;0

AB 



, suy ra





1 2

, . 10

u u AB

 



 

, nên

1 2

;

d d

là chéo nhau.

Vậy mặt phẳng





cách đều hai đường thẳng

1 2

d d

là đường thẳng song song với

1 2

d d

và

đi qua trung điểm





2;2;0

I của đoạn thẳng

Vậy phương trình mặt phẳng





cần lập là:

5 2 12 0

x y z

   

3 0

x y z

   

3 0

x y z

   

2 1 0

1 2

2 2 0

1 1

x y

x z x z













  





 



 

 

   





























2 1 2 0

x y m x z

     









2 1 2 0

m x y mz m

     













2;1; ; 2; 1; 2

n m m n

    

 





   

2 2 2

2 2 1 2

5 5 1 5

cos

3 3

3 2 4 5

2 1 4 1 4 2 1 3

m m

n n

m m

n n

m m m



  

    

 

      

 





cos









: 3 0

R x y z

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay

Câu 17: Trong không gian với hệ toạ độ

Oxyz

,cho hai đường thẳng

1 2

d d

lần lượt có phương trình

2 2 3

2 1 3

x y z

  

  ,

1 2 1

2 1 4

x y z

  

 



. Phương trình mặt phẳng







cách đều

hai đường thẳng

1 2

d d

là:

7 2 4 0

x y z

  

. B.

7 2 4 3 0

x y z

   

2 3 3 0

x y z

   

. D.

14 4 8 3 0

x y z

   

Hướng dẫn giải:

Ta có

đi qua





2;2;3

A và có





2;1;3

u 



đi qua





1;2;1

B và có





2; 1;4

u  



   

1 2

1;1; 2 ; ; 7; 2; 4

d d

AB u u

 

     

 

  

;

1 2

; 1 0

d d

u u AB

 

   

 

  

nên

1 2

d d

chéo nhau.







cách đều

1 2

d d

nên







song song với

1 2

d d

 

1 2

; 7; 2; 4

d d

n u u

 

    

 

  











có dạng

7 2 4 0

x y z d

   

Theo giả thiết thì

















, ,d A d B

 

2 1

69 69

d d

 

   





:14 4 8 3 0

x y z

    



Câu 18: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng song song và cách

đều hai đường thẳng và

A. . B. .

C. . D. .

Hướng dẫn giải:

Ta có: đi qua điểm và có VTCP .

và đi qua điểm và có VTCP Vì song songvới hai đường

thẳng và nên VTPT của là

Khi đó có dạng loại đáp án A và C.





1 1 1

x z



 



: .

2 1 1

x z



 

 





: 2 2 1 0

xP z

  





: 2 2 1 0

yP z

  





: 2 2 1 0

xP y

  





: 2 2 1 0

yP z

  





2;0;0





1;1;1

u  







0;1;2





2; 1; 1 .

  















1 2

, 0;1; 1

n u u

    

 

  





y z D

  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay

Lại có cách đều và nên đi qua trung điểm của . Do đó

Chọn B.

Câu 19: Trong hệ trục tọa độ

Oxyz

cho mặt phẳng





:5 4 0

P x z

  

và hai đường thẳng

1 2

;

d d

lần

lượt có phương trình

1 1 1 2 1

; .

1 1 2 2 1 1

x y z x y z

    

   



Viết phương trình của mặt

phẳng









/ / ,

Q P

theo thứ tự cắt

1 2

d d

tại

A B

sao cho

4 5

AB 

   

1 2

25 331 25 331

:5 0; :5 0

7 7

Q x z Q x z

   

     









1 2

:5 2 0; :55 11 14 0

Q x z Q x z

     









1 2

: 5 2 0; : 55 11 14 0

Q x z Q x z

       









1 2

:5 4 0; :55 11 7 0

Q x z Q x z

     

Hướng dẫn giải:

 

   

1 2

1 1 2 '

: , : 2 ' ; :5 0, 4

1 2 1 '

3 6 15 2 3 2 12 30 5

; ; , ; ;

3 3 3 9 9 9

x t x t

d y t d y t Q x z d d

z t z t

d d d d d d

Q d A Q d B

   

 

 

        

 

 

     

 

        

   

   

   

   

Suy ra

 

6 6 4 30 5 1

; ; 6 ; 6 4 ;30 5

9 9 9 9

d d d

AB d d d

   

 

     

 

 



     

 

2 2 2

4 5 1

6 6 4 30 5

3 8

AB d d d

       

25 331

42 300 252 0

25 331

d d



 





     



 







Vậy, tìm được hai mặt phẳng thỏa mãn:

   

1 2

25 331 25 331

:5 0; :5 0

7 7

Q x z Q x z

   

     

Chọn A.

Câu 20: Trong không gian với hệ tọa độ

Oxyz

cho điểm





1;2;3

A và đường thẳng

. Mặt phằng





chứa đường thẳng

và có khoảng cách từ

đến





là

lớn nhất. Khi đó





có một véctơ pháp tuyến là









0; ;1

 

 

 





: 2 2 1 0

yP z

  

3 1

2 1 1

 

 



x y z

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24

Facebook: https://www.facebook.com/dongpay

A. B. C. D.

Hướng dẫn giải:

Gọi H,K lần lươt là hình chiếu vuông góc của A lên d và (P)

Khi đó: d(A,(P)) = AK AH hay d(A,(P)) lớn nhất khi và chỉ khi

Ta có: và

Suy ra:

Hay một véctơ pháp tuyến của (P) là

Chọn A.

Câu 21: Trong không gian với hệ tọa độ , cho hai đường thẳng và

. Viết phương trình mặt phẳng chứa sao cho góc giữa mặt

phẳng và đường thẳng là lớn nhất.

6 0

   

x y z . B.

7 5 9 0

   

x y z . C.

6 0

x y z

   

. D.

3 0

   

x y z .

Hướng dẫn giải:

Ta có: đi qua và có .

Phương trình mặt phẳng có dạng: .

Ta có:

Gọi

Với

Với . Đặt , ta được

Xét hàm số . Ta có:

4 5 13

( ; ; )

n 



4 5 13

( ; ; )

 



4 5 13

( ; ; )

n  



4 5 13

( ; ; )

n  





H K



3 2 1 2 1 1

( ; ; ); ( ; ; )

H t t t a

      



.AH a t

  

 

4 5 13

3 3 3

( ; ; )

AH    



4 5 13

( ; ; )

n 



Oxyz

1 2

1 2 1

x y z

 

 



2 1

2 1 2

x y z

 

 



( )

(1; 2;0)



(1;2; 1)

VTCPu

 



( )

2 2 2

( 1) ( 2) 0,( 0)

A x B y Cz A B C

       

( ) . 0 2

d P u n C A B

     

 

2 2

4 3

1 (4 3 )

(( ), ) sin .

2 4 5

3 2 4 5

A B

P d

A AB B

 



   

 



2 2

sin



 





1 (4 3)

sin .

2 4 5

t t







 

(4 3)

( )

2 4 5

f t

t t





 

2 2

16 124 84

'( )

(2 4 5)

t t

f t

t t

 



 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25

Facebook: https://www.facebook.com/dongpay

Dựa vào BBT ta có: khi

Khi đó:

Vậy khi Phương trình mặt phẳng

Chọn B.

Câu 22: Trong không gian với hệ tọa độ cho điểm Viết phương trình mặt phẳng

đi qua gốc tọa độ và cách một khoảng lớn nhất.

A. B. C. D.

Hướng dẫn giải:

Gọi là hình chiếu của trên vuông tại

. Khi đó đi qua và vuông góc với là vecto

pháp tuyến của phương trình của mặt phẳng là

hay

Chọn A.

Câu 23: Trong không gian với hệ trục tọa độ

Oxyz

, cho hai đường thẳng

1 2

1 2 1

x y z

 

 



và

2 1

2 1 2

x y z

 

 



. Gọi





là mặt phẳng chứa

sao cho góc giữa mặt phẳng





và

đường thẳng

là lớn nhất. Chọn mệnh đề đúng trong các mệnh đề sau:





có vectơ pháp tuyến là





1; 1;2

n  







qua điểm





0;2;0

A .





song song với mặt phẳng





:7 5 3 0

Q x y z

   





cắt

tại điểm





2; 1;4

B  .

Hướng dẫn giải:

qua





1; 2;0

M  và có VTCP





1;2; 1

 



. Vì





d P

 nên





M P

 .

'( ) 0

f t



 



 



 





max ( )

f t 

 

  

5 3

sin ( 7)



  

5 3

sin





 



( ):7 5 9 0

P x y z

   

Oxyz





1;2; 1 .













0;0;0

2 0.

x y z

  

1 2 1

x z

  



x y z

  

2 0.

x y z

   

( )

MHO

 

MH MO

 

max

MH



( )

(1;2; 1)

 



( )



( )

1( 0) 2( 0) 1( 0) 0

x y z

     

2 0.

x y z

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26

Facebook: https://www.facebook.com/dongpay

Pt mặt phẳng





có dạng:













2 2 2

1 2 0 0

A x B y Cz A B C

       

Ta có:





. 0 2

d P u n C A B

     

 

Gọi

 



 

2 2

4 3

, sin

3 2 4 5

A B

P d

A AB B



   

 

 

TH1: Với



thì

2 2

sin





TH2: Với



. Đặt



, ta được:

 

4 3

sin

3 2 4 5

t t





 



Xét hàm số

 

4 3

2 4 5

f t

t t





 

. Dựa vào bảng biến thiên ta có:

 

max

f x  khi

 

khi

 

Khi đó

 

5 3

sin 7

f  



So sánh TH1 và TH2





lớn nhất với

5 3

sin





khi

 

Vậy phương trình mặt phẳng





:7 5 9 0

P x y z

   

Chọn B.

Câu 24: Trong không gian với hệ trục toạ độ

Oxyz

,cho tứ diện

ABCD

có điểm









1;1;1 , 2;0;2

A B ,









1; 1;0 , 0;3;4

C D  . Trên các cạnh , ,

AB AC AD

lần lượt lấy các điểm

', ', '

B C D

thỏa:

' ' '

AB AC AD

  

. Viết phương trình mặt phẳng





' ' '

B C D

biết tứ diện

' ' '

AB C D

có

thể tích nhỏ nhất?

16 40 44 39 0

x y z

   

. B.

16 40 44 39 0

x y z

   

16 40 44 39 0

x y z

   

. D.

16 40 44 39 0

x y z

   

Hướng dẫn giải:

Áp dụng bất đẳng thức

AM GM



ta có:

. .

4 3

' ' ' '. '. '

AB AC AD AB AC AD

   

'. '. ' 27

. . 64

AB AC AD

 



' ' '

'. '. ' 27

. . 64

AB C D

ABCD

V AB AC AD

 

' ' '

AB C D ABCD

V V 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27

Facebook: https://www.facebook.com/dongpay

Để

' ' '

AB C D

nhỏ nhất khi và chỉ khi

' ' ' 3

AB AC AD

  

3 7 1 7

' ' ; ;

4 4 4 4

AB AB B

 

  

 

 

 

Lúc đó mặt phẳng





' ' '

B C D

song song với mặt phẳng





BCD

và đi qua

7 1 7

' ; ;

4 4 4

 

 

 





' ' ' :16 40 44 39 0

B C D x y z

    

Câu 25: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng







đi qua điểm





1;2;3

M và cắt các

trục Ox, Oy, Oz lần lượt tại

( khác gốc toạ độ

) sao cho

là trực tâm tam giác

ABC

. Mặt phẳng







có phương trình là:

2 3 14 0

x y z

   

. B.

1 0

1 2 3

x y z

   

3 2 10 0

x y z

   

. D.

2 3 14 0

x y z

   

Hướng dẫn giải:

Cách 1:Gọi

là hình chiếu vuông góc của

trên

là hình chiếu vuông góc

trên

là trực tâm của tam giác

ABC

khi và chỉ khi

M BK CH

 

Ta có:

 

(1)

AB CH

AB COH AB OM

AB CO





   







(1)

Chứng minh tương tự, ta có:

AC OM



(2).

Từ (1) và (2), ta có:





OM ABC



Ta có:





1;2;3



Mặt phẳng







đi qua điểm





1;2;3

M và có một VTPT là





1;2;3



nên có phương trình

là:













1 2 2 3 3 0 2 3 14 0

x y z x y z

          

Cách 2:

+) Do

, ,

A B C

lần lượt thuộc các trục

, ,

Ox Oy Oz

nên

( ;0;0), (0; ;0), (0;0; )

A a B b C c

(

, , 0

a b c



Phương trình đoạn chắn của mặt phẳng

( )

ABC

là:

x y z

a b c

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28

Facebook: https://www.facebook.com/dongpay

+) Do

là trực tâm tam giác

ABC

nên

. 0

( )

AM BC

BM AC

M ABC



















 

. Giải hệ điều kiện trên ta được

, ,

a b c

Vậy phương trình mặt phẳng:

2 3 14 0

x y z

   

Câu 26: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): và đường thẳng

. Phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt

phẳng (Q) một góc nhỏ nhất là

A. B.

C. D.

Hướng dẫn giải:

PT mặt phẳng (P) có dạng: . Gọi .

Chọn hai điểm . Ta có:

 (P): 

TH1: Nếu a = 0 thì  .

TH2: Nếu a  0 thì . Đặt và

Xét hàm số .

Dựa vào BBT, ta thấy

Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn .

Vậy: (P): .

Chọn A.

x y z

2 5 0

   

x y z

1 1 3

2 1 1

  

 





  

: 4 0

P y z





  

:x 4 0

P z





   

:x 4 0

P y z





  

: 4 0

P y z

ax by cz d a b c

2 2 2

0 ( 0)

      



P Q

(( ),( ))

a

M N d

( 1; 1;3), (1;0;4)

  

M P c a b

N P d a b

( )

( ) 7 4

 

   



 

  

 

ax by a b z a b

( 2 ) 7 4 0

      

a b

a ab b

2 2

cos .

5 4 2







 

3 3

cos .



 

a

b b

a a

cos .

5 4 2







 

 

 

 



f x

( ) cos





x x

f x

x x

9 2 1

( ) .

5 4 2

 



 

f x

0 0

min ( ) 0 cos 0 90 30



     a

b c d

1, 1, 4

  

y z

4 0

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29

Facebook: https://www.facebook.com/dongpay

Câu 27: Trong không gian

Oxyz

, cho hai điểm





3;0;2

A ,





3;0;2

B và mặt cầu

2 2 2

( 2) ( 1) 25

x y z

    

. Phương trình mặt phẳng







đi qua hai điểm

và cắt mặt

cầu





theo một đường tròn bán kính nhỏ nhất là:

4 5 17 0

x y z

   

. B.

3 2 7 0

x y z

   

4 5 13 0

x y z

   

. D.

3 2 –11 0

x y z

  

Hướng dẫn giải:

Mặt cầu





có tâm





0; 2;1

I  , bán kính



. Do

17 R

 

nên

luôn cắt





Do đó

( )



luôn cắt





theo đường tròn





có bán kính

 

,r R d I 



. Đề bán

kính

nhỏ nhất









d I P

 lớn nhất.

Mặt phẳng







đi qua hai điểm

và vuông góc với mp





ABC

Ta có

AB (1; 1; 1)

  



AC ( 2; 3; 2)

   



suy ra





ABC

có véctơ pháp tuyến

, ( 1;4; 5)

n AB AC

 

   

 

  

(α) có véctơ pháp tuyến

, ( 9 6; 3) 3(3;2;1)

n n AB

 

      

 

  



Phương trình

















: 3 – 2 2 –1 1 – 3 0 3 2 –11 0

x y z x y z

      



Câu 28: Trong không gian với hệ toạ độ

Oxyz

,cho





: 4 2 6 0

P x y z

   





: 2 4 6 0

Q x y z

   

Lập phương trình mặt phẳng







chứa giao tuyến của









P Q

và cắt các trục tọa độ tại các

điểm

, ,

A B C

sao cho hình chóp .

O ABC

là hình chóp đều.

6 0

x y z

   

. B.

6 0

x y z

   

. C.

6 0

x y z

   

. D.

3 0

x y z

   

Hướng dẫn giải:

Chọn









6;0;0 , 2;2;2

M N thuộc giao tuyến của









P Q

Gọi













;0;0 , 0; ;0 , 0;0;

A a B b C c

lần lượt là giao điểm của







với các trục

, ,

Ox Oy Oz



   

: 1 , , 0

x y z

a b c

   









chứa

M N

2 2 2

a b c













  





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30

Facebook: https://www.facebook.com/dongpay

Hình chóp .

O ABC

là hình chóp đều

OA OB OC a b c

     

Vây phương trình

6 0

x y z

   

Câu 29: Trong không gian với hệ toạ độ

Oxyz

, cho điểm





1;1;1

N . Viết phương trình mặt phẳng





cắt các trục

, ,

Ox Oy Oz

lần lượt tại

, ,

A B C

(không trùng với gốc tọa độ

) sao cho

là tâm đường tròn ngoại tiếp tam giác

ABC





: 3 0

P x y z

   

. B.





: 1 0

P x y z

   





: 1 0

P x y z

   

. D.





: 2 4 0

P x y z

   

Hướng dẫn giải:

Gọi













;0;0 , 0; ;0 , 0;0;

A a B b C c

lần lượt là giao điểm của





với các trục

, ,

Ox Oy Oz



   

: 1 , , 0

x y z

P a b c

a b c

   

Ta có:

 

1 1 1

1 1 3 3 0

1 1

N P

a b c

NA NB a b a b c x y z

NA NC a c



  







             

 

 

   







Câu 30: Phương trình của mặt phẳng nào sau đây đi qua điểm





1;2;3

M và cắt ba tia

lần lượt tại

sao cho thể tích tứ diện

OABC

nhỏ nhất?

6 3 2 18 0

x y z

   

. B.

6 3 3 21 0

x y z

   

6 3 3 21 0

x y z

   

. D.

6 3 2 18 0

x y z

   

Hướng dẫn giải:

Giả sử

( ;0;0), (0; ;0), (0;0; ) ( , , 0)

A a B b C c a b c



(ABC):

x y z

a b c

  

(1)

M(1;2;3) thuộc (ABC):

1 2 3

a b c

  

Thể tích tứ diện OABC:

V abc



Áp dụng BDT Côsi ta có:

1 2 3 6 27.6 1

1 3 1 27 27

abc V

a b c abc abc

         

Ta có: V đạt giá trị nhỏ nhất

1 2 3 1

27 6

V b

a b c







       









ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31

Facebook: https://www.facebook.com/dongpay

Vậy (ABC):

6 3 2 18 0

x y z

   

. Chọn (D)

Câu 31: Trong không gian với hệ tọa độ

Oxyz

cho điểm

E(8;1;1)

.Viết phương trình mặt phẳng

( )



qua E và cắt nửa trục dương

, ,

Ox Oy Oz

lần lượt tại

, ,

A B C

sao cho

nhỏ nhất với

là

trọng tâm tam giác

ABC

2 11 0

x y z

   

. B.

8 66=0

x y z

  

2 18 0

x y z

   

. D.

2 2 12 0

x y z

   

Hướng dẫn giải:

Chọn D.

Cách 1 :

Với đáp án A:

11 11 11 11 121

(11;0;0);B(0;11;0);C(0;0; ) ( ; ; ) OG

2 3 3 6 4

A G  

Với đáp án B:

33 11 15609

( ;0;0);B(0;66;0);C(0;0;66) ( ;22;22) OG

4 4 16

A G  

Với đáp án C:

18 18

(9;0;0);B(0;18;0);C(0;0;18) (3; ; ) OG 81

3 3

A G

  

Với đáp án D:

( 12;0;0);B(0;6;0);C(0;0;6) ( 4;2;2) OG 24

A G

    

Cách 2 :

Gọi













;0;0 , 0; ;0 , 0;0;

A a B b C c

với

, , 0

a b c



. Theo đề bài ta có :

8 1 1

a b c

  

. Cần tìm

giá trị nhỏ nhất của

2 2 2

a b c

 

Ta có





   





 

2 2

2 2 2 2 2 2

4 1 1 .2 .1 .1 6. 2

a b c a b c a b c a b c

            

Mặt khác





   

 

2 2 2

4 1 1 .2 .1 .1

8 1 1

4 1 1 36

a b c a b c

a b c

      

 

    

 

 

   

Suy ra

2 2 2 3

a b c

  

. Dấu

'' ''



xảy ra khi

2 2

2 2 .

b c a b c

    

Vậy

2 2 2

a b c

 

đạt giá trị nhỏ nhất bằng 216 khi

12, 6

a b c

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32

Facebook: https://www.facebook.com/dongpay

Vậy phương trình mặt phẳng là : 1

12 6 6

x y z

   hay 2 2 12 0x y z    .

Câu 32: Trong không gian với hệ toạ độ Oxyz cho 2;1;6 , 1;( ) ( )2;4A B và 1;3( ;2 .)I Viết phương

trình mặt phẳng (P) đi qua ,A B sao cho khoảng cách từ I đến (P) lớn nhất.

A. 3 7 6 35 0   x y z . B. 7 5 9 0   x y z .

C. 6 0x y z    . D. 3 0   x y z .

Hướng dẫn giải:

Ta có

2 2 2

3 2 4 29   IA và

2 2 2

0 5 2 29   IB . Gọi M là trung điểm của

đoạn thẳng AB, vì IA=IB nên IM AB, ta

có

1 1

; ;5 ;

2 2

 

 

 

IM

Gọi H là hình chiếu vuông góc của I lên

mặt phẳng (P):

Nếu H, M là hai điểm phân biệt thì tam

giác IHM vuông tại H, IH<IM hay

IH

Nếu H trùng với M thì

 IH IM

. Vậy ta có

IH

, IH lớn nhất khi H  M.

Khi đó (P) có vectơ pháp tuyến là

3 7

; ;3

2 2

 

  

 

 

  

n IH IM . Vậy phương trình mặt phẳng

(P) là

     

3 7

2 1 3 6 0

2 2

     x y z

hay 3 7 6 35 0   x y z

Chọn A.

Câu 33:

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm và . Mặt phẳng

(P) đi qua M, N sao cho khoảng cách từ đến (P) đạt giá trị lớn nhất. (P) có vectơ

pháp tuyến là:

A. B. C. D.

Hướng dẫn giải:

- Khoảng cách từ K đến (P) lớn nhất bằng KH, khi H’

trùng H

- Vậy mặt phẳng (P) qua MN và vuông góc với KH.

(0; 1;2)



( 1;1;3)







0;0;2

(1;1; 1)



(1; 1;1)



(1; 2;1)



(2; 1;1)



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33

Facebook: https://www.facebook.com/dongpay

- Tìm H và viết (P) hoặc:

- (P) chứa MN và vuông góc với (MNP).

Gọi H, H’ là hình chiếu của K lên MN và (P).

Ta có: không đổi.

Vậy lớn nhất khi và chỉ khi H’ trùng H hay (P) vuông góc với KH.

;

(MNK) có vtpt là

Do nên HK có vtcp là .

Chọn A.

Câu 34: Trong không gian

Oxyz

cho các điểm





1;0;0 ,





2;0;3 ,

B 





0;0;1

và





0;3;1 .

Mặt

phẳng





đi qua các điểm

sao cho khoảng cách từ điểm

đến





gấp hai lần

khoảng cách từ điểm

đến





Có bao mặt phẳng





thỏa mãn đầu bài?

A. Có vô số mặt phẳng





B. Chỉ có một mặt phẳng





C. Không có mặt phẳng





nào. D. Có hai mặt phẳng





Hướng dẫn giải:

Chọn A.

Giả sử





có phương trình là:





2 2 2

z 0 0

ax by c d a b c

      

Vì





0 .

M P c d d c

      

Vì





3 0

N P b c d

    

hay



vì

c d

 





: 0.

P ax cz c

   

Theo bài ra:

















, 2 ,

d B P d A P





2 2 2 2

2 3

a c c a c

a c a c

   



 

c a a c

   

Vậy có vô số mặt phẳng





Câu 35: Trong không gian tọa độ Oxyz, cho phương trình mặt phẳng

 

( ,( )) '

d k P KH KH

( ,( ))

d K P

   

 

(0;1;0); (1; 1; 1)

MK NK  



( 1;2;1)

 

   

 

  

, ( 1;0; 1)

n MK NK











( )

HK MNK

HK MN

 

 

 

 

, (2;2; 2)

MN n

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34

Facebook: https://www.facebook.com/dongpay

Xét các mệnh đề sau:

(I) Với mọi thì các mặt phẳng luôn tiếp xúc với một mặt cầu không đổi.

(II) Với mọi thì các mặt phẳng luôn cắt mặt phẳng (Oxz).

(III) .

Khẳng định nào sau đây đúng?

A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III) D. Cả 3 đều đúng.

Hướng dẫn giải:

+ Ta có , với mọi .

Do đó với mọi m thay đổi trên thì các mặt phẳng luôn tiếp xúc với mặt cầu tâm

O, bán kính . Khẳng đinh (I) đúng.

+ Vectơ pháp tuyến của mặt phẳng là và vectơ pháp tuyến

của mặt phẳng (Oxz) là .

cắt (Oxz) khi và chỉ khi . Khẳng đinh (II) đúng.

+ Khẳng đinh (III) sai.

Chọn A.

Câu 36: Cho mặt phẳng





đi qua hai điểm









3,0,4 , 3,0,4

A B  và hợp với mặt phẳng





xOy

một góc

và cắt

y Oy

tại

Tính khoảng cách từ

đến





4 3

. B.

. C.

3 3

. D.

2 3

Hướng dẫn giải:

Vẽ

OH KC



với

là giao điểm

của

và trục

z Oz

Ta có:

0 0

30 60 ; 4

C K OK

 

   





: 3 5 1 4 20 0, 1;1

mx m y mz m

 

      

 

 

1;1

 

 

 

 



















; 5, 1;1

d O m

 

   

 

 

 





2 2 2

; 4

9 25 1 16

d O

m m m



 

  

 

 

  

1;1

 

 

 

 

1;1

 



 

 



















3 ;5 1 ;4

n m m m

 







0;1;0

j 









; 0 0

n j m

 

  

 

 

 

-3

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35

Facebook: https://www.facebook.com/dongpay





, .sin60

4. 2 3.

d O P OH OK  

 

Chọn D.

Câu 37: Trong không gian với hệ tọa độ

Oxyz

, hai mặt phẳng

4 4 2 7 0

x y z

   

và

2 2 1 0

x y z

   

chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là

V  B.

81 3

V 

9 3

V  D.

V 

Hướng dẫn giải:

Theo bài ra hai mặt phẳng

4 4 2 7 0

x y z

   

và

2 2 1 0

x y z

   

chứa hai mặt của hình

lập phương. Mà hai mặt phẳng

( ): 4 4 2 7 0

P x y z

   

và

( ) : 2 2 1 0

Q x y z

   

song

song với nhau nên khoảng cách giữa hai mặt phẳng sẽ bằng cạnh của hình lập phương.

Ta có

(0;0; 1) ( )

M Q

 

nên

2 2 2

2 7 3

(( ),( )) ( ,( ))

4 ( 4) 2

d Q P d M P

 

  

  

Vậy thể tích khối lập phương là:

2 2 2 8

. .

3 3 3 27

V   .

Câu 38:

Trong không gian với hệ toạ độ , gọi là mặt phẳng qua hai điểm và

đồng thời hợp với mặt phẳng một góc . Khoảng cách từ O tới là:

A. B. C. D.

Hướng dẫn giải:

Gọi lần lượt là hình chiếu vuông góc điểm lên đường thẳng và mặt phẳng

Ta có:

Oxyz











2;0;1





2;0;5







Oxz







;

K H











A B Oxz











Oxz AB



  





HK AB

OK AB













 









ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36

Facebook: https://www.facebook.com/dongpay

Suy ra tam giác vuông cân tại

Khi đó:

Mặt khác:

Khi đó:

Chọn A.

Câu 39: Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng





: 0

Q x y z

  

và hai điểm









4, 3,1 , 2,1,1 .

A B Tìm điểm

thuộc mặt phẳng





sao cho tam giác

ABM

vuông

cân tại





1; 2;1

17 9 8

; ;

7 7 7





 



 

 



 



. B.





1;2;1

17 9 8

; ;

7 7 7





 



 



 







1;2;1

13 5 9

; ;

7 7 7





 



 

 



 



. D.





1;1;1

9 9 8

; ;

7 7 7





 



 

 



 



Hướng dẫn giải:

Gọi













, , . 0 1 .

M a b c M Q a b c    

Tam giác

ABM

cân tại

khi và chỉ khi:

             

2 2 2 2 2 2

2 2

4 3 1 2 1 1 2 5 0 2

AM BM a b c a b c a b                 

Từ





và





ta có:

 

0 2 5

2 5 0 5 3

a b c a b

a b c b

    

 



 

      

 

Trung điểm

là





3; 1;1 .

I  Tam giác

ABM

cân tại

suy ra:

       

2 2 2

3 1 1 5 3

MI a b c       

Thay





và





ta được:

     

2 2 2

2 2 1 6 3 5

b b b

 





       



 



   















, ,

Oxz KH OK OKH



  

OHK

 

, .

d O OH



 

 

, .

OA AB

OK d O AB



  

 



 

, .

d O OH



  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37

Facebook: https://www.facebook.com/dongpay





2 1, 1 1; 2;1

9 17 8 17 9 8

, ; ;

7 7 7 7 7 7

b a c M

      

 

        

 

 

Chọn A.

Câu 40: Trong không gian với hệ tọa độ

Ox ,

cho 2 điểm









1;3;2 , 3;2;1

A B và mặt phẳng





: 2 2 11 0.

P x y x

   

Tìm điểm

trên





sao cho

2 2, 30 .

MB MBA



 





 

1;2;3

1;4;1







. B.





 

1; 2;3

1; 4;1











. C.





 

2;1;3

4;1;1







. D.





 

1; 2;3

1;4;1











Hướng dẫn giải:

Nhận thấy









, , 6.

A P B P AB  

Áp dụng định lý côsin trong tam giác

MAB

ta có:

2 2 2 0 2 2 2

2 . . os30 2

MA MB BA MB BAc MB MB BA

      

Do đó tam giác

MAB

vuông tại

Ta có:

   

, 0; 5;5 : 3 1;3 ;2

AM p

u AB n AM y t M t t

z t







 

        



 



 



  

Ta có

2 2 2

2 2 1

MA t t t

      

Với









1 1;2;3 ; 1 1;4;1

t M t M    

Chọn A.

Câu 41: Trong không gian tọa độ , cho tám điểm , , ,

, , , , . Hỏi hình đa diện tạo bởi

tám điểm đã cho có bao nhiêu mặt đối xứng.

A. 3. B. 6. C. 8. D. 9

Hướng dẫn giải:

Vì tám điểm đã chõ tạo nên một hình lập phương, nên hình đa diện tạo bởi tám điểm này có

9 mặt đối xứng.

Chọn D.

Câu 42: Trong không gian với hệ tọa độ

Oxyz

, cho bốn điểm





1; 2;0 ,

A 





0; 1;1 ,

B 





2;1; 1 ,







3;1;4

D . Hỏi có bao nhiêu mặt phẳng cách đều bốn điểm đó?

D. Vô số.

Hướng dẫn giải:

Ta có





1;1;1 ,

 







1;3; 1 ,

 







2;3;4





AD .

Oxyz





2; 2;0

A  





3; 2;0

B 





3;3;0





2;3;0

D 





2; 2;5

M  





2; 2;5

N  





3; 2;5

P 





2;3;5

Q 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38

Facebook: https://www.facebook.com/dongpay

Khi đó

 

, 4;0; 4

 

  

 

 

AB AC suy ra

, . 24 0

 

  

 

  

AB AC AD .

Do đó

, , ,

A B C D

không đồng phẳng và là 4 đỉnh của một tứ diện.

Khi đó sẽ có 7 mặt phẳng cách đễu bốn đỉnh của tứ diện. Bao gồm: 4 mặt phẳng đi qua trung

điểm của ba cạnh tứ diện và 3 mặt phẳng đi qua trung điểm bốn cạnh tứ diện (như hình vẽ).

Chọn C.

Câu 43: Trong không gian cho điểm

(1; 3;2)



.Có bao nhiêu mặt phẳng đi qua

và cắt các trục

tọa độ tại

, ,

A B C

mà

OA OB OC

  

A. 1. B. 2. C. 3. D. 4.

Hướng dẫn giải:

Chọn C.

Giả sử mặt phẳng

( )



cần tìm cắt

, ,

Ox Oy Oz

lần lượt tại

(a,0,0),B(0,b,0),C(0,0c)(a,b,c 0)



( ): 1

x y z

a b c

  



;

( )



qua

(1; 3;2)



nên:

1 3 2

( ): 1(*)

a b c

  



(1)

(2)

0 0

(3)

(4)

a b c

OA OB OC a b c

a b c

 





  



       



  



   



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39

Facebook: https://www.facebook.com/dongpay

Thay

(1)

vào (*) ta có phương trình vô nghiệm

Thay

(2),(3),(4)

vào (*) ta được tương ứng

4, 6,

a a a



   

Vậy có 3 mặt phẳng.

Câu 44: Có bao nhiêu mặt phẳng đi qua điểm

(1;9;4)

M và cắt các trục tọa độ tại các điểm

(khác gốc tọa độ) sao cho

OA OB OC

 

. B.

. C.

. D.

Hướng dẫn giải:

Chọn D.

Giả sử mặt phẳng

( )



cắt các trục tọa độ tại các điểm khác gốc tọa độ là

( ;0;0), (0; ;0), (0;0; )

A a B b C c

với

, , 0.

a b c



Phương trình mặt phẳng

( )



có dạng

x y z

a b c

  

Mặt phẳng

( )



đi qua điểm

(1;9;4)

M nên

1 9 4

1 (1).

a b c

  

Vì

OA OB OC

 

nên

a b c

  do đó xảy ra 4 trường hợp sau:

+) TH1:

a b c

 

Từ

(1)

suy ra

1 9 4

1 14,

a a a

     nên phương trình mp

( )



là

14 0.

x y z

   

+) TH2:

a b c

  

Từ

(1)

suy ra

1 9 4

1 6,

a a a

    

nên pt mp

( )



là

6 0.

x y z

   

+) TH3:

a b c

  

Từ

(1)

suy ra

1 9 4

1 4,

a a a

     

nên pt mp

( )



là

4 0.

x y z

   

+) TH4:

a b c

   

Từ

(1)

có

1 9 4

1 12,

a a a

     

nên pt mp

( )



là

12 0.

x y z

   

Vậy có 4 mặt phẳng thỏa mãn.

Câu 45: Trong không gian với hệ tọa độ

Oxyz

, cho điểm

(2; 2;0)



, đường thẳng

1 2

1 3 1

x y z

 

  



. Biết mặt phẳng

( )

có phương trình

ax by cz d

   

đi qua

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40

Facebook: https://www.facebook.com/dongpay

song song với



và khoảng cách từ



tới mặt phẳng

( )

lớn nhất. Biết

a b

là các số

nguyên dương có ước chung lớn nhất bằng 1. Hỏi tổng

a b c d

  

bằng bao nhiêu?

. B.

. C.

. D.



Hướng dẫn giải:

Gọi

là hình chiếu vuông góc của

trên đường thẳng



( 1 ;3 ;2 )

H H t t t

    

( 3;3 2; 2)

AH t t t

     



. 0

AH AH u



   

 

với

( 1;3;1)



 



1.( 3) 3.(3 2) 1.( 2) 0 11 11

t t t t

           

  





0; 3;1

H 

Gọi

là hình chiếu vuông góc của

trên

( )

, khi đó: ( ,( )) ( ,( ))

d P d H P HF HA

   

Suy ra

max

( ,( ))

d P HA

 

. Dấu “=” xảy ra khi

F A



( )

AH P

 

, hay bài toán được phát

biểu lại là:

“ Viết phương trình mặt phẳng

( )

đi qua

và vuông góc với

”

Ta có





2; 1;1 (2;1; 1)

     



, suy ra

( )

(2;1; 1)

 



Suy ra phương trình mặt phẳng

( )

là:

2( 2) 2 0 2 2 0

x y z x y z

         

, * 2, 1

( , ) 1 1, 2

a b a b

a b c d

  

 

     

 

    

 



Chọn B.

Câu 46: Trong không gain Oxyz, cho hai đường thẳng

1 2 1

x y z

  

 



và

: 3

x t

d y t

 





 





 



Mặt phẳng





: 0

P ax by cz d

   

(với ; ; ;a b c d





) vuông góc với đường thẳng

và

chắn

1 2

d d

đoạn thẳng có độ dài nhỏ nhất. Tính

a b c d

  



Hướng dẫn giải:

Ta có mặt phẳng (P) vuông dóc với đường thẳng

nên (P) có véctơ pháp tuyến





1;2;1

n 



Phương trình (P) có dạng





: 2 0

P x y z d

   

Gọi M là giáo điểm của (P) với

và N là giao của (P) với

suy ra

2 2 10

; ;

6 3 6

d d d

  

 

 

 

4 1

; ; 2

3 3

d d

   

 



 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41

Facebook: https://www.facebook.com/dongpay

Ta có

16 155

18 9 9

d d

MN   

Để MN nhỏ nhất thì

nhỏ nhất, nghĩa là

 

Khi đó

a b c d

    

Chọn A.

Câu 47: Trong không gian với hệ trục toạ độ Oxyz, cho điểm





10;2;1

A và đường thẳng

1 1

2 1 3

x y z

 

  . Gọi





là mặt phẳng đi qua điểm

, song song với đường thẳng

sao cho khoảng cách giữa

và





lớn nhất. Khoảng cách từ điểm





1;2;3

M  đến mp





là

97 3

76 790

790

2 13

3 29

Hướng dẫn giải::





là mặt phẳng đi qua điểm

và

song song với đường thẳng

nên





chứa đường thẳng



đi qua điểm

và

song song với đường thẳng

Gọi

là hình chiếu của

trên

là hình chiếu của

trên





Ta có









d d P HK AH

  (

không đổi)



GTLN của

( , ( ))

d d P

là











d d P

lớn nhất khi

vuông góc với





Khi đó, nếu gọi





là mặt phẳng chứa

và

thì





vuông góc với





 

   

 

, 98;14; 70

97 3

:7 5 77 0 , .

P d Q

n u n

P x y z d M P

 

   

 

      

  

Câu 48: Trong không gian với hệ trục toạ độ

Oxyz

cho điểm





2;5;3

A và đường thẳng

1 2

2 1 2

x y z

 

  . Gọi





là mặt phẳng chứa đường thẳng

sao cho khoảng cách từ

đến





lớn nhất. Tính khoảng cách từ điểm





1;2; 1



đến mặt phẳng





11 18

3 2.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải::

Gọi

là hình chiếu của

trên

;

là hình chiếu của

trên





Ta có









d A P AK AH

  (Không

đổi)



GTLN của

( , ( ))

d d P

là

⟹









d A P

lớn nhất khi

K H



Ta có





3;1;4

H ,





qua

và







: 4 3 0

P x y z

    

Vậy

 

11 18

d M P  .

Câu 49: Trong không gian với hệ tọa độ

Oxyz

, cho













;0;0 , 0; ;0 , 0;0;

A a B b C c

với

, ,

a b c

dương. Biết

, ,

A B C

di động trên các tia

, ,

Ox Oy Oz

sao cho

a b c

  

. Biết rằng khi

, ,

a b c

thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện

OABC

thuộc mặt phẳng





cố

định. Tính khoảng cách từ





2016;0;0

M tới mặt phẳng





2017

. B.

2014

. C.

2016

. D.

2015

Hướng dẫn giải:

Chọn D.

Gọi







là mặt phẳng trung trực của đoạn









đi qua điểm

;0;0

 

 

 

và có VTPT









;0;0 1;0;0

OA a a 



 

: 0

  



Gọi







là mặt phẳng trung trực của đoạn









đi qua điểm

0; ;0

 

 

 

và có VTPT









0; ;0 0;1;0

OB a a 



 

: 0

  



Gọi







là mặt phẳng trung trực của đoạn









đi qua điểm

0;0;

 

 

 

và có VTPT









0;0; 0;0;1

OC a a 



 

: 0

  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43

Facebook: https://www.facebook.com/dongpay

Gọi

là tâm mặt cầu ngoại tiếp tứ diện

OABC

     

; ;

2 2 2

a a a

I I

 

    

 

 

  

Mà theo giả thiết,

 

2 1 : 1

2 2 2

a b c

a b c I P x y z

           

Vậy,

 

2016 1

2015

3 3

d M P



  .

Câu 50: Trong không gian với hệ trục tọa độ

Oxyz

cho mặt phẳng





:3 5 0

P x y z

   

và hai

điểm





1;0;2





2; 1;4 .

B 

Tìm tập hợp các điểm





; ;

M x y z

nằm trên mặt phẳng





sao

cho tam giác

MAB

có diện tích nhỏ nhất.

7 4 7 0

3 5 0

x y z

   





   



7 4 14 0

3 5 0

x y z

   





   



7 4 7 0

3 5 0

x y z

   





   



3 7 4 5 0

3 5 0

x y z

   





   



Hướng dẫn giải:

Chọn C.

Ta thấy hai điểm

A B

nằm cùng 1 phía với mặt phẳng





và

song song với





Điểm





M P

 sao cho tam giác

ABM

có diện tích nhỏ nhất

. ( ; )

ABC

AB d M AB



  nhỏ nhất





;

d M AB

 nhỏ nhất, hay













M P Q Q

   là

mặt phẳng đi qua

và vuông góc với





Ta có





1; 1;2

AB  



, vtpt của





 





3;1; 1

 



Suy ra vtpt của





   

 

, 1;7;4

Q P

n AB n

 

  

 

  

PTTQ













: 1 1 7 4 2 0

Q x y z

     

7 4 7 0

x y z

    

Quỹ tích

là

7 4 7 0

3 5 0

x y z

   





   



Câu 51: Trong không gian

Oxyz

, cho hình hộp chữ nhật .

ABCD A B C D

   

có điểm

trùng với gốc

của hệ trục tọa độ,

( ;0;0)

B a

(0; ;0)

D a

(0;0; )

A b



( 0, 0)

a b

 

. Gọi

là trung điểm của

cạnh



. Giá trị của tỉ số

để hai mặt phẳng

( )

A BD



và





MBD

vuông góc với nhau là:

. B.

. C.



. D. 1.

Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44

Facebook: https://www.facebook.com/dongpay

Ta có

   

; ;0 ' ; ; ; ;

AB DC C a a C a a b M a a

 

   

 

 

 

Cách 1.

Ta có

0; ;

MB a

 

  

 

 



;





; ;0

BD a a

 



và





' ;0;

A B a b

 



Ta có

; ; ;

2 2

ab ab

u MB BD a

 

 

  

 

 

 

  

và





2 2 2

; ;; 'BD A aB

 

 

 

 

 

Chọn





1;1;1

v 



là VTPT của





A BD

   

' . 0 0 1

2 2

ab ab a

A BD MBD u v a a b

          

 

Cách 2.

' ' '

A B A D A X BD

AB AD BC CD a

MB MD MX BD

 

 

     

 

 

 

với

là trung điểm

   







' ; ' ;

A BD MBD A X MX

 

 

 

; ;0

2 2

a a

 

 

 

là trung điểm

' ; ;

2 2

a a

A X b

 

 

 

 



; ;

2 2 2

a a b

 

   

 

 











' '

A BD MBD A X MX

  

' . 0

A X MX

 

 

2 2

2 2 2

a a b

   

    

   

   

 

Câu 52: Trong không gian với hệ trục toạ độ cho 3 điểm .

Gọi là mặt phẳng đi qua sao cho tổng khoảng cách từ và đến lớn nhất

biết rằng không cắt đoạn . Khi đó, điểm nào sau đây thuộc mặt phẳng ?

A. B. C. D. .

Hướng dẫn giải:

Oxyz













1;0;1 ; 3; 2;0 ; 1;2; 2

A B C

 





















2; 0; 3 .

G 





3; 0; 2 .







1;3;1 .





0;3;1

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45

Facebook: https://www.facebook.com/dongpay

Gọi là trung điểm đoạn ; các điểm

lần lượt là hình chiếu của

trên .

Ta có tứ giác là hình thang và là

đường trung bình.

Mà (với không đổi)

Do vậy, lớn nhất khi

đi qua và vuông góc với

Câu 53: Trong không gian với hệ trục toạ độ cho các điểm

trong đó dương và mặt phẳng . Biết rằng vuông góc với

và , mệnh đề nào sau đây đúng?

A. B. C. D.

Hướng dẫn giải:

Ta có phương trình mp( là

Ta có

Từ (1) và (2) .

Câu 54: Cho hình lập phương .

ABCD A B C D

   

có cạnh bằng 2. Tính khoảng cách giữa hai mặt phẳng









và

AB D BC D

  

Hướng dẫn giải:

Chọn A.

Ta chọn hệ trục tọa độ sao cho các đỉnh của hình lập phương có tọa độ như sau:

, ,

B C I

 



, ,

B C I





BCC B

 



















, , 2 .

d B P d C P BB CC II



    

 

II IA





















, ,

d B P d C P



I A

















2;0; 1 .















: 2 1 0 1;3;1 .

P x z E P

      

Oxyz













1;0;0 , 0; ;0 , 0;0;

A B b C c

b c





: 1 0

P y z

  





mp ABC





mp P

 

d O ABC



b c

 

2 1.

b c

 

3 1.

b c

 

3 3.

b c

 

)

ABC

x y z

b c

  

   

1 1

0 (1)

ABC P b c

b c

     

 

2 2

1 1 1 1 1

, 8(2)

3 3

1 1

d O ABC

b c

     

 

b c b c

     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46

Facebook: https://www.facebook.com/dongpay

















       

0;0;0 2;0;0 2;2;0 0;2;0

0;0;2 2;0;2 2;2;2 0;2;2

A B C D

   









   

2;0;2 , 0;2;2 ,

2;2;0 , 0;2;2

AB AD

BD BC

 

 



  

 

* Mặt phẳng





AB D

 

qua





0;0;0

A và nhận véctơ

 

, 1; 1;1

n AB AD

 

 

   

 

 



làm véctơ pháp tuyến.

Phương trình





AB D

 

là:

x y z

  

* Mặt phẳng





BC D



qua





2;0;0

B và nhận véctơ

 

, 1;1; 1

m BD BC

 



  

 

 



làm véctơ

pháp tuyến.

Phương trình





BC D



là:

2 0.

x y z

   

Suy ra hai mặt phẳng





AB D

 

và





BC D



song song với nhau nên khoảng cách giữa hai

mặt phẳng chính là khoảng cách từ điểm

đến mặt phẳng





BC D



 

2 2 3

, .

d A BC D



 

Cách khác: Thấy khoảng cách cần tìm

   

 

1 1 2 3

, .2 3 .

3 3 3

d AB D BC D AC

   

  

Câu 55: Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm













5;5;0 , 1;2;3 , 3;5; 1

A B C



và mặt

phẳng





:x 5 0

P y z

   

Tính thể tích

của khối tứ diện

SABC

biết đỉnh

thuộc mặt

phẳng





và

SA SB SC

 

145

V  . B.

145



. C.

V  . D.

127

V  .

Hướng dẫn giải:

Gọi













; ; 5 0 1

S a b c P a b c      .

Ta có:

   

2 2

5 5 ,

AS a b c

    

           

2 2 2 2 2 2

1 2 3 , 3 5 1

BS a b c CS a b c           

           

         

2 2 2 2 2 2

2 2 2 2 2

1 2 3 3 5 1

5 5 3 5 1

4 6 8 21 0

4 2 15 0

a b c a b c

SA SB SC

a b c a b c

a b c

a c



          



  





         



   







  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47

Facebook: https://www.facebook.com/dongpay

Ta có hệ:

4 6 8 21 0

23 13 9

4 2 15 0 6; ;

2 2 2

5 0

a b c

a c b S

a b c







   





 

 

         

 

 

 

 

   





 





. Lại có:









4; 3;3 , 2;0; 1

AB AC

   

 

 

23 9 145

3; 10; 6 ; 1; ; 145

2 2 6

S ABC

AB AC AS AB AC AS V

 

            

 

 

     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48

Facebook: https://www.facebook.com/dongpay

PHƯƠNG TRÌNH ĐƯỜNG THẲNG NÂNG CAO

A - LÝ THUYẾT CHUNG

1. Định nghĩa

Phương trình tham số của đường thẳng



đi qua điểm





0 0 0 0

; ;

M x y z

và có vec tơ chỉ phương





1 2 3

; ; , 0

a a a a a

 

  

0 1

0 2

0 3

x x a t

y y a t

z z a t

 





 





 



Nếu

1 2 3

; ;

a a a

đều khác không. Phương trình đường thẳng



viết dưới dạng chính tắc như sau:

0 0 0

1 2 3

x x y y z z

a a a

  

 

Ngoài ra đường thẳng còn có dạng tổng quát là:

1 1 1 1

2 2 2 2

A x B y C z D

   





   



với

1 1 1 2 2 2

, , , , ,

A B C A B C



thỏa

2 2 2 2 2 2

1 1 1 2 2 2

0, 0.

A B C A B C

     

2. Vị trí tương đối của hai đường thẳng

Chương trình cơ bản Chương trình nâng cao

1 )Vị trí tương đối của hai đường thẳng

Trong không gian

cho hai đường thẳng

0 1 0 1

0 2 0 2

0 3 0 3

' ' '

: ; ': ' ' '

' ' '

x x a t x x a t

d y y a t d y y a t

z z a t z z a t

   

 

 

   

 

 

   

 

Vtcp



đi qua

và

có vtcp



đi qua

, '

u u

 

cùng phương:

0 0

' '

/ / ' ; '

' '

u ku u ku

d d d d

M d M d

 

 

 

  

 

 

 

 

   

, '

u u

 

không cùng phương:

 

0 1 0 1

0 2 0 2

0 3 0 3

' ' '

x a t x a t

y a t y a t I

z a t y a t

  





  





  





d chéo d’



hệ phương trình





vô nghiệm



d cắt d’



hệ phương trình





có 1 nghiệm

1 ) Vị trí tương đối của hai đường thẳng

Trong không gian

cho hai đường thẳng

0 1 0 1

0 2 0 2

0 3 0 3

' ' '

: ; ': ' ' '

' ' '

x x a t x x a t

d y y a t d y y a t

z z a t z z a t

   

 

 

   

 

 

   

 

Vtcp



đi qua

và

có vtcp



đi qua

   

, ' 0

/ / '

u u

d d

M d



 





 











  

   

, ' 0

u u

d d

M d



 





 

 









  

   

, ' 0

at '

, ' . 0

u u

d c d

u u MM



 



 





 





 



  

  

   

' , ' . 0

d cheo d u u MM

 

 

 

  

3. Vị trí tương đối của đường thẳng và mặt phẳng

Phương pháp 1 Phương pháp 2

Trong không gian

cho: Trong không gian

cho đường thẳng d

qua





0 0 0

; ;

M x y z

có vtcp:





1 2 3

; ;

a a a a





và

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49

Facebook: https://www.facebook.com/dongpay





:Ax+By+Cz+D=0



và

0 1

0 2

0 3

x x a t

d y y a t

z z a t

 





 





 



Pt:

















0 1 0 2 0 3

0 1

A x a t B y a t C z a t D      

Phương tr

ình





vô nghiệm thì





/ /d



Phương tr

ình





có 1 nghiệm thì

cắt







Phương tr

ình





có vô số nghiệm thì









Đặc biệt:





d a n



 

 

cùng phương





:Ax+By+Cz+D=0



có vtpt





; ;

n A B C









cắt





. 0

a n



 

 

   

 

. 0

/ /

a n



















 





nằm trên mp







 

. 0

a n



















 

4. Khoảng cách

Khoảng cách từ





0 0 0

; ;

M x y z

đến mặt phẳng





:Ax+By+Cz+D=0



cho bởi công thức

 

0 0 0

2 2 2

By Cz D

d M

A B C



  



 

Khoảng cách từ M đến đường thẳng





Phương pháp 1:

ập ptmp







đi qua

và vuông góc với d.

Tìm t

ọa độ giao điểm

của mp







và





d M d MH



Kho

ảng cách giữa hai đường thẳng chéo nhau

Phương pháp 1:

đi qua





0 0 0

; ;

M x y z

; có vtpt





1 2 3

; ;

a a a a





đi qua





0 0 0

' '; '; '

M x y z

; vtpt





1 2 3

' '; '; '

a a a a





Lập phương trình mp







chứa d và song song

với d’:













, ' ',d d d d M





Kho

ảng cách từ M đến đường thẳng





Phương pháp 2:

(

đi qua

có vtcp



)

 

M M u

d M

 

 

 

 



Kho

ảng cách giữa hai đường thẳng chéo nhau

Phương pháp 2:

đi qua





0 0 0

; ;

M x y z

; có vtpt





1 2 3

; ;

a a a a





đi qua





0 0 0

' '; '; '

M x y z

; vtpt





1 2 3

' '; '; '

a a a a





 

, ' . '

, '

hop

day

a a MM

a a

 

 

   

 

 

  

 

5. Góc giữa hai đường thẳng

 Góc giữa hai đường thẳng







đi qua





0 0 0

; ;

M x y z

có VTCP





1 2 3

; ;

a a a a











đi qua





0 0 0

' '; '; '

M x y z

có VTCP





1 2 3

' '; '; '

a a a a





 

1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

. '

. ' . ' . '

cos cos , '

. '

. ' ' '

a a

a a a a a a

a a

a a a a a a



 

  

   

 

6. Góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng và mặt phẳng







đi qua

có VTCP



, mặt phẳng







có VTPT





; ; .

n A B C





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50

Facebook: https://www.facebook.com/dongpay

Gọi



là góc hợp bởi







và mặt phẳng

 

1 2 3

2 2 2 2 2 2

1 2 3

:sin cos ,

Ba Ca

a n

A B C a a a

 

 

 

   

 

B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Đường thẳng



song song với

4 5 2

3 4 1

x y z

  

 



và cắt cả hai đường thẳng

1 1 2

3 1 2

  

 

x y z

và

2 3

2 4 1

 

 

x y z

. Phương trình nào không phải đường

thẳng



4 1 1

3 4 1

  

  



x y z

7 2

3 3

3 4 1

 



  



y z

9 7 2

3 4 1

  

  



x y z

4 1 1

3 4 1

  

  



x y z

Hướng dẫn giải:

Giải: Gọi M, N là giao điểm của



và

1 2

d d

Khi đó M, N thuộc

1 2

d d

nên

2 2 '

1 3

1 , 3 4 '

2 2 '

  

 



 

    

 

 

  



M N

x t

y t y t

z t z t

Vector chỉ phương của



là





3 2 ' 3 ;4 4 ' ; 2 ' 2

        



MN t t t t t t



song song với

4 5 2

3 4 1

  

 



x y z

nên

3 2 ' 3 4 4 ' 2 ' 2

3 4 1

       

 



t t t t t t

Giải hệ ta được

' 1;

   

t t

. Vậy

 

7 2

4; 1; 1 , 3; ;

3 3

 

     

 

 

N M

Vậy

4 1 1

3 4 1

  

  



x y z

Chọn A.

Câu 2: Cho đường thẳng

( ): 1

x t

d y t

z t

 





 









và mp (P) :

2 0

x y

  

. Tìm phương trình đường thẳng

nằm trong mặt phẳng (P) cắt và vuông góc với (d).

1 2

x t

y t

 





 









1 3

x t

y t

 





 









1 2

x t

y t

 





 









x t

y t

 





 









Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51

Facebook: https://www.facebook.com/dongpay

Gọi I là giao điểm của (d) và (P):

(1 ;1 ;2 ), ( ) 0 (1;1;0)

I t t t I P t I

     

(d) có vectơ chỉ phương

( 1; 1;2)

u   



, (P) có vectơ pháp tuyến

(1;1;0)

n 



Vectơ pháp tuyến của mặt phẳng cần tìm là

u u v



 



 

  

=(-2 ;2 ;0)

Phương trình mặt phẳng cần tìm là

1 2

x t

y t

 





 









Chọn A.

Câu 3: Trong không gian với hệ tọa độ cho đường thẳng và mặt phẳng

Phương trình đường thẳng nằm trong sao cho cắt và

vuông góc với đường thẳng là

A. . B. .

C. . D. .

Hướng dẫn giải:

Chọn C.

Vectơ chỉ phương của , vectơ pháp tuyến của





là

 





1;2;2

n 



Vì .

Tọa độ giao điểm là nghiệm của hệ

Lại có , mà . Suy ra .

Vậy đường thẳng đi qua và có VTCP nên có phương trình

Oxyz

1 2

1 1 1

x y z

 

  







: 2 2 4 0.

P x y z

   







 

: 1 2

x t

d y t t

z t

  





  





 





 

: 2

2 2

x t

d y t t

z t







  





 





 

2 4

: 1 3

x t

d y t t

z t

  





   





 





 

: 3 3

3 2

x t

d y t t

z t

  





  





 









: 1;1; 1



 



 

; 4; 3;1

d P

u u

u u n

d P

u n





 

 

 

 

    

 

 











 

  

 





H P

  

 

2 2; 1;4

2 2 4 0

x t

y t

t H

z t

x y z







 



     



 



   











;

d P d

  





H P

  

H d







2; 1;4

H  





4; 3;1

u  



 

2 4

: 1 3

x t

d y t t

z t

  





   





 





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52

Facebook: https://www.facebook.com/dongpay

Câu 4: Trong không gian với hệ tọa độ

cho đường thẳng

2 2

2 1 1

x y z

 

 

và mặt phẳng





: 2 3 0.

P x y z

   

Viết phương trình đường thẳng



nằm trong





sao cho



vuông

góc với

và khoảng cách giữa hai đường thẳng



và

bằng

7 4

1 1 1

x y z

 



  



 







  



  

. B.

7 4

1 1 1

x y z

 



  











  



 

7 4

2 1 1

1 4 1

x y z

 



  











  





. D.

7 4

1 1 1

3 1

1 1 1

x y z

  



  



 



  



  



  

Hướng dẫn giải:

Đường thẳng d có VTCP





2;1;1 .

u 



Mặt phẳng





có VTPT





1;2; 1 ,

 



ta có

 

, 3; 3; 3

p d

n u

 

  

 

 

Vì

   

, ; 0; 1;1

P d VTPT u u u

 

 

       

 

  

Khi đó, phương trình mặt phẳng





: 0

Q y z m

  

Chọn





1; 2;0 ,

A d

 

ta có:

 

; ; 2 2

d A Q d d



 



     







Với





4 : 4 0

m Q y z

    

Vì









P Q

    

đi qua

 

7 4

7;0;4 :

1 1 1

x y z

 

   

 

Với





0 : 0

m Q y z

   

Vì









P Q

    

đi qua

 

3;0;0 :

1 1 1

x y z



   

 

Chọn A.

Câu 5: Cho hai điểm









3;3;1 , 0;2;1

A B và mặt phẳng





: 7 0

x y z

   



. Đường thẳng

nằm

trên







sao cho mọi điểm của

cách đều 2 điểm

A B

có phương trình là

7 3 .

x t

y t

z t







 









7 3 .

x t

y t

z t







 









7 3 .

x t

y t

z t

 





 









7 3 .

x t

y t

z t







 









Hướng dẫn giải:

Chọn A.

Mọi điểm trên

cách đều hai điểm

A B

nên

nằm trên mặt phẳng trung trực của đoạn

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 53

Facebook: https://www.facebook.com/dongpay

Có





3; 1;0

AB   



và trung điểm

là

3 5

; ;1

2 2

 

 

 

nên mặt phẳng trung trực của

là:

3 5

3 0 3 7 0

2 2

x y x y

   

        

   

   

Mặt khác





d 



nên

là giao tuyến của hai mặt phẳng:

3 7 0 7 3

7 0 2

x y y x

x y z z x

    

 



 

    

 

Vậy phương trình

 

: 7 3

x t

d y t t

z t







  











Câu 6: Trong không gian với hệ tọa độ

cho đường thẳng

2 1

1 2 1

x y z

 

 

 

và mặt phẳng





: 3 0.

P x y z

   

Gọi

là giao điểm của





, .

d P

Tìm





M P

 sao cho

vuông góc

với

và

4 14.

MI 





 

5;9; 11

3; 7;13





 





. B.





 

5;7; 11

3; 7;13





 









 

5;9; 11

3; 7;13

 











. D.





 

5; 7;11

3;7; 13











Hướng dẫn giải:

Vì

I d



nên





2 ; 1 2 ; .

I t t t

   

Hơn nữa









2 1 2 3 0 1 1;1;1

I P t t t I          

Gọi





; ; .

M a b c

Do:





. 0 2 2 0

M P a b c

MI d IM u a b c

    





       





 

   





1; 1; 1 , 1; 2; 1

IM a b c u

      

 

     

2 2 2

4 14 1 1 1 224.

MI a b c       

Khi đó ta có hệ phương trình:

       

2 2 2 2

3 2 1 5 3

2 2 0 4 3 9 7

11 13

1 1 1 224 1 16

a b c b a a a

a b c c a b b

c c

a b c a

 

       

 

 

   

           

   

   

  

 

       

 

 

Với













; ; 5;9; 11 5;9; 11

a b c M   

Với













; ; 3; 7;13 3; 7;13

a b c M     

Chọn A.

Câu 7: Trong không gian

Ox ,

cho hai mặt phẳng









: 2 2 0, :2 2 1 0.

P x y z Q x y z

      

Viết phương trình của đường thẳng

đi qua





0;0;1 ,

A nằm trong mặt phẳng





và tạo

với mặt phẳng





một góc bằng

45 .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 54

Facebook: https://www.facebook.com/dongpay

1 2

: ; :

1 4 1

x t x t

d y t d y t

z t z

 

 

 

  

 

 

  

 

. B.

1 2

: 2 1; : 1

1 4 1

x t x t

d y t d y t

z t z

 

 

 

   

 

 

  

 

1 2

: 1 ; :

1 4 1 4

x t x t

d y t d y t

z t z t

 

 

 

   

 

 

   

 

. D.

1 2

1 4

: 1 ; :

1 4 1

x t x t

d y t d y t

z t z

  

 

 

   

 

 

  

 

Hướng dẫn giải:

Ta có





2;2;1

n 



là vecto pháp tuyến của









, 1; 2;2

Q b  



là vec tơ pháp tuyến của





Gọi





2 2 2

; ; , 0

a a b c a b c

   



là một vecto chỉ phương của

Vì đường thẳng

đi qua





0;0;1

A mà









0;0;1 ,

A A Q



Do đó





. 0 2 2 0 2 2

d Q a n a n a b c c a b

            

   

Góc hợp bởi

và





bằng

45 :

 

2 2 2

2 2

sin 45 cos ;

18( ) 4 2 2

a b

a b c

a b

a b c

a b c a b c a b

 

    

 

        

 





 

1 1; 4

1 1; 0

a b b a c

     

      

Vậy

1 2

: ; :

1 4 1

x t x t

d y t d y t

z t z

 

 

 

  

 

 

  

 

là các đường thẳng cần tìm.

Chọn A.

Câu 8: Trong không gian với hệ tọa độ

Ox ,

cho hình thang cân

ABCD

có hai đáy

AB CD

thỏa

mãn 2

CD AB



và diện tích bằng 27; đỉnh





1; 1;0 ;

A   phương trình đường thẳng chứa

cạnh

là

2 1 3

2 2 1

x y z

  

 

Tìm tọa độ các điểm

biết hoành độ điểm

lớn hơn

hoành độ điểm





2; 5;1

D   . B.





3; 5;1

D   . C.





2; 5;1

D  . D.





3; 5;1

D 

Hướng dẫn giải:

Đường thẳng

qua





2; 1;3

M  có vec tơ chỉ phương





2;2;1

u 



Gọi





2 2 ; 1 2 ;3

H t t t

   

là hình chiếu của A lên CD, ta có:













. 2 3 2 ;2.2 (3 1 0; 3;2 , , 3

AH u t t t t H d A CD AH

          

 

Từ giả thiết ta có:

3 18 6; 3; 9

ABCD

AB CD AB AB DH HC

       

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 55

Facebook: https://www.facebook.com/dongpay

Đặt

       

2 ;2 ; 0 2 4;4;2 3;3;2

B A

AB tu t t t t x x t AB B

         



  



   

6;6;3 6;3;5

2; 2; 1 2; 5;1

HC AB C

HD AB D

  

        

 

Chọn A.

Câu 9: Trong không gian với hệ tọa độ

Ox ,

cho hai đường thẳng

1 2

: ;

1 2 1

x y z

 

 

2 1 1

x y z

  

 

và mặt phẳng





: 2 5 0.

P x y z

   

Lập phương trình đường

thẳng d song song với mặt phẳng





và cắt

1 2

d d

lần lượt tại

A B

sao cho độ dài đoạn

đạt giá trị nhỏ nhất.

1 2 2

1 1 1

x y z

  

 

. B.

1 2 2

1 1 1

x y z

  

 



1 2 2

1 1 1

x y z

  

 

. D.

2 2 2

1 1 1

x y z

  

 

Hướng dẫn giải:

Vì









1 2

; 1 ; 2 2 ; , 2 2 ;1 ;1

A d B d A a a a B b b b

         

Ta có





2 3; 2 3; 1

AB a b a b a b

         







có vec tơ pháp tuyến

   

 

1;1; 2 , / /

AB n

n AB P

A P







  









 







. 0 2 3 2 3 2 2 2 0 4 5; 1; 3

AB n AB n a b a b a b b a AB a a

                      

    

Do đó:

       

2 2 2 2

5 1 3 2 2 27 3 3

AB a a a          

min 3 3

AB  khi





2 1;2;2

a A 













3; 3; 3 , 1;2;2

AB A P

    



Vậy phương trình đường thẳng

1 2 2

: .

1 1 1

x y z

  

 

Chọn A.

Câu 10: Trong không gian với hệ tọa độ

Ox ,

cho đường thẳng

3 2 1

2 1 1

x y z

  

 



và mặt

phẳng





: 2 0.

P x y z

   

Gọi

là giao điểm giữa

và





. Viết phương trình đường

thẳng



nằm trong mặt phẳng





, vuông góc với

đồng thời khoảng cách từ

đến



bằng

42.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 56

Facebook: https://www.facebook.com/dongpay

5 2 5

2 3 1

3 4 5

2 3 1

x y z

  



  







  



  







. B.

5 2 5

2 3 1

3 4 5

2 3 1

x y z

  



  



 



  



  



 



5 2 5

2 3 1

3 4 5

2 3 1

x y z

  



  







  



  







. D.

5 2 5

2 3 1

3 4 5

2 3 1

x y z

  



  



  



  





Hướng dẫn giải:

Phương trình tham số của

3 2

: 2

x t

d y t

z t

 





  





  



Mặt phẳng





có VTPT





1;1;1 ,

n 



d có VTCP





2;1; 1

 



Vì









1; 3;0

M d P M   

Vì



nằm trong





và vuông góc với d nên:

 

; 2; 3;1

d P

VTCP u u n



 

  

 

  

Gọi





; ;

N x y z

là hình chiếu vuông góc của

trên



, khi đó:





1; 3;

MN x y z

  



Ta có:

 

   

 

2 2

2 0

5; 2; 5

2 3 11 0

3; 4;5

1 3 42

MN u

x y z

N P x y z

x y z







   

 





      



 

 



 



    







 

Với

 

5 2 5

5; 2; 5 :

2 3 1

x y z

  

     



Với

 

3 4 5

3; 4;5 :

2 3 1

x y z

  

     



Chọn A.

Câu 11: Trong không gian với hệ tọa độ

cho điểm





1;2;3 ,

A đường thẳng

2 1 2

x y z



 



và mặt phẳng





: 2 1 0.

P x y z

   

Gọi

là đường thẳng đối xứng với d qua





Tìm

tọa độ điểm

trên

sao cho



62 16 151 26 2 151 31 8 151

; ;

27 27 27

62 16 151 26 2 151 31 8 151

; ;

27 27 27



 

   



 



 



 

   



 



 



62 151 26 151 31 151

; ;

27 27 27

62 151 26 151 31 151

; ;

27 27 27



 

   



 



 



 

   



 



 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 57

Facebook: https://www.facebook.com/dongpay

16 151 2 151 8 151

; ;

27 27 27

16 151 2 151 8 151

; ;

27 27 27



 



 



 



 

  



 



 



62 4 151 26 2 151 31 8 151

; ;

27 27 27

62 4 151 26 2 151 31 8 151

; ;

27 27 27



 

   



 



 



 

   



 



 



Hướng dẫn giải:

Có

cắt





tại





2; 1;1 .

I  Chọn





0;0; 1

M d

 

và

là điểm đối xứng của

qua





Khi đó





' ' .

M d

 Ta tìm

Gọi



là đường thẳng đi qua

và vuông góc với mặt phẳng





 

1;2 1 :

1 2 1

x y z

VTCP u VTPT n





       



 

Gọi

là trung điểm

thì tọa độ

định:

1 2 2 1 2 2

; ; ; ; .

1 2 1

3 3 3 3 3 3

2 1 0

x y z

x y z H

x y z





 



 

          





 

 



   



Từ đó:

 

2 4 1

' 2 ;2 ;2 ; ;

3 3 3

H M H M H M

M x x y y z z

 

      

 

 

Suy ra d’ là đường thẳng đi qua





2; 1;1

I  nhận VTCP:

8 1 4 2 1 1

' ; ; ':

3 3 3 8 1 4

x y z

M I d

  

 

   

 

 







' 2 8 ; 1 ;1 4

B d B t t t

     

Theo đề bài ta phải có:

     

2 2 2

1 2 151

9 1 8 3 4 2 81 81 6 67 0

AB t t t t t t



             

62 16 151 26 2 151 31 8 151

; ;

27 27 27

62 16 151 26 2 151 31 8 151

; ;

27 27 27



 

   



 



 





 

   



 



 



Chọn A.

Câu 12: Cho hai điểm và hai mặt phẳng

. Viết phương trình đường thẳng qua cắt lần lượt tại

sao cho tam giác cân tại và nhận là đường trung tuyến.









1;2;3 , 2;4;4

M A





: 2 1 0,

P x y z

   





: 2 4 0

Q x y z

   











B C

ABC

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 58

Facebook: https://www.facebook.com/dongpay

A. B.

C. D.

Hướng dẫn giải:

Gọi , từ giả thiết suy ra là trung điểm của , suy ra .

nên có hai pt:

Tam giác cân tại nên:

Từ và có hệ:

Đường thẳng qua và có pt .

Chọn D.

Câu 13: Trong không gian với hệ trục tọa độ Oxyz, gọi d là đường thẳng đi qua điểm





1;0; 1

 

cắt

1 2 2

2 1 1

x y z

  

 



, sao cho





cos ;d



là nhỏ nhất, biết phương trình của đường thẳng

3 2 3

1 2 2

x y z

  

  



. Phương trình đường thẳng d là?

1 1

2 2 1

x y z

 

 



1 1

4 5 2

x y z

 

 



1 1

4 5 2

x y z

 

 

 

1 1

2 2 1

x y z

 

 

Hướng dẫn giải:

Gọi





1 2 ;2 ; 2

M d M t t t

       

d có vectơ chỉ phương là





2 2; 2; 1

u AM t t t

     

 



có vectơ chỉ phương





1;2;2

u  



 

cos ;

3 6 14 9

t t

 

 

1 2 3

1 1 1

x y z

  

  

 

1 2 3

2 1 1

x y z

  

  



1 2 3

1 1 1

x y z

  

  

1 2 3

1 1 1

x y z

  

  







; ;

B a b c





2 ;4 ;6

C a b c

  









B P C Q

 









2 1 0 1 2 8 0 2 .

a b c a b c         ;









1; 2; 1 , 2 2 ;4 2 ;6 2 .

AM BC a b c

     

 

ABC





. 0 2 8 0 3 .

AM BC a b c     

 









1 , 2





   

2 1 0 0

2 8 0 3 0;3;2 , 2;1;4 .

2 8 0 2

a b c a

a b c b B C

a b c c

    

 

 

       

 

 

    

 



1 2 3

1 1 1

x y z

  

  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 59

Facebook: https://www.facebook.com/dongpay

Xét hàm số

 

6 14 9

f t

t t



 

, ta suy ra được









min 0 0

f t f

 

Do đó





min cos ; 0

 

 

 

khi



. Nên





2;2; 1

 



Vậy phương trình đường thẳng d là:

1 1

2 2 1

x y z

 

 



Chọn A.

Câu 14: Trong không gian với hệ tọa độ cho điểm và đường thẳng có phương

trình: . Viết phương trình đường thẳng đi qua , vuông góc và cắt .

A. . B. .

C. . D. .

Hướng dẫn giải:

Do cắt nên tồn tại giao điểm giữa chúng. Gọi .

Phương trình tham số của : . Do , suy ra

Do nên là vectơ chỉ phương của .

Theo đề bài, vuông góc nên ( là vector chỉ phương của ). Suy ra

. Giải được . Vậy

Chọn B.

Câu 15: Trong không gian tọa độ Oxyz cho M(2;1;0) và đường thẳng d có phương trình:

1 1

2 1 1

x y z

 

 



. Gọi



là đường thẳng đi qua M, cắt và vuông góc với d. Viết phương

trình đường thẳng



1 4

x t

y t

z t

 





 





 



1 4

3 2

x t

y t

z t

 





 





 



1 4

x t

y t

z t

 





 





 



1 4

x t

y t

z t

 





 





 



Hướng dẫn giải:

Oxyz





1;0; 2

1 1

1 1 2

x z

 

 



1 2

1 1 1

x z

 

  

1 2

1 1 1

x z

 

  



1 2

2 1 1

x z

 

  

1 2

1 3 1

x z

 

  





B d

 

  







x t

y t t

z t

  



 





 





B d







1; ; 1

B t t t

 





; ;2 3

AB t t t

  



A B







AB u







(1;1;2)





. 0

ABu







t 1







1;1; 1

  



1 2

: .

1 1 1

x z

 

  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 60

Facebook: https://www.facebook.com/dongpay

PTTS của d là

1 2

x t

y t

z t

 





  





 



Gọi H là hình chiếu vuông góc của M lên d, đường thẳng



cần tìm là đường thẳng MH.

Vì H thuộc d nên





1 2 ; 1 ;

H t t t

   

suy ra

(2 1; 2 ; )

MH t t t

    



Vì

MH d



và d có 1 VTCP là

(2;1; 1)

 



nên

. 0

MH u



 





. Do đó

1 4 2

; ;

3 3 3

 

 



 

 



Vậy PTTS của



là:

1 4

x t

y t

z t

 





 





 



Chọn A.

Câu 16: Trong không gian với hệ tọa độ





; 5 2 ;1

MN N t t t

    

gọi

đi qua





1;0; 1

 

, cắt

1 2 2

2 1 1

x y z

  

  



, sao cho góc giữa

và

3 2 3

1 2 2

x y z

  

  



là nhỏ nhất.

Phương trình đường thẳng

là

1 1

2 2 1

x y z

 

 



1 1

4 5 2

x y z

 

 



1 1

4 5 2

x y z

 

 

 

1 1

2 2 1

x y z

 

 

Hướng dẫn giải:

Gọi





1 2 ;2 ; 2

M d M t t t

       

có vectơ chỉ phương





2 2; 2; 1

a AM t t t

     

 



có vectơ chỉ phương





1;2;2

a  



 

cos ;

3 6 14 9

t t

 

 

Xét hàm số

 

6 14 9

f t

t t



 

, ta suy ra được









min 0 0 0

f t f t

   

Do đó









min cos , 0 0 2;2 1

d t AM

      

 

 



Vậy phương trình đường thẳng

là

1 1

2 2 1

x y z

 

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 61

Facebook: https://www.facebook.com/dongpay

Câu 17: Trong không gian với hệ tọa độ

3 2

1 2

x t

y t

z t

 





  





  



cho hai đường thẳng

1 2

2 1 1

x y z

 

 



và

1 2 2

1 3 2

x y z

  

 



. Gọi



là đường thẳng song song với





: 7 0

P x y z

   

và cắt

1 2

d d

lần lượt tại hai điểm

A B

sao cho

ngắn nhất. Phương trình của đường thẳng



là.

5 .

x t

z t

 











  



x t

z t





 









  





y t

z t









 





  





6 2

x t

y t

z t





 



 





  





Hướng dẫn giải:





 

1 2 ; ; 2

1 ; 2 3 ;2 2

A d A a a a

B d B b b b

    

     



có vectơ chỉ phương





2 ;3 2; 2 4

AB b a b a b a

      







có vectơ pháp tuyến





1;1;1

n 



Vì





/ /

 nên

. 0 1

P P

AB n AB n b a

     

   

.Khi đó





1;2 5;6

AB a a a

    



     

2 2 2

1 2 5 6

6 30 62

5 49 7 2

6 ;

2 2 2

AB a a a

a a

      

  

 

     

 

 



Dấu

" "



xảy ra khi

5 5 9 7 7

6; ; , ;0;

2 2 2 2 2

a A AB

   

    

   

   



Đường thẳng



đi qua điểm

5 9

6; ;

2 2

 



 

 

và vec tơ chỉ phương





1;0;1

u  



Vậy phương trình của



là

x t

z t





 









  





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 62

Facebook: https://www.facebook.com/dongpay

Câu 18: Trong không gian với hệ tọa độ

Oxyz

cho hai đường thẳng

1 2

2 1 1

x y z

 

 



và

1 2

: 1

x t

d y t

  





 









. Phương trình đường thẳng vuông góc với





:7 4 0

P x y z

  

và cắt hai

đường thẳng

1 2

d d

là:

7 4

2 1 1

x y z

 

  B.

2 1

7 1 4

x y z

 

 



2 1

7 1 4

x y z

 

 

 

2 1

7 1 4

x y z

 

 

Hướng dẫn giải:

Gọi

là đường thẳng cần tìm

Gọi

1 2

A d d B d d

   





 

2 ;1 ; 2

1 2 ;1 ;3

2 2 1; ; 5

A d A a a a

B d B b b

AB a b a b a

    

    

      







có vectơ pháp tuyến





7;1; 4 ,

 







d P AB n

 

 

cùng phương



có một số

thỏa

AB kn



 

2 2 1 7 2 2 7 1 1

0 2

5 4 4 5 1

a b k a b k a

a b k a b k b

a k a k k

        

  

  

         

  

  

         

  

đi qua điểm





2;0; 1



và có vectơ chỉ phương





7;1 4

d P

a n

  

 

Vậy phương trình của

là

2 1

7 1 4

x y z

 

 



Câu 19: Trong không gian với hệ tọa độ

Oxyz

cho hai đường thẳng

1 2 1

3 1 2

x y z

  

   và

1 1

1 2 3

x y z

 

   . Phương trình đường thẳng song song với

: 1

d y t

z t







  





 



và cắt hai

đường thẳng

1 2

;

 

là:

3 .

y t

z t







 





 



3 .

y t

z t

 





  





  



3 .

y t

z t

 





  





  



3 .

y t

z t







  





 



Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 63

Facebook: https://www.facebook.com/dongpay

Gọi



là đường thẳng cần tìm

Gọi

1 2

,A B

     





 

1 3 ;2 ;1 2

1 ;2 ; 1 3

3 2; 2 2; 2 3 2

A A a a a

B B b b b

AB a b a b a b

     

    

         



có vectơ chỉ phương





0;1;1

a 



/ / ,

d AB a

 

 

cùng phương



có một số

thỏa

AB ka



 

3 2 0 3 2 1

2 2 2 2 1

2 3 2 2 3 2 1

a b a b a

a b k a b k b

a b k a b k k

        

  

  

           

  

  

         

  

Ta có









2;3;3 ; 2;2;2

A B



đi qua điểm





2;3;3

A và có vectơ chỉ phương





0; 1; 1

  



Vậy phương trình của



là

y t

z t







 





 



Câu 20: Trong không gian

Oxyz

, cho điểm





3;3; 3

 

thuộc mặt phẳng





2 – 2 0

: 15x y z

  



và

mặt cầu





2 2 2

:(x 2) (y 3) (z 5) 100

S      

. Đường thẳng



qua A, nằm trên mặt phẳng







cắt

( )

tại

. Để độ dài

lớn nhất thì phương trình đường thẳng



là:

3 3 3

1 4 6

x y z

  

  . B.

3 3 3

16 11 10

x y z

  

 



3 5

3 8

x t

z t

  











  



. D.

3 3 3

1 1 3

x y z

  

  .

Hướng dẫn giải:

Mặt cầu





có tâm





2;3;5

I , bán kính



. Do

(I,( )) R





nên



luôn cắt





tại

Khi đó

 

(I, )

AB R d  

. Do đó,

lớn nhất thì









,d I



nhỏ nhất nên



qua

với

là hình chiếu vuông góc của I lên







. Phương trình

x 2 2t

y 3

z t

 





 





 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 64

Facebook: https://www.facebook.com/dongpay









( ) 2 2 2 2 3– 2 5 15 0

H t t t

       







2; 7;

t 2

H     .

Do vậy

AH (1;4;6)





là véc tơ chỉ phương của



. Phương trình của

3 3 3

1 4 6

x y z

  

 

Câu 21: Phương trình nào sau đây không phải là phương trình hình chiếu vuông góc của đường thẳng

d: trên mặt phẳng (Oxy):

A. B. C. D.

Hướng dẫn giải:

A(1;-2;3), B(3;1;4) thuộc d. Hình chiếu của A,B trên mặt phẳng (Oxy) là A

(1;-2;0),

(3;1;0)

Phương trình hình chiếu đi qua hoặc và nhận véc tơ cùng phương với

làm véc tơ chỉ phương.

Chọn C.

Câu 22: Trong không gian với hệ tọa độ

Oxyz

cho đường thẳng

12 9 1

: ,

4 3 1

x y z

  

  và mặt

thẳng





:3 5 2 0

P x y z

   

. Gọi

là hình chiếu của

lên





Phương trình tham số của

là

25 .

2 61

x t

y t

z t

 











 



25 .

2 61

x t

y t

z t







 





 



25 .

2 61

x t

y t

z t







 





  



25 .

2 61

x t

y t

z t







 





 



Hướng dẫn giải:

Cách 1:

Gọi





A d P

 





   

12 4 ;9 3 ;1

3 0;0; 2

A d A a a a

A P a A

    

     

đi qua điểm





12;9;1

1 2

2 3 ,

x t

y t t R

z t

 





   





 



3 2 '

1 3 ' , '

x t

y t t R

 





  









1 4 '

2 6 ', '

x t

y t t R

 





   









1 2 '

2 3 ', '

x t

y t t R

 





  









5 2 '

4 3 ', '

x t

y t t R

 





  









 

/ /

2;3;0

A B 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 65

Facebook: https://www.facebook.com/dongpay

Gọi

là hình chiếu của

lên









có vectơ pháp tuyến





3;5; 1

 



đi qua





12;9;1

B và có vectơ chỉ phương





3;5; 1

BH P

a n

  

 

 

12 3

: 9 5

12 3 ;9 5 ;1

78 186 15 113

; ;

35 35 7 35

186 15 183

; ;

35 7 35

x t

BH y t

z t

H BH H t t t

H P t H

 





 





 



    

 

     

 

 

 

 

 

 



đi qua





0;0; 2



và có vectơ chỉ phương





62; 25;61

a  



Vậy phương trình tham số của

là

2 61

x t

y t

z t







 





  



Cách 2:

 Gọi





qua

và vuông góc với





đi qua điểm





12;9;1

B và có vectơ chỉ phương





4;3;1

a 







có vectơ pháp tuyến





3;5; 1

 







qua





12;9;1

B có vectơ pháp tuyến

 

, 8;7;11

Q d P

n a n

 

  

 

  





:8 7 11 22 0

Q x y z

   



là giao tuyến của





và





Tìm một điểm thuộc

, bằng cách cho



Ta có hệ

 

3 2 0

0;0; 2 '

8 11 22 2

x z x

M d

x z y

  

 

   

 

   

 

đi qua điểm





0;0; 2



và có vectơ chỉ phương

 

; 62; 25;61

d P Q

a n n

 

  

 

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 66

Facebook: https://www.facebook.com/dongpay

Vậy phương trình tham số của

là

2 61

x t

y t

z t







 





  



Câu 23: Trong không gian với hệ tọa độ

cho đường thẳng

1 2

: 2 4

x t

d y t

z t

 





  





 



. Hình chiếu song

song của





1; 2;2

BH Q

a n  

 

lên mặt phẳng

 

: 1 2

3 2

1 ; 1 2 ;3 2

10 1 11 7

; ;

9 9 9 9

x t

BH y t

z t

H BH H t t t

H P t H

 





  





 



     

 

     

 

 

theo

phương

1 6 2

1 1 1

x y z

  

  

 

có phương trình là:

3 2

0 .

1 4

x t

z t

 











 



0 .

1 2

x t

z t

 











 



1 2

0 .

5 4

x t

z t

  











 



3 2

0 .

x t

z t

 











 



Hướng dẫn giải:

Giao điểm của d và mặt phẳng

 

: 1 2

3 2

1 ; 1 2 ;3 2

10 1 11 7

; ;

9 9 9 9

x t

BH y t

z t

H BH H t t t

H P t H

 





  





 



     

 

     

 

 

là:

(5;0;5)

Trên

1 2

: 2 4

x t

d y t

z t

 





  





 



chọn M bất kỳ không trùng với

(5;0;5)

; ví dụ:

(1; 2;3)



. Gọi A

là hình chiếu song song của M lên mặt phẳng

 

: 1 2

3 2

1 ; 1 2 ;3 2

10 1 11 7

; ;

9 9 9 9

x t

BH y t

z t

H BH H t t t

H P t H

 





  





 



     

 

     

 

 

theo

phương

1 6 2

1 1 1

x y z

  

  

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 67

Facebook: https://www.facebook.com/dongpay

+/ Lập phương trình d’ đi qua M và song song hoặc trùng với

1 6 2

1 1 1

x y z

  

  

 

+/ Điểm A chính là giao điểm của d’ và

 

: 1 2

3 2

1 ; 1 2 ;3 2

10 1 11 7

; ;

9 9 9 9

x t

BH y t

z t

H BH H t t t

H P t H

 





  





 



     

 

     

 

 

+/ Ta tìm được

(3;0;1)

Hình chiếu song song của

1 2

: 2 4

x t

d y t

z t

 





  





 



lên mặt phẳng

 

: 1 2

3 2

1 ; 1 2 ;3 2

10 1 11 7

; ;

9 9 9 9

x t

BH y t

z t

H BH H t t t

H P t H

 





  





 



     

 

     

 

 

theo phương

1 6 2

1 1 1

x y z

  

  

 

là đường thẳng

đi qua

(5;0;5)

và

(3;0;1)

A .

Vậy phương trình là:

1 2

x t

z t

 











 



Câu 24: Trong không gian với hệ tọa độ





: 2 2 1 0

Q x y z

   

gọi

đi qua





3; 1;1

A  , nằm trong

mặt phẳng





: 5 0

P x y z

   

, đồng thời tạo với

1 2 2

x y z



  

một góc

. Phương

trình đường thẳng

là

3 7

1 8 .

1 15

x t

y t

z t

 





  





  



1 .

x t

y t

 





  









3 7

1 8 .

1 15

x t

y t

z t

 





  





 



x t

y t

 





  









và

3 7

1 8 .

1 15

x t

y t

z t

 





  





 



Hướng dẫn giải:



có vectơ chỉ phương





1;2;2







ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 68

Facebook: https://www.facebook.com/dongpay

có vectơ chỉ phương





; ;

a a b c









có vectơ pháp tuyến





1; 1;1

n  











   

 

0 0

2 2 2

; 1

, 45 cos , cos45

2 2

2 2 2 9 ; 2

d P

d P a n b a c

d d

a b c

a b c a b c

     

    

 

 

 

     

 

Từ

1 2

1 2 1

x y z

 

  

và

1 1

1 2 3

x y z

 

   , ta có:

14 30 0

15 7 0

c ac

a c





  



 



Với



, chọn

a b

 

, phương trình đường thẳng

là

x t

y t

 





  









Với

15 7 0

a c

 

, chọn

7 15; 8

a c b

     

, phương trình đường thẳng

là

3 7

1 8

1 15

x t

y t

z t

 





  





 



Câu 25: Trong không gian với hệ tọa độ

Oxyz

gọi

đi qua điểm





1; 1;2

A , song song với





: 2 3 0

   

P x y z , đồng thời tạo với đường thẳng

1 1

1 2 2

 

  



x y z

một góc lớn

nhất. Phương trình đường thẳng

là.

1 1 2

1 5 7

  

 



x y z

1 1 2

4 5 7

  

 



x y z

1 1 2

4 5 7

  

 

x y z

1 1 2

1 5 7

  

 

 

x y z

Hướng dẫn giải:



có vectơ chỉ phương





1; 2;2



 



có vectơ chỉ phương





; ;





a a b c





có vectơ pháp tuyến





2; 1; 1

  



Vì





d P

 nên . 0 2 0 2

         

   

d P d P

a n a n a b c c a b

 

2 2

5 4 5 4

cos ,

3 5 4 2

 

  

 

a b a b

a ab b

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 69

Facebook: https://www.facebook.com/dongpay

Đặt



, ta có:

 

5 4

cos ,

3 5 4 2



 

 

t t

Xét hàm số

 

5 4

5 4 2





 

f t

t t

, ta suy ra được:

 

1 5 3

max

5 3

 

  

 

 

f t f

Do đó:

 

5 3 1 1

max cos ,

27 5 5

       

 

 

d t

Chọn

1 5, 7

    

a b c

Vậy phương trình đường thẳng

là

1 1 2

1 5 7

  

 



x y z

Chọn A.

Câu 26: Trong không gian cho đường thẳng

3 1

1 2 3

x y z

 

   và đường thẳng

3 1 2

x y z

  

  . Viết phương trình mặt phẳng





đi qua



và tạo với đường thẳng

một góc lớn nhất.

A. 19 17 2 77

0 0

x y z

   

B. 19 17 2 34

0 0

x y z

   

C. 31 8 5 91

x y z

   

D. 31 8 5 98

x y z

   

Hướng dẫn giải:

Chọn D.

Đường thẳng

có VTCP là





3;1;2

u 



Đường thẳng



đi qua điểm





3;0; 1



và có VTCP là





1;2;3

u 







  nên





M P

 . Giả sử VTPT của





là









2 2 2

; ; , 0

n A B C A B C

   



Phương trình





có dạng









3 1 0

A x By C z

    





  nên

. 0 2 3 0 2 3

u n A B C A B C

        

 

Gọi



là góc giữa

và





. Ta có

 

2 2 2 2

2 2

3 2 3 2

3 2

14.

14. 2 3

u n

B C B C

A B C

sin

u n

A B C

B C B C

   

 

  

 

   

 



 

2 2

5 7 5 7

5 12 10

14. 5 12 10

B C B C

B BC C

 

 

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 70

Facebook: https://www.facebook.com/dongpay

TH1: Với



thì

5 70

14 14

sin  



TH2: Với



đặt



ta có

 

5 7

5 12 10

sin

t t





 



Xét hàm số

 

5 7

5 12 10

f t

t t





 

trên



Ta có

 

50 10 112

5 12 10

t t

f t

t t

  





 

 

8 8 75

5 5 14

0 50 10 112 0

7 7

5 5

t f

f t t t

t f



 

  

 



 





      



 

    



 

 



Và

 

5 7

lim lim 5

5 12 10

x x

f t

t t

 



 

 

Bảng biến thiên

Từ đó ta có

 

Maxf t  khi

8 8

5 5

  

. Khi đó

1 8 75

5 14

sin f

 

 

 

 



So sánh TH1 và Th2 ta có

sin



lớn nhất là

sin 



khi



Chọn

8 5 31

B C A

      

Phương trình





là









31 3 8 5 1 0 31 8 5 98 0

x y z x y z

         

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 71

Facebook: https://www.facebook.com/dongpay

Câu 27: Trong không gian với hệ trục toạ độ

Oxyz

cho mặt phẳng





: 2 0

P x y z

   

và hai

đường thẳng

2 2

x t

d y t

z t

 











 



;

': 1 .

1 2

x t

d y t

z t



 







 







 



Biết rằng có 2 đường thẳng có các đặc điểm: song song với





; cắt

d d



và tạo với

góc

Tính cosin góc tạo bởi hai đường thẳng đó.

Hướng dẫn giải::

Gọi



là đường thẳng cần tìm,



là VTPT của mặt phẳng





Gọi





1 ; ;2 2

M t t t

  là giao điểm của



và

; là giao điểm của

và

Ta có:

Ta có

Vậy, có 2 đường thẳng thoả mãn là .

Khi đó,

Câu 28: Trong không gian với hệ tọa độ Oxyz, cho hai điểm và . Đường

thẳng cắt mặt phẳng tại điểm . Tính tỉ số .

A. . B. . C. . D. .

Hướng dẫn giải:

Ta có:

;

và

Ta có:

thẳng hàng





3 ;1 ;1 2

M t t t

   

  







' 2 ;1 ; 1 2 2

MM t t t t t t

  

      





 





 

2 4 ; 1 ;3 2

M P

P t MM t t t

MM n







 

       













 

 

6 9

cos30 cos ,

36 108 156

MM u

t t



 





   



 

 



 

1 2

: 4 ; : 1

x x t

y t y

z t z t



 

 

 

     

 

 



  

 

 

1 2

cos , .

  





2;3;1

A 





5; 6; 2





Oxz











;0;

M Oxz M x z

 





; ;

7 31 59

AB AB  







; ;

2 3 1

AM x z

   



, ,

A B M





.AM k AB k  

 



2 7 9

3 3 1

1 0

x k x

k k

z k z

     

 

     

 

 

  

 





;0;

9 0 .

M 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 72

Facebook: https://www.facebook.com/dongpay

và

Chọn A.

Câu 29: Trong không gian với hệ tọa độ Oxyz, cho hai điểm

( 2; 2; 1),

 





1; 2; 3



và đường

thẳng

1 5

2 2 1

x y z

 

 



. Tìm vectơ chỉ phương



của đường thẳng



qua A, vuông góc

với d đồng thời cách điểm B một khoảng bé nhất.

(2;1;6)

u 



(2;2; 1)

 



(25; 29; 6)

  



(1;0;2)

u 



Hướng dẫn giải:

Cách 1 (Tự luận)

Gọi (P) là mặt phẳng qua A và vuông góc với d, B’ là hình chiếu của B lên (P)

Khi đó đường thẳng



chính là đường thẳng AB’ và

B'A

u 

 

Ta có

 

( 2; 2;1)

: (P): 2 2 9 0

(2;2; 1)

P d

Qua A

P x y z

VTPT n u

 





    



  





 

Gọi d’ là đường thẳng qua B và song song d’

1 2

' 2 2

x t

d y t

z t

 





  





  



B’ là giao điểm của d’ và (P)

'( 3; 2; 1) ' (1;0;2)

B u B A      

 



Chọn D

Cách 2: Không cần viết phương trình mặt phẳng (P) qua A và vuông góc với d.

Gọi d’ là đường thẳng qua B và song song d’

1 2

' 2 2

x t

d y t

z t

 





  





  



B’



d’





' 2 3; 2 4; 4

B A t t t

      



AB’



. ' 0 2 ' (1;0;2)

u B A t u B A       

   



Chọn D

Câu 30: Trong không gian với hệ toạ độ Oxyz, cho hai điểm









1;2; 1 , 7; 2;3

A B  và đường thẳng

có phương trình

2 3

2 (t R)

4 2

x t

y t

z t

 





  





 



. Điểm M trên

sao cho tổng khoảng cách từ

đến

và

là nhỏ nhất có tổng các tọa độ là:





2;0;4 .

M  B.





2;0;1 .

M  C.





1;0;4 .

M  D.





1;0;2 .

M 

Hướng dẫn giải:





; ;

14 6 2 118 2 .

BM BM AB

      



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 73

Facebook: https://www.facebook.com/dongpay

Nếu M nằm trên d thì điểm I có tọa độ là M=(2+3t;-2t;4+2t). Từ đó ta có:

       

2 2 2

3 1; 2 2 ;2 5 3 1 2 2 2 5

            



AM t t t AM t t t

Tương tự:

       

2 2 2

3 5;2 2 ;2 1 3 5 2 2 2 1

           



BM t t t BM t t t

Từ (*): MA=MB =

     

2 2 2

3 1 2 2 2 5

    t t t

     

2 2 2

3 5 2 2 2 1

    t t t

Hay:

2 2

17 34 30 17 36 30 34 36 0 11 70 0 0

             

t t t t t t t t

Tọa độ M thỏa mãn yêu cầu là: M=(2;0;4 ).

Chọn A.

Câu 31: Trong không gian với hệ trục tọa độ

Oxyz

cho điểm

(2;3;0),

(0; 2;0),

B 

; 2;2

 



 

 

và đường thẳng

: 0 .

x t

d y

z t













 



Điểm

thuộc

sao cho chu vi tam giác

ABC

là nhỏ nhấ thì độ

dài

bằng

2 3.

2 6

Hướng dẫn giải:

có độ dài không đổi nên chu vi tam giác

ABC

nhỏ nhất khi

AC CB



nhỏ nhất.

Vì

 

   

2 2

;0;2 2 2 2 9, 2 2 4

C d C t t AC t BC t

         

   

2 2

2 2 2 9 2 2 4.

AC CB t t

       

Đặt









2 2 2;3 , 2 2;2

u t v t    

 

ápdụngbấtđẳngthức

u v u v

  

   

     

2 2 2

2 2 2 9 2 2 4 2 2 2 25.

t t         Dấubằngxảyrakhivàchỉ

khi

2 2

2 2 2 3 7 7 3 6 7 3

;0; 2 2 2.

2 5 5 5 5 5 5

2 2

t C CM



     

          

     

 

     

Chọn C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 74

Facebook: https://www.facebook.com/dongpay

Câu 32: Trong không gian với hệ tọa độ., cho bốn điểm. và. Kí hiệu

là đường thẳng đi qua

sao

cho tổng khoảng cách từ các điểm

, ,

A B C

đến

lớn nhất. Hỏi đường thẳng

đi qua

điểm nào dưới đây?





1; 2;1

M   . B.





5;7;3

N . C.





3;4;3

P . D.





7;13;5

Q .

Hướng dẫn giải:

Ta có phương trình mặt phẳng qua A,B,C là:

 

: 1 2 3 6 0

3 2 6

x y z

ABC x y z

       

Dễ thấy





D ABC

 .Gọi. lần lượt là hình chiếu vuông góc của

, ,

A B C

trên

Suy ra













, , , ' ' '

d A d d B d d C d AA BB CC AD BD CD

        .Dấu bằng xảy ra khi

' ' '

A B C D

  

. Hay tổng khoảng cách từ các điểm

, ,

A B C

đến

lớn nhất khi d là

đường thẳng qua D và vuông góc với mặt phẳng

 

1 2

: 1 3 ;

x t

ABC d y t N d

z t

 





   





 



chọn B.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 75

Facebook: https://www.facebook.com/dongpay

PHƯƠNG TRÌNH MẶT CẦU NÂNG CAO

A - LÝ THUYẾT CHUNG

1. Định nghĩa mặt cầu

Tập hợp các điểm trong không gian cách điểm

cố định một khoảng cách

cho trước là mặt cầu

tâm

và bán kính

Kí hiệu





; .

S O R

Trong không gian với hệ trục

Ox :

- Mặt cầu





tâm





, ,

I a b c

bán kính

có phương trình là:

     

2 2 2

x a y b z c R

     

- Phương trình:

2 2 2

2 2 2 0,

x y z ax by cz d       với

2 2 2

a b c d

   

là phương trình mặt cầu

tâm





; ; ,

I a b c

bán kính

2 2 2

R a b c d

   

2. Vị trí tương đối của mặt phẳng





và mặt cầu















d I P R



khi và chỉ khi





không cắt mặt cầu















d I P R



khi và chỉ khi





tiếp xúc mặt cầu















d I P R



khi và chỉ khi





cắt mặt cầu





theo

giao tuyến là đường tròn nằm trên mặt phẳng





có tâm

và có bán kính

2 2

r R d

 

3. Vị trí tương đối giữa mặt cầu và đường thẳng

a) Cho mặt cầu





;

S O R

và đường thẳng



. Gọi

là hình

chiếu của

lên



và

d OH



là khoảng cách từ

đến



 Nếu

d R



thì



cắt mặt cầu tại 2 điểm phân biệt (H.3.1)

 Nếu

d R



thì



cắt mặt cầu tại 1 điểm duy nhất (H.3.2)

 Nếu

d R



thì



không cắt mặt cầu (H.3.3)

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 76

Facebook: https://www.facebook.com/dongpay

B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Trong không gian với hệ trục tọa độ , cho ba điểm và

. Mặt cầu tâm I đi qua và độ dài

(biết tâm I có hoành độ nguyên, O là

gốc tọa độ). Bán kính mặt cầu là

A. B. C. D.

Hướng dẫn giải:

Phương trình mặt cầu (S) có dạng:

Vì điểm thuộc mặt cầu (S) nên ta có hệ:

Suy ra

Chọn B.

Câu 2: Trong không gian với hệ tọa độ

Ox ,

cho













1;0;0 , 2; 1;2 , 1;1; 3 .

A B C

  

Viết phương

trình mặt cầu có tâm thuộc trục

đi qua

và cắt mặt phẳng





ABC

theo một đường

tròn có bán kính nhỏ nhất.

2 2

1 5

2 4

x y z

 

   

 

 

. B.

2 2

1 5

2 4

x y z

 

   

 

 

2 2

1 9

2 4

x y z

 

   

 

 

. D.

2 2

3 5

2 4

x y z

 

   

 

 

Hướng dẫn giải:

Mặt phẳng





ABC

có phương trình:

1 0

x y z

   

Gọi





là mặt cầu có tâm

I Oy



và cắt





ABC

theo một đường tròn bán kính r nhỏ nhất.

Vì

I Oy



nên





0; ;0 ,

I t gọi

là hình chiếu của

lên





ABC

khi đó là có bán kính

đường tròn giao của





ABC

và





là

2 2

r AH IA IH

  

Ta có

 

2 2

2 2 2

2 1 2 2 2

1, , 1 .

3 3

t t t t

IA t IH d I ABC r t



   

        

Do đó, r nhỏ nhất khi và chỉ khi



Khi đó

1 5

0; ;0 ,

2 4

I IA

 



 

 

Oxyz









0;2;0 , 1;1;4

A B 





3; 2;1

C 





, ,

A B C

OI 







R 

2 2 2

2 2 2 0

x y z ax by cz d

      

, , ,

O A B C

( ) 4 4 0

( ) 2 2 8 18 0

( ) 6 4 2 14 0

A S b d

B S a b c d

C S a b c d

   

 

 

       

 

 

     

 

2 2 2 2

5 5 5

OI OI a b c

      

1; 0; 2; 4 3

a b c d R

        

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 77

Facebook: https://www.facebook.com/dongpay

Vậy phương trình mặt cầu cần tìm là:

2 2

1 5

2 4

x y z

 

   

 

 

Chọn A.

Câu 3: Trong không gian với hệ tọa độ

Ox ,

viết phương trình mặt cầu có tâm





1;2;3

I và tiếp

xúc với đường thẳng

1 2 2

x y z



 



   

2 2

233

1 2 ( 3)

x y z      . B.

   

2 2

243

1 2 ( 3)

x y z      .

   

2 2

2223

1 2 ( 3)

x y z      . D.

   

2 2

333

1 2 ( 3)

x y z     

Hướng dẫn giải:

+ Đường thẳng

đi qua





0; 2;0

M  có vec tơ chỉ phương





1; 2;2 .

u  



Tính được





1;4;3 .

MI 



+ Khẳng định và tính được

 

233

MI u

d I d

 

 

 

 



+ Khẳng định mặt cầu cần tìm có bán kính bằng





d I d

và viết phương trình:

   

2 2

233

1 2 ( 3)

x y z     

Chọn A.

Câu 4: Trong không gian với hệ tọa độ

Ox ,

cho mặt cầu có phương trình

2 2 2

4 2 6 12 0

x y z x y z

      

và đường thẳng

: 5 2 ; 4; 7 .

d x t y z t

    

Viết

phương trình đường thẳng



tiếp xúc mặt cầu





tại điểm





5;0;1

M biết đường thẳng



tạo với đường thẳng

một góc



thỏa mãn

cos .





5 3 5 13

: 5 : 5

1 1 11

x t x t

y t y t

z t z t

   

 

 

     

 

 

   

 

. B.

5 3 5 13

: 5 : 5

1 1 11

x t x t

y t y t

z t z t

   

 

 

     

 

 

   

 

5 3 5 13

: 5 : 5

1 1 11

x t x t

y t y t

z t z t

   

 

 

    

 

 

   

 

. D.

5 3 5 13

: 5 : 5

1 1 21

x t x t

y t y t

z t z t

   

 

 

     

 

 

   

 

Hướng dẫn giải:

         

2 2 2

: 2 2 3 26

S x y z S

       có tâm





2; 1; 3

 

và bán kính

26.

R 









3;1;4 , 2;0;1

IM u 

 

là 1 VTVP của





Giả sử





; ;

u a b c





là 1 VTCP của đường thẳng





2 2 2

a b c

   

Do tiếp xúc mặt cầu





tại





3 4 0 3 4 1

M IM u a b c b a c         

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 78

Facebook: https://www.facebook.com/dongpay

Mà góc giữa đường thẳng



và đường thẳng

bằng



 

1 2

2 2 2

1 2

1 1

cos , os 2

7 7

. 5

u u

a c

u u c

u u

a b c





     

 

 

Thay





vào





ta được:

 

   

2 2 2 2 2 2 2 2

7 2 5. 3 4 7 4 4 5 9 24 16

a c a a c c a ac c a a ac c c

            

2 2

22 92 78 0

a c

a ac c

a c

 





    



 



Với

a c

 

2 2 2

a b c

  

nên chọn

1 3; 5

c a b

     



phương trình đường thẳng là:

5 3

: 5

x t

y t

z t

 





  





 



Với

a c

  do

2 2 2

a b c

  

nên chọn

11 13; 5

c a b

    



phương trình đường thẳng là:

5 13

: 5

1 11

x t

y t

z t

 





 





 



Chọn A.

Câu 5: Trong không gian với hệ tọa độ

Ox ,

cho đường thẳng

1 2

: .

1 2 2

x y z

 

 



Tìm tọa độ

điểm

thuộc đường thẳng

sao cho mặt cầu





tâm

tiếp xúc với trục

có bán

kính bằng 2.

 

6 8 2

2;0; 2 ; ;

5 5 5

M M

 

  

 

 

. B.

 

6 8 2

2;0;2 ; ;

5 5 5

M M

 



 

 

 

7 8 4

2;0; 2 ; ;

5 5 5

M M

 

  

 

 

. D.

 

6 8 2

4;0; 2 ; ;

5 5 5

M M

 

  

 

 

Hướng dẫn giải:

Vì





1 ; 2 2 ; 2 .

M d M t t t

      Trục

đi qua điểm





O 0;0;0

và có vtcp





0;0;1 ;

k 



   

1 ; 2 2 ; 2 ; 2 2 ; 1 ;0

; 5 6 5

OM t t t OM k t t

OM k t t

 

          

 

 

   

 

  

 

Gọi

là bán kính mặt cầu





, ta có:

 

; 5 6 5

R d M Oz t t

   





2 2

2; 2;0

2 5 6 5 2 5 6 5 0

6 8 2

; ;

5 5 5

R t t t t











          

 







 





 



Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 79

Facebook: https://www.facebook.com/dongpay

Câu 6: Trong không gian với hệ tọa độ

Ox ,

cho hai đường thẳng

1 2

 

có phương trình:

1 2

2 1 1 2 3 1

: ; :

1 4 2 1 1 1

x y z x y z

     

     



. Viết phương trình mặt cầu có bán kính

nhỏ nhất và tiếp xúc với hai đường thẳng

1 2

, ?

 

 

2 2

2 6

x y z

   

. B.

 

2 2

2 6

x y z

   

 

2 2

2 6

x y z

   

. D.

 

2 2

2 6

x y z

   

Hướng dẫn giải:

Mặt cầu có bán kính nhỏ nhất và tiếp xúc với hai đường thẳng

1 2

 

là mặt cầu nhận đoạn

vuông góc chung của

1 2

 

làm đường kính. Giả sử mặt cầu cần lập là





và

A B

lần

lượt là tiếp điểm của





với

1 2

 

. Viết phương trình

1 2

 

dưới dang tham số thì ta có:









2 ;1 4 ;1 2 , 2 ;3 ; 1

A m m m B n n n

       

là đoạn vuông góc chung của

1 2

 

nên:

   

. 0

3 21 0

0 2;1;1 , 2;3; 1

3 0

. 0

ABU

n m

m n A B

n m

ABU







 





      

 

 









 

Trung điểm

của

có tọa độ là





0;2;0

I nên phương trình mặt cầu cần lập là:

 

2 2

2 6

x y z

   

Chọn A.

Câu 7: Trong không gian với hệ tọa độ

Ox ,

cho mặt cầu





2 2 2

: 2 4 2 3 0.

S x y z x y z

      

Viết phương trình mặt phẳng





chứa trục

và cắt mặt cầu





theo một đường tròn có

bán kính bằng 3.





: 2 0

P y z

 

. B.





: 2 0

P x z

 

. C.





: 2 0

P y z

 

. D.





: 2 0

P x z

 

Hướng dẫn giải:





có tâm





1; 2; 1

 

và bán kính







chứa trục

và cắt mặt cầu





theo một đường tròn có bán kính bằng 3 nên





chứa

và đi qua tâm

của mặt cầu.

Ta có:









1; 2; 1 ,

OI P

 



có vec tơ pháp tuyến

 

, 0; 1; 2

n i OI

 

   

 

  

và





qua

Vậy





: 2 0.

P y z

 

Chọn A.

Câu 8: Trong không gian với hệ tọa độ

Oxyz,

cho đường thẳng

1 1

2 1 1

x y z

 

 



và cắt mặt

phẳng





: 2 6 0

P x y z

   

tại điểm

Viết phương trình mặt cầu





có tâm

thuộc

đường thẳng

và tiếp xúc với mặt phẳng





tại điểm

biết diện tích tam giác

IAM

bằng

3 3

và tâm

có hoành độ âm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 80

Facebook: https://www.facebook.com/dongpay

     

2 2

: 1 1 6

S x y z

    

. B.

     

2 2

: 1 1 36

S x y z

    

     

2 2

: 1 1 6

S x y z

    

. D.

     

2 2

: 1 1 6

S x y z

    

Hướng dẫn giải:

Một vec tơ chỉ phương của đường thẳng

là





2;1; 1 .





Một vec tơ pháp tuyến của đường

thẳng và mặt phẳng





là





1;2;1 .

n 



Gọi



là góc giữa đường thẳng

và mặt phẳng





Ta có

 



2 2 1

sin cos , 30

6. 6

u n IMA

 

 

     

 

Gọi

bán kính mặt cầu





S IA R

 

Tam giác

IAM

vuông tại

có

30 3. 3 3 . 3 3 6

IMA

IMA AM R S IA AM R



       

Giả sử:

 

1 2 ;1 ; ,

I t t t t

   

Từ giả thuyết ta có khoảng cách:

 

3 3

, 1 3

d I P R t t



      

(loại)





1;0;1

I 

Phương trình mặt cầu

     

2 2

: 1 1 6.

S x y z

    

Chọn A.

Câu 9: Trong không gian tọa độ

Ox ,

viết phương trình mặt cầu đi qua ba điểm









1; 1;2 , 2;1; 1

A B

 





1;2; 3

 

biết tâm của mặt cầu nằm trên mặt phẳng

Oxz

 

2 2

12 4 1326

11 11 121

S x y z

   

    

   

   

. B.

 

2 2

12 4 1327

11 11 121

S x y z

   

    

   

   

 

2 2

12 4 1328

11 11 121

S x y z

   

    

   

   

. D.

 

2 2

12 4 1329

11 11 121

S x y z

   

    

   

   

Hướng dẫn giải:





Oxz

I  nên





;0; ,

I x z IA IB IC

  nên:

       

2 2 2 2

1 1 2 2 1 1

1 1 2 1 4 3

x z x z



        





        





Giải hệ ta được

12 4 12 4

; ;0;

11 11 11 11

x z I

 

      

 

 

Bán kính

1326

121

R 

Phương trình mặt cầu

 

2 2

12 4 1326

11 11 121

S x y z

   

    

   

   

Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 81

Facebook: https://www.facebook.com/dongpay

Câu 10: Trong không gian

cho 3 điểm













13; 1;0 , 2;1; 2 , 1;2;2

A B C   và mặt cầu





2 2 2

: 2 4 6 67 0.

S x y z x y z

      

Viết phương trình mặt phẳng





đi qua qua

song song với

và tiếp xúc với mặt cầu









S S

có tâm





1;2;3

I và có bán kính







: 2 2 28 0

P x y z

    

hoặc





:8 4 100 0

P x y z

   





: 2 2 28 0

P x y z

    

hoặc





:8 4 100 0

P x y z

   





: 2 2 28 0

P x y z

    

hoặc





:8 4 100 0

P x y z

   





: 2 2 2 28 0

P x y z

    

hoặc





:8 4 1000 0

P x y z

   

Hướng dẫn giải:

Giả sử





có vtpt













2 2 2

; ; , 0 , / /

n A B C A B C P BC

   



nên:









, 1;1;4 . 0 4 4 ; ;

n BC BC n BC A B C n B C B C

          

     





đi qua





13; 1;0A

 

phương trình:









: 4 12 52 0

P B C x By Cz B C

     





tiếp xúc với

   

 

2 2

4 2 3 12 52

, 9

B C B C B C

S d I P R

B C B C

    

   

 

 

  

  

2 2

2 0

2 8 0 2 4 0

4 0

B C

B BC C B C B C

B C

 



        



 



Với

2 0

B C

 

chọn







 



ta được phương trình:





: 2 2 28 0

P x y z

    

Với

4 0

B C

 

chọn











ta được phương trình:





:8 4 100 0

P x y z

   

Chọn A.

Câu 11: Trong không gian

Ox ,

cho mặt cầu





2 2 2

: 4 2 2 3 0,

S x y z x y z

      

mặt phẳng





: 1 0

P x y z

   

và hai điểm









1;1;0 , 2;2;1 .

A B

Viết phương trình mặt phẳng







song song với

vuông góc với mặt phẳng





và cắt mặt cầu





theo một đường tròn





có bán kính bằng





: 2 1 0

x y z



   

và mp





: 2 11 0

x y z



   





: 5 2 1 0

x y z



   

và mp





: 2 11 0

x y z



   





: 2 1 0

x y z



   

và mp





: 5 2 11 0

x y z



   





: 5 2 1 0

x y z



   

và mp





: 5 2 11 0

x y z



   

Hướng dẫn giải:





viết dưới dạng

       

2 2 2

: 2 1 1 9

S x y z

     

Suy ra





có tâm





2; 1; 1

 

, bán kính



Ta có





3;1;1

AB 



một VTPT của mặt phẳng





là





1; 1;1

n  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 82

Facebook: https://www.facebook.com/dongpay

Do đó

 

. 2; 2;4 0

AB n

 

  

 

  

Gọi vec tơ là một VTPT của mặt phẳng







Ta có:





   

/ /AB

u AB

u n







 

 

 







 



 

cùng phương với

. .

AB n

 

 

 

Chọn

 

. 1; 1; 2

u AB n u

 

    

 

   

Mặt phẳng







có một VTPT



nên phương trình có dạng

2 0

x y z D

   

Gọi

là khoảng cách từ

đến mặt phẳng







cắt





theo một đường tròn





có bán

kính

r  Nên

2 2

9 3 6

d R r    

Ta có:









2 1 2 1

6 6 5 6

d D

    





      



 



Với



thì





: 2 1 0

x y z



   

không qua





1;1;0

A  (vì

1 1 2.0 1 0

    

)

Nên





/ / .



Tương tự, mặt phẳng cũng song song với

Vậy có hai mặt phẳng







thỏa mãn yêu cầu bài toán có phương trình:





: 2 1 0

x y z



   

và mp





: 2 11 0

x y z



   

Chọn A.

Câu 12: Trong không gian

Oxyz,

cho hai điểm









2;0;0 , 0;2;0 .

A B Điểm

thuộc trục

sao

cho tam giác

ABC

là tam giác đều, viết phương trình mặt cầu





có tâm

tiếp xúc với ba

cạnh của tam giác

ABC





2 2 2

: 2

S x y z

  

. B.





2 2 2

: 2

S x y z

   





2 2 2

: 2

S x y z   . D.





2 2 2

: 2

S x y z   

Hướng dẫn giải:

Vì





Oz C 0;0;

C c

  và tam giác

ABC

đều khi và chỉ khi:

2 2 2 2 2 2

2 2 2 2

AB AC BC AB AC BC c c

           

Vậy





0;0;2

C hoặc





0;0; 2



Lập luận được tứ diện

OABC

đều vì

OA OB OC

  

và tam giác

ABC

đều.

Gọi

là trung điểm của

thì

IO AB



tại

2 2 2 2

1 1

2 2 2

2 2

I OI AB OA OB      

(Tam giác

OAB

vuông tại

)

Lập luận được mặt cầu





có tâm

tiếp xúc với 3 cạnh của tam giác

ABC

có bán kính





, 2.

R d O AB IO  

Do đó phương trình có mặt cầu





2 2 2

: 2.

S x y z

  

Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 83

Facebook: https://www.facebook.com/dongpay

Câu 13: Trong không gian với hệ tọa độ

Ox ,

cho đường thẳng

2 1 1

1 2 1

x y z

  

 

 

và mặt cầu

       

2 2 2

: 1 2 1 25.

S x y z      Viết phương trình đường thẳng



đi qua điểm





1; 1; 2 ,

  

cắt đường thẳng

và mặt cầu





tại hai điểm

A B

sao cho



1 6

: 1 2

2 9

x t

y t

z t

  





   





  



. B.

1 6

: 1 2

2 9

x t

y t

z t

  





   





  



1 6

: 1 2

2 9

x t

y t

z t

  





  





 



. D.

2 6

: 3 2

2 9

x t

y t

z t

  





   





  



Hướng dẫn giải:

Gọi:









1 1 1

2 ;1 2 ;1 3 ;2 2 ;3

M d M t t t MM t t t

           



Mặt cầu có tâm





1;2;1

I 

Mặt phẳng

 





 





1;2;1

: :

qua I

P P

VTPT n MM

 



 



 

 







 





























: 3 1 2 2 2 3 1 0

P t x t y t z

         

Gọi

là trung điểm

thì

, 3

IH AB IH

 

 

3 15

3 2 3 ,

6 8 22

IM MH d M P

t t

 







     





 



Với

1 2

1 : 1 2 .

x t

t y t

z t

  





      





  



Với

1 6

: 1 2 .

2 9

x t

t y t

z t

  





     





  



Chọn A.

Câu 14: Trong không gian

Ox ,

viết phương trình mặt cầu





tiếp xúc với mặt phẳng





:2 2 1 0

Q x y z

   

tại





1; 1; 1

 

và tiếp xúc mặt phẳng





: 2 2 8 0

P x y z

   

     

       

2 2

2 2 2

: 3 1 9

: 1 2 3 9

c x y z



    



     



. B.

     

       

2 2

2 2 2

: 3 1 9

: 1 2 3 9

c x y z



    



     



     

       

2 2

2 2 2

: 3 1 9

: 1 2 3 9

c x y z



    



     



. D.

     

       

2 2

2 2 2

: 3 1 81

: 1 2 3 81

c x y z



    



     



Hướng dẫn giải:

Mặt phẳng





có vec tơ pháp tuyến





2;1;2 .

n 



Đường thẳng

đi qua

và vuông góc

với





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 84

Facebook: https://www.facebook.com/dongpay

có phương trình là

1 2

1 .

1 2

x t

y t

z t

 





  





  



Lấy





1 2 ; 1 ; 1 2

I t t t d

     

 

       

         

2 2 2

2 2

2 2 2

1 2 2 2 2 4 8

, 4 4

1 4 4

1 3;0;1 , 3 : 3 1 9

1 1; 2; 3 , 3 : 1 2 3 9

t t t

MI d I P t t t t

t I R S x y z

     

       

 

        

             

Chọn A.

Câu 15: Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng:

, và mặt cầu

Viết phương trình mặt phẳng song song với hai đường thẳng và cắt mặt cầu (S)

theo giao tuyến là đường tròn (C) có chu vi bằng .

Chọn B.

Hướng dẫn giải:

+ qua và có vectơ chỉ phương .

qua và có vectơ chỉ phương .

+ Mặt phẳng () song song với nên có vectơ pháp tuyến:

Phương trình mặt phẳng () có dạng:

+ Mặt cầu (S) có tâm và bán kính .

Gọi r là bán kính đường tròn (C), ta có:

2 1 1

1 2 3

x y z

  

  



: 2

1 2

x t

y t

z t







  





 



2 2 2

( ): 2 2 6 5 0

S x y z x y z

      

( )



1 2

 

2 365



5 3 4 0; 5 3 10 0

x y z x y z

       

5 3 10 0

x y z

   

5 3 3 511 0; 5 3 3 511 0

x y z x y z

         

5 3 4 0

x y z

   



(2; 1;1)

M 

(1;2; 3)

 





(0;2;1)

(1; 1;2)

u  



1 2

 

1 2

, (1; 5; 3)

u u

 

  

 

 



5 3 0

x y z D

   

I(1; 1;3)





2 365 365

5 5

r r



  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 85

Facebook: https://www.facebook.com/dongpay

Khi đó:

+ Phương trình mặt phẳng .

Vì nên M

và M

không thuộc loại (1).

Vậy phương trình mặt phẳng () cần tìm là: .

Chọn B.

Câu 16: Trong không gian Oxyz, cho điểm và mặt phẳng . Mặt cầu S

có tâm I nằm trên mặt phẳng , đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác

OIA bằng . Phương trình mặt cầu S là:

A. hoặc

B. hoặc

C. hoặc

D. hoặc

Hướng dẫn giải:

Gọi là tâm của S.

Khi đó nên ta suy ra hệ

Giải hệ ta tìm được hoặc

Chọn D.

Câu 17: Cho điểm





1;7;5

I và đường thẳng

1 6

2 1 3

x y z

 

 



. Phương trình mặt cầu có tâm

và

cắt đường thẳng d tại hai điểm A, B sao cho tam giác diện tích tam giác IAB bằng

2 6015

là:

     

2 2 2

1 7 5 2018.

x y z      B.

     

2 2 2

1 7 5 2017.

x y z     

     

2 2 2

1 7 5 2016.

x y z      D.

     

2 2 2

1 7 5 2019.

x y z     

 

2 2

,( )

d I R r



  

 





  







( ): 5 3 4 0 (1) hay 5 3 10 0 (2)

x y z x y z



       

1 2

/ /( ), / /( )

 

 

( )





5 3 10 0

x y z

   





1,0, 1







: 3 0

P x y z

   





6 2



     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

2 2 1 9.

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

1 2 2 9

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

2 2 1 9

x y z

     

     

2 2 2

1 2 2 9

x y z

     





, ,

I x y z





, , 6 2

I P IO IA IO IA AO     

   

2 2

2 2 2 2

2 2 2 2 2 2

1 1

1 0

2 2 6 2 9

3 0

x y z x y z

x z

x y z x y z

x y z



      

   





        

 

 

   











2,2,1





1,2, 2

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 86

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Gọi H là hình chiếu của





1;7;5

I trên d





0;0; 4

 





; 2 3

IH d I d  

8020

AIB

IH AB

S AB



   

2 2

2017

R IH

 

   

 

 

Vậy phương trình mặt cầu là:

     

2 2 2

1 7 5 2017.

x y z     

Chọn B.

Câu 18: Cho điểm

(0;0;3)

I và đường thẳng

: 2 .

x t

d y t

z t

  











 



Phương trình mặt cầu (S) có tâm

và cắt

đường thẳng

tại hai điểm

A B

sao cho tam giác

IAB

vuông là:

 

2 2

3 .

x y z

   

 

2 2

3 .

x y z

   

 

2 2

3 .

x y z

   

 

2 2

3 .

x y z

   

Hướng dẫn giải:

 Gọi





1 ;2 ;2

H t t t d

   

là hình chiếu vuông góc của

lên đường thẳng





1 ;2 ; 1

IH t t t

     



 Ta có vectơ chỉ phương của





1;2;1

a 



và

IH d



1 2 2 7

. 0 1 4 1 0 2 6 0 ; ;

3 3 3 3

IH a t t t t t H

 

                

 

 

 

2 2 2

2 2 2 2 3

3 3 3 3

     

    

     

     

 Vì tam giác

IAB

vuông tại

và

IA IB R

 

. Suy ra tam giác

IAB

vuông cân tại

, do đó

bán kính:

2 2 3 2 6

cos45 2 . 2 2.

2 3 3

R IA AB IH IH     

 Vậy phương trình mặt cầu

   

2 2

: 3

S x y z

   

Chọn B.

Câu 19: Cho điểm





2;5;1

A và mặt phẳng

( ):6 3 2 24 0

P x y z

   

, H là hình chiếu vuông góc của

trên mặt phẳng





. Phương trình mặt cầu

( )

có diện tích

784



và tiếp xúc với mặt

phẳng





tại H, sao cho điểm A nằm trong mặt cầu là:

     

2 2 2

8 8 1 196.

x y z      B.

     

2 2 2

8 8 1 196.

x y z     

     

2 2 2

16 4 7 196.

x y z      D.

     

2 2 2

16 4 7 196.

x y z     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 87

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

 Gọi

là đường thẳng đi qua

và vuông góc với





. Suy ra

2 6

: 5 3

1 2

x t

d y t

z t

 





 





 



 Vì H là hình chiếu vuông góc của

trên





nên

( )

H d P

 

Vì

H d



nên





2 6 ;5 3 ;1 2

H t t t

   .

 Mặt khác,

( )

H P



nên ta có:













6 2 6 3 5 3 2 1 2 24 0 1

t t t t

         

Do đó,





4;2;3

H  .

 Gọi

I R

lần lượt là tâm và bán kính mặt cầu.

Theo giả thiết diện tích mặt cầu bằng

784



, suy ra

4 784 14

R R

  

 

Vì mặt cầu tiếp xúc với mặt phẳng





tại H nên ( )

IH P I d

  

Do đó tọa độ điểm

có dạng





2 6 ;5 3 ;1 2

I t t t

   , với

 

 Theo giả thiết, tọa độ điểm

thỏa mãn:













     

2 2 2

6 2 6 3 5 3 2 1 2 24

( ,( )) 14

6 3 ( 2)

2 2

6 3 2 14

t t t

d I P

t t t



     

 











 



  

   

 

  







 

  



   





Do đó:





8;8; 1



 Vậy phương trình mặt cầu

     

2 2 2

( ): 8 8 1 196

S x y z      .

Chọn A.

Câu 20: Cho mặt phẳng





: 2 2 10 0

P x y z

   

và hai đường thẳng

2 1

1 1 1

x y z

 

  



2 3

1 1 4

x y z

 

   . Mặt cầu





có tâm thuộc



, tiếp xúc với



và mặt phẳng





có phương trình:

2 2 2

( 1) ( 1) ( 2) 9

x y z

     

hoặc

2 2 2

11 7 5 81

2 2 2 4

x y z

     

     

     

     

2 2 2

( 1) ( 1) ( 2) 9

x y z

     

hoặc

2 2 2

11 7 5 81

2 2 2 4

x y z

     

     

     

     

2 2 2

( 1) ( 1) ( 2) 9.

x y z

     

2 2 2

( 1) ( 1) ( 2) 3.

x y z

     

Hướng dẫn giải:



x t

y t

z t

 





 





 



;



đi qua điểm

(2;0; 3)



và có vectơ chỉ phương

(1;1;4)

a 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 88

Facebook: https://www.facebook.com/dongpay

 Giả sử

(2 ; ;1 )I t t t

  

là tâm và

là bán kính của mặt cầu





 Ta có:

( ; ;4 )

AI t t t

 





, (5 4;4 5 ;0)

AI a t t

 

  

 

 



 

5 4

;

AI a

d I

 



 

  

 



2 2 2(1 ) 10

( ,( ))

1 4 4

t t t

d I P

    



 

 







tiếp xúc với



và







( , ) ( ,( ))

d I d I P

  

5 4 10

t t

  









 



 Với





11 7 5

; ;

2 2 2

 



 

 





 

2 2 2

11 7 5 81

2 2 2 4

S x y z

     

     

     

     

 Với

 



(1; 1;2), 3

I R

 







2 2 2

:( 1) ( 1) ( 2) 9

S x y z

     

Chọn A.

Câu 21: Trong không gian với hệ tọa độ

Oxyz

cho ba đường thẳng

: 1, ;

d y t

z t







 











: , ;

d y u u

z u







 





 





1 1

: .

1 1 1

x y z

 

   Viết phương trình mặt cầu tiếp xúc với cả

1 2

d d

và có tâm thuộc đường thẳng



   

2 2

1 1 1

x y z

    

. B.

2 2 2

1 1 1 5

2 2 2 2

x y z

     

     

     

     

2 2 2

3 1 3 1

2 2 2 2

x y z

     

     

     

     

. D.

2 2 2

5 1 5 9

4 4 4 16

x y z

     

     

     

     

Hướng dẫn giải:

Chọn A.

Đường thẳng

đi qua điểm





1;1;0

M và có véc tơ chỉ phương





0;0;1

u 



Đường thẳng

đi qua điểm





2;0;1

M và có véc tơ chỉ phương





0;1;1

u 



Gọi

là tâm của mặt cầu. Vì





nên ta tham số hóa





1 ; ;1

I t t t

 

, từ đó









1 2

;1 ; 1 , 1 ; ;

IM t t t IM t t t

        

 

Theo giả thiết ta có









1 2

; ;

d I d d I d

 , tương đương với

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 89

Facebook: https://www.facebook.com/dongpay

   

1 2

2 2

1 2

; ;

1 2 1

d d

IM u IM u

t t t

u u

   

  

   

    

   

 

Suy ra





1;0;1

I và bán kính mặt cầu là





; 1

R d I d

 

. Phương trình mặt cầu cần tìm là

   

2 2

1 1 1

x y z

    

Câu 22: Cho mặt cầu





2 2 2

: 2 4 1 0

     

S x y z x z và đường thẳng

: .

 











 



x t

d y t

z m t

Tìm

để

cắt





tại hai điểm phân biệt

A B

sao cho các mặt phẳng tiếp diện của





tại

và tại

vuông góc với nhau.

 

m hoặc

 

m B.



m hoặc

 

m hoặc



m D. Cả

, ,

A B C

đều sai

Hướng dẫn giải:

Để thỏa mãn yêu cầu đề bài thì trước tiên d phải cắt mặt cầu, tức là phương trình

       

2 2

2 2. 2 4. 1 0

         

t t m t t m t có hai nghiệm phân biệt.





2 2

3 2 1 4 1 0

      

t m t m m

Phương trình có hai nghiệm phân biệt khi

 

' 0 1 3 12 3 0

       

m m m

5 1 0

   

m m .

Với phương trình có hai nghiệm phân biệt, áp dụng định lí Viet ta có

 

1 2 1 2

4 1 2

; 1

3 3

  

   

m m

t t t t m

Khi đó









1 1 1 2 2 2

1 ; ; 2 , 1 ; ; 2

       

 

IA t t m t IB t t m t

Vậy

















1 2 1 2 1 2

. 1 1 2 2 0

         

 

IA IB t t t t m t m t

    

1 2 1 2

3 1 2 1 0

       

t t m t t m

   

2 2

4 1 1 2 1 0

        

m m m m

 







 



(TM).

Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 90

Facebook: https://www.facebook.com/dongpay

Câu 23: Trong không gian Oxyz, cho mặt cầu





2 2 2

: 4 6 0

     

S x y z x y m và đường thẳng

 

1 1

2 1 2

 

 

x y z

. Tìm m để (d) cắt (S) tại hai điểm M, N sao cho độ dài MN bằng 8.

 

m B.



m C.



m D.

 

Hướng dẫn giải:

(S) có tâm





2;3;0

I và bán kính

   

2 2

2 3 0 13 13

       R m m m

Gọi H là trung điểm M, N

 

Đường thẳng (d) qua





0;1; 1



A và có vectơ chỉ phương

   

2;1;2 ; 3

 

 

   

 



u AI

u d I d

Suy ra

 

2 2 2 2

; 4 3 5

    

R MH d I d

Ta có

13 5 13 25 12

       

m m m

Chọn D.

Câu 24: Cho đường thẳng d là giao tuyến của hai mặt phẳng

và mặt cầu S có phương trình .

Tìm m để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho AB = 8.

A. 9 B. 12 C. 5 D. 2

Hướng dẫn giải:

Ta có lần lượt là VTPT của (α) và (β)

Suy ra VTCP của đường thẳng d là

Ta có A(6;4;5) là điểm chung của hai mặt phẳng (α) và (β) nên Ad.

Mặt cầu (S) có tâm I(-2;3;0), bán kính với m < 13.

Gọi H là trung điểm của AB  .

Trong tam giác vuông IHA ta có:

( ): x 2y 2z 4 0

    

( ): 2x 2y z 1 0,

    

2 2 2

x y z 4x 6y m 0

     

1 2

n (2; 2; 1), n (1;2; 2)

    

 

1 2

u n ;n (2;1;2),

 

 

 

  

R 13 m

 

IA (8;1;5) IA,u ( 3; 6;6) d(I,d) 3

 

      

 

  

AH 4 vµ IH 3

  

2 2 2 2

IA IH AH R 9 16

    

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 91

Facebook: https://www.facebook.com/dongpay

. Vậy m = 12 là giá trị cần tìm.

Chọn B.

Câu 25: Trong không gian với hệ trục tọa độ Oxyz, cho

(1;0;2), (3;1;4), (3; 2;1)

A B C



. Tìm tọa độ

điểm S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng

3 11

và S có cao độ âm.

( 4; 6;4)

 

. B.

(3;4;0)

S . C.

(2;2;1)

S . D.

(4;6; 4)



Hướng dẫn giải:

Ta có

(2;1;2); (2; 2; 1)

AB AC

   

 

, suy ra

AB AC



 

Tam giác ABC vuông nên I và S có thể sử dụng các tính chất của phép

dụng tâm để tính.

Tính được IM.

( ) ,

MI ABC MI k AB AC k

 

   

 

  

AS MI



 

, tìm S.

, (3;6; 6)

AB AC

 

 

 

 

Gọi

1 5

3; ;

2 2



 

 

 

là trung điểm

Ta có:

2 2 2

3 11 9 81 9

2 2 4 2

IM IB BM IM

 

      

 

 

( ) , (3;6; 6) 9 .

MI ABC MI k AB AC k MI k

 

      

 

  

Suy ra

9 1

2 2

k k

   



thì









2 3;6; 6 4;6; 4

AS MI S

    

 

Chọn D.

Câu 26: Trong không gian với hệ tọa độ

Oxyz

, cho điểm





0;0;4

A , điểm

nằm trên mặt phẳng





Oxy

và

M O



. Gọi

là hình chiếu vuông góc của

lên

và

là trung điểm của

. Biết đường thẳng

luôn tiếp xúc với một mặt cầu cố định. Tính bán kính mặt cầu

đó.



. B.



. C.



. D.

R 

Hướng dẫn giải:

Chọn A.

13 m 25 m 12

     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 92

Facebook: https://www.facebook.com/dongpay

Ta có tam giác

OAM

luôn vuông tại

Gọi

là trung điểm của

(Điểm

cố định)

Ta có tam giác

ADO

vuông tại

có

là

đường trung tuyến nên

 

2 1

ID OA 

Ta có

là đường trung bình của tam giác

OAM

nên

song song với

mà

OD AM OD IE

  

Mặt khác tam giác

EOD

cân tại

. Từ đó suy ra

là đường trung trực của

Nên



 

; 90 2

DOE ODE IOD IDO IDE IOE ID DE       

Vậy

luôn tiếp xúc với mặt cầu tâm

bán kính

 

Câu 27: Trong không gian với hệ tọa độ

Oxyz

xét các điểm





0;0;1





;0;0

B m





0; ;0

C n





1;1;1

với

0; 0

m n

 

và

m n

 

Biết rằng khi

thay đổi, tồn tại một mặt cầu cố

định tiếp xúc với mặt phẳng





ABC

và đi qua

. Tính bán kính

của mặt cầu đó?



. B.

R  . C.



. D.

R  .

Hướng dẫn giải:

Gọi

(1;1;0)

I là hình chiếu vuông góc của

lên mặt phẳng

( )

Oxy

Ta có: Phương trình theo đoạn chắn của mặt phẳng

( )

ABC

là:

  

x y

m n

Suy ra phương trình tổng quát của

( )

ABC

là

   

nx my mnz mn

Mặt khác

2 2 2 2

( ,( )) 1



 

 

d I ABC

m n m n

(vì

 

m n

) và

1 ( ,( ))

 

ID d I ABC

Nên tồn tại mặt cầu tâm

(là hình chiếu vuông góc của

lên mặt phẳng

Oxy

) tiếp xúc

với

( )

ABC

và đi qua

Chọn A.

Câu 28:

Trong không gian tọa độ Oxyz cho điểm và mặt cầu (S) có

phương trình: .Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện

ABCD

có thể tích lớn nhất.

A. B. C. D.

Hướng dẫn giải:

(0;1;1), (1;0; 3), ( 1; 2; 3)

A B C

   

2 2 2

2 2 2 0

x y z x z

     

7 4 1

; ;

3 3 3

 

 

 

 

1 4 5

; ;

3 3 3

 

 

 

 

7 4 1

; ;

3 3 3

 

 

 

7 4 1

; ;

3 3 3

 



 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 93

Facebook: https://www.facebook.com/dongpay

Ta có (S) suy ra (S) có tâm I(1;0;-1), bán kính

Và

Mặt phẳng (ABC) có một vectơ pháp tuyến là

Suy ra mp(ABC) có phương trình:

Ta có nên lớn nhất khi và chỉ khi lớn nhất.

Gọi là đường kính của mặt cầu (S) vuông góc với mp(ABC). Ta thấy với D là 1 điểm

bất kỳ thuộc (S) thì .

Dấu “=” xảy ra khi D trùng với D

hoặc D

Đường thẳng đi qua I(1;0;-1), và có VTCP là

Do đó (D

) có phương trình: .

Tọa độ điểm D

và D

thỏa mãn hệ:

Ta thấy: . Vậy điểm là điểm cần tìm

Chọn D.

Câu 29: Trong không gian với hệ tọa độ

, cho đường thẳng

1 3

1 2 1

x y z

 

 

 

và mặt cầu





tâm

có phương trình

       

2 2 2

: 1 2 1 18

S x y z

     

. Đường thẳng

cắt





tại hai điểm

A B

. Tính diện tích tam giác

IAB

8 11

16 11

8 11

Hướng dẫn giải:

Chọn A.

2 2 2

:( 1) ( 1) 4

    

x y z

R 2



(1; 1; 4); ( 1; 3; 4)

AB AC

      

 

, ( 8;8; 4)

n AB AC

 

   

 

  

8x 8(y 1) 4(z 1) 0 2x 2y z 1 0

          

( ;( )).

ABCD ABC

V d D ABC S



ABCD

( ;( ))

d D ABC

1 2

D D





1 2

( ;( )) max ( ;( )); ( ;( ))

d D ABC d D ABC d D ABC



1 2

D D

(2; 2;1)

ABC

n  



1 2

 





 





  



x t

y t

z t

2 2 2

1 2

( 1) ( 1) 4

x t

y t

z t

x y z

 











 









   













    



1 2

7 4 1 1 4 5

; ; & ; ;

3 3 3 3 3 3

   

   



   

   

D D

1 2

( ;( )) ( ;( ))

d D ABC d D ABC



7 4 1

; ;

3 3 3

 

 

 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 94

Facebook: https://www.facebook.com/dongpay

Đường thẳng

đi qua điểm

 

1;0; 3C  và có vectơ chỉ phương

 

1;2; 1u   



Mặt cầu

 

S có tâm

 

1;2; 1I  , bán kính

3 2R 

Gọi H là hình chiếu vuông góc của I lên đường thẳng

Khi đó:

,IC u

 

 



 



, với

 

0; 2; 2IC   



;

2 3 4 0x y z   

Vậy

2 2 2

6 2 2 66

1 4 1

 

 

 

Suy ra

22 4 6

3 3

HB   

Vậy,

1 1 66 8 6 8 11

2 2 3 3 3

IAB

S IH AB



     

Câu 30: Trong không gian Oxyz , cho điểm

1 3

; ;0

2 2

 

 

 

M và mặt cầu

 

2 2 2

: 8.  S x y z Đường

thẳng d thay đổi, đi qua điểm ,M cắt mặt cầu

 

S tại hai điểm phân biệt. Tính diện tích lớn

nhất S của tam giác .OAB

A. 7S . B. 4S . C. 2 7S . D. 2 2S .

Hướng dẫn giải:

Mặt cầu

 

S có tâm

 

0;0;0O và bán kính 2 2R .

Vì 1 OM R nên M thuộc miền trong của

mặt cầu

 

S . Gọi A , B là giao điểm của đường

thẳng với mặt cầu. Gọi H là chân đường cao hạ

từ O của tam giác OAB .

Đặt x OH , ta có 0 1  x OM , đồng thời

2 2 2

8   OHHA R x . Vậy diện tích tam

giác OAB là

. . 8

  

OAB

S OH AB OH HA x x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 95

Facebook: https://www.facebook.com/dongpay

Khảo sát hàm số

( ) 8

 

f x x x

trên





0;1

, ta được













0;1

max 1 7

 f x f

Vậy giá trị lớn nhất của





OAB

S , đạt được khi



hay



H M

, nói cách khác là



d OM

Chọn A.

Câu 31: Trong không gian với hệ tọa độ

Oxyz

, cho điểm





2;11; 5



và mặt phẳng













2 2

:2 1 1 10 0

P mx m y m z

     

. Biết rằng khi

thay đổi, tồn tại hai mặt cầu cố

định tiếp xúc với mặt phẳng





và cùng đi qua

. Tìm tổng bán kính của hai mặt cầu đó.

2 2

. B.

5 2

. C.

7 2

. D.

12 2

Hướng dẫn giải:

Gọi





; ; ,

I a b c r

lần lượt là tâm và bán kính của mặt cầu. Do mặt cầu tiếp xúc với





nên ta

có

 









 

2 2

2 1 1 10

2 10

1 2 1 2

ma m b m c

b c m ma b c

r d I P

m m

    

    

  

 









 

2 2

2 10 1 2

2 2 2 10 0 1

2 2 2 10 0 2

b c m ma b c r m

b c r m ma b c r

      



       







       





TH1:





 

2 2 2 10 0 1

b c r m ma b c r       

Do m thay đổi vẫn có mặt cầu cố định tiếp xúc với





nên yêu cầu bài toán trờ thành tìm

điều kiện

, ,

a b c

sao cho





không phụ thuộc vào

. Do đó





luôn đúng với mọi

2 0

2 10 0

b c r



  



 





   



2 5 0

b r



  



 





 



Suy ra





 





 

2 2

0;5 2; 5 : 5 2 5

I r S x y r z r

        

Lại có





A S

 nên suy ra:

 

2 2

4 11 5 2 12 2 40 0

10 2

r r r r





         









ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 96

Facebook: https://www.facebook.com/dongpay

TH2:

 

2 2 2 10 0b c r m ma b c r       

làm tương tự TH1 (trường hợp này

không thỏa đề bài )

Tóm lại: Khi m thay đổi, tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng

 

P và cùng đi

qua A và có tổng bán kính là:

12 2

suy ra chọn D

Câu 32: Cho hình chóp SABC có đáy là tam giác đều cạnh bằng

6cm

và

 

4 3SA SB SC cm  

.Gọi D là điểm đối xứng của B qua C. Khi đó bán kính mặt cầu ngoại tiếp hình chóp

SABD bằng?

5cm

3 2cm

C. 26cm D. 37cm

Hướng dẫn giải:

Cách 1: Dựng CG vuông góc với

 

ABC , Qua E dựng mặt phẳng vuông góc với

, mặt

phẳng này cắt CG tại F. Suy ra F là tâm mặt cầu ngoại tiếp hình chóp S.ABD.Đặt

SF R

Xét hình chữ nhật:

 

2 2

FGSH FC SH FG SH R CH     

Lại có:

 

2 2

2FC R CB  .Từ (1) và (2)

suy ra

2 2 2 2

SH R CH R CB   

 

2 2 2

6 12 36 5 12 0 37R R R R cm         

Suy ra chọn D

Cách 2:

Chọn hệ trục tọa độ như hình vẽ.

Ta có:

 

     

0;0;0 , 3 3; 3;0 , 3 3;3;0 , 2 3;0;6C A B S   

   

0;0; 36 12 6F CG F t FA FS t t        

 

1 37t SC cm    suy ra chọn D

Câu 33: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng

2 1 4

x y z



 



và mặt cầu

       

2 2 2

: 1 2 1 2S x y z      . Hai mặt phẳng

 

P và

 

Q chứa

và tiếp xúc với

 

. Gọi ,M N là tiếp điểm. Tính độ dài đoạn thẳng

.MN

2 2.

C. 6. D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 97

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Chọn B.

Mặt cầu

 

S có tâm

 

1;2;1 , 2I R 

Đường thẳng

nhận

 

2; 1;4u  



làm vectơ chỉ phương

Gọi H là hình chiếu của I lên đường thẳng d.

 

2 2; ;4H d H t t t   

Lại có:

   

. 0 2 1; 2;4 1 . 2; 1;4 0IH u t t t       

 

   

2 2 1 2 4 4 1 0 0t t t t        

Suy ra tọa độ điểm

 

2;0;0H .

Vậy 1 4 1 6IH    

Suy ra: 6 2 2HM   

Gọi K là hình chiếu vuông góc của M lên

đường thẳng HI .

Suy ra:

2 2 2

1 1 1 1 1 3

4 2 4MK MH MI

     .

Suy ra:

2 4

3 3

MK MN  

Câu 34: Trong không gian với hệ tọa độ ,Oxyz cho

điểm

     

;0;0 , 0; ;0 , 0;0; ,A a B b C c trong

đó

0a 

0b 

0c 

và

1 2 3

a b c

   Biết mặt phẳng

 

ABC tiếp xúc với mặt cầu

       

2 2 2

: 1 2 3 .

S x y z      Thể tích của khối tứ diện

OABC

là

Hướng dẫn giải:

Chọn A.

Cách 1: Ta có

 

: 1.

x y z

ABC

a b c

  

Mặt cầu

 

S có tâm

 

1;2;3I và bán kính

R 

Mặt phẳng

 

ABC tiếp xúc với

   

 

2 2 2

1 2 3

; .

1 1 1

a b c

S d I ABC R

a b c

  

   

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 98

Facebook: https://www.facebook.com/dongpay

Mà

2 2 2

1 2 3 1 1 1 7

7 .

a b c a b c

      

Áp dụng BĐT Bunhiacopski ta có

 

2 2 2 2

2 2 2 2 2 2

1 1 1 1 2 3 1 1 1 7

1 2 3 7 .

a b c a b c a b c

   

           

   

   

Dấu

" "



xảy ra

1 2 3

1 1 1

2, 1, ,

1 2 3

a b c



 



    





  





khi đó

1 2

6 9

OABC

V abc

 

Cách 2: Ta có

 

: 1,

x y z

ABC

a b c

  

mặt cầu





có tâm

(1;2;3),

I R  .

Ta có





ABC

tiếp xúc với mặt cầu





 

2 2 2

1 2 3

,( )

1 1 1

a b c

d I P R

a b c

  

   

 

2 2 2 2 2 2

2 2 2

7 1

72 1 1 1 7 1 1 1 7

7 2 2

1 1 1

a b c a b c

a b c



          

 

2 2 2

1 1 1 1 2 3 7

a b c a b c

      

2 2 2

1 1 1 1 3

1 0

2 2a b c

     

      

     

     









 









1 2

6 9

OABC

V abc

  

Cách 3: Giống Cách 2 khi đến

2 2 2

1 1 1 7

a b c

  

Đến đây ta có thể tìm a, b, c bằng bất đẳng thức như sau:

Ta có

 

2 2

2 2 2 2

2 2 2 2 2 2

1 2 3 1 1 1 1 1 1 1 1 1 7

7 1. 2. 3. 1 2 3

a b c a b c a b c a b c

     

              

     

     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 99

Facebook: https://www.facebook.com/dongpay

Mà

2 2 2

1 1 1 7

a b c

   

Dấu “=” của BĐT xảy ra

1 1 1

1 2 3

a b c

 

, kết hợp với giả thiết

1 2 3

a b c

  

ta được



. Vậy:

1 2

6 9

OABC

V abc

 

Ta có









 









1 2

6 9

OABC

V abc

  

Cách 4: Mặt cầu





có tâm





1;2;3

I và bán kính

R 

Phương trình mặt phẳng

( ) : 1

x y z

ABC

a b c

  

Ta có:

1 2 3

7 7 7

7 1

a b c a b c

      

nên

 

1 2 3

; ;

7 7 7

M ABC

 



 

 

Thay tọa độ

1 2 3

; ;

7 7 7

 

 

 

vào phương trình mặt cầu

( )

ta thấy đúng nên

( )

M S



Suy ra:

( )

ABC

tiếp xúc với

( )

thì

là tiếp điểm.

Do đó:

( )

ABC

qua

1 2 3

; ;

7 7 7

 

 

 

, có VTPT là

 

6 12 18

; ; 1;2;3

7 7 7

MI n

 

  

 

 

 

( )

ABC

có phương trình:

2 3 2 0 1 2

2 1

x y z

x y z a

         



Vậy

1 2

6 9

V abc

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 100

Facebook: https://www.facebook.com/dongpay

GTLN, GTNN TRONG HÌNH HỌC TỌA ĐỘ OXYZ

Câu 1: Trong không gian với hệ tọa độ cho hai điểm và mặt phẳng

Tìm tọa độ điểm thuộc sao cho nhỏ nhất?

A. . B. .

C. . D.

2 11 18

; ;

5 5 5

 

 

 

 

Hướng dẫn giải:

Chọn D.

Thay tọa độ vào phương trình mặt phẳng , ta được



hai điểm

cùng phía với đối với mặt phẳng .

Gọi là điểm đối xứng của

qua





. Ta có

Nên





min

MA MB A B



  khi và chỉ khi

là giao

điểm của

A B



với





Phương trình ( đi qua và

có véctơ chỉ phương

 





1;2; 1

 



Gọi

là giao điểm của



trên





, suy ra tọa độ của

là





0; 2;4

H  , suy ra





1; 4;6



  , nên phương trình

: 1 3

2 4

x t

A B y t

z t









  





 



Vì

là giao điểm của

A B



với





nên ta tính được tọa độ

Câu 2: Cho hai điểm









1,3, 2 ; 9,4,9

A B   và mặt phẳng





:2 1 0.

P x y z

   

Điểm M thuộc

(P). Tính GTNN của

AM BM



A. B. C. D.

Hướng dẫn giải:

Ta có:





















2. 1 3 2 1 2. 9 4 9 1 72 0

          

A B



nằm cùng phía so với mặt

phẳng (P).

Oxyz









1;0;2 ; 0; 1;2

A B 





: 2 2 12 0.

P x y z

   





MA MB







2;2;9

6 18 25

; ;

11 11 11

 

 

 

 

7 7 31

; ;

6 6 4

 

 

 









1;0;2 ; 0; 1;2

A B 













P A P B









MA MB MA MB A B

 

   

: 2

2 2

x t

AA y t

z t

 













 









1;0;2

2 11 18

; ; .

5 5 5

 

 

 

 

6 204



7274 31434



2004 726



3 26

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 101

Facebook: https://www.facebook.com/dongpay

Gọi A’ là điểm đối xứng của A qua (P). Mặt phẳng (P) có vtpt

Đường thẳng

’

đi qua





1,3, 2

 

có vtcp có pt:

Gọi H là giao của

’

và





ta có:

















2 1 2 3 2 1 0 1 1,2, 1 .

t t t t H

            

Ta có H là trung điểm của





’ ’ 3,1,0 .

AA A

Đường A’B đi qua A’(3, 1, 0) có vtcp có pt:

Gọi N là giao điểm của A’B và mặt phẳng





ta có:













2. 3 4 – 1 3 1 0 1 1,2,3 .

t t t t N        

Để

MA MB



nhỏ nhất thì khi đó

’

MA MB A B

 

Chọn D.

Câu 3: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng và hai điểm

. M là một điểm trên mặt phẳng . Giá trị lớn nhất của

là:

A. B. C. D.

Hướng dẫn giải:

Ta có: A, B nằm khác phía so với (P). Gọi B’ là điểm đối xứng với B qua (P). Suy ra

Đẳng thức xảy ra khi

, , ’

M A B

thẳng hàng.

Chọn A.

Câu 4: Trong không gian với hệ trục tọa độ

Oxyz

cho mặt phẳng (P) có phương trình

2 – 1 0

x y z

  

và hai điểm









3;1;0 , 9;4;9 .

M N  Tìm điểm





; ;

I a b c

thuộc mặt phẳng

(P) sao cho đạt giá trị lớn nhất. Biết

, ,

a b c

thỏa mãn điều kiện:

A. B. C. D.

Hướng dẫn giải:

Nhận thấy 2 điểm M, N nằm về hai phía của mặt phẳng (P).





2, 1,1

n 







2, 1,1

n 



1 2

x t

y t

z t

  





 





  







' 12,3,9

A B 



3 4

x t

y t

z t

 





 









M N



 

2 2

12 3 9 234 3 26

    

( ): 1 0

P x y z

   





(1; 3;0), 5; 1; 2

A B

  

( )

T MA MB

 

2 5.

T 

2 6.

T 

4 6

T 

2 3

T 

'( 1; 3;4)

 

' ' 2 5.

T MA MB MA MB AB     

IM IN



a b c

  

a b c

  

a b c

  

19.

a b c

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 102

Facebook: https://www.facebook.com/dongpay

Gọi R là điểm đối xứng của M qua mặt phẳng (P), khi đó đường thẳng MR đi qua điểm M(3;

1; 0) và vuông góc với mặt phẳng (P) có phương trình: . Gọi

Ta có . Đẳng thức xảy ra khi I, N, R thẳng hàng. Do đó tọa độ

điểm I là giao điểm của đường thẳng NR: (t là tham số ) và mặt phẳng (P).

Dễ dàng tìm được I(7; 2; 13).

Chọn A.

Câu 5: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm









1;2;2 , 5;4;4

A B và mặt phẳng





:2 – 6 0.

P x y z

  

Tọa độ điểm M nằm trên (P) saocho

2 2

MA MB



nhỏ nhất là:





1;3;2

 B.





2;1; 11

 C.





1;1;5

 D.





1; 1;7



Hướng dẫn giải:

+ Kiểm tra phương án A không thuộc (P).

+ Tính trực tiếp MA

+ MB

trong 3 phương án B,C,D và so sánh.

Chọn C.

Câu 6: Trong không gian tọa độ

Oxyz

cho mặt phẳng













:2 1 0, 8; 7;4 , 1;2; 2 .

P x y z A B

      

Tìm tọa độ điểm

thuộc mặt phẳng





sao cho

2 2

MA MB



nhỏ nhất.





0;0; 1



. B.





0;0;1

M . C.





1;0;1

M . D.





0;1;0

Hướng dẫn giải:

Gọi

là điểm thỏa mãn





2 0 2; 1;0

IA IB I   

 

Có









2 2

2 2 2 2 2

2 2 3 2

MA MB MI IA MI IB MI IA IB

       

   

Vì

IA IB

không đổi nên





2 2

min

MA MB MI M

   là hình chiếu vuông góc của

lên mặt phẳng





Đường thẳng

đi qua

và vuông góc với





   

2 2

: 1 ; 0;0; 1

x t

d y t d P M

z t

 





      









Chọn A.

3 1

2 1 1

x y z

 

 



(P) (1;2; 1) ( 1;3; 2)

H MR H R

      

IM IN IR IN RN

   

1 8

2 11

x t

y t

z t

  





 





  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 103

Facebook: https://www.facebook.com/dongpay

Câu 7: Cho 2 điểm









0,0, 3 , 2,0, 1

A B

 

và mặt phẳng





:3 8 7 1 0.

P x y z

   

Tìm





M P



sao cho

2 2

MA MB



nhỏ nhất.

283 104 214

; ;

183 183 183

 

 

 

 

. B.

283 104 214

; ;

183 183 183

 

 

 

 

283 14 14

; ;

183 183 183

 

 

 

 

. D.

283 14 14

; ;

183 183 183

 

 

 

Hướng dẫn giải:

Gọi

sao cho

4 5

2 0 ;0;

3 3

IA IB I

 

  

 

 

 





 

2 2 2

2 2 2 2 2 2 2 2

2 .

2 3 2 2 3 2

MA MA MI IA MI IA MI IA

MB MB MI IB MI IB MI IB

MA MB MI IA IB MI IA IB MI IA IB

     

        

    

  

Suy ra





2 2

min

2MA MB khi

bé nhất hay

là hình chiếu của

trên





Tìm được tọa độ

283 104 214

; ;

183 183 183

 

 

 

 

Chọn A.

Câu 8:

Trong không gian với hệ tọa độ , cho đường thẳng hai điểm

và . Biết điểm thuộc thì nhỏ nhất.Tìm

A. B. C. D.

Hướng dẫn giải:

Phương trình đường thẳng AB là: . Dễ thấy đường thẳng và AB cắt

nhau tại điểm suy ra AB và đồng phẳng.

Lại có .

Ta có: .

Do đó nhỏ nhất khi trùng với điểm

Oxyz

 

x t

y t t

z t

: 1 2



 



    















2;0;3





2; 2; 3

 





M x y z

0 0 0

; ;



MA MB

4 4





 

y t t

z t

1 1

3 3







 





 











2; 1;0













IA IB IA IB IA IB AB

0;1;3 , 0; 1; 3       

   

 

   

MA MB MA MB MA MB AB IA IB

2 4

4 4 2 2 4

1 1 1 1 1

2 2 2 8 8

 

       

 

 

MA MB

4 4







2; 1;0



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 104

Facebook: https://www.facebook.com/dongpay

Chọn C.

Câu 9: Trong không gian với hệ trục toạ độ cho 3 điểm .

Điểm sao cho giá trị của biểu thức nhỏ

nhất. Khi đó, điểm cách một khoảng bằng

A. B. C. D.

Hướng dẫn giải:

Gọi . Ta có

với

nhỏ nhất khi nhỏ nhất là hình chiếu vuông góc của trên

Câu 10: Trong không gian với hệ trục tọa độ

Oxyz

, cho





1;1;1

A ,





0;1;2

B ,





2;0;1

C 





: 1 0

P x y z

   

. Tìm điểm





N P

 sao cho

2 2 2

S NA NB NC

   đạt giá trị nhỏ

nhất.

1 5 3

; ;

2 4 4

 



 

 

. B.





3;5;1

N . C.





2;0;1

N  . D.

3 1

; ; 2

2 2

 

 

 

 

Hướng dẫn giải:

Chọn A.

Gọi

là trung điểm

và

là trung điểm

. Do đó

1 3

1; ;

2 2

 



 

 

và

3 5

0; ;

4 4

 

 

 

Khi đó

2 2 2 2 2 2

1 1

2 2 4

2 2

S NA NI BC NJ IJ BC

      .

Do đó

nhỏ nhất khi

nhỏ nhất. Suy ra

là hình chiếu của

trên





Phương trình đường thẳng

x t

NJ y t

z t









 





 





Oxyz













1;2;3 ; 0;1;1 ; 1;0; 2

A B C







: 2 0

M P x y z

    

2 2 2

2 3

T MA MB MC

  





:2 2 3 0

Q x y z

   

121

24.

2 5

101





; ;

M x y z

2 2 2

6 6 6 8 8 6 31

T x y z x y z

      

2 2 2

2 2 1 145

3 3 2 6

T x y z

 

     

      

 

     

     

 

 

145

T MI  

2 2 1

; ;

3 3 2

 



 

 







5 5 13

; ;

18 18 9

 

   

 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 105

Facebook: https://www.facebook.com/dongpay

Tọa độ điểm

là nghiệm của hệ:

1 0

x y z

x t

y t

z t

   



 







 

 

 

 

 



 

 



Câu 11: rong không gian với hệ tọa độ Oxyz cho ba điểm

     

1;01;1 , 1;2;1 , 4;1; 2A B C  và mặt

phẳng

 

: 0P x y z   . Tìm trên (P) điểm M sao cho

2 2 2

MA MB MC  đạt giá trị nhỏ

nhất. Khi đó M có tọa độ

 

1;1; 1M  B.

 

1;1;1M C.

 

1;2; 1M  D.

 

1;0; 1M 

Hướng dẫn giải:

Gọi G là trọng tâm của tam giác ABC, ta có

 

2;1;0G , ta

có

 

2 2 2 2 2 2 2

3 1MA MB MC MG GA GB GC     

Từ hệ thức (1) ta suy ra:

2 2 2

MA MB MC  đạt GTNN

MG

đạt GTNN  M

là hình chiếu vuông góc của G trên (P).

Gọi (d) là đường thẳng qua G và vuông góc với (P) thì (d) có phương trình tham số là

x t

y t

z t

 





 









Tọa độ M là nghiệm của hệ phương trình

 

2 1

1 1

1;0; 1

0 1

x t t

y t x

z t y

x y z z

   

 

 

  

 

  

 

 

 

    

 

Chọn D.

Câu 12: (Hình Oxyz) Cho

     

1;3;5 , 2;6; 1 , 4; 12;5A B C    và điểm

 

: 2 2 5 0P x y z    .

Gọi M là điểm thuộc

 

P sao cho biểu thức

4S MA MB MA MB MC    

    

đạt giá trị

nhỏ nhất. Tìm hoành độ điểm M.

x 

x  

x 

x  

Hướng dẫn giải:

Gọi I là điểm

 

4 0 3;7; 3 .IA IB I   

  

Gọi G là trọng tâm ta m giác ABC

 

1; 1;3G  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 106

Facebook: https://www.facebook.com/dongpay

Nhận thấy, M,I nằm khác phía so với mp(P).

Có





3 3

S MI MG GI

   . Dấu bằng xảy ra khi M là giao điểm của GI và (P)





1;3;1

M

Chọn C.

Câu 13: Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm





2;1; 1







0;3;1

B và mặt phẳng





: 3 0

P x y z

   

. Tìm tọa độ điểm

thuộc

( )

sao cho

MA MB



 

có giá trị nhỏ

nhất.





4; 1;0

M   . B.





1; 4;0

M   . C.





4;1;0

M . D.





1; 4;0

M  .

Hướng dẫn giải:

Gọi





; ;

I a b c

là điểm thỏa mãn

2 0

IA IB

 

 



, suy ra





4; 1; 3

 

Ta có

2 2 2 .

MA MB MI IA MI IB MI

     

      

Suy ra

MA MB MI MI

  

  

Do đó

MA MB



 

nhỏ nhất khi

nhỏ nhất hay

là hình chiếu của

trên mặt phẳng





Đường thẳng đi qua

và vuông góc với





có là

4 1 3

1 1 1

x y z

  

 



Tọa độ hình chiếu

của

trên





thỏa mãn

 

4 1 3

4;0

y z



   

  



 













Chọn D.

Câu 14: Trong không gian

Oxyz

, cho mặt phẳng

2 2 9 0

x y z

   

và mặt cầu

2 2 2

( ):( 3) ( 2) ( 1) 100

S x y z      . Tọa độ điểm

nằm trên mặt cầu

( )

sao cho

khoảng cách từ điểm

đến mặt phẳng

( )

đạt giá trị nhỏ nhất là:

11 14 13

; ;

3 3 3

 



 

 

. B.

29 26 7

; ;

3 3 3

 

 

 

 

29 26 7

; ;

3 3 3

 

 

 

 

. D.

11 14 13

; ;

3 3 3

 



 

 

Hướng dẫn giải:

Mặt cầu

( )

có tâm

(3; 2;1)



Khoảng cách từ

đến mặt phẳng

( )

: ( ;( )) 6

d I P R

 

nên

( )

cắt

( )

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 107

Facebook: https://www.facebook.com/dongpay

Khoảng cách từ

thuộc

( )

đến

( )

lớn nhất



( )

M d



đi qua

và vuông góc với

( )

Phương trình

3 2

( ): 2 2

x t

d y t

z t

 





  





 



Ta có:

( ) (3 2 ; 2 2 ;1 )

M d M t t t

     

Mà:

( )

M S



10 29 26 7

; ;

3 3 3 3

10 11 14 13

; ;

3 3 3 3

t M



 

   

 



 







 

   



 

 



Thử lại ta thấy:

1 2

( ,( )) ( ,( ))

d M P d M P



nên

11 14 13

; ;

3 3 3

 



 

 

thỏa yêu cầu bài toán

Câu 15: Trong không gian

Oxyz

, cho mặt phẳng

( ): 2 2 4 0

P x y z

   

và mặt cầu

2 2 2

( ): 2 2 2 1 0.

S x y z x y z

      

Giá trị của điểm

trên





sao cho









d M P

đạt

GTNN là:





1;1;3

. B.

5 7 7

; ;

3 3 3

 

 

 

. C.

1 1 1

; ;

3 3 3

 

 

 

 

. D.





1; 2;1

 .

Hướng dẫn giải::

Ta có:

( ,( )) 3 2 ( ) ( ) .

d M P R P S

      

Đường thẳng d đi qua I và vuông góc với (P) có pt:

1 2 , .

1 2

x t

y t t

z t

 





  





 





Tọa độ giao điểm của d và (S) là:

5 7 7

; ;

3 3 3

 

 

 

1 1 1

; ;

3 3 3

 

 

 

 

Ta có:

( ,( )) 5 ( ,( )) 1.

d A P d B P

  

( ,( )) ( ,( )) ( ,( )).

d A P d M P d B P

  

Vậy:

min

( ,( )) 1 .

d M P M B

   

Câu 16: Trong không gian

Oxyz

cho mặt cầu

       

2 2 2

: 1 2 3 9

S x y z

     

và mặt phẳng





:2 2 3 0

P x y z

   

. Gọi





; ;

M a b c

là điểm trên mặt cầu





sao cho khoảng cách từ

đến





là lớn nhất. Khi đó

a b c

  

a b c

  

a b c

  

a b c

  

Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 108

Facebook: https://www.facebook.com/dongpay

Chọn C.

Mặt cầu

       

2 2 2

: 1 2 3 9

S x y z

     

có tâm





1;2;3

I và bán kính



Gọi

là đường thẳng đi qua





1;2;3

I và vuông góc





Suy ra phương trình tham số của đường thẳng

là

1 2

2 2

x t

y t

z t

 





 





 



Gọi

A B

lần lượt là giao của

và





, khi đó tọa độ

A B

ứng với

là nghiệm của

phương trình

     

2 2 2

1 2 1 2 2 2 3 3 9

t t t





         



 



Với

   

1 3;0;4 ;( ) .

t A d A P   

Với

   

1 1;4;2 ;( ) .

t B d B P

     

Với mọi điểm





; ;

M a b c

trên





ta luôn có













;( ) ;( ) ;( ) .

d B P d M P d A P

 

Vậy khoảng cách từ

đến





là lớn nhất bằng

khi





3;0;4

Do đó

a b c

  

Câu 17: Trong không gian Oxyz cho 4 điểm , , , . Gọi

M là một điểm nằm trên đường thẳng CD sao cho tam giác MAB có chu vi bé nhất. Khi đó

toạ độ điểm M là:

A. B. C. D.

Hướng dẫn giải:

Tam giác MAB có độ dài cạnh không đổi, do đó chu vi bé nhất khi và chỉ khi

bé nhất.

; . Vì nên , suy ra điểm M cần tìm là

hình chiếu vuông góc của A, cũng là hình chiếu vuông góc của B lên đường thẳng

. Từ

đó tìm ra điểm .

Chọn A.

Câu 18: Cho hình chóp

O ABC

có , ,

OA a OB b OC c

  

đôi một vuông góc với nhau. Điểm M cố

định thuộc tam giác

ABC

có khoảng các lần lượt đến các mặt phẳng





2;3;2





6; 1; 2

 





1; 4;3

C  





1;6; 5







0;1; 1







2;11; 9







3;16; 13

M 





1; 4;3

M  

4 3

AB 

MA MB







4; 4; 4

  







2;10; 8

 



. 0

ABCD



 

AB CD







0;1; 1



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 109

Facebook: https://www.facebook.com/dongpay













, ,

OBC OCA OAB

là 1,2,3. Khi tồn tại

, ,

a b c

thỏa thể tích khối chóp

O ABC

nhỏ

nhất, giá trị nhỏ nhất của thể tích khối chóp

O ABC

là

A. 18 B. 27

C. 6 D. Không tồn tại

, ,

a b c

thỏa yêu cầu bài toán

Hướng dẫn giải:

Chọn hệ trục tọa độ thỏa

















0,0,0 , ,0,0 , 0, ,0 , 0,0,

O A a B b C c

Điểm M cố định thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng









, ,

OBC OCA





OAB

là 1,2,3 nên tọa độ điểm M là (1,2,3)

Phương trình mặt phẳng (ABC) là

Vì M thuộc mặt phẳng (ABC) nên

OABC

Áp dụng bất đẳng thức Cauchy ta có

Chọn B.

Câu 19: Trong không gian với hệ tọa độ

Oxyz

, cho điểm





1;2;1

M . Mặt phẳng





thay đổi đi qua

lần lượt cắt các tia

, ,

Ox Oy Oz

tại

, ,

A B C

khác

. Tính giá trị nhỏ nhất của thể tích

khối tứ diện

OABC

54.

18.

Hướng dẫn giải:

Chọn C.

Gọi













;0;0 , 0; ;0 , 0,0,

A a B b C c

với

, , 0

a b c



Phương trình mặt phẳng





x y z

a b c

  

Vì:

 

1 2 1

M P

a b c

    

Thể tích khối tứ diện

OABC

là:

OABC

V abc



Áp dụng bất đẳng thức Cauchy ta có:

1 2 1 1 2 1

3 .

a b c a b c

  

Hay

2 54

1 3 1

abc abc

  

. Suy ra:

54 9

abc abc

  

x y z

a b c

  

1 2 3

a b c

  

abc

1 2 3 1 1 1 1

1 3 . . 27

abc

a b c a b c

     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 110

Facebook: https://www.facebook.com/dongpay

Vậy:

OABC



Câu 20: Trong hệ trục tọa độ Oxyz cho 3 điểm với .Giả sử

thay đổi nhưng thỏa mãn không đổi. Diện tích tam giác ABC đạt giá

trị lớn nhất bằng

A. B. C. D.

Hướng dẫn giải:

Phương trình (ABC):

Gọi là hình chiếu vuông góc của O lên

Khi đó

Ta có

Áp dụng bất đẳng thức Cosi ta có

Dấu “=” xảy ra khi và chỉ khi

Vậy

Chọn B.

Câu 21: Trong không gian với hệ toạ độ

Oxyz

phương trình mặt phẳng (P) đi qua điểm ,

cắt các tia

, ,

Ox Oy Oz

tại

, ,

A B C

sao cho thể tích tứ diện

OABC

có giá trị nhỏ nhất là













;0;0 , 0; ;0 , 0;0;

A a B b C c

, , 0

a b c



, ,

a b c

2 2 2 2

a b c k

  

x y z

a b c

  





; ;

H x y z





ABC

 

     

2 2

2 2 2

2 2

2 2 2

2 2

2 2 2

ab c

ab bc ca

H ABC

bcx cay abz abc

a bc

OH AB ax by y

ab bc ca

OH AC ax cz

a b c

ab bc ca







 





  





  

      

  

 

   

 









 





     

2 2 2

abc

ab bc ca

 

 

1 1

. .

6 6

OABC

V OAOB OC abc

 

     

2 2 2

3 1

ABCD

ABC

S ab bc ca



    

4 4 4 4 4 4

2 2 2 2 2 2 4 4 4

2 2 2

a b b c c a

a b b c c a a b c

  

       

a b c

 

4 2

1 3

max

2 3 6

k k

S  

(9;1;1)

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 111

Facebook: https://www.facebook.com/dongpay

A. B. C. D.

Hướng dẫn giải:

Giá sử .

Khi đó PT mặt phẳng (P) có dạng: .

Ta có:  (1); (2)

(1)  ≥ 

Dấu "=" xảy ra   (P): .

Chọn B.

Câu 22: Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật

ABCD A B C D

   

có điểm A

trùng với gốc tọa độ,

( ;0;0), (0; ;0), (0;0; )

B a D a A b



với

( 0, 0)

a b

 

. Gọi M là trung điểm

của cạnh



. Giả sử

a b

 

, hãy tìm giá trị lớn nhất của thể tích khối tứ diện

A BDM



max

A MBD



 B.

max 1

A MBD





max

A MBD



  D.

max

A MBD





Hướng dẫn giải:

Ta có:

( ; ;0), ( ;0; ), (0; ; ), ( ; ; ) ; ;

C a a B a b D a b C a a b M a a

 

  



 

 

Suy ra:

( ;0; ), (0; ; ), ; ;

A B a b A D a b AM a a

 

 

     

 

 

  

2 2

, ( ; ; ) , .

2 4

A MBD

a b a b

A B A D ab ab a A B A D A M V



   

    

     

   

    

, 0

a b



nên áp dụng BĐT Côsi ta được:

2 2

1 1 1 64

4 3

2 2 4 27

a b a a b a b a b       

Suy ra:

max

A MBD



 .

Chọn A.

  

7 3 3

x y z

  

27 3 3

x y z

  



27 3 3

x y z

   

27 3 3

x y z

A a Ox B b Oy C c Oz

( ;0;0) , (0; ;0) , (0;0; )

  

a b c

( , , 0)



x y z

a b c

  

M P

(9;1;1) ( )



a b c

9 1 1

  

OABC

V abc



abc bc ac ab

  

abc

3 9( )

abc abc abc

3 2

( ) 27.9( ) 243

  

bc ac ab

a b c

9 1 1







 



 



  







x y z

27 3 3

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Hình Học Tọa Độ Oxyz

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 112

Facebook: https://www.facebook.com/dongpay

Câu 23: Trong không gian với hệ tọa độ Oxyz, cho hai điểm









1;5;0 , 3;3;6

A B và đường thẳng



có phương trình tham số

1 2

x t

y t

z t

  





 









. Một điểm M thay đổi trên đường thẳng



sao cho

chu vi tam giác MAB đạt giá trị nhỏ nhất. Tọa đô điểm M và chu vi tam giác ABC là





1;0;2 ;

M P =

2( 11 29)

 B.





1;2;2 ;

M P =

2( 11 29)







1;0;2 ;

M P =

11 29

 D.





1;2;2 ;

M P =

11 29



Hướng dẫn giải:

Gọi P là chu vi của tam giác MAB thì

P AB AM BM

  

Vì AB không đổi nên P nhỏ nhất khi và chỉ khi

AM BM



nhỏ nhất.

Điểm

 

nên





1 2 ;1 ;2

M t t t

   .

2 2 2 2

(3 ) (2 5) (3 6) (2 5)

AM BM t t     

Trong mặt phẳng tọa độ Oxy, ta xét hai vectơ





3 ;2 5

u t



và





3 6;2 5

v t  



Ta có

2 2 2 2

(3 ) (2 5) ; (3 6) (2 5)

u t v t    

 



| | | |

AM BM u v

  

 

và

(6;4 5) | | 2 29

u v u v    

   

Mặt khác, ta luôn có

| | | | | |

u v u v

  

   

Như vậy

2 29

AM BM 

Đẳng thức xảy ra khi và chỉ khi

u v

 

cùng hướng

3 2 5

3 6

2 5

   

 

(1;0;2)



và

min( ) 2 29

AM BM  . Vậy khi M(1;0;2) thì minP =

2( 11 29)



Chọn A.

Bấm Tải xuống để xem toàn bộ.

| 1/112

| | Tải xuống

Preview text:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
TỌA ĐỘ CỦA ĐIỂM VÀ VÉCTƠ TRONG KHÔNG GIAN A - LÝ THUYẾT CHUNG
1. Véc tơ trong không gian * Định nghĩa
Trong không gian, vecto là một đoạn thẳng có định hướng tức là đoạn thẳng có quy định thứ tự của hai đầu
Chú ý: Các định nghĩa về hai vecto bằng nhau, đối nhau và các phép toán trên các vecto trong
không gian được xác định tương tự như trong mặt phẳng.
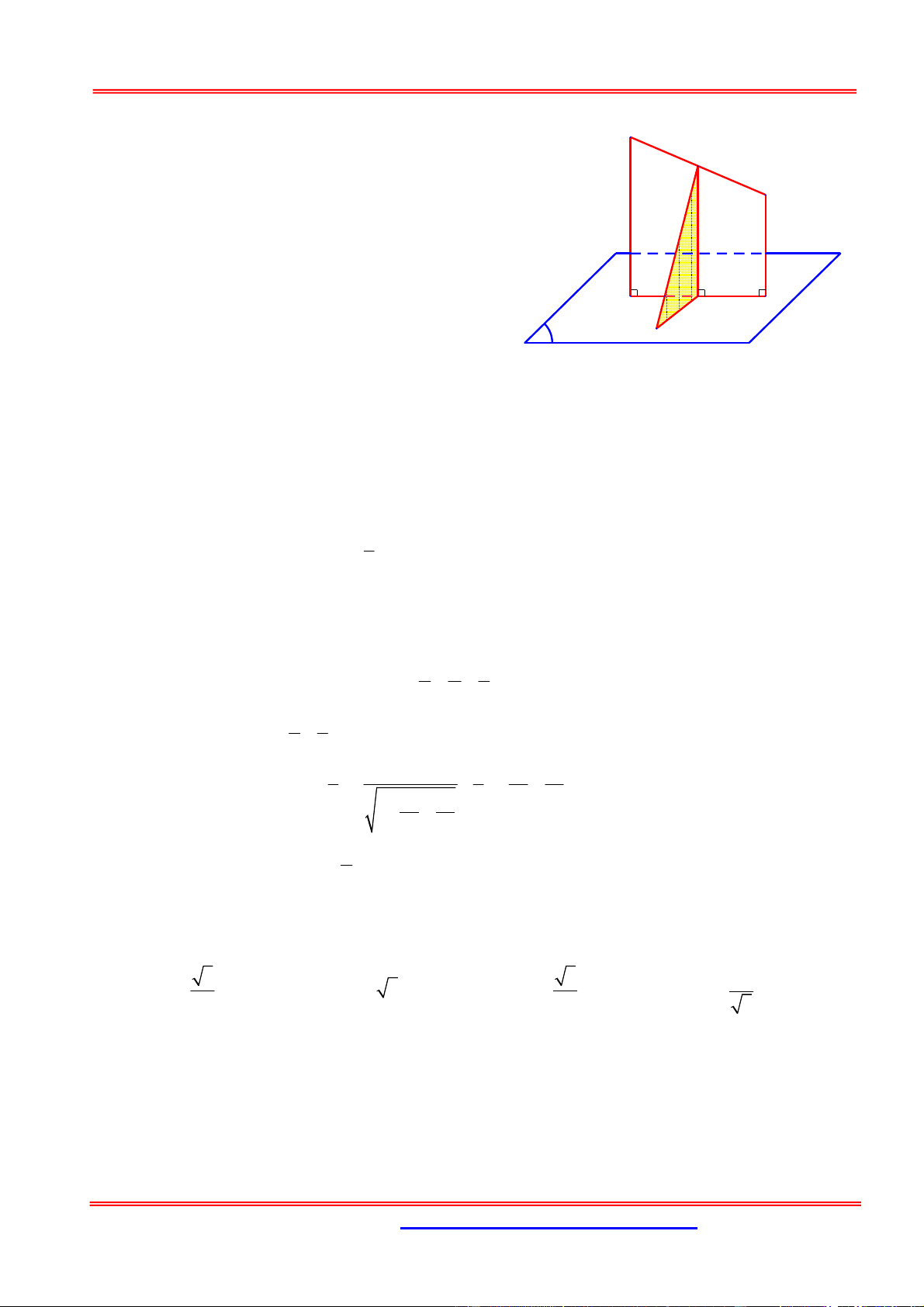
2. Vecto đồng phẳng     D3 c
* Định nghĩa: Ba vecto a, ,
b c khác 0 gọi là đồng
phẳng khi giá của chúng cùng song song với một D2 b mặt phẳng. Chú ý:  a
n vecto khác 0 gọi là đồng phẳng khi giá D1
của chúng cùng song song với một mặt phẳng.
Các giá của các vecto đồng phẳng có thể Δ3 Δ2
là các đường thẳng chéo nhau. 
* Điều kiện để 3 vecto khác 0 đồng phẳng Định lý 1:    Δ    1 P a, ,
b c đồng phẳng  m
 , n   : a  mb  nc
* Phân tích một vecto theo ba vecto không đồng phẳng    
Định lý 2: Cho 3 vecto e , e , e không đồng phẳng. Bất kì một vecto a nào trong không gian cũng 1 2 3
có thể phân tích theo ba vecto đó, nghĩa la có một bộ ba số thực  x , x , x duy nhất 1 2 3     
a  x e  x e  x e 1 1 2 2 3 3    
Chú ý: Cho vecto a, , b c khác 0 :       1. a, ,
b c đồng phẳng nếu có ba số thực , m ,
n p không đồng thời bằng 0 sao cho: ma  nb  pc  0       2. a, ,
b c không đồng phẳng nếu từ ma  nb  pc  0  m  n  p  0 3. Tọa độ của vecto
Trong không gian xét hệ trục Oxyz, có trục Ox vuông góc với trục Oy tại O, và trục Oz vuông góc
với mặt phẳng Oxy tại O. Các vecto đơn vị trên từng trục Ox,Oy, Oz lần lượt là   
i  1;0;0, j  0;1;0 , k  0;0;  1 .     
a) a  a ; a ;a  a  a i  a j  a k 1 2 3  1 2 3    
b) M  x , y , z
 OM  x i  y j  z k M M M  M M M
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
c) Cho A x , y , z  , B  x , y , z ta có: A A A B B B   2 2 2
AB   x  x ; y  y ; z  z và AB   x  x  y  y  z  z B A   B A   B A  . B A B A B A   x  x y  y z  z 
d) M là trung điểm AB thì B A M ; B A ; B A    2 2 2   
e) Cho a  a ; a ; a và b  b ;b ;b ta có: 1 2 3  1 2 3  a  b 1 1   
a  b  a  b 2 2 a  b  3 3  
a  b  a  b ; a  b ;a  b 1 1 2 2 3 3  
k.a  ka ; ka ;ka 1 2 3        .
a b  a . b cos  ;
a b  a b  a b  a b 1 1 2 2 3 3  2 2 2
a  a  a  a 1 2 3  
a b  a b  a b     cos  cos  ; a b 1 1 2 2 3 3 
(với a  0,b  0 ) 2 2 2 2 2 2
a  a  a . b  b  b 1 2 3 1 2 3    
a và b vuông góc:  .
a b  0  a b  a b  a b  0 1 1 2 2 3 3 a  kb   1 1   
a và b cùng phương:  k
  R : a  kb  a  kb 2 2 a  kb  3 3
4. Tích có hướng và ứng dụng  
Tích có hướng của a  a ; a ; a và b  b ;b ;b là: 1 2 3  1 2 3     a a a a a a  2 3 3 1 1 2  , a b   ; ;
  a b  a b ; a b  a b ; a b  a b 2 3 3 2 3 1 1 3 1 2 2 1    b b b b b b 2 3 3 1 1 2   a. Tính chất:      
a,b  a, a,b  b          
a,b  a . b sin   a,b     
a và b cùng phương: a,b  0         a, ,
b c đồng phẳng   , a b .c  0  
b. Các ứng dụng tích có hướng 1  
Diện tích tam giác: S   AB, AC ABC 2  
1   
Thể tích tứ diện V 
 AB, AC.AD ABCD 6  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
  
Thể tích khối hộp: V
  AB, AD .AA'
ABCD. A' B 'C ' D '  
5. Một số kiến thức khác  
a) Nếu M chia đoạn AB theo tỉ số k MA  k MB thì ta có: x  kx y  ky z  kz A B x  ; A B y  ; A B z  với k  1 M 1 M  k 1 M  k 1 k
x  x  x
y  y  y
z  z  z
b) G là trọng tâm tam giác A B C ABC  x  ; A B C y  ; A B C z  G 3 G 3 G 3
    
G là trọng tâm tứ diện ABCD  GA  GB  GC  GD  0
B – BÀI TẬP TRẮC NGHIỆM Câu 1:
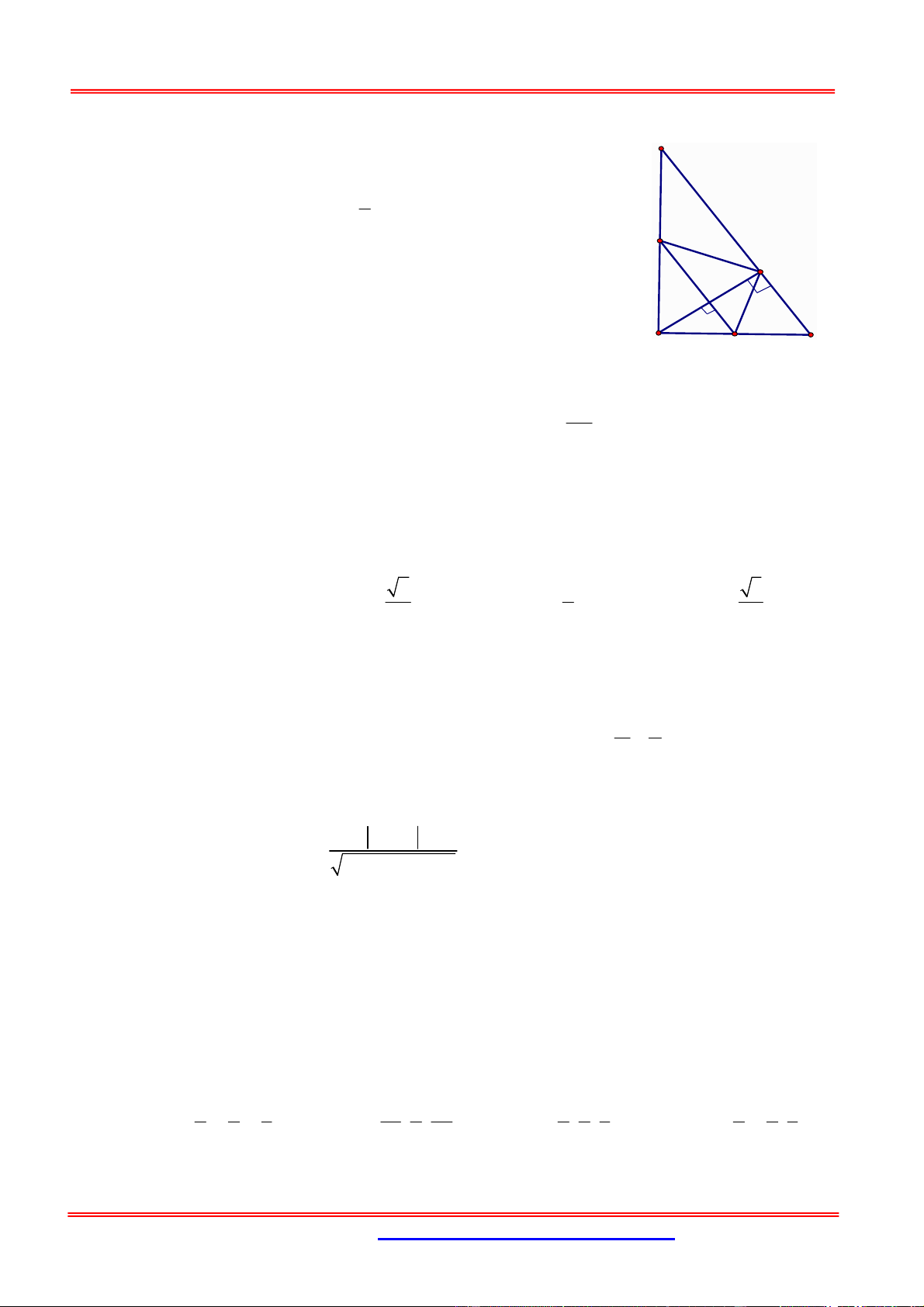
Cho 4 điểm S 1, 2, 3; A2, 2,3; B 1,3,3;C 1, 2, 4. SABC là: A. Tứ diện. B. Hình chóp đều. C. Tứ diện đều. D. Hình thang vuông Hướng dẫn giải:    AB   1
 ;1; 0; BC  0;1;  1 ; AC   1  ;0;  1
 AB  BC  CA  2  ABC là tam giác đều   
SA  1;0;0; SB  0;1;0; SC  0;0; 
1  SA  SB  SC  1 1 0 0 D S ,
A SB, SC   0 1 0  1  0 0 0 1
   
Hay ta có thể tính S ; A SB SC  0  
    S ,
A SB, SC không đồng phẳng.
 SABC là hình chóp đều, đỉnh S. Chọn B. Câu 2:
Cho bốn điểm S 1, 2, 3; A2, 2,3; B 1,3,3;C 1, 2, 4.Gọi M , N, P lần lượt là trung điểm
của BC,CA và AB. Khi đó SMNP là: A. Hình chóp. B. Hình chóp đều. C. Tứ diện đều. D. Tam diện vuông Hướng dẫn giải: 2
Tam giác: ABC có AB  BC  CA  2  MN  NP  PM  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz   
SA  1;0;0; SB  0;1;0; SC  0;0  ;1 S    S .
A SB  0  SA  SB
Tương tự SA  SC, SB  SC
Các tam giác vuông SAB, SBC, SCA vuông
tại S, có các trung tuyến: AB 2
SP  SM  SN  
 MN  NP  PM 2 2 A C
Ta có: SP   SAB; SM  SBC ; SN   SCA N
  
 SP, SM , SN không đồng phẳng P M
 SMNP là tứ diện đều. B Chọn C. Câu 3:
Cho bốn điểm S 1, 2, 3; A2, 2,3; B 1,3,3;C 1, 2, 4.Xác định tọa độ trọng tâm G của hình chóp SABC.  5 13   7 9   5 9 13  A. 5,9,13 . B. , 3,   . C. 1, ,   . D. , ,    3 3   4 4   4 4 4  Hướng dẫn giải:
   
    
Ta có GS  GA  GB  GC  4OG  OA  OB  OC  OS  1 5 x  2 11  1   4 4   1 9
 G  y  2  3  2  2  4 4   1 13 z  3  3  4  3    4 4 Chọn D.     Câu 4:
Cho 3 vectơ a  1,1, 2  ;b  2, 1  , 2;c   2  , 3, 2
 . Xác định vec tơ d thỏa mãn       . a d  4; . b d  5; . c d  7.  3 5   5  A. 3, 6,5 . B.  3  , 6, 5 . C. , 6,   . D. 3, 6,   .  2 2   2  Hướng dẫn giải:    . a d  4
x  y  2z  4   1      .
b d  5  2x  y  2z  5 2    . c d  7 2
 x  3y  2z  7 3     
1  2 : 3x  9  x  3 và 2  3 : 2 y  12  y  6 1 1 5   5    1 : z 
 x  y  4  3  6  4   d  3;6;   2 2 2  2  Chọn D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Câu 5:
Trong không gian Oxyz, cho điểm A2;0;2, B 3;1; 4  ,C  2
 ; 2;0 . Điểm D trong mặt
phẳng (Oyz) có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách
từ D đến mặt phẳng (Oxy) bằng 1 có thể là: A. D 0; 3  ;   1 B. D 0;2;  1 
C. D 0;1;  1
D. D 0;3;  1 Hướng dẫn giải:
Do D  Oyz   D 0; ;
b c với c  0 c   1 loai
Theo giả thiết: d D,Oxy  1  c  1       D 0; ; b   1 c  1     Ta có AB  1; 1  ; 2  , AC   4
 ; 2; 2, AD   2  ; ; b  1  
  
Suy ra  AB, AC  2;6; 2   
  AB, AC .AD  6b  6    
1    b  3
Cũng theo giả thiết, ta có: V 
 AB, AC.AD  b 1  2  ABCD    6 b  1  Chọn D. Câu 6:
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A1; 2;0 , B 3; 4 
;1 , D 1;3; 2 . Tìm
tọa độ điểm C sao cho ABCD là hình thang có hai cạnh đáy AB , CD và có góc C bằng 45 . 
A. C 5;9;5 .
B. C 1;5;3 .
C. C 3;1  ;1 .
D. C 3;7;4 . Hướng dẫn giải: Chọn D. 
Cách 1. AB  (2; 2;1) .
x  1 2t 
Đường thẳng CD có phương trình là CD : y  3  2t . z  2  t    Suy ra C  1
  2t;3  2t; 2  t  ; CB  (4  2t;1 2t;1 t), CD  ( 2  t; 2  t; t) .  (4  2t)( 2
 t)  (1 2t)(2t)  ( 1   t)( t  ) Ta có cos BCD  2 2 2 2 2 2
(4  2t)  (1 2t)  ( 1   t) (2t)  ( 2  t)  ( t  ) (4  2t)( 2
 t)  (1 2t)(2t)  ( 1   t)(t) 2 Hay  (1). 2 2 2 2 2 2 2
(4  2t)  (1 2t)  (1 t) ( 2  t)  ( 2  t)  ( t  )
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Lần lượt thay t bằng 3;1; 1; 2 (tham số t tương ứng với toạ độ điểm C ở các phương án A,
B, C, D), ta thấy t  2 thoả (1). Cách 2.  
Ta có AB  (2; 2;1), AD  ( 2  ;1; 2) . Suy ra A B  
AB  CD và AB  AD . Theo giả thiết, suy  
ra DC  2 AB . Kí hiệu C(a; ; b c) , ta có  
DC  (a 1;b  3; c  2) , 2AB  (4; 4; 2) . Từ
đó C(3; 7; 4) . D C Câu 7:
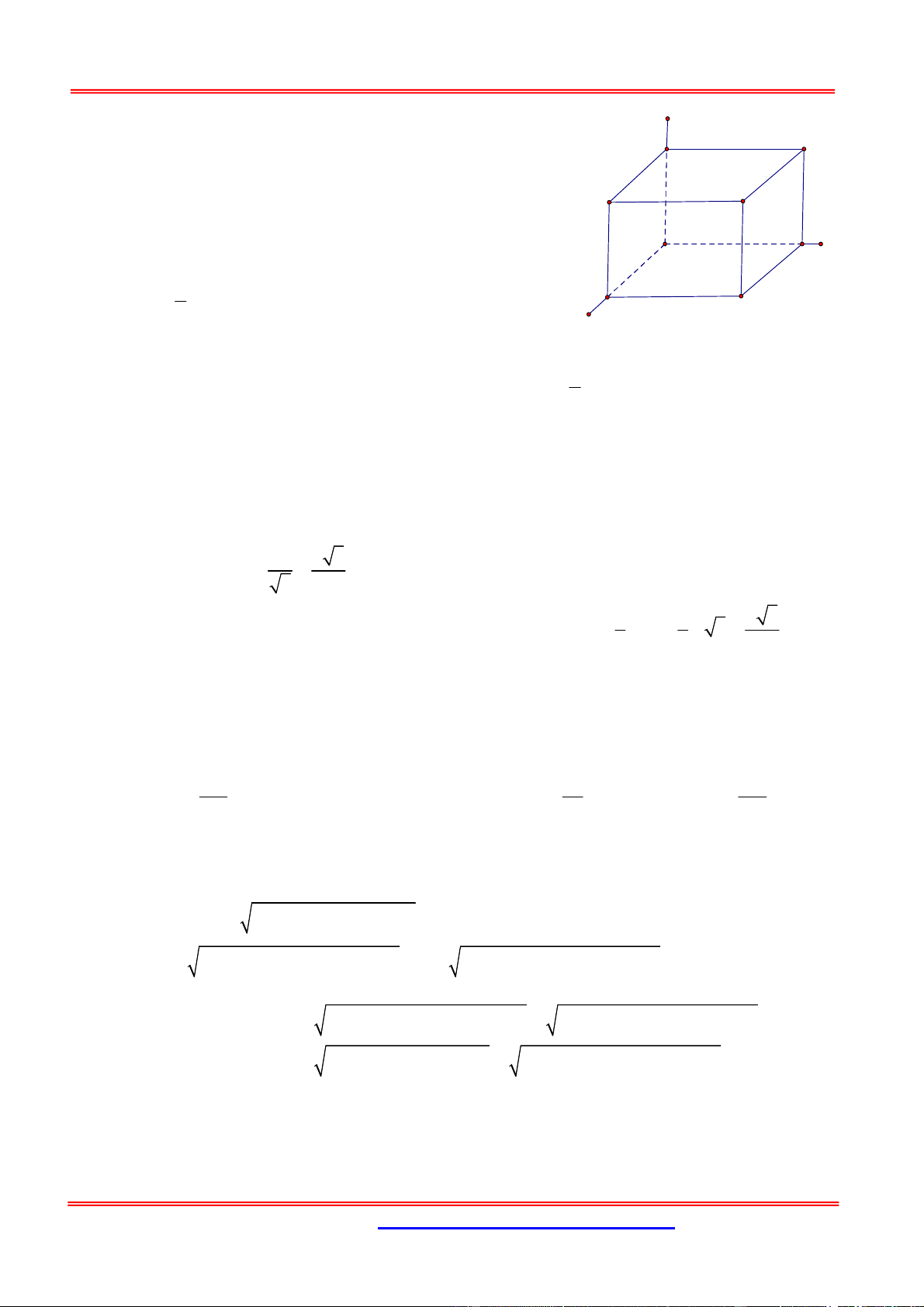
Trong không gian với hệ tọa độ Oxy , cho hình hộp chữ nhật ABC . D AB C  D   có A trùng
với gốc tọa độ O , các đỉnh B( ; m 0; 0) , D(0; ; m 0) , A (
 0; 0; n) với m, n  0 và m  n  4 . Gọi
M là trung điểm của cạnh CC . Khi đó thể tích tứ diện BDA M 
đạt giá trị lớn nhất bằng 245 9 64 75 A. . B. . C. . D. . 108 4 27 32 z Hướng dẫn giải: A' B'  n 
Tọa độ điểm C( ; m ; m 0), C (  ; m ;
m ; n), M  ; m ; m D'  C'  2  n     n  AO B BA   ;
m 0; n, BD   ; m ;
m 0 , BM   0; ; m m  x m  2  D C   2 y
BA , BD  m ; n m ; n m  2
1    m n V 
BA , BD.BM  BDA M  6 4 3
 m  m  2n  512 256 Ta có 2 . m . m (2n)      m n   3  27 27 64  V  BDAM 27 Chọn C. Câu 8:
Cho ba điểm A3;1;0, B 0; 1  ;0,C 0;0; 6
  . Nếu tam giác AB C
  thỏa mãn hệ thức
   
AA  B B   C C
  0 thì có tọa độ trọng tâm là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz A. 1;0; 2  . B. 2;3;0. C. 3; 2  ;0. D. 3; 2   ;1 . Hướng dẫn giải: Chọn A
* Cách diễn đạt thứ nhất:
Gọi G, G’ theo thứ tự lần lượt là trọng tâm tam giác ABC, A’B’C’. Với mọi điểm T trong không gian có:
            
1 : A' A  B ' B  C 'C  0  TATA'  TB TB'  TC TC '  0
     
 TA  TB  TC  TA '  TB '  TC ' 2
   
   
Hệ thức (2) chứng tỏ. Nếu T  G tức là TA  TB  TC  0 thì ta cũng có TA '  TB '  TC '  0
hay T  G ' hay (1) là hệ thức cần và đủ để hai tam giác ABC, A’B’C’ có cùng trọng tâm.
 3  0  0 11 0 0  0  6 
Ta có tọa độ của G là: G  ; ;  1;0; 2      3 3 3 
Đó cũng là tọa độ trọng tâm G’ của A  ' B 'C '
* Cách diễn đạt thứ hai:
   
Ta có: AA '  BB '  CC '  0 (1)
  
  
   
  A'G ' G 'G  GA  B'G ' G 'G  GB  C 'G '  G 'G  GC  0
  
    
 GA GB  GC   A'G '  B 'G '  C 'G '  3G 'G  0 (2)
Nếu G, G’ theo thứ tự lần lượt là trọng tâm tam giác ABC, A’B’C’ nghĩa là
       
GA  GB  GC  A 'G '  B 'G '  C 'G ' thì 2  G 'G  0  G '  G
Tóm lại (1) là hệ thức cần và đủ để hai tam giác ABC, A’B’C’ có cùng trọng tâm.
 3  0  0 11 0 0  0  6 
Ta có tọa độ của G là: G  ; ;  1;0; 2   
. Đó cũng là tọa độ trọng  3 3 3  tâm G’ của A  ' B 'C ' Câu 9:
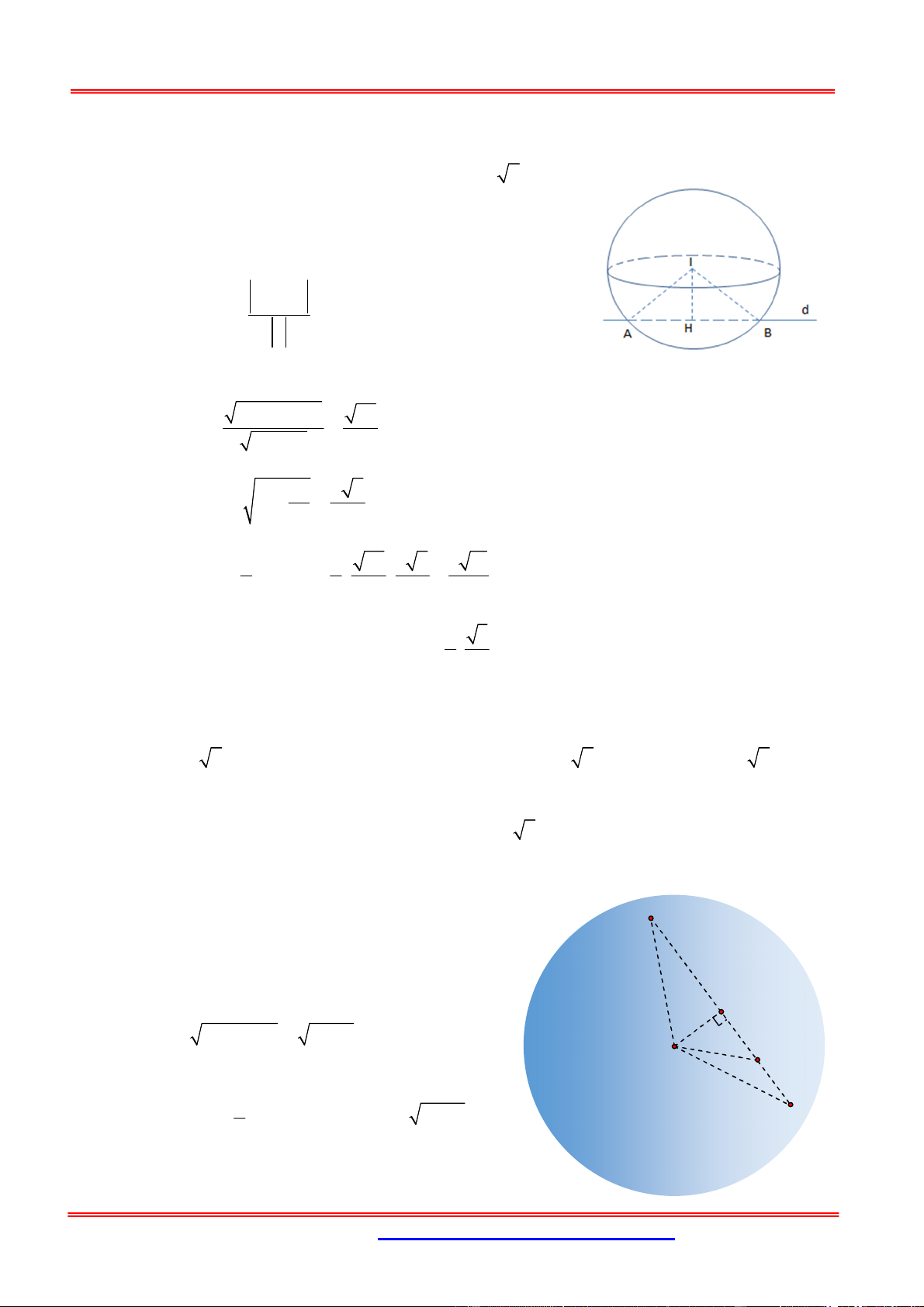
Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm M 3;0;0 , N  , m ,
n 0, P 0;0; p .  Biết 0
MN  13, MON  60 , thể tích tứ diện OMNP bằng 3. Giá trị của biểu thức 2 2
A  m  2n  p bằng A. 29. B. 27. C. 28. D. 30. Hướng dẫn giải:    
OM  3;0;0,ON   ; m ;
n 0  OM .ON  3m
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz       OM .ON 1 m 1 0
OM .ON  OM . ON cos 60       2 2 OM . ON 2 2 m  n
MN  m  2 2 3  n  13
Suy ra m  2; n  2 3
   1
OM , ON  .OP  6 3 p  V 
6 3 p  3  p   3   6
Vậy A  2  2.12  3  29.
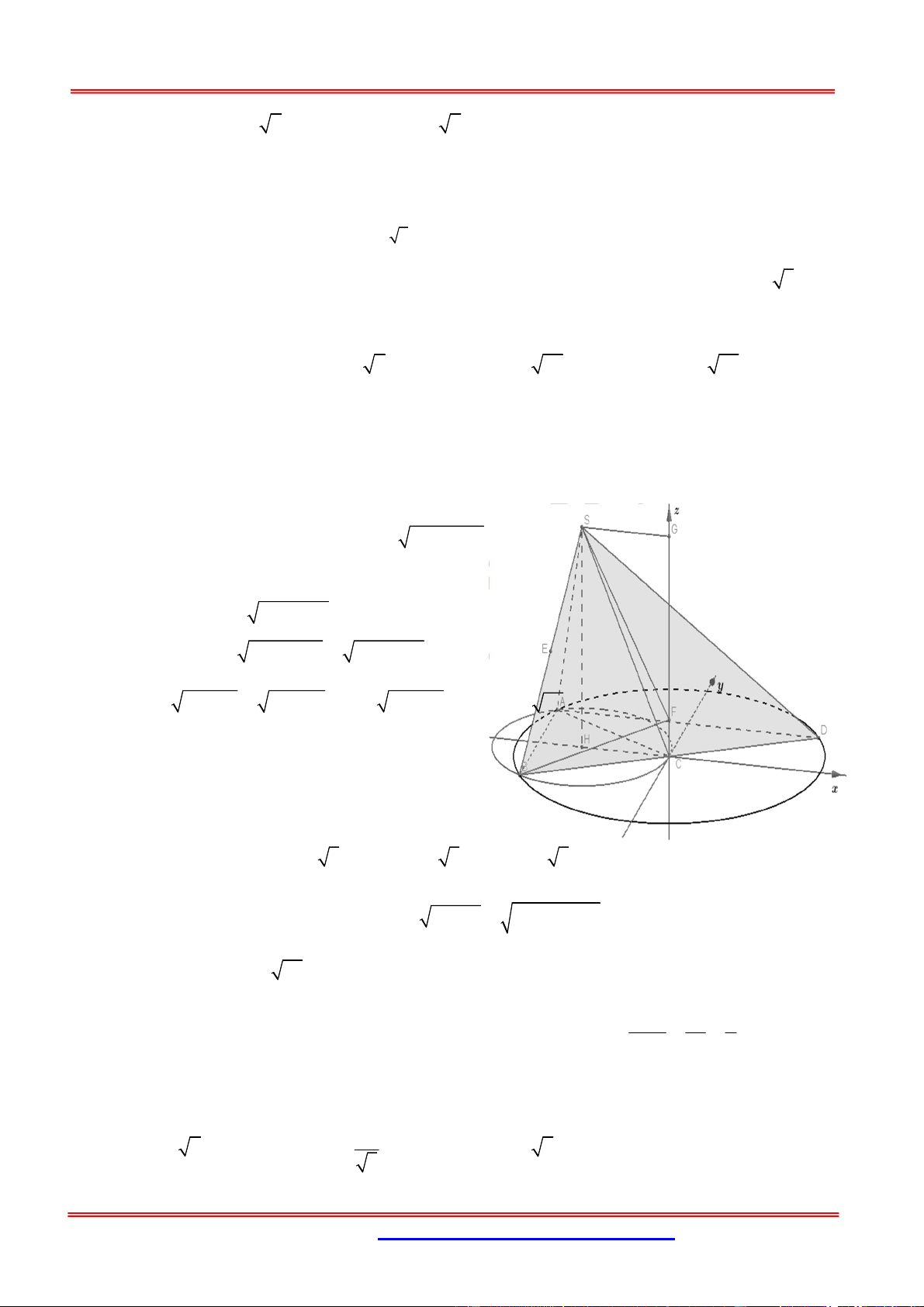
Câu 10: Cho hình chóp S.ABCD biết A 2  ; 2; 6, B  3  ;1;8 ,C  1
 ; 0; 7, D 1;2;3 . Gọi H là trung 27
điểm của CD, SH   ABCD . Để khối chóp S.ABCD có thể tích bằng (đvtt) thì có hai 2
điểm S , S thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm I của S S 1 2 1 2 A. I 0; 1  ; 3 . B. I 1;0;3
C. I 0;1;3 . D. I  1  ; 0; 3  . Hướng dẫn giải:   1   3 3
Ta có AB  1; 1
 ; 2, AC  1; 2   ;1  S 
 AB, AC   ABC 2   2     DC  2; 2
 ; 4, AB   1
 ; 1; 2  DC  2.AB  ABCD là hình thang và 9 3 S  3S  ABCD ABC 2 1 Vì V  SH.S  SH  3 3 S .ABCD 3 ABCD
Lại có H là trung điểm của CD  H 0;1;5     Gọi S  ; a ;
b c  SH   ;1 a  ;
b 5  c  SH  k  AB, AC  k 3;3;3  3k;3k;3k    Suy ra 2 2 2
3 3  9k  9k  9k  k  1  
+) Với k  1  SH  3;3;3  S  3  ; 2  ; 2 
+) Với k  1  SH   3
 ; 3; 3  S 3; 4;8 Suy ra I 0;1;3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 11: Trong không gian với hệ tọa độ Oxyz , cho hình vuông ABCD , B(3;0;8) , D( 5  ; 4  ; 0) . Biết  
đỉnh A thuộc mặt phẳng ( Oxy ) và có tọa độ là những số nguyên, khi đó CA  CB bằng: A. 5 10. B. 6 10. C. 10 6. D. 10 5. Hướng dẫn giải:
Ta có trung điểm BD là I ( 1  ; 2
 ; 4) , BD  12 và điểm A thuộc mặt phẳng (Oxy) nên ( A a; ; b 0) . 2 2 AB  AD 2 2 2 2 2  
(a  3)  b  8  (a  5)  (b  4)
ABCD là hình vuông  2   1   2  2 2 2 AI   BD 
(a 1)  (b  2)  4  36    2   17 a  b   4  2a a  1   5  17 14      hoặc 
 A(1; 2; 0) hoặc A ; ;0 2 2  
(a  1)  (6  2a)  20  b  2  1  4  5 5  b     5 (loại). Với (
A 1; 2; 0)  C( 3  ; 6  ;8) .
Câu 12: Trong không gian với hệ toạ độ Oxyz , cho 4 điểm ( A 2; 4; 1
 ) , B(1;4;1) , C(2;4;3) D(2; 2; 1
 ) . Biết M  ;x y; z , để 2 2 2 2  
MA  MB  MC  MD đạt giá trị nhỏ nhất thì x y z bằng A. 7. B. 8. C. 9. D. 6. Hướng dẫn giải:  7 14 
Gọi G là trọng tâm của ABCD ta có: G  ; ; 0  .  3 3  Ta có: 2 2 2 2 2 2 2 2 2
MA  MB  MC  MD  4MG  GA  GB  GC  GD  7 14   2 2 2 2
GA  GB  GC  GD . Dấu bằng xảy ra khi M  G ;
; 0  x  y  z    7 .  3 3 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 10
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
PHƯƠNG TRÌNH MẶT PHẲNG NÂNG CAO A - LÝ THUYẾT CHUNG 1. Định nghĩa
Trong không gian Oxyz phương trình dạng Ax  By  Cz  D  0 với 2 2 2
A  B  C  0 được gọi là
phương trình tổng quát của mặt phẳng.
Phương trình mặt phẳng  P : Ax  By  Cz  D  0 với 2 2 2
A  B  C  0 có vec tơ pháp tuyến là  n   ; A ; B C .   
Mặt phẳng  P đi qua điểm M x ; y ; z
và nhận vecto n   ; A ;
B C , n  0 làm vecto pháp tuyến 0  0 0 0 
dạng  P : A x  x  B y  y  C z  z  0. 0   0   0   
Nếu  P có cặp vecto a  a ; a ; a ;b  b ;b ;b không cùng phương, có giá song song hoặc 1 2 3   1 2 3    
nằm trên  P. Thì vecto pháp tuyến của  P được xác định n  a,b .  
2. Các trường hợp riêng của mặt phẳng
Trong không gian Oxyz cho mp  :Ax  By  Cz  D  0, với 2 2 2
A  B  C  0. Khi đó:
D  0 khi và chỉ khi   đi qua gốc tọa độ.
A  0, B  0, C  0, D  0 khi và chỉ khi   song song trục Ox.   Oxy.
A  0, B  0, C  0, D  0 khi và chỉ khi song song mặt phẳng D D D x y c a   , b   , c   .
  :    1 ,
A B, C, D  0. Đặt A B C Khi đó: a b z
3. Vị trí tương đối của hai mặt phẳng
Trong không gian Oxyz cho   : Ax  By  Cz  D  0 và  ' : A' x  B ' y  C ' z  D '  0
 AB '  A' B    '  cắt
 BC '  B 'C
CB'  C ' B 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 11
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
 AB '  A' B    '  //
 BC '  B 'C
va AD '  A' D
CB'  C 'B 
 AB '  A ' B      '
BC '  B 'C 
 CB'  C 'B 
 AD '  A' D   
Đặt biệt:     '  n .n  0  . A A ' .
B B ' C.C '  0 1 2
4. Góc giữa hai mặt phẳng
Gọi  là góc giữa hai mặt phẳng  0 0 0    90 
P : Ax  By  Cz  D  0 và Q : A' x  B ' y  C ' z  D'  0     n .n     A A B B C C n n     P Q  P Q . ' . ' . ' cos = cos , 2 2 2 2 2 2 n . n
A  B  C . A '  B '  C ' P Q
B – BÀI TẬP TRẮC NGHIỆM  y  0 Câu 1:
Trong không gian với hệ tọa độ 
Oxyz cho điểm M 1;0;0 và
2x  y  2z  2  0  N 0;0;  1
 , mặt phẳng  P qua điểm M , N và tạo với mặt phẳng Q : x  y  4  0 một góc bằng O
45 . Phương trình mặt phẳng  P là  y  0  y  0 A.  . B.  .
2x  y  2z  2  0 
2x  y  2z  2  0 
2x  y  2z  2  0
2x  2z  2  0 C.  . D. . 
2x  y  2z  2  0 
2x  2z  2  0  Hướng dẫn giải:  
Gọi vectơ pháp tuyến của mp  P và Q lần lượt là n a b c  2 2 2
a  b  c  0 , n P  ; ;  Q
P qua M 1;0;0  P : a x  
1  by  cz  0
P qua N 0;0;  1
  a  c  0   a  b 1 a  0
P hợp với Q góc O
45  cos n ,n cos P Q  O  45     2 2 2 2 2 a  2    b a b
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 12
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Với a  0  c  0 chọn b  1 phương trình  P : y  0
Với a  2b chọn b  1  a  2 phương trình mặt phẳng  P  : 2x  y  2z  2  0 . Chọn A. Câu 2:
Trong không gian với hệ toạ độ Oxyz ,cho  P : x  4 y  2z  6  0 , Q : x  2 y  4z  6  0 .
Lập phương trình mặt phẳng   chứa giao tuyến của  P ,Q và cắt các trục tọa độ tại các điểm ,
A B, C sao cho hình chóp O.ABC là hình chóp đều.
A. x  y  z  6  0 .
B. x  y  z  6  0 .
C. x  y  z  6  0 .
D. x  y  z  3  0 . Hướng dẫn giải:
Chọn M 6;0;0, N 2; 2; 2 thuộc giao tuyến của  P ,Q Gọi A ;
a 0; 0, B 0; ;
b 0, C 0;0;c lần lượt là giao điểm của   với các trục Ox, Oy, Oz x y z    :    1a, , b c  0 a b c  6 1    a
  chứa M , N  2 2 2     1  a b c
Hình chóp O.ABC là hình chóp đều  OA  OB  OC  a  b  c
Vây phương trình x  y  z  6  0 . Chọn B. Câu 3:
Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng: x  t x  2 y 1 z 1   :   ,  : 2 2 2
 y  2  t và mặt cầu (S ) : x  y  z  2x  2 y  6z  5  0 1 1 2 3 2 z  1 2t 
Viết phương trình mặt phẳng ( ) song song với hai đường thẳng  ,  và cắt mặt cầu (S) 1 2 2 365
theo giao tuyến là đường tròn (C) có chu vi bằng . 5
A. x  5y  3z  4  0; x  5y  3z 10  0
B. x  5y  3z 10  0
C. x  5 y  3z  3  511  0; x  5 y  3z  3  511  0
D. x  5y  3z  4  0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 13
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Chọn B. Hướng dẫn giải: 
+  qua M (2; 1;1) và có vectơ chỉ phương u  (1; 2; 3  ) . 1 1 1 
 qua M (0; 2;1) và có vectơ chỉ phương u  (1; 1; 2) . 2 2 2  
+ Mặt phẳng () song song với  ,  nên có vectơ pháp tuyến: u ,u   (1; 5; 3  ) 1 2 1 2  
 Phương trình mặt phẳng () có dạng: x  5y  3z  D  0
+ Mặt cầu (S) có tâm I(1; 1
 ;3) và bán kính R  4 . 2 365 365
Gọi r là bán kính đường tròn (C), ta có: 2 r   r  5 5 35 D  3 35 D  4
Khi đó: d  I , ( ) 2 2  R  r      5 35 5 D  10 
+ Phương trình mặt phẳng () : x  5y  3z  4  0 (1) hay x  5y  3z 10  0 (2) .
Vì  / /( ),  / /( ) nên M1 và M2 không thuộc ()  loại (1). 1 2
Vậy phương trình mặt phẳng () cần tìm là: x  5y  3z 10  0 . Chọn B. Câu 4:
Cho tứ giác ABCD có A0;1;  
1 ; B 1;1; 2;C 1;1;0; D 0;0 
;1 . Viết phương trình của
mặt phẳng  P qua ,
A B và chia tứ diện thành hai khối ABCE và ABDE có tỉ số thể tích bằng 3.
A. 15x  4 y  5z 1  0 .
B. 15x  4 y  5z 1  0 .
C. 15x  4 y  5z 1  0 .
D. 15x  4 y  5z 1  0 Hướng dẫn giải:
P cắt cạnh CD tại E, E chia đoạn CD theoo tỷ số 3  A  x  3x 1 3.0 1 C D x    F  4 4 4   y  3y 1 3.0 1 N C D  E y    4 4 4   z  3z 0  3.1 3 C D z      4 4 4 B D   E  1 5 7  1
AB  1; 0;3; AE  ;  ;    1;5;7  4 4 4  4 C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 14
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Vecto pháp tuyến của   
P : n  AB, AE  15; 4  ; 5
    P :  x  015   y   1  4
    z   1 5  0  
 15x  4 y  5z 1  0 Chọn A.  y  0 Câu 5:
Trong không gian với hệ tọa độ 
Oxyz cho điểm M 1;0;0 và
2x  y  2z  2  0  N 0;0; 
1 , mặt phẳng  P qua điểm M , N và tạo với mặt phẳng Q : x  y  4  0 một góc bằng O
45 . Phương trình mặt phẳng  P là  y  0  y  0 A.  . B.  .
2x  y  2z  2  0 
2x  y  2z  2  0 
2x  y  2z  2  0
2x  2z  2  0 C.  . D. . 
2x  y  2z  2  0 
2x  2z  2  0  Hướng dẫn giải:  
Gọi vectơ pháp tuyến của mp  P và Q lần lượt là n a;b;c  2 2 2
a  b  c  0 , n P  Q
P qua M 1;0;0  P : a x  
1  by  cz  0
P qua N 0;0; 
1  a  c  0   a  b 1 a  0
P hợp với Q góc O
45  cos n , n  cos    P Q  O 45  2 2 2  2 2 a  2  b a b 
Với a  0  c  0 chọn b  1 phương trình  P : y  0
Với a  2b chọn b  1  a  2 phương trình mặt phẳng  P : 2x  y  2z  2  0 . Chọn A. Câu 6:
Cho tứ giác ABCD có A0;1;  
1 ; B 1;1; 2;C 1;1;0; D 0;0 
;1 . Viết phương trình tổng
quát của mặt phẳng Q song song với mặt phẳng  BCD và chia tứ diện thành hai khối 1
AMNF và MNFBCD có tỉ số thể tích bằng . 27
A. 3x  3z  4  0 .
B. y  z 1  0 .
C. y  z  4  0 .
D. 4x  3z  4  0 Hướng dẫn giải: 3  AM  1
Tỷ số thể tích hai khối AMNF và MNFBCD :     AB  27 AM 1  
 M chia cạnh AB theo tỉ số 2 AB 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 15
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  1 2.0 1 x    3 3   1 2.1    E  y   1 ; BC  2  0;1 
;1 ; BD   1;1  ;1 3   2  2  1 x   0  3 
Vecto pháp tuyến của Q : n  0;1;   1  1 
 M  Q  Q : x  0     y  
1 1  z  0  1  0  3 
  P : y  z 1  0 Chọn B. Câu 7:
Từ gốc O vẽ OH vuông góc với mặt phẳng  P ,OH  p ; gọi ,  , lần lượt là các góc
tạo bởi vec tơ pháp tuyến của  P với ba trục Ox,Oy,O .
z Phương trình của  P là:
A. x cos  y cos   z cos   p  0 .
B. x sin  y sin   z sin   p  0 .
C. x cos  y cos   z cos   p  0 .
D. x sin  y sin   z sin   p  0 Hướng dẫn giải: 
H  p cos , p cos  , c cos   OH   p cos, p cos  , c cos  
Gọi: M  x, y, z   P  HM   x  p cos , y  p cos  , z  c cos    OH  HM
  x  p cos  p cos   y  p cos   p cos    z  c cos  p cos
  P : x cos  y cos   z cos  p  0 Chọn A. Câu 8:
Viết phương trình tổng quát của mặt phẳng  P cắt hai trục y 'Oy và z 'Oz tại A0, 1
 , 0 , B 0, 0, 
1 và tạo với mặt phẳng  yOz một góc 0 45 .
A. 2x  y  z 1  0 .
B. 2x  y  z 1  0 .
C. 2 x  y  z 1  0; 2 x  y  z 1  0 .
D. 2 x  y  z 1  0; 2 x  y  z 1  0 Hướng dẫn giải:
Gọi C a, 0,0 là giao điểm của  P và trục x 'Ox    BA  0, 1  ,  
1 ; BC  a, 0,   1   
Vec tơ pháp tuyến của  P là n  B ,
A BC  1, a, a   
Vec tơ pháp tuyến của  yOz là: e  1, 0, 0 1   1 2 1
Gọi  là góc tạo bởi  P và  yOz  0 2  os c 45  
 4a  2  a   2 2 1 2a 2
Vậy có hai mặt phẳng  P :  2x  y  z  1  2x  y  z 1  0; 2x  y  z 1  0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 16
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Chọn D. Câu 9:
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình: 2 2 2
x  y  z  2x  6 y  4z  2  0 . Viết phương trình mặt phẳng (P) song song với giá của 
véc tơ v  (1;6;2) , vuông góc với mặt phẳng ( ) : x  4 y  z 11  0 và tiếp xúc với (S).
2x  y  2z  3  0
2x  y  2z  3  0 A.  . B.  .
2x  y  2z  21  0 
2x  y  2z  21  0 
2x  y  z  3  0
2x  y  z  13  0 C.  . D. 
2x  y  z  1  0 
2x  y  z  1  0  Hướng dẫn giải:
Vậy: (P): 2x  y  2z  3  0 hoặc (P): 2x  y  2z  21  0 
(S) có tâm I(1; –3; 2) và bán kính R = 4. VTPT của ( ) là n  (1; 4;1) .   
 VTPT của (P) là: n  n,v   (2; 1; 2)  PT của (P) có dạng: 2x  y  2z  m  0. P m  21 
Vì (P) tiếp xúc với (S) nên d (I ,(P))  4  . m  3 
Vậy: (P): 2x  y  2z  3  0 hoặc (P): 2x  y  2z  21  0 . Chọn B. 2 2 2 Câu 10: Cho điểm (
A 0;8; 2) và mặt cầu (S) có phương trình (S) : (x  5)  (y  3)  (z  7)  72 và điểm B(9; 7
 ; 23) . Viết phương trình mặt phẳng (P) qua Atiếp xúc với (S) sao cho khoảng 
cách từ B đến (P) là lớn nhất. Giả sử n  (1; ;
m n) là một vectơ pháp tuyến của (P) . Lúc đó A. . m n  2. B. . m n  2  . C. . m n  4. D. . m n  4  . Hướng dẫn giải: Chọn D.
Mặt phẳng (P) qua A có dạng a(x  0)  b( y  8)  c(z  2)  0  ax  by  cz  8b  2c  0 . Điều kiện tiếp xúc:
5a  3b  7c  8b  2c
5a 11b  5c
d (I; (P))  6 2   6 2   6 2 . (*) 2 2 2 2 2 2
a  b  c
a  b  c
9a  7b  23c  8b  2c
9a 15b  21c Mà d ( ; B (P))   2 2 2 2 2 2
a  b  c
a  b  c
5a 11b  5c  4(a  b  4c)   2 2 2
a  b  c 2 2 2 2 2 2
5a 11b  5c
a  b  4c
1  (1)  4 . a  b  c   4  6 2  4  18 2 . 2 2 2 2 2 2 2 2 2
a  b  c
a  b  c
a  b  c
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 17
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz a b c Dấu bằng xảy ra khi  
. Chọn a  1;b  1; c  4 thỏa mãn (*). 1 1  4
Khi đó (P) : x  y  4z  0 . Suy ra m  1
 ; n  4 . Suy ra: . m n  4  .
Câu 11: Cho mặt phẳng  P đi qua hai điểm A3, 0, 4, B  3
 , 0, 4 và hợp với mặt phẳng  xOy một góc 0
30 và cắt y 'Oy tại C. Viết phương trình tổng quát mặt phẳng  P.
A. y  3z  4 3  0 .
B. y  3z  4 3  0 .
C. y  3z  4 3  0 .
D. x  y  3z  4 3  0 Hướng dẫn giải:  
C 0, c, 0; AC   3  , , c 4
 ; AB  6, 0, 0   
Vec tơ pháp tuyến của  P : n   AC, AB  60, 4, c   
Vec tơ pháp tuyến của  xOz : e  0, 0,1 3   c 3  0 2 cos 30  
 c  48  c  4 
3  n  6 0, 4, 4 3 2   2 16  c
  P :  x  3.0   y  0 4   z  4 4 
3   0  y  z 3  4 3  0 Chọn C. x  t x  1 1  
Câu 12: Trong không gian với hệ tọa độ Oxyz , cho ba đường thẳng d :  y  0 , d :  y  t , 1 2 2 z  0   z  0  x  1 
d : y  0 . Viết phương trình mặt phẳng đi qua điểm H 3;2 
;1 và cắt ba đường thẳng d , 3 1 z  t  3
d , d lần lượt tại A , B , C sao cho H là trực tâm tam giác ABC . 2 3
A. 2x  2 y  z 11  0 .
B. x  y  z  6  0 .
C. 2x  2 y  z  9  0 .
D. 3x  2 y  z 14  0 . Hướng dẫn giải: Chọn A.
Gọi Aa; 0; 0 , B 1; ;
b 0 , C 1;0;c .    
AB  1 a;b;0, BC  0;  ;
b c, CH  2;2;1 c, AH  3  a; 2;  1 . Yêu cầu bài toán
  
 AB, BC .CH  0  
2bc  2c a  
1  1 cb a   1  0  b   0    2 3  A . B CH 0 a b 1 9b 2b 0          9   b    c  2 .  0 b BC AH  2   
Nếu b  0 suy ra A  B (loại).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 18
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 9  11   9  Nếu b  , tọa độ A ; 0; 0   , B 1; ;0 
 , C 1; 0;9 . Suy ra phương trình mặt phẳng 2  2   2 
 ABC  là 2x  2 y  z 11  0 .
 x  3  t  x  t '  
Câu 13: Trong không gian Oxyz, cho 2 đường thẳng d:  y  2
  t và d’:  y  5  t '   z  2  t z  2t ' 3 2  5 
Viết phương trình mặt phẳng () chứa (d) và tạo với mặt phẳng Oyz một góc nhỏ nhất.
A. 3x  y  2z  7  0 .
B. 3x  y  2z  7  0 . C. 3
 x  y  2z  7  0 .
D. 3x  y  2z  7  0 . Hướng dẫn giải: 
Giả sử (β): Ax  By  Cz  D  0 (đk: 2 2 2
A  B  C  0), (β) có vtpt là n  ( ; A B;C)  A( ) 
3A  2B  D  0  
D   A  2C 2 d  (β)        n . a  0 
 A  B  C 2  0 
B  A  C 2     A
cos(( ), (Oyz))  cos(n, i ) = 2 2 2
A  ( A  C 2)  C
TH 1: A = 0 (không thoả đb hoặc 
( ), (Oyz) không nhỏ nhất) TH 2: A ≠ 0, ta có:  1 1
cos(( ),(Oyz)) = = = C 2 C 2 1 (1  2 )  ( ) C C 6 12 2 2 ( 3)  2. 2  ( )  A A A A 3 9 1 C 6 12 2 ( 3  )  A 3 9  C 6
( ), (Oyz) nhỏ nhất  
cos(( ),(Oyz)) lớn nhất  2 ( 3  ) nhỏ nhất  A 3 C 6 3   0 A 3  1  A  1 (choïn) B     3  nên . Vậy: (β):  2 
3x  y  2z  7  0 C    7   3 D     3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 19
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Chọn D. x  2 y 1 z
Câu 14: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   . Viết phương 1 2 1 
trình mặt phẳng (P) chứa đường thẳng d và cắt các trục Ox, Oy lần lượt tại A và B sao cho
đường thẳng AB vuông góc với d.
A.  P : x  2y  5z  4  0.
B.  P : x  2 y  5z  5  0.
C.  P : x  2 y  z  4  0.
D.  P : 2x  y  3  0. Hướng dẫn giải:
Cách 1 (Tự luận) 
Đường thẳng d qua M(2;1;0) và có VTCP u  1;2;  1 d   
Ta có: AB  d và AB  Oz nên AB có VTCP là: u
 u , k   2; 1  ;0 AB d      
(P) chứa d và AB nên (P) đi qua M(2;1; 0), có VTPT là: n  u ,u   1;2;5 d AB   
  P : x  2y  5z  4  0  Chọn A
Cách 2: Dùng phương trình mặt phẳng theo đoạn chắn.
Đường thẳng d qua 2 điểm M(2;1;0) và N(3;3;-1)
Giả sử mp(P) cắt Ox, Oy, Oz lần lượt tại A(a;0;0), B(0;b;0), C(0;0;c) x y z   P :    1 a b c   AB  d  A .
B u  0  a  2b (1) d   2 1 3 3 1
P chứa d nên d cũng đi qua M, N    1 (2),    1 (3) a b a b c 4
Từ (1), (2), (3)  a = 4, b = 2, c =
  P : x  2y  5z  4  0  Chọn A 5 x  t    
Câu 15: Trong không gian tọa độ Oxyz cho đường thẳng d : y 1 2t và mp
z  2t 
P: 2x  y2z 2  0 . Viết phương trình mặt phẳng R qua d và tạo với P một góc nhỏ nhất.
A. x  y  z  3  0
B. x  y  z  3  0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 20
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
C. x  y  z  3  0
D. x  y  z  3  0 Hướng dẫn giải:  x y 1     
2x  y 1 0 1 2 
Đường thẳng d là giao tuyến của hai mặt phẳng:    .  x z  2
x  z 2  0     1 1
Do vậy mặt phẳng R qua d thì R thuộc chùm mặt phẳng:
2x  y 1 mx  z 2  0 .
Hay mp R : 2  m x  y  mz 1 2m  0 (*). Mp R có  
n  m  2;1;m ;n  2; 1  ; 2  1   P  . Vậy:  n .n
2m  21 2m 5 5 1 5 1 cos P        n n m    m   m  m    P  22 2 3 1 4 1 4 3 2 4 5 2m 2 2 3 3 1 1 3
Do  nhỏ nhất cho nên cos  lớn nhất khi m  1  .
Vậy thay vào (*) ta có mp R: x  y  z  3  0 . Chọn B. x  2  t
x  2  2t  
Câu 16: Cho hai đường thẳng d :  y  1 t và d :  y  3
. Mặt phẳng cách đều hai đường 1 2 z  2t   z  t 
thẳng d và d có phương trình là 1 2
A. x  5 y  2z 12  0.
B. x  5 y  2z  12  0.
C. x  5y  2z 12  0.
D. x  5 y  2z 12  0. A
Hướng dẫn giải: Chọn D. M  B
d qua A2;1;0 và có VTCP là u  1; 1  ; 2 ; 1   1 P 
d qua B 2;3;0 và có VTCP là u  2;0;1 . 2   2       Có u ,u  1  ; 5
 ; 2 ; AB  0;2;0 , suy ra u ,u .AB  10 , nên d ; d là chéo nhau. 1 2  1 2    1 2
Vậy mặt phẳng  P cách đều hai đường thẳng d , d là đường thẳng song song với d , d và 1 2 1 2
đi qua trung điểm I 2; 2;0 của đoạn thẳng AB .
Vậy phương trình mặt phẳng  P cần lập là: x  5 y  2z 12  0 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 21
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 17: Trong không gian với hệ toạ độ Oxyz ,cho hai đường thẳng d , d lần lượt có phương trình 1 2 x  2 y  2 z  3 x 1 y  2 z 1 d :   , d :  
. Phương trình mặt phẳng   cách đều 1 2 1 3 2 2 1 4
hai đường thẳng d , d là: 1 2
A. 7x  2 y  4z  0 .
B. 7x  2 y  4z  3  0 .
C. 2x  y  3z  3  0 .
D. 14x  4 y  8z  3  0 . Hướng dẫn giải:  
Ta có d đi qua A2;2;3 và có u  2;1;3 , d đi qua B 1;2  ;1 và có u  2; 1  ; 4 d  d  1 1 2 2    AB   1  ;1; 2
 ; u ;u   7; 2  ; 4  ; d d  1 2  
    u  ;u  AB  1
  0 nên d , d chéo nhau. d d 1 2 1 2     
Do   cách đều d , d nên   song song với d , d  n  u ;u    7; 2  ; 4  d d  1 2 1 2 1 2  
   có dạng 7x  2 y  4z  d  0 d  2 d 1 3
Theo giả thiết thì d  ,
A    d B,     d  69 69 2
   :14x  4 y  8z  3  0
Câu 18: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng P song song và cách x  2 y z x y  1 z  2
đều hai đường thẳng d :   và d :   . 1 1 1 1 2 2 1 1
A. P : 2x  2z  1  0 .
B. P : 2y  2z  1  0 .
C. P : 2x  2y  1  0 .
D. P : 2y  2z  1  0 . Hướng dẫn giải: 
Ta có: d đi qua điểm A 2; 0; 0 và có VTCP u  1;1; 1 1  . 1 
và d đi qua điểm B 0;1; 2 và có VTCP u  2; 1; 1 . P 2   Vì song songvới hai đường 2   
thẳng d và d nên VTPT của P là n  u ,u   0;1; 1  1 2    1 2
Khi đó P có dạng y  z  D  0  loại đáp án A và C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 22
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  1 
Lại có P cách đều d và d nên P đi qua trung điểm M 0; ;1 của AB. Do đó 1 2    2 
P : 2y  2z  1  0 Chọn B.
Câu 19: Trong hệ trục tọa độ Oxyz cho mặt phẳng  P : 5x  z  4  0 và hai đường thẳng d ; d lần 1 2 x 1 y z  1 x 1 y  2 z  1 lượt có phương trình   ;  
. Viết phương trình của mặt 1 1 2 2 1 1 4 5
phẳng Q / /  P, theo thứ tự cắt d , d tại ,
A B sao cho AB  . 1 2 3 25  331 25  331
A. Q : 5x  z 
 0; Q : 5x  z   0 . 1   2  7 7
B. Q : 5x  z  2  0; Q : 55x 11z 14  0 . 1   2 
C. Q : 5x  z  2  0; Q : 5
 5x 11z 14  0 . 1   2 
D. Q : 5x  z  4  0; Q : 55x 11z  7  0 1   2  Hướng dẫn giải: x  1 t
x  1 2t '  
d : y  t 
, d :  y  2  t ' ; Q : 5x  z  d  0, d  4  1 2   z 1 2t     z  1   t '    3
  d 6  d 1  5  2d   3
  2d 12  d 30  5d  
Q  d  A ; ;
, Q  d  B ; ; 1     2    3 3 3   9 9 9 
  6  d 6  4d 30  5d  1 Suy ra AB  ; ;   
6  d;6  4d;30  5d   9 9 9  9 4 5 1 2 2 2 Do AB  
6 d  6
  4d   30  5d   3 8  2  5  331 d  80 2 7 
 42d  300d  252  0   9  2  5  331 d   7
Vậy, tìm được hai mặt phẳng thỏa mãn: 25  331 25  331
Q : 5x  z 
 0; Q : 5x  z   0 1   2  7 7 Chọn A.
Câu 20: Trong không gian với hệ tọa độ Oxyz, cho điểm A1;2;3 và đường thẳng d : x  3 y 1 z   2 1 1
 . Mặt phằng P chứa đường thẳng d và có khoảng cách từ A đến P là
lớn nhất. Khi đó  P có một véctơ pháp tuyến là
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 23
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz    
A. n  (4; 5;13)
B. n  (4; 5; 1  3)
C. n  (4; 5;13)
D. n  (4; 5;13) Hướng dẫn giải:
Gọi H,K lần lươt là hình chiếu vuông góc của A lên d và (P)
Khi đó: d(A,(P)) = AK  AH hay d(A,(P)) lớn nhất khi và chỉ khi H  K    4 Ta có: H( 3   2t; 1   t; t  ); a  (2;1; 1
 ) và AH.a  0  t  3  4 5 13
Suy ra: AH  ( ;  ;  ) 3 3 3 
Hay một véctơ pháp tuyến của (P) là n  (4; 5;13) Chọn A. x 1 y  2 z
Câu 21: Trong không gian với hệ tọa độ Oxyz , cho hai đường thẳng d :   và 1 1 2 1 x  2 y 1 z d :  
. Viết phương trình mặt phẳng (P) chứa d sao cho góc giữa mặt 2 2 1  2 1
phẳng (P) và đường thẳng d là lớn nhất. 2
A. x  y  z  6  0 .
B. 7x  y  5z  9  0 . C. x  y  z  6  0 .
D. x  y  z  3  0 . Hướng dẫn giải: 
Ta có: d đi qua M(1; 2
 ; 0) và có VTCPu  (1; 2; 1) . 1
Phương trình mặt phẳng (P) có dạng: 2 2 2 (
A x 1)  B(y  2)  Cz  0,(A  B  C  0) .  
Ta có: d  (P)  .
u n  0  C  A  2B 2 4A  3B 1 (4A  3B)
Gọi   ((P),d )  sin   . 2 2 2 2 2 3 2A  4AB  5 3 2  4  5 B A AB B 2 2
Với B  0  sin  3 A 2 1 (4t  3)
Với B  0 . Đặt t 
, ta được sin  . B 2 3 2t  4t  5 2 (4t  3) 2
16t 124t  84
Xét hàm số f (t) 
. Ta có: f '(t)  2 2t  4t  5 2 2
(2t  4t  5)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 24
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
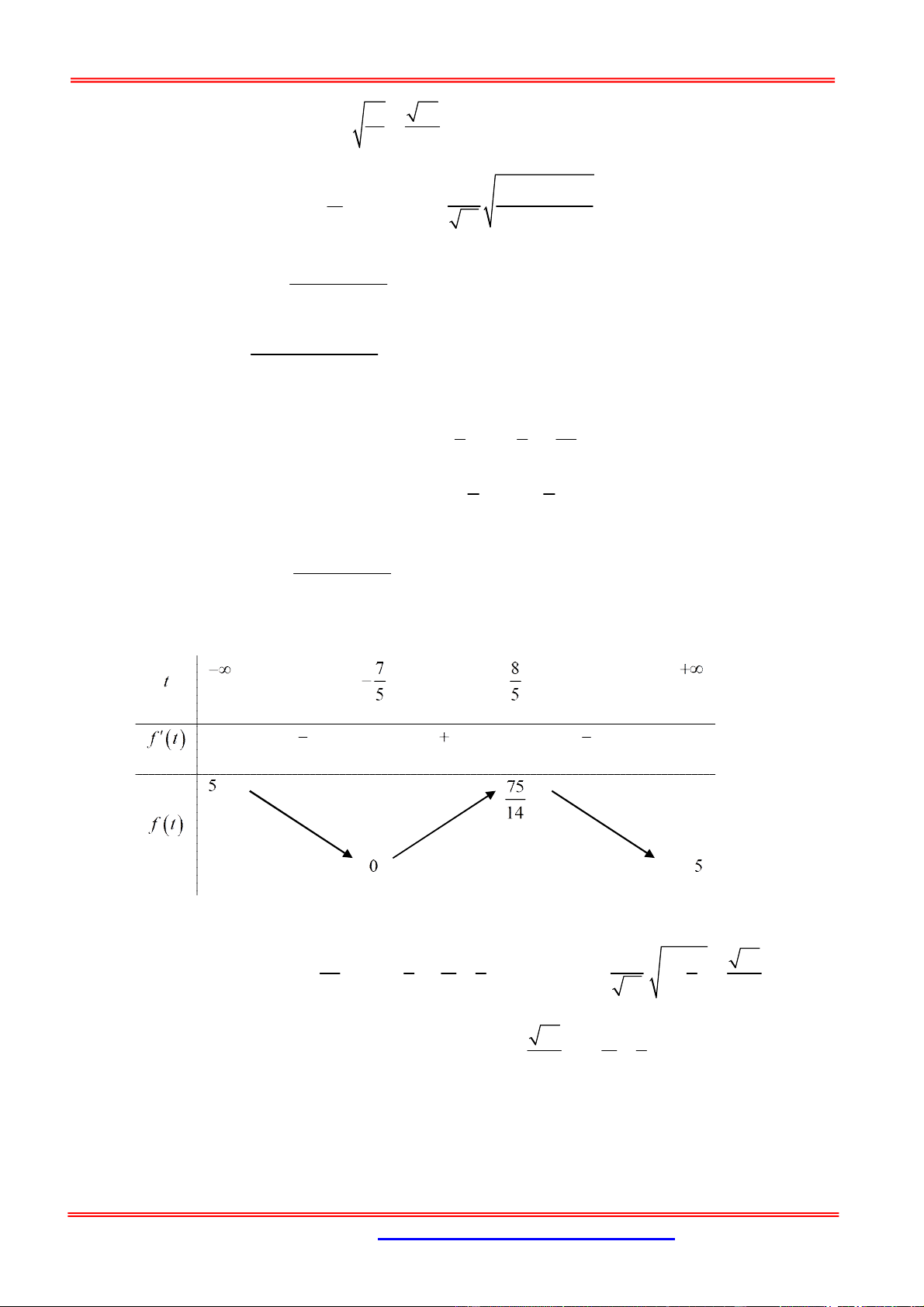
Hình Học Tọa Độ Oxyz  3 t   f '(t) 0    4  t  7   25 A
Dựa vào BBT ta có: max f (t)  khi t  7   7 3 B 5 3
Khi đó: sin  f (7)  9 5 3 A Vậy sin  khi  7
  Phương trình mặt phẳng (P) : 7x  y  5z  9  0 9 B Chọn B.
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho điểm M 1; 2;  
1 . Viết phương trình mặt phẳng
  đi qua gốc tọa độ O 0;0; 0 và cách M một khoảng lớn nhất. x y z
A. x  2y  z  0. B.    1.
C. x  y  z  0.
D. x  y  z  2  0. 1 2 1  Hướng dẫn giải:
Gọi H là hình chiếu của M trên (P)  MHO vuông tại H  MH  MO   MH
 MO . Khi đó (P) đi qua M và vuông góc với MO  M ( O 1; 2; 1  ) là vecto max
pháp tuyến của (P)  phương trình của mặt phẳng (P) là 1(x  0)  2(y  0)  1(z  0)  0
hay x  2y  z  0. Chọn A. x 1 y  2 z
Câu 23: Trong không gian với hệ trục tọa độ Oxyz , cho hai đường thẳng d :   và 1 1 2 1  x  2 y 1 z d :  
. Gọi  P là mặt phẳng chứa d sao cho góc giữa mặt phẳng  P và 2 2 1  2 1
đường thẳng d là lớn nhất. Chọn mệnh đề đúng trong các mệnh đề sau: 2 
A.  P có vectơ pháp tuyến là n  1; 1  ; 2 .
B.  P qua điểm A0; 2;0 .
C.  P song song với mặt phẳng Q : 7x  y  5z  3  0 .
D.  P cắt d tại điểm B 2; 1  ; 4 . 2 Hướng dẫn giải:  d qua M 1; 2
 ;0 và có VTCP u  1; 2;  
1 . Vì d  P nên M   P . 1   1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 25
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Pt mặt phẳng  P có dạng: A x    B  y    Cz   2 2 2 1 2
0 A  B  C  0 .  
Ta có: d  P  u.n  0  C  A  2B . 1   4A  3B 1 4 A  3B
Gọi    P   ,d   2  sin    . 2 2 2 2 2 3
2 A  4 AB  5 3 2  4  5 B A AB B 2 2
TH1: Với B  0 thì sin  . 3 A 1 4t  32
TH2: Với B  0 . Đặt t 
, ta được: sin   . B 2 3 2t  4t  5 4t  32 25
Xét hàm số f t  
. Dựa vào bảng biến thiên ta có: max f  x  khi t  7 2 2t  4t  5 7 A khi  7 . B 5 3
Khi đó sin  f  7    . 9 5 3 A
So sánh TH1 và TH2   lớn nhất với sin  khi  7 . 9 B
Vậy phương trình mặt phẳng  P : 7x  y  5z  9  0 . Chọn B.
Câu 24: Trong không gian với hệ trục toạ độ Oxyz ,cho tứ diện ABCD có điểm A1;1  ;1 , B 2;0; 2 , C 1; 1
 ; 0 , D 0;3;4 . Trên các cạnh AB, AC, AD lần lượt lấy các điểm B ', C ', D ' thỏa: AB AC AD  
 4 . Viết phương trình mặt phẳng  B 'C ' D ' biết tứ diện AB 'C ' D ' có AB ' AC ' AD ' thể tích nhỏ nhất?
A. 16x  40 y  44z  39  0 .
B. 16x  40 y  44z  39  0 .
C. 16x  40 y  44z  39  0 .
D. 16x  40 y  44z  39  0 . Hướng dẫn giải: AB AC AD A . B AC.AD
Áp dụng bất đẳng thức AM  GM ta có: 3 4     3 AB ' AC ' AD '
AB '.AC '.AD '
AB '.AC '.AD ' 27 V
AB '.AC '.AD ' 27 27   
AB 'C ' D '    V  V A . B AC.AD 64 V A . B AC.AD 64
AB 'C ' D ' 64 ABCD ABCD
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 26
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz AB ' AC ' AD ' 3  3   7 1 7  Để V
nhỏ nhất khi và chỉ khi     AB '  AB  B ' ; ; AB 'C 'D'   AB AC AD 4 4  4 4 4   7 1 7 
Lúc đó mặt phẳng  B 'C ' D ' song song với mặt phẳng  BCD và đi qua B ' ; ;    4 4 4 
  B 'C ' D ' :16x  40y  44z  39  0 .
Câu 25: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng   đi qua điểm M 1; 2;3 và cắt các
trục Ox, Oy, Oz lần lượt tại A , B , C ( khác gốc toạ độ O ) sao cho M là trực tâm tam giác
ABC . Mặt phẳng   có phương trình là: x y z
A. x  2 y  3z 14  0 . B.   1  0 . 1 2 3
C. 3x  2 y  z 10  0 .
D. x  2 y  3z 14  0 . Hướng dẫn giải:
Cách 1:Gọi H là hình chiếu vuông góc của C trên AB , K là hình chiếu vuông góc B trên
AC . M là trực tâm của tam giác ABC khi và chỉ khi M  BK  CH AB  CH  Ta có: z
  AB  COH   AB  OM (1) AB  CO  C (1) K M
Chứng minh tương tự, ta có: AC  OM (2). A
Từ (1) và (2), ta có: OM   ABC  O x H 
Ta có: OM 1; 2;3 . B y 
Mặt phẳng   đi qua điểm M 1; 2;3 và có một VTPT là OM 1; 2;3 nên có phương trình là:  x  
1  2  y  2  3 z  3  0  x  2y  3z 14  0 . Cách 2: +) Do ,
A B, C lần lượt thuộc các trục Ox, Oy, Oz nên (
A a; 0; 0), B(0; ;
b 0), C(0; 0; c) (
a, b, c  0 ). x y z
Phương trình đoạn chắn của mặt phẳng ( ABC) là:    1 . a b c
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 27
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz    AM .BC  0 
 
+) Do M là trực tâm tam giác ABC nên BM .AC  0 . Giải hệ điều kiện trên ta được a,b, c M (ABC)  
Vậy phương trình mặt phẳng: x  2 y  3z 14  0 .
Câu 26: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x  2y  z  5  0 và đường thẳng x  1 y  1 z  3 d :  
. Phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt 2 1 1
phẳng (Q) một góc nhỏ nhất là
A. P  : y  z  4  0
B. P  : x z  4  0
C. P  : x y  z  4  0
D. P  : y  z  4  0 Hướng dẫn giải: 
PT mặt phẳng (P) có dạng: ax  by  cz  d 
a2  b2  c2 0 (
 0) . Gọi a  ((P), Q ( )) . M (P)
c  a  b
Chọn hai điểm M(1; 1;3), N (1; 0; 4)  d . Ta có:   N (P)   d  a 7  4b   3 a  b
 (P): ax  by  (2a  b)z  7a  4b  0  cos  . 6 a2 5  4ab  2b2 3 b 3
TH1: Nếu a = 0 thì cos  .   0 a  30 . 6 2b2 2 b 1 3 a b
TH2: Nếu a  0 thì cos  . . Đặt x  và f x 2 ( )  cos  2 6 a b  b  5  4  2  a  a 
9 x2  2x  1
Xét hàm số f (x)  . .
6 5  4x  2x2 Dựa vào BBT, ta thấy f x 0 0
min ( )  0  cos  0  a  90  30
Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn b  1,c  1, d  4 .
Vậy: (P): y  z  4  0 . Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 28
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 27: Trong không gian Oxyz , cho hai điểm
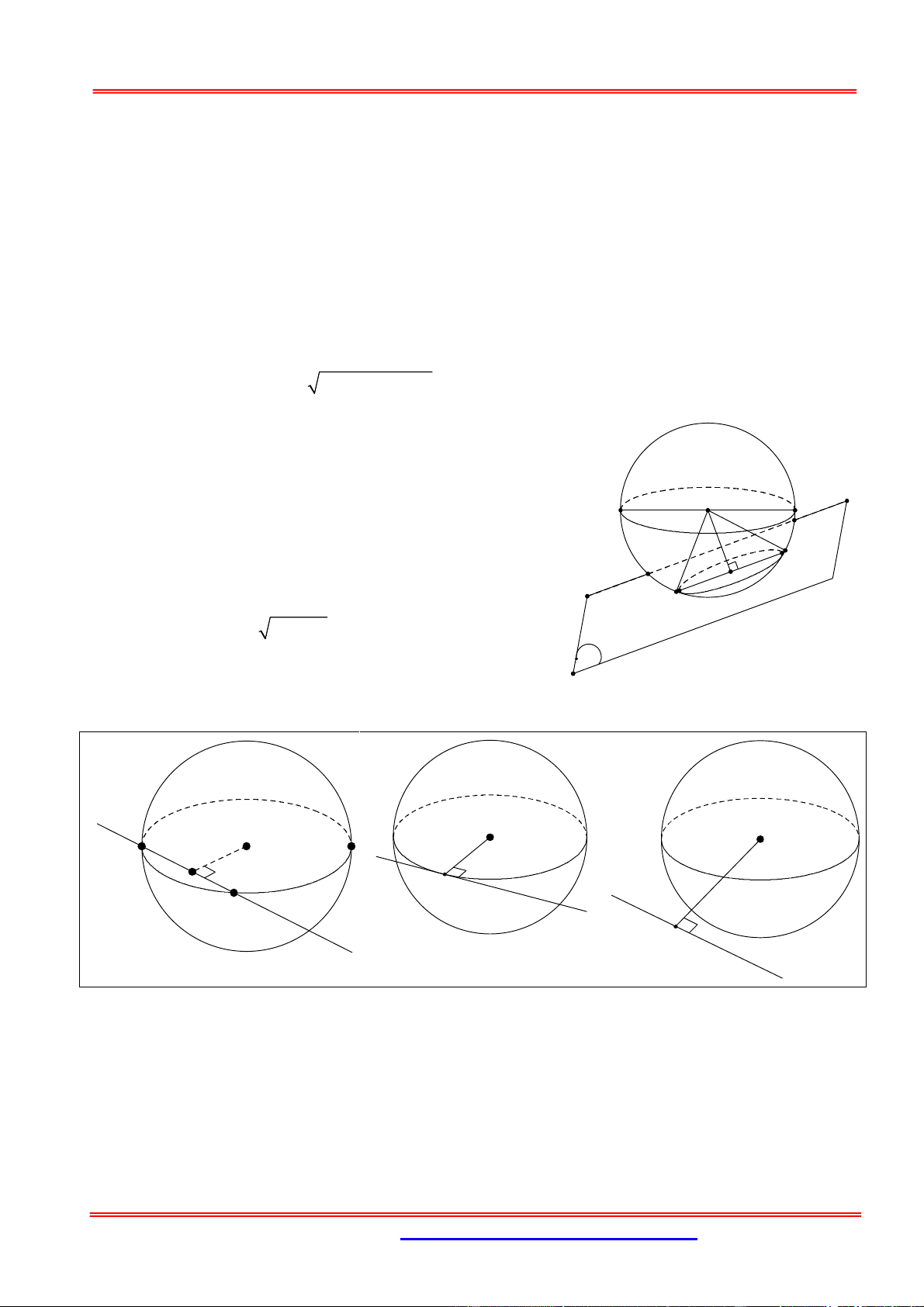
A3;0; 2 , B 3;0; 2 và mặt cầu 2 2 2
x  ( y  2)  (z 1)  25 . Phương trình mặt phẳng   đi qua hai điểm A , B và cắt mặt
cầu  S  theo một đường tròn bán kính nhỏ nhất là:
A. x  4 y  5z  17  0 .
B. 3x  2 y  z  7  0 .
C. x  4 y  5z 13  0 .
D. 3x  2 y  z – 11  0 . Hướng dẫn giải:
Mặt cầu  S  có tâm I 0; 2  
;1 , bán kính R  5 . Do IA  17  R nên AB luôn cắt S .
Do đó ( ) luôn cắt  S  theo đường tròn C  có bán kính r  R  d I  2 2 , . Đề bán
kính r nhỏ nhất  d I,P lớn nhất.
Mặt phẳng   đi qua hai điểm A , B và vuông góc với mp  ABC  .   Ta có AB  (1; 1; 1  ) , AC  ( 2  ; 3; 2
 ) suy ra  ABC  có véctơ pháp tuyến   
n   AB, AC   (1; 4; 5  )     
(α) có véctơ pháp tuyến n   , n AB  ( 9   6; 3  )  3  (3; 2;1)   
Phương trình   : 3 x – 2  2 y –  1  
1 z – 3  0  3x  2 y  z –11  0 .
Câu 28: Trong không gian với hệ toạ độ Oxyz ,cho  P : x  4 y  2z  6  0 , Q : x  2y  4z  6  0 .
Lập phương trình mặt phẳng   chứa giao tuyến của  P ,Q và cắt các trục tọa độ tại các điểm ,
A B, C sao cho hình chóp .
O ABC là hình chóp đều.
A. x  y  z  6  0 .
B. x  y  z  6  0 .
C. x  y  z  6  0 .
D. x  y  z  3  0 . Hướng dẫn giải:
Chọn M 6;0;0, N 2; 2; 2 thuộc giao tuyến của  P ,Q Gọi A ;
a 0;0, B 0; ;
b 0,C 0;0;c lần lượt là giao điểm của   với các trục Ox, Oy, Oz x y z    :    1a, , b c  0 a b c  6 1    a
  chứa M , N   2 2 2    1   a b c
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 29
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Hình chóp .
O ABC là hình chóp đều  OA  OB  OC  a  b  c
Vây phương trình x  y  z  6  0 .
Câu 29: Trong không gian với hệ toạ độ Oxyz , cho điểm N 1;1 
;1 . Viết phương trình mặt phẳng
P cắt các trục Ox,Oy,Oz lần lượt tại ,
A B, C (không trùng với gốc tọa độ O ) sao cho N
là tâm đường tròn ngoại tiếp tam giác ABC
A.  P : x  y  z  3  0 .
B.  P : x  y  z 1  0 .
C.  P : x  y  z 1  0 .
D.  P : x  2y  z  4  0 . Hướng dẫn giải: Gọi A ;
a 0;0, B 0; ;
b 0,C 0;0;c lần lượt là giao điểm của  P với các trục Ox, Oy, Oz x y z   P :  
 1a,b, c  0 a b c  1 1 1   
 N   P 1  a b c  
Ta có: NA  NB   a 1  b 1  a  b  c  3  x  y  z  3  0 NA NC  
a 1  c 1   
Câu 30: Phương trình của mặt phẳng nào sau đây đi qua điểm M 1; 2;3 và cắt ba tia Ox , Oy , Oz
lần lượt tại A , B , C sao cho thể tích tứ diện OABC nhỏ nhất?
A. 6x  3y  2z  18  0 .
B. 6x  3y  3z  21  0 .
C. 6x  3y  3z  21  0 .
D. 6x  3y  2z 18  0 . Hướng dẫn giải: Giả sử (
A a; 0; 0), B(0; ;
b 0), C(0;0;c) (a, b, c  0) x y z (ABC):    1 (1) a b c 1 2 3 M(1;2;3) thuộc (ABC):    1. a b c 1
Thể tích tứ diện OABC: V  abc 6 1 2 3 6 27.6 1 Áp dụng BDT Côsi ta có: 3 1     3  1  
abc  27  V  27 a b c abc abc 6 a  3 1 2 3 1 
Ta có: V đạt giá trị nhỏ nhất  V  27      b   6 a b c 3 c  9 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 30
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Vậy (ABC): 6x  3y  2z 18  0 . Chọn (D)
Câu 31: Trong không gian với hệ tọa độ Oxyz cho điểm E(8;1;1) .Viết phương trình mặt phẳng ( )
qua E và cắt nửa trục dương Ox, Oy, Oz lần lượt tại ,
A B, C sao cho OG nhỏ nhất với G là
trọng tâm tam giác ABC .
A. x  y  2z 11  0 .
B. 8x  y  z  66=0 .
C. 2x  y  z 18  0 .
D. x  2 y  2z 12  0 . Hướng dẫn giải: Chọn D. Cách 1 : 11 11 11 11 121 Với đáp án A: 2 (
A 11; 0;0); B(0;11; 0);C(0;0; )  G( ; ; )  OG  2 3 3 6 4 33 11 15609 Với đáp án B: 2 ( A
;0; 0); B(0;66; 0); C(0; 0; 66)  G( ; 22; 22) OG  4 4 16 18 18 Với đáp án C: 2 (
A 9; 0; 0); B(0;18;0); C(0;0;18)  G(3; ; )  OG  81 3 3 Với đáp án D: 2 ( A 1
 2; 0; 0); B(0;6; 0); C(0; 0; 6)  G(4; 2; 2)  OG  24 Cách 2 : 8 1 1 Gọi A ;
a 0;0, B 0; ;
b 0,C 0;0;c với a,b, c  0 . Theo đề bài ta có :    1. Cần tìm a b c
giá trị nhỏ nhất của 2 2 2
a  b  c . 2 2 Ta có  2 2 2
a  b  c      a  b  c    2 2 2 4 1 1 .2 .1 .1
6. a  b  c   2a  b  c Mặt khác  2 2 2
a  b  c 4 1  1  a.2  . b 1 . c  1  8 1 1  
 2a  b  c      a b c   4 1 2 1  36 2 a Suy ra 2 2 2 3
a  b  c  6 . Dấu '  ' xảy ra khi 2 2
 b  c  a  2b  2 . c 4 Vậy 2 2 2
a  b  c đạt giá trị nhỏ nhất bằng 216 khi a  12, b  c  6 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 31
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x y z
Vậy phương trình mặt phẳng là :  
 1 hay x  2 y  2z 12  0 . 12 6 6
Câu 32: Trong không gian với hệ toạ độ Oxyz cho ( A 2;1; 6 , ) B 1 ( ; 2; 4) và I 1 ( ; 3; 2 . ) Viết phương
trình mặt phẳng (P) đi qua ,
A B sao cho khoảng cách từ I đến (P) lớn nhất.
A. 3x  7 y  6z  35  0 .
B. 7x  y  5z  9  0 .
C. x  y  z  6  0 .
D. x  y  z  3  0 . Hướng dẫn giải: Ta có 2 2 2
IA  3  2  4  29 và 2 2 2
IB  0  5  2 
29 . Gọi M là trung điểm của
đoạn thẳng AB, vì IA=IB nên IM  AB, ta  1 1  94 có M ; ;5 ;   IM  .  2 2  2
Gọi H là hình chiếu vuông góc của I lên mặt phẳng (P):
Nếu H, M là hai điểm phân biệt thì tam giác IHM vuông tại H, IH94 IH  . 2 94 94
Nếu H trùng với M thì IH  IM  . Vậy ta có IH 
, IH lớn nhất khi H  M. 2 2     3 7 
Khi đó (P) có vectơ pháp tuyến là n  IH  IM 
; ;3 . Vậy phương trình mặt phẳng P    2 2  3 7
(P) là  x  2   y  
1  3 z  6  0 hay 3x  7 y  6z  35  0 2 2 Chọn A. M(0;1;2) N(1;1; 3)
Câu 33: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm và . Mặt phẳng
(P) đi qua M, N sao cho khoảng cách từ K 0; 0;2 đến (P) đạt giá trị lớn nhất. (P) có vectơ pháp tuyến là: A. (1;1; 1  ) B. (1; 1  ;1) C. (1; 2  ;1) D. (2; 1  ;1) Hướng dẫn giải:
- Khoảng cách từ K đến (P) lớn nhất bằng KH, khi H’ K trùng H
- Vậy mặt phẳng (P) qua MN và vuông góc với KH.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Tr H ang ' 32 M
Facebook: https://www.facebook.com/dongpay N P H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
- Tìm H và viết (P) hoặc:
- (P) chứa MN và vuông góc với (MNP).
Gọi H, H’ là hình chiếu của K lên MN và (P).
Ta có: d(k,(P))  KH  KH ' không đổi.
Vậy d(K,(P)) lớn nhất khi và chỉ khi H’ trùng H hay (P) vuông góc với KH.   
MK  (0;1;0); NK  (1; 1; 1) ; MN  (1;2;1)    (MNK) có vtpt là  
n  MK, NK  (1;0;1)     HK  (MNK) Do nên HK có vtcp là  
MN,n  (2;2;2). HK     MN Chọn A.
A1;0;0, B  2
 ; 0;3, M 0;0  ;1 N 0;3  ;1 .
Câu 34: Trong không gian Oxyz, cho các điểm và Mặt P P phẳng
đi qua các điểm M , N sao cho khoảng cách từ điểm B đến gấp hai lần  P. P
khoảng cách từ điểm A đến Có bao mặt phẳng thỏa mãn đầu bài?
A. Có vô số mặt phẳng  P.
B. Chỉ có một mặt phẳng  P.
C. Không có mặt phẳng  P nào.
D. Có hai mặt phẳng  P. Hướng dẫn giải: Chọn A.
Giả sử  P có phương trình là: ax  by  c  d   2 2 2 z
0 a  b  c  0
Vì M   P  c  d  0  d   . c
Vì N  P  3b  c  d  0 hay b  0 vì c  d  0.
  P :ax  cz  c  0. 2
 a  3c  c a  c
Theo bài ra: d  B, P  2d  ,
A  P   2
 c  a  a  c 2 2 2 2 a  c a  c
Vậy có vô số mặt phẳng  P.
Câu 35: Trong không gian tọa độ Oxyz, cho phương trình mặt phẳng
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 33
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  mx m y mz m          m  2 : 3 5 1 4 20 0, 1;1 .   Xét các mệnh đề sau: (I) Với mọi m  1;1  
thì các mặt phẳng 
luôn tiếp xúc với một mặt cầu không đổi.    m
(II) Với mọi m  0 thì các mặt phẳng m  luôn cắt mặt phẳng (Oxz).   (III) d O;   m       m  5, 1;1 .      
Khẳng định nào sau đây đúng? A. Chỉ (I) và (II) B. Chỉ (I) và (III) C. Chỉ (II) và (III)
D. Cả 3 đều đúng. Hướng dẫn giải: 20 20  
+ Ta có d O;      m   1;1 m  4 , với mọi .     2 9m  25 2 1  m  2  16m 25
Do đó với mọi m thay đổi trên  1;1 
thì các mặt phẳng 
luôn tiếp xúc với mặt cầu tâm    m
O, bán kính R  4 . Khẳng đinh (I) đúng.  2
+ Vectơ pháp tuyến của mặt phẳng 
n  3m;5 1m ;4m m  là và vectơ pháp tuyến 
của mặt phẳng (Oxz) là j  0;1;  0 .       n
 ; j  0  m  0
m  cắt (Oxz) khi và chỉ khi . Khẳng đinh (II) đúng.   + Khẳng đinh (III) sai. Chọn A.
Câu 36: Cho mặt phẳng  P đi qua hai điểm A3, 0, 4, B  3
 , 0, 4 và hợp với mặt phẳng  xOy một góc 0
30 và cắt y 'Oy tại C. Tính khoảng cách từ O đến  P. A. 4 3 . B. 3 . C. 3 3 . D. 2 3 z B Hướng dẫn giải: K x'
Vẽ OH  KC với K là giao điểm H
của AB và trục z 'Oz . A P   Ta có: 0 0
C  30  K  60 ;OK  4 -3 y 30
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com O Trang C 34
Facebook: https://www.facebook.com/dongpay 3 x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  d O P 0 ,
 OH  OK.sin 60 3  4.  2 3. 2 Chọn D.
Câu 37: Trong không gian với hệ tọa độ Oxyz , hai mặt phẳng 4x  4 y  2z  7  0 và
2x  2 y  z 1  0 chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là 27 81 3 9 3 64 A. V  B. V  C. V  D. V  8 8 . 2 27 Hướng dẫn giải:
Theo bài ra hai mặt phẳng 4x  4 y  2z  7  0 và 2x  2 y  z 1  0 chứa hai mặt của hình
lập phương. Mà hai mặt phẳng (P) : 4x  4 y  2z  7  0 và (Q) : 2x  2 y  z  1  0 song
song với nhau nên khoảng cách giữa hai mặt phẳng sẽ bằng cạnh của hình lập phương. 2   7 3 Ta có M (0; 0; 1
 )  (Q) nên d ((Q), (P))  d (M , (P))   2 2 2 2 4  ( 4  )  2 2 2 2 8
Vậy thể tích khối lập phương là: V  . .  . 3 3 3 27   A2; 0  ;1
Câu 38: Trong không gian với hệ toạ độ Oxyz , gọi
là mặt phẳng qua hai điểm và B 2  ;0; 
5 đồng thời hợp với mặt phẳng Oxz một góc 0
45 . Khoảng cách từ O tới   là: 3 3 1 2 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải:
Gọi K; H lần lượt là hình chiếu vuông góc điểm O lên đường thẳng AB và mặt phẳng . Ta có: , A B Oxz
    Oxz  AB O O 
 H    HK  AB    O  K  AB OK  AB   K 450
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com H
Trang 35
Facebook: https://www.facebook.com/dongpay 
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
 Oxz        KH OK   , ,  OKH
Suy ra tam giác OHK vuông cân tại H OK
Khi đó: d O,   OH  . 2   OA  AB 3
Mặt khác: OK  d  , O AB    . AB 2 OK
Khi đó: d O   3 ,  OH   . 2 2 Chọn A.
Câu 39: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng Q : x  y  z  0 và hai điểm A4, 3  ,  1 , B 2,1, 
1 . Tìm điểm M thuộc mặt phẳng Q sao cho tam giác ABM vuông cân tại M . M 1; 2  ;  1 M 1;2;  1   A.  17 9 8  . B.  17 9 8  . M ;  ;    M ; ;      7 7 7    7 7 7  M 1;2;  1 M 1;1;  1   C.  13 5 9  . D.   9 9 8  M ;  ;    M ;  ;       7 7 7    7 7 7  Hướng dẫn giải: Gọi M  , a ,
b c.M Q  a  b  c  0   1 .
Tam giác ABM cân tại M khi và chỉ khi:
AM  BM  a  2  b  2  c  2  a  2  b  2  c  2 2 2 4 3 1 2 1 1
 a  2b  5  0 2
a  b  c  0
a  2b  5 Từ   1 và 2 ta có:    *
a  2b  5  0 c  5   3b  
Trung điểm AB là I 3; 1; 
1 . Tam giác ABM cân tại M , suy ra: AB MI 
 a  2  b  2  c  2 3 1 1  5 3 2 b  2 2 2 2
Thay * và 3 ta được: 2b 2 b  1  6 3b 5          9 b    7
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 36
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz b  2
  a  1,c  1  M 1;2  ;1 9 17 8  17 9 8  b    a  , c    M ;  ;    7 7 7  7 7 7  Chọn A.
Câu 40: Trong không gian với hệ tọa độ Oxyz, cho 2 điểm A1;3; 2, B 3; 2  ;1 và mặt phẳng 
P : x  2y  2x 11  0. Tìm điểm M trên P sao cho 0
MB  2 2, MBA  30 . M 1; 2;3 M 1;2;3 M 2;1;3 M 1;2;3 A.  . B.  . C.  . D.  M 1; 4;  1  M 1; 4;  1  M 4;1;  1  M 1; 4;  1  Hướng dẫn giải:
Nhận thấy A   P , B  P, AB  6.
Áp dụng định lý côsin trong tam giác MAB ta có: 2 2 2 0 2 2 2
MA  MB  BA  2M . B B . A o
c s30  2  MB  MB  BA
Do đó tam giác MAB vuông tại . A x  1     Ta có: u
  AB, n   
 AM  y   t  M  t  t AM p 0; 5;5 : 3 1;3 ; 2    z  2  t  Ta có 2 2 2
MA  2  t  t  2  t  1 
Với t  1  M 1; 2;3; t  1  M 1; 4;  1 Chọn A.
Câu 41: Trong không gian tọa độ Oxyz , cho tám điểm A 2; 2; 0 , B 3; 2; 0 , C 3;3; 0 ,
D 2; 3; 0 , M  2; 2; 5 , N 2; 2; 5 , P 3; 2; 5 , Q  2;3;5 . Hỏi hình đa diện tạo bởi
tám điểm đã cho có bao nhiêu mặt đối xứng. A. 3. B. 6. C. 8. D. 9 Hướng dẫn giải:
Vì tám điểm đã chõ tạo nên một hình lập phương, nên hình đa diện tạo bởi tám điểm này có 9 mặt đối xứng. Chọn D.
Câu 42: Trong không gian với hệ tọa độ Oxyz , cho bốn điểm A1; 2  ;0, B 0; 1   ;1 , C 2;1;  1 ,
D 3;1; 4 . Hỏi có bao nhiêu mặt phẳng cách đều bốn điểm đó? A. 1. B. 4. C. 7. D. Vô số. Hướng dẫn giải:   
Ta có AB  1;1; 
1 , AC  1;3; 
1 , AD  2;3;4 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 37
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  
  
Khi đó  AB, AC    4  ;0; 4
  suy ra  AB, AC.AD  2  4  0 .     Do đó ,
A B,C, D không đồng phẳng và là 4 đỉnh của một tứ diện.
Khi đó sẽ có 7 mặt phẳng cách đễu bốn đỉnh của tứ diện. Bao gồm: 4 mặt phẳng đi qua trung
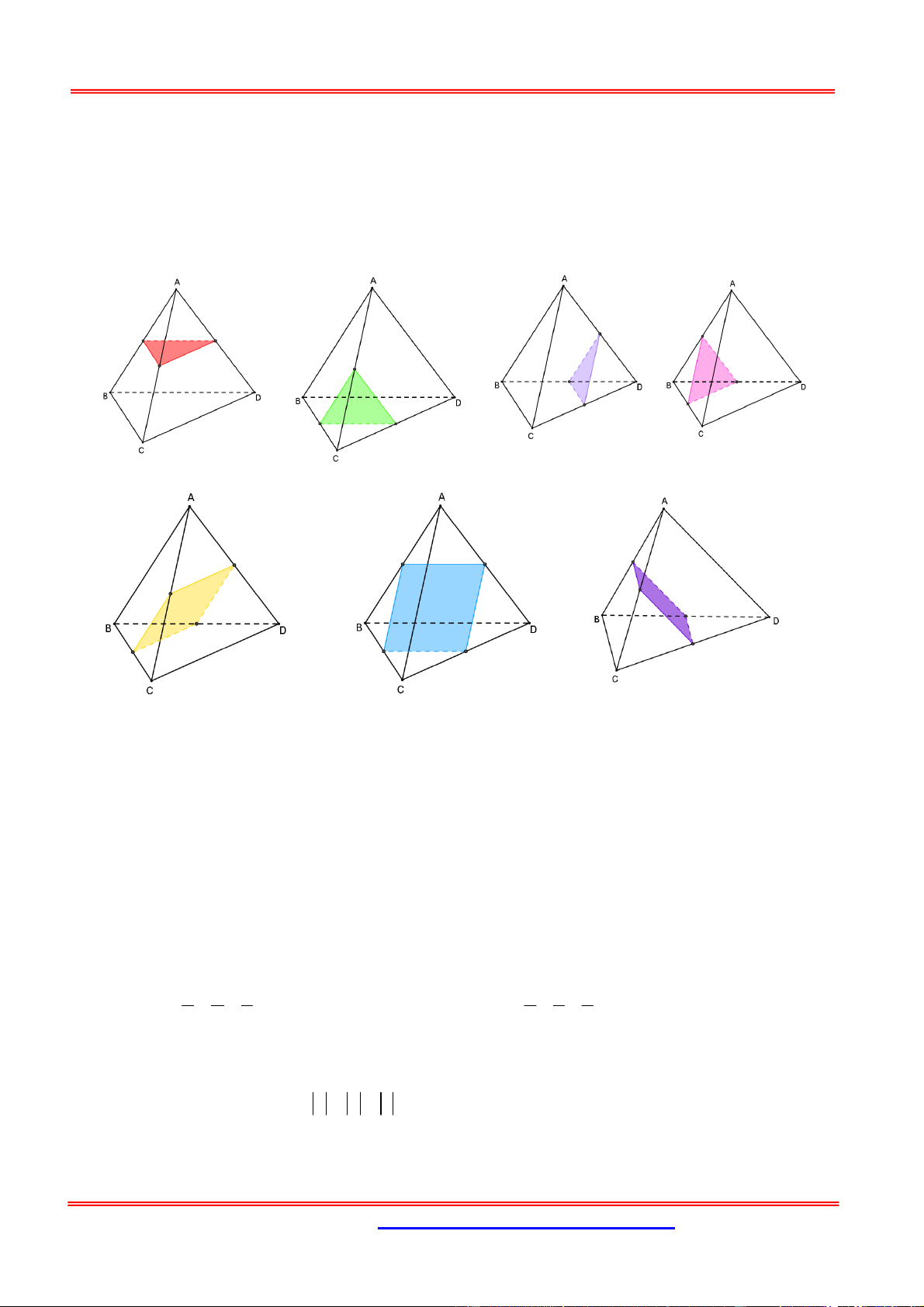
điểm của ba cạnh tứ diện và 3 mặt phẳng đi qua trung điểm bốn cạnh tứ diện (như hình vẽ). Chọn C.
Câu 43: Trong không gian cho điểm M (1; 3; 2) .Có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại ,
A B, C mà OA  OB  OC  0 A. 1. B. 2. C. 3. D. 4. Hướng dẫn giải: Chọn C.
Giả sử mặt phẳng ( ) cần tìm cắt Ox, Oy, Oz lần lượt tại (
A a, 0, 0), B(0, b, 0), C(0, 0 c)(a, b, c  0) x y z 1 3 2 ( ) :  
 1 ; ( ) qua M (1; 3; 2) nên: ( ) :    1(*) a b c a b c
a  b  c(1)
a  b  c(2) OA OB OC 0 a b c 0          a  b   c(3) a  b   c(4) 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 38
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Thay (1) vào (*) ta có phương trình vô nghiệm 3 
Thay (2), (3), (4) vào (*) ta được tương ứng a  4
 , a  6, a  4 Vậy có 3 mặt phẳng.
Câu 44: Có bao nhiêu mặt phẳng đi qua điểm M (1;9; 4) và cắt các trục tọa độ tại các điểm A , B , C
(khác gốc tọa độ) sao cho OA  OB  OC . A. 1. B. 2 . C. 3 . D. 4 . Hướng dẫn giải: Chọn D.
Giả sử mặt phẳng ( ) cắt các trục tọa độ tại các điểm khác gốc tọa độ là (
A a; 0; 0), B(0; ;
b 0), C(0; 0; c) với a, b, c  0. x y z
Phương trình mặt phẳng ( ) có dạng    1. a b c 1 9 4
Mặt phẳng ( ) đi qua điểm M (1;9; 4) nên    1 (1). a b c
Vì OA  OB  OC nên a  b  c , do đó xảy ra 4 trường hợp sau:
+) TH1: a  b  . c 1 9 4 Từ (1) suy ra  
 1  a  14, nên phương trình mp ( ) là x  y  z 14  0. a a a 1 9 4
+) TH2: a  b   . c Từ (1) suy ra  
 1  a  6, nên pt mp ( ) là x  y  z  6  0. a a a 1 9 4 +) TH3: a  b   . c Từ (1) suy ra  
 1  a  4, nên pt mp ( ) là a a a
x  y  z  4  0. 1 9 4 +) TH4: a  b    . c Từ (1) có    1  a  12 
, nên pt mp ( ) là a a a
x  y  z 12  0.
Vậy có 4 mặt phẳng thỏa mãn.
Câu 45: Trong không gian với hệ tọa độ Oxyz , cho điểm ( A 2; 2  ; 0) , đường thẳng x 1 y z  2  :  
. Biết mặt phẳng (P) có phương trình ax  by  cz  d  0 đi qua A , 1  3 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 39
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
song song với  và khoảng cách từ  tới mặt phẳng (P) lớn nhất. Biết a, b là các số
nguyên dương có ước chung lớn nhất bằng 1. Hỏi tổng a  b  c  d bằng bao nhiêu? A. 3 . B. 0 . C. 1 . D. 1. Hướng dẫn giải:
Gọi H là hình chiếu vuông góc của A trên đường thẳng  . 
Do H    H (1 t;3t; 2  t)  AH  ( t
  3;3t  2;t  2)   
Do AH    AH .u  0 với u  ( 1  ;3;1)    1
 .(t  3)  3.(3t  2)  1.(t  2)  0  11t  11  t  1  H 0; 3   ;1
Gọi F là hình chiếu vuông góc của H trên (P) , khi đó: d (, (P))  d (H , (P))  HF  HA Suy ra d( ,  ( ) P )
 HA . Dấu “=” xảy ra khi F  A  AH  (P) , hay bài toán được phát max biểu lại là:
“ Viết phương trình mặt phẳng (P) đi qua A và vuông góc với AH ”   Ta có AH   2  ; 1  ;  1  (2;1; 1  ) , suy ra n  (2;1; 1  ) ( P)
Suy ra phương trình mặt phẳng (P) là: 2(x  2)  y  2  z  0  2x  y  z  2  0 . a,b   *
a  2,b  1 Do   
 a  b  c  d  0 . (a, b)  1 c  1  , d  2    Chọn B. x  2  t x 1 y  2 z 1 
Câu 46: Trong không gain Oxyz, cho hai đường thẳng d :  
và d : y  3  t . 1 1 2 1  2 z  2  
Mặt phẳng  P : ax  by  cz  d  0 (với a; ;
b c; d   ) vuông góc với đường thẳng d và 1
chắn d , d đoạn thẳng có độ dài nhỏ nhất. Tính a  b  c  d . 1 2 A. 14 B. 1 C. 8 D. 12 Hướng dẫn giải: 
Ta có mặt phẳng (P) vuông dóc với đường thẳng d nên (P) có véctơ pháp tuyến n  1; 2;  1 . 1
Phương trình (P) có dạng  P : x  2y  z  d  0 .
Gọi M là giáo điểm của (P) với d và N là giao của (P) với d suy ra 1 2
 2  d 2  d 10  d   4  d 1   d  M ; ;   , N ; ; 2    .  6 3 6   3 3 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 40
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 2 d 16d 155 Ta có 2 MN    . 18 9 9 Để MN nhỏ nhất thì 2
MN nhỏ nhất, nghĩa là d  16 .
Khi đó a  b  c  d  14 . Chọn A.
Câu 47: Trong không gian với hệ trục toạ độ Oxyz, cho điểm A10; 2  ;1 và đường thẳng x 1 y z 1 d :  
. Gọi  P là mặt phẳng đi qua điểm A , song song với đường thẳng d 2 1 3
sao cho khoảng cách giữa d và  P lớn nhất. Khoảng cách từ điểm M  1  ; 2;3 đến mp P là 97 3 76 790 2 13 3 29 A. . B. . C. . D. . 15 790 13 29
Hướng dẫn giải:: d  H
P là mặt phẳng đi qua điểm A và
song song với đường thẳng d nên  P
chứa đường thẳng d  đi qua điểm A và
song song với đường thẳng d . K d'
Gọi H là hình chiếu của A trên d , K A
là hình chiếu của H trên  P . P
Ta có d d, P  HK  AH ( AH không đổi)
 GTLN của d (d, (P)) là AH
 d d, P lớn nhất khi AH vuông góc với  P .
Khi đó, nếu gọi Q là mặt phẳng chứa A và d thì  P vuông góc với Q .     n    P
ud , nQ 98;14; 70   97 3
  P :7x  y  5z  77  0 d M ,P  . 15
Câu 48: Trong không gian với hệ trục toạ độ Oxyz, cho điểm A2;5;3 và đường thẳng x 1 y z  2 d :  
. Gọi  P là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A 2 1 2
đến  P lớn nhất. Tính khoảng cách từ điểm M 1;2;  
1 đến mặt phẳng  P . 11 18 11 4 A. . B. 3 2. C. . D. . 18 18 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 41
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Hướng dẫn giải:: A
Gọi H là hình chiếu của A trên d ;
K là hình chiếu của A trên  P . Ta có d  ,
A  P  AK  AH (Không đổi) K d
 GTLN của d (d, (P)) là AH ⟹ H d  ,
A  P lớn nhất khi K  H . P
Ta có H 3;1;4 ,  P qua H và  AH
  P :x  4 y  z  3  0
Vậy d M  P 11 18 ,  . 18
Câu 49: Trong không gian với hệ tọa độ Oxyz , cho A ;
a 0; 0, B 0; ;
b 0, C 0;0;c với a, b, c dương. Biết ,
A B, C di động trên các tia Ox, Oy, Oz sao cho a  b  c  2 . Biết rằng khi
a, b, c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng P cố
định. Tính khoảng cách từ M 2016;0;0 tới mặt phẳng  P . 2014 2016 2015 A. 2017 . B. . C. . D. . 3 3 3 Hướng dẫn giải: Chọn D.
Gọi   là mặt phẳng trung trực của đoạn OA  a  
   đi qua điểm D ; 0; 0 
 và có VTPT OA   ;
a 0;0  a 1;0;0  2  a
   : x   0 . 2
Gọi   là mặt phẳng trung trực của đoạn OB  a  
    đi qua điểm E 0; ;0 
 và có VTPT OB  0; a; 0  a 0;1; 0  2  a
   : y   0 . 2
Gọi   là mặt phẳng trung trực của đoạn OC  a  
   đi qua điểm F 0;0; 
 và có VTPT OC  0;0; a   a 0; 0;  1  2  a
   : z   0 . 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 42
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  a a a 
Gọi I là tâm mặt cầu ngoại tiếp tứ diện OABC  I           I ; ;   .  2 2 2  a b c
Mà theo giả thiết, a  b  c  2   
 1  I   P : x  y  z  1. 2 2 2 2016 1 2015
Vậy, d M , P   . 3 3
P :3x  y  z  5  0
Câu 50: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng và hai
A1;0; 2 B 2;1;4. M  ; x y; z  P điểm ,
Tìm tập hợp các điểm nằm trên mặt phẳng sao
cho tam giác MAB có diện tích nhỏ nhất.
x  7 y  4z  7  0
x  7 y  4z  14  0 A.  . B.  .
3x  y  z  5  0 
3x  y  z  5  0 
x  7 y  4z  7  0 3
 x  7 y  4z  5  0 C.  . D.  .
3x  y  z  5  0 
3x  y  z  5  0  Hướng dẫn giải: Chọn C. Ta thấy hai điểm ,
A B nằm cùng 1 phía với mặt phẳng  P và AB song song với  P .
Điểm M   P sao cho tam giác ABM có diện tích nhỏ nhất A .
B d (M ; AB)  S 
nhỏ nhất  d  M ; AB nhỏ nhất, hay M     P  Q,Q là A  BC 2
mặt phẳng đi qua AB và vuông góc với  P .   Ta có AB  1; 1
 ; 2 , vtpt của  P n   P 3;1;  1     
Suy ra vtpt của Q : n   AB, n    1  ;7; 4 Q P        PTTQ Q : 1   x  
1  7 y  4  z  2  0
 x  7 y  4z  7  0
x  7 y  4z  7  0 Quỹ tích M là  .
3x  y  z  5  0 
Câu 51: Trong không gian Oxyz , cho hình hộp chữ nhật ABC . D AB C  D
  có điểm A trùng với gốc 
của hệ trục tọa độ, B(a;0;0) , D(0; a; 0) , A (0; 0;b) (a  0, b  0) . Gọi M là trung điểm của a 
cạnh CC . Giá trị của tỉ số
để hai mặt phẳng ( A BD) và  MBD vuông góc với nhau là: b 1 1 A. . B. . C. 1  . D. 1. 3 2 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 43
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz    b 
Ta có AB  DC  C  ; a ;
a 0  C ' ; a ; a b  M ; a ; a    2  Cách 1.   b    Ta có MB  0;  ; a  
 ; BD  a; a; 0 và A ' B   a;0; b  2      ab ab    Ta có 2 u   ; MB BD  ; ; a 2 2 2           và B ; D A' B
 a ; a ; a   2 2    
Chọn v  1;1; 
1 là VTPT của  A' BD   ab ab a
 A BD  MBD 2 '
 u.v  0  
 a  0  a  b   1 2 2 b Cách 2.
 A' B  A' D
 A' X  BD
AB  AD  BC  CD  a    
với X là trung điểm BD MB  MD MX  BD   
  A' BD; MBD  
  A' X ;MX     a a  X ; ; 0 
 là trung điểm BD  2 2    a a    a a b  A' X  ; ; b 
 , MX   ;  ;     2 2   2 2 2 
 A'BD  MBD  A' X  MX
  2 2 2  a   a  b a
 A ' X .MX  0      0       1  2   2  2 b
Câu 52: Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A1;0;  1 ; B 3; 2  ; 0;C 1;2; 2   .
Gọi  P là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến  P lớn nhất
biết rằng  P không cắt đoạn BC . Khi đó, điểm nào sau đây thuộc mặt phẳng P ? A. G  2  ; 0; 3. B. F 3; 0; 2  .
C. E 1;3;  1 .
D. H 0;3;  1 . Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 44
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Gọi I là trung điểm đoạn BC ; các điểm B B ,
 C , I  lần lượt là hình chiếu của B, C , I I trên  P . C Ta có tứ giác BCC B
  là hình thang và IIlà đường trung bình.
 d  B, P  d C, P  BB  CC  2II .
Mà II   IA (với IA kh ông đổi) B' I' C'
Do vậy, d B, P  d C, P lớn nhất khi P A I   A 
  P  đi qua A và vuông góc IA với I 2; 0; 1.
  P : x  2z 1  0  E 1;3;  1   P .
Câu 53: Trong không gian với hệ trục toạ độ Oxyz, cho các điểm A1;0;0, B0; ;
b 0,C 0;0;c
trong đó b, c dương và mặt phẳng  P : y  z 1 0 . Biết rằng mp  ABC  vuông góc với
mp  P  và d O  ABC  1 ,
 , mệnh đề nào sau đây đúng? 3
A. b  c 1.
B. 2b  c 1.
C. b  3 c 1.
D. 3b  c  3. Hướng dẫn giải: x y z
Ta có phương trình mp( ABC) là    1 1 b c 1 1
 ABCP    0b  c (1) b c 1 1 1 1 1
Ta có d O, ABC        8 (2) 2 2 3 1 1 3 b c 1  2 2 b c 1
Từ (1) và (2)  b  c 
 b  c 1 . 2
Câu 54: Cho hình lập phương ABC . D AB C  D
  có cạnh bằng 2. Tính khoảng cách giữa hai mặt phẳng  AB D   và  BC D  . 3 3 2 A. . B. 3. C. . D. . 3 2 3 Hướng dẫn giải: Chọn A.
Ta chọn hệ trục tọa độ sao cho các đỉnh của hình lập phương có tọa độ như sau:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 45
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
A0;0;0 B 2;0;0 C 2; 2;0 D 0; 2;0 A' D'
A 0;0; 2 B2;0;2 C2; 2; 2 D0; 2; 2  
AB  2;0; 2, AD  0; 2; 2, C'   B'
BD  2; 2; 0 , BC  0; 2; 2 A
* Mặt phẳng  AB D
  qua A0;0;0 và nhận véctơ D 1    B n 
 AB , AD  1; 1  ;  1 làm véctơ pháp tuyến. 4   C
Phương trình  AB D
  là: x  y  z  0. 1   
* Mặt phẳng  BC D
  qua B 2;0;0 và nhận véctơ m  BD, BC  1;1;   1 làm véctơ 4   pháp tuyến.
Phương trình  BC D
  là: x  y  z  2  0.
Suy ra hai mặt phẳng  AB D   và  BC D
  song song với nhau nên khoảng cách giữa hai
mặt phẳng chính là khoảng cách từ điểm A đến mặt phẳng  BC D   :
d  A  BC D   2 2 3 ,   . 3 3
Cách khác: Thấy khoảng cách cần tìm d  AB D   BC D   1 1 2 3 ,  AC  .2 3  . 3 3 3
Câu 55: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A5;5;0, B 1;2;3, C 3;5;   1 và mặt
phẳng  P : x y  z  5  0 Tính thể tích V của khối tứ diện SABC biết đỉnh S thuộc mặt .
phẳng  P và SA  SB  SC . 145 45 127 A. V  . B. V  145 . C. V  . D. V  . 6 6 3 Hướng dẫn giải: Gọi S  ; a ;
b c  P  a  b  c  5  0  1 . 2 2
Ta có: AS  a    b   2 5 5  c ,
BS  a  2  b  2  c  2 CS  a  2  b  2  c  2 1 2 3 , 3 5 1  a  2
1  b  22  c  32  a  32  b  52  c  2 1 
SA  SB  SC   2 2 2 2 2 2  Do
a  5  b  5  c  a  3  b  5  c   1 
4a  6b  8c  21  0
 4a 2c 15  0 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 46
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  a  6
4a  6b  8c  21  0    23  13 9 
Ta có hệ: 4a  2c 15  0  b    S  6;  ;    . Lại có: 2  2 2  a b c 5 0        9 c     2   AB  4
 ; 3;3, AC 2;0;   1     23 9 
   145
 AB  AC  3; 1
 0; 6; AS  1; ; 
  AB  AC  AS  145  V    S.  2 2 ABC  6
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 47
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
PHƯƠNG TRÌNH ĐƯỜNG THẲNG NÂNG CAO A - LÝ THUYẾT CHUNG 1. Định nghĩa
Phương trình tham số của đường thẳng  đi qua điểm M x ; y ; z
và có vec tơ chỉ phương 0  0 0 0   
 x  x  a t 0 1 
a  a ; a ; a , a  0 :  y  y  a t 1 2 3  0 2
z  z  a t  0 3
Nếu a ; a ; a đều khác không. Phương trình đường thẳng  viết dưới dạng chính tắc như sau: 1 2 3 x  x y  y z  z 0 0 0   a a a 1 2 3
A x  B y  C z  D  0
Ngoài ra đường thẳng còn có dạng tổng quát là: 1 1 1 1
A x  B y  C z  D  0  2 2 2 2 với A
 , B ,C , A , B , C thỏa 2 2 2 2 2 2
A  B  C  0, A  B  C  0. 1 1 1 2 2 2 1 1 1 2 2 2
2. Vị trí tương đối của hai đường thẳng
Chương trình cơ bản
Chương trình nâng cao
1 )Vị trí tương đối của hai đường thẳng
1 ) Vị trí tương đối của hai đường thẳng
Trong không gian Oxyz cho hai đường thẳng
Trong không gian Oxyz cho hai đường thẳng
x  x  a t
x  x ' a 't '
x  x  a t
x  x ' a 't ' 0 1 0 1 0 1 0 1    
d :  y  y  a t
; d ' :  y  y ' a 't '
d :  y  y  a t
; d ' :  y  y ' a 't ' 0 2 0 2 0 2 0 2 z z a t   
z  z ' a 't '   
z  z  a t
z  z ' a 't ' 0 3  0 3     0 3 0 3  
Vtcp u đi qua M và d ' có vtcp u ' đi qua M '
Vtcp u đi qua M và d ' có vtcp u ' đi qua M ' 0 0   0 0   
u, u ' cùng phương: 
 u,u '  0    
d  / / d '      u  ku '  u  ku ' M  d '  d / /d '  0 
; d  d '      M  d '  M  d ' 0  0   
 u,u '  0   u, u '
d   d '  
không cùng phương: M  d '  0
x  a t  x ' a 't '    0 1 0 1 
u,u '  0
 y  a t  y ' a 't ' I   0 2 0 2   d  a
c t d '      
z  a t  y ' a 't '  
 u, u ' .MM  0 0 3 0 3 0  
d chéo d’  hệ phương trình   1 vô nghiệm   
d  cheo d '  u,u '.MM  0 0  
d cắt d’  hệ phương trình   1 có 1 nghiệm
3. Vị trí tương đối của đường thẳng và mặt phẳng Phương pháp 1 Phương pháp 2
Trong không gian Oxyz cho:
Trong không gian Oxyz cho đường thẳng d 
qua M  x ; y ; z có vtcp: a  a ;a ; a và 1 2 3  0 0 0 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 48
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 
x  x  a t   0 1
 :Ax+By+Cz+D=0 có vtpt n  ; A ; B C     
 :Ax+By+Cz+D=0 và d : y  y  a t 0 2 d     . a n  0  cắt
z  z  a t  0 3     . a n  0 Pt:
d  / /    
A  x  a t  B y  a t  C z  a t  D  0 1 M      0 1   0 2   0 3        1 d / /    Phương trình vô nghiệm thì d     . a n  0 nằm trên mp     1   M      Phương trình
có 1 nghiệm thì d cắt   1 d    Phương trình có vô số nghiệm thì  
Đặc biệt: d     a, n cùng phương 4. Khoảng cách
Khoảng cách từ M  x ; y ; z đến mặt phẳng  :Ax+By+Cz+D=0 cho bởi công thức 0 0 0 
Ax  By  Cz  D
d M ,  0 0 0  0 2 2 2
A  B  C
Khoảng cách từ M đến đường thẳng d 
Khoảng cách từ M đến đường thẳng d  Phương pháp 1: Phương pháp 2: 
Lập ptmp   đi qua M và vuông góc với d.
( d đi qua M có vtcp u ) 0 
Tìm tọa độ giao điểm H của mp   và d M M , u 0  
d M ,   
d  M , d   MH u
Khoảng cách giữa hai đường thẳng chéo nhau
Khoảng cách giữa hai đường thẳng chéo nhau Phương pháp 1:  Phương pháp 2: 
d đi qua M  x ; y ; z ; có vtpt a  a ;a ; a 1 2 3  0 0 0 
d đi qua M  x ; y ; z ; có vtpt a  a ;a ; a 1 2 3  0 0 0   d ' đi qua
M ' x '; y '; z ' ; vtpt 0 0 0  
d ' đi qua M ' x '; y '; z ' ; vtpt a '  a ';a ';a ' 1 2 3  0 0 0    
a '  a ';a ';a ' 1 2 3 
a, a '.MM ' V   hop
Lập phương trình mp   chứa d và song song d ,  '      , ' S a a day  
với d’: d d, d '  d M ', 
5. Góc giữa hai đường thẳng
Góc giữa hai đường thẳng 
 đi qua M x ; y ; z có VTCP a  a ;a ; a 1 2 3  0 0 0  
 ' đi qua M ' x '; y '; z ' có VTCP a '  a ';a ';a ' 1 2 3  0 0 0      . a a '
a a  a a  a a
cos  cos a, a ' . ' . ' . ' 1 1 2 2 3 3     2 2 2 2 2 2 a . a '
a  a  a . a '  a '  a ' 1 2 3 1 2 3
6. Góc giữa đường thẳng và mặt phẳng 
Góc giữa đường thẳng và mặt phẳng  đi qua M có VTCP a , mặt phẳng   có VTPT 0  n   ; A B;C .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 49
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz   Aa  Ba  Ca
Gọi  là góc hợp bởi  và mặt phẳng   : sin  cos a, n 1 2 3  2 2 2 2 2 2
A  B  C . a  a  a 1 2 3
B – BÀI TẬP TRẮC NGHIỆM x  4 y  5 z  2 Câu 1:
Đường thẳng  song song với d :  
và cắt cả hai đường thẳng 3 4 1 x  1 y  1 z  2 x  2 y  3 z d :   và d :  
. Phương trình nào không phải đường 1 3 1 2 2 2 4 1 thẳng  7 2 y  z  x  4 y  1 z  1 x  3 A.  :   B. 3 3  :   3 4  1 3 4  1 x  9 y  7 z  2 x  4 y  1 z  1 C.  :   D.  :   3 4 1 3 4 1 Hướng dẫn giải:
Giải: Gọi M, N là giao điểm của  và d , d . 1 2 x
 1  3t x  2   2t ' M N  
Khi đó M, N thuộc d , d nên y  1   t , y t . M   3  4 ' 1 2 N z 2 2    t z  t '  M  N 
Vector chỉ phương của  là MN   3
  2t ' 3t;4  4t ' t;2  t ' 2t  x  4 y  5 z  2
3  2t ' 3t 4  4t ' t
2  t ' 2t  song song với d :   nên   3 4  1 3 4  1 4  7 2 
Giải hệ ta được t '  1;t   . Vậy N  4  ; 1  ;  1 , M 3;  ;    3  3 3  x  4 y  1 z  1 Vậy  :   3 4  1 Chọn A. x  1 t  Câu 2:
Cho đường thẳng (d ) :  y  1 t và mp (P) : x  y  2  0 . Tìm phương trình đường thẳng z  2t 
nằm trong mặt phẳng (P) cắt và vuông góc với (d). x  1 2t x  1 3t x  1 2t x  1 t    
A. y  1 2t
B. y  1 3t
C. y  1 2t
D.  y  1 t z  0     z  5  z  0  z  5  Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 50
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Gọi I là giao điểm của (d) và (P): I (1 t;1 t; 2t), I  (P)  t  0  I (1;1;0)  
(d) có vectơ chỉ phương u  (1; 1
 ; 2) , (P) có vectơ pháp tuyến n  (1;1; 0)   
Vectơ pháp tuyến của mặt phẳng cần tìm là u    
u, v =(-2 ;2 ;0)   x  1 2t 
Phương trình mặt phẳng cần tìm là y  1 2t z  0  Chọn A. x y 1 z  2 Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng  :   và mặt phẳng 1 1 1
P : x  2 y  2z  4  0. Phương trình đường thẳng d nằm trong P sao cho d cắt và
vuông góc với đường thẳng  là
x  3  t  x  3t  
A. d :  y  1 2t t   .
B. d :  y  2  t t   .      z  1 t   z  2  2t 
x  2  4t
x  1 t  
C. d :  y  1 3t t   .
D. d :  y  3  3t t   .    
 z  4  t   z  3  2t  Hướng dẫn giải: Chọn C.  
Vectơ chỉ phương của  : u  1;1; 1 , vectơ pháp tuyến của  P là n  1;2; 2 . P      d   u    d  u    Vì      u    d
u ; nP  4; 3;  1 . d P     
ud  nP 
Tọa độ giao điểm H     P là nghiệm của hệ x  t   y  1 t   t  2   H  2  ; 1  ; 4 . z  2  t 
x  2y  2z  4  0 
Lại có d;    P  d , mà H     P . Suy ra H  d . 
Vậy đường thẳng d đi qua H 2; 1; 4 và có VTCP ud  4; 3;1 nên có phương trình
x  2  4t 
d :  y  1 3t t   .
 z  4  t 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 51
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x  2 y  2 z Câu 4:
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d :   và mặt phẳng 2 1 1
P : x  2 y  z  3  0. Viết phương trình đường thẳng  nằm trong P sao cho  vuông
góc với d và khoảng cách giữa hai đường thẳng  và d bằng 2.  x  7 y z  4  x  7 y z  4  :     :   1 1  1   1 1 1 A.  . B.  . x  3 y z  x  3 y z  :    :    1 1  1  1 1 1   x  7 y z  4  x  7  y z  4  :     :   2 1 1  1 1  1  C.  . D.  x  3 y z  x  3  y z 1  :    :    1 4 1  1 1  1 Hướng dẫn giải:  
Đường thẳng d có VTCP u  2;1; 
1 . Mặt phẳng  P có VTPT n   ta có p 1;2;  1 , d  
n ,u   3; 3  ; 3  p d   
 1  
Vì    P,   d  VTPT u  u ;u      0; 1;  1 3 d  
Khi đó, phương trình mặt phẳng Q : y  z  m  0
Chọn A1;2;0  d, ta có: 2   m m  4 d  ;
A Q  d ;d   2   2   2 m  0 
Với m  4  Q : y  z  4  0 x  7 y z  4
Vì    P  Q   đi qua B 7; 0; 4   :   1 1 1
Với m  0  Q : y  z  0 x  3 y z
Vì    P  Q   đi qua C 3;0; 0   :   1 1  1 Chọn A. Câu 5:
Cho hai điểm A 3;3;  1 , B 0;2; 
1 và mặt phẳng   : x  y  z  7  0 . Đường thẳng d nằm
trên   sao cho mọi điểm của d cách đều 2 điểm ,
A B có phương trình là x  t x  t x  t  x  2t    
A.  y  7  3t .
B.  y  7  3t .
C.  y  7  3t .
D.  y  7  3t . z  2t     z  2t  z  2t  z  t  Hướng dẫn giải: Chọn A.
Mọi điểm trên d cách đều hai điểm ,
A B nên d nằm trên mặt phẳng trung trực của đoạn AB .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 52
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz   3 5  Có AB   3
 ; 1; 0 và trung điểm AB là I ; ;1 
 nên mặt phẳng trung trực của AB là:  2 2   3   5  3  x   y 
 0  3x  y  7  0     .  2   2  3
 x  y  7  0
 y  7  3x
Mặt khác d    nên d là giao tuyến của hai mặt phẳng:    .
x  y  z  7  0 z  2x   x  t 
Vậy phương trình d :  y  7  3t t   . z  2t  x  2 y 1 z Câu 6:
Trong không gian với hệ tọa độ Oxyz cho đường thẳng d :   và mặt phẳng 1 2 1 
P : x  y  z  3  0. Gọi I là giao điểm của d, P. Tìm M P sao cho MI vuông góc
với d và MI  4 14. M 5;9;1  1 M 5;7; 1   1 A.  . B.  . M  3  ; 7  ;13  M  3  ; 7  ;13  M  5  ;9; 1   1 M 5; 7  ;1  1 C.  . D.  . M 3; 7  ;13  M 3; 7; 1  3  Hướng dẫn giải:
Vì I  d nên I 2  t;1 2t; t  .
Hơn nữa I   P  2  t 1 2t  3  0  t  1   I 1;1;  1 M  
 P  a  b  c  3 Gọi M a; ; b c. Do:   
MI  d  IM .u  0  a  2b  c  2  0  d  
IM  a 1;b 1;c  
1 ,u  1;2;   1 d  2 2 2
Do MI  4 14  a   1  b   1  c   1  224.
Khi đó ta có hệ phương trình: a b c 3     b  2a 1 a  5 a  3       
a  2b  c  2  0
 c  4  3a  b  9  b  7      
 a  2  b  2  c  2   a  2 c  11  c  13 1 1 1 224 1  16   
Với a;b;c  5;9;1  1  M 5;9; 1   1 Với a; ; b c   3
 ; 7;13  M 3; 7  ;13 Chọn A. Câu 7:
Trong không gian Oxyz, cho hai mặt phẳng  P : x  2y  2z  0,Q : 2x  2 y  z 1  0.
Viết phương trình của đường thẳng d đi qua A0;0; 
1 , nằm trong mặt phẳng Q và tạo
với mặt phẳng  P một góc bằng 0 45 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 53
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x  t x  t x  t x  t    
A. d :  y  t
; d :  y  t  .
B. d :  y  2t 1;d :  y  1 t . 1 2 1 2 z 1 4t    z  1     z  1 4t z  1   x  t x  3t x  1 4t x  t    
C. d :  y  t 1 ; d : y  t  .
D. d :  y  1 t ;d :  y  t  1 2 1 2 z 1 4t    z  1 4t     z  1 4t z  1   Hướng dẫn giải:  
Ta có n  2;2; 
1 là vecto pháp tuyến của Q,b  1;2; 2 là vec tơ pháp tuyến của  P . 
Gọi a  a b c 2 2 2 ; ;
, a  b  c  0 là một vecto chỉ phương của d.
Vì đường thẳng d đi qua A0;0;  1 mà A0;0; 
1 , A  Q    
Do đó d  Q  a  n  .
a n  0  2a  2b  c  0  c  2  a  2b
Góc hợp bởi d và  P bằng 0 45 :     . a b 2
a  2b  2c 0  sin 45  cos  ; a b      2 2 2 a . b 2
3 a  b  c
 18(a  b  c )  4 a  2b  2c2 2 2 2  a  b
a  b b  1 a  1;c  4 a  b  b  1
  a  1; c  0 x  t x  t  
Vậy d :  y  t
; d :  y  t
 là các đường thẳng cần tìm. 1 2 z 1 4t    z  1   Chọn A. Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa
mãn CD  2AB và diện tích bằng 27; đỉnh A 1
 ; 1; 0; phương trình đường thẳng chứa x  2 y  1 z  3 cạnh CD là  
. Tìm tọa độ các điểm D biết hoành độ điểm B lớn hơn 2 2 1 hoành độ điểm . A A. D  2  ; 5  ;  1 . B. D  3  ; 5  ;  1 . C. D 2; 5  ;  1 . D. D 3; 5  ;  1 Hướng dẫn giải: 
Đường thẳng CD qua M 2; 1
 ;3 có vec tơ chỉ phương u  2;2;  1
Gọi H 2  2t; 1
  2t;3  t  là hình chiếu của A lên CD, ta có:  
AH .u  2 3  2t;2.2t  (3  t   t  1   H 0; 3  ; 2, d  ,
A CD  AH  3 Từ giả thiết ta có: 2S AB  CD  3 ABCD AB 
 18  AB  6; DH  3; HC  9 AH
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 54
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz    AB 
Đặt AB  tu  2t;2t;t   t  0 x  x   t    2  AB 4; 4; 2  B 3;3; 2 B A  u  9  HC 
AB  6;6;3  C 6;3;5 6  3  HD   AB   2  ; 2  ;   1  D 2; 5  ;  1 6 Chọn A. x 1 y  2 z Câu 9:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   ; 1 1 2 1 x  2 y 1 z 1 d :  
và mặt phẳng  P : x  y  2z  5  0. Lập phương trình đường 2 2 1 1
thẳng d song song với mặt phẳng  P và cắt d , d lần lượt tại ,
A B sao cho độ dài đoạn 1 2
AB đạt giá trị nhỏ nhất. x 1 y  2 z  2 x 1 y  2 z  2 A. d :   . B. d :   . 1 1 1 1 1 1 x 1 y  2 z  2 x  2 y  2 z  2 C. d :   . D. d :   1 1 1 1 1 1 Hướng dẫn giải:
Vì A  d ; B  d  A 1   a; 2
  2a; a , B 2  2 ; b 1 ; b 1 b 1 2     
Ta có AB  a  2b  3; 2
 a  b  3; a  b   1      AB  n
P có vec tơ pháp tuyến n  1;1;2, AB / / P   A  P      
AB  n  A .
B n  0  a  2b  3  2a  b  3  2a  2b  2  0  b  a  4  AB  a  5; a 1;3 2 2 2 2
Do đó: AB  a  5  a  
1  3  2a  2  27  3 3
 min AB  3 3 khi a  2  A1;2;2  AB   3  ; 3  ; 3
 , A1;2; 2   P x 1 y  2 z  2
Vậy phương trình đường thẳng d :   . 1 1 1 Chọn A. x  3 y  2 z  1
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và mặt 2 1 1
phẳng  P : x  y  z  2  0. Gọi M là giao điểm giữa d và  P . Viết phương trình đường
thẳng  nằm trong mặt phẳng  P , vuông góc với d đồng thời khoảng cách từ M đến  bằng 42.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 55
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  x  5 y  2 z  5  x  5 y  2 z  5  :     :   2 3  1  2 3  1 A.  . B.  . x  3 y  4 z  5  x  3 y  4 z  5  :    :    2 3  1  2 3  1  x  5 y  2 z  5  x  5 y  2 z  5  :     :   2 3 1  2 3 1 C.  . D.  x  3 y  4 z  5  x  3 y  4 z  5  :    :    2 3  1  2 3 1 Hướng dẫn giải:
x  3  2t 
Phương trình tham số của d : y  2   t z  1   t   
Mặt phẳng  P có VTPT n  1;1;  1 , d có VTCP u   d 2;1;  1 P
Vì M  d   P  M 1;3;0   
Vì  nằm trong  P và vuông góc với d nên: VTCP u  u ;n     2; 3;  1 d P    Gọi N  ;
x y; z  là hình chiếu vuông góc của M trên  , khi đó: MN   x 1; y  3; z    MN  u  
x  y  z  2  0    N  5; 2  ; 5
Ta có: N  P
 2x  3y  z 11  0      N 3; 4  ;5 2 2    MN  42    x   1   y  3 2  z  42  x  5 y  2 z  5
Với N 5; 2; 5   :   2 3  1 x  3 y  4 z  5
Với N 3; 4;5   :   2 3 1 Chọn A. x y z 1
Câu 11: Trong không gian với hệ tọa độ Oxyz cho điểm A1; 2;3, đường thẳng d :   2 1 2
và mặt phẳng  P : x  2 y  z 1  0. Gọi d ' là đường thẳng đối xứng với d qua  P. Tìm
tọa độ điểm B trên d ' sao cho AB  9.   62 16 151 2
 6  2 151 31 8 151  B  ; ;   27 27 27     A.  .
 62 16 151 26  2 151 31 8 151  B  ; ;    27 27 27       62  151 2  6  151 31 151  B  ; ;   27 27 27     B.  .  62  151 2  6  151 31 151  B  ; ;    27 27 27    
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 56
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  16 151 2 151 8 151  B  ; ;   27 27 27     C.  .  1  6 151 2  151 8 151  B  ; ;    27 27 27       62  4 151 2
 6  2 151 31 8 151  B  ; ;   27 27 27     D.   624 151 2
 6  2 151 31 8 151  B  ; ;    27 27 27     Hướng dẫn giải:
Có d cắt  P tại I 2; 1; 
1 . Chọn M 0;0; 
1  d và M ' là điểm đối xứng của M qua
P. Khi đó M 'd '. Ta tìm M '.
Gọi  là đường thẳng đi qua M và vuông góc với mặt phẳng  P   x y z 1
 VTCP u  VTPT n        P 1;2  1 : 1 2 1 
Gọi H là trung điểm MM ' thì tọa độ H định:  x y z 1    1 2 2  1 2 2  1 2 1 
 x   ; y   ; z    H  ;  ;  .   3 3 3  3 3 3 
x  2y  z 1  0   2 4 1 
Từ đó: M '2x  x ; 2 y  y ; 2z  z     H M H M H M  ; ;    3 3 3 
Suy ra d’ là đường thẳng đi qua I 2; 1;  1 nhận VTCP:   8 1 4  x  2 y 1 z 1 M ' I  ; ;  d ' :      3 3 3  8 1 4
B  d '  B 2  8t; 1
  t;1 4t 
Theo đề bài ta phải có: 1 2 151
AB  9  1 8t 2  t  32  4t  22 2
 81  81t  6t  67  0  t  27
  62 16 151 26  2 151 31 8 151  B  ; ;   27 27 27    
   6216 151 262 151 318 151 B ; ;    27 27 27     Chọn A.
Câu 12: Cho hai điểm M 1; 2;3, A2;4; 4 và hai mặt phẳng  P : x  y  2z 1  0,
Q : x  2y  z  4  0 . Viết phương trình đường thẳng  qua M cắt  P, Q lần lượt tại , B C
sao cho tam giác ABC cân tại A và nhận AM là đường trung tuyến.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 57
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x 1 y  2 z  3 x 1 y  2 z  3 A.  :   B.  :   1  1  1 2 1  1 x 1 y  2 z  3 x 1 y  2 z  3 C.  :   D.  :   1 1 1 1 1  1 Hướng dẫn giải: Gọi B  ; a ;
b c , từ giả thiết suy ra M là trung điểm của BC , suy ra C 2  ; a 4  ; b 6  c.
B  P, C
Q nên có hai pt: a  b  2c 1  0  
1 ;  a  2b  c  8  0 2.   AM 1; 2  ;   1 , BC 2  2 ; a 4  2 ; b 6  2c.  
Tam giác ABC cân tại A nên: AM .BC  0  a  2b  c  8  0 3.
a  b  2c 1  0 a  0   Từ  
1 , 2 và 3 có hệ: a  2b  c  8  0  b  3  B 0;3;2, C 2;1; 4. a 2b c 8 0      c  2   x 1 y  2 z  3
Đường thẳng  qua B và C có pt  :   . 1 1  1 Chọn D.
Câu 13: Trong không gian với hệ trục tọa độ Oxyz, gọi d là đường thẳng đi qua điểm A  1  ; 0;   1 , x 1 y  2 z  2 cắt  
, sao cho cos d; là nhỏ nhất, biết phương trình của đường thẳng 2  2 1 1  x  3 y  2 z  3  :  
. Phương trình đường thẳng d là? 2 1  2 2 x 1 y z 1 x 1 y z 1 A.   B.   2 2 1  4 5 2  x 1 y z 1 x 1 y z 1 C.   D.   4 5 2  2 2 1 Hướng dẫn giải:
Gọi M  d    M 1 2t; 2  t; 2   t . 1    
d có vectơ chỉ phương là ud  AM  2t  2;t  2; 1   t  . 
 có vectơ chỉ phương u2   1  ; 2; 2 . 2 2 2 t cos d;   . 2  2 3 6t 14t  9
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 58
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 2 t
Xét hàm số f t  
, ta suy ra được min f t   f 0  0 . 2 6t 14t  9 
Do đó min cos d;    0
t  . Nên AM  2; 2;   1 . 2    khi 0 x 1 y z 1
Vậy phương trình đường thẳng d là:   . 2 2 1  Chọn A.
Câu 14: Trong không gian với hệ tọa độ Oxyz, cho điểm A 1; 0; 2 và đường thẳng d có phương x  1 y z  1 trình:  
. Viết phương trình đường thẳng  đi qua A , vuông góc và cắt d . 1 1 2 x  1 y z  2 x  1 y z  2 A.  :   . B.  :   . 1 1 1 1 1 1  x  1 y z  2 x  1 y z  2 C.  :   . D.  :   . 2 1 1 1 3 1 Hướng dẫn giải: B  
Do  cắt d nên tồn tại giao điểm giữa chúng. Gọi B    d  .  Bd  x  t  1 
Phương trình tham số của d :  y  t ,t   . Do B  d , suy ra Bt  1;t; t  1 z  t 1  
 AB  t;t; 2t  3 
Do A, B   nên AB là vectơ chỉ phương của  .   
Theo đề bài,  vuông góc d nên AB  u ( u  (1; 1; 2) là vector chỉ phương của d ). Suy ra    x  1 y z  2 A .
B u  0 . Giải được t  1  AB  1;1; 1   . Vậy  :   . 1 1 1  Chọn B.
Câu 15: Trong không gian tọa độ Oxyz cho M(2;1;0) và đường thẳng d có phương trình: x 1 y 1 z  
. Gọi  là đường thẳng đi qua M, cắt và vuông góc với d. Viết phương 2 1 1 
trình đường thẳng  ? x  2  t x  2  t x  1 t x  2  t    
A. y  1 4t
B. y  1 4t
C. y  1 4t
D. y  1 4t z  2t     z  3  2t  z  2t  z  2t  Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 59
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x  1 2t 
PTTS của d là y  1   t . z  t 
Gọi H là hình chiếu vuông góc của M lên d, đường thẳng  cần tìm là đường thẳng MH. 
Vì H thuộc d nên H 1 2t; 1   t; t
  suy ra MH  (2t 1;2  t; t  ) .    2
Vì MH  d và d có 1 VTCP là u  (2;1; 1
 ) nên MH .u  0  t  . Do đó 3   1 4  2   MH  ; ;    3 3 3  x  2  t 
Vậy PTTS của  là: y  1 4t . z  2t  Chọn A.
Câu 16: Trong không gian với hệ tọa độ MN  N t; 5
  2t;1 t  gọi d đi qua A 1  ; 0;   1 , cắt x 1 y  2 z  2 x  3 y  2 z  3  :  
, sao cho góc giữa d và  :   là nhỏ nhất. 1 2 1 1  2 1  2 2
Phương trình đường thẳng d là x 1 y z 1 x 1 y z 1 x 1 y z 1 x 1 y z 1 A.   . B.   . C.   . D.   . 2 2 1  4 5 2  4 5 2 2 2 1 Hướng dẫn giải:
Gọi M  d    M 1 2t; 2  t; 2   t 1    
d có vectơ chỉ phương a  AM  2t  2;t  2; 1   t d  
 có vectơ chỉ phương a  1; 2; 2 2   2 2 2 t cos d;   2  2 3 6t 14t  9 2 t
Xét hàm số f t  
, ta suy ra được min f t   f 0  0  t  0 2 6t 14t  9 
Do đó min cos , d   0  t  0  AM  2; 2   1   x 1 y z 1
Vậy phương trình đường thẳng d là   2 2 1 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 60
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x  2  t  x 1 y z  2
Câu 17: Trong không gian với hệ tọa độ  y  3  2t cho hai đường thẳng d :   và 1  2 1 1  z  1   2t  x 1 y  2 z  2 d :  
. Gọi  là đường thẳng song song với  P : x  y  z  7  0 và cắt 2 1 3 2
d , d lần lượt tại hai điểm ,
A B sao cho AB ngắn nhất. Phương trình của đường thẳng  1 2 là.    x  6  t x  6
x  6  2t
x  12  t      5  5  5 A.  y  5 . B.  y  .
C.  y   t .
D.  y   t .  2 2 2 z  9  t      9  9  9 z    t  z    t z    t  2   2   2 Hướng dẫn giải:
A d  A 1 2a; a; 2   a 1  
B  d  B 1 ; b 2  3 ; b 2  2b 2   
 có vectơ chỉ phương AB  b  2a;3b  a  2; 2
 b  a  4 
P có vectơ pháp tuyến n  1;1;  1 P     
Vì  / /  P nên AB  n  A .
B n  0  b  a 1.Khi đó AB  a 1; 2a  5;6  a P P
AB  a  2
1  2a  52  6  a2 2
 6a  30a  62 2  5  49 7 2  6 a    ; a       2  2 2 5  5 9    7 7 
Dấu "  " xảy ra khi a   A 6; ;  , AB   ; 0;     2  2 2   2 2   5 9  
Đường thẳng  đi qua điểm A 6; ;  
 và vec tơ chỉ phương u   1  ; 0;  1 d  2 2   x  6  t   5
Vậy phương trình của  là  y  2   9 z    t   2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 61
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x y 1 z  2
Câu 18: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   và 1 2 1  1 x  1   2t 
d :  y  1 t
. Phương trình đường thẳng vuông góc với  P : 7x  y  4z  0 và cắt hai 2 z  3 
đường thẳng d , d là: 1 2 x  7 y z  4 x  2 y z 1 A.   . B.   . 2 1 1 7 1 4  x  2 y z 1 x  2 y z 1 C.   . D.   . 7  1  4 7 1 4 Hướng dẫn giải:
Gọi d là đường thẳng cần tìm
Gọi A  d  d , B  d  d 1 2
A  d  A 2a;1 a; 2  a 1  
B  d  B 1   2 ; b 1 ; b 3 2    AB   2
 a  2b 1; a  ; b a  5   
P có vectơ pháp tuyến n  7;1;4, d  P  AB,n cùng phương P p  
 có một số k thỏa AB  k np
2a  2b 1  7k  2
 a  2b  7k  1 a  1   
 a  b  k
 a  b  k  0  b   2   a 5 4k  a 4k 5          k  1     
d đi qua điểm A2; 0;  
1 và có vectơ chỉ phương a  n  7;1 4 d P  x  2 y z 1
Vậy phương trình của d là   7 1 4 x 1 y  2 z 1
Câu 19: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng  :   và 1 3 1 2 x  3 x 1 y z 1   :  
. Phương trình đường thẳng song song với d :  y  1
  t và cắt hai 2 1 2 3 z  4  t 
đường thẳng  ;  là: 1 2 x  2 x  2  x  2  x  2    
A. y  3  t .
B. y  3  t .
C. y  3  t .
D. y  3  t . z  3  t     z  3  t  z  3  t  z  3  t  Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 62
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Gọi  là đường thẳng cần tìm
Gọi A     , B     1 2
A    A 1 3a; 2  a;1 2a 1  
B    B 1 b; 2b; 1   3b 2   
AB  3a  b  2; a  2b  2; 2
 a  3b  2 
d có vectơ chỉ phương a  0;1;  1 d  
 / /d  AB, a cùng phương d  
 có một số k thỏa AB  k ad
3a  b  2  0  3
 a  b  2  a  1   
 a  2b  2  k  a  2b  k  2  b  1
 2a 3b 2 k  2a 3b k 2          k  1    
Ta có A2;3;3; B 2;2;2 
 đi qua điểm A 2;3;3 và có vectơ chỉ phương AB  0; 1  ;   1 x  2 
Vậy phương trình của  là y  3  t z  3  t  A  3  ;3; 3
  : 2x – 2 y  z 15  0
Câu 20: Trong không gian Oxyz , cho điểm thuộc mặt phẳng và S  2 2 2
: (x 2)  (y 3)  (z 5)  100 mặt cầu
. Đường thẳng  qua A, nằm trên mặt phẳng
  cắt (S) tại A , B . Để độ dài AB lớn nhất thì phương trình đường thẳng  là: x  3 y  3 z  3 x  3 y  3 z  3 A.   . B.   . 1 4 6 16 11 10
x  3  5t  x  3 y  3 z  3 C. y  3 . D.   .  1 1 3 z  3   8t  Hướng dẫn giải:
Mặt cầu S  có tâm I 2;3;5 , bán kính R  10 . Do d(I, ( ))  R nên  luôn cắt S tại A , B . Khi đó AB  R  d  2 2 (I, )
. Do đó, AB lớn nhất thì d  I, nhỏ nhất nên  qua H , x  2  2t 
với H là hình chiếu vuông góc của I lên   . Phương trình BH : y  3  2t z  5  t 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 63
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
H  ( )  2 2  2t   2 3 – 2t   5  t 15  0  t  2   H  2  ; 7; 3 .  x  3 y  3 z  3
Do vậy AH  (1; 4; 6) là véc tơ chỉ phương của  . Phương trình của   1 4 6
Câu 21: Phương trình nào sau đây không phải là phương trình hình chiếu vuông góc của đường thẳng x  1 2t  d:  y  2
  3t , t  R trên mặt phẳng (Oxy): z  3  t 
x  3  2t '
x  1 4t '
x  1 2t '   
A.  y  1 3t ' ,t ' R B.  y  2
  6t ',t ' R C. y  2  3t ',t ' R D. z  0    z  0  z  0 
x  5  2t ' 
 y  4  3t ',t '  R z  0  Hướng dẫn giải:
A(1;-2;3), B(3;1;4) thuộc d. Hình chiếu của A,B trên mặt phẳng (Oxy) là A/(1;-2;0), B/(3;1;0) 
Phương trình hình chiếu đi qua / A hoặc /
B và nhận véc tơ cùng phương với / / A B  2;3;0 làm véc tơ chỉ phương. Chọn C. x 12 y  9 z 1
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   , và mặt 4 3 1
thẳng  P: 3x  5y  z  2  0 . Gọi d 'là hình chiếu của d lên  P.Phương trình tham số của d ' là x  62t x  62t x  62t x  62t    
A.  y  25t .
B.  y  25t .
C. y  25t .
D.  y  25t .
z  2  61t     z  2  61t  z  2   61t  z  2  61t  Hướng dẫn giải: Cách 1:
Gọi A  d   P
A  d  A12  4a;9  3 ; a 1 a
A  P  a  3   A0;0; 2  
d đi qua điểm B 12;9;  1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 64
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Gọi H là hình chiếu của B lên  P 
P có vectơ pháp tuyến n  3;5;   1 P  
BH đi qua B 12;9; 
1 và có vectơ chỉ phương a
 n  3;5;   1 BH P
x  12  3t 
BH : y  9  5t z 1 t 
H  BH  H 12  3t;9  5t;1 t 78  186 15 113 
H  P  t    H ;  ;   35  35 7 35   186 15 183  AH  ;  ;    35 7 35  
d ' đi qua A0;0; 2 và có vectơ chỉ phương a  62; 25; 61 d '   x  62t 
Vậy phương trình tham số của d ' là  y  25t z  2   61t  Cách 2:
Gọi Q qua d và vuông góc với  P 
d đi qua điểm B 12;9; 
1 và có vectơ chỉ phương a  4;3;  1 d 
P có vectơ pháp tuyến n  3;5;   1 P   
Q qua B 12;9; 
1 có vectơ pháp tuyến n  a , n   8;7;  11 Q d P  
Q : 8x  7 y 11z  22  0
d ' là giao tuyến của Q và  P
Tìm một điểm thuộc d ' , bằng cách cho y  0 3
 x  z  2 x  0 Ta có hệ   
 M 0;0;2  d ' 8x 11z  22 y  2     
d ' đi qua điểm M 0; 0; 2
  và có vectơ chỉ phương a  n ;n   62; 25  ;  61 d P Q  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 65
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x  62t 
Vậy phương trình tham số của d ' là  y  25t z  2   61t  x  1 2t 
Câu 23: Trong không gian với hệ tọa độ BH cho đường thẳng d :  y  2
  4t . Hình chiếu song z  3 t  x  1 t  BH : y  1   2t
z  3  2t    song của a  n  1; 2  ; 2
lên mặt phẳng H  BH  H 1 t; 1
  2t;3  2t  theo BH Q  10  1 11 7 
H  P  t    H  ; ;   9  9 9 9  x 1 y  6 z  2 phương  :   có phương trình là: 1  1 1
x  3  2t x  3  t x  1   2t
x  3  2t     A. y  0 . B. y  0 . C. y  0 . D. y  0 . z 1 4t     z  1 2t  z  5  4t  z  1 t  Hướng dẫn giải: x  1 t  BH : y  1   2t
z  3  2t 
Giao điểm của d và mặt phẳng H  BH  H 1 t; 1
  2t;3  2t  là: M (5; 0;5) . 0 10  1 11 7 
H  P  t    H  ; ;   9  9 9 9  x  1 2t 
Trên d :  y  2
  4t chọn M bất kỳ không trùng với M (5; 0;5) ; ví dụ: M (1; 2;3) . Gọi A 0 z  3 t  x  1 t  BH : y  1   2t
z  3  2t 
là hình chiếu song song của M lên mặt phẳng H  BH  H 1 t; 1
  2t;3  2t  theo 10  1 11 7 
H  P  t    H  ; ;   9  9 9 9  x 1 y  6 z  2 phương  :   . 1  1 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 66
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x 1 y  6 z  2
+/ Lập phương trình d’ đi qua M và song song hoặc trùng với  :   . 1  1 1 x  1 t  BH : y  1   2t
z  3  2t 
+/ Điểm A chính là giao điểm của d’ và H  BH  H 1 t; 1
  2t;3  2t  10  1 11 7 
H  P  t    H  ; ;   9  9 9 9  +/ Ta tìm được ( A 3; 0;1) x  1 2t 
Hình chiếu song song của d :  y  2
  4t lên mặt phẳng z  3 t  x  1 t  BH : y  1   2t
z  3  2t  x 1 y  6 z  2
H  BH  H 1 t; 1
  2t;3  2t  theo phương  :   là đường thẳng 1  1 1 10  1 11 7 
H  P  t    H  ; ;   9  9 9 9 
đi qua M (5; 0;5) và ( A 3; 0;1) . 0 x  3  t 
Vậy phương trình là: y  0 z  1 2t 
Câu 24: Trong không gian với hệ tọa độ Q : x  2y  2z 1  0 gọi d đi qua A3; 1  ;  1 , nằm trong x y  2 z
mặt phẳng  P : x  y  z  5  0 , đồng thời tạo với  :   một góc 0 45 . Phương 1 2 2
trình đường thẳng d là
x  3  7t x  3  t  
A. y  1 8t .
B.  y  1 t . z  1  15t   z  1 
x  3  7t x  3  t
x  3  7t    C. y  1   8t . D. y  1
  t và y  1   8t . z  115t    z  1  z  115t  Hướng dẫn giải: 
 có vectơ chỉ phương a   1; 2;2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 67
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 
d có vectơ chỉ phương a  a; ; b c d  
P có vectơ pháp tuyến n  1; 1  ;  1 P  
d   P  a  n  b  a  ; c d P   1 , d  0
 45  cos , d  0  cos 45
a  2b  2c 2   2 2 2 2
3 a  b  c
 2 a  2b  2c2  9 2 2 2
a  b  c ; 2 x 1 y  2 z x 1 y z 1 c  0 Từ  :   và  :   , ta có: 2
14c  30ac  0  1  1 2 1 2 1 2 3 15a  7c  0  x  3  t 
Với c  0 , chọn a  b  1 , phương trình đường thẳng d là y  1   t z  1 
Với 15a  7c  0 , chọn a  7  c  1  5;b  8
 , phương trình đường thẳng d là
x  3  7t   y  1   8t z 115t 
Câu 25: Trong không gian với hệ tọa độ Oxyz, gọi d đi qua điểm A1;1;2 , song song với x  1 y  1 z
P : 2x  y  z  3  0 , đồng thời tạo với đường thẳng  :   một góc lớn 1 2  2
nhất. Phương trình đường thẳng d là. x  1 y  1 z  2 x  1 y  1 z  2 A.   . B.   . 1 5 7 4 5  7 x  1 y  1 z  2 x  1 y  1 z  2 C.   . D.   . 4 5 7 1 5 7 Hướng dẫn giải: 
 có vectơ chỉ phương a  1; 2  ;2   
d có vectơ chỉ phương a  a b c d  ; ;  
P có vectơ pháp tuyến n  P 2;1;  1    
Vì d   P nên a  n  a .n  0  2a  b  c  0  c  2a  b d P d P 5a  4b 1 5a  4b2 cos, d    2 2 2 2
3 5a  4ab  2b
3 5a  4ab  2b
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 68
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz a 1 5t  42 Đặt t 
, ta có: cos, d   b 2
3 5t  4t  2 5t  42  1  5 3
Xét hàm số f t  
, ta suy ra được: max f t   f   2   5t  4t  2  5  3 5 3 1 a 1
Do đó: max cos, d    t        27 5 b 5
Chọn a  1  b  5  ,c  7 x  1 y  1 z  2
Vậy phương trình đường thẳng d là   1 5  7 Chọn A. x  3 y z 1 Câu 26: Trong không gian cho đường thẳng  :   và đường thẳng 1 2 3 x  3 y 1 z  2 d :  
. Viết phương trình mặt phẳng  P đi qua  và tạo với đường thẳng 3 1 2
d một góc lớn nhất.
A. 19x 17 y  20z  77  . 0
B. 19x 17 y  20z  34  . 0
C. 31x  8 y  5z  91  . 0
D. 31x  8 y  5z  98  . 0 Hướng dẫn giải: Chọn D. 
Đường thẳng d có VTCP là u  3;1; 2 . 1   
Đường thẳng  đi qua điểm M 3;0;  
1 và có VTCP là u  1; 2;3 . 
Do    P nên M  P . Giả sử VTPT của  P là n   A B C  2 2 2 ; ;
, A  B  C  0 .
Phương trình  P có dạng A x  3  By  C  z   1  0 .  
Do    P nên u.n  0  A  2B  3C  0  A  2  B  3C .
Gọi  là góc giữa d và  P . Ta có   u .n 1
3A  B  2C 3 2
 B  3C   B  2C
sin      2 2 2 u . n
14. A  B  C
14. 2B  3C 2 2 2 1  B  C 5B  7C 1 5B  7C2   . 2 2 2 2 14. 5 12 10 14
5B 12BC 10C B BC C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 69
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 5 70
TH1: Với C  0 thì sin   . 14 14 B 1 5t  72
TH2: Với C  0 đặt t  ta có sin  . C 2 14 5t 12t 10 5t  72
Xét hàm số f t   trên  . 2 5t 12t 10 2
50t 10t 112
Ta có f t   .
5t 12t 102 2  8  8  75 t   f     5  5  14 f t 2
 0  50t 10t 112  0   .  7  7  t    f   0    5   5  5t  72
Và lim f t   lim  5 . 2 x
x 5t  12t 10 Bảng biến thiên 0 0 75 8 B 8 1  8  75
Từ đó ta có Maxf t   khi t    . Khi đó sin  . f    . 14 5 C 5 14  5  14 75 B 8
So sánh TH1 và Th2 ta có sin lớn nhất là sin  khi  . 14 C 5
Chọn B  8  C  5  A  31.
Phương trình  P là 31 x  3  8y  5 z  
1  0  31x  8 y  5z  98  0 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 70
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 27: Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng  P : x  y  z  2  0 và hai x  1 t
x  3  t  
đường thẳng d : y  t
; d ' : y  1 t .
z  2  2t   z  1 2t 
Biết rằng có 2 đường thẳng có các đặc điểm: song song với  P ; cắt d, d và tạo với d góc O
30 . Tính cosin góc tạo bởi hai đường thẳng đó. 1 1 2 1 A. . B. . C. . D. . 5 2 3 2
Hướng dẫn giải:: 
Gọi  là đường thẳng cần tìm, n là VTPT của mặt phẳng  P . P
Gọi M 1 t;t; 2  2t  là giao điểm của  và d ; M 3  t ;1 t ;1 2t là giao điểm của 
và d ' 
Ta có: MM '2  t  t;1 t  t;1 2t  2t  M    P 
MM  //  P     t  2 MM 4  t; 1
  t;3  2t  MM   n  P   3 6  t  9 t  4 Ta có O
cos30  cos MM ,ud     2 2 t  1 36t 108t 156     x  5 x  t  
Vậy, có 2 đường thẳng thoả mãn là  : y  4  t ;  : y  1  . 1 2 z 10  t z  t   1
Khi đó, cos  ,   . 1 2  2
Câu 28: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 2; 3;1 và B5; 6; 2 . Đường AM
thẳng AB cắt mặt phẳng Oxz tại điểm M . Tính tỉ số . BM AM 1 AM AM 1 AM A.  . B.  2 . C.  . D.  3 . BM 2 BM BM 3 BM Hướng dẫn giải:  
M  Oxz  M  ;
x 0;z ; AB  7; ;
3 1  AB  59 AM  x  ; 2  ; 3 z  1 và Ta có: ;  
x  2  7k x  9     Ta có: A, B, M thẳng hàng  AM  .
k AB k     3   3k   1   k z 1 k    z  0    M  ; 9 0;0.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 71
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz  BM  1 ; 4  ;
6  2  BM  118  2A . B và Chọn A.
Câu 29: Trong không gian với hệ tọa độ Oxyz, cho hai điểm ( A 2; 2
 ; 1), B 1; 2; 3 và đường x 1 y  5 z  thẳng d :  
. Tìm vectơ chỉ phương u của đường thẳng  qua A, vuông góc 2 2 1
với d đồng thời cách điểm B một khoảng bé nhất.    
A. u  (2;1; 6)
B. u  (2; 2; 1  )
C. u  (25; 29; 6)
D. u  (1; 0; 2) Hướng dẫn giải:
Cách 1 (Tự luận)
Gọi (P) là mặt phẳng qua A và vuông góc với d, B’ là hình chiếu của B lên (P)  
Khi đó đường thẳng  chính là đường thẳng AB’ và u  B'A Q  ua ( A 2; 2  ;1)  Ta có  P :   
 (P) : 2x  2 y  z  9  0 V
 TPT n  u  (2; 2; 1  )  P d x  1 2t 
Gọi d’ là đường thẳng qua B và song song d’  d '  y  2  2t
z  3 t   
B’ là giao điểm của d’ và (P)  B '( 3  ; 2
 ; 1)  u  B ' A  (1; 0; 2)  Chọn D
Cách 2: Không cần viết phương trình mặt phẳng (P) qua A và vuông góc với d. x  1 2t 
Gọi d’ là đường thẳng qua B và song song d’  d '  y  2  2t
z  3 t  
B’ d’  B ' A   2  t  3; 2
 t  4;t  4    
AB’  d  u . B ' A  0  t  2
  u  B ' A  (1;0; 2)  Chọn D d
Câu 30: Trong không gian với hệ toạ độ Oxyz, cho hai điểm A 1; 2;  
1 , B 7; 2;3 và đường thẳng
x  2  3t 
d có phương trình  y  2  t
(t  R) . Điểm M trên d sao cho tổng khoảng cách từ M
z  4  2t 
đến A và B là nhỏ nhất có tổng các tọa độ là:
A. M  2;0; 4 .
B. M  2;0;  1 .
C. M  1;0;4 .
D. M  1;0;2 . Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 72
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Nếu M nằm trên d thì điểm I có tọa độ là M=(2+3t;-2t;4+2t). Từ đó ta có: 
 AM   t    t t    AM   t  2    t 2   t  2 3 1; 2 2 ;2 5 3 1 2 2 2 5  2 2 2
Tương tự:  BM  3t  5;2  2t;2t  
1  BM  3t  5  2  2t   2t   1 2 2 2 2 2 2
Từ (*): MA=MB = 3t  
1  2  2t  2t  5 = 3t  5  2  2t   2t   1 Hay: 2 2
 17t  34t  30  17t  36t  30  34t  36t  0 11  70t  0  t  0
Tọa độ M thỏa mãn yêu cầu là: M=(2;0;4 ). Chọn A.  6 
Câu 31: Trong không gian với hệ trục tọa độ Oxyz, cho điểm (
A 2;3;0), B(0;  2; 0), M ;  2; 2    5  x  t 
và đường thẳng d : y  0
.Điểm C thuộc d sao cho chu vi tam giác ABC là nhỏ nhấ thì độ z  2  t  dài CM bằng 2 6 A. 2 3. B. 4. C. 2. D. . 5 Hướng dẫn giải:
Do AB có độ dài không đổi nên chu vi tam giác ABC nhỏ nhất khi AC  CB nhỏ nhất. 2 2
Vì C  d  C t;0; 2  t   AC   2t  2 2  9, BC   2t  2   4
 AC  CB   t 
2    t  2 2 2 2 9 2 2  4.      
Đặt u   2t  2 2;3, v   2t  2;2 ápdụngbấtđẳngthức u  v  u  v   t 
2    t  2     2 2 2 2 9 2 2 4 2 2 2
 25. Dấubằngxảyrakhivàchỉ 2 2 2t  2 2 3 7  7 3   6 7   3  khi   t   C ; 0;  CM    2  2   2.        2t  2 2 5  5 5   5 5   5  Chọn C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 73
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 32: Trong không gian với hệ tọa độ., cho bốn điểm. và. Kí hiệu d là đường thẳng đi qua D sao
cho tổng khoảng cách từ các điểm ,
A B, C đến d lớn nhất. Hỏi đường thẳng d đi qua
điểm nào dưới đây? A. M  1  ; 2;  1 .
B. N 5;7;3 .
C. P 3;4;3 .
D. Q 7;13;5 . Hướng dẫn giải: x y z
Ta có phương trình mặt phẳng qua A,B,C là:  ABC  :  
 1  2x  3y  z  6  0 . 3 2 6
Dễ thấy D   ABC  .Gọi. lần lượt là hình chiếu vuông góc của ,
A B,C trên d . Suy ra d  ,
A d   d  B, d   d C, d   AA' BB ' CC '  AD  BD  CD .Dấu bằng xảy ra khi
A '  B '  C '  D . Hay tổng khoảng cách từ các điểm ,
A B, C đến d lớn nhất khi d là x  1 2t 
đường thẳng qua D và vuông góc với mặt phẳng  ABC   d :  y  1 3t ; N  d z  1 t  chọn B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 74
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
PHƯƠNG TRÌNH MẶT CẦU NÂNG CAO A - LÝ THUYẾT CHUNG 1. Định nghĩa mặt cầu
Tập hợp các điểm trong không gian cách điểm O cố định một khoảng cách R cho trước là mặt cầu
tâm O và bán kính .
R Kí hiệu S O; R.
Trong không gian với hệ trục Oxyz : 2 2 2
- Mặt cầu S  tâm I a,b, c bán kính R có phương trình là:  x  a   y  b   z  c 2  R . - Phương trình: 2 2 2
x  y  z  2ax  2by  2cz  d  0, với 2 2 2
a  b  c  d  0 là phương trình mặt cầu
tâm I a;b;c, bán kính 2 2 2 R 
a  b  c  d .
2. Vị trí tương đối của mặt phẳng  P và mặt cầu S 
d  I, P  R khi và chỉ khi  P không cắt mặt cầu S . I P
d  I, P  R khi và chỉ khi
tiếp xúc mặt cầu  S . R
d  I, P  R khi và chỉ khi  P cắt mặt cầu S  theo H
giao tuyến là đường tròn nằm trên mặt phẳng  P có tâm H và có bán kính 2 2 r  R  d .
3. Vị trí tương đối giữa mặt cầu và đường thẳng P
a) Cho mặt cầu S O; R và đường thẳng  . Gọi H là hình
chiếu của O lên  và d  OH là khoảng cách từ O đến  O O O A H H B H
Nếu d  R thì  cắt mặt cầu tại 2 điểm phân biệt (H.3.1)
Nếu d  R thì  cắt mặt cầu tại 1 điểm duy nhất (H.3.2)
Nếu d  R thì  không cắt mặt cầu (H.3.3)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 75
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
B – BÀI TẬP TRẮC NGHIỆM Câu 1:
Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm A0; 2;0, B  1
 ;1;4 và C 3; 2  ;  1
. Mặt cầu  S  tâm I đi qua , A ,
B C và độ dài OI  5 (biết tâm I có hoành độ nguyên, O là
gốc tọa độ). Bán kính mặt cầu  S  là A. R  1 B. R  3 C. R  4 D. R  5 Hướng dẫn giải:
Phương trình mặt cầu (S) có dạng: 2 2 2
x  y  z  2ax  2by  2cz  d  0 Vì 4 điểm , O , A ,
B C thuộc mặt cầu (S) nên ta có hệ:  A  (S )
4b  d  4  0  
B  (S )   2
 a  2b  8c  d 18  0 C  (S)  
6a  4b  2c  d 14  0   2 2 2 2
OI  5  OI  5  a  b  c  5 Suy ra a  1
 ;b  0;c  2  ;d  4   R  3 Chọn B. Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho A1;0;0 , B 2; 1
 ; 2,C 1;1; 3  . Viết phương
trình mặt cầu có tâm thuộc trục Oy, đi qua A và cắt mặt phẳng  ABC  theo một đường
tròn có bán kính nhỏ nhất. 2 2  1  5  1  5 A. 2 2 x  y   z  2 2   .
B. x  y   z    .  2  4  2  4 2 2  1  9  3  5 C. 2 2 x  y   z  2 2   .
D. x  y   z     2  4  2  4 Hướng dẫn giải:
Mặt phẳng  ABC  có phương trình: x  y  z 1  0
Gọi S  là mặt cầu có tâm I Oy và cắt  ABC  theo một đường tròn bán kính r nhỏ nhất.
Vì I  Oy nên I 0;t;0, gọi H là hình chiếu của I lên  ABC  khi đó là có bán kính
đường tròn giao của  ABC  và S  là 2 2 r  AH  IA  IH . 2 2 t 1 t  2t 1 2t  2t  2 Ta có 2 2
IA  t 1, IH  d  I , ABC  2 
 r  t  1  . 3 3 3 1  1  5
Do đó, r nhỏ nhất khi và chỉ khi t  . Khi đó 2 I 0; ;0 , IA    2  2  4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 76
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 2  1  5
Vậy phương trình mặt cầu cần tìm là: 2 2 x  y   z     2  4 Chọn A. Câu 3:
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu có tâm I 1; 2;3 và tiếp x y  2 z xúc với đường thẳng   . 1 2  2 2 2 233 2 2 243 A.  x   1   y  2 2  (z  3)  . B.  x   1   y  2 2  (z  3)  . 9 9 2 2 2223 2 2 333 C.  x   1   y  2 2  (z  3)  . D.  x   1   y  2 2  (z  3)  9 9 Hướng dẫn giải: 
+ Đường thẳng d đi qua M 0; 2
 ;0 có vec tơ chỉ phương u  1; 2; 2. Tính được  MI  1; 4;3.   MI ,u   233
+ Khẳng định và tính được d  I , d     u 3
+ Khẳng định mặt cầu cần tìm có bán kính bằng d  I , d  và viết phương trình: 233  x  2 1   y  22 2  (z  3)  9 Chọn A. Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình 2 2 2
x  y  z  4x  2 y  6z 12  0 và đường thẳng d : x  5  2t; y  4; z  7  t. Viết
phương trình đường thẳng  tiếp xúc mặt cầu S  tại điểm M 5;0;  1 biết đường thẳng  1
tạo với đường thẳng d một góc  thỏa mãn cos  . 7
x  5  3t
x  5 13t
x  5  3t
x  5 13t    
A.  :  y  5t   :  y  5t .
B.  :  y  5t   :  y  5t . z 1 t    z  111t     z  1 t z  111t  
x  5  3t
x  5 13t
x  5  3t
x  5 13t    
C.  :  y  5t
  :  y  5t .
D.  :  y  5t   :  y  5t z 1 t    z  111t     z  1 t z  1 21t   Hướng dẫn giải:
S   x  2   y  2   z  2 : 2 2 3
 26   S  có tâm I 2; 1
 ; 3 và bán kính R  26.  
IM  3;1; 4,u  2;0;1 là 1 VTVP của d  1   
Giả sử u  a; ;
b c là 1 VTCP của đường thẳng   2 2 2
a  b  c  0 2    
Do tiếp xúc mặt cầu S  tại M  IM  u  3a  b  4c  0  b  3a  4c 1 2  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 77
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Mà góc giữa đường thẳng  và đường thẳng d bằng .     u .u    u u  1 2 1 2a c 1 cos ,  o
c s       2 1 2   2 2 2 u . u 7
a  b  c . 5 7 1 2 Thay   1 vào 2 ta được: a  c 
a   a  c2 2 2  c   2 2
a  ac  c    2 2 2 2 7 2 5. 3 4 7 4 4
5 a  9a  24ac 16c  c  a  3c 2 2 22a 92ac 78c 0       13 a   c  11 Với a  3  c do 2 2 2
a  b  c  0 nên chọn c  1  a  3;b  5 
x  5  3t 
 phương trình đường thẳng là:  :  y  5  t z  1 t  13 Với a   c do 2 2 2
a  b  c  0 nên chọn c  1
 1  a  13;b  5 11
x  5 13t 
 phương trình đường thẳng là:  :  y  5t z  111t  Chọn A. x 1 y  2 z Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   . Tìm tọa độ 1 2 2 
điểm M thuộc đường thẳng d sao cho mặt cầu S  tâm M tiếp xúc với trục Oz có bán kính bằng 2.  6 8 2   6 8 2 
A. M 2; 0; 2  M ;  ;   .
B. M 2; 0; 2  M ; ;   .  5 5 5   5 5 5   7 8 4   6 8 2 
C. M 2; 0; 2  M ;  ;   .
D. M 4; 0; 2  M ;  ;    5 5 5   5 5 5  Hướng dẫn giải: 
Vì M  d  M 1 t; 2   2t; 2
 t . Trục Oz đi qua điểm O0;0;0 và có vtcp k  0;0;  1 ;   
OM  1 t; 2   2t; 2  t   O
 M ;k   2  2t; 1   t; 0     2
 OM ; k   5t  6t  5  
Gọi R là bán kính mặt cầu S  , ta có: R  d  M Oz  2 ;
 5t  6t  5 t  1 M 2; 2  ; 0 2 2  R 2 5t 6t 5 2 5t 6t 5 0            1    6 8 2  t  M ;  ;   5     5 5 5  Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 78
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng  ,  có phương trình: 1 2 x  2 y 1 z 1 x  2 y  3 z 1  :   ;  :  
. Viết phương trình mặt cầu có bán kính 1 2 1 4 2 1 1 1 
nhỏ nhất và tiếp xúc với hai đường thẳng  ,  ? 1 2
A. x   y  2 2 2 2  z  6 .
B. x   y  2 2 2 2  z  6 .
C. x   y  2 2 2 2  z  6 .
D. x   y  2 2 2 2  z  6 Hướng dẫn giải:
Mặt cầu có bán kính nhỏ nhất và tiếp xúc với hai đường thẳng  ,  là mặt cầu nhận đoạn 1 2
vuông góc chung của  ,  làm đường kính. Giả sử mặt cầu cần lập là S  và , A B lần 1 2
lượt là tiếp điểm của S  với  ,  . Viết phương trình  ,  dưới dang tham số thì ta có: 1 2 1 2 A 2  ; m 1 4 ;
m 1 2m, B  2   n;3  ; n 1 n
Do AB là đoạn vuông góc chung của  ,  nên: 1 2   A . B U  0   3
 n  21m  0 1    
 m  n  0  A2;1  ;1 , B  2  ;3;   1 3n  m  0 A . B U  0    2
Trung điểm I của AB có tọa độ là I 0; 2;0 nên phương trình mặt cầu cần lập là:
x   y  2 2 2 2  z  6 Chọn A. Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu  S  2 2 2
: x  y  z  2x  4 y  2z  3  0.
Viết phương trình mặt phẳng  P chứa trục Ox và cắt mặt cầu S  theo một đường tròn có bán kính bằng 3.
A.  P : y  2z  0 .
B.  P : x  2z  0 .
C.  P : y  2z  0 .
D.  P : x  2z  0 Hướng dẫn giải:
S  có tâm I 1; 2  ;  
1 và bán kính R  3.
P chứa trục Ox và cắt mặt cầu S  theo một đường tròn có bán kính bằng 3 nên P
chứa Ox và đi qua tâm I của mặt cầu.     Ta có: OI 1; 2  ;  
1 ,  P có vec tơ pháp tuyến n  i
 ,OI   0;1; 2
  và  P qua . O  
Vậy  P : y  2z  0. Chọn A. x 1 y 1 z Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và cắt mặt 2 1 1 
phẳng  P : x  2 y  z  6  0 tại điểm M . Viết phương trình mặt cầu S  có tâm I thuộc
đường thẳng d và tiếp xúc với mặt phẳng  P tại điểm ,
A biết diện tích tam giác IAM
bằng 3 3 và tâm I có hoành độ âm.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 79
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 2 2 2 2
A. S   x   2 : 1
 y   z   1  6 .
B. S   x   2 : 1
 y   z   1  36 . 2 2 2 2
C.  S   x   2 : 1
 y   z   1  6 .
D. S   x   2 : 1
 y   z   1  6 Hướng dẫn giải: 
Một vec tơ chỉ phương của đường thẳng d là u 2;1;  
1 . Một vec tơ pháp tuyến của đường 
thẳng và mặt phẳng  P là n  1; 2; 
1 . Gọi  là góc giữa đường thẳng d và mặt phẳng P.   2  2 1 1
Ta có sin   cos u, n  0  
   IMA  30 6. 6 2
Gọi R bán kính mặt cầu S   IA  .
R Tam giác IAM vuông tại A có  1 0
IMA  30  AM  R 3.S  3 3  I .
A AM  3 3  R  6 IMA 2 1
Giả sử: I 1 2t;1 t; t  ,t  2 3t  3
Từ giả thuyết ta có khoảng cách: d  I, P  R 
 t  1 t  3 (loại) 6  I  1  ;0;  1 2 2
Phương trình mặt cầu S   x   2 : 1
 y   z   1  6. Chọn A. Câu 9:
Trong không gian tọa độ Oxyz, viết phương trình mặt cầu đi qua ba điểm
A1;1; 2, B 2;1;   1 C  1  ; 2; 3
  biết tâm của mặt cầu nằm trên mặt phẳng Ox . z 2 2 2 2  12   4  1326  12   4  1327 A.  S  2 : x   y  z   2     .
B.  S  : x   y  z       .  11   11  121  11   11  121 2 2 2 2  12   4  1328  12   4  1329 C.  S  2 : x   y  z   2     .
D.  S  : x   y  z        11   11  121  11   11  121 Hướng dẫn giải:   x  2
1 1  z  22   x  22 1  z   2 1
I  Oxz nên I  ;
x 0; z , IA  IB  IC nên: x 2
1 1  z  22   x  2
1  4   z  32  12 4  12 4 
Giải hệ ta được x   ; z    I  ; 0;    11 11  11 11  1326 Bán kính R  121 2 2  12   4  1326
Phương trình mặt cầu  S  2 : x   y  z        11   11  121 Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 80
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 10: Trong không gian Oxyz cho 3 điểm A  1
 3; 1; 0, B 2;1;2 ,C 1; 2; 2 và mặt cầu S  2 2 2
: x  y  z  2x  4 y  6z  67  0. Viết phương trình mặt phẳng  P đi qua qua , A
song song với BC và tiếp xúc với mặt cầu S .S  có tâm I 1; 2;3 và có bán kính R  9. A.  P : 2
 x  2 y  z  28  0 hoặc  P :8x  4 y  z 100  0 . B.  P : 2
 x  2 y  z  28  0 hoặc  P :8x  4 y  z 100  0 . C.  P : 2
 x  2 y  z  28  0 hoặc  P :8x  4 y  z 100  0 . D.  P : 2
 x  2 y  2z  28  0 hoặc  P :8x  4y  z 1000  0 Hướng dẫn giải: 
Giả sử  P có vtpt n   A B C   2 2 2 ; ;
, A  B  C  0,P / /BC nên:      
n  BC, BC  1;1;4  .
n BC  0  A  B  4C  n   B  4C; ; B C 
P đi qua A13; 1
 ;0  phương trình:  P :  B  4C  x  By  Cz 12B  52C  0
B  4C  2B  3C 12B  52C
P tiếp xúc với S   d I,P  R   9   B  4C 2 2 2  B  C
B  2C  0 2 2
 B  2BC  8C  0   B  2C  B  4C   0  B  4C  0  B  2
Với B  2C  0 chọn 
, ta được phương trình:  P : 2
 x  2 y  z  28  0 C  1   B  4
Với B  4C  0 chọn 
, ta được phương trình:  P : 8x  4 y  z 100  0 C  1  Chọn A. S  2 2 2
: x  y  z  4x  2 y  2z  3  0,
Câu 11: Trong không gian Oxyz, cho mặt cầu mặt phẳng
P : x  y  z 1  0
A1;1;0, B 2; 2;  1 .   và hai điểm
Viết phương trình mặt phẳng P S 
song song với AB, vuông góc với mặt phẳng và cắt mặt cầu theo một đường tròn
C có bán kính bằng 3.
A.   : x  y  2z 1  0 và mp   : x  y  2z 11  0 .
B.   : x  5y  2z 1  0 và mp   : x  y  2z 11  0 .
  : x  5y  2z 11  0
C.   : x  y  2z 1  0 và mp .
D.   : x  5y  2z 1  0 và mp   : x  5y  2z 11  0 Hướng dẫn giải: 2 2 2
Pt S  viết dưới dạng  S  :  x  2   y   1   z   1  9
Suy ra S  có tâm I 2;1; 
1 , bán kính R  3.  
Ta có AB  3;1; 
1 một VTPT của mặt phẳng  P là n  1; 1  ;  1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 81
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz    Do đó  A . B n  2; 2  ; 4  0  
Gọi vec tơ là một VTPT của mặt phẳng  . Ta có:        / / AB u    AB      
  u cùng phương với  A . B n .       P u    n   1    Chọn u   A .
B n  u  1;1; 2   2   
Mặt phẳng   có một VTPT u nên phương trình có dạng x  y  2z  D  0
Gọi d là khoảng cách từ I đến mặt phẳng   cắt S  theo một đường tròn C  có bán kính r  3. Nên 2 2 d 
R  r  9  3  6 2    1  2  1  D D  1 Ta có: d  6 
 6  5  D  6   6 D  1  1 
Với D  1 thì   : x  y  2z 1  0 không qua A 1  ;1; 0 (vì 1  1 2.0 1  0 )
Nên   / / A .
B Tương tự, mặt phẳng cũng song song với A . B
Vậy có hai mặt phẳng   thỏa mãn yêu cầu bài toán có phương trình:
  : x  y  2z 1  0 và mp   : x  y  2z 11  0 . Chọn A.
Câu 12: Trong không gian Oxyz, cho hai điểm A2;0;0, B 0;2;0. Điểm C thuộc trục Ox sao
cho tam giác ABC là tam giác đều, viết phương trình mặt cầu S  có tâmO tiếp xúc với ba
cạnh của tam giác ABC. A.  S  2 2 2
: x  y  z  2 . B.  S  2 2 2
: x  y  z  2  . C.  S  2 2 2
: x  y  z  2 . D.  S  2 2 2
: x  y  z   2 Hướng dẫn giải:
Vì C  Oz  C 0;0;c và tam giác ABC đều khi và chỉ khi: 2 2 2 2 2 2
AB  AC  BC  AB  AC  BC  2  2  2  c  c  2 
Vậy C 0;0; 2 hoặc C 0;0;2
Lập luận được tứ diện OABC đều vì OA  OB  OC  2 và tam giác ABC đều.
Gọi I là trung điểm của AB thì IO  AB tại 1 1 2 2 2 2 I  OI 
AB  OA  OB  2  2  2 2 2
(Tam giác OAB vuông tại O )
Lập luận được mặt cầu S  có tâm O tiếp xúc với 3 cạnh của tam giác ABC có bán kính
R  d O, AB  IO  2.
Do đó phương trình có mặt cầu  S  2 2 2
: x  y  z  2. Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 82
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x  2 y 1 z 1
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và mặt cầu 1  2  1
S   x  2   y  2   z  2 : 1 2 1
 25. Viết phương trình đường thẳng  đi qua điểm M  1  ; 1; 2
 , cắt đường thẳng d và mặt cầu S  tại hai điểm ,
A B sao cho AB  8. x  1   6t x  1   6t  
A.  : y  1   2t .
B.  : y  1   2t . z  2   9t   z  2   9t  x  1   6t x  2   6t  
C.  : y  1 2t .
D.  : y  3   2t
z  2  9t   z  2   9t  Hướng dẫn giải: 
Gọi: M  d    M
2  t;1 2t;1 t  MM  3  t; 2  2t;3  t 1 1   1  
Mặt cầu có tâm I  1  ; 2;  1 qua I   1  ; 2;  1 qua I  1; 2;  1
Mặt phẳng  P :    P :     P    V   TPT n  MM  P 1
  P : 3  t  x  
1  2  2t  y  2  3  t   z   1  0
Gọi H là trung điểm AB thì IH  AB, IH  3 t  1  3t 15 Do IM 3 2 MH 3
d M , P        3 2 6t  8t  22 t   5 x  1   2t x  1   6t  3 
Với t  1   : y  1
  2t . Với t    :  y  1   2t .  5 z  2  t   z  2   9t  Chọn A.
Câu 14: Trong không gian Oxyz, viết phương trình mặt cầu S  tiếp xúc với mặt phẳng
Q : 2x  y  2z 1  0 tại M 1; 1  ;  
1 và tiếp xúc mặt phẳng  P : x  2y  2z  8  0  2 2
c :  x  32  y   z  2 2 1  9
c :  x  3 2
 y   z   1  9 A.  . B.  .  2 2 2
c :  x  2
1   y  22   z  32  9  
c :  x  
1   y  2   z  3  9   2 2
c :  x  32  y   z  2 2 1  9
c : x  3 2
 y   z   1  81 C.  . D.   2 2 2
c :  x  2
1   y  22   z  32  9  
c :  x  
1   y  2   z  3  81  Hướng dẫn giải: 
Mặt phẳng Q có vec tơ pháp tuyến n  2;1; 2. Đường thẳng d đi qua M và vuông góc với Q
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 83
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x  1 2t 
có phương trình là y  1   t . z  1   2t 
Lấy I 1 2t; 1
  t; 1 2t   d       MI  d  1 2t 2 2t 2 4t 8 I,  P 2 2 2 
4t  t  4t   t   1 4  4
t  1  I 3;0; 
1 , R  3  S  :  x  32  y   z  2 2 1  9 t  1   I 1; 2  ; 3
  , R  3   S  :  x  2
1   y  22   z  32  9 Chọn A.
Câu 15: Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng: x  t x  2 y 1 z 1   :   ,  : 2 2 2
 y  2  t và mặt cầu (S ) : x  y  z  2x  2 y  6z  5  0 1 1 2 3 2 z  1 2t 
Viết phương trình mặt phẳng ( ) song song với hai đường thẳng  ,  và cắt mặt cầu (S) 1 2 2 365
theo giao tuyến là đường tròn (C) có chu vi bằng . 5
A. x  5y  3z  4  0; x  5y  3z 10  0
B. x  5y  3z 10  0
C. x  5 y  3z  3  511  0; x  5y  3z  3  511  0
D. x  5y  3z  4  0 Chọn B. Hướng dẫn giải: 
+  qua M (2; 1;1) và có vectơ chỉ phương u  (1; 2; 3  ) . 1 1 1 
 qua M (0; 2;1) và có vectơ chỉ phương u  (1; 1; 2) . 2 2 2  
+ Mặt phẳng () song song với  ,  nên có vectơ pháp tuyến: u ,u   (1; 5; 3  ) 1 2 1 2  
 Phương trình mặt phẳng () có dạng: x  5y  3z  D  0
+ Mặt cầu (S) có tâm I(1; 1
 ;3) và bán kính R  4 . 2 365 365
Gọi r là bán kính đường tròn (C), ta có: 2 r   r  5 5
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 84
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 35 D  3 35 D  4
Khi đó: d  I , ( ) 2 2  R  r      5 35 5 D  10 
+ Phương trình mặt phẳng () : x  5y  3z  4  0 (1) hay x  5y  3z 10  0 (2) .
Vì  / /( ),  / /( ) nên M1 và M2 không thuộc ()  loại (1). 1 2
Vậy phương trình mặt phẳng () cần tìm là: x  5y  3z 10  0 . Chọn B.
Câu 16: Trong không gian Oxyz, cho điểm A1, 0,  
1 và mặt phẳng  P : x  y  z  3  0 . Mặt cầu S
có tâm I nằm trên mặt phẳng  P , đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác
OIA bằng 6  2 . Phương trình mặt cầu S là: 2 2 2 2 2 2
A.  x  2   y  2   z   1
 9 hoặc  x  2   y  2   z   1  9. 2 2 2 2 2 2
B.  x  2   y  2   z   1
 9 hoặc  x   1
  y  2   z  2  9 2 2 2 2 2 2
C.  x  2   y  2   z   1
 9 hoặc  x  2   y  2   z   1  9 2 2 2 2 2 2
D.  x  2   y  2   z   1
 9 hoặc  x  
1   y  2   z  2  9 Hướng dẫn giải: Gọi I  ,
x y, z  là tâm của S.
Khi đó I   P, IO  I ,
A IO  IA  AO  6  2 nên ta suy ra hệ  x  2
1  y   z  2 2 2 2 2 1 
x  y  z 
x  z 1  0  2 2 2  2 2 2
2 x  y  z  2  6  2
 x  y  z  9
x  y  z 3  0
x  y  z  3  0   
Giải hệ ta tìm được I 2, 2, 
1 hoặc I 1, 2, 2   Chọn D. x 1 y  6 z
Câu 17: Cho điểm I 1;7;5 và đường thẳng d :  
. Phương trình mặt cầu có tâm I và 2 1  3
cắt đường thẳng d tại hai điểm A, B sao cho tam giác diện tích tam giác IAB bằng 2 6015 là: 2 2 2 2 2 2 A.  x  
1   y  7   z  5  2018. B.  x  
1   y  7   z  5  2017. 2 2 2 2 2 2 C.  x  
1   y  7   z  5  2016. D.  x  
1   y  7   z  5  2019.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 85
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Hướng dẫn giải:
Gọi H là hình chiếu của I 1;7;5 trên d H 0;0;4  IH  d  I ;d   2 3 2 IH .AB 2S  AB  A  IB S   AB   8020 2 2  R  IH   2017 A  IB   2 IH  2  2 2 2
Vậy phương trình mặt cầu là:  x  
1   y  7   z  5  2017. Chọn B. x  1   t 
Câu 18: Cho điểm I (0; 0;3) và đường thẳng d :  y  2t
. Phương trình mặt cầu (S) có tâm I và cắt z  2  t 
đường thẳng d tại hai điểm ,
A B sao cho tam giác IAB vuông là: 3 8
A. x  y   z  32 2 2  .
B. x  y   z  32 2 2  . 2 3 2 4
C. x  y   z  32 2 2  .
D. x  y   z  32 2 2  . 3 3 Hướng dẫn giải:
 Gọi H 1 t; 2t;2  t  d là hình chiếu vuông góc của I lên đường thẳng d 
 IH  1 t; 2t;1 t 
 Ta có vectơ chỉ phương của d : a  1;2  ;1 và IH  d d   1  2 2 7 
 IH .a  0  1
  t  4t 1 t  0  2
  6t  0  t   H  ; ; d   3  3 3 3  2 2 2  2   2   2  2 3  IH            3   3   3  3
 Vì tam giác IAB vuông tại I và IA  IB  R . Suy ra tam giác IAB vuông cân tại I , do đó bán kính: 2 2 3 2 6 0
R  IA  AB cos 45  2IH .  2IH  2.  2 3 3 8
 Vậy phương trình mặt cầu S  : x  y   z  32 2 2  . 3 Chọn B.
Câu 19: Cho điểm A2;5; 
1 và mặt phẳng (P) : 6x  3y  2z  24  0 , H là hình chiếu vuông góc của
A trên mặt phẳng  P . Phương trình mặt cầu (S) có diện tích 784 và tiếp xúc với mặt
phẳng  P tại H, sao cho điểm A nằm trong mặt cầu là: 2 2 2 2 2 2
A.  x  8   y  8   z   1  196.
B.  x  8   y  8   z   1  196. 2 2 2 2 2 2
C.  x 16   y  4   z  7  196.
D.  x 16   y  4   z  7  196.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 86
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Hướng dẫn giải:
x  2  6t 
 Gọi d là đường thẳng đi qua A và vuông góc với P . Suy ra d :  y  5  3t z  1 2t 
 Vì H là hình chiếu vuông góc của A trên P nên H  d  (P) .
Vì H  d nên H 2  6t;5  3t;1 2t  .
 Mặt khác, H  (P) nên ta có: 62  6t   35  3t   21 2t   24  0  t  1  Do đó, H  4  ; 2;3 .
 Gọi I , R lần lượt là tâm và bán kính mặt cầu.
Theo giả thiết diện tích mặt cầu bằng 784 , suy ra 2
4 R  784  R  14 .
Vì mặt cầu tiếp xúc với mặt phẳng  P tại H nên IH  (P)  I  d .
Do đó tọa độ điểm I có dạng I 2  6t;5  3t;1 2t  , với t  1  .
 Theo giả thiết, tọa độ điểm I thỏa mãn:
 6 2  6t  35  3t   21 2t   24 t  1   14
d (I ,(P))  14  2 2 2   6 3 ( 2)        t  3  t  1  AI  14   
  t 2   t 2   t 2 2   t  2 6 3 2  14  
Do đó: I 8;8;   1 .  2 2 2
Vậy phương trình mặt cầu (S) :  x  8   y  8   z   1  196 . Chọn A. x  2 y z 1
Câu 20: Cho mặt phẳng  P : x  2y  2z 10  0 và hai đường thẳng  :   , 1 1 1 1  x  2 y z  3  :  
. Mặt cầu S  có tâm thuộc  , tiếp xúc với  và mặt phẳng  P , 2 1 1 4 1 2 có phương trình: 2 2 2  11   7   5  81 A. 2 2 2
(x 1)  ( y 1)  (z  2)  9 hoặc  x     y     z    .  2   2   2  4 2 2 2  11   7   5  81 B. 2 2 2
(x  1)  ( y 1)  (z  2)  9 hoặc  x     y     z    .  2   2   2  4 C. 2 2 2
(x 1)  ( y 1)  (z  2)  9. D. 2 2 2
(x 1)  ( y 1)  (z  2)  3. Hướng dẫn giải: x  2  t  
  :  y  t ;  đi qua điểm (
A 2;0; 3) và có vectơ chỉ phương a  (1;1; 4) . 1 2 2 z 1 t 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 87
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
 Giả sử I (2  t;t;1 t)   là tâm và R là bán kính của mặt cầu S  . 1       AI , a    5t  4
 Ta có: AI  (t;t; 4  t)   AI , a   (5t  4; 4  5t; 0) 
 d  I;     2  2 2  a 3 2
2  t  2t  2(1 t)  10 t 10
d (I, (P))   . 1 4  4 3  7 t 
 S  tiếp xúc với  và P  d(I,  )  d(I,(P))  5t  4  t 10   . 2 2 2 t  1  2 2 2 7  11 7 5  9  11   7   5  81  Với t   I  ; ;   , R 
  S  :  x     y     z    . 2  2 2 2  2  2   2   2  4  Với t  1
  I (1; 1; 2), R  3  S  2 2 2
: (x 1)  ( y  1)  (z  2)  9 . Chọn A.  x  1 
Câu 21: Trong không gian với hệ tọa độ Oxyz, cho ba đường thẳng d :  y  1,t  ;  1  z  t   x  2  x 1 y z 1
d :  y  u , u  ;   :  
. Viết phương trình mặt cầu tiếp xúc với cả d , d 2 1 2  1 1 1 z  1 u 
và có tâm thuộc đường thẳng  ? 2 2 2 2 2  1   1   1  5 A.  x   2
1  y   z   1  1. B. x   y   z         .  2   2   2  2 2 2 2 2 2 2  3   1   3  1  5   1   5  9 C. x   y   z         . D. x   y   z         .  2   2   2  2  4   4   4  16 Hướng dẫn giải: Chọn A. 
Đường thẳng d đi qua điểm M 1;1; 0 và có véc tơ chỉ phương u  . d 0;0  ;1 1   1 1 
Đường thẳng d đi qua điểm M
2; 0;1 và có véc tơ chỉ phương u  . d 0;1  ;1 2   2 2
Gọi I là tâm của mặt cầu. Vì I   nên ta tham số hóa I 1 t;t;1 t  , từ đó  
IM  t;1 t; 1   t ,
IM  1 t; t; t  . 1   2  
Theo giả thiết ta có d  I; d  d I ;d , tương đương với 1   2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 88
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz     2 2 2 IM ;u  IM ;u  1 d d 1 t  t 2 1 t 1 2 2               t  0 u u 1 2 1 d d2 Suy ra I 1;0; 
1 và bán kính mặt cầu là R  d  I;d  1. Phương trình mặt cầu cần tìm là 1 
 x  2  y   z  2 2 1 1  1.
 x  2  t 
Câu 22: Cho mặt cầu S  2 2 2
: x  y  z  2x  4z  1  0 và đường thẳng d :  y  t . Tìm m để d z  m   t
cắt S  tại hai điểm phân biệt ,
A B sao cho các mặt phẳng tiếp diện của S  tại A và tại B vuông góc với nhau. A. m  1  hoặc m  4 
B. m  0 hoặc m  4  C. m  1  hoặc m  0 D. Cả ,
A B,C đều sai Hướng dẫn giải:
Để thỏa mãn yêu cầu đề bài thì trước tiên d phải cắt mặt cầu, tức là phương trình
  t 2  t  m  t 2 2 2
 2.2  t   4.m  t  1  0 có hai nghiệm phân biệt. 2
 t  m   2 3 2
1 t  m  4m  1  0
Phương trình có hai nghiệm phân biệt khi    m  2 2 ' 0 1
 3m  12m  3  0 2
 m  5m  1  0 .
Với phương trình có hai nghiệm phân biệt, áp dụng định lí Viet ta có 2 m  4m  1 2  t t  ;t  t  m  1 1 2 1 2   3 3  
Khi đó IA  1 t ;t ;m  2  t , IB  1  t ;t ;m  2  t . 1 1 1   2 2 2    Vậy I .
A IB  1 t 1  t
 t t  m  2  t m  2  t  0 1   2  1 2  1   2 
 3t t  m  
1 t  t   m  22 1  0 1 2 1 2 2 m  1 
 m  4m  1  m  2 1  m  22 2  1  0   (TM). 3 m  4   Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 89
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 23: Trong không gian Oxyz, cho mặt cầu  S  2 2 2
: x  y  z  4x  6 y  m  0 và đường thẳng x y  1 z  1 d  :  
. Tìm m để (d) cắt (S) tại hai điểm M, N sao cho độ dài MN bằng 8. 2 1 2 A. m  2  4 B. m  8 C. m  16 D. m  1  2 Hướng dẫn giải: 2
(S) có tâm I 2;3;0 và bán kính R    2 2 2
 3  0  m  13  m m  13
Gọi H là trung điểm M, N  MH  4
Đường thẳng (d) qua A0;1; 
1 và có vectơ chỉ phương     u, AI  u   
 2;1; 2  d  I;d     3 u Suy ra 2 2 R 
MH  d  I d  2 2 ;  4  3  5
Ta có 13  m  5  13  m  25  m  1  2 Chọn D.
Câu 24: Cho đường thẳng d là giao tuyến của hai mặt phẳng ( )
 : x  2y  2z  4  0
() : 2x  2y  z 1  0, và mặt cầu S có phương trình 2 2 2
x  y  z  4x  6y  m  0 .
Tìm m để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho AB = 8. A. 9 B. 12 C. 5 D. 2 Hướng dẫn giải:   Ta có n  (2; 2; 1
 ), n  (1; 2; 2) lần lượt là VTPT của (α) và (β) 1 2  1  
Suy ra VTCP của đường thẳng d là u  n ;n   (2;1; 2), 1 2 3  
Ta có A(6;4;5) là điểm chung của hai mặt phẳng (α) và (β) nên Ad.
Mặt cầu (S) có tâm I(-2;3;0), bán kính R  13  m với m < 13.   
IA  (8;1;5)  IA, u   (3; 6;6)  d(I, d)  3   AB
Gọi H là trung điểm của AB  AH   4 vµ IH  3 . 2
Trong tam giác vuông IHA ta có: 2 2 2 2
IA  IH  AH  R  9  16
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 90
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
 13  m  25  m  1
 2 . Vậy m = 12 là giá trị cần tìm. Chọn B.
Câu 25: Trong không gian với hệ trục tọa độ Oxyz, cho (
A 1; 0; 2), B(3;1; 4),C(3; 2  ;1) . Tìm tọa độ
điểm S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng
3 11 và S có cao độ âm. 2 A. S (4; 6  ; 4) . B. S (3; 4; 0) . C. S (2; 2;1) .
D. S (4;6; 4) . Hướng dẫn giải:    
Ta có AB  (2;1; 2); AC  (2; 2  ; 1
 ) , suy ra AB  AC . S
Tam giác ABC vuông nên I và S có thể sử dụng các tính chất của phép dụng tâm để tính. N Tính được IM. I    A C
MI  ( ABC)  MI  k  AB, AC   k   M   B
AS  2MI , tìm S.  
 AB, AC   (3;6; 6)     1  5  Gọi M 3; ; 
 là trung điểm BC. Ta có:  2 2  2  3 11  9 81 9 2 2 2
IM  IB  BM       IM   2  2 4 2      9 1
MI  ( ABC)  MI  k  AB, AC   k (3; 6; 6) 
 MI  9 k . Suy ra
 9 k  k     2 2 1   k 
thì AS  2MI  3;6; 6
   S 4;6;4 2 Chọn D.
Câu 26: Trong không gian với hệ tọa độ Oxyz , cho điểm A 0;0; 4 , điểm M nằm trên mặt phẳng
Oxy và M  O . Gọi D là hình chiếu vuông góc của O lên AM và E là trung điểm của
OM . Biết đường thẳng DE luôn tiếp xúc với một mặt cầu cố định. Tính bán kính mặt cầu đó. A. R  2 . B. R  1 . C. R  4 . D. R  2 .
Hướng dẫn giải: Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 91
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Ta có tam giác OAM luôn vuông tại O . A
Gọi I là trung điểm của OA (Điểm I cố định)
Ta có tam giác ADO vuông tại D có ID là 1
đường trung tuyến nên ID  OA  2   1 2 I
Ta có IE là đường trung bình của tam giác OAM
nên IE song song với AM mà OD  AM  OD  IE D
Mặt khác tam giác EOD cân tại E . Từ đó suy ra
IE là đường trung trực của OD M O Nên E      
DOE  ODE; IOD  IDO  IDE  IOE  90  ID  DE 2 OA
Vậy DE luôn tiếp xúc với mặt cầu tâm I bán kính R   2 2 A0;0;  1 B  ;
m 0; 0 C 0; ; n 0
Câu 27: Trong không gian với hệ tọa độ Oxyz, xét các điểm , , , D 1;1; 
1 với m  0;n  0 và m  n 1. Biết rằng khi m , n thay đổi, tồn tại một mặt cầu cố  ABC
định tiếp xúc với mặt phẳng
và đi qua d . Tính bán kính R của mặt cầu đó? 2 3 3 A. R  1 . B. R  . C. R  . D. R  . 2 2 2 Hướng dẫn giải:
Gọi I (1;1;0) là hình chiếu vuông góc của D lên mặt phẳng (Oxy) x y
Ta có: Phương trình theo đoạn chắn của mặt phẳng ( ABC) là:   z  1 m n
Suy ra phương trình tổng quát của ( ABC) là nx  my  mnz  mn  0 1  mn
Mặt khác d (I,( ABC)) 
 1 (vì m  n  1) và ID  1  d (I,( ABC)) 2 2 2 2
m  n  m n
Nên tồn tại mặt cầu tâm I (là hình chiếu vuông góc của D lên mặt phẳng Oxy ) tiếp xúc
với ( ABC) và đi qua D Chọn A.
Câu 28: Trong không gian tọa độ Oxyz cho điểm (
A 0;1;1), B(1;0; 3  ),C( 1  ; 2  ; 3  ) và mặt cầu (S) có phương trình: 2 2 2
x  y  z  2x  2z  2  0 .Tìm tọa độ điểm D trên mặt cầu (S) sao cho tứ diện
ABCD có thể tích lớn nhất.  7 4 1   1  4 5   7 4 1   7 4 1  A. D ;  ;  B. D ; ; C. D ; ; D.       D ;  ;    3 3 3   3 3 3   3 3 3   3 3 3  Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 92
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Ta có (S) 2 2 2
: (x 1)  y  (z 1)  4 suy ra (S) có tâm I(1;0;-1), bán kính R  2  
Và AB  (1; 1; 4); AC  (1; 3; 4)   
Mặt phẳng (ABC) có một vectơ pháp tuyến là n   AB, AC   ( 8  ;8; 4)   
Suy ra mp(ABC) có phương trình: 8
 x  8(y 1)  4(z 1)  0  2x  2y  z 1  0 1 Ta có V  d ( ;
D ( ABC)).S nên V
lớn nhất khi và chỉ khi d( ;
D ( ABC)) lớn nhất. ABCD 3 ABC ABCD
Gọi D D là đường kính của mặt cầu (S) vuông góc với mp(ABC). Ta thấy với D là 1 điểm 1 2
bất kỳ thuộc (S) thì d ( ;
D ( ABC))  maxd (D ;(ABC)); d (D ;(ABC)) 1 2  .
Dấu “=” xảy ra khi D trùng với D1 hoặc D2 
Đường thẳng D D đi qua I(1;0;-1), và có VTCP là nABC  (2; 2  ;1) 1 2 x  1 2t 
Do đó (D1D2) có phương trình: y  2  t . z  1    t x  1 2t  2  t   y  2  t  3
Tọa độ điểm D1 và D2 thỏa mãn hệ:    z  1 t 2   t  2 2 2
 (x 1)  y  (z 1)  4  3   7 4  1    1  4 5   D ; ; & D ; ; 1   2    3 3 3   3 3 3   7 4 1 
Ta thấy: d (D ; ( ABC))  d (D ; ( ABC)) . Vậy điểm D ;  ;  là điểm cần tìm 1 2    3 3 3  Chọn D. x 1 y z  3
Câu 29: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt cầu 1 2 1  2 2 2
S  tâm I có phương trình  S  :  x  
1   y  2   z   1
 18 . Đường thẳng d cắt S  tại hai điểm ,
A B . Tính diện tích tam giác IAB . 8 11 16 11 11 8 11 A. . B. . C. . D. . 3 3 6 9 Hướng dẫn giải: Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 93
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 
Đường thẳng d đi qua điểm C 1;0; 3
  và có vectơ chỉ phương u   1  ; 2;   1
Mặt cầu S  có tâm I 1; 2;  
1 , bán kính R  3 2
Gọi H là hình chiếu vuông góc của I lên đường thẳng d .   IC,u    Khi đó: IH   , với IC  0; 2  ; 2   ; u
2x  y  3z  4  0 2 2 2 6  2  2 66 Vậy IH   1 4 1 3 22 4 6 Suy ra HB  18   3 3 1 1 66 8 6 8 11 Vậy, S  IH  AB     . IAB 2 2 3 3 3  1 3 
Câu 30: Trong không gian Oxyz , cho điểm M  ;
;0  và mặt cầu S  2 2 2
: x  y  z  8. Đường  2 2   
thẳng d thay đổi, đi qua điểm M , cắt mặt cầu S  tại hai điểm phân biệt. Tính diện tích lớn
nhất S của tam giác OA . B A. S  7 . B. S  4 . C. S  2 7 . D. S  2 2 . Hướng dẫn giải:
Mặt cầu S  có tâm O0;0;0 và bán kính R  2 2 .
Vì OM  1  R nên M thuộc miền trong của
mặt cầu S  . Gọi A , B là giao điểm của đường A
thẳng với mặt cầu. Gọi H là chân đường cao hạ
từ O của tam giác OAB .
Đặt x  OH , ta có 0  x  OM  1, đồng thời H 2 2 2 HA 
R  OH  8  x . Vậy diện tích tam giác OAB là O M B 1 2 S 
OH .AB  OH .HA  x 8  x . OAB 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 94
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Khảo sát hàm số 2
f (x)  x 8  x trên 0; 
1 , ta được max f  x  f   1  7 . 0;  1
Vậy giá trị lớn nhất của S
 7 , đạt được khi x  1 hay H  M , nói cách khác là OAB d  OM . Chọn A.
Câu 31: Trong không gian với hệ tọa độ Oxyz , cho điểm A 2;11;5 và mặt phẳng
P mx   2
m   y   2 : 2 1 m  
1 z 10  0 . Biết rằng khi m thay đổi, tồn tại hai mặt cầu cố
định tiếp xúc với mặt phẳng  P và cùng đi qua A . Tìm tổng bán kính của hai mặt cầu đó. A. 2 2 . B. 5 2 . C. 7 2 . D. 12 2 . Hướng dẫn giải:
Gọi I a;b;c , r lần lượt là tâm và bán kính của mặt cầu. Do mặt cầu tiếp xúc với  P nên ta có 2ma   2 m   1 b   2 m   1 c 10 b  c 2
m  2ma  b  c 10
r  d  I,  P    2 m   1 2  2 m   1 2 b  c 2
m  2ma  b  c 10  r  2 m   1 2
b  c  r 2 2
m  2ma  b  c  r 2 10  0   1 
 bcr 2 2m 2mabcr 2100 2 
TH1: b  c  r  2
2 m  2ma  b  c  r 2 10  0   1
Do m thay đổi vẫn có mặt cầu cố định tiếp xúc với  P nên yêu cầu bài toán trờ thành tìm điều kiện , a , b c sao cho  
1 không phụ thuộc vào m . Do đó   1 luôn đúng với mọi b
  c  r 2  0   a  0
b  c  r 2 10  0 
b  r 2  5  0  2 2  2 2 a  0
Suy ra I 0;5  r 2; 5
   S  : x   y  5  r 2  z  5  r . c  5   r  2 2
Lại có A  S  nên suy ra: 4   11   5  r 2 2 2 2
 r  r 12 2r  40  0   r  10 2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 95
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
TH2: b  c  r  2
2 m  2ma  b  c  r 2 10  0 làm tương tự TH1 (trường hợp này không thỏa đề bài )
Tóm lại: Khi m thay đổi, tồn tại hai mặt cầu cố định tiếp xúc với mặt phẳng  P và cùng đi
qua A và có tổng bán kính là: 12 2 suy ra chọn D
Câu 32: Cho hình chóp SABC có đáy là tam giác đều cạnh bằng 6cm và SA  SB  SC  4 3 cm
.Gọi D là điểm đối xứng của B qua
C. Khi đó bán kính mặt cầu ngoại tiếp hình chóp SABD bằng? A. 5cm
B. 3 2cm C. 26cm D. 37cm Hướng dẫn giải:
Cách 1: Dựng CG vuông góc với  ABC  , Qua E dựng mặt phẳng vuông góc với SB , mặt
phẳng này cắt CG tại F. Suy ra F là tâm mặt cầu ngoại tiếp hình chóp S.ABD.Đặt SF  R Xét hình chữ nhật: 2 2
FGSH  FC  SH  FG  SH  R  CH   1 Lại có: 2 2 FC 
R  CB 2 .Từ (1) và (2) suy ra 2 2 2 2
SH  R  CH  R  CB 2 2 2 6  R 12 
R  36  5  R 12  0  R  37 cm Suy ra chọn D Cách 2:
Chọn hệ trục tọa độ như hình vẽ.
Ta có: C 0;0;0 , A3 3;3;0, B  3 
3;3; 0, S 2 3;0;6
F CG  F 
t   FA  FS   t   t  2 2 0; 0; 36 12 6
 t  1  SC  37 cm suy ra chọn D x  2 y z
Câu 33: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và mặt cầu 2 1 4
S   x  2   y  2   z  2 : 1 2 1
 2 . Hai mặt phẳng  P và Q chứa d và tiếp xúc với S 
. Gọi M , N là tiếp điểm. Tính độ dài đoạn thẳng MN. 4 A. 2 2. B. . C. 6. D. 4. 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 96
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Hướng dẫn giải: Chọn B.
Mặt cầu S  có tâm I 1; 2  ;1 , R  2 
Đường thẳng d nhận u  2; 1
 ; 4 làm vectơ chỉ phương
Gọi H là hình chiếu của I lên đường thẳng d. H  d  H 2t  2;t; 4t  Lại có:  
IH.u  0  2t 1; t   2; 4t   1 .2; 1
 ; 4  0  22t  
1  t  2  4 4t   1  0  t  0
Suy ra tọa độ điểm H 2;0;0 .
Vậy IH  1 4  1  6
Suy ra: HM  6  2  2
Gọi K là hình chiếu vuông góc của M lên đường thẳng HI . 1 1 1 1 1 3 Suy ra:      . 2 2 2 MK MH MI 4 2 4 2 4 Suy ra: MK   MN  . 3 3
Câu 34: Trong không gian với hệ tọa độ Oxyz, cho
điểm A a;0;0, B 0; ;
b 0, C 0;0;c , trong 1 2 3
đó a  0 , b  0 , c  0 và  
 7. Biết mặt phẳng  ABC  tiếp xúc với mặt cầu a b c
S   x  2   y  2   z  2 72 : 1 2 3 
. Thể tích của khối tứ diện OABC là 7 2 1 3 5 A. . B. . C. . D. . 9 6 8 6 Hướng dẫn giải: Chọn A. x y z
Cách 1: Ta có  ABC  :    1. a b c 72
Mặt cầu S  có tâm I 1; 2;3 và bán kính R  . 7 1 2 3   1 a b c 72
Mặt phẳng  ABC  tiếp xúc với  S   d  I; ABC   R   . 1 1 1 7   2 2 2 a b c
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 97
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 1 2 3 1 1 1 7 Mà    7     . 2 2 2 a b c a b c 2
Áp dụng BĐT Bunhiacopski ta có 2   1 1 1   1 2 3  1 1 1 7 2 2 2 1  2  3  2       7     .  2 2 2    2 2 2  a b c   a b c  a b c 2  1 2 3    1 1 1  2 1 2
Dấu "  " xảy ra   a b c
 a  2, b  1, c  , khi đó V  abc  . 3 OABC  6 9 1 2 3     7  a b c x y z 72
Cách 2: Ta có  ABC  :  
 1, mặt cầu S  có tâm I (1;2;3), R  . a b c 7 1 2 3   1 a b c 72
Ta có  ABC  tiếp xúc với mặt cầu S   d  I , (P)  R   1 1 1 7   2 2 2 a b c 7 1 72 1 1 1 7 1 1 1 7           7  2 2 2 2 2 2 1 1 1 7 a b c 2 a b c 2   2 2 2 a b c  a  2 2 2 2 1 1 1 1 2 3 7  1 1   1   1 3             1    0  b   1 2 2 2       a b c a b c 2  a 2   b   c 2   2 c   3 1 2  V  abc  . OABC 6 9 1 1 1 7
Cách 3: Giống Cách 2 khi đến    . 2 2 2 a b c 2
Đến đây ta có thể tìm a, b, c bằng bất đẳng thức như sau: Ta có 2 2  1 2 3   1 1 1   1 1 1  1 1 1 7 2 7     1.  2.  3.   2 2 2 1  2  3             2 2 2  2 2 2  a b c   a b c   a b c  a b c 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 98
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 1 1 1 1 1 1 7 Mà   
 Dấu “=” của BĐT xảy ra a b c  
, kết hợp với giả thiết 2 2 2 a b c 2 1 2 3 1 2 3 2 1 2  
 7 ta được a  2 , b  1, c  . Vậy: V  abc  . a b c 3 OABC 6 9  a  2  1 2 Ta có  b   1  V  abc  . OABC  6 9 2 c   3 72
Cách 4: Mặt cầu S  có tâm I 1; 2;3 và bán kính R  . 7 x y z
Phương trình mặt phẳng ( ABC) :    1. a b c 1 2 3 1 2 3  1 2 3  Ta có: 7 7 7    7     1 nên M ; ;     ABC  a b c a b c  7 7 7   1 2 3  Thay tọa độ M ; ; 
 vào phương trình mặt cầu (S ) ta thấy đúng nên M  (S ) .  7 7 7 
Suy ra: ( ABC) tiếp xúc với (S ) thì M là tiếp điểm.  1 2 3 
  6 12 18  
Do đó: ( ABC) qua M ; ; 
 , có VTPT là MI  ; ;  n    1; 2;3  7 7 7   7 7 7  x y z 2
( ABC) có phương trình: x  2 y  3z  2  0   
 1  a  2 , b  1, c  . 2 1 2 3 3 1 2 Vậy V  abc  6 9
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 99
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
GTLN, GTNN TRONG HÌNH HỌC TỌA ĐỘ OXYZ Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1; 0; 2; B 0; 1; 2 và mặt phẳng
P : x  2y  2z 12  0. Tìm tọa độ điểm M thuộc P sao cho MA  MB nhỏ nhất?  6 18 25 A.  M 2; 2;9 . B. M  ;  ; .    11 11 11   7 7 31   2 11 18  C. M ; ; . D. M  ;  ;     .  6 6 4   5 5 5  Hướng dẫn giải: Chọn D.
Thay tọa độ A 1;0; 2; B 0; 1; 2 vào phương trình mặt phẳng P , ta được
P  A P  B  0  hai điểm ,
A B cùng phía với đối với mặt phẳng P . B
Gọi A là điểm đối xứng của A qua  P . Ta có A
MA  MB  MA  MB  AB .
Nên min  MA  MB  A B
 khi và chỉ khi M là giao
điểm của AB với  P . H M  x  1 t P 
Phương trình AA :  y  2t
( AA đi qua A1;0; 2 và
 z  2  2t   A'
có véctơ chỉ phương n   ). P 1;2;  1  
Gọi H là giao điểm của AA trên  P , suy ra tọa độ của H là H 0;2; 4 , suy ra x  t  A  1  ; 4
 ; 6 , nên phương trình AB :  y  1   3t .
z  2  4t   2 11 18
Vì M là giao điểm của AB với  P nên ta tính được tọa độ  M  ;  ; .    5 5 5  Câu 2: Cho hai điểm A 1
 ,3, 2; B  9
 , 4, 9 và mặt phẳng  P : 2x  y  z 1  0. Điểm M thuộc
(P). Tính GTNN của AM  BM . 7274  31434 2004  726 A. 6  204 B. C. D. 3 26 6 3 Hướng dẫn giải: Ta có: 2.  1  3   2    
1 2.9  4  9   1  72  0  ,
A B nằm cùng phía so với mặt phẳng (P).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 100
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz 
Gọi A’ là điểm đối xứng của A qua (P). Mặt phẳng (P) có vtpt n 2, 1,  1 
x  1 2t  Đường thẳng A ’
A đi qua A  1  ,3, 2
  có vtcp n2, 1  , 
1 có pt:  y  3  t z  2   t 
Gọi H là giao của A ’
A và  P ta có: 2 1
  2t   3  t    2
  t  1  0  t  1  H 1, 2,  
1 . Ta có H là trung điểm của A ’ A  ’ A 3,1, 0. 
x  3  4t 
Đường A’B đi qua A’(3, 1, 0) có vtcp A' B  1
 2,3,9 có pt: y  1 t z  3t 
Gọi N là giao điểm của A’B và mặt phẳng  P ta có:
2.3  4t  – 1 t   3t 1  0  t  1  N  1  , 2,3.
Để MA  MB nhỏ nhất thì M  N khi đó MA  MB  ’ A B =  2 2 2 12  3  9  234  3 26 Chọn D. Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x  y  z 1  0 và hai điểm ( A 1; 3  ;0), B 5; 1
 ;2 . M là một điểm trên mặt phẳng (P) . Giá trị lớn nhất của
T  MA  MB là: 4 6 2 3 A. T  2 5. B. T  2 6. C. T  . D. T  . 2 3 Hướng dẫn giải:
Ta có: A, B nằm khác phía so với (P). Gọi B’ là điểm đối xứng với B qua (P). Suy ra B '( 1  ; 3  ;4) .
T  MA  MB  MA  MB '  AB '  2 5. Đẳng thức xảy ra khi M , , A ’ B thẳng hàng. Chọn A. Câu 4:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình
2x – y  z 1  0 và hai điểm M 3;1;0, N  9
 ; 4;9. Tìm điểm I a; ;
b c thuộc mặt phẳng
(P) sao cho IM  IN đạt giá trị lớn nhất. Biết a,b, c thỏa mãn điều kiện:
A. a  b  c  21
B. a  b  c  14
C. a  b  c  5
D. a  b  c  19. Hướng dẫn giải:
Nhận thấy 2 điểm M, N nằm về hai phía của mặt phẳng (P).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 101
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Gọi R là điểm đối xứng của M qua mặt phẳng (P), khi đó đường thẳng MR đi qua điểm M(3; x  3 y 1 z
1; 0) và vuông góc với mặt phẳng (P) có phương trình:   . Gọi 2 1 1
H  MR  (P)  H (1; 2; 1
 )  R(1;3; 2) .
Ta có IM  IN  IR  IN  RN . Đẳng thức xảy ra khi I, N, R thẳng hàng. Do đó tọa độ x  1   8t 
điểm I là giao điểm của đường thẳng NR:  y  3  t
(t là tham số ) và mặt phẳng (P).
z  2 11t 
Dễ dàng tìm được I(7; 2; 13). Chọn A. Câu 5:
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 1; 2; 2, B 5;4;4 và mặt phẳng
P : 2x  y – z  6  0. Tọa độ điểm M nằm trên (P) saocho 2 2
MA  MB nhỏ nhất là: A.  1  ;3; 2 B. 2;1; 1   1 C.  1  ;1;5 D. 1; 1  ; 7 Hướng dẫn giải:
+ Kiểm tra phương án A không thuộc (P).
+ Tính trực tiếp MA2 + MB2 trong 3 phương án B,C,D và so sánh. Chọn C. Câu 6: Trong không gian tọa độ Oxyz, cho mặt phẳng
P : 2x  y  z 1  0, A8; 7
 ; 4 , B 1; 2;2. Tìm tọa độ điểm M thuộc mặt phẳng  P sao cho 2 2
MA  2MB nhỏ nhất.
A. M 0;0;   1 . B. M 0;0;  1 . C. M 1;0;  1 . D. M 0;1;0 Hướng dẫn giải:  
Gọi I là điểm thỏa mãn IA  2IB  0  I 2;1;0     2 2 Có 2 2
MA  MB  MI  IA  MI  IB 2 2 2 2 2
 3MI  IA  2IB Vì I ,
A IB không đổi nên  2 2 MA  2MB   MI
 M là hình chiếu vuông góc của I min min
lên mặt phẳng  P .
Đường thẳng d đi qua I và vuông góc với  P. x  2  2t 
 d :  y  1 t;d   P  M 0;0;  1 z  t  Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 102
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Câu 7:
Cho 2 điểm A0, 0, 3
 , B 2, 0,  
1 và mặt phẳng  P : 3x  8y  7z 1  0. Tìm M  P sao cho 2 2
MA  2MB nhỏ nhất.  283 104 2  14   2  83 104 214  A. M ; ;   . B. M ; ;   .  183 183 183   183 183 183   283 14 1  4   283 14 14  C. M ; ;   . D. M ; ;    183 183 183   183 183 183  Hướng dẫn giải:    4 5 
Gọi I sao cho IA  2IB  0  I ;0;    3 3       2 2
MA  MA  MI  IA2 2 2
 MI  IA  2MI.IA      2 2
MB  MB  MI  IB2 2 2
 MI  IB  2MI.IB
   2 2 2 2 2
MA  2MB  3MI  IA  2IB  2MI IA  IB 2 2 2
 3MI  IA  2IB Suy ra  2 2 MA  2MB 
khi MI bé nhất hay M là hình chiếu của I trên  P. min  283 104 2  14 
Tìm được tọa độ M ; ;   .  183 183 183  Chọn A. x   2  t Oxyz   : y   1   t 2 t  Câu 8:
Trong không gian với hệ tọa độ , cho đường thẳng  hai điểm   z   t 3 
A 2;0;3 và B 2; 2  ; 3 
. Biết điểm M x ;y ;z thuộc  thì MA4 MB4  nhỏ nhất.Tìm      0 0 0  x0 A. x  0 B. x  1 C. x  2 D. x  3 0 0 0 0 Hướng dẫn giải: x   2 
Phương trình đường thẳng AB là: y   t
t   . Dễ thấy đường thẳng  và AB cắt 1  1  z   3  t 3 1 
nhau tại điểm I 2; 1; 0 suy ra AB và  đồng phẳng.      
Lại có IA 0;1; 3 , IB 0; 1  ; 3   IA  I
 B  IA  IB  AB .     2 2 1 1  1  1 1 Ta có: 2 4 MA4  MB4  MA2  MB2  MA  MB  AB4  IA  IB .         2 2 2 8 8   Do đó MA4 MB4 
nhỏ nhất khi M trùng với điểm I 2;1;0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 103
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Chọn C. Câu 9:
Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A1;2;3; B0;1;  1 ;C 1;0; 2 . Điểm M 
 P :x  y  z  2  0 sao cho giá trị của biểu thức 2 2 2
T  MA  2MB  3MC nhỏ
nhất. Khi đó, điểm M cách Q :2x  y  2z  3  0 một khoảng bằng 121 2 5 101 A. . B. 24. C. . D. . 54 3 54 Hướng dẫn giải: 2 2 2 Gọi M  ; x ;
y z . Ta có T  6x  6y  6z 8x 8y  6z  31 2 2 2  2 2 1        145
 T  6  x   y  z           3   3   2  6   145  2 2 1 2  T  6MI  với I ; ;    6  3 3 2 
 T nhỏ nhất khi MI nhỏ nhất  M là hình chiếu vuông góc của I trên P  5 5 13   M  ;  ;  .    18 18 9 
Câu 10: Trong không gian với hệ trục tọa độ Oxyz , cho A1;1; 
1 , B 0;1;2 , C  2  ; 0;  1
P : x  y  z 1  0 . Tìm điểm N  P sao cho 2 2 2
S  2NA  NB  NC đạt giá trị nhỏ nhất.  1 5 3   3 1  A. N  ; ;   . B. N 3;5;  1 . C. N  2  ;0;  1 . D. N ;  ; 2    .  2 4 4   2 2  Hướng dẫn giải: Chọn A.  1 3   3 5 
Gọi I là trung điểm BC và J là trung điểm AI . Do đó I 1  ; ;   và J 0; ;   .  2 2   4 4  1 1 Khi đó 2 2 2 2 2 2
S  2NA  2NI 
BC  4NJ  IJ  BC . 2 2
Do đó S nhỏ nhất khi NJ nhỏ nhất. Suy ra J là hình chiếu của N trên  P .  x  t   3
Phương trình đường thẳng NJ :  y   t . 4   5 z   t   4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 104
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
x  y  z 1  0  1 x   x t   2     5 Tọa độ điểm 3
J là nghiệm của hệ:      y y t  4  4    3 5 z z t       4 4
Câu 11: rong không gian với hệ tọa độ Oxyz cho ba điểm A 1;01;  1 , B 1;2; 
1 , C 4;1; 2 và mặt
phẳng  P : x  y  z  0 . Tìm trên (P) điểm M sao cho 2 2 2
MA  MB  MC đạt giá trị nhỏ
nhất. Khi đó M có tọa độ
A. M 1;1;  1 B. M 1;1;  1
C. M 1;2;   1
D. M 1;0;  1 Hướng dẫn giải:
Gọi G là trọng tâm của tam giác ABC, ta có G 2;1;0 , ta có 2 2 2 2 2 2 2
MA  MB  MC  3MG  GA  GB  GC   1
Từ hệ thức (1) ta suy ra: 2 2 2
MA  MB  MC đạt GTNN  MG đạt GTNN  M
là hình chiếu vuông góc của G trên (P).
Gọi (d) là đường thẳng qua G và vuông góc với (P) thì (d) có phương trình tham số là x  2  t   y  1 t z  t  x  2  t t   1    y  1 t x  1
Tọa độ M là nghiệm của hệ phương trình     M 1;0;   1 z  t y  0  
x  y  z  0 z  1    Chọn D.
Câu 12: (Hình Oxyz) Cho A  1
 ;3;5, B 2;6;  1 , C  4  ; 1
 2;5 và điểm  P : x  2 y  2z  5  0 .  
  
Gọi M là điểm thuộc  P sao cho biểu thức S  MA  4MB  MA  MB  MC đạt giá trị
nhỏ nhất. Tìm hoành độ điểm M. A. x  3 B. x  1  C. x  1 D. x  3  M M M M Hướng dẫn giải:   
Gọi I là điểm IA  4IB  0  I 3;7; 3
 .Gọi G là trọng tâm ta m giác ABC  G 1; 1  ;3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 105
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Nhận thấy, M,I nằm khác phía so với mp(P).
Có S  3MI  MG  3GI . Dấu bằng xảy ra khi M là giao điểm của GI và (P)  M 1;3;  1 Chọn C.
Câu 13: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2;1;  1 , B 0;3;  1 và mặt phẳng  
P : x  y  z  3  0 . Tìm tọa độ điểm M thuộc (P) sao cho 2MA  MB có giá trị nhỏ nhất. A. M 4; 1  ; 0 . B. M 1; 4  ; 0 .
C. M 4;1;0 . D. M 1; 4  ;0 . Hướng dẫn giải:    Gọi I a; ;
b c là điểm thỏa mãn 2IA  IB  0 , suy ra I 4; 1  ; 3 .   
      
Ta có 2MA  MB  2MI  2IA  MI  IB  MI. Suy ra 2MA  MB  MI  MI .  
Do đó 2MA  MB nhỏ nhất khi MI nhỏ nhất hay M là hình chiếu của I trên mặt phẳng x  4 y 1 z  3
P Đường thẳng đi qua I và vuông góc với P có là d :   . 1 1 1
Tọa độ hình chiếu M của I trên  P thỏa mãn  x  4 y  1 z  3     1 1 1   M 1; 4  ; 0 .
x  y  z  3  0  Chọn D.
Câu 14: Trong không gian
Oxyz , cho mặt phẳng
2x  2 y  z  9  0 và mặt cầu 2 2 2
(S) : (x  3)  ( y  2)  (z 1)  100 . Tọa độ điểm M nằm trên mặt cầu (S ) sao cho
khoảng cách từ điểm M đến mặt phẳng (P) đạt giá trị nhỏ nhất là:  11 14 13   29 26 7  A. M  ; ;   . B. M ;  ;    .  3 3 3   3 3 3   29 26 7   11 14 13  C. M  ; ;    . D. M ; ;    .  3 3 3   3 3 3  Hướng dẫn giải:
Mặt cầu (S ) có tâm I (3; 2  ;1) .
Khoảng cách từ I đến mặt phẳng (P) : d (I; (P))  6  R nên (P) cắt (S ) .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 106
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Khoảng cách từ M thuộc (S ) đến (P) lớn nhất  M  (d ) đi qua I và vuông góc với (P)
x  3  2t 
Phương trình (d ) :  y  2  2t . z 1 t 
Ta có: M  (d )  M (3  2t; 2
  2t;1 t)  10  29 26 7  t   M ;  ;   1   3  3 3 3  Mà: M  (S)    10  11 14 13  t    M  ; ;  2   3   3 3 3   11 14 13 
Thử lại ta thấy: d(M , (P))  d (M , (P)) nên M  ; ; thỏa yêu cầu bài toán 1 2    3 3 3 
Câu 15: Trong không gian Oxyz , cho mặt phẳng (P) : x  2 y  2z  4  0 và mặt cầu 2 2 2
(S) : x  y  z  2x  2y  2z 1  0.Giá trị của điểm M trên S  sao cho d M ,P đạt GTNN là:  5 7 7   1 1 1  A. 1;1;3 . B. ; ;   . C. ;  ;    . D. 1; 2;  1 .  3 3 3   3 3 3 
Hướng dẫn giải::
Ta có: d (M , (P))  3  R  2  (P)  (S )  .   x  1 t 
Đường thẳng d đi qua I và vuông góc với (P) có pt: y  1 2t ,t  .   z 1 2t   5 7 7   1 1 1 
Tọa độ giao điểm của d và (S) là: A ; ;   , B ;  ;     3 3 3   3 3 3  Ta có: d ( ,
A (P))  5  d (B, (P))  1.  d ( ,
A (P))  d (M , (P))  d (B, (P)).
Vậy:  d (M , (P))  1  M  . B min 2 2 2
Câu 16: Trong không gian Oxyz cho mặt cầu  S  :  x  
1   y  2   z  3  9 và mặt phẳng
P : 2x  2y  z  3  0 . Gọi M a; ;
b c là điểm trên mặt cầu S  sao cho khoảng cách từ
M đến  P là lớn nhất. Khi đó
A. a  b  c  5.
B. a  b  c  6.
C. a  b  c  7.
D. a  b  c  8. Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 107
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Chọn C. 2 2 2
Mặt cầu  S  :  x  
1   y  2   z  3  9 có tâm I 1; 2;3 và bán kính R  3.
Gọi d là đường thẳng đi qua I 1; 2;3 và vuông góc  P x  1 2t 
Suy ra phương trình tham số của đường thẳng d là y  2  2t . z  3 t  Gọi ,
A B lần lượt là giao của d và S  , khi đó tọa độ ,
A B ứng với t là nghiệm của 2 2 2 t   1
phương trình 1 2t  
1  2  2t  2  3  t  3  9  t  1   13
Với t  1  A3;0; 4  d  ; A (P)  . 3 5 Với t  1   B  1
 ; 4; 2  d  ; B (P)  . 3
Với mọi điểm M a; ;
b c trên S  ta luôn có d  B;(P)  d M ;(P)  d  ; A (P). 13
Vậy khoảng cách từ M đến  P là lớn nhất bằng khi M 3;0;4 3
Do đó a  b  c  7.
Câu 17: Trong không gian Oxyz cho 4 điểm A2;3;2 , B 6; 1  ; 2 , C  1
 ; 4;3 , D1;6; 5   . Gọi
M là một điểm nằm trên đường thẳng CD sao cho tam giác MAB có chu vi bé nhất. Khi đó
toạ độ điểm M là:
A. M 0;1;   1 B. M 2;11; 9   C. M 3;16; 1   3 D. M 1; 4  ;3 Hướng dẫn giải:
Tam giác MAB có độ dài cạnh AB  4 3 không đổi, do đó chu vi bé nhất khi và chỉ khi
MA  MB bé nhất.     AB  4;4; 4
  ; CD  2;10; 8   . Vì .
AB CD  0 nên AB  CD , suy ra điểm M cần tìm là
hình chiếu vuông góc của A, cũng là hình chiếu vuông góc của B lên đường thẳng CD . Từ
đó tìm ra điểm M 0;1;  1 . Chọn A.
Câu 18: Cho hình chóp .
O ABC có OA  a, OB  ,
b OC  c đôi một vuông góc với nhau. Điểm M cố định thuộc tam giác
ABC có khoảng các lần lượt đến các mặt phẳng
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 108
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
OBC,OCA,OAB là 1,2,3. Khi tồn tại a,b,c thỏa thể tích khối chóp . O ABC nhỏ
nhất, giá trị nhỏ nhất của thể tích khối chóp . O ABC là A. 18 B. 27 C. 6
D. Không tồn tại a,b, c thỏa yêu cầu bài toán Hướng dẫn giải:
Chọn hệ trục tọa độ thỏa O 0, 0, 0, Aa, 0, 0 , B 0,b, 0 ,C 0, 0, c
Điểm M cố định thuộc tam giác ABC có khoảng các lần lượt đến các mặt phẳng
OBC ,OCA, OAB là 1,2,3 nên tọa độ điểm M là (1,2,3) x y z
Phương trình mặt phẳng (ABC) là    1 a b c 1 2 3
Vì M thuộc mặt phẳng (ABC) nên    1 a b c 1 VOABC= abc 6 1 2 3 1 1 1 1
Áp dụng bất đẳng thức Cauchy ta có 3 1     3 . .  abc  27 a b c a b c 6 Chọn B.
Câu 19: Trong không gian với hệ tọa độ Oxyz , cho điểm M 1; 2; 
1 . Mặt phẳng  P thay đổi đi qua
M lần lượt cắt các tia Ox, Oy, Oz tại ,
A B,C khác O . Tính giá trị nhỏ nhất của thể tích
khối tứ diện OABC . A. 54. B. 6. C. 9. D. 18. Hướng dẫn giải: Chọn C.
Gọi Aa;0;0, B 0; ;
b 0,C 0, 0, c với , a , b c  0 . x y z
Phương trình mặt phẳng  P :    1 . a b c 1 2 1
Vì: M   P     1. a b c 1
Thể tích khối tứ diện OABC là: V  abc OABC 6 1 2 1 1 2 1
Áp dụng bất đẳng thức Cauchy ta có: 3    3 . a b c a b c 2 54 1 Hay 3 1  3  1 
. Suy ra: abc  54  abc  9 abc abc 6
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 109
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz Vậy: V  9 . OABC
Câu 20: Trong hệ trục tọa độ Oxyz cho 3 điểm A ;
a 0; 0, B 0; ;
b 0 ,C 0;0;c với a, , b c  0 .Giả sử , a ,
b c thay đổi nhưng thỏa mãn 2 2 2 2
a  b  c  k không đổi. Diện tích tam giác ABC đạt giá trị lớn nhất bằng 2 k 3 2 k 3 A. B. C. 2 k 3 D. 2 k 2 6 Hướng dẫn giải: x y z Phương trình (ABC):    1 a b c Gọi H  ; x ;
y z  là hình chiếu vuông góc của O lên  ABC  2 2  ab c x  
ab2  bc2  ca2
H   ABC  b
 cx  cay  abz  abc 2 2     a bc Khi đó O
 H  AB  ax  by  0  y  O  H  AC
ax  cz  0   
ab2  bc2  ca2 2 2  a b c z   
ab2  bc2  ca2  abc  OH 
ab2  bc2  ca2 1 1 Ta có V  O . A O . B OC  abc OABC 6 6 3V 1 ABCD  S   ab  bc  ca ABC  2  2  2 OH 2
Áp dụng bất đẳng thức Cosi ta có 4 4 4 4 4 4 a  b b  c c  a 2 2 2 2 2 2 4 4 4
a b  b c  c a   
 a  b  c 2 2 2
Dấu “=” xảy ra khi và chỉ khi a  b  c 4 2 1 k k 3 Vậy max S   2 3 6 Chọn B.
Câu 21: Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M(9;1;1) ,
cắt các tia Ox, Oy, Oz tại ,
A B,C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất là
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 110
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz x y z x y z x y z x y z A.    1 B.    1 C.    1 D.    1 7 3 3 27 3 3 27 3 3 27 3 3 Hướng dẫn giải:
Giá sử A(a;0; 0)Ox, B(0;b;0)Oy,C(0;0;c) Oz (a,b,c  0) . x y z
Khi đó PT mặt phẳng (P) có dạng:    1 . a b c 9 1 1 1
Ta có: M(9;1;1) (P)     1 (1); V  abc (2) a b c OABC 6 3
(1)  abc  9bc  ac  ab ≥ 3 9(abc 2 )  abc 3  abc 2 ( ) 27.9( )  abc  243
9bc  ac  ab a  27   x y z Dấu "=" xảy ra  9 1 1
 b  3  (P):    1.    1  c 27 3 3  a b c  3  Chọn B.
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A B  C  D   có điểm A
trùng với gốc tọa độ, B( ; a 0; 0), D(0; ; a 0), A (  0; 0; )
b với (a  0,b  0) . Gọi M là trung điểm
của cạnh CC . Giả sử a  b  4 , hãy tìm giá trị lớn nhất của thể tích khối tứ diện A B  DM ? 64 A. maxV  B. maxV  1 A M  BD  27 A MBD 64 27 C. maxV   D. maxV  AMBD  27 A MBD 64 Hướng dẫn giải:  b  Ta có: C( ; a ; a 0), B (  ; a 0; ) b , D (  0; ; a ) b ,C (  ; a ; a b)  M ; a ; a    2      b 
Suy ra: AB  ( ; a 0; b  ), A D   (0; ; a b  ), AM  ; a a;     2  2 2  
   3a b a b 2   A B  , A D    (a ; b a ;
b a )   AB, A D
  .AM   V       2 A MBD 4 1 1 1 64
Do a,b  0 nên áp dụng BĐT Côsi ta được: 2 2 3
4  a  b  a  a  b  3 a b  a b  2 2 4 27 64 Suy ra: maxV  . A M  BD 27 Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 111
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Hình Học Tọa Độ Oxyz
Câu 23: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A1;5;0, B 3;3;6 và đường thẳng  x  1   2t 
có phương trình tham số  y  1 t
. Một điểm M thay đổi trên đường thẳng  sao cho z  2t 
chu vi tam giác MAB đạt giá trị nhỏ nhất. Tọa đô điểm M và chu vi tam giác ABC là
A. M 1;0;2; P = 2( 11  29)
B. M 1; 2; 2; P = 2( 11  29)
C. M 1;0;2; P = 11  29
D. M 1; 2; 2; P = 11  29 Hướng dẫn giải:
Gọi P là chu vi của tam giác MAB thì P  AB  AM  BM .
Vì AB không đổi nên P nhỏ nhất khi và chỉ khi AM  BM nhỏ nhất.
Điểm M   nên M  1
  2t;1 t; 2t  . 2 2 2 2
AM  BM  (3t)  (2 5)  (3t  6)  (2 5)  
Trong mặt phẳng tọa độ Oxy, ta xét hai vectơ u  3t;2 5 và v   3  t  6; 2 5  .   Ta có 2 2 2 2
u  (3t)  (2 5) ; v  (3t  6)  (2 5)        AM  BM |
 u |  | v | và u  v  (6; 4 5) |
 u  v | 2 29    
Mặt khác, ta luôn có | u |  | v | |
 u  v | Như vậy AM  BM  2 29   3t 2 5
Đẳng thức xảy ra khi và chỉ khi u, v cùng hướng    t  1 3  t  6 2 5
 M (1; 0; 2) và min( AM  BM )  2 29 . Vậy khi M(1;0;2) thì minP = 2( 11  29) Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 112
Facebook: https://www.facebook.com/dongpay

Trắc nghiệm nâng cao hình học tọa độ Oxyz – Đặng Việt Đông Toán 12

Thông tin :

Tài liệu liên quan:

Bài giảng vectơ và hệ trục tọa độ trong không gian Toán 12 KNTTVCS

Toán ứng dụng thực tế vectơ và hệ trục toạ độ trong không gian

Chuyên đề hình học giải tích không gian – Lưu Huy Thưởng Toán 12

Chuyên đề HH giải tích không gian – Trung tâm LTĐH Vĩnh Viễn Toán 12

Bài tập tọa độ không gian phân theo dạng có lời giải chi tiết – Trần Sĩ Tùng Toán 12