Trắc nghiệm nâng cao khối đa diện – Đặng Việt Đông Toán 12

Tài liệu gồm 125 trang được biên soạn bởi thầy Đặng Việt Đông tuyển tập các bài toán trắc nghiệm nâng cao khối đa diện có đáp án và lời giải chi tiết.Mời các bạn đón xem.

60 30 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

125 trang 8 tháng trước

Tác giả:

Profile Lan Tường
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 0
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
THỂ TÍCH KHỐI CHÓP
A- LÝ THUYẾT CHUNG
Trước khi vào phần bài tập bạn đọc cần trang bị cho mình các kiến thức căn bản tối thiểu:
1. Thể tích khối chóp
Công thức tính:
1
.
3
V B h
với
B
diện tích đáy,
h
là chiều cao khối chóp.
2. Định lý tỉ số thể tích khối tứ diện hoặc khối chóp tam giác
Cho khối tứ diện
SABC
và
', ', '
A B C
là các điểm tùy ý lần lượt thuộc
SA SB SC
ta có:
' ' '
' ' '
SABC
SA B C
V
SA SB SC
V SA SB SC
Chúng ta sẽ cùng đi ngay vào các ví dụ minh họa để thấy rằng có những bài liên quan đến thể tích khối
đa diện rất khó, đòi hỏi khả năng vận dụng cao.
h
B
B
A
S
C
A'
B'
C'
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
B – BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho khối tứ diện đều
D
ABC
cạnh
a
. Gọi
E
là điểm đối xứng của
A
qua
D
. Mặt phẳng
qua
CE
và vuông góc với mặt phẳng
D
AB
cắt cạnh
AB
tại điểm
F
. Tính thể tích
V
của
khối tứ diện
E
A CF
.
A.
3
2
30
a
V B.
3
2
60
a
V C.
3
2
40
a
V D.
3
2
15
a
V
Câu 2: Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng tâm tam giác
BCD
. Tính thể tích
V
của khối chóp
.
AGBC
.
A.
3
V
. B.
4
V
. C.
6
V
. D.
5
V
.
Câu 3: Cho tứ diện đều cạnh
a
và điểm
I
nằm trong tứ diện. Tính tổng khoảng cách từ
I
đến các
mặt của tứ diện.
A.
2
a
. B.
6
3
a
. C.
3
2
a
. D.
34
2
a
.
Câu 4: Cho khối tứ diện
ABCD
có
0
3, 4, 90
BC CD ABC BCD ADC
. Góc giữa hai
đường thẳng
AD
và
BC
bằng
0
60
. Tính cosin góc giữa hai mặt phẳng
ABC
và
ACD
?
A.
2 43
43
B.
43
86
C.
4 43
43
D.
43
43
Câu 5: Cho hình chóp tứ giác
.
S ABCD
có
SA ABCD
,
ABCD
là hình thang vuông tại
A
và
B
biết
2
AB a
,
3 3
AD BC a
. Tính thể tích khối chóp
.
S ABCD
theo
a
, biết khoảng cách
từ A đến mặt phẳng
( )
SCD
bằng
3 6
4
a
.
A.
3
6 6
a
. B.
3
2 6
a
. C.
3
2 3
a
. D.
3
6 3
a
.
Câu 6: Cho hình chóp
.
S ABC
có
, 2
SA a BC a
và tất cả các cạnh còn lại đều bằng
x
. Tìm
x
biết thể tích khối chóp đã cho có thể tích bằng
3
11
6
a
.
A.
3
2
a
x . B.
7
2
a
x . C.
9
2
a
x . D.
5
2
a
x .
Câu 7: Cho hình chóp đều
.
S ABC
có đáy cạnh bằng
a
, góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
60
. Gọi
A
,
B
,
C
tương ứng là các điểm đối xứng của
A
,
B
,
C
qua
S
.
Thể tích của khối bát diện có các mặt
,
ABC
A B C
,
A BC
,
B CA
,
C AB
,
AB C
,
BA C
,
CA B
là
A.
3
2 3
3
a
. B.
3
2 3
a
. C.
3
3
2
a
. D.
3
4 3
3
a
.
Câu 8: Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông cân,
AB AC a
,
SC ABC
và
SC a
. Mặt phẳng qua
C
, vuông góc với
SB
cắt
,
SA SB
lần lượt tại
E
và
F
. Tính thể
tích khối chóp
.
S CEF
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
A.
3
2
36
SCEF
a
V . B.
3
18
SCEF
a
V
. C.
3
36
SCEF
a
V . D.
3
2
12
SCEF
a
V .
Câu 9: Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng a. Gọi
P
là mặt phẳng đi qua
A
và
song song
BC
và vuông góc với
,
SBC
góc giữa
P
với mặt phẳng đáy là
0
30 .
Thể tích
khối chóp
.
S ABC
là:
A.
3
3
24
a
B.
3
3
8
a
C.
3
8
a
D.
3
3
8
a
Câu 10: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng 4, mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Gọi
, ,
M N P
lần lượt là trung điểm của các
cạnh
, , .
SD CD BC
Thể tích khối chóp
.
S ABPN
là
,
x
thể tích khối tứ diện
CMNP
là
.
y
Giá
trị
,
x y
thỏa mãn bất đẳng thức nào dưới đây:
A.
2 2
2 160
x xy y B.
2 2
2 2 109
x xy y
C.
2 4
145
x xy y D.
2 4
125
x xy y
Câu 11: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng a, mặt bên
SAB
là tam giác đều,
3.
SC SD a Tính thể tích khối chóp
. .
S ABCD
A.
3
2
2
a
V B.
3
2
3
a
V C.
3
2
6
a
V D.
3
6
a
V
Câu 12: Cho hình chóp
. ,
S ABCD
đáy
ABCD
là hình thang vuông tại
, ; 2 , .
A D AB AD a CD a
Góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
0
60 .
Gọi
I
là trung điểm của
,
AD
biết
hai mặt phẳng
,
SBI SCI
cùng vuông góc với mặt phẳng
.
ABCD
Tính thể tích khối
chóp
. .
S ABCD
A.
3
3 15
5
a
B.
3
3 17
5
a
C.
3
3 19
5
a
D.
3
3 23
5
a
Câu 13: Cho hình chóp
.
S ABC
có chân đường cao nằm trong tam giác
;
ABC
các mặt phẳng
; ;
SAB SAC SBC
cùng tạo với mặt phẳng
ABC
một góc bằng nhau. Biết
25, 17, 26,
AB BC AC
đường thẳng SB tạo với đáy một góc bằng
0
45 .
Tính thể tích V
của khối chóp
.
SABC
A.
680
V
B.
408
V
C.
578
V
D.
600
V
Câu 14: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
8
AB
,
6
BC
. Biết
6
SA
và vuông góc với mặt phẳng đáy
ABC
. Một điểm
M
thuộc phần không gian bên trong
của hình chóp và cách đều tất cả các mặt của hình chóp. Tính thể tích của khối tứ diện
.
M ABC
.
A.
24
V
. B.
64
3
V . C.
32
3
V . D.
12
V
.
Câu 15: Cho khối đa diện đều
n
mặt có thể tích
V
và diện tích mỗi mặt của nó bằng
.
S
Khi đó,
tổng các khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
A.
.
nV
S
B.
.
V
nS
C.
3
.
V
S
D.
.
3
V
S
Câu 16: Cho hình chóp S.ABCD có đáy là nửa lục giác đều với cạnh a (a> 0). Cạnh SA vuông góc
với đáy và SA =
3
a
. M là một điểm khác B trên SB sao cho AM
.
MD
Tính tỉ số
SM
SB
.
A.
3
4
B.
1
4
C.
3
5
D.
5
4
Câu 17: Cho hình chóp
.
S ABC
có
1
SA SB SC
. Tìm thể tích lớn nhất của khối chóp
.
S ABC
.
A.
1
3
. B.
1
6
. C.
1
4
. D.
1
12
.
Câu 18: Cho hình chóp
.
S ABC
có , ,
1.
ABSA x BC Sy AC SB C
Thể tích khối chóp
.
S ABC
lớn nhất khi tổng
x y
bằng:
A.
3
B.
2
3
C.
4
3
D.
4 3
Câu 19: Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ diện đó lớn nhất là
bao nhiêu?
A.
1
4
B.
3
4
C.
1
8
D.
5
8
Câu 20: Khối tứ diện
ABCD
có
1
AB
và tất cả các cạnh còn lại có độ dài không vượt quá
1
. Hỏi
thể tích lớn nhất của khối tứ diện đó là?
A.
3
8
. B.
1
8
. C.
1
24
. D.
3
.
Câu 21: Khối tứ diện
ABCD
có
1
AB x x
và có tất cả các cạnh còn lại có độ dài không vượt
quá
1
. Tính
x
khi thể tích của khối tứ diện đó lớn nhất.
A.
2 3
3
x . B.
6
2
x . C.
3 2
2
x . D.
2 6
3
x .
Câu 22: Cho tứ diện
ABCD
có 4 ,
AB a CD x
và tất cả các cạnh còn lại bằng
3 .
a
Tìm
x
để
khối
tứ diện
ABCD
có thể tích lớn nhất.
A.
2 10 .
x a
B.
10 .
x a
C.
6
x a
. D.
3
a
.
Câu 23: Cho khối tứ diện
ABCD
có
AB x
, tất cả các cạnh còn lại bằng nhau và bằng
2
x
. Hỏi
có bao nhiêu giá trị của
x
để khối tứ diện đã cho có thể tích bằng
2
12
.
A.
1
. B.
6
. C.
4
D.
2
.
Câu 24: Xét khối tứ diện
ABCD
có
AB x
và các cạnh còn lại đều bằng
2 3
. Tìm
x
để thể tích
khối tứ diện
ABCD
đạt giá trị lớn nhất.
A.
6
x . B.
14
x
. C.
3 2
x
. D.
3 3
x .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
Câu 25: Cho khối chóp
.
S ABC
có
SA a
,
2
SB a
,
3
SC a
. Thể tích lớn nhất của khối chóp
là
A.
3
6
a . B.
3
6
2
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Câu 26: Cho khối chóp
.
S ABC
có
SA a
,
2
SB a
,
3
SC a
. Thể tích lớn nhất của khối chóp
là
A.
3
6
a . B.
3
6
2
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Câu 27: Cho hình chóp
.
S ABC
có
1
SA SB SC
. Tìm thể tích lớn nhất của khối chóp
.
S ABC
.
A.
1
3
. B.
1
6
. C.
1
4
. D.
1
12
.
Câu 28: Cho hình chóp
.
S ABC
có
2
SA SB SC
, đáy
ABC
là tam giác vuông tại
A
,
1
AB
.
Tìm thể tích lớn nhất của khối chóp
.
S ABC
.
A.
5
8
. B.
5
4
. C.
2
3
. D.
4
3
.
Câu 29: Cho hình chóp
.
S ABC
có
1
SA SB SC BA BC
. Tìm thể tích lớn nhất của khối chóp
.
S ABC
?
A.
1
6
. B.
2
12
. C.
1
8
. D.
3
12
.
Câu 30: Trong các khối tứ diện
ABCD
có tam giác
ABC
đều cạnh
2
a
và tam giác
ABD
vuông tại
D
,
2
a
AD
. Khoảng cách lớn nhất từ
B
đến mặt phẳng
ACD
là?
A.
2 2
3
a
. B.
3
a
. C.
3
3
a
. D.
2 3
a
.
Câu 31: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
C
, cạnh bên
SA
vuông góc
với mặt phẳng đáy
ABC
. Biết
1
SC
, tìm thể tích lớn nhất của khối chóp
.
S ABC
.
A.
3
12
. B.
2
12
. C.
2 3
27
. D.
3
27
.
Câu 32: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
C
,
2
AB
. Cạnh bên
1
SA
và
vuông góc với mặt phẳng đáy. Thể tích lớn nhất của khối chóp
.
S ABC
là?
A.
1
3
. B.
1
4
. C.
1
12
. D.
1
6
.
Câu 33: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
C
,
2
SA AB a
. Cạnh bên
SA
vuông góc với mặt phẳng đáy
ABC
. Gọi
,
H K
lần lượt là hình chiếu vuông góc của
A
lên
SB
và
SC
. Tìm thể tích lớn nhất
max
V
của khối chóp
.
S AHK
.
A.
3
max
2
6
a
V . B.
3
max
3
6
a
V . C.
3
max
3
3
a
V . D.
3
max
2
3
a
V .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
Câu 34: Cho tam giác
ABC
vuông cân tại
B
,
2
AC
. Trên đường thẳng qua
A
vuông góc với mặt
phẳng
ABC
lấy điểm
,
M N
khác phía với mặt phẳng
ABC
sao cho
. 1
AM AN
. Tìm
thể tích nhỏ nhất của khối tứ diện
MNBC
.?
A.
1
3
. B.
1
6
. C.
1
12
. D.
2
3
.
Câu 35: Cho hình chóp tam giác đều
.
S ABC
có
1
SA
. Thể tích lớn nhất của khối chóp
.
S ABC
là?
A.
1
6
. B.
2
12
. C.
3
12
. D.
1
12
.
Câu 36: Cho hình chóp tam giác
.
S ABC
có đáy
ABC
là tam giác vuông cân đỉnh
C
và
SA
vuông
góc với mặt phẳng
, , .
ABC SC a SCA
Xác định góc
để thể tích khối chóp
SABC
lớn nhất.
A.
1
arcsin
3
B.
2
arcsin
7
C.
1
arcsin
5
D.
1
3arcsin
3
Câu 37: Cho hình chóp
.
S ABCD
có
,
SA x
các cạnh còn lại bằng 2. Tìm giá trị của
x
để thể tích
khối chóp lớn nhất
A.
6
B.
2
C.
7
D.
2 6
Câu 38: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Kí hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm di
động trên đoạn
CB
sao cho
45
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là?
A.
2 1
9
. B.
2 1
3
. C.
2 1
6
. D.
2 1
9
.
Câu 39: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Ký hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm
di động trên đoạn
CB
sao cho
60
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là
A.
2 3
3
. B.
2 3
9
. C.
2 3 3
3
. D.
2 3 3
9
.
Câu 40: Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc,
I
là tâm nội tiếp tam giác
ABC
. Mặt phẳng
P
thay đổi qua
I
, cắt các tia
SA
,
SB
,
SC
lần lượt tại
, ,
A B C
. Biết
2
SA SB
,
7
SC . Hỏi thể tích của khối chóp
.
S A B C
có giá trị nhỏ nhất là?
A.
243 7
256
. B.
7
3
. C.
81 7
256
. D.
27 7
256
.
Câu 41: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
4
AD
, các cạnh bên bằng
nhau và bằng
6
. Tìm thể tích lớn nhất của khối chóp
.
S ABCD
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
A.
130
3
. B.
128
3
. C.
125
3
. D.
250
3
.
Câu 42: Cho hình chóp
.
S ABCD
có
SB x
0 3
x
. Tất cả các cạnh còn lại bằng nhau và
bằng
1
. Với giá trị nào của
x
thì thể tích khối chóp
.
S ABCD
lớn nhất?
A.
3
3
x . B.
2
2
x . C.
6
2
x . D.
3
2
x .
Câu 43: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
4
AB
. Cạnh bên
SA
vuông
góc với mặt phẳng đáy
ABCD
và
6
SC
. Thể tích lớn nhất của khối chóp
.
S ABCD
là?
A.
40
3
. B.
80
3
. C.
20
3
. D. 24.
Câu 44: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi tâm
O
, cạnh bằng 1,
SO ABCD
và
1
SC
. Thể tích lớn nhất của khối chóp
.
S ABCD
là?
A.
2 3
9
B.
2 3
3
. C.
2 3
27
. D.
4 3
27
.
Câu 45: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Kí hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm di
động trên đoạn
CB
sao cho
45
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là?
A.
2 1
9
. B.
2 1
3
. C.
2 1
6
. D.
2 1
9
.
Câu 46: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Ký hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm
di động trên đoạn
CB
sao cho
30
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là?
A.
1
9
. B.
1
3
. C.
2
27
. D.
4
27
.
Câu 47: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Ký hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm
di động trên đoạn
CB
sao cho
60
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là
A.
2 3
3
. B.
2 3
9
. C.
2 3 3
3
. D.
2 3 3
9
.
Câu 48: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành với
4
AD a
. Các cạnh bên của
hình chóp bằng nhau và bằng
6
a
. Tìm thể tích
max
V
của khối chóp
.
S ABCD
.
A.
3
max
8
3
a
V . B.
3
max
4 6
3
a
V . C.
3
max
8
V a
. D.
3
max
4 6
V a
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
Câu 49: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành và thể tích bằng
V
. Gọi
,
M N
lần lượt là các điểm di động trên các cạnh
AB
và
AD
sao cho
2 4
AB AD
AM AN
. Gọi
'
V
là
thể tích khối chóp
.
S MBCDN
. Tìm giá trị nhỏ nhất của
'
V
.
A.
1
4
V
. B.
2
3
V
. C.
3
4
V
. D.
1
3
V
.
Câu 50: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
', '
A C
thỏa mãn
1
'
3
SA SA
,
1
'
5
SC SC
. Mặt phẳng
P
chứa đường thẳng
' '
A C
cắt các cạnh
,
SB SD
lần
lượt tại
', '
B D
và đặt
. ' ' ' '
.
S A B C D
S ABCD
V
k
V
. Giá trị nhỏ nhất của
k
là?
A.
1
60
. B.
1
30
. C.
3
4
V
. D.
15
16
.
Câu 51: Cho hình chóp
có đáy
ABCD
là hình vuông cạnh
,
a SA
vuông góc với mặt phẳng
đáy và góc giữa
SC
với mặt phẳng
SAB
bằng
0
30 .
Gọi M là điểm di động trên cạnh CD
và H là hình chiếu vuông góc của S trên đường thẳng BM. Khi điểm M di động trên cạnh
CD thì thể tích của khối chóp SABH đạt giá trị lớn nhất bằng:
A.
3
2
3
a
B.
3
2
2
a
C.
3
2
6
a
D.
3
2
12
a
Câu 52: Cho hình chóp tứ giác
.
S ABCD
có
2
SA SB SC a
. Tìm thể tích lớn nhất của khối chóp
.
S ABCD
.
A.
3
2 6
3
a
. B.
3
32 3
9
a
. C.
3
4 6
9
a
. D.
3
32 3
27
a
.
Câu 53: Khối chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
.
SA SB SC a
, Cạnh
SD
thay
đổi. Thể tích lớn nhất của khối chóp
.
S ABCD
là:
A.
3
8
a
. B.
3
4
a
. C.
3
3
8
a
. D.
3
2
a
.
Câu 54: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a SA
vuông góc với mặt phẳng
đáy và góc giữa
SC
với mặt phẳng
SAB
bằng
0
30 .
Gọi
M
là điểm di động trên cạnh
CD
và
H
là hình chiếu vuông góc của
S
trên đường thẳng
.
BM
Khi điểm
M
di động trên
cạnh
CD
thì thể tích của khối chóp
.
S ABH
đạt giá trị lớn nhất bằng:
A.
3
2
6
a
. B.
3
2
3
a
. C.
3
2
2
a
. D.
3
2
12
a
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
C – HƯỚNG DẪN GIẢI
Câu 1: Cho khối tứ diện đều
D
ABC
cạnh
a
. Gọi
E
là điểm đối xứng của
A
qua
D
. Mặt phẳng
qua
CE
và vuông góc với mặt phẳng
D
AB
cắt cạnh
AB
tại điểm
F
. Tính thể tích
V
của
khối tứ diện
E
A CF
.
A.
3
2
30
a
V B.
3
2
60
a
V C.
3
2
40
a
V D.
3
2
15
a
V
Hướng dẫn giải:
Áp dụng định lý Menelaus:
A
. . 1
A
HB F EM
HM FB E
A 3 A 2
2. . 1
4 3
F F
FB FB
2
5
AF AB
và
E 2AD
A
. Ta có:
E
D
E 4
.
D 5
A F
AB
S A AF
S A AB
3 3
E D
4 4 2 2
.
5 5 12 15
A CF ABC
a a
V V .
Câu 2: Cho tứ diện
ABCD
có thể tích bằng 12 và
G
là trọng tâm tam giác
BCD
. Tính thể tích ----
--------------------------------------------- của khối chóp
.
AGBC
.
A.
3
V
. B.
4
V
. C.
6
V
. D.
5
V
.
Chọn B.
Cách 1:
Phân tích: tứ diện
ABCD
và khối chóp
.
AGBC
có cùng đường cao là khoảng cách từ
A
đến mặt phẳng
BCD
. Do
G
là trọng tâm tam giác
BCD
nên ta có
BGC BGD CGD
S S S
3
BCD BGC
S S
(xem phần chứng minh).
Áp dụng công thức thể tích hình chóp ta có:
.
.
1
1
.
.
3
3
3
1
1
.
.
3
3
ABCD BCD
BCD
ABCD BCD
A GBC GBC
GBC
A GBC GBC
V h S
h S
V S
V S
h S
V h S
.
1 1
.12 4
3 3
A GBC ABCD
V V
.
Chứng minh: Đặt ;
DN h BC a
.
Từ hình vẽ có:
+)
1 1
//
2 2 2
MF CM h
MF ND MF DN MF
DN CD
.
+)
2 2 2
// .
3 3 3 2 3
GE BG h h
GE MF GE MF
MF BM
G
B
C
D
A
F
E
G
M
N
B
C
D
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay
+)
1 1
.
2 2
3 3
1 1
.
2 2 3
BCD
BCD GBC
GBC
DN BC ha
S
S S
h
S
GE BC a
+) Chứng minh tương tự có 3 3
BCD GBD GCD
S S S
BGC BGD CGD
S S S
.
Cách 2:
;
1 1
; ;
3 3
;
d G ABC
GI
d G ABC d D ABC
DI
d D ABC
.
Nên
.
1 1
; . . 4.
3 3
G ABC ABC DABC
V d G ABC S V
Câu 3: Cho tứ diện đều cạnh
a
và điểm
I
nằm trong tứ diện. Tính tổng khoảng cách từ
I
đến các
mặt của tứ diện.
A.
2
a
. B.
6
3
a
. C.
3
2
a
. D.
34
2
a
.
Hướng dẫn giải:
Chọn B.
2 2 3 3
.
3 3 2 3
a a
AH AM .
2
2 2 2
6
3 3
a a
SH SA AH a .
Ta có
2 3
1 1 3 6 2
. . .
3 3 4 3 12
SABC ABC
a a a
V S SH .
Mặt khác,
SABC ISAB IABC ISAC ISBC
V V V V V
1
. ; ; ; ;
3
ABC
S d I SAB d I ABC d I SAC d I SBC
3
; ; ; ;
SABC
ABC
V
d I SAB d I ABC d I SAC d I SBC
S
3
2
2
3.
6
12
3
3
4
a
a
a
.
Câu 4: Cho khối tứ diện
ABCD
có
0
3, 4, 90
BC CD ABC BCD ADC
. Góc giữa hai
đường thẳng
AD
và
BC
bằng
0
60
. Tính cosin góc giữa hai mặt phẳng
ABC
và
ACD
?
A.
2 43
43
B.
43
86
C.
4 43
43
D.
43
43
H
1
G
I
D
C
B
A
H
M
C
B
A
S
I
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Ta dựng
AE BCD và dễ dàng chứng minh được
BCDE
là hình chữ nhật. Khi đó
0
, 60AD BC ADE khi đó ta suy ra
3 3 6 3
ABCD
AE V .
Mặt khác ta chú ý công thức tính nhanh:
2 sin ,
3
ABC ACD
ABCD
S S ABC ACD
V
AC
Do vậy đặt
,ABC ACD
và theo định lý
Pythagoras ta suy ra 43; 6; 2 13AB AD AC .
Khi đó:
2 1
6 3 3 43 12 sin
2
6 13
2 43
cos
43
.
Câu 5: Cho hình chóp tứ giác
.S ABCD
có
SA ABCD ,
ABCD
là hình thang vuông tại A và B
biết
2AB a
,
3 3AD BC a
. Tính thể tích khối chóp
.S ABCD
theo a , biết khoảng cách
từ A đến mặt phẳng ( )SCD bằng
3 6
4
a .
A.
3
6 6a . B.
3
2 6a . C.
3
2 3a . D.
3
6 3a .
Hướng dẫn giải:
Dựng
AM CD
tại M .
Dựng
AH SM
tại H .
Ta có:
3 6
4
AH a .
2
. 4
2
ABCD
AD BC
S AB a
2
2
2 2CD AD BC AB a
2
1
.
2
ABC
S AB BC a
2
3
ACD ABCD ABC
S S S a
21 3 2
.
2 2
ACD
ACD
S
S AM CD AM a
CD
Ta có:
2 2 2
2 2
1 1 1 . 3 6
2
AH AM
AS a
AH AM AS
AM AH
3
.
1
. 2 6
3
S ABCD ABCD
V SA S a
M
A
D
B
C
S
K
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay
Câu 6: Cho hình chóp
.
S ABC
có
, 2
SA a BC a
và tất cả các cạnh còn lại đều bằng
x
. Tìm
x
biết thể tích khối chóp đã cho có thể tích bằng
3
11
6
a
.
A.
3
2
a
x . B.
7
2
a
x . C.
9
2
a
x . D.
5
2
a
x .
Hướng dẫn giải:
Chọn D
Gọi
,
E F
lần lượt là trung điểm của các cạnh
,
BC SA
.
Khi đó ta có ,
FE SA FE BC
và
BC SAE
nên
BC SA
.
Và
2 2 2 2 2 2
FE AE FA AB BE FA
2 2 2 2
2
2 4 3
4 4 4
a a x a
x
Áp dụng công thức:
.
1
. . . ; .sin ;
6
S ABC
V SA BC d SA BC SA BC
Suy ra:
2 2
1 4 3
. . 2. .sin90
6 4
x a
V a a
3
2 2
11 1
. . 2. 4 3
6 12
a
a a x a
5
2
a
x .
Câu 7: Cho hình chóp đều
.
S ABC
có đáy cạnh bằng
a
, góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
60
. Gọi
A
,
B
,
C
tương ứng là các điểm đối xứng của
A
,
B
,
C
qua
S
.
Thể tích của khối bát diện có các mặt
,
ABC
A B C
,
A BC
,
B CA
,
C AB
,
AB C
,
BA C
,
CA B
là
A.
3
2 3
3
a
. B.
3
2 3
a
. C.
3
3
2
a
. D.
3
4 3
3
a
.
Hướng dẫn giải:
Chọn A.
Cách 1: Ta tính thể tích khối chóp
.
S ABC
:
Gọi H là tâm tam giác ABC đều cạnh a
3
3
a
CH . Góc giữa đường thẳng SA và mặt
phẳng (ABC) bằng
0
60
2 3
.
1 1 3 3
60 .S . . .
3 3 4 12
o
S ABC ABC
a a
SCH SH a V H S a
a
a 2
x
x
x
x
E
F
A
C
B
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay
3
. ' ' .ACS .
2 3
2 2.4 8
3
B ACA C B S ABC
a
V V V V .
Cách 2: Ta có thể tích khối chóp
.
S ABC
là:
3
.
3
12
S ABC
a
V .
Diện tích tam giác
SBC
là:
2
39
12
SBC
a
S
.
Khoảng cách từ
A
đến mặt phẳng
SBC
là:
3
,
13
a
d A SBC
.
Tứ giác
' '
BCB C
là hình chữ nhật vì có hai đường chéo
bằng nhau và cắt nhau tại trung điểm mỗi đường.
Có
2 3 2 3 39
' '
3 3 3
a a a
SB BB B C .
Diện tích
' '
BCB C
là:
2
' '
39
3
BCB C
a
S .
Thể tích khối 8 mặt cần tìm là:
3
' '
1 2 3
2. , . .
3 3
BCB C
a
V d A SBC S
Cách 3
Thể tích khối bát diện đã cho là
' ' ' '. .
1
2 2.4 8 8. .
3
A B C BC A SBC S ABC ABC
V V V V SG S
Ta có:
0
; 60 .
SA ABC SAG Xét
SGA
vuông tại
G
:
tan .tan .
SG
SAG SG AG SAG a
AG
Vậy
2 3
1 1 3 2 3
8. . 8. . . .
3 3 4 3
ABC
a a
V SG S a
Câu 8: Cho hình chóp
SABC
có đáy
ABC
là tam giác vuông cân,
AB AC a
,
SC ABC
và
SC a
. Mặt phẳng qua
C
, vuông góc với
SB
cắt
,
SA SB
lần lượt tại
E
và
F
. Tính thể
tích khối chóp
.
S CEF
.
A.
3
2
36
SCEF
a
V . B.
3
18
SCEF
a
V
. C.
3
36
SCEF
a
V . D.
3
2
12
SCEF
a
V .
Hướng dẫn giải:
Từ
C
hạ
,
CF SB F SB
,
,
CE SA E SA
H
B'
A'
C'
C
A
B
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay
a
a
a
E
F
B
C
A
S
Ta có
AB AC
AB SAC AB CE
AB SC
CE SAB CE SB
Vậy mặt phẳng qua
C
và vuông góc
SB
là mặt
CEF
.
Ta có
.
SCEF
SCAB
V
SE SF
V SA SB
Tam giác vuông
SAC
vuông tại
C
ta có:
2 2
2
SA SC AC a
và
2 2
2 2
1
2 2
SE SC a SE
SA SA a SA
Tam giác vuông
SBC
vuông tại
C
ta có:
2 2
3
SB SC BC a
và
2 2
2 2
1
3 3
SF SC a SF
SB SB a SC
Do đó
3
1 1 1 1 1 1 1
. . .
2 3 6 6 6 3 36
SCEF
SCEF SABC ABC
SCAB
V
V V SA S a
V
.
Chọn C.
Câu 9: Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng a. Gọi
P
là mặt phẳng đi qua
A
và
song song
BC
và vuông góc với
,
SBC
góc giữa
P
với mặt phẳng đáy là
0
30 .
Thể tích
khối chóp
.
S ABC
là:
A.
3
3
24
a
B.
3
3
8
a
C.
3
8
a
D.
3
3
8
a
Hướng dẫn giải:
Tổng quát: Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
.
a
Gọi
P
là mặt phẳng đi
qua
A
và song song
BC
và vuông góc với
,
SBC
góc giữa
P
với mặt phẳng đáy là
Thể tích khối chóp
.
S ABC
là:
3
.
cot
24
S ABC
a
V
S
H
F
G
M
A
B
C
E
x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay
Áp dụng bài này:
3 0 3
.
cot30 3
24 24
S ABC
a a
V
+
ABC
đều
2
3
4
ABC
a
S
+ Gọi G là trọng tâm
+ Gọi
=EF EF//BC =Ax
P SBC P SBC với
/ / / /
Ax EF BC
+ Gọi
M
là trung điểm ,
BC SM EF N
.
Ta có:
,
AM BC SG BC BC SAM AN BC AN Ax
Mà
0
A , / / Ax , 30
M BC BC Ax AM P ABC NAM
Ta có:
GSM NAM
(cùng phụ với
SMA
)
Xét
SGM
vuông tại
G
có:
0
1 1 3
.cot .cot30 . . 3
3 3 2 2
a a
SG GM GSM AM
Vậy:
2 3
.
1 1 3 3
. . . .
3 3 4 2 24
S ABC ABC
a a a
V S SG
.
Chọn A.
Câu 10: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng 4, mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Gọi
, ,
M N P
lần lượt là trung điểm của các
cạnh
, , .
SD CD BC
Thể tích khối chóp
.
S ABPN
là
,
x
thể tích khối tứ diện
CMNP
là
.
y
Giá
trị
,
x y
thỏa mãn bất đẳng thức nào dưới đây:
A.
2 2
2 160
x xy y B.
2 2
2 2 109
x xy y
C.
2 4
145
x xy y D.
2 4
125
x xy y
Hướng dẫn giải:
+ Gọi
H
là trung điểm
.
AB
Do
ABC
đều và
SAB ABCD SH ABCD
Xét
ABC
đều:
3
2 3
2
AB
SH
+ Ta có:
ABPN ABCD ADN CND
S S S S
2 2
. . 4.2 2.2
4 10
2 2 2 2
AD DN CN CP
AB
.
1 1 20 3 20 3
. . .10.2 3
3 3 3 3
S ABPN ABPN
V S SH x
+ Gọi
AN HD K
ta có
MK
là đường trung bình của
DHS
K
P
N
M
H
C
B
A
D
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay
1 1 1 1 1 1 2.2 2 3 2 3 2 3
. . . . . . . . .
2 3 3 2 2 3 2 2 3 3
CMNP CNP
HK SH V S MK CN CP SH y
Thay vào các đáp án.
Chọn C.
Câu 11: Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng a, mặt bên
SAB
là tam giác đều,
3.
SC SD a Tính thể tích khối chóp
. .
S ABCD
A.
3
2
2
a
V B.
3
2
3
a
V C.
3
2
6
a
V D.
3
6
a
V
Hướng dẫn giải:
Gọi
I
là trung điểm AB;J là trung điểm của
CD
từ giả thiết ta có:
3
;
3
a
IJ a SI và
2
2 2 2
11
3
4 2
a a
SJ SC JC a
Áp dụng định lý cosin cho tam giác
IJ
S
ta có:
2 2
2
2 2 2
2
2
3 11
IJ +IS
4 4
cos IJ
2.IJ.IS
3
2. .
2
3
0
3
3
a a
a
SJ
S
a
a
a
a
Suy ra, tam giác
SIJ
là tam giác có
IJ
S
tù. Từ
giả thiết tam giác
SAB
đều và tam giác
SCD
là
cân đỉnh
.
S
Gọi
H
là hình chiếu của
S
trên
,
ABCD
ta có
H
thuộc
IJ
và
I
nằm giữa
HJ
tức là tam giác vuông
SHI
có
0
90 .
H
Góc
I
nhọn và
3 6
cos os os IJ IJ sin .
3 3
I c SIH c S S va SIH ke bu SIH
Xét tam giác SHI ta có
3 6 2
.sin .
2 3 2
a a
SH SI SIH
Vậy
3
2
.
1 1 2 2
. . .
3 3 2 6
S ABCD ABCD
a a
V S SH a
Chọn C.
Câu 12: Cho hình chóp
. ,
S ABCD
đáy
ABCD
là hình thang vuông tại
, ; 2 , .
A D AB AD a CD a
Góc giữa hai mặt phẳng
SBC
và
ABCD
bằng
0
60 .
Gọi
I
là trung điểm của
,
AD
biết
hai mặt phẳng
,
SBI SCI
cùng vuông góc với mặt phẳng
.
ABCD
Tính thể tích khối
chóp
. .
S ABCD
I
A
B
J
C
D
M
N
S
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay
A.
3
3 15
5
a
B.
3
3 17
5
a
C.
3
3 19
5
a
D.
3
3 23
5
a
Hướng dẫn giải:
Gọi
H
trung điểm của
,
BC I
là hình chiếu của
H
lên
,
BC J
là trung điểm
.
AB
Ta có
2 2
, 2
SI mp ABCD IC ID DC a
2 2
5
IB IA AB a
và
2 2
5
BC IB CJ JB a
2 2
1 1
3 ; . .
2 2
ABCD IAB
S AD AB CD a S IA AB a
và
2
1 1
. .
2 2
CID
S DC DI a
2
3
.
2
IBC ABCD IAB DIC
a
S S S S
Mặt khác
1
. ,
2
IBC
S IH BC
nên
2
3 3
.
5
IBC
S
IH a
BC
0
9 3
.tan60 .
5
SI IH a
Do đó
3
.
1 3 15
. .
3 5
S ABCD ABCD
V SI S a
Chọn A.
Câu 13: Cho hình chóp
.
S ABC
có chân đường cao nằm trong tam giác
;
ABC
các mặt phẳng
; ;
SAB SAC SBC
cùng tạo với mặt phẳng
ABC
một góc bằng nhau. Biết
25, 17, 26,
AB BC AC
đường thẳng SB tạo với đáy một góc bằng
0
45 .
Tính thể tích V
của khối chóp
.
SABC
A.
680
V
B.
408
V
C.
578
V
D.
600
V
Hướng dẫn giải:
Gọi J là chân đường cao của hình chóp
. ; ,
S ABC H K
và L lần lượt là hình chiếu
của J trên các cạnh AB, BC và
.
CA
Suy ra
,
SHJ SLJ
và
SKJ
lần lượt là góc
tạo bởi mặt phẳng
ABC
với các mặt
z
=17
x
=8
x
=8
y
=9
y
=9
z
=17
K
B
A
L
C
J
S
H
H
I
B
J
A
D
C
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay
A
C
B
S
M
phẳng
, , .
SAB SAC SBC
Theo giả thiết ta có:
SHJ SLJ SKJ
,
suy ra các tam giác vuông , ,
SJH SJL SJK
bằng nhau.
Từ đó,
.
JH JL JK
Mà J nằm trong tam giác ABC nên J là tâm đường tròn nội tiếp tam
giác
.
ABC
Áp dụng công thức Hê- rông, ta tính được diện tích của tam giác ABC là
204.
S
Kí hiệu P
là nửa chu vi tam giác ABC,
r
là bán kính
đường tròn
nội tiếp của
.
ABC
Ta có
204
6.
34
S
r
P
Đặt
, , .
x BH BL y CL CK z AH AK
Ta có hệ phương trình:
7
25.
26
x y
x z
y z
Giải hệ phương trình ta được
; ; 8;9;17
x y z
2 2 2 2
6 8 10
JB JH BH
Ta có
0
, 45 ,
SBJ SB ABC suy ra SJB là
tam giác vuông cân tại J.
10.
SJ JB
Thể tích V của khối chóp
.
S ABC
là
1
. 680
3
ABC
V SJ S
Chọn A.
Câu 14: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
B
,
8
AB
,
6
BC
. Biết
6
SA
và vuông góc với mặt phẳng đáy
ABC
. Một điểm
M
thuộc phần không gian bên trong
của hình chóp và cách đều tất cả các mặt của hình chóp. Tính thể tích của khối tứ diện
.
M ABC
.
A.
24
V
. B.
64
3
V . C.
32
3
V . D.
12
V
.
Hướng dẫn giải:
Chọn C
Vì
BC BA
BC SB
BC SA
. Khi đó
1
. 24
2
SAB
S SA AB
,
2 2
1 1
. .6. 8 6 30
2 2
SAC
S SA AC
,
2 2
1 1
. 8 6 .6 30
2 2
SBC
S SB BC
,
1
.6.8 24
2
ABC
S
.
z
z
y
y
x
x
L
H
K
J
A
C
B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay
Thể tích khối chóp đã cho là:
1 1
. . . 48
3 2
V SA AB BC
.
Theo bài ra điểm
M
thuộc phần không gian bên trong của hình chóp và cách đều tất cả các
mặt của hình chóp nên ta gọi khoảng cách từ điểm
M
đến các mặt của hình chóp là
d
thì:
.
1
.
3
S ABC SAB SAC SBC ABC
V d S S S S
.
3
S ABC
SAB SAC SBC ABC
V
d
S S S S
3.48 4
30 30 24 24 3
d
. Khi đó:
.
1 1 4 32
. . . .24
3 3 3 3
M ABC ABC
V d S .
Câu 15: Cho khối đa diện đều
n
mặt có thể tích
V
và diện tích mỗi mặt của nó bằng
.
S
Khi đó,
tổng các khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng
A.
.
nV
S
B.
.
V
nS
C.
3
.
V
S
D.
.
3
V
S
Hướng dẫn giải:
Chọn C.
Xét trong trường hợp khối tứ diện đều.
Các trường hợp khác hoàn toàn tương tự.
. 1 . 2 . 3 . 4
1 1 1 1
. ; . ; . ; .
3 3 3 3
H ABC H SBC H SAB H SAC
V h S V h S V h S V h S
3
1 2 4
1 2 3 4
1 2 3 4
1 2 3 4
3
3 3 3
; ; ;
3
3
V
V V V
h h h h
S S S S
V V V V
V
h h h h
S S
Câu 16: Cho hình chóp S.ABCD có đáy là nửa lục giác đều với cạnh a (a> 0). Cạnh SA vuông góc
với đáy và SA =
3
a
. M là một điểm khác B trên SB sao cho AM
.
MD
Tính tỉ số
SM
SB
.
A.
3
4
B.
1
4
C.
3
5
D.
5
4
Hướng dẫn giải: :
Đặt hình chóp vào hệ trục toạ độ như
hình vẽ. Suy ra ta có: A = (0; 0; 0), D =
(2a; 0; 0), S = (0; 0; a
3
) và
B =
3
; ;0
2 2
a a
. Suy ra phương trình
của SB là:
2 2 3
3 3
x y z a
a
a a
Gọi M(x
0
; y
0
; z
0
) thuộc cạnh SB, ta có:
A
C
B
S
H
A
D
B
C
S
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay
0 0
0 0
3
3 2 3
y x
z a x
.
Mặt khác AMDN
. 0AM DM

x
0
2
– 2ax
0
+ y
0
2
+ z
0
2
= 0
0
3
8
a
x
3 3 3 3
; ;
8 8 4
a a a
M
3
4
SM SB
hay
3
4
SM
SB
.
Chọn A.
CỰC TRỊ THỂ TÍCH KHỐI CHÓP
Câu 17: Cho hình chóp
.S ABC
có
1SA SB SC
. Tìm thể tích lớn nhất của khối chóp
.S ABC
.
A.
1
3
. B.
1
6
. C.
1
4
. D.
1
12
.
Hướng dẫn giải:
Chọn B
.
Gọi H là hình chiếu của A lên mặt phẳng
SBC
.
Ta có
1 1 1 1
. . . . . .sin . . .
3 6 6 6
SBC
V AH S AH SB SC BSC AS SB SC
.
Dấu “=” xảy ra khi và chỉ khi
, ,
sin 1
AH AS
AS SBC
SA SB SB SC SC SA
SB SC
BSC
.
Câu 18: Cho hình chóp
.S ABC
có
, , 1.ABSA x BC Sy AC SB C Thể tích
khối chóp
.S ABC
lớn nhất khi tổng x y bằng:
A. 3 B.
2
3
C.
4
3
D. 4 3
Hướng dẫn giải: Ta gọi ,M N lần lượt là trung điểm
của , .SA BC
Dễ chứng minh được ( )SA MBC và
MBC
cân tại
M
Tính được:
2 2 2 2 2
2 2 2
1 .
4 4 4 4
BC SA BC x y
MN MB AB
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay
Do đó:
2 2
.
1
1 .
6 4
S ABC
x y
V V xy
Vì
2 2
2
x y xy
nên
2
1 2
1 ( ) . 2
6 2 12
xy
V xy xy xy
. Dấu bằng xảy ra khi
.
x y
Đến đây, có hai hướng xử lý:
Thứ nhất, sử dụng BĐT Côsi:
3
2
2
32
2 2
( ) 2 4. . (2 ) 4. .
2 2 3 27
xy xy
xy
xy xy
xy xy xy
Dấu bằng xảy ra
2 4
.
2
3 3
2
x y
x y x y
xy
xy
Thứ hai, đặt
t xy
và xét
2
( ) (2 )
f t t t
, đạt GTLN khi
4
3
t
, suy ra
2 4
.
3 3
x y x y
Câu 19: Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ diện đó lớn nhất là
bao nhiêu?
A.
1
4
B.
3
4
C.
1
8
D.
5
8
Hướng dẫn giải:
Giả sử tứ diện
ABCD
có cạnh lớn nhất là
AB
, suy ra các
tam giác ACD và BCD có tất cả các cạnh đều không lớn
hơn 1. Các chiều cao AF và BE của chúng không lớn hơn
2
1 ,
4
a
trong đó
1.
CD a
Chiều cao hình tứ diện
2
AF 1
4
a
AH
(do tam giác AHF vuông tại H có AF là cạnh huyền)
Thể tích của khối tứ diện là:
2
2
1 1 1 1 1 1
. . . . . . . . 1 4
3 3 2 3 2 4 24
BCD
a
V S AH BE CD AH a a a
Để tìm giá trị lớn nhất của V ta xét biểu thức
2
4 .
a a
Vì
0 1
a
nên
2
4 3
a a
và
2
1 1
4 .
24 8
V a a
Chọn C.
F
H
B
C
D
A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay
Câu 20: Khối tứ diện
ABCD
có 1AB và tất cả các cạnh còn lại có độ dài không vượt quá 1. Hỏi
thể tích lớn nhất của khối tứ diện đó là?
A.
3
8
. B.
1
8
. C.
1
24
. D.
3
.
Hướng dẫn giải:
Chọn B
Tứ diện
ABCD
có 1AB , các cạnh còn lại đều
không lớn hơn 1. Đặt
, 0;1CD a x
Gọi M là trung điểm của
BC
, K là hình chiếu của
B lên
CD
và H là hinfhc hiếu của A trên
mp BCD . Khi đó ta có
1 1
. . . (1)
3 6
ABCD BCD
V AH S x BK AH
Có
2 2 2 2
2 2
1
1 4
2 4 4 2
BC BD CD x
BM BM x
Tương tự ta cũng có
2
1
4
2
AM x
Mà
2 2
1 1
4 (2), 4 3
2 2
BK BM BK x AH AM x
Từ (1), (2), (3) suy ra
2
1
4 ; 0;1
24
ABCD
V x x x
Xét hàm số
2
1
4 , 0;1
24
f x x x x là hàm đồng biến nên
1 1
1
8 8
ABCD
f x f V
(Dấu bằng xẩy ra khi hai tam giác ,ACD BCD là hai tam giác đều có cạnh bằng 1 và ,H K
trùng với M . Khi đó
3
1
2
AB )
Chọn B.
Câu 21: Khối tứ diện
ABCD
có
1AB x x và có tất cả các cạnh còn lại có độ dài không vượt
quá 1. Tính x khi thể tích của khối tứ diện đó lớn nhất.
A.
2 3
3
x . B.
6
2
x . C.
3 2
2
x . D.
2 6
3
x .
Hướng dẫn giải:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay
2 2
2 2
20
.
. 20
2
.
5 2 5
a x
x
IK CD x a x
CH
ID
a a
Thể tích khối tứ diện lớn nhất khi
CH
lớn nhất.
2 2 2
2 2 2
20
20 10 5.
2
x a x
x a x a CD a
Đạt được khi
2 2 2
20 10.x a x x a
Câu 23: Cho khối tứ diện
ABCD
có
AB x
, tất cả các cạnh còn lại bằng nhau và bằng
2 x
. Hỏi
có bao nhiêu giá trị của x để khối tứ diện đã cho có thể tích bằng
2
12
.
A. 1. B.
6
. C. 4 D. 2 .
Hướng dẫn giải:
Chọn D
Ta có
2 2 2 2
2
2
1
cos 1 ,cos
2 . 2(2 ) 2
CA CB CD x
CA CB AB x
ACB BCD
CACB x
Vậy
2
2 2
3 2 2
2
2
(2 ) 1 1 1 1
1 2 1 1
6 2 2 2 2
2 2
2 2
x x x
V
x
x
.
2
1
2
6 6 2
0,275842
6 2 12
x
x x
x x
x
.
Câu 24: Xét khối tứ diện
ABCD
có
AB x
và các cạnh còn lại đều bằng 2 3 . Tìm x để thể tích
khối tứ diện
ABCD
đạt giá trị lớn nhất.
A. 6x . B.
14x
. C.
3 2x
. D. 3 3x .
Hướng dẫn giải:
Chọn D.
Gọi E là trung điểm của AB , ta có các tam giác
,CAB DAB lần lượt cân tại ,C D nên
,CE AB DE AB AB ECD . Suy ra
1
.
3
ABCD CDE
V AB S
Ta có
2
2 2
12
4
x
CE DE AD AE
Gọi F là trung điểm của
CD
, ta có
EF CD
và
2 2
2 2
12
12 9
4 4 4
x x
FE DE DF , Suy ra
2
1
. 3. 9
2 4
CDE
x
S FE CD
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay
Khi đó
2 2 2
2
3 3 3 36
9 36 3 3
3 4 6 6 2
x x x
V x x x
.
Câu 25: Cho khối chóp
.
S ABC
có
SA a
,
2
SB a
,
3
SC a
. Thể tích lớn nhất của khối chóp
là
A.
3
6
a . B.
3
6
2
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Chọn D.
Gọi
H
là hình chiếu của
A
lên
1
( ) .
3
SBC
SBC V AH S
.
Ta có
AH SA
; dấu “=” xảy ra khi
AS SBC
.
1 1
. .sin .
2 2
SBC
S SB SC SBC SB SC
, dấu “=” xảy ra khi
SB SC
.
Khi đó,
1 1 1 1
.
3 3 2 6
SBC
V AH S AS SB SC SA SB SC
.
Dấu “=” xảy ra khi
SA SB SC
đôi một vuông góc với
nhau.
Suy ra thể tích lớn nhất của khối chóp là
3
1 6
. .
6 6
a
V SA SB SC .
Câu 26: Cho khối chóp
.
S ABC
có
SA a
,
2
SB a
,
3
SC a
. Thể tích lớn nhất của khối chóp là
A.
3
6
a . B.
3
6
2
a
. C.
3
6
3
a
. D.
3
6
6
a
.
Hướng dẫn giải: :
Gọi
H
là hình chiếu của
A
lên
1
( ) .
3
SBC
SBC V AH S
.
Ta có
AH SA
; dấu “=” xảy ra khi
AS SBC
.
1 1
. .sin .
2 2
SBC
S SB SC SBC SB SC
, dấu “=” xảy ra
khi
SB SC
.
Khi đó,
1 1 1 1
.
3 3 2 6
SBC
V AH S AS SB SC SA SB SC
.
Dấu “=” xảy ra khi
SA SB SC
đôi một vuông góc với
a
a 2
a 3
A
S
B
C
H
a
3
a
2
a
A
S
B
C
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay
nhau.
Suy ra thể tích lớn nhất của khối chóp là
3
1 6
. .
6 6
a
V SA SB SC .
Chọn D.
Câu 27: Cho hình chóp
.S ABC
có
1SA SB SC
. Tìm thể tích lớn nhất của khối chóp
.S ABC
.
A.
1
3
. B.
1
6
. C.
1
4
. D.
1
12
.
Hướng dẫn giải:
Chọn B
.
Gọi H là hình chiếu của A lên mặt phẳng
SBC
.
Ta có
1 1 1
. . . . . .sin . . .
3 6 6
SBC
V AH S AH SB SC BSC AS SB SC
.
Dấu “=” xảy ra khi và chỉ khi
, ,
sin 1
AH AS
AS SBC
SA SB SB SC SC SA
SB SC
BSC
.
Câu 28: Cho hình chóp
.S ABC
có
2SA SB SC
, đáy
ABC
là tam giác vuông tại A , 1AB .
Tìm thể tích lớn nhất của khối chóp
.S ABC
.
A.
5
8
. B.
5
4
. C.
2
3
. D.
4
3
.
Hướng dẫn giải:
Chọn A
Gọi H là hình chiếu của
S
lên
ABC . Khi đó H là tâm
đường tròn ngoại tiếp
ABC
. Hay H là trung điểm
BC
.
Đặt
AC x
. Khi đó
2
1BC x ,
2
15
2
x
SH
.
Ta có:
2
2 2
1 1 1 15
. . . . . . .
3 6 6 2
15
1 5
.
12 2 8
ABC
x
V SH S SH AB AC x
x x
.
Dấu “=” xảy ra khi và chỉ khi
2 2
15
15
2
x x x .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay
Câu 29: Cho hình chóp
.S ABC
có
1SA SB SC BA BC
. Tìm thể tích lớn nhất của khối chóp
.S ABC
?
A.
1
6
. B.
2
12
. C.
1
8
. D.
3
12
.
Hướng dẫn giải:
Chọn C
Cách 1:
Gọi H là hình chiếu của
S
lên
ABC . Khi đó H là tâm đường tròn ngoại tiếp
ABC
.
Vì
ABC
cân tại B nên H thuộc đường trung trực BM của
AC
.
Đặt
AC x
.
Ta có:
2 2
1 1 4
. . . . 1
2 2 4 4
ABC
x x x
S BM AC x
và
2
1
4
4
ABC
abc
R
S
x
.
Mặt khác chiều cao của khối chóp:
2
2 2 2 2
2
3
4
x
SH SB BH SB R
x
.
Thể tích khối chóp:
2 2
2 2
2
3
1 1 3 4 1
. . . .
3 3 4 4 12 8
ABC
x x
x x x
V SH S
x
.
Dấu “=” xảy ra khi và chỉ khi
2 2
3
3
2
x x x .
Cách 2:
Gọi ,K I lần lượt là hình chiếu của
C
lên
SAB và
SB
.
Thể tích khối chóp:
1 1 1 3 3 1
. . . . . . .
3 3 3 2 4 8
SAB SAB
V CK S CI S
Dấu “=” xảy ra khi và chỉ khi hình chiếu của
C
lên
SAB trùng trung điểm
SB
.
Câu 30: Trong các khối tứ diện
ABCD
có tam giác
ABC
đều cạnh
2a
và tam giác ABD vuông tại
D ,
2
a
AD . Khoảng cách lớn nhất từ B đến mặt phẳng
ACD là?
A.
2 2
3
a
. B. 3a . C.
3
3
a
. D. 2 3a .
Hướng dẫn giải:
Chọn B
Ta có
2 ,
2
1 1
cos ,cos ,cos
2 4
a
AB AC a AD
BAC DAB CAD x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay
Khi đó
3 2
2
2 .2 .
1 1 1 1 16 4 11
2
1 2. . .
6 4 16 2 4 12
a
a a
a x x
V x x
.
Khi đó
2
2
3 16 4 11 1
3
2 1 2
B
ACD
V a x x
d f x f a
S x
.
Câu 31: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
C
, cạnh bên
SA
vuông góc
với mặt phẳng đáy
ABC . Biết
1SC
, tìm thể tích lớn nhất của khối chóp
.S ABC
.
A.
3
12
. B.
2
12
. C.
2 3
27
. D.
3
27
.
Hướng dẫn giải:
Chọn D
Đặt
2 2 2
1AC x SA SC AC x và
2
2
1
2 2
ABC
x
S CA .
Vì vậy
2 2 2
2
2
3
2 2 2
. 2 2
1 1
. . 1
3 3 2
6 2
2 2
2
3
27
6 2
ABC
x x x
x
V S SA x
x x x
Dấu bằng xảy ra khi
2 2
2
2 2
3
x x x .
Câu 32: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
C
, 2AB . Cạnh bên
1SA
và
vuông góc với mặt phẳng đáy. Thể tích lớn nhất của khối chóp
.S ABC
là?
A.
1
3
. B.
1
4
. C.
1
12
. D.
1
6
.
Hướng dẫn giải:
Chọn A
Đặt
CA x
,
2 2 2
4CB AB CA x
2
. 4
2 2
ABC
CACB x x
S
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay
Suy ra
2 2 2
1 4 4
.
3 6 6
ABC
x x x x
V SA S
2 2
4 1
2.6 3
x x
Dấu bằng đạt tại
2 2
4x x
2x
.
Câu 33: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
C
,
2SA AB a
. Cạnh bên
SA
vuông góc với mặt phẳng đáy
ABC . Gọi , H K lần lượt là hình chiếu vuông góc của A
lên
SB
và
SC
. Tìm thể tích lớn nhất
max
V của khối chóp
.S AHK
.
A.
3
max
2
6
a
V . B.
3
max
3
6
a
V . C.
3
max
3
3
a
V . D.
3
max
2
3
a
V .
Hướng dẫn giải:
Chọn A.
Đặt
AC x
2 2 2 2
4BC AB AC a x
Ta có
1
. . .
6
SABC
V SA BC AC
2 2
1
.2 . 4
6
a x a x
2 2
4
3
ax a x
Vì vậy
. .
.
S AHK S ABC
SH SK
V V
SB SC
2 2 2
2
1 4
. .
2 3
SA ax a x
SC
3 2 2 3
2 2
2 4 2
.
3 4 6
a x a x a
a x
3
max
2
6
a
V .
Câu 34: Cho tam giác
ABC
vuông cân tại B ,
2AC
. Trên đường thẳng qua A vuông góc với mặt
phẳng
ABC lấy điểm ,M N khác phía với mặt phẳng
ABC sao cho
. 1AM AN
. Tìm
thể tích nhỏ nhất của khối tứ diện
MNBC
.?
A.
1
3
. B.
1
6
. C.
1
12
. D.
2
3
.
Hướng dẫn giải:
Chọn D.
Tam giác
ABC
vuông cân tại B ,
2 2AC AB BC
.
Ta có
1 1 1 1
. . . .
3 3 2 3
MNBC ABC
V AM AN S AM AN AB BC AM AN
Sử dụng BĐT cauchy ta có
2
2 . 2
3
MNBC
AM AN AM AN V .
A
B
C
S
H
K
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay
Câu 35: Cho hình chóp tam giác đều
.S ABC
có
1SA
. Thể tích lớn nhất của khối chóp
.S ABC
là?
A.
1
6
. B.
2
12
. C.
3
12
. D.
1
12
.
Hướng dẫn giải:
Chọn A.
Gọi
O
là tâm của tam giác đều
ABC
. Gọi
0 1R OA x x
Ta tính được
2 2
1SO SA R x
Cạnh của tam giác đều
ABC
là
0 2 0 2
1 3 3
2 sin60 3 sin60
2 4
ABC
a R x S a x
Vậy
2 2
.
4 2 4 6
1 3
. 1
3 4
3 3
1
8 4
S ABC ABC
V SO S x x
x x x x
Cách 1: Dùng Cauchy: Có
2 2 2 4 2 4 2
3
.
1 1 1 4 1
1 1 3 1 1
2 2 4 27 6
S ABC
x x x x x x x V .
Cách 2: Dùng hàm
4 6 3 5
3
0 1 4 6 ; 0
2
f x x x x f x x x f x x
.
Dùng bảng biế thiên thì
f x đạt giá trị lớn nhất tại
3
2
x khi đó
.
0 1
4 1
max
27 6
S ABC
x
f x V
Câu 36: Cho hình chóp tam giác
.S ABC
có đáy
ABC
là tam giác vuông cân đỉnh
C
và
SA
vuông
góc với mặt phẳng
, , .ABC SC a SCA
Xác định góc
để thể tích khối chóp
SABC
lớn nhất.
A.
1
arcsin
3
B.
2
arcsin
7
C.
1
arcsin
5
D.
1
3arcsin
3
Hướng dẫn giải:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay
3 2
3 2
. os ; .sin
1 1 1
. . . . sin . os
3 6 6
1
sin 1 sin
6
SABC ABC
BC AC a c SA a
V S SA AC BC SA a c
a
Xét hàm số:
3
f x x x trên khoảng
0;1 .
Ta có:
2
1
' 1 3 , ' 0 .
3
f x x f x x
Từ đó ta thấy trên khoảng
0;1 hàm số
f x liên tục và có một điểm cực trị là điểm cực
đại, nên tại đó hàm số đạt
GTLN
hay:
0;1
1 2
max
3 3 3
x
f x f
hay
1
arcsin , 0
2
3
Chọn A.
Câu 37: Cho hình chóp
.S ABCD
có ,SA x các cạnh còn lại bằng 2. Tìm giá trị của x để thể tích
khối chóp lớn nhất
A. 6 B.
2
C. 7 D. 2 6
Hướng dẫn giải:
Gọi O là giao điểm của AC và
.BD
Ta có OD=OB và SB=SD nên
SO BD
, do đó
BO SAC .
Mặt khác
2 2 2 2 2 2
SO SB OB AB OB OA
nên
SO OA OC
. Do đó tam giác
SAC vuông tại S.
Ta có
2 2 2 2
4 4 4AC x OA x .
Do đó
2 2
4 12 0 2 3OB x x .
Và
2 2 2 2 2
16 4 4
SOA
S x OA x x .
Để
.S ABCD
V đạt giá trị lớn nhất khi và chỉ khi
SOAB
V đạt giá trị lớn nhất.
Do đó
.S ABCD
V đạt giá trị lớn nhất khi và chỉ khi
2 2
12x x đạt giá trị lớn nhất.
Suy ra
2 2 2
12 6 6x x x x .
Câu 38: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông, 1AB , cạnh bên
1SA
và vuông
góc với mặt phẳng đáy
ABCD . Kí hiệu M là điểm di động trên đoạn
CD
và
N
là điểm di
động trên đoạn
CB
sao cho
45MAN
. Thể tích nhỏ nhất của khối chóp
.S AMN
là?
A.
2 1
9
. B.
2 1
3
. C.
2 1
6
. D.
2 1
9
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn B
Đặt
DM x
,
BN y
ta có
tan tan
tan 45 tan
1
1 tan .tan
DAM BAN x y
DAM BAN
xy
DAM BAN
. Suy ra
1
1
x
y
x
.
và
2 2 2
1
AM AD DM x
,
2
2
2 2 2
1 2 1
1 1
1 1
x x
AN AB BN y
x x
.
Vì vậy
2
1 1 1 2 1
. . . sin 45 2 1
3 6 6 1 3
AMN
x
V SA S SA AM AN f x f
x
.
Câu 39: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Ký hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm
di động trên đoạn
CB
sao cho
60
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là
A.
2 3
3
. B.
2 3
9
. C.
2 3 3
3
. D.
2 3 3
9
.
Hướng dẫn giải:
Chọn C
Đặt ,
DM x BN y
. Ta có:
tan tan
tan60 tan
1
1 tan .tan
DAM BAN x y
DAM BAN
xy
DAM BAN
1 3
3
x
y
x
.
2 2 2
1
AM AD DM x
,
2
2 2 2
1 3
1 1
3
x
AN AB BN y
x
.
Vì vậy
2
.
3 1
1 1
. . . . . .sin60
3 6
6 3
S AMN AMN
x
V SA S SA AM SN
x
.
Ta có
2
3 1
2 3 3
2 3
3
6 3
x
f x f
x
.
Câu 40: Cho hình chóp
.
S ABC
có
SA
,
SB
,
SC
đôi một vuông góc,
I
là tâm nội tiếp tam giác
ABC
. Mặt phẳng
P
thay đổi qua
I
, cắt các tia
SA
,
SB
,
SC
lần lượt tại
, ,
A B C
. Biết
2
SA SB
,
7
SC . Hỏi thể tích của khối chóp
.
S A B C
có giá trị nhỏ nhất là?
A.
243 7
256
. B.
7
3
. C.
81 7
256
. D.
27 7
256
.
Hướng dẫn giải:
Chọn A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay
· Ta có
. .
. . .
S A B C S ABC
SA SB SC
V V
SA SB SC
· Ta có 2, 7SA SB SC
.
1 1
. . 7
6 3
S ACB
V SASB SC
· Từ 2, 7 2, 3SA SB SC AB BC AC
· Do I là tâm đường tròn nội tiếp tam giác
ABC
nên:
. . . 0BC IA CA IB AB IC
. . 0BC SA SI CA SB SI AB SC SI

BC CA AB
SI SA SB SC
AB BC CA AB BC CA AB BC CA
. . . .
BC SA CA SB AB SC
SA SB SC
AB BC CA SA AB BC CA SB AB BC CA SC
.
· Do bốn điểm , , ,A B C I
đồng phẳng nên
. . . 1
BC SA CA SB AB SC
AB BC CA SA AB BC CA SB AB BC CA SC
· Sử dụng bất đẳng thức AM-GM ta có
1 . . .
BC SA CA SB AB SC
AB BC CA SA AB BC CA SB AB BC CA SC
3
3
. .
3 . . .
AB BC CA SA SB SC
SA SB SC
AB BC CA
3
3 3
. . 27. . .
1 3 . . . . .
AB BC CA SA SB SC SA SB SC AB BC CA
SA SB SC SA SB SC
AB BC CA AB BC CA
·
. . .
3 3
27. . . 27.2.3.3 1 81 7
. . . 7
3 256
2 3 3
S A B C S ABC S ABC
SA SB SC AB BC CA
V V V
SA SB SC
AB BC CA
Dấu bằng xảy ra
. . . 1
. . .
BC SA CA SB AB SC
AB BC CA SA AB BC CA SB AB BC CA SC
BC SA CA SB AB SC
AB BC CA SA AB BC CA SB AB BC CA SC
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay
8 9
2
9
8
4
3
7
3 4
SB SA
SA SB
SB SA
SC
SC
SC
.
Câu 41: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với 4AD , các cạnh bên bằng
nhau và bằng
6
. Tìm thể tích lớn nhất của khối chóp
.S ABCD
A.
130
3
. B.
128
3
. C.
125
3
. D.
250
3
.
Hướng dẫn giải:
Chọn B
Đặt
AB x
và
O
là tâm của mặt đáy, ta có
SO ABCD và
2 2 2
2
4
6 32
4 4
x x
SO
.
Vì vậy sử dụng bất đẳng thức
AM GM
, ta co có:
2 2 2
2 2
1 2 2 128 128
4 . 32 128 .
3 4 3 3 2 3
x x x
V x x x
.
Câu 42: Cho hình chóp
.S ABCD
có
SB x
0 3x
. Tất cả các cạnh còn lại bằng nhau và
bằng 1. Với giá trị nào của x thì thể tích khối chóp
.S ABCD
lớn nhất?
A.
3
3
x . B.
2
2
x . C.
6
2
x . D.
3
2
x .
Hướng dẫn giải:
Chọn C
Theo giả thiết
ABCD
là hình thoi và gọi
O AC BD
.
SAC BAC c c c OS OB OD SBD
vuông tại
S
.
Vì
SA SC SD
chân đường cao H của khối chóp
nằm trên đường thẳng BD và
2 2 2
.
1
SB SD x
SH
SB SD x
Ta có
2 2 2 2
1, 2 2 3BD x AC OA AB OB x .
Vì vậy
2 2
1 1
. 3 1
2 2
ABCD
S AC BD x x .
Suy ra
2 2
2 2 2
3
3 3 1
6 6 2.6 4
x x
x x x x
V
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay
Dấu bằng xảy ra khi
2 2
6
3
2
x x x .
Câu 43: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
4
AB
. Cạnh bên
SA
vuông
góc với mặt phẳng đáy
ABCD
và
6
SC
. Thể tích lớn nhất của khối chóp
.
S ABCD
là?
A.
40
3
. B.
80
3
. C.
20
3
. D. 24.
Hướng dẫn giải:
Chọn A.
Đặt
AD=x
, ta có
2 2 2
16
AC AB AD x
và
2 2 2 2 2
6 16 20
SA SC AC x x
.
Vì vậy
2 2
2
1 1 4 20
. 20 .4
3 3 3
ABCD
x x
V SA S x x
2 2
2 20 40
3 3
x x
Dấu bằng xảy ra khi
2 2
20
x x
10
x
Câu 44: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi tâm
O
, cạnh bằng 1,
SO ABCD
và
1
SC
. Thể tích lớn nhất của khối chóp
.
S ABCD
là?
A.
2 3
9
B.
2 3
3
. C.
2 3
27
. D.
4 3
27
.
Hướng dẫn giải:
Chọn D
Đặt
OC x
2 2 2
1
OB BC OC x
2
4 2 1
ABCD OBC
S S x x
và
2 2 2
1
SO SC OC x
vì vậy
2
1 2 1
.
3 3
ABCD
x x
V S SO
=
2 2 2
2 2 1 1
3
x x x
3
2 2 2
2 2 1 1 4 3
3 3 27
x x x
.
Dấu bằng xảy ra khi
2 2
2 1
x x
1
3
x
.
Câu 45: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Kí hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm di
động trên đoạn
CB
sao cho
45
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là?
A.
2 1
9
. B.
2 1
3
. C.
2 1
6
. D.
2 1
9
.
Hướng dẫn giải:
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay
Đặt
DM x
,
BN y
ta có
tan tan
tan 45 tan
1
1 tan .tan
DAM BAN x y
DAM BAN
xy
DAM BAN
. Suy ra
1
1
x
y
x
.
và
2 2 2
1
AM AD DM x
,
2
2
2 2 2
1 2 1
1 1
1 1
x x
AN AB BN y
x x
.
Vì vậy
2
1 1 1 2 1
. . . sin 45 2 1
3 6 6 1 3
AMN
x
V SA S SA AM AN f x f
x
.
Câu 46: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Ký hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm
di động trên đoạn
CB
sao cho
30
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là?
A.
1
9
. B.
1
3
. C.
2
27
. D.
4
27
.
Hướng dẫn giải:
Chọn A
Đặt ,
DM x BN y
. Ta có:
tan tan
tan30 tan
1
1 tan .tan
DAM BAN x y
DAM BAN
xy
DAM BAN
3
1 3
x
y
x
.
2 2 2
1
AM AD DM x
,
2
2 2 2
3
1 1
1 3
x
AN AB BN y
x
.
Vì vậy
2
.
1 1 1
. . . . . .sin30
3 6
6 3 1
S AMN AMN
x
V SA S SA AM SN
x
.
Ta có
2
1 1 1
9
3
6 3 1
x
f x f
x
.
Câu 47: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
1
AB
, cạnh bên
1
SA
và vuông
góc với mặt phẳng đáy
ABCD
. Ký hiệu
M
là điểm di động trên đoạn
CD
và
N
là điểm
di động trên đoạn
CB
sao cho
60
MAN
. Thể tích nhỏ nhất của khối chóp
.
S AMN
là
A.
2 3
3
. B.
2 3
9
. C.
2 3 3
3
. D.
2 3 3
9
.
Hướng dẫn giải:
Chọn C
Đặt ,
DM x BN y
. Ta có:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay
tan tan
tan60 tan
1
1 tan .tan
DAM BAN x y
DAM BAN
xy
DAM BAN
1 3
3
x
y
x
.
2 2 2
1
AM AD DM x
,
2
2 2 2
1 3
1 1
3
x
AN AB BN y
x
.
Vì vậy
2
.
3 1
1 1
. . . . . .sin60
3 6
6 3
S AMN AMN
x
V SA S SA AM SN
x
.
Ta có
2
3 1
2 3 3
2 3
3
6 3
x
f x f
x
.
Câu 48: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành với
4
AD a
. Các cạnh bên của
hình chóp bằng nhau và bằng
6
a
. Tìm thể tích
max
V
của khối chóp
.
S ABCD
.
A.
3
max
8
3
a
V . B.
3
max
4 6
3
a
V . C.
3
max
8
V a
. D.
3
max
4 6
V a
.
Hướng dẫn giải:
Chọn A
Do
6
SA SB SC SD a
nên hình chiếu vuông góc của
S
lên mặt phẳng
ABCD
trùng với tâm đường tròn ngoại tiếp đáy, do vậy
ABCD
là một hình chữ nhật và
H
là giao
điểm của
AC
và
BD
.
Đặt
0
AB x
ta có:
2 2 2 2
16
AC AD AB x a
,
2
2 2 2
1
8
4 2
AC
SH SA a x
.
Vì vậy
2 2
1 2 8
. . . .
3 3
ax a x
S ABCD SO AB AD
.
Sử dụng bất đẳng thức AM – GM ta có:
2 2 2 3 3
2 2 2
max
8 8 8
8 4
2 3 3
x a x a a
x a x a V V
.
Câu 49: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành và thể tích bằng
V
. Gọi
,
M N
lần lượt là các điểm di động trên các cạnh
AB
và
AD
sao cho
2 4
AB AD
AM AN
. Gọi
'
V
là
thể tích khối chóp
.
S MBCDN
. Tìm giá trị nhỏ nhất của
'
V
.
A.
1
4
V
. B.
2
3
V
. C.
3
4
V
. D.
1
3
V
.
Hướng dẫn giải:
Chọn B.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay
Ta có
1
' 1 . .
2
AM AN
V V
AB AD
1
2
xy
V
Trong đó
, 0< , <1
1 2
4
AM AN
x y x y
AB AD
x y
2 1
1
4 1 4
x
y x
x
Vì vậy
2
2
' 1
4 1 3
x
V V V
x
min
2
'
3
V V
.
Câu 50: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
', '
A C
thỏa mãn
1
'
3
SA SA
,
1
'
5
SC SC
. Mặt phẳng
P
chứa đường thẳng
' '
A C
cắt các cạnh
,
SB SD
lần
lượt tại
', '
B D
và đặt
. ' ' ' '
.
S A B C D
S ABCD
V
k
V
. Giá trị nhỏ nhất của
k
là?
A.
1
60
. B.
1
30
. C.
3
4
V
. D.
15
16
.
Hướng dẫn giải:
Chọn A.
Đặt
.
S ABCD
V V , ta có
' '
SB SD
SB SD
' '
SA SC
SA SC
3 5 8
Mặt khác
. ' ' '
' ' ' 1
. .
1
15
2
S A B C
V
SA SB SC
x
SA SB SC
V
. ' ' '
1
30
S A B C
V xV
. ' ' '
. ' ' '
' ' ' 1 1
. .
1
15 30
2
S A C D
S A C D
V
SA SD SC
y V yV
SA SD SC
V
. ' ' '
1
30
S A B C
V xV
Do đó
. ' ' ' '
.
1
30
S A B C D
S ABCD
V
k x y
V
, trong đó
'
SB
x
SB
,
'
SD
y
SD
Và
1 1
4
x y
x y
4 1
8 2
x y
1
60
k .
Câu 51: Cho hình chóp
có đáy
ABCD
là hình vuông cạnh
,
a SA
vuông góc với mặt phẳng
đáy và góc giữa
SC
với mặt phẳng
SAB
bằng
0
30 .
Gọi M là điểm di động trên cạnh CD
và H là hình chiếu vuông góc của S trên đường thẳng BM. Khi điểm M di động trên cạnh
CD thì thể tích của khối chóp SABH đạt giá trị lớn nhất bằng:
A
D
B
C
S
M
N
A
D
B
C
S
A'
B'
C'
D'
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay
A.
3
2
3
a
B.
3
2
2
a
C.
3
2
6
a
D.
3
2
12
a
Hướng dẫn giải:
Ta có góc giữa SC và mặt phẳng
SAB
là
0
30
CSB
Trong tam giác SBC có
0
.cot30 3
SB BC a
Trong tam giác SAB có
2 2
2
SA SB AB a
Thể tích khối chóp
.
S ABH
là:
.
1 1 1 2
. . . 2 .
3 3 2 6
S ABH ABH
a
V S SA HA HB a HA HB
Ta có
2 2 2 2
HA HB AB a
và theo bất đẳng thức
AM GM
ta có:
2
2 2 2
2 . .
2
a
a HA HB HA HB HA HB
Đẳng thức xảy ra khi
0
45
HA HB ABM M D
Khi đó
2 3
.
2 2 2
. .
6 6 2 12
S ABH
a a a a
V HA HB
Chọn D.
Câu 52: Cho hình chóp tứ giác
.
S ABCD
có
2
SA SB SC a
. Tìm thể tích lớn nhất của khối chóp
.
S ABCD
.
A.
3
2 6
3
a
. B.
3
32 3
9
a
. C.
3
4 6
9
a
. D.
3
32 3
27
a
.
Hướng dẫn giải:
Chọn D
Ta có:
SA SB SC SD
ABCD
nội tiếp đường tròn bán kính
R
.
Ta có:
2 2 2 2
4
h cb R a R
và
2
2 sin 2 sin sin ,
. sin ,
2
2 2
R ABC R BAD AC DB
AC BD AC BD
S R
2 2 2 3
(0;2 )
2 4 2 6 32 3
( ) ( )
3 3 3 27
a
Sh R a R a a
V f R max f R f
Câu 53: Khối chóp
.
S ABCD
có đáy
ABCD
là hình thoi cạnh
a
.
SA SB SC a
, Cạnh
SD
thay
đổi. Thể tích lớn nhất của khối chóp
.
S ABCD
là:
A.
3
8
a
. B.
3
4
a
. C.
3
3
8
a
. D.
3
2
a
.
Hướng dẫn giải:
Chọn D.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay
Khi
SD
thay đổi thi
AC
thay đổi. Đặt
AC x
.
Gọi
O AC BD
.
Vì
SA SB SC
nên chân đường cao
SH
trùng
với tâm đường tròn ngoại tiếp tam giác
ABC
.
H BO
.
Ta có
2
2 2 2 2
2
4 4
2 4 2
x a x a x
OB a
2 2 2 2
1 1 4 4
. .
2 2 2 4
ABC
a x x a x
S OB AC x
2 2
2 2 2 2
. .
4
4 4
4.
4
ABC
a a x a x a
HB R
S
x a x a x
.
4 2 2
2 2 2
2 2
2 2
3
4
4
a a a x
SH SB BH a
a x
a x
2 2 2 2
. .
2 2
1 2 3 4
2 2. . . .
3 3 4
4
S ABCD S ABC ABC
a a x x a x
V V SH S
a x
2 2 2 3
2 2
1 1 3
. 3
3 3 2 2
x a x a
a x a x a
Câu 54: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a SA
vuông góc với mặt phẳng
đáy và góc giữa
SC
với mặt phẳng
SAB
bằng
0
30 .
Gọi
M
là điểm di động trên cạnh
CD
và
H
là hình chiếu vuông góc của
S
trên đường thẳng
.
BM
Khi điểm
M
di động trên
cạnh
CD
thì thể tích của khối chóp
.
S ABH
đạt giá trị lớn nhất bằng:
A.
3
2
6
a
. B.
3
2
3
a
. C.
3
2
2
a
. D.
3
2
12
a
.
Hướng dẫn giải:
Chọn D
Góc giữa
SC
và
SBC
là
0
30
CSB CSB
Ta có
2 2
tan 3; 2
BC
CSB SB a SA SB AB a
SB
Đặt
, 0 ,
CM x x a DM a x
Ta có
BM SH
BM SAH BM AH
BM SA
Ta có
2
1 1 1 1
. , . . ;
2 2 2 2 2
BMC ADM ABM ABCD AMC ADM
a
S BC CM ax S AD DM a a x S S S S
x
a
O
A
S
D
C
B
H
C
D
B
A
S
M
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay
Ta có
2
2 2
1
.
2
ABM
a
S AH BM AH
a x
;
2 2
2 2
ax
BH AB AH
a x
Thể tích của khối chóp
.
S ABH
là
2
4
2 2
2 2 2 2
1 1 1 1 2
. . . 2. . .
3 3 2 6 6
ABH
a ax x
V SA S SA BH AH a a
a x
a x a x
(*)
Xét hàm số
2 2
, 0;
x
f x x a
a x
Ta có
2 2
2
2 2
; 0
a x
f x f x x a
a x
Trên đoạn
0;
a
ta có
0, 0;
f x x a
Vậy giá trị lớn nhất của
V
tại
x a
3
2
12
mzx
V a
Cách 2: Từ
(*)
3
4 4
2 2
2 2 1 2
. .
6 6 2 12
x a
V a a
a x a
. Dấu
khi:
x a
.
Cách 3: Dễ thấy
H
nhìn
AB
dưới góc vuông nên
.
S ABH
V lớn nhất khi
ABH
S
lớn nhất khi và
chỉ khi
H O
(tâm của hình vuông )
x a
. Từ đó có kết quả.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay
THỂ TÍCH KHỐI LĂNG TRỤ
A- LÝ THUYẾT CHUNG
1. Thể tích khối lăng trụ
.
V B h
với
B
diện tích đáy,
h
là chiều cao lăng trụ.
2. Thể tích khối hộp chữ nhật
. .
V a b c
với
, ,
a b c
là ba kích thước.
3. Thể tích khối lập phương
3
V a
với
a
là độ dài cạnh.
B
h
b
c
a
a
a
a
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay
B – BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho lăng trụ đứng
ABCA B C
có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa
mặt phẳng
( )
AB C
và mặt phẳng
( )
BB C
bằng
0
60
.Tính thể tích lăng trụ
ABCA B C
.
A.
3
2
a
B.
3
2
a
C.
3
6
a D.
3
3
a
Câu 2: Cho khối lăng trụ tam giác
. ’ ’ ’.
ABC A B C
Gọi
,
M N
lần lượt thuộc các cạnh bên
’, ’
AA CC
sao cho
'
MA MA
và
4 '
NC NC
. Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ
diện
’ ’ ’, ’ , ’ ’
GA B C BB MN ABB C
và
’ ,
A BCN
khối tứ diện nào có thể tích nhỏ nhất?
A. Khối
’
A BCN
B. Khối
’ ’ ’
GA B C
C. Khối
’ ’
ABB C
D. Khối
’
BB MN
Câu 3: Cho lăng trụ tam giác
. ' ' '
ABC A B C
có
'
BB a
, góc giữa đường thẳng
'
BB
và
ABC
bằng
60
, tam giác
ABC
vuông tại
C
và góc
60
BAC
. Hình chiếu vuông góc của điểm
'
B
lên
ABC
trùng với trọng tâm của
ABC
. Thể tích của khối tứ diện
'.
A ABC
theo
a
bằng
A.
3
13
108
a
. B.
3
7
106
a
. C.
3
15
108
a
. D.
3
9
208
a
.
Câu 4: Cho hình lăng trụ đứng
. ' ' '
ABC A B C
, biết đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách
từ tâm
O
của tam giác
ABC
đến mặt phẳng
'
A BC
bằng
6
a
.Tính thể tích khối lăng trụ
. ' ' '
ABC A B C
.
A.
3
3 2
8
a
. B.
3
3 2
28
a
. C.
3
3 2
4
a
. D.
3
3 2
16
a
.
Câu 5: Cho hình lăng trụ có tất cả các cạnh đều bằng
a
, đáy là lục giác đều, góc tạo bởi cạnh bên
và mặt đáy là
60
. Tính thể tích khối lăng trụ
A.
3
27
8
V a
. B.
3
3
4
V a
. C.
3
3
2
V a
. D.
3
9
4
a
.
Câu 6: Cho lăng trụ
. ' ' '
ABC A B C
có đáy là tam giác đều cạnh
.
a
Hình chiếu vuông góc của điểm
'
A
lên mặt phẳng
ABC
trùng với trọng tâm tam giác
.
ABC
Biết khoảng cách giữa hai
đường thẳng
AA'
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là:
A.
3
3
12
a
B.
3
3
6
a
C.
3
3
3
a
D.
3
3
24
a
Câu 7: Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
, một mặt phẳng
cắt các cạnh
AA
,
BB
,
CC
,
DD
lần lượt tại
M
,
N
,
P
,
Q
. Biết
1
3
AM a
,
2
5
CP a
. Thể tích khối
đa diện .
ABCD MNPQ
là:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay
A.
3
11
30
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
11
15
a
.
Câu 8: Cho khối hộp
. ' ' ' '
ABCD A B C D
có cạnh bên bằng 1.; đáy
ABCD
là một hình chữ nhật có
các cạnh
3, 7;
BA AD các mặt bên
' '
ABB A
và
' '
ADD A
hợp với mặt đáy các
góc theo thứ tự
0 0
45 ;60 .
Thể tích khối hộp là:
A.
4
(đvdt) B.
3
(đvdt) C.
2
(đvdt) D.
6
(đvdt)
Câu 9: Cho khối hộp
. ' ' ' '
ABCD A B C D
có độ dài cạnh bên bằng a; đáy là hình thoi, diện tích của
hai mặt chéo là
1
S
và
2
S
; góc giữa hai mặt phẳng chứa hai mặt chéo là
.
Tính thể tích V
của khối hộp đã cho.
A.
1 2
cos
S S
V
a
B.
1 2
cos
3
S S
V
a
. C.
1 2
cos
4
S S
V
a
D.
1 2
cos
2
S S
V
a
Câu 10: Cho khối hộp
. ' ' ' '
ABCD A B C D
có tất cả các cạnh bên bằng
a
và các góc
' , , '
A AB BDA A AD
đều bằng
0 0
0 90 .
Tính thể tích
V
của khối hộp.
A.
3 2 2
sin 2 cos os arcsin
2
a
V a c
B.
3 2 2
2 sin cos os
2
a
V a c
C.
3 2 2
2 sin cos os
2 2
a
V a c
D. Đáp số khác.
Câu 11: Cho khối hộp đứng
. ' ' ' '
ABCD A B C D
có
, , ;
AB a AD b BAD
đường chéo
'
AC
hợp
với đáy góc
.
Tính thể tích khối hộp đứng đã cho là:
A.
2 2
4 2 . os . os .cos
V ab a b ab c c
B.
2 2
2 2 . os . os .cos
V ab a b ab c c
C.
2 2
3 2 . os .sin .tan
V ab a b ab c
D.
2 2
2 . os .sin .tan
V ab a b ab c
CỰC TRỊ THỂ TÍCH KHỐI LĂNG TRỤ
Câu 12: Cho hình hộp chữ nhật
.
ABCD A B C D
có tồng diện tích của tất cả các mặt là
36
, độ dài
đường chéo
AC
bằng
6
. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu?
A.
8
. B.
8 2
. C.
16 2
. D.
24 3
.
Câu 13: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng
36
và độ dài đường chéo bằng
6
.
Tìm thể tích lớn nhất
max
V
của hình hộp chữ nhật đã cho?
A.
max
8
V
. B.
max
12
V
. C.
max
8 2
V . D.
max
6 6
V .
Câu 14: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng
2 6
. Tìm thể tích lớn nhất
max
V
của hình hộp đã cho.
A.
max
16 2
V . B.
max
16
V
. C.
max
6 6
V . D.
max
12 3
V .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay
Câu 15: Tìm
max
V là giá trị lớn nhất của thể tích các khối hộp chữ nhật có đường chéo bằng
3 2
cm
và diện tích toàn phần bằng
2
18 .
cm
A.
3
max
6 .
V cm
B.
3
max
5 .
V cm
C.
3
max
4 .
V cm
D.
3
max
3 .
V cm
Câu 16: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng
36
và độ dài đường chéo bằng
6
.
Tìm thể tích lớn nhất
max
V
của hình hộp chữ nhật đã cho?
A.
max
8
V
. B.
max
12
V
. C.
max
8 2
V . D.
max
6 6
V .
Câu 17: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng
2 6
. Tìm thể tích lớn nhất
max
V
của hình hộp đã cho.
A.
max
16 2
V . B.
max
16
V
. C.
max
6 6
V . D.
max
12 3
V .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay
60
0
H
M
I
A
C
B
A'
B'
C'
B'
B
C
M
I
C – HƯỚNG DẪN GIẢI
Câu 1: Cho lăng trụ đứng
ABCA B C
có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa
mặt phẳng
( )
AB C
và mặt phẳng
( )
BB C
bằng
0
60
.Tính thể tích lăng trụ
ABCA B C
.
A.
3
2
a
B.
3
2
a
C.
3
6
a D.
3
3
a
Hướng dẫn giải:
Từ A kẻ AI
BC
I là trung điểm
BC
AI
(BC
C B
)
AI
B
C (1)
Từ I kẻ IM
B
C (2)
Từ (1), (2)
B
C
(IAM)
Vậy góc giữa (A
B
C) và (
B
CB) là
AMI
= 60
0
Ta có AI=
1
2
BC a
; IM=
0
tan60
3
AI a
2
2
3
a
BH IM
;
2 2 2 2 2 2
1 1 1 3 1 1
' 4 4 2
B B BH BC a a a
.
Suy ra
BB
=
2
a
;
2
1 1
. .2
2 2
ABC
S AI BC a a a
2 3
2. 2
ABC A B C
V a a a
Chọn A.
Câu 2: Cho khối lăng trụ tam giác
. ’ ’ ’.
ABC A B C
Gọi
,
M N
lần lượt thuộc các cạnh bên
’, ’
AA CC
sao cho
'
MA MA
và
4 '
NC NC
. Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ
diện
’ ’ ’, ’ , ’ ’
GA B C BB MN ABB C
và
’ ,
A BCN
khối tứ diện nào có thể tích nhỏ nhất?
A. Khối
’
A BCN
B. Khối
’ ’ ’
GA B C
C. Khối
’ ’
ABB C
D. Khối
’
BB MN
Hướng dẫn giải:
+ Nhận thấy khoảng cách từ G và A xuống mặt phẳng
’ ’ ’
A B C
là bằng nhau ( do G,A thuộc mặt phẳng
/ / ’ ’ ’
ABC A B C
' ' ' . ' ' '
GA B C A A B C
V V
Mà
. ' ' ' ' '
A A B C ABB C
V V (Do 2 hình chóp này có 2 đáy
’ ’
AA B
và
’
ABB
diện tích bằng nhau;chung đường cao hạ từ C’)
' ' ' ' '
GA B C ABB C
V V
=> Không thế khối chóp
’ ’ ’
GA B C
hoặc
’ ’
ABB C
thể thích nhỏ
G
A'
C'
B'
C
B
A
M
N
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay
60°
60°
C'
A'
G
M
N
B
C
A
B'
nhất → Loại B,C
+ So sánh Khối
’
A BCN
và Khối
’
BB MN
Nhận thấy khoảng cách từ M và A’ xuống mặt
’
BBCC
là bằng nhau → Khối
’
A BCN
và
Khối
’
BB MN
có đường cao hạ từ M và A’ bằng nhau. Mặt khác Diện tích đáy
’
BNB
>
Diện tích đáy BCN
=> Khối
’
A BCN
< Khối
’ .
BB MN
=> Khối
’
A BCN
có diện tích nhỏ hơn.
Chọn A.
Câu 3: Cho lăng trụ tam giác
. ' ' '
ABC A B C
có
'
BB a
, góc giữa đường thẳng
'
BB
và
ABC
bằng
60
, tam giác
ABC
vuông tại
C
và góc
60
BAC
. Hình chiếu vuông góc của điểm
'
B
lên
ABC
trùng với trọng tâm của
ABC
. Thể tích của khối tứ diện
'.
A ABC
theo
a
bằng
A.
3
13
108
a
. B.
3
7
106
a
. C.
3
15
108
a
. D.
3
9
208
a
.
Hướng dẫn giải:
Gọi
,
M N
là trung điểm của
,
AB AC
và
G
là trọng tâm của
ABC
.
'
B G ABC
0
', ' 60
BB ABC B BG .
'.
1 1
. . ' . . . '
3 6
A ABC ABC
V S B G AC BC B G
Xét
'
B BG
vuông tại
G
, có
0
' 60
B BG
3
'
2
a
B G . (nửa tam giác đều)
Đặt
2
AB x
. Trong
ABC
vuông tại
C
có
0
60
BAC
tam giác
ABC
là nữa tam giác đều
, 3
2
AB
AC x BC x
Do
G
là trọng tâm
ABC
3 3
2 4
a
BN BG .
Trong
BNC
vuông tại
C
:
2 2 2
BN NC BC
2 2 2
2 2
3
2 13
9 9 3
3
16 4 52
2 13
3 3
2 13
a
AC
a x a a
x x x
a
BC
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay
Vậy,
3
'
1 3 3 3 3 9
. . .
6 2 208
2 13 2 13
A ABC
a a a a
V .
Câu 4: Cho hình lăng trụ đứng
. ' ' '
ABC A B C
, biết đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách
từ tâm
O
của tam giác
ABC
đến mặt phẳng
'
A BC
bằng
6
a
.Tính thể tích khối lăng trụ
. ' ' '
ABC A B C
.
A.
3
3 2
8
a
. B.
3
3 2
28
a
. C.
3
3 2
4
a
. D.
3
3 2
16
a
.
Hướng dẫn giải:
Gọi
M
là trung điểm của
BC
,
ta có
' '
A AM A BC
theo giao tuyến
'
A M
.
Trong
'
A AM
kẻ
' ( ' )
OH A M H A M
.
'
OH A BC
Suy ra:
, '
6
a
d O A BC OH
.
2
3
4
ABC
a
S
.
Xét hai tam giác vuông
'
A AM
và
OHM
có góc
M
chung nên chúng đồng dạng.
Suy ra:
2 2 2
2
1 3
.
1 3
6 3 2
' ' ' '
'
3
'
2
a a
OH OM
A A A M A A A A
A A AM
a
A A
.
6
'
4
a
A A . Thể tích:
2 3
. ' ' '
6 3 3 2
. ' .
4 4 16
ABC A B C ABC
a a a
V S A A
.
Câu 5: Cho hình lăng trụ có tất cả các cạnh đều bằng
a
, đáy là lục giác đều, góc tạo bởi cạnh bên
và mặt đáy là
60
. Tính thể tích khối lăng trụ
A.
3
27
8
V a
. B.
3
3
4
V a
. C.
3
3
2
V a
. D.
3
9
4
a
.
Hướng dẫn giải:
Chọn D.
Ta có
ABCDEF
là lục giác đều nên góc ở đỉnh bằng
120
.
ABC
là tam giác cân tại
B
,
DEF
là tam giác cân tại
E
.
2
1 3
. .sin120
2 4
ABC DEF
a
S S a a
O
C'
B'
M
A
B
A'
C
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay
2 2
2. . .cos
AC AB BC AB BC B
2 2
1
2. . . 3
2
a a a a a
2
. 3. 3
ACDF
S AC AF a a a
2 2 2
2
3 3 3 3
3
4 4 2
ABCDEF ABC ACDF DEF
a a a
S S S S a
3
' 60 ' '.sin 60
2
a
B BH B H BB
Suy ra
Câu 6: Cho lăng trụ
. ' ' '
ABC A B C
có đáy là tam giác đều cạnh
.
a
Hình chiếu vuông góc của điểm
'
A
lên mặt phẳng
ABC
trùng với trọng tâm tam giác
.
ABC
Biết khoảng cách giữa hai
đường thẳng
AA'
và
BC
bằng
3
4
a
. Khi đó thể tích của khối lăng trụ là:
A.
3
3
12
a
B.
3
3
6
a
C.
3
3
3
a
D.
3
3
24
a
Hướng dẫn giải:
Gọi M là trung điểm BC, dựng MH vuông
góc với
'.
AA
Suy ra
3
, '
4
a
MH d BC A A
Đặt
,
AH x
ta có:
2
2
'
3
a
A A x
Từ
' . ' . .
3
a
A A MH A G AM x
Vậy
2 3
3 3
. .
3 4 12
a a a
V
Chọn A.
Câu 7: Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
, một mặt phẳng
cắt các cạnh
AA
,
BB
,
CC
,
DD
lần lượt tại
M
,
N
,
P
,
Q
. Biết
1
3
AM a
,
2
5
CP a
. Thể tích khối
đa diện
.
ABCD MNPQ
là:
A.
3
11
30
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
11
15
a
.
Hướng dẫn giải:
2
3
3 3 9
'. 3.
4 4
ABCDEF
a
V BH S a a
M
A
B'
A'
C'
C
B
H
60°
C'
E'
F'A'
D'
E
F
B
C
D
A
B'
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay
Tứ giác MNPQ là hình bình hành có tâm là I
thuộc đoạn OO’.
Ta có:
11
2 30 2
AM CP a
OI a
Gọi O
1
là điểm đối xứng O qua I thì:
OO
1
=2OI=
11
15
a
< a. Vậy O
1
nằm trong đoạn OO’.
Vẽ mặt phẳng qua O
1
song song với (ABCD) cắt
các cạnh AA’; BB’;CC’; DD’ lần lượt tại
A
1
, B
1
,C
1
, D
1
. Khi đó I là tâm của hình hộp
1 1 1
. .
ABCD AB C D
Vậy
1 1 1 1
. .V ABCD MNPQ V MNPQ A B C D
2 3
1 1 1 1 1
1 1 11
( . )
2 2 30
V ABCD A B C D a OO a
Câu 8: Cho khối hộp
. ' ' ' '
ABCD A B C D
có cạnh bên bằng 1.; đáy
ABCD
là một hình chữ nhật có
các cạnh
3, 7;
BA AD
các mặt bên
' '
ABB A
và
' '
ADD A
hợp với mặt đáy các
góc theo thứ tự
0 0
45 ;60 .
Thể tích khối hộp là:
A.
4
(đvdt) B.
3
(đvdt) C.
2
(đvdt) D.
6
(đvdt)
Hướng dẫn giải:
Dựng
'
A H ABCD
và
' , ' , .
A I AB A J AD HI AB HJ AD
Ta có
0 0
' 45 ; ' 60 .
A IH A JH
Đặt
' .
A H h
Tam giác
'
HA J
vuông có
0
' 60
A JH
nên là
nửa tam giác đều có cạnh
'
A J
, đường cao
' ,
A H HJ
là nửa cạnh
2 2
2 2 2
2 3
'
2
3
2
12 9 12
' ' ' 1
9 9
h h
A J
h h
A J AA A J
2
9 12
AJ
3
h
với
3
0
2
h
Tam giác
'
HA I
vuông cân tại '
H IH A H h
IHJ
A là hình chữ nhật.
Q
O
1
I
O'
O
A'
C'
D'
C
B
D
A
B'
N
M
P
45
0
60
0
I
H
J
B'
A'
C'
B
C
D
A
D'
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay
2
2 2
9 12 3
9 12 9
3
21
h
AJ IH h h h h
Thể tích khối hộp
3
. ' ' ' ': . ' 3. 7. 3
21
ABCD
ABCD A B C D V S A H
(đvdt)
Chọn B.
Câu 9: Cho khối hộp
. ' ' ' '
ABCD A B C D
có độ dài cạnh bên bằng a; đáy là hình thoi, diện tích của
hai mặt chéo là
1
S
và
2
S
; góc giữa hai mặt phẳng chứa hai mặt chéo là
.
Tính thể tích V
của khối hộp đã cho.
A.
1 2
cos
S S
V
a
B.
1 2
cos
3
S S
V
a
. C.
1 2
cos
4
S S
V
a
D.
1 2
cos
2
S S
V
a
Hướng dẫn giải:
Gọi
O
và
'
O
theo thứ tự là tâm của hai mặt
đáy
, ' ' ' '.
ABCD A B C D
Hai mặt chéo
' '
ACC A
và
DD' '
B B
có
giao tuyến là
OO',
có diện tích theo thứ tự
1 2
, .
S S
Dựng mặt phẳng
P
vuông góc với
OO'
tại
,
I
cắt các cạnh bên
AA', ', ',DD'
BB CC
theo thứ tự tại
, , ,
E F G H
(
P
các cạnh
bên).
Ta có:
, OO'
EG HF
tại
I EIH
là
góc giữa hai mặt phẳng chéo
' '
ACC A
và
DD' '
B B
.
- EF
GH
là một thiết diện thẳng của hình hộp và là một hình bình hành.
Do đó, ta có thể tích V của hình hộp là:
1
. ' . . . '.sin
2
EFGH
V S AA EG HF AA
Ta lại có:
1 2
1 ' ' 2 DD' '
.AA' EG= ; . '
ACC A B B
S S
S S EG S S HF BB HF
a a
1 2 1 2
cos
1
. . .sin .
2 2
S S S S
V a
a a a
Chọn D.
Câu 10: Cho khối hộp
. ' ' ' '
ABCD A B C D
có tất cả các cạnh bên bằng
a
và các góc
' , , '
A AB BDA A AD
đều bằng
0 0
0 90 .
Tính thể tích
V
của khối hộp.
I
G
F
H
E
B'
B
C'
D'
A'
C
D
A
P
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay
A.
3 2 2
sin 2 cos os arcsin
2
a
V a c
B.
3 2 2
2 sin cos os
2
a
V a c
C.
3 2 2
2 sin cos os
2 2
a
V a c
D. Đáp số khác.
Hướng dẫn giải:
Dựng
' ; ' '
A H AC A K AD A BD
cân tại ' '
A A O BD
Ta có
'
'
A O BD
BD A AC BD AH
AC BD
AH ABCD HK AD
Đặt
' . '
A AO HAA
vuông tại
os =
'
AH
H c
AA
ABCD
là hình thoi
AC
là phân giác
góc
,
BAD KAH
vuông tại K
2
2 2
2
os os . os . os
2 2 ' '
os cos
os ' '.sin .sin ' 1 os cos
2
os os os
2 2 2
AK AH AK AK
c c c c
AH AA AH AA
c a
c A H AA a A H a c
c c c
Do đó ta có:
2 2 2
. ' ' ' '
. ' .sin . os cos
2
cos
2
ABCD A B C D ABCD
a
V S A H a c
3 2 2
2 sin cos os .
2 2
a
a c
Chọn C.
Câu 11: Cho khối hộp đứng
. ' ' ' '
ABCD A B C D
có
, , ;
AB a AD b BAD
đường chéo
'
AC
hợp
với đáy góc
.
Tính thể tích khối hộp đứng đã cho là:
A.
2 2
4 2 . os . os .cos
V ab a b abc c
B.
2 2
2 2 . os . os .cos
V ab a b abc c
C.
2 2
3 2 . os .sin .tan
V ab a b ab c
D.
2 2
2 . os .sin .tan
V ab a b abc
Hướng dẫn giải:
2 2
2 . os .sin .tan
V ab a b abc
K
H
O
B'
A'
C'
B
D'
A
D
C
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 53
Facebook: https://www.facebook.com/dongpay
Ta có:
'
CC ABCD
'
CAC
là góc của
'
AC
và mặt đáy
ABCD
.
Xét
ABC
, ta có:
2 2 2
2 . . os
AC AB BC AB BC c ABC
2 2 0 2 2
2 . os 180 2 . os .
a b ab c a b ab c
2 2
2 . os
AC a b ab c
Do đó ta có:
2 2
' .tan 2 . os .tan
CC AC a b abc
.
Thể tích của hình hộp đứng:
2 2
. ' sin . 2 . os .tan
ABCD
V S CC ab a b ab c
2 2
2 . os .sin .tan
V ab a b abc
Chọn D.
CỰC TRỊ THỂ TÍCH KHỐI LĂNG TRỤ
Câu 12: Cho hình hộp chữ nhật .
ABCD A B C D
có tồng diện tích của tất cả các mặt là
36
, độ dài
đường chéo
AC
bằng
6
. Hỏi thể tích của khối hộp lớn nhất là bao nhiêu?
A.
8
. B.
8 2
. C.
16 2
. D.
24 3
.
Hướng dẫn giải:
Chọn C.
Gọi chiều dài 3 cạnh của hình hộp chữ nhật lần lượt là:
a
,
b
,
0
c
Ta có
2 2 22 2
36; 2 2 2 36 ( ) 72 6 2
a b c S ab bc cAC a a b c a b c
3
3
3
6 2
16 2
3 3 3
a b c a b c
abc abc
. Vậy
16 2
Max
V
Câu 13: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng
36
và độ dài đường chéo bằng
6
.
Tìm thể tích lớn nhất
max
V
của hình hộp chữ nhật đã cho?
A.
max
8
V
. B.
max
12
V
. C.
max
8 2
V . D.
max
6 6
V .
Hướng dẫn giải:
Chọn C
Gọi
, ,
a b c
là các kích thước của hình hộp chữ nhật. Ta có
a
b
B'
B
A
D
C
A'
D'
C'
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 54
Facebook: https://www.facebook.com/dongpay
* Độ dài đường chéo
2 2 2
6d a b c .
* Tổng diện tích các mặt
2 36S ab bc ca .
Ta tìm giá trị lớn nhất của V abc .
Ta có
2 2 2
6 2a b c a b c ab bc ac .
Mà
2
2
4 6 2 4 18 4 18 6 2 0 4 2
b c bc a a b c a a a
.
Khi đó
3 2
18 6 2 6 2 18V abc a a a a a a f a .
Khảo sát hàm số
y f a trên
0;4 2
.
Ta có
2
0
3 2
a
f a
a
.
So sánh
0 0, 2 8 2, 3 2 0, 4 2 8 2f f f f
ta được
max
8 2V .
Câu 14: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng 2 6
. Tìm thể tích lớn nhất
max
V của hình hộp đã cho.
A.
max
16 2V . B.
max
16V . C.
max
6 6V . D.
max
12 3V .
Hướng dẫn giải:
Chọn B
Gọi , ,a b c là kích thước của hình hộp chữ nhật, ta có
2 2 2
2 2 2
4 32
8
24
2 6
a b c
a b c
a b c
a b c
Suy ra
2
2 2 2
20
2
a b c a b c
ab bc ca
2 2
4 8 4 20 8 0 4b c bc a a a a
.
2
20 8 8 20V abc a a a f a a a a
.
Suy ra
max
0;4
max 2 4 16V f a f f
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 55
Facebook: https://www.facebook.com/dongpay
Câu 15: Tìm
max
V là giá trị lớn nhất của thể tích các khối hộp chữ nhật có đường chéo bằng
3 2
cm
và diện tích toàn phần bằng
2
18 .
cm
A.
3
max
6 .
V cm
B.
3
max
5 .
V cm
C.
3
max
4 .
V cm
D.
3
max
3 .
V cm
Hướng dẫn giải:
Chọn C.
Đặt
, ,
a b c
là kích thước của hình hộp thì ta có hệ
2 2 2
18
9
a b c
ab bc ac
.
Suy ra
6.
a b c
Cần tìm GTLN của
.
V abc
Ta có
6 9 9 6 .
b c a bc a b c a a
Do
2 2
4 6 4 9 6 0 4.
b c bc a a a a
Tương tự
0 , 4
b c
.
Ta lại có
9 6
V a a a
. Khảo sát hàm số này tìm được GTLN của
V
là 4.
Câu 16: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng
36
và độ dài đường chéo bằng
6
.
Tìm thể tích lớn nhất
max
V
của hình hộp chữ nhật đã cho?
A.
max
8
V
. B.
max
12
V
. C.
max
8 2
V . D.
max
6 6
V .
Hướng dẫn giải:
Chọn C
Gọi
, ,
a b c
là các kích thước của hình hộp chữ nhật. Ta có
* Độ dài đường chéo
2 2 2
6
d a b c
.
* Tổng diện tích các mặt
2 36
S ab bc ca
.
Ta tìm giá trị lớn nhất của
V abc
.
Ta có
2 2 2
6 2
a b c a b c ab bc ac .
Mà
2
2
4 6 2 4 18 4 18 6 2 0 4 2
b c bc a a b c a a a
.
Khi đó
3 2
18 6 2 6 2 18
V abc a a a a a a f a
.
Khảo sát hàm số
y f a
trên
0;4 2
.
Ta có
2
0
3 2
a
f a
a
.
So sánh
0 0, 2 8 2, 3 2 0, 4 2 8 2
f f f f
ta được
max
8 2
V .
Câu 17: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng
2 6
. Tìm thể tích lớn nhất
max
V
của hình hộp đã cho.
A.
max
16 2
V . B.
max
16
V
. C.
max
6 6
V . D.
max
12 3
V .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 56
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn B
Gọi , ,a b c là kích thước của hình hộp chữ nhật, ta có
2 2 2
2 2 2
4 32
8
24
2 6
a b c
a b c
a b c
a b c
Suy ra
2
2 2 2
20
2
a b c a b c
ab bc ca
2 2
4 8 4 20 8 0 4b c bc a a a a
.
2
20 8 8 20V abc a a a f a a a a
.
Suy ra
max
0;4
max 2 4 16V f a f f
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 57
Facebook: https://www.facebook.com/dongpay
TỈ LỆ THỂ TÍCH
A- LÝ THUYẾT CHUNG
1. Hai khối chóp
1 2
. ...
n
S A A A
và
1 2
. ...
m
S B B B
có chung đỉnh
S
và hai mặt đáy cùng nằm trên một mặt
phẳng, ta có:
1 2 1 2
1 2 1 2
. ... ...
. ... ...
n n
m m
S A A A A A A
S B B B B B B
V S
V S
2. Hai khối chóp tam giác .
S ABC
có , , '
A SA B SB C SC
ta có:
. ' ' '
.
. .
S A B C
S ABC
V
SA SB SC
v SA SB SC
3. Kiến thức cần nhớ đối với khối lăng trụ tam giác và khối hộp.
.
3
A ABC
V
V
,
.
2
3
A BCC B
V
V
.
.
6
A ABD
V
V
,
3
BDA C
V
V
.
4. Một số công thức nhanh cho các trường hợp hay gặp
Tam giác
ABC
vuông tại
A
có đường cao
AH
có
2
,
BH AB
BC BC
2
.
CH AC
CB BC
Mặt phẳng
song song với mặt đáy của khối chóp
1 2
. ...
n
S A A A
cắt
k
SA
tại điểm
k
M
thỏa mãn
,
k
k
SM
p
SA
ta có
1 2
1 2
. ...
3
. ...
.
n
n
S M M M
S A A A
V
p
V
Hình lăng trụ tam giác .
ABC A B C
có , ,
AM BN CP
x y z
AA BB CC
có
.
.
3
ABC MNP
x y z
V V
Hình hộp .
ABCD A B C D
có , ,
AM BN CP
x y z
AA BB CC
. Mặt phẳng
MNP
cắt
'
DD
tại
Q
thì ta
có đẳng thức
x z y t
với
DQ
t
DD
và
.
.
4
ABCD MNPQ
x y z t
V V
Hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành và , ,
SM SN SP
x y z
SA SB SC
. Mặt phẳng
MNP
cắt
SD
tại
Q
thì ta có đẳng thức
1 1 1 1
x z y t
với
SQ
t
SD
và
.
1 1 1 1 1
4
S MNPQ
V xyzt V
x y z t
.
Định lí Meneleus cho 3 điểm thẳng hàng
. . 1
MA NB PC
MB NC PA
với
MNP
là một đường thẳng cắt ba
đường thẳng
, ,
AB BC CA
lần lượt tại
, , .
M N P
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 58
Facebook: https://www.facebook.com/dongpay
B – BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho hình chóp .
S ABC
.Trên cạnh
SA
lấy các điểm
,
M N
sao cho
SM MN NA
.Gọi
,
là các mặt phẳng song song với mặt phẳng
ABC
và lần lượt đi qua
,
M N
.Khi đó
hai mặt phẳng
,
chia khối chóp đã cho thành 3 phần.Nếu phần trên cùng có thể tích
là
3
10
dm
tích hai phần còn lại lần lượt là?
A.
3
80
dm
và
3
190
dm
. B.
3
70
dm
và
3
190
dm
.
C.
3
70
dm
và
3
200
dm
. D.
3
80
dm
và
3
180
dm
.
Câu 2: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành và có thể tích bằng
V
. Gọi
, ,
M N P
lần lượt là các điểm trên các cạnh
, ,
SA SB SC
sao cho
1 2 1
, ,
2 3 3
SM SN SP
SA SB SC
.
Mặt phẳng
MNP
cắt cạnh
SD
tại điểm
Q
. Tính thể tích khối đa diện .
ABCD MNPQ
.
A.
5
63
V
. B.
10
63
V
. C.
53
63
V
. D.
58
63
V
.
Câu 3: Cho khối chóp .
S ABCD
có đáy là hình chữ nhật,
3
AB a
,
AD a
,
SA
vuông góc với
đáy và
SA a
. Mặt phẳng
qua
A
vuông góc với
SC
cắt
SB
,
SC
,
SD
lần lượt tại
M
,
N
,
P
. Tính thể tích khối chóp .
S AMNP
.
A.
3
3 3
40
a
. B.
3
3
40
a
. C.
3
3
10
a
. D.
3
3
30
a
.
Câu 4: Cho khối chóp .
S ABCD
có thể tích
V
và đáy là hình bình hành. Điểm
S
thỏa mãn
0
SS kDC k
. Biết thể tích phần chung của hai khối chóp .
S ABCD
và .
S ABCD
là
7
25
V
. Tìm
k
.
A.
9
k
. B.
6
k
. C.
11
k
. D.
4
k
.
Câu 5: Cho hình chóp .
S ABC
có tất cả các cạnh đều bằng
a
. Một mặt phẳng
P
song song với
mặt đáy
ABC
cắt các cạnh
SA
,
SB
,
SC
lần lượt tại
M
,
N
,
P
. Tính diện tích tam giác
MNP
biết
P
chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau.
A.
2
. 3
8
MNP
a
S
. B.
3
. 3
16
MNP
a
S
. C.
2
3
. 3
4 2
MNP
a
S
D.
2
3
. 3
4 4
MNP
a
S
.
Câu 6: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật với ,
AB a AD b
và cạnh bên
SA c
vuông góc với mặt phẳng
ABCD
. Gọi
M
là một điểm trên cạnh
SA
sao cho
0
AM x x c
. Tìm
x
để mặt phẳng
MBC
chia khối chóp thành hai khối đa diện có
thể tích bằng nhau.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 59
Facebook: https://www.facebook.com/dongpay
A.
3 2
2
c
x
. B.
2 3
2
ab
x
c
. C.
3 5
2
c
x
. D.
5 1
2
ab
x
c
.
Câu 7: Cho hình chóp
có đáy
ABCD
là hình thang với
/ /
AB CD
và 4
CD AB
.Gọi
M
là 1 điểm trên cạnh
SA
sao cho 0
AM SA
. Tìm tỉ số
SM
SA
sao cho mặt phẳng
CDM
chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau:
A.
3 13
2
SM
SA
. B.
4 26
2
SM
SA
. C.
3 17
2
SM
SA
. D.
3 23
2
SM
SA
.
Câu 8: Cho điểm
M
trên cạnh
SA
, điểm N trên cạnh
SB
của hình chóp tam giác .
S ABC
có thể tích
bằng
V
sao cho
1
,
3
SM SN
x
SA SB
. Mặt phẳng
P
qua
MN
và song song với
SC
chia khối
chóp .
S ABC
thành hai khối đa diện có thể tích bằng nhau. Tính
x
.
A.
4 5
3
x
B.
8 10
6
x
C.
4 5
6
x
D.
8 10
9
x
Câu 9: Cho khối tứ diện đều
ABCD
cạnh bằng
a
, Gọi
M
,
N
là trung điểm các cạnh
AB
,
BC
svà
E
là điểm thuộc tia đối
DB
sao cho
BD
k
BE
. Tìm
k
để mặt phẳng
MNE
chia khối tứ
diện thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
B
có thể tích là
3
11 2
294
a
.
A.
6
5
k
. B.
6
k
. C.
4
k
. D.
5
V
.
Câu 10: Cho khối tứ diện đều
ABCD
cạnh bằng
2 .
cm
Gọi
, ,
M N P
lần lượt là trọng tâm của ba tam
giác
, , .
ABC ABD ACD
Tính thể tích
V
của khối chóp
.
AMNP
A.
3
2
162
V cm
. B.
3
2 2
81
V cm
. C.
3
4 2
81
V cm
. D.
3
2
144
V cm
.
Câu 11: Cho hình chóp tứ giác đều .
S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một góc
60
. Gọi
M
là điểm đối xứng của
C
qua
D
,
N
là trung điểm
.
SC
Mặt phẳng
BMN
chia khối chóp .
S ABCD
thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé)
bằng:
A.
7
5
. B.
1
7
. C.
7
3
. D.
6
5
.
Câu 12: (Hình học không gian) Cho tứ diện
ABCD
và
, ,
M N P
lần lượt thuộc
, ,
BC BD AC
sao cho
4 , 2 , 3 .
BC BM BD BN AC AP
Mặt phẳng
MNP
cắt
AD
tại Q. Tính tỷ số thể tích hai
phần khối tứ diện
ABCD
bị chia bởi mặt phẳng
.
MNP
A.
2
3
B.
7
13
C.
5
13
D.
1
3
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 60
Facebook: https://www.facebook.com/dongpay
Câu 13: Cho hình lăng trụ tam giác đều
. ' ' ',
ABC A B C
có cạnh đáy bằng
a
và cạnh bên bằng
a 2
.
Lấy M, N lần lượt trên cạnh
', '
AB A C
sao cho
' 1
.
' ' 3
AM A N
AB A C
Tính thể tích V của khối
' .
BMNC C
A.
3
6
108
a
B.
3
2 6
27
a
C.
3
3 6
108
a
D.
3
6
27
a
Câu 14: Cho hình chóp tứ giác đều .
S ABCD
có đáy là hình vuông
ABCD
cạnh
,
a
góc giữa mặt bên
và phẳng đáy là
thỏa mãn
1
cos = .
3
Mặt phẳng
P
qua AC và vuông góc với mặt
phẳng
SAD
chia khối chóp .
S ABCD
thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện
là gần nhất với giá trị nào trong các giá trị sau:
A.
0,11
B.
0,13
C.
0,7
D.
0,9
Câu 15: Cho tứ diện .
S ABC
,
M
và
N
là các điểm thuộc các cạnh
SA
và
SB
sao cho 2
MA SM
,
2
SN NB
,
( )
là mặt phẳng qua
MN
và song song với
SC
. Kí hiệu
1
( )
H
và
2
( )
H
là các
khối đa diện có được khi chia khối tứ diện .
S ABC
bởi mặt phẳng
( )
, trong đó,
1
( )
H
chứa
điểm
S
,
2
( )
H
chứa điểm
A
;
1
V
và
2
V
lần lượt là thể tích của
1
( )
H
và
2
( )
H
. Tính tỉ số
1
2
V
V
.
A.
4
5
B.
5
4
C.
3
4
D.
4
3
Câu 16: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình vuông cạnh a, SA =
3
a
và SA vuông góc
với mặt phẳng đáy. Mặt phẳng (P) đi qua điểm A và vuông góc với
SC
cắt
, ,
SB SC SD
lần
lượt tại
’, ’, ’.
B C D
Tính thể tích khối chóp
. ’ ’ ’
S AB C D
theo a.
A.
3
3 3
20
a
B.
3
3
20
a
C
3
3 3
10
a
D.
3
3 5
10
a
Câu 17: Cho tứ diện đều ABCD cạnh a. Mặt phẳng (P) chứa cạnh BC cắt cạnh AD tại E. Biết góc
giữa hai mặt phẳng (P) và (BCD) có số đo là
thỏa mãn
5 2
tan
7
. Gọi thể tích của hai
tứ diện ABCE và tứ diện BCDE lần lượt là
1
V
và
2
V
. Tính tỷ số
1
2
V
V
.
A.
3
8
B.
1
8
C.
3
5
D.
5
8
Câu 18: Cho khối chóp .
S ABC
có
6, 2, 4, 2 10
SA SB SC AB
và
90 , 120
SBC ASC
.
Mặt phẳng
P
qua
B
và trung điểm
N
của
SC
và vuông góc với mặt phẳng
SAC
cắt
cạnh
SA
tại
M
. Tính tỉ số thể tích
.
.
S MBN
S ABC
V
V
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 61
Facebook: https://www.facebook.com/dongpay
A.
2
9
. B.
2
5
. C.
1
6
. D.
1
4
.
Câu 19: Khối tứ diện
ABCD
có thể tích
V
, khối tứ diện
1 1 1 1
A B C D
có thể tích
1
V
, các đỉnh
1 1 1 1
, , ,
A B C D
lần lượt là trọng tâm của các tam giác , , ,
BCD CDA DAB ABC
. Khối tứ diện
2 2 2 2
A B C D
có thể tích
2
V
, các đỉnh
2 2 2 2
, , ,
A B C D
lần lượt là trọng tâm của các tam giác
1 1 1
B C D
,
1 1 1
C D A
,
1 1 1
D A B
,
1 1 1
A B C
. Cứ tiếp tục như thế ta được khối tứ diện
n n n n
A B C D
có thể
tích
n
V
, các đỉnh
, , ,
n n n n
A B C D
lần lượt là trọng tâm của các tam giác
1 1 1
n n n
B C D
,
1 1 1
n n n
C D A
,
1 1 1
n n n
D A B
,
1 1 1
n n n
A B C
. Tính
1 2 2018
...
S V V V
?
A.
2018
2018
3 1
2.3
V
S
. B.
2019
2019
27 1
26.27
V
S
.
C.
2018
2018
27 1
26.27
V
S
. D.
2019
2019
3 1
2.3
V
S
.
Câu 20: Cho khối lăng trụ tam giác .
ABC A B C
. Gọi
,
M N
lần lượt thuộc các cạnh bên ,
AA CC
sao cho ; 4
MA MA NC NC
. Gọi
G
là trọng tâm tam giác
ABC
. Hỏi trong bốn khối tứ
diện , ,
GA B C BB MN ABB C
và
A BCN
, khối tứ diện nào có thể tích nhỏ nhất?
A. Khối
A BCN
. B. Khối
GA B C
. C. Khối
ABB C
. D. Khối
BB MN
.
Câu 21: Cho hình lăng trụ tam giác đều
. ’ ’ ’
ABC A B C
, có cạnh đáy bằng và cạnh bên bằng .
Lấy
,
M N
lần lượt trên cạnh
’, ’
AB A C
sao cho . Tính thể tích V của khối
’ .
BMNC C
A. B. C. D.
Câu 22: Cho khối lập phương .
ABCD A B C D
cạnh
a
. Các điểm
E
và
F
lần lượt là trung điểm
của
C B
và
C D
. Mặt phẳng
AEF
cắt khối lập phương đã cho thành hai phần, gọi
1
V
là
thể tich khối chứa điểm
A
và
2
V
là thể tich khối chứa điểm
'
C
. Khi đó
1
2
V
V
là
A.
25
47
. B. 1. C.
17
25
. D.
8
17
.
Câu 23: Cho hình lập phương
. ' ' ' '
ABCD A B C D
cạnh
.
a
Gọi
,
M N
lần lượt là trung điểm của
' '
A B
và
.
BC
Mặt phẳng
DMN
chia khối lập phương đã cho thành hai khối đa diện. Gọi
H
là khối đa diện chứa đỉnh
, '
A H
là khối đa diện còn lại. Tính tỉ số
'
H
H
V
V
.
A.
'
37
48
H
H
V
V
B.
'
55
89
H
H
V
V
C.
'
2
3
H
H
V
V
D.
'
1
2
H
H
V
V
a
2
a
' 1
' ' 3
AM A N
AB A C
3
6
108
a
3
2 6
27
a
3
3 6
108
a
3
6
27
a
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 62
Facebook: https://www.facebook.com/dongpay
Câu 24: Cho hình lập phương .
ABCD A B C D
cạnh
.
a
Gọi
,
M N
lần lượt là trung điểm của các
cạnh
A B và BC
. Mặt phẳng (
)
DMN
chia hình lập phương thành 2 phần. Gọi
1
V
là thể tích
của phần chứa đỉnh
2
,
A V
là thể tích của phần còn lại. Tính tỉ số
1
2
V
V
.
A.
2
3
. B.
55
89
. C.
37
48
. D.
1
2
.
Câu 25: Cho hình hộp
’ ’ ’ ’.
ABCDA B C D
Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng
thời song song với
’ ’.
B D
Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là
1 2
,
V V
(Trong đó V
1
là thể tích khối chứa A). Tính tỉ số
1
2
V
F
V
.
A.
7
17
. B.
1.
C.
17
25
. D.
8
17
.
Câu 26: Cho khối lăng trụ tam giác ABC. A’B’C’. Gọi I, J, K lần lượt là trung điểm của các cạnh AB,
AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai
phần đó.
A.
25
47
. B. 1. C.
49
95
. D.
8
17
.
CỰC TRỊ TỈ LỆ THỂ TÍCH
Câu 27: Cho hình chóp tứ giác .
S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
A
,
C
thỏa
mãn
1 1
,
3 5
SA SA SC SC
. Mặt phẳng
P
chứa đường thẳng
A C
cắt các cạnh
,
SB SD
lần lượt tại
,
B D
và đặt
.
.
S A B C D
S ABCD
V
k
V
. Giá trị nhỏ nhất của
k
là bao nhiêu?
A.
1
60
. B.
1
30
. C.
4
15
. D.
15
16
.
Câu 28: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
C
là trung điểm cạnh
SC
.
Mặt phẳng
P
chứa đường thẳng
AC
cắt các cạnh
,
SB SD
tại
,
B D
. Đặt
.
.
S B C D
S ABCD
V
m
V
.
Giá trị nhỏ nhất của
m
bằng :
A.
2
27
. B.
4
27
. C.
1
9
. D.
2
9
.
Câu 29: Cho khối tứ diện đều .
S ABC
cạnh bằng
a
. Mặt phẳng
P
đi qua
S
và trọng tâm của tam
giác
ABC
cắt các cạnh
,
AB AC
lần lượt tại
,
M N
. Đặt
.
.
S AMN
S ABC
V
m
V
. Giá trị nhỏ nhất của
m
bằng
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 63
Facebook: https://www.facebook.com/dongpay
A.
2
3
. B.
2
9
. C.
4
9
. D.
1
3
.
Câu 30: Cho hình chóp .
S ABCD
có thể tích
V
và đáy
ABCD
là hình bình hành. Mặt phẳng qua
A
và trung điểm
N
cạnh
SC
cắt cạnh
,
SB SD
lần lượt tại
,
M P
. Tính thể tích nhỏ nhất của
khối chóp .
S AMNP
.
A.
8
V
. B.
3
8
V
. C.
4
V
. D.
3
V
.
Câu 31: Cho hình chóp tứ giác .
S ABCD
có đáy
ABCD
là hình hình hành. Các điểm
A
,
C
thỏa
mãn
1 1
,
3 5
SA SA SC SC
. Mặt phẳng
P
chứa đường thẳng
A C
cắt các cạnh
,
SB SD
lần lượt tại
,
B D
và đặt
.
.
S A B C D
S ABCD
V
k
V
. Tính giá trị lớn nhất của
k
là bao nhiêu?
A.
4
105
. B.
1
30
. C.
4
15
. D.
4
27
.
Câu 32: Cho hình chóp .
S ABCD
có
ABCD
là hình bình hành và có thể tích
V
. Gọi
,
M N
thứ tự là
các điểm di động trên các cạnh
,
AB AD
sao cho
2
4
AB AD
AM AN
. Gọi
'
V
là thể tích khối
chóp .
S AMN
. Tìm giá trị nhỏ nhất của
'
V
.
A.
1
4
V
B.
1
6
V
C.
1
8
V
D.
1
3
V
Câu 33: Cho hình chóp .
S ABCD
có
ABCD
là hình bình hành và có thể tích
V
. Gọi
,
M N
thứ tự là
các điểm di động trên các cạnh
,
AB AD
sao cho
2
4
AB AD
AM AN
. Gọi
'
V
là thể tích khối
chóp .
S MBCDN
. Tìm giá trị lớn nhất của
'
V
.
A.
1
4
V
B.
2
3
V
C.
3
4
V
D.
1
3
V
Câu 34: Cho hình chóp .
S ABCD
có thể tích
V
, đáy là hình bình hành. Mặt phẳng
đi qua
A
,
trung điểm
I
của
SO
cắt các cạnh
, ,
SB SC SD
lần lượt tại
, ,
M N P
. Tính thể tích nhỏ nhất
của khối chóp .
S AMNP
.
A.
18
V
. B.
3
V
. C.
6
V
. D.
3
8
V
.
Câu 35: Cho hình chóp
. ,
S ABCD SA
là đường cao, đáy là hình chữ nhật với
, , .
SA a AB b AD c
Trong mặt phẳng
SDB
lấy G là trọng tâm tam giác
SDB
, qua G kẻ đường thẳng
d
cắt
cạnh BS tại M, cắt cạnh SD tại N, mp
AMN
cắt SC tại K. Xác định M thuộc SB sao cho
SAMKN
V đạt giá trị lớn nhất và nhỏ nhất. Hãy tìm giá trị lớn nhất và nhỏ nhất đó.
A.
ax min
,
8 9
SAMKN m SAMKN
abc abc
V V
B.
ax min
,
8 10
SAMKN m SAMKN
abc abc
V V
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 64
Facebook: https://www.facebook.com/dongpay
C.
ax min
,
9 10
SAMKN m SAMKN
abc abc
V V
D.
ax min
,
10 11
SAMKN m SAMKN
abc abc
V V
Câu 36: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
', '
A C
thỏa mãn
1
'
3
SA SA
,
1
'
5
SC SC
. Mặt phẳng
P
chứa đường thẳng
' '
A C
cắt các cạnh
,
SB SD
lần
lượt tại
', '
B D
và đặt
. ' ' ' '
.
S A B C D
S ABCD
V
k
V
. Giá trị lớn nhất của
k
là?
A.
4
105
. B.
1
30
. C.
4
15
. D.
4
27
.
Câu 37: Cho khối chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật. Một mặt phẳng song song với đáy
cắt các cạnh bên
SA
,
SB
,
SC
,
SD
lần lượt tại
M
,
N
,
P
,
Q
. Gọi
M
,
N
,
P
,
Q
lần lượt
là hình chiếu của
M
,
N
,
P
,
Q
trên mặt phẳng đáy. Tìm tỉ số
SM
SA
để thể tích khối đa diện
.
MNPQ M N P Q
đạt giá trị lớn nhất.
A.
3
4
. B.
2
3
. C.
1
2
D.
1
3
.
Câu 38: Cho khối chóp .
S ABC
. Một mặt phẳng song song với đáy cắt các cạnh bên
SA
,
SB
,
SC
lần lượt tại
M
,
N
,
P
. Gọi
M
,
N
,
P
lần lượt là hình chiếu của
M
,
N
,
P
trên mặt phẳng
đáy. Tìm tỉ số
SM
SA
để thể tích khối đa diện .
MNP M N P
đạt giá trị lớn nhất.
A.
3
4
. B.
2
3
. C.
1
2
. D. .
.
.
Câu 39: Cho hình chóp
.
S ABCD
có đáy là hình bình hành và có thể tích là
.
V
Điểm
P
là trung
điểm của
,
SC
một mặt phẳng qua
AP
cắt hai cạnh
SD
và
SB
lần lượt tại
M
và
.
N
Gọi
1
V
là thể tích của khối chóp
. .
S AMPN
Tìm giá trị nhỏ nhất của
1
V
V
?
A.
1
8
. B.
2
3
. C.
3
8
. D.
1
3
.
Câu 40: Cho hình chóp
.
S ABC
có
30
ASB BSC CSA
và
SA SB SC a
. Mặt phẳng
P
qua
A
cắt hai cạnh
,
SB SC
lần lượt tại
,
B C
sao cho chu vi tam giác
AB C
nhỏ nhất.
Gọi
1 2
,
V V
lầ lượt là thể tích các khối chóp . , .
S AB C S ABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
3 2 2
V
V
. B.
1
2
3 1
V
V
. C.
1
2
4 2 3
V
V
. D.
1
2
2 1
V
V
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 65
Facebook: https://www.facebook.com/dongpay
Câu 41: Cho khối chóp
.
S ABC
có
SA SB SC a
60
ASB
,
90
BSC
,
120
ASC
. Gọi
,
M N
lần lượt là các điểm trên cạnh
AB
và
SC
sao cho
CN AM
SC AB
. Khi khoảng cách giữa
M
và
N
nhỏ nhất, tính thể tích
V
của khối chóp
.
S AMN
.
A.
3
2
72
a
. B.
3
5 2
72
a
. C.
3
5 2
432
a
. D.
3
2
432
a
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 66
Facebook: https://www.facebook.com/dongpay
C – HƯỚNG DẪN GIẢI
Câu 1: Cho hình chóp
.S ABC
.Trên cạnh
SA
lấy các điểm ,M N sao cho
SM MN NA
.Gọi
,
là các mặt phẳng song song với mặt phẳng
ABC
và lần lượt đi qua ,M N .Khi đó
hai mặt phẳng
,
chia khối chóp đã cho thành 3 phần.Nếu phần trên cùng có thể tích
là
3
10dm
tích hai phần còn lại lần lượt là?
A.
3
80dm
và
3
190dm
. B.
3
70dm
và
3
190dm
.
C.
3
70dm
và
3
200dm
. D.
3
80dm
và
3
180dm
.
Hướng dẫn giải:
Chọn B
Đặt
. 1 .
,
S ABC S MNP
V V V S
ta có:
3
1
1 1
. . .
3 27
SM SP SQ
V V V V
SA SB SC
3
270V dm
.
Tương tự ta có :
3
3
1 2
2 8
. . . 80
3 27
SN SE SF
V V V V V dm
SA SB SC
.
Do đó:
3
2 1
80 70V V dm
,
3
3 1 2
190V V V V dm
.
Chọn B.
Câu 2: Cho hình chóp .S ABCD có đáy ABCD là hình bình hành và có thể tích bằng V . Gọi
, ,M N P lần lượt là các điểm trên các cạnh , ,SA SB SC sao cho
1 2 1
, ,
2 3 3
SM SN SP
SA SB SC
.
Mặt phẳng
MNP
cắt cạnh SD tại điểm Q . Tính thể tích khối đa diện .ABCD MNPQ .
A.
5
63
V . B.
10
63
V . C.
53
63
V . D.
58
63
V .
Hướng dẫn giải:
Chọn D
Đặt
1
2
SM
x
SA
,
2
3
SN
y
SB
,
1
3
SP
z
SC
,
SQ
t
SD
.
Ta có
1 1 1 1 3 1 2
2 3
2 7
t
x z y t t
.
F
Q
E
P
B
C
S
M
N
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 67
Facebook: https://www.facebook.com/dongpay
Do đó
. . .
1 1 1 5
. .
2 2 2 63
S MNPQ S MNP S PQM
V V V xyz V zxt V xz y t V V .
Suy ra
.
5 58
1
63 63
ABCD MNPQ
V V V .
Câu 3: Cho khối chóp
.S ABCD
có đáy là hình chữ nhật,
3AB a
,
AD a
,
SA
vuông góc với
đáy và
SA a. Mặt phẳng
qua A vuông góc với SC cắt SB , SC , SD lần lượt tại M , N , P .
Tính thể tích khối chóp .S AMNP .
A.
3
3 3
40
a
. B.
3
3
40
a
. C.
3
3
10
a
. D.
3
3
30
a
.
Hướng dẫn giải:
Chọn B
Ta có
, ,
SC SC AM SC AN SC AP
.
Mặt khác
CB SAB AM CB AM SBC AM SB
. Tương tự ta có AP SD .
Thể tích khối chóp ban đầu là
3
2
1 3
3 .
3 3
a
V a a
.
Tính các tỉ số
1
SA
x
SA
,
2
2
2 2
1
3 4
SM SA a
y
SB SB a a
,
2
2
2 2 2
1
3 5
SN SA a
z
SC SC a a a
,
2
2
2 2
1
2
SP SA a
t
SD SD a a
.
Vậy
3
1 1 1 1 3 3
4 40 40
xyzt a
V V V
x y z t
.
Câu 4: Cho khối chóp .S ABCD có thể tích V và đáy là hình bình hành. Điểm
S thỏa mãn
0
SS kDC k . Biết thể tích phần chung của hai khối chóp .S ABCD và .
S ABCD là
7
25
V . Tìm k .
A. 9k . B. 6k . C. 11k . D. 4k .
Hướng dẫn giải:
Chọn D
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 68
Facebook: https://www.facebook.com/dongpay
Ta có AB //CD //
SS nên ,
B S A SB C S D SC .
Theo Thales ta cũng có
, 1
1
B S C S S S SB SC k SD
k t
B B C C DC SB SC k SD
.
Do đó
2
.
2
2 1
1 1 1 1 1
.1.1. .
4 1 1 1 1
2 1
1 1
S ADC B
k k
k k
V V V
k k
k k
k k
k k
.
Vậy thể tích phần chung là
2
.
2
2 1
7
1 4 0
25
2 1
S ADC B
k k
V V V V V k k
k k
.
Câu 5: Cho hình chóp
.S ABC
có tất cả các cạnh đều bằng
a
. Một mặt phẳng
P
song song với
mặt đáy
ABC
cắt các cạnh
SA
,
SB
,
SC
lần lượt tại M ,
N
, P . Tính diện tích tam giác
MNP
biết
P
chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau.
A.
2
. 3
8
MNP
a
S
. B.
3
. 3
16
MNP
a
S
. C.
2
3
. 3
4 2
MNP
a
S
D.
2
3
. 3
4 4
MNP
a
S
.
Hướng dẫn giải:
Chọn D.
3
.
.
. . 1
S MNP
S ABC
V SM SN SP SM
V SA SB SC SA
Theo bài ra:
.
.
1
2
2
S MNP
S ABC
V
V
Từ
1
,
2
ta có
3
1
2
SM
SA
3
1
2
SM
SA
Lại có:
.
.
1
, .
1
3
= 3
1
2
, .
3
MNP
S MNP
S ABC
ABC
d S MNP S
V
V
d S ABC S
Mà
3
,
1
= 4
,
2
d S MNP
SM
SA
d S ABC
Từ
3
,
4
ta có được
3
2
=
2
MNP
ABC
S
S
2 2
3 3
3
2 2 . 3 . 3
= .
2 2 4
4. 4
MNP ABC
a a
S S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 69
Facebook: https://www.facebook.com/dongpay
Câu 6: Cho hình chóp .
S ABCD
có đáy
ABCD
là hình chữ nhật với ,
AB a AD b
và cạnh bên
SA c
vuông góc với mặt phẳng
ABCD
. Gọi
M
là một điểm trên cạnh
SA
sao cho
0
AM x x c
. Tìm
x
để mặt phẳng
MBC
chia khối chóp thành hai khối đa diện có
thể tích bằng nhau.
A.
3 2
2
c
x
. B.
2 3
2
ab
x
c
. C.
3 5
2
c
x
. D.
5 1
2
ab
x
c
.
Hướng dẫn giải:
Chọn C
Ta có
SM SN c x
SA SD c
Vì vậy
.
. .
.
2
S MBC
S MBC S ABCD
S ABC
V SM c x c x
V V
V SA c c
Và
2 2
. .
2 2
.
. 2
SMNC
S MNC S ABCD
SADC
c x c x
V
SM SN
V V
V SA SD c c
Vậy
2 2
2
2 2
1
.
2 2
SMNBC SABCD SABCD
c x c x c cx
c x
V V V
c c c
Từ giả thiết ta có
2
2
2 2
2
3 5
1 3 0
2
c
c x c cx
c cx x x
c
.
Câu 7: Cho hình chóp
có đáy
ABCD
là hình thang với
/ /
AB CD
và
4
CD AB
.Gọi
M
là
1 điểm trên cạnh
SA
sao cho
0
AM SA
. Tìm tỉ số
SM
SA
sao cho mặt phẳng
CDM
chia
khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau:
A.
3 13
2
SM
SA
. B.
4 26
2
SM
SA
. C.
3 17
2
SM
SA
. D.
3 23
2
SM
SA
.
Hướng dẫn giải:
Chọn B
Đặt
,0 1
SM SN
x x
SA SB
.
D
A
B
C
S
M
N
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 70
Facebook: https://www.facebook.com/dongpay
Ta có
4
4 1
,
5 5
SADC ADC
SABC ABC
SADC SABDC SABC SABDC
V S AD
V S AB
V V V V
.
Ta có
4
5
SMCD
SMCD SABDC
SACD
V SM x
V V
V SA
2
2
.
5
SMNC
SMNC SABC
SABC
V
SM SN x
x V V
V SA SB
Vậy
2
4
5 5 2
SABCD
SMNCD SABCD
V
x x
V V
Suy ra
2
4 1 4 26
5 5 2 2
x x
x
.
Câu 8: Cho điểm M trên cạnh
SA
, điểm N trên cạnh
SB
của hình chóp tam giác
.S ABC
có thể tích
bằng
V
sao cho
1
,
3
SM SN
x
SA SB
. Mặt phẳng
P qua
MN
và song song với
SC
chia khối
chóp
.S ABC
thành hai khối đa diện có thể tích bằng nhau. Tính
x
.
A.
4 5
3
x
B.
8 10
6
x
C.
4 5
6
x
D.
8 10
9
x
Hướng dẫn giải:
Chọn B
Trong
:ABS MN AB E , trong
: / / ,SAC MQ SC Q AC , trong
:ABC EQ BC P
.
Khi đó
1
/ / / / ,
3
SM CQ SN CP
NP SC MQ x
SA CA SB CB
.
Trong tam giác
: . . 1
1 1 2 3 1
. . 1
2 1 1
NB MS EA
SAB
NS MA EB
x EA EA x AB x
x EB EB x EB x
Ta có
.
2 2 2 8 8
. . . .
3 3 3 1 9 3 1 9 3 1
EAMQ
EAMQ
S ABC
V
AM AQ EA x x x
V V
V AS AC BA x x x
E
P
Q
A
B
C
S
M
N
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 71
Facebook: https://www.facebook.com/dongpay
3 3
2
.
3 3
1 1
1
. . 1 .
3 1 3 1 3 1
1 1
8 1 8 1 8 10
9 3 1 3 1 2 9 3 1 3 1 2 6
EBNP
EBNP
S ABC
AMQBNP
x x
V
BN BP EB x
x V V
V BS BC AB x x x
x x
x x
V V V V x
x x x x
Câu 9: Cho khối tứ diện đều
ABCD
cạnh bằng
a
, Gọi
M
,
N
là trung điểm các cạnh
AB
,
BC
svà
E
là điểm thuộc tia đối
DB
sao cho
BD
k
BE
. Tìm
k
để mặt phẳng
MNE
chia khối
tứ diện thành hai khối đa diện, trong đó khối đa diện chứa đỉnh
B
có thể tích là
3
11 2
294
a
.
A.
6
5
k
. B.
6
k
. C.
4
k
. D.
5
V
.
Hướng dẫn giải:
Chọn C
Ta có diện tích khối tứ diện đều cạnh
a
bằng
3
0
2
12
a
V
0
. .
1
4
BMNE
ABCD
BMQE
V
BM BN BE
V BA BC BD
V V
Theo ta let ta có:
2 1
1
1
2 1
1
2
k
EP EQ k
EN EM k
k
2
0
2
4 1
11
. . .
4
2 1
EDPQ BMQE
k
EP EQ DE k
V V V
EN EM BE k
k
Do đó
2 3
0 0 0
2 2
4 1 4 1
11
. 1
4 4 4
2 1 2 1
BMNPQD
k k
k k k
V V V V
k
k k k
0
22
49
BMNPQD
V V
hay
3
0 0
2
4 1
1 4
4 4
2 1
k
k k
V V k
k k
Câu 10: Cho khối tứ diện đều
ABCD
cạnh bằng
2 .
cm
Gọi
, ,
M N P
lần lượt là trọng tâm của ba tam
giác
, , .
ABC ABD ACD
Tính thể tích
V
của khối chóp
.
AMNP
C
B
A
D
E
M
N
Q
P
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 72
Facebook: https://www.facebook.com/dongpay
P
N
M
H
K
F
E
A
B
C
D
A.
3
2
162
V cm
. B.
3
2 2
81
V cm
. C.
3
4 2
81
V cm
. D.
3
2
144
V cm
.
Hướng dẫn giải:
Chọn C.
Tam giác
BCD
đều
2 3
3
3
DE DH
2 2
2 6
3
AH AD DH
EF
, D,BC
1 1 1 1 3
. . . .
2 2 2 2 4
K
E FK
S d FK d BC
EF
1 1 2 6 3 2
. . .
3 3 3 4 6
SKFE K
V AH S
.
Mà
2
3
AM AN AP
AE AK AF
Lại có:
8 8 4 2
. .
27 27 81
AMNP
AMNP AEKF
AEKF
V AM AN AP
V V
V AE AK AF
.
Câu 11: Cho hình chóp tứ giác đều .
S ABCD
có cạnh đáy bằng
a
, cạnh bên hợp với đáy một góc
60
. Gọi
M
là điểm đối xứng của
C
qua
D
,
N
là trung điểm
.
SC
Mặt phẳng
BMN
chia khối chóp .
S ABCD
thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé)
bằng:
A.
7
5
. B.
1
7
. C.
7
3
. D.
6
5
.
Hướng dẫn giải:
Chọn A.
Giả sử các điểm như hình vẽ.
E SD MN E
là trọng
tâm tam giác
SCM
,
//
DF BC F
là trung
điểm
BM
.
Ta có:
, 60
6
2
SD ABCD SDO
a
SO
,
E
N
M
FO
AB
C
D
S
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 73
Facebook: https://www.facebook.com/dongpay
2 2
7
2
a
SF SO OF
2
6 1 7
, ; .
2 4
2 7
SAD
a a
d O SAD OH h S SF AD
1
6
MEFD
MNBC
V ME MF MD
V MN MB MC
3
5 5 1 1 5 1 5 6
, 4
6 6 3 2 18 2 72
BFDCNE MNBC SBC SAD
a
V V d M SAD S h S
3 3
. .
1 6 7 6
.
3 6 36
S ABCD ABCD SABFEN S ABCD BFDCNE
a a
V SO S V V V
Suy ra:
7
5
SABFEN
BFDCNE
V
V
Câu 12: (Hình học không gian) Cho tứ diện
ABCD
và
, ,
M N P
lần lượt thuộc
, ,
BC BD AC
sao cho
4 , 2 , 3 .
BC BM BD BN AC AP
Mặt phẳng
MNP
cắt
AD
tại Q. Tính tỷ số thể tích hai
phần khối tứ diện
ABCD
bị chia bởi mặt phẳng
.
MNP
A.
2
3
B.
7
13
C.
5
13
D.
1
3
Hướng dẫn giải:
Gọi
, ,
I MN CD Q PI AD
kẻ
/ / , / / .
DH BC H IM DK AC K IP
1
.
3
ID DH BM
NMB NDH
IC CM CM
1 1 2
3 2 3 3
IK DK ID DK
DK
IP CP IC AP
.
APQ DKQ
Suy ra
2 3
3 5
AQ AP AQ
DQ DK AD
Đặt
.
ABCD
V V Ta có:
1
. ;
5
ANPQ
ANCD
V
AP AQ
V AC AD
1 1
2 10
ANCD DACN
ANPQ
ABCD DABC
V V DN
V V
V V DB
.
1 1
.
2 2
1 1 1
2 2 4
CDMP
CDMP
CDBA
V ABMP DABMP CDMP
V CM CP
V V
V CB CA
V V V V V
Q
K
I
P
M
N
B
C
A
D
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 74
Facebook: https://www.facebook.com/dongpay
.
7 7
20 13
ABMNQP
ABMNQP ANPQ N ABMP
CDMNQP
V
V V V V
V
Vậy mặt phẳng
MNP
chia khối chóp thành hai phần với tỉ lệ thể tích
7
.
13
Chọn B.
Câu 13: Cho hình lăng trụ tam giác đều
. ' ' ',
ABC A B C
có cạnh đáy bằng
a
và cạnh bên bằng
a 2
.
Lấy M, N lần lượt trên cạnh
', '
AB A C
sao cho
' 1
.
' ' 3
AM A N
AB A C
Tính thể tích V của khối
' .
BMNC C
A.
3
6
108
a
B.
3
2 6
27
a
C.
3
3 6
108
a
D.
3
6
27
a
Hướng dẫn giải:
Gọi G, K lần lượt tâm các hình chữ
nhật
' '
ABB A
và
AA' ' .
C C
Ta có:
1 2
' 3 3
AM AM
AB AG
(Do G trung điểm AB’)
Xét tam giác
'
ABA
có AG là trung
tuyến và
2
.
3
AM
AG
Suy ra
M
là trọng
tâm tam giác
'.
ABA
Do đó BM đi q
ua trung điểm I của AA’.
Ta có:
' 1 ' 2
' 3 ' 3
A N A N
A C A K
(Do K là trung điểm A’C)
Xét tam giác
AA' '
C
có
'
A K
là trung tuyến
và
' 2
.
' 3
A N
A K
Suy ra N là trọng tâm của tam giác
AA' '.
C
Do đó
'
C N
đi qua trung điểm I
của AA’.
Từ M là trọng tâm tam giác
'
ABA
và N trọng tâm của tam giác
AA' '.
C
Suy ra:
1
.
' 3
IM IN
IB IC
Gọi
1 2
,
V V
lần lượt là thể tích các khối chóp
; '.
IMNC IBCC
Ta có:
1
2
1
. .
' 9
V IM IN IC
V IB IC IC
Mà
1 2 2
8
.
9
V V V V V
K
G
N
M
I
H
A'
B'
C'
B
C
A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 75
Facebook: https://www.facebook.com/dongpay
Hạ AH vuông góc với BC tại H thuộc
.
BC
Ta được AH vuông góc với mặt phẳng
' ' . AA'
BB C C song song với mặt phẳng
' '
BB C C
nên khoảng cách từ I đến mặt phẳng
' '
BB C C
bằng khoảng cách từ A đến
' '
BB C C
và bằng AH.
Ta có:
2 3
2 '
3 1 1 3 2 6
; , ' ' . . . .
2 3 3 2 2 12
BCC
a a a a
AH V d I BB C C S
Suy ra:
3
2
8 2 6
.
9 27
a
V V
Chọn B.
Câu 14: Cho hình chóp tứ giác đều
.
S ABCD
có đáy là hình vuông
ABCD
cạnh
,
a
góc giữa mặt bên
và phẳng đáy là
thỏa mãn
1
cos = .
3
Mặt phẳng
P
qua AC và vuông góc với mặt
phẳng
SAD
chia khối chóp
.
S ABCD
thành hai khối đa diện. Tỉ lệ thể tích hai khối đa
diện là gần nhất với giá trị nào trong các giá trị sau:
A.
0,11
B.
0,13
C.
0,7
D.
0,9
Hướng dẫn giải:
.
S ABCD
là hình chóp tứ giác đều
.
SO ABCD
Gọi
N
là trung điểm CD
,
,
CD SN CD ON
SCD ABCD CD
SCD ABCD SNO
Kẻ
.
CM SD
Ta có:
AC BD
AC SBD
AC SO
AC SD SD ACM ACM SAD
nên mặt phẳng
P
là
ACM
.
+ Xét tam giác
SON
vuông tại N có:
3
.
2
cos
ON a
SN
SNO
2 2
2 2
3
2.
2 2
a a
SO SN ON a
+ Xét tam giác
SOD
vuông tại O có:
N
O
C
B
A
D
S
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 76
Facebook: https://www.facebook.com/dongpay
2
2
2 2
2 10
2 ` .
2 2
a a
SD SO OD a
Ta có:
1 1 . 3 10
. . .
2 2 10
SCD
SN CD a
S CM SD SN CD CM
SD
Xét tam giác
MCD
vuông tại M có:
2
2 2 2
3 10 10
D .
10 10
a a
M CD CM a
Ta có:
.
10
1 1 1 1
10
. . .
2 2 2 10 10
10
2
M ACD MACD
MACD SABCD
SABCD SACD
a
V V
DM DA DC
V V
V V DS DA DC
a
Mặt phẳng
P
chia khối chóp
.
S ABCD
thành hai khối
.
M ACD
và
9
.
10
SABCD MACD SABCM SABCM SABCD
S ABCM V V V V V
Do đó:
1
0,11
9
MACD
SABCM
V
V
Chọn A.
Câu 15: Cho tứ diện
.
S ABC
,
M
và
N
là các điểm thuộc các cạnh
SA
và
SB
sao cho
2
MA SM
,
2
SN NB
,
( )
là mặt phẳng qua
MN
và song song với
SC
. Kí hiệu
1
( )
H
và
2
( )
H
là các
khối đa diện có được khi chia khối tứ diện
.
S ABC
bởi mặt phẳng
( )
, trong đó,
1
( )
H
chứa
điểm
S
,
2
( )
H
chứa điểm
A
;
1
V
và
2
V
lần lượt là thể tích của
1
( )
H
và
2
( )
H
. Tính tỉ số
1
2
V
V
.
A.
4
5
B.
5
4
C.
3
4
D.
4
3
Hướng dẫn giải:
Kí hiệu
V
là thể tích khối tứ diện
SABC
.
Gọi
P
,
Q
lần lượt là giao điểm của
( )
với
các đường thẳng
BC
,
AC
.
Ta có
// //
NP MQ SC
. Khi chia khối
1
( )
H
bởi
mặt phẳng
( )
QNC
, ta được hai khối chóp
.
N SMQC
và .
N QPC
.
Ta có:
.
.
( ,( ))
(B,( ))
N SMQC SMQC
B ASC SAC
V S
d N SAC
V d SAC S
;
( ,( )) 2
(B,( )) 3
d N SAC NS
d SAC BS
;
P
N
Q
M
A
B
C
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 77
Facebook: https://www.facebook.com/dongpay
2
4 5
9 9
AMQ SMQC
ASC ASC
S S
AM
S AS S
.
Suy ra
.
.
2 5 10
3 9 27
N SMQC
B ASC
V
V
.QP
.
( ,(QP ))
(S,(A ))
1 1 2 2
3 3 3 27
QPC
N C
S ABC ABC
S
V
d N C
V d BC S
NB CQ CP
SB CA CB

. .QP
1 1
1 2
. . 1 2
10 2 4 4
5 4
27 27 9 9
N SMQC N C
B ASC S ABC
V
V
V V
V V
V V V V V
1
2
4
5
V
V
Câu 16: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh a, SA =
3
a
và SA vuông góc
với mặt phẳng đáy. Mặt phẳng (P) đi qua điểm A và vuông góc với
SC
cắt
, ,
SB SC SD
lần
lượt tại
’, ’, ’.
B C D
Tính thể tích khối chóp
. ’ ’ ’
S AB C D
theo a.
A.
3
3 3
20
a
B.
3
3
20
a
C
3
3 3
10
a
D.
3
3 5
10
a
Hướng dẫn giải:
, ( ) '
BC AB BC SA BC SAB BC AB
( ) ' ' ( ) '
SC P SC AB AB SBC AB SB
Tương tự
'
AD SD
. ' ' ' . ' ' . ' '
S AB C D S AB C S AD C
V V V
. ' '
2 2
.
2 2
2 2
' ' '. '.
. .
3 3 9
. .
4 5 20
S AB C
S ABC
V
SB SC SB SB SC SC
V SB SC SB SC
SA SA
SB SC
(1)
2 2
. ' '
2 2 2 2
.
' ' '. '. 3 3 9
. . . .
4 5 20
S AD C
S ADC
V
SD SC SD SD SC SC SA SA
V SD SC SD SC SD SC
(2)
Do
3
2
. .
1 1 3
. . 3
3 2 6
S ABC S ADC
a
V V a a
Cộng (1) và (2) theo vế ta được
3 3
. ' ' . ' '
. ' ' '
3 3
9 9 9 3 3 3
.
20 20 10 6 20
3 3
6 6
S AB C S AD C
S AB C D
V V
a a
V
a a
Chọn A.
C'
D'
B'
C
A
B
D
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 78
Facebook: https://www.facebook.com/dongpay
Câu 17: Cho tứ diện đều ABCD cạnh a. Mặt phẳng (P) chứa cạnh BC cắt cạnh AD tại E. Biết góc
giữa hai mặt phẳng (P) và (BCD) có số đo là
thỏa mãn
5 2
tan
7
. Gọi thể tích của hai
tứ diện ABCE và tứ diện BCDE lần lượt là
1
V
và
2
V
. Tính tỷ số
1
2
V
V
.
A.
3
8
B.
1
8
C.
3
5
D.
5
8
Hướng dẫn giải:
+) Gọi M là trung điểm
.
BC
Khi đó BC
(MAD) nên (P)(AMD);
(P)(AMD) =ME.
Kẻ AHME thì AH(BCE) (do AH
(AMD))
Kẻ DKME nên DK(BCE) (do DK
(AMD)). Hiển nhiên AH song song DK
Khi đó
.
1
2 .
A BCE
D BCE
V
V
AH
V V DK
+) Gọi là góc giữa (P) và (ABC) (
0
2
). Hiển nhiên
DME
;
AME
.
Vì AM = DM nên:
1
2
sin
sin .sin .sin
sin
VAH
t
DK V
(1)
+) Trong tam giác OMA:
1 1
os( ) os cos sin
3 3
MO
c c sin
MA
. (2)
Từ (1) có:
2 2 2 2
os 1 sin 1 .sin 1 .
c t t x
; với x=sin
2
.
Thay vào (2) ta có:
2 2
1 1
1 . 1 . (1 )(1 ) .
3 3
t x x t x t x x t x
.
+) Giải phương trình có:
2
8
.
(9 6 9)
x
t t
Vì
2
2 2
2 2 2
8 9 6 9 8
sin tan .
1 9 6 9 9 6 1 9 6 1
x t t
x
x t t t t t t
Theo giả thiết suy ra
2 2
2
3
8 50 196 171
5
9 6 1 9 6 0
19
9 6 1 49 25 25
15
t
t t t t
t t
t
M
A
B
C
D
E
H
K
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 79
Facebook: https://www.facebook.com/dongpay
Vậy
3
5
ABCE
DBCE
V
V
Chọn C.
Câu 18: Cho khối chóp
.
S ABC
có
6, 2, 4, 2 10
SA SB SC AB và
90 , 120
SBC ASC
.
Mặt phẳng
P
qua
B
và trung điểm
N
của
SC
và vuông góc với mặt phẳng
SAC
cắt
cạnh
SA
tại
M
. Tính tỉ số thể tích
.
.
S MBN
S ABC
V
V
.
A.
2
9
. B.
2
5
. C.
1
6
. D.
1
4
.
Hướng dẫn giải:
Chọn C
Ta có:
.
.
1
.
2
S MBN
S ABC
V
SM SN
k
V SA SC
với
SM
k
SA
.
Áp dụng định lý hàm số cosin ta có:
90 ; 60 ; 120
ASB BSC ASC
Đặt
6, 2, 4
; ;
. 0; . 4; . 12
a b c
SA a SB b SC c
a b b c a c
Vì
BMN SAC
nên kẻ
,
BH MN H MN BH SAC
.
Khi đó:
. 1 1
BH x BM x BN x SM SB x SN SB
1 1
1
2 2
x
x ka b x c b kxa b c
.
Lại có:
1
0
. 0
2
1
. 0
0
2
x
a kxa b c
BH SA BH SA
BH SAC
BH SC
x
BH SC
c kxa b c
1
36 6 1 0
3
1
12 4 8 1 0
3
k
kx x
kx x
x
.
Vậy
.
.
1 1 1 1
. .
2 2 3 6
S MBN
S ABC
V
SM SN
k
V SA SC
.
N
S
B
C
A
M
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 80
Facebook: https://www.facebook.com/dongpay
Câu 19: Khối tứ diện
ABCD
có thể tích
V
, khối tứ diện
1 1 1 1
A B C D
có thể tích
1
V
, các đỉnh
1 1 1 1
, , ,
A B C D
lần lượt là trọng tâm của các tam giác , , ,
BCD CDA DAB ABC
. Khối tứ diện
2 2 2 2
A B C D
có thể tích
2
V
, các đỉnh
2 2 2 2
, , ,
A B C D
lần lượt là trọng tâm của các tam giác
1 1 1
B C D
,
1 1 1
C D A
,
1 1 1
D A B
,
1 1 1
A B C
. Cứ tiếp tục như thế ta được khối tứ diện
n n n n
A B C D
có thể
tích
n
V
, các đỉnh
, , ,
n n n n
A B C D
lần lượt là trọng tâm của các tam giác
1 1 1
n n n
B C D
,
1 1 1
n n n
C D A
,
1 1 1
n n n
D A B
,
1 1 1
n n n
A B C
. Tính
1 2 2018
...
S V V V
?
A.
2018
2018
3 1
2.3
V
S
. B.
2019
2019
27 1
26.27
V
S
.
C.
2018
2018
27 1
26.27
V
S
. D.
2019
2019
3 1
2.3
V
S
.
Hướng dẫn giải:
Chọn C
Ta có
3
1
1 1
3 27
V V V
3 2
2 1 1
1 1 1
3 27 27
V V V V
…
3 2018
2018 2017
1 1
3 27
V V V
2018
2018
2 2018
2018
1
1
27 1
1 1 1 1
27
... . .
1
27 27 27 27 26.27
1
27
V
S V V
Câu 20: Cho khối lăng trụ tam giác
.
ABC A B C
. Gọi
,
M N
lần lượt thuộc các cạnh bên ,
AA CC
sao cho ; 4
MA MA NC NC
. Gọi
G
là trọng tâm tam giác
ABC
. Hỏi trong bốn khối tứ
diện , ,
GA B C BB MN ABB C
và
A BCN
, khối tứ diện nào có thể tích nhỏ nhất?
A. Khối
A BCN
. B. Khối
GA B C
. C. Khối
ABB C
. D. Khối
BB MN
.
Hướng dẫn giải:
Chọn A.
Gọi
V
là thể tích khối lăng trụ đã cho.
Ta có: . .
2
3
M BB C C A BB C C A BB C C
V V V V
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 81
Facebook: https://www.facebook.com/dongpay
Và
. .
1 1 1
2 2 3
BB N CBB BB C C A BB C A BB C C
S S S V V V
Và
.
1 1 1
2 2 3
BB N CBB BB C C BB MN M BB C C
S S S V V V
Chú ý:
. .
4 2 2 4
5 3 3 15
BCN BCC BB C C A BCN A BB C C
S S S V V V
.
Chọn A.
Câu 21: Cho hình lăng trụ tam giác đều
. ’ ’ ’ABC A B C
, có cạnh đáy bằng và cạnh bên bằng .
Lấy ,M N lần lượt trên cạnh ’, ’AB A C sao cho . Tính thể tích V của khối
’ .BMNC C
A. B. C. D.
Hướng dẫn giải:
Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ và
AA’C’C.
Ta có: (Do G trung điểm AB’).
Xét tam giác ABA’ có AG là trung tuyến và .
Suy ra là trọng tâm tam giác ABA’. Do đó BM đi qua
trung điểm I của AA’.
Ta có: (Do K là trung điểm
A’C).
Xét tam giác AA’C’ có A’K là trung tuyến và .
Suy ra N là trọng tâm của tam giác AA’C’. Do đó C’N đi
qua trung điểm I của AA’.
Từ là trọng tâm tam giác ABA’ và N là trọng tâm của tam giác AA’C’. Suy ra:
.
Gọi lần lượt là thể tích các khối chóp IMNC; IBCC’. Ta có:
a
2
a
' 1
' ' 3
AM A N
AB A C
3
6
108
a
3
2 6
27
a
3
3 6
108
a
3
6
27
a
1 2
' 3 3
AM AM
AB AG
2
3
AM
AG
M
' 1 ' 2
' 3 ' 3
A N A N
A C A K
' 2
' 3
A N
A K
M
1
' 3
IM IN
IB IC
1 2
;
V V
H
K
G
M
N
I
B'
C'
A
C
B
A'
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 82
Facebook: https://www.facebook.com/dongpay
. Mà . Suy ra .
Hạ AH vuông góc với BC tại H thuộc
.BC
Ta được AH vuông góc với mặt phẳng
(BB’C’C). AA’ song song với mặt phẳng nên khoẳng cách từ I đến mặt phẳng
(BB’C’C) bằng khoẳng cách từ A đến (BB’C’C) và bằng AH. Ta có: .
. Suy ra .
Chọn B.
Câu 22: Cho khối lập phương
.ABCD A B C D
cạnh a . Các điểm E và F lần lượt là trung điểm
của
C B
và
C D
. Mặt phẳng
AEF cắt khối lập phương đã cho thành hai phần, gọi
1
V là
thể tich khối chứa điểm A
và
2
V là thể tich khối chứa điểm
'C
. Khi đó
1
2
V
V
là
A.
25
47
. B. 1. C.
17
25
. D.
8
17
.
Hướng dẫn giải:
Đường thẳng EF cắt A D
tại
N
, cắt
A B
tại M ,
AN
cắt DD
tại P , AM cắt
BB
tại Q . Từ đó mặt phẳng
AEF cắt
khối lăng trụ thành hai khối đó là
ABCDC QEFP
và AQEFPB A D
.
Gọi
.ABCD A B C D
V V
,
3 .A A MN
V V
,
4 4
,
PFD N QMB E
V V V V
.
Do tính đối xứng của hình lập phương nên
ta có
4 5
V V .
3
3
1 1 3 3 3
. . . .
6 6 2 2 8
a a a
V AA A M A N a
,
3
4
1 1
. . . . .
6 6 3 2 2 72
a a a a
V PD D F D N
3
1 3 4
25
2
72
a
V V V ,
3
2 1
47
72
a
V V V . Vậy
1
2
25
47
V
V
.
Chọn A.
1
2
1
. .
' 9
V
IM IN IC
V IB IC IC
1 2
V V V
2
8
9
V V
' '
BB C C
3
2
a
AH
2 3
2 '
1 1 3 2 6
. ; ' ' . . .
3 3 2 2 12
BCC
a a a
V d I BB C C S
3
2
8 2 6
9 27
a
V V
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 83
Facebook: https://www.facebook.com/dongpay
Câu 23: Cho hình lập phương
. ' ' ' '
ABCD A B C D
cạnh
.
a
Gọi
,
M N
lần lượt là trung điểm của
' '
A B
và
.
BC
Mặt phẳng
DMN
chia khối lập phương đã cho thành hai khối đa diện. Gọi
H
là khối đa diện chứa đỉnh
, '
A H
là khối đa diện còn lại. Tính tỉ số
'
H
H
V
V
.
A.
'
37
48
H
H
V
V
B.
'
55
89
H
H
V
V
C.
'
2
3
H
H
V
V
D.
'
1
2
H
H
V
V
Hướng dẫn giải:
, '
AN ND J JM BB K
. Ta có:
2 ' ; ' '.
BK B K I A D
Ta có:
1
' ' '
4
A I D D
. Suy ra thiết diện là
KMIDN
' . ' . . '
ABA KMIDN D ABKMA D BKN D MA I
H
V V V V V
3
2
3 3
3
'
'
1 1 1 1 2 1 1 55
. . . . . . . . . .
3 2 3 2 3 2 2 3 3 2 2 4 144
55 89 55
.
144 144 89
H
H
H
a a a a a a a
a a a a
Va a
V a
V
Chọn B.
Câu 24: Cho hình lập phương
.
ABCD A B C D
cạnh
.
a
Gọi
,
M N
lần lượt là trung điểm của các cạnh
A B và BC
. Mặt phẳng (
)
DMN
chia hình lập phương thành 2 phần. Gọi
1
V
là thể tích của phần chứa đỉnh
2
,
A V
là thể tích
của phần còn lại. Tính tỉ số
1
2
V
V
.
A.
2
3
. B.
55
89
. C.
37
48
. D.
1
2
.
N
M
K
I
C'
C
D
A
B
D'
A'
B'
J
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 84
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải
Gọi
H AB DN
;
MH
cắt
'
B B
tại
K
, cắt
'
A A
tại
S
;
SD
cắt
' '
A D
tại
E
.
Thiết diện tương ứng là ngũ giác
DNKME
.
Phần đa diện chứa
A
có thể tích là:
1 . . ' .
S ADH S A EM K BNH
V V V V .
Dùng tam giác đồng dạng kiểm tra được:
BA BH
;
4 '
AH A M
;
4 '
AD A E
và
1
' ' '
3
SA B K A A
.
Đặt độ dài cạnh hình lập phương bằng
1
thì:
1 2
' ;
3 3
SA KB
.
Ta có:
.
1 1 1 4
. . 1 .1.2
6 6 3 9
S ADH
V SA AD AH
.
. ' .
1 1
64 144
S A EM S ADH
V V ;
. .
1 1
8 18
K BNH S ADH
V V
Vậy thì phần đa diện chứa
A
có thể tích là:
4 1 1 55
9 144 18 144
.
Suy ra phần đa diện không chứa
A
có thể tích là:
3
55 89
1
144 144
.
Chọn B.
Câu 25: Cho hình hộp
’ ’ ’ ’.
ABCDA B C D
Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng
thời song song với
’ ’.
B D
Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là
1 2
,
V V
(Trong đó V
1
là thể tích khối chứa A). Tính tỉ số
1
2
V
F
V
.
A.
7
17
. B.
1.
C.
17
25
. D.
8
17
.
Hướng dẫn giải:
*Gọi N là trung điể A’D’. Khi đó
)
.
P BDNM
E
K
N
M
A'
A
N
M
A'
A
D
C
B
B'
C'
D'
D'
C'
B'
B
C
D
S
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 85
Facebook: https://www.facebook.com/dongpay
Thấy BMDNAA’=I.
Khi đó: V
1
=V(A’MNABD); V
2
=V-V
1
. (Với V là thể tích hình hộp)
* Ta có:
( ' ) ( ) 1
( A'B'D') ( ' ' ') 4
V IA MN S AMN
V A S A B D
* Mà:
(AA'B'D') 1
6
V
V
nên có:
1
( ' )
24
V IA MN V
* Lại có:
( ' ) '. . 1
( ) . . 8
V IA MN IA IM IN
V IABD IA IB ID
*Vậy:
1
( )
3
V IABD V
* Do đó:
1
1 1 7
3 24 24
V V V V
nên
2 1
17
24
V V V V
.
Vậy:
1
2
7
17
V
V
Chọn A.
Câu 26: Cho khối lăng trụ tam giác ABC. A’B’C’. Gọi I, J, K lần lượt là trung điểm của các cạnh AB,
AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai
phần đó.
A.
25
47
. B. 1. C.
49
95
. D.
8
17
.
Hướng dẫn giải:
Chứng minh EI = IJ = JF. Từ đó suy ra
' 1
' ' 3
EB EM FA
EB EK FB
. Lại từ đó suy ra
1
2
FN
FK
.
Ta có: d(K, A'B') = (1/2)d(C', A'B'), FB' = (3/2)A'B'. Suy ra
S
KFB’
= (3/4)S
A’B’C’
.
Mặt khác vì
1
' 3
EB
EB
nên suy ra d(E, (KFB’)) = (3/2)h (h là
chiều cao lăng trụ).
Do đó V
EKFB’
= (3/8)V (V là thể tích lăng trụ).
'
1 1 1 1
. . . .
' 3 3 3 27
EBIM
EB FK
V EI EM EB
V EF EK EB
nên V
EBIM
=
1 3 1
.
27 8 72
V V
.
'
'
' 1 1 1 1
. . . .
' 3 3 2 18
FA JN
FB EK
V
FJ FA FN
V FE FB FK
nên V
FA’JN
=
1 3 1
.
18 8 48
V V
.
Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Gọi V
1
là thể tích phần chứa điểm B' và
V
2
là thể tích phần chứa điểm
.
C
C
I
N
M
D
B
C'
A'
B'
D'
A
N
F
M
E
K
J
I
B'
C'
A'
C
B
A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 86
Facebook: https://www.facebook.com/dongpay
Ta có V
1
= (3/8 – 1/72 – 1/48)V = (49/144)V nên V
2
= (95/144)V.
Do đó
1
2
49
95
V
V
.
Chọn C.
CỰC TRỊ TỈ LỆ THỂ TÍCH
Câu 27: Cho hình chóp tứ giác .
S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
A
,
C
thỏa
mãn
1 1
,
3 5
SA SA SC SC
. Mặt phẳng
P
chứa đường thẳng
A C
cắt các cạnh
,
SB SD
lần lượt tại
,
B D
và đặt
.
.
S A B C D
S ABCD
V
k
V
. Giá trị nhỏ nhất của
k
là bao nhiêu?
A.
1
60
. B.
1
30
. C.
4
15
. D.
15
16
.
Hướng dẫn giải:
Chọn A
Đặt
.
S ABCD
V V , ta có:
3 5 8
SB SD SA SC
SB SD SA SC
.
Đặt
0, 0
SB SD
x y
SB SD
1 1
4
x y
x y
.
.
1 1
. .
1
15 30
2
S A B C
S A B C
V
SA SB SC
x V xV
SA SB SC
V
.
.
.
1 1
. .
1
15 30
2
S A D C
S A D C
V
SA SD SC
y V yV
SA SD SC
V
.
Do đó
.
.
1
30
S A B C D
S ABCD
V
k x y
V
4 1 1
8 2 60
x y k .
Câu 28: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Gọi
C
là trung điểm cạnh
SC
.
Mặt phẳng
P
chứa đường thẳng
AC
cắt các cạnh
,
SB SD
tại
,
B D
. Đặt
.
.
S B C D
S ABCD
V
m
V
.
Giá trị nhỏ nhất của
m
bằng :
A.
2
27
. B.
4
27
. C.
1
9
. D.
2
9
.
Hướng dẫn giải:
Chọn C
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 87
Facebook: https://www.facebook.com/dongpay
Đặt
.
.
1
. .
1
2
2
S B C D
S ABCD
V
SB SC SD
V V xy
SB SC SD
V
.
1
;
2
SB SD
m xy x y
SB SD
;
1 1
1 2 3
SA SC
x y SA SC
.
Sử dụng bất đẳng thức
AM GM
ta có
1 1 2 4 1
9 9
xy m
x y
xy
.
Câu 29: Cho khối tứ diện đều
.
S ABC
cạnh bằng
a
. Mặt phẳng
P
đi qua
S
và trọng tâm của tam
giác
ABC
cắt các cạnh
,
AB AC
lần lượt tại
,
M N
. Đặt
.
.
S AMN
S ABC
V
m
V
. Giá trị nhỏ nhất của
m
bằng
A.
2
3
. B.
2
9
. C.
4
9
. D.
1
3
.
Hướng dẫn giải:
Chọn C
Ta có .
AMN
ABC
S
AM AN
m xy
S AB AC
.
Gọi
O
là trọng tâm tam giác
ABC
, đặt
; , 0;1
AM AN
x y x y
AB AC
Ta có
D
là trung điểm của
AB
, giả sử
AM AD
đặt
AB a
Áp dụng định lí Meneleuys cho tam giác
ACD
có
. . 1
MD OC NA
MA OD NC
.
2
.2. 1
a
xa
ya
xa a ya
2 1 1 3 2
x y x y xy x y xy
4
9
m xy
.
Câu 30: Cho hình chóp
.
S ABCD
có thể tích
V
và đáy
ABCD
là hình bình hành. Mặt phẳng qua
A
và trung điểm
N
cạnh
SC
cắt cạnh
,
SB SD
lần lượt tại
,
M P
. Tính thể tích nhỏ nhất của
khối chóp
.
S AMNP
.
A.
8
V
. B.
3
8
V
. C.
4
V
. D.
3
V
.
Hướng dẫn giải:
Chọn C
Ta có
1
1, , ,
2
SA SN
x y z t
SA SB SC
M
S
S SP
D
.
D
O
B
C
A
M
N
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 88
Facebook: https://www.facebook.com/dongpay
Và
1 1 1 1 1 1
1 2 3
x z y t y t
.
Do đó
.
1 1 1 1 1 3
3 3 .1.
4 4 2 4
S AMNP
xyzt V
V V yt ytV
x y z t
.
Mặt khác
.
2
4
3 3 9 3
S AMNP
yt
y t V
yt yt V
.
Câu 31: Cho hình chóp tứ giác .
S ABCD
có đáy
ABCD
là hình hình hành. Các điểm
A
,
C
thỏa
mãn
1 1
,
3 5
SA SA SC SC
. Mặt phẳng
P
chứa đường thẳng
A C
cắt các cạnh
,
SB SD
lần lượt tại
,
B D
và đặt
.
.
S A B C D
S ABCD
V
k
V
. Tính giá trị lớn nhất của
k
là bao nhiêu?
A.
4
105
. B.
1
30
. C.
4
15
. D.
4
27
.
Hướng dẫn giải:
Chọn A
Đặt
.
S ABCD
V V , ta có:
3 5 8
SB SD SA SC
SB SD SA SC
.
Đặt
0, 0
SB SD
x y
SB SD
.
.
.
1 1
. .
1
15 30
2
S A B C
S A B C
V
SA SB SC
x V xV
SA SB SC
V
.
.
.
1 1
. .
1
15 30
2
S A D C
S A D C
V
SA SD SC
y V yV
SA SD SC
V
.
Do đó
.
.
1
30
S A B C D
S ABCD
V
k x y
V
và
1 1
8
x y
.
Không mất tính tổng quát, giả sử
1 1
x
4 4
y
, từ
1 1
8
8
y
x
x y y
1 1
30 30 8
y
k x y y
y
với
1
1
4
y
. Ta có
2
1 8 1
1 0, y ;1
30 4
8
k
y
.
Vậy
max
1 1 4
1 1
30 7 105
k k
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 89
Facebook: https://www.facebook.com/dongpay
Câu 32: Cho hình chóp
.
S ABCD
có
ABCD
là hình bình hành và có thể tích
V
. Gọi
,
M N
thứ tự là
các điểm di động trên các cạnh
,
AB AD
sao cho
2
4
AB AD
AM AN
. Gọi
'
V
là thể tích khối
chóp
.
S AMN
. Tìm giá trị nhỏ nhất của
'
V
.
A.
1
4
V
B.
1
6
V
C.
1
8
V
D.
1
3
V
Hướng dẫn giải:
Chọn A
Đặt
1 1 1 2 2 1
; 4 1
4 1 4
AB AD x
y x
AM x AN y x y x
2 2
.
1 1
. '
2 2 4 1 4 1
SAMN
S ABCD
V
AM AN x x
xy V V
V AB AD x x
2
1
;1
4
1 1
min
4 1 4 2
x
x
x
Câu 33: Cho hình chóp
.
S ABCD
có
ABCD
là hình bình hành và có thể tích
V
. Gọi
,
M N
thứ tự là
các điểm di động trên các cạnh
,
AB AD
sao cho
2
4
AB AD
AM AN
. Gọi
'
V
là thể tích khối
chóp
.
S MBCDN
. Tìm giá trị lớn nhất của
'
V
.
A.
1
4
V
B.
2
3
V
C.
3
4
V
D.
1
3
V
Hướng dẫn giải:
Chọn C
Đặt
1 1 1 2 2 1
; 4 1
4 1 4
AB AD x
y x
AM x AN y x y x
2 2
.
1 1
. ' 1
2 2 4 1 4 1
SAMN
S ABCD
V AM AN x x
xy V V
V AB AD x x
2
1
;1
4
3 1
max 1
4 1 4 2
x
x
x
Câu 34: Cho hình chóp
.
S ABCD
có thể tích
V
, đáy là hình bình hành. Mặt phẳng
đi qua
A
,
trung điểm
I
của
SO
cắt các cạnh
, ,
SB SC SD
lần lượt tại
, ,
M N P
. Tính thể tích nhỏ nhất
của khối chóp
.
S AMNP
.
A.
18
V
. B.
3
V
. C.
6
V
. D.
3
8
V
.
D
A
B
C
S
N
M
D
A
B
C
S
N
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 90
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn C
Với
1
SA
x
SA
,
2
3
SM
y
SB
,
1
2
SN
z
SC
,
SP
t
SD
ta có
1 1 1 1
x z y t
. Xét tam giác
SAC
ta có
1 1
2 2
1 1
4
SO SC
SO SA SC SI SA SN
SI SN
SI SA SN
z
Mặt khác 3 điểm
, ,
A I N
thẳng hàng nên
1 1 1
1
4 4 3
z
z
.
Vậy
2
.
1
;1
4
1 1 1 1 2 1
min
4 3 4 1 2 6
S AMNP
xyzt t V
V V f t V f t f
x y z t t
Dấu bằng xảy ra khi
1 1
;
2 2
t y
tức
đi qua trung điểm của
,
SB SD
.
Câu 35: Cho hình chóp
. ,
S ABCD SA
là đường cao, đáy là hình chữ nhật với
, , .
SA a AB b AD c
Trong mặt phẳng
SDB
lấy G là trọng tâm tam giác
SDB
, qua G kẻ đường thẳng
d
cắt
cạnh BS tại M, cắt cạnh SD tại N, mp
AMN
cắt SC tại K. Xác định M thuộc SB sao cho
SAMKN
V đạt giá trị lớn nhất và nhỏ nhất. Hãy tìm giá trị lớn nhất và nhỏ nhất đó.
A.
ax min
,
8 9
SAMKN m SAMKN
abc abc
V V
B.
ax min
,
8 10
SAMKN m SAMKN
abc abc
V V
C.
ax min
,
9 10
SAMKN m SAMKN
abc abc
V V
D.
ax min
,
10 11
SAMKN m SAMKN
abc abc
V V
Hướng dẫn giải:
Gọi O là tâm hình chữ nhật
.
ABCD
Ta có:
2
3
SG SO
và
K AG SC
và K là trung điểm
SC
1 1 1
. . . . . . . .
2 4 12
SMAK
SMAK SBAC SBAC
SBAC
V
SM SA SK SM SM SM
V V V a b c
V SB SA SC SB SB SB
Tương tự
1
. . .
12
SNAK
SN
V a b c
SC
.
M
G
K
O
C
D
A
B
S
N
P
N
I
O
C
A
D
B
S
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 91
Facebook: https://www.facebook.com/dongpay
Do đó:
1
. .
12
SAMKN
SM SN
V a b c
SB SC
Trong mp
SBD
:
. . . 1
.
2 2 2 2. . 2. . . 3
SMN SMG SGN SMG SGN
SBD SBO SBO SBO
S S S S S
SM SN SG SM SG SN SM SN SM SN
S SB SC S S S SO SB SO SB SB SC SB SC
Do M, N lần lượt nằm trên cạnh SB, SD nên:
1
1
2 2
SB SM
SM SB
SB
Đặt
1
, 1
2
SM
t t
SN
thì
1
. .
3 3 1
SN SN SN t
t t
SC SC SC t
Nhận thấy
SAMKN
V đạt GTLN, GTNN nếu:
3 1
SM SN t
f t t
SB SC t
với
1
1.
2
t
Ta có
2
2 2
1 9 6
' 1
3 1 3 1
t t
f t
t t
Nên
2
' 0 , 0
3
f t t t
(loại).
1 3 3 2 4
, 1 , .
2 2 2 3 3
f f f
Do vậy
8
SAMKN
abc
V là GTLN khi M là trung điểm SB hoặc M trùng với
.
B
9
SAMKN
abc
V là GTNN khi MB chiếm 1 phần
.
SB
Chọn A.
Câu 36: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành. Các điểm
', '
A C
thỏa mãn
1
'
3
SA SA
,
1
'
5
SC SC
. Mặt phẳng
P
chứa đường thẳng
' '
A C
cắt các cạnh
,
SB SD
lần
lượt tại
', '
B D
và đặt
. ' ' ' '
.
S A B C D
S ABCD
V
k
V
. Giá trị lớn nhất của
k
là?
A.
4
105
. B.
1
30
. C.
4
15
. D.
4
27
.
Hướng dẫn giải:
Chọn A.
H
M
G
O
D
B
S
N
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 92
Facebook: https://www.facebook.com/dongpay
Đặt
.S ABCD
V V , ta có
' '
SB SD
SB SD
' '
SA SC
SA SC
3 5 8
Mặt khác
. ' ' '
' ' ' 1
. .
1
15
2
S A B C
V
SA SB SC
x
SA SB SC
V
. ' ' '
1
30
S A B C
V xV
. ' ' '
. ' ' '
' ' ' 1
. .
1
15
2
1
30
S A C D
S A C D
V SA SD SC
y
SA SD SC
V
V yV
Do đó
. ' ' ' '
.
1
30
S A B C D
S ABCD
V
k x y
V
, trong đó
'SB
x
SB
,
'SD
y
SD
Và
1
;1
8
1 4
( ) max ( ) (1)
30 8 1 105
x
k f x x f x f
x
.
Câu 37: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Một mặt phẳng song song với đáy
cắt các cạnh bên
SA
,
SB
,
SC
,
SD
lần lượt tại M ,
N
, P , Q . Gọi M
,
N
, P
,Q
lần lượt
là hình chiếu của M ,
N
, P , Q trên mặt phẳng đáy. Tìm tỉ số
SM
SA
để thể tích khối đa diện
.MNPQ M N P Q
đạt giá trị lớn nhất.
A.
3
4
. B.
2
3
. C.
1
2
D.
1
3
.
Hướng dẫn giải:
Chọn B.
Đặt
SM
x
SA
0 1x , kí hiệu
V
,
h
lần lượt
là thể tích và chiều cao của khối chóp đã cho,
theo Thales ta có:
MN NP PQ SM
x
AB BC CD SA
;
và
,
1
,
d M ABCD
AM
x
SA
d S ABCD
, 1d M ABCD x h .
Vì vậy:
.
. . ,
MNPQ M N P Q
V MN MQ d M ABCD
2
1 . . .x x AB AD h
2
3 1x x V .
P'
Q'
N'
A
P
M'
Q
D
C
B
N
M
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 93
Facebook: https://www.facebook.com/dongpay
Sử dụng bất đẳng thức
AM GM
ta có:
2
1
x x
1
. . 2 2
2
x x x
3
1 2 2 4
2 3 27
x x x
.
Do đó
.
4
9
MNPQ M N P Q
V V
. Dấu
" "
xảy ra
2 2
x x
2
3
x
.
Chọn B.
Câu 38: Cho khối chóp
.
S ABC
. Một mặt phẳng song song với đáy cắt các cạnh bên
SA
,
SB
,
SC
lần lượt tại
M
,
N
,
P
. Gọi
M
,
N
,
P
lần lượt là hình chiếu của
M
,
N
,
P
trên mặt phẳng
đáy. Tìm tỉ số
SM
SA
để thể tích khối đa diện .
MNP M N P
đạt giá trị lớn nhất.
A.
3
4
. B.
2
3
. C.
1
2
. D.
1
3
.
Hướng dẫn giải:
Chọn B.
Đặt
SM
x
SA
0 1
x
, kí hiệu
V
,
h
lần lượt
là thể tích và chiều cao của khối chóp đã cho,
theo Thales ta có:
MN NP MP SM
x
AB BC CA SA
;
và
,
1
,
d M ABC
AM
x
SA
d S ABC
, 1
d M ABC x h
;
2
MNP ABC
S x S
.
Vì vậy:
.
. ,
MNP M N P MNP
V S d M ABC
2
1 . .
ABC
x x S h
2
3 1
x x V
.
Sử dụng bất đẳng thức
AM GM
ta có:
2
1
x x
1
. . 2 2
2
x x x
3
1 2 2 4
2 3 27
x x x
.
Do đó
4
9
MNPQM N P
V V
. Dấu
" "
xảy ra
2 2
x x
2
3
x
.
Chọn B.
Câu 39: Cho hình chóp
.
S ABCD
có đáy là hình bình hành và có thể tích là
.
V
Điểm
P
là trung
điểm của
,
SC
một mặt phẳng qua
AP
cắt hai cạnh
SD
và
SB
lần lượt tại
M
và
.
N
Gọi
1
V
là thể tích của khối chóp
. .
S AMPN
Tìm giá trị nhỏ nhất của
1
V
V
?
A.
1
8
. B.
2
3
. C.
3
8
. D.
1
3
.
B
N'
P'
A
P
M'
N
C
M
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 94
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn D.
Gọi
O
là tâm của hình bình hành
ABCD
. G là trọng tâm tam giác
SAC
.
Ta có
, ,
M G N
thẳng hàng. Do
ABCD
là hình bình hành nên
. . .
1
2
S ADC S ABC S ABCD
V V V .
Theo công thức tỉ số thể tích ta có:
. . .
. .
.
1 1
.
1
2 4
2
S AMP S AMP S AMP
S ADC S ABCD
S ABCD
V V V
SM SP SM SM
V SD SC SD V SD
V
Tương tự
. . .
. .
.
1 1
.
1
2 4
2
S ANP S ANP S ANP
S ABC S ABCD
S ABCD
V V V
SN SP SN SN
V SB SC SB V SB
V
Từ đó suy ra
. .
. .
.
.
1
4
1
4
S AMP S ANP
S ABCD S ABCD
S AMNP
S ABCD
V V
SM SN
V V SD SB
V
SM SN
V SD SB
Hay
1
1
4
V
SM SN
V SD SB
Ta chứng minh
3
SD SB
SM SN
.
Thậy vậy, qua
,
B D
kẻ các đường song song với
MN
cắt
SO
lần lượt tại
,
E F
.
Ta có: ;
SD SF SB SE SD SB SE SF
SM SG SN SG SM SN SG
2 3
2. 3
2
SD SB SO
SM SN SG
Đặt ;
SD SB
x y
SM SN
. Ta có
3
x y
Mặt khác
1
2
1 1 1 1 3 3 1
4 4 4 4 3
V SM SN x y
V SD SB x y xy xy
x y
Vậy
1
V
V
nhỏ nhất bằng
1
3
.
Câu 40: Cho hình chóp
.
S ABC
có
30
ASB BSC CSA
và
SA SB SC a
. Mặt phẳng
P
qua
A
cắt hai cạnh
,
SB SC
lần lượt tại
,
B C
sao cho chu vi tam giác
AB C
nhỏ nhất.
Gọi
1 2
,
V V
lầ lượt là thể tích các khối chóp . , .
S AB C S ABC
. Tính tỉ số
1
2
V
V
.
A.
1
2
3 2 2
V
V
. B.
1
2
3 1
V
V
. C.
1
2
4 2 3
V
V
. D.
1
2
2 1
V
V
.
Hướng dẫn giải:
Chọn C
S
B
D
O
G
M
N
E
F
S
A
B
C
D
O
N
P
M
G
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 95
Facebook: https://www.facebook.com/dongpay
Đặt
1
2
, . .
VSB SC SB SC
x y x y
SB SC V SB SC
.
Khi đó:
2 2 2
2
2 2 2
2. . .cos
2. . .cos30 1 3
AB SA SB SA SB ASB
a ax a ax a x x
.
2
1 3
AB a x x
Tương tự:
2
1 3
AC a y y
,
2 2
3
B C a x xy y
Ta có:
2 2 2 2
2
1 3 1 3 3
p AB AC B C
a x x y y x xy y
2 2
2 2
2
3 1 3 1
1 3
2 2 2 2
a y y x x x x
2
2
2 2 2
3 3 1 1
1 3 ( 1 1 3 )
2 2 2 2
a x x a x x a x x x x
.
2 2 2 2
2 2
1 3 3 1 3 1 1 3
2
2 2 2 2 2 2 2 2
a x x a a
.
Dấu bằng xảy ra khi:
2
1
2
3
2
, 3 1 3 1 3 1 4 2 3
3
2
y x
V
x x x y
V
y
.
Câu 41: Cho khối chóp
.
S ABC
có
SA SB SC a
60
ASB
,
90
BSC
,
120
ASC
. Gọi
,
M N
lần lượt là các điểm trên cạnh
AB
và
SC
sao cho
CN AM
SC AB
. Khi khoảng cách giữa
M
và
N
nhỏ nhất, tính thể tích
V
của khối chóp
.
S AMN
.
A.
3
2
72
a
. B.
3
5 2
72
a
. C.
3
5 2
432
a
. D.
3
2
432
a
.
Hướng dẫn giải:
Chọn C
S
A
C
B
C'
B'
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 96
Facebook: https://www.facebook.com/dongpay
Ta có thể tích khối chóp
.
S ABC
à
2 2
3 3
0
1 1 2
1
6 2 2 12
a a
V
.
Đặt
0 1
CN AM
m m
SC AB
, ta có
, ,
SA a SB b SC c
,
a b c a
,
2 2
. , . 0, .
2 2
a a
a b b c a c
.
Theo đẳng thức trên ta có đẳng thức vectơ
1 , .
SN m c SM SA AM a mAB a m b a
1
1 1
MN SN SM m c a m b a
m a mb m c

.
Do đó
2
2
2
2 2
1 1
11
3 5 3
12
MN m a mb m c
a
m m a
.
Dấu bằng xảy ra tại
. 0
3 3
0
5
. . .
6
5 1 2 5 2
1 . .
6 6 12 432
S AMC
SN SN AM
m V V V
SC SC AB
a a
m m V
.
b
c
a
C
A
B
S
M
N
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 97
Facebook: https://www.facebook.com/dongpay
1,8
dm
1
dm
1
dm
3
m
1,2
m
ỨNG DỤNG THỰC TẾ
A – BÀI TẬP TRẮC NGHIỆM
Câu 1: Kim tự tháp Cheops (có dạng hình chóp) là kim tự tháp cao nhất ở Ai Cập. Chiều cao của
kim tự tháp này là 144m , đáy của kim tự tháp là hình vuông có cạnh dài 230m . Các lối đi
và phòng bên trong chiếm
30%
thể tích của kim tự tháp. Biết một lần vận chuyển gồm
10
xe, mỗi xe chở
6
tấn đá, và khối lượng riêng của đá bằng
3 3
2,5.10 /kg m . Số lần vận
chuyển đá để xây đủ dựng kim tự tháp là:
A.
740600
. B.
76040
. C.
7406
. D.
74060
.
Câu 2: Một hộp đựng chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một
phần tư thể tích phía trên của hộp được dải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa
đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi
0
x x là giá trị làm cho hộp
kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị là
0
V . Tìm
0
V .
A. 48 đvtt B. 16 đvtt C. 64 đvtt D.
64
3
đvtt
Câu 3: Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình
vuông trên một mặt) là 4cm.
A. 27 cm
3
. B. 1728 cm
3
. C. 1 cm
3
. D. 9 cm
3
.
Câu 4: Cắt một miếng giấy hình vuông ở hình 1 và xếp thành một hình chóp tứ
giác đều như hình 2 . Biết cạnh hình vuông bằng
20cm
,
OM x cm .
Tìm x để hình chóp đều ấy có thể tích lớn nhất?
A.
9x cm
. B.
8x cm
.
C.
6x cm
. D.
7x cm
.
Câu 5: Người ta muốn xây một bể chứa nước dạng khối
hộp chữ nhật trong một phòng tắm. Biết chiều dài,
chiều rộng, chiều cao của khối hộp đó lần lượt là
3m
; 1,2m ; 1,8m (người ta chỉ xây hai mặt thành
bể như hình vẽ bên). Biết mỗi viên gạch có chiều
dài
20cm
, chiều rộng
10cm
, chiều cao
5cm
. Hỏi
người ta sử dụng ít nhất bao nhiêu viên gạch để
xây bể đó và thể tích thực của bể chứa bao nhiêu
lít nước? (Giả sử lượng xi măng và cát không đáng
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 98
Facebook: https://www.facebook.com/dongpay
kể).
A.
738
viên,
5742
lít. B.
730
viên,
5742
lít.
C.
738
viên,
5740
lít. D.
730
viên,
5740
lít.
Câu 6: Cho một cây nến hình lăng trụ lục gác đều có chiều cao và độ dài cạnh đáy lần lượt là
15cm
và
5cm
. Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho
cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng
A.
1500 ml
. B. 600 6 ml . C.
1800 ml
. D. 750 3 ml.
Câu 7: Một miếng bìa hình tròn có bán kính là
20cm
. Trên biên của miếng bìa, ta xác định 8 điểm
, , , , , , ,A B C D E F G H theo thứ tự chia đường tròn thành 8 phần bằng nhau. Cắt bỏ theo các
nét liền như hình vẽ để có được hình chữ thập ABNCDPEFQGHM rồi gấp lại theo các nét
đứt , , ,MN NP PQ QM tạo thành một khối hộp không nắp. Thể tích của khối hộp thu được
là:
A.
4000 2 2 4 2 2
2
B.
3
4000 2 2
2
.
C.
4000 2 2 4 2 2
. D.
3
4000 2 2 .
Câu 8: Cho một tấm nhôm hình chữ nhật
ABCD
có
60AD cm
,
40AB cm
. Ta gập tấm nhôm
theo hai cạnh
MN
và PQ vào phía trong cho đến khi AB và
DC
trùng nhau như hình vẽ
bên để dược một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể
tích lớn nhất bằng
A. 4000 3
3
cm B. 2000 3
3
cm C. 400 3
3
cm D.
4000 2
3
cm
Câu 9: Cho một tấm nhôm hình chữ nhật
ABCD
có
60AD cm
. Ta gấp tấm nhôm theo 2 cạnh
MN
và PQ vào phía trong đến khi AB và
DC
trùng nhau như hình vẽ dưới đây để được
một hình lăng trụ khuyết hai đáy. Tìm x để thể tích khối lăng trụ lớn nhất?
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 99
Facebook: https://www.facebook.com/dongpay
A.
20x
. B.
15x
. C.
25x
. D.
30x
.
Câu 10: Một khối gỗ hình lập phương có độ dài cạnh bằng
.x cm Ở chính giữa mỗi mặt của hình
lập phương, người ta đục một lỗ hình vuông thông sang mặt đối diện, tâm của lỗ hình vuông
là tâm của mặt hình lập phương, các cạnh lỗ hình vuông song song với các cạnh của hình lập
phương và có độ dài
y cm như hình vẽ bên. Tìm thể tích V của khối gỗ sau khi đục biết
rằng 80 ; 20 .x cm y cm
A.
3
490000cm . B.
3
432000cm . C.
3
400000cm . D.
3
390000cm .
Câu 11: Một khối gỗ hình lập phương có độ dài cạnh bằng
x cm .Ở chính giữa mỗi mặt của hình lập
phương, người ta đục một lỗ hình vuông thông sang mặt đối diện,tâm của lỗ hình vuông là
tâm của mặt hình lập phương,các cạnh lỗ hình vuông song song với cạnh của hình lập
phương và có độ dài
y cm (như hình vẽ bên).Tính tỉ số
S
V
,trong đó
V
của khối gỗ sau khi
đục và
S
là tổng diện tích mặt (trong và ngoài)khối gỗ sau khi đục.
A.
6 3
2
x y
S
V x y x y
. B.
3 3
2
x y
S
V x y x y
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 100
Facebook: https://www.facebook.com/dongpay
C.
2 3
2
x y
S
V x y x y
. D.
9 3
2
x y
S
V x y x y
.
Câu 12: Cần phải xây dựng một hố ga, dạng hình hộp chữ nhật có thể tích
3
V m
, hệ số
k
cho trước
(
k
- tỉ số giữa chiều cao của hố và chiều rộng của đáy). Gọi
, , 0
x y h
lần lượt là chiều
rộng, chiều dài và chiều cao của hố ga. Hãy xác định
, , 0
x y h
xây tiết kiệm nguyên vật
liệu nhất.
, ,
x y h
lần lượt là
A.
33
3
2
2
2 1 2 1
2
2 ; ; .
4 4
2 1
k V k k V
kV
x y h
k
k
B.
33
3
2
2
2 1 2 1
2
; ; 2 .
4 4
2 1
k V k k V
kV
x y h
k
k
C.
33
3
2
2
2 1 2 1
2
; 2 ; .
4 4
2 1
k V k k V
kV
x y h
k
k
D.
33
3
2
2
2 1 2 1
2
; 6 ; .
4 4
2 1
k V k k V
kV
x y h
k
k
Câu 13: Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt bỏ các tam giác
cân bên ngoài của tấm nhôm, phần còn lại gập thành một hình chóp tứ giác đều có cạnh đáy
bằng
x m
, sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Tìm
x
để
khối chóp nhận được có thể tích lớn nhất.
A.
2 2
5
x B.
1
2
x
C.
2
4
x D.
2
3
x
Câu 14: Một viên đá có dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng
a
, người ta cưa viên
đá theo mặt phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có
thể tích bằng nhau. Tính diện tích thiết diện của viên đá bị cưa bởi mặt phẳng nói trên.
A.
2
3
4
a
. B.
2
3
4
a
. C.
2
3
4
a
. D.
2
3
4
a
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 101
Facebook: https://www.facebook.com/dongpay
Câu 15: Người thợ cần làm một bể cá hai ngăn, không có nắp ở
phía trên với thể tích
3
1,296 .m Người thợ này cắt các
tấm kính ghép lại một bể cá dạng hình hộp chữ nhật
với ba kích thước , ,a b c như hình vẽ. Hỏi người thợ
phải thiết kế các kích thước , ,a b c bằng bao nhiêu để
đỡ tốn kính nhất, giả sử độ dày của kính không đáng
kể.
A. 3,6 ; 0,6 ; 0,6a m b m c m B. 2,4 ; 0,9 ; 0,6a m b m c m
C. 1,8 ; 1,2 ; 0,6a m b m c m D. 1,2 ; 1,2 ; 0,9a m b m c m
Câu 16: Khi xây nhà, chủ nhà cần làm một hồ nước bằng gạch và xi măng có dạng hình hộp đứng
đáy là hình chữ nhật có chiều dài gấp ba lần chiều rộng và không nắp, có chiều cao là
h
và
có thể tích là . Hãy tính chiều cao của hồ nước sao cho chi phí xây dựng là thấp nhất?
A. m B. 2h m C.
3
2
h m D.
5
2
h m
Câu 17: Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích
3
72dm và chiều cao
là
3 .dm
Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích
thước , a b (đơn vị dm) như hình vẽ.
Tính , a b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bề dày các tấm kính
như nhau và không ảnh hưởng đến thể tích của bể.
A. 24, 24.a b B. 3, 8.a b C. 3 2, 4 2.a b D. 4, 6.a b
Câu 18: Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 1,296 m
3
.
Người thợ này cắt các tấm kính ghép lại một bể cá dạng hình
hộp chữ nhật với 3 kích thước a, b, c như hình vẽ. Hỏi người
thợ phải thiết kế các kích thước a, b, c bằng bao nhiêu để đỡ
tốn kính nhất, giả sử độ dầy của kính không đáng kể.
A. 3,6 ; 0,6 ; 0,6a m b m c m
B. 2,4 ; 0,9 ; 0,6a m b m c m
C. 1,8 ; 1,2 ; 0,6a m b m c m
D. 1,2 ; 1,2 ; 0,9a m b m c m
b dm
a dm
3 dm
c
b
a
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 102
Facebook: https://www.facebook.com/dongpay
Câu 19: Từ một tấm tôn có kích thước 90cmx3m người ta làm một máng xối nước trong đó mặt cắt
là hình thang ABCD có hinh dưới. Tính thể tích lớn nhất của máng xối.
A.
3
40500 3
cm
B.
3
40500 2
cm
C.
3
40500 6
cm
D.
3
40500 5
cm
Câu 20: Để làm một máng xối nước, từ một tấm tôn kích thước
0,9 3
m m
người ta gấp tấm tôn đó
như hình vẽ dưới. Biết mặt cắt của máng xối (bị cắt bởi mặt phẳng song song với hai mặt
đáy) là một hình thang cân và máng xối là một hình lăng trụ có chiều cao bằng chiều dài của
tấm tôn. Hỏi
x m
bằng bao nhiêu thì thể tích máng xối lớn nhất?
A.
0,5
x m
. B.
0,65
x m
. C.
0,4
x m
. D.
0,6
x m
.
Câu 21: Khi xây dựng nhà, chủ nhà cần làm một bể nước bằng gạch có dạng hình hộp có đáy là hình
chữ nhật chiều dài
d m
và chiều rộng
r m
với
2 .
d r
Chiều cao bể nước là
h m
và thể
tích bể là
3
2 .
m
Hỏi chiều cao bể nước như thế nào thì chi phí xây dựng là thấp nhất?
A.
3 3
2 2
m
. B.
3
2
3
m
. C.
3
3
2
m
. D.
2 2
3 3
m
.
Câu 22: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là
V
. Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng
A.
2
3
x V
B.
3
x V
C.
1
4
x V
D.
x V
Câu 23: Nhân ngày quốc tế phụ nữ 8-3 năm 2017, ông A quyết định mua tặng vợ một món quà và
đặt nó vào trong một chiếc hộp có thể tích là 32 ( đvtt ) có đáy hình vuông và không có nắp.
Để món quà trở nên thật đặc biệt và xứng đáng với giá trị của nó ông quyết định mạ vàng
cho chiếc hộp, biết rằng độ dạy lớp mạ tại mọi điểm trên hộp là như nhau. Gọi chiều cao và
cạnh đáy của chiếc hộp lần lượt là . Để lượng vàng trên hộp là nhỏ nhất thì giá trị của
phải là?
A. B. C. D.
3m
90cm
3m
30cm
30cm
30cm
D
B
C
A
h;x
h;x
x 2;h 4
x 4;h 2
3
4;
2
x h
1; 2
x h
3
m
0,9
m
0,3
m
0,3
m
xm
0,3
m
3
m
0,3
m
x
x
(a) T
ấ
m tôn
(b) Máng x
ố
i
(c) M
ặ
t c
ắ
t
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 103
Facebook: https://www.facebook.com/dongpay
Câu 24: Một ngôi nhà có nền dạng tam giác đều
ABC
cạnh dài
10
m
được đặt song song và cách
mặt đất
h m
. Nhà có 3 trụ tại
, ,
A B C
vuông góc với
ABC
. Trên trụ
A
người ta lấy hai
điểm
,
M N
sao cho ,
AM x AN y
và góc giữa
MBC
và
NBC
bằng
90
để là mái và
phần chứa đồ bên dưới. Xác định chiều cao thấp nhất của ngôi nhà.
A.
5 3
. B.
10 3
. C.
10
. D.
12
.
Câu 25: Một nhà sản xuất sữa có hai phương án làm hộp sữa. Hộp sữa có dạng khối hộp chữ nhật
hoặc hộp sữa có dạng khối trụ. Nhà sản xuất muốn chi phí bao bì càng thấp càng tốt(tức diện
tích toàn phần của hộp nhỏ nhất), nhưng vẫn phải chứa được một thể tích xác định là
V
cho
trước. Khi đó diện tích toàn phần của hộp sữa bé nhất trong hai phương án là
A.
3
2
2
V
.
B.
3
2
6
V
.
C.
3
2
3 6
V
.
D.
3
2
3 2
V
.
Câu 26: Một bác thợ gò hàn làm một chiếc thùng hình hộp chữ nhật (không nắp) bằng tôn thể tích
3
665,5
dm
. Chiếc thùng này có đáy là hình vuông cạnh
( )
x dm
, chiều cao
( )
h dm
. Để làm
chiếc thùng, bác thợ phải cắt một miếng tôn như hình vẽ. Tìm
x
để bác thợ sử dụng ít
nguyên liệu nhất.
A.
10,5( )
dm
. B.
12( )
dm
. C.
11( )
dm
. D.
9( )
dm
.
Câu 27: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là
V
. Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng
A.
2
3
x V
B.
3
x V
C.
1
4
x V
D.
x V
Câu 28: Người ta muốn xây một bồn chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết
chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là 5m, 1m, 2m (hình vẽ bên). Biết
mỗi viên gạch có chiều dài 20cm, chiều rộng 10cm, chiều cao 5cm. Hỏi người ta sử dụng ít
nhất bao nhiêu viên gạch để xây bồn đó và thể tích thực của bồn chứa bao nhiêu lít nước?
(Giả sử lượng xi măng và cát không đáng kể)
A. 1180 viên, 8820 lít B. 1180 viên, 8800 lít
C. 1182 viên, 8820 lít D. 1180 viên, 8800 lít
Câu 29: Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng
lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác
cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng
trụ tam giác đều (như hình vẽ). Gọi
1 2
,
V V
lần lượt là thể tích của lăng trụ tứ giác đều và lăng
trụ tam giác đều. So sánh
1
V
và
2
V
.
h
h
h
h
x
x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 104
Facebook: https://www.facebook.com/dongpay
A.
1 2
V V B.
1 2
V V C.
1 2
V V D. Không so sánh
được
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 105
Facebook: https://www.facebook.com/dongpay
B – HƯỚNG DẪN GIẢI
Câu 1: Kim tự tháp Cheops (có dạng hình chóp) là kim tự tháp cao nhất ở Ai Cập. Chiều cao của
kim tự tháp này là 144m , đáy của kim tự tháp là hình vuông có cạnh dài 230m . Các lối đi
và phòng bên trong chiếm
30%
thể tích của kim tự tháp. Biết một lần vận chuyển gồm
10
xe, mỗi xe chở
6
tấn đá, và khối lượng riêng của đá bằng
3 3
2,5.10 /kg m . Số lần vận
chuyển đá để xây đủ dựng kim tự tháp là:
A.
740600
. B.
76040
. C.
7406
. D.
74060
.
Hướng dẫn giải:
Chọn D.
Gọi cạnh của hình chóp là
230a
,chiều cao
144h
Thể tích kim tự tháp:
2 3
2539 00
1
2
3
V ha m
Thể tích khối đá cần vận chuyển
3
0.7 1777440V m .
Gọi x là số lần vận chuyển. Để đủ đá xây dựng kim tự
tháp thì
Câu 2: Một hộp đựng chocolate bằng kim loại có hình dạng lúc
mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên của hộp được dải một lớp bơ
sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình
vẽ, gọi
0
x x là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate
nguyên chất có giá trị là
0
V . Tìm
0
V .
A. 48 đvtt B. 16 đvtt C. 64 đvtt D.
64
3
đvtt
Hướng dẫn giải:
Phân tích: Đây là một dạng bài toán ứng dụng thực thể kết hợp với cả phần tính thể tích khối
đa diện ở hình học và phần tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức đã học ở
chương I phần giải thích.
Trước tiên ta nhận thấy
2
6 12 2 2 6V x x x x x
2 3 2
2 12 36 2 24 72x x x x x x
Xét hàm số
3 2
2 24 72f x x x x trên
0;6
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 106
Facebook: https://www.facebook.com/dongpay
2
6
' 6 48 72; ' 0
2
x
f x x x f x
x
Khi đó
0;6
max 2 64f x f đvtt. Đến đây nhiều quý độc gỉ vội vã khoanh C mà không
đắn đo gì. Tuy nhiên, nếu vội vã như vậy là bạn đã sai, bởi đề bài yêu cầu tìm thể tích
chocolate nguyên chất mà không phải là thể tích hộp do đó ta cần. Tức là
1 3
1
4 4
thể tích
hộp. tức là
3
.64 48
4
đvtt
Câu 3: Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình
vuông trên một mặt) là 4cm.
A. 27 cm
3
. B. 1728 cm
3
. C. 1 cm
3
. D. 9 cm
3
.
Hướng dẫn giải:
Đây là một bài toán ăn điểm, nhưng nếu đọc không kĩ từng câu chữ trong đề bài các độc giả
rất có thể sai
Ta có khối rubic như sau:
Hướng sai 1: Nghĩ rằng mỗi cạnh của ô vuông là 4 nên chiều dài mỗi cạnh của khối rubic là
3
4.3 12 12 1728a V B
Hướng sai 2: Nghĩ rằng chu vi mỗi ô vuông là tổng độ dài của cả 12 cạnh nên chiều dài mỗi
cạnh là
1
3
, nên độ dài của khối rubik là
3
1
.3 1 1 1
3
a V C
Hướng sai 3: Nhầm công thức thể tích sang công thức tính diện tích nên suy ra ý D.
Cách làm đúng: Chu vi của một ô nhỏ là 4 cm nên độ dài mỗi cạnh nhỏ là 1cm, vậy độ dài
cạnh của khối rubic là
3
3.1 3 3.3.3 27a cm V cm .
Chọn A.
Câu 4: Cắt một miếng giấy hình vuông ở hình 1 và xếp thành một hình chóp tứ
giác đều như hình 2 . Biết cạnh hình vuông bằng
20cm
,
OM x cm .
Tìm x để hình chóp đều ấy có thể tích lớn nhất?
A.
9x cm
. B.
8x cm
.
C.
6x cm
. D.
7x cm
.
Hướng dẫn giải:
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 107
Facebook: https://www.facebook.com/dongpay
1,8
dm
1
dm
1
dm
3
m
1,2
m
Ta có:
2
OM x AC x
,
2
AM x
.
Suy ra:
2
x
OH
,
2
x
MH
,
10 2
2
x
SH
.
2 2
2 2
10
20 10
2 2 2
x x
SO SH OH x
2 2
1 1 20
. 20 10 .2 40 4 .
3 3 3
đáy
V SO S x x x x
5
15
2
20 20 40 4 20
40 4 . . . . .2
3 3 5 3
x x x x x
V x x x x
Dấu
" "
xảy ra khi
40 4 8
x x x
.
Câu 5: Người ta muốn xây một bể chứa nước dạng khối
hộp chữ nhật trong một phòng tắm. Biết chiều dài,
chiều rộng, chiều cao của khối hộp đó lần lượt là
3
m
;
1,2
m
;
1,8
m
(người ta chỉ xây hai mặt thành
bể như hình vẽ bên). Biết mỗi viên gạch có chiều
dài
20
cm
, chiều rộng
10
cm
, chiều cao
5
cm
. Hỏi
người ta sử dụng ít nhất bao nhiêu viên gạch để
xây bể đó và thể tích thực của bể chứa bao nhiêu
lít nước? (Giả sử lượng xi măng và cát không đáng
kể).
A.
738
viên,
5742
lít. B.
730
viên,
5742
lít.
C.
738
viên,
5740
lít. D.
730
viên,
5740
lít.
Hướng dẫn giải:
Chọn A.
Thể tích của bể là
18.11.29 5742
V l
.
Thể tích của
1
viên gạch là
3
1
dm
, thể tích cần xây dựng là
3
(30 11).18 738
dm
, suy ra số
viên ít nhất cần dùng là
738
viên.
Câu 6: Cho một cây nến hình lăng trụ lục gác đều có chiều cao và độ dài cạnh đáy lần lượt là
15cm
và
5cm
. Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho
cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng
A.
1500 ml
. B.
600 6 ml
. C.
1800 ml
. D.
750 3 ml
.
Hướng dẫn giải:
Ta có
10 cm,AD=5 3 cm
AB
50 3
ABCD
S
H
x
O
M
D
A
C
S
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 108
Facebook: https://www.facebook.com/dongpay
. 750 3
ABCD
V S h
Chọn D
Câu 7: Một miếng bìa hình tròn có bán kính là
20cm
. Trên biên của miếng bìa, ta xác định 8 điểm
, , , , , , ,A B C D E F G H theo thứ tự chia đường tròn thành 8 phần bằng nhau. Cắt bỏ theo các
nét liền như hình vẽ để có được hình chữ thập ABNCDPEFQGHM rồi gấp lại theo các nét
đứt , , ,MN NP PQ QM tạo thành một khối hộp không nắp. Thể tích của khối hộp thu được
là:
A.
4000 2 2 4 2 2
2
B.
3
4000 2 2
2
.
C.
4000 2 2 4 2 2
. D.
3
4000 2 2 .
Hướng dẫn giải:
Chọn C.
Theo giả thuyết ta có
2
2 sin
8.2
AB CD EF GH MN NP PQ QM r
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 109
Facebook: https://www.facebook.com/dongpay
1 cos
4
40sin 40 20 2 2
8 2
Và
10 4 2 2
2
AH
MH MA NB NC PD PE QG QH
Vì vậy
2
. . 20 2 2 .10 4 2 2 4000 2 2 4 2 2V MN MQ MA
Câu 8: Cho một tấm nhôm hình chữ nhật
ABCD
có
60AD cm
,
40AB cm
. Ta gập tấm nhôm
theo hai cạnh
MN
và PQ vào phía trong cho đến khi AB và
DC
trùng nhau như hình vẽ
bên để dược một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể
tích lớn nhất bằng
A. 4000 3
3
cm
B. 2000 3
3
cm
C. 400 3
3
cm
D.
4000 2
3
cm
Hướng dẫn giải:
Chọn A.
Đáy của lăng trụ là tam giác cân có
cạnh bên bằng x , cạnh đáy bằng
60 2x
Đường cao tam giác đó là
2
2
60 2
60 900
2
x
AH x x
,
với H là trung điểm
NP
Diện tích đáy là
1 1
. 60 900. 30 60 900 900 30 900 30
2 30
ANP
S S AH NP x x x x x
3
2
1 900
100 3
30 3
S cm
Diện tích đáy lớn nhất là
2
100 3cm nên thể tích lớn nhất là
3
40.100 3 4000 3V cm .
Câu 9: Cho một tấm nhôm hình chữ nhật
ABCD
có
60AD cm
. Ta gấp tấm nhôm theo 2 cạnh
MN
và PQ vào phía trong đến khi AB và
DC
trùng nhau như hình vẽ dưới đây để được
một hình lăng trụ khuyết hai đáy. Tìm x để thể tích khối lăng trụ lớn nhất?
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 110
Facebook: https://www.facebook.com/dongpay
A.
20x
. B.
15x
. C.
25x
. D.
30x
.
Hướng dẫn giải:
Chọn A.
Ta có
60 2PN x
, gọi H là trung điểm của
PN
suy ra 60 900AH x
1
. 60 2 60 900 60 2 15 225
2
ANP
S x x x x f x
, do chiều cao của khối
lăng trụ không đổi nên thể tích khối lăng trụ max khi
f x max.
45 20
' 0 20, 20 100 3, 15 0
15 225
x
f x x f f
x
maxf 100 3x khi
20x
Câu 10: Một khối gỗ hình lập phương có độ dài cạnh bằng
.x cm Ở chính giữa mỗi mặt của hình
lập phương, người ta đục một lỗ hình vuông thông sang mặt đối diện, tâm của lỗ hình vuông
là tâm của mặt hình lập phương, các cạnh lỗ hình vuông song song với các cạnh của hình lập
phương và có độ dài
y cm như hình vẽ bên. Tìm thể tích V của khối gỗ sau khi đục biết
rằng 80 ; 20 .x cm y cm
A.
3
490000cm . B.
3
432000cm . C.
3
400000cm . D.
3
390000cm .
Hướng dẫn giải:
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 111
Facebook: https://www.facebook.com/dongpay
Thể tích cần tìm bằng thể tích khối lập phương ban đầu trừ đi 6 khối hộp chữ nhật có đáy là
hình vuông cạnh
y cm , chiều cao
;
2
x y
cm
rồi trừ đi thể tích khối lập phương có độ dài
cạnh bằng
y cm . Vì vậy,
3 2 3 3 2 3 3
80 20
6 80 6. .20 20 432000 .
2 2
x y
V x y y cm
Câu 11: Một khối gỗ hình lập phương có độ dài cạnh bằng
x cm .Ở chính giữa mỗi mặt của hình lập
phương, người ta đục một lỗ hình vuông thông sang mặt đối diện,tâm của lỗ hình vuông là
tâm của mặt hình lập phương,các cạnh lỗ hình vuông song song với cạnh của hình lập
phương và có độ dài
y cm (như hình vẽ bên).Tính tỉ số
S
V
,trong đó
V
của khối gỗ sau khi
đục và
S
là tổng diện tích mặt (trong và ngoài)khối gỗ sau khi đục.
A.
6 3
2
x y
S
V x y x y
. B.
3 3
2
x y
S
V x y x y
.
C.
2 3
2
x y
S
V x y x y
. D.
9 3
2
x y
S
V x y x y
.
Hướng dẫn giải:
Chọn A
Thể tích hình cần tính bằng thể tích khối lập phương ban đầu trừ đi 6 khối hộp chữ nhật có
đáy là hình vuông cạnh y cm ,chiều cao
2
x y
cm
,rồi trừ đi thể tích khối lập phương có độ
dài cạnh bằng y cm .
Vì vậy:
2
3 2 3
6 2
2
x y
V x y y x y x y
.
Tổng diện tích các mặt của khối gỗ sau khi đục là
2 2
( )
6 6.4. 6 3
2
y x y
V x y x y x y
Vậy
6 3
2
x y
S
V x y x y
.
Chọn A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 112
Facebook: https://www.facebook.com/dongpay
Câu 12: Cần phải xây dựng một hố ga, dạng hình hộp chữ nhật có thể tích
3
V m
, hệ số
k
cho trước
(
k
- tỉ số giữa chiều cao của hố và chiều rộng của đáy). Gọi
, , 0
x y h
lần lượt là chiều
rộng, chiều dài và chiều cao của hố ga. Hãy xác định
, , 0
x y h
xây tiết kiệm nguyên vật
liệu nhất.
, ,
x y h
lần lượt là
A.
33
3
2
2
2 1 2 1
2
2 ; ; .
4 4
2 1
k V k k V
kV
x y h
k
k
B.
33
3
2
2
2 1 2 1
2
; ; 2 .
4 4
2 1
k V k k V
kV
x y h
k
k
C.
33
3
2
2
2 1 2 1
2
; 2 ; .
4 4
2 1
k V k k V
kV
x y h
k
k
D.
33
3
2
2
2 1 2 1
2
; 6 ; .
4 4
2 1
k V k k V
kV
x y h
k
k
Hướng dẫn giải:
Chọn C.
Gọi
, , , , 0
x y h x y h
lần lượt là chiều rộng, chiều dài và chiều cao của hố ga.
Ta có:
h
k h kx
x
và
2
V V
V xyh y
xh kx
.
Nên diện tích toàn phần của hố ga là:
2
2 1
2 2 2
k V
S xy yh xh kx
kx
Áp dụng đạo hàm ta có S nhỏ nhất khi
3
2
2 1
4
k V
x
k
Khi đó
3
3
2
2 1
2
2 ,
4
2 1
k k V
kV
y h
k
.
Câu 13: Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt bỏ các tam giác
cân bên ngoài của tấm nhôm, phần còn lại gập thành một hình chóp tứ giác đều có cạnh đáy
bằng
x m
, sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Tìm
x
để
khối chóp nhận được có thể tích lớn nhất.
x
y
h
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 113
Facebook: https://www.facebook.com/dongpay
A.
2 2
5
x B.
1
2
x
C.
2
4
x D.
2
3
x
Hướng dẫn giải:
Ta có:
2
1 2 1
2 4
x
y z y
Chiều cao của hình chóp:
2 2
2 2
2 1 2 1 2
2 4 2 2 2
h z x y x x
2
1 1 2
.
3 2 2
chop
V x x
chop
V
lớn nhất khi hàm số
2
1 2
2 2
y x x
đạt GTLN
2
5 2 4
'
1 2
4
2 2
x x
y
x
2
0
' 0 5 2 4 0
2 2
5
x
y x x
x
Chọn A.
1
x
x
z
y
h
x
2
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 114
Facebook: https://www.facebook.com/dongpay
Câu 14: Một viên đá có dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng
a
, người ta cưa viên
đá theo mặt phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có
thể tích bằng nhau. Tính diện tích thiết diện của viên đá bị cưa bởi mặt phẳng nói trên.
A.
2
3
4
a
. B.
2
3
4
a
. C.
2
3
4
a
. D.
2
3
4
a
.
Hướng dẫn giải:
Chọn D.
Từ giả thiết
. .
1
2
S A B C D S ABCD
V V
. .
1
2
S A B C S ABC
V V
( Do khối chóp tứ giác đều)
.
.
1
2
S A B C
S ABC
V
V
3
3 3
2 2
SA SA a
SA
SA
A B SA
3
2
a
2
2
3
4
td
a
S A B
.
Câu 15: Người thợ cần làm một bể cá hai ngăn, không có nắp ở
phía trên với thể tích
3
1,296 .
m
Người thợ này cắt các
tấm kính ghép lại một bể cá dạng hình hộp chữ nhật
với ba kích thước
, ,
a b c
như hình vẽ. Hỏi người thợ
phải thiết kế các kích thước
, ,
a b c
bằng bao nhiêu để
đỡ tốn kính nhất, giả sử độ dày của kính không đáng
kể.
A.
3,6 ; 0,6 ; 0,6
a m b m c m
B.
2,4 ; 0,9 ; 0,6
a m b m c m
C.
1,8 ; 1,2 ; 0,6
a m b m c m
D.
1,2 ; 1,2 ; 0,9
a m b m c m
Hướng dẫn giải:
Với
a
là chiều dài của cả 2 ngăn của bể cá. Ta có:
1,296 1
V abc
3
6
2 2 2 3 2 3 3
2 2 2 2
a a a a abc abc abc
S c bc b c bc b ac bc ab abc
b a c abc
B'
A'
O
D'
C'
D
C
B
A
S
c
b
a
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 115
Facebook: https://www.facebook.com/dongpay
b dm
a dm
3 dm
Dấu “=” xảy ra khi
3
2 3 1
2
2
a b
b
a a c
c
Thay vào
3 3
3 1,296.4 6
1 : 1,296 ; 1,8; 0,6.
4 3 5
b b b a c
Chọn C.
Câu 16: Khi xây nhà, chủ nhà cần làm một hồ nước bằng gạch và xi măng có dạng hình hộp đứng
đáy là hình chữ nhật có chiều dài gấp ba lần chiều rộng và không nắp, có chiều cao là
h
và
có thể tích là . Hãy tính chiều cao của hồ nước sao cho chi phí xây dựng là thấp nhất?
A. m B.
2
h m
C.
3
2
D.
5
2
Hướng dẫn giải:
Gọi x, y, h lần lượt là chiều rộng, chiều dài và chiều cao của hình hộp
Theo đề bài ta có
3
y x
và
2
3
V V
V hxy h
xy x
Để tiết kiệm nguyên vật liệu nhất ta cần tìm các kích thước sao cho diện tích toàn phần của
hồ
nước là nhỏ nhất.
Khi đó ta có:
2
2 2
8
2 2 2 2.3 . .3x 3
3 3 3
tp
V V V
S xh yh xy x x x x
x x x
Ta có
2
2 2
3
8 4 4 16
3 3 3 36
3 3 3 3
Cauchy
tp
V V V V
S x x
x x x
.
Dấu “=” xảy ra khi và chỉ khi
2
3
2
4 4 3
3 2
3 9 3 2
V V V
x x h
x x
.
Vậy chọn C.
Câu 17: Người ta muốn thiết kế một bể cá bằng kính
không có nắp với thể tích
3
72
dm
và chiều
cao là
3 .
dm
Một vách ngăn (cùng bằng
kính) ở giữa, chia bể cá thành hai ngăn, với
các kích thước
,
a b
(đơn vị dm) như hình
vẽ.
Tính
,
a b
để bể cá tốn ít nguyên liệu nhất
(tính cả tấm kính ở giữa), coi bề dày các
tấm kính như nhau và không ảnh hưởng đến thể tích của bể.
A.
24, 24.
a b B.
3, 8.
a b
C.
3 2, 4 2.
a b D.
4, 6.
a b
Chọn D.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 116
Facebook: https://www.facebook.com/dongpay
Có:
24
72 3. 72V ab a
b
(1)
Bể cá tốn ít nguyên liệu nhất nghĩa là diện tích toàn phần nhỏ nhất.
Ta có diện tích toàn phần của bể cá là:
216
3.3 2. 3 6 24
tp
S a ab b b
b
Áp dụng bất đẳng thức Côsi:
216 216
6 24 2 .6 24 96
tp
S b b
b b
Dấu bằng xảy ra khi và chỉ khi:
216
6 6 0b b b
b
. Từ (1), ta suy ra:
4a
.
Câu 18: Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 1,296 m
3
.
Người thợ này cắt các tấm kính ghép lại một bể cá dạng hình
hộp chữ nhật với 3 kích thước a, b, c như hình vẽ. Hỏi người
thợ phải thiết kế các kích thước a, b, c bằng bao nhiêu để đỡ
tốn kính nhất, giả sử độ dầy của kính không đáng kể.
A. 3,6 ; 0,6 ; 0,6a m b m c m
B. 2,4 ; 0,9 ; 0,6a m b m c m
C. 1,8 ; 1,2 ; 0,6a m b m c m
D. 1,2 ; 1,2 ; 0,9a m b m c m
Hướng dẫn giải:
Thể tích bể cá là: 1,296V abc
Diện tích tổng các miếng kính là
2 3S ab ac bc
(kể cả miếng ở giữa)
Ta có:
3 3
3
1 2 3
3 , ,
1 2 3 1 2 3 3 6 3 6
3 . .
1,296
Cauchy cho so
c b a
S
abc c b a c b a
abc

Dấu “=” xảy ra khi
1,8
1 2 3
1,2
1,296
0,6
a
b
c b a
abc
c
.
Chọn C.
Câu 19: Từ một tấm tôn có kích thước 90cmx3m người ta làm một máng xối nước trong đó mặt cắt
là hình thang ABCD có hinh dưới. Tính thể tích lớn nhất của máng xối.
A.
3
40500 3cm B.
3
40500 2cm
C.
3
40500 6cm D.
3
40500 5cm
3m
90cm
3m
30cm
30cm
30cm
D
B
C
A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 117
Facebook: https://www.facebook.com/dongpay
Thể tích máng xối:
2
.300 ( )
ABCD
V S cm
.
Vậy thể tích lớn nhất khi diện tích hình thang là lớn nhất.
1
( ).
2
ABCD
S BC AD CE
CE CDsin
30.
sin
2 30 60
AD BC ED cos
90
90 2
2
ABCD
S sin sin
Đặt
90
( ) 90 2 , [0; ]
2
f sin sin
90
'( ) 90 .2 2
2
f cos cos
2
1
cos
'( ) 0 cos cos2 0 2cos cos 1 0
3
2
cos 1
f
.
(0) ( ) 0; 135 3
3
f f f
. Vậy GTLN của diện tích ABCD là
2
135 3
cm
.
Vậy thể tích máng xối lớn nhất bằng
3
40500 3
cm
khi ta cạnh CD tạo với BC góc
0
60
.
Câu 20: Để làm một máng xối nước, từ một tấm tôn kích thước
0,9 3
m m
người ta gấp tấm tôn đó
như hình vẽ dưới. Biết mặt cắt của máng xối (bị cắt bởi mặt phẳng song song với hai mặt
đáy) là một hình thang cân và máng xối là một hình lăng trụ có chiều cao bằng chiều dài của
tấm tôn. Hỏi
x m
bằng bao nhiêu thì thể tích máng xối lớn nhất?
A.
0,5
x m
. B.
0,65
x m
. C.
0,4
x m
. D.
0,6
x m
.
Hướng dẫn giải:.
Chọn D.
Gọi
h
là chiều cao của lăng trụ
Vì chiều cao lăng trụ bằng chiều dài tấm tôn nên thể tích máng xối lớn nhất khi diện tích
hình thang cân (mặt cắt) lớn nhất
Ta có
0,3
2
h
S x
3
m
0,9
m
0,3
m
0,3
m
xm
0,3
m
3
m
0,3
m
x
x
(a) T
ấ
m tôn
(b) Máng x
ố
i
(c) M
ặ
t c
ắ
t
θ
θ
30cm
30cm
30cm
E
D
B C
A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 118
Facebook: https://www.facebook.com/dongpay
h
0.3m
0.3m
B
A
C
2
2
0,3
0,3
2
0,3
0,3
4
x
BC x
x
h
ĐK:
2
2
0,3
0,3 0; 0,3 0,9
4
x
x
Khi đó:
2 2
1
0,3 4. 0,3 0,3
4
S x x
Xét hàm số
2 2
0,3 4. 0,3 0,3 ; 0,3 0,9
f x x x x
2 2
2 2
2 0,3
4. 0,3 0,3 0,3
4. 0,3 0,3
x
f x x x
x
2 2
2 2 2 2
4. 0,3 0,3 0,3 0,3 0,36 2 0,3
4. 0,3 0,3 4. 0,3 0,3
x x x x x
x x
2
0,3
0 0,3 0,18 0
0,6
x
f x x x
x
x
0,3
0,6
0,9
f x
0
f x
Dựa vào bảng biến thiên ta thấy
f x
lớn nhất khi
0,6
x
Vậy thể tích máng xối lớn nhất khi
0,6
x m
.
Câu 21: Khi xây dựng nhà, chủ nhà cần làm một bể nước bằng gạch có dạng hình hộp có đáy là hình
chữ nhật chiều dài
d m
và chiều rộng
r m
với
2 .
d r
Chiều cao bể nước là
h m
và thể
tích bể là
3
2 .
m
Hỏi chiều cao bể nước như thế nào thì chi phí xây dựng là thấp nhất?
A.
3 3
2 2
m
. B.
3
2
3
m
. C.
3
3
2
m
. D.
2 2
3 3
m
.
Hướng dẫn giải:
Gọi
0
x x
là chiều rộng của đáy suy ra thể tích bể nước bằng
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 119
Facebook: https://www.facebook.com/dongpay
2
2
1
2 . 2V x h h
x
Diện tích xung quanh hồ và đáy bể là
2 2
6
6 . 2 2 0
S x h x x x
x
Xét hàm số
2
6
2
f x x
x
với
0.
x
Hàm số đạt giá trị nhỏ nhất tại
3
3
.
2
x
Vậy chiều cao cần xây là
2
2
3
1 1 2 2
.
3 3
3
2
h m
x
Câu 22: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là
V
. Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng
A.
2
3
x V
B.
3
x V
C.
1
4
x V
D.
x V
Hướng dẫn giải:
Gọi
a
là độ dài cạnh đáy,
x
là độ dài đường cao của thùng đựng đồ
, 0
a x
Khi đó,
2 2
2a 4 2 4
tp
V V
V a x a S ax Vx
x x
Để làm thùng hàng tốn ít nguyên liệu nhất thì
tp
S
nhỏ nhất 2 4
V
Vx
x
nhỏ nhất.
Cách 1 : Xét hàm số
2 4
V
f x Vx
x
trên
0;

Ta có
1
2
3
2
2 2
' ; ' 0
V V
f x f x x V V x x V
x
x
Từ BBT ta thấy để làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ
bằng
1
3
V
.
f x( )
f' x( )
x
f
(V
1
3
)
0
+ ∞
0
+
V
1
3
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 120
Facebook: https://www.facebook.com/dongpay
Cách 2: ta có
3
2
2 4 2 2 2 6
V V
Vx Vx Vx V
x x
Dấu
" "
xảy ra tại
3
3
x
V
V x V x V
x
Chọn B.
Câu 23: Nhân ngày quốc tế phụ nữ 8-3 năm 2017, ông A quyết định mua tặng vợ một món quà và
đặt nó vào trong một chiếc hộp có thể tích là 32 ( đvtt ) có đáy hình vuông và không có nắp.
Để món quà trở nên thật đặc biệt và xứng đáng với giá trị của nó ông quyết định mạ vàng
cho chiếc hộp, biết rằng độ dạy lớp mạ tại mọi điểm trên hộp là như nhau. Gọi chiều cao và
cạnh đáy của chiếc hộp lần lượt là . Để lượng vàng trên hộp là nhỏ nhất thì giá trị của
phải là?
A. B. C. D.
Hướng dẫn giải:
Chọn B.
Ta có , để lượng vàng cần dùng là nhỏ
nhất thì Diện tích S phải nhỏ nhất ta có
,
Câu 24: Một ngôi nhà có nền dạng tam giác đều
ABC
cạnh dài
10
m
được đặt song song và cách
mặt đất
h m
. Nhà có 3 trụ tại
, ,
A B C
vuông góc với
ABC
. Trên trụ
A
người ta lấy hai
điểm
,
M N
sao cho ,
AM x AN y
và góc giữa
MBC
và
NBC
bằng
90
để là mái và
phần chứa đồ bên dưới. Xác định chiều cao thấp nhất của ngôi nhà.
A.
5 3
. B.
10 3
. C.
10
. D.
12
.
Hướng dẫn giải:
Đáp án B
h;x
h;x
x 2;h 4
x 4;h 2
3
4;
2
x h
1; 2
x h
x
x
h
S xh x
S x. x x
V
x
V x h h
x
x x
2
2 2
2
2
2 2
4
32 128
4
32
S x f x f' x x x
x
x
2
2
128 128
2 0 4
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 121
Facebook: https://www.facebook.com/dongpay
Để nhà có chiều cao thấp nhất ta phải chọn
N
nằm trên mặt đất. Chiều cao của nhà là
NM x y
.
Gọi
I
là trung điểm của
BC
. Ta có
ABC
đều
AI BC
, vì
MN ABC MN BC
, từ đó suy ra
0
90
MI BC
BC MNI MIN
NI BC
IMN
vuông tại
I
nhận
AI
là đường cao nên
2
2
10 3
. 75
2
AM AN AI xy
Theo bất đẳng thức Côsi:
2 2. 75 10 3 5 3
x y xy x y
Do đó chiều cao thấp nhất của nhà là
10 3.
Câu 25: Một nhà sản xuất sữa có hai phương án làm hộp sữa. Hộp sữa có dạng khối hộp chữ nhật
hoặc hộp sữa có dạng khối trụ. Nhà sản xuất muốn chi phí bao bì càng thấp càng tốt(tức diện
tích toàn phần của hộp nhỏ nhất), nhưng vẫn phải chứa được một thể tích xác định là
V
cho
trước. Khi đó diện tích toàn phần của hộp sữa bé nhất trong hai phương án là
A.
3
2
2
V
.
B.
3
2
6
V
.
C.
3
2
3 6
V
.
D.
3
2
3 2
V
.
Hướng dẫn giải:
Chọn D
Trường hợp 1: Hộp sữa hình trụ
Thể tích không đổi
2 2 2
2
2
, 2 2 2
tp
V V
V R h h S R Rh R
R R
Áp dụng bất đẳng thức Cauchy cho bộ ba số dương
2
2 , ,
V V
R
R R
Ta có
3
2 2 2
3
2 3 2 . . 3 2
tp
V V V V
S R R V
R R R R
(*)
Trường hợp 2: Hộp sữa hình hộp chữ nhật
Thể tích không đổi
h
b
a
R
h
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 122
Facebook: https://www.facebook.com/dongpay
; 2 2 2 2 . 2 . 2
tp
V V V V V
V abh h S ab a b h ab a b ab
ab ab ab b a
Áp dụng bất đẳng thức Cau chy cho bộ ba số dương
; ;
V V
ab
a b
Ta có
3
2
3
2.3 . . 6
tp
V V
S ab V
a b
(**)
Xét hai kết quả ta thấy (*) nhỏ hơn
Vậy diện tích toàn phần của hộp sữa bé nhất là
3
2
3 2
tp
S V
(đvdt)
Câu 26: Một bác thợ gò hàn làm một chiếc thùng hình hộp chữ nhật (không nắp) bằng tôn thể tích
3
665,5
dm
. Chiếc thùng này có đáy là hình vuông cạnh
( )
x dm
, chiều cao
( )
h dm
. Để làm
chiếc thùng, bác thợ phải cắt một miếng tôn như hình vẽ. Tìm
x
để bác thợ sử dụng ít
nguyên liệu nhất.
A.
10,5( )
dm
. B.
12( )
dm
. C.
11( )
dm
. D.
9( )
dm
.
Hướng dẫn giải:
Chọn C.
Ta có thể tích hình hộp là:
2
2
665,5
665,5V x h h
x
Diện tích toàn phần là
2 2
2
2662 2662
4 ' 2S x xh x S x
x x
;
' 0 11
S x
Lập bảng biến thiên ta thấy khi
11
x
thì S đạt giá trị nhỏ nhất
Vậy để sử dụng ít nguyên liệu nhất thì bác thợ xây phải cắt một miếng tôn có đáy là hình
vuông cạnh
11( )
dm
.
Câu 27: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là
V
. Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng
A.
2
3
x V
B.
3
x V
C.
1
4
x V
D.
x V
Hướng dẫn giải:
Gọi
a
là độ dài cạnh đáy,
x
là độ dài đường cao của thùng đựng đồ
, 0
a x
Khi đó,
2 2
2a 4 2 4
tp
V V
V a x a S ax Vx
x x
Để làm thùng hàng tốn ít nguyên liệu nhất thì
tp
S
nhỏ nhất 2 4
V
Vx
x
nhỏ nhất.
Cách 1 : Xét hàm số
2 4
V
f x Vx
x
trên
0;

h
h
h
h
x
x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 123
Facebook: https://www.facebook.com/dongpay
Ta có
1
2
3
2
2 2
' ; ' 0
V V
f x f x x V V x x V
x
x
Từ BBT ta thấy để làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ
bằng
1
3
V
.
Cách 2: ta có
3
2
2 4 2 2 2 6
V V
Vx Vx Vx V
x x
Dấu
" "
xảy ra tại
3
3
x
V
V x V x V
x
Câu 28: Người ta muốn xây một bồn chứa nước dạng khối hộp
chữ nhật trong một phòng tắm. Biết chiều dài, chiều
rộng, chiều cao của khối hộp đó lần lượt là 5m, 1m,
2m (hình vẽ bên). Biết mỗi viên gạch có chiều dài
20cm, chiều rộng 10cm, chiều cao 5cm. Hỏi người ta
sử dụng ít nhất bao nhiêu viên gạch để xây bồn đó và
thể tích thực của bồn chứa bao nhiêu lít nước? (Giả sử
lượng xi măng và cát không đáng kể)
A. 1180 viên, 8820 lít B. 1180 viên, 8800 lít
C. 1182 viên, 8820 lít D. 1180 viên, 8800 lít
Hướng dẫn giải:
Phân tích:
* Theo mặt trước của bể:
Số viên gạch xếp theo chiều dài của bể mỗi hàng là
500
25
20
x
viên
Số viên gạch xếp theo chiều cao của bể mỗi hàng là:
200
40
5
. Vậy tính theo chiều cao thì
có 40 hàng gạch mỗi hàng 25 viên. Khi đó theo mặt trước của bể.
25.40 1000
N
viên.
f x( )
f' x( )
x
f
(V
1
3
)
0
+ ∞
0
+
V
1
3
5m
2m
1dm
1dm
1m
V
H'
V
H
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 124
Facebook: https://www.facebook.com/dongpay
* Theo mặt bên của bể: ta thấy, nếu hàng mặt trước của bể đã được xây viên hoàn chỉnh
đoạn nối hai mặt thì ở mặt bên viên gạch còn lại sẽ được cắt đi còn
1
2
viên. Tức là mặt bên
sẽ có
1 100 20
.40 .40 180
2 20
viên.
Vậy tổng số viên gạch là 1180 viên.
Khi đó thể tích bờ tường xây là
1180.2.1.0,5 1180 lít
Vậy thể tích bốn chứa nước là:
50.10.20 1180 8820
lít
Câu 29: Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng
lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác
cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng
trụ tam giác đều (như hình vẽ). Gọi
1 2
,V V lần lượt là thể tích của lăng trụ tứ giác đều và lăng
trụ tam giác đều. So sánh
1
V và
2
V .
A.
1 2
V V B.
1 2
V V C.
1 2
V V D. Không so sánh
được
Hướng dẫn giải:
Ta có
3
1
. .
4 4 16
a a a
V a
và
3
2
1 3 3
. . . .
2 3 2 3 36
a a a
V a . Do đó
1 2
V V .
Ta chọn phương án C.
| 1/125
| | Tải xuống

Có thể bạn quan tâm:

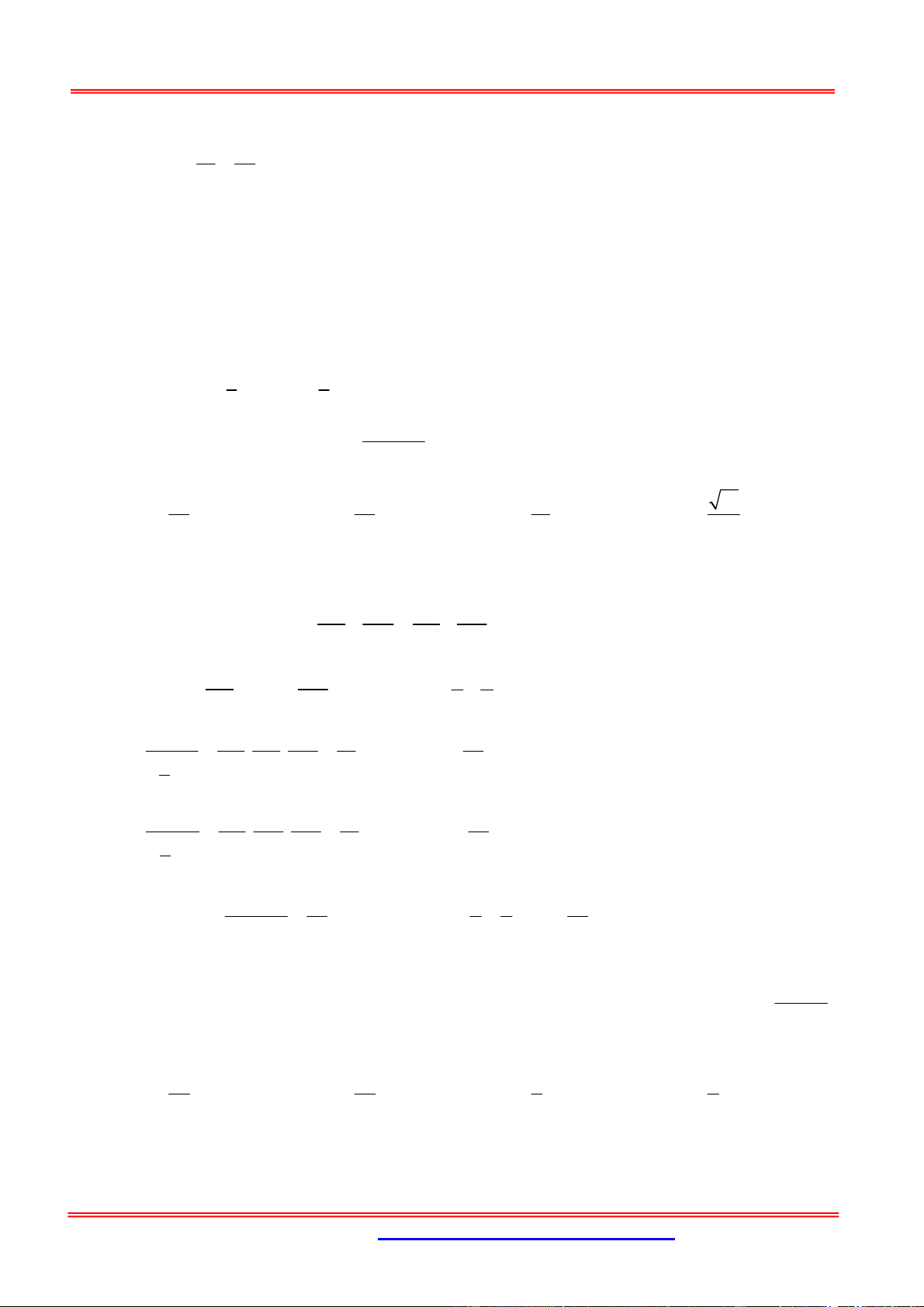
Preview text:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 0
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
THỂ TÍCH KHỐI CHÓP A- LÝ THUYẾT CHUNG
Trước khi vào phần bài tập bạn đọc cần trang bị cho mình các kiến thức căn bản tối thiểu:
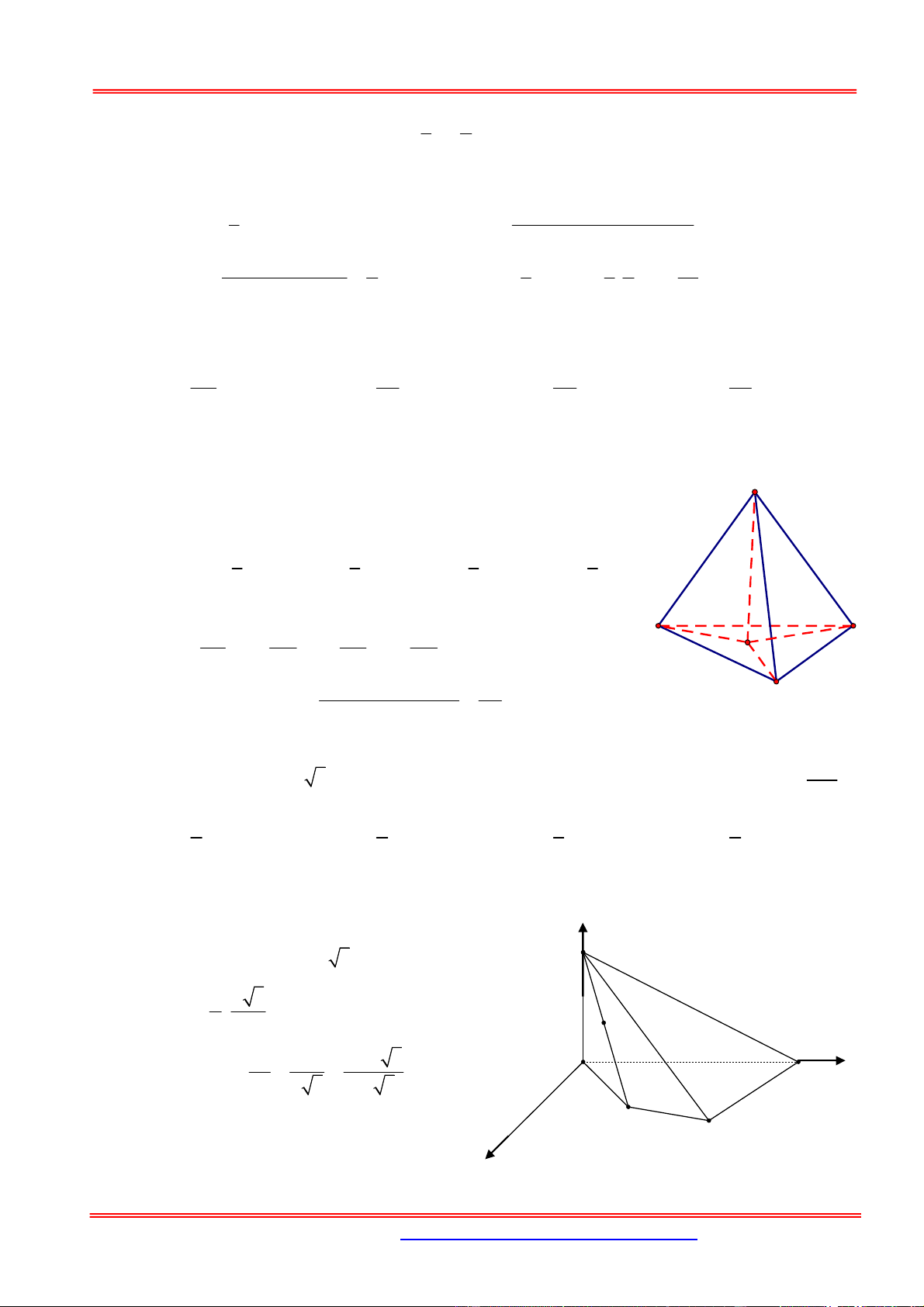
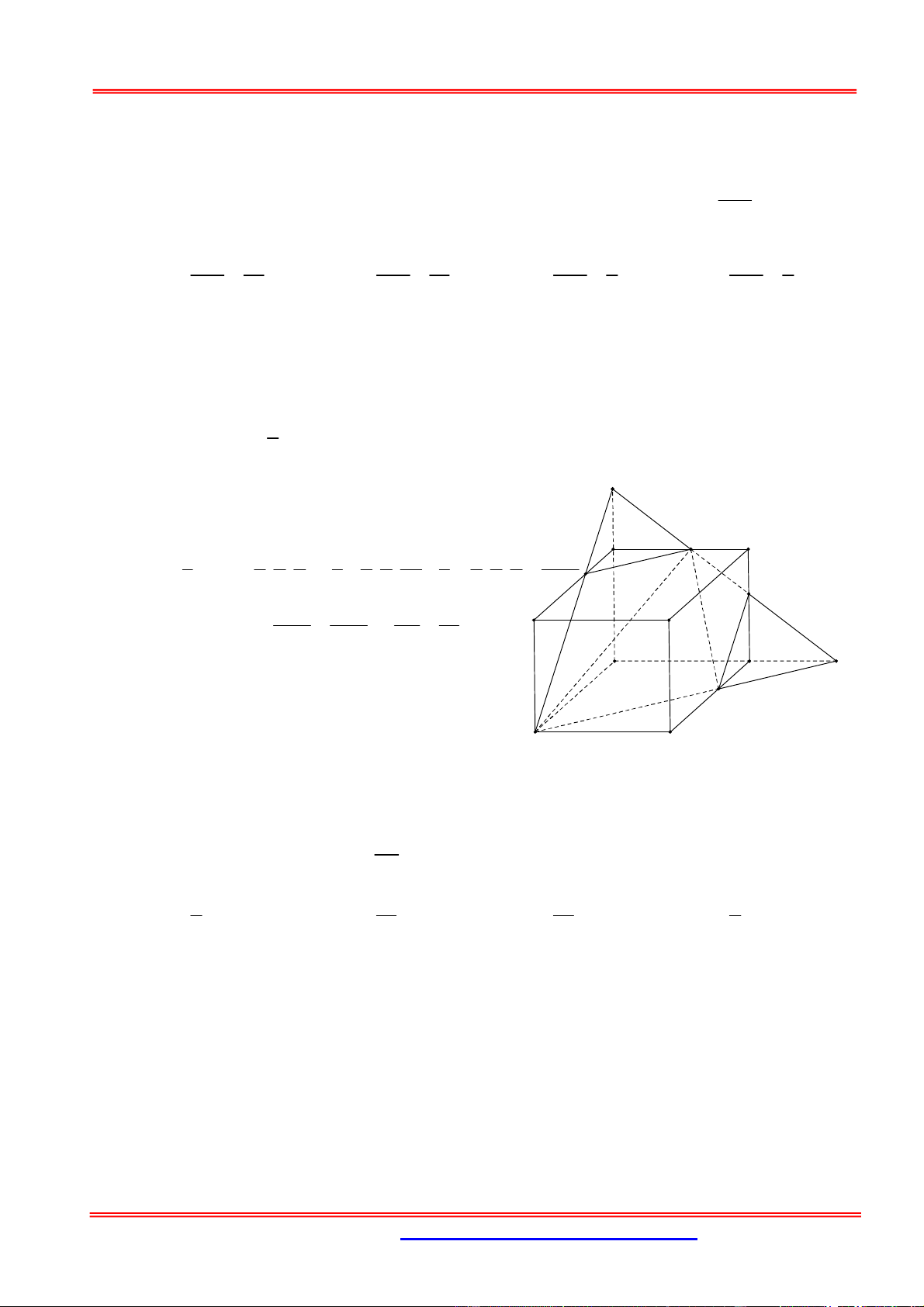
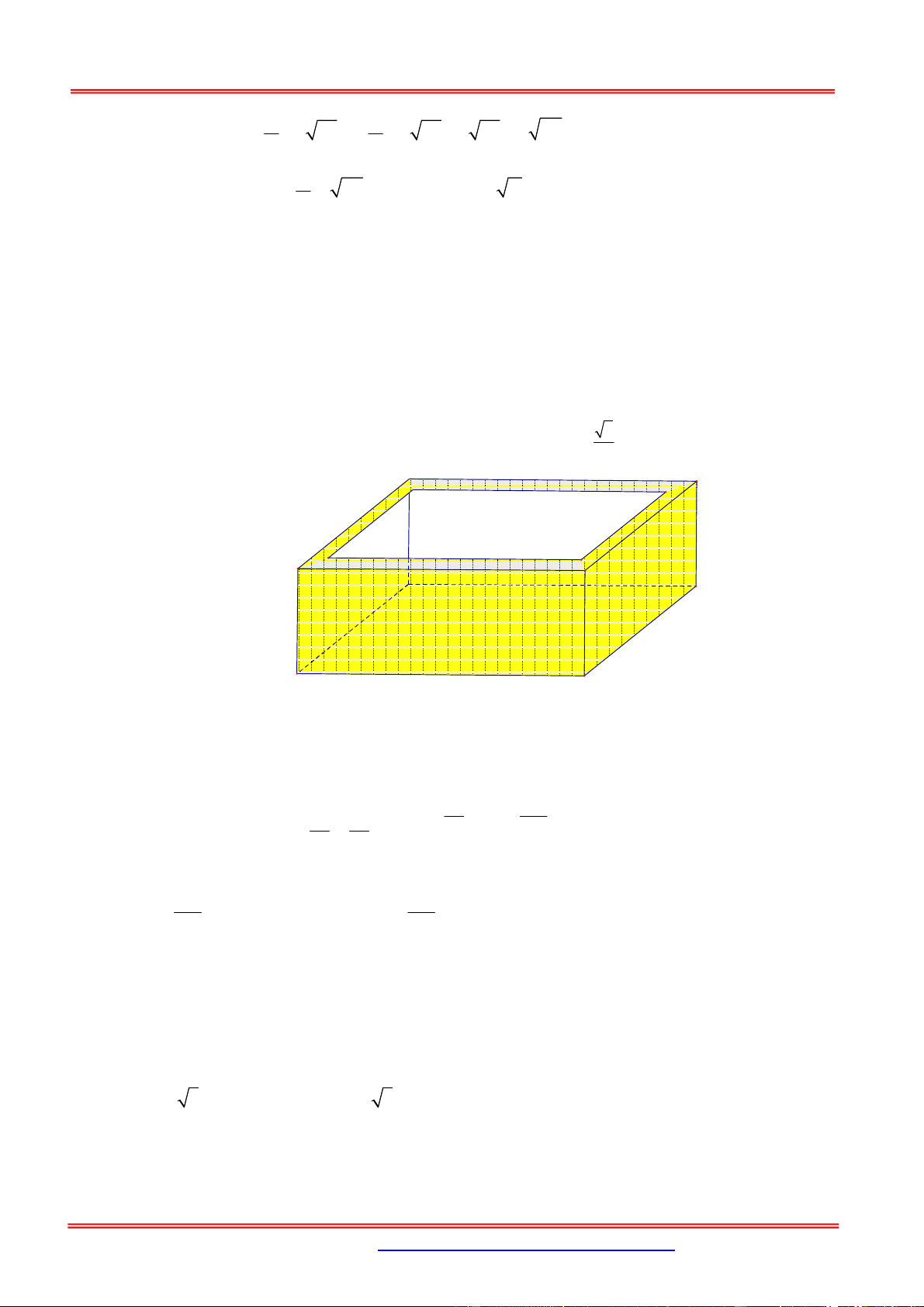
1. Thể tích khối chóp 1
Công thức tính:V  .
B h với B diện tích đáy, h là chiều cao khối chóp. 3 h B
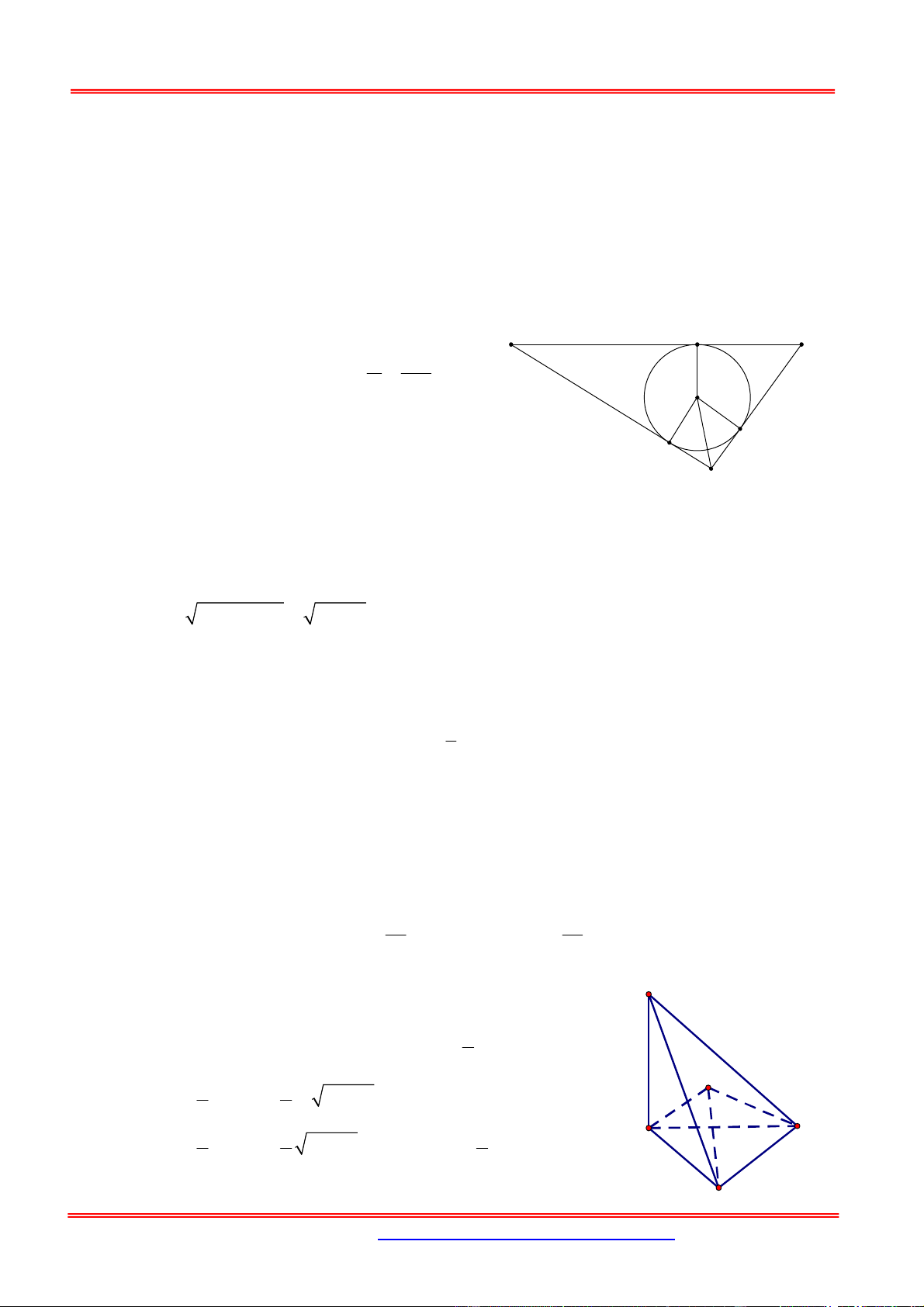
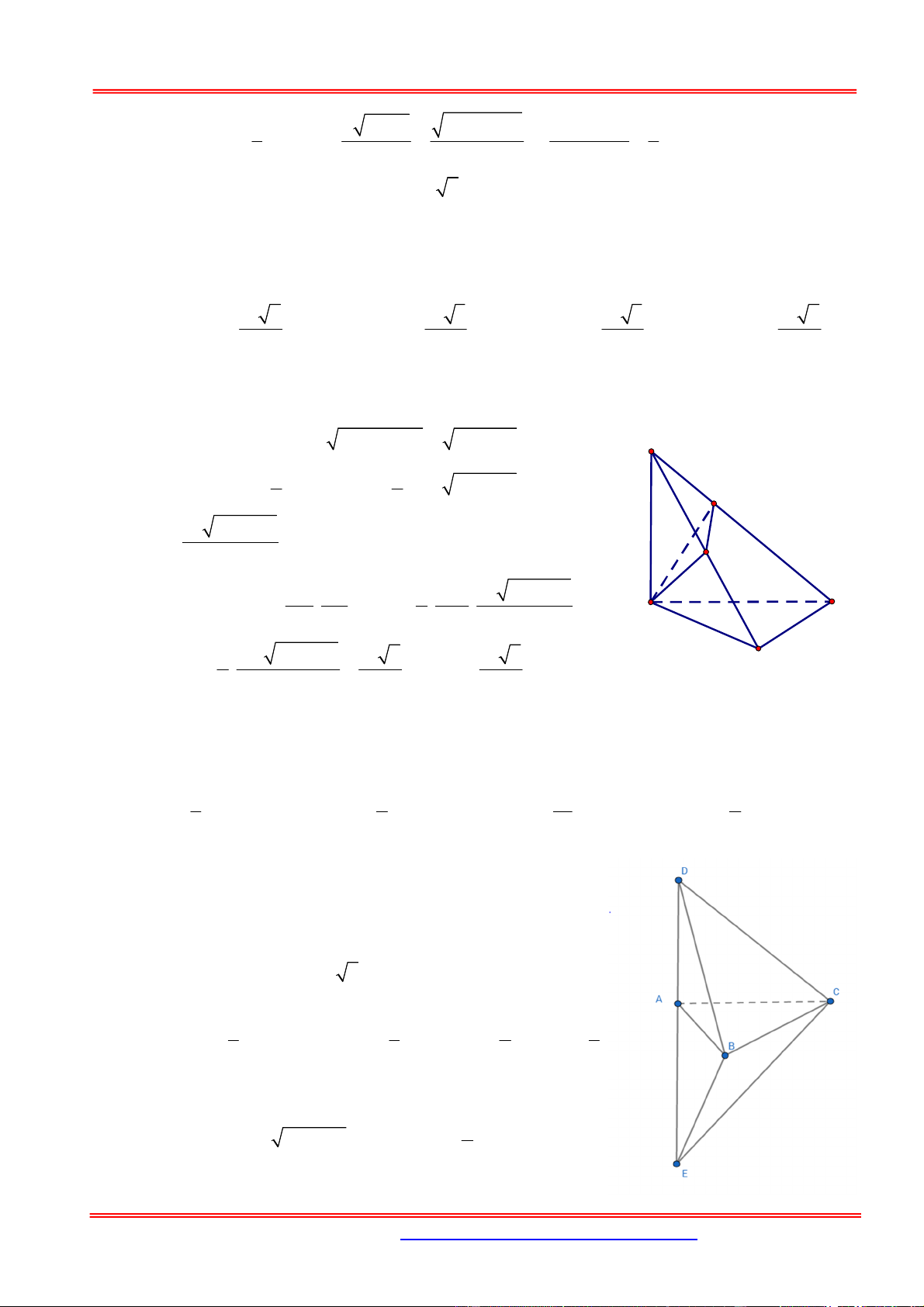
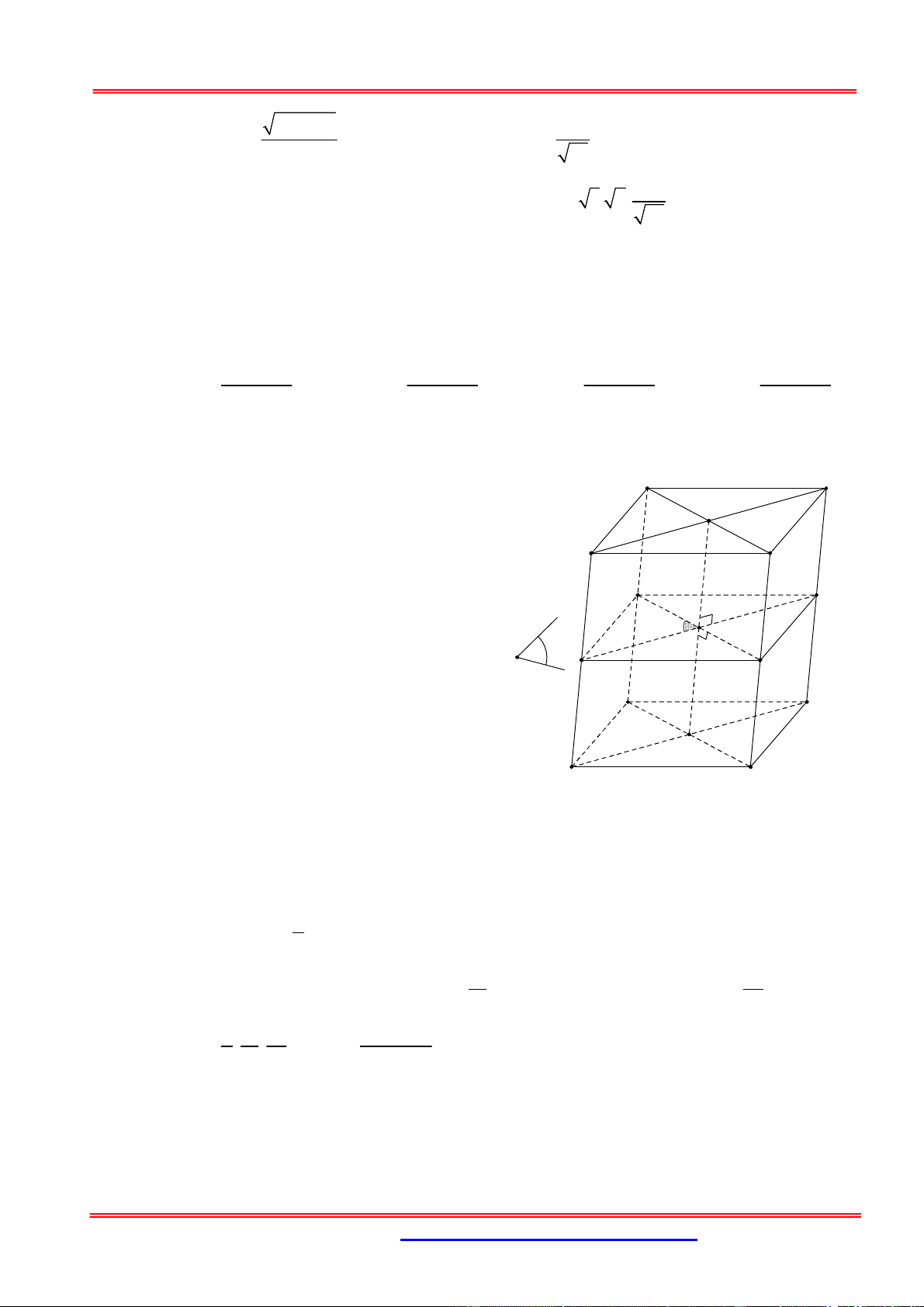
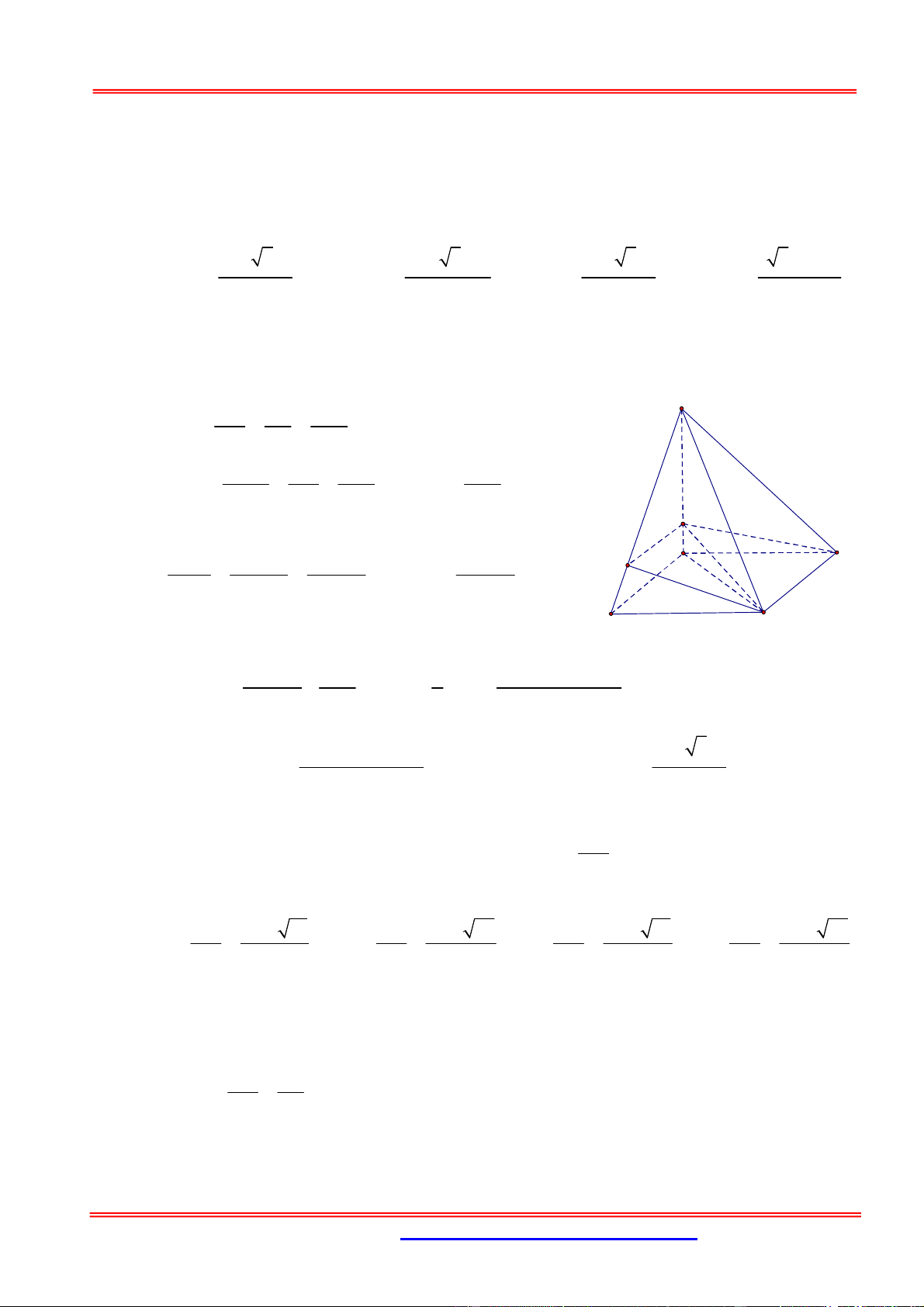
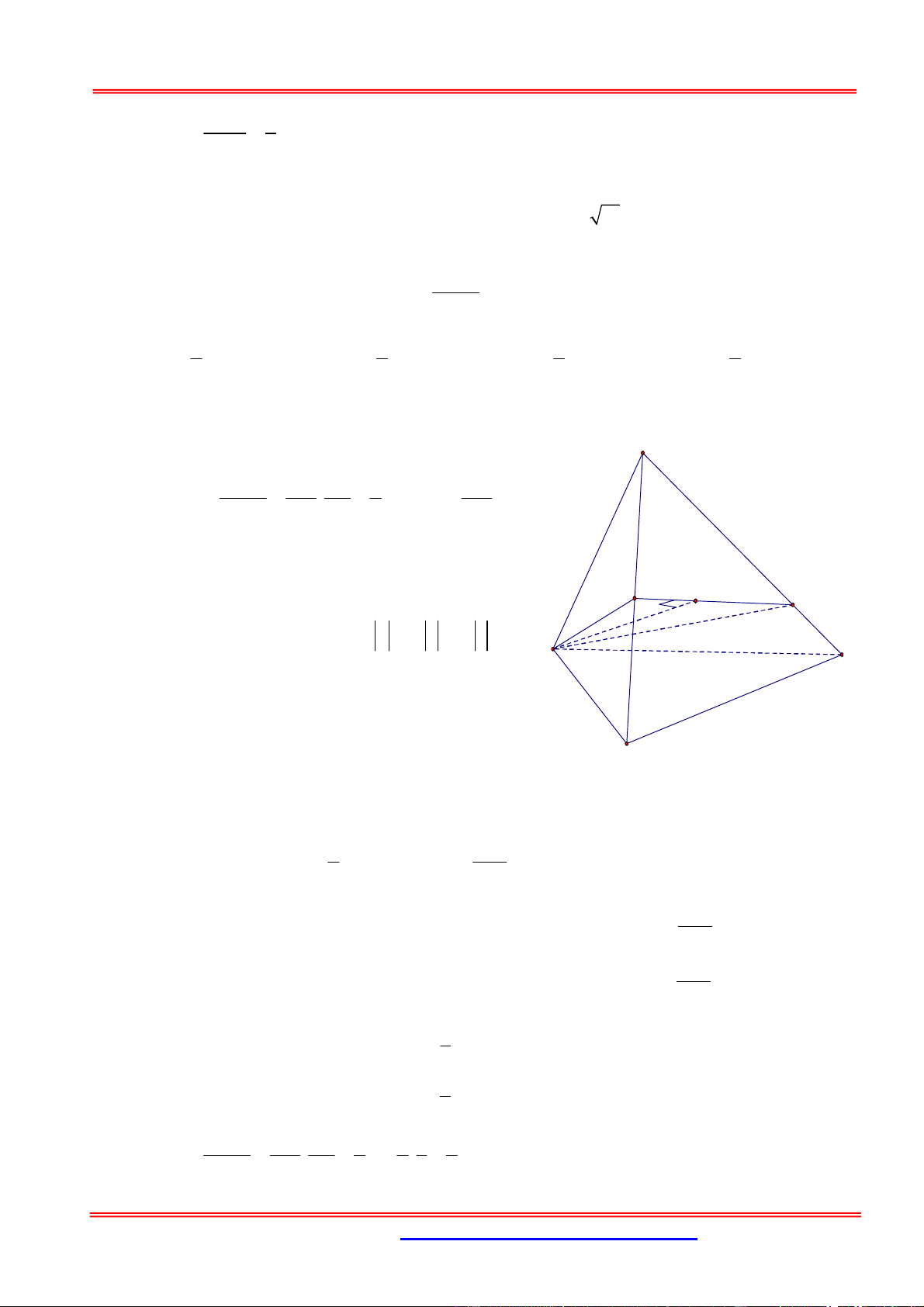
2. Định lý tỉ số thể tích khối tứ diện hoặc khối chóp tam giác S A' C' B' C A B
Cho khối tứ diện SABC và A', B ',C ' là các điểm tùy ý lần lượt thuộc S ,
A SB, SC ta có: V SA SB SC SABCV
SA' SB ' SC '
SA' B 'C '
Chúng ta sẽ cùng đi ngay vào các ví dụ minh họa để thấy rằng có những bài liên quan đến thể tích khối
đa diện rất khó, đòi hỏi khả năng vận dụng cao.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
B – BÀI TẬP TRẮC NGHIỆM Câu 1:
Cho khối tứ diện đều ABCD cạnh a . Gọi E là điểm đối xứng của A qua D . Mặt phẳng
qua CE và vuông góc với mặt phẳng  A D
B  cắt cạnh AB tại điểm F . Tính thể tích V của
khối tứ diện AECF . 3 2a 3 2a 3 2a 3 2a A. V B. V C. V D. V  30 60 40 15 Câu 2:
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD . Tính thể tích V của khối chóp . A GBC . A. V  3 . B. V  4 . C. V  6 . D. V  5 . Câu 3:
Cho tứ diện đều cạnh a và điểm I nằm trong tứ diện. Tính tổng khoảng cách từ I đến các mặt của tứ diện. a a 6 a 3 a 34 A. . B. . C. . D. . 2 3 2 2 Câu 4:
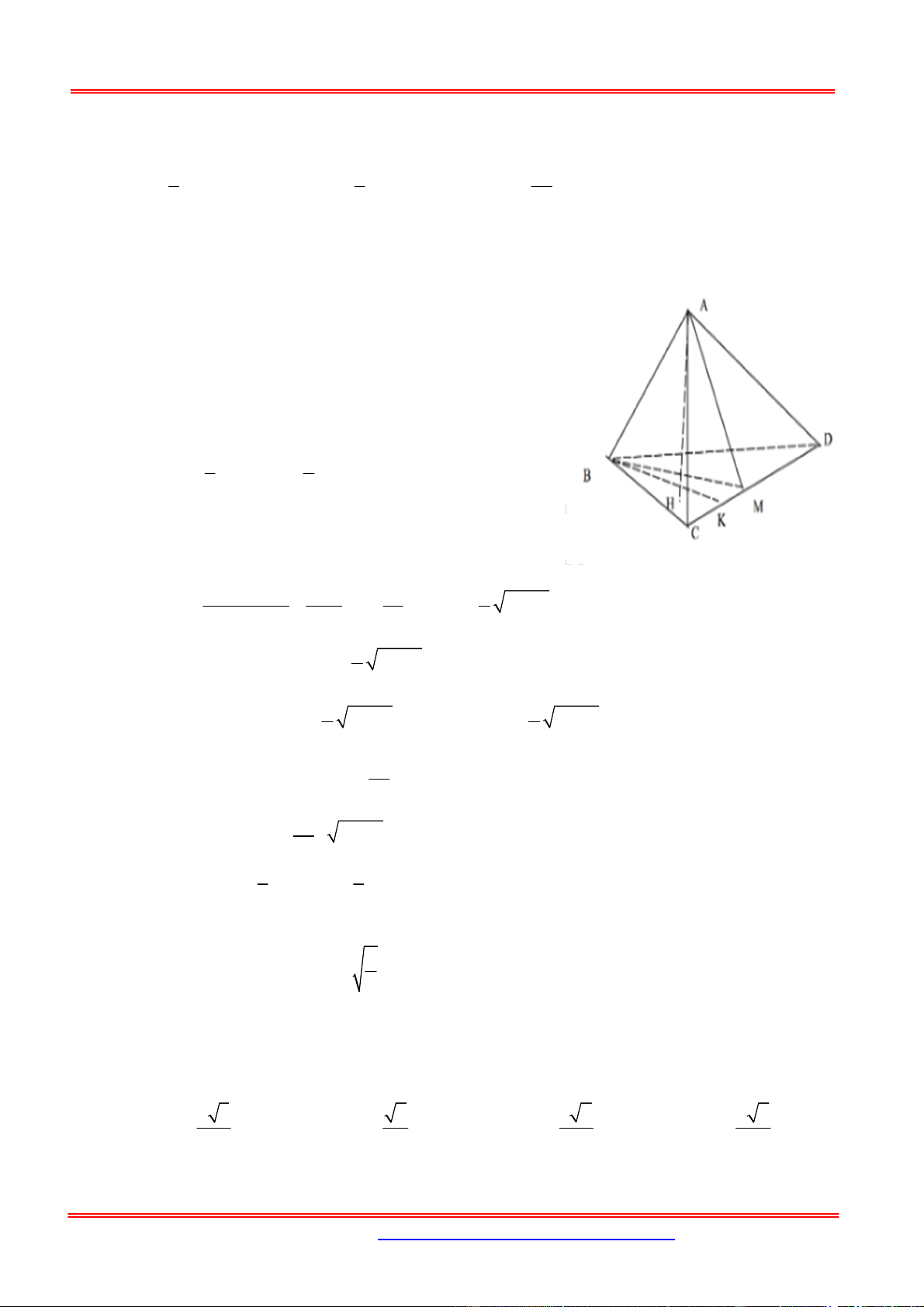
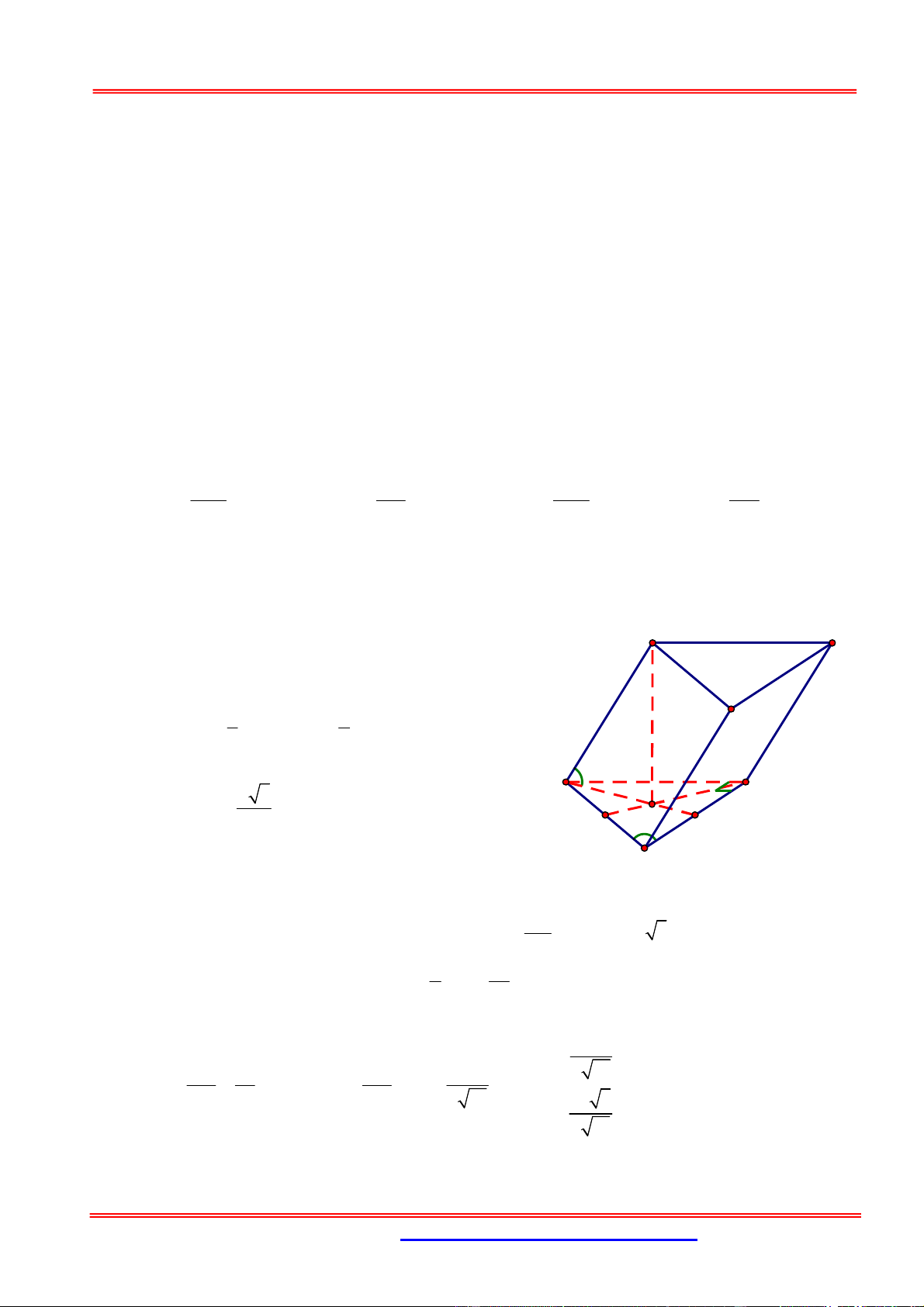
Cho khối tứ diện ABCD có 0
BC  3,CD  4, A
BC  BCD  ADC  90 . Góc giữa hai
đường thẳng AD và BC bằng 0
60 . Tính cosin góc giữa hai mặt phẳng  ABC  và  ACD ? 2 43 43 4 43 43 A. B. C. D. 43 86 43 43 Câu 5:
Cho hình chóp tứ giác S.ABCD có SA   ABCD , ABCD là hình thang vuông tại A và B
biết AB  2a , AD  3BC  3a . Tính thể tích khối chóp S.ABCD theo a , biết khoảng cách 3 6
từ A đến mặt phẳng (SCD) bằng a . 4 A. 3 6 6a . B. 3 2 6a . C. 3 2 3a . D. 3 6 3a . Câu 6:
Cho hình chóp S.ABC có SA a, BC a 2 và tất cả các cạnh còn lại đều bằng x . Tìm x 3 a 11
biết thể tích khối chóp đã cho có thể tích bằng . 6 3a 7a 9a 5a A. x  . B. x  . C. x  . D. x  . 2 2 2 2 Câu 7:
Cho hình chóp đều S.ABC có đáy cạnh bằng a , góc giữa đường thẳng SA và mặt phẳng
ABC  bằng 60 . Gọi A, B, C tương ứng là các điểm đối xứng của A , B , C qua S .
Thể tích của khối bát diện có các mặt ABC, AB C
  , ABC , B CA , C AB , AB C   , BA C   , CAB là 3 2 3a 3 3a 3 4 3a A. . B. 3 2 3a . C. . D. . 3 2 3 Câu 8:
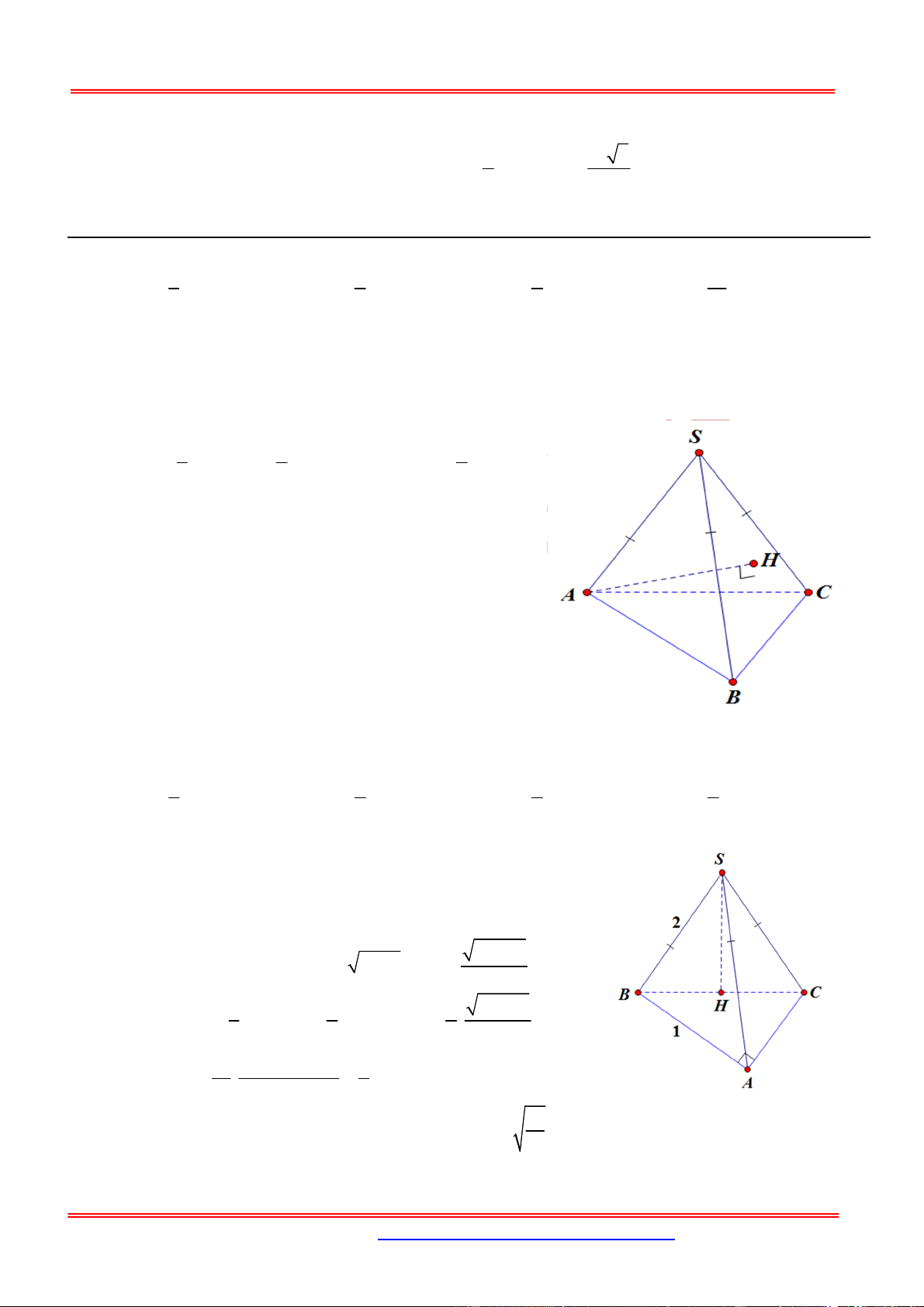
Cho hình chóp SABC có đáy ABC là tam giác vuông cân, AB AC a , SC   ABC  và
SC a . Mặt phẳng qua C , vuông góc với SB cắt S ,
A SB lần lượt tại E và F . Tính thể
tích khối chóp S.CEF .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 3 2a 3 a 3 a 3 2a A. V  . B. V  . C. V  . D. V  . SCEF 36 SCEF 18 SCEF 36 SCEF 12 Câu 9:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi  P là mặt phẳng đi qua A và
song song BC và vuông góc với  SBC , góc giữa  P với mặt phẳng đáy là 0 30 . Thể tích
khối chóp S.ABC là: 3 a 3 3 a 3 3 a 3 3a A. B. C. D. 24 8 8 8
Câu 10: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4, mặt bên SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Gọi M , N, P lần lượt là trung điểm của các
cạnh SD,CD, BC. Thể tích khối chóp S.ABPN là ,
x thể tích khối tứ diện CMNP là . y Giá
trị x, y thỏa mãn bất đẳng thức nào dưới đây: A. 2 2
x  2xy y  160 B. 2 2
x  2xy  2 y  109 C. 2 4
x xy y  145 D. 2 4
x xy y  125
Câu 11: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều,
SC SD a 3. Tính thể tích khối chóp S.ABC . D 3 a 2 3 a 2 3 a 2 3 a A. V B. V C. V D. V  2 3 6 6
Câu 12: Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại , A ;
D AB AD  2 , a CD  . a
Góc giữa hai mặt phẳng  SBC  và  ABCD bằng 0
60 . Gọi I là trung điểm của AD, biết
hai mặt phẳng  SBI , SCI  cùng vuông góc với mặt phẳng  ABCD. Tính thể tích khối chóp S.ABC . D 3 15 3 17 3 19 3 23 A. 3 a B. 3 a C. 3 a D. 3 a 5 5 5 5
Câu 13: Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC; các mặt phẳng
SAB;SAC;SBC cùng tạo với mặt phẳng  ABC  một góc bằng nhau. Biết
AB  25, BC  17, AC  26, đường thẳng SB tạo với đáy một góc bằng 0 45 . Tính thể tích V
của khối chóp SABC. A. V  680 B. V  408 C. V  578 D. V  600
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB  8 , BC  6 . Biết SA  6
và vuông góc với mặt phẳng đáy  ABC  . Một điểm M thuộc phần không gian bên trong
của hình chóp và cách đều tất cả các mặt của hình chóp. Tính thể tích của khối tứ diện M .ABC . 64 32 A. V  24 . B. V  . C. V  . D. V  12 . 3 3
Câu 15: Cho khối đa diện đều n mặt có thể tích V và diện tích mỗi mặt của nó bằng S. Khi đó,
tổng các khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao nV V 3V V A. . B. . C. . D. . S nS S 3S
Câu 16: Cho hình chóp S.ABCD có đáy là nửa lục giác đều với cạnh a (a> 0). Cạnh SA vuông góc SM
với đáy và SA = a 3 . M là một điểm khác B trên SB sao cho AM  M . D Tính tỉ số . SB 3 1 3 5 A. B. C. D. 4 4 5 4
Câu 17: Cho hình chóp S.ABC có SA SB SC  1 . Tìm thể tích lớn nhất của khối chóp S.ABC . 1 1 1 1 A. . B. . C. . D. . 3 6 4 12
Câu 18: Cho hình chóp S.ABC có SA x, BC y, AB AC SB SC  1. Thể tích khối chóp
S.ABC lớn nhất khi tổng x y bằng: 2 4 A. 3 B. C. D. 4 3 3 3
Câu 19: Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ diện đó lớn nhất là bao nhiêu? 1 3 1 5 A. B. C. D. 4 4 8 8
Câu 20: Khối tứ diện ABCD có AB  1 và tất cả các cạnh còn lại có độ dài không vượt quá 1. Hỏi
thể tích lớn nhất của khối tứ diện đó là? 3 1 1 A. . B. . C. . D. 3 . 8 8 24
Câu 21: Khối tứ diện ABCD có AB x x  
1 và có tất cả các cạnh còn lại có độ dài không vượt
quá 1. Tính x khi thể tích của khối tứ diện đó lớn nhất. 2 3 6 3 2 2 6 A. x  . B. x  . C. x  . D. x  . 3 2 2 3
Câu 22: Cho tứ diện ABCD có AB  4a, CD x và tất cả các cạnh còn lại bằng 3a.Tìm x để khối
tứ diện ABCD có thể tích lớn nhất. A. x  2 10 . a
B. x  10a.
C. x  6a . D. 3a .
Câu 23: Cho khối tứ diện ABCD có AB x , tất cả các cạnh còn lại bằng nhau và bằng 2  x . Hỏi 2
có bao nhiêu giá trị của x để khối tứ diện đã cho có thể tích bằng . 12 A. 1. B. 6 . C. 4 D. 2 .
Câu 24: Xét khối tứ diện ABCD có AB x và các cạnh còn lại đều bằng 2 3 . Tìm x để thể tích
khối tứ diện ABCD đạt giá trị lớn nhất. A. x  6 . B. x  14 . C. x  3 2 . D. x  3 3 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 25: Cho khối chóp S.ABC có SA a , SB a 2 , SC a 3 . Thể tích lớn nhất của khối chóp là 3 a 6 3 a 6 3 a 6 A. 3 a 6 . B. . C. . D. . 2 3 6
Câu 26: Cho khối chóp S.ABC có SA a , SB a 2 , SC a 3 . Thể tích lớn nhất của khối chóp là 3 a 6 3 a 6 3 a 6 A. 3 a 6 . B. . C. . D. . 2 3 6
Câu 27: Cho hình chóp S.ABC có SA SB SC  1 . Tìm thể tích lớn nhất của khối chóp S.ABC . 1 1 1 1 A. . B. . C. . D. . 3 6 4 12
Câu 28: Cho hình chóp S.ABC có SA SB SC  2 , đáy ABC là tam giác vuông tại A , AB  1.
Tìm thể tích lớn nhất của khối chóp S.ABC . 5 5 2 4 A. . B. . C. . D. . 8 4 3 3
Câu 29: Cho hình chóp S.ABC có SA SB SC BA BC  1. Tìm thể tích lớn nhất của khối chóp S.ABC ? 1 2 1 3 A. . B. . C. . D. . 6 12 8 12
Câu 30: Trong các khối tứ diện ABCD có tam giác ABC đều cạnh 2a và tam giác ABD vuông tại a D , AD
. Khoảng cách lớn nhất từ B đến mặt phẳng  ACD là? 2 2a 2 a 3 A. . B. a 3 . C. . D. 2a 3 . 3 3
Câu 31: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C , cạnh bên SA vuông góc
với mặt phẳng đáy  ABC  . Biết SC  1, tìm thể tích lớn nhất của khối chóp S.ABC . 3 2 2 3 3 A. . B. . C. . D. . 12 12 27 27
Câu 32: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , AB  2 . Cạnh bên SA  1 và
vuông góc với mặt phẳng đáy. Thể tích lớn nhất của khối chóp S.ABC là? 1 1 1 1 A. . B. . C. . D. . 3 4 12 6
Câu 33: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , SA AB  2a . Cạnh bên SA
vuông góc với mặt phẳng đáy  ABC  . Gọi H , K lần lượt là hình chiếu vuông góc của A
lên SB và SC . Tìm thể tích lớn nhất V
của khối chóp S.AHK . max 3 a 2 3 a 3 3 a 3 3 a 2 A. V  . B. V  . C. V  . D. V  . max 6 max 6 max 3 max 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 34: Cho tam giác ABC vuông cân tại B , AC  2 . Trên đường thẳng qua A vuông góc với mặt
phẳng  ABC  lấy điểm M , N khác phía với mặt phẳng  ABC  sao cho AM .AN  1. Tìm
thể tích nhỏ nhất của khối tứ diện MNBC .? 1 1 1 2 A. . B. . C. . D. . 3 6 12 3
Câu 35: Cho hình chóp tam giác đều S.ABC có SA  1 . Thể tích lớn nhất của khối chóp S.ABC là? 1 2 3 1 A. . B. . C. . D. . 6 12 12 12
Câu 36: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân đỉnh C và SA vuông 
góc với mặt phẳng  ABC , SC a, SCA . Xác định góc để thể tích khối chóp SABC lớn nhất. 1 2
A.  arcsin
B.  arcsin 3 7 1 1
C.  arcsin
D.  3arcsin 5 3
Câu 37: Cho hình chóp S.ABCD có SA x, các cạnh còn lại bằng 2. Tìm giá trị của x để thể tích
khối chóp lớn nhất A. 6 B. 2 C. 7 D. 2 6
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD  . Kí hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  45 . Thể tích nhỏ nhất của khối chóp S.AMN là? 2 1 2 1 2 1 2 1 A. . B. . C. . D. . 9 3 6 9
Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD . Ký hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  60 . Thể tích nhỏ nhất của khối chóp S.AMN là 2  3 2  3 2 3  3 2 3  3 A. . B. . C. . D. . 3 9 3 9
Câu 40: Cho hình chóp S.ABC có SA , SB , SC đôi một vuông góc, I là tâm nội tiếp tam giác ABC
. Mặt phẳng  P thay đổi qua I , cắt các tia SA , SB , SC lần lượt tại A , B ,C . Biết SA SB
2 , SC  7 . Hỏi thể tích của khối chóp S.A BC
  có giá trị nhỏ nhất là? 243 7 7 81 7 27 7 A. . B. . C. . D. . 256 3 256 256
Câu 41: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  4 , các cạnh bên bằng
nhau và bằng 6 . Tìm thể tích lớn nhất của khối chóp S.ABCD
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 130 128 125 250 A. . B. . C. . D. . 3 3 3 3
Câu 42: Cho hình chóp S.ABCD có SB x 0  x  3 . Tất cả các cạnh còn lại bằng nhau và
bằng 1. Với giá trị nào của x thì thể tích khối chóp S.ABCD lớn nhất? 3 2 6 3 A. x  . B. x  . C. x  . D. x  . 3 2 2 2
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  4 . Cạnh bên SA vuông
góc với mặt phẳng đáy  ABCD  và SC  6 . Thể tích lớn nhất của khối chóp S.ABCD là? 40 80 20 A. . B. . C. . D. 24. 3 3 3
Câu 44: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , cạnh bằng 1, SO   ABCD và
SC  1. Thể tích lớn nhất của khối chóp S.ABCD là? 2 3 2 3 2 3 4 3 A. B. . C. . D. . 9 3 27 27
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD  . Kí hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  45 . Thể tích nhỏ nhất của khối chóp S.AMN là? 2 1 2 1 2 1 2 1 A. . B. . C. . D. . 9 3 6 9
Câu 46: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD . Ký hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  30 . Thể tích nhỏ nhất của khối chóp S.AMN là? 1 1 2 4 A. . B. . C. . D. . 9 3 27 27
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD . Ký hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  60 . Thể tích nhỏ nhất của khối chóp S.AMN là 2  3 2  3 2 3  3 2 3  3 A. . B. . C. . D. . 3 9 3 9
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với AD  4a . Các cạnh bên của
hình chóp bằng nhau và bằng a 6 . Tìm thể tích V
của khối chóp S.ABCD . max 3 8a 3 4 6a A. V  . B. V  . C. 3 V  8a . D. 3 V  4 6a . max 3 max 3 max max
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
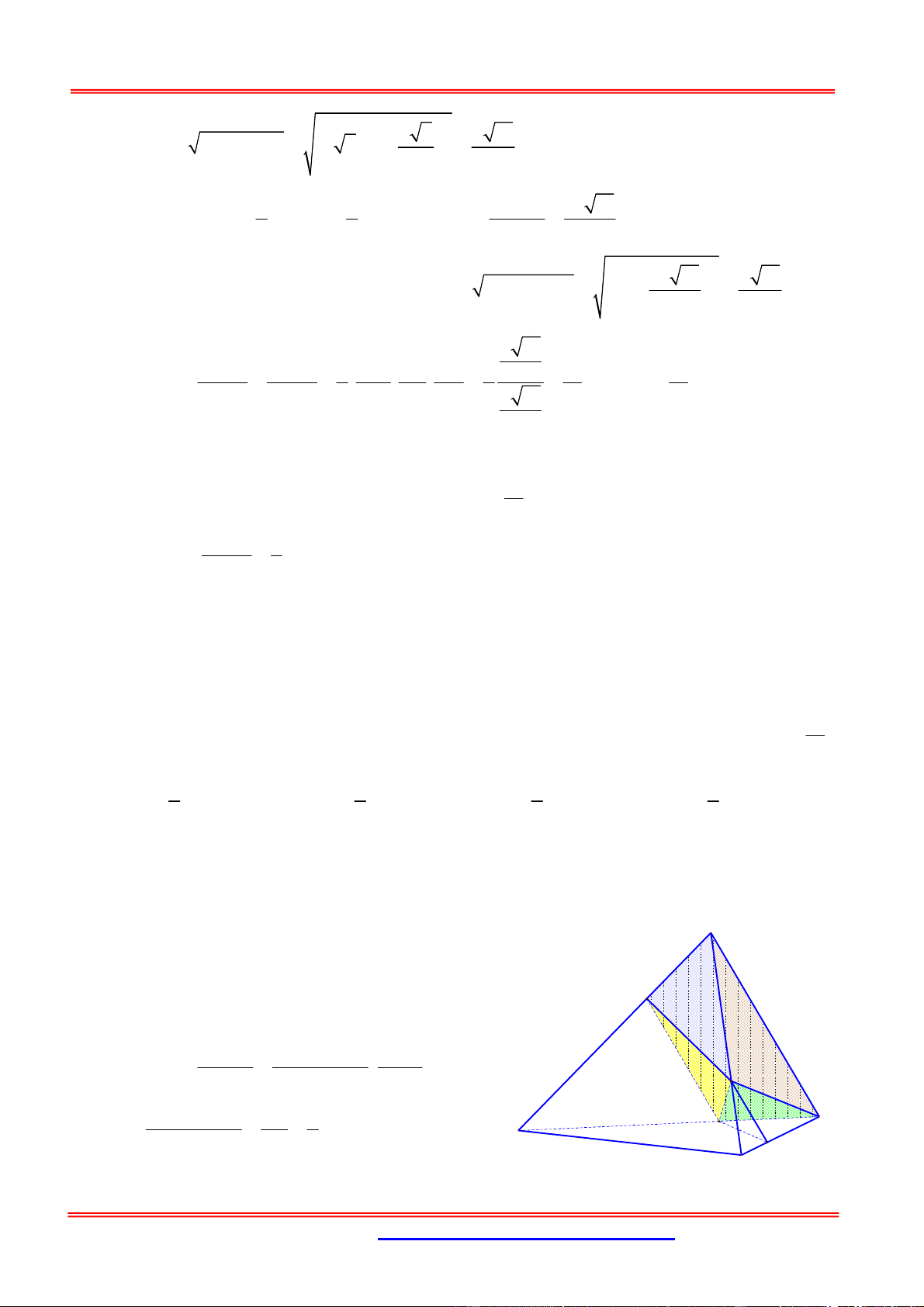
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và thể tích bằng V . Gọi M , N AB AD
lần lượt là các điểm di động trên các cạnh AB và AD sao cho  2  4 . Gọi V ' là AM AN
thể tích khối chóp S.MBCDN . Tìm giá trị nhỏ nhất của V ' . 1 2 3 1 A. V . B. V . C. V . D. V . 4 3 4 3
Câu 50: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Các điểm A ',C ' thỏa mãn
 1   1  SA '  SA , SC ' 
SC . Mặt phẳng  P chứa đường thẳng A'C ' cắt các cạnh SB, SD lần 3 5 V
lượt tại B ', D ' và đặt
S. A' B 'C ' D ' k
. Giá trị nhỏ nhất của k là? VS.ABCD 1 1 3 15 A. . B. . C. V . D. . 60 30 4 16
Câu 51: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh ,
a SA vuông góc với mặt phẳng
đáy và góc giữa SC với mặt phẳng  SAB bằng 0
30 . Gọi M là điểm di động trên cạnh CD
và H là hình chiếu vuông góc của S trên đường thẳng BM. Khi điểm M di động trên cạnh
CD thì thể tích của khối chóp SABH đạt giá trị lớn nhất bằng: 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 2 6 12
Câu 52: Cho hình chóp tứ giác S.ABCD có SA SB SC  2a . Tìm thể tích lớn nhất của khối chóp S.ABCD . 3 2 6a 3 32 3a 3 4 6a 3 32 3a A. . B. . C. . D. . 3 9 9 27
Câu 53: Khối chóp S.ABCD có đáy ABCD là hình thoi cạnh a . SA SB SC a , Cạnh SD thay
đổi. Thể tích lớn nhất của khối chóp S.ABCD là: 3 a 3 a 3 3a 3 a A. . B. . C. . D. . 8 4 8 2
Câu 54: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA vuông góc với mặt phẳng
đáy và góc giữa SC với mặt phẳng  SAB bằng 0
30 . Gọi M là điểm di động trên cạnh CD
và H là hình chiếu vuông góc của S trên đường thẳng BM . Khi điểm M di động trên
cạnh CD thì thể tích của khối chóp S.ABH đạt giá trị lớn nhất bằng: 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 6 3 2 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
C – HƯỚNG DẪN GIẢI Câu 1:
Cho khối tứ diện đều ABCD cạnh a . Gọi E là điểm đối xứng của A qua D . Mặt phẳng
qua CE và vuông góc với mặt phẳng  A D
B  cắt cạnh AB tại điểm F . Tính thể tích V của
khối tứ diện AECF . 3 2a 3 2a 3 2a 3 2a A. V B. V C. V D. V  30 60 40 15 Hướng dẫn giải: HB A F EM FA 3 FA 2
Áp dụng định lý Menelaus: . .  1  2. .  1   HM FB A E FB 4 FB 3 2 S E A AF 4  AF
AB và AE  2AD . Ta có:  E A F  .  5 S AD AB 5 ABD 3 3 4 4 a 2 a 2  VV  .  . AECF AB D 5 C 5 12 15 Câu 2:
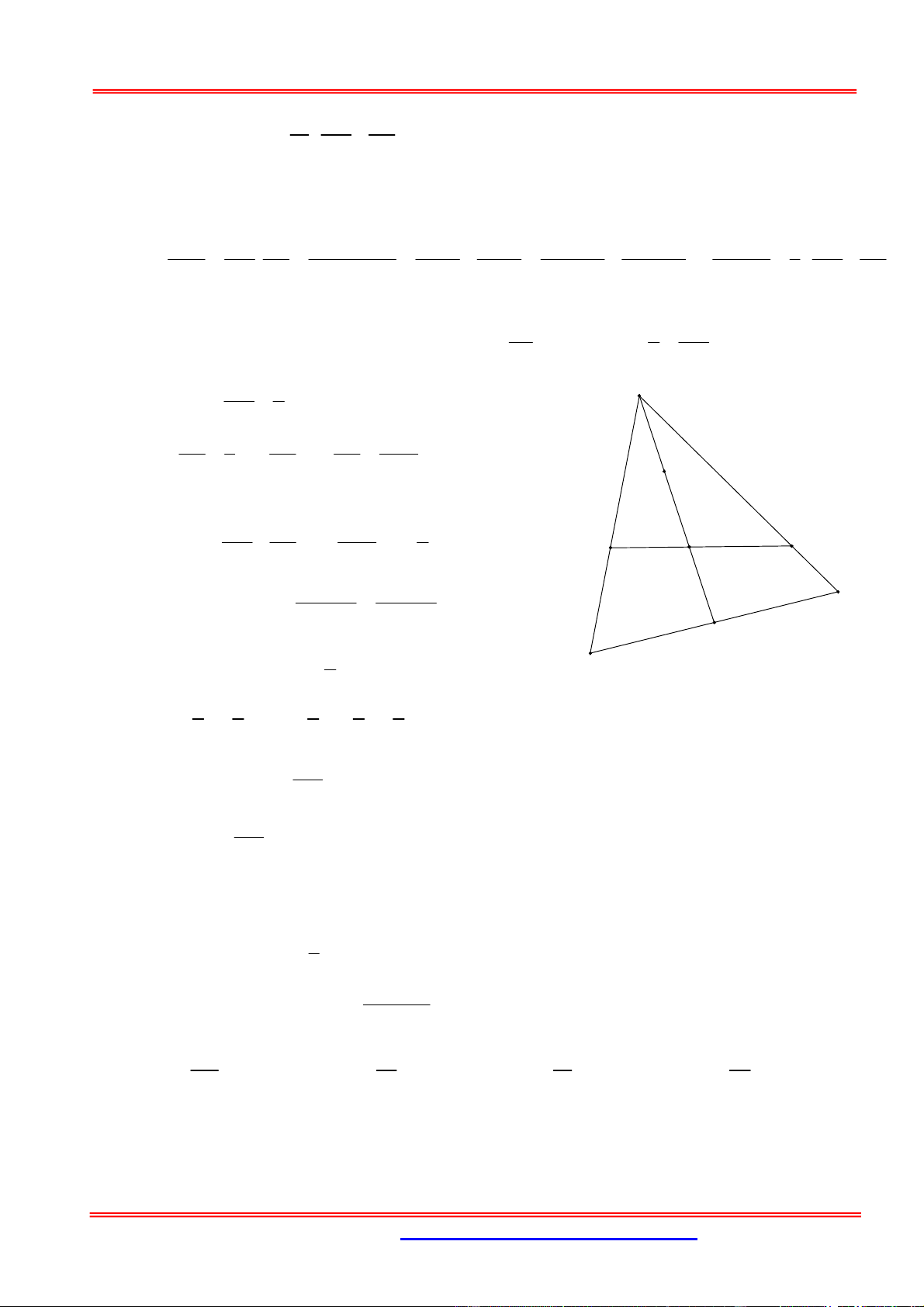
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm tam giác BCD . Tính thể tích ----
--------------------------------------------- của khối chóp . A GBC . A. V  3 . B. V  4 . C. V  6 . D. V  5 . Chọn B.Cách 1:
Phân tích: tứ diện ABCD và khối chóp .
A GBC có cùng đường cao là khoảng cách từ A
đến mặt phẳng  BCD . Do G là trọng tâm tam giác BCD nên ta có SSSBGCBGD CGDS  3S (xem phần chứng minh). BCD BGC
Áp dụng công thức thể tích hình chóp ta có: A 1  1 V  . h S ABCDBCD . h S 3   V 3 BCD S ABCDBCD      3 1 V 1 S A. V . GBC h S   . GBC h S . GBC A GBC 3 GBC  3 1 1  VV  .12  4 . B D A.GBC 3 ABCD 3
Chứng minh: Đặt DN  ; h BC a . G Từ hình vẽ có: C +) B D MF CM 1 1 h MF // ND     MF DN MF  . DN CD 2 2 2 N G E +) M GE BG 2 2 2 h h F GE // MF     GE MF  .  MF BM 3 3 3 2 3 C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 1 DN.BC ha S +) BCD 2 2    3  S  3S D S 1 1 BCD GBC h GBC GE.BC a 2 2 3
+) Chứng minh tương tự có S  3S  3SBCDGBDGCD GSSS . A CBGCBGDCGD H Cách 2: H1 I
d G; ABC  B GI 1    d  1
G; ABC   d  ;
D ABC  . d  ; D ABC  DI 3 3 1 1 Nên V
d G; ABC .S  .V  4. G. ABC    3 ABC 3 DABC Câu 3:
Cho tứ diện đều cạnh a và điểm I nằm trong tứ diện. Tính tổng khoảng cách từ I đến các mặt của tứ diện. a a 6 a 3 a 34 A. . B. . C. . D. . 2 3 2 2 Hướng dẫn giải: S Chọn B. 2 2 a 3 a 3 AH AM  .  . 3 3 2 3 2 a a 6 2 2 2 SH SA AH a   . 3 3 A C I 2 3 1 1 a 3 a 6 a 2 H Ta có VS .SH  . .  . SABC M 3 ABC 3 4 3 12 Mặt khác, VVVVV B SABC ISAB IABC ISAC ISBC 1  S
. d I;SAB  d I; ABC   d I;SAC   d I;SBC  3 ABC   3 a 2 3. a 6   V
d I SAB  d I ABC   d I SAC   d I SBC  3 ; ; ; ; SABC  12   . S 2 a 3 3 ABC 4 Câu 4:
Cho khối tứ diện ABCD có 0
BC  3,CD  4, A
BC  BCD  ADC  90 . Góc giữa hai
đường thẳng AD và BC bằng 0
60 . Tính cosin góc giữa hai mặt phẳng  ABC  và  ACD ? 2 43 43 4 43 43 A. B. C. D. 43 86 43 43
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 10
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Hướng dẫn giải:
Ta dựng AE   BCD và dễ dàng chứng minh được
BCDE là hình chữ nhật. Khi đó   AD BC 0 ,
 ADE  60 khi đó ta suy ra AE  3 3  V  6 3 . ABCD
Mặt khác ta chú ý công thức tính nhanh: 2S S sin ABC ACD ABC ACD  ,  VABCD 3AC
Do vậy đặt   ABC  , ACD  và theo định lý
Pythagoras ta suy ra AB
43; AD  6; AC  2 13 . 2  1  Khi đó: 6 3  3 43   12sin 6 13  2  2 43  cos . 43 Câu 5:
Cho hình chóp tứ giác S.ABCD có SA   ABCD , ABCD là hình thang vuông tại A và B
biết AB  2a , AD  3BC  3a . Tính thể tích khối chóp S.ABCD theo a , biết khoảng cách 3 6
từ A đến mặt phẳng (SCD) bằng a . 4 A. 3 6 6a . B. 3 2 6a . C. 3 2 3a . D. 3 6 3a . Hướng dẫn giải:
Dựng AM CD tại M .
Dựng AH SM tại H . S 3 6 Ta có: AH a . 4 AD BC 2 S  .AB  4a ABCD K 2
CD   AD BC 2 2  AB  2a 2 A D 1 2 SA . B BC a ABC 2 M 2 SSS  3a ACD ABCD ABC B C 1 2S 3 2 SAM . ACD CD AM   a ACD 2 CD 2 1 1 1 AH .AM 3 6 Ta có:    AS   a 2 2 2 2 2 AH AM AS 2 AM AH 1 3 VS . A S  2 6a S . ABCD 3 ABCD
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 11
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Câu 6:
Cho hình chóp S.ABC có SA a, BC a 2 và tất cả các cạnh còn lại đều bằng x . Tìm x 3 a 11
biết thể tích khối chóp đã cho có thể tích bằng . 6 3a 7a 9a 5a A. x  . B. x  . C. x  . D. x  . 2 2 2 2 Hướng dẫn giải: Chọn D
Gọi E, F lần lượt là trung điểm của các cạnh BC, SA .
Khi đó ta có FE S ,
A FE BC và BC   SAE  nên BC SA . Và 2 2 2 2 2 2
FE AE FA AB BE FA S 2 2 2 2 2a a 4x  3a 2  x    4 4 4 Áp dụng công thức: a 1 V  . .
SA BC.d SA; BC .sin SA; BC S . ABC     6 F x 2 2 1 4x  3a x Suy ra: V  . . a a 2. .sin 90 6 4 3 a 11 1 2 2 5a   . .
a a 2. 4x  3a x  . x A C 6 12 2 E x a 2 B Câu 7:
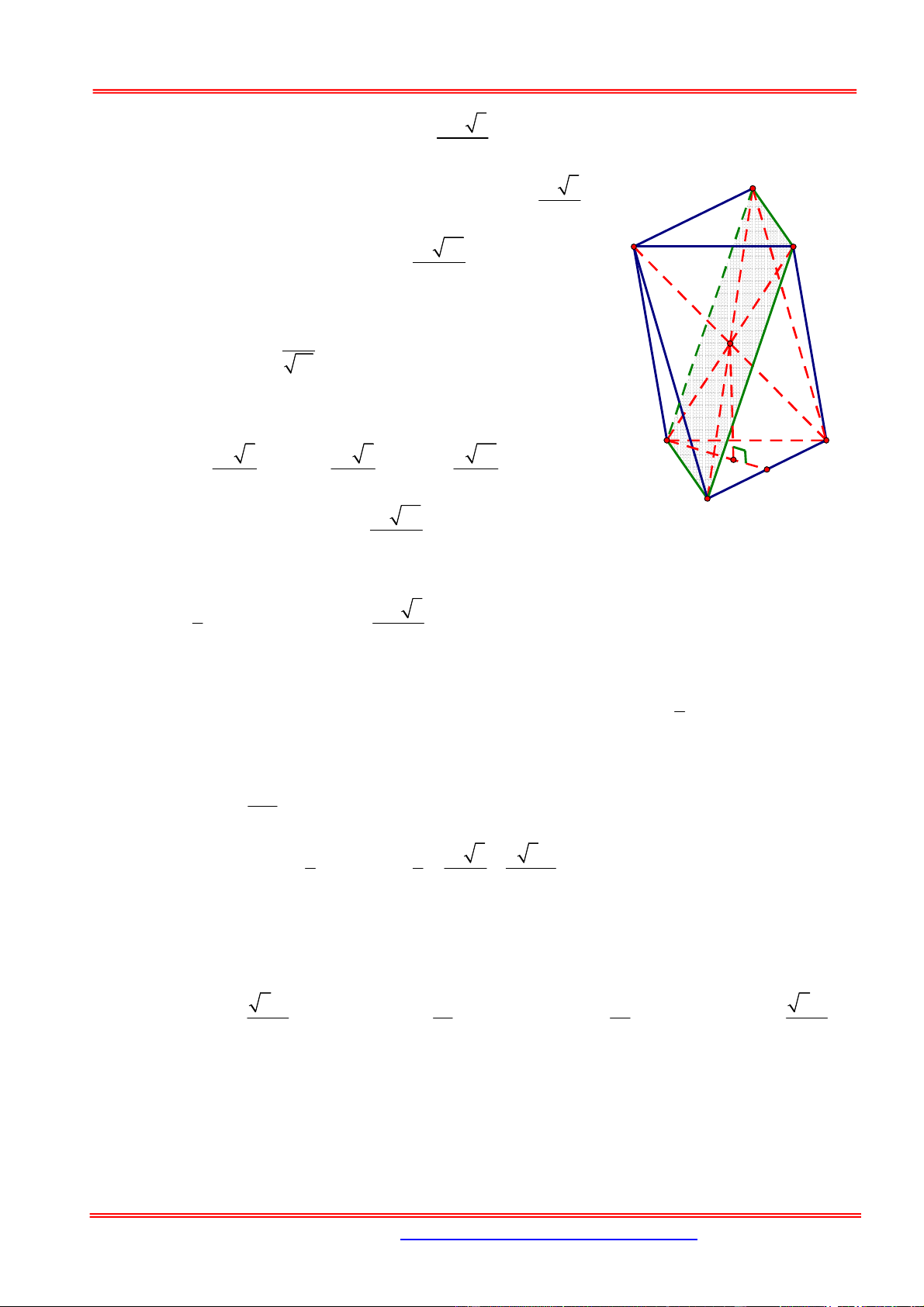
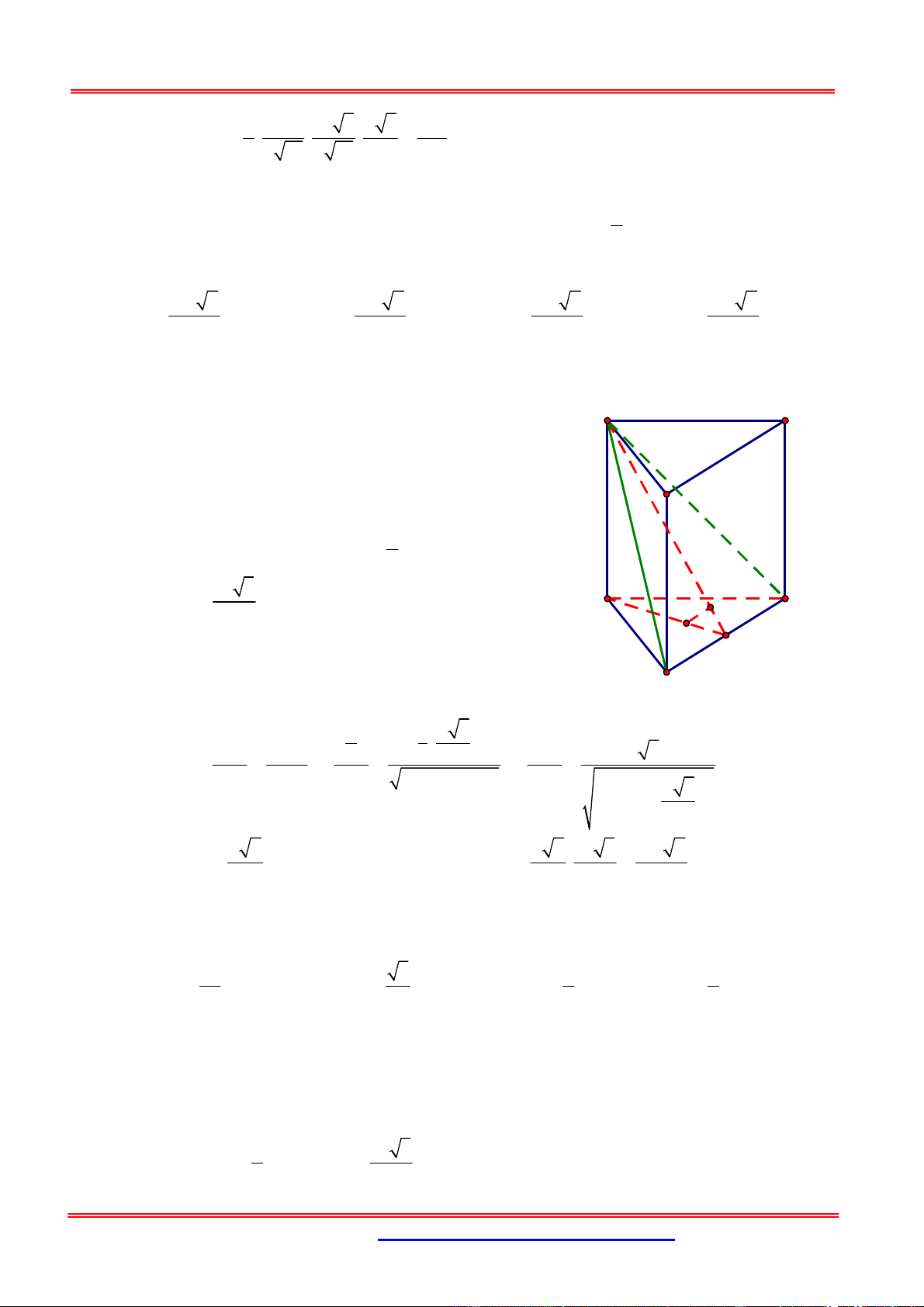
Cho hình chóp đều S.ABC có đáy cạnh bằng a , góc giữa đường thẳng SA và mặt phẳng
ABC  bằng 60 . Gọi A, B, C tương ứng là các điểm đối xứng của A , B , C qua S .
Thể tích của khối bát diện có các mặt ABC, AB C
  , ABC , B CA , C AB , AB C   , BA C   , CAB là 3 2 3a 3 3a 3 4 3a A. . B. 3 2 3a . C. . D. . 3 2 3 Hướng dẫn giải: Chọn A.
Cách 1: Ta tính thể tích khối chóp S.ABC : a 3
Gọi H là tâm tam giác ABC đều cạnh a  CH
. Góc giữa đường thẳng SA và mặt 3 phẳng (ABC) bằng 0 60  2 3 a a o 1 1 3 3
SCH  60  SH a V  .S H .S  . a  . S. ABC 3 ABC 3 4 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 12
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 3 2a 3 V  2V  2.4V  8V  .
B. ACA'C ' B.ACS S. ABC 3 A' 3 a 3
Cách 2: Ta có thể tích khối chóp S.ABC là:V  . S . ABC 12 2 B' C' a 39
Diện tích tam giác SBC là: S  . SBC 12
Khoảng cách từ A đến mặt phẳng  SBC  là:  a
d A SBC  3 ,  . S 13
Tứ giác BCB 'C ' là hình chữ nhật vì có hai đường chéo
bằng nhau và cắt nhau tại trung điểm mỗi đường. C B 2a 3 2a 3 a 39 Có SB   BB '   B 'C  . H 3 3 3 2 a 39 A
Diện tích BCB 'C ' là: S  . BCB 'C ' 3
Thể tích khối 8 mặt cần tìm là: 3 1 V d  2a 3 2. ,
A SBC .S  . BCB 'C ' 3 3 Cách 3 1
Thể tích khối bát diện đã cho là V  2V  2.4V  8V  8. . SG S
A' B 'C ' BC A'.SBC S. ABC 3 ABC
Ta có: SA ABC    0 ;
SAG  60 . Xét S
GA vuông tại G :  SG  tan SAG
SG AG. tan SAG  . a AG 2 3 1 1 a 3 2 3a
Vậy V  8. S . G S  8. . . a  . 3 ABC 3 4 3 Câu 8:
Cho hình chóp SABC có đáy ABC là tam giác vuông cân, AB AC a , SC   ABC  và
SC a . Mặt phẳng qua C , vuông góc với SB cắt S ,
A SB lần lượt tại E và F . Tính thể
tích khối chóp S.CEF . 3 2a 3 a 3 a 3 2a A. V  . B. V  . C. V  . D. V  . SCEF 36 SCEF 18 SCEF 36 SCEF 12 Hướng dẫn giải:
Từ C hạ CF SB, F SB , CE S ,
A E SA
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 13
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao AB AC
AB   SAC   AB CE Ta có AB SCS
CE  SAB  CE SB
Vậy mặt phẳng qua C và vuông góc SB là mặt FCEF  . a V SE SF Ta có SCEF  . V SA SB SCAB E
Tam giác vuông SAC vuông tại C ta có: B C 2 2 SA
SC AC a 2 a a 2 2 SE SC a SE 1 và     2 2 SA SA 2a SA 2 A
Tam giác vuông SBC vuông tại C ta có: 2 2 SB
SC BC a 3 2 2 SF SC a SF 1 và     2 2 SB SB 3a SC 3 V 1 1 1 1 1 1 1 Do đó SCEF 3  .   VV  . S . A Sa . V 2 3 6 SCEF 6 SABC 6 3 ABC 36 SCAB Chọn C. Câu 9:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi  P là mặt phẳng đi qua A và
song song BC và vuông góc với  SBC , góc giữa  P với mặt phẳng đáy là 0 30 . Thể tích
khối chóp S.ABC là: 3 a 3 3 a 3 3 a 3 3a A. B. C. D. 24 8 8 8 Hướng dẫn giải:
Tổng quát: Cho hình chóp tam giác đều S S.ABC có cạnh đáy bằng .
a Gọi  P là mặt phẳng đi F
qua A và song song BC và vuông góc với SBC , H
góc giữa  P với mặt phẳng đáy là E
Thể tích khối chóp S.ABC là: C A 3 a cot VG S . ABC x 24 M B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 14
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 3 0 3 a cot 30 a 3 Áp dụng bài này: V   S . ABC 24 24 2 a 3 + A
BC đều  S  ABC 4 + Gọi G là trọng tâm
+ Gọi  P  SBC  =EF  EF//BC   P   SBC  =Ax với Ax / /EF / / BC
+ Gọi M là trung điểm BC, SM EF N .
Ta có: AM BC, SG BC BC   SAM   AN BC AN Ax Mà M BC BC Ax AM
  P  ABC    0 A , / / Ax ,  NAM  30   
Ta có: GSM NAM (cùng phụ với SMA )  1 1 a 3 a Xét S
GM vuông tại G có: 0
SG GM .cot GSM AM .cot 30  . . 3  3 3 2 2 2 3 1 1 a 3 a a 3 Vậy: V  .S .SG  . .  . S . ABC 3 ABC 3 4 2 24 Chọn A.
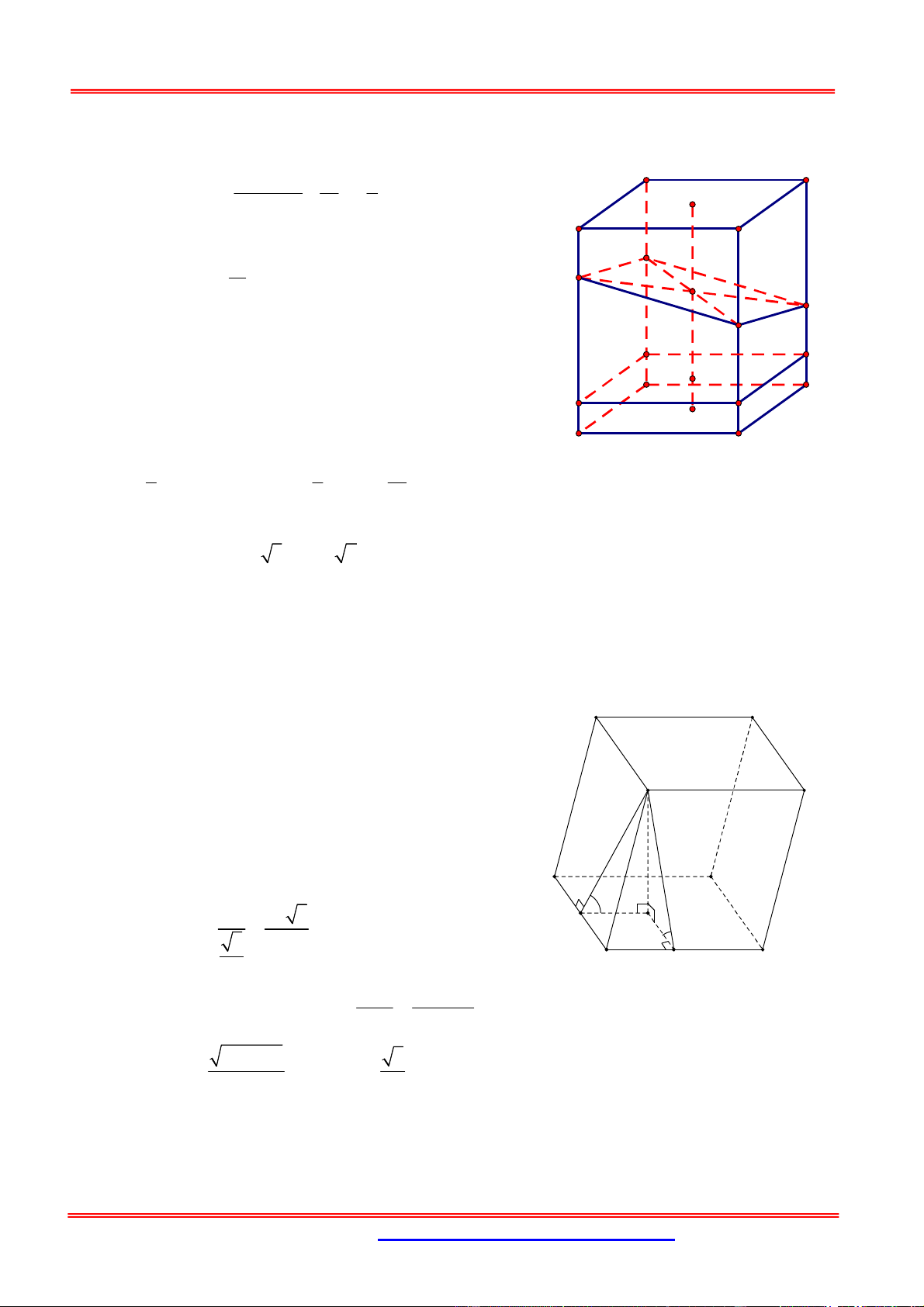
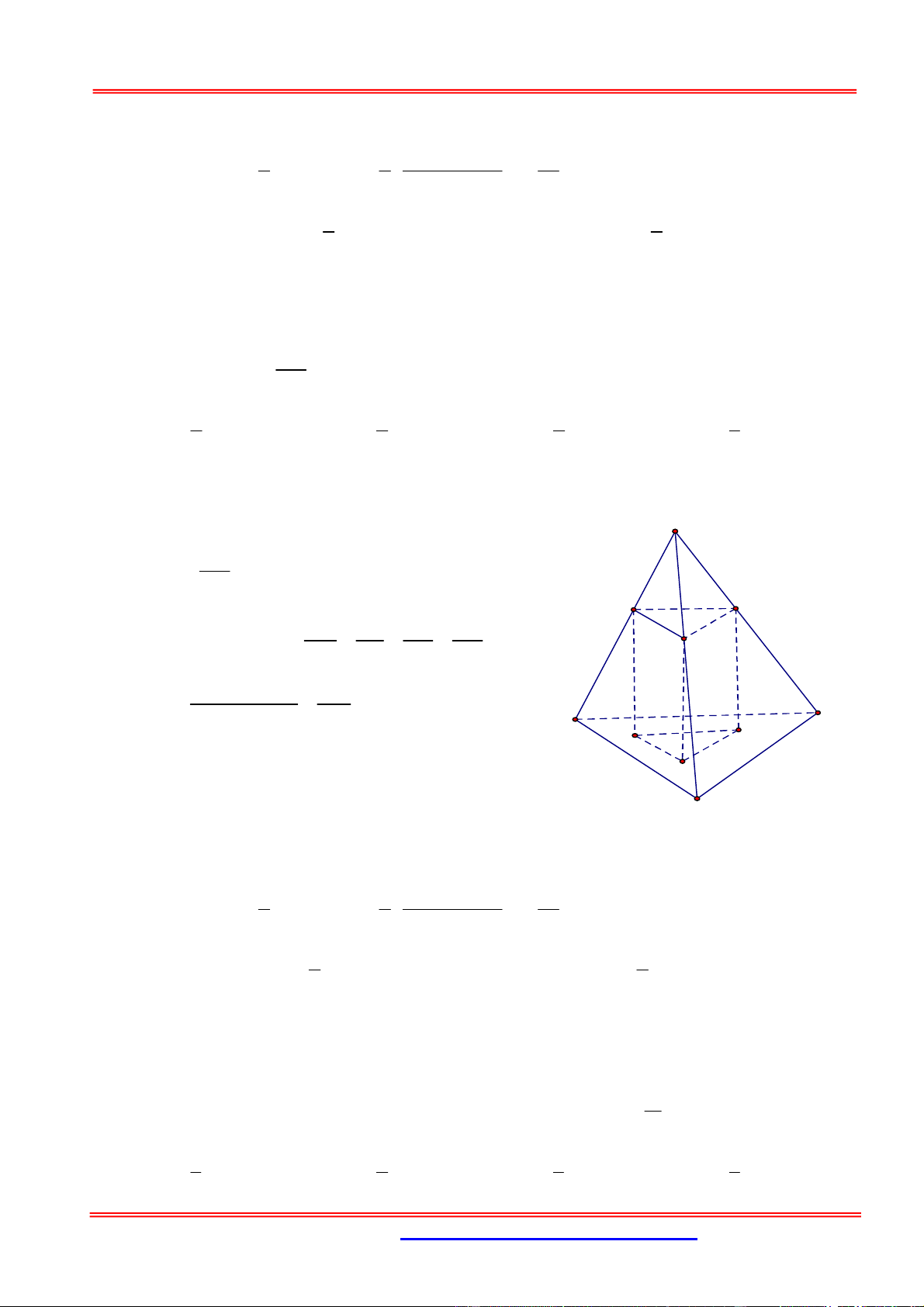
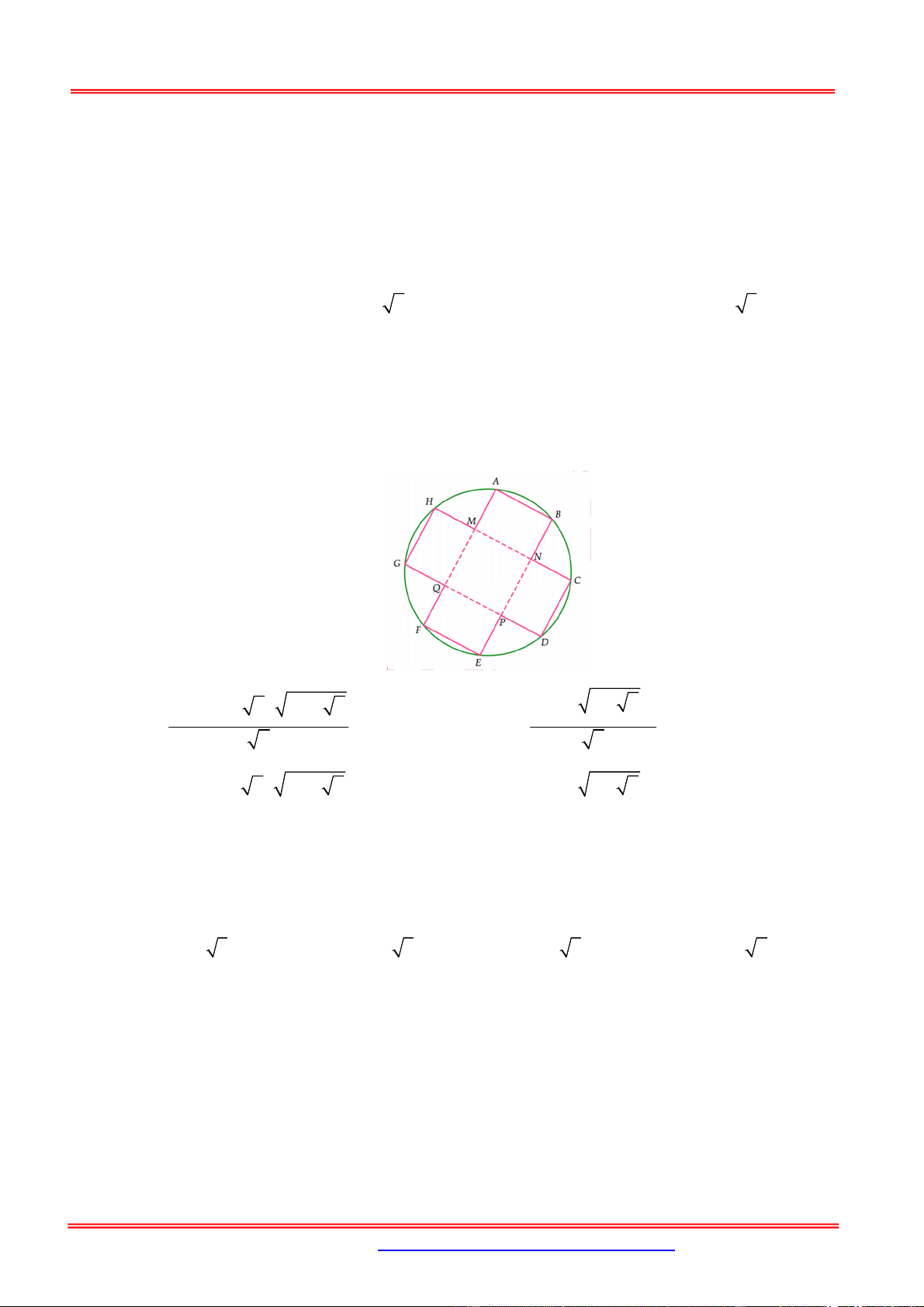
Câu 10: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4, mặt bên SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Gọi M , N, P lần lượt là trung điểm của các
cạnh SD,CD, BC. Thể tích khối chóp S.ABPN là ,
x thể tích khối tứ diện CMNP là . y Giá
trị x, y thỏa mãn bất đẳng thức nào dưới đây: A. 2 2
x  2xy y  160 B. 2 2
x  2xy  2 y  109 C. 2 4
x xy y  145 D. 2 4
x xy y  125 Hướng dẫn giải: S
+ Gọi H là trung điểm A . B Do A
BC đều và  SAB   ABCD  SH   ABCDM 3AB Xét A
BC đều: SH   2 3 2 A D + Ta có: SSSS K ABPN ABCD ADN CND H N B P C A . D DN CN.CP 4.2 2.2 2 2  AB    4    10 2 2 2 2 1 1 20 3 20 3  V  .S .SH  .10.2 3   x S. ABPN 3 ABPN 3 3 3
+ Gọi AN HD  K ta có MK là đường trung bình của DHS
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 15
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 1 1 1 1 1 2.2 2 3 2 3 2 3  HK SH V  .S
.MK  . .CN.C . P .SH  . .   y  2 CMNP 3 CNP 3 2 2 3 2 2 3 3 Thay vào các đáp án. Chọn C.
Câu 11: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều,
SC SD a 3. Tính thể tích khối chóp S.ABC . D 3 a 2 3 a 2 3 a 2 3 a A. V B. V C. V D. V  2 3 6 6 Hướng dẫn giải:
Gọi I là trung điểm AB;J là trung điểm của CD từ giả thiết ta có: a 3 2 a a 11 IJ  ; a SI  và 2 2 2 SJ
SC JC  3a   3 4 2
Áp dụng định lý cosin cho tam giác SIJ ta có: S 2 2 2 3a 11a a    2 2 2   S  IJ +IS SJ 4 4 cos IJ   2.IJ.IS a 3 2. . a 2 2 a 3      0 2 a 3 3 D MA
Suy ra, tam giác SIJ là tam giác có SIJ tù. Từ H I J
giả thiết tam giác SAB đều và tam giác SCD là N B C
cân đỉnh S. Gọi H là hình chiếu của S trên  
ABCD, ta có H thuộc IJ và I nằm giữa HJ tức là tam giác vuông SHI có 0 H  90 .    3   6
Góc I nhọn và cos I  o c sSIH   o c sSIJ 
SIJ va SIH ke bu   sin SIH  . 3 3  a 3 6 a 2
Xét tam giác SHI ta có SH SI.sin SIH  .  2 3 2 3 1 1 a 2 a 2 Vậy 2 VS .SH a .  . S . ABCD 3 ABCD 3 2 6 Chọn C.
Câu 12: Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại , A ;
D AB AD  2 , a CD  . a
Góc giữa hai mặt phẳng  SBC  và  ABCD bằng 0
60 . Gọi I là trung điểm của AD, biết
hai mặt phẳng  SBI , SCI  cùng vuông góc với mặt phẳng  ABCD. Tính thể tích khối chóp S.ABC . D
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 16
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 3 15 3 17 3 19 3 23 A. 3 a B. 3 a C. 3 a D. 3 a 5 5 5 5 Hướng dẫn giải:
Gọi H trung điểm của BC, I là hình chiếu của H
lên BC, J là trung điểm A . B S
Ta có SI mp ABCD 2 2 , IC
ID DC a 2 2 2 IB
IA AB a 5 và 2 2
BC IB CJ JB a 5 J 1 1 B S
AD AB CD a SIA AB a A ABCD   2 2 3 ; . . 2 IAB 2 I H 1 1 và 2 S  .DC.DI a CID D 2 2 C 2 3aSSSS  . IBC ABCD IAB DIC 2 1 2S 3 3 Mặt khác SIH.BC, nên IBC IH   . a IBC 2 BC 5 9 3 0
SI IH .tan 60 . a 5 1 3 15 Do đó 3 VSI.Sa . S . ABCD 3 ABCD 5 Chọn A.
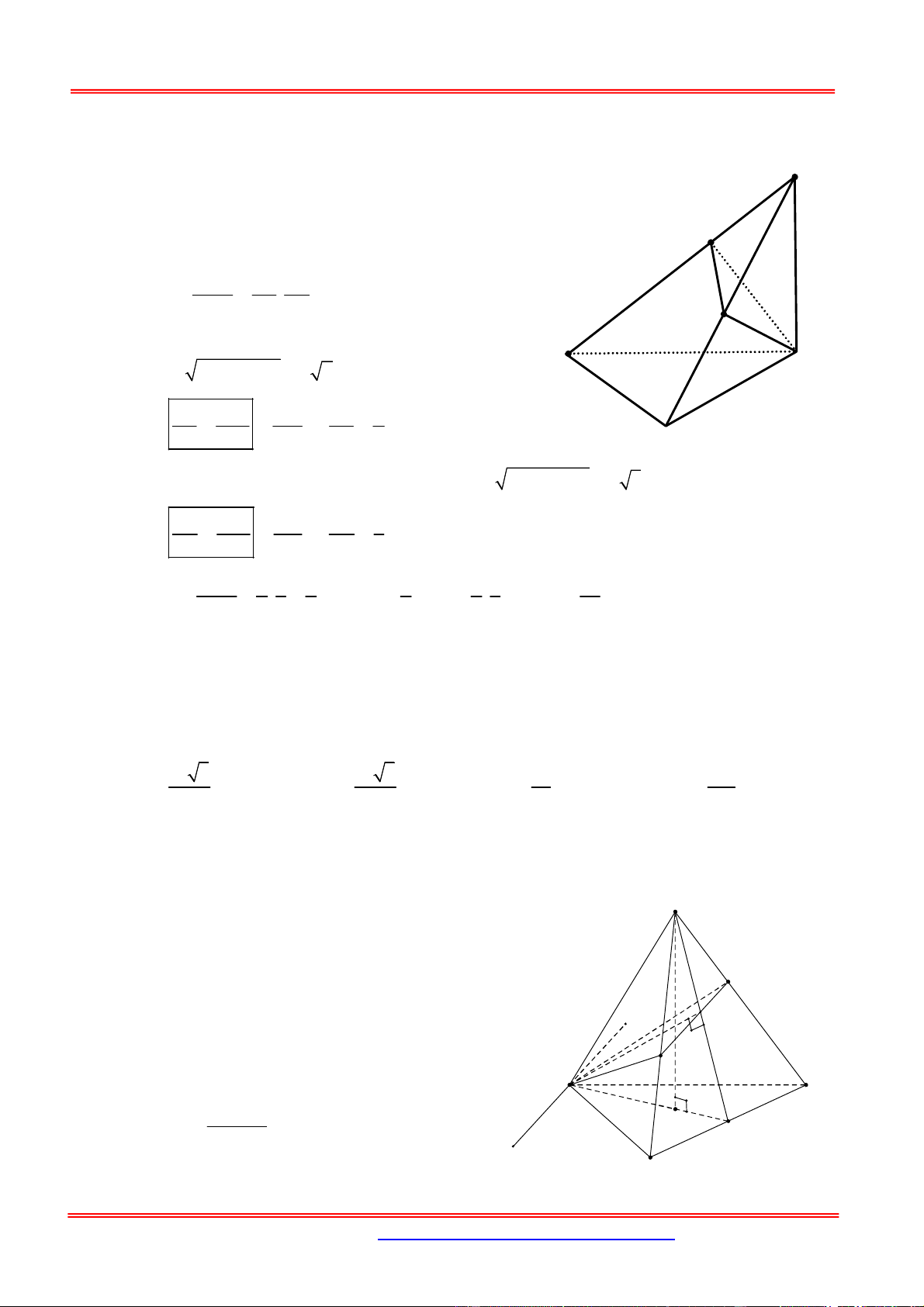
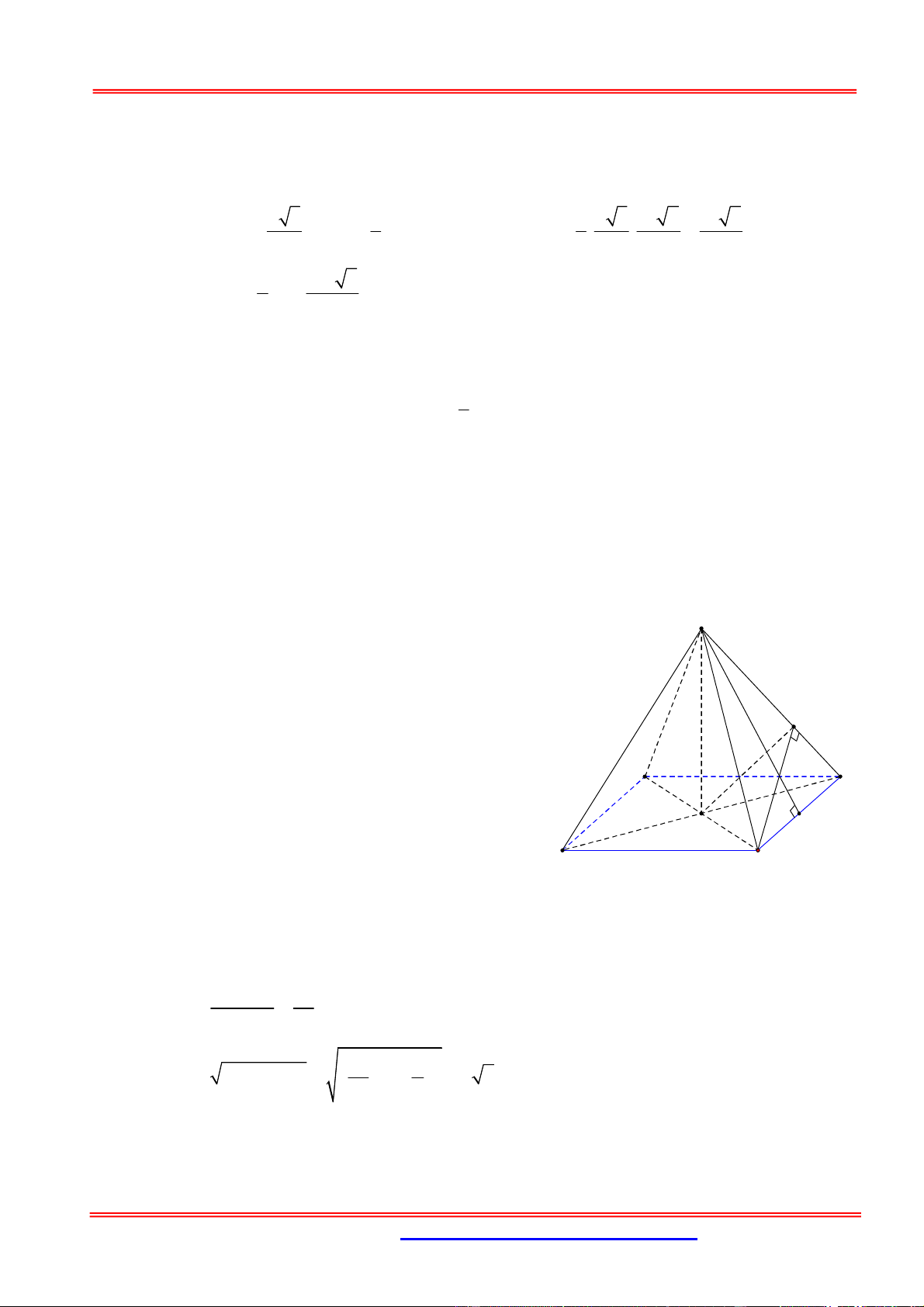
Câu 13: Cho hình chóp S.ABC có chân đường cao nằm trong tam giác ABC; các mặt phẳng
SAB;SAC;SBC cùng tạo với mặt phẳng  ABC  một góc bằng nhau. Biết
AB  25, BC  17, AC  26, đường thẳng SB tạo với đáy một góc bằng 0 45 . Tính thể tích V
của khối chóp SABC. A. V  680 B. V  408 C. V  578 D. V  600 Hướng dẫn giải: S
Gọi J là chân đường cao của hình chóp
S.ABC; H , K và L lần lượt là hình chiếu
của J trên các cạnh AB, BC và C . A y=9 C    z=17
Suy ra SHJ , SLJ và SKJ lần lượt là góc y=9 K A z=17 J L
tạo bởi mặt phẳng  ABC  với các mặt H x=8 x=8 B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 17
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
phẳng  SAB, SAC  ,SBC .   
Theo giả thiết ta có: SHJ SLJ SKJ ,
suy ra các tam giác vuông SJH , SJ , L SJK bằng nhau.
Từ đó, JH JL JK. Mà J nằm trong tam giác ABC nên J là tâm đường tròn nội tiếp tam giác ABC.
Áp dụng công thức Hê- rông, ta tính được diện tích của tam giác ABC là S  204. Kí hiệu P
là nửa chu vi tam giác ABC, r là bán kính đường tròn z K y A C S 204
nội tiếp của ABC. Ta có r    6. z y P 34 J Đặt
x BH BL, y CL CK , z AH AK. L H xx y  7 x B
Ta có hệ phương trình: x z  25 .
y z  26 
Giải hệ phương trình ta được  ;
x y; z   8;9;17 2 2 2 2 JB
JH BH  6  8  10 
Ta có SBJ   SB ABC   0 ,  45 , suy ra SJB là
tam giác vuông cân tại J. SJ JB  10. 1
Thể tích V của khối chóp S.ABC là V SJ.S  680 3 ABC Chọn A.
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB  8 , BC  6 . Biết SA  6
và vuông góc với mặt phẳng đáy  ABC  . Một điểm M thuộc phần không gian bên trong
của hình chóp và cách đều tất cả các mặt của hình chóp. Tính thể tích của khối tứ diện M .ABC . 64 32 A. V  24 . B. V  . C. V  . D. V  12 . 3 3 Hướng dẫn giải: S Chọn C BC BA 1 Vì 
BC SB . Khi đó S  . SA AB  24 , BC SA SAB  2 M 1 1 2 2 S  . SA AC  .6. 8  6  30 , SAC 2 2 A C 1 1 1 2 2 S  . SB BC  8  6 .6  30 , S  .6.8  24 . SBC 2 2 ABC 2 B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 18
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 1
Thể tích khối chóp đã cho là: V  . SA .A . B BC  48 . 3 2
Theo bài ra điểm M thuộc phần không gian bên trong của hình chóp và cách đều tất cả các
mặt của hình chóp nên ta gọi khoảng cách từ điểm M đến các mặt của hình chóp là d thì: 1 3V Vd. SSSS S. ABCd S . ABCSAB SAC SBC ABC  3 SSSS SAB SAC SBC ABC 3.48 4 1 1 4 32  d   . Khi đó: V  .d.S  . .24  . 30  30  24  24 3 M . ABC 3 ABC 3 3 3
Câu 15: Cho khối đa diện đều n mặt có thể tích V và diện tích mỗi mặt của nó bằng S. Khi đó,
tổng các khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng nV V 3V V A. . B. . C. . D. . S nS S 3S Hướng dẫn giải: Chọn C. S
Xét trong trường hợp khối tứ diện đều.
Các trường hợp khác hoàn toàn tương tự. 1 1 1 1 Vh .S; Vh .S; Vh .S; Vh .S H . ABC 1 H .SBC 2 H .SAB 3 H .SAC 4 3 3 3 3 3V 3V 3V 3V A C 1 2 3 4 h  ; h  ; h  ; h  1 2 3 4 H S S S S
3V V V V 1 2 3 4  3V
h h h h   B 1 2 3 4 S S
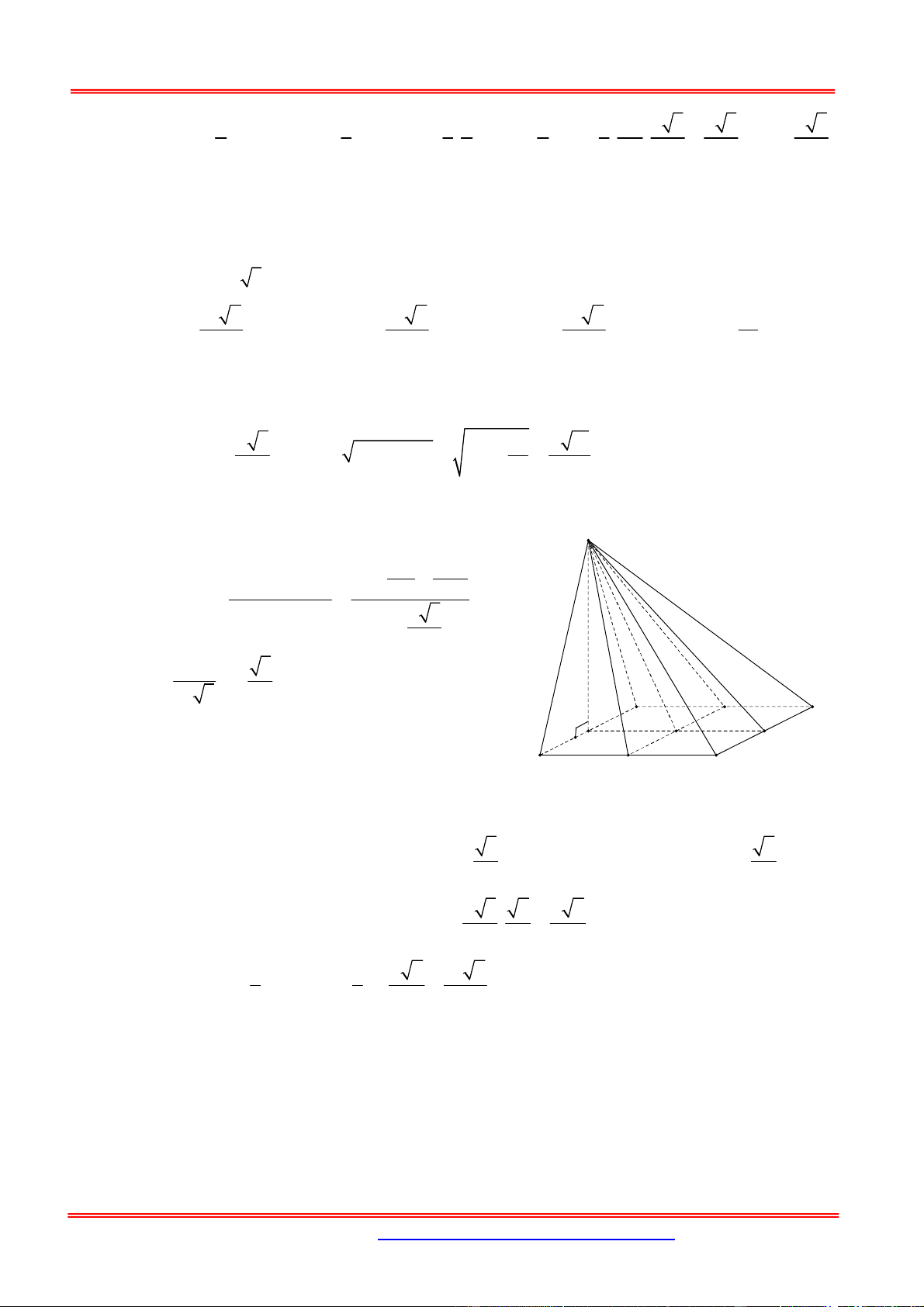
Câu 16: Cho hình chóp S.ABCD có đáy là nửa lục giác đều với cạnh a (a> 0). Cạnh SA vuông góc SM
với đáy và SA = a 3 . M là một điểm khác B trên SB sao cho AM  M . D Tính tỉ số . SB 3 1 3 5 A. B. C. D. 4 4 5 4
Hướng dẫn giải: :
Đặt hình chóp vào hệ trục toạ độ như
hình vẽ. Suy ra ta có: A = (0; 0; 0), D =
(2a; 0; 0), S = (0; 0; a 3 ) và S  a a 3  B =  ;
; 0  . Suy ra phương trình  H 2 2    2x 2 y z a 3 A D của SB là:   a a 3 a 3 Gọi M(x B C
0; y0; z0) thuộc cạnh SB, ta có:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 19
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao   y  3x 0 0  .
z a 3  2 3x  0 0
 
Mặt khác AMDN  AM .DM  0 3a  x 2 2 2
0 – 2ax0 + y0 + z0 = 0  x  0 8
 3a 3a 3 a 3   3  SM 3  M   ; ;   SM SB hay  .  8 8 4    4 SB 4 Chọn A.
CỰC TRỊ THỂ TÍCH KHỐI CHÓP
Câu 17: Cho hình chóp S.ABC có SA SB SC  1 . Tìm thể tích lớn nhất của khối chóp S.ABC . 1 1 1 1 A. . B. . C. . D. . 3 6 4 12 Hướng dẫn giải: Chọn B .
Gọi H là hình chiếu của A lên mặt phẳng SBC . Ta có 1 1  1 1
V  .AH .S  .AH. .
SB SC.sin BSC  .AS. . SB SC  3 SBC 6 6 6 . Dấu “=” xảy ra khi và chỉ khi  AH AS  
AS  SBC     
SA SB, SB SC, SC SA s  in BSC  1 SB SC   . Câu 18: Cho hình chóp S.ABC có
SA x, BC y, AB AC SB SC  1. Thể tích
khối chóp S.ABC lớn nhất khi tổng x y bằng: 2 4 A. 3 B. C. D. 4 3 3 3
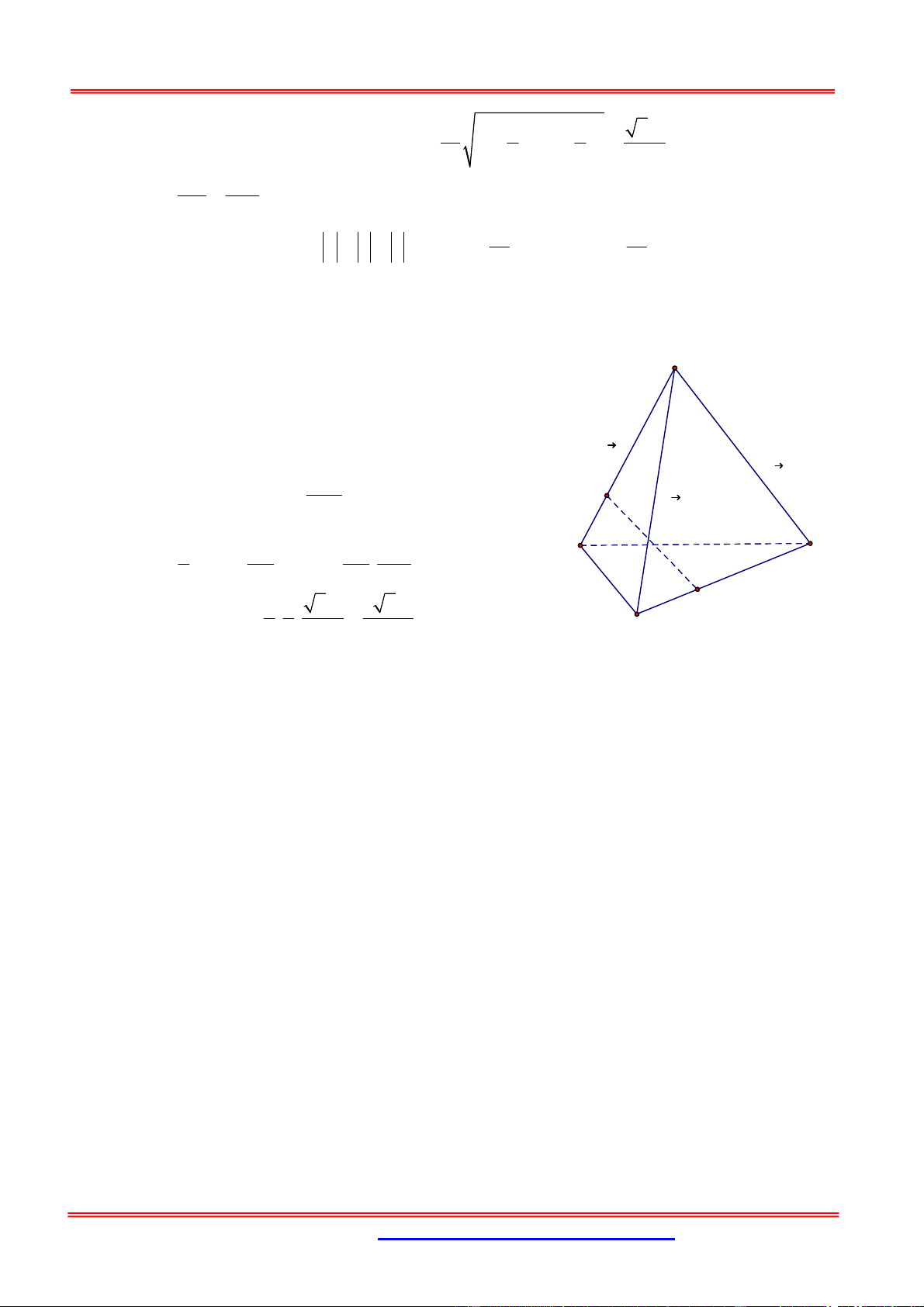
Hướng dẫn giải: Ta gọi M , N lần lượt là trung điểm của S , A BC.
Dễ chứng minh được SA  (MBC) và MBC cân tại M Tính được: 2 2 2 2 2 BC SA BC x y 2 2 2 MN MB   AB    1 . 4 4 4 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 20
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 1 x y Do đó: V Vxy 1 . S. ABC 6 4 1 xy 2 Vì 2 2
x y  2xy nên 2 V xy 1 
(xy) .2  xy . Dấu bằng xảy ra khi x  . y 6 2 12
Đến đây, có hai hướng xử lý:
Thứ nhất, sử dụng BĐT Côsi: 3  xy xy    2  xy xy xy   32 2 xy   xy 2 2 ( ) 2  4. . (2  xy)  4.  .   2 2 3 27     x y  2 4
Dấu bằng xảy ra   xyx y   x y  .  2  xy 3 3   2 4
Thứ hai, đặt t xy và xét 2
f (t)  t (2  t) , đạt GTLN khi t  , suy ra 3 2 4 x y   x y  . 3 3
Câu 19: Nếu một tứ diện chỉ có đúng một cạnh có độ dài lớn hơn 1 thì thể tích tứ diện đó lớn nhất là bao nhiêu? 1 3 1 5 A. B. C. D. 4 4 8 8 Hướng dẫn giải:
Giả sử tứ diện ABCD có cạnh lớn nhất là AB , suy ra các
tam giác ACD và BCD có tất cả các cạnh đều không lớn A
hơn 1. Các chiều cao AF và BE của chúng không lớn hơn 2 a 1
, trong đó CD a  1. 4 2 a
Chiều cao hình tứ diện AH  AF  1 4 B D
(do tam giác AHF vuông tại H có AF là cạnh huyền) H F
Thể tích của khối tứ diện là: 2 C 1 1 1 1 1  a  1 V S
.AH  . .BE.C . D AH  . . . a 1  aa BCD    2 4  3 3 2 3 2 4 24  
Để tìm giá trị lớn nhất của V ta xét biểu thức a  2 4  a . 1 1
Vì 0  a  1 nên a  2
4  a   3 và V a  2 4  a   . 24 8 Chọn C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 21
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 20: Khối tứ diện ABCD có AB  1 và tất cả các cạnh còn lại có độ dài không vượt quá 1. Hỏi
thể tích lớn nhất của khối tứ diện đó là? 3 1 1 A. . B. . C. . D. 3 . 8 8 24 Hướng dẫn giải: Chọn B
Tứ diện ABCD có AB  1, các cạnh còn lại đều
không lớn hơn 1. Đặt CD a, x  0;  1
Gọi M là trung điểm của BC , K là hình chiếu của
B lên CD và H là hinfhc hiếu của A trên
mp BCD . Khi đó ta có 1 1 VAH .S  . x BK.AH (1) ABCD 3 BCD 6 Có 2 2 2 2 BC BD CD x 1 2 2 BM    1  BM  4  x 2 4 4 2 1 Tương tự ta cũng có 2 AM  4  x 2 1 1 Mà 2 2
BK BM BK
4  x (2), AH AM  4  x 3 2 2 1
Từ (1), (2), (3) suy ra Vxx x ABCD  2 4 ; 0;  1 24 1
Xét hàm số f x 2 
x 4  x , x  0; 
1 là hàm đồng biến nên 24 1 1
f x  f   1   V  8 ABCD 8
(Dấu bằng xẩy ra khi hai tam giác AC ,
D BCD là hai tam giác đều có cạnh bằng 1 và H , K 3
trùng với M . Khi đó AB   1 ) 2 Chọn B.
Câu 21: Khối tứ diện ABCD có AB x x  
1 và có tất cả các cạnh còn lại có độ dài không vượt
quá 1. Tính x khi thể tích của khối tứ diện đó lớn nhất. 2 3 6 3 2 2 6 A. x  . B. x  . C. x  . D. x  . 3 2 2 3 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 22
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 20a x . x 2 2 IK.CD x 20 2 a x CH    . ID a 5 2a 5
Thể tích khối tứ diện lớn nhất khi CH lớn nhất. 2 2 2
x  20a x 2 2 2
x 20a x
 10a CD a 5. 2 Đạt được khi 2 2 2
x  20a x x a 10.
Câu 23: Cho khối tứ diện ABCD có AB x , tất cả các cạnh còn lại bằng nhau và bằng 2  x . Hỏi 2
có bao nhiêu giá trị của x để khối tứ diện đã cho có thể tích bằng . 12 A. 1. B. 6 . C. 4 D. 2 . Hướng dẫn giải: Chọn D C
A CB CD  2  x  Ta có   2 2 2 2
CA CB AB x  1 cos ACB   1 , cos BCD   2 2C . A CB 2(2  x) 2  2 2 2 3 2 2 (2 x)  x    1   1   x   1   1  Vậy V  1 21   1            . 6 
22  x2  2  2   2    2 2  x    2   2    x 2  x 2 x  6x  6 2 x  1     . 6 2 12 x  0, 275842 
Câu 24: Xét khối tứ diện ABCD có AB x và các cạnh còn lại đều bằng 2 3 . Tìm x để thể tích
khối tứ diện ABCD đạt giá trị lớn nhất. A. x  6 . B. x  14 . C. x  3 2 . D. x  3 3 . Hướng dẫn giải: Chọn D.
Gọi E là trung điểm của AB , ta có các tam giác
CAB, DAB lần lượt cân tại C, D nên
CE AB, DE AB AB   ECD . Suy ra 1 VA . B S ABCD 3 CDE 2 x Ta có 2 2 CE DE
AD AE  12  4
Gọi F là trung điểm của CD , ta có EF CD và 2 2 x 12 x 2 1 x 2 2 FE
DE DF  12    9  , Suy ra S
FE.CD  3. 9  4 4 4 CDE 2 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 24
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 2 3 x 3
3  x  36  x  Khi đó 2 V x 9   x 36  x   3 3   . 3 4 6 6 2  
Câu 25: Cho khối chóp S.ABC có SA a , SB a 2 , SC a 3 . Thể tích lớn nhất của khối chóp là 3 a 6 3 a 6 3 a 6 A. 3 a 6 . B. . C. . D. . 2 3 6 Chọn D. 1
Gọi H là hình chiếu của A lên (SBC)  V AH .S . 3 SBC
Ta có AH SA ; dấu “=” xảy ra khi AS  SBC  . 1  1 S  .
SB SC.sin SBC  .
SB SC , dấu “=” xảy ra khi SBC 2 2 A SB SC . Khi đó, 1 1 1 1 V AH .SAS SB SC
SA SB SC . a 3 SBC 3 2 6
Dấu “=” xảy ra khi S ,
A SB, SC đôi một vuông góc với a 3 nhau. S C H
Suy ra thể tích lớn nhất của khối chóp là 3 1 a 6 V S . A S . B SC  . a 2 6 6 B
Câu 26: Cho khối chóp S.ABC có SA a , SB a 2 ,
SC a 3 . Thể tích lớn nhất của khối chóp là 3 a 6 3 a 6 3 a 6 A. 3 a 6 . B. . C. . D. . 2 3 6
Hướng dẫn giải: : A
Gọi H là hình chiếu của A lên 1 (SBC)  V AH .S . 3 SBC
Ta có AH SA ; dấu “=” xảy ra khi AS  SBC  . a 1  1 S  .
SB SC.sin SBC  .
SB SC , dấu “=” xảy ra SBC a 3 2 2 C khi SB SC . S H Khi đó, 1 1 1 1 a 2 V AH .SAS SB SC
SA SB SC . 3 SBC 3 2 6 B
Dấu “=” xảy ra khi S ,
A SB, SC đôi một vuông góc với
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 25
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao nhau. 3 1 a 6
Suy ra thể tích lớn nhất của khối chóp là V S . A S . B SC  . 6 6 Chọn D.
Câu 27: Cho hình chóp S.ABC có SA SB SC  1 . Tìm thể tích lớn nhất của khối chóp S.ABC . 1 1 1 1 A. . B. . C. . D. . 3 6 4 12 Hướng dẫn giải: Chọn B .
Gọi H là hình chiếu của A lên mặt phẳng SBC . Ta có 1 1  1
V  .AH .S  .AH. .
SB SC.sin BSC  .AS. . SB SC  3 SBC 6 6 . Dấu “=” xảy ra khi và chỉ khi  AH AS  
AS  SBC     
SA SB, SB SC, SC SA s  in BSC  1 SB SC   .
Câu 28: Cho hình chóp S.ABC có SA SB SC  2 , đáy ABC là tam giác vuông tại A , AB  1.
Tìm thể tích lớn nhất của khối chóp S.ABC . 5 5 2 4 A. . B. . C. . D. . 8 4 3 3 Hướng dẫn giải: Chọn A
Gọi H là hình chiếu của S lên  ABC  . Khi đó H là tâm
đường tròn ngoại tiếp A
BC . Hay H là trung điểm BC . 2 15  x
Đặt AC x . Khi đó 2 BC x 1 , SH  . 2 2 1 1 1 15  x
V  .SH.S  .SH .A . B AC  . .x 3 ABC 6 6 2 Ta có: .  2 2 15 1
x x  5  .  12 2 8 15
Dấu “=” xảy ra khi và chỉ khi 2 2
15  x x x  . 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 26
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 29: Cho hình chóp S.ABC có SA SB SC BA BC  1. Tìm thể tích lớn nhất của khối chóp S.ABC ? 1 2 1 3 A. . B. . C. . D. . 6 12 8 12 Hướng dẫn giải: Chọn C Cách 1:
Gọi H là hình chiếu của S lên  ABC  . Khi đó H là tâm đường tròn ngoại tiếp ABC . Vì A
BC cân tại B nên H thuộc đường trung trực BM của AC .
Đặt AC x . Ta có: 2 2 1 1 x x 4  x S  .BM .AC  . . x 1  và ABC 2 2 4 4 abc 1 R   . 2 4SABC 4  x
Mặt khác chiều cao của khối chóp: 2 3  x 2 2 2 2 SH SB BH SB R  . 2 4  x
Thể tích khối chóp: 2 x    2 2 2 3 1 1 3 4  x x x x  1
V  .SH.S  . .   ABC 2 3 3 4  x 4 12 8 . 3
Dấu “=” xảy ra khi và chỉ khi 2 2
x  3  x x . 2 Cách 2:
Gọi K, I lần lượt là hình chiếu của C lên  SAB và SB . 1 1 1 3 3 1
Thể tích khối chóp: V  .CK.S  .CI.S . .  . 3 SAB 3 SAB 3 2 4 8
Dấu “=” xảy ra khi và chỉ khi hình chiếu của C lên  SAB trùng trung điểm SB .
Câu 30: Trong các khối tứ diện ABCD có tam giác ABC đều cạnh 2a và tam giác ABD vuông tại a D , AD
. Khoảng cách lớn nhất từ B đến mặt phẳng  ACD là? 2 2a 2 a 3 A. . B. a 3 . C. . D. 2a 3 . 3 3 Hướng dẫn giải: Chọn Ba
AB AC  2a, AD    2 Ta có    1  1  cos BAC  , cos DAB  , cos CAD x   2 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 27
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Khi đó a 2 . a 2 . a 3 2 1 1 1 1 a 16  x  4x 11 2 2 V  1 
x  2. . .x  6 4 16 2 4 12 . Khi đó 2 3V a 1
 6x  4x 11  1  d   f x   fa . B   3 2   S 2 1 x  2  ACD
Câu 31: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C , cạnh bên SA vuông góc
với mặt phẳng đáy  ABC  . Biết SC  1, tìm thể tích lớn nhất của khối chóp S.ABC . 3 2 2 3 3 A. . B. . C. . D. . 12 12 27 27 Hướng dẫn giải: Chọn D Đặt 2 2 2
AC x SA
SC AC  1 x và 2 1 x 2 SCA  . ABC 2 2 2 2 x .x  2 2 2  2 1 1 x x  2 V S .SA  . 1 x  3 ABC 3 2 6 2 Vì vậy 3 2 2 2
x x  2  2x    2   3   6 2 27 2 Dấu bằng xảy ra khi 2 2
x  2  2x x  . 3
Câu 32: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , AB  2 . Cạnh bên SA  1 và
vuông góc với mặt phẳng đáy. Thể tích lớn nhất của khối chóp S.ABC là? 1 1 1 1 A. . B. . C. . D. . 3 4 12 6 Hướng dẫn giải: Chọn A 2 C . A CB x 4  x
Đặt CA x , 2 2 2 CB AB CA  4  x S   . ABC 2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 28
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 xx x  2 1 4 4  x  2 2 x  4  x 1 Suy ra V  . SA S     3 ABC 6 6 2.6 3 Dấu bằng đạt tại 2 2
x  4  x x  2 .
Câu 33: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , SA AB  2a . Cạnh bên SA
vuông góc với mặt phẳng đáy  ABC  . Gọi H , K lần lượt là hình chiếu vuông góc của A
lên SB và SC . Tìm thể tích lớn nhất V
của khối chóp S.AHK . max 3 a 2 3 a 3 3 a 3 3 a 2 A. V  . B. V  . C. V  . D. V  . max 6 max 6 max 3 max 3 Hướng dẫn giải: Chọn A. Đặt AC x 2 2 2 2  BC AB AC  4a x S 1 1 Ta có V  . . SA BC.AC 2 2  .2 .
a x 4a x SABC 6 6 H 2 2
ax 4a x  3 K SH SK 2 2 2 1 SA
ax 4a x Vì vậy V  . V  . . S . AHK S . ABC A B SB SC 2 2 SC 3 3 2 2 3
2 a x 4a x a 2 3 a 2  .   V  . C 2 2 3 4a x 6 max 6
Câu 34: Cho tam giác ABC vuông cân tại B , AC  2 . Trên đường thẳng qua A vuông góc với mặt
phẳng  ABC  lấy điểm M , N khác phía với mặt phẳng  ABC  sao cho AM .AN  1. Tìm
thể tích nhỏ nhất của khối tứ diện MNBC .? 1 1 1 2 A. . B. . C. . D. . 3 6 12 3 Hướng dẫn giải: Chọn D.
Tam giác ABC vuông cân tại B ,
AC  2  AB BC  2 . Ta có 1 1 1 1 VAM AN SAM AN AB BC AM AN MNBC  . ABC  . . .   3 3 2 3
Sử dụng BĐT cauchy ta có 2
AM AN  2 AM .AN  2  V  . MNBC 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 29
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 35: Cho hình chóp tam giác đều S.ABC có SA  1 . Thể tích lớn nhất của khối chóp S.ABC là? 1 2 3 1 A. . B. . C. . D. . 6 12 12 12 Hướng dẫn giải: Chọn A.
Gọi O là tâm của tam giác đều ABC . Gọi R OA x 0  x   1 Ta tính được 2 2 SO
SA R  1 x
Cạnh của tam giác đều ABC là 1 3 3 0 2 0 2
a  2R sin 60  3x Sa sin 60  x ABC 2 4 1 3 2 2 VSO.Sx 1 x S . ABC 3 ABC 4 Vậy 3 3 4  x  2 1 x  4 6  x x 8 4
Cách 1: Dùng Cauchy: Có 1 1 1 4 1 2 2 2 4 1  x
x 1 x  3 x  2 1 x  4  x  2 3 1 x    V  . S . 2 2 4 27 ABC 6 3
Cách 2: Dùng hàm f x 4 6
x x  0  x  
1  f  x 3 5
 4x  6x ; f  x  0  x  . 2 3
Dùng bảng biế thiên thì f x đạt giá trị lớn nhất tại x  khi đó 2 4 1
max f x   VS. ABC 0x 1  27 6
Câu 36: Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân đỉnh C và SA vuông 
góc với mặt phẳng  ABC , SC a, SCA . Xác định góc để thể tích khối chóp SABC lớn nhất. 1 2
A.  arcsin
B.  arcsin 3 7 1 1
C.  arcsin
D.  3arcsin 5 3 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 30
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
BC AC a. os c ; SA  . a sin 1 1 1 3 2 VS .SA
.AC.BC.SA a sin . os c SABC 3 ABC 6 6 1 3  a sin  2 1 sin  6 Xét hàm số:   3
f x x x trên khoảng 0;  1 . 1
Ta có: f ' x 2
 1 3x , f ' x  0  x   . 3
Từ đó ta thấy trên khoảng 0; 
1 hàm số f x liên tục và có một điểm cực trị là điểm cực
đại, nên tại đó hàm số đạt GTLN hay:  1  2 1 
max f x  f    hay  arcsin ,  0     x   0;  1  3  3 3 3  2  Chọn A.
Câu 37: Cho hình chóp S.ABCD có SA x, các cạnh còn lại bằng 2. Tìm giá trị của x để thể tích
khối chóp lớn nhất A. 6 B. 2 C. 7 D. 2 6 Hướng dẫn giải:
Gọi O là giao điểm của AC và B . D Ta có OD=OB và SB=SD nên
SO BD , do đó BO   SAC  . Mặt khác 2 2 2 2 2 2
SO SB OB AB OB OA
nên SO OA OC . Do đó tam giác SAC vuông tại S. Ta có 2 2 2 2
AC x  4  4OA x  4 . Do đó 2 2
4OB  12  x  0  x  2 3 . Và 2 2 Sx  2 2 OA x  2 16 4  4x . SOA Để V
đạt giá trị lớn nhất khi và chỉ khi V
đạt giá trị lớn nhất. S . ABCD SOAB Do đó V
đạt giá trị lớn nhất khi và chỉ khi 2 x  2
12  x  đạt giá trị lớn nhất. S . ABCD Suy ra 2 2 2
x  12  x x  6  x  6 .
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD  . Kí hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  45 . Thể tích nhỏ nhất của khối chóp S.AMN là? 2 1 2 1 2 1 2 1 A. . B. . C. . D. . 9 3 6 9
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 31
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Hướng dẫn giải: Chọn B
Đặt DM x , BN y ta có        1 x   DAM BAN  tan DAM tan BAN x y tan 45 tan     . Suy ra y  .
1 tan DAM .tan BAN 1 xy 1 x và 2 2 2 AM AD DM x 1 , 2  1 x  2 2 x   1 2 2 2 AN
AB BN  1 y    1  .  1 x x 1 2 1 1 x 1 2 1 Vì vậy V  . SA S  .
SA AM .AN sin 45  f x   f  2   1  . 3 AMN 6 6 x   1 3
Câu 39: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD . Ký hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  60 . Thể tích nhỏ nhất của khối chóp S.AMN là 2  3 2  3 2 3  3 2 3  3 A. . B. . C. . D. . 3 9 3 9 Hướng dẫn giải: Chọn C Đặt DM  ,
x BN y . Ta có:        1 3x   DAM BAN  tan DAM tan BAN x y tan 60 tan      y  .
1 tan DAM .tan BAN 1 xy 3  x 2  1 3x  2 2 2 AM AD DM x 1 , 2 2 2 AN AB BN y  1    1 .  3 x     3  2 x   1 1 1 Vì vậy V  .S . A S  .S .
A AM .SN.sin 60  . S . AMN 3 AMN 6 6 3  x  2 3 x   1 2 3  3
Ta có f x   f 2  3  . 6  3  x 3
Câu 40: Cho hình chóp S.ABC có SA , SB , SC đôi một vuông góc, I là tâm nội tiếp tam giác ABC
. Mặt phẳng  P thay đổi qua I , cắt các tia SA , SB , SC lần lượt tại A , B ,C . Biết SA SB
2 , SC  7 . Hỏi thể tích của khối chóp S.A BC
  có giá trị nhỏ nhất là? 243 7 7 81 7 27 7 A. . B. . C. . D. . 256 3 256 256 Hướng dẫn giải: Chọn A
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 32
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao · Ta có
SASBSCV  . . .V S . A BC   S. ABC SA SB SC
· Ta có SA SB  2, SC  7 1 1  V  . SA . SB SC  7 S. ACB 6 3
· Từ SA SB
2, SC  7  AB  2, BC  3  AC
· Do I là tâm đường tròn nội tiếp tam giác ABC nên:   
BC.IA C . A IB A . B IC  0       
BC SA SI   C .
A SB SI   A .
B SC SI   0  BC  CA  AB   SI SA SB SC
AB BC CA
AB BC CA
AB BC CA BC SA  CA SB  AB SC   . .SA  . SB  . SC .
AB BC CA SA
AB BC CA SB
AB BC CA SC · Do bốn điểm A ,
B ,C , I đồng phẳng nên BC SA CA SB AB SC .  .  .  1
AB BC CA SA
AB BC CA SB
AB BC CA SC
· Sử dụng bất đẳng thức AM-GM ta có BC SA CA SB AB SC 1  .  .  .
AB BC CA SA
AB BC CA SB
AB BC CA SCA . B BC.CA SA SB SC  33 . . .
AB BC CA3 SASBSC   A . B BC.CA SA SB SC
SASBSC 27.A . B BC.CA 3  1  3 . . .  . . 
AB BC CA3 SASBSC   SA SB SC
AB BC CA3
SASBSC 27.A . B BC.CA 27.2.3.3 1 81 7 · V  . . VV  . 7  S . A BC   S. ABC SA SB SC
AB BC CA3 S.ABC 2  3  33 3 256 Dấu bằng xảy ra  BC SA CA SB AB SC .  .  .  1 
AB BC CA SA
AB BC CA SB
AB BC CA SC   BC SA CA SB AB SC  .  .  . 
AB BC CA SA
AB BC CA SB
AB BC CA SC
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 33
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao SB SA 8  9  
SA  SB  2
SBSA 9    8     . SC 4 3    SC  7   SC 3   4
Câu 41: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AD  4 , các cạnh bên bằng
nhau và bằng 6 . Tìm thể tích lớn nhất của khối chóp S.ABCD 130 128 125 250 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải: Chọn B
Đặt AB x và O là tâm của mặt đáy, ta có 2 2 2 x  4 x
SO   ABCD và 2 SO  6   32  . 4 4
Vì vậy sử dụng bất đẳng thức AM GM , ta co có: 2 2 2 1 x 2 2 x 128  x 128 V  4x 2 . 32   x  2 128  x   .  3 4 3 3 2 3 .
Câu 42: Cho hình chóp S.ABCD có SB x 0  x  3 . Tất cả các cạnh còn lại bằng nhau và
bằng 1. Với giá trị nào của x thì thể tích khối chóp S.ABCD lớn nhất? 3 2 6 3 A. x  . B. x  . C. x  . D. x  . 3 2 2 2 Hướng dẫn giải: Chọn C
Theo giả thiết ABCD là hình thoi và gọi O AC BD . S
AC  BAC c c c  OS OB OD SBD vuông tại S .
Vì SA SC SD  chân đường cao H của khối chóp nằm trên đường thẳng BD và S . B SD x SH   2 2 2 SB SD x 1 Ta có 2 2 2 2 BD
x 1, AC  2OA  2 AB OB  3  x . 1 1 Vì vậy 2 2 SAC.BD  3  x x 1 . ABCD 2 2 2 x   2 2  x x x  2 2 3 3 x  3  x 1 Suy ra V     . 6 6 2.6 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 34
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 6 Dấu bằng xảy ra khi 2 2
x  3  x x  . 2
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  4 . Cạnh bên SA vuông
góc với mặt phẳng đáy  ABCD  và SC  6 . Thể tích lớn nhất của khối chóp S.ABCD là? 40 80 20 A. . B. . C. . D. 24. 3 3 3 Hướng dẫn giải: Chọn A. Đặt AD=x , ta có 2 2 2 AC AB AD x  16 và 2 2 2 2 2 SA
SC AC  6  x 16  20  x . 2 1 1 4 x  2 20  x   2 2
2 x  20  x  40 Vì vậy 2 V  . SA S  20  x .4x    3 ABCD 3 3 3 3 Dấu bằng xảy ra khi 2 2
x  20  x x  10
Câu 44: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , cạnh bằng 1, SO   ABCD và
SC  1. Thể tích lớn nhất của khối chóp S.ABCD là? 2 3 2 3 2 3 4 3 A. B. . C. . D. . 9 3 27 27 Hướng dẫn giải: Chọn D
Đặt OC x  2 2 2 OB
BC OC  1 x  2 S  4S  2x 1 x ABCD OBC và 2 2 2 SO
SC OC  1 x vì vậy x  2 1 2 1 x  2 x  2  x   2 2 2 1 1 x V S .SO  = 3 ABCD 3 3 3 2 2 2 2
 2x 1 x 1 x  4 3     . 3  3  27 1 Dấu bằng xảy ra khi 2 2
2x  1 x x  . 3
Câu 45: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD  . Kí hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  45 . Thể tích nhỏ nhất của khối chóp S.AMN là? 2 1 2 1 2 1 2 1 A. . B. . C. . D. . 9 3 6 9 Hướng dẫn giải: Chọn B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 35
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Đặt DM x , BN y ta có        1 x   DAM BAN  tan DAM tan BAN x y tan 45 tan     . Suy ra y  .
1 tan DAM .tan BAN 1 xy 1 x và 2 2 2 AM AD DM x 1 , 2  1 x  2 2 x   1 2 2 2 AN
AB BN  1 y    1  .  1 x x 1 2 1 1 x 1 2 1 Vì vậy V  . SA S  .
SA AM .AN sin 45  f x   f  2   1  . 3 AMN 6 6 x   1 3
Câu 46: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD . Ký hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  30 . Thể tích nhỏ nhất của khối chóp S.AMN là? 1 1 2 4 A. . B. . C. . D. . 9 3 27 27 Hướng dẫn giải: Chọn A Đặt DM  ,
x BN y . Ta có:        3  x   DAM BAN  tan DAM tan BAN x y tan 30 tan      y  .
1 tan DAM .tan BAN 1 xy 1 3x 2  3  x  2 2 2 AM AD DM x 1 , 2 2 2 AN AB BN y  1    1 .  1 3x     2 1 1 x 1 Vì vậy V  . . SA S  . .
SA AM .SN.sin 30  . S . AMN 3 AMN 6 6 3x   1 2 x 1  1  1
Ta có f x   f    . 6  3x   1  3  9
Câu 47: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB  1, cạnh bên SA  1 và vuông
góc với mặt phẳng đáy  ABCD . Ký hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạ 
n CB sao cho MAN  60 . Thể tích nhỏ nhất của khối chóp S.AMN là 2  3 2  3 2 3  3 2 3  3 A. . B. . C. . D. . 3 9 3 9 Hướng dẫn giải: Chọn C Đặt DM  ,
x BN y . Ta có:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 36
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao        1 3x   DAM BAN  tan DAM tan BAN x y tan 60 tan      y  .
1 tan DAM .tan BAN 1 xy 3  x 2  1 3x  2 2 2 AM AD DM x 1 , 2 2 2 AN AB BN y  1    1 .  3 x     3  2 x   1 1 1 Vì vậy V  .S . A S  .S .
A AM .SN.sin 60  . S . AMN 3 AMN 6 6 3  x  2 3 x   1 2 3  3
Ta có f x   f 2  3  . 6  3  x 3
Câu 48: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với AD  4a . Các cạnh bên của
hình chóp bằng nhau và bằng a 6 . Tìm thể tích V
của khối chóp S.ABCD . max 3 8a 3 4 6a A. V  . B. V  . C. 3 V  8a . D. 3 V  4 6a . max 3 max 3 max max Hướng dẫn giải: Chọn A
Do SA SB SC SD a 6 nên hình chiếu vuông góc của S lên mặt phẳng  ABCD
trùng với tâm đường tròn ngoại tiếp đáy, do vậy ABCD là một hình chữ nhật và H là giao
điểm của AC và BD .
Đặt AB x  0 ta có: 2 AC 1 2 2 2 2 AC AD AB x 16a , 2 2 2 SH SA   8a x . 4 2 2 2 1
2ax 8a x
Vì vậy S.ABCD  . . SO A . B AD  . 3 3
Sử dụng bất đẳng thức AM – GM ta có: 2 2 2 3 3
x  8a x 8a 8a 2 2 2
x 8a x   4a V   V  . max 2 3 3
Câu 49: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và thể tích bằng V . Gọi M , N AB AD
lần lượt là các điểm di động trên các cạnh AB và AD sao cho  2  4 . Gọi V ' là AM AN
thể tích khối chóp S.MBCDN . Tìm giá trị nhỏ nhất của V ' . 1 2 3 1 A. V . B. V . C. V . D. V . 4 3 4 3 Hướng dẫn giải: Chọn B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 37
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao  1 AM AN   xy  Ta có V '  1 . . V    1 V   S  2 AB AD   2   AM AN x  , y  0<x, y<1   AB AD Trong đó 1 2    4  x y DA N 2x  1  My   x  1   4x 1  4  B C 2  x  2 2 Vì vậy ' V  1 V V   V'  V . 4x 1 3 min   3
Câu 50: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Các điểm A ',C ' thỏa mãn
 1   1  SA '  SA , SC ' 
SC . Mặt phẳng  P chứa đường thẳng A'C ' cắt các cạnh SB, SD lần 3 5 V
lượt tại B ', D ' và đặt
S. A' B 'C ' D ' k
. Giá trị nhỏ nhất của k là? VS.ABCD 1 1 3 15 A. . B. . C. V . D. . 60 30 4 16 Hướng dẫn giải: Chọn A. SB SD SA SC S Đặt V V , ta có    S. ABCD SB' SD' SA' SC'  3  5  8 A' D' V SA' ' SB SC' 1
Mặt khác S.A'B'C '  . .  x B' 1 SA SB SC 15 D V A C' 2 1  VxV B
S. A' B 'C ' C 30 V ' SA ' SD ' SC 1 1 1
S . A'C ' D '  . .  y VyV VxV
S. A'C ' D ' 1 SA SD SC 15 30
S. A' B 'C ' 30 V 2 V 1 SB' ' SD Do đó
S. A' B 'C ' D ' k  
x y , trong đó x  , y V 30 SB SD S. ABCD  1 1  4 1 1
Và  x y   4    x y    k  . x y   8 2 60
Câu 51: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh ,
a SA vuông góc với mặt phẳng
đáy và góc giữa SC với mặt phẳng  SAB bằng 0
30 . Gọi M là điểm di động trên cạnh CD
và H là hình chiếu vuông góc của S trên đường thẳng BM. Khi điểm M di động trên cạnh
CD thì thể tích của khối chóp SABH đạt giá trị lớn nhất bằng:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 38
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 3 a 2 3 a 2 3 a 2 3 a 2 A. B. C. D. 3 2 6 12 Hướng dẫn giải:
Ta có góc giữa SC và mặt phẳng  SAB là 0 CSB  30 Trong tam giác SBC có 0
SB BC.cot 30  a 3 Trong tam giác SAB có 2 2 SA
SB AB a 2 1 1 1 a 2
Thể tích khối chóp S.ABH là: VS SA  . H . A H . B a 2  H . A HB S . ABH 3 ABH 3 2 6 Ta có 2 2 2 2
HA HB AB a và theo bất đẳng thức AM GM ta có: 2 a 2 2 2
a HA HB  2H . A HB H . A HB  2 Đẳ  ng thức xảy ra khi 0
HA HB ABM  45  M D 2 3 a 2 a 2 a a 2 Khi đó VH . A HB  .  S . ABH 6 6 2 12 Chọn D.
Câu 52: Cho hình chóp tứ giác S.ABCD có SA SB SC  2a . Tìm thể tích lớn nhất của khối chóp S.ABCD . 3 2 6a 3 32 3a 3 4 6a 3 32 3a A. . B. . C. . D. . 3 9 9 27 Hướng dẫn giải: Chọn D
Ta có: SA SB SC SD ABCD nội tiếp đường tròn bán kính R . Ta có: 2 2 2 2
h cb R  4a R và  
 2R sin ABC 
2Rsin BADsinAC, . sin , DB AC BD AC BD  2 S    2R 2 2 2 2 2 3 Sh 2R 4a R  2 6a  32 3a V   f (R)   max
f (R)  f    (0;2a ) 3 3  3  27  
Câu 53: Khối chóp S.ABCD có đáy ABCD là hình thoi cạnh a . SA SB SC a , Cạnh SD thay
đổi. Thể tích lớn nhất của khối chóp S.ABCD là: 3 a 3 a 3 3a 3 a A. . B. . C. . D. . 8 4 8 2 Hướng dẫn giải: Chọn D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 39
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Khi SD thay đổi thi AC thay đổi. Đặt AC x . S
Gọi O AC BD .
Vì SA SB SC nên chân đường cao SH trùng
với tâm đường tròn ngoại tiếp tam giác ABC .  H BO . 2 2 2 2 2  x  4a x 4a x Ta có 2 OB a       2  4 2 A 2 2 2 2 B 1 1 4a x
x 4a x SO . B AC  . xABC 2 2 2 4 x O H a 2 2 . a . a x a x a HB R    . 2 2 2 2 4SABC
x 4a x 4a x 4. D C 4 4 2 2 a
a 3a x 2 2 2 SH SB BH a   2 2 2 2 4a x 4a x 2 2 2 2 1
2 a 3a x
x 4a x V  2V  2. SH .S  . . S . ABCD S. ABC ABC 2 2 3 3 4 4a x 2 2 2 3 1      a  1 x 3a x a 2 2 .
x 3a x   a    3 3 2 2  
Câu 54: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a SA vuông góc với mặt phẳng
đáy và góc giữa SC với mặt phẳng  SAB bằng 0
30 . Gọi M là điểm di động trên cạnh CD
và H là hình chiếu vuông góc của S trên đường thẳng BM . Khi điểm M di động trên
cạnh CD thì thể tích của khối chóp S.ABH đạt giá trị lớn nhất bằng: 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 6 3 2 12 Hướng dẫn giải: Chọn D S  
Góc giữa SC và  SBC  là 0
CSB CSB  30 Ta có  BC 2 2 tan CSB
SB a 3; SA
SB AB a 2 SB A
Đặt CM x, 0  x a  DM a x, DBM SH Ta có H
BM   SAH   BM AH M BM SAB C Ta có 2 1 1 1 1 a SBC.CM a , x SA . D DM
a. a x SSSSBMC ADM  ; 2 2 2 2 ABM ABCD AMC ADM 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 40
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 1 a ax Ta có S
AH .BM AH  ; 2 2 BH AB AH ABM 2 2 2 a x 2 2 a x
Thể tích của khối chóp S.ABH là 2 1 1 1 1 a ax 2 x 4 V  . SA S  . SA BH .AH a 2. .  a . (*) ABH 2 2 2 2 2 2 3 3 2 6 6 a x a x a x x
Xét hàm số f x  , x  0; a 2 2   a x 2 2 a x
Ta có f  x 
; f x  0  x a 2    2 2 a x
Trên đoạn 0; a ta có f  x  0, x  0;a 2
Vậy giá trị lớn nhất của V tại x a 3  Va mzx 12 3 2 x 2 1 2a Cách 2: Từ (*) 4 4 V a .  a . 
. Dấu  khi: x a . 2 2 6 a x 6 2a 12
Cách 3: Dễ thấy H nhìn AB dưới góc vuông nên V lớn nhất khi S lớn nhất khi và S . ABH ABH
chỉ khi H O (tâm của hình vuông )  x a . Từ đó có kết quả.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 41
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
THỂ TÍCH KHỐI LĂNG TRỤ A- LÝ THUYẾT CHUNG
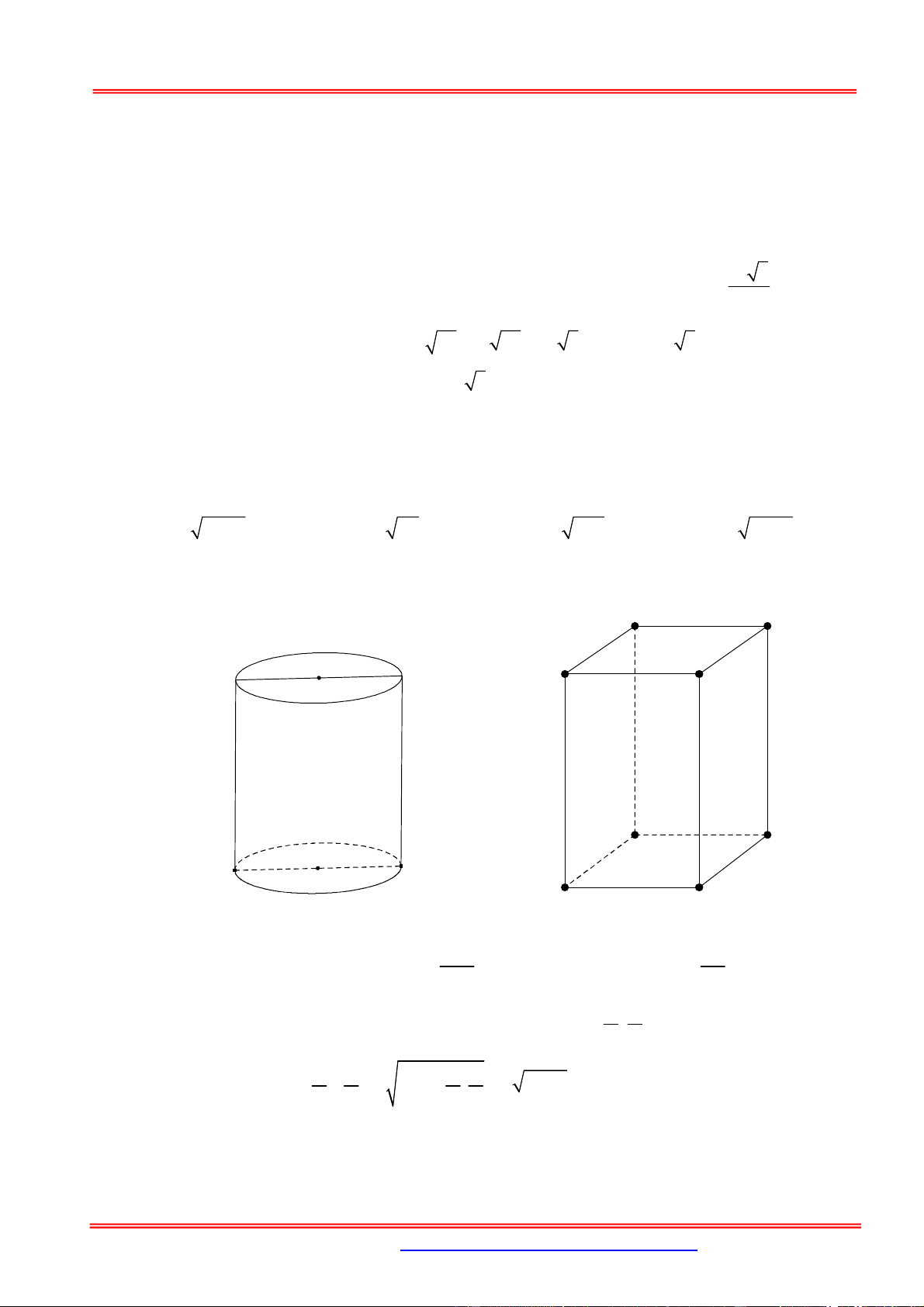
1. Thể tích khối lăng trụ V  .
B h với B diện tích đáy, h là chiều cao lăng trụ. h B
2. Thể tích khối hộp chữ nhật V a. . b c với , a ,
b c là ba kích thước. a c b
3. Thể tích khối lập phương 3
V a với a là độ dài cạnh. a a a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 42
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
B – BÀI TẬP TRẮC NGHIỆM
Câu 1: Cho lăng trụ đứng ABCA BC
  có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa mặt phẳng ( AB C
 ) và mặt phẳng (BB C  ) bằng 0
60 .Tính thể tích lăng trụ ABCA BC   . A. 3 a 2 B. 3 2a C. 3 a 6 D. 3 3a
Câu 2: Cho khối lăng trụ tam giác ABC. ’ A ’
B C’. Gọi M , N lần lượt thuộc các cạnh bên A ’ A ,C ’ C
sao cho MA MA ' và NC  4NC ' . Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ diện G ’ A ’ B ’ C , B ’ B MN , AB ’ B C’ và ’
A BCN, khối tứ diện nào có thể tích nhỏ nhất? A. Khối ’ A BCN B. Khối G ’ A ’ B C’ C. Khối AB ’ B ’ C D. Khối B ’ B MN
Câu 3: Cho lăng trụ tam giác ABC.A' B 'C ' có BB '  a , góc giữa đường thẳng BB ' và  ABC  bằng 
60 , tam giác ABC vuông tại C và góc BAC  60 . Hình chiếu vuông góc của điểm
B ' lên  ABC  trùng với trọng tâm của A
BC . Thể tích của khối tứ diện A '.ABC theo a bằng 3 13a 3 7a 3 15a 3 9a A. . B. . C. . D. . 108 106 108 208
Câu 4: Cho hình lăng trụ đứng ABC.A' B 'C ' , biết đáy ABC là tam giác đều cạnh a . Khoảng cách a
từ tâm O của tam giác ABC đến mặt phẳng  A' BC  bằng .Tính thể tích khối lăng trụ 6
ABC.A ' B 'C ' . 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. . 8 28 4 16
Câu 5: Cho hình lăng trụ có tất cả các cạnh đều bằng a , đáy là lục giác đều, góc tạo bởi cạnh bên
và mặt đáy là 60 . Tính thể tích khối lăng trụ 27 3 3 9 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 a . 8 4 2 4
Câu 6: Cho lăng trụ ABC.A' B 'C ' có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của điểm
A ' lên mặt phẳng  ABC  trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai a 3
đường thẳng AA ' và BC bằng
. Khi đó thể tích của khối lăng trụ là: 4 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 6 3 24
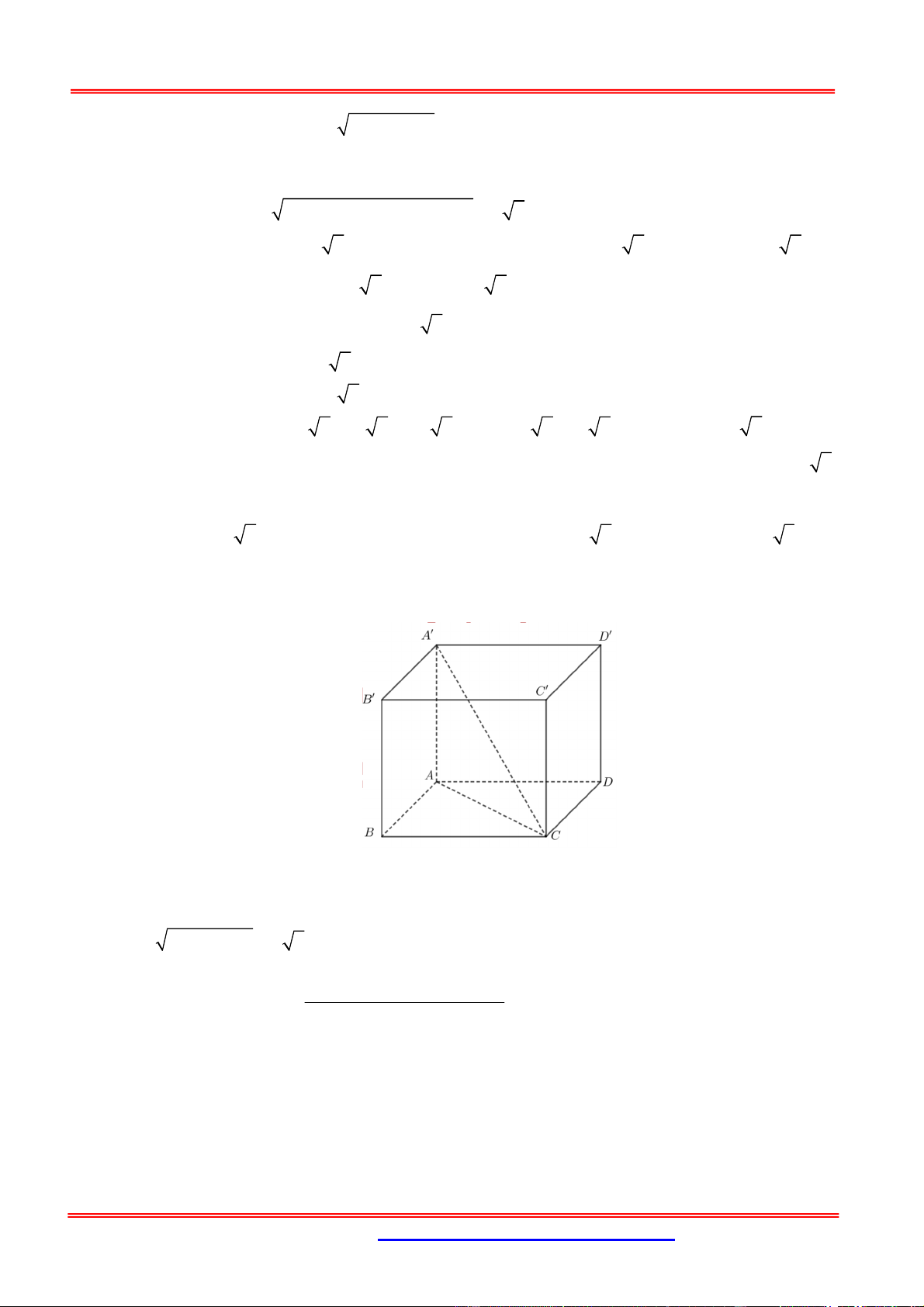
Câu 7: Cho hình lập phương ABC . D AB CD
  có cạnh bằng a , một mặt phẳng  cắt các cạnh 1 2
AA , BB , CC , DD lần lượt tại M , N , P , Q . Biết AM a , CP a . Thể tích khối 3 5 đa diện ABC . D MNPQ là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 43
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 11 3 a 3 2a 11 A. 3 a . B. . C. . D. 3 a . 30 3 3 15
Câu 8: Cho khối hộp ABC .
D A ' B 'C ' D ' có cạnh bên bằng 1.; đáy ABCD là một hình chữ nhật có
các cạnh BA  3, AD  7; các mặt bên  ABB ' A' và  ADD ' A' hợp với mặt đáy các góc theo thứ tự 0 0
45 ; 60 . Thể tích khối hộp là: A. 4 (đvdt) B. 3 (đvdt) C. 2 (đvdt) D. 6 (đvdt)
Câu 9: Cho khối hộp ABC .
D A ' B 'C ' D ' có độ dài cạnh bên bằng a; đáy là hình thoi, diện tích của
hai mặt chéo là S và S ; góc giữa hai mặt phẳng chứa hai mặt chéo là . Tính thể tích V 1 2 của khối hộp đã cho. S S cos S S cos S S cos S S cos A. 1 2 V B. 1 2 V  . C. 1 2 V D. 1 2 V a 3a 4a 2a
Câu 10: Cho khối hộp ABC .
D A ' B 'C ' D ' có tất cả các cạnh bên bằng a và các góc
A ' AB, BD ,
A A' AD đều bằng  0 0
0   90 . Tính thể tích V của khối hộp. a a A. 3 2 2
V a sin 2cos  os c arcsin B. 3 2 2
V  2a sin cos  os c 2 2 a C. 3 2 2 V  2a sin cos  os c D. Đáp số khác. 2 2 Câu 11:
Cho khối hộp đứng ABC .
D A ' B 'C ' D ' có AB a, AD b, BAD ; đường chéo AC ' hợp
với đáy góc . Tính thể tích khối hộp đứng đã cho là: A. 2 2
V  4ab a b  2a . b o c s. o
c s.cos B. 2 2
V  2ab a b  2a . b o c s. o
c s.cos C. 2 2
V  3ab a b  2a . b o
c s.sin .tan D. 2 2
V ab a b  2a . b o
c s.sin .tan
CỰC TRỊ THỂ TÍCH KHỐI LĂNG TRỤ
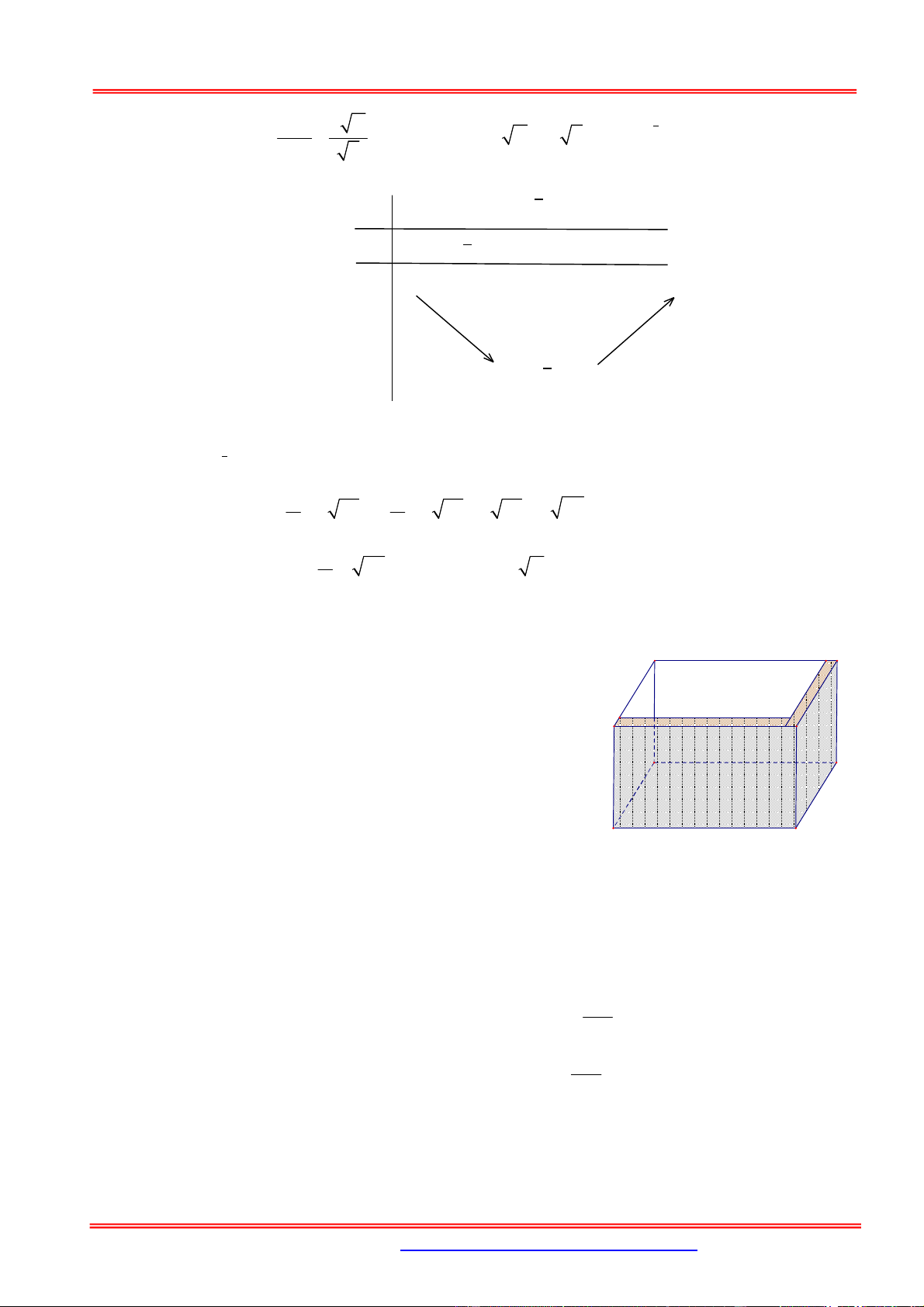
Câu 12: Cho hình hộp chữ nhật ABC . D AB CD
  có tồng diện tích của tất cả các mặt là 36 , độ dài
đường chéo AC bằng 6 . Hỏi thể tích của khối hộp lớn nhất là bao nhiêu? A. 8 . B. 8 2 . C. 16 2 . D. 24 3 .
Câu 13: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng 36 và độ dài đường chéo bằng 6 .
Tìm thể tích lớn nhất V
của hình hộp chữ nhật đã cho? max A. V  8 . B. V  12 . C. V  8 2 . D. V  6 6 . max max max max
Câu 14: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng 2 6
. Tìm thể tích lớn nhất V của hình hộp đã cho. max A. V  16 2 . B. V  16 . C. V  6 6 . D. V  12 3 . max max max max
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 44
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Câu 15: Tìm m
V ax là giá trị lớn nhất của thể tích các khối hộp chữ nhật có đường chéo bằng 3 2cm
và diện tích toàn phần bằng 2 18cm . A. 3 V  6cm . B. 3 V  5cm . C. 3 V  4cm . D. 3 V  3cm . max max max max
Câu 16: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng 36 và độ dài đường chéo bằng 6 .
Tìm thể tích lớn nhất V
của hình hộp chữ nhật đã cho? max A. V  8 . B. V  12 . C. V  8 2 . D. V  6 6 . max max max max
Câu 17: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng 2 6
. Tìm thể tích lớn nhất V của hình hộp đã cho. max A. V  16 2 . B. V  16 . C. V  6 6 . D. V  12 3 . max max max max
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 45
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
C – HƯỚNG DẪN GIẢI
Câu 1: Cho lăng trụ đứng ABCA BC
  có đáy là tam giác ABC vuông cân tại A, BC=2a. Góc giữa mặt phẳng ( AB C
 ) và mặt phẳng (BB C  ) bằng 0
60 .Tính thể tích lăng trụ ABCA BC   . A. 3 a 2 B. 3 2a C. 3 a 6 D. 3 3a Hướng dẫn giải:
Từ A kẻ AI BCI là trung điểm A' BC C' AI  (BC C B
  )  AI BC (1) B'
Từ I kẻ IM B C (2) B' H
Từ (1), (2)  BC  (IAM) M
Vậy góc giữa (A BC) và ( BCB) là MB C 600 AMI = 600 I A C 1 Ta có AI=
BC a ; IM= I 2 B AI a  0 tan 60 3 2a 1 1 1 3 1 1 BH  2IM  ;      . 3 2 2 2 2 2 2 B ' B BH BC 4a 4a 2a 1 1
Suy ra BB = a 2 ; 2 SAI.BC  .
a 2a aABC 2 2 2 3 V
a 2.a a 2 ABC AB C   Chọn A.
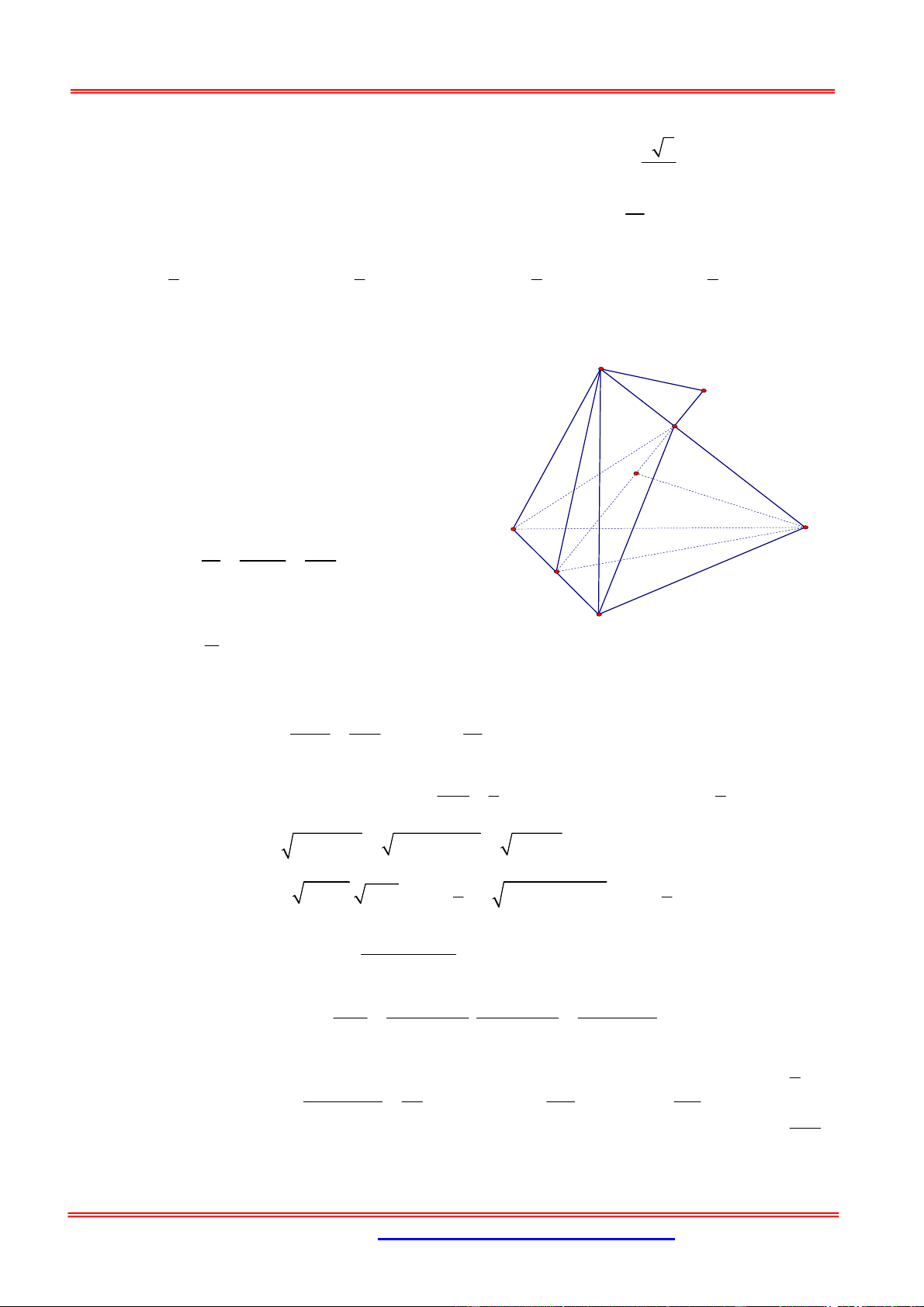
Câu 2: Cho khối lăng trụ tam giác ABC. ’ A ’
B C’. Gọi M , N lần lượt thuộc các cạnh bên A ’ A ,C ’ C
sao cho MA MA ' và NC  4NC ' . Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ diện G ’ A ’ B ’ C , B ’ B MN , AB ’ B C’ và ’
A BCN, khối tứ diện nào có thể tích nhỏ nhất? A. Khối ’ A BCN B. Khối G ’ A ’ B C’ C. Khối AB ’ B ’ C D. Khối B ’ B MN Hướng dẫn giải: C A
+ Nhận thấy khoảng cách từ G và A xuống mặt phẳng G  ’ A ’ B ’
C  là bằng nhau ( do G,A thuộc mặt phẳng BABC / /  ’ A ’ B ’ C N M VV
GA' B 'C '
A. A' B 'C ' Mà VV
(Do 2 hình chóp này có 2 đáy A ’ A ’ B và .
A A' B 'C ' ABB 'C ' C' AB ’
B diện tích bằng nhau;chung đường cao hạ từ C’) A'VV
GA' B 'C ' ABB 'C '
=> Không thế khối chóp G ’ A ’
B C’ hoặc AB ’ B ’ C thể thích nhỏ B'
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 46
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao nhất → Loại B,C + So sánh Khối ’
A BCN và Khối B ’ B MN
Nhận thấy khoảng cách từ M và A’ xuống mặt BBCC’ là bằng nhau → Khối ’ A BCN và Khối B ’
B MN có đường cao hạ từ M và A’ bằng nhau. Mặt khác Diện tích đáy BN ’ B > Diện tích đáy BCN => Khối ’
A BCN < Khối B ’ B MN. => Khối ’
A BCN có diện tích nhỏ hơn. Chọn A.
Câu 3: Cho lăng trụ tam giác ABC.A' B 'C ' có BB '  a , góc giữa đường thẳng BB ' và  ABC  bằng 
60 , tam giác ABC vuông tại C và góc BAC  60 . Hình chiếu vuông góc của điểm
B ' lên  ABC  trùng với trọng tâm của A
BC . Thể tích của khối tứ diện A '.ABC theo a bằng 3 13a 3 7a 3 15a 3 9a A. . B. . C. . D. . 108 106 108 208 Hướng dẫn giải:
Gọi M , N là trung điểm của AB, AC B' C'
và G là trọng tâm của ABC .
B 'G   ABC   BB ABC      0 ',
B ' BG  60 . A' 1 1 V  .S .B 'G
.AC.BC.B 'G A'. ABC 3 ABC 6  Xét B  ' BG 0 B ' BG  60 60° vuông tại G , có B C a 3  B 'G  . (nửa tam giác đều) G 2 M N 60° A Đặt 
AB  2x . Trong ABC 0
vuông tại C có BAC  60 AB
 tam giác ABC là nữa tam giác đều  AC   ,
x BC x 3 2 3 3a
Do G là trọng tâm A
BC BN BG  . 2 4 Trong B
NC vuông tại C : 2 2 2
BN NC BC  3a AC  2 2 2  9a x 9a 3a  2 13 2 2    3x x   x    16 4 52 2 13 3a 3 BC    2 13
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 47
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 3 1 3a 3a 3 a 3 9a Vậy, V  . . .  . A' ABC 6 2 13 2 13 2 208
Câu 4: Cho hình lăng trụ đứng ABC.A' B 'C ' , biết đáy ABC là tam giác đều cạnh a . Khoảng cách a
từ tâm O của tam giác ABC đến mặt phẳng  A' BC  bằng .Tính thể tích khối lăng trụ 6
ABC.A ' B 'C ' . 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. . 8 28 4 16 Hướng dẫn giải: A' C'
Gọi M là trung điểm của BC ,
ta có  A' AM    A' BC  theo giao tuyến A' M .
Trong  A' AM  kẻ OH A ' M (H A' M ) .
OH   A' BC B' a
Suy ra: d O, A ' BC   OH  . 6 2 a 3 S  . AABC C 4 HO M
Xét hai tam giác vuông A ' AM và OHM có góc M
chung nên chúng đồng dạng. B a 1 a 3 . OH OM 1 3 Suy ra: 6 3 2      . 2 2 2 A ' A A' M A' A A' ' A A A AM   2 a 3 A' A    2   a 6 2 3 a 6 a 3 3a 2  A' A  . Thể tích: VS .A' A  .  . 4
ABC . A' B 'C ' ABC 4 4 16
Câu 5: Cho hình lăng trụ có tất cả các cạnh đều bằng a , đáy là lục giác đều, góc tạo bởi cạnh bên
và mặt đáy là 60 . Tính thể tích khối lăng trụ 27 3 3 9 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 a . 8 4 2 4 Hướng dẫn giải: Chọn D.
Ta có ABCDEF là lục giác đều nên góc ở đỉnh bằng 120 .
ABC là tam giác cân tại B , DEF là tam giác cân tại E . 2 1 a 3 SS  . a . a sin120  ABC DEF 2 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 48
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 AC
AB BC  2.A . B BC.cos B A' F'  1 2 2 
a a  2. . a . a   a 3   B' E'  2  2 C' D' S
AC.AF a 3.a a 3 ACDF 2 2 2 a 3 a 3 3a 3 2 SSSS   a 3   ABCDEF ABC ACDF DEF 4 4 2 A F 60°  a 3
B ' BH  60  B ' H BB '.sin 60  B 2 H E 2 3a 3 9 C 3 D
V BH '.Sa 3.  a ABCDEF Suy ra 4 4
Câu 6: Cho lăng trụ ABC.A' B 'C ' có đáy là tam giác đều cạnh .
a Hình chiếu vuông góc của điểm
A ' lên mặt phẳng  ABC  trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai a 3
đường thẳng AA ' và BC bằng
. Khi đó thể tích của khối lăng trụ là: 4 3 a 3 3 a 3 3 a 3 3 a 3 A. B. C. D. 12 6 3 24 Hướng dẫn giải: C' B'
Gọi M là trung điểm BC, dựng MH vuông a 3
góc với AA'. Suy ra MH d BC, A' A  A' 4 2 a
Đặt AH x, ta có: 2 A' A x H M 3 C B a Từ A ' .
A MH A 'G.AM x  . 3 A 2 3 a a 3 a 3 Vậy V  .  . 3 4 12 Chọn A.
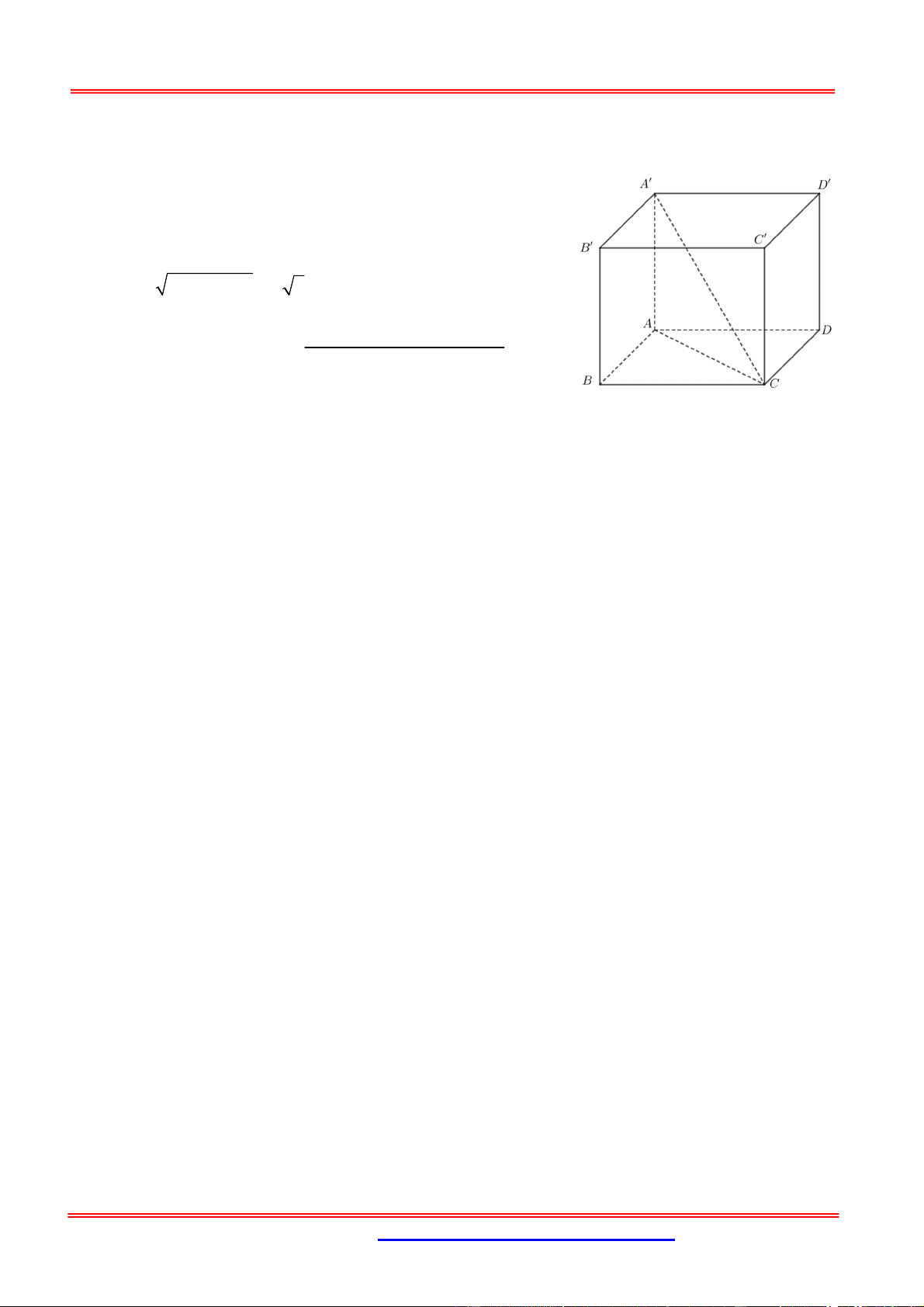
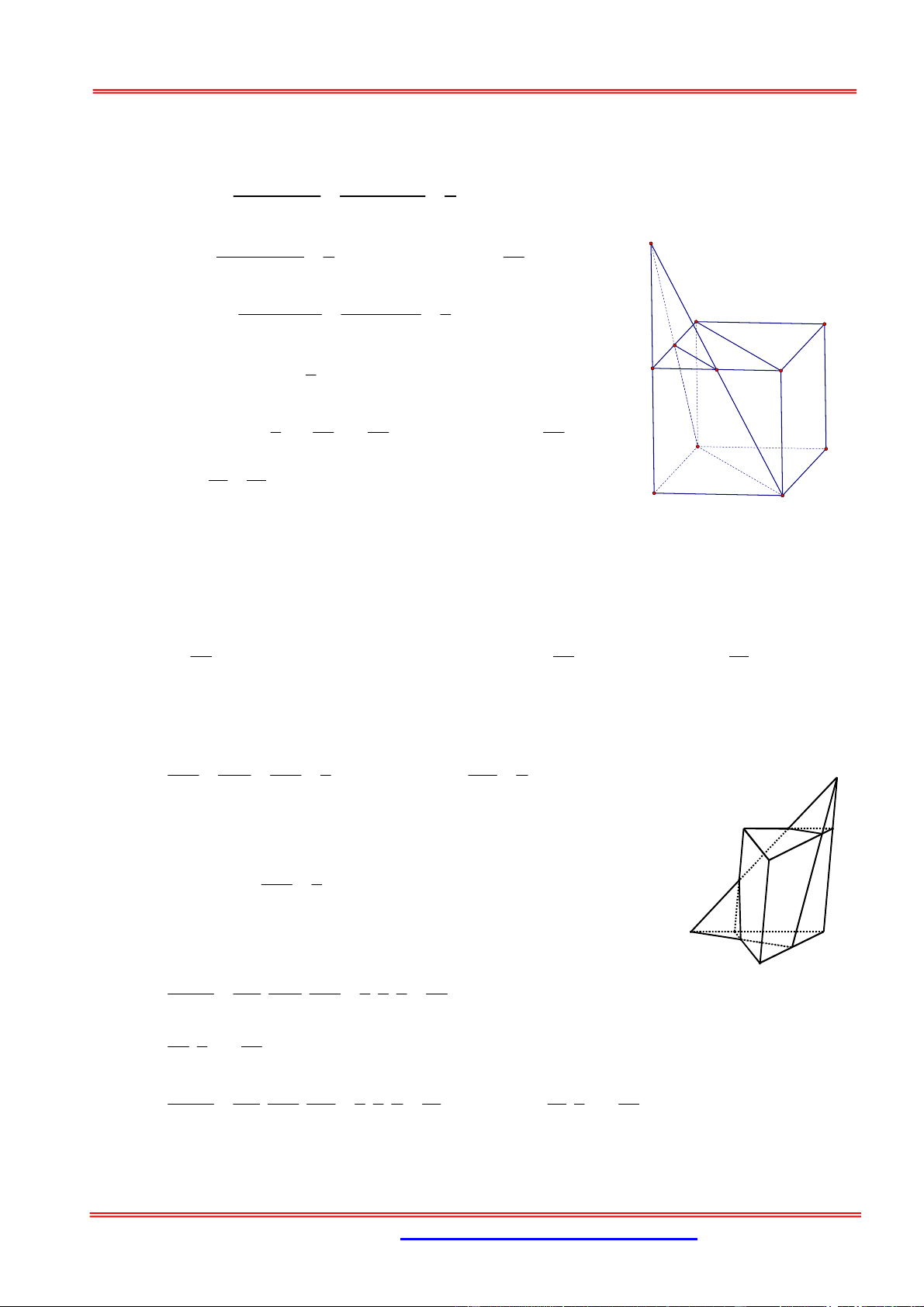
Câu 7: Cho hình lập phương ABCD.AB CD
  có cạnh bằng a , một mặt phẳng  cắt các cạnh 1 2
AA , BB , CC , DD lần lượt tại M , N , P , Q . Biết AM a , CP a . Thể tích khối 3 5 đa diện ABC . D MNPQ là: 11 3 a 3 2a 11 A. 3 a . B. . C. . D. 3 a . 30 3 3 15 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 49
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Tứ giác MNPQ là hình bình hành có tâm là I thuộc đoạn OO’. B C AM CP 11 a Ta có: OI   a O 2 30 2 Gọi O A
1 là điểm đối xứng O qua I thì: D N 11 OO1=2OI=
a < a. Vậy O1 nằm trong đoạn OO’. M 15 I P
Vẽ mặt phẳng qua O1 song song với (ABCD) cắt Q
các cạnh AA’; BB’;CC’; DD’ lần lượt tại O A B' 1
1, B1,C1, D1. Khi đó I là tâm của hình hộp C' ABC .
D AB C D . Vậy 1 1 1 O' V ABC .
D MNPQ  V MNP . Q A B C D A' D' 1 1 1 1  1 1 2 11 3
V ( ABCD.A B C D )  a OO a 1 1 1 1 1 2 2 30
Câu 8: Cho khối hộp ABC .
D A' B 'C ' D ' có cạnh bên bằng 1.; đáy ABCD là một hình chữ nhật có
các cạnh BA  3, AD  7; các mặt bên  ABB ' A ' và  ADD ' A ' hợp với mặt đáy các góc theo thứ tự 0 0
45 ;60 . Thể tích khối hộp là: A. 4 (đvdt) B. 3(đvdt) C. 2 (đvdt) D. 6 (đvdt) Hướng dẫn giải:
Dựng A ' H   ABCD  và D' C'
A ' I AB, A ' J AD HI AB, HJ AD. Ta có  0  0
A ' IH  45 ; A ' JH  60 . A'
Đặt A' H  . h B'
Tam giác HA' J vuông có 0
A ' JH  60 nên là
nửa tam giác đều có cạnh A' J , đường cao
A ' H , HJ là nửa cạnh D C 600 h 2h 3  A ' J   J H 450 3 2 A 2 I B 2 2 12h 9 12h 2 2 2
A ' J AA '  A ' J  1  9 9 2 9 12h 3  AJ  với 0  h  3 2
Tam giác HA ' I vuông cân tại H IH A' H h
AIHJ là hình chữ nhật.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 50
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 9 12h 3 2 2 AJ IH
h  9 12h  9h h  3 21 3
Thể tích khối hộp ABC .
D A' B 'C ' D ' :V S .A' H  3. 7.  3 (đvdt) ABCD 21 Chọn B.
Câu 9: Cho khối hộp ABC .
D A' B 'C ' D ' có độ dài cạnh bên bằng a; đáy là hình thoi, diện tích của
hai mặt chéo là S và S ; góc giữa hai mặt phẳng chứa hai mặt chéo là . Tính thể tích V 1 2 của khối hộp đã cho. S S cos S S cos S S cos S S cos A. 1 2 V B. 1 2 V  . C. 1 2 V D. 1 2 V a 3a 4a 2a Hướng dẫn giải:
Gọi O và O ' theo thứ tự là tâm của hai mặt
đáy ABCD, A ' B 'C ' D '. D' C'
Hai mặt chéo  ACC ' A ' và  BDD ' B ' có
giao tuyến là OO ', có diện tích theo thứ tự A' B' S , S . 1 2 H G
Dựng mặt phẳng  P  vuông góc với OO' I P
tại I , cắt các cạnh bên AA ', BB ', CC ', DD ' F E
theo thứ tự tại E, F , G, H (  P  các cạnh D C bên). 
Ta có: EG, HF  OO' tại I EIH là A B
góc giữa hai mặt phẳng chéo  ACC ' A ' và
BDD ' B ' .
- EFGH là một thiết diện thẳng của hình hộp và là một hình bình hành.
Do đó, ta có thể tích V của hình hộp là: 1 V S .AA ' 
.EG.HF.AA '.sin EFGH 2 S S Ta lại có: 1 2 S SEG.AA'  EG= ; S S
HF.BB '  HF  1 ACC ' A' 2 BDD ' B ' a a 1 S S S S cos 1 2 1 2  V  . . . a sin . 2 a a 2a Chọn D.
Câu 10: Cho khối hộp ABC .
D A' B 'C ' D ' có tất cả các cạnh bên bằng a và các góc
A ' AB, BD ,
A A ' AD đều bằng  0 0
0   90 . Tính thể tích V của khối hộp.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 51
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao a a A. 3 2 2
V a sin 2cos  o
c s arcsin B. 3 2 2
V  2a sincos  o c s 2 2 a C. 3 2 2 V  2a sin cos  o c s D. Đáp số khác. 2 2 Hướng dẫn giải:
Dựng A ' H AC; A ' K AD A  ' BD D' C'
cân tại A'  A'O BD Ta có
A'O BD A'
BD   A' AC   BD AH B' AC BDD
AH   ABCD  HK AD C K Đặt 
A ' AO .HAA ' vuông tại H O AH
H cos= AA' A B
ABCD là hình thoi  AC là phân giác góc 
BAD ,KAH vuông tại K AK AH AK AK  os c   os c . os c  .   os c  2 AH 2 AA' AH AA' 2 os c  cos a 2 2  os c 
A' H AA'.sin  .
a sin A ' H a 1  os c  cos 2 2 os c os c os c 2 2 2 a Do đó ta có: 2 2 2 VS
.A ' H a .sin . o c s  cos
ABCD. A' B 'C ' D ' ABCD 2 cos 2 a 3 2 2  2a sin cos  o c s . 2 2 Chọn C.
Câu 11: Cho khối hộp đứng ABC .
D A' B 'C ' D ' có 
AB a, AD b, BAD ; đường chéo AC ' hợp
với đáy góc . Tính thể tích khối hộp đứng đã cho là: A. 2 2
V  4ab a b  2a . b o c s. o
c s.cos B. 2 2
V  2ab a b  2a . b o c s. o
c s.cos C. 2 2
V  3ab a b  2a . b o
c s.sin.tan D. 2 2
V ab a b  2a . b o
c s.sin.tan Hướng dẫn giải: 2 2
V ab a b  2a . b o
c s.sin. tan
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 52
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Ta có: CC '   ABCD 
CAC '  là góc của AC ' và mặt đáy D'C' ABCD  . Xét ABC , ta có: 2 2 2 
AC AB BC  2 A . B BC. os c ABC A' B' 2 2
a b ab c  0  2 2 2 . os 180
a b  2a . b o c s. b D C 2 2  AC
a b  2a . b o c s Do đó ta có: 2 2 A a CC '  A .
C tan a b  2a . b o
c s.tan . B
Thể tích của hình hộp đứng: 2 2 V S
.CC '  ab sin . a b  2a .
b cos. tan ABCD 2 2
V ab a b  2a . b o
c s.sin.tan Chọn D.
CỰC TRỊ THỂ TÍCH KHỐI LĂNG TRỤ
Câu 12: Cho hình hộp chữ nhật ABC . D A BCD
  có tồng diện tích của tất cả các mặt là 36 , độ dài
đường chéo AC bằng 6 . Hỏi thể tích của khối hộp lớn nhất là bao nhiêu? A. 8 . B. 8 2 . C. 16 2 . D. 24 3 . Hướng dẫn giải: Chọn C.
Gọi chiều dài 3 cạnh của hình hộp chữ nhật lần lượt là: a , b , c  0 Ta có 2 2 2 2 2
AC  a b c  36; S  2ab  2bc  2ca  36  (a b c)  72  a b c  6 2 3 3
a b c
a b c   6 2  3  abc abc        16 2 . Vậy V  16 2 3 3  3  Max    
Câu 13: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng 36 và độ dài đường chéo bằng 6 .
Tìm thể tích lớn nhất V
của hình hộp chữ nhật đã cho? max A. V  8 . B. V  12 . C. V  8 2 . D. V  6 6 . max max max max Hướng dẫn giải: Chọn C
Gọi a, b, c là các kích thước của hình hộp chữ nhật. Ta có
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 53
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao * Độ dài đường chéo 2 2 2
d a b c  6 .
* Tổng diện tích các mặt S  2 ab bc ca  36 .
Ta tìm giá trị lớn nhất của V abc . Ta có 2 2 2
a b c a b c ab bc ac  6 2 . 2 2
Mà b c  4bc  6 2  a  418  a b c  418  a6 2  a  0  a  4 2 .
Khi đó V abc a   a  a 3 2 18 6 2
a  6 2a 18a f a .
Khảo sát hàm số y f a trên 0; 4 2  .   a  2
Ta có f a  0   . a  3 2 
So sánh f 0  0, f  2  8 2, f 3 2  0, f 4 2   8 2 ta được V  8 2 . max
Câu 14: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng 2 6
. Tìm thể tích lớn nhất V của hình hộp đã cho. max A. V  16 2 . B. V  16 . C. V  6 6 . D. V  12 3 . max max max max Hướng dẫn giải: Chọn B
Gọi a, b, c là kích thước của hình hộp chữ nhật, ta có
4a b c  32 
a b c  8    2 2 2 2 2 2
a b c  24
a b c  2 6  
a b c2   2 2 2
a b c
Suy ra ab bc ca   20 2
b c2  bc    a2 4 8
 4 20  a 8  a  0  a  4   .
V abc a
a   a   f a  a    2 20 8
a  8a  20 . Suy ra V
 max f a f 2  f 4  16 max       0;4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 54
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Câu 15: Tìm m
V ax là giá trị lớn nhất của thể tích các khối hộp chữ nhật có đường chéo bằng 3 2cm
và diện tích toàn phần bằng 2 18cm . A. 3 V  6cm . B. 3 V  5cm . C. 3 V  4cm . D. 3 V  3cm . max max max max Hướng dẫn giải: Chọn C. 2 2 2
a b c  18 Đặt , a ,
b c là kích thước của hình hộp thì ta có hệ  .
ab bc ac  9 
Suy ra a b c  6. Cần tìm GTLN của V ab . c
Ta có b c  6  a bc  9  a b c  9  a 6  a. 2 2
Do b c  4bc  6  a  4 9  a 6  a  0  a  4.   Tương tự 0  , b c  4 .
Ta lại có V a 9  a 6  a 
 . Khảo sát hàm số này tìm được GTLN của V là 4.
Câu 16: Cho hình hộp chữ nhật có tổng diện tích các mặt bằng 36 và độ dài đường chéo bằng 6 .
Tìm thể tích lớn nhất V
của hình hộp chữ nhật đã cho? max A. V  8 . B. V  12 . C. V  8 2 . D. V  6 6 . max max max max Hướng dẫn giải: Chọn C
Gọi a, b, c là các kích thước của hình hộp chữ nhật. Ta có * Độ dài đường chéo 2 2 2
d a b c  6 .
* Tổng diện tích các mặt S  2 ab bc ca  36 .
Ta tìm giá trị lớn nhất của V abc . Ta có 2 2 2
a b c a b c ab bc ac  6 2 . 2 2
Mà b c  4bc  6 2  a  418  a b c  418  a6 2  a  0  a  4 2 .
Khi đó V abc a   a  a 3 2 18 6 2
a  6 2a 18a f a .
Khảo sát hàm số y f a trên 0; 4 2  .   a  2
Ta có f a  0   . a  3 2 
So sánh f 0  0, f  2  8 2, f 3 2  0, f 4 2   8 2 ta được V  8 2 . max
Câu 17: Cho hình hộp chữ nhật có tổng độ dài tất cả các cạnh bằng 32, độ dài đường chéo bằng 2 6
. Tìm thể tích lớn nhất V của hình hộp đã cho. max A. V  16 2 . B. V  16 . C. V  6 6 . D. V  12 3 . max max max max
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 55
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Hướng dẫn giải: Chọn B
Gọi a, b, c là kích thước của hình hộp chữ nhật, ta có
4a b c  32 
a b c  8    2 2 2 2 2 2
a b c  24
a b c  2 6  
a b c2   2 2 2
a b c
Suy ra ab bc ca   20 2
b c2  bc    a2 4 8
 4 20  a 8  a  0  a  4   .
V abc a
a   a   f a  a    2 20 8
a  8a  20 . Suy ra V
 max f a f 2  f 4  16 max       0;4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 56
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao TỈ LỆ THỂ TÍCH A- LÝ THUYẾT CHUNG
1. Hai khối chóp S.A A ...A và S.B B ...B có chung đỉnh S và hai mặt đáy cùng nằm trên một mặt 1 2 n 1 2 m V S phẳng, ta có: S. 1 A 2 A ... n A 1 A 2 A ... n AV S
S .B B ...B B B ...B 1 2 m 1 2 m V
SASBSC
2. Hai khối chóp tam giác S.ABC có A  S ,
A B  SB, C ' SC ta có: S.A'B'C'  . . v SA SB SC S . ABC
3. Kiến thức cần nhớ đối với khối lăng trụ tam giác và khối hộp. V 2V V, V. A .  ABC    3 A .BCC B 3 V V V, V. A .  ABD   6 BDA C 3
4. Một số công thức nhanh cho các trường hợp hay gặp 2 2 BHAB CHAC
Tam giác ABC vuông tại A có đường cao AH có  ,    .   BCBC CBBC
Mặt phẳng  song song với mặt đáy của khối chóp S.A A ...A cắt SA tại điểm M thỏa mãn 1 2 n k k SM V k
S.M M ...Mp, ta có 1 2 n 3  p . SA V k
S. A A ...A 1 2 n AM BN CP
x y z
Hình lăng trụ tam giác ABC.A BC   có  x,  y,  z có VV . AABBCCABC.MNP 3 AM BN CP Hình hộp ABC . D A BCD   có  x,  y,
z . Mặt phẳng  MNP cắt DD ' tại Q thì ta AABBCCDQ
x y z t
có đẳng thức x z y t với t  và VV . DDABCD.MNPQ 4 SM SN SP
Hình chóp S.ABCD có đáy ABCD là hình bình hành và  x,  y,  z . Mặt phẳng SA SB SC 1 1 1 1 SQ
MNP cắt SD tại Q thì ta có đẳng thức    với t  và x z y t SD 1  1 1 1 1  Vxyzt    V . S .MNPQ   4 x y z t   MA NB PC
Định lí Meneleus cho 3 điểm thẳng hàng . .
 1 với MNP là một đường thẳng cắt ba MB NC PA
đường thẳng AB, BC, CA lần lượt tại M , N , . P
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 57
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
B – BÀI TẬP TRẮC NGHIỆM Câu 1:
Cho hình chóp S.ABC .Trên cạnh SA lấy các điểm M , N sao cho SM MN NA .Gọi
, là các mặt phẳng song song với mặt phẳng  ABC  và lần lượt đi qua M , N .Khi đó
hai mặt phẳng ,  chia khối chóp đã cho thành 3 phần.Nếu phần trên cùng có thể tích là 3
10 dm tích hai phần còn lại lần lượt là? A. 3 80 dm và 3 190 dm . B. 3 70 dm và 3 190 dm . C. 3 70 dm và 3 200 dm . D. 3 80 dm và 3 180 dm . Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng V . Gọi SM 1 SN 2 SP 1
M , N , P lần lượt là các điểm trên các cạnh S ,
A SB, SC sao cho  ,  ,  . SA 2 SB 3 SC 3
Mặt phẳng  MNP cắt cạnh SD tại điểm Q . Tính thể tích khối đa diện ABC . D MNPQ . 5 10 53 58 A. V . B. V . C. V . D. V . 63 63 63 63 Câu 3:
Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB  3a , AD a , SA vuông góc với đáy và
SA a . Mặt phẳng  qua A vuông góc với SC cắt SB , SC , SD lần lượt tại M , N , P
. Tính thể tích khối chóp S.AMNP . 3 3 3a 3 3a 3 3a 3 3a A. . B. . C. . D. . 40 40 10 30 Câu 4:
Cho khối chóp S.ABCD có thể tích V và đáy là hình bình hành. Điểm S  thỏa mãn  
SS   k DC k  0 . Biết thể tích phần chung của hai khối chóp S.ABCD và S .ABCD là 7 V . Tìm k . 25 A. k  9 . B. k  6 . C. k  11. D. k  4 . Câu 5:
Cho hình chóp S.ABC có tất cả các cạnh đều bằng a . Một mặt phẳng  P song song với
mặt đáy  ABC  cắt các cạnh SA , SB , SC lần lượt tại M , N , P . Tính diện tích tam giác
MNP biết  P chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau. 2 a . 3 3 a . 3 2 a . 3 2 a . 3 A. S  . B. S  . C. SD. S  . MNPMNPMNP 8 MNP 16 3 4 2 3 4 4 Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD b và cạnh bên
SA c vuông góc với mặt phẳng  ABCD . Gọi M là một điểm trên cạnh SA sao cho
AM x 0  x c . Tìm x để mặt phẳng  MBC  chia khối chóp thành hai khối đa diện có thể tích bằng nhau.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 58
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 3 2c 2 3ab 3 5c  5  1ab A. x  . B. x  . C. x  . D. x  . 2 2c 2 2c Câu 7:
Cho hình chóp SABCD có đáy ABCD là hình thang với AB / /CD và CD  4AB .Gọi M SM
là 1 điểm trên cạnh SA sao cho 0  AM SA . Tìm tỉ số
sao cho mặt phẳng CDM SA
chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau: SM 3   13 SM 4   26 SM 3   17 SM 3   23 A.  . B.  . C.  . D.  . SA 2 SA 2 SA 2 SA 2 Câu 8:
Cho điểm M trên cạnh SA , điểm N trên cạnh SB của hình chóp tam giác S.ABC có thể tích SM 1 SN bằng V sao cho  ,
x . Mặt phẳng  P qua MN và song song với SC chia khối SA 3 SB
chóp S.ABC thành hai khối đa diện có thể tích bằng nhau. Tính x . 4  5 8  10 4  5 8  10 A. x B. x C. x D. x  3 6 6 9 Câu 9:
Cho khối tứ diện đều ABCD cạnh bằng a , Gọi M , N là trung điểm các cạnh AB , BC svà BD
E là điểm thuộc tia đối DB sao cho
k . Tìm k để mặt phẳng  MNE  chia khối tứ BE 3 11 2a
diện thành hai khối đa diện, trong đó khối đa diện chứa đỉnh B có thể tích là . 294 6 A. k  . B. k  6 . C. k  4 . D. V  5 . 5
Câu 10: Cho khối tứ diện đều ABCD cạnh bằng 2c .
m Gọi M , N , P lần lượt là trọng tâm của ba tam
giác ABC, ABD, AC .
D Tính thể tích V của khối chóp AMN . P 2 2 2 4 2 2 A. 3 V cm . B. 3 V cm . C. 3 V cm . D. 3 V cm . 162 81 81 144
Câu 11: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy một góc
60 . Gọi M là điểm đối xứng của C qua D , N là trung điểm SC. Mặt phẳng  BMN
chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng: 7 1 7 6 A. . B. . C. . D. . 5 7 3 5
Câu 12: (Hình học không gian) Cho tứ diện ABCD và M , N , P lần lượt thuộc BC, BD, AC sao cho
BC  4BM , BD  2BN , AC  3A .
P Mặt phẳng  MNP cắt AD tại Q. Tính tỷ số thể tích hai
phần khối tứ diện ABCD bị chia bởi mặt phẳng  MNP. 2 7 5 1 A. B. C. D. 3 13 13 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 59
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 13: Cho hình lăng trụ tam giác đều ABC.A ' B 'C ', có cạnh đáy bằng a và cạnh bên bằng a 2 . AM A ' N 1
Lấy M, N lần lượt trên cạnh AB ', A 'C sao cho 
 . Tính thể tích V của khối AB ' A 'C 3 BMNC 'C. 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. 108 27 108 27
Câu 14: Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên 1
và phẳng đáy là thỏa mãn cos= . Mặt phẳng  P qua AC và vuông góc với mặt 3
phẳng SAD chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện
là gần nhất với giá trị nào trong các giá trị sau: A. 0,11 B. 0,13 C. 0, 7 D. 0, 9
Câu 15: Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA  2SM ,
SN  2NB , () là mặt phẳng qua MN và song song với SC . Kí hiệu (H ) và (H ) là các 1 2
khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng () , trong đó, (H ) chứa 1 V
điểm S , (H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . Tính tỉ số 1 . 2 1 2 1 2 V2 4 5 3 4 A. B. C. D. 5 4 4 3
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a 3 và SA vuông góc
với mặt phẳng đáy. Mặt phẳng (P) đi qua điểm A và vuông góc với SC cắt SB, SC, SD lần lượt tại ’ B , C’, ’
D . Tính thể tích khối chóp S.A ’ B C’ ’
D theo a. 3 3 3a 3 3a 3 3 3a 3 3 5a A. B. C D. 20 20 10 10
Câu 17: Cho tứ diện đều ABCD cạnh a. Mặt phẳng (P) chứa cạnh BC cắt cạnh AD tại E. Biết góc 5 2
giữa hai mặt phẳng (P) và (BCD) có số đo là thỏa mãn tan  . Gọi thể tích của hai 7 V
tứ diện ABCE và tứ diện BCDE lần lượt là V và V . Tính tỷ số 1 . 1 2 V2 3 1 3 5 A. B. C. D. 8 8 5 8
Câu 18: Cho khối chóp S.ABC có SA  6, SB  2, SC  4, AB  2 10 và SBC 90 , ASC 120     .
Mặt phẳng  P qua B và trung điểm N của SC và vuông góc với mặt phẳng SAC  cắt V
cạnh SA tại M . Tính tỉ số thể tích S.MBN . VS.ABC
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 60
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 1 1 A. . B. . C. . D. . 9 5 6 4
Câu 19: Khối tứ diện ABCD có thể tích V , khối tứ diện A B C D có thể tích V , các đỉnh 1 1 1 1 1
A , B , C , D lần lượt là trọng tâm của các tam giác BCD, CD ,
A DAB,ABC . Khối tứ diện 1 1 1 1
A B C D có thể tích V , các đỉnh A , B , C , D lần lượt là trọng tâm của các tam giác 2 2 2 2 2 2 2 2 2
B C D , C D A , D A B , A B C . Cứ tiếp tục như thế ta được khối tứ diện A B C D có thể 1 1 1 1 1 1 1 1 1 1 1 1 n n n n
tích V , các đỉnh A , B , C , D lần lượt là trọng tâm của các tam giác B C D , n n n n n n 1  n 1  n 1  C D A , D A B , A B C
. Tính S V V  ...  V ? n 1  n 1  n 1  n 1  n 1  n 1  n 1  n 1  n 1  1 2 2018  2018 3   1 V  2019 27   1 V A. S  . B. S  . 2018 2.3 2019 26.27  2018 27   1 V  2019 3   1 V C. S  . D. S  . 2018 26.27 2019 2.3
Câu 20: Cho khối lăng trụ tam giác ABC.A BC
  . Gọi M , N lần lượt thuộc các cạnh bên AA ,CC
sao cho MA MA ;
NC  4NC . Gọi G là trọng tâm tam giác ABC . Hỏi trong bốn khối tứ diện GAB C  , BB MN , ABB C   và A B
CN , khối tứ diện nào có thể tích nhỏ nhất? A. Khối A BCN . B. Khối GA BC   . C. Khối ABB C   . D. Khối BB MN .
Câu 21: Cho hình lăng trụ tam giác đều ABC. ’ A ’ B ’
C , có cạnh đáy bằng a và cạnh bên bằng a 2 . AM A' N 1
Lấy M , N lần lượt trên cạnh A ’ B , ’ A C sao cho 
 . Tính thể tích V của khối AB ' A'C 3 BMNC’C. 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. 108 27 108 27
Câu 22: Cho khối lập phương ABC . D A BCD
  cạnh a . Các điểm E và F lần lượt là trung điểm của C B   và C D
  . Mặt phẳng  AEF  cắt khối lập phương đã cho thành hai phần, gọi V là 1 V
thể tich khối chứa điểm A và V là thể tich khối chứa điểm C ' . Khi đó 1 là 2 V2 25 17 8 A. . B. 1. C. . D. . 47 25 17
Câu 23: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh .
a Gọi M , N lần lượt là trung điểm của
A' B ' và BC. Mặt phẳng  DMN  chia khối lập phương đã cho thành hai khối đa diện. Gọi V  H
H  là khối đa diện chứa đỉnh ,
A H ' là khối đa diện còn lại. Tính tỉ số . VH ' V V V VH  37 H  55  H  2  H  1 A. B. C. D. V 48 V 89 V 3 V 2  H '  H ' H ' H '
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 61
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 24: Cho hình lập phương ABC . D A BCD   cạnh .
a Gọi M , N lần lượt là trung điểm của các
cạnh ABvà BC . Mặt phẳng (DMN ) chia hình lập phương thành 2 phần. Gọi V là thể tích 1 V1 của phần chứa đỉnh ,
A V là thể tích của phần còn lại. Tính tỉ số . 2 V 2 2 55 37 1 A. . B. . C. . D. . 3 89 48 2
Câu 25: Cho hình hộp ABCD ’ A ’ B C’ ’
D . Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng thời song song với ’ B ’
D . Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V
V ,V (Trong đó V F  . 1 2
1 là thể tích khối chứa A). Tính tỉ số 1 V2 7 17 8 A. . B. 1. C. . D. . 17 25 17
Câu 26: Cho khối lăng trụ tam giác ABC. A’B’C’. Gọi I, J, K lần lượt là trung điểm của các cạnh AB,
AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó. 25 49 8 A. . B. 1. C. . D. . 47 95 17
CỰC TRỊ TỈ LỆ THỂ TÍCH
Câu 27: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Các điểm A , C thỏa
 1   1  mãn SA  S , A SC 
SC . Mặt phẳng  P chứa đường thẳng A C
  cắt các cạnh SB, SD 3 5 V lần lượt tại B ,  D và đặt
S. AB CD k   
. Giá trị nhỏ nhất của k là bao nhiêu? VS.ABCD 1 1 4 15 A. . B. . C. . D. . 60 30 15 16
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi C là trung điểm cạnh SC . V
Mặt phẳng  P chứa đường thẳng AC cắt các cạnh SB, SD tại B , D . Đặt S .B CD m    . VS.ABCD
Giá trị nhỏ nhất của m bằng : 2 4 1 2 A. . B. . C. . D. . 27 27 9 9
Câu 29: Cho khối tứ diện đều S.ABC cạnh bằng a . Mặt phẳng  P đi qua S và trọng tâm của tam V
giác ABC cắt các cạnh AB, AC lần lượt tại M , N . Đặt S . AMN m
. Giá trị nhỏ nhất của m VS.ABC bằng
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 62
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 4 1 A. . B. . C. . D. . 3 9 9 3
Câu 30: Cho hình chóp S.ABCD có thể tích V và đáy ABCD là hình bình hành. Mặt phẳng qua A
và trung điểm N cạnh SC cắt cạnh SB, SD lần lượt tại M , P . Tính thể tích nhỏ nhất của
khối chóp S.AMNP . V 3V V V A. . B. . C. . D. . 8 8 4 3
Câu 31: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình hình hành. Các điểm A , C thỏa
 1   1  mãn SA  , SA SC 
SC . Mặt phẳng  P chứa đường thẳng A C
  cắt các cạnh SB, SD 3 5 V lần lượt tại B ,  D và đặt
S. AB CD k   
. Tính giá trị lớn nhất của k là bao nhiêu? VS.ABCD 4 1 4 4 A. . B. . C. . D. . 105 30 15 27
Câu 32: Cho hình chóp S.ABCD có ABCD là hình bình hành và có thể tích V . Gọi M , N thứ tự là AB 2 AD
các điểm di động trên các cạnh AB, AD sao cho 
 4 . Gọi V ' là thể tích khối AM AN
chóp S.AMN . Tìm giá trị nhỏ nhất của V ' . 1 1 1 1 A. V B. V C. V D. V 4 6 8 3
Câu 33: Cho hình chóp S.ABCD có ABCD là hình bình hành và có thể tích V . Gọi M , N thứ tự là AB 2 AD
các điểm di động trên các cạnh AB, AD sao cho 
 4 . Gọi V ' là thể tích khối AM AN
chóp S.MBCDN . Tìm giá trị lớn nhất của V ' . 1 2 3 1 A. V B. V C. V D. V 4 3 4 3
Câu 34: Cho hình chóp S.ABCD có thể tích V , đáy là hình bình hành. Mặt phẳng  đi qua A ,
trung điểm I của SO cắt các cạnh SB, SC, SD lần lượt tại M , N , P . Tính thể tích nhỏ nhất
của khối chóp S.AMNP . V V V 3V A. . B. . C. . D. . 18 3 6 8
Câu 35: Cho hình chóp S.ABCD, SA là đường cao, đáy là hình chữ nhật với SA a, AB b, AD  . c
Trong mặt phẳng SDB lấy G là trọng tâm tam giác SDB , qua G kẻ đường thẳng d cắt
cạnh BS tại M, cắt cạnh SD tại N, mp  AMN  cắt SC tại K. Xác định M thuộc SB sao cho V
đạt giá trị lớn nhất và nhỏ nhất. Hãy tìm giá trị lớn nhất và nhỏ nhất đó. SAMKN abc abc abc abc A. V  ,VB. V  ,VSAMKN max SAMKN min 8 9 SAMKN max SAMKN min 8 10
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 63
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao abc abc abc abc C. V  ,VD. V  ,VSAMKN max SAMKN min 9 10 SAMKN max SAMKN min 10 11
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Các điểm A ', C ' thỏa mãn
 1   1  SA '  SA , SC ' 
SC . Mặt phẳng  P chứa đường thẳng A'C ' cắt các cạnh SB, SD lần 3 5 V
lượt tại B ', D ' và đặt
S . A' B 'C ' D ' k
. Giá trị lớn nhất của k là? VS.ABCD 4 1 4 4 A. . B. . C. . D. . 105 30 15 27
Câu 37: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng song song với đáy
cắt các cạnh bên SA , SB , SC , SD lần lượt tại M , N , P , Q . Gọi M  , N , P , Q lần lượt SM
là hình chiếu của M , N , P , Q trên mặt phẳng đáy. Tìm tỉ số
để thể tích khối đa diện SA MNP . Q M NPQ
  đạt giá trị lớn nhất. 3 2 1 1 A. . B. . C. D. . 4 3 2 3
Câu 38: Cho khối chóp S.ABC . Một mặt phẳng song song với đáy cắt các cạnh bên SA , SB , SC
lần lượt tại M , N , P . Gọi M  , N , P lần lượt là hình chiếu của M , N , P trên mặt phẳng SM đáy. Tìm tỉ số
để thể tích khối đa diện MN . P M NP
  đạt giá trị lớn nhất. SA 3 2 1 A. . B. . C. . D. . . 4 3 2 .
Câu 39: Cho hình chóp S .ABC D có đáy là hình bình hành và có thể tích là V. Điểm P là trung
điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N . Gọi V
V là thể tích của khối chóp S .AM PN . Tìm giá trị nhỏ nhất của 1 ? 1 V 1 2 3 1 A. . B. . C. . D. . 8 3 8 3 
Câu 40: Cho hình chóp S.ABC có A
SB  BSC  CSA  30 và SA SB SC a . Mặt phẳng
P qua A cắt hai cạnh SB, SC lần lượt tại B ,C sao cho chu vi tam giác AB C   nhỏ nhất. V
Gọi V ,V lầ lượt là thể tích các khối chóp S.AB C
 , S.ABC . Tính tỉ số 1 . 1 2 V2 V V V V A. 1  3  2 2 . B. 1  3 1 . C. 1  4  2 3 . D. 1  2 1 . V V V V 2 2 2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 64
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao   
Câu 41: Cho khối chóp S.ABC có SA SB SC a ASB  60 , BSC  90 , ASC  120 . Gọi CN AM
M , N lần lượt là các điểm trên cạnh AB và SC sao cho  . Khi khoảng cách giữa SC AB
M và N nhỏ nhất, tính thể tích V của khối chóp S.AMN . 3 2a 3 5 2a 3 5 2a 3 2a A. . B. . C. . D. . 72 72 432 432
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 65
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
C – HƯỚNG DẪN GIẢI Câu 1:
Cho hình chóp S.ABC .Trên cạnh SA lấy các điểm M , N sao cho SM MN NA .Gọi
, là các mặt phẳng song song với mặt phẳng  ABC và lần lượt đi qua M , N .Khi đó
hai mặt phẳng ,  chia khối chóp đã cho thành 3 phần.Nếu phần trên cùng có thể tích là 3
10 dm tích hai phần còn lại lần lượt là? A. 3 80 dm và 3 190 dm . B. 3 70 dm và 3 190 dm . C. 3 70 dm và 3 200 dm . D. 3 80 dm và 3 180 dm . Hướng dẫn giải: Chọn B S Đặt V V ,V S ta có: S . ABC 1 S .MNP M Q 3 SM SP SQ  1  1 V  . . .V V V N P F 3
V  270 dm . 1   SA SB SC  3  27 C Tương tự ta có : E 3 SN SE SF  2  8 3 V V  . . .V V V  80 dm . 1 2   SA SB SC  3  27 B Do đó: 3
V  80 V  70 dm , 3
V V V V  190 dm . 2 1 3 1 2 Chọn B. Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng V . Gọi SM 1 SN 2 SP 1
M , N , P lần lượt là các điểm trên các cạnh S ,
A SB, SC sao cho  ,  ,  . SA 2 SB 3 SC 3
Mặt phẳng  MNP cắt cạnh SD tại điểm Q . Tính thể tích khối đa diện ABC . D MNPQ . 5 10 53 58 A. V . B. V . C. V . D. V . 63 63 63 63 Hướng dẫn giải: Chọn D SM 1 SN 2 SP 1 Đặt x   , y   , z   , SA 2 SB 3 SC 3 SQ t  . SD 1 1 1 1 3 1 2 Ta có     2  3    t  . x z y t 2 t 7
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 66
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 1 1 5 Do đó VVVxy . z
V zxt. V xz y t V V . S .MNPQ S .MNP S .PQM   2 2 2 63  5  58 Suy ra V  1 V V . ABCD.MNPQ    63  63 Câu 3:
Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB  3a , AD a , SA vuông góc với đáy và
SA a . Mặt phẳng  qua A vuông góc với SC cắt SB , SC , SD lần lượt tại M , N , P .
Tính thể tích khối chóp S.AMNP . 3 3 3 3 3a 3 3a 3a 3a A. . B. . C. . D. . 40 40 10 30 Hướng dẫn giải: Chọn B Ta có
SC    SC AM , SC AN, SC AP . Mặt khác
CB  SAB  AM CB AM  SBC  AM SB
. Tương tự ta có AP SD .
Thể tích khối chóp ban đầu là 3 1 3a 2 V  3a .a  . 3 3 SA
Tính các tỉ số x   1 , SA 2 2 SMSA a 1 y       , 2 2 SBSB a  3a 4 2 2 2 SNSA a 1 2 SPSA a 1 z       , t     . 2 2 2   SC 2 2  SC
a  3a a 5 SDSD a a 2 3 xyzt  1 1 1 1  3 3a Vậy V      V V    . 4 x y z t 40 40   Câu 4:
Cho khối chóp S.ABCD có thể tích V và đáy là hình bình hành. Điểm S  thỏa mãn  
SS  k DC k  0 . Biết thể tích phần chung của hai khối chóp S.ABCD và S .ABCD là 7 V . Tìm k . 25 A. k  9 . B. k  6 . C. k  11. D. k  4 . Hướng dẫn giải: Chọn D
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 67
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Ta có AB // CD // SS  nên B  SA SB, C  SD SC . Theo Thales ta cũng có BS CS SS SBSCk SD    k    , t   1. BB CC DC SB SC k  1 SD   2 1 k k  1 1 1 1  k 2k   1 Do đó V  .1.1. . V V . S ADC B       .   4
k 1 k 1 1 1 k k 2k k    2 1  k 1 k 1  2  k 2k  1   7
Vậy thể tích phần chung là V   V V  1 V
V k  4 k  0 .
S. ADCB 2    2k k  1   25   Câu 5:
Cho hình chóp S.ABC có tất cả các cạnh đều bằng a . Một mặt phẳng  P song song với
mặt đáy  ABC cắt các cạnh SA , SB , SC lần lượt tại M , N , P . Tính diện tích tam giác
MNP biết P chia khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau. 2 a . 3 3 a . 3 2 a . 3 2 a . 3 A. S  . B. S  . C. SD. S  . MNP 8 MNP 16 MNP 3 MNP 4 2 3 4 4 Hướng dẫn giải: Chọn D. 3 V SM SN SPSM S .MNP  . .      1 V SA SB SCSA S . ABCV 1
Theo bài ra: S.MNP  2 V 2 S. ABC 3  SM  1 Từ   1 , 2 ta có     SA  2 SM 1   3 SA 2 Lại có:
1 d S,MNP.S MNP V 1 S .MNP 3  = 3 V 1 2 S. ABC
d S, ABC .S 3 ABC
d S, MNP SM 1 Mà =  4
d S, ABC 3 SA 2 3 S 2 3 3 2 2 2 2 a . 3 a . 3
Từ 3 , 4 ta có được MNP =  S = S  .  MNP ABC S 2 3 2 2 4 4. 4 ABC
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 68
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD b và cạnh bên
SA c vuông góc với mặt phẳng  ABCD . Gọi M là một điểm trên cạnh SA sao cho
AM x 0  x c . Tìm x để mặt phẳng  MBC chia khối chóp thành hai khối đa diện có thể tích bằng nhau. 3 2c 2  3ab 3 5c  5   1 ab A. x  . B. x  . C. x  . D. x  . 2 2c 2 2c Hướng dẫn giải: Chọn C S SM SN c x Ta có   SA SD c V SM c x c x
Vì vậy S.MBC    VV S .MBC S . V SA c 2 ABCD c S . ABC M Và A V B SM .SN c x c x N SMNC  2  2    VV 2 S.MNC 2 S. V S . A SD c 2 ABCD c SADC D C Vậy
 c x2 c x   1 c x2 2  c cx V    VV . SMNBC 2 SABCD SABCD 2  2c c  2 c     2 2 3  5 c c xc cx 2 2   Từ giả thiết ta có
 1  c  3cx x  0  x  . 2 c 2 Câu 7:
Cho hình chóp SABCD có đáy ABCD là hình thang với AB / /CD và CD  4 AB .Gọi M là SM
1 điểm trên cạnh SA sao cho 0  AM SA . Tìm tỉ số
sao cho mặt phẳng CDM  chia SA
khối chóp đã cho thành hai khối đa diện có thể tích bằng nhau: SM 3   13 SM 4   26 SM 3   17 SM 3   23 A.  . B.  . C.  . D.  . SA 2 SA 2 SA 2 SA 2 Hướng dẫn giải: Chọn B SM SN Đặt x   , 0  x  1. SA SB
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 69
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V S AD SADC ADC    4 V S AB Ta có SABC ABC . 4 1  VV ,VV SADC 5 SABDC SABC 5 SABDC V SM 4x Ta có SMCD   VV SMCD V SA 5 SABDC SACD 2 V SM SN x SMNC 2  .  x VV SMNC V SA SB 5 SABC SABC 2  4x x V Vậy SABCD V   VSMNCD   5 5 SABCD 2   2 4x x 1 4   26 Suy ra    x  . 5 5 2 2 Câu 8:
Cho điểm M trên cạnh SA , điểm N trên cạnh SB của hình chóp tam giác S.ABC có thể tích SM 1 SN bằng V sao cho  ,
x . Mặt phẳng  P qua MN và song song với SC chia khối SA 3 SB
chóp S.ABC thành hai khối đa diện có thể tích bằng nhau. Tính x . 4  5 8  10 4  5 8  10 A. x B. x C. x D. x  3 6 6 9 Hướng dẫn giải: Chọn B S
Trong  ABS  : MN AB E , trong M
SAC  : MQ / /SC, Q AC , trong  ABC  : EQ BC P . SM CQ 1 SN CP N Q
Khi đó NP / /SC / /MQ    ,   x . C A SA CA 3 SB CB Trong tam giác P NB MS EA B SAB : . .  1 E NS MA EB 1 x 1 EA EA 2x AB 3x 1  . .  1     x 2 EB EB 1 x EB 1 x VEAMQ AM AQ EA 2 2 2x 8x 8x Ta có  . .  . .   VV V AS AC BA 3 3 3x 1 9 3x 1 EAMQ 9 3x 1 S . ABC    
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 70
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V BN BP EB 2 1 xxx EBNP 1 3 1 3  . .  1 x .   VV V BS BC AB 3x 1 3x 1 EBNP 3x 1 S .ABC 8x 1 x3 1 8x 1 x3 1 8  10  VV V V     x AMQBNP 9 3x   1 3x 1 2 93x   1 3x 1 2 6 Câu 9:
Cho khối tứ diện đều ABCD cạnh bằng a , Gọi M , N là trung điểm các cạnh AB , BC BD
svà E là điểm thuộc tia đối DB sao cho
k . Tìm k để mặt phẳng MNE chia khối BE 3 11 2a
tứ diện thành hai khối đa diện, trong đó khối đa diện chứa đỉnh B có thể tích là . 294 6 A. k  . B. k  6 . C. k  4 . D. V  5 . 5 Hướng dẫn giải: Chọn C A
Ta có diện tích khối tứ diện đều cạnh 3 a 2 a bằng V  0 12 M V BM BN BE BMNE  . . Q V BA BC BD ABCD E 1  VV B D BMQE 0 4 Theo ta let ta có: P N EP EQ k 1 2k   1    EN EM 1 2k 1 k 1  C 2 EP EQ DE 4 k  2 1 k 1 1  V  . . V  . V EDPQ BMQE EN EM BE 2k  2 0 1 k 4 k 4k 2 1 k 1 1 k  4k 3 1    Do đó VV  . V V 1  BMNPQD 0 4 2k 2 0 0 1 k 4 4  k 2k 2 1      3 22 k k  4k  1   V
V hay V V 1
  k  4 BMNPQD 0 49 0 0 4 4  k 2k 2 1    
Câu 10: Cho khối tứ diện đều ABCD cạnh bằng 2c .
m Gọi M , N , P lần lượt là trọng tâm của ba tam
giác ABC, ABD, A .
CD Tính thể tích V của khối chóp AMN . P
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 71
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 2 4 2 2 A. 3 V cm . B. 3 V cm . C. 3 V cm . D. 3 V cm . 162 81 81 144 Hướng dẫn giải: Chọn C. A 2 3
Tam giác BCD đều  DE  3  DH  3 2 6 2 2 AH AD DH  3 N 1 1 1 1 3 M S  .d .FK  . d . BC  EFKE ,FK  D,BC P B 2 2 2 2 4 K D 1 1 2 6 3 2  VAH.S  . .  . SKFE E  FK H 3 3 3 4 6 E F AM AN AP 2 Mà    AE AK AF 3 C Lại có: V AM AN AP 8 8 4 2 AMNP  . .   VV  . V AE AK AF 27 AMNP 27 AEKF 81 AEKF
Câu 11: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , cạnh bên hợp với đáy một góc
60 . Gọi M là điểm đối xứng của C qua D , N là trung điểm SC. Mặt phẳng  BMN
chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng: 7 1 7 6 A. . B. . C. . D. . 5 7 3 5 Hướng dẫn giải: Chọn A. S
Giả sử các điểm như hình vẽ.
E SD MN E là trọng tâm tam giác SCM , N
DF // BC F là trung E điểm BM . H Ta có: C D M SD ABCD     ,  SDO  60 , O F a 6  SO  2 B A
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 72
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 a 7 SF SO OF  2 2  d a 6 1 a 7
O, SAD  OH h  ; SSF.AD SAD 2 7 2 4 V ME MF MD 1 MEFD     V MN MB MC 6 MNBC 3 5 5 1 a           B V FDCNE M V NBC d  1 5 1 5 6 M , SAD S 4 SBC h SSAD 6 6 3 2 18 2 72 3 3 1 a 6 7a 6        S V . S . ABCD O SABCD S V ABFEN VS.ABCD VBFDCNE 3 6 36 V 7 Suy ra: SABFEN   V 5 BFDCNE
Câu 12: (Hình học không gian) Cho tứ diện ABCD và M , N, P lần lượt thuộc BC, BD, AC sao cho
BC  4BM , BD  2BN , AC  3A .
P Mặt phẳng MNP cắt AD tại Q. Tính tỷ số thể tích hai
phần khối tứ diện ABCD bị chia bởi mặt phẳng  MNP. 2 7 5 1 A. B. C. D. 3 13 13 3 Hướng dẫn giải:
Gọi I MN CD, Q PI AD, A
kẻ DH / /BC H IM , DK / / AC K IP. ID DH BM 1 NMB NDH     . IC CM CM 3 P Q IK DK ID 1 DK 1 2 K       DK IP CP IC 3 2 AP 3 3 I H A
PQ  DKQ. B D N M AQ AP 2 AQ 3 Suy ra      DQ DK 3 AD 5 C VANPQ AP AQ 1 Đặt V V . Ta có:  .  ; ABCD V AC AD 5 ANCD V V DN 1 1 ANCD DACN     VV V V DB 2 ANPQ 10 ABCD DABC V CM CP 1 1 CDMP  .   VV V CB CA 2 CDMP 2 CDBA 1 1 1  VVV VV V . ABMP 2 DABMP 2 CDMP 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 73
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 7 VABMNQP 7  VVVV   ABMNQP ANPQ N . ABMP 20 V 13 CDMNQP 7
Vậy mặt phẳng MNP chia khối chóp thành hai phần với tỉ lệ thể tích . 13 Chọn B.
Câu 13: Cho hình lăng trụ tam giác đều ABC.A' B 'C ', có cạnh đáy bằng a và cạnh bên bằng a 2 . AM A ' N 1
Lấy M, N lần lượt trên cạnh AB ', A'C sao cho 
 . Tính thể tích V của khối AB ' A 'C 3 BMNC 'C. 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. 108 27 108 27 Hướng dẫn giải:
Gọi G, K lần lượt tâm các hình chữ A' C'
nhật ABB ' A ' và AA 'C 'C. AM 1 AM 2 Ta có:    N AB ' 3 AG 3 K B' (Do G trung điểm AB’) I
Xét tam giác ABA ' có AG là trung G M AM 2 tuyến và 
. Suy ra M là trọng AG 3 C A
tâm tam giác ABA '. Do đó BM đi q H
ua trung điểm I của AA’. A ' N 1 A ' N 2 Ta có:    B A 'C 3 A ' K 3
(Do K là trung điểm A’C)
Xét tam giác AA 'C ' có A ' K là trung tuyến A ' N 2 và 
. Suy ra N là trọng tâm của tam giác AA 'C '. Do đó C ' N đi qua trung điểm I A ' K 3 của AA’.
Từ M là trọng tâm tam giác ABA ' và N trọng tâm của tam giác AA 'C '. Suy ra: IM IN 1   . IB IC ' 3 V IM IN IC 1
Gọi V ,V lần lượt là thể tích các khối chóp IMNC; IBCC '. Ta có: 1  . .  1 2 V IB IC ' IC 9 2 8
Mà V V V V V . 1 2 2 9
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 74
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Hạ AH vuông góc với BC tại H thuộc BC. Ta được AH vuông góc với mặt phẳng
BB 'C 'C . AA ' song song với mặt phẳng BB 'C 'C  nên khoảng cách từ I đến mặt phẳng
BB 'C 'C  bằng khoảng cách từ A đến BB 'C 'C  và bằng AH. 2 3 a 3 1 1 a 3 a 2 a 6 Ta có: AH  ; V
d I , BB 'C 'C  .S  . .  . 2     BCC ' 2 3 3 2 2 12 3 8 2a 6
Suy ra: V V  . 2 9 27 Chọn B.
Câu 14: Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên 1
và phẳng đáy là thỏa mãn cos= . Mặt phẳng  P qua AC và vuông góc với mặt 3
phẳng  SAD chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa
diện là gần nhất với giá trị nào trong các giá trị sau: A. 0,11 B. 0,13 C. 0, 7 D. 0,9 Hướng dẫn giải:
S.ABCD là hình chóp tứ giác đều
SO   ABCD. S
Gọi N là trung điểm CD C
D SN ,CD ON   SCD
   ABCD  CDM
  SCD, ABCD    SNO Kẻ CM S . D Ta có: AAC BD D
AC   SBDAC SON O
AC SD SD   ACM    ACM   SADB C
nên mặt phẳng  P là  ACM  .
+ Xét tam giác SON vuông tại N có: ON 3a SN    . cosSNO 2 2 2  3a   a 2 2  SO SN ON    a 2.      2   2 
+ Xét tam giác SOD vuông tại O có:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 75
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2      aa SD SO OD a 2 2 2 10 2 2 `    .  2  2   1 1 SN.CD 3a 10 Ta có: SCM .SD
SN.CD CM   . SCD 2 2 SD 10 2  3a 10  a 10
Xét tam giác MCD vuông tại M có: 2 2 2
DM CD CM a     .  10  10   a 10 V V 1 DM DA DC 1 1 1 Ta có: M .ACD MACD 10   . . .    VV V 2V 2 DS DA DC 2 MACD SABCD a SABCD SACD 10 10 10 2
Mặt phẳng  P chia khối chóp S.ABCD thành hai khối M .ACD và 9
S.ABCM VVVVV SABCD MACD SABCM SABCM 10 SABCD V 1 Do đó: MACD   0,11 V 9 SABCM Chọn A.
Câu 15: Cho tứ diện S.ABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA  2SM ,
SN  2NB , () là mặt phẳng qua MN và song song với SC . Kí hiệu (H ) và (H ) là các 1 2
khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng () , trong đó, (H ) chứa 1 V
điểm S , (H ) chứa điểm A ; V và V lần lượt là thể tích của (H ) và (H ) . Tính tỉ số 1 . 2 1 2 1 2 V2 4 5 3 4 A. B. C. D. 5 4 4 3 Hướng dẫn giải:
Kí hiệu V là thể tích khối tứ diện SABC .
Gọi P , Q lần lượt là giao điểm của () với
các đường thẳng BC , AC . S
Ta có NP//MQ//SC . Khi chia khối (H ) bởi 1
mặt phẳng (QNC) , ta được hai khối chóp M
N.SMQC và N.QPC . V d N SAC S N SMQC ( , ( )) Ta có: . SMQC   ; V d (B, (SAC)) S N B. ASC SAC
d (N , (SAC)) NS 2 C   ; A Q d (B, (SAC)) BS 3 P B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 76
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 SAM S AMQ  4 SMQC 5       . SAS  9 S 9 ASC ASC VN SMQC 2 5 10 Suy ra .    V 3 9 27 B. ASC V d N C S N .QPC ( , (QP )) QPC   V
d (S, (A BC)) S S . ABC ABC NB CQ CP 1 1 2 2        SB CA CB 3 3 3 27 V V V N .SMQC N .QP C 10 2 4 V 4 V 4 1 1         5V  4V 1   1 2 V V V 27 27 9 V V 9 V 5 B. ASC S. ABC 1 2 2
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a 3 và SA vuông góc
với mặt phẳng đáy. Mặt phẳng (P) đi qua điểm A và vuông góc với SC cắt SB, SC, SD lần lượt tại ’ B , ’ C , ’
D . Tính thể tích khối chóp S.A ’ B ’ C ’
D theo a. 3 3 3a 3 3a 3 3 3a 3 3 5a A. B. C D. 20 20 10 10 Hướng dẫn giải:
BC AB, BC SA BC  (SAB)  BC AB ' S
SC  (P)  SC AB '  AB '  (SBC)  AB '  SB C'
Tương tự AD '  SD D' VVV
S . AB 'C ' D '
S . AB 'C '
S. AD 'C ' B' V SB ' SC '
SB '.SB SC '.SC
S . AB 'C '  .  . 2 2 V SB SC SB SC S. ABC (1) D C 2 2 SA SA 3 3 9  .  .  2 2 SB SC 4 5 20 A B 2 2 V SD ' SC '
SD '.SD SC '.SC SA SA 3 3 9
S . AD 'C '  .  .  .  .  (2) 2 2 2 2 V SD SC SD SC SD SC 4 5 20 S. ADC 3 1 1 a 3 Do 2 VV  . a .a 3  S . ABC S . ADC 3 2 6
Cộng (1) và (2) theo vế ta được 3 3 V V 9 9 9 a 3 3 3a
S . AB 'C '
S . AD 'C '     V  . 
S . AB 'C ' D ' 3 3 a 3 a 3 20 20 10 6 20 6 6 Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 77
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 17: Cho tứ diện đều ABCD cạnh a. Mặt phẳng (P) chứa cạnh BC cắt cạnh AD tại E. Biết góc 5 2
giữa hai mặt phẳng (P) và (BCD) có số đo là thỏa mãn tan  . Gọi thể tích của hai 7 V
tứ diện ABCE và tứ diện BCDE lần lượt là V và V . Tính tỷ số 1 . 1 2 V2 3 1 3 5 A. B. C. D. 8 8 5 8 Hướng dẫn giải:
+) Gọi M là trung điểm BC. A
Khi đó BC  (MAD) nên (P)(AMD); H (P)(AMD) =ME.
Kẻ AHME thì AH(BCE) (do AH  E (AMD)) K
Kẻ DKME nên DK(BCE) (do DK 
(AMD)). Hiển nhiên AH song song DK B D V V AH Khi đó 1 . A BCE   V V DK M 2 D.BCE
+) Gọi  là góc giữa (P) và (ABC) ( C  0 
). Hiển nhiên DME ; 2  AME . sin AH V Vì AM = DM nên: 1   sin  .sin  . t sin (1) sin DK V2 MO 1 1 +) Trong tam giác OMA: os
c ()    os
c  cos  sin  sin  . (2) MA 3 3 Từ (1) có: 2 2 2 2 o
c s 1 sin  1 t .sin  1 t .x ; với x=sin2. 1 1 Thay vào (2) ta có: 2 2
1 t x. 1 x t.x  
(1 t x)(1 x)  t.x  . 3 3 8
+) Giải phương trình có: x  . 2
(9t  6t  9) 2 x 8 9t  6t  9 8 Vì 2 2
sin x  tan   .  2 2 2 1 x
9t  6t  9 9t  6t 1 9t  6t 1  3 t  8 50 196 171  5 Theo giả thiết suy ra 2 2 
 9t  6t  1 
 9t  6t   0   2 9t  6t  1 49 25 25 19 t   15
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 78
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V 3 Vậy ABCE V 5 DBCE Chọn C.
Câu 18: Cho khối chóp S.ABC có SA  6, SB  2, SC  4, AB  2 10 và SBC 90, ASC 120     .
Mặt phẳng  P qua B và trung điểm N của SC và vuông góc với mặt phẳng  SAC  cắt V
cạnh SA tại M . Tính tỉ số thể tích S.MBN . VS.ABC 2 2 1 1 A. . B. . C. . D. . 9 5 6 4 Hướng dẫn giải: Chọn C S V SM SN 1 SM
Ta có: S.MBN  .  k với k  . V SA SC 2 SA S . ABC
Áp dụng định lý hàm số cosin ta có: ASB 90; BSC 60; ASC 120       H N M Đặt   
     
a  6, b  2, c  4  SA  ; a SB  ;
b SC c         . a b  0; . b c  4; . a c  12  BA
Vì  BMN    SAC  nên kẻ
BH MN , H MN BH  SAC  . C        Khi đó: BH  .
x BM  1 xBN x SM SB  1 xSN SB             1  1 x
x k a b  1 x
c b kxa b c   .  2  2     1 x    a kxa b c  0    BH SA  BH .SA  0   2 
Lại có: BH   SAC   
     BH SC      BH .SC  0  1 x  
c kxa b c  0      2   1 k  36kx  6  1 x  0   3     . 12kx  4  8  1 x  0 1  x    3 V SM SN 1 1 1 1 Vậy S.MBN  .  k  .  . V SA SC 2 2 3 6 S . ABC
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 79
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 19: Khối tứ diện ABCD có thể tích V , khối tứ diện A B C D có thể tích V , các đỉnh 1 1 1 1 1
A , B ,C , D lần lượt là trọng tâm của các tam giác BCD,CD ,
A DAB,ABC . Khối tứ diện 1 1 1 1
A B C D có thể tích V , các đỉnh A , B ,C , D lần lượt là trọng tâm của các tam giác 2 2 2 2 2 2 2 2 2
B C D , C D A , D A B , A B C . Cứ tiếp tục như thế ta được khối tứ diện A B C D có thể 1 1 1 1 1 1 1 1 1 1 1 1 n n n n
tích V , các đỉnh A , B ,C , D lần lượt là trọng tâm của các tam giác B C D , n n n n n n 1  n 1  n 1  C D A , D A B , A B C
. Tính S V V  ...  V ? n 1  n 1  n 1  n 1  n 1  n 1  n 1  n 1  n 1  1 2 2018  2018 3   1 V  2019 27   1 V A. S  . B. S  . 2018 2.3 2019 26.27  2018 27   1 V  2019 3   1 V C. S  . D. S  . 2018 26.27 2019 2.3 Hướng dẫn giải: Chọn C Ta có 3  1  1 V V V 1    3  27 3 2  1  1  1  V V V V 2   1 1    3  27  27  … 3 2018  1   1  VVV 2018   2017    3   27  2018  1  2 2018 1            2018 27   1 1 1 1 1 27 VS V    ...        V . .  2018 27   27   27  27 1 26.27   1 27
Câu 20: Cho khối lăng trụ tam giác ABC.AB C
  . Gọi M , N lần lượt thuộc các cạnh bên AA ,CC
sao cho MA MA ;
NC  4NC . Gọi G là trọng tâm tam giác ABC . Hỏi trong bốn khối tứ diện GA BC  , BB MN , ABB C   và A B
CN , khối tứ diện nào có thể tích nhỏ nhất? A. Khối A BCN . B. Khối GA BC   . C. Khối ABB C   . D. Khối BB MN . Hướng dẫn giải: Chọn A.
Gọi V là thể tích khối lăng trụ đã cho. 2 Ta có: VVVV M .BB CCA.BB CCA BB CC  3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 80
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Và 1 1 1 SSSVVV BB NCBBBB CC  . A BB C   .   2 2 A BB C C 3 Và 1 1 1 SSSVVV BB NCBBBB CCBB MN M .   2 2 BB C C 3 Chú ý: 4 2 2 4 SSSVVV BCN BCCBB CCA .  BCN A .    5 3 3 BB C C 15 . Chọn A.
Câu 21: Cho hình lăng trụ tam giác đều ABC. ’ A ’ B ’
C , có cạnh đáy bằng a và cạnh bên bằng a 2 . AM A'N 1
Lấy M , N lần lượt trên cạnh A ’ B , ’ A C sao cho 
 . Tính thể tích V của khối AB ' A'C 3 BMN ’ C C. 3 a 6 3 2a 6 3 3a 6 3 a 6 A. B. C. D. 108 27 108 27 Hướng dẫn giải:
Gọi G, K lần lượt là tâm các hình chữ nhật ABB’A’ và AA’C’C. A' C' AM 1 AM 2 Ta có:  
 (Do G trung điểm AB’). AB ' 3 AG 3 AM 2 N
Xét tam giác ABA’ có AG là trung tuyến và  . AG 3 K B' I
Suy ra M là trọng tâm tam giác ABA’. Do đó BM đi qua trung điểm I của AA’. A ' N 1 A ' N 2 G M Ta có:    (Do K là trung điểm A 'C 3 A ' K 3 A’C). A C A ' N 2
Xét tam giác AA’C’ có A’K là trung tuyến và  . A ' K 3 H
Suy ra N là trọng tâm của tam giác AA’C’. Do đó C’N đi
qua trung điểm I của AA’. B
Từ M là trọng tâm tam giác ABA’ và N là trọng tâm của tam giác AA’C’. Suy ra: IM IN 1   . IB IC ' 3
Gọi V ; V lần lượt là thể tích các khối chóp IMNC; IBCC’. Ta có: 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 81
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V IM IN IC 1 8 1  . . 
. Mà V V V . Suy ra V V . V IB IC ' IC 9 1 2 2 9 2
Hạ AH vuông góc với BC tại H thuộc BC. Ta được AH vuông góc với mặt phẳng
(BB’C’C). AA’ song song với mặt phẳng BB 'C 'C  nên khoẳng cách từ I đến mặt phẳng a 3
(BB’C’C) bằng khoẳng cách từ A đến (BB’C’C) và bằng AH. Ta có: AH  . 2 1 1 a 3 a 2 a 6 3 8 2a 6 V .d I
 ; BB 'C 'C   .S  . .  V V  2    2 3 . Suy ra .   BCC ' 3  3 2 2 12 2 9 27 Chọn B.
Câu 22: Cho khối lập phương ABC . D AB CD
  cạnh a . Các điểm E và F lần lượt là trung điểm của C B   và C D
  . Mặt phẳng  AEF  cắt khối lập phương đã cho thành hai phần, gọi V là 1 V
thể tich khối chứa điểm A và V là thể tich khối chứa điểm C ' . Khi đó 1 là 2 V2 25 17 8 A. . B. 1. C. . D. . 47 25 17 Hướng dẫn giải:
Đường thẳng EF cắt AD tại N , cắt
AB tại M , AN cắt DD tại P , AM cắt
BB tại Q . Từ đó mặt phẳng  AEF  cắt
khối lăng trụ thành hai khối đó là ABCDC Q
EFP và AQEFPB A  D . Gọi V V , V V ,
ABCD. AB CD   3 A. A MN V V , V V . 4 PFD N  4 QMB E
Do tính đối xứng của hình lập phương nên
ta có V V . 4 5 3 1 1 3a 3a 3a V AA .A M  .AN  . a .  , 3 6 6 2 2 8 3 1 1 a a a a V PD .D F  .D N   . . .  4 6 6 3 2 2 72 3 25a
V V  2V  , 1 3 4 72 3 47a V 25
V V V  . Vậy 1  . 2 1 72 V 47 2 Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 82
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 23: Cho hình lập phương ABC .
D A ' B 'C ' D ' cạnh .
a Gọi M , N lần lượt là trung điểm của
A ' B ' và BC. Mặt phẳng  DMN  chia khối lập phương đã cho thành hai khối đa diện. Gọi V   H
H  là khối đa diện chứa đỉnh ,
A H ' là khối đa diện còn lại. Tính tỉ số . VH ' V V V VH  37  H  55  H  2  H  1 A. B. C. D. V 48 V 89 V 3 V 2  H '  H '  H '  H ' Hướng dẫn giải:
AN ND J , JM BB '  K . Ta có: BK  2B ' K; I A' D '. 1 Ta có: A' I
D ' D ' . Suy ra thiết diện là KMIDN 4 VVVVVH ABA' KMIDN D. ABKMA' D.BKN D.MA' I A' M B' 3 1  1 a a  1 1 a 2a 1 1 a a 55a 2  . a a  . .  . a . .  . . a . .    I 3  2 3 2  3 2 2 3 3 2 2 4 144 K 3 3 55a 89a V 55 C' 3 H D'Va     .  H ' 144 144 V 89 H ' A B J Chọn B. N D C
Câu 24: Cho hình lập phương ABC . D AB CD   cạnh .
a Gọi M , N lần lượt là trung điểm của các cạnh ABvà BC . Mặt phẳng (DMN )
chia hình lập phương thành 2 phần. Gọi V là thể tích của phần chứa đỉnh ,
A V là thể tích 1 2 V1
của phần còn lại. Tính tỉ số . V 2 2 55 37 1 A. . B. . C. . D. . 3 89 48 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 83
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao S A' M A' M E B' B' K D' C' D' C' A A B B H N N D C D C Hướng dẫn giải
Gọi H AB DN ; MH cắt B ' B tại K , cắt A ' A tại S ; SD cắt A' D ' tại E .
Thiết diện tương ứng là ngũ giác DNKME .
Phần đa diện chứa A có thể tích là: V VVV . 1 S . ADH S. A' EM K .BNH
Dùng tam giác đồng dạng kiểm tra được: BA BH ; AH  4 A ' M ; AD  4 A ' E và 1
SA '  B ' K A ' A . 3 1 2
Đặt độ dài cạnh hình lập phương bằng 1thì: SA '  ; KB  . 3 3 1 1  1  4 Ta có: VS . A A . D AH  1 .1.2  . S . ADH   6 6  3  9 1 1 1 1 VV  ; VVS . A' EM S . 64 ADH 144 K .BNH S . 8 ADH 18 4 1 1 55
Vậy thì phần đa diện chứa A có thể tích là:    . 9 144 18 144 55 89
Suy ra phần đa diện không chứa A có thể tích là: 3 1   . 144 144 Chọn B.
Câu 25: Cho hình hộp ABCD ’ A ’ B ’ C ’
D . Gọi M là trung điểm A’B’. Mặt phẳng (P) qua BM đồng thời song song với ’ B ’
D . Biết mặt phẳng (P) chia khối hộp thành hai khối có thể tích là V
V ,V (Trong đó V F  . 1 2
1 là thể tích khối chứa A). Tính tỉ số 1 V2 7 17 8 A. . B. 1. C. . D. . 17 25 17 Hướng dẫn giải:
*Gọi N là trung điể A’D’. Khi đó  P  BDNM ).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 84
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Thấy BMDNAA’=I.
Khi đó: V1=V(A’MNABD); V2=V-V1. (Với V là thể tích hình hộp)
V (IA' MN ) S (AMN ) 1 * Ta có:   V ( A A 'B'D')
S ( A' B ' D ') 4 V (AA'B'D') 1 1 I * Mà: 
nên có: V (IA ' MN )  V V 6 24
V (IA' MN )
IA'.IM .IN 1 * Lại có:   D' C' V (IABD) I . A I . B ID 8 N 1 M
*Vậy: V (IABD)  V A' B' 3 1 1 7 17
* Do đó: V V V
V nên V V V V . 1 3 24 24 2 1 24 D C V 7 Vậy: 1  V 17 2 A B Chọn A.
Câu 26: Cho khối lăng trụ tam giác ABC. A’B’C’. Gọi I, J, K lần lượt là trung điểm của các cạnh AB,
AA’ và B’C’. Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó. 25 49 8 A. . B. 1. C. . D. . 47 95 17 Hướng dẫn giải:
Chứng minh EI = IJ = JF. Từ đó suy ra EB EM FA ' 1 FN 1    . Lại từ đó suy ra  . EB ' EK FB ' 3 FK 2 E
Ta có: d(K, A'B') = (1/2)d(C', A'B'), FB' = (3/2)A'B'. Suy ra I A B
SKFB’ = (3/4)SA’B’C’. M EB 1 C Mặt khác vì 
nên suy ra d(E, (KFB’)) = (3/2)h (h là J EB ' 3 chiều cao lăng trụ). F A' B' Do đó V N
EKFB’ = (3/8)V (V là thể tích lăng trụ). K C' V EI EM EB 1 1 1 1 EBIM  . .  . .  nên VEBIM = V EF EK EB ' 3 3 3 27 EB ' FK 1 3 1 . V V . 27 8 72 V FJ FA' FN 1 1 1 1 1 3 1 FA' JN  . .  . .  nên VFA’JN = . V V . V FE FB ' FK 3 3 2 18 18 8 48 FB ' EK
Mặt phẳng (IJK) chia khối lăng trụ thành hai phần. Gọi V1 là thể tích phần chứa điểm B' và
V2 là thể tích phần chứa điểm C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 85
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Ta có V1 = (3/8 – 1/72 – 1/48)V = (49/144)V nên V2 = (95/144)V. V 49 Do đó 1  . V 95 2 Chọn C.
CỰC TRỊ TỈ LỆ THỂ TÍCH
Câu 27: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Các điểm A , C thỏa
 1   1  mãn SA  S , A SC 
SC . Mặt phẳng  P chứa đường thẳng AC cắt các cạnh SB, SD 3 5 V lần lượt tại B ,  D và đặt S. A BCD k   
. Giá trị nhỏ nhất của k là bao nhiêu? VS.ABCD 1 1 4 15 A. . B. . C. . D. . 60 30 15 16 Hướng dẫn giải: Chọn A SB SD SA SC Đặt V V , ta có:     3  5  8 . S. ABCD SBSDSASCSBSD  1 1  Đặt x   0, y
 0   x y   4   SB SD x y   V
SASBSC 1 1 S . A BC    . .  x VxV . S. 1 SA SB SC 15 A BC   30 V 2 V
SASDSC 1 1 S . A DC    . .  y VyV . S. 1 SA SD SC 15 A DC   30 V 2
VS AB CD   1 4 1 1 Do đó . k  
x y  x y    k  . V 30 8 2 60 S. ABCD
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi C là trung điểm cạnh SC . V
Mặt phẳng  P chứa đường thẳng AC cắt các cạnh SB, SD tại B , D . Đặt S.B CD m    . VS.ABCD
Giá trị nhỏ nhất của m bằng : 2 4 1 2 A. . B. . C. . D. . 27 27 9 9 Hướng dẫn giải: Chọn C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 86
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V
SBSCSD 1 Đặt S .B CD V V     . .  xy . S. ABCD 1 SB SC SD 2 V 2 1  SBSD  1 1 SASCm xy x  ; y    ;     1 2  3 . 2  SB SD x y SA SC 1 1 2 4 1
Sử dụng bất đẳng thức AM GM ta có    xy   m  . x y xy 9 9
Câu 29: Cho khối tứ diện đều S.ABC cạnh bằng a . Mặt phẳng  P đi qua S và trọng tâm của tam V
giác ABC cắt các cạnh AB, AC lần lượt tại M , N . Đặt S. AMN m
. Giá trị nhỏ nhất của m VS.ABC bằng 2 2 4 1 A. . B. . C. . D. . 3 9 9 3 Hướng dẫn giải: Chọn C S AM AN Ta có AMN m   .  xy . A S AB AC ABC
Gọi O là trọng tâm tam giác ABC , đặt AM AN D x  ; y
x, y 0;  1  O N AB AC M
Ta có D là trung điểm của AB , giả sử
AM AD đặt AB a B C
Áp dụng định lí Meneleuys cho tam giác MD OC NA ACD có . .  1. MA OD NC a xa  2 ya 4  .2.  1  2x  
1 y x 1 y  3xy x y  2 xy m xy  . xa a ya 9
Câu 30: Cho hình chóp S.ABCD có thể tích V và đáy ABCD là hình bình hành. Mặt phẳng qua A
và trung điểm N cạnh SC cắt cạnh SB, SD lần lượt tại M , P . Tính thể tích nhỏ nhất của
khối chóp S.AMNP . V 3V V V A. . B. . C. . D. . 8 8 4 3 Hướng dẫn giải: Chọn C SA SM SN 1 SP Ta có x   1, y  , z   ,t  . SA SB SC 2 SD
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 87
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 1 1 1 1 1 Và       1 2  3 . x z y t y t xyzt  1 1 1 1  1 V 3 Do đó V     V  3  3 yt.1.  ytV . S . AMNP     4 x y z t 4 2 4   y t 2 yt 4 V Mặt khác yt    yt   V  . S. 3 3 9 AMNP 3
Câu 31: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình hình hành. Các điểm A , C thỏa
 1   1  mãn SA  , SA SC 
SC . Mặt phẳng  P chứa đường thẳng AC cắt các cạnh SB, SD 3 5 V lần lượt tại B ,  D và đặt S. A BCD k   
. Tính giá trị lớn nhất của k là bao nhiêu? VS.ABCD 4 1 4 4 A. . B. . C. . D. . 105 30 15 27 Hướng dẫn giải: Chọn A SB SD SA SC Đặt V V , ta có:     3  5  8 . S. ABCD SBSDSASCSBSD Đặt x   0, y   0 . SB SD V
SASBSC 1 1 S . A BC    . .  x VxV . S. 1 SA SB SC 15 A BC   30 V 2 V
SASDSC 1 1 S . A DC    . .  y VyV . S. 1 SA SD SC 15 A DC   30 V 2
VS AB CD   1 1 1 Do đó . k  
x y và   8 . V 30 x y S. ABCD 1 1 1 1 y
Không mất tính tổng quát, giả sử x   y  , từ   8  x  4 4 x y 8  y 1 1  y  1  k
x y   y   với  y  1. Ta có 30 30 8  y   4 1  8   1  k   1  0, y  ;1 . 30     8  y2   4    1  1  4 Vậy kk 1  1  . max     30  7  105
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 88
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 32: Cho hình chóp S.ABCD có ABCD là hình bình hành và có thể tích V . Gọi M , N thứ tự là AB 2 AD
các điểm di động trên các cạnh AB, AD sao cho 
 4 . Gọi V ' là thể tích khối AM AN
chóp S.AMN . Tìm giá trị nhỏ nhất của V ' . 1 1 1 1 A. V B. V C. V D. V 4 6 8 3 Hướng dẫn giải: Chọn A S Đặt AB 1 AD 1 1 2 2x 1  ;     4  y    x  1 AM x AN y x y 4x 1 4 2 2 V 1 AM AN 1 x x SAMN  .  xy   V '  V D V 2 AB AD 2 4x 1 4x 1 S . ABCD C N 2  x  1 1 min   x A M B    1  ;1 4x 1 4 2      4 
Câu 33: Cho hình chóp S.ABCD có ABCD là hình bình hành và có thể tích V . Gọi M , N thứ tự là AB 2 AD
các điểm di động trên các cạnh AB, AD sao cho 
 4 . Gọi V ' là thể tích khối AM AN
chóp S.MBCDN . Tìm giá trị lớn nhất của V ' . 1 2 3 1 A. V B. V C. V D. V 4 3 4 3 Hướng dẫn giải: Chọn C Đặt S AB 1 AD 1 1 2 2x 1  ;     4  y    x  1 AM x AN y x y 4x 1 4 2 2 V 1 AM AN 1 xxSAMN  .  xy   V '  1 V   V 2 AB AD 2 4x 1 4x 1 D S . ABCD   C 2  x  3 1 N max 1   x     1  A M B ;1 4x 1 4 2      4 
Câu 34: Cho hình chóp S.ABCD có thể tích V , đáy là hình bình hành. Mặt phẳng  đi qua A ,
trung điểm I của SO cắt các cạnh SB, SC, SD lần lượt tại M , N, P . Tính thể tích nhỏ nhất
của khối chóp S.AMNP . V V V 3V A. . B. . C. . D. . 18 3 6 8
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 89
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Hướng dẫn giải: Chọn C SA SM 2 SN 1 Với x   1 , y   , z   , S SA SB 3 SC 2 SP 1 1 1 1 t  ta có  
 . Xét tam giác SAC SD x z y t ta có N  P 1          SO 1  SCSO SA SC SI SA SN   2 SI 2  SNI  1   1   MSI SA SN   4  z  Mặt khác 3 điểm ,
A I , N thẳng hàng nên A D 1 1 1   1  z  . 4 4z 3 O Vậy C B 2 xyzt  1 1 1 1  2t  1  V V     V f t
V  min f t fS . AMNP         4 x y z t 3   4t    1 1  ;1  2  6  4    1 1
Dấu bằng xảy ra khi t  ; y
tức  đi qua trung điểm của SB, SD . 2 2
Câu 35: Cho hình chóp S.ABCD, SA là đường cao, đáy là hình chữ nhật với SA a, AB  , b AD  . c
Trong mặt phẳng  SDB lấy G là trọng tâm tam giác SDB , qua G kẻ đường thẳng d cắt
cạnh BS tại M, cắt cạnh SD tại N, mp  AMN  cắt SC tại K. Xác định M thuộc SB sao cho V
đạt giá trị lớn nhất và nhỏ nhất. Hãy tìm giá trị lớn nhất và nhỏ nhất đó. SAMKN abc abc abc abc A. V  ,VB. V  ,VSAMKN max SAMKN min 8 9 SAMKN max SAMKN min 8 10 abc abc abc abc C. V  ,VD. V  ,VSAMKN max SAMKN min 9 10 SAMKN max SAMKN min 10 11 Hướng dẫn giải: S
Gọi O là tâm hình chữ nhật ABC . D 2 Ta có: SG
SO và K AG SC và K là trung điểm 3 SC K V SM SA SK 1 SM 1 SM 1 SM SMAK  . .  V  . .V  .VN M . . a . b c SMAK V SB SA SC 2 SBAC SB 4 SBAC SB 12 SB G SBAC A D 1 SN Tương tự V  . . a . b c . O SNAK 12 SC B C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 90
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1  SM SN  Do đó: V   . a . b c SAMKN   12  SB SC  Trong mp  SBD : S SM SN SS S S . SG SM . SG SN SM .SN 1  SM SN SMN  . SMG SGN SMG SGN           S SB SC 2S 2S 2S 2. . SO SB 2. . SO SB . SB SC 3  SB SC SBD SBO SBO SBOSB 1 SM
Do M, N lần lượt nằm trên cạnh SB, SD nên:
SM SB    1 2 2 SB SM  1  Đặt t  ,  t  1 S   thì SN  2  SN 1  SN SN t t.  t    .   SC 3  SC SC 3t 1 H Nhận thấy V đạt GTLN, GTNN nếu: SAMKN SM SN t 1 f t    t  với  t  1. G N M SB SC 3t 1 2 2 1 9t  6t
Ta có f 't   1  D 3t  2 1 3t  2 1 O 2
Nên f 't   0  t  ,t  0 (loại). B 3  1  3 3  2  4 f  , f     1  , f  .    2  2 2  3  3 abc Do vậy V
là GTLN khi M là trung điểm SB hoặc M trùng với . B SAMKN 8 abc V
là GTNN khi MB chiếm 1 phần S . B SAMKN 9 Chọn A.
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Các điểm A ',C ' thỏa mãn
 1   1  SA '  SA , SC ' 
SC . Mặt phẳng  P chứa đường thẳng A'C ' cắt các cạnh SB, SD lần 3 5 V
lượt tại B ', D ' và đặt
S. A' B 'C ' D ' k
. Giá trị lớn nhất của k là? VS.ABCD 4 1 4 4 A. . B. . C. . D. . 105 30 15 27 Hướng dẫn giải: Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 91
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao SB SD SA SC Đặt V V , ta có     3  5  8 S. ABCD SB' SD' SA' SC' V SA' ' SB SC' 1 1
Mặt khác S.A'B'C '  . .  x VxV 1 SA SB SC 15
S. A' B 'C ' 30 V 2 V ' SA ' SD SC' 1
S . A'C ' D '  . .  y 1 SA SD SC 15 V 2 1  VyV
S. A'C ' D ' 30 V 1 Do đó
S. A' B 'C ' D ' k  
x y , trong đó V 30 S. ABCD SB' ' SD x  , y SB SD Và 1  x  4
k f (x)  x
 max f (x)  f (1)     1 30  8x 1   ;1 105  8    .
Câu 37: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật. Một mặt phẳng song song với đáy
cắt các cạnh bên SA , SB , SC , SD lần lượt tại M , N , P , Q . Gọi M  , N  , P , Q lần lượt SM
là hình chiếu của M , N , P , Q trên mặt phẳng đáy. Tìm tỉ số
để thể tích khối đa diện SA MNP . Q M NPQ
  đạt giá trị lớn nhất. 3 2 1 1 A. . B. . C. D. . 4 3 2 3 Hướng dẫn giải: Chọn B. S SM Đặt
x 0  x  
1 , kí hiệu V , h lần lượt SA
là thể tích và chiều cao của khối chóp đã cho, Q M MN NP PQ SM theo Thales ta có:     x ; AB BC CD SA N P A
d M , ABCD D AM và   1 x M' Q'
d S, ABCD SA
d M , ABCD  1 xh . P' N' B C Vì vậy: VMN.M . Q d M , ABCD MNPQ.M NPQ      2
x 1 x.A . B A . D h 2
 3x 1 xV .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 92
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Sử dụng bất đẳng thức AM GM ta có: 3 1
1  x x  2  2x  4 2
x 1 x  . x .
x 2  2x     . 2 2  3  27 4 2 Do đó V
V . Dấu "  " xảy ra  x  2  2x x  . MNPQ.M NPQ   9 3 Chọn B.
Câu 38: Cho khối chóp S.ABC . Một mặt phẳng song song với đáy cắt các cạnh bên SA , SB , SC
lần lượt tại M , N , P . Gọi M  , N  , P lần lượt là hình chiếu của M , N , P trên mặt phẳng SM đáy. Tìm tỉ số
để thể tích khối đa diện MN . P M NP
  đạt giá trị lớn nhất. SA 3 2 1 1 A. . B. . C. . D. . 4 3 2 3 Hướng dẫn giải: Chọn B. S SM Đặt
x 0  x  
1 , kí hiệu V , h lần lượt SA
là thể tích và chiều cao của khối chóp đã cho, P M MN NP MP SM theo Thales ta có:     x ; N AB BC CA SA
d M , ABC  AM và   1 x A C
d S, ABC  SA M' P'
d M , ABC   1 xh ; 2 Sx S . MNP ABC N' Vì vậy: VS .d M , ABC MNP.M NP   MNP    B 2
x 1 x.S .h 2
 3x 1 xV . ABC
Sử dụng bất đẳng thức AM GM ta có: 3 1
1  x x  2  2x  4 2
x 1 x  . x .
x 2  2x     . 2 2  3  27 4 2 Do đó V
V . Dấu "  " xảy ra  x  2  2x x  . MNPQM NP   9 3 Chọn B.
Câu 39: Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích là V . Điểm P là trung
điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi V
V là thể tích của khối chóp S.AMPN. Tìm giá trị nhỏ nhất của 1 ? 1 V 1 2 3 1 A. . B. . C. . D. . 8 3 8 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 93
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao Hướng dẫn giải: Chọn D.
Gọi O là tâm của hình bình hành ABCD . G là trọng tâm tam giác SAC . 1
Ta có M ,G, N thẳng hàng. Do ABCD là hình bình hành nên VVV . S . ADC S . ABC S . 2 ABCD
Theo công thức tỉ số thể tích ta có: V SM SP V 1 SM V 1 SM S . AMP S . AMP S.  . AMP     V SD SC 1 2 SD V 4 SD S . ADC S. ABCD VS. 2 ABCD Tương tự V SN SP V 1 SN V 1 SN S. ANP S . ANP S .  . ANP     S V SB SC 1 2 SB V 4 SB S . ABC S. ABCD VS. 2 ABCD V V 1  SM SN S . AMP S. ANP      V V 4  SD SB M
Từ đó suy ra S.ABCD S . ABCD V 1  SM SN P S . AMNP    G   V 4  SD SB S. ABCDD A V 1  SM SN  Hay 1   N   V 4  SD SB O SD SB Ta chứng minh   3 . B C SM SN
Thậy vậy, qua B, D kẻ các đường song song với MN cắt SO lần lượt tại E, F . SD SF SB SE SD SB SE SF Ta có:  ;     S SM SG SN SG SM SN SG SD SB 2SO 3     2.  3 SM SN SG 2 M G SD SB N E Đặt  ; x
y . Ta có x y  3 SM SN D B O F V 1  SM SN  1  1 1  x y 3 3 1 Mặt khác 1             V 4  SD SB  4 x y 4xy 4xy    x y2 3 V 1 Vậy 1 nhỏ nhất bằng . V 3
Câu 40: Cho hình chóp S.ABC có ASB BSC CSA 30      
và SA SB SC a . Mặt phẳng
P qua A cắt hai cạnh SB, SC lần lượt tại B ,C sao cho chu vi tam giác AB C   nhỏ nhất. V
Gọi V ,V lầ lượt là thể tích các khối chóp S.AB C
 , S.ABC . Tính tỉ số 1 . 1 2 V2 V V V V A. 1  3  2 2 . B. 1  3 1 . C. 1  4  2 3 . D. 1  2 1 . V V V V 2 2 2 2 Hướng dẫn giải: Chọn C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 94
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao SBSCV SBSC Đặt 1  , xy   .  . x y . SB SC V SB SC 2 Khi đó: 2 2 2
AB  SA SB  2. . SA SB .cos ASB . S
a  ax2 2  2  2. . a .
ax cos 30  a  2
1 3x x C' B' 2
AB  a 1 3x x Tương tự: 2
AC  a 1 3y y , B 2 2 B C
   a x  3xy y A Ta có:
2 p AB  AC  B C   C  2 2 2 2 a 1 3x x 1 3y y x 3xy y             2 2  2 2   3  1  3     1  2 a   y     y x x 1 3x x               2  2  2  2            2 2  3 3   1 1  2 2 2  a   x    x
a 1 3x x a( 1 x x  1 3x x )   .  2 2   2 2    2 2 2 2  2 2  1  3   3  1  3 1   1 3      a x      x          a           a 2 .   2   2   2   2    2 2   2 2             3 y x V Dấu bằng xảy ra khi: 2 x
, x  3 1  x y  3 1    3  2 1 1  4  2 3 . 3 V2  y 2   
Câu 41: Cho khối chóp S.ABC có SA SB SC a ASB  60 , BSC  90 , ASC  120 . Gọi CN AM
M , N lần lượt là các điểm trên cạnh AB và SC sao cho  . Khi khoảng cách giữa SC AB
M và N nhỏ nhất, tính thể tích V của khối chóp S.AMN . 3 2a 3 5 2a 3 5 2a 3 2a A. . B. . C. . D. . 72 72 432 432 Hướng dẫn giải: Chọn C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 95
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 3 3 a  1   1  2a
Ta có thể tích khối chóp S.ABC à V  1    . 0     6  2   2  12 CN AM Đặt 
m 0  m   1 , ta có SC AB
         2 2   a     a
SA a, SB b, SC c , a b c a , . a b  , . b c  0, . a c   . 2 2
Theo đẳng thức trên ta có đẳng thức vectơ 
        
SN  1 mc, SM SA AM a mAB a mb a.
       MN SN SM
1 mc a m b a           S    .  m  
1 a mb  1 mc Do đó    MN   2 2 m  
1 a mb  1 mc c . 2 a   11a 2
3m  5m  3 2 a N 12 b Dấu bằng xảy ra tại 5 SN SN AM C A m   V  .V  . .V S . AMC 0 6 SC SC AB . 3 3 5 1 2a 5 2a M
m 1 mV  . .  0 6 6 12 432 B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 96
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
ỨNG DỤNG THỰC TẾ
A – BÀI TẬP TRẮC NGHIỆM Câu 1:
Kim tự tháp Cheops (có dạng hình chóp) là kim tự tháp cao nhất ở Ai Cập. Chiều cao của
kim tự tháp này là 144 m , đáy của kim tự tháp là hình vuông có cạnh dài 230 m . Các lối đi
và phòng bên trong chiếm 30% thể tích của kim tự tháp. Biết một lần vận chuyển gồm 10
xe, mỗi xe chở 6 tấn đá, và khối lượng riêng của đá bằng 3 3
2,5.10 kg / m . Số lần vận
chuyển đá để xây đủ dựng kim tự tháp là: A. 740600 . B. 76040 . C. 7406 . D. 74060 . Câu 2:
Một hộp đựng chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một
phần tư thể tích phía trên của hộp được dải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa
đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi x x là giá trị làm cho hộp 0
kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị là V . Tìm V . 0 0 64 A. 48 đvtt B. 16 đvtt C. 64 đvtt D. đvtt 3 Câu 3:
Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình
vuông trên một mặt) là 4cm. A. 27 cm3. B. 1728 cm3. C. 1 cm3. D. 9 cm3. Câu 4:
Cắt một miếng giấy hình vuông ở hình 1 và xếp thành một hình chóp tứ
giác đều như hình 2 . Biết cạnh hình vuông bằng 20cm , OM x cm .
Tìm x để hình chóp đều ấy có thể tích lớn nhất?
A. x  9cm .
B. x  8cm .
C. x  6cm .
D. x  7cm . Câu 5:
Người ta muốn xây một bể chứa nước dạng khối 1dm
hộp chữ nhật trong một phòng tắm. Biết chiều dài,
chiều rộng, chiều cao của khối hộp đó lần lượt là 1dm
3m ; 1, 2m ; 1,8m (người ta chỉ xây hai mặt thành
bể như hình vẽ bên). Biết mỗi viên gạch có chiều
dài 20cm , chiều rộng 10cm , chiều cao 5cm . Hỏi 1,8dm
người ta sử dụng ít nhất bao nhiêu viên gạch để
xây bể đó và thể tích thực của bể chứa bao nhiêu 1,2m
lít nước? (Giả sử lượng xi măng và cát không đáng 3m
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 97
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao kể).
A. 738 viên, 5742 lít. B. 730 viên, 5742 lít.
C. 738 viên, 5740 lít. D. 730 viên, 5740 lít. Câu 6:
Cho một cây nến hình lăng trụ lục gác đều có chiều cao và độ dài cạnh đáy lần lượt là 15cm
và 5cm . Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho
cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng A. 1500 ml . B. 600 6 ml . C. 1800 ml . D. 750 3 ml . Câu 7:
Một miếng bìa hình tròn có bán kính là 20cm . Trên biên của miếng bìa, ta xác định 8 điểm , A B,C, ,
D E, F,G, H theo thứ tự chia đường tròn thành 8 phần bằng nhau. Cắt bỏ theo các
nét liền như hình vẽ để có được hình chữ thập ABNCDPEFQGHM rồi gấp lại theo các nét
đứt MN, NP, PQ,QM tạo thành một khối hộp không nắp. Thể tích của khối hộp thu được là: 4000 2  2  4  2 2   3 4000 2 2 A. B. . 2 2
C. 40002  2 4  2 2 . D.   3 4000 2 2 . Câu 8:
Cho một tấm nhôm hình chữ nhật ABCD có AD  60cm , AB  40cm . Ta gập tấm nhôm
theo hai cạnh MN và PQ vào phía trong cho đến khi AB và DC trùng nhau như hình vẽ
bên để dược một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể tích lớn nhất bằng A. 4000 3  3 cm B. 2000 3  3 cm C. 400 3  3 cm D. 4000 2  3 cm Câu 9:
Cho một tấm nhôm hình chữ nhật ABCD có AD  60cm . Ta gấp tấm nhôm theo 2 cạnh
MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ dưới đây để được
một hình lăng trụ khuyết hai đáy. Tìm x để thể tích khối lăng trụ lớn nhất?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 98
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao A. x  20 . B. x  15 . C. x  25 . D. x  30 .
Câu 10: Một khối gỗ hình lập phương có độ dài cạnh bằng x cm. Ở chính giữa mỗi mặt của hình
lập phương, người ta đục một lỗ hình vuông thông sang mặt đối diện, tâm của lỗ hình vuông
là tâm của mặt hình lập phương, các cạnh lỗ hình vuông song song với các cạnh của hình lập
phương và có độ dài y cm như hình vẽ bên. Tìm thể tích V của khối gỗ sau khi đục biết
rằng x  80 c ; m y  20 c . m A. 3 490000 cm . B. 3 432000 cm . C. 3 400000 cm . D. 3 390000 cm .
Câu 11: Một khối gỗ hình lập phương có độ dài cạnh bằng x cm .Ở chính giữa mỗi mặt của hình lập
phương, người ta đục một lỗ hình vuông thông sang mặt đối diện,tâm của lỗ hình vuông là
tâm của mặt hình lập phương,các cạnh lỗ hình vuông song song với cạnh của hình lập S
phương và có độ dài y cm (như hình vẽ bên).Tính tỉ số
,trong đó V của khối gỗ sau khi V
đục và S là tổng diện tích mặt (trong và ngoài)khối gỗ sau khi đục. S
6  x  3yS 3 x  3yA.  . B.  . V
x y x  2yV
x y x  2y
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 99
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao S
2  x  3yS 9 x  3yC.  . D.  . V
x y x  2yV
x y x  2y
Câu 12: Cần phải xây dựng một hố ga, dạng hình hộp chữ nhật có thể tích  3
V m  , hệ số k cho trước
( k - tỉ số giữa chiều cao của hố và chiều rộng của đáy). Gọi x, y, h  0 lần lượt là chiều
rộng, chiều dài và chiều cao của hố ga. Hãy xác định x, y, h  0 xây tiết kiệm nguyên vật
liệu nhất. x, y, h lần lượt là 2k   1 V 2kV k 2k   1 V A. 3 3 x  2 ; y  3 ; h  . 2 4k 2k  2 1 4 2k   1 V 2kV k 2k   1 V B. 3 3 x  ; y  3 ; h  2 . 2 4k 2k  2 1 4 2k   1 V 2kV k 2k   1 V C. 3 3 x  ; y  2 3 ; h  . 2 4k 2k  2 1 4 2k   1 V 2kV k 2k   1 V D. 3 3 x  ; y  6 3 ; h  . 2 4k 2k  2 1 4
Câu 13: Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt bỏ các tam giác
cân bên ngoài của tấm nhôm, phần còn lại gập thành một hình chóp tứ giác đều có cạnh đáy
bằng x m , sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Tìm x để
khối chóp nhận được có thể tích lớn nhất. 2 2 1 2 2 A. x B. x C. x D. x  5 2 4 3
Câu 14: Một viên đá có dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng a , người ta cưa viên
đá theo mặt phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có
thể tích bằng nhau. Tính diện tích thiết diện của viên đá bị cưa bởi mặt phẳng nói trên. 2 a 2 a 2 a 2 a A. . B. . C. . D. . 3 4 3 4 3 4 3 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 100
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 15: Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 3
1, 296m . Người thợ này cắt các
tấm kính ghép lại một bể cá dạng hình hộp chữ nhật với ba kích thước , a ,
b c như hình vẽ. Hỏi người thợ c
phải thiết kế các kích thước , a ,
b c bằng bao nhiêu để
đỡ tốn kính nhất, giả sử độ dày của kính không đáng kể. b a A. a  3, 6 ; m b  0, 6 ; m c  0, 6m B. a  2, 4 ; m b  0,9 ; m c  0, 6m C. a  1,8 ; m b  1, 2 ; m c  0, 6m D. a  1, 2 ; m b  1, 2 ; m c  0,9m
Câu 16: Khi xây nhà, chủ nhà cần làm một hồ nước bằng gạch và xi măng có dạng hình hộp đứng
đáy là hình chữ nhật có chiều dài gấp ba lần chiều rộng và không nắp, có chiều cao là h và
có thể tích là . Hãy tính chiều cao của hồ nước sao cho chi phí xây dựng là thấp nhất? 3 5 A. m
B. h  2 m C. h m D. h m 2 2
Câu 17: Người ta muốn thiết kế một bể cá bằng kính không có nắp với thể tích 3 72dm và chiều cao là 3d .
m Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước ,
a b (đơn vị dm) như hình vẽ. 3 dm b dm a dm Tính ,
a b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bề dày các tấm kính
như nhau và không ảnh hưởng đến thể tích của bể. A. a  24, b  24.
B. a  3, b  8.
C. a  3 2, b  4 2. D. a  4, b  6.
Câu 18: Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 1,296 m3.
Người thợ này cắt các tấm kính ghép lại một bể cá dạng hình
hộp chữ nhật với 3 kích thước a, b, c như hình vẽ. Hỏi người
thợ phải thiết kế các kích thước a, b, c bằng bao nhiêu để đỡ
tốn kính nhất, giả sử độ dầy của kính không đáng kể. A. a  3, 6 ; m b  0, 6 ; m c  0, 6m B. a  2, 4 ; m b  0, 9 ; m c  0, 6m C. a  1,8 ; m b  1, 2 ; m c  0, 6m D. a  1, 2 ; m b  1, 2 ; m c  0,9m
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 101
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 19: Từ một tấm tôn có kích thước 90cmx3m người ta làm một máng xối nước trong đó mặt cắt
là hình thang ABCD có hinh dưới. Tính thể tích lớn nhất của máng xối. A D 30cm 30cm 90cm 3m 3m B 30cm C A. 3 40500 3cm B. 3 40500 2cm C. 3 40500 6cm D. 3 40500 5cm
Câu 20: Để làm một máng xối nước, từ một tấm tôn kích thước 0,9m 3m người ta gấp tấm tôn đó
như hình vẽ dưới. Biết mặt cắt của máng xối (bị cắt bởi mặt phẳng song song với hai mặt
đáy) là một hình thang cân và máng xối là một hình lăng trụ có chiều cao bằng chiều dài của
tấm tôn. Hỏi x m bằng bao nhiêu thì thể tích máng xối lớn nhất? x 3 m 0, 3 m x m x 0, 9 m 0, 3 m 3 m 0, 3 m 0, 3 m (a) Tấm tôn (b) Máng xối (c) Mặt cắt
A. x  0,5m .
B. x  0, 65m .
C. x  0, 4m .
D. x  0, 6m .
Câu 21: Khi xây dựng nhà, chủ nhà cần làm một bể nước bằng gạch có dạng hình hộp có đáy là hình
chữ nhật chiều dài d m và chiều rộng r m với d  2r. Chiều cao bể nước là hm và thể tích bể là 3
2 m . Hỏi chiều cao bể nước như thế nào thì chi phí xây dựng là thấp nhất? 3 3 2 3 2 2 A.m . B. 3 m . C. 3 m . D.m . 2 2 3 2 3 3
Câu 22: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là V . Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng 2 1 A. 3 x V B. 3 x V C. 4 x V
D. x V
Câu 23: Nhân ngày quốc tế phụ nữ 8-3 năm 2017, ông A quyết định mua tặng vợ một món quà và
đặt nó vào trong một chiếc hộp có thể tích là 32 ( đvtt ) có đáy hình vuông và không có nắp.
Để món quà trở nên thật đặc biệt và xứng đáng với giá trị của nó ông quyết định mạ vàng
cho chiếc hộp, biết rằng độ dạy lớp mạ tại mọi điểm trên hộp là như nhau. Gọi chiều cao và
cạnh đáy của chiếc hộp lần lượt là h; x . Để lượng vàng trên hộp là nhỏ nhất thì giá trị của h; x phải là?
A. x  2; h  4 B. x  4; h  3 2
C. x  4; h
D. x  1;h  2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 102
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 24: Một ngôi nhà có nền dạng tam giác đều ABC cạnh dài 10 m được đặt song song và cách
mặt đất h m . Nhà có 3 trụ tại ,
A B, C vuông góc với  ABC  . Trên trụ A người ta lấy hai
điểm M , N sao cho AM x, AN y và góc giữa  MBC  và  NBC  bằng 90 để là mái và
phần chứa đồ bên dưới. Xác định chiều cao thấp nhất của ngôi nhà. A. 5 3 . B. 10 3 . C. 10 . D. 12 .
Câu 25: Một nhà sản xuất sữa có hai phương án làm hộp sữa. Hộp sữa có dạng khối hộp chữ nhật
hoặc hộp sữa có dạng khối trụ. Nhà sản xuất muốn chi phí bao bì càng thấp càng tốt(tức diện
tích toàn phần của hộp nhỏ nhất), nhưng vẫn phải chứa được một thể tích xác định là V cho
trước. Khi đó diện tích toàn phần của hộp sữa bé nhất trong hai phương án là A. 3 2 2V . B. 3 2 6 V . C. 3 2 3 6V . D. 3 2 3 2V .
Câu 26: Một bác thợ gò hàn làm một chiếc thùng hình hộp chữ nhật (không nắp) bằng tôn thể tích 3
665,5 dm . Chiếc thùng này có đáy là hình vuông cạnh x(d ) m , chiều cao ( h d ) m . Để làm
chiếc thùng, bác thợ phải cắt một miếng tôn như hình vẽ. Tìm x để bác thợ sử dụng ít nguyên liệu nhất. h h x x h h A. 10, 5(dm) . B. 12(dm) . C. 11(dm) . D. 9(dm) .
Câu 27: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là V . Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng 2 1 A. 3 x V B. 3 x V C. 4 x V
D. x V
Câu 28: Người ta muốn xây một bồn chứa nước dạng khối hộp chữ nhật trong một phòng tắm. Biết
chiều dài, chiều rộng, chiều cao của khối hộp đó lần lượt là 5m, 1m, 2m (hình vẽ bên). Biết
mỗi viên gạch có chiều dài 20cm, chiều rộng 10cm, chiều cao 5cm. Hỏi người ta sử dụng ít
nhất bao nhiêu viên gạch để xây bồn đó và thể tích thực của bồn chứa bao nhiêu lít nước?
(Giả sử lượng xi măng và cát không đáng kể)
A. 1180 viên, 8820 lít
B. 1180 viên, 8800 lít
C. 1182 viên, 8820 lít
D. 1180 viên, 8800 lít
Câu 29: Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng
lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác
cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng
trụ tam giác đều (như hình vẽ). Gọi V ,V lần lượt là thể tích của lăng trụ tứ giác đều và lăng 1 2
trụ tam giác đều. So sánh V và V . 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 103
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
A. V V
B. V V
C. V V D. Không so sánh 1 2 1 2 1 2 được
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 104
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
B – HƯỚNG DẪN GIẢI Câu 1:
Kim tự tháp Cheops (có dạng hình chóp) là kim tự tháp cao nhất ở Ai Cập. Chiều cao của
kim tự tháp này là 144 m , đáy của kim tự tháp là hình vuông có cạnh dài 230 m . Các lối đi
và phòng bên trong chiếm 30% thể tích của kim tự tháp. Biết một lần vận chuyển gồm 10
xe, mỗi xe chở 6 tấn đá, và khối lượng riêng của đá bằng 3 3
2,5.10 kg / m . Số lần vận
chuyển đá để xây đủ dựng kim tự tháp là: A. 740600 . B. 76040 . C. 7406 . D. 74060 . Hướng dẫn giải: Chọn D.
Gọi cạnh của hình chóp là a  230 ,chiều cao h  144 1 Thể tích kim tự tháp: 2 3 V ha  2 539 00 2 m 3
Thể tích khối đá cần vận chuyển 3
0.7V  1777 440m .
Gọi x là số lần vận chuyển. Để đủ đá xây dựng kim tự tháp thì Câu 2:
Một hộp đựng chocolate bằng kim loại có hình dạng lúc
mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên của hộp được dải một lớp bơ
sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình
vẽ, gọi x x là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate 0
nguyên chất có giá trị là V . Tìm V . 0 0 64 A. 48 đvtt B. 16 đvtt C. 64 đvtt D. đvtt 3 Hướng dẫn giải:
Phân tích: Đây là một dạng bài toán ứng dụng thực thể kết hợp với cả phần tính thể tích khối
đa diện ở hình học và phần tìm giá trị lớn nhất, giá trị nhỏ nhất của một đa thức đã học ở
chương I phần giải thích.
Trước tiên ta nhận thấy
V    x
xx x x  2 6 12 2 2 6  x  2 x x   3 2 2 12
36  2x  24x  72x
Xét hàm số f x 3 2
 2x  24x  72x trên 0;6
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 105
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao x  6 f ' x 2
 6x  48x  72; f ' x  0  x  2 
Khi đó max f x  f 2  64 đvtt. Đến đây nhiều quý độc gỉ vội vã khoanh C mà không 0;6
đắn đo gì. Tuy nhiên, nếu vội vã như vậy là bạn đã sai, bởi đề bài yêu cầu tìm thể tích 1 3
chocolate nguyên chất mà không phải là thể tích hộp do đó ta cần. Tức là 1  thể tích 4 4 3
hộp. tức là .64  48 đvtt 4 Câu 3:
Tính thể tích khối rubic mini (mỗi mặt của rubic có 9 ô vuông), biết chu vi mỗi ô (ô hình
vuông trên một mặt) là 4cm. A. 27 cm3. B. 1728 cm3. C. 1 cm3. D. 9 cm3. Hướng dẫn giải:
Đây là một bài toán ăn điểm, nhưng nếu đọc không kĩ từng câu chữ trong đề bài các độc giả rất có thể sai Ta có khối rubic như sau:
Hướng sai 1: Nghĩ rằng mỗi cạnh của ô vuông là 4 nên chiều dài mỗi cạnh của khối rubic là 3
a  4.3  12  V  12  1728  B
Hướng sai 2: Nghĩ rằng chu vi mỗi ô vuông là tổng độ dài của cả 12 cạnh nên chiều dài mỗi 1 1 cạnh là
, nên độ dài của khối rubik là 3
a  .3  1  V  1  1  C 3 3
Hướng sai 3: Nhầm công thức thể tích sang công thức tính diện tích nên suy ra ý D.
Cách làm đúng: Chu vi của một ô nhỏ là 4 cm nên độ dài mỗi cạnh nhỏ là 1cm, vậy độ dài cạnh của khối rubic là 3
a  3.1  3cm V  3.3.3  27 cm . Chọn A. Câu 4:
Cắt một miếng giấy hình vuông ở hình 1 và xếp thành một hình chóp tứ
giác đều như hình 2 . Biết cạnh hình vuông bằng 20cm , OM x cm .
Tìm x để hình chóp đều ấy có thể tích lớn nhất?
A. x  9cm .
B. x  8cm .
C. x  6cm .
D. x  7cm . Hướng dẫn giải: Chọn B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 106
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Ta có: OM x AC  2x , AM  2x . x x x Suy ra: OH  , MH  , SH  10 2  . S 2 2 2 2 2  10 x   x 2 2  SO SH OH     20     10  xA M  2 2   2  x H O D C 1 1 20 V S . O S  20  x x   x x đáy 10  2 2 .2 40 4 . 3 3 3 5 15 20 20
 40  4x x x x x  20  V  40  4x 2 . . x . x . x   .2   3 3  5  3
Dấu "  " xảy ra khi 40  4x x x  8 . Câu 5:
Người ta muốn xây một bể chứa nước dạng khối 1dm
hộp chữ nhật trong một phòng tắm. Biết chiều dài,
chiều rộng, chiều cao của khối hộp đó lần lượt là 1dm
3m ; 1, 2m ; 1,8m (người ta chỉ xây hai mặt thành
bể như hình vẽ bên). Biết mỗi viên gạch có chiều
dài 20cm , chiều rộng 10cm , chiều cao 5cm . Hỏi 1,8dm
người ta sử dụng ít nhất bao nhiêu viên gạch để
xây bể đó và thể tích thực của bể chứa bao nhiêu 1,2m
lít nước? (Giả sử lượng xi măng và cát không đáng kể). 3m
A. 738 viên, 5742 lít. B. 730 viên, 5742 lít.
C. 738 viên, 5740 lít. D. 730 viên, 5740 lít. Hướng dẫn giải: Chọn A.
Thể tích của bể là V  18.11.29  5742 l  .
Thể tích của 1 viên gạch là 3
1dm , thể tích cần xây dựng là 3
(30 11).18  738dm , suy ra số
viên ít nhất cần dùng là 738 viên. Câu 6:
Cho một cây nến hình lăng trụ lục gác đều có chiều cao và độ dài cạnh đáy lần lượt là 15cm
và 5cm . Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho
cây nến nằm khít trong hộp. Thể tích của chiếc hộp đó bằng A. 1500 ml . B. 600 6 ml . C. 1800 ml . D. 750 3 ml . Hướng dẫn giải:
Ta có AB  10 cm,AD=5 3 cm S  50 3 ABCD
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 107
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V S .h  750 3 ABCD Chọn D Câu 7:
Một miếng bìa hình tròn có bán kính là 20cm . Trên biên của miếng bìa, ta xác định 8 điểm , A B,C, ,
D E, F,G, H theo thứ tự chia đường tròn thành 8 phần bằng nhau. Cắt bỏ theo các
nét liền như hình vẽ để có được hình chữ thập ABNCDPEFQGHM rồi gấp lại theo các nét
đứt MN, NP, PQ,QM tạo thành một khối hộp không nắp. Thể tích của khối hộp thu được là: 4000 2  2  4  2 2   3 4000 2 2 A. B. . 2 2
C. 40002  2 4  2 2 . D.   3 4000 2 2 . Hướng dẫn giải: Chọn C. Theo giả thuyết ta có 2
AB CD EF GH MN NP PQ QM  2r sin 8.2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 108
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 cos 4  40sin  40  20 2  2 8 2 Và AH
MH MA NB NC PD PE QG QH   10 4  2 2 2 2  
Vì vậy V MN.M . Q MA  20 2  2 .10 4  2 2  4000   2  2 4  2 2   Câu 8:
Cho một tấm nhôm hình chữ nhật ABCD có AD  60cm , AB  40cm . Ta gập tấm nhôm
theo hai cạnh MN và PQ vào phía trong cho đến khi AB và DC trùng nhau như hình vẽ
bên để dược một hình lăng trụ khuyết hai đáy. Khi đó có thể tạo được khối lăng trụ với thể tích lớn nhất bằng A. 4000 3  3 cm B. 2000 3  3 cm C. 400 3  3 cm D. 4000 2  3 cm Hướng dẫn giải: Chọn A.
Đáy của lăng trụ là tam giác cân có
cạnh bên bằng x , cạnh đáy bằng 60  2x
Đường cao tam giác đó là 2  60  2x 2  AH x   60x  900   ,  2 
với H là trung điểm NP Diện tích đáy là 1 1 S S
AH .NP  60x  900.  x x   xx ANP 30  60
900900 30 900 30  2 30 3 1  900   S   100 3    2 cm  30  3 
Diện tích đáy lớn nhất là 2
100 3cm nên thể tích lớn nhất là V    3 40.100 3 4000 3 cm  . Câu 9:
Cho một tấm nhôm hình chữ nhật ABCD có AD  60cm . Ta gấp tấm nhôm theo 2 cạnh
MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ dưới đây để được
một hình lăng trụ khuyết hai đáy. Tìm x để thể tích khối lăng trụ lớn nhất?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 109
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao A. x  20 . B. x  15 . C. x  25 . D. x  30 . Hướng dẫn giải: Chọn A.
Ta có PN  60  2x , gọi H là trung điểm của PN suy ra AH  60x  900 1 S  .  x x    x x
f x , do chiều cao của khối ANP 60 2  60 900 60 2  15 225    2
lăng trụ không đổi nên thể tích khối lăng trụ max khi f x max. 45 x  20 f ' x 
 0  x  20, f 20  100 3, f 15  0 15x  225
max f  x  100 3 khi x  20
Câu 10: Một khối gỗ hình lập phương có độ dài cạnh bằng x cm. Ở chính giữa mỗi mặt của hình
lập phương, người ta đục một lỗ hình vuông thông sang mặt đối diện, tâm của lỗ hình vuông
là tâm của mặt hình lập phương, các cạnh lỗ hình vuông song song với các cạnh của hình lập
phương và có độ dài y cm như hình vẽ bên. Tìm thể tích V của khối gỗ sau khi đục biết
rằng x  80 c ; m y  20 c . m A. 3 490000 cm . B. 3 432000 cm . C. 3 400000 cm . D. 3 390000 cm . Hướng dẫn giải: Chọn B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 110
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Thể tích cần tìm bằng thể tích khối lập phương ban đầu trừ đi 6 khối hộp chữ nhật có đáy là x y
hình vuông cạnh y cm , chiều cao
cm; rồi trừ đi thể tích khối lập phương có độ dài 2
cạnh bằng y cm . Vì vậy,  x y  80  20 3 2 3 3 2 3 V x  6
y y  80  6. .20  20  432000    3 cm .  2  2
Câu 11: Một khối gỗ hình lập phương có độ dài cạnh bằng x cm .Ở chính giữa mỗi mặt của hình lập
phương, người ta đục một lỗ hình vuông thông sang mặt đối diện,tâm của lỗ hình vuông là
tâm của mặt hình lập phương,các cạnh lỗ hình vuông song song với cạnh của hình lập S
phương và có độ dài y cm (như hình vẽ bên).Tính tỉ số
,trong đó V của khối gỗ sau khi V
đục và S là tổng diện tích mặt (trong và ngoài)khối gỗ sau khi đục. S
6  x  3yS 3 x  3yA.  . B.  . V
x y x  2yV
x y x  2yS
2  x  3yS 9 x  3yC.  . D.  . V
x y x  2yV
x y x  2yHướng dẫn giải: Chọn A
Thể tích hình cần tính bằng thể tích khối lập phương ban đầu trừ đi 6 khối hộp chữ nhật có x y
đáy là hình vuông cạnh y cm ,chiều cao
cm ,rồi trừ đi thể tích khối lập phương có độ 2
dài cạnh bằng y cm .  x y  2 Vì vậy: 3 2 3 V x  6 y y   
x y  x  2y .  2  Tổng diện tích các mặt của khối gỗ sau khi đục là y x y V  6  ( ) 2 2
x y   6.4.
 6 x y x  3y 2 S
6  x  3y Vậy  . V
x y x  2yChọn A
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 111
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 12: Cần phải xây dựng một hố ga, dạng hình hộp chữ nhật có thể tích  3
V m  , hệ số k cho trước
( k - tỉ số giữa chiều cao của hố và chiều rộng của đáy). Gọi x, y, h  0 lần lượt là chiều
rộng, chiều dài và chiều cao của hố ga. Hãy xác định x, y, h  0 xây tiết kiệm nguyên vật
liệu nhất. x, y, h lần lượt là 2k   1 V 2kV k 2k   1 V A. 3 3 x  2 ; y  3 ; h  . 2 4k 2k  2 1 4 2k   1 V 2kV k 2k   1 V B. 3 3 x  ; y  3 ; h  2 . 2 4k 2k  2 1 4 2k   1 V 2kV k 2k   1 V C. 3 3 x  ; y  2 3 ; h  . 2 4k 2k  2 1 4 2k   1 V 2kV k 2k   1 V D. 3 3 x  ; y  6 3 ; h  . 2 4k 2k  2 1 4 Hướng dẫn giải: Chọn C.
Gọi x, y, h x, y, h  0 lần lượt là chiều rộng, chiều dài và chiều cao của hố ga. h V V Ta có: k
h kx và V xyh y   . x 2 xh kx
Nên diện tích toàn phần của hố ga là: 2k   1 V 2
S xy  2 yh  2xh   2kx kx
Áp dụng đạo hàm ta có S nhỏ nhất khi h 2k   1 V 3 x y 2 4k x 2kV k 2k   1 V Khi đó 3 y  2 3 , h  . 2k  2 1 4
Câu 13: Cho một tấm nhôm hình vuông cạnh 1m như hình vẽ dưới đây. Người ta cắt bỏ các tam giác
cân bên ngoài của tấm nhôm, phần còn lại gập thành một hình chóp tứ giác đều có cạnh đáy
bằng x m , sao cho bốn đỉnh của hình vuông gập lại thành đỉnh của hình chóp. Tìm x để
khối chóp nhận được có thể tích lớn nhất.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 112
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 2 2 1 2 2 A. x B. x C. x D. x  5 2 4 3 Hướng dẫn giải: h x 2 1 x z y x 1 2x 1 Ta có: 2 y   z   y 2 4 2 2  2  1  2  1 2
Chiều cao của hình chóp: 2 2 h z   x    y   x    x  2  4  2  2 2     1 1 2 2  Vx .  x chop 3 2 2 1 2 V lớn nhất khi hàm số 2 y xx đạt GTLN chop 2 2 2 5  2x  4x y '  1 2 4  x 2 2  x  0 2 y ' 0 5 2x 4x 0        2 2  x   5 Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 113
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Câu 14: Một viên đá có dạng khối chóp tứ diện đều và tất cả các cạnh đều bằng a , người ta cưa viên
đá theo mặt phẳng song song với mặt đáy của khối chóp để chia viên đá thành hai phần có
thể tích bằng nhau. Tính diện tích thiết diện của viên đá bị cưa bởi mặt phẳng nói trên. 2 a 2 a 2 a 2 a A. . B. . C. . D. . 3 4 3 4 3 4 3 4 Hướng dẫn giải: Chọn D. S A' D' B' C' A D O B C 1 1
Từ giả thiết  VVVV
( Do khối chóp tứ giác đều) S. A BCD   S .    2 ABCD S . A B C S . 2 ABC 3 V 1  SA  SA a a 2 a S . A BC       SA   2    A B    SA   S A B    . V 2 3 3 tdSA  2 2 3 2 3 4 S. ABC
Câu 15: Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 3
1, 296m . Người thợ này cắt các
tấm kính ghép lại một bể cá dạng hình hộp chữ nhật với ba kích thước , a ,
b c như hình vẽ. Hỏi người thợ c
phải thiết kế các kích thước , a ,
b c bằng bao nhiêu để
đỡ tốn kính nhất, giả sử độ dày của kính không đáng kể. b a A. a  3, 6 ; m b  0, 6 ; m c  0, 6m B. a  2, 4 ; m b  0,9 ; m c  0, 6m C. a  1,8 ; m b  1, 2 ; m c  0, 6m D. a  1, 2 ; m b  1, 2 ; m c  0,9m Hướng dẫn giải:
Với a là chiều dài của cả 2 ngăn của bể cá. Ta có: V abc  1, 296   1  aa a a abc abc abc 6 3 S  2 c bc b  2 c bc
b  2ac  3bc ab  2  3   abc3    2  2 2 2 b a c abc
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 114
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao  3 a b 2 3 1   2 Dấu “=” xảy ra khi     a a c bc    2 3 1, 296.4 6 Thay vào   3 3 1 :
b  1, 296  b   b
; a  1,8; c  0, 6. 4 3 5 Chọn C.
Câu 16: Khi xây nhà, chủ nhà cần làm một hồ nước bằng gạch và xi măng có dạng hình hộp đứng
đáy là hình chữ nhật có chiều dài gấp ba lần chiều rộng và không nắp, có chiều cao là h và
có thể tích là . Hãy tính chiều cao của hồ nước sao cho chi phí xây dựng là thấp nhất? 3 5 A. m
B. h  2 m C. h m D. h m 2 2 Hướng dẫn giải:
Gọi x, y, h lần lượt là chiều rộng, chiều dài và chiều cao của hình hộp V V
Theo đề bài ta có y  3x và V hxy h   2 xy 3x
Để tiết kiệm nguyên vật liệu nhất ta cần tìm các kích thước sao cho diện tích toàn phần của hồ nước là nhỏ nhất. V V 8V Khi đó ta có: 2
S  2xh  2 yh xy  2x  2.3 . x  . x 3 x   3x tp 2 2 3x 3x 3x 2 8V 4V 4 Cauchy V 16V Ta có 2 2 3 S   3x    3x  3  36 . tp 3x 3x 3x 3 4V 4V V 3
Dấu “=” xảy ra khi và chỉ khi 2 3  3x x   2  h   . 2 3x 9 3x 2 Vậy chọn C.
Câu 17: Người ta muốn thiết kế một bể cá bằng kính
không có nắp với thể tích 3 72dm và chiều cao là 3d .
m Một vách ngăn (cùng bằng
kính) ở giữa, chia bể cá thành hai ngăn, với 3 dm các kích thước ,
a b (đơn vị dm) như hình vẽ. Tính ,
a b để bể cá tốn ít nguyên liệu nhất b dm a dm
(tính cả tấm kính ở giữa), coi bề dày các
tấm kính như nhau và không ảnh hưởng đến thể tích của bể. A. a  24, b  24.
B. a  3, b  8.
C. a  3 2, b  4 2. D. a  4, b  6. Chọn D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 115
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 24
Có: V  72  3.ab  72  a  (1) b
Bể cá tốn ít nguyên liệu nhất nghĩa là diện tích toàn phần nhỏ nhất. 216
Ta có diện tích toàn phần của bể cá là: S  3.3a ab  2. 3 b   6b  24 tp b 216 216
Áp dụng bất đẳng thức Côsi: S   6b  24  2 .6b  24  96 tp b b 216
Dấu bằng xảy ra khi và chỉ khi:
 6b b  6 b  0 . Từ (1), ta suy ra: a  4 . b
Câu 18: Người thợ cần làm một bể cá hai ngăn, không có nắp ở phía trên với thể tích 1,296 m3.
Người thợ này cắt các tấm kính ghép lại một bể cá dạng hình
hộp chữ nhật với 3 kích thước a, b, c như hình vẽ. Hỏi người
thợ phải thiết kế các kích thước a, b, c bằng bao nhiêu để đỡ
tốn kính nhất, giả sử độ dầy của kính không đáng kể. A. a  3, 6 ; m b  0, 6 ; m c  0, 6m B. a  2, 4 ; m b  0, 9 ; m c  0, 6m C. a  1,8 ; m b  1, 2 ; m c  0, 6m D. a  1, 2 ; m b  1, 2 ; m c  0,9m Hướng dẫn giải:
Thể tích bể cá là: V abc  1, 296
Diện tích tổng các miếng kính là S ab  2ac  3bc (kể cả miếng ở giữa) 3 3 S 1 2 3 1 2 3 3 6 3 6 Ta có: 3     3 . .   abc c b a c b a abc 1, 296  1 2 3 Cauchy cho 3 so , , c b a  a  1,8 1 2 3    
Dấu “=” xảy ra khi c b ab   1, 2 . abc 1, 296    c  0, 6  Chọn C.
Câu 19: Từ một tấm tôn có kích thước 90cmx3m người ta làm một máng xối nước trong đó mặt cắt
là hình thang ABCD có hinh dưới. Tính thể tích lớn nhất của máng xối. A D 30cm 30cm 90cm 3m 3m B 30cm C A. 3 40500 3cm B. 3 40500 2cm C. 3 40500 6cm D. 3 40500 5cm
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 116
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Thể tích máng xối: 2 V S .300 (cm ) . ABCD
Vậy thể tích lớn nhất khi diện tích hình thang là lớn nhất. 1 S
(BC AD).CE A E D ABCD 2 θ
CE CDsin  30.sin 30cm
AD BC  2ED  30  60cos 30cm θ 90 S  90sin sin2 B C ABCD 30cm 2 90
Đặt f ()  90sin sin2
,[0;] 2 90
f '()  90cos  .2cos2 2  1  cos 2 f '() 0 cos cos 2 0 2 cos cos1 0           2   3 .   cos 1    
f (0)  f ()  0; f  135 3  
. Vậy GTLN của diện tích ABCD là 2 135 3cm .  3 
Vậy thể tích máng xối lớn nhất bằng 3
40500 3cm khi ta cạnh CD tạo với BC góc 0 60 .
Câu 20: Để làm một máng xối nước, từ một tấm tôn kích thước 0,9m 3m người ta gấp tấm tôn đó
như hình vẽ dưới. Biết mặt cắt của máng xối (bị cắt bởi mặt phẳng song song với hai mặt
đáy) là một hình thang cân và máng xối là một hình lăng trụ có chiều cao bằng chiều dài của
tấm tôn. Hỏi x m bằng bao nhiêu thì thể tích máng xối lớn nhất? x 3 m 0, 3 m x m x 0, 9 m 0, 3 m 3 m 0, 3 m 0, 3 m (a) Tấm tôn (b) Máng xối (c) Mặt cắt
A. x  0,5m .
B. x  0, 65m .
C. x  0, 4m .
D. x  0, 6m .
Hướng dẫn giải:. Chọn D.
Gọi h là chiều cao của lăng trụ
Vì chiều cao lăng trụ bằng chiều dài tấm tôn nên thể tích máng xối lớn nhất khi diện tích
hình thang cân (mặt cắt) lớn nhất h Ta có S   x  0,3 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 117
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao x  0,3 BC   x  0,3 2 B C 2  x  0,32  h  0,3  4 h 0.3m  x  2 2 0,3 ĐK: 0,3 
 0;0,3  x  0,9 4 0.3m A Khi đó: 1 S
x  0,3 4.0,32   x  0,32 4 Xét hàm số
f x   x    2   x  2 0, 3 4. 0, 3
0, 3 ;0,3  x  0, 9 2 2 2   x  0,3
f   x  4.0,3   x  0,3   x  0, 3
4.0,32   x  0,32
4.0,32   x  0, 32   x  0,3 x  0,3
0,36  2x x  0,3  
4.0,32   x  0,32
4.0, 32   x  0,32 x  0  , 3 f  x 2
 0  x  0,3x  0,18  0  x  0,6  x 0,3 0, 6 0,9 f  x  0  f x
Dựa vào bảng biến thiên ta thấy f x lớn nhất khi x  0, 6
Vậy thể tích máng xối lớn nhất khi x  0, 6m .
Câu 21: Khi xây dựng nhà, chủ nhà cần làm một bể nước bằng gạch có dạng hình hộp có đáy là hình
chữ nhật chiều dài d m và chiều rộng r m với d  2r. Chiều cao bể nước là hm và thể tích bể là 3
2 m . Hỏi chiều cao bể nước như thế nào thì chi phí xây dựng là thấp nhất? 3 3 2 3 2 2 A.m . B. 3 m . C. 3 m . D.m . 2 2 3 2 3 3 Hướng dẫn giải:
Gọi x x  0 là chiều rộng của đáy suy ra thể tích bể nước bằng
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 118
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 2
V  2x .h  2  h  2 x
Diện tích xung quanh hồ và đáy bể là 6 2 2 S  6 . x h  2x
 2x x  0 x 6
Xét hàm số f x 2 
 2x với x  0. x 3
Hàm số đạt giá trị nhỏ nhất tại 3 x  . 2 1 1 2 2
Vậy chiều cao cần xây là h    m. 2 2 x 3 3  3  3    2 
Câu 22: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là V . Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng 2 1 A. 3 x V B. 3 x V C. 4 x V
D. x V Hướng dẫn giải:
Gọi a là độ dài cạnh đáy, x là độ dài đường cao của thùng đựng đồ a, x  0 V V Khi đó, 2 2
V a x a
S  2a  4ax  2  4 Vx tp x x V
Để làm thùng hàng tốn ít nguyên liệu nhất thì S nhỏ nhất  2
 4 Vx nhỏ nhất. tp x V
Cách 1 : Xét hàm số f x  2
 4 Vx trên 0;  x 1 2V 2 V
Ta có f ' x   ; f ' x 2 3  0  x
V V x x V 2 x x 1 x 0 V 3 + ∞ f' x ( ) 0 + f(x) 1 f (V 3 )
Từ BBT ta thấy để làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ 1 bằng 3 V .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 119
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V V Cách 2: ta có 3 2 2  4 Vx  2
 2 Vx  2 Vx  6 V x x V Dấu "  " xảy ra tại 3 3
Vx  x V x V x Chọn B.
Câu 23: Nhân ngày quốc tế phụ nữ 8-3 năm 2017, ông A quyết định mua tặng vợ một món quà và
đặt nó vào trong một chiếc hộp có thể tích là 32 ( đvtt ) có đáy hình vuông và không có nắp.
Để món quà trở nên thật đặc biệt và xứng đáng với giá trị của nó ông quyết định mạ vàng
cho chiếc hộp, biết rằng độ dạy lớp mạ tại mọi điểm trên hộp là như nhau. Gọi chiều cao và
cạnh đáy của chiếc hộp lần lượt là h; x . Để lượng vàng trên hộp là nhỏ nhất thì giá trị của h; x phải là? 3
A. x  2; h  4
B. x  4; h  2
C. x  4; h
D. x  1;h  2 2 h x x Hướng dẫn giải: Chọn B. S   4xh  x2  32 128 Ta có   S  4x.x2 
x2 , để lượng vàng cần dùng là nhỏ 2 V 32 V
  x h h    x2 x  x2 x2
nhất thì Diện tích S phải nhỏ nhất ta có 128 128 S
x2  f   x f '  x  2x   0  x  4 , x x2
Câu 24: Một ngôi nhà có nền dạng tam giác đều ABC cạnh dài 10 m được đặt song song và cách
mặt đất h m . Nhà có 3 trụ tại ,
A B, C vuông góc với  ABC  . Trên trụ A người ta lấy hai
điểm M , N sao cho AM x, AN y và góc giữa  MBC  và  NBC  bằng 90 để là mái và
phần chứa đồ bên dưới. Xác định chiều cao thấp nhất của ngôi nhà. A. 5 3 . B. 10 3 . C. 10 . D. 12 . Hướng dẫn giải: Đáp án B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 120
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
Để nhà có chiều cao thấp nhất ta phải chọn N nằm trên mặt đất. Chiều cao của nhà là
NM x y .
Gọi I là trung điểm của BC . Ta có A
BC đều  AI BC , vì MI BC
MN   ABC   MN BC , từ đó suy ra  BC  MNI   0    MIN  90 NI BC  2  10 3  I
MN vuông tại I nhận AI là đường cao nên 2
AM .AN AI xy     75  2   
Theo bất đẳng thức Côsi: x y  2 xy  2. 75  10 3  x y  5 3
Do đó chiều cao thấp nhất của nhà là 10 3.
Câu 25: Một nhà sản xuất sữa có hai phương án làm hộp sữa. Hộp sữa có dạng khối hộp chữ nhật
hoặc hộp sữa có dạng khối trụ. Nhà sản xuất muốn chi phí bao bì càng thấp càng tốt(tức diện
tích toàn phần của hộp nhỏ nhất), nhưng vẫn phải chứa được một thể tích xác định là V cho
trước. Khi đó diện tích toàn phần của hộp sữa bé nhất trong hai phương án là A. 3 2 2V . B. 3 2 6 V . C. 3 2 3 6V . D. 3 2 3 2V . Hướng dẫn giải: Chọn D h h R a b
Trường hợp 1: Hộp sữa hình trụ V 2V Thể tích không đổi 2 2 2
V  R h h
, S  2 R  2 Rh  2 R  2 tp  R R V V
Áp dụng bất đẳng thức Cauchy cho bộ ba số dương 2 2 R , , R R V V V V Ta có 2 2 3 2 3 S  2 R    3 2 R . .  3 2V (*) tp R R R R
Trường hợp 2: Hộp sữa hình hộp chữ nhật Thể tích không đổi
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 121
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao V V VV V
V abh h
; S  2ab  2a bh  2ab  2 . a  2 . b  2 ab   tp   ab ab abb a V V
Áp dụng bất đẳng thức Cau chy cho bộ ba số dương ; ab ; a b V V Ta có 3 2 3 S  2.3 . ab .  6 V (**) tp a b
Xét hai kết quả ta thấy (*) nhỏ hơn
Vậy diện tích toàn phần của hộp sữa bé nhất là 3 2
S  3 2V (đvdt) tp
Câu 26: Một bác thợ gò hàn làm một chiếc thùng hình hộp chữ nhật (không nắp) bằng tôn thể tích 3
665,5 dm . Chiếc thùng này có đáy là hình vuông cạnh x(d ) m , chiều cao ( h d ) m . Để làm
chiếc thùng, bác thợ phải cắt một miếng tôn như hình vẽ. Tìm x để bác thợ sử dụng ít nguyên liệu nhất. A. 10, 5(dm) . B. 12(dm) . C. 11(dm) . D. 9(dm) . Hướng dẫn giải: h h Chọn C. 665,5
Ta có thể tích hình hộp là: 2
V x h  665, 5  h  2 x x 2662 2662 Diện tích toàn phần là 2 2
S x  4xh x
S '  2x ; 2 x x x h h
S '  0  x  11
Lập bảng biến thiên ta thấy khi x  11 thì S đạt giá trị nhỏ nhất
Vậy để sử dụng ít nguyên liệu nhất thì bác thợ xây phải cắt một miếng tôn có đáy là hình vuông cạnh 11(dm) .
Câu 27: Một người dự định làm một thùng đựng đồ hình lăng trụ tứ giác đều có thể tích là V . Để
làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ bằng 2 1 A. 3 x V B. 3 x V C. 4 x V
D. x V Hướng dẫn giải:
Gọi a là độ dài cạnh đáy, x là độ dài đường cao của thùng đựng đồ a, x  0 V V Khi đó, 2 2
V a x a
S  2a  4ax  2  4 Vx tp x x V
Để làm thùng hàng tốn ít nguyên liệu nhất thì S nhỏ nhất  2
 4 Vx nhỏ nhất. tp x V
Cách 1 : Xét hàm số f x  2
 4 Vx trên 0;  x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 122
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao 1 2V 2 V
Ta có f ' x   ; f ' x 2 3  0  x
V V x x V 2 x x 1 x 0 V 3 + ∞ f' x ( ) 0 + f(x) 1 f (V 3 )
Từ BBT ta thấy để làm thùng hàng tốn ít nguyên liệu nhất thì chiều cao của thùng đựng đồ 1 bằng 3 V . V V Cách 2: ta có 3 2 2  4 Vx  2
 2 Vx  2 Vx  6 V x x V Dấu "  " xảy ra tại 3 3
Vx  x V x V x
Câu 28: Người ta muốn xây một bồn chứa nước dạng khối hộp 1dm
chữ nhật trong một phòng tắm. Biết chiều dài, chiều
rộng, chiều cao của khối hộp đó lần lượt là 5m, 1m, VH'
2m (hình vẽ bên). Biết mỗi viên gạch có chiều dài 1dm VH
20cm, chiều rộng 10cm, chiều cao 5cm. Hỏi người ta
sử dụng ít nhất bao nhiêu viên gạch để xây bồn đó và 2m
thể tích thực của bồn chứa bao nhiêu lít nước? (Giả sử 1m
lượng xi măng và cát không đáng kể) 5m
A. 1180 viên, 8820 lít
B. 1180 viên, 8800 lít
C. 1182 viên, 8820 lít
D. 1180 viên, 8800 lít Hướng dẫn giải: Phân tích:
* Theo mặt trước của bể: 500
Số viên gạch xếp theo chiều dài của bể mỗi hàng là x   25 viên 20 200
Số viên gạch xếp theo chiều cao của bể mỗi hàng là:
 40 . Vậy tính theo chiều cao thì 5
có 40 hàng gạch mỗi hàng 25 viên. Khi đó theo mặt trước của bể. N  25.40  1000 viên.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 123
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Khối Đa Diện Nâng Cao
* Theo mặt bên của bể: ta thấy, nếu hàng mặt trước của bể đã được xây viên hoàn chỉnh 1
đoạn nối hai mặt thì ở mặt bên viên gạch còn lại sẽ được cắt đi còn viên. Tức là mặt bên 2 sẽ có 1 100  20 .40  .40  180 viên. 2 20
Vậy tổng số viên gạch là 1180 viên.
Khi đó thể tích bờ tường xây là 1180.2.1.0,5  1180 lít
Vậy thể tích bốn chứa nước là:
50.10.20 1180  8820 lít
Câu 29: Từ một mảnh giấy hình vuông cạnh là a, người ta gấp nó thành 4 phần đều nhau rồi dựng
lên thành một hình lăng trụ tứ giác đều (như hình vẽ). Từ một mảnh giấy hình vuông khác
cũng có cạnh là a, người ta gấp nó thành 3 phần đều nhau rồi dựng lên thành một hình lăng
trụ tam giác đều (như hình vẽ). Gọi V ,V lần lượt là thể tích của lăng trụ tứ giác đều và lăng 1 2
trụ tam giác đều. So sánh V và V . 1 2
A. V V
B. V V
C. V V D. Không so sánh 1 2 1 2 1 2 được Hướng dẫn giải: 3 a a a Ta có V  . a .  1 4 4 16 3 1 a 3 a a 3 và V  . a . . . 
. Do đó V V . 2 2 3 2 3 36 1 2
Ta chọn phương án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 124
Facebook: https://www.facebook.com/dongpay