Thông tin
Quiz

Trắc nghiệm nâng cao nguyên hàm, tích phân và ứng dụng – Đặng Việt Đông Toán 12

Trắc nghiệm nâng cao nguyên hàm, tích phân và ứng dụng – Đặng Việt Đông Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

Chủ đề:

Chương 3: Nguyên hàm - Tích phân và ứng dụng 199 tài liệu

Môn:

Toán 12 3.9 K tài liệu

Thông tin:

122 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Trắc nghiệm nâng cao nguyên hàm, tích phân và ứng dụng – Đặng Việt Đông Toán 12

82 41 lượt tải Tải xuống

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1

Facebook: https://www.facebook.com/dongpay

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2

Facebook: https://www.facebook.com/dongpay

MỤC LỤC

NGUYÊN HÀM NÂNG CAO ........................................................................................................... 3

A – LÝ THUYẾT CHUNG ............................................................................................................ 3

B – BÀI TẬP TRẮC NGHIỆM ..................................................................................................... 4

TÍCH PHÂN NÂNG CAO .............................................................................................................. 15

A – LÝ THUYẾT CHUNG .......................................................................................................... 15

B – BÀI TẬP TRẮC NGHIỆM ................................................................................................... 16

ỨNG DỤNG TÍCH PHÂN NÂNG CAO ........................................................................................ 55

A – LÝ THUYẾT CHUNG .......................................................................................................... 55

B – BÀI TẬP TRẮC NGHIỆM ................................................................................................... 55

ỨNG DỤNG THỰC TẾ .................................................................................................................. 87

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3

Facebook: https://www.facebook.com/dongpay

NGUYÊN HÀM NÂNG CAO

A – LÝ THUYẾT CHUNG

1. Định nghĩa

Cho hàm số





y f x

 xác định trên tập K (khoảng, nửa khoảng, đoạn của R). Nếu Ta có hàm số





F x

xác định trên K sao cho









F x f x

 thì





F x

được gọi là nguyên hàm của hàm số





f x

trên K.

Định lí 1. Nếu





F x

là một nguyên hàm của hàm số





f x

trên K thì với mỗi hằng số C, hàm số









G x F x C

 

cũng là một nguyên hàm của hàm số





f x

trên K.

Định lí 2. Nếu





F x

là một nguyên hàm của hàm số





f x

trên K thì mọi nguyên hàm của





f x

trên K đều có dạng









G x F x C

 

với C là hằng số.

Định lí 3. Mọi hàm số





f x

liên tục trên K đều có nguyên hàm trên K.

2. Tính chất:









f x dx f x C

 



với C là hằng số.









kf x dx k f x dx



 

với k là hằng số khác 0.





















f x g x f x dx f x dx g x dx

    

 

  

Bảng nguyên hàm

Chú ý: công thức tính vi phân của





f x

là









d f x f x dx

  

 

Nguyên hàm cơ bản Nguyên hàm của hàm hợp

dx C





du C





dx x C

 



du u C

 



 

x dx x C

 





   





 

u du u C

 





   





dx x C

 



du u C

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4

Facebook: https://www.facebook.com/dongpay

x x

e dx e C

 



u u

e du e C

 



a dx C

 



a dx C

 



cos sin

xdx x C

 



cos sin

udu u C

 



sin cos

xdx x C

  



sin cosu

udu C

  



tan

cos

dx x C

 



tan

cos

du u C

 



cot

sin

dx x C

  



cot

sin

du u C

  



B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho





F x

là nguyên hàm của hàm số

 

f x





và

 

0 ln 4

F   . Tập nghiệm

của phương trình









3 ln 3 2

F x x

  

là:





S  . B.





2;2

S   . C.





1;2

S  . D.





2;1

S   .

Hướng dẫn giải:

Ta có:

 

d 1 1

1 d ln 3

3 3 3 3

x x

x e

F x x x e C

e e

 

      

 

 

 

 

 

0 ln 4

F   nên



. Vậy

 





ln 3

F x x e   .

Do đó:









3 ln 3 2 2

F x e x

    

Chọn A.

Câu 2: Cho

( )

F x x



là một nguyên hàm của hàm số

( )

f x e

. Tìm nguyên hàm của hàm số

( )

f x e



2 2

( ) 2

f x e dx x x C



   



2 2

( )

f x e dx x x C



   



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5

Facebook: https://www.facebook.com/dongpay

2 2

( ) 2 2

f x e dx x x C



  



2 2

( ) 2 2

f x e dx x x C



   



Hướng dẫn giải:

Từ giả thiết





















2 2 2 2

' . ' . 2 .e

x x x

F x f x e x f x e x f x      (1)

Đặt





' .

A f x e dx





. Đặt

u e



du e dx

 

,dv=f’(x)dx chọn v=f(x)













2 2 2

. 2 . 2 2 2 2

x x

A e f x f x e dx x F x C x x C

         



Chọn D.

Câu 3: Cho

( ) ( 1)

F x x e

  là một nguyên hàm của hàm số

( )

f x e

. Tìm nguyên hàm của hàm số

( )

f x e



( ) d (4 2 )

x x

f x e x x e C



  



( ) d

x x

f x e x e C





 



( ) d (2 )

x x

f x e x x e C



  



( ) d ( 2)

x x

f x e x x e C



  



Hướng dẫn giải:

Từ giả thiết

       

2 2

' . 1 . .

x x x

F x f x e x e f x e

 

    

 

   

. .

x x

x e x

x e f x e f x

e e

    

 

' ...

x x

f x

e e



 

   

 

 

Đặt

   

2 2

' . . 1

x x x

A f x e dx e dx x e dx



   

  

Đặt

choïn

x x

u x du dx

dv e dx v e

    





 















1 1 2

x x x x x

A x e e dx x e e C e x C

          



Chọn C.

Câu 4: Cho

( )

F x

  là một nguyên hàm của hàm số

( )

f x

. Tìm nguyên hàm của hàm số

( )ln

f x x



3 5

ln 1

( )ln

f x xdx C

x x



  



3 5

ln 1

( )ln

f x xdx C

x x



  



3 3

ln 1

( )ln

f x xdx C

x x



  



3 3

ln 1

( )ln

f x xdx C

x x



   



Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6

Facebook: https://www.facebook.com/dongpay

Từ giả thiết

 













 

3 4 3

1 1 1

f x f x f x

F x f x

x x x x x x

 

        

 

 

 

' 3.

f x

  

Đặt

 

4 4

3ln ln

' .ln . 3

x x

A f x x dx dx dx

x x



   

  

Đặt

4 3

ln 3

1 1

choïn

u x du dx

dv dx v

x x



  







  





3 4 3 3

1 1 1 ln 1

3 ln

3 3 3

A x dx C

x x x x

 

       

 

 



Chọn C.

Câu 5: Cho

( )

F x

 là một nguyên hàm của hàm số

( )

f x

. Tìm nguyên hàm của hàm số

( )ln

f x x



2 2

ln 1

( )ln

f x xdx C

x x

 



   

 

 



2 2

ln 1

( )ln

f x xdx C

x x



  



2 2

ln 1

( )ln

f x xdx C

x x

 



   

 

 



2 2

ln 1

( )ln

f x xdx C

x x



  



Hướng dẫn giải:

Từ giả thiết

 













 

2 3 2

1 1 1

f x f x f x

F x f x

x x x x x x

 

         

 

 

 

2 3

1 2

'f x

x x

 

   

 

 

Đặt

 

3 3

2 ln

' .ln . .ln . 2

A f x x dx x dx dx

x x

  

  

Đặt

3 2

1 1

choïn

u x du dx

dv dx v

x x



  







  





2 3 2 2 2 2

ln 1 ln 1 ln 1

2 2

2 2 2 4 2

x x x

A dx C C

x x x x x x

     

           

     

     



Chọn A.

Câu 6: Hàm số nào dưới đây là nguyên hàm của hàm số

 

f x





trên khoảng





;

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7

Facebook: https://www.facebook.com/dongpay

 





ln 1

F x x x C

   

. B.

 





ln 1 1

F x x C

   

 

F x x C

  

. D.

 

F x C

 



Hướng dẫn giải:

Ta có bài toán gốc sau:

Bài toán gốc: Chứng minh

 

x x a c a

x a

    







Đặt

2 2

x x x a

t x x a dt dx dt dx

x a x a

 

 

       

 

 

 

tdx

x a

 



dt dx

x a

 



Vậy khi đó

ln ln

dx dt

t c x x a c

x a

      



 

( điều phải chứng minh).

Khi đó áp dụng công thức vừa chứng minh ta có

 





2 2

ln 1 ln 1

F x dx x x c x x c

        





Chọn A.

Câu 7: Cho F(x) là một nguyên hàm của

 

tan

cos 1 cos

f x

x a x





, biết





0 0



 



 

 



Tính

3 4

F F

   



   

   

 

5 3

 . B.

5 1



. C.

3 5

 . D.

5 2



Hướng dẫn giải:

 

4 4 4 4

2 2 2 2

0 0 0 0

tan tan 1

tan 1

cosx 1 cos cos tan 1 2 tan 1

x x

f x dx dx dx d x a

a x x x a x a

    

    

   

   

2 2

tan 1 tan 0 1 3 2

a a       



2 1 3 2

a a     

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8

Facebook: https://www.facebook.com/dongpay





2 1 2 1 3 2 5 2 6

3 6

1 1

3 2

a a a

a a

        



    



Do đó

tan

3 4

cos 1 cos

F F dx

x x

   

  

   

   







 

2 2

tan 2 tan 2 5 3

3 4

    

 

Chọn A.

Câu 8: Biết

 

2 2

cos 2

cos sin .sin 4

x x xdx C

   



. Với a là số nguyên. Tìm a?



12.



14.



Hướng dẫn giải:

Đặt

 





2 2

cos sin .sin 4

f x x x xdx

 



, Ta có:

 





 

2 2

cos sin .sin4 cos2 .2sin 2 .cos2

2 cos 2 .sin2

f x x x xdx x x x

x xdx

  



 



Đặt cos2 2sin2

t x dt xdx

   

Vậy

 

7 7

cos 2

7 7

t x

F x t dt C C



      



Chọn C.

Câu 9: Biết

sin cos

ln sin cos

sin cos

x x

dx a x x C

x x



  





. Với a là số nguyên. Tìm a?



Hướng dẫn giải:

Vì

 

sin cos

ln sin cos

sin cos sin cos

x x

a x x C

x x x x









     

 

 



nên

Nguyên hàm của:

sin cos

x x





là: ln sin cos

x x C

 

Chọn A.

Câu 10: Tìm một nguyên hàm của:

tan

1 4.

tan 1



 



 

 

biết nguyên hàm này bằng 3 khi





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9

Facebook: https://www.facebook.com/dongpay

cos



sin



tan 2



. D.

cot 2



Hướng dẫn giải:

 

tan 2tan

2 2

1 4. 1 1 tan

cos

1 tan

tan 1

x x

f x x

 

 

      

 

 

 





 

 

Nguyên hàm của





tan

F x x C

 

Ta có:

 

3 tan 3 2 tan 2

4 4

F C C F x x

 

        

 

 

 

Chọn C.

Câu 11:





ln 2sin cos

F x x x x

  

là nguyên hàm của:

sin cos

sin 3cos

x x





. B.

sin 2cos

2sin cos

x x





. C.

sin cos

sin 3cos

x x





. D.

3sin cos

2sin cos

x x





Hướng dẫn giải:

Ta chỉ cần đạo hàm của F(x), rồi sau đó quan sát kết quả đúng.

Ta có:

 





2sin cos '

2sin cos 3sin cos

' 1 1

2sin cos 2sin cos 2sin cos

x x

x x x x

F x

x x x x x x



 

    

  





F x

 là một nguyên hàm của

3sin cos

2sin cos

x x





Chọn D.

Câu 12: Biết

 

1 1

25 20 4

5 2

dx C

x x

a x

  

 





. Với a là số nguyên. Tìm a?



100.



25.



Hướng dẫn giải:

Chú ý nếu chúng ta biến đổi:

 





25 20 4

x x

dx x x dx C

x x



 

    



 

 

. Là sai

Điều sau đây mới đúng:

   





2 2

25 20 4

25 20 4 25 20 4

x x

x x d x x C



 

     





Trở lại bài, ta sẽ biến đổi biểu thức





25 20 4

x x 

về dạng

 

ax b

 như sau:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10

Facebook: https://www.facebook.com/dongpay

 

3 6

1 1

5 2

25 20 4

5 2

1 1

5 5

25 5 2

dx dx x dx

x x

C C



  



 



    



  

Chọn D.

Câu 13: Biết

ln 2 7

2 5 7

x a

dx x C

x x b



  

 



, với a, b là cá số nguyên. Tính S = a + b?



Hướng dẫn giải:

Ta quan sát mẫu cso thể phân tích được thành nhân tử, sử dụng MTCT bấm giải phương

trình bậc 2:

2 5 7 0

x x

  

thấy có hai nghiệm là:

x x

  

Áp dụng công thức









1 2

ax bx c a x x x x

     với

1 2

x x

là hai nghiệm ta có:









2 5 7 1 2 7

x x x x

    

Do đó:

  

1 1 1 1

ln 2 7

2 5 7 1 2 7 2 7 2

x x

dx dx dx x C

x x x x x

 

    

    

  

Chọn C.

Câu 14: Biết

 

sin 2 cos2 cos4

x x dx x x C

   



, với a, b là cá số nguyên. Tính S = a + b?



Hướng dẫn giải:

Nếu áp dụng ngay:

t dt C



 





thì ta có:

 

sin 2 cos2

x x

x x dx C



  



. Là sai.

Ta phải khai triển

 

sin 2 cos 2

x x

 để xem thử

   

sin 2 cos2 1 sin 4 4

x x dx x dx x cos x C

    

 

Chọn D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11

Facebook: https://www.facebook.com/dongpay

Câu 15: Biết

1 cos

dx a tan C

x b

 





, với a, b là cá số nguyên. Tính S = a + b?



Hướng dẫn giải:

Chưa áp dụng ngay được công thwucs nguyên hàm cơ bản, ta quan sát mẫu và thấy rằng có

thể biến đổi

1 cos 2cos

x  dựa trên công thức hạ bậc:

1 cos2

cos







. Do đó:

1 1

tan

1 cos 2

2cos

dx dx C

  



 

Ta thấy rằng

1, 2

a b

 

do đó S=3.

Chọn C.

Câu 16: Biết

tan

1 sin 2 4

dx x C

x b

 

  

 



 





, với a, b là cá số nguyên. Tính S = a + b?



Hướng dẫn giải:

1 1 1

1 sin2

1 cos 2 2cos

2 4

dx dx dx

x x

  



   

  

   

   

  

 

1 1

tan tan

2 4 2 4

x C x C

   

      

   

   

 

Ta thấy a=1,b=2 suy ra S=3

Chọn C.

Câu 17: Cho

 

8sin

f x x

 

 

 

 



. Một nguyên hàm





F x

của





f x

thỏa





0 8



là:

4 2sin 2 9

x x

 

  

 

 



. B.

4 2sin 2 9

x x

 

  

 

 



4 2sin 2 7

x x

 

  

 

 



. D.

4 2sin 2 7

x x

 

  

 

 



Hướng dẫn giải:

Ta cần phải tính

 

8sin

f x dx x dx

 

 

 

 

 



. Đầu tiên sử dụng công thức hạ bậc để đổi





f x

như sau:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12

Facebook: https://www.facebook.com/dongpay

 

1 cos 2

8sin 8

12 2

f x x

 

 

 

 

 

 

  

 

 

 

 



   

4 4cos 2 4 2sin 2

6 6

f x x F x x x C

   

       

   

   

 

 

0 8 2sin 8 9

f C C

 

      

 

 



Chọn B.

Câu 18: Cho





f x x

 

. Một nguyên hàm





F x

của





f x

thỏa





1 1



là:

x x

 

khi 0

2 2

khi 0

x x

x C x



  







  





khi 0

x C x



  







  





. D.

khi 0

x x C x

x C x



   





  





Hướng dẫn giải:

Ta có:

 

1 khi 0

x x

f x

x x

 







 



 

khi 0

x C x

F x

x C x



  



 





  





Theo đề

 

1 1

F C

   

do đó:

khi 0

2 2

khi 0

x x

x C x



  







  





Chọn B.

Câu 19: Biết

( )

F x

là nguyên hàm của

 

5 8 4

x x

 





với

0 1

 

và

 



 

 

. Giá trị nhỏ

nhất của

( )

F x

là:

24.

20.

25.

26.

Hướng dẫn giải:

Ta có:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13

Facebook: https://www.facebook.com/dongpay

 





 

2 2

9 4 2 1

5 8 4

9 4 4 9

x x x

x x

F x dx dx

x x

dx C

x x x

  

 

 



 

 

    



 

 

 



Vì

 



 

 

nên

4 9

26 0

C C

    

 



 

 

Lúc này

 

4 9

F x

x x

 



với

0 1

 

. Sử dụng MTCT bấm Mode 7 chọn start 0 end 1

Step 0.1:

Quan sát bảng giá trị ta thấy giá trị nhỏ nhất của F(x) là 25 xảy ra khi x =0,4

Chọn C.

Câu 20: Khi tính nguyên hàm

  

2 1 1

x x 



người ta đặt





t g x

 (một hàm biểu diễn theo

biến x) thì nguyên hàm trở thành



. Biết

 

g  , giá trị của









0 1

g g

 là:

3 6



1 6



2 6



2 3 6



Hướng dẫn giải:

Đối với bài này HS cần pahir nắm được kĩ thuật biến đổi khi tính nguyên hàm. Hs cần phải

dự đoán phép đặt ẩn phụ, đầu tiên ta thấy nguyên hàm có thể biến đổi thành:

  

 

1 1

2 1

2 1 1

dx dx

x x





 



 

Do đó ta đặt:

   

2 2

2 1

2 1 2 1

2 1 1

1 1

x dx dx

t dt dt

x x



    



 

Vì vậy suy ra

  

2 1 1

dx dt

x x



 

 

Tuy nhiên đây là lời giải sai, ta có thể thấy khi đặt

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14

Facebook: https://www.facebook.com/dongpay

   

2 2

2 1

2 1 2 1

2 1 1

1 1

x dx dx

t C dt dt

x x



     



 

Với C là hằng số, kết quả không thay đổi. Vì vậy chính xác ở đây là:

 

2 1

t C g x



  



. Theo đề

 

g  n33n suy ra C=0.

Cuối cùng ta được

 

2 1

g x







vì vậy

   

2 6

0 1

g g



 

Chọn C.

Chú ý: Bài toán này hoàn toàn có thể dùng MTCT để chọn kết quả, Ta có:

     

 

  

3 3

1 1 1

2 1 1 2 1 1

1 1

2 1 1

dt dx t dx

x x x x

g x dx

x x

  

   

 

 

  



Do đó





g x

là nguyên hàm của

  

1 1

2 1 1

x x 

. Suy ra:

   

  

 

  

 

0 0

3 3

4 4

1 1 1 1

0 4 0 4

2 2

2 1 1 2 1 1

g g dx g dx g

x x x x

    

   

 

Và:

   

  

 

  

 

1 1

3 3

4 4

1 1 1 1

1 4 1 4

2 2

2 1 1 2 1 1

g g dx g dx g

x x x x

    

   

 

Sử dụng MTCT bấm:

  

 

  

 

0 1

3 3

4 4

1 1 1 1

4 4

2 2

2 1 1 2 1 1

dx g dx g

x x x x

  

   

 

Là kết quả C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15

Facebook: https://www.facebook.com/dongpay

TÍCH PHÂN NÂNG CAO

A – LÝ THUYẾT CHUNG

1. Định nghĩa

Cho hàm số





y f x

 thỏa:

+ Liên tục trên đoạn





;

a b





F x

là nguyên hàm của





f x

trên đoạn





;

a b

Lúc đó hiệu số









F b F a

 được gọi là tích phân từ a đến b và kí hiệu

     

f x dx F b F a

 



Chú ý:

+ a, b được gọi là 2 cận của tích phân.

+ a = b thì

 

f x dx





+ a > b thì

   

b a

a b

f x dx f x dx

 

 

+ Tích phân không phụ thuộc và biến số, tức là

       

b b

a a

f x dx f t dt F b F a

  

 

2. Tính chất

       

b c b

a a c

f x dx f x dx f x dx a c b

   

  

   

b b

a a

kf x dx k f x dx



 

với k là hằng số khác 0.

       

b b b

a a a

f x g x dx f x dx g x dx

  

 

 

  

Chú ý:

Để tính tích phân từ a đến b, ta tiến hành tìm nguyên hàm rồi sau đó thay cận vào theo công thức

     

f x dx F b F a

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16

Facebook: https://www.facebook.com/dongpay

B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Xét tích phân

2 2

3sin 2cos 2

A dx

x x





 



. Bằng cách đặt

tan ,

t x



tích phân A được

biến đổi thành tích phân nào sau đây.

t 



. B.

t 



. C.

t 



. D.

t 



Hướng dẫn giải:

Ta có:

2 2 2 2

3sin 2cos 2 cos 3tan 2

cos

x x x x

 

    

 

 









2 2 2 2 2

cos 3tan 2 2 1 tan cos tan 4

x x x x x

 

     

 

Vậy:

 

2 2

cos tan 4

A dx

x x









, lúc này đặt

tan

t x



và đổi cận ta đc:

A dx







Chọn A.

Câu 2: Đặt

tan

t 

thì

cos

I dx







được biến đổi thành

 

f t dt



. Hãy xác định





f t





2 4

1 2 .

f t t t

  





2 4

1 2 .

f t t t

  





1 .

f t t

 





1 .

f t t

 

Hướng dẫn giải:

2 2

2 2 2

0 0

1 1 1

. 1 tan .

cos cos cos

2 2 2

I dx dx

x x x

 

 

 

 

  

 

 

 

 

 

Đặt

1 1

cos

tan

0 0; 1

dt dx

x t x t









 





     





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17

Facebook: https://www.facebook.com/dongpay

Vậy:

   

 

1 1

2 2 4 2 4

0 0

1 .2 2 1 2 1 2

I t dt t t dt f t t t

        

 

Chọn B.

Câu 3: Biết rằng

 

1 3 2

3 , ,

5 3

a b

e dx e e c a b c



   





. Tính

2 3

b c

T a

  



10.



Hướng dẫn giải

Chọn C.

Đặt

Đổi cận: +

nên câu C đúng.

Câu 4: Biết

2 2 1

4 ln 2 ln5

I dx a b

 

   



, với

a b

là các số nguyên. Tính

S a b

 



11.



 

Hướng dẫn giải

Chọn B.

Ta có:

5 2 5

1 1 2

2 2 1 2 2 1 2 2 1

d d d

x x x

I x x x

x x x

     

  

  









2 5

1 2

2 2 1 2 2 1

5 2 2 3

x x

dx dx dx dx

x x x x

   

 

   

   

   

2 5

1 2

5 3

2 5ln 2 3ln

x dx dx x x x x

x x

   

       

   

   

 

8ln2 3ln5 4

  

11.

a b





   



 



Câu 5: Biết

 

ln 2 1 d ln3 ,

I x x x c

   



trong đó

, ,

a b c

là các số nguyên dương và

là phân

số tối giản. Tính

S a b c

  

60.



70.



72.



68.



Hướng dẫn giải

1 3 1 3 2 3

t x t x tdt dx

      

0 1

x t

  

1 2

x t

  









 

1 2 2

2 2 2

1 3 2 2 2

1 1 1

0 1 1

3 2 2 2 2 2 2 .

x t t t t t

e dx te dt te e dt te e e e e e e



          

  

b c





  



 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18

Facebook: https://www.facebook.com/dongpay

Chọn B.

Ta có

 

ln 2 1 d

I x x x

 



. Đặt

 

u d

ln 2 1

2 1

d d

d x

u x

v x x







 

  



 















 

4 4

0 0

ln 2 1

2 2 1

x x

I x x dx dx



   



 

 

1 1 1 1 63

8ln9 16ln3 ln 2 1 ln3 3

2 4 4 2 1 4 4 8 4

x x

dx x x

 

          

 



 



ln3 ln3 3 4 70

c b S







       









Câu 6: Giả sử tích phân

 

2017

.ln 2 1 d ln3

x x x a

  



. Với phân số

tối giản. Lúc đó

6057.

b c

 

6059.

b c

 

6058.

b c

 

6056.

b c

 

Hướng dẫn giải

Chọn B.

Ta có

   

1 1

2017

0 0

.ln 2 1 d 2017 .ln 2 1 d

I x x x x x x

   

 

Đặt

 

d d

ln 2 1

2 1

d d

2 8

u x

v x x







 

  



 









 





Do đó

   

 

1 1

2 2

0 0

1 1 2

.ln 2 1 d ln 2 1 d

2 8 2 8 2 1

x x

x x x x x

 

   

     

 

   



   

 

 

3 3

ln3 ln3

8 4 8

x x

 



  

 

 

 

2017

3 6051

.ln 2 1 d 2017 ln3 ln3.

8 8

I x x x

 

    

 

 



Khi đó

6059.

b c

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19

Facebook: https://www.facebook.com/dongpay

Câu 7: Tính tích phân

 

6 2

4 2

4 3 2

d 3 4

1 8

x x

x a b c



  

   







. Với

là các số

nguyên. Khi đó biểu thức

2 4

a b c

 

có giá trị bằng

. B.

241

. C.

196

. D.

Hướng dẫn giải

Chọn B.

Ta có

6 2 6 2 6 2 6 2

4 2 2 2

2 2 2 2

4 4 4

1 1 1 1

4 3 1 1

d 4 d 4 d d

1 1 1

x x x x

x x x x I J

x x x

   

 

    

       

 

  

 

   

Tính

6 2

4 d 4 2 6 2 2 4

I x x



       



Tính

6 2 6 2 6 2

2 2 2

2 2

1 1 1

1 1

d d d .

x x

J x x x

  

 



  



 



 

 

 

  

Đặt

1 1

1 d

t x dt x

x x

 

    

 

 

. Khi

1 0

6 2

x t

  









  





Khi đó

 







. Đặt





2 tan d 2 1 tan d

t u t u u

    . Khi

0 0

t u

  







  







Suy ra

 

4 4

0 0

2 1 tan

2 2 2

du du

2 2 8

2 1 tan

J u



   



 

 



Vậy

 

6 2

4 2

4 3 2

d 16 3 16 4

1 8

a b

x x



  



  

     













Vậy

2 4

241

a b c  

Câu 8: Tích phân

d ln2

1 cos2

x a b

 







, với

là các số thực. Tính

16 8

a b



Hướng dẫn giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20

Facebook: https://www.facebook.com/dongpay

Chọn A

Đặt

d d

d 1

tan

1 cos2

u x

v x



 

 



 



 





. Ta có

1 1 1 1 1 1 1 1

tan tan d ln cos ln ln2 ,

4 4

2 2 8 2 8 2 8 4 8 4

0 0

I x x x x x a b

           





 

  

Do đó,

16 8 4

a b

 

Câu 9: Cho biết tích phân với là các ước nguyên của 4.

Tổng

A. 2. B. 4. C. 3. D. 1

Hướng dẫn giải

Ta có

Chọn A.

Câu 10: Tích phân

ln2

2 1

e a

x e

e b



 



. Tính tích

a b

12.

Hướng dẫn giải

Chọn B.

   

ln2 ln2 ln2 ln 2 ln 2

2 1

1 1

0 0 0 0 0

d d d d 1 d

x x x x

x e x e x e x e x



   



     

    

 

ln2

1 1

2 1

2 2

e e e e e





 

       

 

 

1, 2 2

a b ab

    

 

4 2

. .

2 ln

a e b e c

I x x x dx

 

  



, ,

a b c

  

 

2 3

1 1 1

2 ln 2 ln

e e e

I x x x dx x dx x xdx

   

  

 

3 4 4

1 1

2 1

2 2

x dx x e

  



2 2 2 2

1 1

1 1 1 1 1

ln ln

1 1

2 2 2 4

e e

x xdx x x x dx e x

 



    

 

 

 

   

2 4 2

2 4

1 1 2e 1

2 ln 1

2 4 4

e e

I x x x dx e

  

     



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21

Facebook: https://www.facebook.com/dongpay

Câu 11: Biết

3 23

6 3

sin 3

d 3

x c d

a b

x x



   

 





 



với

, , ,

a b c d

là các số nguyên. Tính

a b c d

  

a b c d

   

. B.

a b c d

   

. C.

a b c d

   

. D.

a b c d

   

Hướng dẫn giải

Chọn A.





 

6 3

3 3 3

6 3

6 6

6 3

3 3 3

1 sin

sin

1 sin

x x x

I dx dx x x xdx

x x

  

 

    

 

 

  

  

Đặt

t x dt dx

    

. Đổi cận

3 3

x t



   







   





 

 

  

   

3 3 3

6 3 6 3 6 3

3 3 3

1 sin 1 sin 1 sin

I t t t dt t t tdt x x xdx



 

            

  

  

Suy ra

 

3 3

2 2 sin sin

I x x dx I x xdx

 

   

 

 

(+)

sin



(–)

cos



(+)

sin



6 (–)

cos



sin



 

3 2

sin 3 cos 6 sin 6sin 2 6 3

27 3

I x x x x x x x



        



 



Suy ra:

27, 3, 2, 6

a b c d

     

. Vậy

a b c d

   

Câu 12: Với các số nguyên

a b

thỏa mãn

 

2 1 ln d ln

x x x a b

   



. Tính tổng

P a b

 



. B.



. C.



. D.



Hướng dẫn giải

Chọn C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22

Facebook: https://www.facebook.com/dongpay

Đặt

 

d 2 1 d

u x

v x x









 





ta có

d d

u x

v x x











 



 

   

 

2 2

2 2 2

1 1

2 1 ln d ln . d

3 3

6ln2 1 d 6ln 2 6ln 2 4 4 ln64

2 2 2

x x x x x x x x x

x x x

    

 

            

 

 

 



4 64 60

P a b

     

Câu 13: Biết

 

4 2

2 . .

x x

e x e dx a e b e c

   



với a, b, c là các số hữu tỷ. Tính

S a b c

  



. B.

 

. C.

 

. D.



Hướng dẫn giải

Ta có

 

2 2 2 2 2

0 0 0 0 0

2 2 . 2 2

2 2 2

x x

x x x x x x

e e

I e x e dx e dx x e dx xe dx xe dx

        

    

Đặt

 

   

4 4

2 2

0 0

2 . 2

2 2

1 3

2 . 2 2

2 2 2 2

x x

u x du dx

I x e e dx

dv e dx v e

e e

x e e e

 

 

     

 

 

 

      



1 3

;

2 2

a c

S a b c



 



     









Chọn D.

Câu 14: Cho hàm số





sin2 cos2

f x a x b x

  thỏa mãn

' 2

 

 

 

 



và

adx





. Tính tổng

a b



bằng:

Hướng dẫn giải

Chọn C.





' 2 cos2 2 sin2

f x a x b x

 

' 2 2 2 1

f a a

 

       

 

 



3 1 3 4

b b

adx dx b b

      

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23

Facebook: https://www.facebook.com/dongpay

Vậy

1 4 5.

a b

   

Câu 15: Có bao nhiêu giá trị của

trong đoạn

 

 

 



thỏa mãn

sin 2

1 3cos







. B.

. C.

. D.

Hướng dẫn giải

Chọn B.

Đặt

1 3cos 1 3cos 2 d 3sin d .

t x t x t t x x

       

Đổi cận: + Với

0 2

x t

  

+ Với

1 3cos .

x a t a A

    

Khi đó

 

sin 2 2 2 2

d d 2 1 1 3cos 1 cos 0

3 3 3 3

1 3cos

x t t A A a a

           



 

 

a k k   





. Do

1 3

;2 2

4 4 2 4 2

a k k





 

         



 



 



  

Bình luận: Khi cho

 



thì tích phân không xác định vì mẫu thức không xác định

(trong căn bị âm). Vậy đáp án phải là B, nghĩa là chỉ chấp nhận





Câu 16: Có bao nhiêu số





0;20

a



sao cho

sin sin 2 .

x xdx





. B.

. C.

. D.

Hướng dẫn giải

Chọn D

Ta có

 

5 6 6 7 7

0 0 0

2 2 2

sin sin 2 2 sin cos 2 sin sin sin sin .

7 7 7

a a a

x xdx x xdx xd x x a

    

  

Do đó

sin 1 sin 1 2

a a a k

     



. Vì





0;20

a



nên

0 2 20 10

2 2

k k

      



 

và k





nên có 10 giá trị của

Câu 17: Nếu

sin cos d

x x x 





thì

bằng

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải

Chọn A.

Đặt

sin d cos d

t x t x x

  

. Đổi cận: khi

0 0;

6 2

x t x t

     



Khi đó:

1 1 1

d .

1 1 2 64

I t t

n n



 

   

 

 

 



Suy ra

1 1

2 64



 



 

 

có nghiệm duy nhất



(tính đơn điệu).

Câu 18: Giá trị của

lim d









bằng



Hướng dẫn giải

Chọn D.

Ta có:

I x









Đặt

1 d d

x x

t e t e x

   

. Đổi cận: Khi

1 ; 1 1

n n

x n t e x n t e



        

Khi đó:

 

1 1

1 1 1 1

d d ln 1 ln 1 ln

1 1 1

n n

e e

I t t t t

t t t t e

 



 



 



 

       

 

  

 

 

Mà

1 1

e e



 



 



 

 



 



 

 

khi

 

, Do đó,

lim 1 ln 0



  

Câu 19: Cho các tích phân

1 tan

I dx









và

sin

cos sin

J dx

x x









với

 



 

 





, khẳng định sai

là

cos

cos sin

I dx

x x









. B.

ln sin os

I J c  

 

ln 1 tan

I  



. D. I J

 



Hướng dẫn giải

Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25

Facebook: https://www.facebook.com/dongpay

Ta có

1 1 cos

sin

1 tan cos sin

cos

 

 





  



nên A đúng.





0 0

cos sin

ln cos sin ln cos sin

cos sin cos sin

d x x

x x

I J dx x x

x x x x





      

 

 

 



 

B đúng

I J dx x

   





D đúng.

Câu 20: Giả sử

 

   

2017

1 1

1 d

a b

x x

x x x C

a b

 

   



với

a b

là các số nguyên dương. Tính

a b



bằng:

2017

. B.

2018

. C.

2019

. D.

2020

Hướng dẫn giải

Ta có:

        

 

   

2018 2019

2017 2017 2017 2018

1 1

1 d 1 1 1 d 1 1 d

2018 2019

x x

x x x x x x x x x C

 

            

  

Vậy

2019, 2018 2 2020

a b a b

    

Chọn D.

Câu 21: Tích phân

2001

2 1002

(1 )

I dx







có giá trị là

1001

2002.2

. B.

1001

2001.2

. C.

1002

2001.2

. D.

1002

2002.2

Hướng dẫn giải

2 2

2004

1002

3 2 1002

1 1 3

. .

(1 )

I dx dx

x x

 



 



 

 

 

. Đặt

2 3

1 2

t dt dx

x x

     .

Câu 22:

Cho tích phân trong đó a là nghiệm của phương trình , b là một

số dương và . Gọi . Tìm chữ số hàng đơn vị của b sao cho .

A. 3. B. 2. C. 4. D. 5

Hướng dẫn giải

Giải phương trình







C dx

2 2







b a





A x dx



C A

2 2 0 0



    

x a

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26

Facebook: https://www.facebook.com/dongpay

Tính tích phân C. Đặt:

Tính tích phân A ta có

Theo giả thiết

Chọn A.

Câu 23: Biết tích phân

1 .

1 2 8

x a b



 









trong đó ,a b





. Tính tổng

a b



A. 0. B. 1. C. 3. D. -1

Hướng dẫn giải

2 2 2

0 0

2 2

1 1 1

1 2 1 2 1 2

x x x

I dx dx dx x dx

 

  

    

  

   

Đặt

sin

x t





 



Chọn C.

Câu 24: Biết rằng:

ln2

1 1 5

d ln 2 ln 2 ln .

2 1 2 3

x x b c

 

   

 



 



Trong đó

, ,

a b c

là những số nguyên.

Khi đó

S a b c

  

bằng:

. B.

. C.

. D.

Hướng dẫn giải

Chọn C.

ln2 ln2 ln2

0 0 0

1 1

d d d

2 1 2 1

x x

x x x x x

e e

 

  

 

 

 

  

Tính

ln2

2 2

ln 2

2 2

x x  



Tính

ln2

2 1

e 



3 3

    

x x

t e t e 2 

tdt e dx







C dt

= 2 2 2 3 4



   



dt t e



7 11 109 109

3 2 3 4 3. 3 ln 3,305053521

3 2 4 4

            

b b b

C A e e e b

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27

Facebook: https://www.facebook.com/dongpay

Đặt

2 1 d 2 d d

x x

t e t e x x

     



. Đổi cận:

ln2 5, 0 3

x t x t

     

 

ln2 5 5

0 3 3

1 d 1 1 5

d d ln 1 ln ln4 ln5 ln2 ln3 ln2 ln

2 1 1 1 3

x t t t

e t t t t

 

           

 

  

 

  

ln2

1 1 5

d ln 2 ln2 ln 2, 1, 1

2 1 2 3

x x a b c

 

        

 



 



Vậy

a b c

  

Câu 25: Trong các số dưới đây, số nào ghi giá trị của

2 .cos

, ,

1 2

x a

dx a b



 









. Khi đó

a b

bằng

. B. 0. C. 2. D. 1

Hướng dẫn giải

Ta có:

   

 

2 2 2

0 0

2 cosx 2 cos 2 cos

1 2

1 2 .2 1 2 .2

x x x

x x

dx dx dx



 



 

  

  



Đặt

x t

 

ta có



thì 0,x

 



thì





và

dx dt

 

 

   

2 2 2 2

0 0 0 0

2 cos

2 cos cos cos

1 2 .2 1 2 .2 1 2 .2 1 2 .2

x t t x

x t x

dx d t dt dx



     

   

   

   

Thay vào (1) có

   

 

2 2 2 2 2

0 0 0 0

1 2 cos

2 cosx 2 cos cos cos sin 1

1 2 2 2 2

1 2 .2 1 2 .2 1 2 .2

x x

x x x

x x x x

dx dx dx dx dx





     



  

    

    



Vậy

2 cosx 1

1 2 2











Chọn C.

Câu 26: Trong các số dưới đây, số nào ghi giá trị của

2 .cos

1 2









ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28

Facebook: https://www.facebook.com/dongpay

. B. 0. C. 2. D. 1.

Hướng dẫn giải

Chọn A.

Ta có:

   

 

2 2 2

0 0

2 cos 2 cos 2 cos

d d d 1

1 2

1 2 .2 1 2 .2

x x x

x x

x x x



 



 

  

  



Đặt

x t

 

ta có



thì 0,x

  



thì





và

d d

x t

 

 

   

2 2 2 2

0 0 0 0

2 cos

2 cos cos cos

d d d d

1 2 .2 1 2 .2 1 2 .2 1 2 .2

x t t x

x t x

x t t x



     

   

   

   

Thay vào (1) có

   

2 2 2

0 0

2 cos 2 cos cos

d d

1 2

1 2 .2 1 2 .2

x x

x x x

x x dx



 



 

  

  



 

2 2

0 0

1 2 cos

cos sin 1

d d

2 2 2

1 2 .2

x x



   



 

 



Vậy

2 cosx 1

1 2 2











Câu 27:

Cho

( ) 5

f x dx





. Tính

(1 )

I f x dx

 



10.

Hướng dẫn giải

Đặt

t x dt dx

   

0 1

1 0

x t

  

( ) 5

I f t dt

  



Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29

Facebook: https://www.facebook.com/dongpay

Câu 28: Giả sử

 

d 3

f x x





và

 

d 9

f z z





. Tổng

   

3 5

1 3

d d

f t t f t t



 

bằng

12.

Hướng dẫn giải

Chọn C.

Ta có

   

1 1

0 0

d 3 d 3

f x x f t t

  

 

;

   

5 5

0 0

d 9 d 9

f z z f t t

  

 

           

   

5 1 3 5 3 5

0 0 1 3 1 3

3 5

1 3

9 d d d d 3 d d

d d 6.

f t t f t t f t t f t t f t t f t t

f t t f t t

      

  

     

 

Câu 29: Cho

( ), ( )

f x g x

là các hàm số liên tục trên đoạn





2;6

và thỏa mãn

3 6 6

2 3 3

( ) 3; ( ) 7; ( ) 5

f x dx f x dx g x dx

  

  

. Hãy tìm mệnh đề KHÔNG đúng.

[3 ( ) ( )] 8

g x f x dx

 



[3 ( ) 4] 5

f x dx

 



[2 ( ) 1] 16

f x dx

 



[4 ( ) 2 ( )] 16

f x g x dx

 



Hướng dẫn giải

3 6 6

2 3 2

( ) ( ) f( ) 10

f x dx f x dx x dx

  

  

Ta có:

6 6 6

3 3 3

[3 ( ) ( )] 3 ( ) ( ) 15 7 8

g x f x dx g x dx f x dx

     

  

nên

đúng

3 3 3

2 2 2

[3 ( ) 4] 3 f( ) 4 9 4 5

f x dx x dx dx

     

  

nên

đúng

ln 6 6 6

2 2 2 2

[2 ( ) 1] [2 ( ) 1] 2 f( ) 1 20 4 16

f x dx f x dx x dx dx

       

   

nên

đúng

ln 6 6 6

3 3 3 3

[4 ( ) 2 ( )] [4 ( ) 2 ( )] 4 f( ) 2 ( ) 28 10 18

f x g x dx f x g x dx x dx g x dx

       

   

Nên

sai

Chọn

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30

Facebook: https://www.facebook.com/dongpay

Câu 30: Cho hàm số

 

4 8

f x t t dt

 



. Gọi

m M

lần lượt là giá trị nhỏ nhất, giá trị lớn nhất

của hàm số





f x

trên đoạn





0;6

. Tính

M m



A. 18 B. 12 C. 16 D. 9

Hướng dẫn giải

 

   

3 4 2 2

4 8 4 4 3

f x t t dt t t x x

      



, với















2 4; 0 2 1;6

f x x f x x

 

      .













0 3; 2 1; 6 15

f f f

   

. Suy ra

15, 1

M m

  

. Suy ra

M m

 

Chọn C.

Câu 31: Nếu





0 1







f x

liên tục và

 

' 9

f x dx





thì giá trị của





là:

A. 3. B. 9. C. 10. D. 5.

Hướng dẫn giải

Ta có:

           

' 3 0 9 3 1 9 3 10

f x dx f x f f f f

        



Chọn C

Câu 32: Cho





f x

và





g x

là hai hàm số liên tục trên





1,1

 và





f x

là hàm số chẵn,





g x

là

hàm số lẻ. Biết

 

f x dx





và

 

g x dx





. Mệnh đề nào dưới đây sai?

 

f x dx







. B.

 

g x dx







   

f x g x dx



 

 

 

. D.

   

f x g x dx



 

 

 

Hướng dẫn giải

Nhớ 2 tích chất sau để làm trắc nghiệm nhanh:

1. Nếu hàm





f x

CHẴN thì

   

a a

f x dx f x dx





 

2. Nếu hàm





f x

LẺ thì

 

f x dx







Nếu chứng minh thì như sau:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31

Facebook: https://www.facebook.com/dongpay

Đặt

     

1 0 1

1 1 0

A A

A f x dx f x dx f x dx

 

  

  



 

A f x dx







. Đặt

t x

 

dt dx

  

Đổi cận:

       

0 1 1

1 0 0

A f t dt f t dt f x dx

       

  

(Do tích phân xác định không phụ thuộc

vào biến số tích phân)

 

f x dx





(Do





f x

là hàm chẵn









f x f x

   )

Vậy

     

1 1 1

1 0 0

A f x dx f x dx f x dx



   

  

(1)

Đặt

     

1 0 1

1 1 0

B B

B g x dx g x dx g x dx

 

  

  



 

B g x dx







. Đặt

t x

 

dt dx

  

Đổi cận:

       

0 1 1

1 0 0

B g t dt g t dt g x dx

       

  

(Do tích phân xác định không phụ thuộc

vào biến số tích phân)

 

g x dx

 



(Do





f x

là hàm chẵn









g x g x

    )

Vậy

     

1 1 1

1 0 0

B g x dx g x dx g x dx



    

  

(2)

Từ (1) và (2)

Chọn B

Câu 33: Cho tích phân

 

f x dx





. Tính tích phân

 

I f x dx







. B.



. C.



. D.



Hướng dẫn giải

 

I f x dx





Đặt

2 2

t x dt dx

  

Đổi cận:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32

Facebook: https://www.facebook.com/dongpay

   

6 6

0 0

1 1

2 2

I f t dt f x dx

  

 

(Do tích phân xác định không phụ thuộc vào biến số tích

phân )

.20 10

 

Chọn B

Câu 34: Cho hàm số





f x

liên tục trên đoạn [0; 6] thỏa mãn

 

f x dx





và

 

f x dx





. Tính

giá trị của biểu thức

   

2 6

0 4

P f x dx f x dx

 

 



.` B.



. C.



. D.



Hướng dẫn giải

Ta có:

         

2 6 6 2 6

0 4 0 6 4

P f x dx f x dx f x dx f x dx f x dx

 

    

 

 

    

           

6 4 2 6 6 2

0 6 4 4 0 4

f x dx f x dx f x dx f x dx f x dx f x dx

 

     

 

 

     

10 6 4

  

Chọn A

Câu 35: Cho tích phân

 

cos . sin 8

I x f x dx

 





. Tính tích phân

 

sin . cos

K x f x dx







 

. B.



. C.



. D.



Hướng dẫn giải

 

cos . sin

I x f x dx







Đặt

t x

 



dt dx

  

Đổi cận:

     

2 2

0 0

cos . sin . sin . cos . sin . cos .

2 2

I t f t dt t f x dt x f x dt

 

   

      

   

 

   

 

  

 



 

(Tích

phân xác định không phụ thuộc vào biến số tích phân)



K I

  

Chọn C

Câu 36: Cho hàm số





f x

liên tục trên đoạn [0; 1] và có

 

3 2 5

f x dx

 

 

 



. Tính

 

f x dx





. B. 2. C. 1. D.



Hướng dẫn giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33

Facebook: https://www.facebook.com/dongpay

Ta có:

 

3 2 5

f x dx

 

 

 



   

1 1 1

0 0 0

3 2 5 3 2 5

dx f x dx x f x dx

     

  

   

1 1

0 0

2 5 3 2 1

f x dx f x dx

       

 

Chọn A

Câu 37: Cho hai hàm số





f x

và





g x

liên tục trên đoạn [0; 1], có

 

f x dx





và

 

g x dx

 



. Tính tích phân

   

I f x g x dx

 

 

 





. B.

. C. 2. D.



Hướng dẫn giải

         

1 1 1

0 0 0

3 3 4 3 2 10

I f x g x dx f x dx g x dx

       

 

 

  

Chọn B

Câu 38: Cho hàm số





y f x

 có đạo hàm là





f x

liên tục trên đoạn [0; 1] và





1 2



. Biết

 

f x dx





, tính tích phân

 

. '

I x f x dx







. B.

 

. C.



. D.

 

Hướng dẫn giải

Ta có:

 

. '

I x f x dx





Đặt

u x du dx

  





dv f x dx

 Chọn









v f x dx f x

 



         

1 1

0 0

. 1. 1 0. 0 2 1 1

I x f x f x dx f f f x dx

        

 

Chọn A

Câu 39: Cho biết

( ) 15

f x dx







. Tính giá trị của

[ (5 3 ) 7]dx

P f x  





Hướng dẫn giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34

Facebook: https://www.facebook.com/dongpay

Để tỉnh

ta đặt

5 3

0 5

2 1

t x dx

x t

    

  

   

nên

1 5 5 5

5 1 1 1

1 1

[ ( ) 7]( ) [ ( ) 7]dt ( ) 7

3 3 3

1 1

.15 .7.(6) 19

3 3

P f t f t f t dt dt



  

 

      

 

 

  

   

Chọn D.

Câu 40: Cho là hàm số chẵn, có đạo hàm trên đoạn Biết rằng và

. Tính

A. B. C. D.

Hướng dẫn giải

Chọn D.

Vì là hàm số chẵn nên

Xét tích phân

Đặt

Đổi cận:

1 2; 3 6

x u x u

     

Vậy

Câu 41: Cho

là hai hàm liên tục trên





1;3

thỏa:

   

3 d 10

f x g x x

 

 

 

   

2 d 6

f x g x x

 

 

 

. Tính

   

f x g x x



 

 



A. 8. B. 9. C. 6. D. 7.





y f x







6;6 .



 

d 8

f x x







 

2 d 3

f x x

 



 

I f x x







11.



14.







f x

     

2 2

1 1

d 0 d d 8

f x x f x x f x x

 

   

  

   

3 3

1 1

2 d 2 d 3

f x x f x x

  

 

 

2 d 3

K f x x

 



2 d 2d d

u x u x x    

     

6 6 6

2 2 2

1 1

d d 3 d 6

2 2

K f u u f x x f x x

    

  

       

6 6 2 6

1 1 1 2

d d d d 8 6 14.

I f x x f x x f x x f x x



      

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải

Chọn C.

 Ta có

       

3 3 3

1 1 1

3 d 10 d 3 d 10

f x g x x f x x g x x

    

 

   

 Tương tự

       

3 3 3

1 1 1

2 d 6 2 d d 6

f x g x x f x x g x x

    

 

   

 Xét hệ phương trình

3 10 4

2 6 2

u v u

u v v

  

 



 

  

 

, trong đó

 

u f x x





 

v g x x





 Khi đó

       

3 3 3

1 1 1

d d d 4 2 6

f x g x x f x x g x x

     

 

   

Câu 42: Cho hàm số

 

ln 1

f x x x

  

. Tính tích phân

 

I f x dx





ln 2

I 

. B.





ln 1 2

I   . C.

ln 2



2ln2



Hướng dẫn giải

Ta có:

   

 

' ln 1 ln 1 2

I f x dx f x x x      



Chọn B

Câu 43: Cho hàm số





f x

có đạo hàm liên tục trên đoạn [1; ln3] và thỏa mãn





f e



 

ln3

' 9

f x dx e

 



. Tính





ln3

I f .

9 2

I e

 

. B.



. C.

 

. D.

2 9

I e

 

Hướng dẫn giải

Ta có:

       

ln3

' ln3 1 9

f x dx f x f f e

    



(gt)









2 2

ln3 9 ln3 9

f e e f

     

Chọn B

Câu 44: Cho hai hàm số





y f x

 và





y g x

 có đạo hàm liên tục trên đoạn [0; 1] và thỏa mãn

   

' . 1

f x g x dx





   

. ' 1

f x g x dx

 



. Tính

   

I f x g x dx



 

 



 

. B.



. C.



. D.



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải

           

1 1

0 0

.g . ' ' .g

I f x x dx f x g x f x x dx

  

   

   

 

       

1 1

0 0

. ' ' . 1 1 0

f x g x dx f x g x dx

    

 

Chọn B

Câu 45: Cho hàm số





y f x

 liên tục trên R, thỏa mãn

 

f x dx





. Tính

 

tan 1 . tan

I f x dx

 







. B.

 

. C.





. D.

 



Hướng dẫn giải

Đặt





tan 1 tan

t x dt x dx

    . Đổi cận:

   

1 1

0 0

I f t dt f x dx

  

 

(Tích phân xác định không phụ thuộc vào biến số tích phân)



Chọn A

Câu 46: Cho hàm số





y f x

 liên tục và thỏa mãn

 

2 3

f x f x

 

 

 

 

với

 



 

 

. Tính





f x



. B.

. C.



. D.



Hướng dẫn giải

Đặt





f x

A dx





(1) Đặt

1 1

t dt dx

x x

   

  

Đổi cận:

 

2 2

1 1

2 2

1 1 1

t f f f

t t x

A dt dt dx

t t

     

     

     

    

  

(Tích phân xác định không phụ thuộc vào

biến số tích phân) (2)

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37

Facebook: https://www.facebook.com/dongpay

Ta có:

   

 

2 2 2

1 1 1

2 2 2

1 2 2 3 3 3

f x f

A dx dx dx x

x x

 



 

 

     

  

9 3

2 2

A A

   

Chọn B

Câu 47: Cho hàm số





y f x

 liên tục trên R và thỏa mãn









2 2cos2

f x f x x

    . Tính

 

I f x dx









 

. B.



. C.

 

. D.



Hướng dẫn giải

 

I f x dx









(1) Đặt

t x dt dx

    

Đổi cận:

       

2 2 2

I f t dt f t dt f x dx



 

       

  

  

(2) (Tích phân xác định không phụ thuộc

vào biến số tích phân)

(1) + (2)

   

2 2

2 2 2cos2

I f x f x dx xdx

 

      

 

 

 

 

2 1 cos2

x dx



  





 

2 2 2

2 2cos 2 cos 2 cos 2sin 2 1 1 4

xdx x dx xdx x



  

      

 

 

  

  



  

 

Chọn D

Câu 48: Biết hàm số

y f x

 

 

 

 



là hàm số chẵn trên đoạn

;

2 2

 



 

 

 

và

 

sin cos

f x f x x x

 

   

 

 



. Tính

 

I f x dx









. B.



. C.



. D.

 

Hướng dẫn giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38

Facebook: https://www.facebook.com/dongpay

Đặt

t x dt dx

    



Đổi cận:

 

2 2

0 0

2 2 2

I f t dt f t dt f x dx

     

       

     

     

  

 



  

(Tích phân xác định không phụ

thuộc vào biến số tích phân)

f x

 

 

 

 











Vì

f x

 



 

 



là hàm số chẵn

2 2

f x f x



   

   

   



   



 

Vậy

     

2 2

0 0

2 sin cos cos sin 1 1 2

I f x f x dx x x dx x x

 

 

           

 

 

 

 

 

 



  

Chọn D

Câu 49: Cho hàm số





y f x

 liên tục trên R, thỏa mãn









2018

f x f x e

  

. Tính

 

I f x dx







2019





. B.

2018





. C.



. D.





Hướng dẫn giải

 

I f x dx







(1) Đặt

t x

 

dt dx

  

Đổi cận:

      

1 1 1

I f t dt f t dt f x dx



 

       

  

(2) (Tích phân xác định không phụ thuộc

vào biến số tích phân).Ta có:

       

1 2018 2 2018 2018

I I f x f x dx



     

 

 



1 1

2019

x x

I e dx e e

e e



     



2019



 

Chọn A

Câu 50: Cho hàm số





f x

thỏa mãn

   

1 ' 10

x f x dx

 



và









2 1 0 2

f f

 

. Tính

 

I f x dx







. B.

 

. C.



. D.

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải

   

1 '

A x f x dx

 



Đặt 1

u x du dx

   





dv f x dx

 Chọn





v f x



           

1 1 1 1

0 0 0 0

1 . 2 (1) (0) 2 10 8

A x f x f x dx f f f x dx f x dx f x dx

            

   

Chọn B

Câu 51: Cho hàm số





f x

thỏa









0 1 1

f f

 

. Biết

   

e f x f x dx ae b

  

 

 



. Tính biểu

thức

2018 2018

Q a b

  .



. B.



. C.



. D.



Hướng dẫn giải

       

1 2

1 1 1

0 0 0

' '

x x x

A A

A e f x f x dx e f x dx e f x dx

    

 

  

 

 

A e f x dx





Đặt









u f x du f x dx

   ,

dv e dx



Chọn

v e



   

. '

x x

A e f x e f x dx

  





Vậy

       

1 1

2 2

0 0

. 1 0 1

x x

A e f x A A e f x e f f e

       

2018 2018

1 1 2

a b





     



 



Chọn D

Câu 52: Cho hàm số





f x

liên tục trên







và thỏa

 

.cos

f t dt x x







. Tính





f .





4 123

f  . B.

 



. C.

 



. D.

 



Hướng dẫn giải

Ta có:

















F t f t dt F t f t

  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40

Facebook: https://www.facebook.com/dongpay

Đặt

   

 

G x f t dt F x F  



 









2 2

' 2 .

G x F x x f x

 

  

 

(Tính chất đạo hàm hợp:













' ' . '

f u x f u u x

 

 

)

Mặt khác, từ gt:

   

.cos

G x f t dt x x

 













' .cos ' sin cos

G x x x x x x

    

   





2 . sin cos

x f x x x x

   

  

(1)

Tính





f  ứng với



Thay



vào (1)





4. 4 2 sin2 cos2 1

    

  

 

 

Chọn D

Câu 53: Cho hàm số





f x

thỏa mãn





. .cos

f x

t dt x x







. Tính





f .





4 2 3

f  . B.





4 1

 

. C.

 



. D.





4 12

f  .

Hướng dẫn giải

 

cos 3 .cos

3 3

f x

t dt x x f x x x

 

 

     

 



 









3 cos 4 12

f x x x f   



Chọn D

Câu 54: Cho hàm số





f x

có đạo hàm liên tục trên đoạn [1, 2] và thỏa mãn





f x



khi





1,2

x .

Biết

 

' 10

f x dx





và





 

ln2

f x





. Tính





f .





2 10

 

. B.





2 20



. C.





2 10



. D.





2 20

 

Hướng dẫn giải

Ta có:

       

' 2 1 10

f x dx f x f f

   



(gt)





 

     





 

' 2

ln ln 2 ln 1 ln ln2

f x f

dx f x f f

f x f

    

     

     



(gt)

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41

Facebook: https://www.facebook.com/dongpay

Vậy ta có hệ:









 

2 1 10

2 20

1 10

f f

  









 







Chọn B

Câu 55: Cho hàm số





y f x

 có đạo hàm liên tục trên đoạn





1;1

 , thỏa mãn





f x



x  R và









' 2 0

f x f x

 

. Biết





1 1



, tính











f e



 

. B.





f e

 

. C.





f e

 

. D.





1 3

 

Hướng dẫn giải

Từ gt:

       





 

' 2 0 ' 2 2

f x

f x f x f x f x

f x

       





 

   

2 ln 2

x C

f x

dx dx f x x C f x e

f x

 

        

 

 

 

Có









2 0 2 2

1 1 1 2

c x

f e e c f x e

   

       





f e

  

Chọn C

Câu 56: Cho hàm số





y f x

 có đạo hàm liên tục trên R, nhận giá trị dương trên khoảng







và thỏa





1 1











' 3 1

f x f x x

 

. Mệnh đề nào đúng?





1 5 2

 

. B.





4 5 5

 

. C.





2 5 3

 

. D.





3 5 4

 

Hướng dẫn giải

Từ gt:

   





 

' 3 1

3 1

f x

f x f x x

f x

   







 

1 2

ln 3 1

3 1

f x

dx dx f x x C

f x

     

 

 



 

 

3 1

x C

f x e

 

 

Vì

 

1 1 1

f e e C



      

   

2 4 4

3 1

3 3 3

5 3,79

f x e f e

 

    

Chọn D

Câu 57: Cho hàm số





y f x

 có đạo hàm liên tục trên R và





f x



khi x  [0; a] (



). Biết









. 1

f x f a x

 

, tính tích phân

 

f x









. B.

I a



. C.



. D.



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải

 

f x







(1) Đặt

t a x dt dx

    

Đổi cận:

     

0 0

1 1

1 1 1

a a

I dt dx

f a t f a t f a x

    

     

  

(2) (Tích phân xác định không

phụ thuộc vào biến số tích phân)

(1) + (2)

   

1 1

I dx

f x f a x

 

  

 

  

 











       









   

0 0

1 1 2

1 . 2

f a x f x f a x f x

dx dx dx a

f x f a x f x f a x f a x f x

      

   

       

 

 

Chọn A

Câu 58: Cho hàm số

   

.cos .

G x t x t dt

 



. Tính

 

 

 



' 1

 

 

 

 



. B.

' 1

 



 

 



. C.

' 0

 



 

 



. D.

' 2

 



 

 



Hướng dẫn giải

Cách 1: Ta có:

















.cos ' .cos

F t t x t dt F x t x t

    



Đặt

       

.cos 0

G x t x t dt F x F   



           

/ /

' 0 ' ' 0 cos 0 ' 1

G x F x F F x F x x x x

         

   

   

' 1

 

 

 

 



Chọn B

Cách 2: Ta có

   

.cos

G x t x t dt

 



. Đặt

u t du dt

  





cos

dv x t dx

  Chọn





sin

v x t

  

         

0 0

.sin sin sin cos cos0 cos 1 cos

x x

G x t x t x t dt x t dt x t x x

             

 

 

' sin ' sin 1

2 2

G x x G

 

    

 

 

 

Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43

Facebook: https://www.facebook.com/dongpay

Câu 59: Cho hàm số

 

cos .

G x t dt



( 0x  ). Tính

 

'G x .

 

' .cosG x x x . B.

 

' 2 .cosG x x x . C.

 

' cosG x x . D.

 

' cos 1G x x 

Hướng dẫn giải

Ta có

   

cos ' cosF t tdt F t t  



 

cos 0

G x tdt F x F   



 

   

/ / /

2 2 2 2

' 0 0 2 .F'G x F x F F x F F x x x

     

       

 

     

2 .cos 2 .cosx x x x 

Chọn B

Câu 60: Tìm giá trị lớn nhất của

 

G x t t dt 



trên đoạn

 

1;1 .

. B.

. C.

 . D.

Hướng dẫn giải

 

3 2 3 2 3 2

1 1 5

3 2 3 2 3 2 3 2 6

t t x x x x

G x t t dt

 

          

 

 



 

'G x x x    bảng biến thiên:

Từ bảng biến thiên

Chọn C

Câu 61: Cho hàm số

 

G x t dt 



. Tính

 

'G x .

x

. B.

1 x . C.

1 x

. D.

 

2 2

1 1x x 

Hướng dẫn giải

Đặt

   

2 2

1 ' 1F t t dt F t t    



             

1 1 ' ' ' 1 '

G x t dt F x F G x F x F F x

        





Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44

Facebook: https://www.facebook.com/dongpay

Câu 62: Cho hàm số

 

sin .

F x t dt





(



). Tính





F x

sin

. B.

sin

. C.

2sin

. D. sin

Hướng dẫn giải

Đặt





sin

F t t dt





 

sin 1

G x t dt F x F  



 





 













sin

' ' ' 1 ' '.sin

G x F x F F x x x

     

Chọn B

Câu 63: Tính đạo hàm của





f x

, biết





f x

thỏa

   

f t f x

t e dt e









f x x



. B.





' 1

f x x

 

. C.

 

'f x



. D.

 

f x





Hướng dẫn giải

Đặt

















. ' .

f t f t

F t t e dt F t t e

  



 

   

. 0

f t

G x t e dt F x F   















' '

f x

G x F x e

   (gt)









f x f x

x e e

 

   

f x f x

x e e

   

 

   





















. ' .e ' .

f x f x f x

e x f x f x e

  

     

1 . ' ' '

x f x f x f x

    



Chọn D

Câu 64: Cho





y f x

 là hàm số chẵn, có đạo hàm trên đoạn





6;6 .

 Biết rằng

 

d 8

f x x







và

 

2 d 3.

f x x

 



Tính

 

d .

f x x







. B.



. C.



. D.



Hướng dẫn giải

Xét tích phân

 

2 d

K f x x

 



Đặt

2 d 2d d

u x u x x       

Đổi cận: Khi

1 2

x u

   

;

3 6

x u

   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45

Facebook: https://www.facebook.com/dongpay

Vậy,

   

6 2

2 6

1 1

d d

2 2

K f u u f x x

 

  

 

. Mà



, nên

 

d 6

f x x







Vì

là hàm chẵn trên





6;6

 nên

   

6 2

2 6

d d 6

f x x f x x



 

 

Từ đó suy ra

     

6 2 6

1 1 2

d d d 8 6 14

I f x x f x x f x x

 

     

  

Chọn D.

Câu 65: Cho hàm số . Biết rằng và . Khi đó tổng

bằng?

A. . B. . C. . D. .

Hướng dẫn giải

Giải hệ (1) và (2) ta được: .

Chọn D.

Câu 66: Cho

là hai hàm liên tục trên





1;3

thỏa:

   

3 d 10

f x g x x

 

 

 

   

2 d 6

f x g x x

 

 

 

. Tính

   

f x g x x



 

 



A. 8. B. 9. C. 6. D. 7.

Hướng dẫn giải

+ Ta có

       

3 3 3

1 1 1

3 d 10 d 3 d 10

f x g x x f x x g x x

    

 

   

+ Tương tự

       

3 3 3

1 1 1

2 d 6 2 d d 6

f x g x x f x x g x x

    

 

   

( ) .

(x 1)

f x b xe

 



'(0) 22

 

( ) 5

f x dx





a b



146



146

'(x) (1 )

(x 1)

'(0) 22 3a b 22 (1)

f be x



  



      

1 1 1

0 0 0

( ) 5 5

(x 1)

5 (2)

f x dx a dx b xe dx

   



  

  

108 38

13 13

a b 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46

Facebook: https://www.facebook.com/dongpay

+ Xét hệ phương trình

3 10 4

2 6 2

u v u

u v v

  

 



 

  

 

, trong đó

 

u f x x





 

v g x x





+ Khi đó

       

3 3 3

1 1 1

d d d 4 2 6

f x g x x f x x g x x

     

 

   

Nên ta có hệ phương trình sau:

 

0 . 10

1 5

402

5 5

40 2

2 2

P y x

b b



  



 

    

 

 

 



 

Ta có thể tích của bê tông là:

2 2 3

0 0

1 5 8

5.2 2 40

40 2 361

V x dx x dx m

 

   

      

 

   

   

 

 

Câu 67: Cho , , . Khẳng định nào sau đây đúng?

A. . B. . C. . D.

Hướng dẫn giải

Với .

Đặt .

Chọn .

Suy ra

Do đó .

Chọn C.

Câu 68: Rút gọn biểu thức:

0 1 2 *

1 1 1

... , .

2 3 1

n n n n

T C C C C n

     





cos

I xdx













n n

I I





n n

I I





n n

I I





n n

I I





0 1

; cos 1

I I xdx



  







1 2

cos 1 cos .sin

n n

u x du n x xdx

 

    

cos

dv xdx



sin

v x



 

2 2

1 2 2

0 0

cos cos .sin 1 cos .sin

n n n

xdx x x n x xdx

 



 

  

 

 

2 2

1 cos . 1 cos

n x x dx





  



   

2 2

0 0

1 cos . 1 cos .

n n

n x dx n x dx

 



   

 

2 2

0 0

cos . cos .

n n

x dx x dx

 





 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47

Facebook: https://www.facebook.com/dongpay





. B.





. C.

2 1







. D.

2 1









Hướng dẫn giải

Ta có

0 1

1 1

...

2 1

n n n

T C C C

   



. Nhận thấy các số

1 1 1 1

; ; ;...;

1 2 3 1



thay đổi ta nghĩ ngay đến

biểu thức

n n

x dx x c



 





Ở đây ta sẽ có lời giải như sau:

 

0 1 2 2 3 3

1 ...

n n

n n n n n

x C xC x C x C x C

       .

Khi đó ta suy ra

 

1 1

0 1 2 2 3 3

0 0

1 ...

n n

n n n n n

x dx C xC x C x C x C dx

      

 

 

2 3 1

0 1 3

1 1

1 ...

0 0

1 2 3 1

n n n n

x x x

x C x C C C

n n



 

      

 

 

 

0 1 2

2 1 1 1 1

...

1 2 3 1

n n n n

C C C C

n n





     

 

Chọn D.

Câu 69: Nếu a là một số thỏa mãn các điều kiện sau:

;

2 2

 

 



 

 

và

 

cos sin

x a dx a

 



thì:









. C.

2 .









Hướng dẫn giải:

     

 

2 2 2 2

cos sin sin sin sin sin

2cos .sin 2sin .cos 1

2 2 2 2

x a dx x a a a a a a

a a a a a

       



 



Vì

;

2 2

 

 



 

 

nên

; sin 0

2 4 4 2

a a

 

 

  

 

 

, vậy:

 

2 2

1 cos cos cos cos 0

2 2 2 2

a a a a a a 

    

 

2 2

sin 0 1

2 2

2sin .sin 0 ,

2 2

sin 0 2

2 2

a a a a

a a a

k l

a a



 

 

 

 



 

     

 

 

 

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48

Facebook: https://www.facebook.com/dongpay

Vì k





nên (1) không thỏa mãn với mọi

;

2 2

 

 



 

 

,hoặc thay 4 vào đáp án (1) ta thấy

đều không thỏa.

Đối với (2). Vì

;

2 2

 

 



 

 

nên Chọn l=1 lúc đó





Chọn D.

Câu 70: Gọi S là tập hợp tất cả các số nguyên dương k thỏa mãn điều kiện

ln 2

dx e

 



. Khi đó:





1 .

S  B.





S  . C.





1,2

S  D.

 

Hướng dẫn giải:



Dùng phương pháp tích phân từng phần

ln ln ln

u k x du dx

x x

dv dx v x



     







  



 

ln ln ln 1

k k

I x dx e k e

x e

      



Vậy

 

ln 2 ln ln 1 2

k k

dx e e k e e

x e

       











ln 1 ln 1 1 ln 1 ln 1

e k k e k e k

          

k e

 

mà k là số nguyên dương nên Chọn





1;2

k  .

Chọn C.

Câu 71: Biết

 

f x dx





và

 

f t dt





. Tính

 

f u du





Hướng dẫn giải:

     

4 3 4

0 0 3

f u du f u du f u du

 

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49

Facebook: https://www.facebook.com/dongpay

Mà

   

3 3

0 0

f u du f x dx

 

 

và

   

4 4

0 0

f u du f t dt

 

 

Nên:

   

4 4

3 3

3 5 3 5 16

5 3 5 3 15

f u du f u du

      

 

Chọn D.

Chú ý: tích phân không phụ thuộc vào biến số.

Câu 72: Biết

dx a









. Tính giá trị của

I dx







I a

 

1 .

I a

 

I a

 

1 .

I a

 

Hướng dẫn giải:

Sử dụng phân tích

1 1 1

2 2

0 0 0

1 1

x x

dx dx x dx

e e



 

 

  

Hoặc máy tính cầm tay để kiểm tra kết quả.

Chọn C.

Câu 73: Đặt

sin

I xdx







. Khi đó:

n n

I I





n n

I I





n n

I I





n n

I I





Hướng dẫn giải:

Khi



 

thì

0 sin 1

 

. Do đó với



 

Ta có:

2 2

1 1

0 0

sin sin sin sin

n n n n

n n

x x I xdx I xdx

 

 

    

 

, tức là:

n n

I I





Chọn A.

Câu 74: Cho

 

2 2

I x x dx

 



và

 

J x x dx

 



. Xét các câu:

(1)

 

2 1





với mọi n.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50

Facebook: https://www.facebook.com/dongpay

(2)

 

2 1





với mọi n.

(3)

 

2 1

n n

I J

 



với mọi n.

A. (1) đúng. B. (1) và (2) đúng. C. Tất cả đều sai. D. cả (1) và (3)

đúng.

Hướng dẫn giải:

Chỉ (1) và (3) đúng. Khẳng định (2) sai.

Ta đặt

cos

x t



để tính

 

2 2

2 2 1

0 0

sin 1 cos cos sin .cos

J t t tdx t tdt

 



  

 

 

2 2

2 1

sin 1

sin sin

2 2 2 1

td t

n n





  

 



Như vậy khẳng định (2) sai. Ngoài ra, để thấy rằng với mọi





0;1

x

x x



nên suy ra với mọi n ta có

 

2 1

n n

I J

 



Vậy: (1) và (3) cùng đúng.

Chọn D.

Câu 75: Tìm số nguyên dương k nhỏ nhất, thỏa mãn

x k









. B.



. C.



. D.



Hướng dẫn giải:





, 0;1 , 2 0

x x x k

     



do đó:

x k







 



Suy ra số nguyên dương k nhỏ nhất thỏa mãn ycbt là k=1

Chọn C.

Câu 76: Cho









f x g x

là các hàm liên tục trên [a; b].

(1) Với mọi số thực y, ta có:

       

2 2 2

2 . 0

b b b

a a a

y f x dx y f x g x dx g x dx

  

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51

Facebook: https://www.facebook.com/dongpay

(2)

       

2 2 2 2

. .

b b b

a a a

f x g x dx f x dx g x dx

 



 

 

  

Trong hai khẳng định trên:

A. Chỉ có (1) đúng. B. Chỉ có (2) đúng.

C. Cả hai khẳng định đều đúng. D. Cả hai khẳng định đều sai.

Hướng dẫn giải:

Với mọi số thực y ta có:

   

0 .

y f x g x

   

 

















2 2 2

. 2 . .

y f x y f x g x g x

   từ đó suy ra (1) đúng:

 

2 2 2

( ) 2 ( ).g ( ) 0

b b b

a a a

y f x dx y f x x dx g x dx

  

  

Vì vế trái của Bất đẳng thức trên là tam thức bậc hai đối với y, nên theo định thức về dấu

của tam thức bậc hai, Ta có:

2 2

' ( ). ( ) ( ) . ( ) 0

b b b

a a a

f x g x dx f x dx g x dx

 

   

 

 

  

2 2

( ). ( ) ( ) . ( )

b b b

a a a

f x g x dx f x dx g x dx

 

 

 

 

  

((2) đúng).

Chọn C.

Câu 77: Cho









f x g x

là các hàm liên tục trên [a; b].









0, ;

f x x a b

   và





 

 

, ;

g x

m M x a b

f x

   

Căn cứ vào giả thiết đó, một học sinh lập luận:

(1) Ta có bất đẳng thức





 





 

 

 

0 . , ; . *

g x g x

m M f x x a b

f x f x

  

    

  

  

(2) Biến đổi, (*) trở thành

















2 2

0 ( ) . . . . ( ), ; .

g x M m f x g x M m f x x a b

      

(3) suy ra

         

2 2

. .

b b b

a a a

g x dx M mx f x dx M m f x g x dx

  

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52

Facebook: https://www.facebook.com/dongpay

Lập luận trên:

A. Đúng hoàn toàn. B. Sai từ (1). C. Sai từ (2). D. Sai từ (3).

Hướng dẫn giải:

Lập luận đúng hoàn toàn. Bất đẳng thức sau cùng được gọi là bất đẳng thức Diza

Chọn A.

Câu 78: Cho hai hàm









f x g x

cùng đồng biến và liên tục trên [a; b]. Với

a b



. Khi đó, xét

khẳng định sau đây:

(1)





;

x a b

  . Ta có:

     

b b b

a a a

f a dx f x dx f b dx

 

  

(2)

   

f x dx f b





(3) Tồn tại





;

x a b

 sao cho

 

f x f x dx

b a







Các khẳng định đúng trong 3 khẳng định trên là:

A. Chỉ (1) và (2). B. Chỉ (2) và (3).

C. Chỉ (1) và (3). D. Cả (1), (2) và (3).

Hướng dẫn giải:

Chỉ (1) và (3) đúng. Khẳng định (2) sai:

Do tính đồng biến nên

a x b

  

ta có













f a f x f b

  , tức là:

     

b b b

a a a

f a dx f x dx f b dx

 

  

vậy (1) đúng

Suy ra:

       

. ( ) .

b a f a f x dx b a f b

   



Do đó





f x

liên tục trên [a;b] nên tồn tại





;

x a b

 sao cho:

 

f x f x dx

b a







. Vậy (3) đúng.

Chọn C.

Câu 79: Ta định nghĩa:

   













     

khi

max ,

khi g

f x f x g x

f x g x

g x x f x

 



  



 







ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 53

Facebook: https://www.facebook.com/dongpay

Cho





f x x



và





3 2

g x x

 

Như thế

 

max ( ), ( )

f x g x dx



bằng:

x dx



. B.

 

1 2

0 1

3 2

x dx x dx

 

 

 

3 2

x dx





. D. 15.

Hướng dẫn giải:

Hoành độ giao điểm của hai đường thẳng là

1; 2

x x

 

Xét





3 2

x x

 

và vẽ Bảng xét dấu để xem trên đoạn nào thì





f x x



và





3 2

g x x

 

hàm có Giá trị lớn hơn.

0 1 2

3 2

x x

 

+ 0 − 0

Do đó

     

2 1 2

0 0 1

max , 3 2

f x g x dx x dx x dx

    

   

Chọn B.

Câu 80: Biết

cos

1 3

dx m











. Tính giá trị của

cos

1 3

I dx



























Hướng dẫn giải:

Sử dụng phân tích:

2 2

cos cos

cos .

1 3 1 3

x x

dx dx xdx

  





  

  

 

  

(sử dụng MTCT để tính

cos .xdx









)

Do đó:

cos

1 3

I dx m





  





Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 54

Facebook: https://www.facebook.com/dongpay

Câu 81: Cho

x m







với m > 0. Tìm các giá trị của tham số m để



 

. B.



. C.

1 1

8 4

 

. D.



Hướng dẫn giải:

Tính tích phân theo tham số m bằng cách đặt

t x m

 

, sau đó tìm m từ Bắt phương

trình



Chọn A.

Câu 82: Cho m là một số dương và

 

4 ln 4 2 ln 2

x x

I dx

 



. Tìm m khi



. B.



. C.



. D.



Hướng dẫn giải:

Tính tích phân theo tham số m ta được:

 

4 ln 4 2 ln 2

x x

I dx

 







4 2 4 2

x x m m

   

sau đó tìm m từ phương trình I =12.

Chọn D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 55

Facebook: https://www.facebook.com/dongpay

ỨNG DỤNG TÍCH PHÂN NÂNG CAO

A – LÝ THUYẾT CHUNG

1. Diện tích hình phẳng

Nếu có hình phẳng giới hạn bởi các đường

( )

y f x

x a

x b





















(Trong đó

1 2

( ), ( )

f x f x

liên tục trên đoạn [a;b]),

thì diện tích S được tính theo công thức

1 2

( ) ( )

S f x f x dx

 



2. Thể tích khối tròn xoay

Quay quanh trục Ox: Cho hình phẳng giới giới hạn bởi các đường





y f x

x a

x b















(Trong đó





f x

liên tục trên đoạn [a;b]), quay quanh trục Ox, ta được khối tròn xoay.

Thể tích

của khối tròn xoay được tính theo công thức

 

( )

V f x dx







Quay quanh trục Oy: Cho hình phẳng giới hạn bởi các đường





x f y

x a

x b















(Trong đó





f y

liên tục trên đoạn [a;b]), quay quanh trục Oy, ta được khối tròn xoay.

Thể tích

của khối tròn xoay được tính theo công thức

 

(y)

V f dx







B – BÀI TẬP TRẮC NGHIỆM

Câu 1: Cho hàm số





y f x

 liên tục trên đoạn





;

a b

. Gọi

là diện tích hình phẳng giới hạn bởi

đồ thị









C y f x

 , trục hoành, hai đường thẳng

x a



x b



(như hình vẽ dưới đây).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 56

Facebook: https://www.facebook.com/dongpay

Giả sử

là diện tích hình phẳng

. Chọn công thức đúng trong các phương án A, B, C, D

cho dưới đây?

   

d d

S f x x f x x 

 

. B.

   

d d

S f x x f x x  

 

   

d d

S f x x f x x 

 

. D.

   

d d

S f x x f x x  

 

Hướng dẫn giải:

Chọn B.

+ Nhìn đồ thị ta thấy:

 Đồ thị ( )C cắt trục hoành tại

 

0;0O

 Trên đoạn

 

;0a , đồ thị ( )C ở dưới trục hoành nên

   

f x f x 

 Trên đoạn

 

0;b , đồ thị

 

C ở trên trục hoành nên

   

f x f x

+ Do đó:

         

0 0

d d d d d

b b b

a a a

S f x x f x x f x x f x x f x x     

    

Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị

 

C của hàm số

 

4 3

y x x   và hai tiếp

tuyến của

 

C xuất phát từ

 

3; 2M  là

Hướng dẫn giải:

Chọn A

Ta có

 

2 4 2

y x x



    .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 57

Facebook: https://www.facebook.com/dongpay

Gọi





0 0

;

x y

là tọa độ tiếp điểm. Khi đó,

 

0 0 0

4 3

y x x

  

và





0 0

y x x



 

Phương trình của tiếp tuyến của





tại điểm có tọa độ





0 0

;

x y

là

  

 

0 0 0 0

2 4 3

y x x x x x

     

Vì tiếp tuyến đi qua điểm





3; 2



nên

  

 

0 0 0 0

1 1

2 2 3 4 3

5 3 11

x y x

x x x x

x y x

    



       



   



Diện tích hình phẳng cần tìm

 

3 5

2 2

1 3

1 1 8

4 3 1 d 4 3 3 11 d

2 2 3

S x x x x x x x x

   

           

   

   

 

Câu 3: Gọi D là miền được giới hạn bởi các đường

3 10, 1,

y x y y x

    

và D nằm ngoài

parabol

y x



. Khi cho D quay xung quanh trục Ox, ta nhận được vaath thể tròn xoay có

thể tích là:

11 .



12 .



Hướng dẫn giải:

Gọi

1 2

;

V V

lần lượt là thể tích tam giác cong

ABH

và tam giác HBC tạo nên khi xoay quanh

trục Ox, phần diện tích được biểu diễn qua đồ thị sau:

Vậy

 

2 3

2 2 2 2

1 2

( ) 1 ( 3 10) 1 (dvtt)

V V V x dx x dx

 

        

 

 



 

Chọn B.

= 1

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 58

Facebook: https://www.facebook.com/dongpay

Câu 4: Gọi d là tiếp tuyến của đồ thị hàm số

y x



tại giao điểm của đồ thị đó với trục Ox. Diện

tích của hình tam giác tạo bởi hai trục tọa độ và đường thẳng d được xác định bởi tích phân:

xdx



. B.



. C.

 

x dx





. D.

 

x dx





Hướng dẫn giải:

Tọa độ giao điểm của đồ thị y=lnx với trục Ox là nghiệm của hệ phương trình:

ln 1

0 0

y x x

y y

 

 



 

 

 

Ta có:

   

' ln , 1 1

y x y



  

Vậy phương trình của tiếp tuyến d là:





0 1 1 1

y x y x

     

Diện tích phải tìm:

 

1 1

0 0

1 1

2 2

S x dx x dx x

 

      

 

 

 

Chọn D.

Câu 5: 1) cho

1 1

( )

y f x



và

2 2

( )

y f x



là hai hàm số liên tục trên đoạn [a;b]. Giả sử:



và



, với

a b

  

 

, là các nghiệm của phương trình

1 2

( ) ( ) 0

f x f x

 

. Khi đó diện tích của hình

phẳng giới hạn bởi 2 đường thẳng và đồ thi của hàm số được cho bởi công thức

1 2 1 2 1 2

( ) ( ) ( ) ( ) ( ) ( ) .

S f x f x dx f x f x dx f x f x dx

     

  





 

(2) Cũng với giải thiết như (1), nhưng:

   

1 2 1 2 1 2

( ) ( ) ( ) ( ) ( ) ( ) .

S f x f x dx f x f x dx f x f x dx

     

  





 

A. (1) đúng nhưng (2) sai. B. (2) đúng nhưng (1) sai.

C. Cả (1) và (2) đều đúng. D. Cả (1) và (2) đều sai.

Hướng dẫn giải:

Chú ý rằng với mọi





1 2

; , ( ) ( ) 0

x f x f x

  

 

và

( )

f x

và

( )

f x

đều liên tục trên khoảng





;

 

, nên

1 2

( ) ( )

f x f x



giữ nguyên dấu.

Nếu

1 2

( ) ( ) 0

f x f x

 

thì ta có:

   

1 2 1 2 1 2

( ) ( ) ( ) ( ) ( ) ( )

f x f x dx f x f x dx f x f x dx

  

  

    

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 59

Facebook: https://www.facebook.com/dongpay

Nếu

1 2

( ) ( ) 0

f x f x

 

thì ta có:

   

1 2 2 1 1 2

( ) ( ) ( ) ( ) ( ) ( )

f x f x dx f x f x dx f x f x dx

    

  

  

  

Vậy trong mọi trường hợp ta đều có:

 

1 2 1 2

( ) ( ) ( ) ( )

f x f x dx f x f x dx

  

 

 

 

Tương tự như thế đối với 2 tích phân còn lại. vì vậy, hai công thức (1) và (2) là như

nhau:

Chọn C.

Câu 6: Gọi là diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục Ox và đường

thẳng với . Kết quả giới hạn là:

A. 1. B. 2. C. 3. D. 4

Hướng dẫn giải:

Ta có

Suy ra ,

Chọn B.

Câu 7: Phần bôi đen trên hình vẽ là hình phẳng (D) giới hạn giữa parabol (P) và tiếp tuyến d của (P)

tại điểm A(1;1) và đường thẳng



. Tính diện tích hình phẳng (D).

. B.

. C.

. D.

Hướng dẫn giải:

Vì parabol (P) nhận gốc O làm đỉnh và đối xứng qua Oy nên phương trình parabol (P) có

dạng

( 0)

y ax a

 

Vì (P) đi qua A(1;1) nên



, suy ra phương trình (P):

y x



x x

y e e

 

x a



ln2



lim



 

ln2

2 2

2 2 2

x x a a

S e e dx e e

    



lim 2





-1

-1-2

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 60

Facebook: https://www.facebook.com/dongpay

Đường thẳng d là tiếp tuyến của (P) tại A nên có phương trình: 2 1y x 

Diện tích hình phẳng (D) là:

2 2

2 2 3

1 1

1 1 1

(2 1) ( 1) ( 1) 0

3 3 3

S x x dx x dx x

 

         

 

 

Chọn A

Lưu ý: Bài này cần phải tìm phương trình của các đường dựa trên hình vẽ.

Câu 8: Diện tích miền phẳng giới hạn bởi các đường: 2 , 3

y y x    và 1y  là:

A. S 

1 1

ln2 2

 . B.

ln2

S   . C.

S  . D.

ln2

S   .

Hướng dẫn giải:

Chọn A.

Xét phương trình hoành độ giao điểm của các đường. Ta có:



2 3 1

x x    



2 1 0

x  

 3 1 2x x    

Diện tích cần tìm là:

 

1 2

0 1

2 1 1

2 1 d 3 1 d 2

ln 2 2 ln2 2

S x x x x x

   



           

   

   

 

Câu 9: Cho ,a b là hai số thực dương. Gọi (K) là hình phẳng nằm trong góc phần tư thứ hai, giới

hạn bởi parabol

y ax và đường thẳng y bx  . Biết thể tích khối tròn xoay tạo được khi

quay (K) xung quanh trục hoành là một số không phụ thuộc vào giá trị của

và b . Khẳng

định nào sao đây là đúng?

4 5

2b a

. B.

4 2

2b a

. C.

3 5

2b a

. D.

5 3

2b a

Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 62

Facebook: https://www.facebook.com/dongpay

Diện tích hình phẳng giới hạn bởi

1 , , 0y x y k x    bằng diện tích hình phẳng giới hạn

bởi :

2 2

1 , 1, , 0.y x y x y k x     

     

   

1 1 1

2 2 2

0 1

1 d 1 d 1 d 1 1 1 1

k k

x k x k x x k x x k k k k

 



             

  

           

1 1 1 1

1 1 1 1 1 1 1 1 1 1

3 3 3 3

k k k k k k k k k k                 

 

2 4

1 1

3 3

k k   

 

1 2k  

4 1.k  

Câu 11: Cho hàm số ( )y f x có đồ thị ( )y f x



 cắt trục Ox tại ba điểm có hoành độ a b c  như

hình vẽ. Mệnh đề nào dưới đây là đúng?

A. ( ) ( ) ( ).f c f a f b 

B. ( ) ( ) ( ).f c f b f a 

C. ( ) ( ) ( ).f a f b f c 

D. ( ) ( ) ( ).f b f a f c 

Hướng dẫn giải:

Chọn A.

Đồ thị của hàm số ( )y f x



 liên tục trên các đoạn

 

;a b và

 

;b c , lại có ( )f x là một nguyên hàm của ( )f x



Do đó diện tích của hình phẳng giới hạn bởi các đường:

( )

y f x

x a

x b























là:

     

( )d ( )d

b b

a a

S f x x f x x f x f a f b

 

      

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 63

Facebook: https://www.facebook.com/dongpay

Vì









S f a f b

  





Tương tự: diện tích của hình phẳng giới hạn bởi các đường:

( )

y f x

x b

x c























là:

     

( )d ( )d

c c

b b

S f x x f x x f x f c f b

 

    

 









S f c f b

  





Mặt khác, dựa vào hình vẽ ta có:

























1 2

S S f a f b f c f b f a f c

      





Từ (1), (2) và (3) ta chọn đáp án A.

(có thể so sánh





f a

với





f b

dựa vào dấu của

( )

f x



trên đoạn





;

a b

và so sánh





f b

với





f c

dựa vào dấu của

( )

f x



trên đoạn





;

b c

Câu 12: Gọi

là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường

y x

 ,



và



quanh trục

. Đường thẳng





0 4

x a a

  

cắt đồ thị hàm

y x



tại

(hình vẽ bên). Gọi

là thể tích khối tròn xoay tạo thành khi quay tam giác

OMH

quanh trục

. Biết rằng

V V



. Khi đó



. B.

2 2

a 

. C.



. D.



Hướng dẫn giải:

Chọn D.

Ta có

0 0

x x

  

. Khi đó

d 8

V x x 



 

Ta có





;

M a a

Khi quay tam giác

OMH

quanh trục

tạo thành hai hình nón có chung đáy:

 Hình nón





có đỉnh là

, chiều cao

h OK a

 

, bán kính đáy

R MK a

  ;

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 64

Facebook: https://www.facebook.com/dongpay

 Hình nón

 

N thứ 2 có đỉnh là

, chiều cao

4h HK a  

, bán kính đáy R MK a 

Khi đó

2 2

1 1 2

1 1 4

3 3 3

V R h R h a  

  

Theo đề bài

2 8 2. 3

V V a a    

 

Câu 13: Cho tam giác đều ABC có diện tích bằng 3 quay xung quanh cạnh AC của nó. Tính thể

tích V của khối tròn xoay được tạo thành.

A. 2 .V 



B. .V 



V 



V 



Hướng dẫn giải:

Chọn A

3 2

ABC

S AB BC CA     . Chọn hệ trục vuông góc

Oxy sao cho

   

 

0;0 , 1;0 , 0; 3O A B  với O là trung

điểm AC . Phương trình đường thẳng

là

 

3 1y x  ,

thể tích khối tròn xoay khi quay ABO quanh trục AC

(trùngOx ) tính bởi

 

3 1V x dx



  



 

. Vậy thể tích cần tìm 2 2V V



 



Câu 14: Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi các đường thẳng

8 ,y x y x  và đồ thị hàm số

y x là

, trong đó ,a b là các số nguyên,

tối giản. Khi

đó a b bằng

A. 68. B. 67 . C. 66 . D. 65

Hướng dẫn giải:

Ta có

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 65

Facebook: https://www.facebook.com/dongpay

3 3

8 0 0;8 0 ; 0

2 2

x x x x x x x









         







Nên

 

1 2 2

0 1

8 8

S x x dx x x dx    

 

Câu 15: Thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn

2 2

( ): ( 3) 1C x y   xung quanh trục hoành là

A. 6V 



. B.

6V 



. C.

3V 



. D.

6V 



Hướng dẫn giải:

Chọn D.

2 2 2

( 3) 1 3 1x y y x       .

   

2 2

3 1 3 1

12 1

V x x dx

x dx



 

     

 

 

 





Đặt sin cos .x t dx t dt   . Với

x t



  







    







ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 66

Facebook: https://www.facebook.com/dongpay

2 2

2 2 2

2 2

12 1 sin .cos 12 cos 6

V t tdt tdt

 

    

 

 

  

Câu 16: Trong mặt phẳng tọa độ

Oxyz

cho





có phương trình

 

2 2

1, , 0

x y

a b

  

và đường

tròn





2 2

: 7.

C x y

 

Để diện tích elip





gấp 7 lần diện tích hình tròn





khi đó



. B.

7 7

ab  . C.

ab  . D.



Hướng dẫn giải:

Chọn D.

 

2 2

1, , 0

x y b

a b y a x

a b a

     

Diện tích





là

 

2 2

0 0

4 4 d

a a

b a x x b

S a x x

a a



  

 

Đặt

sin t, t ; d costdt

2 2

x a x a

 

    

 

 

 

Đổi cận: 0 t 0; t

x x a

     



 

2 2

0 0

4 a .cos tdt 2 1+cos2t dt

a a

S ab ab

  

 



Mà ta có

 

. 7 .

S R 

 

Theo giả thiết ta có

   

7. 49 49.

E C

S S ab ab    

 

Câu 17: Gọi





S t

là diện tích hình phẳng giới hạn bởi các đường

  

1 2

x x



 



( 0)

x t t

 

. Tìm





lim .

S t



ln2

 

. B.

ln2



. C.

ln2

 . D.

ln2



Hướng dẫn giải:

Chọn B.

Cách 1:

*Tìm

, ,

a b c

sao cho

  

1 ( 2)

1 2

a bx c

x x



 

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 67

Facebook: https://www.facebook.com/dongpay

    

1 2 1

a x bx c x

     

2 2

1 4 4

ax ax a bx bx cx c

       









1 4 4

a b x a b c x a c

       

0 1

4 0 1

4 1 3

a b a

a b c b

a c c

  

 

 

      

 

 

   

 

*Vì trên





  

1 2

x x

 

 

nên ta có:

Diện tích hình phẳng:

 

    

2 2

0 0

1 1 3

d d

1 2 2

t t

S t x x

x x x

   



  

   



  

   

 

 

1 1 1 1 1

d ln

1 2 2 2

x x x x

 



 

    

 

   

 



 



1 1 1

ln ln 2

2 2 2

t t



   

 

*Vì

1 1

lim 1 lim ln 0

2 2

t t

 

 

   

  

   

 

   

và

lim 0







Nên

 

1 1 1 1

lim lim ln ln2 ln 2

2 2 2 2

t t

S t

t t

 



 

     

 

 

 

Cách 2: Dùng Máy tính cầm tay.

Diện tích hình phẳng:

 

  

1 2

S t x

x x

 



 

 

 



Cho

100



ta bấm máy

  

100

d 0,193

1 2

x x

 

 

 

 

 



Dùng máy tính kiểm tra 4 kết quả ta được đáp án B.

Câu 18: Gọi H là phần mặt phẳng giới hạn bởi đường thẳng

y mx



với



và parabol (P) có

phương trình





y x x

 

. H có diện tích:

   

2 2 5

m m

 

. B.

   

2 5 2

m m

 

 



. D.

 

m 

Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 68

Facebook: https://www.facebook.com/dongpay

Gọi diện tích cần tính là

, Ta có:

1 ln

S dx







Đặt

1 ln ,

u x

 

khi



thì 1,

u x e

 

thì

u du dx

 



 

2 2

2 2 1

3 3

udx u

 

  

 

 



Chọn C.

Câu 19: Gọi

là diện tích hình phẳng giới hạn bởi các đường

2 ,

my x



mx y









. Tìm

giá trị của

để



Hướng dẫn giải:

Chọn A.

Ta có

2 2

2 0

my x y x

   

(do



và

2 2

2 0

y mx

mx y y mx

y mx



 

   



  





Xét phương trình hoành độ giao điểm của

my x



và

mx y

 ta có

2 2 4 3

2 2 2 8 0

x mx x m mx x m x

x m





      







Khi đó

2 2

0 0

1 1

2 d 2 d

2 2

m m

S x mx x x mx x

m m

 

   

 

 

 

3 2

1 2 2 4

2 3 3 3

x m m

x x

  

Để

4 9 3

3 3

3 4 2

S m m

      

(do



Câu 20: Gọi

là diện tích của mặt phẳng giới hạn bởi đường thẳng

y mx



với m < 2 và parabol

(P) có phương trình





y x x

 

. Gọi

là diện tích giới hạn bởi (P) và Ox. Với trị số nào

của m thì

1 2

S S

 ?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 69

Facebook: https://www.facebook.com/dongpay

2 4

. B.

2 2

. C.

. D.

Hướng dẫn giải:

Ta tính

trước, phương trình hoành độ giao điểm:

 

2 0

x x





  







, do đó

S x x dx  



Ta tính

, phương trình hoành độ giao điểm:

 

2 2

2 2 0

mx x x x m x

x m





      



 



, do đó:

 

2 2

0 0

2 2

3 2

m m

m x

S x x mxdx x mx dx



 

 



         

 

 

 

 

1 4

. 2 4

6 2 3



    

(Chú ý: muốn đường thẳng cắt parabol tại 2 điểm phân biệt thì trong tinhd huống này

parabol phải có phần chứa đỉnh nằm trên đường thẳng).

Chọn A.

Câu 21: Cho hình thang cong (H) giới hạn bởi các đường

; 0; 0

y e y x

  

và ln4x  . Đường

thẳng

 

, 0 ln 4x k k   chia (H) thành hai phần có diện tích

và

như hình vẽ bên.

Tìm k để

1 2

2S S

ln4

k  . B. ln2k  . C.

k  . D. ln3k  .

Trích đề Minh họa 2 - 2017

Hướng dẫn giải:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 70

Facebook: https://www.facebook.com/dongpay

Ta có:

ln4

1 2

1, 4

x x k x x k

S e dx e e S e dx e e

       

 

Do đó:

 

1 2

2 1 2 4 3 ln3

k k k

S S e e e k          .

Chọn D.

Câu 22: Gọi





là hình phẳng giới hạn bởi đồ thị hàm số:

4 4

y x x

  

, trục tung và trục hoành.

Xác định

để đường thẳng





đi qua điểm





0;4

A có hệ số góc

chia





thành hai

phần có diện tích bằng nhau.

 

. B.

 

. C.

 

. D.

 

Hướng dẫn giải:

Chọn C.

Phương trình hoành độ giao điểm của đồ thị hàm số

4 4

y x x

  

và trục hoành là:

4 4 0 2

x x x

    

Diện tích hình phẳng





giới hạn bởi đồ thị hàm số:

4 4

y x x

  

, trục tung và trục

hoành là:

 

2 2

0 0

4 4 d 4 4 d

S x x x x x x

     

 

2 4

3 3

x x

 

   

 

 

Phương trình đường thẳng





đi qua điểm





0;4

có hệ số góc

có dạng:

y kx

 

Gọi

là giao điểm của





và trục hoành. Khi đó



 

 

 

Đường thẳng





chia





thành hai phần có diện tích

bằng nhau khi

B OI



và

1 4

2 3

OAB

S S



 

0 2

1 1 4 4 6

. .4.

2 2 3

OAB

S OAOB







 



 





    

 

  





  





Câu 23: Cho hàm số

4 2

y x x m

  

có đồ thị





với

là tham số thực. Giả sử





cắt trục

tại bốn điểm phân biệt như hình vẽ :

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 71

Facebook: https://www.facebook.com/dongpay

Gọi

và

là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm

để

1 2 3

S S S

 

 

. B.

 

. C.



. D.



Hướng dẫn giải:

Chọn D

Giả sử

x b



là nghiệm dương lớn nhất của phương trình

4 2

3 0

x x m

  

. Khi đó ta có

4 2

3 0

b b m

  

(1)

Nếu xảy ra

1 2 3

S S S

 

thì

 

5 4

4 2 3 2

3 d 0 0 0 (2) do 0

5 5

b b

x x m x b mb b m b

           



Từ (1) và (2), trừ vế theo vế ta được

4 2 2

4 5

2 0 (do 0)

5 2

b b b b

    

Thay trở ngược vào (1) ta được



Câu 24: Tìm giá trị của tham số m sao cho: và y = m(x+2) giới hạn bởi hai hình

phẳng có cùng diện tích

A. 0 < m < 1. B. m = 1. C. . D. m = 9

Hướng dẫn giải:

Phương trình hoành độ giao điểm:

Điều kiện d: y = m(x+2) và (C): giới hạn 2 hình phẳng:

Gọi S

, S

lần lượt là diện tích các hình phẳng nhận được theo thứ tự từ trái sang phải.

y x 3x 2

  

1 m 9

 

x 3x 2 m(x 2)

   

x 2 hoÆc x 1 m, m 0.

     

y x 3x 2

  

0 m 9.

 





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 72

Facebook: https://www.facebook.com/dongpay

Nếu m = 1: d đi qua điểm uốn (0;2) của (C). Khi đó S

= S

Nếu 0 < m < 1: S

> 4 > S

Nếu 1 < m < 9: S

< 4 < S

Nếu m > 9  Khi đó:

 S

= 2m

Vậy m = 1 thỏa yêu cầu bài toán.

Chọn B.

Câu 25:

Cho hàm số có đồ thị (C). Tìm sao cho hình

phẳng giới hạn bởi đồ thị (C) và các đường thẳng và có diện tích bằng

A. . B. . C. . D.

Hướng dẫn giải:

Xét hàm số trên . Ta có ,

. Do nên

và

Ta có bảng biến thiên trong

0 2



(x 4x)dx 4



 



1 m 2;1 m 4.

    

2 1 m

3 3

1 2

1 m

S x 3x 2 m(x 2) dx; S x 3x 2 m(x 2) dx

 



         

 

m 0



3 2

1 1

2 2

3 3

y x mx x m

    

 















 

0, 2, 0

x x y

  



3 2

1 1

2 2

3 3

y x mx x m

    





0;2

2 2

y x mx



  

x m m



  





 



  



 















 

2 2

2 0, 0 2 2

m m m m

       

   

1 5

0 2 0, 2 2 0.

3 3

y m y m

     





0;2

m m

  













ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 73

Facebook: https://www.facebook.com/dongpay

Dựa vào BBT suy ra

Gọi S là diện tích hình phẳng cần tìm. Ta có:

Chọn C.

Câu 26: Cho hàm số

2 2

y m x

  

. Tập hợp tất cả các giá trị của tham số thực

sao cho đồ

thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục

hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng

là



. B.







. C.

; 1

 

 

 

 

 

 

. D.

; 1

 

 

 

 

Hướng dẫn giải:

Tập xác định









3 2 2 2

2 4 2 2

y x m x x x m



    ;

0 2

y x m

x m









  



 



Đồ thị của hàm số đã cho có cực đại và cực tiểu

 

Vì

 

nên hàm số đạt cực đại tại



suy ra điểm cực đại của đồ thị hàm số là





0;2

Đường thẳng cùng phương với trục hoành qua điểm cực đại có phương trình là

: 2

d y



Phương trình hoành độ giao điểm của





và

là:

2 2

2 2 2 2

m x x m

x m







 

     









 



Diện tích hình phẳng cần tìm là: (chú ý rằng hàm số đã cho là hàm chẵn)





0, 0;2

y x

  

3 2

1 1

4 2 2 4

3 3

1 1 4 10 1

2 2 4 4

3 3 3 2

S x mx x m dx

x mx x m dx m

      

 







          









 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 74

Facebook: https://www.facebook.com/dongpay

2 2 2

4 4 4

2 2 2 2 2 2

2 0 0

2 3

2 d 2 2 d 2 2 d

2 2 2

2 64

10 3 15

m m m

x x x

S m x x m x x m x x

m x m



 

     

 

 

 

  

 

 

  

Ta có

S m





   



 



Chọn B.

Câu 27:

Trong hệ trục Oxy, cho tam giác OAB vuông ở A, điểm B nằm trong góc phàn tư thứ nhất.

A nằm trên trục hoành, OB = 2017. Góc Khi quay tam giác đó

quanh trục Ox ta được khối nón tròn xoay. Thể tích của khối nón lớn nhất khi:

A. . B. . C. . D.

Hướng dẫn giải:

Phương trình đường thẳng

tan , 2017 os

y x OA c

 

 

Khi đó thể tích nón tròn xoay là:

Đặt Xét hàm số .

Ta tìm được lớn nhất khi

Chọn A.

Câu 28: Cho hàm số









3 2

, , , , 0

y f x ax bx cx d a b c a

      



có đồ thị





. Biết rằng đồ thị





tiếp xúc với đường thẳng



tại điểm có hoành độ âm và đồ thị hàm số





y f x





cho bởi hình vẽ dưới đây:



, 0 .

AOB



 

 

  

 

 

sin





cos





cos





sin





 

2017.cos

3 3

2 2 2 2

2017 . 2017 .

tan . .cos .sin .cos 1 cos .

3 3

V x dx



 

     

   



cos 0; .

t t



 

  

 

 

 

1 , 0;

f t t t t

 

  

 

 





f t

3 3 6

cos sin .

3 3 3

 

    

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 75

Facebook: https://www.facebook.com/dongpay

Tính diện tích S của hình phẳng giới hạn bởi đồ thị

 

C và trục hoành.

A. 9S  . B.

S  . C.

. D.

Hướng dẫn giải:

Chọn B.

Từ đồ thị suy ra

 

3 3f x x



  .

   

 

2 3

3 3 3f x f x dx x dx x x C



     

 

 

C tiếp xúc với đường thẳng 4y  tại điểm có hoành độ

âm nên

 

0 0 0

0 3 3 0 1f x x x



       .

Suy ra

 

1 4 2f C   

 

: 3 2C y x x   

Xét phương trình

3 2 0

x x

 



   







Diện tích hình phẳng cần tìm là:

 

3 2

x x dx



  



Câu 29: Đường cong được cho bởi phương trình

 

x g y , với đạo hàm

 

g y



là hàm liên tục, gọi





m n m n



tương ứng là tung độ các điểm M và N thuộc đồ thị





x g y

 . Độ dài đường

cong

 

x g y từ điểm M tới điểm N là:

 

1 ( )

g y dx



. Áp dụng tính độ dài đường cong

y x từ

 

1;1 đến

 

2;2 .

A. 1,07. B. 1,06. C. 1. D. 2.

Hướng dẫn giải:

Ta có:

y x x y x

     .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 76

Facebook: https://www.facebook.com/dongpay

Do đó độ dài cần tính:

1 1.06

 



Chọn B.

Câu 30: Đường cong được cho bởi phương trình





x g y

 , với đạo hàm





g y



là hàm liên tục, gọi





m n m n



tương ứng là tung độ các điểm M và N thuộc đồ thị





x g y

 . Độ dài đường

cong





x g y

 từ điểm M tới điểm N là:

 

1 ( )

g y dx





. Áp dụng tính độ dài đường cong

x y



từ





1;1

đến





4;2

A. 1,07. B. 7,27. C. 7,2 D. 2.

Hướng dẫn giải:

Ta có:

' 2

x y



Độ dài cần tính là:

1 2 7.27

ydx 



Chọn B.

Câu 31: Đường cong được cho bởi phương trình





x g y

 , với đạo hàm





g y



là hàm liên tục, gọi





m n m n



tương ứng là hoành độ các điểm M và N thuộc đồ thị. Độ dài đường cong





y g x

 từ điểm M tới điểm N là:

 

1 ( )

g y dx





. Tìm độ dài của đường cong

y x



từ điểm





0;0

đến điểm





2;4 2

. Tích phân cần tính để giải bài này là:

4 2

1 9

xdx





. B.

1 9

xdx





4 2

1 4

x dx





. D.

1 4

x dx





Hướng dẫn giải:

Cung cần tính là phần của đường cong nằm trong góc vuông thứ nhất. Ta có:

y x

 nên

y x



 . Độ dài cung cần tìm bằng:

2 2

0 0

1 1 9

y dx xdx



  

 

Chọn D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 77

Facebook: https://www.facebook.com/dongpay

Câu 32: Xét hàm số





y f x

 liên tục trên miền





;

D a b

 có đồ thị là một đường cong

. Gọi

là phần giới hạn bởi

và các đường thẳng

x a



x b



. Người ta chứng minh được rằng

diện tích mặt cong tròn xoay tạo thành khi xoay

quanh

bằng

   

 

2 1 d

S f x f x x



 





. Theo kết quả trên, tổng diện tích bề mặt của khối tròn xoay

tạo thành khi xoay phần hình phẳng giới hạn bởi đồ thị hàm số

 

2 ln

x x

f x





và các

đường thẳng



x e



quanh

là

2 1

e 



. B.

4 9

e 



. C.

4 2

4 16 7

e e 



. D.

4 9

e 



Hướng dẫn giải:

Ta có

     

 

2 ln ln 1 1 1 1

4 2 4 4 4 16 2

x x x x

f x f x x f x x x

x x x



 

 

           

 

 

Lại có

   

0, 1;

f x x x e



     , nên





f x

đồng biến trên





. Suy ra

   

 

1 0, 1;

f x f x e

     .

Từ đây ta thực hiện phép tính như sau

   

 

ln 1 1

2 1 d 2 1 d

2 4 16 2

b e

x x

S f x f x x x x

 



      

 

 

 

 

 

2 2

1 1

1 2 3

ln 1 1 ln 1

2 d 2 d

2 4 16 2 2 4 4

ln 1

2 d

2 4 4

1 1 1 1 ln

2 ln d

2 8 4 16

e e

x x x x

S x x x x

x x

x x x x x

I I I

   

 

      

   

 

 

   

 

  

 

 

 

   

 

 

  

 



 



Với

4 2 4 2

1 1 2 3

2 8 8 16 16

x x e e

I x x x

 

 

 

    

 

 



 

2 2

1 1 1 1 1

ln d 2ln 1

4 4 4 16 16

I x x x x x e

 

       

 

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 78

Facebook: https://www.facebook.com/dongpay

1 ln 1 1

d ln

16 32 32

I x x

 

     

 

 



Chọn D.

Câu 33: Tính độ dài đường cong

4 2

y x

 

, từ điểm A có hoành độ a = 0 đến điểm B có hoành

độ b = 1. Kết quả là:

. B.

. C.

. D.

Hướng dẫn giải:

Ta có:





( ) 2 2 , ( ) 8 .

f x x f x x

 

  

thay vào Công thức ta được

1 8

T xdx

 



. Đổi biến

1 8

u x

 

. Ta có:

Khi

0 1.

1 9

x u

  





  



Vậy

1 1 2 13

8 8 3 6

T udu u

  



Chọn A.

Câu 34: Cho hai mặt cầu









có cùng bán kính

thỏa mãn tính chất: tâm của





thuộc





và ngược lại. Tính thể tích phần chung

của hai khối cầu tạo bởi

( )

và

( )

V R



 . B.





. C.





. D.





Hướng dẫn giải:

Chọn C

Gắn hệ trục

Oxy

như hình vẽ

Khối cầu





S O R

chứa một đường tròn lớn là





2 2 2

C x y R

 

Dựa vào hình vẽ, thể tích cần tính là

 

3 3

2 2 2

2 d 2

3 12

x R

V R x x R x



 

 

    

 

 



2 2 2

( ) :

C x y R

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 79

Facebook: https://www.facebook.com/dongpay

Câu 35: Gọi

là thể tích khối tròn xoay tạo thành do quay xung quanh trục hoành một elip có

phương trình

2 2

25 16

x y

 

có giá trị gần nhất với giá trị nào sau đây?

A. 550. B. 400. C. 670. D. 335.

Hướng dẫn giải:

Chọn C.

Ta có

2 2

1 25

25 16 5

x y

y x

     

Do elip nhận

làm các trục đối xứng nên thể tích

cần tính bằng 4 lần thể tích hình

sinh bởi hình phẳng giới hạn bởi các đồ thị hàm số

y x

 



và các đường

thẳng



quay xung quanh

4 640

V 4. 25 d 670,2

5 3

x x=



 

   

 

 



Câu 36: Gọi

và

lần lượt là thể tích khối tròn xoay tạo nên bởi phép quay hình elip

 

2 2

x y

a b

  

. Xung quanh trục

Ox Oy

. Hỏi khẳng định nào dưới đây đúng?

x y

V V



. B.

x y

V V



. C.

x y

V V



. D.

x y

V V



Hướng dẫn giải:

2 2

y b

x y

a b

x a



 

 



 

  

  



 



 

 



 



2 3 2

2 2 2

2 2

0 0

4 4

2 2 1 2 .

3 3 3

a a

x x ab ab

V y dx b dx b x b

a a

   

      

   

   

 

 

  

2 3 2

2 2 2

2 2

0 0

4 4

2 2 1 2 .a

3 3 3

b b

y x

y x a b ab

V V x dx a dx a x

b a

   

       

   

   

 

 

  

Vì b > a nên

x y

V V



Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 80

Facebook: https://www.facebook.com/dongpay

Câu 37: Cho hàm số có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi

đồ thị (C) với y<0 và trục hoành, S’ là diện tích hình phẳng giới hạn bởi đồ thị (C) với y>0

và trục hoành. Với giá trị nào của m thì ?

A. B. C. D.

Hướng dẫn giải

Phương trình hoành độ giao điểm (*)

Đặt , phương trình trở thành: (**)

Để S>0, S’>0 thì 0<m<4. Khi đó (*) có 4 nghiệm phân biệt với

là hai nghiệm dương phân biệt của (**)

Do ĐTHS hàm bậc 4 nhận Oy làm trục đối xứng nên

Kết hợp với (**) ta được .

Chọn C.

Câu 38: Cho parabol





: 1

P y x

 

và đường thẳng

: 2

d y mx

 

. Biết rằng tồn tại

để diện tích

hình phẳng giới hạn bởi





và

đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó.



Hướng dẫn giải:

Chọn B.

Phương trình hoành độ giao điểm của





và

là





2 2

1 2 1 0 *

x mx x mx      

Ta có

4 0, .

m m

     



Nên phương trình





luôn có 2 nghiệm phân biệt

x a



và





x b a b

 

Do đó





luôn cắt

tại 2 điểm phân biệt





; 2

A a ma



và





; 2 .

B b mb 

Với mọi

đường thẳng

luôn đi qua điểm





0;2 .

Mà



Suy ra





2 1, ; .

mx x x a b

    

4 2

y x x m

  

S S



m 



4 2

4 0

x x m

  

; 0

x t t

 

4 0

t t m

  

2 1 1 2

; ; ;

t t t t

 





1 2 1 2

; ,

t t t t



   

 

1 1

4 2 4 2

4 2

2 2

' 4 4

4 0 0

5 3

t t

S S x x m dx x x m dx

t t

x x m dx m

      

       

 



m 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 81

Facebook: https://www.facebook.com/dongpay

Do đó diện tích hình phẳng giới hạn bởi

 

và d là

 

   

 

     

2 2

2 1 d 1 d

2 3

1 1 1

1 1

2 3 2 3 3

1 1

2 3 3

1 1

4 1

2 3 3

b b

a a

mx x

S mx x x mx x x x

m m

b a b a a b ab b a b a a b ab

S b a b a a b ab

b a ab b a a b ab

 

         

 

 

   

             

   

   

 

       

 

 

 

       

 

 

 

Vì

,a b

là nghiệm của phương trình

 

nên ta có

a b m

 





 



Khi đó

 

2 2

2 4 16

4 4. .

6 3 9 9

S m

 

    

 

 

Đẳng thức xảy ra khi 0.m  Vậy

min

S 

Câu 39: Cho parabol (P) và hai điểm A, B thuộc (P) sao cho AB = 2. Tìm A, B sao cho diện

tích hình phẳng giới hạn bởi (P) và đường thẳng AB đạt giá trị lớn nhất

A. B. C. D.

Hướng dẫn giải

Giả sử sao cho AB = 2

Phương trình đường thẳng AB:

Gọi S là diện tích hình phẳng cần tìm, ta có

y x



















2 2

; , ,

A a a B b b P b a

 





y b a x ab

  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 82

Facebook: https://www.facebook.com/dongpay

Vì AB = 2 nên

Chọn B.

Câu 40: Parabol

y 

chia hình tròn có tâm là gốc tọa độ, bán kính bằng 2 2 thành hai phần có

diện tích là

và

, trong đó

1 2

S S

. Tìm tỉ số

3 2

21 2







3 2

9 2







3 2





9 2

3 2







Hướng dẫn giải:

Chọn B.

Diện tích hình tròn là

8S r

 

  .

Ta có

8 d 2

2 3

S x x





    



Suy ra

2 1

S S S



   

Vậy

3 2

9 2









Câu 41: Xét hàm số

 

y f x liên tục trên miền

 

;D a b có

đồ thị là một đường cong

. Gọi

là phần giới hạn bởi

và các đường thẳng

x a

x b

. Người ta chứng minh được rằng diện tích mặt cong tròn xoay tạo thành khi xoay

quanh

bằng

   

 

2 1 d

S f x f x x





 



. Theo kết quả trên, tổng diện tích bề mặt

của khối tròn xoay tạo thành khi xoay phần hình phẳng giới hạn bởi đồ thị hàm số

 

2 ln

x x

f x





và các đường thẳng

1x 

x e

quanh

là

2 1





. B.

4 9





. C.

4 2

4 16 7

e e



 

. D.

4 9





     

2 2

| | [ ]

b b

a a

S b a x ab x dx b a x ab x dx b a

         

 

| b a | b a 2

   

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 83

Facebook: https://www.facebook.com/dongpay

Hướng dẫn giải:

Chọn D.

Cách 1. (Giải tự luận)

Ta có

     

 

2 ln ln 1 1 1 1

4 2 4 4 4 16 2

x x x x

f x f x x f x x x

x x x



 

 

           

 

 

Lại có

   

0, 1;

f x x x e



     , nên





f x

đồng biến trên





. Suy ra

   

 

1 0, 1;

f x f x e

     .

Từ đây ta thực hiện phép tính như sau

   

 

ln 1 1

2 1 d 2 1 d

2 4 16 2

b e

x x

S f x f x x x x

 

 



      

 

 

 

 

2 2

1 1

1 2 3

ln 1 1 ln 1

2 d 2 d

2 4 16 2 2 4 4

ln 1

2 d

2 4 4

1 1 1 1 ln

2 ln d

2 8 4 16

e e

x x x x

S x x x x

x x

x x x x x

I I I

 



   

 

      

   

 

 

   

 

  

 

 

 

   

 

 

  

 



Với

4 2 4 2

1 1 2 3

2 8 8 16 16

x x e e

I x x x

 

 

 

    

 

 



 

2 2

1 1 1 1 1

ln d 2ln 1

4 4 4 16 16

I x x x x x e

 

       

 

 



1 ln 1 1

d ln

16 32 32

I x x

 

    

 

 



Cách 2.

Học sinh có thể trực tiếp bấm máy tính tích phân

ln 1 1

2 1 d

2 4 16 2

x x

S x x



 

    

 

 



để có kết quả

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 84

Facebook: https://www.facebook.com/dongpay

Câu 42: Diện tích hình phẳng giới hạn bởi hàm số

2 2

1y x x  , trục

và đường thẳng

1x 

bằng

 

ln 1a b b

 

với

là các số nguyên dương. Khi đó giá trị của

a b c 

là

. B.

. C.

. D.

Hướng dẫn giải:

Chọn C.

Cách 1 (dùng máy tính):

Phương trình hoành độ giao điểm

2 2

1 0 0x x x   

Diện tích hình phẳng cần tìm là

2 2

1dS x x x 



vì

 

2 2

1 0, 0;1x x x   

 

2 2

ln 1

a b b

x x x

 

 



Bước 1: Bấm máy tính tích phân

2 2

1d 0,4201583875S x x x  



( Lưu D)

Bước 2: Cơ sở: Tìm nghiệm nguyên của phương trình

   

ln 1 ln 1a b b a b b

D c

c D

   

   (coi

 

c f x ,

a x

b

và ta thử các

giá trị

... 5; 4;..0,1;2;3;4.....b   

)

Thử với

1b 

Thử với

2b 

: Mode + 7

 

2 ln 1 2X

F X

 

 ;

Kết quả:

3;c 8,b 2a   

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 85

Facebook: https://www.facebook.com/dongpay

Cách 2 (giải tự luận):

Phương trình hoành độ giao điểm

2 2

1 0 0x x x   

Diện tích hình phẳng cần tìm là

2 2

1dS x x x 



vì

 

2 2

1 0, 0;1x x x   

Đặt

 

tan d 1 tan dx t x t t   

Đổi cận 0 0; 1

x t x t



     

Khi đó

 

2 2

4 4 4

2 2 2

2 2

0 0 0

sin 1 1 sin .cos

tan 1 tan 1 tan d . d d

cos cos cos

cos

t t t

S t t t t t t

t t t

  

    

  

Đặt

sin d cos du t u t t  

Đổi cận

0 0;

4 2

t u t u



     

 

     

2 2 2

3 3 3 2

2 2 2 2

0 0 0

1 1

d d d

1 1 1 1

S u u u

u u u u

 

 

 

   

 

   

 

  

Ta có

 

  

2 2 2

0 0 0

1 1 1 1 1 1 1

d d d

8 1 1 8 1 1

u u

H u u u

u u u u

 

  

 

   

 

   

 



 

  

   

3 3

1 1 1 3 1 1

8 1 1 1

1 1

u u u

u u

 

    

 

  

 

 

 



   

 

3 3 2

1 1 1 6

1 1

u u

 

 

  

 

 



 



   

 

2 2 2

1 1 1 6

16 1 16 1

u u

 



  

 

 



 



 

2 1 6

2 8

 





Tính

 

K u







ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 86

Facebook: https://www.facebook.com/dongpay

 

  

2 2 2

0 0 0

6 3 1 1 3 1 1

d d d

2 1 1 2 1 1

u u

K u u u

u u u u

 

  

 

   

 

   

 



 

  

   

  

 

2 2

3 1 1 2 3 1 1 1

d ln 3 2 3ln 1 2

2 1 1 2 1 1 1

1 1

u u u u u

u u

 

  

        

 

    

 

 



Vậy









3 2 3ln 1 2 7 2 3ln 1 2

2 8 8

   

  

Khi đó





7 2 3ln 1 2

8 6

S K

 

 





 





7 2 3ln 1 2 3 2 ln 1 2

3 2 3ln 1 2

8 6 8

   

    

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 87

Facebook: https://www.facebook.com/dongpay

ỨNG DỤNG THỰC TẾ

Câu 1: Một vật chuyển động chậm dần đều với vận tốc

( ) 160 10 ( / )

v t t m s

 

. Quãng đường mà

vật chuyển động từ thời điểm

0( )

t s



đến thời điểm mà vật dừng lại là

1028 .

1280 .

1308 .

1380 .

Hướng dẫn giải

Chọn B.

Khi vật dừng lại thì





160 10 0 16

v t t t

    

Suy ra:

   

 

16 16

0 0

d 160 10 d 160 5 1280 .

s v t t t t t t m

     

 

Câu 2: Một chiếc ô tô chuyển động với vận tốc





( / )

v t m s

, có gia tốc

( ) ( ) , ( / )

2 1

a t v t m s



 



. Vận tốc của ô tô sau 10 giây (làm tròn đến hàng đơn vị) là

4,6 /

m s

. B.

7,2 /

m s

. C.

1,5 /

m s

. D.

2,2 /

m s

Hướng dẫn giải

Chọn A.

Vận tốc của ô tô sau 10 giây là:

3 3 3

d ln 2 1 ln 21 4,6 ( / ).

2 1 2 2

v t t m s

    





Câu 3: Một hạt proton di chuyển trong điện trường có biểu thức gia tốc ( theo

cm s

) là

 

( )

1 2

a t







(với t tính bằng giây). Tìm hàm vận tốc

theo t, biết rằng khi



thì





30 /

v cm s



1 2



1 2



 

1 2 30



 

 

1 2t





Hướng dẫn giải

Chọn B.



   

 

20 10

d d

1 2

v t a t t t C



   



 

 Do





0 30



, suy ra

30 20

1 2.0

C C

   



 Vậy, hàm

 

1 2

v t

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 88

Facebook: https://www.facebook.com/dongpay

Câu 4: Một vật chuyển động với vận tốc

( ) 1 2sin 2 (m/s)

v t t

 

. Quãng đường mà vật chuyển động

trong khoảng thời gian

0 (s)



đến thời điểm

(s)

t 



là





. B.

3 1





. C.

3 1





. D.





Hướng dẫn giải

Chọn A.

Quãng đường cần tìm

   

1 2sin 2 d cos2 1

s t t t t

     





Câu 5: Một người lái xe ô tô đang chạy với vận tốc

20 /

m s

thì người lái xe phát hiện có hàng rào

ngăn đường ở phía trước cách

(tính từ vị trí đầu xe đến hàng rào) vì vậy, người lái xe đạp

phanh. Từ thời điểm đó xe chuyển động chậm dần đều với vận tốc





5 20

v t t

  

(

m s

trong đó

là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp

phanh đến khi dừng hẳn, xe ô tô còn cách hàng rào ngăn cách bao nhiêu mét (tính từ vị trí đầu

xe đến hàng rào)?

. B.

. C.

. D.

Hướng dẫn giải

Chọn A.

Xe đang chạy với vận tốc

20 /

v m s



tương ứng với thời điểm





t s



Xe đừng lại tương ứng với thời điểm





t s



Quảng đường xe đã đi là

   

5 20 d 20 40

S t t t t m

 

      

 

 



Vậy ô tô cách hàng rào một đoạn





45 40 5

 

Câu 6: Một vật chuyển động với vận tốc

10 /

m s

thì tăng tốc với gia tốc

( ) 3

a t t t

 

. Tính quãng

đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.

4300

4300 .

430 .

430

Hướng dẫn giải

Chọn A.

 Hàm vận tốc

   

 

2 3

d 3 d

2 3

t t

v t a t t t t t C

     

 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 89

Facebook: https://www.facebook.com/dongpay

 Lấy mốc thời gian lúc tăng tốc





0 10 10

v C

   

Ta được:

 

2 3

t t

v t

  

 Sau 10 giây, quãng đường vật đi được là:

2 3 3 4

3 4300

10 d 10 .

2 3 2 12 3

t t t t

s t t m

   

      

   

   



Câu 7: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc (m/s). Đi được (s),

người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần

đều với gia tốc (m/s

). Tính quãng đường (m) đi được của ô tô từ lúc bắt đầu

chuyển bánh cho đến khi dừng hẳn.

A. (m). B. (m). C. (m). D. (m).

Hướng dẫn giải

Chọn D.

Quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh:

(m).

Vận tốc (m/s) của ô tô từ lúc được phanh đến khi dừng hẳn thoả mãn

, . Vậy .

Thời điểm xe dừng hẳn tương ứng với thoả mãn (s).

Quãng đường ô tô đi được từ lúc xe được phanh đến khi dừng hẳn:

(m).

Quãng đường cần tính (m).

Câu 8: Một ôtô đang chạy đều với vận tốc

m/s thì phía trước xuất hiện chướng ngại vật nên

người lái đạp phanh gấp. Kể từ thời điểm đó, ôtô chuyển động chậm dần đều với gia tốc



m s

. Biết ôtô chuyển động thêm được

thì dừng hẳn. Hỏi

thuộc khoảng nào dưới

đây.





3;4

. B.





4;5

. C.





5;6

. D.





6;7

Hướng dẫn giải

( ) 7

v t t



 

95,70



87,50



94,00



96,25



5 5

1 1

0 0

( )d 7 d 7 87,5

S v t t t t   

 

( )

v t

( ) ( 70)d = 70

v t t t C

   



2 1

(5) (5) 35 385

v v C   

( ) 70 t 385

v t   

( ) 0 5,5

v t t  

5,5 5,5

2 1

5 5

( )d ( 70 385)d 8,75

S v t t t t    

 

1 2

96,25

S S S  

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 90

Facebook: https://www.facebook.com/dongpay

Chọn C.

Gọi





x t

là hàm biểu diễn quãng đường,





v t

là hàm vận tốc.

Ta có:

     

0 d

v t v a t at

    







v t at

   

       

0 0

0 d 15 d 15

t t

x t x v t t at t at t

       

 

 

x t at t

  

Ta có:

 

15 0

15 20

v t

at t

x t

  





 



 

  







15 8 45

15 20

2 3 8

t t t a        .

Câu 9: Một ôtô đang chạy với vận tốc

18 /

m s

thì người lái hãm phanh. Sau khi hãm phanh, ôtô

chuyển động chậm dần đều với vận tốc





36 18

v t t

  

(

m s

) trong đó

là khoảng thời

gian tính bằng giây kể từ lúc bắt đầu hãm phanh. Quãng đường ôtô di chuyển được kể từ lúc

hãm phanh đến khi dừng hẳn là bao nhiêu mét?

5,5

. B.

3,5

. C.

6,5

. D.

4,5

Hướng dẫn giải

Chọn D.

Lấy mốc thời gian là lúc ô tô bắt đầu hãm phanh. Gọi

là thời điểm ô tô dừng. Ta có





v T



. Suy ra

36 18 0 0,5

T T

    

(s)

Khoảng thời gian từ lúc hãm phanh đến lúc dừng hẳn ô tô là 0,5 s. Trong khoảng thời gian

đó, ô tô di chuyển được quãng đường là

 

0,5

36 18 18 18 4,5( )

s t dt t t m

      



Câu 10: Một vật di chuyển với gia tốc . Khi thì vận tốc của vật là

. Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng

đơn vị).

A. . B. . C. . D. .

Hướng dẫn giải:

Chọn C.

   

20 1 2

a t t



  





m s



30 /

m s

106

S m



107

S m



108

S m



109

S m



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 91

Facebook: https://www.facebook.com/dongpay

Ta có . Theo đề ta có

. Vậy quãng đường vật đó đi được sau 2 giây là:

Câu 11: Một vật chuyển động với vận tốc

( ) 1,5 (m/s)

v t



 



. Quãng đường vật đó đi được

trong 4 giây đầu tiên bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).

A. 12,60 m. B. 12,59 m. C. 0,83 m. D. 6,59 m.

Hướng dẫn giải

Chọn B.

 Quãng đường trong 4 giây đầu tiên (từ



đến



) là

4 4

0 0

2 6

1,5 d 1,5 2 d

2 2

s t t t

t t

 



 

     

 

 

 

 

1,5 2 6ln 2 12,59 .

t t t m

 

     

 

 

Câu 12: Một tia lửa được bắn thẳng đứng từ mặt đất với vận tốc

15 /

m s

. Hỏi sau 2,5 giây, tia lửa ấy

cách mặt đất bao nhiêu mét, biết gia tốc là

9,8 /

m s

30,625 .

37,5 .

68,125 .

6,875 .

Hướng dẫn giải

Chọn C.

 Hàm vận tốc





15 9,8

v t v at t

   

 Quãng đường tia lửa đi được sau 2,5 giây là:

 

2,5

15 9,8 d 15 4,9 68,125 .

s t t t t m

    



Câu 13: Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là





24,5 /

m s

và

gia tốc trọng trường là





9,8 /

m s

. Quãng đường viên đạn đi từ lúc bắn lên cho tới khi rơi

xuống đất là (coi như viên đạn được bắn lên từ mặt đất)





61,25

. B.





30,625

. C.





29,4

. D.





59,5

Hướng dẫn giải

Chọn A.

Chọn chiều dương từ mặt đất hướng lên trên, mốc thời gian



bắt đầu từ khi vật chuyển

động.

     

20 1 2

1 2

v t a t dt t dt C



     



 





0 30 10 30 20

v C C

     

 

20 5ln 1 2 20 5ln5 100 108

1 2

S dt t t m

 

       

 



 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 92

Facebook: https://www.facebook.com/dongpay

Ta có vận tốc viên đạn theo thời gian

là









24,5 9,8 /

v t v gt t m s

   

Khi vật ở vị trí cao nhất thì có vận tốc bằng 0 tương ứng tại thời điềm



Quãng đường viên đạn đi được từ mặt đất đến vị trí cao nhất là

   

5 5

2 2

0 0

245

24,5 9,8

S t v t dt t dt   

 

Vậy quãng đường viên đạn đi từ lúc bắn lên cho tới khi rơi xuống đất là

 

245

2. 61,25

 .

Câu 14: Một lực 50 N cần thiết để kéo căng một chiếc lò xo có độ dài tự nhiên 5 cm đến 10 cm. Hãy

tìm công sinh ra khi kéo lò xo từ độ dài từ 10 cm đến 13 cm?

A. 1,95J. B. 1,59 J. C. 1000 J. D. 10000 J

Hướng dẫn giải

Theo định luật Hooke, khi chiếc lò xo bị kéo căng thêm

m so với độ dài tự nhiên thì chiếc

lò xo trì lại với một lực ( )

f x kx



.Khi kéo căng lò xo từ 5 cm đến 10 cm, thì nó bị kéo căng

thêm 5 cm = 0,05 m. Bằng cách này, ta được

(0,05) 50



bởi vậy:

0.05 50 1000

0.05

k k   

Do đó:

( ) 1000

f x x



và công được sinh ra khi kéo căng lò xo từ 10 cm đến 13 cm là:

0,08

0,05

W 1000 1000 1,95

xdx J

  



Chọn A.

Câu 15: Một ôtô đang chạy đều với vận tốc

m/s thì phía trước xuất hiện chướng ngại vật nên

người lái đạp phanh gấp. Kể từ thời điểm đó, ôtô chuyển động chậm dần đều với gia tốc



m s

. Biết ôtô chuyển động thêm được

thì dừng hẳn. Hỏi

thuộc khoảng nào dưới

đây.





3;4

. B.





4;5

. C.





5;6

. D.





6;7

Hướng dẫn giải

Chọn C.

Gọi





x t

là hàm biểu diễn quãng đường,





v t

là hàm vận tốc.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 93

Facebook: https://www.facebook.com/dongpay

Ta có:

     

0 d

    



v t v a t at





   

v t at

       

0 0

0 d 15 d 15

       

 

t t

x t x v t t at t at t

 

  

x t at t

Ta có:

 

15 0

15 20

  





 



 

  







v t

at t

x t

15 8 45

15 20

2 3 8

       t t t a .

Câu 16: Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt

đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã

chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật





v t t t

 

, trong đó

(phút) là thời gian tính từ lúc bắt đầu chuyển động,





v t

được tính theo đơn vị mét/phút (

m p

). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc

của khí cầu là





5 /

v m p



. B.





7 /

v m p



. C.





9 /

v m p



. D.





3 /

v m p



Hướng dẫn giải

Chọn C.

Gọi thời điểm khí cầu bắt đầu chuyển động là



, thời điểm khinh khí cầu bắt đầu tiếp đất

là

Quãng đường khí cầu đi được từ thời điểm



đến thời điểm khinh khí cầu bắt đầu tiếp

đất là

là

 

2 2

10 d 5 162

t t t t   



4,93 10,93 9

t t t

      





0 0 10

v t t

   

nên chọn



Vậy khi bắt đầu tiếp đất vận tốc

của khí cầu là









9 10.9 9 9 /

v m p

  

Câu 17: Một ô tô đang chạy với vận tốc

10 /

m s

thì người lái đạp phân, từ thời điểm đó, ô tô chuyển

động chậm dần đều với vận tốc









5 10 /

v t t m s

  

, trong đó

là khoảng thời gian tính

bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn ô tô còn di

chuyển bao nhiêu mét?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 94

Facebook: https://www.facebook.com/dongpay

0,2

. B.

. C.

. D.

Hướng dẫn giải

Chọn C.

Ta có ô tô đi được thêm

giây nữa với vận tốc chậm dần đều









5 10 /

v t t m s

  

ứng dụng tích phân, ta có quãng đường cần tìm là:

     

2 2

0 0

d 5 10 d 10 10

S v t t t t t t m

 

       

 

 

 

* Lúc dừng thì ta có:





0 5 10 0 2

v t t t

      

Từ lúc đạp phanh đến lúc dừng hẳn, ô tô đi được quãng đường:

S v t at

 

Với

   

2 10.2 5 .2 10

t S m

 





     









* Áp dụng công thức lý 10 ta có:

2 2

2 1

2. .

v v a s

 

Ta còn có công thức liên hệ giữa vận tốc và gia tốc:

v v a t

 

Dựa vào phương trình chuyển động thì





5 /

a m s

 

Khi dừng hẳn thì ta có





0 /

v m s



Theo công thức ban đầu, ta được

 

2 2

2 1

0 10

2 2. 5

v v

s m

 

  



Câu 18: Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây.

Cho





3’

a b

h tt

 

và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là

150

. Sau 10 giây thì thể tích nước trong bể là

1100

. Hỏi thể tích nước trong bể sau khi

bơm được 20 giây là bao nhiêu.

8400

. B.

2200

. C.

6000

. D.

4200

Hướng dẫn giải

Ta có

 

2 3

(3 )

at bt dh t t at   



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 95

Facebook: https://www.facebook.com/dongpay

Khi đo ta có hệ:

3 2

5 . . .5 150

1 2

10 . . .10 1100

a b



 











 







 





Khi đó





3 2

h t

t t

 

Vậy thể tích nước trong bể sau khi bơm được 20 giây là





20 8400

h m



Chọn A.

Câu 19: Gọi





h t





là mức nước trong bồn chứa sau khi bơm được

giây. Biết rằng

 

h t t



 

và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước

được

giây (chính xác đến

0,01

)

2,67 .

2,66 .

2,65 .

2,68 .

Chọn B.

 Hàm

   

3 3

1 3

8d 8 8

5 20

h t t t t t C

     



 Lúc



, bồn không chứa nước. Suy ra

 

12 12

0 0 0

5 5

h C C

      

Vậy, hàm

   

3 12

8 8

20 5

h t t t

   

 Mức nước trong bồn sau 6 giây là





6 2,66 .

h cm



Câu 20: Khi quan sát một đám vi khuẩn trong phòng thí nghiệm người ta thấy tại ngày thứ x có số

lượng là





N x

. Biết rằng

 

2000

N x







và lúc đầu số lượng vi khuẩn là 5000 con.Vậy ngày

thứ 12 số lượng vi khuẩn là?

A. 10130. B. 5130. C. 5154. D. 10129.

Hướng dẫn giải

Chọn A.

Thực chất đây là một bài toán tìm nguyên hàm. Cho





N x



và đi tìm





N x

Ta có

2000

d 2000.ln 1 5000

x x

  





( Do ban đầu khối lượng vi khuẩn là 5000).Với



thì số lượng vi khuẩn là

10130



con.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 96

Facebook: https://www.facebook.com/dongpay

Câu 21: Một đám vi trùng tại ngày thứ t có số lượng là





N t

. Biết rằng

 

4000

1 0,5

N t







và lúc đầu

đám vi trùng có

250000

con. Hỏi sau 10 ngày số lượng vi trùng gần với số nào sau đây

nhất?

251000

con. B.

264334

con. C.

261000

con. D.

274334

con.

Chọn B.



 

4000

d 8000.ln 1 0,5

1 0,5

N t t t C

   





 Lúc đầu có 250000 con, suy ra





0 250000 250000

N C  

 Vậy









8000.ln 1 0,5 250000 10 264334,0758

N t t N    

Câu 22: Một đám vi trùng tại ngày thứ

có số lượng

( )

N t

, biết rằng

7000

( )

N t







và lúc đầu đám

vi trùng có

300000

con. Sau 10 ngày, đám vi trùng có khoảng bao nhiêu con?

302542

con. B.

322542

con. C.

312542

con. D.

332542

con.

Hướng dẫn giải

Chọn C.

Ta có

7000

( ) ( )d d 7000ln | 2|

N t N t t t t C



    



 

(0) 300000 300000 7000ln 2

N C

   

Khi đó

(10) 7000ln12 300000 7000ln 2 312542

   

. Chọn C

Câu 23: Tốc độ phát triển của số lượng vi khuẩn trong hồ bơi được mô hình bởi hàm số

 

1000

, 0

1 0,3

B t t



 



, trong đó





B t

là số lượng vi khuẩn trên mỗi

nước tại ngày thứ

. Số lượng vi khuẩn ban đầu là

500

con trên một

nước. Biết rằng mức độ an toàn cho

người sử dụng hồ bơi là số vi khuẩn phải dưới

3000

con trên mỗi

nước. Hỏi vào ngày

thứ bao nhiêu thì nước trong hồ không còn an toàn nữa?

10.

11.

12.

Hướng dẫn giải

Chọn B

Ta có

 

1000 1000

' d d

0,3 1 0,3

1 0,3

B t t t C

   



 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 97

Facebook: https://www.facebook.com/dongpay

Mà

 

10000 11500

0 500 500

3 1 0,3.0 3

B C C      



Do đó:

 

10000 11500

3 1 0,3 3

B t

  



Nước trong hồ vẫn an toàn khi chỉ khi

 

10000 11500

3000 3000 10

3 1 0,3 3

B t t

      



Vậy kể từ ngày thứ 10, nước hồ không còn an toàn.

Câu 24: Ông An có một mảnh vườn hình elip có độ dài trục

lớn bằng

và độ dài trục bé bằng

. Ông muốn

trồng hoa trên một dải đất rộng

và nhận trục bé

của elip làm trục đối xứng (như hình vẽ). Biết kinh phí

để trồng hoa là

100.000

đồng/

. Hỏi ông An cần

bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền

được làm tròn đến hàng nghìn).

7.862.000

đồng. B.

7.653.000

đồng. C.

7.128.000

đồng. D.

7.826.000

đồng.

Hướng dẫn giải

Chọn B.

Giả sử elip có phương trình

2 2

x y

a b

 

, với

a b

 

Từ giả thiết ta có

2 16 8

a a

  

và

2 10 5

b b

  

Câu 25: Trên cánh đồng cỏ có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa 2

cọc là 4 mét còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn

nhất mà 2 con bò có thể ăn chung (lấy giá trị gần đúng nhất).

1,034

1,574

1,989

2,824

Hướng dẫn giải

Diện tích mặt cỏ ăn chung sẽ lớn nhất khi 2 sợi dây được kéo căng và là phần giao của 2

đường tròn.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 98

Facebook: https://www.facebook.com/dongpay

Xét hệ trục tọa độ như hình vẽ, gọi ,O M là vị trí của cọc. Bài toán đưa về tìm diện tích

phần được tô màu.

Ta có phương trình đường tròn tâm

 

2 2 2

: 3O x y 

và phương trình đường tròn tâm

   

2 2

: 4 2M x y  

Phương trình các đường cong của đường tròn nằm phía trên trục Ox là:

9y x  và

 

4 4y x  

Phương trình hoành độ giao điểm:

 

4 4 9 4 8 16 9

x x x x         

Diện tích phần được tô màu là:

 

2 4 4 9 1,989S x dx x dx

 

 

     

 

 

 

. Ta có thể

giải tích phân này bằng phép thế lượng giác, tuy nhiên để tiết kiệm thời gian nên bấm máy.

Chọn C.

Vậy phương trình của elip là

 

2 2

64 25

y y E

x y

y y E



  



  



 





Khi đó diện tích dải vườn được giới hạn bởi các đường

   

1 2

; ; 4; 4E E x x  

và diện

tích của dải vườn là

4 4

2 2

4 0

5 5

2 64 d 64 d

8 2

S x x x x



   

 

Tính tích phân này bằng phép đổi biến 8sinx t , ta được

6 4

 

 

 

 



Khi đó số tiền là

80 .100000 7652891,82 7.653.000

6 4

 

  

 

 





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 99

Facebook: https://www.facebook.com/dongpay

Câu 26: Một mảnh vườn hình tròn tâm O bán kính 6m . Người ta cần

trồng cây trên dải đất rộng 6m nhận O làm tâm đối xứng, biết

kinh phí trồng cây là 70000 đồng

/ m

. Hỏi cần bao nhiêu tiền

để trồng cây trên dải đất đó (số tiền được làm tròn đến hàng

đơn vị)

A. 8412322 đồng. B. 8142232 đồng.

C. 4821232 đồng. D. 4821322 đồng.

Hướng dẫn giải

Chọn D

Xét hệ trục tọa độ oxy đặt vào tâm khu vườn, khi đó phương trình đường tròn tâm O là

2 2

x y 36 

. Khi đó phần nửa cung tròn phía trên trục Ox có phương trình

36 (x)y x f  

Khi đó diện tích S của mảnh đất bằng 2 lần diện tích hình phẳng giới hạn bởi trục hoành, đồ

thị (x)y f và hai đường thẳng 3; 3x x  

2 36 x dxS



  



Đặt 6sin 6cosx t dx tdt   . Đổi cận: 3

x t    



; 3

x t  



6 6

2 36cos 36 (cos2t+1)dt 18(sin2t 2t) 18 3 12S tdt

 



      

 



 



Do đó số tiền cần dùng là 70000. 4821322S  đồng

Câu 27: Một thùng rượu có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách đều hai

đáy có bán kính là 40cm , chiều cao thùng rượu là 1m (hình vẽ). Biết rằng mặt phẳng chứa

trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu (

đơn vị lít) là bao nhiêu?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 100

Facebook: https://www.facebook.com/dongpay

425,2

lit. B.

425162

lit. C.

212581

lit. D.

212,6

lit.

Hướng dẫn giải

Chọn A.

 Gọi





P y ax bx c

  

là parabol đi qua điểm





0,5;0,3

và có đỉnh





0;0,4

(hình vẽ).

Khi đó, thể tích thùng rượu bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi





, trục hoành và hai đường thẳng

0,5

 

quay quanh trục

 Dễ dàng tìm được

 

: 0,4

P y x  

 Thể tích thùng rượu là:

2 2

0,5 0,5

2 2

0,5 0

2 2 203

0,4 2 0,4 425,5 (l)

5 5 1500

V x dx x dx



   

       

   

   

 



 

Câu 28: Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m, có bán kính

đáy 1m, với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn

tương ứng với 0,5m của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại

trong bồn (theo đơn vị

)

A. 11,781

B. 12,637

C. 1

14,923 .

8,307 .

Hướng dẫn giải

Chọn B.

0,4m

0,3m

0,5m

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 101

Facebook: https://www.facebook.com/dongpay

 Thể tích của bồn (hình trụ) đựng dầu là:

2 2 3

.1 .5 5 ( )

V r h m

  

  

 Thể tích phần đã rút dầu ra (phần trên mặt (ABCD)) là:

.5 3,070 ( )

3 4

V m

 

  

 

 



 Vậy thể tích cần tìm là:

2 1

5 3,07 12,637 ( ).

V V V m

    



Câu 29: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2,25 mét,

chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy số

tiền bác Năm phải trả là:

A. 33750000 đồng. B. 12750000 đồng. C. 6750000 đồng. D. 3750000 đồng.

Hướng dẫn giải

Chọn C.

 Gắn parabol





và hệ trục tọa độ sao cho





đi qua

(0;0)

 Gọi phương trình của parbol là (P):





P y ax bx c

  

Theo đề ra,





đi qua ba điểm

(0;0)

O ,

(3;0)

A ,

(1,5;2,25)

B .

Từ đó, suy ra





: 3

P y x x

  

 Diện tích phần Bác Năm xây dựng:

S x x dx

   



 Vậy số tiền bác Năm phải trả là:

1500000 675 0

000

 (đồng)

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 102

Facebook: https://www.facebook.com/dongpay

Câu 30: Trong chương trình nông thôn mới, tại một xã X có xây một cây cầu bằng bê tông như hình

vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu. (Đường cong trong hình vẽ là các đường

Parabol).

. B.

. C.

18 .

. D.

Hướng dẫn giải

Chọn D.

Chọn hệ trục

Oxy

như hình vẽ.

Gọi





P y ax c

 

là Parabol đi qua hai điểm

 

;0 , 0;2

A B

 

 

 

Nên ta có hệ phương trình sau:

 

0 . 2

: 2

361

P y x



 

 

 

 

 

    

 

 

 



 



Gọi





P y ax c

 

là Parabol đi qua hai điểm

 

10;0 , 0;

C D

 

 

 

0,5

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 103

Facebook: https://www.facebook.com/dongpay

Nên ta có hệ phương trình sau:

 

0 . 10

1 5

402

5 5

40 2

2 2

P y x

b b



  



 

    

 

 

 



 

Ta có thể tích của bê tông là:

2 2 3

0 0

1 5 8

5.2 2 40

40 2 361

V x dx x dx m

 

   

      

 

   

   

 

 

Câu 31: Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng

giới hạn bởi các đường

y x

 

và trục

quay quanh trục

biết đáy lọ và miệng lọ

có đường kính lần lượt là

và

, khi đó thể tích của lọ là:

8 .



Hướng dẫn giải

Chọn B.



1 1 1

1 0

r y x

   



2 2 2

2 3

r y x

   

Suy ra:

 

3 3

2 3

0 0

d 1 d

2 2

V y x x x x

 

     

 

 

 

   

Câu 32: Hạt electron có điện tích âm là

1,6.10



. Nếu tách hai hạt eletron từ

đếm 4

thì

công

sinh ra là

3,194.10 .





-16

1,728.10



1,728.10 .





3,194.10 .





Hướng dẫn giải

Chọn B.

 Áp dụng công thức

1 2

kq q

A x





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 104

Facebook: https://www.facebook.com/dongpay

Trong đó:

9 12 12

9.10 ; 1 10 ; 4 4.10

k a pm m b pm m

 

    

;

1 2

1,6.10

q q C



 

 Suy ra:





4.10

9 19

4.10

28 16

9.10 . 1,6.10

d 2,304.10 1,728.10

A x J

x x



 

 

   

 

 



Câu 33: Trong mạch máy tính, cường độ dòng điện (đơn vị

) là một hàm số theo thời gian t, với

( ) 0,3 0,2

I t t

 

. Hỏi tổng điện tích đi qua một điểm trong mạch trong 0,05 giây là bao

nhiêu?

0,29975 .

0,29 .

0,01525 .

0,01475 .

Hướng dẫn giải

Chọn D.

   

0,05

0,05 0,05

0 0

d 0,3 0,2 d 0,3 0,01475 .

q I t t t t t mC

 

     

 

 

 

Câu 34: Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có có biểu thức cường độ là

 

cos

i t I t

 

 

 

 





. Biết

i q





với

là điện tích tức thời ở tụ điện. Tính từ lúc



, điện

lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng





là





. B. 0. C.







Hướng dẫn giải

Chọn C.

Điện lượng chuyển qua tiết diện của dây dẫn của đoạn mạch trong thời gian từ 0 đến





là

 

0 0

d cos d sin

2 2

I I

q i t t I t t t

   

     

   

   

 

 



 



 

 

Câu 35: Khi một chiếc lò xo bị kéo căng thêm





x m

so với độ dài tự nhiên là





0,15

của lò xo thì

chiếc lò xo trì lại (chống lại) với một lực





800 .

f x x



Hãy tìm công

sinh ra khi kéo lò

xo từ độ dài từ





0,15

đến





0,18 .

36.10 .

W J





72.10 .

W J





36 .

W J



72 .

W J



Hướng dẫn giải

Chọn A.

Công được sinh ra khi kéo căng lò xo từ 0,15m đến 0,18m là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 105

Facebook: https://www.facebook.com/dongpay

0,03

2 0,03 2

800 .d 400 36.10 .

W x x x J



  



Chú ý: Nếu lực là một giá trị biến thiên (như nén lò xo) và được xác định bởi hàm





F x

thì

công sinh ra theo trục

từ

tới

là

 

d .

A F x x





Câu 36: Một dòng điện xoay chiều i = I

sin t

 



 

 





chạy qua một mạch điện có điện trở thuần

R.Hãy tính nhiệt lượng Q tỏa ra trên đoạn mạch đó trong thời gian một chu kì T.

. B.

. C.

. D.

Hướng dẫn giải

Chọn A.

Ta có: Q =

2 2 2

0 0

sin

T T

Ri dt RI t dt

 

 

 

 

 





1 2

cos

RI dt

 

 

 

 









2 2

0 0

sin 2

2 4 2

RI RI

t t T

 

   

  

 







Câu 37: Đặt vào một đoạn mạch hiệu điện thế xoay chiều u = U

sin



. Khi đó trong mạch có

dòng diện xoay chiều i = I

sin t

 



 

 





với



là độ lệch pha giữa dòng diện và hiệu

điện thế.Hãy Tính công của dòng diện xoay chiều thực hiện trên đoạn mạnh đó trong

thời gian một chu kì.

0 0

U I

cos



. B.

0 0

sin

U I



. C.

0 0

( )

U I

Tcos



 

. D.

0 0

U I

Tcos



Lời giải

Ta có:

A =

0 0

2 2

sin sin

T T

uidt U I t tdt

T T

 

 

 

 

 

 



0 0

1 4

U I cos cos t dt

 

  

 

 





 

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 106

Facebook: https://www.facebook.com/dongpay

0 0

1 4

2 2

U I

cos cos t dt

 

  

 

 





 

0 0 0 0

sin

2 4 2

U I U I

tcos t Tcos

 

   

  

 



  



Hướng dẫn giải

Chọn D.

Câu 38: Để kéo căng một lò xo có độ dài tự nhiên từ

đến

cần lực

. Tính công (

)

sinh ra khi kéo lò xo có độ dài từ

đến

1,56 ( )

A J



. B.

1 ( )

A J



. C.

2,5 ( )

A J



. D.

2 ( )

A J



Hướng dẫn giải

Chọn A.

Theo Định luật Hooke, lực cần dùng để giữ lò xo giãn thêm

mét từ độ dài tự nhiên là





f x kx



, với





k N m

là độ cứng của lò xo. Khi lò xo được kéo giãn từ độ dài

đến

, lượng kéo giãn là

5 0.05

cm m



. Điều này có nghĩa





0.05 40



, do đó:

 

0,05 40 800 /

0,05

k k N m

   

Vậy





800

f x x



và công cần để kéo dãn lò xo từ

đến

là:

     

0,08

2 2

0,05

800d 400 400 0,08 0,05 1,56

A x x J

 

    

 



Câu 39: Một thanh AB có chiều dài là 2a ban đầu người ta giữ thanh ở góc nghiêng



 

, một đầu

thanh tựa không ma sát với bức tường thẳng đứng. Khi buông thanh, nó sẽ trượt xuống dưới

tác dụng của trọng lực. Hãy biểu diễn góc



theo thời gian t (Tính bằng công thức tính

phân)

(sin sin )

 







 

. B.

(sin sin )

 







 





f x k x



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 107

Facebook: https://www.facebook.com/dongpay

(sin sin )

 







 

. D.

(sin sin )

 







 

Hướng dẫn giải

Do trượt không ma sát nên cơ năng của thanh được bảo toàn

sin sin

o q tt

mga mga K K  

 

(1)

Do khối tâm chuyển động trên đường tròn tâm O bán kính a nên:

2 2

K ma 





Động năng quay quanh khối tâm:

2 2 2 2 2

1 1 1 1

(2 ) ' '

2 2 12 6

K I m a ma  

  

Thay vào (1) ta được:

' (sin sin )

a g 

  

' (sin sin )

  

  

(sin sin )

 







 

Chọn D.

Câu 40:

Trong kinh tế học, thặng dư tiêu dùng của hàng hóa được tính bằng công thức

 

( ) .d .

I p x P x 



Với ( )p x là hàm biểu thị biểu thị giá mà một công ty đưa ra để bán được x đơn vị hàng hóa.

a là số lượng sản phẩm đã bán ra, ( )P p a là mức giá bán ra ứng với số lượng sản phẩm là

Cho

1200 0,2 0,0001p x x  

, (đơn vị tính là USD). Tìm thặng dư tiêu dùng khi số lượng

sản phẩm bán là 500.

A. 1108333,3 USD. B. 570833,3 USD. C. 33333,3 USD. D. Đáp án khác.

Hướng dẫn giải

Chọn C.

Áp dụng công thức trên với

   

500; 500 1075a P p a p   

Suy ra

 

500

2 3

1200 0,2 0,0001 1075 d 125 33333,3

10 30000

x x

I x x x x

 

       

 

 



USD

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 108

Facebook: https://www.facebook.com/dongpay

Câu 41:

Một khối cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông góc bán kính

và cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được.

A. (dm

). B. (dm

). C. (dm

). D. (dm

)

Hướng dẫn giải:

Đặt hệ trục với tâm O, là tâm của mặt cầu; đường thẳng

đứng là Ox, đường ngang là Oy; đường tròn lớn có phương

trình .

Thể tích là do hình giới hạn bởi Ox, đường cong

, quay quanh Ox.

= (bấm máy).

Chọn A.

Câu 42:

Từ một khúc gõ hình trụ có đường kính 30cm, người ta cắt khúc gỗ bởi một mặt phẳng đi

qua đường kính đáy và nghiêng với đáy một góc để lấy một hình nêm (xem hình minh

họa dưới đây)

Hình 1 Hình 2

Kí hiệu là thể tích của hình nêm (Hình 2). Tính .

A. . B. . C. . D.

Hướng dẫn giải

Chọn hệ trục tọa độ như hình vẽ.Khi đó

hình nêm có đáy

132



100



2 2

x y

 

y x

 

3, 3

x x

  

(25 )

V x dx





 



132







V cm

2250

 

V cm

225









V cm

1250





V cm

1350

5dm

3dm

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 109

Facebook: https://www.facebook.com/dongpay

là nửa hình tròn có phương trình:

Một một mặt phẳng cắt vuông góc với trục Ox tại điểm có hoành độ ,

cắt hình nêm theo thiết diện có diện tích là (xem hình).

Dễ thấy và khi đó

suy ra thể tích hình nêm là:

Chọn A.

Câu 43: Người ta dựng một cái lều vải





có dạng hình “chóp lục giác cong đều” như hình vẽ bên.

Đáy của





là một hình lục giác đều cạnh

. Chiều cao

SO m



(

vuông góc với

mặt phẳng đáy). Các cạnh bên của





là các sợi dây

nằm trên các

đường parabol có trục đối xứng song song với

. Giả sử giao tuyến (nếu có) của





với

mặt phẳng





vuông góc với

là một lục giác đều và khi





qua trung điểm của

thì lục giác đều có cạnh

. Tính thể tích phần không gian nằm bên trong cái lều





đó.

135 3

(

). B.

96 3

(

). C.

135 3

(

). D.

135 3

(

Hướng dẫn giải

y x x

225 , 15;15

 

   

 





15;15

 

 

 





S x



NP y

   

0 2

tan45 15

MN NP y x

 

  

1 1

. . 225

2 2

S x MN NP x

 







V S x dx

   

x dx cm

2 3

. 225 2250



  



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 110

Facebook: https://www.facebook.com/dongpay

Đặt hệ trục tọa độ như hình vẽ, ta có parabol cần tìm đi qua 3 điểm có tọa độ lần lượt là

 

0;6A

 

1;3B

 

3;0C

nên có phương trình là

1 7

2 2

y x x  

Theo hình vẽ ta có cạnh của “thiết diện lục giác” là

. Nếu ta đặt t OM thì

7 1

2 4

BM t   (chú

ý là ta phải lấy giá trị có dấu “



” trước dấu căn và

cho

chạy từ C đến

Khi đó, diện tích của “thiết diện lục giác” bằng

 

3 3 3 7 1

6. 2

4 2 2 4

S t t

 

   

 

 

với

 

0;6t

Vậy thể tích của “túp lều” theo đề bài là:

 

6 6

0 0

3 3 7 1 135 3

d 2 d ...

2 2 4 8

V S t t t t

 

     

 

 

 

Chọn D.

Câu 44: Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn bán kinh 4 cắt

vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là tam giác đều. Thể tích của

vật thể là:

256

V  B.

V  C.

256 3

V 

32 3

V 

Hướng dẫn giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 111

Facebook: https://www.facebook.com/dongpay

Chọn tâm đường tròn làm gốc.

Diện tích thiết diện là

2 2

3(4 )

S AB x  

2 2

32 3

( ) 3 (4 )

V S x dx x dx

 

   

 

Chọn D.

Câu 45: Một người có mảnh đất hình tròn có bán kính 5m, người này tính trồng cây trên mảnh đất

đó, biết mỗi mét vuông trồng cây thu hoạch được giá 100 nghìn. Tuy nhiên cần có khoảng

trống để dựng chồi và đồ dùng nên người này căng sợi dây 6m sao cho 2 đầu mút dây nằm

trên đường tròn xung quanh mảnh đất. Hỏi người này thu hoạch được bao nhiêu tiền (tính

theo đơn vị nghìn và bỏ phần số thập phân).

.A. 3722. B. 7445. C. 7446 . D. 3723

Hướng dẫn giải

Đặt hệ trục tọa độ 4349582 như hình vẽ.

Phương trình đường tròn của miếng đất sẽ là

2 2

25x y 

Diện tích cần tính sẽ bằng 2 lần diện tích phần tô

đậm phía trên.

Phần tô đậm được giới hạn bởi đường cong có

phương trình là

25y x  , trục

; 5; 4Ox x x   (trong đó giá trị 4 có được dựa

vào bán kính bằng 5 và độ dài dây cung bằng 6)

Vậy diện tích cần tính là

2 25 74,45228...S x dx



  



Chọn B.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 112

Facebook: https://www.facebook.com/dongpay

Câu 46: Trong Công viên Toán học có những mảnh đất mang hình dáng khác nhau. Mỗi mảnh được

trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán

học. Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có

phương trình trong hệ tọa độ

Oxy

là

 

2 2 2

16 25y x x  như hình vẽ bên.

Tính diện tích

của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ tọa độ

Oxy

tương

ứng với chiều dài

mét.

 

125

S m B.

 

125

S m C.

 

250

S m D.

 

125

S m

Hướng dẫn giải

Chọn D.

Vì tính đối xứng trụ nên diện tích của mảnh đất tương ứng với 4 lần diện tích của mảnh đất

thuộc góc phần tư thứ nhất của hệ trục tọa độ

Oxy

Từ giả thuyết bài toán, ta có

y x x   .

Góc phần tư thứ nhất

 

25 ; 0;5

y x x x  

Nên

2 3

( )

1 125 125

25 d ( )

4 12 3

S x x x S m    



Câu 47: Gọi

 

là phần giao của hai khối

hình trụ có

bán kính

, hai trục hình trụ vuông góc với nhau.

Xem hình vẽ bên. Tính thể tích của

 



. B.

 



 



. D.

 





Hướng dẫn giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 113

Facebook: https://www.facebook.com/dongpay

Chọn A.

Ta gọi trục tọa độ Oxyz như hình vẽ. Khi đó phần giao

 

là

một vật thể có đáy là một phần tư hình tròn tâm O bán kính

, thiết

diện của mặt phẳng vuông góc với trục Ox là một hình vuông có

diện tích

 

2 2

 S x a x

Thể tích khối

 

là

 

2 2

0 0

 

 

a a

S x dx a dx .

Câu 48: Một khối cầu có bán kính là

 

5 dm

, người ta cắt bỏ hai

phần của khối cầu bằng hai mặt phẳng song song cùng

vuông góc đường kính và cách tâm một khoảng

 

3 dm

để

làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà

chiếc lu chứa được.

 

100



 



 

41 dm



 

132 dm



Hướng dẫn giải

Chọn D.

Cách 1: Trên hệ trục tọa độ Oxy , xét đường tròn

2 2

( ):( 5) 25C x y  

. Ta thấy nếu cho

nửa trên trục Ox của

 

quay quanh trục Ox ta được mặt cầu bán kính bằng 5. Nếu cho

hình phẳng

 

giới hạn bởi nửa trên trục Ox của

 

, trục Ox , hai đường thẳng

0, 2x x  quay xung quanh trục Ox ta sẽ được khối tròn xoay chính là phần cắt đi của

khối cầu trong đề bài.

Ta có

2 2 2

( 5) 25 25 ( 5)x y y x       

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 114

Facebook: https://www.facebook.com/dongpay

 Nửa trên trục Ox của

 

có phương trình

2 2

25 ( 5) 10y x x x    

 Thể tích vật thể tròn xoay khi cho

 

quay quanh Ox là:

 

2 2

10 d 5

3 3

V x x x x

 

    

 

 





 

Thể tích khối cầu là:

4 500

V .5

3 3

 



Thể tích cần tìm:

 

2 1

500 52

2 2. 132

3 3

V V V dm    

 



Câu 49: Một cái chuông có dạng như hình vẽ. Giả sử khi cắt chuông bởi mặt phẳng qua trục của

chuông, được thiết diện có đường viền là một phần parabol ( hình vẽ ). Biết chuông cao 4m,

và bán kính của miệng chuông là

2 2

. Tính thể tích chuông?

A. 6



B. 12



D. 16



Hướng dẫn giải

Xét hệ trục như hình vẽ, dễ thấy parabol đi qua ba

điểm

 

   

0;0 , 4;2 2 , 4; 2 2 nên có phương trình



. Thể tích của chuông là thể tích của khối tròn

xoay tạo bởi hình phẳng

2 , 0, 4  y x x x

quay

quanh trục Ox. Do đó

Ta có

 

2 16  



V xdx x

  

Câu 50: Một mảnh vườn hình tròn tâm O bán kính 6m . Người ta cần trồng cây trên dải đất rộng 6m

nhận O làm tâm đối xứng, biết kinh phí trồng cây là 70000 đồng

/ m

Hỏi cần bao nhiêu

tiền để trồng cây trên dải đất đó (số tiền được làm tròn đến hàng đơn vị)

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 115

Facebook: https://www.facebook.com/dongpay

8412322

đồng. B.

8142232

đồng. C.

4821232

đồng. D.

4821322

đồng

Hướng dẫn giải

Xét hệ trục tọa độ oxy đặt vào tâm khu vườn, khi đó phương trình đường tròn tâm O là

2 2

x y 36

 

. Khi đó phần nửa cung tròn phía trên trục Ox có phương trình

36 ( )

  

y x f x

Khi đó diện tích S của mảnh đất bằng 2 lần diện tích hình phẳng giới hạn bởi trục hoành, đồ

thị

( )



y f x

và hai đường thẳng

3; 3

  

x x

2 36



  



S x dx

Đặt

6sin 6cos

  

x t dx tdt

. Đổi cận: 3

    

x t



; 3

  

x t



6 6

2 36cos 36 (cos2t+1)dt 18(sin 2t 2t) 18 3 12

 



      

 

S tdt



 



Do đó số tiền cần dùng là

70000. 4821322



S đồng

Câu 51: Cho một vật thể bằng gỗ có dạng khối trụ với bán kính đáy bằng R. Cắt khối trụ bởi một mặt

phẳng có giao tuyến với đáy là một đường kính của đáy và tạo với đáy góc . Thể tích

của khối gỗ bé là:

A. B. C. D.

Hướng dẫn giải

V 





V 





ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 116

Facebook: https://www.facebook.com/dongpay

Chọn hệ trục Oxy như hình vẽ. Cắt khối gỗ bé bởi các mặt phẳng vuông góc với Ox tại điểm

có hoành độ x ta được thiết diện là tam giác vuông có diện tích bằng .

Vậy thể tích khối gỗ bé bằng:

Chọn A.

Câu 52: Vòm cửa lớn của một trung tâm văn hoá có dạng hình Parabol. Người

ta dự định lắp cửa kính cường lực cho vòm cửa này. Hãy tính diện tích

mặt kính cần lắp vào biết rằng vòm cửa cao 8m và rộng 8m (như hình

vẽ)

( )

m B.

( )

m C.

128

( )

m D.

131

( )

Hướng dẫn giải:

Đáp án đúng: C

Các phương án nhiễu:

A. HS tính tích phân sai

1 28

2 3



   



S x dx

( )m

B. HS tính tích phân sai

1 26

2 3



   



S x dx

( )m

)

D. HS nhầm a =

 , b= 8, c = 0 =>

1 131

2 3



   



S x x dx

( )m

2 2

( )

A x R x

 

2 2

1 2

2 3

V R x



  



2 2

R x



2 2

R x



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 117

Facebook: https://www.facebook.com/dongpay

Câu 53: Một khuôn viên dạng nửa hình tròn có đường kính bằng

4 5

(m). Trên đó người thiết kế

hai phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa

hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau

một khoảng bằng

(m), phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ

Nhật Bản.

Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là

100.000

đồng/m

Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến

hàng nghìn)

3.895.000

(đồng). B.

1.948.000

(đồng). C.

2.388.000

(đồng). D.

1.194.000

(đồng).

Hướng dẫn giải:

Chọn B

Đặt hệ trục tọa độ như hình vẽ. Khi đó phương

trình nửa đường tròn là

 

2 2 2 2

2 5 20y xR x x     .

Phương trình parabol

 

P có đỉnh là gốc

sẽ

có dạng

y ax

. Mặt khác

 

qua điểm

 

2;4M

do đó:

 

4 2 1a a    .

Phần diện tích của hình phẳng giới hạn bởi

 

P và nửa đường tròn.( phần tô màu)

Ta có công thức

 

2 2 2

11,920 4S x x dx m



  



Vậy phần diện tích trồng cỏ là   

19,47592654

trongco hinhtron

S S S

Vậy số tiền cần có là

100000 1.948.000

trongxo

S  

(đồng).đồng.

Câu 54: Một công ty quảng cáo X muốn làm một bức tranh

trang trí hình MNEIF ở chính giữa của một

bức tường hình chữ nhật ABCD có chiều cao

6 BC m , chiều dài 12 CD m (hình vẽ bên).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 118

Facebook: https://www.facebook.com/dongpay

Cho biết

MNEF

là hình chữ nhật có

MN m



; cung

EIF

có hình dạng là một phần của

cung parabol có đỉnh

là trung điểm của cạnh

và đi qua hai điểm

. Kinh phí làm

bức tranh là

900.000

đồng/

Hỏi công ty X cần bao nhiêu tiền để làm bức tranh đó?

20.400.000

đồng. B.

20.600.000

đồng. C.

20.800.000

đồng. D.

21.200.000

đồng.

Câu 55: Một sân chơi cho trẻ em hình chữ nhật có chiều dài

100

và chiều rộng là

người ta làm

một con đường nằm trong sân (như hình vẽ). Biết rằng viền ngoài và viền trong của con

đường là hai đường elip, Elip của đường viền ngoài có trục lớn và trục bé lần lượt song song

với các cạnh hình chữ nhật và chiều rộng của mặt đường là

. Kinh phí cho mỗi

làm

đường

600.000

đồng. Tính tổng số tiền làm con đường đó. (Số tiền được làm tròn đến hàng

nghìn).

293904000.

283904000.

293804000.

283604000.

Hướng dẫn giải:

Chọn A.

Xét hệ trục tọa độ

Oxy

đặt gốc tọa độ

vào tâm của hình Elip.

Phương trình Elip của đường viền ngoài của con đường là

 

2 2

: 1

50 30

x y

 

. Phần đồ thị

của





nằm phía trên trục hoành có phương trình

 

30 1

y f x

  

Phương trình Elip của đường viền trong của con đường là

 

2 2

: 1

48 28

x y

 

. Phần đồ thị

của





nằm phía trên trục hoành có phương trình

 

28 1

y f x

  

100

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 119

Facebook: https://www.facebook.com/dongpay

Gọi

là diện tích của





và bằng hai lần diện tích phần hình phẳng giới hạn bởi trục

hoành và đồ thị hàm số





y f x



. Gọi

là diện tích của





và bằng hai lần diện tích

phần hình phẳng giới hạn bởi trục hoành và đồ thị hàm số





y f x



Gọi

là diện tích con đường. Khi đó

50 48

2 2

2 30 d 21 28 1

50 48

x x

S S S

x x

 

    

 

Tính tích phân

 

2 1 d , ,

I b a





  





Đặt

sin , d cos d

2 2

x a t t x a t t

 

 

     

 

 

Đổi cận ;

2 2

x a t x a t

 

       

Khi đó

 

2 2 2

2 2

2 2 2

sin cos d co2 1 s d 1 co.

2 s2

t a t t t t t

I b ab b

  

  

   

  

sin 2

ab ab





 



 









Do đó

1 2

50.30 48.28 156

S S S

  

    

Vậy tổng số tiền làm con đường đó là 600000. 600000.

156 294053000







(đồng).

Câu 56: Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây

Người ta đo được đường kính của miệng ly là

và chiều cao là

. Biết rằng thiết

diện của chiếc ly cắt bởi mặt phẳng đối xứng là một parabol. Tính thể tích





V cm

của vật

thể đã cho.





. B.





 . D.

V  .

Hướng dẫn giải:

Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 120

Facebook: https://www.facebook.com/dongpay

Chọn gốc tọa độ

trùng với đỉnh

của parabol

 

Vì parabol

 

đi qua các điểm

   

2;6 , 2;6A B

và

 

0;0I

nên parabol

 

có phương trình

y x

Ta có

2 2

3 2

2 3

  y x x y . Khi đó thể tích của vật thể đã cho là

 

12 .

V y dy cm

 

 

 

 

 



Câu 57: Trong mặt phẳng tọa độ, cho hình chữ nhật

 

có một cạnh nằm trên trục hoành, và có hai

đỉnh trên một đường chéo là

 

1;0A 

và

 

;B a a , với

0a 

. Biết rằng đồ thị hàm số

y x

chia hình

 

thành hai phần có diện tích bằng nhau, tìm

9a 

. B.

4a 

. C.

a  . D.

3a 

Hướng dẫn giải:

Chọn D.

Gọi

ACBD

là hình chữ nhật với

nằm trên trục

 

1;0A 

và

 

;B a a

Nhận thấy đồ thị hàm số

y x

cắt trục hoành tại điểm có hoành độ bằng 0 và đi qua

 

;B a a . Do đó nó chia hình chữ nhật

ACBD

ra làm 2

phần là có diện tích lần lượt là

. Gọi

là diện tích

hình phẳng giới hạn bởi các đường

y x

và trục

0,x x a 

và

là diện tích phần còn lại. Ta lần lượt tính

Tính diện tích

S x x



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 121

Facebook: https://www.facebook.com/dongpay

Đặt

2 d d

t x t x t t x

    

; Khi

0 0;

x t x a t a

     

Do đó

2 2

2 d

3 3

t a a

S t t

 

  

 

 



Hình chữ nhật

ACBD

có

AC a AD a

  

nên

 

1 2

2 1

3 3

ACBD

a a

S S S a a a a a

      

Do đồ thị hàm số

y x



chia hình





thành hai phần có diện tích bằng nhau nên

1 2

2 1

3 3

a a

S S a a a a a a a

       

(Do



)

Câu 58: Sân trường có một bồn hoa hình tròn tâm

. Một nhóm học sinh lớp 12 được giao thiết kế

bồn hoa, nhóm này định chia bồn hoa thành bốn phần, bởi hai đường parabol có cùng đỉnh

và đối xứng nhau qua

. Hai đường parabol này cắt đường tròn tại bốn điểm

tạo thành một hình vuông có cạnh bằng

(như hình vẽ). Phần diện tích

dùng

để trồng hoa, phần diện tích

dùng để trồng cỏ (Diện tích làm tròn đến chữ số thập

phân thứ hai). Biết kinh phí trồng hoa là

150.000

đồng /1m

, kinh phí để trồng cỏ là

100.000

đồng/1m

. Hỏi nhà trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm

tròn đến hàng chục nghìn)

6.060.000

đồng. B.

5.790.000

đồng. C.

3.270.000

đồng. D.

3.000.000

đồng.

Hướng dẫn giải:

Chọn C.

Chọn hệ trục tọa độ như hình vẽ

Parabol có hàm số dạng

y ax bx c

  

có đỉnh là gốc tọa độ và đi qua điểm





2;2

nên

có phương trình

y x



Đường tròn bồn hoa có tâm là gốc tọa độ và bán kính

2 2

OB 

nên có phương trình là

2 2

x y

 

. Do ta chỉ xét nhánh trên của đường tròn nên ta chọn hàm số nhánh trên là

y x

 

Vậy diện tích phần

2 2

8 d

S x x x



 

  

 

 



Do đó, diện tích trồng hoa sẽ là

2 2

1 2

2 8 d 15,233...

S S x x x



 

    

 

 



ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng

File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 122

Facebook: https://www.facebook.com/dongpay

Vậy tổng số tiền để trồng bồn hoa là:









15,233 150.000 2 2 15,233 100.000 3.274.924



     đồng.

Làm tròn đến hàng chục nghìn nên ta có kết quả là

3.270.000

đồng.

Bấm Tải xuống để xem toàn bộ.

| 1/122

| | Tải xuống

Preview text:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng MỤC LỤC
NGUYÊN HÀM NÂNG CAO ........................................................................................................... 3
A – LÝ THUYẾT CHUNG ............................................................................................................ 3
B – BÀI TẬP TRẮC NGHIỆM ..................................................................................................... 4
TÍCH PHÂN NÂNG CAO .............................................................................................................. 15
A – LÝ THUYẾT CHUNG .......................................................................................................... 15
B – BÀI TẬP TRẮC NGHIỆM ................................................................................................... 16
ỨNG DỤNG TÍCH PHÂN NÂNG CAO ........................................................................................ 55
A – LÝ THUYẾT CHUNG .......................................................................................................... 55
B – BÀI TẬP TRẮC NGHIỆM ................................................................................................... 55
ỨNG DỤNG THỰC TẾ .................................................................................................................. 87
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng NGUYÊN HÀM NÂNG CAO
A – LÝ THUYẾT CHUNG 1. Định nghĩa
Cho hàm số y  f  x xác định trên tập K (khoảng, nửa khoảng, đoạn của R). Nếu Ta có hàm số
F  x xác định trên K sao cho F ' x  f  x thì F  x được gọi là nguyên hàm của hàm số f  x trên K.
Định lí 1. Nếu F  x là một nguyên hàm của hàm số f  x trên K thì với mỗi hằng số C, hàm số
G  x  F  x  C cũng là một nguyên hàm của hàm số f  x trên K.
Định lí 2. Nếu F  x là một nguyên hàm của hàm số f  x trên K thì mọi nguyên hàm của f  x
trên K đều có dạng G  x  F  x  C với C là hằng số.
Định lí 3. Mọi hàm số f  x liên tục trên K đều có nguyên hàm trên K. 2. Tính chất:
f ' x dx  f  x  C  với C là hằng số.
kf  x dx  k f  x dx  
với k là hằng số khác 0.
 f  x  g  x f  x  dx  f  x dx  g  x dx      Bảng nguyên hàm
Chú ý: công thức tính vi phân của f  x là d  f  x  f ' x dx   Nguyên hàm cơ bản
Nguyên hàm của hàm hợp 0dx  C  0du  C 
dx  x  C 
du  u  C   1   1 1 x dx x  
 C     1   1 u du u  
 C     1   1   1 1 1
dx  ln x  C 
du  ln u  C  x u
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng x x
e dx  e  C  u u
e du  e  C  x a u a x a dx   C  u a dx   C  ln a ln a
cos xdx  sin x  C 
cos udu  sin u  C 
sin xdx   cos x  C 
sin udu   cosu C  1 1
dx  tan x  C 
du  tan u  C 2  cos x 2 cos u 1 1
dx   cot x  C 
du   cot u  C 2  sin x 2 sin u
B – BÀI TẬP TRẮC NGHIỆM 1 1 Câu 1:
Cho F  x là nguyên hàm của hàm số f  x 
và F 0   ln 4 . Tập nghiệm S x e  3 3
của phương trình F  x   3 3
ln x  3  2 là: A. S    2 .
B. S  2;  2 .
C. S  1;  2 .
D. S  2;  1 . Hướng dẫn giải: dx 1 x  e  1
Ta có: F  x   1 dx  x  e   C  . x  x   ln x 3 e  3 3 e  3 3   1 1
Do F 0   ln 4 nên x
C  0 . Vậy F  x  
x ln e 3 . 3 3
Do đó: 3    ln  x F x
e  3  2  x  2 Chọn A. Câu 2: Cho 2
F (x)  x là một nguyên hàm của hàm số 2 ( ) x
f x e . Tìm nguyên hàm của hàm số 2 (  ) x f x e . A. 2 x 2 f (
 x)e dx  x  2x  C  B. 2 2 (  ) x
f x e dx   x  x  C 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng C. 2 x 2 f (
 x)e dx  2x  2x  C  D. 2 x 2 f (
 x)e dx  2x  2x  C  Hướng dẫn giải: Từ giả thiết 
     2x   2     2x     2 ' . ' . 2 .e x F x f x e x f x e x f x (1) Đặt    2 ' . x A f x e dx  . Đặt 2 x u  e 2   2 x du
e dx ,dv=f’(x)dx chọn v=f(x) 2 x        2x A e f x
f x e dx  x  F  x 2 . 2 . 2 2  C  2
 x  2x  C  Chọn D. Câu 3: Cho ( )  ( 1) x F x x
e là một nguyên hàm của hàm số 2 ( ) x
f x e . Tìm nguyên hàm của hàm số 2 (  ) x f x e .  x x 2 A. 2 (
 ) xd  (4  2 ) x f x e x x e  C  B. 2 f (  x)e d x x  e  C  2 C. 2 (
 ) xd  (2  ) x f x e x x e  C  D. 2 (
 ) xd  (  2) x f x e x x e  C  Hướng dẫn giải: / Từ giả thiết 
     2x     x     2 ' . 1 . . x F x f x e x e f x e   / x e x  x  1 x x x . x  .
x e  f  x 2 .e
 f  x  
 f ' x   ...  2 x x   e e x x  e  e  x x 1 Đặt A  f ' x 2 2 .e dx  . x
e dx  1 x x e dx   x  e u
  1 x  du  dx Đặt x x x x x 
 A  1 x e  e dx  1 x e  e  C  e 2  x  C x 
dv  e dx choïn x v  e  Chọn C. 1 f (x) Câu 4:
Cho F (x)  
là một nguyên hàm của hàm số
. Tìm nguyên hàm của hàm số 3 3x x f (  x) ln x . ln x 1 ln x 1 A. f (
 x) ln xdx    C  B. f (
 x) ln xdx    C 3 5  x 5x 3 5 x 5x ln x 1 ln x 1 C. f (
 x) ln xdx    C  D. f (
 x) ln xdx     C 3 3  x 3x 3 3 x 3x Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng f  x /  1  f  x 1 f  x 1
Từ giả thiết  F ' x        f x   3  4   3 x  3x  x x x x 1
 f ' x  3. 4 x 3ln x ln x Đặt A  f ' x.ln . x dx  dx  3  dx   4  4 x x  1
u  ln x  3du  dx   x  1 1 1  ln x 1 Đặt   A  3   ln x  dx    C    1 1 3 4 3 3   3x 3 x  x 3x dv 
dx choïn v   4 3   x 3x Chọn C. 1 f (x) Câu 5: Cho F (x) 
là một nguyên hàm của hàm số
. Tìm nguyên hàm của hàm số 2 2x x f (  x) ln x  ln x 1  ln x 1 A. f (
 x) ln xdx     C   B. f (
 x) ln xdx    C 2 2   2 2  x 2x  x x  ln x 1  ln x 1 C. f (
 x) ln xdx     C   D. f (
 x) ln xdx    C 2 2   2 2  x x  x 2x Hướng dẫn giải: f  x /  1  f  x 1 f  x 1
Từ giả thiết  F ' x        f x    2  3   2 x  2x  x x x x /  1  2
 f ' x     2  3  x  x 2 ln x Đặt A  f ' x.ln . x dx  .ln . x dx  2 dx   3  3 x x  1
u  ln x  du  dx   x Đặt  1 1 dv 
dx choïn v   3 2   x 2x  ln x 1   ln x 1   ln x 1   A  2   dx  2    C     C  2  3   2 2   2 2   2x 2x   2x 4x   x 2x  Chọn A. 1 Câu 6:
Hàm số nào dưới đây là nguyên hàm của hàm số f  x  trên khoảng  ;   ? 2 1 x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
A. F  x   2
ln x  1 x   C .
B. F  x   2
ln 1 1 x   C . 2x
C. F  x 2
 1 x  C .
D. F  x   C 2 1 x Hướng dẫn giải:
Ta có bài toán gốc sau: dx
Bài toán gốc: Chứng minh 2  ln x 
x  a  c a     2 x  a 2  2x 
x  x  a tdx Đặt 2
t  x  x  a  dt  1
 dx  dt  dx  dt  2 2  2 x  a  x  a 2 x  a dt dx   2 t x  a dx dt Vậy khi đó 2 
 ln t  c  ln x 
x  a  c  
( điều phải chứng minh). 2 t x  a
Khi đó áp dụng công thức vừa chứng minh ta có 1 F  x 2 
dx  ln x  1 x  c  ln   2 x  1 x  c . 2  1 x Chọn A.    F  1 tan x   Câu 7:
Cho F(x) là một nguyên hàm của f  x 
, biết F 0  0 ,  4  . 2
cos x 1 a cos x       F  F     Tính  3   4  ? A. 5  3 . B. 5 1. C. 3  5 . D. 5  2 Hướng dẫn giải:     4 4 4 4 tan x tan x 1 f  x 2 dx  dx  dx 
d tan x 1 a     2 2 2 2 0 0 cos x 1 a cos x 0 cos
x tan x  1 a 0 2 tan x 1 a  2 2  tan
1 a  tan 0 1 a  3  2 . 4
 a  2  a 1  3  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
 a  2  a 1 2 a 1  3  2   5  2 6 3  6  
a 1  a  1 3  2  3       tan x   Do đó F  F  dx  2 2      tan  2  tan  2  5  3 . 2  3   4  3 4
 cos x 1  cos x 4 Chọn A. 7 5 cos 2x Câu 8: Biết  2 2
cos x  sin x .sin 4xdx  
 C . Với a là số nguyên. Tìm a? a A. a  6. B. a  12. C. a  7. D. a  14. Hướng dẫn giải:
Đặt f  x   x  x5 2 2 cos sin .sin 4xdx , Ta có: 5
f  x  cos x sin x .sin 4xdx  cos 2x5 2 2 .2 sin 2 . x cos 2x  6  2 cos 2 . x sin 2xdx 
Đặt t  cos 2x  dt  2  sin 2xdx 7 7 t cos 2x Vậy F  x 6   t dt   C    C  7 7 Chọn C. sin x  cos x Câu 9: Biết
dx  a ln sin x  cos x  C 
. Với a là số nguyên. Tìm a? sin x  cos x A. a  1. B. a  2. C. a  3. D. a  4. Hướng dẫn giải: 
sin x cos x  sin x  cos x
Vì a ln sin x  cos x  C       nên sin x  cos x sin x  cos x sin x  cos x Nguyên hàm của:
là: ln sin x  cos x  C . sin x  cos x Chọn A. 2 x tan 
Câu 10: Tìm một nguyên hàm của: 2 1 4.
biết nguyên hàm này bằng 3 khi x  . 2  x 4 2  tan 1    2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 1 A.  3. B.  3. C. tan x  2 . D. cot x  2 . 2 cos x 2 sin x Hướng dẫn giải: 2 x  x 2  tan 2 tan   1 f  x 2 2 2  1 4.  1  1 tan x  2   2 x  x cos x 2  2  1 tan tan 1     2 2   
Nguyên hàm của F  x  tan x  C     Ta có: F  3  tan
 C  3  C  2  F  
 x  tan x  2  4  4 Chọn C.
F  x  x  ln 2sin x  cos x Câu 11: là nguyên hàm của: sin x  cos x
sin x  2 cos x sin x  cos x 3sin x  cos x A. . B. . C. . D. . sin x  3cos x 2sin x  cos x sin x  3cos x
2 sin x  cos x Hướng dẫn giải:
Ta chỉ cần đạo hàm của F(x), rồi sau đó quan sát kết quả đúng.
2sin x  cos x' 2sin x  cos x 3sin x  cos x
Ta có: F ' x  1  1  2sin x  cos x
2 sin x  cos x
2 sin x  cos x 3sin x  cos x
 F  x là một nguyên hàm của .
2 sin x  cos x Chọn D. 1 1 Câu 12: Biết dx    C 
. Với a là số nguyên. Tìm a?  2
25x  20x  4
a 5x  25 A. a  4. B. a  100. C. a  5. D. a  25. Hướng dẫn giải:
Chú ý nếu chúng ta biến đổi:  3
25x  20x  4 1 2   4 2 dx 
25x  20x  4 dx   C  . Là sai 3    2 x x  4 25 20 4     
25x  20x  4 2 2   4 2 3
Điều sau đây mới đúng: 25x  20x  4 d 25x  20x  4   C 4 
Trở lại bài, ta sẽ biến đổi biểu thức  x  x  3 2 25 20 4 về dạng   n ax b như sau:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 1  dx  dx  5x  2 dx  3  6   6   2
25x  20x  4 5x  2  1 5x  2 5 1   C    C 5 5  255x  25 Chọn D. 1 x a Câu 13: Biết dx 
ln 2x  7  C 
, với a, b là cá số nguyên. Tính S = a + b? 2 2x  5x  7 b A. S  4. B. S  2. C. S  3. D. S  5. Hướng dẫn giải:
Ta quan sát mẫu cso thể phân tích được thành nhân tử, sử dụng MTCT bấm giải phương trình bậc 2: 7 2
2x  5x  7  0 thấy có hai nghiệm là: x  1  , x  . 2 Áp dụng công thức 2
ax  bx  c  a  x  x x  x
với x , x là hai nghiệm ta có: 1   2  1 2 2
2x  5x  7   x   1 2x  7 Do đó: 1 x x 1 1 1 dx  dx  dx 
ln 2x  7  C  2   2x  5x  7  x   1 2x  7 2x  7 2 Chọn C. a Câu 14: Biết  x  x2 sin 2 cos 2 dx  x  cos 4x  C 
, với a, b là cá số nguyên. Tính S = a + b? b A. S  4. B. S  2. C. S  3. D. S  5. Hướng dẫn giải: n 1 t  Nếu áp dụng ngay: n t dt   C  thì ta có: n  1 2
sin 2x  cos 2x3
sin 2x  cos 2x dx   C  . Là sai. 3 Ta phải khai triển  x  x2 sin 2 cos 2 để xem thử  x  x2 1 sin 2 cos 2
dx  1 sin 4x dx  x cos4x  C   4 Chọn D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 10
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 x Câu 15: Biết
dx  a.tan  C 
, với a, b là cá số nguyên. Tính S = a + b? 1 cos x b A. S  4. B. S  2. C. S  3. D. S  5. Hướng dẫn giải:
Chưa áp dụng ngay được công thwucs nguyên hàm cơ bản, ta quan sát mẫu và thấy rằng có x 1 cos 2 thể biến đổi 2 1 cos x  2 cos
dựa trên công thức hạ bậc: 2 cos   . Do đó: 2 2 1 1 x dx  dx  tan  C   . 1 cos x x 2 2 2 cos 2
Ta thấy rằng a  1, b  2 do đó S=3. Chọn C. 1 a    Câu 16: Biết dx  tan x   C   
, với a, b là cá số nguyên. Tính S = a + b? 1 sin 2x b  4  A. S  4. B. S  2. C. S  3. D. S  5. Hướng dẫn giải: 1 1 1 dx  dx  dx     1 sin 2x     2   1 cos  2x 2 cos  x      2   4  1    1      tan  x  C  tan x   C     2  4  2  4  Ta thấy a=1,b=2 suy ra S=3 Chọn C.   
Câu 17: Cho f  x 2  8sin x  
 . Một nguyên hàm F  x  của f  x thỏa F 0  8 là:  12       
A. 4x  2 sin 2x   9   .
B. 4x  2 sin 2x   9   .  6   6       
C. 4x  2 sin 2x   7   .
D. 4x  2 sin 2x   7   .  6   6  Hướng dẫn giải:    Ta cần phải tính f  x 2 dx  8sin x  dx    
. Đầu tiên sử dụng công thức hạ bậc để đổi  12 
f  x như sau:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 11
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng      1 cos 2x           f  x 2 6  8sin x   8     12   2           
f  x  4  4 cos 2x   F  
 x  4x  2sin 2x   C    6   6     f 0  8  2  sin
 C  8  C  9    6  Chọn B.
Câu 18: Cho f  x  1 x . Một nguyên hàm F  x của f  x thỏa F   1  1 là: 2  x 1 x   khi x  0   2 2 A. 2 x  x 1 B.  . 2 x x 
 C khi x  0 2   2 2
 x  x C khi x  0 2 
x  x  C khi x  0 1  1 2  C.  . D. 2  . 2 x x  x   C khi x  0 x   C khi x  0 2 2   2  2 Hướng dẫn giải: 2  x x 
 C khi x  0 1
  x khi x  0  1  2
Ta có: f  x  
 F  x   .
1 x khi x  0 2  x x 
 C khi x  0 2   2 2  x 1 x   khi x  0 1   2 2 Theo đề F   1  1  C   do đó: . 1  2 2 x x 
 C khi x  0 2   2 Chọn B. 2 5x  8x  4  1 
Câu 19: Biết F (x) là nguyên hàm của dx 
với 0  x  1 và F  26   . Giá trị nhỏ x 1 x2 2  2 
nhất của F (x) là: A. 24. B. 20. C. 25. D. 26. Hướng dẫn giải: Ta có:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 12
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 9x  4  2 2 x  2x x x     1 5 8 4 F  x  dx  dx   2 x 1 x2 2 x  2 1 x   9 4  4 9     dx    C   2 1 x  2 x  x 1 x    1  4 9 Vì F  26   nên 
 C  26  C  0  2  1  1  1 2    2  4 9
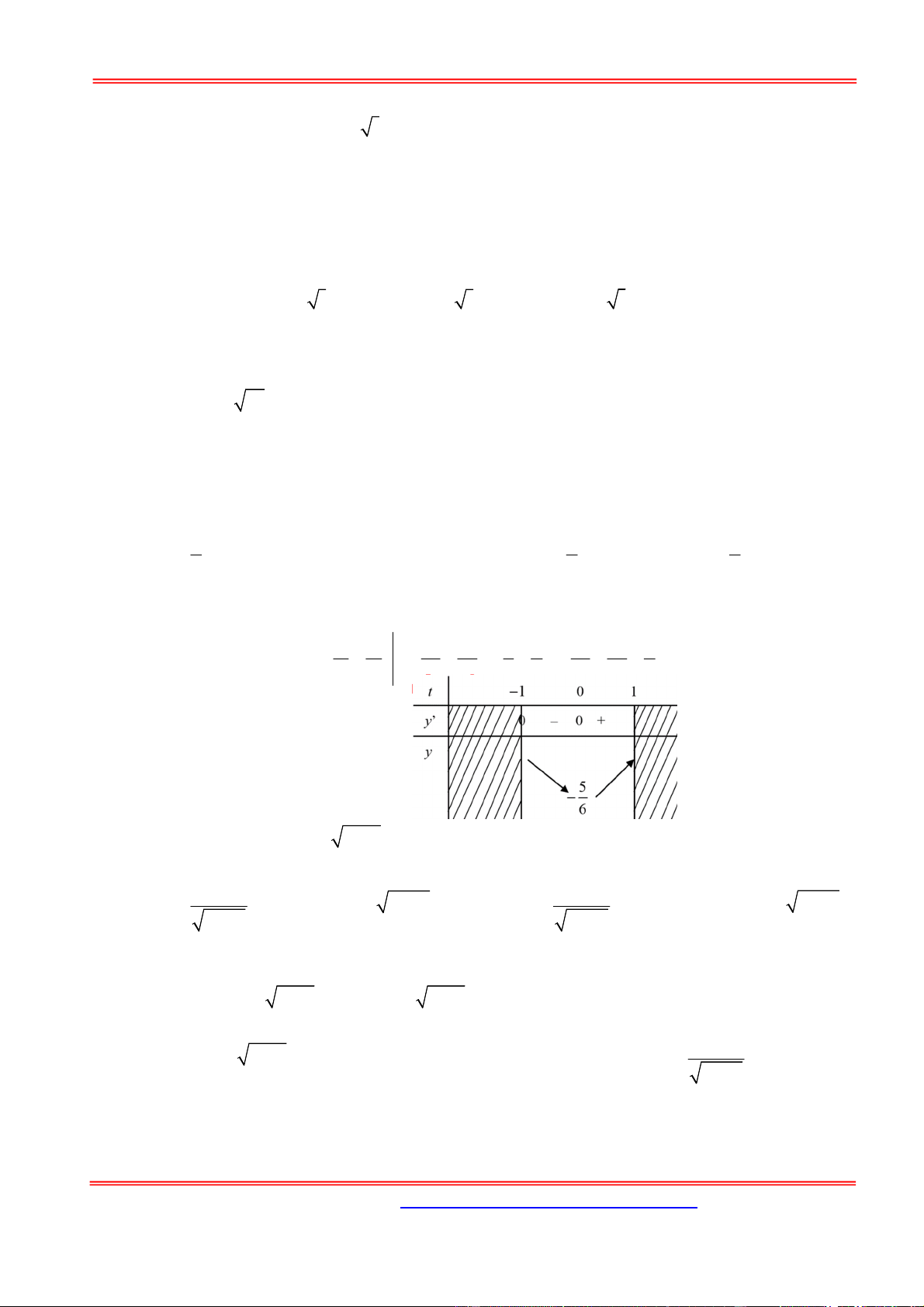
Lúc này F  x  
với 0  x  1. Sử dụng MTCT bấm Mode 7 chọn start 0 end 1 x 1 x Step 0.1:
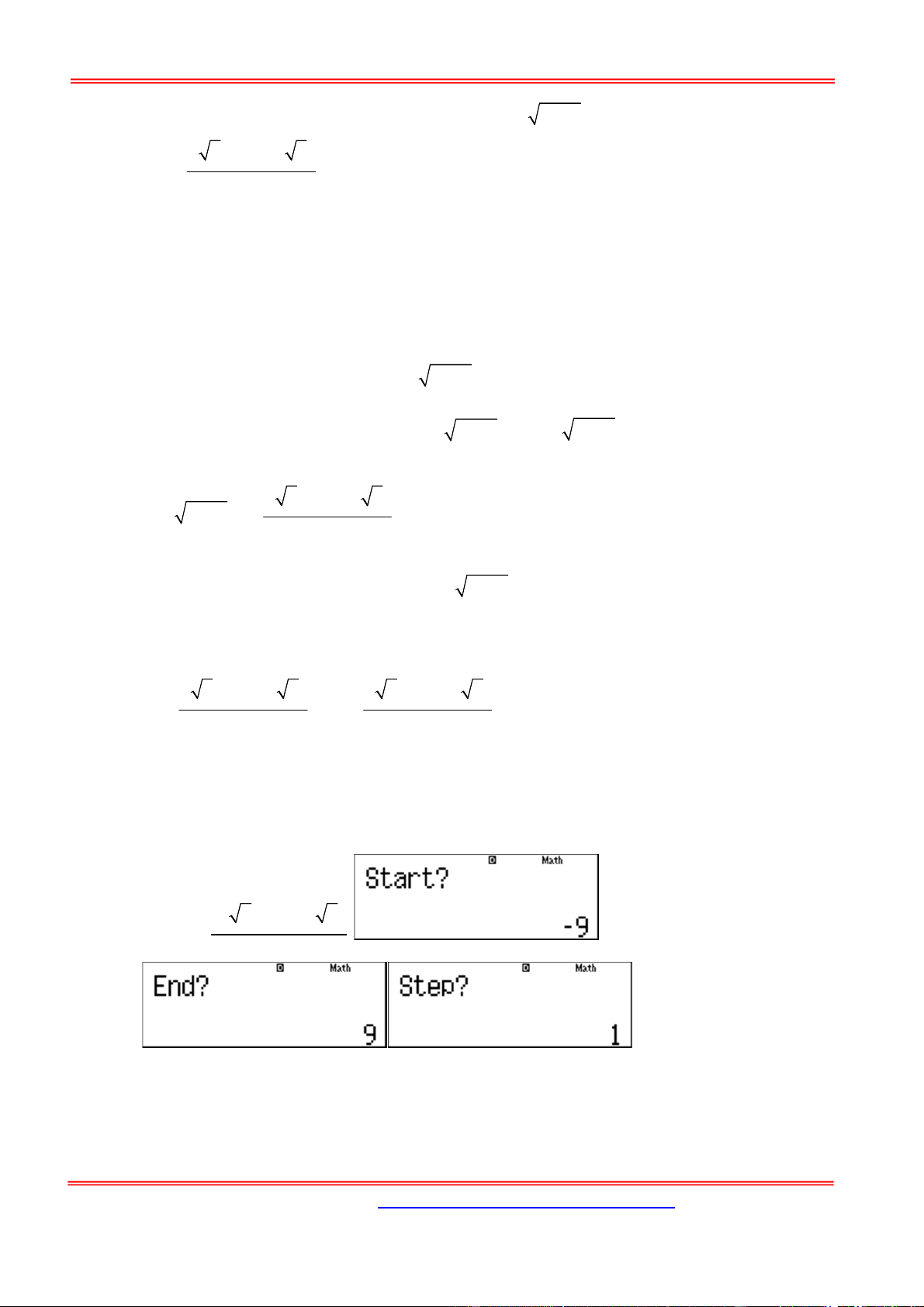
Quan sát bảng giá trị ta thấy giá trị nhỏ nhất của F(x) là 25 xảy ra khi x =0,4 Chọn C. 1
Câu 20: Khi tính nguyên hàm dx 
người ta đặt t  g  x (một hàm biểu diễn theo 2x   1  x  3 1 3
biến x) thì nguyên hàm trở thành 2dt  . Biết g 4 
, giá trị của g 0  g   1 là: 5 3  6 1 6 2  6 2  3 6 A. . B. . C. . D. . 2 2 2 2 Hướng dẫn giải:
Đối với bài này HS cần pahir nắm được kĩ thuật biến đổi khi tính nguyên hàm. Hs cần phải
dự đoán phép đặt ẩn phụ, đầu tiên ta thấy nguyên hàm có thể biến đổi thành: 1 1 dx  dx  
 x   x  3 2x 1 2 1 1  x  2 1 x 1 Do đó ta đặt: 2x  1 dx dx t   dt   2dt  x 1 2x  1 2x 1 2  x  2 1  x  2 1 x  1 x  1 1 Vì vậy suy ra dx  2dt   2x   1  x  3 1
Tuy nhiên đây là lời giải sai, ta có thể thấy khi đặt
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 13
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2x 1 dx dx t   C  dt   2dt  x 1 2x 1 2x 1 2  x  2 1  x  2 1 x 1 x 1
Với C là hằng số, kết quả không thay đổi. Vì vậy chính xác ở đây là: 2x  1 3 t 
 C  g  x . Theo đề g 4  n33n suy ra C=0. x 1 5 2x  1 2  6
Cuối cùng ta được g  x 
vì vậy g 0  g   1  x 1 2 Chọn C.
Chú ý: Bài toán này hoàn toàn có thể dùng MTCT để chọn kết quả, Ta có: 1 1 1 2dt  dx  t  dx   
 x   x  3 2 2 1 1 2x   1  x  3 1 1 1
 g  x  dx  2 2x   1  x  3 1 1 1
Do đó g  x là nguyên hàm của . Suy ra: 2 2x   1  x  3 1 0 0 1 1 1 1
g 0  g 4 
dx  g 0  dx  g 4   2
 x   x  3 2 2 1 1 2x   1  x  3 4 4 1 Và: 1 1 1 1 1 1 g   1  g 4  dx  g   1  dx  g 4   2
 x   x  3 2 2 1 1 2x   1  x  3 4 4 1 Sử dụng MTCT bấm: 0 1 1 1 1 1
dx  g 4  dx  g 4   2
 x   x  3 2 2 1 1 2x   1  x  3 4 4 1 Là kết quả C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 14
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng TÍCH PHÂN NÂNG CAO
A – LÝ THUYẾT CHUNG 1. Định nghĩa
Cho hàm số y  f  x thỏa:
+ Liên tục trên đoạn  ; a b .
+ F  x là nguyên hàm của f  x trên đoạn  ; a b . b
Lúc đó hiệu số F b  F a được gọi là tích phân từ a đến b và kí hiệu f  x dx  F b  F a  a Chú ý:
+ a, b được gọi là 2 cận của tích phân. b + a = b thì
f  x dx  0.  a b a + a > b thì
f  x dx   f  x dx   . a b b b
+ Tích phân không phụ thuộc và biến số, tức là
f  x dx  f t  dt  F b  F a   . a a 2. Tính chất b c b +
f  x dx  f  x dx  f  x dx, a  c  b    . a a c b b +
kf  x dx  k f  x dx,  
với k là hằng số khác 0. a a b b b +
 f  x  g  x dx  f  x dx  g  x dx      . a a a Chú ý:
Để tính tích phân từ a đến b, ta tiến hành tìm nguyên hàm rồi sau đó thay cận vào theo công thức b
f  x dx  F b  F a  . a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 15
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
B – BÀI TẬP TRẮC NGHIỆM  4 1 Câu 1: Xét tích phân A  dx 
. Bằng cách đặt t  tan ,
x tích phân A được 2 2
3sin x  2cos x  2 0
biến đổi thành tích phân nào sau đây. 1 1 1 1 1 1 1 1 A. dt  . B. dt dt dt 2  . C.  . D.  . t  4 2 t  4 2 t  2 2 t  2 0 0 0 0 Hướng dẫn giải:  2  Ta có: 2 2 2 2
3sin x  2 cos x  2  cos x 3 tan x  2   2   cos x  2 2  x  x    2  x 2   x  2 cos 3 tan 2 2 1 tan cos tan x  4    4 1 Vậy: A  dx 
, lúc này đặt t  tan x và đổi cận ta đc: 2 cos x  2 tan x  4 0  1 dt A  dx  . 2 t  4 0 Chọn A.  x 2 1 1 Câu 2: Đặt t  tan thì I  dx 
được biến đổi thành 2 f t dt 
. Hãy xác định f t  : 2 x 6 0 cos 0 2
A. f t  2 4
 1  2t  t . B. f t  2 4
 1  2t  t . C. f t  2  1  t .
D. f t  2  1  t . Hướng dẫn giải: 2     2 2  1  1  x  1 2 I  . dx  1  tan . dx     2 x 2 x  2 2 x  0 0  cos  cos cos  2  2 2  1 1 dt  . dx  2 x 2 x  cos Đặt t  tan   2 2  
x  0  t  0; x   t  1  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 16
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 1 2 Vậy: I   2
1  t  .2dt  2 2 4
1  2t  t dt  f t  2 4
 1  2t  t 0 0 Chọn B. 1 b c  a b Câu 3: Biết rằng 1 3 x 2 3e dx  e 
e  c a,b, c   
 . Tính T  a   . 0 5 3 2 3 A. T  6. B. T  9. C. T  10. D. T  5. Hướng dẫn giải Chọn C. Đặt 2
t  1 3x  t  1 3x  2tdt  3dx
Đổi cận: + x  0  t  1
+ x  1  t  2 1 2 2 2 2 2 13x t t t t t 2 2 2  3e dx 2 te dt 2 te  e dt  2 te  e
 2 2e  e  e  e  2e .    0 1  1 1   1 1    a  10  
 T  10 nên câu C đúng. b  c  0  5 2 x  2 1 Câu 4: Biết I 
dx  4  a ln 2  b ln 5 
, với a , b là các số nguyên. Tính S  a  . b x 1 A. S  9. B. S  11. C. S  5. D. S  3  . Hướng dẫn giải Chọn B. 5 2 5 2 x  2  1 2 x  2 1 2 x  2  1 Ta có: I  dx  dx  dx    x x x 1 1 2 2 22  x 5 1 2  x  2 1 2 5 5  2x 2x  3  dx  dx  dx  dx     1 2 x x x x 1 2 2 5  5   3    x dx  2  dx       
5ln x  x 2  2x 3ln x  5 1 2 1 2  x   x  a  8
 8 ln 2  3ln 5  4  
 a  b  11. b  3   4 a b Câu 5:
Biết I  x ln 2x   1 dx  ln 3  c, 
trong đó a, b, c là các số nguyên dương và là phân b c 0
số tối giản. Tính S  a  b  . c A. S  60. B. S  70. C. S  72. D. S  68. Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 17
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Chọn B.  2 u d  dx 4 u   ln 2x  1     2x 1
Ta có I  x ln 2x   1 dx  . Đặt    2 dv  d x x x 0  v    2 4 4 2
x ln 2x   4 2 1 x
I  x ln 2x   1 dx   dx   2 2x 1 0 0 0 4 4 2  x 1 1   x 1 1  63  8 ln 9      dx  16 ln 3   x  ln 2x 1  ln 3  3     2 4 4 2x 1   4 4 8 4 0       0 a  63 a 63   ln 3  c 
ln 3  3  b  4  S  70 . b 4 c  3  1 2017 b b Câu 6: Giả sử tích phân .
x ln 2x   1 dx  a  ln 3 
. Với phân số tối giản. Lúc đó c c 0
A. b  c  6057.
B. b  c  6059.
C. b  c  6058.
D. b  c  6056. Hướng dẫn giải Chọn B. 1 1 2017 Ta có I  .
x ln 2x   1 dx  2017 .
x ln 2x   1 dx   . 0 0  2 du  dx u   ln 2x  1     2x 1 Đặt    2 dv  d x x x 1  v     2 8 1 1 2 1 2  x 1    x 1  2  Do đó .
x ln 2x   1 dx   ln 2x   1            dx 2 8 2 8 2x 1 0   0    0  1 2 3  x  x  3  ln 3   ln 3   8 4 8   0 1  3  6051  I  .
x ln 2x  2017 1 dx  2017 ln 3  ln 3.     8  8 0
Khi đó b  c  6059.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 18
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 6  2 3 4 2 4
 x  x  3 2 Câu 7: Tính tích phân dx 
a 3  b  c  4  
. Với a , b , c là các số 4   x  1 8 1
nguyên. Khi đó biểu thức 2 4
a  b  c có giá trị bằng A. 20 . B. 241. C. 196 . D. 48 . Hướng dẫn giải Chọn B. 6  2 6  2 6  2 6  2 2 4 2 2 2 2 2 2 4
 x  x  3  x 1  x  1 Ta có dx  4   dx  4  dx 
dx  I  J  4   4    . 4 x 1 x 1 x  1 1 1   1 1 6  2 2 6  2 Tính 2 I  4  dx  4  x  2 6  2 2  4  . 1 1 6  2 6  2 6  2 1 1 2 2 2 1 2 1 2 2 x 1 Tính  d x  d x J x x  d . x  4   2 x 1 1 2 1 1 1  1 x   2 x   2 x    x 
x  1  t  0 1  1  
Đặt t  x   dt  1 dx  . Khi  . 2  6  2 x  x  x   t  2   2 t   0  u  0 2 dt  Khi đó J   . Đặt t  u  t   2 2 tan d
2 1 tan u du . Khi   . t   22 2 t  2  u  0   4    2  2 4 1 tan u  4 4 2 2 2 Suy ra J  du  du  u     . 2  2 1 tan u 2 2 8 0  0 0 6  2 2 4 2 4
 x  x  3 2 a  b  1  6 Vậy dx  16 3 16   4     . 4   x 1 8 c  1 1  Vậy 2 4
a  b  c  241.  4 x Câu 8: Tích phân
dx  a  b ln 2 
, với a , b là các số thực. Tính 16a  8b 1 cos 2x 0 A. 4. B. 5. C. 2. D. 3. Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 19
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Chọn A u   x du  dx   Đặt  dx   1 . Ta có dv  v  tan x   1 cos 2x    2   1 1   1  1 1  1 1 1 4 I  x tan x 4  tan d x x   ln cos x 4   ln   ln 2  a  ,b   0 2 2 8 2 8 2 2 8 4 8 4 0 0
Do đó, 16a  8b  4 . e 4 2 . a e  . b e  c Câu 9:
Cho biết tích phân I  x   2
2x  ln xdx  với , a ,
b c là các ước nguyên của 4. 4 1
Tổng a  b  c  ? A. 2. B. 4. C. 3. D. 1 Hướng dẫn giải e e e I  x   2 2x  ln x 3
dx  2 x dx  x ln xdx .   1 1 1 e e 1 1 3 4 2 x dx  x   4 e    1 2 2 1 1 e e 2 1  e 1  1  1 e e 1 Ta có 2 2 2 2 x ln xdx  x ln x  x dx  e  x      2 1 x 2 2 1 4 1  1    e 2 4 2    I  x  1 e 1 2e e 1 2
2x  ln xdx   4 e   1    2 4 4 1 Chọn A. ln 2 2 x 1 e   1 a Câu 10: Tích phân dx  e   . Tính tích . a b . x e b 0 A. 1. B. 2. C. 6. D. 12. Hướng dẫn giải Chọn B. ln 2 2 x 1  ln 2 ln 2 ln 2 ln 2 e  1 x 1   x x 1 dx  e dx  e dx  e  d x   e x  x   1 x d       e 0 0 0 0 0  x  ln2 ln 2 1  1  1  x  e  e
 2e  e  1  e   
 a  1, b  2  ab  2 . 0 0  2  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 20
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  3 3 2 sin x  3 Câu 11: Biết dx    c  d 3 
với a, b, c, d là các số nguyên. Tính 6 3  1 a b  x  x  3
a  b  c  d .
A. a  b  c  d  28 .
B. a  b  c  d  16 . C. a  b  c  d  14 . D.
a  b  c  d  22 . Hướng dẫn giải Chọn A.    sin x  6 3 3 3
1 x  x sin x 3 I  dx  dx      6 3
1 x  x sin xdx . 6 6 6 3  1  1  x  x  x  x      3 3 3    x    t    3 3
Đặt t  x  dt  dx . Đổi cận  .    x   t     3 3     3 3 3 I    6 3
1 t  t sin tdt     6 3
1 t  t sintdt     6 3
1 x  x sin xdx      3 3 3   3 3 Suy ra 2I    3 2  x sin x 3 dx  I  x sin xdx  .     3 3 3
x (+)  sin x 2
3x (–)  cos x
6x (+)  sin x 6 (–)  cos x 0  sin x  3 2   I   3 3 2
x sin x  3x cos x  6x sin x  6 sin x 3    2  6 3   27 3 3
Suy ra: a  27, b  3  , c  2
 , d  6 . Vậy a  b  c  d  28 . 2 3
Câu 12: Với các số nguyên a, b thỏa mãn 2x   1 ln d x x  a   ln b 
. Tính tổng P  a  b . 2 1 A. P  27 . B. P  28 . C. P  60 . D. P  61 . Hướng dẫn giải Chọn C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 21
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  1 u   ln x  du  dx Đặt  ta có  x dv  2x    1 dx  2
v  x  x  2 2 1 2x   1 ln d x x    2 x  x 2 ln x   2
x  x . dx 1  x 1 1 2 2  x   3  3
 6 ln 2   x   2 1 dx  6 ln 2   x  6 ln 2  4   4    ln 64    1   2    2  2 1
P  a  b  4   64  60 . 2 Câu 13: Biết x  2 x e x  e  4 2 dx  . a e  .
b e  c với a, b, c là các số hữu tỷ. Tính S  a  b  c 0 A. S  2 . B. S  4  . C. S  2  . D. S  4 Hướng dẫn giải 2 2 2 2 2 x 2 x 2 e e x x x x x 1 Ta có I  e
 2x  e  2
dx  e dx  2 . x e dx   2 xe dx    2 x xe dx     2 2 2 0 0 0 0 0 0 4 2 u   x du  dx e 1     I    2 . x
x e  2  2 x e dx x x  0 dv  e dx v  e 2 2 Đặt   0 4 4 e 1     e 2 .
x e  2  2 x e  2 3 2 2   2e  0 0 2 2 2 2  1 3 a  ; c    2
2  S  a  b  c  4 b   2  Chọn D.    b
Câu 14: Cho hàm số f  x  a sin 2x  b cos 2x thỏa mãn f '  2    và adx  3 
. Tính tổng a  b  2  a bằng: A. 3. B. 4. C. 5. D. 8. Hướng dẫn giải Chọn C.
f ' x  2a cos 2x  2bsin 2x    f '
 2  2a  2  a  1    2  b b
adx  dx  3  b 1  3  b  4   a 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 22
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Vậy a  b  1 4  5.   a sin x 2
Câu 15: Có bao nhiêu giá trị của a trong đoạn ; 2   thỏa mãn dx   . 4    1 3cos x 3 0 A. 2 . B. 1. C. 4 . D. 3 . Hướng dẫn giải Chọn B. Đặt 2
t  1 3cos x  t  1 3cos x  2 d t t  3  sin d x . x
Đổi cận: + Với x  0  t  2
+ Với x  a  t  1 3cos a  . A Khi đó a 2 2 sin x 2 2 2 2 dx  dt  t 
2  A   A  1 1 3cos a  1 cos a  0   1 3cos x 3 3 3 3 0 A A      1 3 k  0  a 
 k k   . Do a  ; 2  
 k  2    k      . 2  4  4 2 4 2 k  1  
Bình luận: Khi cho a 
  thì tích phân không xác định vì mẫu thức không xác định 2 
(trong căn bị âm). Vậy đáp án phải là B, nghĩa là chỉ chấp nhận a  . 2 a 2
Câu 16: Có bao nhiêu số a 0;20  sao cho 5
sin x sin 2xdx  .  7 0 A. 20 . B. 19 . C. 9 . D. 10 . Hướng dẫn giải Chọn D a a a 2 a 2 2 Ta có 5 6 6
sin x sin 2xdx  2 sin x cos xdx  2 sin xd sin x 7 7  sin x  sin a  . 0    7 7 7 0 0 0  Do đó 7
sin a  1  sin a  1  a 
 k 2 . Vì a 0;20  nên 2  1 0 
 k 2  20  
 k  10 và k   nên có 10 giá trị của k 2 2  6 n 1
Câu 17: Nếu sin x cos d x x   thì n bằng 64 0 A. 3. B. 4. C. 5. D. 6.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 23
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Hướng dẫn giải Chọn A.  1
Đặt t  sin x  dt  cos d
x x . Đổi cận: khi x  0  t  0; x   t  6 2 1 1 n 1 2 n 1   2 t n 1  1  1
Khi đó: I  t dt   .     . n 1 n 1  2  64 0 0 n 1   1  n 1 Suy ra   
có nghiệm duy nhất n  3 (tính đơn điệu).  2  64 n 1  1 lim dx   1 x n  e
Câu 18: Giá trị của n bằng A. 1  . B. 1. C. . e D. 0. Hướng dẫn giải Chọn D. n 1  1 Ta có: I  dx  1 x  e n Đặt  1 x   d x t e
t  e dx . Đổi cận: Khi n n 1 x n t 1 e ; x n 1 t 1 e           n 1  n 1 1e 1e  n 1  n 1 1  1 1 e  1 e Khi đó: I  dt   dt     
ln t 1  ln t   1 ln n e t t   t  t   e   n   n 1 1 1 n 1 1 1e 1e n  1  1 1 n e     e  1 1 Mà  
khi n   , Do đó, lim I  1 ln  0 n 1 1  n  e  1 e  n e  e    e   1  sin x   
Câu 19: Cho các tích phân I  dx  và J  dx  với   0; 
 , khẳng định sai 1 tan x cosx  sin x  4  0 0 là  cos x A. I  dx  .
B. I  J  ln sin   o c s . cosx  sin x 0
C. I  ln 1 tan  .
D. I  J   . Hướng dẫn giải Chọn C
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 24
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 1 cos Ta có   nên A đúng. 1 tan  sin 
cos  sin  1 cos
 cos x  sin x
 d cos x  sin x I  J  dx 
 ln cos x  sin x   ln cos  sin  B đúng 0   cos x  sin x cos x  sin x 0 0 
I  J  dx  x    D đúng. 0  0 a b 2017 1 x 1 x Câu 20: Giả sử x 1 x dx    C 
với a, b là các số nguyên dương. Tính a b
2a  b bằng: A. 2017 . B. 2018 . C. 2019 . D. 2020 . Hướng dẫn giải Ta có: 2018 2019 1 x 1 x
x 1 x2017 dx   x 1 
1 1 x2017 dx   
1 x2017 1 x2018      dx     C 2018 2019
Vậy a  2019, b  2018  2a  b  2020 . Chọn D. 2 2001 x
Câu 21: Tích phân I  dx  có giá trị là 2 1002 (1 x ) 1 1 1 1 1 A. . B. . C. . D. . 1001 2002.2 1001 2001.2 1002 2001.2 1002 2002.2 Hướng dẫn giải 2 2004 2 x 1 1 2 I  .dx  .dx  t  1  dt   dx . 3 2 10 02  . Đặt 1002 x (1 x ) 2 3 x x 1 1 3  1  x  1  2   x  b x e 2 x 1  
Câu 22: Cho tích phân C 
dx trong đó a là nghiệm của phương trình 2 2 , b là một  x a e  3 2 số dương và 2
b  a . Gọi A 
x dx . Tìm chữ số hàng đơn vị của b sao cho C  3A.  1 A. 3. B. 2. C. 4. D. 5 Hướng dẫn giải 2 Giải phương trình x 1
2   2  x  0  a  0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 25
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Tính tích phân C. Đặt: x 2   3   x t e t e  3  2  x tdt e dx b e 3 b 2t e 3 b e 3 C   dt = 2  2  2 b dt t e  3  4  t 2 2 2 7
Tính tích phân A ta có A  3 Theo giả thiết b 7 b 11 b 109 109
C  3A  2 e  3  4  3.  e  3   e   b  ln  3,305053521 3 2 4 4 Chọn A. 2 2 2 1 x . a   b
Câu 23: Biết tích phân dx  
trong đó a, b   . Tính tổng a  b ? 1 2x 8 2  2 A. 0. B. 1. C. 3. D. -1 Hướng dẫn giải 2 2 2 2 2 1 x 0 2 2 2 2 1 x 1 x 2 I  dx  dx  dx  1 x dx     1 2x 1 2x 1 2x 2 2 0 0   2 2   2
Đặt x  sin t  I  . 8 Chọn C. ln 2  1  1 a 5
Câu 24: Biết rằng: x  dx 
ln 2  b ln 2  c ln .   
Trong đó a, b, c là những số nguyên.  2 x e 1  2 3 0
Khi đó S  a  b  c bằng: A. 2 . B. 3 . C. 4 . D. 5 . Hướng dẫn giải Chọn C. ln 2 ln 2 ln 2  1  1 x  dx  d x x  dx      .  2 x e 1  2 x e  1 0 0 0 ln 2 ln 2 2 2 x ln 2 Tính d x x    2 2 0 0 ln 2 1 Tính dx  2 xe 1 0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 26
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng t x x d
Đặt t  2e 1  dt  2e dx  dx 
. Đổi cận: x  ln 2  t  5, x  0  t  3 . t 1 ln 2 5 5 1 dt  1 1  x    t  t   t        x      5 5 d d ln 1 ln ln 4 ln 5 ln 2 ln 3 ln 2 ln 2e 1 t t   3 1  t 1 t  3 0 3 3 . ln 2  1  1 5 2 x  dx  ln 2  ln 2  ln
 a  2, b  1, c  1      2 x e 1  2 3 0
Vậy a  b  c  4 .  2 x 1 2  .cos x a
Câu 25: Trong các số dưới đây, số nào ghi giá trị của dx  , , a b   . Khi đó . a b bằng 1 2x b   2 1 A. . B. 0. C. 2. D. 1 2 Hướng dẫn giải     2 x 1  2 x 2 2 x cosx 2 cos x 2 cos x Ta có: dx  dx  dx  x   1   1 2  1 2x .2 1 2x .2 0   0    2  
Đặt x  t ta có x  0 thì t  0, x  thì t 
và dx  dt 2 2     2 x 2 2 cos x 2t cos  t   2 2 cos t cos x dx  d  t     dt   dx     1 2x .2 1 2t .2 1 2t .2 1 2x .2 0   0   0   0   Thay vào (1) có       2 x 1  2 x 2 2 x 2 cosx 2 cos x cos x 1 2  2 cos x 2 cos x sin x 1 dx  dx  dx  dx  dx        1 2x  1 2x .2 1 2x .2 1 2x .2 2 2 2 0   0   0   0 0  2  2 x 1 2  cosx 1 Vậy dx   1 2x 2   2 Chọn C.  2 x 1 2  .cos x
Câu 26: Trong các số dưới đây, số nào ghi giá trị của dx  12x   2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 27
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 A. . B. 0. C. 2. D. 1. 2 Hướng dẫn giải Chọn A.     2 x 1  2 x 2 2 cos x 2 cos x 2x cos x Ta có: dx  dx  dx  x   1   1 2  1 2x .2 1 2x .2 0   0    2  
Đặt x  t ta có x  0 thì t  0, x   thì t 
và dx  dt 2 2     2 x 2 2 cos x 2t cos  t   2 2 cos t cos x dx  d  t     dt   dx     1 2x .2 1 2t .2 1 2t .2 1 2x .2 0   0   0   0   Thay vào (1) có    2 x 1  2 x 2 2 cos x 2 cos x cos x dx  dx  dx    1 2x  1 2x .2 1 2x .2 0   0    2    2 1 2x  2 cos x 2 cos x sin x 1  dx  dx     1 2x .2 2 2 2 0   0 0  2 x 1 2  cosx 1 Vậy dx   1 2x 2   2 1 1
f (x)dx  5  I 
f (1 x)dx  Câu 27: Cho 0 . Tính 0 1 A. 5. B. 10. C. . D. 5 5 Hướng dẫn giải
x  0  t  1
Đặt t  1 x  dt  dx , x 1 t  0 0
I   f (t)dt  5  1 Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 28
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 5 3 5 Câu 28: Giả sử
f  x dx  3  và
f  z  dz  9  . Tổng
f t  dt  f t dt   bằng 0 0 1 3 A. 12. B. 5. C. 6. D. 3. Hướng dẫn giải Chọn C. 1 1 5 5 Ta có
f  x dx  3  f t  dt  3   ;
f  z  dz  9  f t  dt  9   0 0 0 0 5 1 3 5 3 5 9 
f t  dt  f t dt  f t  dt  f t  dt  3  f t  dt  f t  dt       0 0 1 3 1 3 3 5 
f t  dt  f t  dt  6.   1 3 Câu 29: Cho
f (x), g( x) là các hàm số liên tục trên đoạn 2;6 và thỏa mãn 3 6 6
f (x)dx  3; f (x)dx  7; g(x)dx  5   
. Hãy tìm mệnh đề KHÔNG đúng. 2 3 3 6 3
A. [3g(x)  f (x)]dx  8 
B. [3 f (x)  4]dx  5  3 2 6 6 ln e ln e C.
[2f (x) 1]dx  16  D.
[4 f (x)  2g(x)]dx  16  2 3 Hướng dẫn giải 3 6 6
f (x)dx  f (x  
)dx  f(x)dx  10  2 3 2 6 6 6
Ta có: [3g(x)  f (x)]dx  3 g(x)dx 
f (x)dx  15  7  8    nên A đúng 3 3 3 3 3 3
[3 f (x)  4]dx  3 f(x)dx  4 dx  9  4  5    nên B đúng 2 2 2 6 ln e 6 6 6
[2f (x) 1]dx  [2f (x) 1]dx  2 f(x)dx 1 dx  20  4  16     nên C đúng 2 2 2 2 6 ln e 6 6 6
[4f (x)  2g(x)]dx  [4f (x)  2g(x)]dx  4 f(x)dx  2 g(x)dx  28 10  18     3 3 3 3 Nên D sai Chọn D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 29
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng x
Câu 30: Cho hàm số f  x    3
4t  8t dt . Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất 1
của hàm số f  x trên đoạn 0;6. Tính M  m . A. 18 B. 12 C. 16 D. 9 Hướng dẫn giải x x
f  x    3 4 2 2
4t  8t dt  t  4t 
 x  4x  3 , với x  0 . 1 1
f   x  2x  4; f  x  0  x  2 1;6 .
f 0  3; f 2  1; f 6  15 . Suy ra M  15, m  1. Suy ra M  m  16 . Chọn C. 3
Câu 31: Nếu f 0  1, f ' x liên tục và f ' x dx  9 
thì giá trị của f   3 là: 0 A. 3. B. 9. C. 10. D. 5. Hướng dẫn giải 3 3 Ta có: f ' x 
dx  f  x  f 3  f 0  9  f 3 1  9  f 3  10 0 0 Chọn C
Câu 32: Cho f  x và g  x là hai hàm số liên tục trên  1  , 
1 và f  x là hàm số chẵn, g  x là 1 1 hàm số lẻ. Biết
f  x dx  5 
và g  x dx  7 
. Mệnh đề nào dưới đây sai? 0 0 1 1 A.
f  x dx  10  . B.
g  x dx  14  . 1 1 1 1 C.
 f  x  g  x dx  10    . D.
 f  x  g  x dx  10    . 1 1 Hướng dẫn giải
Nhớ 2 tích chất sau để làm trắc nghiệm nhanh: a a
1. Nếu hàm f  x CHẴN thì
f  x dx  2 f  x dx  
2. Nếu hàm f  x LẺ thì a 0 a
f  x dx  0 a
Nếu chứng minh thì như sau:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 30
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 0 1 Đặt A 
f  x dx 
f  x dx  f  x dx    1 1 0    1 A A2 0 A  f x dx
   dt  dx 1    . Đặt t x 1  Đổi cận: 0 1 1  A  f t  . dt  f t  dt  f x dx 1           
(Do tích phân xác định không phụ thuộc 1 0 0 1
vào biến số tích phân) 
f  x dx 
(Do f  x là hàm chẵn  f x  f  x ) 0 1 1 1 Vậy A 
f  x dx  f  x dx  f  x dx  10    (1) 1  0 0 1 0 1 Đặt B 
g  x dx  g  x dx  g  x dx    1 1 0     1 B B2 0 B  g x dx
   dt  dx 1    . Đặt t x 1 Đổi cận: 0 1 1
 B  g t . dt  g t
 dt  g x dx 1           
(Do tích phân xác định không phụ thuộc 1 0 0 1
vào biến số tích phân)   g  x dx 
(Do f  x là hàm chẵn  g x  g  x ) 0 1 1 1 Vậy B 
g  x dx   g  x dx  g  x dx  0    (2) 1  0 0 Từ (1) và (2) Chọn B 6 3
Câu 33: Cho tích phân
f  x dx  20 
. Tính tích phân I 
f 2x dx  . 0 0 A. I  40 . B. I  10 . C. I  20 . D. I  5 . Hướng dẫn giải 3 I 
f 2x dx 
Đặt t  2x  dt  2dx Đổi cận: 0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 31
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 6 6 1 1  I 
f t dt 
f  x dx  
(Do tích phân xác định không phụ thuộc vào biến số tích 2 2 0 0 phân ) 1  .20  10 2 Chọn B 6 4
Câu 34: Cho hàm số f  x liên tục trên đoạn [0; 6] thỏa mãn f  x dx  10  và
f  x dx  6  . Tính 0 2 2 6
giá trị của biểu thức P 
f  x dx  f  x dx   . 0 4 A. P  4 .` B. P  16 . C. P  8 . D. P  10 . Hướng dẫn giải 2 6 6 2 6   Ta có: P  f  
x  dx  f  x dx   f  x dx  f  x dx   f  x dx     0 4  0 6  4 6 4 2 6 6 2   
f  x dx   f  x dx  f  x dx   f  x dx  f  x dx  f  xdx        10  6  4 0  6 4  4 0 4 Chọn A   2 2
Câu 35: Cho tích phân I  cos .
x f sin x dx  8 
. Tính tích phân K  sin .
x f cos x dx  . 0 0 A. K  8  . B. K  4 . C. K  8 . D. K  16 . Hướng dẫn giải  2  I  cos .
x f sin x dx  Đặt t 
 x  dt  dx Đổi cận: 2 0   0 2 2         I  cos  t . f sin  t .     
 dt   sin t. f cos x.dt  sin .
x f cos x.dt    (Tích   2    2  0 0 2
phân xác định không phụ thuộc vào biến số tích phân)  K  K  I  8 Chọn C 1 1
Câu 36: Cho hàm số f  x liên tục trên đoạn [0; 1] và có 3
  2 f  x dx  5    . Tính
f  x dx  . 0 0 A. 1  . B. 2. C. 1. D. 2  . Hướng dẫn giải
File Word liên hệ: 0978064165
- Email: dangvietdong.bacgiang.vn@gmail.com
Trang 32
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 1 1 1 1 Ta có: 3
  2 f  x dx  5   
 3dx  2 f  x dx  5  3x  2 f  x dx  5    0 0 0 0 0 1 1  2 
f  x dx  5  3  2  f  x dx  1   0 0 Chọn A 1 1
Câu 37: Cho hai hàm số f  x và g  x liên tục trên đoạn [0; 1], có f  x dx  4 
và g  x dx  2   0 0
. Tính tích phân I   f  x  3g  x dx    . A. 1  0 . B. 10 . C. 2. D. 2  . Hướng dẫn giải 1 1 1
I   f  x  3g  
 x dx 
f  x dx  3 g  x dx  4  32  10    0 0 0 Chọn B
Câu 38: Cho hàm số y  f  x có đạo hàm là f ' x liên tục trên đoạn [0; 1] và f   1  2 . Biết 1 1
f  x dx  1 
, tính tích phân I  .
x f ' x dx  . 0 0 A. I  1. B. I  1  . C. I  3 . D. I  3  . Hướng dẫn giải 1 Ta có: I  . x f '   x dx 0
Đặt u  x  du  dx , dv  f ' x dx Chọn v  f ' x dx  f  x  1 1  I  .
x f  x 1  f  x dx  1. f  
1  0. f 0  f  x dx  2 1  1   0 0 0 Chọn A 5 2 Câu 39: Cho biết
f (x)dx  15 
. Tính giá trị của P  [f (5  3x)  7]dx  1 0 A. P  15 B. P  37 C. P  27 D. P  19 Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 33
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng dt
t  5  3x  dx   3
Để tỉnh P ta đặt x  0  t  5 nên
x  2  t  1 1  5 5 5 dt 1 1  
P  [f (t)  7]( ) 
[f (t)  7]dt  
f (t)dt  7 dt      3 3 3 5 1   1 1  1 1  .15  .7.(6)  19 3 3 Chọn D. 2
Câu 40: Cho y  f  x là hàm số chẵn, có đạo hàm trên đoạn  6  ;6. Biết rằng
f  xdx  8 và 1 3 6
f 2xdx  3 . Tính  I 
f  xdx  1 1  A. I  11. B. I  5. C. I  2. D. I  14. Hướng dẫn giải Chọn D. a 2 2
Vì f  x là hàm số chẵn nên
f  xdx  0 
f  xdx  f  xdx  8     a 1  1 3 3
f 2x dx  f 2xdx  3   1 1 3 Xét tích phân K 
f 2xdx  3 1 du
Đặt u  2x  du  2dx  dx  2
Đổi cận: x  1  u  2; x  3  u  6 . 6 6 6 1 1 K 
f u du 
f  x dx  3  f  xdx  6    2 2 2 2 2 6 6 2 6 Vậy I 
f  xdx  f  xdx  f  xdx  f  x dx  8  6  14.     1  1 1 2 3 Câu 41: Cho f , g là hai hàm liên tục trên 1;  3
thỏa:  f  x  3g  x dx  10    . 1 3 3
2 f  x  g  x dx  6    . Tính
 f  x  g  x dx    . 1 1 A. 8. B. 9. C. 6. D. 7.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 34
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Hướng dẫn giải Chọn C. 3 3 3
Ta có  f  x  3g  x dx  10  f  x dx  3 g  x dx  10      . 1 1 1 3 3 3
Tương tự 2 f  x  g  x dx  6  2 f  x dx  g  x dx  6      . 1 1 1 u   3v  10 u  4 3 3 Xét hệ phương trình    , trong đó u 
f  x dx 
, v  g  x dx  . 2u  v  6 v  2   1 1 3 3 3
Khi đó  f  x  g  x dx  f  x dx  g  x dx  4  2  6      . 1 1 1 1
Câu 42: Cho hàm số f  x 2  ln x 
x 1 . Tính tích phân I 
f ' x dx  . 0 A. I  ln 2 .
B. I  ln 1 2  . C. I  ln 2 D. I  2ln 2 Hướng dẫn giải 1 1 1 Ta có: I  f ' 2 
x dx  f  x  ln x  x  1  ln 1 2 0   0 0 Chọn B
Câu 43: Cho hàm số f  x có đạo hàm liên tục trên đoạn [1; ln3] và thỏa mãn f   2 1  e , ln 3 f ' x 2 dx  9  e 
. Tính I  f ln 3 . 1 A. 2 I  9  2e . B. I  9 . C. I  9  . D. 2 I  2e  9 . Hướng dẫn giải ln 3 ln 3 Ta có: f ' x 2 
dx  f  x
 f ln 3  f   1  9  e (gt) 1 1  f   2 2
ln 3  e  9  e  f ln 3  9 Chọn B
Câu 44: Cho hai hàm số y  f  x và y  g  x có đạo hàm liên tục trên đoạn [0; 1] và thỏa mãn 1 1 1 /
f ' x.g  x dx  1  ,
f  x.g ' x dx  1 
. Tính I   f  x.g  x dx    . 0 0 0 A. I  2  . B. I  0 . C. I  3 . D. I  2 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 35
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Hướng dẫn giải 1 1
I   f  x.g  /  
x dx   f  x.g ' x  f ' x.g  x dx     0 0 1 1 
f  x.g ' x dx  f ' x.g  x dx  11  0   0 0 Chọn B 1 Câu 45: Cho hàm số
y  f  x liên tục trên R, thỏa mãn
f  x dx  1  . Tính 0  4 I   2 tan   
1 . f  tan x dx . 0   A. I  1. B. I  1  . C. I  . D. I   . 4 4 Hướng dẫn giải Đặt t  x  dt   2 tan
1 tan xdx . Đổi cận: 1 1  I 
f t  dt  f  x dx  
(Tích phân xác định không phụ thuộc vào biến số tích phân)  1 0 0 Chọn A  1   1 
Câu 46: Cho hàm số y  f  x liên tục và thỏa mãn f  x  2 f  3x   với x  ; 2   . Tính  x   2 
2 f  x dx  . x 1 2 9 3 9 3 A. . B. . C.  . D.  . 2 2 2 2 Hướng dẫn giải 2 f  x 1 1 dt Đặt A  
dx (1) Đặt t   dt   dx    dx Đổi cận: x 2 x x 2 t 1 2 1  1   1   1  t. f f f 2   2   2    t   t   x   A  dt  dt  dx  2    
(Tích phân xác định không phụ thuộc vào t t 2 2 1 1 2 2 biến số tích phân) (2)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 36
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  1 
f  x  2 f 2 2   2 2  x  3x 9 3 Ta có:  
1  2 2  3A  dx 
dx  3dx  3x     3A   A  x x 1 2 2 1 1 1 2 2 2 2 Chọn B
Câu 47: Cho hàm số y  f  x liên tục trên R và thỏa mãn f  x  f x  2  2 cos 2x . Tính  2 I 
f  x dx  .   2 A. I  1  . B. I  1. C. I  2  . D. I  2 . Hướng dẫn giải  2 I 
f  x dx 
(1) Đặt t  x  dt  dx Đổi cận:   2     2 2 2  I  f  t
 .dt   f  t   dt 
f x dx   
(2) (Tích phân xác định không phụ thuộc      2 2 2 vào biến số tích phân)    2 2 2 (1) + (2)  2I 
 f  x  f x dx  2  2 cos 2xdx     
2 1 cos 2xdx         2 2 2     2 2 2 2 2 2 2 cos xdx  2 cos x dx  2
cos xdx  2 sin x  2 1     1   4              2 2 2 2  I  2 Chọn D        Câu 48: Biết hàm số y  f x    là hàm số chẵn trên đoạn  ;   và  2   2 2      2
f  x  f x 
 sin x  cos x   . Tính I 
f  x dx  .  2  0 1 A. I  0 . B. I  1. C. I  . D. I  1  . 2 Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 37
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  Đặt t 
 x  dt  dx Đổi cận: 2   0 2 2           I  f  t .    dt   f  t dt  f  x dx      
(Tích phân xác định không phụ   2   2   2  0 0 2  2       
thuộc vào biến số tích phân)  f  x     Vì f  x   là hàm số chẵn  2   2  0          f  x  f  x       2   2      2 2 2     Vậy 2I 
f  x  f x 
dx  sin x  cos x dx  cos x  sin x  1  1  2       2     0  0 0  I  1  Chọn D
Câu 49: Cho hàm số y  f  x liên tục trên R, thỏa mãn    2018   x f x
f x  e . Tính 1 I 
f  x dx  . 1  2 e 1 2 e 1 2 e 1 A. I  . B. I  . C. I  0 . D. I  . 2019e 2018e e Hướng dẫn giải 1 I 
f  x dx 
( 1) Đặt t  x  dt  dx Đổi cận: 1  1  1 1  I 
f t dt   f  t   dt 
f x dx   
(2) (Tích phân xác định không phụ thuộc 1 1 1  1
vào biến số tích phân).Ta có:  
1  20182  I  2018I   f  x  2018 f x dx    1 1 2 2 1 1 e 1 e 1  2019 x x I  e dx  e  e     I  1 e e 2019e 1  Chọn A 1 Câu 50: Cho hàm số
f  x thỏa mãn  x  
1 f ' x dx  10  và 2 f  
1  f 0  2 . Tính 0 1 I 
f  x dx  . 0 A. I  8 . B. I  8  . C. I  4 . D. I  4  .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 38
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Hướng dẫn giải 1
A   x   1 f ' 
x dx Đặt u  x 1  du  dx , dv  f ' x dx Chọn v  f  x 0 1 1 1 1
 A   x  
1 . f  x 1  f  x dx  2 f (1)  f (0)  f  x dx  2  f  xdx  10  f  x dx  8      0 0 0 0 0 Chọn B 1
Câu 51: Cho hàm số f  x thỏa f 0  f   1  1. Biết x
e  f  x  f ' x dx  ae  b    . Tính biểu 0 thức 2018 2018 Q  a  b . A. Q  8 . B. Q  6 . C. Q  4 . D. Q  2 . Hướng dẫn giải 1 1 1 x
A  e  f  x x x  
 f ' x dx  e f  x dx  e f ' x dx    0 0 0
  A A 1 2 1 x A  e f x dx 1    0 1 1
Đặt u  f  x  du  f ' x dx , x
dv  e dx Chọn x v  e x  A  e . x f x  e f ' x dx 1      0 0  A2 1 1 Vậy x    x A e f x
 A  A  e f x  .
e f 1  f 0  e 1 2 2       0 0 a  1 2018 2018    a  b  11  2 b  1   Chọn D 2 x
Câu 52: Cho hàm số f  x liên tục trên 0; và thỏa
f t  dt  . x cos x 
 . Tính f 4 . 0 2 3 1
A. f 4  123 . B. f 4  . C. f 4  . D. f 4  . 3 4 4 Hướng dẫn giải
Ta có: F t   f t  dt  F 't   f t  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 39
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 x
Đặt G  x 
f t dt  F   2
x   F 0 0 /
 G  x  F  2
x   x f  2 ' 2 .
x  (Tính chất đạo hàm hợp: f ' u  x  f 'u.u ' x     ) 2 x
Mặt khác, từ gt: G  x 
f t  dt  . x cos x   0
 G ' x   .
x cos x '  x sin x  cos x  x f  2 2 .
x   x sin  x  cos x (1)
Tính f 4  ứng với x  2 1
Thay x  2 vào (1)  4. f 4  2
  sin 2  cos 2  1  f 4  4 Chọn D f  x
Câu 53: Cho hàm số f  x thỏa mãn 2 t .dt  . x cos x 
 . Tính f 4 . 0 1
A. f 4  2 3 .
B. f 4  1  . C. f 4  . D. f   3 4  12 . 2 Hướng dẫn giải f  x f  x t  f  x 3 3  3 2 t dt    
 x cos x   f  x  3 . x cos x    3 3   0 0  f  x 3
 3x cos  x  f 4 3  12 Chọn D
Câu 54: Cho hàm số f  x có đạo hàm liên tục trên đoạn [1, 2] và thỏa mãn f  x  0 khi x 1, 2 . 2 2 f ' x Biết
f ' x dx  10  và dx  ln 2  . Tính f 2 . f x 1   1
A. f 2  1  0 .
B. f 2  20 .
C. f 2  10 .
D. f 2  2  0 . Hướng dẫn giải 2 2 Ta có: f ' x 
dx  f  x  f 2  f   1  10 (gt) 1 1 2 f ' x 2 f 2
dx  ln  f  x  ln  f 2  ln  f   1   ln  ln 2  (gt) f  x       1 f 1 1  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 40
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
 f 2  f   1  10  f    2  20
Vậy ta có hệ:  f 2    2 f     1  10 f   1   Chọn B
Câu 55: Cho hàm số y  f  x có đạo hàm liên tục trên đoạn  1  
;1 , thỏa mãn f  x  0 x  R và
f ' x  2 f  x  0 . Biết f  
1  1, tính f   1 . A. f   2 1 e   . B. f   3 1  e . C. f   4 1  e . D. f   1  3 . Hướng dẫn giải f ' x
Từ gt: f ' x  2 f  x  0  f ' x  2
 f  x   2  f  x f ' x  dx  2
 dx  ln  f  x  2
 x  C  f  x 2 xC  e   f  x   Có f   2  c 0   e
  e  c   f  x 2  x2 1 1 1 2  e
 f   4 1  e Chọn C
Câu 56: Cho hàm số y  f  x có đạo hàm liên tục trên R, nhận giá trị dương trên khoảng 0; và thỏa f  
1  1, f  x  f ' x 3x 1 . Mệnh đề nào đúng?
A. 1  f 5  2 .
B. 4  f 5  5 .
C. 2  f 5  3 .
D. 3  f 5  4 . Hướng dẫn giải 1 f ' x
Từ gt: f  x  f ' x 3x 1   3x 1 f  x f ' x 1 2 2 3x 1  C  dx 
dx  ln  f  x  3x  1  C    f  x 3  e f  x   3x 1 3 2 2 4 4 .2C 4 3 x 1   Vì f   0 3 1  1  e
 1  e  C  
 f  x 3 3  e  f   3
5  e  3, 79 3 Chọn D
Câu 57: Cho hàm số y  f  x có đạo hàm liên tục trên R và f  x  0 khi x  [0; a] ( a  0 ). Biết a dx
f  x. f a  x  1, tính tích phân I   . 1 f x 0   a a a A. I  .
B. I  2a . C. I  . D. I  . 2 3 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 41
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Hướng dẫn giải a dx I  
( 1) Đặt t  a  x  dt  dx Đổi cận: 1 f x 0   0 a dt 1 a 1  I    dt  dx   
(2) (Tích phân xác định không 1 f a  t  f a  t  f a  x a   1 1 0   0  
phụ thuộc vào biến số tích phân) a  1 1 
(1) + (2)  2I     dx
 1 f x 1 f a  x 0       1    1  
2 2        a f a x f x f a x f x a  dx 
dx  dx  a    I 
1 f  x. f a  x  f  x  f a  x
2  f a  x  f x 2 0     0 Chọn A x   
Câu 58: Cho hàm số G  x  t.cos  x  t .dt  . Tính G '  .  2  0             A. G '  1   . B. G '  1   . C. G '  0   . D. G '  2   .  2   2   2   2  Hướng dẫn giải
Cách 1: Ta có: F t   t.cos  x  t  dt  F ' x  t.cos  x  t   x
Đặt G  x  t.cos  x  t  dt  F  x  F 0  0   
 G  x  F  x  F   /
  F  x  F    x  x  x / ' 0 ' ' 0 cos  0  x '  1      G '  1    2  Chọn B x
Cách 2: Ta có G  x  t.cos  x  t  dt 
. Đặt u  t  du  dt , dv  cos  x  t  dx Chọn 0
v   sin  x  t  x x    x x G x  t
 .sin  x  t   sin  x  t  dt  sin  x  t  dt  cos  x  t   cos 0  cos x  1 cos x   0 0 0 0    
 G ' x  sin x  G '  sin  1    2  2 Chọn B
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 42
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 x
Câu 59: Cho hàm số G  x  cos t.dt 
( x  0 ). Tính G ' x . 0
A. G  x 2 '  x .cos x .
B. G ' x  2 .
x cos x . C. G ' x  cos x .
D. G ' x  cos x 1 . Hướng dẫn giải 2 x
Ta có F t  
cos tdt  F 't   cos t 
 G  x  cos tdt  F   2
x   F 0 0 / / /
 G  x  F  x   F    F  x   F   / 2 2   F        2
x   x  2 ' 0 0 2 .F' x    2  2 . x cos x  2 . x cos x Chọn B x
Câu 60: Tìm giá trị lớn nhất của G  x   2t  tdt trên đoạn  1   ;1 . 1 1 5 5 A. . B. 2 . C.  . D. . 6 6 6 Hướng dẫn giải x x 3 2 3 2 3 2  t t  x x  1 1  x x 5 G  x 2  t  t  dt              3 2 3 2    3 2  3 2 6 1 1  G  x 2 '
 x  x  bảng biến thiên: Từ bảng biến thiên Chọn C x
Câu 61: Cho hàm số G  x 2  1  t dt 
. Tính G ' x . 1 x 1 A. . B. 2 1 x . C. . D.  2 x   2 1 x 1 . 2 1 x 2 1 x Hướng dẫn giải
Đặt F t  2 
 t dt  F t  2 1 '  1 t  x x G  x 2 
1 t dt  F  x  F  
1  G ' x  F ' x  F ' 
1  F ' x   2 1 1 x Chọn A
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 43
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng x
Câu 62: Cho hàm số F  x 2  sin t .dt 
( x  0 ). Tính F ' x . 1 sin x 2sin x A. sin x . B. . C. . D. sin x . 2 x x Hướng dẫn giải x
Đặt F t  2  sin 2 t dt  , G  x  sin t dt  F 
 x  F  1 1 x
 G  x  F  x   F    F  x    x   x 2 sin ' ' ' 1 ' '.sin  2 x Chọn B x
Câu 63: Tính đạo hàm của f  x , biết f  x thỏa f t f  x t.e dt  e  . 0 1 1
A. f ' x  x .
B. f  x 2 '  x 1.
C. f ' x  .
D. f ' x  . x 1 x Hướng dẫn giải x Đặt   f t  f t F t  t e  f t
dt  F t    . '  t.e  G  x    t.e
dt  F  x  F 0  0 /         ' ' f x G x F x  e (gt)      . f x f x x e  e       . f x f x x e   e      f  x 1  e
 x f  x f x  f  x f x . ' .e ' .e  1 .
x f ' x  f ' x  f ' x  1 x Chọn D 2
Câu 64: Cho y  f  x là hàm số chẵn, có đạo hàm trên đoạn  6  ; 6. Biết rằng
f  x dx  8  và 1 3 6 f  2
 x dx  3.  Tính f  x d . x  1 1 A. I  11. B. I  5 . C. I  2 . D. I  14 . Hướng dẫn giải 3
Xét tích phân K  f  2  x dx  1 du
Đặt u  2x  du  2d 
x  dx   2
Đổi cận: Khi x  1  u  2
 ; x  3  u  6 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 44
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 6 2 1 1  2 Vậy, K  
f u du 
f  x dx   . Mà K  3 , nên
f  xdx  6  . 2 2 2 6  6 6 2 
Vì f là hàm chẵn trên  6
 ; 6 nên f  x dx 
f  x dx  6   . 2 6  6 2 6 Từ đó suy ra I 
f  x dx 
f  x dx  f  x dx  8  6  14    . 1 1 2 Chọn D. 1 a
Câu 65: Cho hàm số f (x)   . x
b xe . Biết rằng f '(0)  22 và
f (x)dx  5 . Khi đó tổng 3  (x1) 0
a  b bằng? 1  46 26 2  6 146 A. . B. . C. . D. . 13 11 11 13 Hướng dẫn giải 3  a f '(x) x   be (1 x) 4 (x 1) f '(0)  22  3  a b  22  (1) 1 1 1 1 ( )  5 x f x dx  a
dx  b xe dx  5   3  (x1) 0 0 0 a   b  5 (2) 4 108 38
Giải hệ (1) và (2) ta được: a  , b  . 13 13 Chọn D. 3 Câu 66: Cho f , g là hai hàm liên tục trên 1;  3
thỏa:  f  x  3g  x dx  10    . 1 3 3
2 f  x  g  x dx  6    . Tính
 f  x  g  x dx    . 1 1 A. 8. B. 9. C. 6. D. 7. Hướng dẫn giải 3 3 3 + Ta có  f  x  
 3g  x dx  10 
f  x dx  3 g  x dx  10    . 1 1 1 3 3 3 + Tương tự
2 f  x  g  x dx  6  2 f  x dx  g  x dx  6      . 1 1 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 45
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng u   3v  10 u  4 3 3
+ Xét hệ phương trình    , trong đó u 
f  x dx 
, v  g  x dx  . 2u  v  6 v  2   1 1 3 3 3 + Khi đó
 f  x  g  x dx  f  x dx  g  x dx  4  2  6      . 1 1 1  5  1 0  . a 102  a     2   40 1 5
Nên ta có hệ phương trình sau:      P  2 : y   x  2 5 5 40 2  b b      2   2 19  10  1 5   8  
Ta có thể tích của bê tông là: 2 2 3 2 V  5.2  x  dx  
x  2 dx  40m        0 0   40 2   361   .  2
Câu 67: Cho I  cosn xdx , , n 
. Khẳng định nào sau đây đúng?  n   2 n 0 n  1 n  2 n  1 A. I  I . B. I  I . C. I  I .
D. I  2I n n 1 n  n n 2 n  n n 2 n  n n 2  Hướng dẫn giải  2  Với I  ; I  cosxdx  1 .  0 1 2 0 n 1  n 2  Đặt u  cos
x  du  n   1 cos x.sin xdx .
dv  cos xdx Chọn v  sin x .   2  2 Suy ra n n 1  2 cos xdx  cos
x.sin x  n    n 2  2 1 cos x.sin xdx  0 0 0    2 2 2 n  n 2 1 cos    x.   2
1  cos x dx   n 2 1 cos    .      1 cosn n x dx n x.dx .  0 0 0   2 2 n  n 1 Do đó n 2 cos x.dx  cos  x.dx .   n 0 0 Chọn C. 1 1 1
Câu 68: Rút gọn biểu thức: 0 1 2 n * T  C 
C  C  ... 
C , n   . n 2 n 3 n n 1 n
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 46
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2n 2n 1 n 1 2  1 A. T  . B. 1 2n T   . C. T  . D. T  n 1 n 1 n 1 Hướng dẫn giải Ta có 1 1 1 1 1 1 0 1 T  C  C  ... n 
C . Nhận thấy các số ; ; ;...;
thay đổi ta nghĩ ngay đến n 2 n n 1 n 1 2 3 n  1 n 1 biểu thức n 1 x dx x    c  . n 1 n
Ở đây ta sẽ có lời giải như sau:   x 0 1 2 2 3 3 1
 C  xC  x C  x C  ... n n  x C . n n n n n 1 1 n
Khi đó ta suy ra 1 x dx    0 1 2 2 3 3
C  xC  x C  x C  ... n n  x C dx n n n n n  0 0 2 3 n 1 1  n 1  x x x  1   x   1 0 1 3 1  C x  C  C  ... n  C   n 1 0 n 2 n 3 n n 1 n 0   n 1 2  1 1 1 1 0 1 2   C  C  C  ... n  C . n  1 n 2 n 3 n n  1 n Chọn D. a  3 
Câu 69: Nếu a là một số thỏa mãn các điều kiện sau: a  ; 2  và cos 
x  a dx  sin a thì: 2 2    0
A. a   . B. a   .
C. a  2  . D. a  2 . Hướng dẫn giải: a a cos   2
x  a dx  sin  2
x  a   sin a  sin  2 a  a  2
 sin a  sin a 0 0 2 a  2a a a a  2 cos .sin  2sin .cos   1 2 2 2 2  3  a  3  a Vì a  ;  nên  ;  sin  0 , vậy: 2 2      2  4 4  2 2 2 a  2a a a  a a   1  cos  cos  cos  cos  0 2 2 2 2 2 2  a  a  a  a sin  0  k 1 2 2     a  a a 2 2  2sin .sin  0    
k,l  . 2 2 2 2  a  a sin  0  l 2  2    2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 47
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  3 
Vì k   nên (1) không thỏa mãn với mọi a  ; 
,hoặc thay 4 vào đáp án (1) ta thấy 2 2    đều không thỏa.  3 
Đối với (2). Vì a  ; 
nên Chọn l=1 lúc đó a  2 . 2 2    Chọn D. e k
Câu 70: Gọi S là tập hợp tất cả các số nguyên dương k thỏa mãn điều kiện ln dx  e  2  . Khi đó: x 1 A. S    1 . B. S    2 .
C. S  1,  2 D. S   . Hướng dẫn giải: e k ln dx  x 1
Dùng phương pháp tích phân từng phần  k 1 u   ln
 ln k  ln x  du   dx  x x
dv  dx  v  x  e e k k  I  x ln  dx  e ln
 ln k  e   1  x e 1 1 e k k
Vậy ln dx  e  2  e ln
 ln k  e   1  e  2  x e 1
 eln k   1  ln k  1   e  
1 ln k  e 1  ln k  1
 k  e mà k là số nguyên dương nên Chọn k 1;  2 . Chọn C. 3 5 4 3 4
f  xdx  
f t dt  
f udu  3 5 Câu 71: Biết 0 và 0 . Tính 3 . 8 14 17 16 A. . B. . C.  . D.  . 15 15 15 15 Hướng dẫn giải: 4 3 4
f u du  f u du  f u du    . 0 0 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 48
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 3 3 5 4 4 3 Mà
f udu  f  xdx    và
f udu  f t dt    3 5 0 0 0 0 4 4 3 5 3 5 16 Nên:  
f udu  f u du       5 3 5 3 15 3 3 Chọn D.
Chú ý: tích phân không phụ thuộc vào biến số. 1 2 x 1 2 x dx  a  I  dx  1 x  e 1 x  e Câu 72: Biết 0 . Tính giá trị của 0 . 1 1 A. I   . a
B. I  1  a. C. I   . a
D. I  1  a. 2 3 Hướng dẫn giải: 1 2 1 2 1 x x Sử dụng phân tích 2 dx  dx  x dx    . 1  x  e 1 x  e 0 0 0
Hoặc máy tính cầm tay để kiểm tra kết quả. Chọn C.  2 I  sinn xdx n  Câu 73: Đặt 0 . Khi đó: A. I  I . B. I  I . C. I  I . D. I  I . n 1  n n 1  n n 1  n n 1  n Hướng dẫn giải:   Khi 0  x 
thì 0  sin x  1 . Do đó với 0  x  Ta có: 2 2   2 2 n 1  n n 1 sin x sin x I sin    
xdx  I  sinn xdx I  I . n n   , tức là: n 1  n 0 0 Chọn A. 1 1 n n 2 I  x  x dx J  x  x dx n   2 1  n   2 1  Câu 74: Cho 0 và 0 . Xét các câu: 1 (1) I  với mọi n. n 2n   1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 49
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 (2) J  với mọi n. n 2n   1 1 (3) I  J  với mọi n. n n 2n   1 A. (1) đúng. B. (1) và (2) đúng.
C. Tất cả đều sai. D. cả (1) và (3) đúng. Hướng dẫn giải:
Chỉ (1) và (3) đúng. Khẳng định (2) sai.   2 2 n
Ta đặt x  cost để tính J sin t t tdx     t tdt n   2 1 cos  2n 1 cos sin .cos  . 0 0   2 2n2 2 n sin 1 2 1  sin
td sin t     . 2n  2 2 n 1 0   0
Như vậy khẳng định (2) sai. Ngoài ra, để thấy rằng với mọi x 0;  1 1 2
x  x nên suy ra với mọi n ta có I  J  . n n 2n   1
Vậy: (1) và (3) cùng đúng. Chọn D. 1 dx
Câu 75: Tìm số nguyên dương k nhỏ nhất, thỏa mãn  0  . 2x  k 0 A. k  3. B. k  4 . C. k  1 . D. k  2 . Hướng dẫn giải: 1 * dx x    , x  0; 
1 , 2x  k  0 do đó:  0  , x    *. 2x  k 0
Suy ra số nguyên dương k nhỏ nhất thỏa mãn ycbt là k=1 Chọn C.
Câu 76: Cho f  x, g  x là các hàm liên tục trên [a; b]. b b b
(1) Với mọi số thực y, ta có: 2 2 y
f  xdx  y f  x g  x 2 2 .
dx  g  xdx  0    . a a a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 50
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 b b b  
(2)  f  x g  x 2 2 dx   f  x 2 2 .
dx . g  xdx    .  a  a a
Trong hai khẳng định trên:
A. Chỉ có (1) đúng.
B. Chỉ có (2) đúng.
C. Cả hai khẳng định đều đúng.
D. Cả hai khẳng định đều sai. Hướng dẫn giải:
Với mọi số thực y ta có:        2 0 . y f x g x    2 2
 y f  x  y f  x g  x 2 . 2 . .
 g  x từ đó suy ra (1) đúng: b b b 2 2 y f x dx  y f x  x 2 ( ) 2 ( ).g
dx  g (x)dx  0    a a a
Vì vế trái của Bất đẳng thức trên là tam thức bậc hai đối với y, nên theo định thức về dấu
của tam thức bậc hai, Ta có: 2 b b b   2 2
 '   f (x).g(x)dx   f (x)d .
x g (x)dx  0     a  a a 2 b b b   2 2
  f (x).g(x)dx   f (x)d . x g (x)dx    ((2) đúng).  a  a a Chọn C.
Câu 77: Cho f  x, g  x là các hàm liên tục trên [a; b]. g  x
f  x  0, x
 a;b và m   M , x
  a;b. f  x
Căn cứ vào giả thiết đó, một học sinh lập luận:
(1) Ta có bất đẳng thức  g  x  g  x  2 0  
 m  M 
. f  x, x   ; a b. *  f x  f  x    
(2) Biến đổi, (*) trở thành 2  g
x  M  m f  x g  x 2 0 ( ) . .  M . .
m f (x), x
 a;b. b b b (3) suy ra 2 g  x 2
dx  M .mx f  xdx  M  m f  x.g  xdx    . a a a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 51
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Lập luận trên: A. Đúng hoàn toàn. B. Sai từ (1). C. Sai từ (2). D. Sai từ (3). Hướng dẫn giải:
Lập luận đúng hoàn toàn. Bất đẳng thức sau cùng được gọi là bất đẳng thức Diza Chọn A.
Câu 78: Cho hai hàm f  x, g  x cùng đồng biến và liên tục trên [a; b]. Với a  b . Khi đó, xét khẳng định sau đây: b b b (1) x
 a;b . Ta có: f adx  f  xdx  f bdx    . a a a b (2)
f  xdx  f b  . a 1 b
(3) Tồn tại x  a;b sao cho f  x  f x dx 0    0    . b  a a
Các khẳng định đúng trong 3 khẳng định trên là: A. Chỉ (1) và (2). B. Chỉ (2) và (3). C. Chỉ (1) và (3).
D. Cả (1), (2) và (3). Hướng dẫn giải:
Chỉ (1) và (3) đúng. Khẳng định (2) sai:
Do tính đồng biến nên a
  x  b ta có f a  f  x  f b , tức là: b b b
f adx  f  xdx  f bdx    vậy (1) đúng a a a b
Suy ra: b  a. f a 
f (x)dx  b  a. f b  a
Do đó f  x liên tục trên [a;b] nên tồn tại x  a;b sao cho: 0   1 b f  x  f x dx 0     . Vậy (3) đúng. b  a a Chọn C.  f
  x khi f  x  g  x 
max  f  x, g  x    g
  x khi g  x  f  x
Câu 79: Ta định nghĩa:  .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 52
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Cho   2
f x  x và g  x  3x  2 . 2
Như thế max  f (x), g(x)dx  bằng: 0 2 1 2 A. 2 x dx  . B. 2
x dx  3x  2dx   . 0 0 1 2 C. 3x  2dx  . D. 15. 0 Hướng dẫn giải:
Hoành độ giao điểm của hai đường thẳng là x  1; x  2 Xét 2
x  3x  2 và vẽ Bảng xét dấu để xem trên đoạn nào thì   2 f x  x và
g  x  3x  2 hàm có Giá trị lớn hơn. x 0 1 2 2 x  3x  2 + 0 − 0 2 1 2
Do đó max  f  x, g  x 2 d
 x  x dx  3x  2dx      0 0 1 Chọn B.  2 cos x  2 cos x dx  m  I  dx  1  3x 1  3x
Câu 80: Biết  . Tính giá trị của  .   A.   . m B.  . m C.   . m D.  . m 4 4 Hướng dẫn giải:  2  2 cos x cos x  Sử dụng phân tích: 2 dx  dx  cos . x dx      1  3x 1  3x     (sử dụng MTCT để tính 2 cos . x dx    )   2 cos x Do đó: I 
dx    m  . 1  3x  Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 53
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1 dx
Câu 81: Cho I  , 
với m > 0. Tìm các giá trị của tham số m để I  1. 2x  m 0 1 1 1 1 A. 0  m  . B. m  . C.  m  . D. m  0 . 4 4 8 4 Hướng dẫn giải:
Tính tích phân theo tham số m bằng cách đặt t 
2x  m , sau đó tìm m từ Bắt phương trình I  1. Chọn A. m
Câu 82: Cho m là một số dương và
 4x ln 4  2x I
ln 2dx . Tìm m khi I  12 . 0 A. m  4 . B. m  3 . C. m  1. D. m  2 . Hướng dẫn giải: m m
Tính tích phân theo tham số m ta được:
 4x ln 4  2x I
ln 2dx 4x 2x  4m 2m     , 0 0
sau đó tìm m từ phương trình I =12. Chọn D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 54
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
ỨNG DỤNG TÍCH PHÂN NÂNG CAO
A – LÝ THUYẾT CHUNG
1. Diện tích hình phẳng
 y  f (x) 1 
 y  f (x)
Nếu có hình phẳng giới hạn bởi các đường 2  . x  a  x  b 
(Trong đó f (x), f (x) liên tục trên đoạn [a;b]), 1 2 b
thì diện tích S được tính theo công thức S 
f (x)  f (x) dx 1 2  . a
2. Thể tích khối tròn xoay
 y  f  x O  x
Quay quanh trục Ox: Cho hình phẳng giới giới hạn bởi các đường  . x  a  x  b 
(Trong đó f  x liên tục trên đoạn [a;b]), quay quanh trục Ox, ta được khối tròn xoay. b
Thể tích V của khối tròn xoay được tính theo công thức V   f x dx . x  2 ( ) x  a
x  f  y O  y
Quay quanh trục Oy: Cho hình phẳng giới hạn bởi các đường x  a  x  b 
(Trong đó f  y liên tục trên đoạn [a;b]), quay quanh trục Oy, ta được khối tròn xoay. b
Thể tích V của khối tròn xoay được tính theo công thức V   f dx . y  2 (y) y  a
B – BÀI TẬP TRẮC NGHIỆM Câu 1:
Cho hàm số y  f  x liên tục trên đoạn  ;
a b . Gọi D là diện tích hình phẳng giới hạn bởi
đồ thị C  : y  f  x , trục hoành, hai đường thẳng x  a , x  b (như hình vẽ dưới đây).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 55
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Giả sử S là diện tích hình phẳng D . Chọn công thức đúng trong các phương án A, B, C, D D cho dưới đây? 0 b 0 b A. S  f x x  f x x
S   f x dx  f x dx D  d  d   . B. D       . a 0 a 0 0 b 0 b C. S  f x x  f x x
S   f x dx  f x dx D  d  d   . D. D       . a 0 a 0 Hướng dẫn giải: Chọn B.
+ Nhìn đồ thị ta thấy:
Đồ thị (C) cắt trục hoành tại O 0;0 Trên đoạn  ;
a 0 , đồ thị (C) ở dưới trục hoành nên f  x   f  x
Trên đoạn 0;b, đồ thị C  ở trên trục hoành nên f  x  f  x b 0 b 0 b + Do đó: S  f x x  f x x  f x x   f x x  f x x D   d   d   d  d  d      a a 0 a 0 1 Câu 2:
Diện tích hình phẳng giới hạn bởi đồ thị C  của hàm số y   2
x  4x  3 và hai tiếp 2
tuyến của C  xuất phát từ M 3; 2   là 8 5 13 11 A. . B. . C. . D. . 3 3 3 3 Hướng dẫn giải: Chọn A 1 Ta có y 
2x  4  x  2 . 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 56
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 1
Gọi  x ; y là tọa độ tiếp điểm. Khi đó, y   2
x  4x  3 và y x  x  2 . 0  0 0 0  0 0  2 0
Phương trình của tiếp tuyến của C  tại điểm có tọa độ  x ; y là 0 0  1
y   x  2 x  x    2 x  4x  3 0 0 0 0  2
Vì tiếp tuyến đi qua điểm M 3; 2   nên 1
x  1  y  x 1 2
   x  23  x    2
x  4x  3  0 0 0 0  0  2
x  5  y  3x 11  0
Diện tích hình phẳng cần tìm 3  1   
S    x  4x  3 5 1 8 2  x   1 dx      2
x  4x  3  3x   11 dx  1 3 2 2      3 Câu 3:
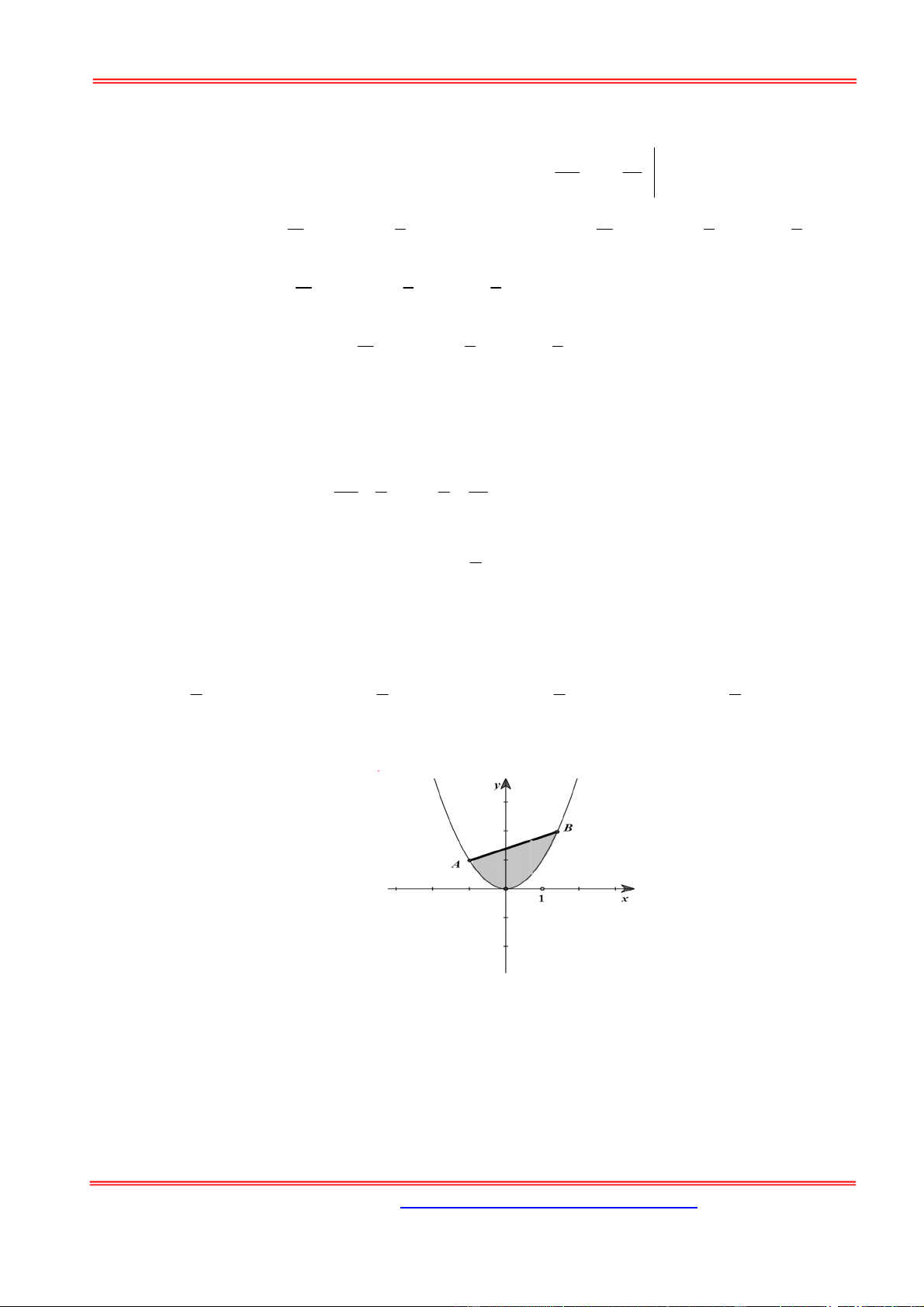
Gọi D là miền được giới hạn bởi các đường 2 y  3
 x 10, y  1, y  x và D nằm ngoài parabol 2
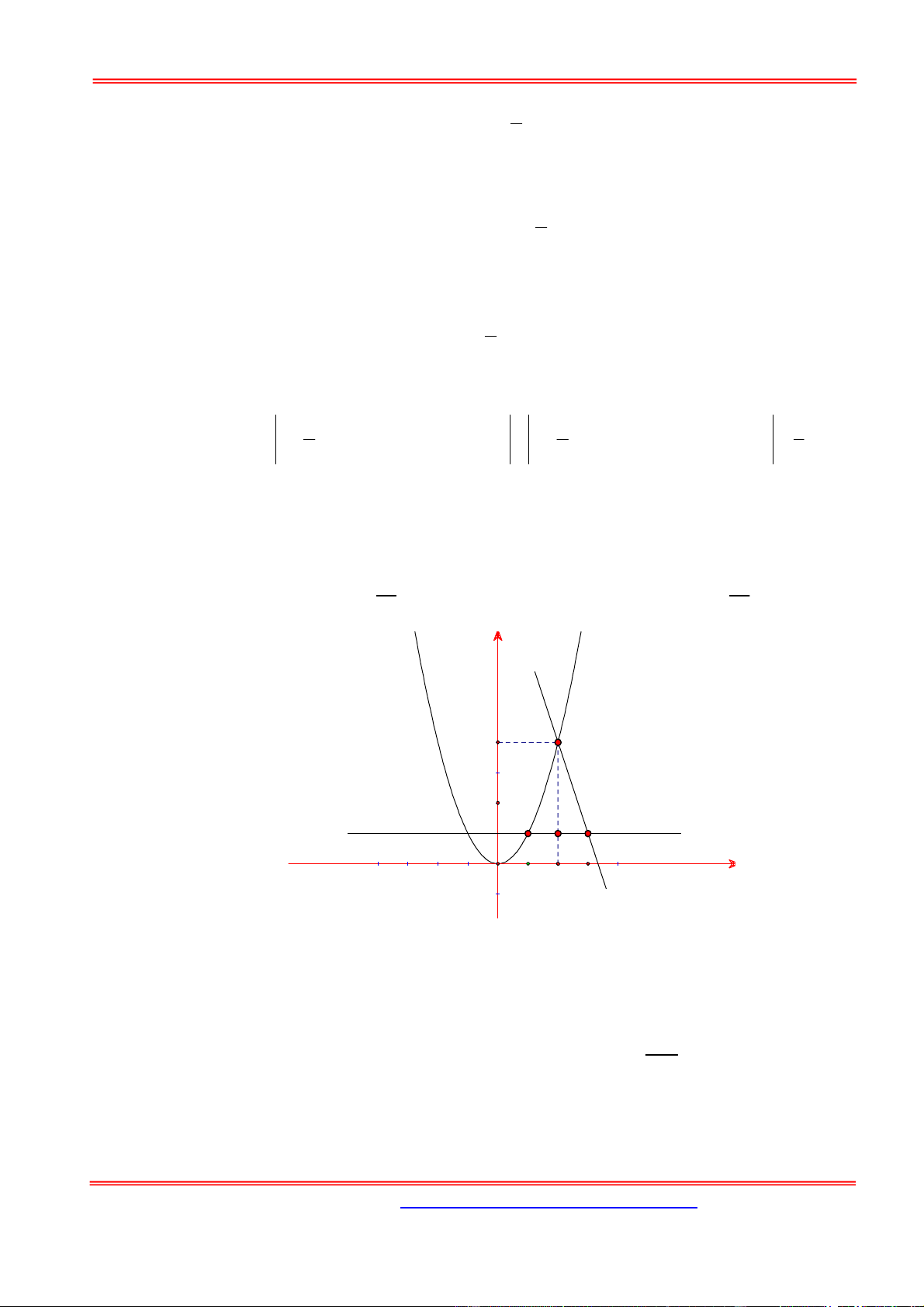
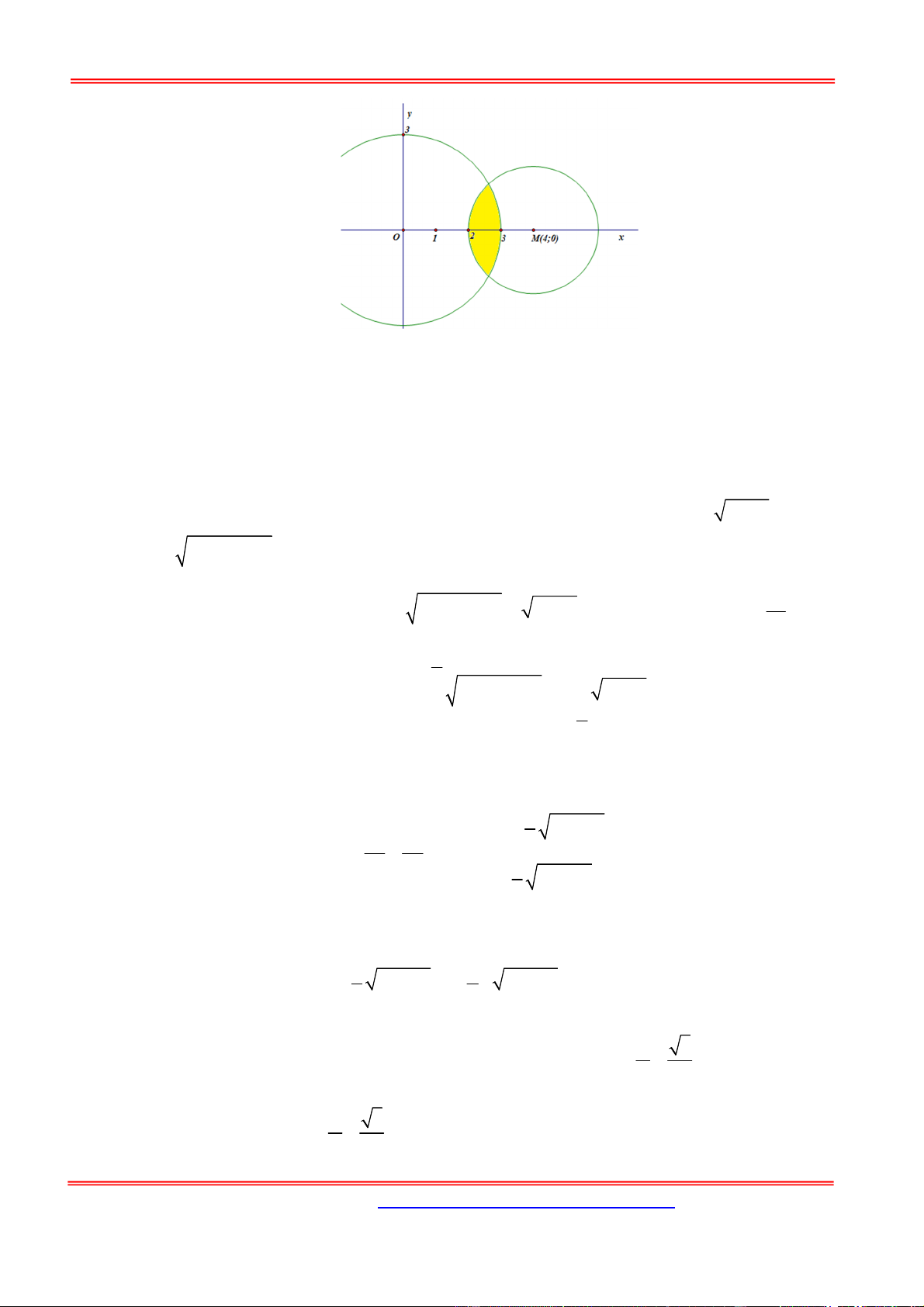
y  x . Khi cho D quay xung quanh trục Ox, ta nhận được vaath thể tròn xoay có thể tích là: 56 25 A. 11. B. . C. 12 . D. . 5 3 y 4 B 2 A C y = 1 H x 2 3 O 1 Hướng dẫn giải:
Gọi V ;V lần lượt là thể tích tam giác cong ABH và tam giác HBC tạo nên khi xoay quanh 1 2
trục Ox, phần diện tích được biểu diễn qua đồ thị sau: 2 3 2 56 Vậy 2 2 2 2
V  V  V   (x ) 1 dx     ( 3  x 10)  1 d  x  (dvtt) 1 2         5 1 2 Chọn B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 57
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Câu 4:
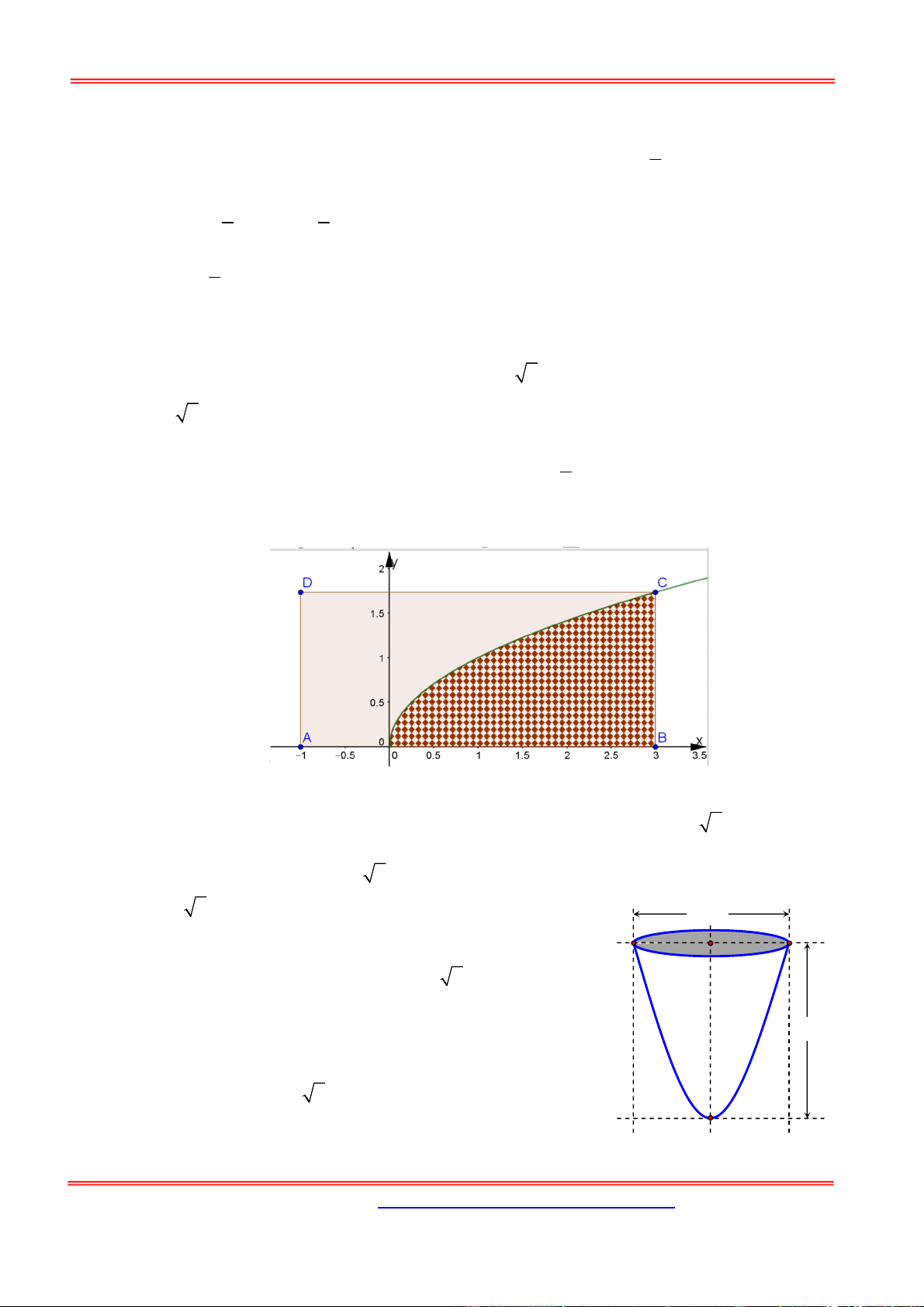
Gọi d là tiếp tuyến của đồ thị hàm số y  ln x tại giao điểm của đồ thị đó với trục Ox. Diện
tích của hình tam giác tạo bởi hai trục tọa độ và đường thẳng d được xác định bởi tích phân: 1 1 ln x 1 1 A. ln xdx  . B. dx  . C.  x   1 dx  . D.  x   1 dx  x 0 0 0 0 Hướng dẫn giải:
Tọa độ giao điểm của đồ thị y=lnx với trục Ox là nghiệm của hệ phương trình:  y  ln x x  1    y  0 y  0   1
Ta có: y '  ln x  , y  1  1. x
Vậy phương trình của tiếp tuyến d là: y  0   1 x  
1  y  x 1. 1 1 1 2  x  1
Diện tích phải tìm: S 
x 1dx  1 xdx  x       . 2 2 0 0   0 Chọn D. Câu 5:
1) cho y  f (x) và y  f (x) là hai hàm số liên tục trên đoạn [a;b]. Giả sử:  và  , với 1 1 2 2
a      b , là các nghiệm của phương trình f (x)  f (x)  0 . Khi đó diện tích của hình 1 2
phẳng giới hạn bởi 2 đường thẳng và đồ thi của hàm số được cho bởi công thức   b S 
f (x)  f (x) dx 
f (x)  f (x) dx 
f (x)  f (x) d . x 1 2 1 2 1 2    a  
(2) Cũng với giải thiết như (1), nhưng:   b S 
 f (x)  f (x) dx 
f (x)  f (x) dx 
f (x)  f (x)dx . 1 2   1 2  1 2    a  
A. (1) đúng nhưng (2) sai.
B. (2) đúng nhưng (1) sai.
C. Cả (1) và (2) đều đúng.
D. Cả (1) và (2) đều sai. Hướng dẫn giải:
Chú ý rằng với mọi x ;   , f (x)  f (x)  0 và f (x) và f (x) đều liên tục trên khoảng 1 2 1 2
;   , nên f (x)  f (x) giữ nguyên dấu. 1 2
Nếu f (x)  f (x)  0 thì ta có: 1 2   
f (x)  f (x)dx 
f (x)  f (x) dx 
f (x)  f (x) dx 1 2  1 2   1 2       
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 58
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Nếu f (x)  f (x)  0 thì ta có: 1 2   
f (x)  f (x) dx 
f (x)  f (x) dx 
f (x)  f (x) dx 1 2  2 1   1 2       
Vậy trong mọi trường hợp ta đều có:  
f (x)  f (x) dx 
f (x)  f (x) dx 1 2  1 2     
Tương tự như thế đối với 2 tích phân còn lại. vì vậy, hai công thức (1) và (2) là như nhau: Chọn C. Câu 6:
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 x   2 x y e
e , trục Ox và đường a
thẳng x  a với a  ln 2 . Kết quả giới hạn lim S là: a a A. 1. B. 2. C. 3. D. 4 Hướng dẫn giải: ln 2 x x 1 Ta có S  e  e dx  e  e  a   2 2  2 a 2 a 2 2 a Suy ra lim S  2 , a a Chọn B. Câu 7:
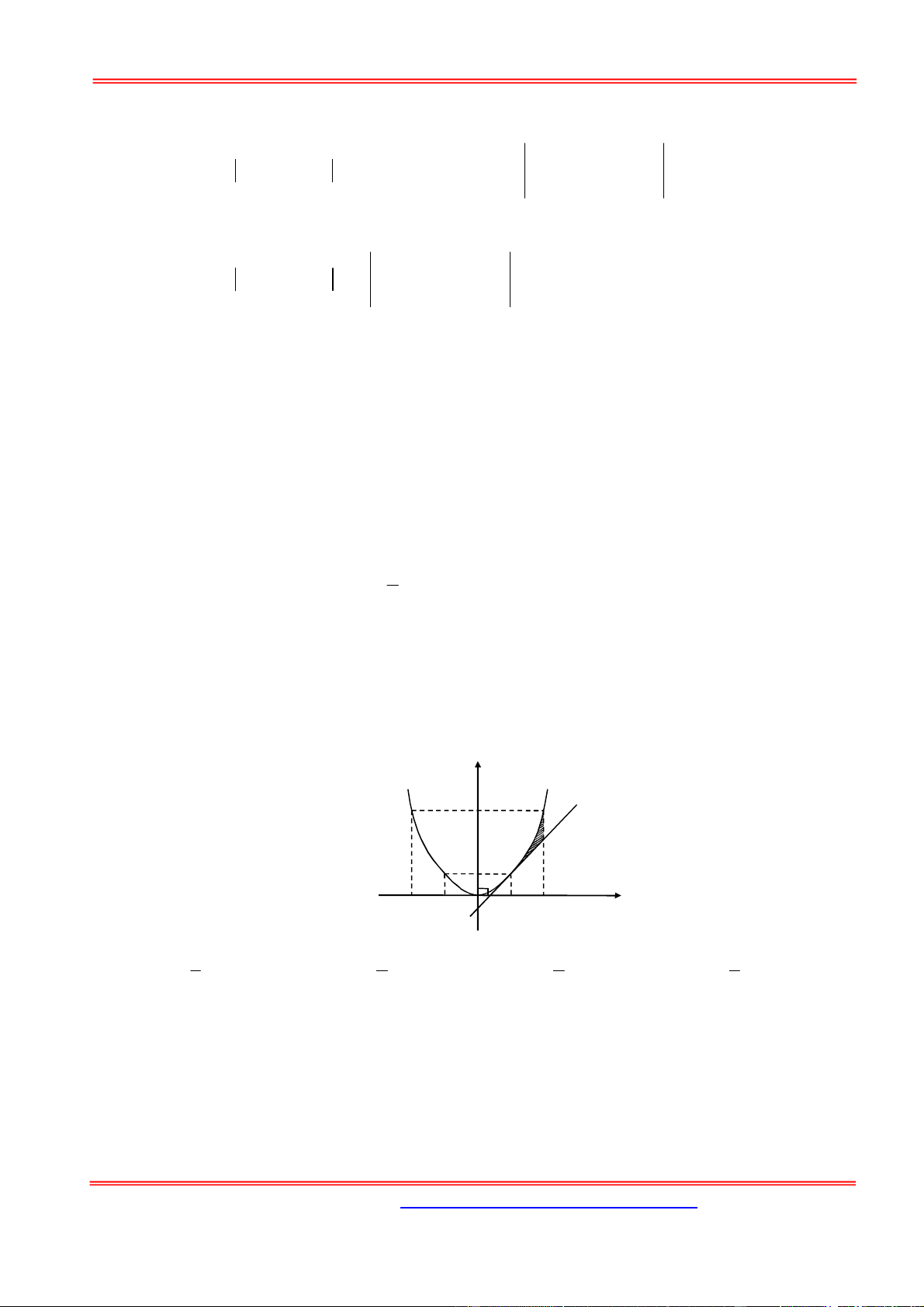
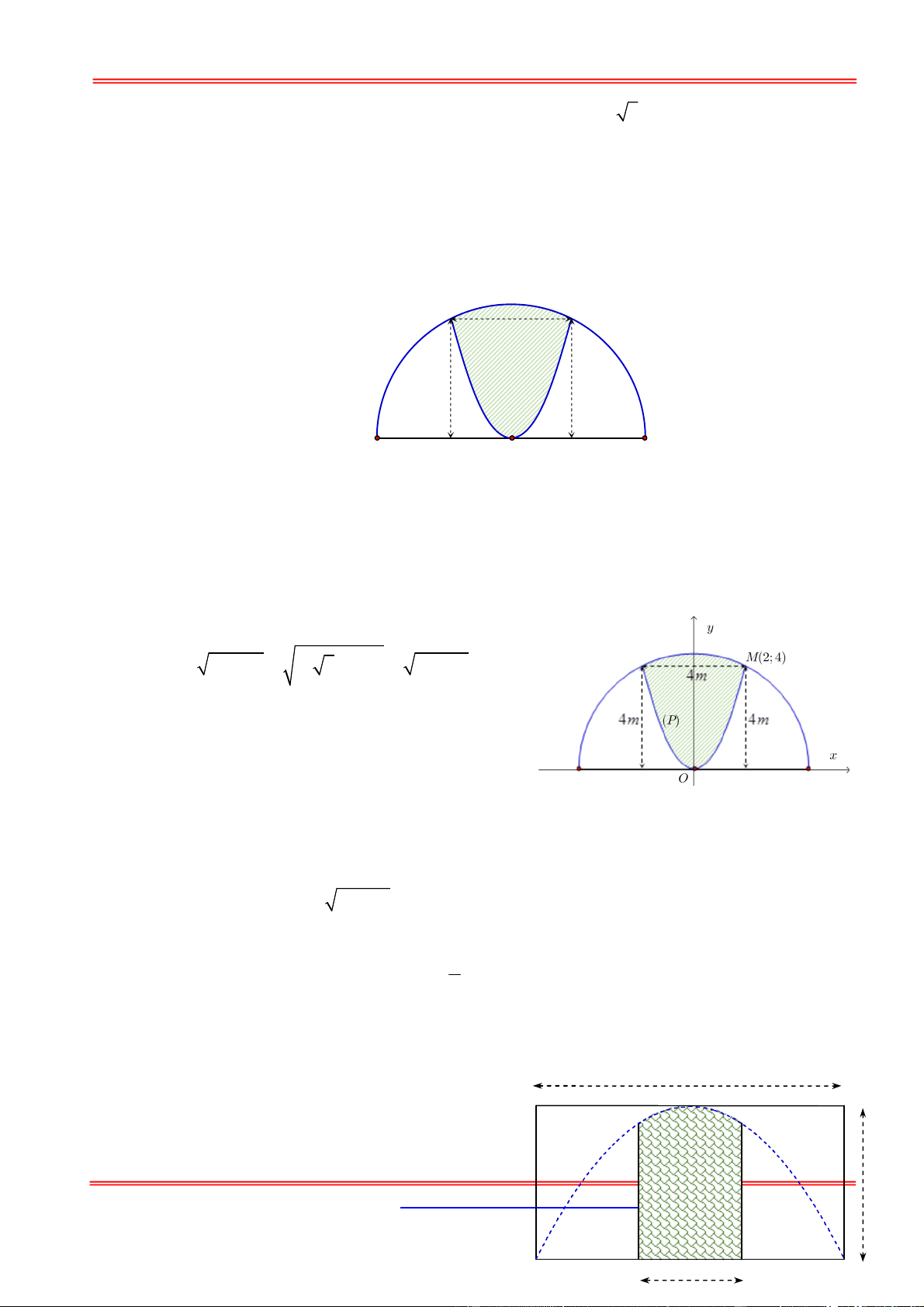
Phần bôi đen trên hình vẽ là hình phẳng (D) giới hạn giữa parabol (P) và tiếp tuyến d của (P)
tại điểm A(1;1) và đường thẳng x  2 . Tính diện tích hình phẳng (D). y 4 1 A 1 x -2 -1 -1 1 2 4 3 A. . B. . C. . D. 3 3 3 5 Hướng dẫn giải:
Vì parabol (P) nhận gốc O làm đỉnh và đối xứng qua Oy nên phương trình parabol (P) có dạng 2
y  ax (a  0) .
Vì (P) đi qua A(1;1) nên a  1 , suy ra phương trình (P): 2 y  x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 59
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Đường thẳng d là tiếp tuyến của (P) tại A nên có phương trình: y  2x 1 2 2 2 1 1 1
Diện tích hình phẳng (D) là: 2 2 3
S   x  (2x 1) d
 x  (x 1) dx  (x 1)   0      . 3 3 3 1 1 1 Chọn A
Lưu ý: Bài này cần phải tìm phương trình của các đường dựa trên hình vẽ. Câu 8:
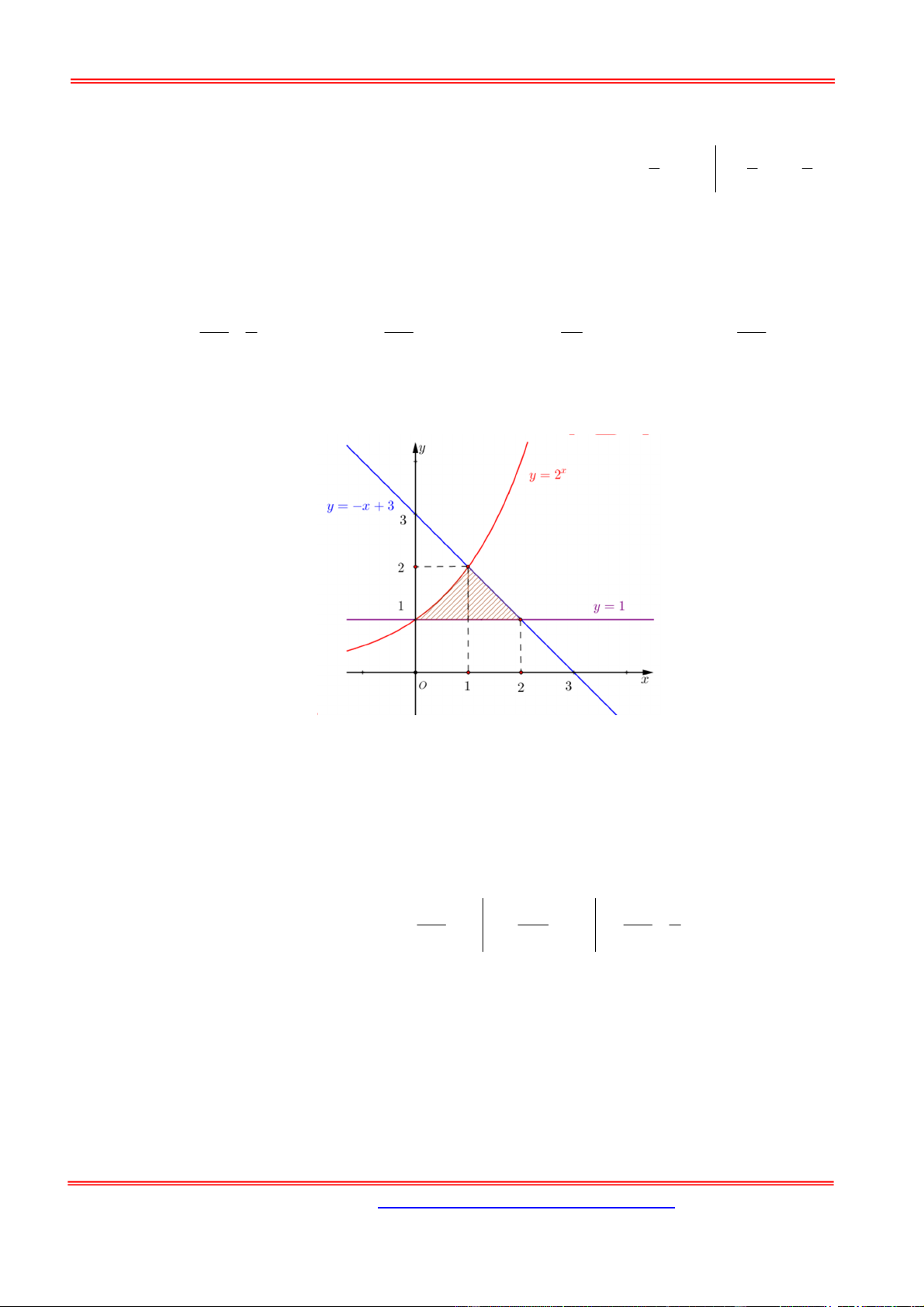
Diện tích miền phẳng giới hạn bởi các đường:  2x y
, y  x  3 và y  1 là: 1 1 1 47 1 A. S   . B. S   1. C. S  . D. S   3 . ln 2 2 ln 2 50 ln 2 Hướng dẫn giải: Chọn A.
Xét phương trình hoành độ giao điểm của các đường. Ta có:
2x   x  3  x  1
2x  1  x  0
x  3  1  x  2 Diện tích cần tìm là: 1 2 1 2 x 2      S   x x   2 1 1 2
1 dx  x  3   1 dx   x   2x        ln 2 2 ln 2 2 0 1     0 1 Câu 9:
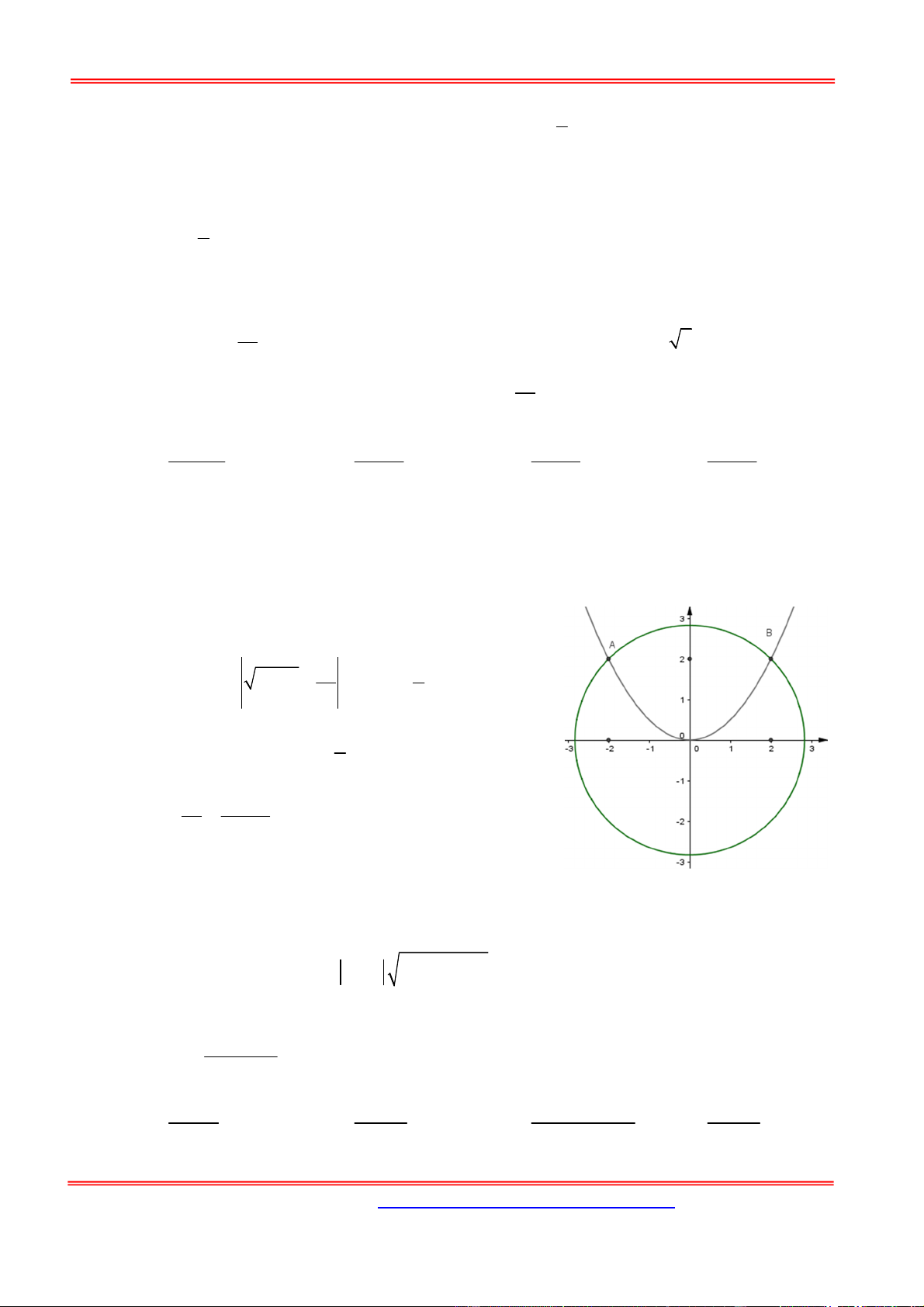
Cho a, b là hai số thực dương. Gọi (K) là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol 2
y  ax và đường thẳng y  b
 x . Biết thể tích khối tròn xoay tạo được khi
quay (K) xung quanh trục hoành là một số không phụ thuộc vào giá trị của a và b . Khẳng
định nào sao đây là đúng? A. 4 5 b  2a . B. 4 2 b  2a . C. 3 5 b  2a . D. 5 3 b  2a . Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 60
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Diện tích hình phẳng giới hạn bởi 2
y  1 x , y  k, x  0 bằng diện tích hình phẳng giới hạn bởi : 2 2
y  1 x , y  x 1, y  k, x  0. 1k 1 1k   1 2
1 x  k dx    2
k 1 x dx    2 k  x  
1 dx  1 k  1 k  1 k  1 k 3 0 1k 1 1 1 1 1 
 1 k   1 k  1 k  1 k  1 k  1 k  1 k  1 k  1 k  1 k   3 3 3 3 2 4 
1 k  1 k     k 3 1  2 3  k  4 1. 3 3
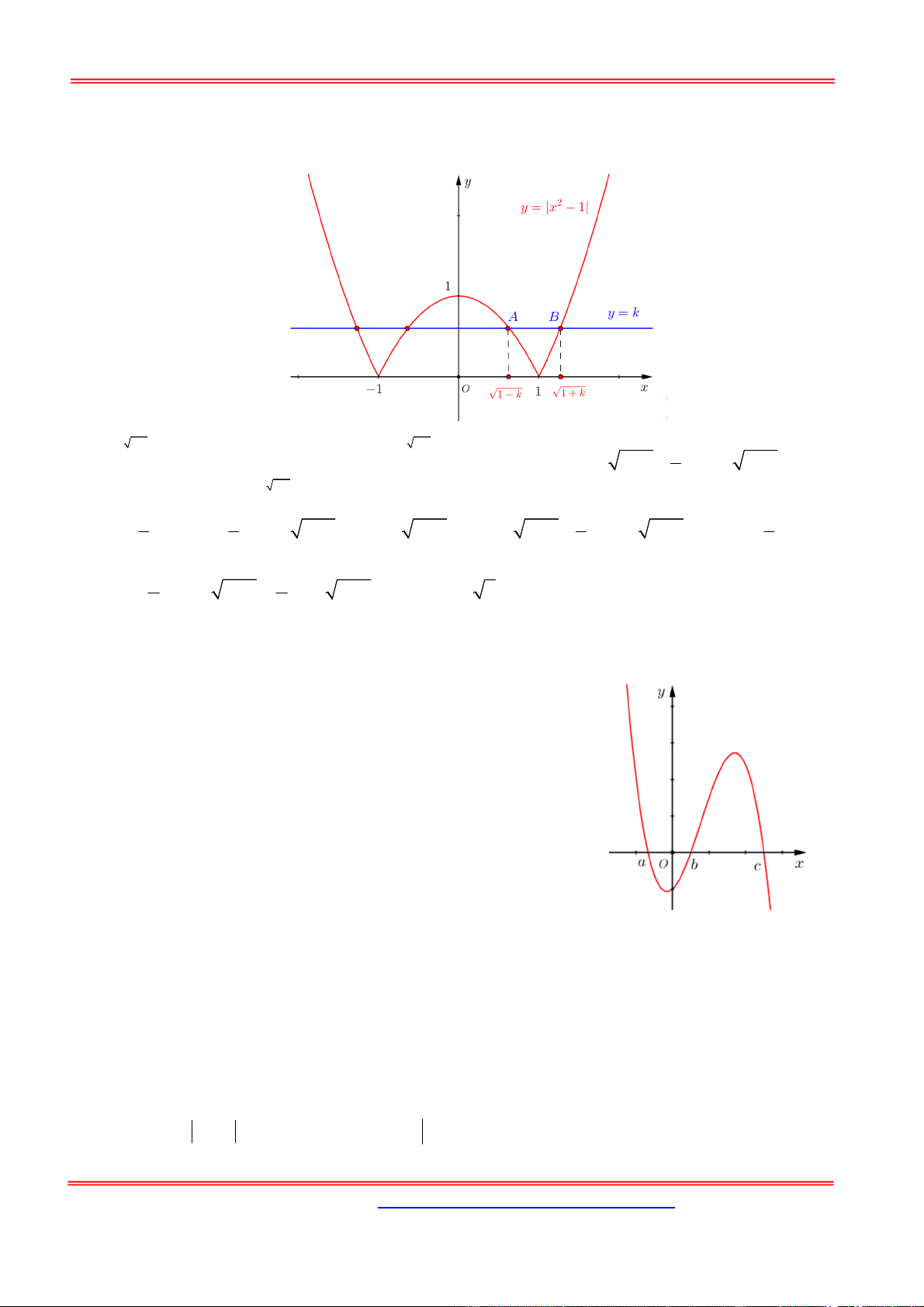
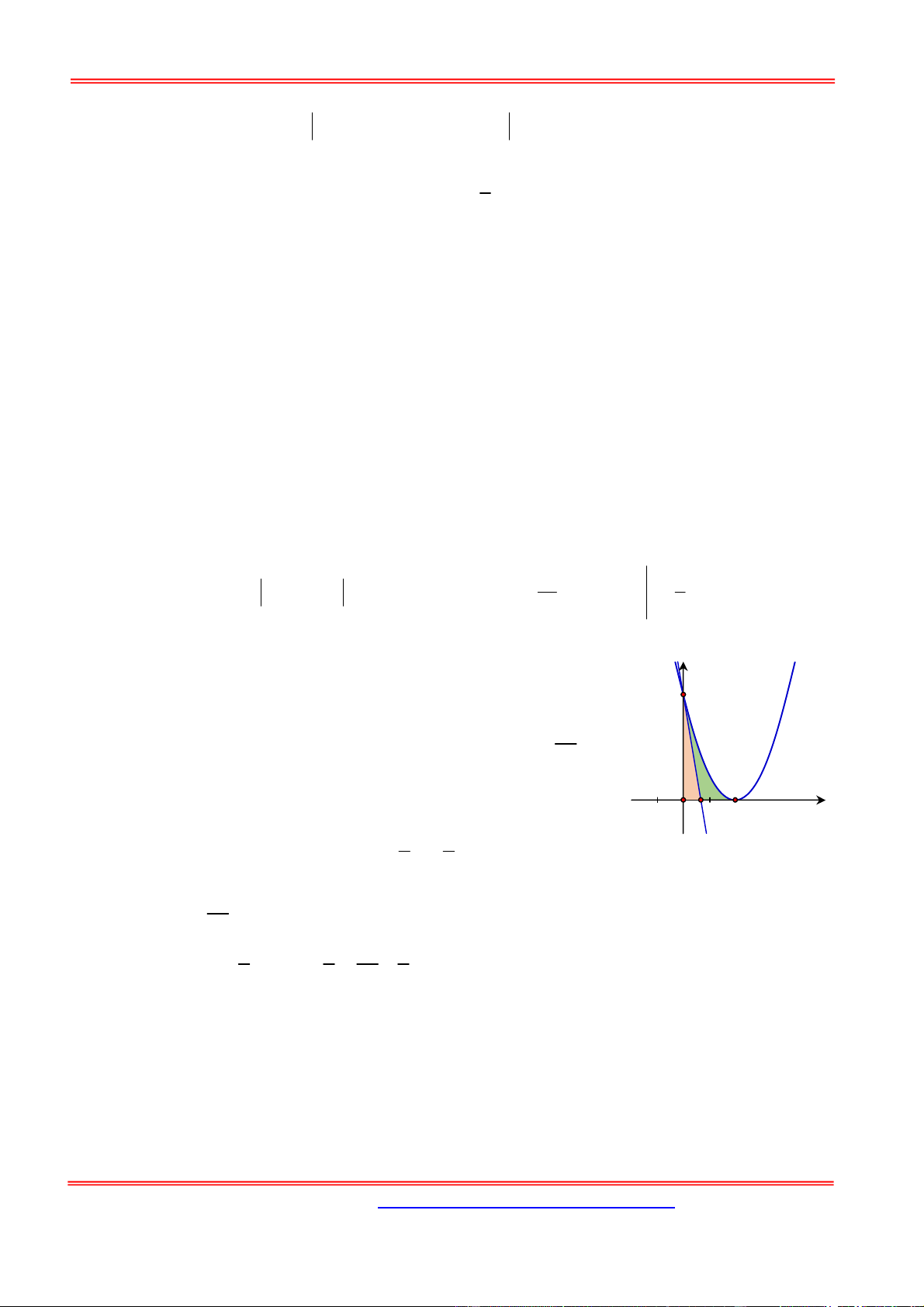
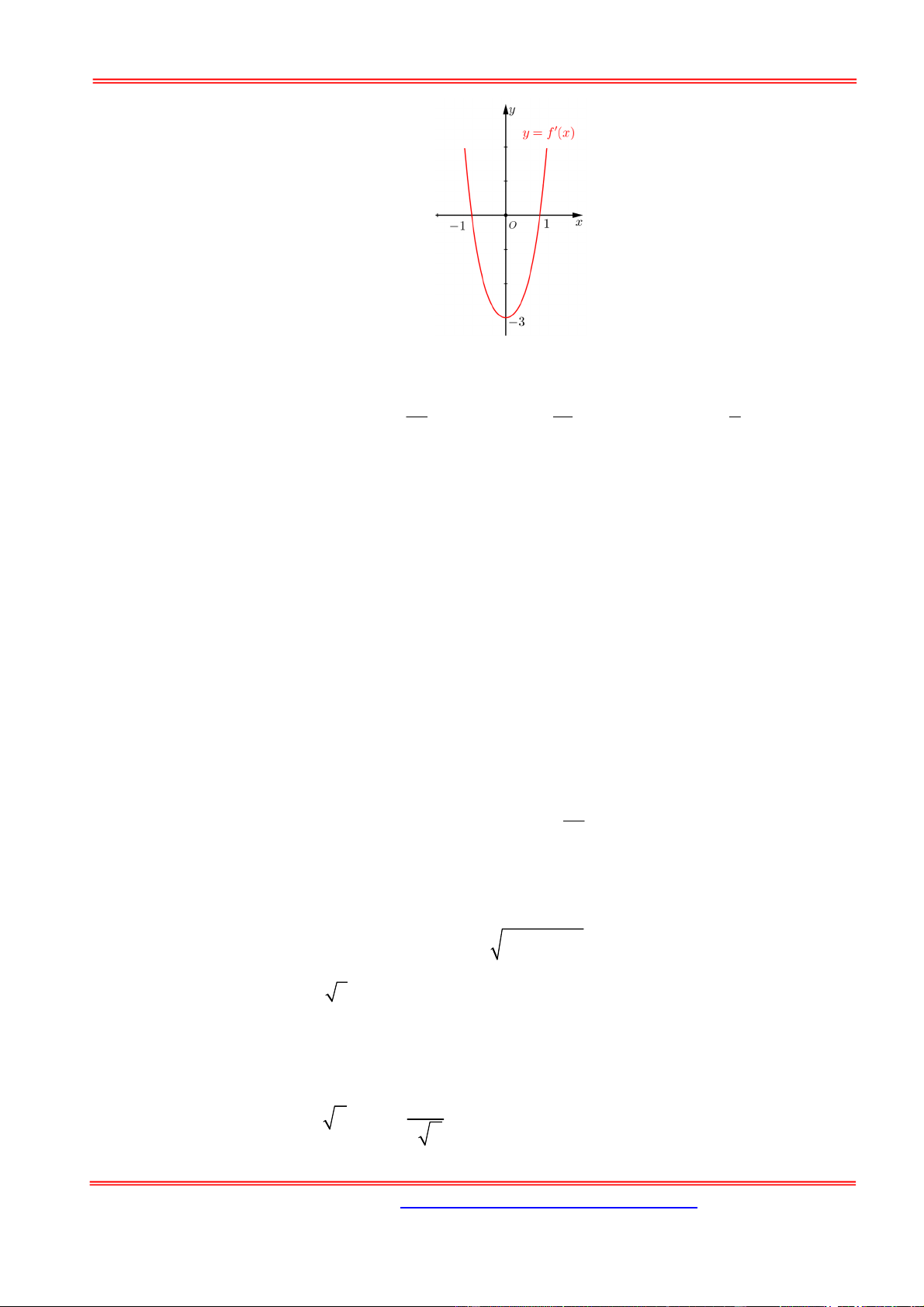
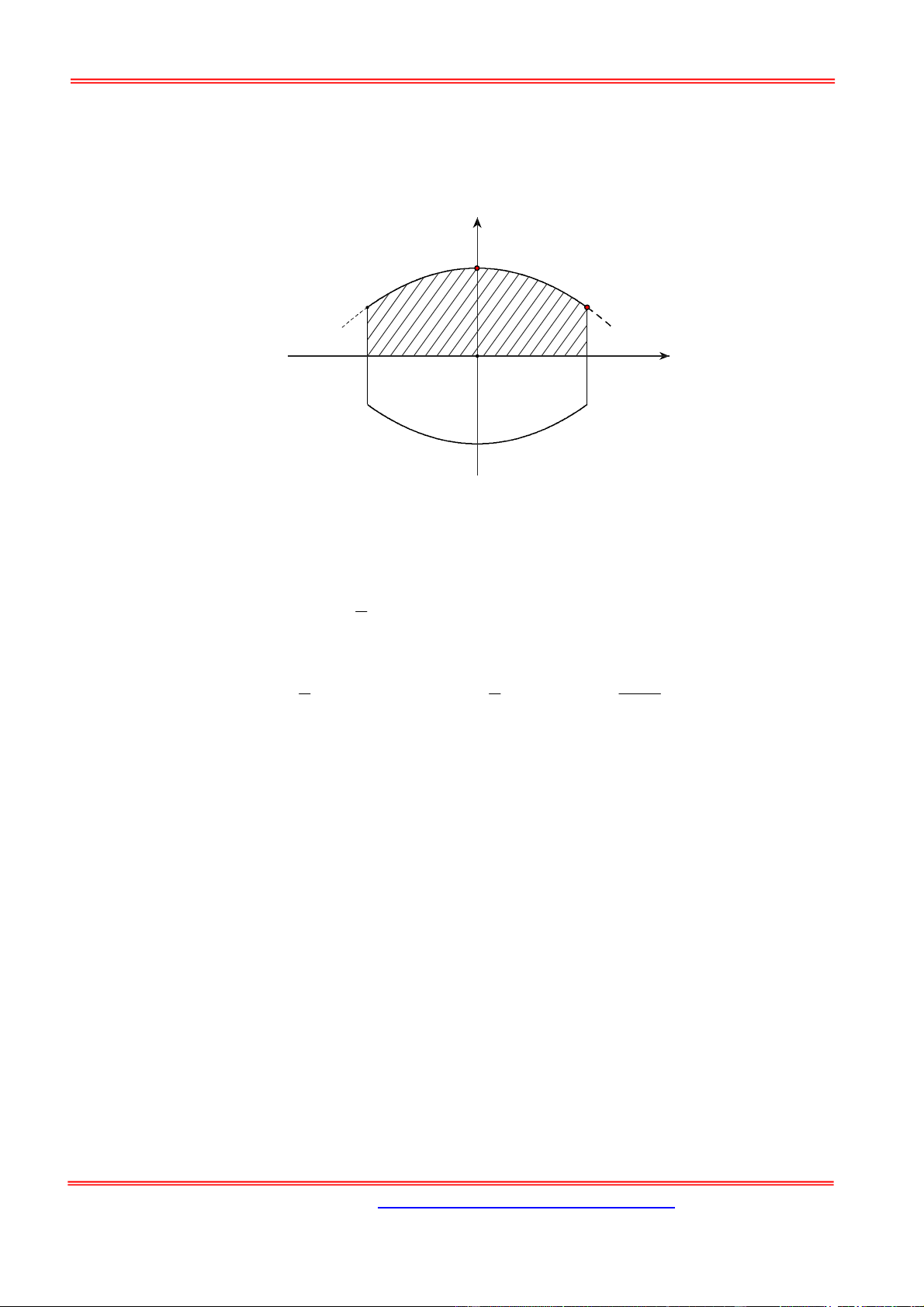
Câu 11: Cho hàm số y  f (x) có đồ thị y  f (
 x) cắt trục Ox tại ba điểm có hoành độ a  b  c như
hình vẽ. Mệnh đề nào dưới đây là đúng?
A. f (c)  f (a)  f (b).
B. f (c)  f (b)  f (a).
C. f (a)  f (b)  f (c).
D. f (b)  f (a)  f (c). Hướng dẫn giải: Chọn A.
Đồ thị của hàm số y  f (
 x) liên tục trên các đoạn  ; a b và  ;
b c , lại có f (x) là một nguyên hàm của f (  x) .  y  f (  x)   y  0
Do đó diện tích của hình phẳng giới hạn bởi các đường:  là: x  a  x  b  b b b S  f (
 x) dx   f (
 x)dx   f x  f a  f b 1         . a a a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 62
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Vì S  0  f a  f b   1 1      y  f (  x)   y  0
Tương tự: diện tích của hình phẳng giới hạn bởi các đường:  là: x  b  x  c  c c c S  f (  x) dx  f (
 x)dx  f x  f c  f b 2         . b b b
S  0  f c  f b 2 . 2    
Mặt khác, dựa vào hình vẽ ta có: S  S  f a  f b  f c  f b  f a  f c 1 2             3 .
Từ (1), (2) và (3) ta chọn đáp án A.
(có thể so sánh f a với f b dựa vào dấu của f (
 x) trên đoạn  ;
a b và so sánh f b
với f c dựa vào dấu của f (
 x) trên đoạn  ; b c ).
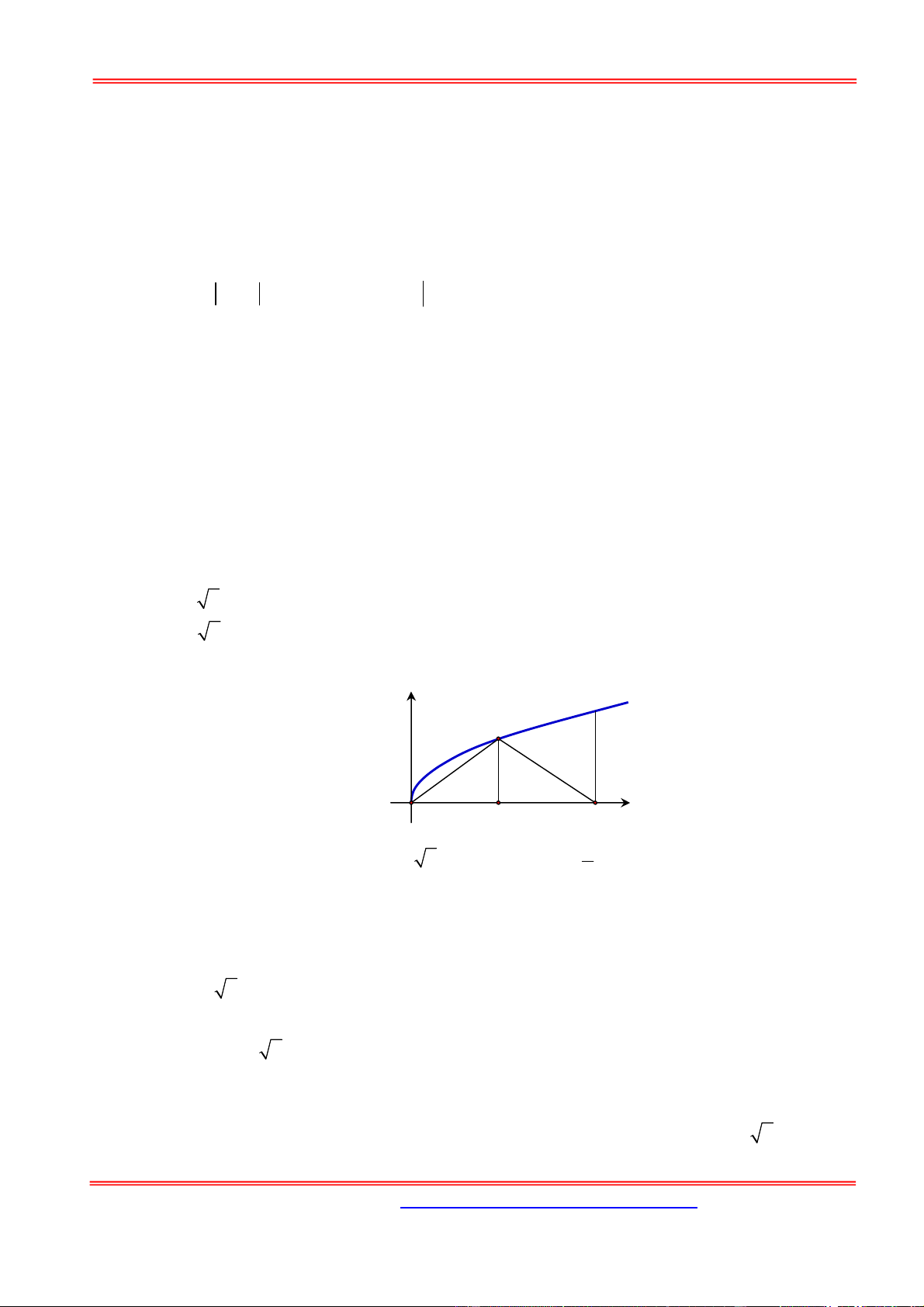
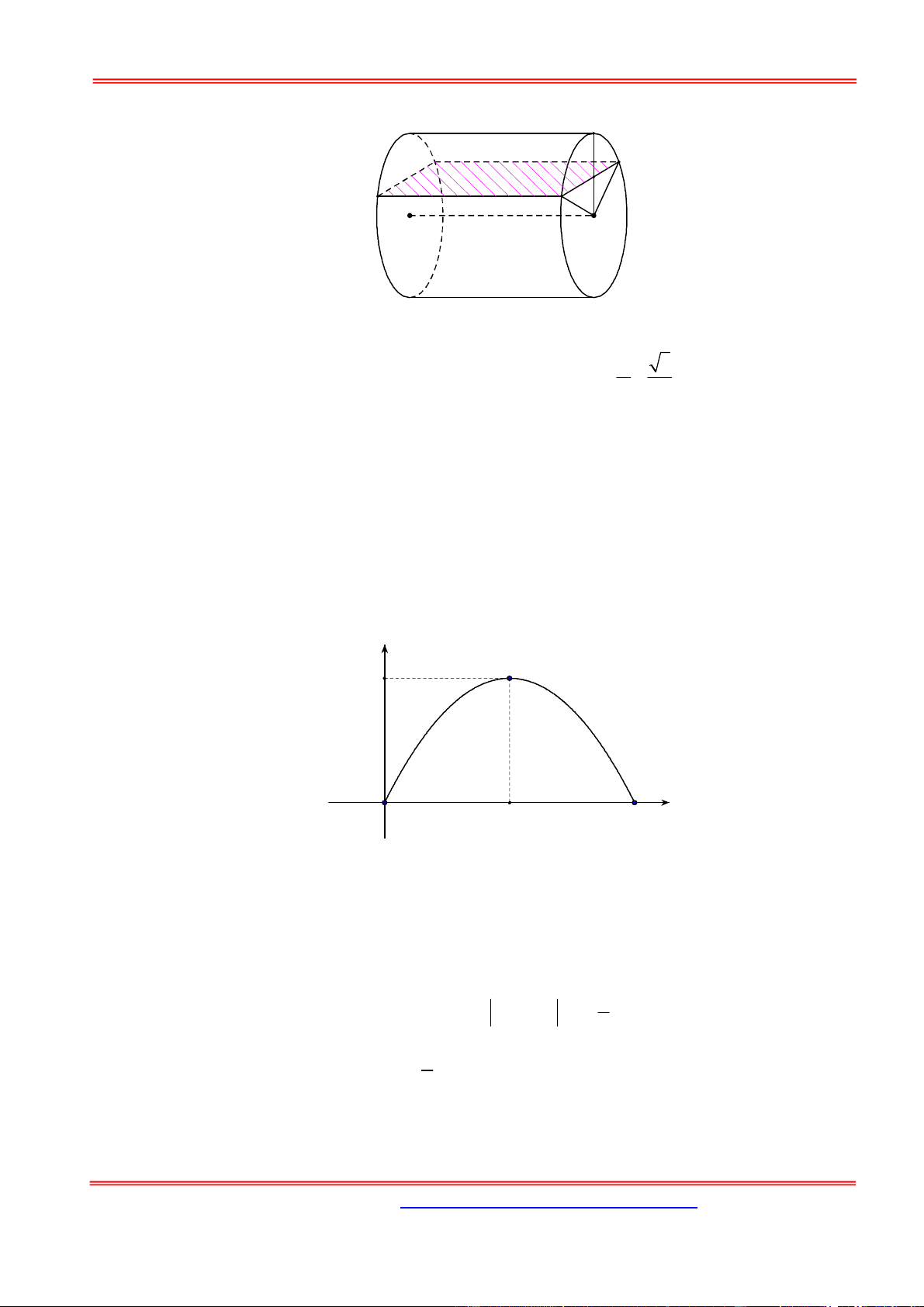
Câu 12: Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y 
x , y  0 và x  4 quanh trục Ox . Đường thẳng x  a 0  a  4 cắt đồ thị hàm y 
x tại M (hình vẽ bên). Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác 1
OMH quanh trục Ox . Biết rằng V  2V . Khi đó 1 y M a H O K 4 x 5 A. a  2 . B. a  2 2 . C. a  . D. a  3 . 2 Hướng dẫn giải: Chọn D. 4
Ta có x  0  x  0 . Khi đó V   d x x  8   0 Ta có M  ; a a 
Khi quay tam giác OMH quanh trục Ox tạo thành hai hình nón có chung đáy:
Hình nón  N có đỉnh là O , chiều cao h  OK  a , bán kính đáy R  MK  a ; 1  1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 63
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Hình nón  N thứ 2 có đỉnh là H , chiều cao h  HK  4  a , bán kính đáy R  MK  a 2  2 1 1 4 Khi đó 2 2
V   R h   R h   a 1 1 2 3 3 3 4
Theo đề bài V  2V  8  2.  a  a  3 . 1 3
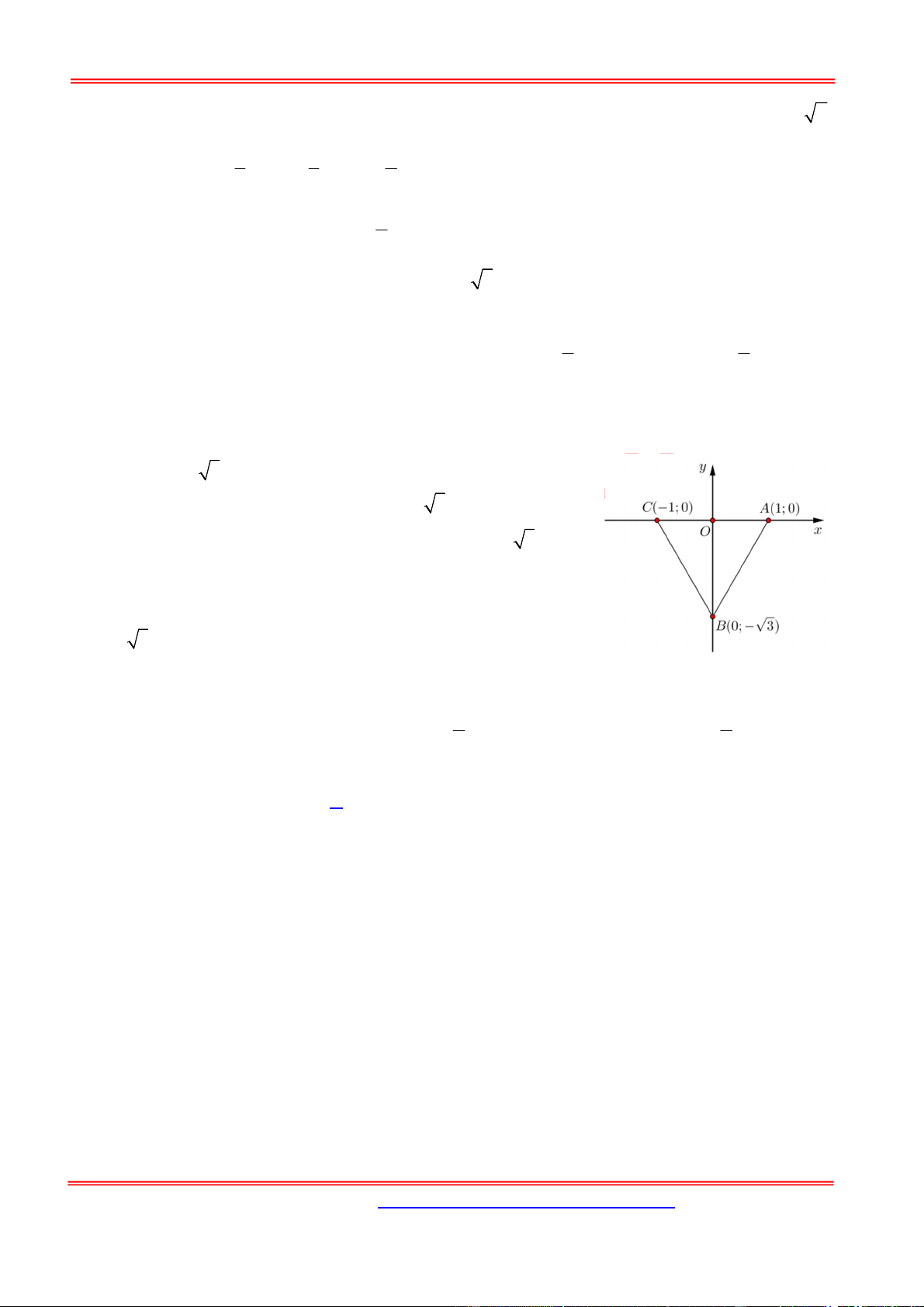
Câu 13: Cho tam giác đều ABC có diện tích bằng 3 quay xung quanh cạnh AC của nó. Tính thể
tích V của khối tròn xoay được tạo thành. 7 7
A. V  2 .
B. V   . C. V   . D. V   . 4 8 Hướng dẫn giải: Chọn A S
 3  AB  BC  CA  2 . Chọn hệ trục vuông góc ABC
Oxy sao cho O 0;0, A1;0, B 0; 3 với O là trung
điểm AC . Phương trình đường thẳng AB là y  3  x   1 ,
thể tích khối tròn xoay khi quay ABO quanh trục AC
(trùng Ox ) tính bởi 1 V    3  x   1 dx  
 . Vậy thể tích cần tìm V  2V   2 . 0
Câu 14: Diện tích hình phẳng nằm trong góc phần tư thứ nhất, giới hạn bởi các đường thẳng a a
y  8x, y  x và đồ thị hàm số 3 y  x là
, trong đó a, b là các số nguyên, tối giản. Khi b b
đó a  b bằng A. 68 . B. 67 . C. 66 . D. 65 Hướng dẫn giải: Ta có
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 64
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  x  0  x  0 3 3
8x  x  0  x  0;8x  x  0  
; x  x  0   x  2 2 x  1   1 2 2 63
Nên S  8x  xdx   3
8x  x  dx    4 0 1 .
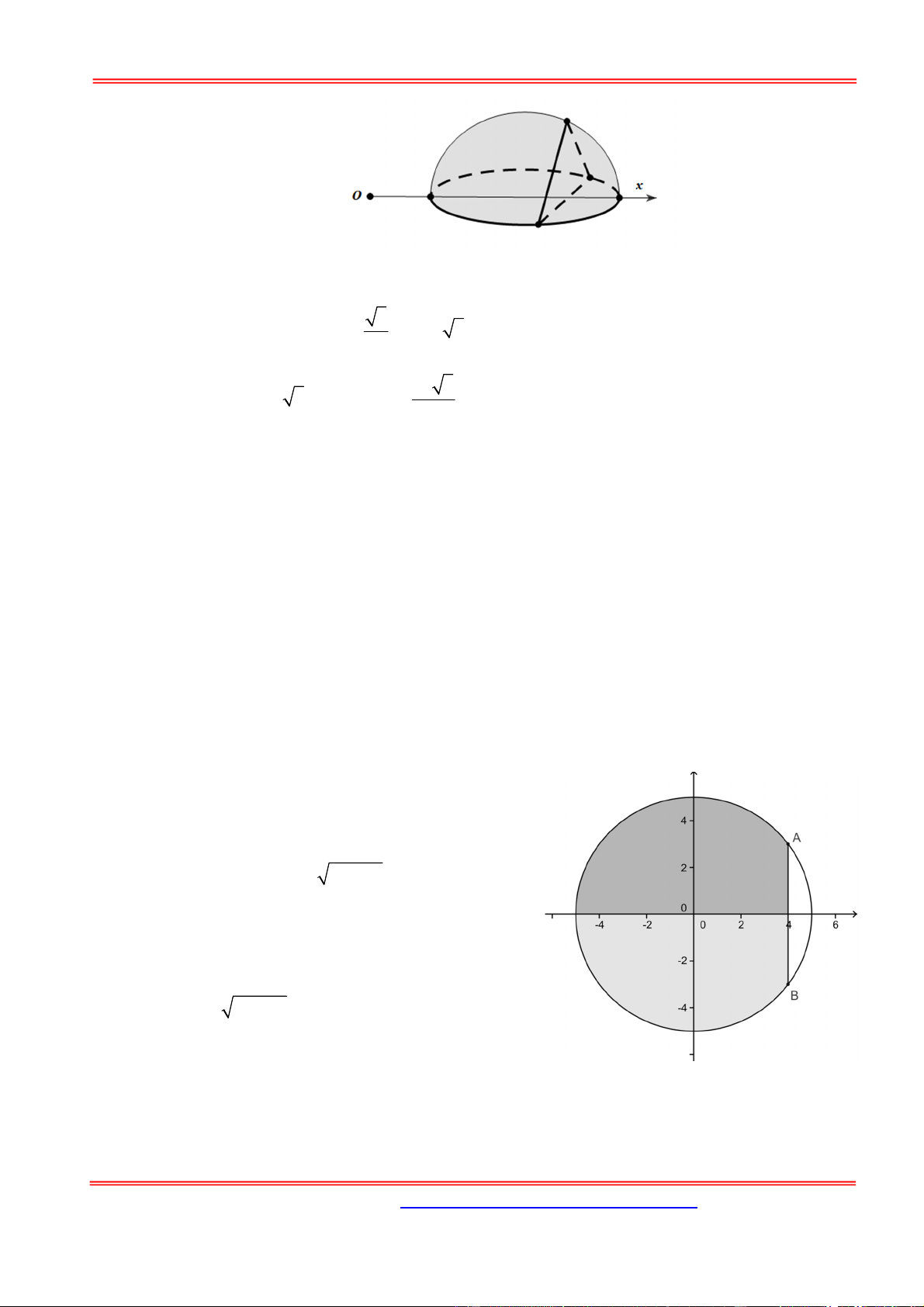
Câu 15: Thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn 2 2
(C) : x  ( y  3)  1 xung quanh trục hoành là
A. V  6 . B. 3 V  6 . C. 2 V  3 . D. 2 V  6 . Hướng dẫn giải: Chọn D. 2 2 2
x  ( y  3)  1  y  3  1 x . 1  
V    3  1 x 
2 3 1 x 2 2 2 dx    1 . 1 2  12 1 x dx 1  
x  1  t    2
Đặt x  sin t  dx  cost.dt . Với  .   x  1  1  t     2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 65
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng   2 2 2 2 2  V  12
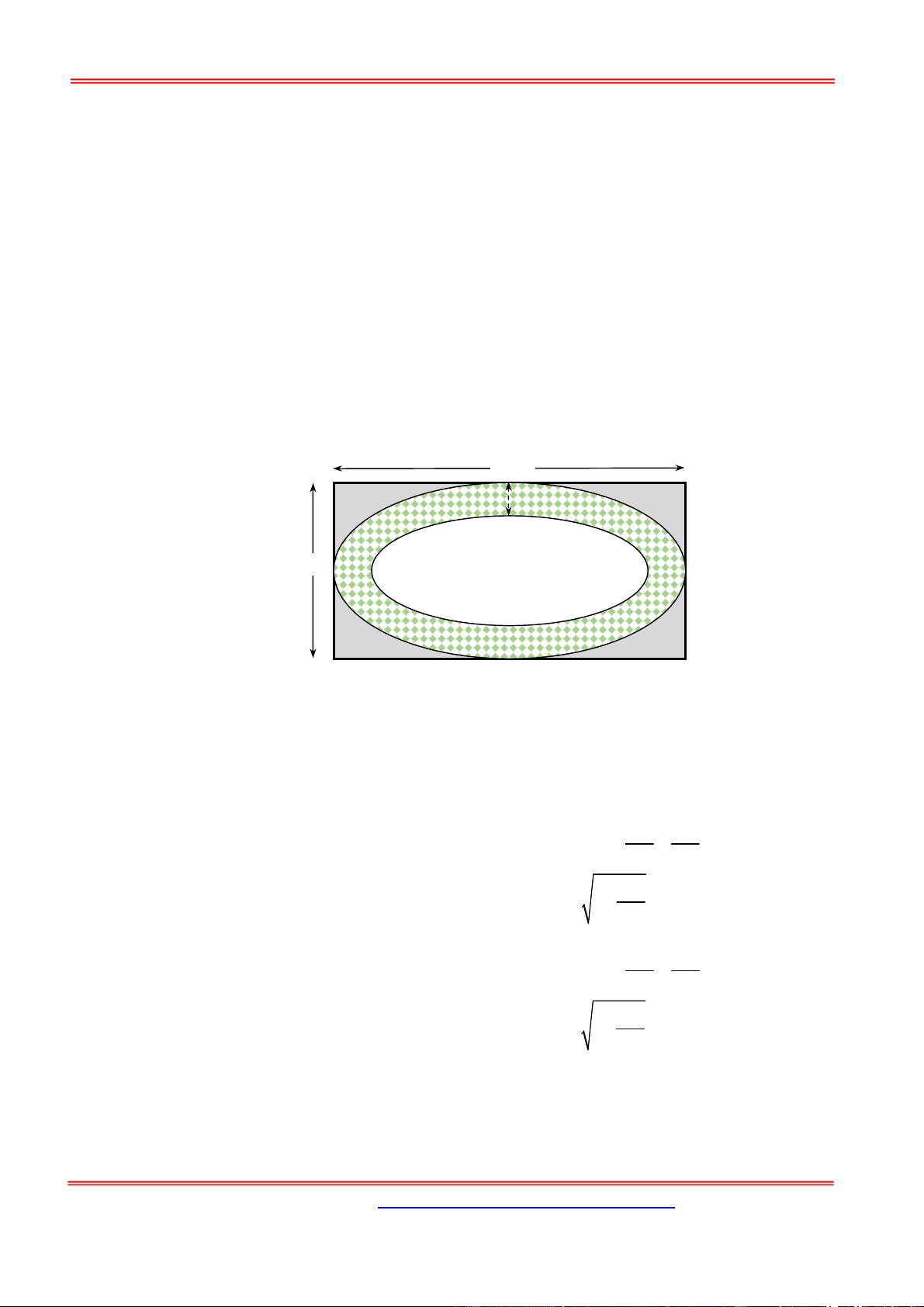
1 sin t.cos tdt  12 cos tdt  6    .     2 2 2 2 x y
Câu 16: Trong mặt phẳng tọa độ Oxyz cho  E  có phương trình 
 1, a,b  0 và đường 2 2 a b tròn C  2 2
: x  y  7. Để diện tích elip  E  gấp 7 lần diện tích hình tròn C  khi đó
A. ab  7 .
B. ab  7 7 . C. ab  7 . D. ab  49 . Hướng dẫn giải: Chọn D. 2 2 x y b 
 1, a,b  0 2 2  y  a  x . 2 2 a b a a 2 2 b a  x d a x b
Diện tích  E  là 2 2 S  4  4
a  x dx  E   a a 0 0    
Đặt x  a sin t, t   ;
 dx  a cos tdt  . 2 2    
Đổi cận: x  0  t  0; x  a  t  2 a a b 2 2 S  4 a .cos tdt  2ab  ab E 1+cos2tdt      a 0 0 Mà ta có 2 S
  .R  7 . C
Theo giả thiết ta có S  7.S
  ab  49  ab  49.  E C 1
Câu 17: Gọi S t  là diện tích hình phẳng giới hạn bởi các đường y 
, y  0 , x  0 ,  x   1  x  22
x  t (t  0) . Tìm lim S t . t  1 1 1 1 A.  ln 2  . B. ln 2  . C.  ln 2 . D. ln 2  . 2 2 2 2 Hướng dẫn giải: Chọn B. Cách 1: 1 a bx  c
*Tìm a, b, c sao cho    x   1  x  22 2 x  1 (x  2)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 66
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
  a  x  2 1 2
 bx  c  x   1 2 2
 1  ax  4ax  4a  bx  bx  cx  c a  b  0 a  1  
  a  b 2 1
x  4a  b  c x  4a  c  4a  b  c  0  b   1  . 4a c 1    c  3    1
*Vì trên 0;t , y   0 nên ta có:  x   1  x  22 t  1 t   1 x 3  
Diện tích hình phẳng: S t     dx    d  x    x   1  x  22 
 x 1 x  22  0 0     t t  1 1 1   x 1 1      d  x  ln    
 x 1  x  2 x  22   x  2 x  2  0 0   t  1 1 1  ln   ln 2  . t  2 t  2 2  t 1   t 1  1 *Vì lim  1  lim ln  0     và lim  0
t   t  2 t    t  2 
t  t  2  t 1 1 1  1
Nên lim S t   lim ln   ln 2   ln 2    . t  t   t  2 t  2 2  2
Cách 2: Dùng Máy tính cầm tay. t  1 
Diện tích hình phẳng: S t     dx
 x 1x 22    0   100  1 
Cho t  100 ta bấm máy    dx  0,193   x  1  x 22    0  
Dùng máy tính kiểm tra 4 kết quả ta được đáp án B.
Câu 18: Gọi H là phần mặt phẳng giới hạn bởi đường thẳng y  mx với m  2 và parabol (P) có
phương trình y  x 2  x . H có diện tích:  2  m2 2 2  5m
2  m 5  2m A. . B. . 6 6   m2 2 m  2 2 C. . D. . 6 6 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 67
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng e 1 ln x
Gọi diện tích cần tính là S , Ta có: S  dx  x 1 1
Đặt u  1 ln x, khi x  1 thì u  1, x  e thì u  2, du  dx x 2 2 3  2  2 S  2 udx  u   2 2    1 . 3 3 1  1 Chọn C. 1
Câu 19: Gọi S là diện tích hình phẳng giới hạn bởi các đường 2 2my  x , 2 mx 
y , m  0 . Tìm 2
giá trị của m để S  3 . 3 1 A. m  . B. m  2. C. m  3. D. m  . 2 2 Hướng dẫn giải: Chọn A. 1 Ta có 2 2
2my  x  y 
x  0 (do m  0 ). 2m 1
 y  2mx  0 và 2 2 mx 
y  y  2mx   . 2
 y   2mx  0  1
Xét phương trình hoành độ giao điểm của 2 2my  x và 2 mx  y ta có 2 1  x  0 2 2 4 3 x 
2mx  x  2m 2mx  x  8m x  0   . 2m x  2m  2m 2 1 m  1  Khi đó 2 2 S 
x  2mx dx 
x  2mx dx     2m  2m  0 0 2m 3 2 1 x 2 2m 4m  .  x x  . 2m 3 3 3 0 2 4m 9 3 Để 2 S  3   3  m   m  (do m  0 ). 3 4 2
Câu 20: Gọi S là diện tích của mặt phẳng giới hạn bởi đường thẳng y  mx với m < 2 và parabol 1
(P) có phương trình y  x 2  x . Gọi S là diện tích giới hạn bởi (P) và Ox. Với trị số nào 2 1 của m thì S  S ? 1 2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 68
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 1 A. 3 2  4 . B. 3 2  2 . C. . D. . 5 4 Hướng dẫn giải:
Ta tính S trước, phương trình hoành độ giao điểm: 2  x  0 2 4
x 2  x  0  2  , do đó S  2x  x dx   . x  2 2  3 0
Ta tính S , phương trình hoành độ giao điểm: 1 x  0 2 2
mx  2x  x  x  m  2 x  0   , do đó: x  2  m  2m 2m 2m 3 2  x 2  m x  2 S 
2x  x  mx dx     2
x  2  mx dx     . 1      3 2 0 0   0 2  m3 1 4 3   .  m  2  4 6 2 3
(Chú ý: muốn đường thẳng cắt parabol tại 2 điểm phân biệt thì trong tinhd huống này
parabol phải có phần chứa đỉnh nằm trên đường thẳng). Chọn A.
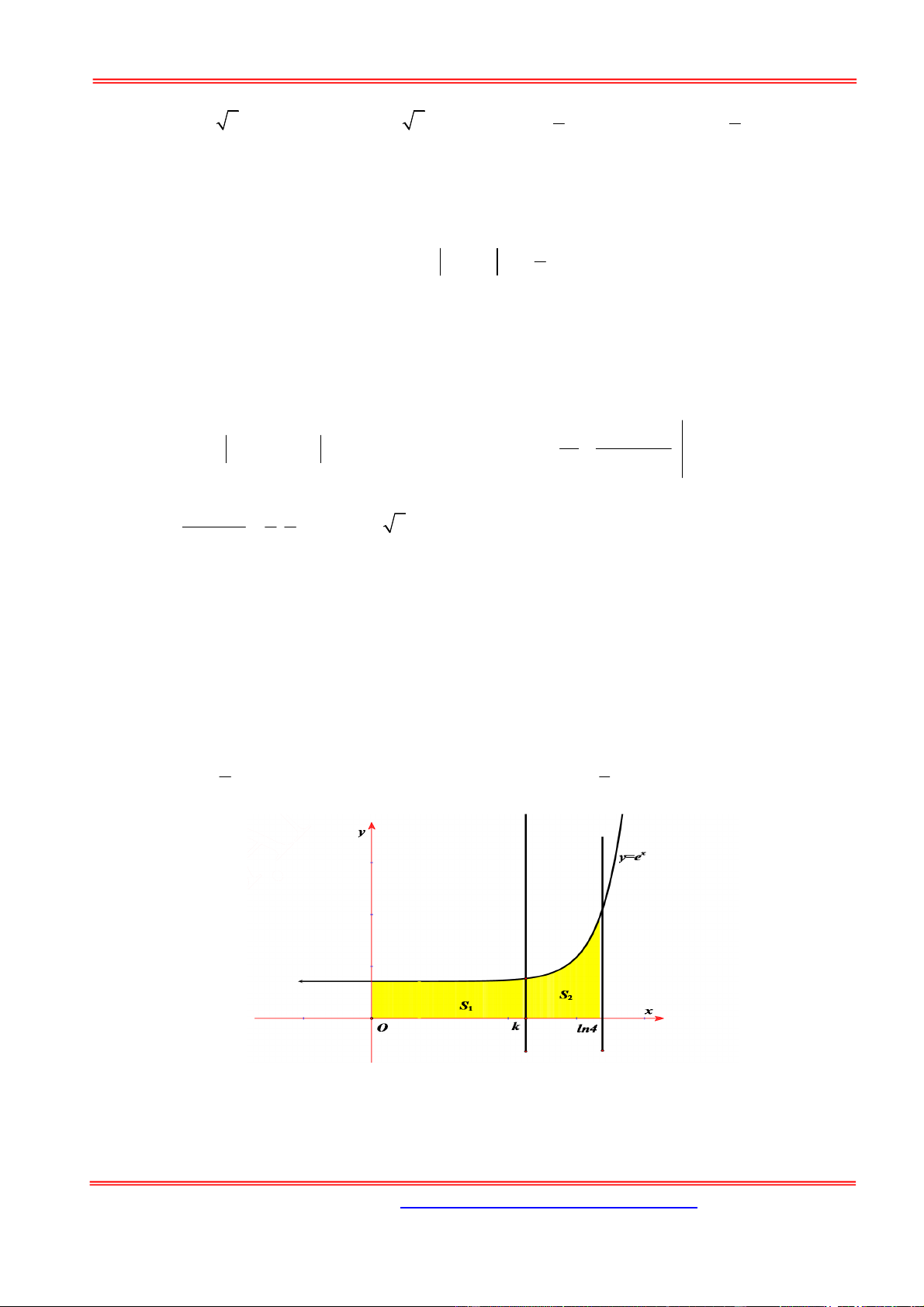
Câu 21: Cho hình thang cong (H) giới hạn bởi các đường x
y  e ; y  0; x  0 và x  ln 4 . Đường
thẳng x  k,0  k  ln 4 chia (H) thành hai phần có diện tích S và S như hình vẽ bên. 1 2
Tìm k để S  2S . 1 2 2 8 A. k  ln 4 . B. k  ln 2 . C. k  ln . D. k  ln 3. 3 3
Trích đề Minh họa 2 - 2017 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 69
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng k ln 4 k ln 4 Ta có: x x k
S  e dx  e  e 1, x x S  e dx  e  4 k  e 1 2   0 k 0 k k k k 9
Do đó: S  2S  e 1  2 4  e  e   3  k  ln 3 . 1 2   3 Chọn D.
Câu 22: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số: 2
y  x  4x  4 , trục tung và trục hoành.
Xác định k để đường thẳng d  đi qua điểm A0; 4 có hệ số góc k chia  H  thành hai
phần có diện tích bằng nhau. A. k  4 . B. k  8 . C. k  6 . D. k  2 . Hướng dẫn giải: Chọn C.
Phương trình hoành độ giao điểm của đồ thị hàm số 2
y  x  4x  4 và trục hoành là: 2
x  4x  4  0  x  2 .
Diện tích hình phẳng  H  giới hạn bởi đồ thị hàm số: 2
y  x  4x  4 , trục tung và trục 2 2 2 3  x  8 hoành là: 2 S 
x  4x  4 dx    2
x  4x  4dx 2   2x  4x    . 3 3 0 0   0
Phương trình đường thẳng d  đi qua điểm A0; 4 y
có hệ số góc k có dạng: y  kx  4 . 4  4  
Gọi B là giao điểm của d  và trục hoành. Khi đó B ; 0   .  k 
Đường thẳng d  chia  H  thành hai phần có diện tích O B 1 I x d 1 4
bằng nhau khi B OI và S  S  O  AB 2 3 .  4  0   2   k  2 k       k  6 . 1 1 4 4 k  6  S  O . A OB  .4.   O  AB   2 2 k 3 Câu 23: Cho hàm số 4 2
y  x  3x  m có đồ thị C
với m là tham số thực. Giả sử C cắt trục m  m 
Ox tại bốn điểm phân biệt như hình vẽ :
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 70
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng y Cm  S3 O x S S 1 2
Gọi S , S và S là diện tích các miền gạch chéo được cho trên hình vẽ. Tìm m để 1 2 3
S  S  S . 1 2 3 5 5 5 5 A. m   . B. m   . C. m  . D. m  . 2 4 2 4 Hướng dẫn giải: Chọn D
Giả sử x  b là nghiệm dương lớn nhất của phương trình 4 2
x  3x  m  0 . Khi đó ta có 4 2
b  3b  m  0 (1)
Nếu xảy ra S  S  S thì 1 2 3 b 5 4  b b 4 2
x  3x  m 3 2 dx  0 
 b  mb  0 
 b  m  0 (2) do b  0 5 5 0 4 5
Từ (1) và (2), trừ vế theo vế ta được 4 2 2
b  2b  0  b  (do b  0) . 5 2 5
Thay trở ngược vào (1) ta được m  . 4
Câu 24: Tìm giá trị của tham số m sao cho: 3
y  x  3x  2 và y = m(x+2) giới hạn bởi hai hình
phẳng có cùng diện tích A. 0 < m < 1. B. m = 1. C. 1  m  9 . D. m = 9 Hướng dẫn giải:
Phương trình hoành độ giao điểm: 3 x  3x  2  m(x  2)
 x  2 hoÆc x  1  m , m  0.
Điều kiện d: y = m(x+2) và (C): 3
y  x  3x  2 giới hạn 2 hình phẳng: 0  m  9.
Gọi S1, S2 lần lượt là diện tích các hình phẳng nhận được theo thứ tự từ trái sang phải.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 71
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 0
Nếu m = 1: d đi qua điểm uốn (0;2) của (C). Khi đó S 3 1 = S2 = (x  4x)dx  4 2
Nếu 0 < m < 1: S1 > 4 > S2
Nếu 1 < m < 9: S1 < 4 < S2
Nếu m > 9  1  m  2; 1 m  4. Khi đó: 2 1 m 3 3 S 
x  3x  2  m(x  2) dx; S 
x  3x  2  m(x  2) dx 1 2   1 m 2  S2  S1 = 2m m  0
Vậy m = 1 thỏa yêu cầu bài toán. Chọn B. 1 1   3 2      5  
Câu 25: Cho hàm số y x mx 2x 2m
có đồ thị (C). Tìm m 0;   sao cho hình 3 3  6
phẳng giới hạn bởi đồ thị (C) và các đường thẳng x  0, x  2, y  0 và có diện tích bằng 4. 1 A. m  1 . B. m  1 . C. m  . D. m  1 4 3 2 Hướng dẫn giải: 1 1 Xét hàm số 3 2 y 
x  mx 2x 2m  trên 0;2 . Ta có 2
y  x  2mx 2 , 3 3  2 x  m   m 2   5 y  0  
. Do m  0;  nên   2    x  m   m 2  6 2 2 m
  m  2  0, 0  m   m  2  2 1 5
và y 0  2m   0, y2  2m   0. 3 3
Ta có bảng biến thiên trong 0;2 x 0 2 2 m   m 2  y 0  y y0 y 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 72
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Dựa vào BBT suy ra y  0, x 0;2
Gọi S là diện tích hình phẳng cần tìm. Ta có: 2 1 1 3 2 S  4 
x  mx  2x  2m  dx  4  3 3 0 2 1 1  4m 10 1 3 2
   x  mx 2x 2m  dx     4   4  m  3 3  3 2 0 Chọn C. 4 x Câu 26: Cho hàm số 2 2 y 
 2m x  2 . Tập hợp tất cả các giá trị của tham số thực m sao cho đồ 2
thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục 64
hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng là 15   2    1  A.  . B.   1  . C.  ; 1   . D.  ;1 .  2     2  Hướng dẫn giải:
Tập xác định D    x  0  3 2
y  x  m x  x  2 2 2 4 2
x  2m  ; y  0  x  2m   x   2m 
Đồ thị của hàm số đã cho có cực đại và cực tiểu  m  0 1 Vì a 
 0 nên hàm số đạt cực đại tại x  0 suy ra điểm cực đại của đồ thị hàm số là 2 A0; 2
Đường thẳng cùng phương với trục hoành qua điểm cực đại có phương trình là d : y  2 .
Phương trình hoành độ giao điểm của C và d là: m  x  0 2 4 x  x  0  2 2
 2m x  2  2    x  2 m  2 2 2 x  4m  x  2  m 
Diện tích hình phẳng cần tìm là: (chú ý rằng hàm số đã cho là hàm chẵn)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 73
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 m 2 m 2 4 4 m 4 x x  x  2 2 2 2 2 2 S 
 2m x dx  2
 2m x dx  2  2m x dx      2 2 2 2  m 0 0   5  x 2  2 m 64 5 2 3  2  m x  m   10 3   0 15 64 m  1 Ta có S   m  1   15 m  1   Chọn B.
Câu 27: Trong hệ trục Oxy, cho tam giác OAB vuông ở A, điểm B nằm trong góc phàn tư thứ nhất.   
A nằm trên trục hoành, OB = 2017. Góc 
AOB   , 0    . Khi quay tam giác đó    3 
quanh trục Ox ta được khối nón tròn xoay. Thể tích của khối nón lớn nhất khi: 6 3 1 2 A. sin  . B. cos  . C. cos  . D. sin  3 2 2 3 Hướng dẫn giải:
Phương trình đường thẳng OB : y  x tan  , OA  2017c os
Khi đó thể tích nón tròn xoay là: 2017.cos 3 3 2 2 2017 . 2 2017 . V  
x tan .dx 
.cos.sin   .cos   2 1  cos  . 3 3 0 Đặt  1  Xét hàm số 2  1  .
t  cos  t  0; .  
f t   t 1 t , t  0;    2   2  Ta tìm được 3 3 6
f t lớn nhất khi t   cos   sin  . 3 3 3 Chọn A.
Câu 28: Cho hàm số y  f  x 3 2
 ax  bx  cx  d ,a, ,
b c  , a  0 có đồ thị C  . Biết rằng đồ thị
C tiếp xúc với đường thẳng y  4 tại điểm có hoành độ âm và đồ thị hàm số y  f  x
cho bởi hình vẽ dưới đây:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 74
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Tính diện tích S của hình phẳng giới hạn bởi đồ thị C  và trục hoành. 27 21 5
A. S  9 . B. S  . C. . D. . 4 4 4 Hướng dẫn giải: Chọn B.
Từ đồ thị suy ra f   x 2  3x  3 .
f  x  f  x dx    2 x   3 3
3 dx  x  3x  C .
Do C  tiếp xúc với đường thẳng y  4 tại điểm có hoành độ x âm nên 0 f  x  2
 0  3x  3  0  x  1  . 0 0 0 Suy ra f  
1  4  C  2  C  3
: y  x  3x  2 x  2  Xét phương trình 3
x  3x  2  0   . x  1  1 27
Diện tích hình phẳng cần tìm là:  3
x  3x  2dx   . 2  4
Câu 29: Đường cong được cho bởi phương trình x  g  y , với đạo hàm g y là hàm liên tục, gọi ,
m n m  n tương ứng là tung độ các điểm M và N thuộc đồ thị x  g  y . Độ dài đường n
cong x  g  y từ điểm M tới điểm N là:   g y 2 1 ( ) dx 
. Áp dụng tính độ dài đường cong m 2
y  x từ 1  ;1 đến  2;2 . A. 1,07. B. 1,06. C. 1. D. 2. Hướng dẫn giải: 1 Ta có: 2
y  x  x  y  x '  . 2 y
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 75
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 1
Do đó độ dài cần tính: 1 dy  1.06  . 2 4 y 1 Chọn B.
Câu 30: Đường cong được cho bởi phương trình x  g  y , với đạo hàm g y là hàm liên tục, gọi ,
m n m  n tương ứng là tung độ các điểm M và N thuộc đồ thị x  g  y . Độ dài đường n
cong x  g  y từ điểm M tới điểm N là:   g y 2 1 ( ) dx 
. Áp dụng tính độ dài đường cong m 2
x  y từ 1  ;1 đến 4;2 . A. 1,07. B. 7,27. C. 7,2 D. 2. Hướng dẫn giải:
Ta có: x '  2 y 4 Độ dài cần tính là: 1 2 ydx  7.27  . 1 Chọn B.
Câu 31: Đường cong được cho bởi phương trình x  g  y , với đạo hàm g y là hàm liên tục, gọi ,
m n m  n tương ứng là hoành độ các điểm M và N thuộc đồ thị. Độ dài đường cong n
y  g  x từ điểm M tới điểm N là:   g y 2 1 ( ) dx 
. Tìm độ dài của đường cong m 3
y  4x từ điểm 0;0 đến điểm 2;4 2  . Tích phân cần tính để giải bài này là: 4 2 2 A. 1  9xdx  . B. 1  9xdx  . 0 0 4 2 25 C. 3 1  4x dx  . D. 3 1  4x dx  . 0 0 Hướng dẫn giải:
Cung cần tính là phần của đường cong nằm trong góc vuông thứ nhất. Ta có: 3 1 2 y  2x nên 2
y  3x . Độ dài cung cần tìm bằng: 2 2 2
1  y dx  1  9xdx   . 0 0 Chọn D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 76
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 32: Xét hàm số y  f  x liên tục trên miền D   ;
a b có đồ thị là một đường cong C . Gọi S
là phần giới hạn bởi C và các đường thẳng x  a , x  b . Người ta chứng minh được rằng
diện tích mặt cong tròn xoay tạo thành khi xoay S quanh Ox bằng b S   f  x  
 f x2 2 1
dx . Theo kết quả trên, tổng diện tích bề mặt của khối tròn xoay a 2 2x  ln x
tạo thành khi xoay phần hình phẳng giới hạn bởi đồ thị hàm số f  x  và các 4
đường thẳng x  1 , x  e quanh Ox là 2 2e 1 4 4e  9 4 2 4e 16e  7 4 4e  9 A.  . B.  . C.  . D.  . 8 64 16 16 Hướng dẫn giải: Ta có 2 2 2 2x  ln x x ln x 1  1  1 1 f  x   
 f   x  x 
  f  x2 2  x   x     2 4 2 4 4x  4x  16x 2 1
Lại có f  x  x 
 0,x 1;e , nên f  x đồng biến trên 1;e . Suy ra 4x 1
f  x  f   1   0, x  1;e . 2
Từ đây ta thực hiện phép tính như sau b e 2  x ln x   1 1  S  2 f  x 1 
 f x2 2 dx  2  1 x   dx    2  2 4    16x 2  a 1 e e 2 2 2  x ln x  1 1  x ln x   1 2  S  2  x   dx  2  x  dx   2     2 4 16x 2 2 4      4x  1 1 e 2  x ln x   1   2  x  dx     2 4    4x  1 e  1 1 1 1 ln x 3   2 x  x  x ln x  dx    2 8 4 16 x  1
 2  I  I  I 1 2 3  e 4 2 4 2 e  1 1   x x  2e  e  3 Với 3 I  x  x dx    1      1  2 8  8 16 16   1 e e  1  1 1 1 1 2 I  
x ln x dx   x    2ln x   2 1   e  2 1  4  4 4 16 16 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 77
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng e e  1 ln x  1 1 2 I   dx   ln x   . 3    1  16 x  32 32 1 Chọn D. 3 4 2
Câu 33: Tính độ dài đường cong 2 y 
x 1, từ điểm A có hoành độ a = 0 đến điểm B có hoành 3
độ b = 1. Kết quả là: 13 21 3 14 A. . B. . C. . D. . 6 4 2 3 Hướng dẫn giải:
Ta có: f  x 
x   f  x 2 ( ) 2 2 , ( )  8 .
x thay vào Công thức ta được 1 T  1  8xdx 
. Đổi biến u  1  8x . Ta có: 0
x  0  u  1.
Khi x 1 u  9  9 9 3 1 1 2 13 Vậy 2 T  udu  . u   . 8 8 3 6 1 1 Chọn A.
Câu 34: Cho hai mặt cầu  S ,  S có cùng bán kính R thỏa mãn tính chất: tâm của  S thuộc 1  2  1 
S và ngược lại. Tính thể tích phần chung V của hai khối cầu tạo bởi (S ) và (S ) . 2  1 2 3  R 3 5 R 3 2 R A. 3 V   R . B. V  . C. V  . D. V  . 2 12 5 Hướng dẫn giải: y 2 2 2 Chọn C
(C) : x  y  R
Gắn hệ trục Oxy như hình vẽ
Khối cầu S O, R  chứa một đường tròn lớn là O R R x 2 C  2 2 2
: x  y  R
Dựa vào hình vẽ, thể tích cần tính là R R 3 3      2 2   R  x  2 x 5 R V 2
dx  2  R x    . 3 R 12 R   2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 78
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 35: Gọi V là thể tích khối tròn xoay tạo thành do quay xung quanh trục hoành một elip có 2 2 x y phương trình 
 1 . V có giá trị gần nhất với giá trị nào sau đây? 25 16 A. 550. B. 400. C. 670. D. 335. Hướng dẫn giải: Chọn C. 2 2 x y 4 Ta có 2   1  y   25  x . 25 16 5
Do elip nhận Ox , Oy làm các trục đối xứng nên thể tích V cần tính bằng 4 lần thể tích hình 4
sinh bởi hình phẳng giới hạn bởi các đồ thị hàm số 2 y 
25  x , y  0 và các đường 5
thẳng x  0 , x  5 quay xung quanh Ox . 5 2  4  640 2 V  4. 25  x dx=  670, 2   .  5  3 0
Câu 36: Gọi V và V lần lượt là thể tích khối tròn xoay tạo nên bởi phép quay hình elip x y 2 2 x y 
 1 a  b . Xung quanh trục Ox, Oy . Hỏi khẳng định nào dưới đây đúng? 2 2 a b
A. V  V .
B. V  V .
C. V  V .
D. V  V . x y x y x y x y Hướng dẫn giải: 2   x  2 2 y  b 1   2  2 2 a x y      1   2 2 2 a b  y   2 2 x  a 1  2   b    a a a 2 3 2  x   x  4 ab 4 ab 2 2 2
V  2 y dx  2 b 1 dx  2 b x    .b x   2   2  a 3a 3 3 0 0     0 b b b 2 3 2  y   x  4 a b 4 ab 2 2 2
V  V  2 x dx  2 a 1 dx  2 a x    .a y x   2   2  b 3a 3 3 0 0     0
Vì b > a nên V  V . x y Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 79
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Câu 37: Cho hàm số 4 2
y  x  4x  m có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi
đồ thị (C) với y<0 và trục hoành, S’ là diện tích hình phẳng giới hạn bởi đồ thị (C) với y>0
và trục hoành. Với giá trị nào của m thì S  S ' ? 2 20 A. m  2 B. m  C. m  D. m  1 9 9 Hướng dẫn giải
Phương trình hoành độ giao điểm 4 2
x  4x  m  0 (*) Đặt 2
x  t; t  0 , phương trình trở thành: 2
t  4t  m  0 (**)
Để S>0, S’>0 thì 0t ;  t ; t ; t với 2 1 1 2
t ; t , t  t
là hai nghiệm dương phân biệt của (**) 1 2  1 2 
Do ĐTHS hàm bậc 4 nhận Oy làm trục đối xứng nên t t 1 1
S  S '    4 2
x  4x  mdx    4 2
x  4x  mdx 0 t2 t 2 2    t 4t 4 2
x  4x  m 2 2 dx  0    m  0 0 5 3 20
Kết hợp với (**) ta được m  . 9 Chọn C.
Câu 38: Cho parabol  P 2
: y  x 1 và đường thẳng d : y  mx  2 . Biết rằng tồn tại m để diện tích
hình phẳng giới hạn bởi  P và d đạt giá trị nhỏ nhất, tính diện tích nhỏ nhất đó. 4 2 A. S  0. B. S  . C. S  . D. S  4. 3 3 Hướng dẫn giải: Chọn B.
Phương trình hoành độ giao điểm của  P  và d là 2 2
x  1  mx  2  x  mx  1  0 * Ta có 2
  m  4  0, m   .
 Nên phương trình * luôn có 2 nghiệm phân biệt x  a và
x  b a  b. Do đó  P  luôn cắt d tại 2 điểm phân biệt Aa; ma  2 và B b; mb  2.
Với mọi m, đường thẳng d luôn đi qua điểm M 0; 2. Mà y  1. CT Suy ra 2
mx  2  x  1, x  a;b.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 80
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Do đó diện tích hình phẳng giới hạn bởi  P  và d là b b 3   S   mx x b mx  2   2 x   1 dx  2
mx  1 x dx   x    2 3 a a a    m 1   m 1 1    b  a
b  a 1 
a  b  ab  b  a
b  a 1 a  b2 2 2  ab 2 3   2 3 3      2  m 1 1 
 S  b  a2
b  a 1 a  b2 2  ab  2 3 3    2  m 1 1  
 b a2 4ab   
b  a 1 a  b2  ab    2 3 3  
a  b  m Vì ,
a b là nghiệm của phương trình * nên ta có  . ab  1   2 2  m 2  4 16 Khi đó 2 S   2 m  4   4.  .   6 3 9 9   4
Đẳng thức xảy ra khi m  0. Vậy S  . min 3
Câu 39: Cho parabol (P) 2
y  x và hai điểm A, B thuộc (P) sao cho AB = 2. Tìm A, B sao cho diện
tích hình phẳng giới hạn bởi (P) và đường thẳng AB đạt giá trị lớn nhất 4 3 2 3 A. B. C. D. 3 4 3 2 Hướng dẫn giải Giả sử A  2 a a  B  2 ; ,
b, b Pb  a sao cho AB = 2
Phương trình đường thẳng AB: y  b  a x  ab
Gọi S là diện tích hình phẳng cần tìm, ta có
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 81
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng b b 1
S  | b  a x  ab  x | dx  [b  a x  ab  x ]dx  b  a 3 2 2   6 a a
Vì AB = 2 nên | b a | b a  2 4  S  3 Chọn B. 2 x
Câu 40: Parabol y 
chia hình tròn có tâm là gốc tọa độ, bán kính bằng 2 2 thành hai phần có 2 S
diện tích là S và S , trong đó S  S . Tìm tỉ số 1 . 1 2 1 2 S2 3  2 3  2 3  2 9  2 A. . B. . C. . D. . 21  2 9  2 12 3  2 Hướng dẫn giải: Chọn B. Diện tích hình tròn là 2
S   r  8 . 2 2 x 4 Ta có 2 S  8  x  dx  2  1  2 3 2  4
Suy ra S  S  S  6  2 1 3 S 3  2 Vậy 1  . S 9  2 2
Câu 41: Xét hàm số y  f  x liên tục trên miền D   ; a b có
đồ thị là một đường cong C . Gọi S là phần giới hạn bởi C và các đường thẳng x  a ,
x  b . Người ta chứng minh được rằng diện tích mặt cong tròn xoay tạo thành khi xoay S b
quanh Ox bằng S   f  x  
 f x2 2 1
dx . Theo kết quả trên, tổng diện tích bề mặt a
của khối tròn xoay tạo thành khi xoay phần hình phẳng giới hạn bởi đồ thị hàm số 2 2x  ln x f  x 
và các đường thẳng x  1 , x  e quanh Ox là 4 2 2e 1 4 4e  9 4 2 4e 16e  7 4 4e  9 A.  . B.  . C.  . D.  . 8 64 16 16
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 82
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Hướng dẫn giải: Chọn D.
Cách 1. (Giải tự luận) Ta có 2 2 2 2x  ln x x ln x 1  1  1 1 f  x   
 f   x  x 
  f  x2 2  x   x     2 4 2 4 4x  4x  16x 2 1
Lại có f  x  x 
 0,x 1;e , nên f  x đồng biến trên 1;e . Suy ra 4x 1
f  x  f   1   0, x  1;e . 2
Từ đây ta thực hiện phép tính như sau b e 2  x ln x   1 1  S  2 f  x 1 
 f x2 2 dx  2  1 x   dx    2  2 4    16x 2  a 1 e e 2 2 2  x ln x  1 1  x ln x   1 2  S  2  x   dx  2  x  dx   2     2 4 16x 2 2 4      4x  1 1 e 2  x ln x   1   2  x  dx     2 4    4x  1 e  1 1 1 1 ln x 3   2 x  x  x ln x  dx    2 8 4 16 x  1
 2  I  I  I 1 2 3  e 4 2 4 2 e  1 1   x x  2e  e  3 Với 3 I  x  x dx    1      1  2 8  8 16 16   1 e e  1  1 1 1 1 2 I  
x ln x dx   x    2ln x   2 1   e  2 1  4  4 4 16 16 1 e e  1 ln x  1 1 2 I   dx   ln x   . 3    1  16 x  32 32 1 Cách 2. e 2 x ln x  1 1 
Học sinh có thể trực tiếp bấm máy tính tích phân 2 S  2  1 x   dx   2  2 4  16x 2  1 để có kết quả
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 83
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 42: Diện tích hình phẳng giới hạn bởi hàm số 2 2 y  x
x 1 , trục Ox và đường thẳng x  1
a b  ln 1 b  bằng
với a , b , c là các số nguyên dương. Khi đó giá trị của a  b  c là c A. 11. B. 12. C. 13 . D. 14. Hướng dẫn giải: Chọn C.
Cách 1 (dùng máy tính):
Phương trình hoành độ giao điểm 2 2 x
x 1  0  x  0 1
Diện tích hình phẳng cần tìm là 2 2 S  x x 1dx  vì 2 2 x x 1  0, x  0;  1 . 0 1
a b  ln 1 b 2 2   x x 1dx   c 0 1
Bước 1: Bấm máy tính tích phân 2 2 S  x
x 1dx  0, 4201583875  ( Lưu D) 0
Bước 2: Cơ sở: Tìm nghiệm nguyên của phương trình
a b  ln 1 b 
a b  ln 1 b  D   c 
(coi c  f  x , a  x , b   và ta thử các c D
giá trị b  ...  5; 4  ;..0,1; 2;3; 4.....)
Thử với b  1:
Thử với b  2 : Mode + 7 X 2  ln 1 2 F  X   ; D
Kết quả: a  3;c  8, b  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 84
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Cách 2 (giải tự luận):
Phương trình hoành độ giao điểm 2 2 x
x 1  0  x  0 1
Diện tích hình phẳng cần tìm là 2 2 S  x x 1dx  vì 2 2 x x 1  0, x  0;  1 . 0 Đặt x  t  x   2 tan d 1 tan t dt 
Đổi cận x  0  t  0; x  1  t  4    4 4 2 4 2 sin t 1 1 sin t.cos t Khi đó 2 2
S  tan t 1 tan t   2
1 tan t dt  . dt  dt  2 2 
cos t cos t cos t  2 0 0 0 cos t 3
Đặt u  sin t  du  cos tdt  2
Đổi cận t  0  u  0;t   u  4 2 2 2 2     2 2 1  2 2 1 u u  2 1 1 S  du  du       du    1 u 3 1 u 3
 1u 3  1u 2 2 2 2 2   0 0 0     2 2 2 3 3 2 2 2 1 1
 1 u 1 u  1  1 1  Ta có H  du    du   du         1 u 3 2 8 1 u 1 u 8 1 u 1 u  0 0      0 2 2 2   1  1 1 3 1 1    2 1 1 1 6       du         du  8   3 3 2 1 u3 1 u3 2
1 u  1 u 1 u   8     0 1 u 1 u 2 0   1 u    2 2 2 2  1 1   1 6 2 2 1 6      d 2 u   du    2 161 u 2 16 1 u 2    8 2 2 8   1 u 2 2 0 0 1 u  0 2 2 6 Tính K  du  1u 22 0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 85
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 2 2 2 2 2 2 2 2 6 3
 1 u 1 u  3  1 1  K  du    du   du         1 u 2 2 2 1 u 1 u 2 1 u 1 u  0 0      0 2 2 2 3  1 1 2  3  1 1 1  u       du    ln  3 2  3ln 1 2  2 2   2   2  1 u 1 u
1 u 1 u 
2 1 u 1 u 1 u 0           0
3 2  3ln 1 2 7 2  3ln 1 2 2  Vậy H    2 8 8 7 2  3ln 1 2  1 Khi đó S   K 8 6 7 2  3ln 1 2 3 2  ln 1 2 1  
 3 2  3ln 1 2  8 6 8
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 86
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
ỨNG DỤNG THỰC TẾ Câu 1:
Một vật chuyển động chậm dần đều với vận tốc v(t)  160 10t (m / s) . Quãng đường mà
vật chuyển động từ thời điểm t  0 (s) đến thời điểm mà vật dừng lại là A. 1028 . m B. 1280 . m C. 1308 . m D. 1380 . m Hướng dẫn giải Chọn B.
Khi vật dừng lại thì v t   160 10t  0  t 16 16 16 16
Suy ra: s  v t dt  160 10t  dt     2
160t  5t   1280 . m 0 0 0 3 Câu 2:
Một chiếc ô tô chuyển động với vận tốc v t (m / s) , có gia tốc 2
a(t)  v (  t)  , (m / s ) 2t 1
. Vận tốc của ô tô sau 10 giây (làm tròn đến hàng đơn vị) là
A. 4, 6 m / s .
B. 7, 2 m / s .
C. 1, 5 m / s .
D. 2, 2 m / s . Hướng dẫn giải Chọn A. 10 10 3 3 3
Vận tốc của ô tô sau 10 giây là: v  dt  ln 2t 1 
ln 21  4, 6 (m / s).  2t 1 2 2 0 0 Câu 3:
Một hạt proton di chuyển trong điện trường có biểu thức gia tốc ( theo 2 cm / s ) là 20  a(t) 
(với t tính bằng giây). Tìm hàm vận tốc v theo t, biết rằng khi t  0 thì 1 2t 2
v  30 cm / s . 10 10  2  0 A. B.  20
C.   t  3 1 2  30 D.  30 1 2t 1 2t 1 2t2 Hướng dẫn giải Chọn B. 20  10
 v t   a tdt  dt   C   12t2 1 2t 10
 Do v0  30, suy ra
 C  30  C  20 1 2.0 10
 Vậy, hàm v t    20 . 1 2t
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 87
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Câu 4:
Một vật chuyển động với vận tốc v(t)  1 2 sin 2t (m/s) . Quãng đường mà vật chuyển động 3
trong khoảng thời gian t  0 (s) đến thời điểm t  (s) là 4 3 3 1 3 1 3 A. 1 . B. . C. . D. 1 . 4 4 4 4 Hướng dẫn giải Chọn A. 3 4 3 3
Quãng đường cần tìm s 
1 2sin 2t dt  t  cos 2t 4  1  . 0 4 0 Câu 5:
Một người lái xe ô tô đang chạy với vận tốc 20 m/s thì người lái xe phát hiện có hàng rào
ngăn đường ở phía trước cách 45m (tính từ vị trí đầu xe đến hàng rào) vì vậy, người lái xe đạp
phanh. Từ thời điểm đó xe chuyển động chậm dần đều với vận tốc v t  5
 t  20 ( m/s ),
trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp
phanh đến khi dừng hẳn, xe ô tô còn cách hàng rào ngăn cách bao nhiêu mét (tính từ vị trí đầu xe đến hàng rào)? A. 5 m . B. 4 m . C. 6 m . D. 3 m . Hướng dẫn giải Chọn A.
Xe đang chạy với vận tốc v  20 m/s tương ứng với thời điểm t  0 s
Xe đừng lại tương ứng với thời điểm t  4 s . 4 4  5 
Quảng đường xe đã đi là S  5t  20 2
dt   t  20t  40    m .  2  0 0
Vậy ô tô cách hàng rào một đoạn 45  40  5m . Câu 6:
Một vật chuyển động với vận tốc 10 m / s thì tăng tốc với gia tốc 2
a(t )  3t  t . Tính quãng
đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc. 4300 430 A. . m B. 4300 . m C. 430 . m D. . m 3 3 Hướng dẫn giải Chọn A. 2 3 3t t
 Hàm vận tốc v t   a t  dt    2
3t  t dt    C 2 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 88
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
 Lấy mốc thời gian lúc tăng tốc  v 0 10  C 10 2 3 3t t
Ta được: v t    10 2 3
 Sau 10 giây, quãng đường vật đi được là: 10 10 2 3 3 4  3t t   t t  4300 s   10 dt   10t  . m      2 3 2 12 3 0     0 Câu 7:
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v (t)  7t (m/s). Đi được 5 (s), 1
người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần
đều với gia tốc a  70 (m/s2 ). Tính quãng đường S (m) đi được của ô tô từ lúc bắt đầu
chuyển bánh cho đến khi dừng hẳn.
A. S  95, 70 (m).
B. S  87,50 (m).
C. S  94, 00 (m).
D. S  96, 25 (m). Hướng dẫn giải Chọn D.
Quãng đường ô tô đi được từ lúc xe lăn bánh đến khi được phanh: 5 5 5 2 t
S  v (t)dt  7tdt  7  87,5 (m). 1 1   2 0 0 0
Vận tốc v (t) (m/s) của ô tô từ lúc được phanh đến khi dừng hẳn thoả mãn 2 v (t)  ( 7
 0)dt=  70t  C , v (5)  v (5)  35  C  385 . Vậy v (t)  7  0 t 385 . 2  2 1 2
Thời điểm xe dừng hẳn tương ứng với t thoả mãn v (t)  0  t  5, 5 (s). 2
Quãng đường ô tô đi được từ lúc xe được phanh đến khi dừng hẳn: 5,5 5,5 S 
v (t)dt  ( 7
 0t  385)dt  8, 75 (m). 2 1   5 5
Quãng đường cần tính S  S  S  96, 25 (m). 1 2 Câu 8:
Một ôtô đang chạy đều với vận tốc 15 m/s thì phía trước xuất hiện chướng ngại vật nên
người lái đạp phanh gấp. Kể từ thời điểm đó, ôtô chuyển động chậm dần đều với gia tốc a 2
m / s . Biết ôtô chuyển động thêm được 20m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây. A. 3; 4 . B. 4;5 . C. 5;6 . D. 6;7 . Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 89
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Chọn C.
Gọi x t  là hàm biểu diễn quãng đường, vt  là hàm vận tốc. t
Ta có: v t   v 0  a dt  at 
 v t   at 15 . 0 t t 1
x t   x 0  v t  dt  at 15 2 dt   at 15t   2 0 0 1 x t  2   at 15t 2    v  t  at 15 0  0  15 8 45 Ta có:    1  
t 15t  20  t   a  . x  t  2  20
 at 15t  20   2 3 8  2 Câu 9:
Một ôtô đang chạy với vận tốc 18 m / s thì người lái hãm phanh. Sau khi hãm phanh, ôtô
chuyển động chậm dần đều với vận tốc v t   3
 6t 18 ( m / s ) trong đó t là khoảng thời
gian tính bằng giây kể từ lúc bắt đầu hãm phanh. Quãng đường ôtô di chuyển được kể từ lúc
hãm phanh đến khi dừng hẳn là bao nhiêu mét? A. 5, 5 m . B. 3, 5 m . C. 6, 5 m . D. 4, 5 m . Hướng dẫn giải Chọn D.
Lấy mốc thời gian là lúc ô tô bắt đầu hãm phanh. Gọi T là thời điểm ô tô dừng. Ta có
v T   0 . Suy ra 3
 6T 18  0  T  0, 5 (s)
Khoảng thời gian từ lúc hãm phanh đến lúc dừng hẳn ô tô là 0,5 s. Trong khoảng thời gian 0,5 0,5
đó, ô tô di chuyển được quãng đường là s 
36t 18 dt    2 1
 8t 18t   4,5(m) . 0 0 
Câu 10: Một vật di chuyển với gia tốc a t     t 2 20 1 2  2
m / s  . Khi t  0 thì vận tốc của vật là
30m / s . Tính quảng đường vật đó di chuyển sau 2 giây (làm tròn kết quả đến chữ số hàng đơn vị).
A. S  106m .
B. S  107m .
C. S  108m .
D. S  109m . Hướng dẫn giải: Chọn C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 90
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 
Ta có v t   a t dt     t 2 10 20 1 2 dt 
 C . Theo đề ta có   1 2t
v 0  30  C  10  30  C  20 . Vậy quãng đường vật đó đi được sau 2 giây là: 2  10  S   20 dt     2
5 ln 1 2t   20t   5ln 5 100  108m . 0  1 2t  0 2 t  2
Câu 11: Một vật chuyển động với vận tốc v(t)  1, 5 
(m/s) . Quãng đường vật đó đi được t  2
trong 4 giây đầu tiên bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm). A. 12,60 m. B. 12,59 m. C. 0,83 m. D. 6,59 m. Hướng dẫn giải Chọn B.
 Quãng đường trong 4 giây đầu tiên (từ t  0 đến t  4) là 4 4 2 4  t  2   6  2  t  s  1,5  dt  1, 5  t  2  dt      1,5t 
 2t  6 ln t  2  12, 59 . m   t  2    t  2  2 0 0   0
Câu 12: Một tia lửa được bắn thẳng đứng từ mặt đất với vận tốc 15 m / s . Hỏi sau 2,5 giây, tia lửa ấy
cách mặt đất bao nhiêu mét, biết gia tốc là 2 9,8 m / s ? A. 30, 625 . m B. 37, 5 . m C. 68,125 . m D. 6, 875 . m Hướng dẫn giải Chọn C.
 Hàm vận tốc vt  v  at 15  9,8t 0
 Quãng đường tia lửa đi được sau 2,5 giây là: 2,5 2,5 s 
15  9,8tdt    2 15t  4,9t  68,125 . m 0 0
Câu 13: Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là 24,5m / s và
gia tốc trọng trường là  2
9, 8 m / s  . Quãng đường viên đạn đi từ lúc bắn lên cho tới khi rơi
xuống đất là (coi như viên đạn được bắn lên từ mặt đất)
A. 61, 25 m .
B. 30, 625 m .
C. 29, 4 m .
D. 59, 5  m Hướng dẫn giải Chọn A.
Chọn chiều dương từ mặt đất hướng lên trên, mốc thời gian t  0 bắt đầu từ khi vật chuyển động.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 91
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Ta có vận tốc viên đạn theo thời gian t là v t   v  gt  24,5  9,8t m / s 0   5
Khi vật ở vị trí cao nhất thì có vận tốc bằng 0 tương ứng tại thời điềm t  2
Quãng đường viên đạn đi được từ mặt đất đến vị trí cao nhất là 5 5 2 2 245
S t   v t  dt  24, 5  9,8t dt    8 0 0 245
Vậy quãng đường viên đạn đi từ lúc bắn lên cho tới khi rơi xuống đất là 2.  61, 25 m . 8
Câu 14: Một lực 50 N cần thiết để kéo căng một chiếc lò xo có độ dài tự nhiên 5 cm đến 10 cm. Hãy
tìm công sinh ra khi kéo lò xo từ độ dài từ 10 cm đến 13 cm? A. 1,95J. B. 1,59 J. C. 1000 J. D. 10000 J Hướng dẫn giải
Theo định luật Hooke, khi chiếc lò xo bị kéo căng thêm x m so với độ dài tự nhiên thì chiếc
lò xo trì lại với một lực f (x)  kx .Khi kéo căng lò xo từ 5 cm đến 10 cm, thì nó bị kéo căng
thêm 5 cm = 0,05 m. Bằng cách này, ta được f (0, 05)  50 bởi vậy: 50
0.05k  50  k   1000 0.05
Do đó: f (x)  1000x và công được sinh ra khi kéo căng lò xo từ 10 cm đến 13 cm là: 2 0,08 x 0,08 W  1000xdx  1000  1, 95J 0,05 0,05 2 Chọn A.
Câu 15: Một ôtô đang chạy đều với vận tốc 15 m/s thì phía trước xuất hiện chướng ngại vật nên
người lái đạp phanh gấp. Kể từ thời điểm đó, ôtô chuyển động chậm dần đều với gia tốc a 2
m / s . Biết ôtô chuyển động thêm được 20m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây. A. 3;4 . B. 4;5 . C. 5;6 . D. 6;7 . Hướng dẫn giải Chọn C.
Gọi x t  là hàm biểu diễn quãng đường, vt  là hàm vận tốc.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 92
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng t
Ta có: v t   v0  a dt   
at  vt   at 15 . 0 t t 1
x t  x0  v t dt  at 15 2
dt   at 15   t 2 0 0 1 x t  2
  at 15t 2 at  v t   15  0  0  15 8 45 Ta có:    1  
t 15t  20  t   a  . x t  2  20
 at 15t  20   2 3 8  2
Câu 16: Tại một nơi không có gió, một chiếc khí cầu đang đứng yên ở độ cao 162 (mét) so với mặt
đất đã được phi công cài đặt cho nó chế độ chuyển động đi xuống. Biết rằng, khí cầu đã
chuyển động theo phương thẳng đứng với vận tốc tuân theo quy luật v t  2
 10t  t , trong đó
t (phút) là thời gian tính từ lúc bắt đầu chuyển động, v t  được tính theo đơn vị mét/phút (
m/p ). Nếu như vậy thì khi bắt đầu tiếp đất vận tốc v của khí cầu là
A. v  5m/p .
B. v  7 m/p .
C. v  9m/p .
D. v  3m/p . Hướng dẫn giải Chọn C.
Gọi thời điểm khí cầu bắt đầu chuyển động là t  0 , thời điểm khinh khí cầu bắt đầu tiếp đất là t . 1
Quãng đường khí cầu đi được từ thời điểm t  0 đến thời điểm khinh khí cầu bắt đầu tiếp đất là t là 1 t1 3  t 2 10t  t  2 1 dt  5t   162 1 3 0  t  4
 , 93  t  10, 93  t  9
Do v t   0  0  t 10 nên chọn t  9 .
Vậy khi bắt đầu tiếp đất vận tốc v của khí cầu là v   2
9 10.9  9  9m/p
Câu 17: Một ô tô đang chạy với vận tốc 10m / s thì người lái đạp phân, từ thời điểm đó, ô tô chuyển
động chậm dần đều với vận tốc v t   5
 t 10m / s , trong đó t là khoảng thời gian tính
bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển bao nhiêu mét?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 93
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng A. 0, 2m . B. 2m . C. 10m . D. 20m . Hướng dẫn giải Chọn C.
Ta có ô tô đi được thêm 2 giây nữa với vận tốc chậm dần đều v t   5
 t 10m / s
ứng dụng tích phân, ta có quãng đường cần tìm là: 2 2 2  5 
S  v t  dt  5t 10 2
dt   t 10t  10     m  2  0 0 0
* Lúc dừng thì ta có: v t   0  5
 t 10  0  t  2 1
Từ lúc đạp phanh đến lúc dừng hẳn, ô tô đi được quãng đường: 2 S  v t  at 0 2 a  5   1 Với t   2  S  10.2  5 2 .2  10 m 2 v 10  0
* Áp dụng công thức lý 10 ta có: 2 2 v  v  2. . a s 2 1
Ta còn có công thức liên hệ giữa vận tốc và gia tốc: v  v  . a t 0
Dựa vào phương trình chuyển động thì a    2 5 m / s 
Khi dừng hẳn thì ta có v  0 m / s 2   2 2 2 v  v 0 10
Theo công thức ban đầu, ta được 2 1 s    10 m . 2a 2.5
Câu 18: Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho ’ h t  2
 3at  bt và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là 3
150m . Sau 10 giây thì thể tích nước trong bể là 3
1100m . Hỏi thể tích nước trong bể sau khi
bơm được 20 giây là bao nhiêu. A. 3 8400m . B. 3 2200m . C. 3 6000m . D. 3 4200m Hướng dẫn giải 2 bt
Ta có h t  2 3
 (3at  bt)dt  at   . 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 94
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  1 3 2 5 .a  . . b 5  150   a  1 2 Khi đo ta có hệ:    1 b  2 3 2 1  0 .a  . . b 10  1100    2 Khi đó   3 2
h t  t  t .
Vậy thể tích nước trong bể sau khi bơm được 20 giây là h  3 20  8400m . Chọn A.
Câu 19: Gọi ht  cm là mức nước trong bồn chứa sau khi bơm được t giây. Biết rằng 1 ht  3 
t  8 và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước 5
được 6 giây (chính xác đến 0, 01 cm ) A. 2, 67 . cm B. 2, 66 . cm C. 2, 65 . cm D. 2, 68 . cm Chọn B. 1 3
 Hàm h t  3  t  8dt 
t  83 t  8  C  5 20 12 12
 Lúc t  0 , bồn không chứa nước. Suy ra h 0  0 
 C  0  C   5 5 3 12
Vậy, hàm h t 
t  8 3 t  8  20 5
 Mức nước trong bồn sau 6 giây là h6  2,66 c . m
Câu 20: Khi quan sát một đám vi khuẩn trong phòng thí nghiệm người ta thấy tại ngày thứ x có số 2000
lượng là N  x . Biết rằng N x 
và lúc đầu số lượng vi khuẩn là 5000 con.Vậy ngày 1 x
thứ 12 số lượng vi khuẩn là? A. 10130. B. 5130. C. 5154. D. 10129. Hướng dẫn giải Chọn A.
Thực chất đây là một bài toán tìm nguyên hàm. Cho N x và đi tìm N  x . 2000 Ta có
dx 2000.ln 1 x  5000 
( Do ban đầu khối lượng vi khuẩn là 5000).Với 1 x
x  12 thì số lượng vi khuẩn là  10130 con.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 95
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 4000
Câu 21: Một đám vi trùng tại ngày thứ t có số lượng là N t  . Biết rằng Nt   và lúc đầu 1 0, 5t
đám vi trùng có 250000 con. Hỏi sau 10 ngày số lượng vi trùng gần với số nào sau đây nhất? A. 251000 con. B. 264334 con. C. 261000 con. D. 274334 con. Chọn B. 4000
 N t  
dt  8000.ln 1 0, 5t  C 1 0,5t
 Lúc đầu có 250000 con, suy ra N 0  250000  C  250000
 Vậy N t  8000.ln 1 0,5t  250000  N 10  264334,0758. 7000
Câu 22: Một đám vi trùng tại ngày thứ t có số lượng N (t) , biết rằng N (  t)  và lúc đầu đám t  2
vi trùng có 300000 con. Sau 10 ngày, đám vi trùng có khoảng bao nhiêu con? A. 302542 con. B. 322542 con. C. 312542 con. D. 332542 con. Hướng dẫn giải Chọn C. 7000
Ta có N (t)  N (  t)dt 
dt  7000 ln | t  2 | C   t  2
Do N (0)  300000  C  300000  7000 ln 2
Khi đó N (10)  7000 ln12  300000  7000 ln 2  312542 . Chọn C
Câu 23: Tốc độ phát triển của số lượng vi khuẩn trong hồ bơi được mô hình bởi hàm số 1000 Bt  
,t  0 , trong đó B t  là số lượng vi khuẩn trên mỗi ml nước tại ngày thứ 1 0,3t2
t . Số lượng vi khuẩn ban đầu là 500 con trên một ml nước. Biết rằng mức độ an toàn cho
người sử dụng hồ bơi là số vi khuẩn phải dưới 3000 con trên mỗi ml nước. Hỏi vào ngày
thứ bao nhiêu thì nước trong hồ không còn an toàn nữa? A. 9 B. 10. C. 11. D. 12. Hướng dẫn giải Chọn B 1000 1000
Ta có B 't  dt  dt    C   10,3t2 0, 31 0, 3t 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 96
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 10000 11500
Mà B 0  500  
 C  500  C  31 0, 3.0 3 10000 11500
Do đó: B t    31 0,3t  3
Nước trong hồ vẫn an toàn khi chỉ khi 10000 11500
B t   3000     3000  t  10 31 0,3t  3
Vậy kể từ ngày thứ 10, nước hồ không còn an toàn.
Câu 24: Ông An có một mảnh vườn hình elip có độ dài trục
lớn bằng 16m và độ dài trục bé bằng10m . Ông muốn
trồng hoa trên một dải đất rộng 8m và nhận trục bé 8m
của elip làm trục đối xứng (như hình vẽ). Biết kinh phí
để trồng hoa là 100.000 đồng/ 2
1m . Hỏi ông An cần
bao nhiêu tiền để trồng hoa trên dải đất đó? (Số tiền
được làm tròn đến hàng nghìn). A. 7.862.000 đồng. B. 7.653.000 đồng. C. 7.128.000 đồng. D. 7.826.000 đồng. Hướng dẫn giải Chọn B. 2 2 x y
Giả sử elip có phương trình 
 1, với a  b  0 . 2 2 a b
Từ giả thiết ta có 2a  16  a  8 và 2b  10  b  5
Câu 25: Trên cánh đồng cỏ có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa 2
cọc là 4 mét còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn
nhất mà 2 con bò có thể ăn chung (lấy giá trị gần đúng nhất). A. 1, 034 m2 B. 1, 574 m2 C. 1, 989 m2 D. 2,824 m2 Hướng dẫn giải
Diện tích mặt cỏ ăn chung sẽ lớn nhất khi 2 sợi dây được kéo căng và là phần giao của 2 đường tròn.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 97
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Xét hệ trục tọa độ như hình vẽ, gọi O, M là vị trí của cọc. Bài toán đưa về tìm diện tích phần được tô màu.
Ta có phương trình đường tròn tâm O 2 2 2
: x  y  3 và phương trình đường tròn tâm
M   x  2 2 2 : 4  y  2
Phương trình các đường cong của đường tròn nằm phía trên trục Ox là: 2
y  9  x và y    x  2 4 4 21
Phương trình hoành độ giao điểm: 4   x  42 2
 9  x  4  8x 16  9  x  8 21   8 3  2 
Diện tích phần được tô màu là: S  2 4   x  4 2 dx  9  x dx  1,989     . Ta có thể 2 21    8 
giải tích phân này bằng phép thế lượng giác, tuy nhiên để tiết kiệm thời gian nên bấm máy. Chọn C.  5 2 y   64  y E 2 2  1 x y  8
Vậy phương trình của elip là   1   64 25 5  2 y  64  y E1   8
Khi đó diện tích dải vườn được giới hạn bởi các đường  E ; E ; x  4
 ; x  4 và diện 1   2  4 4 5 5 tích của dải vườn là 2 2 S  2 64  x dx  64  x dx   8 2 4 0   3 
Tính tích phân này bằng phép đổi biến x  8sin t , ta được S  80    6 4    3 
Khi đó số tiền là T  80 
.100000  7652891,82  7.653.000 .  6 4 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 98
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 26: Một mảnh vườn hình tròn tâm O bán kính 6m . Người ta cần
trồng cây trên dải đất rộng 6m nhận O làm tâm đối xứng, biết
kinh phí trồng cây là 70000 đồng 2
/ m . Hỏi cần bao nhiêu tiền
để trồng cây trên dải đất đó (số tiền được làm tròn đến hàng 6m đơn vị) O A. 8412322 đồng. B. 8142232 đồng. C. 4821232 đồng. D. 4821322 đồng. Hướng dẫn giải Chọn D
Xét hệ trục tọa độ oxy đặt vào tâm khu vườn, khi đó phương trình đường tròn tâm O là 2 2
x  y  36 . Khi đó phần nửa cung tròn phía trên trục Ox có phương trình 2
y  36  x  f (x)
Khi đó diện tích S của mảnh đất bằng 2 lần diện tích hình phẳng giới hạn bởi trục hoành, đồ
thị y  f (x) và hai đường thẳng x  3  ; x  3 3 2  S  2 36  x dx  3   
Đặt x  6sin t  dx  6 cos tdt . Đổi cận: x  3   t  
; x  3  t  6 6    6 6 6 2  S  2 36cos tdt  36
(c os2t+1) dt  18(sin 2 t 2 t)  18 3 12         6 6  6
Do đó số tiền cần dùng là 70000.S  4821322 đồng
Câu 27: Một thùng rượu có bán kính các đáy là 30cm , thiết diện vuông góc với trục và cách đều hai
đáy có bán kính là 40cm , chiều cao thùng rượu là 1m (hình vẽ). Biết rằng mặt phẳng chứa
trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu (
đơn vị lít) là bao nhiêu?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 99
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng A. 425, 2 lit. B. 425162 lit. C. 212581 lit. D. 212, 6 lit. Hướng dẫn giải Chọn A. y S A 0,4m 0,3m x O 0,5m  Gọi  P 2
: y  ax  bx  c là parabol đi qua điểm A0,5;0, 
3 và có đỉnh S 0;0, 4 (hình vẽ).
Khi đó, thể tích thùng rượu bằng thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi
P , trục hoành và hai đường thẳng x  0,5 quay quanh trụcOx . 2
 Dễ dàng tìm được P 2 : y   x  0, 4 5
 Thể tích thùng rượu là: 0,5 2 0,5 2  2   2  203 2 2 V    x  0, 4 dx  2  x  0, 4 dx   425,5 (l)        5   5  1500 0,5 0
Câu 28: Một bồn hình trụ đang chứa dầu, được đặt nằm ngang, có chiều dài bồn là 5m, có bán kính
đáy 1m, với nắp bồn đặt trên mặt nằm ngang của mặt trụ. Người ta đã rút dầu trong bồn
tương ứng với 0,5m của đường kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn (theo đơn vị 3 m ) A. 11,781 3 m . B. 12,637 3 m . C. 1 3 14, 923 m . D. 3 8, 307 m . Hướng dẫn giải Chọn B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 100
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng H C B A D O' O
 Thể tích của bồn (hình trụ) đựng dầu là: 2 2 3
V   r h   .1 .5  5 (m )   3 
 Thể tích phần đã rút dầu ra (phần trên mặt (ABCD)) là: 3 V    .5  3, 070 (m ) 1  3 4   
 Vậy thể tích cần tìm là: 3
V  V  V  5  3, 07  12, 637 (m ). 2 1
Câu 29: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2,25 mét,
chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy số
tiền bác Năm phải trả là: A. 33750000 đồng. B. 12750000 đồng. C. 6750000 đồng. D. 3750000 đồng. Hướng dẫn giải Chọn C. y B x O A
 Gắn parabol  P và hệ trục tọa độ sao cho  P đi qua O(0;0)
 Gọi phương trình của parbol là (P):P 2
: y  ax  bx  c
Theo đề ra,  P đi qua ba điểm O(0; 0) , (
A 3; 0) , B(1, 5; 2, 25) .
Từ đó, suy ra  P 2
: y  x  3x 3 9
 Diện tích phần Bác Năm xây dựng: 2 S 
 x  3x dx   2 0 9
 Vậy số tiền bác Năm phải trả là: 1500 . 000  67500 0 0 (đồng) 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 101
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 30: Trong chương trình nông thôn mới, tại một xã X có xây một cây cầu bằng bê tông như hình
vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu. (Đường cong trong hình vẽ là các đường Parabol). 0, 5m 2m 5m 0, 5m 19m 0, 5m A. 3 19m . B. 3 21m . C. 3 18m . . D. 3 40m . Hướng dẫn giải Chọn D.
Chọn hệ trục Oxy như hình vẽ. y O x  19  Gọi  P  2
: y  ax  c là Parabol đi qua hai điểm A ; 0 , B   0;2 1  2  2   19   8 0  . a  2 a   8
Nên ta có hệ phương trình sau:    2   361   P  2 : y   x    2 1 361  b   2 2  b    5  Gọi  P  2
: y  ax  c là Parabol đi qua hai điểm C 10;0, D 0; 2    2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 102
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  5  1 0  . a 102  a     2   40 1 5
Nên ta có hệ phương trình sau:      P  2 : y   x  2 5 5 40 2  b b      2   2 19  10  1 5   8  
Ta có thể tích của bê tông là: 2 2 3 2 V  5.2  x  dx  
x  2 dx  40m        0 0   40 2   361  
Câu 31: Một Bác thợ gốm làm một cái lọ có dạng khối tròn xoay được tạo thành khi quay hình phẳng
giới hạn bởi các đường y 
x 1 và trục Ox quay quanh trục Ox biết đáy lọ và miệng lọ
có đường kính lần lượt là 2dm và 4dm , khi đó thể tích của lọ là: 15 14 15 A. 2 8 dm . B. 3  dm . C. 2  dm . D. 2 dm . 2 3 2 Hướng dẫn giải Chọn B. y x O 3
 r  y  1  x  0 1 1 1
 r  y  2  x  3 2 2 2 3 3 2  x  15 Suy ra: 2
V   y dx    x   3 1 dx    x       0 2 2 0 0  
Câu 32: Hạt electron có điện tích âm là 19 1, 6.10
C . Nếu tách hai hạt eletron từ 1pm đếm 4 pm thì công W sinh ra là A. 28 W  3,194.10 J . B. -16 W  1, 728.10 J . C. 28 W  1, 728.10 J . D. 16 W  3,194.10 J . Hướng dẫn giải Chọn B. b kq q  Áp dụng công thức 1 2 A  dx  . 2 x a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 103
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Trong đó: 9 12 12
k  9.10 ; a  1 pm  10 ;
m b  4 pm  4.10 m ; 19
q  q  1, 6.10 C 1 2 9   9.10 . 19 4.10 1, 6.10 2 12 12 4.10  1   Suy ra: 2  8 16 A  dx  2, 304.10   1, 728.10 J  . 2    x  x 12 1  2  10 10
Câu 33: Trong mạch máy tính, cường độ dòng điện (đơn vị mA) là một hàm số theo thời gian t, với
I (t)  0, 3  0, 2t . Hỏi tổng điện tích đi qua một điểm trong mạch trong 0,05 giây là bao nhiêu? A. 0, 29975 mC. B. 0, 29 mC. C. 0, 01525 mC. D. 0, 01475 mC. Hướng dẫn giải Chọn D. 0,05 0,05 0,05 2  t  q 
I t  dt 
0,3  0,2tdt  0,3t   0, 01475 mC.     10 0 0   0
Câu 34: Dòng điện xoay chiều hình sin chạy qua một đoạn mạch LC có có biểu thức cường độ là   
i t   I cos t 
. Biết i  q với q là điện tích tức thời ở tụ điện. Tính từ lúc t  0 , điện 0    2  
lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng là   2I 2I  I A. 0 . B. 0. C. 0 . D. 0 .    2 Hướng dẫn giải Chọn C. 
Điện lượng chuyển qua tiết diện của dây dẫn của đoạn mạch trong thời gian từ 0 đến là         I      2I
q  i t  0 0 dt  I cos t  dt  sin t   0        2    2   0 0 0
Câu 35: Khi một chiếc lò xo bị kéo căng thêm x m so với độ dài tự nhiên là 0,15m của lò xo thì
chiếc lò xo trì lại (chống lại) với một lực f  x  800 .
x Hãy tìm công W sinh ra khi kéo lò
xo từ độ dài từ 0,15m đến 0,18m. A. 2 W  36.10 J . B. 2 W  72.10 J .
C. W  36J.
D. W  72J. Hướng dẫn giải Chọn A.
Công được sinh ra khi kéo căng lò xo từ 0,15m đến 0,18m là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 104
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng 0,03 2 0,03 2 W 800 . x dx 400x 36.10    J. 0 0
Chú ý: Nếu lực là một giá trị biến thiên (như nén lò xo) và được xác định bởi hàm F  x thì b
công sinh ra theo trục Ox từ a tới b là A  F  x d . x  a  2
Câu 36: Một dòng điện xoay chiều i = I  0 sin t  
  chạy qua một mạch điện có điện trở thuần  T 
R.Hãy tính nhiệt lượng Q tỏa ra trên đoạn mạch đó trong thời gian một chu kì T. 2 RI 2 RI 2 RI 2 RI A. 0 T . B. 0 T . C. 0 T . D. 0 T 2 3 4 5 Hướng dẫn giải Chọn A.  2  T T  cos   T 1 2  2    Ta có: Q = 2 2 2 Ri dt  RI sin t   dt 2  T  0      RI dt   T  0 0 0 2 0 T 2 2 RI  T  2   RI 0 0  t  sin 2 t    T     . 2 4    T  2  0 2
Câu 37: Đặt vào một đoạn mạch hiệu điện thế xoay chiều u = U0 sin
t . Khi đó trong mạch có T  2
dòng diện xoay chiều i = I  0 sin t  
  với  là độ lệch pha giữa dòng diện và hiệu  T 
điện thế.Hãy Tính công của dòng diện xoay chiều thực hiện trên đoạn mạnh đó trong thời gian một chu kì. U I U I U I U I A. 0 0 cos . B. 0 0 T sin  . C.
0 0 Tcos(   ) . D. 0 0 Tcos 2 2 2 2 Lời giải Ta có: T T  2  2 T 1   4  
A = uidt  U I sin t   sin tdt 0 0      U I cos  cos t   dt      T  T 0 0  0 0 2   T  0 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 105
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng T U I 1   4   0 0  cos  cos t   dt      2 2   T  0  T U I  T  4   U I 0 0 0 0  tcos  sin t    Tcos      . 2 4    T  2  0 Hướng dẫn giải Chọn D.
Câu 38: Để kéo căng một lò xo có độ dài tự nhiên từ 10cm đến 15cm cần lực 40N . Tính công ( A )
sinh ra khi kéo lò xo có độ dài từ 15cm đến 18cm .
A. A  1, 56 (J ) .
B. A  1 (J ) .
C. A  2, 5 (J ) .
D. A  2 (J ) . Hướng dẫn giải Chọn A. x
f  x  k.x O M x x
Theo Định luật Hooke, lực cần dùng để giữ lò xo giãn thêm x mét từ độ dài tự nhiên là
f  x  kx , với k  N /m là độ cứng của lò xo. Khi lò xo được kéo giãn từ độ dài 10cm đến
15cm , lượng kéo giãn là 5 cm  0.05 m . Điều này có nghĩa f 0.05  40, do đó: 40
0, 05k  40  k 
 800  N /m 0, 05
Vậy f  x  800x và công cần để kéo dãn lò xo từ 15cm đến 18cm là: 0,08 0,08 A 800 dx 400x
400 0, 082 0, 052 2       1,56  J   0,05   0,05
Câu 39: Một thanh AB có chiều dài là 2a ban đầu người ta giữ thanh ở góc nghiêng    , một đầu o
thanh tựa không ma sát với bức tường thẳng đứng. Khi buông thanh, nó sẽ trượt xuống dưới
tác dụng của trọng lực. Hãy biểu diễn góc  theo thời gian t (Tính bằng công thức tính phân)  d  d A. t    . B. t    . 3 3g o
(sin   sin  ) o
(sin   sin  ) 2 o a 2 o a
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 106
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng  d  d C. t    . D. t    3g 3g o
(sin   sin ) o
(sin   sin ) o a 2 o a Hướng dẫn giải
Do trượt không ma sát nên cơ năng của thanh được bảo toàn
mga sin   mga sin   K  K (1) o q tt 2 2 ma  1
Do khối tâm chuyển động trên đường tròn tâm O bán kính a nên: 2 2 K   ma  ' tt 2 2 1 1 1 1
Động năng quay quanh khối tâm: 2 2 2 2 2 K  I 
m(2a)  '  ma  ' q 2 2 12 6 2 Thay vào (1) ta được: 2
a '  g(sin   sin  ) 3 o 3g  '  
(sin   sin  ) 2 o a  d t    3g o
(sin   sin ) 2 o a . Chọn D.
Câu 40: Trong kinh tế học, thặng dư tiêu dùng của hàng hóa được tính bằng công thức a
I   p(x)  P.d . x  0
Với p(x) là hàm biểu thị biểu thị giá mà một công ty đưa ra để bán được x đơn vị hàng hóa.
a là số lượng sản phẩm đã bán ra, P  p(a) là mức giá bán ra ứng với số lượng sản phẩm là a. Cho 2
p  1200  0, 2x  0, 0001x , (đơn vị tính là USD). Tìm thặng dư tiêu dùng khi số lượng sản phẩm bán là 500.
A. 1108333,3 USD. B. 570833,3 USD. C. 33333,3 USD. D. Đáp án khác. Hướng dẫn giải Chọn C.
Áp dụng công thức trên với a  500; P  p a  p500  1075 . 500 500 2 3  x x  Suy ra I    2
1200  0, 2x  0, 0001x 1075dx  125x    33333, 3   USD 10 30000 0   0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 107
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 41: Một khối cầu có bán kính 5dm, người ta cắt bỏ 2 phần bằng 2 mặt phẳng vuông góc bán kính
và cách tâm 3dm để làm một chiếc lu đựng. Tính thể tích mà chiếc lu chứa được. 100
A. 132 (dm3).
B. 41 (dm3). C.  (dm3).
D. 43 (dm3) 3 Hướng dẫn giải:
Đặt hệ trục với tâm O, là tâm của mặt cầu; đường thẳng
đứng là Ox, đường ngang là Oy; đường tròn lớn có phương trình 2 2
x  y  25 . 3dm 5dm
Thể tích là do hình giới hạn bởi Ox, đường cong 3dm 2 y 
25  x , x  3, x  3  quay quanh Ox. 3 2
V   (25  x )dx = (bấm máy).  132 3 Chọn A.
Câu 42: Từ một khúc gõ hình trụ có đường kính 30cm, người ta cắt khúc gỗ bởi một mặt phẳng đi
qua đường kính đáy và nghiêng với đáy một góc 0
45 để lấy một hình nêm (xem hình minh họa dưới đây) Hình 1 Hình 2
Kí hiệuV là thể tích của hình nêm (Hình 2). Tính V . 225 A. V  cm3 2250 . B. V 
cm3 . C. V  cm3 1250 . D.       V  cm3 1350  4 Hướng dẫn giải
Chọn hệ trục tọa độ như hình vẽ.Khi đó hình nêm có đáy
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 108
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
là nửa hình tròn có phương trình: y   x 2 225 ,x   1  5;15  
Một một mặt phẳng cắt vuông góc với trục Ox tại điểm có hoành độ x , x   15  ;15   
cắt hình nêm theo thiết diện có diện tích là S x (xem hình).  
Dễ thấy NP  y và MN  0 NP  y   2 tan 45 15 x khi đó 1 1 15
S x  MN.NP  . 225  2
x suy ra thể tích hình nêm là:    
V   S xdx 2 2 15 15 1  .
 225  x2 dx  2250cm3 . 2 15 Chọn A.
Câu 43: Người ta dựng một cái lều vải  H  có dạng hình “chóp lục giác cong đều” như hình vẽ bên.
Đáy của  H  là một hình lục giác đều cạnh 3 m . Chiều cao SO  6 m ( SO vuông góc với
mặt phẳng đáy). Các cạnh bên của  H  là các sợi dây c , c , c , c , c , c nằm trên các 1 2 3 4 5 6
đường parabol có trục đối xứng song song với SO . Giả sử giao tuyến (nếu có) của  H  với
mặt phẳng  P vuông góc với SO là một lục giác đều và khi  P qua trung điểm của SO
thì lục giác đều có cạnh 1 m . Tính thể tích phần không gian nằm bên trong cái lều  H  đó. S c6 c5 c 1m 1 c2 c3 c4 O 3m 135 3 96 3 135 3 135 3 A. ( 3 m ). B. ( 3 m ). C. ( 3 m ). D. ( 3 m ). 5 5 4 8 Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 109
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Đặt hệ trục tọa độ như hình vẽ, ta có parabol cần tìm đi qua 3 điểm có tọa độ lần lượt là 1 7
A0;6 , B 1;3 , C 3;0 nên có phương trình là 2 y  x  x  6 2 2
Theo hình vẽ ta có cạnh của “thiết diện lục giác” là 7 1
BM . Nếu ta đặt t  OM thì BM   2t  (chú 2 4
ý là ta phải lấy giá trị có dấu “ ” trước dấu căn và
cho B chạy từ C đến A ).
Khi đó, diện tích của “thiết diện lục giác” bằng 2 2 BM 3 3 3  7 1 
S t   6.    2t   với 4 2  2 4    t 0;  6 .
Vậy thể tích của “túp lều” theo đề bài là: 2 6 6 3 3  7 1  135 3
V  S t  dt    2t   dt  ...    2  2 4  8 0 0   Chọn D.
Câu 44: Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn bán kinh 4 cắt
vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là tam giác đều. Thể tích của vật thể là: 256 64 256 3 32 3 A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 110
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Chọn tâm đường tròn làm gốc. 3
Diện tích thiết diện là 2 2 S 
AB  3(4  x ) 4 2 2 32 3 2 V 
S(x)dx  3 (4  x )dx    . 3 2  2  Chọn D.
Câu 45: Một người có mảnh đất hình tròn có bán kính 5m, người này tính trồng cây trên mảnh đất
đó, biết mỗi mét vuông trồng cây thu hoạch được giá 100 nghìn. Tuy nhiên cần có khoảng
trống để dựng chồi và đồ dùng nên người này căng sợi dây 6m sao cho 2 đầu mút dây nằm
trên đường tròn xung quanh mảnh đất. Hỏi người này thu hoạch được bao nhiêu tiền (tính
theo đơn vị nghìn và bỏ phần số thập phân). .A. 3722 . B. 7445 . C. 7446 . D. 3723 Hướng dẫn giải
Đặt hệ trục tọa độ 4349582 như hình vẽ.
Phương trình đường tròn của miếng đất sẽ là 2 2 x  y  25
Diện tích cần tính sẽ bằng 2 lần diện tích phần tô đậm phía trên.
Phần tô đậm được giới hạn bởi đường cong có phương trình là 2 y  25  x , trục
Ox; x  5; x  4 (trong đó giá trị 4 có được dựa
vào bán kính bằng 5 và độ dài dây cung bằng 6)
Vậy diện tích cần tính là 4 2 S  2
25  x dx  74, 45228...  5 Chọn B.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 111
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 46: Trong Công viên Toán học có những mảnh đất mang hình dáng khác nhau. Mỗi mảnh được
trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán
học. Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemmiscate có
phương trình trong hệ tọa độ Oxy là 2 2 y  x  2 16
25  x  như hình vẽ bên. y x
Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ tọa độ Oxy tương
ứng với chiều dài 1 mét. 125 125 250 125 A. S   2 m  B. S   2 m  C. S   2 m  D. S   2 m  6 4 3 3 Hướng dẫn giải Chọn D.
Vì tính đối xứng trụ nên diện tích của mảnh đất tương ứng với 4 lần diện tích của mảnh đất
thuộc góc phần tư thứ nhất của hệ trục tọa độ Oxy . 1
Từ giả thuyết bài toán, ta có 2 y   x 5  x . 4 1 Góc phần tư thứ nhất 2 y 
x 25  x ; x  0;5 4 5 1 125 125 Nên 2 3 S 
x 25  x dx   S  (m ) (I )  4 12 3 0 1
Câu 47: Gọi  H  là phần giao của hai khối hình trụ có 4
bán kính a , hai trục hình trụ vuông góc với nhau.
Xem hình vẽ bên. Tính thể tích của  H  . 3 2a 3 3a A. V  . B. V  .  H  3  H  4 3 a 3  a C. V  . D. V  . H  2  H  4 Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 112
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Chọn A.
Ta gọi trục tọa độ Oxyz như hình vẽ. Khi đó phần giao  H  là
một vật thể có đáy là một phần tư hình tròn tâm O bán kính a , thiết
diện của mặt phẳng vuông góc với trục Ox là một hình vuông có
diện tích S  x 2 2  a  x a a 3 2a
Thể tích khối  H  là S  x dx   2 2 a    x dx  . 3 0 0
Câu 48: Một khối cầu có bán kính là 5dm , người ta cắt bỏ hai
phần của khối cầu bằng hai mặt phẳng song song cùng
vuông góc đường kính và cách tâm một khoảng 3dm để
làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được. 100 43 A.   3 dm  B.   3 dm  C. 3 3   3 41 dm  D.   3 132 dm  Hướng dẫn giải Chọn D.
Cách 1: Trên hệ trục tọa độ Oxy , xét đường tròn 2 2
(C ) : ( x  5)  y  25 . Ta thấy nếu cho
nửa trên trục Ox của C quay quanh trục Ox ta được mặt cầu bán kính bằng 5. Nếu cho
hình phẳng  H  giới hạn bởi nửa trên trục Ox của C , trục Ox , hai đường thẳng
x  0, x  2 quay xung quanh trục Ox ta sẽ được khối tròn xoay chính là phần cắt đi của
khối cầu trong đề bài. Ta có 2 2 2
(x  5)  y  25  y   25  ( x  5)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 113
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
 Nửa trên trục Ox của C có phương trình 2 2 y 
25  (x  5)  10x  x
 Thể tích vật thể tròn xoay khi cho  H  quay quanh Ox là: 2 2 3    V    x 52 2 10x  x  2
dx   5x   1   3 3 0   0 4 500 Thể tích khối cầu là: 3 V   .5  2 3 3 500 52
Thể tích cần tìm: V  V  2V   2.  132  3 dm 2 1  3 3
Câu 49: Một cái chuông có dạng như hình vẽ. Giả sử khi cắt chuông bởi mặt phẳng qua trục của
chuông, được thiết diện có đường viền là một phần parabol ( hình vẽ ). Biết chuông cao 4m,
và bán kính của miệng chuông là 2 2 . Tính thể tích chuông? A. 6 B. 12 C. 3 2 D. 16 Hướng dẫn giải
Xét hệ trục như hình vẽ, dễ thấy parabol đi qua ba
điểm 0;0,4;2 2,4;2 2  nên có phương trình 2 y x 
. Thể tích của chuông là thể tích của khối tròn 2
xoay tạo bởi hình phẳng y 
2x, x  0, x  4 quay quanh trục Ox. Do đó 4 4
Ta có V   2xdx    2
 x  16 0 0
Câu 50: Một mảnh vườn hình tròn tâm O bán kính 6m . Người ta cần trồng cây trên dải đất rộng 6m
nhận O làm tâm đối xứng, biết kinh phí trồng cây là 70000 đồng 2
/ m Hỏi cần bao nhiêu
tiền để trồng cây trên dải đất đó (số tiền được làm tròn đến hàng đơn vị)
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 114
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng A. 8412322 đồng. B. 8142232 đồng. C. 4821232 đồng. D. 4821322 đồng Hướng dẫn giải
Xét hệ trục tọa độ oxy đặt vào tâm khu vườn, khi đó phương trình đường tròn tâm O là 2 2
x  y  36 . Khi đó phần nửa cung tròn phía trên trục Ox có phương trình 2
y  36  x  f (x)
Khi đó diện tích S của mảnh đất bằng 2 lần diện tích hình phẳng giới hạn bởi trục hoành, đồ
thị y  f (x) và hai đường thẳng x  3  ; x  3 3 2  S  2 36   x dx 3   
Đặt x  6sin t  dx  6 cos tdt . Đổi cận: x  3   t  
; x  3  t  6 6    6 6 6 2  S  2 36cos tdt  36
(c os2t+1) dt  18(sin 2 t 2 t)  18 3 12         6 6  6
Do đó số tiền cần dùng là 70000.S  4821322 đồng
Câu 51: Cho một vật thể bằng gỗ có dạng khối trụ với bán kính đáy bằng R. Cắt khối trụ bởi một mặt
phẳng có giao tuyến với đáy là một đường kính của đáy và tạo với đáy góc 0 45 . Thể tích của khối gỗ bé là: 3 2R 3  R 3 R 3  R A. V  . B. V  . C. V  . D. V  . 3 6 3 3 Hướng dẫn giải
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 115
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng O y x 2 2 R  x 2 2 R  x
Chọn hệ trục Oxy như hình vẽ. Cắt khối gỗ bé bởi các mặt phẳng vuông góc với Ox tại điểm 1
có hoành độ x ta được thiết diện là tam giác vuông có diện tích bằng 2 2 ( A x)  R  x . 2 R 3 1 2R
Vậy thể tích khối gỗ bé bằng: 2 2 V  R  x  .  2 3  R Chọn A.
Câu 52: Vòm cửa lớn của một trung tâm văn hoá có dạng hình Parabol. Người
ta dự định lắp cửa kính cường lực cho vòm cửa này. Hãy tính diện tích
mặt kính cần lắp vào biết rằng vòm cửa cao 8m và rộng 8m (như hình vẽ) 28 26 128 131 A. 2 (m ) B. 2 (m ) C. 2 (m ) D. 2 (m ) 3 3 3 3 Hướng dẫn giải: Đáp án đúng: C
Các phương án nhiễu: 4 1 28
A. HS tính tích phân sai 2 S   x  8 dx   2 (m ) 2 3 4  4 1 26
B. HS tính tích phân sai 2 S   x  8 dx   2 (m ) ) 2 3 4  4 1 1 131 D. HS nhầm a =  , b= 8, c = 0 => 2 S   x  8x dx   2 (m ) 2 2 3 4 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 116
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Câu 53: Một khuôn viên dạng nửa hình tròn có đường kính bằng 4 5 (m). Trên đó người thiết kế
hai phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa
hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau
một khoảng bằng 4 (m), phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản.
Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100.000 đồng/m2.
Hỏi cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến hàng nghìn) 4m 4m 4m
A. 3.895.000 (đồng).
B. 1.948.000 (đồng). C. 2.388.000 (đồng). D. 1.194.000 (đồng). Hướng dẫn giải: Chọn B
Đặt hệ trục tọa độ như hình vẽ. Khi đó phương
trình nửa đường tròn là y  R  x   2 2 2 2 2 2 5
 x  20  x .
Phương trình parabol P có đỉnh là gốc O sẽ có dạng 2
y  ax . Mặt khác  P qua điểm
M 2;4 do đó:  a 2 4 2  a  1.
Phần diện tích của hình phẳng giới hạn bởi P và nửa đường tròn.( phần tô màu) 2 Ta có công thức 2 2 2 S 
20  x  x dx  11,94m . 1    2  1
Vậy phần diện tích trồng cỏ là S  S  S  trongco hinhtron 1 19, 47592654 2
Vậy số tiền cần có là S
 100000  1.948.000 (đồng).đồng. trongxo
Câu 54: Một công ty quảng cáo X muốn làm một bức tranh 12 m
trang trí hình MNEIF ở chính giữa của một A I B
bức tường hình chữ nhật ABCD có chiều cao F E
BC  6 m , chiều dài CD  12 m (hình vẽ bên). 6 m
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 117
Facebook: https://www.facebook.com/dongpay M N D 4 m C
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Cho biết MNEF là hình chữ nhật có MN  4 m ; cung EIF có hình dạng là một phần của
cung parabol có đỉnh I là trung điểm của cạnh AB và đi qua hai điểm C , D . Kinh phí làm
bức tranh là 900.000 đồng/ 2 m .
Hỏi công ty X cần bao nhiêu tiền để làm bức tranh đó? A. 20.400.000 đồng.
B. 20.600.000 đồng. C. 20.800.000 đồng. D. 21.200.000 đồng.
Câu 55: Một sân chơi cho trẻ em hình chữ nhật có chiều dài 100 và chiều rộng là 60m người ta làm
một con đường nằm trong sân (như hình vẽ). Biết rằng viền ngoài và viền trong của con
đường là hai đường elip, Elip của đường viền ngoài có trục lớn và trục bé lần lượt song song
với các cạnh hình chữ nhật và chiều rộng của mặt đường là 2m . Kinh phí cho mỗi 2 m làm
đường 600.000 đồng. Tính tổng số tiền làm con đường đó. (Số tiền được làm tròn đến hàng nghìn). 100m 2m 60m A. 293904000. B. 283904000. C. 293804000. D. 283604000. Hướng dẫn giải: Chọn A.
Xét hệ trục tọa độ Oxy đặt gốc tọa độ O vào tâm của hình Elip. 2 2 x y
Phương trình Elip của đường viền ngoài của con đường là  E :   1 . Phần đồ thị 1  2 2 50 30 2 x
của  E nằm phía trên trục hoành có phương trình y  30 1  f x . 2 1   1  50 2 2 x y
Phương trình Elip của đường viền trong của con đường là  E :   1. Phần đồ thị 2  2 2 48 28 2 x
của  E nằm phía trên trục hoành có phương trình y  28 1  f x . 2 2   2  48
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 118
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Gọi S là diện tích của  E và bằng hai lần diện tích phần hình phẳng giới hạn bởi trục 1  1
hoành và đồ thị hàm số y  f x . Gọi S là diện tích của  E và bằng hai lần diện tích 2  1   2
phần hình phẳng giới hạn bởi trục hoành và đồ thị hàm số y  f x . 2  
Gọi S là diện tích con đường. Khi đó 50 2 48 2 x x
S  S  S  2 30 1 dx  2 28 1 dx 1 2  2  . 2 50 48 5  0 48 a 2 x
Tính tích phân I  2 b 1 d , x a,b     . 2   a a    
Đặt x  a sin t,   t 
 dx  a cos tdt   .  2 2   
Đổi cận x  a  t  
; x  a  t  . 2 2    2 2 2 Khi đó 2 2 I  2
b 1 sin t .a cos t dt  2ab
cos t dt  b a
1 cos 2tdt          2 2 2  2  sin 2t   ab t  ab    .  2    2
Do đó S  S  S  50.30  48.28  156 . 1 2
Vậy tổng số tiền làm con đường đó là 600000.S  600000.156  294053000 (đồng).
Câu 56: Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây
Người ta đo được đường kính của miệng ly là 4cm và chiều cao là 6cm . Biết rằng thiết
diện của chiếc ly cắt bởi mặt phẳng đối xứng là một parabol. Tính thể tích  3 V cm  của vật thể đã cho.
A. V  12 . B. V  12 . 72 72 C. V   . D. V  . 5 5 Hướng dẫn giải: Chọn A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 119
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Chọn gốc tọa độ O trùng với đỉnh I của parabol  P. Vì parabol  P đi qua các điểm 3 A 2
 ;6, B2;6 và I 0;0 nên parabol  P có phương trình 2 y  x . 2 3 2 Ta có 2 2 y  x  x 
y . Khi đó thể tích của vật thể đã cho là 2 3 6  2  V   y dy  12    3 cm .  3  0
Câu 57: Trong mặt phẳng tọa độ, cho hình chữ nhật  H  có một cạnh nằm trên trục hoành, và có hai
đỉnh trên một đường chéo là A 1  ;0 và B ; a
a  , với a  0 . Biết rằng đồ thị hàm số y 
x chia hình  H  thành hai phần có diện tích bằng nhau, tìm a . 1 A. a  9 . B. a  4 . C. a  . D. a  3 . 2 Hướng dẫn giải: Chọn D.
Gọi ACBD là hình chữ nhật với AC nằm trên trục Ox , A 1  ;0 và B ; a a 
Nhận thấy đồ thị hàm số y 
x cắt trục hoành tại điểm có hoành độ bằng 0 và đi qua B  ; a
a  . Do đó nó chia hình chữ nhật ACBD ra làm 2 4 cm A B
phần là có diện tích lần lượt là S , S . Gọi S là diện tích 1 2 2 O
hình phẳng giới hạn bởi các đường y 
x và trục Ox ,
x  0, x  a và S là diện tích phần còn lại. Ta lần lượt tính 1 6 cm S , S . 1 2 a
Tính diện tích S  xdx 2  . 0 I
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 120
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng Đặt 2 t 
x  t  x  2tdt  dx ; Khi x  0  t  0; x  a  t  a . a a 3  2t  2a a Do đó 2 S  2t dt   . 2    3 3 0   0
Hình chữ nhật ACBD có AC  a 1; AD  a nên 2a a 1 S  S
 S  a a  1   a a  a 1 ACBD 2   3 3
Do đồ thị hàm số y 
x chia hình  H  thành hai phần có diện tích bằng nhau nên 2a a 1 S  S  
a a  a  a a  3 a  a  3 (Do a  0 ) 1 2 3 3
Câu 58: Sân trường có một bồn hoa hình tròn tâm O . Một nhóm học sinh lớp 12 được giao thiết kế
bồn hoa, nhóm này định chia bồn hoa thành bốn phần, bởi hai đường parabol có cùng đỉnh
O và đối xứng nhau qua O . Hai đường parabol này cắt đường tròn tại bốn điểm A , B , C ,
D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích S , S dùng l 2
để trồng hoa, phần diện tích S , S dùng để trồng cỏ (Diện tích làm tròn đến chữ số thập 3 4
phân thứ hai). Biết kinh phí trồng hoa là 150.000 đồng /1m2, kinh phí để trồng cỏ là
100.000 đồng/1m2. Hỏi nhà trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm
tròn đến hàng chục nghìn) A. 6.060.000 đồng. B. 5.790.000 đồng. C. 3.270.000 đồng. D. 3.000.000 đồng. Hướng dẫn giải: Chọn C.
Chọn hệ trục tọa độ như hình vẽ Parabol có hàm số dạng 2
y  ax  bx  c có đỉnh là gốc tọa độ và đi qua điểm B 2; 2 nên 1 có phương trình 2 y  x 2
Đường tròn bồn hoa có tâm là gốc tọa độ và bán kính OB  2 2 nên có phương trình là 2 2
x  y  8 . Do ta chỉ xét nhánh trên của đường tròn nên ta chọn hàm số nhánh trên là 2 y  8  x . 2  1  Vậy diện tích phần 2 2 S  8  x  x dx 1     2  2  2  1 
Do đó, diện tích trồng hoa sẽ là 2 2 S  S  2 8  x  x dx  15, 233... 1 2     2  2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 121
Facebook: https://www.facebook.com/dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Nguyên Hàm-Tích Phân-Ứng Dụng
Vậy tổng số tiền để trồng bồn hoa là:     2 15, 233 150.000 2 2
15, 233100.000  3.274.924 đồng.
Làm tròn đến hàng chục nghìn nên ta có kết quả là 3.270.000 đồng.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 122
Facebook: https://www.facebook.com/dongpay